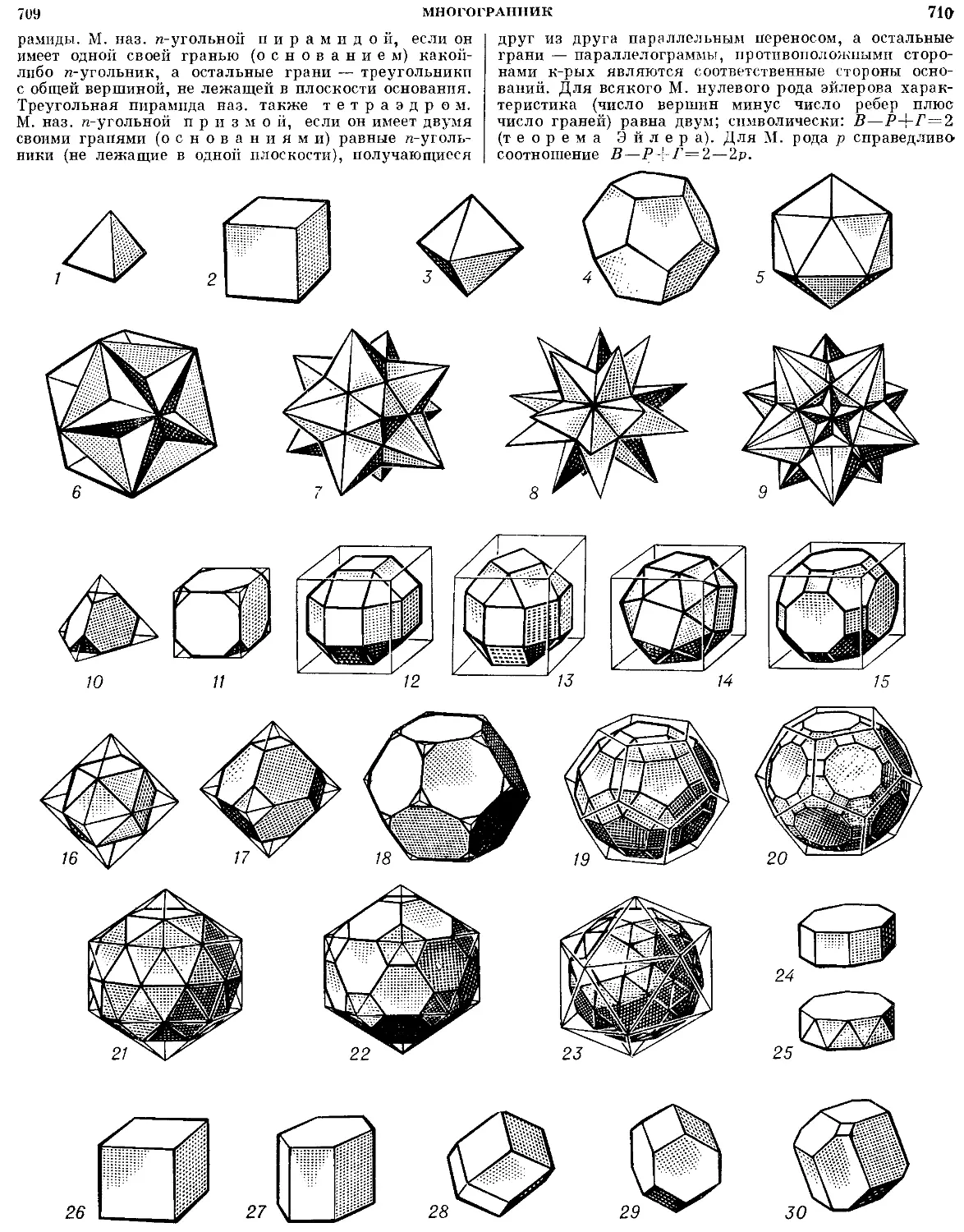
Текст
КООРДИНАТЫ — числа, величины, по к-рым на-
находится (определяется) положение какого-либо элемен-
элемента (точки) в некоторой совокупности (множестве М), на-
например на плоскости поверхности, в пространстве, на
многообразии. В ряде разделов математики и физики
К. именуются по-другому, напр. К. элемента (вектора)
векторного пространства наз. его компонентами, К.
в произведении множеств — проекции на один из его
сомножителей, в теории относительности системы К.—
это системы отсчета, и т. п. Часто встречается ситуация,
когда ввести достаточно разумные и удобные К. гло-
глобально на всем множестве невозможно (напр., точкам
сферы в отличие от плоскости нельзя взаимно одноз-
однозначно и непрерывно сопоставить пары чисел), и тогда
вводят понятие локальных координат. Таково, напр.,
положение в теории многообразий.
Совокупность К. организуется в систему коор-
координат (систему отнесения, систему
референци и), или карту, причем К. взаимно
однозначно соответствуют элементам множества М.
В этом — основа метода координат, истока-
истоками к-рого принято считать работы П. Ферма (P. Fermat,
1636) и Р. Декарта (R. Descartes, 1637). Впрочем, еще
Аполлоний Пергский C—2 вв. до н. э.) определял ко-
нич. сечения с помощью того, что сейчас [следуя
Г. Лейбницу (G. Leibniz, 1694)] называют К., хотя
числовых значений они не имели. Но широта и долгота
в «Географии» Птолемея B в. н. э.) были уже числовыми
К. В 14 в. Н. Орем (N. Oresme) пользовался К. на пло-
плоскости для построения графиков, называя долготой
и широтой то, что теперь называется абсциссой и ор-
ординатой.
Попытки обойтись без введения К. извне, сохранить,
так сказать, «чистоту» теории, себя не оправдали [напр.,
синтетические конструкции проективных координат,
культивировавшиеся К. Штаудтом (Ch. Staudt, 18i7),
оказалось возможным заменить простыми алгеоряич.
эквивалентами, что привело к понятию проективной
геометрии над телом]. Впрочем но прогшл вкус и, так
сказать, к внутреннему способу введения
К. (в отличие от внешнего способа при-
привнесения К. извне), основанному на оценке положения
координируемого объекта относительно нек-рых, вы-
выбранных a priori стандартных подмножеств, напр, ли-
линий, поверхностей и т. п. (называемых в этом случае
координатными линиями, поверхностя-
поверхностями и т. п.). Это в особенности относится к множест-
множествам, в определении к-рых участвуют числа (напр., мет-
рпч. и векторные пространства), т. е. к весьма обшир-
обширному и практически важному классу математич. объек-
объектов, чем и объясняется их широкое распространение.
Среди систем К. точек (точечных К.) выделяют
т. н. линейные координаты, в к-рых коор-
координатными линиями служат прямые. Таковы, напр.,
декартова прямоугольная система координат, тре-
треугольные К. (см. Тетраэдральные координаты), бари-
барицентрические координаты, проективные координаты.
Системы К., для к-рых не все координатные линии
прямые, наз. криволинейными координатами. Такие К.
используются как на плоскости (напр., полярные ко-
координаты, эллиптические координаты, параболические
координаты, биполярные координаты), так и на поверх-
поверхностях (геодезические координаты, изотермические коор-
координаты и др.)- Многие специальные виды систем кри-
криволинейных К. вводятся при использовании сетей ли-
линий, отвечающих тем или иным условиям. Из них на-
наиболее важный класс — ортогональные системы коор-
координат, в к-рых координатные линии пересекаются под
прямым углом.
Различные виды К. на плоскости (или на поверхно-
поверхности) обобщаются на случай пространства. Напр., поня-
понятие полярных К. на плоскости приводит к понятию по-
полярных К. в пространстве (сферических координат и ци-
цилиндрических координат); понятие биполярных К. на
плоскости — к понятиям тороидальных координат,
бицилиндрических координат и биполярных К. в прост-
пространстве; понятие эллиптических К. на плоскости — к
понятию эллипсоидальных координат в пространстве.
Иногда потребности удобства и наглядности приво-
приводят к отступлению от равенства количества чисел, яв-
являющихся К. точек множества и его размерностью.
По тем же причинам допускается нарушение в отдель-
отдельных точках взаимной однозначности координатного
отображения (таковы, напр., полярные К.).
В тех случаях, когда изучаемое многообразие М
негомеоморфно области евклидова пространства, бывает
удобно использовать избыточные К., в к-рых
число К. больше размерности М. Такие К., как пра-
правило,— однородные координаты.
Часто говорят о К. прямых, плоскостей и других гео-
метрич. объектов, понимая под этим К. в каком-либо
пространстве, точками к-рого являются прямые, пло-
плоскости и т. д. (см., напр., Грассмана многообразие).
Равноправие точек и прямых в геометрии двух измере-
измерений и равноправие точек и плоскостей в геометрии трех
измерений согласно двойственности принципу позво-
позволяют ввести К., с помощью к-рых могут быть определе-
определены положения прямых и плоскостей. Таковы, напр.,
тангенциальные координаты.
Метод К. стал полезным не только на пути алгорит-
алгоритмизации рассуждений (сведению их к вычислениям),
но и для обнаружения новых фактов и связей (так,
напр., непротиворечивость евклидовой геометрии по-
посредством К. сводится к непротиворечивости арифмети-
арифметики). И хотя ряд разделов математики, напр, римано-
еа геометрия, может быть изложен в «бескоординат-
«бескоординатном» виде, конкретные результаты чаще добываются
методом К., а точнее, выбором удобных для данной за-
задачи координатных систем (напр., выразительность
ряда задач механики достигается именно в специальных
К., в к-рых «разделяются» переменные).
М. И. Войцеховский, А. Б. Иванов.
КОПРЕДСТАВЛЕНИЕ группы— задание груп-
группы ее образующими и соотношениями между ними.
КОПРИСОЕДИНЕННОЕ ПРЕДСТАВЛЕНИЕ —
представление группы Ли G, контрагредиентное к
присоединенному представлению Ad этой группы. К. п.
действует в пространстве д*, дуальном к пространству
алгебры Ли ц группы G.
Если G — вещественная матричная группа, т. е. под-
подгруппа в GL (n, R), то g — подпространство в прост-
пространстве Mat,, (R) вещественных матриц порядка п.
Пусть g-1- — ортогональное дополнение к g относи-
относительно билинейной формы
(X, У)н-»и- XY в Matn(R),
V — какое-нибудь подпространство в Mat,,(R), допол-
дополнительное к g-1-, P — оператор проектирования на V
параллельно д-Ч Тогда д* отождествляется с V п
К. п. задается формулой
Соответствующее представление алгебры д также наз.
К. п. В рассматриваемом случае оно имеет вид
K(X)Y=P(XY — YX), Х?д, Y?V.
К. п. играет основную роль в орбит методе (см. [2]).
Каждая G-орбита Q в К. п. несет на себе каноническую
G-инварпантную гампльтонову структуру (см. Гамилъ-
тонова система). Другими словами, на каждой орбите
Q имеется однозначно определенная невырожденная
G-инвариантная замкнутая дифференциальная 2-форма
Вд (откуда все G-орбиты в К. п. четномерны). Явное вы-
выражение для BQ можно получить следующим образом.
Пусть F??j*, Q — орбита, проходящая через точку F,
а ? и т] — 1:_сг.тельные векторы к Q в точке F. Найдутся
такие X и Y из Д, что
l=K(X)F, x)=K(Y)F.
Тогда
Ва(?, T]) = <f, [X, У]>.
Для каждого Х?д векторное иоле i,x(P) = K(X)F яв-
является гамильтоновыы относительно BQ; в качестве его
производящей функции (генератора) можно взять эле-
элемент X, рассматриваемый как линейная функция на д*.
Стабилизатор точки, орбита которой имеет максималь-
максимальную размерность в К. п., коммутативен [1]. Возникаю-
Возникающие на каждой орбите скобки Пуассона порождают еди-
единую скобку Березина, задающую структуру Ли локаль-
локальной алгебры в пространстве гладких функций на д*
(см. [3]). Координатное выражение этой скобки имеет
вид
где с,/ — структурные константы алгебры Ли д.
Лит.: [1] В е г n a t Р. [и др.], Representations des groupes
de Lie re'bohiUes, P., 1972; [2] К и р и л л о в А. А., Элементы
теории представлений, М., 1972; [3] его же, «Успехи матем.
наук», 137В, т. 31, в. 4, с. 57—7В. А. А. Кириллов.
КОПРОИЙВЕДЕНИЕ семейства объектов
категории — понятие, описывающее на языке
морфизмов конструкции прямой суммы модулей или
разъединенного объединения (букета) множеств. Пусть
^м *€Л— индексированное семейство объектов кате-
категории ЗЛ. Объект S, вг-есте с морфнзмами а,- : А[-+ S,
наз. к о п р о и з в е л е н и е м семейства A,, i?I,
если для всякого семейства морфизмов а; : Aj —>- X,
i?I, существует такой единственный морфизм а : S —>-
—>- X, что а,а=а,-, i?l. Морфизмы а,- наз. в л о ж е-
пиями копроизведения; К. обозначается
П*6Г4;(а,-) или П*еГ4 ,-, или S=A1*. . .*Ап в случае
/={1, . . ., и}. Морфизм а, входящий в определение
К., иногда обозначается П4буа,- или (*)igJa/. К. семей-
семейства объектов определено однозначно с точностью до
изоморфизма, оно ассоциативно и коммутативно. Поня-
Понятие К. двойственно понятию произведения.
К. пустого (емейства объектов является левым нулем
(инициальным объектом) категории. В абелевой катего-
категории К. часто наз. прямой суммой семей-
ства о б ъ е к т ов Л,-, i ?/, и обозначается V .4,-
или А!+. . .+Ап в случае /= {1, ... , п}. В большин-
большинстве категорий структуризованных множеств К. семей-
семейства объектов совпадает со свободным произведением
этого семейства и, как правило, требует специального
описания. Так, в категории групп К.— это свободное
произведение групп, в категориях модулей — прямая
сумма модулей и т. д.
В категории с нулевыми морфизмами для К. 5=
= ni6 jAi(aj) существуют такие однозначно определен-
определенные морфизмы я,-: 5->-Л,-, что сг,-я,-=1^, а/Яу=0.
В абелевой категории К. и произведение конечного се-
семейства объектов совпадают.
Лит.: [1] Ц а л е н к о М. III., III у л ь г е Й ф е р Е. Г.,
Основы теории категорий, М., 1974. М. Ш. Цаленко.
КО--Н-ПРОСТРАНСТВО — топологическое прост-
пространство, двойственное Н-пространству.
КОПСЕВДОГАЛИЛЕЕВО ПРОСТРАНСТВО — про-
пространство, двойственное псеедогалилееву пространству.
Оно является частным случаем полугиперболического
пространства.
Лит.: [1J Розенфельд Б. А., Неевклидовы прострпн-
ства, М., 1969. Л. А. Сидоров.
КОПСЕВДОЕВКЛИДОВО ПРОСТРАНСТВО — про-
пространство, получаемое из псевдоевклидова путем при-
применения принципа двойственности проективного прост-
пространства такой же размерности; обозначение lR*n. К. п.
lR*n является пространством с проективной метрикой,
к-рая вводится в соответствии с общим определением
проективных метрик путем выделения абсолюта в соот-
соответствующем по размерности проективном пространст-
пространстве. Проективная метрика псевдоевклидова простран-
пространства lRn определяется абсолютом, состоящим из сово-
совокупности (п—1)-плоскости и вещественной (п—2)-квад-
рики в этой плоскости, поэтому проективная метрика
соответствующего двойственного К. п. lRn определяет-
определяется двойственным к указанному абсолютом: веществен-
вещественным (абсолютным) конусом 2-го порядка с точечной вер-
вершиной, принимаемой в качестве абсолютной точки. Аб-
Абсолютный конус делит К. п. lRn на две области, в к-рых
скалярный квадрат векторов имеет постоянный знак.
Эти области изображают многообразия соответствую-
соответствующих плоскостей псевдоевклидова пространства, двойст-
двойственного для данного lRn- Изотропные плоскости псевдо-
псевдоевклидова пространства изображают точки абсолюта
lRn- В зависимости от расположения относительно аб-
абсолютного конуса и абсолютной точки (вершины) раз-
различают четыре типа прямых: эллиптические
прямые, пересекающие абсолютный конус в двух
мнимо сопряженных точках; гиперболически е
прямые, пересекающие абсолютный конус в двух
вещественных точках; параболические пря-
м ы е, проходящие через абсолютную точку; изо-
изотропные прямые — параболические, к-рые ка-
касаются абсолютного конуса.
В соответствующем по принципу двойственности псрв-
доевклидовом пространстве прямые первых двух типов
изображаются пучками плоскостей, пересекающихся
соответственно по евклидовым и псевдоевклидовым
(п—2)-плоскостям, параболические прямые — пучками
параллельных плоскостей, а изотропные — пучками
плоскостей, пересекающихся по изотропным (п—2)-
плоск остям.
Расстояние между точками К. п. lRn определяется
с учетом двойственного характера этого пространства
по отношению к соответствующему псевдоевклидову
пространству lRn. Пусть точкам X ц YclRn соответст-
соответствуют плоскости в lRn с нормальными уравнениями
(и, ж) + ио = О; (v,
так, что
причем
(uEu) = ±i, (vEv) =
где Е — линейный оператор, определяющий скалярное
произведение в lRn- Расстояние б между точками X (х°,
№) и Y (у0, у) определяется соотношением
cos? ± =
р (x
где р — мнимое или действительное число, называемое
радиусом кривизны пространства lRn.
В случае, когда плоскости в пространстве lR,n отве-
отвечающие точкам X и Y, параллельны, за расстояние ме-
между точками принимается расстояние d между этими
параллельными плоскостями:
d = | у°~х°\, когда (жЕж) > О,
d = i\ у° — х°\, когда (хЕж) < 0.
Геометрия на различных типах прямых пространства
lRn определяется типом проективной метрики на этих
прямых. Так, гиперболич. прямая несет на себе проек-
проективную метрику гиперболич. пространства и т. д.
За величину уяла между двумя плоскостями в К. п.
lR*i принимается нормированное расстояние между
соответствующими им по принципу двойственности точ-
точками псевдоевклидова пространства lRn. Угол между
двумя плоскостями равен нормированному расстоянию
между точками этих плоскостей, являющихся полюсами
(п — 2)-плоскости их пересечения относительно квад-
квадрик, высекаемых абсолютным конусом на данных пло-
плоскостях, причем во всех случаях определяется тот угол,
к-рый не содержит абсолютной точки. В частности, в
пространстве 1Л2 угол между двумя прямыми равен
нормированному расстоянию между такими двумя точ-
точками данных прямых, к-рые вместе с точкой пересече-
пересечения этих прямых гармонически делят точки пересече-
пересечения с абсолютными прямыми.
Движениями К. п. lRn наз. такие его преобразова-
преобразования, к-рые индуцируются движениями двойственного
ему псевдоевклидова пространства. Движения К. п.
lRr. описываются (как и движения псевдоевклидова
пространства lRn) псевдоортогональными операторами
индекса I.
Вследствие двойственного характера свойств плоско-
плоскостей ХЛ2 и 1Ri геометрия плоскости ^г может быть по-
получена из геометрии плоскости 1Л2? в частности геомет-
геометрия треугельника в плоскости 1Лг- Основные соотно-
соотношения между длинами сторон и величинами углов вы-
выражаются формулами, аналогичными для треугольни-
треугольников в коевюшдовой плоскости (см. Неевклидово прост-
пространство), но с применением гиперболич. функций вме-
вместо соответствующих тригонометрических.
Пусть в треугольнике ABC внутренний угол В содер-
содержит абсолютную точку. Между длинами сторон а, Ь, с
и величинами углов А , Ё, С имеют место соотношения
Ь=а+с,
, а , Ъ . с '
sh — sh — sh —•
р Р Р
А- = В2 + С- — ZBCch -2-.
На плоскости х/?2 метрика расстояний является ги-
гиперболической проективной, а метрика углов — пара-
болической. В 3-пространстве 1Йз проективная метрика
на плоскости является гиперболической, на прямой —
эллиптической, а метрика в пучках плоскостей — пара-
параболической (псевдоевклидовой) метрикой.
К. п.— предельный случай гиперболических прост-
пространств.
Лит.: [1] Розенфельд Б. А., Неевклидовы простран-
пространства, М., 1969; [2] Я г л о м И. М., Розенфельд Б. А.,
Ясинская Е. У., «Успехи матем. наук», 1964, т. 19, в. 5,
с. 51—113. Л. А. Сидоров.
КОРАЗМЕРНОСТЬ —1) К. (или факторраз-
мерность) подпространства L в вектор-
векторном пространстве V — размерность факторпространства
V/L; она обозначается codim^ L или просто codim L
п совпадает с размерностью прямого дополнения к L
в Тг. Справедливо равенство
dim L-\- codim L=dim Г.
Если М и N — два подпространства в V, имеющие ко-
конечные К., то Mf)N и M-j-N также имеют конечные
К., причем
codim (Af+iV)-rcodim (Mf) N)=codim Af+codim N.
2) К. подмногообразия Лгв дифференци-
дифференцируемом многообразии М — К. касательного подпро-
подпространства TX(N) в касательном пространстве Т^М1)
в точке x^N. Если М и Лг конечномерны, то
codim iV=dim Af—dim N.
Если М и N — дифференцируемое многообразия, L —
подмногообразие в Лг, / : М —>- Л — дифференцируемое
отображение, трансверсальное подмногообразию L, то
codim /~1(i) = codim L.
3) К. алгебраического подмногооб-
подмногообразия (или аналитического прост-
пространства) 7в алгебраическом многообразии (анали-
(аналитическом пространстве) X — разность
codim y=dim X—dim Y.
Лит.: [1] Б у р б а к и Н., Алгебра. Алгебраические струк-
структуры. Линейная и полилинейная алгебра, пер. с франц., М., 1962;
[2] е г о же, Дифференцируемые и аналитические многообра-
многообразия. Сводка результатов, пер. с франц., М., 1975; [3] Г о л у-
б и ц к и й М., Г и й е м и и В., Устойчивые отображения и
их особенности, пер. с англ., М., 1977.
В. Е. Говоров, А. Ф. Харшалпдзё.
КОРАССЛОЕНИЕ — тройка (X, i, Y), где X, Y —
топологич. пространства, i : X —*¦ Y — вложение, об-
обладающее следующим свойством существова-
существования продолжающей го м отопи и для
полиэдров: для любых полиэдра К, отображения
/ : Y —v К и гомотопии
F:XX[0, 1]-+ К
с
существует гомотопия
G : YX10, 1]-^ К
с
Go(iXid)=F,
где
(iXid): ХХ[0, 1]~>ГХ[0, 1].
Если это свойство выполнено для любых топологич.
пространств, то К. (X, г, Y) наз. парой Борсука
(впрочем, термин «К.» употребляется и в смысле «пара
Борсука»). Пространство Yh(X) наз. к о с л о е м К.
(X, i, Y). Цилиндрическая конструкция превращает
любое непрерывное отображение в К. и позволяет по-
построить последовательность
X ~> Y -> Y/i (X) -> С1 -> С2 -+ . . .
топологич. пространств, в к-рой С1—SX (SX — над-
надстройка над X) — кослой отображения Y^-Yli(X),
превращенного в К., С2—SY — кослой отображения
Yli(X) -> Cj и т. д. Если (X, i, У) — К. пунктирован-
пунктированных пространств, то для любого пунктированного поли-
полиэдра К индуцированная последовательность
[X, К] ч- [Y, К] ч- [F/i(X), #] ч- [Сх, К] ч- . . .
есть точная последовательность пунктированных мно-
множеств; здесь все члены, начиная с четвертого,— группы,
а начиная с седьмого,— абелевы группы.
Лит.: [1] С п е н ь е р Э., Алгебраическая топология, пер.
с англ., М., 1971. Л. Ф. Харшиладве.
КОРЕНЬ — 1) К. с т е п о н и п из числа а —
число х= у/а, п-я степень хп к-рого равна а.
2) К. алгебраического уравнения
над полем К
— элемент с?К, к-рый после подстановки его вместо
х обращает уравнение в тождество. К. этого уравне-
уравнения наз. также и К. многочлена
1 + . . . + а„ _ 1* 4-а„.
Если с является К. многочлена / (х), то f(x) делится без
остатка на х—с (см. Безу теорема). Всякий многочлен
f(x) с действительными или комплексными коэффициен-
коэффициентами имеет, по крайней мере, один, вообще говоря, ком-
комплексный К. Многочлен /(х) можно записать в виде
f(x) = ao(x—сх)(х—Со). . .(х—с„),
где сх, с2, ... , с„ — К. многочлена f(x). Если среди К.
с,, с.2, ... , сп многочлена fix) встречаются равные, то
общее их значение на,!. кратным корнем.
3) К. н з единицы — элемент поля к, удовлетво-
удовлетворяющий уравнению жга = 1 при нек-ром натуральном т.
К. из единицы образуют подгруппу в мультипликатив-
мультипликативной группе поля к. Обратно, любая конечная подгруппа
мультипликативной группы поля А; состоит нз К. из еди-
единицы н является циклической. В частности, такова
подгруппа Uп всех К. из единицы заданной степени п,
содержащихся в алгебраич. замыкании к поля к, т. е.
всех Z,?k, удовлетворяющих уравнению ?"=1. Если п
взаимно просто с характеристикой поля к (или эта ха-
характеристика равна 0), то порядок группы Un равен п
и образующие этой группы наз. первообразны-
м и корнями степени п из единицы. Число таких
корней в группе Un равно значению функции Эйлера
ц>(п), т. е. числу вычетов по модулю п, взаимно про-
простых с га. В поле характеристики р>0 не существует
К. из единицы степени р, отличных от 1.
В случае, когда поле к конечно порождено над своим
простым подполем, число К. нз единицы, содержащихся
в к, конечно.
В поле комплексных чисел число z является К. пз
единицы степени п тогда и только тогда, когда |z| = l и
arg 2=2яш/п с целыми т и п, т. е. когда
z = е**Ь*/п = см 2ят + . ; 2лт
п г п '
при этом первообразные К. выделяются условием
(т, п)=1. На комплексной плоскости К. из единицы
степени п лежат в вершинах правильного «-угольника,
вписанного в единичную окружность, что объясняет
связь К. из единицы с задачей о делении круга.
К. из единицы появляются в теории чисел в качестве
значений ряда важных теоретико-числовых функций
(абелевы числовые характеры, символ Лежандра, функ-
функция Мёбиуса, символ норменного вычета и т. д.). В тео-
теории полей и алгебранч. теории чисел важную роль иг-
играют поля, получаемые присоединением К. из единицы
к нек-рому основному полю (см. Круговое поле, Круго-
Круговое расширение, Куммера расширение).
Лит.: [1] Ван-дер-Варден Б. Л., Алгебра, пер.
с нем., М., 1976; [2] Л е н г С, Алгебра, пер. с англ., М., 1968.
Л. В. Кузьмин.
КОРНА НЕРАВЕНСТВО — неравенство для вектор-
функций V((xJ), i, /=1, ... , п, и их производных, опре-
определенных в нек-рой ограниченной области А простран-
пространства R":
dv. dv ¦ \2
dxJ Ox1
П vl^c\\vi, A)
J А A = l
где
fV" v\\dx. B)
К. н. справедливо и для вектор-функций из пространст-
пространства Н^А), полученного пополнением пространства
Сг(А) по норме B). Иногда неравенство A) наз. вто-
вторым К. н., а нервы м К. н. считается неравен-
неравенство A) без второго слагаемого в левой части.
К. н. предложено А. Корном (А. Когп, 1908) для по-
получения априорной оценки решения неоднородных
уравнении теории упругости.
Лит.: [1] Ф и к е р а Г., Теоремы существования в теории
упругости, пер. с англ., М., 1974. М. И. Войцеховскип.
КОРНЕВАЯ СИСТЕМА — конечное множество R
векторов векторного пространства V над полем R, обла-
обладающее следующими свойствами: 1) Л не содержит ну-
нулевого вектора и порождает V; 2) для каждого a?R
существует такой элемент а* сопряженного к V прост-
пространства У*,что <х*(а)=2 и что эндоморфизм sa : х\—*¦
i—*¦ х—а*(ж)а пространства V переводит R в себя;
3) п{а, р)=р*(а) $ г для всех а, р?Я.
Впервые наборы векторов, обладающие перечислен-
перечисленными свойствами, возникли в теории полупростых ком-
комплексных алгебр Ли как системы весов присоединенного
представления максимального тора такой алгебры (см.
Вес представления, Ли полупростая алгебра). Позже
было обнаружено, что такие системы векторов естест-
естественно появляются и во многих других разделах мате-
математики, напр, в алгебраической геометрии [4], [7], в
теории особенностей [71, в теории целочисленных квад-
квадратичных форм [5]. С К. с. оказались также связанны-
связанными нек-рые вопросы теории чисел [6].
Общие свойства К. с. Эндоморфизм sa является
отражением относительно а. и определен свойствами 1)
и 2) однозначно. Кег а* является множеством неподвиж-
неподвижных точек эндоморфизма sa и sa(oc)^ —а. Элементы из R
наз. корнями К. с. R, dim V — рангом.
К. с. R наз. приведенной, если для любого
а?Я вектор —а является единственным корнем, кол-
линеарным с а. Множество Я*={а*|а?Д} есть К. с.
в V*, для к-рой а**=а при всех а?Д; она наз. д у-
а л ь н о й (или обратной) К. с. к Я. Конечная
группа A (R), образованная всеми автоморфизмами
пространства V, переводящими R в себя, наз. груп-
группой автоморфизмов К. с. Я. Подгруппа
W(R) в A(R), порожденная отражениями sa, a?R,
наз. группой В е и л я К. с. Я. Если V — пря-
прямая сумма своих подпространств V;, г=1, ... , Z, и
R; — К. с. в F/, то R= \Ji=iRj — К. с. в V, она наз.
прямой суммой К. с. Я,-. Непустая К. с. Я
наз. неприводимой, если R не является прямой
суммой двух непустых К. с. Всякая К. с. является пря-
прямой суммой некоторого набора неприводимых К. с. и
это разложение определено однозначно с точностью до
порядка слагаемых.
Связные компоненты множества V—(JccgflKera* яв~
ляются открытыми симплициальными конусами и наз.
камерами К. с. R в V (см. Камера). Группа Вейля
действует просто транзитивно на множестве всех камер.
Замыкание С камеры С является фундаментальной об-
областью дискретной группы W{R). Пусть Lx, . . ., Lr —
стенки камеры С. Для каждой стенки ?,¦ существует
единственный корень а,- такой, что L, = Ker ai и а,-
лежит по ту же сторону от ?,-, что и С. Семейство корней
аь . . ., аг образует базис в V, который наз. бази-
базисом К. с, определенным камерой С.
Говорят также, что ах, . . ., аг — набор простых
корней, определенный камерой С. Группа W(R)
порождена отражениями sa , i=l, . . ., г, причем
(sasaynij=i, где niij — порядок sasa_,— система оп-
определяющих соотношений для W(R), так что W(R) —
Кокстера группа. Группа A (R) есть полупрямое произ-
произведение подгруппы всех элементов из A (R), оставляю-
оставляющих множество ах, . . ., аг инвариантным, и W(R).
Выбор камеры С определяет отношение порядка в V
(согласованное со структурой векторного пространства),
при к-ром положительными считаются линейные ком-
комбинации простых корней аи . . ., <хг с неотрицательны-
неотрицательными коэффициентами. Всякий корень оказывается либо
положительным, либо отрицательным, а все его коор-
координаты в базисе ах, . . ., <zr — целочисленными. Под-
Подгруппа Q{R) в V, порожденная К. с. R, является решет-
решеткой (т. е. дискретной подгруппой ранга г), инвариант-
инвариантной относительно группы Вейля W(R). Ее элементы
наз. радикальными весами К. с. Д. Груп-
Группы Вейля К. с. могут быть охарактеризованы среди всех
дискретных линейных групп, порожденных отражения-
отражениями, как такие, к-рые не имеют ненулевых неподвижных
векторов и обладают инвариантной решеткой. Если
Q(R) рассматривать как группу параллельных перено-
переносов пространства V, то полупрямое произведение
Wa(R) группы W(R) на Q{R) наз. аффинной
группой Вейля К. с. Л. Wa(R) является ди-
дискретной группой преобразований пространства V,
порожденной отражениями в гиперплоскостях
La, k= {v?V\a*(v)=k},
где <x?R, k^Z- Факторпространство пространства V
по Wa(R) компактно; если R неприводима, то
фундаментальной областью для Wa(R) будет симп-
симплекс.
На V может быть выбрана (неоднозначно) билинейная
симметрическая положительно определенная форма (,),
инвариантная относительно W(R). Эта форма снабжает
V структурой евклидова пространства, в к-ром элемен-
элементы из И (R) являются ортогональными преобразования-
преобразованиями, а отражение sa, а(;Я, имеет для всех ж^Увид
sa(x)=x—2(x, а) а/(а, а).
С помощью формы ( , ) пространства V и F* могут
быть отождествлены, и тогда <x*=2al(a, а), а усло-
условие 3) определения К. с. означает, что п (а, E)=
=2 (а, Р)/(Р, P)€Z для всех a, P?R.
Введение формы (,) позволяет говорить о метрических
соотношениях между корнями, в частности об угле меж-
между корнями и о длине корня. Величина угла оказывает-
оказывается не зависящей от выбора формы (,), а если К. с. R
неприводима, то это верно и для отношения длин двух
корней.
Классификация К. с. Пусть аь . . ., аГ — некото-
некоторый фиксированный базис приведенной К. с. Л и п,/=
= ге(а,-, a.j). Матрица ||ге,-у-||, 1<г, /<г, наз. матрицей
К а р т а н а К. с. Л; в ней пц=2, а пц при i-ф] могут
быть равны 0, —1, —2 или —3. С точностью до переста-
перестановки индексов эта матрица не зависит от выбора бази-
са. Две К. с. с одинаковыми матрицами Картана изо-
изоморфны.
С К. с. обычно связывают граф Кокстера
К. с, вершичамп к-рого служат элементы базиса аь
. . ., аг, причем вершины а,- и ау соединены одним, дву-
двумя, тремя ребрами или не соединены вовсе в случаях,
когда произведение га,-,"/' равно соответственно 1, 2, 3
или 0. К. с. неприводима тогда и только тогда, когда ее
граф Кокстера связен. Граф Кокстера определяет лишь
углы между парами корней базиса; по нему не восста-
восстанавливается матрица Картана (но восстанавливается
группа Вейля): существуют дуальные неизоморфные
К. с. с одинаковыми графами Кокстера. Однако матри-
матрица Картана (а с ней и К. с.) полностью определяется
ориентированным графом Кокстера,
наз. также схемой простых корней К. с.
R. Ориентация вводится по правилу: если простые
корни а,- и а,- не ортогональны и имеют разную длину,
то на двух или трех ребрах, соединяющих г-го и /-ю
вершины, ставится знак неравенства >, ориентирован-
ориентированный в сторону вершины, отвечающей корню меньшей
длины. В нек-рых случаях над каждой вершиной графа
Кокстера надписывают число, пропорциональное квад-
квадрату длины соответствующего корня (с общим для всех
корней коэффициентом пропорциональности); по тако-
такому взвешенному графу также однозначно восстанавли-
восстанавливается К. с.
Полный список попарно неизоморфных неприводи-
неприводимых приведенных К. с, заданных своими схемами про-
простых корней, следующий:
Ап о——О • • •—о—о П вершин ( п & 7 )
П вершин (»>г)
П вершин (Л > 3 )
Л вершин (/7 >4)
Конструкция неприводимых К. с.
Пусть еи . . ., еп — канонический базис в Rn, (,) —
скалярное произведение в R", для к-poro {е,-, еу-) =
= &ij, и Г„ — решетка в Rn, порожденная векторами
«1, • • •. еп.
1) Пусть V — гиперплоскость в Rn + 1, ортогональ-
ортогональная вектору «i+. . . + е,1 + 1. Тогда
= {«1—е/М^/; *. 7 = 1. •¦••
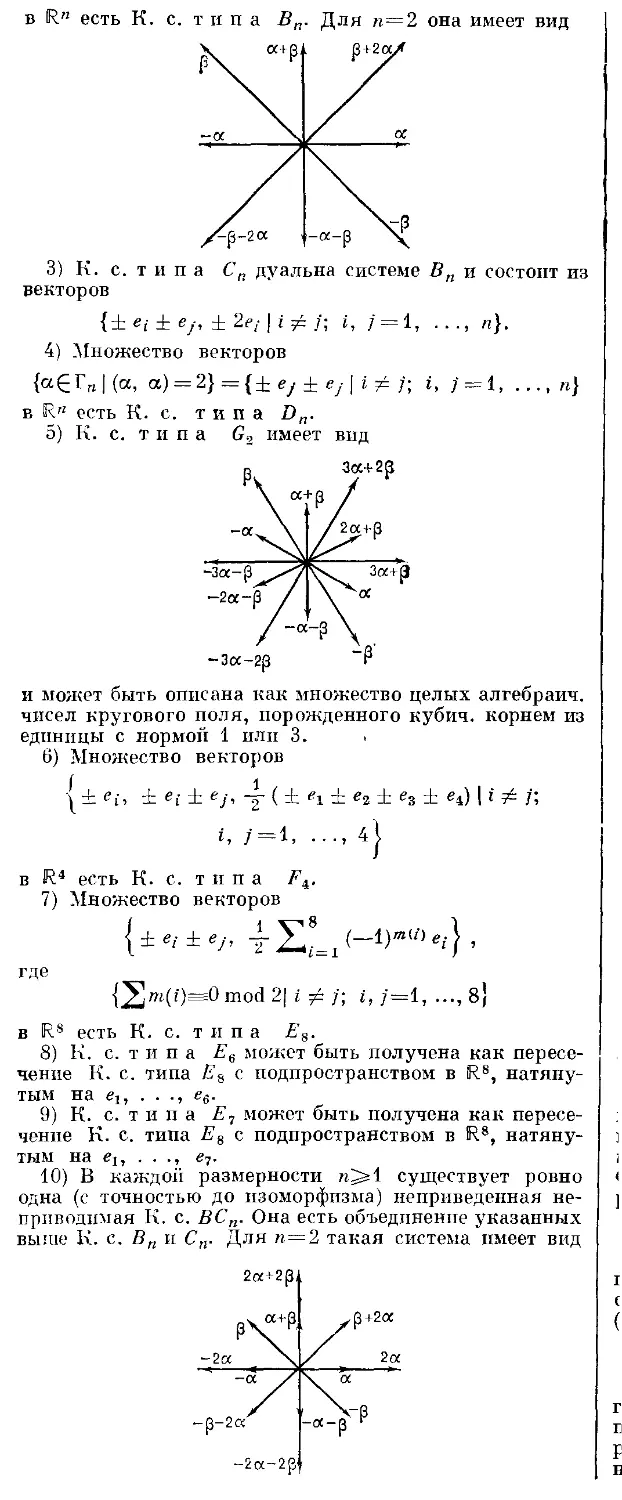
есть К. с. типа Ап. Для п=2 она имеет вид
/-«-p -p
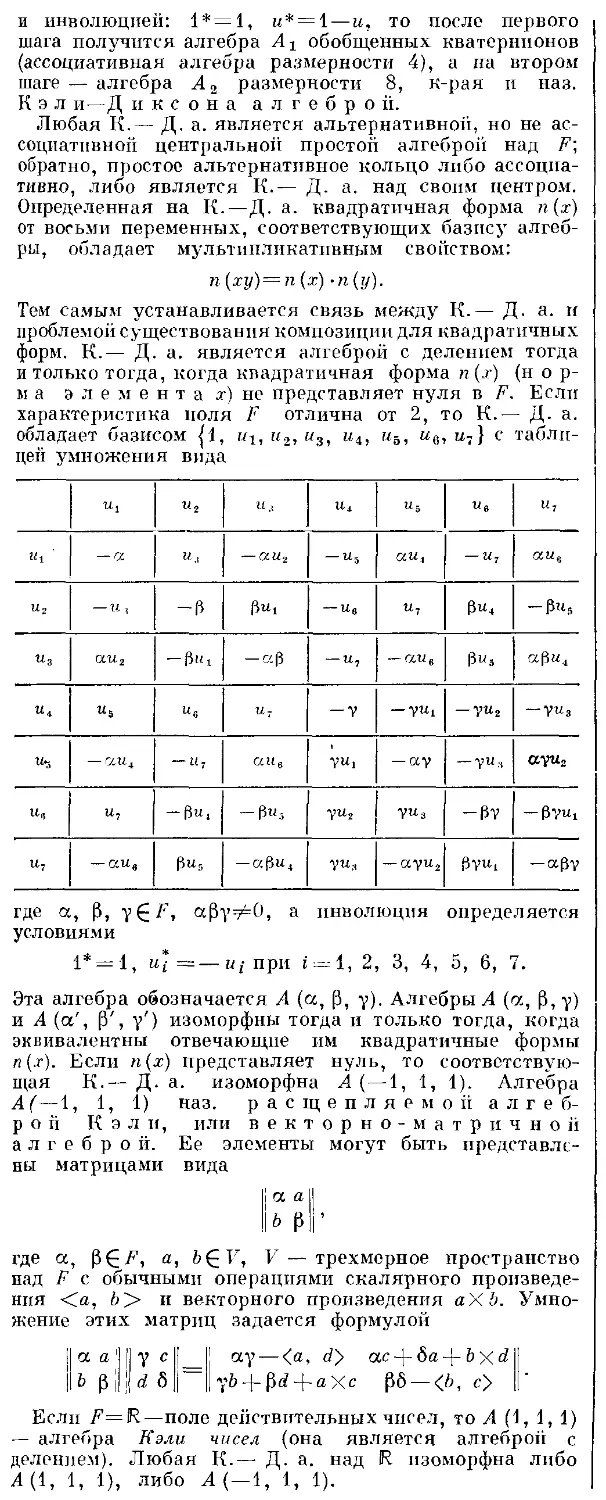
2) Множество векторов
{а?Г„|(а, а) = 1 или 2} =
= {±«i, ± ei ±ej\i Ф j; i, /=1, ..., п}
в R" есть К. с. типа Вп. Для «=2 она имеет вид
3) К. с. т и п а Сп дуальна системе Вп и состоит из
векторов
{± е,' ± ej, ± 2е; \\фу, i, / = 1, . . ., п).
4) Множество векторов
в R" есть К. с. типа Dn.
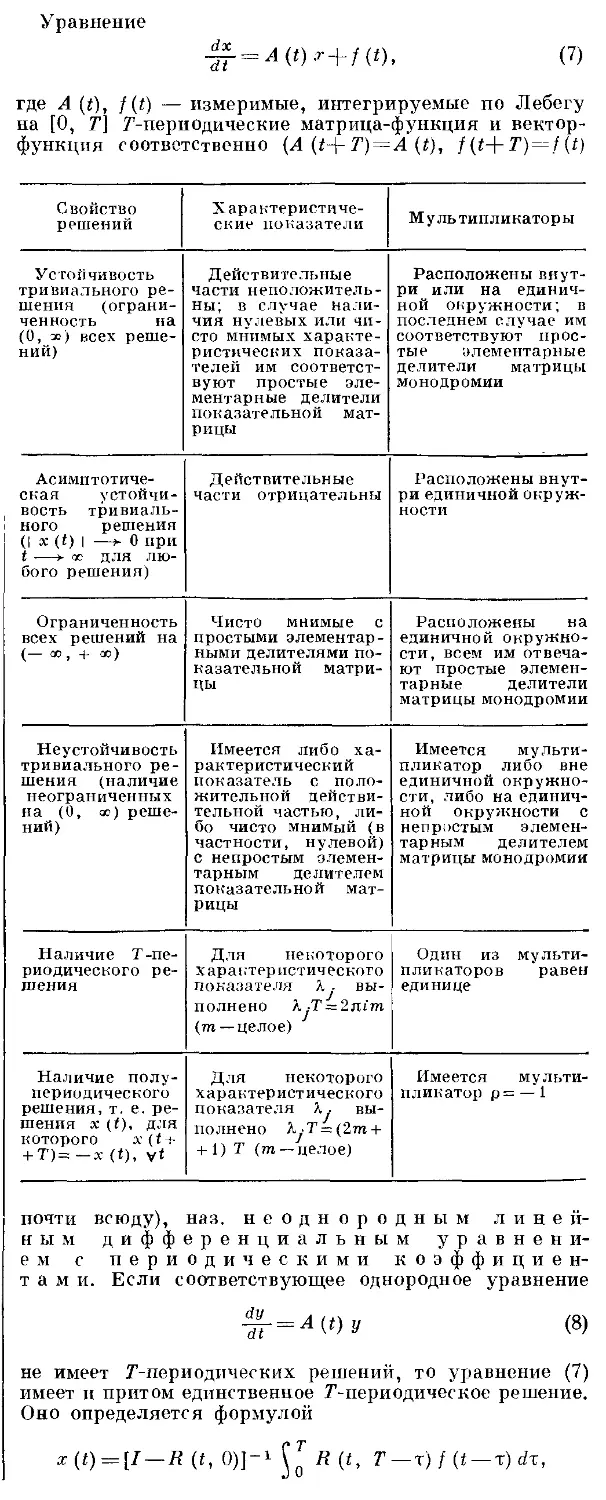
5) К. с. типа G2 имеет вид
-Р'
и может быть описана как множество целых алгебраич.
чисел кругового поля, порожденного кубич. корнем из
единицы с нормой 1 или 3.
6) Множество векторов
у
ej, -у ( ± «1 ± «г ± е3 ± е4)
i, /=1, ..., 4\
в R4 есть К. с. т и п а
7) Множество векторов
{±e,±ej, т
где
в R8 есть К. с. типа Е8.
8) К. с. т и п а Е6 может быть получена как пересе-
пересечение К. с. типа Еъ с подпространством в R.8, натяну-
натянутым на еь . . ., е6.
9) К. с. т и п а Е7 может быть получена как пересе-
пересечение К. с. типа Е8 с подпространством в R8, натяну-
натянутым на в], . . ., е7.
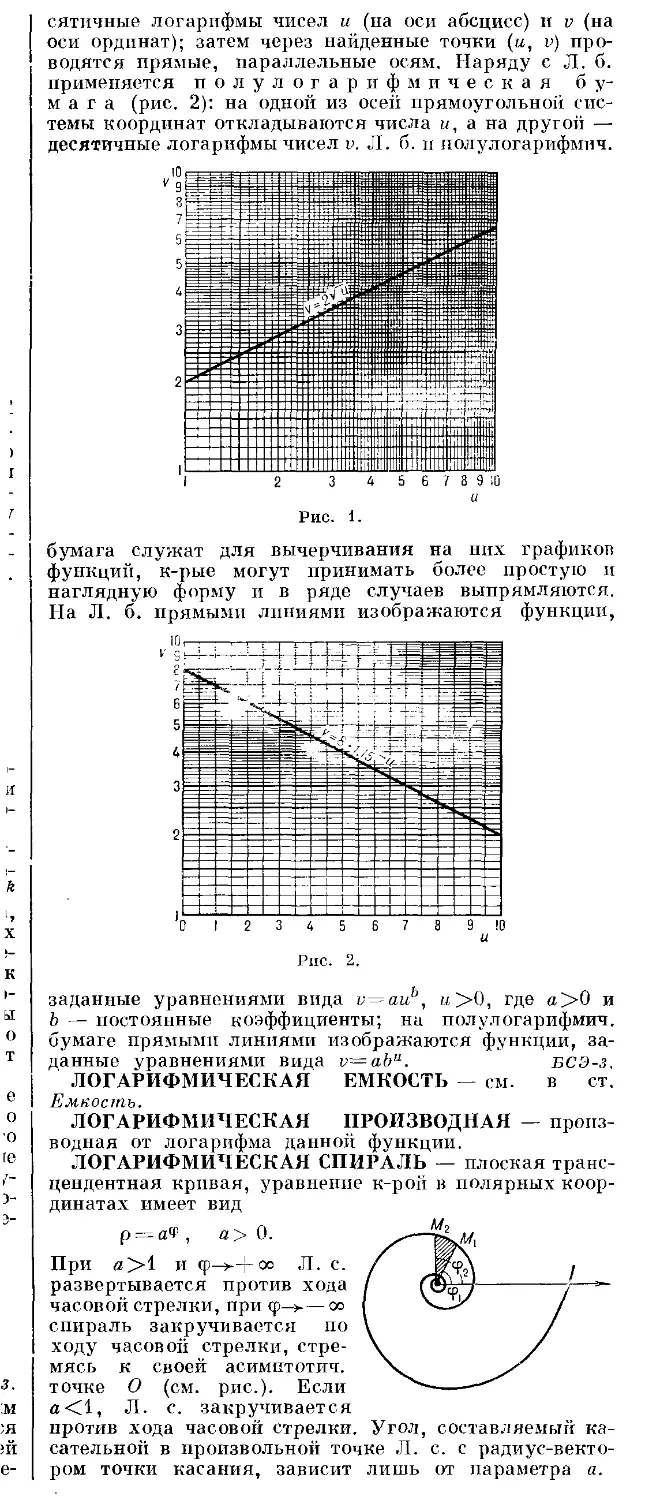
10) В каждой размерности «>1 существует ровно
одна (с точностью до изоморфизма) неприведенная не-
неприводимая К. с. ВСп. Она есть объединение указанных
выше К. с. Вп и Сп. Для « = 2 такая система имеет вид
2а
¦то
-2а
-а
-C-2 а
+2Р,
а+р
\
/
,C+2а
^/
/ 2а
\ а
ч-р
Об аффинных К. с. см. [6].
Лит.: [1] Б у р б а к и Н., Группы и алгебры Ли..., пер.
с франц., М., 1972; [2] С е р р Ж.-П., Алгебры Ли и группы
Ли, пер. с англ. и франц., М., 1969; [3] Стейнберг Р.,
Лекции о группах Шевалле, пер. с англ., М., 1975; [41 М а-
н и н Ю. И., Кубические формы, М., 1972; [5] Milnor J.,
Husemoller D., Symmetric bilinear forms, B.—Hdlb.—
N. Y., 1973; [6] M а к д о н а л ь д И. Г., «Математика»,
1972, т. 16, Л» 4, с. 3—49; [7] А р н о л ь д В. И., «Успехи ма-
тем. наук», 1975, т. 30, в. 5, с. 3—65. В. Л. Попов.
КОРНЕВОЙ ВЕКТОР линейного преоб-
преобразования А векторного простран-
пространства V над полем к — вектор v ? V, лежащий
в ядре линейного преобразования (А—ХЕ)п, где Х?к,
п — целое положительное число, зависящее от А и v.
Число Я будет непременно собственным значением пре-
преобразования А. Если при этом (А—ХЕ)п~1иф0, то го-
говорят, что v — К. в. высоты п, принадлежащей Я.
Понятие К. в. обобщает понятие собственного векто-
вектора преобразования А: собственные векторы — это в точ-
точности К. в. высоты 1. Множество F^,K. в., принадлежа-
принадлежащих фиксированному собственному значению Я, яв-
является линейным подпространством в V, инвариантным
относительно А. Оно наз. корневым подпро-
подпространством, принадлежащим собственному зна-
значению Я. К. в., принадлежащие различным собствен-
собственным значениям, линейно независимы; в частности,
V% Л Рц=°. если к^=ц.
Пусть V конечномерно. Если все корни характери-
стич. многочлена преобразования А лежат в к (напр.,
когда к алгебраически замкнуто), то "V раскладывается
в прямую сумму различных корневых подпространств:
Это разложение является частным случаем весового
разложения векторного пространства V относительно
расщепляемой нильпотентной алгебры Ли L линейных
преобразований: алгеброй L в этом случае служит одно-
одномерная подалгебра, порожденная преобразованием А
в алгебре Ли всех линейных преобразований простран-
пространства V (см. Вес представления).
Если в нек-ром базисе матрица преобразования А
является жордановой матрицей, то компоненты разло-
разложения (*) могут быть описаны следующим образом:
корневое подпространство V% есть линейная оболочка
множества тех векторов базиса, к-рые отвечают жорда-
новым клеткам с собственным числом Я.
Лит.: 11] Воеводин В. В., Линейная алгебра, М.,
1974; [2] М а л ь ц е в А. И., Основы линейной алгебры, 3 изд.,
М., 1970. В. Л. Попов.
КОРНИША — ФИШЕРА РАЗЛОЖЕНИЕ — асимп-
асимптотическое разложение разности между соответствую-
соответствующими квантилями нормального распределения и какого-
либо близкого к нему распределения по степеням мало-
малого параметра; изучено Э. Корнишем и Р. Фишером [1].
Если F(x, t) — функция распределения, зависящая от
параметра t, Ф (х) — функция нормального распределе-
распределения с параметрами @, 1), причем F(х, ?)-+Ф(х) при
t—»-0, то при определенных условиях на F(x, t) К.—
Ф. р. функции x=F-1[<D (z), t] (F'1 — функция, об-
обратная к F) имеет вид
x = z + '?"i'~i1Si(z)ti + O(t>»), A)
где Sj(z) — некоторые многочлены от z. Аналогично
определяется К.— Ф. р. функции г=Ф~1[Р(х, t)]
(ф-1 — функция, обратная к Ф) по степеням х:
где Qi(x) — некоторые многочлены от х. Формула B)
получается при разложении функции Ф-1в ряд Тейло-
Тейлора в точке Ф (х) и использовании Эджворта разложе-
разложения. Разложение A) является обращением формулы B).
Если X — случайная величина с функцией распреде-
распределения F(x, t), то величина Z=Z(X)=<D-1[F(X, t)]
имеет нормальное распределение с параметрами @, 1)
и, как следует из B), функция распределения величины
лучше аппроксимируется при t —>- 0 функцией Ф(х),
чем функция F (х, t). Если X имеет нулевое математич.
ожидание и единичную дисперсию, то первые члены
разложения A) имеют следующий вид
где Vi=x3'/x2/2, Y2=xj/z2, кг есть r-fi семиинвариант
X, М2)=4"Я2B), ЛоB)=-^[2Я3B) + Я1B)], Hr(z) -
многочлены Эрмита, определяемые соотношением
<!(z)Hr(z) = (-\yd-^l (ФB)=Ф'B)).
О разложениях для величин с предельными законами
из семейства распределений Пирсона см. [3]. См. также
Случайных величин преобразование.
'Лит.: [1] С о г n i s h E. A., Fisher R. A., «Rev.
Inst. internal:, statist.», 1937, v. 5, p. 307—20; [2] К е н д а л л М.,
Стьюарт А., Теория распределений, пер. с англ., М., 1966;
13] Б о л ь ш е в Л. Н., «Теория вероятн. и ее примен.», 1963,
т. 8, с. 129—55. В. И- Пагуроеа.
КОРНЮ СПИРАЛЬ, клотоида, клофоид а,—
плоская трансцендентная кривая (см. рис.), натураль-
натуральное уравнение к-рой имеет вид
где г — радиус кривизны^ а= const, s — длина дуги.
Параметрические уравнения:
-?-ds' у=Js0 sin -?•ds-
К. с. касается оси абсцисс в начале координат. Асим-
Асимптотические точки: М±( У~ла/2, У па/2) и Мг{—У па/2,
— УИа/2).
К. с. иногда наз. спи-
спиралью Эйлера по име-
имени Л. Эйлера (L. Euler), у
к-рого она впервые встре-
встречается A744). Начиная с
работ А. Корню (А. Согни,
1874) К. с. широко исполь-
используется в практике расчета
дифракции света.
Лит.: [1] С а в е л о в А. А.,
Плоские кривые, М., 1960.
Д. Д. Соколов. ~
КОРРЕКТНАЯ ЗАДАЧА — задача определения ре-
решения z—R(u) из метрического пространства Z (с рас-
расстоянием Pz(-,-)) по исходным данным и из метрическо-
метрического пространства U (с расстоянием Ри( •,•))» для к-рой
выполнены следующие условия: а) для всякого u?U
существует решение z?Z; б) решение определяется од-
однозначно; в) задача устойчива на пространствах (Z, U):
для всякого е>0 существует такое б(е)>0, что для лю-
любых «J, u2?i/ из неравенства рц(и1, г/2)<б(е) следует
неравенство pz(zii zi)-^-ei гДе 2i==^Gt1), z2=i? (и2).
Задачи, не удовлетворяющие хотя бы одному из пере-
перечисленных условий корректности, наз. некорректными
задачами.
КОРРЕЛОГРАММА временного ряда хг,
. . . , хТ — совокупность сериальных (выборочных)
коэффициентов корреляции
Г^Т — • «=1,2,...,
где .г — выборочное среднее ряда
Иногда К. наз. график rj как функции от t. К. является
эмпирической мерой статистической связи между чле-
членами последовательности {xt}. В анализе временных
рядов К. используется для статистпч. выводов о вероят-
вероятностной модели, предлагаемой для описания и объясне-
объяснения наблюдаемой последовательности данных.
Теоретической К. иногда наз. нормирован-
нормированную корреляционную функцию (стационарной) случай-
случайной последовательности {X}
где
cov(X,, Xs + t) = B(Xs-BXs)(Xs + t-EXs + f)
— ковариация случайных величин XS1 Xs + t, a D(XS) —
дисперсия случайной величины Xs. Если рассматри-
рассматривать {xf} как реализацию случайной последовательно-
последовательности {Xt}, то выборочная К. {rt} при достаточно общих
предположениях дает состоятельные и асимптотически
нормальные оценки для теоретической К. {р^} (см. [3]).
Хотя описания стационарной случайной последова-
последовательности в корреляционных и спектральных терминах
с математич. точки зрения эквивалентны, в статистич.
анализе временных рядов области применений корре-
корреляционных и спектральных методов разделяются в за-
зависимости от исходного материала и конечной цели ана-
анализа. Если спектральный анализ дает представление о
наличии и интенсивностях периодич. компонент вре-
временного ряда, то корреляционные методы удобнее при-
применять при исследовании статистич. связей между по-
последовательными значениями наблюдаемых данных.
В статистич. практике методы, основанные на К., ис-
используются обычно в тех случаях, когда есть основа-
основания предполагать наличие достаточно простой стоха-
стич. модели (авторегрессия, скользящие средние или
смешанная модель авторегрессии и скользящих сред-
средних невысоких порядков), порождающей данный вре-
временной ряд (напр., в эконометрии). В таких моделях
теоретическая К. {р^} обладает выраженной особен-
особенностью (обращение в нуль для всех достаточно больших
значений t в модели скользящих средних, экспоненци-
экспоненциальное убывание с возможной осцилляцией в моделях
авторегрессии), наличие подобной особенности у вы-
выборочной К. может служить указанием на ту или
иную гипотетическую вероятностную модель. Для про-
проверки согласия и оценки параметров выбранной моде-
модели разработаны статистические методы, основанные
на распределениях сериальных коэффициентов кор-
корреляции.
Лит.: [1] Андерсон Т., Статистический анализ вре-
временных рядов, пер. с англ., М., 1976; [2] Кен да л л М.,
С т ь ю а р т А., Многомерный статистический анализ и времен-
временные ряды, пер. с англ., М., 1976; [3] Хеннан 3., Много-
Многомерные временные ряды, пер. с англ., М., 1974. А. С. Холево.
КОРРЕЛЯЦИИ КОЭФФИЦИЕНТ — числовая ха-
характеристика совместного распределения двух случай-
случайных величин, выражающая их взаимосвязь. К. к.
р=р(А'1, Х2) для случайных величин Хг и Х2 с
математич. ожиданиями а1=ЕД*1 и а,=ЕА'2 и ненулевы-
ми дисперсиями ol=DX1 и ol=DX2 определяется ра-
равенством
р (Хъ Х2) = — .
К. к. для Xj и Х2 совпадает с ковариацией для норми-
нормированных величин (Xj—а1)/о1 и (Z2—a2)/a2. К. к. сим-
симметричен относительно Хг и Х2 и инвариантен относи-
относительно изменения начала отсчета и масштаба. При этом
— 1<р<:1. Значение К. к. как одной из возможных мер
взаимосвязи определяется следующими его свойствами:
1) если величины Хх и Х2 независимы, то p(Xj, Х2)=0
(обратное утверждение в общем случае неверно), о ве-
величинах, для к-рых р=0, говорят, что они некоррели-
рованы; 2) |р| = 1 тогда и только тогда, когда величины
связаны линейной функциональной зависимостью:
Трудность интерпретации р как меры взаимозависимо-
взаимозависимости заключается в том, что равенство р=0 может иметь
место как для независимых, так и для зависимых слу-
случайных величин, в общем случае для независимости
необходимо и достаточно равенство нулю их макси-
максимального коэффициента корреляции. Таким образом,
К. к. не исчерпывает все виды связи между случайными
величинами и является лишь мерой линейной зависимо-
зависимости. При этом степень линейной зависимости характери-
характеризуется следующим образом: величина
дает линейное представление Х2 по Xlt наилучшее в
том смысле, что
Е (Х2-Х2J = min E (Х2~с1Х1 — с2)\
Си С2
см. также Регрессия. Характеристиками корреляции
между несколькими случайными величинами служат
частный коэффициент корреляции и множественный
коэффициент корреляции. О способах проверки гипотез
независимости и исследования корреляции с помощью
К. К. СМ. Корреляция. А- В. Прохоров.
КОРРЕЛЯЦИОННАЯ МАТРИЦА — матрица коэф-
коэффициентов корреляции нескольких случайных величин.
Если Х1у . . ., Хп — случайные величины с ненулевы-
ненулевыми дисперсиями al, . . . , oft, то элементы рц при 1Ф]
равны корреляции коэффициентам р(Х/, Ху), а при г=/
равны 1. Свойства К. м. Р определяются свойствами
ковариационной матрицы 2 в силу соотношения: 2 =
= ВРВ, где В — диагональная матрица с диагональны-
диагональными элементами СГЬ ... , Оп. д. В. Прохоров.
КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ действи-
действительного случайного процесса {X (t);
t?T} — функция аргументов t, s?T, определяемая
равенством
В (t, s) =Е [X (О — ЕХ (*)] [X (s)-EX(s)].
Для того чтобы К. ф. была определена, следует предпо-
предположить, что процесс X (t) при всех t? T имеет конечный
второй момент EX (iJ. Параметр t пробегает здесь не-
некоторое подмножество Т действительной прямой и обыч-
обычно интерпретируется как «время», однако совершенно
аналогично определяется К. ф. случайной функции, за-
заданной на множестве произвольной природы, в частно-
частности К. ф. случайного поля, когда Т — подмножество
конечномерного пространства. Если JC(t) = [X1(t), . . .,
Xn(t)] — многомерный случайный процесс (случайная
функция), то его К. ф. наз. матричнозначная функция
В (t,s) = l\Bif(t, s)\\l /=1,
где
Ви (t, s) =Е [X,- (О-ЕХ,- (*)] [Xj (s)~EXj («)]
— взаимная корреляционная функ-
функция процессов Xi(t), Xj(t).
К. ф. является важной характеристикой случайного
процесса. Если X (t) — гауссовский процесс, то его К. ф.
В (t, s) и среднее значение EX (t) (т. е. первые и вторые
моменты) однозначно определяют конечномерные рас-
распределения, а значит и процесс в целом. В общем случае
первых двух моментов заведомо недостаточно для пол-
полного описания случайного процесса. Напр., одинако-
одинаковую К. ф. В (t, s) = e~a^~sl имеют гауссовский марков-
марковский стационарный процесс, траектории к-рого непре-
непрерывны, и так наз. телеграфный сигнал —
точечный марковский стационарный процесс, прини-
принимающий два значения ±1. Однако К. ф. определяет ряд
важных свойств процесса — так наз. свойства
второго порядка (т. е. выражающиеся в тер-
терминах вторых моментов). В силу этого, а также благо-
благодаря своей относительной простоте, корреляционные
методы широко используются как в теории случайных
процессов, так и в ее статистич. приложениях (см. Кор-
релограмма).
Скорость и характер убывания корреляций при
\t—s\ -*- оо дают представление об эргодических свой-
свойствах процесса. Условия на скорость убывания корре-
корреляций в той или иной форме^присутствуют в предель-
предельных теоремах для случайных процессов. Локальные
свойства 2-го порядка, такие как среднеквадратичные
непрерывность, дифференцируемость, дают полезную,
хотя и весьма грубую характеристику локального по-
поведения процесса. Исследование свойств траекторий в
терминах К. ф. с большой полнотой проведено в гаус-
совском случае (см. Выборочная функция). Одним из на-
наиболее завершенных разделов теории случайных про-
процессов является теория линейной экстраполяции и
фильтрации, позволяющая находить оптимальные ли-
линейные алгоритмы прогноза и аппроксимации случай-
случайных процессов, основываясь на знании К. ф.
Характеристическим свойством К. ф. является поло-
положительная определенность:
для любого п, любых комплексных сг, . . ., сп и
любых tu . . ., tn?T. В наиболее важном случае ста-
стационарного в широком смысле процесса В (t, s) зависит
от разности аргументов: B{t, s)=R(t—s). Условие по-
положительной определенности принимает тогда вид
Если R (t) дополнительно непрерывна при t=0 (что со-
соответствует среднеквадратичной непрерывности про-
процесса X(t)), то
R «) =
(<)=f eit^F (dk),
где F (dX) — положительная конечная мера; здесь А,
пробегает всю действительную прямую, если Г=
= (—со, оо) (случай «непрерывного времени»), или отре-
отрезок [—л, я], если Т={. . . , —1, О, 1, . . .} (случай
«дискретного времени»). Мера F(dk) наз. спект-
спектральной мерой случайного процесса. Таким
образом, корреляционные и спектральные свойства
стационарного случайного процесса оказываются тесно
связанными; напр., скорость убывания корреляций при
t —>- оо соответствует степени гладкости спектральной
плотности f{X)=F(d%)ldX и т. п.
В статистической механике К. ф. наз. также совмест-
совместная плотность вероятности р(хг, . . . , хт) нахождения
т различных частиц рассматриваемой системы в точках
хх, ... , хт; совокупность этих функций однозначно
определяет соответствующее точечное случайное поле
Лит.: [1] Д у б Дж., Вероятностные процессы, пер. с англ., I
М., 1956; [2] Л о э в М., Теория вероятностей, пер. с англ., М.,
1962; [3] Г и х м а н II. И., Скороход А. В., Введение в
теорию случайных процессов, М-, 1965. А. С. Холево.
КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ в статисти-
статистической механике — функция, описывающая
влияние частиц или групп частиц друг на друга и эф-
эффекты взаимодействия подсистем рассматриваемой сис-
системы.
В классической статистич. механике К. ф. G2(l, 2),
G3(l, 2, 3), ... определяются соотношениями
F2(l, 2) = F1(l)F1B)+Gt(.i, 2),
F3(\,2,3)=F1(i)F1B)F1(S)+F1(l)G2B, 3)+F1B)G2(i,3)+
+ F1C)Gt(U 2)+G,(l, 2, 3), . . . ,
где символами 1, 2, ... в аргументах функций обозна-
обозначена совокупность координат г и импульсов р соответ-
соответственно 1-й, 2-й, . . . частицы, ^A, . . ., s) — приве-
приведенные функции распределения
Fs(l, 2. ..., ,)=V
^i) J Dtd(s+i)...dN,
V— объем системы, N — число частиц, Df=Df(i, 2i
... , jV) — функция распределения в фазовом прост-
пространстве в момент времени t с нормировкой
Dt{i, 2, ..., N)di...dN = l.
Закон изменения Di во времени характеризуется урав-
уравнением Лиувилля dD^ldt=AD-t, в к-ром А представляет
не зависящий явно от времени оператор Лиунилля.
Обычно рассматривается случай, когда Л состоит из
суммы аддитивной части и бинарной части, характери-
характеризующей взаимодействия между частицами:
2 -4-У
Согласно принципу ослабления корреляции К. ф. удов-
удовлетворяют граничным условиям Gs A, 2, . . ., s) -+ 0
при max {li'i—га|, . . ., |гх—г^1, . . ., |rJ_1—vs\ }->-co.
К. ф. G1(l) = /1(l), G2(l, 2), . . . , G8(l *) яв-
ляются функциональными производными функционала
6sAf(u)
au A) вu B). . .6u
(и), связанного с так наз. производящим функцио-
функционалом
соотношением
Функционал Af(u) удовлетворяет уравнению
ВА. (и) С 6Af (и)
4)(VA(VJdi+
(и) )
В квантовой статпстич. механике К. ф. являются
операторными величинами и определяются соотноше-
соотношениями:
F2(i, 2) =5A, 2){F1(l)i?1B)} + G2(l, 2),
F,(l, 2, 3)=SA, 2, 3) {^A)^B) F,C)} +
+ ~S(i, 2, 3) {F, A)G2 B, 3)+fxB) G2(l, 3)+
l, 2, 3), .... (*)
где 5A, 2), 5A, 2, 3) — операторы симметризации
для бозе-систем и антисимметризации для ферми-сис-
тем. К. ф. (*), наз. матрицей плотности,
удовлетворяет квантовомеханич. уравнению Лиувилля
(см. [2]).
В квантовой статистич. механике помимо К. ф. (*)
рассматриваются К. ф., построенные на обычных термо-
термодинамических средних (см. [3]), и К. ф., построенные
на квазисредних (см. [3]).
Билинейные комбинации К. ф. (как квантовые, так
и классические) дают функции Грина (см. [5]). Для
К. ф. справедливы спектральные представления, Бого-
Боголюбова неравенство, вариации среднего значения тео-
теорема (см. [4]).
Иногда используют К. ф., соответствующие так
наз. разложению Кирквуда (см. [6]); пространственно-
временную К. ф. (см. [8]).
К. ф. могут быть интерпретированы как характери-
характеристики вероятностных мер (см. [9]).
Лит.: [1] Б о г о л ю б о в Н. Н., Проблемы динамической
теории в статистической физике, М.— Л., 1946; [2] Б о г о л ю-
б о в Н. Н., Гуров К. П., «Ж. экспериментальной и теоре-
тич. физики», 1947, т. 17, в. 7, с. 614—28; [3] Боголюбов
Н. Н., Избранные труды, т. 3, К., 1971; [4] Боголю-
Боголюбов Н. Н., (м л.), Садовников Б. И., Некоторые воп-
вопросы статистической механики, М., 1975; [5] Б о г о л ю-
бов Н. Н., Т я б л и к о в С. В., «Докл. АН СССР», 1959,
т. 126, JMj 1, с. 53—56; [6] Л и б о в Р., Введение в теорию кине-
кинетических уравнений, пер. с англ., М., 1974; [7] II с и х а р а А.,
Статистическая физика, пер. с англ., М., 1973; [8] Р ю э л ь Д.,
Статистическая механика. Строгие результаты, пер. с англ.,
М., 1971; [9] Престон К. Дж., Гиббсовские состояния на
счетных множествах, пер. с англ., М., 1977.
А. Н. 'Ермилов, А. М. Н'/рбатов.
КОРРЕЛЯЦИОННОЕ ОТНОШЕНИЕ — характерис-
характеристика зависимости между случайными величинами.
Именно, К. о. случайной величины Y по случайной ве-
величине X называется выражение
1
где DY — дисперсия Y, D(Y\X) — условная диспер-
дисперсия Y при данном X, характеризующая рассеяние }'
около условного математич. ожидания B(Y\X) при
данном значении X. Всегда 0<T]y|X<:l. Равенство
Tiy|jr=0 соответствует некоррелированным случайным
величинам; ^у^х = 1 тогда и только тогда, когда имеется
точная функциональная связь между Y и X; в случае
линейной зависимости Y от X К. о. совпадает с квадра-
квадратом коэффициента корреляции. К. о. несимметрично от-
относительно X и Y, поэтому наряду с ily|jf рассматри-
рассматривается y\xiY — К. о. X по Y, определяемое аналогичным
образом. Между Цу1Х и tfxtY нет какой-либо простой
зависимости. См. также Корреляция. А. в. Прохоров.
КОРРЕЛЯЦИЯ — зависимость между случайными
величинами, не имеющая, вообще говоря, строго функ-
функционального характера. В отличие от функциональной
зависимости К., как правило, рассматривается тогда,
когда одна из величин зависит не только от данной
другой, но и от ряда случайных факторов. Зависимость
между двумя случайными событиями проявляется в том,
что условная вероятность одного из них при наступле-
наступлении другого отличается от безусловной вероятности.
Аналогично, влияние одной случайной величины на
другую характеризуется условными распределениями
одной из них при фиксированных значениях другой.
Пусть X и Y — случайные величины с заданным
совместным распределением вероятностей, тх и ту—
математич. ожидания X и Y, а\ и оу — дисперсии X
и Y, р — коэффициент К. между X и Y. Если для каж-
каждого возможного значения Х=х определено условное
математич. ожидание у (ж) = Ё[У I X = z] величины Y, то
функция у(х) наз. регрессией величины У по X, а ее
график — линией р е г р е с с и и У по X. Зави-
Зависимость У от X проявляется в изменении средних значе-
значений У при изменении X, хотя при каждом фиксирован-
фиксированном значении Х=х величина У остается случайной ве-
величиной с определенным рассеянием. Для выяснения
вопроса, насколько точно регрессия передает изменешге
У при изменении X, используется условная дисперсия
У при данном значении Х = х или ее средняя величина
(мера рассеяния У около линии регрессии)
п2 _ с [V FfflV- 11'
Uy I у -— t^ -I Г. li Л. ¦—- XI I .
J. | .Л. *- ^ ¦ ' '
Если X и У независимы, то все условные математич.
ожидания У не зависят от х и совпадают с безусловным:
у (х)=ту, при этом Оу^= Оу. При точной функциональ-
функциональной зависимости У от X величина У при каждом дан-
данном Х=х принимает лишь одно определенное значение
и oY{X = 0. Аналогично определяется x(y) = E[X\Y=
= у] — регрессия X по У. Естественным показателем
концентрации распределения вблизи линии регрессии
у(х) служит корреляционное отношение
1
,Y = 1 — aY\xl°Y-
Величина i]yt y=0 тогда и только тогда, когда регрессия
имеет вид у(х)=ту, в атом случае коэффициент К. р
равен 0 и величина Y не коррелирована с X. Если ре-
регрессия У по X линейна, т. е. линия регрессии—прямая
если, кроме того, |р| = 1, то У связана с X точной линей-
линейной зависимостью, если же "Пу|^=Р2<1, то между У и X
нет функциональной зависимости. Точная функцио-
функциональная зависимость У от X, отличная от линейной,
имеет место тогда и только тогда, когда p2<r|v \-=l-
Практическое использование коэффициента К. в каче-
качестве меры отсутствия зависимости справедливо (за
редким исключением) лишь тогда, когда совместное
распределение X и У нормально (или близко к нор-
нормальному распределению), так как в этом случке из
равенства р=0 следует независимость X п У. Исполь-
Использование р как меры зависимости для произвольных
случайных величин X и У приводит часто к ошибочным
выводам, так как р может равняться 0 даже при функци-
функциональной зависимости между величинами. Если дву-
двумерное распределение X и У нормально, то обе линии
регрессии суть прямые и р полностью определяет кон-
концентрацию распределения вблизи линий регрессии:
при |р| = 1 прямые регрессии сливаются в одну, что со-
соответствует линейной зависимости между X и У, при
р=0 величины независимы.
При изучении связи между несколькими случайными
величинами Х5, . . . , Хп с заданным совместны.м рас-
распределением пользуются множественными и частными
корреляционными отношениями и коэффициентами К.
Последние вычисляются с помощью обычных коэффици-
коэффициентов К. между X; и А',-, в совокупности образующих
корреляционную матрицу. Мерой линейной связи
между Xj и совокупностью всех остальных величин
Х2, . . . , Хп служит множественный коэффициент кор-
корреляции. Если взаимосвязь величин Х± и Х.2 предполо-
предположительно определяется влиянием остальных величин
Xs, . . . , Хп, то показателем линейной связи между
Xj и Х2 при исключении влияния Х?, . . . , Хп является
частный коэффициент корреляции ХЛ и Х.г относлтель-
но Х.2, . . . , Хп.
О мерах К., основанных на ранговых статистиках,
см. ст. Кендалла коэффициент ранговой корреляции,
Спирмена коэффициент ранговой корреляции.
В математич. статистике разработаны методы оценки
коэффициентов, характеризующих К. между случайны-
случайными величинами или признаками, и методы проверки ги-
гипотез об их значениях, использующие их выборочные
аналоги. Совокупность таких методов наз. корре-
корреляционным анализом. Корреляционный
анализ статистич. данных заключает в себе следующие
основные практич. приемы: 1) построение корреляцион-
корреляционного поля и составление корреляционной таблицы;
2) вычисление выборочных корреляционных отношений
или коэффициентов К.; 3) проверка статистич. гипотезы
значимости связи. Дальнейшее исследование может за-
заключаться в установлении конкретного вида зависимо-
зависимости между величинами (см. Регрессия).
Вспомогательными средствами при анализе выбороч-
выборочных двумерных данных являются корреляционное ноле
и корреляционная таблица. При нанесении на коорди-
координатную плоскость выборочных точек получают кор-
корреляционное поле. По характеру расположе-
расположения точек поля можно составить предварительное мне-
мнение о форме зависимости случайных величин (напр., о
том, что одна величина в среднем возрастает или убы-
убывает при возрастании другой). Для численной обработ-
обработки результаты обычно группируют и представляют в
форме корреляционной таблицы. В каж-
каждой клетке этой таблицы приводятся численности п,у
тех пар (х, у), компоненты к-рых попадают в соответст-
соответствующие интервалы группировки по каждой перемен-
переменной. Предполагая длины интервалов группировки (по
каждому из переменных) равными между собой, выби-
выбирают центры х; (соответственно г/,) этих интервалов и
числа п,у в качестве основы для расчетов.
Более точную информацию о характере и силе связи,
чем картина корреляционного поля, дают коэффициент
К. п корреляционное отношение. Выборочный
коэффициент корреляции определяется
по формуле
22
Г)
где
При большом числе независимых наблюдений, подчи-
подчиненных одному и тому же распределению, близкому к
нормальному, р близок к истинному коэффициенту К. р.
Во всех других случаях в качестве характеристики силы
связи рекомендуется использовать корреляционное
отношение, интерпретация к-рого не зависит от вида ис-
исследуемой зависимости. Выборочное значение г|у,у вы-
вычисляется по данным корреляционной таблицы:
— У п
'Mi - у)'1
Пк|х= , -V ;
где числитель характеризует рассеяние условных
средних значений у, около безусловного среднего у
(аналогично определяется выборочное значение *] \-|У).
Величина Цу\Х—Р2 используется в качестве индикатора
отклонения регрессии от линейной.
Проверка гипотезы значимости связи основывается
на распределениях выборочных корреляционных ха-
характеристик. В случае нормального распределения
величина выборочного коэффициента К. 7> считается
значимо отличной от нуля, если выполняется неравен-
неравенство
где ta есть критическое значение «-распределения Стью-
дснта с (п—2) степенями свободы, соответствующее вы-
выбранному уровню значимости а. В случае р^О обычно
используют так наз. z-преобразование Фишера, заменяя
величину р на z по формуле
2 1 -р
Уже при сравнительно небольших п распределение ве-
величины z хорошо приближается нормальным распреде-
распределением с математич. ожиданием, равным
1 In 1 + Р | р
и дисперсией, равной И(п — 3). Исходя из этого, можно
определить приближенные интервалы для истинного
коэффициента К. р.
О распределении выборочного корреляционного от-
отношения и о способах проверки гипотез о линейности
регрессии см. [3].
Лит.: [11 Крамер Г., Математические методы статисти-
статистики, пер. с англ., 2 изд., М., 1975; [2] Ван-дер-Вар-
ден Б. Л., Математическая статистика, пер. с нем., М.,1960;
[3]КендаллМ., СтьюартА., Статистические выводы
и связи, пер. с англ., М., 1973; [4] Айвазян С. А., Стати-
Статистическое исследование зависимостей, М., 1968.
Л. Б. Прохоров.
КОРРЕЛЯЦИЯ, дуальное,преобразова-
н и е,— взаимно однозначное отображение % проектив-
проективного пространства П„ на себя такое, что из Sp(^Sq
следует k(Sp)ZDK{Sq). При К. образом суммы подпрост-
подпространств является пересечение их образов и, наоборот,
образом пересечения является сумма образов, в част-
частности образ точки — гиперплоскость, а образ гипер-
гиперплоскости — точка. Для существования К. простран-
пространства Пп(К) над телом К необходимо и достаточно, чтобы
в К существовал инверсный автоморфизм:
взаимно однозначное отображение а : К —>- К, при
к-ром a(k1+k2)=a(ki)+a(k2), а(клкг)=^а(к2)а(к1); в
этом случае ПП(К) оказывается двойственным самому
себе. Примерами пространств, для к-рых существует К.,
являются вещественные (K=R, a=id), комплексные
(К=С, а : z —>- z), кватернионные (ЛГ=Н, а : Q —>- Q)
проективные пространства.
Пусть П„ интерпретируется как совокупность ли-
линейных подпространств (левого) линейного простран-
пространства A n+i{K) над телом К; полубилинейной
формой на Ап + ] наз. функция fa(x, у), зависящая от
инверсного автоморфизма а тела К и обладающая сле-
следующими свойствами:
y, z),
x, z),
fa(kx, y) = kfa(x, y),
fa(-r, ky)=a(k) fa(x, y).
В частности, если a=id, то fa(x, у) наз. билиней-
билинейной ф oj) м о и,— напр., если A'=R; в случае К=С
и а : z —>- z, то /а наз. эрмитовой; если же К=Н
и а : Q —>- Q, то /а наз. симплектической.
Тогда для любого x?Aln+i(K) образ К. к(х) совпадает
с совокупностью решений х уравнения fa(x, X)=0
(говорят также, что каждая К. х представима полубили-
полубилинейной формой fa (х, у) — теорем аБиркгофа —
Нейман а).
Подпространство W наз. нулевым относительно
К. х, если x{P)Z)P для любой точки P?W. Если х
представима формой /а(х, у), то fa{x, х) = 0 для всех
x?W (в частности, fa(x, y)=—fa(y, х)). Напр., стро-
строго изотропное подпространство
(т. е. подпространство U такое, что t/czx(t/)) является
нулевым, причем на нем f(U, U)=0; нулевая прямая
либо неизотропна, либо строго изотропна. Все макси-
максимальные нулевые подпространства К. х имеют одну и
ту же размерность. Если ш=П,;, то К. наз. н у л ь-
полярной (нулевой) и является (спмплектц-
ческим) поляритетом.
Обобщение понятия К.— дуальное отобра-
отображение х проективных пространств: П„(К) —>-
—>- Пп(/>) — взаимно однозначное отображение такое,
что если ГсХ^П,,, то х(.У)сх(У)?П„; оно сущест-
существует, если есть инверсный изоморфизм а : К —>- L.
Напр., пусть L= К* — совокупность элементов А", в
к-рой операции сложения и умножения определены сле-
следующим образом: х-\-у=х-{-у, х-у=у-х (см. Проектив-
Проективная алгебра, конструкция II). Тогда К* — тело,
инверсно изоморфное К; если Т1п(К) — левое, то
ЙП(Я*) — правое проективные пространства, п они
канонически двойственны друг другу.
М. И- Войцеховский.
КОРТЕВЕГА — де ФРИСА УРАВНЕНИЕ, КдФ-
уравнение,— уравнение вида
предложено Д. Кортевегом п Г. де Фрисом [1] для
описания распространения волн на мелкой воде. Оно
может быть проинтегрировано с помощью метода об-
обратной задачи теории рассеяния, к-рый основан на пред-
представлении К.— де Ф. у. в виде
^~ = [L, M] =LM — ML,
где L=—q^-\-u(x, t) — одномерный оператор Шрё-
дингера, а
М = ^i~ —
Для К.— де Ф. у. однозначно разрешима задача Koran
в классе быстроубывающих функций с начальным ус-
условием: и (х) ? S (R1) (здесь S (R1) — пространство Швар-
Шварца). Пусть
s = {r (k)?S (R1); xy, mj > 0, ху, Ф Kjx ПРН h Ф h*
7=1, -.., п)
— данные рассеяния для оператора Шрёдингера с по-
потенциалом и(х).
Т0ГДЙ 8X*t
г (k, t)=es'^lr(k), mj(t)=e > m}, Xy(O=>Sy,
и решение и (г, t) определяется по данным рассеяния
s(t) с помощью нек-рого интегрального уравнения.
В случае г (fc)=0 последнее уравнение явно решается;
возникающие таким образом потенциалы наз. без-
безотражательными, а соответствующие решения
К.— де Ф. у.— /г-солитонными (см. Солшпои).
К.— до Ф. у. записывается в гамнльтоновом виде
— Я(") = з1+Ы; )dx'>
здесь фазовым пространством является пространство
^(R1), а скобки Пуассона задаются билинейной формой
оператора ^. Отображение и (х) —*- s представляет со-
собой каноническое преобразование к переменным типа
действие — угол. В новых переменных гамильтоновы
уравнения явно интегрируются, и их решение дается
указанными выше формулами. К.— де Ф. у. обладает
бесконечным набором интегралов движения:
/' n>
Все эти интегралы движения находятся в инволюции,
и порождаемые ими гамильтоновы системы (так наз.
высшие уравнения Кортевега — де
Ф р и с а) вполне интегрируемы.
С помощью интегральных уравнений обратной задачи
также находится решение задачи Коши для начального
данного типа ступеньки:
lim и(х)=с<0, lim u(x)=0.
X -* — оо * ->- + оо
При t —>- + оо в окрестности фронта решение и (х, t) рас-
распадается на невзаимодействующие солитоны — проис-
происходит распад ступеньки.
В случае задачи Коши с периодическим начальным
условием и(х-гТ)=и(х), х? R1, аналогом безотража-
безотражательных потенциалов являются потенциалы, для к-рых
оператор Шрёдингера имеет конечное число запрещен-
запрещенных зон,— конечнозонные потенциалы.
Периодические и почти периодические конечнозонные
потенциалы являются стационарными решениями выс-
высших К.— де Ф. у.; последние представляют собой впол-
вполне интегрируемые конечномерные гамильтоновы сис-
системы. Произвольный периодич. потенциал аппроксими-
аппроксимируется конечнозонными. Пусть E/^R1; Ej^Ej^ при
)гФ]2; /=1, . . . , 2g+l — края зон; а Г — гиперэл-
гиперэллиптическая кривая
над полем С. Тогда действительнозначные почти пери-
периодические потенциалы с указанными краями зон, а
также решения задачи Коши выражаются через б-функ-
ции на многообразии Якоби /(Г) кривой Г. При опре-
определенных соотношениях на края зон полученные реше-
решения будут периодическими. Если отказаться от условий
Ej^R1, то получатся компле-кснозначные (возможно с
полюсами) решения К.— де Ф. у., к-рые также наз.
конечнозонными.
Лит.: [1] Korteweg D., d e VriesG., «Phil. Mag.»,
1895, v. 39, p. 422—43; [2] «Phys. Rev. Lett.», 1967, v. 19,
p. 1095—97; [3] 3 a x a p о в В. Е., Ф а д д е е в Л. Д.,
«Функциональный анализ и его приложения», 1971, т. 5, в. 4,
с. 18—27; [4] М а р ч е н к о В. А., Спектральная теория опе-
операторов Штурма — Лиувилля, К-, 1972; [5] Дубро-
Дубровин Б. А., Матвеев В. Б., Новиков С. П., «Ус-
«Успехи матем. наук», 1976, т. 31, в. 1, с. 55—136; [6] К у-
н и н И. А., Теория упругих сред с микроструктурой, М., 1975.
Л. А. Тахтаджян.
КОРТЕЖ — конечная последовательность (допус-
(допускающая повторения) элементов какого-нибудь множе-
множества X. К. обозначается посредством (хь х2, . ¦ . , хп)
или x1,x2l. . .,хп, где п — длина К. (п^О), а х,- есть
г-й член К. и х;^Х A<г<га). При гс=0 получается
пустой кортеж, не имеющий членов.
В качестве синонимов термина «К.» можно использо-
использовать следующие понятия: слово в алфавите X (в этом
случае обычно предполагается, что X конечно); эле-
элемент нек-рой декартовой степени множества X; элемент
свободной полугруппы с множеством образующих X
и единицей; функция, определенная на первых п нату-
натуральных числах (п^О), со значениями в множестве X.
В. Н. Гришин.
КОС ТЕОРИЯ — раздел топологии и алгебры, изуча-
изучающий косы п группы, составленные из их классов эк-
эквивалентности, и различные обобщения этих групп [1].
Коса из п нитей — объект, состоящий из
двух параллельных плоскостей Ро и Рг в трехмерном
пространстве R3, содержащих упорядоченные множест-
множества точек aL, . . . , ап?Р0 и Ьи . . . , bn?Plt и из re
простых дуг ?],... , 1п, пересекающих каждую парал-
параллельную плоскость Pf между Ро и Р1 однократно и сое-
соединяющих точки {а,-} с точками {&,}, i=l, ... , п.
Рис. 1.
Рис. 2.
/
to
/
О)
/
<C (
' У
-A
)/
V
Считается, что а,- лежат на прямой La в Ро, точки Ь,- —
на прямой Ьь в Рг, параллельной La, причем 6,- распо-
расположены под а,- для каждого i (см. рис. 1). Косы изобра-
изображаются в проекции на плоскость, проходящую через
La и Lb; эта проекция может быть приведена в общее
положение так, что имеется только конечное число
двойных точек, попарно лежащих в разных уровнях, и
пересечения трансверсальны.
Нить 1{ косы со соединяет а,- с bk и определяет под-
1 2 ... п 1
становку Sa={k1 к2 . . . кп). Если эта подстановка
тождественна, то шназ. кра-
крашеной (или чистой) ко-
с о й. Транспозиции (г г+1)
отвечает простейшая
коса <х,- (см. рис. 2).
Во множестве всех кос с п
нитями и с фиксированными
Ро, Ри {а,}, {&,-} вводится от-
отношение эквивалентности. Оно
определяется гомеоморфизма-
гомеоморфизмами h : П —>- П, где П — об-
область между Ро и Ри тож-
тождественными на .PoU-Pi, к-рые
можно считать такими, что
h{Pf) = Pf. Косы аи Р эквива-
эквивалентны, если существует такой
гомеоморфизм h и /i(a)=p.
Классы эквивалентности, далее также называемые
косами, образуют группу кос В (п) относительно
операции, определяемой следующим образом. Экзем-
Экземпляр П' области П помещается над другим экземпляром
П" так, чтобы Р'о совпала с Р[, а\ — с b[, а затем П' (J
(JII" сжимается,-вдвое. Образы кос ш'^П' и а>"?П"
дают косу со' со'
1\ с помощью
класс эквивалентности, содержащий косу из п парал-
параллельных отрезков, коса ш, обратная косе со, опреде-
определяется отражением в плоскости Pi/2- Условие йш=
= е — на рис. 3. Отображение w-+Sa определяет эпи-
эпиморфизм В (п) на группу S (п) перестановок п элемен-
элементов, ядром к-рого является подгруппа К(п), соответст-
соответствующая всем чистым косам, так что имеется точная по-
последовательность
Группа кос В (и) имеет две основные интерпретации.
Первая — пространство конфигураций —
получается отождествлением плоскостей Pf с помощью
вертикальной проекции на Ро, при к-рой образы точек
Рис. 3.
нить Z,- к-рой получается продолжением
1к-, где А,-? «У*0'**'. Единичная коса —
t при изменении t от 0 до 1 образуют след изо-
изотопии (ft множества (Ja,- по Ро, причем q>?(\Jai)= Uai-
Косе однозначно соответствует класс гомотопных пе-
петель в пространстве неупорядоченных наборов G (п) из
п попарно различных точек плоскости, и имеет место
изоморфизм
Для крашеных кос аналогично строится изоморфизм
a: K(n)-+niF(n),
где F(л) — пространство упорядоченных наборов из п
различных точек плоскости, так что К(п) можно отож-
отождествить с подгруппой, отвечающей накрытию
р : F(n)-+G(n)=F(n)IS(n).
Вторая — группа гомеотопий — получается
продолжениями изотопии q>f до изотопии ф" плоскости
Ро, тождественной вне нек-рого диска, причем q>®=id.
При каждом t два такие продолжения отличаются на
гомеоморфизм, тождественный в точках ац. Косе одно-
однозначно соответствует компонента пространства гомео-
гомеоморфизмов Y (п) плоскости, отображающих множество
(J о,- на себя, и имеет место изоморфизм
у : В (п) -+ n0Y (п).
Каждому гомеоморфизму h ? Y сопоставляется авто-
автоморфизм свободной группы ранга п : Fn=n1(R2\{Jai),
определенный с точностью до внутреннего, к-рый в свою
очередь дает гомоморфизм 5(n)—>-Out Fn=AutFn/lnnFn.
Элементы образа наз. косовыми автомор-
автоморфизмами свободной группы. В частности, косе а,-
отвечает автоморфизм
если j—i, г+1 ({х,} — базис Fn). Любой косовой авто-
автоморфизм а обладает свойствами:
a(xi)=AixiAJ1, a
с точностью до внутреннего (смысл А ,• — ниже), эти
свойства характеризуют косовые автоморфизмы.
Косы a,-, l<:i<re—1, являются образующими группы
В (и), т. е. a=akiaka. . .<зк причем
= ajOi при | i —;
— 2.
A)
Оказывается, что A) — копредставление для В (п) (см.
рис. 4). Имеет место расщепляющая точная последова-
а, о,+| а, - о^,о, а,+,
Рис. 4.
Рис. 5.
тельность (получающаяся из локально тривиального
расслоения F (п) ->- F (п—1) со слоем Л2\(а1, . . . ,
en-i)):
1 -> Fn_t ~^К(п)-^К (п — 1) —>- 1,
к-рая приводит к нормальному ряду
К (п) = А„ з. . . => Ах Г) Ао = Fn _ j
со свободными факторами ^4,/у!f — i, причем А; имеет
«дополнение» [/„_,-, изоморфное К(п— i—1). Каждый
элемент ш^В(и) может быть представлен единственным
образом в виде
Ш =@2. . .(ОпЛ(о,
где яа — выбранный представитель для 5Ш в В(п), а
a>i?An^[ + 1f) [/;. Приведение косы к такой форме наз.
ее причесыванием. Это решает проблему тож-
тождества в В (ге).
Копредставление для К (и) таково: образующие (см.
рис. 5)
соотношения
ArsA(j = AijArs, если r<s < г < / или i < г < s < /;"
ArjAij = Arj, если i = s;
A;jAsjA[jAij = Asj, если r = i < / < s;
Оно может быть получено как копредставление ядра ес-
естественного гомоморфизма в 5 (ге) абстрактной группы
В (л), заданной копредставлением A) с помощью Шрей-
ера системы 11/=2-<и .ft., j^kj^n, где Mjj=Oj_1. . .<т,ч
Центр группы В (ге) — бесконечная циклич. группа,
порожденная элементом (с^. . .оп)п. Коммутант В'(п)
совпадает с В"{п) при ге>5; -В'(З) изоморфна свободной
группе ранга 2, а В'D) — полупрямому произведению
двух таких групп. Фактор по коммутанту — бесконеч-
бесконечная циклич. группа, порожденная образами а;. Эле-
Элементы конечного порядка в В (ге) отсутствуют. Группа
К (ге) переходит в себя при эндоморфизмах с неабелевым
образом. В частности, Я(ге)П^'(ге) — вполне характе-
ристич. подгруппа в В(п), а также ив К (ге) (см. [15]).
Проблема сопряженности в В (ге) решается существен-
существенно сложнее проблемы тождества. Имеется единственная
нормальная по Гарсайду форма косы
— так наз. элемент Гарсайда, Q — положительная, т. е.
имеющая запись через <т,- с положительными показате-
показателями, коса. Косе со конечным числом операций, опреде-
определяемых по i (сопряжение с нек-рыми элементами, вы-
выбор элементов максимальной степени и т. п.), сопостав-
сопоставляется нек-рое множество слов 2 (со), из к-рого выби-
выбирается слово в нормальной форме Д+ Т с минимальным
Т. Это — так наз. верхняя форма косы ш.
Оказывается, что две косы сопряжены тогда и только
тогда, когда их верхние формы совпадают (см. [7]).
Представление Бурау группы кос В (ге)
в группу матриц над кольцом целочисленных много-
многочленов одной переменной определяется соответствием:
где Ik — единичная матрица порядка к. Матрица
Ь((о)—/„ есть приведенная матрица Александера (см.
Александера инварианты) зацепления, полученного
замыканием косы со (см. ниже). Для крашеной косы из
аналогичной матрицы Гаснера получается полная
матрица Александера. Проблема точности этих пред-
представлений не решена A982) (см. [2]).
То, что пространства F(ге) и G(n) асферичны, дает
возможность вычислить гомологии групп кос.
Гомологии К(п) (см. [16]): гомологически К (ге)
совпадает с произведением букетов окружностей, в
к-рых число окружностей увеличивается от одной до
ге—1. Кольцо когомологии изоморфно внешнему граду-
градуированному кольцу, порожденному одномерными эле-
элементами ш,у= со/,-, 1 <:?«:/<:ге, с соотношениями
0
0
0
0
I — t
1
0
0
t
0
0 1
0
0
0
Wft;G>fm+cu/ot comfc+coOTfcCOftr^O. В качестве a»,i можно
взять формы ^—. aZk~ 2l отвечающие обходу диагона-
/лг zfc—zi
лей zfc=?j.
Гомологии В (п) (см. [81, [12]): гомоморфизм
В (га) -> S (га) может быть продолжен вложением S (га) —>
—>- О (га); индуцированный гомоморфизм в когомологиях
Н*(О (п)) -> Н*(В (га)) апиморфен, т.е. когомологии
mod 2 группы .5 (я) порождаются классами Штифеля—
Уитни.
Имеется естественное отображение G(n) в Q2S2 —
пространство сфероидов S2 —<- S2 (вокруг га точек берут-
берутся малые диски, к-рые канонически со степенью I ото-
отображаются в сферу, а все дополнение — в точку). Это
отображение (см. [14]) устанавливает гомологич. экви-
эквивалентность предельного пространства С(оо) и (Q2S2H
(индекс означает, что берется компонента сфероидов
степени 0). Относительно нестабильных групп гомоло-
гомологии В (га) доказано [16], что они конечны, стабилизиру-
стабилизируются с ростом п и имеется правило повторения Н'В Bre-f-
-{-!) —Н1 В Bге). Дано |17] описание вычисления этих
групп.
Приложения и обобщения. ^Замк-
^Замкнутой косой наз. зацепление (га-компонентный
узел) в R3, каждая компонента к-рого трансверсально
пересекает полуплоскости, ограниченные одной и той
же прямой — осью I замкнутой косы (см. рис. 6). Коса со
порождает замкнутую косу со (з а м ы к а н и е со) сле-
следующим образом. Цилиндр с основа-
]'_ „-^ ниями на РоиР], содержащий внут-
внутри себя со, изгибается в R3 так, что
образующие переходят в окружности
с центрами на прямой 1, а основания
совмещаются и каждая точка а,- сов-
совпадает с 6/. Тогда объединение нитей
' г,-перейдет в w.. Обратно, каждое за-
иь' цепление в R3 может быть представ-
представлено замкнутой косой. Эквивалентным косам отвечают
изотопные зацепления и, более того, сопряженные косы
дают изотопные зацепления. Обратное неверно, так как
зацепление может быть представлено косами с разным
числом нитей. Кроме того, косы аап_1 и соой-i не со-
сопряжены в В(п), но отвечают изотопным зацеплениям.
Если две замкнутые косы эквивалентны как зацепления,
то они могут быть получены одна из другой цепочкой
элементарных преобразований двух типов (см. рис. 7).
Пти операции интерпретируются в терминах копредстав-
лоний группы зацеплений, что дает алгебраич. перефор-
переформулировку проблемы изотопности зацеплений в виде
вопроса о системе групп В(п). Копредставление группы
зацепления со имеет вид
ъ •••, Уп, yi=-AiVhiAI1} .
где соотношения определены косовым автоморфизмом
Ъш. Обратно, каждое такое соотношение определяет
косу.
2) Если разрезать поверхность рода g с помощью g
непересекающихся сечений так, что получится сфера с
2g дырами, то гомеоморфизмы этой сферы с дырами, ос-
оставляющие на месте точки на краях дыр, определяют
гомеоморфизмы поверхности, неподвижные на сечени-
сечениях, и сами определяются с точностью до изотопии эле-
элементами группы KBg). Это дает представление группы
кос в группе гомеотопий поверхности. Аналогично
строится и представление BBg). Эти представления ис-
используются при изучении диаграмм Хегора трехмер-
трехмерных многообразий.
3) Отождествлением R2 с комплексной прямой С1
и сопоставлением неупорядоченному набору из га точек
плоскости многочлена степени га, имеющего эти точки
своими корнями, получается возможность отождествить
G(n) с пространством многочленов с ненулевым дискри-
дискриминантом. Так, этот факт позволил получить ряд резуль-
результатов о непредставимости алгебраич. функций супер-
суперпозицией функций от меньшего числа переменных
(см. [16]).
4) Пространства конфигураций для любого простран-
пространства X определяются аналогично G(n) и F(п) с заменой
R2 на X. Фундаментальные группы этих пространств
В (X) и К (X) наз. группами кос простран-
пространства X и чистых кос соответственно. Для многообра-
многообразия Мп размерности больше 2 Я]^„(Х)«П"Ш1Я,- М (i),
и эти группы интереса не представляют. Для двумер-
двумерного многообразия имеется естественное вложение
В (п) и К (п) в Вп(М2) и Кп{М2), индуцированное вло-
вложением R2CT,1/2. Для М2, отличного от сферы и проек-
проективной плоскости, получается точная последователь-
последовательность
1 -> л,К B) -^ nyKn {M*) —> ПЧ^щМ"^
для сферы гомоморфизм е является эпиморфизмом, по-
полученным добавлением к A) еще одного соотношения
5) Если р : X —*¦ Y есть /с-листное накрытие, то р~1а,
где а — петля в У, является петлей в пространстве кон-
конфигураций X, чем определяется гомоморфизм nxY —>-
—>- Вь(Х), к-рый усиливает монодромию накрытия и на-
находит применение в алгебраич. геометрии.
С
61 Пусть V — комплексификация действительного
векторного простран-
пространства V, а W — ко-
конечная неприводимая
группа, порожден-
ная отражениями, . )
действующая в V У
(и, следовательно, в
V ). Пусть s/ — порож-
порождающие отражения
В ПЛОСКОСТЯХ PjCZVii Рис- "<¦
D — их объединение.
V
Пусть, наконец, V /D=YW a Xw — факторпространст-
во. Группы k,Yw и щХуу наз. группами Брис-
корна, они естественно обобщают К(п) и В (п).
Если ord (.?,Sy)=m,y, то я^Х^ имеет непредставление
вида
где число сомножителей с каждой стороны равно т;у
(о,- здесь соответствует камере Вейлж. Для этих групп
доказано, что .XV и Yw являются пространствами типа
К (к, 1), решена проблема сопряженности. В алгебраич.
геометрии пространства Х-уг появляются как дополне-
дополнения к дискриминанту версальных деформаций рацио-
рациональных особенностей (см. [12],[13]).
Лит.: [llArttn E., «Ann. Math.», 1947, v. 48, p. 101—26,
643—49; [2] Birman J., «Ann. Math. St.», 1974, №82; [3]
Buran W., «Hamburg Abh.», 1P32, Bd 9, S. 117—24; [4]
Марков А. А., «Тр. Матем. ин-та АН СССР». 1945, т. 16;
[5] Gassner В., «Hamburg Abh.», 1961, Bd 25, S. 10—22;
[6] F a d e 1 1 E., NeuwirthL., «Math. Scand.», 1962,
v. 10, p. Ill —18; [7] Г а р с а й д Ф., «Математика», 1970, т. 14,
№ 4, с. 116—32; [8] Ф у к с Д. Б., «Функциональный анализ
и его приложения», 1970, т. 4, Л» 2, с. 62—73; [9] Арнольд
В. И., там же, № 1, с. 84—85; [10] Горин Е. А., Л и н В. Я.,
«Матем. сб.», 1969, т. 78, с. 579—610; [11] Арнольд В. И.,
«Тр. Моск. матем. об-ва», 1970, т. 21, с. 27—46; [12] Б р и с-
корнЭ., «Математика», 1974, т. 18, №3, с. 46 — 59; [13]
Б р и с к о р н Э., С а й т о К., там же, № 6, с. 56—79; [14]
D е 1 1 g n e P., «Invent. Math.», 1972, v. 17, № 4, p. 273—302;
[15] Л и н В. Я., «Успехи матем. наук». 1974, т. 29, в. 1,
с. 173—74; [16] Арнольд В. И., «Матем. заметки», 1969,
т. 5, J\Ts 2, с. 227—31; [17] Лин В. Я., в кн.: Итоги науки и
техники. Алгебра. Топология. Геометрия, т. 17. М., 1979,
с. 159—227. А. В. Чернаеский.
КОСАЯ ПРОИЗВОДНАЯ, наклонная про-
производи а я,— производная функции /, заданной в
окрестности точек нек-рой поверхности S, по направле-
направлению /, не совпадающему с направлением конормали
нек-рого эллинтнч. оператора в точках S. В краевых за-
задачах для эллиптич. уравнений 2-го порядка К. п. мо-
может фигурировать в граничных условиях. В этом случае
краевая задача наз. задачей с косой производной. См.
Дифференциальное уравнение с частными производными;
задача с косой (наклонной) производной.
Если поле направлений I на S имеет вид Z=(Zlt ...,
In), гДе li — функции точки P?S, удовлетворяющие
соотношению ?i=1Vi)~ = ^, то К. п. функции / как про-
производная по направлению I имеет вид
LY h()M, (!. . »),
где xl, . . . , xn — декартовы координаты в евклидовом
пространстве R".
Лит.: [1] Миранда К., Уравнения с частными произ-
производными эллиптического типа, пер. с итал., М., 1957.
А. И. Янушаускас.
КОСЕКАНС — одна из тригонометрических функций:
другие обозначения: esc ,r, cose x. Область определе-
определения — вся числовая прямая за исключением точек,
абсциссы к-рых
х=^пп, и = 0, —1, —2, ...
К.— функция неограниченная нечетная периодическая
(с периодом 2я). Производная К.:
(cosec х)' — с°зд __ — cigX cosec x.
Интеграл от К.:
\ cosec х dx = In
К. разлагается в ряд
х ' 6 ' 360 ! 15120 ' •••' ^ ! ! ^ "•
Ю. А. 1'орьков.
КОСИНУС — одна из тригонометрических функций:
Область определения — вся числовая прямая, область
значений — отрезок [ — 1; 1]; К.— функция четная пе-
периодическая с периодом 2я. К. и синус связаны форму-
формулой
sin2 .r-|-cos2 x=i.
К. и секанс связаны формулон
cos х = .
sec x
Производная К.:
(cos х)' = —sin х.
Интеграл от К.:
\ сos xd.c -— sin x-\-C.
К. разлагается в степенной ряд:
cos x = i — -^у- + -?7 •••> — оо<а< оэ.
Функция, обратная К., наз. арккосинусом.
К. и синус комплексного аргумента z связаны с по-
показательной функцией формулой Эйлера
e'-z = cos г-j- г sin г.
Если х — действительное число, то
Jx . „-ix
COS J = -
Если z=ix (чисто мнимое число), то
COS IX = g = ell х,
где ch x — гиперболический косинус. Ю. А. горъкоо.
КОСИНУС АМПЛИТУДЫ, эллиптический
косину с,— одна из трех основных Якоби эллипти-
эллиптических функций, обозначаемая
en « = cn(«, k) = cos am и.
К. а. выражается следующим образом через сигма-
функции Вейерштрасса, тета-функции Якоби или с по-
помощью степенного ряда:
, ,, (Ti (и) O0@)O,(w)
где к—модуль эллиптической функции, 0<;/с<:1;
v=ui2a>, 2ю~ л"&з@). При к = 0, 1 имеем соответственно
cn(«, O) = cos и, сп(и, l) = l/ch и.
Лит.: [1] Гурвиц А., Курант Р., Теория функций,
пер. [с нем.), М., 1988, ч. 2, гл. :i. Е. Д. Соломеицев.
КОСИНУС ГИПЕРБОЛИЧЕСКИЙ — см. Гипербо-
Гиперболические функции.
КОСИНУСОВ ТЕОРЕМА: квадрат стороны тре-
треугольника равен сумме квадратов двух других его сто-
сторон без удвоенного произведения этих сторон на коси-
косинус угла между ними, т. е.
c2=a2+b2—2ab cos С,
где а, Ь, с — стороны треугольника, а С — угол между
Сторонами а И 6. ю- А- Горькое.
КОСИНУС-ПРЕОБРАЗОВАНИЕ ФУРЬЕ — см.
Фурье преобразование.
КОСМОЛОГИЧЕСКАЯ ПОСТОЯННАЯ — физиче-
физическая постоянная, характеризующая свойства вакуума,
к-рая иногда вводится в общей теории относительности.
С учетом К. п. уравнения Эйнштейна имеют вид
где Л — К. п., gij — метрический тензор, R;j— тензор
Риччи, R — кривизна пространства, Tij — тензор
энергии-импульса, с — скорость света, G — гравита-
гравитационная постоянная. Эти уравнения являются уравне-
уравнениями Лагранжа для действия
д — о0—
где So — действие для вещества, V — четырехмерный
объем. К. п. была введена в общую теорию относитель-
относительности [1] для того, чтобы уравнения гравитационного
поля допускали пространственно однородное статиче-
статическое решение (так. наз. космологическая модель Эйн-
Эйнштейна). После построения теории эволюционирующей
космологич. модели Фридмана и получения ее наблюда-
наблюдательных подтверждений, отсутствие такого решения у
исходных уравнений Эйнштейна не рассматривается
как недостаток теории. Достоверных указаний на отли-
отличие К. п. от нуля нет. Однако наличие достаточно малой
К. и. (|Л|^10~55 см~г) не противоречит наблюдатель-
наблюдательным данным и общим физическим принципам.
Наличие К. п. может существенно изменять некоторые
этапы эволюции наиболее распространенных космоло-
космологич. моделей (см. [2]). В связи с этим космологич. моде-
модели с К. п. предлагалось использовать для объяснения
нек-рых свойств распределения квазаров (см. [3], [4],
[5]).
Член Agij в уравнениях гравитационного поля можно
включить в тензор энергии-импульса и рассматривать
как тензор энергии импульса вакуума (см. [2]). В этом
случае вакуум имеет плотность энергии e=c4A/8nG и
давление р =—с4Л/8тсС, что соответствует уравнению
состояния р=—е. В теории с К. п. свойства вакуума
сказываются уже в нерелятивистском приближении.
Так, гравитационный потенциал точечной массы в тео-
теории с К. п. равен (см. [6]):
Стп Л 9 п
_ _ Г2С2.
Член Ag[/ инвариантен по отношению к преобразова-
преобразованиям локальной группы Лоренца, что соответствует
принципу лоренц-инвариавтности вакуума в квантовой
теории поля. Представление о К. п. как о величине,
характеризующей плотность энергии и давление ваку-
вакуума, в принципе позволяет связать представление о
К. п. с представлениями квантовой теории поля. Имеет-
Имеется ряд формул, связывающих значение К. п. с фунда-
фундаментальными физическими постоянными и возрастом
Вселенной (см. [2]).
Лит.: [1] Э й нш т е й н А., Собр. научных трудов, т. 1,
М., 1965, с. 601—12; [2] Зельдович Я. Б., Новиков
И. Д., Строение и эволюция Вселенной, М., 1975; [3] Р е t-
rosianV., SalpeterE., SzekeresP., «Astrophys. J.»,
1967, v. 147, p. 1222—26; [4] Шкловский И. С,
«Астрономический циркуляр», 1967, № 429; [5] Карда-
ш ё в Н. С, там же, № 430; [6] Т о л м е н Р., Относитель-
Относительность, термодинамика и космология, пер. с англ., М., 1974.
Д. Д. Соколов.
КОСМОЛОГИЧЕСКИЕ МОДЕЛИ — одно из основ-
основных понятий космологии как науки, описывающей Все-
Вселенную (окружающий нас мегамир) как целое, отвле-
отвлекаясь от несущественных в этой связи деталей.
Математич. форма К. м. зависит от того, какая физич.
теория кладется в основу описания движущейся мате-
материи: в соответствии с этим различают общерелятивист-
общерелятивистские, ньютонианские модели, модели стационарного
состояния, модели с изменяющейся константой тяготе-
тяготения и т. д. Из них наиболее важны общерелятивистские.
К К. м. можно отнести и астрономич. системы мира:
системы Птолемея, Коперника и др. В современных
К. м. для учета лишь существенных деталей вводится
понятие об усереднении физич. характеристик по физи-
физически большому объему. Усередненные значения пред-
предполагаются непрерывными и (обычно) много раз диффе-
дифференцируемыми. Возможность такого усереднения не
является самоочевидной. Можно представить себе
иерархическую модель Вселенной, в к-рой существуют
качественно различные объекты все возрастающих
масштабов. Однако имеющиеся наблюдательные данные
не согласуются с такой моделью.
Процедура усереднения для общерелятивистских
К. м. еще недостаточно обоснована математически.
Трудность здесь состоит в том, что различные «микро-
«микросостояния», дающие одну и ту же К. м. при усередне-
усереднении, являются различными псевдоримановыми много-
многообразиями, обладающими, возможно, даже различной
топологич. структурой (см. также Геометродинамика).
Физической основой общерелятивистских
К. м. является общая теория относительности Эйн-
Эйнштейна (иногда включая вариант с космологической по-
постоянной, см. Относительности теория). Математич.
формой общерелятивистских К. м. является геометрия
в целом псевдоримановых многообразий. Считается, что
топологич. структура многообразия должна предска-
предсказываться теоретически. Выбор того или иного тополо-
топологич. строения К. м. затруднен тем, что модели, имею-
имеющие различную топологию и другие глобальные свой-
свойства, могут быть локально изометричны. Один из мето-
методов решения вопроса о топологии К. м. состоит в зада-
задании дополнительных постулатов, либо вытекающих из
общетеоретич. соображений (напр., принцип причинно-
сти), либо являющихся опытными фактами (напр., по-
постулат в [1] исходит из СР-неинвариантности). Обычно
построение К. м. начинают с предположения того или
иного типа симметрии, в связи с чем выделяются одно-
однородные и изотропные К. м., анизотропные однородные
К. м. и др. (см. [2]). Впервые общерелятивистская
К. м. была предложена А. Эйнштейном в 1917 (см. [3]).
Эта модель была статистической однородной и изотроп-
изотропной и содержала Л-член. Впоследствии была разрабо-
разработана нестационарная однородная изотропная модель,
к-рая наз. фридмановской [4]. Предсказанная
этой моделью нестационарность была обнаружена в
1929 (см. [5]). Фридмановская модель имеет варианты
в зависимости от значений входящих в нее параметров.
При плотности вещества р, меньшей или равной нек-рой
критической плотности р0, имеет место так наз. откры-
открытая модель, при р>Ро — закрытая. Метрика
фридмановской К. м. имеет в нек-рых координатах вид
¦ г~1 J
где t — время, р и р0 — средняя и так наз. критическая
плотности вещества в данный момент времени, с — ско-
скорость света, г, 9 и ф — координаты. Критическая плот-
плотность р0 является нек-рой функцией времени, причем
оказывается, что величина р—р0 не меняет знак. При
fe <1 пространственное сечение t= const
является пространством Лобачевского, при &=0 —
евклидовым пространством (однако сама К. м. не яв-
является плоской), при &>0 — сферическим пространст-
пространством. Функция R(t) (радиус мира) определяется из
уравнений Эйнштейна и уравнений состояния. При
одном (&<0) или двух (&>0) значениях t функция R
обращается в нуль. Одновременно обращаются в бес-
бесконечность средняя плотность, кривизна и другие фи-
зич. характеристики модели. Принято говорить, что в
подобных точках К. м. имеет сингулярность.
В зависимости от уравнения состояния говорят о хо-
холодной (давление р=0) или о горячей (р=е/3, е — плот-
плотность энергии) моделях. Открытие в 1965 изотропного
равновесного излучения (Т»3°К) подтверждает горя-
горячую модель. Несмотря на грубый характер фридманов-
ских моделей, уже они передают основные черты
строения Вселенной. О дальнейшем построении К. м.
на их основе см. [1]. Развита теория эволюции малых от-
отклонений К. м. от фридмановской модели. В резуль-
результате этой эволюции, по-видимому, образуются скопле-
скопления галактик и другие астрономич. объекты. Имеющие-
Имеющиеся наблюдательные данные свидетельствуют в пользу
того, что реальная Вселенная с хорошей степенью точ-
точности описывается фридмановской К. м. Эти данные,
однако, не позволяют определить знак величины к
(несколько более вероятным представляется к<0).
Возможны иные топологич. интерпретации фридманов-
фридмановской К. м., к-рые получаются различными факториза-
циями (склейками) пространственного сечения. Наблю-
Наблюдательные данные накладывают лишь очень слабые ог-
ограничения на характер этих факторизации (см. [1]).
В логически последовательной теории построение К. м.
должно начинаться с выбора многообразия — носителя
псевдоримановой метрики. Однако метода такого выбо-
выбора еще нет. Имеется лишь несколько ограничений воз-
возможного глобального строения К. м., основанных на
принципе причинности и на факте несохранения комби-
комбинированной четности (см. [1]).
Предлагались многие иные К. м., в частности ани-
анизотропные однородные (см. [1], [6]).
До появления общерелятивистских К. м. неявно
предполагалось, что распределение масс является изо-
изотропным, однородным и статическим. Однако это пред-
предположение приводит к так наз. гравитационному, фото-
метрическому и другим парадоксам (бесконечно боль-
большой гравитационный потенциал, бесконечно большая
освещенность и др.)- Общерелятивистские К. м. не
содержат этих парадоксов (см. [2]). Рассматривая
распределения масс, аналогичные тем, к-рые имеют
место в общерелятивистских К. м., удалось получить
хорошие ньютонианские приближения к нек-рым обще-
общерелятивистским К. м. (см. [1]). Эти К. м. также не со-
содержат упомянутых парадоксов.
Лит.: [1] 3 е л ь д о в и ч Я. В., Новиков И. Д.,
Релятивистская астрофизика, М., 1967; [2] П е т р о и А. 3.,
Новые методы в общей теории относительности, М., 1966; [3]
Эйнштейн А., Собр. научных трудов, т. 1 М., 1965;
[4] Friedman A. A., «Z. Phys.», 1922, Bd 10, S. 377—86;
[5] Ни b b I e E. P., «Proc. Nat. Acad. Sci.», 1929, v. 15, № 3,
p. 168—73; [6] P e n z i a s A. A., W i 1 s о n R. W., «Astro-
phys. J.», 1965, v. 142, p. 419—21; [7] Heckmann O.,
Schiick ing E., в кн.: Handbuch der Physik, Bd 53, В.,
1959, S. 489—519; [8] Б е л и н с к и й В. А., Л и ф ш и ц Е. М.,
Халатников И. М., «Успехи физ. наук», 1970, т. 102,
в. 3, с. 463—500; [9] П е н р о у з Р., Структура пространства —
времени, пер. с англ., М., 1972. Д. Д. Соколов.
КОСОЕ ПРОИЗВЕДЕНИЕ — 1) К. п. векторов —
то же, что псевдоскалярное произведение векторов.
2) К. п. в эргодической теории — авто-
автоморфизм Т пространства с мерой Е (и порожденный им
каскад {Тп}) такой, что Е является прямым произве-
произведением двух пространств с мерой X X Y и действие Т
в Е специальным образом согласовано с этой структу-
структурой прямого произведения. А именно:
Т(х, y)=(R(x), S(x, у)),
где R — автоморфизм пространства с мерой X («базы»),
a S (х, ¦) при фиксированном х является автоморфиз-
автоморфизмом пространства с мерой У («слоя»). Понятие К. п.
непосредственно переносится на случай эндоморфиз-
эндоморфизмов, потоков и более общих групп и полугрупп преоб-
преобразований.
Во многих примерах геометрия, и алгебраич. проис-
происхождения фазовое пространство Е естественно опреде-
определяется как нек-рое К. п. в топологич. смысле (расслое-
(расслоение). Однако это не вызывает необходимости в обобще-
обобщении приведенного определения К. п. в эргодической
теории, ибо с метрической (в смысле теории меры) точки
зрения нет различия между прямыми и косыми произ-
произведениями пространств. д. в, Аносов.
3) К. п. в топологии — устаревшее название
расслоения со структурной группой.
КОСОСИММЕТРИЧЕСКАЯ БИЛИНЕЙНАЯ ФОРМА,
ант и симметрическая билинейная
форм а,— билинейная форма / на унитарном Л-моду-
Л-модуле V (где А — коммутативное кольцо с единицей),
удовлетворяющая условию:
/ (i>!, v2) = — /(i>2> vi) Для любых vlt v2?V.
Строение любой К. б. ф. / на конечномерном векторном
пространстве V над полем характеристики Ф 2 пол-
полностью определяется ее индексом Витта w (/) (см. Bumma
теорема, Витта разложение). А именно, V будет орто-
ортогональной (относительно /) прямой суммой ядра F-1-
формы / и подпространства размерности 2w(f), на к-ром
сужение формы / является нейтральной формой. Две
К. б. ф. на V изометричны тогда и только тогда, когда
их индексы Витта равны между собой. В частности,
невырожденная К. б. ф. нейтральна, а размерность
пространства V в этом случае четна.
Для любой К. б. ф. / на V существует базис elt ...,
е„, в к-ром матрица формы / имеет вид
0 Ет 0[|
-Ет 0 0 , (*)
О 0 0||
где m=w(f), а Ет — единичная матрица порядка т.
Матрица К. б. ф. в произвольном базисе кососиммет-
рична. Поэтому указанные выше свойства К. б. ф.
могут быть сформулированы и следующим образом:
для любой кососимметрич. матрицы М над полем ха-
характеристики ф2 найдется такая невырожденная
матрица Р, что PrMP имеет вид (*). В частности ранг
матрицы М четен, а определитель кососимметрич. мат-
матрицы нечетного порядка равен 0.
В случае поля характеристики 2 перечисленные
утверждения сохраняют силу, если заменить условие
кососимметричности формы / более сильным условием
знакопеременности: f(v,v) = O для любых v?V (для
полей характеристики ф2 эти условия эквивалентны).
Эти результаты допускают обобщение на случай, ког-
когда Л — коммутативное кольцо главных идеалов, V —
свободный Л-модуль конечной размерности и / — зна-
знакопеременная билинейная форма на V. А именно, в этих
условиях существует такой базис ех, ..., еп модуля V
и целое неотрицательное число т<:ге/2, что
0 Ф / (е,-, ei + m)=a.i?A, i = l, ..., т,
а,- делит а,- + 1 при ?=1, ¦. ., т—1, а в остальных слу-
случаях /(г,, еу-) = 0. Идеалы А а,; однозначно определяются
указанными условиями, а модуль V^- порождается эле-
элементами e2m + i, . . ., е„.
Определитель знакопеременной матрицы нечетного
порядка равен 0 для любого коммутативного кольца А
с единицей. В случае, когда порядок знакопеременной
матрицы М над А четен, элемент det M?A является
квадратом в А (см. Пфаффиан).
Лит.: [11 Б у р б а к и Н., Алгебра. Модули, кольца, фор-
формы, пер. с франц., М., 1966; [2] Л е н г С, Алгебра, пер. с
англ., М., 1968; [3] Ар тин Э., Геометрическая алгебра, пер.
с англ., М., 1969. В. Л. Попов.
КОСОСИММЕТРИЧЕСКАЯ МАТРИЦА — квадрат-
квадратная матрица А над полем характеристики рф2 такая,
что А т = —А. Ранг К. м.— число четное. Любая квад-
квадратная матрица В над полем характеристики, отличной
от 2, есть сумма симметрической и кососимметрической
матриц:
Ненулевые корни характеристич. многочлена действи-
действительной К. м.— чисто мнимые числа. Действительная
К. м. подобна матрице
где о/=а/
[alt ..., at, 0, ..., 0],
01
a i a/ — действительные числа, /=1
-1 и J
..., t. Жорданова форма / комплексной К. м. обла-
обладает свойствами: 1) жорданова клетка Jт(к) с элемен-
элементарным делителем (х—Х)т, где ХфО, повторяется в /
столько же раз, сколько и клетка Jт(—X); 2) при четном
т жорданова клетка Jm@) с элементарным делителем
хт повторяется в / четное число раз. Любая комплекс-
комплексная Ж. м. со свойствами 1) и 2) подобна нек-рой К. м.
Множество всех К. м. порядка п над полем к образует
алгебру Ли над к относительно сложения матриц и ком-
коммутирования: А В—В А.
Лит.: [1] Гантмахер Ф. Р., Теория матриц, 3 изд.,
М., 1967. Д. А. Супруненпо.
КОСОСИММЕТРИЧЕСКИЙ ТЕНЗОР — тензор над
re-мерным векторным пространством Е, инвариантный
относительно операции альтернирования по нек-рой
группе его индексов. Координаты К. т. обладают косой
симметрией по соответствующей группе индексов, т. е.
при перестановке местами двух индексов они изменяют
свое значение на противоположное (в смысле аддитив-
аддитивного закона в поле К, над к-рым определено Е), а при
равенстве двух индексов они равны нулю.
Наиболее важное значение имеют К. т., не изменя-
изменяющиеся при альтернировании по всей группе ковариант-
ных или контравариантных индексов. Контравариант-
ный или ковариантный К. т. валентности г наз. г- в е к-
тором, или поливектором, над Е, соот-
соответственно над Е* — сопряженном к Е пространством;
они являются элементами внешней алгебры векторного
пространства Е. Внешнюю алгебру над Е* обычно наз.
алгеброй внешних форм, отождествляя ковариантные
К. т. валентности г с г-формами.
Лит. см. при ст. Внешняя алгебра. II. X. Сабитов.
КОТАНГЕНС — одна из тригонометрических функ-
функций:
. cos х
у ¦— ctg х = — ;
другие обозначения: cot ,r, cotg x. Область определе-
определения — вся числовая ось, за исключением точек, абс-
абсциссы к-рых х=пп, п=0, —1, ±2, ... . К.— функция
неограниченная нечетная периодическая (с периодом
я). К. и тангенс связаны соотношением
ctg х— 1/tg x.
Функция, обратная К., наз. арккотангенсом.
Производная К.:
(ctg .)¦)' = — l/sin2.r.
Интеграл от К.:
\ ctg х dx — In | sin x | -\- С.
К. разлагается в ряд
^l&" - х з 45 ¦••>^\|^)^- —•
К. комплексного аргумента z — мероморфная функ-
функция, нули к-рой находятся в точках z=nn, где п —О,
it 1 , ±2, ... . Ю. А. Горькое.
КОТЕЛЬНИКОВА ИНТЕРПРЕТАЦИЯ — интерпре-
интерпретация многообразия прямых трехмерного Лобачевского
пространства 16'3 на комплексной плоскости S2(i)
(или на 1S2(i)). Всякой прямой пространства 1.S'3 ста-
ставятся в соответствие плюккеровы координаты, опреде-
определенные в этом случае с точностью до знака. С помощью
этих координат прямых устанавливается соответствие
между прямыми и их полярами в пространстве Х53, а
также определяются векторы прямых и их поляр. Одна
из двух взаимных поляр изображается вектором еди-
единичной длины, а другая — вектором мнимоеднничной
длины. Многообразие пар взаимно полярных прямых
пространства 1S3 изображается плоскостью S2(i) с ра-
радиусом кривизны, равным 1 или г, причем это соответст-
соответствие является непрерывным. Изотропные прямые про-
пространства 153 изображаются точками абсолюта плоско-
плоскости S2(i). Связная группа движений пространства
153(г) изоморфна группе движений плоскости S2(i).
Иногда К. и. понимается в более широком смысле
как интерпретация многообразий прямых трехмерных
пространств в виде комплексных или др. двумерных
плоскостей (см. Фубини интерпретация).
К. и. впервые была предложена А. П. Котельнико-
вым (см. [i]) и независимо от него Э. Штуди (см. [2]).
Лит.: [1] Котельников А. П., Проективная теория
векторов, Казань, 1899; [2] S t u d у Е., Geometrie derDynamen,
Lpz., 1903; [3] Р о з е н ф е л ь д Б. А., Неевклидовы прост-
пространства, М., 1969. Л. А. Сидоров.
КОТЕСА ФОРМУЛЫ — формулы для приближен-
приближенного вычисления определенных интегралов по значе-
значениям подинтегральной функции в конечном числе рав-
равноотстоящих точек, т. е. квадратурные формулы с рав-
равноотстоящими узлами. К. ф. имеют вид
Числа адГ' наз. коэффициентами Коте-
с а, они определяются из того условия, чтобы формула
(*) была точной для случаев, когда f(x) является много-
многочленом степени не выше п.
К. ф. предложены Р. Котесом (R. Cotes, 1722), в бо-
более общей форме были рассмотрены И. Ньютоном
(I. Newton). См. Ньютона — Котеса квадратурная
формула. ВСЭ'З.
КОХЛЕОИДА — плоская трансцендентная кривая,
уравнение к-рой в полярных координатах имеет вид
1 ф
К. имеет бесчисленное множество завитков, проходя-
проходящих через полюс и касающихся
полярной оси (см. рис.); полюс —
особая точка бесконечной крат-
кратности. Каждая прямая, проведен-
проведенная через полюс О, пересекает
К. в точках, касательные в кото-
которых проходят через одну и ту же
точку.
Лит.: [1] С а в с л о в А. А.,
Плоские кривые, М., 19И0.
Д. Д. Соколов.
КОЦЕПЬ — однородный элемент коцепной абелевой
группы С* (или, в общем случае, модуля), т. е. градуи-
градуированной абелевой группы, снабженной эндоморфиз-
эндоморфизмом б степени +1, обладающим свойством бб=О. Эндо-
Эндоморфизм б наз. кограничным отображе-
отображение м, или кограницей.
Обычно коцеиная группа С* возникает как группа
Нот (С*. Ж), или Нот (С*, G), где G — произвольная
абелева группа, наз. группой коэффициен-
коэффициентов^ С*—группа цепей, т. е. градуированная абелева
группа, снабженная эндоморфизмом д степени —1 —
граничным отображением, или границей, причем дд=О.
При этом отображение б в группе С* — Нот (С*, G)
определяется как сопряженное к д : (б/)<т=/(да), где
Для топологич. пространства X определена группа
С„,(Х) сингулярных цепей — абелева группа формаль-
формальных конечных сумм 2a,-s,-, где а(? Ж, a s,- — произволь-
произвольные сингулярные симплексы пространства X, т. е. не-
непрерывные отображения в X стандартного симплекса.
Сингулярной коцепью пространства X с
коэффициентами в G наз. однородный элемент группы
С*(Х, G)=~Hom(C*(X), G).
Аналогично, с и м и л и ц и а л ь н о й п - к о-
цепью симплициального разбиения X с коэффициен-
коэффициентами в абелевой группе G наз. гомоморфизм Сп(Х) —*¦ G,
где Сп(Х) — группа re-цепей разбиения X, т. е. группа
формальных конечных сумм 2a,-s,-, где a,?Z, a s,- суть
n-симплексы разбиения X. В частности, коцепь в смыс-
смысле Александрова — Чеха произвольного топологич.
пространства X есть К. нерва нек-рого открытого по-
покрытия пространства X.
Если X — клеточное разбиение (Хп— ^-мерный ос-
остов X), то абелева группа Нп(Хп, Х„_0 наз. группой
n-мерных клеточных коцепей разбиения X.
Кограничный гомоморфизм б : Нп(Хп, Хп-г) —>-
->- Нп + 1(Х,! + 1, Хп) полагается совпадающим со связы-
связывающими отображениями тройки (Хп + 1, Хп, Хп_1).
На практике часто группа С* снабжается дополни-
дополнительно мультипликативной структурой, т. е. представ-
представляет собой градуированную алгебру. В этих случаях
кограничное отображение б обладает свойством Лейбни-
Лейбница: б(хг/) = (бх)гН-( — l)degxx(&y), здесь элемент х?С*
полагается однородным степени deg x. Такой градуиро-
градуированной концепной алгеброй является, напр., алгебра
дифференциальных форм на гладком многообразии, в
к-рой внешний дифференциал играет роль конграницн.
А. Ф. Харшиладлс
КОЦИКЛ — коцепь, аннулируемая кограничным ото-
отображением, другими словами, коцепь, обращающаяся
в нуль на ограничивающих цепях. Понятие К. обоб-
обобщает понятие замкнутой дифференциалр>ноГ1 формы на
гладком многообразии, интеграл к-рой по ограничиваю-
ограничивающей цепи равен нулю.
В соответствии с различными вариантами понятия
коцепи имеются различные варианты понятия К. Напр.,
К. в смысле Александрова — Чеха топологич. прост-
пространства есть К. нерва нек-рого открытого покрытия
его. Лишь одномерные К. с неабелевыми коэффициен-
коэффициентами требуют отдельного обсуждения. Одномерный
коцикл симплициального множества К с коэффициен-
коэффициентами в неабелевой группе G представляет собой такую
функцию o->/(cr)?G, определенную на множестве К1
одномерных симплексов из К, что/(a("))/(o<2)) = /(crA))
для любого двумерного симплекса в?К. Два К. /
и g наз. к о г о м о л о г и ч н ы м it, если существует
такая функция h : KB-+G, что /(т)/г(т<°>)^/г(т11>)я(т)
для любого одномерного симплекса х?К. Классы кого-
мологии одномерных К. образуют пунктированное
множество Н1{К; G). Аналогично определяются одно-
одномерные К. и их когомологич. классы в смысле Алексан-
Александрова — Чеха с коэффициентами в пучке неабелевых
групп. Классы когомологии этих К. связаны с расслое-
расслоениями СО Структурной группой. Л. Ф. Харшилндзе.
КОШИ ЗАДАЧА — одна из основных задач теории
дифференциальных уравнений (обыкновенных и с част-
частными производными); состоит в отыскании решения (ин-
(интеграла) дифференциального уравнения, удовлетворяю-
удовлетворяющего так наз. начальным условиям (начальным данным).
К. з. обычно возникает при анализе процессов, опреде-
определяемых дифференциальным законом и начальным со-
состоянием, математич. выражением к-рых и являются
уравнение к начальное условие (откуда терминология и
выбор обозначений: начальные данные задаются при
i=0, а решение отыскивается при i^O). От краевых за-
задач К. з. отличается тем, что область, в к-рой должно
Г.ыть определено искомое решение, здесь заранее не
указывается. Тем не менее и К. з. можно рассматривать
как одну из краевых задач.
Основные вопросы, к-рые связаны с К. з., таковы.
1) Существует ли (хотя бы локально) решение К. з.?
2) Если решение существует, то какому пространству
оно принадлежит, в частности, какова область его су-
существования?
3) Является ли решение единственным?
4) Если решение единственно, то будет ли оно кор-
корректным, т. е. непрерывным (в каком-либо смысле) отно-
относительно начальных данных?
Простейшая К. з. состоит в том, что требуется найти
определенную на полупрямой х^хп функцию и(х),
к-рая удовлетворяет обыкновенному дифференциально-
дифференциальному уравнению 1-го порядка
du , i ч /1,
(/ — данная функция) и при х=ха принимает значе-
значение и0:
и(хо) = ио. B)
Геометрически это означает, что в семействе интеграль-
интегральных кривых уравнения A) на плоскости (х, и) разыски-
разыскивается кривая, проходящая через точку (х0, и0).
Первое утверждение о существовании такой функции
(при условии непрерывности / для всех х и непрерыв-
непрерывной дифференцируемое™ ее по и) доказано О. Коти
(A. Cauchy, 1820—30) и обобщено Э. Пикаром (Е.
Picard, 1S91 — 96) (заменившим дифференцируемость
условием Липшица но и). При этом решение К. з.
оказывается единственным и непрерывно зависящим
от начальных данных. Современные представления о
К. з.— по существу далеко идущее обобщение этой
задачи.
То, что вопросы 1) — 4) глубоко затрагивают суть
дела, т. е. для утвердительного ответа на них требуются
определенные условия, иллюстрируется уже теорией
обыкновенных дифференциальных уравнений. Так,
решение К. з. для уравнения A) с условием B), где /
задана на открытом множестве G и лишь непрерывна,
существует на нек-ром интервале, зависящем от G и
(-fii! "о) (см- Леано теорема), но может быть неединствен-
неединственным. Решение может существовать не во всех точках,
где определено /.
Дословно так же формулируется К. з. для систем
обыкновенных дифференциальных уравнений, т. е. для
обыкновенного дифференциального уравнения вида A)
с начальным условием B), где и=и(?) — функция со
значением в конечномерном векторном пространстве
Е, и(хо)=ио?Е, a f(x, и) — функция, определенная в
R + XE. Для существования, единственности и коррект-
корректности решения К. з. и здесь достаточны условия Пи-
кара.
Для обыкновенных дифференциальных уравнений
высших порядков
dftu
п — / (.г, и, и\ . •-, и*-п~1^).
К. з., в начальных данных к-рой участвуют, помимо
самой функции, и ее производные
// (.?()) — Uq, ll' (Xq) - II ц. . . . , 'J *• 1 ~ ^ (•?(}) " и0 »
стандартным приемом сводится к соответствующей за-
задаче вида A), B).
В случае обыкновенных дифференциальных уравне-
уравнений 1-го порядка, не разрешимых относительно произ-
производной искомой функции, постановка К. з.— та же,
разве что в большей степени опирается на ее геометрич.
трактовку, но исследование может осложняться невоз-
j можностью (даже локальной) редукции уравнения к
нормальной форме A).
Если для обыкновенного дифференциального уравне-
уравнения постановка и исследование К. з. не содержит прин-
принципиальных затруднений, то в случае дифференциаль-
дифференциальных уравнений с частными производными положение
(и, в частности, ответы на вопросы 1) — 4)) существен-
существенно усложняется, даже если рассматриваемые функции
достаточно регулярны. Это в значительной мере обус-
i ловлено многомерностью пространства независимых
переменных и вытекающими из этого (алгебраическими)
вопросами разрешимости. Так, условие разрешимости
К. з. (в нек-ром смысле промежуточной между «обыкно-
«обыкновенностью» и «частностью») для системы уравнений в
полных дифференциалах
соа = А? (х) d.r> =0, ?= 1, . . ., п, а=1, . . ., к < п,
состоящей в отыскании (л—/с)-мерной интегральной
поверхности, проходящей через данную точку, имеет
вид
du>a л ш1 л . .. л <й* = О
(в окрестности этой точки; здесь d, л — символы внеш-
внешнего дифференциала и внешнего произведения соответ-
соответственно) (см. Фробениуса теорема).
Для линейных дифференциальных уравнений с част-
частными производными
К. з. ставится следующим образом. В нек-рой области
G переменных х=(х1, . . . , хп) найти решение, удовле-
удовлетворяющее начальным условиям, т. е. принимающее
вместе со своими производными до (т—1)-го порядка
включительно заданные значения на нек-рой располо-
расположенной в G (п—1)-мерной гиперповерхности S (носи-
(носители начальных условий). Начальные ус-
ловия можно задавать в виде производных от и по на-
направлению единичной нормали v к S:
= фй, 0</cs?m— 1, D)
S
где фй(г), x?S — известные функции (данные
Коши).
Аналогичным образом ставится К. з. и для нелиней-
нелинейных дифференциальных уравнений.
С К. з. связано понятие нехарактеристич. поверхно-
поверхности. Если неособое преобразование переменных х —>- х'
«выпрямляет» поверхность S в окрестности точки х0,
переводя ее в участок гиперплоскости хп = 0, то в пре-
/ д
образованном уравнении C) коэффициент при I 7~г
\охп,
пропорционален величине
/~i i \ ^^i / \ d A di da dn
f/ t% \t — ^ d'y. (*^J V \ — у \ . . .V •
""¦] О | =¦ fiX
Поверхность S наз. нехарактеристической
в точке х0, если
Q(x0, v)=jtO. E)
В этом случае вблизи точки х0 уравнений C) можно
записать в так наз. нормальной форме
,m "
дх'п \ dx'
= (dlt ..., dn), dn<m. F)
К. з. обычно рассматривается, когда носителем на-
начальных данных является характеристич. поверхность,
т. е. когда условие E) выполнено для всех xo?S.
В теории К. з. важное место занимает Коши — Кова-
Ковалевской теорема: если S — аналитич. поверхность в ок-
окрестности своей точки х0, функции аа,/и ф^, 0<:/с-<т—1,
аналитичны в этой окрестности и выполнено условие
E), то в окрестности точки существует аналитич. ре-
решение и(х) К. з. C), D), к-рое в классе аналитич. функ-
функций единственно. В предположении аналитичности эта
теорема справедлива и для общих нелинейных уравне-
уравнений, если они могут быть приведены к нормальной фор-
форме F), а также для систем таких уравнений. Эта теорема
носит универсальный характер, поскольку она приме-
применима к аналитич. уравнениям независимо от их типа
(эллиптического, гиперболического и т. д.) и дает су-
существование решения в малом. Решение единственно
в классе неаналитич. функций.
Для дифференциальных уравнений с частными про-
производными порядка выше 1-го К. з. может оказаться
некорректной, если в условиях теоремы Коши —
Ковалевской отказаться от аналитичности уравнения
или данных Коши. Иллюстрацией служит пример
А д а м а р а: К. з. для уравнения Лапласа
с начальными условиями
и(х, у, О)=фо(ж, у), ~(х, у, 0)=0
не имеет решения, если функция фо(я, у) не является
аналитической.
Широкий класс уравнений, для к-рых К. з. поставле-
поставлена корректно, составляют гиперболич. уравнения.
В этом случае К. з. носит глобальный характер, однако
условия нехарактеристичности S при этом недостаточ-
недостаточно. Необходимо, чтобы S была поверхностью простран-
пространственного типа. Модельным уравнением гиперболич.
типа является волновое уравнение
д' п в2и „ ._.
-^р°' G)
рассматриваемое в (и+1)-мерной области переменных
(x, t)={x1, . . ., xn, t). K. 3. для этого уравнения
с данными
и(х, О)=фо(х), §?(*, 0) = ф1(х)
на гиперплоскости г=0 однозначно разрешима для
любых достаточно гладких функций ф0, ф1? и решение
непрерывно зависит в метрике пространств Ск от этих
функций. Для случаев ге= 1, п= 2 и п= 3 явный вид это-
этого решения дается формулами Д'А л а м б е р а,
Пуассона и Кирхгофа соответственно:
где
и(х, t)=±t
где х=(хи х2, х3), I— (lu g2, |3) и da — элемент поверх-
поверхности единичной сферы |?| = 1.
Множество точек на плоскости <=0, данные Коши
на к-ром вполне определяют значение и (х, t) решения
волнового уравнения G) в точке (х, t), наз. областью
зависимости для этой точки. Областями зависи-
зависимости точки (х, t) в случаях ге=1, и=2 и и=3 являются
отрезок, круг и шар, определяемые соотношением
\у—а;|2<:г2 (в соответствующем пространстве IR"). Если
носителем данных Коши является нек-рая область S
гиперплоскости t=0, то данные Коши в этой области
влияют на решение во всех точках (х, t) множества, для
к-рого пересечение Sf\{\y—х|2<?2} не пусто; это мно-
множество наз. областью влияния.
Множество точек (х, t)?Rn + 1, на к-ром решение и
вполне определяется по данным Коши на S, наз. о б-
ластью определения и(х, t) с начальными
данными на S. В случае га=1, и=2 и га=3 область опре-
определения образуют все точки (х, t), для к-рых отрезок,
круг и шар \у—x|2<:<2 соответственно расположены в S.
Эти результаты распространяются на более общий
случай, когда носителем данных Коши является по-
поверхность S пространственного типа, то есть поверх-
поверхность, для к-рой величина Q в E) сохраняет на S поло-
положительное значение.
Кроме К. з., для гиперболич. уравнений корректно
поставлены и другие задачи, напр. Коши характери-
характеристическая задача, смешанная начально-краевая задача;
в последней задаче решение имеется в (и+1)-мерном
цилиндре с образующей, параллельной оси /, и с основа-
основанием S, представляющем собой нек-рую область в про-
пространстве переменных х—(хл, . . ., хп) с границей Г.
Носителем начальных условий служит S, а на боковой
поверхности ГХ {t>0} цилиндра задается значение
функции или ее нормальной производной (в случае
уравнений 2-го порядка) или более общие краевые ус-
условия.
Для вырождающихся уравнений К. з. имеет свои осо-
особенности. Напр., если уравнение гиперболич. типа и
носителем данных Коши является поверхность, на к-рой
уравнение параболически вырождается, то в зависимо-
зависимости от характера вырождения принятие начальных ус-
условий может осуществляться с нек-рым весом.
Лит. : [1] К о в а л е в с к а я С. В., Научные работы, М.,
1948; [21 А д а м а р Ж., Задача Коши для линейных уравнений
с частными производными гиперболического типа, пер. с франц.,
М.,1978; [3] БерсЛ., ДжонФ.,ШехтерМ., Уравнения
с частными производными, пер. с англ., М., 1966; [4] Б и ц а д-
з е А. В., Уравнения математической физики, М., 1976; [5]
Курант Р., Уравнения с частными производными, пер.
с англ., М., 1964; [6] М и з о х а т а С, Теория уравнений с
частными производными, пер. с япон., М., 1977; [7] Тихо-
Тихонова. Н., Самарский А. А., Уравнения математиче-
математической физики, 4 изд., М., 1972; [8]Хёрмандер Л., Линей-
Линейные дифференциальные операторы с частными производными,
пер. с англ., М., 1965. А. П. Солдатов.
КОШИ ЗАДАЧА; численные методы ре-
решения для обыкновенного диффе-
дифференциального уравнения. Задачей Ко-
ши наз. задача определения функции или нескольких
функций, удовлетворяющих одному или, соответствен-
соответственно, системе дифференциальных уравнений и прини-
принимающих заданные значения в нек-рой фиксированной
точке. Пусть
У (х) = {Ух(х), Уз(х), •••, Уп(х)},
/ (¦*> J/) = {/i(*> У), /г (*. У), •••> fn(x, У)}
— вектор-функции, определенные и непрерывные со-
соответственно на отрезке /={#, | х—а |<:^4} и в замк-
замкнутой области U={(x, у), \х—а|<Л, \\у—Ь\\*?В}, где
||-Ц — некоторая норма в конечномерном пространстве
R". В этих обозначениях К. з. для системы обыкно-
обыкновенных дифференциальных уравнений 1-го порядка
записывается в виде
y'(x)=f(x, у), y(xo) = yQ, хо?1, г/о€п- С1)
Вводя соответствующим образом новые неизвестные
функции, можно привести к такому виду К. з. для любой
системы обыкновенных дифференциальных уравнений
произвольного порядка.
Решение задачи A) существует, если функция f(x, у)
непрерывна в П. Для того чтобы это решение было един-
единственным, достаточно, чтобы выполнялось условие
О с г у д а:
\lf(x, yi) — f(x, J/2)IK« (|| г/! — у2\\), B)
где функция со(<) — такова, что
или более сильное условие Липшица:
11/C. У\) — / (г. 2/г)И < Ь |] Ух — Уг^' ~ №
Величина L наз. постоянной Липшица.
Если функция f(x, у) непрерывно дифференцируема по
у, то в качестве постоянной Липшица можно взять ве-
величину
L= SUP Ш • D)
Оценка C) с постоянной Липшица D) оказывается в
ряде случаев слишком грубой для успешного примене-
применения численных методов решения К. з., несмотря на то,
что теоретически решение этой задачи существует и
оно единственно. Это происходит, в частности, в тех
случаях, когда собственные значения матрицы -g- име-
имеют «большой разброс», т. е. наибольшее собственное
лначение в сотни или даже тысячи раз больше наимень-
наименьшего собственного значения. Такие системы дифферен-
дифференциальных уравнений наз. жесткими систем а-
м и, а соответствующие задачи — жесткими за-
задачами Кош и. Одним из источников возникнове-
возникновения жестких систем является сведение уравнений с
частными производными к системе обыкновенных диф-
дифференциальных уравнений, напр, с помощью метода
прямых.
Численные методы для обыкновенных дифференци-
дифференциальных уравнений представляют собой, как правило,
одно или несколько соотношений, связывающих иско-
искомую функцию у(х) в дискретной последовательности
точке Xk, &=0, 1, ..., множество к-рых наз. сеткой. Ос- j
новы численных методов вообще и для дифференциаль-
дифференциальных уравнений в частности были заложены Л. Эйле-
Эйлером (L. Euler). Его именем называется один из самых
простых методов решения К. з., к-рый состоит в сле-
следующем. Пусть решение задачи A) в окрестности точки
хк разложено в ряд Тейлора
уП = у (**) + у' (**) (*-**) + у" (**) (*х*)а + • • •
Если величина х—хк мала, то, отбрасывая члены поряд-
порядка (х—хк)г и более высокого, получают приближенное
равенство
у{х)ку (хк) + у' (хк) (х — хк), у' (хк) = / (хк, у (хк)).
В точке х/г + 1 приближенное решение может быть вы-
вычислено по формуле
Ук + 1=Ук + (хк + 1 — *k) f (хк, Ук)-
Это соотношение и наз. методом Эйлера.
В дальнейшем численные методы были значительно
усовершенствованы. Это развитие велось в основном
в двух направлениях: методы, получившие в дальней-
дальнейшем название Рунге—Кутта методов и конечнораз-
ностные методы, важнейшим представителем к-рых
является Адамса метод.
К достоинствам методов Рунге — Кутта следует от-
отнести то, что алгоритмы, получающиеся на их основе,
являются однородными, т. е. не изменяющимися при
переходе от одной точки сетки к другой. Кроме того,
в методах Рунге — Кутта можно изменять шаг интег-
интегрирования в соответствии с требуемой точностью вы-
вычислений без значительного усложнения самого алго-
алгоритма (см. Кутта — Мерсона метод, Рунге правило).
На основе этих методов созданы достаточно надежные
двусторонние методы. Основным недостатком является
то, что для вычисления приближенного решения в одной
точке сетки требуется несколько вычислений правой
части f(x, у) дифференциального уравнения A). Это
приводит, в особенности при сложных правых частях,
к значительному увеличению времени вычислений.
В конечноразностных методах, в том числе в методе
Адамса, требуется лишь одно вычисление правой части
на один узел сетки. Это является главным достоинством
конечноразностных методов. Однако для того чтобы
начать вычисления по какой-либо конечноразностной
формуле, необходимо прежде вычислить дополнитель-
дополнительные «начальные значения». Это приводит к тому, что
алгоритм оказывается неоднородным — первые не-
несколько значений должны вычисляться по другим фор-
формулам. Более существенным недостатком конечнораз-
конечноразностных методов является невозможность простого
изменения шага интегрирования, т. е. необходимость
использовать сетки с постоянным шагом.
На основе конечноразностных методов разработаны
так. наз. методы предсказания — уточнения, к-рые
представляют собой пару конечноразностных формул,
одна из к-рых (предсказывающая) является, как пра-
правило, явной, а вторая (уточняющая) — неявной, напр.,
предсказывающая:
У У + Cf f)
уточняющая:
/п = /(*!.. Уп)> Tn = f(xn, Уп)-
Предсказывающе-уточняющие методы находят успеш-
успешное применение при решении жестких систем обыкновен-
обыкновенных дифференциальных уравнений.
Несмотря на то, что дифференциальные уравнения
высокого порядка формально сводятся к системе урав-
нений 1-го порядка, методы, приспособленные к кон-
конкретному виду дифференциального уравнения, иногда
оказываются значительно более эффективными. В свя-
связи с этим развиваются конечноразностные методы, ис-
использующие производные высшего порядка, напр.
Штермера метод.
Лит.: [1] Б е р е з и н И. С, Ж и Д к о в Н. П., Методы
вычислений, 2 изд., т. 2, М., 1962; [2] Бахвалов Н. С,
Численные методы, 2 изд., М., 1975; [3] Modern Numerical Me-
Methods for ordinary differential equations, Oxf., 1976.
В. В. Поспелов.
КОШИ ИНТЕГРАЛ — 1) К. и,— определенный ин-
интеграл от непрерывной функции одного действительного
переменного. Пусть функция /(а-) непрерывна на отрезке
[а, Ь] и а=хо<х1<... <-r,_i <.r,-<... <.т„=6,
Ax[=Xj—?|'-i, '=1, 2, . . ., п; предел
наз. определенным интегралом по
К о ш и от функции /(х) на отрезке [а, Ь] и обозначают
К. и.— частный случай Римана интеграла. Определе-
Определение дано О. Коши в [1].
Лит.: [1] С а и с h у A. L., Resume des lecons donnees a
l'Ecole Royale Polytechnique sur le calcul infinitesimal, t. 1,
P., 1823. Л. Д. Кудрявцев.
2) К. и.— интеграл с я д р о м Коши
1
выражающий значения регулярной аналлтич. функции
f(z) внутри контура L через ее значения на L. Точнее,
пусть /(г) — регулярная аналитич. функция комплек-
комплексного переменного z в области D и L — замкнутая ку-
кусочно гладкая жорданова кривая, расположенная в D
вместе со своей внутренностью G, причем обход L со-
совершается против часовой стрелки. Тогда справедлива
основная в теории аналитич. функций одного комплек-
комплексного переменного интегральная формула
Коши:
Стоящий справа в фop^fyлe A) интеграл и наз. интег-
интегралом Коши.
Впервые, по-видимому, К. и., применительно к ча-
частным ситуациям, появляется в работах О. Коши [1].
К. и. характеризуется, таким образом, двумя усло-
условиями: 1) К. и. берется по замкнутой гладкой или хотя
бы кусочно гладкой кривой L; 2) подинтегральная функ-
функция К. и. имеет вид
/(?>
где ??L, a f(z) — регулярная аналитич. функция на L
и внутри L. Если в К. и. z?CG, т. е. если z расположена
во внешности кривой L, то при сохранении условий 1)
$4^ * B)
В частности, если L — окружность радиуса р с центром
z, т. е.
? = {? = *+рв'в; 0<9<2л},
то из A) следует
т. е. значение /(z) в любой точке z?D равно среднему
арифметическому ео значений на любой достаточно ма-
малой окружности LczD с центром г. Формула A) позво-
ляет получить и все остальные элементарные свойства
аналитич. функций.
Если, с другой стороны, flz) является регулярной
аналитич. функцией в бесконечной области CG — внеш-
внешности замкнутой кривой L и на L,
/(»)== lim/(z),
то справедлива интегральная формула
Коши для бесконечной области:
_if(co)-f<z). z
\
Пусть теперь Г — некоторая, не обязательно замк-
замкнутая, кусочно гладкая кривая, расположенная в ко-
конечной плоскости z=<fc оо, <р(?) — непрерывная комплекс-
комплексная функция на Г иг — точка, не лежащая на Г. И н-
тегралом типа Коши (и. т. К.) наз. обобще-
обобщение К. и. в виде
Функцию ф(?) наз. иногда плотностью интег-
интеграла типа Коши. Простейшие свойства и. т. К.:
1) F(z) — регулярная аналитич. функция переменно-
переменного z в любой области, не содержащей точек Г;
2) производные /"<">(z) выражаются формулами
3) функция F(z) регулярна в бесконечности, причем
F(oo) = 0, F(z) = O(llz) при z->-oo.
С точки зрения общей теории аналитич. функций и
применений к механике и физике, основное значение
имеет вопрос о существовании граничных значений
н. т. К. при приближении к Г и об их аналитич. выра-
выражении. К.и. A) всюду внутри L равен /(z), а во внешно-
внешности он тождественно равен нулю. Поэтому, когда и.т.К.
C) обращается в К. и., т. е. когда выполняются условия
1) и 2), функция F(z) при приближении к L слева (т. е.
изнутри) имеет граничные значения F+ (?o) = /(?o)>
и при этих значениях на L она непрерывна в каждой
точке Со€^ слева от L; при приближении к L справа
(т. е. извне) F(z) имеет граничные значения нуль,
F~(?,o) = O, и при этих значениях на L она непрерывна
в каждой точке Со6^ справа от L. Т. обр., для К. и.
F+E0)-F- (?„) = /(?„).
Для и. т. К. общего вида дело обстоит несколько
сложнее. Пусть кривая Г задана уравнением ?=?(«),
s — длина ее дуги, отсчитываемая от какой-либо фик-
фиксированной точки, Со=?(хо) — произвольно фикси-
фиксированная точка на Г и Ге — та часть кривой Г, к-рая
остается после удаления из Г меньшей дуги с концами
?(«„—е) и СК+8)- Если существует конечный предел
imj_r Ф«>"С LT Ф<»^ г <=Г D)
то он наз. сингулярным, или особым, ин-
интегралом. Доказано, напр., что сингулярный
интеграл D) существует, если кривая Г гладкая в ок-
окрестности отличной от концов Г точки Со, а плотность
ф(С) удовлетворяет условию Гёльдера
При этих условиях существуют и граничные значе-
значения, к-рые выражаются формулами Сохоц-
к о г о:
F ± (Со) = J: ~ Ф (Со) ~Ь 2^7 j г г-г—' ?о€Г, E)
а функции F+(z) и F~(z) — непрерывны в окрестности
Со^Г соответственно слева и справа от Г. В случае
К. и. сингулярный интеграл равен
В эквивалентной форме формулы E) записываются так:
F)
5о€г. (?)
Формулы Сохоцкого E) — G) имеют основное значе-
значение при решении граничных задач теории аналитиче-
аналитических функций, сингулярных интегральных уравнений,
связанных с и. т. К., а также при решении ряда задач
гидродинамики, теории упругости и др.
Пусть Г — произвольная, для простоты замкнутая,
спрямляемая кривая длины I, t()=tJ>(s) — угол между
ваправлением оси Ох и касательной к Г в точке ?—
= ?(s)?r, рассматриваемый как функция длины дуги s,
Ф(«) — комплексная функция длины дуги s ограничен-
ограниченной вариации на [О, I]. Выражение
ваз. интегралом типа Кош и — Стиль-
ес а (и. т. К.—С). Иначе говоря, и. т. К.— С. есть
и. т. К. по произвольной конечной комплексной боре-
левской мере, сосредоточенной на Г. Если функция
<D(s) абсолютно непрерывна, то и. т. К.—С. превраща-
превращается в интеграл типа Коши — Лебега
(и. т. К.—Л.), часто называемый также просто и н-
тегралом типа Коши:
ГДе <p(?)=<p[?(s)] = <»'(s).
Пусть ?0—точка Г , в к-рой существует определенная
касательная, наклоненная к оси Ох под углом i|H; такие
точки имеются на спрямляемой кривой почти всюду.
Пусть точка z находится на нек-рой прямой, проходя-
проходящей через ?0 и наклоненной к нормали под углом а0, на
расстоянии |г—?0| = е, т. е. z= ?0=teiel (г|'0 + а°\
Разность между и. т. К.— С. (8) и интегралом по Ге
Jre z-u J
определена во всех точках ?о€Г, в к-рых существует
определенная касательная, т. е. почти всюду на Г.
В теории и. т. К.—С. важное значение имеет основ-
основная лемма Привалова: предельный переход
UmWiU, e, ao)=± Ф'(?„)
осуществляется для всех точек ?о€Г, кроме, быть мо-
может, точек множества меры нуль на Г, не зависящего от
а0, равномерно относительно а0 в любом угле |ао| <
<я/2—6, 6>0. Если сингулярный интеграл существует
почти всюду на Г, то и. т. К.—С. имеет почти всюду
на Г угловые граничные значения F±(l,l>), для к-рых
справедливы формулы Сохоцкого:
Верво и обратное: если и. т. К.—С. почти всюду на Г
имеет угловые граничные значения изнутри и извне Г,
то сингулярный интеграл существует и формулы A0)
справедливы почти всюду на Г. Полного решения проб-
проблемы необходимых и достаточных условий существова-
существования граничных значений в достаточно простых терми-
терминах для и. т. К.—С. и даже для и. т. К.—Л. пока A982)
не получено.
В отличие от рассмотренного выше случая и. Т.К.
по гладкой кривой Г, даже при наличии угловых гра-
граничных значений, и. т. К.—С. уже, вообще говоря,
не является непрерывной функцией в окрестности точки
?0?Г слева пли справа от Г. Здесь известно, напр., что
и. т. К.—Л. (9) непрерывен в замкнутой области D,
ограниченной спрямляемым контуром Г, при дополни-
дополнительном условии, что его плотность ср(?) удовлетворяет
на Г условию Липшица
Относительно и. т. К.—Л. (9) говорят, что он обра-
обращается в К. и.
4[ ФЯ"е, A1)
понимаемый в смысле Лебега, если угловые граничные
значения F + (t,0) изнутри Г совпадают с ф(?0) почти всю-
всюду на контуре Г. Иначе говоря, интеграл (9) обращается
в К. и. (И), если угловые граничные значения f ~(?о)
извне Г равны нулю почти всюду на Г. Относящаяся
сюда теорема Голубева — Привалова
гласит: суммируемая функция (f (?) на Г тогда и только
тогда представляет собой угловые граничные значения
нек-рого К. и. изнутри Г, когда равны нулю все мо-
моменты
=0, п = 0, 1, 2, ... A2)
Если выполнены аналогичные A2) условия
) = 0, я-0, 1, 2, ..., A3)
?
то и. т. К.—С. (8) обращается в интеграл К о-
ш и — С т и л т ь е с а (и. К.—С):
т. е. угловые граничные значения F + (t,0) изнутри Г
совпадают с производной Ф'(в0) почти всюду на Г или,
иначе говоря, угловые граничные значения F~ (?„)
извне Г равны нулю почти всюду на Г. Условия A3)
сразу обеспечивают абсолютную непрерывность функ-
функции Ф(в) на отрезке [0, I], а следовательно, на самом деле
в этом случае и. К.—С. A4) является и н т е г р алом
Кош и — Лебега (и. К.—Л.) с плотностью ф(?)~
= cp[?(s)]=<D'(s). Таким образом, класс функций, пред-
ставимых и. К.— С, совпадает с классом функций,
представимых и. К.—Л.
Важной задачей представляется внутренняя харак-
теризация классов функций, регулярных в области D,
ограниченной замкнутой спрямляемой кривой Г, и пред-
представимых К. и. A1), и. т. К.-Л. (9) илии. т. К.—С. (8)
(о наиболее важных классах A (D), B(D)=H00(D), Hp(D)
и N*{D) см. в ст. Граничные свойства аналитических
функции).
В простейшем случае, когда Z)={z:|z|<l}— еди-
единичный круг и r={z:|z| = l} — единичная окружность,
н. т. К.—С, принимающий в этом случае вид
изображает всегда функцию класса Нр, 0<р<1. Об-
Обратная теорема неверна: совокупность функций классов
Нр, 0<р<1, шире, чем совокупность функций, пред-
ставнмых в виде A5). Напротив, совокупность функ-
функций, представимых в D и. К.—С. или К. и., совпадает
с классом #!.
В случае произвольной односвязной области D, огра-
ограниченной спрямляемой кривой Г, класс функций, пред-
представимых в D и. К.—С. или К. и., совпадает с классом
Смирнова Ег (см. Граничные свойства аналитических
функций). Характеристики классов функций, пред-
ставимых и. т. К.—С. или и. т. К.—Л., значительно
сложнее.
Пусть /(г) — произвольная (не аналитическая) функ-
функция класса С1 в конечной замкнутой области D, огра-
ограниченной кусочно гладкой жордановои кривой L. Иног-
Иногда интегральной формулой Коши наз.
также следующее обобщение классич. формулы A):
_i с /<?)dc 1 се э/ djdn _ f/OO. z€#i_ ,16)
где
Эта формула встречается, начиная, по-видимому, с
работ Д. Помпею (D. Pompeiu, 1912). Она известна также
как формула Помпею, формула Боре-
ля — Помпею, формула Коши — Грина
и находит многочисленные приложения в теории обоб-
обобщенных аналитич. функций, сингулярных интеграль-
интегральных уравнений и в различных прикладных вопросах.
Пусть f(z) — регулярная аналитич. функция многих
комплексных переменных z=(zt, . . ., zn) в замкнутом
поликруге D, D= {z?C":\zv—avl<rv}. Тогда в каждой
точке D функция /(г) представима кратным ин-
интегралом Коши:
SZgf' A7)
где Г={??СП: |?v—av\ = rv, v=l, . . ., я} — остов
поликруга, ?=(?.!, . . ., ?„), d?=^i- ¦ Жп, l~z=
= (?i—zi) • • ¦ (S«—гп)' Формула A7) дает простейший
аналог К. и. для окружности L={z?C: |z—а\ = г}, но
при п>1 интегрирование в A7) распространено уже не
на всю границу поликруга, а лишь'на его остов. Вооб-
Вообще, пусть D=D1XD2X . . -XDn — поликруговая об-
область в С", составленная как произведение односвяз-
ных плоских областей Dv с гладкими границами dDv=
= {zv=zv(iv), 0<?v«l}, 77=5JD1X5?JX. . .dDn — ос-
остов D, представляющий собой гладкое я-мерное много-
многообразие. Формула A7) распространяется и на этот слу-
случай.
Большое значение в теории аналитич. функций мно-
многих комплексных переменных имеют более глубокие
обобщения интегральной формулы Коши, в первую оче-
очередь такие, как Л ере формула, названная самим Ж. Лере
(J. Leray) формулой Коши — Фантапье,
и Бохнера — Мартинелли представление. В связи
с этим при я>1 изучаются в основном граничные свой-
свойства интегральных представлений, отличных от A7).
Лит.: [1] С а и с h у A. L., Sur la mecanique celeste et sur
un nouveau calcul appele calcul des limites, Turin, 1831 (или
CEuvres completes, ser. 1, t. 8, P., 1892); [2] Шабат Б. В.,
Введение в комплексный анализ, 2 изд., ч. 1—2, 1976; [3] М а р-
кушевич А. И., Теория аналитических функций, 2 изд.,
т. 1, М., 1967; [4] М у с х е л и ш в и л и Н. И., Сингулярные
интегральные уравнения, 3 изд., М., 1968; [5] Владими-
Владимиров В. С, Методы теории функций многих комплексных пере-
переменных, М., 1964; [6] П р и в а л о в И. И., Интеграл Cauchy,
Саратов, 1918; [7] его же, Граничные свойства аналитиче-
аналитических функций, 2 изд., М.— Л., 1950; [8] X а в и н с о н С. Я.,
в кн.: Итоги науки. Математический анализ. 1963, М., 1965,
с. 5—80; [9] X в е д е л и д з е Б. В., в кн.: «Современные про-
проблемы математики», т. 7, М., 1975, с. 5—162; [10] С а 1 d е-
г д п А. Р., «Ргос. Nat. Acad. Sci. USA», 1977, v. 74, Mi,
p. 1324—27. E. Д. Соломенцев.
КОШИ ИНТЕГРАЛЬНАЯ ТЕОРЕМА: если
f(z) — регулярная аналитич. функция комплексного
переменного z в односвязной области D на комплексной
плоскости С = С1, то интеграл от f(z), взятый по любой
замкнутой спрямляемой кривой у, расположенной в D,
равен нулю, т. е.
]rf(z)dz = (
Эквивалентная формулировка К. и. т. утверждает, что
интеграл
не зависит от выбора пути интегрирования, соединяю-
соединяющего фиксированные точки а и Ь в области D. Именно
такой в сущности и была первоначальная формулиров-
формулировка К. и. т., предложенная О. Коши в 1825 (см. [1]);
близкие формулировки имеются в письмах К. Гаусса
(С. Gauss, 1811). Доказательство О. Коши содержало
дополнительное предположение непрерывности произ-
производной/'(z); первое полное доказательство дано Э. Гурса
[2]. Свойство аналитич. функций, выражаемое К. и. т.,
полностью характеризует последние (см. Мореры теоре-
теорема), и потому из К. и. т. выводятся все основные свой-
свойства аналитич. функций.
В случае произвольной области D на плоскости С или
на римановой поверхности К. и. т. может быть сформу-
сформулирована так: если /(z) — регулярная аналитич. функ-
функция в области D, то интеграл от /(z) по любой спрямля-
спрямляемой замкнутой кривой yCD, гомотопной нулю в D,
равен нулю.
Распространением К. и. т. на случай аналитич. функ-
функций многих комплексных переменных является тео-
теорема Коши — Пуанкаре: если /(z), z=(zx,
. . ., zn),— регулярная аналитич. функция в области D
комплексного пространства С", ra^l, то для любой
(п+1)-мерной поверхности GczD с гладкой границей
y=dG интеграл
где f(z)dz — сокращенное обозначение голоморфной
дифференциальной формы
f(z)dz = f(z1, ..., zn)dz1A.../\azn. '
При п=1 поверхность G и область D имеют одинаковую
размерность, п+1 = 2ге (случай классической К. и. т.);
при га>1 размерность G меньше размерности D, и+1<
<2я. См. также Вычет, Коши интеграл.
Лит.: [1] С а и с h у A. L., CEuvres completes, ser. 1, t. 4,
P., 1890, p. 285; [2] G о u r s a t E., «Acta math.», 1884, v. 4,
p. 197—200; [3] Маркушевич А. И., Теория аналитиче-
аналитических функций, 2изд., т. 1, М., 1967; [4] В л а д и м и р о в В. С,
Методы теории функций многих комплексных переменных, М.,
1964; [5] Ш а 6 a t Б. В., Введение в комплексный анализ,
2 изд., ч. 1 — 2, М., 1976. Е. Д. Соломенцев.
КОШИ КРИТЕРИЙ — 1) К. к. сходимости
числовой последовательности: для
того чтобы последовательность чисел (действительных
или комплексных) хп, ге=1, 2, . . ., имела предел, необ-
необходимо и достаточно, чтобы для любого е>0 существо-
существовал такой номер N, что для всех n^-N и m^-N выпол-
выполнялось неравенство
К. к. сходимости числовой последовательности обоб-
обобщается в критерий сходимости точек полного метрич.
пространства.
Последовательность точек {хп} полного метрич. про-
пространства сходится в том и только в том случае, когда
для любого е>0 существует такое N, что для всех
ri^-N и rri^N выполняется неравенство р{х„, хт)<^е.
2) К. к. существования предела фун-
функций п переменных (ri^i). Пусть функция
/ определена на множестве X га-мерного пространства
Rn и принимает числовые (действительные или комп-
комплексные) значения, а — предельная точка множества
X (или символ оо, в этом случае множество X неограни-
чено). Конечный предел lim / (.г) существует тогда
и только тогда, когда для любого r>0 найдется та-
кая окрестность U=U(a) точки а, что для любых
х'?U [\Х и x"?Uf\X выполняется неравенство
|/(*")--/(*') К е.
Этот критерий обобщается на более общие отображе-
отображения: пусть X — топологич. пространство, а — его пре-
предельная точка, в к-рой выполняется первая аксиома
счетности, Y— полное метрич. пространство и /•—ото-
/•—отображение X в Y. Для того чтобы существовал предел
lim f(x),
необходимо и достаточно, чтобы для любого е>0 су-
существовала окрестность U=U(a) точки а такая, что
для всех х' ? U и x"^U выполнялось неравенство
р (/(*"), /(*'))<е.
3) К. к. равномерной сходимости
семейства функций. Пусть X — некоторое
множество, Y — топологич. пространство, удовлетво-
удовлетворяющее в предельной точке yo?Y первой аксиоме счет-
счетности, Л — полное метрич. пространство, f(x, у) —
отображение множества XXY в Л, х?Х, y?Y. Семей-
Семейство отображений f(x, у), отображающих при фикси-
фиксированном y?Y множество X в Л, является равномер-
равномерно сходящимся на X при у —>- у0, если для любого
8>0 существует такая окрестность U=U(y0) точки
г/о, что для всех у' ? ?/, y"?U и всех х?Х
выполняется неравенство
У"), /(*,
В частности, если У — множество натуральных чисел
и fn{x)=f(x, я), то последовательность {fn(x)} равно-
равномерно сходится на множестве X при я —>- оо тогда и
только тогда, когда для любого е>0 существует такой
номер N, что для всех х?Х и всех номеров ri^N и
nC^N выполняется неравенство
I/»(*)-/« (*I <е.
4) К. к. сходимости ряда: числовой ряд
?,n=ian сходится тогда и только тогда, когда для любого
8>0 существует такой номер N, что для всех n^-N и
всех целых р^О выполняется неравенство
< е.
Для кратных рядов аналогичный критерий сходимости
наз. критерием Кош и— Штольца. Напр.,
для того чтобы двойной ряд
сходился по прямоугольным частичным суммам
необходимо и достаточно, чтобы для любого е>0 на-
нашлось такое N, что при всех n^N, rn^-N и всех целых
р^О и д^О выполнялось неравенство
\$п + р, m + q — $пт I < 6.
Эти критерии обобщаются на ряды в банаховых прост-
пространствах (вместо абсолютной величины берутся нормы
соответствующих элементов).
5) К. к. равномерной сходимости
ряда: пусть и„=и„(х), я=1, 2, ... ,— функции,
определенные на нек-ром множестве X и принимающие
числовые значения. Для того чтобы ряд
2L, »»(*>¦
равномерно сходился на множестве X, необходимо и
достаточно, чтобы для любого е>0 существовал такой
номер N, что для всех n^N, целых р^О и х?Х выпол-
выполнялось неравенство
< е.
Этот критерий также переносится на кратные ряды,
причем не только на числовые, но и на ряды, члены
к-рых принадлежат банаховым пространствам, т. е.
когда ип (х) являются отображениями множества X в
нек-рое банахово пространство.
6) К. к. сходимости несобственных
интегр ало в: пусть функция / определена на полу-
полуинтервале [а, Ъ), —оо<а<Ь<:+оо, принимает на нем
числовые значения и при любом с?(а, Ь) интегрируема
(по Риману или по Лебегу) на отрезке [а, с]. Для того
чтобы несобственный интеграл
fb
/ (х) dx
Ja
сходился, необходимо и достаточно, чтобы для любого
е>0 существовало такое Т]?(а, 6), что для всех т|' и ц",
удовлетворяющих УСЛОВИЮ Т)<Т]'<&, Т) <Т)"<Ь, ВЫПОЛ-
ВЫПОЛНЯЛОСЬ неравенство
< 8.
Аналогичным образом критерий формулируется и для
несобственных интегралов других типов, а также обоб-
обобщается на случай, когда функция / зависит от несколь-
нескольких переменных и ее значения лежат в банаховом
пространстве.
7) К. к. равномерной сходимости не-
несобственных интегралов: пусть функция
f(x, у) при каждом фиксированном y?Y, где У — не-
некоторое множество, определена на полуинтервале
[а, 6), —оо <a<fe<:-j- °o, принимает числовые значения
и при любом eg (a, 6) интегрируема по х на отрезке
[а, с]. Для того чтобы интеграл
$*/(*. y)dx, y?Y,
равномерно сходился на множестве У, необходимо и
достаточно, чтобы для любого е>0 нашлось такое г\?
^ (а, Ь), что для любых г\' д т]", удовлетворяющих ус-
условиям т)<т)'<Ь, т)<Т]"<& и всех y?Y, выполнялось
неравенство
J(x, y)dx
< 8.
Этот критерий также переносится на несобственные ин-
интегралы других типов, на случай функций многих пере-
переменных и на функции, значения к-рых лежат в банахо-
банаховых пространствах.
Лит.: [1] С а и с h у A. L., Analyse algebrique, P., 1821:
[2] Stolz О., «Math. Ann.», 1884, Bd 24, S. 154—71; [3]
Дьедонне Ж., Основы современного анализа, пер. с англ!.,
М., 1964; [4] И л ь и н В. А., П о з н я к Э. Г.. Основы мате-
математического анализа, 3 изд., т. 1, М., 1971, т. 2, М., 1973; [5]
Кудрявцев Л. Д., Курс математического анализа, • т. 11—
2, М., 1981; [б] Никольский С. М. Курс математическо-
математического анализа, 2 изд., т. 1—2, М., 1975; [7] Уиттекер Э.- Т.,
В а т с о н Дш. - Н., Курс современного анализа, пер. с англ.,
2 изд., ч. 1, М., 1963. Л. Д'. Кудрявцев.
КОШИ МАТРИЦА линейной системы обыкновенных
дифференциальных уравнений — матрица, задающая
Коши оператор X @, т) этой системы в нек-ром базисе
пространства R" (или С"), не зависящем от 0 и ¦%.
, В. М. Миллионщиков,
КОШИ НЕРАВЕНСТВО— 1) К. н.— неравенство для
конечных сумм, имеющее вид:
Доказано О. Коши (A. Cauchy, 1821); интегральный
аналог — Буняковского неравенство.
2) К. н.— неравенство для модуля ]f<-k)(a)\ производ-
производной регулярной аналитич. функции /(г) в фиксирован-
фиксированной точке а комплексной плоскости С или для модуля
коэффициента \ск\ разложения f(z) в степенной ряд
К. н. имеют вид
где г — радиус любого круга <7={z?C; \z—<z| «:<¦},
на к-ром функция /(г) регулярна; М(г) — максимум
модуля \f(z)\ на окружности \z—a\ = r. Неравенства (*)
встречаются в работах О. Коши (A. Cauc)iy,CM., напр.,
[1]). Из них непосредственно вытекает неравен-
неравенство Ко in и — Адамара (см. |2]):
где d(a, 0D) — расстояние от точки а до границы dD
области голоморфности функции /(г). В частности, для
целой функции /(z) в любой точке а?С имеем
A^tc
sup
=¦-=0.
Для голоморфной функции /(z) многих комплексных
переменных г=(гл, . . . , zn), п>1, К. н. имеют вид
или
1 " ' ' "' ,ki ... rkn
1 n
м (r,,..., rn)
где ск
пенной ряд'
— коэффициенты разложения /(z) в сте-
сте?i, ...,/¦„ — радиусы поликруга <7"={zgCf!: U/—
—ву|<г;, /= 1, ... , м), на к-ром f(z) голоморфна;
М{г\, . . ., г„) — максимум |/(z)| на остове поликруга
i/".
Лит. см. при ст. Ноши — Адамара теорема.
Е. Д. Соломенцее.
КОШИ ОПЕРАТОР системы обыкновенных диффе-
дифференциальных уравнений
.с = / (t, x), x^R», A)
— зависящий от параметров 9 и т оператор Х(б, т):
R™ _». R", сопоставляющий значению всякого решения
x(t) системы A) в точке (=т значение этого же решения
в точке t=Q:
Если система A) линейная, т. е.
х=А (t)x, B)
где А(-)—суммируемое на каждом отрезке отображение
(а, Р)—>HomfR'S R") (или (а, Р)—>¦ Нот (С, С")),
то К. о. при всяких 8, т?(а,,Р) есть невырожденное
линейное отображение R™ —*¦ R" (соответственно
С"), удовлетворяющее при всяких 6, т, п?
(а, Р) равенствам:
л: (в, в)=/, х(в, т)=л:-1(т, е
ДГ(в, T])X(ii, т)=Х(в, т)
С"
C)
и неравенству
\)Х (Q, т)|]<ехр [
(Для нелинейной системы A), удовлетворяющей усло-
условиям теоремы существования и единственности решения
задачи Копш, равенства C) тоже верны, с должными
оговорками относительно областей определения входя-
входящих в них операторов.) Общее решение системы
()+(),
где h(-)— суммируемое на каждом отрезке отображение
(а, Р)—^R" (или (а, f>)—*С»).
записывается чере.ч К. о. X (в, т) системы B) формулой
произвольных постоянных вариации:
а' (t, Q)h(Q)dQ.
Для К. о. системы B) имеет место Лиувилля—Остро-
Лиувилля—Остроградского формула
det X F, т) = ехр \в tr А (?) d%,
где tr А (?) — след оператора А (|).
Производная К. о. X(Q, т) системы A) в точке x?R"
равна К. о. системы уравнений в вариациях вдоль ре-
решения x(t) системы A), равного х при *=т (предпола-
(предполагается, что график решения x(t) при всех t, принадле-
принадлежащих отрезку с концами в и т, содержится в области
GczR" + l такой, что / — непрерывное отображение
G—v R", имеющее непрерывную в G производную f'x;
это — одна из формулировок теоремы о диффе-
ренцируемости решения по началь-
начальному значен и ю).
Для линейной системы B) с постоянными коэффици-
коэффициентами (A (t)=A) К. о. задается формулой
X(Q, т)=ехр((в-т)Л) D)
(ехр В для линейного оператора В определяется как
^ -jfi\ Bk; при другом подходе за определение ехр А
можно принять формулу D), положив в ней 6 —т+1).
Из формулы D) видно, что К. о. зависит только от раз-
разности параметров 8—т:
ХF-Н, т-М)=Х(в, т).
Это равенство — следствие автономности системы, име-
имеющее место для всякой автономной системы
x = f(x), x?R", E)
обозначив для системы E) К. о. Х(в, х) через !®~%,
получают из формул C) следующие формулы:
(см. также Динамическая система, Действие группы).
Для линейной системы B) с периодическими коэффи-
коэффициентами:
A(t+T)=A(i)
при нек-ром 7>0 и всех <?R — выполняется тождество
XF-f Г, т-f Т)=Х(в, т)
при всех 6, t?R; для такой системы оператор
Х(х+Т, х), где x^R — любое, наз. операто-
оператором м о н о д р о м и и. Матрица, задающая оператор
Х(х-\-Т, х) (или, напр., Х(Т, 0)) в каком-либо базисе,
наз. монодромии матрицей. Все операторы монодромии
фиксированной линейной системы с периодическими
коэффициентами подобны друг другу:
Х(в+Т, в)=Х(в, х)Х(х+Т, т)Х-1F, т),
поэтому спектр оператора монодромии Х(т-\-Т, т) не
зависит от т. Собственные значения оператора монодро-
монодромии наз. мультипликаторами такой системы, через
них выражаются условия устойчивости и условной ус-
ToiraimoCTH системы (см. Ляпунова характеристический
показатель, Устойчивость по Ляпунову, Устойчивости
теория). Для систем B) с периодическими комплексны-
комплексными коэффициентами:
A(.):R-^-Kom(C", С"), A(t + T) = A(t)
для нек-рого Г>0 и всех i?R — имеет место теоре-
теорема Ляпунова:
Хф, т) = 6Ч(е)ехр((е-т)Дт),
где #T=-jr 1п Х(х+Т, т), а 5т(в) при любых 0, t?R
является невырожденным линейным оператором С" —»-
—>- С", периодически зависящим от 0:
5(Э+Г) 5'(е)
) (
Иногда К. о. наз. по-другому (напр., «матрицантом»—
для линейной системы, или «оператором сдвига по тра-
траекториям»). В. М. Миллионщиков.
КОШИ ПОСЛЕДОВАТЕЛЬНОСТЬ — то же, что
фундаментальная последовательность.
КОШИ ПРИЗНАК — 1) К. п. сходимости
числового ряда: если для числового ряда
Zun с неотрицательными членами существует такое
71=1
число д, 0<:д<1, что, начиная с нек-рого номера, вы-
п/
полняется неравенство у "„«:?, равносильное условию
lim у ич< 1, то данный ряд сходится. Если же, начи-
п/
ная с нек-рого номера, имеет место неравенство у «„^1
или даже менее того существует подпоследовательность
й„ А = 1,2,..., для членов к-рой имеет место нера-
венство т/ ип ^1, то ряд расходится.
У k
п /
В частности, если существует limy и„<1, то ряд
^n^!un сходится, если существует lim у ип~>\, то ряд
П-»-°о
расходится. Установлен О. Коши [1]. Для рядов "V°° un
с членами ип произвольных знаков из условия
!i?Lj/!ип1 >1 слеДУет расходимость ряда; из условия
П-*оо
lim у )ип]<С\ — абсолютная сходимость ряда.
2) К. п. интегральный, интеграль-
интегральный признак Коши — Маклорена:
если для числового ряда ^п=1мп с неотрицательными
членами существует такая невозрастающая неотрица-
неотрицательная функция /(ж), определенная при х^\, что
f(n)=un, n=l, 2, . . ., то данный ряд сходится в том
и только в том случае, когда сходится интеграл
f(x)dx. Впервые дан в геометрич. форме К. Макло-
реном [2], а впоследствии вновь открыт О. Коши [3].
Лит.: [1] Cauchy A. L.. Analyse algebrique, P., 182!
p. 132—35; [21 M а с L a u г i n C, A treatise of fluxions
v. 1, Edinburgh, 1742, p. 289—90; [3] С a u с h v A. L., CEuv
res completes, s6r. 2, t. 7, P., 1889, p. 268—79; [4l H и к о л ь
с кий С. М., Курс математического анализа, 2 изд., т. 1, М.
1975. Л. Д. Кудрявцев
КОШИ РАСПРЕДЕЛЕНИЕ — непрерывное распре-
распределение вероятностей с плотностью
р(х;
и функцией распределения
F (х; Л, (X) =—
где —oo<u<oo н ^>0 — параметры. К. р. одновер-
одновершинно и симметрично относительно точки х=[х, являю-
являющейся модой и медианой этого распределения. Моменты
положительного порядка, в том числе и математич. ожи-
ожидание, не существуют. Характеристик функция имеет
вид е№-^П. Класс К. р. замкнут относительно ли-
линейных преобразований: если случайная величина X
имеет К. р. с параметрами X и (X, то случайная величина
Y=aX-\-b также имеет К. р. с параметрами к'=\а\Х и
ц' — a\i-{-b. Класс К. р. замкнут относительно операции
свеотки:
Р (х; А.1, Hi) *... * р (х; Х,„ (х„) =
= р (х;
иначе, сумма независимых случайных величин с К. р.
снова имеет К. р. Таким образом, К. р., также как нор-
нормальное распределение, принадлежит к классу устой-
устойчивых распределений, а именно, является симметрич-
симметричным устойчивым распределением с показателем 1. След-
Следствием соотношения (*) является следующее свойство
К. р.: если случайные величины Xlt . . ., Хп незави-
независимы и имеют одно и то же К. р., то арифметическое
среднее —(Xlt . . ., Х„) имеет такое же распределение,
как и каждая величина Х^. Еще одна особенность К. р.
состоит в том, что в семействе К. р. распределение сум-
суммы случайных величин может быть задано формулой
(*), даже если величины зависимы: напр., если X и У
независимы и имеют одинаковое К. р., то случайные ве-
величины Х-\-X и Х + У имеют одно и то же К. р. К. р.
с параметрами Х—1 и [i—О есть «-распределение Стьго-
Стьгоде нт а с числом степеней свободы, равным 1. К. р. с
параметрами (X, ц) совпадает с распределением случай-
случайной величины j.i-]—уг, где X и У независимы и нормаль-
нормально распределены с параметрами @, к2) и @, 1) соответст-
соответственно. Такое же К. р. имеет функция \i-\-X tg z случай-
случайной величины z, равномерно распределенной на отрезке
[—я/2, я/2|. К. р. определяется также и в пространствах
размерности больше единицы. К. р. рассмотрено О. Ко-
ши (A. Cauchy).
Лит.: [1] Ф е л л е р В., Введение в теорию вероятностей и
ее приложения, пер. с англ., т. 2, М., 1967. А. В. Прохоров.
КОШИ ТЕОРЕМА — 1) К. т. о многогран-
многогранника х: два замкнутых выпуклых многогранника
конгруэнтны, если между их истинными гранями, реб-
ребрами и вершинами имеется сохраняющее инцидент-
инцидентность взаимно однозначное соответствие, причем соот-
соответствующие грани многогранников конгруэнтны.
К. т.— первая теорема об однозначной определенности
выпуклых поверхностей, поскольку многогранники,
о к-рых идет речь в К. т., изометричны в смысле внут-
внутренней метрики. К. т. является частным случаем теоре-
теоремы о том, что всякая замкнутая выпуклая поверхность
однозначно определяется своей метрикой (см. [4|).
К. т. установлена О. Коти (см. [1]).
Лит..-'[1] С а и с h у A. L., «J. Ecole polytechn.», 1813, t. 9,
p. 87—98; [2] А л е к с а н д р о в А. Д., Выпуклые многогран-
многогранники, М.— Л., 1950; [3] Адамар Ж., Элементарная геомет-
геометрия, 3 изд., ч. 2, М., 1958; [4] Погорелов А. В., Одно-
Однозначная определенность выпуклых поверхностей М.— Л.
1949 (Тр. Матем. ин-та АН СССР, т. 29). Е. В. Шикин.
2) К. т. о промежуточных значениях
непрерывной функции на отрезке:
если функция /, значениями к-рой являются действи-
действительные числа, непрерывна на [а, Ь] и число С лежит
между /(а) и f(b), то существует такая точка 16(а> ''!,
что /(|) = С. В частности, если f(a) и /F) имеют разные
знаки, то существует такая точка |, что /(|) = 0. В этой
форме К. т. используют для выделения промежутков,
в к-рых заведомо имеются нули рассматриваемой функ-
функции. Из К. т. следует, что образом промежутка число-
числовой прямой при его непрерывном отображении в число-
числовую прямую является также промежуток. К. т. до-
пускает обобщение на топология, пространства: всякая
непрерывная функция / : X —»- Я1, определенная на
связном топологич. пространстве X (Я1 — множество
действительных чисел), принимающая какие-либо два
значения, принимает и любое лежащее между ними,
поэтому образ пространства X также промежуток
числовой прямой.
К. т. была сформулирована независимо Б. Больцано
(В. Bolzano, 1817) и О. Коши (A. Cauchy, 1821).
3) К. т. о среднем значении — обобщение
формулы конечных приращений Лагранжа. Если функ-
функции fug принимают действительные значения, непре-
непрерывны на [а, Ь] и дифференцируемы на (а, Ь), причем
g'фE на (а, Ь), а потому g(a)^=g(b), то существует такая
точка |?(а, Ь), что
f(b)-f(a) =Г (?)
g(b)-g(a) g'F) *
При g(t) = t, a^.t<cb, получается формула конечных
приращений Лагранжа. Геометрич. смысл К. т. состоит
в том, что на всякой непрерывной кривой x=f(t), y=
=g(t), a<:i<:6, лежащей на плоскости хОу и имеющей
в каждой точке (/(г), g(t)) касательную, есть точка
(/(?), #(?)), в к-рой касательная параллельна хорде,
соединяющей концы (/(a), g{a)) и (f(b), g(b)) рассматри-
рассматриваемой кривой.
Лит.: [1] Ильин В. А., П о з н я к Э. Г., Основы ма-
математического анализа, 3 изд., ч. 1, М., 1971; [2] Кудряв-
ц е в Л. Д., Математический анализ, 2 изд., т. 1, М., 1973;
[3J Н и к о л ь с к и й С. М., Курс математического анализа,
2 изд., т. 1, М., 1975. Л. Д. Кудрявцев.
4) К. т. в теории групп: если порядок конеч-
конечной группы G делится на простое число р, то G обладает
элементами порядка р.
Теорема была доказана О. Коши (см. [1]) для групп
подстановок.
Лит.: [1] Cauchy A. L., в кн.: Exercices d'analyse et
de physique mathematique, t. 3, P., 1844, p. 151—252; [2] К у-
p о ш А. Г., Теория групп, 3 изд., М.,' 1967.
КОШИ ФИЛЬТР — фильтр F в равномерном прост-
пространстве X такой, что для любого окружения V равно-
равномерной структуры пространства X существует множест-
множество, малое порядка V и принадлежащее F. Другими
словами, К. ф.— это фильтр, содержащий сколь угодно
малые множества в равномерном пространстве X. Поня-
Понятие К. ф. обобщает понятие последовательности Коши
в метрич. пространстве.
Всякий сходящийся фильтр есть К. ф. Всякий
фильтр, мажорирующий К. ф., также есть К. ф. При
равномерно непрерывном отображении образ базиса
К. ф. есть базис К. ф. Равномерное пространство, в
к-ром всякий К. ф. сходится, является полным
пространством.
Лит.: [1] БурбакиН., Общая топология. Основные
структуры, пер. с франц., М., 1968. Б. А. Ефимов.
КОШИ ХАРАКТЕРИСТИЧЕСКАЯ ЗАДАЧА — за-
задача отыскания решения дифференциальных уравнений
или систем уравнений с частными производными по за-
заданным его значениям на характеристических много-
многообразиях.
Для широкого класса уравнений гиперболического
и параболического типов в пространстве Еп + 1 незави-
независимых переменных хх, х2, . . ., хп, t носителями дан-
данных могут служить определенным образом ориентиро-
ориентированные незамкнутые я-мерные поверхности S. Если,
напр., S является поверхностью пространственного
типа, то Коши задача (с начальными данными на S)
поставлена всегда корректно. В К. х. з. носителем дан-
данных является исключительно характеристическое мно-
многообразие (или ее определенная часть). В этом случае
задача Коши может и вовсе не иметь решения, а если и
имеет таковое, то оно может быть неединственным.
Напр., К. х. з. для уравнения (я=1, хх=х)
uxt = 0
с данными на характеристике t=0
и(х, О)=тМ, щ(х, O)=v(z)
некорректна. Если решение К. х. з. существует, то из
уравнения и из второго начального условия вытекает
необходимое условие ее разрешимости: v'(x) = 0, то
есть решение К. х. з. может существовать лишь при
v(;r)=const=a. В этом случае, если т(х)?С2, t^O,
решение действительно существует и задается формулой
и(х, t) = t(x)+at+p(t),
где p(i) — любая функция класса С2, t^O, удовлетво-
удовлетворяющая условиям р(О) = р'(О) = О.
Для существования решения К. х. з. для линейных
систем гиперболических уравнений требуется, чтобы
ранг расширенной матрицы системы был равен вдоль
характеристической поверхности S рангу вырожденной
матрицы.
Существует широкий класс гиперболических уравне-
уравнений и систем, для к-рых в качестве носителя данных
могут служить характеристические поверхности. Так,
напр., для уравнения
когда характеристическая поверхность 5 представляет
собой конус
2"=1(*;-*?J-(«-*оJ=О, B)
К. х. з. ставится так: найти регулярное внутри конуса
B) решение и(х, t) уравнения A), принимающее на ко-
конусе B) наперед заданные значения.
В случае пространственного переменного (я=1,
хх=х) конус B) представляет собой пару прямых
(х—xoJ=(t—10J, проходящих через точку (х0, t0). Эти
прямые разбивают плоскость Е2 переменных х, t на
четыре угла. Пусть область Q представляет один из этих
углов. В этом случае характеристическую задачу при-
принято наз. задачей Гурса: определить регулярное в об-
области Q решение и (х, t) уравнения
удовлетворяющее условиям
м=Ф при х—xo=t—10, u=iK при х—xo—t(,—t,
ф(з0, to)=ty(xo, t0).
Если характеристическая поверхность 5 является одно-
одновременно поверхностью вырождения типа или порядка,
то К. х. з. может оказаться корректной.
Для уравнения
Утиуу — uxx + aux + bui/ + cu = f, C)
к-рое является гиперболическим при i/>0, линия вы-
вырождения у=0 является характеристикой. При 0 <т<1
задача Коши
и(х, 0) = т(*), иу (х, 0)=v(x) D)
для уравнения C) является корректной, а при от^1
она становится некорректной. В этом случае естествен-
естественно исследовать эту задачу как с видоизмененными на-
начальными данными:
lim a (ж, у) и(х, у)=х(х), lim P (х, у) и (х, у) =v (x),
lim a(x, y)=0, lim p (х, г/)=0,
у -+ о у ^- о
так и с неполными начальными данными, т. е. при от-
отсутствии одного из условий D).
Лит.: [1] Владимиров В. О., Уравнения математи-
математической физики, 3 изд., М., 1976; [2J Г о д у н о в С. К., Урав-
Уравнения математической физики, М., 1971; [3] Три к о ми Ф.,
Лекции по уравнениям в частных производных, пер. с итал.,
М., 1957; [4] Б е р с Л., Джон Ф., Ш е х т е р М., Уравне-
Уравнения с частными производными, пер. с англ., М., 1966; [5] Б и-
цадзеА. В., КалиниченкоД. Ф., Сборник задач
по уравнениям математической физики, М., 1977; [6] Б и ц а д-
з е А. В., Линейные уравнения с частными производными сме-
смешанного типа, в кн.: Тр. третьего Всесоюзного математического
съезда, т. 3, М., 1958. В. А. Елеее.
КОШИ ЯДРО — функция вида II(t—х), являющаяся
ядром Коши интеграла. Между К. я. и Гильберта яд-
ядром в случае единичной окружности существует связь:
dt
<
где
t = e'x, x = eis.
Иногда К. я. наз. функцию вида 2лг (t - х) '
А. Б. Иванов.
КОШИ — АДАМАРА ТЕОРЕМА: пусть задан степен-
степенной ряд
Л= lim sup у \ck\ •
k -»- оо
Если Л=оо, то ряд A) сходится только в точке z=a;
если 0<Л<оо, то ряд A) абсолютно сходится в круге
|z—а\ <Л радиуса
Л = Х B)
и расходится вне этого круга при |г—а\ >Л; если Л=0,
то ряд A) абсолютно сходится при всех z?C. Содержа-
Содержание К.— А. т. выражается, таким образом, форму-
формулой Коши — Адамара B), к-рую при этом сле-
следует понимать в расширенном смысле, включая равен-
равенства 1/оо = 0 и 1/0=оо. Иначе говоря, содержание К.—
А. т. состоит в том, что внутренность множества точек
(абсолютной) сходимости ряда, A) есть круг \z—a\ <if
радиуса B). В случае действительного степенного ряда
A) формула B) определяет радиус интервала сходимо-
сходимости а—ДО<а+Д. В основном К.— А. т. была вы-
высказана О. Коши (A. Cauchy) в его лекциях [1], опубли-
опубликованных в 1821, полную ясность в формулировку и до-
доказательство внес Ж. Адамар [2].
Для степенных рядов
/(г) = 2*1 *„ = оС*« ¦ ¦ • *» (zi-fll)*'- •• (zn-«n)*" C)
no я комплексным переменным z=(zj, ... , zn), ,
обобщением формулы Коши — Адамара является сле-
следующее соотношение:
к-рому удовлетворяют сопряженные радиусы сходимо-
сходимости rlf . . . , гп ряда C) (см. Круг сходимости). Записав
соотношение D) в виде Ф (ги . . . , г„)=0, получают
уравнение, определяющее границу нек-рой логарифми-
логарифмически выпуклой кратно круговой области с центром а,
к-рая и является внутренностью множества точек аб-
абсолютной сходимости ряда C) при я>1.
Лит.: [1] Коше О. Л., Алгебраический анализ, пер.
с франц., Лейпциг, 1864; [2] Н a d a m а г d J., «J. math, pures
et appl.» D), 1892, t. 8, p. 101—86; [3] M a p к у ш е в и ч А. И.,
Теория аналитических функций, 2 изд., т. 1, М., 1967; [4] Ш а-
б а т Б. В., Введение в комплексный анализ, 2 изд., М., 1976.
Е. Д. Соломенцев.
КОШИ — КОВАЛЕВСКОЙ ТЕОРЕМА — теорема,
утверждающая существование (единственного) анали-
тич. решения задачи Коши в малом, если функции, за-
задающие дифференциальное уравнение или систему этих
уравнений и все начальные данные вместе с их нехарак-
нехарактеристическим носителем, являются аналитическими.
Для системы к дифференциальных уравнений с част-
частными производными с к неизвестными функциями
иг(х, х0), ... , ик(х, х0) вида
где
1 =
т,
К.— К. т. формулируется следующим образом: задача
Коши
д'и.
Эх/
= ф,у(х), i = l, ..., к; j=0, 1, ..., то —1, B)
х/
где а= {(х, х0), хо=О, x?Q0}— носитель начальных
данных ф,у, всегда имеет и притом единственное анали-
тич. решение и (х, х0) в нек-рой области Q пространства
переменных хо,х, содержащей Qo, если F[ и <р,у являются
аналитич. функциями всех своих аргументов.
Пусть дана линейная система дифференциальных
уравнений вида
Р(х, D)u^Y
где а=(а0, аи . . . , а„) — вектор с неотрицательными,
целочисленными координатами;
— порядок дифференциального оператора
А<х(х), х=(х0, . . -,хп) — заданная квадратная матрица
порядка N; u(x)=\\uj(x)\\, /=1, . . . , N,— искомый
вектор-столбец; В (х) — заданный вектор с N компо-
компонентами.
Вообще говоря, К.— К. т. не исключает существова-
существования неаналитических, помимо аналитического, решений
задачи Коши. Однако для линейной системы дифферен-
дифференциальных уравнений C) с аналитич. коэффициентами
Аа(х) и условиями Коши на аналитической нехаракте-
ристич. поверхности а задача Коши имеет не более од-
одного решения в нек-рой окрестности Qo поверхности а.
При этом не предполагается аналитичность начальных
данных и решения и(х).
Решение задачи Коши A), B), существование к-рого-
гарантируется К.— К. т., может оказаться неустойчи-
неустойчивым (т. к. малое изменение начальных данных ф,у(ж)
может вызвать сильное изменение решения), напр.,.
в том случае, когда система A) принадлежит эллиптич.
типу. При неаналитических начальных данных задача
Коши A), B) может потерять смысл, если не ограничить-
ограничиться случаем, когда система A) является гиперболиче-
гиперболической.
К.— К. т. для широкого класса уравнений обобщена
на случай, когда начальное многообразие является ха-
характеристическим в каждой точке (см. [1], [2]). В этом
случае начальные функции не могут быть заданы про-
произвольно; они должны удовлетворять определенным
условиям, к-рые диктуются дифференциальным уравне-
уравнением.
Характеристическая задача Коши может иметь не-
неединственное решение. В частности, имеет место сле-
следующее утверждение. Пусть Р (х, D) — дифференци-
дифференциальный оператор порядка т с главной частью Рт(х, D}
и с вещественными аналитич. коэффициентами, опреде-
определенный в окрестности Q точки х° из евклидова прост-
ранства Л", ф — вещественная аналитическая в Й
функция такая, что
grad ф (х°) ф 0 и Рт (х, gradф)=O,
но Р^(х, grad ф)=?^0 для некоторого / при х=х°. Тогда
существует такая окрестность Qo точки х° и аналитиче-
аналитическая при ц>(х)ФЦ)(х11) функция и(х) из класса Cm(Q0),
что Р(х, D)u=Q и
sup и —- {.г [ х ? Qo, ф (х) ==?:ф (¦*¦„)}.
Если начальное многообразие является характери-
характеристическим вдоль нек-рых кривых, то, вообще говоря,
решение характеристич. задачи Коши многозначно в
нек-рой окрестности начальной поверхности и степень
ветвления определяется геометрич. природой соответст-
соответствующих характеристич. поверхностей. Теорема доказа-
доказана С. В. Ковалевской A875).
Лит.: [1] Б е р с Л., Джон Ф., Ш е х т е р М., Уравне-
Уравнения с частными производными, пер. с англ., М., 1966; [2] Б и-
Мд з е А. В., Уравнения математической физики, М., 1976;
Владимиров В. С, Уравнения математической физи-
физики, 2 изд., М., 1971; [4] К у р а н т Р., Уравнения с частными
производными, пер. с англ., М., 1964; [5] Хёрмандер Л.,
Линейные дифференциальные операторы с частными производ-
производными, пер. с англ., М., 1965. А. М. Нахушев.
КОШИ—РИМАНА УСЛОВИЯ, Д'Аламбера —
Эйлера у с л о в и я,— условия на действительную
и= и (х, у) и мнимую v= и (х, у) части функции комплекс-
комплексного переменного w=f(z) = u^-iv, z=x^t-iy, обеспечиваю-
обеспечивающие моногенность и аналитичность /(z) как функции
комплексного неременного.
Для того чтобы функция ш=/(г), определенная в
нек-рой области D комплексной плоскости z, была
моногенноп в точке zo= xo-\-iy0, т. е. имела
производную в точке z0 как функция комплексного пере-
переменного z, необходимо и достаточно, чтобы ее действи-
действительная и мнимая части и и v были дифференцируемы
в точке (х0, у0) как функции действительных перемен-
переменных х и у и чтобы, кроме того, в этой точке выполня-
выполнялись условия Коти — Римана:
ди dv ди dv ...
дх ду ' ду дх * '
Если К.— Р. у. выполнены, то производная f'(z)
представима в любой из следующих форм:
f I \ ди . . ду _ ду . ди ди . ди _??_ г "-22-
•> * ' дх ' дх ду ду дх ду ду * дх '
Для того чтобы однозначная в области D функция
/(г) была аналитической в D, необходимо и достаточно,
чтобы ее действительная и мнимая части были диффе-
дифференцируемыми функциями, удовлетворяющими К.—
Р. у. всюду в D. Функции и и v класса C2(Z>), удовлет-
удовлетворяющие К.— Р. у. A), являются, каждая по отдель-
отдельности, гармоническими функциями от х и у; условия A)
суть условия сопряженности этих двух
гармонич. функций: зная одну из них, вторую можно
найти интегрированием.
Условия (I) справедливы для любых двух ортогональ-
ортогональных направлений s и и, ориентированных взаимно так
же, как оси Ох и О у в виде:
Эц __ ду ди йг>
д.< дп ' дп ЫГ
Напр., в полярных координатах (г, ц>) при гфО:
дг г d(f ' г д(р дг
Введя операторы комплексного диф-
дифференцирования
дг 2 V дх ду ) ' дТ 2 \ дх "^ ~ду~) '
К.— Р. у. A) можно записать в виде
Эг
Таким образом, дифференцируемая функция /(г, z)
переменных гиг является аналитич. функцией от z
тогда и только тогда, когда dfldz=O.
Для аналитич. функций многих комплексных пере-
переменных z^={zu z2, . . ., zn), zk = xk+iyk, к=1, 2, . . ., n,
К.— P. у. записываются в виде переопределенной
при ге>1 системы уравнений с частными производными
для функций
u = ~Ref(z) = u(x1, ,r2, ..., т„; уг, уг, ..., уп),
у = Im/ (z) =v (хи r2, ..., хп; уи у2, ..., у„):
""^' • ¦¦¦' •
или, при помощи операторов комплексного дифферен-
дифференцирования, в виде:
-!?-=--О, /fc-1, 2, ..., я\
9z?
Функции и и у класса С2, удовлетворяющие условиям
B), являются при п>1, каждая по отдельности, плюр и-
гармоническими функциями от переменных х^ и г/^. Плю-
ригармонич. функции при я>1 составляют собственный
подкласс класса гармонич. функций. Условия B) суть
условия сопряженности двух плюригар-
монич. функций и и v: зная одну из них, другую можно
найти интегрированием.
Условия A) впервые, по-видимому, появились в ра-
работе Ж. Д'Аламбера [1]. В работе Л. Эйлера, доложен-
доложенной Петербургской академии наук в 1777 (см. [2]),
условия A) получили впервые характер общего призна-
признака аналитичности функций. О. Копти пользовался со-
соотношениями A) для построения теории функций, на-
начиная с мемуара, представленного Парижской академии
наук в 1814 (см. [3]). Знаменитая диссертация Б. Ри-
мана (В. Riemann) об основах теории функций относит-
относится к 1851 (см. [4]).
Лит.: [11 D ' Alembert J., Essai d'une nouvelle theo-
rie de la resistance des fluides, P., 1752; [2] E и 1 e r L., «Nova
Acta Acad. Sc. Petrop.». 1797, v. 10, p. 3—19; t3j С a u с h у A.-L.,
(Euvres completes, ser. 1, t. 1, P., 1S82, p. 319—506; [4] P и-
м а н В., Соч., пер. с нем., М.— Л., 1948, с. 49 — 87; [5] М а р-
кушевич А. И., Теория аналитических функций, 2 изд.,
т. 1, М., 1967, гл. 1; [6] Ш а б а т Б. В., Введение в комплекс-
комплексный анализ, 2 изд., М., 1976, ч. 1, гл. 1, ч. 2, гл. 1.
Е. Д. Соломенцев.
КОЭНА — МАКОЛЕЯ КОЛЬЦО, маколеево
кольцо,— коммутативное локальное нётерово коль-
кольцо А, глубина prof Л к-рого равна его размерности
dim А. Гомологич. характеризация К.— М. к. А со-
состоит в том, что группы ExtlA(k, А) или группы локаль-
локальных когомологий Н\а(А) обращаются в нуль при всех
i<dim А; здесь т — максимальный идеал, а к — поле
вычетов А. Можно дать определение К.— М. к.,
используя понятие регулярной последова-
последовательности. Так называется последовательность
«i, . . ., а/, элементов m такая, что для всех i элемент
а,- не делит нуль в А/(аь . . ., а,_!), Локальное кольцо
А наз. К.— М. к., если существует регулярная после-
последовательность а1, . . ., <z?, для к-рой факторкольцо
Al(a1, . . ., afc) артиново. В этом случае A-=prof A =
= dim A.
Если р — простой идеал в К.— М. к. А , то для его
высоты ht(\>) (см. Высота идеала) выполняется соотно-
соотношение
U (р) -|- dim (Alp) = dim A.
В частности, К.— М. к. равноразмерное и цепное. Фун-
Фундаментальным результатом о К. —М. к. является еле-
дующая теорема о несмешанности.
Пусть А есть d-мерное К.— М. к., а аи . . ., а^ — по-
последовательность элементов А и dim(A/(a1, . . ., а^)) =
= d—k. Тогда последовательность alt . . ., а^ регу-
регулярна, и идеал 91=(ах, . . ., ак) несмешанный,
т. е. любой простой идеал, ассоциированный с 91, имеет
высоту к и ковысоту d—к. Теорема о несмешанностй
была доказана Ф. Маколеем [1] для кольца многочленов
и И. Коэном [2] для кольца формальных степенных
рядов.
Примеры К.— М. к. Регулярное локальное коль-
кольцо (и, вообще, любое кольцо Горенштейна) является
К.— М. к.; любое артиново кольцо, любое одномерное
приведенное кольцо, любое двумерное нормальное
кольцо являются К.— М. к. Если А — локальное К.—
М. к., то такими же будут его пополнение, кольцо фор-
формальных степенных рядов над А и любое конечное пло-
плоское расширение. К.— М. к. будет и полное пе-
пересечение вК.— М. к. Л, т. е. факторкольцо ви-
вида А/(а1, . . ., а^), где последовательность аь . . ., а^
регулярна. Наконец, локализация К.— М. к. в прос-
простом идеале снова является К.— М. к. Это позволяет
расширить определение К.— М. к. на произвольные
кольца и схемы. А именно, нётерово кольцо А (схема X)
наз. кольцом Коэна — Маколея (схемой Ко э-
на — Маколея), если для любого простого идеала
\)СА (соответственно любой точки х?Х) локальное
кольцо А^ (соответственно Qx, х) является К.— М. к.
В этом более широком смысле К.— М. к. является
кольцо многочленов над полем и даже над любым
К.— М. к., а также полугрупповое кольцо К [G|~| %,"],
где G — выпуклый многогранный конус в R™ (см. [6]).
К.— М. к. стабильны и при переходе к кольцам ин-
инвариантов. Если G — конечная группа, действующая
на К.— М. к. А, причем ее порядок обратим в А, то
кольцо инвариантов А0 также есть К.— М. к.
Для градуированного кольца А свойство быть К.—
М. к. проявляется в когомологиях обратимых пучков
на проективной схеме Proj(j4) (см. [4]). Если однород-
однородное кольцо А конуса ъ Ап + 1, связанного с проективным
многообразием ХсгР", является К.— М. к., то X наз.
арифметическим многообразием Ко-
Коэна — Маколея. В этом случае кольцо А изоморф-
но ®ve ZH°(X, 6x(v)), и Н'(Х, 6x(v)) = 0 для всех v^ Z
и для 0<!<dim X, где Cx(v) есть v"H тензорная степень
поляризующего обратимого пучка (ЗхA) на %• Этим
свойством обладают проективные пространства и их
произведения, полные пересечения, многообразия Грас-
смана и подмногообразия Шуберта [7], многообразие
флагов и обобщенное многообразие флагов [8].
Модуль М над локальным кольцом А наз. моду-
модулем Коэна — Маколея, если его глубина рав-
равна размерности. На модули Коэна — Маколея распро-
распространяются многие результаты о К.— М. к.; напр.,
носитель такого модуля равноразмерен. Существует
гипотеза, что любое полное локальное кольцо обладает
модулем Коэна — Маколея М таким, что dim M=
= dim A.
Лит.: [1] М а с а и 1 а у F. S., The algebraic theory of
modular systems, Camb., 1916; [2] С о h e n I. S., «Trans.
Amer. Math. Soc», 1946, v. 59, p. 54—106; [3J 3 a p и с с к и й О.,
Самюэль П., Коммутативная алгебра, пер* с англ., т. 2,
М., 1963; [4] М а м ф о р д Д., Лекции о кривых на алгебраи-
алгебраической поверхности, пер. с англ., М., 1968; [5] С е р р Ж.-П.,
«Математика», 1963, т. 7, X 5, с. 3—93; [6] Н о с h s t е г М.,
«Ann. Math.», 1972, v. 96, p. 318—37; [7] e г о те, «J. Algebra»,
1973, v. 25, p. 40—57; [8] К e m p f G. R., «Ann. Math.», 1976,
V. 103, p. 557—91. В. И. Данилов.
КОЭРЦИТИВНАЯ КРАЕВАЯ ЗАДАЧА — краевая
задача, удовлетворяющая коэрцитиености неравенст-
неравенству. Иногда К. к. з. для эллиптич. уравнений наз. э л-
липтическими краевыми задачами
[41.
Пусть Р (%,i, . . ., s«) — однородный многочлен
степени 2т и
— эллиптич. уравнение порядка 2т. Для уравнения A)
в полупространстве Дп : {а:„>0} рассматривается крае-
краевая задача с граничными условиями
q}(D)u - фу, / ^1, . . ., т, при хп--=0, B)
где <//Ei, • . ., i,i) — однородные многочлены степеней
^у. j=l, ¦ . ¦, т.
Задача A), B) коэрцитивна в Я,{, если порядки всех
операторов </у относительно д/дх„ меньше 2т и если эта
задача не имеет ограниченных решений вида
и (x) = w(xn) exp i (x-lI-l^- . . . + xn-iln-i), C)
Многочлен Р (?', т) относительно т имеет в верхней по-
полуплоскости Im т>0 ровно т корней тх, . . ., тт. Если
все эти корни различны, то отсутствие ограниченных
решений вида C) у задачи A), B) эквивалентно выпол-
выполнению неравенства
[П, <;. (ту-т,)]-1 det (qj (g\ т,-)) ФО, V ф 0. D>
Это условие иногда наз. условием дополнительности.
Краевая задача
г (х, l))u = f, х?&, (Ц(х, ХУ)в = ф/, x^aG, E)
/ = 1, .. ¦, /га,
для линейного эллиптич. уравнения порядка 2т в об-
области G коэрцитивна в точке х„ границы Г области G%
если коэрцитивна задача
где Р2т и qH) — однородные составляющие самой высо-
высокой степени соответствующих полиномов.
Для исследования К. к. з. успешно применяется ме-
метод выпрямления границы. Некоторым гомеоморфным
отображением окрестность U (X) точки X границы Г
области G отображается так, чтобы пересечение U (Х)()
Г) Г переходило в нек-рую область плоскости уп=0,
a U(X)f)G — в полупространство Д« переменных ylf
. . . , уп. В результате такого отображения К. к. з.
для произвольной области G с достаточно гладкой
границей Г редуцируется к исследованию задачи для
Условие D) для задачи E) означает, что характери-
стич. направление системы дифференциальных опера-
операторов
qj(x, D)u, /=1, . . . , т,
заданных в окрестности точек границы Г области Gf
ни в одной точке Г не является касательным к Г. При
выполнении этого условия для решения и задачи E)
имеет место коэрцитивная оценка
-ц г + П11о,
где норма в пространстве Соболева w\m(G) оценивается
через норму ив L2(G)h нормы/в L2(G) и фу в W^m~)lj(T)f
;=1, . . . , т, причем |ху— порядок оператора д/.
Понятие К. к. з. обобщается и на эллиптич. системы
уравнений. Методы исследования и результаты, спра-
справедливые для К. к. з. для одного эллиптич. уравнения,,
обобщаются и на К. к. з. для эллиптич. систем C). Ис-
Исследование К. к. з. для эллиптич. уравнений и систем
часто редуцируется, напр, параметрикса методом, кис-
следованию системы сингулярных интегральных урав- I
пений. Эта система является нётеревой системой интег-
интегральных уравнений (см. [2], [6]), а условие D), или в
случае системы аналог этого условия, гарантирует нор-
нормальность системы интегральных уравнений. К. к. з.
всегда нётерова, т. е. неоднородная задача разрешима
при соблюдении конечного числа условий ортогональ-
ортогональности, наложенных на правые части уравнений системы
и на заданные функции в краевых условиях, а соответ-
соответствующая однородная задача имеет конечное число ли-
линейно независимых решений.
Примером К. к. з. для любого эллиптич. уравнения
сможет служить задача Дирихле. В этом случае
gj-l
qj(x,D)= —— , / = 1, ..., то,
тде д/дп означает производную по направлению конор-
мали для данного эллиптич. оператора. Однако задача
Дирихле уже не для всякой эллиптич. системы является
К. к. з. Примером таких систем может служить сис-
система двух уравнений, к-рая в комплексной записи наз.
Вицадзе уравнением.
Лит.: [1] Бицадзе А. В., Краевые задачи для эллип-
эллиптических уравнений второго порядка, М., 1966; [2] Лопа-
Лопатин с к и й Я. Б., «Укр. матем. ж.», 1953, т. 5, X» 2, с. 123—
51; [3J Миранда К., Уравнения с частными производными
эллиптического типа, пер. с итал., М., 1957; [4] X ё р м а н-
дер Л., Линейные дифференциальные операторы с частными
производными, пер. с англ., М., 1965; [5] е г о ж е, «Математи-
«Математика», 1960, т. 4, № 4, с. 37—73; [6] Шапиро 3. Я., «Матем.
¦сб.», 1951, т. 28, с. 55—78. А. И. Янушаускас.
КОЭРЦИТИВНОСТИ НЕРАВЕНСТВО — неравен-
неравенство, дающее оценку снизу нек-рой билинейной формы
либо дающее оценку сверху нормы решения нек-рого
зллиптич. уравнения через норму известной функции
и нормы граничных данных.
Пусть
i = 2|a|<2m°«Waa,(-l)"'Re2|a| = 2me<xHga=S
— равномерно эллиптический в области Qt из простран-
-ства R™ оператор с коэффициентами aa(x)?C00(Q1),
пусть область Q содержится в области Qt и в нек-рой
окрестности границы S области Q заданы дифференци-
дифференциальные операторы Му, /=0, 1, . . ., т — 1, порядков /
такие, что характеристики этих операторов ни в одной
точке поверхности S не являются касательными к 5.
Тогда в нек-рой окрестности S существуют дифференци-
дифференциальные операторы Nj порядков у, у=то, . . ., 2га—1,
такие, что
2|a|<m, |РКЛЛ' aafidtv)-(v,L(u)) =
= 2Г=~оХ S.
d0
для всех у и и из С°°(й). Здесь ( , ) обозначает скалярное
произведение в L2(fi).
Форма
D(v, «) = 2, „ | < m, | р | < m {dav, aap д^и)
наз. коэрцитивной формой на пространст-
пространстве X, W%l(Q)cz.X<^W2'(Q), если существуют постоянные
¦С>0 и Х^О такие, что
Re.DK «)=sC|M^n-M"f0,Q ¦ ¦ B)
для всех и?Х. Здесь W™— Соболева пространство, а,
Wi — его подпространство элементов с компактными
носителями, т. е. обращающихся в нуль в окрестности
границы области Q. Неравенство B) является К. н. для
формы D (v, и). Если в B) можно положить Х=0, то:
D (г, и) наз. строго коэрцитивной.
Если решение и уравнения L(u)=/ удовлетворяет на
S условиям Mj(u) = 0, / = 0, . . ., т—1, то справедливо
неравенство
IMIsm, Q<ClllL (")[[„, Q+M"Ho, a C)
с нек-рыми постоянными С1>0 и Х{^0. Когда решение
и уравнения L(u)=f удовлетворяет на S условиям
Мj(u) = <fj, ; = 0, . . ., то—1, вместо неравенства C)
имеет место следующее неравенство
}- D>
+ 11-11., й
Это неравенство дает оценку нормы решения и уравне-
уравнения L(u)=/ в пространстве Соболева wlm(Q) через
норму и в пространстве L2(Q) и нормы функций / и фу,
.7 = 0, . . ., то—1, в соответствующих пространствах.
Неравенство D) является К. н. для краевой задачи для
эллиптич. уравнения.
При помощи неравенства D) получается более общее
неравенство
л*,
7
}-
К. н. играет важную роль в исследовании коэрцитив-
коэрцитивных краевых задач и в доказательствах гладкости реше-
решений эллиптич. уравнений и, в частности, в доказатель-
доказательствах аналитичности решений аналитических эллиптич.
уравнений.
Лит.. [1] Agmon S., Lectures on elliptic boundary value
problems, [N. Y.J, 1965; [2] M о г г е у С. В., N i г e n b e г g L.,
«Comm. Pure Appl. Math.», 1957, v. 10, № 2, p. 271—90.
A. H. Янушауспас.
КОЭФФИЦИЕНТ — числовой множитель при бук-
буквенном выражении, известный множитель при той или
иной степени неизвестного или постоянный множитель
при переменной величине. Так, в одночлене —сРЪ2
К. ость — —, в уравнении x2-{-2px-\-q=Q К. при х2 есть
1, а К. при х равен 2р; в формуле длины окружности
2=2лг К. есть 2я. В уравнении прямой у=кх-\-Ъ число
fe, выражающее тангенс угла наклона прямой к оси Ох,
наз. угловым коэффициентом. всэ-з.
КОЭФФИЦИЕНТОВ ПРОБЛЕМА для клас-
класса S — проблема для класса функций
/ B) = 2 + ?j c«2"i
регулярных и однолистных в круге |z|<l, заключаю-
заключающаяся в определении для каждого п, п^2, области зна-
значений Vn системы коэффициентов {с2, с3, . . ., сп}
функций этого класса и, в частности, в нахождении
точных оценок для \сп\, ге>2, в классе S (см. Вибербаха
гипотеза). К. п. для нек-рого класса R функций, регу-
регулярных в \z\ <1, заключается в определении в классе Л
для каждого п, га>1, области значений системы первых п
коэффициентов разложения функции класса R в ряд
по степеням z и, в частности, в получении точных оце-
оценок этих коэффициентов в классе R. К. п. решена для
Каратеодори класса, для класса регулярных типично
вещественных в круге функций, для класса однолист-
однолистных звездообразных функций, для класса функций, ре-
регулярных и ограниченных в |z|<l.
Известно, что V2 — круг: |с2|<2. Получены глубокие
качественные результаты по К. п. в классе S (см. [7]).
Множество Vn — ограниченная замкнутая область,
точка с2=0, с3 = 0, . . .,.с„=0 — внутренняя точка
Vn\ Vn гомеоморфно замкнутому Bга—2)-мерному шару,
граница Vn состоит из конечного числа частей Щ, П2,
. . ., Пдг; координаты точки (с2, с3, . . ., с„) на любой
одной из этих частей — функции конечного числа пара-
параметров (<:2и—3). Каждой граничной точке Vn соответ-
соответствует единственная функция класса S. Граница V3
состоит из двух гиперповерхностей Щ и П2 размерно-
размерности 3 и их пересечения: поверхностей П3 и П4 и кривой
П5. Для Щ и П2 получены параметрич. формулы в тер-
терминах элементарных функций. Сечение V3 плоскостью
Im c2=0 симметрично относительно плоскостей Re с2=
= 0 и Im с3=0. Сечение V3 плоскостью Im с3=0 сим-
симметрично относительно плоскостей Im с2=0 и Re c2=0.
Функция w=/(z), соответствующая точке поверхности
IIj, отображает \z\ <1 на плоскость w с единственным
аналитич. разрезом, уходящим в бесконечность. Функ-
Функция u;=/(z), соответствующая точке поверхности П2,
отображает |z|<l на плоскость w с разрезом по трем
аналитич. дугам, исходящим из нек-рой конечной точки
под углом 2я/3 друг к другу, одна из этих дуг лежит на
прямой arg w= const и уходит в бесконечность.
Были исследованы также: область значений {с2, с3}
в подклассе функций из S с действительными с2 и с3;
области значений {Ic^ + il, |с2? + 1|}и {сд + 1, с2^ + 1}, если
Im C? + 1=Im c2/i + i=0, на подклассе ограниченных
функций из S вида
область значений {с2, с3] на подклассе ограниченных
функций из S; область значений {с2, с3, с4} в подклассе
функций из S с действительными с2) с3 и с4.
Точные оценки для коэффициентов вида |с„| <Л„,
п^2, получены в подклассе выпуклых функций из S
с Ап~1, в подклассе звездообразных функций из S с
Лп=п, в подклассе нечетных звездообразных функций
из 5 с Ап=\, п=3, 5, . . ., в классе однолистных функ-
функций с действительными коэффициентами с Ап=п, в под-
подклассе близких к выпуклым функций из S с Ап—п.
В классе функций
регулярных и типично вещественных в |z|<l, имеет
место точная оценка |с„|-<п, га^2, а в классе Биберба-
ха — Эйленберга функций f (z)=a1z-\-a2z2-j-. . . — точ-
точная оценка |о„|<:1, п^1.
Для класса 2 функций
мероморфных и однолистных в |?|>1, известны точные
оценки:
Для подкласса звездообразных функций из 2 справед-
справедлива точная оценка
Имеются точные оценки коэффициентов и в других под-
подклассах из S и 2 (см. [1] — [4]), а также в нек-рых клас-
классах р-листных функций и в классах р-листных в сред-
среднем функций (см. [5]).
Лит.: [1]Голузин Г. М., Геометрическая теория функ-
функций комплексного переменного, 2 изд., М., 1966; [2J Б а з и л е-
в и ч И. Е., в кн.: Математика в СССР за сорок лет. 1917—•
1957, т. 1, М., 1959, с. 444—72; [3]Дженкинс Дж., Од-
Однолистные функции и конформные отображения, пер. с англ.,
М., 1962; [4] Н а у m a n W. К., «J. London Math. Soc», 1965,
v. 40, pt 3, p. 385—406; [5] G о о d m a n A. W., «Bull. Amer.
Math. Soc», 1968, v. 74, N6, p. 1035—50; [61 P helps D.,
«{Trans. Amer. Math. Soc>>, 1969, v. 143, p. 475—85; [7] S с h a-
effer A. C, Spencer D. C, Coefficient regions f6r
schlicht functions, N..Y.r 1950. E. Г.,Голузина.
КОЯДРО морфизма категории — поня-
понятие, двойственное понятию ядра морфизма. В катего-
категориях векторных пространств, групп, колец и т. п. оно
описывает наибольший факторобъект объекта В, анну-
аннулирующий образ гомоморфизма а: А —*• В.
Пусть $ — категория с нулевыми морфизмами. Мор-
Морфизм v : В —*• С наз. коядром морфизма
а : А —v В, если av=0 и всякий морфизм <р, для к-рого
аф=0, однозначно представим в виде <р=уф. К. морфиз-
морфизма а обозначается coker a.
Если v=coker a и v' = coker a, то v'=v? для единст-
единственного изоморфизма ?.
Обратно, если v= coker a и | — изоморфизм, то
v' = v| есть К. морфизма а. Таким образом, все К. мор-
морфизма а образуют факторобъект объекта В, к-рый обоз-
обозначается Coker a. Если v= coker a, то v — нормальный
эпиморфизм. Обратное, вообще говоря, неверно. К.
нулевого морфизма 0: 4->fl равно 1д. К. единичного
морфизма \А существует тогда и только тогда, когда в й
имеется нулевой объект.
В категории й с нулевым объектом морфизм a : А —>-
—V В обладает К. в том и только в том случае, когда в fit
существует коуниверсальный квадрат относительно
морфизмов а и 0 : А —*• 0. Это условие выполнено, в
частности, для любого морфизма локально малой спра-
справа категории с нулевым объектом и произведениями.
М. Ш. Цаленко.
КРАВЧУКА МНОГОЧЛЕНЫ — многочлены, орто-
ортогональные на конечной системе JV+1 целочисленных то-
точек при условии, что функция распределения сг(х) есть
ступенчатая функция со скачками
а(ж + 0) — о (ж—O)=(N')pxqN-x, x = 0, 1, 2, ..., N,
\ х /
где ( J — биноминальный коэффициент, р>0, д>0
и p-\-q=i. К. м. имеют представление
Впервые рассмотрены М. Ф. Кравчуком [1].' '
Лит.: II] К г а w t с h о u k M., «С. г. Acad. sci.», 1929,
I. 189, p. 620—22; 12] Cere Г., Ортогональные многочлены,
пер. с англ., М., 1962. П. К. Суетиц.
КРАЕВАЯ ЗАДАЧА для обыкновенного
дифференциального уравнения — за-
задача о нахождении решения уравнения
принадлежащего заданному множеству D пространства
D (/, R") абсолютно непрерывных на / функций от t со
значениями в R":
B)
Здесь функция f(t, x) определена на /XR", принимает
значения в R" и удовлетворяет условиям Каратеодори;
J — промежуток числовой прямой R.
1) К. з. A), B) наз. линейной, если
/(/, x)=A(t)z+b(t),
где функции A (t) и b(t) суммируемы на каждом ком-
компактном промежутке из /; множество Ц является ли-
линейным многообразием в D (/, R"). В частности, может
быть
J=[t0, h],
[ R»):
где функция Ф (t) имеет ограниченную вариацию. Ли-
Линейная К. з. порождает линейный оператор
Lx (t) = x' — A(t)x, x
собственные значения к-poro являются теми значения-
значениями параметра Я, при к-рых однородная К. з.
имеет нетривиальные решения. Ути нетривиальные ре-
решения суть собственные функции оператора L. Если
обратный оператор Z, существует и имеет место ин-
интегральное представление
x(t)=L-1b(t)^jG (t, s)b(s)ds, t?J,
то функция G(t, s) наз. ф у н к ц и е и Грина.
2) Пусть /=(—оо, оо), функция /(t, х) почти перио-
периодична по t равномерно относительно я на каждом ком-
компактном подмножестве из R", D — множество абсолют-
абсолютно непрерывных на / почти периодлч. функций от t.
Тогда К. з. A), B) наз. задачей о почти пе-
периодических решениях.
3) В теории управления рассматриваются К. з. с
функциональным параметром — управлением. Напр.,
пусть задано уравнение
|f = /(*, х, и), *€/ = [*„, *,], x?R", C)
множество допустимых управлений U и два множества
Мо, Л/jCR". Пусть D — множество абсолютно непре-
непрерывных функций от t, удовлетворяющих включениям
x(to)?Mo, x(t1)^M1. К. з. состоит в нахождении такой
пары (хо(-), ио( •)), что "()(•)?U и решение xo(t) уравне-
уравнения C) при u=uo(?) удовлетворяет условию ж-0(-)^/>.
4) Имеется большое количество разнообразных не-
необходимых и достаточных условий существования, един-
единственности решения разных К. з. и методов построения
приближенного решения (см. [4] — [7]). Рассмотрим,
напр., задачу
x'=A(t)x + f(t, x),
в которой
\\i(t, х)[\^
для нек-рых постоянных а>0, Ь>0, а^О. Пусть соот-
соответствующая однородная задача
x'r=A(t)x, [[' [d(b(t))x(t)=O E)
регулярна, т. е. имеет только тривиальное реше-
решение. Тогда задача D) имеет по крайней мере одно реше-
решение, если либо а<1, либо а^1 и Ь достаточно мало.
Исследование задачи E) на регулярность является
довольно сложной проблемой. Однако, напр., линейная
К. з. (скалярная)
x" + q(t)x' + p(t)x = O, *(*„) = 0, x(t1) = O
регулярна, если при \g(t)\-^.2m найдется такое
что
V'\p(t)-k]+dt^2\F(k, m) — m],
J * О
где
У к — m- ctg — !Ц3
m2 < A; < m2 + л
Г
2 —A; ctg — ^ , к < m2.
Лит.: [1] X а р т м а н Ф-, Обыкновенные дифференциаль-
дифференциальные уравнения, пер. с англ., М., 1970; [2J К р а с н о с с л ь-
с к и й М. А., Б у р д В. Ш., Колосов Ю. С, Нели-
Нелинейные почти периодические колебания, М., 1970; L3] П о н-
т р я г и н Л. С, [и др.), Математическая теория оптимальных
процессов, 3 изд., М., 1976; [4] Красовский Н. Н., Тео-
Теория управления движением. Линейные системы, М., 1968; [5]
Зубов В. И., Лекции по теории управления, М., 1075;
[til К а м к е Э., Справочник по обыкновенным дифференциаль-
дифференциальным уравнениям, пер. с нем., 5 изд., М., 1976; [7] К и г у р а д-
з е И. Т., Некоторые сингулярные краевые задачи для обык-
обыкновенных Дифференциальных уравнений, Тб., 1975.
Ю. В. Номленко, Е. Л. Тонкое.
КРАЕВАЯ ЗАДАЧА для уравнения с час т-
н ы м 11 производя ы м и — задача определения в
нек-рой области D переменных j; = (j-1, . . ., хп) реше-
решения и (.г) уравнения
(Lu) (*)=/(¦*¦), z?D, A)
удовлетворяющего на границе S этой области (или ее
части) определенным краевым условиям
(Ви)(у)=<р(у), y?S. B)
Как правило, краевые условия связывают граничные
значения решения с его производными до нек-рого по-
порядка, т. е. В является дифференциальным оператором.
Однако встречаются и краевые условия других типов.
Для данного дифференциального уравнения целесо-
целесообразность рассмотрения той или иной К. з. часто опре-
определяется понятием ее корректной постановки. Именно,
К. з. корректно поставлена, если ее решение существу-
существует, единственно и непрерывно зависит от данных этой
задачи. Различные типы дифференциальных уравнений
требуют различных корректно поставленных К. з.,
и обратно, корректные постановки К. з. иногда могут
служить основой для классификации типов дифферен-
дифференциальных уравнений.
К. з. наз. линейной, если операторы L и В ли-
линейны, и однородной, если / и ф в A), B) равны нулю.
Линейная К. з. наз. нётеровой, если: а) однород-
однородная задача имеет конечное число к линейно независимых
решений; б) неоднородная задача разрешима тогда и
только тогда, когда / и <р удовлетворяют I линейно не-
независимым условиям типа условий ортогональности;
в) при условии однозначной разрешимости решение
непрерывно зависит от / и ср.
Если к=1, то задача наз. фредгольмовой.
Разность к—I определяет индекс задачи.
Широкий класс К. з. для линейных уравнений с част-
частными производными 2-го порядка
. .=о
У" ь<(*)-§г
охватывается задачей Пуанкаре. В этой за-
задаче носителем краевых условий является вся граница,
к-рая предполагается (п—1)-мерным многообразием, а
граничный оператор В в B) имеет вид
(Ви)(у) = У" P,-M-|j7 + p(!/)u--=q>M, y?S. D)
Задача Пуанкаре хорошо исследована в ограничен-
ограниченной области D с достаточно гладкой границей, при
условии равномерной эллиптичности оператора L.
В предположении достаточной гладкости коэффици-
коэффициентов операторов L и В в C), D) и границы области D
задача Пуанкаре нётерова, если п-=2, ^р?>0, и фред-
гольмова, если п>2, ^р/>0и вектор р=(рх, . . ., р„)
некасателен к S. При исследовании задачи Пуанкаре
в двумерном случае широкое применение находят мето-
методы теории функций комплексного неременного (см. Кра-
Краевая задача; методы комплексного переменного).
Для общего эллиптич. уравнения порядка 2т.
Lu = V, , ., аа(.г)^=/(з-), if» E)
краевые условия могут задаваться с помощью линейных
дифференциальных операторов
F)
порядка nij<.2m с коэффициентами, определенными на
границе S области Z). Если операторы L и By- удовлетво-
удовлетворяют так наз. условию дополнительности, то производ-
производные порядка 2т функции и, удовлетворяющей гранич-
граничным условиям, можно оценить (в нек-рой норме) через
норму / в E) и подходящие нормы граничных функций
<ру в F). К. з. такого типа наз. коэрцитивными К. з.
Другой тип К. з. представляют так наз. смешанные
задачи, в к-рых на смежных участках границы задаются
различные краевые условия.
Для эллиптич. уравнений характерно то, что краевые
условия задаются на всей границе. Однако в полной
мере это относится только к равномерно эллиптич.
уравнениям. Если оператор L в C) эллиптичен внутри
области и на части S0<^S параболически вырождается,
то в зависимости от характера вырождения участок Sf,
от задания краевых условий может освобождаться. См.
тэкже Краевая задача для эллиптического уравнения.
Если уравнение C) не принадлежит к эллиптич. ти-
типу, то часть границы от задания краевых условий, как
правило, освобождается. Напр., для простейшего урав-
уравнения параболич. типа — уравнения теплопроводности
Т д2и ди л
Lu = -г— тт- = 0
дхг dt
задача Дирихле в области D, ограниченной прямыми
л-— — 1, 1= — 1, состоит в задании граничных значений
функции и на отрезках {t=—1, —1<:т<:-)-1}и {.t= —1,
ll}
}
Специальным образом ставятся К. з. для уравнений
смешанного эллиптико-гиперболич. типа.
Важное место занимают К. з. в теории аналитич.
функций. Пусть S — кусочно гладкая линия на плос-
плоскости, т. е. объединение конечного числа простых
ориентируемых дуг. Задача линейного со-
сопряжения заключается в определении аналитиче-
аналитической вне S функции ф(г), имеющей предельные значения
<Р±(')> t?S, с обеих сторон S и удовлетворяющей крае-
краевому условию
Ф+ (O-G(f)(p- (t) = g(t), t?S,
где G(t) и g(t) — заданные функции. С помощью пред-
представлений аналитич. функций интегралами типа Коши
при некоторых предположениях относительно функций
G, g и линии S решения этой задачи выписываются в
явном виде. См. Граничные задачи теории аналитиче-
аналитических функций.
Для изучения К. з. предложен ряд методов. Шварца
альтернирующий метод и связанные с ними выметания
метод Пуанкаре и Перрона метод опираются на при-
применение принципа максимума. Решение К. з. с помощью
интегральных уравнений основано на различных ин-
интегральных представлениях решений. Исследование К.
з. с помощью априорных оценок относится к функцио-
функциональным методам. Широко применяется теория обоб-
обобщенных функций. В практических приложениях значи-
значительное распространение получили различные конечно-
разностные методы.
Лит.: [1] Б е р с Л., Джон Ф., Ш е х т е р М., Урав-
Уравнения с частными производными, пер. с англ., М., 19A6'; [2]
Бицадзе А. В., Краевые задачи для эллиптических урав-
нений второго порядка, М., 1966; [3] К у р а н т Р., Уравнения
с частными производными, пер. с англ., М., 1964; [4] Лады-
Ладыженская О. А., Краевые задачи математической физики,
М., 1973; [5] М и р а н д а К., Уравнения с частными производ-
производными эллиптического типа, пер. с итал., М., 1957: [6] М у с х е-
л и ш в и л и Н. И., Сингулярные интегральные уравнения,
3 изд., М., 1968; [7] Т и х о н о в А. Н., Самарский А. А.,
Уравнения математической физики, 4 изд., М., 1972.
А. П. Солдатов.
КРАЕВАЯ ЗАДАЧА для эллиптического
уравнения — задача отыскания регулярного в об-
области D решения и эллиптического уравнения
удовлетворяющего нек-рым дополнительным условиям
на границе Г области D.
Классические К. з. являются частными случаями сле-
следующей задачи: найти регулярное в области D решение
уравнения A), удовлетворяющее на границе Г условию
a^. + bu=g, B)
где dldl — производная по нек-рому направлению;
а, Ь и g — заданные непрерывные на Г функции, причем
|а| + |6|>0 всюду на Г (см. [1]).
При a^sO, b=l К. з. есть Дирихле задача; при Ь=0,
а=1 — задача с косой производной (см. Дифферен-
Дифференциальное уравнение с частными производными; задача с
косой производной), к-рая переходит в Неймана зада-
задачу, если направление I совпадает с направлением ко-
нормали. Если Г=Г!иГ2, где 1\ и Г2 — непересекаю-
непересекающиеся открытые подмножества Г, а 1\ [) Г2 либо являет-
является (п—2)-мерным многообразием, либо пусто, и а=1,
6=0 на Гх, а=0, 6=1 на Г2, то получается смешанная
задача.
Задача B) изучалась для эллиптич. уравнений с дву-
двумя независимыми переменными (см. [2]). Довольно пол-
полно исследованы задача Дирихле для эллиптич. уравне-
уравнений с любым конечным числом независимых переменных
(см. [1], [3], [4]) и задача с косой производной в том слу-
случае, когда направление I ни в одной точке Г не выходят
в касательную к Г плоскость. В этом случае задача с
наклонной производной — фредгольмова и решение
имеет такую же гладкость, как и поле направлений I
и функция g (см. [1]). Изучался случай, когда I выходит
в касательную к Г плоскость в нек-рых точках Г (см.
[3]). Были исследованы локальные свойства решений
задачи с косой производной (см. [5]). В точках выхода
поля I в касательную к Г плоскость решение задачи ме-
менее гладкое, чем поле I и функция g. На основании этого
исследована задача в обобщенной постановке (см. [7],
[8]).
Пусть краевое условие для регулярных в единичном
шаре 2cR:l гармонич. функций имеет вид
К — множество точек единичной сферы S, в к-рых
обращается в нуль функция a>=ax-\-by-rcz. Векторное
поле Р (а, Ь, с) по множеству К выходит в касательную к
единичной сфере S плоскость. Пусть, кроме того, К
состоит из конечного числа непересекающихся кривых,
К+ — подмножество К, состоящее из таких точек, в
к-рых grad to составляет острый угол с проекцией поля
Р на сферу S, и К~ — оставшаяся часть К. Обобщенная
постановка задачи заключается в дополнительном зада-
задании значений м на Х + , но на множестве К ~ допуска-
допускаются интегрируемые особенности у решения и. В случае,
когда К~ пусто, за счет повышения гладкости допол-
дополнительных данных задачи можно сделать сколь угодно
гладким решение обобщенной задачи. Решение смешан-
смешанной задачи на множестве Г0=Г1ЛГ2, вообще говоря,
имеет особенности (см. [1]). Для того чтобы это решение
не имело особенностей на Го, необходимо накладывать
дополнительные условия на данные задачи (см. [11]).
Широкий класс К. з. составляют так наз. задачи со
свободными границами. В этих задачах требуется найти
не только решение уравнения A), но и область его регу-
регулярности. Граница Г области неизвестна, но на ней
должны удовлетворяться два краевых условия. Приме-
Примером таких задач является задача о волновых
движениях идеальной жидкости.
В этой задаче ищется регулярная в нек-рой области D
гармонич. функция и, причем часть Гг границы извест-
известна и на Г\ нормальная производная ди/дп равна нулю,
а другая часть границы Г2 неизвестна и на ней выпол-
выполняются два краевых условия:
где д>0 — заданная функция.
Для гармонич. функций двух независимых перемен-
переменных используется аппарат конформных отображений
(см. [12], [13], [14]). См. также Дифференциальное урав-
уравнение с частными производными; задача со свободными
границами.
Исследовалась следующая задача: найти регулярную
в области jD гармонич. функцию и, удовлетворяющую
на границе Г области условию
|grad u|2 = g,
где <?>0 — заданная функция. Для гармонич. функ-
функций двух независимых переменных эта задача решена
полностью (см. [14]).
Для уравнения Lu=f, где L — равномерно эллипти-
эллиптический в замыкании D области jD оператор порядка
2т, рассматривается задача отыскания регулярного в jD
решения и, удовлетворяющего на границе Г области D
условиям:
Ду-и = Ф;-, / = 1, ..., т, C)
где Bj(x, D), /=1, . . ., то,— дифференциальные опе-
операторы, удовлетворяющие следующему условию
дополнительности.
(ft В \
х, —, . . ., ) — главная часть опе-
ратора L, В/ — главная часть оператора В j, n — нор-
нормаль к Г в точке х, ХфО — произвольный вектор, па-
параллельный Г. Через Jk(k) обозначены корни L'(x,
Х-\-тп) с положительными мнимыми частями. Много-
Многочлены В)(х, X-\-in), /=1, . . ., т, относительно перемен-
переменного т должны быть линейно независимыми по модулю
многочлена Пь=1(т—т?(А.)). И в этом случае задача
является нормально разрешимой. Нарушение условия
дополнительности может повлечь существенное изме-
изменение характера задачи (см. [171).
Задача B) — частный случай задачи C). Для задачи
B) при assl условие дополнительности эквивалентно
тому, что направление I ни в одной точке границы об-
области не выходит в касательную к границе плоскость.
Другим частным случаем задачи C) является задача
с краевыми условиями:
±^. = фу, /=0,1 i«-l,
dnJ
к-рая есть некоторый аналог задачи Дирихле для эл-
липтич. уравнений высших порядков.
Изучена К. з. для полигармонич. уравнения Д*и=0,
когда граница области состоит из многообразий раз-
различной размерности (см. [15]).
При исследовании К. з. для нелинейных уравне-
уравнений (напр., задач Дирихле и Неймана) важную роль
играют априорные оценки решений A), различные
принципы неподвижной точки (см. [17], [18]) и обобще-
обобщения Морса теории на бесконечномерный случай
(см. [19]).
Лит.: [1] Миранда К., Уравнения с частными произ-
производными эллиптического типа, пер. с итал., М., 1957; [2] В е к у а
И. Н., Обобщенные аналитические функции, М., 1959; [3] Б и-
цадзе А. В., Краевые задачи для эллиптических уравнений
второго порядка, М., 1966; [4] К е л д ы ш М. В., «Успехи ма-
тем. наук», 1941, в. 8, с. 171—292; [5] Hormander L.,
«Ann. Math.», 1966, v. 83, № 1, p.129—209; [6] В о г r e 1 1 i R. L.,
«J. Math, and Mech.», 1966, v. 16, № 1, p. 51—81; [7] Его-
Егоров Ю. В., Кондратьев В. А., «Матем. сб.», 1969, т. 78,
JMs 1, с. 148—76; [81 М а з ь я В. Г., «Матем. сб.», 1972, т. 87,
№ 3, с. 417—53; [9] Я н у ш а у с к а с А., «Докл. АН СССР»,
1965, т. 164, №4, с. 753 — 55; [10J В и шик М. И., Э с-
к и н Г. И., «Сиб. матем. ж.», 1968, т. 9, №5, с. 973—97;
[11] Giraud G., «Ann. Soc. Polon. de Math., annee 1933»,
Krakow, 1934, t. 12, p. 35—54; [12] Лаврентьев М. А., Ва-
Вариационный метод в краевых задачах для систем уравнении эл-
эллиптического типа, М., 1962; [13] Некрасов А. И., Точная
теория волн установившегося вида на поверхности тяжелой
жидкости, в кн.: Собр. соч., т. 1, М., 1961; [14] Г а х о в Ф. д.,
Краевые задачи, 2 изд., М., 1963; [15] Соболев С. Л.,
«Матем. сб.», 1937, т. 2, № 3, с. 465—99; [16] А г м о н С,
ДуглисА., НиренбергЛ., Оценки вблизи границы
решений эллиптических уравнений в частных производных при
общих граничных условиях, пер. с англ., М., 1962; [17] S с h a u-
der J., «Math. Z.». 1931, Bd 33, S. 602—40; [18] Leray J.,
Schauder J., «Ann. sci. Ecole norm, sup.», ser. 3, 1934,
t. 51, p. 45—78; [19] P a 1 a i s R. S., «Topology», 1963, v. 2,
№ 4, p. 299—340. А. И. Янушаускас.
КРАЕВАЯ ЗАДАЧА; методы комплекс-
комплексного переменного — методы изучения К. з.
для дифференциальных уравнений с частными произ-
производными, в к-рых используется представление решений
через аналитич. функции комплексного переменного.
Пусть для уравнения 2-го порядка эллиптич. типа
Аи + а(х, y)^L + b(x, y)^L+c(x, y)u=0, A)
где а, Ь, с — аналитич. функции действительных пере-
переменных х, у в нек-рой области плоскости z=x-\-iy,
поставлена К. з.: найти регулярное в односвязной об-
области ScDa решение уравнения A), удовлетворяющее
краевому условию
дх-1 дук
где a,jk(t), f(t)?Ca(dS), 0<а<1, Т]k — линейные опе-
операторы, отображающие С (dS) в Са (OS), причем
Тт-к,к — вполне непрерывны.
Эта задача охватывает известные классические крае-
краевые задачи Дирихле, Неймана, Пуанкаре и др.
При помощи формулы общего представления решений
(см. Дифференциальное уравнение с частными производ-
производными; методы комплексного переменного):
и(х, у) = Яе {g(z, 1o z, 1)Ф (г) —
эта задача приводится к эквивалентной К. з. для ана-
аналитич. функций:
где ak(t) — заданные непрерывные в смысле Гёльдера
функции, t?dS, Tm — вполне непрерывный оператор,
a Tfi (fe=0, 1, . . ., m—1) — линейные операторы.
Пусть конечная односвязная область S ограничена
замкнутым контуром Ляпунова (см. Ляпунова поверх-
поверхности и кривые) dS и пусть производная порядка т^0
голоморфной в S функции Ф (z) принимает на dS зна-
значения функции класса Са, 0<а<1. Тогда, считая, что
точка z=0 принадлежит S, функцию Ф (z) представляют
в виде
+ \ as fi (i) ds + ic, если m^si,
где (i(i) — действительная функция класса Ca(dS),
0<а<1, а с — действительная постоянная; ц.(?) и с
определяются по Ф (z) единственным образом.
Подстановка этих выражений в краевое условие C)
позволяет получить для искомой функции (х эквива-
эквивалентное задаче B) сингулярное интегральное уравне-
уравнение вида
где Т — вполне непрерывный оператор.
Для нормальной разрешимости К. з. B) необходимо
и достаточно, чтобы
а (t) = 2Г= о * *"» -* (О Ф °. * 6 OS, m ^ 0. D)
Задача Дирихле (т=0) всегда нормально разрешима.
(Ниже всюду предполагается, что условие D) соблю-
соблюдено.)
Индекс К.з. B) вычисляется по формуле
х = 2 (то + р), го^ 1,
где р — приращение функции -g^r arg a (t) при одно-
однократном обходе контура dS в положительном направ-
направлении. Индекс задачи Дирихле равен нулю.
Однородная К. з. R (ц)=0 имеет конечное число fe^O
линейно независимых решений, причем fe^x, а неод-
неоднородная задача B) имеет решение тогда и только тог-
тогда, когда выполняются равенства
/(Ov/(*)d5 = O, / = 1, 2, ..., к',
где V/ — полная система линейно независимых решений
союзного однородного интегрального уравнения
Необходимым и достаточным условием для того, что-
чтобы К. з. B) имела решение для любой правой части,
является наличие ровно х линейно независимых реше-
решений у соответствующей однородной задачи Д(и) = 0.
Следовательно, в случае х>0 однородная К. з. R(u) = 0
всегда имеет не меньше, чем х, линейно независимых
решений, а при х<0 неоднородная задача B) не до-
допускает решения для любой правой части, причем чис-
число условий разрешимости не меньше |х|.
Необходимые и достаточные условия разрешимости
неоднородной К. з. могут быть сформулированы в тер-
терминах замкнутости относительно рассматриваемой об-
области нек-рого ядра, а также полноты определенной
системы функций. Эти ядра и системы функций строят-
строятся в явном виде при помощи функции Римана уравне-
уравнения A) и коэффициентов краевого условия. Напр.,
пусть {«&}—некоторая полная система решений
относительно основной области jD0 уравнения A) и
пусть ScD0. Тогда необходимым и достаточным усло-
условием разрешимости задачи B) для любой правой части
является полнота системы функций {R (и^)} на границе.
Весьма полные результаты получены относительно
следующей К. з. (обобщенной задачи Рима-
на — Гильберта): найти решение уравнения
d-w-\-A (z) w-\-B (z) w =f (z), w = u-\-iv, E)
2d-=dx-idy,
непрерывное в S-\-dS и удовлетворяющее краевому
условию
Re [X(z), w(z)] =au + py = 7, z?dS, F)
где а, р, у — заданные действительные функции, при-
принадлежащие классу Ca(dS), 0<а<1, причем а2+р2=1.
Область S, вообще говоря, многосвязна. Такая задача
может быть редуцирована к эквивалентному сингуляр-
сингулярному интегральному уравнению. Этим путем удается
получить полный качественный анализ К. з. F).
Пусть граница dS области S состоит из конечного
числа простых замкнутых кривых dS0, . . ., dSm,
удовлетворяющих условиям Ляпунова. Так как при
конформных отображениях вид уравнения и краевого
условия сохраняются, то без ущерба для общности
можно считать, что dS0 — единичная окружность с
центром в точке z=0, лежащей в рассматриваемой об-
области S, a dSlt . . ., dSm — окружности, лежащие вну-
внутри dSa.
Индексом задачи F) наз. целое число п,
равное приращению -=—arg [a(?)+iP(?)], когда точка
? один раз обойдет OS в положительном направлении.
Краевое условие можно привести к более простому
виду
Re [г?'И w(z)]=y,
где с (z) = Cj- на dSj, причем со=О, а сь . . ., ст — неко-
некоторые действительные постоянные, к-рые однозначно
выражаются через аир. Индекс сопряженной задачи
Re {(cc+ip) -^- w(z)| =0, z?dS,
вычисляется по формуле: n' = — n+m—1.
Задача F) имеет решение тогда и только тогда, когда
где Wjf — произвольное решение сопряженной задачи.
Пусть еже' — числа линейно независимых решений
однородных задач F) и G) соответственно. Тогда
е — е' = п — п' = 2п-\-\. — т.
Если п<0, то однородная задача F) не имеет не-
нетривиальных решений. Если n>m—1, то однородная
задача F) имеет ровно е=2п-\-1 — т линейно независи-
независимых решений, а неоднородная задача F) всегда разре-
разрешима. Если и<0, то неоднородная задача F) имеет ре-
решение тогда и только тогда, когда
(a+Ф) w,yds = 0, / = 1,2, ...; e' — m — 2n — i,
где w%j — полная система решений однородной зада-
задачи G). Если т=0 и п=0, то е=\ и все решения одно-
однородной задачи [6] имеют вид
где с — действительная постоянная, а (о0 — непрерыв-
непрерывная в S + dS функция.
Приведенные результаты полностью характеризуют
задачу в односвязном (т=0) и многосвязном (п<0,
n>m—1) случаях. Особого рассмотрения требуют
случаи 0<п«?то—1, к-рые также в достаточной мере
детально разработаны.
Для уравнения E) изучена также К. з. типа Пуанка-
Пуанкаре задачи.
Лит. см. при ст. Дифференциальное уравнение с часгп}1ыми
производными; методы комплексного переменного. И- Н. Вепуа.
КРАЕВАЯ ЗАДАЧА теории потенциала—
основная задача потенциала теории как классической,
так и абстрактной. Поскольку классические ньютонов
и логарифмич. потенциалы удовлетворяют определен-
определенным дифференциальным уравнениям с частными произ-
производными эллиптич. типа, а именно Лапласа уравнению
в областях, свободных от порождающих эти потенциа-
потенциалы масс, и Пуассона уравнению в областях, занятых мас-
массами, к числу К. з. теории потенциала относят в первую
очередь краевые задачи для эллиптич. уравнений и сис-
систем.
1) Дирихле задача, или первая краевая
задача, когда требуется найти потенциал и(х) в
нек-рон области D по заданным его непрерывным зна-
значениям u(x)=j (x), х? Г, на границе области dD=V,
причем распределение масс внутри D предполагается
известным. Эта задача в теории потенциала является
основной.
2) Неймана задача, пли вторая краевая
задача, когда требуется найти потенциал в D по
заданным непрерывным значениям его нормальной
производной
Ой (ж) , , тл
=(Р <*) на Г
3) Смешанная задача, или третья краевая
задача, когда на Г задается линейная комбинация
4) Задача с косой производной, когда на Г в условии
(*) вместо производной по нормали ди(х)/дп к Г фигу-
фигурирует производная ди (x)ldl по произвольному, вообще
говоря, направлению 1=1 (х), х?Г.
Кроме перечисленных общих задач, в теории потен-
потенциала возникли также следующие специфические про-
проблемы.
5) Робела задача, когда на Г ищется такое распреде-
распределение масс, потенциал к-рого и(х) постоянен внутри
области D. Эта задача возникает как электростатич.
проблема определения такого равновесного распреде-
распределения зарядов на проводнике Г, к-рое ничем не прояв-
проявляет себя внутри D.
6) Выметания метод, к-рын в своем простейшем из-
изложении, ведущем начало от А. Пуанкаре (Н. Poin-
сагё), состоит в отыскании такого распределения масс
на границе Г, потенциал к-рого в дополнительной об-
области CD совпадал бы с потенциалом данных «выме-
«выметаемых» масс, расположенных внутри D. В потенциала
теории абстрактной две последние задачи имеют осо-
особенно большое значение.
См. также Бесселев потенциал, Нелинейный потен-
потенциал, Рисса потенциал.
Лит.: [1] Г ю н т е р Н. М., Теория потенциала и ее приме-
применение к основным задачам математической физики, М., 1953;
[2] Л а н д к о ф Н. С, Основы современной теории потенциа-
потенциала, М., 1966; [3] Брело М., Основы классической теории
потенциала, пер. с франц., М., J964; [4] Constantines-
cuC, Cornea A., Potential theory on harmonic spaces, В.,
1!O2. " E. Д. Соломенцев.
КРАЕВАЯ ЗАДАЧА, численные методы
решения для уравнений с частными
производными — приближенные методы реше-
решения, в результате к-рых решение задачи представляется
таблицей чисел. Точно решения (в виде явных формул,
рядов и т. п.) К. з. можно построить лишь в редких
случаях. Из приближенных методов решения наиболь-
наибольшее распространение получили разностные методы (см.
[1]); они применимы к самым общим задачам и удобны
для реализации на ЭВМ. Сущность разностных методов
состоит в том, что исходная область изменения незави-
независимых переменных заменяется дискретным множеством
точек — сеткой, а производные, входящие в уравнение
и в граничные условия, аппроксимируются на этой сетке
разностными отношениями. В результате такой ироце-
дуры исходной задаче сопоставляется система конеч-
конечного числа алгебраич. уравнений (линейных или нели-
нелинейных), называемая разностной схемой. За прибли-
приближенное решение исходной задачи принимается решение
разностной схемы. Точность приближения зависит от
способа аппроксимации и от густоты сетки, т. е. от того,
насколько плотно сетка заполняет исходную область.
В дальнейшем рассматриваются только линейные К. з.
для уравнении с частными производными, причем ис-
исходная задача считается корректно поставленной. Обос-
Обоснование разностных методов связано с исследованием
корректности разностной задачи и ее сходимости при
измельчении сетки. Разностная задача нал. к о р р е к т-
н о й, если при любых правых частях ее решение су-
существует, единственно и устойчиво. Под устойчивостью
разностной схемы понимается непрерывная зависимость
ее решения от правой части, равномерная относительно
шагов сетки.
Пусть, напр., требуется решить задачу Дирихле для
уравнения Пуассона в квадрате С={0<х1, х,2<1}
с границей Г:
и(хи з-2) = ц(хи хг), (хъ
Область G заменяется квадратной сеткой Gh с шагом h,
т. е. множеством точек
/ = 1, 2, ..., JV-l}
с границей
а производные, входящие в уравнение,— разностными
отношениями
Д2Л 21 1ч J
где ы/( у= и (xi°, ДУ>). Разностная схема имеет вид
i, j = l, 2, ..., JV—1; Vi,j\T=\>-i.j,
h
где y;,j — ее решение.
Решение задачи A) существует и единственно при лю-
любых правых частях / и при любых граничных условиях
(х (см. [2]). Более того, решение разностной задачи
A) сходится при h —>- 0 к решению исходной задачи,
причем схема имеет второй порядок точности в норме с,
то есть
max | у (х1, г3) — и (хг, хг) |< МЛ2,
где Л/ — постоянная, не зависящая от h.
Разностная схема A) представляет собой систему
линейных алгебраич. уравнений, для к-рой характерно
большое число уравнений (именно (Л — 1) 2 уравнений,
причем 7V —>- оо при h —*- 0), большое число нулей в мат-
матрице этой системы и плохая обусловленность (отноше-
(отношение наименьшего собственного числа к наибольшему
есть величина порядка h2 при h —>- 0). Для решения по-
подобных систем уравнений, возникающих при аппрокси-
мацип дифференциальных уравнений разностными, су-
существуют эффективные прямые и итерационные методы.
Прямые методы дают точное решение разностной задачи
после выполнения конечного числа арнфметич. дейст-
действий. К прямым методам относятся различные варианты
метода прогонки, включая матричную прогонку, метод
декомпозиции, быстрое преобразование Фурье, метод
суммарных представлений (см. [1], |2], [3], [6]). Эффек-
Эффективность прямых методов оценивается порядком числа
действий при Л —>- 0. Так, матричная прогонка требует
для решения задачи A) числа действий C(й~4), в то
время как метод быстрого преобразования Фурье тре-
требует для решения той же задачи Q{h~2 In h~x) дейст-
действий. Из итерационных методов решения разностных
задач используется метод Ричардсона с чебышевским
набором параметров, попеременно-треугольный итера-
итерационный метод, различные методы переменных на-
направлений (см. [2]). Эффективность итерационных ме-
методов оценивается порядком минимального числа ите-
итераций пп(е), необходимых для того, чтобы уменьшить
погрешность начального приближения в 1/е раз. Напр.,
при решении задачи A) методом Ричардсона величина
по(е) имеет порядок Л~Чп —, а при решении методом
переменных направлений с оптимальным выбором
итерационных параметров n0(e) = O (In It'1 In—). Ите-
Итерационные методы более универсальны и более просты
в реализации, чем прямые, и вследствие этого полу-
получили большое распространение при решении разност-
разностных задач.
Пусть, напр., требуется решить первую К. з. для
уравнения теплопроводности:
dt dxr dxi
. п. . , \ B)
и (хи х2, «)=0, (*]. .г2)?Г. )
Для решения этой задачи задается сетка по времени
с шагом т>0
(от = {tn = nx, n=0, 1, 2, ...}
и сетка G^ по пространственным переменным. Пусть
u'l /=m(j-i'), жг", tn). Производная u't аппроксимирует-
аппроксимируется отношением
а лапласиан А — разностным оператором ДЛ. Исход-
Исходному уравнению B) ставится в соответствие разностная
схема
*, / = 1, 2, .... ЛГ-1;
Параметр о, входящий в эти уравнения, определяет
устойчивость и точность схемы. Если а^0,5, то схема C)
устойчива при любых шагах сетки т и h (абсолютно ус-
устойчивая разностная схема). Если же ст<С0,5, то схема
(о) устойчива при нек-ром ограничении на величину
7=т/А3 (условно устойчивая разностная схема); напр.,
явная схема (ст=0) устойчива при условии у<1/4. При
ст=0,5 схема имеет второй порядок точности по т и по h,
при остальных а — первый порядок точности по т и
второй — по h. Разностная задача C) решается «по
слоям». Слоем номера п наз. множество всех точек сетки
(*h ^ tt>t при нек-ром фиксированном h. На нулевом
слое (при п = 0) значения </?, / известны из начальных
условий. Если значения y?t / на нек-ром слое п уже из-
П1 1
вестны, то значения (/,- j=yi, / на следующем слое на-
находятся из системы уравнений
.-¦.,1г.--.
)
где
Для нахождения решения задачи D) можно воспользо-
воспользоваться любым из методов решения стационарной зада-
задачи A). Существуют, однако, более экономичные алго-
алгоритмы решения многомерных нестационарных К. з.,
а именно методы переменных направлений (см. [1] —
[5]), позволяющие сводить решение многомерной задачи
к решению последовательности одномерных задач. Так,
для решения уравнения теплопроводности можно вос-
воспользоваться следующей схемой переменных направ-
направлений:
"', ; '.у .
673т = Л
»7V - уГ)и
Эта схема абсолютно устойчива, имеет второй порядок
точности и решается путем последовательного обраще-
обращения одномерных разностных операторов.
Решение разностной задачи, даже если оно получено
точно, может не только количественно, но и качествен-
качественно отличаться от решения исходной дифференциальной
задачи. Особенно сильно это отличие сказывается при
счете уравнений, имеющих особенности в коэффициен-
коэффициентах или в самом решении (так, при расчете разрывных
решений уравнений газовой динамики обычно появ-
появляются зоны сильного «размазывания» разрывов).
Таким образом, непосредственная аппроксимация диф-
дифференциальной задачи разностной, когда производные
заменяются с большой степенью произвола разностны-
разностными отношениями, не всегда приводит к хорошей разност-
разностной схеме. Выработан ряд принципов построения раз-
разностных схем, позволяющих получить схемы хорошего
качества. Так, успешно применяется метод баланса и
методы аппроксимации вариационного функционала
(см. [1] — [3]). Полученные этими методами разностные
схемы правильно отражают интегральные законы со-
сохранения, справедливые для исходных уравнений, и
обеспечивают знакоопределенность соответствующих
разностных операторов. В теории разностных однород-
однородных схем (см. [7]) рассматриваются вопросы построения
и исследования сходимости разностных схем для урав-
уравнений с переменными (в том числе и разрывными) ко-
коэффициентами.
Лит.: [1] Тихонов А. Н., Самарский А. А.,
Уравнения математической физики, 5изд.,М., 1977; [2] С а м а р-
ский А. А.. Теория разностных схем, М., 1977; [3] М а р-
чук Г. И., Методы вычислительной математики, М., 1977;
[4] Я н е н к о Н. Н., Методы дробных шагов решения много-
многомерных задач математической физики, Новосиб., 1967; [5]
Дьяконов Е. Г., Разностные методы решения краевых
задач, в. 1—2, М., 1971—72; [6] Положив Г. Н., Числен-
Численное решение двумерных и трехмерных краевых задач математи-
математической физики и функции дискретного аргумента, Киев, 1962;
[7] Тихонов А. Н., Самарский А. А., «Ж. вы-
вычислит, матем. и матем. физ.», 1981, т. 1, в. 1, с. 5—63.
А. В. Гулин.
КРАЕВЫЕ УСЛОВИЯ, граничные у с л о-
в и я,— условия, к-рым должно удовлетворять искомое
решение заданного дифференциального уравнения на
границе (или ее части) области, где это решение ищется.
К. у. обычно задаются с помощью дифференциальных
операторов, однако встречаются К. у. и других типов.
Л. П. Солдатов.
КРАЙ — подмножество замыкания М" (открытого)
действительного и-мерного многообразия Мп, каждая
точка к-рого гомеоморфна нек-рой области W" замкну-
замкнутого полупространства R", открытой в R+ (но не в R").
Точка а?Мп, соответствующая краевой точке области
W"dRi, т. е. точке пересечения W" с границей полу-
полупространства R", наз. краевой точкой Мп.
Многообразие, обладающее краевыми точками, наз.
многообразием с краем. Компактное мно-
многообразие без К. наз. замкнутым многооб-
многообразием. Совокупность всех краевых точек Мп есть
(ге—1)-мерное многообразие без края. м. И. Войцеховский.
КРАМЕРА ПРАВИЛО: если определитель D квад-
квадратной системы линейных уравнений
021*1 + • • • + ainxn = Z>2,
anlxl + • • • + &nnxn ^^ bn
не равен нулю, то эта система имеет единственное реше-
решение и это решение находится по формулам
*ft = -g-, k = l, 2, ..., п. (*)
Здесь Df; — определитель, получаемый из D заменой
fe-ro столба на столбец свободных членов. Формулы (*)
наз. формулами Крамера; они были найдены
Г.Крамером [1].
Лит.: [1] Cramer G., Introduction' a l'analyse des lignes
courbes, Gen., 1750, p. 657; [2] К у р о ш А. Г., Курс высшей ал-
алгебры, 11 изд., М., 1975. И. В. Проскуряков.
КРАМЕРА ТЕОРЕМА — интегральная предельная
теорема для вероятностей больших отклонений (укло-
(уклонений) сумм независимых случайных величин. Пусть
Х1, Х2, ¦ ¦ ¦— последовательность независимых случай-
случайных величин с общей невырожденной функцией распре-
распределения F(х) такой, что ЕХХ^О и производящая функ-
функция моментов Eetxi конечна в нек-ром интервале |(| <Я
(последнее условие наз. условием Крамера).
Пусть
Если ж>1, x=o(Y~n) при п—>- сх>, то
\ ~ 1",<Ж) = ехр / -^L-
Здесь Ф (x) — нормальная (О, 1) функция распределе-
распределения, M0 = 5. cktk — так наз- РЯД Крамера,
коэффициенты к-рого зависят только от моментов слу-
случайной величины X-l, этот ряд сходится для всех до-
достаточно малых t. Несколько более слабый по сравнению
с приведенным выше результат был получен Г. Краме-
Крамером (Н. Cramer) в 1938.
Лит.: [1] К р а м е р Г., «Успехи матем. наук», 1944, в. 10,
с. 166—78; [2] И б р а г и м о в И. А., Л и н н и к Ю. В.,
Независимые и стационарно связанные величины, М., 1965;
[3] П е т р о в В. В., Суммы независимых случайных величин,
М., 1972. В. В. Петров.
КРАМЕРА — МИЗЕСА КРИТЕРИЙ — непарамет-
непараметрический критерий для проверки гипотезы Но, согласно
к-рой независимые одинаково распределенные случай-
случайные величины Х1г . . . , Хп имеют заданную непрерыв-
ную функцию распределения F(x). К.— М. к. основан
на статистике вида
(x))dF(x),
где Fn(x) — функция эмпирического распределения,
построенная по выборке Х1г . . . , Хп, Т (t) — некото-
некоторая неотрицательная функция, определенная на отрезке
[О, 1] и такая, что Т (t), № (t) и i2xF (t) интегрируемы на
[О, 1]. Критерии такого типа, основанные на квадратич-
квадратичной метрике, впервые были рассмотрены Г. Крамером
[1] и Р. Мизесом [2]. Н. В. Смирнов предложил выбрать
Y (f)=l и показал, что в этом случае при справедливо-
справедливости гипотезы Но и п-> и статистика ш«= &п [1] имеет
в пределе «омега-квадрат» распределение, не завися-
зависящее от гипотетич. функции распределения F(x). Стати-
стич. критерий для проверки гипотезы Яо, основанный
на статистике со,2, наз. критерием ^(крите-
^(критерием Крамера — Мизеса — Смирнова),
при этом для нахождения численного значения статис-
статистики con пользуются следующим ее представлением:
где ХA)<. . .<:Х(„) — вариационный ряд, построен-
построенный по выборке Хг, . . . , Хп. Согласно критерию ш2
с уровнем значимости а, гипотеза На отвергается, коль
скоро (Ол=><Ва, где и>%, — верхняя а-квантиль распре-
распределения ш2, т. е. Р {@2<к>а}=1—а. Аналогично уст-
устроен критерий, предложенный Т. Андерсоном и Д. Дар-
лингом (см. [5]), основанный на статистике a%[ilF(x)(l —
— F(x))].
Лит.: [1] Cramer H., Sannolikhetskalkylen och nugra
av dess anvandningar, Stockh., [19261; [2] MisesB. V.,
Wahrscheinlichkeitsrechnung und ihre Anwendung in der Statis-
tik und theoretischen Physik, Lpz.—W., 1931; [3] Смир-
Смирнов H. В., «Матем. сб.», 1937, т. 2, №5, с. 973—93; [4]
Большей Л. Н., Смирнов Н. В., Таблицы матема-
математической статистики, 2 изд., М., 1968; [5] A n d е г s о n T. W.,
D а г 1 i n g D. A., «Ann. Math. Stat.», 1952, v. 23, p. 193—212.
M. С. Никулин,
КРАТНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ, k - к р а т-
ная последовательность, элементов дан-
данного множества X — отображение fe-ii степени Nk
множества натуральных чисел N в множество X. Эле-
Элементом (или членом) К. п. /: Nk—>- X наз. упо-
упорядоченный комплекс из к-\-\. элементов (nlt . . . ,
пк, х), где x=f(n1, . . . , nk), х?Х, (и,, . . . ,
k т. е. iij^N, /=1, 2, . . ., к, к-рый обознача-
обозначащ . Л. Д. Кудрявцев.
КРАТНАЯ ТОЧКА плоской кривой F(x, y)~0 —
особая точка, в к-рой обращаются в нуль частные про-
производные до порядка п включительно и не равна нулю
хотя бы одна из частных производных (re-rl)-ro поряд-
порядка. Так, например, если F(x0, i/0) = 0, F'x{xn, yo) = O,
Fy(x0, уо) = О, но из производных Fxx(x0, у о), Fxy(x0, y0),
Fyy(x0, у0) хотя бы одна не равна 0, то К. т. М (х0, у0)
наз. двойной точкой; если в точке М (х0, у0) равны
нулю первые и вторые частные производные и не равна
нулю хотя бы одна из трех производных, то К. т.—
тройная Т О Ч К а И Т. Д. А. Б. Иванов.
КРАТНО КРУГОВАЯ ОБЛАСТЬ, область
Рейнхарт а,— область D комплексного простран-
пространства С", п>1, с центром в точке а=(аи . . .,о„)^С"
такая, что вместе с каждой точкой zo=(z1, . . ., zan)?D
ей принадлежат и все точки вида
{z = Bj, . . ., zn):\ zv — av| =] z° — av\, v = l, 2, . . ., n}.
К. к. o. D с а=0 инвариантна относительно преобразо-
преобразований {z°}->- {z°e' v }, 0<9v<2n, v=l, ... , n.
К. к. о. составляют подкласс Гартогса областей и под-
класс класса круговых областей, опреде-
определяемых условием: вместе с каждой точкой z°?D они
содержат и все точки вида
{z = (zb ..., zn):z = a+(z° — a) e™, 0<6 < 2л},
т. е. все точки окружности с центром а и радиусом
Sz°—el = (^,"=1|2v—Ovl2I/2, расположенной на комплекс-
комплексной прямой, проходящей через а и z°.
К. к. о. D наз. полной кратно круговой
областью, если вместе с каждой точкой z°?D en
принадлежит поликруг
[z = (zu ..., zB):| zv—av|<| z° —av|, v=l, ..., re}.
Полная К. к. о. звездообразна относительно ее цент-
центра а.
Примеры полных К. к. о.: шары и поликруги в С™.
Круговая область D наз. полной круговой
областью, если вместе с каждой точкой z°?D она
содержит и весь круг {z=a-\-(z°—a)?, |?]<:1}.
К. к. о. D наз. логарифмически выпук-
выпуклой кратно круговой областью, если
образ X(D*) множества
D* = {z = (z1, ..., zn)?D:Z)Z2. . .гп ф 0}
при отображении
А,:*—>*(*) = (In I*!! 1п|*„|)
является выпуклым множеством в действительном про-
пространстве R". Важное свойство логарифмически вы-
выпуклых полных К. к. о. состоит в том, что каждая та-
такая область в С™ есть внутренность множества точек
абсолютной сходимости (т. е. область сходимости)
нек-рого степенного ряда по переменным z1—аи . . . ,
zn—an, и обратно: область сходимости любого степен-
степенного ряда по гь . . ., гп есть логарифмически выпуклая
полная К. к. о. с центром а=0.
Лит.: [1] Владимиров В. С, Методы теории функ-
функций многих комплексных переменных, М., 1964; [2] Ш а-
б а т Б. В., Введение в комплексный анализ, 2 изд., М., 1976.
Е. Д. Соломенцев.
КРАТНОГАРМОНИЧЕСКАЯ ФУНКЦИЯ — гармо-
гармоническая функция, у к-рой операторы Лапласа по от-
отдельным группам независимых переменных обращаются
в нуль. Точнее, функция и=и{х1, х2, . . ., хп), га>2,
класса С2 в области D евклидова пространства R" наз.
К. ф. в D, если существуют такие натуральные числа
пи ;г2! • • •» nki rai+re2+- ¦ --\~nk=ni ra^&=&2, что всю-
всюду в D выполняются тождества:
-=0.
Важный собственный подкласс класса К. ф. составляют
плюригармонические функции, для к-рых и=2го, п/=2,
/=1,2,... , т, т. е. к—т, и к-рые, кроме того, удов-
удовлетворяют нек-рым дополнительным условиям.
Лит.: [1] С т е й н И., В е й с Г., Введение в гармонический
анализ на евклидовых пространствах, пер. с англ., М., 1974,
iS. Д. Соломенцев.
КРАТНОЕ натурального числа а —
натуральное число, делящееся на а без остатка. Число
и, к-рое делится на каждое из чисел а, Ъ, , . . , т, наз.
общим кратным этих чисел. Из всех общих К.
двух или нескольких чисел одно (не равное нулю)
является наименьшим (наименьшее общее
к р а т н о е), а остальные будут К. этого наименьшего.
Зная наибольший общий делитель d двух чисел а и Ь,
находят наименьшее общее К. т по формуле m=abfd.
КРАТНОСТЬ ВЕСА М представления р
алгебры Ли t в векторном простран-
пространстве V ¦— размерность пм весового подпространства
VmCV, соответствующего весу М (см. Вес представле-
представления).
Пусть t — Картана подалгебра полупростой алгеб-
алгебры Ли й над алгебраически замкнутым полем нулевой
характеристики, ар — ограничение на t конечномер-
конечномерного представления сг алгебры (J. В этом случае прост-
пространство V является прямой суммой весовых подпро-
подпространств алгебры t, соответствующих различным ве-
весам. Эти веса и их кратности часто наз. весами и крат-
ностями весов представления сг алгебры д.
Пусть представление а неприводимо и Л — его стар-
старший вес (см. Картана теорема о старшем векторе).
Тогда гаЛ=1. Для весов, отличных от старшего, извест-
известно несколько способов вычисления их кратностей. Два
из них являются классическими результатами теории
представлений — формула Фрейденталя и формула
Костанта.
1. Формула Фрейденталя (см. [4], [1]).
Пусть ( , ) — естественное скалярное произведение на
сопряженном к t пространстве t*, индуцированное-
Киллинга формой на t, R — система корней алгебры
д относительно t и > — отношение частичного по-
порядка на t*, определенное какой-либо фиксированной
системой простых корней (Xj, . . ., <хг в R. Тогда
((Л + 6, Л+6) — (М + 6, М+6))гам =
= 2 У У" ;гм+ь„ (M + fca, а),
где 8=A/гJаб/? а>0 а и'по определению, п^=0, если
N не вес представления сг. Для любого веса М^Л.
множитель при пм в левой части формулы отличен or
нуля. Эта формула имеет рекуррентный характер: она
позволяет выразить гам через гадг, если iV>M. Посколь-
Поскольку известно, что геЛ=1, формула фрейденталя дает эф-
эффективный способ нахождения кратностей гам.
2. Формула Костанта (см. [5], [1]). Пусть
Г = {М? t*l 2 (М, a,-)/(a,-, a,)? Ж для всех i = l, ..., г}.
Множество Г является подгруппой по сложению в t*,
инвариантной относительно группы Вейля W, к-рая
действует в t* естественным образом. Элемент 8, а
также все веса представления сг лежат в Г. Пусть для
каждого М?Г число Р (М) равно количеству способов
записи М в виде суммы положительных корней, т. е.
Р (М) — это число решений {ka\a?R, a>0} уравнения
~ ¦Z-asR, a>0 a '
где fca?Z, fca>0 при всех а. Функция Р (М) на Г
наз. функцией разбиения. Тогда
вМ = 2св w (det5) P (S (Л+о)-(М+о)).
Практическое использование приведенных выше фор-
формул связано с громоздкими вычислениями. Для полу-
полупростых алгебр ранга 2 имеются более удобные геомет-
геометрические правила подсчета К. в. (см. [2]).
Лит.: [1] Джекобсон Н., Алгебры Ли, пер. с англ.,
М., 1964; [2] Ж е л о б е н к о Д. П., Лекции по теории групп
Ли, Дубна, 1965; [3] е г о же, Компактные группы Ли и их
представления, М., 1970; [4] Preudenthal H., «Indag.
Math.», 1954, v. 16, p. 369—76, 487 — 91; 1956, v. 18, p. 511 — 14;
E] Kostant В., «Trans. Amer. Math. Soc», 1959, v. 93,
p. 53—73. В. Л. Попов.
КРАТНОСТЬ ОСОБОЙ ТОЧКИ алгебраиче-
алгебраического многообразия — целое число, изме-
измеряющее степень особенности многообразия в этой точке.
Кратностью |х (X, х) многообразия X в точке х наз. крат-
кратность максимального идеала m в локальном кольце
Qx, х- Кратность X в точке х совпадает с кратностью
касательного конуса С(Х, х) в вершине, а также со-
степенью специального слоя а~1(х) раздутия сг: X' —у X
точки х на X, где а-1(х) рассматривается погруженным
в проективное пространство Р (m/Ш2) (см. [3]). Крат-
Кратность (х(Х, ,г)=1 тогда и только тогда, когда х неособая
(регулярная) точка X. Если X является гиперповерх-
гиперповерхностью в окрестности х (т. е. X задается одним уравне-
уравнением /=0 в аффинном пространстве Z), то fi(X, x) сов-
совпадает с числом п таким, что /?п"—nn + 1, где 11 —
максимальный идеал локального кольца Qz, x. Крат-
Кратность не меняется при пересечении X общей гипер-
гиперплоскостью, проходящей через х. Если через Xд обо-
обозначить множество точек .т?Х таких, что \i(X, x)~^d,
то Ха является замкнутым подмножеством (подмного-
(подмногообразием).
Лит.: [1] Samuel P.. Methodes d'algebre abstraite en
Seometrie algebrique, 2 ed., В., 1967; [2] Cepp Ж.-П., «Мате-
«Математика», 1963, т. 7, JMS 5, с. 3—93; [3] R a m a n u ] a m C. P.,
Invent, math.», 1973, v. 22, № 1, p. 63—67. В. И. Данилов.
КРАТНЫЙ ИНТЕГРАЛ — определенный интеграл
от функции нескольких переменных. Имеются различ-
различные понятия К. и. (интеграл Римана, интеграл Лебега,
интеграл Лебега — Стилтьеса и др.).
Кратный интеграл Римана вводится на основе Жор-
дана меры (х. Пусть Е — измеримое по Жордану мно-
множество n-мерного евклидова пространства R", (х„ есть
7г-мерная мера Жордана и т= {Е; }j=i — разбиение мно-
множества Е, т. е. такая система измеримых по Жордану
множеств Е;, что (ji=iE, = E и \in(Ei(\Ej) — 0, 1ф],
i, / = 1, 2, . . ., п. Величину
8Т = max d (Ei),
i=i, 2 *
где d (Ei) — диаметр множества Е,-, наз. мелкостью
разбиения т. Если функция f(x), х=(х1, . . ., хп),
определена на множестве Е, то всякую сумму вида
наз. интегральной суммой Римана
функции /. Если для функции / существует lim От ,
бт ->-о
независящий от разбиения, то этот предел наз. «-к рат-
ратным интегралом Римана и обозначают
Е f
или
Саму функцию / наз. в этом случае интегрируе-
интегрируемой по Р и м а н у, короче — R-u нтегрируе-
м о и.
В случае и—1 в качестве множества Е, по к-рому
производится интегрирование, обычно берется отрезок,
а в качестве его разбиений т рассматриваются разбие-
разбиения, состоящие также только из отрезков (см. Римана
интеграл). Таким образом, в этом случае как множество,
по к-рому производится интегрирование, так и элемен-
элементы разбиения представляют собой измеримые но Жор-
Жордану множества весьма специального вида — отрезки.
Поэтому не все свойства Д-интегрируемых на отрезке
функций справедливы для функции Л-интегрируемых
на произвольных нзмеримых по Жордану множествах.
Напр., из того, что любая функция, определенная на
множестве жордановой меры нуль, Л-интегрируема
на нем, следует, что Л-интегрируемые функции могут
быть неограниченными, это невозможно для Л-интег-
рируемых функций на отрезках. Чтобы из Л-интегри-
руемости функции на нек-ром множестве следовала ог-
ограниченность функции, на рассматриваемое множество
налагают дополнительные условия, напр, чтобы у него
существовали сколь угодно мелкие разбиения, все
элементы к-рых имеют положительную меру Жордана.
К таким множествам относятся все измеримые по Жор-
дану открытые множества и их замыкания, в частное! и
измеримые по Жордану области и их замыкания. Имен-
Именно для таких множеств большей частью и используется
кратный интеграл Римана.
В случае /i = 2 (n=--3) К. и. наз. двойным (т р о й-
н ы м). Поскольку кратный интеграл Римана можно
брать только по множествам, измеримым по Жордану
(в случае п =2 они наз. также к в а д р и р у е м ы м и,
а при п=3 — кубируемыми множества-
м и), то двойной (тройной) интеграл Римана рассмат-
рассматривают только на множествах (обычно областях или их
замыканиях), границы к-рых имеют площади (обьемы)
в смысле Жордана, равные нулю.
Интеграл Римана от ограниченных функций га пере-
переменных (п~^\) обладает обычными свойствами интегра-
интеграла (линейность, аддитивность относительно множеств,
по к-рым производится интегрирование, сохранение
при интегрировании нестрогих неравенств, интегри-
интегрируемость произведения интегрируемых функций и т. п.).
Кратный интеграл Римана может быть сведен к
повторному интегралу. Пусть ж=(.х', x")?R",
Е — измеримое в Rn по Жордану множество, Я(а-о) =
= Е[) {х' = х'о} — сечение множества Е (п—то)-мерной
гиперплоскостью х' = х'о, ЕХ" — проекция Е на гипер-
гиперплоскость Rm -- {х : х"=0}, причем Е(х') и Ех- изме-
измеримы соответственно в смысле (п—то)-мерной и то-мер-
ной меры Жордана. Тогда, если функция / Я-интегри-
руема на множестве Е и для всех х' ? Ех« существуют
(га—т)-кратные интегралы от ее сужения на множестве
Е(х'), то существует повторный интеграл
где внешний интеграл является m-кратным интегралом
Римана, и
Для случая п=3 отсюда следуют формулы: 1) Если
EcRxyz, Еху — проекция Е на плоскость хОу, а функ-
функции ф(х, у) И1|)(з;, у), (х, у)?Еху, таковы, что множество
Е ограничено в направлении оси z их графиками, т. е.
Е -={(х, у, z):(x, у)?Еху, ф (лг, i/)<z<\()(x, у)},
то
dxdy[f(x, v, z)dz.
Еху J<P (*</)
2) Пусть проекцией множества Е на ось Ох яиляется
отрезок [а, Ь\, а Е (.г) — сечение множества Е пло-
плоскостью, параллельной плоскости yOz и проходящей
через точку х, тогда
В случае, когда G является измеримой по Жордану
областью в пространстве R?, a x=<f(t) — взаимно одно-
значное отображение G на измеримую область Г прост-
пространства Rx, причем ф непрерывно дифференцируемо на
замыкании G области G, для интегрируемой на Г=
= ф(б) функции f(x) справедлива формула замены пере-
переменного в интеграле
где J (t) — якобиан отображения ср.
Геометрический смысл кратного интеграла Римана
от функции га переменных связан с понятием (га+1)-мер-
ной меры Жордана |xn + 1: если функция/(ж) интегрируе-
интегрируема на множестве EczR*, /(x)>0 на Я и
то
B)
Кратным интегралом Лебега наз.
Лебега интеграл от функций многих переменных, его
определение базируется на понятии Лебега меры в га-мер-
га-мерном евклидовом пространстве. Кратный интеграл
Лебега может быть сведен к повторному интегралу (см.
Фубини теорема). Для непрерывно дифференцируемых
взаимно однозначных отображений областей справед-
справедлива формула замены переменного A), а также форму-
формула B), выражающая геометрич. смысл кратного интег-
интеграла Лебега, в к-рой под мерой Lin-t-i следует понимать
(п+1)-мерную меру Лебега.
Понятие К. и. переносится на функции, интегрируе-
интегрируемые по множеству А, принадлежащему произведению
XX Y пространств X и Y, в каждом из к-рых заданы
с-конечные полные неотрицательные меры, соответст-
соответственно цх и Ну, при этом интегрирование по множеству
А производится по мере (х, являющейся произведением
мер \lx и|1}.
Для функций многих переменных существует также
понятие несобственного К. и. (см. Несобствелный ин-
интеграл). Понятие К. и. применяется также к неопреде-
неопределенным интегралам функций многих переменных. Под
неопределенным К. и. понимают функцию множества
F(E)={ f(x)dx,
где Е — измеримое множество. Если, напр., f(x) интег-
интегрируема по Лебегу на нек-ром множестве, то ее неопре-
неопределенный интеграл F(E) почти всюду на этом множестве
имеет функцию }(х) своей симметричной производной.
В этом смысле (аналогично случаю функций одной пере-
переменной) взятие неопределенного К. и. является опера-
операцией, обратной к операции дифференцирования функ-
функции множества.
Лит.: [1] И л ь и и В. А., Лозняк Э. Г., Основы мате-
математического анализа, 2 изд., ч. 2, М., 1980; [2] К о лмо го-
ров А. Н., ФоминС. В., Элементы теории функций и
функционального анализа, 5 изд., М., 1981; [31 Николь-
Никольский С. М., Курс математического анализа, 2 изд., т. 2, М.,
1975. Л. Д. Кудрявцев.
КРАТНЫЙ РЯД, s-к р а т н ьт ft p я д,— выражение
вида
составленное из членов таблицы \\ит, „,..., р\\- Каж-
Каждый член этой таблицы занумерован х^2 индексами то,
п, . . . , р, к-рые пробегают независимо друг от друга
все натуральные числа. Теория К. р. аналогична тео-
теории двойных рядов. См. также Абсолютно сходящийся
ряд.
Лит.: [1] Ф и х т е н г о л ь ц Г. М., Курс дифференциаль-
дифференциального и интегрального исчисления, 4 изд., т. 2, М., 1959.
Е. Г. Соболевская,
КРАТЧАЙШАЯ — линия в метрическом прост-
пространстве, соединяющая две его точки и не превосходя-
превосходящая по длине любую другую линию с теми же концами.
На плоскости К.— отрезки прямых, на сфере — дуги
больших полуокружностей. В римановых пространствах
геодезические линии являются К. на малых участках;
длины подобных участков оцениваются в зависимости
от кривизны и топологии пространства. Важную роль
играют К. в геометрии в целом поверхностей и метрик,
не подчиненных требованиям регулярности. Так, по-
понятие К.— одно из основных и исходных в аксиоматпч.
построениях общих пространств с внутренней метри-
метрикой; многие внутренние и внешние геометрич. характе-
характеристики общих выпуклых поверхностей устанавливают-
устанавливаются с помощью свойств принадлежащих им К. и т. п.
А. Д. Милка.
КРЕАТИВНОЕ МНОЖЕСТВО, творческое
множеств о,— рекурсивно перечислимое множест-
множество А натуральных чисел, дополнение к-рого А до нату-
натурального ряда является продуктивным множеством;
иными словами, множество А креативно, если оно ре-
рекурсивно перечислимо и существует такая частично ре-
рекурсивная функция ф (х), что для всякого содержащего-
содержащегося в А рекурсивно перечислимого множества Wx с гё-
делевым номером х
К. ы. часто встречаются в различных алгоритмически
неразрешимых проблемах, в силу чего образуют важ-
важнейший класс рекурсивно перечислимых множеств, не
являющихся рекурсивными. Креативными оказываются
множества номеров доказуемых и опровержимых фор-
формул многих формальных теорий (при естественной ну-
нумерации всех формул теории); в частности, так обстоит
дело в арифметике Пеано и вообще во всех рекурсивно'
неотделимых теориях (т. е. в теориях, множества дока-
доказуемых и опровержимых формул к-рых эффективно не-
неотделимы). Все К. м. рекурсивно изоморфны между
собой (т. е. для каждой пары К. м. существует рекур-
рекурсивное взаимно однозначное преобразование натураль-
натурального ряда, отображающее одно из них на другое) я
принадлежат одной тьюринговой степени, наибольшей
среди степеней рекурсивно перечисленных множеств.
Понятие креативности обобщается на последователь-
последовательности множеств и другие объекты.
Лит.: [1] Роджерс X., Теория рекурсивных функций
и эффективная вычислимость, пер. с англ., М., 1972; [2] III e н-
фи лд Дж., Математическая логика, пер. с англ., М., 1975.
В. А. Дутспий.
КРЕМОНОВО ПРЕОБРАЗОВАНИЕ — бйрацш-
нальное преобразование проективного пространства Р$,
п^2, над полем к. Бирациональные преобразования
плоскости и трехмерного пространства систематически
изучал (начиная с 1863) Л. Кремона (L. Cremona).
Группа К. п. также называется его именем — груп-
группа Кремоны и обозначается Сг(Р^).
Простейшими примерами К. п., отличными от про-
проективных преобразований, являются квадратичные би-
бирациональные преобразования плоскости. В неодно-
неоднородных координатах (г, у) их можно записать в виде
дробно-линейных преобразований
х ^ "i*4 Ь,г/+с, ^ a,x + bzy + cs
a2x + b2y + c2 ' а4х+Ь4У + с4
Среди них выделяется так наз. стандартное
квадратичное преобразование т:
(*. У) —
' V
или в однородных координатах
Оно является изоморфизмом вне координатных осей
имеет три фундаментальные точки (точки неопреде-
неопределенности) @, 0, 1), @, 1, 0), A, 0, 0) и отображает в
каждую из этих точек координатную ось, не содержа-
содержащую эту точку.
По теореме Нётера (см. Кремоны группа) над алгебра-
алгебраически замкнутым полем к каждое К. п. плоскости Р\
может быть представлено в виде композиции квадратич-
квадратичных преобразований.
В теории К. п. плоскости важную роль играют не-
к-рые специальные классы преобразований, в частности
инволюции Гейзера и инволюции Бертини (см. [1]).
Инволюция Гейзера а: Р\ —у Р\ опреде-
определяется с помощью линейной системы кривых степени 8
на р\, проходящих с кратностью 3 через 7 точек в об-
общем положении. Инволюция Бертини E:
Pk —у Р\ определяется с помощью линейной системы
кривых степени 17 на Pk, проходящих с кратностью 6
через 8 точек в общем положении.
К. п. вида
X *• X,
Pjx)y+Q(x) р 0 R
наз. преобразованиями Жонкьера.
Наиболее естественно они интерпретируются как бира-
тгиональные преобразования квадрики PkX Pk, сохра-
сохраняющие проекцию на один из множителей. Теорема
Нётера допускает при этом следующую переформули-
переформулировку: группа Bir(P1XP1) бирациональных автомор-
автоморфизмов квадрики порождена инволюцией о" и преобра-
преобразованиями Жонкьера, где o'gAut (РХХ Р1) — автомор-
автоморфизм перестановки множителей.
Всякий бирегулярный автоморфизм аффинного про-
пространства А\ в Pi продолжается дб К. п. пространства
Pi, так что Aut(A^)czCr(P'k). В случае га=2 группа
Aut(^l) порождена подгруппой аффинных преобразо-
преобразований и подгруппой преобразований вида
х —>¦ аж + Ь, а ф 0, с ф 0, а,
более того, она является амальгамированным произве-
произведением этих подгрупп [5]. Как устроены группы AutD?)
при га^З неизвестно. Вообще, о К. п. в размерности
п^З не получено к настоящему времени A982) сколь
либо существенных результатов.
Лит.: [1] Hudson H., Cremona transformations in plane
and space, Camb., 1927; [2] G о d e a u x L., Les transformations
birationnelles du plan, P., 1927; [3] Coble A., Algebraic geo-
geometry and theta functions, N. Y.,1929; [4] H а г а т а М., «Ма-
«Математика», 1964, т. 8, JSa 4, с. 75—94; [5] Шафаревич И. Р.,
¦«Rend, math.», 1966, v. 25, p. 208—12. В. А. Исковских.
КРЕМОНЫ ГРУППА — группа Cr{Pnk) бирацио-
бирациональных автоморфизмов проективного пространства
P'k над полем к, или, что то же, группа кремоновых пре-
преобразований пространства Р%.
Группа Сг(Р^) естественным образом содержит в ка-
качестве подгруппы группу PGL(n+l, к) проективных
преобразований пространства Р%, причем при га^2 эти
группы не совпадают. Группа Ст(Р%) будет изоморфна
группе Aut к(хх, . . . , хп) автоморфизмов над к поля
рациональных функций от п переменных над к.
Основным результатом о К. г. проективной плоскости
является теорема Нётера: группа Ct(Pk) над
алгебраически замкнутым полем порождается квадра-
квадратичными преобразованиями или, что эквивалентно,
стандартным квадратичным преобразованием и проек-
проективными преобразованиями (см. [1], [7]). Неизвестно
<A982), является ли эта группа простой. Существует
обобщение теоремы Нётера на случай, когда основное
поле к не является алгебраически замкнутым (см. [5]).
Одна из труднейших проблем бирациональной гео-
геометрии — проблема описания строения группы Сг(Р^),
к-рая уже не порождается квадратичными преобразова-
преобразованиями. Почти во всех работах о кремоновых преобразо-
преобразованиях 3-мерного пространства изучаются лишь кон-
конкретные примеры таких преобразований. О строении
К. г. пространства размерности выше 3 почти ничего
не известно.
Важное направление исследований К. г. связано с
изучением подгрупп группы Сг(Р^). С точностью до со-
сопряженности описаны конечные подгруппы в Cr(Pjt)
над алгебраически замкнутым полем к (см. [8], а также
[6]). Классификация всех инволюций вСг(Р|) получена
еще в 1877 Э. Бертини (Е. Bertini, см., напр., [4], [5]).
Вопрос об описании всех инволюций в Сг(Р&), га^З,
открыт. Все максимальные связные алгебраич. под-
подгруппы в Сг(Р|) описаны Ф. Энрикесом (F. Enriques)
в 1893 (см. [4]). Это в точности группы автоморфизмов
всех минимальных моделей рациональных поверхно-
поверхностей, т. е. плоскости Р%, квадрики ЯхР1 и серии ли-
линейчатых поверхностей Fдг, N^2. Имеются нек-рые об-
обобщения этого результата (см. [3], [9]) на случай груп-
группы Cr(Pk), га>3.
Лит.: [1] Алгебраические поверхности, М., 1965 (Тр. Матем.
ин-та АН СССР, т. 75); [2] С о b I e A., Algebraic geometry and
theta functions, N. Y., 1929; [3] Demazure M., «Ann. sci.
EC. norm, sup.», seT. 4, 1970, t. 3, № 4, p. 507—88; [4] G o-
d e a u x L., Les transformations birationnelles du plan, P.,
1927; [5] Hudson H., Cremona transformations in plane and
space, Camb., 1927; [6] Манин Ю. И., «Матем. сб.», 1967,
т. 72, №2, с. 161—92; [7] Нагата М., «Математика», 1964,
т. 8, № 4, с. 75—94; [8] W i m a n A., «Math. Ann.», 1897, Bd 48,
S. 195—240; [9] Umemura H., «Nagoya Math. J.», 1980,
v. 79, p. 47—67. В. А. Псковских.
КРИВАЯ — обычно линия вообще, не исключая и
частного случая — прямой,
КРИВИЗНА — собирательное название ряда коли-
количественных характеристик (численных, векторных,
тензорных), описывающих отклонение свойств того или
иного объекта (кривой, поверхности, риманова прост-
пространства и др.) от соответствующих объектов (прямая,
плоскость, евклидово пространство и др.), к-рые счи-
считаются плоскими. Обычно понятия К. вводятся локаль-
локально, то есть в каждой точке. Эти понятия К. связаны с
рассмотрением отклонений 2-го порядка малости, поэ-
поэтому предполагается задание изучаемого объекта С--
гладкими функциями. В ряде случаев вводят интеграль-
интегральные понятия, к-рые сохраняются и при отказе от С2-
гладкости. Как правило, тождественное обращение в
нуль К. во всех точках приводит к совпадению (на ма-
малых участках, но не в целом) изучаемого объекта с
«плоским» объектом.
Кривизна кривой. Пусть у — регулярная
кривая в ?г-мерном евклидовом пространстве, парамет-
параметризованная натуральным параметром t. Пусть далее
а(Р, Р]) и s(P, Pj) — соответственно угол между ка-
касательными к кривой у в точках Р и Рх этой кривой
и длина дуги кривой между Р и Р±. Тогда предел
*=¦- lima (Р, Px)ls(P, Px)
Р1-*Р
наз. кривизной кривой у в точке Р. К. кривой
у равна модулю вектора d2y(t)/dt2, а направление этого
вектора совпадает с направлением главной нормали
кривой. Для того чтобы кривая у совпадала с нек-рым
отрезком прямой или со всей прямой, необходимо и
достаточно, чтобы К. кривой к тождественно равнялась
нулю.
Кривизна поверхности. Пусть Ф —
регулярная поверхность в трехмерном евклидовом про-
странстве. Пусть Р — точка Ф, ТР — касательная пло-
плоскость к Ф в точке Р, п — нормаль к Ф в точке Р, а —
плоскость, проходящая через п и нек-рый единичный
вектор I в ТР. Кривая у1 , получающаяся при пересече-
пересечении плоскости а и поверхности Ф, наз. нормаль-
нормальным сечением поверхности Ф в точке Р в на-
направлении I. Величина
5*3-'
где t — натуральный параметр на кривой у, наз. нор-
нормальной кривизной поверхности Ф в на-
направлении I. С точностью до знака нормальная К. рав-
равна К. кривой у, .
В касательной плоскости Тр существуют два перпен-
перпендикулярных направления Zi и 12 такие, что нормальную
К. в произвольном направлении можно представить с
помощью так наз. формулы Эйлера:
kr = fcj cos2 0 + к? sin2 0,
где 9 — угол между 1Х и 12. Величины &х и к2, являющие-
являющиеся нормальными К. в направлениях 1Х и 12, наз. глав-
главными кривизнами, а направления 1± и 12 —
главными направлениями поверхности.
Главные К. являются экстремальными значениями нор-
нормальных К. Структуру нормальных К. в данной точке
поверхности удобно графически изображать следующим
образом. При kt фО уравнение
1
1/2
где гA) — радиус-вектор, задает в касательной пло-
плоскости ТР нек-рую кривую 2-го порядка, к-рая наз.
индикатрисой Дюпена. Индикатриса Дю-
Дюпена может быть одной из следующих трех кривых:
эллипсом, гиперболой или парой параллельных пря-
прямых. Соответственно этому точки поверхности подразде-
подразделяются на эллиптические, гиперболические и парабо-
параболические. В эллиптич. точке 2-я квадратичная форма
поверхности знакоопределенна, в гиперболической точ-
точке — знаконеопределенна, а в параболич. точке — вы-
вырождена. В случае, если все нормальные К. в точке
равны нулю, точка паз. точкой уплощения.
Если индикатриса Дюпена является кругом, то такую
эллиптич. точку наз. шаровой (или о м б и л и-
ческой) точкой.
Главные направления определены однозначно (с точ-
точностью до перенумерации) в том случае, если точка не
является шаровой точкой или точкой уплощения.
В этих случаях любое направление является главным.
Имеет место теорема Родрига, в силу к-рой
необходимым и достаточным условием того, что направ-
направление I — главное, является выполнение условия
d»==— Ыг,
где г — радиус-вектор поверхности, п — вектор еди-
единичной нормали.
Линия на поверхности наз. линией к р и в и з-
н ы, если ее направление в каждой точке является глав-
главным. В окрестности каждой точки Р поверхности, к-рая
не является шаровой точкой или точкой уплощения,
поверхность можно параметризировать так, что ее ко-
координатные линии будут линиями К.
Величина
наз. средней кривизной поверхности. Ве-
Величина
К = 1Чк2
наз. гауссовой (или полной) кривизной
поверхности. Гауссова К. является объектом внутрен-
внутренней геометрии поверхностей, т. е. может быть выраже-
выражена только через 1-ю квадратичную форму:
К. = ¦
E Eu Ev
F F F
G Gu Gv
{(-
Fv-Gu
\ A)
Veg-f* Jv \Veg~f- Jui
где Е, F, G — коэффициенты 1-й квадратичной формы
поверхности.
С помощью формулы A) гауссова К. вводится для
абстрактного двумерного риманова многообразия с ли-
линейным элементом dn2. Для того чтобы поверхность была
локально изометрична плоскости, необходимо и доста-
достаточно, чтобы ее гауссова К. была тождественно равна
нулю.
Кривизна риманова пространства.
Пусть М" — регулярное и-морное риманово простран-
пространство, ВМ'1 — пространство регулярных векторных по-
полей на Мп. К. риманова пространства М" обычно ха-
характеризуют с помощью Римана тензора, т. е. полили-
полилинейного отображения
R: ВМ" X ВМ" X ВМ" —>• ВМ",
к-рое задано соотношением
П(Х, Y)Z=?X
где у — связность Леви-Чивита; на М", [ , ) —
скобка Ли. Если в нек-рой локальной системе коорди-
координат х' положить X——г , У= —у , то формуле B) можно
Эх дх1
придать следующий вид:
Z/ k; I - % i; k =Z"flLw,
где ; — знак ковариантной производной.
Таким образом, тензор Римана является количествен-
количественной характеристикой некоммутативности вторых кова-
риантных 71роизводных в римановом пространстве.
С помощью тензора Римана количественно описывается
и ряд других свойств римановых пространств, отличаю-
отличающих их от евклидовых.
Коэффициенты тензора Римана в локальной системе
координат х1 могут быть выражены через символы Кри-
стоффеля п коэффициенты метрич. тензора следующим
образом:
эг' эг'
эг
ik 'JLa-г1 гг г1 тг
7J~ 'k~~ ' ""
»,,, — 1 / "" ' "«"» <-_rm !??_ i
\ dx Ox dx1 dx1 3x dx( Ox1 dxm J
_L „ / rP r" rP тп \
где .R/wra — тензор Римана с опущенным индексом,
или — в бескоординатных обозначениях — отображение
<R(X, Y)U, Zy (где <•, •> — знак скалярного произ-
произведения).
Тензор Римана имеет следующие свойства симметрии:
R (X, Y)Z = —R(Y, X)Z,
<Л (X, Y)Z, U> = — <Д (X, Y)U, Zy,
<Л (X, Y) Z, U> = <R (Z, U) X, У>,
R(X, Y)Z + R(Y, Z)X + R(Z, X)Y = 0,
к-рые в локальных координатах можно записать в виде
iklm-\- R imkl-\- R ilmk — Q-
Тензор Римана имеет «2(га2—1)/12 алгебраически неза-
независимых компонент. Справедливо так наз. тожде-
тождество Бьянки для ковариантных производных тен-
тензора Римана
(VVR)(Y,Z, U) + (vvR) (Z, X, U) + {\7R){X,Y, U) = 0,
где (A^R)(Y, Z, U) — ковариантная производная
R (Y, Z)U no X. В локальных координатах это тождест-
тождество имеет вид
Rlkl; т + Rlmk; I + Ritm; k = 0.
Иногда тензор Римана определяют с обратным знаком.
Необходимым и достаточным условием локальной
изометричности риманова пространства евклидову яв-
является равенство нулю его тензора Рпмана.
Используют и иной, эквивалентный подход к описа-
описанию свойств К. риманова пространства М". Пусть а —
двумерное линейное пространство касательного прост-
пространства ТМ" к М" в точке Р. Тогда секционной
кривизной Мп в точке Р в направлении о наз.
величина
<Л (V, W) W, V>
<V, Vy <W, Wy- <y, W>2 '
где V и W — векторы, определяющие а. Одна и та же
площадка а может определяться разными векторами V
и W, однако Kg не зависит от выбора различных векто-
векторов, определяющих одну и ту же площадку. Для дву-
двумерного риманова пространства секционная К. совпа-
совпадает с гауссовой К. Тензор Римана может быть восста-
восстановлен по секцпонным кривизнам следующим образом:
<R(X, Y)Z, U> = ^-
— k(X + U, Z) — k(X,Y + Z) — k(U, Y + Z) + k(X, Z) +
+ k(U, Y)-k(Y+U, X + Z)^k(Y + U, X) +
+ k(Y+U, Z) + k{Y, Z + X) +
+ k{U, Z+X)-k(Y, Z)-k(U, X)},
где
к (V, W)=Ko«V, Vy<\V, W>-<F, Wy-).
Используют и менее детальные характеристики К. ри-
риманова пространства — тензор Риччи:
и скалярную кривизну, или кривизну
Риччи:
k
Тензор Риччи симметричен: Rik=Rki-
Иногда для характеристики К. употребляют п более
сложные, в частности квадратичные, конструкции, по-
построенные из тензора Рпмана. Одним из наиболее упо-
употребительных инвариантов такого рода является инва-
инвариант
= HklmRi '
используемый при изучении поля тяготения Шварц-
шильда.
Для двумерного пространства тензор Римана имеет
вид
R(X, Y)Z = K«Y, Z>X — (X, Z>Y), C)
где К — Гауссова К. В этом случае кривизна Рпччи
равна К. Для трехмерного пространства тензор Римана
имеет вид
R iklm = RilSkm — R im8kl-\- ^-kmSil —
+ (
где gjj— метрический тензор, R,-j — тензор Риччи,
li — кривизна Риччи.
В том случае, если секционные К. не зависят ни от
точки, ни от двумерного направления, пространство
Мп наз. пространством постоянной
кривизны; тензор Римана такого пространства
имеет вид C) (константа К наз. кривизной про-
пространства М"). При га>2 оказывается, что если
во всех точках К. не зависят от направления, то прост-
пространство Мп является пространством постоянной К.
(теорема Шура).
Кривизна подмногообразий. Пусть
Ф — регулярная поверхность в Ел, у — кривая на Ф,
ар — касательная плоскость к Ф в точке Р, через к-рую
проходит кривая у. Пусть малая окрестность точки Р
проектируется на плоскость а.р п пусть у — проекция
кривой у на плоскость ар. Геодезической кривизной и
кривой у в точке Р наз. число, равное по модулю К.
кривой у в точке Р. Геодезическая К. считается положи-
положительной, если вращение касательной кривой у при про-
прохождении точки Р образует с направлением нормали к
поверхности правый винт. Геодезическая К. является
объектом внутренней геометрии поверхности Ф. Геоде-
Геодезическая К. может быть вычислена по формуле
( d2xl d*xJ i dxk dxl dx1 \
*= dS2 /'' dxi Jwt . D>
\8i; ~dTUs~J
где x'(s) — натуральное уравнение кривой у в локаль-
локальных координатах х' на Ф, g[j — компоненты метрич.
тензора поверхности Ф в этих координатах, Y\i— сим-
символы Кристоффеля, eij — вполне дискримннантный тен-
тензор. С помощью формулы D) вводится понятие геодези-
геодезической К. для кривой на абстрактном двумерном рима-
новом пространстве. Необходимым и достаточным ус-
условием того, что кривая на римановом многообразии
совпадает с геодезической или с ее отрезком, является
тождественное равенство нулю геодезической К.
Пусть Ф — двумерное подмногообразие трехмерного
риманова пространства М. К определению К. для Ф
можно подойти двумя способами. С одной стороны, мож-
можно рассматривать Ф как риманово пространство, метри-
метрика к-рого индуцирована метрикой М, и определить его
К. по формуле A). Полученная таким образом К.
наз. внутренней кривизной. С другой сто-
стороны, можно провести построение, приводящее к поня-
понятию К. для поверхности в евклидовом пространстве и
для подмногообразия риманова пространства. В резуль-
результате получается иное понятие К.; эта К. наз. вне ш-
н е й кривизной. Справедливо следующее соот-
соотношение:
где Кс — К. пространства М в направлении касатель-
касательной плоскости к Ф.
Понятия нормальной, внешней и внутренней К. до-
допускают обобщение на размерности и коразмерности
изучаемого подмногообразия.
Понятие тензора Римана обобщено на ряд прост-
пространств, имеющих менее сильные структуры, чем рима-
риманово пространство. Напр., тензоры Римана и Риччн
зависят лишь от аффинной структуры риманова прост-
пространства и могут быть введены и для пространства аф-
аффинной связности (однако в этом случае тензоры Рима-
Римана и Риччи обладают не всеми свойствами симметрии).
Напр., Й1кфЙк1. Другими примерами такого рода яв-
являются тензор конформной К. и тензор проективной К.
Тензор конформной кривизны (тен-
(тензор Вопля) имеет вид
ciklm = "-iklm "¦UiSk'i
где квадратные скобки означают альтернацию по за-
ключенным в них индексам. Равенство нулю тензора
конформной К. является необходимым и достаточным
условием того, что данное пространство локально сов-
совпадает с конформно-евклидовым пространством. Тен-
Тензор проективной кривизны имеет вид
где 67 — символ Кронекера, п — размерность про-
пространства. Равенство нулю тензора проективной К.
является необходимым и достаточным условием
того, что данное пространство локально совпадает с
проективно-евклидовым пространством.
Понятие К. обобщено на случай нерегулярных объек-
объектов, в частности на случай теории двумерных многооб-
многообразий ограниченной кривизны. К. в пространстве здесь
рассматривается не в точке, а в области, и говорят о
полной, или интегральной, кривизне области. В регу-
регулярном случае полная К. равна интегралу от гауссовой
К. Полная К. геодезич. треугольника может быть вы-
выражена через углы Р,- при вершинах этого треугольника
соотношением
А" = 2 Pi-л. E)
являющимся частным случаем Гаусса — Бонне теоре-
теоремы. Формула E) была положена в основу определения
полной К. для многообразий ограниченной К.
Понятие К. является одним из основных понятий сов-
современной дифференциальной геометрии. Ограничения
на К. дают обычно содержательную информацию об
объекте. Так, в теории поверхностей Е3 знак гауссо-
гауссовой К. определяет тип точки (эллиптический, гипербо-
гиперболический, параболический). Поверхности с всюду не-
неотрицательной гауссовой К. обладают целым набором
общих свойств, к-рые позволяют объединять их в один
естественный класс (см. [4]; [6]). Много специфических
свойств имеют поверхности нулевой средней К. (см.
Минимальная поверхность). В теории нерегулярных
поверхностей специально изучают классы поверхностей
ограниченной интегральной абсолютной гауссовой или
средней К.
В римановых пространствах равномерное ограниче-
ограничение секционных кривизн Ко пространства в любой его
точке и любом двумерном направлении позволяет ис-
использовать теоремы сравнения. Последние позволяют
сравнивать скорость расхождения геодезических и объ-
объемы областей в рассматриваемом пространстве с харак-
характеристиками соответствующих линий и областей в
пространстве постоянной К. Некоторые из ограниче-
ограничений на А'а даже предопределяют топологпч. строение
пространства в целом. Например.
Теорема о сфере. Пусть М полное односвяз-
ное рнманово пространство размерности п^2 и х/4<
<6<А'о <:1. Тогда М гомеоморфно сфере S".
Теоремы Ада мара — Картана и Г р fl-
flit о л а — М а й е р а. Пусть М полное риманово про-
пространство размерности п~^2. Если всюду Кс <0 и М
односвязно или всюду Ко >0 и М некомпактно, то М
гомеоморфно евклидову пространству Е".
Понятия К. используются в различных естественных
науках. Так, при движении тела по траектории с ее К.
связана центробежная сила. Гауссова К. возникла в
связи с. работами К. Гаусса (К. Gauss) по картографии.
Со средней К. поверхности жидкости связан капилляр-
капиллярный эффект. В относительности теории с распределе-
распределением вещества и энергии (точнее, с тензором энергии-
импульса) связана К. пространства-времени (см. Прос-
Пространство-время). Тензор конформной К. находит
применение в теории рождения частиц в гравитацион-
гравитационном поле.
Лит.: [1] Р а ш е в с к и й П. К., Риманова геометрия и
тензорный анализ, 3 изд., М., 1967; [2] II о г о р с л о в А. В.,
Дифференциальная геометрия, 5 изд., М., 1969; [3J Бляш-
Бляшке В., Дифференциальная геометрия..., пер. с нем., т. 1, М.—
Л., 1935; [4] Александров А. Д., Внутренняя геометрия
выпуклых поверхностей, М.— Л., 1948; [5] Г р о м о л Д.,
К л'и нгенберг В., М е й е р В. Риманова геометрия
в целом, пер. с нем., М., 1971; [б] ПогореловА. В.,
Внешняя геометрия выпуклых поверхностей, М., 1969.
Д. Д. Соколов.
КРИВИЗНЫ ЛИНИЙ СЕТЬ — ортогональная сеть
на гладкой гиперповерхности Vn-\ евклидова прост-
пространства Еп(п^3), образованная кривизны- линиями.
К. л. с. на Fn_i является сопряженной сетью. Напр.,
на поверхности вращения V2cE3 меридианы и парал-
параллели образуют К. л. с. Если на гладкой р-мерной по-
поверхности VpCzEn B<:p<re) задано поле одномерных
нормалей такое, что нормаль [х, то] этого поля принад-
принадлежит дифференциальной окрестности 2-го порядка
точки x?Vp, то относительно этого поля нормалей на
Vр определяются линии кривизны и К. л. с. точно так-
также, как и на \Тп-\. Но К. л. с. на Vp(p<Cn—1), вообще
говоря, не является сопряженной.
Лит.: [1] Э й з е н х а р т Л. П., Риманова геометрия,
пер. с англ., М., 1948; [2] Ш у л и к о в с к и й В. И., Класси-
Классическая дифференциальная геометрия в тензорном изложении,
М. 1963. В. Т. Базылев.
КРИВИЗНЫ ЛИНИЯ — линия на поверхности, в
каждой точке к-рой касательная имеет одно из главных
направлений. К. л. определяется уравнением
dv2 —dudv du-
Е F G
L M jy
= 0,
где E, F, G — коэффициенты первой, a L, M, N — коэф-
коэффициенты второй квадратичных форм поверхности.
Нормали поверхности вдоль К. л. образуют разверты-
развертывающуюся поверхность. На поверхностях вращения
К. л.— меридианы и параллели. К. л. развертываю-
развертывающейся поверхности — ее прямолинейные образующие
и линии, ортогональные к ним. а. Б. Иванов
КРИВИЗНЫ ПРЕОБРАЗОВАНИЕ — отображение
R {X, Y) пространства $~(М) векторных полей на мно
гообразии М, линейно зависящее от X, Y?<0~(М) и
задаваемое формулой
R(X, Y)Z=--VxvvZ-VrVxZ~Vix,YiZ;
здесь \7„ — ковариантная производная вдоль X,
[X, Y] -— коммутатор X и Y. Отобраягенпе
ость кривизны тензор определяемой у линейной связ-
связности, м. И. Войцеховспий.
КРИВИЗНЫ ТЕНЗОР — тензор типа A,3), получаю-
получающийся в разложении кривимы формы в локальном ко
базисе на многообразии М". В частности, в голономно.м
кобазисе dx', г=1, . . . , п, компоненты К. т. Ищ аф-
аффинной связности выражаются через объекты связно-
, сти Тij и их производные
/[/ ' // / a ~т~ ip ji jp и*
Аналогично определяется К. т. для произвольной связ-
связности на главном расслоенном пространстве со струк-
структурной группой Ли G через разложение соответствую-
соответствующей формы кривизны, в частности для конформной
связности и проективной связности. Оп принимает
значения в алгебре Ли группы G и представляет собой
пример так наз. тензоров с нескалярными компонен-
компонентами. М. И. Войцеховспий.
Лит. см. при ст. Кривизна.
КРИВИЗНЫ ФОРМА — 2-форма Q на главном
расслоенном пространстве Р со структурной группой
Ли ?, принимающая значения в алгебре Ли g группы
G и определяемая связности формой 0, заданной на Р,
по формуле
dQ = dQ +-1 [6, 6].
К. ф. является мерой отклонения данной связности от
локально плоской связности, к-рая
характеризуется условием Q=0. К. ф. удовлетворяет
тождеству Бланки
dQ=\Q, 6]
и определяет алгебру голономии (см. Голоиомии группа).
Ю. Г. Лумисте.
КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ — интеграл по
кривой. Пусть в re-мерном евклидовом пространстве R"
задана спрямляемая кривая y={x=x(s), 0<:s<:5},
х=(хг, . . . , хп), s — длина дуги и на кривой у задана
функция F= F(x(s)). К. и.
F (x) ds
У
определяется равенством
F (х (s)) ds A)
(справа — интеграл по отрезку) и наз. к р и в о л и-
нейным интегралом первого рода,
или криволинейным интегралом по
длине дуги. Он является пределом соответствую-
соответствующих интегральпых сумм, к-рые могут быть описаны в
терминах, связанных с кривой. Напр., если функция
F(x(s)) интегрируема по Риману (см. Римана инте-
интеграл), т= {s;}Т=о — разбиение отрезка [0, 5], бт =
= max (s[—s,-_i) — его мелкость, 5/?[si-i, si), As,=
i=l,2,...,n
=s,-—s,-_i— длина части кривой у от точки x(.s,-_i) до
точки x(sj), i=l, 2, . . . , m, и
огт=У F(x(l;))Ash
*~^i= 1
TO
\ F (x) ds— lim a .
Если спрямляемая кривая у задана параметрическим
представлением х= х(t)= (<fi(t), . . . , <pn(t)), a<:<<:fe,
и на ней задана функция F= F(x(t)), то интеграл
С F(x)dxk, fc=l, 2, . . ., га,
J v
определяется равенством
\h F (x(t)) dyk (t) B)
(справа — Стилтпъеса интеграл) и наз. к р н в о л и-
нейным интегралом второго рода,
или криволинейным интегралом по
координате х^. Он также является пределом
соответствующих интегральных сумм: если т= ¦'
разбиение отрезка [а, Ъ], r>,-?U,_i, ?,], Аж/;; =
?= 1,2,... т, и
то
1 F (ж) d.r^ = lim
Если i7 — непрерывная на спрямляемой кривой функ-
функция, то К. и. A) и B) всегда существуют. Если А —
начало, а В — конец кривой у, то К. и. A) и B) обозна-
обозначаются также через
f F (х) ds и С F (х) dxk.
•JAB •> АВ
К. и. первого рода не зависит от ориентации кривой:
„F(i)ii!=[ F (x) ds,
В А •> АВ
а К. и. второго рода меняет знак при изменении ориен-
ориентации кривой:
F(x)dxk = ~ С F(x)dxk.
A -JAB
Если 7 — непрерывно дифференцируемая кривая,
x(t)=D>i(t), ¦ ¦ ¦ , Фп@) — ее непрерывно дифференци-
дифференцируемое представление, a<:i<:b, и F — непрерывная на
7 функция, то
2mdk=l [ч'к1
, * = 1, 2, ..., и,
и тем самым интегралы, стоящие в правой части этих
равенств, не зависят от выбора параметра на кривой у.
Если t=(cos cxj, . . . , cos а„) — единичный касатель-
касательный вектор к кривой у, то К. и. второго рода выражает-
выражается через К. и. первого рода но формуле
F (х) dxk = ^ F (x) cos ак ds.
Если кривая у задана векторным представлением
r(t)=(fpi(t), . . . , ц>п(ф, a a(x(t))=(a1(x(t)), . . . ,
an(x(t))) — векторная функция, определенная на у, то,
по определению,
\ a(x)dr=\ (а. %) ds—\ \ ак(х) dxk.
Связь между К. и. и интегралами других видов устанав-
устанавливается Грина формулой и Стокса формулой.
С помощью К. и. можно вычислять площади плоских
областей: если конечная плоская область G ограничена
спрямляемым простым контуром у, то ее площадь равна
mesG=\ xtdx2 = — \ x2dx1 = —\ x1dxi — ,r2dx1,
J V J V l J V
где контур у ориентирован против часовой стрелки.
Если вдоль кривой у распределена нек-рая масса М
с линейной плотностью р(х), то
М=[ p{x)ds.
Если F (x) — напряженность силового поля (т. е. сила,
действующая на единицу массы), тогда
J,
_ F (x) dr
равен работе силового поля вдоль кривой 7 при переме-
перемещении вдоль 7 единичной массы.
К. н. используются в теории векторных полей. Если
непрерывное векторное поле а = а(х)=(а1(х), . . . ,
ап(х)) определено на нек-рой га-мерной области G, ге>1,
то следующие три свойства эквивалентны.
1) Для любой замкнутой спрямляемой кривой yCzG
справедливо равенство
\ а (х) dr = О
(векторное поле, обладающее этим свойством, наз. по-
потенциальным).
2) Для любой пары точек A?G, B^G и для любых
i двух спрямляемых кривых (АВ)г, (АВJ с началом в точ-
ке А и концом в точке В:
\ ^ a(x)dr=\ a(x)dr.
3) В области G существует такая функция и (х) (назы-
(называемая потенциальной функцией векторного поля «(ж)),
что уи(х) = а (х), т. е. ди (x)/dx^=ati(x), ?=1,2, ... , п,
при этом для любых А , В ?G и любой кривой JG
С a(x)dr = u(B)-u(A).
•> АВ
Если гс—2 или га=3 и область б1 односвязна при п=2
и поверхностно односвязна при га=3, а поле а(х) не-
непрерывно дифференцируемо, то свойства 1) — 3) экви-
эквивалентны следующему свойству.
4) Вихрь векторного поля в области G равен нулю:
rota (ж) = 0, z?G.
Если условие односвязности области G не выполнено,
то свойство 4) не эквивалентно, вообще говоря, свойст-
свойствам 1) — 3). Напр., для поля
а(хи
определенного на плоскости с выброшенным началом
координат, имеем rot a{x) = 0, хфО, но
Лит.: [1] Ильин В. А.,Позняк З.Г., Основы мате-
математического анализа, 2 И8Д., ч. .2, М., 1980; [2] Кудряв-
Кудрявцев Л. Д., Курс математического анализа, т. 2, М., 1981;
[3J Никольский С. М., Курс математического анализа,
2 изд., т. 2, М., 1975. Л. Д. Кудрявцев.
КРИПКЕ МОДЕЛИ — структуры, состоящие из
нек-рого множества обычных моделей для классической
логики, упорядоченных между собой нек-рым отноше-
отношением, и служащие для интерпретации в них различных
неклассических логик (интуиционистской, модальных
л др.). Точнее, К. м. для языка L имеют вид
K=(S, R, D, W),
где 5 — некоторое непустое множество («миров», «си-
«ситуаций»); R — некоторое бинарное отношение на S
(напр., для системы / интуиционистской логики R
является частичным порядком, для модальной системы
54 — нредпорядком, для системы S5 — отношением
эквивалентности); отображение D сопоставляет каждо-
каждому a?S нек-рую непустую область Da так, что если
ai?P, то .Da<=Dp; оценка W сопоставляет всякой инди-
индивидной константе а элемент W [а] ? П a 6 я^сч вгякой ин-
индивидной переменной х— элемент W(x)? Uaes^a> Для
каждого a?S всякой пропозициональной переменной
р — истинностное значение \?а(р)?{Ш, Л} (для сис-
системы / требуется также, чтобы если аЯр и И/а(р) = И,
то Wfi(p)=H), всякой re-местной (п^1) предикатной
константе Р — некоторое подмножество Wa(P)'={Da)"
[для системы /, если аЛ|5, то Wa(P)^W$ (P)], всякой
«-местной функциональной константе / — функцию
Wad) из (Da)" в Da [для системы /, если аЯ|5, то Waif)
есть ограничение VFp (/) на Da].
Для всяких a?S и формулы А языка L такой, что
для любой свободной переменной х в A W{x)?Da,
индуктивно определяется истинностное значение
WaG4)G {И, Л }. Для системы / значение Wa(A) опре-
определяется следующим образом:
а) если А — элементарная формула, то значение
Wa(A) уже задано моделью;
б) Wa(B&C)=H t; (Wa(B)=H и Wa(C)=H);
Ht^(Wa.(B)=Vi. или Wa(C) = tt);
г) Wa(BZ)C)=J/i t^. (для всякого fi?S, если аЯВ и
p(B) = ll, то И^(С)=И);
д) ^а(~|5)=И t^ (для всякого Рб'5, если а/?В, то
(В) Л)
р() );
о) Wa(VxB)=M t^ (для
если айВ и ГН^р, то
ж) WaCx5) = H t^ (существует W' = W такое, что
W'(x)?Da и Wa(B) = H) (здесь W'=W означает, что
оценка W совпадает с W всюду, кроме, быть может, на
ж). Иногда вместо И/«(Л) = И пишут а\=-А.
Для модальных логик определение Wa(A) в случаях
(г), (д) и (ж) происходит иначе:
г') Wa(BzDC)=ll X (W E)=Л или Wa(C)=U);
д') WanS)=ntZ Wa(B)=J[;
ж') Wa(VxB)=H t^ (для всякого W'=W, если
то И^(В)=И);
кроме того, добавляется
з) Wa(OB)=VL t; (для всякого #?.5, если ссйВ, то
(B) U)
p() )
Формула А наз. истинной в К. м. K=(S, R, D,
W) (пишут К \=А), если Wa(A) = V. для всякого a?S.
Для каждой из систем /, S4, S5 справедлива теоре-
теорема о полноте: всякая формула выводима в этой
системе тогда и только тогда, когда она истинна во всех
К. м. из соответствующего класса. Существенно, что
области Da являются, вообще говоря, различными, по-
поскольку формула
где х но входит свободно в А , не выводима в системе /,
но истинна во всех К. м. с постоянной областью. Сис-
Система, полученная из / добавлением схемы (*), полна
относительно К. м. с постоянной областью (см. [4]).
Пропозициональный фрагмент каждой из систем /,
SA, S5 является финитно аппроксимируемым, т. е. вся-
всякая невыводимая в нем формула опровержима на
нек-рой конечной К. м. из соответствующего класса.
Понятие «К. м.» родственно понятию вынуждения
(см. Вынуждения метод). К. м. введены С. А. Крипке
(S. A. Kripke).
Лит.: [1] К р и п к е С. А., Семантический анализ модаль-
модальной логики, в кн.: Ф е й с Р., Модальная логика, пер. с англ.,
М., 1974, с. 254—323; [2] Шютте К., Полные системы мо-
модальной и интуиционистской логики, там же, с. 324—421; [3]
G б г d е г m а n n S., «J. Symb. Logic», 1971, v. 36, p. 249—61;
[4] К о э н Пол Дт., Теория множеств и континуум-гипо-
континуум-гипотеза, пер. с англ., М., 1969. С. Я. Соболев.
КРИСТАЛЛОГРАФИЧЕСКАЯ ГРУППА — дискрет-
дискретная группа движений n-мерного евклидова пространст-
пространства Е", имеющая ограниченную фундаментальную об-
область. Две К. г. считаются эквивалентными,
если они сопряжены в группе аффинных преобразова-
преобразований пространства Е".
Происхождение теории К. г. связано с изучением
симметрии орнаментов (п=2) и кристаллических струк-
структур (га=3). Классификация всех плоских (двумер-
(двумерных) и пространственных (трехмерных)
К. г. была получена в конце 19 в. Е. С. Федоровым и
несколько позже А. Шёнфлисом (см. [2], [3], а также
[6], [7], [9]). С точностью до эквивалентности имеется
17 плоских и 219 пространственных К. г.; если же рас-
рассматривать пространственные группы с точностью до
сопряженности при помощи аффинных преобразова-
преобразований, сохраняющих ориентацию, то их будет 230.
В 1910 Л. Бибербахом были исследованы К. г. в про-
произвольной размерности [4]. Он доказал, в частности,
следующие теоремы.
1) Всякая га-мерная К. г. Г содержит п линейно не-
независимых параллельных переносов; группа G линей-
линейных частей преобразований из Г конечна. (Для п=3
это было доказано в [3].)
2) Две К. г. эквивалентны тогда и только тогда, ког-
когда они изоморфны как абстрактные группы.
3) При любом п имеется лишь конечное число п-мер-
ных К. г., рассматриваемых с точностью до эквивалент-
эквивалентности (что является решением 18-й проблемы Гильбер-
Гильберта).
Теорема 1) позволяет дать следующее описание строе-
строения К. г. как абстрактных групп. Пусть L — совокуп-
совокупность всех параллельных переносов, принадлежащих
К. г. Г. Тогда L — нормальная подгруппа конечного
индекса, изоморфная %п и совпадающая со своим цент-
централизатором в Г. Наличие такой нормальной подгруппы
L в абстрактной группе Г является и достаточным ус-
условием того, чтобы группа Г была изоморфна К. г. [7].
Группа G линейпых частой К. г. Г сохраняет решетку
L; иными словами, в базисе решетки L преобразования
из G записываются целочисленными матрицами.
Для того чтобы задать К. г. Г, нужно, помимо Git L,
указать для каждого g?G такой вектор a(g), что преоб-
преобразование
принадлежит группе Г. Вектор a (g) определен с точ-
точностью до прибавления вектора из L. Отображение
a:g \—>a {g)+L
является одномерным коциклом на G со значениями в
V/L, где V — векторное пространство, ассоциирован-
ассоциированное с Еп.
Любая тройка {G, L, а}, где GcGL(F) — конечная
линейная группа, L — G-пнвариантная решетка па —
одномерный коцикл на G со значениями в V/L, соответ-
соответствует указанным образом нек-рой К. г. При этом трой-
тройки {G, L, ах} и {G, L, а2}, где ах и а2 — когомологичиые
коциклы, соответствуют эквивалентным К. г. Нулевому
классу когомологий соответствует расщепляе-
расщепляемая (пли с и м м о р ф н а я) К. г., к-рая, при под-
подходящем выборе начала отсчета, состоит из всех преоб-
преобразований вида
g?, ?
В матричной интерпретации описание всех ?г-мерных
К. г. сводится к описанию всех конечных групп цело-
целочисленных матриц порядка п (с точностью до сопряжен-
сопряженности в группе GLn(g)) и, для каждой такой группы G,
к вычислению группы когомологий ff1(G, R"/gn).
Двум классам когомологий отвечают эквивалентные
К. г. тогда и только тогда, когда они переводятся друг
в друга нормализатором группы G в GLn(Z). Теорема
2) Бибербаха и результат X. Цассенхауза [7] означают,
что естественный гомоморфизм
является изоморфизмом. Это легко может быть выведе-
выведено из точной последовательности когомологнй груп-
группы G.
Две К. г. относятся к одному классу (соответст-
(соответственно арифметическому классу), если
их группы линейных частей сопряжены в GL,,(R)
(соответственно в GLn(Z))- При ге=3 имеется 32 класса
п 73 арифметических класса К. г.
Среди конечных групп целочисленных матриц можно
выделить группы симметрии решеток, т. е. группы всех
ортогональных преобразований, сохраняющих какую-
либо заданную решетку в векторном пространстве (и
записанных в базисе этой решетки). В 1848 О. Браво
(A. Bravais) определил все возможные группы симмет-
симметрии 3-мерных решеток и разбил в соответствии с этим
все 3-мерные решетки на 44 типов (так наз. типы
Б р а в е). Подгруппы группы GLn(g), являющийся
группами симметрии решеток, наз. подгруппами
Б р а в е.
Подгруппы Браве можно интерпретировать также
как стационарные подгруппы для естественного дейст-
действия группы GLn(g) на множестве положительно опре-
определенных квадратичных форм от п переменных. Поэтому
для их нахождения может быть использована теория
приведения (см. [11]). Всякая максимальная конечная
подгруппа группы GLnB) является подгруппой Браве
(но не наоборот).
Приводимая таблица дает число конечных подгрупп
в группе GLn(^) (рассматриваемых с точностью до
сопряженности).
п
1
2
3
4
5
Число макси-
максимальных конеч-
конечных подгрупп
1
2
4
9
17
Число
подгрупп
Браве
1
5
14
64
?
Число конечных
подгрупп
2
13
73
710
Пересечение подгрупп Браве также есть подгруппа
Браве. Наименьшая подгруппа Браве G, содержащая
группу G линейных частей К. г. Г и рассматриваемая с
точностью до сопряженности в GLn(R) (соответственно
в GLn(Z)), наз. геометрической (соответст-
(соответственно арифметической) голоэдрией
группы Г. Если Г — К. г. общего положения
в том смысле, что ее нельзя аффинным преобразованием
перевести в К. г., решетка параллельных переносов
к-рой обладает меньшей симметрией, то G совпадает с
группой симметрии решетки параллельных переносов
группы Г. Две К. г. относятся к одной сингонии
(соответственно типу Браве), если их геометри-
геометрические (соответственно арифметические) голоэдрии сов-
совпадают. При 71 — 3 имеется 7 сингонии и 14 типов Браве
крнсталлографич. групп.
Линейные представления К. г. Не-
Неприводимые конечномерные комплексные линейные
представления К. г. Г описываются следующим обра-
образом. Пусть % — какой-либо характер (гомоморфизм в
мультипликативную группу комплексных чисел) груп-
группы L,
и а — такое неприводимое представление группы Гх,
что a(l) = %(l)-i при l?L. Тогда представление группы
Г, индуцированное представлением а подгруппы Гх
(см. Индуцированное представление), ноприводимо.
Всякое неприводимое представление группы Г полу-
получается описанным способом (см. [9], [10]).
Лит.: [1] Браве О., Избр. научные труды, Л., 1974,
с. 41 —138; [2] Ф е д о р о в Е. С, Симметрия и структура крис-
кристаллов. Основные работы, М., 1949, с. 111 — 255; [3] S с h о е п-
flies A., Kristallsysteme und Kristallstruktur, Lpz., 1891;
[4] В 1 e b e г b а с h L., «Math. Ann.», 1911, Bd 70, S. 297—336;
1912, Bd 72, S. 400—12; [5] Д е л о н е В., Па Дуров Н.,
Александров А., Математические основы структурного
анализа кристаллов..., Л.— М., 1934; [61 Ш у б и и к о в А. В.,
Атлас кристаллографических групп симметрии, М.—Л., 1946; [7]
Zassenhaus H., «Comm. math, helv.», 1948, v. 21, p. 117—
141; [8] M а л ь ц е в А. И., Избр. труды, т. 1— Классическая
алгебра, М., 1976, с. 371—75; [9] Л ю б а р с к и й Г. Я., Тео-
Теория групп и ее применение в физике, М., 1957; [10] Фадде-
Фаддеев Д. К., Таблицы основных унитарных представлений федо-
федоровских групп, М.— Л., 1961; [И] Д е л о н е Б. Н., Гали у-
л и н Р. В., Ш т о г р и н М. И., в кн.: Итоги науки и техни-
техники. Современные проблемы математики, т. 2, М., 1973, с. 119—
254. Э. Б. Винберг.
КРИСТАЛЛОГРАФИЯ МАТЕМАТИЧЕСКАЯ — со-
совокупность методов описания внешних форм кристал-
кристаллов и их внутреннего пространственного строения.
В основе К. м. лежит представление об упорядоченном
трехмерно периодическом расположении в кристалле
составляющих его частиц, к-рые образуют кристаллич.
решетку. Выросшие в равновесных условиях кристаллы
имеют форму правильных выпуклых многогранников
той или иной симметрии. Группы симметрии классифи-
классифицируют: по числу п измерений пространства, в к-ром
они определены; по числу т измерений пространства,
в к-рых объект периодичен (их соответственно обозна-
обозначают Gm) и по нек-рым другим признакам. Для описа-
описания кристаллов используют различные группы симмет-
симметрии, из к-рых важнейшими являются пространственные
группы Gg, описывающие атомную структуру кристал-
кристаллов, и точечные группы симметрии Go, описывающие их
внешнюю форму.
Операциями точечной группы симметрии
являются: повороты вокруг оси симметрии порядка N
на 360сМг, отражение в плоскости симметрии (зеркаль-
(зеркальное отражение), инверсия / (симметрия относительно
точки), инверсионные повороты N (комбинация поворо-
поворота на 360°/iV с одновременной инверсией). Вместо ин-
инверсионных поворотов иногда рассматривают зеркаль-
зеркальные повороты N. Число групп Go бесконечно. Однако в
кристаллах ввиду наличия кристаллич. решетки воз-
возможны только операции и соответственно оси симмет-
симметрии до 6-го порядка (кроме 5-го), к-рые обозначаются
символами 7, 2, 3, 4, 6, а также инверсионные оси: /
(она же центр симметрии), 2=т (она же плоскость сим-
симметрии, 3, 4, 6). Количество точечных кристаллографич.
групп, описывающих внешнюю форму кристаллов, ог-
ограничено: 32 группы.
Группы, содержащие лишь повороты, описывают
кристаллы, состоящие только из совместимо равных
частей. Эти группы наз. группами 1-го рода. Группы,
содержащие отражения, или инверсионные повороты,
описывают кристаллы, в к-рых есть зеркально равные
части (но могут быть и совместимо равные части). Эти
группы наз. группами 2-го рода. Кристаллы, описывае-
описываемые группами 1-го рода, могут кристаллизоваться в
двух энантиоморфных формах, условно наз. «правой»
и «левой», каждая из них не содержит элементов сим-
симметрии 2-го рода, но они зеркально равны друг другу.
Многие свойства кристаллов, принадлежащих к опре
деленным классам, описываются предельными
точечными группами, содержащими оси
симметрии бесконечного порядка. Наличие такой оси
означает, что объект совмещается с собой при по-
повороте на любой, в том числе бесконечно малый угол.
Таких групп семь.
Пространственная группа симметрии
кристаллич. решетки описывается группами G%. Ха-
Характерными для решетки операциями являются три
некомпланарных переноса а, Ь, с, к-рыо отвечают трех-
трехмерной периодичности атомной структуры кристаллов.
Вследствие возможности комбинирования в решетке
трансляций и операций точечной симметрии в группах
С% возникают операции и соответствующие элементы
симметрии с трансляционной компонентой — винто-
винтовые оси различных порядков и плоскости скользящего
отражения.
Всего известно 230 пространственных (федоровских)
групп симметрии G%, и любой кристалл относится к од-
одной из этих групп. Трансляционные компоненты эле-
элементов микросимметрии микроскопически не проявля-
проявляются; поэтому каждая из 230 групп G% макроскопиче-
макроскопически сходственна с одной из 32 точечных групп. Сово-
купность переносов, присущих данной пространствен-
пространственной группе, есть ее трансляционная подгруппа, пли
решетка Враве; таких решеток существует 14.
См. также Кристаллографическая группа.
Лит.: [1] Шубников А. В., Флинт Е. Е., Б о-
к и й Г. Б., Основы кристаллографии, М.— Л., 1940; [2] Ф с-
доров Е. С, Симметрия и структура кристаллов, [М.],
1949; [3] Ш а с к о л ь с к а я М., Кристаллы, м., 1959.
По материалам ст. Симметрия кристаллов
из БСЭ-3.
КРИСТОФФЕЛЯ СИМВОЛ дифференциаль-
дифференциальной квадратичной формы
— символ для сокращенного обозначения выражения
Символ Yk ij наз. К. с. 1-го рода, в отличие от К. с.
2-го рода Г ? у, определяемого соотношением
где gkt определяется из равенств
1, если t = s,
3, если t Ф s.
К. с. введен Э. Кристоффелем (Е. Christoffe], 1869).
КРИСТОФФЕЛЯ ЧИСЛА, К р и с т о ф ф е л я
коэффициенты,- коэффициенты к^ квадратур-
квадратурной формулы
точной для алгебраич. многочленов степени <;2ге—1.
Узлы Xfr такой квадратурной формулы являются нуля-
нулями многочлена рп(х) степени п, ортогонального на [а, 6]
относительно распределения da (x) всем многочленам
степени п—1; если Xi<x2<. . .<х„, то К. ч. определя-
определяются однозначно. К. ч. Л^>0, 2^=1Xj. = aF) — a(a) и
), k=i,2, ..., п.
Если многочлены рп(х) ортонормированны, то К. ч.
представимы в виде
1 ¦ ¦ ¦ +Рп (xk), к=1, 2, ..., п,
¦, к= 1,2, ..., га,
1-1 Рп-1 (X
где Х„ — старший коэффициент многочлена р„(х).
В случае а= — 1, 6=1 и da(x)=dx pn{x) являются Ле-
жандра многочленами, а К. ч.
Эти выражения указаны 0. Кристоффелем [1]. Для
гс=1, 2, . . . , 7 эти коэффициенты были вычислены
К. Гауссом (С. Gauss). См. также Гаусса квадратурная
формула.
Лит.: [1] Christoffe] Б. В., «J. reine und angew.
Math.», 1858, Bd 55, S. 61—82; L2] Сегё Г., Ортогональные
многочлены, пер. с англ., М., 1962; [3] Натансон И. П.,
Конструктивная теория функций, М.— Л., 1949.
Н. П. Корнейчук, В. П. Моторный.
КРИСТОФФЕЛЯ — ДАРБУ ФОРМУЛА для много-
многочленов {Рп(х)}, ортонормированных с интегральным ве-
сом da(x) на некотором интервале (а, Ъ),— формула
вида
г (x)Pn(t)-Pn(x)Pn
где \in — старший коэффициент многочлена Рп(х)-
К.— Д. ф. применяется при исследовании условий схо-
сходимости рядов Фурье по ортогональным многочленам в
отдельной точке. К.— Д. ф. в случае, когда а(х) сту-
ступенчатая функция, была опубликована П. Л. Чебышо-
вым в 1855 (см. [1J). Затем Э. Кристоффель [2] устано-
установил ее для Лежандра многочленов, а Г. Дарбу [3] распро-
распространил эту формулу на общий случай произвольного
веса.
Лит.: [1] Ч е б ы ш е в П. Л., Поли. собр. соч., т. 2, М.,
1947, с. 103—106; [2] Chris toff el Е. В., «J. reine und
angew. Math.», 1858, Bd 55, S. 61—82; [3] D a r b о u x M. G.,
«J. math, pures et appl.», 1878, ser. 3, t. 4, p. 5—56, 377—416.
См. также лит. при статье Ортогональные многочлены.
П. К. Суетин.
КРИСТОФФЕЛЯ — ШВАРЦА ФОРМУЛА — фор-
формула
дающая интегральное представление функции /(z),
конформно отображающей верхнюю полуплоскость
Im z>0 на внутренность ограниченного многоуголь-
многоугольника с вершинами А^ и углами эта^ при вершинах @<
<ccfe<2, k=i, . . . , п). При этом z0, с, с1 — некоторые
постоянные, ^4fc=/(«ft), &=1, . . . , п. Постоянную z0
можно фиксировать произвольно в верхней полупло-
полуплоскости. Тройку точек из аи . . . , ап, напр. %, а2, а3,
можно задавать произвольно; остальные п—3 точки а#,
а также постоянные с, с1 определяются однозначно, если
вершины Аи . . . , Ап многоугольника заданы (см. [3]).
Формула (*) была получена независимо Э. Кристоффе-
лем A867, см. [1]) и Г. Шварцем A869, см. [2]). Инте-
Интеграл в правой части (*) наз. интегралом Кри-
стоффеля — Шварца.
Основная трудность при применении формулы (*)
состоит в нахождении неизвестных параметров. При
/г>4 общие методы неизвестны.
Разработаны методы приближенного отыскания пара-
параметров К.— Ш. ф. (см. [4], [5]).
К.— Ш. ф. остается справедливой и для многоуголь-
многоугольников, у к-рых одна или несколько вершин лежат в бес-
бесконечно удаленной точке. В этом случае угол между
сторонами многоугольника в бесконечности определяет-
определяется как угол, взятый со знаком минус, между этими же
сторонами или их продолжениями в конечной точке.
Если прообраз а, одной из вершин многоугольника на-
находится в бесконечно удаленной точке, то соответствую-
соответствующий множитель (t—ai)ai~1 в формуле (*) выпадает.
К.— Ш. ф. справедлива также для функции, отобра-
отображающей единичный круг |г| <1 на рассмотренный выше
многоугольник. В этом случае |о^| = 1, к=1, ... , п,
|zo|«:l. Видоизменения этой формулы охватывают слу-
случаи отображения верхней полуплоскости, а также вну-
внутренности и внешности единичного круга на внешность
многоугольника (см. [3]).
К.— Ш. ф. обобщена на случай, когда функция f(z)
конформно отображает круговое кольцо 0<g<|z|<l
или, в более общем случае, многосвязную область, со-
состоящую из круга с выброшенными из него п кругами,
на область соответствующей связности, ограниченную
многоугольниками (см. [6], [7]).
Лит.: [1] Chris toff el E. В., «Arm. math, pura ed
appl.», Ser. 2, 1868, t. 1, p. 89—103; 1871, t. 4, p. 1—9; [2]
Schwarz H. A., Gesammelte mathematische Abhandlungen,
Bd 1—2, В., 1890; [3] Л а в р е н т ь е в М. A., HI а б а т Б. В.,
Методы теории функций комплексного переменного, 4 изд., М.,
1973; [4] К а н т о р о в и ч Л. В., Крылов В. И., При-
ближенные методы высшего анализа, 5 изд., М.— Л., 1962;
[5] К о и п е н ф е л ь с В., ШтальманФ., Практика кон-
конформных отображений, пер. с нем., М., 1963; [6] А х и е-
зер Н. И., Элементы теории эллиптических функций, 2 изд.,
М., 1970; [7] Максимов Ю. Д., «Докл. АН СССР», 1960,
т. 136, JV» 2, с. 284—87. Ю. Д. Максимов.
КРИТИЧЕСКАЯ ОБЛАСТЬ — часть выборочного
пространства такая, что попадание в нее наблюденного
значения случайной величины, с распределением к-рой
связана проверяемая гипотеза, влечет отказ от этой
гипотезы. Пусть нужно проверить гипотезу Но о рас-
распределении случайной величины X, принимающей зна-
значения в выборочном пространстве (!', 2д). При по-
построении нерандомизированного критерия для провер-
проверки гипотезы Но пространство Ж разбивают на два^е-
пересекающихся множества К я К таких, что К[)К=
= S, i??5B. При этом критерий проверки представляет
собой правило, согласно к-рому гипотеза Но отклоняет-
отклоняется, если в результате эксперимента окажется, что реа-
реализация х случайной величины X попадает в множество
К, в противном случае (т. е. при х?К) гипотезу Но
следует принять. Множество К наз. К. о. критерия, а
его дополнение К — областью принятия гипотезы.
В этом смысле задача выбора К. о. эквивалентна по-
построению нерандомизировашюго статистич. критерия
для проверки гипотезы Но. Естественно, что К. о. выби-
выбирается до проведения эксперимента, связанного с про-
проверкой гипотезы #0, а сам выбор К. о. в рамках теории
Неймана — Пирсона определяется вероятностями оши-
ошибок первого и второго рода, возникающими в задачах
статистич. проверки гипотез.
Лит.: [1] Крамер Г., Математические методы статисти-
статистики, пер. с англ., 2 изд., М., 1975; [2] Л е м а н Э., Проверка ста-
статистических гипотез, пер. с англ., 2 изд., М., 1979; [3] В ан-
дер-Варден Б. Л., Математическая статистика, пер. с
нем., М., 1960. М. С. Никулин.
КРИТИЧЕСКАЯ ТОЧКА — 1) К. т. порядка т —
такая точка а комплексной плоскости, в к-рой аналитич.
функция /(z) регулярна, а ее производная /'(z) имеет
нуль порядка т., где т. — натуральное число. Иными
словами, К. т. определяется условиями:
Бесконечно удаленная К. т. а= оо порядка т для
функции/(z), регулярной в бесконечности, определяет-
определяется условиями:
lim [f(z)-f(ao)]z>"=0, lim [/ (z)-/ (oo)] z» + i фО.
При аналитическом отображении w=f(z) угол между
двумя кривыми, выходящими из К. т. порядка т, уве-
увеличивается в m-\-i раз. Если функция /(z) рассматри-
рассматривается как комплексный потенциал нек-рого плоского
течения несжимаемой жидкости, то К. т. характерна
тем, что через нее проходит не одна, а т+1 линий
тока, причем скорость течения в К. т. обращается в
нуль. Для обратной функции z=ty(w) такой, что
/ [i|;(ii>)]=ii>, К. т. а является алгебраич. точкой ветвле-
ветвления порядка т+1.
2) Точка а комплексного (п—т)-мерного неприво-
неприводимого аналитического множества
M = {z?V; /i(z) = /2(z)=...=/m(z)=0},
заданного в окрестности V точки а комплексного прост-
пространства С" условиями /1(z)=/2(z)=. . ¦=fm(z)=O, где
/ii /2» • ¦ • i fm — голоморфные на V функции п комп-
комплексных переменных, z=(zl, z2, . . . , zn), наз. К. т.,
если ранг матрицы Якоби \\dfjldz^\\, j—i, . . . , m;
k=i, ... , n, меньше числа т.. Прочие точки М наз.
правильными. К. т. на Я сравнительно мало —
они образуют аналитическое множество комплексной
размерности не выше п—т—1. В частности, при то=1,
т. е. если Af={/1(z) = O} и размерность М равна ге—1,
размерность множества К. т. не выше п—2.
Лит.: [1] Гур ввц А., Курант Р., Теория функ-
функций, пер. с нем., М., 1968; 12] Шабат Б. В., Введение в
комплексный анализ, 2 изд., М., 1976. Е. Д. Соломенцев.
3) К. т. гладкого (т. е. непрерывно диффе-
дифференцируемого) отображения / к-м е р н о г о
дифференцируемого многообразия
М в 1-м е р н о е дифференцируемое мно-
многообразие N — такая точка хо^М, что ранг
RkXo/ отображения / в этой точке (т. е. размерность об-
образа df(TXoM) касательного пространства к М под
действием дифференциала df : ТХйМ —>- Тf(x^N) мень-
меньше I. Совокупность всех К. т. наз. критическим
множеством, образ / (х0) К. т. х0— критиче-
критическим значением, а точка y?N, не являющаяся
образом никакой К. т.,— регулярной т о ч-
к о й, или регулярным значением (хотя
она может вообще не принадлежать образу j(M)); не-
некритические точки из М тоже наз. регулярными.
Согласно теореме Сарда, если / имеет класс
гладкости Cm, m>min(k—l, 0), то образ критического
множества имеет первую категорию в N (т. е. является
объединением не более чем счетной системы нигде не
плотных множеств) и имеет Z-мерную меру нуль (см.
[1], [2]). Условие на т не может быть ослаблено [3].
Чаще всего бывает нужен случай т= оо (при этом
доказательство упрощается, см. [4]). Эта теорема широ-
широко используется для приведения в общее положение
посредством «малых шевелений»; напр., с ее помощью
легко доказать, что если в R™ имеются два гладких под-
подмногообразия, то сколь угодно малым сдвигом одного
из них можно достичь, чтобы их пересечение тоже было
подмногообразием (см. [2], [4], а также Трансверсаль-
Трансверсальность отображений).
Согласно приведенному определению, при к<1 каж-
каждую точку хо(~М надо считать критической. Но при этом
существенно различаются свойства тех точек х0, для
к-рых Rkxo/=/c, и тех, для к-рых Rkxo/</c. В первом
случае в нек-рой окрестности точки х0 отображение
/ выглядит приблизительно как стандартное вложение
R* в R'; точнее, имеются такие локальные координаты
xj, . . . , Z? вблизи х0 (на М) я уг, . . . , уг вблизи f (х0)
(на N), что в этих координатах / представляется в виде
Во втором случае образ окрестности точки х0 может
не быть многообразием, а иметь различные особенно-
особенности — заострения, самопересечения и т. д. Поэтому оп-
определение К. т. часто модифицируют, понимая под
К. т. те точки х0, для которых RkXo/ < min (к, I);
соответственно модифицируется и смысл других приве-
приведенных выше терминов [5].
Поведение отображений в окрестности К. т. изучает-
изучается в теории особенностей дифференцируемых отобра-
отображений (см. [5], [6]). При этом рассматриваются не про-
произвольные К. т. (о к-рых мало что можно сказать), а
К. т., удовлетворяющие условиям «не слишком силь-
сильной вырожденности» и «типичности». Так, рассматри-
рассматриваются К. т. достаточно гладких отображений или се-
семейств отображений (достаточно гладко зависящих от
конечного числа параметров), являющиеся «неустрани-
«неустранимыми» в том смысле, что при малом (в смысле Ст с под-
подходящим т) возмущении исходного отображения или
семейства у возмущенного отображения (семейства) в
нек-рой окрестности исходной К. т. имеется К. т. того
же типа. Для отображения М —>- R (т. е. обычной ска-
скалярной функции; в этом случае К. т. часто наз. ста-
стационарными точками) типичными в указан-
указанном смысле являются так наз. невырожденные
К. т., в к-рых гессиан — невырожденная квадратичная
форма. О типичных К. т. для семейства функций см.
[6], [7].
Лит.: [llSard A., «Bull. Amer. Math. Soc», 1942, v. 48,
p. 883—90; L2] С т е р н б е р г С, Лекции по дифференциаль-
дифференциальной геометрии, пер. с англ., М., 1970; L3] Whitney Ы.,
«Duke Math. J.», 1935, v. 1, J4S 4, p. 514—17; 14] M и л н о р Д ж.,
Топология с дифференциальной точки зрения, в кн.: М и л-
норДж., Уоллес А., Дифференциальная топологии.
Начальный курс, пер. с англ., М., 1972; [5] Г о л у б и ц к и й М.,
Гийемин В., Устойчивые отображения и их особенности,
пер. с англ., М., 1977; [6] Б р ё к е р Т., Л а н д е р Л., Диф-
Дифференцируемые ростки и катастрофы, пер. с англ., М., 1977;
[7] Арнольд В. И., «Функцион. анализ и его прилож.»,
1972, т. 6, № 4, с. 3—25. Д. В. Аносов.
КРИТИЧЕСКАЯ ФУНКЦИЯ — статистика, значе-
значения к-рой суть условные вероятности отклонения про-
проверяемой гипотезы при заданном значении результата
наблюдения. Пусть X — случайная величина, прини-
принимающая значения в выборочном пространстве (!', 58),
распределение вероятностей к-рой принадлежит семей-
семейству {Ре }, 0€®1 и пусть проверяется гипотеза На:
0?восв против альтернативы #х: 6^в1=в\ви.
Далее, пусть на ЗЕ задана измеримая функция <р(-'
такая, что 0<:ф(х)<:1 при всех ж?ЗЕ. Если для провер-
проверки гипотезы воспользоваться рандомизированным кри-
критерием, согласно к-рому гипотеза Но отвергается с ве-
вероятностью ф(х), когда в результате эксперимента уста-
установлено, что Х = х, и принимается с вероятностью
1—ф (х), то функция ф (•) наз. К. ф. этого критерия. При
построении нерандомизированного критерия К. ф. вы-
выбирают так, чтобы она принимала только значения О
и 1. В этом случае К. ф. является индикатором нек-рого
множества К?$В, называемого критической областью
критерия, т. е. ф(ж)=1 при х?К и ф(ж) = 0 при х (? К.
Лит.: [1] Леман Э., Проверка статистических гипотез,
пер. с англ., 2 изд. М., 1979. М. С. Никулин.
КРИТИЧЕСКИЙ ИДЕАЛ — простой идеал дедекин-
дова кольца А, делящий дискриминант конечного се-
парабельного расширения К/k, где к — поле частных
кольца А. К. и. и только такие идеалы разветвлены в
расширении К/к. Простой идеал р кольца А наз. раз-
разветвленным в К /к, если в целом замыкании В
кольца А в поле К имеет место равенство
где Sgj., • • • 1 *$s — некоторые простые идеалы кольца
В и хотя бы одно из чисел /; больше 1. Число Z,- наз.
индексом ветвления идеала $$,-.
Если К/к — расширение Галуа с группой Галуа
G(Klk), то i1=J2=- • - = ls и индекс I; совпадает с поряд-
порядком подгруппы инерции Т(ф,) группы
G(K/k):
Т ($i) = {o?G (К/к)\оа-а?$; для всех а
Другой, более тонкой характеристикой ветвления
является подгруппа высшего ветвле-
ветвления Т(Ц${)пс:Т(tyi), re=l, 2, ... , определяемая
следующим образом:
Т №i)n = {o?G (К/к)\о (a)-a€ffl+1 для всех а?В}.
Пусть А = Z ; согласно теореме Минковс-
к о г о в любом конечном расширении поля рациональ-
рациональных чисел Q существуют К. и. Для произвольных полей
алгебраич. чисел это не так: если поле к не одноклас-
сно, т. е. имеет нетривиальную группу классов идеалов,
то над к существуют неразветвленные рас-
расширения, т. е. расширения, не имеющие критич.
идеалов. Пример такого расширения —• гильбертово
поле классов поля к: так, поле Q ( Y~5^ У—5) совпадает
с гильбертовым полем классов поля Q (У—5) и не раз-
разветвлено над полем Q ( У—5).
Лит.: [1] Б о р е в и ч 3. И., Шафаревич И. Р.,
Теория чисел, 2 изд., М., 1972; [2] Алгебраическая теория чисел,
пер. с англ., М., 1969; [3] Ленг С, Алгебраические числа,
пер. с англ., М., 1966. л: В. Кузьмин.
КРИТИЧЕСКИЙ УРОВЕНЬ — дополнение крити-
критической функции до единицы. Пусть для проверки нек-рой
гипотезы Но относительно распределения вероятностей
случайной величины А' применяется критерий, осно-
основанный на статистике Т (X), функция распределения
к-рой при гипотезе //0 есть G(t). Если критич. область,
соответствующая данному критерию, задается неравен-
неравенством вида T(X)>t, то К. у. выражается формулой
1G {Т(Х)}
Лит.: II] Ломан Э., Проверка статистических гипотез,
пер. с англ., 2 изд., М., 1979; [2] Гаек Я., Ш и д а к 3., Теория
ранговых критериев, пер. с англ., М., 1971. М. С. Никулин.
КРИТИЧЕСКОЕ ЗНАЧЕНИЕ — значение дифферен-
дифференцируемого отображения в критической точке.
КРОНЕКЕРА МЕТОД — метод разложения много-
многочлена с рациональными коэффициентами на неприводи-
неприводимые множители над полем рациональных чисел; пред-
предложен в 1882 Л. Кронекером [1]. Пусть d — общий зна-
знаменатель всех коэффициентов многочлена ср(ж). Тогда
f(x)=d<p(x) — многочлен с целыми коэффициентами;
причем из любого разложения ф (х) на неприводимые
множители с рациональными коэффициентами можно
получить разложение f{x) на неприводимые множители
с целыми коэффициентами, множители к-рого отлича-
отличаются от соответствующих множителей ф (х) лить по-
постоянными множителями, и обратно.
Пусть / (х) имеет степень п>0 л к — наибольшее на-
натуральное число, для к-рого к<.п12. Если f(x)-—g(x)X
Xh(x) — разложение f(x) на множители с целыми ко-
коэффициентами, где степень g(x) не больше степени h(x),
то степень g(x) не превосходит к. Давая х любые ft-f-1
различных иелых значений х=с;, г=1, 2, ... , &+1,
получают равенства
1(ci)=g(ci)h(Ci), j = l, 2, ..., ft+1,
где g(cj) и h(c[) — целые числа. Таким образом, g(c,-)
делит /(с,-). Беря произвольные делители dj чисел /(с,),
получают
g{ci) = dh г = 1, 2, ..., k + i.
Из этих равенств многочлен g (x) находится по интер-
интерполяционной формуле Лагранжа или проще — из урав-
уравнений для коэффициентов. Найденный многочлен g(x)
надо испытать, проверив, делит ли он f(x). Это построе-
построение многочлена и проверка проводятся для всевозмож-
всевозможных наборов делителей чисел /(с,-).
Далее этот же процесс применяется к g(x) и h(x)
и т. д., пока не приходят к неразложимым множителям.
К. м. приводит к громоздким вычислениям. Для уп-
упрощения можно сначала понизить степень /(х), выделив
его рациональные корни (см. [3] с. 355).
Пример. f(x) = xb—xi—2хъ—ва^+баг—1 (это мно-
многочлен с целыми коэффициентами и без рациональных
корней). Если f(x)=g(x)h(x), где степень к многочлена
g(x) не больше степени h(x), то 2<fc<s/2, т. е. fc=2.
Пусть Cl=0, с2=1, с3=2. Тогда /@)-=1; f(l)=—5;
/B)= — 21. Делители этих чисел: ^=±1, d2= — i, ±5,
rfs= —1, —3, ±7, ±21. Всего получается 2 -4 -8=64 ком-
комбинации. Две комбинации d,-, отличающиеся лишь зна-
знаком, дают два многочлена ±g(j). Поэтому можно про-
проверять лишь #@) = -|-1. Остаются 32 случая. Перебирая
все эти случаи, можно найти лишь один многочлен
2-й степени, делящий /(.г). Это g(z) = z2—Зх+1. Откуда
/(х) = (х2—Зх-(-1)(х3-|-2г2-г За- — 1). Оба сомножителя
этого разложения неприводимы (как многочлены 2-й
и 3-й степеней, не имеющие рациональных корней).
Лит.: [1] Kronecker L., «J. reine und angew. Math.»,
1882, Bd 92, S. 1 — 122; [2] О к у н е в Л. Я., Высшая алгебра,
М. 1937; [3] К у р о ш А. Г., Курс высшей алгебры, 11 изд.,
М. 1975. И. В. Ироспуряпов.
КРОНЕКЕРА СИМВОЛ — величина б/, определяе-
определяемая равенствами
6, A, если| = /,
' \0, если г ^ /.
При 1<;г, /<ге К. с. 6/ имеет га2 компонент, матрица
к-рых |]6/|| является единичной. К. с. введен Л. Кроне-
кером (L. Kronecker, 1866).
Обобщением К. с. является совокупность величин
ty,\ )l '".}Р< имеющих 2р целых (верхних и нижних)
индексов, га, гр = 1, 2, ... , п, равных +1 (или —1),
если строка индексов (iu i2, ... , ip) — четная (нечет-
(нечетная) перестановка строки различных индексов (/ь /2,
, )р), и нулю — во всех остальных случаях. Числа
2 через е]1 '")р)
наз. компонентами К. с. Аффинный тензор
типа (р, р), имеющий в нек-ром базисе компоненты, рав-
равные компонентам К. с, имеет те же самые компоненты
в любом другом базисе.
К. с. удобен в различных задачах тензорного ис-
исчисления. Напр., определитель
а\ а\ ... с
6j" '"jp (часто обозначаемые при
П
. ап
равен сумме
4 elll2 . ¦ • 1П 1 2 n
^- 12 ... n tj i2 ' in'
в к-рой суммирование производится по всем га! пере-
перестановкам чисел 1, 2, . . . , п. Операция альтерниро-
альтернирования тензора {аа' '¦ аР, 1<ау<:п} имеет вид
„[а, ... ар] = J_^_ 6а, ... аРан ... 1р.
Лит.: [1] Kronecker L., Vorlesungen iiber die Theorie
der Determinanten, Lpz., 1903. Л. П. Купцов.
КРОНЕКЕРА ТЕОРЕМА: пусть даны «, = («,,,
. . . , ain)?Rn, г=1, . . . , т, и Ь=(Ьи . . . , bn)?R";
для того чтобы при любом е>0 существовали целые чис-
числа <37, г=1, ... , »г, и ру, /=1, ... , п, такие, что
< е, 1 </<ге,
необходимо и достаточно, чтобы для любых таких
ги ¦ ¦ ¦ > Г«€ 2, что
'/=1
., m,
J-* 1=1
также было целым. Эта теорема была доказана в 1884
Л. Кронекером (см. [1])..
К. т. является частным случаем следующей теоремы,
описывающей замыкание подгруппы тора Tn=RnllZn,
порожденной элементами e,-+Z", *=1, . . . , т: это
замыкание состоит в точности из таких классов
что для любых чисел rt, ... , тп?_% таких, что
i = i, ¦ ¦¦, п,
выполнено
В условиях К. т. указанное замыкание совпадает со
всем Тп. Это означает, что подгруппа элементов вида
плотна в Т", а подгруппа векторов вида
где
где p?zn, плотна в R". К. т. можно вывести из теории
двойственности для коммутативных топологических
групп [3].
В случае т=1 К. т. превращается в следующее
утверждение: для того чтобы класс co+Z", где со=
— (toi, . . . , (i)n)?R", порождал Тп как топологич.
группу, необходимо и достаточно, чтобы числа 1, щ,
... , й)„ были линейно независимы над полем Q рацио-
рациональных чисел. В частности, тор Тп как топологич.
группа монотети чей, т. е. порождается одним
элементом.
Лит.: [1] К г о п е с к е г L., Werke, Bd 3, Halbbd 1, Lpz.,
1899; [2] Бур баки Н., Общая топология. Топологические
группы. Числа и связанные с ними группы и пространства, пер.
с франц., М., 1969; [3] ПонтрягинЛ. С, Непрерывные
группы, 3 изд., М., 1973. А. Л. О пищик.
КРОНЕКЕРА ФОРМУЛА — формула, выражающая
алгебраич. сумму значений нек-рой функции на мно-
множество корней системы уравнений; установлена Л. Кро-
некером [1], [2]. Пусть F1(xx, . . . , хп), t=Q, 1, ... , п,
fix1, . . . , хп) — действительнозначные непрерывно
дифференцируемые в R" такие, что система уравнений
Fs ix1, ...,*»)= О, s = l, ..., п, A)
имеет конечное число корней. Пусть уравнение
F0 (а-1, . .., х")=0
определяет замкнутую поверхность Р, не проходящую
через корни системы A), и /1°<0 внутри Р. Если функ-
функции Fs, s=l, ... , я, рассматриваются как кол!поненты
векторного поля в пространстве R", то его особые точ-
точки (по определению) соответствуют корням системы A).
Пусть ха — некоторый корень, a %ixa) — индекс этой
особой точки. Тогда
— У
к it 7
J Я><0
dV
X (л-а) =
o = 0 QR"
dS
B)
(суммирование по всем корнял1), где К'1 — объем еди-
единичной сферы Sn~x,
Л =
F\
in
Fn
г n
D =
F° Fi
F1 f\
и для функции Ф через Ф,- обозначены ее производные
дФ/дх'. формула B) и есть формула Кроне-
Кронекера.
При /=1 пространственный интеграл в B) исчезает,
и получается выражение для суммы индексов %р особых
точек векторного поля {Fs}, расположенных внутри
поверхности Р, т. е. для степени отображения поверх-
поверхности Р в сферу S"*1, определяемого как ограничение
на множество Р отображения FS=FS/R,s=i, ... , re.
При нек-рых дополнительных условиях величина %р
равна так наз. характеристике Кронекера системы функ-
функций F\ Я, ... , F" (см. [3]).
Лит.: [1] К г о п е с к е г L., «Monatsbericht», 1869, S.159—
19.9, С88—98; [2] его же, там же, 1878, S. 95—121; [3] Ч е-
таев Н. Г., Устойчивость движения. Работы по аналитиче-
ской механике, М., 1962, с. 273—313; L4J Пуанкаре А.,
О кривых, определяемых дифференциальными уравнениями,
пер. с франц., М.—Л., 1947. М. И. Войцеховский.
КРОНЕКЕРА — КАПЕЛЛИ ТЕОРЕМА, к р и т е-
рий совместности системы линейных
уравнений: для совместности системы уравнений
«22^2 + • ¦ • + а2пхп = 62,
необходимо и достаточно, чтобы ранг матрицы А —
= ||а(-у|| из коэффициентов при неизвестных был равен
рангу расширенной матрицы А, получающейся из мат-
матрицы А добавлением столбца, свободных членов Ь;.
У Л. Кронекера эта теорема содержится в его лек-
лекциях, читавшихся в Берлинском университете в 1883—
1891 (ом. [1]). Л. Капелли, по-видимому, впервые дал
приведенную выше формулировку теоремы с использо-
использованием термина «ранг матрицы» (см. [2]).
Лит.: [1] К г о п е с k e r L., Vorlesungen iiber die Theorie
der Determinanten, Lpz., 1903; [2] С a p e 1 1 i A., «Revista di
Matematica», 1892, v. 2, p. 54—58; 13] Курош А. Г., Курс
высшей алгебры, 11 изд., М., 1975. И. В. Проскуряков.
КРОНЕКЕРОВО ПРОИЗВЕДЕНИЕ колец, ал-
алгебр — то же, что их тензорное произведение.
КРУГ — часть плоскости, ограниченная окружнос-
окружностью и содержащая ее центр. Площадь К.: «?=лг2, где
г — радиус окружности.
КРУГ КРИВИЗНЫ, окружность к р и в и з-
н ы,— окружность, имеющая с кривой в данной точке
соприкосновение не ниже 2-го порядка. Центр К. к. наз.
центром кривизны кривой в точке соприкос-
соприкосновения, а радиус К. к.— радиусом к р и в и з-
н ы. К. к. располагается в соприкасающейся плоскости
кривой. . бсэ-з
КРУГ СХОДИМОСТИ степенного ряда
fW = Yt°° си(*~*Г A)
— круг вида A={z: |z—a|</?}, z?C, в к-ром ряд A)
абсолютно сходится, а вне его, при \z—а|>Л, расхо-
расходится. Иными словами, К. с. А есть внутренность мно-
множества точек сходимости ряда A). Радиус R К. с. наз.
радиусом сходимости ряда A). К. с. может
вырождаться в точку а, когда Л = 0, и может совпадать
со всей открытой плоскостью переменного z, когда R =
=^00. Радиус сходимости R равен расстоянию от центра
ряда а до множества особых точек функции / (z) (об оп-
определении R по коэффициентам ряда с& см. Коши —
Адамара теорема). Любой круг Д= {z: |z|</?}, 0<:i?<:
<:оо, на плоскости z является К. с. нек-рого степенного
ряда.
В случае степенного ряда
/(*)=/(«!, ...,*„) =
по нескольким комплексным переменным zlt . . . , zn,
и>1, поликругом сходимости ряда B) наз. всякий по-
поликруг
An = {z-—(z1, . . ., z,,): | zv — av | < Rv, v = 1, . . ., n}
такой, что во всех его точках ряд B) абсолютно сходит-
сходится, а в любом поликруге вида
{z = (zu ..., zn): | zv — ov| < Rv, v = l, ...,/;},
где Rv^Rv и по крайней мере одно из последних не-
неравенств строгое, найдется хотя бы одна точка, в к-рои
ряд B) расходится. Радиусы Rv , v=l, . . . , n, 0-<i?v ¦<
<:oo, поликруга сходимости наз. сопряженными
радиусами сходимости ряда B). Они связа-
связаны определенным соотношением с коэффициентами ряда
B), так что любой поликруг с центром а, радиусы к-ро-
го удовлетворяют этому соотношению, является поли-
поликругом сходимости ряда B) (см. Коши — Адамара
теорема). Любой поликруг вида Д„, 0</?v<oo, v=l,
... , п, в комплексном пространстве С" есть поликруг
сходимости нек-рого степенного ряда по п комплексным
переменным. Вся внутренность множества точек абсо-
абсолютной сходимости ряда B) при ге>1 имеет более слож-
сложный вид — это логарифмически выпуклая полная крат-
кратно круговая область пространства С" с центром а.
Лит.: [1] Маркушевич А. И., Теория аналитических
функций, 2изд., т. 1, М., 1967; [2] Ш а б а т Б. В., Введение в
комплексный анализ, 2 изд., ч. 1, М., 1976. Е. Д. Соломенцее.
КРУГА ПРОБЛЕМА — проблема наилучшей асимп-
тотич. оценки числа А (х) целых точек (и, v) в круге
243 Пусть 0 — нижняя грань числа а в равенстве
А (х)
К. Гаусс (см. [1]) доказал, что Q^U- В. Серпиньский
[2] по методу Г. Ф. Вороного [3] установил, что B-^Vg.
Последней A982) является оценка в<:13/41| (см. [4]). Су-
Существует гипотеза, что остаточный член в формуле (*)
есть
Среднее значение для К. п.:
где С — некоторая абсолютная постоянная, е>0 —
любое.
К. п. по содержанию и методам исследования во мно-
многом аналогична проблеме делителей Дирихле (см. Дели-
Делителей проблемы). Обобщением К. п. является проб-
проблема шара — проблема оценки В (х) — числа це-
целых точек (и, v, w) в таре M2+i;2+uJ<:a;. Исходной для
оценки является формула
B(x) = 2AG(x)+O(V'lc),
где
к-рая получается за счет разбиения шара шестью пло-
плоскостями
u=v, u = w, v — w, v = 0, u=0, w = 0
на 24 части, имеющие одинаковое число целых точек,
если считать точки на плоскостях сечений с коэффици-
коэффициентами 1/2. Главный член роста В (х) равен объему шара
проблема сводится к оценке Р(х)=В(х)—V(x) — вели-
величины суммы дробных долей функций, стоящих под зна-
знаком [ ] в выражении для G(x). Наиболее глубокие
оценки для Р (х) получены на основе метода тригоно-
метрич. сумм И. М. Виноградовым [5], [6]:
Существует гипотеза, что
Обобщением К. п. и проблемы шара является пробле-
проблема оценки Af(x) — числа целых точек в n-мерных эл-
эллипсоидах
F{ux, ..., ии)=^" v = 1 arv
где F — положительно определенная квадратичная
форма (см. [7]).
Лит.: [1] G a u s s С. F., Werke, Bd 2, Gottingen, 1863,
S. 269—91; [2] S i e г p i n s k i W., «Prace Mat.— Fiz.», 1906,
t. 17, p. 77—118; [3] Вороной Г. Ф., Собр. соч., т. 1, К.,
1952, с. 5; [4] X у а Л о - г е н, Метод тригонометрических сумм
и его применения в теории чисел, пер. с нем., М., 1964; [ft]
Виноградов И. М., «Изв. АН СССР. Сер. матем.», 1963,
т. 27, № 5, с. 957—68; [6] е г о же, Особые варианты метода
тригонометрических сумм, М., 1976; [7] Novak В., Lattice
points in moredimensional ellipsoids, «Тр. матем. ин-та АН
СССР», 1973, т. 132, с. 145—50. А. Ф. Лаврип.
КРУГОВАЯ СИММЕТРИЗАЦИЯ — геометрическое
преобразование открытого (замкнутого) плоского мно-
множества G относительно луча X с началом в точке Р во
множество G*, определяемое следующими условиями: 1)
пересечение G* с нек-рой окружностью с центром в Р
пусто или состоит из всей этой окружности, в зависимо-
зависимости от того, является ли пересечение G с выбранной ок-
окружностью соответственно пустым или совпадающим
со всей окружностью; 2) если пересечение G и окружно-
окружности с центром в точке Р имеет угловую меру Лебега Ф,
то пересечение этой окружности с G* состоит из откры-
открытой (замкнутой) дуги, пересекающей X, симметричной
относительно X и видимой из Р под углом, равным Ф.
Определение К. с. естественным образом переносится
на пространственный случай (симметризация
относительно полуплоскост и). См.
также Симметризация.
Лит.: [1] Полна Г., Сеге Г., Изопериметрические
неравенства в математической физике, пер. с англ., М., 1962;
[2] Хейман В. К., Многолистные функции, пер. с англ.,
М., 1960; [3]Дженкинс Д ж., Однолистные функции и кон-
конформные отображения, пер. с англ., М., 1962.
И- П. Митюк.
КРУГОВОЕ ПОЛЕ, поле деления круг а,—
поле Kn=Q(t,nI получающееся присоединением к по-
полю Q рациональных чисел первообразного корня ?„
из единицы степени п, где и — некоторое натуральное
число. Иногда (локальным) круговым по-
полем наз. также поле вида Qp(t,n), где QP — поле ра-
рациональных р-адических чисел. Так как Кп~К2п при
нечетном га, обычно предполагается, что пф2 (mod 4).
Тогда различным п соответствуют неизоморфные
поля Кп.
К. п. естественно возникают в задаче о делении кру-
круга — деление окружности на п равных частей эквива-
эквивалентно построению на комплексной плоскости перво-
первообразного корня ?„. К. п. устроены «достаточно просто»,
и поэтому дают удобный экспериментальный материал
для создания общих понятий теории чисел. Напр., по-
понятие целого алгебраич. числа и дивизора возникли
первоначально при рассмотрении К. п.
Место К. п. среди всех полей алгебраич. чисел выяс-
выясняет теорема Кронекера — Вебера,
утверждающая, что конечное расширение K/Q абелево
тогда и только тогда, когда KczKn для нек-рого п.
Аналогичное утверждение выполняется и для локаль-
локальных К. п.
Алгебраическая теория. Поле Кп яв-
является абелевым расширением поля Q с группой Галуа
G (Kn/Q) s= (Z/reZ)*,
где (z/reZ)* — мультипликативная группа кольца вы-
вычетов по модулю п. В частности, степень [Кп : Q] равна
ф(ге), где ф(«) — функция Эйлера. Поле Кп чисто мни-
мнимое и имеет степень 2 над своим максимальным вполне
вещественным подполем Кп
Если п=р11, . . . , р/ — разложение п на простые
множители, то Кп является свободным композитом
полей KJ, . . . , Klf. В поле К t простой дивизор р
имеет индекс ветвления е=(р— l)pi~1=cp(pi). В К t
имеет место равенство главных дивизоров (р)=A— ьр')е-
Все остальные простые дивизоры поля Q не разветвле-
разветвлены в К t, откуда следует, что р разветвлен в поле Кп
тогда и только тогда, когда р\п.
Числа 1, ?,п, . . . , ^л'"'" образуют фундаменталь-
фундаментальный базис поля К„. Дискриминант поля Kpt равен
+ppt~1{pt-t-i)_ Для линейно разделенных над Q полей
Е и F со взаимно простыми дискриминантами DЕ и Dp
выполняется соотношение DEf=D'eD'f , где n=[F : Q],
т=\Е : Q]. Это позволяет вычислить D^ для произ-
произвольного п (см. [3]).
Для поля К t числа вида
где а, ЬфО (mod p), порождают подгруппу конечного
индекса в группе всех единиц. Элементы этой подгруп-
подгруппы наз. круговыми единицами.
Закон разложения для К. п., т. е. закон, по к-рому
простые дивизоры (р) поля Q разлагаются в произве-
произведение простых дивизоров в Кп,— частный случай об-
общего закона разложения в абелевых расширениях, до-
доставляемого теорией noneii классов (см. [4]). А именно,
если (р, п) = 1 и / — наименьшее натуральное число,
для к-рого р-^=1 (mod n), то в Кп
где простые дивизоры ?х, . . . , pg попарно различ-
различны, N(pi) = pf и /g=<p(n). Таким образом, тип разло-
разложения (р) зависит только от вычета р (mod n). В случае,
когда р\п, точный вид разложения (р) можно получить,
учитывая, что К„= KmKpt, где, (т., р)=1 и (р) вполне
разветвлен в Kpt.
Если К — максимальное абелево расширение Q,
то K=\JnKn и
G (K/Q) -= lim С (KJQ) -= lim (Z/reZ)*^- Z*,
где X — пополнение кольца целых чисел z по всем
идеалам конечного индекса. В частности, для любого
простого I существует единственное расширение
Oco.j/Q с группой Галуа, изоморфной группе целых
/-адических чисел Z;.
Согласно теории полей классов существует отобра-
отображение взаимности
xp:JQ—+G(K/Q),
где Jq — группа иделей поля Q. В случае К. п. ото-
отображение гЬ допускает простое и явное описание (см.
[4]).
Аналитическая теория. Многие резуль-
результаты о строении группы классов дивизоров поля Кп
удается получить с помощью аналитич. методов. Если
hn — число классов поля Кп, то
A, х),
где w, D и R — число корней из единицы, дискриминант
и регулятор поля Kn, i=<p(re)/2 и F A) — некоторая яв-
явно вычислимая константа, L(\, X) — L-функция Дирих-
Дирихле, соответствующая характеру х, где % пробегает все
нетривиальные мультипликативные характеры mod re.
В свою очередь, для L(\, %) существуют явные выраже-
выражения в терминах гауссовых сумм (см. [7] гл. 5). Этим
решается вопрос о вычислении hn при заданном и.
Существует естественное разложение hn на два мно-
множителя hn=hnh% — первый и второй множители числа
классов, причем h% интерпретируется как число клас-
классов поля К„. В случае, когда n=pf, h^ = (E : Ео), где
Е — группа единиц поля К t и Ео — группа круговых
единиц (любая круговая единица становится действи-
действительной после умножения на подходящий корень из
единицы).
Для задач, связанных с проблемой Ферма, важную
роль играет вопрос о делимости числа классов поля
Кi на I для простых I. Известно, что fej=0 (mod I) для
бесконечного числа простых I (такие I наз. иррегу-
иррегулярными). Относительно регулярных простых чисел
I, т. е. чисел, для к-рых /i;^0(mod l), до сих пор не
известно A982), конечно или бесконечно их число. Су-
Существует гипотеза, что /i/"^0(mod/) для всех I. Эта
гипотеза проверена для большого числа примеров. Лег-
Легче поддается исследованию множитель hf. Существует
относительно простой критерий делимости hf (и ht) на
I в терминах чисел Вернулли [7]. Известно, что hf ->¦ оо
при i —>- оо и что hb=i тогда и только тогда, когда ?<:
<19 (см. [6]).
Для исследования группы классов К. п. успешно
применяются так наз. р-адические L-функции (см. [5],
[8]).
Лит.: [1] Kummer E., «J. reine und angew. Math.»,
1847, Bd 35, S. 327—67; [2] В е й л ь Г., Алгебраическая теория
чисел, пер. с англ., М-, 1947; [3] Ленг С, Алгебраические
числа, пер. с. англ., М., 1966; [4] Алгебраическая теория чисел,
пер. с англ., М., 1969; [5] Ш а ф а р е в и ч И. Р., Дзета-функ-
Дзета-функция, М., 1969; [6] U с h i d а К., «T6hoku Math. J.», 1971,
v. 23, p. 573—80; [7] Б о р е в и ч 3. И., Шафар е ви ч И. Р.,
Теория чисел, 2 изд., М., 1972; [8] Iwasawa К., Lectures
on p-adic L-functions, N. Y. — Tokyo, 1972; [9] Lang S., Cyc-
lotomic fields, Priceton — Hdlb.— В., 1978. Л. В. Кузьмин.
КРУГОВОЕ ПРЕОБРАЗОВАНИЕ, преобразо-
преобразование Мёбиус а,— преобразование, переводя-
переводящее окружности в окружности. Рассматриваемое как
точечное преобразование, К. п. является преобразова-
преобразованием расширенной (дополненной бесконечно удаленной
точкой) евклидовой плоскости, при к-ром окружность
или прямая переходят в окружность или прямую. В этом
случае говорят о точечной аналлагмати-
ческой геометрии.
Как неточечное преобразование К. п.— частный слу-
случай преобразований прикосновения (или касательных
К. п., или К. п. Ли); основным элементом является
не точка, а окружность. В этом случае говорят о круго-
круговой аналлагматической геометрии.
Лит.: [1] Энциклопедия элементарной математики, кн. 4,
М., 1963. А. В. Иванов.
КРУГОВОЕ РАСШИРЕНИЕ поля к — расшире-
расширение К, получаемое присоединением к к первообразного
корня из единицы нек-рой степени п. Иногда термин
«К. р.» относят и к любому промежуточному подполю
расширения К над к. К. р. наз. также бесконечное ал-
гебраич. расширение, являющееся объединением коноч-
коночных К. р. Важный пример К. р.— круговые поля,
отвечающие случаю, когда k=Q — поле рациональ-
рациональных чисел.
Пусть поле к имеет характеристику 0 и к(?,п) — его
К. р., полученное присоединением первообразного кор-
корня ?„. Тогда поле к{?,п) является композитом к и кру-
кругового поля Q (?„). Поэтому многие свойства круговых
полей переносятся и на К. р. Напр., &(?„) будет нор
мальным абелевым расширением поля к (причем ото
справедливо и для полей положительной характери-
характеристики), группа Галуа расширения k(Z,n)lk является под-
подгруппой группы Галуа расширения Q (Z,n)/Q, в част-
частности, ее порядок делит ср(«), где ц>(п) — функция Эй-
Эйлера.
Если к — поле алгебраич. чисел, то в расширении
кAп)/к могут ветвиться только простые девизоры, де-
делящие п, хотя при кф*0 дивизор поля к, делящий п,
может остаться неразветвленным в &(?„). К. р. поля ал-
гебраич. чисел с группой Галуа Г, изоморфной адди-
аддитивной группе целых Z-адических чисел 2г, наз. круго-
круговыми Г-расширениями (см. [2], [3], [4]). Такое Г-расши-
рение в случае, когда Z,i?k, имеет вид к„,= [)пкп, где
kn=k(t,ln).
Лит.: [1] Ленг С, Алгебра, пер. с англ., М., 1968; [2]
Ш а ф а р е в и ч И. Р., Дзета-функция, М., 1969; [3] К у з ь-
м и н Л. В., «Изв. АН СССР. Сер. матем.», 1972, т. 36, № 2,
с. 267—327; [4] I w a a a w а К., «Ann. Math.», 1973, v. 98, № 2,
p. 246 — 326. Л. В. Кузьмин.
КРУГОВОЙ МЕТОД — один из наиболее общих ме-
методов аддитивной теории чисел. Пусть Хх, Х2, . . . ,
Xk — произвольные множества натуральных чисел,
N — натуральное число и Jk(N) — число решений
уравнения
где п1^Х1, п%?Х.2, . . . , пк^Хк. Изучением величин
/fc(iV) занимается аддитивная теория чисел; напр., если
доказать, что Jk(N) больше нуля при всех N, то это бу-
будет означать, что любое натуральное число является
суммой it слагаемых чисел множеств Xlt Х2, . . . , Х^.
Пусть, далее, s — комплексное число, |s|<l, и
Тогда функция g (s)
g (*)=gi (*) 82 (*)• ¦ -gk (*) =
является производящей функцией величин J^{N). По
формуле Коти
Последний интеграл изучается при R —>- 1—0. Окруж-
Окружность интегрирования |s| = i? разбивается на «большие»
и «малые» дуги, центрами к-рых являются рациональ-
рациональные числа. Для целого ряда аддитивных задач удается
достаточно полно исследовать интегралы по «большим»
дугам, к-рые дают «главную» часть величины /ft(JV), и
оценить интегралы по «малым» дугам, к-рые дают «ос-
«остаточный» член асимптотич. формулы для J^N).
Введение И. М. Виноградовым в К. м. тригономет-
тригонометрич. сумм не только сильно упростило его применения,
но и дало возможность единым способом решать широ-
широкий круг самых разных аддитивных задач. Основой
К. м. в форме тригонометрич. сумм является следую-
следующая формула:
i = 0,
т Ф 0, т — целое.
Г1 г-Иат , \ 1'
)ое da=\0,
Из этой формулы следует, что
где
Конечные суммы sm(a) наз. тригонометрическими. Для
исследования /^(iV) отрезок интегрирования [0, 1] раз-
разбивается на «большие» и «малые» дуги — отрезки с
центрами в рациональных точках с «малыми» и «боль-
«большими» знаменателями. Для многих аддитивных задач
удается с хорошей точностью вычислить интегралы по
«большим» дугам (тригонометрич. суммы для а из
«больших» дуг близки к рациональным тригонометрич.
суммам с малым знаменателем, хорошо вычисляются и
являются «большими»); на «малых» же дугах, к-рые со-
содержат основную долю точек отрезка [0, 1], тригоно-
метрич. суммы «малы»; их удается нетривиально оце-
оценить (см. Тригонометрических ci/мм метод, Виноградова
метод), что позволяет получить асимптотич. формулу
для /^(iV).
С помощью К. м. в форме тригонометрич. сумм и .ме-
.метода И. М. Виноградова оценок тригонометрич. сумм
получены наиболее сильные результаты в аддитивной
теории чисел (см. Варипга проблема, Гольдбаха пробле-
проблема, Гольдбаха—Варипга проблема, Гильберта — Кам-
Камке проблема).
Лит.: [1] Виноградов И. М., Метод тригонометриче-
тригонометрических сумм в теории чисел, М., 1971; [2] X у а Л о - г е н, Ме-
Метод тригонометрических сумм и его применения в теории чисел,
пер. с нем., М., 1964; [3] К а р а ц у б а А. А., Основы анали-
аналитической теории чисел, М., 1975. А. А. Нарацуба.
КРУГОВЫЕ ТОЧКИ, циклические точки,
на плоскости, дополненной мнимыми и бесконечно
удаленными точками,— две мнимые бесконечно удален-
удаленные точки, однородные координаты A, г, 0) и A, —г, 0)
к-рых удовлетворяют уравнению любой окружности.
Прямые, проходящие через К. т., наз. и з о т р о п-
н ы м и прямы м н. БСЭ-2.
КРУ Л ЛЯ КОЛЬЦО — коммутативное целостное
кольцо А, для к-poro существует семейство (iv)isz
дискретных нормирований поля частных К кольца А,
удовлетворяющее следующим условиям: а) для любого
х? #\{0} и для всех i, исключая, быть может, конечное
число, Vj(x) = Q\ б) для г?#\{0} условие х?А эквива-
эквивалентно тому, что V{(x)~^0 для всех z?/. Нормирования
vi наз. при этом существенными.
К. к. были рассмотрены В. Круллем [1] под названи-
названием колец конечного дискретного
главного порядка. Они являются наиболее
естественным классом колец, в к-рых существует теория
дивизоров (см. также Дивизориалъный идеал, Классов
дивизоров группа). Упорядоченная группа дивизоров
К. к. А канонически изоморфна упорядоченной группе
2(/). Существенные нормирования К. к. могут быть
отождествлены с множеством простых идеалов высоты 1.
К. к. вполне целозамкнуто. Любое цолозамкнутое нё-
терово кольцо, в частности дедекиндово кольцо,.является
К. к. Кольцо k [X-l, . . . , Хп, . . .] многочленов от бес-
бесконечного числа переменных — пример К. к., не яв-
являющегося кётеровым. Вообще, любое факториальное
кольцо — К. к. Для того чтобы К. к. было факториаль-
но, необходимо и достаточно, чтобы любой его простой
идеал высоты 1 был главным.
Класс К. к. замкнут относительно операций локали-
локализации, перехода к кольцу многочленов или формаль-
формальных степенных рядов, а также целого замыкания в ко-
конечном расширении поля частных К.
Лит.: [1] Krull W., «J. reine und angew. Math.», 1931,
Bd 167, S. 160—96; [2] 3 a p и с с к и й О., Самюэль П.,
Коммутативная алгебра, пер. с англ:, т. 2, М., 1963; [3] Бур-
баки Н., Коммутативная алгебра, пер. с франц., М., 1971.
КРУЛЛЯ — РЕМАКА — ШМИДТА ТЕОРЕМа"""—
группа утверждений, касающихся связи между прямы-
прямыми разложениями группы или кольца. Теоретико-струк-
Теоретико-структурная форма этого результата известна как теорема
Оре (см. Дедепиндова решетка). Для группы G с произ-
произвольной системой операторов имеет место теорема
Шмидта (Р. Ремак получил этот результат для ко-
конечных групп [2], а В. Крулль — для колец [1]): если
такая группа обладает главным рядом, то любые два ее
разложения в прямое произведение с неразложимыми
сомножителями центрально изоморфны, т. е. между
множествами сомножителей каждого из этих разложе-
разложений может быть установлено взаимно однозначное соот-
соответствие и, если А ж А' — соответствующие друг другу
сомножители, то существует такой изоморфизм ф."
А —>- А', что a~1q>(a) для всякого а?А лежит в центре
группы G ([3], см. также [4]). А. Г. Курош установил,
Здесь Х{= {х, у, z}, t — время, p — плотность, v=
= {«,}= {и, v, w} — скорость, E — полная удельная
энергия, Р — давление. Для замыкания системы A)
используется уравнение состояния
P=P(p,J),
где
J=E-±\v\*
— внутренняя удельная энергия.
Процесс решения эволюционной системы A) разби-
разбивается на шаги по времени, каждый из к-рых состоит
из трех этапов: эйлерова, лагранжева и заключитель-
заключительного. Вначале рассматривается изменение внутреннего
состояния подсистемы — «крупной частицы» (эйлеров
этап), а затем — перемещение этой подсистемы без
изменения внутреннего состояния (лагранжев и зак-
заключительный этапы).
Эйлеров этап. Область интегрирования покры-
покрывается неподвижной (эйлеровой) разностной сеткой про-
что ложно ограничиться требованием существования
главного ряда лишь у факторгрупп группы G, вложимых
в ее центр. Теорема Шмидта, как теорема для групп с
операторами, в частности, справедлива для модуля над
любым кольцом. Однако модуль М неразложим, если
его кольцо эндоморфизмов локально (см. Локальное
кольцо), а при нек-рых ограничениях (напр., если М —
модуль конечной длины) справедливо и обратное. В свя-
связи с этим К.— Р.— Ш. т. для модулей может быть
сформулирована так: два разложения
где кольца эндоморфизмов модулей М( и М) локальны,
изоморфны. При этом каждое слагаемое одного из раз-
разложений может быть заменено нек-рым слагаемым дру-
другого. В нек-рых случаях такую замену можно осущест-
осуществить н для бесконечного множества слагаемых. К ис-
исследованию вопросов, связанных с К.— Р.— Ш. т.,
разработан теоргтнко-категорный подход, использую-
использующий рассмотрение категории подмодулей прямых сумм
данных модулей.
Лит.: [UKrull W., «Math. Ann.», 1924, Bd 91, S. 1 — 46;
[2] Remak R., «J. reine und angew. Math.», 1911, Bd 139,
S. 293—308; [3] Шмидт О. Ю., «Math. Z.», 1928, Bd 29,
S. 34—41; [4] К у р о ш А. Г., Теория групп, 5 изд., М., 1967;
{5] Лам бе к И., Кольца и модули, пер. с англ., М., 1971; i
[6] Ф е й с К., Алгебра: кольца, модули и категории, пер. с
англ., т. 1 — 2, М., 1977—79; [7] Итоги науки и техники. Алгебра.
Топология. Геометрия, т. 14, М., 1976, с. 57—190.
Л. А. Скор}1яков.
КРУПНЫХ ЧАСТИЦ МЕТОД — метод для расчета
сжимаемых течений сплошной среды [1]. К. ч. м. основы-
основывается на расщеплении исходной системы дифференци-
дифференциальных уравнений по физическим процессам (см. [3]).
Им решается эволюционная система уравнений. Допус-
Допускается стационарное решение в результате установле-
установления. К. ч. м, является развитием метода «частиц в |
ячейках» Харлоу. •
К. ч. м. широко используется для исследования
аэрогазодинамич. течений, дифракционных задач, транс-
трансзвуковых потоков, явлений взаимодействия излучения
с веществом и др.
Разностная схема К. ч. м. может быть описана
на примере движения идеального сжимаемого газа
(уравнения неразрывности, импульса п энергии):
|?- + div (рг) =
до I
(Г)
liv(i>w)=0.
извольной формы [для краткости изложения рассмат-
рассматривается прямоугольная сетка в двумерной (плоской)
области (см. рис.)]. На этом этапе расчета изменяются
лишь величины, относящиеся к ячейке в целом, а жид-
жидкость предполагается моментально заторможенной.
Поэтому конвективные члены вида div (typv), я|)=A, и,
v, E), соответствующие эффектам перемещения, из урав-
уравнений A) опускаются. В оставшихся уравнениях A) р
выносится из-под знака дифференциала, и уравнения
A) разрешаются относительно временных производных
от и, v, E:
ди . дР n dv . ар п дЕ . -,.
Простейшая конечноразностная аппроксимация
(центральные разности) приводит к следующим выраже-
выражеt.J
р _ р
i +'/г, ! i-Чг.
Ш
1.1
П ~П „Л ~п
i+Чг, j"' + '/», Г i-Чг, l" С-Чг,
-[
р" Т>" _р" Z," 1
I ', i + 4*vi,j + 4i ', i+42Vi, /-'/, | At
+ Ay Qn ¦
J ' '. /
МИ ОТНОСЯТСЯ
P1-l.l+pli
Здесь величины с дробными индексами относятся к гра-
границам ячеек, напр.
и, v, E — промежуточные значения параметров пото-
потока, полученные в предположении «замороженности» по-
поля р на слое tn-\- At. Хотя схема эйлерова этапа в дан-
данном виде неустойчива, при определенных формах запи-
записи последующих этапов вся схема в целом — устойчи-
устойчива. Устойчивости эйлерова этапа можно достигнуть,
напр., путем введения в него элементов интегральных
соотношений метода. При этом аппроксимация подш;-
тегральных функций производится в направлении, па-
параллельном оси тела (см. рис.), т. е. как в схеме 1 ме-
метода интегральных соотношений: исходная система
уравнений берется в интегральном виде, в ней аппрок-
аппроксимируются интегралы
/ = \ ри dx, 0=\ j)vd%, г))= V рЕ dr.
Лагранжев этап. На данном этапе находятся
при tnJr At потоки массы через границы ячеек. При этом
полагают, что масса крупной частицы переносится
только за счет нормальной к границе составляющей ско-
скорости. Так, напр.,
и т. д. Знак < > определяет параметры риа на гра-
границе ячейки. Выбор этих величин имеет важное зна-
значение, так как сильно влияет на устойчивость и точ-
точность счета. Возможны различные разностные представ-
представления для AM": разного порядка точности, с учетом
и без учета направления потока, центральные разно-
разности, Z/P-аппроксимации и т. д. Потоки импульса
(энергии) равны произведению AM" на соответствую-
соответствующие значения скорости (полной удельной энергии).
Проводились также аппроксимации не только потоков
массы, но и потоков импульса и энергии.
Заключительный этап. На этом этапе
находятся окончательные поля эйлеровых параметров
потока в момент t" + l = t"^- At. Уравнения этого этапа
представляют собой законы сохранения массы М, им-
импульса р и полной энергии Я, записанные для данной
ячейки (крупной частицы) в разностной форме М" + 1~
= Л#«+2ДЛ/"«, рп + 1 = р-2Ар", Еп + 1=Е"+2АЕ".
Окончательные значения параметров потока р, X—
= {«, у, Е} на следующем временном слое вычисляются
по формулам (поток течет слева направо и снизу вверх):
Дх Ау
"i, f
p-j Дх Ду
Консервативность и полную дивергентность раз-
разностной схемы (схема дивергентно-консервативная)
обеспечивает уравнение для полной энергии Е. На за-
заключительном этапе (в случае использования дискрет-
дискретной модели среды) целесообразно производить дополни-
дополнительный пересчет плотности, что сглаживает флуктуа-
флуктуации и повышает точность вычислений. Комбинируя
различные представления этапов, получают серию раз-
разностных схем К. ч. м., что позволяет осуществить
широкий класс численных экспериментов.
К. ч. м. допускает трактовку с различных точек зре-
зрения: метод расщепления, смешанный эйлерово-лагран-
жевый метод, расчет в локально лагранжевых коорди-
координатах (эйлеров этап) с пересчетом на прежнюю сетку
.лагранжев и заключительный этапы), разностная
.(апись законов сохранения для элемента жидкости —
«крупной частицы», эйлерова разностная схема.
Граничные условия ставятся с помощью рядов фик-
фиктивных ячеек (чтобы каждую расчетную точку сделать
внутренней и сохранить единый алгоритм для всех
ячеек). Для схемы 1-го порядка аппроксимации доста-
достаточно одного слоя, для 2-го порядка — два слоя и т. д.
Пусть, напр., рассматривается задача о расчете обтека-
обтекания осесимметричных и плоских тел с образующей
произвольной формы (см. рис.). Приведенные ранее
расчетные формулы справедливы для внутренних ячеек
поля, со всех сторон окруженных жидкостью, и для
ячеек, прилегающих к твердому телу, контур к-рого
совпадает с границами ячеек.
При расчете обтекания тел конечноразностными ме-
методами можно использовать два подхода: расчет в коор-
динатах s, n\ введение в рассмотрение дробных ячеек
(см. [2]). В первом случае затруднительно рассчитывать
тела с изломами и с вогнутостями. Второй подход сво-
свободен от этих недостатков.
Граничные условия на теле в случае дробных ячеек
ставятся, как и в случае целых ячеек, с помощью вве-
введения фиктивных ячеек. Внутри тела формируется слой
фиктивных ячеек, прилегающих к дробным ячейкам.
Для определения параметров газа в этих фиктивных
ячейках из центра фиктивной ячейки а на контур тела
опускают нормаль и в точке их пересечения А проводят
касательную к—к (см. рис.). Затем в поле течения стро-
строят нек-рую ячейку р\ симметричную данной фиктивной
ячейке а относительно касательной Л;—к. Газодинамич.
параметры g в ячейке Р определяют путем «взвешива-
«взвешивания» gfi --2,-S$. g; B;5з(-=1), где суммирование произ-
производится по тем ячейкам i, часть площади Se,. к-рых по-
попала в ячейку р. Постановка условий непротекания тре-
требует для каждой фиктивной ячейки задания еще одного
параметра у: угла наклона радиус-вектора, пересекаю-
пересекающего контур тела в точке А. При использовании усло-
условий прилипания (обе компоненты скорости при переходе
через поверхность тела меняют знак) не требуется за-
задания дополнительного параметра у. Параметры газа
в фиктивной ячейке а тогда будут
!} =
Л I a
Граничные условия для тела, контур к-рого совпада-
совпадает с границами ячеек, являются частным случаем изло-
изложенных здесь граничных условий.
Для каждой дробной ячейки (см. рис.) необходимо
знать 5 геометрич. характеристик: Ai_J/ j, Аг j_i/2,
^г + '/2 j< ^i } + чг и ft',/' ГДе ft./ — доля объема дроб-
дробной ячейки по отношению к объему полной ячейки
ДхЛг/, Ai_1^ j — часть площади стороны (г—V2, ;'),
открытой для течения жидкости, и т. п.
Размещение твердой границы внутри ячейки вносит
две особенности: оно смещает центр масс из геометрич.
центра ячейки ближе к границе я уменьшает реальные
размеры ячейки. При рассмотрении как целых, так и
дробных ячеек все параметры потока относятся к центру
массы. Именно между центрами масс производится ин-
интерполяция газодинамич. функций. В случае целых яче-
ячеек центр масс либо совпадает с геометрич. центром яче-
ячеек (плоская декартова система координат), либо бли-
близок к нему (цилиндрич. система координат). В реальных
расчетах разница даже для прилегающего к оси ряда
ячеек не превышает 0,2 -Дг. В результаты расчетов это
обстоятельство не вносит существенных искажений.
При надлежащем введении дробных ячеек смещение
центра массы относительно геометрич. центра также не
превышает этой величины. Более серьезным является
вопрос, связанный с уменьшением эффективных разме-
размеров ячейки. Чтобы при уменьшении размеров ячейки
At ,
не нарушалось условие устойчивости стг<^^, гДе л — х
или у, ячейки с /</min уст. присоединяются к соседним
целым ячейкам внутри потока и полученные комплексы
рассчитываются по формулам дробных ячеек. В этой
случае геометрич. размеры укрупненной ячейки не
меньше размеров целой ячейки: A;_i/2 j^^i^t j—72^
Jsl, . . . , /|/>1, поэтому вопрос об устойчивости дроб-
дробных ячеек снят.
В плоском случае геометрич. характеристики дроб-
дробных ячеек можно получить непосредственным измере-
измерением. В осесимметричном случае необходимо произвес-
произвести дополнительный пересчет с учетом расстояния дан-
данной дробной ячейки до оси симметрии. Разностные фор-
формулы для дробных ячеек получаются путем незначи-
тельного изменения разностных выражений для целых
ячеек.
Исследование разностных схем К. ч. м. (аппрокси-
(аппроксимации, вязкостных эффектов, устойчивости) проводи-
проводилось с помощью дифференциальных приближений (см.
[4]). Проведено обобщение К. ч. м. на пространственно-
трехмерный случай.
Лит.: [1] Белоцерковский О. М., Давы-
Давыдов Ю. М., «Ж. вычисл. матем. и матем. физ.», 1971, т. 11,
N! 1, с. 182—207; [2] Давыдов Ю.М., там же, з\Г» 4,с. 1056—
63; [3] М а р ч у к Г. И., Методы вычислительной математики,
Новосчб., 1973; [4] Белоцерковский О. М., Давы-
Давыдов Ю. М., Исследование схем метода «крупных частиц»
с помощью дифференциальных приближений, в кн.: Проблемы
прикладной математики и механики, М., 1971, с. 145—55.
Ю. М. Давыдов.
КРУЧЕНИЕ — 1) К. кривой — величина, ха-
характеризующая отклонение пространственной кривой
у от соприкасающейся плоскости. Пусть Р — произ-
произвольная точка кривой у и Q — точка кривой у, близкая
Р, Д8 — угол между соприкасающимися плоскостями
кривой у в точках Р и Q, a | As| — длина отрезка PQ
кривой у. Абсолютным кручением |А-2|
кривой у в точке Р наз. величина
К. кривой определяется равенством к2= — \к2\ и счи-
считается положительным (отрицательным), если вращение
соприкасающейся плоскости при движении вдоль кри-
кривой в сторону возрастания s от вектора бинормали к
вектору главной нормали происходит против часовой
стрелки (по часовой стрелке) при наблюдении из точ-
точки Р.
Регулярная (трижды непрерывно дифференцируемая)
кривая в каждой точке, где ее кривизна отлична от
нуля, имеет К. Если r=r(s) — естественная параметри-
параметризация кривой, то
(г1, г", г'")
к, = —
[»•', г"]
К. иногда наз. второй кривизной.
Кривизна и К., заданные как функции длины дуги,
определяют кривую с точностью до положения в про-
пространстве.
Кривая, у к-рой К. в каждой точке равно нулю,—
плоская. е. В. Шикин.
2) К. геодезическое — обобщение К. кри-
кривой, инвариант полосы в пространстве Е3, определяе-
определяемый формулой
а = (х1, xs, x's),
где х1 — касательный вектор к базовой кривой Г поло-
полосы, х3 — нормальный вектор полосы. Обычное К. х
кривой Г ненулевой кривизны выражается через а и
нормальную и геодезич. кривизны Ь и с по формуле
, Ъ'с—Ъс'
* = « + -STj^r ¦
Равенство нулю геодезич. К. характеризует полосы
кривизны, в частности для полос, принадлежащих
поверхности в Е3, — кривизны линии.
Аналогичные понятия вводятся для полос в римано-
вом пространстве (см. [1], [2]).
3)К, подмногообразия— обобщение К.
кривой, кривизна связности, индуцированной в нор-
нормальном расслоении v(Mk) многообразия Mk, по-
погруженного в риманово пространство V". Пусть юр1 —
формы связности в v(Mk), ш" — формы эйлеровых кри-
кривизн Mk в V", s=l, . . . , к; а, р=1, . . . , п—к.
Тогда формы
определяют риманово кручение, а формы
QaG = Ша Л 03s
— гауссово кручение Мк в V". Риманово К.
и гауссово К. связаны соотношением
где Rakh — компоненты тензора кривизны V" в на-
направлении бивектора, касательного к Mh, a as— орто-
ортогональный кобазис касательного пространства к Мк.
Тензоры S\i, получающиеся в разложении форм К.
QaR.(&aG) по формам а' АО-1, нэз. тензорами
гауссова и риманова кручения (см.
[1],'[4]).
Пример. Пусть М2 — поверхность в евклидовом
пространстве ?4. Тогда гауссово и риманово К. равны
и сводятся к единственному числу
Е F G
EG-F2
N1
где Е, F, G — коэффициенты первой, a L,-, Mt, N; —
второй квадратичных форм М2 в ?4. Равенство и=0
в нек-рой окрестности геометрически интерпретируется
как вырождение эллипса кривизны в отрезок, тогда су-
существует два семейства ортогональных линий кривиз-
кривизны, касательные к к-рым соответствуют концам этого
отрезка. Условие х=0 локально необходимо и доста-
достаточно для того, чтобы М" располагалась в римановом
пространстве V3, погруженном в ?4, и нормаль к М2
в касательном пространстве к Vs была направлена по
главному вектору Риччи тензора Vs. В частности, нуле-
нулевое К. необходимо для уплощения М2 в Е3.
4) К. аффинной связности Г — величина,
выражающая отклонение от перестановочности кова-
риантных производных какой-либо функции на много-
многообразии М" с этой связностью Г. Она определяется пре-
преобразованием
где X, Y — векторные поля на Мп, V% Y — ковариант-
ная производная Y вдоль X, \Х, Y] — коммутатор X и
Y. В локальных координатах х', ?=1, ... , п, таких,
что Х = —/ и У=—, , преобразование S имеет вид
дх' dxJ r
S (— —\ — S^ в- •
\дх' дх-' J 11 дхк
тензор S^j—Tij—rfi, где Г/j — компоненты связности
Г в выбранном базисе, наз. тензором круче-
кручения.
Эквивалентным образом К. определяется ковариант-
ным дифференциалом векторнозначной 1-формы ш*
смещения данной связности
к-рый наз. формой кручения; здесь 9/ —
связности формы для Г. В локальном кобазисе dxl
(дуальном базису —-.) форма
V дх1}
h • '
где Sij имеет те же значения, что и выше.
Геометрич. смысл К. аффинной связности Г заклю-
заключается в том, что развертка каждого бесконечномалого
контура L, выходящего из точки х?М" и возвращаю-
возвращающегося в нее на касательное пространство к М" в х,
уже не будет замкнутой кривой. Векторная разность
между концами развертки с точностью до малых 2-го
порядка имеет компоненты fiA, А=1, ... , п. Други-
Другими словами, этот вектор пропорционален ограничен-
ограниченной контуром L двумерной площадке с бивектором
df'J:Qk=Sijdf'J. Эти представления лежат в основе ин-
интерпретации упругой среды с непрерывным распреде-
распределением источников внутренних напряжений в виде дис-
дислокаций, вектор Q* тогда оказывается аналогом так
наз. вектора Бюргерса (см. [4] — [7]).
Прим о р. В двумерном рпмановом пространстве
М2 с .метрической связностью тензор К. сводится к век-
вектору: Sij=Skeij, здесь etj — метрич. бивектор. Пусть
в М2 дан малый треугольник, образованный отрезками
геодезических длины а, Ъ, с, с углами А, В, С. Тогда
главная часть проекций вектора Sk в точке А на сторо-
сторону АВ равна отношению величины с—a cos В—b cos A
к площади треугольника ст, а на перпендикуляр к АВ —
величине a sin В — b sin А, деленной на а. Таким об-
образом, в Л/2 нулевого К. имеют место теоремы косину-
косинусов и синусов обыкновенной тригонометрии с точностью
до величин, малых в сравнении с о.
5) К. пространства А — элемент т(Х, А)
Уайтхеда группы Wh A, определяемый парой (X, А),
где А — конечное клеточное пространство, и вложение
AczX является гомотопич. эквивалентностью. Эквива-
Эквивалентно, К.— элемент группы "Уайтхеда Wh Ях фунда-
фундаментальной группы Я]. К. инвариантно при клеточных
распшрениях и стягиваниях и при клеточных измель-
измельчениях. Доказана топологич. инвариантность К. Если
А односвя.чно, то его К. равно нулю.
Если (W; Mo, Mj) — произвольный fe-кобордизм,
то t(W, Ма} = т(/Г, Мо), где К — клеточное пространст-
пространство, ассоциированное с данным разложением на ручки
многообразия W (от многообразия Мо), это — кру-
кручение й-к обордизма.
Пусть М f — цилиндр клеточного отображения /:
X —>- Y, являющегося гомотопич. эквивалентностью.
Тогда т(Mf, У) = 0, нот(Mf, X)?Wh ntX не всегда
равно нулю. Оно определяет по формуле
т(/)=/*т(Л4>, X) € Whnir
элемент т(/), наз. кручением отображения
/ (иногда К. наз. сам т(М^, X)). Если т(/) = 0, то наз.
простой гомотопической эквива-
эквивалентностью (см. [8]).
6) К. конечно порожденной абеле-
вой группы G — группа Т, состоящая из всех
элементов конечного порядка v группы G. Числа v>l
могут быть однозначно с точностью до перестановки
выбраны в виде степеней простых чисел, и тогда они
наз. к о э ф ф п*ц центами кручения груп-
группы С (см. [9]).
Лит.: [1] К а р т а я Э., Риманова геометрия в ортогональ-
ортогональном репере, пер. с франц., М., 1960; [2] Б л я ш к е В., Введе-
Введение в дифференциальную геометрию, пер. с нем., М., 1957;
[3] Итоги науки. Алгебра. Топология. Геометрия. 1969, М., 1971,
с. 123—68; [4] 3 у л а н к е Р., В и н т г е н П., Дифференци-
альная геометрия и расслоения, пер. снем.,М., 1975; [5]Нор-
ден А. П., Пространства аффинной связности, 2 изд., М.,
1976; 16] К а р т а п Э., Пространства аффинной, проективной и
конформной связности, [пер. с франц.], Казань, 1962; [7] С х о у-
тен Я.-А., Тензорный анализ для физиков, пер. с англ., М.,
1965; [8] Р у р к К., Сандерсон Б., Введение в кусочно
линейную топологию, пер. с англ., М., 1974; [9]К у р о ш А. Г.,
Теория групп, 3 изд., М., 1967. М. И. Войцеховский.
КРУЧЕНИЯ ТЕНЗОР — кососимметрический по
нижним индексам тензор типа A, 2), получающийся в
разложении кручения формы в локальном кобазисе на
многообразии М". В частности, в голономном кобазисе
dx', i=l, ... , п, компоненты К. т. Si/ выражаются
через объекты связности Г,у:
JV/. И. Войцеховский.
КРУЧЕНИЯ ФОРМА — ковариантный дифференци-
дифференциал векторнозначной 1-формы смещения аффинной связ-
связности — 2-форма
Q = Da> = da» -\- Э л со,
где в — форма связности. К. ф. удовлетворяет так наз.
первому тождеству Бианки
Л 0 + со Л Н,
д р форма данной связности. Аналогич-
Аналогично определяется К. ф. для редуктивных связностей.
М. 11. Войцеховспий.
КРЫЛА ТЕОРИЯ — раздел аэродинамики, изучаю-
изучающий взаимодействие тел с потоками жидкости и газа.
Основная задача К. т.— определение аэродинамич.
сил, действующих на тело, и нахождение поля скорос-
скоростей и и давления р как функций времени t и декартовых
координат %=[х1, . . . , ¦?„), п=2 для плоских и ?г=3
для пространственных течений.
Для безвихревых баротропных течений в отсутствие
вязких и массовых сил плотность газа р — известная
функция давления р=р(р), компоненты скорости «,¦ —
частные производные потенциала ср, ы/=——. В области,
дх,-
занятой газом, ц> удовлетворяет кразилинейному урав-
уравнению
' '
где c=(-?) — скорость звука, S/y— символы Кро-
покера. Давление р определяется потенциалом из ин-
интеграла Коши — Лагранжа
Граница области течения состоит тга кусочно гладкой
поверхности крыла S и конечного числа поверхностей
контактного разрыва 2у, /=1, ... , т, к-рые пересе-
пересекаются с 5 по ребрам заострения кромок крыла либо
касаются 5. В плоских течениях S, 2у — кусочно глад-
гладкие кривые, кромки крыла — угловые точки S. На S
потенциал удовлетворяет условию непротекания, а на
2у — условиям контактного разрыва:
+vFV4> = 0 на S, B)
где F(ae, t) — 0, Fj(ac, г) = 0 — уравнения поверхностей
5, 2у, ф* — предельные значения (г при подходе к раз-
различным сторонам поверхности 2у. На линиях пересече-
пересечения S П 2у ставится условие Жуковского — Кутта —
Чаплыгина о конечности давлений в кромках крыла
lim | р (х) | < со при ж0 € $ П 2у . D)
В стационарном случае D) совпадает с условием ко-
конечности скоростей в точках Sf|2y. Форма поверхнос-
поверхностей 2у неизвестна и определяется вместе с решением
задачи.
Поверхности Бу моделируют вихревой след, возни-
возникающий за обтекаемым телом в реальных течениях
(см. Аэродинамики математические задачи). Этот факт
согласуется с тем, что в рамках гипотезы о безвихре-
безвихревом характере движения непрерывного решения задачи
об обтекании крыла с конечной величиной давления в
острых кромках в общем случае не существует. В ис-
исключительных случаях, напр, для плоских ставдю-
нарных течений с постоянной циркуляцией скорости
вокруг крылового профиля, поверхности разрыва мо-
могут отсутствовать.
Уравнения A)—D) вместе с начальными данными об-
образуют краевую задачу для нахождения <р, 2_,-. Ее тип
определяется характером течения и числом Маха М=
= |уф|с-1. Для неустановившихся движений сжимае-
мои жидкости и стационарных ( д^=0 ) сверхзвуковых
) течений уравнение A) имеет гиперболич. тип,
для движений несжимаемой жидкости (p=const, c=oo)
и стационарных дозвуковых (М<1) течений уравнение
A) эллиптическое. В последнем случае в предположе-
предположении, что S — кусочно гладкая кривая, имеющая одну
угловую точку ж0 с углом ая, а?[0, 1], справедливо ут-
утверждение: для любого вектора к, |7с| = 1, существует
Я>0 такое, что при gfc[0, X) задача A)—B) имеет един-
единственное решение, удовлетворяющее в аз0 условию Жу-
Жуковского — Кутта — Чаплыгина и условию на бес-
бесконечности:
lim | v<p | < °о, Hm V<p (ж) = Qk,
X -> Х0 | X \ ->¦ оо
причем М (q) —>- 0 при q -*. 0 и М (q) —>- 1 при q -+¦ Я, где
М E[) = sup М (ас) — число Маха течения.
Для стационарных плоских дозвуковых течений спра-
справедлива основная теорема Жуковского (см. [1] —[3]):
при обтекании профиля полная сила, действующая на
него со стороны жидкости, перпендикулярна к, а ее
величина R равна
-д7 ds, pco= lim р(аз).
s | ж |-> »
Для таких течений доказана математич. корректность
более общих задач: о совместном обтекании нескольких
профилей; об обтекании крыла со срывом струй и с об-
образованием застойной зоны (струйные течения); обрат-
обратные задачи, определяющие формы крыла и его части по
заданной эпюре давлений [4].
В связи с трудностями решения задач К. т. в точной
постановке большое значение имеют приближенные мо-
модели: теория тонкого крыла, К. т. малого удлинения
и т. д. Наиболее распространенной из них является ли-
линейная теория слабого изогнутого тонкого крыла (см.
[1], [5] — [И]). В ее основе лежат следующие предполо-
предположения: потенциал течения имеет вид (p=qx1-\-U>, тол-
толщина крыла и уФ малы по отношению к хорде крыла и
скорости невозмущенного потока 9>0. В теории тон-
тонкого крыла поверхность S моделируется ее проекцией
Sfj на плоскость хп = 0, а поверхность контактного раз-
разрыва 2 — полуполосой 20=Q\50, где Q — объедине-
объединение всех лучей, параллельных оси Охх, выходящих из
точек 50 в положительном направлении этой оси. Функ-
Функция Ф (ас, t) удовлетворяет линеаризованным уравне-
уравнениям и граничным условиям:
1 дщ> , „ Мп д'Ф ,, ,,2 v 9!Ф V^« 92ф ^
ЭФ , Г'ЭФ Г ЭФ ЭФ "I
lim g^r =и на о0,' | а^~ 1 = 1 "аТ + 9 а^~~ 1=0 на 20;
.-г— ЭФ ЭФ I _ „
lim -gj- -j- 9 g~J~ I < °° при ж0 с ^о П 20)
где Се», Л/», — постоянные скорость звука и число Маха,
соответствующие равномерному потоку со скоростью q,
через [/] обозначен скачок величины / при переходе че-
через 20, v± — заданные функции, определенные формой
и условиями движения крыла.
К этим уравнениям добавляются соотношения, опре-
определяющие поведение решений на бесконечности: в за-
дачах о стационарных дозвуковых (М0о<_\) течениях —
затухание возмущений при \ж\ —>- оо, в задачах о малых
дозвуковых колебаниях крыла — условие излучения
Зоммерфельда (излучения условия), в задачах о сверх-
сверхзвуковых (Л/те>1) течениях добавляется равенство Ф =
= 0 на головной волне возмущений (огибающей харак-
характеристических конусов с центрами на SQ).
Основной метод решения задач теории тонкого кры-
крыла — представление So, 20 в виде вихревых поверхно-
поверхностей и сведение краевых задач к сингулярным интег-
интегральным уравнениям для плотности вихря. При этом
в точках границы So, не принадлежащих 20, производ-
производные Ф, как правило, обращаются в бесконечность. Ли-
Линейная теория пригодна для описания реальных тече-
течений лишь вне нек-рой окрестности передней кромки
крыла.
В линейной теории тонкого крыла получены решения
в виде бесконечных рядов, содержащих специальные
функции, плоской задачи о малых гармонич. колебани-
колебаниях крылового профиля, пространственной стационарной
задачи в случае, когда S является эллипсом (см. [1],
[5] — [9]). Для расчета крыльев произвольной формы в
плане разработаны численные методы (см. [10], [11]).
Лит.: [1] Седов Л. И., Плоские задачи гидродинамики
и аэродинамики, 2 изд., М., 1966; [2] К о чин II. Е., К и-
бель И. А., Розе Н. В., Теоретическая гидромеханика,
6 изд., ч. 1, М., 1963; [3] Б е р ct Л., Математические вопросы
дозвуковой и околозвуковой газовой динамики, пер. с англ.,
М., 1961; [4] М о н а х о в В. Н., Краевые задачи со свободными
границами для эллиптических систем уравнений, Новосиб.,
1977; [5] Н е к р а с о в А. И., Теория крыла в нестационарном
потоке, М.—Л., 1947; [6] Горелов Д. Н., Теория крыла в
нестационарном потоке, Новосиб., 1975; [71 Майлс Дж.,
Потенциальная теория неустановившихся сверхзвуковых тече-
течений, пер. с англ., М., 1963; [8] Г о л у б е в В. В., Труды по
аэродинамике, М.— Л., 1957; [9] К о ч и н Н. Е., «Прикл. ма-
тем. и механ.», 1945, т. 9, в. 1, с. 13—66; [10] К р а с и л ь щ и-
к о в а Е. А., Крыло конечного размаха в сжимаемом пото-
потоке, М.—Л., 1952; [11] Б е л о ц е р к о в с к и й О. М.,
Ништ М. И., Отрывное и безотрывное обтекание тонких
крыльев идеальной жидкостью, М., 1978.
В. Н. Монахов, П. II. Плотников.
КРЫЛОВА — БОГОЛЮБОВА МЕТОД УСРЕДНЕ-
УСРЕДНЕНИЯ — метод, применяемый в теории нелинейных
колебаний для исследования колебательных процессов,
основанный на принципе усреднения (осреднения), за-
заменяющем точное дифференциальное уравнение движе-
движения усредненным.
Различные схемы усреднения (Гаусса, Фату, Дело-
Делоне — Хилла и др.) широко применялись в небесной ме-
механике еще задолго до работ Н. М. Крылова и Н. Н. Бо-
Боголюбова. Разработка общего алгоритма, получившего
название метода усреднения Крылова —
Боголюбова, и теорема о близости решении точ-
точной и усредненной систем принадлежат Н. М. Крыло-
Крылову и Н. Н. Боголюбову (см. [1], [2]). Создание строгой
теории метода усреднения, исчерпывающее выяснение-
сущности общего принципа усреднения принадлежат
Н. Н. Боголюбову (см. [3], [4]), к-рый показал, что ме-
метод усреднения связан с существованием нек-рой заме-
замены переменных, позволяющей исключить время t из
прсвых частей рассматриваемых уравнений с наперед
заданной степенью точности относительно малого пара-
параметра е; он же обосновал асимптотич. характер прибли-
приближений, получаемых методом усреднения, и установил
соответствие между решениями точных и усредненных
уравнений на бесконечном временном интервале. Этк
результаты получили дальнейшее развитие в работах
Ю. А. Митропольского и др. (см. [5]—[8]) и применяют-
применяются для изучения нелинейных колебаний.
Система уравнений, для к-рых разработан К.— Б. м.
у., имеет стандартный вид:
где t — время, 8 — малый положительный параметр.
Основные предположения, при к-рых рассматривается
система A), сводятся к достаточной гладкости функции
X по t, х и нек-рой «возвращаемости» ее по t, обеспечи-
обеспечивающей существование среднего значения
lim -jr \ X(t, x)dt=X0(x),
напр, периодичности или почти периодичности X по t.
Согласно К.— Б. м. у. т-е приближение к решению
x=x(t) системы A) определяется выражением
)
в к-ром |=^(i) — решение «усредненного» уравнения
%
п E).
Flt F/, Pj, /=2, . . . , те,— функции, подбираемые из
условия, чтобы выражение B) удовлетворяло уравне-
уравнению A) с точностью до величин порядка em + l и чтобы
F i обладали по I той же возвращаемостью, что и правая
часть системы A). Функции Fj находятся элементарно,
функции Рj определяются в результате усреднения
правой части системы A) после подстановки в нее вы-
выражения B). Так, в частности, для системы A) с пери-
периодической по t правой частью, когда
X (t, х) = X (t +2л, х) = >Г_ ^ < k < ^ Xk (x) e'*f, C)
функция Fx определяется по C) согласно формуле
функции Fт и Рт при т^2 определяются по соотно-
соотношению
X(t,
аналогичными формулами.
Обоснование метода усреднения сводится к следую-
следующему: 1) установление оценки
11*(')-Б(О|1<11(е), * € [0,
где г\ (е) —*¦ 0 при е —>- 0, /, — постоянная, не завися-
зависящая от е, ж@)=2;@); 2) доказательство существования
решения x=xo(t) системы A), находящегося в достаточ-
достаточно малой окрестности положения равновесия \=
= !о : Хо(§о)=О усредненной системы:
sup \\x(t)~ |0||<т)(е),
и установление свойств устойчивости, периодичности
или почти периодичности этого решения; 3) доказатель-
доказательство существования интегрального многообразия т:
x=f(t, ф, е), f(t, ф+2л, e)=/(i, ф, е),
системы A), находящегося вблизи периодической тра-
траектории ?=§о(фI ф=8V, v=const, усредненной системы:
sup II/C, ф, е) —?о(ф)И<П(е),
t, ф6(-оо, «,)
и исследование поведения решений системы A), начи-
начинающихся в окрестности многообразия т.
Лит.: [1] К р ы я о в Н. М., Боголюбов Н. Н., При-
Приложение методов нелинейной механики к теории стационарных
колебаний, К., 1934; [2] их же, Введение в нелинейную ме-
механику, К., 1937; [3] Б о г о л ю б о в Н. Н., О некоторых ста-
статических методах в математической физике, К., 1945; [4] его
ж е, «Сб. трудов Ин-та строительной механики АН УССР»,
1950, Лг« 14, с. 9—34; [5] Боголюбов Н. Н., М и т р о-
польский Ю. А., Асимптотические методы в теории нели-
нелинейных колебаний, 3 изд., М., 19G3; 16] Митрополь-
с к и й Ю. А., Метод усреднения в нелинейной механике, К.,
1971; [7] е г о же, Нестационарные процессы в нелинейных
колебательных системах. К., 1955; [8] В о л о с о в В. М., в кн.:
Механика в СССР за 50 лет, т. 1, М., 1968, с. 115—35.
А. М. Самойлснко.
КУБ — 1) К.— один из пяти типов правильных мно-
многогранников; имеет 6 квадратных граней, 12 ребер,
8 вершин, в каждой вершине сходятся 3 ребра (они
взаимно перпендикулярны). К. иногда наз. гекса-
гексаэдром.
2) К. числа а — третья степень а3 этого числа.
КУБАТУРНАЯ ФОРМУЛА — формула для при-
приближенного вычисления кратных интегралов вида
deff
\
Интегрирование выполняется по Q-множеству в евкли-
евклидовом пространстве R", х={хх, хг, . . . , хп). К. ф. наз.
приближенное равенство
-2^=1 с,/
Подинтеградьная функция записана в виде произведе-
произведения двух функций: первая р (х) считается фиксирован-
фиксированной для данной К. ф. и наз. весовой функцией, вторая
f (х) принадлежит достаточно широкому классу функ-
функций, напр., непрерывных и таких, что интеграл / (/)
существует. Сумма в правой части A) наз. кубатурной
суммой, точки х^} наз. узлами К. ф., а числа С. — ее
коэффициентами. Обычно ж(-"?Й, хотя это требование
не является обязательным. Нахождение приближенного
значения / (/) с помощью формулы A) сводится к вы-
вычислению кубатурной суммы. При и=1 формула A)
и сумма в правой ее части наз. квадратурными
(см. Квадратурная формула).
del
Пусть а = (<х1, а2, . . . , а„) — мультииндекс, здесь
а,- — неотрицательные целые числа;
def def
| а | = а Л? "
— одночлен степени |а| от и переменных;
def def
|x = 7lf (n, m) — (n-\-m)\ln\m\
— число одночленов степени не выше т от п перемен-
переменных; <Pj(x), /=1, 2, ... ,— одночлены, занумерован-
занумерованные так, что одночлены меньшей степени имеют мень-
меньший номер, а одночлены одной и той же степени
нумеруются в любом порядке, напр, лексикографиче-
лексикографическом. При указанной нумерации ср1(х)=1, а среди
ф/(х), / = 1, 2, . . . , jx, содержатся все одночлены
степени не выше т. Пусть <р (х) — многочлен степени
т. Множество точек в комплексном пространстве С",
удовлетворяющих уравнению <р(ж) = О, наз. алгебраич.
гиперповерхностью порядка т.
Один из способов получения К. ф. основан на алгеб-
алгебраич. интерполировании. Точки xV^Q, /=1, 2, . . . ,
jx, выберем так, чтобы они не лежали на алгебраич.
гиперповерхности порядка т или, что равносильно,
чтобы матрица Вандермонда
def
F = [ф1 (*<Л, ф2 (*<Л), . . ., фд (*</>)] f=1
была неособенной. Интерполяционный многочлен функ-
функции f(x) по ее значениям в хУ> в форме Лагранжа имеет
вид
где ?j(x) — многочлен влияния /-го узла: i?y(x('))=6,;-
(б,у — символ Кронекера). Умножение приближенного
равенства /(ж)э=5>(ж) на р (х) и интегрирование по Q
приводит к К. ф. A), в к-рой N=\i и
/ = 1,2, ..., ,i. B)
Существование интегралов B) равносильно существо-
def
ванию моментов весовой функции р,- = !(<(;), i=l, 2,
. . ., ц. Здесь и далее предполагается, что требуемые
моменты р (х) существуют. К. ф. A), узлы к-рой не ле-
лежат на алгебраич. гиперповерхности порядка т, их
число N=n и коэффициенты определяются равенствами
B), наз. интерполяционной К. ф. Фор-
Формула A) обладает т-с войством, если она обра-
обращается в точное равенство, когда /(х) — любой много-
многочлен степени не выше т; интерполяционная К. ф. обла-
обладает m-свойством. Для того чтобы К. ф. A), обладаю-
обладающая m-свойством и с числом узлов iV«:u., была интер-
интерполяционной, необходимо и достаточно, чтобы ранг
матрицы
был равен N. При п= 1 это условие выполнено, так что
квадратурная формула, обладающая ?ге-свойством и с
числом узлов iV<:m+l, является интерполяционной.
Фактич. построение интерполяционной К. ф. сводится
к выбору узлов и вычислению коэффициентов. Коэф-
Коэффициенты Cj можно находить из линейной алгебраич.
системы
spV- q (x(J>) — п ' 12 и
которую получают, записывая, что К. ф. A) (при N=\i)
точна для одночленов степени не выше т. Матрица сис-
системы совпадает с V.
Пусть требуется построить К. ф. A), к-рая обладает
m-свойством, а число ее узлов меньше ц. За счет выбора
коэффициентов это сделать невозможно, поэтому неиз-
неизвестными в A) считаются не только коэффициенты, но и
узлы. Таким образом, имеется N(n-{-l) неизвестных.
Так как К. ф. должна обладать m-свойством, то это дает
и уравнений
У N_ Cm (*<Л) =Pi, I = 1, 2, .. ., а. C)
Естественно потребовать, чтобы число неизвестных
совпадало с числом уравнений: N (п-{-1)=ц. Это ра-
равенство ориентировочно определяет число узлов иско-
искомой К. ф. Если iV=u/(rc-f-l) — не целое, то полагаем
.V=[{i/(re+l)]+l, где [[х/(и+1I означает целую часть
[i/(«-j-l). Требуемая К. ф. с указанным числом узлов не
всегда существует. Если К. ф. существует, то она име-
имеет в (га+1) раз меньше узлов, чем интерполяционная
К. ф. Однако в этом случае узлы и коэффициенты опре-
определяются из нелинейной системы уравнений C). Метод
неопределенных параметров построения К. ф. состоит
в том, что К. ф. ищется в таком виде, к-рый приводит
к упрощению системы C). Это возможно в тех случаях,
когда Q и р (х) обладают симметрией. Расположение уз-
узлов согласуется с симметрией Q и р (х), при этом сим-
симметричным узлам сопоставляются одинаковые коэффи-
коэффициенты. Упрощение системы C) связано с риском: сис-
тедга C) может иметь решение, а упрощенная — не
имеет.
def
Пример. Пусть Q=K2= {—1-^агх, ж2<:1}, р(%\,
х2)=\. Требуется построить К. ф. с 7-свойством; ге=2,
ц=МB, 7) = 36 и число узлов равно 12. Узлы распо-
расположим следующим образом. Первую группу узлов об-
образуют точки пересечения окружности с центром в на-
начале координат и радиусом а с координатными осями.
Вторая группа узлов состоит из точек пересечения ок-
окружности с тем же центром и радиусом Ъ с прямыми
ху=±х2. Третья группа узлов образуется как и вто-
вторая, при этом радиус окружности обозначается с.
Коэффициенты, отвечающие узлам одной и той же груп-
группы, считаются одинаковыми и равными А, В, С для уз-
лов первой, второй и третьей групп соответственно.
Такой выбор узлов и коэффициентов обеспечивает точ-
точность К. ф. для одночленов xlxi, у к-рых хоть одно из
чисел i и ; нечетно. Чтобы К. ф. имела 7-свойство, дос-
достаточно потребовать, чтобы она была точна для 1, х\.
х\, х\х\, xf, x\x\. Это приводит к нелинейной системе
шести уравнений относительно шести неизвестных а,
Ь, с, А, В, С. Решая ее, получаем К. ф., узлы к-рой
принадлежат Кг и коэффициенты положительны.
Пусть G — конечная подгруппа группы ортогональ-
ортогональных преобразований О(п) пространства R", оставляю-
оставляющих неподвижным начало координат. Множество Q
и функция р (х) наз. инвариантными относительно G,
если g(Q)=Q и р (g(x))=p (x) при x?Q для любого
g?G. Совокупность точек вида ga, где а — фиксирован-
фиксированная точка R" и g пробегает все элементы группы G,
наз. орбитой, содержащей а. К. ф. A) наз. инвариант-
инвариантной относительно G, если Q и р (х) инвариантны относи-
относительно G и совокупность ее узлов представляет собой
объединение орбит, при этом узлам одной и той же
орбиты сопоставляются одинаковые коэффициенты. Ин-
Инвариантными относительно G множествами являются
все пространство R", шар и сфера с центром в начале
координат, а если G — группа преобразований правиль-
правильного многогранника U в себя, то инвариантен и U.
Таким образом, инвариантные К. ф. можно рассмат-
рассматривать, когда в качестве Q берутся R", шар, сфера, куб
и любой правильный многогранник, а в качестве р (х) —
любая инвариантная относительно G функция, напр.,
р(г), где r=V ;ri+a|+- ¦ ¦+•?«. Теорема 1. Чтобы инва-
инвариантная относительно G К. ф. обладала тте-свойством,
необходимо и достаточно, чтобы она была точна для тех
многочленов степени не выше т, к-рые инвариантны от-
относительно G (см. [5]). Метод неопределенных парамет-
параметров можно определить как метод построения инвари-
инвариантных К. ф., обладающих m-свойством. В приведенном
выше примере в качестве G можно взять группу симмет-
симметрии квадрата. Теорема 1 имеет существенное значение
при построении инвариантных К. ф.
Для простых областей интегрирования, таких, как
куб, симплекс, шар, сфера, и для веса р(х)=1 можно
построить К. ф. кратным применением квадратурных
def
формул. Напр., когда Q=Kn = {—l<:x,<:i, i=l,
2, ... , п} — куб, то с помощью квадратурной форму-
формулы Гаусса с к узлами i,- и коэффициентами А; может
быть получена К. ф.
J{x)dx^ ^A^ ...Ainf(th,...,tin),
имеющая кп узлов и точная для всех одночленов ха
таких, что 0<:а,-<:2&—1, г=1, 2, ... , п, в частности
для всех многочленов степени не выше 2к—1. Число
узлов таких К. ф. быстро возрастает. Этим фактом опре-
определяются границы их применимости.
Всюду в дальнейшем считается, что весовая функция
сохраняет знак, для определенности
р (ж)ЗзО в Q и Pi > 0. D)
Положительность коэффициентов К. ф. с таким весом
является ценным ее свойством. Теорема 2. Если область
интегрирования Q замкнута и р (х) удовлетворяет D),
то существует интерполяционная К. ф. A), обладаю-
обладающая m-свойством, 7V<:[i, с положительными коэффици-
коэффициентами и узлами, принадлежащими Q. Вопрос о факти-
фактическом построении такой К. ф. остается открытым.
Теорема 3. Если К. ф. с весом, удовлетворяющим D),
имеет действительные узлы и коэффициенты и обладает
m-свойством, то среди ее коэффициентов не менее
def
к = М(п, I) положительных, 1=[т/2] — целая часть
числа т/2. При условиях теоремы 3 число X является
нижней границей для числа узлов:
Ото неравенство остается справедливым и без предполо-
предположения о действительности x{ii и Сj.
Среди К. ф. с m-свойством большой интерес представ-
представляют те, к-рые имеют наименьшее число узлов. В случае
т—1, 2 такие формулы легко найти при любом п и для
произвольных Q и р (х)^0, при этом наименьшее число
узлов совпадает с нижней границей к: равно 1 в первом
случае и re+l — во втором. При то^З наименьшее чис-
число узлов зависит от области и веса. Напр., нрн т—3
для области с центральной симметрией и р(х)=\ наи-
наименьшее число узлов равно 2и, а для симплекса и
р(х)=1 оно равно га+2. При п^З эти числа различны.
В силу D)
def _
(Ф, г|з) = /(Фг|з) E)
является скалярным произведением в пространстве
многочленов. Пусть 5°/к — векторное пространство
многочленов степени к, к-рые ортогональны в смысле
скалярного произведения E) ко всем многочленам
степени не выше к—1. Размерность jjp^ равна М (п—1,
к) — числу одночленов степени к. Многочлены из fpk
наз. ортогональными многочленами Q и р(х). Теорема 4.
Чтобы существовала К. ф. A), обладающая Bк — 1)-
свойством и с числом узлов N=M(n, к—1), равным
нижней границе, необходимо и достаточно, чтобы ее
узлы были общими корнями всех ортогональных много-
многочленов Q и р (х) степени к. Теорема 5. Если п ортого-
ортогональных многочленов степени к имеют к" конечных и
попарно различных общих корней, то эти корни можно
взятъ в качестве узлов К. ф. A), к-рая обладает Bк—1)-
свойством.
Погрешность К. ф. ('!), в к-рой р(х)=1 и Q ограниче-
ограничено, определяется равенством
def
Пусть В — банахово пространство функций такое, что
l(f) является линейным функционалом в В. Норма функ-
функционала ||J||=sup U(/)| характеризует качество рас-
рассматриваемой К. ф. для всех функций пространства В.
Другой подход к построению К. ф. основан на миними-
минимизации ||{|| как функции узлов и коэффициентов искомой
кубатурной формулы (при фиксированном числе узлов).
Даже при п= 1 реализация этого подхода связана с
трудностями. Для любого п~^2 важные результаты по-
получил С. Л. Соболев [4]. Вопрос о минимизации ||Zjj по
коэффициентам при заданных узлах решается до конца;
задача выбора узлов рассматривается в предположении,
что узлы образуют параллелешшедальную решетку и
минимизация осуществляется лишь за счет параметров
этой решетки. В качестве В, в частности, берется прост-
пространство L™(R"), где m>n/2, при этом искомая К. ф.
считается точной для многочленов степени не выше
т—\.
Лит.: [1] К р ы л о в В. И., Приближенное вычисление
интегралов, 2 изд., М., 1967; [2] К р ы-л о в В. И., Шуль-
Шульгина Л. Т., Справочная книга по численному интегрированию,
М., 1966; [3] S t г о u d A. H., Approxlmale calculation of
multiple integrals, [N. Y.], 1971; [4] Соболев С. Л., Введе-
Введение в теорию кубатурных формул, М., 1974; [51 е г о же, «Сиб.
матем. т.», 1962, т. 3, № 5, с. 769—96; [6] М ы с о в с к и х И. П.,
Интерполяционные кубатурные формулы, М., 1981.
И. П. Мысовспих.
КУБИКА — плоская кривая 3-го порядка, т. е.
множество точек плоскости (проективной, аффинной, ев-
евклидовой), однородные координаты х0, хи х2 к-рых (от-
(относительно проективной, аффинной или декартовой
системы координат) удовлетворяют однородному урав-
уравнению третьей степени
F И = 2il ik = Q >4jkxixjxk = 0, aiJk = ajik = aik/.
Количество касательных, к-рые можно провести к К. из
находящейся вне ее точки, наз. классом К. Коника
2 if-/- П
e*t 1=0
наз. конической (или первой) полярой
точки М'(ло, х[, х'г) — полюса; прямая
> 7 X; = О
наз. прямолинейной (или второй) по л я-
р о й точки относительно К. Если полюс М' лежит на
К., то его прямолинейная поляра касается в точке М'
К. и конической поляры точки М'. Гессианом К.
наз. множество точек, конич. поляры к-рых распадают-
распадаются на две прямые; она определяется уравнением
К. пересекается со своей гесснаной в девяти общих
точках перегиба. Прямые, на к-рые распадаются конич.
поляры точек гессианы, а также прямые, соединяющие
нары соответствующих точек гессианы, огибают кривую
6-го порядка 3-го класса — к э л и а н у К. Все К.
плоскости, проходящие через девять точек перегиба
К., образуют с и з и г е т и ч е с к и и пучок, со-
содержащий гессианы всех кривых пучка и четыре кри-
кривые, каждая из к-рых распадается на три прямые и об-
образует с и з и г е т и ч е с к и й треугольник.
Конич. поляра точки перегиба М' распадается на две
прямые: касательную к К. в точке М' и гармони-
гармоническую поляру точки М' — множество точек,
гармонически сопряженных с М' относительно двух то-
точек пересечения К. с секущей, проведенной через М'.
Гармонич. поляры трех лежащих на одной прямой точек
перегиба пересекаются в одной точке. Существуют раз-
различные проективные, аффинные и метрич. классифика-
классификации К.: по типам канонич. уравнений; по характеру не-
несобственных точек К.; по характеру асимптот и др.
Из К. на евклидовой плоскости наиболее известны:
декартов лист (х'д-\-у3—Ъаху — iS), локон Аньези (у (а2-\-
+ ж2)=ай), кубнч. парабола (у — ах3), полукубич. пара-
парабола (у--^= ах'-'), строфоида (у2 (а—а;) = х2(а+ж)), циссоида
Диоклеса (г/2Bа—х)=х3), трисектриса (х(х'~-гу2) =
= аCж2—у2))., конхоида Слюза (а(х—а)(х2-{-у2) = к2х2).
В алгебраич. геометрии кубикой наз. как кубическую
гиперповерхность, так и пространственную кубическую
кривую.
Лит.: [1] С м о г о р ж е в с к и й А. С, Столона Е. С.,
Справочник по теории плоских кривых третьего порядка, М.,
1961. В. С. Малаховский,
КУБИЧЕСКАЯ ГИПЕРПОВЕРХНОСТЬ — проектив-
проективное алгебраич. многообразие, задаваемое однородным
уравнением F3(x0, . . . , х„) = 0 3-й степени с коэффи-
коэффициентами из нек-poro основного поля к.
Кубические кривые. Неприводимая кубич.
кривая является либо гладкой (в этом случае ее кано-
канонич. класс равен 0, а род 1), либо имеет одну особую
двойную точку (в этом случае она рациональна). Кубич.
кривые — кривые наименьшей степени, для к-рых су-
существуют модули. Каждая гладкая кубич. кривая X
над алгебраически замкнутым полем к, характеристика
к-рого отлична от 2 и 3, бирациональными преобразо-
преобразованиями может быть приведена к вейерштрассовой фор-
форме, в неоднородных координатах плоскости (х, у) имею-
имеющей вид
г/2 = 4ж3 — g2x — g3,
гДе #2> ?з€^) ?2—27g-i=7fcO. Две кубич. кривые с коэффи-
циентами (g2, gs) и (g'2, g'3) в вейерштрассовой форме изо-
изоморфны тогда и только тогда, когда
«1-27*5
Функция
принимает любые значения из к и зависит только от
кривой X, она наз. абсолютным инвариан-
инвариантом кубич. кривой X.
На множестве точек X (к) кубич. кривой определен
бинарный закон композиции (хг, х2) -> х1 о хг, где
xl-x2 — третья точка пересечения кривой X с прямой,
проходящей через точки хг и хг. Бели фиксировать
нек-рую точку хо?Х(к), то композиция
(.Tj, .Т2) , Хо° {Х1ох2)
превращает множество X (к) в абелеву группу с нулем
х0. Кубич. кривая, снабженная этой структурой, яв-
является одномерным абелевым многообразием (эллип-
тич. кривой).
В случае, когда к=С — поле комплексных чисел,
Х(С) есть риманова поверхность рода 1, т. е. одномер-
одномерный комплексный тор — факторгруппа С/Г(Х), где
Г(А') — двумерная решетка периодов. Поле к рацио-
рациональных функций кривой X в этом случае изоморфно
полю эллиптич. функций на С с решеткой периодов
Т(Х). Коэффициенты g.2 и g3 интерпретируются как мо-
модулярные формы весов 4 и 6 соответственно, совпадаю-
совпадающие с точностью до постоянного множителя с формами,
определяемыми рядами Эйзенштейна наименьших весов.
Функция j в этом случае есть не что иное, как модуляр-
модулярный инвариант.
Для кубич. кривых над алгебраически незамкнутым
полем к также развита содержательная арифметич. тео-
теория (см. [2]). Существенную часть ее достижений со-
составляют теорема Морделла — Вейля, теория комплекс-
комплексного умножения и когомологическая теория главных
однородных пространств. Основные нерешенные A982)
проблемы этой теории: проблема ограниченности ран-
ранта над полем алгебраич. чисел, гипотеза конечности
для группы главных однородных локально тривиальных
пространств, гипотеза Берча и Суиннертон-Дайера
о дзета-функции, гипотеза Вейля об униформизации
и др.
Кубические поверхности. Над алгебра-
алгебраически замкнутым полем к каждая неприводимая ку-
кубич. поверхность (если она не вырождается в конус)
является рациональной поверхностью. Класс гиперпло-
гиперплоского сечения h поверхности F совпадает с канониче-
каноническим классом (— Кр). Любая гладкая кубич. поверх-
поверхность получается из проективной плоскости Р2 разду-
раздутием (т. е. моноидальиым преобразованием) 6 точек, ни-
никакие 3 из к-рых не лежат на одной прямой, а все 6 не
лежат на одной конике. Соответствующее бирациональ-
ное отображение <р: Р2 -+¦ F задается линейной системой
кубич. кривых, проходящих через эти 6 точек. На F
лежат 27 прямых, каждая из к-рых является исключи-
исключительной (см. Исключительное подмногообразие). Ими
исчерпываются все исключительные кривые на F. Кон-
Конфигурация 27 прямых богата симметриями: группа ав-
автоморфизмов соответствующего графа изоморфна груп-
группе Вейля Е6. Кубич. поверхности принадлежат к серии
поверхностей дель Пеццо — проективных
поверхностей с обильным обратным канонич. классом.
Над алгебраически незамкнутым полем к имеются
гладкие кубич. поверхности F, для к-рых не существует
бирационального изоморфизма с Р2 над к (т. е. F не !
рационален над к). Среди них есть поверхности, обла-
обладающие fc-точками, в этом случае они унирационалъны
над к. Такие кубич. поверхности являются контрприме-
контрпримером для Люрота проблемы о поверхностях над незамк-
незамкнутыми полями. Над нек-рыми к существуют минималь-
минимальные кубич. поверхности. Критерий минималь-
минимальности Сегре [6]: Pic(F)~%. Вычислена группа
бирациональных автоморфизмов минимальной кубич.
поверхности (найдены ее образующие и определяющие
соотношения) и развита арифметич. теория кубич. по-
поверхностей [4]. Для описания множества точек F(к)
привлечены неассоциативные структуры: квазигруппы
и лупы Муфанг.
Кубические гиперповерхности раз-
размерности 3. Все гладкие К. г. размерности ^2
над алгебраически замкнутым полем унирациональны.
В 80-е гг. 19 в. был поставлен вопрос: будет ли гладкая
трехмерная К. г. рациональна? На него получен отри-
отрицательный ответ [3]. Тем самым дано и отрицательное
решение проблемы Люрота для трехмерных многообра-
многообразий. С каждой гладкой К. г. V размерности 3 связано
главное поляризованное пятимерное абелево многооб-
многообразие — промежуточный якобиан J3(V). В случае /с=С
он определяется как комплексный тор
IP'*(V, C)/#3(F, Ж),
где Я1'2 (V, С) — соответствующая компонента Ходжа
в разложении пространства когомологип H3(V, С).
Для доказательства нерациональности V было показа-
показано, что J3(V) не является якобианом никакой кривой
рода 5. Нерациональность К. г. над полем конечной
характеристики установлена в [5].
К. г. V однозначно определяется своей Фано поверх-
поверхностью Ф (V). ДляФ(Т') справедлива Торелли теорема
(и тем самым теорема Торелли справедлива и для F).
Нерешенной проблемой о К. г. размерности 3 является
проблема описания ее группы бирациональных авто-
автоморфизмов.
Неизвестно A982), будет ли каждая гладкая К. г.
размерности ^ 4 рациональна. Рациональность уста-
установлена в этом случае для иек-рых К. г. специально-
специального вида; напр.:
1+1 „,*? = <), тЗ*2.
Лит.: [1] Г у р в и ц А., Курант Р., Теория функций,
пер. [с нем.], М., 1968; [2] КасселсД ж., «Математика»,
1968, т. 12, № 1, с. 113 — 60; т. 12, Л1 2, с. 3—48: [3] Кли-
Климе н с К. Г., Г р и ф ф и т с Ф. А., там же, 1972, т. 16,
№ 6, с. 3 — 32; 1973, т. 17, Ni 1, с. 3—41; [4] М а н и н Ю. И.,
Кубические формы, М., 1972; [5] М и г г е J. Р., «Сотр. math.»,
1973, v. 27, р. 63—82; [6] Segre В., The non-singular cubic
surfaces, Oxf., 1942; [7] T ю р и н А. Н., «Успехи матем. наук»,
1972, т. 27, в. 5, с. 3—50; [8] е г о ж е, «Изв.
АН СССР. Сер. матем.», 1971, т. 35, с. 498—
529; [9] Ш а ф а р е в и ч И. Р., Основы ал-
алгебраической геометрии, М., 1972.
В. А. Псковских.
КУБИЧЕСКАЯ ПАРАБОЛА — пло
екая кривая (см. рис.), выражаемая в
прямоугольной системе координат урав-
уравнением у=ах3.
КУБИЧЕСКАЯ ФОРМА — однород-
однородный многочлен третьей степени от не-
нескольких переменных с коэффициентами
из нек-рого фиксированного поля или
кольца. Пусть к — нек-рое поле и F3(x0, . . . , хп) —
К. ф. с коэффициентами из к (говорят, что это —
К. ф. над к). Уравнение
F3{x0, . . . , я„) = 0
определяет кубическую гиперповерхность в проективном
пространстве Рп, что сводит алгебро-геометрическую
теорию К. ф. над алгебраически замкнутым полем к
к теории кубических гиперповерхностей (см. [1]).
Арифметич. теория К. ф. над числовыми полями (и их
кольцами целых) развита пока A982) недостаточно
полно по сравнению с богатой и содержательной ариф-
арифметич. теориой квадратичных форм. Для К. ф. от двух
переменных арифметич. теория — это теория кубич.
расширений числовых полей (см. [2]). Для К. ф. от трех
переменных арифметич. теория — это часть арифметич.
теории эллиптич. кривых (см. [3]). В частности, для К.
ф. от трех переменных известны примеры нарушения
принципа Хассе. Для К. ф. от четырех переменных
(см. [1, 4, 6]) также известны примеры нарушения
принципа Хассе. Для К. ф. от большего числа перемен-
переменных нет никакой общей теории.
В чисто алгебраич. теории К. ф. кроме результатов
о структуре множеств точек на кубич. гиперповерхно-
гиперповерхностях имеется еще ряд результатов классич. теории ин-
инвариантов. А именно, известно строение алгебры (аб-
(абсолютных) инвариантов К. ф. от двух и трех перемен-
переменных; в зтих случаях она не имеет сизигий и является
алгеброй многочленов соответственно от одного (степени
4) и двух (степени 4 и 6) алгебраич. независимых одно-
однородных образующих. Если число переменных больше
трех, указанная алгебра имеет сизигии [5] и устроена
весьма сложно. Орбиты, их стабилизаторы и канонич.
представители, а также семейства орбит относительно
естественного действия группы SLn на пространстве
всех К. ф. от трех и четырех переменных изучались
А. Пуанкаре [6].
Лит.: [1] Манин Ю. И., Кубические формы. Алгебра,
геометрия, арифметика, М., 1972; [2] Д е л о н е Б. Н., Фад-
Фаддеев Д. К., Теория иррациональностей третьей степени,
М.—Л., 1940 (Тр. Матем. ин-та АН СССР, т. 11); [3] К а с-
с е л с Д ж., «Математика», 1968, т. 12, N, I, с. 113—60; JVJ 2,
с. 3—48: [4] Segre В., «Math. Notae», [Univ. Rosario], 1951,
v. 11, p. 1—68; [5] К а ц В. Г., П о п о в В. Л., В и н-
б е р г Е. Б., «С. г. Acad. sci.», 1976, t. 283, p. 875—78; [6]
Пуанкаре А., Избр. труды, пер. с франц., т. 2, М., 1972,
с. 819—900. В. А. Псковских, В. Л. Попов.
КУБИЧЕСКИЙ ВЫЧЕТ по'модулю т — це-
целое число а, для к-рого сравнение х3^^а (mod го) разре-
разрешимо. Если указанное сравнение не разрешимо, то
число а наз. кубическим невычетом по
модулю го. В случае простого модуля р вопрос о
разрешимости сравнения a:3=a(mod p) может быть вы-
выяснен с помощью критерия Эйлера: для раз-
разрешимости сравнения xss=a(mo& p), (а,р) = 1 необходи-
необходимо и достаточно, чтобы
р-1
a q =1 (mod p),
где ?=C, р—1), и при выполнении последнего условия
исходное сравнение имеет q различных по модулю р
решений. Из критерия следует, в частности, что среди
чисел 1, 2, ... , р — 1 имеется ровно (q—1) -—- кубиче-
кубических невычетов и ^—^ К. в. по простому модулю р.
С. А. Степанов.
КУБИЧЕСКОЕ УРАВНЕНИЕ — алгебраическое
уравнение третьей степени, т. е. уравнение вида
ах*-\-Ъх* + сх-\- d = 0,
где афО. Заменяя в этом уравнении х новым неизвест-
неизвестным г/, связанным с х равенством х=у — Ь/За, К. у. мож-
можно привести к более простому (каноническому) виду:
где
Ь2 с
Р~~~ зЗг 5" '
2b3 be } d
У 27а3 3~аг'~а '
решение жо этого уравнения можно получить с помощью
Кардано формулы; таким образом, К. у. решается в ра-
радикалах.
Решение К. у. было найдено в 16 в. В начале 16 в.
С. Ферро (S. Ferro) решил уравнение вида xSJrpx=q,
где р>0, д>0, но не опубликовал решения. Затем
Н. Тарталья (N. Tartaglia) заново открыл результат
С. Ферро, а также дал решение уравнения вида х3=
= px-{-q (p>0, д>0) и без доказательства сообщил, что
к уравнению этого вида сводится уравнение вида с3+
-\-q=pX^ где р>0, <?>0. Свои результаты Н. Тарталья
сообщил Дж. Кардано (G. Cardano), к-рый опубликовал
решение уравнения третьей степени общего вида в 1545.
Лит.: [1] Курош А. Г., Курс высшей алгебры, 11 изд.,
М., 1975. И. В. Проскуряков.
КУБОВИДНЫЙ КОНТИНУУМ, га-кубовид-
га-кубовидный к о н т и н у у м,— компакт (метризуемын би-
бикомпакт), обладающий для любого 8>0 «-отображением
на обычный куб I". Если компакт X является пределом
счетного спектра из компактов, вложимых в /", то X
является подмножеством К. к. В классе К. к. сущест-
существует универсальный элемент, т. е. такой К. к. U, что
каждый К. к. гомеоморфен нек-рому подпространству
пространства U.
Лит.: [1] П а с ы н к о в Б. А., «Успехи матем. наук»,
1966, т. 21, в. 4, с. 91 —100. Л. Г. Замбахидзе.
КУЗЕНА ПРОБЛЕМЫ — проблемы, названные по
имени П. Кузена [1], к-рый впервые решил их для про-
простейших областей в пространстве п комплексных пере-
переменных С".
Первая (аддитивная) проблема Ку-
Кузена (I К. п.). Дано покрытие 11 = {Ua} комплексно-
комплексного многообразия М открытыми подмножествами Ua и в
каждом Uа задана мероморфная функция /а, причем
функции /<хр=/<х—/р голоморфны в Сар= Са П ?7р лля
всех индексов а, [5 (условие согласования).
Требуется построить функцию /, мероморфную на всем
многообразии М и такую, что функции /—fa голоморф-
голоморфны в Ua для всех а. Другими словами, надо построить
глобальную мероморфную функцию с локально задан-
заданными полярными особенностями.
Функции /ар, определенные в попарных пересече-
пересечениях иа$ элементов покрытия 11, определяют голо-
голоморфный коцикл 1-го порядка для 11, т. е. удовлетворя-
удовлетворяют условию
/«P+/(ta = 0 в С7ар,
/ap + /pv+ 'v<* = ° в Ua П <7р П Uy A)
для всех а, C, у. Более общая проблема (так наз. I К. п.
в когомологической формулировке)
заключается в следующем. На попарных пересечениях
?7<хр покрытия 11 заданы голоморфные функции /гар,
удовлетворяющие условию коцикличности A). Требует-
Требуется найти функции ha, голоморфные в Ua и такие, что
для всех а, C. Если /ар соответствуют данным I К. п.
и указанные ha существуют, то функция
f = {fa + ha в Ua)
определена и мероморфна на всем многообразии М и
является решением данной I К. п. Обратно, если / —
решение I К. п. с данными {fa}, то голоморфные функ-
функции ha=f—fa удовлетворяют B). Таким образом,
конкретная I К. п. разрешима тогда и только тогда,
когда соответствующий ей коцикл является голоморф-
голоморфной кограницей (т. е. выполняется условие B)).
I К. п. можно формулировать в локализованном ва-
варианте. Каждому набору данных {Ua, fa} с условием
согласования соответствует однозначно определенное
глобальное сечение пучка aSlQ, где аМ к Q — пучки
ростков мероморфных и голоморфных функций соот-
соответственно, причем любое глобальное сечение aS/Q со-
соответствует какой-нибудь I К. п. (значение сечения к,
соответствующего данным {fa}, в точке z? Ua есть эле-
элемент aSzl6z с представителем /«). Отображение гло-
ф
бальных сечений Г (сЖ) -*¦ Г (aSlQ) переводит каждую
мероморфную на М функцию / в сечение v,f пучка aMIQ,
где y.f(z) — класс в a/flzlQz ростка / в точке z, z?M.
Локализованная IK. п. заключается в том,
чтобы для данного глобального сечения и пучка оМЩ
найти мероморфную на М функцию / (т. е. сечение q$)
такую, что ф(/)=х.
Теоремы о разрешимости I К. п. можно рассматри-
рассматривать как многомерное обобщение Миттаг-Леффлера
теоремы о построении мероморфной функции с данными
полярными особенностями. I К. п. в когомологич. фор-
формулировке с фиксированным покрытием 11 разрешима
(для произвольных согласованных {/а}) тогда и только
тогда, когда НхA1, 0) = О (когомологии Чеха для по-
покрытия % с голоморфными коэффициентами триви-
тривиальны) .
Конкретная I К. п. на М разрешима тогда и только
тогда, когда соответствующее ей сечение aSlfy принад-
принадлежит образу отображения <р. Произвольная I К. п. на
М разрешима тогда и только тогда, когда <р — отобра-
отображение на (сюръективно). На любом комплексном мно-
многообразии М имеет место точная последовательность
> т (М, Q).
Если когомологии Чеха для М с коэффициентами в Q
тривиальны (т. е. H1(Q/M, 6)=0), то <р — отображение
на и Hl(Qd, E) = 0 для любого покрытия 11 многообра-
многообразия М. Таким образом, если Н1 (М, C) = 0, то на М
разрешима любая I К. п. (в классической, когомоло-
когомологической и локализованной формулировках). В част-
частности, I К. п. разрешима во всех областях голоморф-
голоморфности и на Штейна многообразиях. Если область
DaC2, то I К. п. в D разрешима тогда и только тогда,
когда D — область голоморфности. Пример неразре-
неразрешимой I К. п.: Vkf=C2\{0}, иа={гаф0}, а=1, 2,
Вторая (мультипликативная) проб-
проблема Кузена (ПК. п.). Дано открытое покрытие
U={Ua} комплексного многообразия Мяв каждом
Ua задана мероморфная функция /а, /«^0 на каждой
компоненте Ua, причем функции /ap=/a/fi1 голоморфны
п нигде не равны нулю в tTa|3 для всех a, p (условие
согласован и я). Требуется построить мероморф-
мероморфную на М функцию / такую, что функции //й1 голоморф-
голоморфны и нигде не равны нулю в Ua для всех а.
Когомологическая формулировка
II К. п. Дано покрытие 11 и в попарных пересечениях
Ua$ заданы голоморфные нигде не равные нулю функции
/ар, образующие мультипликативный коцикл первого
порядка, т. е.
/га|3/|3га = 1 В Uар,
= l В Uа (] ?/р П #v •
Требуется найти функции ha, голоморфные и нигде не
равные нулю в Ua такие, что /гар=^р^а1 в [/гар для
всех а, р. Если коцикл {/ар} соответствует данным II
К. п. и указанные ha существуют, то функция /=
= {faha в Uа} определена и мероморфна всюду на М
и является решением данной II К. п. Обратно, если
данная II К. п. разрешима, то соответствующий ей
коцикл является голоморфной кограницей.
Локализованная II К. п. Каждому набору
данных {Ua, fa} П К. п. соответствует однозначно
определенное глобальное сечение пучка &#*/0* (ана-
(аналогично I К. п.), где сЖ* = рМ\{0} @ — нулевое сече-
сечение) — мультипликативный пучок ростков мероморф-
ных функций и 6*— подпучок 0, у к-рого каждый
слой C* состоит из ростков голоморфных функций,
отличных от нуля в точке z. Отображение глобальных
сечений
Г (а?*) ^ Г (Ж 16*)
сопоставляет мероморфной функции / сечение х?пучка
a/ft*lQ*, где щ (z) — класс в qSzIQz ростка /в точке
z, z?M. Локализованная II К. п. заключается в сле-
следующем: дано глобальное сечение х* пучка a/ft*IQ*,
требуется найти мероморфную функцию / на М, /=Й0
на компонентах М (т. е. глобальное сечение &#*)> та-
такую, что г|з(/) = х*.
Сечениям o/ft*lQ* однозначно соответствуют диви-
зоры, поэтому пучок aM*lQ* = 3) наз- пучком ро-
ростков дивизоров. Дивизор на комплексном
многообразии М — это формальная локально конечная
сумма "Zkjhj, где kj — целые числа и Ду — аналитиче-
аналитические подмножества М чистой коразмерности 1. Каждой
мероморфной функции / соответствует дивизор, слагае-
слагаемые к-рого — неприводимые компоненты нулевого и
полярного множеств / с соответствующими кратностями
kj, причем кратности нулей берутся со знаком плюс,
а кратности полюсов— со знаком минус. Отображение^
сопоставляет каждой функции / ее дивизор (/); такие
дивизоры наз. собственными. II К. п. в тер-
терминах дивизоров заключается в следующем:
на многообразии М задан дивизор Д, требуется пост-
построить мероморфную на М функцию / такую, что Д=
= (/)•
Теоремы о разрешимости II К. п. можно рассматри-
рассматривать как многомерные обобщения теоремы Вейерштрасса
0 построении мероморфной функции с данными нулями
и полюсами. Аналогично I К. п., для разрешимости
всякой II К. п. в когомологич. формулировке необхо-
необходимо и достаточно условие Я1 (М, Q*) = 0. К сожалению,
пучок 0* не когерентен, и это условие менее эффек-
эффективно. При попытке свести данную II К. п. к I К. п.
путем логарифмирования возникает препятствие в виде
целочисленного коцикла 2-го порядка и получается
точная последовательность
№(М, 6)-^ Н1(М, 6*)-^НЦМ, z),
где % — постоянный пучок целых чисел. Таким обра-
образом, если Н1(М, Q)=H2(M, Z) = 0, то на М разрешима
любая II К. п., любой дивизор является собственным.
Если М — многообразие Штейна, то а — изоморфизм,
поэтому топологич. условие Я2(М, Z) = 0 на многооб-
многообразии Штейна М является необходимым и достаточным
для разрешимости II К. п. в когомологич. формули-
формулировке. Сквозное отображение с=а°Р,
г (&» -^ л1 (м, q*) -Д п* (м, %)
сопоставляет каждому дивизору Д элемент с(Д) группы
Н2(М, 2), к-рый наз. классом Чжэня диви-
дивизора Д. Конкретная II К. п., соответствующая диви-
дивизору Д, разрешима при условии II1 (М, Q)=0 тогда и
только тогда, когда класс Чжэня дивизора Д тривиа-
тривиален, т. е. е(Д) = О. На многообразии Штейна отображе-
отображение с сюръективно, более того, любой элемент ил
Л2(М, Z) имеет вид с(Д) для нек-рого дивизора Л
с положительными кратностями kj. Таким образом,
препятствия для решения II К. п. на многообразии
Штейна М полностью описываются группой IP(M, Z).
Примеры. 1) M=C2\{z1=z2, UiHl}; I К. п.
неразрешима, II К. п. неразрешима, напр, для дивизора
A=Mf\{z1=z2, |zjj<l} с кратностью 1.
2) М= {jzi + zf+zf—1|<1}с:С3, Д — одна из компо-
компонент пересечения М плоскостью z2=:iz1 с кратностыо
1; II К. п. неразрешима (М — область голоморфности,
1 К. п. разрешима).
3) I К. п. и II К. п. разрешимы в областях D =
—/JjX. . .ХД„сС", где Dj — плоские области и все
I).-, кроме, быть может, одной, односвязны.
Лит.: [1] С о u s i n P., «Acta math.», 1895, v. 19, p. 1—62;
12] Ш а б а т Б. В., Введение в комплексный анализ, 2 изд.,
ч. 2, М., 1976; [3] Г а н н и и г Р., Р о с с и X., Аналитиче-
Аналитические функции многих комплексных переменных, пер. с англ.,
М., 1969. Е. М. Чирка.
КУММЕРА ГИПОТЕЗА — предположение о пове-
поведении кубической Гаусса суммы
где х{п, р) = ехрBя/ ind n/3) — кубический характер
по модулю р=1 (mod 3), а р — простое число. Изве-
Известно, что
При этом argx(x) лежит либо в первом, либо в третьем,
либо в пятом секстанте. В соответствии с этим Э. Куммер
(Е. Kummer) разбил все простые числа р=1 (mod 3)
на три класса Plt Р3 и Ръ. Согласно К. г. в каждом из
классов Ра, Ръ и Р3 находится бесконечное множество
простых чисел, причем эти классы имеют соответствен-
соответственно асимптотич. плотности 1/2, 1/я и 1/(i. Существуют
различные обобщения К. г. на характеры более высо-
высокого порядка, чем 3. К. г. доказана в модифицирован-
модифицированном виде (см. [3]).
Лит.: [1] X а с с е Г., Лекции по теории чисел, пер. с нем.,
М., 1953; [2] Д э в е н п о р т Г., Мультипликативная теория
чисел, пер. с англ., М., 1971; [3] Heath-Brown D. R.,
Pattersons. I. «J. reine und angew. Math.», 1979, Bd
130, S. 111 — 30. Б. М. Бредихин.
КУММЕРА ПОВЕРХНОСТЬ — алгебраич. поверх-
поверхность четвертого порядка и класса, сама себе взаимная,
имеющая 16 двойных точек, из к-рых 16 групп (по 6 то-
точек каждая) расположены в одной двойной касатель-
касательной плоскости к поверхности (т. е. плоскости, касаю-
н;ейся поверхности по конич. сечению). Уравнение
16-й степени, определяющее двойной элемент, приво-
приводится к одному уравнению 6-й степени и нескольким
квадратным. Найдена Э. Куммером (Е. Kummer,
1864). К. п. принадлежит классу КЗ-поверхностей и
выделяется среди них условием существования на ней
16 неприводимых рациональных кривых.
Лит.: [1] Клейн Ф., Лекции о развитии математики в
XIX столетии, пер. с нем., М.— Л., 1937; [2] Hudson R.,
Rummer's quartic surface, Camb., 1905; [3] E n r i q u e s F.,
Le superficie algebriche, Bologna, 1949. M. И. Войцеховгкии.
КУММЕРА ПРЕОБРАЗОВАНИЕ — одно из преоб-
преобразований числовых рядов, улучшающее сходимость;
предложено Э. Куммером (Е. Kummer). Пусть
V ak = A я V bh = B
— сходящиеся ряды и пусть существует предел
Тогда
Если сумма В известна, то К. п. может оказаться
полезным при вычислениях, так как ряд в правой части
сходится быстрее ряда в левой.
Лит.: [1] Ф и х т е н г о л ь ц Г. М., Курс дифференциаль-
дифференциального и интегрального исчисления, 7 изд., т. 2, М., 1970.
В. В. Сенатов.
КУММЕРА ПРИЗНАК — общий признак сходи-
сходимости рядов с положительными членами, предложен-
предложенный Э. Куммером (Е. Kummer). Пусть дан ряд
V ап = а1+а2+... 4 <*„+••• (*)
и ci, c2J. . ., с,,,. . .— произвольная последовательность
^» 1
положительных чисел такая, что ряд > — расхо-
¦*—'п — 1
дится. Если для п > N выполняется неравенство
где б — постоянное положительное число, то ряд (*)
сходится. Если Кп <: 0 для п > /V, то ряд (*) расхо-
расходится.
В предельной форме К. п. формулируется следую-
следующим образом: пусть
lim К„ — К,
п —>- °°
тогда при К > 0 ряд (*) сходится, при А* < 0 — рас-
расходится.
Лит.: [1] Ф и х т е и г о л ь ц Г. М., Курс дифференциаль-
дифференциального и интегрального исчисления, 7 изд., т. 2, М., 1970.
Е. Г. Соболевская.
КУММЕРА РАСШИРЕНИЕ — расширение поля
к характеристики р ^ 0 вида
, .... п/щ), A)
где oci,. . ., oc/^fe, n — некоторое натуральное число,
причем предполагается, что поле к содержит первообраз-
первообразный корень ?„ из 1 степени га (в частности, п взаимно
просто с р при рф 0). К. р. названы по имени Э. Кум-
мера (Е. Кшшпег), впервые подробно рассмотревшего
расширения вида Q (Х,пу а)> гДе Q;— поле рациональ-
рациональных чисел и
Основной результат теории К. р. состоит в том, что
для поля к, содержащего первообразный корень ?„,
конечное расширение К!к является куммеровым (для
данного п) тогда и только тогда, когда К/к — нормаль-
нормальное абелево расширение и группа Галуа G(Klk) имеет
период га. Любое К. р. поля к полностью характеризу-
характеризуется своей группой Кум мера A (Klk) = Blk*,
где к* — мультипликативная группа поля к, а
fi = {ig K*\r» б 'со-
'сосуществует невырожденное спаривание Кум-
мера, т. е. отображение
G(K/k) xA(K/k)—^ii(n),
где ц(п) — подгруппа группы к*, порожденная ?„.
Для a^G(Klk) и а^А (К/к) это спаривание задается
формулой (а, а) = (y/a)E~1G(i(n), где <х?к, a^/ag
(з-В — некоторый представитель элемента а. Это спа-
спаривание определяет канонический изоморфизм
G (К/к) ^ Rom (А (К/к), \х(п)). B)
Другими словами, всякий автоморфизм o?G(K/k)
определяется своим действием на корни ^/а,- в A),
и это действие может быть произвольным, если только
корни у/а,- независимы. В частности, если G(Klk) —
цнклич. группа, то К=к^^/а), где а?к*.
Пусть к — нормальное расширение поля к0 и Как.
Поле К тогда и только тогда нормально над А0) когда
А (К/к) переходит в себя под действием G(klk0). В этом
случае изоморфизм B) является ?(?/7с0)-операторным,
т.'е. если T^G(klk0), a^G(Klk) и
то ф(а*)=тх, где (i%) (а) = т(х(т-1а)). (Группа G(k/k0)
действует на G(Klk) с помощью сопряжения в G(Klk^).)
Это обстоятельство позволяет сводить многие вопросы
об абелевых расширениях периода п поля к к тео-
теории К. р. даже в том случае, когда ?« С &• ^ имен-
но, если К/к — такое расширение, то расширение
K{Z,n)!k(C,n) является куммеровым, причем его группа
Куммера характеризуется условием: для %^G{k{t,n)!k)
и а?А (К(?„)/'к(?„)) будет т(а) = а', где i — натураль-
натуральное число, определенное по модулю п условием т(?„) =
= Е».
Основные результаты о К. р. могут быть получены
как следствие Гильберта теоремы о циклич. расшире-
расширениях, утверждающей тривиальность одномерной груп-
группы Галуа когомологий //1(G(Z/fc), A"*).
Теория К. р. переносится на случай бесконечных
абелсвых расширений периода п. При этом спаривание
Куммера устанавливает двойственность Понтрягина
между проконечной группой G(Klk) (наделенной топо-
топологией Крулля) и дискретной группой А (К/к) ( м.
[1] гл. 8, § 8; [2] гл. 3, § 2).
Теория К. р., называемая также теорией К у м-
м е р а, имеет аналог для случая расширений вида A),
но с п=р (так наз. теория Артина — Шрей-
е р а). Роль группы \.i(n) в этом случае играет аддитив-
аддитивная группа простого подполя Fр поля к. Основное утвер-
утверждение этой теории: любое абелево расширение К
периода р поля к имеет вид к (Pi, ..., Cf), где рь ...,
Р/ — корни уравнений вида хР—г=а (см. [1] гл. 8,
\ 8). Существует также принадлежащее Э. Витту
(Е. Witt) обобщение этой теории для случая n~ps,
где «>1, использующее Витта векторы.
Имеется, наконец, попытка построения неабелевой
«теории Куммера» [3], где роль мультипликативной
группы поля играет группа матриц GL(n, К).
Лит.: [1] Лен г С, Алгебра, пер. с англ., М., 1968; [2]
Алгебраическая теория чисел, пер. с англ., М.. 1969; [3] Т а-
kahashi S., «J. Math. Soc. Japan», 1968, v. 20, Л^ 1—2,
p. 365—70. Л. В. Кузьмин.
КУММЕРА ТЕОРЕМА: пусть к — поле частных де-
декиндова кольца А, К — расширение поля к степени
п, В — целое замыкание А в К и р — некоторый про-
простой пдеал кольца А: пусть Ж=/с[6], где 6^5, и эле-
элементы 1, 0, О2,. . ., б" образуют базис Л-модуля В;
наконец, пусть / (х) — минимальный многочлен эле-
элемента 0, /* (х) — образ f(x) в кольце А/р[х] п. f* (х) =
=/i (x)li . . . fr (x) — разложение многочлена /* (х)
на неприводимые множители в кольце у4/р[.т]; тогда в
кольце В идеал рВ распадается в произведение простых
идеалов
при этом степень многочлена fi (x) совпадает со сте-
степенью [В/р; : А/$] расширения полей вычетов.
К. т. позволяет определить разложение простого
идеала при расширении основного поля через разло-
разложение на неприводимые множители в поле вычетов ми-
минимального многочлена подходящего примитивного
элемента данного расширения.
Эта теорема в нек-рых частных случаях была дока-
доказана Э. Куммером [I] и применена для получения зако-
закона разложения в круговых полях и нск-рых циклич.
расширениях круговых полей.
Лит.: [1] К u m m е г Е., «J. reine und anpew. Math.»,
1847, Bd 35, S. 319—26; [2] Алгебраическая теория чисел, пер.
с англ., М., 19В0. Л. В. Кузьмин.
КУМУЛЯНТ — то же, что семиинвариант..
КУРАНТ — термин, употребляемый при рассмотре-
рассмотрении разностных схем интегрирования одномерных
гиперболических систем. Если т — шаг по t, h —
шаг по х, % — максимальный из наклонов характери-
характеристик, то курант разностной схемы равен kx/h.
Лит.: [1] Годунов С. К., Рябенький В. С, Раз-
Разностные схемы, М., 1973. Н. С. Бахвалов.
КУРАНТА ТЕОРЕМА о конформном отоб-
отображении областей с переменными
границами: пусть {Dn} — последовательность
вложенных односвязных областей плоскости комплек-
комплексного переменного z, Dn + iCDn, сходящаяся к своему
ядру DZo относительно нек-рой точки z0, причем область
DZo ограничена жордановой кривой; тогда последова-
последовательность функций {w=fn (z)}, конформно отображаю-
отображающих области Dn па круг Д= {w: |гс|<1}, /„(zo) = 0,
/«(zo)>O, равномерно сходится в замкнутой области
^г0 к функции w=f(z), конформно отображающей Ого
на А, причем /(zo) = O, /'(zo)>O.
К. т., полученная Р. Курантом [i], дополняет Кара-
теодори теорему.
Лит.: [1] С о u r a n t R., «Gott. Nachr.», 1914, S. 101 — 109;
1922, S. 89—70; [2] M a p к у ш е в и ч А. И., Теория аналити-
аналитических функций, 2 иад., т. 2, М., 1968. К. Д. Соломенцее.
КУРАНТА — ФРИДРИХСА — ЛЕВИ УСЛОВИЕ —
необходимое условие устойчивости разностных схем в
классе бесконечно дифференцируемых коэффициентов.
Пусть Q (Р) — область зависимости значения решения
по какому-либо из коэффициентов (в частности, им
может быть начальное условие), Qfl(P)— область за-
зависимости значения uh (P) решения соответствующего
разностного уравнения. Для сходимости uh( P) —>-
—>и(Р) необходимо, чтобы при мельчении шага h об-
область зависимости разностного уравнения покрывала
область зависимости дифференциального уравнения
Q{P)cz lim Qn{P).
h -* 0
Лит.: [1] К у р а н т Р., Ф р и д рихеК., Леви Г.,
«Успехи матем. наук», 1940, в. 8, с. 125—60; [2] Г о д у н о в С. К.,
Рябенький В. С., Разностные схемы. Введение в теорию,
М., 197 3. Я. С. Бахвалов.
КУРАТОВСКОГО ГРАФИК — плоский одномерный
континуум, во всех точках (кроме счетного числа) имею-
имеющий размерность 0. Построен К. Куратовским [1] в
связи с задачей о размерности подмножества N (X)
данного гс-мерного пространства X, состоящего из
всех точек z?X, в к-рых
mdz X = ind X — п
(N{X) наз. размерным ядром пространства X).
Для метрич. пространства со счетной базой X всегда
inAN (X)^indX — I,
и К. г. показывает, что этот результат — окончатель-
окончательный.
К. г. строится так. Пусть П — канторово множество
на отрезке [0, 1] оси абсцисс декартовой системы
координат на плоскости. Для каждого
полагается
л /@)—0. График этой функции, т. е. множество К
точек {х, /(х)), х^П, плоскости и есть К. г. Если
z — правый конец смежного к П интерпала, то
шс!гА"=1, а во всех остальных точках — indzK>-0.
Лит.: [1] Kuratowski К., «Mathematica», 1932, t. 6;
[2] Александровы. С, Пасынков Б. А., Введе-
Введение в теорию размерности..., М., 1973. Л. А. Мальцев.
КУРАТОВСКОГО ПОЛИЭДР — некоторая одномер-
одномерная фигура в трехмерном пространстве. К. п. первого
типа состоит из ребер тетраэдра и еще одного отрезка,
соединяющего середины непересекающихся ребер.
К. п. второго типа есть полный граф, натянутый на
вершины тетраэдра и нек-рую точку, взятую внутри
него. Необходимое и достаточное условие, при выпол-
выполнении к-рого граф G является плоским, состоит в том,
что граф G не должен содержать К. п. первого или вто-
рого типа (теоремаКуратовского — Понт-
р я г и н а).
Лит.: [1J Kuratowski к., «Fund, math.», 1930, t. 15,
p. 271—83; [2] X a p a p и Ф., Теория графов, пер. с англ., М.,
1973. Б. А. Ефимов.
КУРАТОВСКОГО — КНАСТЕРА ВЕЕР — вполне
несвязное плоское множество, становящееся связным
после прибавления к нему одной точки. Построено
К. Куратовским и Б. Кнастером [1] следующим обра-
образом. Пусть С — канторово совершенное множество,
Р — подмножество множества С, состоящее из точек
Р=2\ ~п таких, что, начиная с нек-рого п, числа ап
либо все равны нулю, либо все равны двум, Q — мно-
множество остальных точек. Пусть, далее, а — точка на
плоскости с координатами A/2, 1/2), L(c) — отрезок,
соединяющий переменную точку с множества С с точ-
точкой а. Пусть, наконец, L* {р) — множество всех точек
отрезка L(p), имеющих рациональные ординаты для
р^Р, и L* (q) —множество всех точек отрезка L(q),
имеющих иррациональные ординаты для q^Q. Тогда
связно, хотя Х\а вполне несвязно, т. е. X есть
К.—К. в.
Лит.: [1] Knaster В., Kuratowski К., «Fund,
math.», 1921, t. 2, p. 206 — 55. Л. Г. Замбахидзе.
КУСОЧНО ЛИНЕЙНАЯ ТОПОЛОГИЯ — раздел то-
топологии, изучающий полиэдры. Под полиэдром
понимается прежде всего подмножество топологиче-
топологического векторного пространства, представимое конеч-
конечным или локально конечным объединением выпуклых
многогранников ограниченной размерности, а также
топологич. полиэдры с фиксированной кусочно линей-
линейной структурой (см. ниже). Локальная конечность
означает, что каждая точка имеет в объемлющем про-
пространстве окрестность, пересекающуюся только с
конечным числом элементов объединения. Понятие
полиэдра является промежуточным между понятиями
топологич. пространства и симплициального комплекса
(последнее вводится для того, чтобы сделать более кон-
конструктивным изучение сначала пространств, гомеомор-
фных полиэдрам, а затем и более общих пространств).
Пространство, гомеоморфное полиэдру, наз. тополо-
топологическим полиэдром (?-п о л и э д р о м).
К классу i-полиэдров относятся важнейшие объекты
конечномерной топологии, прежде всего сглаживаемые
многообразия.
Имея в виду финитизацию изучения полиэдров, рас-
рассматриваются следующие четыре категории т, $*, &С,
А- В т объектами служат t-полиэдры, а морфизмами —
непрерывные отображения. В 5s объекты — полиэдры,
а морфизмы — кусочно линейные отобра-
отображения (pl-o т о б р а ж е н и я), т. е. отображения,
линейно переводящие выпуклые многогранники
нек-рого покрытия прообраза в многогранники нек-рого
покрытия образа. Объектами в SK являются с и м п л и-
циальные комплексы, т. е. полиэдры с
фиксированным правильным его покрытием симплек-
симплексами — таким покрытием, что два симплекса могут
пересекаться только по общей грани; морфизмы в г/Г —
симплициальные отображения, т. е.
/Л-отображения, линейно переводящие каждый симп-
симплекс прообраза на нек-рый симплекс образа. Наконец,
Л состоит из абстрактных комплексов
(а-комплексов) и их симплициальных отображений,
а-к омплекс в Л, есть не более чем счетное множе-
множество А с выделенной системой его конечных подмно-
подмножеств ограниченной мощности, к-рые наз. его сим-
симплексам и, удовлетворяющей условиям: 1) с каж-
каждым симплексом а выделяются и все содержащиеся в
нем подмножества — грани а; 2) каждый симплекс
служит гранью не более чем конечного числа других
симплексов. Отображение множеств, на к-рых опре-
определено строение а-комплекса, наз. симплипиальным, ес-
если оно переводит симплексы прообраза в симплексы
образа. Размерностью симплекса в а-комплек-
се наз. уменьшенное на единицу число его элементов.
Каждый элемент множества А является гранью комп-
комплекса А и наз. его вершиной. Удобно считать,
что каждый а-комплекс содержит пустой симплекс,
обозначаемый 1.
Имеются функторы забывания
Именно, полиэдр определяет топологич. пространство,
а р.-отображение непрерывно; это задает t, t(p) наз.
пространством полиэдра Р. Каждый
комплекс определяет полиэдр, а симплициальное отоб-
отображение комплексов есть pi-отображение; это задает р,
р {К) наз. телом комплекса и обозначается
\К\. Наконец, множество вершин комплекса К имеет
выделенные подмножества — множества вершин симп-
симплексов К, что определяет а-комплекс, причем симп-
симплициальное отображение комплексов определяет симп-
симплициальное отображение соответствующих а-комплек-
сов; это задает а, а (К) наз. схемой комплекса
К. Построенные функторы не имеют естественных обра-
обращений. Они, однако, становятся эквивалентностями,
если перейти к факторкатегориям. Естественные изо-
изоморфизмы наз. соответственно гомеоморфиз-
гомеоморфизмом в т, pl-т о м е о м о р ф и з м о м в 5\ с и м п -
лициальным изоморфизмом в Ж1 и в ,i.
Каждому а-комплексу следующим образом можно по-
поставить в соответствие его реализации. В топо-
топологич. векторном пространстве R выбирается множе-
множество точек Ь[ во взаимно однозначном соответствии с
вершинами а-комплекса А, к-рые находятся в общем
положении в Д (для этого достаточно, напр., чтобы
размерность R была больше удвоенной размерности
А), причем в ограниченной части пространства может
лежать только конечное число точек. Если на каждое
множество точек Ь,-, отвечающих одному симплексу в
А, натянуть симплекс в i?, то объединение этих симп-
симплексов дает комплекс, схемой к-рого служит А; он п
наз. реализации"! а-комплекса. Все реализации одного
и того же а-комплекса изоморфны, так что функтор а
устанавливает взаимно однозначное соответствие между
классами изоморфных комплексов в К и в Л. Любой
полиэдр Р является телом нек-рого комплекса К,
и в этом случае К наз. прямолинейной три-
триангуляцией Р, или просто триангуля-
триангуляцией, схема К наз. абстрактной триангу-
триангуляцией Р. Для pZ-отображения / : Р —>• Q сущест-
существуют триангуляции К для Р и L для Q, так что / симп-
лициально отображает К в L. Различные триангу-
триангуляции полиэдра не обязательно изоморфны, вследствие
чего вводится более грубое отношение эквивалентности
в Ж'. Подразделением комплекса К± наз.
комплекс К2 такой, что \К2\ = \КХ\, и каждый симплекс
К2 лежит в нек-ром симплексе A'i. Комплекс К ком-
комбинаторно эквивалентен К', если К
и К' имеют изоморфные подразделения. Комплексы К
и К' комбинаторно эквивалентны тогда и только тогда,
когда \К\ pZ-гомеоморфно \К'\. Иначе говоря, функтор
р устанавливает естественное соответствие между клас-
классами комбинаторно эквивалентных комплексов и pl~
гомеоморфных полиэдров. Функтор t эпиморфен (по
определению). Полиэдр Р наз. прямолинейной
реализацией i-полиэдра t(P). Предположение о
том, что любые две реализации /-полиэдра р/-гомео-
морфны между собой, известное как основная
гипотеза комбинаторной топологии
(Hauptvermutung), оказалось неверным [3]. В связи
с этим говорят о pZ-строениях на г-полиэдрах:
pl-c троение задается гомеоморфизмом т : Т -> Р
(-полиэдра на полиэдр, причем два гомеоморфизма
Ti: Т —>- Р и т2 : Т —>- Р2 определяют одну и ту же
структуру, если т^тг" является pZ-гомеоморфизмом;
( б
рууру, ^ pрф
и т2 определяют эквивалентные (но не обязатель-
обязательно совпадающие) структуры, если Рг и Р2 pZ-гомеоморф-
ны. i-полиэдр с фиксированной ^/-структурой также
наз. полиэдром. Наконец, отношение комбинаторной
эквивалентности в К приводит с помощью функтора а
к новому отношению эквивалентности в А- Для выра-
выражения этого отношения внутренними средствами в и€
удобна операция звездного подразделения, определяе-
определяемая следующим образом. Д ж о й н о м (или соеди-
соединением) двух симплексов а и а, вер-
вершины к-рых находятся в общем положении в вектор-
векторном пространстве R, наз. их выпуклая оболочка; это —
симплекс размерности re!+«2—1, обозначаемый Oi*ot.
Джойн а с пустым симплексом 1 совпадает со. Джой-
ном двух комплексов К1 и К2, расположен-
расположенных в топологич. векторном пространстве R так, что
каждый симплекс Кх находится в общем положении
с каждым симплексом К2, наз. комплекс, составленный
из попарных джойнов симплекса из Кг и симплекса из К2
(считается, что 1 лежит и в К\ и в К2). Звездой
симплексаств комплексе К наз. подкомплекс St^a,
состоящий из всех замкнутых симплексов, имеющих а
своей гранью. Звезда может быть представлена как
джойн а и нек-рого комплекса Ik^a, наз. л и н к о м
(или поясом) ав К и составленного из тех симп-
симплексов звезды, к-рые не пересекают а. Пусть х — про-
произвольная точка внутри а. Заменой в К симплексов
звезды симплексами вида х*о1*о2, где at— симплекс из
(ijc, a ст2 — одна из граней а, при сохранении осталь-
остальных симплексов получается подразделение К, к-рое
и наз. звездным подразделением К с
центром в а и обозначается аК. Два комплекса ком-
комбинаторно эквивалентны тогда и только тогда, когда
они имеют изоморфные подразделения, получаемые
последовательностями звездных подразделений (т е о-
рема Александера, [4]).
Понятие звездного подразделения переносится в ка-
категорию и€. Для этого комплексы записываются в виде
многочленов специального вида: переменными служат
вершины комплекса, а одночлены — его симплексы,
включая 1. При сложении многочленов повторяющиеся
симплексы заменяются одним одночленом. Умножение
многочленов (определенное, только если они не имеют
общих переменных) интерпретируется как джойн соот-
соответствующих комплексов. Пусть фиксирован симплекс
а в комплексе А, и А записан в виде А = о*1кьО-\-
-{-Ai, где а вынесено за скобки из объединения тех
одночленов, к-рые содержат а, т. е. входят в звезду
St^a. То, что остается в скобке, есть линк а; Ах — объ-
объединение остальных симплексов. После замены ст на
х*да, где да — объединение граней а, кроме самого а,
но включающее 1, получится новый комплекс оА =
=х*да*1к^а-^Аг. Переход А —>- оА, а также и сам
аА, наз. (абстрактным) звездным под-
подразделением А. Операции звездного подразде-
подразделения в К и в с/1 согласованы с действием функтора а,
и можно представить Л как формальную систему со
счетным алфавитом, с многочленами указанного вида в
качестве конструктивных объектов и звездным подразде-
подразделением в качестве элементарных переходов от одного
объекта к другому. Вместе с тем в <А становятся оправ-
оправданными вопросы об алгоритмической разрешимости. В
частности, неразрешим вопрос о комбинаторной экви-
эквивалентности а-комплексов (и, следовательно, о pZ-гомео-
морфизме полиэдров) (теорема Маркова, [5]).
Финитизм комплексов первоначально имел целыо
введение инвариантов: инвариант определяется по три-
триангуляции, а его инвариантность проверяется только
при элементарных преобразованиях (моделью здесь
служило введение эйлеровой характеристики). Однако
этот метод не получил широкого распространения в
связи с тем, что, во-первых, из-за нарушения Haupt-
vermutung он не дает доказательства топологич. ин-
инвариантности, а во-вторых, вычисление инвариантов
по триангуляции является часто безнадежной задачей.
Более или менее систематически этот путь применяется
в топологии трехмерных многообразий и в теории узлов.
В гомотопической топологии это привело к технике
клеточных разбиений. Развитие идеи а-комплексов
привело к теории полусимплициалъных комплексов,
позволяющих в гомотопич. топологии избегать несуще-
несущественных топологич. трудностей.
Основным объектом К. л. т. являются pZ-многообра-
зия, играющие важную роль соединяющего звена меж-
между дифференцируемыми и топологич. многообразиями.
Понятие многообразия естественно вводится в каждую
из четырех категорий т, !р, <5Г, Л. В т это просто топо-
топологич. многообразия, к-рые могут быть триангулиро-
триангулированы, в 53 это pl-м ногообразия — полиэдры,
каждая точка к-рых имеет окрестность, pZ-гомеоморф-
ную кубу соответствующей размерности, в SfC и в ,Л
рассматриваются соответственно комбинатор-
комбинаторные и формальные многообразия —
комплексы (а-комплексы), звезды вершин к-рых ком-
комбинаторно эквивалентны стандартной триангуляции
симплекса, состоящей из самого симплекса и всех его
граней. В классе pi-многообразий также не верна Haupt-
vermutung. Построен пример некомбинаторной три-
триангуляции топологич. многообразия (см. [7], [8]), в
к-ром вложения нек-рых симплексов не локально пло-
плоски. Если предположить локальную плоскостность
всех симплексов и, сверх того, выполнимость Пуанкаре
гипотезы в размерностях 3 и 4, то можно доказать,
что триангуляция многообразия является комбинатор-
комбинаторным многообразием. Наконец, не выяснен A982) вопрос
о триангулируемости произвольного (метризуемого)
многообразия, хотя построены примеры многообразий
без комбинаторной триангуляции.
Лит.: [1] Рур к К., Сандерсон Б., Введение в
кусочно линейную топологию, пер. с англ., М., 1974; [2]
М а н к р с Дж., Элементарная дифференциальная топология,
в кн.: Ми л нор Дж., Сташеф Дш., Характеристические
классы, пер. с англ., М., 1979, с. 270—359; [3] М i I n о г .Т.,
«Ann. of Math.», 1961, v. 74, p. 575—90; U] A 1 e x a n d e г J.,
«Trans. Amer. Math. Soc», 1926, v. 28, p. 301—29; [5] M a p-
к о в А. А., «Докл. АН СССР», 1958, т. 121, № 2. с. 218—20;
[6]KirbyR., Siebenmann L., «Bull. Amer. Math. Soc»,
1969, v. 75, p. 742—49; [7] Edwards R., «Notices Amer.
Math. Soc», 1975, v. 22. № 2, A—334. А. В. Чернавский.
КУТТА — MEPCOHA МЕТОД — пятиэтапный метод
Рунге — Кутта 4-го порядка точности. Применительно
к задаче Коиш
у' (x) = f(x, у (х)), xo*Czs^X, у(хо) = уо, A)
метод имеет вид:
k1 = hf(x0, y0), i/o=!/(^o).
+ -Lh, Уо-f х
l — hf ( %о~т~ ~~2~
x0+h, yoJrl-k1-~k3-{-2ki),
1
y1 (zo+ h) = j/0 + -l *!_—JL ks + 2k4,
Величина R = 0,2\y1 — у2\ служит для оценки погрешно-
погрешности метода и для автоматического выбора шага интегри-
интегрирования. Если е — предписанная точность вычислений,
то шаг интегрирования выбирается следующим обра-
образом. Берется нек-рый начальный шаг и производятся
вычисления по формулам B). Вычисляется величина R.
При R >е шаг интегрирования уменьшается в два раза.
При 7f<:s/64 шаг увеличивается вдвое. Если же е/64<
<Я<е, то шаг считается выбранным правильно. После
этого в качестве начальной точки х0 берется точка
¦r.0-\-h и весь процесс повторяется снова. В качестве
приближенного решения выступает величина у2. Ве-
Величина у1 носит вспомогательный характер.
В связи с тем, что
то есть формула для вычисления у1 является как бы
«вложенной» в формулу для вычисления у2, описанный
выше метод оценки погрешности и выбора шага интег-
интегрирования наз. методом вложенных форм.
Имеются стандартные программы К.— М. м. на языке
алгол [1], [2].
Лит.: [1] Christiansen J., «Numer. Mach.», 1970,
Bd 14, S. 317—24; [2] Lukehart P.M., «Commuris Assoc.
Comput. Math.», 1963, v. ti, Л» 12, p. 737 — 38; [3] F о х L., Nu-
Numerical solution of ordinary and partial differential equations,
Oxf., 1962; [4] L a n с e G. N., Numerical methods for high speed
computers, L., 1960. В. В. Поспелов.
КЭЛЕРА МЕТРИКА, кэлерова метрик а,—
эрмитова метрика на комплексном многообразии,
фундаментальная форма со к-рой замкнута, т. е. удов-
удовлетворяет условию dco=O. П р и м е р ы К. м.: эрмито-
эрмитова метрика 'S)n \dzk\2 в пространстве С", Фубиии —
Штуди метрика в комплексном проективном простран-
пространстве СР", метрика Бергмана (см. Бергмана керифунк-
ция) в ограниченной области пространства С". К. м.
на комплексном многообразии индуцирует К. м. на
любом его подмногообразии. Всякая эрмитова метрика
на одномерном многообразии кэлерова.
Понятие К. м. было впервые рассмотрено Э. Кэлером
[1]. В то же время в алгебраич. геометрии система-
систематически использовалась метрика на проективных алгеб-
алгебраич. многообразиях, индуцированная метрикой Фу-
бгшн — Штуди (см. [5]). Эта метрика является мет-
метрикой Ходжа, т. е. ее фундаментальная форма
имеет целочисленные периоды.
Эрмитова метрика h на комплексном многообразии
является кэлеровой тогда и только тогда, когда она
удовлетворяет любому из следующих условий: парал-
параллельный перенос вдоль любой кривой (относительно
связности Леви-Чивнта) является комплексным линей-
линейным отображением, т. е. перестановочен с оператором
комплексной структуры; соответствующий метрике
h комплексный оператор Лапласа ? на дифференциаль-
дифференциальных формах удовлетворяет условию П = Пь т. е. Лап-
Лапласа оператор А совпадает с 2HJ; b окрестности каждой
точки существуют локальные координаты, в к-рых мат-
матрица метрики h совпадает с единичной матрицей с точ-
точностью до бесконечно малых 2-го порядка (см. [3], [6]).
Лит.: [1J К a h I e r E., «Abh. Math. Semin. Univ. Ham-
Hamburg», 1933, Bd 9, S. 173—8ti; [2] В е и л ь А., Введение в теорию
кэлеровых многообразий, пер. с франц., М., 1961; [31 Л и х н е-
р о в и ч А., Теория связностей в целом и группы голономий,
пер. с франц., М., 1960: Г4] Уэллс Р., Дифференциальное
исчисление на комплексных многообразиях, пер. с англ., М.,
1976; [5] Н о d g e W. V. D.. The theory and applications of
harmonic integrals, 2 ed., Camb., 1952; [6] Г р и ф ф и т с Ф.
[и др.], «Успехи матем. наук», 1977, т. 32, в. 3, с. 119—52.
А. Л. Опищик.
КЭЛЕРОВА ФОРМА — фундаментальная форма
Кэлера метрики на комплексном многообразии. К. ф.
является гармонической вещественной дифференциаль-
дифференциальной формой типа A, 1). Дифференциальная форма со
ла комплексном многообразии М служит К. ф. для
нек-рой кэлеровои метрики тогда и только тогда, когда
со в окрестности U каждой точки х?М записывается в
виде
iJ^^-dZa A d7^
где р — строго плюрисубгармонич. функция в U, zj,...,
zn — локальные комплексные координаты.
К. ф. наз. формой Ходжа, если она соответ-
соответствует метрике Ходжа, т. е. имеет целочисленные пе-
периоды или, что то же, определяет целочисленный класс
когомологий.
Лит.: [1] Уэллс Р., Дифференциальное исчисление на
комплексных многообразиях, пер. с англ., М., 1976.
А. Л. Онищип.
КЭЛЕРОВО МНОГООБРАЗИЕ — комплексное мно-
многообразие, на к-ром можно ввести Кэлера метрику.
Иногда такие многообразия нал. многообразия-
многообразиями кэлерова типа, а термин «К. м.» оставля-
оставляется для многообразий, снабженных кэлеровой метр и
кой 11]. Всякое подмногообразие К. м. является
К. м. В частности, все проективные комплексные алгео-
раич. многообразия без особых точек являются К. ы.,
причем кэлерова метрика на них индуцируется Ф;/-
бини — Штуди метрикой на комплексном проективном
пространстве. Аналогично, всякое подмногообразие и
аффинном пространстве С" (в частности, всякое Штейна
многообразие) является кэлеровым. Другие примеры
К. м. получаются, если рассматривать факторпрост-
ранство M/V К. м. М по дискретной группе аналитич.
автоморфизмов Г, сохраняющих кэлерову метрику.
В частности, любой комплексный тор есть К. м. Всякое
одномерное комплексное многообразие кэлерово.
Теория гармонич. форм на компактном К. м. дает
следующие свойства групп когомологий де Рама п
Дольбо на таком многообразии М (см. [1], [2], а такж(-
[5], где эти свойства были впервые доказаны для про-
проективных алгебраич. многообразий):
dim H2r + 1 (M, С) четна,
H-r (M, С) Ф О при r = 1, 2, ..., ~ dimcM.
Голоморфные формы на компактном К. м. замкнуты.
В частности,
где А1— пространство всех голоморфных 1-форм на М.
В случае A\m^M=i число
dim Л1 = -g- dim Н1 (М, С)
есть род компактной римановой поверхности М. На
указанных выше свойствах основано построение приме-
примеров некэлеровых компактных многообразий, простей-
простейшим из к-рых является поверхность Хонфа, дпффеомор-
фная S1XS3.
К. м. М наз. многообразием Ходжа,
если кэлерова метрика на М является метрикой Ходжа.
Всякое проективное алгебраич. многообразие без осо-
особых точек является многообразием Ходжа относитель-
относительно метрики, индуцированной метрикой Фубинн —
Штуди. Обратно, всякое компактное комплексное мно-
многообразие М, снабженное кэлеровой метрикой Ходжа
т), допускает биголоморфное вложение в комплекс-
комплексное проективное пространство, причем метрика на М,
индуцированная метрикой Фубини — Штуди, имеет
вид Л-г], где к — натуральное число [1], [3] (теорема
Кодаиры о проективном вложен и и).
Таким образом, компактное комплексное многообразие
М изоморфно проективному алгебраич. многообразию
тогда и только тогда, когда М — многообразие Ходжа.
Другая форма этого критерия состоит в том, что ком-
компактное комплексное многообразие М является проек-
проективным алгебраич. многообразием тогда и только тогда,
когда на М существует отрицательное расслоение на
комплексные прямые. Теорема Кодаиры допускает
обобщение на комплексные пространства (см. [4],
[6]). Компактные К. м., не являющиеся многообразиями
Ходжа, можно найти среди двумерных комплексных
торов. Напр., этим свойством обладает тор С2/Г, где
Г — решетка, натянутая на векторы A,0), @,1), ( V —2,
У^З), ( V — 5, V~~) (см. [1], [3]). Другое необходимое
и достаточное условие проективности re-мерного ком-
компактного кэлерова многообразия М состоит в нали-
наличии на М п алгебраически независимых мероморфных
функций.
Всякое некомпактное полное К. м., имеющее поло-
положительную секционную кривизну, является многооб-
многообразием Штейна. Тем же свойством обладает любое одно-
связное полное К. м. неположительной секционной
кривизны [71.
Лит.: [1] Уэллс Р., Дифференциальное исчисление на
комплексных многообразиях, пер. с англ., М., 1976; [2]
В е й л ь А., Введение в теорию кэлеровых многообразий, пер.
с франц., М., 1961; [3] Чшэнь Шэн-шэнь, Комплексные
многообразия, пер. с англ., М., 1961; [4] Ганнинг Р.,
Росси X., Аналитические функции многих комплексных
переменных, пер. с англ., М., 1969; [5] Hodge W. V. D.,
The theory and applications of harmonic integrals, 2 ed., Camb.,
1952; [6] Г р а у э р т Г., в кн.: Комплексные пространства.
Сб. пер., М., 1965, с. 45—104; 17] Greene R. E., W u H.,
веб.: Value-Distribution Theory. Part A, N. Y., 1974, p. 145—67.
А. Л. Онищик.
КЭЛИ АЛГЕБРА — алгебра Кэли чисел.
КЭЛИ ПОВЕРХНОСТЬ — алгебраическая линейча-
линейчатая поверхность, являющаяся поверхностью переноса
с ел1 сетями переноса. Ее уравнение в декартовых коор-
координатах
х3 — 6xi/ —|— 6z = 0.
Название в честь А. Кэли [1], рассматривавшего эту
поверхность как геометрич. иллюстрацию своих иссле-
исследований по теории пучков бинарных квадратичных
форм.
Лит.: [1] С а у 1 е у A., «Philos. Trans. Roy. Soc. London»,
1858, v. 148, p. 415—27; [2] Ш у л и к о в с к и й В. И., Клас-
Классическая дифференциальная геометрия в тензорном изложении,
М., 1963. М. И. Войцеховский.
КЭЛИ ПРЕОБРАЗОВАНИЕ линейного (диссипатив-
ного) оператора А с областью определения DomA,
плотной в гильбертовом пространстве Н,— оператор
Сд= (А — И) (А + ?/)~°, определенный на подпростран-
подпространстве DomCj[=(A-\-iI)DomA. Матричный вариант та-
такого преобразования рассматривал А. Кэли (A. Cay-
ley). К. п. устанавливает соответствие между свойст-
свойствами операторов А, чей спектр а (А) «близок» к дей-
действительной прямой, и операторов с околоунитарным
спектром (близким к окружности {??С : |?| = 1}).
Так, имеют место утверждения: 1) если А — линейный
диссипативпый оператор, то СА—сжатие (т. е. ||С_4х||^
<IN|, x?DomA) и КегG—СА)= {0}; 2) если Г —
сжатие, КегG— Т)= {0} и (/— T)DomT плотно в Н,
то Т=Сд при нек-ром линейном диссипативном опе-
операторе А: именно А = i(/-f T)(I—Т)~1ш, 3) симметрич-
симметричность А равносильна изометричности (унитарности)
СА; 4) о(А)=а(о(СА)), где co(g)=i A + g) (I —S),
в частности ограниченность А эквивалентна тому, что
14а(Сл); 5) если у — идеал операторов в Н, то из
А— В?у следует СА—Св?:Т'> если же А, В — ограни-
ограниченные операторы, то верно и обратное: из СА—Cj^y
следует А—В?у. К. п. устанавливает соответствие и
между нек-рыми другими характеристиками операто-
операторов А и СА: классификациями частей спектра, крат-
ностями спектров, структурами инвариантных подпро-
странств, функциональными исчислениями, спектраль-
спектральными разложениями и т. д. Так, если А — самосопря-
самосопряженный оператор с разложением единицы {-?(}, i?R,
то {Fs}, Fs=Ef при s^—2 arctg t, — разложение еди-
единицы для С & и
Лит.: [1] А х и е з е р Н. И., Глазная И. М., Теория
линейных операторов в гильбертовом пространстве, 2 изд., М.,
1966; [2]Секефальви-Надь Б., Ф о я ш Ч., Гармони-
Гармонический анализ операторов в гильбертовом пространстве, пер.
с англ., М., 1970. Я- К. Никольский.
КЭЛИ ТАБЛИЦА — квадратная таблица умножения
произвольного конечного группоида. Заглавная строка
таблицы заполняется в нек-ром порядке символами,
обозначающими различные элементы группоида, теми
же символами и в том же порядке заполняется заглав-
заглавный столбец. Если группоид обладает единицей, то
единичный символ, как правило, помещается на первом
месте. Если на ?-м месте в заглавном столбце стоит
символ а; и на /-м место в заглавной строке — символ:
а/, то на пересечении г-й строки и /~го столбца записы-
записывается символ, обозначающий произведение а,-яу. К. т.
введена А. К эли (A. Caylcy) в 1854 для групп.
Для того чтобы К. т. определяла нек-рую квазигруп-
квазигруппу, необходимо и достаточно, чтобы в каждой строке
(столбце) таблицы, не считая заглавных, каждый сим-
символ встречался ровно один раз. К. т. группы, кроме
того, должна удовлетворять следующему условию:
на местах, соответствующих произведениям (а/а^а^ и
ai(a,jak), стоят одинаковые элементы. Симметричные-
относительно главной диагонали К. т. соответствуют
коммутативным бинарным операциям; в частности, та-
таковы К. т. абелевых групп.
Лит.: [1] Гроссман И., М а г н у с В., Группы и их
графы, пер. с англ., М., 1971; [2] Клиффорд А., И р е о-
тон Г., Алгебраическая теория полугрупп, пер. с англ.,
т. 1, М., 1972. Н. П. Вильяме.
КЭЛИ ФОРМА — форма от (п+1) (Лг-М) перемен-
переменных, где n=dim X, а X — замкнутое алгебраическое-
подмногообразие TV-мерного проективного простран-
пространства PjV, однозначно с точностью до умножения на кон-
константу определяемая по X и сама однозначно опре-
определяющая X. Точное определение К. ф. состоит в
следующем. Пусть Р-^ есть jV-мерное проективное
пространство всех гиперплоскостей в PN, Г — под-
подмножество в многообразии
Р^х ... хР'' х I,
состоящее из всех таких наборов. (ль. . ., я„ + ], х),.
что точка х-? X лежит в пересечении гиперплоскостей
"i,. • ., яи + 1 и
Ф : PNX ...xFxX-
п +1 п л-1
— естественная проекция. Тогда ф(Г) есть неприводи-
неприводимое подмногообразие коразмерности 1 в
и потому ф(Г) является многообразием нулей нек-poir
формы Fx на
PN X • • • X Р*.
Всегда можно считать, что Fx не имеет кратных
множителей, и это условие определяет Fx по X одноз-
однозначно с точностью до умножения на константу. Наобо-
рот, F% однозначно определяет множество всевозмож-
всевозможных наборов га+1 гиперплоскостей в PN, пересекаю-
пересекающихся по точкам из X, и потому F% однозначно опреде-
определяет X. Форма Fx и наз. формой К э л и многооб-
многообразия X.
Часто К. ф. наз. также формойЧжоу, или ассо-
ассоциированной формой многообразия
X. Идея определения X комплексом линейных подпро-
подпространств размерности N—п—1 в PN, пересекающих X,
восходит к А. Кэли [5], к-рый применил ее для случая
n=l, N—3. Коэффициенты К. ф. наз. координа-
координатами Чжоу многообразия X.
К. ф. Fx однородна по каждой из ге+1 систем коор-
координат пространства
(i-я система координат — это система координат t-ro
сомножителя указанного пространства). Степени одно-
однородности Fx по каждой из систем координат совпадают.
Эта общая степень d обозначается через deg X, наз.
степенью подмногообразия X, и име-
имеет следующий гсометрич. смысл: d есть максимум числа
точек пересечения X со всевозможными (N—п)-мерными
линейными пространствами L в PN t для к-рых Xf)L—
конечное множество (т. е. d — это число точек пересе-
пересечения X с «общим» (Л'—«)-мерным линейным подпро-
подпространством).
Множество всех форм (рассматриваемых с точностью
до умножения на ненулевую константу) от тг+1 групп
переменных по JV+1 переменных, имеющих степень
d по каждой группе, образует проективное пространст-
пространство Р N.n.d нек-рой размерности v^y, „, а- К. ф. Fx можно
отождествить с точкой Р N< "• d. Множество Сдг_П|
точек в Р N'"< d, являющихся К. ф. re-мерных замкнутых
подмногообразий степени d в Р-?*, есть квазипроектив-
квазипроективное многообразие; оно параметризует семейство всех
таких подмногообразий, причем указанное семейство
является алгебраическим относительно этой параметри-
параметризации. В общем случае Сдг,п, d не замкнуто в Р JV. ".<*.
Конструкция К. ф. естественно распространяется на
замкнутые n-мерные циклы в Р-", т. е. формальные
линейные комбинации miXi~\-. . .-\-msXs замкнутых
и-мерных подмногообразий Хг,. . ., Xs в Р^ с целыми
коэффициентами т,-> 0. А именно, полагают
deg Х = V5 m,deg X/
л Fx^F1^1 ¦ ¦ -Fixs- Множество CNytlid всех К. ф.
n-мерных циклов степени d в Р^ замкнуто в Р N<n-d.
Изучение К. ф. п свойств многообразий Cjy>rlyC( и
Сдг, „_ л является важным моментом в проблеме класси-
классификации подмногообразий и циклов в PN. Первый шаг
в этой классификации состоит в изучении разбиения
C'N, n, d па неприводимые компоненты. Напр., для jV=3,
п—\\ d=1 (кривые степени 2 в трехмерном простран-
пространстве) многообразие С3 х> 2 состоит из двух неприводи-
неприводимых компонент размерности 8. Первая компонента
¦соответствует плоским кривым второго порядка, а
вторая — парам прямых. Бирациональная классифика-
классификация многообразий Сн „_ ^ является важной проблемой
(во всех известных примерах такие многообразия рацио-
рациональны).
Лит.: ШШафаревич И. Р., Основы алгебраической
теометрии, М., 1972; [2] X о д ж В., П и д о Д., Методы алгеб-
алгебраической геометрии, пер. с англ., т. 2, М., 1954; [3] Samu-
Samuel P., Mfithodes d'algebre abstraite en geometric algebrique,
2 id., В., 1967; [4] Chow W.- L., van der Waerden
В. L., «Math. Ann.», 1937, Bd 113, S. 692—704; 15J С а у 1 e у А.,
Collected mathematical papers, v. 4, Gambr., 1891, p. 446—55.
В. Л. Попов.
КЭЛИ ЧИСЛО — гиперкомплексное число, а именно,
элемент 8-мерной алгебры над полем действительных
чисел (алгебры Кэли), впервые рассмотренной
А. Кэли (A. Cayley). Алгебра Кэли может быть полу-
получена применением процесса Кэли—Диксона из алгебры
кватернионов (см. Кэли—Диксона алгебра). Она является
единственной 8-мерной действительной альтернативной
алгеброй без делителей нуля (см. Фцобениуса теорема).
Алгебра Кэли является алгеброй с однозначным деле-
делением и с единицей, альтернативной, но неассоциативнол
и некоммутативной.
Лит.: [1] К у р о ш А. Г., Лекции по общей алгебре, 2 изд..
М., 1973. Н. Я. Вильяме.
КЭЛИ — ДАРБУ УРАВНЕНИЕ — дифференциаль-
дифференциальное уравнение с частными производными третьего по-
порядка, к-рому должна удовлетворять функция и(х1у
х2, х3) для того, чтобы семейство поверхностей и(х1,
Х2, x3) = const могло быть дополнено до трижды ортого
нальной системы поверхностей. К.— Д. у. может быть
записано в виде
= 0,
где
К.— Д. у. получено в раскрытом виде А. Кэли [1].
В приведенном виде выведено Г. Дарбу [2].
Лит.: [1] Gay ley А., «С. г. Acad. sci.», 1872, t. 75, p.
324—30; 381—85; [21 D а г b о u x G., Legons sur les systemes
orthogonaux et les coordonnees curvilignes, P., 1898; [3] К а-
г ан В. Ф., Основы теории поверхностей в тензорном изложе-
изложении, ч. 2, М.— Л., 1948. Е. В. Шикип.
КЭЛИ — ДИКСОНА АЛГЕБРА — альтернативная
8-мерная алгебра, получающаяся из алгебры обобщен-
обобщенных кватернионов применением процесса Кэл и—
Диксона. Этот процесс заключается в построении
по заданной алгебре А новой алгебры А^ (удвоенной
размерности) и является обобщением процесса удвоения
(см. Гиперкомплексное число). А именно, пусть А —
алгебра с единицей 1 над полем F, б — некоторый
ненулевой элемент из F и задано F-линейное отобра-
отображение х —*¦ х*, являющееся инволюцией, причем
1
1
0
0
«22
1
0
u2
0
c33
«33
1
0
0
M3
2cI2
2u12
0
u2
«l
0
2c23
23
0
0
"s
u.
2c
2ь
0
«3
0
«i
На прямой сумме линейных пространств AQ}A = A1
формулой
(°i, а2> Фг, Ь2) — \аф1 — бЬ2а2 , aib2-\-b1a2)
определяется умножение, превращающее At в алгебр)'.
Алгебра А вкладывается в Ах в качество подалгебры:
х _> (х, 0) и инволюция * продолжается до инволюции
в Ах'.
(аь а2)* = {а1, — а2).
При этом
tr (a1, a2)=tr(a1), п (ага2) = п (at) -\- 6л (а2)¦
Процесс перехода от алгебры А к алгебре А± можно
продолжить, получая возрастающую цепочку алгеор
AczAiCA2C- . .; параметр б на каждом шаге может
меняться. Если процесс Кэли — Диксона начинается с
алгебры А с базисом {1, и], таблицей умножения
и инволюцией: 1*=1, и* = 1 — и, то поело первого
шага получится алгебра Аг обобщенных кватернионов
(ассоциативная алгебра размерности 4), а на втором
шаге — алгебра А 2 размерности
к-рая и наз.
К э л и—Д и к с о н а алгеброй.
Любая К.— Д. а. является альтернативной, но не ас-
ассоциативной центральной простой алгеброй над F;
обратно, простое альтернативное кольцо либо ассоциа-
ассоциативно, либо является К.— Д. а. над своим центром.
Определенная на К.—Д. а. квадратичная форма п(.г)
от восьми переменных, соответствующих базису алгеб-
алгебры, обладает мультипликативным свойством:
п(ху)=п{х)-п(у).
Тем самым устанавливается связь между К.— Д. а. и
проблемой существования композиции для квадратичных
форм. К.— Д. а. является алгеброй с делением тогда
и только тогда, когда квадратичная форма п (х) (н о р-
м а э л е м е н т а х) не представляет нуля в F. Если
характеристика поля F отлична от 2, то К.— Д. а.
обладает базисом {1, иг, м2, и3, и4, иъ, ив, и,} с табли-
таблицей умножения вида
щ
U,
«4
lh
и,
U;
щ
— а
— и t
аи,
— аи,
Щ
— аи,
и2
ил
-Р
U6
—
-Р«.
Р«5
U Л
— ии2
Р
-аР
и-
-Р«г,
— afjut
и4
— «5
— и„
-и,
— 7
7«i
7«2
7«я
U5
аи,
и,
— аи.
— 7«i
— «7
7«з
— ауи2
"в
— и,
ри,
Р«5
— 7«2
-37
PVU,
и7
аи,
-Р«»
ар«4
— 7и3
ауи2
-P7"i
-ар7
где а, Р, 7^F, аРу^О, а инволюция определяется
условиями
1* = 1, Uf=—u/при г = 1,2, 3, 4, 5, 6, 7.
Эта алгебра обозначается А (а, [3, у). Алгебры Л (а, E, у)
и 4 (а', C', у') изоморфны тогда и только тогда, когда
эквивалентны отвечающие им квадратичные формы
п (х). Если п(х) представляет нуль, то соответствую-
соответствующая К.—Д. а. изоморфна А ( — 1, 1, 1). Алгебра
А (—1, 1, 1) наз. расщепляемой алгеб-
алгеброй К э л и, или векторно-матричной
могут быть представле-
представле, или
алгеброй. Ее элементы
ны матрицами вида
а а
где a, Pdi-F, a, b?V, V — трехмерное пространство
над F с обычными операциями скалярного произведе-
произведения <а, 6> и векторного произведения аХЬ. Умно-
Умножение этих матриц задается формулой
a a
у с
d S
— <а, dy
— <6, су
Если F=R—поле действительных чисел, то А A, 1, 1)
— алгебра Кэли чисел (она является алгеброй с
делением). Любая К.— Д. а. над R изоморфна либо
А A, 1, 1), либо А ( — 1, 1, 1).
Построение К.— Д. а. над произвольным полем при-
принадлежит Л. Диксону (L. Dickson), к-рый изучил также
их основные свойства (см. [1], [2]).
Пусть А— альтернативное кольцо, ассоциативно-ком-
ассоциативно-коммутативный центр С к-рого отличен от нуля и не содер-
содержит делителей нуля, a F — поле частных кольца С.
Тогда имеется естественное вложение А —>- A(/)cl'\
Если A@cF есть К.— Д. а. над F, то А наз. коль-
кольцом К з л и — Диксона.
Лит.: [1] Д и к с о н Л. Э., Линейные алгебры, пер. с англ.,
Харьков, 1935; [2] S с h a f е г R. D., An introduction to nonas-
sociative algebras, N. Y., 1966; [3] Ж е в л а к о в К. А.,
С л и н ь к о А. М., Ш е с т а к о в И. П., Шир-
Ширшов А. И., Кольца, близкие к ассоциативным, М., 1978.
Е. Н. Кузьмин.
КЭЛИ — КЛЕЙНА ПАРАМЕТРЫ — некоторые спе-
специальные координаты в группе вращений трехмерного
пространства SOC), построение к-рых в конечном счете
основано на связи между SO C) и группой SUB)
унитарных матриц 2-го порядка с единичным определи-
определителем. Существует отображение ф : SUB) —>- S0C),
являющееся эпиморфизмом по своим алгебраич. свой-
свойствам и двулистным накрытием — по топологическим.
(Рассматриваемое в нек-рой окрестности единичной
матрицы, это отображение обладает свойствами изе-
морфизма, поэтому говорят, что S0C) и SUB) ло-
локально изоморфны.) Каждая матрица V?SUB) имеет
вид
— — , где а, р — комплексные числа, связанные
ра
соотношением |а|2+|(М2=1- Их и'"принимают за К.—
К. п. для A=q>(V). (Иногда под К.— К. п. понимают
все четыре коэффициента матрицы V.) Построение кон-
конкретного отображения ф с указанными свойствами
можно осуществить по-разному, поэтому у различных
авторов имеются нек-рые различия в определении
К.™ К. п. (см. [2], [3]).
Поскольку ф является не настоящим изоморфизмом,
а только двулистным накрытием, то невозможно опре-
определить К.— К. п. как (непрерывные) координаты на
всей группе S0{3); это можно сделать лишь локаль-
локально. Однако К.— К. п. можно использовать для изу-
изучения процесса вращения, при к-ром А непрерывно
зависит от действительного параметра t (причем здесь
нет необходимости как-либо ограничивать область
возможных значений А). Действительно, если для нек-
рого t=t0 выбрано какое-то фиксированное значение
прообраза V(t0) ?ф-1 (A {t0)), то но непрерывности для
всех t однозначно определяются соответствующие V(t).
(Двузначность полного прообраза ф проявляется
лишь в том, что равенство A(t) = A(s) имеет место не
только при V(t)=V(s), но и при V(t) = — V(s).) По-
Поэтому К.— К. п. можно применять при исследовании
движений твердого тела с неподвижной точкой (его
конфигурационное пространство совпадает с SOC)).
Такой подход принят в [1], однако он не получил широ-
широкого распространения.
Группа S U B) изоморфна группе кватернионов с
единичной нормой, поэтому, переходя от V к соответ-
соответствующему кватерниону p-f-Xi+uj+v/c, можно вместо
К.— К. п. пользоваться параметрами Эйле-
Эйлера — Родрига — четырьмя действительными чис-
числами р, >., u, v, удовлетворяющими соотношению
p2+>.2-)-u.2-r v2—1. Они связаны простыми формулами
с К.— К. и. (см. [1], [3]) и обладают тем же свойством
«двузначности» (историю вопроса см. в [1]). По суще-
существу, в относящихся сюда исследованиях впервые рас-
рассматривались двузначные представления группы вра-
вращений (см.- Спинор).
Лит.: [1] К 1 е i n F., Sommerfeld A., Ober die Tlieo-
rie des Kreisels, Ш. 1—2, Lpz., 1897—98 (перепечатка N. Y.—
Stuttg., 1965); [2] Голдстейн Г., Классическая механика,
пер. с англ., 2 изд., М., 1975; [3] С и н г Д ж.- Л., Классическая
динамика, пер. с англ., М., 1963. Д. В. Аносов.
КЭМПБЕЛЛА — ХАУСДОРФА ФОРМУЛА — форму-
формула для вычисления выражения
ii> = ln (eaev)
в алгебре формальных степенных рядов от некоммути-
некоммутирую щих ассоциативных и и v. Более точно, пусть А —
свободная ассоциативная алгебра с единицей над полем
Q со свободными образующими и и i;, a L — ее подал-
подалгебра Ли, порожденная этими же элементами относи-
относительно операции коммутирования [х, у\ = ху—ух; и
пусть А и L — пополнения алгебр А и L степенными
рядами элементов из А и L. Тогда отображение
ехр: х —> ех = У
является непрерывной биекциеи алгебры А на мульти-
мультипликативную группу \-\-A 1, где Аг — совокупность
рядов без свободного члена. Обратным к этому отобра-
отображению является отображение
In: у — In (j,) = V" ^ШИ (y-i)«.
¦*"""п = 1 п
Ограничение отображения ехр на L является биекциеи
алгебры А на группу 1 + Z. Это позволяет ввести груп-
групповую операцию хоу=]ц (ехеУ) на множестве элементов
алгебры Ли L, причем в получаемой таким образом
группе подгруппа, порожденная элементами и и v,
оказывается свободной. К.— X. ф. дает выражение для
uov в виде степенного ряда от и и v:
1m
.[••• [... [•-. Ни, u] ц] v, ...., г], ..., т>1, ..., -в]
Р/л! 9т!
или (в терминах присоединенного представления
(ad x)(y) = [x, у]):
w= Z_i Zj (""г sН~ "'г s)>
где
w, =у« (-I)"-' v '
' '¦ s Z-im > 1 m X
"'—• (adu)ri(adr)siN (adu)rOT
Здесь 2* означает суммирование по гх+. .
суммирование по rx+. . .-f-rm_i^r—1,
+ + 1 l
Первым задачу о разыскании выражения w рассмот-
рассмотрел Дж. Кэмпбелл [1]. Ф. Хаусдорф [2] доказал, что w
выражается через коммутаторы от элементов и и v,
т. е. принадлежит алгебре Ли L.
Если cj — нормированная алгебра Ли над полным
недискретно нормированным полем К, то ряд (*),
где м, v?q, сходится в окрестности нуля. Это поз-
позволяет определить в окрестности нуля пространства С[
структуру локальной банаховой группы Ли над А*
(в ультрамотрическом случае — структуру банаховой
группы Ли), алгеброй Ли к-роп является Д. Этот факт
дает одно из доказательств существования локальной
группы Ли с заданной алгеброй Ли C-я теорема
Л и). Обратно, во всякой локальной группе Ли умно-
умножение в канонических координатах задается К.—
X. ф.
Лит.: [1] Campbell J. E., «Proc. London Math. Soc»,
1897 v. 28. p. 381 — 90; 1898, v. 29, p. 14 — 32; [2] H a u s-
dorff F., «Leipziger Ber.», 1906, Bd 58, S. 19 — 48; [3] Бур-
баки H., Группы и алгебры Ли. Алгебры Ли, свободные ал-
алгебры Ли и группы Ли, пер. с франц., М., 1976; [4] С е р р Ж.-
П., Алгебры Ли и группы Ли, пер. с франц., М., 1969; [5] Теория
алгебр Ли. Топология групп Ли. Семинар «Софус Ли», пер. с
франц., М., 1962; [6] Магнус В., К а р р а с А., С о л и-
тэр Д., Комбинаторная теория групп, пер. с англ., М., 1974.
Ю. А. Бахтурин.
КЮННЕТА ФОРМУЛА — формула, выражающая го-
гомологии (или когомологии) тензорного произведения
комплексов или прямого произведения пространств
через гомологии (когомологии) сомножителей.
Пусть Л — ассоциативное кольцо с единицей, А
и С — цепные комплексы соответственно правых и
левых Л-модулей. Пусть А(®С — комплекс, ассо-
ассоциированный с тензорным произведением комплексов А
и С над Л. Если
ТоГ1 (В (А), В (С)) = Тог, (П,(А), В (С)) =
Тог1(Ян, (A), Z(C))=0,
то имеет место точная последовательность градуиро-
градуированных модулей
^)-К A)
где а — гомоморфизм степени 0, а- E — степени —1
(см. [2]). Для коцепных комплексов имеется аналогич-
аналогичная точная последовательность с гомоморфизмом Р сте-
степени + 1. Если Я*(Тогх (А, С)) = 0 (напр., А или С~
плоский Л-модуль) и Л наследственно, то последова-
последовательность A) существует и расщепляется [2], [3], так что
2P + , n#/>H). П, (С)).
Эта формула наз. формулой Кюннета; иногда
формулой, или соотношением, Кюннета
называют и точную последовательность A). Имеет место
обобщение формулы A), в к-ром тензорное произведе-
произведение заменяется произвольным двойным функтором
Т(А, С) на категории Л-модулей со значениями в той
же категории, ковариантным по каждому аргументу.
Рассматривается также случай функтора Т, ковариант-
ного по А и контравариантного по С. В частности,
функтор Т (А, С)=Нот(Л, С) приводит к формуле,
выражающей когомологии Я* (Нот (Л, С)), где А —
правый цепной, а С — левый коцепной комплексы над
Л, через Н*(А) и Н*(С), а именно, если Л наслед-
наследственно и Н* (Ext1 (А, С))-—0 (напр., А свободен), то
имеет место расщепляемая точная последовательность
О —>¦ Ext1 (Я, (А), Н* (С)) -^ И* (Нош (А, С)) X
где а' — гомоморфизм степени 0, а В' — степени -|~1
(см. [2], [31).
Пусть X, Y — топология, пространства, a L, М —
модули над кольцом главных идеалов R, причем
Toi"! (L, Л/) = 0. Тогда сингулярные гомологии прост-
пространств X, У, XX Y связаны следующей расщепляемой
точной последовательностью
О —* Н* (X, L) ® Я, (Y, М) ^ Я* (ХХУ, L ® М) Л-
Л ТоГ1 (Я* (X, L), Я* (Y, М))-*0,
где а — гомоморфизм степени 0, а [3 — степени —1. Ес-
Если предположить дополнительно, что либо все Hk (X, R)
и Hk(Y, Я), либо все Я^(У, К) и М конечно по-
рождены, то аналогичная точная последовательность
имеется для сингулярных когомологпй:
0-^Я*(Х, L)®H*(Y, М) -^ Я*(Хх^, Ь®М) --
Д> Тог2 (Я* (X, L), Я* (У, М)) —-> О,
причем а — гомоморфизм степени 0, а E — степени
+ 1. Например., если R — поле, то
а если при этом все Я&(Х, Я) или все H^{Y, R) ко-
конечномерны, то
Имеются также аналогичные формулы для относитель-
относительных гомологии и когомологий [3], [4].
В случае L=M=R модуль Я* (X, Я)®Я* (У, Я)
обладает структурой косого тензорного произведения
алгебр, при этом а — гомоморфизм алгебр. Таким
образом, если ТО1'!(Я*(Х, Я), H*(Y, Я)) = 0 и все
Нк(Х, Я) или все Hk(Y, Я) конечно порождены, то
имеет место изоморфизм алгебр [3]:
Я* (XxY, R) s Я* (X, Я) (g) II* (У, Я).
В случае, когда X и У — конечные полиэдры,
К. ф. позволяет найти числа Бетти и коэффициенты
кручения полиэдра XX У через аналогичные инварианты
полиэдров X и У. Именно эти результаты были полу-
получены самим Г. Кюннетом [1]. В частности, если Ьк(Х)
есть к-е число Бетти полиэдра X и
P(x)=Hk>obk(X)t«
— многочлен Пуанкаре полиэдра X, то
p(XXY) = p(X)p(Y).
В теории когомологий со значениями в пучке имеет-
имеется следующий вариант К. ф. [6]. Пусть X и У —
топологич. пространства со счетными базами, JF и
% — пучки Фреше на X и У (см. Когерентный ана-
аналитический пучок). И пусть JF (или %) — ядерный
пучок (т. е. §~(U) — ядерное пространство для
всех открытых UdX). Тогда на XX У определен пучок
Фреше flgjg такой, что
(П,
где (X) — знак пополненного тензорного произведения,
a UdX, V'czY открыты. Если пространства Н*(Х, §~)
и H*(Y, <g) отделимы, то справедлива К. ф.
Я*(ХХУ, f ®S) ^U*(X,g-)®H*(Y, •§).
В частности, когерентные аналитич. пучки JF, g на
комплексных аналитич. пространствах X, У со счет-
счетными базами являются ядерными и
где If *, g* — аналитические обратные образы пучков
fug при проекциях УхУ-+Хи ХХУ^-У. Таким
образом, если Н*(Х, §") и II* (Y, %) отделимы, то
(У, S).
В алгебраической геометрии К. ф. обычно встреча-
встречаются в таком варианте. Пусть X и У — алгебраичес-
алгебраические многообразия над полем к, а §~ и g — когерент-
когерентные алгебраич. пучки на X и У соответственно. Тогда
[9]:
H*(XXY, §-®k%)siH*(X, $r)®kH*(Y,%).
Здесь §~®1г§ — пучок на XX У, модули сечений кото-
которого над UX V (U — открытое аффинное подмножество
в X, V — в У) суть
Г A7, Г)®*ГA', S).
Более общо, пусть р : X ->- S и q : У —>- 5 — морфиз-
мы в категории схем, h : XXY -+ S — их расслоенное
S
произведение, |р и # — квазикогерентные пучки моду-
модулей на X и У. Обобщая конструкцию пучка §~®^
можно ввести пучки модулей Тог^ (JF, <§) на XX У,
модули сечения которых для аффинных S, X и Y
изоморфны То4(Г(Х, f), Г (У, ?)), где Л=ГE, б,)-
Тогда существуют [7] две спектральные последователь-
последовательности (Ег) и (' Ег) с начальными членами
имеющие один и тот же предел. Эта громоздкая форму-
формулировка К. ф. приобретает более привычный вид в
терминах производных функторов [11]:
L / L \
s
Если пучок JF или g является плоским над S, то
спектральная последовательность (Ег) вырождается.
Аналогично, ('Ег) вырождается, если все R^p^iF)
(или все Rkq* C§)) плоские над S. Если обе спектраль-
спектральные последовательности (Ег) и ('Ег) вырождаются, то
К. ф. приобретает вид
) * Ш ®q k «
К. ф. имеется и для этальных пучков Л-модулей на
схемах X и У, где А — конечное кольцо. Ее можно
записать в виде
где ! означает, что когомологии берутся с компактными
носителями. В частности (см. [8]), для полных алгеб-
раич. многообразий X и У К. ф. для /-адических
когомологии имеет вид
Я*(ХХУ, Qt)=H*(X, Q
Для произвольных многообразий такая формула дока-
доказана лишь в предположении о возможности разреше-
разрешения особенностей, напр., для многообразий надполем
нулевой характеристики.
Вариант К. ф. имеется и в Х-теории. Пусть X —
такое пространство, что группа К* {X) конечно порож-
порождена, и пусть У — клеточное пространство. Тогда имеет
место точная последовательность 2,-градуированных
модулей
О —> К*(Х) ® K*(Y) -Л- K*(XxY) Л-
K*(Y))—»0,
где а — гомоморфизм степени 0, a E — степени 1
(см. [5]). Частным случаем этого утверждения явля-
является Ботта теорема периодичности для комплексных
расслоений. Известна также К. ф. в теории бордизмов
[10].
Лит.: [1] Kiinneth H., «Math. Ann.», 1923, Bd 90,
S. 65—85; 1924, Bd 91, S. 125—34; [2] К а р т а н А., Э й л е н-
берг С, Гомологическая алгебра, пер. с англ., М., I960;
[3] Д о л ь д А., Лекции по алгебраической топологии, пер. с
англ., М., 1976; [4] G п е н ь е р Э., Алгебраическая топология,
пер. с англ., М., 1971; [5] А т ь я М., Лекции по К-теории, пер-
с англ., М., 1967; [6] К a u p L., «Math. Z.», 1967, Bd 97, № 2,
S. 158—68; [7] G г о t h e n d i e с k A., D i e и d о n n ё J.,
Elements de g<5ometrie algebrique, ch. 3, pt. 2, P., 1963. (Publ.
Math. IHES, .№ 17); [8] Theorie des topos et cohomologie etale des
schemas, t. 3, В.— [a. o.], 1973; [9J Sampson J., W a s h-
n i t z e r G., «111. J. Math.», 1959, v. 3, Л5 3, p. 389—402; LlOl
Коннер Э., Флойд Э., Гладкие периодические отображе-
отображения, пер. с англ., М., 1969; [11] Harts home R., Residues
and duality, В.— Hdlb.— N. Y., 1966.
В. И. Данилов, А. Л. Опищик-
ЛАВРЕНТЬЕВА ТЕОРЕМА — 1) Л. т. в де-
дескриптивной теории множеств: тополо-
топологии, отображение между двумя множествами в R" можно
продолжить до гомеоморфизма нек-рых содержащих
их множеств типа Ge. Следствием этой Л. т. является
топологич. инвариантность хаусдорфова типа множе-
множества (см. [1]).
2) Л. т. в т е о р и и приближен» и, критерий
возможности равномерной аппроксимации: для того
чтобы любую непрерывную на компакте А'сС функцию
можно было равномерно на К аппроксимировать много-
многочленами, необходимо и достаточно, чтобы К был не
разбивающим комплексную плоскость компактом без
внутренних точек (см. [2]).
3) Л. т. в теории квазиконформных
отображен и й: если Dz и Dw — две односвязные
плоские области, ограниченные кусочно гладкими кри-
кривыми, а 2Ь z2, z3 и u>i, w.2, w3 — положительно зану-
занумерованные тройки точек на их границах, то какова
бы ни была сильно эллиптическая система уравнений
Ч>1 (*, У, и, v, u'x, u'y, v'x, v'y)=0,
Ф2 (х, у, и, v, и'х, и'у, г/, ^)=0
с равномерно непрерывными частными производными
функций, задающих уравнения характеристик, всегда
существует единственное гомеоморфное отображение
D2 на Dw, осуществляемое решением и(.т, у), v(x, у)
системы, с соответствием указанных троек граничных
точек.
4) Л. т. в области механики (теория кры-
крыла, уединенная волна, формы динамич. потери устой-
устойчивости, струпные течения, теория кумулятивного за-
заряда, направленный взрыв) см. в [4].
Теоремы 1) — 4) получены М. А. Лаврентьевым.
Лит.: [11 Лаврентьев М. A., «Fundam. math.», 1924,
t. в, p. 149—60; [2] его же, «Тр. физико-матем. ин-та АН
СССР, Отдел матем.», 1934, т. 5, с. 159—245; [3] его же,
«Изв. АН СССР. Сер. матем.», 1948, т. 12, Л", fi, с. 513 — 54; [4]
Михаил Алексеевич Лаврентьев, М., 1971 (АН СССР. Материалы
к биобиблиографии ученых СССР. Сер. математики, в 12).
ЛАГЕРРА МНОГОЧЛЕНЫ, м н о г о ч л е и ы' Ч е-
б ы ш е в а — Лагерра,— многочлены, ортогональ-
ортогональные на интервале @, оо) с весовой функцией ц>(х) =
= хае~х, где сс> — 1. Стандартизованные Л. м. опре-
определяются формулой
Ц?'-*Ь п = 0, 1, 2, ...;
представление с помощью гамма-функции:
¦"" Г (a + n+l) <-x)K
В применениях наиболее важны формулы:
+ n)
(x),
Многочлен Ln (x) удовлетворяет дифференциальному
уравнению (уравнению Лагерра)
0, п = 1, 2, ....
Производящая функция Л. м. имеет вид
Ортонормированпые Л. м. выражаются через стандарти-
стандартизованные многочлены:
Множество всех Л. м. плотно в пространстве функций,
квадрат к-рых интегрируем с весом ср (x) на интервале
(О, оо).
Наиболее часто употребляются Л. м. при условии
а=0, исследованные Э. Лагерром [1], обозначаются в
этом случае Ьп(х) (в отличие от них Л. м. Ь% (х) иногда
называют обобщенным н). Несколько первых
Л. м. Ln(x) имеют вид
LQ(x)=i,
L{i
2()
L3 (x) =l—
Li(x) = i—
Л. м. Ln' (x) иногда обозначается Ln(x; a).
Лит.: [1] Laguerre Б., «Bull. Soc. math. France»,
1878, t. 8, p. 72—78; F2] С т е к л о в В. А., «Изв. Ими. АН»,
1916, [т. 10], с. 633—42; [3] G е г ё Г., Ортогональные много-
многочлены, пер. с англ., М., 1962; [4] С у е т и н П. К., Классиче-
Классические ортогональные многочлены, 2 изд., М., 1979. П. К. Суетин.
ЛАГЕРРА ПРЕОБРАЗОВАНИЕ — интегральное пре-
преобразование вида
f(n) = T{F(x)} = ^ e-*Ln(x)F(x)dx, n = 0, 1, 2, ...,
где Ln (x) — Лагерра многочлен степени п. Формула
обращения имеет вид
Т-1 {/ (n)} = F (*) = 2;"=0/ (n)Ln(x), 0<x< оо,
если ряд сходится. Если функция F (х) непрерывна,
F' (х) кусочно непрерывна на [0, оо) и F(х) = О(еах),
х —>- оо, а<1, то
Если функции F(x), F' (х) непрерывны, F" (х) кусочно
непрерывна на [0, оо) и | F(x)\-r\F' (x)\-—0 (еах), х->-<х,
а<1, то
Если F(x) кусочно непрерывна на [0, со) и F(х) =
— 0(еах), х—»-оо, а<1, то для
и при п^=0
e(O)=f(O).
Пусть функции F(x) и G(x) кусочно непрерывны на
[О, х) и
(x)\ = O(e"x), z^oo, a < 1/2,
T{F} = f(n), T{G}=g(n).
Тогда
T-4f(n)j(n)} =
XG (z+i —2 y^cosB^
Обобщенное Л. п. имеет вид
e-^^aL«(x)F(.r)d^, n = 0, 1, 2, ...,
где Z/" (z) — обобщенный многочлен Лагерра (см. [4]).
Лит.: [1] 3 е м а н я н А. Г., Интегральные преобразова-
преобразования обобщенных функций, пер. с англ., М., 1974; [2] М с
Cully J., «SIAM Rev.», 1960, v. 2, .№ 3, р. 185—91; [3] D e b-
n a t h L., «Bull. Calcutta Math. Soc», 1960, v. 52, j\° 2, p. 69—
77; [4] Итоги науки. Математический анализ. 196rt, M., 1967,
с. 7—82. Ю. А. Бричков, А. П. Прудников.
ЛАГЕРРА УРАВНЕНИЕ — см. Лагерра многочлены.
ЛАГЕРРА ФОРМУЛА — 1) Формула для вычисле-
вычисления угла между прямыми в евклидовом и псевдоевкли-
псевдоевклидовом пространствах. Пусть X и У — бесконечно
удаленные точки прямых а и b, a G и К — точки пере-
пересечения этих прямых с абсолютом пространства. Тогда
угол ф между этими прямыми выражается с помощью
двойного отношения W(G, К, X, У):
ф= -|-lnJF(G, А', А', У)
Для двумерного пеевдоевклидова пространства G и К —
направляющие векторы изотропных прямых, проходя-
проходящих через точку пересечения прямых а и h.
Формула выведена Э. Лагерром [1].
2) Формула, согласно к-рой для всех кривых на дан-
данной поверхности, имеющих касание в нек-рой точке,
совпадают величины
где fcj и k2 — кривизна и кручение кривой, угол между
главной нормалью кривой и нормалью к поверхности,
s — натуральный параметр на кривой. Формула полу-
получена Э. Лагерром A870, см. [2]).
Лит.: [1] La;«erre E., «Nouv. arm. math.», 1853, t. 12,
;>. 57—63; [2] его же, (Euvres, t. 2, P., 1905; [3] Розен-
t> e л ь д Б. А., Неевклидовы пространства, М., 1969.
Д. Д. Соколов.
ЛАГЕРРА ФУНКЦИИ — функции, являющиеся ре-
решениями уравнения
где а, п — произвольные параметры. Л. ф. могут
»1ыть выражены через вырожденную гипергеометричес-
•:ую функцию или через Уиттекера функцию. В случае
/i = 0, 1, 2. . . решения уравнения (*) наз. Лагерра
многочленами. Иногда Л. ф. наз. функцию
где Л1"' {х) — многочлены Лагерра.
Лит.: [1] Я н к е Е., Э м д е Ф., Леш Ф., Специальные
Функции. Формулы, графики, таблицы, пер. с нем., 2 изд., М.,
1368. А- Б. Иванов.
ЛАГРАНЖА ЗАДАЧА — одна из основных задач
классич. вариационного исчисления. Состоит в мини-
минимизации функционала
J(y)=\x*i{x, у, y')dx, f: RxR"xR"—-R,
при наличии дифференциальных ограничений типа ра-
равенств:
Ф (х, У, у') = 0, ф: RxK"xK"—>R'n,m<n, A)
и граничных условий:
¦ф(^1, j/(*i), хг, V {гг)) ¦--=-¦ Q, г|э: Rx R"xRx Rn —>¦ RP,
Обычно Л. з. рассматривается при условии, что имеет
место регулярность системы A), состоящая в том, что
матрица ||d<p/di/'|l имеет максимальный ранг:
При этом условии систему A) можно разрешить отно-
относительно части переменных и, используя иные обозна-
обозначения (t, х вместо х, у), привести Л. з. к виду
F{t,X, «,*,*': RXR»xRr_R, | B)
г = Ф((, /, и), Ф: RxR»XRr—у R". ./
Функцию F и отображение Ф предполагают обычно
непрерывно дифференцируемыми. Задачи оптимального
управления задаются обычно в форме B) (р а з р о-
m e н и а я, или понтрягинская, форма),
и при этом накладываются еще ограничения на управ-
управление u?U. Необходимые условия сильного якстре-
мума для задачи B) (для простоты — с закрепленным
левым х0 и свободным правым концом хх) имеют сле-
следующий вид. Пусть
L (t, х, х, и, р (i)) = (p (t)) —х-\-Ф (t, х, и))—F (t, .r, и)
— Л агранжа функция. Для того чтобы вектор-функция
(x*(t), и* (t)) доставляла сильный минимум в Л. я. B),
необходимо, чтобы были выполнены соотношения:
dx
U*, и*) Но
?
dx
(AT*, U*)
dt=°-
P(«l)=0, D)
g^LU, x*(t), x, u, p(t))-
L(t, x*(t), x*(t), u*(l), p(t)) —
(t))\Lx(t, x*\t),i*(t), u*(t), p(t)) =
)|O(t, x*(t), u)-F(t, x*(t), u))-
x*(t), U*(t)) + F(t, x*(t), u*(«)))<0 E)
при всевозмо?кпых допустимых значениях х, и.
Если провести дифференцирование в C) по t и
воспользоваться обозначением
ffi(t, х, и, р) = (р|Ф)—/\
то необходимое условие сильного минимума сформули-
сформулируется в форме принципа максимума, в к-ром соединены
Эйлера уравнение C), трансверсальности условие D) и
Вейерштрасса условие E). Для того чтобы вектор-функ-
вектор-функция (х*, и*) доставляла сильный минимум в задаче B)
с закрепленным левым и свободным правым концами,
необходимо, чтобы нашлось решение системы
'?¦"*¦»> p(i)=o
р@ = ? , p(il)=o,
при к-ром
$C{t, x*(t), u*(t), p@) = max^f(t, x* (t), и, p(t)).
Ж. Лагранж (J. Lagraoge) рассматривал подобные
задачи в связи с исследованиями по механике B-я пол.
18 в .)•
Лит. см. при статье Вариационное исчисление.
И. В. Вапнярский, В. М. Тихомиров.
ЛАГРАНЖА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА —
форма записи многочлена степени п (интерполя-
(интерполяционного многочлена Л агранжа),
интерполирующего заданную функцию f(x) в узлах
х0, xlv . ., х„:
~~ П -^- A)
В случае, когда значения х,- являются равноотстоя-
равноотстоящими, т.е. хх — хо = х2 — х1=...=х„ — xn_l = h,
с помощью обозначений (x—xo)lh=t формула A) может
быть приведена к виду
t (t-1) ... (t-n)
ХИ-_0<-1)<^. B)
В выражении B), наз. Л. и. ф. для равноотсто-
равноотстоящих узлов, коэффициенты, стоящие перед f(x[):
( 1)С
( ' п (t-i) и! '
наз. коэффициентами Лагранжа.
Если функция / имеет производную порядка п+1
на отрезке [а, Ь], все узлы интерполяции лежат на
этом отрезке и для любой точки х?[а, Ь]:
ax = min{i0, xlt ...,х„,х}, рх==шах {х0, хи . . ., х„, х},
то существует такая точка |?[ал, $х], что
/ (x)-Ln (x) = /(« + i) (I) ш„ (.т)/
где
Если абсолютная величина производной /(" + ') огра-
ограничена на отрезке [а, 6] постоянной М и если в каче-
качестве узлов интерполяции выбраны точки, в к-рые перей-
перейдут корни многочлена Чебышева степени п+1 при ли-
линейном отображении отрезка [ — 1, 1] на отрезок \а, 6],
то для любого ,r?[a, b] справедливо неравенство
Если узлы интерполяции — комплексные числа z0,
%,..., zn п лежат в нек-рой области G, ограниченной
кусочно гладким контуром у, а функция / является
однозначной аналитич. функцией в замыкании области
G, то Л. и. ф. имеет вид
причем
Л. и. ф. для интерполирования с помощью тригоно-
тригонометрия, полиномов наз. формула
т ы-
дающая тригонометрич. полином порядка и, принимаю-
принимающий в заданных узлах х0, ху,. . ., хп данные значения
г/0, г/1,- ¦ -, Уп-
Формула предложена Ж. Лагранжем (.Т. Lagrange,
1795).
Лит.: [1] Б е р е з и н И. С, Ж и д к о в Н. II., Методы
вычислений, 3 изд., т. 1, М., 1966; [2] Бахвалов Н. С,
Численные методы, 2 изд., М., 1975.
Л. Д. Кудрявцев, М. И. Самарин.
ЛАГРАНЖА МЕТОД — метод приведения квадра-
квадратичной формы к сумме квадратов, указанный в 1-759
Ж. Лагранжем (J. Lagrange). Пусть дана квадратичная
форма
/ (х) = 2" /= 1 aVxixj> аЧ = аЛ> (*)
от п переменных ху, х2,. . ., хп с коэффициентами из
поля к характеристики Ф2. Требуется привести эту
форму к канонич. виду
при помощи невырожденного линейного преобразования
переменных. Л. м. состоит в следующем. Можно счи-
считать, что не все коэффициенты формы A) равны нулю.
Поэтому возможны два случая.
1) При некотором g, l<:g<:n, диагональный коэф-
коэффициент agg^0. Тогда
где форма /i (х) не содержит переменную xg.
2) Если же все «?¦?¦= а/гл = О, но о^^О, то
где форма /2(я) но содержит двух переменных xg и а-/;.
Формы, стоящие под знаками квадратов в D), линейно
независимы. Применением преобразований вида C) и
D) форма A) после конечного числа шагов приводится
к сумме квадратов линейно независимых линейных
форм. С помощью частных производных формулы C)
и D) можно записать в виде
JL i 1LY fit 1LY1
Лит.: [1] Гантмахер Ф. P., Теория матриц, 2 изд.,
М., 1966; [2] К у р о ш А. Г., Курс высшей алгебры, 11 изд.,
М., 1975; [3] Александров П. С, Лекции но анали-
аналитической геометрии..., М., 1968. И. В. Проскуряков.
ЛАГРАНЖА МНОЖИТЕЛИ — переменные, с по-
помощью к-рых строится Лагранжа функция при иссле-
исследовании задач на условный экстремум. Использование
Л. м. и функции Лагранжа позволяет единообразным
способом получать необходимые условия оптималь-
оптимальности в задачах на условный экстремум. Метод получе-
получения необходимых условий в задаче определения экстре-
экстремума функции
/Oi, ...,*„) A)
при ограничениях
g/(xlt ..., а-„) = 6,-, i = l, ..., т, т < п, B)
заключающийся в использовании Л. м. Я,,-, i=l,. . ., пг,
построении функции Лагранжа
F (х, X) =/ (*) + 2Г=1 Я' [b'-gi {x)]
и приравнивании к нулю ее частных производных но xj
и X/, наз. методом Лагранжа. В этом методе
оптимальное значение х* = (х\,. . ., хп) находится
вместо с соответствующим ему вектором Л. м. Х* =
= (Xlv . ., %т) из решения системы т-\-п уравнений.
Л. м. К( , i=l,. .., т, допускают следующую интерпре-
интерпретацию [1]: пусть х* доставляет относительный экстре-
экстремум функции A) при условиях B); z* = f(x*). Значения
х*, X* и z* зависят от значений Ь; — правых частей
ограничений B). Формулируются достаточно общие
предположения, при к-рых все xj и X; являются непре-
непрерывно дифференцируемыми функциями вектора Ь=
= (&i,. . ., Ьт) в нек-рой s-окрестности его значения,
задаваемого в B). При этих предположениях непрерыв-
непрерывно дифференцируемой по 6,- будет и функция z *. Частные
производные от экстремума z* по 6,- равны соответству-
соответствующим Л. м. k'i, вычисленным при данном &=(&!,. . .,
«:
^- = JtJ, 1 = 1, .... т. C)
Z
В прикладных задачах z часто интерпретируется как
доход или стоимость, а правые части />,- — как затраты
некоторых ресурсов. Тогда размерностью Я,- будет
отношение единицы стоимости к единице ?-го вида
ресурсов. Числа Я; показывают, как изменится мак-
максимальный доход (или максимальная стоимость), если
количество i-ro вида ресурсов увеличится на единицу.
Приведенная интерпретация Л. м. распространяется
также на случай ограничений в виде неравенств и на
случай, когда переменные xj подчинены требованиям
неотрицательности.
В вариационном исчислении с помощью Л. м. удобно
получать необходимые условия оптимальности в задаче
на условный экстремум как необходимые условия
безусловного экстремума нек-рого составного функцио-
функционала. Л. м. в вариационном исчислении являются уже
не константами, а нек-рыми функциями. В теории опти-
оптимального управления и в Понтрягина принципе мак-
максимума Л. м. получили название сопряженных
переменных.
Лит.: [1] X е д л и Д ж., Нелинейное и динамическое про-
программирование, пер. с англ., М., 1967; [2] Б ли ее Г. А.,
лекции по вариационному исчислению, пер. с англ., М., 1950.
И. Б. Вапнярский.
ЛАГРАНЖА ПРИНЦИП, принцип стацио-
стационарного действи я,—вариационный интеграль-
интегральный принцип динамики голономных систем, стесненных
идеальными стационарными связями и находящихся
под действием потенциальных сил, не зависящих явно
от времени.
Согласно Л. п., в действительном движении голоном-
ной системы, для к-рой существует интеграл энергии
T-\-V=h, между нек-рым начальным Ао и конечным
А1 положениями, действие по Лагранжу
имеет стационарное значение по сравнению с кинемати-
кинематически возможными движениями между теми же поло-
положениями и с топ же энергией 1г, что и в действительном
движении. Здесь Т и V — кинетическая и потенци-
потенциальная энергии системы, mv vv — количество движения
v-ii точки системы, t0 и t — моменты времени прохож-
прохождения системы через положения Ао и А1.
Если начальное и конечное положения системы дос-
достаточно близки одно к другому, то действие но Лагран-
Лагранжу имеет минимум для действительного движения, в
связи с чем Л. п. наз. также принципом н а и-
меньшего действия в форме Лагран-
ж а.
Л. п. приводит задачу определения действительного
движения системы к вариационной Лагранжа задаче;
он выражает условие, необходимое и достаточное для
действительного движения [4].
Л. п. в неявной форме впервые был высказан П. Мо-
пертюи [1]; Л. Эйлер [2] дал его обоснование для случая
движения одной материальной точки в центральном
поле. Ж. Лагранж [3] распространил этот принцип на
многие более общие задачи.
Лит.: [11 М a u p e r t и i s P. L. M., «Histoire de l'Acad.
Royale des Sci.», aim. 1744, P., 1748, p. 417; [2] Euler L.,
Methodus inveniendi lineas curvas maximi minimive proprietate
gaudentes sive solutio problematis isoperimetrici latissimo sensu
accepti, Lausannae-Genevae, 1744; [31 La grange j., Essai
d'une nouvelle methode pour determiner les maxima et les minima
des formules integrates indefinies, Turin, 1762; Ul Суслов Г.
К., Теоретическая механика, 3 изд., М.— Л., 1946.
В. В. Румянцев.
ЛАГРАНЖА РЯД — степенной ряд, дающий реше-
решение задачи локального обращения голоморфной функ-
функции комплексного переменного. Первоначальное реше-
решение задачи обращения, данное Ж. Лагранжем (J. Lag-
range, 1770), было затем усовершенствовано А. Бюрма-
ном (Н. Burmann, 1779). См. Бюрмана — Лагранжа
ряд. Е. Д. Соломенцев.
ЛАГРАНЖА СКОБКИ относительно пе-
переменных и и v — суммы вида
уп
t=1 eiT Sv до ди
где q= (qu. . ., qn) и р= (Ри. . ., р„) — нек-рые функ-
функции от и и v.
Если q= (qx,. . ., qn) и р = = (рь. . ., р„) — канонич.
переменные и Q=Q{q, p), P=P(q, p) — канонические
преобразования, то Л. с. являются инвариантами
этого преобразования
[«. v\q, /7 = [и, »]Q, Р-
По этой причине индексы q, p в правой части (*) часто
опускают. Л. с. наз. фундаментальными, когда пере-
переменные и и v совпадают с какой-либо парой из 2ге
переменных q, p. Из i:nx можно составить три матрицы
[Р, P] = {[Pi, Р/]}"._ /=1, [я, q], [1, Р],
первые две из к-рых нулевые, а последняя единичная.
Между Л. с. и Пуассона скобками имеется определенная
связь. Именно, если функции u;=ui(q, p), 1<:г<:Хп,
осуществляют диффеоморфизм R2n —v R2", то матрицы,
составленные из элементов [u,-, uj] и (uj, u,), взаимно
обратны.
Лит.: [1] La grange J. L., CEuvres, t. 6, P., 1873; [2]
Уиттекер Э. Т., Аналитическая динамика, пер. с англ.,
М.— Л., 1937; [3] Лурье А. И., Аналитическая механика,
М., 1961; ['i] Г о л д с т е й н Г., Классическая механика, пер.
с англ., 2 изд., М., 1975. А. П. Солдатов,
ЛАГРАНЖА СПЕКТР — множество постоянных Лаг-
Лагранжа в проблеме рациональных приближений дей-
действительных чисел. Л. с. содержится в спектре Маркова
(см. Маркова проблема спектра).
ЛАГРАНЖА ТЕОРЕМА — 1) Л. т. в дифференциаль-
дифференциальном исчислении — см. Конечных приращений формула.
2) Л. т. в теории групп: порядок |G| любой конеч-
конечной группы G делится на порядок \Н\ любой ее под-
подгруппы Н. Фактически теорема была доказана Ж. Лаг-
Лагранжем (J. Lagrange, 1771) при изучении свойств под-
подстановок в связи с исследованиями разрешимости
алгебраич. уравнений в радикалах.
Лит.: [1] Каргаполов М. И., Мерзляков Ю. И.,
Основы теории групп, 2 изд., М., 1977. Н. Н. Вильяме.
3) Л. т. о сравнениях: число решений сравнения
айхп + а-^х" -1 -j- ... -\- а„ = 0 (mod p), а0ф0 (mod p),
по простому модулю р не превосходит его степени п.
Доказана Ж. Лагранжем (см. [1]). Обобщается на много-
многочлены с коэффициентами из произвольной области це-
целостности.
Лит.: [1] Lagrange J. L., CEuvres, t. 2, P., 1868,
p. 667; [2] Виноградов И. М., Основы теории чисел,
8 изд., М., 1972. С. А. Степанов.
4) Л. т. о сумме четырех квадратов:
всякое натуральное число можно представить в виде
суммы четырех квадратов целых чисел. Установлена
Ж. Лагранжем [1]. Об обобщении Л. т. см. Варинга
проблема.
Лит.: fU L a g r a n g e J. L., «Nouv. mem. Acad. roy. sci.
de Berlin, ann. 1770», В., 1772, p. 123—33; [2] С е р р Ж.-П.,
Курс арифметики, пер. с франц., М., 1972. С. М. Воронин.
5) Л. т. о цепных дробях: всякая цепная
дробь, представляющая кеадратическую иррациональ-
иррациональность, является периодической. Установлена Ж. Лаг-
Лагранжем [1].
Лит.: [1] L a g r a n g e J. L., «Mem. Acad. roy. sci. de Ber-
Berlin, aim. 1767», t. 23, В., 1769, p. 165—310; [2] X и н ч и н А. Я.,
Цепные дроби, 3 изд., М., 1961, с. 62. С. М. Воронин.
ЛАГРАНЖА УРАВНЕНИЕ — обыкновенное диффе-
дифференциальное уравнение 1-го порядка, не разрешенное
относительно производной, но линейное относительно
независимой переменной и неизвестной функции:
F(y')x+G(y')y=H(y'). A)
Это уравнение названо по имени Ж. Лагранжа (J. La-
granite, 1759, см. [1]); уравнение A) исследовал также
Ж. Д'Аламбер (J. D'Alembert), и потому оно иногда
наз. уравнением Д'А л а м б е р а. Частным
случаем Л. у. является Клеро уравнение.
Л. у. всегда разрешимо в квадратурах методом
введения параметра (методом диф-
ференцир ования). Пусть, напр., уравнение
A) приводится к виду
y=f(y')x+g(y'), f(y')^y'. B)
Вводя параметр р = у' и взяв полный дифференциал
от обеих частей равенства B), с учетом соотношения
dy=pdx приходят к Л1 нейному уравнению 1-го порядка
Если г=Ф (р, С) — решение этого уравнения (где С —
произвольная постоянная), то решение уравнения B)
записывается в параметрич. виде
х=Ф(р, С), у = 1(р)Ф(р, C) + g(p).
Если р0 — изолированный корень уравнения р = (р,
то y=r:f(po)-vJrg(Po) —также решение уравнения B);
это решение может оказаться особым.
Лит.: [l]Lagrange J. L., CEuvres, t. I , P., 1867, p. 23 —
36; 12] С т е и а н о в В. В Курс дифференциальных уравне-
уравнений, 8 изд., М., 1959. Н. X. Розов.
ЛАГРАНЖА УРАВНЕНИЯ м ех аники — обык-
обыкновенные дифференциальные уравнения 2-го порядка,
описывающие движения механич. систем под действием
приложенных к ним сил. Л. у. установлены Ж. Лаг-
ранжем [1] в двух формах: Л. у. 1-го рода, или уравне-
уравнения в декартовых координатах с неопределенными
множителями Лагранжа, и 2-го рода, или уравнения в
обобщенных лагранжевых координатах.
Л. у. 1-го рода описывают движения как голономных
систем, стесненных только геометрич. связями вида
/,(*i. .... *злг.0 = 0, » = 1, .... k,fs(x, t)?C\ A)
так и неголономных систем, на к-рые наложены, поми-
помимо связей A), кинематич. связи вида
г = 1, ..., Л1, ф, (х, х,
dxv
где o-v , a:v = -JT- — декартовы координаты и скорости
точек, N — число точек системы, t — время, т3р_2 =
= т3р-\ = т3р — масса р-й точки, имеющей координаты
Связи A) и B) предполагаются независимыми, т. е.
ранги матриц
_! равны соответствен-
но к н т.
Л. у. 1-го рода имеют вид
-~ik ди sr<m д'('г
s=\ г= 1 •v
v = l 3N,
где ).s, \лг — неопределенные множители Лагранжа,
пропорциональные реакциям связей, Xv — проекции
на оси координат заданных активных сил, причем сила
Fр, действующая на р-ю точку, имеет проекции Х3/7_2,
d
К дифференциальным уравнениям C) надлежит
присоединить /с+тге уравнений A) и B), в результате
чего получается система ZN-\-k-\-m уравнений с таким
же числом неизвестных xv , %s, цг. Л. у. 1-го рода на
практике обычно применяются для систем с неболь-
небольшим числом неизвестных.
Л. у. 2-го рода описывают движения лишь голоном-
ных систем, стесненных связями вида A). Введением
в рассмотрение n=3N—к независимых обобщенных
лагранжевых координат ?,-, с помощью к-рых любое
возможное положение системы может быть получено
при нек-рых значениях q, из равенств
xv-=xv(9u ¦¦¦, In, t), \(qi, t)?C", D)
обращающих уравнения A) в тождества, устанавлива-
устанавливается для каждого t взаимно однозначное соответствие
между возможными положениями системы и точками
нск-рой области n-мерного конфигурационного про-
пространства (q1,. . ., qn). В случае стационарных связей
A) всегда возможно выбрать переменные <?,- так, что
время t не будет входить в уравнения D). Далее запи-
записываются с помощью уравнений D) выражения для
суммы элементарных работ всех активных сил Fр на
возможных перемощениях системы
и кинетич. энергии системы
TDi, h, 0=тУМ т
Здесь
t=l l
— обобщенная сила, соответствующая координате
lii Ts(qi, q,-, t) — однородные степени s формы обоб-
обобщенных скоростей qi, причем
3N dxv
X
9xv
9xv 9xv
9xv 9xv
dt
В случае стационарных связей Т= Т2.
Л. у. 2-го рода имеют вид
d дТ ОТ _ . .
Уравнения E) представляют собой систему п обыкно-
обыкновенных дифференциальных уравнений 2-го порядка с
неизвестными q;. Они инвариантны по форме относи-
относительно выбора лагранжевых координат. Эта система
уравнений движения имеет наименьший возможный
порядок 2п. В этом, а также в отсутствии в уравне-
уравнениях E) реакций связей, состоит большое преимущест-
преимущество уравнений E) по сравнению с Л. у. 1-го рода C).
После интегрирования системы E) реакции связей мо-
могут быть определены из уравнений, выражающих вто-
второй закон Ньютона для точек системы.
В случае потенциальных обобщенных сил, когда су-
существует силовая функция f/(?i, •-., qn, t) такая, что
Qj =д— , i=l, . . ., и, уравнения E) принимают вид
Ат—г1 т—= 0, s = l, ..., п, F)
dt ад( dqt '
где L{qi, qi, t)=T-\-U носит название функции
Лагранжа, или кинетич. потенциала.
Если -^=0, или -^-=0, то уравнения F) допус-
допускают обобщенный интеграл энергии
V" -2?- (Ц — L — T2 — Г о — 6r = const
или циклический интеграл
—; = р^ = COnSt,
соответствующий: циклической координате qa.
Лит.: [1] Lagrange J., Mecanique analytique, P., 1788
(рус. пер.— Л а г р а н ж Ж., Аналитическая механика, 2 изд.,
т. 1, М.— Л. 1950). В. В. Румянцев.
ЛАГРАНЖА ФУНКЦИЯ — функция, используе-
используемая при решении задач на условный экстремум функ-
функций многих переменных и функционалов. С помощью
Л. ф. записываются необходимые условия оптималь-
оптимальности в задачах на условный экстремум. При атом не
требуется выражать одни переменные через другие
или учитывать, что не все переменные являются неза-
независимыми. Получаемые с помощью Л. ф. необходимые
условия представляют замкнутую систему соотноше-
соотношений, среди решений к-рой содержится искомое опти-
оптимальное решение задачи на условный экстремум.
Л. ф. используется как при рассмотрении теоретич.
вопросов линейного и нелинейного программирования,
так и при построении нек-рых вычислительных методов.
Пусть, напр., поставлена задача на условный экст-
экстремум функции многих переменных: найти максимум
или минимум функции
/ (Zl, . . ., Хп) A)
при условиях
gj (х1у . . ., хп) = b(, г = 1, . . ., т; т < п. B)
Функция F(x, X), определенная выражением
F (x, X) = Xof (ж) + Ях [by — gy (я)] + ...+
наз. функцией Лагранжа, а числа X; —
Лагранжа множителями. Имеет место следующее ут-
утверждение, называемое правилом множите-
л е и: если х* — (п ,. . ., х„) — решение задачи на услов-
условный экстремум A), B), то существует хотя бы одна не-
ненулевая система множителей Лагранжа Х*=(Хо , >ч , ...,
\т) такая, что точка (х*, к*) является точкой стацио-
стационарности Л. ф. по переменным х;- и X;, 1ф0, рас-
рассматриваемым как независимые переменные. Необходи-
Необходимые условия стационарности Л. ф. приводят к системе
т-\-п уравнений
3F(x*. к*) , , Э/ (.х*) '"Г-чт , dg.(x*)^
дх. о дх. Zm^i--\ "I Эх. ' D)
/ = 1 п,
dF (х*, к*) , . ,. „ . . ,_.
^т - = о;—g/(z*)=0, i = l, ..., т. E)
I
Соотношения E) полученной системы представляют
условия связи B). Точка х* доставляет обычный (безу-
(безусловный) экстремум Л. ф. F (х, X*) по х.
Для большинства практич. задач значение %о в C),
D) можно принять равным единице. Однако имеются
примеры (см. [1]), в к-рых правило множителей при
Х,о = 1 не выполняется, а выполняется при ко --0. Для
определения условий, позволяющих отличить случаи
Хо — 1 и %о— 0, рассматриваются (см. [2]) матрицы G и
¦V-
ag,
ax,
dgm
Эг,
agi
axn
agm
дх„
G,=
dg,
Эх,
agm
fix,
a/
Ox,
agi
dxn
dgm
¦¦¦ dxn
at
Пусть r(G) — ранг матрицы G, рассматриваемой в опти-
оптимальной точке х*. Тогда если r(G^) = r(G), то Хо = 1;
если же r(Gf)>r(G), то для выполнения правила мно-
множителей необходимо положить Хй —0. Кроме того,
если r(Gj) = r(G)=m (наиболее распространенный случай
в практич. задачах), то Xi определены однозначно, а
если r(Gj)>r(G) или r(Gf) = r(G)<im, то Xi определяют-
определяются не единственным образом. В зависимости от рассмот-
рассмотренных случаев Хо полагается равным 0 или 1. Тогда
система D), E) превращается в систему т^п уравнений
с т+ге неизвестными xi ,. . ., хп, Xi,. . ., Х*т. Множи-
Множителям Лагранжа Xi можно дать интерпретацию, имею-
имеющую определенный физич. смысл (см. Лагранжа мно-
множители).
В случае, когда оптимизируемая функция /(х) яв-
является квадратичной, а условия связи B) линейны,
система необходимых условий D), E) оказывается ли-
линейной, и ее решение но вызывает затруднений. В об-
общем случае система необходимых условий D), E) в за-
задаче на условный экстремум, получаемая с помощью
Л. ф., оказывается нелинейной, и ее решение возможно
лишь с применением итерационных методов, напр.
Ньютона метода. Основной трудностью при этом,
помимо вычислительных трудностей решения системы
нелинейных уравнений, оказывается проблема полу-
получения всех решений, удовлетворяющих необходимым
условиям. Не существует вычислительного процесса,
обеспечивающего получение всех решений системы D1,
E), и это является одним из обстоятельств, ограничи-
ограничивающих применение метода множителей Лагранжя.
Л. ф. применяется в задачах нелинейного программы
рования, отличающихся от классич. задач на условный
экстремум наличием, помимо условий типа равенства,
ограничений типа неравенства: найти минимум или
максимум
/ И F)
при условиях
gi И < bh i
Si (х) Зг bt, i ¦-
m, m2
0)
x^sO. (8)
Для вывода необходимых условий оптимальности в за-
задаче F) — (8) вводится Л. ф.
F (х, X) = / (х)
(9)
Для определенности рассматривается случай максиму-
максимума f{x). Пусть x* = (xi,. . ., хп)^0 доставляет макси-
максимум f(x) при ограничениях G), (8) и пусть в точке х*
выполнено требование регулярности ограничений (см.
[2]); пусть / — множество индексов j из /=1,. . ., ;',
для к-рых xj >0, Jo — множество индексов /, для к-рых
27=0, и / — множество индексов i из г=1,. . ., т2,
для к-рых ограничения G) в точке х* выполняются как
строгие неравенства. Тогда существует такой вектор
k*=(klt. . ., к*т):
к* 5э 0 при i = 1, . . ., т1,
к* < 0 при г = тя1 + 1, ¦••, »<2>
к* любого знака при i = m2-\-\, .. ., т, f ^ '
ki — О при if-I,
с) У
к*
dF
(X
д:
dg
*, Я*)
¦¦ (х*)
ах.
(х*. Я*)
С Эг 0 При 1=1, . . ., П?1,
= 6/— ^/(ж*) J <0 при i = mi + l, . .., m2, A2)
V =0 при i = m«-\-i, ..., т.
Сформулированные необходимые условия обобщают
условия D), E). Эти условия можно интерпретировать,
используя понятие седловой точки функции Р(х, к).
В седловой точке (.г*, %*) функция F(x, X) удовлетво-
удовлетворяет неравенствам
F (х, X*XF(a*, )i
Точка (х*, К*), в к-рой выполняются условия A0) —
A2), удовлетворяет необходимым условиям существо-
существования седловой точки Л. ф. F(x, К) на множестве х^О
п к, удовлетворяющем ограничениям A0). В том случае,
когда f (х) — вогнутая при х^О функция, a g[{x) —
выпуклая, если %i >0, и вогнутая, если %i <0, i=l,. . .,
т, сформулированные необходимые условия оказы-
оказываются п достаточными, т. е. найденная нз необходи-
необходимых условий точка (х*, к*) является седловой точкой
Л. ф. F(х, к) при х^0 и к, удовлетворяющем огра-
ограничениям A0), и f(x*) является абсолютным максиму-
максимумом f(x) при ограничениях G), (8).
Наряду с Л. ф., записываемой в виде (9), использу-
используется и другая форма записи Л. ф., отличающаяся зна-
знаком множителей Лагранжа. При этом изменяется и
форма записи необходимых условий. Пусть поставлена
задача нелинейного программирования: найти максимум
/(*) A3)
при ограничениях
gi(x)^0, i = l, ..., т, A4)
х^О. A5)
Ограничения G) при t—1,. . ., т2 сводятся к A4)
простым переобозначением. Условия типа равенства
gi(x) = bi, it>m^ заменяются неравенствами g;{x) —
— 6/>0 и bj—gi(x)^O и также приводятся к виду A4).
Пусть Л. ф. записана в виде
f(x, я)=/(*)+27=1%igi{x) A6)
и пусть / — множество индексов i из г=1,. . ., т, для
к-рых ограничения A4) выполняются как строгие не-
неравенства. Тогда если х*~^0 — оптимальное решение
задачи A3) — A5), то при выполнении требования
регулярности ограничений существует такой вектор
к*=(К,. . ., к*т):
Д.* 5& 0, г = 1, ..., т; к* = 0, i?I, A7)
что
dF {ж*, Я.*)
A9)
(cm. [2], [3]). Условия A7) — A9) с учетом положи-
положительных и нулевых значений х/ и X; иногда записы-
записывают следующим образом:
Если ограничения G) или A4) линейны, то упоминае-
упоминаемое выше условие регулярности ограничений всегда
выполнено. Поэтому для линейных ограничений един-
единственным предположением при выводе необходимых
условий является дифференцируемость функции /(.г).
Если в задаче A3) — A5) функции f(x) и gt(x),
t=l,. . ., т, вогнутые, то точка (х*, %*), удовлетворяю-
удовлетворяющая необходимым условиям A7) — A9), является сед-
ловой точкой Л. ф. A6) и х* доставляет абсолютный
максимум. То что Л. ф. имеет в этом случае седловую
точку, может быть доказано и без предположений о
дифференцируемости функций /(х) и gi(x).
Аналог Л. ф. применяется и в вариационном исчисле-
исчислении при рассмотрении задач на условный экстремум
функционалов. Здесь также необходимые условия опти-
оптимальности в задаче на условный экстремум оказывается
удобным записывать как необходимые условия для нек-
рого составного функционала (аналога Л. ф.), построен-
построенного с помощью множителей Лагранжа. Пусть, напр.,
поставлена Болъца задача: найти минимум функционала
J(x) = V'f(t, х, '^dt + g^, x(t{), t2, x(t2)),
/ -. R x R" X R" —>¦ R, g : R x R" x R x Rn —>¦ R,
при наличии дифференциальных ограничений типа
равенств
ф(«, х, х)=0, 9:RxR"xR"—>¦ Rm, m < п,
и граничных условий
¦ф(*!, x(tt), t2, x(t2))=0, if: RxR«xRxR"-^R/),
Необходимые условия в этой условноакстремальной за-
задаче получаются как необходимые условия безуслов-
безусловного экстремума функционала (см. [4])
/ (х, к, е)=^ (Я„/ (t, х, *) + 2Г=1 Kt О fl С ', *
составленного с помощью множителей Лагранжа
>ч>, l-i (t), i = l, ..., m, ец, (Х = 1, ..., p.
Эти необходимые условия, представляющие собой зам-
замкнутую систему соотношений для определения оптималь-
оптимального решения х* (t) и соответствующих множителей
Лагранжа Я ,¦ (г) и ец, в конкретных постановках записы-
записываются в виде Эйлера уравнения, Вейерштрасса усло-
условия и трансверсальности условия.
Лит.: [1] Смирнов В. И., Курс высшей математики,
23 изд., т. 1, М,., 1974; [2] X е д л и Д ж-, Нелинейное и динами-
динамическое программирование, пер. с англ., М., 1967; [3] К u h n H.
W., T u с к е г A. W., в кн.: Proceedings of the Second Berkeley
Symposium on Mathematical Statistics and Probability, Berk.—
Los Ang., 1951, p. 481—92; [4] Б л и с с Г. А., Лекции по вариа-
вариационному исчислению, пер. с англ., М., 1950. И. Б. Вапнярский.
ЛАГРАНЖЕВО МНОГООБРАЗИЕ — «мерное диф-
дифференцируемое подмногообразие L" 2п-мерного сим-
плектического многообразия М"п такое, что внешняя
форма ш, задающая симплектпч. структуру на М2п,
обращается в нуль тождественно на L" (т. е. для любой
точки x?Ln и любых векторов X, Y, касающихся L"
в этой точке, <й(Х, У) = 0). В наиболее важном случае,
когда M2n — Rin с координатами (pi, ..., р„, qu ..., qn),
а со =Jj._ dpiAdqi, условие лагранжевости подмного-
подмногообразия L", заданного параметрич. уравнениями
Pi = Pi(u1, ..., и„), 9/ = ?,-("i, ..., ип),
имеет вид
[u,-, и/] = 0, i, / = 1, . . ., я,
где [и,-, иу] — Лагранжа скобки.
Лит.: [1] М а с л о в В. П., Теория возмущений и асимпто-
асимптотические методы, М., 1965; [2] е г о же, Метод ВКБ в многомер-
чом случае, в кн.: Хединг Дж., Введение в метод фазовых ин-
интегралов (метод ВКБ), пер. с англ., М., 1965; [3] А р-
Еильд В. И., Математические методы классической механи-
механики, М., 1974; [4] М а с л о в В. П., Федор юк М. В.,
Квазиклассическое приближение для уравнений квантовой ме-
механики, М., 1976; [5] М и щ е н к о А. С, Стернин Б. Ю.,
Шаталов В. Е., Лагранжевы многообразия и метод кано-
канонического оператора, М., 1978. Д. В. Аносов.
ЛАГРАНЖИАН, функция Л агранжа, и н-
т е г р а н т,— подннтегральная функция L (q, q, t) в
задаче на экстремум для функционала
<•>-$::
L(q(t),q(t),t)dt;
экстремальная задача решается при возможном нало-
наложении связей и граничных условий; здесь q—(qi, ...,
}„), q=dq!dt, L — произвольное дифференцируемое
отображение L : R"XR"-XR -*-R.
Термин «Л.» возник в классич. механике, где в про-
простейшем случае Л. наз. разность кинетической и по-
потенциальной энергии системы, причем движения систе-
системы совпадают с экстремалями соответствующего ин-
интегрального функционала (принцип стациокарного дей-
действия). В общем случае в классич. механике Л. наз.
произвольное дифференцируемое отображение L : ТМХ
XR—>- R, где ТМ— касательное расслоение нек-рого
дифференцируемого многообразия М (конфигурацион-
(конфигурационного многообразия системы).
Необходимое условие слабого экстремума функцио-
функционала (*) при отсутствии связей дается уравнением Эй-
Эйлера — Лагранжа
дьd Э? „
Наличие связей типа равенств учитывается при по-
.ющи множителей Лагранжа. При наличии «некласси-
«неклассических» связей типа неравенств в теории оптимального
управления необходимое условие сильного экстремума
функционала (*) дает Понтпрягина принцип максимума.
При помощи понятия Л. удобно рассматривать различ-
различные симметрии системы, поскольку всякой однопарамет-
рич. группе диффеоморфизмов конфигурационного мно-
многообразия, сохраняющих Л., соответствует первый
интеграл уравнений движения (теорема Нётер).
Во многих задачах полезным оказывается переписать
уравнения Эйлера — Лагранжа в виде Гамильтона
уравнений, что позволяет, в частности, использовать
метод каноннч. преобразований и Гамильтона —
Якоби теорию. Переход к гамильтоновой форме записи
полезен также при квантовании исходной классич. си-
системы. Если Л. не вырожден, то переход к гамильтоно-
гамильтоновой формулировке производится с помощью Лежапдра
преобразования, в случае вырождения применяется
более сложная процедура редукции (см. [1], [6]).
В механике сплошных сред и квантовой теории поля,
к-рые можно рассматривать как механич. системы с бес-
бесконечным числом степеней свободы, рассматриваются
экстремальные задачи для функционалов вида
где
L (t) = \ X (q, q, </', f, x) dx,
x = (x-i, ..., a^), CcR', Q = <l(t, a') = (<?ii •••> 9«)i
q = (dqi/dt, ..., dqjdt), q' = (dqi/dxj).
В этом случае функционал L (г) наз. лагранжиа-
лагранжианом, а функция X (q, q, q', ?, х) — плотностью
лагранжиана. Основные понятия для таких
систем (гамильтониан и др.) вводятся по аналогии с
классич. механикой.
Лит.: [1] А р н о л ь д В. И., Математические методы клас-
классической механики, М., 1974; [2] Боголюбов Н. Н.,
Ширков Д. В., Введение в теорию квантованных полей,
3 изд., М., 1976; [3] И о ф ф е А. Д., Тихомиров В. М.,
Теория экстремальных задач, М., 1974; [4] Понтряги н Л.С.
[и др.], Математическая теория оптимальных процессов,
2 изд., М., 1969; L5] С т е р н б е р г С., Лекции по дифферен-
дифференциальной геометрии, пер. о англ., М., 1970; [6] Ф а д д е е в
Л. Д., «Теоретич. и матем. физика», 1969, т. 1, JM» 1, с. 1—18.
И. В. Волович.
ЛАКУНА — 1) Л. в теории функций —
см. Адамара теорема о лакунах, Л акунарный степенной
ряд.
2) Л. в геометрии — см. Движений группа,
Лакунарное пространство.
3)Л. в теории дифференциальных
уравнений с частными производны-
производными — одна из областей D, на к-рые разбивается внут-
внутренность характеристич. конуса линейной гипербо-
лич. системы
а и, _._ ь
—~=\ Luuj, \<i<k, A)
at ' /=i
с вершиной в точке (х0, t0) плоскостью t=tr, обладаю-
обладающая следующим свойством: малые достаточно глад-
гладкие изменения начальных данных внутри D не влияют
на значение решения и в точке (х0, t0). В A) предпола-
предполагается, что L;j — линейный дифференциальный опе-
оператор порядка nj и порядок дифференцирований в нем
по t не превосходит пу=1. Под «изменением внутри»
понимается изменение в нек-рой области, входящей в
D вместе со своей границей.
Для волнового уравнения
решение и задачи Копш
= <Pi C)
в точке (хй, t0), io>0> вполне определяется значениями
функций ф0. фх на сфере \у—xo\ = tB при нечетном п>1
и на шаре \у—xo\<?tg при четном п и и=1, поэтому
область \у—хо\ <i0 на плоскости i=0 является Л. для
уравнения B) при нечетном п>1. Для четного п и
ге=1 уравнение B) Л. не имеет. Это согласуется с
Гюйгенса принципом для решений волнового уравне-
уравнения.
Возмущение начальных данных C) в малой окрест-
окрестности точки х0 приводит к сферич. волне с центром
в этой точке, к-рая при нечетном га>1 имеет передний и
задний фронты. При остальных значениях п задний
фронт этой волны «размыт», это явление наз. диффу-
диффузией волн. Диффузия волн типична для всех линей-
линейных гиперболич. уравнений 2-го порядка, если число
п пространственных переменных четно (см. [1]). Ана-
Аналогичный вопрос для ге=3 изучался в [2], где был
описан класс гиперболич. уравнении 2-го порядка, для
к-рых диффузия волн отсутствует. Уравнения этого
класса тесно связаны с волновым уравнением. Для
общих гиперболич. систем A) найдена связь «в малом»
между существованием Л. для системы A) и аналогич-
аналогичным вопросом для соответствующей системы с постоян-
постоянными коэффициентами (см. [3]). Для последних систем
получены необходимые и достаточные условия алгеб-
раич. характера, обеспечивающие наличие Л.
Лит.: ШАдамар Ж., Задача Коши для линейных урав-
уравнений с частными производными гиперболического типа, пер.
с франц., М., 1978; [2]Mathisson M., «Acta math.», 1939,
t. 71, J4» 3—4, p. 249—82; [3] П е т р о в с к и й И. Г., «Матем.
сб.», 1945, т. 17, с. 289 — 370; [4! К у р а н т Р., Уравнения с
частными производными, пер. с англ., М-, 1964. А. П. Солдатов.
ЛАКУНАРНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ — после-
последовательность чисел {п/;} таких, что п^ + 1/;ц^Х>1;
обозначается А и применяется, в частности, в теории
лакунарных рядов и в теории лакунарных тригономет-
тригонометрич. рядов. Существуют обобщения класса А. Напр.,
класс В2 : {«fc}?S2, если существует такое А, что число
решений уравнений [nkl^n]i2]=m (nfc,>n/jj, [a] —
целая часть числа а) не превосходит А при любом
целом т; класс R : {п^^Я, если существует такое А,
что число решений уравнения [«&,— "а2— ¦ • - — nk 1 = "(
(nftl>»^2>. . . >;?? ) не превосходит Ар при любом
р=2, 3, ... и любом целом т; классы Л0, S,o, Ra ,
состоящие из последовательностей, разбивающихся на
конечное число последовательностей, соответственно
из классов А, В„, R.
Лит.: Бари Н. К., Тригонометрические ряды, М., 1961.
В. Ф. Емельянов.
ЛАКУНАРНАЯ СИСТЕМА порядка р>2, Sр-
система,— ортонормированная система функций
{фя}/Г=1 пространства LP такая, что если ряд
сходится в пространстве L2, то его сумма принадлежит
классу Lp. Если система функций {ф„} есть ^-система
при любом р>2, то она наз. S^-c и с т е м о й. С. Банах
(S. Banach) доказал (см. [2]), что из всякой ограничен-
ограниченной в пространстве LP ортонормированной в L2 системы
функций можно выбрать ^^-систему. Для того чтобы
ортонормированная система функций {срп} была Sp-
систомой, необходимо и достаточно, чтобы существова-
существовала постоянная цр, зависящая только от р и такая, что
для всех N, {а}. Если система функций {ср„} есть Sp-
система при некотором р>2, то найдется постоянная т
такая, что
2Г=.
1п = 1а„Фп
для всех ,V, {«„}. Система функций, обладающая этим
свойством, наз. системой Банаха. Эти опреде-
определения распространяются и на не ортогональные систе-
системы функций (см., напр., [3]). Иногда под Л. с. пони-
понимают систему функций, ряды к-рой обладают одним
или несколькими свойствами лакунарных тригономет-
тригонометрических рядов, в зависимости от к-рых ей придают раз-
различные названия. Напр., с теоремой единственности
для лакунарных тригонометрич. рядов связано понятие
Л. с. е-единственности. Система функций {фп}™=1
I наз. системой s-единственности, если существует число
8>0 такое, что из сходимости ряда (*) к нулю всюду,
за исключением быть может множества меры, меньшей
f, следует равенство всех его коэффициентов нулю.
Лит.: [11 К а ч м а ж С, Штейн га уз Г., Теория ор-
ортогональных рядов, пер. с нем., М., 1958; [2] А л е к с и ч Г.,
Проблемы сходимости ортогональных рядов, пер. с англ., М.,
19E3; [3] Г а п о ш к и н В. Ф., «Успехи матем. наук», 1966,
т. 21 в. 6, с. 3—82. В. Ф. Емельянов.
ЛАКУНАРИОЕ ПРОСТРАНСТВО — пространство
аффинной связности или риманово пространство
нек-рой определенной степени подвижности. Л. п. опре-
определяется порядком полной движений группы, т. е. наи-
наибольшим числом ее параметров для данного простран-
пространства. Так, обычное re-мерное аффинное пространство
Табл. 1.—Порядки полных групп
автоморфизмов в пространствах аффинной
связности Ап размерности п
Аг
6
4
i
А,
12
9
i
П2+П
п2
п2 — 1
7!2 —П + 1
Г!2— П— 2
п2 — 2п -г 5
3
2
1
Типы пространств и
лакун
Пространства первое
лакунарности
Первая лакуна
Пространства второй
лакунарности
Вторая лакуна
Пространства третьей
лакунарности
Третья лакуна
Пространства четвертой
лакунарности
допускает группу движении максимального порядка
п2-\-п. Порядки полных групп движений других про-
пространств аффинной связности принадлежат отрезку на-
натурального ряда [1, я2-)-и], но не каждое число из этого
отрезка может быть порядком полной группы движений.
Интервалы наибольшей длины, составленные из чисел,
не являющихся порядком полных групп движений, наз.
лакунами, а дополнения к ним до указанного от-
отрезка натурального ряда — отрезками конден-
конденсации. Пространство наз. пространством k-ii лаку-
лакунарности, если порядок его полной группы движе-
движений принадлежит отрезку конденсации, имеющему
номер к. Счет ведется с отрезка конденсации, содержа-
содержащего максимальный порядок. Об известном распреде-
распределении подвижности «твердых» тел в пространствах аф-
аффинной связности см. таблицу 1. Речь идет о порядках
полных групп движений — синонимах степени подвиж-
подвижности, степени свободы твердых тел. Вопрос об опре-
определении возможных степеней подвижности твердых
и подобно изменяемых тел в римановмх пространст-
пространствах частично решен лишь для пространств знакоопре-
деленной метрики. В общем случае известны те степе-
степени подвижности и реализующие их римановы прост-
пространства, к-рые приведены в таблице 2.
Табл. 2.—Порядки полных групп
автоморфизмов в римановых
пространствах Vn размерности п
3
1
()
4
1
v4
10
8
1
Vs
1Г>
11
1
Vn
n (n + 1)
n(n-i)
П G1 — 1)
2
G1—1) (n-2) , r
2 ' °
3
2
1
Типы пространств и Ла-
КуН
Пространства первой
лакунарности (постоян-
(постоянной кривизны)
Первая лакуна
Пространства второй
лакунарности
Вторая лакуна
Пространства третьей
лакунарности
Лит.: [I] Егоров И. П., в сб.: Итоги пауки. Алгебра.
Топология. Геометрия. 1965, М., 1967, с. 375 — 428; [2] его
ж е, в сб.: Итоги науки и техники. Проблемы геометрии, т. 10,
М., 1978, с. 147—91; [3J е г о же, Геометрия, М., 1979.
И. П. Егоров.
ЛАКУН АРНЫЙ РЯД — ряд по лакунарной системе
функций. Примерами служат лакунарные тригономет-
рич. ряды, лакунарные степенные ряды, ряды Радома-
хера, ряды независимых функций с нулевыми матема-
тич. ожиданиями, ряды Дирихле с показателями,
независимыми над полем рациональных чисел, и т. д.
В. Ф. Емельянов.
ЛАКУНАРНЫЙ СТЕПЕННОЙ РЯД — ряд
с пропусками (лакунами), в к-ром показатели Я,1т А2,. . .
пробегают не все числа из натурального ряда. В зави-
зависимости от свойств последовательности {К/,} получено
много свойств ряда (*). Так, если
h+i~kk > е^' /с=о, l, 2, ..., е > о,
и ряд (*) сходится в круге \z\ <Д, 0<Л<оо, то все
точки окружности I z| = R — особые для / (z) (т е о р е м а
А д а м а р а о лакунах). Усиленггем отой теоремы
является Фабри теорема о лакунах. Если нижняя плот-
плотность
lim v =0,
то /(г) — однозначная аналитич. функция с односвяз-
ной областью существования (теорема II о й а).
См. также Сверхсходимость.
Лит.: [1] Б и б е р б а х Л-, Аналитическое продолжение,
пер. с нем., М., 1967. А. у». Леоуипъев.
ЛАКУНАРНЫЙ ТРИГОНОМЕТРИЧЕСКИЙ РЯД —
ряд вида
2Г=1 ак cos n^r + b/, sinner, A)
lim ^1
^Л>1.
к» *
Рядом типа A) К. Вейерштрасс (К. Weierstrass) в
1872 представил непрерывную нигде не дифференцируе-
дифференцируемую функцию. Ж. Адамар (J. Hadamard) в 1892 при-
применил ряды (П, назвав их лакуяарными, к изучению
аналитич. продолжения функции. Системами, изуче-
изучение Л. т. р. началось с работы П. Фату (P. Fatou,
1906), в к-рой доказано, что из сходимости всюду Л. т. р.
при Я>3 следует
Л. т. р. обладают свойствами, существенно отличающи-
отличающими их от общих тригонометрии, рядов. Напр., А. Н. Кол-
Колмогоров, построив первый пример A923) суммируемой
функции с расходящимся почти всюду рядом Фурье,
в 1924 доказал сходимость почти всюду лакунарного
ряда Фурье; А. Зигмунд (A. Zygmund, 1948) доказал,
что если суммы двух Л. т. р. совпадают на множестве
положительной меры, то эти ряды тождественны. Для
многих приложений Л. т. р. важна обнаруженная
Зигмундом в 30-е гг. 20 в. зависимость свойств ряда
A) от его коэффициентов. Так, если
то ряд A) есть ряд Фурье функции /(.г), принадлежа-
принадлежащей всем пространствам Lp@, 2я), 1<:р<+оо, и,
следовательно, сходится почти всюду. При этом суще-
существуют постоянные Л/7>0, Sjt7>0, зависящие только от
р и Л такие, что
Если условие C) не выполнено, то ряд A) расходится
почти всюду и, более того, почти всюду не суммируется
никаким методом Теплица (следовательно, не является
рядом Фурье). Если ряд A) сходится в каждой точке
нек-рого интервала (Т* — ограничен в каждой точке
пек-рого интервала), то выполнено условие B). Если
коэффициенты ряда A) есть оA/п^), то ого сумма есть
непрерывная гладкая функция, дифференцируемая в
тех и только в тех точках, в к-рых сходится формально
продифференцированный ряд A).
Лит.: [1J Бари Н. К., Тригонометрические ряды, М.,
1961; [2] Зигмунд А., Тригонометрические ряды, пер. с
англ., 12 изд.], т. 1—2, Ы., 1965; [3] У л ь и н о в П. л., «Успе-
«Успехи матем. наук», 1964, т. 19, в. 1, с. 3—69: [4] Г а п о ш к и н
В. Ф., «Успехи матем. наук», 1966, т. 21, в. 6, с. 3—83; [5] К а-
х а н Ж.- П., Случайные функциональные ряды, пер. с англ.,
М., 1973; [В] К а Ь а п е J.- P., Series de Fourier absolument
convergentes, В.— Hdlb.— N. Y., 1970; [7] Rudin W., Fou-
Fourier analysis on groups, N. Y.— L., 1962. В. Ф. Емельянов.
ЛАМБЕРТА МЕТОД СУММИРОВАНИЯ — один из
методов суммирования числовых рядов. Ряд
гуммируем методом Ламберта к числу
S, если
lim F(y) = S,
где
ап ——з— при у > О,
п=1 * ~е
п ряд справа сходится. Метод предложен И. Ламбер-
Ламбертом A). Из суммируемости ряда Чезаро методом сум-
суммирования (С, к) для нек-рого/с>—1 к сумме S следует
его суммируемость Л. м. с. к той же сумме, и если ряд
суммируем Л. м. с. к сумме S, то он суммируем и
Абеля методом суммирования к той же сумме. Л. м. с.
регулярен (см. Регулярные метода суммирования).
Лит.: [1] Lambert J. H., Anlage zur Architektonik,
Bd 2, Riga, 1771; [2] Харди Г., Расходящиеся ряды, пер.
с англ., М., 1951. И. И. Волков.
ЛАМБЕРТА ПРЕОБРАЗОВАНИЕ — интегральное
преобразование вида
Л. п. является непрерывным аналогом Ламберта ряда
(при соответствии ta(tL-*an, е*<-*1/г). Имеет место
следующая формула обращения. Пусть
a(t)?L (О, оо)
и
lim a(t) *i-6=o, б > 0;
0
тогда если т>0 и функция a(t) непрерывна при
<=т, то
то (т) = lim —^— (-
к-уоо ' ч
где ц. (и) — Мёбиуса функция.
Лит.: [1] Widder Ь. V., «Math. Mag.», 1950, v. 23,
p. 171—82; [2] Итоги науки. Математический анализ. 1966,
М., 1967, с. 7—82. Ю. А. Брычков, А. П. Прудников.
ЛАМБЕРТА РЯД — функциональный ряд
Рассмотрен И. Ламбертом (см. [1]) в связи с вопросами
сходимости степенных рядов. Если сходится ряд
то Л. р. сходится при всех значениях х, кроме ж=
= ±1; в противном случае он сходится для тех значений
х, для к-рых сходится ряд
Л. р. применяется в нек-рых задачах теории чисел.
Так, при Ы<1 сумма <р(х) ряда A) представляется в
виде степенного ряда:
где
а суммирование распространяется на делители к числа
п. В частности, если ал=1, то а„=т(п) — число дели-
делителей и, если ап=п, то а„=о(п) — сумма делителей п.
Поведение ф(.г) (с надлежащими ап) при х —>- 1—О
используется, напр. (см. [3]), в задаче Харди и Рама-
нуджана для получения асимптотич. формулы для ко-
количества «неограниченных разбиений» натурального
числа.
Лит.: [1] Lambert J. H., Opera mathematica, v. 1—2,
Zurich, 1946—48; [2] Ф и х т е н г о л ь ц Г. М., Курс дифферен-
дифференциального и интегрального исчисления, 4 изд., т. 2,М., 1959;
[3] Постников А. Г., Введение в аналитическую теорию
чисел, М., 1971. М. II. Вайцехсвский.
ЛАМБЕРТА ЧЕТЫРЕХУГОЛЬНИК, трипрямо-
у г о л ь н и к,— четырехугольник, в к-ром при трех
вершинах прямые углы. Рассматривался И. Ламбертом
(J. Lambert, 1766) при попытках доказать постулат
Евклида о параллельных. Из трех возможных предпо-
предположений о величине четвертого угла: либо угол прямой,
либо угол тупой, либо угол острый; первая гипотеза
является утверждением, эквивалентным постулату Евк-
Евклида о параллельных; вторая приводит к противоречию
с др. аксиомами и постулатами Евклида. Относительно
третьей гипотезы И. Ламберт сделал предположение,
что она выполняется на нек-рой мнимой сфере.
Лит.: [1] Каган В. Ф., Основания геометрии, ч. 1,
М.— Л., 1949; [2] II о г о р е л о в А. В., Основания геомет-
геометрии, 3 изд., М., 1968. А. Б. Иванов.
ЛАМЕ КОЭФФИЦИЕНТЫ ортогональной
криволинейной системы координат
и, v, w в пространстве — величины
г _-|//Эх
dw
аналогично определяются Л. к. на плоскости. Через
Л. к. в координатах и, v, w выражаются элемент длины:
dl=V L
элемент площади поверхности:
da = \f(LaLv du dvJ + (LULW du dwJ+(LvLw du dwf;
элемент объема:
dV=LULVLW du dv dw.
Л. к. входят в выражения векторных дифференциаль-
дифференциальных операций в координатах и, и, w:
1 Эф 1 (Эф 1 6ф
div a = -p-j—j— т- (auLvLw) -f- — (avLuLw) +
, 9
^а==ьЬ^ \_L (a»L^ —k (a«^
, д / LuLw Эф \ | д / T.nLv Эф
Л. к. для различных ортогональных криволинейных
координат см. в соответствующих статьях.
Л. к. введены Г. Ламе [1].
Лит.: [1] Lam ё G'., Lecons sur les coordonnees curvilignes
et leurs diverses applications, P., 1859; [2] Лаптев Г. Ф.,
Элементы векторного исчисления, М., 1975; [3] Морс Ф. М.,
Ф е ш б а х Г., Методы теоретической физики, пер. с англ.,
т. 1, М., 1958. В. И. Битюцков.
ЛАМЕ КРИВАЯ — плоская алгебраич. кривая, урав-
уравнение к-рой в декартовых прямоугольных координатах
имеет вид
\~а ) ' \1Г
где m=p/q, p и q — взаимно простые числа, а>0 и
Ь>0. Порядок Л. к. равен pq при га>0 и 2pq при m<0.
При то=1 Л. к.— прямая, при т=2 — эллипс, при
т=2/3 и о=Ь — астроида. Л. к. названы по имени
Г. Ламе (G. Lame), рассмотревшего их в 1818.
Лит.: [1] Саве лов А. А., Плоские кривые, М-, 1960.
Д. Д. Соколов.
ЛАМЕ ПОСТОЯННЫЕ — величины, связывающие
компоненты упругого напряжения в какой-либо точке
твердого изотропного деформируемого тела с компонен-
компонентами деформации в этой же точке:
где ант — нормальная и касательная составляющие
напряжения, s — компоненты деформации, а коэффи-
коэффициенты лиц — постоянные Ламе. Л. п. зависят от
материала и его температуры. Л. п. связаны с модулями
упругости и коэффициентом Пуассона v:
„ Е ¦ _ Ev
^~~ 2(l+v)'
где Е — модуль продольной упругости, G — модуль
сдвига.
Л. п. наз. по имени Г. Ламе (G. Lame). БСЭ-з.
ЛАМЕ УРАВНЕНИЕ — линейное обыкновенное диф-
дифференциальное уравнение 2-го порядка в комплексной
области
где V? (z) — Вейерштрасса эллиптическая функция,
А и В — константы. Это уравнение было впервые
изучено Г. Ламе [1]; оно возникает при разделении
переменных в уравнении Лапласа в эллиптич. коорди-
координатах. Уравнение A) наз. формой Вейершграс-
с а для Л. у. Существует такая замена независимой
переменной в уравнении A), в результате к-рой полу-
получается форма Якоб и для Л. у.:
sn2 и] w.
Имеются также многочисленные алгебраич. формы
Л. у., переход к к-рым осуществляется различными
преобразованиями независимой переменной уравнения
A), напр.:
dHu .1/1 . 1 . 1 n. dm
Л + В1
Для практич. приложений форма Якоби является
наиболее подходящей.
Особенно важен случай, когда в уравнении A) (или
B)) 5=n(n-f 1), где ?г — натуральное число. В этом
случае решения уравнения A) мероморфны во всей
плоскости и их свойства довольно хорошо изучены.
Среди решений уравнения B) при 5=д(п+1) перво-
первостепенное значение имеют Ламе функции.
Лит.: [1] Lame G., «J. math, pures et appl.», 1837, t. 2,
p. 147—88; [2] Стретт М. Д. О., Функции Ляме, Матье и
родственные им в физике и технике, пер. с нем., Хар.— К.,
1935; [3] Уиттекер Э.-Т., Ватсон Д.-Н., Курс со-
современного анализа, пер. с англ., 2 изд., ч. 2, М., 19ВЗ; [4]
Б е й т м е н Г., Э р д е й и А., Высшие трансцендентные
функции. Эллиптические н автоморфные функции. Функции
Ламе ,и Матье, пер. с англ., М., 1967; [5] Г о б с о н Е. В.,
Теория сферических и эллипсоидальных функций, пер. с англ.,
М., 1952. Н. X. Розов.
ЛАМЕ ФУНКЦИЯ, эллипсоидальная
гармоническая функция,— функция спе-
специального вида, удовлетворяющая Ламе уравнению.
Если уравнение Ламе в алгебраич. форме
A + n (n + 1)
где n — натуральное число, a elt e2, e3 и А — констан-
ты, имеет решение одного из следующих видов:
РA),
Vt-eiP(l), i = l, 2, 3,
где Р(§) — многочлен с единичным старшим коэффи-
коэффициентом, то это решение ваз. соответственно функ-
функцией Ламе степени п первого рода
1-го, 2-го, 3-го или 4-го вида.
При фиксированном четном п всегда найдутся такие
значения параметра А (собственные значения), что
существует (л + 2)/2 Л. ф. 1-го вида и Зи/2 Л. ф. 3-го
вида с многочленами Р(§) степени и/2 и (п—2)/2 соот-
соответственно. При фиксированном нечетном п всегда
найдутся такие значения Л, что существует 3(л+1)/2
Л. ф. 2-го вида и (и—1)/2 Л. ф. 4-го вида с многочленами
Р (Ъ) степени (га—1)/2 и {п—3)/2 соответственно. Всего
при заданном натуральном и существует 2/г—f-1 линейно
независимых Л. ф.
Решения уравнения (*), линейно независимые с Л. ф.
первого рода и получающиеся с помощью Лиувилля —
Остроградского формулы, наз. функциями
Ламе второго рода.
Лит. см. при ст. Ламе уравнение. Н. X. Розов.
ЛАНДАУ КИНЕТИЧЕСКОЕ УРАВНЕНИЕ — кине-
кинетическое уравнение для слабо взаимодействующего
газа, в частности уравнение переноса заряженных
частиц в плазме с учетом кулоновских столкновений.
Получено Л. Д. Ландау (см. [1], [2]). Для систем с ку-
лоновским взаимодействием при выводе Л. к. у. коэф-
коэффициенты уравнения содержат расходящийся интеграл
(«кулоновский логарифм»: 1пЛа[, — логарифм отноше-
отношения максимального и минимального прицельного пара-
параметра при столкновении двух заряженных частиц а и
Ь). Чтобы получить приближенный нерасходящийся
результат, интеграл «обрезают»: за верхний предел
интегрирования берется длина электростатич. экрани-
экранирования Дебая, за нижний — расстояние ближнего
взаимодействия (или квантовомеханич. длина волны).
Наложенное извне «обрезание» интеграла, не вытекаю-
вытекающее из самого вывода Л. к. у., оставляет открытым
вопрос о построении адекватного кпнетич. уравнения
для систем с кулоновским взаимодействием. Были
предложены (см., напр., [3]) различные виды таких
уравнений (также не свободные от расходимостей).
В этих уравнениях учитывается динамич. экранирова-
экранирование, зависящее от скоростей частиц.
Для разреженного газа пробных частиц, взаимодей-
взаимодействующих с равновесным фоном, Л. к. у. переходит в
линейное уравнение Фоккера — Планка. Для неодно
родной плазмы интеграл столкновений Ландау следует
добавить в правую часть Власова кинетического урав-
уравнения. Полученное уравнение наз. уравнением
Власова — Ландау (см. [3]).
Для смеси частиц нескольких типов систему Л. к. у.
можно записать в виде
— = Ia + Sa, A)
где fa=fa (r, v< t) — функция распределения для
частиц типа а в 6-мерном фазовом пространстве коор-
координат г и скоростей v (t — время). Функция Sa(r, v,
t)=S описывает источники частиц, 1а — интеграл
столкновений, к-рый можно привести к виду
a~ a \_ де; \'a dv{ ) "г 2 dv. dvj \Ia dv; d
где суммирование подразумевается по одинаковым
индексам i, j от 1 до 3, Ya=^nZaei!m\; ma, Zae —
масса и заряд частиц типа а, е — заряд электрона,
ва = ^ь {^aflnAab \ fb (Г' "'' t] ' V~V> ' UV'
h — V (m« + mb\ f/z&Y2ln \ „ f f,. tr v' Ox
X i v — v' 1 ~4v'
— потенциалы, введенные в [2], 1пЛа(, — кулоыовские
логарифмы, зависящие от средних энергий частиц.
Интеграл столкновений B) содержит эллиптнч. диффе-
дифференциальный оператор по скорости, коэффициенты к-рого
выражаются через интегральные операторы типа потен-
потенциала от fa(r, v, t). Для неоднородной плазмы
dfg _ dfg , dfa_ . Zaf у. 8fa
dt dt ' di- "T~ma dv '
где ZaeF—сила, действующая на частицы типа а.
Л. к. у. позволяют получить гидродинампч. уравне-
уравнения сохранения для плотностей массы, импульса и
внутренней энергии, а также Болъцмана Н-теорему.
Существование обобщенного решения Л. к. у. дока-
доказано в малом (см. [4]).
Численное решение Л. к. у. на ЭВМ проводилось
для расчета утечки частиц из открытых магнитных ло-
ловушек (см. [5]), определения коэффициента умножения
энергии в тороидальных термоядерных реакторах (см.
[6]), оценки дополнительных методов нагрева плазмы
в токамаках. В условиях хорошего удержания плазмы
в магнитных ловушках необходимо использовать пол-
полностью консервативные разностные схемы (см. [7]),
точно сохраняющие для решения Л. к. у. полное число
частиц и их энергию.
Лит.: [1] Ландау Л. Д., «Phys. Z. Sowjetunion», 1936,
Bd 10, Hft 2, S. 154—64; его же, «Ж. эксперимент, и теоретич.
физики», 1937, т. 7, Л'» 2, с. 203—209; [2] Трубников Б. А.,
в кн.: Вопросы теории плазмы, в. 1, М., 1963, с. 98 —182; [3]
Б а л е с к у Р., Равновесная и неравновесная статистическая
механика, пер. с англ., т. 1—2, М., 1978; [4] А р с ен ье в А. А-.,
Песков Н. В., «VK. вычисл. матем. и матсм. физики»,
1977, т. 17, .\« 4, с. 1063—68; [5] Киллин Д ж., Маркс
К. Д., в кн.: Вычислительные методы в физике плазмы, пер. с
англ., М., 1974; с. 417 — 82; [6] Киллин Дж., М и р и н А.,
V е н с и н к М., в кн.: Управляемый термоядерный синтез,
пер. с англ., М., 1980, с. 419—67; [7] Самарский А. А.,
Теория разностных схем, М., 1977. В. А. Чуянов.
ЛАНДАУ ТЕОРЕМЫ — теоремы для регулярных
в круге функций, устанавливающие нек-рые связи меж-
между геометрич. свойствами производимого этими функ-
функциями конформного отображения и начальными коэффи-
коэффициентами представляющих их степенных рядов.
В 1904 Э. Ландау показал [1], что если функция
f(z) регулярна в круге \z\ <Д и не принимает в нем зна-
значений 0 и 1, то Л ограничено сверху положительной
постоянной, зависящей только от ао=/(О) и a1=f @).
В 1905 К. Каратеодори (С. Caratheodory) установил,
что роль экстремальной функции в этой теореме играет
модулярная функция. Эти результаты Э. Ландау и
К. Каратеодори известны в виде следующей теоремы.
Теорема Ландау — Каратеодори.
Если функция
/(z) = e0 + o1z+..., в^О,
регулярна и не принимает значений 0 и 1 в круге
\z\<R, то
здесь т=т(Х) — какая-либо ветвь функции, обратной к
классич. модулярной функции А:г(т) = Х(т) группы Л/2
дробно-линейных преобразований
ах + Ь , , .
т—* ;, аа — ос = 1,
где a, d — нечетные, а Ь, с — четные числа. Функция
^,(т) отображает фундаментальную область Т2 группы
М2;
4", | Rex | < 1, Imx>o|
(Т.г получается присоединением к Int T2 той части гра-
границы этой области, для к-рой Кет^О), на всю расширен-
расширенную Х-плоскость таким образом, что Я(оо) = 0, Я@)=1,
ХA)=оо. При этом для каждого значения % уравнение
к2(х)=Х имеет одно и только одно решение т, принад-
принадлежащее Т.,. Под функцией х(к) в теореме Ландау —
Каратеодор[г можно понимать ту ветвь указанной
обратной функции, к-рая отображает расширенную
Х-плоскость на Тг.
Пример функции f(z) = k(i "jrrjj, регулярной в круге
!z|<l и не обращающейся в нуль и 1 при \z\ <1, пока-
показывает, что теорема Ландау — Каратеодори неулучшае-
ма. Из теоремы Ландау — Каратеодори вытекает Пи-
кара теорема о значениях, не принимаемых целыми
функциями.
9. Ландау нашел точное значение постоянной Q (М),
фигурирующей в следующей формулировке теоремы
Коши об обратных функциях. Пусть функция ш=/(г)
регулярна в круге !z|'<l, /@)=0, /'@)=1 и \f(z)\<M
в круге lz|<l, М^\; тогда существует такая постоян-
постоянная Q (М), что обратная функция z=(p(w), обращающая-
обращающаяся в нуль при w=0, регулярна в круге \w\<CQ (M) и
|()|1 в этом круге. Э. Ландау установил, что
Q (М) = М (М— Умг — IJ.
Экстремальной функцией этой оценки является
t - Mz
fM (z) =
M-z
Та же функция /уц (z) является экстремальной в сле-
следующей Л. т. Если функция / (z) удовлетворяет ука-
указанным выше условиям, то f(z) однолистна в круге \z\ <
р), где ()(М) = М— У~ЛГ2 — 1.
Э. Ландау принадлежит ряд теорем покрытия в тео-
теории конформного отображения, устанавливающих су-
существование и оценки соответствующих постоянных.
Ниже приведена одна из них. Пусть И — класс функ-
функций /(г), регулярных в круге lz|<l и нормированных
условиями /@) = 0, /'@)=1. Из теоремы Блоха (см.
Блоха константа) вытекает следующая Л. т.: сущест-
существует абсолютная постоянная
inf {L
где Lf — радиус наибольшего круга ш-плоскости,
целиком накрываемого образом круга \z\ <1 при отоб-
отображении w—f(z); В — константа Блоха. Постоянная L
наз. постоянной Ландау. Для L известны
оценки (см. [5], [8]): 1/2<:L<;0,55. . . Из сформулиро-
сформулированной Л. т. вновь следует теорема Пикара.
Лит.: [1] Landau E., «Sitzungsber. Preuss. Akad. Wiss.»,
1904, S. 1118 — 33; [2] e г о ж e, Darstellung und Begriindung
einiger neuerer Ergebnisse der Funklionentheorie, 2 Aufl., В.,
1929; [3] его же, «Rend. Circolo mai. Palermo», 1922, t. 46,
p. 347—48; [4] его же, «Sitzungsber. Preuss. Akad. Wiss.
Phys.-Math. Kl», 1926, S. 467—74; [5] его же, «Math. Z.»,
1929, Bd 30, S. 608—34; [6] его же, «Тр. Тбилисск. матем.
ин-та. АН СССР», 1940, т. 8, с. 23 —68; [7] Стой лов С,
Теория функций комплексного переменного, пер. с рум., т. 1,
М., 1962; [8] Г о л у з и н Г. М., Геометрическая теория функ-
функций комплексного переменного, 2 изд., М., 1966; [9] Вал и-
рон Ж., Аналитические функции, пер. с франц., М., 1957;
[10] Б е р м а н т А., «Матем. сб.», 1944, т. 15, М 2, с. 285—318.
Г. В. Кузьмина.
ЛАПЛАСА ВЕКТОР — интеграл движения точки
постоянной массы т в поле потенциала Ньютона —
Кулона V(r)==tt/r:
hi = {xlxi — х^г) = — (x2L3~.r3L2) +И-7-
Л2 = (х2т4 — ж) (xL xL) + х
Л3 = (х8х4—
где
, , L3) — момент импульса — определяет
плоскость орбиты (при L Ф Q), а совместно с интегра-
интегралом энергии
— ее конфигурацию. Л. в. определяет ориентацию
кеплеровой орбиты и пропорционален радиус-вектору
ее второго фокуса.
Аналог интеграла Л. в. существует также для потен-
потенциала изотропного гармонич. осциллятора, к-рый
вместе с ньютоновым занимает исключительное поло-
положение среди потенциалов центрального поля.
В центрально-возмущенном ньютоновом поле Л. в.
не является интегралом, а прецессирует. Напр., в за-
задаче Кеплера с релятивистским 4-импульсом угол пово-
поворота Л. в.
за период г. В квантовой теории существование интег-
интеграла Л. в. объясняет «случайное вырождение» уровней
энергии водородоподобного атома по азимутальному
квантовому числу I в дополнение к вырождению по маг-
магнитному квантовому числу т, обязательному для про-
произвольного центрального потенциала V (г). Уравнение
Шрёдингера кулонова осциллятора соответствует
двум тождественным частицам, одна из к-рых движется
в поле кулонова центра, расположенного в первом
фокусе кеплерова эллипса, а другая—в поле второго
фокуса. Гамильтониан каждой частицы инвариантен
относительно группы ортогональных преобразований
ее координат О C), а вся система в целом относительно
группы О C)ХО C) = О D) ортогональных преобразова-
преобразований 4-мерного евклидова пространства.
Л. в. введен в рассмотрение Я. Германом (см. [1])
и П. Лапласом (см. [2]), по-видимому, независимо.
Иногда Л. в. называют вектором Рунге —
Ленца.
Лит.: [1] Hermann J., «Giornale de Letterati d'Italia>>,
Venecia, 1710, v. 2, p. 447—67; [2] Laplace P., Traite" de
mecanique celeste, t. 1, P., 1798; [3] V 0 1 k O., «Celestial Mecha-
Mechanics», 1976, v. 14, p. 365—82; [4] Д у б о ш и н Г. Н., Небесная
механика. Основные задачи и методы, М., 1975; [5] П о п о в В.
С, Физика высоких энергий и теории элементарных частиц,
К., 1967, с. 702—27. В. В. Охрименко.
ЛАПЛАСА ИНТЕГРАЛ — 1) Интеграл вида
осуществляющий интегральное Лапласа преобразова-
преобразование функции j (t) действительного переменного t,
0<г<оо, в функцию F(p) комплексного переменного р.
Был рассмотрен П. Лапласом (P. Laplace) в кон. 18—
нач. 19 вв.; применялся Л. Эйлером (L. Euler, 1737).
2) Интегралы, зависящие от параметров а, E>0:
В. И. Витюцков.
ЛАПЛАСА МЕТОД асимптотических
оценок — метод вычисления асимптотики при Я>0,
Я-^-+оо интегралов Лапласа
где Q=[a, Ь] — конечный отрезок, S — действитель-
действительная, / — комплексная функции, достаточно гладкие при
x?Q. Асимптотика F(А) равна сумме вкладов от точек,
в к-рых достигается max S(x), если число их конечно.
1) Если максимум достигается при х=а и S' (а)фО,
то вклад Va (к) от точки а в асимптотику интеграла A)
равен
2) Если максимум достигается во внутренней точке
х° отрезка Q и S" (х°)фО, то вклад от нее равен
Эта формула получена П. Лапласом [1]. Полностью
исследован случаи, когда функции f(x), S'(х) имеют
нули конечной кратности в точках максимума функции
S, и получены асимптотич. разложения (см. [2] — [8]).
Л. м. распространяется и на случай контура Q, рас-
расположенного на комплексной плоскости (см. Перевала
метод).
Пусть Q — ограниченная область в IR.", наибольшее
значение функции S (х) в замыкании Q достигается
только во внутренней точке х", и х° — невырожденная
стационарная точка функции S. Тогда
В огом случае также получены асимптотич. разложения
для F(X). Все приведенные выше формулы справед-
справедливы при комплексных Я, |л| —»- оо, |arg K\ <:я/2 — е.
Имеются также модификации Л. м. на случай более
сложной зависимости от параметра (см. [4], [8]):
Лит.: [1] Laplace P. S., Essai philosophique sur les
probabilit6s, CEuvres completes, t. 7, P., 1886 (в рус. пер.—
Опыт философии теории вероятностей, М., 1908); [2] Э р-
д е й и А., Асимптотические разложения, пер. с англ., М.,
1962; [3] Брёйн Н. Г., Асимптотические методы в анализе,
пер. с англ., М., 1961; [4] Евграфов М. А., Асимптоти-
Асимптотические оценки и целые функции, 2 изд., М., 1962; [5] Кон-
сон Э.-Т., Асимптотические разложения, пер. с англ., М.,
1966; [6] О 1 v е г F. W. J., Asymptotics and special functions,
N. Y.— [a. o.], 1974; [7] Риекстыньш Э. Я., Асимптоти-
Асимптотические разложения интегралов, т. 1, Рига, 1974; [8] Ф е д о-
рюк М. В., Метод перевала, М., 1Н77. м. В. Феворюк.
ЛАПЛАСА ОПЕРАТОР, л а и л а с и а н,— диффе-
дифференциальный оператор Д в R", определяемый формулой
дХудХу ' дх% { '
(здесь хг, х2,. . ., хп— координаты в R"), а также некото-
некоторые его обобщения. Л. о. A) является простейшим эл-
липтич. дифференциальным оператором 2-го порядка.
Л. о. играет важную роль в математич. анализе, ма-
тематич. физике и геометрии (см., напр., Лапласа
уравнение, Лапласа — Белътрами уравнение, Гармо-
Гармоническая функция, Гармоническая форма).
Пусть М есть n-мерное риманово пространство с
метрикой
пусть \\g'J\\ — матрица, обратная к матрице ||g,y|l,
g=det||g,y||. Тогда Л. о. (или оператор Лап-
ласа — Бельтрами) римановой метрики B)
на М имеет вид
где (х1, . . ., х") — локальные координаты на М. Опе-
Оператор A) отличается знаком от Л. о. стандартной евк-
евклидовой метрики ds2= (da;1J-!-. ¦ . + {dxn)i на R".
Обобщение.м onepaTOj>a C) является Л. о. на диффе-
дифференциальных формах. Именно, в пространстве всех
внешних дифференциальных форм на М Л. о. имеет
вид
A = {d-\-d*f = dd* + d*d, D)
где d — оператор внешнего дифференцирования формы,
d* — формально сопряженный к d оператор, опреде-
определяемый с помощью следующего произведения на глад-
гладких финитных формах:
(a, Р) = $ал*Р, E)
где * — оператор Ходжа, порожденный метрикой B)
и переводящий р-формы в (п—р)-формы. В формуле
E) формы а и Р считаются действительными, на комп-
комплексных формах нужно использовать эрмитово продол-
продолжение скалярного произведения E). Сужение опера-
оператора D) на О-формы (т. е. функции) задается формулой
C). На р-формах при произвольном целом р^О Л. о. в
локальных координатах записывается в виде
лК,..л d-7'' A...Adxcp) =
л ... Adxp.
Здесь v'i V/ — ковариантные производные по .г',
R'^'j— тензор кривизны, R%~= Rn'i'k — тензор Риччи.
Пусть дан произвольный эллиптич. комплекс
...Т(Ер-г)-^Т (Ер) Л Г (Ер + 1) —. .., F)
где Ер — действительные или комплексные расслоения
на многообразии М, Г (Ер) — пространства их гладких
сечений. Введя в каждом расслоении Ер эрмитову мет-
метрику, а также задав произвольным образом элемент
объема на М, можно определить эрмитово скалярное
произведение в пространствах гладких финитных се-
сечений расслоений Ер. Тогда определены операторы d*,
формально сопряженные к операторам d. По формуле
C) строится Л. о. на каждом пространстве Т(Ер).
Если в качестве комплекса F) взять комплекс де Рама,
то при естественном выборе метрики в р-формах и эле-
элемента объема, порожденных метрикой B), получается
в качестве Л. о. комплекса де Рама описанный выше
Л. о. на формах.
На комплексном многообразии М наряду с комплек-
комплексом де Рама имеются эллиптич. комплексы
. ..Л^-1- Ч-^АР-Ч-^AP + i'Q _+ ..., G)
э э
.. .АР-ч-1 —+ АР'Ч—>ля-ог + 1-^ . . ., (8)
где АР' ч — пространство гладких форм типа (р, q)
на М. Вводя эрмитову структуру в касательном рас-
расслоении на М, можно построить Л. о. D) комплекса
де Рама и Л. о. комплексов G), (8):
Каждый из этих операторов переводит в себя простран-
пространство АР' Ч. Если М — кэлерово многообразие, а эрми-
эрмитова структура на М индуцирована кэлеровой метри-
метрикой, то
Д = 2П=2П-
Важным фактом, определяющим роль Л. о. эллмптич.
комплекса, является существование в случае компакт-
компактного многообразия М ортогонального раз-
разложения Ходжа:
Г (Ер) = d (Г (?„_!» 0 Жр (Е) Ф d* (Г (Ер + 1)). (9)
В этом разложении fflP (Е)=КегА\г^Е ,, где А — Л. о.
комплекса F), так что fflp(E) — пространство «гармо-
«гармонических» сечений расслоения Ер (в случае комплекса
де Рама — это пространство всех гармонических форм
степени р). Прямая сумма первых двух слагаемых в пра-
правой части формулы (9) равна Кег d|r(E ч, а прямая сум-
сумма двух последних слагаемых совпадает с Kerd*\T(E *,,
В частности, разложение (9) задает изоморфизм про-
пространства когомологий комплекса F) в члене Г (Ер) и
пространства гармонич. сечений jfflP(E).
Лит.: [1] Рам Ж. д е, Дифференцируемые многообразия,
пер. с франц., М., 1956; [2] Ч ж э н ь Ш э н - ш э н ь, Комп-
Комплексные многообразия, пер. с англ., М., 1961; [3] У э л л с Р.,
Дифференциальное исчисление на комплексных многообразиях,
пер. с англ., М., 1976. М. А. Шубин,
ЛАПЛАСА ПОСЛЕДОВАТЕЛЬНОСТЬ — последова-
последовательность конгруэнции в трехмерном проективном (аф-
(аффинном, евклидовом) пространстве, в к-рой каждые две
соседние конгруэнции образованы касательными к двум
семействам линий сопряженной сети одной поверхности
(фокальной поверхности конгруэнции). Каждая из
двух соседних конгруэнции Л. п. наз. преобразо-
преобразованием Лапласа другой. Аналитич. преобра-
преобразования уравнения Лапласа связаны с геометрич. пере-
переходом от одной фокальной поверхности конгруэнции к
другой ее фокальной поверхности (см. [1]). С каждой
Л. п. конгруэнции связана Л. п. фокальных поверх-
поверхностей (см. [2]). Л. п. р-мерных многообразий Картана
особого проективного типа в проективном п-простран-
стве Рп (см. [3]) обобщена на случай произвольных
р-сопряженных систем в Рп (см. [4J).
Лит.: [1] Darboux G., Lecons sur la theorie generate
des surfaces, 2 ed., pt. 2, P., 1915; [2] Фиников С. П.,
Теория конгруэнции, М.— Л., 1950; [3] С h е г n S.- S., «Ргое
Nat. Acad. Sci. USA», 1944, v. 30, p. 95—97; [4] Смирнов Р
В., «Докл. АН СССР», 1950, т. 71, JV« 3, с. 437 — 39.
ЛАПЛАСА ПРЕОБРАЗОВАНИЕ, транс фор-
формация Лаплас а,— в широком смысле — и н-
теграл Лапласа вида
F (p) = \jLf(z)e-P*dz, A)
где интегрирование производится по нек-рому контуру
L в плоскости комплексного переменного z, ставящий
в соответствие функции/(z), определенной на /., анали-
аналитич. функцию F (р) комплексного переменного р = а+
+ iT. Многие интегралы вида A) были рассмотрены
П. Лапласом (см. [1]).
В узком смысле под Л. п. подразумевают одно-
одностороннее преобразование Лапла-
с а
^ B)
называемое так в отличие от двустороннего
преобразования Лапласа
tat. C)
Л. п.— частный вид интегральных преобразований;
преобразования вида B) или C) тесно связаны с Фурье
преобразованием. Двустороннее Л. п. C) можно рас-
рассматривать как преобразование Фурье функции / (t)e~ot,
одностороннее Л. к. B) — как преобразование Фурье
функции ф(?)> равной f(t)e~ot при 0<?<оо и равной
нулю при —oo<Z<0.
Подынтегральная комплексная локально суммируе-
суммируемая функция /(t) наз. функцией-оригина-
л о м, или просто оригиналом; в приложениях
часто удобно трактовать переменное t как время.
Функция F{p) = L[f\{p) наз. также преобразо-
преобразованием Лапласа оригинала f(t) или изоб-
изображением по Лапласу. Интеграл B) пони-
понимается, вообще говоря, как условно сходящийся на
бесконечности. Априори возможны три случая: 1)
существует действительное число ас такое, что интег-
интеграл B) сходится при Rep=a>ac, а при Rep=a<aG—
расходится; это число ас наз. а б с ц и с с о й (у с л о в-
ной) сходимости; 2) интеграл B) сходится при
всех р, в этом случае полагают ас= — оо; 3) интеграл
B) расходится при всех р, в этом случае полагают вс=
=-}-оо. Если ас<-(-со, то интеграл B) представляет
однозначную аналитич. функцию F(p) в полупло-
полуплоскости сходимости Re/7>ov Обычно огра-
ограничиваются рассмотрением абсолютно сходящихся
интегралов B). Точная нижняя грань тех а, для к-рых
существует интеграл
наз. абсциссой абсолютной сходимо-
сходимости аа, o><aa. Если а есть нижняя грань тех а,
для к-рых \f(t)\ = O (ect), г—>-+°о, то аа=а; число а
иногда наз. показателем роста оригинала
/(«)¦
При нек-рых дополнительных условиях оригинал
f(t) однозначно восстанавливается по своему Л. п.
F(p). Напр., если f{t) имеет ограниченную вариацию в
окрестности точки г„ или если f(t) кусочногладкая, то
имеет место формула обращения Л. п.:
/ (h) =L———i =
= ^ lim [o+iR F (p)epi dp, a > aa. D)
z m Д _>. со J o-iR
Формулы B) и D) позволяют получить ряд соотно-
соотношений между операциями, производимыми над ориги-
оригиналами и изображениями, а также таблицу изображений
для часто встречающихся оригиналов. Все это состав-
составляет элементарную часть операционного исчисления.
В математич. физике важные применения находит
многомерное Л. п.
J(t)e-lP'1>dt, E)
где t^ (ti, . . ., tn) — точка re-мерного евклидова про-
пространства R", p= (pi, . . ., pn)=o+ix= (au . . ., а„)+
-Н(ть . . ., т„) — точка комплексного пространства
С", п>1,
— скалярное произведение, dt=dt1. . .dtn — элемент
объема в R™. Комплексная функция /(t) в E) определе-
определена и локально суммируема в области интегрирования
C*={z?R«; tjj>0, 7 = 1, . . ., re} — положительном
координатном угле пространства Rn. Если функция
/(() ограничена в С*, то интеграл E) существует во всех
точках р?Сп, удовлетворяющих условию Re(/j, /)>
>(), i?C*, к-рое определяет снова положительный
координатный угол S={a?Rn; оу>0, ;=1, . . ., ге}.
Интеграл E) определяет голоморфную функцию комп-
комплексных переменных р= (plt . . ., рп) в трубчатой об-
ласти Ts=S+iRn={p=e+ix?Cn; e?S, t?R«}
пространства С™ с основанием S. В более общем случае
в качестве области интегрирования С* в E) и основания
S трубчатой области можно взять любую пару сопря-
сопряженных замкнутых выпуклых острых конусов в про-
пространстве R" с вершиной в начале координат. При
ге=1 формула E) переходит в B), причем С*={г?К;
(>0} — положительная полуось и Ts— {p=a-j-ix?C;
a>0} — правая полуплоскость. Л. п. E) определено
и голоморфно и для функций / (t) гораздо более широ-
широких классов, напр, для всех быстро убывающих функ-
функций, составляющих класс Y=vCR™)> T- е- Для бесконеч-
бесконечно дифференцируемых в R" функций /(?), убывающих
при U| —>- оо вместе со всеми производными быстрее
любой степени величины М. Элементарные свойства
Л. п. с соответствующими изменениями остаются
справедливыми и для многомерного случая.
Развитием Л. п. является Л. п. мер и вообще обоб-
обобщенных функций. Наиболее полно теория Л. п. обоб-
обобщенных функций развита для важного в математич.
физике класса y' = y'(Rn) обобщенных функций мед-
медленного роста, определяемых как линейные непрерыв-
непрерывные функционалы на пространстве быстро убывающих
основных функций y=y(R"). Такое Л. п. L[g] обобщен-
обобщенной функции медленного роста g?y' снова является
обобщенной функцией медленного роста, L[g]?y'.
Численное преобразование Лапла-
Лапласа — численное выполнение преобразования B), пере-
переводящего оригинал f{t), 0<?<oo, в изображение F(p),
р=а+гт, а также численное обращение Л. п., т. е.
численное нахождение /(?) из интегрального уравнения
B) либо по формуле обращения D).
Необходимость применения численного Л. п. возни-
возникает вследствие того, что таблицы оригиналов и изоб-
изображений охватывают далеко не все встречающиеся в
практике случаи, а также вследствие того, что оригинал
или изображение зачастую выражаются слишком слож-
сложными, неудобными для применений формулами.
В случае действительных значений параметра р
формулу B) при нек-рых дополнительных предполо-
предположениях можно свести к вычислению интеграла с ве-
весом Лагерра:
lx'e~x4>lx)dx F)
при нек-ром s^O. При нек-рых условиях к интегралу
F) приводится и Л. п. для комплексных р (см. [9]).
Для вычисления интеграла в F) применима квадра-
квадратурная формула
где коэффициенты Aii> и узлы х^ выбираются так,
чтобы равенство G) при фиксированном п было точным
или для всех многочленов степени <:2п—1, или для нек-
некрой системы рациональных функций в зависимости от
свойств функции ср(ж). Коэффициенты А{^ и узлы a4s)
для таких квадратурных формул просчитаны для мно-
многих значений параметра s (см. [9] — [11]).
Проблема обращения Л. п., как задача отыскания
решения f (х) интегрального уравнения первого рода
B), относится к классу некорректных задач и может
быть решена, в частности, посредством регуляризирую-
щего алгоритма.
Задачу численного обращения Л. п. можно также ре-
решать методами, основанными на разложении функции-
оригинала в функциональный ряд. Сюда в первую оче-
очередь можно отнести разложение в степенной ряд, в
обобщенный степенной ряд, в ряд по показательным
функциям, а также в ряды по ортогональным функ-
функциям, в частности по многочленам Чебышева, Лежандра,
Якоби и Лагерра. Задача разложения оригинала в ряды
по многочленам Чебыпюва, Лежандра, Якоби в оконча-
окончательном своем виде сводится к проблеме моментов на
конечном промежутке. Пусть известно Л. п. F(p)
функции $(t)f(t):
тце f (t) — искомая функция, а р (() — неотрицательная,
интегрируемая на [0, со) функция. Предполагается,
что функция /(*) интегрируема на любом конечном
отрезке [О, Т] и принадлежит классу L2(p"(i), 0, со).
По изображению F (р) функции C (t) /(t) функция f{t)
строится в виде ряда по смещенным многочленам Якобн,
в частности по смещенным многочленам Лежандра,
Чебышева первого и второго рода, коэффициенты к-рого
0^ вычисляются по формуле
где а\ ) — коэффициенты смещенного многочлена Ле-
Лежандра, Чебышева первого и второго рода соответст-
соответственно, записанных в виде 5"*=i а\ь х' (см. [4]).
Пусть задано Л. п. F(p) функции f(t), причем f(t)
удовлетворяет условию
e-<t->-\i(t) \*dt < оо, X >— 1.
Тогда / (t) можно разложить в ряд по обобщенным
многочленам Лагерра
сходящийся к f (t) в среднем. Коэффициенты ak этого
ряда вычисляются по формуле
* <1к I 1
(-П*
Другим приемом численного обращения Л. п. явля-
является построение квадратурных формул для интеграла
обращения D).
Изображение F (р) стремится к нулю, если точка р
удаляется на бесконечность так, что Вер при этом
неограниченно растет. Предполагается, что F(p) убы-
убывает по степенному закону, т. е. что F (р) представима в
виде
а ф(р) регулярна в полуплоскости RejD>cra и непре-
непрерывна при Rep^aa. Интеграл D) при этом имеет вид
Ф(р)^. (8)
Для интеграла (8) построена интерполяционная квад-
квадратурная формула, основанная на интерполировании
ф(р) многочленами от Ир:
'@=2й=04*)(')фЫ + я», (9)
гДе Pk — узлы интерполирования, произвольные,
расположенные справа от прямой Rep=aa, Rn — оста-
остаточный член формулы и
Коэффициенты a^y зависят только от выбранных узлов
Рй и для нек-рых способов их выбора (в частности, для
равноотстоящих узлов) вычислены (см. [12]). Задача
исследования сходимости интерполяционных квадра-
квадратурных формул заключается в выяснении связей между
свойствами ср(р) и узлами р^, при к-рых можно быть
уверенным в стремлении остаточного члена Rn формулы
(9) к нулю. Эта задача решена для нек-рых конкретных
узлов pft и для нек-рых частных классов функций ср(р)
(см. ИЗ]).
Для интеграла D) можно строить квадратурные
формулы наивысшей степени точности в классе рацио-
рациональных функций частного вида. Чтобы параметры
формулы не зависели от аа и t, выполняется замена
переменной p = z/t-\-aa. Интеграл D) принимает вид
e > 0, F*(z) = F {-Y + Oa
Как и прежде, предполагается, что F* (z) = z~sfp(z)
и для вычисления интеграла / (s) строится квадра-
квадратурная формула
/(«)«2*=14*ЧЮ- <10>
точная для любого многочлена степени <:2п — 1 от
переменной Mz. Для этого необходимо и достаточно,
чтобы формула A0) была интерполяционной и чтобы
узлы z^s> были корнями нек-рой системы ортогональ-
ортогональных многочленов co(ns)(l/z). Окончательно это условие
приводит к формуле
где z/;S) — корни ортогональных многочленов wj,s)(l/z).
Для многочленов co,(jS) (Mz) известны явное выражение,
рекуррентное соотношение, дифференциальное уравне-
уравнение, решением к-рого они являются, производящая
функция. Для нек-рых частных значений s показано,
что корни многочленов шлA/г) лежат в правой полу-
полуплоскости (см. [13]). В [12] приведены значения узлов и
коэффициентов A(i) формулы A1) для s=l, 2, 3, 4, 5;
п—1AI5 с 20 верными десятичными знаками и для
s=0,01 @,01K; ге=1A) 10 с 7—8 верными десятичными
знаками.
Лит.: [1] Laplace P. S., Theorie analytique des proba-
bilit&s, P., 1812; [2] Ван дер Поль В., Времмер X..
Операционное исчисление на основе двустороннего преобразова-
преобразования Лапласа, пер. с англ., М., 1952; [3] Б о х н е р С, Лекции
об интегралах Фурье, пер. с англ., М., 1962; [41 Д и т-
к и н В. А., Прудников А. П., Операционное исчисле-
исчисление, М., (966; [5] их же, Интегральные преобразования и
операционное исчисление, 2 изд., М., 1974; [6] D о е t s с h G.,
Handbuch der Laplace-Transformation, Bd 1—3, Basel, 1950—56;
[7] Владимиров В. С, Обобщенные функции в матема-
математической физике, М., 1976; [8] 3 е м а н я н А. Г., Интеграль-
Интегральные преобразования обобщенных функций, пер. с англ., М.,
1974; [9] А й з е н ш т а т В. С, 'Крылов В. И., М е-
тельский А. С, Таблицы для численного преобразования
Лапласа и вычисления интегралов вида \ xse-xf(x)dx, Минск,
1962; [10] S а 1 z е г Н. Е., Z u с к с г R. «Bull. Amer. Math.
Soc», 1949, J\I5 55, p. 1004—12; [11] Пальцев А. А., С к о б-
л я Н. С, «Изв. АН БССР. Сер. физ.-матем. наук», 1905, Д5 3,
с. 15—23; [12] Крылов В. И., Скобля Н. С, Спра-
Справочная книга по численному обращению преобразования Лапла-
Лапласа, Минск, 1968; [13] их же. Методы приближенного преоб-
преобразования Фурье и обращения преобразования Лапласа, М.,
1974. Н. С. Жаврид.
ЛАПЛАСА ПРЕОБРАЗОВАНИЕ в геометрии—
переход от одной фокальной сети конгруэнции к другой
фокальной сети той же конгруэнции. Понятие Л. п.
сети ввел Г. Дарбу (G. Darboux, 1888), обнаружив-
обнаруживший, что аналитич. преобразование решений уравнения
Лапласа
эге _ _эе_ . , т
dudv а ди ' I
где а, Ь, с — известные функции переменных и, v,
может быть интерпретировано геометрически как пе-
реход от одной фокальной сети конгруэнции к другой
ее фокальной сети. Л. п. сетей устанавливает связь
теории сопряженных сетей с линейчатой геометрией.
Существуют различные обобщения Л. п. сети.
Лит.: [11 Т г i t z e i с a G., Geometrie differentielle projec-
tive des reseaux, P.—Bucarest, 1924; [2] Итоги науки. Геометрия.
1963, M., 19В5. В. Т. Базылев.
ЛАПЛАСА РАСПРЕДЕЛЕНИЕ — непрерывное рас-
распределение вероятностей с плотностью
р(х)==±ае-а\х-Я\г _ оо < .г < оо,
где р, —оо<р<оо, — параметр сдвига, а а >0, —
масштабный параметр. Плотность Л. р. симметрична
относительно точки х~$, производная плотности имеет
разрыв при ж=р. Характеристич. функция Л. р. с
параметрами а и В равна
Л. р. имеет конечные моменты любого порядка, в част-
частности его математич. ожидание равно р\ а дисперсия
равна 2/а3.
Л. р. было впервые введено П. Лапласом [1] и часто
наз. «первым законом распределения
Лаплас а» в отличие от «второго закона
распределения Лапласа», как иногда наз.
нормальное распределение. Л. р. наз. также двусто-
двусторонним показательным распреде-
распределен и е м в силу того, что Л. р. совпадает с распределе-
распределением случайной величины
где Х1 и Х2 — независимые случайные величины,
имеющие одинаковое показательное распределение с
плотностью ае-ах, ж>0. Л. р. с плотностью j-e~[xl и
Коши распределение с плотностью — ^ +х, связаны сле-
следующим образом:
ettxe-\x\ dx =
1
i + t'
А. С"
я J - =
. ium.: [1] Laplace P. S., Theorie analytique des proba-
bilites, P., 1812; [2] Ф е л л е р В., Введение в теорию вероят-
вероятностей и ее приложения, пер. с англ., т. 2, М., 1967.
А. В. Прохоров.
ЛАПЛАСА ТЕОРЕМА — 1) Л. т. об опреде-
определителях — см. ст. Алгебраическое дополнение.
2) Л. т. об а п п р о к с и м а ц и и биномиа-
биномиального распределения нормальным
распределением; первый вариант центральной
предельной теоремы теории вероятностей: если Sn —
число «успехов» в п Бернулли испытаниях с вероятно-
вероятностью уепеха р, 0<р<1, то при п —>- оо для любых,
действительных чисел хг и х2 (?\<С-*''г)
< S"-»P < Xt\ _> ф (х2)-Ф (т,), (*)
> пр A-р) 1
где
4 ' 1 2я J-oo
— функция распределения стандартного нормального
закона.
Самостоятельное значение имеет т. н. локальная
Л. т.: для вероятности
Р {5„ = т}= С™рт A— р)п~т, 0<т<ге, т — целое,
справедливо равенство
Р {Я„ = т} = —=1==ф (*) A + е„),
\ ар A-р) т
где
— плотность стандартного нормального распределения
ие„^-0 при и —>- оо равномерно для всех то, для к-рых
т—пр
х= г ¦=. принадлежит какому-либо конечному ин-
Knp(l-p)
тервалу.
В общем виде Л. т. была доказана П. Лапласом [1].
Один частный случай Л. т. (р=1/2) был изучен А. Му-
авром [2], в связи с чем Л. т. иногда наз. теоремой
М у а в р а — Лапласа.
Для нрактич. применения Л. т. важно иметь пред-
представление об ошибках, возникающих при использо-
использовании приближенных формул. В более точной (по срав-
сравнению с [1]) асимптотич. формуле
p A-
остаточный член Rn(y) имеет порядок 0A/ У~п) равно-
равномерно для всех действительных у. Из равномерных
аппроксимаций биномиального распределения по-
посредством нормального распределения наиболее удачна
формула Я. Успенского A937): если a— V^np (I—p),
ТО ДЛЯ ЛЮбыХ 1I И у2
где
и при а:==5
|Д| < @,13 + 0,18 |1 — 2р|)а-2 + е
Для улучшения относительной точности аппроксимации
С. Н. Бернштейном A943) и В. Феллером (W. Feller,
1945) были предложены другие формулы.
Лит.: [1] L а р 1 а с е P. S.,'Theorie analytique des probabi-
lites, P., 1812; [2] M о i v r e A. d e, Miscellanea analytica de
seriebus et quadraturis, L., 1730; [3] Прохоров Ю. В.,
Розанов Ю. А., Теория вероятностей, 2 изд., М., 1973;
[41 F е 1 1 е г W., «Ann. Math. Statistics», 1945, v. 16, p. 319—29;
[5] Ф е л л е р В., Введение в теорию вероятностей и ее при-
приложения, пер. с англ., 2 изд., т. 1, М. 19C7. А. В. Прохоров,
ЛАПЛАСА УРАВНЕНИЕ — однородное дифферен-
дифференциальное уравнение с частными производными вида
. д2и , дги . . дги п ,,
Аи^-^+—7,+ • • •+—72 = 0, 1)
где u=u(x)-—u{xi, х2, . . ., хп) — функция от п дей-
действительных переменных. Левая часть Л. у. наз. Лап-
Лапласа оператором от функции и. Регулярные решения
Л. у. класса С2 в нек-рой области D евклидова про-
пространства R", п~^2, т. е. решения, имеющие непрерыв-
непрерывные частные производные до 2-го порядка в D, наз.
гармоническими функциями в D. Л. у. является основ-
основным представителем дифференциальных уравнений с
частными производными 2-го порядка эллиптич. типа,
на к-ром вырабатывались и вырабатываются основные
методы решения краевых задач для эллиптических урав-
уравнений.
Пусть v — потенциальное векторное
поле в D, т. е. «=—grad и, где и=и(х1, х2, . . .,
хп) — потенциал. Так как
Дм see div grad и = — div v,
то физич. смысл Л. у. состоит в том, что оно выполня-
выполняется для потенциала любого такого поля в областях
D, свободных от источников поля. Напр., Л. у. удов-
удовлетворяет гравитационный потенциал сил тяготения в
областях, свободных от притягивающих масс, потен-
потенциал электростатпч. поля в областях, свободных от
зарядов, и т. д. Таким образом, Л. у. выражает закон
сохранения для потенциального поля. С этой точки
зрения форма A) Л. у. получается при выборе декарто-
декартовой прямоугольной системы координат; в других систе-
системах координат оператор Лапласа и Л.у. принимают
другой вид. При наличии источников поля в правой
части A) появляется функция, пропорциональная
плотности источников, и Л. у. переходит в Пуассона
уравнение. Л. у. возникает и во многих других вопросах
математич. физики, в к-рых рассматриваются стацио-
стационарные поля, напр, при изучении стационарного рас-
распределения температур, статических задач теории упру-
упругости и др.
Основными для Л. у. являются следующие краевые
задачи теории потенциала: 1) Дирихле задача, пли
первая краевая задача, когда ищется
гармонич. функция, принимающая на границе области
3D заданные непрерывные значения; 2) Неймана зада-
задача, или вторая краевая задача, когда ищет-
ищется гармонич. функция и такая, что ее нормальная про-
производная ди/дп принимает на дО заданные непрерывные
значения; 3) смешанная задача, когда ищется гармо-
гармонич. функция и, удовлетворяющая на границе линей-
линейному соотношению а{у)ди (i/)/dre-|-p (y)u(y) = g (у), y?dD,
а(у)фО.
В случае п=2 Л. у. тесно связано с теорией аналптич.
функций комплексного переменного z=x1-\-ix2, харак-
характеризующихся тем, что их действительная и мнимая
части являются сопряженными гармонич. функциями.
Л. у. встречается у Л. Эйлера и Ж. Д'Аламбера
(см. [1], [2]) в связи с задачами гидромеханики и перво-
первоначальным рассмотрением функций комплексного пере-
переменного. Однако широкую известность оно получило
после появления работ П. Лапласа (см. [3], [4]) по
теории гравитационного потенциала и небесной меха-
механике.
Уравнение A) иногда наз. скалярным Л. у. в
отличие от в е к т о р н о г о Л. у.
div v— rot rot v — 0. B)
V3
В случае, напр., векторного поля v = 2Ji=iviei' заданно-
заданного в прямоугольной декартовоп системе координат про-
пространства R:t, векторное Л. у. B) равносильно трем
скалярным Л. у. Л;;, —0 для каждой из компонент
Vi=V{(xi, х2, хя), i=l, 2, 3. В других системах коор-
координат векторное Л. у. равносильно системе трех урав-
уравнений с частными производными 2-го порядка относи-
относительно компонент векторного поля г1, получающейся
из B) после выполнения указанных там операций
векторного анализа в соответствующих координатах
(см. [7]).
Лит.: [1] Е и 1 е г L., «Novi Commentarii Acad. Sci. Petro-
politanae», 1761, t. 6; [2] D'A 1 e m b e r t J. le R о n d,
Opuscules mathematiques, t. 1, P., 1701; [3] L a p 1 а с e P. S.,
«Mem. Acad. Paris A782)», 1785; [41 e г о же, Traite de mecani-
que celeste, t. 2, P., 1799; [5] В л а д и м и р о в B.C., Уравне-
Уравнения математической физики, 2 изд., М., 1971; [6] М а р к у ш е-
в и ч А. И., Теория аналитических функций, 2 изд., т. 2, М.,
1968; [7] Морс Ф. М., Ф е ш б а х Г., Методы теоретической
физики пер. с англ., т. 2, М., 1960. Е. Д. Соломенцев.
ЛАПЛАСА УРАВНЕНИЕ; численные мето-
методы решения — методы, заменяющие исходную
краевую задачу дискретной задачей, содержащей ко-
конечное число N неизвестных, нахождение к-рых с
соответствующей точностью позволяет определить ре-
решение исходной задачи с заданной точностью s; N
зависит от s и стремится к оо при s —>- 0.
Л. у. в случае d пространственных переменных
xss (a'i, х2) . . ., х^) имеет вид
V^ d д2и (х)
и является однородным уравнением Пуассона. Краевые
задачи для уравнения Лапласа являются частными
случаями краевых задач для уравнения Пуассона и
более общих уравнений эллиптич. типа (см. [1]), а
численные методы решения краевых задач для уравне-
уравнений эллиптич. типа (см. [2]) содержат в себе многие
численные методы для уравнения Лапласа. Специфика
Л. у. позволяет конструировать и использовать методы,
обладающие существенно лучшими характеристиками,
чем методы для более общих уравнений, хотя на прак-
практике часто этим возможностям предпочитают простоту
реализации метода на ЭВМ.
Основными численными методами для уравнений
эллиптич. типа являются: вариационно-разностные
методы (проекционно-разностные, методы конечных эле-
элементов) и разностные методы (методы сеток). Оба
класса методов связаны с аппроксимацией исходной
области Q нек-рой сеточной областью ?1р/, содержащей
N узлов сетки, и построением системы алгебраич. урав-
уравнений
относительно значений функции, определяемой в этих
узлах. В вариационно-разностных методах, являющих-
являющихся специальными случаями вариационных и проекцион-
проекционных методов, используется идея аппроксимации рас-
рассматриваемого пространства функций, содержащего
решение исходной задачи, нек-рыми специальными
конечномерными подпространствами с заданными ба-
базисными функциями, а в системе (*) вектор и^ состоит
из коэффициентов разложения получаемой аппрокси-
аппроксимации искомого решения по выбранному базису. В
предположении, что решение исходной задачи в огра-
ограниченной области Q на плоскости имеет вид
где uo(x)?Wl+rn(Q), m>0, W\+m(Q) — пространство
Соболева, а функции lk(x)? W\(Q) заданы и отражают
асимптотич. поведение и (х) вблизи особых точек (угло-
(угловых точек границы, точек перемены типа граничного
условия), для многих типов областей Q и смешанных
краевых задач эти методы позволяют, напр., найти ре-
решение и(х) с точностью s в VF^fi) при затрате
O(s~2<mln2 е) арифметич. действий (см. [3]), а в ряде
более частных случаев оценки вычислительной работы
уменьшаются до O(e~2/m;ln s!) и O(s~2/m).
R разностных методах обычно используется в той или
иной форме аппроксимация производных разностями,
и в системе (*) вектор состоит из компонент, аппрокси-
аппроксимирующих значения решения в узлах сетки йдг. РГаибо-
лее изучены характеристики упомянутых методов для
краевых задач в ограниченных областях Q на плоскости.
Напр., для условия Дирихле и|г = ф (s), где Г — граница
Q и ф (s) — достаточно гладкие, можно на основе
улучшения дифференциальных свойств решения Л. у.
по мере удаления от Г так построить систему (*), что
число N по порядку равно числу NT точек на Г, ис-
используемых для задания q>(s) с точностью е, а идг мо-
может быть найдено с точностью е при затрате О (A'rln2iVr)
арифметич. действий и дает возможность найти решение
исходной задачи с точностью г в любой фиксированной
точке из строго внутренней подобласти при затрате
конечного числа действий (см. 14]). Методы такого
типа являются асимптотически оптимальными; в случае
же использования, напр., более простых методов с
прямоугольной сеткой, обладающих точностью О(Лг-1),
затраты на нахождение идг с точностью е составияют
0(./VlnA'|lne|); N^N\ (cm. [4]). Наиболее детально
изучены оценки погрешности метода сеток для Л. у.
(см. [4], [5]); при наличии особых точек на Г целесооб-
целесообразно использовать специальную структуру сеток
вблизи этих точек (см. [6]). Часто используются и раз-
разностные методы, основанные на аппроксимации нек-рых
интегральных характеристик для Л. у. (см. [7] — [9]).
Относительно редко применяется метод коллокаций,
в к-ром система (*) получается как следствие выпол-
выполнения исходного уравнения в узлах сетки и предполо-
предположения, что приближение к решению исходной задачи
ищется в нек-ром конечномерном подпространстве.
Специальный класс численных методов решения крае-
краевых задач для Л. у. основан на сведении этих задач к
сингулярным интегральным уравнениям (см. [11) и
последующему решению полученных интегральных
уравнений численными методами (см. [16], [11]).
Лит.: [1] Владимиров В. С, Уравнения математи-
математической физики, 2 изд., М., 1971; [2] М а р ч у к Г. И., Методы
вычислительной математики, 2 изд., М., 1980; [3] Дьяконов
Е. Г., веб.: Вариационно-разностные методы в математической
физике, НовосиО., 1978, с. 149—64; [4] В а х в а л о в Н. С, в сб.:
Международный конгресс математиков в Ницце. 1970, М., 1972,
с. 27—33; [5] В о л к о в Е. А., «Ж. вычислит, матем. и матем.
физики», 1969, т. 9, № 3, с. 573—84; [6] е г о же, «Тр. матем.
ин-та АН СССР», 1979, т. 150, с. 67—98; [7] Люстер'ник Л.
А., «Успехи матем. наук», 1954, т. 9, в. 2, с. 3—66; [8] Самар-
Самарский А. А., Фрязинов II. В., «Успехи матем. наук»,
1976, т. 31, в. 6, с. 167—97; [9] Волков Е. А., «Докл. АН
СССР», 1978, т. 238, JSB 5, с. 1036—39; [10] П а р т о н В. 3.,
П е р л и н П. И., Интегральные уравнения теории упругости,
М., 1977; [11] Иванов В. В., в сб.; Механика сплошной
среды и родственные проблемы анализа, М., 1972, с. 209—19.
Е. Г. Дьяконов.
ЛАПЛАСА — БЕЛЬТРАМИ УРАВНЕНИЕ, Б е л ь-
1 р а л и уравнен л е,— обобщение Лапласа
уравнения для функций на плоскости на случай функ-
функций и на произвольном двумерном римановом многооб-
многообразии R класса С2. Для поверхности R с локальными
координатами |, Т) и первой квадратичной форл'ой
Л.— Б. у. имеет вид
ди ди\ Г ди
При E=G и F=0, т. е. для случая, когда (|, г)) —
изотермич. координаты на R, уравнение (*) переходит
в уравнение Лапласа. Л.— Б. у. было введено Э. Бельт-
рами в 1864—65 (см. [1]).
Левая часть уравнения (*), поделенная на У EG—F2,
наз. вторым дифференциальным пара-
параметром Бельтрами.
Регулярные решения и Л.— Б. у. являются обоб-
обобщениями гармонич. функций и наз. обычно гар-
гармоническими функциями на поверх-
поверхности R. Физически эти решения интерпретируются
подобно обычным гармонич. функциям, напр, как по-
потенциал скоростей потока несжимаемой жидкости,
текущего по поверхности R, или как потенциал элект-
ростатич. поля на R, и т. п. Гармонич. функции на
поверхности сохраняют свойства обычных гармонич.
функций. Для них справедливо обобщение Дирихле
принципа: среди всех функций v класса C"(G)f\C{G)
в области GczR, принимающих на границе dG те же
значения, что гармонич. функция v?C(G), последняя
дает минимум интегралу Дирихле
где
*"~ EG-F*
— первый дифференциальный пара-
параметр Б е л ь т р а м и, являющийся обобщением
квадрата градиента grad2i/ на случай функций на по-
поверхности.
По поводу обобщения Л.— Б. у. на римановы многооб-
многообразия высших размерностей см. Лапласа оператор.
Лит.: [1] Beltrami E., Richerche di analisi applicata
alia geometria, в кн.: Opere matematiche, t. 1, Milano, 1902,
p. 107 — 98; [2] Шиффер М., Спенсер Д. К., Функ-
Функционалы на конечных римановых поверхностях, пер. с англ.,
М. 1957. Е. Д. Соломенцев, Е. В Шикин.
ЛАРМОРОВСКИЙ РАДИУС, радиус Л а р м о-
р а,— радиус окружности, по к-рой движется заряжен-
заряженная частица в плоскости, перпендикулярной магнит-
магнитному полю Н. Движение заряда е в однородном магнит-
магнитном поле происходит под действием силы Лоренца и
описывается уравнением
dt с ^ ' *т
где р — импульс заряженной частицы, с — скорость
света, V — скорость заряда в лабораторной системе
отсчета. Решение уравнения A) в декартовой системе
координат с осью z, направленной по нолю И, имеет
вид
Fx = T'Of cos (Ш -f-oc), l'y = —VOf sin (oji-f-a), VZ = VOZ,
x = xo-\-r sin (cof-f-a), y=y,
B)
где ш=есНЫ — т. н. частота Л ариора, е —
энергия заряженной частицы, не меняющаяся при
движении в однородном магнитном поле, Vof, l'oz,
a, x0, j/0, zu — постоянные, определяемые из начальных
условий,
v
V — ¦
@ ecH
— Л. р. В однородном магнитном поле заряд движется
по винтовой линии с осью вдоль магнитного поля с Л. р.
г. Скорость частицы при этом постоянна по величине.
Если скорость частицы мала по сравнению со скоро-
скоростью света, то можно приближенно положить г=тс2
и выражение для Л. р. принимает вид
г = Vtf /a>0 = Votmc/eH.
В результате вращения заряженных частиц в магнит-
магнитном ноле возникает магнитный момент системы.
Лит.: [1] Та мм И. Е., Основы теории электричества,
7 изд., М-, 1957; [2] Ландау Л. Д., Л и ф ш и ц Е. М.,
Теория поля, 6 изд., М., 1973. В. В. Параил.
ЛАСКЕРА КОЛЬЦО — коммутативное кольцо, в
к-ром любой идеал обладает примерным разложением,
т. е. представляется в виде пересечения конечного
числа примерных идеалов. Аналогично, Л-модуль
наз. модулем Ласкера, если любой его под-
подмодуль обладает примерным разложением. Любой мо-
модуль конечного типа над Л. к. является ласкеровым.
Э. Ласкер [1] доказал наличие примерного разложения
в кольцах многочленов. Э. Нётер [2] установила, что
любое нётерово кольцо является Л. к.
Лит.: [1] L а s k е г Е., «Math. Ann.», 1905, Bd 60, S. 20—
116; [2] Noether E., там же, 1921, Bd 83, S. 24—06; [3]
Б у р б а к и Н., Коммутативная алгебра, пер. с франц., М.,
1971. В. И. Данилов.
ЛАТИНСКИЙ КВАДРАТ — квадратная матрица по-
порядка п, каждая строка и каждый столбец к-рой явля-
являются перестановкой элементов конечного множества S,
состоящего из п элементов. Говорят, что Л. к. по-
строен на множестве S; обычно 5={1, 2, . . ., п).
Л. к. существует для любого п\ напр., л = ||а,у||, где
aijss i-\-j — I (mod и), i, / = 1, 2, . . ., п,
есть Л. к.
Каждый Л. к. можно рассматривать как таблицу ум-
умножения квазигруппы; верно и обратное: таблица ум-
умножения конечной квазигруппы есть Л. к. Для того
чтобы Л. к. A = \\aij\\ был Кэли таблицей группы,
необходимо и достаточно выполнение условия (к р и-
терпя квадрата):
если aik=^a
По двум
порядка т
порядка тп,
an=ai
А
a/k—ajiki
k l
Л. к. А = \\аы\\ порядка
можно всегда построить Л. к.
напр, следующим образом:
то ajl=aj,u.
п и B~\\brs\\
Для числа Ln Л. к.
порядка п верна
\(n— I)! ...2!1!
оценка снизу:
Л. к. наз. редуцированным (или Л. к.
стандартного вида), если элементы его пер-
первой строки и первого столбца расположены в натураль-
натуральном порядке. Для числа 1п редуцированных Л. к.
порядка п верны соотношения:
Ln = n\(n-\)\ln, ZnS=mn = (rc —2)!(n-3)! ...2!l!
Два Л. к., построенные на одном и том же множестве
S, наз. эквивалентными, если один из дру-
другого получается перестановкон строк, столбцов и пере-
переименованием элементов. Пусть кп — число классов
эквивалентности Л. к. порядка п. Известны следующие
первые значения 1п и кп:
п
hn . . . .
la . . . .
тп . . . .
3
1
1
1
4
2
4
2
5
2
56
12
в
22
9408
288
16
7
563
942
34
080
560
1
535 281
2 4
8
676
401
883
257
856
200
, д
1<сс, E«п, сущест-
сущестКроме того, г9 = 377 597 570 964 258 816. Задача полу-
получения оценок для 1п остается нерешен-ной A982).
В теории планирования экспериментов требуется
строить Л. к. с различными ограничениями на располо-
расположения элементов в них. Л. к. наз. полным, если для
любых натуральных а, р\ аР E
вуют такие i, j, к, I, что
(°i7' ai.j + i) — (a' Р) и (
Известны алгоритмы построения полных Л. к. только
в случае четных п, для нек-рых нечетных п имеются
примеры полных Л. к.
Латинским подквадратом данного
Л. к. порядка п наз. такая его подматрица, что она
сама является Л. к. порядка к, к<Сп. Любой Л. к.
порядка к может быть латинским подквадратом Л. к.
порядка п при п^2к.
При построении ортогональных латинских квадратов
существенную роль играет понятие трансверсали Л. к.
Частичной трансверсалью длины t
Л. к. 4 = j|a,y|| наз. такое множество Т, состоящее из
t клеток Л. к.
T = {(h,ii), (н, /г), • • •, (if, it)},
что
Всегда <<п; при t=n частичная трансверсаль наз.
трансверсалью. Существование в Л. к. поряд-
порядка п множества из п непересекающихся трансверсалеи
является необходимым и достаточным условием суще-
ствования для него ортогонального соквадрата. Л. к.
6-го порядка
012 345
120 453
201 534
345 012
453 120
534 201
нс имеет ни одной трансворсали.
В любом Л. к. порядка /г^=7 существует цо крайней
мере одна частичная трансверсаль длины ?^Bя—1)/3.
При я^=4 всегда можно построить Л. к. такой, что обе
его главные диагонали являются трансверсалями.
Несколько обобщений Л. к. Частичным, или
неполным, Л. к. порядка п наз. матрица порядка п,
у к-рой только часть клеток заполнена элементами мно-
множества S мощности п, но в каждой строке и в каждом
столбце элементы S встречаются не более одного раза.
Существуют частичные Л. к., к-рые нельзя дополнить
до Л. к., напр.:
1 ...
.234
Неполный Л. к., содержащий точпо п — 1 элементов,
может быть дополнен до Л. к. Известно, что две таб-
таблицы Кэли двух разных групп порядка п отличаются
друг от друга но крайней .мере на 2п местах.
Бесконечным Л. к. наз. бесконечная матрица,
элементы к-рой — натуральные числа, встречающиеся в
каждой строке и в каждом столбце точно один раз.
Имеется несколько обобщений понятия Л. к. на
многомерный случай. Так, m-yi р р н ы м переста-
перестановочным кубом порядка п наз. т-мерная
матрица
порядка п, элементами к-рой являются первые п
натуральных чисел и для любого к набор
есть перестановка первых п натуральных чисел. А
т-и е р н ы м гиперкубом порядка п и класса
г наз. от-мерная матрица порядка п, элементы к-рой
принадлежат множеству vis nr элементов, каждый эле-
элемент встречается в матрице пт~г раз, а в каждом
(п — 1)-мерном сечении матрицы (т. е. среди элементов
"•¦•¦¦л-! «2'fc+i-v
где г/;—const, а остальные индексы пробегают все п
значений) встречается пт~г~1 раз.
Лит.: [1] Сачков В. Н., Комбинаторные методы дис-
дискретной математики, М., 1977; [2] Denes J., Keed well А-
D., Latin Squares and their Applications, Budapest, 1974; [3]
Холл М., Комбинаторика, пер. с англ., М., 1970; [4] Р а й-
зер Г.- Д ж., Комбинаторная математика, пер. с англ. М.,
196В. В. М. Михеев.
ЛАТИНСКИЙ ПРЯМОУГОЛЬНИК — прямоуголь-
прямоугольная матрица размера тХп, т^п, каждая строка к-рой
является перестановкой (без повторений) элементов
множества S, состоящего из п элементов, причем в
столбцах каждый элемент встречается не более одного
раза. При т=п Л. п. является латинским квадратом
порядка п. Обычно S= {1, 2,. . ., п}, и о Л. п. говорят,
что он построен на множестве S.
Л. п. существует при любых натуральных т, п,
(и<п. Примером Л. п. может служить матрица, пер-
первая строка к-рой есть A,2,..., п), а все последую-
последующие получаются из предыдущей циклич. сдвигом на
один шаг. Л. п. размера тХп, т<.п, всегда может быть
дополнен до латинского квадрата порядка п так, что
первые т строк латинского квадрата будут совпадать
со строками Л. п.
Для числа L (т, п) Л. п. размера тХ п верна следую-
следующая оценка снизу:
L (т, п) 5э п\ (л — 1)! . . . (и —т + 1)!
Л. п. наз. нормализованным, если его первая
строка есть A, 2,. . ., ?г). Число К(т, п) нормализо-
нормализованных Л. п. связано с L(m, n) соотношением:
L (т, п) = п\ К (т, п).
Подсчет L(m, п) при яг=2,3 связан с классич.
комбинаторными задачами: с задачей о числе беспоряд-
беспорядков (см. Инверсия) и с задачей о супружеских парах.
Так, число беспорядков Dn=K{2, n), а число разме-
размещений Un в задаче о супружеских парах есть число
Л. п. размера ЗХп, первые две строки к-рых суть:
23...П
п \ 2 . ..л—1
Для Un верны формулы:
'¦ ¦¦)'
(m)k = m{m-\) ...(m — k+\).
Число ^C, ti) выражается через Dk и Uf.
К(Ъ, п) =2Г=о (
где m=[n/2], tr0=l. Верна также следующая асимп-
асимптотика:
К(А,п)~(п\)е (l_-L_— + . .. + ^—+. ..)
где bs=Hs( —1/2), Hs(t) — Эрмигпа многочлен. Из-
Известно также, что
К C, r + s) = 2ГК C, s) (mod r).
Задача о перечислении Л. п., имеющих более трех
строк, не решена A0S2). При т<п1/3~б, где 8=6 (л)—».
->-т О так, что п-6<л> _». О, получена асимптотика:
L(ffl,n)~.(n!)»exp{-
На Л. п. распространяются нек-рыо понятия и
теоремы, связанные с латинскими квадратами. Так,
два Л. п. ||я,у|| и |16,у|! размера тХп наз. ортого-
ортогональным и, если все пары вида (а,-у, Ь,/) различны.
Множество Л. п., в к-ром любые два Л. п. ортогональ-
ортогональны, имеет не более т — 1 Л. п.
Часто под Л. п. понимают следующее обобщение
Л. п.: латинским прямоугольником
размера rXs, построенным на множестве S, состоящем
из » элементов, наз. матрица размера rXs с элементами
из S, встречающимися в каждой строке п каждом стол-
столбце не болое одного раза. Л. п. размера rXs, построен-
построенный на п символах, может быть расширен до латинского
квадрата порядка п тогда и только тогда, когда каждый
символ встречается в Л. п. не менее r-~s—п раз.
Лит.: [1] Р и о р д а н Д ж., Введение в комбинаторный
анализ, пер. с англ., М., 1963.
См. также лит. при ст. Латинский квадрат. В. М. Михеев.
ЛЕБЕГА ИНТЕГРАЛ — одно из наиболее важных
обобщений понятия интеграла. Пусть (X, р.) — про-
пространство с неотрицательной полной счетноаддитивной
мерой ц, причем (j,X<+oo. Простой ф у н к ц и-
е й наз. измеримая функция g : X —>- R1, принимаю-
( щая не более счетного множества значений:
g{ yn
упфуь при пфк, если х?Хп, \Jn=iX,,= X. Простая
функция g наз. суммируемо и, если ряд
сходится абсолютно; сумма этого ряда есть интег-
интеграл Лебега:
Функция / : X —>¦ R1 суммируема на X, /?L(X, (x),
если существует равномерно сходящаяся на множестве
полной меры к f последовательность простых сумми-
суммируемых функции gn п предел
hm \ gnd\i = I
конечен. Число / есть интеграл Лебега:
Определение корректно: предел / существует и не
зависит от выбора последовательности gn. Если
f?L(X, (x), то / — измеримая почти всюду конечная
функция на X. Л. и. ость линейный неотрицательный
функционал на L(X, jx), обладающий следующими
свойствами:
1) если f(x)?L(X, u) и
fi{x^X, f(x) *h(x)} = 0,
то h{.r)^L(X, [i) и
2) если f?L{X, [x), то \f\?L(X, ц) и
3) если f?L(X, u), |й|</ и А измерима, то
L(A\ ц) и
4) если m</«:Af и / измерима, то f?L(X, u.) n
m[xA' < f f rfu < Л/uX.
В случае, когда иХ = + со и X=\Jn-*iXn, [хХ„<~|-со,
интеграл Лебега
определяется как
lim \ f
П -* со Jtn
при условии, что этот предел существует и конечен
для любой последовательности Еп такой, что [j,?'n<-j-oo,
ЕпаЕп + 1, \)n=iEn=X. В этом случае свойства 1),
2), 3) сохраняются, а свойство 4) нарушается.
О переходе к пределу под знаком Л. и. см. Лебега
теорема.
Если А есть измеримое множество X, то Л. и.
определяется или, как указано выше, заменой X на А ,
или как
гДе Ха — характеристич. функция А; эти определения
эквивалентны. Если f?L(A, ц), то f?L(A', jx) для
любого измеримого A'czA. Если
Ап измеримо для каждого п, для пфк
Ап П Ак = 0
и 1?L(A, ц), то
Обратно, если при тех же условиях на Ап для
каждого п, f?L(An, ц) и
?(, (х) и верно предыдущее равенство (о-адди-
тивность Л. и.).
Функция множества АсХ
абсолютно непрерывна относительно [х; если /15=0, то
F(A) есть неотрицательная абсолютно непрерывная
относительно (х мера. Обратное утверждение представ-
представляет Радона — Никодима теорему.
Для функций / : R" —>. R1 название «интеграл Лебе-
Лебега» применяется к соответствующему функционалу,
если мера (х есть Лебега мера; при этом множество сум-
суммируемых функций обозначается просто L (X) и интег-
интеграл
Для других мер этот функционал наз. Лебега—Стилть-
еса интегралом.
Если / : R1 -» R1, /??[а, ')] и х : [а, р] _> [a, ft],—
неубывающая абсолютно непрерывная функция, то
Если / : R1 -у R1, /gi [а, Ъ] и g : [а, Ь] -^- R1,—мо-
R1,—монотонна на [а, Ь], то fg?L\a, Ь] и существует точка
5^[ Ъ\ такая, что
/ (х) ^ (*) dj: = g (a) J^ / (х) dx + g (Ь) J* / (х) dx
(вторая теорема о средне >0.
А. Лебег дал в 1902 (см. [1]) определение интеграла
для XaR1 и моры [х, являющейся мерой Лебега. Он
строил простые функции, равномерно приближающие
почти всюду на множестве конечной меры Е измеримую
неотрицательную функцию f : Е —у R1, и доказал су-
существование общего предела (конечного или бесконеч-
бесконечного) интегралов этих простых функций при стремле-
стремлении их к /. Л. и. является базой для различных обоб-
обобщений понятия интеграла. Как отметил Н. Н. Лузин
[2], свойство 2) — т. п. абсолютная интегрируемость,
выделяет Л. к. для / : R1 —». R1 из всевозможных обоб-
обобщенных интегралов.
Лит.: [1] Лебег А., Интегрирование и отыскание при-
примитивных функций, пер. с франц., М.— Л., 1Й34; [2] Л у-
зин Н. Н., Р1нтеграл и тригонометрический ряд, М.— Л.,
j!M1; [3] Колмогоров А. Н., Фомин С. В., Эле-
Элементы теории функций и функционального анализа, 5 изд., М.,
1981. Ц. А. Виноградова.
ЛЕБЕГА КОНСТАНТЫ — 1) Величины
где
n /M_sin(n+l/2) t
2 sin /2
есть Дирихле ядро. Л. к. L,, при каждом я является:
1) максимальным значением | Sn(f, x) | для всех
х и функций /(t) таких, что |/(?)!<:1 при почти всех t;
2) точной верхней гранью \Sn(f, x)\ для всех х
и всех непрерывных функций /(?) таких, что |/(()|<:1;
3) точно11 верхней гранью интегралов
!•?„(/, x)\dx
для всех функций f(t) таких, что
Здесь Sn(f, x) есть частная сумма ряда Фурье по
тригонометрич. системе 2я-периодической функции
/(*)• Справедлива асимптотич. формула:
В частности, Ln —>. 00 при п —>. оо, что связано с расхо-
расходимостью тригонометрич. рядов Фурье нек-рых непре-
непрерывных функций. В более широком смысле Л. к. опре-
определяются для других ортонормированных систем как
величины
Ln = vrai sup [Ь \Dn (x, t)\dt,
t(b) >"
где Df!(x, t) есть ядро Дирихле для данной ортонорми-
рованной на (а, Ъ) системы функций, и играют важную
роль в вопросах сходимости рядов Фурье по этим систе-
системам. Л. к. введены А. Лебегом (Н. Lebesgue, 1909).
См. также Лебега функции.
Лит.: [1] Зигмунд А., Тригонометрические ряды, пер.
с англ., т. 1, М., 1965. К. И. Осколков.
2) Л. к. интерполяционного процес-
процесса — числа
= max ^" \lnk(x)\, n = i, 2, . ..,
где
я0, хг, . . ., хп — попарно различные узлы интерполя-
интерполяции, лежащие на нек-ром отрезке [а, Ь\.
Пусть С[а, ЭДи^/Дя» Ь\ — соответственно простран-
пространства непрерывных на отрезке [а, Ь] функций и много-
многочленов степени не выше чем п, рассматриваемых на том
же отрезке, с равномерной метрикой, и пусть Рп (х, /) —
интерполяционный многочлен степени п, принимающий
в узлах Xk, &=0,1,. . ., п, те же значения, что и функ-
функция /. Если через Рп обозначить оператор, ставящий в
соответствие функции /(ж) многочлен Рп(х, /),
Рп : С[а, Ъ]-*~д>п[а, Ь], то [\PJ=Xn, где слева стоит
норма оператора в пространстве линейных ограничен-
ограниченных операторов X (С \а, Ь], Рп[а, Ъ\) и
]|/ (х)~Рп (х, /) j|c [а> Ь] < A +А,„) Еп (/),
где En(f) — наилучшее приближение функции / алгеб-
раич. многочленами степени <:п.
При любом выборе на отрезке [а, Ъ\ узлов интерпсь
ляции НтХ„= + оо. Для равноотстоящих узлов суще-
"->¦¦» _,,
ствует такая постоянная с>0, что \,1^с2пп 1г. Для
узлов, совпадающих с нулями многочлена Чебышева,
Л. к. имеют минимальный порядок возрастания,
именно:
Х„ж In п.
Если функция / т раз дифференцируема на отрезке
[a, b], y={.!/fe}i?=o — заданный набор чисел («прибли-
(«приближений значений /(-t>)»), Рп(х, Y) — интерполяционный
многочлен степени п, принимающий в узлах х^, к=0,
1, . . ., и, значения у^,
max 2
2. lnk(x)\, n = 0, 1,...,
a <
TO
+ A,,;m max I/W) —г/fe |-
ft=o, l п
Л. к. Х„т произвольного отрезка [а, Ъ] связаны с
аналогичными константами Апт для отрезка [ — 1, 1]
соотношением
В частности Х„ = Л„. Л. Д. Кудрявцев.
ЛЕБЕГА МЕРА в R" — счетно-аддитивная мера
X, являющаяся продолжением объема как функции
n-мерных интервалов на более широкий класс jl мно-
множеств, измеримых по Лебегу. Класс Л содержит в себе
класс Si борелевских множеств и состоит из множеств
вида A\JB, где BcBj, A, B1c:Si и \(В1) = 0. Не всякое
подмножество R" принадлежит Ji- Для любого А?,Л
где inf берется по всевозможным счетным семействам
интервалов {/у} таким, что Ac[]Ij. Формула (*) имеет
смысл для каждого AdR" и определяет функцию мно-
множеств 'К* (совпадающую на Jl с К), называемую внеш-
внешней меройЛебега. Множество А принадлежит
Л тогда и только тогда, когда
для любого конечного интервала /; при всех
X* (A) = ini {X(U):Ac:U, U — открыто}
i' при всех А ? Л
\ (A)--=l* (A) = sup {к (F):A-=>F, F — компактно};
если ).* (Л)<оо, то последнее равенство достаточно для
включения А ?Л- Если О — ортогональный оператор в
R" и a?Rn, то Х(ОА + а) = Х(А) для любого А?Л-
Л. м. введена А. Лебегом [1].
Лит.: [1] lebesgue H., «Ann. mat. pura ed appl.»,
C) 1902, v. 7, p. 231; [2] Сакс С, Теория интеграла, пер.
с англ., М., 1949; [3] X а л м о ш П., Теория меры, пер. с англ.,
М., 1953; [4] Колмогоров А. Н., Фомин С. В.,
Элементы теории функций и функционального анализа, 5 изд.,
М., 1981. В. В. Сазонов.
ЛЕБЕГА МЕТОД СУММИРОВАНИЯ — один из ме-
методов суммирования тригонометрич. рядов. Ряд
¦~- + ^n^l ancosnx + bnsmnx (*)
суммируем в точке ха методом суммирова-
суммирования Лебега к сумме s, если в нек-рой окрестности
(х0—/г, xo-{-h) этой точки сходится проинтегрированный
ряд
НГ + 2Т=1 1Г {а" s[n пх~ъп cos пу)
и его сумма F (х) в точке ,т0 имеет симметрич. производ-
производную, равную s:
ц F(x^h)F(xh)
2"
Последнее условие можно представить также в виде
22_ ^
Л. м. с. не является регулярным в том смысле, что не
может суммировать любой сходящийся тригонометрия,
ряд (*) (см. Регулярные методы суммирования), од-
однако если ряд (*) есть ряд Фурье суммируемой функции
f(x), то он суммируем Л. м. с. почти всюду к f(x).
Метод предложен А. Лебегом [1].
Лит.: [1] Lebesgue H., Lecons sur les series trigonome-
triques. P., 190G; [2] Бари Н. К., Тригонометрические ряды,
M., 1961. Я. И. Волков.
ЛЕБЕГА МНОЖЕСТВО функции /, определен-
определенной на открытом множестве GcrR*,— множество точек
?G таких, что
Я (Д)->- 0 л (a)J Д
где Д — замкнутый куб, содержащий точку ;/, и X —
мера Лебега. Функция / здесь может быть действитель-
действительной ИЛИ векторной. В. В. Сазонов.
ЛЕБЕГА НЕРАВЕНСТВО — оценка уклонения част-
частных сумм ряда Фурье с помощью наилучших прибли-
приближений. Л. н. в случае тригонометрич. системы пони-
понимается как соотношение
max \Rn(f, *)|<(?„+1) ?„(/)> n = l, 2, . . . ,
x
где Rn (/, x) есть n-ii остаток (тригонометрического)
ряда Фурье непрерывной 2л-периодической функции /,
Ln — Лебега константа, En(j) — равномерное наилуч-
наилучшее приближение тригонометрич. полиномами порядка
п. Л. и.— соотношение общего характера: его аналоги
выполнены для произвольных ортонормированных си-
систем при соответствующих определениях констант
Лебега и наилучших приближений, а также для срав-
сравнения остатков рядов Фурье с наилучшими приближе-
приближениями в нормах других пространств, напр. Lp, 1<:р<эо.
Л. н. и подобные ому соотношения часто используются
в теории аппроксимации для получения оценок наи-
наилучших приближений снизу. Л. н. доказано А. Лебегом
(Н. Lebesguo).
Лит.: [1] Зигмунд А., Тригонометрические ряды,
пер. с англ., т. 1, М., 1965. К. И. Осколков.
ЛЕБЕГА ПРИЗНАК — признак точечной сходимос-
сходимости ряда Фурье. Если 2я-периодическая интегрируемая
на отрезке [0, 2я] функция f(x) в точке х0 при нек-ром
б>0 удовлетворяет условию
г^ /+\
dt=O, (*)
+ U j» t + h
где
то ряд Фурьо функции f (х) в точке х0 сходится к числу
S. Л. п. доказан А. Лебегом [1]. Условие (*) равносиль-
равносильна совокупности двух условий
ф*0М1 dt = 0A),A_+0.
Л. п. сильнее Дирихле признака, Жордана признака,
Дини признака, Балле Пуссена признака и Юнга приз-
признака.
Лит.: [1] Lebesgue H., «Math. Ann.», 1905, Bd 61,
S. 251—80; [2] Б а р и Н. К., Тригонометрические ряды, М.,
1961. Б. И. Голубое.
ЛЕБЕГА ПРОСТРАНСТВО — пространство с мерой
(М, $3, (х) (где М — нек-рое множество, S3 — нек-рая
а-алгебра его подмножеств, именуемых измеримыми, а
p, — нек-рая мера, определенная на измеримых мно-
множествах), изоморфное «стандартному образцу», состоя-
состоящему из нек-рого отрезка Д и не более чем счетного
множества точек а,- (в «крайних» случаях этот «образец»
может состоять только из отрезка Д или только из точек
о,-) и снабженному следующей мерой т: на Д берется
обычная Лебега мера, а каждой из точек а,- приписыва-
приписывается мера то(а,-)=то;>0; при этом мера предполагается
нормированной, т.е. [х (Af)=ro(A)+2ro/=l. «Изомор-
«Изоморфизм» здесь можно понимать в строгом смысле или по
mod 0; соответственно получается более узкий или более
широкий вариант понятия Л. п. (в последнем случае
можно говорить о Л. п. по mod 0). Можно дать опреде-
определение Л. п. в терминах «внутренних» свойств простран-
пространства с мерой (М, ф, (i) (см. [\\ — |3]).
Л. п.— наиболее часто встречающийся тип прост-
пространств с нормированной мерой, ибо любое полное сепа-
рабельное метрнч. пространство с нормированной мерой
(определенной на его борелевских подмножествах и
затем обычным образом пополненной) является Л. п.
Помимо свойств, общих всем пространствам с мерой,
Л. п. обладает рядом специфических «хоропшх» свойств.
Напр., любой автоморфизм булевой а-алгебры с ме-
мерой (iB, и.) порождается нек-рым автоморфизмом
Л. п. М. При ряде естественных операций из Л. п.
снова получается Л. п. Так, подмножество А положи-
положительной меры в Л. п. М само является Л. п. (его измери-
измеримыми подмножествами считаются те, которые измеримы
в М, а мора ц^ (Х)=ц (X)/fi (А)); прямое произведение
конечного или счетного числа Л. п. есть Л. п. Другие
свойства Л. п. связаны с измеримыми разбиениями.
Лит.: [1] Halmos P. R., Neumann J., «Ann.
Math.», 1Й42, v. 43, Л{« 2, p. 332—50; [2] P о х л и н В. А.,
«Матем. сб.», 1949, т. 25, Лг 1, с. 107—50; [3] Н а е г е п-
d о п с k J., «.Bull. Soc. math. Belg-.», 1973, t. 25, M 3, p. 243—58.
Д. В. Аносов.
ЛЕБЕГА РАЗЛОЖЕНИЕ — 1) Л. р. функции
ограниченной вариации — каноническое
представление функции ограниченной вариации в виде
суммы не более чем трех слагаемых. Если / (х) — функ-
функция ограниченной вариации на отрезке [а, Ъ], то она
может быть представлена в виде
f(x) = A(x)+S(x)+D(x),
где А (х) — абсолютно непрерывная функция (см.
Абсолютная непрерывность), S (х) — сингулярная
функция, a D (х) — скачков функция. В нек-рых слу-
случаях, напр., если f(a)=A (а), это представление един-
единственно. Л. р. установлено А. Лебегом (Н. Lebesgue,
1904, см. [1]).
Лит.: [1] Лебег А., Интегрирование и отыскание при-
примитивных функций, пер. с франц., М,— Л., 1934; [2] Н а т а н-
сон И. II., Теория функций вещественной переменной,
3 изд. М. 1974; [3] X а л ы о ш П., Теория меры. пер. с англ.,
М., 1953. Б. И. Голубое.
2) Л. р. з а д а н н о й на измеримом п р о-
странстве (X, 21) C1 есть а-алгебра) а-к о н е ч-
н о й обобщенной меры ц относительно опре-
определенной там же а-конечной обобщенной меры v — пред-
представление и. в виде (х=а+р, где а, р" суть а-конечные
обобщенные меры, причем а абсолютно непрерывна
относительно v, a P сингулярна относительно v. Такое
представление всегда возможно и единственно.
Лит.: [1] X а л м о ш П., Теория меры, пер. с англ., М.,
1953; [2] Дан форд Н., Шварц Д ж. Т., Линейные
операторы, пер. с англ., М., 1962. В. В. Сазонов.
ЛЕБЕГА РАЗМЕРНОСТЬ — размерность, определен-
определенная посредством покрытий; важнейший размерностный
инвариант dim X топологич. пространства X, откры-
открытый А. Лебегом [1]. Он высказал гипотезу, что dim In=n
для n-мерного куба /«. Л. Брауэр [21 впервые доказал
это, а также более сильное тождество: dim /n=Ind /"=
= п. Точное определение инварианта dim X (для класса
метрич. компактов) дал П. С. Урысон, доказавший для
пространств X этого класса тождество
dim X-^ind X=Ind X
(тождество Урысон а, см. Размерности тео-
теория), распространенное на класс всех сепарабельных
метрич. пространств в 1925 В. Гуревичем (W. Hurewicz)
и Л. А. Тумаркиным.
Для компактов X Л. р. определяется как наимень-
наименьшее целое число п, обладающее том свойством, что при
любом е>0 существует конечное открытое е-покрытие
компакта X, имеющее кратность <п+1; при атом е-
покрытием метрич. пространства наз. покрытие,
все элементы к-рого имеют диаметр <е, а кратно-
кратностью конечного покрытия пространства X наз.
наибольшее такое целое число к, что существует точка
пространства X, содержащаяся в к элементах данного
покрытия. Для произвольного нормального (в част-
частности, мотризуемого) пространства X Л. р. наз. наи-
наименьшее целое число п такое, что ко всякому конечному
открытому покрытию к» пространства X существует
вписанное в него (конечное открытое) покрытие а крат
ности п-\-\. При этом покрытие а наз. вписанный
в покрытие к», если каждый элемент покрытия гх яв-
является подмножеством хотя бы одного элемента покры-
покрытия к».
Лит.: [1] Lebesgue H., «Math. Ann.», 1911, Bd 70,
S. 166—68; [2] Brouwer L. E. J «J. reine und angew.
Math.», 1913, Bd 142, S. 146 — Ь2; [З] Александров И. С,
И а с ы н к о в Б. А., Введение в теорию размерности..., М.,
1973. П. С. Александров.
ЛЕБЕГА ТЕОРЕМА — 1) Л. т. в т е о р и и раз-
размерности: «-мерный куб для любого е>0 обладает
конечным замкнутым е-покрытием кратности ¦<«+],
it в то же время существует такое ео=е,и (и) >0, что любое
конечное замкнутое Е,|-покрытпе я-мерк-ого куба имеет
кратность r>n-f-l. Это утверждение привело в даль-
дальнейшем к определению основного размерност-
ного инварианта — Лебега размерности dim X нор-
нормального ТОПОЛОГИЧ. пространства X. В. А. Пасынков.
2) Л. т. о предельном переходе под
знаком интеграла; пусть на множестве Е
задана последовательность измеримых функций fn(x),
к-рая сходится почти всюду (или по мере) на Е к функ-
функции f(x)\ если на Е существует такая суммируемая
функция Ф(х), что при всех п и х
то }„(х) и f(x) суммируемы на Е и
I'm \ /„(*) dx
Впервые доказана А. Лебегом [1]. Важный частный слу-
случай Ф (.r) = const и Е с конечной мерой, также назы-
называемый Л. т., был им получен раньше [2].
Иногда Л. т. называют теорему, впервые доказанную
Б. Лови [3]: пусть на множестве Е задана неубываю-
неубывающая последовательность измеримых неотрицательных
функций 0</! (ж)</2 (#)•<. . . и
/(*)= lim /„(*)
П ->- оо
почти всюду, тогда
Лит.: [1] Lebesg-ue H., «Ann. Fac. sci. Univ. Touiouse
sci. math, et sci. phys.», 1909, v. 1, p. 25—117; [2] Lebes-
Lebesgue H., «Ann. mat. pura ed appl.», C), 1902, v. 7, p. 231; [3]
Levi В., «Rend. 1st. Lombardo sue lett», B), 1906, v. 39,
p. 775—80; [4] Сакс С, Теория интеграла, пер. с англ., М.,
1949; [5] Натансон И. П., Теория функций вещественной
переменной, 3 изд., М., 1974. Т. П. Лукашенко.
ЛЕБЕГА ТОЧКА — значение действительной пере-
переменной х такое, что для данной суммируемой по Ле-
'"'сту на (а, Ъ) функции f(x) выполнены соотношения
Согласно теореме Лебега множество точек, в
к-рых эти соотношения выполнены (т. н. множест-
множество Лебега), имеет полную меру (Лебега) на интер-
интервале (а, Ь), т. е. в почти каждой точке х, а именно, во
всех Л. т. функция f(x) в среднем мало отличается от ее
значения в близлежащих точках ,r=t/. Понятие Л. т.
имеет аналоги и для функций многих неременных. Это
понятие и утверждения типа приведенной теоремы Ле-
fiera лежат в основе различных исследований проблем
сходимости почти всюду, в частности исследований
сингулярных интегралов.
Лит.: [1] Колмогоров А. Н., Фомин С. В.,
Элементы теории функций и функционального анализа, л изд.,
М., 1981. Н. И. Осколпов.
ЛЕБЕГА ФУНКЦИИ — функции
dx, t?[a, b),
по Ф={ф&}/?=1 — заданная ортонормированная по
мере Лебега на отрезке \а, Ь] система функций, п--
— \, 2,. . . Аналогично определяются Л. ф. в случае,
когда ортонормированная система Ф задана на произ-
произвольном пространстве с мерой. Справедливо равенство
?*(*)= _ sup \Sn(f)(t)\, t?[a, b],
где
— частная сумма ряда Фурье функции / по системе Ф.
И случае, когда Ф — тригонометрия, система, Л. ф.
постоянны и сводятся к Лебега константам. Л. ф. вве-
введены А. Лебегом (Н. Lebesgno).
Лит.: [1] Качмаш С, Штейнгауз Г., Теория
[|Тогональных рядов, пер. с нем. М., 1958. Б. С. Кпшии.
ЛЕБЕГА ЧИСЛО — 1) Л. ч. открытого и о-
к р ы т и я о) метрич. пространства X — любое такое
число к>0, что как только подмножество А простран-
пространства X имеет диаметр <(•¦, так А содержится хотя бы
и одном элементе покрытия со. Для любого открытого
покрытия компакта существует хотя бы одно Л. ч.;
можно построить двухэлементное покрытие прямой,
для к-рого нот ни одного Л. ч.
2) Л. ч. системы замкнутых подмно-
подмножеств \ метрич. пространства X — любое такое число
€>(), что как только множество АаХ диаметра <:g пе-
пересекает все моменты какой-нибудь подсистемы К'
i истемы ?i, так пересечение элементов системы непусто.
Любая конечная система замкнутых подмножеств
компакта обладает хотя бы одним Л. ч. б. а. Пасынков.
ЛЕБЕГА — СТИЛТЬЕСА ИНТЕГРАЛ — обобщение
,1ебега интеграла. Для неотрицательной меры ц, назва-
название «интеграл Лебега—Стилтьеса» употребляется п том
(лучае, когда X=R" и и, не есть мора Лебега; тогда
интеграл \ fd\i определяется так же, как интеграл Ле-
йога в общем случае. Если мера [i знакопеременная, то
(i=(ii—|^о, где \1г и (х.2 — неотрицательные меры, и
Л,—С. и."
при условии, что оба интеграла в правой части суще-
существуют. Для X=R1 счетная аддитивность и ограничен-
ограниченность меры (х эквит!алентна тому, что мера порождена
нек-рой функцией Ф ограниченной вариации. В таком
случае Л.— С. и. записывается в виде
Для дискретной меры Л.— С. и. представляет собой
числовой ряд.
Лит.: [1] Камке Е., Интеграл Лебега — Стилтьеса,
пер. с нем., М., 1959. И. А. Виноградова.
ЛЕБЕГОВСКИЙ СПЕКТР — термин спектральной
теории. Пусть А — самосопряженный, a U — уни-
унитарный операторы, действующие в гильбертовом про-
пространстве Н. Оператор А, соответственно U, имеет
простой спектр Лебега, если он унитарно
эквивалентен оператору умножения на /. в пространстве
комплекснозначных Лункций /(X), к-рые определены на
действительной оси R, соответственно на окружности
и для которых
imp = 5 i/wi2dx.< оо,
где интегрирование ведется по обычной Лебега мере
на Rj соответственно на S1, откуда и назв. Л. с. (см.
Унитарно эквивалентные операторы). Для U это опре-
определение экпивалентно следующему: в // существует
такой ортонормироваиный базис е/, /=0, ±\, ±2,. . .,
что Uej=ej + l. Далее, оператор имеет спектр Ле-
Лебега, если // можно разложить в ортогональную
прямую сумму инвариантных подпространств, в каж-
каждом из к-рых оператор имеет простой Л. с. Хотя для
данного оператора может быть много таких разложений,
число «.слагаемых» для ка;г.;;ого из них одно и то же
(оно может быть и бесконечным кардинальным числом).
Это число наз. кратностью Л. с. Наконец, ана-
аналогичные понятия можно ввести для однопараметрич.
группы унитарных операторов U(t), непрерывной в
слабой (или, что в данном случае то же, сильной) опе-
операторной топологии. По теореме Стоуна U(t)--=elAi,
где А — нек-рый самосопряженный оператор. Если А
имеет Л. с. нек-рой кратности, то говорят, что теми же
свойствами обладает и U(t). Напр., группа U(t) имеет
простой Л. с, если она унитарно эквивалентна группе
f(X) —,-e'Mf(X) bL2(R), а та в свою очередь эквивалент-
эквивалентна группе сдвигов f (X) —>- f(X-\-t) в том же пространстве
L2 (R). Д. В. Аносов.
ЛЕБЕДЕВА ПРЕОБРАЗОВАНИЕ — интегральное
преобразование вида
F (т) = $ ~ I lix (¦'-) -\-I-H П1 Kit (or) f (x) dx, 0 < т < ой,
где /v (x), Kv (х) — модифицированные цилиндрич.
функции. Введено Ы. Н. Лебедевым [1]. Если
(О, 1), x^j{x)^L(\, oo),
то почти при всех х имеет место формула обращения
F (т> т sh л
о
Лит.: [1] Лебедев Н. Н., «Сиб. матем. ж.», 1962, т. 3,
№ 2, с. 213 — 22. Ю. А. Брычков, А. П. Прудников.
ЛЁВЕНХЕЙМА — СКОЛЕМА ТЕОРЕМА — см.
Гё'деля теорема о полноте.
ЛЕВИ КАНОНИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ —
формула для логарифма характеристич. функции 1пф (к)
безгранично делимого распределения:
где характеристики Л. к. и, у, а2, М, N удовлетворяют
следующим условиям: —оо<^<оо, а3^0, М (х) и
Лт (х) — неубывающие непрерывные слева функции на
(—оо, 0) и @, оо) соответственно и такие, что
lim N(x) = lim М(г)=0
f ° x* dM (х) < оо, V х* dN (x) < оо .
Каждому безгранично делимому распределению соот-
соответствует единственный набор характеристик Л. к. п.
у, а'1, М, N, и обратно, при приведенных выше ус-
условиях на у, о-, М п N по любому такому набору
Л. к. п. определяет логарифм характернстич. функции
нек-рого безгранично делимого распределения.
Так, для нормального распределения со средним a
п дисперсией а2
у=а, о*=о2, Лг(ж)=0, М(:г)=О.
Для распределения Пуассона с параметром А,
у = А/2, а2 = 0, М (х) — 0, N(x) = —k при ,г<1,
N (а-) =0 при х > 1.
Устойчивому распределению с показателем а, 0<
<а<2, соответствует Л. к. п. с
а'2-=0 и нек-рым у, М (х) =cj\ x \a, N(x) = —cjxa,
где с,-^0, i=l, 2, — постоянные (с!+с2>0). Л. к. п.
безгранично делимого распределения было предложено
П. Леви (P. Levy, 1934). Оно является обобщением
формулы А. Н. Колмогорова, найденной им в 1932 для
случая, когда безгранично делимое распределение
имеет конечную дисперсию. Для 1пф (К) имеется экви-
эквивалентная Л. к. п. формула, предложенная в 1937
А. Я. Хинчиным и называемая Леей— Хинчина кано-
каноническим представлением. Вероятностный смысл функ-
функций Л' и М и область использования Л. к. п. опреде-
определяются следующим: каждой безгранично делимой функ-
функции распределения F (х) соответствует стохастически
непрерывный однородный процесс с независимыми
приращениями
X = {X(t), 0<t < оо}, Х@)=0,
такой, что
В свою очередь сепарабельнын процесс X упомянутого
типа имеет с вероятностью 1 выборочные траектории
без разрывов второго рода, и поэтому для Ь>а>0
определена случайная величина Y ([а, Ь]), равная числу
элементов в множестве
i:a< lim X (t + т)— lim X (t — т) < Ь, О < t «s l\ •
т i 0 т | 0 I
В этих обозначениях для функции N, соответствующей
F(x), имеет место следующее соотношение
Е {Y ([a, b])} = N (b) — N (a).
Аналогичное соотношение имеет место и для функ-
функции М.
В терминах характеристик Л. к. п. функции распре-
распределения Р {X A) <>} легко выражаются многие свойства
поведения выборочных траекторий сепарабельного
процесса X. В частности, при а2=0
lim N (х) > — оо, lim M (х) < оо,
х -> о х ^ О
почти все выборочные функции X с вероятностью 1 будут
ступенчатыми функциями с конечным числом скачков
на любом конечном интервале. Если о=0 и
то выборочные траектории X с вероятностью 1 имеют
ограниченную вариацию на любом конечном интервале.
Непосредственно через характеристики Л. к. п.
Р{ХA) < .г} определяется инфинитезимальный опе-
оператор, соответствующий процессу X, рассматриваемому
как марковская случайная функция. Многие аналитнч.
свойства безгранично делимой функции распределения
непосредственно выражаются в терминах характери-
характеристик ее Л. к. п.
Имеются аналоги Л. к. п. для безгранично делимых
распределений, задаваемых на широком классе алгсб-
раич. структур.
Лит.: [1] Г н е д е н к о Б. В., Колмогоров А. Н.,
Предельные распределения для сумм независимых случайных
величин, М.— Л., 1949; [2] Петров В. В., Суммы незави-
независимых случайных величин, М., 1972; [3] Прохоров Ю. В.,
Розанов Ю. А., Теория вероятностей, 2 изд., М., 1973;
[4] Г и х м а н И. И., Скороход А. В., Теория случай-
случайных процессов, т. 2, М., 1973; [5] И т о К., Вероятностные про-
процессы, пер. с япон., т. 2, М., 1963. В. А. Рогозин.
ЛЕВИ МЕТРИКА — метрика L в пространстве Jf
функций распределения одномерных случайных вели-
величин:
L^=L(F, G) = inf{e:F (.r — e) —
— e<G(.r)</'1(a- + s) + s, V4
для любых F, G??f. Введена П. Леви (см. [1]). Если
между графиками функций F и G вписывать квадраты
со сторонами, параллельными осям координат (в точ-
точках разрыва графики дополняются вертикальными
отрезками), то сторона наибольшего из них равна L.
Л. м. можно рассматривать как частный случай Леви,—
Прохорова метрики. Определение Л. м. переносится
на множество М всевозможных неубывающих функции,
заданных на R1 (при этом допускаются бесконечные
значения метрики).
Важнейшие свойства Л. м.:
1) Л. м. индуцирует в ^слабую топологию. Метрич.
пространство (§~, L) является сепарабельным и полным.
Сходимость последовательности функций из М в метри-
метрике L эквивалентна полной сходимости.
2) Если F?M it
F_1(x) = ini{t: F (t) < х},
то для любых F, G?M
L(F, G)=L(F_U С_г).
3) Регулярность Л. м.: для любых F, G, II ^^
L (F * Н, G * #)< L (F, G),
следствием этого свойства является свойство полу-
полуаддитивности:
L(F1*F2, G1h-.G2XL(Fu G^ + L^F^ G2)
и «неравенство сглаживания»:
L(F, GXL(F*H, G X H) + 2L(E, H)
(E — распределение, вырожденное в нуле).
4) Если aft>0, Fk, Gft?f~, то
A> Zj Mft) maxL (Fk, G^).
5) Если f>r (/<'), r>0,— абсолютньп! момент распре-
распределения F, то
L (F, ?)ss {Рл (^)}r/(r: X)-
6) Л. м. на М связана со средней метрикой
Pi = Pi (Л G)=\ \F(x)-G(x)\dx
неравенством
7) Л. м. на М связана с равномерной метрикой
соотношениями
L<p<L + min{<?F(L), Qo(L)}, (*)
где
<?F(x) = sup \F (t + x) — F (t)\
t
(Qf(x) — концентрации функция, если F(^{jf). В ча-
частности, если одна из функций, напр. G, имеет равно-
равномерно ограниченную производную, то
p<(l+supG' (x))L.
X
Следствием (*) является теорема Попа — Гливенко об
эквивалентности слабой и равномерной сходимости
в том случае, когда предельное распределение непре-
непрерывно.
8) Если Fa, o(x)= F(ахлса), где а и а>0 — кон-
константы, то для любых F, G?(|F
L(aF, oG)<aL(Fo a, GO<J)
(в частности, Л. м. инвариантна относительно сдвига
распределений) и
Jf* L (Fa, о- Ge>a)=p(F,G).
9) Если /, g — характеристич. функции, соответст-
вующие распределениям F, G, то для любых Т
Понятие Л. м. можно распространить на случай рас-
распределений в R".
Лит.: [1] Levy P., Theorie de l'addition des variables
lioatoires, P., 1937; 2 ed., P., 1954; [2] Золотарев В. М.,
Тр. Матем. ин-та АН СССР», 1971, т. 112, с. 224 — 31; [3] 3 о л о-
: а р е в В. М., Сенатов В. В., «Теория вероятн. и ее
пимен.», 1975, т. 20, № 2, с. 239 — 50; [4] Линии к Ю. В.,
петровский И. В., Разложения случайных величин и
векторов, М., 1972. В. М. Золотарев.
ЛЕВИ НЕРАВЕНСТВО — неравенство для распре-
распределения максимума сумм независимых случайных
ирлпчпн, центрированных соответствующими медиа-
медианами. Именно, пусть X], . . ., Хп — независимые слу-
случайные величины, Sfi = 2il^1X; и тХ — медиана слу-
случайной величины X, тогда для любого х имеет место
• I. н.
Р{ max (Sk-m(Sk-Sn))^x}<2P {Sn^x}
1 < ft < n
P{ max \Sk — m(Sk — Sn)\^x}<2?{\Sn\^x}.
Непосредственным следствием этих неравенств являют-
п Л. н. для симметрично распределенных случайных
¦;«шчин Xt, . . ., Хп:
Р { max Sk Ss x} s? 2P {Sn ^s x}
1< ft<
P{ max | Sk | 5э л-} s? 2P {| Sn | 5эх}.
1 < A < n
Л. н. можно рассматривать как обобщение Колмого-
Колмогорова неравенства. Л. н. было получено П. Леви [1]
при исследовании общих проблем сходимости распре-
распределений сумм независимых случайных величин к устой-
устойчивым законам. Существует обобщение Л. н. для мар-
мартингалов.
Лит.: [1] Levy P., Theorie de l'addition des variables
aleatoires, P., 1937; 2 <5d., P., 1(^54; [2] Л о э в М., Теория веро-
вероятностей, пер. с англ., М., 11N2. А. В. Прохоров.
ЛЕВИ ПРОБЛЕМА — проблема геометрич. характе-
ризации областей данного аналитич. пространства,
являющихся пространствами Штейна; была поставлена
Э. Леви [1] для областей аффинного пространства С" в
следующей форме. Пусть D — область в С™, каждая
граничная точка ? к-рой обладает следующим свойством:
существуют окрестность U течки ? в Си голоморфная
функция в Uf]D, не продолжаемая гололюрфно в точ-
точку ?. Является ли D голоморфности областью? Ука-
Указанное свойство равносильно любому из следующих
утверждений об области D: 1) ни для какой ±€.dD
не существует последовательности ограниченных голо-
голоморфных поверхностей Л\> , сходящейся к голоморфной
поверхности S, причем dSv -+.0S, Sv, dSaD, ц"^5;
2) область D псевдовыпукла, т. е. — logplz, dD), z?Z),
где р — евклидово расстояние,—¦ плюрисубгармоничная
функция в D; 3) D — псовдовыпуклое многообразие,
т. е. в D существует плюрисубгармонич. функция,
стремящаяся к +оо при приближении к dD. Л. п. для
С" была положительно решена в 1953—54 независимо
К. Ока (К. Ока), X. Бремерманом (Н. Bremer-
mann) и Ф. Норге (F. Norguet), причем К. Ока решил
проблему в более общей постановке, относящейся к
наложения областям над С" (см. [2] — [6]). Результат
К. Ока обобщается на области наложения над любым
многообразием Штейна: если такая область D является
псевдовыиуклым многообразием, то D — многообразие
Штейна. Л. п. положительно решена it в ряде других
случаев, напр, для некомпактных областей наложения
над проективным пространством СР" или над кэлеровым
многообразием, на к-ром существует строго плюрисуб-
плюрисубгармонич. функция (см. [2]), для областей в кэлеровом
многообразии с положительной голоморфной бисекци-
онной кривизной [7]. В то же время известны примеры
псовдовыпуклых многообразий и областей, не являю-
являющихся многообразиями Штейна и даже не голоморфно
выпуклых. Необходимым и достаточным условием
штейновости комплексного пространства является его
сильная псевдовыпуклость (см. Псевдовыпуклостъ и
псевдовогнутоетъ). Далее, сильно псевдовыпуклая
область любого комплексного пространства голоморф-
голоморфно выпукла и является собственной модификацией не-
некоторого пространства Штейна (см. [2], 14]).
Л. п. может быть поставлена также для областей D
в бесконечномерном топологич. комплексном векторном
пространстве Е. Если Е локально выпукло и D —
область голоморфности, то D псевдовыпукла, т. е. в D
существует плюрисубгармонич. функпия, стремящая-
стремящаяся к +оо при приближении к 3D. Обратная теорема
неверна даже в банаховых пространствах, но доказана
для банаховых пространств со счетным базисом и ряда
других классов пространств Е (см. [2]).
Лит.: [1] Le v i E. E., «Ann. mat. pura ed appl.», 1911,
v. 18, p. 69—79; [2] Итоги науки и техники. Алгебра. Тополо-
Топология. Геометрия, т. 11, М., 1974, с. 125 — 51; 1977, т. 15, с. 93 —
171; [3] Владимиров В. С., Методы теории функций мно-
многих комплексных переменных, М., 1964; [4] Г а н н и н г Р.,
Р о с с и X., Аналитические функции многих комплексных пе-
переменных, пер. с англ., М., 1969; [о] Фукс Б. А., Спспиаль-
ные главы теории аналитических функций многих комплексных
переменных, М., 1963; [б] Шабат Б. В., Введение в ком-
комплексный анализ, 2 изд., ч. 2 — Функции нескольких перемен-
переменных, М., 1976; [7] Suzuki О., «Publ. Res. Inst. Math. Sci.
Kyoto Univ.», 1976, v. 12, p. 439 — 45. А. Л. Онищик.
ЛЕВИ УСЛОВИЕ — поддающееся эффективной про-
проверке условие псевдовыпуклостн в смысле Леви обла-
областей комплексного пространства С", предложенное
Э. Леви [1] и состоящее в следующем. Пусть область
граничной точки
задана ус-
усD в окрестности
ловием
D Г) Ul ={z = (zb . . ., zn) ? Ut,; ф (г) = ф (z, ~z) < 0},
где действительная функция ф принадлежит классу
С2 (Ut,) и grad ф (^)фО. Тогда, если область D псевдовы-
пукла в точке ? в смысле Леви, то неотрицателен (ком-
(комплексный) гессиан
~" *'" =0 A)
при всех а== (а1; . . ., а„)?С", комплексно ортогональ-
ортогональных grad ф(?)> т. е. таких, что
Лу [и) (lfc = U. ynj
Обратно, если в точке L,?dD выполнено условие
И (I; Ф) (а, а) > 0 C)
при всех аФО, удовлетворяющих условию B), то об-
область D псевдовыпукла в смысле Леви в точке ?.
При п = 2 в приведенных формулировках неравенства
A), C) можно заменить соответственно еще более про-
простыми равносильными неравенствами L (
Ь(Ч>)@>0, где
„ 9ф Эф
92ф
9г, Эг, dz1
9ф 92ф
9г2 9г., с*г2
9z2 9z2
— определитель Леви функции ф (z).
Л. у. A) — C) обобщается также для областей
на комплексных многообразиях (см. [4]).
Лит.: [1] Levi E. E., «Ann. mat. pura ed app].», 1910,
v. 17, p. 61—87; 1911, v. 18, p. B9—79; [2j В л а д и м и р о в В. С,
Методы теории функций многих комплексных переменных,
М., 1964; [3] Ш а б а т Б. В., Введение в комплексный анализ,
2 изд., ч. 2, М., 1978; [4] Г а н н и н г Р., Р о с с и X., Ана-
Аналитические функции многих комплексных переменных, нер. с
англ., М., 1969. Е. Д. Соломенцев.
ЛЕВИ — КРАМЕРА ТЕОРЕМА: если сумма двух
независимых непостоянных случайных величин нор-
нормально распределена, то и каждое из слагаемых нор-
нормально распределено; высказана П. Леви [1] и дока-
доказана Г. Крамером [2]. Эквивалентные формулировки:
1) если композиция двух собственных распределений
является нормальным распределением, то и каждое
из них является нормальным распределением; 2) если
фх (() и ф2(?) —характеристич. функции и
Ф1 (*)
= ехр (-
— оо <Р< оо,
ф(),
(*)
В формулировке 1) Л.— К. т. допускает обобщение
на композицию двух знакопеременных мер с ограниче-
ограничениями на отрицательную вариацию; в формулировке
2) — на случаи, когда вместо условия (*) рассматри-
рассматривается условие
IT"
-oo<p< оо,
где 4>i(t), . . ., <Pm(t) — характеристич. функции,
ai, ¦ ¦ •> ат — положительные числа, Е — множество
действительных чисел с точкой сгущения в нуле.
Имеются обобщения Л.— К. т. на случайные величины
в евклидовых пространствах и в локально компактных
абелевых группах.
Л.—К. т. обладает свойством устойчивости, т. е.
близость распределения суммы независимых случайных
величин к нормальному влечет близость распределения
каждого из слагаемых к нормальному; известны коли-
количественные оценки устойчивости.
Теоремы, аналогичные Л.— К. т., получены для рас-
распределения Пуассона, для композиции распределения
Пуассона и нормального, для других классов безгра-
безгранично делимых распределений (см. [6]).
Лит.: [1] Levy P., «J. math, pures et appl.», 1935, t. 14,
p. 347 — 402; [2] Cramer H., «Math. Z.», 1936, Bd 41, S. 405 —
14; [3] Райков Д. А., «Докл. АН СССР», 1937, т. 14,
с. 9 —12; [4] Л и и и и к Ю. В., «Теория вероятн. и ее примен.»,
1957, т. 2, с. 34—59; [5] Сапогов Н. А., «Вестн. Ленингр.
ун-та. Сер. матем., механ. и астр.», 1959, .№ 19, о. 78—105; [в]
Л и н н и к Ю. В., Островский И. В., Разложения слу-
случайных величин и векторов, М., 1972; [7] Ф е л ь д м а н Г. М.,
«Теория вероятн. и ее примен.», 1977, т. 22, вып. 1, с. 136 — 43.
К. В. Островский.
ЛЕВИ — МАЛЬЦЕВА РАЗЛОЖЕНИЕ — представ-
представление конечномерной алгебры Ли L над полем харак-
характеристики нуль в виде прямой суммы (векторных про-
пространств) ее радикала R (максимального разрешимого
идеала в L) и нек-рой нолупростой подалгебры Ли
SaL. Получено Э. Леви [1] и А. И. Мальцевым [21.
Теорема Леви — Мальцева утверждает, что такое раз-
разложение L = R-\- S всегда существует; при этом подал-
подалгебра S определена однозначно с точностью до автомор-
автоморфизма вида exp(adz), где adz — внутреннее дифферен-
дифференцирование алгебры Ли /., определяемое нек-рым эле-
элементом z нильрадикала (наибольшего ннлытотентного
идеала) алгебры /.. Если G — связная односвязная
вещественная группа Ли, то в группе G существуют
замкнутые односвязные аналитич. подгруппы R и S,
где R — максимальный связный замкнутый разреши-
разрешимый нормальный делитель в G, S — полупростая под-
подгруппа в G, Rf\S^ {е} и отображение (г, s) —>- rs,
r?R, s?S, является аналитич. изоморфизмом многооб-
многообразия RXS на О; разложение G=RS= SR также наз.
в этом случае Л.— М. р.
Лит.: [1] Levi E. E., «Atti Accad. sci. Torino. Cl. sci.
fis., mat. e natur.», 1905, v. 40, p. 3 — 17; [2] Мальцев А. И.,
«Докл. АН СССР», 1942, т. 36, № 2, с. 46 — 50; [3] Джекоб-
сон Н., Алгебры Ли, пер. с англ., М., 1964; [4] К и р и л-
лов А. А., Элементы теории представлении, М., 1972; [5]
Наймарк М. А., Теория представлений групп, М., 1976.
А. И. Штерн.
ЛЕВИ — ПРОХОРОВА МЕТРИКА — метрика в про-
пространстве ЗЛ конечных борелевских мер на метрич.
пространстве (U, d), определяемая равенством:
к(Р, <?)=inf{e: Р (/!)<<? (Л?)+е, Q (А) *? Р (А* )+е;
МА с= Щ,
где 5Р есть а-алгебра борелевских множеств из (U, d) и
A* ={z: d(x, y)<e, у ? А}.
Л.— П. м. введена Ю. В. Прохоровым [1] как обоб-
обобщение Леви метрики. Величина я не изменится, если в
ее определении оставить одно из двух неравенств и
заменить 58 системой всех открытых или всех замкну-
замкнутых множеств из !8 (см. [2]).
Важнейшие свойства Л.— П. м.
1) Метрич. пространство (ЩГ[, я) сепарабельно тогда
и только тогда, когда сепарабельно (U, d).
2) Пространство (U, d) полно, если полно простран-
пространство EJJ, я). Обратное верно, если меры из ЭЛ имеют
сепарабольиые носители.
3) В пространстве QJ@ Л.— П. м. обладает свойства-
свойствами, аналогичными свойствам метрики Леви. Именно,
свойством регулярности 3) и его следствиями, свойст-
свойствами 4), 5), свойством G) (в случае C/=R.X), частично
свойством 7) (именно, я<:ТО, а также аналогом свой-
свойства 8), если (U, d) является линейным нормированным
пространством: если Ра,п (А) ~Р{аА-\-а), где <т>0,
a?U, то для любых Р
л(аР, oQ)^an.(Pa,a, Qa.o),
lim л(Ра о. Qa <j)^var(P, <?).
<J->- О
4) В случае U—Rk Л.— П. м. в <Ш0 оценивается
с помощью характерпстич. функций /, g, соответст-
соответствующих мерам Р, Q (см. [3], 14]).
5) Л.— П. м. является минимальной метрикой по от-
отношению к расстоянию по вероятности
х(Х, F) = inf {t: P {d{X, Y) > е} < е}
iCM. [5]).
Лит.: [1] Прохоров Ю. В., «Теория вероятн. и ее
||.», 1956, т. 1, в. 2, с. 177—238; [2] Dudley R. М.
•lath. Statistics», 1968, v. 39, К. 5, p. 1563—72; [3] Ю р и н-
,| В. В. «Теория вероятн. и ее примени», 1975, т. 20, в. 1
с. о —12: [4] Абрамов В. А., там ше, 1976, т. 21, в. 2,
с. 406—1М; [5] Strassen V., «Ann. Math. Statistics», 1965,
v. 36, ,\'j 2, p. 423—39; [6] Биллингслей П., Сходимость
вероятностных мер, пер. с англ., М., 1977. В. М. Золотарев.
ЛЕВИ - ХИНЧННА КАНОНИЧЕСКОЕ ПРЕД-
ПРЕДСТАВЛЕНИЕ — формула для логарифма характерис-
тич. функции 1пф (/„) безгранично делимого распределе-
распределения:
где подинтегральная функция при х=0 равна — Х2/2
п характеристики Л.— X. к. п. у и G удовлетворяют
следующим условиям: у — действительное число,
G(x) — неубывающая непрерывная слева функция
ограниченной вариации.
Л. — X. к. п. было предложено А. Я. Хинчиным
A937) и эквивалентно формуле, предложенной несколь-
несколько ранре П. Леви (P. Levy, 1934) и называемой Леей
каноническим представлением. Каждому безгранично
делимому распределению соответствует единственный
набор характеристик Л.— X. к. п. у и G, и обратно,
при условиях на у и G, приведенных выше, по любому
такому набору Л.— X. к. п. определяет логарифм ха-
характерпстич. функции нек-рого безгранично делимого
распределения. Для слабой сходимости последователь-
последовательности безгранично делимых распределений, определяе-
определяемых характеристиками уп, Gn, n=l, 2, . . ., к распре-
распределению (которое необходимо будет безгранично де-
делимым) с характеристиками у и G необходимо и доста-
.очно, чтобы liniYn"=Y и Gn вполне сходились к G при
п —>- оо.
Лит. см. при ст. Лови Каноническое представление.
ЛЕВИ-ЧИВИТА СВЯЗНОСТЬ — аффинная^Твяз-
несть на римановом пространстве М, к-рая является
ии.чановой связностью (т. е. связностью, относительно
к-рой метрич. тензор ковариантно постоянный) и имеет
нулевое кручение. Аффинная связность на М опреде-
определяется этими условиями однозначно, так что каждое
риманово пространство М обладает единственной
Л.-Ч. с. Впервые это понятие возникло в 1917 у
Т. Леви-Чивита [1] в виде понятия параллельного пере-
перенесения вектора в римановой геометрии. Сама идея
посходит еще к Ф. Миндингу (F. Minding), к-рый в 1837
ввел понятие развертки линии на поверхности.
Относительно локальной координатной системы в
М, где ds2=g;jdx'dxj', Л.-Ч. с. на At определяется
формами а>)= }.Adxk, где
ее тензор кривизны Rjki определяется формулой
da)-}-(Ok Л wf = y R'jkidxk Л dxl.
Пусть Rij,ki=gimR?ki, тогда
n l ) jk /i ik
dxJ'o.vk)
при этом:
¦R;y, « = — fi;y, ift! -Я/у, /м = Rki,
Тензор кривизны Л.-Ч. с. имеет и-(и- —1)'12 сущест-
существенных компонент, где «=dim М. Напр., при я=2
имеется только одна существенная компонента Л12> i2 =
= Jfdet|g,y|, где X — гауссова кривизна.
Если риманово пространство М изометрически по-
погружено в евклидово пространство Ь'дг, то его Л.-Ч. с.
характеризуется следующим образом: для произволь-
произвольных двух векторных полей X, У на MdE^ ковариант-
ная производная (VyX)x в точке х?М является
ортогональной проекцией на касательную плоскость
Tx(M)aEjy обычного дифференциала (dYX)x поля Л"
в Eji/ относительно вектора YX?TX(M). Другими
словами, отображение соседней бесконечно близкой
касательной плоскости на исходную совершается пу-
путем ортогонального проектирования.
Лит.: [1] Lcvi-Givita Т., «Rend. Circolo math. Pa-
Palermo», 1917, v. 42, p. 173—205; [2] Громол Д., К л и н-
генберг В., Мейер В., Риманова геометрия в целом,
пер. с нем., М., 1971; [3] Р а ш е в с к и й П. К., Риманова
геометрия и тензорный анализ, 3 изд., М., 1967. Ю. Г. Лутистс
ЛЁВНЕРА МЕТОД, метод Л ё в н е р а пара-
параметрических представлений одно-
однолистных функций, параметричес-
параметрический метод Лёвнер а,— метод в теории одноли-
однолистных функций, заключающийся в использовании
Лёвиера уравнения для решения экстремальных задач.
Метод был предложен К. Лёвнером [1]. Он основан на
том, что множество функций /(z), /@) = 0, регулярных
и однолистных в круге Е= \z : \z\ <1} и отображающих
Е на области типа (s), получаемые из круга |ш1<1 про-
проведением разреза вдоль части нек-рой жордяновой
дуги, исходящей пз точки окружности |и>| = 1 и не
проходящей через точку ш=0, плотно (в топологии
равномерной сходимости функций внутри круга Е) во
всем семействе функций /(z), /@) = 0, регулярных п
однолистных в Е и таких, что |/(z)|<l в Е. Связывая
длину удаляемой дуги с параметром t, удается устано-
установить, что функция w=f(z), /@) = 0, однолистно отобра-
отображающая Е на область D типа (s), является решением
дифференциального уравнения (см. Лёвнера уравнение)
df(z, t)_ ,, tS l + fe(t)/(z, t) .
—qI — 7 (z. 4 x_k (t)f(Z, t) ' (">
f(z, t(j) = f(z), удовлетворяющим начальному условию
f(z, 0)=z. Здесь t?[0, t0], к(t) — непрерывная комп-
лекснозначная функция на промежутке [0, if0), соот-
соответствующая области D, причем |fc(f)| = l. К. Лёвнеь
использовал этот метод для получения точных оценок
коэффициентов с3 и Ьп, п=2, 3,. . ., разложений
в классе S функций ш=/(г), /@) = 0, /'@) = 1, регуляр-
регулярных и однолистных в Е.
Л. м. был использован (см. [3]) для получения основ-
основных результатов теории однолистных функций (тео-
(теорем искажения, взаимного роста, теорем вращения).
Пусть S' — подкласс функций f(z) класса S, имеющих в
Е представление
1(z)= lim e'/(z, t),
где/(г, t) как функция от z регулярна и однолистна в
Е, |/B, t)l<! в ^./@, i) = 0, /z@, г)>0, а как функ-
функция от I, 0<?<оо, является решением дифференциаль-
дифференциального уравнения (*), удовлетворяющим начальному
условию /(г, 0) = z; k(t) в уравнении (*) — любая
комплекснозначная функция, кусочно непрерывная и
по модулю равная единице на промежутке [0, оо).
Для того чтобы оценить какую-либо величину в классе
S, достаточно оценить ее в подклассе S', поскольку
любую функцию f(z) класса S можно аппроксимиро-
аппроксимировать функциями /„(г), /л@) = 0, /п@)>0, каждая из
к-рых однолистно отображает Е на плоскость ш с раз-
разрезом по жордановой дуге, уходящей в оо и не прохо-
проходящей через w=0, а значит и функциями /п(г)//л@)??'.
При этой аппроксимации оцениваемые величины для
аппроксимирующих функций сходятся к той же величи-
величине, что и для функции /(z).
Л. м. используется в работах по теории однолист-
однолистных функций (см. [3] с. 536—37); он часто приводит
к успеху при получении явных оценок, но, как прави-
правило, не обеспечивает описания всех экстремальных
функций и полной информации об их единственности.
Для полного решения экстремальных задач Л. м. обыч-
обычно сочетают с вариационным методом (см. [3] с. 538—
539 и Вариационно-параметрический метод). Л. м.
распространен на двусвязные области. Получено обоб-
обобщенное уравнение типа уравнения Лёвнера для много-
связных областей, для автоморфных функций (см. [4]).
Л™.: [lllijwner К., «Math. Ann.», 1923, Bd 89. S. 103—
21; [2] P e s с h 1 E., «J. reine und angew. Math.», 1936, Bd 176,
S. fil—94; [3] Г о л у з и н Г. М., Геометрическая теория функ-
функций комплексного переменного, 2 изд., М., 1966; [4] Алек-
Александров И. А., Параметрические продолжения в теории
однолистных функций, М., 1976. Е. Г. Голузина.
ЛЁВНЕРА УРАВНЕНИЕ — дифференциальное урав-
уравнение вида
dw I +eia{t) w
- JD
dt i_e aa> w '
где a (t) — действительная непрерывная на интервале
— оо <?<оо функция. Обобщением Л. у. является урав-
уравнение Куфарева — Лёвнера (у. К. — Л.):
dw „ , .,
¦гг = — wP (и>, t),
где Р (w, t), Ы<1, —оо <?<оо,— измеримая по t
при фиксированном w и регулярная по w функция с
положительной действительной частью, нормирован-
нормированная условием Р@, t)=i. Л. у. и у. К.— Л., возник-
возникшие в теории однолистных функций, лежат в основе
параметрич. метода исследования экстремальных
проблем конформного отображения.
Решение w(t, z, т), w(r, z, x) = z, у. К.— Л., рас-
рассматриваемое как функция начального значения z,
при всяком t~>x конформно отображает круг Ы <1
на однолистную односвязную область, принадлежащую
кругу |ц>1<1. По формуле
/ (z) = a + b\\metw{t, z, 0)
при надлежащем выборе Р (ш, /) в у. К.— Л. и комплек-
комплексных постоянных а. Ь можно получить произвольную
регулярную однолистную функпию в круге 1г|<1.
Л. у. порождает на этом пути, в частности, конформные
отображения круга на области, получаемые из всей
плоскости проведением разреза вдоль нек-рой дуги
Жордана (см. [1] — [4]).
Дифференциальное уравнение с частными производ-
производными
к-рому удовлетворяет функция
f (z, x) = lim e*w (t, s, i),
также называют у. К.— Л.
Л. у. было установлено К. Лёвнером [1]; у. К.— Л.
впервые было получено П. П. Куфаревым (см. [5]).
Лит.: [1] L 6 w n е г К.. «Math. Ann.», 1923, Bd S9, Ms 2,
S. 103 — 21; [2] К у ф а р е в П. П., «Ученые зап. Томск, ун-та»,
1947, т. 5, с. 20—21; [3] Pommerenke С, «J. reme und ап-
gew. Math.», 1965, Bd 218, S. 159 — 73; [4] Г у т л я н с к и й В. Я.,
«Докл. АН СССР», 1970, т. 194, М5 4, с. 750 — 53; [5] К у-
фарев П. П., «Матем. сб.», 1943, т. 13, № 1, с. К7 — 118;
[6] Г о л у з и н Г. М., Геометрическая теории функций
комплексного переменного, 2 изд., М., 1966. В. Я. Гцтляиский.
ЛЕЖАНДРА МНОГОЧЛЕНЫ, сферические
многочлен ы,— многочлены, ортогональные на
сегменте [ —1,1] с единичным весом ф(х)=1. Стандарти-
Стандартизованные Л. м. определяются Родрига формулой
¦Р«^)=^2И^г(ж2^1)П' « = 0,1,2,...,
и имеют представление
Наиболее употребительны формулы
(n + i) Pn + 1(x) = Bn + i) хР„(х)-пР„_1(г),
Р„(-х) = (-1)пРп(х); Р„A) = 1, Р„(—1) = (—1)»,
A-х2) Р'п {х) = пРп_1 (х) — хпРп(х),
P'n+i {х) — Р'„^ (х) = Bп + 1) Рп (х).
Л. м. можно определить как коэффициенты разложения
производящей функции
Vi-Zxt + t' ^-л = 0
где ряд в правой части сходится, если ,г?[ — 1, 1].
Несколько первых стандартизованных Л. м. имеют
вид
(х) = E.т3 — Зж)/2, Pt (x) = C5^ —ЗОх2-}- 3)/8,
Ръ (х) = F3г5 —70ж3 + 15ж)/8,
Л. м. порядка п удовлетворяет дифференциальному
уравнению (уравнению Л е ж а н д р а)
к-рое появляется при решении уравнения Лапласа
в сферич. координатах методом разделения перемен-
переменных. Ортонормированпые Л. м. имеют вид
9~- Рп{х), n = 0,l,2,...t
и допускают равномерную и весовую оценки
Ряды Фурье по Л. м. внутри интервала (—1, 1) анало-
аналогичны тригонометрич. рядам Фурье; есть теорема о
равносходимости этих двух рядов, к-рая означает,
что ряд Фурье — Лежандра функции f{x) в точке
x?(—1, 1) сходится тогда и только тогда, когда в точке
6=arccos х сходится тригонометрия, ряд Фурье функции
F@) = (sin0)'/l!/(cosG).
В окрестности концов положение иное, ибо последова-
последовательность {Р„(±1)} возрастает со скоростью V^n.
Если функция f(x) на сегменте [ — 1, 1] непрерывна и
удовлетворяет условию Липшица порядка а>1/2, то ряд
Фурье — Лежандра сходится к функции / (х) равномер-
равномерно на всем сегменте [ — 1, 1]. При условии <х=1/2 этот
ряд, вообще говоря, расходится в точках .r==tl.
Эти многочлены введены А. Лежандром [1].
Лит.: [1] Legendrc A. M., «Memoires de mathematique
ct de physique, presentes a l'Academie royale des sciences par
divers savants», 1785, t. 10, p. 411 — 34; [2] Го б со и Е. В.,
Теория сферических и эллипсоидальных функций, пер. с англ.,
М., 1952; см. также лит. при статье Ортогональные многочлены.
П. К. Суетии.
ЛЕЖАНДРА ПРЕОБРАЗОВАНИЕ — 1) Преобразо-
Преобразование математич. анализа, осуществляющее двойствен-
двойственность между объектами в дуальных пространствах
(наряду с проективной двойственностью в аналитич.
геометрии и полярной двойственностью в выпуклой гео-
геометрии). Пусть f : А -*¦ R — гладкая функция, рас-
рассматриваемая на открытом множестве А нормирован-
нормированного пространства X и обладающая тем свойством, что
отображение х —*¦ f (х) (здесь /' (х) — Фреше производ-
производная /) взаимно однозначно отображает А на множество
ВсХ*. Тогда Л. п. / — это функция на В, определен-
определенная формулой
/*(**)=<.г*, (л-г (**)>-/ал-1 (-г*))- а)
В случае, если / — функция на R" и при этом опре-
определитель det ( —j—у 1 отличен от нуля в области А,
Л. п. задается формулами
f'(x) = y, f*(y)=<x, /'(*)>-/(*); A')
здесь
Vn . . / в/ в/
- • .. ^1=1*'У' f (*) = (в?Г> •••'
Преобразование .г —v /* (/' (х)) встречается еще у
Г. Лейбница (G. Leibnitz), в общем виде определено
А. Лежаидром (A. Legendre, 1789), хотя ранее рассмат-
рассматривалось также Л. Эйлером (L. Euler, 1776).
В случае, если / ¦— конечномерная функция, являю-
являющаяся гладкой, строго выпуклой и растущей на беско-
бесконечности быстрее линейной функции, то Л. п. можно
определить так:
/*(¦<¦*)= max «х*, x>—f(x)). B)
Выражение B) с заменой max на sup было положено
(см. [2]) в основу теории двойственности выпуклых
функций (см. Сопряженная функция)
Примеры. Л. п. функции
одного переменного будет функция
/Р Ш— р, . р -Гр, — h
Л. п. функции (х, х)/2 в гильбертовом пространстве X
со скалярным произведением (•, •) будет функция
(у, г/)/2.
Л. п., основанное на замене переменных х —>¦ y=f (x),
является частным случаем прикосновения преобразова-
преобразования; сущность Л. п. заключается в возможности двойст-
двойственного описания поверхности в пространстве — как
множества точек (х, f(x)) и как огибающей семейства
ее касательных плоскостей, задаваемых парой (х*,
<.x*, •>—f*(x*)), состоящей из линейного функцио-
функционала х* и аффинной касательной функции х -> <.г*,
х>-1*{х*).
Л. п. играет важную роль в анализе, особенно в
выпуклом анализе (см. [1], [2], [4]), в теории дифферен-
дифференциальных уравнений, в вариационном исчислении
(см. [6]), в классич. механике, термодинамике, теории
упругости и других разделах математич. физики. Так,
применение Л. п. к решению у дифференциального
уравнения F(x, у, у') = 0 переводит его в решение
У уравнения F(Y', XY' — Y, X), где Х = у' (х), У(Х) =
= у* (X), к-рое иногда интегрируется проще исходного.
Применение Л. п. к лагранжиану задачи классического
вариационного исчисления переводит его в Гамильтона
функцию. При этом система уравнений Эйлера (в вари-
вариационном исчислении) и уравнения Лаграижа (в клас-
классич. механике) переходят в эквивалентную систему
канонич. уравнений. В термодинамике Л. п. осуществ-
осуществляет переход от одних функций состояния к другим,
напр, от удельного объема и энтропии к температуре
и давлению.
Лит.: [1] Фихтенгольц Г. М., Курс дифференци-
дифференциального и интегрального исчисления, т. 1, М., 1970; [2] Г у р-
са Э., Курс математического анализа, пер. с франц., 3 изд ,
т. 1, М.—Л., 1936; [3] Арнольд В. И., Математические
методы классической механики, М., 1974; [4] Р о к а Ф е л-
л а р Р., Выпуклый анализ, пер. с англ., М., 1973; [5] F с п-
с h e I W., «Canad. J. Math.», 1949, v. 1, p. 73—77; [6] Сага-
theodory с., Variations rechnung und partielle Differential-
gleichungen erster Ordnung, Lpz.— В., 1933. В. М. Тихомиров.
2) Интегральное преобразование вида
f(n) = T{F (x)}^-^j1_iPn(x)F (x)dx, n = 0, 1, 2, ...,
где Рп(х) — Лежандра многочлен порядка п. Формула
обращения имеет вид
—1 < х < 1,
если ряд сходится. Л. п. сводит дифференциальную
операцию
#-A-*2)|"
dxK ' dx
к алгебраической по формуле
Т [±{l-x*J*?>.}=-n(n + i)f(n), n = 0, 1, 2, ...
Для Л. п. имеет место теорема о свертке: если
T{Ft(x)} = fi(n), i = l, 2,
то
h(n)f2(n) = T [h(.r)},
где
h (х) =
/^ (S) A-^-1--ц*+ 2х?Л) /г d\ dr\,
, h (E) /^ (S) Aц+ ?
Е (х) — внутренность эллипса s2+tJ—2хЪ,г\ = 1—х2.
Л. п. является частным случаем Лкоби преобразова-
преобразования.
Лит.: [1] Tranter С. J., «Quart. J. Math.», 1950, v. 1,
p. 1—8; [2] Итоги науки. Математический анализ, 19(i(i, M ,
1967, с. 7—82. Ю. А. Брычков, А. П. Прудтюм.
ЛЕЖАНДРА СИМВОЛ — арифметическая функция
чисел р и а, определенная для простых нечетных р ц
целых а, не делящихся на р. Л. с. обозначается ( —
Л. с. Г-^Л = 1, если сравнение х'г=а (mod p) разрешимо;
в противном же случае ( — ) = —1. Иногда Л. с. доопре-
доопределяют и для чисел а, делящихся на р, полагая, что в
этом случае ( — ) = 0. Л. с. обладает следующими свой-
свойствами:
1) если a = 6(mod.p), то (—J = (—J ;
2) (yj=l;
3) (±)=a(P-Vi
1 \ -n /
7) ecjii p и q — простые нечетные, то
JL*) ( JL
Последний факт, впервые доказанный К. Гауссом
(С. Gauss, 1796), носит название квадратичного
закона взаимности. Перечисленные свойства
позволяют легко вычислять Л. с, не прибегая к реше-
решению сравнений. Напр.,
593^ ^593у1 ^593,1 ^593 )
Еще более облегчает вычисление Л. с. использование
Якоби символа. При фиксированном р Л. с. является,
действительным характером мультипликативной группы
классов вычетов по модулю р.
Введен А. Лежандром (A. Legendre, 1785).
Лит.: [1] Виноградов И. М., Основы теории чисел,
8 изд., М., 1972. Ю. В. Нестеренко.
ЛЕЖАНДРА ТЕОРЕМА — 1) Неопределенное (дио-
d) уравнение
коэффициенты к-рого а, Ъ и с — попарно взаимно
простые целые рациональные числа, свободные от
квадратов и не все одного знака, имеет ненулевое рацио-
рациональное решение тогда и только тогда, когда разре-
разрешимы все три сравнения:
ж2 = — 6с (mod | о|),
х2 ss — c.a (mod | Ъ |),
ж2 = — a6 (mod | с I).
К Л. т. сводится вопрос о представлении нуля
произвольной тернарной квадратичной формой с рацио-
рациональными коэффициентами.
Доказана А. Лежандром (A. Legendre, 1785).
Лит.: [1] Боревич 3. И., Шафаревич И- Р.,
Теория чисел, 2 изд., М., 1972, гл. 1, § 7. Ю. В. Нестеренко.
2) Сумма углов треугольника не может быть больше
двух прямых углов.
3) Если в одном треугольнике сумма углов равна
двум прямым углам, то она равна двум прямым углам
ro всяком другом треугольнике.
Теоремы 2), 3) были доказаны А. Лежандром
(A. Legendre, 1800, 1833) при попытках обосновать
постулат Евклида о параллельных. Аналогичные ут-
утверждения были установлены Дж. Саккери (G. Saccheri,
см. Саккери четырехугольник).
Лит.: [1] Каган В. Ф., Основания геометрии, ч. 1, М.—
Л., 1949; [2] Погорело! А. В., Основания геометрии,
3 изд., М., 1968. А. Б. Иванов.
ЛЕЖАНДРА УРАВНЕНИЕ — см. Лежандра функции.
ЛЕЖАНДРА УСЛОВИЕ — необходимое условие для
решения простейшей задачи вариационного исчисления,
I предложенное А. Лежандром (A. Legendre, 1786):
для того чтобы кривая уй (х) доставляла минимум функ-
функционалу
J =
=\г F (х, у, у') dx, y{x1) = y1, у(х.2) = у2,
необходимо, чтобы во всех точках кривой у (х) вторая
производная от подиптегральной функции по у' была
неотрицательна
F , t(x, у(х), у'(х))^0, хг^х^х2.
Если у есть n-мерный вектор с координатами ylt . . ., уп
то Л. у. требует неотрицательности квадратичной форм1,1
X" 5Г F-Л*' уП, у' (x))r\i4;-s?o,
J~^ i = l ¦*—«у = 1 У V' j
•г 6 [*i. «гЬ 1 = (»U. •••> 1н) 6 Rn-
Для случая максимума функционала знак неравенства
в Л. у. меняется на противоположный. Для вариацион-
вариационных задач на условный акстре.мум аналогом Л. у. яв-
является Клебша условие.
Л. у., так же как и Эйлера уравнение, является
необходимым условием слабого экстремума. При нару-
нарушении Л. у. вторая вариация функционала не сохраня-
сохраняет свой знак и кривая у (х) не доставляет экстремум
функционалу.
Если в Л. у. знак нестрогого неравенства заменен
на знак строгого неравенства, то такое условие наз.
усиленным условием Лежандра. Уси-
Усиленное Л. у. в отличие от Л. у. не является необходи-
необходимым. Усиленное Л. у. участвует в формулировке
достаточных условий экстремума. Экстремаль, на к-рой
выполняется усиленное Л. у., наз. не особой (не-
(неособенной) экстремалью. Такая экстре-
экстремаль дважды непрерывно дифференцируема, и уравне-
уравнение Эйлера для нее можно представить в виде обыкно-
обыкновенного дифференциального уравнения 2-го порядка,
разрешенного относительно старшей производной.
Если на неособой экстремали выполняется усиленное
Якоби условие, то можно построить поле экстремален,
окружающее данную экстремаль, что является первым
шагом при исследовании достаточных условий экстре-
экстремума.
Лит.: Ш Лаврентьев М. А., Люстерник Л. А.,
Курс вариационного исчисления, 2 изд., М., 1950; [2]
Б ли ее Г. А., Лекции по вариационному исчислению, пер.
с англ., М., 1950. И. Б. Вапнярский.
ЛЕЖАНДРА ФУНКЦИИ — функции, являющиеся
решениями дифференциального уравнения
Лежандра:
g ^ ^Jo, (•)
где v и fi — произвольные числа. Если v=0, i, 2, . . .,
а Ц--0, то ограниченные на [—1, 1] решения уравнения
(*) наз. Лежандра многочленами; при целых ц,, —v<:
<(i<:v, ограниченные на [ —1,1] решения уравнения
(*) наз. присоединенными функциями
Лежандра. А. Б. Иванов.
ЛЕЖАНДРОВО МНОГООБРАЗИЕ — такое «мер-
«мерное гладкое подмногообразие Ln Bn-V 1)-мерного
контактного многообразия М""+ 1 (т. е.
многообразия, снабженного пфаффовой формой а,
внешнее произведение к-рой на ге-ю внешнюю степень
ее внешнего дифференциала ал {йа)пф0 во всех точках
М2п + Х), что пфаффова форма а, задающая контактную
структуру на М2п + 1, обращается в нуль тождественно на
L" (т. е. <х(Х) = 0 для любого вектора X, касающегося
L" в какой-нибудь точке последнего). В важном частном
случае, когда М°" + 1~R2n + 1 с координатами (рь . . .,
Pni (h, ¦ ¦ ¦, ап, '') и а = 2. i=1Pidq,-—dr, a Ln расположено
тяк, что д,- можно принять за координаты на нем, усло-
условно, чтобы L" было Л. м., означаем, что оно задается
уравнениями вида
r = f(ii, .... 'In), Ру = г^ •••'P" = d^ '
ш при этом pi также можно принять за координаты
ли L", то координаты </,- и р,- связаны Лежандра преоб-
преобразованием; если же в окрестности нек-рой точки этого
сделать нельзя, то преобразование Лежандра имеет в
этой точке особенность.
Примеры Л. м. уже давно встречались в различных
гопросах анализа и геометрии, но само понятие Л. м.
введено сравнительно недавно по аналогии с лпгранже-
вым многообразием. Д- В. Аносов.
ЛЕЙБНИЦА ПРИЗНАК сходимости зна-
знакочередующегося ряда: если члены знако-
знакочередующегося ряда
монотонно убывают (я„>а„ + 1, ге—1, 2, . . .) и стремятся
к нулю (lira. а„=0),то ряд сходится; при этом остаток
п-»-°°
рята
имеет знак своего первого члена и меньше его по аб-
абсолютной величине. Признак установлен Г. Лейбницем
(G. Leibniz, 1682). В. И. Битюцков.
ЛЕЙБНИЦА РЯД — знакочередующийся ряд
сходящийся к я/4. Рассмотрен Г. Лейбницем (G. Leib-
Leibniz 1673 — 74). в- И. Битюцков.
ЛЕЙБНИЦА ФОРМУЛА для производных
произведения — формула, дающая выражение
для производной порядка п от произведения двух
функций через их производные порядков к= О, 1, . . ., п
(под производными нулевого порядка понимаются сами
функции). А именно, если функции и=и(х) и v=v(x)
имеют в нек-рой точке производные до порядка п вклю-
включительно, то их произведение uv имеет в этой точке про-
производные тех же порядков и
Эта формула была сообщена Г. Лейбницем (G. Leibniz)
в письме к И. Бернулли (J. Bernoulli) в 1695.
.''/. Д. Кудрявцев.
ЛЕКСИКОГРАФИЧЕСКИЙ ПОРЯДОК — порядок на
прямом произведении
частично упорядоченных множеств Ха, где множество
индексов L — вполне упорядочено, определяемый
следующим образом: если {ха}, {уа}?Х, то {.га}-<
<{;/«} тогда и только тогда, когда либо ха=-]1а для всех
a?L, либо существует такое a?L, что ха<;/а и хр —Уа
для всех |5<а. Множество X, упорядоченное лексико-
графич. порядком, наз. лексикографичес-
лексикографическим, или о р д и н а л ь н ы м, п р о и з в е д е и и е м
множеств Ха- Если все множества Ха совпадают между
собой {Xa.= Y для всех a?L), то их лексикографич.
произведение наз. ординальной степенью множества У
и обозначается LY. Говорят также, что X упорядочено
по принципу первого различия (как слова упорядочены
в словаре). Таким образом, если L — натуральный ряд,
то
{х1г . .., х„, ...} < {ух, . .., у„, .. .}
означает, что для нек-рого к
xk < У к и xi = Vi Для всзх * < '¦'•
Л. п. является частным случаем упорядоченного про-
произведения частично упорядоченных множеств (см.
[З]). Л. п. может быть определен аналогично и для
любого частично упорядоченного множества индексов
L (см. [1]), однако в этом случае отношение на мно-
множество ТТ Ха но обязано быть порядком в обычном
смысле.
Лексикография, произведение конечного чи"ла впол-
вполне упорядоченных множеств вполне упорядочено. Лек-
енкографич. произведение цепей есть цепь.
Для конечного L Л. п. рассматривался фактически
еще Г. Кантором [4] при определении произведения
порядковых типов линейно упорядоченных множеств.
Л. п. широко используется вне математики, на-
например при упорядочении слов в словарях, справоч-
справочниках и т. п.
Лит.: [1] Б и р к г о ф Г., Теория структур, пер. с англ.
М., 1952; [2] Куратовский К., М о с т о в с к и й А.
Теория множеств, пер. с англ., М-, J 970; [3] С тс о р н я к и в Л. А.
Элементы теории структур М., 1970; ['(] С а и t n г G.
«Math. Ann.», 1895, Bd46, N5 4, S. 481 —512; [5] Hnusdorf f P.
Grundzuge der Mengenlehre, Lpz., 1914. Т. С. Фофанова
ЛЕМНИСКАТНЫЕ ФУНКЦИИ, л о м и и с к а т п-
ческие функции, — частный случаи эллипти-
эллиптических функций, возникающий при обращении эллип-
тнч. интеграла частного вида
Эти интегралы появились впервые при вычислении дли-
длины дуги Берпулли лемнискаты в работах Дж. Фаньяно
(G. Fagnano, 1715). Сами Л. ф. ввел К. Гаусс (С. Gauss,
1797).
Л. ф. две:
« = cos lomn z = cl z,
sin lemn z = sl z = cos lemn ( —— z
где
Л. ф. выражаются через Лкоби эллиптические функции
с модулем к= У 2/2:
- dn (z V 2 )
В теории Вейерштрасса эллиптических функций Л. ф.
появляются вт. н. гармоническом случае,
когда инварианты g%=^, ?з=0.
Лит.: [11 Уиттекер Э.-'т., В а т с о и Д. Н., Курс
современного анализа, пер. с англ., 2 изд., ч. 2, М., 19U3. гл. 22.
Е. Д. Соломеицев.
ЛЕМНИСКАТЫ — 1) Плоские алгебраич. кривые по-
порядка 2п, произведение расстояний каждой точки
к-рых до заданных точек (фокусов) F,, F.2, . . ., Flt
равно заданному числу г (р а д и у с у Л.). Уравнение
Л. в декартовых прямоугольных координатах
I / „ 2. \ ( 7 2 ) ( Z Z ) I ^ Гп Г ~> О Z = X -^- 111
Окружность есть Л. с одним,фокусом, Кассили овал —
Л. с двумя фокусами. См. также Бернулли лемниската
и Бута лемниската. Д- Д- Соколов.
2) Л.— кривая уровня многочлена. Если все фокусы
Fk- zk=xk~<~iykik=i, 2, . . ., п, различны и радиус Л.
достаточно мал, то Л. состоит из п континуумов, попар-
попарно не имеющих общих точек. При достаточно большом
радиусе Л. состоит из одной связной компоненты. Как
показал Д. Гильберт (D. Hilbei't, 1897), границу Г
произвольной односвязной конечной области можно
I сколь угодно хорошо приблизить Л., т. е. для любого
е>0 можно указать Л. Л такую, что в е-окрестности
каждой точки Г существуют точки Л и каждая точка Л
попадает в F-окреетноеть соответствующей точки Г.
Лит.: [1] M а р к у ш е в и ч Л. И., Теория аналитических
функций, 2 цзд., т. 1, М., 1И67; [2] У о л ш Д ж.- Л., Интер-
Интерполяция и аппроксимация рациональными функциями в комп-
комплексной области, пер. с англ., М., 1961. Е. Д. Соломенцев.
ЛЕРЕ СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ,
спектральная последовательность
непрерывного отображен и я,— спект-
спектральная последовательность, связывающая когомоло-
гии со значениями в пучке абелевых групп §~ на топо-
логич. пространстве X с когомологиями его прямых об-
образов fgrf при непрерывном отображении / : X —>- У.
Точнее, нторой член Л. с. п. имеет вид
а ее предел Ет есть биградуированная группа, связан-
связанная с нек-рой фильтрацией градуированной группы
Н*(Х,$~). Конструкция Л. с. п. может быть обобще-
обобщена на когомологии с носителями в заданных семействах.
В случае локально компактных пространств и когомо-
когомологии с компактными носителями Л. с. п. была по-
построена Ж. Лере в 1946 (см. [1], [2]).
Если §~=А — постоянный пучок, отвечающий абе-
левой группе А, / — проекция локально тривиального
расслоения со слоем F, а пространство У локально
стягиваемо, то fq (§~) будут локально постоянными
пучками со слоем Hq (F, А). Если, кроме того, У одно-
связно или же X — расслоенное пространство со
связной структурной группой, то fq (JT) — постоянные
пучки и член Е2 принимает особенно простой вид:
El' q = Hp (Y, II" (F, A)).
Условие локальной стягиваемости может быть заменено
другими топологич. условиями на X, У, F (напр., У
локально компактно, F компактно).
Используя сингулярные когомологии, можно постро-
построить для любого расслоения в смысле Серра с линейно
связными слоями аналог Л. с. п., обладающий всеми
перечисленными выше свойствами Л. с. п. локально
тривиального расслоения (спектральная пос-
последовательность Серра). Аналогичная
спектральная последовательность существует в сингу-
сингулярных гомологиях.
Лит.:[1~\ L е г а у J., «J. math, pures et appl.», 1950, t. 29,
p. 1 — 139; [2] e г о ж е, там же, р. 169—213; [3] Г о д е-
ман Р., Алгебраическая топология и теория пучков, пер. с
франц., М., 1961; [4] X у С ы - ц з я н, Теория гомотопий, пер.
с англ., Ы., 1964. Д. А. Пономарев.
ЛЕРЕ ФОРМУЛА, Кош и — Фантапье фор-
формула,— формула интегрального представления голо-
голоморфных функций /(z) многих комплексных перемен-
переменных z= (zb z2, . . ., z,,), n^l, обобщающая интеграль-
интегральную формулу Коши (см. Коши интеграл).
Пусть D—конечная область комплексного пр<}'
странства С" с кусочно гладкой границей д?>;
%(?; z) : 3D —>. С" — любая гладкая вектор-функция
от t^OD со значениями в С" такая, что скалярное про-
произведение
всюду на 3D для всех z?D. Тогда любая голоморфная в
D функция /(z), непрерывная в замкнутой области D,
представима в виде
f(Q6(x(X,; г» л dz
Формула (*) обобщает классическую интегральную
формулу Коши для аналитич. функций одного комплекс-
комплексного переменного и наз. формулой Лере. Ж. Лере
(J. Leray), получивший эту формулу (см. [1]), назвал ее
формулой Коши — Фантапье. В этой фор-
муле дифференциальные формы 6(х(?; z)) и dt, состав-
составляются по законам:
6(x(S; 2)) = ^"^ (—IL' Xv(S; z)dXia; z) л ...
... Л rfxv-i (?; г) Л dxv+1 (?; z) л . . . Л dXn (?; z)
где Л — знак внешнего умножения (см. Внешнее про-
произведение). Выбирая вид функции "/., из формулы (*:
можно получить различные интегральные представле-
представления. При этом следует иметь в виду, что, вообще говоря,
интеграл Л е р е в формуле (*) не равен тожде-
тождественно нулю, когда z находится вне D.
См. также Бохнера — Мартинелли представление.
Лит.: [1] Л ере Ж., Дифференциальное и интегрально'
исчисление на комплексном аналитическом многообразии, г,с];.
с франц., М., 1961; [2] Ш а б а т Б. В., Введение в комп.-iei i-
ный анализ, 2 изд., ч. 2, М., 1976. Е. Д. Солош-.ще;..
ЛЕФШЕЦА ДВОЙСТВЕННОСТЬ, Л е ф ш е ц а -
Пуанкаре двойственность,— утвержде-
утверждение о двойственности между гомологиями и когомоло-
гиямн, установленное С. Лефшецем (S. Lefschctzi.
Более точно, если (X, А) — такая пара пространств,
что Хччу1 есть n-мерное топологич. многообразие, то
для любой абелевой группы G и для любого i имеет место
изоморфизм
здесь в правой части стоят когомологии с компактными
носителями; если многообразие Х\/1 неориентируемо,
то нужно, как обычно, брать когомологии с локальными
Коэффициентами. Ю. Б. Рудяк
ЛЕФШЕЦА ТЕОРЕМА — 1) Л. т. о неподвиж-
неподвижных точках, Лефшеца — Хопфа теоре-
теорема,— теорема, позволяющая выразить число непод-
неподвижных точек непрерывного отображения через его
Лефшеца число. Так, если непрерывное отображение / :
X —>- X конечного клеточного пространства X не име-
имеет неподвижных точек, то его число Лефшеца L(f\
равно нулю. Частным случаем последнего утверждения
является Брауэра теорема о неподвижной точке.
Ю. Б. Рудяк.
2) Л. т. о гиперплоском сечении, сла-
слабая Л. т.: пусть X — алгобраич. подмногообразие
комплексной размерности п в комплексном проектив-
проективном пространстве <CPN и пусть Pcz.CPN — гиперплос-
гиперплоскость, проходящая через все особые точки многообразия
X (если они есть), a Y=X[)P — гиперплоское сечение
многообразия X; тогда относительные группы гомоло-
гомологии Н,(Х, Y, Z) равны нулю при ?<п. Отсюда выте-
вытекает, что естественный гомоморфизм
является изоморфизмом для i<Cn—1 и сюръективен для
i=n — i (см. [1]).
По формулам универсальных коэффициентов отсюда
получаются соответствующие утверждения для групп
целочисленных когомологпй. Во всяком случае для
когомологии с коэффициентами в поле рациональных
чисел имеют место двойственные утверждения: гомо-
гомоморфизм пространств когомологии
Я' (X; Q)— +//' (У; Q),
индуцированный вложением YczX, является изомор-
изоморфизмом для г<п—1 и инъективен для i=— п — 1 (см. [6]j.
Аналогичное утверждение справедливо для гомото-
пич. групп: П((Х, У) = 0 при i<_n. В частности, кано-
нич. гомоморфизм Л! (У) —>- пх (X) является изоморфиз-
изоморфизмом при п^З и сюръективен при п=2 (теорема
Лефшеца о фундаментальной группе).
Существует обобщение этой теоремы на случай произ-
вольного алгебраически замкнутого поля (см. [7]), а
также на случай, когда Y — нормальное полное пере-
пересечение в X (см. [81).
3) Сильная Л. т.— теорема о существовании
разложения Лефшеца когомологий комплексного кэле-
рова многообразия на примитивные составляющие.
Пусть V — компактное кэлерово многообразие раз-
размерности п с кэлеровой формой ч> и пусть
11 ? Я1-1 (У, С) сй!(Г, С)
— класс когомологнй типа A, 1), соответствующий
форме (о при изоморфизме де Рама (если V — проек-
проективное алгебраич. многообразие над С с естественной
метрикой Ходжа, то ц — класс когомологий, двойст-
двойственный классу гомологии гиперплоского сечения) и
L:H' (V, С) —¦> Я<+2(Г, С)
— линейный оператор, определяемый умножением на
Л, т. е.
Lz=--z-r\, z ?Я< (V, С).
Имеет место изоморфизм (см. [1])
Lk:Hn- k(V, С) -^ tf"-*(F, С)
для любого к— 0, 1,. . ., п. Ядро оператора
Lk+i. нп~к (V, С) —* Я" + *+2 V, С)
обозначается Н'1~ (V, С) и наз. примитивной
частью (п—к)-к огомологий многообра-
многообразия V. Элементы из Но" (V, С) наз. примитив-
примитивными к о г о м о л о г и я м и, а соответствующие
лм циклы — примитивными циклами.
Сильная Л. т. устанавливает следующее разложение ко-
когомологий в прямую сумму примитивных (наз. разло-
разложением Л е ф ш е ц а):
я» (V, С)=ф|["/в2]/.*я7-2*(|/, с)
для всех т=0, 1,2,.. ., 2п. Отображения
являются вложениями. Разложение Лефшеца коммути-
коммутирует с разложением Ходжа
H*{V, C)=^p+<i=mHP^{V, С)
(см. [13]). В частности, определена примитивная часть
HP*"{V, С) в H"-q(V, С) и
Hf(V, С)=ф/, + в = тяг-«G, С).
Сильная Л. т. и разложение Лефшеца имеют аналоги
в абстрактной алгебраич. геометрии для Z-адических и
кристальных когомологий (см. [4], [14]).
4) Л. т. о к о г о м о л о г и я х типа A,1) —
теорема о соответствии между двумерными алгебраич.
классами когомологий комплексного проективного ал-
1ебранч. многообразия и классами когомологий типа
A, !)•
Пусть V — неособое проективное алгобраич. много-
многообразие над полем С. Элемент z?H2(V, %) наз. ал-
алгебраическим, если двойственный ему (в смыс-
смысле Пуанкаре) класс гомологии определяется нек-рым
.швп.чором. Л. т. о когомологиях типа A,1) утвержда-
утверждает, что класс z?H2(V, %) алгебрапчен тогда и только
тогда, когда
z 6 i(H*(V, Z)) Г\Н1а(У, С),
где II1'1 (V, С) — компонента Ходжа типа A, 1) дву-
двумерных комплексных когомологий #2(V, С), а отоб-
отображение j :H2(V, 1,)—>-H2(V, С) индуцировано есте-
естественным вложением % -> С (см. [1], а также [6], [12]).
По поводу алгебраич. классов когомологий в размер-
размерностях, больших 2, см. Ходжа гипотеза.
Для произвольного комплексного аналитич. много-
многообразия V существует аналогичная характеризация
элементов группы H2(V, g), являющихся классами
Чжэня расслоений на комплексные прямые над V
(см. [И]).
Лит.: [1] Lefschetz S., L'analysis situs et la geometrie
algebrique, P., 1924; [2] его ж е, «Trans. Amer. Math. Soc»,
1921, v. 22, p. 327 — 482; [3] его ж е, «Ann. Math.», 1937, v. 38,
p. 819—22; [4] Berthelot P., Cohomologie cristallme des
schemes de earacteristique p>0, B.— [a. o.], 1974; [5] D e 1 i g-
n e P., К a t z N., Groupes dc monodromie en geometric algeb-
rique, В.— [a. o.], 1973; [6] Griffiths P., Harris J.,
Principles of algebraic geometry, N. Y., 1978; [7] G г о t h e n-
d i e с k A., Cohomologie locale des faisceaux cohfirents et theore-
mes de Lefschetz locaux et, globaux, P.— Amst., 1968; [8] Hart-
shorne R., Ample subvarieties of algebraic variefies, B.—
[u. a.], 1970; [9] M а м ф о р д Д., Абелевы многообразия, пер.
с англ., М., 1971; [101 М и л н о р Д ж., Теория Морса, пер.
с англ., М., 1965; [11] Уэллс Р., Дифференциальное исчис-
исчисление на комплексных многообразиях, пер. с англ., М., 1976;
[12] Чжэнь Шэн-шэнъ, Комплексные многообразия,
пер. с англ., М., 1961; [13] Вейль А., Введение в теорию
кэлеровых многообразий, нер. с франц., М., 1961; [14] Д е-
л и н ь П., «Успехи матсм. наук», 1975, т. 30, в. 5, с. 159—90.
В. Л. Псковских.
ЛЕФШЕЦА ФОРМУЛА — формула, выражающая
число неподвижных точек эндоморфизма топологич.
пространства через следы соответствующих эндоморфиз-
эндоморфизмов в пространствах когомологий.
Эта формула была установлена впервые С. Лефгпецом
для конечномерных ориентируемых топологич. многооб-
многообразий [1] и для конечных клеточных комплексов (см.
[2, 3]). Этим работам С. Лефшеца предшествовала
работа Л. Брауэра (L. Brouwer, 1911) о неподвижной
точке непрорывного отображения n-мерной сферы в
себя. Некоторый новый вариант доказательства Л. ф.
для конечных клеточных комплексов был дан X. Хоп-
фом (Н. Hopf, см. [9]).
Пусть X — связное ориентируемое га-мерное ком-
компактное топологич. многообразие или n-мерный конеч-
конечный клеточный комплекс, / : X —*¦ X — непрерывное
отображение, Л(/, X) — Лефшеца число отображения
I /. Предполагается, что все неподвижные точки отобра-
отображения / : X —>- X изолированы. Для каждой неподвиж-
неподвижной точки х?Х пусть i (х) — ее индекс Крон е-
к е р а (локальная степень отображения / в окрест-
окрестности точки х). Тогда Л. ф. для X и / имеет вид
Имеется [8] обобщение Л. ф. на случай произвольных
непрерывных отображений компактных евклидовых
окрестностных ретрактов.
Пусть X — дифференцируемое компактное ориенти-
ориентированное многообразие, / : X —>• X — дифференцируе-
дифференцируемое отображение. Неподвижная точка i?X для отоб-
отображения / наз. невырожденной, если она
изолирована и dol(dfx—Е)Ф0, где dfx : Тх(Х)—*¦
-*-Тх(Х) — дифференциал отображения / в точке х,
а Е — тождественное преобразование. Для невырожден-
невырожденной точки х'?Х ее индекс i (x) совпадает с числом sgn det
(dfx—Е). В этом случае Л. ф. A) показывает, что число
Лефшеца Л(/, X) равно разности между числом непод-
неподвижных точек с индексом +1 и числом неподвижных
точек с индексом —1, в частности не превосходит общего
числа неподвижных точек. Левую часть формулы A)
в этом случае можно определить так же, как индекс
пересечения ГуА на XXX, где Г^ — график отображе-
отображения / и АсХ XX — диагональ.
Следствием Л. ф. является формула Хопфа,
утверждающая, что эйлерова характеристика %(Х)
равна сумме индексов нулей глобального С°"-векторного
поля v на X (предполагается, что все нули векторного
поля v изолированы) (см. [5]).
Существует вариант Л. ф. для компактных комплекс-
комплексных многообразий ц когомологии Долъбо (см. [5]).
Пусть X — компактное комплексное многообразие
размерности т и / : X —*¦ X — голоморфное отобра-
жепио с невырожденными неподвижными точками.
Пусть Нр''' (X) — когомологии Дольбо многообразия X
типа (;>, q) и /* : Пр'ч (X) ->- Нр' " (X) — индуциро-
индуцированный отображением / эндоморфизм. Число
л (/, вх)=2"=о (™1)? Тг
паз. голоморфным числом Л е ф га е ц а.
Тогда имеет место следующая голоморфная
Л. ф.
А (/, бх) ]?
где dfv — голоморфный дифференциал отображения /
в точке х.
В а5;трактноп алгебраич. геометрии Л. ф. послужила
отправной точкой для поиска Вейля когомологии в
свя:ш с гипотезами Вейля о дзета-функциях алгебраич.
многообразий, определенных над конечными полями.
Аналог Л. ф. в абстрактной алгобраич. геометрии
устанавливается для /-адических когомологии с ком-
компактными носителями и с коэффициентами в конструк-
конструктивных Qt -пучках, где Qt — поле ^-адических чисел,
I — простое число, отличное от характеристики поля к.
Эту формулу часто называют формулой следа.
Пусть X — алгебраич. многообразие (или схема)
над конечным полем к, F : X —*¦ X — морфизм Фробе-
ниуса и CJF — пучок на X и Нс(Х, Щ~) — когомологии
с компактными носителями многообразия (схемы) X
с коэффициентами в пучке |р. Тогда морфизм F опре-
определяет эндоморфизм когомологии
F*:Hcc (X> S7) -^ Щ (Х> Я7)-
Если fc,,r>fc — расширение степени п поля к, Х„=
~Х@к,„ cf,r~3~®k,l — многообразие (схема) и пу-
пучок, полученные пз X и f посредством расширения
поля скаляров, то соответствующий морфизм Фро-
бенпуса Fн : Хп —>- Хп совпадает с п-й степенью Г'1
морфизма F.
Пусть теперь X — отделимая схема конечного типа
над конечным полем к из q элементов, $ — конструк-
конструктивный Qj-пучок на X, I — простое число, отличное от
характеристики ноля к, Xh" — множество неподвиж-
неподвижных геометрпч. точек морфизма F" или, что то же са-
самое, множество X (к„) геометрич. точек схемы X со
значениями в поле кп. Тогда для любого целого n^l \
имеет место следующая Л. ф. (или формула еле- i
да) (см. [6], [7]):
= 2/-1)'' Tr (f*"' ЯЬ (Х> ^))' B)
где (ТХ—слон пучка §~ в точке х. В случае постоянного
пучка EГ=Ог имеем Tr(F"*, Сг) —1 и левая часть форму-
формулы B) представляет собой не что иное, как число гео-
метрнч. точек схемы X со значениями в поле кп. В ча-
частности, при п—\ — это просто число точек схемы X
со значениями в основном поле к. Если схема X является
собственной яад к (напр., если X —полное алгобраич.
многообразие над к), то Н 1С (X, ^Г) = Я'(Я, f) и правая
часть формулы B) является альтернированной суммой
следов эндоморфизма Фробепиуса в обычных когомо-
погиях схемы X.
Имеются (см. [7]) обобщения формулы B).
Лит,: [1] -L e f s с h e t z S. «Trans. Amer. Math. Soc»,
1926, vv 28, ,Л*2 1, p. 1—49; [2] e г о же, «Proc. Nat. Acad. Sci.
USA», 1927, л'. 13, p. 614—22; [3] его же, «Ann. Math.» B),
1937, v. 38, Кч 4, p. 819 — 22; [4] Kleiman S. L., в кн.: Dix ex-
exposes sur la cohomologie des schemas. Amst.— P., 1968, p. 359—
386; [5] Griffiths P., Harris J., Principles of algebraic
geometry, N. Y., 1978; [6] Cohomologie etale. SG-A 4V2, В.—
Hdlh.— N. Y., 1977; [7l Cohomologie (-adique et fonctions L,
SGA 5, B.— Hdlb.— N. Y., 1977; [8] Д о л ь д А., Лекции по
алгебраической топологии, пер. с англ., М., 1976; [9] 3 е ii-
ф е р т Г., Т р е л ь ф а л л ь В., Топология, пер. е нем., М.
Л., 1938. В. А. Исковскь..
ЛЕФШЕЦА ЧИСЛО — инвариант отображения цеп-
цепного (коцепного) комплекса или топологич. простран-
пространства в себя. Пусть X — цепной комплекс абелевых
групп (соответственно топологич. пространство), / ¦
X —»- X — эндоморфизм степени 0 (соответственно непре-
непрерывное отображение), Н,(Х, Q) — гомологии группы
объекта X с коэффициентами в поле рациональных чи
сел Q, причем
У, сИтГ|Я/(Х, Q) < оо.
и пусть t{ — след линейного преобразования
/,: Ht(X, Q)—*H,(X, <Q).
По определению, число Лефгаеца отображения /
есть
В случае коцепного комплекса определение аналогично
В частности, Л. ч. тождественного отображения ел
равно эйлеровой характеристике %(Х) объекта А'.
Если X — цепной (коцепной) комплекс свободных
абелевых групп или тоиологич. пространство, то число
А(/) всегда целое. Л. ч. было введено С. Лефшецем
[1] для решения задачи о числе неподвижных точек
непрерывного отображения (см. Лефшеца формула).
Для нахождения Л. ч. эндоморфизма / комплекса
X, состоящего из конечномерных векторных прост-
пространств X над Q, можно воспользоваться следующе;'
формулой (к-рая иногда наз. формулой следа
X о п ф а)
Л (/) = 2™_ (—1)' Т1>
где Тi — след линейного преобразования / : X,- —>- X,.
В частности, если X — конечное клеточное простран-
пространство, ф : X —>- X — его непрерывное отображение is
себя и г|) : X —>- X — нек-рая клеточная аппроксимация
отображения ф, то
где Тj — след преобразования
г|,;+ :Ci(X, Q)—*Ci(X,Q),
индуцированного отображением 1|з, а С,(Х,-, Q) — груп-
группа рациональных г-мерных цепей клеточного простран-
пространства X.
Все сказанное выше допускает обобщение на cnyqaii
произвольного поля коэффициентов.
Лит.: [1] Lefschetz S., «Trans Amer. Math. Soc»,
1926, v. 28, p. 1—49; [2] 3 e йферт Г., Т р е л ь ф а л л i. В.,
Топология, пер. с нем.. М.— Л., 1938. 10. Б. Рудяк.
ЛЖЕЦА ПАРАДОКС — см. А нтиномия.
ЛИ р-АДИЧЕСКАЯ ГРУППА — аналитичегая
группа над полом Qp р-адических чисел (более об;т;.о —
над любым локально компактным неархимедовым но-
нолем if). Естественными примерами Ли р-а. г. являются
группы Галуа нек-рых бесконечных расширений полей.
Напр., если <Q(?pv)—поле, полученное присоедине-
присоединением к полю Q рациональных чисел первообразного кор-
корня t,pv степени pv из единицы, и k=Q(Z,p), K=
= U^=l'?(Spv), то при рф2 группа Галуа расширения
Юк изоморфна Ли р-а. г., %р — группе целых р-ади-
ческих чисел.
Многие результаты теории обычных групп Ли (связь
между группами и алгебрами Ли, конструкция и
свойства экспоненциального отображения) имеют ана-
аналоги и в р-адическом случае. Эти результаты находят
применение в алгебраич. теории чисел и в теории
групп.
Лит.: [1] Б у р б а к и Н., Группы и алгебры Ли. Алгебры
Ли, свободные алгебры Ли и группы Ли, пер. с франц., М.,
1976; [2] С е р р Ж,- П., Алгебры Ли и группы Ли, пер. с англ.
и Лранц., М., 1969; [3] L а г а г d М., «Publ. Math. IHES»
1065, t. 26, p. 389—603. А. А. Кириллов.
ЛИ АЛГЕБР МНОГООБРАЗИЕ над кольцом
к — класс Ж алгебр Ли над к, удовлетворяющих нек-
некрой фиксированной системе тождеств. К наиболее рас-
распространенным Ли а. м. относятся многообразия: Я —
абелевых алгебр Ли, заданное тождеством от/=0, Эсс —
нилыютентных класса с алгебр Ли, в к-рых любые
произведения длины больше с равны нулю, (?г —
разрешимых длины <:i! алгебр Ли, в к-рых производ-
производный ряд сводится к нулю не более чем за I шагов.
Совокупность v(k) всех алгебр Ли а. м. над к — груп-
группоид относительно умножения: 2B = U??, где Ж —
класс расширений алгебр из SB при помощи идеалов
из U; ©;—2t'; алгебры из 312 наз. метабеле-
в ы м п.
Центральная проблема теории Ли а. м.— описание
базисов тождеств Ли а. м., в частности с точки зрения
их конечности или бесконечности (если кольцо к нё-
терово). В случае, если к — поле характеристики р>0,
имеются примеры локально конечных Ли а. м., лежа-
лежащих в 2t3 и не обладающих конечным базисом тождеств.
В случае поля к характеристики 0 примеров бесконечно
базируемых многообразий пока нет A982). Коночная
базируемость сохраняется при умножении справа на
нильпотентное многообразие или при объединении с
таким многообразием. К числу ш п е х т о в ы х (т. е.
таких, в к-рых каждое многообразие конечно базируе-
базируемо) Ли а. м. относятся Ли а. м. Ш^Г\ЗШ[ над любым
нётеровым кольцом, 9i C2t ГШ г9? с над любым полем
характеристики ф2, Ли а. м. var(&2), определенное
тождествами, справедливыми в алгебре Ли к2 матриц
порядка 2 над полем к, char(/c) = O. Над полем к харак-
характеристики 0 нет пока примера конечномерной алгебры
Ли А такой, что уах(А) бесконечно базируемо, над
бесконечным полем к характеристики р>0 такие при-
примеры имеются. Над конечным полем или, общее, над
любым конечным кольцом к с единицей тождества конеч-
конечной алгебры Ли А следуют из своей конечной подси-
подсистемы.
Ли а. м. var(yl), порожденное конечной алгеброй
А, наз. многообразием Кросса и содер-
содержится в многообразии Кросса Q, (/, т, с), состоящем из
алгебр Ли, в к-рых все главные факторы имеют порядок
</», все нильпотентные факторы имеют класс -<е,
все внутренние дифференцирования ad x аннулируются
унитарным многочленом f^k[t]. Почти кросс о-
вы многообразия (т. е. некроссовы многооб-
многообразия, все собственные подмногообразия к-рых крос-
совы) описаны в разрешимом случае, имеются примеры
неразрешимых почти кроссовых многообразий. Группо-
Группоид v (к) над бесконечным полем — свободная полугруппа
с 0 и 1, над конечным полем v(k) может не быть ассо-
ассоциативным. Решетка Jf(S5) подмногообразий Ли а. м. 33
над полем к модулярна, но не дистрибутивна в общем
случае. Дистрибутивность решетки JC (W) имеет место
лишь в случае бесконечного поля. Базисы тождеств
конкретных алгебр Ли найдены лишь в немногих нетри-
нетривиальных случаях: для к2 (char (к) = 0 либо char (к) = 2),
а также для некоторых метабелевых алгебр Ли.
Важные результаты получены об алгебрах Ли с тожде-
тождеством (adx)"=0 (см. Ли нильалгебра).
Лит.: [1] Артамонов В. А., «Успехи ыатем. наук»,
1978, т. 33, в. 2, с. 135—67; [2] A m а у о В., Stewart I.,
Infinite-dimensional Lie algebras, Leyden, 1974; [3] Вахт y-
рин Ю. A., Lectures on Lie algebras, В., 1978.
Ю. А. Бахтурин.
ЛИ АЛГЕБРА, лиева алгебр а,— унитарный
fc-модуль L над коммутативным кольцом к с единицей,
к-рый снабжен билинейным отображением (х, у) i—=>•
i—=>• [х, у] прямого произведения LXL в L, обладаю-
обладающим следующими двумя свойствами:
1) [х, г] = 0 (откуда вытекает антикоммутативность
[х, у] —— [у, ж]);
2) [х, [у, z]] + [у, [z, х\] + [z, [х, у]] = 0 (т о ж-
дество Якоб и).
Таким образом, Ли а. является алгеброй над к (не
обязательно ассоциативной); обычным образом опре-
определяются понятия подалгебры, идеала, факторалгебры
и гомоморфизма алгебр Ли. Ли a. L наз. к о м м у т а-
т и в н о й, если [х, г/] = 0 для всех х, y?L.
Наиболее важным является случай, когда к — ио-
иоле (в особенности к— R или С), a L — векторное прост-
пространство (вообще говоря, бесконечномерное) над к.
Ли а. появились в математике в кон. 19 в. в связи с
изучением Ли групп (см. также Ли локальная группа,
Ли группа преобразований, Ли теорема), а в неявной
форме несколько раньше в механике. Общей предпо-
предпосылкой возникновения этого понятия было понятие
«инфинитезимального преобразования», воеходяхцее по
меньшей мере ко времени возникновения исчисления
бесконечно малых. Замкнутость интегралов класса С.2
уравнения Гамильтона относительно скобок Пуассона,
удовлетворяющих тождеству Якоби,— одно из самых
ранних замечаний, выраженное, собственно, на языке
Ли а. (см. [8], [10]). Сам термин «Ли а.» был введен
Г. Вейлем (Н. Weyl) в 1934 (до этого времени исполь-
использовались термины «ипфинитезимальные преобразова-
преобразования рассматриваемой группы», или «инфиннтезпмаль-
ная группа»). С течением времени роль Ли а. возрастала
пропорционально месту, занимаемому группами Ли в
математике (особенно в геометрии), а также в классичес-
классической и квантовой механике. Этим в первую очередь объяс-
объясняется особое место Ли а. среди многих других много-
многообразий универсальных алгебр. В наше время аппарат
Ли а. воспринимается уже не только как полезное п
мощное средство линеаризации теоретико-групповых
задач (будь то в теории групп Ли или в значительной
мере поглотившей ее и чрезвычайно разросшейся
теории алгебраических групп, или же в стоящей несколь-
несколько особняком теории конечных групп); это также источ-
источник красивых и трудных задач линейной алгебры.
Имеется несколько естественных источников, достав-
доставляющих важнейшие примеры Ли а.
1) В рамках общей алгебры значение Ли а. опреде-
определяется прежде всего тем, что множество Dor (А) всех
дифференцирований любой А-алгебры является Ли а.
с операцией
Дифференцирования Ли a. L вида
ad х: у ь-» [х, у], .г, у ? L,
наз. внутренними дифференцирова-
дифференцированиям и, или присоединенными эндомор-
эндоморфизмам и. Они образуют в Der(L) подалгебру ad L,
а отображение х—>-ad x является гомоморфизмом Ли а.
L —>¦ Dor(L) (присоединенное представ-
представление Ли a. L); его образ ad L изоморфен фактор-
алгебре алгебры L по ее центру
Z{L) = {x ?L\[x, y\ = 0 Vy ?L].
2) Еще один существенный источник Ли а. связан
со следующим простым наблюдением. Если L — ассо-
циативная алгебра над к с умножением {х, у) \—*¦ ху,
то умножение в fc-модуле L, задаваемое правилом
(*, У)
[х, у] = ху—уг,
наделяет L структурой Ли а. над к. Говорят, что (L,
I , ]) — Ли а., ассоциированная с ассоциативной алгеб-
алгеброй (L, •)• Так, классич. пример Ли a. (L, [ , ])
получится, если в качестве (L, •) взять (ассоциативную)
алгебру Мл (к) всех квадратных матриц порядка п
над к.
Следующие четыре бесконечные серии подалгебр в
Ли а. указанного типа наз. классическими
(к — поле нулевой характеристики):
Bn
5 =
{.г
{х
Ап
= {
111
= 0
|о
= {х
Е Л:?
* 6 М2п +
0
0
-Е„
2И I X
0 I
?"
0 II
п + 1 (fe) 1
tra- =
1(к)\хВ + В*х
, Еп =
1
f
D V = 0}
n :
= 0},
1
6
c =
A ^
!;
nS&2
Mn(k
0
0
En
0
E
0
При этом dim Ап=п (и+2), dim Ви~ гс Bn-i-l), dim Cn =
= иB«-^1), dim ?>„=иBи—1).
Если, кроме того, поле к алгебраически замкнуто,
то эти Ли а. замечательны тем, что ими и еще пятью
Ли особыми алгебрами G2, F$, Eg, E7, Es размерностей
14, 52, 78, 133 и 248 соответственно исчерпываются,
с точностью до изоморфизма, все простые (т. е. некомму-
некоммутативные и не содержащие идеалов, отличных от 0 и
самой алгебры) конечномерные Ли а. над к.
3) Еще один источник Ли а.— векторные поля на
многообразии (см. [13], [14]). Пусть F — кольцо С°°-
гладких функций на С°°-гладком многообразии М.
Векторное пространство Vect(Af) всех С"-гладких век-
векторных полей на М образует Ли а. относительно опе-
операции коммутирования (см. Ли скобка), играющую
важную роль в теории многообразий; Ли a. Vect(Af)
совпадает с Ли a. Der(F). Эта алгебра, вообще говоря,
бесконечномерна. Если М — группа Ли, то подпрост-
подпространство в Vect (M), состоящее из всех левоинвариантных
векторных полей, является конечномерной подалгеброй
ж наз. алгеброй Ли группы Ли М; она
играет важную роль в теории групп Ли, позволяя пере-
переформулировать многие свойства групп Ли в терминах
Ли а. См. также Ли алгебра алгебраической группы,
Ли алгебра аналитической группы.
Если в приведенном выше примере заменить кольцо F
на коммутативную алгебру 0n(k) = k[[X1, . . ., Хп]}
формальных степенных рядов над полем к, то вместо
Vect (М) получается Ли a. Wn формальных векторных
полей, состоящая из дифференциальных операторов
Подалгебры Srl cz W,, + 1, //„crW2,M состоящие из диф-
дифференцирований, аннулирующих соответственно внеш-
внешние дифференциальные формы
л ... Л
dXi Л
а также подалгебра KnC^Win--L дифференцированшг,
умножающих форму
на элементы изC„(/с), вместе с алгеброй Wn составляют
важный класс простых бесконечномерных Ли а. (а л-
гебры Ли картаповского типа). Ал-
Алгебра Wn наз. общей, Su — специальной,
//„ — гамильтоновой, Кп — контактной.
Эти алгебры встречались еще у С. Ли (S. Lie) при изу-
изучении псевдогрупп преобразований (fc—-R. или С), а
затем исследовались по разным поводам 3. Картаном
(Е. Cartan) и др. (см. [151, [17], [18], [19]).
4) Следующая общая конструкция позволяет строить
% -алгебру Ли L по любой группе G; она находит
применение в теории групп (см. Бёрнсайда проблема,
[16]). Пусть
— нижний центральный ряд группы G. Тогда L —
это прямая сумма аддитивно записанных факторгрупп
G,7G,- + 1, причем, по определению, произведение эле-
элементов х ? G,7G,- + 1 и у ? GjlGj + l есть элемент из
G,-+//G/+у _j, являющийся классом коммутатора элемен-
элементов х ? Gj и у ? Gj, представляющих соответственно х и у.
На произвольные элементы из L эта операция распро-
распространяется по дистрибутивности. Имеются (см. [16])
нек-рые обобщения этой конструкции.
Строение алгебр Ли. Одним из общих результатов,
показывающих, в частности, что конструкция 2) име-
имеет в известном смысле универсальный характер, явля-
является Виркгофа — Витта теорема, согласно к-рой для
любой Ли a. L над полем к существует такая ассоциа-
ассоциативная fe-алгебра U, что L изоморфно вкладывается в
Ли a. (U, [ , ]), ассоциированную с U. Если при этом
L конечномерна, то можно считать, что и U конечно-
конечномерна (см. Универсальная обертывающая алгебра).
Пусть L — конечномерная Ли а. над полем к пуле-
пулевой характеристики. Тогда L линейна, т. е. изоморфна
подалгебре нек-рой Ли а. Мп(к) (теорема Ад о).
В L имеется наибольший разрешимый идеал Д, назы-
называемый радикалом (см. Ли разрешимая алгебра).
Кроме того, в L существует подалгебра S (называемая
подалгеброй Лев и) такая, что L — прямая
сумма векторных пространств S и R, причем любая
другая подалгебра с таким свойством переводится в 5
автоморфизмом алгебры L (теорема Леви —
Мальцева). Подалгебра 5 является полупростои
(т. е. ее радикал равен нулю), и она может быть охарак-
охарактеризована как максимальная полупростая подалгебра
в L. Таким образом, L является полупрямой суммой
полупростой и разрешимой Ли а., что сводит задачу
классификации конечномерных Ли а. над полем нуле-
нулевой характеристики к описанию Ли а. этих двух типов.
Хотя разрешимые Ли а. в нек-ром смысле «получаются»
из тривиально устроенных одномерных (а именно,
обладают цепочкой подалгебр ?=Lnr)L,3 . . . ?„=0
таких, что L; — идеал в Ь[ — \ и L; — \IL{ одномерна);
строение их настолько сложно, что к настоящему
времени A982) фактически отсутствует даже корректная
постановка задачи о классификации разрешимых Ли а.
Напротив, конечномерные полупростые Ли а. над по-
полем нулевой характеристики допускают полное описа-
описание (см. Ли полупростая алгебра): всякая такая алгебра
разлагается в прямую сумму простых идеалов (и об-
обратно, прямая сумма простых Ли а.— полупроста).
В случае алгебраически замкнутого поля все простые
Ли а. явно перечислены (см. п. 2); в случае произволь-
произвольного поля к имеется процедура их нахождения, с
помощью к-рой в ряде случаев (напр., при k=R) также
найдена явная классификация.
Конечномерные Ли а. над полем характеристики
р>0 исследованы значительно менее полно (даже
для алгебраически замкнутых полей). Эти Ли а. обла-
обладают многими специфич. свойствами. Напр., весьма
нетривиальным оказался даже вопрос описания полу-
полупростых Ли а. в терминах простых алгебр (см. [23]).
При любом р существуют параметрич. семейства про-
простых Ли а., попарно неизоморфных друг другу. Теория
Ли а. для этого случая находится в процессе становле-
становления, причудливым образом отражая в себе черты двух
разных классов комплексных Ли а.— конечномерных
простых и бесконечномерных транзитивных простых,
соответствующих примитивным псевдогруппам Ли
(см. [17J, [18], [19]).
Изучение бесконечномерных Ли а. началось еще в
19 в. одновременно с изучением конечномерных. Такие
Ли а. естественно появляются при классификации при-
примитивных псевдогрупп преобразований, предпринятой
в 1909 Э. Картаном [20]. Эти алгебры обладают фильт-
фильтрацией, для к-рой ассоциированная градуированная
Ли а. имеет вид Cbi°=L^i и транзитивна. Бесконечно-
Бесконечномерные градуированные Ли а. являются предметом
интенсивных исследований, в к-рых обнаруживаются
связи этих Ли а. не только с классическими геометрич.
вопросами, но и со многими другими областями мате-
математики (см. Ли градуированная алгебра, а также [17],
[22]). Важные примеры бесконечномерных Ли а. появ-
появлялись в последнее время в теории уравнений матема-
тич. физики (напр., для уравнения Кортевега — де
Фриса) и в формальном вариационном исчислении (см.
[14]).
Абстрактная теория бесконечномерных Лн а. (см.,
напр., [9]) находится пока в начальной фазе своего
развития. Для построения структурной теории Ли а. и
для большинства приложений в физике важную роль
играет теория представлений Ли а.
См. также Супералгебра, Ли алгебр многообразие.
Лит.: [1] Б у р б а к и Н., Группы и алгебры Ли, пер. с
франц., [гл. 1 — 8], М., 1972—78; [2] Джекобсон Н.,
Алгебры Ли. пер. с англ., М., 1964; [3] Капланский И.,
Алгебры Ли и локально компактные группы, пер. с англ., М.,
1974; [4] Магнус В., Кар рас А., С о лит эр Д.,
Комбинаторная теория групп, пер. с англ., М., 1974; [5] П о н т-
рягин Л. С, Непрерывные группы, 3 изд., М., 1973; [6]
Теория алгебр Ли. Топология групп Ли, Семинар «Софус Ли»,
пер. с франц., М., 1962; [7] С е р р Ж. П., Алгебры Ли и группы
Ли, пер. с англ. и франц., М., 1969; [8] Ш е в а л л е К., Теория
групп Ли, пер. с франц., т. 3, М..1958;[9] Amayo R. К., Ste-
Stewart Ian, Infinite-dimensional Lie algebras, Leyden, 1974;
[10] Humphreys J. E., Introduction to Lie algebras and
representation theory, N. Y.— Hdlb.— В., 1972; [11] S e 1 i g-
man G. В., Modular Lie algebras, В.— Hdlb.—N. Y., 1967;
[12] Арнольд В. И., Математические методы классической
механики, М., 1974; [13] Годбийон К., Дифференциальная
геометрия и аналитическая механика, пер. с франц., М., 1973;
[14] Дубровин Б. А., Новиков С. П., Ф о м е н-
к о А. Т., Современная геометрия, М., 1979; [15] Международ-
Международный конгресс математиков. Ницца. 1970. Доклады советских
математиков, М., 1972, с. 111 —17; [16] Кострикин А. И.,
«Изв. АН СССР. Сер. матем.», 1957, т. 21, с. 289 — 310; 1959,
т. 23, с. 3—34; 1970, т. 34, с. 744—56; [17] Гийемин В.,
«Математика», 1966, т. 10, № 4, с. 3—31; U8] К а ц В. Г., «Изв.
АН СССР. Сер. матем.», 1968, т. 32, с. 1323—67; 1974, т. 38,
с. 800—34; [19] Кострикин А. И., III а ф а р е в и ч И. Р.,
«Изв. АН СССР. Сер. матем.», 1969, т. 33, с. 251 — 322; [20]
С art an E., «Ann. Scient. Ecole norm, super.», 1909, t. 26,
p. 93—161; [21] L a z a r d M., там же, 1954, t. 71, p. 101—90; [22]
Singer I. M., S t e r n b e r g S., «J. Analyse Math.», 1965
v. 15, p. 1 — 114; [23] Block R. E., «Ann. Math.», 1969, v. 90,
№ 3, 433—59. А. И. Кострикин, В. Л. Попов.
ЛИ АЛГЕБРА АЛГЕБРАИЧЕСКОЙ ГРУППЫ —
аналог Ли алгебры аналитической группы, относящийся
к случаю аффинных алгебраич. групп. Как и в анали-
тич. случае, Ли а. а. г. G есть касательное пространство
к G в единице, а структура алгебры Ли определена в
нем с помощью левоинвариантных дифференцирований
алгебры функций на G. Точное определение состоит в
следующем.
Пусть К — алгебраически замкнутое поле, G —
аффинная алгебраич. ЛГ-группа, A = K[G] — алгебра
регулярных функций на G и Lie (G) — множество всех
дифференцирований Z-алгебры А , к-рые коммутируют
с автоморфизмами алгебры А, определенными левыми
сдвигами из G. Пространство Lie(G) является алгеброй
Ли с операцией [D\, Di\=^D1°Di—ZJ0-C*i (CM- Ли ли-
линейная алгебра), а операция DlPl=D°. . .oD (p сомножи-
сомножителей) определяет на Lie (G) структуру р-алгебры Ли
(р равно характеристике поля К, если она положитель-
положительна, и равно 1, если она нулевая). Пусть L (G) — каса-
касательное пространство к G в единице е, т. е. векторное
пространство над К всех ^-дифференцирований из А в
Л-модуль А/те, где те — максимальный идеал точки
е, и пусть фр : А —>- А/те канонич. гомоморфизм. Для
любого D ?Lie(G) композиция фгг0 является элемен-
элементом из L(G), а отображение Lie(G) —>- L(G), определен-
определенное формулой D —>- фе D, является изоморфизмом век-
векторных пространств над К. Это позволяет перенести с
Lie(G) на L(G) структуру р-алгебры Ли. Эта р-алгебра
Ли L (G) и наз. Ли а. а. г. G. Если к — подполе в К
и G определена над к, то левоинвариантные fc-дифферен-
цирования /с-алгобрыЛ ^сА , определяющей fc-структуру
на G, образуют /с-структуру на Lie(G), а указанный
выше изоморфизм определен над к.
Пример. Пусть V — конечномерное векторное про-
пространство над К и G = GL(V) — алгебраич. группа
всех автоморфизмов пространства V. Тогда касательное
пространство к G в точке е естественно отождествля-
отождествляется с векторным пространством End V всех эндомор-
эндоморфизмов пространства V, а структура Ли а. а. г. G на
End V задастся формулами: [X, Y] = XY — YX,
Х1Р]=ХР. Полученная алгебра Ли обозначается rtl(F).
Ли а. а. г. обладают рядом свойств, аналогичных
свойствам алгебр Ли аналитич. групп. Так, дифферен-
дифференциал гомоморфизма алгебраич. групп в единице есть
гомоморфизм их алгебр Ли. Размерность Ли а. а. г. G
равна размерности группы G. Ли а. а. г. G и ее связ-
связной компоненты единицы совпадают. Дифференциал
присоединенного представления алгебраич. группы яв-
является присоединенным представлением ео алгебры
Ли. Если Н — алгебраич. подгруппа в алгебраич.
группе G, то L(H) есть подалгебра в L(G). Более того,
пусть / ¦— идеал всех регулярных функций на G, об-
обращающихся в нуль на Н. Тогда, отождествляя L (G)
с Lie (G), можно описать L (Н) как множество всех таких
элементов из Lie(G), к-рые аннулируют /. Это описа-
описание особенно удобно при рассмотрении линейных ал-
алгебраич. групп, т. е. алгебраич. подгрупп G в GL(F).
А именно, пусть / — идеал if[End V], состоящий из эле-
элементов, равных нулю на G. Тогда L(G)cz#l(V) состоит
в точности из таких эндоморфизмов X пространства V,
что дифференцирование алгебры К [End V], порожден-
порожденное эндоморфизмом У 1—*¦ XY пространства End V,
переводит / в себя. Операции же в L (G) индуцированы
описанными выше операциями в ftl(F).
Если р = 1, то связь между аффинными алгебраич.
группами и их алгебрами Ли является по существу
столь же тесной, как связь между аналитич. группами
и их алгебрами Ли. Это позволяет в значительной сте-
степени сводить изучение аффинных алгебраич. групп к
изучению их алгебр Ли и обратно. При этом алгебры Ли
линейных алгебраич. групп (т. е. алгебраич. подгрупп
в GL(V)) выделяются среди всех подалгебр Ли в Cj((F)
с помощью внутреннего критерии (см. Ли алгебраичес-
алгебраическая алгебра). В случае р > 1 указанная связь не явля-
является столь тесной и в значительной степени теряет свое
значение. А именно, в этом случае в общем справедли-
справедливыми остаются лишь результаты, позволяющие извле-
извлекать из свойств группы сведения о свойствах ее алгебры
Ли. Напротив, многие теоремы, устанавливающие в
случае р = 1 эту связь в обратную сторону, перестают
быть справедливыми. Напр., могут существовать раз-
различные связные подгруппы данной группы, алгебры
Ли к-рых совпадают; алгебра Ли неразрешимой алгеб-
рапч. группы может быть разрешимой (это так, напр.,
для группы матриц порядка 2 с определителем 1 при
р~-2) и т. п.
Slum.: [J] Б о р е л ь А., Линейные алгебраические группы,
пер. с anr.i.. M., 1972; [2] Ш е в а л л е К., Теория групп Ли,
пор. с франц., т. 2, М., 1958. В. Л. Попов.
ЛИ АЛГЕБРА АНАЛИТИЧЕСКОЙ ГРУППЫ, а л-
г о б р а Л и группы Л и G, определенной над
полем к, полным относительно нек-рого нетривиального
абсолютного .значения,—алгебра Ли g группы G, рассмат-
рассматриваемой как Ли локальная группа. Таким образом, $
как векторное пространство отождествляется с каса-
касательным пространством к G в точке е. Операция умно-
умножения 1 , ] в алгебре Ли й может быть определена
любым из следующих эквивалентных способов.
1) Пусть ad — дифференциал присоединенного пред-
представления группы G. Тогда adX для любого вектора
X(; й является линейным преобразованием простран-
пространства с}, причем adX (У)=[Х, Y] для любого У?д.
2) Пусть k— R, X и У?с| — два касательных век-
вектора к G в точке е и х (t) и у (t) — гладкие кривые в
G, для к-рых X и У являются касательными векторами
при t~ 0. Тогда [X, У] есть касательный вектор при
s=0 к кривой q(t) = x(s)y (s)x(s)~1y (s) ~x, где s^O,
a s2=/.
3) Пусть U (G) — ассоциативная fc-алгебра обоб-
обобщенных функций на G с носителем вепс умножением,
определяемым сверткой*. Пространство <\ отождеств-
отождествляется с множеством примитивных элементов в биалгеб-
ре U (G) и для любых X, У?й вектор Х*У—У*Х так-
также лежит в q. Тогда Х*У— У*Х=[Х, У].
4) Пусть X — векторное пространство всех век-
векторных нолей на G, инвариантных относительно левых
сдвигов на элементы из G. Сопоставление векторному
нолю его значения в точке e?G является изоморфизмом
векторных пространств X и Д. С другой стороны, вся-
всякому векторному полю L?X сопоставляется левоинва-
риантное дифференцирование fe-алгобры А аналитич.
функции на G по формуле L(f) (g)= (d[)g(Lg) для лю-
любых f?A, g(zG, и это сопоставление является изомор-
изоморфизмом пространства X с векторным пространством D
всех левоинвариантных дифференцирований алгебры
А. Для любого Х?а, через Lx^X обозначается лево-
инвариантное векторное поле, для к-рого (Lx)e~--X.
Если X, У(;Я, то произведение [X, У] может быть
определено как такой вектор из ег, что поле Lfx, Y] за~
дает дифференцирование L-x-Ly—LyLx алгебры А.
Пример. Пусть G — аналитич. группа всех невы-
невырожденных матриц порядка п с коэффициентами в к.
Тогда касательное пространство а, к G в единице
отождествляется с пространством всех матриц порядка
п с коэффициентами в к, а структура алгебры Ли на д
определяется формулой [X, Y]= XY—УХ.
Сопоставление аналитич. группе ее алгебры Ли
обладает важными функториальными свойствами и в
значительной степени сводит изучение аналитич. групп
к изучшнш их алгебр Ли. А именно, пусть Gt и G2 —
аналитич. группы с алгебрами Ли йх и з2, ф'- Gt —*- G2 —
аналитнч. гомоморфизм. Тогда d(fe '¦ Й! —>- й2 гомомор-
гомоморфизм алгебр Ли. Ли а. а. г. Gj X Gi изоморфна cliffy.
Если й — Ли а. а. г. G, // — подгруппа Ли в G (см.
Mj, группа) и ft — Ли а. а. г. Н, то ft — подалгебра
в й, причем, если Н нормальна, то (i — идеал в й-
Пусть характеристика поля к равна 0. Алгебра Ли
пересечения подгрупп Ли совпадает с пересечением
их алгебр Ли. Алгебра Ли ядра гомоморфизма ср ана-
аналитнч. групп ость ядро гомоморфизма dq>e их алгебр Ли.
Алгебра Ли факторгруппы G/H, где // — аналитич.
нормальная подгруппа в G, есть факторалгебра алгеб-
ры Ли группы G по идеалу, отвечающему подгруппе Н.
Если д — Ли а. а. г. G и ft — подалгебра в G, то
существует единственная связная подгруппа Ли 7/сС
с алгеброй Ли ft; при этом Н не обязательно замкнута в
G. Ли а. а. г. разрешима (нильпотентна, полупроста)
тогда и только тогда, когда сама группа разрешима
(ннлыютентна, полупроста).
Указанная связь между категориями аналитич.
групп и алгебр Ли не является все же, в отличие от
случая локальных групп Ли, эквивалентностью этих
категорий. А именно, ноизоморфные аналитич. группы
могут иметь изоморфные алгебры Ли. Аналитич.группы
с изоморфными алгебрами Ли наз. локально изо-
изоморфны м и. В случае поля к нулевой характеристи-
характеристики каждой конечномерной алгебре Ли над к отвечает
нок-рый класс локально изоморфных аналитич. групп.
Пусть /с— R или С. Среди всех локально изоморфных
аналитич. групп имеется единственная с точностью
до изоморфизма связная и односвязная группа; кате-
категория аналитич. групп такого типа эквивалентна ка-
категории конечномерных алгебр Ли над к. В частности,
всякий гомоморфизм алгебр Ли индуцирован аналитич.
гомоморфизмом соответствующих связных и односвяз-
ных аналитич. групп. Любая связная группа Ли, ло-
локально изоморфная данной связной и односвя;шой
группе Ли G, имеет вид G/D, где D — дискретный
нормальный делитель, лежащий в центре группы G.
Лит.: [1] Бурбаки Н., Группы и алгебры Ли. Алгебры
Ли, свободные алгебры Ли и группы Ли, пер. с франц., М., 197В:
[2] П о н т р я г и н Л. С, Непрерывные группы, 3 изд., М.,
1973; [3] С е р р Ж.-II., Алгебры Ли и группы Ли. пер. с англ.
и франц., М., 1969; [4] Кириллов А. А., Элементы теории
представлений, 2 изд., М., 1978; [5] Шевалле К., Теории
групп Ли, пер. с англ., т. 1, М., 1948. В. Л. Попов.
ЛИ р- АЛГЕБРА, ограниченная алгебра
Л и,— алгебра L над полем к характеристики р > О
(или, более общо, над кольцом простой характеристики
р> 0), снабженная р-отображением х —>- х1^ таким, что
выполняются следующие соотношения:
ad (zW) = (ad з-)[рЭ,
'.*, У)-
Здесь ad x : у —>- [х, у] — внутреннее дифференци-
дифференцирование алгебры L, определяемое элементом x^L
(оператор присоединенного представления), а Ар(х, у)
элемент из L, являющийся линейной комбинацией од-
одночленов Ли
(ad х1... ad rp _ j) x
с ж,- = .т или у для всех г=1, . . ., р — 1.
Типичный пример Ли р-а. получается, если рас-
рассмотреть произвольную ассоциативную алгебру А над
к как универсальную алгебру с двумя производными
операциями:
i) (.г, у)—>-[х, у] = ху— ух,
и) х-+хр.
В частности, свойство ad(.r.P) = (adx)P является прямым
следствием тождества
(ad х)" у = 2"_ (—V
при п=р, когда ( п. ) = 0, /=1, . . ., р — 1. Так как всякая
Ли алгебра вложима в подходящим образом выбранную
ассоциативную алгебру А с операциями i) — ii) ( т е о-
рема Пуанкаре — Биркгофа — Витта),
то часто х1Р1 заменяют, с нек-рой долей двусмысленно-
двусмысленности, на х1'.
Для всякой Ли р-а. L существует р-у ниверсаль-
ная (ограниченная универсальная)
обертывающая ассоциативная алгеб-
р a Up{L). Если dim^^='!, то AimtiUp{L) = pn. Это же
замечание показывает, что для произвольной алгебры
Ли имеет смысл говорить о ее наименьшей р-оболочке,
или о /'-замыкании.
Обычная подалгебра Ли М (идеал Ли) в L наз.
р-п одалгеброй (р-и д е а л о м), если х(Р1 ? М
для всех х(^М. Гомоморфизм ф :/>-*¦ А' Ли р-а. наз.
^-гомоморфизмом, коль скоро
Если при этом К — линейная Ли р-а. над к, то говорят
также о р-продставленин <р алгебры L.
Задание р-структуры х —v х1Р] на алгебре Ли L с ба-
базисом {<?i, е2, . . .} и нулевым центром Z (L) единственно
и вполне определяется заданием образов е\р^ базисных
элементов е,-. С другой стороны, коммутативная алгебра
Лп L, для к-рон всегда, очевидно, Лр(х, у) = 0, снаб-
снабжается р-структурой путем рассмотрения пары (L, л),
где я — произвольное р-полулинейное отображение
Над алгебраически замкнутым полем к всякая конеч-
конечномерная коммутативная Ли р-а. L разлагается в пря-
прямую сумму L=L(,Q;LX тора
и нильпотентной подалгебры Lx с тождеством
;1.чя достаточно большого т (см. [1]).
Важным источником Ли р-а. служат теория алгеб-
ранч. групп, теория формальных групп и теория не-
сепарабельных полей (см. [2]). Алгебра Ли Der/, (А)
все дифференцирований произвольной алгебры А яв-
является р-подалгеброн в EndftD). Если, в частности,
А=к\Х]1Хрк\Х], то W1=I)ovk{A) натянута на диффе-
дифференцирования d; : X —>- A'' + 1, i= — 1, 0, 1, . . ., р—2,
с правилом коммутирования
[dh d/] = (i — i) d!+J- при i + /</j —2,
[d;, dj] = O при i+i>p + 2,
и р-структурон
d\p]=0 при i^ 0, dlp] = d0.
Этот пример простой Ли р-а. послужил поводом к
поискам других простых алгебр. Все известные к на-
настоящему времени A982) конечномерные простые Ли
р-а. над алгебраически замкнутым полем к характе-
характеристики р > 5 исчерпываются алгебрами клагеич.
типа (вместе с пятью исключительными). Это А„, п^А,
В,„ /!>2, Сп, н>3, Dn, n>4, Go, Fi, Etl, Е,, Е, и ал-
алгебрами картановского типа И7,,, n^l, Srn n^s2, Hn,
n^i, Kn, п^2. Размерности последних четырех алгебр
равны соответственно пр", ге(р" + 1 — 1), р2"—2 и
р-"-1—е, где е = 0 при я + 2^0(р) и е=1 при п-г2=з0(р).
Все эти алгебры определены над простым подполем поля
к, так что неизоморфных простых р-алгебр фиксиро-
фиксированной размерности — конечное число (как правило,
0, 1 или 2). Недоказанная пока A982) гипотеза, воз-
возникшая в связи с работой [3], заключается в том, что
других конечномерных простых Ли р-а. в этом случае
не существует. При р = 2, 3, 5, однако, ситуация заве-
заведомо сложнее.
Лит.: [1] Д ж е к о б о о н Н., Алгебры Ли, пер. е англ.,
М., 19В4: [2] Seligman G. В., Modular Lie algebras, В.—
Hdlb.— N. Y., 1967; 13] Кострики н А. II., Ш а ф а р е-
вич И. Р., «Докл. АН СССР», 1966. т. 1G8, с. 740 — 42: [4]
Zassenhaus H., «Hamb. Abh.», 1939, Bd 13, S. 1 — 100.
A. II. KocmpuKuii.
ЛИ АЛГЕБРАИЧЕСКАЯ АЛГЕБРА — 1) Алгебра
Ли алгебраич. подгруппы (см. Алгебраическая группа)
полной линейной группы всех автоморфизмов конечно-
мерного векторного пространства V над полем к.
Если Я — произвольная подалгебра в алгебре Ли всех
эндоморфизмов V, то существует наименьшая Ли а.
а., содержащая д; она паз. алгебраической
оболочкой подалгебры Ли q. Для ал-
алгебраичности алгебры Ли д над произвольным алгеб-
алгебраически замкнутым полем к необходимо, чтобы вместе
с каждым линейным оператором u?i) в g лежали его
полупростая и нильпотентная компоненты sure (см.
Жордана разложение). Это условие определяет т. н.
почти алгебраические алгебры Ли.
Оно не является достаточным для того, чтобы С( была
Ли а. а. В случае ноля к характеристики 0 необ-
необходимое и достаточное условие алгебраичности алгебры
Ли Д состоит в том, что вместе с ге и s=diag(su . . .,
sm) в g лежат все операторы вида (f(s)~ diag(cp (s^, . . .,
cp(sm)), где ср — произвольное Q-линейное отображение
из к в к. Исследовано [3] строение Ли а. а. в случае
ноля характеристики р > 0.
2) Алгебра Ли L над коммутативным кольцом к,
в к-рой для любого элемента ж ?//-эндоморфизм ad ж : у->
—>-[х, у], заданный на L, является корном нек-рого
многочлена со старшим коэффициентом 1 и остальными
коэффициентами из к- Конечномерная над полем к
алгебра Ли является Ли а. а. Обратное неверно: над
любым полем к существуют бесконечномерные Ли а. а.
с конечным числом порождающих [4]. Ряд вопросов о
Ли а. а. получает решение уже в классе Ли нильал-
гебр.
Лит.: [1] Б о р е л ь А., Линейные алгебраические группы,
пер. с англ., М., 1972: [2] Ш е в а л л е К., Теория групп Ли,
пер. с франц., т. 2, М., 1958; [3] S е 1 i g m a n G., Modular Lie
algebras, В.— Hdlb.— N. Y., 1967: Ш Голод Е. С, «Изв.
АН СССР. Сер. матем.». 1984, т. 28, J4» 2, с. 273—78.
Ю. А. Бахтурин.
ЛИ БАНАХОВА ГРУППА — множество G, снаб-
снабженное одновременно структурой группы и структурой
аналитич. банахова многообразия; эти две структуры
согласованы в следующем смысле: отображение (g, h)-*-
—>- gh~1 из GXG в G является аналитическим. В случае,
если банахово многообразие конечномерно, это понятие
совпадает с обычным понятием группы Ли.
Пример ы. Банахово пространство с операцией
сложения, множество А* обратимых элементов в бана-
банаховой алгебре А с операцией умножения, множество
Ск (М, G) fr-гладких функций на гладком многообразии
со значениями в группе Ли G с операцией поточечного
умножения являются Ли б. г. С другой стороны, мно-
множество Diff* M fc-гладких взаимно однозначных отобра-
отображений гладкого многообразия М на себя не является
Ли б. г.: естественные структуры банахова многообра-
многообразия и группы (относительно операции композиции) в
этом случае не согласованы.
Для Ли б. г. остаются справедливыми нек-рые ос-
основные теоремы теории групп Ли: каждой Ли б. г.
соответствует банахова алгебра Ли, по к-рой,
в свою очередь, восстанавливается локальная Ли б. г.
Известно, однако, что не всякая локальная Ли б. г.
продолжается до глобальной [2]; окрестность единицы
в Ли б. г. покрывается образом экспоненциальною
отображения; имеется соответствие между связными
замкнутыми подгруппами Ли б. г. и замкнутыми под-
подалгебрами соответствующей алгебры Ли.
Имеются различные обобщения понятия Ли б. г.
(см. [3]), в к-рых структура банахова пространства за-
заменяется структурой линейного топология, простран-
пространства более общего типа.
Лит.: [1] Б у р б а к и Н., Группы и алгебры Ли. Алгебры
Ли, свободные алгебры Ли и группы Ли, пер. с франц., М.,
1976; [2] D e la Harpe P., Classical Banach — Lie algebiii-
and Banach — Lie groups of operators in Hilbert space, B.-
La. o.], 1972; [3] О m о r i H., Infinite dimensional Lie transfor-
malJOn groups B.— [a. 0.], 1974. А. А. Кириллов.
ЛИ ВПОЛНЕ РАЗРЕШИМАЯ АЛГЕБРА, т р е у-
гольная алгебра Л и,— конечномерная ал-
гебра Ли g над полем к, для к-рой собственные значе-
значения операторов присоединенного представления ad X
принадлежат к для всех Х?д.
Ли в. р. а. разрешима, класс всех Ли в. р. а. содер-
содержит класс нильпотентных алгебр Ли и содержится
в классе экспоненциальных алгебр Ли. Он замкнут
относительно перехода к подалгебрам, факторалгебрам
и конечным прямым суммам, но не замкнут относитель-
относительно расширений.
Ли в. р. а. над совершенным полем обладают многи-
многими свойствами разрешимых алгебр Ли над алгебраичес-
алгебраически замкнутым полем (теорема Ли, наличие цепочки
идеалов д = g0 гз (}i ГЭ ... ГЭ $„= {0}, для к-рых
dim Cj,—dim g—i, и др.). В произвольной конечномер-
конечномерной алгебре Ли g существуют максимальные вполне
разрешимые подалгебры, они содержат нильрадикал.
Если fe=R пли С или если к совершенно и Д — алгеб-
раич. линейная алгебра Ли, то все'вполне разрешимые
подалгебры сопряжены. Алгебра Ли ft над /с, отвечаю-
отвечающая ^-разложимой алгебраич. группе над совершенным
полем к, есть Ли в. р. а.
Любая Ли в. р. а. над полем характеристики 0 изо-
изоморфно вкладывается в алгебру Ли верхних треуголь-
треугольных матриц с коэффициентами из к (которая сама
есть Ли в. р. а.). Простейший пример Ли в. р. а., не
являющейся нильпотентной,— ато двумерная алге-
алгебра Ли с базисом X, Y и определяющим соотношением
[X, Y]=X.
Лит. см. при ст. .Ни вполне разрешимая группа.
В. В. Горбацееич.
ЛИ ВПОЛНЕ РАЗРЕШИМАЯ ГРУППА, треу-
треугольная группа Л п,— связная вещественная
группа Ли G, для любого элемента g к-рой собствен-
собственные значения оператора присоединенного представ-
представления Ad g действительны.
Связная группа Ли G будет Ли в. р. г. тогда и только
тогда, когда ее алгебра Ли о, вполне разрешима,
поэтому ряд свойств класса Ли в. р. г. параллелен
свойствам Ли вполне разрешимых алгебр.
Для Ли в. р. г. справедлива следующая теорема о
неподвижной точке [2]: всякая вполне разрешимая
подгруппа Ли G проективной группы имеет неподвиж-
неподвижную точку в каждом G-инвариантном замкнутом подмно-
подмножестве действительного проективного пространства.
Имеют место также другие аналоги свойств комплек-
комплексных разрешимых групп Ли. Произвольная связная
группа Ли G обладает максимальными связными вполне
разрешимыми подгруппами Ли Т, все они сопряжены в
G (см. [2]). При изучении строения вещественных полу-
полупростых групп Ли подгруппа Т часто используется
как вещественный аналог борелевской подгруппы.
Односвязная Ли в. р. г. изоморфно вкладывается в
группу вещественных верхних треугольных матриц над
R с положительными диагональными элементами (к-рая
сама есть Ли в. р. г.).
Лит.: [1] Б о р е л ь А., Линейные алгебраические группы,
пер. с франц., М., 1972; [2] В и н б е р г Э. Б., «Докл. АН
СССР», 1961, т. 14), с. 270 —73. В. В. Горбацееич.
ЛИ ГРАДУИРОВАННАЯ АЛГЕБРА — алгебра Ли
(\ над полем К, градуированная при помощи нек-рой
абелевой группы А, т. е. разложенная в прямую сумму
подпространств ?«, а?А, таким образом, что [g«, gg ]c=
&}а+р- Если А — упорядоченная группа, то для каж-
каждой фильтрованной алгебры Ли ассоциированная с ней
градуированная алгебра является Ли г. а.
Ли г. а. играют важную роль в классификации прос-
простых конечномерных алгебр Ли, Йордановых алгебр и их
обобщений, примитивных псевдогрупп преобразова-
преобразований (см. [3], [4]). Для любой полупроотой веществен-
вещественной алгебры Ли ее Картана разложение может рас-
рассматриваться как Е2"гРаДУировка. Локальная клас-
классификация римановых симметрич. пространств сво-
дится к классификации й2~гРаДУиРованнь1Х простых
комплексных алгебр Ли [6].
Некоторые конструкции градуи-
градуированных алгебр Ли. 1) Пусть U — ассо-
ассоциативная алгебра, снабженная возрастающей филь-
фильтрацией {Uk : к?%), причем [Uk, Ut\CLUk + l _rf, где
d — фиксированное натуральное число, и и^ =
= Uk + dlUk-trd-i- Тогда операция коммутирования в U
индуцирует в пространстве "&=2-,k<=-o^k структуру
2-градуированной алгебры Ли. Таким путем могут
быть получены нек-рые алгебры Ли функции с Пуассо-
Пуассона скобкой в качестве коммутатора. В следующих двух
примерах Uk=Ui при/с>0 и Г/fc=0 при fc<0. а) Пусть
U — алгебра линейных дифференциальных операторов с
полиномиальными коэффициентами, U1— подпростран-
подпространство, натянутое на ее образующие Pi = s^r. i 4i=xi,
i=l, . . -, т. Тогда [U^, Ui\^zUk + i_t и ц есть алгебра
Лп многочленов от р,-, щ с обычной скобкой Пуассо-
Пуассона, б) Пусть U — универсальная обертывающая алгеб-
алгебра конечномерной алгебры Ли д, причем ?/, = д. Тогда
[t/fc, !7(]с^ + (_) и и канонически изоморфна (как век-
векторное пространство) симметрии, алгебре над д, т. е.
алгебре многочленов на сопряженном пространстве fl*
(теорема Пуанкаре — Биркгофа — В и т-
т а). Если (( — алгебра Ли связной группы Ли G, то
коммутатор элементов из и можно интерпретировать
либо как скобку Пуассона для соответствующих лево-
инвариантных функций на кокасательном расслоении
T*G, либо как скобку Пуассона на каждой орбите ко-
ирисоединенного представления, определяемую пос-
посредством стандартной симплектич. структуры на этих
орбитах.
2) Пусть char Кф2, Е есть re-мерное векторное
[ пространство над К, снабженное невырожденной квад-
квадратичной формой Q; <гх, . . ., еп — нек-рый ортогональ-
ортогональный базис в Е. Разложение Клиффорда алгебры С (Q)
в сумму одномерных подпространств {e;t . . . ei/;),
j'i< . . . <г/г, является ее ^"-градуировкой. При п = 2т
элементы алгебры С (Q) с нулевым следом образуют
простую Ли г. а. типа А^, N=2m — 1; ее градуировка
обладает высокой степенью симметрии; в частности,
все градуирующие подпространства равноправны. Ана-
Аналогичные градуировки (при помощи различных ко-
конечных групп) имеются и у других простых алгебр Ли
fll.
3) Каждой псевдогруппе Ли преобразований отве-
отвечает нек-рая алгебра Ли векторных полей. Росток I
этой алгебры Ли в любой точке обладает естественной
2-фильтрацией
/ = *_!=> Zo г> ZjID...,
где к 1к относятся ростки тех векторных полей, коор-
координаты к-рых разлагаются в степенные ряды без членов
степени меньше чем fc+1. Ассоциированная Ли г. а.
может быть интерпретирована как нек-рая алгебра Ли
полиномиальных векторных полей.
Классификация простых градуи-
градуированных алгебр Ли. Простым примитив-
примитивным псевдогруппам Ли соответствуют следующие 4 се-
серии простых бесконечномерных Ли г. а. (см. [5]):
Wn— алгебра Ли всех полиномиальных векторных
полей в n-мерном аффинном пространстве;
Sn — ее подалгебра, состоящая из векторных полей
с нулевой дивергенцией;
//„, где п=2пг,— подалгебра, состоящая из векторных
полей, аннулирующих дифференциальную форму
V"lOT 7 7
2л =i dx' А dxm + i
(гамильтоиовых векторных полей);
Кп, где n=2m-j-l,— подалгебра, состоящая из век-
векторных полей, умножающих дифференциальную форму
2Г=1 (a'« + i d:ri ~xi dxm + i) + dxn
на функцию.
Над полями характеристики р>0 могут быть опре-
определены простые конечномерные Ли г. а., аналогичные
Wn, Sn, Hn и К„ (см. [5]).
Простые Ли г. а. другого типа получаются сле-
следующим образом [4]. Пусть д=д(Л) —алгебра Ли,
определяемая при помощи неразложимой матрицы Кар-
Картана А =|| я.у ||, i, /=1, . . ., и (здесь и далее употребля-
употребляются обозначения статьи Картана матрица). Алгебра д
снабжается 2*-градуировкой так, что &j?<Joi ei€fta.>
//€?!_« , где а/ —строка @. . .1. . .0), причем 1 стоит
на г-м месте. Элементы cc?g", для к-рых $«,=^0, наз.
корнями, а а,- — простыми корнями. Всякий корень
есть линейная комбинация простых корней с целыми
коэффициентами одного знака п dim Да<оо для любо-
любого сс? %п. Факторалгебра д' (А) алгебры q по ее цент-
центру, лежащему в д0, проста как градуированная алге-
алгебра,!, е. не имеет нетривиальных градуирован, идеалов.
Пусть Р — совокупность линейных комбинаций
строк матрицы А с положительными коэффициентами.
Имеет место один из следующих случаев:
(П) Р содержит ст.року, все элементы к-рой положи-
положительны;
(Н) Р содержит нулевую строку;
(О) Р содержит строку, все элементы к-рой отрица-
отрицательны.
В случае (П) $(А)=-$' (А) —простая конечномер-
конечномерная алгебра Ли. В случае (О) д(А) — простая
бесконечномерная алгебра Ли. В случае (Н) алгебра
д' = д' (А) проста лишь как градуированная алгебра.
Она может быть превращена в К [и, «"Ч-алгебру так,
что: а) ид,'а=$'а+х, где v — нек-рая строка из поло-
положительных чисел; б) факторалгебра $7A—и)Д' = Д
есть простая конечномерная алгебра Ли. Наибольший
общий делитель всех компонент v,- строки V, равный 1, 2
или 3, наз. индексом алгебры д'.
В следующей таблице приведен список всех простых
Ли г. а. с матрицей Картана типа (Н). Здесь алгебра д'
обозначается так же, как и д, но с добавлением ее
индекса, указываемого в скобках.
Схема простых корней описывает матрицу А. Ее
вершины соответствуют простым корням; 1-я и j-я
вершины соединены (а,-уау,-)-кратным ребром, ориен-
ориентированным от i-i'i вершины к /-Й, если |а,у| >|а/,-|,
и неориентированным, если |а,у| = [ау,-|. Возле вершин
указаны числа V,-.
С помощью Ли г. а. с матрицей Картана типа (Н)
классифицируются ЕИ"гРаДУированные простые ко-
конечномерные алгебры Ли (см. [4], [2]). А именно, пусть
ц' = (\'(А), где А удовлетворяет условию (Н), и р : 1"^
->¦% —такой гомоморфизм, что р (a;)SsO и р(х)=т.
Тогда 1Чй=2п(со=? Йа при любом fc? Z изоморфно ото-
отображается на подпространство д& с Д, зависящее
только от вычета к по модулю т, и разложение Д=
= 2&=ofl* есть 2т-градуировка алгебры д. Если
поле К алгебраически замкнуто, то описанным спосо-
способом получаются, причем без повторений, все %т-
градуированные простые конечномерные алгебры Ли
над К. Индекс алгебры д' равен порядку автоморфиз-
автоморфизма 8 : /я—>f exp 'z~-) x, x?#k, алгебры Д по модулю
группы внутренних автоморфизмов.
Имеется классификация простых 2-градуированных
алгебр Ли Й=2&=~.* 9*. удовлетворяющих ус-
Обозначение
д2Л-2'
Сл-,
?121
Ei
(II
Схема простых корней
1 1
г (И
ловиям: a) dim $k<z.C\k\N для нек-рых С и TV; б) ft по-
порождается подпространством <t-i+So~bfiii B) пред-
представление д0 на Я-1 неприводимо. В этом случае либо
Й конечномерна, либо g есть одна из алгебр Wn, Sn,
Нп, Кп, либо g есть алгебра #'(А), определяемая
матрицей Картана типа (Н), снабженная подходящей
2-градуировкой [4].
Иногда % ,-градуированной алгеброй Ли наз.
супералгебра Ли.
Лит.: [1] А л е к с е е в с к и й А. В., «Функциональный
анализ и его приложения», 1974, т. 8, № 4, с. 1—4; [21 В и н-
бер г Э. Б., «Изв. АН СССР. Сер. матем.», 1976, т. 40, Л« .;,
с. 488—52В; [3] К а н т о р И. Л., «Тр. семинара по векторному
и тензорному анализу...», 1972, в. 16, с. 407—99; [4] К а ц В. Г.,
«Изв. АН СССР. Сер. матем.», 1968, т. 32, Mi 6, с. 1323—67;
[5] К о с т р и к и н А. И., Ш а ф а р е в и ч И. Р., «Изв.
АН СССР. Сер. матем.», 1969, т. 33, № 2, о. 252—322; [6]
HelgasonS., Differential geometry. Lie groups, and symmetric
spaces, N. Y., 1978. Э. Б. Винбепг.
ЛИ ГРУППА — группа G, обладающая такой струк-
структурой аналитического многообразия, что отображение
р. : (х, у)-^-ху~1 прямого произведения GXG в G ана-
литично. Другими словами, Ли г.— это множество,
наделенное согласованными структурами группы и
аналитич. многообразия. Ли г. наз. вещественной,
комплексной или р-адической в зависимости от поля,
над к-рым рассматривается ее аналитич. многообразие.
В дальнейшем, как правило, рассматриваются вещест-
вещественные Ли г. (всякая комплексная Ли г. естественно
наделяется структурой вещественной Ли г.— с по-
помощью конструкции ограничения основного поля; о
Ли г. над полями р-адических чисел см. Ли р-адическая
группа, Аналитическая группа).
Примеры Ли г. Полная линейная группа
GL(n. R) пая полем R действительных чисел (см.
Линейная группа) и ее подгруппы, замкнутые в есте-
естественной евклидовой топологии.
Основные понятия теории Ли г. введены в матема-
математику в 70-е гг. 19 в. С. Ли (S. Lie). Ли г. возникли в
связи с проблемой разрешимости дифференциальных
уравнений в квадратурах и исследованием непрерыв-
непрерывных групп преобразований. Успешное применение те-
теории групп к решению алгебраич. уравнений высших
степеней, выразившееся в создании теории Галуа,
повлекло за собой попытку построения аналога теории
Галуа для дифференциальных уравнений. И хотя груп-
группы в теории дифференциальных уравнении заняли не-
несколько иное место, нежели в теории алгебраич. урав-
уравнений, это привело к созданию теории Ли г., а также
теории алгебраич. групп, глубоко связанных со мно-
многими областями математики. Первоначально Ли г.
определялись как локальные группы преобразований,
т. е. как семейства локальных аналитич. преобразо-
преобразований re-мерного пространства R" (или С"), анали-
аналитически зависящих от конечной системы параметров,
причем требовалось, чтобы параметры произведения
преобразований выражались через параметры сомно-
сомножителей посредством аналитич. функций. Позже пере-
перешли к абстрактному рассмотрению Ли г., но также с
локальной точки зрения (см. Ли локальная группа).
Спстоматич. исследование глобального строения Ли г.
первыми начали 9. Картан (Е. Cartan) и Г. Вепль
(Н. Weyl). Первое современное изложение теории Ли
г. было дано в 1938 Л. С. Понтрягиным (см. [1]).
Возникает вопрос, не приведет ли замена аналитич-
аналитичности многообразия G и отображения и. дпфференцпру-
емостыо к расширению класса Ли г.? Этот вопрос был
решен еще С. Ли: если ц дважды непрерывно дифферен-
дифференцируемо, то G является Ли г. Значительно более слож-
сложной оказалась пятая проблема Г и л ь б е р-
т а: пусть G есть «-мерное толологич. многообразие и
отображение и. : (х,у)-^-ху~1 непрерывно, будет ли G
Ли г.? Для компактных групп эта проблема была реше-
решена положительно Дж. Нейманом (J. Neumann) в 1933, а
для локально компактных абелевых групп — Л. С.
Понтрягнным в 1934. В общем случае положительное
решение было получено в 1952 А. М. Глисоном
(А. М. Gleason), Д. Монтгомери и Л. Зипшшом (см.[131,
а также [18]). Таким образом, можно определить Ли г.
как топологич. группу, топологич. пространство к-рой
является конечномерным (или локально евклидовым)
многообразием, что весьма важно для общей теории
тонологич. групп.
Подмножество Н Ли г. G наз. подгруппой
(точнее, подгруппой Л и), если Н является
подгруппой абстрактной группы G и подмногообразием
аналитич. многообразия G. М о р ф и з м Лиг. Gx
Ли г. G2— это аналитич. отображение / : Gx-^Gi4 явля-
являющееся гомоморфизмом абстрактных групп; если к тому
же / биективно, а /-1 аналитично, то / наз. изомор-
изоморфизмом Ли г.; в случае локальной биективности
/, говорят, что Ли г. Gt и G2 локально и з о м о р-
ф н ы. Пусть Н — замкнутая нормальная подгруппа
Ли г. G. Тогда факторгруппа GIH наделяется такой
структурой аналитич. многообразия, что G/II превра-
превращается в Ли г., а канонпч. отображение G-+GIH яв-
является морфизмом. Размерностью Ли г. G наз.
размерность G как аиалитич. многообразия. В дальней-
дальнейшем рассматриваются только конечномерные Ли г.,
хотя многие результаты обобщаются на случай Ли
банаховых групп.
Соответствие между группами и алгебрами Ли.
Основным методом исследования в теории Ли г. являет-
является инфинитезимальный метод, созданный С. Ли. Этот
метод позволяет в значительной мере редуцировать
изучение такого сложного объекта, как Ли г., к изу-
изучению чисто алгебраич. объекта — Ли алгебры. Каж-
дой Ли г. G сопоставляется алгебра Ли L(G), к-рая
строится следующим образом (см. также Ли алгебра
аналитической группы). Левоинвариантным вектор-
векторным полем на G наз. векторное поле, инвариантное
относительно дифференциалов левых сдвигов, т. е.
X — левоинвариантное векторное поле, если
(dLg)X{h) = X{gh) для любых g, h?G, где Lg(h) = gh.
Лев'оинвариантные векторные поля на G образуют век-
векторное пространство, к-рое можно отождествлять с
касательным пространством Te(G) в единице е группы
G, сопоставляя полю X его значение в е. Если X,
Y? Te(G), то скобка Ли X°Y—YoX также бу-
будет левоинвариантным полем и это задает в Те (G) би-
билинейную операцию, относительно к-рой Te(G) ста-
становится алгеброй Ли L (G) (здесь о означает компози-
композицию векторных долей, рассматриваемых как дифферен-
дифференцирования алгебры бесконечно дифференцируемых дей-
ствительно-значных функций на многообразии G).
Можно дать более явную конструкцию операции ком-
коммутирования [X, Y] в L(G). Пусть x(t), y(t) —ин-
—интегральные кривые полей X, У в G, проходящие через
единицу группы. Тогда [X, Y] будет касательным век-
вектором в точке е к кривой
Восстановить группу Ли G по ее алгебре Ли L (G)
позволяет экспоненциальное отображение ехр : L (G)—*¦
—yG, сопоставляющее полю X?L(G) элемент х A) его
интегральной кривой x(t). Если G — линейная Ли г.,
т. е. подгруппа полной линейной группы GL (n, R),
то L(G) отождествляется с подалгеброй полной мат-
матричной алгебры Ли L (n, R) и экспоненциальное ото-
отображение принимает вид
Отображение ехр : L (G)—^G аналитично и локально изо-
изоморфно, и поэтому определяет в окрестности едини-
единицы группы G локальную карту (к а н о н и ч е с к и о
координат ы). Согласно К эмпбелла — Хаусдорфа
формуле запись умножения в G в канонич. координа-
координатах, т. е. отображение
(X, У) —> ехр-1 (ехр X ехр У), X, Y?L (G),
выражается через операции в алгебре Ли L(G). Таким
образом, локально Ли г. полностью определяется
своей алгеброй Ли.
Соответствие между группами и алгебрами Ли об-
обладает глубокими функториальными свойствами. Ли г.
определяется своей алгеброй Ли с точностью до ло-
локального изоморфизма; в частности, если Ли г. G± и
G2 связны и односвязны, то из изоморфизма их алгебр
Ли следует изоморфизм G^G.2- Связные подгруппы
Ли г. G взаимно однозначно соответствуют подалгебрам
алгебры Ли L(G). Пусть / : G1-y-G2— морфизм двух Ли
г. Тогда дифференциал морфизма в единице оказывает-
оказывается гомоморфизмом алгебр Ли:
dfe: L(G1)—^L(Gi).
Вообще говоря, не всякий гомоморфизм L (G^—t-L (G.,)
имеет вид dje, однако в случае односвязной группы G,
это так. Связная подгруппа Н связной Ли г. G тогда
и только тогда нормальна, когда L (Л) является идеа-
идеалом в алгебре Ли L (G); если к тому же // замкнута в G,
то
По построению алгебра Ли L (G) данной Ли г. G являет-
является аналитически инвариантной. В действительности
же L (G) топологически инвариантна, что непосредст-
непосредственно вытекает из следующей теоремы Карта-
Н а: непрерывное гомоморфное отображение (веще-
ственпой) Ли г. G в Ли г. Н является морфпзмом.
Для комплексных Ли г. последнее утверждение не
всегда верно, хотя оно сохраняет силу для /з-адиче-
ских Ли г. (см. [3]). Группа автоморфизмов Aut(G)
связной Ли г. G является Ли г., к-рая отождествляет-
отождествляется с подгруппой группы Aut (L(G)). В частности, если
Ли г. G односвязна, то
Aut (G) s* Aut (L (G)) и L (Aut (G)) es D (L (G)),
где D (L (G)) обозначает алгебру Ли дифференциро-
дифференцирований алгебры L(G). Соответствие
где Int (g)— внутренний автоморфизм, порожденный
элементом g ? G, наз. присоединенным пред-
представлением Ли г. G; его дифференциал бу-
будет присоединенным представлением х—>&Ах алгебры
Ли L(G).
Глобальное строение групп Ли. Важным результатом
здесь является теорема существования глобальной
Ли г. с заданной вещественной алгеброй Ли, доказан-
доказанная в 1930 Э. Картаном. Он показал также, что зам-
замкнутая подгруппа вещественной Ли г. является под-
подгруппой Ли. К этому времени выявилась особая роль
двух типов Ли г.: полупростых и разрешимых (см. Ли
полупростая группа, Ли разрешимая группа). Связная
Ли г. G наз. полупростой, если она не содержит
неединичных связных разрешимых нормальных под-
подгрупп; если к тому же G не содержит и других нетри-
нетривиальных связных нормальных подгрупп, то она наз.
простой. Алгебра Ли L (G) полупростой, простой
пли разрешимой Ли г. G является соответственно полу-
полупростой, простой или разрешимой алгеброй Ли. Иссле-
Исследование произвольных Ли г. в существенной степени
сводится к изучению полупростых и разрешимых. Вся-
Всякая Ли г. G обладает наибольшей связной разрешимой
нормальной подгруппой, к-рая наз. разрешимым
радикалом и обозначается R (G). В группе G
существуют максимальные полупростые подгруппы.
Если S — одна из них, то G=S -R (G), причем все
максимальные полупростые подгруппы сопряжены;
если G односвязна, то Sf)R(G)=(e) и произведение
будет полупрямым (теорема Л ев и — Маль-
Мальцева). Существование этого разложения доказано
впервые Э. Леви (Е. Levi) в 1905 для комплексных ал-
алгебр Ли, сопряженность полупростых компонент уста-
установлена А. И. Мальцевым в 1942 (см. [16], а также
Леви — Мальцева разложение).
Наиболее общий факт о разрешимых Ли г. получен
еще С. Ли: всякая связная разрешимая линейная груп-
группа над полем С приводится к треугольному виду, т. е.
описание связных разрешимых Ли г. сводится к описа-
описанию подгрупп полной треугольной группы Т(п)с
С GL(n, С). Детальное исследование разрешимых Ли
г. провел А. И. Мальцев в [16].
При изучении строения полупростых Ли г. важную
роль играют их максимальные компактные подгруп-
подгруппы, изученные Э. Картаном в тесной связи с теорией
симметрич. пространств (см. [10]). Согласно классич.
теореме Картапа максимальные компактные подгруппы
полуиростой Ли г. G сопряжены; если В — максималь-
максимальная компактная подгруппа в G, то существует такое
подмногообразие EcG, аналитически изоморфное ев-
евклидову пространству, что G~BE, причем отображе-
отображение ВХ Е—^-ВЕ, (Ь, е)-^-Ье, является изоморфизмом апа-
литич. многообразий. Таким образом, топологич. стро-
строение группы G определяется топологич. строением
группы В. А. И. Мальцев [16] распространил
теорему Картана на произвольные связные Ли г. Дру-
Другое разложение связной Ли г. в произведение макси-
максимальной компактной подгруппы и евклидова простран-
гтва было найдено К. Ивасавой (см. Иеасавы разложе-
разложение).
Линейная представимость. С самого начала разви-
развития теории Ли г. было ясно, что произвольные Ли г.
близки к линейным группам Ли. С. Ли доказал, что
во многих случаях Лп г. локально изоморфны линей-
линейным Ли г. Общая теорема была получена И. Д. Адо
в 1935: всякая Ли г. локально изоморфна линейной
(см. [15]). В то же время нетрудно указать примеры
Ли г., не являющихся линейными: такой будет одно-
связная накрывающая группы SLB, R) или (в случае
поля С) комплексный компактный тор. Если G — од-
носвязная разрешимая группа Ли, то всякая ее под-
подгруппа Ли односвязна и изоморфна линейной группе Ли.
В общем случае найден следующий критерий для ли-
линейной представимости [16]: связная Ли г. G тогда и
только тогда является линейной, когда линейны ее
радикал R (G) и полупростая факторгруппа G/R(G);
в свою очередь, для линейной представимости радикала
R (G) необходимо и достаточно, чтобы его коммутант
был односвязен, а линейность полупростой Ли г.
G/R (G) зависит от строения ее центра. Компактные,
а также комплексные полупростые Ли г. не только ли-
линейны, но и являются линейными алгебраическими
группами [12].
Классификация. Одной из главных проблем теории
Ли г. является проблема классификации произволь-
произвольных связных Ли г. с точностью до изоморфизма. В клас-
классе всех локально изоморфных связных Ли г., имеющих
одну и ту же алгебру Ли, существует единственная
односвязная Ли г. Go, и всякая Ли г. G из этого класса
изоморфна GJN, где 7V — нек-рая дискретная цент-
центральная нормальная подгруппа. Поэтому классифи-
классификация Ли г. сводится к классификации конечномерных
алгебр Ли и вычислению центров односвязных Ли г.
С другой стороны, она сводится к классификации двух
принципиально различных типов групп: полупростых
и разрешимых (см. Ли полупростая группа, Ли разре-
разрешимая группа). На первый взгляд разрешимые Ли г.
устроены проще и их классификация, казалось бы,
не должна быть трудной. Однако это впечатление об-
обманчиво и пока A982) нет никакой надежды получить,
классификацию разрешимых Ли г. Полупростые Ли г.,
напротив, удалось полностью классифицировать. Пол-
Полную классификацию комплексных полупростых алгебр
Ли получил В. Киллинг (W. Killing) в 1888—90 (см.
[1], [3]). Так как комплексная полупростая алгебра Ли
является прямой суммой простых подалгебр, то доста-
достаточно классифицировать простые алгебры Ли. Оказа-
Оказалось, что существует лишь девять различных типов ком-
комплексных простых алгебр Ли, а именно, четыре беско-
бесконочные серии
А„, n^sl, Вп, reS2=2, С„, n5s2, Dn, n 5= 4,
и пять исключительных алгебр
(см. также Ли полупростая алгебра). Бесконочным се-
сериям комплексных простых алгебр Ли соответствуют
классические линейные группы Ли. Соответствующие
односвязные группы имеют вид: тип А„—SL(re+l, С),
тип Вп—Spin(/2n + 1), гДе Spin(/,,, + i) обозначает спи-
норную группу, соответствующую невырожденной
квадратичной форме /2n + i размерности 2п + 1; тип
Сп — симплектическая группа степени 2п; тип Dn —
Spin (/2„). Нетрудно вычисляются центры этих групп.
Напр., центр SL(re-f 1, С) — циклич. группа порядка
и+1, а центры Spin (/2n + i) п спмплектич. группы —
циклич. группы 2-го порядка. Так получается класси-
классификация комплексных полупростых Лп г. Классифи-
Классификация вещественных полупростых Ли г. оказывается
значительно сложнее и опирается на классификацию.
их вещественных форм. Наиболее важен здесь факт су-
существования у всякой комплексной полупростой группы
G единственной компактной вещественной формы В;
это означает, что алгебра Ли L(G) изоморфна L(B)(g)R?,
т. е. получается комплексификацией алгебры Ли L(B).
Основываясь на этом, Э. Картан в 30-х гг. 20 в. полу-
получил полную классификацию вещественных форм ком-
комплексных полупростых Ли г. В терминах Галуа ко-
гомологий это равносильно описанию множества Нг(К,
Aut(G)) (см. также Линейная алгебраическая группа).
Впоследствии метод Киллинга был усовершенство-
усовершенствован 0. Картаном и Г. Вейлем, что дало возможность
решить ряд других классификационных проблем, а
также развить важную теорию представлений Ли г.
Получена классификация полупростых подгрупп клас-
сич. комплексных простых Ли г. (см. [17]).
Современное развитие и применения. В 50-х гг.
20 в. в теории Ли г. начался новый этап развития, что
выразилось, в частности, в создании теории алгебраич.
групп (см. Линейная алгебраическая группа). Еше ра-
ранее К. Шевалло (С. Chevalley, см. [12]) детально объяс-
объяснил алгебраич. природу основных результатов теории
Ли. Привлечение методов алгебраич. геометрии позво-
позволило но-новому осветить эти классич. результаты и
открыло новые глубокие связи с теорией функций, те-
теорией чисел и т. д. Значительное развитие получила
теория р-адических групп Ли (см. [3], [6]). Ли г. свя-
связаны практически со всеми основными разделами ма-
математики: с геометрией и топологией — через теорию
Ли групп преобразований, с анализом — через теорию
линейных представлений и т. д. Чрезвычайно важны
также разнообразные применения Ли г. в физике и
механике.
Лит.: [1] П о н т р я г и н Л. С, Непрерывные группы,
3 изд., М., 1973; [2] Б о р е л ь А., Линейные алгебраические
группы, пер. с англ., М., 1972; [3] Б у р б а к и Н., Группы и
алгебры Ли, пер. с франц., [гл. 1—8], М., 1972—78; [4]
Вей л ь Г., Классические группы, их инварианты и представ-
представления, пер. с англ., М., 1947; [5] В и г н е р Е., Теория групп
и ее приложения к квантомеханической теории атомных спект-
спектров, пер. с англ., М., 1961; [6] С е р р Ж.- П., Алгебры Ли и
группы Ли, пер. с англ. и франц., М., 1969; [7] С т е й н-
берг Р., Лекции о группах Шевалле, пер. с англ., М., 1975;
18] Теория алгебр Ли. Топология групп Ли. Семинар«Софус Ли»,
пер. с франц., М., 1962; [9J Хамермеш М., Теория групп
и ее применение к физическим проблемам, пер. с англ., М., 1966;
[101 Хелгасон С, Дифференциальная геометрия и симмет-
симметрические пространства, пер. с англ., М., 1964; [11] Чебота-
Чеботарев Н. Г., Теория групп Ли, М.— Л., 1940; [12] Шевал-
Шевалле К. Теория групп Ли, пер. с англ. и франц., т. 1 — 3, М.,
1948 — 58; [13] Hochschild G., The Structure of Lie
Groups, S. F., 1965; [14] Montgomery D., Z i p p i n L.,
Topological transformation groups, N. Y.— L., 1955; [15]
А до И. Д., «Изв. Физ.-матем. об-ва» (Казань), 1935, т. 7,
с. 1—43; [16] Мальцев А. И., «Матем. сб.», 1945. т. 16,
с. 163—90; [17] е г о ж е, «Изв. АН СССР. Сер. матем.», 1944,
т. 8, Л» 4, с. 143—74; [18] Скляренко Е., в кн.; Проблемы
Гильберта, М., 1969, с. 101 —15. В. П. Платонов.
ЛИ ГРУППА ПРЕОБРАЗОВАНИЙ — гладкое дейст-
действие связной группы Ли G на гладком многообразии М,
т. е. гладкое (класса С°°) отображение А : GMM
такое, что:
(I) A(g'g", m)-.-=A (gr, A (g", m)) vg', g"?
(II) А (е, т) = т ут?М
(е — единица группы G).
Ли г. п., удовлетворяющая также условию:
(III) если A(g, m,) = m ут?М, то g = e,
наз. эффективной.
Примеры Ли г. п. Любое гладкое линейное
представление группы Ли С в конечномерном вектор-
векторном пространстве М; действие группы Ли G на себе с
помощью левых или правых сдвигов A (g, m) = gm или
A (g, m)'-=mg~1 соответственно (g, m?G); действие груп-
группы Ли G на себе с помощью внутренних автоморфизмов
A (g, т) = gmg~1 (g, m?G); одпопараметрическая группа
преобразований, т. е. гладкое действие группы R на
многообразии М.
Наряду с определенными выше глобальными Ли г. п.
рассматриваются также локальные Ли г. п.,
являвшиеся основным объектом классич. теории групп
Ли [1]. При этом вместо G рассматривается локальная
группа Ли, т. е. окрестность U единицы в нек-рой
группе Ли, а вместо М — открытое подмножество
WczR".
Если G — Ли г. п. на М, то, выбрав подходящие
окрестность U^e в G и открытое подмножество WdM,
получают локальную Ли г. п. Обратный переход —
от локальной Ли г. п. к глобальной (глобализа-
(глобализация) — возможен не всегда. Однако если dim M<:4
и W достаточно мало, то глобализация возможна
(см. [2]).
Иногда рассматриваются Ли г. п. класса Ck, I <fc<:oo ,
или С<° (аналитические), т. е. предполагается принад-
принадлежность отображения А соответствующему классу.
Если А непрерывно, то для его принадлежности клас-
классу С* или С40 достаточно, чтобы для любого g^G пре-
преобразование Ag : m-^-A (g, m) многообразия М при-
принадлежало этому классу (см. [3]). В частности, задание
Ли г. п. G на М эквивалентно заданию непрерывного
гомоморфизма G—>-Diff M в группу Diff M диффеомор-
диффеоморфизмов многообразия М, снабженную естественной то-
топологией.
Любой Ли г. п. соответствует гомоморфизм А* : д—>-
—>- Ф(М) алгебры Ли Д группы G в алгебру Ли Ф (М)
гладких векторных полей на М, сопоставляющий эле-
элементу Х?д поле скоростей однопараметрич. группы
преобразований
(t, m)^A (exp tX, m),
где t?R, т?М, охр : Д —>- G — экспоненциальное ото-
отображение (см. [5]). Если G эффективна, то гомоморфизм
А% инъективен. Для связной группы G гомоморфизм
А* полностью определяет Ли г. п. Обратно, любому
гомоморфизму Р : д —*-Ф(М) отвечает локальная Ли
г. п. [6]. Если все векторные поля из Р (д) полны
(т. е. их интегральные кривые x{t) определены для всех
t), то существует глобальная Ли г. п. G на М, для к-рой
Imis^9. Достаточно потребовать, чтобы р (д) как
алгебра Ли порождалась полными векторными поля-
полями; условие полноты автоматически выполнено, если
М компактно [4].
Если G — Ли г. п. многообразия М, то стационар-
стационарная подгруппа Gm= {g?G\A (g, m) = m} для любой
точки т?М является замкнутой подгруппой Ли в G;
ее называют также стабилизатором, или под-
подгруппой изотропии, точки т. Соответствую-
Соответствующая подалгебра Ли йтСД состоит из всех таких
Х?8, что А* (Х)т=0. Подалгебра (\т непрерывно
зависит от т в естественной топологии на множестве
всех подалгебр в д [7]. Орбита G(m)~{A (g, m), g?G}
точки т является погруженным подмногообразием в
М, диффеоморфным GlGm. Если G компактна, то все
орбиты являются компактными вложенными подмно-
подмногообразиями. Примеры невложенных орбит дает дей-
действие группы R на торе
T' = {(ZU *g)|*,-€C, | Z; | = 1, J = l, 2},
заданное формулой
A (t, (Zl, z3))^.(e'tzlt e^h2),
где a^R иррационально.
Ли г. п. А, : GX М,—>-М,-, ?=1, 2, наз. подобны-
м и, если существует такой диффеоморфизм / : М1-+М2,
что A1(g, m) — A2(g, f(m)), g?G, m^Mx. Важной зада-
задачей теории групп преобразований является задача
классификации Ли г. п. с точностью до подобия. В на-
настоящее время A982) она решена лишь в нек-рых част-
частных случаях. Еще С. Ли [1] дал классификацию ло-
локальных Ли г. п. в областях пространства R1 и R2 с
точностью до локального подобия. Частичная класси-
классификация проведена для Ли г. п. на трехмерных мно-
многообразиях. Хорошо изучены также компактные Ли
г. п. О транзитивных Ли г. п. см. Однородное простран-
пространство.
Лит.: [1] L i с S., «Math. Ann.», 1880, Bd 16, S. 441 — 528;
[2] Mostow G., «Ann. Math.», 1950, v. 52, p. 606 — 36; [3]
Bochner S., Montgomery D., «Ann. Math.», 1945
v. 46, p. 685—94; [4] P a 1 a i s R., «Mem. Amer. Math. Soc.»
1957, v. 22, p. 1 —123; 15] 3 у л а н к е Р., В и н т г е н П.
Дифференциальная геометрия и расслоения, пер. с нем., М.
1975; [6] П о н т р я г и н Л. С, Непрерывные группы, 3 изд.,
М., 1973; [7] Richardson R., в кн.: Proceedings of the
conference on transformation groups, New Orleans, 1967, B.—
[a. o.], 1968, p. 429—40; [8] Чеботарев Н. Г., Теория
групп Ли, М Л., 1940. В. В. Горбпцевич.
ЛИ ДИФФЕРЕНЦИАЛ тензорного поля
Q п о направлению векторного поля
X — главная линейная часть приращения тензорного
поля Q при его преобразовании, к-рое индуцировано
локальной однопараметрич. группой ср( преобразова-
преобразований многообразия, порожденной полем X. Ли д. bvQ
тензорного поля Q по направлению векторного ноля X
равен (X'xQ) dt, где XxQ — Ли производная тензорного
поля Q по направлению X.
Понятие Ли д. допускает следующую физич. интер-
интерпретацию. Если однопараметрич. группа преобразова-
преобразований ф( области евклидова пространства описывает
стационарный поток жидкости с полем скоростей
X, t — время, a Q есть тензорное поле, описывающее
ту или иную характеристику жидкости (тензор ско-
скоростей деформации, тензор напряжений, плотность
и т. п.), то Ли д. 6xQ описывает главную линейную
часть изменения со временем поля Q с точки зрения
наблюдателя, движущегося вместе с жидкостью, т. е.
В переменных Лагранжа. Д. В. АлекссеескиИ.
ЛИ ДИФФЕРЕНЦИРОВАНИЕ — естественная опе-
операция на дифференцируемом многообразии, сопостав-
сопоставляющая дифференцируемому векторному нолю X и '
дифференцируемому геометрич. объекту Q на многооб-
многообразии М нек-рый новый геометрич. объект XxQ,
описывающий скорость изменения геометрич. объекта Q
относительно однопараметрич. группы преобразований
(pf многообразия М, порожденной полем X. Геометрич.
объект XxQ наз. производной Ли геоме-
геометрического объекта Q относительно век-
векторного доля X.
В частном случае, когда Q есть векторнозначная
функция на М, ее производная Ли X%Q совпадает с
производной dxQ функции Q по направлению вектор-
векторного поля X и задается формулой
гДе ф| — локальная однопараметрич. группа преобра-
преобразований многообразия М, порожденная полем X, или в
локальных координатах х' — формулой
где
В общем случае определение Ли д. состоит в следую-
следующем. Пусть W — пек-рое GL* (п)-пространство, т. е.
многообразие с фиксированным действием полной диф-
дифференциальной группы GL* (п) порядка к (группы
i-струй в нуле диффеоморфизмов ср : R" -> R", (р @)^0).
Пусть Q : PkM^>-W — геометрич. объект порядка к
типа w на и-мерном многообразии М, рассматриваемый
как GL* (ге)-эквивариантное отображение главного
GL* (и)-расслоения кореперов PkM fc-ro порядка на
М в W. Локальная однопараметрич. группа преобра-
зований ср. многообразия М, порожденная векторным
нолем X на М, индуцирует локальную однопараметрич.
группу преобразований ф^*' многообразия кореперо»
РкМ. Ее поле скоростей
наз. полным лифтом поля X на РкМ. Произ-
Производная Ли геометрич. объекта Q типа М относительно
векторного поля X на М определяется как геометрич.
объект &xQ типа TW (где TW — касательное расслое-
расслоение многообразия W, рассматриваемое естественным
образом как GL* (и)-пространство), задаваемый фор-
формулой
Значение производной Ли XXQ B точке рк?РкМ
зависит, и притом линейно, только от 1-струи в точке
Pli отображения Q и от значения в этой точке векторного
ноля Х(*> (или, что эквивалентно, от fc-струи поля X
в соответствующей точке х?М).
Если геометрич. объект Q линеен, т. е. соответствую-
соответствующее GL* (ге)-пространство W является векторным про-
пространством с линейным действием группы GL*(?i), то
касательное многообразие TW естественным образом
отождествляется с прямым произведением WXW, и
поэтому производную Ли
XXQ ¦ Р"М —+ Т11' г. -WXW
можно рассматривать как пару геометрич. объектов
типа W. Первый из них есть само Q, а второй, обычно
отождествляемый с самой производной Ли линейного
геометрия, объекта Q, равен производной д Q
А.
функции Q по направлению векторного поля
Таким образом, производную Ли линейного геометрич.
объекта можно рассматривать как геометрич. объект
того же типа, что и Q.
Локальные координаты х! в многообразии М оп-
определяют локальные координаты х1, у/ в многообразии
Р1М кореперов 1-го порядка:
В этих координатах производная Ли любого геометрич.
объекта Q = Q(x'\ Vj) 1-го порядка (напр., тензорного-
поля) по направлению векторного поля
±-Ч их'
задастся формулой
где
Аналогичная формула справедлива для производной
Ли геометрич. объекта любого порядка.
Производная Ли Хх в пространстве дифференциаль-
дифференциальных форм на многообразии М выражается через опе-
оператор внешнего дифференцирования d и оператор вну-
внутреннего умножения ix (определяемый как свертка
векторного поля с дифференциальной формой) с по-
помощью следующей формулы гомотошш:
X х ~ d о lx -|- i\r о d.
Обратно, оператор внешнего дифференцирования dr
действующий на р-форму со, выражается через Ли д.
по формуле
da(X, Х„.,)=--УР+] <—i
Х(А',, ..., А',-, ..., A'/J + 1) +
+ Ъ< /(-II"+J> «(^A-,,Yy, X, Xh ..., Xj,..., Xp + 1),
где ~ означает, что соответствующий символ должен
¦быть пропущен, Хх, . . ., А'^ + 1 — векторные поля.
В отличие от ковариантпого дифференцирования,
требующего введения связности, операция Ли д. оп-
определяется структурой дифференцируемого многообра-
многообразия, а производная Ли геометрич. объекта Q по на-
направлению векторного поля X является конкомитантом
геометрич. объектов X и Q.
Лит.: [l]Slebodzinski W., «Bull. cl. sci. Acad. roy.
Belgique», 1931, v. 17, p. 864—70; Г2] Итоги науки. Алгебра. То-
Топология. Геометрия. 19И5, М., 1967, с. 429 — 65; [3] Y а п о К.,
The theory of Lie derivatives and its applications, Amst., 1957;
[4] С т е р н б е р г С, Лекции по дифференциальной геомет-
геометрии, пер. с англ., М., 1970; L5] Вагнер В., «Докл. АН
СССР», 1945, т. 46, с. 383—86; [6] Лаптев Б. Л., «Тр. Се-
Семинара по вект. и тенз. анализу», 1956, т. 10, с. 227 — 48; [7]
Е в т v ш и к Л. Е., «Докл. АН СССР», I960, т. 132, о. 998 —
1001; [8] Р а 1 a i s R. S., «Proc. Amer. Math. Soc», 1954, v. 5,
p. 902—08. Д. В. Алексесвский.
ЛИ КВАДРИКА — одна из соприкасающихся квад-
квадрик к поверхности в геометрии эквиаффинной или
проективной группы. В гиперболич. точке Мо она
определяется следующим образом.
Пусть дано векторное поле v' (t) вдоль линии L : и' (t),
к-рая является асимптотической (или, по крайней ме-
мере, имеет в Мо касание 2-го порядка с асимптотической).
Квадрика, содержащая три бесконечно близкие пря-
прямые, проходящие через три точки линии и' (t) в направ-
направлении векторов v'{t)ri(t) = c'ri+cN, 7-ь г2, N — репер в
О О О О О
Мо, Лг — аффинная нормаль, и наз. квадрикой
Л и. Ее уравнение имеет вид
где (I1 : g2 : 5 : 1) вместе с (с1 : с" : с : 1) — однородные
координаты указанных прямых, g;j — асимптотич. тен-
тензор, Я — аффинная средняя кривизна.
Ли к. (наряду с квадрикой Вильч и неко-
некого и квадрикой Ф у б и н и) принадлежат пучку
Дарбу квадрик. Первая имеет уравнение
j
.для нее L — геодезическая 1-го рода, а вторая — урав-
ТТРТТТТР
нение
для нее L имеет Мо касание 3-го порядка; здесь х — га-
гауссова кривизна тензора g,y.
Понятие Ли к. введено в его письме к Ф. Клейну
(F. Klein) от 18.12.1878 (см. [1]).
Лит.: [1] L i e S., Gesammelte Abhandlungen. Anraerkungen
zum 3-ten Bd, Lpz.— Oslo, 1922, S. 718; [2l Ш и р о к о в П. А.,
Широков А. II., Аффинная дифференциальная геометрия,
М., 1959; [3] Фиников С. II., Ироективно дифференциаль-
дифференциальная геометрия, М.—Л., 1937. М. 11. Войцсховский.
ЛИ КОЛЬЦО, лиево кольц о,— кольцо А,
удовлетворяющее следующим условиям:
а2 = 0
и
(ab)c+(bc)a-\-(ca)b=O
(тождество Якоб и), где а, Ь, с — любые эле-
элементы из кольца А. Первое из этих условий влечет ан-
антикоммутативность кольца А:
Ьа=- —ah.
Ли к. образуют многообразие колец, в общем случае
ноассоциативных. В него входят, однако, все кольца с
нулевым умножением.
См. также Неассоциативные кольца и алгебры.
О. А. Иванова.
ЛИ КОМПАКТНАЯ ГРУППА — компактная груп-
группа, являющаяся конечномерной вещественной группой
Ли. Ли к. г. могут быть охарактеризованы как конечно-
конечномерные локально связные компактные топологич.
группы.
Если G0 — связная компонента единицы Ли к. г. G,
то группа связных компонент GIG0 конечна. Собственно
к теории групп Ли относится изучение строения связ-
связных Ли к. г.
Следующие примеры связных Ли к. г. играют важ-
важную роль в общей структурной теории Ли к. г.
1) Мультипликативная группа Т1 всех комплексных
чисел, равных по модулю 1.
2) Группа SU(re) всех комплексных унитарных мат-
матриц порядка п с определителем 1.
3) Группа SO (п) всех вещественных ортогональных
матриц порядка п с определителем 1.
4) Группа Sp(re) всех матриц X?SUBre), для к-рых
XJXT=J, где /— L ^ « , Т — знак транспонирова-
транспонирования и 1„ — единичная матрица порядка п.
Полная классификация связных Ли к. г. была полу-
получена в трудах Э. Картана [1] и Г. Вейля [2]. Она со-
состоит в следующем.
Имеются два основных типа связных Ли к. г.
1) Связные коммутативные Ли к. г.
Это в точности торы, т. е. группы вида Т"=
71! V у Т1
— 1 у\ . .. /\ 1 .
п раз
2) Связные полупростые Ли к. г. (см.
Ли полупростая группа). Если G — связная молупрос-
тая Ли к. г., то универсальная накрывающая группа G
группы G также является Ли к. г. (т е о р е м a Be й-
л я). Центр Z группы G конечен, а все связные группы
Ли, локально изоморфные G, компактны и исчерпыва-
исчерпываются с точностью до изоморфизма группами вида G/D,
где DczZ. Алгебры Ли полупростых Ли к. г. могут
быть внутренне охарактеризованы среди всех конечно-
конечномерных вещественных алгебр Ли как алгебры с отрица-
отрицательно определенной Киллинга формой.
Указанные два основных типа связных Ли к. г.
определяют строение произвольных связных Ли к. г.
А именно, последние с точностью до изоморфизма ис-
исчерпываются всевозможными факторгруппами вида
(Gx T)/D, где G — связная односвязная Ли к. г. с цент-
центром Z, Т — тор, а О — конечная подгруппа в группе
ZXT, пересекающаяся с Т лишь по единице. Алгебры
Ли произвольных Ли к. г. также могут быть внутренне
охарактеризованы среди всех конечномерных вещест-
вещественных алгебр Ли: это в точности алгебры Ли д, обла-
обладающие таким положительно определенным скалярным
произведением ( , ), что (\х, у], z)-\- (у, [х, z])==0 для
любых х, у, г?д. Они наз. к о м и а к т н ы м и а л-
гебрами Ли.
Таким образом, классификация связных Ли к. г.
сводится к классификации связных односвязных полу-
полупростых Ли к. г. (или, что то же, полупростых компакт-
компактных алгебр Ли) и описанию их центров. Оказывается,
что полупростые компактные алгебры Ли находятся во
взаимно однозначном соответствии с полупростыми ком-
комплексными алгебрами Ли (и тем самым с приведенными
корневыми системами). А именно, если Д — полупро-
полупростая компактная алгебра Ли, то ее комплексификация
QC = 3(X)rC полупроста. Обратно, в любой полупро-
полупростой алгебре Ли над С существует, и притом единст-
единственная с точностью до сопряженности, компактная ве-
вещественная форма. В частности, окончательный резуль-
тат классификации простых компактных алгебр Ли и
соответствующих им связных односвязных Ли к. г.
таков. Имеется 4 бесконечных серии т. н. класс и-
ч е с к и х простыхкомпактных алгебр
Л и, соответствующих следующим сериям неприводи-
неприводимых приведенных систем корней: Ак, п>1, Вп, и>2,
Сп, п^З и Dn, ?г^4. Ото соответственно алгебры Ли
групп SU (ra+1), SO Bи + 1), Sp (re) и SO Bre). Кроме
них имеется еще лишь пять т. н. исключитель-
исключительных простых компактных алгебр Ли,
соответствующих системам корней типов G2, /\, Еа,
Е7 п Е„. Всякая компактная простая алгебра Ли изо-
изоморфна одной из этих алгебр Ли, а сами они попарно
неиаоморфны друг другу. Ли к. г. SU(n) и Sp(ra), и^1,
связны и односвязны. Группа SO (re), ге^З, связна, но
неодносвязна. Ее универсальная накрывающая наз.
спи норной Ли к. г. и обозначается Spin (n).
Центры связных односвязных нолупростых Ли к. г.
совпадают с центрами соответствующих односвязных
комплексных групп Ли (см. Ли полупростая группа).
Всякая Ли к. г. допускает точное линейное представ-
представление; образ такого представления является вещест-
вещественной алгебраич. группой. Любая Ли к. г. G обладает
комплексификациен G^ (см. Комплексификация групп»
Ли). При этом Gp является комплексной редуктивной
алгебраич. группой, аффинная алгебра A q к-рой может
быть описана как алгебра всех представляю-
представляющих функций на G, т. е. таких непрерывных
комлекснозначных функций, что линейная оболочка
сдвигов / на элементы из G конечномерна. Алгебра A q
¦обладает естественной вещественной структурой и по-
потому определяет нек-рую алгебраич. группу над R.
Вещественные точки этой группы образуют G, а ком-
комплексные — G,p. Группа G является максимальной
компактной подгруппой в Gg. В результате получается
взаимно однозначное соответствие между классами изо-
изоморфных Ли к. г. и редуктпвных алгебраич. групп над С.
Всякая Ли к. г. является вещественной аналитич.
труппой. Комплексные компактные аналитич. группы
наз. также комплексными Ли к. г. Всякая
связная комплексная Ли к. г. (как комплексная груп-
группа Ли) изоморфна комплексному тору Сл/Г, где Г — дис-
дискретная подгруппа ранга 2в в С", и (как вещественная
труппа Ли) изоморфна Т-". Два комплексных тора
С"/Г1 и С"/Г2 изоморфны (как комплексные группы
Ли) тогда н только тогда, когда Г2=?(Г1) для нек-
рого g?GLn(C).
Лит.: [1] К а р т а н Э., Геометрия групп Ли и симметри-
симметрические пространства, пер. с франц., М., 1949; [2] В е й л ь Г.,
-«Успехи матеы. наук», 1938, в. 4, с. 201—46; [3] II о н т р я-
г и н Л. С, Непрерывные группы, 3 изд., М., 1973; [4] Теория
алгебр Ли. Топология групп Ли. Семинар «Софус Ли», пер. с
франц.. М., 1962; [5] Ж е л о б е и к о Д. П., Компактные груп-
группы Ли и их представления, М., 1970; [6] Н а й м а р к М. А.,
Теория представлений групп, М., 1976; [7] В и н б е р г Э. Б.,
О и и щ и к А. Л., Семинар по алгебраическим группам и
группам Ли. 1967/68, М., 1969; [8] Бур бак и Н., Группы
и алгебры Ли. Алгебры Ли, свободные алгебры Ли и группы Ли,
пер. с франц., М., 1976; [9] С е р р Ж.- П., Алгебры Ли и груп-
группы Ли, пер. с англ. и франц., М., 1969; [10] Адаме Д ж.,
Лекции по группам Ли, пер. с англ., М., 1979. В. Л. Попов.
ЛИ ЛИНЕЙНАЯ АЛГЕБРА над полем к —
алгебра Ли $, элементы к-рой являются линейными
преобразованиями нек-рого векторного пространства V
над к; сложение элементов и их умножение на элементы
из к определяются обычным образом, а коммутатор
\х, у] элементов х, у^З задается формулой
(ху п ух — обычные произведения линейных преобра-
преобразований). Ли л. а., состоящая из всех линейных пре-
преобразований пространства V, обозначается fll(F).
Если V=k", то ftt(F) естественно отождествляется с
множеством всех квадратных матриц порядка п над к
и обозначается fit (и, к.). Произвольная Ли л. а.— ото
подалгебра нек-рой алгебры Ли et(V).
Примеры. 1) Пусть V наделено структурой ассо-
ассоциативной алгебры. Тогда все дифференцирования ал-
алгебры V образуют Ли л. а. Если V — алгебра Ли, то
для фиксированного элемента г?7присоединен-
ное к х линейное преобразование
пространства V, определенное формулой у—>-[х, у], у? V,
будет дифференцированием алгебры V; оно обозначается
ad х. Множество
является Ли л. а., она наз. присоединенной
линейной алгеброй Ли, или алгеброй
Ли внутренних дифференцирований
алгебры V. 2) Пусть к — поле, полное относительно нок-
рого нетривиального абсолютного значения, V — н(р-
мируемое полное пространство над к и G — л и н о й-
н а я группа Ли преобразований пространства V,
т. е. подгруппа Ли в группе Ли всех автоморфизмов
пространства V. Тогда Ли алгебра аналитической груп-
группы G естественно отождествляется с подалгеброй Ли в
fll(F), т. е. является Ли л. а.
Проблема существования изоморфизма произвольной
конечномерной алгебры Ли с нек-рой Ли л. а. возник-
возникла уже в первых работах по теории групп и алгебр Л it,
но была положительно решена лишь в 1935 теоре-
теоремой А до (см. [4]): каждая конечномерная алгебра
Ли д над полем нулевой характеристики обладает точ-
точным конечномерным представлением р (и, более того,
если П •— наибольший нильпотентный идеал в д, то
представление р можно выбрать так, чтобы все элементы
из р (п) были нильпотентны). Для групп Ли аналог
этой теоремы, вообще говоря, не имеет места: напр.,
универсальная накрывающая группы вещественных
упимодулярных матриц порядка 2 не допускает точ-
точного линейного представления.
См. также Ли алгебраическая алгебра.
Лит.: [1] II о н т р я г и н Л. С, Непрерывные группы,
3 изд., М., 1973; [2] Б у р б а к и Н., Группы и алгебры Ли.
Алгебры Ли, свободные алгебры Ли и группы Ли, пер. с франц.,
М., 1976; [3] С е р р Ж.- П., Алгебры Ли и группы Ли, пер. с
англ. и франц., М., 1969; [4] А д о И. Д., «Успехи матем. наук»,
1947, т. 2, в. 6, с. 159—73. В. Л. Попов.
ЛИ ЛОКАЛЬНАЯ АЛГЕБРА — алгебра Ли, эле-
элементами к-рой являются гладкие функции на гладком
вещественном многообразии М (или, более общо, глад-
гладкие сечения гладкого векторного расслоения Е над М),
а операция коммутирования непрерывна в С00-топо-
С00-топологии и носит локальный характер, т. е.
supp[/i, /2]c:supp/insupp/2,
где supp / — носитель функции (сечения) /. Известна
полная классификация Ли л. а. для расслоений Е с
одномерным слоем (в частности, для обычных функций)
(см. [3]). А именно, операция коммутирования в этом
случае является бидифференциальным оператором пер-
первого порядка, т. е. имеет вид
/«1=2. eii
где д(=д1дх1 — частные производные по локальным ко-
координатам на М. Далее, пусть Р (х) — подпростран-
подпространство в касательном пространстве ТХМ к многообразию
М в точке х?М, порожденное векторами
а (х) = 2fc а* (х) dk и с' (*) = 2 . cU (*) д/'
i=l,2, .... и. '
Тогда распределение {Р(х)у х?М} интегрируемо,
так что многообразие М распадается в объединение
UasA-^a интегральных многообразий. Операция
коммутирования перестановочна с ограничением на
Ма, п возникающие таким образом структуры Ли л.а. на
Ма транзитивны в том смысле, что Р (х) для любой точ-
точки х совпадает с касательным пространством к интег-
интегральному многообразию Ма, содержащему х.
Каждая транзитивная Ли л. а. локально определя-
определяется размерностью подстилающего многообразия с точ-
точностью до замены переменных в базе и слое. Для чет-
номерного многообразия она изоморфна алгебре скобок
Пуассона, а для нечетномерных — алгебре скобок
Лагранжа (см. [1]).
Примером Ли л. а., иллюстрирующим общую теорию,
является структура алгебры Ли в С°° (R") , в к-рой
lh, /2] = 2. . ^"Sihdjh,
i,j. ft
где с ft' — структурные константы нек-poii «-мерной
алгебры Ли <} (см. [2]). В этом случае многообразие
Л/—R" естественно отождествляется с пространством
Д*, двойственным к д, а разбиение на подмногообразия
Ма совпадает с разбиением д* на орбиты коприсоеди-
ненного представления.
Ли л. а. возникают как алгебры Ли пек-рых беско-
бесконечномерных групп Ли. В частности, они являются
алгебрами Ли для дифференциальных групп в смысле
Дж. Ритта [4]. Из работы [6] вытекает описание всех
Ли л. а., связанных с расслоениями на прямой с дву-
двумерным слоем. Все такие Ли л. а. являются расшире-
расширениями алгебры скобок Лагранжа (которая в этом случае
совпадает с алгеброй Ли векторных полей) с помощью
тривиальной Ли л. а. с одномерным слоем. Анонсиро-
Анонсирована [6] классификация «простых» Ли л. а.
Лит.: [1] Арнольд В. И., Математические методы клас-
классической физики, М., 1974; [2] Б е р е з и н Ф- А., «Функцио-
«Функциональный анализ и его приложения», 1967, т. 1, и. 2, с. 1—14;
[3] Кириллов А. А., «Успехи матем. наук», 197S, т. 31,
в. 4, с. 57—76; [4] R 1 t t J. P., «Ann. Math.», 1950, v. 52,
p. 708—26; [5] e г о же, там же, 1951, v. 53, p. 491—519; [6]
Weisfeiler В., «Bull. Amer. Math. Soc», 1978, v. 84
.Vs 1, p. 127 — 30. А. А. Кириллов]
ЛИ ЛОКАЛЬНАЯ ГРУППА, аналитическая
локальная групп а,— аналитическое много-
многообразие G над полем к, полным относительно нек-рого
нетривиального абсолютного значения, снабженное от-
отмеченным элементом е (единицей), открытым подмноже-
подмножеством U^en парой аналитич. отображений (g, h)\—з> gh
многообразия U'XU в G и gt—> g'1 окрестности U в
себя, для которых:
1) в некоторой окрестности точки е выполняется
тождество ge=eg;
2) в некоторой окрестности точки е выполняется
тождество e-=gg-1=g~'Lg;
3) для некоторой окрестности U'cz.U точки е вы-
выполняется включение U'U'ezU, причем g(hr)=(gh)r,
где g, ft, г — любые элементы из U'.
Ли л. г. впервые появились в трудах С. Ли (S. Lie)
и его школы (см. [1]) как локальные Ли группы преобра-
преобразований.
Пусть G1 и G2— две Ли л. г. с единицами е± и е.2 со-
соответственно. Локальным гомоморфизмом
Gj в G2 (обозначается / : Gy-^G^) наз. аналитич. отобра-
отображение / : U—>-G2 нек-рой окрестности U^et в С1у для
к-рого f(e1) = e2 и )(gh)=f{g)f(h) для g,h из нек-рой
окрестности UyCZ.U точки et. Определяемая естествен-
естественным образом композиция локальных гомоморфизмов
также есть локальный гомоморфизм. Локальные гомо-
гомоморфизмы Gy-^-Gz, совпадающие в нек-рой окрестно-
окрестности точки e-i, наз. эквивалентными. Если су-
существуют такие локальные гомоморфизмы /: G^-^-G^ и
/, : G2-*-Gi, что композиции /2°/v и /i°/2 эквивалентны
тождественным отображениям, то Ли л. г. Gx и G2 наз.
эквивалентными.
Пример. Пусть G — аналитич. группа с едини-
единицей е и G — открытая окрестность точки е в G. Тогда
аналитич. структура на G индуцирует аналитич. струк-
структуру на G, причем операции умножения и взятия об-
обратного элемента в G превращают G в Ли л. г. (в част-
частности, сама G может рассматриваться как Ли л. г.).
Все Ли л. г. G, получаемые таким способом из фикси-
фиксированной аналитич. группы G, эквивалентны между
собой.
Один из принципиальных вопросов теории групп Ли
состоит в том, насколько общий характер имеет приве-
приведенный выше пример, т. е. будет ли всякая Ли л. г.
(с точностью до эквивалентности) окрестностью нек-
некрой аналитич. группы. Ответ на этот вопрос положите-
положителен (см. [2], [3], [4]), в случае банаховых Ли л. г. ответ
отрицателен (см. [4]).
Важнейшим средством изучения Ли л.г. является
сопоставление Ли л. г. ее алгебры Ли. А именно,
пусть G — Ли л. г. над полем к и е — ее единица. Вы-
Выбор карты с аналитич. многообразия G в точке е позво-
позволяет отождествить нек-рую окрестность точки е в С с не-
к-рой окрестностью U нуля в ге-мериом координатном
пространстве к", так что U становится Ли л. г. Пусть
Ua— такая окрестность нуля в Ли л. г. U, что для
любых х, у?и0 определено произведение z=xy? U. То-
Тогда в координатной форме умножение в Ли л. г. [/в
окрестности Uo задается п аналитич. функциями
zi = fi(xi, •••> хп, Ул., ¦¦¦, Уп), i = i, -.., п,
где (хи . . ., хп), (уи . . ., у,,), (z,, . . ., z,,) — соответ-
соответственно координаты точек х, ydzUo n z—xy?U. В до-
достаточно малой окрестности нуля функция /, представ-
представляется в виде суммы сходящегося степенного ряда (так-
(также обозначаемого далее через /,•), а наличие в U еди-
единицы и ассоциативного закона выражается следующими
свойствами этих рядов, рассматриваемых как формаль-
формальные степенные ряды от 2п переменных:
) ( 0 0) = а,- и /,-@, . . ., 0; уи
in
a) /,(x
., yn)~ij
6) fi(Ul
(vu . ¦ .,
'i для
, . . .,
, v- i
, xn,
всех
"«;
о,
i
/i
vn; wu . . ., wn), . . .,
(f1(uu . . ., и„; ь-и . . .,
Vn)i ¦ ¦ •> /n("l» ¦ • •> un\ v\, • • •, vn)\ ^1, • • •, wn)) ДЛЯ
всех i.
Свойства а) и б) означают, что система формальных
степенных рядов Fc—{f\, ¦ ¦ ¦, in) является формальной
группой. В частности, однородная компонента степени 2
каждого из рядов /,¦ является билинейной формой на
к'1, т. е. имеет вид
^j,ibjlx/yi^bi (х' У)' Х=(Х1, ¦¦¦^,г), У = (Уь ••-,!/«),
что позволяет определить на к" умножение [ , ] по пра-
правилу:
U, y] = (bi(x, У) — Ъх(у, х), ..., Ь„(х, у) — Ъп(у, х)).
Относительно этого умножения к" является алгеброй
Ли. Указанная структура алгебры Ли переносится в
касательное пространство <\ к многообразию G в точке е
с помощью определенного картой с изоморфизма g^k".
Формальные группы Fc и Fc, определенные разными
картами, изоморфны, а указанная структура алгебры
Ли на Я не зависит от выбора карты с. Алгебра Ли $
наз. алгеброй Ли локальной группы
Л и. Для любого локального гомоморфизма Ли л. г.
его дифференциал в единице является гомоморфизмом
алгебр Ли, откуда следует, что сопоставление Ли л. г.
ее алгебры Ли является функториальным. В частности,
эквивалентные Ли л. г. имеют изоморфные алгебры Ли.
Если поле к имеет характеристику 0, указанная выше
конструкция, восходящая к С. Ли [1], позволяет све-
свести изучение свойств Ли л. г. к изучению соответству-
соответствующих свойств их алгебр Ли. В этом случае алгебра Ли
д определяет Ли л. г. G однозначно с точностью до
эквивалентности. А именно, карта с может быть выбра-
на так, что произведение ху в Ли л. г. U выражается
в виде нек-рого сходящегося ряда (т. н. ряда Кэмпбел-
ла — Хаусдорфа) от элементов пространства к", полу-
полученных из х и у с помощью операции коммутирования
[ , ] н умножения на элементы из к (см. Кэмпбелла —
Хаусдорфа формула). Обратно, для произвольной ко-
конечномерной алгебры Ли I) над к ряд Кэмпбелла — Ха-
Хаусдорфа сходится в нек-рой окрестности нуля в i)
и определяет в этой окрестности структуру Ли л. г. с
алгеброй Ли I). Таким образом, для любой заданной
алгебры Ли I) существует единственная с точностью
до эквивалентности Ли л. г., алгеброй Ли к-рой явля-
является f|. Более того, всякий гомоморфизм алгебр Ли
индуцирован нек-рым единственным гомоморфизмом
соответствующих Ли л. г. Иначе говоря, сопоставление
Ли л. г. ее алгебры Ли определяет эквивалентность ка-
категории Ли л. г. и категории конечномерных алгебр Ли
над к. Кроме того, сопоставление Ли л. г. соответствую-
соответствующей формальной группы определяет эквивалентность
категории Ли л. г. и категории формальных групп
над к.
Алгебра Ли может быть определена н для любой
банаховой Ли л. г.; основной результат об эквивалент-
эквивалентности категорий Ли л. г. и алгебр Ли обобщается на
этот случай (см. [21).
Лит.: [1] L i e S., E n g e I F., Theorie der Transformations-
gruppen, Bd 1 — 3, Lpz., 1888—93; [2] Б у р б а к и Н., Группы
и алгебры Ли. Алгебры Ли, свободные алгебры Ли и группы Ли,
пер. с франц., М., 19715; [3] П о н т р я г и н Л. С, Непрерыв-
Непрерывные группы, 3 изд., М., 1973; [4] С е р р Ж.- П., Алгебры Ли
и группы Ли, пер. с англ. и франц., М., 1969; [5] Чебот а-
рев Н. Г., Теория групп Ли, М.— Л., 1940. В. Л. Попов.
ЛИ НИЛЬАЛГЕБРА — алгебра Ли Я над полем к,
определяемая наличием функции п : qXq->N такой,
что (ad х)п1х'У) (j/) = 0, где (ad х) (у)=[х, у], для любых
xi !/?й- Основной вопрос о Лин.— условия на я. fc, n,
при к-рых я (локально) нильпотентна (см. Ли нилъ-
потентная алгебра). Конечномерная над к Ли н.—
нильпотентна. С другой стороны, над любым полем су-
существуют конечно порожденные ненильпотентные Ли н.
[1J. Пусть п — константа. Ли н. локально нильпотент-
нильпотентна, если charA = 0 или если п<р+1, где p^=charfc > 0
(теорема Кострнкина [21). Локальная ниль-
нильпотентность имеет место и в случае, когда Д локально
разрешима. Бесконечно порожденная Ли н. ненильпо-
тентна при п^р—2 (см. [3]), а при п^р-{-1 ненильпо-
ненильпотентность сохраняется и при условии разрешимости.
Неизвестно A982), нильпотентны ли Ли н., если char
к=0 (при гс<4 ответ положительный). Открыт A982)
вопрос о локальной нильпотентности Ли н. при ге>р+1.
Изучение Ли н. над полем к, char &=p>0, тесно связа-
связано с Бёрнсайда проблемой.
Лит.: [1] Голод Е. С, «Изв. АН СССР. Сер. матем.»,
1964, т. 28, -V» 2, с. 273 — 76; [2] К о с т р и к и н А. И., «Изв.
АН СССР. Сер. матем.», 1959, т. 23, № 1, с. 3—34; [3] р а з-
м ы с л о в Ю. П., Алгебра и логика, 1971, т. 10, Л"« 1, с. 33—
44; [41 Бахтурин Ю. A., Lectures on Lie algebras, В.,
1978; [5] Braun A., «J. Algebra», 1974, v. 31, p. 287 — 92.
Ю. А. Бахтурин.
ЛИ НИЛЫ1ОТЕНТНАЯ АЛГЕБРА — алгебра Ли я
над полем К, удовлетворяющая одному из следующих
эквивалентных условий:
1) существует конечная убывающая цепочка идеалов
{Я,-}о<!<п алгебры Я таких, что Яо = Й, Й„={0}
и [Я, Й/]с:Й1 + 1 Для 0<г<7?;
2) С*я= {0} (аналогично СьЯ={0}) для достаточно
большого к, где С*й и С^Я — члены соответственно
нижнего и верхнего центральных рядов;
3) существует такое А-, что &dx: ... ad .т^ = 0 для
любых хг, . . ., .т/г?Я-
Абелева алгебра нильпотентна. Если V — конечно-
конечномерное векторное пространство над К, a F={Vi) —
флаг в нем, то
?EdV\VV;-1 для I}
является нильпотентной подалгеброй в алгебре Ли
Д1 (V) всех линейных преобразований пространства V.
Если в V выбрать базис, согласованный с флагом F,
то в нем элементы алгебры n(F) представятся верхними
треугольными матрицами с нулями на главной диаго
нали. Если F — полный флаг (т. е. dim V^fc), то
соответствующая матричная Ли н. а. н (т, к) состоит
из всех верхних треугольных матриц порядка то=
= dim V с нулями на главной диагонали.
Для любой неодномерной Ли н. а. коразмерность
ее коммутатора codim [д, д]^2. В частности, если
dim д < д2, то д абелепа. Единственная неабелева
трехмерная Ли п. a. if изоморфна П C, К). Ли н. а.
перечислены еще в нескольких малых размерностях
(для dim Д<7 при К—С), но общего подхода к их
классификации пока A982) нет.
Ли н. а. (ранее их называли специальными
алгебрами Ли, или алгебра ми Ли ран
г а 0) встретились уже на первых шагах исследований
С. Ли (S. Lie) по интегрированию дифференциальных
уравнении. Классификация Ли разрешимых алгебр све-
сведена в нек-ром смысле к перечислению Ли н. а. В про-
произвольной конечномерной алгебре Ли существует наи-
наибольший нильпотентный идеал (нильрадикал
в терминологии [2]). Рассматривается и другой ниль-
нильпотентный идеал — пересечение ядер неприводимых
конечномерных представлений (нильпотентный радикал)
(см. [1], J4]). Если г — радикал алгебры Д, то ниль-
нильпотентный радикал п совпадает с
[Я, г] = [Д
Факторалгебра д/lt редуктивна и П есть минималь-
минимальный из идеалов, обладающих этим свойством. В слу-
случае char К—-0 нильрадикал состоит из всех таких
х?х, что ad х нильпотентен.
При изучении редуктивной алгебры Ли Д над С
естественно возникают ее нильпотентные подалгебры,
являющиеся нилыютентными радикалами в параболи-
параболических подалгебрах алгебры Д. В случае Д=Д1 (V)
эти ннльпотентные подалгебры совпадают с рассмотрен-
рассмотренными выше подалгебрами П(/?). Нильпотентный ра-
радикал борелевской подалгебры (см. Бореля подгруппа)
в g есть максимальная подалгебра в д, состоящая из
нильпотентных элементов,— единственная с точностью
до сопряженности. Более широкий класс Ли н. а.
образуют произвольные идеалы параболич. подалгебр
алгебры д, состоящие из нильпотентных элементов.
В случае д=д1(К) эти Ли н. а. были классифицирова-
классифицированы в [6] (стандартные нуль-алгебр ы),
а в общем случае в [7].
Центр Ли н. а. нетривиален и любая Ли н. а. может
быть получена рядом центральных расширений с по-
помощью Ли н. а. Класс Ли н. а. замкнут относительно
перехода к подалгебре, факторалгебре, центральному
расширению и конечной прямой сумме. В частности,
любая подалгебра в n(m, К) нильпотентна. Обратно,
произвольная конечномерная Ли н. а. изоморфна под-
подалгебре в п(т, К) при нек-ром т (если char К=0) —
это частный случай теоремы Адо (см. [1], [2]).
Если Д — произвольная конечномерная алгебра Ли,
то любой ее нильпотентный идеал ортогонален ей от-
относительно Киллинга формы, в частности для Ли н. а.
эта форма тривиальна.
Одной из основных в теории Ли н. а. является тео-
теорема Энгеля: если р : Д—>-Д[ (V) — конечномерное
представление Ли нильпотентной алгебры Д, причем
р(.г) нильпотентно для любого ж?д, то существует та-
такой полный флаг F, что p(g)czn(F). Из теоремы Эн-
Энгеля следует, что конечномерная алгебра Ли Д ниль-
нильпотентна тогда и только тогда, когда ad"a:=0 при
нек-ром п и всех x?q, т. е. когда любой ж?д яв-
является нильпотентным элементом.
В теореме Энгеля содержится описание нильпотент-
ных представлений Ли н. а.; описание произвольных
конечномерных представлении принадлежит X. Цас-
сенхаузу (Н. Zassenhaus, см. [2]): если поле К алгебраи-
алгебраически замкнуто, а V — конечномерный ft-модуль, то
1/=©"=1.У;> гДе подмодули V,- таковы, что ограничение
действия любого х?# на них есть сумма скалярного
и нильпотентного операторов. Если V — конечномерное
векторное пространство над полем К характеристики О,
то любая алгебраическая Ли н. a. ftCIftl(F) имеет
вид ft —а+п, где а и п — идеалы, состоящие соот-
соответственно из полупростых и нильпотентных линейных
преобразований, принадлежащих алгебре ft [5].
Лит.: [1] Б у р б а к и Н., Группы и алгебры Ли. Алгебры
Ли, свободные алгебры Ли и группы Ли, пер, с франц., М.,
197В; [2] Дшекобсон Н., Алгебры Ли, пер, с англ., М.,
1964; [3] С е р р Ж.- П., Алгебры Ли и группы Ли, пер. с англ,
и франц., М., 1969; [4] Теория алгебр Ли. Топология групп Ли.
Семинар «Софус Ли», пер, с франц., М., 1961; [5] Ш е в а л-
л е К., Теория групп Ли, пер. с франц., т. 3, М., 1958; [6]
Г у р а в и ч Г. Б., «Матем. сб.», 1954, т. 35, с. 437 — 60; [71
X а к и м д ж а н о в Ю. Б., «Вестн. Моск. ун-та. Матем.,
механ.», 1974, Л» E, с. 49 — 55. В. В. Горбацееич.
ЛИ НИЛЬПОТЕНТНАЯ ГРУППА — группа Ли,
ннлыютентная как абстрактная группа. Абелева группа
Ли нильпотентна. Если F=^{Vi} — флаг в конечномер-
конечномерном векторном пространстве V над полем К, то
Л' (F) = {g? GL (V) | gv ее= v mod F,- V " € V;, I =э= 1}
будет нилыютентной алгебраич. группой над К; в ба-
базисе, согласованном с флагом F, ее элементы представ-
представляются верхними треугольными матрицами с единица-
единицами на главной диагонали. Бели F — нолный флаг (т. е.
dim Vk — k), то соответствующая N (F) матричная Ли
н. г. N (н, к) состоит из всех матриц порядка »=dim V
указанного выше вида.
Если К — полное нормированное поле, то N (F) —
Ли н. г. над К. Ее алгеброй Ли служит n(F) (см. Ли
нилъпотентная алгебра). Вообще, алгебра Ли группы
Ли G над полем К характеристики 0 нильпотентна тогда
н только тогда, когда нильпотентна связная компонента
единицы Go группы G. Это позволяет перенести на Ли
н. г. свойства нильпотентных алгебр Ли (см. [2], [4],
[5]). Групповой вариант теоремы Энгеля при этом до-
допускает следующее усиление (теорема К о л ч и-
н а): если G — подгруппа в GL(T), где V — конечно-
конечномерное векторное пространство над произвольным полем
К, а каждый g?G унипотентен, то существует такой
полный флаг F в V, что GdN (F) (при этом G автома-
автоматически оказывается нильпотентной) (см. [3]).
Ли н. г. разрешимы, поэтому свойства. Ли разреши-
разрешимых групп переносятся и на них, причем часто в уси-
усиленной форме, ибо всякая Ли н. г. треугольна. Связ-
Связная группа Ли G нильпотентна тогда и только тогда,
когда в канонич. координатах (см. Ли группа) групповая
операция в G записывается полиномиально [4]. Вся-
Всякая односвязная вещественная Ли н. г. G изоморфна
алгебраич. группе, более того — алгебранч. подгруппе
в N (и, R). При этом точное представление группы G
в N {п, R) можно выбрать так, чтобы группа автомор-
автоморфизмов Aut G вкладывалась в GLG?, R) — нормализа-
нормализатор образа группы G [см. [1]).
Если G — связная матричная вещественная Ли н. г.,
то она разлагается в прямое произведение компактной
абелевой и односвязной групп Ли. Связная линейная
алгебраич. группа G над полем характеристики 0 раз-
разлагается в прямое произведение абелева нормального
делителя, состоящего из полупростых элементов, ц нор-
нормального делителя, состоящего из унипотентных эле-
элементов [5].
Ранее Ли н. г. наз. специальными груп-
группами Ли, или группами Ли ранга 0. В те-
теории представлений полупростых групп Ли при изуче-
изучении дискретных подгрупп в таких группах существен-
но используются орисферич. группы Ли, являющиеся
Ли н. г.
Лит.: [1] Birkhoff G., «Arm. Math.», 1937, v. 38,
p. 526 — 32; [2] Б у р б а к и Н., Группы и алгебры Ли. Алгеб-
Алгебры Ли, свободные алгебры Ли и группы Ли, пер. с франц.,
М., 1976; [31 С е р р Ж.- П., Алгебры Ли и группы Ли, пер. с
англ. и франц., М-, 1969; [4] Хелгасон С., Дифференци-
Дифференциальная геометрия и симметрические пространства, пер. с англ.,
М., 1964; [5] Ш е в а л л е К., Теория групп Ли, пер. с франц.,
т. 3, М., 1958. В. В. Горбацевич.
ЛИ ОСОБАЯ АЛГЕБРА — простая алгебра Ли
(см. Ли полупростая алгебра), не являющаяся классиче-
классической. Над алгебраически замкнутым полем нулевой
характеристики существует всего 5 Ли о. а.: Е,;, Е7, Es,
Ец и G2 размерностей 78, 133, 248, 52 и 14 соответ-
соответственно. Индексы в обозначениях равны рангам этих
алгебр Ли. Простейшие линейные представления этих
Ли о. а. имеют размерности 27, 56, 248, 26 и 7 соответ-
соответственно. Алгебра G2 есть алгебра дифференцирований
Кэли—Диксона алгебры, a F±— алгебра дифференциро-
дифференцирований единственной особой йорданоеой алгебры, к-рую
можно представить как алгебру эрмитовых матриц
третьего перядка над алгеброй Кэли—Диксона. Алгеб-
Алгебра Ец есть линейная оболочка дифференцирований и
умножений на элементы особой йордановой алгебры.
Алгебры Е-, и Es и формы всех Ли о. а. над алгебраиче-
алгебраически незамкнутыми полями также связаны с алгеброй
Кэли — Диксона. Различные модели Ли о. а. получают-
получаются при рассмотрении их градуировок посредством цик-
лич. групп. Связные группы Ли, соответствующие Ли
о. а., наз. особыми группами Ли и часто
обозначаются теми же буквами. Напр., комплексная
группа G2— это группа автоморфизмов алгебры Кэлп—
Диксона над С; комплексная группа Ft— это группа
автоморфизмов особой Йордановой алгебры над С.
Лит.: [1] Джекобсон Н., Алгебры Ли, пер. с англ.,
М., 1964; [2] е г о же, Exceptional Lie Algebras, N. Y., 1971;
[3] Фрейденталь Г., «Математика», 1957, т. 1, № 1,
с. 117—53; [4] Р о з е н ф е л ь д Б. А., в кн.: Algebraical and
Topological Foundations of Geometry, Oxf.— [a. o.], 1962,
p. 135—55; [5] В и н б е р г Э. Б., в кн.: Тр. Семинара по век-
векторному и тензорному анализу..., в. 13, М., 1966, с. 7—9; [61
Tits J., «Judag. Math.», 1966, v. 28, M 2, p. 223—37; [7}
его же, Tabellen zu den einfachen Lie Gruppen und ihren Dar-
stellungen, В.— [u. a.], 1967. 9. Б. Винберг.
ЛИ ПОЛУПРОСТАЯ АЛГЕБРА — алгебра Ли, не
имеющая ненулевых разрешимых идеалов (см. Ли раз-
разрешимая алгебра). В дальнейшем рассматриваются ко-
конечномерные Ли п. а. над полем к характеристики 0 (о
Ли п. а. над полем ненулевой характеристики см.
Ли алгебра).
Полупростота конечномерной алгебры Ли Д рав-
равносильна выполнению любого из следующих условий:
1) Д не содержит ненулевых абелевых идеалов;
2) Киллинга форма алгебры д невырождена (к р и-
т е р. и й К а р т а н а);
3) Д разлагается в прямую сумму неабелевых про-
простых идеалов;
4) всякое конечномерное линейное представление
алгебры д вполне приводимо (иначе: всякий конечно-
конечномерный д-модуль пол.упрост);
5) одномерные когомологпи алгебры д со значения-
значениями в любом конечномерном д-модуле тривиальны.
Любой идеал и любая факторалгебра Ли п. а. также
полупросты. Разложение Ли п. а., указанное в усло-
условии 3), единственно. Частным случаем свойства 5) яв-
является следующее утверждение: все дифференцирова-
дифференцирования Ли п. а. являются внутренними. Свойство полупрос-
полупростоты алгебры Ли сохраняется как при расширении,
так и при сужении основного поля.
Пусть д — Ли п. а. над алгебраически замкнутым
полем к. Присоединенное представление изоморфно ото-
отображает алгебру Д на линейную алгебру Ли ad д,
к-рая является алгеброй Ли алгебранч. группы Aut д
всех автоморфизмов алгебры Д и тем самым Ли алгебра-
алгебраической алгеброй. Элемент X ? Д наз. п о л у п р о с т ы м
(нильпотентным), если ad X полупрост (соответ-
(соответственно нильпотснтен). Это свойство элемента X сохра-
сохраняется при любом гомоморфизме алгебры Д в другую
Ли п. а. Связная компонента единицы (Aut д)° совпа-
совпадает с группой внутренних автоморфизмов алгебры
т. е. порождается автоморфизмами вида exp (ad X),
При изучении Ли п. а. над алгебраически замкнутым
полем к существенную роль играют корни Ли п. а.,
к-рые определяются следующим образом. Пусть () —
подалгебра Картана алгебры д. Для ненулевой ли-
линейной функции а?Ь* через Да обозначается линей-
линейное подпространство в д, заданное условием:
Яа = {*¦€<* I 1Н> А'] =« (Я) X,
Если С)а?=0, то а наз. корнем алгебры д от-
относительно ft. Множество 2 всех ненулевых корней
наз. корневой системой, или системой
корней, алгебры д. Имеет место корневое
разложение:
Корневая система и корневое разложение Ли п. а.
обладают следующими свойствами:
1) 2 порождает ft* и является приведенной корневой
системой в абстрактном смысле (в линейной оболочке
системы 2 над полем действительных чисел). Система 2
непрпводима тогда и только тогда, когда д проста.
2) Для любого а ?2
dim да г= dim [да , д_а] = 1.
Существует единственный элемент Яа?[Да, Д-а1 та-
такой, что а(Яа)^2.
3) Для каждого ненулевого Ха?$а существует
единственный Уа^Д-а такой, что [Ха, Ya] = Ha, при-
причем
[На, *а] = 2Ха и [На , Уа]=-2Уа.
Кроме того,
Р(Яа)= (а, а) , а, Р€2,
где ( , ) — скалярное произведение, индуцированное
формой Киллинга.
4) Если а, Р? 2 и а+Р?=0, то Да и дР ортогональны
относительно формы Киллинга и [да, ДР] = Да+Р.
Базис {а.\, . . ., а„} корневой системы 2 наз. также
системой простых корней алгебры
д. Пусть 2 + — система положительных корней относи-
относительно данного базиса и пусть X-a = Ya(a? 2 + ). Тог-
Тогда элементы
составляют базис алгебры д, наз. базисом Кар-
Картана. С другой стороны, элементы
составляют систему образующих алгебры д, причем
определяющие соотношения имеют следующий вид:
(adA'a.)i-n(',/) Xa =0,
(ad A'_a.)!-«('. /)Х_а_ = 0;
здесь i, ; = 1, . . ., п и
2 (а,., оу)
n(i, /) = а/(Я,-)= (а^ а^) .
Из свойства 4) следует равенство
Лта, pXa+|5, если
(| , если
1 "'
Е +) можно выбрать та-
тагде jVa,p?/c. Элементы Ха (а
ким образом, чтобы
#«,0 = —Л'_а, _р и
где р — наибольшее целое число такое, что р—р
Соответствующий базис Картана наз. баз псом
Ш е в а л л е. Структурные константы алгебры д в
этом базисе являются целыми, что позволяет связать
с д алгебры Ли и алгебраич. группы (см. Шевалле
группа) над полями произвольной характеристики.
Если к—С, то линейная оболочка над R векторов
ша, ха-х„а, i(xa+X-a) («€2+)
является компактной вещественной формой алгебры д.
Ли п. а. определяется с точностью до изоморфизма
своей подалгеброй Картана и соответствующей корне-
корневой системой. Точнее, если cji и д2— Ли п. а. над к,
l)i и fJ — их подалгебры Картана, 1ц и 22— соответ-
соответствующие корневые системы, то всякий изоморфизм
|)г—>-(J, индуцирующий изоморфизм корневых систем
2t и 22> продолжается до изоморфизма tjj —>- д2. С дру-
другой стороны, любая приведенная корневая система
может быть реализована как корневая система нек-рой
Ли п. а. Таким образом, классификация Ли п. а. (соот-
(соответственно простых неабелевых алгебр Ли) над ал-
алгебраически замкнутым полем к по существу совпадает
с классификацией приведенных корневых систем (со-
(соответственно неприводимых приведенных корневых
систем).
Простые алгебры Ли, отвечающие корневым систе-
системам типов А — D, наз. классическими и имеют
следующий вид.
Тип An(rC^i). fl--g((n-|-l, к) — алгебра линейных
преобразований пространства к" + 1 со следом 0; dim д =
= п(п+2).
Тип Вп(п^2). я=§оBп+1, к) — алгебра линей-
линейных преобразований пространства к2п + 1, кососиммет-
рических относительно заданной невырожденной сим
метрической билинейной формы; dim fl = 7iBra+l).
Тип Сп(п^Ъ). g=gp(n, к) — алгебра линейных
преобразований пространства к-п, кососимметрических
относительно заданной невырожденной кососимметри-
ческой билинейной формы; dim a, = nBn-\-i).
Тип Dn(n^sA). cj = go Bn, к) — алгебра линейных
преобразований пространства к'1", кососимметрическич
относительно заданной невырожденной симметриче-
симметрической билинейной формы; dimc(=nBn—1).
Простые алгебры Ли, отвечающие корневым системам
типов Ев, Ei, Ея, Ft, G2, наз. особыми, или и с-
ключительиыми (см. Ли особая алгебра).
Картана матрица Ли п. а. над алгебраическим зам-
замкнутым полем также определяет эту алгебру однознач-
однозначно с точностью до изоморфизма. Матрицы Картаня
простых алгебр Ли имеют следующий вид:
Ап-
В„:
2
—1
0
0
0
2
—1
0
0
0
0
— 1
2
— 1
0
0
1
2
—1
0
0
0
0
—1
2
0
0
0
—1
2
0
0
0
0
... 0
0
2
'.'.'. — 1
... 0
... 0
... 0
... —1
... 2
... —1
0
0
0
—1
2
0
0
0
0
— 2
2
Cn:
2
—1
0
0
0
0
0
2
1
0
0
0
—1
2
—1
0
0
—1
2 -
-1
0
0
0
0
0 ...
—1 ...
о
0 ...
0 ...
0 ...
-1
2 '.'.'.
0 ...
0 ... -
0 ...
0 ...
0
0
0
2
_j
0
0
0
0
0
1
0
0
0
0
2
2
0
0
0
-1
2
-1
_4
0
о
0
— 1
0
0
0
0
— 1
2
0
2
0
0
0
0
-1
0
2
Ея:
Dn:
2 0—1 0 0 0
0 2 0 — 1 0 0
— 1 0 2—1 0 0
0 —1 —1 2 —1 0
О О 0 —1 2 —1
0 0 0 0 —1 2
2 0—1 0 0 0 0
0 2 0—1 0 0 0
—1 0 2—1 0 0 0
Е7: 0 —1 —1 2—1 0 0
0 0 0 —1 2 —1 0
0 0 0 0—1 2 —1
0 0 0 0 0—12
2 0—1 0 0 0 0 0
0 2 0—1 0 0 0 0
—1 0 2—1 0 0 0 0
0—1—1 2—1 0 0 0
0 0 0—1 2—1 0 0
0 0 0 0—1 2 —1 0
0 0 0 0 0—1 2—1
0 0 0 0 0 0—12
2—100
— 1 2—2 0 ,, i! 2 —11
0 —1 2 —1 ' 2'||— 3 2
0 0 —1 2
Классификация расщепляемых Ли п. а. над произ-
произвольным полем к характеристики 0 (расщепля-
е м о й наз. Ли п. а. ц, обладающая такой подалгеб-
подалгеброй Картана fjcft, что все характеристич. корни опе-
операторов adX, X?{), лежат в к) выглядит аналогично
случаю алгебраически замкнутого поля. А именно,
каждой неприводимой приведенной корневой системе
соответствует единственная расщепляемая Ли п. а.
В частности, расщепляемые Ли п. а. типов А —D имеют
указанный выше вид с той разницей, что в случаях В
и D нужно рассматривать невырожденные симметри-
симметрические билинейные формы индекса Витта п.
Проблема классификации произвольных Ли п. а.
над к сводится к следующей задаче: перечислить с
точностью до изоморфизма все й-формы flodij, т. е.
такие fc-подалгебры CJoCi}, что Д = До®&^- Здесь
К — алгебраически замкнутое расширение поля к,
ад — заданная Ли п. а. над К. Решение этой задачи
также можно получить в терминах корневых систем
(см. Форма алгебраической группы). В случае, когда
Д — классическая простая алгебра Ли над к (отлич-
(отличная от D}), существует другой метод классификации
А-форм в й, основанный на рассмотрении простых
ассоциативных алгебр (см. [3]).
В случае, когда /c = R, классификации Ли п. а. вы-
выглядит следующим образом (см. [6], 17], [8]). Всякая
простая неабелева алгебра Ли над R либо является
простой алгеброй Ли над С (рассматриваемой как ал-
алгебра над R), либо есть вещественная форма простой
алгебры Ли над С. Классификация вещественных форм
До в простых классич, алгебрах Ли g над С имеет
следующий вид.
"I. Тип Ап : q=gl(ra+l, С), и>1.
Ах ; c]0-=gl(n+l, R).
Ли : п-\-\ = 2т четно, cjo=§u* Bга) — подал-
подалгебра элементов из giBm, С), сохраняющих
нек-рую кватернионную структуру.
лш : flo=8U(p, ге+1— р) — подалгебра эле-
элементов из §1(ге-|-1, С), кососимметрических
относительно невырожденной эрмитовой формы
положительного индекса р, 0<р< (и- -1)/2.
II. Тип ?„: я=ёзB«+1, С), п>2.
Bi : i]o~:§Li (р, 2n + l, —р) — алгебра линейных
преобразований пространства R'ln + 1, кососим-
кососимметрических относительно невырожденноГ[ сим-
симметрической билинейной формы положитель-
положительного индекса р, 0<р<?г.
III. Тип С„: й = §^> («, С), j?>3.
^'i : tfu=SP(«> R) —алгебра линейных пре-
преобразований пространства R2", кососпммет-
рических относительно невырожденной косо-
симметрической билинейной формы.
Си ¦ Йо=8Р(р, п—р), 0<р<п/2,— подал-
подалгебра в §11B/7, 2(п—р)), состоящая из пре-
преобразований, сохраняющих нек-рую кватер-
кватернионную структуру.
IV. Тип Dn : д=ё0Bп, С), п>4.
Di '¦ До—§"(/>, 2?г— р) — алгебра линейных
преобразований пространства R2", кососим-
метрических относительно невырожденной би-
билинейной симметрия, формы положительного
индекса р, 0<р<:п.
¦Dill : Йо--811*B«) — подалгебра в go B«, С),
состоящая из преобразований, сохраняющих
нек-рую кватернионную структуру.
Ли ц. а. над полем С были впервые рассмотрены в
работах В. Киллинга [1], к-рый дал их классифика-
классификацию, хотя в его доказательствах имелись пробелы, вос-
восполненные Э. Картаном [2]. Уже в работах В. Киллинга
и Э. Картана появились корни алгебры Ли как харак-
теристич. корни оператора adX. Э. Картан дал также
классификацию вещественных Л. п. а., установив глу-
глубокую связь между этими алгебрами и глобально сим-
симметрическими риманоеыми пространствами.
Лит.: [1] Killing W., «Math. Ann.», 1888, Bd :>1, S.
252—90; 1889, Bd 33, S. 1 — 48, Bd 34, S. 57 — 122; 1890, Bd 36,
S. 161—89; [2] С а г t a n E., (Euvres completes, pt. 1, t. 1,
P., 1952, p. 137 — 287; [3j Д ж е к о б с о н Н., Алгебры Ли,
пер. с англ., М., 1964; [4] С е р р Ж.-П., Алгебры Ли и группы
Ли, пер. с англ. и франц., М., 1969; [51 С т е й н б е р г Р.,
Лекции о группах Шевалле, пер. с англ., М., 1975; [В] X е л-
г а с о н С, Дифференциальная геометрия и симметрические
пространства, пер. с англ., М., 1964; [7] Helgason S.,
Differential geometry, Lie groups, and symmetric spaces, N. Y.—
San Francisco — L., 1978; [8] Араки III., «Математика»,
1966, т. 10, № 1, с. 90 — 126. А. Л. Онищик.
ЛИ ПОЛУПРОСТАЯ ГРУППА — связная группа
Ли, не содержащая нетривиальных связных разреши-
разрешимых (или, что равносильно, связных абелевых) нор-
нормальных делителей. Связная группа Ли полупроста
тогда и только тогда, когда ее алгебра Ли полупроста.
Связная группа Ли G наз. п р о с т о й, если ее алгебра
Ли проста, т. е. если G не содержит нетривиальных
связных нормальных делителей, отличных от G. Связ-
Связная группа Ли является полупростой тогда и только
тогда, когда она разлагается в локально прямое произ-
произведение простых неабелевых нормальных делителей.
Классификация Ли п. г. сводится к локальной клас-
классификации, т. е. к классификации Ли полупростых
алгебр, а также к глобальной классификации групп
Ли G, отвечающих заданной полупростой алгебре
Ли д.
В случае групп Ли над полем С комплексных чисел
основной результат локальной классификации со-
состоит в том, что всякая односвязная простая нсабе-
лева комплексная группа Ли изоморфна одной из
групп SL,,(C), n^l, Spinn(C), re^5 (универсальная
накрывающая группы SOn(C)), Spn(C), п^'д (см. Клас-
Классическая группа) или же одной из особых комплексных
групп Ли (см. Ли особая алгебра). Глобальная клас-
классификация групп Ли, отвечающих полупростой ал-
алгебре Ли д над С, выглядит следующим образом.
Пусть I) — подалгебра Картана в д, 2 — система
корней алгебры д относительно I). Каждой Ли п. г.
G с алгеброй Ли д соответствует решетка Г (G)clj,
являющаяся ядром экспоненциального отображения
ехр: () —>- G. В частности, если G односвязна, то Г (G)
совпадает с решеткой Г0=Г0(д), порожденной эле-
элементами 2jiiIIa, а?2 (см. Ли полупростая алгебра),
а если G — группа без центра (присоединенная груп-
группа), то Г (G) есть решетка
ri=--r1(ci) = {A'gl)|a(X)g2niZ для всех сс?2}.
В общем случае Г0С1Г (GJcir!. Для любой аддитивной
подгруппы Mat), удовлетворяющей условию ГосМс
СГ,, существует единственная с точностью до изо-
изоморфизма связная группа Ли G с алгеброй Ли д такая,
что T(G) — M. При этом центр группы G изоморфен
l\/T(G), а фундаментальная группа
Jij (G) ~ Г (G)/To.
Факторгруппа Z11=r1/T0 (центр односвязной группы
Ли с алгеброй Ли Д) конечна и для различных типов
простых алгебр Ли Д имеет следующий вид:
ft
Cn
E7
Eg, Fit G2
It 2® It 2
Жз
7,2
0
Порядок группы Fj/Fq совпадает с числом вершин
расширенной диаграммы простых корней алгебры д,
при отбрасывании к-рых получается диаграмма про-
простых корней. Аналогичная классификация имеет место
для компактных вещественных Ли п. г., каждая из
к-рых вкладывается в единственную комплексную
Ли п. г. в качестве максимальной компактной под-
подгруппы (см. Ли компактная группа).
Глобальная классификация некомпактных вещест-
вещественных Ли п. г. может быть проведена аналогично,
но более сложным образом. В частности, центр Z^
односвязной группы Ли, отвечающей полупростой ал-
алгебре Ли Д над R, можно вычислить следующим
способом. Пусть Д=!-{-!р — Картана разложение,
где I — максимальная компактная в Д подалгебра,
а J.1 — ее ортогональное дополнение относительно
формы Киллинга, 9 — соответствующий пнволютив-
. С ,
цыи автоморфизм, продолженный в Д , I) — подал-
подалгебра Картана в Д , содержащая подалгебру Картана
I)'df, Эо — автоморфизм алгебры д , совпадающий
с 8 на корнях относительно I) и продолженный на
корневые векторы соответствующим образом, До^оН"
+!Ро — разложение Картана вещественной формы
ДОДС, отвечающей 60. Тогда Z% s=Tx(\a)ITu [t, f]
(см. 13], где :>та группа вычислена для всех типов про-
простых алгебр д над IR).
Всякая комплексная Ли п. г. G обладает единст-
единственной структурой аффинной алгебраич. группы, со-
гласованиой с заданной на ней аналитич. структурой,
причем любой аналитич. гомоморфизм группы G в
алгебраич. группу является рациональным. Соответст-
Соответствующая алгебра регулярных функций на G совпадает
с алгеброй голоморфных представляющих функций.
С другой стороны, некомпактная вещественная Ли п. г.
не всегда допускает точное линейное представление —
простейшим примером является односвязная группа
Ли, соответствующая алгебре Ли yl B, R). Если Д —
иолупростая алгебра Ли над R, то в центре Zu одно-
связной группы Со, отвечающей Д, существует наи-
наименьшая подгруппа X (д), называемая л и п о а р п-
затором, такая, что GJ X (д) изоморфна линейной
Ли п. г. Если U=f+iu — компактная вещественная
С
форма алгебры g , то
(см. [3], где эта группа вычислена для всех типов
простых алгебр Ли д).
Лит.: [1] Адаме Д ж., Лекции по группам Ли, пер. с
англ., М., 1979; [2] С е р р Ж.- П., Алгебры Ли и группы Ли,
пер. с англ. и франц., М., 1969; [3] С и р о т а А. И., Соло-
Солодовников А. С, «Успехи матем. наук», 1963, т. 18, в. 3,
с. 87 — 144. А. Л. Отпцик.
ЛИ ПРОИЗВОДНАЯ тензорного поля Q по направ-
направлению векторного поля X на многообразии М — тен-
тензорное поле XxQ на многообразии М того же типа,
что и Q, к-рое задается формулой
где ф( — локальная однопараметрич. группа преоб-
преобразований пространства тензорных полей, порожден-
порожденная векторным полем X. В локальных координатах
х1 Л. п. тензорного поля Q=(q)\ " )k) типа (к, I)
по направлению векторного поля X— (X1) имеет
координаты (д:=—.
\ Эх'
а. х/о ''' '-*
= 1 'Р v/..../p//
| См. также Дм дифференцирование. д. в. Алексеевский.
ЛИ ПРОИЗВОДНАЯ ГРУППА — коммутант груп-
группы Ли. Для любой группы Ли G ее Ли п. г. [G, G]
является нормальной (не обязательно замкнутой!
подгруппой Ли в G. Соответствующий идеал в алгебре
Ли g группы G совпадает с коммутантом [д, д]
(называемым также производной алгеброй
Л и для д). Коммутант односвязной (или связной
линейной) группы Ли G всегда замкнут в G.
Лит.: [1] Ш е в а л л е К., Теория групп Ли, пер. с англ.,
т. 1, М., 1948. А. Л. Онищик.
ЛИ РАЗРЕШИМАЯ АЛГЕБРА — алгебра Ли д
над полем К, удовлетворяющая одному из следующих
эквивалентных условий:
1) члены производного ряда /?*Д для д равны {0}
при достаточно большом к;
2) существует конечная убывающая цепочка идеалом
foi}0<i<n. апгебРы Я таких, что До=--Д, Д„={0}
и [д,-, Д,-]сгд,- + 1 (т. е. алгебры Ли Д,7д,- + 1 — абелевы)
для всех 0<:?<п;
3) существует конечная убывающая цепочка подал-
подалгебр {fli-}0<i<m таких, что До —Д, Ят={0}, fii+i —
идеал в д'; и Д//д,- + 1 — одномерная (абелева) алгебра
Ли для 0<i<m.
Нильпотентная алгебра Ли разрешима. Если F=
= {V,-} — полный флаг в конечномерном векторном
пространстве V над К, то
b (/¦) = {*€{?! (F) I xVi<=vi «ля всех *}
есть разрешимая подалгебра в алгебре Ли ftl(F)
всех линейных преобразований пространства V. Если
в V выбрать базис, согласованный с флагом F, то в
нем элементы алгебры b(F) представятся верхними
треугольными матрицами; полученная матричная
Ли р. а. обозначается t{n, К), где п — dimF.
Класс Ли р. а. замкнут относительно перехода к
подалгебре, факторалгебре и расширению. В част-
частности, любая подалгебра в t(n, К) разрешима. Если
char/v=-0 и поле К алгебраически замкнуто, то любая
конечномерная Ли р. а. изоморфна подалгебре в
t(n, К) при нек-ром п. Одним из основных свойств
Ли р. а. является теорема Ли: пусть ft —
Ли р. а. над алгебраически замкнутым полем харак-
характеристики 0 и р: з —>- д1 (V) —ее конечномерное ли-
линейное представление. Тогда в V существует такой
полный флаг F, что p(ft)c:b (f). В частности, если р
неприводимо, то dim.F=l. Идеалы алгебры ft можно
выбрать образующими полный флаг, т. е. такими, что
dim ft, —dim ft — i.
Конечномерная алгебра Ли ft над полем харак-
характеристики 0 разрешима тогда и только тогда, когда
алгебра ZJft = [ft, ft] нилыготентна. Другой кри-
критерий разрешимости (критерий Картана):
алгебра ft разрешима тогда и только тогда, когда
D1^ ортогонально всей ft относительно Киллинга
формы (или любой билинейной формы, ассоциированной
с точным конечномерным представлением алгебры ft).
Ли р. а. впервые рассмотрел С. Ли (S. Lie) в связи
с изучением разрешимых групп Ли преобразований.
Изучение Ли р. а. приобрело большое значение после
введения понятия радикала (т. е. наибольшего
разрешимого идеала) произвольной конечномерной
алгебры Ли ft и доказано, что в случае char)?—О
алгебра ft является полупрямой суммой своего ра-
радикала и максимальной полупростой подалгебры (см.
Леей — Мальцева разложение). Это позволило свести
задачу классификации произвольных алгебр Ли к
перечислению полупростых (что для К=С было сде-
сделано уже В. Киллингом) и разрешимых алгебр. Клас-
Классификация же Ли р. а. проведена (для К=С и R)
лишь в размерностях <:6.
Если ft — разрешимая алгебраич. подалгебра в
ftl(F), где V — конечномерное пространство над
полем К характеристики 0, то ft разлагается в полу-
полупрямое произведение нилыютентного идеала, образу-
образуемого всеми нильпотентными преобразованиями из С\
и нек-рой абелевой подалгебры, состоящей из полу-
полупростых преобразований [6]. Аналогичное строение
имеет вообще любая расщепляемая Ли р. а.,
т. е. конечномерная Ли р. а. над К, каждый элемент х
к-рой разлагается в сумму x=-s^n, где s, re?jft, [s, re] —
= 0, s полупрост, а п нильпотентеи [81. Каждой ко-
конечномерной Ли р. а. над К однозначно сопостав-
сопоставляется минимальная содержащая ее расщепляемая
Ли р. а. (расщепление Мальцева). Ре-
Решена [8] также задача классификации Ли р. а., имею-
имеющих заданное расщепление Мальцева. Таким образом,
задача классификации Ли р. а. сводится, в известном
смысле, к изучению нильпотентных алгебр Ли.
Кроме радикала, в произвольной конечномерной
алгебре Ли ft выделяют максимальные разрешимые
подалгебры. Если К — алгебраически замкнутое поле
характеристики 0, то все такие подалгебры в ft (они
паз. б о р е л е в с к и м и) сопряжены. Напр., t (n, К)
является борелевской подалгеброй в алгебре Ли всех
матриц порядка п. Если К не является алгебраически
замкнутым или charA' конечна, то теорема Ли, вообще
говоря, не верна. Однако она распространяется на
случай, когда К совершенно и содержит характери-
стич. корни всех р(х), -r^jft. Если это условие выпол-
выполнено для присоединенного представления Ли p. a. ft,
то д наз. треугольной. На треугольные ал-
алгебры Ли переносятся многие свойства Ли р. а. над
алгебраически замкнутым полем. В частности, если
char К—О, то все максимальные треугольные подал-
подалгебры в произвольной конечномерной алгебре Ли
сопряжены (см. [1], [7]). Максимальные треугольные
подалгебры используются при изучении полупростых
алгебр Ли над алгебраически незамкнутым полем в
качестве хорошего аналога борелевских подалгебр.
Они играют также основную роль в описании связных
равномерных подгрупп в группах Лн [9].
Лит.: [1] Б о р е л ь А., Тите Ж., «Математика», 1967,
т. 11, № 1, с. 43—111; [2J Б у р б а к и Н., Группы и алгебры
Ли. Алгебры Ли, свободные алгебры Ли и группы Ли, пер. о
франц., М., 1976; [3] Джекобсон Н., Алгебры Ли, пер.
с англ., М., 1964; [4] Б о р е л ь *., Линейные алгебраические
группы, пер. с англ., М., 1972; [5] С е р р Ж.-П., Алгебры Ли
и группы Ли, пер. с англ. и франц., М., 1969; [6] Ш е в а л л е К.,
Теория групп Ли, пер. с франц., т. 3, М., 1958; [7] Вин-
берг Э. Б., «Докл. АН СССР», 1961, т. 141, с. 270—73; [8}
Мальцев А. И., Избр. труды, т. 1, М., 1976, с. 155—76;
[9] О н и щ и к А. Л., «Матем. сб.», 1967, т. 74, с. 398 —'.16.
В. В. Горйацевич.
ЛИ РАЗРЕШИМАЯ ГРУППА — группа Ли, раз-
разрешимая как абстрактная группа. В дальнейшем рас-
рассматриваются вещественные или комплексные Ли р. г.
Нилыютентная, в частности абелева, группа Ли
разрешима. Если F—-{Vi} — полный флаг в конечно-
конечномерном векторном пространстве V (над R или С), то
является разрешимой алгебраич. подгруппой в GL(F)
и, в частности, Ли р. г. Если в V выбрать базис, со-
согласованный с флагом F, то в нем элементы группы
В (F) представятся невырожденными верхними тре-
треугольными матрицами; полученная матричная Ли р. г.
обозначается через Т(п, К), где K=R или С.
Алгебра Ли д группы G разрешима тогда и только
тогда, когда разрешима связная компонента единицы
(G)o группы G. Алгебрами Ли групп В (F) и Т (п, К)
являются соответственно t{F) и Х(п, К) (см. Ли
разрешимая алгебра). В силу соответствия между под-
подалгебрами в я и связными подгруппами Ли в G на
Ли р. г. переносятся все свойства разрешимой алгеб-
алгебры Ли (см. [1], [3]).
Для Ли р. г. справедлив аналог теоремы Ли о раз-
разрешимых алгебрах Ли: если р : G —>~ GL(V) — конеч-
конечномерное комплексное представление Ли р. г. G, то
существует полный флаг F в V такой, что p(G)^S(G).
В частности, в V существует общий собственный век-
вектор для всех p(g), g?G.
Ли р. г. были впервые рассмотрены С. Ли (S. Lie),
предполагавшим, что непрерывные группы могут иг-
играть в теории интегрирования в квадратурах диффе-
дифференциальных уравнений ту же роль, что группа Га-
луа в теории алгебраич. уравнений. Однако, кообще
говоря, группа автоморфизмов дифференциального
уравнения тривиальна, и поэтому только для линей-
линейных и нек-рых других уравнений в этом направлении
получены содержательные результаты. Так, для этих
уравнений выразимость решений через квадратуры
и экспоненты от них фактически эквивалентна разреши-
разрешимости соответствующей (матричной) группы Галуа [2].
Если же эта группа нильпотентна, то экспоненты от
квадратур в решение не входят.
В силу теоремы Леви — Мальцева о разложении в
нолупрямое произведение произвольной связной од-
носвязной группы Ли Ли р. г. играют существенную
роль при изучении произвольных групп Ли. В произ-
произвольной связной группе Ли G рассматриваются также
максимальные разрешимые подгруппы. Если А'=С,
то они наз. борелевскими и сопряжены в
группе G. Напр., В (F) — борелевская подгруппа в
GL(F).
Односвязная Ли р. г. всегда имеет точное конечно-
конечномерное представление, для неодносвязных это не
всегда так. 13 односвязной Ли р. г. произвольная связ-
связная подгруппа замкнута и односвязна [6]. Экспонен-
Экспоненциальное отображение exp: ff —>- G даже для одно-
связной Ли р. г. не обязано быть ни инъективным,
ни сюръективным. Ли р. г., для к-рых. ехр — диф-
диффеоморфизм, наз. экспоненциальными (см.
Ли экспоненциальная группа). Односвязная Ли р. г.
диффеоморфна R-^, а произвольная связная Ли р. г.—
R"X Tm, где Тт есть m-мерный тор.
Связная линейная Ли р. г. над R. представляется в
виде полупрямого произведения K-S, где К — ком-
компактная абелева подгруппа, a S — односвязный нор-
нормальный делитель. Алгебраическая связная раз-
разрешимая группа над любым полем характеристики О
разлагается в полупрямое произведение нормального
делителя, состоящего из унипотентных элементов, и
абелевой подгруппы, состоящей из полупростых эле-
элементов [3]. Для связных Ли р. г. можно определить
[4] аналог расщепления Мальцева.
Если алгебра Ли связной группы Ли G треугольна
(над R), то G наз. треугольной. Для треуголь-
треугольных групп Ли справедлив аналог Ли теоремы о раз-
разрешимых алгебрах. Максимальные связные треуголь-
треугольные подгруппы в произвольной связной группе Ли
сопряжены [5]. Связная треугольная группа Ли изо-
изоморфна подгруппе в Т(п, R) и является экспоненци-
экспоненциальной группой, если она односвязна.
Лит.: [1] Б у р б а к и II., Группы и алгебры Ли. Алгебры
Ли, свободные алгебры Ли и группы Ли, пер. с франц., М., iiO6;
[2] Капланский И., Введение в дифференциальную
алгебру, пер. с англ., М., 1959; [3] Шевалле К., Теория
групп Ли, пер. с франц., т. 3, М., 1958; [4] Auslander L.,
«Bull. Amer. Math. Soc», 1973, у. 79, p. 227—61; [5] В и н б е р г
Э. Б., «Докл. АН СССР» 1961 т. 141, с. 270—73; [6] Маль-
Мальцев А. И., Избр. труды, т. 1, М., 1976, с. 177 — 200.
В. В. Горбацевич.
ЛИ РЕДУКТИВНАЯ АЛГЕБРА — конечномерная
алгебра Ли над полем к характеристики 0, присоеди-
присоединенное представление к-рой вполне приводимо. Свой-
Свойство редуктивности алгебры Ли g равносильно лю-
любому из следующих свойств:
1) радикал г (д) алгебры Ли g совпадает с центром
а (в);
2) Я—:э (Я)+Яо. гДе до — полупростой идеал в д;
3) Я—2f=iflM где Я< — простые идеалы;
4) д допускает точное вполне приводимое конечно-
конечномерное линейное представление.
Свойство редуктивности алгебры Ли сохраняется
как при расширении, так и при сужении основного
поля к.
Важный класс Ли р. а. над fc=R составляют ком-
компактные алгебры Ли (см. Ми компактная группа).
Группу Ли, алгебра Ли к-рой редуктивна, часто наз.
редуктивнои группой Ли. Если к алге-
алгебраически замкнуто, то алгебра Ли над к является
редуктивнои тогда и только тогда, когда она изоморфна
алгебре Ли нек-рой редуктивнои алгебраич. группы
над к.
Обобщением понятия Ли р. а. является следующее
понятие. Подалгебра I) конечномерной алгебры Ли
Я над к наз. редуктивнои в д, если присо-
присоединенное представление ad: f) —>- gi (д) вполне при-
приводимо. В этом случае [) будет Ли р. а. Если к алге-
алгебраически замкнуто, то для редуктивности подалгебры
6 в g необходимо и достаточно следующее условие:
ad r (t)) состоит из полупростых линейных преоб-
преобразований.
Лит.: [1] С е р р Ж.- П., Алгебры Ли и группы Ли, пер.
с англ. и франц., М., 1969. А. Л. Онищип.
ЛИ СВОБОДНАЯ АЛГЕБРА над кольцом
R — алгебиа Ли L = L(X) над R, в к-рой выделено
свободное порождающее множество X, любое отобра-
отображение к-рого в произвольную алгебру G над R про-
продолжается до гомоморфизма из L в G. Мощность мно-
множества X вполне определяет L(X) и наз. ее р а н г о м.
Ли с. а. есть свободный 7?-модуль (о базисах к-рого-
см. Базисный коммутатор). Подалгебра М Ли с. а.
над полем сама является Ли с. а. (теорема Шир-
Ширшова [1]). Если же Я=2, то это верно лишь при
условии, что ЫМ — свободная абелева группа [2].
Конечно порожденные подалгебры в Ли с. а. над
полем образуют подрегаетку в решетке всех подалгебр
[3]. Установлены [4] канонич. связи Ли с. а. со свобод-
свободными группами и свободными ассоциативными алгеб-
алгебрами.
Лит.: [1] Ширшов А. И., «Матем. сб.», 1953, т. 33,
№ 2, с. 441 — 52; [2] W i t t E., «Math. Z.», 1956, Bd 64, S. 195 —
216; [3] К у к и и Г. П., «Алгебра и логика», 1977, т. 16,
№ 5, с. 577—85; [4l Magnus W. «J. relnc und angew. Math.»,.
1937, Bd 177, S. 105—15. Ю. А. Бахтурип.
ЛИ СКОБКА — коммутатор векторных полей на
дифференцируемом многообразии. Если интерпрети-
интерпретировать векторные поля класса С00 на дифференциру-
дифференцируемом (класса С") многообразии М как дифференци-
дифференцирования алгебры F(М) функций класса С°° на М,.
то Ли с. полей ХяУ задается формулой
[X Y]f=X(Yf)-Y(Xf),
где f?F(M). Совокупность всех векторных полей
класса С°° на М является алгеброй Ли относительно
Ли С. А. Л. Онищик.
ЛИ ТЕОРЕМА — 1) Ли т.— одна из трех классич.
теорем теории групп Ли, описывающих связь Ли
локальной группы с ее алгеброй Ли. Ли т. составляют
фундамент теории, развитой в 19 в. С. Ли (S. Lie)
и его школой (см. [1]).
Пусть G — r-мерная вещественная эффективная ло-
локальная Ли группа преобразований области QdR",.
е — единица группы G и пусть в локальных коорди-
координатах в окрестности множества {е} X Q в G X Q дей-
действие группы G на Q задано набором аналитич. функций
yi = fi(8u ¦¦¦, Sri xi, •¦•, *«), г = 1, •¦•, п. A>
где g=- (gu . . ., gr)^G, x--= (xu . . ., .rn)€Q и g(xY-=y=
= (у\, . ¦ ¦, г//г)€^- Указанное действие определяет
на й г аналитич. векторных полей
*'^X" М*)эГТ' » = 1, .... г, B>
где 1и(х)=^(е, х).
Первая теорема Ли устанавливает, что-
функции /у, /=—1, . . ., п, определяющие действие-
группы С, сами определяются по нек-рому вспомога-
вспомогательному набору аналитич. функций ^,- (g), k, s=lr
. . ., г, на С, удовлетворяющих условию
1>*.-(е) = hi, О)
б/;,- — символ Кронекера. Точнее, (tyki(g)) — это мат-
матрица дифференциала правого сдвига на группе G на
элемент g~x в точке g, а набор функций A) — ото и
точности решение системы уравнений
/ = 1, ..., п, D)
удовлетворяющее начальным условиям f/(e, x) = x,
; = 1, . . ., п).
Вторая теорема Ли описывает свойства
функций li/(x) и %,(§¦)¦ А именно, 1;/(х) удовлетво-
ряют системе уравнений
1<;, 7 <r, К J s?n
(эта система есть условие интегрируемости системы
{4)), а функции i[>/ (g) — в системе уравнений
где с,/ — нек-рые константы. Соотношения E) озна-
означают, что коммутатор (скобка Ли) [X;, Х}] векторных
полей X; и Xj является линейной комбинацией полей
Xi, . • ., Хг с постоянными коэффициентами
[*/. */] =2* =,<•?,*», F)
-г. е. что линейная оболочка д полей Xlt . . ., Хг яв-
является алгеброй относительно скобки Ли.
Обращение первой и второй теорем Ли состоит в
следующем: если функции /3, . . ., /„ дают решение
системы D), в к-рой матрица ||?,у|| имеет максимальный
ранг, и выполнены условия C) и E), то формула A)
определяет локальную эффективную группу Ли пре-
преобразований. Эта локальная группа порождена одно-
нараметрич. группами преобразований, заданными
формулой B).
Третья теорема Ли утверждает, что кон-
константы ctj удовлетворяют следующим соотношениям:
с*.= —с*.,
ч и
Х1Г (гт А _!_/¦»!/./ \стг1\—n \ ^ri i h 1 т -сГ г ПЛ
Z*i=\*- a jk^ ы ij^ ji ki>-~v> l s= 'y' ' > ms^r' \'i
т. е. Д является алгеброй Ли. Важное значение имеет
обращение третьей теоремы Лн: если с{/ — любые
константы, удовлетворяющие соотношениям G), то
существует система векторных полей Xlt . . ., Хг,
удовлетворяющих соотношениям F), и эти векторные
поля возникают с помощью описанной выше конст-
конструкции нз нек-рой локальной группы Лн преобразо-
преобразований (иначе говоря, всякая конечномерная алгебра
Ли есть алгебра Ли нек-рой локальной группы Ли
преобразований). Иногда (см., напр., [4]) третьей
теоремой Ли наз. утверждение о существовании для
каждой конечномерной алгебры Ли д над полем R
или С глобальной группы Ли с алгеброй Ли д (см.
-Ли алгебра аналитической группы).
2) Л и т. о разрешимых алгебрах Ли:
пусть ф — линейное представление конечномерной
разрешимой алгебры Ли b в векторном пространстве
V над алгебраически замкнутым полем характеристики
0; тогда в V существует такой базис, в к-ром все опе-
операторы X из ф(Ь) записываются верхнетреугольными
матрицами. Аналогичное утверждение справедливо и
для линейного непрерывного представления связной
¦топологической разрешимой группы в конечномерном
комплексном векторном пространстве (теоретико-груп-
(теоретико-групповой аналог Ли т.); предположение о связности груп-
группы является существенным. Вариант теоретико-груп-
теоретико-группового аналога Ли т. известен под названием Ли —
Колчипа теорема.
Лит.: [1] Lie S., E n g е 1 F., Theorie der Transforma-
tionsgruppen, Bd 1—3, Lpz., 1888—93; [2J Бур баки Н.,
Группы и алгебры Ли. Алгебры Ли, свободные алгебры Ли и
группы Ли, пер. с франц., М., 1976; [3] Понтрягин Л. С.
Непрерывные группы, 3 изд., М., 1973; [4] Сер р Ж. -П.,
Алгебры Ли и группы Ли, пер. с англ. и франц., М., 1969; [6]
Шевалле К., Теория групп Ли, пер. с франц., т. 3, М.
1958; [о] Чеботарев Н. Г., Теория групп Ли, М. —Л.
1940. В. Л. Попов
ЛИ ТРОЙНАЯ СИСТЕМА — векторное простран-
пространство m с трилинейной композицией
ntxmxm—>m, (X, У, Z) —> [X, У, Z],
удовлетворяющей следующим условиям:
\Х X УI О
[X, Y, Z] + [Y,'z, 'x] + [z' X, Y]=0,
[X, Y, [Z, U, V]] = [[X, Y, Z], U, V] + [Z, [X,
Y, U], V] + [Z, U, [X, Y, V]].
Если й — алгебра Ли и raci) — такое подпро-
подпространство, что [[X, Y], Z]?m для любых X, Y, Zgnt,
то операция
[X, Г, Z] = [[X, У], Z]
превращает m в Ли т. с. Обратно, всякая Ли т. с.
может быть получена таким способом из нек-рой ал-
алгебры Ли.
Категория конечномерных Ли т. с. над полем !\
эквивалентна категории односвязных симметрически а
однородных пространств (см. Симметрическое прост-
пространство).
Лит.: [1] Хелгасон С, Дифференциальная геометри:
и симметрические пространства, пер. с англ., М., 1964; L-!
Loos О., Symmetric spaces, v. 1, N. Y.— Amst., 1969.
А. С. ФеОетю.
ЛИ ЭКСПОНЕНЦИАЛЬНАЯ АЛГЕБРА, алгеб-
алгебра Ли типа (Е),— конечномерная вещественная
алгебра Ли ft, для любого элемента X к-рой оператор
присоединенного представления adX lie имеет чисто
мнимых собственных значений. Экспоненциальное ото-
отображение ехр : я —>- G в соответствующую алгебру д
односвязную группу Ли G является диффеоморфизмом,
a G — Ли экспоненциальной группой.
Каждая Ли э. а. разрешима. Нилыготентная ал-
алгебра Ли над R есть Ли э. а. Класс Ли э. а. является
промежуточным между классами всех разрешимых и
вполне разрешимых алгебр Ли; он замкнут относи-
относительно перехода к подалгебрам, факторалгебрам и
конечным прямым суммам, но не замкнут относительно
расширений.
Простейшим примером Ли э. а., не являющейся
вполне разрешимой алгеброй Ли, является трехмерная
алгебра Ли с базисом X, Y, Z и умножением, задан-
заданным формулами
[X, У] = 0, [Z, X] = ailX + a12Y, [Z, Y] = a21X + a22Y,
где [ajj] — действительная матрица, имеющая комп-
комплексные, но не чисто мнимые собственные значения.
Трехмерная алгебра Ли ft0 с базисом X, Y, Z и опре-
определяющими соотношениями
[X, У] = 0, [Z, Х1 = У, [Z, У] = -Х
разрешима, но не является Ли :>. а.
Алгебра Ли $ экспоненциальна тогда и только тог-
тогда, когда все корни алгебры с] имеют вид а+ф, где
а, [5 — вещественные линейные формы на д, причем р
пропорциональна а (см. [1]), или же когда д не имеет
факторалгебр, содержащих подалгебру, изоморфную
во-
Лит. см. при ст. Ли экспоненциальная группа.
В. В. Горбацевич.
ЛИ ЭКСПОНЕНЦИАЛЬНАЯ ГРУППА, группа
Ли типа (Е),—вещественная конечномерная группа
Ли G, для к-рой экспоненциальное отображение ехр:
ft ->- С, где ft — алгебра Ли группы G, являете;:
диффеоморфизмом.
Любая Ли э. г. разрешима, односвязна, а ее алгебра
Ли является Ли экспоненциальной алгеброй. Класс
Ли э. г. замкнут относительно перехода к связной
подгруппе, факторгруппе по связному нормальному
делителю и к конечному прямому произведению, но
не замкнут относительно расширений. Всякая Ли
вполне разрешимая группа (в частности, нильпотент-
ная группа Ли) экспоненциальна, если она односвязна.
Пересечение связных подгрупп в Ли э. г. связно.
Централизатор произвольного подмножества тоже свя-
связен. Связная группа Ли экспоненциальна тогда и
только тогда, когда она не имеет факторгрупп, содер-
содержащих в качестве подгруппы универсальную накры-
накрывающую группы движений евклидовой плоскости.
Лит.: [1] D i х m i e r J., «Bull. Soc. Math. France», 1957,
t. 85, p. 113—21; [2] S a i t б М., «Coll. Gen. Educ. Univ. Tokyo
Sci. Papers», 1957, v. 7, p. 1 — 11, p. 157—68. В. В. Горбацееич.
ЛИ — КОЛЧИНА ТЕОРЕМА: разрешимая подгруп-
подгруппа G группы GL(F) (V — конечномерное векторное
пространство над алгебраически замкнутым полем)
имеет нормальный делитель Ga индекса не более р,
где р зависит только от dimF, такой, что в V сущест-
существует флаг F— {Vt}, инвариантный относительно G1.
Другими словами, в V найдется базис, в к-ром эле-
элементы из G1 записываются треугольными матрицами.
Если G связна в топологии Зариского, то G1=^G; в
этом случае Л. — К. т. является обобщением теоремы
С. Ли (S. Lie), доказанной им для комплексных связ-
связных (в евклидовой топологии) разрешимых групп Ли
(см. Ли разрешимая группа, Ли теорема). Это утверж-
утверждение можно рассматривать также как частный случай
Бореля теоремы о неподвижней точке.
Для произвольного поля справедлив следующий
аналог Л. — К. т.: разрешимая группа матриц содер-
содержит нормальный делитель конечного индекса, ком-
коммутант к-рого нильпотентен.
Л. — К. т. была доказана Э. Колчиным [1] (для связ-
связных групп) и А. И. Мальцевым [21 (в общей формули-
формулировке). Ее наз. также иногда теоремой Кол-
чина — Мальцева.
Лит.: [1] К о 1 с h i n E. R., «Ann. Math.», 1948, v. 40,
№ 4, p. 1 — 42; [2] M а л ь ц е в А. И., Избр. труды, т. 1, М.,
1976, с. 294—313; [3] К а р г а п о л о в М. И., Мерзля-
Мерзляков Ю. И., Основы теории групп, 2 изд., М., 1977.
В. В. Горбацевич.
ЛИНДЕБЕРГА — ФЕЛЛЕРА ТЕОРЕМА — теорема,
устанавливающая условия асимптотич. нормальности
функции распределения суммы независимых случай-
случайных величин, обладающих конечными дисперсиями.
Пусть Х1у Х2, . . .— последовательность независимых
случайных величин с математич. ожиданиями аи
а2, . . . и конечными дисперсиями ol, at, . . ., не все
из к-рых равны нулю. Пусть
Для того чтобы
В~2 max (У2. —>¦ О
1 < / < п '
для любого х при п —>- оо, необходимо и достаточно
выполнение следующего условия (условия Л и н-
д е б е р г а):
при п —>¦ оо для любого е>0. Достаточность была до-
доказана Дж. Линдебергом [1], необходимость — В. Фел-
лером [2].
Лит.: [1] Lindeberg J. W., «Math. Z.», 1922, Bd 15,
S. 211—25; [2] Feller W., «Math. Z.», 1935, Bd 40, S. 521 —
559; [3] Л о э в М., Теория вероятностей, пер. с англ., М., 1962;
[4] П е т р о в В. В., Суммы независимых случайных величин,
М., 1972. В. В. Петров.
ЛИНДЕЛЁФА ГИПОТЕЗА о поведении ?-
функции Р и м а н а: для любого 8>0 выпол-
выполняется
hm р =0
<^=о | t |'
Высказана Э. Линделёфом [1]. Л. г. эквивалентна ут-
утверждению: при фиксированном o^KVs. 1) число ну-
нулей ?(s), лежащих в области Re s>o, f<Im s< Г+l.
есть оAпТ). Поэтому Л. г. является следствием ги-
гипотезы Римана о нулях t,(s). Известно A982), что
г— I; с/24-it) i
где с — нек-рая постоянная, 0<с<6/з7-
Имеются обобщения Л. г. на L-функции Дирихле:
для любого е>0 имеет место
где к — модуль характера у.
Лит.: [1] L i n d о 1 б f E., Le calcul des residus et ses appli-
applications a la theorie des fonctions, P., 1905; [2] Титчмарш Е.
К., Теория дзета-функций Римана, пер. с англ., М., 1953, гл.
XIII. С. М. Воронин.
ЛИНДЕЛЁФА КОНСТРУКЦИЯ — геометрическое
построение для исследования сопряженных точек в
задаче о минимальной поверхности вращения (рис.).
Л. к. остается пригодной для любой простейшей ва-
вариационной задачи на плоскости (х, у), для к-рой
общий интеграл урав-
уравнения Эйлера можно А/
представить в виде
у_ /х-сг
с =/ (, ^
При этом касатель,
ные к экстремали
в сопряженных точ-
точках А та А' пере-
пересекаются в нек-рой f ~~
точке на оси х, а
значение варьируемого интеграла вдоль дуги ААГ
равно его значению на ломаной AT А' (см. [2]). При-
Примером является катеноид с образующей
v v
С1
Лит.: [ll Lindelo'f E., Lejons de calcul des variations,.
P., 1861; [2] В о 1 z a O., «Bull. math, soc», 1911, t. IS, N 3,
p. 107—10; [3] С a r a t h ё о d о г у С, Variationsrechnung und
partielle Differentialgleichungen, B.— Lpz., 1935.
В. В. Охримепко.
ЛИНДЕЛЁФА МЕТОД СУММИРОВАНИЯ — полу-
полунепрерывный метод суммирования числовых и функ-
функциональных рядов, определенный последовательно-
последовательностью функций
goF) = l, gftF) = exp( — 6k In k), б > 0, к = 1, 2, ...
Ряд
суммируем методом суммирования Л и н-
д е л ё ф а к сумме s, если
lim ио + 2Г-п ехР ^ — б*1п Щ ии j =s
и ряд под знаком предела сходится. Метод был введен
Э. Линделёфом [1] для суммирования степенных рядов.
Л. м. с. является регулярным (см. Регулярные ме-
методы суммирования) и применяется как аппарат для
аналитич. продолжения функций. Если / (z) — главная
ветвь аналитич. функции, регулярной в нуле и пред-
ставимой рядом
2LC
akzk
для малых z, то этот ряд суммируем Л. м. с. к f(z)
во всей звезде функции /(z), причем равномерно во-
всякой замкнутой ограниченной области, содержа-
содержащейся внутри звезды.
Из методов суммирования, определенных преобра-
преобразованием последовательности в последовательность
полунепрерывными матрицами а^(и) типа
с (О* + *
Е (и)
где
— целая функция, Э. Линделёфом рассматривался
случай, когда
Матрицу || «ft (со) || с такой целой функцией наз. мат-
матрицей Л и н д е л ё ф а.
Лит.: [1] L i n d е 1 б f E., «J. math.», 1903, t. В, р. 213 —
221; [2] его же, Le calcul des residua ct ses applications a la
thebrie des fonctions, P., 1905; [3] X a p ди Г., Расходящиеся
ряды, пер. с англ., М., 1951; [4] Кук Р., Бесконечные матрицы
и пространства последовательностей, пер. с англ., М., 19В0.
ЛИНДЕЛЁФА ПРИНЦИП — основной качествен-
качественный вариационный принцип в теории конформного
отображения, найденный Э. Линделёфом [1]. Пусть
односвязные области D и D на плоскости комплекс-
комплексного переменного z таковы, что их границы Г и Г
соответственно состоят из конечного числа жордановых
дуг, причем D содержится вВ,и пусть точка zo?Dc:D.
Пусть, кроме того, w—f(z) и w=J(z) — функции,
реализующие конформное отображение соответственно
D и D на единичный круг Д= {и>:[и>| <1}, причем
/(zo) = O, 7(zo) = O. П р и и ц и п Л и н д е л ё ф а со-
состоит в том, что при этих условиях: 1) прообраз Dp
области 1ш|<р, 0<р<1, при отображении u>=/(z)
лежит внутри прообраза Dp этой же области |ш|<р
при отображении w — f(z), причем соприкосновение их
границ Гр и Гр возможно лишь, если D = D; 2) l/'(zo)|^:
Ss=l/'(zo)ij причем знак равенства возможен лишь, если
D = D; 3) если существует общая точка zx контуров
Г и Г, то
причем знак равенства возможен лишь, если I) = D.
Иными словами, при вдавливании внутрь границы Г
области D: 1) все линии у р о в н я Гр , т. е. про-
прообразы окружностей |ш| = (>, сжимаются; 2) растяжение
в точке z0 увеличивается; 3) растяжение в неподвижных
точках г, границы уменьшается.
Из приведенной формулировки Л. п. вытекает так-
также, что длина образа дуги у границы Г, подверг-
подвергшейся вдавливанию до дуги у, всегда не превосходит
длины образа у (длина /(-)')<:длины /(у)), причем ра-
равенство имеет место только в случае Г= Г. Это след-
следствие Л. п. известно также как принцип М о н-
*г е л я.
В более общей ситуации, когда D и D — конечно-
связные области, ограниченные конечным числом жор-
жордановых кривых и расположенные соответственно в
плоскостях z и w, w=f(z) — мероморфная функция
в D, значения к-рой лежат в Z), Л. п. состоит в сле-
следующем. Если w0 — точка образа f(D) области D',
{zv }, v = 0, I, . . .,— множество точек D, для к-рых
/(zv)— w0; mv — кратность нуля zv функции /(z) — w0;
g(z, zv) —'Грина функция области D с полюсом zv,
a g(w, wa) — функция Грина области D с полюсом u>0,
то имеет место неравенство
g (w, wt)^^\^
для всех z?D, w^-f(z). При этом если в A) имеет
место равенство хотя бы в одной точке z?/), то оно
выполняется всюду в В. В частности, неравенство
g{w, wo)^~g(z, z0), B)
вытекающее из A), и было получено Э. Линделёфом
в [1]. Оно означает, что образ области {z:g(z, zo)>X}
всегда расположен внутри области {w : g(w, u>0)>X}.
Л. п. в общем виде A) применим и для произвольных
областей I), D, но заключение, относящееся к случаю
равенства, здесь уже, вообще говоря, не справедливо.
Л. п. позволяет получить многие количественные
оценки изменения конформного отображения при
вариации области (см. [3]). Он тесно связан с подчи-
подчинения принципом, и его можно также рассматривать
как обобщение Шварца леммы.
Лит.: [1] L i n d е 1 б ( Е., «Acta soc. scient. fennica», 1908,
v. 35, №7; [2] Го л узин Г. М., Геометрическая теорл
функций комплексного переменного, 2 изд., М., 1966; ['
Лаврентьев М. А., Щабат Б. В., Методы теории
функций комплексного переменного, C изд., М., 1965; [4]
С той лов С, Теория функций комплексного переменного,
пер. с рум., т. 2, М., 1962; [5] Лаврентьев М. А., Ва-
Вариационный метод в краевых задачах для систем уравнений
эллиптического типа, М., 1962. Е. Д. Соломенцт.
ЛИНДЕЛЕФА ПРОСТРАНСТВО, финально
компактное пространство,— топологиче-
топологическое пространство X такое, что всякое его открытое
покрытие содержит счетное подпокрытие. Напр., вся-
всякое пространство со счетной базой есть Л. п.; всякое
квазикомпактное пространство есть Л. п. Всякое
замкнутое подпространство Л. п. есть Л. п. Для каж-
каждого непрерывного отображения / Л. п. в топологич.
пространство X' подпространство f(X') последнего —
Л. п. Всякое отделимое пространство, являющееся
объединением счетного семейства (би)компактных
множеств,— Л. п. Всякое регулярное Л. и. параком-
пактно. Произведение Л. п. и (би)компактного про-
пространства есть Л. П. м. И. Войцеховский.
ЛИНДЕЛЕФА ТЕОРЕМА об асимптотиче-
асимптотических значениях: 1) Пусть w-=f(z) — огра-
ограниченная регулярная аналитич. функция в единичном
круге D— {z:|z|<l} и пусть а — асимптотич. значение
f (z) вдоль жорданового пути L, расположенного в D
и оканчивающегося в точке ег{", т. е. f(z)—>-a, когда
z -+ егв° вдоль L. Тогда а есть угловое предельное
значение функции /(z) в точке егв", т. е. /(z) равно-
равномерно стремится к а, когда z —>- ег1~'° внутри любого
угла с вершиной ег0°, образованного двумя хордами
круга \z\ <1.
Эта Л. т. верна и в областях D других типов, при-
причем условия на / (z) удается значительно расширить.
Достаточно, напр., потребовать, чтобы /(z) была ме-
роморфной функцией в D, не принимающей трех раз-
различных значений. Л. т. обобщается также для функ-
функций / (z) многих комплексных переменных, z—(zb
. . ., zn). Напр., если /(z) — ограниченная голоморф-
голоморфная функция в шаре Z>= {z:|z| <1 }, имеющая асимпто-
асимптотич. значение а вдоль некасательного пути L в точке
??еШ, то а есть некасательное предельное значение
/ (z) в точке ? (см. [4]).
2) Пусть u;=/(z)— ограниченная регулярная ана-
аналитич. функция в круге D= {z:\z\ <1}, имеющая вдоль
двух различных путей Ьг и L2, оканчивающихся в
точке егв", асимптотич. значения аир- Тогда а=-р
и /(z) —>-а равномерно внутри угла между путями
/,г и L2. Эта Л. т. верна и для областей D других типов.
Для неограниченных функций она, вообще говоря,
неверна.
Л. т. найдены О. Линделёфом [1].
Лит.: [1] Lindelof E., «Acta Soc. sclent, fennica»,
1915, t. 46, № 4; 12] Г о л у з и н Г. М., Геометрическая теория
функций комплексного переменного, 2 изд., М., 1966; [3] К о л-
л и н г в у д Э. Ф., Л о в а т е р А. Д ж., Теория предель-
предельных множеств, пер. с англ., М., 1971; [4J X е н к ин Г. М.,
Чирка И. М., в кн.: Итоги науки и техники. Современные
проблемы математики, т. 4, М., 1975, с. 13 —142.
Е. Д. Соломенцев.
ЛИНДЕМАНА ТЕОРЕМА: показательная функция
ег в любой алгебраич. точке z=t 0 принимает транс-
трансцендентное значение; доказана Ф. Линдеманом (F. Lin-
demauri, 1882). Л. т. называют также следующее
более общее утверждение, сформулированное без дока-
доказательства Ф. Линдеманом и доказанное К. Вейер-
штрассом (К. Weierstrass) в 1885.
Пусть <jj, . . ., ат — алгебраич. числа, lajl--)-. . .-(-
-\-\ат\ф0 и а1? . . ., ат — попарно различимые алге-
алгебраич. числа, тогда
«!<?"' + . . . + атеа"> ф 0.
Это утверждение эквивалентно следующему: если р1?
. . ., Р„ — алгебраич. числа, линейно независимые
над полем рациональных чисел, то числа е^', . . .,
е$" алгебраически независимы.
Метод доказательства Л. т. получил название м е-
тода Эрмита — Линдемана. Он представ-
представляет собой развитие метода Эрмита, при помощи к-рого
в 1873 была доказана трансцендентность числа е, и
основывается на применении Эрмита тождества к
нек-рым специально построенным многочленам.
Из Л. т. может быть выведена трансцендентность
числа я, отрицательное решение проблемы квадратуры
круга, а также трансцендентность значений функций
sinz, cosz, tgz при алгебраическом гфО и значений
функций lnz при алгебраическом z?=0, 1.
Лит.: [11 Гельфонд А. О., Трансцендентные и алгеб-
алгебраические числа, М., 1952; [2] Фельдман Н. И., Ш и Д-
лоиский А. Б., «Успехи матем. наук», 1967, т. 22, в. 3,
с. 3 — 81. А. И. Галочкчн.
ЛИНЕАРИЗАЦИИ МЕТОДЫ —методы, позволяющие
свести решение нелинейных задач к последовательному
решению родственных линейных задач.
Пусть рассматривается нелинейное операторное урав-
уравнение
L(u) = f, A)
где оператор L отображает банахово пространство //
в себя, L@) = 0, и дифференцируем по Фреше. Одним
из классич. методов решения A), связанным с линеа-
линеаризацией A), является итерационный метод Нью-
Ньютона — Канторовича, в к-ром при известном прибли-
приближении и" новое приближение мл + 1 определяется как
решение линейного уравнения
L'un(un + 1 — W)+L(u») = f; B)
основой метода служит аппроксимация L(un-\-z) (при
малых ||z||) выражением Lun z, где Lun — производная
Фреше оператора L в точке и". Различные модифика-
модификации итого метода и соответствующие оценки скорости
сходимости могут быть найдены в [1] — [4]. Само опе-
операторное уравнение A) может соответствовать, напр.,
нелинейной краевой задаче для уравнения с частными
производными (см. [2], [4], [5]), и тогда на каждом шаге
в B) должна решаться линейная краевая задача, что
вызывает необходимость применения численных ме-
методов и той или иной дискретизации исходной задачи
и родственных ей линейных задач. С вычислительной
точки зрения более естественно рассматривать методы
линеаризации после соответствующей дискретизации
исходной задачи, считая A) операторным уравнением
в конечномерном пространстве.
Другим примером Л. м. для приближенного решения
A) может служить итерационный метод секущих
(ложного положения) (см. [2], [3]). Во многих случаях
для задач A), являющихся задачами математич. фи-
физики, линеаризацию L(u"-\-z) предпочитают проводить
на основе физич. соображений, заменяя L(u"-^-z)
на М „z с линейным оператором М „ (см. [5] — [И]).
Тогда получаемые итерационные методы записыва-
записываются в виде
Munun^ = f-(L(u")-Munun). C)
Таковы, напр., методы упругих решений и перемен-
переменных параметров для решения нелинейных задач тео-
теории упругости (см. [5] — [8]); при этом для метода
упругих решений линейный оператор М п — М соот-
соответствует оператору линейной теории упругости. К ним
же примыкают итерационный метод Качанова (см.
[9], [10]) и метод последовательных нагружений (см.
[6) — [8)), сочетающий в себе идеи линеаризации и
продолжения по параметру. Иногда вместо методов
C) используются более общие итерационные методы
типа
МпП(ип + 1-ип) = -Уч{Ь (u")~f) D)
с итерационным параметром у> подлежащим выбору.
При реализации упомянутых методов следует учи-
учитывать и приближенность решения систем (напр., как
следствие применения вспомогательных итерацион-
итерационных методов) (см., напр., [1], [12], [13]). При рассмот-
рассмотрении нелинейных задач на собственные значения
(задач нахождения точек бифуркации), напр, вида
Ци) = Ш(и), L@) = 0, Af(O) = O, E)
идея линеаризации E), сводящая исследование задачи
E) к исследованию линейной задачи на собственные
значения
оказалась Еесьма плодотворной (см. [14] — [16]). Ча-
Часто используется та или иная линеаризация и в сеточ-
сеточных методах решения нестационарных нелинейных
задач (см., напр., [17] — [21]), проводимая за счет
известных решений в моменты времени до tn и дающая
линейные уравнения для решения в следующий диск-
дискретный момент <n+i=f,i-T"T (т — шаг по времени).
Лит.: [1] Красносельский М. А. [и др.], Прибли-
Приближенное решение операторных уравнений, т. 1, М., 1969 ; [2]
Коллатц Л., Функциональный анализ и вычислительная
математика, пер. с нем., М., 1969; [3] О р т е г а Д ж., Р е й н-
б о л д т В., Итерационные методы решения нелинейных систем
уравнений со многими неизвестными, пер. с англ., М., 1975; [4]
Б е л л м а н Р., К а л а б а Р., Квазилинеаризация и нелинейные
краевые задачи, пер. с англ., М., 1968; [5] П о б е д р я Б. Е.,
в кн.: Упругость и неунругость, в. 3, М., 1973, с. 95—173;
[6] О д е н Д ж-, Конечные элементы в нелинейной механике
сплошных сред, пер. с англ., М., 1976; [7] Зенкевич О.,
Метод конечных элементов в технике, пер. с англ., М., 1975;
[8] С в и р с к и й И. В., Методы типа Бубнова — Галеркина
и последовательных приближений, М., 1968; [9] М и х л и н
С. Г., Численная реализация вариационных методов, М., 1966;
[10] Fucik S., Kratochvil A., Necas Т., «Acta
Univ. Corolinae. Math, et Phys.», 1974, v. 15, .\L> 1—2, p. 31—33;
[11] Амосов А. А., Бахвалов Н. С, Оси-
пи к Ю. И., «Ж. вычисл. матем. и матем. физики» 1980, т. 20,
N° 1, с. 104—11; [12] Eisenstat S. С, S с h u I t z M. H.,
Sherman A. H., «Lect. Notes Math.», 1974, № 430, p. 131 —
53; [131 Дьяконов Е. Г., в кн.; Численные методы меха-
механики сплошной среды, т. 7, ."N5 5, М., 1976, с. 14—78; [14] В о-
р о в и ч И. И., в кн.: Проблемы гидродинамики и механики
сплошной среды. К шестидеентилетию акад. Л. И. Седова, М-,
1969; [15] Бергер М. С, в кн.: Теория ветвления и нели-
нелинейные задачи на собственные значения, пер. с англ., М-, 1974,
с. 71—128; [ 161 С к р ы ц н и к И. В., Нелинейные эллиптиче-
эллиптические уравнения высшего порядка, К., 1973; [17] Л а д ы ж е н-
ская О. А., Математические вопросы динамики вязкой не-
несжимаемой жидкости, 2 изд., М., 1970; [18] Дьяконов Е. Г.,
Разностные методы решении краевых задач, в. 2 —¦ Нестацио-
нарные задачи, М., 1972; [lfl] Ривкинд В. Я., У р а л ь-
ц е в а Н. Н., в кн.: Проблемы математического анализа, в. 3,
Л., 1972, с. 69—111; [20] Fairweather G., Finite element
Galerkin methods for differential equations, N. Y., 1978. [Lect.
Notes pure and appl. math., v. 3i]; [21] Luskin M., «SIAM
J. Numer. Analysis», 1979, v. 1«, jvs 2, p. 284—99.
E. Г. Дьяко)Юв.
ЛИНЕЙНАЯ АЛГЕБРА — частный случай опера-
операторного кольца.
ЛИНЕЙНАЯ АЛГЕБРА — раздел алгебры, в к-ром
изучаются векторные (линейные) пространства, линей-
линейные операторы (линейные отображения), линейные,
билинейные и квадратичные функции (функционалы
или формы) на векторных пространствах.
Исторически первым разделом Л. а. была теория
линейных уравнений (алгебраических). В связи с ре-
решением систем линейных уравнений возникло понятие
определителя. В 1750 было получено Крамера правило
для решения системы линейных уравнений, в к-рой
число уравнений равно числу неизвестных и опреде-
определитель из коэффициентов при неизвестных отличен
от нуля. В 1849 был предложен Гаусса метод решения
систем линейных уравнений с числовыми коэффициен-
коэффициентами. Этот метод является простейшим по числу при-
применяемых операций и используется с различными из-
изменениями также для приближенного решения систем
уравнений, коэффициенты к-рых также известны при-
приближенно.
В связи с изучением систем линейных уравнений
и их определителей появилось понятие матрицы.
Понятие ранга матрицы, предложенное Г. Фробениу-
сом (G. Frobenius) в 1877, позволило явно выразить
условия совместности и определенности системы ли-
линейных уравнений в терминах коэффициентов этой
системы (см. Кронекера — Капелли теорема). Тем
самым в конце 19 в. было завершено построение об-
общей теории систем линейных уравнений.
Если в 18 и 19 вв. основное содержание Л. а. со-
составляли системы линейных уравнений и теория опре-
определителей, то в 20 в. центральное положение зани-
занимают понятие векторного пространства и связанные
с ним понятия линейного преобразования, линейной,
билинейной и полилинейной функции на векторном
пространстве.
Векторным, или линейным, простран-
пространств о м над полем К наз. множество V элементов
(называемых векторами), в к-ром заданы операции
сложения векторов и умножения вектора на элементы
из поля К, удовлетворяющие ряду аксиом (см. Век-
Векторное пространство). Рассматриваются также век-
векторные пространства над телами. Одним из важнейших
понятий теории векторных пространств является по-
понятие линейного отображения, т. о. гомоморфизма
векторных пространств над одним и тем же полем.
Линейным оператором, или линейным
преобраз о в а н и е м, наз. линейное отображе-
отображение пространства в себя (т. е. эндоморфизм векторного
пространства). Если пространство V конечномерно,
то, выбирая в V базис ех, е2) . . ., е.г и полагая
Ч>(<7) = 2"_ a'Jen / = 1' 2' •••' п'
получают квадратную матрицу Л = [[а,-у|| порядка п,
к-рая наз. матрицей линейного преоб-
преобразования фв данном базисе.
Векторное пространство V над полем К, снабжен-
снабженное дополнительной операцией умножения векторов,
удовлетворяющей нек-рым аксиомам, наз. алгеб-
алгеброй над f (см. Кольца и алгебры, Операторное
кольцо).
Все линейные преобразования пространства V от-
относительно естественно определенных операций сло-
сложения, умножения и умножения линейных преобра-
зований на элементы поля К образуют алгебру над
полем К. Все квадратные матрицы фиксированного
порядка с элементами из поля К также образуют
алгебру над К. Указанное выше соответствие между
линейными преобразованиями пространства V и их
матрицами в заданном базисе является изоморфизмом
этих алгебр, что позволяет формулировать теоремы
о линейных преобразованиях параллельно на мат-
матричном языке и при их доказательстве использовать
теорию матриц.
Большое значение в теории линейных преобразо-
преобразовании имеет выбор базиса, в к-ром матрица преобразо-
преобразования принимает в каком-то смысле простейший вид.
В случае алгебраически замкнутого поля таким видом
будет, напр., жорданова нормальная форма матрицы.
Важным случаем линейного отображения является
линейная функция (линейный функционал) — ли-
линейное отображение V в Л. Все линейные функции
на V относительно естественным образом определенных
операций сложения и умножения на элементы из поля
К сами образуют векторное пространство Г* над К,
наз. пространством, сопряженным с
пространством V. Векторы пространства V
можно в свою очередь рассматривать как линейные
функции на сопряженном пространстве V*, полагая
x\j) = f(x) для всех x?V, /? F*. Если V конечно-
конечномерно, то тем самым устанавливается естественный
изоморфизм между V и I7**.
Обобщением понятия линейной функции является
понятие полилинейной функции, т. е. функции со зна-
значениями в К, зависящей от нескольких аргументов
(из к-рых одни принадлежат векторному пространству
V, а другие — сопряженному пространству V*), ли-
линейной по каждому аргументу. Эти функции наз.
также тензорами. Их изучением занимается полили-
Iейная алгебра. Частный случай полилинейных функ-
функций — билинейные функции (см. Билинейное отобра-
отображение). Коеосимметрич. полилинейные функции наз.
также внешними формами.
На основе понятия векторного пространства опре-
определяются различные классич. пространства, изучаемые
в геометрии: аффинные пространства, проективные
пространства и др.
Теория векторных пространств имеет важные связи
с теорией групп. Все автоморфизмы n-мерного зек-
торного пространства V над полем К образуют группу
относительно умножения, изоморфную группе невырож-
невырожденных квадратных матриц порядка п с элементами
из А'. Гомоморфное отображение нек-рой группы G
в эту группу автоморфизмов наз. линейным
представлением группы G в простран-
пространстве V. Изучение свойств представлений составляет
предмет теории линейных представлений групп.
Классич. теория линейных уравнений и определи-
определителей была обобщена на случай, когда вместо чисел
или элементов поля рассматриваются элементы произ-
произвольного тела.
Естественным обобщением понятия векторного про-
пространства над полем К является понятие модуля над
произвольным кольцом. Основные теоремы Л. а. пере-
перестают быть верными при замене векторного простран-
пространства на модуль. Изучение возможностей таких обоб-
обобщений, к-рые справедливы и для модулей, привело к
возникновению алгебраической К-теории.
Лит.: [11 Кострикин А. И., Введение в алгебру, М.,
1977; [2] К у р о ш А. Г., Курс высшей алгебры, 11 изд., М.,
1975; [3] Гсльфанд И. М., Лекции по линейной алгебре,
4 изд., М., 1971; [4] Мальцев А. И., Основы линейной ал-
алгебры, 4 изд., М., 1975; ?5] Ефимов Н. В., Розен-
дорн Э. Р., Линейная алгебра и многомерная геометрия,
2 изд., М., 1974; [6] Шилов Г. Е., Введение в теорию линей-
линейных пространств, 2 изд., М., 1956; [71 Г а н т м а х е р Ф. Р.,
Теория матриц, 2 изд., М., 1966; [81 А р ти н Э., Геометричс-
екая алгебра, пер. с англ., М., 1969; [9] Б у р б а к и Н., Ал-
гебра. Алгебраические структуры. Линейная и полилинейная
алгебра, пер. с франц., М., 1962; [10] Бэр Р., Линейная ал-
алгебра и проективная геометрия, пер. с англ., М., 1955.
И. В. Проскуряков.
ЛИНЕЙНАЯ АЛГЕБРА; численные мето-
методы — раздел вычислительной математики, посвящен-
посвященный математич. описанию и исследованию процессов
численного решения задач линейной алгебры.
Среди задач Л. а. наибольшее значение имеют две:
решение системы линейных алгебраич. уравнений и
определение собственных значений и собственных век-
векторов матрицы. Другие часто встречающиеся задачи:
обращение матрицы, вычисление опре-делителя и на-
нахождение корней алгебраич. многочлена, как правило,
не имеют самостоятельного значения в Л. а. и носят
вспомогательный характер при решении основных
задач Л. а.
Любой численный метод в Л. а. можно рассматри-
рассматривать как нек-рую последовательность выполнения
арифметич. операций над элементами входных данных.
Если при любых входных данных численный метод
позволяет найти решение задачи за конечное число
арифметич. операций, то такой метод наз. прям ы м.
В противоположном случае численный метод наз.
итерационным.
Прямые методы решения системы линейных алгеб-
алгебраических уравнений. Пусть дана система
Ах=Ь A)
с матрицей системы А и правой частью Ь. Если мат- (
рица А невырожденная, то решение дается формулой |
х=А~1Ь, где Л есть матрица, обратная к матрице А.
Основная идея прямых методов заключается в преоб-
преобразовании системы A) в такую эквивалентную систему,
для к-рой матрица системы легко обращается и, следо-
следовательно, легко находится решение исходной системы.
Пусть обе части равенства A) умножены слева на
невырожденные матрицы Lu L2, . . ., L^. Тогда новая
система
эквивалентна системе A). При этом матрицы L,- всегда
можно подобрать такими, что матрица системы B)
будет достаточно простои, напр, треугольной, диаго-
диагональной или унитарной. В этом случае легко вычис-
вычисляются А и | АI.
Одним из первых прямых методов является Гаусса
метод. Он использует левые треугольные матрицы
L; и позволяет привести исходную систему уравнений
к системе с правой треугольной матрицей. Этот метод
легко реализуется на ЭВМ, его схема с выбором глав-
главного элемента позволяет решать системы с произволь-
произвольной матрицей, а компактная схема — получать ре-
результаты с повышенной точностью за счет накопления
скалярных произведении. Среди прямых методов,
применяемых на практике, метод Гаусса требует ми-
минимального объема вычислительной работы.
Непосредственно к методу Гаусса примыкают метод
Жордана и его модификация — метод оптимального
исключения (см. [2]). Эти методы используют треуголь-
треугольные матрицы L; как левые, так и правые и позволяют
привести исходную систему к системе с диагональной
матрицей. По своим характеристикам оба метода
мало чем отличаются от метода Гаусса, но второй I
позволяет решать системы вдвое большего порядка
при одной и той же памяти ЭВМ.
Перечисленные методы входят в группу т. н. мето-
методов исключения. Это название объясняется тем, что
при каждом умножении на матрицу L,- в матрице си-
системы исключается один или несколько элементов.
Исключение можно производить не только с помощью
треугольных матриц, но и с помощью унитарных.
Различные модификации методов исключения по су-
ществу связаны с разложением матрицы системы A)
в произведение двух треугольных или треугольной и
унитарной матриц.
Некоторые методы, такие как окаймления метод,
пополнения метод, не являются методами исключения,
хотя и близки к методу Гаусса.
Большое распространение получили методы, осно-
основанные на построении вспомогательной системы век-
векторов, так или иначе связанных с матрицей исходной
системы и ортогональных в нек-рой метрике. Одним
из первых методов этой группы был метод ортогонали-
зации строк. Матрицы L,- в нем — левые треугольные,
матрица системы B) — унитарная. Методы, основан-
основанные на ортогонализации, обладают многими достоин-
достоинствами, но чувствительны к влиянию ошибок округ-
округления. На основе развития методов типа ортогона-
ортогонализации был создан весьма эффективный (при реше-
решении нек-рых систем с разреженными матрицами)
сопряженных направлений метод (см. [9], [10J).
Прямые методы определения собственных значений
и собственных векторов матрицы. Пусть для мат-
матрицы А требуется определить собственное значение к
и собственный вектор х, т. е. решить уравнение
Ах=кх. C)
При замене х=Су, где С — невырожденная матрица,
уравнение C) перейдет в уравнение Ву = ку при В —
= С~1АС. Прямые методы решения данной задачи
состоят в том, что с помощью конечного числа подобных
j преобразований исходная матрица А приводится к
матрице В настолько простого вида, чтобы для нее
легко находились коэффициенты характеристич. мно-
многочлена и собственные векторы. При этом собственные
значения находятся как корни характеристич. много-
многочлена каким-либо из известных методов. Численные
методы перехода от матрицы А к матрице В по суще-
существу мало чем отличаются от численных методов пре-
преобразования системы A) в систему B). Известно много
методов подобного типа (методы Крылова, Данилев-
Данилевского, Хессенберга и т. д., см. [1]), однако они не
нашли широкого применения на практике в силу зна-
значительной численной неустойчивости (см. [3]).
Различают полную проблему собственных значений,
когда ищутся все собственные значения, и частичную
проблему, когда отыскивают нек-рые из них; послед-
последняя задача более типична в случае сеточных задач,
возникающих при аппроксимации дифференциальных
и интегральных уравнений.
Итерационные методы решения системы линейных
алгебраических уравнений. Эти методы дают решение
системы A) в виде предела последовательности нек-рых
векторов; построение их осуществляется посредством
единообразного процесса, наз. процессом и т е р а-
ц и й. Основные итерационные процессы для решения
системы A) могут быть описаны посредством едино-
единообразного процесса следующей общей схемой. Стро-
Строится последовательность векторов х{1), х('->, . . .,
а-1*1, ... по рекуррентным формулам
где ЯA), //(-', . . .— нек-рая последовательность
матриц, х@) — начальное приближение, вообще го-
говоря, произвольное. Различный выбор последователь-
последовательности матриц #(*> приводит к различным итерацион-
итерационным процессам.
Простейшими итерационными процессами являются
стационарные процессы, в к-рых матрицы Я1*1 не
зависят от номера шага /с; их также наз. метода-
методами простой итерации (см. [5]). Если по-
последовательность 11{к) периодична, то процесс наз.
циклическим. Всякий циклич. процесс может
быть преобразован в стационарный, но обычио такое
преобразование усложняет метод. Нестационарные
процессы, в частности циклические, используются
для ускорения сходимости итерационных процессов
(см. [5], [6]). Среди методов ускорения сходимости
особое место занимают методы, использующие много-
многочлены Чебышева (см. [5], [6]) и сопряженные направ-
направления (см. [10]).
Выбор матрицы Н для стационарного процесса и
матриц Н<к> для нестационарного может осуществ-
осуществляться различными способами. Возможно построение
матриц Я1*' таким образом, чтобы итерационный
процесс сходился к решению и по возможности быстро
для широкого класса систем уравнений (см. [5]). Воз-
Возможен и противоположный подход, когда при пост-
построении матриц 111к) максимально используются част-
частные особенности данной системы для получения ите-
итерационного процесса с наибольшей скоростью сходи-
сходимости (см. [6]). Второй способ построения матриц
Д<*> является наиболее распространенным.
Одним из наиболее распространенных принципов
построения итерационных процессов является принцип
релаксации (см. Релаксации методы). В этом случае
матрицы Hik) выбираются из заранее описанного
класса матриц так, чтобы на каждом шаге процесса
уменьшалась какая-либо величина, характеризующая
точность решения системы. Среди релаксационных
методов наиболее разработаны координатные и гра-
градиентные методы. В координатных методах матрицы
//(ft) подобраны так, что на каждом шаге меняются
одна или несколько компонент последовательных при-
приближений. О точности приближенного решения х
чаще всего судят по величине вектора невязки r=ii—Ь.
В случае стационарных итерационных методов глав-
главный член погрешности можно оценить также с помощью
б2-процесса (см. [5]).
Среди других итерационных методов можно отме-
отметить простой итерации метод, переменных направле-
направлений метод, методы полной и неполной релаксации
и т. д. (см. [1], [6], [10]). Как правило, итерационные
методы удобны для реализации на ЭВМ, однако в от-
отличие от прямых методов они чаще всего обладают ве-
весьма ограниченной областью применения. В области
же их применения итерационные методы нередко суще-
существенно превосходят прямые методы по объему вычи-
вычислений. Поэтому вопрос сравнения прямых и итераци-
итерационных методов .может быть решен лишь при детальном
изучении свойств конкретной системы. Наибольшее рас-
распространение нашли итерационные методы для реше-
решения систем, возникающих при разностной аппрокси-
аппроксимации дифференциальных уравнений (см. [5], [6]).
Итерационные методы решения полной проблемы
собственных значений. В итерационных методах собст-
собственные значения вычисляются как пределы нек-рых
числовых последовательностей без предварительного
определения коэффициентов характеристич. много-
многочлена. Как правило, при этом одновременно находятся
и собственные векторы или нек-рые другие векторы,
связанные с собственными простыми соотношениями.
Большинство итерационных методов менее чувстви-
чувствительны к ошибкам округления, чем прямые, но значи-
значительно более трудоемки. Развитие этих методов и их
применение в практике вычислений стало возможным
лишь после создания ЭВМ.
Среди итерационных методов особое место занимает
метод вращений (Якоби метод) решения полной про-
проблемы собственных значений действительной симмет-
симметричной матрицы. Основан он на построении последо-
последовательности матриц, ортогонально подобных исходной
матрице А и имеющих монотонно убывающие до нуля
суммы квадратов всех внедиагональных элементов.
Метод вращений очень прост, легко реализуется на
• IBM и всегда сходится. Независимо от расположения
собственных значений он обладает асимптотически
квадратичной сходимостью. Наличие кратных и близ-
близких собственных значений не только не замедляет
сходимость метода, но, напротив, приводит к ее уско-
ускорению. Метод вращений устойчив к влиянию ошибок
округления результатов промежуточных вычислений.
Свойства этого метода послужили причиной его рас-
распространения на решение полной проблемы матриц
более общего вида. Без существенных изменений метод
вращений переносится на эрмитовы и косоэрмитовы
матрицы. Незначительное его изменение позволяет с
успехом решать полную проблему для матриц А *А п
А А* одновременно, не вычисляя сами произведения
матриц. Эффективное распространение этого метода на
произвольные матрицы простой структуры реализуется
обобщенным методом вращений.
Среди итерационных методов решения полной про-
проблемы собственных значений значительную группу со-
составляют степенные методы. Большинство их вычисли-
вычислительных алгоритмов укладывается в следующие схемы:
AG = G1S1 A=L1R1
или
Rk-1Lk_1 = LkRk
Здесь на каждом шаге матрица, стоящая в левой
части равенства, раскладывается в произведение двух
матриц. Пусть одна из них треугольная, а вторая уни-
унитарная или треугольная другого наименования. Тогда
при нек-рых дополнительных предположениях мат-
матрицы Gk1AGf! и Rk^k сходятся к квазитреугольной
матрице, подобной матрице А. Как правило, порядки
диагональных клеток квазитреугольной матрицы не-
невелики, поэтому полная проблема собственных зна-
значений для предельной матрицы решается достаточно
просто.
Известно несколько методов такого типа. Одним из
лучших среди них является QR-a л г о р и т м (см.
[7]). Вычислительные схемы степенных методов во
многом совпадают с вычислительными схемами реше-
решения систем уравнений прямыми методами.
Исследование и классификация численных методов.
Огромное количество численных методов Л. а. ставит
актуальной задачей не столько создание новых, сколь-
сколько исследование и классификацию существующих
методов (одна из самых полных классификаций методов
с точки зрения их математич. построения содержится
в монографии [1]; описанию методов с точки зрения
возможности их реализации на ЭВМ посвящены мо-
монографии [2], [3], [71).
Первые фундаментальные работы по анализу устой-
устойчивости и ошибок округления в численных методах
решения задач Л. а. появились лишь в 1947—48 и
посвящены исследованию обращения матриц и решению
систем уравнений методами типа Гаусса. Практич.
ценность этих результатов была невелика. Сущест-
Существенный сдвиг в изучении данного вопроса произошел в
середине 60-х гг. (см. [3]), когда был сделан решаю-
решающий шаг к анализу и оценке эквивалентных возмуще-
возмущений. Реально вычисленное решение нек-рой задачи
стало рассматриваться как точное решение той же
задачи, но с возмущенными входными данными. Это
возмущение, наз. эквивалентным, полностью характе-
характеризует влияние ошибок округления. Исследовано боль-
большое кол-во методов с точки зрения мажорантной оцен-
оценки нормы эквивалентного возмущения (см. [3], [7]).
При фиксированном вычислительном алгоритме и
способе округления вся совокупность ошибок округ-
округления является однозначной векторной функцией
Ф((Л), зависящей от числа разрядов t, с к-рыми ве-
ведется счет, и от входных данных А. Главный член
функции (ff (A) при t -*- оо не имеет сколько-нибудь
приемлемого явного выражения. Однако весьма эффек-
эффективным оказалосьисследование ф( (А) на классе случай-
случайно заданных входных данных. Оно показало, что на-
наиболее вероятное значение отклонения вычисленного
решения от точного за счет ошибок округления суще-
существенно меньше, чем максимально возможное (см. [7]).
Анализ влияния ошибок округления показал, что
между лучшими методами нет принципиальной раз-
разницы с точки зрения устойчивости к ошибкам округле-
округления. Этот вывод заставляет по-новому взглянуть на
проблему выбора того или иного численного метода в
практич. деятельности вычислителя. Создание мощных
ЭВМ существенно ослабило значение различия между
методами в таких характеристиках, как объем требу-
требуемой памяти ЭВМ и количество арифметпч. операций, и
привело к возросшим требованиям на гарантию точ-
точности решения. В этих условиях наиболее предпочти-
предпочтительными становятся те методы, к-рые, не очень отли-
отличаясь от лучших по скорости и удобству реализации
на ЭВМ, позволяют решать широкий класс задач как
хорошо, так и плохо обусловленных и давать при этом
оценку точности вычисленного решения.
Классификация и сравнение численных методов, о
к-рых говорилось выше, относятся в основном к тому
случаю, когда вся совокупность входных данных
целиком помещается в оперативную память ЭВМ.
Однако особый интерес представляют два крайних
случая — решение задач Л. а. на малых и сверхмощ-
сверхмощных ЭВМ. Решение задач на таких ЭВМ имеет свою
специфику. В первом случае — это малая память,
ограниченная разрядная сетка и счет в режиме фик-
фиксированной запятой, во втором — наличие мульти-
мультипрограммного режима работы ЭВМ, режима разделе-
разделения времени и т. д.
Лит.: [1] Фаддеев Д. К., Фаддеева В. Н., Вы-
Вычислительные методы линейной алгебры, 2 изд., М.— Л., 1963;
[2] Воеводин В. В., Численные методы алгебры. Теория
и алгорифмы, М., 1966; [3] У и л к и н с о н Д ж.- X., Алгеб-
Алгебраическая проблема собственных значений, пер. с англ., М.,
1970: [4] Воеводин В. В., «Вестн. Моск. ун-та. Матем.,
механ.», 1970, Л» 2, с. 69—82; [э] Бахвалов Н. С, Чис-
Численные методы, 2 изд., М., 1975; [6] Самарский А. А.,
Николаев Е. С, Методы решения сеточных уравнений,
М., 1978; G] В о е в о д и к В. В., Вычислительные основы ли-
линейной алгебры, М., 1977; [8] Фаддеева В. Н. [и др.],
Вычислительные методы линейной алгебры. Библиографический
указатель. 1828—1974 гг., Новосиб., 1976; [9] Воеводин
В. В., Линейная алгебра,2 изд., М., 1980; [10] М а р ч у к Г. И.,
Кузнецов Ю. А., Итерационные методы и квадратичные
функционалы, Новосиб., 1972. В. В. Воеводин.
ЛИНЕЙНАЯ АЛГЕБРАИЧЕСКАЯ ГРУППА — ал-
алгебраическая группа, бирационально изоморфная ал-
гебраич. подгруппе полной линейной группы. Алгебра-
пч. группа G линейна тогда и только тогда, когда алге-
браич. многообразие G аффинно, т. е. изоморфно замк-
замкнутому (в топологии Зариского) подмногообразию
аффинного пространства.
Теория Л. а. г. возникла из потребностей решения
линейных дифференциальных уравнений в квадрату-
квадратурах (теория Галуа дифференциальных уравнений) в
конце 19 в. (С. Ли, S. Lie; Э. Пикар, Е. Picard; Л. Мау-
рер, L. Маигег), и первоначальное изучение Л. а. г.
над полем комплексных чисел проводилось по анало-
аналогии с теорией групп Ли методом алгебр Ли. Л. а. г.
G над полем комплексных чисел С может рассматри-
рассматриваться как аналитич. подгруппа группы GL(rc, С).
Обычным образом определяемая алгебра Ли группы G
будет тогда подалгеброй в алгебре Ли группы GL (п, С)
(т. е. в полной линейной алгебре Ли всех (пХгс)-матриц
с комплексными коэффициентами). На возникающий
здесь вопрос — какие подалгебры Ли полной линейной
алгебры соответствуют алгебраическим (а не только
аналитическим) подгруппам группы GL (га, С) — может
быть дан исчерпывающий ответ (см. Ли алгебраическая
алгебра 1)).
Методы теории групп и алгебр Ли в середине 20 в.
были существенно усовершенствованы и обобщены
К. Шевалле (С. Chevalley), что позволило ему приме-
применить их к изучению Л. а. г. над произвольными по-
полями нулевой характеристики (см. [6]). Для полей
ненулевой характеристики метод алгебр Ли является
менее эффективным, так что естественно возникла не-
необходимость глобального исследования Л. а. г. с по-
помощью методов алгебраич. геометрии. Основы глобаль-
глобального исследования Л. а. г. были заложены А. Борелем
(см. [2]), после чего теория Л. а. г. приобрела вид
стройной дисциплины (см. [8]). Одной из основных
проблем теории Л. а. г. является проблема класси-
классификации Л. а. г. с точностью до изоморфизма. Эта
проблема в основном сводится к ее решению для двух
типов Л. а. г.: полупростых и разрешимых. Произ-
Произвольная Л. а. г. обладает такой максимальной связной
разрешимой нормальной подгруппой Н, что фактор-
факторгруппа G/H является полупростой Л. а. г. Фундамен-
Фундаментальным результатом является классификация Шевалле
полупростых Л. а. г. над алгебраически замкнутыми
полями любой характеристики (см. [7]). Эта класси-
классификация аналогична классификации Картана — Кил-
линга комплексных полупростых групп Л п. Класси-
Классификация Шевалле основывается на том, что в полупро-
полупростой алгебраич. группе строятся аналоги элементов
теории Картана — Киллинга — картановская под-
подгруппа, корни и т. д. Важную роль при этом играют
подгруппы Бореля и максимальные алгебрапч. торы.
Пусть G — полупростая Л. а. г. Т — ее макси-
максимальный тор, Nq(T) — нормализатор Т в G, W=
= Nа(ТI Т — Вейля группа группы G. Тор Т содер-
содержится лишь в конечном числе подгрупп Бореля груп-
группы G, к-рые транзитивно переставляются при сопря-
сопряжении элементами из Nq(T). При помощи подгрупп
Бореля, содержащих Г, строятся нек-рые мономорфиз-
мономорфизмы аддитивной группы поля в подгруппы Бореля (со-
(содержащие Г), играющие роль корней. С помощью
техники Брюа разложений доказывается, что указан-
указанная система структурных элементов допускает полную
классификацию и определяет группу G с точностью
до изоморфизма (см. [7]). Окончательная классифи-
классификация полупростых групп не зависит от характери-
характеристики основного поля и поэтому совпадает с класси-
классификацией комплексных полупростых алгебраич. групп.
Классификация с точностью до fc-изоморфияма полу-
полупростых Л. а. г., определенных над алгебраически
незамкнутым полем к, значительно сложнее; она су-
существенно зависит от поля к и сводится к классификации
fc-форм алгебраич. групп (см. Форма алгебраической
группы). Множество /с-форм алгебраич. группы G,
определенной над алгебраич. замыканием К поля к,
находится во взаимно однозначном соответствии с мно-
множеством одномерных Галуа когомологий H1(k, Aut(G)),
где Aut(G) — группа автоморфизмов G. В тех случаях,
когда известна группа Галуа Gal(K/k) расширения
К/к (напр., если к — поле действительных чисел или
конечное поле), это дает значительную информацию
о формах группы G. Но главная трудность в исследо-
исследовании этой глубокой и пока A982) еще далекой от
своего решения проблемы ложится на изучение к-
структуры полупростых Л. а. г.
В случае произвольного поля к максимальные
/с-разложимые торы играют роль, аналогичную роли
максимальных алгебраич. торов в группе G над ал-
алгебраически замкнутым полем. Ar-разложимый тор —
это тор, /с-изоморфный прямому произведению А-оп-
ределенных одномерных групп GLA). Максимальные
/с-разложимые торы в G сопряжены посредством эле-
элементов из Gfc и их размерность наз. к-р а н г о м G
(что обозначается rang^G). Если rangftG>0, то G наз.
к-н зотропной, в противном случае — ft-a н и-
з о т р о п н о й. ^-изотропность для полупростой груп-
группы G эквивалентна тому, что группа Gj, имеет не-
неединичные уншштентные элементы. Для простой одно-
связной группы G существовала Кнезера — Титса ги-
гипотеза, что при rangfcG>0 группа G& порождается
унипотеятными элементами (см. [13J), в общем случае
решенная отрицательно (см. [16]). Роль подгруппы
Бореля в случае произвольного поля к играет мини-
минимальная параболич. /с-подтруппа, т. е. минимальная
/с-определенная подгруппа G, содержащая подгруппу
Бореля. Естественно определяется корневая система
относительно максимального fc-разложимого тора в G
и относительная группа Вейля (см. [3]). Если группа
G обладает /с-разложимым максимальным тором, то
эти структурные элементы не зависят от поля к и
определяют такие группы с точностью до /с-изомор-
физма. Группы, обладающие fc-разложимыми макси-
максимальными торами, наз. fc-p азложимыми, или
Шевалле группами. Именно К. Шевалле классифици-
классифицировал ^--разложимые алгебрапч. группы и доказал, что
всякая полупростая группа обладает единственной
(с точностью до fc-нзоморфнзма) /с-формой такого типа
(см. [7], [14]).
В общем случае А. Борелем и Ж. Титсом [3] дока-
доказано существование аналога разложения Бргоа для
группы G;;, в к-ром роль подгрупп Бореля играют
минимальные параболич. ^-подгруппы, сопряженные
посредством элементов из G^. Это позволяет в сущест-
существенной мере редуцировать классификацию полупростых
¦Ч. а. г. положительного /с-ранга к классификации
иолулростых групп fc-ранга нуль, т. е. к классифи-
классификации ^-анизотропных групп. А именно, нолунроетая
группа G определяется с точностью до /с-изоморфпзма
своим классом изоморфизма над универсальным полем,
своим А:-нндексом и полупростым А--анизотропным ядром
(см. Анизотропное ядро) (см. [9]). В некоторых случаях
удалось получить классификацию fc-анизотропных по-
луоростых групп. Так, напр., над конечным полем
анизотропных полупростых групп не существует, а
для широкого класса локальных полей к доказано
(см. [15]), что всякая /с-аннзотропная простая Л. а. г.
G является внутренней формой тина Ап, т. е. G^ в од-
носвязном случае изоморфна SLA, D), где D—тело ко-
конечной степени над к. В основе этих результатов ле-
лежит понятие Титса системы, представляющее глубо-
глубокое аксиоматич. обобщение разложений Брюа в клас-
сич. случае.
Из других общих результатов следует отметить
унирациональность многообразия редуктнвной к-ол-
ределенной Л. а. г., а также теорему Гротендика о
существовании во всякой ^-определенной Л. а. г. к-оп-
ределенного максимального тора (см. [1], [10], [12]).
Если группа G определена над полем алгебраич.
чисел или над полем алгебраич. функций одной пере-
переменной, то возникают проблемы об арифметич. свой-
свойствах G, изучением к-рых занимается линейных алге-
алгебраических групп арифметическая теория (см. [12]).
Идеи и техника Л. а. г. были применены к изучению
произвольных линейных групп, что привело к созданию
одного из основных методов в теории линейных групп
(см. [11]).
Лит.: [1] Б о р е л ь А., Линейные алгебраические группы
пер. с англ., М., 1972; [2] Borel A., «Ann. Maih.», 1956, v. 64
.№ 1, р. 20— 82; [3] Б о р е л ь А., Тите Ж., «Математика».
J967, т. 11, .№ 1, с. 43 —111; № 2, с. 3 —31; [4] Серр Ж.-П.
Алгебраические группы и поля классов, пер. с франц., М., 1968
[5] его же, Когомологии Галуа, пер. с франц., М., 11N8
[б] Шевалле К., Теория групп Ли, дер. с англ. и франц.,
т. 1—3, М., 1948—58; [7] С h e v а 1 1 е у С, Classification des
sroupes de Lie algebriques, t. 1—2, P., 1950— 58; [8] III e в а л-
ле К., Теория алгебраических групп, в кн.: Международный
математический конгресс в Эдинбурге, 1958 г., М., 1962, с. 74—
92; [9] Тите Ж., «Математика», 1968, т. 12, .№ 2, с. 110 — 43;
[10] Demazure M., Grothendieck A., Schemas en
groupes, t. 1—3, В.— [u. a.], 1970; [11] Платонов В. П..
«Изв. АН СССР. Сер. матем.», 19С6, т. 30, № 3, с. 573 — 620; [121
Итоги науки и техники. Алгебра. Топология. Геометрия, т. 11,
М., 1974, 0. 5—36; [13] Tits J.. «Ann. Math.», 1964, v. 80,
p. 313 — 29; [14] Стейнберг Р., Лекции о группах Шевал-
ле, пер. с англ., М., 1975; [15] Б р ю а Ф., Тите Ж., «Мате-
«Математика», 1968, т. 12, № 5, с. 3 — 18; [16J Платоно в В. П.,
«Изв. АН СССР. Сер. матем.», 1976, т. 40, К. 2, с. 227 — 61; [17]
Хамфри Д ж., Линейные алгебраические группы, пер. с
англ., М., 1 <180. В. П. Платонов.
ЛИНЕЙНАЯ ГИПОТЕЗА — статистическая гипоте-
гипотеза, согласно к-рой математпч. ожидание а п-мерного
нормального закона Nn(a, о2/) (где / — единичная
матрица), лежащее в линейном подпространстве lIsCZRn
размерности s<", принадлежит линейному подпро-
подпространству Ifd/7S размерности r<s.
Многие задачи математич. статистики можно реду-
редуцировать к задаче проверки Л. г., к-рая часто форму-
формулируется в следующем т. н. каноническом виде. Пусть
X=(Xt, . . ., Хп) — нормально распределенный век-
вектор, компоненты к-рого независимы и
ЕА';- = а,- для г = 1, . . ., s, BXi = () для i = s -)- 1, . . ., п
и
DX,- = 02 для i = l, ..., n,
причем величины а,, . . ., as, а2 неизвестны. Тогда
гипотеза Нв, согласно к-рой
ах = . . . = аг = 0, г < s < п,
является канонической линейной ги-
гипотезой.
Пример. Пусть У,, . . ., У„ и Zb . . ., Zm суть п-\-т
независимых случайных величин, подчиняющихся нор-
нормальным распределениям N1 (а, 02) и Nt (?>, cr2) соот-
соответственно, причем параметры a, ft, а2 неизвестны.
Тогда гипотеза IIn: a~b~Q является Л. г., в то время
как гипотеза а — а0, Ь~Ь0 при аафЪа не является та-
таковой.
Лит.: [1] Л е м а н Э., Проверка статистических гипотез,
пер. с англ., М., 1964. М. С. Никулин.
ЛИНЕЙНАЯ ГРУППА — группа линейных преоб-
преобразований векторного пространства V конечной раз-
размерности п над нек-рым телом К. Выбор базиса в
пространстве V реализует Л. г. как группу невырож-
невырожденных квадратных матриц степени п над телом К.
Тем самым устанавливается изоморфизм между ли-
линейными и матричными группами.
Группа всех автоморфизмов свободного А*-модуля V
нал. также полной линейной группой и
обозначается GL(F), а группа всех обратимых матриц
порядка п над А' (также называемая полной Л. г.)
обозначается GL(«, Л') или GLn(K). Всякая под-
подгруппа группы GL (V) наз. линейной группой
степени п. Наиболее развитая часть теории .11. г.
относится к случаю, когда тело К коммутативно, т. е.
является полем. Поэтому в дальнейшем (если не ого-
оговорено противное) рассматриваются только Л. г. над
полем.
Теория Л. г. зародилась в середине 19 в. и разви-
развивалась в тесной связи с теорией групп Ли, теорией
представлений групп и теорией Галуа. Начало систе-
матич. исследованию Л. г. было положено работами
К. Жордана (см. [1]). На первом этапе развития тео-
теории Л. г. в связи с потребностями теории Галуа изу-
изучались главным образом конечные Л. г., в особенности
разрешимые и классические (см. Классическая группа).
Было установлено и несколько общих фактов, связан-
связанных с приводимостью или неприводимостью Л. г, G,
т. е. со свойствами G-модуля V. Для всякой Л. г. G
существует композиционный ряд G-подмодулей
т. е. такой ряд, что все фактормодули F,- + i/F,- непри-
водимы. Другими словами, всякая матричная группа
сопряжена в GLn(K) нек-рой группе квазитреуголь-
квазитреугольного вида с неприводимыми диагональными блоками.
Пусть Go — подгруппа в G, состоящая из всех эле-
элементов, действующих тождественно на факторах
y, + i/F,-, г=0, . . ., m—1. Тогда Go — нормальная
нильпотентная подгруппа, элементы к-рой удовлетво-
удовлетворяют (в А-алгебре End (К) всех линейных преобразо-
преобразований пространства V) уравнению (х—1)" = 0; такие
Л. г. наз. у н и п о т е н т н ы м и. Всякая унипо-
тентная группа, рассматриваемая как матричная груп-
группа, сопряжена в GL (п. К) с нек-рой подгруппой группы
верхних треугольных матриц с единичной диагональю.
В существенной мере строение группы С по модулю
Go определяется строением неприводимых Л. г. G,- + ],
индуцируемых G в факторах 1'*,- + 1/1*,-. Если Л. г. G
неыриводима над алгебраически замкнутым полем А,
то G содержит ге2 линейно независимых над А элемен-
элементов А-алгебры End (Г), т. е. А-линейная оболочка G
совпадает с End(F). Всякая нормальная подгруппа
вполне приводимой Л. г. вполне приводима.
Бесконечные линейные группы. Хотя теория Л. г,
имеет довольно большую историю, общие методы в
ней были созданы сравнительно недавно. Исключение
составляют только разрешимые и классические Л. г.
Еще К. Жордан в 1870 исследовал структуру разре-
разрешимых Л. г. над конечными полями и получил ряд
классификационных результатов об этих группах.
Эти исследования получили дальнейшее развитие (см.
[13]): детально изучено строение и классифицированы
максимальные разрешимые и локально нпльпотентные
подгруппы в GL (/г, А') над алгебраически замкнутым
полем А'. Основная структурная теорема о разрешимых
Л. г. была получена А. И. Мальцевым (см. [8] с. 294—
313) в 1951: разрешимая Л. г. Г степени п над алгеб-
алгебраически замкнутым полем обладает такой нормальной
подгруппой Н конечного индекса, что Н сопряжена
подгруппе треугольной группы, а индекс [Г : //] меньше
р(п), где р{п) — нек-рая эффективно определяемая
функция от п; в частности, коммутант группы Н яв-
является унипотентной группой и, с абстрактной точки
зрения, группа Г есть конечное расширение группы Н
с нильпотентным коммутантом.
Важный и весьма разветвленный раздел теории Л. г.
представляют классич. группы (см., напр., [4], [7]).
Новый этап в развитии теории Л. г. начался в 60-е
гг. 20 в., когда был создан общий метод исследования,
базирующийся на технике алгебраич. групп (см. Ли-
Линейная алгебраическая группа, а также [9], [18]). Этот
метод позволил решить ряд проблем теории Л. г.
Напр., с его помощью доказана теорема о сво-
свободных подгруппах Л. г. (см. [14]): всякая
Л. г. над нолем нулевой характеристики либо содер-
содержит неабелеву свободную подгруппу, либо обладает
разрешимой подгруппой конечного индекса, и построе-
построена теория периодич. Л. г. (см. [9]) (оказалось, что основ-
основные структурные результаты теории конечных групп
сохраняются и в более общем случае периодич. Л. г.).
Другой важный метод теории Л. г., т. н. метод ап-
аппроксимации, был впервые применен А. И. Мальцевым
в 1940 (см. [8] с. 58—73). Он годится для исследования
Л. г. над областями целостности конечного типа, в
частности для Л. г. с конечным числом образующих.
Суть метода заключается в следующем: пусть GL (n,F)—
полная Л. г. над конечно порожденным нод-
кольцом F поля А; тогда F по модулю максимальных
идеалов аппроксимируется конечными полями /',-, что
влечет аппроксимацию группы GL(«, F) конечными
матричными группами GL(/?, F,). Для всякой под-
подгруппы FcGL(n, F) получается индуцируемая ап-
аппроксимация конечными Л. г. Г/. Оказывается, во
многих случаях свойства группы Г в сильной степени
определяются свойствами групп Г,-. Этот метод был
позднее усовершенствован (см. [18]), что привело к
доказательству общей аппроксимационной теоремы,
из к-рой выводится большинство результатов о бес-
бесконечных Л. г. с конечным числом образующих.
Конечные линейные группы. Наиболее крупным
структурным результатом о коночных Л. г. до сих
пор остается теорема Жордана A878): су-
существует такая целозначная функция /(/г), что каждая
конечная Л. г. степени п над нолем нулевой характе-
характеристики обладает абелсвой нормальной подгруппой
индекса меньше / (п). Для полей положительной ха-
характеристики существуют бесконечные серии простых
конечных групп степени п и поэтому непосредственное
перенесение теоремы Жордана на этот случай невоз-
невозможно. Тем не менее с помощью техники модулярных
представлений конечных групп доказано, что сущест-
существует целозначная функция f(m, n) такая, что конечная
Л. г. степени п над полем характеристики /¦>>(), по-
порядок силовской р-подгруппы к-рой не превосходит
рт, обладает абелевой нормальной подгруппой индекса
меньше f(m, и) (см. [16]).
Одной из главных проблем теории конечных Л. г.
является проблема классификации простых конечных
Л. г. С тех пор как в 1901 Л. Диксон изложил [2]
основные факты о классич. простых конечных Л. г.,
было получено много новых результатов. Среди них
центральное место занимают результаты К. Шевалле
(см. [15]), применившего для исследования простых
конечных Л. г. методы теории алгебраич. групп, что
привело к открытию новых типов простых конечных
Л. г. и позволило почти все известные простые конеч-
конечные Л. г. получать единообразным методом (подробнее
см. [11], [12])'.
Лишенные группы над телами и кольцами. Система-
тпч. исследование Л. г. над некоммутативным телом К
началось после работы Ж. Дьедонне (J. Dieudonne,
1943, см. 15]), в к-рой была описана конструкция
определителя над толом (см. Определитель). Под-
Подгруппа группы GL((?, К) с определителем 1 наз. спе-
специальной линейной группой и обозначается SL(/?, А).
Она порождается трансвекциями (преобразо-
(преобразованиями t такими, что dim(l—t)V=i и tc=v при
v?{i — t)V), и всякая подгруппа группы GL(n, А),
инвариантная относительно GL(n, А), либо скалярна,
либо содержит SL(n, А), за исключением случаев
п —2, |А| — 2, 3, когда группа GL B, А) разрешима.
Если тело А конечномерно над своим центром Z, то
существует единственный определитель со значениями
в Z, называемый приведенной нормой (см. [5]), причем
SL(«, А') содержится в группе \JL(n, К) элементов с
приведенной нормой 1. Вопрос о совпадении этих
групп, поставленный в 1943 (проблема Т а н а-
к и — А р т и н а), был решен отрицательно в [10].
Группа UL(h, А) и факторгруппа SK1=UL(n,A')/SL(n,
А), называемая приведенной группой
У а й т х е д а, играют важную роль в теории линей-
линейных алгебраич. групп и алгебраич. А-теории [5].
Основные вопросы теории Л. г. над кольцами от-
относятся к описанию нормальных подгрупп полной
Л. г. и других классич. групп. Прогресс в этой области
теснейшим образом связан с развитием алгебраич. А-
теории (см. [51). Так, задача описания нормальных
подгрупп группы Gh(n, Ч), где % — кольцо целых
чисел, фактически эквивалентна конгруанц-проблеме
для группы SL(n, Z) при гс>2. А именно, всякая
нескалярная нормальная подгруппа группы SL(?j, Z),
;г>2, имеет конечный индекс и является конгруэнц-
подгруппой, в то время как группа SLB, Z) есть ко-
конечное расширение свободной группы и потому обла-
обладает разнообразными нормальными подгруппами бес-
бесконечного индекса.
Изучались также автоморфизмы классических Л. г.
над кольцами (см. [3], [19]).
Лит.: [11 Jordan С, Traite des substitutions et des equa-
equations algebriques. P., 1870; [2] D i с k s о n L. E., Linear groups,
Lpz., 1901; [3] Автоморфизмы классических групп, пер. с англ.
и франц., М., 1976; [4] А р т и н Э., Геометрическая алгебра.
пер. с англ., М., 1969; [5.1 Басе X., Алгебраическая К-тео-
рия, пер. с анг.![., М., 1973; [6] Б о р е л ь А., Линейные алгеб-
алгебраические группы, пер. с англ., М., 1972; [7] Дьедонне Ж.,
Геометрия классических групп, пер. с франц., М., 1974; [8]
Мальцев А. И., Избранные труды, т. 1— Классическая ал-
алгебра, М., 1976, с. 58—73, 294 — 313: [9] Платонов В. П.,
«Изв. АН СССР. Сер. матем.», 1966, т. 30, № 3, с. 573—620;
[10] его ж е, там же, 1976, т. 40, .№ 2, с. 227—61; [11] Семи-
Семинар по алгеораическим группам, пер. с англ., М., 1973; [12]
С т с и н и с р г Р., Лекции о группах Шевалле, пер. с англ.,
М., 1975; [13] Супруненко Д. А., Группы матриц, М.,
1972; [14] Тите Ж., «Математика», 1972, т. 16, № 2, с. 47 — 66;
[15] Шевалле К., там же, 1958, т. 2, Ms 1, с. 3—53; [16]
Brauer R., Feit W., «Ann. Math.», 1966, v. 84, № 1,
p. 119—31; [17] Draxl P., Kneser M., SKt von Schief-
korpern, В.— Hdlb.—N. Y., 1980; [18] Wehrfritz В.,
Infinite linear «roups, В.— Hdlb.— N. Y., 1973; [191 Итоги нау-
науки. Алгебра. Топология. Геометрия, 1970, М., 1971, с. 75 —110.
В. П. Платонов.
ЛИНЕЙНАЯ ЗАВИСИМОСТЬ — см. в статье Ли-
Линейная независимость.
ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ — способ прибли-
приближенного вычисления значения функции f{x), основан-
основанный на замене функции / (ж) линейной функцией
L(x) = a(x-x1) + b,
параметры а и Ь к-рой выбираются таким образом,
чтобы значения L (х) совпадали со значениями / (х)
в заданных точках х1 и хг:
L(x1) = /(.r1), L (*„)=/(*„).
Этим условиям удовлетворяет единственная функция
, , . / (X;)-/ (Ж,)
L(x)= Ж8-х,- (* — -4)+f Ы,
приближающая заданную функцию / (х) на отрезке
[xlt x.2] с погрешностью
/ (х)— L (x) =~y- (x — Xi) (г — x2), 1?[хи х2].
Вычисления, необходимые для Л. и., легко реализу-
реализуются при ручном счете, благодаря чему этот способ
широко используется при интерполировании табличных
данных.
Лит.: [1] Б а х в а л о в Н. С, Численные методы, 2 изд.,
М., 1975; |2] Б е р е з и н И. С, Жидков Н. II., Методы
вычислений, 3 изд., т. 1, М., 1966. М. К. Самарин.
ЛИНЕЙНАЯ КЛАССИЧЕСКАЯ ГРУППА — группа
невырожденных линейных преобразовании конечно-
конечномерного векторного пространства Е над телом К,
являющаяся классической группой (см. также Линей-
Линейная группа). Важнейшими типами Л. к. г. являются
следующие: полная линейная группа Ghn(K), специ-
специальная линейная группа SLn(A'), симплектическая
группа Sp,;(A'), ортогональная группа Оп(К, /), уни-
унитарная группа Un(K, /) (здесь n=dim?\ / — соот-
соответствующая полуторалинейная форма на Е).
В. л. Попов.
ЛИНЕЙНАЯ КРАЕВАЯ ЗАДАЧА — задача опреде-
определения в нек-рой области D переменных х= (хг, х2,
. . ., хп) решения и (х) линейного дифференциального
уравнения
(Lu)(x) = f(x), x?D,
удовлетворяющего на границе S этой области (или
ее части) линейным краевым условиям
См. также Краевая задача. А. П. Солватов.
ЛИНЕЙНАЯ КРАЕВАЯ ЗАДАЧА; численные
методы решения — методы, позволяющие по-
получить решение Л. к. з. в виде таблицы его прибли-
приближенных значений в точках сетки, не используя пред-
предварительной информации об ожидаемом виде решения.
Для теории этих методов типично предположение о
том, что решение исходной задачи существует и имеет
достаточное число производных. Благодаря отсут-
ствию других предположении численные методы отли-
отличаются своей универсальностью.
Основой численных методов решения Л. к. з. явля-
является замена исходной системы уравнений ее сеточной
аппроксимацией. В случае интегр о-дифференциальных
уравнений такая аппроксимация обычно строится с
помощью разностных схем и квадратурных формул.
При этом возникают следующие проблемы:
1) насколько быстро точное решение сеточной за-
задачи сходится к решению исходной задачи при из-
измельчении сетки;
2) насколько решение сеточной задачи чувстви-
чувствительно к изменениям исходных данных;
3) как найти, хотя бы приближенно, решение се-
сеточной задачи.
При решении первой и второй проблем использу-
используется следующий аппарат. Пусть в замкнутой области
D задано уравнение
Lu = f, A)
а на ее границе Г, состоящей из компонент Г,-,— гра-
граничные условия
l[u = (fi на Г,-, i = l, 2, ..., s. B)
Здесь заданные непрерывные функции /, ср,- принад-
принадлежат нормированным линейным пространствам F, Ф,
соответственно, а линейные операторы L и I; преоб-
преобразуют нек-рое линейное подмножество W нормиро-
нормированного линейного пространства U функций, непре-
непрерывных в D, в F и Ф,- соответственно.
Пусть для аппроксимации уравнения A) выбраны
сетки Dn и DfrClD, зависящие от положительного
параметра h; нормированные линейные пространства
U^ и Ffr функций uh и fn, определенных в точках сеток
Dn и Dft соответственно, а также линейный оператор
Ln, преобразующий V'^ в Fh. Для аппроксимации
граничного условия B) выбирается сетка Г,тгС:Г,
нормированное линейное пространство Ф,л функций
Ф/ft, определенных в точках сетки Г(Л, и линейный
оператор Z,-#, преобразующий Un в Ф{п. Кроме того,
выбираются линейные операторы Р'h и р,^, преобра-
преобразующие F и Ф, в Ffi и Ф,л соответственно. В резуль-
результате получается сеточная аппроксимация
lihufi = Pifi4>i на Г,-ft, ? = 1, 2, ..., s, D)
исходной задачи A), B). Пусть через [u]h, {/}ft, {ф,}/л
обозначены следы функций и, /, ф,- из пространств
U, F, Ф, на сетках Dft, Dii, Г,л соответственно. Ис-
Исследование сходимости сеточных аппроксимаций uft
к решению и исходной задачи при h —*- 0 имеет смысл
производить лишь в сеточных нормах, согласованных
с нормами в пространствах U, F, Ф,-, т. е. при условии,
что для любых функций и, /, ф,- выполняются предель-
предельные соотношения
II На Иид — IIuПи. «{fhiFh —>¦ II/Wf,
И{ф|}|-Л||ф.ь—*11фA1ф.-
in i
Если u?W, f?F, Ф/?Ф/, то величина
z(h)=--\\Lh[u]h-{Lu}l\F +\\Phf-{f}h\\F +
h h
наз. погрешностью аппроксимации за-
задачи A), B) задачей C), D). Если и — решение задачи
A), B), то величина
наз. погрешностью аппроксимации на этом решении.
Говорят, что задача C), D) аппроксимирует задачу
A), B) (или аппроксимирует ее на решении и), если
z(h) —*- 0 (или p(h) —>- 0) при h -*- 0. Порядок малости
величины z(h) (или величины р (h)) наз. порядком
аппр оксимации (или порядком аппроксима-
аппроксимации на решении и).
Пусть, напр., аппроксимируется уравнение тепло-
теплопроводности. В квадранте D (ж^О, t~^0) решается
уравнение A), где
. ди д2и
при начальном условии 11и = ц>1 (х) на полуоси Г, (/=0,
х^О) и граничном условии l2u = (f2(t) на полуоси
Тг(х=0, t^O), где 11и = и, 12и=ди/дх, причем (pi@) =
=ф2@). В качестве F берется пространство непрерыв-
непрерывных функций / (t, x) с нормой
, х)\,
а в качестве Фх и Ф2 — пространства непрерывных
функций фх (х) и ф2 (х) с нормами
II ф1 Иф, = SUP I Ф1 (х) I и II фг |1ф2 = sup | ф2 (О I
Г, Г2
соответственно. Пространство U можно считать сов-
совпадающим с F, а в качестве W берется подмножество
функций u^U, имеющих непрерывные частные про-
производные duldt, ди/дх, д2и/дх2 в области D. Пусть
.Dft — множество точек (пх, mh), и=0, 1,2,.. .; т —
= — 1, 0, 1, . . ., где шаги сетки связаны функцио-
функциональной зависимостью вида т=т(/») такой, что т —>-О
при h —»- 0. Множество D^ будет состоять из точек
((п+1/2)-с, mh), п=0, 1, 2, . . .; т=0, 1, 2, ... В ка-
качестве Ff, и f/ft выбираются пространства сеточных
функций /ft (t, x) и «ft (t, x) с согласованными нормами
II/а И/7 =sup|/ft(i, x)\ и ||MA||c/ft = sup|Mft(t, x)\.
h A
Оператор L^ может быть определен соотношением
Lhuh(t, x)= —
и пусть
(или Pnf(t, .T)=
Для аппроксимации начального условия берется сет-
сетка Г1Л, состоящая из точек @, mh), то=0, 1, 2, . . .;
пространство (Djft сеточных функций (pi/;(s) с согласо-
согласованной нормой
II «Pift 11Ф ь = sup | ф1Л (ж) |
1Л rlft
) = "Л (°. л').
Для аппроксимации граничного условия берется сетка
F2ft, состоящая из точек (п%, 0), га = 0, 1, 2, . . .; про-
пространство Ф2л сеточных функций ф2у; (t) с согласо-
согласованной нормой
I! Ф2А 11ф2Л = SUPI Фгл @1.
оператор Uh, определяемый равенством
hhuh(t)=J-hlun(t, h) — uh(t, —A)],
и оператор р2лфг^ (фгЬл- Тогда
и z (й) —>- 0 при й —>- 0. Если в качестве W взять более
узкое множество функций u^U, имеющих, кроме
указанных ранее, ограниченные частные производные
d2u/dt2 и д*и/дх* в области D, то при %=h получают
аппроксимацию второго порядка.
Сеточную задачу
?а»а = /л. C')
hhuh = fih на Г(Л D')
наз. корректной, если при достаточно малом h
выполняются следующие условия: эта задача разре-
разрешима при любых данных функциях /й ?/¦"/;, Ф,7г€ф/7г;
существует функция т|з (к), не зависящая от /г, стремя-
стремящаяся к нулю вместе с % и такая, что
(и ?л
Цл)
для любой функции u-h^Ufi. Решение корректной се-
сеточной задачи равномерно по h непрерывно зависит
от данных функций. Корректность сеточной задачи
является необходимым условием малой чувствитель-
чувствительности Ре решения к округлениям в процессе его вы-
вычисления. Если и — решение задачи A), B) и задача
C'), D') корректна, то
ll"ft-[»]ftll^^4'(pW). F)
Если, кроме того, задача C), D) аппроксимирует за-
задачу A), B) на решении и, то
IK-Mftllu,,—-0
п
при к —у 0. Если выполняются условия согласования
норм, условие z(/i)—»-0 и условие E), то, полагая
uft=[u]ft и переходя к пределу в неравенстве E) при
li _»- 0, получают неравенство
справедливое для любой функции u?W. Таким об-
образом, для исследования корректности краевых задач
вида A), B) можно использовать такой путь: сначала
получить оценку E), а из нее оценку G). С помощью
оценок типа E) часто удается доказать существование
решения и задачи A), B) как предела сеточной аппрок-
аппроксимации и/, при h —*- 0.
Для полного решения проблемы нахождения при-
приближенного решения задачи A), B) необходимо по-
построить точный или приближенный метод нахождения
решения аппроксимации C), D), обладающий свой-
свойством устойчивости к округлениям. При исследовании
устойчивости полезно использовать понятие замыкания
вычислительного алгоритма. В приведенном примере
уравнение целесообразно решать прогонки методом,
по переменной х.
Оценка F) погрешности сеточного метода обладает
тем недостатком, что в выражение функции \|з (Л) обычно
входят производные от точного решения и. В нек-рых
случаях удается априори (т. е. еще до решения задачи)
оценить эти производные, однако такие оценки обычно
оказываются грубыми. Несколько более точными яв-
являются оценки, в к-рых производные заменяются раз-
разностными отношениями приближенного решения и^.
В основном же практич. оценка погрешности сеточных
методов производится при помощи повторного решения
задачи C), D) с различными h и последующего выде-
выделения главной части погрешности вида h~? [z]ft, где у —
известный порядок малости погрешности. Так, если
справедливо аснмптотич. соотношение
Иногда удается получить уравнения для функции г,
содержащие производные от точного решения и. Тогда
можно решать их численно на более грубой сетке
после решения исходной задачи и по получении глав-
главной части погрешности добавить ее к приближенному
решению uft и тем самым уточнить его.
В некоторых случаях при специальном выборе коор-
координатных функций вариационного или проекционного
метода решения задачи A), B) получаются уравнения
вида C), D), обеспечивающие сходимость не только к
классическому, но и к обобщенному решению. Этот
способ построения аппроксимаций, наз. иногда м е-
тодом конечных элементов, предостав-
предоставляет большую свободу в выборе сетки. Возможность
целесообразно располагать узлы позволяет достигать
требуемой точности при меньшем числе узлов сетки.
Лит.: [1] Бабушка И., В и т а с е к Э., И р а-
г е р М., Численные процессы решения дифференциальных
уравнений, пер. с англ., М., 1969; [2] Бахвалов Н. С,
Конспекты по курсу «Основы вычислительной математики»,
ч. 4, М., 1068; [31 его же, Численные методы, 2 изд., М., 1975;
[4] Варга Р., Функциональный анализ и теория аппрокси-
аппроксимации в численном анализе, пер. с англ., М., 1974; [о] Г а в у-
рин М. К-, Лекции по методам вычислений, М., 197); [В]
Годунов С. К., Рябенький В. С, Разностные схемы,
2 изд., М., 1977; 17] Д ь я к о н о в Е. Г., Разностные методы
решения краевых задач, в. 1—2, М., 1971—72; [8] Канторо-
Канторович Л. В., Акилов Г. П., Функциональный анализ,
2 изд., М., 1977; [9] М а р ч у к Г. И., Методы вычислитель-
вычислительной математики, 2 изд., М., 1980; [10] М и х л и н С. Г., С м о-
лицкий X. Л., Приближенные методы решения дифферен-
дифференциальных и интегральных уравнений, М., 1965; [11] Р н х т-
майер Р. Д., Мортон К., Разностные методы решения
краевых задач, [пер. с англ.], М., 1972; [12] Рябенький
В. С, Филиппов А. Ф., Об устойчивости разностных урав-
уравнений, М., 1956; [131 Самарский Л. А., Теория разност-
разностных схем, М., 1977; [14] Самарский А. А., Никола-
е в Е. С, Методы решения сеточных уравнений, М., 1978.
А. Ф. Шапкин.
ЛИНЕЙНАЯ НЕЗАВИСИМОСТЬ — одно из основ-
основных понятий линейной алгебры. Пусть V — векторное
пространство над полем к; векторы ал, . . ., ап наз.
линейно независимыми, если
к1а1 -f- . . . + к„ап Ф 0
для любого набора к[?К, кроме кг~-. . . = &„=0.
В противном случае векторы а1у . . ., ап наз. лине й-
н о зависимыми. Векторы alt . . ., ап линейно
зависимы в том и только в том случае, когда по край-
крайней мере один из них является линейной комбинацией
остальных. Бесконечное подмножество векторов из V
наз. линейно зависимым, если линейно зависимо его
нек-рое конечное подмножество, и линейно независи-
независимым, если любое его конечное подмножество линейно
независимо. Число элементов (мощность) максималь-
максимального линейно независимого подмножества пространства
не- зависит от выбора этого подмножества и наз. р а н-
г о м, или размерностью, пространства, а
само это подмножество — базисом (базой).
В частном случае, когда векторы а,, . . ., ап — эле-
элементы нек-рого числового поля К, а к — подполе в К,
возникает понятие линейной независимо-
независимости ч и с е л. Л. н. чисел над полем рациональных
чисел Q можно рассматривать также, как обобщение
понятия иррациональности. Так, числа а и 1 линейно
независимы тогда и только тогда, когда а иррацио-
иррационально.
Понятие линейной зависимости и независимости
элементов вводится также в абелевых группах и мо-
модулях.
Линейная зависимость — частный случай более ши-
широкого понятия — абстрактного отношения зависи-
зависимости На множестве. О. А. Иванова.
ЛИНЕЙНАЯ ОБОЛОЧКА — пересечение М всех
подпространств, содержащих множество А векторного
пространства Е. При этом М наз. также подпро-
подпространством, порожденным А . М. И. Войцеховский.
ЛИНЕЙНАЯ ОЦЕНКА — линейная функция от на-
наблюдаемых случайных величин, используемая (при
подстановке в нее конкретных значений наблюденных
величин) в качестве приближенного значения (оценки)
неизвестного параметра анализируемой стохастич. схе-
схемы (см. Оценка статистическая). Специальное выде-
выделение класса Л. о. оправдано следующими обстоятель-
обстоятельствами. Л. о. легче поддаются статистич. анализу, в
частности исследованию на состоятельность, несме-
несмещенность, эффективность, построению соответствующих
доверительных интервалов и т. п. В то же время в до-
достаточно широком диапазоне случаев поиск «наилуч-
«наилучших» (в определенном смысле) оценок не выводит за
пределы класса Л. о. Так, напр., статистич. анализ
линейной регрессионной модели (см. Линейная регрес-
регрессия) вида
дает в качестве наилучшей (в смысле метода наимень-
наименьших квадратов) оценки параметров в оценку
к-рая является линейной относительно наблюденных
значении исследуемой случайной величины Y. Здесь
У есть га-мерный вектор-столбец наблюденных зна-
значений у,, г = 1, . . ., п, исследуемого результирующего
признака (случайной величины), X — матрица раз-
размера пХр (ранга ;>) наблюденных значений xi \ i=l,
..., п, fc=l, ..., р, р неслучайных факторов-аргу-
факторов-аргументов, от к-рых зависит результирующий признак Y,
в есть р-мерный вектор-столбец неизвестных парамет-
параметров Qk, ft—1, . . ., р, и е есть гс-мерный случайный
вектор-столбец остаточных компонент, удовлетворяю-
удовлетворяющий условия Ее=О, Е(гг')=а21 (I — единичная матри-
па).
Лит.: [1] Крамер Г., Математические методы статис-
статистики, пер. с англ., 2 изд., М., 1975; [21 Р а о С. Р., Линейные
статистические методы и их применения, пер. с англ.. М., 1968;
[3] 3 а к с IU., Теория статистических выводов, пер. с англ.,
М., 1975; [4] Шеффе Г., Дисперсионный анализ, пер. с
англ., М. 1963. С. А. Айвазян.
ЛИНЕЙНАЯ РЕГРЕССИЯ одной случай-
случайной переменной Y= (УA), . . ., У<т>)' по
другой Х= (ХA), . . ., Х^Р})' — линейная по ж
m-мерная векторная форма, описывающая зависимость
условного математич. ожидания (при условии Х=.х)
случайного вектора Y от значений as= (xA), . . .,
^"'Соответствующие уравнения
.т<о> = 1, ft = l, 2, ..., т,
наз. уравнениями линейной регрес-
регрессии Y по X, а параметры b^j — коэффициен-
коэффициентами регрессии (см. также Регрессия).
В приложениях допускается интерпретация перемен-
переменной X как наблюдаемого параметра (не обязательно
случайного), от к-рого зависит математич. ожидание ис-
исследуемого результирующего показателя Y(X). Кроме
того, часто под Л. р. У1*' по X понимают «наилучшую»
(в определенном смысле) линейную аппроксимацию
У<*> посредством величин Хили результат наилучшего
(в определенном смысле) выравнивания имеющейся
системы экспериментальных точек («наблюдении») (Y\ \
X,), i=l, • . ., п, с помощью гиперплоскости в про-
пространстве (У1*', X) в ситуациях, когда интерпретация
совокупности этих точек как выборки из соответству-
соответствующей генеральной совокупности может и не быть пра-
правомочной. При таком определении приходится разли-
различать разные варианты Л. р. и зависимости от выбора
способа вычисления ошибки линейной аппроксимации
У**1 посредством величин X (или в зависимости от
конкретного выбора критерия качества выравнивания).
Наиболее распространенными критериями качества
аппроксимации У(*> с помощью линейных комбинаций
А (линейного выравнивания точек (Y't \ X;)) являются:
Q1(b)=E
i (») = E {
= Е {со (X)
В этих соотношениях выбор «весов» со (Л) или со,-
зависит от природы конкретной исследуемой схемы.
Так, напр., если у(*> (X) интерпретируются как слу-
случайные величины, дисперсия к-рых DYKk) (X) (или
их оценки) известны, то со2 (X)-^[Dy<*> (А')]-1. В по-
последних двух критериях «невязки» аппроксимации
или выравнивания измеряются расстояниями р(-, •)
от Y{k) (X) или Y\ ' до искомой гиперплоскости ре-
регрессии. Если коэффициенты bkj определяются из
условия минимизации величин Qi(b) пли Qi(b), то
Л. р. наз. средней квадрат и ческой; при
использовании критериев Q2{b) и Q-i(b) Л. р. наз.
средней модульной (или средней аб-
абсолютной); при использовании критериев Q3 (Ь)
и ()з(Р) — ортогональной.
В нск-рых случаях Л. р. в классич. смысле (*)
совпадает с Л. р., определенной с использованием функ-
функционалов типа Q[. Так, напр., если вектор (X', У(А))
подчиняется многомерному нормальному закону, то
регрессия У(*> по X в смысле (*) совпадает со средней
квадратической Л. р. (при со(ЛГ)^1).
Лит.: [1] Линии к Ю. В., Метод наименьших квадратов
и основы деатематико-статистической теории обработки наблю-
наблюдений, 2 изд., М., 1962; 12] Крамер Г., Математические ме-
методы статистики, пер. с англ., 2 изд., М., 1975: [3] К е н-
д а л л М. Д ж., С т ь ю а р т А., Статистические выводы и
связи, пер. с англ., М-, 1973; [4] Р а о С. Р., Линейные стати-
статистические методы и их применения, пер. с англ., М., 1968.
ЛИНЕЙНАЯ СВЯЗНОСТЬ — 1) Л. г. па'дифф™-
ренцируемом многообразии М — диф-
ференциально-геометрич. структура на М, связанная
с аффинной связностью на М. В каждой аффинной
связности определяется параллельное перенесение век-
вектора, позволяющее для каждой кривой L (з-0, х\) в М
определить линейное отображение касательных век-
векторных пространств ТХ1(М) —>- ТХо(М). В этом смысле
аффинная связность определяет нек-рую Л. с. на М,
к к-рой относятся все понятия и конструкции, связан-
связанные только с перенесением векторов и вообще тензоров.
Л. с. на М является связностью в главном расслоении
В (М) базисов в касательных векторных пространствах
ТХ(М), х?М, и определяется одним из следующих
трех эквивалентных между собой способов:
1) объектом связности Г/k, преобразующимся на
пересечениях областей локальных карт по формулам
Г»' вх'' вх1 вх" Г1 I в'х' вх1' .
/'*'~ дх' вх.' 9хк' >k dxi'dxk' дх' '
2) матрицей 1-форм (о/ на главном расслоенном про-
пространстве В(М), состоящем из всех базисов во всех
касательных пространствах ТХ(М), х?М, такой, что
2-формы
в каждой локальной координатной системе выража-
выражаются в виде
3) билинейным оператором V ковариантного диффе-
дифференцирования, к-рый двум векторным полям X, Y на
М ставит в соответствие третье \JyX и обладает свой-
свойствами:
где / — гладкая функция на М.
Каждая Л. с. на М определяет однозначно нек-рую
аффинную связность на М, канонически присоединен-
присоединенную к ней, к-рая определяется путем развертки любой
кривой L (ж0, хх) в М. Для получения этой развертки
следует сначала определить п= &\тМ линейно неза-
независимых параллельных векторных полой Хх, . . ., Х„
вдоль L, затем разложить но ним касательное к L
векторное поле:
и, наконец, найти в ТХо(М) решение x(t) дифферен-
дифференциального уравнения
при начальном значении x(t) = 0. В произвольной
точке Xf кривой L аффинное отображение касательных
аффинных пространств
определяется теперь отображением реперов
{*,, Л',-(«)} —*{Vt, Xi («)},
где .royt---r(l).
Л. с. часто отождествляется с аффинной связностью,
канонически к ней присоединенной, используя взаимно
однозначное соответствие между ними.
2) Л. с. в векторном расслоении —
дифференциально-геометрич. структура на дифферен-
дифференцируемом векторном расслоении я: X —*- В, к-рая
каждой кусочно гладкой кривой L в В с началом ж0
и концом хх сопоставляет линейный изоморфизм слоев
п~1(хо) и Il~1(-ri) как векторных пространств — па-
параллельное перенесение вдоль L. Л. с. определяется
горизонтальным распределением на главном расслоен-
расслоенном пространство Р базисов в слоях, к к-рому при-
присоединено данное векторное расслоение. Аналити-
Аналитически Л. с. задается такой матрицей 1-форм ша на Р,
где а, р, ... пробегают множество значений, мощ-
мощность к-рого равна размерности слоев, что 2-формы
полубазовы, т. е. над каждой локальной кооодинатной
системой (х') на В выражаются в виде
G& = ?-*?,/**' Л d*A
Горизонтальное распределение определяется при этом
дифференциальной системой со« = О на Р. 2-формы
Й« наз. формами кривизны. Согласно тео-
теореме о голономии они определяют группу голономии
Л. с.
3) Л. с. в расслоенном пространстве —
связность, при к-рой касательные векторы горизонталь-
горизонтальных кривых с началом в данной точке у расслоенного
пространства Е образуют векторное подпространство
Ду в Ту(Е); Л. с. определяется горизонтальным рас-
распределением Д: у н* Ду.
Лит.: [II Лихнерович А., Теория связностей в це-
целом л группы голономии, пер. с франц., М., 1960; [2] К о b э-
у a s lii S., X о m i z u K., Foundations of differential geomet-
geometry, v. 1, N. Y.— L., 1963. Ю. Г. Лумисте.
ЛИНЕЙНАЯ СИСТЕМА — семейство аффективных
линейно эквивалентных дивизоров на алгебраич. мно-
многообразии, параметризованное проективным прост-
пространством.
Пусть X — неособое алгебраич. многообразие над
полем к, X — обратимый пучок на X, Г (А",
X) — пространство глобальных сечений пучка X, а
LaT (X, X) — некоторое конечномерное подпростран-
подпространство. Если dim?>0, то дивизоры, определяемые ну-
нулями сечений из L, линейно эквивалентны и эффек-
эффективны. Линейной системой наз. проек-
проективное пространство |Ь| = Р(Л) одномерных подпро-
подпространств в L, параметризующее эти дивизоры. Если
dimr(A\ JP)<oo, то Л. с. \Т(Х, Х)\ наз. полной;
она обозначается также \L\,
Пусть s0, . . ., sn — базис в L. Он определяет рацио-
рациональное отображение (р? : X —>- Р" по формуле
zH» (so(x), ..., sn(x)), х?Х.
Обычно говорят, что <pL задано Л. с. \L\. Образ ф?(А")
не лежит ни в какой гиперплоскости в Рп (см. [2]).
Обратно, каждое рациональное отображение т|): X —>-
—>- Р'п, обладающее этим свойством, задается нек-роп
Л. с.
Неподвижной компонентой Л. с. \Ь\
наз. такой эффективный дивизор D* на X, что D = D'-\-
+ J9* для любого D?\L\, где D' — эффективный ди-
дивизор. Когда D пробегает Л. с. \L\, дивизоры D' об-
образуют нек-рую Л. с. \L'\ той же размерности, что и
Л. с. \L\. Отображение <pL, совпадает с ф;.. Поэтому
при рассмотрении отображения ф/ можно предпола-
предполагать, что Л. с. \L\ не имеет неподвижных компонент.
В этом случае ф? не определено в точности на базисном
множестве Л. с. |L|.
Примеры. 1) Пусть Х = Р2 и X = QP*(d), й>1,
тогда сечения Т(Р", Qp2 (d)) отождествляются с фор-
формами степени d на Р2, а полная Л. с. \Qp2 (d)\ — с
множеством всех кривых степени d.
2) Стандартное квадратичное преобразование т:
J9? —> Р2 (см. Кремоново преобразование) задается Л. с.
коник, проходящих через точки @, 0, 1), @, 1, 0),
A, 0, 0).
3) Инволюция Гейзера а: Р2 —>- Р2 задается Л. с.
кривых степени 8, проходящих с кратностью 3 через
7 точек в общем положении.
4) Инволюция Бертини р : Рг —>- Р2 задается Л. с.
кривых степени 17, проходящих с кратностью 6 через
8 точек в общем положении.
Лит.: [1] Алгебраические поверхности, М., 1965 (Тр. Ма-
тем. ин-та АН СССР, т. 75); [2] Мамфорд Д., Лекции о
кривых на алгебраической поверхности, пер. с англ., М., 1968;
[3] Z a r i s k i О., Algebraic surfaces, 2 ed., В.— Hdlb. —
N. Y., 1971. В. А. Псковских.
ЛИНЕЙНАЯ СИСТЕМА ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ С ПЕРИОДИЧЕСКИМИ КОЭФФИЦИ-
КОЭФФИЦИЕНТАМИ — система п линейных дифференциальных
уравнений вида
7Г = ан (*) *i + •••+am(*)aV»
A)
d-~ = anl (t) Zj-f . .. -f а„„ @ xn,
где t — действительная переменная, ajh (t), x/l=x/l(t) —
комплекснозначные функции, причем
C-jhKi + T)---o.jh(t) для любых /, h. B)
Число 7>0 наз. периодом коэффициен-
коэффициентов системы A). Систему A) удобно записывать в
виде одного векторного уравнения
? = A(t)x, C)
где
*r = (*i, .... *„>. A(t) = || a/h (t) ||, /, Л = 1, ..., п.
Предполагается, что функции ау/г (i) определены для
t?R, измеримы и интегрируемы по Лебегу на [О, Т]
и почти всюду выполнены равенства B), т. е. A (t-{-T) =
= А {t). Решение уравнения C) — вектор-функция х—
= .r(t) с абсолютно непрерывными компонентами такая,
что C) выполнено почти всюду. Пусть io€^i а — за"
данные (произвольно) число и вектор. Существует и
определяется единственным образом решение x(t),
удовлетворяющее условию ж(*0) = а. Матрица X (t)
порядка п с абсолютно непрерывными элементами наз.
матрицантом (или эволюционной мат-
матрице и, или Коши матрицей) уравнения C), если
почти всюду на R выполняется равенство
где / — единичная (пХ «)-матрица. Матрицант X (t)
удовлетворяет соотношению
X(t-\-T) = X(t)X(T), f?R.
Матрица X (Т) наз. матрицей монодромии,
а ее собственные значения ру — мультиплика-
мультипликаторами уравнения C). Уравнение
det[X(T)-pI] = O D)
для мультипликаторов ру наз. характеристи-
характеристическим уравнением уравнения C) (систе-
(системы A)). Каждому собственному вектору а<0) матрицы
монодромии с мультипликатором р0 соответствует
решение ж<0) (t)= X (t)a'-0) уравнения C), удовлетворяю-
удовлетворяющее условию
7') = рв.г«»(*).
Имеет место теорема Флоке — Ляпунова:
матрицант уравнения C) с Т-периодической матрицей
A (t) представим в виде
X(t) = F(t)e«, E)
где К — постоянная матрица, F(t) — периодическая
с периодом Т, абсолютно непрерывная неособая для
всех t?R матрица-функция и ^@)=/. Обратно:
если F(?) и К — матрицы с указанными свойствами,
то матрица E) является матрицантом нек-рого урав-
уравнения C) с У-периодической матрицей A (t). Матрица
К, наз. показательной матрицей, и
матрица-функция F(t) в представлении E) определи-
ются неоднозначно, В случае действительных коэф-
коэффициентов a.jh (t) в E) X (t) — действительная мат-
матрица, a F (t) и А', вообще говоря,— комплексные
матрицы. Для этого случая справедливо уточнение
теоремы Флоке — Ляпунова: матрицант уравнения C)
с У-периодической действительной матрицей A (t)
представим в виде E), где К — постоянная действи-
действительная матрица, F (t) —действительная абсолютно
непрерывная неособая для всех t матрица-функция,
удовлетворяющие соотношениям
F (t + T) = F (t)L, F@) = /, KL = LK,
где L — некоторая действительная матрица такая, что
В частности, F(t+2T)=F{t). Обратно: если F(t),
A, L — произвольные матрицы, обладающие указан-
указанными свойствами, то E) — матрицант нек-рого урав-
уравнения C) с У-периодической действительной матрицей
A(t).
Из E) сразу следует теорема Флоке, утверж-
утверждающая, что уравнение C) обладает фундаментальной
системой решений, распадающейся на групиы, каждая
из к-рых имеет вид
ж«> (t) = ef-tu1 (t),
@+ • • ¦ + tum-t (t) + um (t)]
где Uj{t)— абсолютно непрерывные 7-периодические
(вообще говоря, комплексные) вектор-функции. (Ука-
(Указанная группа решений соответствует одному (тХт)-
ящику жордановои формы матрицы К.) Если все эле-
элементарные делители матрицы К простые (в частности,
если все корни характеристич. уравнения D) простые),
то имеется фундаментальная система решений вида
Формула E) означает приводимость уравнения C)
(см. Приводимая линейная система) к уравнению
посредством замены х= F(t)y (теорема Ляпу-
Ляпунова).
Пусть pj, . . ., рп — мультипликаторы уравнения
C) и К — произвольная показательная матрица, т. е.
еТК = Х(Т). F)
Собственные значения к1, . . ., Хп матрицы К наз.
характеристическими показателя-
м и уравнения C). Из F) имеем е J=P/, / = 1, . . .,
и. Характеристич. показатель X можно определить
так же, как комплексное число, для к-рого уравнение
C) имеет решение, представимое в виде
где u(t) есть У-периодическая вектор-функция. Ос-
Основные свойства решений, к-рыми обычно интересу-
интересуются в приложениях, определяются характернстич.
показателями или мультипликаторами заданного урав-
уравнения (см. табл.). В приложениях часто коэффициенты
системы A) зависят от параметров; в пространстве
параметров нужно выделить области, для точек к-рых
решения системы A) обладают определенными свой-
свойствами (обычно это — первые четыре свойства, ука-
указанные в таблице, либо справедливость оценки |.z(t)|<:
<:const-e-a' с заданным а). Эти задачи сводятся,
таким образом, к вычислению или к оценке характе-
характеристич. показателей (мультипликаторов) системы A).
Уравнение
dx
dt
где A (t), f(t) — измеримые, интегрируемые по Лебегу
на [О, Т] У-периодические матрица-функция и вектор-
функция соответственно (A (i-j- T) = A (t), f{t+T) = f(t)
Свойство
решений
Характеристиче-
Характеристические показатели
Мультипликаторы
Устойчивость
тривиального ре-
решения (ограни-
(ограниченность на
(О, и) всех реше-
решений)
Действительные
части неположитель-
неположительны; в случае нали-
наличия нулевых или чи-
чисто мнимых характе-
характеристических показа-
показателей им соответст-
соответствуют простые эле-
элементарные делители
показательной мат-
матрицы
Расположены внут-
внутри или на единич-
единичной окружности; в
последнем случае им
соответствуют прос-
простые олементарные
делители матрицы
монодромии
Асимптотиче-
Асимптотическая устойчи-
устойчивость тривиаль-
тривиального решения
(I ж (f) | —». О при
( —>• ос для лю-
любого решения)
Действительные
части отрицательны
Расположены внут-
внутри единичной окруж-
окружности
Ограниченность
всех решений на
(— X, + X)
Чисто мнимые с
простыми элементар-
элементарными делителями по-
показательной матри-
матрицы
Расположены на
единичной окружно-
окружности, всем им отвеча-
отвечают простые элемен-
элементарные делители
матрицы монодромии
Неустойчивость
тривиального ре-
решения (наличие
неограниченных
на @, ос) реше-
решений)
Имеется либо ха-
характеристический
показатель с поло-
положительной действи-
действительной частью, ли-
либо чисто мнимый (в
частности, нулевой)
с непростым элемен-
элементарным делителем
показательной мат-
матрицы
Имеется мульти-
мультипликатор либо вне
единичной окружно-
окружности, либо на единич-
единичной окружности с
непростым элемен-
элементарным делителем
матрицы монодромии
Наличие Т -пе-
-периодического ре-
решения
Для некоторого
характеристического
показателя Я - вы-
выполнено Л,Т = 2я(т
(т — целое)
Один из мульти-
мультипликаторов равен
единице
Наличие полу-
полупериодического
решения, т.е. ре-
решения ж ((), для
которого x(t +
+ Т)=-*@, V*
Для некоторого
характеристического
показателя
Имеется мульти-
мультипликатор р= — 1
У
-
+ 1) Г (т — целое)
почти всюду), наз. неоднородным линей-
линейным дифференциальным уравнени-
уравнением с периодическими коэффициен-
коэффициентами. Если соответствующее однородное уравнение
(8)
не имеет Г-периодических решений, то уравнение G)
имеет и притом единственное Т-периодическое решение.
Оно определяется формулой
х @ = [/-Д (t, 0)]
R (t, Т-х) f (t-т) dx,
где R (t, s)=Y {t+ T)Y (t+s)-1, a Y (t) — матрицант од-
однородного уравнения (8), при этом R(t-\-T, s) — R(t, s),
Ael[I—R(t, 0))ф0.
Пусть уравнение (8) имеет d>l линейно независи-
независимых Г-периодических решении </i(i), • • •, УаA)- Тогда
сопряженное уравнение
dt — А (г' z
имеет также d линейно независимых Т-периодических
решений: z1(t), . . ., z^(t). Для того чтобы неоднород-
неоднородное уравнение G) имело 7-периодическое решение,
необходимо и достаточно выполнения соотношений
ортогональности
d. (9)
При выполнении (9) произвольное Г-периодическое
решение уравнения G) имеет вид
где 7г> • • •> 7d — произвольные числа, а ж<0) (() —
нек-рое Т-периодическое решение уравнения G). При
дополнительных условиях
'Т ((t), yj(t))dt=O, /=1, ..., d,
Г-периодическое решение х (t) определяется однознач-
однозначно; при этом существует такая не зависящая от f(t)
постоянная 6>0, что
|/(s)|=dS)l/2, tg[O, Г].
Пусть задано уравнение
~ = A(t, г)х A0)
с матричным коэффициентом, голоморфно зависящим
от комплексного «малого» параметра 8:
A(t, 8) = Л0(г) + ЁЛ1(«) + 82Л2@+... (И)
Пусть при |е|<80 сходится числовой ряд
Мо (•) 11 + 6 || Л (.)|| + е2!М2 (•)[!+•¦•,
где
S \Aj(t) \dt.
что гарантирует сходимость (поэлементно) ряда A1)
при |8|<80 в пространстве L @, Т). Тогда матрицант
X ((, е) уравнения A0) для фиксированного t^[U, T]
есть аналитич. функция от в при |е|<е0. Пусть A0(t) =
= С — постоянная матрица с собственными значе-
значениями Xj, j~\., 2, . . ., п. Пусть Ру (е) — мультиплика-
мультипликаторы уравнения A0), ру- @) = ехр (Kj T). Если рл(О) =
= ехр (а<0) Т) — мультипликатор кратности г (h=h1,
. . ., hr , hj — некоторые числа из 1, 2, . . ., п), то
-kh^a>v + ~mh, h = hlt ...,hr, A2)
где ид — целые числа. Если этому мультипликатору
отвечают простые элементарные делители матрицы
монодромии, или, иначе, если каждому ~kh, И = кл,
. . ., kr , отвечают простые элементарные делители
матрицы С (напр., все числа Х/г различны), то а(|))
наз. r-к ратным характеристическим
показателем (уравнения A0) при е=0) и р о-
стого типа. Оказывается, что соответствующие г
характеристич. показателей уравнения A0) с малым
е>0 в первом приближении вычисляются весьма
просто. Именно, пусть ад, b/i — соответствующие нор-
мированные собственные векторы матриц С и С*:
Cah^Xhah, C*bh=\hbh,
(aj, Ьл) = 6ул, ;, h = h1, ..., hr ;
пусть
— ряд Фурье для 4j(?) и пусть
где mj — числа из A2). Тогда для соответствующих
г характеристич. показателей ctft(s), h = ku . . ., hr ,
уравнения A0), обращающихся в а("> при 8 = 0, спра-
справедливы разложения в ряды по дробным степеням 8,
начинающиеся с членов первого порядка:
аЛ(е) = а|-°>+Рл? + о(е1 + '/"'г), h~-=hx, ..., hr, A3)
где Рл — корни (написанные столько раз, какова их
кратность) уравнения
det||a/ft —Рб А1| = 0,
ад/, — натуральные числа, равные кратностям соот-
соответствующих C/г (буу=1, бу-ft —О при )фК). Если ко-
корень рй просто!!, то 9л=1 и соответствующая функция
а/, (е.) аналитична при е=0. Из формулы A3) следует,
что возможны случаи, когда «невозмущенная» (т. е.
с 8 = 0) система устойчива (все kj чисто мнимы и им
соответствуют простые элементарные делители), но
«возмущенная» система (малое 8=^=0) неустойчива (Rc|3/i>
>0 хотя бы для одного рй). Это явление потери устой-
устойчивости при сколь угодно малом периодич. изменении
параметров (во времени) наз. параметриче-
параметрическим резонансом. Аналогичные, но более
сложные формулы имеют место для характеристич.
показателей непростого типа.
Пусть рA), . . ., р(<?> — различные мультиплика-
мультипликаторы уравнения C) и к,, . . ., пц — их кратности,
ях+. . .-\-nq = n. Пусть точки р*-'1 на комплексной
плоскости ? окружены непересекающимися кругами
IS—(liJ)\<-R/ и из точки 5=0 в точку ?=0° проведен
непересекающпй эти круги разрез. С помощью этого
разреза определяются ветви логарифма (ln?)m. Пусть
каждому мультипликатору р1^' сопоставлено произ-
произвольное целое число т и U = Х(Г,г) —матрпцант урав-
уравнения A0). Матрица InV («матричный логарифм») мо-
может быть определена формулой
где Г/ — окружность [Z,— рУ'\ = Н/. Набор чисел ти
. . . , m.q определяет ветвь матричного логарифма.
При этом ехр(]п?/)=?/ для малых е. Формула A4)
при всевозможных mi, . . ., ml не охватывает, вообще
говоря, всех значений матричного логарифма, т. е.
всех решений Z уравнения exp Z-- U. Однако решение,
даваемое формулой A4), обладает важным свойством
голоморфности: элементы матрицы lnf/ в A4) суть
голоморфные функции элементов матрицы U. Для
уравнения A0) формула E) принимает вид
X (t, e) = /¦(*, е)ехр[(А'(е)], A5)
где F(t+T, z)=F{t, в),, К (е)= Г'ЧпХ (Т, г). Если
\пХ(Т, е) определяется согласно A4), то
А'(е)=А'0+еЛ'1+..., F(t, s)=F0(i)-fef1@ + ... A6)
— ряды, сходящиеся при малых |е|. Основная инфор-
информация о поведении решении при t —>- -j- oo, к-рой обыч-
обычно интересуются в приложениях, заключена в показа-
показательной матрице К (е). Ниже описан метод аспмпто-
тич. интегрирования уравнения A0), т. е. метод по-
последовательного определения коэффициентов К/, Fj{t)
в A6).
Пусть в A1) А 0(г)=С. При этом, хотя X ((,0) = ехр (tC),
вообще говоря, не существует ветви матричного лога-
логарифма такой, что матрица К(е) аналитична при е = 0
и АГ(О)— С. Указанная ветвь логарифма будет сущест-
существовать в так наз. нерезонансном случае,
когда среди собственных значений Xj матрицы С нет
чисел, для к-рых
(т — целое число). В резонансном случае
(когда такие собственные значения существуют) урав-
уравнение A0) подходящей заменой x = P(t)y, где P{t-\-T) =
~P(t), сводится к аналогичному уравнению, для
к-рого имеет место нерезонансный случай. Матрица
Р (t) определяется по матрице С.
В нерезонансном случае в A6) К0=С, F0(t)=I, a
матрицы Fj(t), К], / = 1, 2, . . ., находятся из урав-
уравнения
¦|f-[С + е^ПО + еМ, (*)+...]^ С e)-F(t, г) К (г)
после приравнивания в этом уравнении коэффициен-
коэффициентов при одинаковых степенях в. Для определения
Z (?) = Fj(t) и L — Kj получается матричное уравнение
вида
-Ц- = сг-2С + Ф(о-?, A7)
тде Ф (t-f-71)—Ф (t). Матрицы Z(t) и L находятся, и
притом однозначно (нерезонансный случай), из A7)
и условия периодичности Z(t-\- T)=Z(t).
Относительно специальных случаев системы A)
¦См. Гамилътопова система линейная, Хилла уравнение.
Лит.: [1] Ш т о к а л о И. 3., Линейные дифференциаль-
дифференциальные уравнения с переменными коэффициентами, К., I960; [2]
Еругин Н. П., Линейные системы обыкновенных диффе-
дифференциальных уравнений с периодическими и квазипериодиче-
квазипериодическими коэффициентами, Минск, 1963; [3] Я к у б о в и ч В. А.,
Старжинский В. М., Линейные дифференциальные
уравнения с периодическими коэффициентами и их приложения,
М., 1972. В. А. Якубович.
ЛИНЕЙНАЯ СИСТЕМА ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ С ПОЧТИ ПЕРИОДИЧЕСКИМИ КОЭФ-
КОЭФФИЦИЕНТАМИ — система дифференциальных урав-
уравнений
x = A(t)x + f(t), xgR", A)
где А(-): R->-Hom(R", R"), /(•): R->-R" — почти
периодические отображения; в координатной записи:
i'=2J"=1a/(«)^+ /'('). *=1> 2, ..., п,
где a,j(t) и /' (t), i, ;' = 1, . . ., п,— почти периодич.
числовые функции. Такие системы возникли в связи
с появлением Бора почти периодических функций
(см. [1]). Интерес к более узкому классу систем (A(t)
и 1 (t) — квазипериодич. отображения) появился зна-
значительно раньше в связи с рассмотрением уравнений в
вариациях вдоль условно периоцич. решений урав-
уравнений небесной механики.
Если однородная система
х=А (t)x B)
есть система с интегральной разделенностью (см. Ин-
Интегральной разделенности условие), то она почти пе-
периодическим по t Ляпунова преобразованием x=L(t)y
приводится к диагональной системе y^B(t)y с почти
периодич. коэффициентами, т. е. к такой, что сущест-
существует не зависящий от t базис в R", состоящий из век-
векторов, являющихся при каждом t?R собственными
векторами оператора В (t); в координатах по этому
базису система y = B(t)y записывается в диагональном
виде:
y'-^i>i(t)y\ 1=1,.... п.
Множество систем с интегральной разделенностью
открыто в пространстве систем B) с почти периодич.
коэффициентами, наделенном метрикой
d(At, Ла) = sup || Лх (*)—^2 (*) fl-
*sR
Имеет место следующая теорема. Пусть A (t) = CJrtD (i),
где C(;Hom(R", R"), причем собственные значения С
все действительны и различны, D (¦) — почти перио-
периодич. отображение R—>-Hom(R™, R"). Тогда найдется
г|>0 такое, что при всех е таких, что |е| <т), система
B) почти периодическим по t преобразованием Ляпу-
Ляпунова приводится к диагональной системе с почти
нериодич. коэффициентами.
Для почти периодич. отображения A (t): R—>¦ Hom(R",
R") следующие четыре утверждения эквивалентны
друг другу: 1) для всякого почти периодич. отобра-
отображения /(•): R —>- Кл у системы A) найдется почти
периодич. решение; 2) имеет место экспоненциальная
дихотомия решений системы B); 3) ни одна из систем
х=А (t)x, где A (t) = limA (tk-\-t), не имеет ненулевых
/г-*- со
ограниченных решений; 4) для всякого ограниченного
отображения /(i): R —>- R" у системы A) найдется ог-
ограниченное решение.
Лит.: [1] Бор Г., Почти периодические функции, пер. с
нем., М.— Л., 1934; [21 Р a v a r d J., Lecons sur les (onctions
presque periodiques, P., 1933; [3] E p у г и н Н. П., Линейные
системы обыкновенных дифференциальных уравнений с перио-
периодическими и квазипериодическими коэффициентами, Минск,
1963: [U М а с с е р а X.- Л., Ш е ф ф е р X.- X., Линейные
дифференциальные уравнения и функциональные пространства,
пер. с англ., М., 1970; [5J М у х а м а д и е в Э., «Докл. АН
СССР», 1971, т. 196, № 1, с. 47 — 49; [В] Итоги науки и техники.
Математический анализ, т. 12, М., 1974, с. 71—146.
В. М. Миллионщиков.
ЛИНЕЙНАЯ ТОПОЛОГИЯ на кольце А ~
кольцевая топология, для к-рой имеется фундамен-
фундаментальная система окрестностей нуля, состоящая из
левых идеалов (в этом случае топология наз. линей-
линейной слева). Аналогично, топология на левом Л-модуле
Е линейна, если имеется фундаментальная система
окрестностей нуля, состоящая из подмодулей. Наи-
Наибольшее распространение имеет адическая топология,
базис к-рой задается степенями нек-рого идеала.
Отделимый линейно топологизированный Л-модуль
Е наз. линейно компактным модулем,
если любой базис фильтра, состоящий из аффинных
линейных подмногообразий в Е (т. е. подмножеств вида
х-\-Е', где r?E, a E'— подмодуль в Е), имеет точку
прикосновения. Любой модуль конечного типа над
полным локальным нётеровым кольцом линейно ком-
компактен.
Лит.: [1] Бур баки Н., Коммутативная алгебра, пер.
с франц., М., 1971. В. И. Данилов.
ЛИНЕЙНАЯ ФОРМА — 1) Однородный многочлен
первой степени.
2) Линейная функция (однородная) на векторном
пространстве V над полем к со значениями в поле к
ЛИНЕЙНАЯ ФОРМА ОТ ЛОГАРИФМОВ алгебраи
ческих чисел — выражение вида
L = р\ log «х + . .. + р„ log an.
Эффективные оценки снизу для \L\ в предположении,
что коэффициенты EЬ . . ., Р„ — рациональные или
алгебраич. числа, a logccb . . ., logan — фиксирован-
фиксированные ветви логарифмов, линейно независимые над
полем Q, играют большую роль в теории чисел.
Когда р1,,. . ., (Зл—рациональны, выполняется неравен-
неравенство |L| > e~ClB, где В = тах |В,!, а ct>0 и зависит
только от чисел аь. . ., ап. Методы, с помощью к-рых
устанавливаются нетравиальные оценки снизу для
\L\, принадлежат теории трансцендентных чисел.
В случае ге=2 ряд неравенств, справедливых для В,
превосходящих нек-рую эффективно вычислимую гра-
границу, получен А. О. Гельфондом A935—49). Лучшее
из них имеет вид \L\ > е~т~ в.
В 1948 им же доказано, что при любом п для всех
достаточно больших В имеет место неравенство
| L \ > е . Последний результат был, однако, лишь
теоремой существования, а граница для В, начиная с
к-рой выполнялось это неравенство, из доказательства
не могла быть определена. Эффективные оценки \L\
при любом п были получены в 1966 А. Бейкером
(см. [2]) на основании метода Гельфонда.
Пусть ге^2, (Xj, . . ., ап — ненулевые алгебраич.
числа, высоты и степени к-рых не превосходят соот-
соответственно А и rf, 4^:4, d~^k. Пусть, далее, 0<8<1
и logab . . ., loga,, — главные значения логарифмов.
Если существуют целые рациональные Ь1у . . ., Ь„,
|6|В, такие, что
U< |*1loga1+...+6nlogan| < е-ев,
В < D»2е-Ч2о
В связи с различньши задачами получено большое
количество эффектных оценок Л. ф. от л. Степенная
по порядку величины В оценка для | L | вчервые была
получена в 1968 Н. И. Фельдманом [3].
Пусть га>2, аь . . ., а„ — алгебраич. числа, logaj,
. . ., logan — фиксированные ветви логарифмов, ли-
линейно независимые над Q. Существуют эффективные
постоянные с2>0, Kj>0 такие, что для любых алге-
алгебраич. чисел р0, Pj, . . ., р„, высота к-рых не превос-
превосходит В, имеет место неравенство
(постоянные с2 и х1 явно выписываются в зависимости
от чисел сед, . . ., ап и степеней E0, . . ., Р„).
С помощью оценок Л. ф. от л. алгебраич. чисел
найдены границы для решений различных классов
диофантовых уравнений (уравнений Туэ, гипер-
эллиптич. уравнений, уравнений, задающих кривые
рода I, и др.). Оценки Л. ф. от л. позволили определить
границы для дискриминантов мнимых квадратичных
полей с числом классов 1 и 2. В теории чисел приме-
применяются также р-адические аналоги теорем об оценках
Л. ф. от л. алгебраич. чисел.
Лит.: [1] Г е л ь ф о н д А. О., Трансцендентные и алгеб-
алгебраические числа, М., 11152; [2] Baker А., в кн.: Actes du
Congrfes International des Mathematiciens, [Nice], 1970, t. 1,
P., 1971, p. 19—2ti: [3] Фельдман Н. И., «Матем. сб.»,
!0S8, т. 77, Л» 3, с. 423—36; [4] его же, «Изв. АН СССР. Сер.
ымтем.», 1971, т. 35, № 5, с. 973—90; [5] Актуальные проблемы
аналитической теории чисел, Минск, 1974. Ю. В. Нестеренко.
ЛИНЕЙНАЯ ФУНКЦИЯ — функция вида y=kx+b.
Основное свойство Л. ф.: приращение функции про-
пропорционально приращению аргумента. Графически
Л. ф. изображается прямой линией.
Л. ф. п переменных хи хг, . . ., хп — функ-
функция вида
где аи а2, . . ., а,п а — некоторые фиксированные
числа. Областью определения Л. ф. является все
и-мерное пространство переменных хи ж2, . . ., х„,
действительных или комплексных. При a=0 JI. ф.
наз. однородной, или линейной, формой.
Если все переменные хг, х2, . . ., хп и коэффици-
коэффициенты аи аг, . . ., ап,а — действительные числа, то гра-
графиком Л. ф. в («+1)-мерном пространстве перемен-
переменных хг, х2, . . ., хп, у является n-мерная гиперплос-
кость y=a1x1Jra,2x2-\-. . ,-\-апхп-\-а, в частности при
n=i—прямая линия на плоскости.
Термин «Л. ф.», или, точнее, линейная однородная
функция, часто применяется для линейного отображе-
отображения векторного пространства X над некоторым полем К
в это поле, т. е. для такого отображения /: X —>- К,
что для любых элементов х' ? X, х"'? X и любых а' ? А',
а"'? К справедливо равенство
причем в этом случае вместо термина «Л. ф.» исполь-
используются также термины — линейный функцио-
функционал и линейная форма. Л Д. Кудрявцев.
ЛИНЕЙНО КОМПАКТНЫЙ МОДУЛЬ — топологи-
топологический модуль над топологии, кольцом, обладающий
базисом окрестностей нуля, состоящим из подмодулей,
и в к-ром всякая центрированная система, состоящая
из классов вычетов по замкнутым подмодулям, имеет
непустое пересечение. Всякий Л. к. м. является пол-
полной топология, группой.
Л. к. м. наз. линейно компактным мо-
модулем в узком смысле, если всякий не-
непрерывный гомоморфизм на топологии, модуль, об-
обладающий базисом окрестностей нуля из подмодулей,
открыт. Топологич. модуль является в узком смысле
Л. к. м. тогда и только тогда, когда он — полная
топологич. группа и всякий его фактормодуль по от-
открытому подмодулю — артинов модуль. В частности,
артинов модуль в дискретной топологии является
Л. к. м. в узком смысле. Таким образом, Л. к. м. в
узком смысле — топологич. аналоги артиновых мо-
модулей.
Прямые произведения, замкнутые подмодули, фак-
тормодули но замкнутым подмодулям и непрерывные
гомоморфные образы, обладающие базисом окрестно-
окрестностей нуля из подмодулей, Л. к. м. (Л. к. м. в узком
смысле) сами будут Л. к. м. (Л. к. м. в узком смысле).
Лит,: [1] Л е ф ш е ц С, Алгебраическая топологии, пер.
с англ., М., 1949; [2] Zelinsky D., «Amer. J. Math.», 1953,
v. 75, № 1, p. 79—90; [31 Leptin H., «Math. Z.». 1955, Bd 62,
S. 241 — 67; 1957, Bd 66, S. 289 — 327. В. II. Арнаутов.
ЛИНЕЙНО РАЗДЕЛЕННЫЕ РАСШИРЕНИЯ и о-
л я к — два подрасширения А и В нек-рого расши-
расширения Q поля к такие, что подалгебра, порожденная
А и В, в Q устроена как тензорное произведение А@В
над к. Пусть А и В — произвольные подкольца рас-
расширения Q поля к, содержащие к, и С — подкольцо
поля Q, порожденное кольцами А и В. Всегда сущест-
существует представление ср: A(g)B на алгебру С, ставящее
в соответствие элементу х(?)у ? A (>?)В, x?A, у(ЦВ,
произведение ху из С. Алгебры А и В наз. лине й и о
разделенными над к, если представление <р
является изоморфизмом A(g)B на С. В этом случае
А[\В = к. Для того чтобы А и В были линейно разде-
разделены над к, достаточно существования базиса алгебры
В над к, к-рый независим над А. Если А конечное
расширение поля к, то степень расширения [В(А):В]
не превосходит степени расширения [А.к] и равенство
имеет место в том и только в том случае, когда А/к
и В/к линейно разделены.
Лит.: [1] Б у р б а к и Н., Алгебра. Многочлены и поля.
Упорядоченные группы, пер. с франц., М., 1965. О. А. Иванова.
ЛИНЕЙНО РЕГУЛЯРНЫЙ СЛУЧАЙНЫЙ ПРО-
ПРОЦЕСС — стационарный в широком смысле случайный
процесс |{i), —oo<t<oo, для к-рого выполнено сле-
следующее условие регулярности:
оо, *) = 0,
где i/j (— оо, () — замкнутая в среднем квадратичном
линейная оболочка значений ?(«)> s<:i (здесь предпо-
предполагается, что Е?(г) = О). Регулярность означает не-
невозможность (линейного) прогнозирования процесса
|(i) на слишком далекое будущее; точнее, если f (i-f-и)
есть наилучший линейный прогноз для ?({+«) по зна-
значениям ?(*), *¦<*:
)-%(t + u)\* = min E|g(t + «)~П|2.
rietfg (-co, <)
то
lim l(t + u) = O.
Ы ~> со
Необходимым и достаточным условием регулярности
(одномерного) стационарного процесса является на-
наличие спектральной плотности j (к) такой, что
Аналитич. условия регулярности многомерных и бес-
бесконечномерных стационарных процессов выглядят слож-
сложнее. В общем случае, когда спектральная плотность
/(Я) представляет собой положительную операторную
функцию в нек-ром гильбертовом пространстве, усло-
условие регулярности равносильно тому, что /(А.) допу-
допускает факторизацию вида
где ф(Х), —оо<Х<оо,— граничное значение опера-
операторной функции ф(Х.-|-ш,), (х —*- О, аналитичной в ниж-
нижней полуплоскости z=A,+ 'H, |л<0.
Всякий стационарный в широком смысле процесс
t,(t) допускает разложение в ортогональную сумму
ми \{t) — линейно регулярный, а т) (t) — линейно
сингулярный процесс, т. е. стационарный
в широком смысле случайный процесс, для к-рого
при этом
У/g ( 00, *)<=#?(— 00, i) И Ят)(—00, t)C=//j(—00. t)
при всех I.
Лит.: Ш Розанов Ю. А., Стационарные случайные
процессы, М., 1963; [2] его же, Теория обновляющих про-
процессов, М., 1974. Ю. А. Розанов.
ЛИНЕЙНО СВЯЗНОЕ ПРОСТРАНСТВО — тополо-
топологическое пространство, в к-ром любые две точки можно
соединить непрерывным образом простой дуги, т. е.
пространство X, для любых двух точек у0 и хх к-рого
существует такое непрерывное отображение /: / —v X
единичного отрезка /=[0, 1], что /@) = ж0 и /A) = ж1.
Эквивалентным образом, Л. с. п.— это пространство,
в к-ром любые две точки можно соединить простой
дугой, или, что то же самое,— это пространство, любое
отображение нульмерной сферы в к-рое гомотопно
постоянному отображению. Всякое Л. с. п. связно.
Непрерывный образ Л. с. п. линейно связен.
Л. с. п. играют важную роль в гомотопич. тополо-
топологии. Если пространство X линейно связно и х0, хг?Х,
то гомотопич. группы л,п(Х, х0) и я„(Х, хг) изоморфны,
причем этот изоморфизм определяется однозначно с
точностью до действия группы лг(Х, х0). Если р:
Е —>¦ В — расслоение с линейно связной базой В, то
любые два слоя имеют один и тот же гомотопический
тип. Если р :Е —>- В — слабое расслоение (Серра
расслоение) над линейно связной базой В, то любые
два слоя имеют один и тот же слабый гомотопич. тип.
Многомерным обобщением линейной связности яв-
является k-c вязность (связность в размерности к).
Пространство X наз. связным в размерно-
размерности к, если любое отображение r-мерной сферы Sr
в X, где /•«:&, гомотопно постоянному отображению.
Лит.: [1] С п е н ь е р Э., Алгебраическая топология, пер.
с англ., М., 1971. С. А. Богатый.
ЛИНЕЙНО УПОРЯДОЧЕННАЯ ГРУППА — алгеб-
алгебраическая система G, являющаяся группой относи-
относительно операции умножения, линейно упорядоченным
множеством относительно бинарного отношения по-
порядка <: и удовлетворяющая аксиоме: для любых
элементов х, у, z?G из х^су следует xz^yz и zx<-zy.
Множество положительных элементов
Р — {x?G, х^е} Л. у. г. G обладает свойствами: 1)
РР^Р, 2J Р[]Р-1=е, 3) g~lPg^P, 4) P{]P-L^G.
Обратно, если в группе G имеется множество Р, удов-
удовлетворяющее свойствам 1) — 4), то G может быть
превращена в Л. у. г., множество положительных
элементов к-рой есть Р.
Имеется большое число признаков упорядочиваемо-
сти группы. Упорядочиваемые группы являются груп-
группами без кручения с однозначным извлечением корня.
Упорядочиваемыми являются все абелевы группы без
кручения, нильпотентные группы без кручения, сво-
свободные группы и свободные разрешимые группы. Суще-
Существуют простые и нехопфовы Л. у. г. Факторгруппа
упорядочиваемой группы по ее центру упорядочиваема.
Прямое, полное прямое и свободное произведения,
а также сплетение Л. у. г. могут быть линейно упоря-
упорядочены с продолжением порядков сомножителей. Груп-
Группа, аппроксимируемая упорядочиваемыми группами,
сама упорядочиваема. Для упорядочиваемых групп
справедлива локальная теорема (см. Мальцева локаль-
локальные теоремы). Л. у. г. вкладывается в мультиплика-
мультипликативную группу линейно упорядоченного тела и в
простую Л. у. г. Класс упорядочиваемых групп —
аксиоматизируемый. Л. у. г. является топологической
группой с интервальной топологией. Л. у. г. является
архимедовой группой тогда п только тогда, когда она
не имеет нетривиальных выпуклых подгрупп. Любая
архимедова Л. у. г. изоморфна нек-рой подгруппе
аддитивной группы действительных чисел с естествен-
естественным порядком. Множество всех выпуклых подгрупп
Л. у. г. образует полную ннфраинвариант-
н у ю систему, факторы к-рой архимедовы, и,
значит, Л. у. г. обладают разрешимыми нормальными
системами (см. Подгрупп система).
Специфическими для теории Л. у. г. являются во-
вопросы, связанные с продолжением частичных порядков
(см. Доупорядочиваемая группа). Имеется ряд обобще-
обобщений понятия Л. у. г.
Лит.: [1] К о к о р и н А. И., К о п ы т о в В. М.,
Линейно "упорядоченные группы, М., 1972; [2] Фукс Л.,
Частично упорядоченные алгебраические системы, пер. г англ.,
М., 1965; [3] Б у р б а к и Н., Алгебра. Многочлены и поля.
Упорядоченные группы, пер. с франц., М., 1965.
А. И. Нокорин, В. М. Когытов.
ЛИНЕЙНО УПОРЯДОЧЕННОЕ МНОЖЕСТВО,
цеп ь,— частично упорядоченное множество, в к-ром
для любых двух элементов а и b имеет место а<.Ь
или 6<:а. Подмножество Л. у. м. само является Л. у. м.
Всякий максимальный (минимальный) элемент Л. у. м.
оказывается наибольшим (наименьшим). Важнейший
частный случай Л. у. м.— вполне упорядоченные мно-
множества. Среди подмножеств частично упорядоченного
множества, являющихся Л. у. м., особенно важную
роль играет композиционный ряд. Сечением Л.у.м.
Р наз. разбиение его на два подмножества А и В так,
что A\JB=P, А [)В — пусто, A^BV и В<=Ай, где
Классы А та В наз. нижним и верхним клас-
классами сечения. Различаются следующие типы сечений:
скачок — в нижнем классе имеется наибольший
элемент, а в верхнем — наименьший; д е д е к и н-
дово сечение — в нижнем (верхнем) классе име-
имеется наибольший (наименьший) элемент, но в верхнем
(нижнем) классе нет наименьшего (наибольшего);
щель — в нижнем классе нет наибольшего элемента,
а в верхнем — наименьшего. Л. у. м. наз. непре-
непрерывным, если все его сечения дедекиндовы. Под-
Подмножество D Л. у. м. Р наз. плотным, если каж-
каждый неодноэлементный интервал множества Р содер-
содержит элементы, принадлежащие D. Л. у. м. действи-
действительных чисел может быть охарактеризовано как не-
непрерывное Л. у. м. в к-ром нет ни наибольшего, ни
наименьшего элементов, но содержится счетное плот-
плотное подмножество. Всякое счетное Л. у. м. изоморфно
некоторому подмножеству Л. у. м. всех двоичных
дробей отрезка [0, 11. Решетка L изоморфна подмно-
подмножеству Л. у. м. целых чисел тогда и только тогда,
когда каждая ее подрешетка является ретрактом.
Лит.: [II Александров П. С, Введение в общую тео-
теорию множеств и функций, М.— Л., 1948; [2] его же. Введе-
Введение в теорию множеств и общую топологию, М., 1977; [3] Б у р-
баки Н., Теория множеств, пер. с франц., М., 19в5.
Л. А. Скорняков.
ЛИНЕЙНОГО ПРЕДСТАВЛЕНИЯ ИНВАРИАНТ —
вектор ?=/=0 в пространстве Е представления я группы
G такой, что я (#)!;=? для всех g?G. Л. п. и. алгебры
Ли X — вектор ?=/=0 в пространстве Е представления
я такой, что я(г)|=0 для всех х?Х. В частности, если
я — представление линейной группы в пространстве
полилинейных функций, данное определение Л. п. и.
совпадает с классическим. Л. п. и., связанные с ог-
ограничениями неприводимых представлений группы на
подгруппу, играют существенную роль в теории пред-
представлений групп и алгебр Ли.
Лит.: [1] В с й л ь Г., Классические группы, их инвариан-
инварианты и представления, пер. с англ., М., 1947; [2] Ж е л о б е н-
к о Д. П., Компактные группы Ли и их представления, М.,
1970. А. И. Штерн.
ЛИНЕЙНОГО СОПРЯЖЕНИЯ ЗАДАЧА, задача
Римана, задача Гильберта, задача
Гильберта — Привалова, задача Ри-
Римана — Привалов а,— одна из основных гра-
граничных задач теории аналитических функций, форму-
формулируемая в простейшем случае следующим образом.
Пусть L — простой гладкий замкнутый контур, де-
делящий плоскость на внутреннюю область D + и до-
дополнительную к ней область D~, содержащую беско-
бесконечно удаленную точку. Пусть на L заданы две функ-
функции G(t) и g(t), удовлетворяющие условию Гёльдера
(условию Н), причем G(t)=^O всюду на L. Требуется
найти две функции Ф±(г), аналитические соответст-
соответственно в D±, непрерывные вплоть до контура, за ис-
исключением конечного числа точек t^, где для них
допустимы разрывы при соблюдении условия
удовлетворяющие на контуре L краевому условию
при этом функция G(t) наз. коэффициентом
задачи. Целое число
x=IndG(t) = Iir^ d arg С (t) = ~ J din G(t)
наз. индексом коэффициента^;) и одно-
одновременно индексом Л. с. з. Пусть отыскивается
решение, удовлетворяющее условию Ф~ (оо) = 0. Тогда
при х>0 однородная Л. с. з. (т. е. когда #(г)=0) и
неоднородная Л. с. з. безусловно разрешимы; решения
зависят линейно от х произвольных постоянных и
выражаются линейно через многочлен степени х — 1
с произвольными коэффициентами. При х = 0 однород-
однородная Л. с. з. имеет лишь тривиальное нулевое решение,
а неоднородная задача разрешима безусловно и одно-
однозначно. При х<0 однородная задача имеет лишь
нулевое решение, неоднородная задача — единствен-
единственное решение лишь при выполнении |х| условий разре-
разрешимости, к-рые могут быть выражены линейно через
многочлен с произвольными коэффициентами.
Решение Л. с. з. во всех случаях представляется
в замкнутой форме — в квадратурах черен
интегралы типа Коши. Предельные значения искомых
функций на контуре необходимо удовлетворяют ус-
условию Н. Перечисленные выше результаты без изме-
изменения переносятся на случай многосвязной области
D +, ограниченной конечным числом простых взаимно
непересекающихся замкнутых кривых. Случай кон-
контура, составленного из разомкнутых кривых, пред-
представляет ту особенность, что на концах кривых кон-
контура решения Л. с. з., в зависимости от выбираемого
класса решений, могут обращаться в бесконечность
или оставаться ограниченными. Индекс зависит or
выбираемого класса решений. Индекс в классе решений
с допустимой на конце бесконечностью порядка меньше
единицы (интегрируемая бесконечность) на единицу
больше, чем индекс в классе ограниченных на этом
конце решении. Соответственно этому на единицу
увеличивается число линейно независимых решений
или уменьшается число условий разрешимости. Ана
логичное положение имеет место в случае, когда коэф-
коэффициент G(t) имеет разрывы 1-го рода; решение в точ-
точках разрыва ведет себя так же, как на концах контура.
В общем случае, когда контур состоит из конечного
числа расположенных как угодно замкнутых и разомк-
разомкнутых кривых, Л. с. з. решается теми же методами,
что и упомянутые выше простые случаи; при этом по-
получаются аналогичные результаты. Нек-рые трудности
представляет исследование решения в точках, где
встречается несколько кривых контура.
В случае, когда G(t), g(t) только непрерывны, но
не удовлетворяют условию Н, сформулированные
выше результаты остаются в силе, за исключением того,
что здесь предельные значения решений существуют
лишь при стремлении к контуру по некасательным
путям, при этом они не непрерывны, а Ф± (t)^Lp <:
любым р>0; если функция G(t) непрерывна, g(t)^Lp,
то и Ф± (t)?Lp. Наиболее общим предположением для
коэффициента G{t), при к-ром решена Л. с. з., яв-
является класс измеримых функций с нек-рым дополни-
дополнительным условием на величину скачка аргумента;
при этом g(t)?Lp.
Рассматривались Л. с. з. с бесконечным индексом,
в к-рых в качестве контуров брались простые гладкие
кривые с одним или обоими концами, уходящими в
бесконечность. Исследованы случаи: 1) степенного
порядка роста, когда при UI —*¦ оо выполняются асимп-
тотич. равенства
IndG(t)~± M|P
@<р<оо для случая одного бесконечного конца,
0<р<1 для обоих бесконечных концов); 2) логариф-
логарифмического порядка, когда при |i| —v оо
IndC(t) ~± |1паг|, 0 < а< оо.
В обоих случаях при положительном бесконечном ин-
индексе число линейно независимых решений бесконечно
и выражается через целую функцию, вид к-рой за-
зависит от порядка индексов. При отрицательном бес-
бесконечном индексе однородная задача не имеет нетри-
нетривиальных решений, а неоднородная разрешима лишь
при выполнении бесконечного множества условий
разрешимости. Главную трудность представляет вы-
выделение конечных решений.
Исследовалось решение Л. с. з. на римановой по-
поверхности и равносильной ей задачи на фундаменталь-
фундаментальной области автоморфной функции, принадлежащей
нек-рой группе подстановок, в автоморфных функциях
этого класса. Число решений или условий разреши-
кости зависит от индекса, а в нек-рых (особых) случаях
также от рода поверхности или фундаментальной
области.
Если в условии (*) считать G матрицей, а Ф^, #
векторами («-мерными), то возникает Л. с. з. для
кусочно аналитического вектора.
Этот случай значительно сложнее, чем рассмотренный
выше скалярный случай (ге=1). Исследование произ-
производится сведением к системе интегральных уравнений.
Число линейно независимых решений или условий
разрешимости зависит от га независимых величин, наз.
частными индексами, зависимость к-рых
от матрицы коэффициентов в явном виде не установ-
установлена. Важную роль играет индекс определителя мат-
матрицы G, наз. суммарным индексом задачи.
Впервые Л. с. з. (для кусочно аналнтич. вектора)
встречается у Б. Римана (В. Riemarm, см. [1]) в связи
с решением задачи о построении линейного дифферен-
дифференциального уравнения по заданной группе подстановок
(группе монодромии). Однако в том примерно виде,
как она сформулирована выше, Л. с. з. была впервые
рассмотрена Д. Гильбертом A905, см. [2]) при менее
общих условиях; первые результаты (альтернативного
характера) были получены им путем сведения к инте-
интегральному уравнению. И. Племель A908, см. [3]),
использовав впервые интегралы типа Копт, свел век-
векторную Л. с. з. к интегральному уравнению и пол-
полностью решил поставленную Риманом задачу диффе-
дифференциальных уравнений. Неоднородную Л. с. з. (в
несколько иной постановке) впервые рассмотрел
И. И. Привалов [4]; его результаты относятся главным
образом к теоретико-функциональным обобщениям.
Л. с. з. имеет большое число приложений. Главные
из них — в теории сингулярных интегральных урав-
уравнений. Даны обобщения в различных направлениях —
т. н. Л. с. з. со сдвигом, сопряжением, дифференци-
дифференциальная, для обобщенных аналитич. функций п другие.
Теория Л. с. з., ее обобщений и приложений наиболее
полно отражена в [5], |6).
Лит.: [1] Р и м а н Б., Сочинения, пер. с нем., М.— Л.,
1948, с. 176—82; [2] Hi lbcrt D., Grundzutte einer allsmet-
nen Theorie der linearen Integralgleichungen, 2 Aufl., Lpz.,— В.,
1924; [3] PI em el] J. «Monatsh. Math.», 1908, Bd 19, S.
211—45; [4] Привалов И. И., «Матем. сб.», 1934, т. 41, J* 4,
с. 519 — 526; [5] М у с х е л и ш в и л и Н. И., Сингулярные ин-
интегральные уравнения, 3 изд., М., 1968, гл. 2; [Н] Г а х о в
Ф. Д., Краевые задачи, 3 изд., М., 1977. Ф. Д. Гахов.
ЛИНЕЙНОЕ ГИПЕРБОЛИЧЕСКОЕ УРАВНЕНИЕ И
СИСТЕМА — дифференциальное уравнение (и система)
с частными производными вида
у к-рого в любой точке х= (х0, .г,, . . ., хп) области его
задания Q среди действительных переменных у0, ух,
. . ., г/„ можно выделить (в случае надобности — после
надлежащего аффинного преобразования независимых
переменных) одно переменное, напр. (/0==л, таким
образом, чтобы для всех точек У= (у1, . . ., у„) из га-
мерного евклидова пространства R" характеристиче-
характеристическое уравнение (относительно Я)
имело ровно Nm действительных корней. Здесь а=
-¦= (а0, . . ., а.,,) — вектор с неотрицательными цело-
целочисленными координатами, |a|=^; ,=oay — порядок
дифференциального оператора Z>a=D™° . . . D"n ,
Dj=dldxj, / = 0, 1, . . ., n, m — порядок системы A),
аа (х) — заданная в области Q квадратная действитель-
действительная матрица порядка N, и (х)= \\uj {x)\\, / = 1, . . .,
N — искомый вектор-столбец, f(x) — заданный в Q
вектор с N компонентами.
Типичным примером является волновое уравнение
ц, , =^ и . C)
К Л. г. у. и с. приводят многие задачи матсматич.
физики.
Поверхность S: ф(г) = 0 наз. характеристи-
характеристической в точке х, если grad ф=^=0 и Q (x, grad ф) —
= 0, где
Q (*, у) = Q (*, г/о, Y) = dot 2, а ,=,„ «а (*) Уа
— характористич. форма системы A). Если Q (х, у) = 0,
то говорят, что вектор у задает в точке жхаракте-
р и с т и ч е с к о е направление. Поверхность
S наз. характеристической поверх-
поверхностью (или характеристикой) для си-
системы A), если
Q (х, grad(p)=O для всех x?S.
Поверхность, не имеющая характерпстпч. направле-
направления нормали ни в одной точке, наз. свободной
поверхностью. На свободной поверхности ранг
характеристической матрицы
А (х, I/) = Л (ж, 1/0, У)^= 2 ct| = maa(-r) Уа> У = grнdф,
равен Лг, в то время как на характеристич. поверх-
поверхности S он меньше Л'. Характеристика S наз. п р о-
с т о и, если для нек-рого / и для всех x?S
Q (.г, grаdф)?i0.
В противном случае характеристику наз. кратной.
Иногда характеристику наз. простой, если ранг матри-
матрицы 4 (х, grad ф) равен N — 1.
Система A) наз. гиперболической в точ-
точке х относительно гиперплоскости
So: z0—0, если матрица А (.г, 1, !/) = я,л,0 , . . ., „ не-
невырожденная (т. е. поверхность S свободная) и все
корни K-^X/i, k=\, . . ., тХ, характеристич. уравнения
Q{x, X, Y)^-0 действительные для всех точек Y?Rn.
Система A) наз. гиперболической в обла-
области Q относительно So, если она гиперболична от-
относительно So в каждой точке x?Q.
Важным классом гиперболич. уравнений и систем
являются строго гиперболич. уравнения и системы,
к-рые иногда наз. вполне гиперболиче-
гиперболическими системам и, или гиперболиче-
гиперболическими в узком смысл е. Система A) наз.
строго гиперболической системой,
когда все корни k=kk характеристич. уравнения раз-
различны для любого ненулевого вектора Y?R". Харак-
Характеристики строго гиперболпч. уравнения (или системы'/
являются простыми. Строго гиперболические (относи-
(относительно So) системы примечательны тем, что для них
корректно поставлена задача Кошн
ж). * = 0, 1, .... in-l, D)
при одних только предположениях достаточной глад-
гладкости коэффициентов аа(х), /(х) системы A) и началь-
начальных данных (начальных функций) г|з^(ж), ж= (аг0, . . .,
хп). Существуют примеры гиперболических, но не
строго гиперболич. уравнений вида A) (даже с постоян
ними коэффициентами при производных порядка т),
для к-рых задача Коши поставлена некорректно.
Решение и (х) задачи Коти D) для волнового урав-
уравнения C) выписывается в явном виде, и оно в случае,
когда re=0 (mod 2) и только тогда, обладает свойством;
значение и (х) в вершине х* характеристиче-
характеристического конуса \Х— Х*\ = хо —ж0, Х-- (х1, . . .,
хп), зависит только от значения начальных данных
i|>o(.?") игр! (х) и их производных на основании \Х — Х*\ =
= хо, хо=О, этого конуса (т.н. Гюйгенса принцип).
Для Строго гиперболических относительно So урав-
уравнений и систем исследован вопрос о диффузии волн
и о лакунах. Исчерпывающий ответ дан в случае
уравнения с постоянными коэффициентами вида
Для одного (скалярного) уравнения с постоянными
коэффициентами аа (я) — «а^const определение строгой
гиперболичности обобщено следующим образом. Урав-
Уравнение A) наз. гиперболическим относи-
относительно ненулевого вектора y?R" + 1,
если
и существует такое действительное число %0, что для
всех ?=(?„, . . ., UeR" + 1 ^Х
Из всех линейных уравнений с постоянными коэф-
коэффициентами только для уравнений, гиперболических
в этом смысле, задача Коши поставлена корректно
при произвольных достаточно гладких начальных
функциях, заданных на гиперплоскости
В частности, волновое уравнение C) является гипер-
гиперболическим в указанном смысле относительно любого
вектора, для к-рого
Существуют различные обобщения определения строго
гиперболич. уравнений и систем. В основном это такие
уравнения и системы, к-рые полностью характеризу-
характеризуются тем, что для них однозначно разрешима задача
Коши с данными на свободной поверхности при любых
достаточно гладких начальных функциях без всяких
ограничений роста на бесконечности.
Другим важным классом линейных гиперболич.
систем 1-го порядка является класс симметрических
гиперболич. систем. Система
2"=0 а/(*) и* +Ь (*)» = /(*), E)
где aj(x), b(x) — заданные в области Q квадратные
матрицы порядка N, а и (х) — искомый вектор из N
компонент, наз. симметрической гипер-
гиперболической системой в области Q, если
матрицы а/ (.г) симметрические (или симметризуемые
одновременно одним и тем же преобразованием) и в
кая^дой точке существует пространственно
ориентированная гиперплоскость,
т. е. гиперплоскость, нормаль к-рой у= (г/0, . . ., уп)
обладает тем свойством, что матрица 7 ff=<tii ,-а ,¦ (х)
положительно определена. Если для симметрической
гиперболич. системы E) с достаточно гладкими коэф-
коэффициентами заданные начальные функции и правая
часть имеют интегрируемые с квадратом обобщенные
частные производные порядка р, то существует един-
единственное обобщенное решение задачи Коши с тем же
числом интегрируемых с квадратом частных производ-
производных. К симметрическим гиперболич. системам сводится
любое строго гиперболич. уравнение 2-го порядка.
Уравнение A) 2-го порядка в классе регулярных
в области ii решений можно записать в виде
+ c(x)u = f(x), @)
где akj(x)~ajk(x), bj(x), с(х) и /(х) — заданные в Q
действительные функции. Уравнение F) гиперболично
в области Q, если в каждой точке этой области все
характеристпч. числа матрицы a(x)=\\ajii(x)\\, к, ; = 0,
. . ., п, старших коэффициентов a.kj(x) отличны от
нуля, причем одно из этих чисел отличается по знаку
от всех остальных. По отношению к уравнению F),
наряду с характеристич. поверхностью, выделяют два
типа гладких поверхностей: пространственно
ориентированные поверхности и
временным образом ориентирован-
ориентированные поверхности. Если поверхности заданы
уравнением вида <р(г) = О, то на поверхности первого
тина Q (,r, gradtp) >0, а на поверхности второго типа
Q{x, grad(p)<0, где
Q (х, у) = 2", /=0 аы (ж) MkV'-
Задача Коши для гиперболич. уравнений с начальными
данными на временным образом ориентированных
поверхностях, вообще говоря, не является корректно
поставленной.
Гиперболич. уравнение
ь>
c(x)u =
наз. равномерно (или регулярн о\ гипер-
гиперболическим в области Q, если существует такое
положительное число 8, что
для всех х из Q и любого ненулевого вектора (?ь . . .,
Sn)€^ra- При п=1 неравенство
aoi — яооаи > 0 для всех x^Q
представляет собой необходимое и достаточное условие
равномерной гиперболичности уравнения F) в обла-
области Q. Уравнение колебания струны
является типичным представителем линейных равно-
равномерно гиперболич. уравнений 2-го порядка с двумя
независимыми переменными. Общее решение этого
уравнения в любой выпуклой области Q плоскости R2
дается Д'Аламбера формулой:
где / и g — произвольные функции.
Гиперболич. уравнение F) при /г=1 после неособой
действительной замены переменных х0 и хг приводится
кнорма л ьному (каноническом у) в иду
"yoyo~"yiy> + ^ (У) "г/о + Я (у) "!/, + C (у) u = F (у), G)
У = (Уо- Ух)-
Для гиперболич. систем, записанных в виде G), где
А (у), В (у) и С (у) — заданные действительные квад-
квадратные матрицы порядка N, F(y) — заданный, аи —
искомый векторы с N компонентами, Римана методом
полностью исследован вопрос о корректности задачи
Коши с начальными данными на нехарактеристиче-
нехарактеристической (свободной) кривой и Гурса задача с данными
на двух пересекающихся характеристиках.
Основными задачами для гиперболич. уравнений
являются: Коши задача, Коши характеристическая
задача и смешанная задача (см. также Смешанная
задача для гиперболического уравнения и системы).
При исследовании основных задач важную роль
играют фундаментальные решения, к-рые позволяют
получать различные (интегральные) представления
регулярных и обобщенных решений и установить их
структурные и качественные свойства, в частности
изучить вопрос о фронте волны и распространении
разрывов.
Уравнение F) паз. у л ь т р а г и н е р б о л и ч р-
с к и м уравнением в области Q, если в
каждой точке z?Q все характеристич. числа мат-
матрицы а (х) отличны от нуля, причем по крайней мере два
из них отличаются по знаку от всех остальных, число
к-рых не ниже двух. Примером ультрагиперболич.
уравнения является уравнение вида
к-рое обладает следующим свойством: если и (,т, у) —
регулярное решение уравнения (8) в области Q ев-
евклидова пространства переменных х= (х0, . . ., х„),
2/= (г/о, ¦ ¦ ., уп) и (**, У*) — произвольная точка Q,
то среднее значение функции и(х*, у*), вычисленное
по сфере 2jj-o(xj — х]J = гг с центром в точке х*= (хо .
. . ., хп) и радиуса г, равно среднему значению функции
и(х*, у), вычисленному по сфере ^/¦=0(y/ — y'j)i=ir2
* *
с центром в точке г/*= (у0 , . . ., уп) и того же радиуса г.
Эта теорема широко применяется в теории линейных
гиперболич. уравнений 2-го порядка с постоянными
коэффициентами.
Лит.: [1] Н a d a m а г d J., Le probleme de Cauchy, P.,
1932; [2] Б е р с Л., Джон Ф., HI е х т е р М., Уравнения
с частными производными, пер. с англ., М., 1966; [3] Б и ц а д-
з е А. В., Уравнения смешанного типа, М., 1959; [4] его же,
Уравнения математической физики, М., 1976; [5] Владими-
Владимиров В. С, Уравнения математической физики, 2 изд., М.,
1971; [6] Гельфанц И. М., Шилов Г. Е., Обобщенные
функции и действия над ними, 2 изд., М., 1959; [7] Г о р-
дин г Л., Задачи Коши для гиперболических уравнений, пер.
с англ., М., 1961; [8] Дезин А. А., «Матем. сб.», 1459,
т. 49, .\в 4, с. 459—84; [9] Курант Р., Уравнения с част-
частными производными, пер. с англ., т. 2, М., 1964; [10] Лады-
Ладыженская О. А., Смешанная задача для гиперболического
уравнения, М., 1953; [11] Л е р е Ж.. Г о р д и н г Л..
Котахе Т., Задача Коши, пер. с франц., М., 1967; [12]
Петровский И. Г., Лекции об уравнениях с частными
производными, 3 изд., М., 1961; [13] Смирнов В. И.,
Курс высшей математики, 20 изд., т. 2, М., 1967; [14] Тихо-
Тихонов А. Н., Самарский А. А., Уравнения математиче-
математической физики, 4 изд., М., 1972; [15] Хёрмандер Л., Линей-
Линейные дифференциальные операторы с частными производными,
пер. с англ., М., 1965. А. М. Нахцшев.
ЛИНЕЙНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
В БАНАХОВОМ ПРОСТРАНСТВЕ — уравнение вида
A)
где A0(t), A1(t) при каждом t — линейные операторы в
банаховом пространстве Е, g(t) — заданная, а и (t) —
искомая функции со значениями в Е; производная и
понимается как предел по норме Е разностного отно-
отношения.
1. Линейное дифференциальное уравнение с ограни-
ограниченным оператором. Пусть An(t) и Ax(t) при каждом
t — ограниченные операторы, действующие в Е. Если
оператор A0(t) имеет при каждом t ограниченный
обратный, то уравнение A) разрешается относительно
производной и принимает вид
u = A(t)u+f(t), B)
где A (t) — ограниченный оператор в пространстве Е,
f(t) и u(t) — функции со значениями в Е. Если функ-
функции A (t) и /(?) непрерывны (или, более общо, изме-
римы и интегрируемы на каждом конечном промежутке),
то решение задачи Коши:
u = A(t)u, u{s)--=u0, C)
существует при любом ио?Е и задается формулой
u(t)=U(t, s)u0,
где
U (t, s) = I-
— эволюционный оператор уравнения и = А (t)u. Ре-
Решение задачи Когаи для уравнения B) определяется
по формуле:
u(t) = U (t, s)«o+^ U (t, T)/(T)dx.
Из D) вытекает оценка
||t' (t, S)||<exp {\[\\A(x)\\dxy, E)
ее уточнение
\\U (t, *)||<ехр(^гд(т)Л}, E')
где г^(т).— спектральный радиус оператора А (т).
Эволюционный оператор обладает свойствами
U(s,s) = I, U {t, т) U (т, s) = U (t, s),
U (t, т) = [Е/ (т, ()]-!.
Основное внимание при изучении уравнения B)
уделяется поведению его решений на бесконечности в
зависимости от поведения A (t) и /((). При этом важной
характеристикой уравнения является генераль-
генеральный (или особый) показатель
х= Urn —In || U (x + s, s)||.
Т. S -»• за
Детально изучены уравнения с периодическими и
почти периодическими коэффициентами (см. Качест-
Качественная теория дифференциальных уравнений в банахо-
банаховом пространстве).
Уравнение B) можно рассматривать и в комплекс-
комплексной плоскости. Если функции A (t) и /(?) голоморфны
в односвязной области, содержащей точку s, то фор-
формулы C), D), E), E') остаются в силе, если под инте-
интегралами понимать интегралы по спрямляемому пути,
соединяющему s и t.
Ряд других вопросов возникает в случае, когда ис-
исходное линейное уравнение неразрешимо относительно
производной. Если оператор A0(t) ограниченно обра-
обратим всюду, за исключением одной точки, напр. ?=0,
то уравнение в пространстве Е приводится к виду
a(t)il = A(t)u+f(t), F)
где a (t) — скалярная функция и а@) = 0. Здесь ос-
основное внимание уделяется изучению поведения ре-
решений в окрестности нуля, при этом различаются
аналитический и неаналитический случаи.
Аналитический случай. Для простей-
простейшего уравнения
с постоянным оператором А эволюционный оператор
U(t)=U(t, 0) имеет вид
решения неоднозначны: при обходе вокруг нуля в по-
положительном направлении они умножаются на опе-
оператор егп1А .
Если для уравнения с регулярной особенностью
где ряд справа сходится в окрестности нуля, оператор
U it) искать в виде ряда
то для определения коэффициентов [Л*> получается
система уравнений
^_ 4и, /с1,2,...
Для разрешимости этой системы, т. е. формальной
разрешимости уравнения G), достаточно, чтобы спект-
спектры операторов Л<"> и Л@) — kl не пересекались или,
что то же, чтобы в спектре оператора Л*0' не было
точек, отличающихся на целое число. При этом ус-
условии ряд
сходится в той же окрестности нуля, что и ряд для
A (t). Если теперь имеется конечное число целых
чисел, представимых в виде разностей точек спектра
оператора Л(о), и каждое из них является изолиро-
изолированной точкой спектра трансформатора
то существует решение вида
и ц)=(/+2Г= 1и" Aп о**)и<с> 1п'- о < м i < р.
где С/й — целые функции аргумента hit, удовлетво-
удовлетворяющие при каждом е>0 условию
Если целые точки спектра трансформатора 31 явля-
являются полюсами его резольвенты, то функции U^ —
многочлены.
В случае иррегулярной особенности рассмотрено
дифференциальное уравнение
в банаховой алгебре 5J3 (напр., в алгебре ограничен-
ограниченных операторов в банаховом пространстве Е). При
нек-рых ограничениях на оператор А 1(|) оно с помощью
интегралов Лапласа сводится к уравнению с регуляр-
регулярной особенностью (т=1) в алгебре матриц с элемен-
элементами из алгебры ig.
Неаналитический случай. Пусть в
уравнении
t"'u = A(t)u + f (t), 0<г<7\
функции A (t) и / (t) бесконечно дифференцируемы.
В конечномерном случае получен исчерпывающий ре-
результат; если уравнение имеет формальное решение в
виде степенного ряда, то оно имеет бесконечно диф-
дифференцируемое на [О, Т] решение, для к-рого фор-
формальный ряд является рядом Тейлора в точке (=0.
В бесконечномерном случае имеется лишь ряд доста-
достаточных условий для существования бесконечно диф-
дифференцируемых решений.
Пусть то>1. Если спектр оператора А @) не пересе-
пересекается с мнимой осью, то существует семейство беско-
бесконечно дифференцируемых решений, зависящее от про-
произвольного элемента g~, принадлежащего инвариант-
инвариантному подпространству оператора А @), отвечающему
части спектра А @), лежащей в левой полуплоскости.
Любое непрерывное на [0, Т] решение входит в это
семейство. Если весь спектр А @) лежит в левой по-
луплоскоети, то существует только одно бесконечно
дифференцируемое решение.
Пусть го=1. Если отрицательные целые числа не
принадлежат спектру оператора А @), то существует
единственное бесконечно дифференцируемое решение.
В аналогичных предположениях относительно опера-
оператора А @) рассмотрены уравнения вида F), в к-рых
a(t) и /(t) имеют конечную гладкость и такой же глад-
гладкостью обладают решения.
Своеобразная картина возникает, когда дифферен-
дифференциальное уравнение неразрешимо относительно про-
производной при всех t, напр, когда А — постоянный
необратимый оператор. Пусть в уравнении
Аи = Ви (8)
операторы А и В — ограниченные в пространстве Е,
оператор А необратим и фредгольмов. Предполагается,
что оператор А -\-гВ непрерывно обратим при доста-
достаточно малых г. Тогда существуют такие разложения
в прямые суммы ?'=Л'A) +Л/A) и Я^=Л'B>+ЛГ<2>,
что операторы А и В отображают ЛгA) в Л'<2) и Ма>
в AfB). Оператор А обратим на Л/A) и отображает
на AfB). Подпространство JVA) конечномерно. Все
решения уравнения (8) лежат в подпространстве Л/A)
и имеют вид exp (A ~1Bt)u0, где А — сужение А на
Л/A). i<0?AfA>. Для неоднородного уравнения Аи =
= Bu-\-f(t) решение существует только при определен-
определенной гладкости i(t) и нек-рых условиях согласования
значений f(t) и ее производных с начальными данными.
Количество производных, к-рые должны иметь нек-рые
компоненты f(t), и количество условий согласования
равны максимальной длине В-присоединенных цепочек
оператора А. При выполнении указанных условий
решение задачи Копти единственно.
Если оператор А-\-гВ необратим при всех е, то все
решения уравнения (8) лежат в подпространстве,
имеющем, вообще говоря, бесконечный дефект. Ре-
Решение задачи Коши для него будет неединственным.
От функции f(t) в неоднородном уравнении требуется
бесконечное число условий дифференцируемости
и условий согласования.
2. Линейное дифференциальное уравнение с неогра-
неограниченным оператором. Пусть A0(t) обратим при каж-
каждом /, так что уравнение A) разрешается относительно
производной и принимает вид
i = A(t)u+f(t), (9)
и пусть здесь A (t) — неограниченный оператор в
пространстве Е с плотной в Е областью определения
D (A (t)), имеющий непустое резольвентное .множество,
f(t) — заданная, a u(t) — искомая функции со зна-
значениями в Е.
Даже для простейшего уравнения и = Аи с неогра-
неограниченным оператором решения задачи Коши u@) — u0
могут не существовать, могут быть неединственными,
могут быть непродолжимыми на всю полуось, поэтому
основные исследования посвящены вопросам сущест-
существования и единственности решений. Под решением
уравнения и=Аи на отрезке [0, Т] понимается функ-
функция, принимающая значения в D(A), дифференциру-
дифференцируемая на [0, Т] и удовлетворяющая уравнению. Иногда
это определение является слишком жестким и вво-
вводится понятие ослабленного решения,
как функции, обладающей теми же свойствами на @, Т],
а в точке 0 лишь непрерывной.
Пусть оператор А имеет резольвенту
R {X, А) = (А — К1)-1
при всех достаточно больших положительных X и
Tim Я-1 In || Л (Я, A)\\ = h < Т.
д—*¦ сю
Тогда ослабленное решение задачи
й = Аи, и @)=и0 A0)
единственно на отрезке [0, Т—h] и может разветвляться
при t= T—h. Если /г = 0, то решение единственно на
всей полуоси. В смысле поведения R (X, А) при X —>- оо
это утверждение является точным.
Если при каждом ua^D (А) существует единственное
непрерывно дифференцируемое на [0, Т] решение
задачи A0), то это решение продолжается на всю по-
полуось и представимо в виде и (t)= U(t)u0, где U (t) —
сильно непрерывная на [0, оо) полугруппа ограничен-
ограниченных операторов, ?/@) = /, для к-рой справедлива
оценка ||f/(t)||<:AfeCl)'. Для того чтобы уравнение
обладало таким свойством, необходимо и достаточно,
чтобы выполнялись неравенства
|1 (X — со)'л Rm (X, Л)||< М (И)
при всех Х>ы и ;«^-1, 2, . . ., где М не зависит от X
и т. Эти условия трудно проверяемы. Они выполнены,
если It (Л— со)/? (X, Л)Ц<1 и тогда ||[/(г)||«;<¦>'. Если
еще м=0, то U (t) — полугруппа сжатий. Ото
будет тогда и только тогда, когда А — максимальный
диссипативный оператор. При uo^_D (А) функция
U(t)u0 не будет дифференцируемой (во всяком случае
при f=0), ее часто наз. обобщенным реше-
решением уравнения A0). Решения уравнения и = Аи
можно строить как предел при п —»- оо решений урав-
уравнений и = Л„гг с ограниченными операторами при
тех же начальных условиях. Для этого достаточно,
чтобы операторы Ап коммутировали, сильно сходились
к А на О D) и
При выполнении условий A1) этими свойствами обла-
обладают операторы ^4„=—nl — пгН (X, А ) (операторы
И о с и д ы).
Другой метод построения решений уравнения и = Аи
основан на преобразовании Лапласа. Если резольвента
оператора А определена на нек-ром контуре Г, то
функция
и (t) = — JL { euR (X, A)uodX A2)
формально удовлетворяет уравнению
й=.= Аи !- _i_ [ ektdXu0.
2 лг J Г
Если обеспечить сходимость интегралов, законность
дифференцирования под знаком интеграла и обращения
в нуль последнего интеграла, то и (t) будет удовле-
удовлетворять уравнению. Трудность состоит в том, что норма
резольвенты не может на бесконечности убывать быст-
быстрее, чем |Я1-1. Однако на нек-рых элементах она убы-
убывает быстрее. Напр., если R {X, А) определена при
ReX^a и
|| R (X, А) 1| =й М | X \к, /с=а — 1,
при достаточно больших \Х\, то для Г= (— гоэ, гоо)
формула A2) дает решение для любого uo?D (Ат + Ъ).
В более «плохом» случае, когда предыдущее неравен-
неравенство выполнено лишь в области
Re X S& a | Im X \а, 0 < а < 1
(слабо гиперболич. уравнение), и Г — граница этой
области, получается решение лишь для и0, принадле-
жащих пересечению областей определения всех сте-
степеней оператора А, с определенным поведением ||^4"«0||
при п —»- оо.
Значительно больше ослабленных решений получа-
получается в том случае, когда Г уходит в левую полупло-
полуплоскость и можно использовать убывание на нем функ-
функции \ё*-Ц. При этом, как правило, решения обладают
повышенной гладкостью при г>0. Если резольвента
ограничена на контуре Г: ReX=—T|.i(|/mA|), где"ф(т) —
гладкая неубывающая вогнутая функция, растущая
на оо как 1пт, то функция A2) при любом и„?Е ста-
становится дифференцируемой и удовлетворяет урав-
уравнению, начиная с нек-рого tB, с дальнейшим увели-
увеличением t ее гладкость повышается. Если "ф(т) растет
как степень т с показателем, меньшим единицы, то
функция A2) бесконечно дифференцируема при <>0;
если 1|л(т) растет как т/1пт, то u{t) принадлежит квази-
аналитич. классу функций; если растет как линейная
функция, то u(t) — аналитична. Во всех этих случаях
она удовлетворяет уравнению и = Аи.
Существование резольвенты на контурах, уходящих
в левую полуплоскость, можно, пользуясь разложе-
разложением в ряд, получить из соответствующих оценок на
вертикальных прямых. Если при R?i
|| Л (X, А) (|< М A + | Im>,|)-P, 0 < р < 1, A3)
то для каждого uo?D (А) существует решение задачи
A0). Все эти решения бесконечно дифференцируемы
при г>0. Они представляются в виде и(t)= U(t)un,
где U(t) — бесконечно дифференцируемая полугруппа
при i>0, имеющая, вообще говоря, особенность при
= 0. Для ее производных справедливы оценки
Если оценка A3) выполнена при Р=1, то все обобщен-
обобщенные решения уравнения и=Аи аналитичны в нек-ром
секторе, содержащем положительную полуось.
Уравнение и = Аи вяз. абстрактным пара-
параболическим, если существует единственное ос-
ослабленное решение на |0, оо], удовлетворяющее на-
начальному условию м@) = мо при любом ио?Е. Если
|| Я (X, -4)|]< М \Х — ш I при Re Я> ш, A4)
то уравнение является абстрактным параболическим.
Все его обобщенные решения аналитичны в нек-ром
секторе, содержащем положительную полуось, и спра-
справедливо неравенство
где С не зависит от и0. Обратно, если уравнение об-
обладает перечисленными свойствами, то для оператора
А выполнено A4).
Если задача A0) имеет единственное ослабленное
решение при любом uo?D (А), производная к-рого
суммируема на каждом конечном интервале, то эти
решения представимы в виде u(t)= U(t)ug, где U(t) —
сильно непрерывная полугруппа на @, оо), а всякое
ослабленное решение неоднородного уравнения v=
= Av-{-f(t) с нулевым начальным условием н@) = н0
представимо в виде
v(t)= J'o U(t-s)f(s)ds. A5)
Функция v(t) определена при любой непрерывной
f(t), поэтому она наз. обобщенным решением неодно-
неоднородного уравнения. Для того чтобы обеспечить ее
дифференцируемость, на функцию /(*) налагаются
условия гладкости, и тем «больше», чем «хуже» полу-
полугруппа U(t). Так, в предыдущих условиях A5) будет
ослабленным решением неоднородного уравнения, если
](t) дважды непрерывно дифференцируема; если вы-
выполнено A1), то A5) будет решением, если f(t) непре-
непрерывно дифференцируема; если выполнено A3) при
р">2/з, то v(t) будет ослабленным решением, если f(t)
удовлетворяет условию Гёльдера с показателем v>
/1 \
>2( д- —1 1. Вместо гладкости / (l) no t можно требовать
принадлежность значений / (t) области определения
соответствующей степени оператора А.
Для уравнения с переменным оператором
u=A(t)u, СКг<Г, A6)
имеется несколько основных теорем существования и
единственности решений (ослабленных решений) за-
задачи Копти u(s) = u0 на отрезке sig.t*g.T. Если область
определения А (?) не зависит от t:
оператор A (i) сильно непрерывен по t на D (А) и
\\\R (X, А @I1=^1
при Х>0, то решение задачи Кошм единственно. Если,
кроме того, A (t) сильно непрерывно дифференцируем
на D (А), то при всяком uo?D (А) решение существует
и представимо в виде
u(t)=U(t, s)u0,
где U(t, s) — эволюционный оператор со свойствами:
1) U(t, s) сильно непрерывен в треугольнике Та'-
0r
<s«<;
2) U(t, s)^U(t, т)С/(т, s), 0<s<x<i<r, U(s, s) = I;
3) U(t, s) отображает D (А) в себя и оператор
A(t)U(t,s)A-*{s)
ограничен и сильно непрерывен в Та;
4) на D (А) оператор U(t, .«) сильно дифференцируем
по t и s и
Конструирование оператора U(t, s) проводится путем
аппроксимации оператора A (t) ограниченными опера-
операторами An(t) и заменой последних кусочно постоян-
постоянными операторами.
Предыдущие условия на оператор A (t) во многих
важных задачах не выполняются. Пусть для оператора
A (t) существуют такие константы М и ш, что
\]Д (к, A (tk)) R (К, A (*ft_!)).. .R (X, A (tj) |!<: М (к-ш)"
для всех Х>ш, ()«:«!«. . .<^<Г, /с = 1, 2 .... Пусть
в пространстве Е плотно вложено банахово простран-
пространство F, содержащееся во всех D (А (?)), и обладающее
свойствами: а) оператор A (t) ограниченно действует
из F в Е и непрерывен по t по норме ограниченных
операторов из F в Е; б) существует ияоморфизм S
пространства F на пространство Е такой, что
где В (t) — ограниченная в Е сильно измеримая опе~
раторная функция, для к-рой \\В (t)|| интегрируема на
[О, Т]. Тогда существует эволюционный оператор
U(t, s), обладающий свойствами 1), 2), 3') U(t, s)FdF
и U(t, s) сильно непрерывен в F на Та, 4') на F опе-
оператор U (t, s) сильно дифференцируем в смысле нормы
Е и -gj-=A(t)U, ~jj"= — UA (s). Сформулированное
утверждение позволило получить теоремы существо-
существования для основных квазилинейных уравнений мате-
матич. физики гиперболич. типа.
В теории параболич. уравнений применяется м е-
тод замороженных коэффициентов.
Предполагается, что при каждом to?[(), T] уравнению
и,-—A (to)u отвечает полугрупповой оператор UAUr,)t-
Искомый эволюционный оператор формально удов-
удовлетворяет интегральным уравнениям
U (t, s) = UA (t)(t-s) +
UA @ (t — s) \A W-A (*)] u (т, s) dx,
U(t, s) = UA{s) t-s) +
U (t, x) [A (x)-A (»)] t/A (J) (T-*) Л.
В условиях, когда ядра этих уравнений имеют слабые
особенности, доказывается существование их решения
и то, что U {t, s) является эволюционным оператором.
Наибольшие приложения нашло утверждение: если
D(A(t))^D(A), Ц Л (X, 4@)||<ЛГ A-|-1Х|)-1
при Re X :& 0 и
UA (t)-A(s)] A-* @)ЖС \t-sf
(условие Гёльдера), то существует эволюционный
оператор U(t, s), дающий при каждом и„^Е ослаб-
ослабленное решение V {t, s)u0 задачи Коши. Единственность
решения имеется при условии лишь непрерывности
оператора 4(г)^4~1@) (в гильбертовом пространстве).
Теорема существования, аналогичная приведенной вы-
выше, справедлива для оператора A (t) с условием типа
A3) при определенном соотношении между Р и р.
Предположение о постоянстве D (A (t)) не позволяет
в приложениях рассматривать краевые задачи с гра-
граничными условиями, зависящими от t. Пусть выполнено
||Д (к, A(t))j<M(i + \k\)-\ ReX > 0;
dt ds
?-R (к, A (t^W^A'iXf-1 , 0<p<l,
в секторе |arg>,|<:n—ф, ф<я/2, тогда существует эво-
эволюционный оператор U (t, s). Здесь постоянство D (А (г))
не предполагается. Имеется вариант последнего ут-
утверждения, приспособленный к рассмотрению парабо-
лич. задач в нецилиндрич. областях, в к-ром D (A (t))
при каждом t лежит в нек-ром подпространстве Е (t)
пространства Е.
Оператор U(t, s) для уравнения A6) формально
удовлетворяет интегральному уравнению
U (t, s) = I-\- Va (t) U (x, s)dx. A7)
В силу неограниченности оператора A (t) это урав-
уравнение нельзя решить методом последовательных при-
приближений. Пусть имеется семейство банаховых про-
пространств Еа, 0<а<:1, обладающее свойством: Ef,czEa
и ||ж||а<1к1!р при <x<fi. Предполагается, что оператор
A (t) ограничен как оператор из ?р в Еа'-
и A (t) непрерывен по t по норме пространства огра-
ограниченных операторов из ?р в Еа- Тогда в этом про-
пространстве метод последовательных приближений для
уравнения A7) будет сходиться при \t—s\ <: (Р—а)(Се).
Таким образом локально строится оператор U (t, s)
как ограниченный оператор из Яр в Еа. В приложениях
этот подход дает теоремы типа Коши — Ковалевской.
Для неоднородного уравнения (9) при известном
эволюционном операторе для уравнения u = A{t)u
решение задачи Коши формально записывается в виде
u(t) = U (t, s)uo+^U (t,i)f (т) dr.
В различных случаях при той или иной гладкости
f(t) эта формула допускает обоснование.
Лит.: [1] И о с и д а К., Функциональный анализ, пер.
с англ., М.. 1967; [2] К р е й н С. Г., Линейные дифференци-
дифференциальные уравнения в банаховом пространстве, М., 1967; L3]
Хилле Э., Ф и л л и и с Р., Функциональный анализ и
in !угруппы. пер. с англ., 2 изд., М., 1962; [4] Функциональный
члиз, 2 изд., М., 1972; [5] Г л у ш к о В. П., Линейные вы-
вырождающиеся дифференциальные уравнения, Воронеж, 1972;
Ы Д а л е ц к и и Ю. Л., Крейн М. Г., Устойчивость
решений дифференциальных уравнений в банаховом простран-
пространстве, М., )0: [7] 3 у 0 о в и С. П., Чернышов К. И.,
в кн.: «Дифференциальные уравнения и их применения», Виль-
Вильнюс, l!Oii, в. 14, с. 21 — 39; [8] Кузнецов А. Н., «Функ-
«Функциональный анализ и его прилож. », 1972, т. 6, JVa 2, с. 41 — 51;
[91 Крейн С. Г., Лаптев Г. И., «Дифференциальные
уравнения», 1969, т. 5, ,М 8, с. 1458 — 69; [10] Л ю б и ч Ю. И.,
«Успехи матем. наук», 1U66, т. 21, в. 3, с. 3—51; [11] Овеян-
н ик о в Л. В., «Докл. АН СССР», 1965, т. 163, № 4, с. 819 —
-822; [12] Соболевский П. Е., «Тр. Моск. матем.
об-ва», 1961, т. 10, с. 297—350; [13] Beals R., в кн.: Ргос.
NATO Adv. Study Inst., Liege, 1976, p. 1 — 26; [14] Friedman
A. «Arch. Rat. Mech. and Anal.», 1964, v. 17 Л1 5, p. 353 — 57;
[15] Kato Т., «J. Math. Soc. Japan», 1973, v. 25, Jsfi 4,
P. 648—66: [16] Treve s F., Basic linear partial differential
equations, N. Y., 1975; [17] Miller J., «Acta math.», 1963,
v. 110, № 3—4, p. 209 — 31. С. Г. Крейн.
ЛИНЕЙНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
ВТОРОГО ПОРЯДКА обыкновенное — урав-
уравнение вида
T(t), A)
где x{f) — искомая функция, а р (t), q(t) и r(t) — за-
заданные функции, непрерывные на нек-ром промежутке
(а, 6), Для любых действительных чисел х0, х'о и t0 ? (а, Ь)
существует единственное решение x(t) уравнения A)
с начальными условиями x(to) — .ro, a'(to)~x'n, причем
x(t) определено для всех t? (а, Ь).
Если xx(t) и x2(t) — линейно независимые решения
соответствующего однородного уравнения
0, B)
a xo(t) — частное решение неоднородного уравнения
A), то общее решение уравнения A) дается формулой
где Cj и С2 — произвольные постоянные. Если из-
известно Одно ненулевое решение x1(t) уравнения B),
то второе его решение x2(i), линейно независимое с
Ж] (t), дается формулой
» - J v W dt
x2(t) = x1 (t) \ -1 dt.
Если известны линейно независимые решения ,rt (t)
и ,г2(г) уравнения B), то частное решение xo(t) урав-
уравнения A) можно найти методом произвольных постоян-
постоянных вариации.
При изучении уравнения B) большую роль играют
его преобразования в уравнения других типов. Так,
напр., заменой ж=г1, х' = х2 уравнение B) приводится
к нормальной системе линейных уравнений 2-го по-
порядка; заменой искомой функции
= у ехр ( y\ Р С) dt)
уравнение B) приводится к уравнению y"+R(t)y=O,
где
Л (t)=--t-p'(t)-{-p2 @ + 9 С)
наз. инвариантом уравнения B); заме-
заменой х' = ух уравнение B) сводится к Риккати уравнению
После умножения на
уравнение B) принимает самосопряженный вид
(P(t)x')' + P(t)q(t)x=0.
Уравнение B) интегрируется в квадратурах лишь
в отдельных случаях. Решения наиболее важных част-
частных типов неинтегрируемых уравнений B) входят в
число специальных функций.
Справедлива теорема Штурма о разде-
разделении нулей: если %(<), х2 (t) — линейно не-
независимые решения уравнения B) и ii<?2 — соседние
нули решения xt (t), то на интервале (flt /2) имеется
в точности один нуль решения x2(t).
Пусть в уравнениях
Q (З)
функции qt и q2 непрерывны и 92(?)>?iM на проме-
промежутке (а, Ь). Справедлива теорема сравне-
н и я: если <!<t2 — последовательные нули ненуле-
ненулевого решения первого уравнения C), то на интервале
(ij, t2) имеется хотя бы один нуль любого решения вто-
второго уравнения C).
Линейная краевая задача для уравне-
уравнения A) ставится следующим образом: найти решение
х (t) уравнения A), удовлетворяющее краевым
условиям
где а,-, Р/, 7/ — заданные постоянные и
det
ФО.
I «2
Штурма — Лиувилля задача для уравнения
где д(?)>0 и непрерывна на [а, Ь'\, ставится следующим
образом: найти те значения параметра X, при к-рых
это уравнение имеет ненулевое решение x(t), удовлет-
удовлетворяющее краевым условиям х(а) = х(Ь) = 0. Эти зна-
значения X наз. собственными значениями,
а соответствующие решения — собственными
функциями.
Если в уравнении B) tux комплексны, а функции
р (t) и q(t) голоморфны в точке t0, то для любых чисел
г, и 2) существует единственное голоморфное в точке
t0 комплексное решение х (t) уравнения B), удовлетво-
удовлетворяющее начальным условиям x(tu) = x0, x' (to) = ^o.
Если в уравнении
функции p(t) и q (t) голоморфны в точке t0, причем
хотя бы одно из чисел р (t0), q (t0), q' (t0) отлично от нуля,
то точка ?0 наз. регулярной особой точ-
к о й для уравнения D). В окрестности такой точки
решение уравнения D) отыскивается в виде обобщен-
обобщенного степенного ряда
здесь р находится из определяющего урав-
уравнения
где po-=p{to) и qo=q(t0). Пусть корни р±<р2 этого урав-
уравнения действительны. Если р2—рх не является целым,
то существуют два линейно независимых решения
вида E): при p = Pi и при р=р2. Если р2—рх — целое,
то, вообще говоря, существует лишь Одно решение
в виде E) при р=р2; второе решение имеет более слож-
сложный вид (см. [3] — [6]).
Лит.: [1] Понтрягин Л. С, Обыкновенные дифферен-
дифференциальные уравнения, 3 изд., М., 1970; [2] Камке Э., Справоч-
ник по обыкновенным дифференциальным уравнениям, пер.
с нем., 5 изд., М., 1976; [3] Сансоне Д ж., Обыкновенные
дифференциальные уравнения, пер. с итал., т. 1—2, М., 1953—
1954; [4] Хартман Ф., Обыкновенные дифференциальные
уравнения, пер. с англ., М., 1970; [5] Т р и к о м и Ф., Диффе-
Дифференциальные уравнения, пер. с англ., М., 1962; [6] Голу-
Голубев В. В., Лекции по аналитической теории дифференциаль-
дифференциальных уравнений, 2 изд., М.— Л., 1950. Н. Н. Лпвис.
ЛИНЕЙНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
ОБЫКНОВЕННОЕ — дифференциальное уравнение,
линейное относительно искомой функции одного не-
независимого переменного и ее производных, т. е. урав-
уравнение вида
¦г«» + в1 @ *«»-«+. . . +а„_! (О х' +а„ @ x = f(t), A)
где x(t) —искомая, а а,-(г), f{t) — заданные функции;
число п наз. порядком уравнения A) (ниже из-
излагается общая теория Л. д. у. о.; об уравнениях 2-го
порядка см. также ст. Линейное дифференциальное
уравнение второго порядка).
1) Если в уравнении A) функции аг, . . ., ап, / непре-
непрерывны на промежутке (а, Ь), то для любых чисел х0,
х'о, • • •, -го*'1' и to?(a, b) существует единственное
решение x(t) уравнения A), удовлетворяющее на-
начальным условиям:
x(to)=xo, х' (to) = x'o, -.., xl"-V(to) = x(on-1>,
причем это решение определено на всем промежутке
(а, Ь).
Уравнение
j,w + al(t)iin-v+...+un_1(t)x' + an (*)* = 0 B)
наз. однородным уравнением, соответст-
соответствующим неоднородному уравнению A).
Если x(t) — решение уравнения B) и
X (i0) = X' (г0) = . . . = г»"» (*0) = 0,
то x(t)=O. Если x-tit), . . ., xm(t) — решения уравне-
уравнения B), то и любая их линейная комбинация
является решением уравнения B). Если п функций
Xl(t), ..., xn(t) C)
являются линейно независимыми решениями уравне-
уравнения B), то для всякого решения x(t) уравнения B)
найдутся такие постоянные Сх, . . ., Сп, что
*(t) = C1xl(t)+...+Cnxa(t). D)
Таким образом, если C) — фундаментальная система
решений уравнения B), то его общее решение
задается формулой D), где С1; . . ., Сп — произволь-
произвольные постоянные. Для всякой невырожденной пХп-
матрицы 2?=||Ь(-у|| и всякого ?0€(", °) существует такая
фундаментальная система решений C) уравнения B),
что
Для функций C) определитель
х, (t) ... х„ (t)
W (i)=det
(t) ... хп (t)
¦* 1 V / • • - >* n V
наз. определителем Вроньского, или
вронскианом. Если C) — фундаментальная система ре-
решений уравнения B), то W(Ь)фО при всех t(z(a, b).
Если W(to) = O хотя бы в одной точке t0, то W (t)=0
и решения C) уравнения B) в этом случае линейно
зависимы. Для определителя Вроньского решений C)
уравнения B) справедлива Лиуеилля — Остроград-
Остроградского формула:
Общее решение уравнения A) является суммой об-
общего решения однородного уравнения B) и частного
решения xo(t) неоднородного уравнения A) и задается
формулой
х (t) = СЛ (*)+...+ Спхп (t) + r0 (О,
где J'i(i), . . ., xu(t) — фундаментальная система ре-
решений уравнения B), а Си . . , С„ — произвольные
постоянные. Если известна фундаментальная система
решений C) уравнения B), то частное решение неодно-
неоднородного уравнения A) можно найти методом произволь-
произвольных постоянных вариации.
2) Нормальной линейной системой
обыкновенных дифференциальных
уравнении n-го порядка наз. система
xi =2nj=l<4j(t)xi + b;(t), i = l, ...,»,
пли в векторной форме
x=A(t)x+b(t), E)
где x(t)?R" — искомый вектор-столбен, A (t) — квад-
квадратная матрица порядка п, b(t) — заданная вектор-
функцня. Далее предполагается, что A (t) и b(t) непре-
непрерывны на нек-ром промежутке (а, Ь). В этом случае для
любых to?(a, b) и xo?R" существует единственное
решение x(t) системы E), удовлетворяющее начальному
условию x(to) = xo, причем это решение определено на
всем промежутке (а, Ь).
Линейная система
'х=А (t)x F)
наз. однородной, соответствующей неодно-
неоднородной системе E). Если x(t) — решение
системы F) и ж(го) = 0, то х(г)=О; если х1(г), . . -,
хт (t) — решения, то и любая их линейная комбинация
x{t)=C1x1(t)+...+Cmxm(t)
является решением системы F); если ^(г), . . .,
xm(t) —линейно независимые решения системы F),
то векторы .г! (г), . . ., xm(t) линейно независимы при
любом i?(a, ()). Если п вектор-функций
хгA), ..., xn(t) G)
являются фундаментальной системой решений системы
F), то для всякого решения x(t) системы F) найдутся
такие постоянные Си . . ., С„, что
x(t) = C1.r1(t)+...-JrCn.rn(t). (8)
Таким образом, формулой (8) задается общее решение
системы F). Для любых io€'a, b) и линейно независи-
независимых векторов аь . . ., an?R" существует такая фун-
фундаментальная система решений G) системы F), что
Для вектор-функций G), являющихся решениями
системы F), определитель W (t) матрицы
i<0
(9)
ш @ • • • *пп («)
X @ =
где первый индекс — номер решения, а второй — номер
компоненты, наз. определителем Бронь-
с к о г о, или вронскианом. Если G) — фун-
фундаментальная система решений системы F), то WD)^=0
при всех t?(a, b), а матрица (9) наз. фундамен-
фундаментальной матрицей. Если решения G) сие-
темы F) линейно зависимы хотя бы в одной точке ?0,
то они линейно зависимы при любом t?(a, b) и в этом
случае TV(i)=--O. Для определителя Вроньского рете-
штй G) системы F) справедлива формула Л и у-
г. и л л я:
($! Sp(i4(T)) <
где SpD (т)) = йп(т)+ . . . + а„„(т) — след матрицы
А (т). Матрица (9) удовлетворяет матричному уравне-
уравнению Х = А (t) X(t). Если X (t) — фундаментальная мат-
матрица системы F), то для всякой другой фундаменталь-
фундаментальной матрицы Y (t) этой же системы существует такая
постоянная невырожденная /iX/г-матрица С, что
Y(t)=X(t)C. Если Х(Ц) = Е, где Е — единичная мат-
матрица, то фундаментальная матрица X (t) наз. норм и-
рованной в точке t0 n формулой ж(/) = Х (t)x0
задается решение системы F), удовлетворяющее на-
начальному условию x(to)-~.ro.
Если матрица A (t) перестановочна со своим интег-
интегралом, то фундаментальная матрица системы F), нор-
нормированная в точке to?(a, b), задается формулой
В частности, для постоянной матрицы А фундамен-
фундаментальная матрица, нормированная в точке @, задается
формулой X (t) = exp(A (t—10)).
Общее решение системы E) является суммой общего
решения однородно!! системы F) и частного решения
z<)(t) неоднородной системы E) и задается формулой
х it) = СЛ @+ • • • +Спхп (t) + .r0 (/),
где Xy(t), . . ., xn(t) — фундаментальная система ре-
решений системы F), a Clt . . ., С„ — произвольные по-
постоянные. Если известна фундаментальная система
решений G) системы F), то частное решение неодно-
неоднородной системы E) можно найти методом вариации
произвольных постоянных. Если X (t) — фундамен-
фундаментальная матрица системы F), то формулой
х @ = X (t) Х-1 (*0) х0 +^UX (t) Х-1 (т) 6 (т) dx
задается решение системы E), удовлетворяющее на-
начальному условию x(to) = xo.
3) Пусть в системах E) и F) A (t) и b(t) непрерывны
на полуоси [а, +оо). Все решения системы E) одно-
одновременно либо устойчивы, либо неустойчивы, поэтому
система E) наз. устойчивой (равномерно
устойчивой асимптотически устой-
устойчиво й), если все ее решения устойчивы (соответст-
(соответственно, равномерно, асимптотически устойчивы). Си-
Система E) устойчива (равномерно, асимптотически ус-
устойчива) тогда и только тогда, когда устойчива (соот-
(соответственно равномерно, асимптотически устойчива)
система F). Поэтому при исследовании вопросов ус-
устойчивости линейных дифференциальных систем доста-
достаточно ограничиться рассмотрением однородных си-
систем.
Система F) устойчива тогда и только тогда, когда
все ее решения ограничены на полуоси [а, -(-оо). Си-
Система (б) асимптотически устойчива тогда и только
тогда, когда
lim cc(t)=Q A0)
для всех ее решений x(t). Последнее равносильно
выполнению соотношения A0) для п ее решений xx(t),
. . ., .г,,(/), образующих фундаментальную систему
решений. Асимптотически устойчивая система F)
асимптотически устойчива в целом.
Линейная система с постоянными коэффициентами
х=Ах A1)
устойчива тогда и только тогда, когда все собственные
значения л,], . . ., \„ матрицы А имеют неположитель-
неположительные действительные части (т. е. ReX,<0, ?=1, . . ., п);
причем собственные значения с нулевой действитель-
действительной частью имеют лить простые элементарные дели-
делители. Система A1) асимптотически устойчива тогда и
только тогда, когда все собственные значения матрицы
А имеют отрицательные действительные части.
4) Система
y = -A^(t)y, A2)
где AT (t) —транспонированная матрица A (t), наз.
сопряженной системой для системы (В).
Если x(t) и у (t) — произвольные решения систем F)
и A2) соответственно, то скалярное произведение
(x(t), у {t))=const.
Если X (t) и Y (t) — фундаментальные матрицы реше-
решений систем F) и A2) соответственно, то
где С — нек-рая невырожденная постоянная матрица.
5) Исследование различных специальных свойсти
линейных систем и, в частности, вопросов устойчи-
устойчивости связано с понятием Ляпунова характеристиче-
характеристического показателя решения и развитым А. М. Ляпуно-
Ляпуновым первым методом в теории устойчивости (см. Пра-
Правильная линейная система, Приводимая линейная си-
система).
6) Две системы вида F) наз. а с и м п т о т и ч е с к и
эквивалентными, если между их решениями
x1(t) и x2(t) можно установить такое взаимно одно-
однозначное соответствие, что
lim (*].(?) — *¦,(«)) = 0.
t -*¦ со
Если система A1) с постоянной матрицей А устойчива,
то она асимптотически эквивалентна системе х=
—-(.4 + 6 (t))x, где матрица В (t) непрерывна на [а, + со^
\\B(t)\\dt < «.. A3)
При выполнении условия A3) система x~B(i)x асим-
асимптотически эквивалентна системе х—0.
Две системы вида A1) с постоянными коэффициен-
коэффициентами наз. топологически эквивалент-
н ы м и, если существует гомеоморфизм h: R"—»-IRft,
переводящий ориентированные траектории одной си-
системы на ориентированные траектории другой. Если
квадратные матрицы А а В порядка п имеют одинако-
одинаковое количество собственных значений с отрицательной
действительной частью и не имеют собственных зна-
значений с нулевой действительной частью, то системы
х=-Ах и х = Вх топологически эквивалентны.
7) Пусть в системе F) матрица A (t) непрерывна и
ограничена на всей действительной оси. Система F)
наз. обладающей свойством экспонен-
экспоненциальной дихотомии, если пространство
R" разлагается в прямую сумму: Rn = R"i ff) R"*,
^, так, что для всякого решения x(t) при
выполняется неравенство
а при х@) ? R'1! неравенство
для всех «0?R и f>f0. гДе 0<с<1и/с>0 — постоян-
ные. Свойством экспоненциальной дихотомии обла-
обладает, напр., система A1) с постоянной матрицей А,
если А не имеет собственных значений с нулевой дейст-
действительной частью (такая система наз. гипербол и-
ч е с к о й). Если вектор-функция b(t) ограниченна на
всей действительной оси, то система E) со свойством
экспоненциальной дихотомии имеет единственное ре-
решение, ограниченное на всей прямой R.
Лит.: [11 Петровский И. Г., Лекции по теории
обыкновенных дифференциальных уравнений, ti изд., М., 1070;
[2] Понтрягин Л. О., Обыкновенные дифференциальные
уравнения, 3 изд., М., 1970; [31 Арнольд В. П., Обыкно-
Обыкновенные дифференциальные уравнения, М., 1971; [4] Ляпу-
Ляпунов А. М., Общая задача об устойчивости движения, М. —
Л-, 1950; Го] Демидович Б. П., Лекции по математиче-
математической теории устойчивости, М., 1967; [6] Б ы л о в Б. Ф.,
Виноград Р. Э., Г р о б м а н Д. М., Н е м ы ц-
кий В. В., Теория показателей Ляпунова..., М., 1%К; [7J
Хартман Ф-, Обыкновенные дифференциальные уравне-
уравнения, пер. с англ., М., 1970. Н. Н, Лпдис.
ЛИНЕЙНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ о б ы к н о-
венное — уравнение вида
xln) + ulx«-V + ...+an-lx' + anx = f(t), A)
где x(t) — искомая функция, а-,, . . ., а„ — заданные
действительные числа, f(t) — заданная действитель-
действительная функция.
Соответствующее A) однородное уравне-
уравнение
xin> + a1x<"-1>+ . . . +an_!x' + апх = 0 B)
интегрируется следующим образом. Пусть A.j, . . .,
Ji/г — все различные корни характеристич. уравнения
Х« + а,Х»-1+...+ап_1Х, + а„ = 0 C)
кратностей 1Л, . . ., 1^ соответственно, 1х-\-. . . + /^=п.
Тогда функции
Л\ «Л*, ..., tlrVe%i\ } = !,..., к, (А)
являются линейно независимыми (вообще говоря»
комплексными) решениями уравнения B), т. е. обра"
л уют фундаментальную систему решений. Общее ре-
решение уравнения B) является линейной комбинацией
с произвольными постоянными коэффициентами фунда-
фундаментальной системы решений. Если X,^=ay-(-p,-i — ком-
комплексное число, то для всякого целого т, 0<т<:Ь—1,
действительная часть tme J cos f>jt и мнимая часть
tme i sin p;z комплексного решения tme i являются
линейно независимыми действительными решениями
уравнения B), а паре комплексно сопряженных кор-
корней a7=tPyt кратности lj соответствует 21 j линейно не-
независимых действительных решений
1">еа'4 cos fyt и tmeaJ4 sin f,jt, m = 0, 1, ..., lj — i.
Неоднородное уравнение A) интегрируется методом
произвольных постоянных вариации. В случае, когда
/ — к в а з и м н о г о ч л о if, т. е.
/ (t)=e"t (Prn (t) cos bt + qm (t) sin bt),
где рт и qm — многочлены степеней -<m, а число
a+bi не является корнем уравнения C), частное ре-
решение уравнения A) ищется в виде
х0 (t) = е«* (Рт (t) cos bt + Qm (t) sin bt). E)
Здесь Рт и Qm — многочлены степени т с неопреде-
неопределенными коэффициентами, к-рые находятся подстанов-
подстановкой E) в A). Если а-\-Ы — корень уравнения C) крат-
кратности к, то частное решение уравнения A) ищется
в виде
х0 = t*e** (P,n (t) cos bt + Qm (t) sin bt)
методом неопределенных коэффициентов. Если xo(t) —
частное решение неоднородного уравнения A), а хх it),
. . ., xn(t) — фундаментальная система решений соот-
соответствующего однородного уравнения B), то общее ре-
решение уравнения A) задается формулой
х it) = х0 it) + Сххх it) + ... + Cnxjt),
где Сь . . ., Сп — произвольные постоянные.
Однородная система линейных дифференциальных
уравнений re-го порядка
х'= Ах, F)
где x?Rn — искомый вектор, а А — постоянная дей-
действительная п хга-матрица, интегрируется следующим
образом. Если X — действительное собственное зна-
значение кратности к матрицы А, то решения х—(х\,
. . ., хп), соответствующие собственному значению Я,
ищутся в виде
г. — P. (t\ /А' г — Р lt\ с^' G\
Здесь Pxit), . . ., Pnit) —многочлены степени /с—1
с неопределенными коэффициентами, к-рые находятся
подстановкой G) в F); при этом существует в точности
к линейно независимых решений вида G). Если X —
комплексное собственное значение кратности к, то
действительные и мнимые части комплексных решений
вида G) образуют 2А линейно независимых действи-
действительных решений системы F), а пара комплексно со-
сопряженных собственных значений X п X кратности к
матрицы А порождает 2к линейно независимых дейст-
действительных решения системы F). Перебирая все собст-
собственные значения матрицы А, находят 2и линейно неза-
независимых решений, т. е. фундаментальную систему ре-
решений. Общее решение системы @) является линейной
комбинацией с произвольными постоянными коэффи-
коэффициентами решений, образующих фундаментальную си-
систему.
Матрица X it) = eAt является фундаментальной мат-
матрицей системы G), нормированной в нуле,
т. к. XiO) = E — единичная матрица. Здесь
At =с. , V" A"tk
"t"^A = l"ftl~7
причем этот матричный ряд абсолютно сходится для
любой матрицы А и всех действительных t. Всякая
другая фундаментальная матрица системы F) имеет
вид eAtC, где С — постоянная невырожденная матрица
порядка п.
Лит.: [1] П о н т р я г и н Л. С, Обыкновенные дифферен-
дифференциальные уравнения, 3 изд., М., 1970; [2] Арнольд В. П.,
Обыкновенные дифференциальные уравнения, М., 1971; [3] Д е-
мидович Б. П., Лекции по математической теории устой-
устойчивости, М., 1967. Н. Н. Ладие.
ЛИНЕЙНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
С ЧАСТНЫМИ ПРОИЗВОДНЫМИ — уравнение вида
F (х, ..., p.t _ .п, ...)=0,
где F — линейная функция действительных перемен-
переменных,
U, ¦ . ., in — неотрицательные целочисленные нн-
дексы, 2jj^,1ij = k, fe = 0, . . ., то, m^l, и по крайней
мере одна из производных
отлична от нуля.
Подробнее см. Дифференциальное уравнение с част-
частными производными. А. Б. Иванов.
ЛИНЕЙНОЕ ЗАМЫКАНИЕ — замыкание линей-
линейной оболочки.
ЛИНЕЙНОЕ ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ — ин-
интегральное уравнение, в к-рое неизвестная функция
<p(s) входит в первой степени:
где А, К, f — заданные функции, D — область евкли-
евклидова пространства, k, s — точки этого пространства,
ds — элемент объема. Подробнее см. Интегральное
А Б И
уравнение.
ЛИНЕЙ
р
А. Б. Иванов.
р
ЛИНЕЙНОЕ МНОГООБРАЗИЕ, а ф ф и и по е п о д-
пространств о,— подмножество М (линейного)
векторного пространства Е, являющееся сдвигом
какого-либо его линейного подпространства L, т. е.
множество М вида xo-j-L при нек-ром хоаМ. Мно-
Множество М определяет L однозначно, тогда как хй оп-
определяется только по mod L:
xo+L=x1+N
в том итольковтом случае, когда L=N и хх—xo?L
Размерность М — это размерность подпространства L.
Л. м., к-рому соответствует подпространство кораз-
коразмерности 1, наз. гиперплоскостью.
М. II. Войцеховспий.
ЛИНЕЙНОЕ НЕРАВЕНСТВО — неравенство вида
иди вида
1(х)~а=?а1х1+...-\-апхп — а<0, B)
где alt . . ., а„, а — любые действительные числа,
а>=(*1, • • -, хп)-
В более широком смысле — это неравенство вида
/(*) — а<0 C)
или вида
/(х)-а<0, D)
где f(x) — линейная (т. е. аддитивная и однородная)
функция на действительном векторном пространстве
L (R) со значениями из поля R дехгствительных чи-
чисел и a^R. Дальнейшее обобщение понятия Л. н.
получается, если вместо поля R взять произвольное
упорядоченное поле Р. На основе именно такого обоб-
обобщения построена современная теория Л. н. (см. [1]).
К исследованию систем Л. н. сводится ряд важных
вопросов аналитич. механики, геометрии чисел, при-
приближения функций. Весьма важные приложения на-
находят результаты, относящиеся к системам Л. н.,
в экономпч. исследованиях. В таких приложениях
возникло, в частности, линейное программирование.
К решению конкретных систем Л. н. сводятся многие
ирактич. задачи технико-экономич. и планово-эконо-
мич. характера, что в значительной мере определило
современное направление исследований в области Л. н.
На этом пути возник, в частности, основной принцип
теории Л. н.— принцип граничных решений, установ-
установленный сначала (см. [4]) для конечных систем Л. н.
в модульной форме, т. е. для систем вида
I V (*) — a.j | = | апхх + .. . + ajnxn — о,-1 < dy, E)
/=1, 2, . . ., т, где все ayj, . . ., ajn, aj — в самом об-
общем случае элементы поля комплексных чисел, а все
dj—неотрицательные действительные числа, 7 = 1, 2,
. . ., т.
Принцип граничных решений за-
заключается в следующем. В любой совместной системе
вида E) ранга г>0 можно выделить такую подсистему
ранга г из г неравенств, что хотя бы одно решение по-
последней, обращающее в равенства все ее неравенства,
удовлетворяет всем неравенствам систрмы E), иначе
говоря, является решением системы E).
Принцип граничных решений был распространен
(см. [5]) на системы вида
I/ (X) — aJ = Й;1Г1 "Г • • • + ajnXn — aJ < 0, F)
; = 1, 2, . . ., т, над полем R (т. е. на системы с дейст-
действительными afi, . . ., aJU, a.j, /=1, 2, . . ., m) в виде
следующего более сильного утверждения. В совмест-
совместной системе F) ранга г>0 можно выделить такую под-
подсистему ранга г из г неравенств, что любое решение
этой подсистемы, обращающее в равенства все ее нера-
неравенства, удовлетворяет всем неравенствам F) (для
систем вида F) это утверждение оказывается эквива-
эквивалентным предыдущему утверждению). Рангом си-
системы линейных неравенств наз. наи-
наибольшее число линейно независимых форм lj(x), вхо-
входящих в ее неравенства.
Принцип граничных решений был распространен
также на системы вида F) над произвольным упорядо-
упорядоченным полем Р и даже на более общие системы, со-
составленные из конечного числа Л. н. вида C) над по-
полем Р (см. [6]). Из этого принципа вытекает следую-
следующее условие совместности систем вида F) над произ-
произвольным упорядоченным полем. Система F) ранга
г>0 тогда и только тогда совместна, когда в матрице
ее коэффициентов существует такой отличный от нуля
минор Д порядка г, что для определителей Ду, /—1,
2, . . ., т, получаемых при окаймлении его с помощью
/-п строки этой матрицы и столбца элементов <2у, все
отношения Ду/Д неотрицательны. В случае совместной
системы линейных уравнений а.-^х^-^. . .-\-ajnxn—ау=О,
/ = 1, 2, . . ., m, такие отношения равны нулю для лю-
любого отличного от нуля минора Д порядка г матрицы ее
коэффициентов.
Разработка теории Л. н. началась в конце 19 в. Одно
из первых предложений общего характера, установ-
установленное в исследованиях [3] и [9], — теорема
Минковского — Фаркаша является и те-
теперь одной из ключевых теорем теории Л. н.: если все
решения совместной системы F) над полем R удовлет-
удовлетворяют нек-рому неравенству
b, 6/?R, i = l, 2, . . ., n, то существуют такие неотри-
неотрицательные числа р0, рх, . . ., рт, что имеет место тож-
тождественное относительно x=(xit . . ., хп) соотношение-
В начале 20 в. в исследованиях Г. Ф. Вороного, т/ос-
т/освященных квадратичным формам целочисленных пере-
переменных, возникла одна из основных задач теории
Л. н.— задача изучения свойств выпуклого много-
многогранника, определяемого в пространстве R" реше-
решениями совместной конечной системы Л. н. отличного
от нуля ранга. Основная теорема Вороного (см. [1])
выражает условия невырожденности такого много-
многогранника или, иначе говоря, условия совместности
конечной системы, составленной из неравенств вида
B). Задачей изучения многогранника решений систем
вида F) и результатами Г. Минковского [3] и Ж. Фар-
Фаркаша [9] на долгое время определилось основное на-
направление исследований по линейным неравенствам
(см. [10]).
В дальнейшем выяснилось, что все результаты теории
Л. н., относящиеся к конечным системам неравенств
вида F) и, в частности, упоминавшиеся выше резуль-
результаты Минковского, Фаркаша и Вороного, могут быть
выведены из принципа граничных решений дискрет-
дискретными методами, т. е. без использования топологич.
свойств поля R действительных чисел (или каких бы
то ни было следствий этих свойств), причем дискрет-
дискретными методами был доказан и сам принцип граничных
решений (см. [1] и [6]). Поэтому в качестве основного
поля при построении теории конечных систем Л. н.
оказалось возможным вместо поля R взять произ-
произвольное упорядоченное поле Р. Таким образом, было
подготовлено построение чисто алгебраич. теории Л. н.,
пользующейся только дискретными методами.
Продолжительное время теория Л. н. не имела эф-
эффективных методов для нахождения решения конеч-
конечных систем Л. н. Метод, состоящий в непосредственном
использовании принципа граничных решений, мало
эффективен. Эффективные методы для нахождения от-
отдельных решений конечной системы Л. н. (в частности,
симплексный метод) появились с возникновением ли-
линейного программирования.
В 1960 — 65 был разработан т. н. метод свер-
свертывания систем линейных нера-
неравенств, позволяющий по любой конечной системе,
составленной в общем случае из неравенств вида C)
и D), в частности из неравенств вида A) и B), и по
заданному подпространству связанного с ней прост-
пространства находить нек-рую новую конечную систему
Л. н., множество решений к-рой совпадает с той или
иной проекцией множества решений рассматриваемой
системы на взятое подпространство (см. [1]). Разрабо-
Разработанный на этой основе алгоритм фундамен-
фундаментального свертывания (особый алгоритм
для последовательного исключения неизвестных из
системы F)) позволяет получать общие формулы, оп-
определяющие все множество решений совместной сис-
системы вида F). Метод свертывания может быть исполь-
использован в задачах линейного программирования для
уменьшения числа неизвестных, а также для получе-
получения общих формул, определяющих все множество оп-
оптимальных решений (см. [1]). Показано также [7], что
с помощью метода свертывания можно выделять мак-
максимальные совместные подсистемы в несовместной
конечной системе Л. н., составленной в общем случае
из неравенств вида C) и D), в частности из неравенств
вида A) и B), что позволяет использовать его при од-
одном из подходов к решению задач распознавания об-
образов (см. (8]).
Среди бесконечных систем Л. н. выделен и изучен
особый класс — полиэдрально замкнутые системы (см.
[1]). В случае действительного векторного пространства
R" полиэдрально замкнутые системы определяются
как бесконечные системы вида aaix^-. . . + ам^„—
—ао: <U, oc?Af, с топологически замкнутым в прост-
пространстве R." сопряженным конусом, т. е. конусом,
порожденным элементами
(аа1, ..., аая, —oj, ccg/W, и F,-1),
где в — нулевой элемент пространства R". Бесконеч-
Бесконечные полиэдрально замкнутые системы Л. н. сохраняют
ряд свойств конечных систем Л. н. и, в частности,
для таких систем справедлива теорема Минковского —
Фаркаша. Полиэдрально замкнутые системы Л. н.
используются в теории приближения функций, в вы-
выпуклом программировании, в теории управления (см.
[8]).
Лит.: [1] Ч е р н и к о в С. Н., Линейные неравенства, М.,
1968; [2] Линейные неравенства и смежные вопросы, пер. с англ.,
М., 1959; [3] Minkowski H.. Georaetrie der Zahlen, Lpz.,
1896; [4] Черников С. Н., «Матем. сб.», 1944, т. 15, JSi» 3,
с. 437—48: [5] его же, «Успехи матем. наук», 1953, т. 8, № 2,
с. 7— 73; [6] его же, «Укр. матем. ж.», 1967, т. 19, М1,с. 36 —
80; [7] его же, «Доповвд АН УРСР. Сер. А», 1969, X: 1,
с. 32—35; [8] К р а с о в с к и и Н. Н., Еремин И. И.,
«Укр. матем. ж.», 1973, т. 25, К» 4, с. 465—78; [9] Farkas J.,
«J. reine und angew. Math.», 1902, v. 124, S. 1—27; [10] D i-
ies L. L., McCoy N. H., «Trans. Roy. Soc. Canada.
.Sec. 3», 1933, v. 27, p. 37 — 70. С. H. Черников.
ЛИНЕЙНОЕ ПАРАБОЛИЧЕСКОЕ УРАВНЕНИЕ И
СИСТЕМА — дифференциальное уравнение (и система)
с частными производными вида
8 'и.
Pk/
с*, о
где l<:j<:A7, fc0, . . ., kjy — натуральные, p — целое,
s=(s1, . . ., sn), \s\=Si~\-. . ,+sn, рассматриваемое в об-
области D переменных (x, t)-=(xx, . . -,xn, t). Система A)
наз. параболической (по Петровскому) в
точке (ж0, t")QD, если корни km(Z,, x, t), l<m<:A;1+
+ . . .+fc/v> многочлена но к
det (У А15
удовлетворяют неравенству
suPm, is | = i ReXm(i, x», <o) <0. B)
Здесь (iiL— (iii)^i ... (^„)s" с мнимой единицей г и
&lj — символ Кронекера.
Система A) параболическая в D, если не-
неравенство B) выполняется для всех (х, г)'6 D, и рав-
равномерно параболическая в?>, если
sup Re>.m(g, x, t)<—b
го, | i| = l, (x, !)В
с нек-poii постоянной ё>0.
Для случая уравнения 2-го порядка
2" 5=о Cifu*iXj
можно дать другое определение параболичности. Для
заданной точки х°-=(х0, . . ., х%) существует аффинное
преобразование, приводящее C) к виду
2" у-=о biiv*i*j + 2"=о biv*i+bv=*'
где b;j(x°) — O при 1ф]. Уравнение C) параболическое
в точке ж0, если одно из Ьц(х°) (пусть Ьво(х°) = 0) равно
нулю, остальные Ьц(х°)фО, t>0, и имеют одинаковые
знаки и Ь0(х°)ф0. Уравнение C) параболиче-
параболическое в области D, если оно параболическое в каж-
каждой ее точке. Если коэффициенты параболического
в D уравнения C) достаточно гладкие, то в окрест-
окрестности каждой точки x°?D невырожденной заменой
переменных его можно привести к виду
t sL.it j=1 '/ х!х/ *Т" .?,-_! 1 х;~Г / К I
с положительно определенной формой ?,<Ч/§&/.
Типичным представителем параболич. уравнения
является теплопроводности уравнение
основные свойства к-рого сохраняются и для общих
параболич. уравнений.
Для уравнения D) основными являются следующие
задачи.
Задача К о ш и — Дирихле: найти функ-
функцию и(х, t), к-рая при x?Rn, t>0 удовлетворяет урав-
уравнению D), а при *=0 — начальному условию
Первая краевая задача, в к-рой урав-
уравнение D) задано в цилиндре
QT=Qx[0, Г],
где Я — нек-рая область пространства R". Требуется
найти функцию и, удовлетворяющую уравнению D),
начальному условию
и краевому условию
ди
Ш
x e dQ, о < 1 < T
а;,-их.Х;=:1Ь (х, t)
или соответственно третьим
ди \ .
—г -f- аи ) = гЬ (х, t),
d/v У л: е эй, о < г < г
где v;, l<:i<:n,— компоненты внешней нормали.
Классич. постановка указанных задач требует от
решения непрерывности в замкнутой области, непре-
непрерывности вторых производных внутри и в случае вто-
второй и третьей краевых задач непрерывности первых
производных вплоть до боковой поверхности ци-
цилиндра Q. Кроме того, для задачи Коти — Дирихле,
а в случае неограниченности Q и для краевых задач
требуется ограниченность решения и при \х\—*-оо (или,
более общо, надлежащим образом заданный рост \и\).
Пусть уравнение D) равномерно параболическое,
коэффициенты уравнения, начальных и краевых усло-
условий и граница области достаточно гладки. Тогда ре-
решения задачи Коши — Дирихле и первой краевой за-
задачи существуют и единственны. Если а^-0, о>0 и
выполнены необходимые условия согласования, то
аналогичный результат справедлив и для второй и
третьей краевых задач.
Единственность указанных задач следует из прин-
принципа максимума. Пусть коэффициенты уравнения D)
непрерывны в Qr, область Q ограничена,
М = max— a, N = max— \f\.
Q f Q f
Тогда для любого решения
уравнения D) справедлива оценка
\и(х, t)\<eMt(Nt+max\u\), (x, t)?QT. '
Г
Принцип максимума допускает распространение и на
случай неограниченных областей. Кроме того, для
параболич. уравнений имеет место аналог принципа
Заремба — Жиро о знаке наклонной производной
в точке экстремума, известного в теории эллиптич.
уравнений.
В теории параболич. уравнений важную роль иг-
играют фундаментальные решения. В случае уравнения
теплопроводности E) им является ф5тнкция
)
Вторая и третья краевые задачи |
отличаются от первой лишь условием F), к-рое заме- • !
няется вторым краевым условием
w{x, t, i, т)= 2/5]R *
при t>T удовлетворяющая уравнению E), причем для
любой ограниченной непрерывной в R" функции ср (х)
равномерно на компактных подмножествах точек
x?R". В частности, при т -0 получается решение
и(х, t)= \Ra«>(*, '. 6. 0)<p(g)rf& G)
задачи Коти — Дирихле. На значение решения и
в точке (х, t), г>0, влияют все значения функции. Ото
служит выражением того факта, что возмущения за-
задачи Коши — Дирихле распространяются с бесконеч-
бесконечной скоростью. В этом существенное отличие парабо-
лич. уравнений от гиперболических, где скорость рас-
распространения возмущений конечна.
Фундаментальные решения могут быть построены и
для общих параболич. уравнений и систем при весьма
широких предположениях относительно гладкости ко-
коэффициентов.
Лит.: [1] Бицадзе А. В., Уравнения математической
физики, М-, 1976; [2] Ладыженская О- А., С о л и н-
ников В. А., У р а л ь ц е в а Н. Н., Линейные и квази-
квазилинейные уравнения параболического типа, М., 1967; [3] Ф р и д-
м а н А., Уравнения с частными производными параболическо-
параболического типа, пер. с англ., М., 1968; [4] Эйдельман С. Д.,
Параболические системы, М., 1964; [51 Ильин А. М.,
Калашников А. С, Олейник О. А., «Успехи ма-
тем. наук», 1962, т. 17, и. 3., с. 3 — 46. А. П. Солдптов.
ЛИНЕЙНОЕ ПОДПРОСТРАНСТВО, векторное
подпространств о,— непустое подмножество L
(линейного) векторного пространства Е над полем К
такое, что L само является векторным пространством
по отношению к определенным в Е действиям сложе-
сложения и умножения на скаляр. Множество L-\-xu, где
хо?Е, наз. линейным многообразием, м. И. Войцеховский.
ЛИНЕЙНОЕ ПРЕДСТАВЛЕНИЕ — гомоморфизм я
группы (соответственно алгебры, кольца, полугруппы)
X в группу всех обратимых линейных операторов
в векторном пространстве Е (соответственно в алгебру,
кольцо, мультипликативную полугруппу всех линей-
линейных операторов в Е). Если Е — топологич. векторное
пространство, то Л. п. X в Е наз. такое, образ к-рого
содержит только непрерывные линейные операторы
в Е. Пространство Е наз. пространством
представления я, а операторы л(х), х?Х,—¦
операторами представления я.
Лит.: [1] Кириллов А. А., Элементы теории представ-
представлений, 2 изд., М., 1978. А. II. Штерн.
ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ — отображение
векторного пространства в себя, при к-ром образом
суммы двух векторов является сумма их образов, а об-
образом произведения вектора на число — произведение
образа вектора на это число. Если V — векторное
пространство, / — заданное в нем Л. п. и а", у — любые
векторы пространства, К — любое число (элемент
поля), то
/ (Ж + у) = f (Ж) + / (у) , / (КХ) = %f @5) .
Если векторное пространство V имеет конечную раз-
размерность п; «»,, е2, . . , <*„ — его базис; хг, х.2, ....
хп — координаты произвольного вектора ж в этом ба-
базисе и ул, i/o, . . ., г/,, — координаты его образа y = f (ж),
то координаты вектора // выражаются через координата
вектора ос линейными однородными функциями
Уп = ап\х\ + а
Матрица
аи а12 ... я,
А =
а2
aul ani . . . an:l
наз. матрицей Л. п. / в базисе еи е2, . . ., еп. В ее столб-
столбцах стоят координаты образов базисных векторов. Если
1сп с12 ... с1п
<?21 С22 ... С2п
Cjl\ сп2 • • • Сп
— матрица перехода от базиса еи е2, . . ., еп к базису
е[, е'г, . . ., е'п:
... +сп1еп,
22в2+ .. . +сп2еп,
е-п = ciney -f с2пе-2 + ... + cnneni
то в базисе е[, е$, . . ., е'п матрица В Л. п. / будет В =
С у м м о й двух Л. п. / и g наз. такое преобразова-
преобразование h, при к-ром для всякого вектора x^V
А (») = /
Произведением Л. п. / на число к
наз. преобразование к, при к-ром к (ж) = Я/ (ж) для вся-
всякого вектора as?F.
Произведением Л. п. / на Л. п. g наз.
преобразование
Z («)==? (/(ж)).
Сумма двух Л. п., произведение Л. п. на число, про-
произведение двух Л. п. являются линейными преобразо-
преобразованиями. Л. п. образуют алгебру. В случае, когда
конечномерное пространство имеет размерность л,
алгебра его Л. п. изоморфна алгебре квадратных мат-
матриц порядка п, элементами к-рых являются элементы
того поля, над к-рым построено векторное прост-
пространство.
Л. и. /, при к-ром векторное пространство отобра-
отображается на себя, наз. обратимым, если сущест-
существует такое преобразование f~x, что
где Е — тождественное преобразование. Преобразова-
Преобразование /-1 является Л. п. и наз. обратным преоб-
преобразованием к преобразованию /. Л. п., задан-
заданное в конечномерном векторном пространстве, обра-
обратимо тогда и только тогда, когда определитель его
матрицы в каком-нибудь (и тогда во всяком) базисе
отличен от нуля. Если А — матрица обратимого Л. п.,
то матрица обратного ему Л. п. /-1 равна Л. Обра-
Обратимые Л. п. образуют группу по отношению к операции
умножения. В случае векторных пространств конеч-
конечной размерности п эта группа изоморфна группе не-
невырожденных квадратных матриц порядка п.
Подпространство V векторного пространства V
наз. инвариантным подпространст-
подпространством относительно Л. п. /, если /(aj)^F' для всякого
вектора ж? V". Ненулевой вектор ж? V наз. собст-
собственным вектором Л. п. /, соответствующим
собственному значению Я, если /(ж) = Яж. В случае
пространства конечной размерности над полем комп-
комплексных чисел всякое Л. п. имеет собственный вектор
(обладает одномерным инвариантным подпространст-
подпространством). В случае конечномерного пространства над полем
действительных чисел у всякого Л. п. имеется одно-
одномерное или двумерное инвариантное подпространство.
Л. п. /, заданное в конечномерном векторном прост-
пространстве, наз. диагонализируемым Л. п.,
«ели в пространстве V существует такой базис, в к-ром
матрица этого преобразования имеет диагональную
форму. Другими словами, Л. п. диагонализируемо,
если пространство обладает базисом, состоящим из
собственных векторов этого Л. п. Однако не всякое
Л. н. даже в пространстве над полем комплексных чи-
чисел обладает базисом из собственных векторов этого
Л. п., напр. Л. п. двумерного пространства, заданное
матрицей
II
/
у к-рой имеется единственное одномерное инвариант-
инвариантное подпространство с базисом {1, 0}.
В конечномерном векторном пространстве над полом
комплексных чисел для всякого Л. л. существует такой
базис, в к-ром матрица этого преобразования имеет
клеточный вид, где по главной диагонали стоят жорда-
новы клетки, а в остальных местах — нули. Жорданопа
клетка 1-го порядка состоит из одного числа к; жорда-
нова клетка порядка к есть квадратная матрица по-
порядка к вида
к 1 0 ... 0 0
0 к 1 ... 0 0
0 0 0 ... к 1
0 О О ... О X
Числа к являются собственными значениями матрицы
Л. п. Одному и тому же к могут соответствовать как
несколько клеток Одного и того же порядка, так и
клетки различных порядков. Матрица, состоящая из
жордановых клеток, наз. нормальной жорда^
новой формой матрицы.
Л. п. /, заданное в евклидовом (унитарном) прост-
пространстве, наз. самосопряженным (соответст-
(соответственно эрмитовы м), если для всяких двух векто-
векторов х-, ?/t V имеет место равенство (ж, / (у))=(у, /(жI
(соответственно (ж, /(?/)) = (?/, fix)).
Л. п., заданное в конечномерном евклидовом (унитар-
(унитарном) пространстве, будет самосопряженным (эрмито-
(эрмитовым) тогда и только тогда, когда его матрица А в каком-
нибудь (а тогда л во всяком) ортонормированном ба-
базисе является симметрической (соответственно эрми-
эрмитовой). Самосопряженное (эрмитово) Л. п., заданное
в конечномерном евклидовом (соответственно унитар-
унитарном) пространстве, обладает ортонормированным ба-
базисом, в к-ром его матрица имеет диагональную форму.
По главной диагонали стоят (всегда действительные)
собственные значения матрицы А Л. п.
Л. п. /, заданное в евклидовом (унитарном) прост-
пространстве V, наз. изометрическим (соответст-
(соответственно унитарным), если для всякого вектора
Ша»I1 = 1И-
Л. п., заданное в конечномерном евклидовом (унитар-
(унитарном) пространстве, изометрично (соответственно уни-
унитарно) тогда и только тогда, когда его матрица А
в каком-нибудь (а тогда и во всяком) ортонормирован-
ортонормированном базисе была ортогональной (соответственно уни-
унитарной). Для всякого изометрич. Л. п., заданного
в конечномерном евклидовом пространстве, сущест-
существует ортонормированный базис, в к-ром матрица пре-
преобразования состоит из клеток 1-го и 2-го порядка,
стоящих на ее главной диагонали. Клетки 1-го порядка
суть действительные собственные значения матрицы
А преобразования, равные -|-1 и —1, а клетки 2-го
порядка имеют вид
;] cos ф — sin ф II
1 sin ф cos ф | '
где cos ф и sin ф — действительная часть и коэффи-
коэффициент при г комплексного собственного значения,
^=cos ф + i sin cp матрицы А, на остальных местах
матрицы А стоят нули. Для всякого унитарного пре-
образования, заданного в унитарном пространстве,
существует ортонормированный базис, в к-ром мат-
матрица этого преобразования является диагональной,
причем на главной диагонали стоят числа, по модулю
равные 1.
Всякое Л. п., заданное в конечномерном евклидовом
(унитарном) пространстве, является произведением
самосопряженного и изометрич. Л. п. (соответственно
эрмитова и унитарного).
Лит.: Ш Александров П. С, Лекции по аналити-
аналитической геометрии..., М., 1968; [2] Гель фанд И. М., Лек-
Лекции по линейной алгебре, 4 изд., М., 1971; [3] Ефимов Н. В.,
Розендорн Э. Р., Линейная алгебра и многомерная гео-
геометрия, М-, 1970; [4] X а л м о ш П., Конечномерные вектор-
векторные пространства, пер. с англ., М., 1963. А. С. Пархоменко.
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ — математи-
математическая дисциплина, посвященная теории и методам
решения задач об экстремумах линейных функций на
множествах п-мерного векторного пространства, зада-
задаваемых системами линейных неравенств и равенств;
Л. п.— один из разделов математического программи-
программирования. Типичной задачей Л. п. является следующая:
найти максимум линейной функции
при условиях
S/ = i "'У*/<ь«". * = *. 2, ...,ш; B)
я/ЗгО, / = 1, 2, ..., п, C)
где cj, a-tj и b, — заданные числа.
Задачи Л. п. являются математич. моделями много-
многочисленных задач техннко-экономпч. содержания. При-
Примером может служить следующая задача планирования
работы предприятия. Для производства однородных
изделий необходимо использовать различные произ-
производственные факторы: сырье, рабочую силу, станочный
парк, топливо, транспорт и т. д. Обычно имеется не-
несколько отработанных технологич. способов произ-
производства, причем в этих способах затраты производст-
производственных факторов в единицу времени для выпуска
изделий различны. Количество израсходованных про-
производственных факторов и количество изготовленных
изделий зависит от того, сколько времени предприятие
будет работать по тому или иному технологич. способу.
Ставится задача рационального распределения времени
работы предприятия по различным технологич. спосо-
способам, т. е. такого, при к-ром будет произведено макси-
максимальное количество изделий при заданных ограничен-
ограниченных затратах каждого производственного фактора.
Формализуем задачу. Пусть имеется п технологич.
способов производства изделий и т производственных
факторов. Пусть cj — количество изделий, выпускае-
выпускаемых в единицу времени при работе по ;-му технологич.
способу; а,у — расход j-ro производственного фактора
в единицу времени при работе по /-му технологич. спо-
способу; Ь,- — имеющиеся ресурсы ?-го производственного
фактора и xj — планируемое время работы по /-му
технологпч. способу. Величина
означает общий расход i-ro производственного фактора
при плане ж = (х1, х,2, . . ., хп). И поскольку ресурсы
ограничены величинами Ь/, то возникают естественные
условия B) и C). Ставится задача отыскания такого
распределения времени (оптимального плана) i* =
= (xi, х-г, . . ., хп) работы по каждому технологич.
способу, при к-ром общий объем продукции 2Lj=icjxJ
был бы максимальным, т. е. задача A) — C). Другим
характерным примером прикладных задач Л. п. яв-
является транспортная задача.
Задачи Л. п. являются вспомогательными во мно-
многих методах решения нелинейных задач математич.
программирования. Так, в методе возможных направ-
направлений (см. Математическое программирование) для
отыскания направления спуска на каждой итерации
необходимо решить соответствующую задачу Л. п.
Смысл термина «Л. п.» в том, что в Л. п. решаются
задачи составления оптимальной программы (плана)
действий. В связи с этим Л. п. можно рассматривать
как один из математич. методов в исследовании опера-
операций.
В задачах Л. п. более общего вида по сравнению
с A) — C) нек-рые (или все) из условий B) могут быть
равенствами, а на нек-рые (либо на все) переменные xj
не накладываются условия неотрицательности. Любая
задача Л. п. может быть приведена к эквивалентной
задаче вида A) — C).
Основу изучения свойств задач Л. п. составляет тео-
теория двойственности. Двойственной зада-
задачей Л. п. к задаче A) — C) наз. задача минимиза-
минимизации функции
при условиях
2[ = i a'fyi S=c/' 7 = 1, 2, ...,n; E)
j/fSsO, i = l, 2, ..., т. F)
Задачи A) — C) и D) — F) либо обе имеют решения,
либо обе неразрешимы. Значения целевых функций A)
и D) на решениях совпадают.
Одним из основных методов решения задач Л. п.
является симплексный метод. Геометрически его идея
состоит в следующем. Допустимое множество B) и
C) представляет собой выпуклое многогранное мно-
множество (если оно ограничено, то — многомерный вы-
выпуклый многогранник). Если задача Л. и. имеет ре-
решение, то существует вершина х* многогранного мно-
множества, являющаяся оптимальным планом. Симплекс-
Симплексный метод состоит в таком направленном переборе вер-
вершин, при к-ром значение целевой функции возрастает
от вершины к вершине. Каждой вершине соответствует
система уравнений, выбираемая специальным образом
из системы неравенств B), C), поэтому вычислитель-
вычислительная процедура симплексного метода состоит в последо-
последовательном решении систем линейных алгебраич. урав-
уравнений. Простота алгоритма делает этот метод удобным
для его реализации на ЭВМ. В Л. п. разработан целый
ряд других конечных методов, напр, двойствен-
двойственный симплексный метод, когда решение
прямой задачи A) — C) получают в результате приме-
применения симплексного метода к двойственной задаче
D) — F). Наряду с терминами «симплексный метод» и
«двойственный симплексный метод» приняты термины
«метод последовательного улучшения плана» и «метод
последовательного уточнения оценок».
При моделировании реальных явлений часто возни-
возникают задачи Л. п. больших размерностей. Содержание
этого термина зависит от возможностей вычислитель-
вычислительных алгоритмов и характеристик, используемых ЭВМ,
таких, как объем оперативной памяти, скорость и др.
Для решения задач больших размерностей создаются
методы, учитывающие специфич. структуру матриц
условий. В основе многих из них лежит идея деком-
декомпозиции — разложения системы ограничений на
подсистемы, для каждой из к-рых необходимо решать
подзадачу Л. п. меньшей размерности по сравнению
с исходной задачей.
Для решения задачи Л. п. наряду с конечными ме-
методами применяются также итерационные методы пост-
построения последовательности приближений, пределом
к-рой является оптимальный план. К ним относятся
методы, основанные на применении штрафных функ-
функций (см. Штрафных функций метод), итерационные
методы теории игр, применение к-рых основано па
эквивалентности любой матричной игры соответствую-
соответствующей паре двойственных задач Л. п., и ряд других ме-
методов.
Существенное место в Л. п. занимает проблема ус-
устойчивости. В реальных задачах (в особенности зада-
задачах технико-экономич. содержания) исходная инфор-
информация обычно известна лишь с определенной степенью
точности, и даже малые возмущения (погрешности)
в исходных данных могут вызывать существенные от-
отклонения возмущенного решения от истинного. При
численной реализации того или иного конечного ме-
метода возникают ошибки округления, накопление к-рых,
особенно в задачах большой размерности, может при-
привести к значительным отклонениям полученного при-
приближенного решения от истинного. Обе эти ситуации
характеризуют свойство неустойчивости и присущи не-
некорректно поставленным задачам. В Л. п. разработаны
методы решения некорректных задач. Так, в методе
регуляризации, используя нек-рую дополнительную
информацию о решении, аппроксимируют исходную
задачу иараметрич. последовательностью устойчивых
задач таким образом, чтобы последовательность их
решений сходилась к решению исходной задачи.
Наряду с конечномерными задачами Л. и. рассмат-
рассматриваются также задачи Л. п. в бесконечномерных про-
пространствах. К этим задачам относятся, напр., линейные
задачи оптимального управления со смешанными ог-
ограничениями.
Лит.: [1] Юдин Д. Б., Го ль штейн Е. Г.
Линейное программирование, М., 1969; [2] Данциг Д ж.
Линейное программирование, его применения и обобщения, М.,
196В; [31 Еремин И. И., Астафьев Н. Н., Введение
в теорию линейного и выпуклого программирования, М., 1976
[4] Карманов В. Г., Математическое программирование.
М., J975; [5] Т е р - К р и к о р о в А. М., Оптимальное уп-
управление и математическая экономика, М., 1977.
В. Г. Карманов.
ЛИНЕЙНОЕ ПРОСТРАНСТВО — то же, что век-
векторное пространство.
ЛИНЕЙНОЕ ТОПОЛОГИЧЕСКОЕ ПРОСТРАНСТВО
— векторное (линейное) пространство L, являющееся
топологич. пространством, в к-ром действия сложения
и умножения на скаляр в L непрерывны относительно
заданной в L топологии. См. Топологическое векторное
пространство. м. И. Войцеховский.
ЛИНЕЙНОЕ УРАВНЕНИЕ — уравнение вида
Ах=Ь, A)
где А — линейный оператор, действующий из вектор-
векторного пространства X в векторное пространство В,
х — неизвестный элемент из X, Ъ — заданный элемент
из В (свободный член). Если 6 — 0, то Л. у. наз. о д н о-
родным. Решением Л. у. наз. элемент х0,
обращающий A) в тождество:
Ахо=Ь.
Простейший пример доставляет линейный оператор
А : х—>-ах (линейная функция) и определяемое им
линейное уравнение (алгебраическое):
ах=Ъ, B)
a, b?R, С (или произвольному полю к); его решение
существует тогда и только тогда, когда либо а^ФО
(и тогда хл—Ыа), либо а = Ь=О (и тогда х0 — любое).
Обобщением уравнения B) является Л. у. вида
Ax=f{x)=b, C)
где f (х)—линейный функционал, определенный на
векторном пространстве X над полем k, b?k. В част-
частности, если размерность X конечна и равна п (так что
X изоморфно к"), f имеет вид линейной формы несколь-
нескольких переменных х1; , . ., хп^_к и уравнение C) может
быть записано в виде
aixi+ • • • -\~anxn = b, »n Ь?к. D)
Если а; одновременно не обращаются в нуль, то мно-
множество решений уравнения D) заполняет (п—1)-мер-
ное линейное многообразие (в однородном случае —
линейное подпространство) в X. Если X бесконечно-
бесконечномерно, то множество решений уравнения C) — линей-
линейное многообразие коразмерности 1.
Несколько уравнений вида D) образуют систему
Л. у.:
«/1^1+ • ¦ • + а/пх„ = Ь;, / = 1, ..., т. E)
При этом систему E) можно интерпретировать как
одно Л. у. вида A), если принять в качестве X прост-
пространство к", в качестве В — пространство кт, а опера-
оператор А задать матрицей i|a,y|), i—l,...,n;j = l,...,m.
Вопрос о совместности системы Л. у. E), т. с. вопрос
о существовании решения системы Л. у., решается
сравнением ранга матриц ||а,-у|| и ||а,-у, bj\\.
Более сложно обстоит дело в случае, когда X н В
являются бесконечномерными векторными простран-
пространствами. При этом играют существенную роль тополо-
топологии пространств X и В и обусловливаемые ими те или
иные свойства ограниченности, непрерывности и пр.
оператора А. В общем случае существование и единст-
единственность решения Л. у. обусловлены обратимостью А
(см. Обратное отображение). Однако эффективно об-
обратить А удается далеко не всегда, н потому для ис-
исследования Л. у. приобретают важную роль качест-
качественные методы, позволяющие без решения Л. у. ука-
указать полезные в том или ином отношении свойства
совокупности решений (в предположении, что они
существуют), напр, единственность, априорные оцен-
оценки и т. д. С другой стороны, оператор А может быть
определен не на всем пространстве X, и уравнение A)
может не иметь решения ни при каких Ь. В этой ситуа-
ситуации разрешимость уравнения A) устанавливается (во
многих практически важных случаях) выбором надле-
надлежащего расширения оператора А.
Для конкретных типов Л. у., напр, для линейных
дифференциальных уравнений как обыкновенных, так
и с частными производными, для линейных интеграль-
интегральных уравнений, разработаны специфические, в том
числе и численные, методы решения и исследования.
Наконец, в ряде случаев (напр., в задачах линейной
регрессии) оказываются полезными значения ас, в оп-
определенном смысле наиболее подходящие для роли
решения Л. у. М. И. Войцеывский.
ЛИНЕЙНОЕ УРАВНЕНИЕ алгебраическое —
алгебраическое уравнение 1-й степени по совокупности
неизвестных, т. е. уравнение вида
а2-Г2 +•••-{- ппХп = Ъ .
Всякая система Л. у. может быть записана в виде
A)
где m и п — натуральные числа; a;j (i=i, 2, . . .,
m, ;'= 1, 2, . . ., п) наз. коэффициентами при
неизвестных и являются заданными; Ь; (г'=1, 2, . . .,
т) наз. свободными членами и также яв-
являются заданными; х,- (i=i, 2, . . ., и) наз. неиз-
неизвестными и являются искомыми. Решением
системы Л. у. A) наз. такой набор значений
с1, с2, ¦ ¦ ., сп, что каждое из уравнений системы об-
обращается в тождество при подстановке с,- вместо соот-
ветствующих неизвестных. Для приложений наиболее
важен тот случай, когда коэффициенты при неизвест-
неизвестных, свободные члены и значения неизвестных явля-
являются числами (комплексными, действительными или
целыми), но можно рассматривать также случай, когда
опи лежат в произвольном поле Р.
По числу решений системы Л. у. делятся на следую-
следующие типы:
совместная система — система Л. у., име-
имеющая хотя бы одно решение;
несовместная система (или противоре-
противоречивая) — система, не имеющая ни одного решения;
определенная система — система, имею-
имеющая единственное решение;
неопределенная система — система,
имеющая более одного решения.
Если рассматриваются решения системы со значе-
значениями неизвестных в данном числовом (или любом
бесконечном) поле, то каждая неопределенная система
Л. у. имеет бесконечно много решений. В отличие от
уравнений степени выше первой, тип системы Л. у.
не меняется при расширении данного поля Р. Так, при
расширении поля несовместная система не может стать
совместной, а определенная — неопределенной. Од-
Однако совокупность решений неопределенной системы
при этом расширяется.
Простейший путь определения типа системы A) и
вычисления ее решений дает Гаусса метод исключения
неизвестных. В случае п=т система A) тогда и только
тогда является определенной, когда определитель, со-
составленный из ее коэффициентов при неизвестных, от-
отличен от нуля. В этом случае единственное решение
системы находится по формулам Крамера (см. Кра-
Крамера правило).
Для решения системы Л. у., коэффициенты к-рой
содержат буквенные параметры, более удобным, чем
метод Гаусса, является применение общей теории Л. у.,
связанной с понятием ранга матрицы. Ранг мат-
матрицы можно определить как максимальное число
линейно независимых строк или столбцов. По теореме
о ранге матрицы ранг системы строк матрицы равен
рангу системы столбцов и равен наибольшему порядку
отличных от нуля миноров этой матрицы. С системой
Л. у. A) связаны две матрицы: матрица
составленная из коэффициентов при неизвестных, и
расширенная матрица
В = \аи, 6,-1|,
получаемая из матрицы А добавлением столбца сво-
свободных членов. Критерий совместности системы A)
дает теорема Кронекера — Капелл и:
система Л. у. A) тогда и только тогда совместна, когда
ранг матрицы А равен рангу матрицы В.
Система Л. у. A) тогда и только тогда имеет единст-
единственное решение, когда ранг матрицы А равен рангу
матрицы Б п равен п.
Неизвестные совместной системы Л. у. подразде-
подразделяются на г л а в н ы е и свободные. При любых
значениях свободных неизвестных существуют одно-
однозначно определенные значения главных неизвестных,
дающие в совокупности решение данной системы. Вы-
Выбор главных и свободных неизвестных не всегда одно-
однозначен. Именно, если ранг А равен рангу Б и равен г,
то любые г неизвестных, из коэффициентов при к-рых
можно составить определитель ИфО, можно считать
главными, а остальные — свободными. Определитель
D в этом случае наз. г л а в п ы м (или базисным)
минором системы. Его можно искать методом
окаймления, начиная с миноров низших порядков. Он
также не всегда определен однозначно. При вычисле-
нии решений надо взять лишь г уравнений, содержа-
содержащих главный минор D, и выразить в общем виде (напр.,
используя формулы Крамера) главные неизвестные
через свободные. Эти выражения наз. общим ре-
решением. Свободные неизвестные играют в нем роль
свободных параметров. Придавая им любые значения,
находят значения главных неизвестных, дающие вместе
с выбранными значениями свободных неизвестных ре-
решение системы. Любое решение совместной системы
может быть получено указанным путем при подходя-
подходящих значениях свободных неизвестных. Если все
коэффициенты при неизвестных и свободные члены ле-
лежат в поле Р, то при выборе для свободных неизвестных
значений из того же поля Р получается решение со
значениями всех неизвестных из того же поля Р.
При г=и все неизвестные являются главными и об-
общего решения не существует.
Система Л. у.
а11х1 + а12х2 +...+аыхп =0, \
аг +^^ \ах 0 I
полученная из системы A) заменой свободных членов
нулями, наз. однородной системой Л. у.,
соответствующей системе A). Система B) всегда со-
совместна (т. к. ей удовлетворяет нулевое решение).
Для того чтобы она имела ненулевое решение, необ-
необходимо п достаточно, чтобы ранг ее матрицы А был
меньше числа неизвестных п. В частности, при т = га
квадратная однородная система Л. у. тогда и только
тогда имеет ненулевое решение, когда ее определитель
равен нулю.
Решения совместной системы Л. у. A) и соответст-
соответствующей однородной системы B) связаны следующим
образом: сумма решения системы A) и решения сис-
системы B) является решением системы A); разность двух
решений системы A) — решением системы B). Все ре-
решения системы A) можно получить, прибавляя к каж-
каждому решению системы B) одно и то же частное решение
системы A).
Геометрическая интерпретация решений системы Л. у.
Любую строку из п элементов поля Р можно рассмат-
рассматривать как строку координат вектора х /(-мерного
векторного пространства V над полем Р в нек-ром фик-
фиксированном базисе. Для краткости формулировок
вектор х отождествляется со строкой его координат.
Все решения однородной системы. B) составляют иод-
пространство U пространства V. Его размерность
равна п—г, где п — число неизвестных, а г — ранг
матрицы А системы. При г<Сп подпространство 1~
отлично от нулевого и его базис наз. также ф у и д а-
ментальной системой решений сис-
системы Л. у. B). Обратно, для каждого подпространства
U пространства V существует однородная система
Л. у., решения к-рой составляют подпространство U.
Множество векторов Z= и-гх0, получаемое прибавле-
прибавлением к каждому вектору подпространства U одного и
того же вектора хв, наз. линейным многооб-
многообразием (или плоскостью, иногда гипер-
гиперплоскостью) пространства V. Все решения сов-
совместной системы Л. у. A) составляют нек-рое линейное
многообразие Z; обратно, для любого линейного много-
многообразия Z существует совместная система, решения
к-рой составляют данное многообразие (см. [3]).
Решение систем линейных уравнений в целых числах.
Пусть дана система уравнений A), где все а,-у и Ь; —
целые числа. И пусть через d^, k=i, 2, . . ., min(m, n),
обозначен наибольший общий делитель всех миноров
порядка к матрицы А из коэффициентов при неизвест-
неизвестных, а через d'k, к=\, 2, . . ., min(m, ге+1),— аналогии-
ное число для расширенной матрицы В. Если все ми- |
норы порядка к в матрице А (или В) равны нулю, то
считают dj>. = 0 (соответственно d'k = O). Для того чтобы
целочисленная система Л. у. A) имела целочисленное
решение, необходимо и достаточно, чтобы d'k нацело
делилось на d^, А-=1, 2, . . ., min (т, п), и при т>л
выполнялось равенство dn+i=0.
Для формулировки метода вычисления всех целочис-
целочисленных решений систем Л. у. вводятся т. н. элементар-
элементарные преобразования целочисленных матриц: 1) прибав-
прибавление к i-й строке /-й строки (i^j), умноженной на
целое число с; 2) умножение г-й строки на —1; 3) пере-
перестановка г-й и /-й строк и аналогнчные преобразования
столбцов. При элементарных преобразованиях строк
система A) переходит в эквивалентную систему и,
значит, совокупность целочисленных решений не ме-
меняется. При элементарных преобразованиях столбцов
матрицы А из коэффициентов при неизвестных проис-
происходят следующие преобразования неизвестных: если
уг, у2, . . ., уп — новые неизвестные, то
при преобразовании 1)
при преобразовании 2)
хк = Ук (к Ф
при преобразовании 3)
/ = — У Г,
хк = Ук (к Ф h j), *! = У/, Zj = yi-
При таких преобразованиях неизвестных целочислен-
целочисленные решения и только они переходят в целочисленные.
Систему A), для к-рой ранг А равен рангу В и ра-
равен г, при помощи элементарных преобразований строк
матрицы В и столбцов матрицы А, а также отбрасыва-
отбрасыванием нулевых уравнений можно привести к следую-
следующему канонич. виду
bi, •• ¦> eryr = b'r. C)
Числа ei удовлетворяют дополнительным условиям:
е,- > 0, i = l, 2, ..., г,
и
et делит е,- + 1, г = 1, 2, ..., г — 1.
Для задачи решения системы в целых числах эти до-
дополнительные условия несущественны.
Для существования целочисленных решений системы
C) необходимо и достаточно, чтобы числа
были целыми. Неизвестные г/ь уг, . . ., уг определены
однозначно, а при r-Сп неизвестные yr + i, . . ., уп
могут принимать любые целые значения.
Для вычисления решений исходной системы A) надо
все преобразования столбцов матрицы А применить
в том же порядке к единичной матрице Е порядка п.
Полученная целочисленная матрица Q дает связь ста-
старых и новых неизвестных:
X = QY,
где
г/i
Y =
г/г
Уп
Затем надо положить у,= с,-, г=1, 2, . . ., г, а при
г<Сп неизвестным yr + i, . . ., уп, играющим роль пара-
параметров, можно придавать любые целые значения.
Указанный метод решения системы A) над кольцом
целых чисел обобщается на любые евклидовы кольца
и кольца главных идеалов.
Разыскание целочисленных решений уравнений и
систем в общем случае — предмет теории диофантоеы.,
уравнений.
Лит.: [1] К у р о ш А. Г., Курс высшей алгебры, 11 изд.
М., 1975; [2] К о с т р п к и н А. И., Введение в алгебру, м.
1977; [3] Мишина А. П., Проскуряков И. В.
Высшая алгебра. Линейная алгебра, многочлены, общая алгебра
2 изд., М., 1965. И. В. Проскуряков.
ЛИНЕЙНОЕ ЭЛЛИПТИЧЕСКОЕ УРАВНЕНИЕ И
СИСТЕМА — дифференциальное уравнение (и система)
с частными производными вида
где L — линейный эллиптич. оператор
Оператор A) с действительными коэффициентами аа(х)
эллиптичен в точке х, если характеристич.
форма
<*. е> = 2, «,=„,-*
является определенной в этой точке. Здесь х=(хг, .....
xn)?Rn, а,= (а1, . . ., а„) — мультииндекс (набо]>
целых неотрицательных чисел), |а| = 2а,-, g=(si, • • ¦,
ности, порядок т оператора L должен быть четным
т=2т'. С точностью до знака условие определенности
форм записывается в виде
(_1)т'ш (*, ЙЗйбШ», б>0. B)
Оператор L эллиптичен в области D, если он эллип-
эллиптичен в каждой точке x?D, н равномерно эллиптичен
в этой области, если б>0 в B) не зависит от х.
В случае уравнения 2-го порядка
, * ди , /v г, \
C)
это определение может быть переформулировано сле-
следующим образом. Уравнение C) эллиптично в об-
области D, если в каждой точке этой области путем за-
замены независимых переменных оно допускает приведе-
приведение к канонич. виду
с оператором Лапласа
Л =-214- 4--21
в главной части. В случае эллиптич. уравнения па
плоскости при весьма широких предположениях отно-
относительно коэффициентов а,у такое преобразование воз-
возможно не только в точке, но и во всей области (см.
[1]).
Простейшим эллиптич. уравнением является Лап-
Лапласа уравнение, его решения наз. гармоническими функ-
функциями. Решения линейного эллиптич. уравнения
(л. э. у.) можно охарактеризовать тем, что они имеют
много общих свойств с гармонич. функциями. В пло-
плоском случае все гармонич. функции описываются как
реальные части аналитич. функций, они являются дейст-
действительными аналитич. функциями двух переменных.
Аналогичным свойством обладают решения общего,
л. э. у. Lu = f. Если коэффициенты аа.(х), |а|<:т, и
правая часть f(x) аналитичны по х=(х1, . . ., хп) в об-
ласти D, то и любое решение этого уравнения также
аналитично.
Существуют и другие утверждения подобного типа.
Напр., если коэффициенты и правая часть уравнения
Lu=f непрерывно дифференцируемы до порядка к
н их к-в производные удовлетворяют условию Гёльдера
с показателем а, 0<сс<1, то любое решение обладает
производными до порядка fe-f-лг, удовлетворяющими
условию Гёльдера с тем же показателем а. Принадлеж-
Принадлежность к классу Гёльдера здесь существенна. Если коэф-
коэффициенты и правая часть просто непрерывны, то реше-
решения могут не иметь непрерывных производных по-
порядка, равного порядку уравнения. Это верно даже
для самого простого л. э. у.— Пуассона уравнения
Au = f.
Вышесказанное относится к классич. решениям, т. е.
решениям, имеющим непрерывные производные до
порядка, равного порядку уравнения. Существуют
различные обобщения понятия решения.
Напр., если коэффициенты аа(х) достаточно гладки,
то для оператора A) можно определить сопряженный
по Лагранжу оператор
ll
Локально интегрируемая функция и (х) наз. слабым
решением уравнения Lu =/, если для всех ц> ? С™
(бесконечно дифференцируемых функций с компакт-
компактным носителем) выполнено тождество
(х) ф (х) dx = ^и (х) ?*ф (х) ex.
Тогда, если коэффициенты и правая часть уравнения
Lu=f непрерывны по Гёльдеру, то всякое слабое ре-
решение является классическим.
Для уравнения Лапласа простейшей корректно по-
поставленной задачей является Дирихле задача. В общем
случае уравнения с оператором A) краевая задача
состоит в отыскании в области D решения и (х) урав-
уравнения Lu = f, удовлетворяющего т' = т/2 граничным
условиям вида
Задаче Дирихле отвечают граничные операторы Ьу =
= (ev)J' где ev означает дифференцирование по на-
направлению внешней нормали.
Для того чтобы краевая задача была нётеровой, гра-
граничные операторы В;- должны удовлетворять усло-
условию дополнительности Шапиро —
Лопат и некого (см. [2]) — алгебраич. условию,
связывающему многочлены
в точках границы x?dD. Граничные операторы за-
задачи Дирихле удовлетворяют этому условию по отно-
отношению к любому эллиптич. оператору L.
Если коэффициенты дифференциального оператора и
решение рассматривать в классе комплексных функций,
то эллиптичность оператора L в (i) определяется усло-
условием <а(х, ?)Ф0, ^фО. Это определение допускает эл-
эллиптич. операторы нечетного порядка, как показывает
пример оператора Кош и — Римана: ^- +
+ i^j-. Кроме того, меняются свойства операторов чет-
ного порядка. Напр., для Бицадзе уравнения (см. [3]):
задача Дирихле не является корректно поставленной:
если D — единичный круг, то функции вида и=
= /(z)(l — |z|2) являются решениями однородной за-
задачи Дирихле в области D для любой аналитич. функ-
функции f(z).
Этот пример привел к необходимости выделять клас-
классы эллиптич. операторов, для к-рых сохраняется нёте-
ровость задачи Дирихле. На этом пути возникло поня-
понятие сильно аллиптич. оператора (см. [4]). Оператор
A) — сильно эллиптический опера-
оператор, если для нек-рой комплексной функции у(х)фО
выполнено условие
Re V (*) Х| а \=т а« <*> *>" ^ 6 I 11"' 6 > °-
В частности, порядок т — необходимо четное число.
Следующим более широким понятием явилось поня-
понятие собственной (правильной) эллиптичности. Опера-
Оператор A) — собственно эллиптический
оператор, если его порядок четен и для любой
пары линейно независимых векторов ? и |' многочлен
по т
имеет ровно m' = m/2 корней с отрицательной мнимой
частью и столько же — с положительной. Любой
эллиптич. оператор при и^З собственно эллиптичен,
так что определение по существу относится только
к случаю и=2.
В теории л. э. у. значительную роль играют апри-
априорные оценки норм решений через нормы правых час-
частей уравнения и граничных условий. Эти оценки на-
начали систематически использоваться С. Н. Бернштен-
ном (см. [6]) и свое дальнейшее развитие получили
у Ю. Шаудера (см. [7]). Шаудеровские оценки отно-
относятся к решениям к. э. у. 2-го порядка в области D
с непрерывными по Гёльдеру коэффициентами и бы-
бывают двух видов. Оценки первого вида (оценки «внут-
«внутри») состоят в том, что на любом компакте K?D про-
производные до 2-го порядка включительно и их гёльде-
ровские константы оцениваются через sup!«| и через
модуль и гёльдеровскую константу правой части урав-
уравнения. Оценки второго вида (оценки «вплоть до гра-
границы») относятся к краевым задачам. Здесь оценивают
те же величины, но уже в замыкании рассматриваемой
области, и в оценке фигурируют нормы правых частей
граничных условий.
Шаудеровские оценки получили дальнейшее рас-
распространение для общих л. э. у. и краевых задач
(см. [7]). Вывод этих оценок основан на теории потен-
потенциала. С помощью разбиения единицы им придается
локальный характер, и дело сводится к оценке норм
сингулярных интегральных операторов, к-рые пред-
представляют собой свертку с функциями, связанными
с фундаментальными решениями (оценки «внутри») или
с функциями Грина соответствующей краевой задачи
в нек-рой стандартной области (оценки «вплоть до гра-
границы»). Эти оценки, полученные первоначально в мет-
метрике пространств Гёльдера Са, распространены на
пространства Соболева Wp (L^-оценки) и относятся
к обобщенным решениям.
Для сильно эллиптич. операторов существует ап-
априорная оценка, наз. неравенством Гёрдинга, к-рая
получена другими методами. Она лежит в основе
функционального подхода к исследованию краевых
задач (методы гильбертовых пространств).
В теории л. э. у. важное место занимают фундамен-
фундаментальные решения. Для оператора A) с достаточно глад-
гладкими коэффициентами фундаментальное ре-
решение определяется как функция /(.г, у), удовлет-
удовлетворяющая условию
*ф (х) J (х, у) dx=(f> (у)
для всех ф?С(Г. С точки зрения теории обобщенных
функций это означает равенство
где справа стоит дельта-функция Дирака.
Фундаментальные решения л. э. у. существуют для
уравнений с аналитич. коэффициентами (и сами тогда
аналнтичны), для уравнений с бесконечно дифферен-
дифференцируемыми коэффициентами (и также принадлежащие
классу Сх) и для ряда других уравнений с более сла-
слабыми ограничениями на коэффициенты. Для эллиптич.
оператора Lo с постоянными коэффициентами, состоя-
состоящего пз членов старшего порядка m=2m', фундамен-
фундаментальное решение зависит только от разности аргумен-
и имеет вид (г/ = 0):
/ (х) = | х |»-« ф ( jiL-) + q (х) In | x |,
где q (x) — многочлен степени т—n при четном п
и m — n^Q, в остальных случаях q (i) = 0, т|з (х) анали-
тична на сфере |х| = 1 (см. [8]).
В частности, для оператора Лапласа (т = 2) q = 0,
¦ф—const для га>2 и g=const, т)з=О для ге=2.
Фундаментальные решения позволяют строить раз-
различные явные представления для решений л. э. у.
Они являются необходимым аппаратом при изучении
краевых задач с помощью интегральных уравнений.
Для уравнения 2-го порядка этот метод является клас-
классическим ц дает наиболее точные результаты (см. [9]).
Многообразные применения в теории л. э. у. 2-го по-
порядка получил принцип максимума. Функции а,у, а;, а
предполагаются непрерывными, оператор C) равно-
равномерно эллиптичным в нек-рой области D. Функция и (х)
непрерывна в замыкании D и принадлежит классу
C2(D).
Принцип максимума в его сильной форме заклю-
заключается в следующем. Пусть М — оператор L в C),
в котором а~^0.
а) Если Ми^О и функция и(х) достигает своего
максимума во внутренней точке, то и постоянна.
б) Если Ми^О и максимум и достигается в нек-рой
граничной точке х0, к-рая расположена на поверхности
нек-рого шара, целиком содержащегося в D, то и (х)
либо постоянна, либо производная в точке sc0 по на-
направлению внешней нормали duid\ положительна.
Аналогичные утверждения справедливы для опера-
оператора L с а(х)<:0, если в а) и б) под максимумом пони-
понимать положительный максимум. Принцип максимума
является существенным элементом в доказательствах
теорем единственности для решений ряда краевых за-
задач. Он также имеет нек-рые аналоги в случае урав-
уравнений высшего порядка.
Лит.: [1] В е к"у а И. Н., Обобщенные аналитические
функции, М., 1959; [2] Бицадзе А. В., Краевые задачи
для эллиптических уравнений второго порядка, М., 1986; [31
А г м о и С, Д у г л и с А., Н и р е н б е р г Л., Оценки
вблизи границы решений эллиптических уравнений в частных
производных при общих граничных условиях, пер. с англ., М.,
1962; [4] Й о н Ф., Плоские волны и сферические средние в при-
применении к дифференциальным уравнениям с частными произ-
производными, пер. с англ., М., 1958; [5J Миранда К., Уравне-
Уравнения с частными производными эллиптического типа, пер. с итал.,
М., 1957; [6] Бернштейн С. Н., Собр. соч., т. 3, М..
1960; [7] S с h a u d e r J., «Math. Z.», 1934, Bd 38, S. 257 — 82;
[8| Л о па ти некий Я. Б.. «Укр. матем. ж.», 1953, т. 5,
As 2, с. 123 — 51; [9] В и ш и к М. II., «Матем. сб.», 1951,
т. 29, „V" 3, с. 615—76. .4. П. СолОптов.
ЛИНЕЙНОЙ НЕЗАВИСИМОСТИ МЕРА чисел
аи . . ., ап — функция
? («i. ..., ап | H) = L (#) = min | a,ccj + . .. + а„а„|,
где минимум берется по всевозможным наборам целых
чисел (аи . . ., ап), удовлетворяющим условиям:
Известно, что
Li ГЧ ГЧ I 1Т\ / t 1 ГЧ 1 [ ' I ГЧ \\ 1Т~ ^ (П~ 1)
\<Xi, . . . , GCjj [ п } <. у j СС] J —\- . . . ~- | ССП |) п ,
где т=1, если все числа <zlt . . ., ап действительные, и
т=1/2 — в противном случае. Получение оценок снизу
L(a.i, . . ., ап\Н) по параметру И для конкретных
наборов чисел ах, . . ., ап является одной из задач
теории диофантовых приближений. ю- В. Нестереико.
ЛИНЕЙНЫЙ ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАТОР
в узком смысле — оператор, действующий на
функции, заданные на открытом множестве PcR",
и принимающий значения в поле /с—R или /с=С по
формуле
\ ^ д и /л \
Au = v = y^ o-i i J[ T— ' *¦ '
где ait in — функции со значениями в том же поле,
наз. коэффициентами А. Если коэффициенты
принимают значения во множестве матриц размера
tXs над полем к, то Л. д. о. А определен на гектор-
функциях «=(«ь . . ., us) и преобразует их в вектор-
функции v=(vt, . . ., Vf). В случае п = \ он наз. обык-
обыкновенным линейным дифференци-
дифференциальным оператором, а в случае и>1 — л и-
нейным дифференциальным опера-
оператором с частными производными.
Пусть X — дифференцируемое многообразие, Е и
F — конечномерные векторные расслоения на X (все
из класса С"). Пусть ?\ F — пучки ростков сечений
этих расслоений соответствующей гладкости. Л. д. о.
в широком смысле А : E^F есть отображе-
отображение пучков E-^-F, удовлетворяющее условию: всякая
точка х?Х имеет координатную окрестность U, в п.ре-
делах к-рой расслоения тривиальны, а отображение
A :T(U, E)-+T{U, F),
где T(U, Е) —пространство сечений над U расслсе-
ния Е, действует по формуле A), в к-рой использованы
локальные координаты х1, . . ., хп и тривиализации
Минимальное число т, пригодное для формулы A)
во всех точках х?Х, наз. п о р я д к о м Л. д. о. А.
Напр., всякая ненулевая связность в расслоении Е
есть нек-рый Л. д. о. E^-EffiQ1 (X) первого порядка.
Другое, эквивалентное определение Л. д. о. А : E—yF
таково: это — линейный оператор А : Г (X,Е) —>-
—>T(X,F), удовлетворяющий условию supp^li/C
Csupp и, где supp и — носитель и.
Л. д. о. может быть задан на более широких функ-
функциональных пространствах. Напр., если на X задан,
положительная мера, а на расслоениях Е и F —
нек-рое скалярное произведение, то определены про-
пространства квадратично суммируемых сечений этих рас-
расслоений. Л. д. о., заданный локальными выраже-
выражениями A), определяет линейный неограниченный опе-
оператор А : Li(E)-^-L2{F). При нек-рых слабых предпо-
предположениях последний может быть замкнут как оператор
в гильбертовых пространствах. Это замыкание также
носит название Л. д. о. Подобным же образом может
быть построен оператор, действующий в пространствах
Соболева или в пространствах более обшпх шкал.
Л. д. о. класса С" может быть расширен до опера-
оператора в пространствах обобщенных сечений. Такое рас-
расширение может быть построено с помощью формально
сопряженного оператора. Пусть Е'— расслоение, со-
сопряженное с Е (т. е. ?" = Hom(i?, /), / — одномерное
тривиальное расслоение), a Q — расслоение нечетных
дифференциальных форм на X максимальной степени.
Определено билинейное отображение
(., ¦)/•: ПХ, Е)ХТ0(Х, ?'<g)Q)—-Л,
включающее интегрирование по X. Здесь Го(. . .) —
пространство сечений с компактными носителями.
Формула
pAv, u)E=(v, Au)p
однозначно определяет нек-рый линейный оператор
>А:Г0 (X, F' ® Q) -^ Го (X, Е' ®Q).
Он порождается Л. д. о. tA : i<"(X)Q—>-i?'(X)Q, к-рый
в пределах координатной окрестности U имеет выра-
выражение
если расслоение Q тривиализовано выбором сечения
dxx/\. . .f\dxn. Л. д. о. (А наз. формально соп-
сопряжены ы м по отношению к А.
В пространстве Т0(Х, ?"(X)Q) задается сходимость
по следующему правилу: /?—>-/, если объединение но-
носителей сечений /^ принадлежит компакту, и в любой
координатной окрестности (lei, над к-рой имеется
тривиализация Е, вектор-функции /^ равномерно схо-
сходятся к / вместе со всеми частными производными по
локальным координатам. Пространство всех линейных
функционалов над Г0(Х, ?"(X)Q), непрерывных отно-
относительно указанной сходимости, наз. простран-
пространством обобщенных сечений Е и обозна-
обозначается D' (Е). Оператор 1А переводит сходящиеся после-
последовательности в сходящиеся и потому порождает соп-
сопряженный оператор D' (?)—>-?>' (F). Последний совпа-
совпадает с А на подпространстве Т(Х, Е) и наз. продол-
продолжением данного Л. д. о. на пространство обобщен-
обобщенных сечений. Рассматриваются также и другие расши-
расширения Л. д. о.: на пространства обобщенных сечений
бесконечного порядка, на различные пространства
гиперфункций и т. д.
Под Л. д. о. бесконечного порядка понимается опе-
оператор, действующий в том или ином пространстве ана-
литич. функций (сечений), заданный формулой A),
в к-рой суммирование производится по бесконечному
множеству индексов iu . . ., in.
Следующее свойство характеризует Л. д. о. После-
Последовательность {//,}сГ(Х, Е) объявляется сходящейся
к сечению /, если /^ равномерно стремится к / вместе
со всеми частными производными в любой координат-
координатной окрестности, имеющей компактное замыкание.
Линейный оператор А : Г0(Х, Е)^-Т(Х, F), перево-
переводящий сходящиеся последовательности в сходящиеся,
является Л. д. о. порядка не выше m тогда и только
тогда, когда для любых /, g?.C°°(X) функция
ехр (- ikg) A (/ exp (ikg)) B)
является полиномом1 по параметру к степени не выше т.
Если это условие заменить предположением, что B)
представляется асимптотич. степенным рядом, то по-
получается определение линейного псевдодифференциалъ-
ного оператора.
Пусть многообразие X, а также расслоения Е и F
снабжены G-структурой, где G — нек-рая группа. Тогда
определено действие этой группы на любой Л. д. о.
А : E—>-F по формуле
g*(A)(u)--=g(A(g-i(u))).
Л. д. о. А наз. инвариантным относи-
относительно G, если g* (А)=А для всех g?G.
Расслоение струй (джетов) есть объект, двойствен-
двойственный пространству Л. д. о. Пусть снова Е — вектор-
векторное расслоение на многообразии X класса С". Р а с-
слоение то - с т р у й сечений Е есть векторное
расслоение Jт(Е) на X, слой к-рого над точкой х
равен Ёх/Ёх(т), где Ёх — слой пучка Ё, а Ёх(т) —
подпространство этого слоя, состоящее ш ростков
сечений, у к-рых в точке х обращаются в нуль все диф-
дифференциалы до порядка т включительно. Л. д. о.
dm : E-+Jт (Е), действующий по правилу: значение
сечения dm (и) в точке х равно образу сечения и в фак-
торпространстве Ёх/Ёх(т), наз. универсаль-
н ы м. Пусть, далее, F — расслоение на X, на : J m (Е)—>-
—>-/<' — гомоморфизм расслоений, т. е. Л. д. о. нуле-
нулевого порядка. Композиция
есть Л. д. о. порядка не выше т. Обратно, всякий
Л. д. о. порядка не выше т может быть представлен
единственным способом в виде композиции C).
Символ (главный символ) Л. д. о.
А : E^F есть семейство линейных отображений
аА(х, l):Ex-^Fx,
зависящее от точки (х, \) кокасательного расслоения
Т* (X). Они действуют по формуле е-+—, а (\'пе), где
а — гомоморфизм, участвующий в факторизации C),
е?Ёх, а %те — элемент Jm(E)x, равный образу fme,
где / — росток функции класса С" такой, что /(.г) = 0,
df (х)=Ъ,. Если А имеет вид A), то
где ^1, • • -1 Ьп — координаты слоя расслоения T*(U) =
=sf/Xfc"; таким образом, символ является однородной
по | формой степени т. В соответствии с этой конст-
конструкцией символа вводится понятие характеристики.
Характеристикой Л. д. о. А наз. точка
(х, |)? Т* {X), в к-рой символ ал имеет ненулевое ядро.
Принятая в теории Л. д. о. классификация отно-
относится главным образом к Л. д. о., действующим в рас-
расслоениях одинаковой размерности, фактически к опе-
операторам вида A), где коэффициенты суть квадратные
матрицы. Л. д. о. наз. эллиптическим, если
он не имеет действительных характеристик (х, |),
%ФО. Этот класс характеризуется наилучшими локаль-
локальными свойствами решений уравнения Au=w, а также
корректностью краевых задач в ограниченных облас-
областях. Класс гиперболических Л. д. о. также
выделяется условием, наложенным лишь на характе-
характеристики. Свойство гиперболичности тесно связано
с корректностью задачи Коши с неаналитич. началь-
начальными данными. Класс Л. д. о. главного типа задается
условием, наложенным лишь на символ. Для таких
операторов развита теория локальной разрешимости
и гладкости решений. Класс параболических
Л. д. о. выделяется условием, касающимся не только
символа, но и нек-рых младших членов. Для парабо-
лич. Л. д. о. характерна смешанная задача и задача
Коши с условиями на бесконечности. Класс г и п о-
эллиптических Л. д. о. задается следующим
неформальным условием: всякое априори обобщенное
решение уравнения Au=w с правой частью из С° само
принадлежит С". Известен ряд формальных условий
на выражение A), обеспечивающих гипоэллиптичность
оператора.
Помимо указанных основных типов Л. д. о., иногда
говорят о Л. д. о. смешанного или переменного типа,
о Л. д. о. составного типа и др. Рассматриваются
также задачи в неограниченных областях с условиями
на бесконечности, краевые задачи со свободной грани-
границей, задачи спектральной теории, задачи оптимального
управления и др.
Комплекс Л. д. о. есть последовательность
Л. д. о.
k k Ч- 1
Е*... —rEk—>- Ek + i *Ek + 2—<-¦¦¦,
в к-рой Л? + 1^4а = 0 для всех к. Когомология комплекса
Л. д. о. Е* есть когомология комплекса векторных"
пространств Г(Х, Е*). Пусть Я* — когомология этого
комплекса в к-и члене. Сумма 2 (— l)*dim //* наз.
индекс ом данного комплекса Л. д. о. Так,
индекс эллиптпч. комплекса Л. д. о. (т. е. такого, что
лишь конечное число Е^ отлично от нулевого, и ком-
комплекс, образованный символами Л. д. о. А^, точен во
всех точках (х, ?)?Г* (X), %фО) конечен в случае
компактного X, и отыскание формул, выражающих
индекс такого комплекса через его символ, является
содержанием ряда исследований, объединяющих тео-
теорию Л. д. о. с алгебраич. геометрией и алгебраич. то-
топологией (см. Индекса формулы).
Описанное определение символа не является вполне
удовлетворительным для Л. д. о., действующих в рас-
расслоениях размерности, большей 1. Одной из причин
этого является тот факт, что равенство Олв^аА°ав
может нарушаться. Следующая усложненная конст-
конструкция, заменяющая понятие символа, является более
адекватной. Для всякого расслоения Е на многообра-
многообразии X класса С°° рассматривается пучок D (Е) рост-
ростков Л. д. о. Е—^-1, где / — одномерное тривиальное
расслоение. По определению, значение этого пучка
на открытом множестве UdX есть совокупность всех
Л. д. о. Е\ц-+1\ц. Пусть Dk(E) — его подпучок, об-
образованный операторами порядка не выше к. В Z>«
=Z) (/) имеется структура пучка (некоммутативных)
алгебр, а в D (Е) — структура левого модуля над D,
причем действие a?D на b?D (E) равно композиции
аЪ. Данный Л. д. о. А : E^yF определяет морфизм
левых ?)-дгодулей А' : D (F)^-D (E) по закону компо-
композиции а~+аА . Пусть М (А) — коядро этого морфпзма.
Имеется точная последовательность левых /^-модулей
D(F)-^D (E) -Д М (Л) —>- 0, D)
О(Х)-подмодули Mk=p(Dk(E)), к = 0, 1, . . ., об-
образуют возрастающую фильтрацию в М(А). Градуиро-
Градуированный 0(Х)-модуль
наз. символическим модулем Л. д. о. А.
Поскольку при любых к ж I действие Dk на М(А)
переводит Mt в Mi + k, то в grM(А) имеется структура
градуированного модуля над градуированной алгеброн
gr ?)=(X)o°?>jt''?)ft-i. Аннулятор этого модуля есть
однородный идеал в gr D. Характеристиче-
Характеристическое многообразие оператора А есть мно-
множество корней этого идеала. Так как алгебра gr D изо-
изоморфна симметрич. алгебре касательного расслоения
Т(Х), то характеристич. многообразие канонически
вкладывается в Т*(Х), причем его пересечение с каж-
каждым слоем есть алгебраич. конус.
Если многообразие X, а также данные расслоения
имеют вещественно или комплексно аналитич. струк-
ТУРУ* т0 характеристич. многообразие совпадает с мно-
множеством корней идеала gr(ann M(A)). В этом случае
оно является замкнутым аналитич. подмножеством
в Т* (X), причем если оно не пусто, то его размерность
не меньше dim X. В случае, когда эта размерность
равна dim X, Л. д. о. А наз. максимально
переопределенным, или голономным.
Формальная теория общих Л. д. о. имеет дело с по-
понятиями формальной интегрируемости и резольвенты.
Свойство формальной интегрируемое-
т и, формулируемое в двойственных терминах струп,
эквивалентно условию: О(Х)-модуль gr M(А) локально
свободен. Под резольвентой Л. д. о. Л пони-
понимается последовательность, продолжающая D)
... —^D (F^-Xd (F)-^D (E)—+M {A),
в к-рой все Akt А=1, 2, . . ., суть Л. д. о. В частности,
А! наз. оператором совместности для А.
Формальная интегрируемость обеспечивает локальное
существование резольвенты.
В литературе используются термины «переопределен-
«переопределенная» и «недоопределенная» система дифференциальных
уравнений, однако удовлетворительное общее опреде-
определение отсутствует. Нек-рым приближением к такому
определению может служить следующее: существует
ненулевой Л. д. о. В такой, что В А—>-0 (п с р е о п р е-
деленность), АВ = 6 (недоопределен-
н о с т ь). Напр., Л. д. о. d, равный ограничению опе-
оператора внешнего дифференцирования на формах сте-
степени к на многообразии X размерности п, является
недоопределенным при /с>0, переопределенным при
&<ге и голономным при А=0.
Основные задачи, изучаемые для общих Л. д. о.:
разрешимость уравнения с правой частью Аи = и> при
выполнении условия совместности А1и=0, возмож-
возможность продолжения решений уравнения Аи=0 в боль-
большую область (эффект, связанный с переопределенно-
переопределенностью), представление общего решения через решения
специального вида. Последняя задача может быть
сформулирована более конкретно для инвариантных
операторов, напр, для Л. д. о. в R" с постоянными
или периодич. коэффициентами: записать представле-
представление группы G в пространстве решений в виде интеграла
(в том или ином смысле) по всем неразложимым под-
представлениям. Для определения операторов с по-
постоянными коэффициентами такое представление за-
задается интегралом по экспонентам (экспоненциальное
представление), для операторов с периодич. коэффи-
коэффициентами — интегралом по обобщенным решениям
Флоке.
Определяются Л. д. о. и на произвольных алгебраич.
структурах. Пусть R — коммутативное кольцо, Е
и F суть Л-модули. Отображение множеств А : E-^>-F
наз. Л. д. о. порядка не выше га, если оно аддитивно
и для любого элемента a?R отображение аА—А а
является Л. д. о. порядка не выше m — 1. При этом
под Л. д. о. порядка не выше —1 понимается лишь
нулевое отображение. В частности, Л. д. о. нулевого
порядка есть гомоморфизм Д-модулей и обратно. Вся-
Всякое дифференцирование v : R-+F является Л. д. о.
1-го порядка (или равно нулю). Если R есть алгебра
над нек-рым полем к, то под Л. д. о. над R понимается
Л. д. о. над кольцом R, к-рый является /с-линейным
отображением. Такой Л. д. о. обладает рядом фор-
формальных свойств обычных Л. д. о. Если R есть алгебра
всех формальных степенных рядов над к или алгебра
сходящихся степенных рядов над к, а Е и F — свобод-
свободные Л-модули конечного типа, то всякий Л. д. о.
А '. E-^r-F порядка не выше ш имеет однозначную
запись A).
Пусть (X, О) — кольцованное пространство, Е и F
суть О-модули. Под Л. д. о. А : E^~F понимается вся-
всякий морфизм пучков, к-рый в слоях над каждой точ-
кой z?X действует как Л. д. о. над кольцом (алгеб-
(алгеброй) Ох. Л. д. о., действующие в модулях или пучках
модулей, используются в ряде вопросов алгебраич.
геометрии.
Лит.: [1] Р е е t г е J., «Math. Scand.», 1960, v. 8, p. 116—
120; [2] X ё р м а н д е р Л., в кн.: Псевдодифференциальные
операторы, пер. с англ., М., 1967, с. 63 — 87, 106 — 296, 297—
367; [3] Б е р н ш т е й н И. Н., «Функц. анализ и его при-
лож.», 1972, т. 6, в. 4, с. 26—40; [4] Курант Р., Уравнения
с частными производными, пер. с англ., М., 1964; [5] Тихо-
Тихонов А. Н., Самарский А. А., Уравнения математиче-
математической физики, 5 изд., М., 1977; [6] Хёрмандер Л., Линей-
Линейные дифференциальные операторы с частными производными,
пер. с англ., М., 1965; [7] Паламодов В. П., Линейные
дифференциальные операторы с постоянными коэффициентами,
М., 1967; [8] X а р т м а н Ф., Обыкновенные дифференциаль-
дифференциальные уравнения, пер. с англ., М., 1970; [9] Пале Р., Семинар
по теореме Атьи-Зингера об индексе, пер. с англ., М., 1970;
[10] Паламодов В. П., в кн.: Итоги науки. Математиче-
Математический анализ. 1968, М., 1969, с. 5—37; [11J Спенсер Д.,
«Математика». 1970, т. 14, Л» 2, с. 66—90; № 3, с. 99—126; [12]
Sato M., Kawai Т., Kashiwara M., Microfunctions
and psendodifferential equations, Kyoto, 1972. В. П. Паламодов.
ЛИНЕЙНЫЙ МЕТОД СУММИРОВАНИЯ — метод
суммирования, обладающий свойствами линейности:
1) если ряд ^k=aaji суммируем Л. м. с. к сумме А,
то ряд 2jk=rfak суммируем этим методом к сумме сА;
2) если ряды ^jfe=00fe и Zjk=o^k сУммиРУемы Л. м. с.
соответственно к А и В, то ряд z^k= ^ак~^^к) суммируем
тем же методом к сумме А +5. Все наиболее распрост-
распространенные методы суммирования линейны. В част-
частности, линейными являются матричный метод сумми-
суммирования и полунепрерывный метод суммирования. Су-
Существуют нелинейные методы суммирования. Напр.,
метод, в к-ром суммируемость ряда к сумме S опреде-
определяется наличием предела S у последовательности {Тп},
гДе
Т —•
* п
(sn — частичные суммы ряда), не является линейным.
Лит.: [1] X а р ди Г., Расходящиеся ряды, пер. с англ.,
М., 1951; [2] Кук Р., Бесконечные матрицы и пространства
последовательностей, пер. с англ., М., 1960; [3] К а н г р о Г.
Ф., в сб.: Итоги науки и техники. Математический аналиа, т. 12,
М., 1974, с. 5—70; [4] Барон С. А., Введение в теорию сум-
суммируемости рядов, 2 изд., Тал., 1977. И. И. Волков.
ЛИНЕЙНЫЙ ОПЕРАТОР, линейное и р е о б-
разовани е,— отображение между двумя вектор-
векторными пространствами, согласованное с их линейными
структурами. Точнее, отображение А : E—>-F, где Е
и F — векторные пространства над полем к, паз. л и-
н е й н ы м оператором из Е в F, если
А (х-гу) = Ах-\-Ау, А ('Кх)
при всех х, у?Е, Х^к. Простейшие примеры — ну-
нулевой Л. о. о, переводящий все векторы в O^F,
и (в случае E=F) тождественный Л. о. 1,
оставляющий векторы на месте.
Понятие Л. о., будучи наряду с понятием вектор-
векторного пространства главным в линейной алгебре, играет
роль в самых разнообразных областях математики и
физики, прежде всего — в анализе и его приложениях.
Современное определение Л. о. впервые дал Дж. Пе-
апо [1] (для к=Щ. Оно было, однако, подготовлено
предшествующим развитием математики, накопившей
(начиная с линейной функции у = ах) огромное число
примеров. В алгебре их неполный перечень включает
линейные подстановки в системах линейных уравне-
уравнений, умножение кватернионов и элементов грассмано-
вой алгебры; в аналитич. геометрии — преобразова-
преобразования координат; в анализе — дифференциальные и ин-
интегральные преобразования и интеграл Фурье.
Вплоть до начала 20 в. систематически изучались
лишь Л. о. между конечномерными пространствами
над полями R и С, Первые «бесконечномерные» на-
блюдения, к тому же касающиеся общих полей, были
сделаны О. Тёплицем [3]. Л. о. между бесконечномер-
бесконечномерными пространствами Е и F изучаются, как правило,
в предположении их непрерывности относительно
нек-рых топологий. Непрерывные Л. о., действующие
в различных классах топологич. векторных прост-
пространств, в первую очередь банаховых и гильбертовых,—
это основной объект изучения линейного функцио-
функционального анализа.
В теории Л. о. два специальных случая F=k и
F=E наиболее важны. В первом случае Л. о. наз.
функционалом (см. Линейный функционал),
во втором — линейным оператором, дей-
действующим в Е, или эндоморфизмом.
Все Л. о. из Е в F образуют векторное пространство
X (Е, F) (вместо X (Е, Е) пишется X (?")) над к отно-
относительно сложения и умножения на скаляр, задавае-
задаваемыми формулами.
= А (Хх), А, В~?Х (Е, F),
нулем является о. Умножение (компози-
(композиция) АВ Л. о. А : El-+Fl и В : E2—^F2 определено
лишь при F2=E1 как последовательное применение В
и А. Относительно трех указанных операций X (Е) —
пример ассоциативной алгебры над к с единицей 1.
Это «больше чем пример»: всякая ассоциативная ал-
алгебра над к вкладывается в X (Е) для нек-рого Е.
Векторные пространства над фиксированным полем
(объекты) и Л. о. (морфизмы) образуют, вместе с зако-
законом композиции, категорию J?tw. Следующие понятия
суть специальные случаи (применительно к J2?in) обще-
категорных. Для Л. о. А : E-+F его ядром наз.
подпространство Кег А={х?Е : Ах~0}, обра-
образом — подпространство Im A={y?F : y = Ax для
нек-рого х?Е}, коядром — факторпространство
Coker A = F/lm А. Л. о. Л наз. мономорфиз-
м о м, если Кег Л = @), и э п и м о р ф и з м о м, если
Im A = F. Л. о. В : F-+E наз. левым (соответ-
(соответственно правым) обратным кЛ, если В А
тождественен в Е (соответственно А В — в F). Л. о. А ~х,
одновременно левый и правый обратный к Л, наз.
обратным к А. Л. о. (соответственно эндомор-
эндоморфизм), обладающий обратным, наз. изоморфиз-
изоморфизмом (соответственно автоморфизмом).
Категория J?*M является абелевой категорией относи-
относительно сложения Л. о.; в частности, Л. о. являющийся
сразу моно- н эпиморфизмом, есть изоморфизм. Более
того, в Jr?tra каждый мономорфизм обладает левым,
а эпиморфизм — правым обратным. По аналогии с Jj?in
вводятся категории ЭЪ-ап и ifCitv; объекты первой суть
банаховы, а второй — гильбертовы пространства; мор-
физмами в обеих являются непрерывные Л. о. Обе
категории аддитивны, но не абелевы. Изоморфизмы
в них паз. топологическими изоморфиз-
изоморфизмами; это Л. о., имеющие непрерывные обратные.
Одной из важнейших типовых проблем «внутренней»
теории Л. о. является проблема класс и фи-
к а ц и и эндоморфизмов (или хотя бы их нек-рых
классов) по отношению к той или иной эквивалент-
эквивалентности. Для Л. о. чистой алгебры рассматривается, как
правило, общекатегорная эквивалентность эндомор-
эндоморфизмов в =$?«'«; она наз. подобием. Иными словами,
Л. о. А и В, действующие соответственно в Ей F,
подобны, если для нек-рого изоморфизма U диаграмма
и\ | и (D)
F-Z+F
коммутативна. Эквивалентность непрерывных Л. о.
в (общих) банаховых пространствах, наз. тополо-
топологической эквивалентностью, также по-
нимается в общекатегориом смысле — на этот раз
в.®^и; эт0 означает коммутативность (D) для нек-рого
топологич. изоморфизма U. Для Л. о. в гильбертовых
пространствах за основу берется т. н. унитарная
эквивалентность А и В, соответствующая
требованию коммутативности диаграммы (D) для нек-
рого унитарного (см. ниже) оператора U.
Помимо этого в теории Л. о. между пространствами
с топологией важны задачи об аппрокси-
аппроксимации различных классов Л. о. операторами срав-
сравнительно простого строения. Значительную роль иг-
играют задачи о нахождении общего вида Л. о. в конкрет-
конкретных, чаще всего функциональных, пространствах.
Среди инвариантов подобия наиболее важны спектр
и количество инвариантных подпространств данной
размерности. Пусть А — Л. о. в Е. Его спектром
наз. подмножество а (А) в к, состоящее из тех к, для
к-рых к\—А не имеет обратного. Подпространство
Ео в Е наз. инвариантным относительно А,
если из х?Е0 следует Ах?Е0. Помимо ядра и образа
Л. о. примерами служат одномерные подпространства,
содержащие т. н. собственные векторы опе-
оператора, т. е. те х?Е, хфО, для к-рых Ах— кх, к?к.
При этом элемент к, наз. собственным значе-
значением Л. о. А, заведомо принадлежит его спектру.
Понятие Л. о. является специальным случаем поня-
понятия морфпзма модулей, к-рое получается при замене
поля на произвольное кольцо. Морфизмы модулей во
многом не похожи по свойствам на Л. о., однако именно
результаты о последних явились одним из стимулов
к их изучению.
Линейные операторы в конечномерных пространствах
{без дополнительной структуры). Основным аналитич.
аппаратом таких Л. о. является матричная
запись. Пусть Е и F — пространства с фиксирован-
фиксированными базисами ef, 1«:/<:т, и /,-; l<j<:rc, A : E^>-F —
Л. о., a,-j?k есть г-й коэффициент разложения Аеу
по второму базису. Тогда (тХ га)-матрица M^=\\aij\\
наз. матрицей Л. о. А в базисах ej и /,-. При
E=F обычно употребляется матричная запись в сов-
совпадающих базисах (т. е. е,-—/,•; 1<:г<т=га). При пере-
переходе к другим базисам матрица Л. о. изменяется по
простым формулам.
Различным характеристикам Л. о. отвечают, как
правило, эффективно вычисляемые характеристики их
матриц. Напр., dim Im A ~r(M^) и dim КегЛ =
= dim Е—г(Мд), где г — ранг матрицы; в частности,
А — изоморфизм, если и только если dim ?=dim F=
= г(МА); последнее условие эквивалентно отличию
от нуля определителя матрицы Мд. Алгебраич. опе-
операциям над Л. о. соответствуют одноименные операции
над их матрицами, взятыми в фиксированных базисах.
Л. о. подобны тогда и только тогда, когда они могут
быть записаны (каждый в «своем» базисе) одной и
тон же матрицей. Собственные значения Л. о. суть кор-
корни характеристич. многочлена его матрицы. Отсюда
следует, что всякий Л. о. в конечномерном пространстве
над алгебраически замкнутым полем (напр., С) обла-
обладает хотя бы одним собственным вектором. Спектр
Л. о. в конечномерном пространстве над любым полем
есть множество его собственных значений.
Проблема классификации эндоморфизмов конечно-
конечномерных пространств над алгебраич. замкнутым полем
полностью решена, и классы подобия описаны в тер-
терминах спектров и инвариантных подпространств. Ос-
Основным шагом здесь является следующая классич.
теорема, открытая К. Жорданом (С. Jordan) (рассмат-
(рассматривавшим поле С). Матрица с фиксированным к?к
на главной диагонали, единицами непосредственно над
ней и нулями на остальных местах наз. ж о р д а и о-
в о й клеткой, а блок-матрица с жордановыми
клетками (разных размеров и с разными к) на главной
диагонали и нулями на остальных местах — ж о р д а-
новой патрицей. Тогда каждый эндоморфизм
может быть записан в нек-ром базисе жордановой мат-
матрицей. Отыскание такого базиса наз. приведе-
приведением Л. о. к жордановой форме. По-
Поскольку Л. о., записанные жордановыми матрицами,
подобны в том и только в том случае, когда эти матриц!.:
совпадают с точностью до перестановки жордановых
клеток, теорема означает, что жордановы матрицы до-
доставляют, после соответствующего отождествления,
полный набор инвариантов подобия.
Непрерывные линейные операторы в банаховых
пространствах. Основы их теории заложены С. Бана-
Банахом (см. [4]).
Пример ы. 1) В 1р (здесь и далее 1<:/?<оо):
Л. о. умножения на ограниченную числовую последо-
последовательность; Л. о. левого (соответственно правого)
сдвига, переводяпшй |= {?,-}?;/р в т|= {т),-=|,- + 1} (соот-
(соответственно в т)= {т|,- : т|„ =^-0; т),-= ?,-_], i>0}).
2) В Ь„[а, Ь] или С[а, Ь]: Л. о. умножения на непре-
непрерывную функцию <р(х), х?[а, &]; Л. о. неопределенного
интегрирования, переводящий /(.г) в
3) В Lp(R): Л. о. сдвига на i?R, переводящий
f(x) в g(x)--=f(x+t).
4). Из L1 (R) в C0(R): «классический» оператор
Фурье, переводящий / (х) в
g(x) =y_lf(t)e-ixldt.
Л. о. А : ?"—>-F между банаховыми пространствами
непрерывен тогда и только тогда, когда он о г р а-
н и ч е н, т. о. образ каждого ограниченного мно-
множества в Е ограничен в F, или, что эквивалентно, су-
существует (конечное) число \\А || = sup{||.4;r||, ||z||<:l},
наз. операторной нормой (аналогичное ут-
утверждение верно и для любых нормированных прост-
пространств). Непрерывные Л. о. из Е в F обрагуют
в L(E, F) подпространство В (Е, F), являющееся бана-
банаховым относительно нормы \\А ||. Подпространство
В (Е, Е), чаще обозначаемое В(Е), является и банахо-
банаховой алгеброй относительно операторного умножения.
Класс указанных алгебр универсален в том смысле,
что всякая банахова алгебра топологически изоморфна
подалгебре в В (Е) для нек-рого Е. Подмножество
в В (Е, F), состоящее из топологич. изоморфизмов,
открыто и при Е /¦' содержит шар единичного радиуса
с центром в 1.
Фундаментальную роль в «банаховой» теории Л. о.
играют две теоремы, к-рые вместе с Хана — Банаха
теоремой (см. также Линейный функционал) наз. тремя
основными принципами линейного
анализа. Простейшая форма «принципа равномер-
равномерной ограниченности» — это теорема Банаха-
Штейн х а у з а: если для непрерывных Л. о.
Ап : E—>-F, re^l, 2, . . ., при каждом х?Е s\i$\\Anx\\<.
<оо, то и supЦ-4„II<оо. Простейшая форма «принципа
п
открытости отображения» — это теорема Ба-
Банаха: если непрерывный Л. о. обладает обратным,
то этот обратный оператор заведомо непрерывен. Тре-
Требование «банаховости» (полноты) пространств сущест-
существенно в обеих теоремах.
Спектр непрерывного Л. о. А : Е-+Е, рассматривае-
рассматриваемый, как правило, для комплексных пространств,
является непустым компактом в С. В случае беско-
нечномерного пространства множество собственных зна-
значений Л. о., называемое точечным спект-
спектром, вообще говоря, составляет лишь часть о(А).
Для остальных к?а(А) всегда lm(ki—A)=?E; эти
числа распадаются на два множества — так наз. н е-
прерывный спектр и остаточный
спектр, смотря по тому, плотен Im (XI—А) в Е
или нет. Напр., спектром Л. о. умножения на <р(х) = х
является отрезок [а, Ь], однако все его точки в случае
пространств Ьр[а, Ь\ принадлежат непрерывному, а
в случае С[а, Ь] — остаточному спектру.
Заданная на С\а(.4) операторнозначная функция
Я(к)=(кЛ —Л-)'1 наз. резольвентой Л. о. А.
Она полезна, в частности, тем, что позволяет для каж-
каждой функции w, голоморфной в нек-рой окрестности U
спектра, рассмотреть обозначаемый w(А) Л. о.
w (к) R (к) dk,
где Г — гладкий контур в U, ограничивающий спектр.
Так строится «голоморфное операторное исчисление»;
что же касается «голоморфного мультиоператорного ис-
исчисления», т. е., говоря нестрого, придания разумного
смысла понятию голоморфной функции от нескольких
«операторных» переменных, то задача его построения
оказалась намного труднее. Результаты, в нек-ром
смысле близкие к окончательным, были получены
с помощью методов гомологич. алгебры [5].
В теории Л. о. между банаховыми пространствами
важна операция перехода от А : E—,~F к его т. н. с о-
пряженному Л. о. А* : F*-*-E*, к-рый опреде-
определяется формулой
A*f{x) = f(Ax).
Эта операция обладает свойствами
(А-\-В)* = А* + В*, (кА)*-=кА*, (АВ)* = В*А*,
1И*||=||лц
(в предположении, что левые части равенств имеют
смысл). Если Е и F рефлексивны, то (А*)* = А.
Некоторые важнейшие классы Л. о. в банаховых
пространствах таковы.
1) А : E-+F наз. компактным операто-
р о м, или вполне непрерывным, если он
отображает любое ограниченное множество в ? во
вполне ограниченное (т. е. нредкомпактное) множество
в F. Всякий Л. о., аппроксимируемый в олераторной
норме конечномерными (имеющими конечномерный
образ) Л. о., компактен. Для подавляющего большин-
большинства классич. банаховых пространств F верно и обрат-
обратное: всякий компактный Л. о. из любого Е в F аппрок-
аппроксимируется конечномерными. Так наз. проблема
аппроксимации (верно ли это для всех F?)
решена отрицательно [6].
Тождественный Л. о. в Е компактен в том и только
в том случае, когда Е конечномерно (теорема
Р и с с а). Сп.ектр компактного Л. о.— не более чем
счетное множество, содержащее О. Если спектр беско-
бесконечен, то О — его единственная предельная точка.
Каждое к?а(А), Х=^=0,— собственное значение, и со-
соответствующие ему собственные векторы образуют
конечномерное пространство.
2) А : E—^F наз. ядерным оператором,
если он представим в виде абсолютно сходящегося ряда
в В (/?, F), состоящего из одномерных Л. о.; такой опе-
оператор необходимо компактен. С помощью ядерных
Л. о. определяется важный для анализа класс тополо-
гич. векторных пространств — ядерные пространства.
3) А : E-+F наз. фредгольмовым опера-
оператором, если его ядро и коядро конечномерны; образ
такого Л. о. необходимо замкнут. Главная характерис-
характеристика фредгольмова Л. о.— его индекс dim Кет А —
dim Cokor А. Множество фредгольмовых Л. о. открыто
в В (Е, F), а индекс на нем (в отличие от отдельно взя-
взятых размерностей ядра и коядра)—локально постоянная
функция. Предтечей теории фредгольмовых Л. о. яви-
явилась теория интегральных уравнений Э. Фредгольма
(Е. Fredholm), к-рый по существу доказал (и эту «гео-
«геометрическую» подоплеку увидел Д. Гильберт, D. Hil-
bert), что Л. о. вида 1+Л с компактным А — фред-
гольмов и притом индекса нуль (см. Фредголъма аль-
альтернатива). Важные конкретные классы фредгольмо-
фредгольмовых Л. о. возникают при рассмотрении эллиптич. диф-
дифференциальных выражений на многообразиях. Задача
о вычислении их индекса потребовала привлечения
аппарата алгебраич. топологии [8].
Проблему классификации эндоморфизмов банаховых
пространств, ввиду теоремы Жордана, дающей ко-
конечномерный образец ее решения, можно «в первом
приближении» трактовать как проблему построения
содержательного бесконечномерного аналога жорда-
новой формы Л. о. Она, однако, далека от решения:
не говоря о «достаточном» наборе инвариантных иод-
пространств, до сих пор A982) неизвестно, всякий ли
о?гератор, действующий в гильбертовом пространст-
пространстве II, обладает хотя бы одним нетривиальным (отлич-
(отличным от (О) и Н) инвариантным подпространством.
Если Л. о. А, действующий в произвольном банаховом
пространстве, не пропорционален 1 и перестаново-
перестановочен с нек-рым компактным Л. о., то у всех Л. о., пе-
перестановочных с А, есть нетривиальное инвариантное
подпространство (см. [9]).
Помимо топологии нормированного пространства,
в В(Е, F) есть н другие топологии, задающие в нем
структуру локально выпуклого пространства. Наибо-
Наиболее важны сильная и слабая оператор-
операторные топологии, задаваемые системами полу-
полунорм соответственно
Теория непрорывных Л. о. в топологич. векторных
пространствах (пример такого Л. о.— преобразование
Фурье обобщенных функций) развилась на основе
«банаховой» теории. Значительное место в ней зани-
занимает исследование возможностей обобщения классич.
теорем Банаха и др.; оно привело к введению ряда
важных классов пространств. Напр., теорема об экви-
эквивалентности непрерывности и ограниченности, теорема
Банаха — Штейнхауза и теорема Банаха об обратном
операторе не верны для произвольных, хотя бы и ло-
локально выпуклых, отделимых и полных пространств.
В то же время первая из теорем верна, если Е — борно-
логич. пространство, вторая — если Е — бочечное
пространство, а третья — если Е совершенно полно,
a F бочечно.
Непрерывные линейные операторы в гильбертовых
пространствах (конечномерных и бесконечномерных).
Их теория начала формироваться в работах Д. Гиль-
Гильберта [10] об интегральных уравнениях и бесконечных
квадратичных формах.
Примеры. 1) Все примеры Л. о. в lp, Lp[a, Ь],
Lp(R)., рассмотренные выше, при р=2.
2) Интегральный оператор в Lz[a, b], переводящий
f{x) в
b
где К — интегрируемая с квадратом функция на мно-
множестве д<:.г, (/<:6. Такой Л. о. всегда компактен.
3) Оператор Фурье в L., (R), однозначно определен-
определенный тем, что он совпадает с классич. оператором Фурье
(см. выше) на L1(R)f\L.2(fi).
Понятия и факты приведены ниже в той форме, ка-
какую они имеют для пространств над С: именно в ком-
комплексных пространствах теория оказалась наиболее
важной и содержательной.
Особое положение «гильбертовой» теории Л. о. на
фоне «банаховой» определяется резко возрастающей
ролью понятия сопряженного оператора. Поскольку
гильбертово пространство // и его сопряженное Н*
антиизоморфны, Л. о. А * : Hi—^Hi естественно отож-
отождествляется с Л. о. из II2 в Н1, однозначно определен-
определенным равенством (Ах, у) = (х, А*у); х?Н1; у?Н2; при
таком отождествлении Л. о., сопряженный к эндомор-
эндоморфизму в //, снова действует в Н. В В (Н) возникает
важная дополнительная структура — операция перо-
хода от Л к Л*, обладающая свойствами инволюции,
относительно к-рой В (II) является С*-алгеброй. На
самом деле всякая С*-алгебра изометрически *-
изоморфна 6'*-подалгебре в В (Н) для нек-рого // (т е о-
рема Гельфанда — На им арка).
Для гильбертовых пространств характерны следую-
следующие классы Л. о.
Л. о. А : //—>-// паз. самосопряженным
оператором, или эрмитовым операто-
оператором, если А* = А. Самосопряженный Л. о., равный
своему квадрату, наз. проектором; такой Л. о.
реализуется как оператор ортогонального проектиро-
проектирования на замкнутое подпространство в Н. Л. о. Л : П\—>-
—>-Я2 наз. унитарным оператором (в слу-
случае поля R — ортогональным операто-
р ом), если А * — А ~1 или, что эквивалентно, (Ах, А ;/) =
= (х, у), х, у^Н1 и Im Л=//2. Л. о. унитарен тогда и
только тогда, когда он является изоморфизмом, сохра-
сохраняющим нормы. Самосопряженный и унитарный эндо-
эндоморфизмы суть специальные случаи нормаль-
нормального оператора: т. н. Л. о. А : Н-+Н такой,
что А*А=АА*.
Л. о. умножения на последовательность (соответст-
(соответственно функцию) в 12 (соответственно L2[a, Ъ]) самосопря-
самосопряжен в том и только в том случае, если эта последова-
последовательность (функция) действительнозначна. Интеграль-
Интегральный Л. о. самосопряжен, если и только если К(х, у) =
= К(у, х) почти всюду. В L<l(R) операторы сдвига и
оператор Фурье унитарны. В 12 Л. о. левого и правого
сдвига сопряжены друг другу и не нормальны. Спектр
самосопряженного Л. о. лежит в R, а спектр унитар-
унитарного — на единичной окружности в С. Спектр проек-
проектора Рф\, о состоит из точек 0 и 1. Спектр нормаль-
нормального Л. о. может быть любым компактом в С. Собст-
Собственные векторы самосопряженного Л. о., соответст-
соответствующие различным собственным значениям, ортого-
ортогональны.
Описанные классы Л. о. используются в целом ряде
разделов математики и физики, в том числе в кванто-
квантовой механике (где самосопряженные Л. о. интерпре-
интерпретируются как наблюдаемые), в теории представлений и
гармонич. анализе, в теории дифференциальных урав-
уравнений и в теории динамич. систем.
Всю информацию о Л. о., действующем в конечно-
конечномерном гильбертовом пространстве, доставляет его
матричная запись в ортонормированном базисе. В та-
такой записи переходу к сопряженному Л. о. соответст-
соответствует взятие матрицы, комплексно сопряженной к тран-
транспонированной; как следствие, для матрицы ||а,у||
самосопряженного Л. о. aji=ajj. Класснч. теорема
«о приведении к диагональному виду» утверждает, что
каждый нормальный (в случае поля R. — каждый само-
самосопряженный) Л. о. может быть записан в нек-ром
ортонормированном базисе диагональной матрицей.
Вместе с тем фактом, что Л. о. унитарно эквивалентны
тогда и только тогда, когда они могут быть записаны
(каждый в своем ортонормированном базисе) одинако-
выми матрицами, эта теорема означает, что наборы
собственных значений с учетом их кратности образуют
полную систему инвариантов унитарной эквивалент-
эквивалентности для нормальных Л. о.
Теорема о приведении к диагональному виду оказа-
оказалась «счастливее» теоремы Жордана в том отношении,
что для нее найден содержательный бесконечномерный
аналог: спектральная теорема для нор-
нормальных Л. о., открытая в 1912 (для самосопряженных
Л. о.) Д. Гильбертом. Одна из се формулировок:
нормальный Л. о. однозначно представим в виде
операторнозначного интеграла Стилтьеса А = \
J О" (А)
XP(dX), где Р (dX) — счетно аддитивная и регулярная
(в смысле, напр., сильной операторной топологии)
функция на борелевских подмножествах в а (А), при-
принимающая значения среди проекторов и такая, что
Р(о(Л)) = 1 (см. Спектральная мера). Следствие:
всякий нормальный Л. о. аппроксимируется линей-
линейными комбинациями проекторов.
На основе теоремы Гильберта получена полная клас-
классификация нормальных линейных операторов (в прост-
пространстве любой размерности) с точностью до унитарной
эквивалентности [11]; в частности, оказывается, что
каждый нормальный Л. о. унитарно эквивалентен опе-
оператору умножения на ограниченную измеримую функ-
функцию в L2B), где S — нек-рое измеримое пространство
с конечной мерой. Для компактных нормальных Л. о.
в сепарабельном пространстве картина упрощается:
такой Л. о. обладает ортонормированным базисом из
своих собственных векторов и тем самым унитарно
эквивалентен действующему в 12 оператору умноже-
умножения на последовательность (необходимо сходящуюся
к нулю).
В случае нормального А спектральная теорема поз-
позволяет придать смысл выражению функции f(А) для
более широкого класса функций на спектре, чем голо-
голоморфные функции, напр, для непрерывной / Л. о.
f{A) определяется как \ f(X)P(dX). При этом, если
J О" (А)
А самосопряжен, то Л. о. ехр(гЛ) унитарен.
Основные усилия сосредоточены на изучении различ-
различных классов не нормальных Л. о., в первую очередь-
абстрактных вольтерровых операторов, сжимающих
операторов и спектральных операторов (см. [11] —
[13]). Хотя закономерностей:, сравнимых по закончен-
законченности со спектральной теоремой, пока A982) не обна-
обнаружено, все же в этом направлении получены глубокие
результаты.
Развитие анализа и его приложений, в первую оче-
очередь дифференциальных уравнений и квантовой меха-
механики, заставило выйти за рамки класса ограниченных
(т. е. непрерывных) Л. о. Строго говоря, неогра-
неограниченный оператор А в Н яв есть Л. о.
в принятом здесь смысле, т. к. он задан не на всем Н,
а лишь на его, как правило, плотном подпространстве.
Типичные примеры — Л. о. умножения на х и диффе-
дифференцирования в Ll(R). Для неограниченных Л. о.
определены аналоги спектра, сопряженного Л. о. и
рассмотренных выше классов Л. о. Хотя их теория
сложнее теории ограниченных Л. о., ряд глубоких ре-
результатов последней нашел содержательные обобще-.
ния. Важнейшим среди них является аналог спект-
спектральной теоремы, найденный Дж. Нейманом (J. Neu-
Neumann) для неограниченных самосопряженных опера-
операторов.
Лит.: [1] Peano G., Calcolo geometrieo secondo l'Aus-
dehnung-slehre di H. Grassmann, Torino, 1888; [2] Г е л ь-
фанд И. М., Лекции по линейной алгебре, 4 изд., М., 1971;
[3] Т о е р ] i t z О., «Rend. Circolo mat. Palermo», 1909,
v. 28, p. 88 — 96; Li] Банах С, Курс функвдонального ана-
Л1зу, Кшв, 1948; [5] Taylor J., «Adwances Math,», 1972,
v. 9, N° 2, p. 183 — 252; [6] Э н ф л о П., «Математика», 1974,
т. 18, .№ 1, с. 14В — 55; [7] Шефер X., Топологические вен-
торные пространства, пер. с англ., М., 1971; [8] Функциональный
анализ, 2 изд., М., 1972 (Справоч. матем. б-ка); [9J Ломо-
Ломоносов В. И., «Функц. анализ и его прилож.», 1973, т. 7,
JV» 3, с. 55—56; [10] Н i I b e r t D., Grundzuge einer allgemeinen
Theorie der linearen Integralgleichungen, Lpz.— В., 1912; N. Y.,
1953; [11] Д а н ф о р д Н., Шварц Д ж., Линейные опе-
операторы. Общая теория, пер. с англ., М., 1962; [12] их же,
Линейные операторы, пер. с англ., т. 2, М., 1966; [13] их же,
Линейные операторы. Спектральные операторы, пер. с англ.,
М., 1974; [14] Гохберг И. Ц., Крейн М. Г., Теория
вольтерровых операторов в гильбертовом пространстве и ее
приложения, М., 1967; [15] Секефальви-Надь Б.,
•Ф о я ш Ч., Гармонический анализ операторов в гильбертовом
пространстве, пер. с франц., М., 1970; [16] Бур баки Н.,
Алгебра. Алгебраические структуры. Линейная и полилинейная
алгебра, nejp. с франц., М., 1962. А. Я. Хелемский.
ЛИНЕЙНЫЙ УГОЛ двугранного угла —
угол между перпендикулярами к ребру двугранного
угла, восстановленными в обеих гранях из одной точки.
ЛИНЕЙНЫЙ ФУНКЦИОНАЛ, линейная
форма, на векторном пространстве L над полем
к — отображение / : L-^-к такое, что
для всех .г, y?L, k?k. Понятие Л. ф., будучи важным
специальным случаем понятия линейного оператора,
является одним из основпых в линейной алгебре и иг-
играет значительную роль в анализе.
На множестве L* Л. ф. на L определены операции
сложения н умножения на скаляр по формулам
Они задают в L* структуру векторного пространства
над к.
Ядром Л. ф. наз. подпространство Ker /= {x(~L :
f(x) = O}. Если /^0?L# (т.е. Цх)фО?к), то Кег /
— гиперплоскость в L. Л. ф. с совпадающими ядрами
пропорциональны.
Если {ev ; v?A} — базис в L, то для
х=2"=, 4V Ч е к'f (x)=2L1Ы (ч) •
Сопоставление /—>-{/(?v); v^A} есть изоморфизм L*
на fcA. Следствие: L изоморфно L* тогда и только
тогда, когда оно конечномерно. При переходе к новому
базису в L элементы f(ev)?k преобразуются по тем же
формулам, что и векторы базиса.
Оператор Qi : L—>-(L*)#, определенный равенством
Qi.x(f) — f(x), инъектнвен. Он является изоморфизмом
тогда и только тогда, когда L конечномерно. Этот изо-
изоморфизм, в отличие от изоморфизма между L и L*,
естествен.
Л. ф. на локально выпуклых пространствах, в част-
частности нормированных пространствах,— важный объект
изучения функционального анализа. Каждый непре-
непрерывный (как отображение топологич. пространств)
Л. ф. / на локально выпуклом пространстве Е ограни-
ограничен, т. е.
sup | / (х) | < оо
лге М
для всех ограниченных MczE. Если Е — нормирован-
нормированное пространство, то верно и обратное; при этом оба
свойства эквивалентны конечности числа
||/||=sup {|/(*)|: Ы<1}.
Непрерывные Л. ф. на локально выпуклом прост-
пространстве Е образуют подпространство Е* в Е*, к-рое
наз. сопряженным к Е. В Е* рассматриваются
различные топологии, в том числе слабая и сильная,
к-рые отвечают соответственно за поточечную и за
равномерную сходимость на ограниченных множест-
множествах. Если Е — нормированное пространство, то Е* —
•банахово пространство относительно нормы ||/||, а соот-
ветствующая топология совпадает с сильной. Единич-
Единичный шар {/: ||/||<:1}, рассматриваемый в слабой то-
топологии, компактен.
Важные приложения к анализу имеет теорема
Хана — Банаха, одна из формулировок к-рой
такова: если || • II — п р е д н о р м а на векторном
пространстве Е, /0 — Л. ф., заданный на подпростран-
подпространстве Ео в Е и такой, что |/0(ж)| <||х|| для всех х?Е0,
то /0 может быть распространен на все Е с сохранением
линейности и указанной оценки. Следствие: любой не-
непрерывный Л. ф., заданный на подпространстве Ео
в локально выпуклом пространстве Е, может быть
продолжен до непрерывного Л. ф. на Е, а если Е —
нормированное пространство, то и с сохранением
нормы. Отсюда для каждого х?Е, х=^0, найдется
f?E с Цх)фО.
Пусть Е — нормированное пространство, а Е* и
затем (Е*)* взяты с соответствующими нормами. Тогда
оператор
ДЕ:? —(?•)*, RBx{f) = f(x)
— изометрическое вложение. Если при этом вложе-
вложении Е совпадает с (?*)*, то такое нормированное прост-
пространство, необходимо полное, наз. рефлексив-
рефлексивным. Напр., Lp[a, b] и lp, 1<р<оо, рефлексивны тогда
и только тогда, когда р>1. Аналогичное понятие реф-
рефлексивности есть и для общих локально выпуклых
пространств.
Для многих конкретных локально выпуклых прост-
пространств описаны все Л. ф.: напр., сопряженное к гиль-
гильбертову пространству Н есть {f:f(x) = (x, x0)} для
фиксированного хо?Н. Сопряженное к С[а, Ь] есть
{/:/(ж)=\ x(t) d[i(t) для фиксированной функции
ограниченной вариации ц (t)}.
Лит.: [1] Бурбаки Н., Алгебра. Алгебраические
структуры. Линейная и полилинейная алгебра, пер. с франц.,
М., 1962; [2] Колмогоров А. Н., Фомин СВ.,
Элементы теории функций и функционального анализа, 5 изд.,
М., 1981. А. Я. Хелемский.
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ ГРУПП АРИФ-
АРИФМЕТИЧЕСКАЯ ТЕОРИЯ — теория, изучающая ариф-
метич. свойства линейных алгебраических групп, опре-
определенных, как правило, над глобальным полем.
Одним из главных объектов изучения Л. а. г. а. т.
являются арифметич. подгруппы алгебраич. группы G
(см. Арифметическая группа), а Одним из основных
технич. инструментов — группа аделей G^. На G^
можно определить нек-рым естественным образом
меру, наз. Тамагавы мерой. Один из первых возникаю-
возникающих здесь вопросов: когда объем факторпространства
группы бд по подгруппе главных аделей бд конечен?
Полный ответ на него был получен А. Борелем (А. Во-
rel). Оказалось, напр., что объем G^lG^ всегда коне-
конечен для полупростой группы. Решению этого вопроса
предшествовало построение теории приведения для
арифметич. групп (см. [5], [6]).
Используя теорию приведения для подгрупп глав-
главных аделей, удалось во многих случаях вычислить
объем GaIGj,, к-рый наз. числом Тамагавы
группы G. Напр., для ортогональной группы G
число Тамагавы F(G) = 2, и это фактически эквива-
эквивалентно основному результату аналитич. теории квадра-
квадратичных форм (см. [1]). Изучение структуры арифметич.
групп (начатое в [6]) было продолжено затем в разных
направлениях. Прежде всего следует отметить иссле-
исследования по конгруэнц-проблеме, по проблеме макси-
максимальности арифметич. подгрупп и проблеме рода в
арифметич. группах.
Во всех основных вопросах Л. а. г. а. т. существен-
существенную роль играют теоремы аппроксимации, редуци-
редуцирующие исследование арифметич. свойств алгебраич.
групп, определенных над глобальными полями к иссле-
дованню арифметич. свойств алгебраич. групп, опре-
определенных над локальными полями. Наибольшее зна-
значение имеет проблема сильной аппрок-
аппроксимации (п. с. а.) в алгебраич. группах, к-рая
состоит в следующем. Пусть V= {v} — множество
всех неэквивалентных нормирований поля к; kv —
пополнение к относительно v; Ov — кольцо целых эле-
элементов kv\ )f>v— максимальный идеал Ov. Для произ-
произвольного конечного подмножества SczV через Gs
обозначается подгруппа в GA, у к-рой все у-компо-
ненты при v(?S равны единице. Спрашивается: когда
GsGk=GAl (Здесь черта означает замыкание в тополо-
топологии GA.) Если 5=оо (оо — множество всех архимедо-
архимедовых нормирований к), то эквивалентная формули-
формулировка этой проблемы: когда для любых vf(?.S, г = 1,
2, . . ., п, любых av (^Gkv, и положительных целых
mv имеет решение в группе G& система сравнений
xss a (mod pm°i ) ,
v< V Ч J
где x^G0 для v?S(J {vx, v2, . . ., ;;„}.
V
M. Эйхлер [13] решил проблему сильной аппрокси-
аппроксимации для групп SL(tt, D), где D —тело конечного
fc-ранга. Позднее различные частные случаи этой
проблемы исследовали М. Кнезер (М. Knescr), Г. Ши-
мура (G. Shimura), А. Вейль (A. Weil, см. [4]). Пробле-
Проблема сильной аппроксимации была решена (см. [9],
[10]) для классич. групп над числовыми полями и
найдены необходимые условия для ее положительного
решения в общем случае; а именно: а) группа G должна
быть односвязной как алгебраич. группа и б) если
F — любая простая компонента полупростой части G,
то группа Fs должна быть некомпактной. Необходи-
Необходимость этих условий доказана [14] для функциональ-
функционального поля. Наконец, была доказана [7] (см. также [16])
достаточность условий а) и б) как над числовыми,
так и над функциональными полями, что дало полное
решение п. с. а. В основе метода доказательства лежит
редукция п. с. а. к доказательству Кнезера — Титса
гипотезы о строении односвязных групп над локаль-
локальными полями: если G есть А^-простая односвязиая
А-у-изотропная группа, то Gkv порождается унипо-
тентными элементами или, эквивалентно, фактор-
факторгруппа группы G/; по ее центру проста в абстрактном
смысле. В качестве простейшего применения сильной
аппроксимацнонной теоремы получается следующий
факт: пусть G обладает свойством сильной аппрокси-
аппроксимации относительно S=oo; если О — кольцо целых
элементов к, то
это показывает, что арифметика Gq в значительной
степени определяется арифметикой локальных компо-
компонент Gqv-
Наряду с сильной аппроксимацией существенную
роль в Л. а. г. а. т. играет свойство слабой ап-
аппроксимации (с. с. а.) алгебраич. группы G
относительно S, к-рое состоит в том, что образ Gk
при канонич. проекции G^—f-Gg плотен в Gs- Все одно-
связные группы обладают с. с. а. С другой стороны,
имеются примеры полупростых групп и алгебраич.
торов, не обладающих с. с. а. (см. [11], [2]). Тем не
менее для широкого класса неодносвязных полупрос-
полупростых групп, в частности для присоединенных групп,
выполнено с. с. а. [12]. Если G — алгебрапч. тор и для
всякого v^S тор С разложим над циклич. расшире-
расширением поля kv, то G обладает с. с. а. относительно S.
В нек-рых случаях с. с. а. выполнено для алгебраич.
групп над произвольным полем (см. [11]). Существо-
Существовала гипотеза (см. fill), что с. с. а. выполнено для
группы SL(«, D), где D — тело конечного fc-ранга
над произвольным бесконечным полем к. Однако раз-
развитие приведенной ЛГ-теории привело к отрицатель-
отрицательному ответу (см. [15]): для группы SL(h, D) отклоне-
отклонение от слабой аппроксимации может быть сколь угодно
большим.
Важную роль в Л. а. г. а. т. играют когомологич.
методы, в частности принцип Хассе (см. Галуа когомо-
логии).
Лит.: [1] Арифметические группы и автоморфные функции,
пор. с англ. и франц., М., 1969; [2] Алгебраическая теория чи-
чисел, пер. с англ., М., 1969; [31 В е й л ь А., Основы теории чи-
чисел, пер. с англ., М., 1972; [4] его же, «Математика», 1969,
т. 13, Л! 6, с. 18—98; [5] Боре ль А., «Математика», 1964,
т. 8, Л» 2, с. 3—17; [61 Б о р е л ь А., X а р и ш - Ч а н д р а,
«Математика», 1964, т. 8, N5 2, с. 19—71; [71 Платонов В. И.,
«Изв. АН СССР. Сер. матем.», 1969, т. 33, Л"» 6, с. 12I — 19;
1970, т. 34, № 4, с. 775—77; [8] его же, «Труды Матем. ин-та
АН СССР», 1973, т. 132, с. 102—68; [9] К n e s е г М., «J. rcine
und angew. Math.», 1965, Bd 218, S. 190—203; [10] его же,
«Proc. Symp. Pure Math.», 1966, v. 9, p. 187—96; [11] его же,
«Colloq. groupes algebriqus. Bruxelles», 1962, p. 41—52; [121
Harder G., «Inventiones Math.», 1967, v. 4, J* 3, p. 165—91;
[13] E i с h 1 e г M., «J. reine und angew. Math.», 1938, Bd 179,
S. 227—51; [14] В e hr H., «J. reine und angew. Math.», 1968,
Bd 229, S. 107—16; [15] Платонов В. П., «Труды Матем.
ин-та АН СССР», 1976, т. 142, с. 198—207; [16] Prasad G.,
«Ann. Math.», 1977, v. 105, p. 553 — 72. В. П. Платонов.
ЛИНЕЙЧАТАЯ ПОВЕРХНОСТЬ в дифферен-
дифференциальной геометрии — поверхность, обра-
образованная движением прямой линии. Прямые, при-
принадлежащие этой поверхности, называются прямо-
прямолинейными о б р а з у ю щ и м и, а каждая кри-
кривая, пересекающая все прямолинейные образующие,—
направляющей кривой. Если р=р (v) —
радиус-вектор направляющей, а m=m(u) — единич-
единичный вектор образующей, проходящей через p(v), то
радиус-вектор Л. п. есть
r=p{v)+um{v),
где и — координата точки на образующей. Линейный
элемент Л. п.:
ds'1 = du'i-\-2 (тр') du dv-\-(p'ij{-2 (m'p') u -)-m'2K2) dv2.
Л. п. характеризуется тем, что ее асимптотич. сеть —¦
полугеодезическая. Л. п. всегда можно и притом един-
единственным образом изогнуть так, что произвольная линия
на ней станет асимптотической (теорема Б е л ь-
т р а м и). Кроме того, если Л. п. F, не являющаяся
развертывающейся, изгибается в Л. п. F*, то либо их
образующие соответствуют друг другу, либо обе они
изгибаются в квадрику, на к-рой сеть, соответствую-
соответствующая семействам образующих,— асимптотическая (т е о-
р е м а Бонне).
Множество точек Л. п., в к-рых обращается в нуль
геодезич. кривизна ортогональных траекторий обра-
образующих, наз. с т р и к ц и о н н о й линией Л. п.
(или линией с ж а т и я, т. к. через каждую точку
ее — стр и кц ионную точку — в пределе про-
проходит общий перпендикуляр двух бесконечно сбли-
сближающихся образующих). Координата стрикционной
точки и =—(p'jn')Im'2; на цилиндре стрпкционная линия
не определена, на других развертывающихся поверх-
поверхностях она является ребром возврата. Предел р от-
отношения кратчайшего расстояния между двумя бес-
бесконечно сближающимися образующими Л. п. к углу
между ними наз. параметром распределения Л. п.:
р — (тт'р)/т'2; развертывающаяся поверхность харак-
характеризуется тем, что для нее р=0. Гауссова кривизна
Л. п.:
К = — р2 (т'Г"
у '
где
Y = р + 2и (р'т') + и~т'г — (р'тJ.
Единственная минимальная Л. п.— геликоид. Л. п.
вращения — однополостный гиперболоид, быть может
вырождающийся в цилиндр, конус или плоскость. Если
в-е прямолинейные образующие Л. п. параллельны
одной плоскости, то она представляет собой Каталана
notepxHocmb.
Лит.: [1] Каган В. Ф., Основы теории поверхностей
Б тензорном изложении, ч. 1, М.— Л., 1947; [2] Ш у л и к о в-
ск»й В. И., Классическая дифференциальная геометрия в
тензорном изложении, М., 1963. И. X. Сабитов.
Л п. к алгебраической геометрии —
гладкая проективная поверхность F над алгебраически
замкнутым полем к, бирационально эквивалентная
поверхности /IхС, где Р1— проективная прямая,
а С — нек-рая гладкая проективная кривая рода
g>0. Примером Л. и. служит проективизация Рс(<д)
локально свободного в топологии Зариского пучка
(§ ранга 2 на С.
Если существует гладкий морфизм р : F—>-C, каждый
слой к-рого изоморфен Р1, то F наз. геометри-
геометрически линейчатой поверхностью с ба-
базой С. В случае, когда С — кривая рода 0, геометри-
геометрически Л. п. наз. рациональной линейча-
линейчатой поверхностью; в случае, когда род кри-
кривой С равен #5*1, — геометрически линей-
линейчатой поверхностью рода g. По теореме
Нётера — Энрикеса морфизм р всегда имеет сечение s:
C-*F (см. [i], [2], [5]).
Свойства Л. п. (см. [1], [2], [6]):
1) Каждая геометрически Л. п. F с базой С имеет
вид Рс(<§), где (§ — нек-рый локально свободный пу-
пучок ранга 2 на С, причем
Рс (?) = Рс (<?')
над С тогда и только тогда, когда существует обрати-
обратимый пучок X на С, что <§=(§'®%.
2) Все рациональные геометрически Л. п. с точностью
до изоморфизма исчерпываются счетной серией поверх-
поверхностей
— целое число, Qpx(n) — обратимый пучок на
Р1 степени га; причем, кроме поверхности Веронезе
1'4с:Р5, все поверхности степени га в рп + г являются
рациональными геометрически Л. п. или конусами над
нормальными рациональными кривыми.
3) Если F — минимальная гладкая проективная по-
поверхность над к, бирационально эквивалентная Р1ХС,
где С — кривая рода g^l, то f — геометрически Л. п.
с базой С, причем кривая С определяется поверх-
поверхностью F однозначно с точностью до изоморфизма.
4) Если F — геометрически Л. п. с базой Сир: F-,-
->С — соответствующий морфизм, то
а) Pic (F) ЗЁ р* Pic (С) фж5,
где S — класс нек-рого сечения,
б) q{F) = g, pg(F) = 0, Pn(F) = 0
для любого п>2, и
K2F = &(i-g),
где g — род С, q(F) = dim HX(F, QF) — иррегуляр-
иррегулярность, /)^.(^') = dim H2{F, Qp) — геометрич. pop,,P!!(F) =
— dim IF (F, Qp(nKp)) есть re-кратный род, Kf ~ ка-
нонич. дивизор поверхности F.
5) Если F — геометрически Л. п. с базой С, S —
класс нек-рого сечения морфизма р : F-+C, то сущест-
существует такой обратимый пучок -X на С, что обратимый
пучок &€ = Qf(S) ®Р*% определяет изоморфное вло-
вложение ц>м : Р-+Рл', при к-ром слои морфизма р от-
отображаются на прямые, лежащие на Р' = ф_л (F) и за-
заметающие F', т. е. F' является Л. п. в обычном смысле.
Л. п. составляют отдельный класс в классификации
Энрикеса алгебраич. поверхностей (см. [1], [2], [3]).
Они характеризуются любым из следующих эквива-
эквивалентных критериев линепчатости (см. [1], [3], [4],
[5], [7]):
1) кодаиры размерность у. (F)= — оо;
2) ;г-кратный род P,l(F) = 0 для и = 12;
3) для нек-рой (равносильно для любой) минималь-
минимальной модели F* поверхности F выполняется условие-
обрыва присоединения, т. с. для любого дивизора
D(^Div(F*) существует такое целое число п0, что ли-
линейная система \D-j-nKp\ пуста для всех п~^пп, где
Кр — канонич. дивизор;
4) на нек-рой (равносильно на любой) минимальной
модели F* существует кривая Е па F* с (Е -KF*)<0.
Лит.: [1] Алгебраические поверхности,'М., 1965 (Тр. Матем.
ин-та АН СССР, т. 75); L2] В е a u v i I 1 е A., «Asterisquo», 1978,
¦N» 54' [3] В о m b i e r i E., Husemoller IJ., «Proc.
Symp. Pure Math.», 1975, v. 29, p. 329—420; [4] В о m h i c-
r i E., Mnmford D., в кн.: Complex analysis and algebraic
geometry, Camb., 1977, p. 23—42; [5] Enriques F., Le
superficie algebriche, Bologna, 1949; [6] Harts horne R.,
Algebraic geometry, N. Y.— Hdlb.— В., 1977; [7] К о d a i-
ra K., «Amer. J. Math.», 1968, v. 90, № 4, p. 1048 — 66.
В. А. Псковских.
ЛИНЗОВОЕ ПРОСТРАНСТВО — многообразие нечет-
нечетной размерности, возникающее как пространство орбит
изометричных свободных действий циклич. групп Z/t
на сфере S'-n~l. Удобно взять в качестве S-"~ единич-
единичную сферу в комплексном пространстве С", в к-ром
фиксирован базис.
Пусть %fi действует на каждой координате z^ умно-
2JXI
—г- т.
жением на Ck==e > гДе mk обратимо по модулю /г,
т. е. существуют числа 1^ такие, что m^l^-^X (re). Это
задает изометричное и свободное (благодаря условию
обратимости m,mod &) действие 1./г на S-"~\ причем
любое такое действие имеет описанный вид в подходя-
подходящей системе координат. Рейдемейстера кручение, отве-
отвечающее корню ? h-й степени из единицы, определяется
для Л. п. L=Sin~xl7Lii, построенного этим способом,
формулой — S?rT (? —1)- Любое кусочно линейное
гомеоморфное ему Л. п. L должно иметь равное (с точ-
точностью до —Z.4) кручение и оказывается, что наборы
чисел {Ifr} и {Ifr} должны совпадать. Таким образом,
эти наборы характеризуют Л. п. однозначно с точ-
точностью до кусочно линейного гомеоморфизма и даже
до изометрии, а с другой стороны, благодаря топологич.
инвариантности кручения — и с точностью до гомео-
гомеоморфизма. Л. п. асферично до размерности 2ге—2
(т. е. Л[Ь=0, 2<:i«:2n—2), а фундаментальная группа
равна Z/г ввиду того факта, что универсальным на-
накрывающим для L служит сфера S'1"'1. Гомологии L
совпадают до размерности 2ге—2 с гомологиямн группы
Za, т. е. равны %h во всех размерностях от 2 до 2ге—2
и H0(L) = H2n-i {L)= Ъ. Прямой предел пространств L
дает Эйленберга — Маклейна пространство типа
¦^(Zft, re). Два Л. п. гомотопически эквивалентны
тогда и только тогда, когда совпадают зацепления коэф-
коэффициенты l(oJ, a"~J)?Q/z, где а — образующая
группы двумерных когомологий. С помощью этих ин-
инвариантов устанавливается существование среди Л. п.
асимметричных многообразий.
В трехмерном случае Л. п. совпадают с многообра-
многообразиями, имеющими Хегора диаграмму рода 1, и поэтому
они являются Зейферта многообразиями. Фундамен-
Фундаментальную область действия Z/i на S3 удобно представ-
представлять себе в виде «линзы» — объединения шарового
сегмента с его зеркальным образом — откуда и воз-
возникло название Л. п.
Лит.: [1]Пуанкаре А., Избранные труды, т. 2, 19 72,
с. 728; [2] де Рам Ж., «Матем. сб.», 1936, т. 1, с. 737—43;
[3] Зейферт Г., Трель фалль В., Топология, пер. с
нем., М.—Л., 1938; [4] Milnor J., В и г 1 е t О., в кн.;
Essays on Topology and Related topics, В., 1970, p. 12—17.
А. В. Чернавский.
ЛИНИЯ, к р и в а я,— геометрическое понятие, точ-
точное и в то же время достаточно общее определенно
к-рого представляет значит, трудности и осуществ-
осуществляется в разных разделах геометрии различно.
В рамках элементарной геометрии понятие Л. не
получает отчетливой формулировки и иногда опреде-
определяется как «длина без ширины» или как «граница по-
поверхности». По существу в элементарной геометрии
изучение Л. сводится к рассмотрению примеров (пря-
(прямая, отрезок, ломаная, окружность и др.). Не распо-
располагая общими методами, элементарная геометрия до-
довольно глубоко проникла в изучение свойств конкрет-
конкретных Л. (конич. сечения, нек-рые алгебраич. Л. высших
порядков и трансцендентные Л.), применяя в каждом
случае специальные приемы.
В аналитич. геометрии Л. на плоскости определяется
как множество точек, координаты к-рых удовлетво-
удовлетворяют уравнению F(x, j/) = 0. При этом на функцию F
должны быть наложены ограничения так, чтобы, с од-
одной стороны, уравнение это имело бесконечное мно-
множество решений и, с другой стороны, чтобы это мно-
множество решений не заполняло «куска плоскости».
Важный класс Л. составляют те, для к-рых функция
F(x, у) есть многочлен от двух переменных; в этом
случае Л., определяемая уравнением F(x, г/) = 0, наз.
алгебраической. Алгебранч. Л., задаваемые
уравнением 1-й степени, суть прямые. Уравнение
2-й степени, имеющее бесконечное множество решений,
определяет эллипс, гиперболу, пара-
параболу или Л., распадающуюся на две прямые. Ал-
Алгебраич. Л., определяемые уравнениями высших степе-
степеней, рассматриваются в алгебраич. геометрии. При этом
большую стройность приобретает их теория, если рас-
рассмотрение ведется на комплексной проективной плос-
плоскости. В этом случае алгебраич. Л. определяется урав-
уравнением вида
где F — однородный многочлен трех переменных, яв-
являющихся проективными координатами точек.
Для тех разделов математики, в к-рых господствуют
методы теории функций (анализ, дифференциальная
геометрия и др.), естественное определение Л.— зада-
задание ее п а р а м е т р it ч е с к и м и уравнения-
уравнениями. Так, в случае плоскости, Л., заданная парамет-
рич. уравнениями
*=<рМ, y=V(t), A)
где ff(t) и г|)(г) — непрерывные функции, определен-
определенные на отрезке о<:/-<6, есть множество точек (х, у),
соответствующих всевозможным значениям параметра t
при условии, что эти точки рассматриваются в опреде-
определенном порядке: если точка Мг соответствует значению
параметра tj, а точка Mt — значению t2, то Mt счи-
считается предшествующей М2 при t1<.t2; точки, отвечаю-
отвечающие различным значениям параметра, считаются раз-
различными. Уравнения x=<p1{t1), j/=J»t'1(t1), ti^Uj, &il,
задают ту же Л., что и уравнения A), если существует
такой гомеоморфизм k(t1) = t отрезка [аи &J на отре-
отрезок [о, Ь], к(а-1) = а, к{Ь1)=Ь, что <р (Mfi)) = <pi (*i) и
ty(h(t1)) = ty1 (ti). Аналогично Л. в произвольном топо-
логич. пространстве X определяется параметрич. урав-
уравнением вида x=<$(t), где ф — функция действитель-
действительного переменного t, непрерывная на отрезке [а, Ъ),
значения к-рон суть точки х пространства X.
Кроме такого подхода существует и другая точка
зрения (К. Жордан, С. Jordan, 1882) на определение
Л. параметрич. уравнениями: Л. наз. множество точек
плоскости, координаты к-рых суть непрерывные функ-
функции x=q>(t), г/=\(>@ параметра t, заданные на отрезке
[а, Ь]; теперь точки, соответствующие различным
значениям параметра, но имеющие одни и те же коор-
координаты, уже не считаются различными, и множество,
составляющее Л., уже не рассматривается как упоря-
Рис. 1.
доченное значениями t. Это определение обобщается
на любое топологич. пространство: множество точек
топологич. пространства, являющееся непрерывным
образом отрезка, наз. ж о р д а н о в о й кривой.
Однако построены такие непрерывные функции <р@
и ty(t), 0<f<l, что множество точек, координаты к-рых
определяются этими функциями, заполняют квадрат
О^х, i/s^l (см. Пеано кривая). Более общо, всякий ло-
локально связный континуум (т. е. континуум, каждая
точка к-рого обладает сколь
угодно малой связной окрест-
окрестностью) является непрерывным
образом отрезка (теорема
Мазуркевича). Таким об-
образом, не только квадрат, но о -
и куб любого числа измерений
и даже бесконечномерный гиль-
гильбертов кирпич являются не-
непрерывными образами отрезка.
Вышеизложенное показывает,
что Л. не может быть определена
как непрерывный образ отрезка, если на отображение
не наложить дополнительных ограничений. Так, в диф-
дифференциальной геометрии эти ограничения выража-
выражаются в том, что на функции, фигурирующие в па-
параметрическом задании Л., налагаются условия суще-
существования производных различных порядков. С дру-
другой стороны, существуют континуумы, которые ес-
естественно рассматривать как Л., по к-рые, не будучи
локально связными, не являются непрерывными обра-
образами отрезка. Таков, напр., континуум, определяемый
условиями: i/=sin— , 0<г<:1,х=0, —1<:г/<:1 (рис. 1).
Общее определение Л. для случая плоскости было
дано (Г. Кантор, G. Cantor, 1870-e гг.) в связи с созда-
созданием теории точечных множеств. Плоский континуум,,
в любой окрестности каждой точки к-рого имеются
точки плоскости, не принадлежащие континууму,
наз. канторовой кривой. Важный пример
канторовой кривой доставляет ковер Серпинь-
с к о г о, строящийся следующим образом. Квадрат Q
со стороной 1 делят на девять равных квадратов пря-
прямыми, параллельными его сторонам, и удаляют все»
?
D
?
а
а
а
D
D
ооооапаап
oDddO а ащп
QODODDDOD
ODD
оП а
ООП
D ПП
D Dn
DaODDDDClQ
Qfja nrjODQn
DDDDoDDaD
л=1 п=2 п=3
f Рис. 2.
внутренние точки центрального квадрата (рис. 2Г
ге=1). Так же поступают и с каждым из оставшихся
восьми квадратов первого ранга, получается 64 квад-
квадрата второго ранга (рис. 2, ге=2). Продолжая процесс
для всех натуральных п, на ге-м шаге получают 8" квад-
квадратов я-го ранга со стороною 1/3". Пересечение полу-
полученных таким образом множеств и есть ковер Серпинь-
Серпиньского (рис. 2).
Какова бы ни была канторова кривая L, она может
быть топологически вложена в ковер Серпиньского S,
т. е. в S содержится континуум V, гомеоморфный Л. L.
Ковер Серпиньского является локально связным кон-
континуумом и потому может быть получен как непрерыв-
непрерывный образ отрезка.
В топологии пользуются понятием Л., введенным
в 1921 П. С. Урысоном и являющимся наиболее общим
(но не чрезмерно). Определение Л. формулируется сле-
следующим образом: линией наз. одномерный кон-
Рис. 3.
ш
ш
ш
1 L
1 W
1 Г
Г
щ
f
ill!
Ч*
jllippj
ш
и
и
_/ ¦¦
тинуум, т. е. связное компактное метрич. простран-
пространство С, каждая точка к-рого обладает сколь угодно
малой окрестностью с границей размерности нуль.
Другими словами, при любом е>0 пространство С
может быть представлено в виде суммы конечного числа
замкнутых множеств диаметра, меньшего г, обладаю-
обладающих тем свойством, что никакие три из этих множеств
не имеют общей точки. Ковер Серпиньского удовлет-
удовлетворяет этому определению Л., так что всякая канто-
рова кривая является также и Л. в смысле П. С. Уры-
сона. Обратно, если плоский континуум является Л.
в смысле П. С. Урысона, то он будет канторовой кри-
кривой. Определение Л., данное
П. С. Урысоном, является внут-
внутренним: оно характеризуется
лишь свойствами самого прост-
пространства С и не зависит от того,
рассматривается ли это прост-
пространство само по себе или как
подмножество другого тополо-
гич. пространства.
Существуют Л., к-рые не гомео-
морфны никакому подмножеству
плоскости. Такова, напр., Л., лежащая в трехмерном
пространстве и состоящая из шести ребер тетраэдра и
четырех отрезков, соединяющих какую-либо точку
пространства, не лежащую ни на одной из его граней,
с его вершинами (рис. 3). Но
всякая Л. (в смысле П. С. Уры-
Урысона) гомеоморфна нек-рому под-
подмножеству трехмерного евклидо-
евклидова пространства (теорема
М е н г е р а). Континуум М, об-
обладающий тем свойством, что ка-
какова бы ни была Л. С, в М най-
найдется подконтинуум С", гомео-
морфный континууму С, стро-
строится следующим образом. Куб
К с ребром 1 делится плоскостя-
плоскостями, параллельными его граням,
на 27 ранных кубов. Из куба
К удаляются центральный куб и
все прилежащие к нему по двумерным граням кубы
этого подразделения. Получается множество A"l7 со-
состоящее из 20 оставшихся замкнутых кубов первого
ранга. Поступая точно так же с каждым из кубов пер-
первого ранга, получим множество А, состоящее из
400 кубов второго ранга (рис. 4). Продолжая этот
процесс бесконечно, получим последовательность кон-
континуумов K-^zdK^dK^. . ., пересечение к-рых есть
одномерный континуум М, наз. универсальной
кривой М е н г е р а.
В исследовании Л. важную роль играет понятие
индекса ветвления. Л. С в точке х имеет
индекс ветвления т, если каково бы ни было число
8>0, существует открытое множество U диаметра,
меньшего, чем е, содержащее точку т, граница к-рого
есть множество мощности, не превосходящей ТП, но
для достаточно малого е' >0 граница всякого откры-
открытого множества, содержащего точку х, диаметр к-рого
меньше г', имеет мощность, не меньшую, чем т. Точки
Л. относительно их индекса ветвления классифици-
классифицируются следующим образом.
1) Точки с индексом ветвления п, п — натуральное.
2) Точки неограниченного индекса ветвления со.
(Точка х Л. С имеет индекс ветвления со, если каково бы
ни было число е>0, существует открытое множество,
содержащее точку х, с диаметром, меньшим, чем е,
граница к-рого состоит из конечного множества точек;
но каково бы ни было натуральное п, найдется такое
е„>0, что граница всякого открытого множества,
Рис. 4.
содержащего х и имеющего диаметр меньший, чем е„г
состоит не менее, чем из га точек.)
3) Точки счетного индекса ветвления #0.
4) Точки континуального индекса ветвления с.
Точка Л. С, индекс ветвления к-рой больше двух,
наз. точкой ветвления; точка, индекс ветвле-
ветвления к-рой равен единице, наз. концевой точ-
к о и.
Примеры, а) Отрезок во всех своих внутренних
точках имеет индекс ветвления, равный двум; индекс
ветвления концов отрезка равен единице, б) Окруж-
Окружность в каждой своей точке имеет индекс ветвления
два. в) Л., состоящая из п прямолинейных отрезков,
Рис. 5.
Рис. 6.
исходящих из одной точки О, имеет в точке О индекс
ветвления га. г) Л., состоящая из отрезков Оа1, Оа„,
.... Оап, . . ., выходящих из начала координат б,
11 1 ,.
имеющих длины -^-, ,-р- , ...,—, ...и ооразующих
с осью Ох углы, соответственно равные у , —2 , • • •,
¦у, , ¦ • •, имеет в точке О неограниченно возрастающий
индекс ветвления со (рис. 5). д) Л., состоящая из от-
отрезка Оа0 длины 1 и отрезков Оах, Оа2, . . ., Оап, . . .
длины 1, выходящих из точки О и образующих с от-
отрезком Оа0 углы, соответственно равные ^- , ~ , . . .,
^ , . . ., имеет в каждой точке отрезка Оа0 счетный
индекс ветвления #0 (рис. 6). е) Л., состоящая из от-
отрезков, соединяющих точку О со всеми точками кан-
торова множества, лежащего на отрезке 0<:г^:1,
Рис. 7.
у = 0, имеет во всех своих точках континуальный индекс
ветвления С (рис. 7). ж) Ковер Серпиньского также
имеет во всех своих точках континуальный индекс
ветвления.
Если у Л. совсем нет точек ветвления, т. е. если
в каждой точке Л. индекс ветвления равен 1 или 2,
то эта Л. есть либо простая дуга — топологич.
образ отрезка, либо простая замкнутая
линия — топологич. образ окружности. При этом,
если индекс ветвления Л. во всех точках равен 2, то
это — простая замкнутая Л., если же у Л., не имеющей
точек ветвления, есть концевые точки (при этом ока-
оказывается, что их непременно две), то она будет простой
дугой. Если Л. имеет лишь конечное число точек вет-
ветвления, причем индекс ветвления каждой из них также
конечен, то такая Л. может быть разбита на конечное
число простых дуг, не имеющих попарно никаких дру-
тпх общих точек, кроме своих концов.
Окружность является единственной Л., все точки
к-рой имеют один и тот же конечный индекс ветвления
2; других Л., имеющих во всех точках один и тот же
конечный индекс ветвления,
нет, более того, если все точ-
точки Л. L имеют индекс ветв-
ветвления больший или равный
п, то на Л. L найдется точка,
индекс ветвления к-рой боль-
больше или равен 2ге—2, и при
всяком натуральном п сущест-
существует Л., состоящая только из
точек, имеющих индекс ветв-
ветвления п и 2п—2 (теорема
У р ы с о н а). Пример Л.,
состоящий только из точек с
Рис. ь. индексом ветвления 3 и 4,
строится следующим образом.
В равностороннем треугольнике со стороною 1 прово-
проводятся три средние линии, и из него выбрасываются
внутренние точки треугольника, ограниченного сред-
средними Л. С каждым из оставшихся трех треугольников
первого ранга проделывается аналогичная операция,
в результате к-рой получается девять треугольников
второго ранга. Поступая с ними так же, получим 27
треугольников третьего ранга и так далее для всякого
натурального п. Пересечение полученных в результате
выполнения этих операций множеств есть линия С
{рис. 8). Л., состоящая из точек с индексом ветвления
.3 и 4,— это два континуума С1 и С2. каждый из к-рых
гомеоморфен Л. С и к-рые не имеют никаких других
общих точек, кроме точек, соответствующих вершинам
¦основного треугольника континуума С.
Существуют также Л., имеющие во всех своих точ-
точках неограниченный индекс ветвления, счетный ин-
индекс ветвления и континуальный индекс ветвления.
Лит.: [1] Александров П. С, Введение в общую
теорию множеств и функций, М.— Л., 1948; [2] К у р а т о в-
с к и й К., Топология, пер. с англ., т. 2, М., 1969; [31 М е п-
g e r К., Kurventheorie, Lpz.—В., 1932; [4] Пархомен-
Пархоменко А. С., Что такое линия, М., 1954; [5] У р ы с о н II. С,
'Труды по топологии и другим областям математики, т. 2, М.—
Л., 1951; [6] X а у с д о р ф Ф., Теория множеств, пер. с нем.,
М.— Д., 1937. А. С. Пархоменко.
ЛИНИЯ ВТОРОГО ПОРЯДКА — плосйая линия, де-
декартовы прямоугольные координаты к-рой удовлетво-
удовлетворяют алгебраич. уравнению 2-й степени
апх2-\- 2а12ху + а2,г/2-f 2ai3x-f 2a23y + а33 = 0. (*)
Уравнение (*) может и не определять действительного
геометрич. образа, но для сохранения общности в таких
•случаях говорят, что оно определяет мнимую Л.
в. п. В зависимости от значений коэффициентов урав-
уравнения (*) оно может быть преобразовано с помощью
параллельного переноса и поворота системы координат
на нек-рый угол к одному из 9 приведенных ниже ка-
нонич. видов, каждому из к-рых соответствует опреде-
определенный класс линк'й. Именно,
нераспадающиеся линии:
——f- p- =1 эллипсы,
х* У2 л г
—¦ — ,-г- =1 гиперболы,
а- Ъ- ' '
у2=2рх параболы,
^5—г р~ =—1 мнимые эллипсы;
распадающиеся линии:
мнимых пересекающихся прямых,
— =0 пары действительных пересекающихся
а2 Ь2
прямых,
х2—а?=0 пары действительных параллельных пря-
мых,
пары мнимых параллельных прямых,
22=0 пары совпадающих действительных прямых.
Л. в. п., имеющие единственный центр симметрии
(центр Л. в. и.), наз. центральной ли-
н и е й. Координаты центра Л. в. п. определяются
решением системы:
Л. в. п. без центра симметрии или с неопределенным
центром наз. нецентральной линией.
Исследование вида Л. в. п. может быть проведено
без приведения общего уравнения к канонич. виду.
Это достигается совместным рассмотрением значений
т. н. основных инвариантов Л. в. п.—
выражений, составленных из коэффициентов уравне-
уравнения (*), значения к-рых не меняются при параллельном
переносе и повороте системы координат (а,-у=ау,-):
Д =
«ЦЙ12
и семиинварианта (полуинвариан-
т а):
А =
а22а23
а32аЗЗ
апа13
к-рый является инвариантом относительно поворота
системы координат (см. табл.).
Многие важные свойства Л. в. п. могут быть изучены
при помощи характеристической квад-
квадратичной формы
Ф (х, у) = a1].i2-J-2a12.r(/-f а22г/2,
соответствующей уравнению (*). В частности, нерас-
нераспадающаяся Л. в. п. оказывается эллипсом, мнимым
эллипсом, гиперболой или параболой в зависимости
от того, будет ли Ф (х, у) положительно определенной,
отрицательно определенной, неопределенной или полу-
полуопределенной квадратичной формой, что устанавли-
устанавливается по корням ее характеристического
уравнения:
ап — к аг
«21
= 0 или X2 — S
Три основных инварианта Д, б и S определяют
Л. в. п. (кроме случая параллельных прямых) с точ-
точностью до движения евклидовой плоскости: если соот-
соответствующие инварианты Д, б и S двух линий равны,
то такие линии могут быть совмещены движением.
Иными словами, эти линии эквивалентны по отношению
к группе движений плоскости (метрически эквивалент-
эквивалентны).
Существует классификация Л. в. п. с точки зрения
других групп преобразований. Так, относительно
более общей (чем группа движений) группы аффинных
преобразований эквивалентными являются любые две
линии, определяемые уравнениями одного канонич.
вида. Напр., две подобные Л. в. п. считаются эквива-
эквивалентными. Связи между различными аффинными клас-
классами Л. в. п. позволяет установить классификация
с точки зрения проективной геометрии, в к-рой беско-
нечпо удаленные элементы не играют особой роли.
Действительные нераспадающиеся Л. в. п.: эллипсы,
гиперболы и параболы образуют один проективный
,ласс — класс действительных овальных линий (ова-
лон). Действительная овальная линия является эллип-
io.v, гиперболой или параболой в зависимости от того,
как она расположена относительно бесконечно уда-
удаленной прямой: эллипс пересекает несобственную пря-
прямую в двух мнимых точках, гипербола — в двух раз-
различных действительных точках, парабола касается
несобственной прямой; существуют проективные пре-
преобразования, переводящие эти линии одна в другую.
Существует 5 классов проективной эквивалентности
Л. в. п. Именно,
и ев ы рождающиеся линии (хх, х2, х3 —
однородные координаты):
хг'-х'о—л-|)-=0 действительный овал,
х1~\-х-2-\-хз=0 мнимый овал;
вырождающиеся линии:
х\—хц — О пара действительных прямых,
Х1-\-х1=0 пара мнимых прямых,
х\=0 пара совпадающих прямых.
Кроме аналитич. способа определения Л. в. п. (зада-
(заданием уравнения) существуют и другие способы. Напр.,
эллипс, гипербола и парабола могут быть получены
как сечения конич. поверхности плоскостью (см. Ко-
Конические сечения).
%
линии б
Центральные
Нецентральные линии 6 = 0
И с с л е д о в
порядка
/\
<о
сэ
V
<о
о
II
ание вида линий второго
с помощью инвариантов
Нераспадающиеся линии
Д ф 0
4-<»
-§->»
Действи-
Действительные
эллипсы
Мнимые
эллипсы
Гиперболы
Параболы
Распадающиеся линии
Д = 0
Пары мнимых пересекаю-
пересекающихся прямых (действи-
(действительная точка)
Пары действительных пе-
пересекающихся прямых
А > 0
Л < 0
А = 0
Пары мнимых па-
параллельных пря-
прямых
Пары действитель-
действительных параллельных
прямых
Пары совпадаю-
совпадающих параллельных
прнмых
Лит.: [1] Александров П. С, Лекции по аналити-
аналитической геометрии, М., 1968; L2] Ефимов Н. В., Краткий
курс аналитической геометрии, 11 изд., М., 1972. А. В. Иванов.
ЛИННИКА ДИСКРЕТНЫЙ ЭРГОДИЧЕСКИЙ МЕ-
МЕТОД — специальный метод аналитич. теории чисел,
использующий некоммутативную арифметику и сво-
сводящий вопросы равномерности распределения целых
точек многообразия к рассмотрению «потоков» целых
точек на этом многообразии и операторов, к-рые соз-
создают эти «потоки». Основы метода заложены Ю. В. Лин-
ннком [1]. Л. д. э. м. получил существенное развитие
и приобрел «эргодические» черты по характеру своих
результатов [2], [3]. Дискретный эргодич. метод при-
применялся к вопросам представления чисел тернарными
квадратичными формами и к вопросам асцмптотич.
распределения целых точек по поверхности соответст-
соответствующего эллипсоида или гиперболоида. Наиболее из-
известный результат — теорема Линника об асимптотич.
равномерности распределения целых точек по поверх-
поверхности сферы растущего радиуса (см. [2] гл. IV).
Лит.: [1] Линии к Ю. В., «Изв. АН СССР. Сер. матсм.»,
1940, т. 4, № 4—5, с. 363—402; [2J его же, Эргодические свой-
свойства алгебраических полей, Л., 1967; [3] Малышев А. В.,
О представлении целых чисел положительными квадратичными
формами, М. —Л., 1962 (Тр. Матем. ин-та АН СССР, т. 65);
L41 его же, «Зап. науч. семинаров ЛОМИ», 1975, т. 50, с. 179 —
86; [5] его же, «Acta arithm.», 1975, v. 27, p. 555—98: [n] P e-
ters M., там же, 1977, v. 34, p. 57—80. А. В. Малышев.
ЛИПШИЦА КОНСТАНТА для заданно й в
промежутке (а, Ь) функции /(х) — ниж-
нижняя грань постоянных М>0 в Липшица условии
I f(y)—fH I < М | у-х | « , 0 < а< 1, х, у?(а, Ъ).
А. В. Ефимов-
ЛИПШИЦА УСЛОВИЕ — ограничение на поведение
приращения функции. Если для любых точек х и х',
принадлежащих отрезку [а, Ь], приращение функции f
удовлетворяет неравенству
\f{x) — f(x')\<M\x-x'\<*, (*>
где 0<а<:1 и М — нек-рая постоянная, то говорят,
что функция f(x) на отрезке [а, Ь] удовлетворяет у с-
ловию Липшица порядка а, н пишут:
/(г)? Lip а, или /^Lip^a, или /?#а(М). Каждая
функция, удовлетворяющая при каком-либо а>0 Л. у.
на отрезке [а, Ь], равномерно непрерывна на [а, Ь], а
функции, удовлетворяющие Л. у. степени а=1,— абсо-
абсолютно непрерывны. Функция, имеющая на [а, Ъ] огра-
ограниченную производную, удовлетворяет на [а, Ь\ Л. у.
с любым а<:1.
Л. у. (¦¦>;¦) эквивалентно условию
со F, /)<М6а,
где со (б, /) — непрерывности модуль функции f (х) на
отрезке {а, Ь]. Л. у. впервые рассматривалось Р. Лип-
Липшицем [1] в качестве достаточного условия для сходи-
сходимости ряда Фурье функции f(x). Условие (*) в случае
0<а<1 наз. также Гёлъдера условием степени а.
Лит.: [1] Li pschi tz R., «J. reine und angew. Math.»,
1864, Bd 63, S. 296 — 308; [2] 3 и г м у и д А., Тригонометриче-
Тригонометрические ряды, пер. с англ., 2 изд., т. 1—2, М., 1965; [3] Нага н-
сон И. П., Конструктивная теория функций, М.— Л., 1949.
ЛИПШИЦА УСЛОВИЕ интегральное '— "ог-
"ограничение на поведение приращения функции в инте-
интегральной метрике, функция I (х) из пространства LF (а,Ъ)
с p^sl удовлетворяет на отрезке [а, Ь] интеграль-
интегральному Липшица условию порядка а >0 с по-
постоянной М>0, если
"А | / (x + h)~f (x) f dxyiP < Mh* (*)¦
при всех h? @, Ь — а). В этом случае пишут/? 1лрЛ1(сс, р),
или f?Hp(M), или /(;Lip (а, р\ или /?Я™. Для слу-
случая периодич. функций (с периодом Ь — а) интегральное
Л. у. определяется аналогично, только в неравенстве
(*) верхний предел интегрирования Ъ—h следует за-
заменить на Ь.
Лит.: [1] Зигмунд А., Тригонометрические ряды,
пер. с англ., 2 изд., т. 1—2, М., 1965: [2] Н и к о л ь с к и й С.
М., Приближение функций многих переменных и теоремы вло-
вложения, 2 изд., М., 1977; [3] Бесов и. В., Ильин В. П.,
Никольский СМ., Интегральное представление функ-
функций и теоремы вложения, М., 1975. А. В. Ефимов.
ЛИСП — алгоритмический язык, разработанный в
1959 — 62 Дж. Маккарти [1]. Характеризуется весьма
однородным синтаксисом, в к-ром как программа, так и
ее объекты выглядят одинаково в виде т. н. с п и с о ч-
ной структуры — графа, в частности дерева,
висячими вершинами к-рого являются атомы (см. ниже),,
а остальными вершинами — списки, т. е. после-
последовательности (возможно, пустые) элементов (списков
или атомов), разделенных пробелами и взятых в скобки,
напр.
(АХ C5 В) 44Z).
Атомы — это непустые слова в алфавите языка, не
содержащие скобок, пробелов и обозначающие перемен-
переменные, константы, функции или самих себя. Списки и
атомы, для к-рых имеет смысл говорить об их значе-
значениях, наз. выражениями. Первым элементом
списка — выражения Е — является атом, обозначаю-
обозначающий функцию, или список, изображающий функцию.
Остальные элементы списка Е — это выражения, к-рые
берутся в качестве аргументов функции, а значением Е
является результат взятия функции от ее аргументов.
Значения переменных и константы понимаются обыч-
обычным образом. Изображение функции имеет вид списка
(lambda (jI, . . ., хп) ехр), где lambda — фиксирован-
фиксированный атом, (,rl, . . ., хп) — список связанных перемен-
переменных, обозначающих аргументы функции, а ехр — вы-
выражение, вычисляющее значение функции и содержа-
содержащее в себе xl, . . ., хп как свободные переменные.
Среди фундаментальных функций Л. имеются: саг(/)
и cdr (l), выдающие соответственно первый элемент
списка I и его «хвост»; quote (I), выдающая I в качестве
своего значения; cons (I т), «продолжающая» список I
списком т; cond ((pi el) (р2 e2)), выбирающая в ка-
качестве своего значения значение выражений el или el
в зависимости от того, какое по порядку из предикат-
предикатных выражений pi и р2 оказывается истинным. Фун-
Фундаментальными предикатами являются: atom (I), про-
проверяющий, является ли I атомом; eq (И 12), истинный,
если И и 12— равные друг другу атомы; null (l), истинный,
если I оказывается пустым списком, фундаментальные
функции и предикаты образуют набор средств, доста-
достаточный, чтобы реализовать в Л. и другие конструкции
алгоритмич. языков, напр, конструкцию присваивания
переменной значения выражения или связывания с ато-
атомом обозначаемого им изображения функции. Програм-
Программой в Л., является произвольный список, образован-
образованный выражениями.
Способность Л. легко образовывать произвольные
списочные структуры, в частности с помощью рекур-
рекурсивных определений, а также формировать выражения
в ходе вычислений обусловила широкое распростране-
распространение Л. как средства экспериментального программиро-
программирования сложных логич. задач.
Лит.: [1] McCarthy J., Recursive functions of sym-
boiic expressions and their computation by machine, Pt. 1, CACM,
3 (Apr. 1960), p. 184; [2] Лавров С. С, С и л а г а л з е Г.
ЛИСТИНГА УЗЕЛ — один из
простейших нетривиальных узлов
(рис.). Л. у. обозначается сим-
символом 4i (см. Узлов таблица) и
наз. иногда восьмеркой или че-
четырехкратным узлом. Группа Л.
у. имеет следующее копредставле-
ние \х, у : ух-1 уху-1 = х~1уху-1х\,
а полином Александера равен
A1 = t2— 3i+l. Рассмотрен И. Ли-
Листингом [11.
Лит.: [1] Listing I. В., Vorstudien zur Topologie,
Gott., 1847. M. Ш. Фарбер.
ЛИТЛВУДА ПРОБЛЕМА — 1) Л. п. д л я сов-
совместных диофантовых приближе-
н и й — вопрос о существовании для любых действи-
действительных чисел а, р\ е>0 натурального числа п такого,
что ге||аге||||Рп||<е, где ||а|| — расстояние от а до бли-
ближайшего целого числа. В нек-рых случаях, напр,
при рациональных а н fS, для чисел а и Р, одно из к-рых
представимо цепной дробью с неограниченными эле-
элементами, Л. п. имеет положительное решение.
2) Л. п. для интегралов — утверждение о
том, что для произвольной возрастающей последова-
последовательности М натуральных чисел т^, k—i, 2, . . .,
выполняется неравенство
V 2"_ ex? Bnimkx) dx>f(n), (*)
где /(n) = C In п, С>0 — абсолютная константа, п>п0.
Получены либо более слабые по сравнению с (¦¦¦¦¦) оценки
для произвольных последовательностей М, либо оценки,
близкие к (*) или даже совпадающие с этой оценкой, но
для специальных последовательностей М.
Л. п. сформулированы Дж. Литлвудом (см. [1]); в
общих случаях обе Л. п. не решены A982).
Лит.: [1] Hardy G. H., Little wood J. E.,
«J. London Math. Soc», 1948, v. 23, p. 163—68; [2] Кас-
Кассе лс Д ж.- В.- С. Введение в геометрию чисел, пер. с англ.,
М., 196Г). Б. М. Бредихин.
ЛИУВИЛЛЯ НОРМАЛЬНАЯ ФОРМА — запись
обыкновенного линейного дифференциального уравне-
уравнения 2-го порядка
^|W)j=c A)
в виде
5 0, B)
где к — параметр. Если р(х)?Сг, q(x)?C, (?
и г(г)>0, то уравнение A) приводится к Л. н. ф. B)
с помощью подстановки
г\(\) = Ф(х) у(х), I =
к-рая паз. преобразованием Лиувилля
(введена в [1]). Л. н. ф. играет важную роль при иссле-
исследовании асимптотич. поведения решений уравнения A)
для больших значений параметра К или аргумента, при
исследовании асимптотики собственных функций и соб-
собственных значений задачи Штурма — Лиувилля (см.
[3]).
Лит.: [1] L i о u v i 1 1 е J., «J. math, pures et appl.», 1837,
t. 2, p. 16 — 35; [2j К а м к е Э., Справочник по обыкновенным
дифференциальным уравнениям, пер. с нем., 5 изд., М., 1976; [3]
Титчмарш Э. Ч., Разложения по собственным функциям,
связанные с дифференциальными уравнениями второго порядка,
пер. с англ., т. 1—2, М., 1960—61. М. В. Федорюп.
ЛИУВИЛЛЯ ПОВЕРХНОСТЬ — поверхность, урав-
уравнения геодезических к-рой допускают квадратичный
интеграл a,-jdulduJ, причем тензор а,-у отличен от ме-
трич. тензора gjj поверхности. Напр., поверхность по-
постоянной гауссовой кривизны — Л. п. Для того чтобы
поверхность допускала геодезическое отображение на
плоскость, необходимо и достаточно, чтобы она явля-
являлась Л. п. (Дини т е о р е м а). См. также Лиувилля
сеть. ц. х. Сабитов.
ЛИУВИЛЛЯ СЕТЬ — сеть линий на поверхности,
в параметрах к-рой линейный элемент поверхности име-
имеет вид
2 (\ 2+2
где U=U{u), V~V(v). В каждом четырехугольнике,
образованном двумя парами линий из различных се-
семейств, две геодезич. диагонали имеют равную длину.
Поверхности, несущие Л. с, являются Лиувилля по-
поверхностями. К ним относятся, напр., центральные по-
поверхности второго порядка. Л. с. введена Ж. Лиувил-
лем (J. Liouville, 1846, см. [1] приложение 3).
Лит.: [1] Monge G.. Application de l'analyse a la geo-
metrie, 5 <5d.., P., 1850; [2] Ш у л и к о в с к и й В. И., Клас-
Классическая дифференциальная геометрия в тензорном изложении,
М., 1963. В. Т. Вазылев.
ЛИУВИЛЛЯ ТЕОРЕМА — 1) Л. т. об ограни-
ограниченных целых аналитических функ-
ц и я х: если целая функция / (z) комплексных пере-
переменных z= (zlf . . ., zn) ограничена, т. е.
то /(z) есть константа. Это предложение, одно из основ-
основных в теории аналитич. функций, впервые, по-видимо-.
му, опубликовано в 1844 О. Коши [1] для случая и = 1;
Ж. Лиувилль (J. Liouville) излагал его на лекциях в
1847, откуда и произошло название.
Л. т. допускает обобщения в различных направле-
направлениях. Напр., если / (z) — целая функция в С" и
для нек-рого целого т^О, то / (z) есть многочлен по пе-
переменным (zj, . . ., z,,) степени не выше т. Далее, если
и (х) — действительная гармонич. функция во всем
числовом пространстве R", x=(xlt . . ., а-„), причем
и (х) < М A +1 х \т) (или — и (х) < 1
z?R", то и (х) есть гармонич. многочлен по переменным
(api, . . ., хп) степени не выше т (см. также [4]).
2) Л. т. о конформных отображениях:
всякое конформное отображение области евклидова
пространства Е" при гС^Ъ можно представить в виде
конечного числа суперпозиций простейших отображе-
отображений четырех видов — переноса, подобия, ортогональ-
ортогонального преобразования и инверсии. Доказана Ж. Лиу-
виллем в 1850 (см. [2] добавление 6).
Эта Л. т. выявляет бедность класса конформных ото-
отображений в пространстве, и с этой точки зрения она
весьма важна в теории аналитич. функций многих комп-
комплексных переменных и в теории квазиконформных
отображений.
Лит.: [1] Cauchy А., «С. г. Acad. sci.», 1844, t. 19,
p. 1377—84; [2] M о n g e G., Application de l'analyse a la
geometrie, 5 ed., P., 1850, p. 609—16; [3] Бицадзе А. В.,
Основы теории аналитических функций комплексного перемен-
переменного, 2 изд., М., 1972; [4] Владимиров В. С, Методы
теории функций многих комплексных переменных, М., 19G4.
Е. Д. Соломенцев.
3) Л. т. о приближении алгебраи-
алгебраических чисел — теорема, устанавливающая, что
алгебраич. иррациональности не могут слишком хоро-
хороню приближаться рациональными числами. Именно,
если а — алгебраич. число степени га^;2, а р и д>0 —
любые целые рациональные числа, то имеет место нера-
неравенств о
а ч I > ч" '
тде С — положительная константа, зависящая только
от а п выражаемая в явном виде через сопряженные с а
величины.
С помощью этой теоремы Ж. Лиувилль [1] впервые
построил неалгебраические (трансцендентные) числа.
Таким числом является, напр., число
представляемое рядом с быстро убывающими членами.
При и=2 Л. т. дает неулучшаемый результат. Для
гс^гЗ Л. т. неоднократно усиливалась. В 1909 А. Туэ
[2] установил, что для алгебраич. чисел а степени
и v> ——1-1 справедливо неравенство
К. Зигель [3] улучшил результат А. Туэ, показав, что
неравенство (*) выполняется при (s — целое)
min (
1<S< Я-1 V 8+1
в частности при v>2J^«. Позже Ф. Дайсон [4] доказал
справедливость неравенства (*) при v~>\r2n. Нако-
Наконец, К. Рот [5] установил, что неравенство (*) спра-
справедливо при любом v>2. Результат К. Рота является
наилучшим в своем роде, т. к. любое иррациональное
число ?, алгебраическое или нет, имеет бесконечно
много рациональных приближений plq, удовлетворяю-
удовлетворяющих неравенству
Все указанные выше усиления Л. т. имеют один су-
существенный недостаток — они неэффективны, а именно:
методы их доказательства не позволяют установить,
каким образом постоянная С = С (a, v) в неравенстве
(*) зависит от величин а и v. Получены (см. [6], [7],
[8]) эффективные усиления Л. т., но лишь для значений
показателя v, мало отличающихся от п.
Лит.: Ш Liouville J., «С. г. Acad, sci.», 1844, t. 18,
p. 883—85, 910—11; [2] Thue A., «J. reine und an?ew. Math.»,
1909, Bd 135, S. 284—305- ft] S i e g e 1 C, «Math. Z.», 1921,
Bd 10, S. 173 — 213; [4] Dyson F. I., «Acta math.», 1947,
t. 79, p. 225—40; [5] Roth K. F., «Mathematika», 1955, v. 2,
p. 1—20; [6] Baker A,, «Phiios. Trans. Roy. Soc. London.
Ser. A», 1968, v. 203, p. 173—91; [7] Спринджук В. Г.,
«Нзв. АН СССР. Сер. матем.», 1971, т. 35, с. 991 — 1007; [8]
Фельдман Н. И., там же, с. 973—90. С. А. Степанов.
4).П. т. о сохранении фазового о б ъ е-
м а: объем V любой области G бЖ-мерного фазового про-
пространства (р, д) (пространства компонент импульсов
P = (Pi, •¦•! Pn) и координат <? = (•»-•,, ¦ . •, t'jv) каждой
из N частиц классич. системы с потенциальными сила-
силами взаимодействия) не изменяется с течением времени
Г =
= \ dp dq = const,
J (С)
если все точки этой области двигаются согласно урав-
уравнениям классич. механики. Утверждение является след-
следствием того, что якобиан перехода от переменных
(р, q) (в момент времени t) к переменным (р', q') (в мо-
момент времени t' >i) согласно уравнениям движения
(напр., в форме уравнений Гамильтона) равен единице.
Величина F является одним из интегральных инвариан-
инвариантов Пуанкаре, а Л. т.— одним из следствий их суще-
существования. Л. т. используется в статистич. механике
классич. систем (см. Лиувилля уравнение). Л. т. дока-
доказана Ж. Лиувиллем (J. Liouville, 1851).
И. А. Квасников.
ЛИУВИЛЛЯ УРАВНЕНИЕ — уравнение движения
для функции распределения шдг(р, q; t) по импульсам
Р = (Р\, ..., P/v) и координатам q= (rlt ..., Гдг) N-
частичной классич. системы
дН 9wN dwN дН \
gt -1-- -iV/KJI.— ^ = 1 ^ д1.. др. a,-. ePi J '
где// — гамильтониан системы, а фигурными скобками
обозначены классич. скобки Пуассона.
Если в фазовом пространстве (р, </) распределению
wn{Pi 1< t) сопоставить плотность фазовых точек (каж-
(каждая из к-рых соответствует определенному механич.
состоянию данной системы N материальных точек), то в
силу того, что траектории движения этих точек не пере-
пересекаются вследствие единственности решений уравнений
движения механики, и того, что фазовый объем соглас-
согласно Лиувилля теореме сохраняется, ансамбль этих то-
точек образует в фазовом пространстве своеобразную не-
несжимаемую жидкость, полная производная плотности
к-рон wyv по времени равна нулю:
dt вГ1"^;-! ^ STJ ~~d
Это приводит к Л. у., если только выразить согласно
Гамильтона уравнениям производные от координат и
импульсов через соответствующие частные производные
от гамильтониана.
Л. у. используется не только при рассмотрении об-
общих вопросов статистич. механики, связанных с вы-
выяснением микроскопической и макроскопической струк-
структур состояния системы многих тел, процессов стремле-
стремления к равновесию, проблем «перемешивания» в фа-
фазовом пространстве, эргодичности и т. д., но и в кон-
конкретных исследованиях, т. к. Л. у. является исходным
уравнением при построении Боголюбова цепочки урав-
уравнений, а следовательно, и для различного типа кнне-
тич. уравнений, с помощью к-рых решаются уже при-
прикладные физич. задачи.
В случае квантовых систем роль Л. у. играет урав-
уравнение движения для статистич. оператора p(t) (плот-
(плотности матрица), к-рое в шрёдингеровском временном
представлении имеет вид
? {*Р>
где Н — оператор Гамильтона, а фигурными скобками
обозначены квантовые скобки Пуассона. Это кванто-
квантовое Л. у. является следствием структуры смешанного
состояния (описываемой данным статистич. оператором),
в к-ром каждое из составляющих его чистых квантово-
механич. состояний эволюционирует согласно Шрёдин-
гера уравнению.
Лит.: [1] Голдстейн Г., Классическая механика,
пер. с англ., М., 1957; [2] У л е н б е к Д., Форд Д ж.,
Лекции по статистической механике, пер. с англ., М., 1965;
[3] Боголюбов Н. Н., Избр. труды, т. 2, К., 1970.
II. А. Квасников.
ЛИУВИЛЛЯ ФУНКЦИЯ — арифметическая функ-
функция Х(и), определяемая равенством
где v(n) — число всех простых сомножителей п. Л. ф.
тесно связана с Мёбиуса функцией \х(п):
В теории чисел важна оценка суммы
при х—>-оо. Существует гипотеза, что
S (х) <^ Y~* ln х-
Последний результат, полученный методом И. М. Ви-
Виноградова, имеет вид
(— с1пзг\г ln-i з in х).
Л. ф. введена Ж. Лиувиллем (J. Liouville).
Лит.: [1] П р а х а р К., Распределение простых чисел,
пер. с нем., М., 1967; [2] Чандрасекхаран К., Ариф-
Арифметические функции, пер. с англ., М., 1975. А. Ф. Лаврик.
ЛИУВИЛЛЯ ЧИСЛО — действительное число а,
для к-рого при любом v^l неравенство
а —у | < g~v
имеет бесконечно много целых решений р и д, удовлет-
удовлетворяющих условиям g>0, (р, д)=1. Трансцендентность
Л. ч. вытекает из Лиувилля теоремы. Изучались Ж. Ли-
увнллем [1].
Примеры Л. ч.:
(-1)-
Лит.: [1] Liouville J., «С. г. Acad. sci.», 1844, t. 18,
p. 88-3—85; [2] Гельфонд А. О., Трансцендентные и ал-
алгебраические числа, М., 1952. С. В. Котов.
ЛИУВИЛЛЯ — ОСТРОГРАДСКОГО ФОРМУЛА, Л и-
увилля формул а,— соотношение, связываю-
связывающее вронскиан системы решений п коэффициенты ли-
линейного обыкновенного дифференциального уравнения.
Пусть x1{t), . . ., xn{t) — произвольная система п
решений линейной однородной системы га-го порядка
x' = A(l)x, .r?R", A)
с непрерывным на интервале / оператором A (t), a
W (.ri(t), ..., xn(t)) = W(t)
— вронскиан этой системы решений. Л. —О. ф. имеет вид
¦?-W(t) = W(t)-SpA(t), t?I, B)
или, что то же самое,
W (Xl(t), ..., xn(t)) =
= W (хг (to),...,xn (*„)) -ехР V SpA (s)ds, t, to?I; C)
здесь SpA(t) — след оператора A (t). Л.—О. ф. можно за-
записать с помощью Коши оператора X (t, t0) системы A):
detX(t, *0) = ехрГ Sp A (s) ds, t, to?I. D)
J to
Геометрический смысл соотношения D) (или C)) состоит
в том, что в результате преобразования X(t, t0): R" —>-R"
ориентированный объем любого тела увеличивается в
exp \ Sp A (s)ds раз.
Если рассматривается линейное однородное урав-
уравнение re-го порядка
Ро (О УМ+Р1 (О У^-^ + . ¦ . + Р„-1 @ у'+рп (t)y = O E)
с непрерывными на интервале / коэффициентами, при-
причем ро(г)ф0 при г?/, то Л.—О. ф. наз. равенство
W (Vl{t), ..., yn(t)) =
F)
где W(г/i (t), ..., yn (t)) — вронскиан системы п реше-
решений yi(t), ..., yn(t) уравнения E). Л. —О. ф. C), F)
обычно используются в случае, когда рассматриваемая
система решений является фундаментальной. Напр.,
формула F) позволяет найти в квадратурах общее ре-
решение линейного однородного уравнения 2-го порядка,
если известно одно его частное нетривиальное решение.
Соотношение F) для уравнения E) при п = 2 найдено
Н. Абелем в 1827 (см. [1]), а при произвольном п —
в 1838 Ж. Лиувиллем [2] и М. В. Остроградским [31;
равенство C) получено Ж. Лиувиллем [2] и К. Якоби
[4] (вследствие чего равенство C) иногда наз. ф о р-
пулой Якоби).
Л. — О. ф. B) допускает обобщение на нелинейную сис-
систему
x'=f(t,x), x^R", G)
в предположении, что вектор-функция
/ {t, X) — (/j (t, ХЪ . . . , Хп), . . . , /„ (t, XL, . . . , X,,))
и матрица dfldx непрерывны. Если Q{ocR" — множест-
множество конечной меры [i(t0), а образ Qi этого множества при
линейном отображении X (t, t0): R" —*¦ Rn, где X (t,t0) —
оператор Коши системы G), имеет меру ц(г), то
^=)Qidiy xf(t,X)dx;
здесь
9f((t, xv . . . , xn)
div»
Отсюда вытекает теорема Лиувилля о со-
сохранении фазового объема, имеющая
важные приложения в теории динамических систем и в
статистической механике: поток гладкой автономной
системы
не меняет объем любого тела в фазовом пространстве R
тогда и только тогда, когда div/(i) —0 при всех х;
в частности, фазовый объем сохраняется потоком га-
милыпоновой системы.
Лит.: [1] Abel N. Н., «J. reine und angew. Math.», 1827,
Bd 2, S. 22—30; [2] L 1 о u v i 1 1 e J., «J. math, pures et appl,»,
1S38, t. 3, p. 342—49; [3] О с т р о г р а д с к и й М. В., Поли,
собр. трудов, т. 3, К., 1961, с. 124—26; [4] J а с о b i К., Ge-
sammclte Werke, Bd 4, В., 1886; [5] Понтрягин Л. С,
Обыкновенные дифференциальные уравнения, 4 изд., М., 1974;
[6] Арнольд В. И., Обыкновенные дифференциальные
уравнения, М., 1971. Я. X. Розов.
ЛОБАТТО КВАДРАТУРНАЯ ФОРМУЛА — наивыс-
наивысшей алгебраич. степени точности квадратурная форму-
формула для промежутка [а, Ь] = [ — 1, 1] и веса р(х) = \ с дву-
двумя фиксированными узлами — концами промежутка
[ — 1, 1]. Л. к. ф. имеет вид
l f (х) dx s±A[f (-1) +/ A)] + 2"=, Cjf M-
Узлы Xj— корни ортогонального на [ — 1, 1] с весом
1—.т2 многочлена Рп' )(х) (многочлена Якоби), А =
= 2/(л + 1)(ге+2), Су>0. Алгебраич. степень точности
равна 2п-\-1. Таблица узлов и коэффициентов Л. к. ф.
для я=ЛAI5 (п меняется от 1 до 15 с интервалом 1)
приведена в [2] (см. также [3]).
Формула установлена Р. Лобатто (см. [1]).
Лит.: [1] Lob at to R., Lessen over de differential en
mtesral-rekening-, v. 1—2, S'Gravenliage, 1851—52; f2] Кры-
Крылов В. 11., Приближенное вычисление интегралов, 2 изд.,
М., 1967; [3] Mi Che Is H. H., «Math. Сотр.», 1963, v. 17,
p. 237 — 44. И. П. Мысовских.
ЛОБАЧЕВСКОГО ГЕОМЕТРИЯ — геометрия, осно-
основанная на тех же основных посылках, что и евклидова
геометрия, за исключением аксиомы о параллельных
(см. Пятый постулат). В евклидовой геометрии соглас-
согласно этой аксиоме на плоскости через точку Р, лежащую
Bi:e прямой А 'А, проходит только одна прямая В'В,
не пересекающая А'А. Прямая В'В наз. парал-
параллелью к А'А. При этом достаточно потребовать,
чтобы таких прямых проходило не более одной, так как
существование непересекающей прямой может быть до-
доказано путем последовательного проведения прямых
PQ_\_A'A и PB\^PQ. В Л. г. аксиома параллельности
требует, чтобы через точку Р (рис. 1) проходило более
A' Q \А
Рис. 1.
одной прямой, не пересекающей А 'А. Непересекающие
прямые заполняют часть пучка с вершиной Р. лежащую
внутри пары вертикальных углов TPU и U'PT', рас-
расположенных симметрично относительно перпендикуля-
перпендикуляра PQ. Прямые, образующие стороны вертикальных
углов, отделяют пересекающие прямые от непересекаю-
непересекающих и сами являются тоже непересекающими. Эти гра-
граничные прямые наз. параллелями в точке Р
к прямой А'А соответственно в двух ее направлениях:
Т'Т параллельно А'А к направлении A'A, a UU' па-
параллельно А'А в направлении АА'. Остальные непе-
ресркающие прямые наз. расходящимися
прямыми с А'А (подробнее см. ниже).
Угол а, 0<а<я/2, к-рый параллель к точке Р об-
образует с перпендикуляром PQ, /_QPT= /_QPV' = a,
наз. углом параллельности отрезка PQ=a
и обозначается через а=П (а). При а —0 угол а=п/2;
при увеличении а угол а уменьшается так, что для каж-
каждого заданного а, 0<а<я72, существует определен-
определенное значение а. Эта зависимость наз. Лобачевского
функцией:
П (a)=2arctg {e-<*>k),
где к — некоторая константа, определяющая фикси-
фиксированный по величине отрезок. Она получила назва-
название радиуса кривизны пространства
Лобачевского. Подобно сферич. геометрии су-
существует бесконечное множество пространств Лоба-
Лобачевского, различающихся величиной к.
Евклидова геометрия может быть получена как пре-
предельный случай Л. г., когда обе параллели, проходя-
проходящие через Р, сливаются в одну, т. е. когда множество
всех прямых, проходящих через точку Р и непересе-
кающнх данную прямую А'А, сводится к единственной
прямон. Тогда угол ос=я/2 при любом а. Это условие
эквивалентно требованию /с=оо. В малых областях
пространства, т. е. когда линейные размеры фигур по
отношению к к бесконечно малы, все соотношения Л. г.
аппроксимируются получающимися в пределе соотно-
соотношениями евклидовой геометрии.
Две различные прямые по плоскости образуют пару
одного из трех типов.
Пересекающиеся прямые. Расстояние
от точек одной прямой до другой прямой неограниченно
увеличивается при удалении точки от пересечения пря-
прямых. Если прямые не перпендикулярны, то каждая про-
проектируется ортогонально на другую в открытый отрезок
конечной величины.
Параллельные прямые. На плоскости че-
через данную точку проходит единственная прямая, па-
параллельная данной прямой в заданном на последней
направлении. Параллель в точке Р сохраняет в каждой
своей точке свойство быть параллелью той же прямой
в том же направлении. Параллелизм обладает взаим-
взаимностью (если а\\Ь в определенном направлении, то и
Ь\\а в соответствующем направлении) и транзитивно-
транзитивностью (если а\\Ь и с\\Ъ в одном направлении, то а\\с в со-
соответствующем направлении). В направлении парал-
параллельности параллельные неограниченно сближаются,
в противоположном направлении — неограниченно
удаляются (в смысле расстояния от перемещающейся
точки одной прямой до другой прямой). Ортогональная
проекция одной прямой на другую является открытой
полупрямой.
Расходящиеся прямые. Они имеют один
общин перпендикуляр, отрезок к-рого дает минимальное
расстояние. По обе стороны от перпендикуляра пря-
прямые неограниченно расходятся. Каждая прямая про-
проектируется на другую в открытый отрезок конечной
величины.
Трем типам прямых соответствуют на плоскости три
типа пучков прямых, каждый из к-рых покрывает всю
плоскость: пучок 1-г о рода — множество всех
прямых, проходящих через одну точку (центр пуч-
пучка); пучок 2-г о рода — множество всех пря-
прямых, перпендикулярных к одной прямоп (базе пуч-
пучка); пучок 3-г о рода — множество всех пря-
прямых, параллельных одной прямой в заданном направ-
направлении, включающее и эту прямую.
Ортогональные траектории прямых этих пучков об-
образуют аналоги окружности евклидовой плоскости:
окружность в собственном смысле; э к в и д и-
с т а н т а, или линия равных р а с с т о я-
ний (если не рассматривать базу), к-рая вогнута в
сторону базы; предельная линия, или о р п-
ц и к л, ее можно рассматривать как окружность с
бесконечно удаленным центром. Предельные линии
конгруэнтны. Они не замкнуты и вогнуты в сторону
параллельности. Две предельные линии, порожденные
одним пучком,— концентричны (высекают на прямых
пучка равные отрезки). Отношение длин концентрич.
дуг, заключенных между двумя прямыми пучка, убы-
убывает в сторону параллельности как показательная функ-
функция расстояния х между дугами:
s'/s =c~A';ft.
Каждый из аналогов окружности может скользить
по самому себе, что порождает три типа однопарамет-
рич. движений плоскости: вращение вокруг собствен-
собственного центра; вращение вокруг идеального центра (од-
(одна траектория — база, остальные — эквидистанты);
вращение вокруг бесконечно удаленного центра (все
траектории — предельные линии).
Вращение аналогов окружностей вокруг прямой по-
порождающего пучка приводит к аналогам сферы: соб-
собственно сфере, поверхности равных
расстояний п о р и с ф е р е, или предель-
предельной поверхности.
Па сфере геометрия больших окружностей — обыч-
обычная сферическая геометрия; на поверхности равных
расстояний — геометрия эквидистант, являющаяся
планиметрией Лобачевского, но с большим значением
к; на предельной поверхности — евклидова геометрия
продельных линий.
Связь между длинами дуг и хорд предельных линий
и евклидовы тригонометрич. соотношения на предель-
предельной поверхности позволяют вывести тригонометрич.
соотношения на плоскости, то есть тригонометрич. фор-
формулы для прямолинейных треугольников. Напр., фор-
формулу для площади а треугольника:
а=А:2(я—А— В — С);
для длины окружности:
I = 2лк sh -?- .
Тригонометрич. формулы Л. г. могут быть получены
из формул сферич. геометрии заменой радиуса R на
мнимое число ki.
Доказательство непротиворечивости Л. г. проводится
с помощью построения интерпретации (модели). Пер-
Первой такой интерпретацией явилась Белътрами интер-
интерпретация, где установлено, что в евклидовом простран-
пространстве внутренняя геометрия поверхности постоянной
отрицательной гауссовой кривизны локально совпадает
с Л. г. (роль прямых играют геодезические линии по-
поверхности). Поверхность тако-
такого типа называется псевдо-
псевдосферой.
Другая интерпретация Бсльт-
рами состоит в геодезическом
отображении поверхности по-
постоянной отрицательной кри-
кривизны во внутренность круга.
Рис 2 Однако интерпретации Бельт-
рами моделируют лишь часть
плоскости Лобачевского. Первая интерпретация всей
плоскости Лобачевского — Клейна интерпретация,
в к-рой использована проективная метрика Кэли.
В этой интерпретации (рис. 2) прямые линии простран-
пространства Лобачевского реализуются хордами абсолюта
(без концевых точек), а расстояния и углы выражаются
с помощью двойных отношений четверок точек (концы
М, N отрезка и концевые точки U, Т хорды, на к-рой
лежит отрезок) и соответствующих четверок прямых
[стороны угла и проходящие через вершину касатель-
касательные (мнимые) к абсолюту]. Параллели через точку Р
к прямой МN реализуются прямыми Р Т и Р U, пере-
пересекающими прямую MN в точках на абсолюте. Точки
абсолюта моделируют «бесконечно удаленные точки»,
не являющиеся точками плоскости Лобачевского.
А. Пуанкаре (Н. Poincare, 1882) при построении
теории автоморфных функций пришел к двум другим
моделям — в круге и на полу-
полуплоскости (Пуанкаре интерпре-
интерпретация). В первой модели (рис.
3) плоскость Лобачевского реа-
реализуется внутренностью круга,
прямые — внутренними частями
дуг окружностей, пересекаю-
пересекающих основной круг ортогональ-
ортогонально. Метрика вводится с помо-
помощью двойных отношений, при-
причем величины углов на модели
такие же, как и на плоскости
Лобачевского (модель конформ-
конформная).
Введение тех или иных координат позволяет получать
различные аналитич. модели плоскости Лобачевского.
А. Пуанкаре была предложена A887) модель Л. г. как
геометрии плоских диаметральных сечений на одной из
полостей двуполостного гиперболоида, к-рую можно
трактовать и как геометрию сферы чисто мнимого ради-
радиуса в псевдоевклидовом пространстве. Указанные мо-
модели обобщаются на случай n-мерного пространства.
Как риманова геометрия, Л. г. есть геометрия рима-
нова пространства постоянной отрицательной кривизны.
Источником создания Л. г. послужила проблема па-
параллелей, т. е. попытки доказательства пятого посту-
постулата Евклида о параллельных. Н. И. Лобачевский
A826, опубл. 1829—30) показал, что допущение посту-
постулата, отличного от постулата Евклида, позволяет по-
построить более общую, чем евклидова, Л. г. Независимо
от Н. II. Лобачевского к этому открытию пришел
Я. Больяй (J. Bolyai, 1832). Не получив открытой под-
поддержки у К. Гаусса (С. Gauss), Я. Больяй не продол-
продолжил своих исследований.
К. Гаусс разрабатывал начала новой геометрии в
значительно более ранние годы, но он не публиковал
этих исследований и никогда не высказывался открыто
об этих идеях. Однако в частной переписке он высоко
оценил труды Я. Больяй и Н. И. Лобачевского, но
открыто в печати все-таки не высказался.
Приложения геометрии Лобачевского. Н. И. Лоба-
Лобачевский уже в первой работе по Л. г. показал, опираясь
на впервые измеренные астрономами в те годы годичные
параллаксы звезд, что если в физич. пространстве
реализуется его геометрия, то в пределах Солнечной
системы отклонения от евклидовой геометрии будут
на несколько порядков меньше возможных ошибок
измерений. Таким образом, первым приложением Л. г.
явилось обоснование практич. точности евклидовой
геометрии.
Н. И. Лобачевский применял свою геометрию в мате-
матич. анализе. Переходя от одной системы координат
к другой в своем пространство, он нашел значения
около 200 различных определенных интегралов. Др.
математич. приложения были найдены А. Пуанкаре
A882), к-рый успешно применял Л. г. при разработке
теории автоморфных функций.
Значение Л. г. для космологии было выявлено
А. А. Фридманом. В 1922 он нашел решение уравнения
Эйнштейна, из к-рого следовало, что Вселенная расши-
расширяется с течением времени. Это заключение впоследст-
впоследствии было подтверждено наблюдениями Э. Хаббла
(Е. Hubble, 1929), обнаружившего разбегание удален-
удаленных туманностей. Метрика, найденная А. А. Фридма-
ном, дает при фиксированном времени пространство
Лобачевского. Пространство скоростей специальной
теории относительности является пространством Лоба-
Лобачевского.
Л. г. с успехом используется при изучении столкнове-
столкновений элементарных частиц и при разработке др. вопро-
вопросов ядерных исследований.
Зрительное (перцептивное) восприятие близких об-
областей пространства человеком порождает эффект
обратной перспективы, объясняемый тем, что геометрия
этих областей перцептивного пространства близка к
Л. г. с радиусом кривизны около 15 м.
Создание Л. г. явилось важным этапом в развитии
учения о возможных свойствах пространства. Особен-
Особенное значение это имело для оснований математики,
т. к. принципы современного аксиоматич. метода вы-
вырабатывались в значительной степени благодаря по-
появлению Л. г.
Лит.: [1] Лобачевский Н. И., Поли. собр. соч.,
т. 1 — 5, М.— Л., 194В—51; [2] Б о л ь аи Я., Appendix, пер.
с латин., М.— Л., 1950; [3] Александров А. Д., Абст-
Абстрактные пространства, в кн.: Математика, ее содержание, мето-
методы и значение, т. 3, М., 1956; [4] Егоров И. П., Введение
в неевклидовы геометрии, Пенза, 1972; [5] Ефимов Н. В.,
Высшая геометрия, 6 изд., М., 1978; [6] Каган В. Ф-, Ос-
Основания геометрии, ч. 1, М,— Л., 1949; [7] Лаптев Б. Л.,
Николай Иванович Лобачевский, Казань, 1976; [8] Н о р-
д е н А. П., Элементарное введение в геометрию Лобачевского.
М., 1953; [9] Нут Ю. Ю., Геометрия Лобачевского в анали-
аналитическом изложении, М., 1961: [10] Раушенбах Б. В.,
Пространственные построения в древнерусской живописи, М.,
1975; [11] Розенфельд Б. А., Неевклидовы простран-
пространства, М., 1969; [12] Широков П. А., Краткий очерк основ
геометрии Лобачевского, Казань, 1964. Б. Л. Лаптев.
ЛОБАЧЕВСКОГО МЕТОД, метод Греффе,
метод Данделена,— метод для одновременно-
одновременного вычисления всех корней многочлена. Пусть корни
гъ г2, . . ., гп многочлена
= а0 (z — rj (z — r2) . . . (z — rn), а0 Ф 0, A)
удовлетворяют неравенствам
К|>|г2|>...>|г„|. B)
В качестве приближений к корням могут быть взяты
отношения «i/a,-!, г=1, . . ., п.
Пусть теперь корни /(г), хотя п не выполнено B),
все же различны по абсолютной величине. Л. м. за-
заключается в применении к уравнению /(z) = 0 процесса
квадрирования, к-рый при достаточном числе пов-
повторений приводит к уравнению с корнями, удовлетво-
удовлетворяющими условиям B). Квадрирование со-
состоит в переходе от очередного многочлена /^ (г) к мно-
многочлену ik + \ (z) т°й же степени, корни к-рого равны
квадратам корней /&(z). Переход выполняется по ре-
рекуррентным формулам.
Применение Л. м. возможно и при наличии групп
равных по абсолютной величине корней, хотя ято при-
приводит к осложнениям в логике и формулах метода. До-
Достоинством метода является то, что не требуется зна-
знания начальных приближений к корням многочлена.
В случае различных по абсолютной величине корней
скорость сходимости процесса асимптотически квадра-
квадратичная.
Л. м. является, однако, численно неустойчивым,
т. к. процесс квадрирования приводит к очень быстро-
быстрому накоплению вычислительной погрешности. В связи
с этим предпринимались попытки придать Л. м. саио-
исправляющуюся форму. Так, напр., для вычисления
корней многочлена A) строится последовательность
многочленов gk(z) степени <я — 1, связанных соотно-
соотношениями
) = zgk (z) — (pkf(z), к = 0, i, ...; ?0(г) = 1;
отсюда
gA(z)=z*(mod/(z)).
При каждом фиксированном к ищутся многочлены
Sk, »(z)i определяемые следующим образом:
8k, I (z)=gk (z);
для р^2 gk, p(z) есть многочлен вида
-i (z) Ыг),
имеющий степень <п—р. Если корни многочлена /(z)
удовлетворяют неравенствам
lim gj, p=/*(z)/(z — rx) (z — r2) . . .(z — rp),
где /* (z) —многочлен /(z), нормированный делением
на коэффициент при старшем члене. Таким образом,
из исходного многочлена выделяются множители, соот-
соответствующие группам равных по абсолютной величине
корней (см. [3]). Л. м. предложен Н. И. Лобачевским
в 1834 (см. [1]).
Лит.: [1] Лобачевский Н. И., Полн. собр. соч.,
т. 4, М.— Л., 1948; [2] Б е р е з и н И. С, Жидков Н. П.,
Методы вычислений, 3 изд., т. 1, М., 196В; [3] Sebastiao e
S i I v a J., «Portug. Math.», 1941, .Vi 2, р: 271—79; [4] Hou-
Householder A. S., Stewart G. W., «SIAM Rev.», 1971,
v. 13, p. 38 — 4И. А'. Д. Икрамов.
ЛОБАЧЕВСКОГО ПРИЗНАК сходимости: чис-
лов он ряд 2j —ian c положительными и монотонно стре-
стремящимися к нулю членами сходится или расходится
одновременно с рядом
гДе Рт— наибольший из номеров членов ап, удовлет-
удовлетворяющих неравенству ап^2~т, и —1, 2, . . ., рп.
Предложен Н. И. Лобачевским A834—36).
В. II. Битюцпов.
ЛОБАЧЕВСКОГО ПРОСТРАНСТВО — пространство,
геометрия к-рого определяется аксиомами Лобачевского
геометрии. В более широком смысле Л. п. понимается
как неевклидово гииерболич. пространство, определе-
определение к-рого связано с понятиями геометрии псевдоевкли-
псевдоевклидова пространства. Пусть "Йп + 1 — псевдоевклидово
(п+1)-пространство индекса п; на н-сфере этого про-
пространства рассматривается множество пар диаметрально
противоположных точек. Множество элементов, изо-
метричное множеству пар указанных выше точек
?!-сферы пространства "Л„ + ], наз. /(-пространством Ло-
Лобачевского п обозначается 1Sn. Такое определение Л. п.
позволяет включить это пространство в проективную
классификацию неевклидовых пространств. Пространст-
Пространство lSn в проективном пространстве Рп изображается
внутренней областью овальной (п—1)-квадрики, к-рая
является пересечением n-сферы мнимого радиуса с бес-
бесконечно удаленной плоскостью пространства "Яп + 1,
дополняющей это пространство до проективного про-
пространства Pn + i. Точки овальной (п—1)-квадрики яв-
являются бесконечно удаленными точками пространства
1Sn, т. е. квадрика является абсолютом этого про-
пространства. Внешняя область квадрики, дополняющая
пространство 1Sn до полного пространства Рп, наз.
идеальной областью пространства 1Sn.
Указанная интерпретация наз. проективной
интерпретацией К э л и — Клейна. Она
может быть получена также путем проектирования
гс-сферы мнимого радиуса пространства nRn + \ из ее
центра на касательную n-плоскость, к-рая является
евклидовым re-пространством; при этом пространство
15„ изображается внутренней областью n-шара в этой
?г-плоскости, граница п-шара является абсолютом про-
пространства xSn (иногда последнюю интерпретацию про-
пространства xStl в евклидовом пространстве Rn наз.
интерпретацией Бельтрами — К л е й-
н а).
Проективная интерпретация 3-пространства Лоба-
Лобачевского позволяет проверить выполнение аксиом гео-
геометрии Лобачевского, дать изображение всех фигур
этой геометрии и установить их свойства. В частности,
в указанной интерпретации просто устанавливаются
геометрич. свойства 2-плоскости Лобачевского, выте-
вытекающие из аксиом геометрии Лобачевского.
Присоединением к пространству 1Sn точек абсолюта
и точек идеальной области определяется расширен-
расширенное Л. п. m-плоскость, т<.п, пересекающаяся с аб-
абсолютом, наз. собственной m-п лоскостью;
не пересекающая абсолюта — идеальной т-плоскостью;
тв-плоскость, касающаяся абсолюта,— изотроп-
изотропной т-п лоскостью. Таким же образом клас-
классифицируются прямые пространства 1Sn. Полюсы соб-
собственных плоскостей являются идеальными
точками, а собственные точки — полю-
полюсами идеальных плоскостей. Вообще, полярные
(га—т — 1)-плоскости собственных m-плоскостеп Л. п.
1Sn суть идеальные (га — т — 1)-плоекостп, и полярные
(га—т—1)-плоскости идеальных m-плоскостей — соб-
собственные (га—т— 1)-плоскости.
В пространстве 1Sn в качестве координат точки X
можно рассматривать координаты вектора ж этой точки
в пространстве "Дп + 1, принадлежащей ?г-сфере мнимого
радиуса. Координаты вектора ас (Вейерштрасса коорди-
координаты) при этом должны удовлетворять условию
Используются также координаты Бельтра-
м и
причем J^,j(X'J<l- В пространстве 1Sn вводятся де-
декартовы координаты и1, и2, . . ., и", связанные с коор-
координатами х' соотношениями
„ , иг , и2 , и"
*° = ch— ch— • ..ch— ,
.r1=-sli — ch ... ch ,
о о о
где га, i2=—1,— радиус кривизны пространства 15„.
Расстояние б между точками X и У определяется
соотношением
, б _ |хЕ„|
а ~~ о'
где ос,, у — определенные выше векторы точек X и
У, Е — линейный оператор, определяющий скалярное
произведение в пространстве этих векторов.
Угол между двумя плоскостями Л. п. 1Sn совпадает
с углом между га-плоскостями псевдоевклидова про-
(транства пВп + 1, соответствующим этим плоскостям.
Угол ф между плоскостями связан с расстоянием б
между полюсами этих плоскостей соотношением
6 <| Ш",
когда угол ф — действительный, а б — чисто мнимое, и
а .
Ч' о '
когда угол ф — чисто мнимый, а расстояние б — дей-
действительное.
Расстояние между точками и величины углов между
плоскостями допускают выражения через двойное от-
отношение точек с помощью точек абсолюта.
В Л. п. 1Sn определяются сферы (шары), эквиди-
эквидистантные поверхности, орисферы (орициклы при п=2),
m-симплексы и т. д.
Классификация движений Л. п. 15„ как коллинеаций,
переводящих точки абсолюта (овальной квадрики) в
себя, сводится к классификации вращений псевдоев-
псевдоевклидова пространства "Rn + 1. Группа движений про-
пространства 1Sn изоморфна факторгруппе группы вра-
вращений пространства ?„ + 1 по ее подгруппе, состоящей
из тождественного преобразования и отражения от
точки; состоит из двух связных компонент, является
группой Ли. Движения Л. п. 1Sn описываются псев-
псевдоортогональными операторами индекса п. Для задания
движения пространства 1Sn достаточно указать, в ка-
какие точки переходят ге+1 точек, не лежащих в одной
(и— 1)-плоскости.
Существует ряд конформных интерпретаций Л. н.,
одной из к-рых является Пуанкаре интерпретация.
Возможна также конформная интерпретация простран-
пространства на его плоскости. Кроме указанных существуют
интерпретации в комплексных пространствах. В част-
частности, для пространства 1Бз строятся Котелъникова
интерпретации многообразий прямых.
С помощью проективных интерпретаций наиболее
полным образом классифицируются квадрики в прост-
пространстве xSn и, в частности, на 2-плоскости lS.2.
Пространство lSn является римановым «-простран-
«-пространством постоянной отрицательной кривизны —На'2,
где oi — радиус кривизны пространства. Геометрия
Л. п. в достаточно малых окрестностях точек близка к
геометрии евклидова пространства такой же размерно-
размерности.
В целом пространство 1Sn гомеоморфно пространству
Rn, оно бесконечно простирается во всех направлениях.
Всякая m-плоскость пространства 1Sn, /га<и, является
пространством 1Srn. Кроме того, прямые линии про-
пространства 1Sn являются его геодезич. линиями, а
7П-ПЛОСКОСТИ — вполне геодезич. то-поверхностями этого
пространства.
В проективной классификации метрик неевклидовых
пространств Л. п. также классифицируется по метри-
метрикам прямых, пучков плоскостей и т-плоскостей. В ча-
частности, на 2-плоскости Л. п. проективная метрика на
прямой является гиперболической, а в пучках пря-
прямых — эллиптической.
Лит.: Ш Ефимов Н. В., Высшая геометрия, 6 изд.,
М., 1978; [2] Клейн Ф., Неевклидова геометрия, пер. с нем.,
М.— Л., 1936; [3] Каган В. Ф., Основания геометрии,
ч. 1—2, М.—Л., 1949—56; [41 Розен фельд Б. А., Не-
Неевклидовы пространства, М-, 1969. Л. А. Сидоров.
ЛОБАЧЕВСКОГО ФУНКЦИЯ — 1) Угол па-
параллельности в Лобачевского геометрии —
функция, выражающая
угол а между прямой кх
(или и2) (см. рис.) и от-
отрезком О А, перпендику-
перпендикулярным к прямой а, па-
параллельной их (или и2),
через длину I отрезка О А :
где R — положительная постоянная, к-рая соответ-
соответствует масштабу измерения расстояний.
Л. ф.— непрерывная монотонно убывающая функ-
функция, значения к-рой заключены между я/2 и 0:
lim П (/)=¦?, lim ПB)=0.
I -+ 0 ^ I -> оо
Л. ф. введена Н. И. Лобачевским в 1-826.
Лит.: [l] Каган В. Ф., Основания геометрии, ч. 1,
М.— Л., 1949; [2] Ефимов Н. В., Высшая геометрия,
С изд., М., 1978.
2) Специальная функция, определяе-
определяемая для действительного х равенством
L (х) =— С * In cos t dt.
Л. ф. представляется в виде ряда
Основные соотношения:
L (—х)= — L (.г), — я/2 < а-< я/2,
L (я — х) =^я In 2 — L (х),
L .;л + х)=л In 1 + L (х).
Л.ф. введена Н. И. Лобачевским в 1829.
Лит.: [1] Рыжик II. М., Градштейн И. С,
Таблицы интегралов, сумм, рядов и произведений, 3 изд., М.—
Л., 1951. А. Б. Иванов.
ЛОГАРИФМ числа N по основанию
а — показатель степени т, в к-рую следует возвести
число «(основание Л.), чтобы получить N; обоз-
обозначается logaAr, т. е. m-=\ogaN, если am = N. Каждому
положительному числу соответствует при данном ос-
основании единственный действительный Л. (Л. отрица-
отрицательных чисел являются комплексными числами).
Основные свойства Л.:
logfl (MN) = \о?а М + loga N,
позволяют сводить умножение и деление чисел к сло-
сложению и вычитанию их Л., а возведение в степень и
извлечение корня — к умножению и делению Л. на по-
показатель степени или корня.
В соответствии с десятичным характером счета наи-
наиболее употребительны десятичные Л. (а=10), обозначае-
обозначаемые lg N. Для рациональных чисел, отличных от 10*
с целым к, десятичные Л. суть трансцендентные числа,
к-рые приближенно выражают в конечных десятичных
дробях. Целую часть десятичного Л. наз. характе-
характеристикой, дробную — мантиссой. Так как
lgA0*.Y)- -A-f-lgA", то десятичные Л. чисел, отличаю-
отличающихся множителем 10fe, имеют одинаковые мантиссы
и различаются лишь характеристиками. Это свойство
лежит в основе построения таблиц Л., к-рые содержат
лишь мантиссы Л. целых чисел.
Большое значение имеют также натуральные
Л., основанием к-рых служит трансцендентное число
е~2,71828...; их обозначают In N. Переход от одного
основания Л. к другому совершается по формуле
log6JV='logaA7loga6, множитель l/loga b наз. моду-
модулем перехода (перевода) от основания а к осно-
основанию Ь. Формулы перехода от натуральных Л. к де-
десятичным или обратно:
In 10 '
^- = 2,30258..., —I—= 0,43429...
lg e In 10 '
См. также Логарифмическая функция.
По материалам одноименной статьи из БСЭ-3.
ЛОГАРИФМИЧЕСКАЯ БУМАГА — специальным
образом разграфленная бумага; обычно изготовляется
типографским способом (рис. 1): на каждой из осей
прямоугольной системы координат откладываются де-
сятичные логарифмы чисел и (на оси абсцисс) и v (на
оси ординат); затем через найденные точки (и, v) про-
проводятся прямые, параллельные осям. Наряду с Л. б.
применяется полулогарифмическая бу-
бумага (рис. 2): на одной из осей прямоугольной сис-
системы координат откладываются числа и, а на другой —-
десятичные логарифмы чисел v. Л. 6. п полулогарифмпч.
ш
"9
=
lip ji
iilnii
И 1 г 44MiU IHI HM1 h 1- -
[ l\i- 1 [{jjf I [IMiff i !
НИР
РЩ нДШпт
* кяЙ 1111 ill: н :
ш 111!
!1! Iм
' I
\\Ш
р
I
S
|ф
\
1
S
э
6 7 3 9 10
и
Рис. 1.
бумага служат для вычерчивания на них графиков
функций, к-рые могут принимать более простую и
наглядную форму и в ряде случаев выпрямляются.
На Л. б. прямыми линиями изображаются функции,
заданные уравнениями вида v—au, u>0, где а>0 и
Ъ — постоянные коэффициенты; на полулогарифмич.
бумаге прямыми линиями изображаются функции, за-
заданные уравнениями вида v=abu. БСЭ-з
ЛОГАРИФМИЧЕСКАЯ ЕМКОСТЬ — см. в ст.
Емкость.
ЛОГАРИФМИЧЕСКАЯ ПРОИЗВОДНАЯ — произ-
производная от логарифма данной функции.
ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ — плоская транс-
трансцендентная кривая, уравнение к-рой в полярных коор-
координатах имеет вид
р = аФ , в> 0.
При д>1 и ф—>-+оо Л. с.
развертывается против хода
часовой стрелки, при <р—>-— оо
спираль закручивается по
ходу часовой стрелки, стре-
стремясь к своей асимптотич.
точке О (см. рис.). Если
в<1, Л. с. закручивается
против хода часовой стрелки. Угол, составляемый ка-
касательной в произвольной точке Л. с. с радиус-векто-
радиус-вектором точки касания, зависит лишь от параметра а.
Длина дуги между точками Мг{рх, <${) и М2(р2, ц>2):
|/"i+ in2 о -j/4 + in2 а
= f2 h^ С1-—Ш7г—
Радиус кривизны: г=рУ^1-\-1п*а. Натурал
ненпе: s=--kr, где А:= 1/1п а. Л. с. переходит
(льное урав-
в себя прл
линейных преобразованиях плоскости. Л. с. относится
к т. н. псевдоспиралям (см. Спирали).
Лит.: [1] Саве лов А. А., Плоские кривые, М., 1960.
Д. Д. Соколов.
ЛОГАРИФМИЧЕСКАЯ ТОЧКА ВЕТВЛЕНИЯ, т о ч-
ка ветвления бесконечного поряд-
к а,— частный вид ветвления точки а аналптич. функ-
функции / (z) одного комплексного переменного z, когда ни
при каком числе последовательных обходов в одном и
том же направлении вокруг а аналитич. продолжение
нек-рого элемента функции /(z) не приводит к исход-
исходному элементу. Точнее, изолированная особая точка а
наз. Л. т. в. для /(z), если существуют: 1) кольцо
F= {z: 0<|z—а|<р}, в к-ром /(z) аналитически про-
продолжается по любому пути, 2) точка Zj? V и какой-либо
элемент функции /(z) в виде степенного ряда П (zx; r) =
= ^7jv=ocv (z—zj)v с центром zx и радиусом сходимости
г>0, аналитич. продолжение к-рого вдоль окружности
|z—o^Ui—а\, проходимой сколько угодно раз в од-
одном и том же направлении, никогда не приводит к
исходному элементу П (zx; r). В случае бесконечно
удаленной Л. т. в. а = оо вместо V следует рассма-
рассматривать окрестность V'= {z:|z| >р}. Л. т. в. относятся
к классу трансцендентных точек ветвления. Поведе-
Поведение римановой поверхности R функции / (z) при наличии
Л. т. в. а характеризуется тем, что над а соединяются
вместе бесконечно много листов той ветви R, к-рая
определяется в V или V элементом II (гх; г).
См. также Особая точка аналитической функции.
Лит.: [1] М а р к у ш е в и ч А. И., Теория аналитических
функций, 2 изд., т. 2, М., 1968. гл. 8. Е. Д. Соломенцев.
ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ — функция, об-
обратная к показательной функции. Л. ф. обозначается
у=1п х; A)
ее значение у, соответствующее значению аргумента х,
наз. натуральным логарифмом числа х.
В силу определения соотношение A) равносильно
х = еУ . B)
Так как е^>0 при любом действительном у, то Л. ф.
определена только при г>0. В более общем смысле
Л. ф. наз. функцию
где а>0 (аф\) — произвольное основание логарифмов;
эта функция выражается через In x по формуле:
\ogax = Mlnx,
где Л/ = 1/1па. Л. ф.— одна из
основных элементарных функции;
ее график (см. рис.) носит на-
название л о г а р и ф м и к и. Ос-
Основные свойства Л. ф. вытекают
из соответствующих свойств по-
показательной функции и лога-
логарифмов; напр., Л. ф. удовлетво-
о
7
рф; р
ряет функциональному уравнению
In ;t+ln г/=1п ху.
Л. ф. j/=ln х является строго возрастающей функцией,
причем lim In x= — оо, lim In ,r= + co. В каждой точке
л—¦- + 0 х-»- + х
г>0 Л. ф. имеет производные всех порядков и в доста-
достаточно малой ее окрестности раскладывается в степен-
степенной ряд, т. е. является аналитической функцией.
Для —1<ж<;1 справедливо разложение Л. ф. в сте-
степенной ряд:
1 /Я I \ ** ! Х3 Х* I
1пA+х)=1 о--Г—3 4~+"« •
Производная Л. ф.:
Многие интегралы выражаются через Л. ф.; напр.:
Впервые зависимость между переменными величинами,
выражаемая Л. ф., рассматривалась Дж. Непером
(J. Napier, 1614).
Л. ф. на комплексной плоскости является многознач-
многозначной (бесконечнозначной) функцией, определенной при
всех значениях аргумента z^=0, и обозначается In z.
Однозначная ветвь этой функции, определяемая как
lnz=ln|z| + i arg z,
где arg z — главное значение аргумента комплексного
числа z, —n<arg z<:n, носит название главного
значения Л. ф. Имеем
Ln z=ln z+2 /глг, &• —0, —г, —2, ± . . .
Все значения Л. ф. для отрицательных действительных
z являются комплексными числами. Первая удовлетво-
удовлетворительная теория Л. ф. в комплексной плоскости была
дана Л. Эйлером (L.Euler, 1749), к-рый исходил из
определения
Ln z = lim n (zl;n — 1).
П —*- ос
Лит.: [1] Никольский С. М., Курс математического
анализа, 2 изд., т. 1, М., 1975: [2] Маркушевич А. П.,
Теория аналитических функций, 2 изд., т. 1, М., 1967. БСЭ-з.
ЛОГАРИФМИЧЕСКИ НОРМАЛЬНОЕ РАСПРЕДЕ-
РАСПРЕДЕЛЕНИЕ — непрерывное, сосредоточенное на @, оо)
распределение вероятностей с плотностью
I log e c-Oogx-a)V2q2
= I ox V2x
р (х) = I ox V2x ' ' (*)
{ 0, 0
где —oo<a<oo, a2>0. Случайная величина X подчи-
подчиняется Л. н. р. с плотностью (*), если ее логарифм
log X имеет нормальное распределение с параметрами
а и а2. Таким образом, а=Е log X и a2=D log X. Л. н. р.
является унимодальным распределением и имеет поло-
положительную асимметрию. Моменты случайной величины
X с Л. н. р. с параметрами а и о2 выражаются формулой
поэтому математич. ожидание и дисперсия равны со-
соответственно
ЕХ = еа + °2'2 и ОХ = е2а + °г(есг -1).
Л. н. р. служит одним из простейших примеров рас-
распределения, к-рое не определяется однозначно своими
моментами. Свойства Л. и. р. определяются свойствами
соответствующего нормального распределения. Важ-
Важнейшее свойство Л. н. р.: произведение независимых
случайных величин с Л. н. р. снова подчиняется
Л. н. р. Имеет место аналог центральной предельной
теоремы: распределение произведения п независимых
положительных случайных величин при нек-рых об-
общих условиях стремится к Л. н. р. при п—>-оо. Л. н. р.
возникает как предельное распределение и в нек-рых
других схемах (напр., в моделях дробления частиц,
моделях роста и т. д.).
Лит.: [1] Колмогоров А. Н., «Докл. АН СССР»,
1941, т. 31, № 2, с. 99—101; [2] Крамер Г., Математические
методы статистики, пер. с англ., 2 изд., М., 1975; [3] A i t с h i-
son J., Brown J. A. C, The lognormal distribution
Camb., 195 7. А. В. Прохоров.
ЛОГАРИФМИЧЕСКИ СУБГ АРМОНИЧЕСКАЯ
ФУНКЦИЯ — положительная функция и (х) в области
евклидова пространства R", п^2, логарифм к-рой
\ogu(x) является субгармонической функцией. Напр.,
модуль |/(z)| аналитнч. функции комплексного пере-
переменного /(z) является Л. с.ф., но существуют непре-
непрерывные Л. с.ф. в плоских областях, к-рые нельзя
представить в виде модуля никакой аналитич. функции.
Л. с. ф. составляют подкласс сильно субгармоннч.
функций. При п=1 им соответствуют логарифмически
выпуклые функции.
Основное свойство Л. с.ф. состоит в том, что не только
произведение, но и положительная линейная комбина-
комбинация нескольких Л. с.ф. также является Л. с.ф.
Лит.: [1] Привалов И. И., Субгармонические функ-
функции, М. —Л., 1937, гл. 3. Е. Д. Сояоменцев.
ЛОГАРИФМИЧЕСКИЙ ВЫЧЕТ мероморфной функ-
функции w=--f{z) в точке а расширенной плоскости комплек-
комплексного переменного z — вычет
resa [/' (z)// (z)]
логарифмич. производной /' (z)//(z) в точке а. Пред-
Представив функцию In f(z) в окрестности V(а) точки аф<х
в виде In f(z) = A In (z—a)-f(p(z), где ф (z) — регулярная
функция в V(a), получают
resa[f (z)/f(z)] = A.
Соответствующие формулы для случая о= оо имеют
вид
res^lf (z)/f(z)] = А.
Если а — нуль кратности т функции /(z) или полюс
кратности т, то Л. в. / (z) в точке а равен соответственно
т или —т\ во всех остальных точках Л. в. равен нулю.
Если /(z) — мероморфная функция в области D и
Г — спрямляемая жорданова кривая, расположенная
в D и не проходящая ни через нули, ни через полюсы
f(z), то Л. в. функции / (z) относительно кон-
контура Г наз. интеграл
к-рый равен разности между числом нулей N функ-
функции /(z) и числом полюсов .Р внутри Г (с учетом их
кратности). Геометрич. смысл формулы A) состоит в
том, что при обходе контура Г в положительном на-
направлении вектор w=f(z) делает N—Р оборотов во-
вокруг начала координат ш=0 плоскости переменного
w (см. Аргумента принцип). В частности, если f (z) ре-
регулярна в D, т. е. Р = 0, из A) получается формула для
вычисления индекса точки ш=0 относительно образа
Г*=/(Г) пути Г при помощи Л. в.:
indor*=-^n- \T^-dz. B)
Формула B) приводит к обобщению понятия Л. в.
для регулярных функций многих комплексных пере-
переменных в области D комплексного пространства С",
п>1. Пусть ш=/(г) = (/],..., /„): D —> С" — голоморфное
отображение такое, что якобиан Jf(z)^O и множество
нулей ? = /~1@) изолировано в D. Тогда для любой
области GcG(Z.D, ограниченной простой гладкой зам-
замкнутой поверхностью Г, не проходящей через нули /,
имеем формулу для индекса точки и>=0 относительно
образа Г*=/(Г):
где интегрирование производится по n-мерному остову
Ге = {z(zG: l/v (z)| = 8, v=l, . . ., n} при достаточно ма-
лом 8 >0. Интеграл в формуле C) выражает также сумму
кратностей нулей отображения / в G (см. [2]).
Лит.: [1] М а р к у ш е в и ч А. И., Теория аналитических
функций, 2 изд., т. 1, М., 1967; [2] Ш а б а т Б. В., Введение
в комплексный анализ, 2 изд., М., 1976. Е. Д. Соломенцев.
ЛОГАРИФМИЧЕСКИЙ МЕТОД СУММИРОВАНИЯ —
один из методов суммирования числовых рядов. Ряд
^k=oak c частичными суммами «„суммируем ло-
логарифмическим методом к сумме s, если
логарифмические средние
при т—>-оо сходятся к s. Л. м. с. есть Рисса метод1
суммирования (R, р„) с р„=1/(гс+1). Он равносилен
и совместен с методом суммирования Рисса (R, К, 1)
при A,,; = ln (n-\-l) и сильнее средних арифметических
метода суммирования.
Лит.: [1] Eiesz М., «С. г. Acad. sci.», 1909, t. 149, p. 18 —
21; [2] Харди Г., Расходящиеся ряды, пер. с англ., М.,
1951. И. И. Волков.
ЛОГАРИФМИЧЕСКИЙ ПОТЕНЦИАЛ — потенциал
с логарифмическим ядром 1пг-^—Г > гДе
\х—у\ — расстояние между точками х и у евклидовой
плоскости R2, т. е. потенциал вида
j^dVi(y), A)
где интегрирование производится, вообще говоря,,
по произвольной борелевской мере и. на R2 с компакт-
компактным носителем S=S (ц). Физически можно предста-
представить, что Л. п. возникает из ньютонова потенциала
сил тяготения, когда распределение притягивающих
масс в евклидовом пространстве R3 точек у=(ул, у2,
у3) не зависит, напр., от координаты у3. Общая масса
при этом, разумеется, бесконечна, но если произвести
регуляризацию получающейся силы притяжения F,
к-рую можно считать действующей в плоскости (х1г
х2, 0), состоящую в отбрасывании бесконечного слагае-
слагаемого, то потенциал конечной части силы F будет иметь
как раз вид A) (см. [2]). В отличие от ньютонова, лога-
рифмич. ядро имеет особенность не только при \х—г/1—>-0,
но и при \х—у\—>-оо, что обусловливает нек-рые отли-
отличия в поведении Л. п. по сравнению с ньютоновым.
Они проявляются главным образом при решении внеш-
внешних краевых задач (см. Внешняя и внутренняя краевые
задачи). Основные применения Л. п. находит при ре-
решении плоских краевых задач теории потенциала (см.
также Краевая задача для эллиптического уравнения).
Основные свойства Л. п.: 1) вне носителя S меры ц
Л. п. является регулярным решением Лапласа уравне-
уравнения Ли = 0, т. е. и(х) — гармонич. функция на откры-
открытом множестве R2\5, не регулярная, однако, на бе-
бесконечности; 2) если мера \i абсолютно непрерывна,
т. е. интеграл A) принимает вид
T^rr/(j/)d(i(y), B)
где D — конечная область, da (у) — элемент площади D
и плотность f(y) принадлежит классу С1 (Z> (J c?Z)), то-
вторые производные и(х) непрерывны в D и удовлетво-
удовлетворяют Пуассона уравнению Д« — —2nf(y).
Если интеграл в B) распространен по замкнутой кри-
кривой Ляпунова L (см. Ляпунова поверхности и кривые),
т. е.
<^:-ds(y), C)
то говорят о логарифмическом потенци-
потенциале простого слоя, распределенного на L.
Если при этом /(j/)^C1(i), то Л. п. простого слоя C)
непрерывен всюду в R2. Его нормальная производная
имеет пределы изнутри и извне L соответственно:
lim
х -» у„
dn0
du
dn0
du (yj
— л/ (Уа),
где
— т. н. прямое значение нормальной производной Л. п.
простого слоя, (у—г/0, п0) — угол между вектором
У—У а п внешней нормалью п0 к L в точке yo(zL. Ин-
Интеграл D) непрерывен на L.
Логарифмический потенциал
двойного слоя имеет вид
/ , COS (У — Х, П) 7 / \ /с\
?(!/)\у-х\ ds(y)> E)
где п — внешняя нормаль к L в точке y?L. Если
g(y)^C1 (L), то Л. п. двойного слоя E) является регу-
регулярной гармонии, функцией внутри и извне L и имеет
пределы по нормали изнутри и извне L соответственно:
lim v (or) \i = v(ya
х ->- г/о
lim v (x) \e = v(ya)— я/ (у0),
->- у„
Где
(Vo) =
— прямое значение Л. п. двойного слоя в точке u^
Нормальная производная Л. п. двойного слоя непрерыв-
непрерывна при переходе через L.
Перечисленные граничные свойства Л. п. простого
и двойного слоя вполне аналогичны соответствующим
свойствам ньютонова потенциала (см. также Потен-
Потенциала теория). Из выражения E) видно, что Л. п.
двоимого слоя уже является регулярной на бесконеч-
бесконечности гармоннч. функцией.
Л. п. также непосредственно связан с граничными
задачами, теории аналитических функций, т. к. интеграл
типа Коши выражается через Л. п. простого и двойного
слоя (см. [3]).
Лит.: [1] Соболев С. Л., Уравнения математической
физики, 4 изд., М., 1966; [21 Вебстер А., С е г е Г.,
Дифференциальные уравнения в частных производных матема-
математической физики, пер. с нем., 2 изд., ч. 1—2, М.— Л., 1934;
[3] М у с х е л и ш в и л и Н. И., Сингулярные интегральные
уравнения, 3 изд., М., 1968; [4] La Vallee-Poussin
С п., Le potentiel Josarithmique; balayage et representation con-
forme, Louvain. 1949.; [5] К vans G. C, The logarithmic po-
potential, discontinuous. Dirichlet and Neumann problems, N. Y.,
1927. E. Д. Соломенцев.
ЛОГАРИФМИЧЕСКИЙ ПРИЗНАК СХОДИМОСТИ:
числовой ряд 2Ln=-ia'" a«->^' сходится, если существует
а>0 такое, что
^^ при n^znB,
и расходится, если
ы±
-j~<i при /г=эя0.
В. И. Битюцпов.
ЛОГИКО-МАТЕМАТИЧЕСКИЕ ИСЧИСЛЕНИЯ,
прикладные исчисления,— формализации
математич. теорий. Л.-м. и. задается своим языком и
перечнем постулатов (эти элементы образуют синтаксис)
и в большинстве случаев снабжается семантикой.
Существенными чертами, отличающими Л.-м. и. от
аксиоматич. теорий традиционной математики, явля-
являются: 1) выявление используемых теорий логпч. средств
путем формулирования всех аксиом и вывода правил,
позволяющих выводить одно суждение из другого;
2) переход от разговорного языка к точному формально-
формальному языку. Обычно Л.-м. и. строится на базе нек-рого
логического исчисления (базисного логиче-
логического исчисления). Язык Л.-м. и. получается
из языка этого логич. исчисления добавлением симво-
символов специальных функций и предикатов (и, быть может,
удалением предикатных переменных и переменных для
функций). Перечень постулатов Л.-м. и. получается
путем добавления к перечню постулатов базисного ло-
логич. исчисления (понимаемых применительно к новому
языку) нек-рых постулатов, описывающих свойства
добавленных функций и предикатов. Напр., язык эле-
элементарной теории груип получается по этой схеме из
языка классич. исчисления предикатов с равенством:
добавляются символы -(умножение), inv (обращение)
и е (единица), а выбрасываются все предикатные сим-
символы, кроме равенства. Дополнительный постулат
у/х у у vz {f-x = х& inv (х) -х = е& (х • у) ¦ z = х ¦ (у ¦ z))
утверждает, что е — групповая единица, inv (x) —
элемент, обратный к х, и умножение ассоциативно.
Л.-м.и., построенные на основе исчисления преди-
предикатов с равенством, служат для описания наиболее ча-
часто встречающихся математич. структур. Среди них
арифметика формальная, формализованный анализ (с
кванторами 1-го и 2-го порядков), аксиоматические
теории множеств и т. д. Семантика Л.-м. и. задает ин-
интерпретацию переменных, математич. символов (симво-
(символов предикатов и функций) и логич. операция. Этим
определяются модели Л.-м. и. Из истинности фор-
формулы на любой модели, где истинны аксиомы нек-рого
Л.-м. и., основанного на классич. исчислении предика-
предикатов с равенством, следует, в силу Гёделя теоремы о пол-
полноте, выводимость этой формулы в рассматриваемом
Л.-м. и.
Простейшими по своей структуре являются б е с-
кванторные Л.-м. и. Они употребляются чаще все-
всего для описания свойств различных классов вычисли-
вычислимых функций. Язык бескванторного Л.-м. и. строится
на основе языка исчисления высказываний с равенством
или даже состоит из одних равенств. В первом случае
логич. аппаратом Л.-м. и. служит классич. исчисление
высказываний, во втором случае Л.-м. и. оформляется
в виде исчисления равенств. Постулатами в обоих случа-
случаях считаются: 1) определяющие равенства рассматри-
рассматриваемых функций (напр., а--0=0, х •у'^=х -у+.г), 2) ос-
основные свойства равенства, 3) рассуждения методом
математич. индукции (чаще всего по образцу «из /@)==
= #@), f(x') = h(x, f(x)), g(x') = h(x, g(x)) можно вывести
f {x) = g(x)»), 4) рассуждение, соответствующее V-
удалению: «из А (х) вывести A(t)» (правило подстановки
вместо свободной предметной переменной). Пример —
система ПРА (примитивно рекурсив-
рекурсивная арифметика).
Предметные переменные ПРА (а), (аа), (ааа), . . .;
функциональные переменные (/), (//), (///), . . .; па-
тура льные числа 0, 0', 0", . . . Функциональные сим-
символы (фупкторы) строятся из исходных—'(«следующий
за»), Z (тождественный 0), [/, п, т] (т — местная функ-
функция, значение к-рой равно n-му аргументу), где п, т —
натуральные числа, n-<m, с помощью подстановки S
и примитивной рекурсии R: если ср есть и-местнын функ-
функтор, трх, . . .,!))„ суть m-местные функторы, то S ftp, 11ри
. . .,фге] (результат подстановки i|)t, . . . ,1|)„ в ф) есть
m-местный функтор; если ф есть п-меетпый функтор, \jj
есть (п-|-2)-местный функтор, то /?[ф, -ф] есть (и-f-l)-
местный функтор [примитивная рекурсия:
Я[ф, г|з](О, Х) = ф(Х); R [у, Ц](у', Х) =
= г|з(гл X, Л[Ф, !))](!/, Л"))].
Термы ПРА: 0, предметные переменные и выражения
вида s', ф(«ь . . ., s,,), где s, sb . . ., s,; — термы,
ф - функтор.
Формулы ПРА: r=s, где г, s — термы. Допустимые
.шачения предметных переменных — натуральные чис-
числи, допустимые значения функциональных перемен-
переменных — примитивно рекурсивные функции (иногда бо-
более широкие классы вычислимых функций).
При описании частичных (не всюду определенных)
функции, кроме предиката равенства, появляется пре-
предикат t, или ! («определено»); r=s интерпретируется
в этом случае как «!тч—>\s и из \г следует, что значение г
равно значению s». Добавляются также средства для
изображения функции, универсальной для рассматри-
рассматриваемого класса: либо символ для этой функции, либо
правило: если t — терм, то <?> — функтор (номер к-рого
в нек-рой заранее фиксированной нумерации рассма-
рассматриваемого класса равен t). Постулаты V-удаления и
3-введения модифицируются:
A (t) &! I —> 3jA (х); у.гА (х) &! t ^ A (t).
Добавляется аксиома \t, где t — предметная перемен-
переменная млн константа, а также аксиомы вида
Употребляются также Л.-м. и. для описания вычис-
вычислимых функционалов различных типов: 0 есть тип
(объекты типа 0 — натуральные числа); если а и т
— типы, то (а—^т) есть тип (операций, перерабатыва-
перерабатывающих объекты типа а в объекты типа т). Это — конеч-
конечные типы (см. Типов теория). Рассматриваются также
трансфинитные типы. Для каждого типа указываются
переменные и константы этого типа, в их число обычно
входит символ операции, все значения к-рой равны О,
а также объект ' типа @->0). Для каждого а в число
констант типа (а —*¦ ((() —>- (а —>¦ а)) —>- @ —»- а))) час-
часто включают оператор примитивной рекурсии. Тер-
Термами типа а наз. переменные и константы типа а,
выражения вида r(s), где г — терм типа (т—>-а), s —
терм типа т, а также выражение вида "kxr, к-рое интер-
интерпретируется как обозначение функционала, перераба-
перерабатывающего х в г (ж), где г типа Р, х типа а и а=(а—>-f5).
Бескванторные Л.-м. и. для функционалов конечных
типов используются для математич. изучения квантор-
ных Л.-м. и. В частности, с помощью бескванторной
системы примитивно рекурсивных функционалов удает-
удается доказать непротиворечивость формальной ариф-
арифметики; добавление оператора т. н. бар-рекурсии
позволяет доказать непротиворечивость формализо-
формализованного анализа.
Важное свойство Л.-м. и.— дедуктивная
полнота: она означает, что каждая формула без
свободных переменных выводима или опровержима.
Из дедуктивной полноты Л.-м. и. следует разрешимость
проблемы выводимости — существование алгоритма,
позволяющего по каждой формуле узнать, выводима она
пли нет. Примером дедуктивно полного Л.-м. и. явля-
является теория алгебраически замкнутых полей (с и с-
тема Тарского). Согласно Гёделя теореме о
неполноте дедуктивно полные теории редки: всякое
Л.-м. и., содержащее нек-рый весьма узкий фрагмент
арифметики, дедуктивно неполно. Для еще более ши-
широкого класса Л.-м. и. проблема выводимости алгорит-
алгоритмически неразрешима.
Важная характеристика Л.-м. и.— его выразитель-
выразительная способность. Часто удлотгя ввести выразительные
средства, не фигурирующие явно в языке рассматривае-
рассматриваемого Л.-м. и. Так, в бескванторных языках удаетск
ввести логич. связки и ограниченные кванторы:
х-— у & и — v означает \х — у \-\-\u — v \ =0,
VX<a(f(x) = g(x)) означает *?х< Jf П~ g {х) \ = 0.
В языке формальной арифметики можно говорить о
конечных множествах, частично рекурсивных функциях
и т. д. Одни логич. связки выражаются через другие;
так, в исчислениях 2-го порядка (в том числе основанных
на интуиционистской логике) все связки выражаются
через Vn^, напр. 3 хА (х) эквивалентно уР (\1х(Ах^-
_^_Р)_^_Р). Принципиальные ограничения выразительной,
способности языка дает теорема Тарского:
при естественной нумерации формул языка, содержа-
содержащего нек-рый минимум арифметики, невозможно ука-
указать формулу Т (х) этого языка такую, что Т (п) истин-
истинно тогда и только тогда, когда п — номер истинной
формулы. Для Л.-м. и., основанных на конструктивной
(интуиционистской) логике, часто имеет место теорема
о «расщеплении» дизъюнкций: из выводимости замкну-
замкнутой формулы А V В следует выводимость одной из фор-
формул А, В. Для исследования структуры таких Л.-м. и.
применяются различные аналоги понятия реализуе-
реализуемости. Вопросы непротиворечивости Л.-м. и., неза-
независимости отдельных постулатов, существования о т-
деленных аксиоматик (т. е. таких, что-
каждая выводимая формула А имеет вывод, использую-
использующий постулаты лишь для импликации и символов, вхо-
входящих в А), существование интерпретаций одних
Л.-м. и. в других исследуются в доказательств теории.
Лит.: [1] Гильберт Д., Б е р н а й с П., Основания
математики. Логические исчисления и формализация арифмети-
арифметики, пер. с нем., М., 1979; [2] Новиков П. С, Элементы ма-
математической логики, 2 изд., М., 1973; [3] К л и и и С. К.,
Введение в метаматематику, пер. с англ., М., 1957; [4] Ч г р ч А.,
Введение в математическую логику, пер. с англ., т. 1, М., 3 960;,
[5] Л и н до н Р., Заметки по логике, пер. с англ., М., 1968.
Г. Е. Минц.
ЛОГИСТИКА — термин, употребляемый для обо-
обозначения систем логики, характеризующихся попыткой
сведения логич. рассуждений к формальным вычисле-
вычислениям. В древности и в средние века термин «Л.» означал
практич. операции арифметмч. вычислений. Г. Лей-
Лейбниц (G. Leibniz, кон. 17 в.) употреблял термин «Л.»
для обозначения исчисления умозаключений. В нач.
20 в. под Л. понимали математическую логику.
В. Е. Плиско.
ЛОГИСТИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ — распреде-
распределение вероятностей с функцией распределения!)) (ax^-b)r
где а — параметр масштаба, b — сдвига,
Функция ij) (х) удовлетворяет дифференциальному урав-
уравнению
Л. р. близко к нормальному распределению:
sup| i|)(l,7a-) — Ф(х) | < 0,01,
х
где Ф (х) — функция нормального распределения с ма-
тематич. ожиданием 0 и дисперсией 1. При проверке
гипотезы о совпадении функций распределения двух
выборок из Л. р. с альтернативой сдвига асимптоти-
асимптотически оптимальным является Вилкоксона критерий
(Манна — Уитни критерий). Л. р. оказывается иног-
иногда более удобным, чем нормальное, при обработке дан-
данных и интерпретации выводов. В приложениях исполь-
используется также многомерное Л. р.
Лит.: [1] К е н д а л л М. Д ж., С г ь ю а р т А.,
Статистические выводы и связи, пер. с англ., М., 1973; [2}
Кокс Д. Р., Хинкли Д. В., Теоретическая статистика,
пер. с англ., М., 1978. А. И. Орлов.
ЛОГИЦИЗМ — одно из направлений в основаниях
математики, ставящее целью обосновать математику пу-
путем сведения ее исходных понятий к понятиям логики.
Мысль о сведении математики к логике высказывалась
Г. Лейбницем (G. Leibniz, кон. 17 в.). Практическое
осуществление логицистич. тезиса было предпринято
в кон. 19 — нач. 20 вв. в работах Г. Фреге и Б. Рассела
(см. [1], [2]). Взгляд на математику как на часть логики
обусловлен тем, что любую математич. теорему в ак~
сиоматич. системе можно рассматривать как нек-рое
утверждение о логич. следовании. Остается только все
встречающиеся в таких утверждениях константы опре-
определить через логич. термины. К концу 19 в. в матема-
математике различные виды чисел, включая комплексные,
были определены в терминах натуральных чисел и опе-
операций над ними. Попытка сведения натуральных чисел
к логич. понятиям была предпринята Г. Фреге. В ин-
интерпретации Г. Фреге натуральные числа были кар-
кардинальными числами нек-рых понятий. Однако систе-
система Фреге не свободна от противоречий. Это выясни-
выяснилось, когда Б. Рассел обнаружил противоречие в кан-
торовой теории множеств (антиномия Рассела), пы-
пытаясь свести ее к логике. Обнаруженное противоречие
побудило Б. Рассела к пересмотру взглядов на логику,
к-рую он сформулировал в виде разветвленной типов
теории. Однако построение математики на основе
теории типов потребовало принятия аксиом, к-рые не-
неестественно считать чисто логическими. К ним отно-
относятся, напр., аксиома бесконечности,
к-рая утверждает, что существует бесконечно много
индивидов, т. е. объектов наинизшего типа. В целом
попытка сведения математики к логике не удалась.
Как показал К. Гёдель [3], никакая формализованная
система логики не может быть адекватной базой мате-
математики.
Лит.: [1] Frege G., Grundgesetze der Arithmetik, begriffs-
echriftlich abgeleitet, Bd 1—2, Jena, 1893—1903; [2] White-
head A. N. Russell В., Principia Mathematica, Camb.,
1910; [3] Godel K., «Monatsh. Math, und Phys.», 1931, Bd 38,
S. 173—98; [4] Kappi X., Основания математической логи-
логики, пер. с англ., М., 1969; [5] Френкель А.- А., Б а р-
X и л л е л II., Основания теории множеств, нер. с англ., М.,
196Н. В. Е. Плиско.
ЛОГИЧЕСКАЯ АКСИОМА — формула логико-мате-
матич. языка, принимаемая в качестве аксиомы при
построении формальной теории, истинная в любой
структуре для данного языка в силу смысла логпч.
символов. Л., а. выбираются таким образом, чтобы мно-
множество логических следствий из аксиом в точности сов-
совпадало с множеством теорем. Так, при построении фор-
формализованной теории в нек-ром языке первого порядка
L в качестве логич. аксиом могут быть выбраны все
формулы, получающиеся подстановкой произвольных
формул языка L вместо предикатных переменных в ак-
аксиомы исчисления предикатов.
Лит.: [1] Мендельсон Э., Введение в математиче-
математическую логику, пер. о англ., М., 1971; [2] Ш е" н ф и л д Д ж.,
Математическая логика, пер. с англ., М., 1975. В. Е. Плиско.
ЛОГИЧЕСКАЯ МАТРИЦА — система
Щ1 = <М; D, &, V, =>, П>,
где М — непустое множество, Dg^M; &, v, ИЗ — дву-
двуместные, а ~] — одноместная операции на М. Любую
формулу логики высказываний, построенную из про-
пропозициональных переменных рг, . . ., рп с помощью
логич. связок &, V, Э, ~), можно рассматривать как
«-местную функцию на М, если рг, . . ., р„ считать |
переменными с областью значений М, а логич. связки
интерпретировать как соответствующие операции Л. м.
HJI. Формула 21 наз. общезначимой в 3J), если
при любых значениях переменных в множестве М зна-
значение 91 принадлежит D. Л. м. 9J) наз. х а р а к т е-
р и с т и ч е с к ой для исчисления высказываний К,
«ели в ffll общезначимы те и только те формулы, к-рые
выводимы в К. Примером Л. м. может служить система
<{0, 1}; {1}, &, V, =>v П>,
где
х& !/=min {х, у},
{x, у},
{1—х, у},
~\ х = 1 — х.
Эта Л. м. является характеристической для классич.
исчисления высказываний. Как доказал К. Гёдель
(К. Godel), нельзя построить Л. м. с конечным множе-
множеством М, характеристическую для интуиционистского
исчисления высказываний. В. Е. Плиско.
ЛОГИЧЕСКАЯ ОПЕРАЦИЯ — способ построения
сложного высказывания из данных высказываний, при
к-ром истинностное значение сложного высказывания
полностью определяется истинностными значениями
исходных высказываний. Примерами Л. о. являются
конъюнкция, дизъюнкция, импликация, отрицание.
К Л. о. относятся также кванторы: они позволяют об-
образовывать высказывания и высказывательные формы
из данных вьтсказывателъных форм. в. Е. Плиско.
ЛОГИЧЕСКАЯ ФОРМУЛА — выражение в языке
формальной логики, являющееся аналогом предложе-
предложения. Точное определение Л. ф. дается для каждого
конкретного логич. языка. Как правило, определение
формулы имеет индуктивный характер: выделяется
класс выражений, называемых элементарны-
м и, или атомарными, формулами, и ука-
указываются правила, позволяющие из уже построенных
формул строить новые формулы, используя символы
логических операций. Наир., формулы логики высказы-
высказываний определяются следующим образом. Всякая пропо-
пропозициональная переменная есть (элементарная) формула.
Если А и В — формулы, то выражения (А&В), (A VB),
(A"Z)B), (~^\A) — формулы. Формулы логики предикатов
строятся из пропозициональных, предикатных и пред-
предметных переменных с использованием логич. связок,
кванторов и вспомогательных символов (скобок и запя-
запятых). Элементарные формулы — это пропозициональ-
пропозициональные переменные и выражения вида Р (у\, . . ., уп),
где Р есть n-местная предикатная переменная, у1,
¦ ¦ -1 Уп — предметные переменные. Формулы ис-
исчисления предикатов определяются сле-
следующим образом: а) всякая элементарная формула
есть формула; б) если А и В — формулы, у — предмет-
предметная переменная, то выражения (^А), (А&В), (AvB),
(A~Z)B), (УуА), (ЗуА) суть формулы. в. Е. Плиско.
ЛОГИЧЕСКАЯ ФУНКЦИЯ — n-местная функция,
определенная на множестве истинностных значений
{И, Л} и принимающая значения в этом множестве.
С каждой логической операцией 31 связана логич. функ-
функция Д1(: если V1, . . ., Vn — нек-рые истинностные зна-
значения, то /j[(Kl7 . . ., Vn) есть истинностное значе-
значение высказывания 31 (Ри . . ., Рп), где Ри . . ., Рп— та-
такие высказывания, что истинностное значение Р,- рав-
равно V;, j=l, . . .,71.
Иногда Л. ф. наз. всякая n-местная функция, опре-
определенная на нек-ром множестве М и принимающая зна-
значения в множестве {И, Л}. Такие функции использу-
используются в математич. логике как аналог понятия пре-
предиката. В. Е. Плиско.
ЛОГИЧЕСКИЕ ИСЧИСЛЕНИЯ — формализации со-
содержательных логич. теорий; выводимые объекты Л. и.
интерпретируются как суждения, составленные из
простейших (имеющих, вообще говоря, субъектно-пре-
дикатную структуру) при помощи пропозициональных
связок и кванторов. Чаще всего используются связки
«не», «и», «или», «если..., то...» и кванторы существо-
существования и всеобщности. От произвольных исчислений
Л. и. отличаются чисто логич. характером интерпрета-
интерпретации п правил вывода, от логико-математических ис-
исчислений — отсутствием в языке символов конкрет-
конкретных математич. предикатов и функций (за исключением
символа « = », добавление к-рого интерпретируется как
введение в рассмотрение равенства и не считается обыч-
обычно нарушающим логич. характер исчисления). Сформу-
лпрованные отличия носят относительный характер,
т. к. Л. и. остаются чисто формальными системами, и
любая возможная их интерпретация и семантика должны
рассматриваться как нечто внешнее, имеющее эвристи-
эвристическую, а не доказательную ценность при изучении
свойств исчисления.
Одно т важнейших Л.и.— классическое
исчисление предикатов с функцио-
функциональными знаками. Язык этого исчисления,
помимо круглых скобок и логич. символов ~~1, &, V,
3, 3, V, содержит три потенциально бесконечных
списка: список предметных переменных, предикатных
переменных и функциональных переменных (каждая
пз предикатных и функциональных переменных снаб-
снабжена информацией о своей размерности, причем для
предикатных переменных наименьшая размерность 1,
а для функциональных — 0). Понятие терм а: 1) вся-
всякая предметная переменная и всякая функциональная
переменная размерности 0 есть терм; 2) если Тг, . . .,
5"(— термы, а / — функциональная переменная раз-
размерности I, то /G\, . . ., Т() тоже терм. Если Tlt
. . ., Tk— термы, а Р — предикатная переменная раз-
размерности к, то РGТ], . . ., Tk) наз. атомарной
ф о р м у л о й. Понятие формулы: 1) всякая ато-
атомарная формула есть формула; 2) если F и G — фор-
формулы, ах — предметная переменная, то выражения
~[F,(F&G), (FvG), (F=)G), 3xF и \fxF
суть тоже формулы. Говорят, что в последних двух
формулах все вхождения переменной х связанные;
вхождения переменных, к-рые в процессе построения
формулы не связываются кванторами, наз. свобод-
н ы м и вхождениями. Терм Т наз. свободным
для х в F, если для любого свободного вхождения х
в F неверно, что оно является вхождением в подформулу
вида JyG или Vj/G, где у — какая-либо пз перемен-
переменных, участвующих в построении Т; [F\т означает резуль-
результат подстановки Т в F вместо всех свободных вхожде-
вхождений X.
Пусть х — произвольная предметная переменная,
А, В, С и D — произвольные формулы, причем D
не содержит х свободно, Т — произвольный терм, сво-
свободный для х в А. Аксиомами рассматриваемого исчис-
исчисления являются любые формулы следующих 10 видов
(каждый пз к-рых наз. схемой а к с и о м):
1. (А=>(В=>А)),
2. ((А 3 В) 3 ((А з (В 3 С)) ZD(A-Z) С))),
3. (А ГЗ(В=>(Л&Л))),
4а. ((А &В) з А), 46. ((А&В)=>В),
5а. (A=)(AvB)), 56. (Bz)(AvB)),
6. ((А ¦=> С) з ({В id С) =э ((AVB) ¦=> С)),
7. ((А ¦=> В) ¦=> ((А ¦=> -\В)=>~\А)),
8. П~"М=>Л),
9. (чхА-=>[А]т),
10. ([Щ ¦=> & А) _
Кроме того, это исчисление имеет три правила вывода:
«из А и (A~Z)B) можно получить В», «из {DzdA) можно
получить (DzD^xA)>i, «из (A~z>D) можно получить
{1хА 3-D)». Доказуемыми формулами (или
теоремами) рассматриваемого исчисления наз.
любые формулы, к-рые могут быть получены из аксиом
исчисления в результате применения (возможно, мно-
многократного) указанных правил (см. Вывод логический).
Основная интерпретация исчис-
исчисления предикатов. Область значения пред-
предметных переменных — непустое множество предметов
М, функциональных переменных — функции из М
в М, предикатных переменных — функции из М в
{О, 1 } (одно из значений интерпретируется как «исти-
«истина», второе — как «ложь»); имеются в виду функции,
определенные на любом наборе предметов, количество
членов к-рого соответствует размерности переменной.
Теперь для любой атомарной формулы, зафиксировав
значение ее предикатной переменной и значения вхо-
входящих в нее предметных и функциональных перемен-
переменных, можно говорить об истинности или ложности
этой формулы. Аналогично, используя таблицы истин-
истинности для пропозициональных связок и обычную ин-
интерпретацию кванторов (как бесконечных конъюнк-
конъюнкций и дизъюнкций), можно судить об истинности про-
произвольной формулы рассматриваемого я.чыка при выб-
выбранном М и выбранных значениях входящих в нее пре-
предикатных, функциональных и свободных предметных
переменных. Формула наз. общезначимой, ес-
если при любом таком выборе она оказывается истинной.
Так, каковы бы ни были значения двуместной преди-
предикатной переменной Р и одноместной функциональной
переменной /, из того, что для нек-рого х формула
Р{К:с), f(y)) истинна при любом у, следует, что найдется
г, для к-poro P(z,f(z)) истинна. Следовательно, фор-
формула
CxvyP(f(x), f(y)) ¦=> 3zP (z, f(z)))
общезначима. Можно доказать, что формула выводима
в построенном исчислении тогда и только тогда, когда
она общезначима. Приведенная интерпретация опира-
опирается на достаточно сложные теоретико-множественные
абстракции и поэтому неприемлема с точки зрения
нек-рых философий математики и метаматематнч. тео-
теорий (напр., таких как интуиционизм, финитизм, кон-
конструктивная математика). В рамках этих теорий при-
приходится вырабатывать другие представления о семан-
семантике Л. и.
Многочисленные Л. и. получаются видоизменением
построенного выше Л. и. Так, добавление в язык сим-
символа « = » вместе со схемами аксиом
11. (Т = Т),
12. ((r1 = r2)=>(U]j.=[^2))
(здесь А и Т произвольны, Т1 и Г2 свободны для х в А)
приводит к классическому исчислению пре-
предикатов с равенством. Выбрасывание из
языка функциональных переменных приводит к чис-
чистому (или узкому) исчислению пре-
предикатов. Схемы аксиом 1—8 в сочетании с пер-
первым правилом вывода дают классическое ис-
исчисление высказываний (т. к. субъектно-
преднкатная структура суждений не анализируется
средствами исчислений высказываний, то обычно вместо
различных типов переменных в языке этих исчислений
употребляется лишь один тип — пропозициональные
переменные, каждая из к-рых выступает как атомарная
формула). Выбрасывание из всех упомянутых исчисле-
исчислений схемы 8 приводит к м и н и м а л ь н ы м Л. и., а
схем 7 и 8 — к позитивным Л. и. Возможны и
другие частичные Л. и., напр, получившиеся
фиксированием части логич. символов или части пере-
переменных языка (в сочетании с возможной перестройкой
системы аксиом) с сохранением всех классически вы-
выводимых формул, составленных из этих символов и
переменных; таковы импликативное пропозициональное
исчисление (единственный символ з), чистое одно-
местное (сингулярное) исчисление пре-
предикатов (в языке содержатся лишь предметные и од-
одноместные предикатные переменные) и др. Наиболее
содержательные примеры частичных Л. и. составляют
интуиционистские (конструктив-
н ы е) исчисления, которые получаются из упомяну-
упомянутых классических заменой схемы 8 на схему
8'. (Л из П л из Я)).
Названия Л. и. естественно складываются из упо-
упоминаемых терминов; так, схемы 1 — 7,8', 11,12 опре-
определяют интуиционистское исчисление
высказываний с равенством.
Рассматриваются также Л. и. с несколькими
сортами переменных (и термов), причем не
допускаются подстановки термов одного сорта вместо
другого. В простых случаях области значения термов
разных сортов интерпретируются как разные множества
предметов (так, удобные формализации планиметрии
могут опираться на Л. и. с предметными переменными
двух сортов — «точки» и «прямые»). Но можно после-
последовательно рассматривать сначала исчисление с един-
единственной областью предметов, затем исчисление с до-
дополнительной областью предметов — предикатов над
1-й областью (т. е. во втором исчислении допускаются
кванторы по предикатным переменным первого)
и т. д. Так возникают Л. и. высших порядков
(ранее упоминавшиеся Л. и. имели 1-й порядок). Стрем-
Стремление формализовать логич. теории с более мощным
запасом понятий приводит к ряду обобщений Л.и.
Рассмотрение наряду с «истиной» и «ложью» различных
степеней неопределенности приводит к различным
формализациям многозначных логик и к исчислениям
частичных предикатов. Последние Л. и.
примыкают к исчислениям логич. следования и строгой
импликации исчислению, к-рые возникли в результате
попыток формализации реального употребления выра-
выражения «из А следует 5» путем снятия парадоксов ма-
материальной импликации и отказа от табличного ее зада-
задания. Для формализации изучаемого в модальной логике
различения «необходимых», «возможных» и «случай-
«случайных» утверждений служат модальные Л. и.
Наряду с заданием Л. и. в терминах схем аксиом
часто встречаются формулировки с конечным числом
конкретных аксиом, но с добавлением различных пра-
правил подстановки вместо переменных. Для многих воп-
вопросов теории логического вывода удобны переформу-
переформулировки Л. и. в виде Генцена формальных си-
систем.
Исчисление вполне адекватно формализуемой тео-
теории, если выводимость в нем формулы эквивалентна ее
тождественной истинности в основной интерпретации.
Истинность выводимых формул связана с непротиворе-
непротиворечивостью (корректностью) исчисления, выводимость
всех истинных формул — с его полнотой. Все упомя-
упомянутые Л. п. корректны, многие из них полны в том
или ином смысле (см. Гёделя теорема о полноте).
Но, по-видимому, лишь для классич. теорий 1-го по-
порядка достигнута бесспорная адекватность формализа-
формализации нашим интуитивным представлениям об истинно-
истинности. Важным свойством Л. и. является разрешимость
(см. Разрешения проблема): почти все построенные
исчисления высказываний разрешимы; напротив, все
упомянутые исчисления предикатов (кроме одномест-
одноместного) неразрешимы. Для неразрешимых Л. и. тем не
менее возможны алгоритмы, к-рые для каждой выво-
выводимой формулы устанавливают ее выв-одимость, но
могут не кончать работу для нек-рых невыводимых
формул.
Лит.: [1] Гильберт Д., Б е р н а й с П., Основания ма-
математики. Логические исчисления и формализация арифметики,
пер. с нем., М., 1979; [2] К л и н и С. К., Введение в метама-
метаматематику, пер. с англ., М., 1957; [3] Новиков П. С, Эле-
Элементы математической логики, 2 изд., М., 1В73; L4] Ч ё р ч А.,
Введение в математическую логику, пер. с англ., т. 1, М., I960;
[5] Математическая теория логического вывода. Сб. перево-
переводов, М., 1967. С. Ю. Маслое.
ЛОГИЧЕСКИЙ ЗАКОН в математической логике —
логическая формула, к-рая является схемой истинных
предложений, т. е. превращается в истинное высказы-
высказывание при любой интерпретации входящих в нее пере-
переменных для высказываний и предикатов. Такие форму-
формулы наз. общезначимыми, или тавтологи-
тавтологиями. Напр., тавтология А V ~\А выражает исключен-
исключенного третьего закон. в. Б. Плиско.
ЛОГИЧЕСКОЕ СЛЕДСТВИЕ из данного мно-
множества посылок — высказывание, являюще-
являющееся истинным при любой интерпретации нелогич.
символов (т. е. имен объектов, функций, предикатов),
при к-рой истинны посылки. Если высказывание А
является Л. с. из множества высказываний Г, то го-
говорят, что Г логически влечет А или что А логически
следует из Г.
Если Г — множество предложений нек-рого форма-
формализованного логико-математич. языка 1-го порядка,
А — предложение того же языка, то отношение «А —
логич. следствие из Г» означает, что всякая модель для
Г является моделью для А. Это отношение обозначается
Гр^Л. Из Г'ёделя теоремы о полноте классического ис-
исчисления предикатов следует, что отношение г[=Л сов-
совпадает с отношением Г(—Л, т. е. Г|=Л тогда и только
тогда, когда предложение А выводимо из множества
предложений Г средствами классич. исчисления пре-
предикатов.
Лит.: [1] Р а с е в а Е., Сикорский Р., Математика
метаматематики, пер. с англ., М., 1972; [2] G 6 d e 1 К., «Мо-
natsh. Math, und Phys.», 1930, Bd 37, S. 349—60. В. E. Плиско.
ЛОГНОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ — см. Лога-
Логарифмически нормальное распределение.
ЛОКАЛИЗАЦИИ ПРИНЦИП: для любого тригоно-
метрич. ряда с коэффициентами, стремящимися к ну-
нулю, сходимость или расходимость ряда в нек-рой точке
зависит от поведения т. н. функции Римана
в окрестности этой точки.
При этом функция Римана F {х) данного тригоно-
метрич. ряда
¦^--f- У , ап cos пх-\-Ьп sin nx
— результат двукратного интегрирования его, т. е.
р 1у.\ ао
"" cos пх+ьп
Имеет место обобщение Л. п. для рядов с коэффициен-
коэффициентами, не стремящимися к нулю (см. [2]).
Пит.: [1] Б а р и Н. К., Тригонометрические ряды, М.,
1961; [2] Зигмунд А., Тригонометрические ряды, т. 1,
пер. с англ., М., 1965. М. И. Войцеховский.
ЛОКАЛИЗАЦИЯ в категориях — специаль-
специальная конструкция, связанная со специальными ради-
радикальными подкатегориями; она впервые появилась в
абелевых категориях для описания т. н. Гротендика
категорий с помощью категорий модулей над ассоциа-
ассоциативными кольцами с единицей. Пусть 21 — абелева
категория. Полная подкатегория ?[' категории 21 наз.
плотной, если она содержит все подобъекты и фак-
торобъекты своих объектов и замкнута относительно
расширений, т. е. в точной последовательности
-В^ОЬЭГ тогда и только тогда, когда А, С?ОЬ2Г.
Факторкатегория 21/31' строится следующим образом.
Пусть (R, и] — подобъект прямой суммы АфВ (л^Яа),
где я1; я2— проекции, и пусть квадрат
R
А
|р
коуниверсален. Подобъект (R, fi] наз. 2Г-подобъектом,
если Coker \inlt KerP?Ob2T. Два ЭГ-подобъскта эк-
эквивалентны, если они содержат нек-рый 21'-иодобъект.
Множество Н^,»х, (А, В) состоит, по определению, из
классов эквивалентных Э('-подобъектов прямой суммы
AQB. Обычное умножение бинарных отношений в
абелевой категории согласовано с введенной эквива-
эквивалентностью, что позволяет определить факторкатего-
рию ЗШГ. Эта факторкатегория оказывается абелевой
категорией. Точный функтор Т : ЭГ —*- 9Г/ЭГ' можно за-
задать, сопоставляя каждому морфизму а : А—>-В его
график в AQjB. Подкатегория W наз. подкатего-
подкатегорией локализации, если функтор Т обладает
полным сопряженным справа функтором S : ЭДУЭГ —>- 31.
Подкатегория Л. всегда является подкатегорией всех
радикальных объектов нек-рого наследственного ра-
радикала.
В категории абелевых групп подкатегория всех
периодич. групп есть подкатегория Л. Факторкате-
Факторкатегория любой категории модулой по подкатегории Л.
является категорией Гротендика. Обратно, всякая
категория Гротендика эквивалентна нек-рой фактор-
категории подходящей категории модулей.
Понятие подкатегории Л. можно определить и для
неабелевых категорий [3]. Однако в неабелевом слу-
случае таких подкатегорий обычно мало. Напр., в кате-
категории всех ассоциативных колец имеется только две
тривиальные подкатегории Л.— вся категория и ее
полная подкатегория, содержащая только нулевые
кольца.
Лит.: [1] Б у к у р И., Деляну А., Введение в теорию
Категорий и функторов, пер. с англ., М., 1972; [2] Gabri-
Gabriel P., «Bull. Soe. math. France», 1962, t. 90, p. 323—448; [3]
Шульгейфер Е. Г., «Тр. Моск. матем. об-ва», 1968, т. 19,
с. 271—301. М. Ш. Цаленко.
ЛОКАЛИЗАЦИЯ в коммутативной ал-
алгебре — переход от коммутативного кольца А к
частных кольцу A [S~x], где S — еек-рое подмножество
А. Кольцо А [5] можно определить как решение
задачи об универсальном отображении А в кольцо,
при к-ром все элементы множества S становятся обра-
обратимыми. Имеются, однако, и явные конструкции
A [S-1]:
1) как множества дробей вида a/s, где а?А, a s
является произведением элементов из S (при этом две
дроби ais и a'ls' считаются эквивалентными тогда и
только тогда, когда найдется s", являющийся произве-
произведением элементов из S и такой, что s"(sa' — s'a) = 0;
складываются и умножаются дроби по обычным пра-
правилам);
2) как факторкольцо кольца многочленов A [Xs],
s?S, по идеалу, порожденному многочленами sXs — 1,
s?S;
3) как индуктивный предел индуктивной системы
Л-модулей (А-И Ц);;), где i пробегает естественно упоря-
упорядоченный свободный коммутативный моноид ЛгE).
При этом все А ,¦ изоморфны А, а гомоморфизмы ср,у : А /—>•
—>А j при /=i-j-n1s1-f-. . -H-ra^Sf, совпадают с умноже-
умножением на s™1 •. . . ¦ s^k ? А.
Кольцо А канонически отображается в ^ [S"!] и
превращает последнее кольцо в А -алгебру. Это ото-
отображение А^А [S~1] инъективно тогда и только тогда,
когда S не содержит ни одного делителя нуля в А.
Напротив, если S содержит нильпотентный элемент,
то A [S-1] = 0.
Без потери общности множество S можно считать
замкнутым относительно произведения (такое множест-
множество наз. мультипликативным, или муль-
мультипликативной системой). В этом слу-
случае кольцо Л [S] обозначается также S~1A или
А?. Важнейшие примеры мультипликативных систем:
а) множество {sn} всех степеней элементов s?A;
б) множество Л\5р, то есть дополнение к простому
идеалу $р. Соответствующее кольцо частных является
локальным и обозначается А ^;
в) множество R всех не делителей нуля в А.
Кольцо R~yA наз. полным кольцом част-
частных кольца А. Если А целостно, R~1A=A(Q) яв-
является полем частных.
Операция локализации без труда переносится на
произвольные Л-модули М, если положить
Переход от М к М [S~x] является точным функтором.
Иначе говоря, Л-модуль A [S] является плоским.
Л. коммутирует с прямыми суммами и индуктивными
пределами.
С геометрич. точки зрения Л. означает переход к
открытому подмножеству. Точнее, для s?A спектр
Spec A [s~1] канонически отожествляется с открытым
(в Зариского топологии) подмножеством D (s)dSpec A ,
состоящим из простых идеалов 5Ц, не содержащих s.
Более того, эта операция позволяет связать с каждым
Л -модулем М квазикогерентный пучок М на аффинной
схеме Spec A, для к-рого
На Л. можно смотреть как на операцию, позволяю-
позволяющую обратить морфизмы умножения на s?S в катего-
категории Л-модулей. При таком подходе операция Л. допу-
допускает широкое обобщение на произвольные категории
(см. Локализация в категориях).
Лит-: [1] Б у р б а к и Н., Коммутативная алгебра, пер.
С франц., М., 1971. В. И. Данилов.
ЛОКАЛЬНАЯ ГРУБОСТЬ компактного инвариант-
инвариантного множества F гладкой динамич. системы — сохра-
сохранение всех топологич. свойств системы в нек-рой ок-
окрестности F при любых достаточно малых (в смысле С1)
возмущениях системы. Точнее, Л. г. состоит в следую-
следующем: имеются такие окрестности VZiVzdP и для лю-
любого е>0 найдется такое б>0, что при возмущении
исходной системы в V, отстоящем от нее в С1-метрике
не более чем на б, существует такое гомеоморфное вло-
вложение F—>-[/', к-рое сдвигает точки не более чем на е и
переводит отрезки траекторий исходной системы, ле-
лежащие в V, в нек-рые отрезки траекторий возмущенной
системы. (Таким образом, Л. г., строго говоря, ее ь
свойство не самого множества F, а системы, рассма-
рассматриваемой в окрестности F.)
Если F — положение равновесия потока (или не-
неподвижная точка каскада, т. е. динамич. системы
с дискретным временем), то Л. г. F означает сохранение
топологич. свойств системы при линеаризации в точке
F. Почти очевидно, что необходимым условием Л. г. в
этом случае является расположение собственных зна-
значений линеаризованной системы вне мнимой оси (соот-
(соответственно непопадание их на единичную окружность).
Это условие является и достаточным (теорема
Гробмана — Хартмана, см. [1] гл. IX).
Отсюда легко выводится необходимое и достаточное ус-
условие Л. г. периодической траектории потока: только
один мультипликатор уравнения в вариациях лежит
на единичной окружности. Имеются также результа-
результаты о Л. г. нек-рых гиперболических множеств (см.
[2], [3]).
Лит.: [1] X а р т м а н Ф., Обыкновенные дифференциаль-
дифференциальные уравнения, пер. с англ., М., 1970; [2] Аносов Д. В.,
в кн.: Тр. 5-й Международной конференции по нелинейным колс-
Паниям, т. 2 — Качественные методы . . . , К., 1970, е. 39—45;
[31 Robinson С, «Ann. Math.,», 1074, v. 90, № 1, p. 154—75.
ЛОКАЛЬНАЯ ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТ-
ГЕОМЕТРИЯ — часть дифференциальной геометрии, изучаю-
изучающая свойства геометрпч. образов, в частности линий и
поверхностей, «в малом». Иными словами, строение
геометрич. образа изучается в нск-роп малой окрест-
окрестности произвольной его точки.
Пусть в трехмерном евклидовом пространстве Е3 за-
задана кривая у своим уравнением
r = r(t).
Изучение этой кривой сводится к нахождению вели-
величин, инвариантных относительно группы движений
пространства Е3. Радиус-вектор г точки М кривой
не является инвариантным, но его производные
It ' 1W ' IT' ' ¦ • • w
инвариантны. Дифференциальной окре-
окрестностью п-т о порядка точки М кривой у
наз. совокупность всех понятий и свойств, связанных с
кривой, к-рые выражаются через первые п векторов
последовательности (*). Так, дифференциальной ок-
окрестности 1-го порядка принадлежат понятия касатель-
касательной к кривой и ее нормальной плоскости. Дифферен-
Дифференциальной окрестности 2-го порядка принадлежат по-
понятия кривизны, соприкасающейся плоскости, трех-
трехгранника Френе, соприкасающейся окружности кри-
кривой. Понятие кручения кривой принадлежит дифферен-
дифференциальной окрестности 3-го порядка. Кривизна и кру-
кручение кривой образуют полную систему ее инвариан-
инвариантов в том смысле, что любой инвариант кривой есть
функция кривизны и кручения и их производных любых
порядков. Аналогично строится локальная теория по-
поверхностей пространства Е3. Локальная теория кри-
кривых и поверхностен пространства Е3— это наиболее
старая часть Л. д. г., созданная в основном в 18 —19 вв.
Уже в 19 в. начали появляться различные обобщения
этой теории. Одно из таких обобщений связано с поня-
понятием однородного пространства. В произвольном диф-
дифференциально-геометрическом однородном пространст-
пространстве GlH можно строить локальную теорию кривых и по-
поверхностей различных размерностей аналогично тому,
как это указано выше для пространства Е3, а именно,
как теорию инвариантов основной группы G. В этом
направлении наибольшее развитие получили аффин-
аффинная дифференциальная геометрия и проективная диф-
дифференциальная геометрия.
Обобщение понятия первой квадратичной формы по-
поверхности пространства Е3 привело к теории римано-
вых пространств. Локальная теория римановых про-
пространств возникла еще в сер. 19 в. и продолжает раз-
развиваться, находя многочисленные приложения.
Понятие параллельного перенесения вектора вдоль
кривой на поверхности пространства привело к теории
пространств аффинной связности. В свою очередь это
явилось началом развития общей теории связностей.
Лит.: [1] Ф а в а р Ж., Курс локальной дифференциальной
геометрии, пер. с франц., М., I960. А. С. Феденко.
ЛОКАЛЬНАЯ РАЗМЕРНОСТЬ нормального
топологического пространства X —
топологический инвариант locdim X, определяемый
следующим образом. Считается locdim Х<?.п, п=—1,
О, 1, . . ., если для любой точки х?Х найдется окрест-
окрестность Ох, для Лебега размерности замыкания к-рой
выполняется соотношение dim [Ох\^.п. Если locdim
Х<:ге для нек-рого п, то Л. р. пространства X конечна,
пишется locdim X<+oo и полагается
locdim X = тт{п: locdim A'< п].
Всегда locdim .Y < dim X; существуют нормальные
пространства X с locdim X<dim .Y; в классе иараком-
пактов всегда locdim X = dim .Y. Если в определении
Л. р. лебегову размерность dim [Ох] заменить на боль-
большую индуктивную размерность Ind [Ox], то получится
определение локальной большой индук-
индуктивной размерности loclnd X.
ЛОКАЛЬНАЯ СТРУКТУРА ТРАЕКТОРИЙ квад-
квадратичного дифференциала — описание
поведения траекторий квадратичного дифференциала
на ориентированной римановой поверхности в окрест-
окрестности любой точки этой поверхности. Пусть R — ориен-
ориентированная рнманова поверхность, О (z) dz-— квадра-
квадратичный дифференциал на R; пусть С — множество всех
нулей и простых полюсов Q(z)dz2, а Л" — множество
всех полюсов О (z)dz2 порядка ^э=2. Траектории Q (z)dz°
образуют регулярное семейство кривых на R х(С|_|/7).
При нек-ром расширении понятия регулярного семей-
семейства кривых это остается верным и на R\H. Поведение
траекторий в окрестностях точек множества Н явля-
является значительно более сложным. Полное описание
Л. с. т. приводится ниже.
1) Для любой точки P?R\(C\JH) существуют
окрестность N точки Р на R и гомеоморфное отображе-
отображение N на круг |и>|<1 (w—u-\-iv) такие, что максималь-
максимальная открытая дуга каждой траектории из Лг переходит
в отрезок, на к-ром v постоянно. Следовательно, через
каждую точку из R\(C[JH) проходит траектория диф-
дифференциала Q(z)dz2, являющаяся либо открытой дугой,
либо жордановой кривой на R.
2) Для любой точки Р?С порядка и. (и,>0, если Р —
нуль, и (х=—1, если Р — простой полюс) существуют
окрестность N точки Р на R и гомеоморфное отображе-
отображение N на круг |ш|<1 такие, что .максимальная дуга
каждой траектории из N переходит в открытую дугу,
на к-рой Im ц;A1 + 2)/2 постоянна. Существуют и.+2
траекторий с концами в Р и с предельными касательны-
касательными направлениями, составляющими друг с другом рав-
равные углы величины 2лУ(ц+2).
3) Пусть Р?Н — полюс порядка jx>2. Если нек-рая
траектория имеет конец в Р, то она стремится к Р
по одному из |л—2 направлений, расположенных поя
равными углами 2лУ(и.—2). Существует окрестность JV
точки Р на R со следующими свойствами: A) каждая
траектория, проходящая через нек-рую точку окрест-
окрестности Лт, в каждом из направлений либо стремится к
Р, либо выходит из N; B) существует окрестность yV*
точки Р, содержащаяся в N и такая, что каждая тра-
траектория, проходящая через нек-рую точку из Л"*, хотя
бы в одном направлении стремится к Р, оставаясь в
N*; C) если нек-рая траектория целиком лежит в JV
и поэтому в обоих направлениях стремится к Р, то
касательная к этой траектории при приближении к Р
в соответствующем направлении стремится к одному из
двух смежных предельных положений. Жорданова кри-
кривая, полученная присоединением к этой траектории
точки Р, ограничивает область D, содержащую точки
угла, образованного двумя соседними предельными
касательными. Касательная к любой траектории, имею-
имеющей общие точки с D, стремится при приближении к Р в
двух направлениях соответственно к этим смежным
предельным положениям. Область D отображается с
помощью надлежащей ветви функции ?= \ [0(z)] ¦- dz
на полуплоскость Im ?>c (с — действительное число);
D) для каждой пары смежных предельных положений
существует траектория, обладающая свойствами, опи-
описанными в C).
4) Пусть Р<^Н — полюс 2-го порядка и z — локаль-
локальный параметр, в терминах к-рого Р представляется
точкой z=0. Пусть [О (z)]~1^2 имеет (при нек-ром выборе
ветви корня) следующее разложение в окрестности
точки z=0:
где а, Ь — действительные, Ьи Ь2, . . . — комплексные
постоянные. Строение образов траекторий дифферен-
дифференциала Q (z)dz2 в плоскости z определяется тем, какой
из следующих трех случаев имеет место.
Случай I: афО, ЬфО. Для достаточно малого а>0 об-
образ каждой траектории, пересекающей круг |z|<a,
в одном направлении стремится к z = 0, а в другом —
выходит из круга \z\ <a. И модуль, п аргумент z изме-
изменяются монотонно на образе траектории в круге
|z| <a. Каждый образ траектории закручивается около
точки z=0 и ведет себя асимптотически, как логариф-
мич. спираль.
Случай II: афОу 6=0. Для достаточно малого а>0
образ каждой траектории, пересекающей круг|г|<а,
в одном направлении стремится к z=0, а в другом —
выходит из круга \z\ <a. Модуль z изменяется монотон-
монотонно на образе траектории в круге |z|<a. Разные образы
траекторий имеют разные предельные направления в
точке z —0.
Случай III: а = 0, ЪфО. Для каждого е>0 можно най-
ти такое число а(е)>0, что при 0<а«:а(е) образ тра-
траектории, пересекающей окружность |г| —а, представ-
представляет собой жорданову кривую, лежащую в круговом
кольце a(l + e)~1<|z|<a(l-re).
Лит.: [1] Д ж е н к и н с Д ж., Однолистные функции и
конформные отображения, пер. с англ., М., 1302.
Г. В. Кузьмина.
ЛОКАЛЬНАЯ ТОПОЛОГИЧЕСКАЯ ГРУППА — то-
топологическая группа, в к-рой групповые операции опре-
определены лишь для элементов, достаточно близких к еди-
единице. Введение Л. т. г. было инспирировано изучением
локальной структуры топологич. групп (т. с. их струк-
структуры в сколь угодно малой окрестности единицы)
(см. [1]). Точное определение Л. т. г. состоит в следую-
следующем.
Пусть G — топологич. пространство, е — нек-рый
его элемент, 0 и Q — нек-рые открытые подмножества
bGhGXG соответственно, е^9 и i : 6-*-G, т : Q—>-G —
нек-рые непрерывные отображения. Тогда система
(G, е, в, Q, г, т) наз. Л. т. г., если выполнены условия:
1) (е, g) и (g, e)'?Q для любого g?G и т ((е, g)) =
= m((g, e)) = g;
2) если g, h, t?G и (g, h), (h, t), ((g, h), t),
(g, (h, t))?Q, то m((m((g, h)),t))=m((g, ?n((h, t))));
3) (g, i(g)) и (i(g), g)?Q для любого g?6
um((g,
Обычно Л. т. г. (G, e, 0, Q, г, т) обозначают просто
через G; элемент m((g, h)) обозначают через gk и наз.
произведением g ш h; элемент i (g) обозначают
через g~x и наз. обратным Kg; элемент е наз.
единицей Л. т. r. G. Если (g, h)?Q, то говорят,
что произведение g и h определено; если g?6, то го-
говорят, что для g определен обратный элемент.
Эти (определенные не для любых элементов) опера-
операции на G индуцируют структуру Л. т. г. на любой ок-
окрестности единицы е ъ G. Пусть Gx и G2— две Л. т. г.
Локальным гомоморфизмом Gj в G2
наз. такое непрерывное отображение / нек-рой окрест-
окрестности U1 единицы е1 Л. т. г. Gj в нек-рую окрестность U2
единицы е2 Л. т. г. G2, что /(е1) = е2 и для любых эле-
элементов g, h?U1, произведение к-рых в Gx определено,
произведение элементов / (g) и / (h) в С2также определе-
определено и f(gh) = f(g) f(h). Два локальных гомоморфизма G1
в G2 наз. эквивалентными, если они совпадают
в нек-рой окрестности единицы Л. т. г. G1. Пусть ло-
локальный гомоморфизм / является гомеоморфизмом
окрестностей U1 и U2, а обратное отображение
/-1: U^-^-Ux является локальным гомоморфизмом Л. т. г.
G2 в Л. т. г. Gj. Тогда / наз. локальным изо-
изоморфизмом Л. т. г. Gt и Л. т. г. G.j. Две Л. т. г..
между к-рыми существует локальный изоморфизм,
наз. локально изоморфными. Напр., любаи
Л. т. г. локально изоморфна любой своей окрестности
единицы.
Примером Л. т. г. может служить любая топологич.
группа (и, значит, любая ее окрестность единицы).
В теории Л. т. г. принципиальным является вопрос о
том, насколько общий характер имеет этот пример, т. е.
является ли всякая Л. т. г. локально изоморфной не-
некоторой топологич. группе. В общем случае ответ
отрицателен (см. [4]), но в важном частном случае ко-
конечномерных Ли локальных групп — положителен.
Как и в теории топологич. групп, в теории Л. т. г.
можно определить понятия (локальных) подгрупп, нор-
нормальных делителей, смежных классов, факторгрупп.
Напр., пусть (G, е, 0, Q, i, т) — Л. т. г., и Я — та-
такое подмножество в G содержащее е, что в нск-рой
окрестности U единицы е в G множество Uf\H замкну-
замкнуто. Пусть также для любого #?ЯП© элемент i(g) при-
принадлежит Я, а множество
открыто в НХН (в предположении, что Я снабжено то-
топологией, индуцированной с G). Тогда система
(Я, е, 6П Я, QH, i\H, m\Q[i)
является Л. т. г., к-рая наз. локальной под-
подгруппой в Л. т. г. G. Определения нормального
делителя, смежных классов по подгруппе, факторгруп-
факторгруппы см. в [1].
Лит.: [1] Ионтрягин Л. С, Непрерывные группы,
3 изд., М., 1973; [2] Б у р б а к и Н., Группы и алгебры Ли.
Алгебры Ли, свободные алгебры Ли и группы Ли, пер. с франц.,
М., 197В; [3] С е р р Ж.- 11., Алгебры Ли и группы Ли, пер.
с англ. и франц., М., 1969; [4] Lie S., Engei F., Theorie
der Transformationsgruppen, 2 AufL, Bd 1—3, Lpz., 1930.
В. Л. Попов.
ЛОКАЛЬНАЯ УНИФОРМИЗАЦИЯ — нахождение
для локального кольца бирационально эквивалентно-
эквивалентного ему регулярного локального кольца. Для неприво-
неприводимого алгебраич. многообразия V над полем к разре-
разрешающей системой наз. семейство проектив-
проективных неприводимых многообразий {Fa}, бирационально
эквивалентных V (т. е. таких, что поля рациональных
функций k(Va) и k(V) изоморфны) и удовлетворяющих
следующему условию: для любого нормирования v
поля к (V) найдется многообразие ^"^{^«} такое, что
центр Р' нормирования v на V является неособой точ-
точкой. Существование разрешающей системы (теоре-
(теорема локальной униформ и зац и и) до-
доказано для любых многообразий над полем нулевой
характеристики (см [1]), а также для двумерных мно-
многообразий над любым полем и трехмерных многообра-
многообразий над алгебраически замкнутым полем характеристи-
характеристики, отличной от 2,3 и 5 (см. [2]). Существование разре-
разрешающей системы для V, состоящей из одного многообра-
многообразия, означает разрешение особенностей V и может быть
получено из теоремы о Л. у. в размерности <:3. В об-
общем случае из теоремы о Л. у. следует существование
конечной разрешающей системы (см. [3]).
Лит.: [1J Z а г i s k i O., «Ann. Math.», 1940, v. 41, p. 852 —
96; [2] Abhyankar S., Resolution of singularities of em-
bedden algebraic surfaces, N. Y.— L., 1966; [3] Ходж В.,
Пи до Д., Методы алгебраической геометрии, пер. с англ.,
т. 3, М., 1955; [4] 3 а р и с с к и й О., С а м ю о л ь П.,
Коммутативная алгебра, пер. с англ., т. 2, М., 1963.
ЛОКАЛЬНО БИКОМПАКТНОЕ ПРОСТРАНСТВО*—
топологическое пространство, у каждой точки к-рого
имеется окрестность с бикомпактным замыканием. Ха-
усдорфово Л. б. п. X является вполне регулярным про-
странством. Частично упорядоченное множество всех
его хаусдорфовых бикомпактных расширений является
полной решеткой. Ее минимальный элемент — Алек-
Александрова бикомпактное расширение аХ. Класс хаус-
хаусдорфовых Л. б. п. совпадает с классом открытых под-
подмножеств бикомпактов. Для хаусдорфова Л. б. п. X его
нарост ЬХ^^Х во всяком хаусдорфовом бикомпактном
расширении ЪХ бикомпактен. Всякое связное параком-
пактное Л. б. п. является суммой счетного числа би-
бикомпактных подмножеств.
Важнейший пример Л. б. п.— n-мерное евклидово
пространство. Хаусдорфово топологическое векторное
пространство Е (не сводящееся к нулевому элементу)
над полным недискретным нормированным телом к
локально бикомпактно тогда и только тогда, когда к
локально бикомпактно, а Е конечномерно над к.
В. В. Федорчук.
ЛОКАЛЬНО ВЫПУКЛАЯ РЕШЕТКА, локаль-
локально выпуклая структур а,— действитель-
действительное топологическое векторное пространство Z?, являю-
являющееся одновременно векторной решеткой, топология
к-рого есть локально выпуклая топология, а отобра-
отображения пространства ЕХЕ в Е, определяемые формула-
формулами
(х, y)^sup(x, у), (ж, y)-+ini(x, у), (х, у)?Е,
непрерывны. Общие вопросы теории Л. в. р.— изу-
изучение связей между тоиологич. свойствами и свойствами
порядка, в частности топологич. свойства полос и по-
положительных конусов в Л. в. р. и связей между реше-
решеточными и топологич. свойствами полноты в Л. в. р.;
изучение свойств Л. в. р., являющейся сильным сопря-
сопряженным пространством к локально выпуклому простран-
пространству и свойств вложения Л. в. р. ? в ее второе сопря-
сопряженное пространство; построение теории продолжения
положительных функционалов и линейных отображе-
отображений Л. в. р.
Важнейший пример Л. в. р.— банахова решетка.
Лит.: [1] Канторович Л. В., А к и л о в Г. П.,
Функциональный анализ, 2 изд., М., 1977; [21 Д е й М. М.,
Нормированные линейные пространства, пер. с англ., М.,
1961; [31 Шефер X., Топологические векторные простран-
пространства, пер. с англ., М., 1971. А. И. Штерн.
ЛОКАЛЬНО ВЫПУКЛАЯ ТОПОЛОГИЯ — такая
(не обязательно отделимая) топология т на действитель-
действительном или комплексном топологическом векторном прост-
пространстве Е, обладающая базисом из выпуклых окрест-
окрестностей точек пространства Е, что линейные операции в Е
непрерывны относительно топологии т. Л. в. т. т на век-
векторном пространстве Е аналитически определяется про-
произвольным семейством преднорм {ра, ®>?А} как топо-
топология, базис окрестностей нуля к-рой состоит из мно-
множеств вида {n~1U}, где п пробегает натуральный ряд,
a U — семейство конечных пересечений множеств вида
{х?Е : ра (#)<:1}, <у.?А; такое семейство преднорм наз.
порождающим для х. Топология, индуциро-
индуцированная данной Л. в. т. на векторном подпространстве,
фактортопология на факторпространстве и топология
произведения Л. в. т. суть также Л. в. т. Топология т
на топологическом векторном пространстве Е тогда
и только тогда есть Л. в. т., когда т есть топология
равномерной сходимости на равностепенно непрерывных
подмножествах сопряженного пространства Е*.
Пусть Е и Еа.1 а(:А,— векторные пространства над R
или С, fa (соответственно ga) — линейное отображе-
отображение Е в Еа (соответственно Еа в Е) и %а —Л. в. т. на
Еа, а?А. Слабейшая из топологий на Е, для к-рон все
отображения /а являются непрерывными отображения-
отображениями пространства Е в (Еа, та), наз. и р о е к т н в н о й
топологией на Е относительно семейства {(Еа,
Та, fa), <х(:А}; проективная топология есть Л. в. т.
В частности, верхняя грань семейства Л. в. т. на дан-
данном векторном пространстве, индуцированная тополо-
топология на подпространстве и топология произведения
Л. в. т. суть проективные топологии (и потому —
Л. в. т.). Сильнейшая Л. в. т. на Е, относительно к-рой
все отображения ga, а?А, являются непрерывными
отображениями пространства (Еа, та) в пространство Е,
наз. индуктивной топологией на Е от-
относительно семейства {(Еа, та, ga), a^A]. В част-
частности, фактортопология данной Л. в. т. и топология
прямой суммы Л. в. т. являются индуктивной тополо-
топологией (и потому — Л. в. т.). Понятия проективной и
индуктивной Л. в. т. позволяют определить операций
проективного и индуктивного пределов в категории ло-
локально выпуклых пространств и их линейных отобра-
отображений.
Лит.: [1] Б у р б а к и Н., Топологические векторные про-
пространства, пер. с франц., М., 1959; [2] Шсфер X., Топологи-
Топологические векторные пространства, пер. с англ., М., 1971; [3] Кан-
Канторович Л. В.. А к и л о в Г. П., Функциональный ана-
анализ 2 изд., М., 1!<Г7. А. И. Штерн,
ЛОКАЛЬНО ВЫПУКЛОЕ ПРОСТРАНСТВО — отде-
отделимое топологическое векторное пространство над по-
полем действительных или комплексных чисел, в к-ром
любая окрестность нулевого элемента содержит выпук-
выпуклую окрестность нулевого элемента; иначе говоря, топо-
топологическое векторное пространство Е тогда и только
тогда есть Л. в. п., когда топология в Е есть отделимая
локально выпуклая топология. Примерами Л. в. п.
(и одновременно важными в теории и приложениях
классами Л. в. п.) являются нормированные простран-
пространства, счетно нормированные пространства, Фреше про-
пространства.
Ряд общих свойств Л. в. п. непосредственно следует
из соответствующих свойств локально выпуклых топо-
топологий; в частности, подпространства и отделимые фак-
торпространства Л. в. п., а также произведения се-
семейств Л. в. п. суть Л. в. п. Пусть А — направленное
вверх множество индексов, {Еа, с/.?А } — семейство
Л. в. п. (над одним и тем же полем) с топологиями
{та, <у.?А }; пусть для любой пары (а, Р), <жр, а, Р^^4,
определено непрерывное линейное отображение gap:
Efj—>-Яа и пусть Е — подпространство произведения
i7aeAZ?a, элементы к-рого х=(ха) удовлетворяют соот-
соотношениям ха~'gafj{x$) для всех а<Р; пространство Е
наз. проективным пределом семейства
{Еа.} относительно отображений {gap} и обозначается
lira gap-Eg; топология в Е есть проективная топология
относительно семейства {Еа, та, /«}, где fa — ограниче-
ограничение на подпространство Е проекции (Пае ^Ео)-+Еа-
С другой стороны, пусть для любой пары (a, P), ос«:[3,
а, P6^i определено непрерывное линейное отобра-
отображение haf$ : Еа—*-Е$ ; пусть ga, a?A,— канонич. вло-
вложение пространства Еа в прямую сумму фаеАЕа и
Я —подпространство в @agAZ?a, порожденное образа-
образами всех пространств Еа при отображениях ga—gp°/iap,
где (а, Р) пробегает все пары в АХА, для к-рых a<ji.
Если II замкнуто в ©абД?а, то Л. в. п. (Фа6А^а)/'Я
наз. индуктивным пределом семейства
Л. в. п. {Еа} относительно отображений {ha.fi} и
обозначается lira ha.pEa. Если {Еа} есть семейство
подпространств векторного пространства Е, упорядо-
упорядоченное по включению, и топология тр индуцирует та на
Еа при а<:Р, то индуктивный предел семейства {Еа}
наз. строги м. Л. в. п. метризуемо в том и только в
том случае, когда его топология порождена последова-
последовательностью полунорм; Л. в. п. нормируемо тогда и
только тогда, когда в нем существует ограниченное от-
открытое множество (теорема Колмогорова).
Всякое конечномерное подпространство в Л. в. п. имеет
дополнительное замкнутое подпространство. Попол-
Пополнение Л. в. п. есть Л. в. п., и всякое полное Л. в. п.
изоморфно проективному пределу некоторого семей-
семейства банаховых пространств. Пространство L (F, Е)
непрерывных линейных отображений топологическо-
го векторного пространства F в Л. в. п. Е естест-
естественно снабжается структурой Л. в. п. (см. также
Операторная топология) по данному семейству у ог-
ограниченных подмножеств пространства F, линейная
оболочка объединения к-рых плотна в F: базис окре-
окрестностей нуля соответствующей топологии есть семей-
семейство множеств {/ : f?L(F, E), /(j)cl'), где « пробегает
семейство у, а V пробегает базу окрестностей нуля в Е.
Центральное место и основное содержание теории
не только Л. в. п., но и топологических векторных про-
пространств составляет изучение Л. в. п. в терминах его
сопряженного пространства. Фундаментом этой теории
двойственности для Л.в.п. является Хана—Банаха тео-
теорема, из к-рой, в частности, следует, что если Е —
Л. в. п., то его сопряженное пространство Е' разделяет
точки пространства Е.
Существенной частью теории Л. в. н. является тео-
теория компактных выпуклых множеств в Л. в. п. Вы-
Выпуклая оболочка со К и выпуклая закругленная обо-
оболочка предкомпактного множества К в Л. в. п. Е пред-
компактны; если Е, кроме того, квазиполно, то зам-
замкнутая выпуклая оболочка со К множества К и его
замкнутая выпуклая закругленная оболочка компакт-
компактны. Если А, К непересекающиеся непустые выпуклые
подмножества в Л. в. п. Е, причем А замкнуто, а К
компактно, то существует такой непрерывный действи-
действительный линейный функционал / на Е, что для нек-рого
действительного а неравенства /(л-)>а, f(y)<^a вы-
выполняются для всех х?А, у?К соответственно; в ча-
частности, любое непустое замкнутое выпуклое множе-
множество А в Л. в. п. есть пересечение всех содержащих
его замкнутых полупространств. Непустое замкнутое
выпуклое подмножество В замкнутого выпуклого мно-
множества А наз. гранью множества А, если
любой замкнутый отрезок в А, внутренняя точка к-рого
содержится в В, целиком лежит в В; точка х^А наз.
крайней точкой множества А, если множество
{х} является гранью в А. Если К — компактное вы-
выпуклое множество в Л. в. п. Е и дК — множество его
крайних точек, то для множества ХсА' следующие
условия эквивалентны: 1) со Х=К; 2) ХадК;
3) sup /(X) = sup f(K) для любого непрерывного дейст-
действительного линейного функционала / на Е. В частно-
частности, со дК= К (теорема К р е и н а — М и л ь м а-
н а). Множество ЭК является бэровским пространст-
пространством в индуцированной топологии (т.е.пересечение любой
последовательности плотных в дК открытых подмно-
подмножеств дК плотно в дК), и для любого х?К существует
такая вероятностная мера и на К, что х=\ yda(y)
и мера ц обращается в нуль на всех бэровскнх подмно-
подмножествах ХсК, не пересекающихся с дК (а если К
метризуемо, то ц(дК) = 1). Всякое непрерывное отобра-
отображение компактного выпуклого множества К в Л. в. п.
в себя имеет неподвижную точку (теорема Ша-
удера — Тихонова); коммутативное семейство
непрерывных аффинных преобразовании множества К
в себя (и равностепенная непрерывная группа непре-
непрерывных аффинных преобразований К в себя) имеет
неподвижную точку.
Еще один важный раздел теории Л. в. п.— теория
линейных операторов в Л. в. п.; в частности — теория
компактных (наз. также вполне непрерывными), ядер-
ядерных и фредгольмовых операторов. Теоремы о замкну-
замкнутом графике и открытом отображении имеют в теории
Л. в. п. далеко идущие обобщения. Л. в. п. Е наз.
обладающим свойством аппрокси-
м а ц и п, если тождественное отображение простран-
пространства Е в себя может быть равномерно аппроксимиро-
аппроксимировано на предкомпактных множествах в Е конечномер-
конечномерными непрерывными линейными отображениями про-
странства Е в себя; если Л. в. п. обладает свойством
аппроксимации, то оно обладает рядом других заме-
замечательных свойств и, в частности, в таком пространстве
любой ядерный оператор имеет однозначно определен-
определенный след. Существуют сепарабсльные банаховы про-
пространства, не обладающие свойством аппроксимации,
но банаховы пространства с базисом Шаудера и под-
подпространства проективных пределов гильбертовых про-
пространств обладают свойством аппроксимации. Некото-
Некоторые варианты этого свойства представляют интерес в
теории вполне непрерывных операторов и теории опе-
операторов Фредгольма.
Заметную роль в теории Л. в. п. играют методы го-
мологич. алгебры, связанные с изучением категории
Л. в. п. и их непрерывных отображений, а также нек-
рых подкатегорий этой категории. В частности, гомо-
логич. методы позволили решить ряд задач, связанных с
продолжением линейных отображений, с существова-
существованием линейного отображения в данное пространство,
накрывающего отображение в факторпространство это-
этого пространства, а также изучить свойства пополнений
факторпространств E/F в связи с пополнением про-
пространств Е и F.
Другими существенными вопросами теории Л. в. п.
являются: теория интегрирования вектор-функций со
значениями в Л. в. п. (как правило, бочечном простран-
пространстве); теория дифференцирования нелинейных ото-
отображений Л. в. п.; теория топологических тензорных
произведений Л. в. п. и связанная с ними теория опе-
операторов Фредгольма, ядерных операторов и ядерных
пространств. Существует содержательная теория ряда
специальных классов Л. в. п. таких, как бочечные про-
пространства, борнологич. пространства (на к-рых любая
полунорма, ограниченная на ограниченных множест-
множествах, непрерывна), рефлексивные и полурефлексивные
пространства (канонич. отображение к-рых в сильное
второе сопряженное пространство является соответ-
соответственно топологическим или линейным изоморфизмом),
ядерные пространства и т. д.
Лит.: [1] Колмогоров А. Н., «Studia math.», 1934,
t. 5, p. 29—33; [2] Б у р б а к и Н., Топологические векторные
пространства, пер. с франц., М., 1959; [3] его же, Интегриро-
Интегрирование, пер. с франц., М., 1970, гл. 6—8; то же, 1977, гл. 3—5, 9;
[4] Ш е ф е р X., Топологические векторные пространства,
пер. с англ., М., 1971; [5] Д э й М. М., Нормированные ли-
линейные пространства, пер. с англ., М., 1961; [6] Д а н ф о р д Н.,
Шварц Д ж., Линейные операторы. Общая теория, пер.
с англ., М., 1962; [7] Пич А., Ядерные локально выпуклые
пространства, пер. с нем., М., 1967; [8] Робертсон А,- П.,
Робертсон В.- Д ж., Топологические векторные прост-
пространства, пер. с англ., М., 1967; [9] Ф е л п с Р., Лекции о тео-
теоремах Шоке, пер. с англ., М., 1968; [10J Э н ф л о П., «Матема-
«Математика», 1974, т. 18, № 1, с. 146—55; [11] Фр ел их ер А.,
Б у хер В,, Дифференциальное исчисление в векторных
пространствах без нормы, пер. с англ., М., 1970; [12] П а л а-
м о д о в В. П., «Успехи матем. наук», 1971, т. 26, в. 1, с. 3—65.
А. И. Штерн.
ЛОКАЛЬНО ИНТЕГРИРУЕМАЯ ФУНКЦИЯ в
точке М — функция, интегрируемая в том или
ином смысле в нек-рой окрестности точки М. Если дей-
действительная функция /, определенная на отрезке [а, Ъ],
есть точная конечная производная функции F, дей-
действительной и определенной на том же отрезке, то /
локально интегрируема по Лебегу в точках нек-рого
открытого всюду плотного на [а, Ь] множества. В дву-
двумерном случае (см. [2]) существует действительная
функция /, определенная на квадрате [0,1] X [0,1], яв-
являющаяся точной конечной повторной производной в
любом порядке -J^- = -щ^ =f(x, у), к-рая не будет
локально интегрируемой по Лебегу ни в одной точке
квадрата.
Лит.: [1] Сакс С, Теория интеграла, пер. с англ., М.,
1949; [2] Толстое Г. П., «Тр. Матем. ин-та АН СССР»,
1950, т. 35, с. 1—101. И. А. Виноградова.
ЛОКАЛЬНО КОМПАКТНОЕ ТЕЛО — множество К,
наделенное алгебранч. структурой тела и локально
компактной топологией. При этом требуется, чтобы
алгебраич. операции, т. е. сложение, умножение, пе-
переход к противоположному л обратному элементам (по-
(последний определен только на множестве ненулевых
элементов А* —А"\0), были непрерывны в заданной то-
топологии. Так как любое тело локально компактно от-
относительно дискретной топологии, предполагается, что
топология тела А" не дискретна.
Изучение Л. к. т. основано на существовании меры
Хаара в локально компактной группе К+ (аддитивной
группе тела). Пусть ц — нек-рая мера Хаара на К+ и
SdK — нек-рый компакт в К положительной меры.
Тогда формула
ч Ц ("S)
определяет гомоморфизм (модуль) мультипликативной
группы К* в мультипликативную группу R+ действи-
действительных положительных чисел. По определению по-
полагают тоAд-@)=0.
Функция «модуль» удовлетворяет неравенству
тос!д- (a -f- b) s? A sup (modA- (a), mod/f (b))
с век-рой константой А >0. Если это неравенство вы-
выполняется для А=\, то тело К наз. неархимедо-
в ы м, или у л ь т р а м е т р и ч е с к и м. В против-
противном случае А наз. архимедовым телом.
Тело К архимедово тогда и только тогда, когда оно
связно. Любое архимедово тело изоморфно либо по-
полю действительных чисел, либо полю комплексных
чисел, либо телу кватернионов.
Ультраметрнческое тело А вполне несвязно. Функ-
Функция «модуль» определяет неархимедову метрику на К.
Любое такое тело является расширением конечной сте-
степени либо поля Qp рациональных р-адических чисел
для нек-рого простого р (в случае, когда К имеет ха-
характеристику 0), либо поля FP(X) формальных сте-
степенных рядов над полем F р из р элементов (в случае,
когда А* имеет характеристику р). Поле Qp (соответ-
(соответственно поле Fp((X))) лежит в центре тела А". В каж-
каждом из этих случаев тело К наз. р-т е л о м, или р-п о-
л е м.
Ультраметрическое тело К содержит единственное
максимальное подкольцо R, определяемое условием
R = {a?K |modA'(a)<l}.
Это кольцо локально. Его максимальный идеал Р
определяется условием
P = {a?R | modA-(a) < 1},
а все элементы с модулем 1 являются обратимыми в R.
Идеал Р — главный, а поле вычетов Rip — конечное
поле характеристики р.
В случае, когда р-тело А' не коммутативно, оно имеет
размерность п- над своим центром Ко и индекс вет-
ветвления п над Ко. Далее, существует промежуточное
поле Кг такое, что К^>К{1^К0, К1 — неразветвленное
расширение Ко степени п, и все автоморфизмы Кх над
Ка индуцируются внутренними автоморфизмами тела
К.
Лит.: [1] Б у р б а к и Н., Коммутативная алгебра, пер.
г. франц., М., 1971; [2J Вейль А., Основы теории чисел,
пер. с англ., М., 1972; [3] В а н дер Варден Б. Л., Ал-
Алгебра, пер. с нем., 2 изд., М., 1979; [4] Алгебраическая теория
чисел, пер. с англ., М., 1969; [5] П о н т р я г и н Л. С, Не-
Непрерывные группы 3 изд., М., 1973, Л. В. Кузьмин.
ЛОКАЛЬНО КОНЕЧНАЯ АЛГЕБРА — алгебра, в
к-рой всякая подалгебра с конечным числом образую-
образующих имеет конечную размерность над основным полем.
Л: к. а. удобно себе представлять как объединение
возрастающей цепочки конечномерных подалгебр. Класс
Л. к. а. замкнут относительно взятия гомоморфных обра-
образов и перехода к подалгебрам. Если ограничиться рас-
смотрением ассоциативных алгебр, то расширение
Л. к. а. с помощью Л. к. а. снова будет Л. к. а. По-
Поэтому во всякой алгебре сумма локально конечных иде-
идеалов представляет собою наибольший локально ко-
конечный идеал, содержащий все локально конечные
идеалы и наз. локально конечным ради-
радикалом.
В ассоциативном случае всякая Л. к. а. является
алгебраической. Обратное неверно (см. [6]). Тем не
менее алгебраич. алгебра, удовлетворяющая полино-
полиномиальному тождеству, локально конечна. Неизвестно
A982), будет ли локально конечной алгебраич. ал-
алгебра с делением. Существует предположение, что
конечно определенная алгебраич. алгебра конечномер-
конечномерна. Радикал Джекобсона локально конечной ассоциа-
ассоциативной алгебры совпадает с верхним нильрадикалом.
Радикал Джекобсона локально конечной йордановой
алгебры также является нильидеалом. Всякая альтер-
альтернативная пли специальная йорданова алгебраич. ал-
алгебра ограниченного индекса (степени минимальных
аннулирующих полиномов всех элементов ограничены
в совокупности) над полем характеристики ф2 ло-
локально конечна. Разрешимая алгебраич. алгебра Ли
(внутренние дифференцирования всех элементов алгеб-
алгебраические) локально конечна. Алгебраич. алгебра Ли
ограниченного индекса локально конечна.
Лит.: [1] Джекобсон Н., Строение колец, пер. с
англ.. М., 1961; [2] Херстейн И., Некоммутативные коль-
кольца, пер. с англ., М., 1972; [3] Ширшов А. Й., «Матем. сб.»,
1957, т. 41, Ли 3, с. 381—94; [4] М с Crimmon К., <.Ргос.
Nat. Acad. Sci. USA», 1969, v. 62, J\!s 3, p. 671 — 78; [5] Л ю III a o-
сюэ, «Матем. сб.», 1956, т. 39, № 3, с. 385 — 96: [в] Голод Е. С,
«Изв. АН СССР. Сер. матем.», 1964, т. 28, A'j 2, с, 273 — 76.
В. Н. Латышев.
ЛОКАЛЬНО КОНЕЧНАЯ ГРУППА — группа, в
к-рой каждая конечно порожденная подгруппа конеч-
конечна. Любая Л. к. г.— периодич. группа, но не наоборот
(см. Бёрнсайда проблема). Расширение Л. к. г. с по-
помощью Л. к. г. будет снова Л. к. г. Всякая Л. к. г.
с условием минимальности для подгрупп (и даже для
абелевых подгрупп) обладает абелевой подгруппой ко-
конечного индекса [3] (см. Группа с условием конечности).
Л. к. г., все абелевы подгруппы к-рой имеют конечные
ранги, сама имеет конечный ранг п содержит локально
разрешимую подгруппу конечного индекса.
Лит.: [1] К у р о ш А. Г., Теория групп, 3 изд., М., 1967;
[2] Черников С. Н., «Успехи матем. наук», 1959, т. 14,
в. 5, с. 45—96; [3] Ш у н к о в В. П., «Алгебра и логика», 1970,
т. 9, № 5, с. 579—615- [4] его же, там же, 1971, т. 10, № 2,
с. 199 — 225. А. Л. Шмелъкин.
ЛОКАЛЬНО КОНЕЧНАЯ ПОЛУГРУППА — полу-
полугруппа, в к-рой каждая конечно порожденная подпо-
подполугруппа конечна. Всякая Л. к. п. будет периодиче-
периодической полугруппой. Обратное неверно: существуют даже
периодич. группы, не являющиеся локально конечными
(см. Бёрнсайда проблема). Задолго до решения пробле-
проблемы Бёрнсайда для групп были построены примеры пе-
периодических, но не локально конечных полугрупп в
классах полугрупп, далеких от групп, прежде всего —
в классе нилъполугрупп; таковы, напр., свободная
полугруппа с двумя образующими в многообразии, за-
заданном тождеством г3 = 0, и свободная полугруппа с
тремя образующими в многообразии, заданном тожде-
тождеством х2 = 0. Вместе с тем для ряда классов полугрупп
условия периодичности и локальной конечности равно-
равносильны. Тривиальный пример доставляют коммутатив-
коммутативные полугруппы. Связка Л. к. п. (см. Связка полугрупп)
сама будет Л. к. п. [1], более того, полугруппа, обла-
обладающая разбиением на локально конечные группы, бу-
будет Л. к. п., в частности всякая идемпотентов полу-
полугруппа будет Л. к. п. [7]. Если п таково, что всякая
группа с тождеством хп = 1 локально конечна, то вся-
всякая полугруппа с тождеством х" + х=х локально конеч-
конечна [6]. Полугруппа, обладающая разбиением на Л. к. и.,
может не быть Л. к. п. [3], но если р — такая конгру-
энция на полугруппе S, что факторполугруппа 5/р есть
Л. к. п. и каждый р-класс, являющийся подполугруп-
подполугруппой, есть Л. к. п., то и 5 будет Л. к. п. (см. [4], [5]);
в частности, идеальное расширение Л. к. п. при по-
помощи Л. к. п. само будет Л. к. п. Если S — периодич.
полугруппа матриц над телом и все подгруппы из S
локально конечны, то S локально конечна [8], откуда
вытекает, что всякая периодич. полугруппа матриц
над произвольным полем будет Л. к. п.
Лит.: [1] Ш е в р и н Л. Н., «Докл. АН СССР», 1965, т. 162,
Не -4, с. 770—73; Ш Шнеперман Л. К., «Изв. АН БССР.
Сер. физ.-матем. наук», 197В, № 4, с. 22—28; [3] Б р а у н Т. К.,
«Укр. матем. ж.», 1968, т. 20, № 6, с. 732—38; [4]
Brown Т. С, «Pacif. J. Math.», 1967, v. 22, .Vs 1, p. 11—14;
[5] его же, там же, 1971, v. 36, № 2, p. 285—89; [6] Gre-
Green J. A., Rees D., «Proc. Cambridge Phil. Soc», 1952,
v. 48, pt 1, p. 35—40; [7J McLean D., «Amer. Math. Month-
Monthly», 1954, v. 61, K» 2, p. 110 — 13; [8] M с N a u g h t о n R.,
Z a 1 с s t e i n Y., «J. Algebra», 1975, v. 34, N- 2, p. 292—99.
Л. Н. Шеврин.
ЛОКАЛЬНО КОНЕЧНОЕ ПОКРЫТИЕ — покрытие
топологич. пространства его подмножествами такое,
что у каждой точки есть окрестность, пересекающаяся
лишь с конечным числом элементов этого покрытия.
Не из всякого открытого покрытия прямой можно вы-
выделить Л. к. п.; достаточно рассмотреть монотонную
последовательность интервалов неограниченно расту-
растущих по длине. Оказывается, возможность выделить из
любого открытого покрытия пространства Л. к. н.
равносильна его бикомпактное™. Существенно новое
содержание несет идея локальной конечности в соеди-
соединении с понятием вписанности. Теорема Стоу-
н а утверждает, что в любое открытое покрытие про-
произвольного метрич. пространства можно вписать Л. к. п.
Хаусдорфовы пространства, обладающие последним
свойством, наз. п а р а к о м п а к т а м н. Л. к. п.
важны не только своим участием в определении пара-
паракомпактности. Требование локальной конечности иг-
играет существенную роль в конструкциях, принадлежа-
принадлежащих теории размерности, в формулировках и доказа-
доказательствах разного рода аддиционных теорем. Существо-
Существование в регулярном пространстве базы, распадающейся
в объединение счетного семейства локально конечных
открытых покрытий, равносильно метризуемости этого
пространства. Открытые Л. к. п. нормальных прост-
пространств служат построению разбиения единицы на этом
пространстве, подчиненного этому покрытию. С по-
помощью разбиений единицы строятся, в частности, стан-
стандартные отображения многообразий в евклидовы про-
пространства. Требование локальной конечности покры-
покрытия не обязательно соединять с предположением о его
открытости. Локальная конечность покрытия простран-
пространства автоматически влечет, что в этом покрытии «доста-
«достаточно много» множеств, близких по свойствам к откры-
открытым. Если в любое открытое покрытие регулярного про-
страдства можно вписать какое-нибудь Л. к. п., то
пространство паракомпактно. Рассматриваются также
локально конечные семейства множеств в пространстве,
определяемые аналогично, но не обязанные покрывать
пространство. Специальный их случай представляют
дискретные семейства множеств — такие
семейства множеств, что у каждой точки всего простран-
пространства есть окрестность, пересекающая не более одного
элемента этого семейства. Дискретные семейства важны
в связи с изучением отделимости в пространстве. Так,
выделяются коллективно нормальные пространства
требованием: любое дискретное семейство множеств
отделяется дискретным семейством окрестностей. С
последним условием прямо связана задача комбина-
комбинаторного продолжения локально конечных семейств
множеств до локально конечных семейств открытых
множеств.
Лит.: [1] Enge iking R., General Topology, Warsz.,
1977; [2] Архангельский А. В., Пономарев В. И.,
Основы общей топологии в задачах и упражнениях, М., 1974;
[3] Александров П. С, «С. г. Acad. sci.», 1924, t, 178.
p. 185—87; [4] Stone A. H., «Bull. Amer. Math. Soc», 1948,
v. 54, p. 977—82; [5] Mihaei E., «Proc. Amer. Math. Soc»,
1953, v. 4, № 5, p. 831 — 38. А. В. Архангельский.
ЛОКАЛЬНО КОНЕЧНОЕ СЕМЕЙСТВО м но
ж е с т в в топологическом простран-
пространстве — семейство F множеств такое, что у каждой
точки пространства есть окрестность, пересекающаяся
лишь с конечным множеством элементов семейства F.
Важны локально конечные семейства открытых мно-
множеств и локально конечные открытые покрытия. Так,
регулярное пространство метризуемо в том и только
в том случае, если оно обладает базой, распадающейся
на счетное множество Л. к. с. В любое открытое покры-
покрытие метрич. пространства можно вписать локально ко-
конечное открытое покрытие. Пространства, обладающие
этим свойством, наз. паракомнактными про-
пространствами. А. В. Архангельский.
ЛОКАЛЬНО ЛИНЕЙНО СВЯЗНОЕ ПРОСТРАН-
ПРОСТРАНСТВО — топологическое пространство X, в к-ром для
любой точки х?Х и любой ее окрестности Ох суще-
существует меньшая окрестность Uxd0x такая, что для
любых двух точек ХоЛё ^х существует непрерывное
отображение / : /—>-Ох единичного отрезка / — [0, 1]
в окрестность Ох с /@) — х0 и/A) — х\. Всякое Л. л. с. п.
локально связно. Всякое открытое подмножество
Л. л. с. п. локально линейно связно. Связное Л. л. с. п.
является линейно связным пространством.
Л. л. с. п. играют важную роль в теории накрытий.
Пусть р : (X, хо)-+(Х, ха) — накрытие, а У — Л. л. с. п.
Тогда необходимым и достаточным условием того, чтобы
отображение / : (У, уо)—*(Х, х0) допускало поднятие,
т. е. существовало такое отображение g : (У, у0) ->-
-*¦ (X, х0), что /=pog, является выполнение соотно-
соотношения
/# (Я! (У,Уо)) <= Р (Щ (X, Х0)),
где ях— фундаментальная группа. Если X — локально
односвязное (локально 1-связное, см. ниже) простран-
пространство и хо?Х, то для любой подгруппы Н группы
л.1{Х, х0) существует накрытие р : (X, хо)—>-(Х, ,т0), для
к-рого р# (nx(X, *„)) = #.
Многомерным обобщением локальной линейной связ-
связности является локальная А;-связность
(локальная связность в размерности к). Пространство
X наз. локально /с-связным, если для любой точки
х^Х и любой ее окрестности Ох существует такая
меньшая окрестность UxczOX! что любое отображение
r-мерной сферы Sr в Uх, где г^.к, гомотопно в ()х по-
постоянному отображению. Метрич. пространстве X ло-
локально fc-связно тогда и только тогда, когда всякое ото-
отображение / : А—*-Х с произвольного замкнутого под-
подмножества А метрич. пространства У с dim У<:й+1
можно продолжить на нек-рую окрестность А в Y
(теорема Куратовского — Дугунд-
Ж и). С. А. Богатый.
ЛОКАЛЬНО НИЛЬПОТЕНТНАЯ АЛГЕБРА — ал-
алгебра, всякая конечно порожденная подалгебра к-рой
нильпотентна. Л. н. а. удобно себе представлять как
объединение возрастающей цепочки нильпотентных
подалгебр. Л. н. а. с ассоциативными степенями явля-
является нильалгеброй. Л. н. а. Ли является энгелевой.
Класс Л. н. а. замкнут относительно взятия гомоморф-
гомоморфных образов и перехода к подалгебрам.
В случае ассоциативных алгебр расширение Л. н. а.
с помощью локально нильпотентной снова будет Л. н. а.
Поэтому сумма всех локально нильпотентных идеалов
ассоциативной алгебры представляет собою наибольший
локально нилыютентный идеал, содержащий все ло-
локально нильпотентные идеалы и наз. радикалом
Левицкого. Аналог радикала Левицкого можно
определить в энгелевой алгебре Ли ограниченного ин-
индекса. Локально нильпотентная алгебра не может быть
простой.
Лит.: [1] Дшекобсон Н., Строение колец, пер. с
англ., М., 1961; [2] Херстейн И., Некоммутативные коль-
кольца, пер. с англ., М., 1972; [,3] Кострикин А. И., «Изв.
АН СССР. Сер. матем.», 1957, т. 21, Л» 4, с. 515 — 40.
В. Н. Латышев.
ЛОКАЛЬНО НИЛЬПОТЕНТНАЯ ГРУППА — груп-
группа, каждая конечно порожденная подгруппа к-рой
нильпотентна (см. Нильпотентная группа). В Л. н. г.
все элементы конечного порядка образуют нормальную
подгруппу, являющуюся периодич. частью этой груп-
группы. Эта подгруппа разлагается в прямое произведение
силовскнх подгрупп, а факторгруппа по ней не имеет
кручения. Л. н. г. без кручения обладает свойством
Однозначности извлечения корня: если для элементов
а и Ъ при каком-либо целом пфО будет ап = Ьп, то а = Ь.
Каждая Л. н. г. G без кручения обладает мальцев-
ским пополнением, т. е. вкладывается в
однозначно определенную Л. н. г. без кручения G*
такую, что в ней разрешимы все уравнения вида ?" = g,
где пфО, a g — любой элемент из G. Ото пополнение
функториалыю, т. е. любой гомоморфизм / : G1-^-G2
Л. н. г. без кручения Gx в G2 однозначно продолжается
до гомоморфизма /* : Gi—П?2.
Лит.: [1] К у р о ш А. Г., Теория групп, 3 изд., М., 1967;
[21 Каргаполов М. И., Мерзляков Ю. И., Ос-
Основы теории групп, 2 изд., М., 1977. А. Л. Шмелъкин.
ЛОКАЛЬНО НОРМАЛЬНАЯ ГРУППА — группа
G, всякое конечное подмножество к-рой содержится в
некотором конечном нормальном делителе группы G.
ЛОКАЛЬНО ПЛОСКОЕ ВЛОЖЕНИЕ — вложение
ц одного топологич. многообразия М" в другое Nn,
для к-рого для каждой точки х?М имеются карты в
окрестности U точки жив окрестности V точки qx в
JV, в к-рых ограничение q на U линейно отображает
U в V. Иными словами, q локально линейно в надлежа-
надлежащих системах координат. Эквивалентно: имеются ок-
окрестность U точки х?М и окрестность V точки qx^N
такие, что пару (V, qU) можно гомеоморфно отобразить
на стандартную пару (D", Dm) или (D", D™), где Dk —
единичный шар пространства R* с центром в начале,
a D* — пересечение этого шара с полупространством
Любое вложение окружности и дуги в плоскость яв-
является Л. п. в., однако окружность или дуга могут
быть вложены в Rk при fc^3 не локально плоско
(см. Дикое вложение, Дикая сфера). Любое гладкое
вложение локально плоско в гладком смысле (т. е.
в определении координаты можно выбрать гладкими).
Кусочно линейное вложение может не быть локально
плоским не только в кусочно линейном, но и в топо-
топологич. смысле, напр, конус с вершиной в R+ над зам-
замкнутой ломаной, заузленной в граничной плоскости R:i.
Для пф4 н тфп—2 имеется гомотопич. критерий того,
чтобы вложение было локально плоским: для каждой
точки х?М и окрестности U точки qx имеется окрест-
окрестность VczU такая, что любая петля в V\qM гомотоп-
гомотопна нулю в UlqM (локальная односвязность). Если
т—п—2, то критерий имеется и при пф^, но сущест-
существенно сложнее. При т = 4 вопрос остается невыяснен-
невыясненным. При т = п—1 и т=п—2 Л. п. в. имеет топологи-
топологическое нормальное расслоение. а. в. ЧерпавскиИ.
ЛОКАЛЬНО РАЗРЕШИМАЯ АЛГЕБРА — алгебра,
для к-рой всякая ее конечно порожденная подалгебра
разрешима. Л. р. а. удобно представлять себе как
объединение возрастающей цепочки разрешимых под-
подалгебр. Класс Л. р. а. замкнут относительно перехода
к подалгебрам и взятия гомоморфных образов.
Лит.: [1] Джекобсон Н., Алгебры Ли, пер. с англ.,
М., 1964. В. Н. Латышев.
ЛОКАЛЬНО РАЗРЕШИМАЯ ГРУППА — группа,
в к-рой каждая конечно порожденная подгруппа разре-
разрешима (см. Разрешимая группа). Класс Л. р. г. замкнут
относительно взятия подгрупп и гомоморфных обрааов,
но не замкнут относительно расширений.
Периодическая Л. р. г. локально конечна.
Лит.: [1] Курош А. Г., Теория групп, 3 изд., М.,
1967. А. Л. Шмелъкип.
ЛОКАЛЬНО СВОБОДНАЯ ГРУППА — группа, каж-
каждая конечно порожденная подгруппа к-рой свободна
(см. Свободная группа). Таким образом, счетная Л. с. г.
является объединением возрастающей цепи свободных
подгрупп.
Говорят, что Л. с. г. имеет конечный ранг п, если
всякое ее конечное подмножество содержится в под-
подходящей свободной подгруппе ранга п, причем п —
наименьшее число с этим свойством. Класс Л. с. г.
замкнут относительно свободного произведения, при-
причем ранг свободного произведения Л. с. г. конечного
ранга равен сумме рангов сомножителей.
Лит.: [1] Курош А. Г., Теория групп, 3 изд., М.,
1967. ' А. Л. Шмелъкин.
ЛОКАЛЬНО СВОБОДНЫЙ ПУЧОК — пучок моду-
модулей, локально изоморфный прямой сумме нескольких
экземпляров структурного пучка. Точнее, пусть
(X, (Од.) — окольцованное пространство. Пучок моду-
модулей JF над Qx наз. локально свободным,
если для каждой точки х?Х существует такая откры-
открытая окрестность РсХ, х? U, что ограничение $~|?/
пучка f на Р является свободным пучком модулей
над QxiUi T- е- изоморфно прямой сумме нек-рого мно-
множества / (х) экземпляров структурного пучка Qx\u-
Если X связно и множество I (х) конечно, напр, состо-
состоит из п элементов, то пне зависит от точки х и наз. ран-
рангом Л. с. п. JF. Пусть V — векторное расслоение ранга
в на X и JF — пучок ростков его сечений, тогда ff" —
Л. с. п. ранга п. Обратно, для каждого Л. с. п. §~
ранга п существует векторное расслоение V ранга п
на X такое, что JF является пучком ростков его сечений
(см. [1], [2]); тем самым существует естественное вза-
взаимно однозначное соответствие между классами изо-
изоморфных Л. с. п. ранга п и классами изоморфных век-
векторных расслоений ранга п на X.
Пример: пусть X — гладкое связное алгебраич.
многообразие размерности п, тогда пучок регулярных
дифференциальных форм Qx является Л. с. п. ранга п.
Пусть X — Spec А — связная аффинная схема —
спектр коммутативного кольца А, §f~ — Л. с. п. ранга
п, М—Г (X, <f") —Л-модуль его глобальных сечений.
Тогда Л-модуль М проективен и отображение §~\^>
Н>Г(Х, <f") устанавливает взаимно однозначное соот-
соответствие между множеством классов (с точностью до
изоморфизма) Л. с. п. ранга п и множеством классов
(с точностью до изоморфизма) проективных Л-модулей
ранга п (см. [2]).
Лит.: [1] Г о д е м а н Р., Алгебраическая топология и тео-
теория пучков, пер. с франц., М., 1961; [21 Harts liorne R.,
Algebraic geometry, N. Y.— Hdlb.— В., 1977. В. А. Псковских.
ЛОКАЛЬНО СВЯЗНОЕ ПРОСТРАНСТВО — тополо-
топологическое пространство X, в к-ром для любой точки х и
любой ее окрестности Ох имеется меньшая связная
окрестность Uх. Всякое открытое подмножество Л. с. п.
локально связно. Всякая компонента связности Л. с. п.
открыто-замкнута. Пространство X локально связно
тогда и только тогда, когда для всякого семейства
{А} подмножеств X имеет место включение
Fr(\JtAt)<zl)tFT(At)
(здесь Кг В — граница В, а В — замыкание В). Всякое
локально линейно связное пространство локально связно.
Частичное обращение этого утверждения: всякое пол-
полное метрич. Л. с. п. является локально линейно связ-
ным (теорема Мазуркевпча— Мура-
Мен г е р а). С. А. Богатый.
ЛОКАЛЬНО СВЯЗНЫЙ КОНТИНУУМ — контину-
континуум, являющийся локально связным пространством.
Примеры Л. с. к.: n-мерный куб, п — 0, 1,2,...;
гильбертов кирпич; все тихоновские кубы. Объединение
графика функции
l/ = sin— , 0 < ж< 1,
с отрезком /={@, у) : —1<:г/<1} дает пример не ло-
локально связного (в точках отрезка /) континуума.
Метризуемый континуум локально связан тогда и
только тогда, когда он является непрерывным образом
отрезка, т. е. линией в смысле Жордана. Любой ме-
тризуемый Л. с. к. линейно связан. Более того, лю-
любые две различные точки такого континуума К со-
содержатся в простой дуге, лежащей в К.
Б. Л. Пасынков.
ЛОКАЛЬНО ТРИВИАЛЬНОЕ РАССЛОЕНИЕ — рас-
расслоение я : Х-+В со слоем F, для любой точки базы
к-рого Ъ^В существует окрестность V^b и гомеомор-
гомеоморфизм Цц : UX F—t-n'1 (U) такой, что лср^т («,/) = и, где
u?U, j?F. Отображение hy=(fu~1 наз. картой
Л. т. р. Совокупность карт \кц}, ассоциированная с
покрытием базы {?/}, образует атлас Л. т. р. Напр.,
главное расслоение, пространство к-рого локально ком-
компактно, a G — группа Ли, является Л. т. р., причем
любая карта hy удовлетворяет соотношению
hu(gx) = ghu(x), x?n-*{U),
где G действует на GX U по формуле g(g', u)--(gg', и).
Для любого Л. т. р. я : Х—>-В и непрерывного отобра-
отображения / .' В'—*В индуцированное расслоение является
Л. т. р.
Лит.: [1] С п е н ь е р Э., Алгебраическая топология, пер.
с англ., М., 1971; [2] С т и н р о д Н., Топология косых про-
произведений, пер. с англ., М., 1953; [3] X у С. ы - ц з я н, Теория
гомотопий, пер. с англ., М., 1964; [4] Хьюзмоллер Д.,
Расслоенные пространства, пер. с англ., М., 1970.
М. И. Войцеховский.
ЛОКАЛЬНОЕ ЗАЦЕПЛЕНИЕ — свойство располо-
расположения замкнутого множества Ф вблизи его точки а в
евклидовом пространстве R", заключающееся в су-
существовании такого числа е>0, что при любом поло-
положительном числе б в открытом множестве О (а, б)\Ф
лежит ^-мерный цикл Z?, <?<«, с целыми коэффициен-
коэффициентами, обладающий свойством: всякий лежащий в
О (а, е) компакт Р, в к-ром цикл Z1 гомологичен нулю,
имеет непустое пересечение с множеством Ф. При этом
О(а, б), О (а, г) суть шары с центром а и радиусами б,
е. Не меняя содержания этого определения, можно огра-
ограничиться компактами Р, являющимися полиэдрами.
При qr=0 понятие Л. з. переходит в понятие локального
разбиения. Теорема Александрова о пре-
препятствиях: для того чтобы сИтФ = р, необходимо
п достаточно, чтобы число п—р — 1 было наименьшим
целым числом q, для к-рого в R" имеется ^-мерное за-
зацепление множества Ф вблизи какой-либо точки а?Ф.
Доказана и аналогичная теорема о препятствиях «по
модулю ,т», характеризующая множества Ф, имеющие
равную р гомологическую размерность «по модулю то».
Далеко идущими обобщениями теорем о препят-
препятствиях являются теоремы о гомологическом опоясыва-
опоясывании компактов.
Лит.: [1] Александров П. С, Введение в гомоло-
гомологическую теорию размерности и общую комбинаторную тополо-
топологию, М., 1975; [2] Ситников К., «Докл. АН СССР», 1951,
т. 81, jNi 2, с. 153 — 56. А. А. Мальцев.
ЛОКАЛЬНОЕ КОЛЬЦО — коммутативное кольцо с
единицей, имеющее единственный максимальный идеал.
Если А — Л. к. с максимальным идеалом тп, то фак-
торкольцо А/т является полем и наз. полем вы-
вычетов Л. к. Л.
Примеры Л. к. Любое поле или кольцо норми-
нормирования является локальным. Локально и кольцо
формальных степенных рядов к [\Х1, . . ., Хп]] над
полем к или над любым Л. к. Напротив, кольцо много-
многочленов к [Xlt . . ., Хп] при п>1 не локально. Пусть
X — топологич. пространство (или дифференцируемое
многообразие, или аналитич. пространство, или ал-
гебранч. многообразие), а х — точка X. Пусть Л —
кольцо ростков в точке х непрерывных функций (соот-
(соответственно дифференцируемых, аналитических или ре-
регулярных функций); тогда А — Л. к., максимальный
идеал к-раго состоит из ростков функций, обращающих-
обращающихся в 0 в точке х.
К Л. к. приводят нек-рые общие теоретико-кольце-
теоретико-кольцевые конструкции, важнейшей из к-рых является лока-
локализация. Пусть А — коммутативное кольцо, ар —
простой идеал А. Кольцо Л„ , к-рое состоит из дробей
вида — , где а?А, s?A—р, является локальным и наз.
локализацией кольца А в р. Максималь-
Максимальным идеалом кольца Ар является идеал рЛ^, , а поле
вычетов Л„ отождествляется с полем частных целост-
целостного факторкольца Л|р. Другие конструкции, приводя-
приводящие к Л. к.,— гензелизация или пополнение кольца
относительно нек-рого максимального идеала. Любое
факторкольцо Л. к. также локально.
Свойство кольца А (или Л-модуля М, или Л-алгебры
В) наз. локальным свойством, если вы-
выполнение его для А (или М, или В) эквивалентно вы-
выполнению его для колец Л„ (соответственно модулей
М(?)аАн > или алгебр -В®л^в) для всех простых иде-
идеалов р кольца А (см. Локальное свойство).
Степени т" максимального идеала U1 Л. к. Л опре-
определяют базис окрестностей нуля так наз. тополо-
топологии локального кольца (или т-а д и-
ческой топологии). Для нётерова Л. к. эта
топология отделима (теорема Крулля), а лю-
любой его идеал является замкнутым.
Далее рассматриваются только нётеровы локальные
кольца. Л. к. наз. полным локальным к о л ь-
ц о м, если оно полно относительно m-адической то-
топологии; в этом случае A=lim А/т". В полном Л. к.
п
m-адическая топология слабее любой другой отделимой
топологии (теорема Шевалле). Любое пол-
полное Л. к. представляется как факторкольцо кольца
S [\Х1, . . ., Хп]\ формальных степенных рядов, где
S — поле (в равнохарактеристическом случае) или
полное кольцо дискретного нормирования (в случае
разпых характеристик). Эта теорема позволяет дока-
доказать, что полные Л. к. обладают рядом специфич.
свойств, отсутствующих у произвольных нётеровых
Л. к. (см. [5]), напр, полное Л. к. является превосход-
превосходным кольцом.
Более тонкое, количественное исследование Л. к.
А связано с применением понятия присоединен-
присоединенного градуированного кольца Gr(yl)--
=@n>o (nWirt" + 1). Пусть НА (п) — размерность вектор-
векторного пространства mnlmn + 1 над полем вычетов Л/т;
как функция целого аргумента п она наз. функци-
функцией Гильберта — Самюэля (или характери-
характеристической функцией) Л. к. Л. При больших п
эта функция совпадает с нек-рым многочленом НА(п)
от п, к-рый наз. многочленом Гильберт а —
Самюэля Л. к. Л (см. также Гильберта много-
многочлен). Этот факт можно выразить в терминах ряда
Пуанкаре: формальный ряд
является рациональной функцией вида /(t) A — t)~d<A\.
где f(t)?z[t] —многочлен, a d(A) — 1 равно степени
Нд. Целое число d (A) совпадает с размерностью (по
Круллю) dim А кольца А и является одним из важней-
важнейших инвариантов кольца. Кроме того, d(A) равно наи-
наименьшему числу элементов oj, . . ., а^(^А, для к-рых
факторкольцо A/ (alt . . ., ad) артиново. Если эти эле-
элементы можно выбрать так, чтобы они порождали мак-
максимальный идеал т, то Л. к. А наз. регулярным
локальным кольцом. Регулярность А эк-
эквивалентна тому, что dim(m/m2) = dim А. Для d-мер-
ного регулярного кольца А
a P^(t)=(l — t)~d. Геометрически регулярность озна-
означает неособость соответствующей точки (аналитиче-
(аналитического или алгебраического) многообразия.
Помимо характеристич. функции Нд и связанных
с ней размерности и кратности у Л. к. имеются раз-
различные инварианты гомологич. природы. Главным из
них является глубина prof А (см. Глубина модуля);
условие prof A = dira А выделяет среди Л. к. так наз.
Коэна — Маколея кольца. Неизвестно A982), для вся-
всякого ли полного Л. к. А существует модуль М с prof M=
= dimA. Другими гомологич. инвариантами являются
т. н. ч и с л а Бетти Ь,- (А) Л. к. А, т. е. размерно-
размерности /с-пространств Torf (k, к), где к — поле вычетов А.
Открыт вопрос о рациональности ряда Пуанкаре
^п>0 bn(A)t", хотя для многих классов колец известен
утвердительный ответ. Имеются также инварианты
алгебро-геометрич. природы; при их определении ис-
используется разрешение особенности, соответствующей
Л. к. *
Аналогичная теория строится для полулокаль-
полулокальных к о л е ц, т. е. колец, имеющих конечное число
максимальных идеалов. Роль максимального идеала
для них при этом играет Джекобсона радикал.
Лит.: [1] К г и 1 1 W., «J. reine und angew. Math.», 1938,
Bd 179, S. 204—26; [2] С h e v a 1 1 e у С, «Ann. Math.», 1943,
v. 44, p. 690—708; [3] Cohen I. S., «Trans. Amer. Math.
Soc», 1946. v. 59, p. 54—106; [4] Samuel P., Algebre locale,
P., 1953; [5] N а к a t a M., Local rings, N. Y.~ L., 1962; [6]
Зарисский О., Самюэль П., Коммутативная алгеб-
алгебра, пер. с англ., т. 2, М., 1963; [7] С е р р Ж.- П., «Математи-
«Математика», 1963, т. 7, № 5, с. 3 — 93; [8] Б у р б а к и Н., Коммута-
Коммутативная алгебра, пер. с франц., М., 1971; [9] Атья М.-Ф.,
Макдональд И., Введение в коммутативную алгебру,
пер. с англ., М., 1972. В. И. Данилов.
ЛОКАЛЬНОЕ ПОЛЕ — полное дискретно нормиро-
нормированное поле с конечным полем вычетов. Структура
Л. п. хорошо известна: 1) если характеристика К
равна 0, то К является конечным расширением поля Qp
р-адических чисел; 2) если характеристика К больше О,
то К изоморфно полю к((Т)) формальных степенных ря-
рядов над конечным полем к. Локальными такие поля на-
называются в противоположность глобальным полям
(конечным расширениям полей Q или к(Т)) и являются
средством изучения последних. О когомологич. свой-
свойствах расширений Галуа локальных полей см. [1], а
также ст. Аделъ и Полей классов теория.
Для построения теории полей классов многомерных
схем используется обобщение понятия Л. п. А именно,
структурой /1-й ерного локального поля
наз. последовательность О0, Ог, . . ., Оп полных колец
дискретного нормирования вместе с изоморфизмами
k(Ot) ^K(Oi + 1),
где к — поле вычетов, а К — ноле частных кольца О;
при этом к (Оп) должно быть конечным. Для п-мерных
Л. п. построена структурная теория (см. [3]).
Лит.: [1] Serre J,- P., Corps locaux, P., 1962; [2] Ал-
Алгебраическая теория чисел, пер. с англ., М., 1969; [3] Пар-
Паршин А. Н., «Докл. АН СССР», 1978, т. 243, № 4, с. 855 — 58.
В. И. Данилов.
ЛОКАЛЬНОЕ ПРИБЛИЖЕНИЕ ФУНКЦИИ
мера приближения (в частности, наилучшего прибли-
приближения) функции f(x) на множестве Ec:Rm, рассматри-
рассматриваемая как функция этого множества. Основной инте-
интерес представляет поведение Л. п. ф., когда mes ?—>-0,
В нек-рых случаях удается охарактеризовать в тер-
терминах Л. п. ф. степень гладкости приближаемой функ-
функции. Пусть ?„(/; (а, Р)) — наилучшее приближение
функции f(.r)?C[a,b\ алгебраич. многочленами сте-
степени п на интервале (а, Р), a<ga<P<6. Справедливо
следующее утверждение: условие, необходимое и доста-
достаточное для того, чтобы функция f(x) имела непрерыв-
непрерывную производную порядка n-fl во всех точках [а, 6|.
заключается в том, что
равномерно при Р—кг, а—кс, а<а<Р, где непрерывная
функция X (х) определяется равенством
(n + l)!22« + ! А,(*) = |/(п + 1> (х)\.
Лит.: [11 Райков Д. А., «Докл. АН СССР», 1939 т. 2'..
,N» 7; [2] Бернштейн С. Н., Собр. соч., т. 2, М., 1954;
[3] Б р у дн ы й Ю. А., «Тр. Моск. матем. об-ва», 1971, т. 24,
с. 69 —132. Н. П. Норнейчук, В. П. Моторный.
ЛОКАЛЬНОЕ РАЗБИЕНИЕ — свойство расположе-
расположения замкнутого множества Ф в пространстве R", за-
заключающееся в существовании такой точки а (точка,
в к-рой множество Ф разбивает пространство) и такого
положительного числа е, что при любом числе б>0 в
открытом множестве О (а, б)\Ф, где О (а, 6) — (откры-
(открытый) шар радиуса б с центром а, содержится пара точек,
обладающая свойством: всякий лежащий в О(а,е)
континуум, содержащий эту пару точек, имеет непустое
пересечение с множеством Ф. К. Менгер (К. Monger)
и П. С. Урысон доказали, что лежащее в плоскости
замкнутое множество Ф тогда и только тогда имеет
размерность 1, когда оно не содержит внутренних
(относительно плоскости) точек и локально разбивает
плоскость (хотя бы в одной точке а).
Аналогичная характеризация замкнутых (п — 1)-
мерных множеств в n-мерном пространстве R" дана
П. С. Александровым (см. Локальное зацепление).
А. А. Мальцев.
ЛОКАЛЬНОЕ СВОЙСТВО в коммутативной
алгебре — свойство Р коммутативного кольца А
или Л-модуля М, к-рое верно для кольца А (модуля М)
тогда и только тогда, когда аналогичное свойство вы-
выполняется для локализаций кольца А (модуля М) от-
относительно всех простых идеалов кольца А., т. е. свой-
свойство, к-рое выполняется глобально тогда и только тогда,
когда оно выполняется всюду локально. Часто вместо
множества всех простых идеалов можно ограничиться
рассмотрением всех максимальных идеалов кольца А.
Эта терминология становится понятной, если сопоста-
сопоставить кольцу А топологич. пространство Spec А (спектр
кольца А), состоящее из всех простых идеалов А. Тогда
утверждение «Р верно для А» эквивалентно утвержде-
утверждению «Р выполняется на всем пространстве Spec A»,
а утверждение «Р верно для всех А^» эквивалентно ут-
утверждению «каждая точка р пространства Spec A
обладает окрестностью, в к-рой выполняется Р».
Примеры Л. с. Область целостности А целозам-
кнута в своем поле частных тогда и только тогда, когда
цслозамкнуты локализации А^ для всех максимальных
идеалов кольца А. Гомоморфизм А -модулей / : М—viV
является изоморфизмом (мономорфизмом, эпиморфиз-
эпиморфизмом, нулевым) тогда и только тогда, когда отображение
локализованных модулей /ъ : М„ —>-
вым для всех максимальных идеалов кольца А.
Напротив, свойство Л-модуля М быть свободным не
является локальным.
Лит.: [!] Б у р 0 а к и Н., Коммутативная алгебра, пер.
с франц., М. 1971. Л. В. Кузьмин.
ЛОКАЛЬНОСТИ ПРИНЦИП — собирательное поня-
понятие, объединяющее ряд утверждений, относящихся в
основном к эллиптическим (в нек-рых случаях к гипо-
эллиптпческим) уравнениям (операторам) и вытекаю-
вытекающих из точечного характера особенности фундамен-
фундаментального решения для этого класса уравнений. Напр.,
эллиптич. оператор L(D, x) с переменными коэффи-
коэффициентами, записанный в виде
представим, в соответствующем смысле, в окрестности
точки хй как сумма
где первое слагаемое — оператор с постоянными ко-
коэффициентами, a L' (х) «достаточно мал» в указанной
окрестности.
Лит.: [1] Данфорд Н., Шварц Д ж.-Т., Линей-
Линейные операторы, пер. с англ., т. 2, М., 1966. А. А. Дезин.
ЛОКАЛЬНЫЕ ГОМОЛОГИИ — гомологии группы
НХ„=НСР (X, Х\х; G),
определенные в точках х?Х, где Н°р — гомологии с ком-
компактными носителями. Эти группы совпадают с пря-
прямыми пределами
UmHcp(X, X\U; G)
по открытым окрестностям U точки х, а для гомологи-
гомологически локально связных X — также с обратными пре-
пределами
lim tf?-i (U\x; G).
Гомологическая размерность конечномерного метризуе-
мого локально компактного пространства X над G сов-
совпадает с наибольшим значением п, для к-рого ?{%фО,
причем множество таких точек х?Х имеет размер-
размерность п.
Пусть С% — дифференциальный пучок над X, опре-
определяемый сопоставлением каждому открытому множе-
множеству UmX комплекса цепей С*(Х, X\U\ G). Груп-
Группы Нхр являются слоями производных пучков $??„ =
= Нр(С%). Для обобщенных многообразий Яр = 0 при
p^n=dim X. В этом случае гомологич. последователь-
последовательность с коэффициентами в G пары (X, А) совпадает с
когомологнями пары (X, Х\А) с коэффициентами в
пучке ^f „ (двойственность Пуанкаре —
Л е ф ш е ц а). Для локальных кого мол о-
г и й локально компактных пространств аналогичные
факты не имеют места.
Лит.: [1] Скляр енко Е. Г., «Изв. АН СССР. Сер.
матем.», 1У71, т. 35, .N5 4, с. 831 — 43; [2] X ар лап А. Э.,
«Матем. сб.», 1975, т. 96, М 3, с. 347—73. Е. Г. Склхренко.
ЛОКАЛЬНЫЕ И РЕЗИДУАЛЬНЫЕ СВОЙСТВА —
абстрактные (т. е. сохраняющиеся при изоморфизме)
свойства алгебраич. систем или универсальных алгебр.
Если Р — нек-рое свойство алгебр, то говорят, что
алгебра А локально обладает свойст-
свойством Р, если существует локальная система подал-
подалгебр алгебры А, каждая из к-рых обладает свойством
Р. Локальной системой подалгебр
алгебры А наз. система непустых подалгебр, на-
направленная по включению, объединение всех подалгебр
к-рой совпадает с А. Если каждая алгебра нек-рого
класса, к-рая локально обладает свойством Р, в дей-
действительности сама обладает свойством Р, то Р наз. л о-
кальным свойством алгебр этого класса.
Напр., свойство быть абелевой группой — локальное
свойство в классе всех групп, а свойство быть конечной
группой — не локальное. Подробнее о локальности
свойств см. Мальцева локальные теоремы.
Говорят, что алгебра Лрезидуально обла-
обладает свойством Р, если существует такое раз-
разделяющее семейство конгруэнции (?^)хел на -^ > чт0
каждая факторалгебра A/q^ обладает свойством Р.
Семейство (g^); 6 v наз. разделяющим семей-
семейством конгруэнции, если пересечение всех
q^ есть максимальная (т. е. самая дробная) конгруэнция
данной алгебры. Алгебра А резидуально обладает свой-
свойством Р тогда и только тогда, когда она может быть пред-
представлена в виде подпрямого произведения однотипных
с ней алгебр, обладающих свойством Р. Свойство Р
наз. резидуальным в нек-ром классе алгебр, если вся-
всякая алгебра этого класса, резидуально обладающая
свойством Р, в действительности сама обладает свой-
свойством Р. В классе всех групп свойство быть абелсвой
группой резидуально, а конечность не резидуальна.
Всякое резидуальное свойство алгебр, сохраняющееся
при переходе к гомоморфным образам, локально.
Лит.: [1] Кон П., Универсальная алгебра, пер. с англ.,
М., 19G8. О. А. Иванова.
ЛОКАЛЬНЫЕ КОГОМОЛОГИИ со значения-
значениями в пучке абелевых групп — когомоло-
когомологии со значениями в пучке, носители к-рых содержатся
в заданном подмножестве. Пусть А — топологич. про-
пространство, Of — пучок абелевых групп на X, Z — ло-
локально замкнутое подмножество в X, т. е. замкнутое
подмножество нек-рого открытого в X подмножества V,
тогда через Tz(X,§~) обозначают подгруппу в Г(Т, F\ V),
состоящую из сечений пучка SjfW с носителями в Z.
Если фиксировать Z, то соответствие F—>~Г^(Х, Ijf)
определяет точный слева функтор из категории пучков
абелевых групп на X в категорию абелевых групп.
Значение соответствующего г-го правого производного
функтора на пучке ^ обозначают через Hlz(X, §r) и
наз. г-й группой локальных когомологии пространства
X со значениями в §^ относительно Z. При этом
11$ (X, «Г) = Г2(А', f).
Пусть H'z(§r) — пучок на X, отвечающий предпуч-
ку, к-рый сопоставляет любому открытому подмноже-
подмножеству UCZX группу rZnl7(tr,(f"| U). Соответствие pf"-v
-*-SFCz(?} является точным слева функтором из катего-
категории пучков абелевых групп на X в нее же. Значение
его г-го правого производного функтора на пучке JF
обозначается через SfCzKW) и наз. пучком г'-х локальных
когомологии пучка $ относительно 7,. Пучок ^fz (IF)
ассоциирован с предпучком, сопоставляющим откры-
открытому подмножеству UczX группу ^znu(U, §r\U).
Существует спектральная последовательность
?>р>", сходящаяся к НР/Ч{Х, f), у к-рой Е?-" =
=Нр(Х, SVQZ(?)) (см. [2], [3]).
Пусть Z — локально замкнутое подмножество в
X, Z'— замкнутое подмножество в Z, Z"=Z\Z',
тогда имеют место точные последовательности:
О — Я°, (А', Г) —-...-* Hlz, (А, §г) _
^HZ(X, f)->tfi,,(A\ f") — Я^1 (X, JF)-> A)
о -^ Ж\Л?) — ...-> Ж1г, (Ю -^
— SKZ (Ж) — Ж12~ (?) — Ж?,1 (Ю — B)
Если Z есть все A', a Z'— замкнутое подмножество в
А, то последовательность B) дает точную последова-
последовательность
о — Ж2, (?) — ? — SV*XSZ (Ю ~*5К\. (Ю
и систему изоморфизмов
Пучки SK%x\z- (aF) наз- i~ml л а к у н а р н ы м и
пучками пучка §~ и имеют важные приложения
к вопросу о продолжении сечений и классов когомологии
пучка <f", заданных на X\Z', на все X (см. [4]).
Если X — локально нётсрова схема, f — квазико-
квазикогерентный пучок на X, Z — замкнутая подсхема в X,
т0 SKlz (aF) ~~ также квазикогерентные пучки на X.
Если ^ — когерентный пучок идеалов на X, задающий
подсхему Z, то имеют место изоморфизмы
Km Extj^ (Qxlfn, g-) = Ж{г (Ю-
п
Важными для приложении являются следующие кри-
критерии тривиальности и когерентности пучков локаль-
локальных когомологии (см. [3], [4]).
Пусть X — локально нётерова схема или комплек-
комплексное аналитич. пространство, Z — локально замкну-
замкнутая подсхема или аналитич. подпространство в I, |" —
когерентный пучок (Зх-модулей, ^ — когерентный пу-
пучок идеалов, задающий Z. Пусть
хе Z
где prof^ §~ — длина максимальной регулярной для
^f" X ,х
gfx последовательности элементов из *?-Х,х или оо, если
JF ж=0. Тогда равенство $%'z (lf) = 0 для i<n равно-
равносильно условию profzfflSz n- Пусть codh^ ^"x = profm gTx
(где m — максимальный идеал колец Qxt x) и пусть
Sm(§r)= {x^X\codhx§r^m}. Если X — комплексное
аналитич. пространство или алгебраич. многообразие,
то все множества Sm(§r) являются аналитическими или
соответственно алгебраическими. Если при этом ^ —
когерентный пучок на X, a Z — соответственно ана-
аналитич. пространство или подмногообразие, то когерент-
когерентность пучков ffClz(ff) для 0^i<iq равносильно условию
r\Sk + q + , (f | X\Z) < к
для всякого целого к.
В терминах Л. к. определяются гиперфунк-
гиперфункции, имеющие важные приложения в теории диффе-
дифференциальных уравнений с частными производными [5].
Пусть Q — открытое подмножество пространства R",
к-рое естественным образом вложено в С". Тогда
ЖЦС",6с„) = 0 прирфп. Предпучока+//?(С»,CС„)
на R" определяет вялый пучок, называемый пучком
гиперфункций.
Аналог Л. к. существует и в теории этальных кого-
когомологии [3].
Лит.: [1] Итоги науки и техники. Алгебра. Топология, Гео-
Геометрия т. 10, М., 1972, с. 47 — 112; [2] G г о t h e n d I e с к А.,
Local cohqmology, В.— Hdlb,—N. Y., 1967; [3] его же,
Gohomologie locale des faisceaux cohfirents et theoremes de Lef-
schetz locaux et globaux, Amst.— P., [1968]; [4] Slu Y.-Т.,
Trautmann G., Gap-sheaves and extension of coherent ana-
analytic subsheaves, B.— [a. o.], 1971; [5] III а п и р а П., Теория
гиперфункций, пер. с франц., М., 1972; [6] В anica С,
St3nS§ilS О., Metode algebrice in teoria globaia a spatiilor
complexe, Buc, 1974. Д. А. Пономарев_
ЛОКАЛЬНЫЕ ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ теории
вероятностей — предельные теоремы для плот-
плотностей, т. е. теоремы, устанавливающие сходимость
плотностей последовательности распределений к плот-
плотности предельного распределения (если указанные
плотности существуют), или классический вариант
Л. п. т. — локальные теоремы для решетчатых распреде-
распределений, простейшей из к-рых является локальная Ла-
Лапласа теорема.
Пусть Xi, Х2, ..• — последовательность незави-
независимых случайных величин, имеющих общую функцию
распределения F (х) с математич. ожиданием а и конеч-
конечной положительной дисперсией а2. Пусть Fn (х) функ-
функция распределения нормированной суммы
и Ф (х) — нормальная @,1) функция распределения.
Сделанные предположения обеспечивают выполнение
соотношения Fn (ж)—>-Ф (х) при я—>-оо для любого х.
Можно показать, что это соотношение не влечет за со-
собой сходимость плотности распределения р„(х) слу-
случайной величины Zn к нормальной плотности
даже если распределение F имеет плотность. Если же
Zn имеет при нек-ром п—па ограниченную плотность
распределения рп (х), то
равномерно относительно х. Условие ограниченности
плотности рп (х) для нек-рого па необходимо для того,
чтобы (*) имело место равномерно относительно х.
Пусть Xlt X2, ... — последовательность независи-
независимых случайных величин, имеющих одинаковое невы-
невырожденное распределение, и Х1 с вероятностью 1 при-
принимает значения вида b-\-Nh, Л'=0, —i, —2, . . .,
где fe>0 и Ь — постоянные (т. е. Хг имеет решетчатое
распределение с шагом К).
Пусть Хх имеет конечную дисперсию а2, а=ЕХх и
Для того чтобы
sup [а Y~^ih-1Pn(N)~
при n—rcc, необходимо и достаточно, чтобы шаг U
был максимальным. Эта теорема Гнеденко представ-
представляет собой обобщение локальной теоремы Лапласа.
Л. п. т. для сумм независимых неодинаково распре-
распределенных случайных величин могут служить основным
математич. аппаратом классической статистич. меха-
механики и квантовой статистики (см. [7], [8]).
Л. п. т. глубоко изучены для сумм независимых
случайных величин и векторов вместе с оценками
скорости сходимости в этих теоремах. Наиболее полно
исследован случай предельного нормального распре-
распределения (см. [3], гл. 7); ряд работ посвящен Л. п. т.
для случая произвольного устойчивого распределения
(см. [2]). Аналогичные исследования проведены также
для сумм зависимых случайных величин, в частности
для сумм случайных величин, образующих цепь Мар-
Маркова (см. [5], [6]).
Лит.: [1] Гнеденко Б. В., Колмогоров А. Н.,
Предельные распределения для сумм независимых случайных
величин, М.— Л., 1949; [2] Ибрагимов И. А., Л и н-
н и к Ю. В., Независимые и стационарно связанные величины,
М., 1965; [3] Петров В. В., Суммы независимых случайных
величин, М., 1972; [4] Прохоров Ю. В., Розанов Ю. А.,
Теория вероятностей, 2 изд., М., 1973; [5] Сирашдинов С.
X., Предельные теоремы для однородных цепей Маркова,
Ташкент, 1955; [6] С т а т у л я в и ч у с В. А., «Литовский
матем. сб.», 1961, т. 1, в. 1—2, с. 231 — 314; 1969, т. 9, в. 2,
с. 345—62; [7] Хин чин А. Я., Математические основания
статистической механики, М.— Л., 1943; [8] X и н ч и н А. Я.,
Математические основания квантовой статистики, М.— Л.,
1951. В. В. Петров.
ЛОКАЛЬНЫЙ ГОМЕОМОРФИЗМ — отображение
/ : X—*-Y топологич. пространств такое, что для каждой
точки х?Х найдется окрестность Ох, к-рая посредством
/ отображается в У гомеоморфно. Иногда в определение
Л. г. автоматически включается требование fX = Y и,
кроме того, отображение / предполагается открытым.
Примеры Л. г.: непрерывно дифференцируемое с от-
отличным от нуля якобианом отображение открытого
подмножества «-мерного евклидова пространства в
n-мерное евклидово пространство; отображение накры-
накрытия и, в частности, естественное отображение тополо-
гич. группы на ее факторпространство по дискретной
подгруппе. Если отображение / : X—t-Y полного по
Чеху, в частности, хаусдорфова локально бикомпакт-
бикомпактного пространства на тихоновское пространство Y
открыто и счетнократно, т. е. \f~xy \ <: /if0, y?Y, то на
нек-ром открытом и всюду плотном в X множестве ото-
отображение / ЯВЛЯОТСЯ Л. Г. В. А. Пасынков.
ЛОКАЛЬНЫЙ УНИФОРМИЗИРУЮЩИЙ ПА-
ПАРАМЕТР, локальная у н и ф о р м и з и р у ю-
ща я, локальный пара мет р,— комплексное
переменное t, определенное как непрерывная функция
tPo=4'po(P) точки р римановой поверхности Й всюду
в нек-рой окрестности Т*(р0) точки po?R, реализую-
реализующая гомеоморфное отображение окрестности V(p0) на
круг D{po)={t?C: \t\<r(p0)), причем фро(р0) = 0. При
этом V(p0) наз. отмеченной, или парамет-
параметрической, окрестностью, <рр„: V(p0)—>
—>-?> (р0) — отмеченным, или параметри-
параметрическим, отображением, D(p0) — о т м е-
ч е н н ы м, или параметрическим, к р у-
г о м. При отмеченном отображении любая функция
точки g(p), определенная в отмеченной окрестности
V(p0), переходит в функцию Л. у. п. t, т. е. g{p) =
= g[<p~al (t)] = G(t). Если V(p0) и V(pi)— две отмеченные
окрестности такие, что V (po)(\V (р1)ф0, tpo и tpi —
соответствующие Л. у. п., то tpi = <ppi{y~al (tpo)] есть
однолистная голоморфная функция на нек-рой под-
подобласти D (р0), осуществляющая биголоморфное отобра-
отображение этой подобласти в D (рх).
Если R = Rp — риманова поверхность аналитич.
функции w=F(z) и р0— регулярный элемент F (z) с
проекцией z0=^oo, то tpo=z—z0; tPo=l/z при z0=oo.
Если р0— особый, или алгебраический, элемент F(z),
соответствующий ветвления точке z0 порядка к — 1 >0,
то tp(= ^/z—z0 при z0=^oo и tpB=--i/y^z при zo= 00. В от-
отмеченной окрестности элемента р0 Л. у. п. t фактически
осуществляет при этом локальную униформизацию,
вообще говоря, многозначного соотношения w = F(z) no
формулам (для примера, при )
В случае, когда R — риманова поверхность с кра-
краем, для точек р0, принадлежащих краю R, Л. у. п.
tpo=(fpo(p) отображает отмеченную окрестность V(p0)
на полукруг
D(po) = {t ? С : |*| < г(р0), IrniS-O}.
Если R — риманова область над комплексным про-
пространством С", п>1, то Л. у. п.
осуществляет гомеоморфное отображение отмеченной
окрестности V(p0) на поликруг
D(Po) = {t = (tu ..., tn)gC» :
:|'il < ri(Po). •••> \fn\ < rn(p0)}.
При этом, если пересечение V(po)C\V(pi) не пусто, то
отображение tpi = (ppi[<p~* (tpo)] биголоморфно отобра-
отображает нек-рую подобласть D (р0) в D (р\)-
Лит.: [ИМаркушевич А. И., Теория аналитических
функций, 2 изд., т. 2, М., 19«8; [2] Спрингер Д ж., Вве-
Введение в теорию римановых поверхностей, пер. с англ., М., 1960;
[3] Ш а б а т Б. В., Введение в комплексный анализ, 2 изд., ч.
1—2, М., 1976. Е. Д. Соломенцев.
ЛОКАЛЬНЫХ ВАРИАЦИЙ МЕТОД — один из пря-
прямых методов численного решения задач оптимального
управления с ограничениями на фазовые координаты
и управляющие функции, основанный на варьировании
в пространстве состояний (см. [1] — [3]).
В Л. в. м. исходная задача оптимального управления,
заданная в форме Лагранжа задачи, приводится в ре-
результате дискретизации по аргументу t и фазовому
вектору х к задаче минимизации аддитивного функцио-
функционала
при условиях
хк + 1~ xk=xF (xk, Xk + U Uk, tk, tft + i),
/r = 0, 1, ..., Ar-1, B)
(xk, uh)-?Gk, fc = 0, 1, ..., N, C)
где x/i, iifr — векторы фазовых координат и управлений
в узле tk (имеющие размерности соответственно п и
т), Gk — заданные области (ге+та)-мерного простран-
пространства (Go и 67дг описывают граничные условия), т =
= (Г—to)lN — шаг разбиения исходного интервала
[t0, T\ для независимого переменного. Существенным
для Л. в. м. является условие равенства размерностей
п==гп векторов х и а, при к-ром построение элементар-
элементарной операции оказывается достаточно простым. Под
элементарной операцией понимается определение уп-
управления U?, переводящего систему из точки (t^, x^) в
близкую точку (tk + 3, x/i + i). При равенстве размерностей
векторов х и и и при нек-рых дополнительных условиях
управление и^ определяется на каждом интервале
(i?, ift + ]) из решения системы п уравнений B), получен-
полученной в результате конечноразностной аппроксимации
системы дифференциальных уравнений исходной вариа-
вариационной задачи.
Пусть в качестве начального приближения задана
нек-рая ломаная Го : (жЛ , . . •, xn), Для к-роц выпол-
выполнены условия B), C). Алгоритм Л. в. м. состоит в
последовательном улучшении положения узлов, через
к-рые проходит ломаная Го, осуществляемом в резуль-
результате поочередного локального варьирования каждой
jf-ii компоненты вектора хк. На каждом участке от i!t
до (^ + 2, к=0, 1, . . ., при фиксированных хк и хк + ^
каждая /-я компонента вектора х^ поочередно варьи-
варьируется с шагом/гу>0. Если в результате этого варьиро-
варьирования значение функционала A) уменьшается (при
выполнении условий B), C)), то аналогичное варьи-
варьирование производится с очередной (/-fl)-ii компонен-
компонентой вектора х^, в противном случае /-я компонента
варьируется с шагом (—hj). Такое локальное варьиро-
варьирование осуществляется последовательно для всех узлов
ломаной Го. В результате к моменту окончания итера-
итерации получается новая ломаная Гх, на к-рой функционал
A) принимает значение, не большее чем на начальном
приближении Го. Последующие итерации выполняются
аналогично. При необходимости производится умень-
уменьшение шагов hj и т. Приближенное решение исходной
вариационной задачи определяется путем интерполя-
интерполяции по найденным значениям управления на каждом
шаге.
При т=тг=1 решение, полученное Л. в. м. при за-
заданных значениях т и h, удовлетворяет конечноразно-
конечноразностной аппроксимации уравнения Эйлера с точностью
до членов порядка max (h, hlx, hit2) (см. [3]).
Если варьирование исходной ломаной Го не ограни-
ограничивается поочередным варьированием ее узлов, а осу-
ществляется на более полном графе, соответствующем
выбранным шагам т и hj и включающем ломаную Го,
то говорят о блуждающей трубки методе.
При т<н выполнение элементарной операции свя-
связано с нек-рыми трудностями. В этом случае вместо
Л. в. м. может применяться близкий к нему бегущей
волны метод.
Л. в. м. непосредственно обобщается на вариацион-
вариационные задачи с неаддитивными функционалами, в к-рых
ограничения носят характер изопериметрич. условий
(см. [3]). Л. в. м. может быть распространен на вари-
вариационные задачи, в к-рых неизвестные функции зависят
от нескольких независимых переменных и соответству-
соответствующие функционалы задаются в виде интегралов по об-
областям различной размерности (см. [2]).
Лит.: [1] М о и с е е в Н. Н., Численные методы в теории
оптимальных систем, М., 1971: [2] Крылов II. А., Ч е р-
н о у с ь к о Ф. Л- «Ж. вычислит, матем. и матем. физ.», 1966,
т. 6, X» 2, с. 203—П; 13] Б а н и ч у к Н. В., Петров В. М.,
Черноусько Ф. Л., там же, 1969, т. 9, Л» 3, с. 5-48—57.
И. В. Вапнярспий.
ЛОКСОДРОМА, локсодромия,— линия на по-
поверхности вращения, пересекающая все меридианы под
постоянным углом а. Ес-
Если а — острый или тупой
угол, то Л. образует бес-
бесконечное число витков
вокруг полюса, все при-
приближаясь к нему. Для
поверхности вращения,
первая квадратичная фор-
форма к-рой записана в ви-
виде
ds2=du2+G(u)dvi,
уравнение Л.:
Для сферы с первой квадратичной формой
ds2=R2 (dw2+cos2 и dv2)
уравнение Л.:
v etc a = R In t
ЛОММЕЛЯ
А. В. Пеанов.
МНОГОЧЛЕН — многочлен i?m>v (z)
для т = 0, 1,2,... и
степени т относительно г"
любого v, определяемый равенством
1-m
Т (v + m)
Z'~ Г (v)
m
- -^- ; v, — m
1 —v — m\ — z:
При этом J]i(z) — Бесселя функция и 2F3 — гипергеоме-
трический ряд, Л. м. удовлетворяют соотношениям:
Jv+m (z)=Jv (z)
> v (z)—/v_i (z)
l, m=l, 2,
_i, v-i (z),
Лит.: [1] Magnus W., Oberhcttineer F., For-
meln und Satze fiir die speziellen Funktionen der mathematischen
Physik, 2 Aufl., В.— Gott.— Hdlb., 1948. А. Б. Иванов.
ЛОММЕЛЯ ФУНКЦИЯ — решение неоднородного
Бесселя уравнения
2 —v2) y =
Если p=v+2n, где п — натуральное число, то
\ V + 2 Я
X(-5-
ft! Г (v+ft+1) '
Если числа p-fv^O и р—v^O не являются целыми, то
X
д. \p+2fe
^ Ы
Если p=v—2и, где n^O — целое число, и v не является
целым числом <п, то
Г (v-n) г„, , . , х
я -1 (n-ft-1)! / х "\ v - 2 л + 2 А
-fc = o Г (v-n+ ft+1)
\ V+2&
Здесь при п=0 первая сумма принимается равной нулю,
/v (х) — Бесселя функция. Известны также Л. ф. от
двух переменных.
См. также Ангера функция, Вебера функция, Струве
функция.
Л. ф. изучалась Э. Ломмелем [1].
Лит.: [1] L о m m e I E., «Math. Ann.», 1880, Bd 16, S. 183 —
208; [2] В а т с о н Г. Н., Теория бесселевых функций, пер. с
англ., ч. 1, М., 1949, [3] К а м к е Э., Справочник по обыкновен-
обыкновенным дифференциальным уравнениям, пер. с нем., 5изд., М., 1976.
Е. Д. Соломенцев.
ЛОНГМАНА МЕТОД — метод приближенного вы-
вычисления определенного интеграла
/ = ^ / И dx,
где /(х) имеет точно п корней х; внутри промежутка
[а, Ь]:
и удовлетворяет формулируемым ниже условиям. Пусть
vi t! (-I)'\x'*1f(x)dx, 1 = 0,1,2, ...,п,
тогда /=5, где
„ def ж-,п ,
Предполагается, что f(x) сохраняет знак на промежутке
[х,, х,+1] и имеет разные знаки на соседних промежут-
промежутках, при этом Ь[фО, г = 0, 1,2,. . ., п. Такую функцию
/(х) наз. колеблющейся. Вычисление / с по-
помощью квадратурной формулы при большом п затруд-
затруднительно, т. к. хорошее приближение колеблющейся
функции на всем промежутке \а, Ь] практически не-
невозможно. Использование равенства I=S приводит
к вычислению всех интегралов vj, что также нецелесооб-
нецелесообразно в случае большого п.
Приближенное вычисление 7 в Л. м. основано на
равенстве (п^р)
A)
В равенство A) входят конечные разности vj как функ-
функции дискретного аргумента j:
def
Дуу = vJ + 1 — Vj, / = 0, 1, 2, ..., re —1;
Д' + Чу = &rvJ + 1-Arvj,
г—I, 2, ..., /? —1, / = 0, 1, 2, ..., л —г—I.
Если функция Vj такова, что в правой части A) можно
пренебречь слагаемыми, содержащими конечные раз-
разности порядка р, то приближенное равенство
можно использовать для вычисления S. Чтобы вы-
вычислить правую часть B), достаточно знать р первых
значений Vj, т. е. значения v0, vy, . . ., Vp_r,iip послед-
последних значений vn, t>n_i, . . ., vn-p + \. Л. м. и состоит в
использовании равенства B) для приближенного вы-
вычисления суммы S.
Если в интеграле / верхний предел интегрирования
Ь= -\- оо и
'=2,1. (-1)'""
то вместо A) следует воспользоваться равенством
(преобразование Эйлера) и ряд в пра-
правой части заменить частичной суммой.
Метод предложен И. Лонгманом [1].
Лит.: [1] L о n g m a n I. М., «Math. Comput.», 1960, v. 14,
Ki 69, p. 53—59; [2] D a v i s P. J., R a b i n о w i t z P.,
Methods of numerical integration, N. Y., 1975.
И. П. Мысовских.
ЛОПИТАЛЯ ПРАВИЛО — раскрытие неопределен-
неопределенностей вида 0/0, оо/оо сведением предела отношения
функций к пределу отношения производных рассмат-
рассматриваемых функций. Так, для случая, когда действи-
действительные функции fug определены в проколотой право-
правосторонней окрестности точки а числовой оси, Л. п.
имеет вид
Как в случае неопределенности типа 0/0, т. е. когда
lim f (х) = \im g (x) = О,
д:->а+0 х ~>- а + 0
так и в случае оо/оо, т. е. когда
lim / (х) — lim g (x) = оо,
х->а + 0 х -у а+0
Л. п. справедливо при условиях, что функции fug
дифференцируемы на нек-ром интервале (а, 6), g' \х)Ф0
для всех точек х? (а, Ь) и существует конечный или
бесконечный предел отношения производных
lim АЦ
(в случае неопределенности типа оо/оо этот предел,
если он бесконечный, может быть только бесконечно-
бесконечностью определенного знака); тогда существует и пре-
предел отношения функций lim ——— и справедливо ра-
x-*a+Q S W
венство (*). Это утверждение с естественными видо-
видоизменениями остается верным как для случая левосто-
левостороннего, так и для случая двустороннего предела, а
также тогда, когда х—>--j-oo или х-*—оо.
При практическом отыскании пределов отношения
функций с помощью Л. п. иногда приходится приме-
применять его несколько раз подряд.
При сделанных выше предположениях существование
предела отношения производных /' (x)lg' (х) является
достаточным условием существования предела отно-
отношения f(x)lg(x) самих функций, но не необходимым.
Лит.: 11] Лопиталь Г. Ф., Анализ бесконечно малых,
пер. с франц., М.— Л., 1935; [2] Никольский С. М.,
Курс математического анализа, 2 изд., т. 1, М., 1975.
Л. Д. Кудрявцев.
ЛОРАНА РЯД — обобщение степенного ряда по це-
целым неотрицательным степеням разности z—а пли по
целым неположительным степеням z—а в виде
Ряд A) понимается как сумма двух рядов:
— правильная часть Л. р. и
— главная часть Л. р. Ряд A) считается схо-
сходящимся тогда и только тогда, когда сходятся его пра-
правильная и главная части. Свойства Л. р.: 1) если об-
область сходимости Л. р. содержит внутренние точки, то
она представляет собой круговое кольцо D= {z?C:
0<r<|z—а|<Л<:+оо} с центром в точке афоо; 2) во
всех внутренних точках кольца сходимости D ряд A)
сходится абсолютно; 3) как и для степенных рядов,
поведение Л. р. в точках граничных окружностей
\z—а|=г и \z—а|=Л может быть самым разнообраз-
разнообразным; 4) на любом компактном множестве KdD ряд
A) сходится равномерно; 5) сумма ряда A) в D есть ана-
литнч. функция /(z); 6) ряд A) можно дифференциро-
дифференцировать и интегрировать в D почленно; 7) коэффициенты
С? Л. р. определяются через его сумму /(z) формулами
где 7= (z: U—al —p, г<р<Д} — любая окружность с
центром а, расположенная в D; 8) разложение в Л. р.
единственно, т. е. если /(z)^tp(z) в D, то все коэффи-
коэффициенты их Л. р. по степеням z—а совпадают.
Для случая центра в бесконечно удаленной точке
а=сс Л. р. принимает вид
•-— + со
\ CuZ* C)
причем теперь правильной частью является
а главной —
Область сходимости ряда C) имеет вид
D'=-- {z: 0<r<UI <Л<-гоо },
а формулы B) переходят в формулы
z*+1/(z)rfz' fc=0> ±4' •••'
где у= {z: ]z] — р, г<р<Л}. В остальном все свойства
те же, что и в случае конечного центра а.
Применение Л. р. основано главным образом на
теореме Лорана A843): любая однозначная
аналитич. функция /(z) в кольцеD— {z: 0<:r<|z—а\ <
<Д<Н-оо} представима в D сходящимся Л. р. A).
В частности, в проколотой окрестности D={z: 0<
<C\z—a\<CR} изолированной особой точки а однознач-
однозначного характера аналитич. функция /(z) представима
Л. р., к-рый и служит основным инструментом иссле-
исследования ее поведения в окрестности изолированной
особой точки.
Для голоморфных функций /(z) многих комплекс-
комплексных переменных z= (zj, z2, . . ., zn) аналогом
теоремы Лорана можно считать следующее
предложение: всякую функцию f(z), голоморфную в
произведении D колец Dv = {zvdC: 0<:rv<|zv—«vK
¦Cflv^^00}] можно представить в D в виде сходяще-
сходящегося кратного Л. р.
в к-ром суммирование распространяется на все цело-
целочисленные мультииндексы
к=(кг, к2, ..., А-„), j к | = k1J\- k2-\- ... -\-кп,
{z — a)b = (z1 — a1)k4z2 — a2)k* ... (zn — ол)*«,
1 С f(Ddz
где у— произведение окружностей т>\: = (zv € С: zv =
= av-bPve'f; rv <.pv <.RV, 0<:?<:2я}, v=l, 2, . . ., n.
Область сходимости ряда D) логарифмически выпук-
выпуклая и является относительно полной кратно круговой
областью. Однако применение кратных Л. р. D) ограни-
ограничено, поскольку при п~^2 голоморфные функции /(z)
не могут иметь изолированных особенностей.
Лит.: [1] М а р к у ш е в и ч А. И., Теория аналитических
функций, 2 изд., т. 1, М., 1967, гл. 4; [21 Ш а б а т Б. В., Вве-
Введение в комплексный анализ, 2 изд., М., 1976, ч. 1, гл. 2, ч. 2,
гл. 1. Е. Д. Соломенцев.
ЛОРЕНЦА АТТРАКТОР — компактное инвариант-
инвариантное множество L в трехмерном фазовом пространстве
гладкого потока {5(}, к-рое имеет указанную ниже
сложную топологич. структуру и является асимптоти-
асимптотически устойчивым (т. е. оно устойчиво по Ляпунову и
все траектории из нек-рой окрестности L стремятся к
L при t—>-oo); в понятие аттрактора, т. с. притяги-
притягивающего множества, часто включают только послед-
последнее из этих двух свойств, однако как Л. а., так и дру-
другие практически важные аттракторы обладают обоими
этими свойствами.
Л. а. впервые появился в численных экспериментах
Э. Лоренца [1], исследовавшего поведение траекторий
системы
я;=—ох-\-оу, у = гх — у — xz, z = — bz-\-.ry (*)
при нек-рых конкретных значениях параметров а, г, Ь.
(Эта система вначале была введена как первое нетри-
нетривиальное галеркинское
приближение для нек-рых
гидродинамич. задач—
чем и мотивировался
выбор значений о=10,
'" г=28, 6=8/3, но она воз-
возникает также и в других
физич. вопросах, см. [2],
[3].) В [4] результаты
[1] и более новые данные численных экспериментов в
общих чертах сопоставлены с теоретич. представления-
представлениями теории гладких динамич. систем, а в [5] результаты
[1] интерпретированы как указание о существовании
у системы (*) аттрактора (получившего назв. аттра-
аттрактора Лоренца), к-рый во многом аналогичен
гиперболическим множествам, но не является таковым
(основное отличие связано с тем, что в состав Л. а.
входит положение равновесия типа седло с одним по-
положительным собственным значением; для системы (*)
это положение равновесия — начало координат). Су-
ществование Л. а. и ряд его свойств следуют из опреде-
определенных особенностей отображения последования на
нек-рой поверхности П (для системы (*) используется
плоскость z=27), точная формулировка к-рых, однако,
весьма громоздка (см. [6], [9]) и при проверке к-рых
для конкретных систем, включая (>:¦¦), приходится при-
прибегать к численному интегрированию. Соответственно,
Л. а. посвящены исследования двух типов.
1) В исследованиях теоретич. характера с самого
начала предполагается, что рассматриваемые потоки
имеют на нек-рой поверхности П надлежащее отобра-
отображение последования, и отсюда извлекаются следствия
о свойствах Л. а. Его строение описывается следующим
образом [8]. Рассмотрим «разветвленное многообразие»
Lo, на к-ром при i>0 задан поток фг, как указано на
рисунке. Пусть отображение последования на линии
разветвления ab является (равномерно) растягивающим,
т. е. во всех точках (кроме с, где оно терпит разрыв)
его производная больше нек-рого Я,>1 (годится любое
такое к, но исследование упрощается при >„>"^2, что
совместимо с вычислительными данными о системе (*)
при указанных а, г, Ь). Пары {(Lo, 4>f)} естественным об-
образом образуют обратный спектр топологич. пространств
и отображений; его предел и есть (L, Sf\L). (Даль-
(Дальнейшее изучение структуры Л. а. [8], [11] основыва-
основывается на этом описании, к-рое поэтому естественно
включить в определение Л. а., особенно если не связы-
связывать определение со специальными свойствами отобра-
отображения последования.) Л. а. обладают топологической
транзитивностью и их периодич. траектории в совокуп-
совокупности плотны в L. При малом (в смысле С1) возмущении
потока с надлежащим отображением последования у
возмущенного потока имеется Л. а., близкий к Л. а.
исходного потока, но, вообще говоря, не гомеоморфный
ему. В этом смысле Л. а. сохраняется при малых воз-
возмущениях (в теории гладких динамич. систем извест-
известны A982) только два класса компактных инвариантных
множеств с этим свойством и сколько-нибудь изученной
структурой: Л. а. и локально максимальные гипербо-
гиперболические множества), но Л. а. (в отличие от последних)
не обладают локальной грубостью.
2) Чтобы обнаружить Л. а. у конкретной системы
типа (*) и уточнить его свойства, приходится наряду
с различными теоретич. соображениями использовать
численное интегрирование (см. [7], [9]). Таким путем бы-
были исследованы бифуркации, происходящие в системе
(*) при изменении г или а и приводящие к появлению
Л. а. [9]. Естественно, численное интегрирование и
само по себе дает нек-рую информацию об аттракторе
(поскольку траектории со временем приближаются
к нему, то на чертеже, изображающем последователь-
последовательные точки пересечения просчитываемых траекторий с
П, возле аттрактора эти точки расположены значитель-
значительно «гуще», чем вдали от него, и это сразу бросается в
глаза). Относящийся сюда материал весьма обширен;
так, обнаружены новые области значений параметров,
при к-рых система (*) имеет Л. а. [10]. Здесь, однако,
остаются невыясненными детали топологич. структуры,
к-рая может и отличаться от описанного выше строения
«стандартных» Л. а.
Теоретич. интерпретации данных численных экспе-
экспериментов для систем порядка выше трех пока A982) не
имеется.
Лит.: [1] Lorenz E. N., «J. Aknos. Sci.», 1963, v. 20,
№2, p. 130—41; [2] Монин А. С, «Успехи физич. наук»
1978, т. 125, в. 1, с. 97 — 122; [3] Рабинович М. И., там
же, с. 123—68; [4] М с L a u g h I i n J. В., М а г t i n P. с.,
«Phys. Rev. Letters», 1974, v. 33, p. 1189 — 92; «Phys. Rev. Scr. A»
1975, v. 12, № 1 p. 186—203; [5J Ruelle D., в кн.: Lecture
Notes in Mathematik, №565, [1976], p. 146—58; [6] M а г s-
d e n J. E., McCrokes M., The Hopt bifurcation and its
applications, В., 1976, p. 368; [7] Нелинейные волны, М., 1979
с. 176, 212; [8] Williams R. F., в кн.: Lecture Notes in
Mathematik, №615, [1977], p. 94—112; [9] А ф р а й м о-
в и ч В. С, Быков В. В., Ш и л ь н и к о в Л. П.,
«Докл. АН СССР», 1877, т. 234, Mi 2, с. 336 — 39; [10] М о г i о-
к a N., Shimizu Т., «Phys. Letters» 1978, v. 66 А, Яг 6,
р. 447—49; [11] R a n d D., "«Math. Proc. Cambr. Phil. Soc»,
1978, v. 83, Я» 3, p. 451—60. Д. В. Аносов.
ЛОРЕНЦА ПРЕОБРАЗОВАНИЕ — преобразование
координат, связывающее две галилеевы системы коор-
координат в каком-либо псевдоевклидовом пространстве;
иными словами, Л. п. сохраняет квадрат т. н. интер-
интервала событий. Л. п. является аналогом ортогональных
преобразований (или обобщением понятия движения)
в евклидовом пространстве. Л. п. образуют группу,
называемую группой Лоренца (или общей
группой Лоренца), к-рая обозначается через
L. Л. п. находят применение в четырехмерном простран-
пространстве-времени специальной теории относительности, для
к-рого в галилеевых координатах х, у, z, t интервал
имеет вид
где с — скорость света в вакууме.
Часто рассматривают более узкие классы Л. п. Так,
Л. п., сохраняющие знак координаты t, образуют
т. н. полную группу Лоренца Lf . Л. п.,
матрицы к-рых имеют положительный определитель,
наз. собственными преобразования-
преобразованиями Лоренца и образуют собственную
группу Лоренца L+. Пересечение L^ и L +
часто наз. просто группой Лоренца.
Общая группа Л. п. состоит из комбинаций простран-
пространственных отражений, отражений во времени, простран-
пространственных поворотов и преобразований, к-рые с физич.
точки зрения являются преобразованиями перехода
от одной инерциальной системы отсчета к другой, дви-
движущейся относительно первой со скоростью V, а с ма-
тематич. точки зрения — гиперболпч. поворотом на
угол г|) в плоскости с псевдоевклидовой метрикой. На-
Наличие последнего типа преобразований является спе-
цифич. чертой группы Л. п.
Для перехода от Галилеев ой системы координат х',
у', z', t' к галилеевой системе координат х, у, z, t,
движущейся относительно первой со скоростью V
параллельно оси х', указанные преобразования имеют
вид
V - — '
х_ X'-VJL-. у = у> z = z' t- cZ X
Если ввести угол гиперболического поворота г|з по
формулам
то Л. п. примут вид
х=ее'chip-]-ct' sh i|), ct = x' shty-^ct' chip, y = y', z=z'.
Эти преобразования часто наз. просто Л. п. Они не об-
образуют группу: действие трех гиперболич. поворотов
с непараллельными векторами скоростей может дать
обычный пространственный поворот — т. н. том а-
совская прецессия.
Часто к общим Л. п. добавляют переносы начала коор-
координат, получая при этом т. н. преобразования
Пуанкаре, образующие группу Пуанка-
р е.
Свойства группы Л. п. сходны со свойствами ортого-
ортогональных групп. Отличия связаны с наличием двух ти-
типов отражений (пространственных и временных) и с
некомпактностью группы Л. п. (т. к. единичная сфера
в псевдоевклидовом пространстве, т. е. множество точек,
для к-рого модуль интервала до начала координат ра-
равен единице, некомпактна).
Физические приложения Л. п. связаны с Эйнштейна
относительности принципом, согласно к-рому все
физич. законы, кроме законов гравитации, инвариант-
инвариантны относительно Л. п. В ряде случаев, напр, в аксио-
аксиоматической квантовой теории поля, использование этого
и других столь же общих постулатов позволяет делать
далеко идущие выводы о видах функциональных за-
зависимостей между различными физич. величинами.
В различных областях физики (в особенности, в тео-
теории элементарных частиц) находят широкое примене-
применение представления групп Л. п. В соответствии с прин-
принципом относительности Эйнштейна физич. величины с
различными законами преобразований — векторы, спи-
спиноры, тензоры — преобразуются по тем или иным пред-
представлениям группы Л. п. При этом оказывается, что
эти представления можно характеризовать двумя ин-
инвариантами, к-рые отождествляются с массой и спи-
спином частиц, описываемых этой физич. величиной.
Инфинитезимальные Л. п., т. е. повороты на беско-
бесконечно малый угол, часто используют для получения
различных законов сохранения.
Находят применения также Л. п. в касательном прост-
пространстве псевдориманова пространства; эти преобразо-
преобразования относятся к т. н. локальным симмет-
симметрия м.
Л. п. получили свое название в связи с работами
Г. Лоренца (Н. Lorentz) по электронной теории, к-рые
сыграли важную роль в формулировании этого по-
понятия.
Лит.: [1] Л а н д а У Л. Д., Л и ф ш и ц Е. М., Теория
поля, 6 изд., т. 2, М., 1973; [2] Н а й м а р к М. А., Линейные
представления группы Лоренца, М., 1958; [3] Физический эн-
энциклопедический словарь, т. 3, М., 1963. Д. Д. Соколов.
ЛОРЕНЦА СИЛА — сила, действующая со стороны
заданного электромагнитного поля на движущуюся за-
заряженную частицу. Выражение для Л. с. F было впер-
впервые дано Г. Лоренцем (см. [1]):
F=eJE+±.[V, В], A)
где Е—напряженность электрич. поля, В— магнит-
магнитная индукция, V — скорость заряженной частицы от-
относительно системы координат, в к-рой вычисляются
величины Е, В, F; е — заряд частицы, с — скорость
света в вакууме. Выражение для Л. с. является реля-
релятивистски инвариантным (т. е. справедливым в любой
инерциальнои системе отсчета); оно позволяет связать
уравнения для электромагнитного поля с уравнениями
движения заряженных частиц.
В постоянном и однородном магнитном поле движение
частицы с массой т и зарядом е в нерелятивистском
приближении (V<^c) описывается уравнением
В прямоугольной системе координат с осью z, направ-
направленной вдоль внешнего магнитного поля В, решение
уравнения B) имеет следующий вид
х = х0 + г sin (a>ot + а), у = уо + г cos (u>ot + а),
где щ=еВ1тс — ларморовская частота вращения час-
частицы, г= Уог1щ— радиус вращения частицы (лармо-
ровский радиус), а — начальная фаза вращения, Fo—
начальная скорость частицы. Таким образом, в одно-
однородном магнитном поле заряд движется по винтовой
линии с осью вдоль магнитного поля.
Если электрич. поле Е не равно нулю, то движение
носит более сложный характер. Происходит перемо-
перемощение центра вращения частицы поперек поля В (т. н.
дрейф). Средняя величина дрейфа в векторном виде
Г = с[Е, В]/В2.
Неусредненное движение частицы в плоскости ху в
этом случае происходит по трохоиде.
Лит.: [lj Lorentz H. A., The theory of electrons and
its applications to the phenomena of light and radiant heat, 2 ed.,
Lpz.— N. Y., 1916 (рус. пер.— Теория электронов и ее приме-
применение к явлениям света и теплового излучения, 2 изд., М., 1956);
[2] Л а н д а у Л. Д., Л и ф ш и ц Е. М., Теория поля, 6 изд.,
М., 1973. В. В. Параил.
ЛУЗИНА ГИПОТЕЗА в теории мно-
множеств: мощность континуума есть мощность мно-
множества всех подмножеств, состоящих из счетных по-
порядковых чисел, т. е. 2^°=2^1. Л. г. совместна с сис-
системой аксиом Цермело — Френкеля теории множеств
и аксиомой выбора. Н. Н. Лузин [1] рассматривал эту
гипотезу как альтернативу к континуум-гипотезе,
т.к. 2^° = #1<2^1. Аксиома Мартина и отрицание
континуум-гипотезы влекут Л. г. Отрицание Л. г.
2^° <2 иногда также наз. гипотезой Лузина. Л. г.,
обозначаемая через (HL), или ее отрицание, к-рое обоз-
обозначается через (LH), используется при доказательстве
ряда теорем общей топологии. Напр., (LH) эквива-
эквивалентна одному из следующих утверждений: всякий
бикомпакт мощности, не превосходящей мощности
континуума, имеет всюду плотное подпространство,
удовлетворяющее 1-й аксиоме счетности; всякий диади-
ческтш бикомпакт мощности, не превосходящей мощ-
мощности континуума, метризуем. Из (LH) вытекают сле-
следующие предложения: всякое нормальное пространст-
пространство, удовлетворяющее 1-й аксиоме счетности и Суслила
условию, является коллективно нормальным; всякое
сепарабельное нормальное пространство Мура метри-
зуемо.
Лит.: [1] Лузин Н. Н., «Fundam. math.», 1935, v. 25,
p. 109—31: [2] M о с т о в с к и и А., Конструктивные множест-
множества и их приложения, пер. с англ., М., 1973.
В. А. Ефимов.
ЛУЗИНА КРИТЕРИЙ измеримости функ-
функции действительного переменного:
для того чтобы функция / (х) почти всюду конечная,
заданная на отрезке [а, Ь], была измеримой, необходи-
необходимо и достаточно, чтобы для любого в>0 существовала
непрерывная на [а, Ь] функция ц> (х) такая, что мера
множества
{х? [а, Ь]:/(*)??ф(*)}
была меньше е. Доказан Н. Н. Лузиным [1]. Другими
словами, почти всюду конечная функция является
измеримой тогда и только тогда, когда она становится
непрерывной, если пренебречь множеством сколь угод-
угодно малой меры.
Лит.: [1] Лузин Н. Н., «С. г. Acad. sci.», 1912, t. 154,
p. 1B88--90; [2] Натансон И. П., Теория функций ве-
вещественной переменной, 3 изд., М., 1974.
В. А. Ефимов.
ЛУЗИНА МНОЖЕСТВО, проективное мно-
множеств о,— подмножество полного сепарабелыюго
метрич. пространства, к-рое определяется по индукции
следующим образом. Л. м. класса 0 — есть борелев-
ские множества. Л. м. класса 2п+1 — это непрерыв-
непрерывные образы Л. м. класса 2п. Л. м. класса 2ге — это
дополнения к Л. м. класса 2п—1. В частности, Л. м.
класса 1, т. е. непрерывные образы борелевских мно-
множеств, наз. аналитическими множест-
множествам и, или А-м ножествами, или с у с л и н-
сними множествами. Понятие Л. м. принад-
принадлежит Н. Н. Лузину [1]. Если Р( есть Л. м. класса п,
то U i=iPi и П i=iPi — также Л. м. класса п. Если
PidX{ есть Л. м. класса л, лежащее в полном сепара-
бельном метрич. пространстве X/, то прямое произве-
произведение (конечное или счетное) 11;Р,- является Л. м.
класса п в пространстве П,Х,-. Л. м. нечетного класса п,
расположенное в пространстве X, совпадает с проек-
проекцией множества класса п — 1, расположенного в про-
произведении XXX. Пространство X иррациональных чи-
чисел интервала [0, 1] содержит для любого ге>0 Л. м.
класса п, к-рое не является Л. м. класса О; простран-
ство X содержит также множества, не являющиеся
Л. м.
Лит.: [1] Лузин Н. Н., «С. г. Acad, sci.», 1925, t. 180,
p. 1318—20; [2] e г о же, Лекции об аналитических множест-
множествах и их приложениях, М., 1953; [3] Куратовский К.,
Топология, т. 1, М., 1966. Б. А. Ефимов.
ЛУЗИНА ПРИМЕРЫ в теории функций
комплексного переменного — приме-
примеры, характеризующие граничные единственности
свойства апалитич. функций (см. [1], [2]).
1) Для любого множества Е меры нуль на единич-
единичной окружности Г= {z: |z| = l} H. H. Лузин построил
A919, см. [1]) функцию f(z), регулярную аналити-
аналитическую и ограниченную в единичном круге ?>={z:
\z\ <1} и такую, что f(z) не имеет радиальных гранич-
граничных значений вдоль каждого из радиусов, оканчиваю-
оканчивающихся в точках Е.
Аналогичный пример Н. Н. Лузина и И. И. При-
Привалова A925, см. [2], [3]) отличается лишь незначитель-
незначительными изменениями.
2) Н. Н. Лузин построил A925, см. [2]) также ре-
регулярные аналитич. функции /х(г) и /2(z)^0 в D, стре-
стремящиеся соответственно к бесконечности и нулю пи
всем радиусам, оканчивающимся в точках нек-рого
множества полной меры 2л на Г. Это множество Е пер-
первой категории по Бэру на Г.
См. также Граничные свойства аналитических функ-
функций, Лузина — Привалова теоремы, Предельное мно-
множество.
Лит.: [11 Лузин Н. Н., Собр. соч., т. 1, М., 1953.
с. 267—С9; [2] е г о же, там же, с. 280—318; [3] Привалов
И. И., Граничные свойства аналитических функций, 2 изд.,
М.—Л., 1950; [4] Л о в а т е р А., в сб.: Итоги науки и техники,
Математический анализ, т. 10, М., 1973, с. 99—259.
Е. Д. Соломеицсв.
ЛУЗИНА ПРИНЦИПЫ ОТДЕЛИМОСТИ — две тео-
теоремы, доказанные Н. Н. Лузиным в 1930 (см. [1]) в
дескриптивной теории множеств. Два множества Е и
Е' без общих точек, лежащие в евклидовом простран-
пространстве, В-отделимы, если существуют два борелев-
ских множества Н и Н' без общих точек, содержащие
соответственно множества Е и Е'. Первый Л. п. о.
состоит в том, что два непересекающихся аналитич.
множества всегда .б-отделимы. Так как существуют
два непересекающихся аналитич. дополнения, к-рые
Д-неот делимы, то имеет смысл определение: два мно-
множества ?\ и Ео без общих точек отделимы при помощи
аналитич. дополнений, если существуют два непере-
непересекающихся множества Н1 и 7/2, содержащие соответ-
соответственно ?j и Е2, каждое из к-рых есть аналитич. до-
дополнение. Второй Л. п.о. состоит в том, что если уда
лить из двух аналитич. множеств их общую часть, тс
оставшиеся части всегда отделимы при помощи ана-
аналитич. дополнедшй.
Лит.: [1] Лузин Н. Н., Лекции об аналитических мно-
множествах и их приложениях, М., 1953.
-Б. А. Ефимов.
ЛУЗИНА ПРОБЛЕМА — 1) Проблема теории три-
гонометрич. рядов, состоявшая в доказательстве
гипотезы Лузина о том, что ряд Фурье
ао(/)+2л=1 {ап (f) COS ПХ + Ь„({) Sin ПХ} (*)
каждой измеримой по Лебегу функции f(x), заданно»
на отрезке [0, 2л1. с конечным интегралом
$*"/»(*)*¦:
сходится почти всюду на [0, 2л]. Гипотеза высказана
Н. Н. Лузиным в 1915 в его диссертации (см. [1]
с. 219). Л. п. решена в 1966 в утвердительном смысле
Л. Карлесоном (см. Карлесоиа теорема). До работы
Л. Карлесона [2] не было даже известно, сходится ли
хотя бы в одной точке ряд Фурье каждой непрерывной
на отрезке [0,2я] функции.
Лит.: []] Л у з и н Н. Н., Интеграл и тригонометрический
ряд, 2 изд., М.— Л., 1951; [2] Carleson L., «Acta math.»
1966, v. 116, p. 135 — 57. Б. С. Кашин.
2) Ряд фундаментальных задач теории множеств,
поставленных Н. Н. Лузиным [1], для решения к-рых
он предложил метод резольвент. Именно,
нек-рая проблема Р теории множеств поставлена в ре-
резольвенту, если можно назвать множество точек Е та-
такое, что проблема Р решается положительно каждый
раз, когда можно назвать точку из Е, н решается отри-
отрицательно, если можно доказать, что множество Е
пусто. Само множество Е наз. резольвентой
проблемы Р.
Проблема 1. Будут ли все аналптич. дополне-
дополнения либо счетны, либо иметь мощность континуума?
Резольвента Е этой проблемы есть Лузина множество
класса не выше 3, т. е. если можно указать точку из
Е, то существует несчетное аналитич. дополнение без
совершенной части, а если Е пусто, то таких анали-
аналитич. дополнений не существует.
Проблема 2. Существуют ли неизмеримые по
Лебегу множества Лузина?
Проблема 3. Существует ли множество Лу-
Лузина без Бэра свойства?
Н. Н. Лузин предполагал, что проблемы 1, 2, 3 не-
неразрешимы. Эта гипотеза подтвердилась (см. [3], [4]).
Установлены связи между этими проблемами. Напр.,
из существования неизмеримого множества типа Аг
следует существование несчетного множества типа С А,
не содержащего совершенного подмножества. Получено
[5] положительное решение Л. п. о частях натурального
ряда, исходя из континуум-гипотезы пли отрицания
гипотезы Лузина.
Лит.: [J] Лузин Н. Н., «С. г. Acad. sci.», 1925, t. 181,
p. 279—8!; [2] e г о же, Собр. соч., т. 2, М., 1958; [3] Н о в и-
к о в П. С, «Тр. Матем. ин-та АН СССР», 1951, т. 38, с. 279—
316; [4] S о 1 о v а у R-, «Ann. Math.», 1970, v. 92,Ле 1, p. 1 —
56; [5] Н о в а к Й., «Чехосл. матем. ж.», 1953, т. 3, с. 385—95.
Б. А. Ефимов.
ЛУЗИНА ПРОСТРАНСТВО — несчетное топологнч.
^-пространство, в к-ром каждое нигде не плотное под-
подмножество счетно. Существование Л. п. на действитель-
действительной прямой вытекает из континуум-гипотезы. Из отри-
отрицания континуум-гипотезы и аксиомы Мартина следует,
что не существует Л. п. со счетной я-базой. В частно-
частности, с системой аксиом Цермело—Френкеля теории мно-
множеств и аксиомой выбора совместно утверждение, что
любое сепарабельное метрич. пространство не содер-
содержит Л. п. Существование метризуемых Л. п. доказано
при весьма широких предположениях о месте мощности
континуума в шкале алефов. Любое Л. п. X, лежащее
в сепарабельном метрич. пространстве У, обладает
следующим свойством: для любой последовательно-
последовательности {л,,} положительных чисел существует последова-
последовательность множеств {Ап} такая, что Х= U n=i.An и
Ь(Ап)<Хп, где б (Л) — диаметр множества А. Оно ин-
инвариантно относительно непрерывных отображений.
Любой непрерывный образ Л. п., лежащий в У, имеет
меру Лебега нуль и является нульмерным пространст-
пространством. Более того, любой непрерывный образ Л. и., ле-
лежащий в У, вполне несовершенен, т. е. не содержит
канторова совершенного множества. Из континуум-
гипотезы вытекает существование регулярного, наслед-
наследственно сепарабельного, наследственно финально ком-
компактного, экстремально несвязного Л. п. счетного
я-веса и мощности континуума.
Лит.: [1] Л у з и н Н. Н., «С. г. Acad. sci.», 1914, t. 158,
p. 1258—61; [2] Куратовский К., Топология, т. 1, М.,
1966. ' Б. А. Ефимов.
ЛУЗИНА РЕШЕТО — произвольное отображение
W : Q0—y2x, к-рое каждой двоичной дроби r?Q0 ста-
ставит в соответствие нек-рое подмножество WrdX.
Как правило, X предполагается полным сепарабель-
ным метрич. пространством. Введено Н. Н. Лузиным
[1]. Множество А точек х?Х таких, что сущест-
существует бесконечная последовательность г1<г2< . . . ,
удовлетворяющая условию x^Wri[)Wr2f\ . . ., наз.
просеянным через Л. p. W. Для каждой 4-опе-
рации существует Л. p. W такое, что результат этой
Л-операции просеивается через решето W. Основной ре-
результат, касающийся Л. р., состоит в том, что Лузина
множество и-го класса (или проективный класс Ln)
инвариантно относительно операции просеивания че-
через Л. р. для 0фпф2.
Лит.: [1] Лузин Н. Н., «Fundam. math.», 1927, t. 10,
p. 1—95; [2]Куратовский К., Топология, т. 1, М., 19f;<i.
Б. А. Ефимов.
ЛУЗИНА С-СВОЙСТВО — характеристическое свой-
свойство измеримой функции, конечной почти всюду на об-
области определения. Функция /(х), конечная почти всю-
всюду на [0, 1], о б л а д а е т на [0, 1] С-с в о п с т в о м,
если для любого е>0 существует на [0, 1] совершенное
множество Q с мерой >1—в, на к-ром f(x) непрерывна,
если ее рассматривать только на Q. Понятие С-свойства
было введено Н. Н. Лузиным [1], к-рый также доказал,
что для того, чтобы функция обладала С-свойством, не-
необходимо и достаточно, чтобы она была измерима и
конечна почти всюду на Е. Эта теорема Лузина (к р и-
терпи Лузина) обобщается на случай функции
многих переменных (см. [3], [4]) и является одной
из основных теорем метрич. теории функций.
Лит.: [1] Лузин Н. Н., «Матем. сб.», 1912, т. 28, в. 2,
с. 266—94; [2] е г о же, Собр. соч., т. 1, М., 1953; [3J С а к с
С, Теория интеграла, пер. с англ., М., 1949; L4] К а м к е Э.,
Интеграл Лебега — Стилтьеса, пер. с нем., М., 1959.
А. А. Конюшков.
ЛУЗИНА Л-СВОЙСТВО, «нуль-свойств о»,
функции f(x), непрерывной на отрезке [а, Ь]: для лю-
любого множества Ed[a, b] с мерой mes ? = 0 образ этого
множества f{E) также имеет меру нуль. Введено
Н. Н. Лузиным в 1915 (см. [1]). Имеют место следую-
следующие утверждения.
1) Функция /^const на [а,Ь] такая, что /' (х) = 0 почти
всюду на [а, Ь], не обладает Л. N-c.
2)" Если f(x) не обладает Л. Аг-с., тона [а, Ь] сущест-
существует совершенное множество Р меры нуль такое, что
mes f(P)>0.
3) Абсолютно непрерывная функция обладает
Л. Л'-с.
4) Если f{x) обладает Л. Л'-с. и имеет на [а, Ь]
ограниченное изменение, то / абсолютно непрерывна на
[а, Ь] (теорема Банаха — Зарецкого).
5) Если f (х) не убывает на [а, Ь], причем f (х) ко-
конечна на [а, Ь], то / обладает Л. Л'-с.
6) Для того чтобы для любого измеримого множест-
множества Еа[а, Ъ\ множество f(E) было измеримым, необхо-
необходимо и достаточно, чтобы / обладала на [а, Ъ] Л. Л'-с.
7) Функция f(x), обладающая Л. N-c, имеет /' (,т)
на множестве, любая непустая порция к-рого имеет
положительную меру.
8) Для любого совершенного нигде не плотного мно-
множества Pd[a, b] существует функция/(х), обладающая
Л. Л'-с. на [я, Ъ], у к-рой /' (х) не существует в каждой
точке множества Р.
Понятие Л. Л'-с. обобщается на функции многих пе-
переменных и функции более общей природы, опреде-
определенные на пространствах с мерой.
Л«т.:[1]Лузин Н. Н., Интеграл и тригонометрически! г
ряд, 2изд.,М.—Л., 1951. А. А. Конюшкаи
ЛУЗИНА ТЕОРЕМА — 1) Л. т. в теории функции
комплексного переменного (локальный прин-
принцип конечной площади) — результат
Н. Н. Лузина, обнаруживающий связь между гранич-
граничными свойствами аналитич. функций в единичном круге
и метрикой римановых поверхностей, на к-рые они
отображают круг (см. [1], [2]).
Пусть V — любая область внутри единичного круга
D={z: |z|<l} плоскости комплексного переменного
z, примыкающая к нек-рой дуге а единичной окружно-
окружности r={z: |z| = l}, a
— регулярная аналитич. функция в D. Тогда, если
площадь римановой поверхности, являющейся образом
области V при отображении w=f(z), конечна, то ряд
сходится почти всюду на дуге а.
В связи с этой теоремой Н. Н. Лузин сформулировал
гипотезу, известную также как проблема Лузи-
н а. Точку е'е° ? Г наз. точкой Лузина
функции w=f(z), если w=f(z) отображает каждый круг,
изнутри касающийся Г в точке е'9°, на область беско-
бесконечной площади на римановой поверхности функции
w—j{z). Гипотеза Лузина состоит в том,
что существуют ограниченные аналитич. функции в D
такие, что каждая точка Г является для них точкой
Лузина. Гипотеза Лузина впервые была подтверждена
полностью в 1955 (см. [3]).
Лит.: 11] Л у 3 и н Н. Н., «Докл. АН СССР», 1947, т. 56, At 5,
с. 447—50; [2] е г о же, Собр. соч., т. 1, М., 1953, с. 318—30;
[3] Л о в а т е р А., в сб.: Итоги науки и техники. Математиче-
Математический анализ, т. 10, М., 1973, с. 99—259.
Е. Д. Соломенцее.
2) Л. т. в дескриптивной теории множеств можно ус-
условно разбить на три цикла. Первый и основной цикл
направлен на изучение эффективных множеств (анали-
(аналитических, борелевских, лузинских (проективных)
множеств). Сюда относится Лузина принципы отделимо-
отделимости и теорема о существовании Лузина множеств любого
класса. Второй цикл представляет собой изучение за-
задач, лежащих на пути к решению континуум-гипотезы
и проблемы мощности С А -множеств. Здесь выделяется
теорема Лузина—Серпиньского о разбиении отрезка на
#i борелевских множеств, к-рое определяется соответ-
соответствующим Лузина решетом, а также Л. т. о покрытии:
пусть Е и А — непересекающиеся аналитич. множества
— разложение множества Х~\А на конституанты, тог-
тогда существует такой индекс а.о<^4)^, что
Третий цикл содержит результаты, полученные с ис-
использованием аксиомы выбора. Сюда же примыкают
философские работы по теории множеств. Здесь выде-
выделяются Л. т. о существовании несчетного множества
1-й категории на всяком совершенном множестве, о раз-
разбиении интервала на несчетное множество неизмеримых
множеств. Завершает этот цикл Л. т. о частях нату-
натурального ряда, отражающие нек-рые свойства нароста
p./V\Ar Стоуна — Чеха бикомпактного расширения
$N натурального ряда N.
Лит.: [1] Л у з и н Н. Н., Собр. соч., т. 2, М., 1958.
Б. А. Ефимов.
ЛУЗИНА — ДАНЖУА ТЕОРЕМА — см. Данжуа —
Лузина теорема.
ЛУЗИНА — ПРИВАЛОВА ТЕОРЕМЫ в теории
функций комплексного переменного —
классические результаты Н. Н. Лузина и И. И. При-
Привалова, выясняющие характер граничного единствен-
единственности свойства аналитич. функций (см. [1]).
1) Пусть f(z) — мероморфная функция комплекс-
комплексного переменного z в односвязной области D со спрям-
спрямляемой границей Г. Если / (z) принимает угловые гра-
граничные значения нуль на множестве EciT положитель-
положительной меры Лебега на Г, то /(z)=0 в В. Не существует
мероморфной в D функции, имеющей бесконечные уг-
угловые граничные значения на каком-либо множестве
ЕаТ положительной меры.
2) Пусть w=f(z) — мероморфная в единичном круге
D= {z: |z|<l} функция, отличная от константы и име-
имеющая радиальные граничные значения (конечные или
бесконечные) на множестве Е, расположенном на дуге о
единичной окружности Г= {z: |z| = l}, метрически
плотном и второй категории по Бэру на а. Тогда мно-
множество W ее радиальных граничных значений на Е
содержит по крайней мере две различные точки. Мет-
Метрическая плотность Е па а означает, что
любая порция Е на а имеет положительную меру. От-
Отсюда следует, что если радиальные граничные значения
f(z) на множестве Е указанного типа равны нулю, то
f(z)=(i в D. Далее, не существует мероморфной функ-
функции в единичном круге, принимающей бесконечные ра-
радиальные граничные значения на множестве Е ука-
указанного типа.
Н. Н. Лузин и И. И. Привалов (см. [1], [2]) построили
примеры, показывающие, что условия метрич. плотно-
плотности и 2-й категории по отдельности не являются доста-
достаточными для того, чтобы выполнялось утверждение
теоремы 2.
См. также Граничные свойства аналитических функ-
функций, Лузина примеры, Предельное множество, Привалова
теорема, Риссов теорема.
Лит.: [1] Лузин Н. Н., Привалов И. И., «Ann.
sci. Ecole norm, super.» C), 1925, t. 42, p. 143—91; [2] Прива-
Привалов И. И., Граничные свойства аналитических функций,
2 изд., М.— Л., 1950; [3] Л о в а т е р А., в сб.: Итоги науки и
техники. Математический анализ, т. 10, М., 1973, с. 99—2Г>9.
Е. Д. Соломенцев.
ЛУПА — квазигруппа с единицей, т. е. с таким эле-
элементом е, что хе^ех = х для любого элемента х из ква-
квазигруппы. Значение Л. в теории квазигрупп определя-
определяется следующей теоремой: всякая квазигруппа изо-
изотопна (см. Изотопия) нек-рой Л. Поэтому одной из
основных задач теории квазигрупп является описание
Л., к-рым изотопны квазигруппы данного класса.
С каждой Л. связаны три ядра. Множество
Nt = {а | ах-у = а-ху, для всех х, у ? Q}
элементов из Л. Q (•) наз. левым ядром. Анало-
Аналогично определяются среднее и правое ядра.
Они всегда существуют в Л. Их пересечение наз. я д-
р о м лупы. Каждое ядро — ассоциативная подлу-
подлупа, т. е. подгруппа в (?(•). Соответственные ядра изо-
изотопных Л. изоморфны. Существуют Л. с любыми напе-
наперед заданными ядрами. Л. Q (•), изотопная группе Q (•),
является сама группой и изоморфна группе Q(-) (тео-
(теорема А л б е р т а). В частности, изотопные группы
изоморфны. Нек-рые другие классы Л. также обладают
этим свойством, напр, свободные лупы. Л. Q(-) наз.
fi-лу пой, если любая Л., изотопная Q(-), будет ей
изоморфна.
На Л. распространяются многие понятия и результа-
результаты теории групп. Однако нек-рые обычные свойства
групп могут и не иметь места для Л. Так, в конечных
Л. теорема Лагранжа (о том, что порядок подгруппы
делит порядок группы), вообще говоря, не имеет места.
Если тем не менее для Л. справедлива теорема Лагран-
Лагранжа, то такую Л. наз. лагранжевой. Если вся-
всякая подлупа Л. <?(•) лагранжева, то говорят, что Q(-)
обладает свойством L'. Необходимым и достаточ-
достаточным условием, чтобы Л. Q (•) обладала свойством L',
является следующее: <?(•) должна обладать такой нор-
нормальной цепью
где Qi нормальная подлупа в Q;-i, что Qi^jQj для всех
? = 1, 2, . . ., п обладает свойством V.
Наиболее изученным и наиболее близким к группам
является класс Муфанг луп. Основная теорема о них
(теорема Муфанг): если три элемента а, Ь, с
такой Л. связаны ассоциативным законом, т. е.
ab -c=a -be,
то они порождают ассоциативную подлупу, т. е. группу.
В частности, всякая лупа Муфанг д и а с с о ц и а т и в-
н а, т. е. любые ее два элемента порождают ассоциатив-
ассоциативную подлупу. Свойство Л. быть лупой Муфанг явля-
является универсальным, т.е. инвариантным при
изотопии: любая Л., изотопная лупе Муфанг, сама
является лупой Муфанг.
Одним из наиболее общих классов Л. является класс
IP -луп, или луп со свойством обрати-
обратимости. Они определяются тождествами
~1х-ху = у и ух-х~1 = у.
Здесь ~хх и х~г соответственно левый и правый обрат-
обратные элементы для х. Всякая лупа Муфанг будет IP-
лупой. В /Р-лупе ядра совпадают. Ядро лупы Муфанг
является нормальной характеристической подлупой.
Свойство Л. быть /Р-лупой не является универсаль-
универсальным. Более того, если всякий изотоп нек-рой /Р-лупы
<?(•) есть 1Р-луп&, то Q(-) является лупой Муфанг.
Более общим, чем класс IP-луп, является класс
WIP -луп, или луп со свойством ослаб-
ослабленной обратимости. Они определяются
тождеством х(ух)~1=у~г. Это тождество универсально,
если
(ух) (®yz-y) = {y-xz) У
для всех х, у, z?Q, где Qy — нек-рый автоморфизм.
В этом случае ядро WI Р-лупы является нормальным и
факторлупа по ядру будет лупой Муфанг. Частным слу-
случаем WIP-луп являются CI-л у п ы, или скрещен-
но-обратимые лупы, определяемые тождест-
тождеством (ху) ж~1 = г/.
Обобщением луп Муфанг являются (левые) лупы
Бола, в них выполняется тождество
x(y-xz) = (x-yx)z.
Они инвариантны при изотопии и моноассоциа-
моноассоциативны, т. е. каждый элемент такой Л. порождает
ассоциативную подлупу.
Важным понятием теории квазигрупп и Л. является
понятие псевдоавтоморфизма. Подстановка ер Л. <?(•)
наз. левым псевдоавтоморфизмом,
если существует такой элемент a?Q, что выполняется
равенство
ф (.гг/)-а = ф (,г) (фг/-а) для всех х, у (= Q,
и наз. правым псевдоавтоморфизмом,
если существует такой элемент b?Q, что
Ь-ф (ху) = (Ь-фг) фу для всех х, у (= Q.
Если ф — одновременно левый и правый псевдоавто-
псевдоавтоморфизм, то ф паз. псевдоавтоморфизмом, а
элементы а и Ь — соответственно левым и пра-
правым компаньонами. В Л. автоморфизм —
частный случай исевдоавтоморфизма. Каждый псевдо-
псевдоавтоморфизм /Р-лупы индуцирует автоморфизм в ее
ядре, а в коммутативной лупе Муфанг всякий псевдоав-
псевдоавтоморфизм является автоморфизмом.
В теории Л. значительную роль играют внутренние
подстановки. Подстановка а из ассоциированной груп-
группы G Л. Q (•) с единицей е наз. внутренней, если
ае=е. Совокупность / всех внутренних подстановок
является подгруппой группы G и наз. группой
внутренних подстановок. Группа / по-
порождается подстановками трех видов:
xy = LxyLL' R ~RxyRR T = RXL
С помощью внутренних подстановок определяются
А- л у п ы — лупы, для к-рых все внутренние подста-
подстановки являются автоморфизмами. Если Д-лупа одно-
одновременно является //"-лупой, то она диассоциативна.
Коммутативные диассоциативные Д-лупы являются лу-
лупами Муфанг. Для коммутативных луп Муфанг внут-
внутренние подстановки являются автоморфизмами.
Нек-рые определения из теории групп переносятся
и на Л. Так, Л. наз. г а м и л ь т о н о в о й, если вся-
всякая ее подлупа нормальна, Абелевы группы также счи-
считаются гамильтоновыми Л. Моноассоциативные га-
мильтоновы Л. с элементами конечного порядка явля-
являются прямыми произведениями гамильтоновых р-луп
(р-лупа определяется аналогично р-группе). Диассоциа-
Диассоциативные гамильтоновы Л. будут либо абелевыми груп-
группами, либо прямым произведением АХ ТХН, где А —
абелева группа, элементы к-рой имеют нечетный по-
порядок, Т — абелева группа экспоненты 2, а Н — не-
некоммутативная Л., удовлетворяющая нек-рым допол-
дополнительным условиям.
Л. Q (•) наз. линейно (ч а с т и ч н о) упоря-
упорядоченной, если Q линейно (частично) упорядочен-
упорядоченное множество (относительно <:) и из а<:& следует
ас < be, ca «^ cb,
и обратно. Если в линейно упорядоченной Л. центр
имеет конечный индекс, то <?(•) центрально нильпо-
тентна. Решеточно упорядоченные Л. с условием ми-
минимальности для элементов являются свободными абеле-
абелевыми группами.
Л. изучались и с помощью ассоциированных групп.
Доказано, напр., что существует взаимно однозначное
соответствие между нормальными подлупами Л. и нор-
нормальными делителями соответствующей ассоциирован-
ассоциированной группы.
Лит. см. при статье Квазигруппа. В. Д. Белоусов.
ЛУПА аналитическая — аналитическое мно-
многообразие М, наделенное структурой Л., основные опе-
операции к-рой (умножение, левое и правое деление) яв-
являются аналитич. отображениями МХМъ М. Если е —
единица лупы М, g{t), h{t) —аналитич. пути, выходя-
выходящие из е и имеющие в точке е касательные векторы а, Ъ,
то касательный вектор c=ab век пути k(t), где
k(fi)=g(t)h(t)![h(t)
есть билинейная функция векторов а, Ь. Касательное
пространство Т(М) в точке е с операцией умножения
с=аЬ наз. касательной алгеброй Л. М.
Координаты (х1, . . ., х") в нек-рой окрестности U
элемента е=@, . . .,0) наз. каноническими
1-го рода, если для любого вектора а —(а1, . . ., ап)
кривая x(t)=(alt, . . ., ant) является локальной одно-
параметрич. подгруппой (|г|<:е) с касательным векто-
вектором а в точке е (см. [1]). Аналптич. Л. с ассоциативны-
ассоциативными степенями обладает канонич. координатами 1-го
рода [2]. В этом случае отображение а^>-х(\), опреде-
определенное для достаточно малых а, позволяет отождест-
отождествить U с окрестностью начала координат в Т (М) и
наделить Т (М) строением локальной аналитич. лупы
Ма. Если аналитич. лупа М альтернативна, т. е. лю-
любые два ее элемента порождают подгруппу, то каса-
касательная алгебра Т(М) бинарно лиева, а умножение
(х, у)—>-х о у в Мо выражается Кэмпбелла — Хаусдорфа
формулой. Любая конечномерная бинарно лиева ал-
алгебра над полем R есть касательная алгебра одной и
(с точностью до локальных изоморфизмов) только одной
локальной альтернативной аналитич. Л. [1].
Наиболее полно изучены аналитические Муфанг лупы.
Касательная алгебра аналитич. лупы Муфанг удовлет-
удовлетворяет тождествам
х2=0, J(r, у, .rz)'-=J(x, у, z)x,
где
J(x, у, z)-=(xy)z+(yz)x-\-(zx)y;
такие алгебры наз. алгебрами Мальцева.
Обратно, любая конечномерная алгебра Мальцева над
R является касательной алгеброй нек-рой односвязной
аналитич. лупы Муфанг М, определенной однозначно
с точностью до изоморфизма (см. [2], [3]). Если М' —
связная аналитич. лупа Муфанг с той же касательной
алгеброй и, следовательно, локально изоморфная М,
то существует эпиморфизм М—уМ', ядро к-рого Н
есть дискретная нормальная подгруппа в М; при этом
фундаментальная группа п(М') пространства М'
изоморфна //. Если ср — локальный гомоморфизм одно-
односвязной аналитич. лупы Муфанг М в связную анали-
аналитич. лупу Муфанг М', то ер однозначно продолжается
до гомоморфизма М в М'. Пространство односвязной
аналитич. лупы Муфанг с разрешимой касательной ал-
алгеброй Мальцева аналитически изоморфно евклидову
пространству R" (см. [3]).
Лит.: [1] М а л ь ц е в А. И., «Матем. сб.», 1955, т. 36,
в. 3, с. 569—76; [2] Кузьки н Е. Н., «Алгебра и логика»,
1971, т. 10, в. 1, с. 3 — 22; [3] Кердмап Ф. С, «Докл. АН
СССР», 1979, т. 249, в. 3, с. 533—36. Е. Н. Кузьмин.
ЛУЧ — то же, что полупрямая.
ЛУЧЕВАЯ ФУНКЦИЯ — действительная функция
F(x), заданная на ге-мернон пространстве R" и удов-
удовлетворяющая следующим условиям: F(х) непрерывна,
неотрицательна и однородна (т. е. F (xx)=-xF (x) для
любого действительного числа т5==0). Л. ф. F{x) наз. п о-
л в ж и т е л ь н о й, если F (х)^>0 для всех хфО, и наз.
симметрической, если F(—x)=F(x). Л. ф. наз.
выпуклой, если для любых х, j/^R"
F(x+y)<.F(x) + F(y).
Для любой Л. ф. F(x) найдется постоянная с=ср,
для к-рой
F(x)*sic\x\, x?R".
Если F(x) положительна, то найдется и постоянная
с' = с^>0, для к-рой
F (я) Зге' | х\, x^R".
Множество E точек x?Rn с условием
является звездным телом. Обратно, для каждого от-
открытого звездного тела (S найдется единственная
Л. ф. F&(x), для к-рой
Звездное тело К/г ограничено тогда и только тогда,
когда его Л. ф. F(x) положительна. Если F(х) — сим-
метрич. функция, то ©/г — симметрично относительно
точки 0; верно и обратное. Звездное тело будет выпук-
выпуклым телом тогда и только тогда, когда F(x) — выпук-
выпуклая Л. ф.
Лит.: [1] Кассе л с Д ш.-В.-С, Введение в геометрию
чисел, пер. с англ., М., 1965. А. В. Малышев.
ЛУЧЕВОЙ МЕТОД — метод формального нахожде-
нахождения высокочастотной асимптотики решения задач тео-
теории дифракции и распространения волн. Л. м. состоит
из совокупности приемов нахождения того или иного
варианта геометрического приближения (г. п.) к реше-
решению соответствующей задачи.
Пусть, напр., волновой процесс описывается волно-
волновым уравнением
l- utt — Аи =0.
1(ж, у, z) п
Подстановка ряда г. п. в волновое уравнение и прирав-
приравнивание нулю коэффициентов при последовательных
степенях l/м (параметр со соответствует частоте коле-
колебаний) приводят к соотношениям
7=0, 1, 2, ...,
пз к-рых первое — эйконала уравнение, остальные урав-
уравнения наз. уравнениями переноса. -Это —
рекуррентная последовательность линейных уравнений
вдоль лучей, т. е. экстремалей функционала Ферма
(см. Ферма принцип).
Если заданы поверхности 25,на к-рых выполняются
классические однородные краевые условия и вектор
ут некасателен к 2 s, то по заданному г. п. можно найти
отраженное или отраженное и преломленное г. гг., к-рые
в сумме будут формально удовлетворять краевым ус-
условиям. Пусть, напр., на 2 выполняется краевое ус-
условие Дирихле u|v = 0, тогда отраженное г. п. ищется в
виде
г • ,t uV-» UTP m
иогр — ехР I— гш " — T0Tp)J > ' . A)
Формальное выполнение краевого условия приводит к
равенствам
„OTD I _ и • I 1 0 4 9
и . к 12 — / | ?' / — ' ' ^, . . .
Из первого условия следует классич. закон отражения
лучен: «угол падения равен углу отражения». Равен-
Равенства для иутр задают начальные данные для уравнений
переноса, к-рым удовлетворяют и°тр. Таким образом,
задание «падающей волны» полностью определяет от-
отраженную волну A). Аналогично рассматривается за-
задача преломления на границе раздела двух сред.
В окрестности особенностей поля лучей г. п. непри-
неприменимо и приходится пользоваться более сложными
разложениями, напр, тем или иным вариантом метода
эталонных задач и дифракционного пограничного слоя
(из вариантов последнего, по-видимому, наиболее важ-
важным является метод параболич. уравнения).
Дополненный указанным образом Л. м. позволяет
строить формально высокочастотные разложения доста-
достаточно широкого класса дифракционных задач. По-
видимому, практически всегда такие разложения яв-
являются асимптотическими разложениями решений.
В такой общности это утверждение не доказано, уста-
установлена его справедливость лишь в частных случаях
(когда удается построить явное решение или получить
равномерную по со оценку нормы оператора, обратного
к волновому при рассматриваемых условиях). Одномер-
Одномерным вариантом Л. м. является метод ВКБ, квантовоме-
ханическим — квазиклассическое приближение. Л. м.
успешно применяется при изучении высокочастотных
волн любой природы (напр., упругих, электромагнит-
электромагнитных). Более далеким аналогом Л. м. является Л. м.
для волн Рэлея, распространяющихся вдоль поверх-
поверхности упругого тела произвольной формы, для волн на
поверхности тяжелой жидкости, слабо изогнутых упру-
упругих или акустич. слоев и т. п.
Одно из обобщений получается, если г. п. заменить
рядом:
и ~ ехр [— ipifi (t, х)] \*°° . ' ¦ • B)
Теорию таких разложений наз. пространственно-вре-
пространственно-временной геометрич. оптикой, или теорией волн, модули-
модулированных как по частоте, так и по амплитуде. Разло-
Разложения вида B) применяют также и в том случае, когда
уравнения, описывающие волновые процессы, не яв-
являются дифференциальными (диспергирующие среды).
Разложения B) используют как в случае дифференци-
дифференциальных, так и для псевдодифференциальпых уравнений.
Разработаны нелинейные аналоги (см. [2]).
Другие варианты Л. м. связаны с рассмотрением раз-
разрывных уравнений: во многих ситуациях разрывы опи-
описываются с помощью нестационарного варианта Л. м. и
распространяются вдоль лучей. На нестационарном
аналоге Л. м. основан т. н. метод Адамара исследования
задачи Коши линейных гиперболич. уравнений 2-го
порядка и его обобщения на системы линейных гипер-
гиперболических дифференциальных и псевдодифференци-
псевдодифференциальных уравнений.
Лит.: [1] Б а б и ч В. М., Булдырев В. С, Асимпто-
Асимптотические методы в задачах дифракции коротких волн, М., 1972;
[2] У и з е м Д ж. Б., Линейные и нелинейные волны, пер. с
англ., М., 1977; [3] Б о р о в и к о в В. А., К и н б е р Б. Е.,
Геометрическая теория дифракции, М., 1978. В. М. Бабич.
ЛЬЕНАРА УРАВНЕНИЕ — нелинейное обыкновен-
обыкновенное дифференциальное уравнение 2-го порядка
х'' + f (х)х' + х = 0. (*)
Это уравнение описывает динамику системы с одной сте-
степенью свободы при наличии линейной восстанавливаю-
восстанавливающей силы и нелинейного затухания. Если функция
f(x) обладает следующим свойством:
/ (х) < О при малых | х |,
¦/ (х) > 0 при больших | х |,
т. е. если при малых амплитудах система поглощает
энергию, а при больших происходит диссипация, то в
системе можно ожидать самовозбуждение колебаний
(возникновение автоколебаний). Впервые достаточные
условия возникновения автоколебаний в системе (*)
доказал А. Льенар [1].
Л. у. тесно связано с Рэлея уравнением. Важным
частным случаем Л. у. является Ван дер Поля уравне-
уравнение. Вместо уравнения (*) часто удобно рассматривать
систему
x' = v, i/ = —х—f(x)v
(автоколебательному процессу в системе (*) адекватен
устойчивый предельный цикл на фазовой плоскости
х, v) или эквивалентное ей уравнение
dv - x-f (x)v
dx v
Если ввести новую переменную y = x'-\-F(x), где F(х) =
= \ /(|) а%, то уравнение (*) переходит в систему
x' = y — F(x), у' = —х.
Более общими, чем Л. у., являются уравнения
x"+<f(x,x')x'
Основной интерес представляет выяснение возможно
более широких достаточных условий, при к-рых эти
уравнения имеют единственное устойчивое периодич.
решение. Подробно изучалось также неоднородное
Л. у.
и его обобщения.
Лит.: [1] L i ё и а г d A., «Rev. gen. electr.», 1928, t. 23,
p. 901 —12, 946 — 54; [2] Андронов А. А., В и т т А. А.,
X a it к и н С. Э., Теория колебаний, 2 изд., М., 1959; [3] Сан-
соне Д ж., Обыкновенные дифференциальные уравнения, пер.
с итал., т. 2, М., 1954; [4] Л е ф ш е ц С, Геометрическая тео-
теория дифференциальных уравнений, пер. с англ., М., 1961;
[5] Р е и с с и г Р., С а н с о н е Г., К о н т и Р., Качест-
Качественная теория нелинейных дифференциальных уравнений, пер.
с нем., М., 1974. Н. X. Розов.
ЛЬЕНАРА — ШИПАРА КРИТЕРИЙ — модифика-
модификация Рауса — Гурвица критерия, сводящая все вы-
вычисления в нем к вычислению главных миноров только
четного (или только нечетного) порядка матрицы Гур-
шща.
Пусть дан многочлен
f (Х) = аох» + а1х"-*+...+а„, а0 > 0, (*)
H — его матрица Гурвица и Л,- — ее главные миноры
порядка i, i=l, 2, . . ., п.
Критерий Льенара — Шипара: любое
из следующих четырех условий является необходимым
и достаточным для того, чтобы все корни многочлена *
с действительными коэффициентами имели отрицатель-
отрицательные действительные части:
1) ап > 0, а„_2 > 0. .. ., Дх > О, Д3 > 0, ...;
2) ап > 0, а„_2 > 0, ..., Д2 > 0, Д4 > 0, ...;
3) а„ > 0, а„_! > 0, а„_3 > 0, ..., Дх > О,
Дз > 0, .. .;
4) а„ > 0, о„_! > 0, а„_3 > 0, ..., Д2 > О,
Д4>0, ....
Критерий установлен А. Льенаром и А. Шппаром [1].
Лит.: [1] L i 6 n a r d А., С h i р а г t H., «J. math, pures
et appl.», 1914, t. 10, p. 291^346; [2] Гантмахер Ф. P.,
Теория матриц, 3 изд., М., 1967. И, В. Проскуряков,
ЛЮКСЕМБУРГА НОРМА — функция
|j х [,Ш) = inf {k:X > 0, См (Х-1^ (<) ^ <1},
где М (и) — четная выпуклая функция, возрастающая
при положительных U.
Игл и'1 М (и) =lim и (М (и))-1 = 0,
и ->¦ о
мно-
мноизучены
М(и)>0 при и>0, G — ограниченное замкнутое
жество в R". СвоIства это!! нормы были изучены
В. Люксембургом [1]. Л. н. эквивалентна норме Ор-
лича (см. Орлича пространство) и
Если функции М (и) и Аг(и) дополнительны друг к дру-
другу (см. Орлича класс), то
|j X ||д, =SUP \^a'(t)y (t) df. [i у \\iN) < 1 j .
Если Хя(*) — характеристич. функция измеримого
подмножества EaG, то
Лит.: [1] Luxemburg W., Banach function spaces,
[s. 1.], 1955; [2] К р а с н о с е л ь с к и й М. А., Р у т и ц-
к и й Я. Б., Выпуклые функции и пространства Орлича, М.,
1958. Е. М. Семенов,
ЛЮРОТА ПРОБЛЕМА — проблема характеризации
подполей поля рациональных функций.
В 1876 Ж. Люрот [1] (см. также [2]) доказал, что
всякое подполе поля рациональных функций от одной
переменной к (х), содержащее поле к и отличное от к,
изоморфно полю к(х) (теорема Л ю р о т а). Во-
Вопрос о том, верно ли аналогичное утверждение для
подполей R поля k(xt, . . ., х„), Л A, Як ^2
вестен как проблема Люрот а.
Пусть X — алтебраич. многообразие, являющееся
моделью (см. Минимальная модель) поля R, тогда вло-
вложение R-=k(X)dk(x1, . . ., х„) определяет рациональ-
рациональное отображение / : Р"^>-Х, образ к-рого плотен в X.
Многообразия, для к-рых существует такое отображе-
отображение на них проективного пространства, ная. у н и р а-
ц и о н а л ь н ы м и. Рациональными наз.
многообразия, бирационально изоморфные Рт. На гео-
метрпч. языке Л. п. может быть сформулирована сле-
следующим образом: является ли всякое унпрациональное
многообразие X рациональным? Без ограничения общ-
общности можно предполагать, что dim Х = п, т. с. что R
имеет степень трансцендентности, равную п.
В случае и=1 положительное решение Л. п. для
любого основного поля к дает сформулированная вы-
выше теорема Люрота. Для п = 2 и алгебраически зам-
замкнутого поля к характеристики 0 проблема положи-
тельно решена Г. Кастельнуово (G. Castelnuovo)
в 1893. Из критерия рациональности Г. Кастельнуово
следует также положительное решение Л. п. для таких
поверхностей X над алгебраически замкнутым полем
произвольной характеристики, для к-рых существует
сепарабельное отображение / : Р2-+Х (см. [7]). Для
несепарабельных отображений / существуют примеры,
дающие отрицательное решение Л. п. для нолей простой
характеристики. В случае алгебраически незамкну-
незамкнутого поля к такими примерами являются минимальные
кубич. поверхности в Р3, обладающие А--точками.
Для трехмерных многообразий Л. п. также решается
отрицательно (см. [4], [5], [6]). Доказана [5] нерацио-
нерациональность трехмерной кубической гиперповерхности,
к-рая, как известно, унирациональна. Для доказа-
доказательства был найден новый метод, основанный на срав-
сравнении промежуточного якобиана кубики с якобианами
кривых. Доказана 14] нерациональность гладких трех-
трехмерных квартик. Для конструкции контрпримеров ис-
использована [6] в качестве инварианта группа Брау-
эра многообразия (группа кручений в трехмерных кого-
мологиях). Этот бирациональный инвариант использо-
использован также для построения контрпримеров во всех раз-
раз^З
мерностях ^
Лит.: [llLiiroth .1., «Math. Ann.», 1876, Bd 9, S. 163 —
Co; [2] Ван дер В а р д е н Б. Л., Алгебра, пер. с нем.,
М., 1976; [3] Манин Ю. И., Кубические формы, М., 1972;
UJ И с к о в с к и х В. А., Манин Ю. И., «Матем. сб.»,
1971 т. 86, № 1, с. 140—66; [5] К л е м е н с К. Г., Г р и ф-
ф и т с Ф. С, «Математика», 1972, т. 16, №6, с. 3—32; 1973,
т. 17, № 1, с. 3 — 41; [6j Art in M., Mnmlord D., «Proc.
London Math. Soc», 1972, v. 25, MS 1, p. 75—95; [7] Z а г i s-
ki O., «Amer. J. Math.», 1958, v. 80, p. 146—84.
ЛЯПУНОВА ПОВЕРХНОСТИ И КРИВЫЕ — класс
поверхностей и кривых, обладающих достаточно хоро-
хорошими свойствами гладкости, введенный в теории по-
потенциала А. М. Ляпуновым в кон. 19 — нач. 20 вв.
Поверхность S в трехмерном евклидовом простран-
пространстве R3 наз. поверхностью Ляпунова,
если выполнены следующие три условия (условия
Ляпунова): 1) в каждой точке S существует опре-
определенная касательная плоскость и, следовательно, нор-
нормаль; 2) существует такое число г>0, одно и то же для
всех точек S, что если взять часть 2 поверхности S,
попавшую внутрь сферы Ляпунова В (j/0, r)
с центром в любой точке yo?S радиуса г, то прямые,
параллельные нормали к S в точке у0, встречают 2
не более чем один раз; 3) существуют такие два числа
А >0 и К, 0<^<:1, одни и те же для всей поверхности S,
что для любых двух точек ylt y2?S выполняется нера-
неравенство:
где 9 — угол между нормалями к S в точках уг и у2.
Иногда к этим трем условиям добавляются требования
замкнутости S и того, чтобы телесный угол, под к-рым
любая часть а поверхности S видна из произвольной
точки x^R3, был равномерно ограничен.
Условия Ляпунова обобщаются для гиперповерхно-
гиперповерхностей в пространстве R", и^З.
Аналогично, простая непрерывная кривая L на
плоскости R2 наз. кривой Ляпунова, если она
удовлетворяет следующим условиям: 1') в каждой точке
L существует определенная касательная и, следова-
следовательно, нормаль; 3') существуют такие два числа А >0 и
Я, 0<Л<:1, одни и те же для всей кривой L, что для
любых двух точек уи уг^Ь выполняется неравенство
(*), где 6 — угол между касательными или нормаля-
нормалями к L в точках уи у2. Условие Ляпунова 2) здесь
вытекает из 1') и 3'). Кривые Ляпунова представляют
собой подкласс простых гладких кривых.
Лит.: [1] Л я п у н о в А. М., О некоторых вопросах, свя-
связанных с задачей Дирихле, в его кн.: Собр. соч., т. 1, М., 1954,
с. 45—47; 48—100; [2] С о б о л е в С. Л., Уравнения математи-
ческой физики, 4 изд., М., 1966; [3] Владимиров В. С,
Уравнения математической физики, 2 изд., М., 1971, гл. 5; [4]
М у с х е л и ш в и л и Н. И., Сингулярные интегральные
уравнения, 3 изд., М., 1968, гл. 1. Е. Д. Соломенцев.
ЛЯПУНОВА ПРЕОБРАЗОВАНИЕ — гладко завися-
зависящее от параметра i?R линейное невырожденное преоб-
преобразование L{t) : R«-^R« (или L(t) : С"-»-С"), удовле-
удовлетворяющее условию:
sup [ULWli+iii-MOP+lli Will < + «>.
te R
Введено А. М. Ляпуновым в 1892 (см. [1]). Л. п. широко
используется в теории линейных систем обыкновенных
дифференциальных уравнений. При этом во многих
случаях от требования
sup (I L (t) j] < + оо
le R
можно отказаться.
Лит.: [1] Л я п у н о в А. М., Собр. соч., т. 2, М,—Л., 1956,
с. 7—263. В. М. Миллионщиков.
ЛЯПУНОВА СТОХАСТИЧЕСКАЯ ФУНКЦИЯ — не-
неотрицательная функция V(t, x), для к-рой пара
(V(t, X (?)), f() —супермартингал для нек-рого слу-
случайного процесса X(t), Ff есть а-алгебра событий,
порожденных течением процесса X до момента t. Если
X (t) — марковский процесс, то Л. с. ф. есть функция,
для к-рой стохастич. оператор Ляпунова
= lim ±M{[V(t + h, X(t + h))-V{t, X(t))]/X(t) = x)
h -<¦ a "
неположителен. Оператор L есть инфинитезимальный
оператор процесса (t, X (?)), и потому проверку условия
LV^-О легко осуществить для конкретных случаев.
Оператор L переходит в обычный оператор Ляпунова
dV(t, X (t))ldt, когда процесс X детерминированный,
описываемый системой дифференциальных уравнений.
С помощью Л. с. ф. удается проверить те или иные ка-
качественные свойства траекторий процесса X (t); их
роль в теории случайных процессов аналогична роли
классич. Ляпунова функций в теории систем дифферен-
дифференциальных уравнений.
Часто Л. с. ф. наз. и такие, для к-рых функция
V(t, X (?)) хотя и не является супермартингалом, но с ее
помощью легко можно сформировать супермартингал.
Ниже приведены типичные результаты качественного
поведения траекторий марковских процессов в терми-
терминах Л. с. ф.
1) Если X (t) — непрерывный справа строго мар-
марковский процесс в R*, определенный до момента т пер-
первого выхода из любого компакта, и существуют Л. с. ф.
V(t, х), f >0, x?Rk, и постоянная с такие, что
inf V (t, x) —-»- оо при R —>¦ оо, LF<cT',
t, \x\ > R
то
Р {т < оо | X @) = х) = 1
для любого x?Rk, т. е. процесс X определен при всех
?>0 (неограниченно продолжаем).
2) Для существования стационарного марковского
процесса в R*, отвечающего переходной функции
Р (t, х, А), достаточно существования функции V(х)~^0,
для к-рой
sup LV (х)—>¦—оо
\x\>R
при R—>-оо.
С помощью Л. с. ф. на марковские процессы переносят-
переносятся основные теоремы прямого метода Ляпунова, эти
функции нашли применение и для исследования про-
процессов с дискретным временем.
Лит.: [1] Куш н ер Г. Д ж., Стохастическая устойчи-
устойчивость и управление, пер. с англ., М., 1969; [2] X а с ь м и н-
ский Р. 3., Устойчивость систем дифференциальных уравне-
уравнений при случайных возмущениях их параметров, М., 1969;
[33 Калашников В. В., Качественный анализ поведения
сложных систем методом пробных функций, М., 1978.
Р. 3. Хасъминский.
ЛЯПУНОВА ТЕОРЕМА — 1) Л. т. в теории
вероятностей — теорема, устанавливающая
весьма общие достаточные условия для сходимости
распределений сумм независимых случайных величин
к нормальному распределению. Точная формулировка
Л. т. такова: пусть независимые случайные величины
Х1, . . ., Xk, . . . имеют конечные математич. ожида-
ожидания EXft, дисперсии DX^ и абсолютные моменты
E\Xk-EXk\*+6, 8>0, и пусть Bn=^k=lOXk~
дисперсия суммы Хи . . ., Х„. Тогда если при нек-ром
6>0 выполнено условие
V" E
lim fe = 1
то вероятность неравенства
стремится при п—>-оо к пределу
— Хг/2 j ,г>\
равномерно относительно всех значений it и ж2. Ус-
Условие A) наз. условием Ляпунова. Л. т.
была сформулирована и доказана А. М. Ляпуновым
A901) и явилась завершающим этапом исследований
П. Л. Чебышева, А. А. Маркова и А. М. Ляпунова по
проблеме об условиях приложимости центральной пре-
предельной теоремы теории вероятностей. В дальнейшем
были установлены условия, расширяющие условие Ля-
Ляпунова и являющиеся не только достаточными, но и
необходимыми. Окончательное решение вопроса в этом
направлении было получено С. Н. Бернштейном, Дж.
Линдебергом (J. Lindeberg) и В. Феллером (W. Feller).
В Л. т. впервые была продемонстрирована сила метода
характеристич. функций.
А. М. Ляпуновым была также дана оценка сверху
при б<:1 для абсолютной величины разности А между
вероятностью неравенства B) и ее приближенным зна-
значением C). Этой оценке можно придать следующий вид:
при б<1
и при 6 = 1
где С1 и С2 — абсолютные постоянные и Ln, 6 — дробь
(дробь Ляпунова), стоящая под знаком пре-
предела в A). См. также Бэрри — Эссеена неравенство.
Лит.: [1] Ляпунов А. М., Собр. соч., т. 1, М., 1954,
с. 157—76; [2] Б е р н ш т е й н С. Н., Теория вероятностей,
4 изд., М.— Л., 1946; [3] Ф е л л е р В., Введение в теорию ве-
вероятностей и ее приложения, пер. с англ., т. 2, М., 1967.
А. В. Прохоров.
2) Л. т. в теории потенциала — теоремы
о поведении потенциалов и решения Дирихле задачи,
полученные А. М. Ляпуновым в 1886 —1902 (см. [1]).
Теорема о теле наибольшего по-
потенциала: если существует однородное тело Т
в евклидовом пространстве R3, ньютонов потенциал
к-рого самого на себя, т. е. интеграл
Е (Г) = С [ dxd\ , A)
при данном объеме достигает наибольшего значения, то
это тело есть шар.
Интеграл A) есть энергия однородного распреде-
распределения масс плотности 1 в теле Т. Позднее Т. Карлеман
(Т. Carleman, 1919) доказал, что такое тело Т, для к-рого
энергия Е (Т) при данном объеме достигает своего на-
наибольшего значения, действительно существует.
Первая теорема о нормальных про-
производных потенциала двойного
слоя: пусть S — замкнутая поверхность Ляпунова в
^3, f (у) — плотность масс, распределенных на S,
причем выполняется одно из следующих двух условий:
1) f(y) непрерывна на S, а показатель ^=1 в условии
Ляпунова на угол Э между нормалями к S в точках
У\1 Уч^.3, т. е. ] Q1 <^j4 | г/х—у2\ (см. Ляпунова поверхно-
поверхности и кривые); 2) /(у) непрерывна по Гёльдеру с пока-
показателем 1, т.е. \f{yi)—f(y2)\<A\y1—y2\', тогда если
двойного слоя потенциал
r cos (у-х, п )
W(x)=\ f (у) . _L- dy B)
имеет в точке г/об:^ °ДНУ из нормальных производных
dWj/dny изнутри S или dWeldn извне S, то он имеет
и другую, причем эти производные совпадают.
Вторая теорема о нормальных
производных потенциала двойного
слоя: в предположениях предыдущей теоремы пусть,
кроме того, плотность / (у) удовлетворяет условию
Ляпунова
e>o, v>o,
где (р, ф, z) — цилиндрич. координаты внутри сферы
Ляпунова (см. Ляпунова поверхности и кривые) с на-
началом в точке yo?S и осью Oz, направленной по нор-
нормали пуо. Тогда потенциал двойного слоя B) имеет обе
нормальные производные в точке у0.
Теорема о первых производных
потенциала простого слоя: пусть S —
замкнутая поверхность Ляпунова и плотность f(y)
непрерывна по Гёльдеру, т. е.
Тогда частные производные первого порядка dV/dx,-,
i=i, 2, 3, x=(xi, хг, х3), простого слоя потенциала
непрерывны по Гёльдеру с тем же показателем X в
замкнутых внутренней D; и внешней De областях.
В этой теореме гёльдерова непрерывность была толь-
только высказана А. М. Ляпуновым, доказательство было
завершено Н. М. Гюнтером (см. [2]).
Эти теоремы послужили А. М. Ляпунову основой при
построении строгой теории разрешимости задачи Дирих-
Дирихле методом интегральных уравнений. Развитию идей
А. М. Ляпунова посвящена монография Н. М. Гюнтера
(см. [2]); обобщения для потенциалов более общего вида
см. в [З].
Лит.: [Ц Ляпунов А. М., Собр. соч., т. 1, М., 1954,
с. 26 — 32, 33—44, 45 — 100, 101—22; [2] Г ю н т е р Н. М.,
Теория потенциала и ее применение к основным задачам мате-
математической физики, М., 1953; L3] Миранда К., Уравнения
с частными производными эллиптического типа, пер. с итал.,
М., 1957. Е. Д. Соломенцев.
ЛЯПУНОВА ТЕОРИЯ УСТОЙЧИВОСТИ — теория
устойчивости движения, построенная А. М. Ляпуновым
в конце 19 — нач. 20 вв. (см. [1]). В основе ее лежат по-
понятия устойчивости по Ляпунову и асимптотич. устой-
устойчивости (см. Асимптотически устойчивое решение),
введенные А. М. Ляпуновым, теорема Ляпунова об
устойчивости по первому приближению (на к-рой ос-
нован первый метод Ляпунова исследования устойчи-
устойчивости) и второй метод Ляпунова (см. Ляпунова функ-
функция). Результаты и методы А. М. Ляпунова, разрабо-
разработанные им при построении теории устойчивости, полу-
получили важные и многочисленные применения в матема-
математике, в механике и технике. См. также Устойчивости
теория.
Лит.: [1] Л я п у н о в А. М., Собр. соч., т. 2, М.— Л., 1956.
В. М. Миллионщиков.
ЛЯПУНОВА ФУНКЦИЯ — функция, определяемая
следующим образом. Пусть х0— неподвижная
точка системы дифференциальных уравнений
(т. е. f(x0, t)=0), где отображение f(x, t) : C/xK+^-R
непрерывно и непрерывно дифференцируемо по х (здесь
U — нек-рая окрестность точки х0 в R"); в координа-
координатах эта система записывается в виде
*' = /<" С*1, •••, *", t), i=i, ..., п.
Л. ф. наз. дифференцируемая функция V(х) : U-+-R,
обладающая свойствами:
1) V (-г) > 0 при хфхй;
2) F(xo) = O;
3) 0 5э ^Г / (*, t) =
*mUi=\ Ox1
Функция V(x) введена А. М. Ляпуновым (см. [1])-
Имеет место лемма Ляпунова: если Л. ф.
существует, то неподвижная точка устойчива по Ля-
Ляпунову. На этой лемме основан один из методов ис-
исследования устойчивости (т.н. второй метод
Ляпунова).
Лит.: [1] Л я п у н о в А. М., Собр. соч., т. 2, М.— Л., 1956,
с. 7—263; [2] Б а р б а ш и н Е. А., Функции Ляпунова, М.,
197Н. В. М. Миллионщиков.
ЛЯПУНОВА ХАРАКТЕРИСТИЧЕСКИЙ ПОКАЗА-
ПОКАЗАТЕЛЬ решения линейной системы — верхний предел
где х((]фО — решение линейной системы обыкновен-
обыкновенных дифференциальных уравнений
х^А (t)x; A)
здесь x?Rn, A(-) —суммируемое на каждом отрезке
отображение R —>-Hom(R", Rn) или х?С, А(-) —
суммируемое на каждом отрезке отображение R —>¦
-*-Нот (С™, С"). В координатной записи
где alj(t) — суммируемые на каждом отрезке функции, а
(или любая другая эквивалентная норма; ХХф не зави-
зависит от выбора нормы в R" или в С").
Теорема Ляпунова. Пусть
lim -—С I] А (т) || di < + оо;
t-++ оо * J О
эквивалентно:
1 С t I ? I
lim — \ | О;- (т) J йт < + оо, i, /=1, ..., и.
Тогда для всякого решения x(t)^O системы A)
Л. х. п. XX(t) — действительное число (т. е. ^=izoo).
Для Л. х. и. ненулевых решений системы A) справед-
справедливы утверждения:
1 ^ Я
) (хЛ(п Х{/), ф,
2) Kx,U) + xM))<ma-x (ЛХгм, XX2-t)),
3) существуют линейно независимые решения ж,- (г),
г = 1, . . ., п, системы A), обладающие свойством:
для всяких п линейно независимых решений .r,(i),
г=1, . . ., п, системы A), занумерованных в порядке
убывания Л. х. п., т. е. Ххщ~^к? ^ при ?<:/, выполня-
выполняются неравенства
Фундаментальная система решений х; (t), (=1, . . ., п,
обладающих этим свойством, наз. нормальной;
при этом:
а) семейство чисел Х;(А) = 'кх ^t>, г=1, . . ., п, не
зависит от выбора нормальной фундаментальной систе-
системы xi (t), i=l, . . ., п;
б) для всякого решения x(t)=?O системы A) Л. х. п.
XX(D равен нек-рому Х{(А)\
в) li(A)^lj(A), г</.
Числа Х\(А)^ . . . ^Хп(А) наз. Л. х. п. системы A);
число Х1(А) наз. часто старшим Л. х. п. систе-
системы A).
Множество всех Л. х. п. ненулевых решений систе-
системы A) наз. ее спектр ом.
Частные случаи. 1) Система с постоянными
коэффициентами (т. е. A (t)=A @)). В этом случае
Xj (А) равны действительным частям собственных зна-
значений оператора А @) (матрицы ||оу'||).
2) Система с периодич. коэффициентами (т. е.
A (t+T)=A{t), T>0). В этом случае
X; (А) = ^ In
и,-
Где (X,-— мультипликаторы системы A), занумерованные
в порядке невозрастания их модулей (каждый берется
столько раз, какова его кратность).
Роль Л. х. п. в теории устойчивости по Ляпунову ос-
основана на следующем утверждении: если >ъХ(Л)<0
(>0), то решения системы A) асимптотически устойчи-
устойчивы (соответственно неустойчивы). Из того, что)п(А) <0,
не следует, что нулевое решение системы
устойчиво но Ляпунову; однако если дополнительно
известно, что система A) правильная линейная система,
то такое заключение справедливо (теорема Ля-
Ляпунова).
Пусть система x—B(t)x получена малым возмущением
системы A), удовлетворяющей условию
sup || A (t) || < + оо,
т. е. расстояние между ними, определяемое формулой
d(A, B)=svLV\A(t) — B{t)l B)
ti R
мало. При ге>1 отсюда не следует, что величина
\Х1(А)-Х1(В)\
мала (следует, если система A) имеет постоянные или
периодич. коэффициенты, а также для нек-рых других
систем); иными словами, функционалы Я,- (А) не всюду
непрерывны на пространстве систем A) (sup \\A (<)||<
te R
<+оо), наделенном указанной метрикой B).
Л. х. п. введены А. М. Ляпуновым, причем не только
для решений системы A), но и для произвольных функ-
функций на R+ (см. [1]).
Лит.: [1] Л я п у н о в А. М., Собр. соч., т. 2, М.— Л.,
1956, с. 7—263; [2] Бы лов Б. Ф., Виноград Р. Э.,
Г р о б м а н Д. М., Н е м ы ц к и й В. В., Теория показателей
Ляпунова и ее приложения к вопросам устойчивости, М., 1966;
[3] Итоги науки и техники. Математический анализ, т. 12, М.,
1974, с. 71 —146. В. М. Миллионщиков.
ЛЯПУНОВА — ШМИДТА УРАВНЕНИЕ — нели-
нелинейное интегральное уравнение вида
и (х) —[пК (х< s) u (s) ds== U»i (у) +
x??Z, A)
М, V
где
Un (*) = Ко (х) v (х) + Jq Кг (х, s) v (S) ds,
а0, ос,, . . ., ос,-, р0, рх, . . ., р,- — неотрицательные це-
целые числа,
Q — ограниченное замкнутое множество конечномер-
конечномерного евклидова пространства, v и функции /Г — задан-
заданные непрерывные функции своих аргументов х, s, sj,
. . ., st?Q, и — искомая функция. Сумма, входящая в
правую часть равенства A), может быть конечной пли
представлять бесконечный ряд. В последнем случае
ряд наз. интегро-степенным рядом от
двух функциональных аргументов. Предполагается, что
этот ряд сходится абсолютно и равномерно.
Если единица но является характеристич. числом
ядра К{х, s), то уравнение A) при достаточно малом
v(x)\ в классе непрерывных функций имеет единствен-
единственное малое решение, представимоо в виде интегро-сте-
пенного ряда. Случай, когда единица есть характери-
характеристич. число ядра К, является более сложным. В этом
случае строится нек-рая система уравнений — урав-
уравнение разветвления:
щAи h, ••¦, In, ") = 0, А=1, ..., п, B)
где о)? — известные степенные ряды, п — кратность
характеристич. числа 1. Система B) в общем случае
имеет неединственное решение. Какова бы ни была фик-
фиксированная достаточно малая функция v, каждому ма-
малому непрерывному решению системы B) (непрерывное
решение системы B) наз. малым, если |,- @) = 0) соот-
соответствует малое решение уравнения A), представнмое
в виде интегро-степенного ряда.
Уравнение типа A) впервые было рассмотрено
А. М. Ляпуновым в 1906, а позднее — в более общем
виде — Э. Шмидтом (Е. Schmidt, 1908).
Лит.: [1] В а й н 6 е р г М. М., Треногий В. А., Тео-
Теория ветвления решений нелинейных уравнений, М., 1969; [2]
Смирнов Н. С, Введение в теорию нелинейных интеграль-
интегральных уравнений, Л.— М., 1936. В. В. Хведелидзе.
МАГИЧЕСКИЙ КВАДРАТ — квадратная гаХи-таб-
лица |]а,у|| целых чисел от 1 до ге2, удовлетворяющая
следующим условиям:
где s=re(re2-j-l)/2. Рассматриваются также более общие
М. к., в к-рых не требуется, чтобы 1<:о,-у-<:ге2.
Любое число а, 1<:а<:«2, однозначно характеризуется
парой вычетов (ос, Р) по модулю п (цифрами по основа-
основанию п числа а—1), т. е. точкой двумерного пространства
(Z/reJ над кольцом %1п вычетов по модулю п. Посколь-
Поскольку координаты (г, /) клеток квадрата также можно
считать элементами пространства (ж/пJ, отсюда сле-
следует, что любое распределение чисел от 1 до п2 в квад-
квадратную иХге-таблицу ||а,-у|| задается нек-рым отобра-
отображением
(Z/«J — (ХМ*,
т.е. парой функций a = a(i, })?ъ1п, P = P(i, j)? %ln
от i, j?'?in- Задача состоит в исследовании таких пар,
дающих М. к. В общем виде это сделано (см. [1]) толь-
только при дополнительном предположении линейности
функций а и р. Оказалось, в частности, что М. к. с ли-
линейными функциями а и Р существуют только при не-
нечетных п.
Уже в средние века был известен ряд алгоритмов по-
построения М. к. нечетного порядка п. Каждый такой
алгоритм характеризуется шестью вычетами г0, /„,
р, q, p, q и Описывается следующими правилами:
1) число 1 вписывается в клетку (?0, /0); 2) если число а
вписано в клетку (i, /), то число а-f-l вписывается в
клетку (?+р, /+?), если эта клетка еще свободна от
чисел, и в клетку (i-\-p, / + ?), если клетка (i+p, j+q)
занята.
Вычеты г0, /0, р, q, p, q но могут быть произвольны, но
должны удовлетворять определенным условиям, обес-
обеспечивающим не только выполнение условий (*), но
и выполнимость алгоритма, т. о. пустоту клетки
(?+р, /+</), если занята клетка (?+р, /+?). Эти усло-
условия легко находятся (см. [1] с. 41), причем оказывается,
что М. к. тогда и только тогда может быть построен
алгоритмом такого вида, когда описывающие этот квад-
квадрат функции ос, Р линейны.
Известно много других алгоритмов построения М. к,
(приводящих к квадратам с нелинейными функциями
а, Р), но никакой общей их теории нет A982). Неиз-
Неизвестно даже общее число М. к. порядка п (при ге^5;
для ;г=3 существует, с точностью до очевидных сим-
симметрии, только один М. к., а для га=4 число М. к. равно
Исследовались также М. к., обладающие дополни-
дополнительными свойствами симметрии, лишь опять в очень
специальных ситуациях (напр., при ?г<:5; см. [2]).
Лит.: [1] П о с т н и к о в М. М., Магические квадраты, М.,
1964; [2] Гуревич Е. Я., Тайна древнего талисмана, М.,
1969. М. М. Постпиков.
МАГНИТНОЙ ГИДРОДИНАМИКИ МАТЕМАТИЧЕ-
МАТЕМАТИЧЕСКИЕ ЗАДАЧИ — задачи, связанные с исследованием
движения электропроводящих жидкостей и газов в
присутствии магнитного поля.
МАЖОРАНТА И МИНОРАНТА — 1) Две функции,
значения первой из к-рых не меньше, а второй не больше
соответствующих значений данной функции (для всех
рассматриваемых значений независимого переменного).
2) Для функций, представимых степенным рядом, под
мажорантой понимают сумму степенного ряда с
положительными коэффициентами, к-рые не меньше
абсолютных величин соответствующих коэффициентов
данного ряда. 3) Мажоранта (миноранта) нек-рого под-
подмножества X упорядоченного множества Е — элемент
у?Е такой, что для всякого х?Х справедливо у^х
(x^sy). 4) В теории интегрирования п в теории дифферен-
дифференциальных уравнений мажорантой (м и н о р а п-
т о й), или мажорантной (м и н о р а н т н о й)
функцией, для нек-рой функции /(?) наз. такая
непрерывная функция, у к-рой в каждой точке t все
производные числа не меньше (не больше), чем значения
/(?), и отличны от — оо(+оо). Разность между любой
мажорантой и любой минорантой является неубываю-
неубывающей функцией. Любая суммируемая на отрезке функ-
функция обладает абсолютно непрерывными М. и м., сколь
угодно близкими к ее неопределенному интегралу Ле-
Лебега. Понятие М. и м. может быть обобщено на случай
аддитивной функции множества, а также на случай,
когда производные числа понимаются в нек-ром обоб-
обобщенном смысле.
Лит.: [1] Б у р 6 а к и Н., Теория множеств, пер. с франц.,
М., 1965; [2] С а к с С, Теория интеграла, пер. с англ., М., 1949.
В. А. Скворцов.
МАЙЕРА ЗАДАЧА — одна из основных задач вариа-
вариационного исчисления на условный экстремум. М. з.
состоит в следующем. Найти минимум функционала
при наличии дифференциальных ограничений типа ра-
равенств
ф (я. у, у') = 0, cp:RxR"XR*—*Rm, m < п,
и граничных условий:
тМ*ъ y(xi), хг, у(х2)) =0, tjj:RxR"XRxR"^R/',
р <2п + 2.
Подробнее см. Больца задача.
М. з. названа по имени А. Майера (A. Mayer), к-рый
изучал необходимые условия ее решения (кон. 19 в.).
И. -Б. Вапнярсгмй.
МАКДОНАЛЬДА ФУНКЦИЯ, модифициро-
модифицированная цилиндрическая функция,
бесселева функция мнимого аргу-
аргумента, — функция
К Ы = -5-
v ^2' 2
sin (vn) '
где v — произвольное нецелое действительное число,
_ m! Г (v + m+i)
— цилиндрич. функция чисто мнимого аргумента.
Рассмотрена X. Макдональдом [1]. Если п — целое чис-
число, то
Kn(z)= lim A'V(Z).
М. ф. К\ (z) является решением дифференциального
уравнения
стремящимся экспоненциально к нулю, когда z—vcc,
принимая положительные значения. Функции /v (z)
и Kv (z) образуют фундаментальную систему решений
уравнения (*).
При v^O функция Kv (z) имеет корни лишь в случае
Re(z)<0. Если л/2<|arg z\ <я, то число всех корней в
этих двух квадрантах равно ближайшему к v ^-чет-
^-четному числу, если только v — не является целым;
в последнем случае число всех корней равно v g- .
При arg г=±я корней нет, если только v 5" не целое.
Ряды и асимптотич. представления:
и— целое неотрицательное;
•Ф A) = — С", г|> (т+1) = 1+х+--+^
= 0,5772157... —постоянная Эйлера;
К 1,\ - 1 V" (-I)*" (n-m- 1)!
т!
1 — целое;
у, Г< I 4V2-!2
Х |Х
велико и | arg 2 | < я/2.
Рекуррентные формулы:
(IKV B)
Лит.: [1] M а с d о n a 1 d H. M., «Proc. London Math. Soc»,
1899, v. 30, p. 165—79; [21 В а т с о н Г. Н., Теория бесселевых
функций, пер. с англ., ч. 1, М., 1949. В. И- Пагурова.
МАККИ БОРЕЛЕВСКАЯ СТРУКТУРА — некото-
некоторая борелевская структура (т. е. борелевская система
множеств) на спектре А сепарабельной С*-алгебры А,
определяемая следующим образом. Пусть //„, п=\, 2,
. . ., — гильбертово пространство размерности п,
\тхп(А) — множество ненулевых неприводимых пред-
представлений С*-алгебры А в пространстве Нп, снабжен-
снабженное топологией простой слабой сходимости. Пусть
множество 1ттп(А) снабжено борелевской системой мно-
множеств, подчиненной его топологии (т. е. наименьшей
борелевской системой множеств, относительно к-рой
все отображения я->(я(х)^, г|), х?А, 5, Ц^.НП,
д?1гг„D),— борелевские функции), и пусть Irr (A) —
объединение подпространств 1ттп(А), ге = 1, 2, . . .,
снабженное борелевской системой множеств таких, что
подмножество в Irr (А) тогда и только тогда является
борелевским, когда его пересечение с каждым из мно-
множеств 1ттп(А) принадлежит соответствующей б'орелев-
ской системе множеств. Пусть ср — отображение боре-
левского пространства 1гт(Л) на спектр А С*-алгеб-
ры А, сопоставляющее представлению его класс уни-
унитарной эквивалентности. Борелевская система мно-
множеств в А, образованная множествами, полные про-
прообразы к-рых при отображении ср принадлежат по-
построенной борелевской системе множеств на 1гг (А), и
называется борелевской структурой
М а4к к и на А. М. б. с. содержит все множества из
борелевской системы множеств на А , подчиненной то-
топологии пространства А; каждая точка в А является
борелевским множеством в М. б. с. Следующие усло-
условия эквивалентны: 1) М. б. с. стандартна (т.е. изоморфна
как борелевская система множеств борелевской системе
подмножеств нек-рого полного сепарабельного метрич.
пространства, подчиненной его топологии); 2) М. б. с.
совпадает с борелевской системой множеств, подчинен-
подчиненной топологии в А; 3) М. б. с. на А счетно отделима;
4) если А — CGR-алгебра, то М. б. с. может быть вве-
введена также на квазиспектре сепарабельной С*-алгебры
Лит.: [1] Д и к с м ь е Ж., С*-алгебры и их представления
пер. с франц., М., 1974; [2] G а г d n е г Т. «Canari. J. Math.»
1971, v. 23, Ni 4, p. 674—78; [3] H a 1 p e г n H., «Canad. J. Math.»
1974, v. 26, № 3, p. 621—28. А. И. Штерн
МАККИ ТОПОЛОГИЯ x(F, G) в F, находящемся в
двойственности с пространством G (над тем же полем),—
топология равномерной сходимости на компактных в
слабой топологии (определяемой двойственностью
между F и G) выпуклых уравновешенных множествах
из G. Введена Дж. Макки [1]. М. т. является сильней-
сильнейшей из отделимых локально выпуклых топологий, сог-
согласованных с двойственностью между F и G (т. е. та-
таких отделимых локально выпуклых топологий ?Г в F,
что совокупность непрерывных линейных функциона-
функционалов на пространстве F, наделенном топологией ?Г, сов-
совпадает с G). Семейства множеств в $~, ограниченных от-
относительно М. т. и слабой топологии, совпадают. Вы-
Выпуклое множество в G равностепенно непрерывно при
наделении пространства F топологией Макки в том и
только в том случае, если оно относительно компактно
в слабой топологии; если отделимое локально выпук-
выпуклое пространство Е бочечно или борнологично (в ча-
частности, метризуемо) и Е' — его сопряженное, то М. т.
в Е (находящемся в двойственности с Е') совпадает с
исходной топологией в Е; для пары пространств (F, G)
в двойственности М. т. в ?Г не обязательно бочечна или
метризуема. Слабо непрерывное линейное отображение
отделимого локально выпуклого пространства Е в
отделимое локально выпуклое пространство F непре-
непрерывно относительно М. т. i(E, E') и %{F, F'). Локально
выпуклое пространство Е наз. пространством
М а к к и, если топология в Е есть %(Е, Е'). Пополне-
Пополнения, факторпространства и метризуемые подпростран-
подпространства, произведения, локально выпуклые прямые суммы
и индуктивные пределы семейств пространств Макки
являются пространствами Макки. Если Е — простран-
пространство Макки им — слабо непрерывное линейное отоб-
отображение пространства Е в локально выпуклое простран-
пространство F, образ к-рого является пространством Макки. то
и — непрерывное линейное отображение Е в F. Если
Е — квазиполное пространство Макки и пространство,
сопряженное к пространству Е, снабженному сильной
Я'-топологней, полурефлексивно, то Е рефлексивно.
Лит.: [1] М а с к е у G. W., <<Trans. Amer. Math. Soc»,
1946, v. 60, p. 519—37; [2] Б у р б а к и Н., Топологические
векторные пространства, пер. с франц., М., 1959; [31 Ш е ф е р X.,
Топологические векторные пространства, пер. с англ., М.. 1971.
А. И. Штерн.
МАКЛОРЕНА РЯД для функции f(z) — сте-
степенной ряд вида
Изучался К. Маклореном [1]. Если аналитическая в
нуле функция /(z) разлагается в степенной ряд, то
этот ряд совпадает с М. р. В случае, когда функция
зависит от т переменных, М. р. есть кратный степенной
ряд
,_,* /<*•>(())... А») @)
ft,!
=*«...**«,
суммирование в к-ром проводится по мультппндексам
к=(к1, кг, . . ., кт), к; — неотрицательные целые.
М. р.— частный случай Тейлора ряда.
Лит.: [1] М а с Laurin С, A treatise of fluxions, v. 1—2,
Edinburgh, 1742. Л. Д. Кудрявцев.
МАКЛОРЕНА ФОРМУЛА — частный случай Тей-
Тейлора формулы. Пусть функция f (х) имеет п производ-
производных в точке я1—0. Тогда в нек-рой окрестности U этой
точки функцию /(х) можно представить в виде
где гп(х) — остаточный член n-го порядка, представи-
мый в том или ином виде.
Термин «М. ф.» используется также для функций т
переменных х= (ж,, хг, . . ., хт). В этом случае в М. ф.
под к понимается мультииндекс /с= (feb fe2, . . ., кт)
(см. Маклорена ряд). Названа по имени К. Маклорена
(С. Maclaurin). л. Д. Кудрявцев.
МАКСВЕЛЛА РАСПРЕДЕЛЕНИЕ — распределение
вероятностей с плотностью вероятности
0 , х < 0,
зависящей от параметра ff>0. Функция распределения
М. р. имеет вид
F(r)=f 2Ф(.г/а)-|/Х^ e-xt'tat-i, .rs.0,
1 0 , х < О,
где Ф (х) — функция стандартного нормального рас-
распределения. М. р. имеет положительный коаффициент
асимметрии; оно унимодально — единственная мода
находится в точке х= }^2о\ М. р. имеет конечные мо-
моменты любого порядка; математич. ожидание и диспер-
дисперсия равны соответственно 2 l/ — а и ' а2.
Если Х1, Х2, Х3— независимые случайные величины,
имеющие нормальное распределение с параметрами 0
и сг2, то случайная величина у Xi-'гХ%-{-Хз имеет
М. р. с плотностью (*). Иначе, М. р. может быть полу-
получено как распределение длины случайного вектора,
координаты к-рого в декартовой системе координат в
трехмерном пространстве независимы и нормально рас-
распределены с параметрами 0 и а2. М. р. при а=1 сов-
совпадает с распределением квадратного корня из величи-
величины, имеющей ^-распределение с тремя степенями сво-
свободы (см. также Рэлея распределение). М. р. широко
известно как распределение скоростей частиц в ста-
тистнч. механике и физике. Впервые установлено
Дж. Максвеллом (J. Maxwell, 1859) при решении за-
задачи о распределении скоростей молекул идеального
газа.
Лит.: [1] Ф е л л е р В., Введение в теорию вероятностей
и ее приложения, пер. с англ., т. 2, М., 1967.
А. В. Прохоров.
МАКСВЕЛЛА УРАВНЕНИЯ — уравнения электро-
электромагнитного поля в материальных средах; установлены
в 60-х гг. 19 в. Дж. Максвеллом (J. Maxwell) на основе
экспериментально найденных к тому времени законов
электрических и магнитных явлений.
В классич. электродинамике для описания электро-
электромагнитного поля в среде вводятся четыре векторных
поля: напряженность электрич. поля Ж, электрич. ин-
индукция Т>, напряженность магнитного поля Н и маг-
магнитная индукция В, к-рые являются непрерывными
и дифференцируемыми функциями г радиус-вектора
точки 3-мерного пространства и времени t. Эти поля
определяются с точностью до постоянных множителей,
позволяющих выбрать соответствующую систему фн-
зич. единиц измерения абсолютной величины этих полей.
М. у. представляют собой систему неоднородных
дифференциальных уравнений с частными производ-
производными 1-го порядка для полей Ж, D, Н, И, к-рая в т. н.
абсолютной системе физпч. единиц Гаусса имеет вид:
-!-!?+rot H=%j, (la)
div.B =0, (le)
divi>=4.Ttp, Aг)
где неоднородные члены p(t, r) — заданное скалярное
поле плотности электрнч. заряда в среде и j (t, r) —
векторное ноле плотности олектрич. тока (заряда, про-
проходящего за единицу времени через единичную пло-
площадку, перпендикулярную направлению движения за-
зарядов) являются источниками поля, а с=3 Л010 см/сек—
постоянная, равная скорости распространения электро-
электромагнитных взаимодействий в вакууме. М. у. могут быть
записаны также и в интегральной форме:
B)
Поля_К, D, H, Buj не являются независимыми, при-
причем в согласии с экспериментальными фактами 1) и ,j
зависят только от Ж, а В зависит только от Н, т. е.
имеют место следующие функциональные зависимости:
П=Г>(Ж), .1 = .)(Ж), В=В(Н), C)
к-рые наз. уравнениями состояния, или
материальными уравнениями сре-
д ы. В рамках классической макроскопич. электроди-
электродинамики уравнения состояния C) должны быть заданы
дополнительно (постулированы или определены по экс-
экспериментальным данным) и с их учетом система М. у.
для двух независимых векторных полей Ж и // становит-
становится замкнутой. Конкретный вид уравнений состояния
C) определяется электрическими и магнитными свой-
свойствами данной среды и ее состоянием. В общем случае
в уравнениях состояния C) векторные поля Z), j и В
в точке г в момент времени t могут зависеть нелинейно
от значений полей Ж ж И соответственно во всех точ-
точках среды (нелокальный случай) во все любые моменты
времени, предшествующие согласно физич. принципу
причинности — данному моменту t (случай среды "с
последействием или с памятью). Большинство имеющих
практич. интерес сред характеризуется локальной ли-
линейной зависимостью Z) и j от Ж и В от If, и в этом слу-
случае М. у. оказываются линейными дифференциальны-
дифференциальными уравнениями, однако в приложениях встречаются
и более сложные случаи (напр., в нелинейной оптике).
Уравнения состояния C) могут быть рассчитаны в
принципе с помощью микроскопич. электродинамики,
если учесть законы движения отдельных частиц среды
и их индивидуальные микроскопич. характеристики
?
= 4л [ р dV.
(значения электрич. зарядов, масс). При этом значения
макроскопич. полей К, If, D, В определяются как усред-
усредненные значения микроскопич. полей, создаваемых
отдельными движущимися заряженными частицами
среды, и для них справедливы М. у.
На поверхности раздела различных сред должны быть
выполнены граничные условия
(п!)г) — (»?>,) = 4л а,
(пВ2) - (пВ^-^0,
*де /пов — плотность поверхностного тока, а — плот-
плотность поверхностного заряда, п — единичный вектор
нормали к поверхности раздела, индексы i и 2 отме-
отмечают значения полей с разных сторон поверхности
раздела.
Следствием М. у. является уравнение не-
непрерывности
выражающее закон сохранения электрич. заряда.
М. у. инвариантны относительно преобразований
Лоренца. Если в псевдоевклидовом пространстве 4-мер-
4-мерном пространстве-времени с координатами х\=х, х2=у,
х3 —z, х4=гсг ввести два антисимметричных 4-мерных
тензора Fki и G^i (к, 1—\, 2, 3, 4) с компонентами
12 = j ^ 23=== **1» У 31 = **2> * ik= l? ki А,= 1, Z, О, 4, J
12=//з» 3 — Л1) ^31 = ¦" 2) ^= г^А> Л= 1, Z, О, 4, У
D)
а также 4-мерный вектор тока )^, k=i, 2, 3, 4, про-
пространственные компоненты к-рого ii~—ix, ]%~]ч, !з~—!г
совпадают с компонентами тока j и четвертая компо-
компонента /4=icp пропорциональна плотности заряда, то
М. у. A) могут быть записаны в релятивистски кова-
риантной форме:
9F. OF, OF
ЪГ1 + ST* + Sir =0' к, I, m=i, 2, 3, А, E)
п
V4
• = ^/fc, A=J, 2, 3, 4. F)
Уравнения E) представляют собой 4-мерную форму за-
записи М.у. A6) и Aв), а уравнения F) — 4-мерную форму
записи М. у. Aа) и Aг).
Для электромагнитного поля в вакууме, по опреде-
определению, 1>=Е, В=Н и, следовательно, G^i^^F^i, и
электромагнитное поле описывается лишь одним тен-
тензором Ff-i. Если ввести 4-мерный вектор электромаг-
электромагнитного потенциала Ak, k=i, 2, 3, 4, пространствен-
пространственные компоненты к-рого At=Ax, А2=Ау, A3 = Az
образуют т. н. 3-мерный вектор-потенциал A (t, r),
а четвертая временная компонента At=i(p пропорцио-
пропорциональна скалярному потенциалу поля (p(t, г), то ком-
компоненты антисимметричного тензора электромагнит-
электромагнитного поля Ffci можно выразить через компоненты 4-мер-
4-мерного вектора электромагнитного потенциала Ак сог-
согласно соотношению
ОА. дА,
рЫ = -о^--оГк> *. 1 = 1, 2, 3,4. G)
С учетом G) уравнения E) удовлетворяются тождест-
тождественно, а уравнения F) принимают вид
Х"Ч 4 /Э2А, я дА,\ л_
L, (vr-eT- ё7-) = Т>*' fc=1« 2- 3' 4' (8)
т. е. неоднородных волновых уравнении для компо-
компоненты Ак. Введение в рассмотрение потенциала Ак
позволяет записать М. у. в простой форме (8), однако
потенциал Ак определен неоднозначно, что отражает
инвариантность М. у. в форме (8) относительно гра-
градиентных преобразований. Указанная неоднозначность
в определении потенциала Ak может быть устранена
(см. Градиентное преобразование).
Согласно D) и G) физически наблюдаемые поля Е
и И можно выразить через вектор-потенциал А и
скалярный потенциал ц>:
1 О А.
И=тоЬА, _Е= —gradcp —T -g^-.
В случае, когда электромагнитное поле в вакууме
является свободным, т. е. отсутствуют источники,
М. у. A) и (8) становятся однородными, и из М. у.
A) и (8) можно получить независимые однородные
волновые уравнения для электрического и магнитного
поля
где А — лапласиан и с — скорость распространения
электромагнитных волн в вакууме.
М. у. для электромагнитного поля применимы лишь
в классич. теории, т. к. в случае, когда переменные
электрическое и магнитное поля имеют очень высокие
частоты и очень малые длины волн (сравнимые с дли-
длинами порядка размеров атомов), становятся сущест-
существенными квантовые эффекты, и теория электромагнит-
электромагнитного поля и его источников должна строиться на основе
квантовой электродинамики.
Лит.: [1] Максвелл Дж.К., Избр. соч. по теории
МАКСИМАЛЬНАЯ КОМПАКТНАЯ ПОДГРУППА
топологической группы G — компактная
подгруппа A'cG, к-рая не содержится в качестве соб-
собственной подгруппы ни в какой компактной подгруппе
группы G. Напр., K=SO(n) для G = SL(?<, R), К= {е}
для разрешимой односвязной группы Ли G.
В произвольной группе G М. к. п. могут и не суще-
существовать (напр., если G = GL(V"), где Г — бесконечно-
бесконечномерное гильбертово пространство), а если они сущест-
существуют, то среди них могут быть неизоморфныо.
Наиболее изучены М. к. п. групп Ли. Если G — связ-
связная группа Ли, то любая компактная подгруппа груп-
группы G содержится в нек-рой максимальной (в частности,
М. к. п. обязательно существуют), и все М. к. п. в С
связны и сопряжены между собой. Пространство груп-
группы G диффеоморфно KXR", поэтому большинство то-
пологцч. вопросов о группах Ли сводится к соответ-
соответствующим вопросам о компактных группах Ли.
Лит.: [1] К а р т а н Э., Геометрия групп Ли и симметриче-
симметрические пространства, пер. с франц., М., 1949; [2] X е л г а с о н С,
Дифференциальная геометрия и симметрические пространства,
пер. с англ., М., 1964. В. В. Горбпцевич.
МАКСИМАЛЬНАЯ ПОДГРУППА — собственная
подгруппа группы G, не содержащаяся ни в какой дру-
другой собственной подгруппе группы G, т. с. максималь-
максимальный элемент в множестве всех собственных подгрупп
группы G, упорядоченных но включению. Существуют
группы без М. п., напр, группа типа р°°.
Обобщением понятия М. п. служит понятие под-
подгруппы, максимальной по некото-
некоторому свойству а, т. е. такой обладающей
свойством а собственной подгруппы Но группы G,
что в G нет другой собственной подгруппы Н, обладаю-
обладающей свойством а и содержащей подгруппу Но.
Лит.: [1] К а р г а п о л о в М. И., Мерзляков Ю. И.,
Основы теории групп, 2 изд., М., 1977. Н. Н. Вильяме.
МАКСИМАЛЬНАЯ ЭРГОДИЧЕСКАЯ ТЕОРЕМА:
если Т — эндоморфизм пространства с мерой (X, [i) и
f^L1{X, |х), а Е — множество тех х?Х, для к-рых
Slip V ._ / (У'л-)Эг О,
га> о ¦^-1-°
ТО
¦) Е
М. э. т. принадлежит К. Иосиде и Ш. Какутани [1],
указавшим, что она может играть роль центрального эта-
этапа в доказательстве Виркгофа эргодической теоремы
(у самого Дж. Биркгофа вместо М. э. т. применялись
несколько иные соображения). В доказательствах
появившихся позднее обобщений теоремы Биркгофа
(а также при исследовании родственного вопроса о
разложении фазового пространства на консервативную
и дисснпатнвную части в условиях, когда действуют
эти обобщения) тоже используется соответствующим
образом обобщенная М. э. т. Имеется обобщение М. э. т.,
принадлежащее Э. Хопфу (Е. Hopf), и простое дока-
доказательство этого обобщения, предложенное А. Гарсиа
(A. Garcia) (см. [2]). См. также [3] и лит. при ст.
Виркгофа эргодическая теорема.
Лит.: [1] Y о s i d а К., Kakutani S., «Proc. Imp.
Acad. Tokyo», 1939, v. 15, p. leb—«8: [2] Неве Ж., Матема-
Математические основы теории вероятностей, пер. с франц., М., '9tjS>'.
[31 В е р ш и к А. М., Ю з в и н с. к и й С. А., в кн.: Итоги на-
науки. Математический анализ. 1967, М., 1069, с. 133—87.
Д. В. Амосов.
МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ МЕТОД —
один из основных общих методов построения оценок
неизвестного параметра в статистич. теории оценива-
оценивания.
Пусть по наблюдению X с распределением Р% , за-
зависящим от неизвестного параметра в?в^К*, оцени-
оценивается в. Предполагая, что Есе меры Pq абсолютно
непрерывны относительно общей меры v, определяют
функцию правдоподобия равенством
<1Рп
М. п. м. рекомендует принять в качестве оценки для
в статистику 0, определяемую соотношением
L(Q)=maxL(Q).
Оценка 0 наз. оценкой максимального
(или наибольшего) правдоподобия (о. м. п.).
В широком классе случаев о. м. п. является решением
уравнений правдоподобия
gf-iogz,(e) = o, i = i, ..., к, в=(в1, ..., в*). A)
Пример 1. Пусть Х= (Xlt . . ., Хч)—последова-
Хч)—последовательность независимых случайных величин (наблюде-
(наблюдений) с общим'распределением 5*9» 6?в. Если сущест-
существует плотность
d°P
1 (х, в) = в {х)
dm
относительно нек-рой меры т, то
L{Q)= H"=1f(Xj; в),
и уравнения A) имеют вид
Пример 2. Пусть в условиях 1-го примера
есть нормальное распределение с плотностью
где .r^R1, 6= (a, a2), —oo<a<oo, a2>0. Уравнения
B) принимают вид
Ba4) - x Уn_ i{Xf~ay1 — ti Ba2) - * = 0;
о. м. п. выражается равенствами:
Пример 3. В условиях 1-го примера Xj прини-
принимают значения 0 и 1 с вероятностями соответственно
1 —в, в. Тогда
а о. м. п. 0=_Y.
Пример 4. Пусть наблюдение X=Xf есть диф-
диффузионный процесс со стохастическим дифференциа-
дифференциалом
dXt = Qat(Xt) + dwu Хо=0, 0<<<7\
где wt — винеровский процесс, а 9 — неизвестный од-
одномерный параметр. Здесь (см. [3])
log L ф) = G J Tg a t (Xt) dXt - ^- J ^ а? (А',) Д,
В основе М. п. м. не лежат никакие четко выражен-
выраженные соображения оптимальности, и широко распростра-
распространенная вера в его хорошие качества основана отчасти
на большом успехе, с к-рым М. п. м. применялся к
многочисленным конкретным задачам, отчасти на стро-
строго установленных асимптотически оптимальных свой-
свойствах. Напр., в ситуации 1-го примера в широких
предположениях 0„—>-в с Ре-вероятностью 1. Если су-
существует информационное количество Фишера
J 1 {х, 0)
то разность У~пфп — 0) асимптотически нормальна с
параметрами @, 1~1F)) и 0„ имеет в определенном
смысле асимптотически минимальный средний квадрат
уклонения от в (см. [4]).
Лит.: [1] Крамер Г., Математические методы статистики,
пер. с англ., 2 изд., М., 1975; [2] 3 а к с Ш., Теория стати-
статистических выводов, пер. с англ., М., 1975; [3] Л и п ц е р Р. Ш.,
Ширяев А. И., Статистика случайных процессов, М., 1974;
[4] Ибрагимов И. А., X а с ь ми некий Р. 3., Асим-
Асимптотическая теория оценивания, М., 1979. И. А. Ибрагимов.
МАКСИМАЛЬНОЕ И МИНИМАЛЬНОЕ РАСШИРЕ-
РАСШИРЕНИЯ симметрического оператора
А — операторы А (замыкание оператора А) и А * (со-
(сопряженный к А оператор) соответственно. Все замкну-
замкнутые снмметрпч. расширения оператора А находятся
между ними. Равенство М. и м. р. эквивалентно само-
самосопряженности оператора А и является необходимым
и достаточным условием единственности самосопря-
самосопряженного расширения. А- Я. Логинов, В. С. Шульман.
МАКСИМАЛЬНЫЙ И МИНИМАЛЬНЫЙ ОПЕРА-
ОПЕРАТОРЫ — максимальное и минимальное расширения
оператора, определяемого данным дифференциальным
выражением на подпространстве финитных функций.
Области определения М. и м. о. могут быть конкретно
описаны в ряде случаев, напр, для обыкновенного
дифференциального оператора, для эллиитич. операто-
оператора, для дифференциального оператора с постоянными
коэффициентами.
Лит.: [1] Береааисиий Ю. М., Разложение по собст-
собственным функциям самосопряженных операторов, К., 19t}5.
А. И. Логинов, В. С. Ш,1лъман.
МАКСИМАЛЬНЫЙ ИДЕАЛ — максимальный эле-
элемент в частично упорядоченном множестве тех или иных
собственных идеалов соответствующей алгебраич. сис-
системы. М. и. играют существенную роль в теории ко-
колец. Всякое кольцо с единицей обладает левыми (а
также правыми и двусторонними) М. и. Фактормодуль
M=R/'I левого (соответственно правого) Д-модуля R
по левому (соответственно правому) М. и. / является
неприводимым; гомоморфизм ср кольца R в тело эндо-
эндоморфизмов модуля М — представление кольца R.
Ядро всех таких представлений, т. е. множество эле-
элементов кольца, переходящих в нуль при всех его пред-
представлениях, наз. радикалом Джекобсона
кольца R, оно совпадает с пересечением всех левых
(а также всех правых) М. и.
В кольце R = C [a, b] непрерывных действительных
функций на отрезке [а, Ь] множество всех функций,
обращающихся в нуль в фиксированной точке .г,ь яв-
является М. и. Такими идеалами исчерпываются все
М. и. кольца R. Это соответствие между точками отрез-
отрезка и М. и. кольца R привело к построению различных
теорий, представляющих кольца, как кольца непрерыв-
непрерывных функций на нек-ром топологич. пространстве.
Зариского топология, вводимая на множестве про-
простых идеалов Spec R кольца R, обладает слабыми свой-
свойствами отделимости (т. е. существуют незамкнутые
точки). Аналогичная топология в некоммутативном
случае вводится на множестве Spec R примитивных
идеалов, являющихся аннуляторамн неприводимых
й-модулей. Множество М. п., а в некоммутативном слу-
случае — примитивных М. и., образует подпространство
Spec mRaSpec R, к-рое удовлетворяет аксиоме отде-
отделимости Тг.
Лит.: [1] Джекобсон Н., Строение колец, пер. с англ.,
М., 1961. В. Е. Говоров.
В теории полугрупп М. и. играют меньшую роль,
нежели минимальные идеалы. Если М — максимальный
двусторонний идеал (м. д. п.) полугруппы S, то либо
Л/=5\ {а}, где а — нек-рып неразложимый элемент
из S (т. е. <z?S2X?), либо М есть простой и д е-
а л (т. е. для любых идеалов А, В из АВ^М следует
Дс=М или ВЯ=М); отсюда следует, что в S всякий м. д. и.
будет простым тогда и только тогда, когда S2=S. В по-
полугруппе S с м. д. и. простой идеал P=?S будет макси-
максимальным тогда (и, очевидно, только тогда), когда Р
содержит пересечение / всех м. д. и. из S. Фактор-
полугруппа Риса S/I есть 0-прямое объединение полу-
полугрупп, каждая из к-рых либо 0-простая, либо двух-
двухэлементная нильпотентная.
Иногда полугруппа S с собственными левыми идеа-
идеалами может иметь среди таких идеалов наибольший
L* (т. е. содержащий все другие собственные левые
идеалы); это, напр., выполняется, если S обладает
правой единицей. Если в этом случае множество S' SL*
неодноэлементно, то оно является подполугруппой.
i> периодич. полугруппе S из существования L * вы-
вытекает, что L* будет (наибольшим собственным) дву-
двусторонним идеалом. Другой пример такой же ситуа-
ситуации доставляют подгруппы с отделяющейся групповой
частью (см. Обратимый элемент), не являющиеся
группами.
Лит.: fl] S с h w я г 7 S., «Чехосл. матем. ж.», 1953, т. 3,
Л" 2, с. 139—53; т. 4, с. 365—83; [2] его же, там же, 1969,
т. 19. № 1, с. 72—9; [3] G г 1 1 1 е t P. A., «Amer. Math. Month-
Monthly», 1909, v. 76, № 5, p. 503—09. Л. Н. Шеврин.
МАКСИМАЛЬНЫЙ ИНВАРИАНТ — инвариант-
инвариантная статистика, принимающая различные значения
на различных орбитах, порожденных группой взаимно
однозначных измеримых преобразований выборочного
пространства. Таким образом, если (ЗЕ, 58) — выбо-
выборочное пространство, a G= {g} — группа взаимно од-
однозначных ©-измеримых преобразований Ж на себя,
то инвариантная статистика Т(х) является М. и., если
из того, что Т (х2)=Т (xt), следует, что x2 = gx1 для нек-
рого элемента g^G. Напр., если j? = R", x= {хи . . .,
.г„)г, С={Г} — группа ортогональных преобразований
R"-^R", у=Тх, то статистика Т(х) = 2Х' является
М. и. Любая инвариантная статистика является функ-
функцией М. и.
М. и. используют при построении инвариантных кри-
критериев.
Лит.: [1] Леиан Э., Проверка статистических гипотез,
пер. с англ., М., 1964; [2J Л а к с Ш., Теория статистически-,
вь водов, пер. с англ., М., 1975; [3] К л и м о в Г. П., Инвариант
ные выводы в статистике, М., 1973. М. С. Никулин.
МАКСИМАЛЬНЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯ-
КОРРЕЛЯЦИИ — характеристика взаимозависимости случай-
случайных величин А" и У, определяемая как точная верхняя
грань значений коэффициентов корреляции между дей-
действительными случайными величинами срх(Х) и ср2(У) —
функциями от случайных величин X и У такими, что
(А' (У = 0 и DVl(A') (y l
Если эта верхняя грань достигается при ф1=ф1 (X)
и ф2=ф2 (У), то М. к. к. между случайными вели
чинами А' и У равен коэффициенту корреляции между
величинами ф1 (А') и ф3 (У)- М- к- к- обладает тем свой-
свойством, что равенство р* (X, У)=0 необходимо и доста-
достаточно для независимости случайных величин X и У.
При линейной корреляции между величинами М. к. к.
совпадает с обычным коэффициентом корреляции.
Лит.: [1] Сарманов О. В., «Докл. АН СССР», 1958,
т. 120, № 4, с. 715—18; [2] его же, там же, 1940, т. 53, М 9,
с. 781—84; [3] П р о х о р о в Ю. В., Розанов Ю. А., Теория
вероятностей, 2 изд., М., 1973. И. О. Сарманов.
МАКСИМАЛЬНЫЙ СПЕКТРАЛЬНЫЙ ТИП — тип
максимальной спектральной меры ц
(т. е. класс эквивалентных ей мер) нормального опера-
оператора А , действующего в гильбертовом пространстве Н.
Эта мера определяется (с точностью до эквивалентно-
эквивалентности) из следующего условия. Пусть Е (X) — разложе-
разложение единицы, фигурирующее в спектральном разложе-
разложении нормального оператора Л=\ Xd?(X), a E (\) =
J
— \ <^Е (X) (где Л обозначает борелевское множество) —
соответствующая «операторнозначная» мера; тогда
?"(Л) = 0 в точности для тех Л, для к-рых [х(Л) = 0. Лю-
Любому х^Н сопоставляется его спектральная
мера j.ix(A) = (.r, Е (А)х); в этих терминах определе-
определение |.i означает, что для любого х мера цх абсолютно
непрерывна относительно |х и существует ,г0, для
к-рого \iXo эквивалентна ц (говорят, что х0 принадле-
принадлежит М. с. т.). Если // сепарабельно, то мера ц с та-
такими свойствами всегда существует, но если Н несе-
парабельно, то такой меры может и не быть; тогда А не
имеет М. с. т. Это обстоятельство усложняет теорию
унитарных инвариантов нормальных операторов в не-
сепарабельном случае.
Лит.: [1] Плеснер А. И., Спектральная теория линей-
линейных операторов, М., 1905. Д. В. Аносов.
МАКСИМАЛЬНЫЙ ТОР — 1) М. т. линейной
алгебраической группы G — алгебраи-
алгебраическая подгруппа в G, являющаяся алгебраическим то-
тором и не содержащаяся ни в какой большей подгруппе
такого типа. Пусть, далее, группа G связна. Объеди-
ненио всех М. т. группы G совпадает с множеством всех
полупростых элементов группы G (см. Жордана раз-
разложение) , а пересечение — с множеством всех полупро-
полупростых элементов центра группы G. Всякий М. т. со-
содержится в нек-рой Бореля подгруппе группы G. Цен-
Централизатор М. т. является Картаиа подгруппой груп-
группы G; он всегда связен. Любые два М. т. группы G
сопряжены в G. Если группа G определена над полем
к, то в G существует М. т., также определенный над к;
его централизатор тоже определен над к.
Пусть G — редуктивная группа, определенная над
полем к. Среди всех алгебранч. подгрупп в G, являю-
являющихся расщешшыми над к алгебранч. торами, также
можно рассматривать максимальные подгруппы. По-
Получающиеся таким образом максимальные /с-расще-
пимые торы сопряжены над к. Общая размерность та-
таких торов наз. к - р а н г о м группы G и обозначается
rkfcG. Максимальный fc-расщепнмый тор не является,
вообще говоря, М. т., т. е. rk^G, вообще говоря, меньше
ранга G (равного размерности М. т. в G). Если
rkkG = 0, то G наз. анизотропной над к
группой, а если rk^G совпадает с рангом G, то G
наз. расщепим о и над к группой. Если к
алгебраически замкнуто, то G всегда расщепима над к.
В общем случае G всегда расщепима над сепарабель-
ным замыканием /,-. _
Пример ы. Пусть к — поле и к — его алгебраич.
замыкание. Группа G = GLn(k) невырожденных матриц
порядка п с коэффициентами в к (см. Классическая
группа, Полная линейная группа) определена и рас-
щеппма над простым подполем поля к. Подгруппа всех
диагональных матриц является М. т. в G.
¦ Пусть характеристика поля к отлична от 2. Пусть
V—м-мерное векторное пространство над к, a F —
невырожденная квадратичная форма на V, определен-
определенная над к (последнее означает, что в нек-ром базисе
<?i, . . ., еп пространства V форма F(x1e1-\- . . . ~\-xnert)
является многочленом от тЛ, . . ., хп с коэффициен-
коэффициентами в к). Пусть G—группа всех невырожденных ли-
линейных преобразований пространства V, имеющих оп-
определитель 1 и сохраняющих форму F. Она определена
над к. Пусть \\ — линейная оболочка над к векторов
elt . . . , еп; она является fc-формой пространства V. В V
всегда существует базис fu . . ., /„, в к-ром форма име-
имеет вид
где р = "/2, если и четно, и p=(re-f-l)/2, если п нечетно.
Подгруппа в G, состоящая из тех элементов, к-рые в
этом базисе имеют матрицу вида ||o,w||, где а,-у=О при
1ф] и ацап_{ + ln_j + Л-={ при i=l, 2, . . ., р, является
М. т. в G (так что ранг О равен целой части числа и/2).
Указанный базис не лежит, вообще говоря, в V^-
Однако в I'k всегда существует базис й15 . . ., hn,
в к-ром квадратичная форма имеет вид
/?(*!*,+ ...+*„»„) =
q + ii- ¦ -i xn-q)i
где Fq— квадратичная форма, не представляющая над к
нуля (т. е. такая, что уравнение Fo=0 имеет в к только
нулевое решение) (см. Витта разложение). Подгруппа
в G, состоящая из всех эле.ментов, к-рые в базисе hi,
. . ., lin имеют матрицу вида ||о,-у||, где а,-у=0 при гф],
ailan.i + li „_,- + 1=1 при г=1, . . ., q и а,-,-=1 при
i=g-j-l, . . ., п—q, является максимальным fc-расще-
im.Mi.i.M тором в G (так что rk^G^^ и G расщепима тогда
и только тогда, когда q равно целой части nil).
Рассмотрение М. т. позволяет сопоставить редуктив-
ной группе G нек-рую корневую систему, что является
основой классификации редуктивных групп. А имен-
но, пусть <\ — алгебра Ли группы G и Т — фикси-
фиксированный М. т. в G. Присоединенное представление
тора Т в пространстве д рациопально и диагонализи-
руемо, так что д раскладывается в прямую сумму ве-
весовых подпространств этого представления. Множество
ненулевых весов этого представления (рассматривае-
(рассматриваемое как подмножество своей линейной оболочки в
векторном пространстве X (Г)(Х)-/7 R, где X (Т) — группа
рациональных характеров тора Т) оказывается (при-
(приведенной) корневой системой. Аналогично определя-
определяется и относительная система корней: если G определе-
определена над k, a S — максимальный fc-расщешшый тор в G,
то множество ненулевых весов присоединенного пред-
представления S в д образует корневую систему (вообще
говоря, неприведенную) в нек-ром подпространстве
пространства А'E)(Х) R. См. также Вейля группа,
lL\
Полупростая группа.
Лит.: 11] Б о р е л ь А., Линейные алгебраические группы,
пер. с англ., М., 1972; [2] Арифметические группы и автоморф-
ные функции, пер. с англ. и франц., М., 1969.
2) М. т. связной вещественной груп-
группы Л и G — связная компактная коммутативная
подгруппа Ли Т в G, не содержащаяся ни в какой боль-
большей подгруппе такого типа. Как группа Ли, М. т. Т
изоморфен прямому произведению нескольких экзем-
экземпляров связной одномерной компактной вещественной
группы Ли, к-рая, с точностью до изоморфизма, су-
существует только одна и может быть отождествлена с
«окружностью» S (мультипликативной группой всех
комплексных чисел, равных по модулю 1). Всякий М. т.
группы G содержится в максимальной компактной под-
подгруппе группы G; любые два М. т. группы G (так же,
как и любые две ее максимальные компактные подгруп-
подгруппы) сопряжены в G. Это в известной степени сводит изу-
изучение М. т. к тому случаю, когда G компактна.
Пусть, далее, G является компактной группой. Объ-
Объединение всех М. т. группы G совпадает с G, а пересе-
пересечение — с центром G. Алгебра Ли М. т. Т является
максимальной коммутативной подалгеброй в алгебре
Ли й группы G, и всякая максимальная коммутатив-
коммутативная подалгебра в д так получается. Централизатор
М. т. Т в G совпадает с Т. Присоединенное представле-
представление Т в д диагонализируемо, и все ненулевые веса это-
этого представления образуют в пространстве X G")(X)_R,
IL>
где X (Т) — группа характеров тора Т, корневую
систему. Последнее обстоятельство служит основой
классификации компактных групп Ли.
Лит.: [1] Понтрягин Л. С, Непрерывные группы,
3 изд., М., 1973; [2] Ж е л о б е н к о Д. П., Компактные груп-
группы Ли и их представления, М., 1970: [3] X е л г а с о н С,
Дифференциальная геометрия и симметрические пространства,
пер. с англ., М., 1964. В. Л. Попов.
МАКСИМАЛЬНЫЙ ЧЛЕН РЯДА — член сходяще-
сходящегося числового или функционального ряда с положи-
положительными членами, значение к-рого не меньше значений
всех членов этого ряда.
Применяя это понятие при изучении степенных ря-
рядов
по комплексному переменному z с положительным
радиусом сходимости Я, 0<Л<оо, имеют в виду
максимальный член |х (г) ряда
2Г=о|с*|г*' 0<r = lz-al<R;
таким образом,
Индекс v(r) М. ч. р. ц(г) наз. центральным
индексом:
Если имеется несколько членов ряда, по модулю рав-
равных (х(г), то за центральный индекс принимается на-
наибольший из индексов этих членов. Функция
у = In и. (ех), — оо < х < оо ,
— неубывающая и выпуклая; функция v (r) — ступен-
ступенчатая, возрастает в точках разрыва на натуральное
число и всюду непрерывна справа.
Лит.: [1] В а л и Р о н Ж., Аналитические функции, пер.
с франц., М., 1957; [2] В и т т и х Г. В., Новейшие исследова-
исследования по однозначным аналитическим функциям, пер. с нем., М.,
1960. Е. Д. Соломенцев.
МАКСИМИЗАЦИЯ И МИНИМИЗАЦИЯ ФУНКЦИЙ
конечного числа переменных — задачи
поиска экстремума функции f(x), х= (х1, . . ., хп)?Хд^
cR»; под этой задачей понимается:
1) нахождение /=sup f{x) или /= inf f (x);
хеХ - хеХ
2) отыскание точек максимума или минимума, если
./ или / достигаются на допустимом множестве (см.
Максимум и минимум функции);
3) построение максимизирующей после-
последовательности {х;} или м и н и м и з и р у го-
щей последовательности {ж,} таких, что
lim f(x-\=u lim f(xj)=f,
I —*- JO j —*- CO
если/ или / недостижимы на X.
Исследованием экстремумов функций дискретных
аргументов занимается дискретное программирование
и целочисленное программирование. Ниже освещены
только методы М. и м. ф. непрерывных аргументов.
Классические (непрямые) методы М. и м. ф. приме-
применимы только для гладких функций. Они используют
необходимое условие экстремума для поиска стацио-
нарных точек. Нули производных —~ , а—1, . . ., п
дха
вычисляются на практике чаще всего одним из много-
многочисленных методов последовательных приближений
(см. [31). С другой стороны, каждую задачу решения
конечных функциональных уравнений вида
фга (ж1, .. ., ж") = 0, m<n,
можно интерпретировать как задачу М. и м. ф., напр,
функции
/ (х) =<Pi (*)+••¦ +фт ix) —* min>
и применить для решения последней один из специфич.
методов М. и м. ф.
Прямые методы М. и м. ф. основываются на непосред-
непосредственном сравнении значений f (х) в двух или несколь-
нескольких точках.
Для практич. отыскания экстремумов применяются
итеративные алгоритмы вида:
где i — номер итерации, а X (•) — нек-рый оператор.
При этом обычно предполагается:
1) сходимость алгоритма в том или ином смысле,
чаще всего в смысле
*„ = 7(х„ =?•) или / (*„) =7 (/ (х„) = /);
2) локальность итерационной процедуры, т. е,
7<^0'==о@ ПРИ ?—>-°°); алгоритм «помнит» значения х
только для итераций в нек-рой окрестности текущего
положения Xj. При /=0 получается простой марков-
марковский вычислительный процесс без памяти.
Оператор X (¦) может быть детерминированным в
детерминированных методах или содержать стохастич.
параметры. В вычислительной практике часто сочета-
сочетают стохастич. методы с детерминированными, напр, в
покоординатного спуска методе направление спуска
может определяться случайным образом. Вероятно-
Вероятностные характеристики стохастических параметров, в
свою очередь, могут меняться от итерации к итера-
итерации (поиск с адаптацией и «самообучением», случай-
случайный поиск).
Широко применяют и комбинирование различных де-
детерминированных методов, к к-рому относится последо-
последовательное и параллельное вычисление экстремума не-
несколькими методами, композиции алгоритмов вида
Х = Х2 (Хг( •)) и т. п. Напр., метод Левенбер-
г а — М а р к в а р д т а
¦>•;+1 = *i — (а; V v/ (¦*/) +¦ ?ч!) ~ * V/ (*,-),
к-рый при а,- —О совпадает с градиентным методом, а
при Р[ = 0 с методом Ньютона.
Одномерная оптимизация, то есть
М. и м. ф. f(x), x?Rl, помимо самостоятельного ин-
интереса, является необходимым этапом большинства
применяемых методов. К специфически одномерным
Относятся, напр., Фибоначчи метод, половинного де-
деления метод (дихотомии метод), парабол метод. Ме-
Методами М. и м. ф. многих переменных являются гра-
градиентный метод, наискорейшего cni/ска метод, покоор-
покоординатного спуска метод, симплексный поиск, сканиро-
сканирования метод, сопряженных градиентов метод, тяжело-
тяжелого шарика метод, установления метод и др.
Алгоритмы большинства из перечисленных методов
укладываются в схему метода спуска (подъ-
(подъема):
причем f(xi + i)<.f(xj) или /(х,- + 1)>/(ж,-) для всех i
(условие релаксации). Они различаются между собой
либо выбором вектора направления у,- спуска, либо
выбором способов движения вдоль вектора спуска,
определяемым шаговым множителем эе.
Овражные методы разработаны для функции, рельеф
к-рых имеет вид «оврагов с крутыми склонами» (см.
Овражных функций методы минимизации). Ординар-
Ординарные (не овражные) методы, будучи примененными
здесь, дают извилистый релаксационный
и у т ь, требующий чрезмерно больших затрат ма-
машинного времени для вычисления экстремума.
Сравнительная эффективность методов оценивается
по многим и противоречивым критериям. Сюда входят:
точность решения, скорость решения, надежность ме-
метода, время подготовки задачи к счету, сходимость ал-
алгоритма и др. Область применения каждого из апроби-
апробированных методов весьма ограничена.
Для испытания методов разработаны наборы стан-
стандартных тест-функций, характерных для раз-
различных функциональных классов (см. [1]). Усиленно
исследуется сходимость методов М. и м. ф. (см. [6], [8]).
Однако сходимость — это качество, к-рое не является
ни необходимым, ни достаточным для эффективного
окончания вычислений.
Все перечисленные выше методы приводят к одному
из- локальных экстремумов, если начальное приближе-
приближение принадлежит области притяжения точки этого экс-
экстремума. Нахождение глобального экстремума гаран-
гарантируется лишь для выпуклых и родственных им
унимодальных функций. Теория отыскания глобального
экстремума находится A982) в начальной стадии раз-
развития (см. Многоэкстремальная задача). Другим раз-
развивающимся направлением М. и м. ф. является опти-
оптимизация негладких функций (см. [4], [13], [16]). В ча-
частности, к негладкой функции, как правило, приводит
задача минимизации функции максимума (см. Макси-
мин; численные методы). По-видимому, все из общеупо-
общеупотребительных методов оптимизации имеют содержатель-
содержательный физический, экономический пли биологический
смысл. Соответствующие исследования только развора-
разворачиваются (см. [9]) и приводят к созданию новых мето-
методов (см. также Непрерывные аналоги итерационных
методов). Если значения исследуемой функции опреде-
определяются статистически со стохастич. помехой, то для
отыскания экстремума применяется один из методов
стохастической аппроксимации. Сюда же примыкает
и планирование эксперимента.
Экспериментальные методы М. и
м. ф. используют воспроизведение различных физич,
процессов для поиска экстремумов. К ним относится и
моделирование на АВМ (см. [17]). Несмотря на удобст-
удобство и дешевизну использования в простейших автома-
тич. оптимизаторах, последнее не обеспечивает вы-
высокой точности вычисления.
Графи ч. методы пригодны только для прики-
дочных расчетов и построения начального приближения
для итеративных методов.
Если допустимое множество задано в виде функцио-
функциональных условий
4>т И < О
(связи и ограничения, условный экстремум), то для
поиска экстремумов применяются методы математич.
программирования. Эта же задача может быть сведена
к последовательности задач на безусловный экстремум с
помощью штрафных и барьерных функций (см. Штраф-
Штрафных функций метод).
Лит.: [1] А о к и М., Введение в методы оптимизации, пер.
с англ., М., 1977; [2] Б а х в а л о в Н. С, Численные методы,
2 изд., М., 1975: [j] Березин И. С, Жидков Н. П.,
Методы вычислений, 3 изд.. т. 1, М., 1966; 2 изд., т. 2, М., 1962;
[4] Васильев Ф. II., Лекции по методам решения экстре-
экстремальных задач, М., 1974; [5] Г у п а л А. М., Стохастические ме-
методы решения негладких экстремальных задач, К., 1979; [б]
Карманов В. Г., Математическое программирование, М.,
1975; [7] М о и с е е в Н. Н., Иванилов Ю. П., Столя-
Столярова Е. М., Методы оптимизации, М., 1978; [8] П ш е н и ч-
н ы й Б. Н., Данилин Ю. М., Численные методы в экстре-
экстремальных задачах, М., 1975; [9] Р а з у м и х и н Б. С, Физиче-
Физические модели и методы теории равновесия в программировании
и экономике, М., 1975; [10] РастригинЛ. А., Системы экс-
экстремального управления, М., 1974; [11] Саульев В. К.,
Самойлова И. И., в сб.: Итоги науки и техники. Матема-
Математический анализ, т. 11, М., 1973, с. 91 — 128; [12] Уайлд
Д.-Д ж., Методы поиска экстремума, пер. с англ., М., 1967;
[131 Федоров В. В., Численные методы максимина, М., 1979;
[14] Ортега Д., Рейнболдт В., Итерационные методы
решения нелинейных систем уравнений со многими неизвест-
неизвестными, пер. с англ., М., 1975; [15] Современное состояние теории
исследования операций, М., 1979; [161 Nonsmooth Optimization,
Oxf., 1978: [17] Towards Global Optimisation, v. 1—2, Amst.—
N. Y., 1075 — 78; [18] Евтушенко Ю. Г., «Ж. вычисл.
матем. и матем. физ.», 1971, т. II, .Vi 6, с. 1390—1403.
Ю. П. Иваиилов, В. В. Охрименко.
МАКСИМИН — смешанные экстремумы
sup inf F (х, у), max min F (x, у) и т. п. (*)
lE.Vl/6 1' x € X у g Y
М. можно интерпретировать (напр., в теории принятия
решений, исследовании операций или теории игр) как
наибольший выигрыш из тех, к-рые могут быть достиг-
достигнуты принимающим решения субъектом в наихудших
для него условиях, и, тем самым, как гарантированный
выигрыш. Поэтому принятие решений, ориентирующее
на М., может считаться разумным, оптимальным.
Значение М. не превосходит значения соответствую-
соответствующего минимакса. Условия их равенства весьма важны
в теории игр (см. Минимакса принцип). Такими усло-
условиями являются, напр., наличие в X линейной струк-
структуры, выпуклость X в ней и вогнутость функции F
по .г^-Х при любом y?Y (или же линейность и выпук-
выпуклость Y и выпуклость F по y?Y при любом х^Х).
Нахождение М. как математич. операция формально
состоит в последовательном вычислении экстремумов,
т. е. в решении стандартных («однокритернальных»)
задач оптимального программирования, и потому
никаких концептуальных сложностей не содержит.
Однако даже в условиях «хорошо устроенного» мно-
множества Y и равностепенно по X непрерывной функции
F на нем функция, выражающая соответствие значения
х значениям г/, на к-рых достигается (или «почти дости-
достигается») экстремум inf F (х, у), может оказаться «плохо
г/6 v
устроенной» и, в частности, разрывной функцией от х.
В этих случаях аналитич. нахождение М. (*) становится
затруднительным, и этот М. приходится определять
численными методами (см. Максимин, численные мето-
методы). Сказанное относится и к нахождению минимаксов.
Н. Н. Воробьев.
МАКСИМИН; численные методы — раздел
вычислительной математики, посвященный решению
максиминных (минимаксных) задач. Задачи вычисле-
вычисления максиминов и минимаксов часто возникают в ис-
исследовании операций и теории игр, напр, при использо-
использовании минимакса принципа или наибольшего гаранти-
гарантированного результата принципа.
Исходной является задача вычисления М.:
sup inf F (х, у), A)
х s А' у б Y
возникающая, напр., при решении антагонистич. игр
с полной информацией. Ее естественным обобщением
является задача нахождения М. со «связанными» пере-
переменными:
sup inf F (х, у), B)
х s X уеВ[х)
причем множество В (х) часто задается в виде
B(x) = {y?.Y\y(x, г/) 5=0} ф 0
для всякого х?Х. Эта задача оказывается основной
в теории игр двух лиц с обменом информацией (см.,
напр., Игра с иерархической структурой). Итериро-
Итерирование исходной задачи приводит к задаче кратного,
или последовательного, М.:
sup inf ... sup inf F (xu yu ..., xn, yn), C)
дг,бХ, г/,бУ! xneXnyn?Yn
к-рая связана с решением нек-рых динамич. игр. Пред-
Представляют интерес стохастич. задачи вычисления М., а
также минимаксные задачи оптимального управления.
В основе большинства способов решения минимаксных
задач лежит градиентный метод или штрафных функ-
функций метод. При применении первого из них задачу A)
рассматривают как задачу оптимального программи-
программирования
sup /И, D)
х е X
где
f(x)=mlF{x,y). E)
УЧУ
Построение численных методов решения задачи
D) — E) связано с дифференцируемостью по направ-
направлению функции минимума E).
Если XczW, Y — компакт в R, — производная
по направлению g?Rn (см [1] — [3]),
Ц&= min (^F(x,y),
)
ytYW F)
Y(x) = {y?Y\F(x, у) =/(*)}, j
то в случае конечного множества Y формула F) по-
позволяет построить итеративную последовательность хи
ж2, . . ., в к-рой ?fc + i"?ft+ctfcftj для к=0, 1, ... и
к-рая при нек-рых дополнительных предположениях
сходится к точке, удовлетворяющей необходимому ус-
условию М.
При использовании метода штрафных функций зада-
задача A) для непрерывной на произведении компакта
¦i" и единичного куба YdRm функции F(x, у)
сводится к нахождению
lim max Jf (х, и, с),
С —у со и, X ? X
где
X (х, и, с) = и — с ^у (min (О, F (x, y) — u)y-dy G)
(и — вспомогательная переменная). При этом если
пара (и (с), х (с)) реализует максимум
max if (г, г/, с),
ы, *еХ
то любая предельная точка (и*, х*) последовательно-
последовательности {(и(с?), a;(Cfc))|c?—э-оо } дает величину
u* = max min /" (г, у)
хеХ yeY
М. A) и одну из оптимальных стратегий ж*, для к-рой
в*= min ^ (ж*, у)
уе У
(см. [4]). Тем самым решение задачи A) с любой точ-
точностью сводится к отысканию максимума функции G)
при достаточно больших значениях штрафа с. Избежать
трудностей, связанных с вычислением интегралов в
G), позволяет метод стохастич. градиента (см. [5], [8]):
ГД° (?fc(cfc), T)ft (eft)) — стохастич. градиент функции
Х{с, у, Cfr), т. е. случайная величина, математич. оя;п-
к-рой совпадает с
ь <*)) •
При нек-рых условиях, налагаемых на последователь-
последовательности {ak } и {с? } и функцию F (х, у), для любого началь-
начального приближения (хи у^ последовательность, опре-
определяемая процессом (8), с вероятностью 1 сходится к
множеству решений задачи нахождения М. A).
Избежать больших значений параметра штрафа с
в G) позволяет т. н. «метод невязок» (см. [6]), представ-
представляющий собой еще один способ преобразования задачи
A). При этом величина а* М. A) определяется как мак-
максимальное значение и, для к-рого
min Ф (х, и)=0, (9)
где
Ф (х, у)=\ (min (О, F (х, y) — u)Jdy.
Здесь значение х*, реализующее
min Ф (х, и*),
хйХ
дает оптимальную стратегию в задаче A). Отыскивать
наибольший корень и* уравнения (9) можно, используя
градиентные методы минимизации функции Ф по х.
Методы преобразования задач, основанные на мето-
методе штрафных функций, позволяют приближенно сво-
сводить к задачам на максимум минимаксные задачи со
связанными переменными B) (см. [7], [8]).
Экстремальные задачи, к-рые получаются при све-
сведении минимаксных задач к задачам на максимум,
весьма сложны, и их решение известными методами
сопряжено с большими, подчас непреодолимыми для
современных ЭВМ трудностями. В особенности это
относится к проблеме отыскания последовательных
М. из C) при большой кратности.
Наряду с указанными общими подходами к решению
минимаксных задач имеется ряд приемов, ориентнро-
ванных на те или иные частные классы задач, напр,
на задачи теории игр двух лиц с передачей информации
(см. 161).
Лит.: [1] Демьянов В. Ф., М а л о з е м о в В. Н.,
Введение в минимакс, М., 1972; [2J Д а н с к и н Д ж. М., Те-
Теория максимина, пер. с англ., М., 1970; [3] Д е м ь я н о в В. Ф-,
Минимакс: дифференцируемость по направлениям, Л., 1974;
[4] Герме й ер Ю. Б., Введение в теорию исследования опе-
операций, М., 1971; [5] Е р м о л ь е в Ю. М., Методы стохастиче-
стохастического программирования, М., 197В; [BJ Герме й е р Ю. Б.,
Игры с непротивоположными интересами, М., 1976: [7] Е р е ш-
к о Ф. И., 3 л о б и н А. С, «Экономика и матем. методы»,
1977, т.13, № 4, с. 703—13; [8] Ф е д о р о в В. В., Численные
методы максимина, М., 1979. В. В. Федоров.
МАКСИМИНА ПРИНЦИП — см. Мипимакса прин-
принцип.
МАКСИМИННЫЙ КРИТЕРИЙ — статистический
критерий для проверки сложной гипотезы Но : в ? 60d
Св против сложной альтернативы Н1 : 0"?в1=0\0о,
минимальное значение мощности к-рого является мак-
максимальным в классе всех статистнч. критериев, пред-
предназначенных для проверки Но против Нх и имеющих
один и тот же размер а, 0<а<1. В задаче статистич.
проверки гипотезы Но против альтернативы Ht M. к.
существует в основном, если сама эта задача является
инвариантной относительно нек-рой группы преобразо-
преобразований G, а в соответствующем классе инвариантных
критериев существует равномерно наиболее мощный
критерии. М. к. существует, если семейство вероятно-
вероятностных распределений, определяемое нулевой и конку-
конкурирующей гипотезами До и Нл, является абсолютно не-
непрерывным относительно нек-рой а-конечноп меры.
Лит.: [1] Леман Э. Л., Проверка статистических гипо-
гипотез, пер. с англ., 2 изд., М., 1979; [2] Г а е к Я., Ш и д а к 3.,
Теория ранговых критериев, пер. с англ., М., 1971.
М. С. Никулин.
МАКСИМУМ И МИНИМУМ ФУНКЦИИ — наиболь-
наибольшее и соответственно наименьшее значения функции,
принимающей действительные значения. Точку обла-
области определения рассматриваемой функции, в к-рой
она принимает максимум или минимум, наз. соответ-
соответственно точкой максимума или точкой минимума (см.
Максимума и минимума точки). Если нек-рая точка
является точкой абсолютного (локального) максимума
или минимума, строгого или нестрогого, то значение
функции в этой точке наз. абсолютным (локальным),
соответственно строгим или нестрогим максимумом или
минимумом. Если функция непрерывна на компакте,
то она всегда принимает на нем максимальное и мини-
минимальное значения.
М. и м. ф. называется ее экстремумом.
Л. Д. Кцбрявцев.
МАКСИМУМА И МИНИМУМА ТОЧКИ — точки,
в к-рых действительная функция принимает наиболь-
наибольшее или наименьшее значения на области определения;
такие точки наз. также точками абсолютного
максимума или абсолютного м и н и-
м у м а. Если функция / определена на топологич.
пространстве X, то точка х0 наз. точкой локаль-
локального максимума (локального мини-
минимума), если существует такая окрестность UczX точ-
точки х0, что для сужения рассматриваемой функции на
этой окрестности точка х0 является точкой абсолют-
абсолютного максимума (минимума). Различают точки стро-
строгого н нестрогого максимума (м и-
н и м у м а) (как абсолютного, так и локального).
Напр., точка жо?Д наз. точкой нестрогого (строгого)
локального максимума функции /, если существует
такая окрестность точки х0, что для всех x?U выпол-
выполняется неравенство / (х) <:/ (х0) (соответственно /(х)<
</() )
/(о). 0)
Для функций, определенных на конечномерных об-
областях, в терминах дифференциального исчисления
существуют условия и признаки того, чтобы данная
точка была точкой локального максимума (минимума).
Пусть функция / определена в нек-рой окрестности
точки х0 числовой осн. Если х0— точка нестрогого ло-
локального максимума (минимума) и в этой точке суще-
существует производная /' (х0), то она равна нулю.
Если заданная функция / дифференцируема в окрест-
окрестности точки х0, кроме, быть может, самой этой точки,
в к-рой она непрерывна, и производная /' по каждую
сторону от точки хп в этой окрестности сохраняет по-
постоянный знак, то для того чтобы х0 была точкой
строгого локального максимума (локального минимума),
необходимо и достаточно, чтобы производная меняла
знак с плюса на минус, т. е. чтобы /' (х)>0 при х<Сх0 и
/' (х) <U при ж>.т0 (соответственно с минуса на плюс:
f'(x)<0 при х<ха и /'(а;)>0 при х>хо). Однако не
для всякой функции, дифференцируемой в окрестности
точки х0, можно говорить о перемене знака производной
в этой точке.
Если функция / имеет в точке х0 т производных, при-
причем /tft>(jo) = 0, А=1, 2, . . ., т—1, Ц'")(хо)фО, то
для того чтобы х0 была точкой строгого локального мак-
максимума, необходимо и достаточно, чтобы т было чет-
четным и чтобы /(/л) (жо)<О, и — локального минимума,
чтобы т было четно и /1'л) (хо)>0.
Пусть функция /(.Г], . . ., хп) определена в «-мерной
окрестности точки ,г@>—(Л"\ • • ., #«") и дифференциру-
дифференцируема в этой точке. Если ж@) является точкой нестрогого
локального максимума (минимума), то дифференциал
функции / в этой точке равен нулю. Это условие равно-
равносильно равенству нулю в этой точке всех частных про-
производных 1-го порядка функции /. Если функция имеет
2-е непрерывные частные производные в точке г@), все ее
1-е производные обращаются в ж@) в нуль, а дифферен-
дифференциал 2-го порядка в точке х{0) представляет собой отри-
отрицательную (положительную) квадратичную форму, то
х{0) является точкой строгого локального максимума
(минимума). Известны условия для М. и м. т. диффе-
дифференцируемых функций, когда на область изменения
аргументов наложены определенные ограничения: удов-
удовлетворяются уравнения связи. Необходимые и доста-
достаточные условиям максимума (минимума) действительной
функции, область определения к-рой имеет более
сложную структуру, изучаются в специальных разде-
разделах математики: напр., в выпуклом анализе, математи-
математическом программировании (см. также Максимизация и
минимизация функций). М. и м. т. функций, опреде-
определенных на многообразиях, изучаются в вариационном
исчислении в целом, а М. и м. т. для функций, задан-
заданных на функциональных пространствах, т. е. для функ-
функционалов, в вариационном исчислении. Существуют
также различные методы численного приближенного
нахождения М. и м. т.
Лит.: ШИльин В. А., II о з н я к Э. Г., Основы матема-
математического анализа, Зизд., ч. 1. М., 1971; [2] Кудрявцев Л.Д.,
Курс математического анализа, т. 1,2, М., 1981; [3] Н и к о л ь-
ск и й С. М., Курс математического анализа, 2 изд., т. 1, М.,
1975; [4] Б а х в а л о в Н. С, Численные методы, 2 изд., т. 1,
М. 1975. Л. Д. Кудрявцев.
МАКСИМУМА МОДУЛЯ ПРИНЦИП — теорема, вы-
выражающая одно из основных свойств модуля апалитич.
функции. Пусть / (z) — регулярная аналитическая,
или голоморфная, функция п комплексных перемен-
переменных z= (zlt . . ., zn), iC^\, в области D комплексного
числового пространства С", отличная от константы,
/C)=^const. M. м. п. в локальной форме ут-
утверждает, что ни в какой точке z°^D не может дости-
достигаться локальный максимум модуля /(z), т. е. не суще-
существует окрестности F(z°) точки z°, в к-рой выполняется
неравенство l/(z)| <|/(z°)|, z?V(z°). Если, кроме того,
f(i^3)ф0, то z° не может быть и точкой локального ми-
минимума модуля /(z). Равносильная формулировка
М. м. п. в глобальной форме состоит в том,
что при тех же условиях модуль аналитнч. функции
/(z) не может достигать своей верхней грани
ни в какой точке z°?D. Следовательно, если f(z) не-
непрерывна в конечной замкнутой области D, то наиболь-
наибольшее значение М достигается только в граничных точ-
точках области/). Приведенные формулировки М. м. п. со-
сохраняют силу и в том случае, если f(z) — голоморф-
голоморфная функция на связном комплексном (аналитическом)
многообразии, в частности на римановой поверхности
пли на римановой области D.
М. м. п. допускает обобщения в различных направле-
направлениях. Во-первых, вместо голоморфности /(z) достаточ-
достаточно предположить только, что /(z) — u{z)-{-iv(z) — (ком-
(комплексная) гармоническая функция. Другое обобщение
связано с тем, что для голоморфной функции / (z) мо-
модуль !/(z)| есть логарифмически субгармоническая функ-
функция. Если /(z) — ограниченная голоморфная функция
в конечной области DcC" и условие
limsup{|/(z)|:z—>?,
выполняется для всех точек ??д?), кроме точек
нек-рого множества EddD внешней емкости нуль
(в пространстве R2" = C"), то |/(z)|<Af всюду в D.
См. также Двух констант теорема, Фрагмена — Лин-
делёфа теорема.
М. м. п. обобщается и на голоморфные отображения.
Пусть / : D—>-Cm — голоморфное отображение области
.DczC", н^1, впространство С", т. е. /= (/i, . . ., fm),
m^l, fj, /'=1, . . ., m, — голоморфные функции в
D, /(z)^const и Ц/11 = ]/'l/il2-K . H-l/mT2 — евклидова
норма. Тогда ни в какой точке zu?D функция |!/(=)|| не
может достигать локального максимума. М. м. п.
справедлив всякий раз, когда выполняется сохране-
сохранения области принцип.
Лит.: [1] С т о и л о в С, Теория функций комплексного
переменного, пер. с рум., М., 1962; [2] В л а д и м и р о в В. С,
Методы теории функций многих комплексных переменных, М.,
1964; [3] Ш а б а т Б. В., Введение в комплексный анализ,
2 изд., ч. 1—2, М., 1976. Е. Д. Соломенцее.
МАКСИМУМА ПРИНЦИП дискретный —
принцип максимума Понтрягина для дискретных по
времени процессов управления. Для такого процесса
М. п. может не выполняться, хотя для его непрерыв-
непрерывного аналога, получающегося заменой конечно раз-
разностного оператора %t + i—Xf на дифференциальный
dxldt, Понтрягина принцип максимума справедлив.
Пусть, напр., имеется задача оптимального управления
max/ (xT+1), A)
/t(*/> Щ), B)
$, t=0, 1, ..., Т, C)
хй = а. D)
Задачу A) — D) можно трактовать как обычную зада-
задачу на экстремум при наличии ограничений. Тогда ус-
i * * 1
ловия оптимальности траектории \xt, ut ) можно полу-
получить с помощью Лагранжа функции
где выражение
Pt + 1ft(rt, ut) = Ht
по аналогии с непрерывным случаем наз. Гамильтона
функцией. Пусть функции /, /f, t=0, I, . . ., Т, диф-
дифференцируемы по совокупности переменных, а мно-
множество U ограничено и замкнуто. Тогда для того
чтобы решение {х/, щ } задачи A) — D) было опти-
оптимальным, необходимо существование Лагранжа множи-
множителей {р*+1} таких, что точка (х*, и*, pt+1) будет ста-
стационарной точкой функции Лагранжа, т. е. в этой точке
выполняются условия
dL n dL n s г ^-^ & п
для всех допустимых вариаций управления ди. Пер-
Первое условие приводит к уравнениям динамики дискрет-
дискретного процесса B) и начальному условию D). Второе —
к граничному условию и сопряженной системе для
импульсов {pt + i}'-
.., 1, 0.
Третье условие — к условию для первой вариации
функции Гамильтона:
ввЯ* = -^-в«(<0. E)
Однако условие E) не означает, что функция Гамиль-
Гамильтона на оптимальном управлении достигает максимума
Ht(xt, щ , pt+i)=maxllt(zt, и*, pUi)
ueU
по всем управлениям, удовлетворяющим ограничениям
C); оно показывает, что щ —стационарная точка функ-
функции Гамильтона. Если первая вариация функции Га-
дН,
мпльтона -~- buf обращается в нуль (это имеет место,
в частности, когда щ—внутренняя точка множества
или когда в точке uf существуют допустимые вариа-
вариации управления 8uf, ортогональные I'lFf/duf), то ха-
характер стационарной точки определяется следующи-
следующими по порядку членами в разложении:
Ht [и] + бби4) —Ht (u't) = е -^- Ьщ <0.
Построены примеры, в к-рых оптимальное управление
щ является точкой локального максимума, локального
минимума и даже седловой точкой функции Гамильто-
Гамильтона. Таким образом, в общем случае для дискретных
систем принцип максимума не имеет места.
Для систем, линейных по фазовым переменным
(ut)
или по управлениям
(xt) щ,
при дополнительном условии линейности критерия
J=cT+1xT+1 в первом или выпуклости множества U
во втором случае принцип максимума выполняется
(см. [1] - [5]).
Трактуя задачу оптимального управления линей-
линейной дискретной системой как задачу линейного програм-
программирования (см. [6], [7]), можно получить двойственную
ей динампч. задачу с дискретным временем. Сопряженная
система для импульсов дает уравнения динамики для
двойственной динампч. задачи. На оптимальной тра-
траектории совпадают не только критерии, но и функции
Гамильтона двойственных динамич. задач.
Лит.: [1] Фан Лянь-цэнь, Ван Ч у - с е н, Ди-
Дискретный принцип максимума, пер. с англ., м., 1967; [2] П р о-
п о ii А. П., Элементы теории оптимальных процессов, М., 1973;
[3] Пшеничный Б. Н., Необходимые условия экстремума,
М., 19Н9; [4J Б о л т я н с к и й В. Г., Оптимальное управле-
управление дискретными системами, М., 1973; [5] Г а б а с о в Р., К и-
р и л л о в а Ф. М., «Автоматика и телемеханика», 1966, Ki 11,
с. 46—51; [6] И в а н и л о в Ю. П., «Прикл. матем. и программи-
программирование», Киш., 1971, в. 4, с. 31 — 40; L7] И в а и и л о в Ю. II.,
Пропой А. И., «Докл. АН СССР», 1971, т. 198, Л» 5, с. 1011 —
1014. Ю. II. Ивппилов.
МАКСИМУМА ПРИНЦИП П о н т р я г н u a —
с ii. Понтрягина принцип максимума.
МАЛАЯ КАТЕГОРИЯ — категория Ш, класс мор-
физмов Мог Я1 к-рой является множеством. М. к. Я
наз. U-к а т е г о р и е ii, если Мог RcU, где U —
универсальное множество. Для каждой М. к. .11' и про-
произвольной категории E можно корректно говорить
о категории одноместных ковариантных (контравари-
антных) функторов из SX в E. В частности, М. к. об-
образуют замкнутую категорию Cat малых категорий —
одну из основных категорий математики [1].
Лит.: [1] Lawvere F. W., The category of categories
as a foundation for mathematics, в кн.: Proc. of the Conference
on categorical algebra, La Jolla, 1963, В.— Hdlb.— N. Y., 1966.
M. Ш. Цаленко.
МАЛЕРА ПРОБЛЕМА — гипотеза в метрнч. теории
диофантовых приближений, высказанная К. Малером
[1]: для почти всех (в смысле меры Лебега) чисел со?Я
неравенство
| Р (со) | < [Н {Р)]-п-г
имеет конечное число решений в многочленах Р^1,{х\
степени не выше п. Здесь е>0, п — натуральное и
Н (Р) —максимум -модулей коэффициентов Р. Эк-
Эквивалентная формулировка: для почти всех со?/{ не-
неравенство
max (|| cog j],
имеет конечное число решений в целых числах q (\\a\\ —
расстояние от а до ближайшего целого числа).
М. п. решена утвердительно в 1964 В. Г. Спринджу-
ком [2]. Им же доказаны аналогичные утверждения для
комплексных и р-адических чисел, а также степенных
рядов над конечными полями.
Лит.: ШМаЫег К., «Math. Ann.», 1932 , Bd 100, S. 131 —
39; [2] С п р и н д ж у к В. Г., Проблема Малера в метрической
теории чисел, Минск, 1967. Ю. В. Нсстереико.
МАЛОГО ПАРАМЕТРА МЕТОД в т е о р и и диф-
дифференциальных уравнений — приемы по-
построения приближенны:: решений дифференциальных
уравнений и систем, з:хисящих от параметра.
1) М. п. м. для обыкновенных диффе-
дифференциальных уравнений. Обыкновенные
дифференциальные уравнения, к к-рым приводят при-
прикладные задачи, обычно содержат один или несколько
параметров. Параметр может входить также в начальные
данные или граничные условия. Поскольку найти точ-
точное решение дифференциального уравнения можно лишь
для отдельных весьма частных классов, возникла задача
о построении приближенного решения. Одна из типич-
типичных постановок ее такова: уравнение и начальные (гра-
(граничные) условия содержат параметр X и решение изве-
известно (или его можно считать известным) при ?v=?v0; тре-
требуется построить приближенное решение при значе-
значениях параметра К, близких к Ко, т. е. построить асимп-
асимптотику решения при е—>-0, где е,=Х—Ко — малый пара-
параметр. М. п. м., возникший в связи с задачей трех тел
небесной механики, восходит к Ж. Д'Аламберу
(J. D'Alembert) и интенсивно развивается с кон. 19 в.
Ниже используются следующие обозначения: t —
независимое переменное, е>0 — малый параметр, / —
отрезок O^t^cT, знак ~ означает асимптотпч. равен-
равенство. Все векторные и матричные функции, входящие в
уравнения и в граничные условия, предполагаются
гладкими (класса С°°) по совокупности неременных в
рассматриваемой области (по 8 — при 0<е<:е0 или
||)
о)
1. Задача Коши для системы n-го порядка:
i = /(t, х, е), х(О) = хо(е). A)
Пусть решение фо(^ предельной задачи (т. е. задачи,
получающейся из A) при е=0) существует и единст-
единственно при t^I. Тогда для решения x(t, е) задачи A)
справедливо асимптотич. разложение при е—>-0
х (t, e) - ф„ (t) + У~=1 еЛру (t), B)
равномерное по г?/. Этот факт вытекает из теоремы
о гладкой зависимости от параметра решений системы
обыкновенных дифференциальных уравнении. Если
вектор-функции / и .т0 голоморфны при |е| <е0, х=фо(г),
t(zl, то ряд B) сходится к решению хA, е) при доста-
достаточно малых |е| равномерно по t?I (теорема Пу-
Пуанкаре). Аналогичные результаты справедливы и
для краевой задачи для системы вида A), если решение
соответствующей предельной задачи существует и един-
единственно.
Различают два вида зависимости уравнения (или
системы) от малого параметра — регулярную
и сингулярную. Система в нормальной форме
регулярно зависит от параметра е, если все правые ее
части — гладкие функции от е при малых е^гО; в про-
противном случае система зависит от параметра е сингу-
сингулярно. При регулярной зависимости системы от е
решение задачи с параметром на конечном отрезке по t,
как правило, равномерно стремится при е-*-0 к реше-
решению предельной задачи.
2. В линейной теории рассматриваются сингулярно
зависящие от параметра г системы n-го порядка
ех = А (t, е)ж-Н(г, е),
где элементы п X л-матрицы А и компоненты вектора
/ —.комплексноаначпые функции. Центральная задача
линейной теории — построение такой фундаменталь-
фундаментальной системы решений (ф. с. р.) однородной системы
(т. о. при /=0), для к-рой асимптотика при е —s—(- О
известна на всем отрезке /.
Основным , результатом линейной теории является
следующая теорема Биркгофа. Пусть: 1) соб-
собственные значения kj(t, 0), 1 </</?, матрицы A (t, 0)
различны при t?I; 2) величины
I\e(Xj (t, O)—Xk(t, 0)), leS/, fr<n, i Ф к,
не меняют знак. Тогда существует ф. ср. x1(t, e),
..., xn(t, e) однородной системы
zx = A(t, e) х,
для к-рой справедливо асимптотпч. разложение при
8^ 0:
х, (t, е) ~ ехр [е-1 J ^ X; (г, г) <*т] 2™=Q e*<pA/ (t), C)
Это разложение равномерно по t^I и его можно диф-
дифференцировать по t и по е любое число раз. Если мат-
матрица А не зависит от 8, т. е. А=А (t), то
[
-
где ej, е,- — левые и правые собственные векторы
матрицы A (t), нормированные условием
(e'f{t), ej(t)) = i, t?I.
Решения, имеющие асимптотику вида C), наз. также
В К Б - р е ш е и и я м и (см. ВКБ-метод). Качест-
Качественная структура этих решений такова. Если
ReXy (t) < 0 [Re Я, (t) > 0] при г?/,
то х/ есть вектор-функция типа пограничного слоя
при to=O (to~T), т. е. заметно отлична от нуля только
в 8-окрестности точки t=0 (t—Т). Если же ЙеЛД*)^),
t?I, то решение xj сильно осциллирует при е —>- -f- 0
н имеет порядок 0A) на всем отрезке /.
Если матрица-функция A (t, e) голоморфна при
Ul <-t0, |s|<:e0 н условие 1) выполнено, то формула C)
справедлива при е—+-+0, 0<;г<4!, где ^>0 достаточно
мало. Трудной проблемой является построение асимп-
асимптотики ф. с. р. при наличии на /точек пово-
поворота, т.е. точек, в к-рых матрица A (t, 0) имеет
кратное собственное значение. Эта проблема полно-
полностью решена только для отдельных типов точек пово-
рота (см. [1]). В окрестности точки поворота имеется
переходная область, в к-рой решение устроено довольно
сложно и в простейшем случае выражается через
Эйри функции.
Аналогичные результаты (см. [1]) справедливы для
скалярных уравнений вида
enz<"> + 2"Г' еЛ»у (t, е) хФ = О,
где ау — комплекснозначные функции; роль функций
Я(?, е) играют корни характерйстич. уравнения
ВКБ-решенпя возникают также и в нелинейных си-
стенах вида
ег = / (t, х, е), xgR".
ВКБ-асимптотика C), в условиях теоремы Биркгофа,
справедлива на бесконечном интервале 0<:i<oo (т. е.
разложение C) — асимптотическое и при е —>- +0,
и при (_^+оо), если матрица A (t, г) достаточно
правильно ведет себя при t—>-+оо, напр, быстро
стремится к постоянной матрице с различными соб-
собственными значениями (см. [2]). К сингулярным за-
задачам с малым параметром приводят многие вопросы
спектрального анализа (см. [3]) и математич. физики.
3. Особый иптерес представляет исследование не-
нелинейных систем вида
ex = f(x,y), х@)=хо, x?Rn, \
\
V = g{x, У), !/(О) = !/о,
где е>0 — малый параметр. Первое уравнение опи-
описывает быстрые движения, второе — мед-
медленные движения. Напр., Ван дер Поля
уравнение с помощью замены
приводится при больших значениях параметра Я а
системе
ei=y —-j-z' + r, y = —x,
имеющей вид D).
При е=0 уравнение быстрых движений вырождается
в уравнение f(x, у) — 0. Пусть это уравнение имеет
в нек-рой ограниченной замкнутой области D изме-
изменения у изолированный устойчивый непрерывный
корень x=q>(y) (т. е. действительные части всех соб-
собственных значений матрицы Якоби — отрицательны
при ж=ф(г/), y(zD); пусть решения задачи D) и вырож-
вырожденной задачи
х = (р(у), y = g(x, у), у(в)=уо E)
существуют и единственны при *?/, причем получаю-
получающаяся при решении задачи E) функция y(t)^_D при
f?/. Если точка (х0, у0) принадлежит области влияния
корня х=ц>(у), то
x(t, е)—>?((), 0 < (<Г,
при е —>- +0, где (х, у) — решение вырожденной задачи
(теорема Тихонова). Вблизи точки (=0 пре-
предельный переход x(t, e)-^-x(t) является неравномер-
неравномерным — возникает пограничный слой. Для задачи D)
построена асимптотика решения:
а асимптотика для y(t, e) имеет аналогичный вид.
В F) первая сумма — регулярная часть асимп-
асимптотики, вторая — пограничный слой. Ре-
Регулярная часть асимптотики вычисляется стандартным
способом: ряды вида B) подставляются в систему D),
правые части разлагаются в ряды по степеням е и
затем приравниваются коэффициенты при одинаковых
степенях е. Для вычисления погранслойной части
асимптотики в окрестности точки i=0 вводится новая
переменная т= tie, (быстрое время) и приме-
применяется описанная выше процедура. Возникает нек-рый
интервал на оси t, на к-ром пригодно и регулярное (или
внешнее) разложение, и погранслойное (или внут-
внутреннее) разложение. Функции xk, Щ определя-
определяются из условия совпадения этих разложений (т. н.
метод сращивания, см. [4], [5]).
Аналогичные результаты справедливы в случае,
когда правые части системы D) явно зависят от ?,
для скалярных уравнений вида
zxW = f(t, х, х, ..., х^-1)) G)
и для краевых задач для таких систем и уравнений
(см. Дифференциальные уравнения с малым параметром
при производных, [6], [7]).
При приближении решения задачи D) к т о ч к е
срыва, где теряется устойчивость (напр., где одно
из собственных значений матрицы dfldx при х = (р(у)
обращается в нуль), ряды вида E) теряют асимптотич.
характер. В окрестности точки срыва асимптотика
имеет совершенно иной характер (см. [8]). Исследо-
Исследование окрестностей точки срыва особенно существенно
для построения асимптотич. теории релаксационных
колебаний.
4. Задачи небесной механики и теории нелинейных
колебаний приводят, в частности, к необходимости
исследовать поведение решения задачи A) не на ко-
конечном интервале, а на большом, порядка е или
более высокого, интервале по t. Для исследования
этих задач широко применяется метод усреднения (см.
Крылова — Боголюбова метод усреднения, Малые зна-
знаменатели, [9] — [И]).
5. Асимптотика решений уравнений вида G) ис-
исследуется, в частности, с помощью т. н. метода
многих масштабов (см. [4], [5]); этот метод
является обобщением ВКБ-метода. Рассмотрим этот
метод на примере скалярного уравнения
еУ+/(г, х)=0, (8)
к-рое имеет периодпч. решения (см. [12]). Решение
ищется в виде
* = <р (Г, t, е) ~ Х"=о е/ФУ (г' 0. Г=ЦР (9)
(функции Т, t наз. масштабами). Если урав-
уравнение (8) — линейное, то фу = ег-фу(?) и (9) есть ВКБ-
решение. В нелинейном случае уравнения первых двух
приближений имеют вид
d4i .
от-- "I
S^ + 1{t, cpo)=O,
df (t, ф„) _ „ д й2ф„ • Эф о
Ф1 ^ ^ Т
от-- "I ta Ф1 —— ^ эГИ'~^ Тт~ '
причем первое уравнение содержит две неизвестные
функции S и «р0. Пусть это уравнение имеет периоди-
периодическое по t решение фо=Фо(Л Т). Тогда недостающее
уравнение, из к-рого определяется S, находится из
условия периодичности по t решения <рх и имеет вид
^: 'ПУ йТ =?е, const,
где интеграл берется по периоду решения ср.
Лит.: [1]Вазов В., Асимптотические разложения реше-
решений обыкновенных дифференциальных уравнений, пер. с англ.,
М., 1968; [2] Ф е д о р ю к М. В., «Матем. сб.», 19В9, т. 7В,
№ 4, с. 477—516; [3] Н а й м а р к М. А., Линейные дифферен-
дифференциальные операторы, 2 изд., М., 1969;^[4] К о у л Д.-Д., Методы
возмущений в прикладной математике'', пер. с англ., М.. 1972; 15]
Найфэ А. X., Методы возмущений, пер. с англ., М., 197ь;
[6] Васильева А. Б., Бутузов В. Ф., Асимптотиче-
Асимптотические разложения решений сингулярно возмущенных уравнений,
М., 1973; [7] и х ж е, Сингулярно возмущенные уравнения в
критических случаях, М., 1978; [8] Мищенко Е. Ф., Р о-
з о в Н. X., Дифференциальные уравнения с малым параметром
и релаксационные колебания, М.,197 5; [9] Боголюбов Н. Н.,
Митропольский Ю. А., Асимптотические методы в тео-
теории нелинейных колебаний, 4 изд., М., 1974; [101 В о л о-
с о в В. М., Моргунов Б. И., Метод осреднения в теории
нелинейных колебательных систем, М., 1971; [11] Ар-
Арнольд В. И., «Успехи матем. наук», 1063, т. 18, в. «, с. 91 —
192; [12] К у з м а к Г. Е., «Прикл. матем. и мех.», 1959, т. 23,
«3, с. 515 — 26; [13] Андронов А. А., В и т т А. А.,
Хайкин С. Э., Теория колебаний, 2 изд., М., 1959; [14]
Джакалья Г. Е., Методы теории возмущений для не-
нелинейных систем, пер. с англ., М., 1979; [15] М о и с е е в Н. Н.,
Асимптотические методы нелинейной механики, М., 19UU: [1В]
Бутузов В. Ф.,Васильева А. Б., Ф е д о р ю к М. В.,
в кн.: Итоги науки. Математический анализ. 1967, М., 1969,
с. 5—73. Н. X. Розов. М. В. Федорюк.
2) М. п. м. для дифференциальных
уравнений с частными производ-
производными. Как и для обыкновенных дифференциальных
уравнений, решения дифференциальных уравнений с
частными производными могут зависеть от малого па-
параметра е (предполагается, что е>0) регулярно или
сингулярно. Грубо говоря, регулярная зависимость
наблюдается тогда, когда старшие члены дифферен-
дифференциального оператора не зависят от е, а младшие чле-
члены — гладкие функции е при малых е. Тогда и решение
является гладкой функцией е. Если же при е _> 0
обращается в нуль какой-либо из старших членов в
уравнении с частными производными, то решение,
как правило, зависит от е сингулярно. В этом случае
часто говорят об уравнении с частными производными
«с малым параметром при старших производных».
Подобная классификация несколько условна, т. к.
само выделение старших членов не всегда очевидно;
к тому же параметр может входить и в граничные
условия. Кроме того, сингулярность может возникнуть
в случае неограниченной области, даже если малый
параметр стоит при младших производных (на беско-
бесконечности они играют в определенном смысле такую же
или даже более главную роль, чем старшие).
Пусть, напр., имеется эллиптич. уравнение с част-
частными производными 2-го порядка в ограниченной
области GcR". Решение задачи
есть гладкая функция е при малых е, если граница
гладкая, ау, Ь, /, ср — гладкие функции от х и е и пре-
предельная краевая задача
однозначно разрешима для любых гладких функций
/(ж, 0), (р(х, 0). Решение разлагается в асимптотич.
ряд по степеням е:
коэффициенты к-рого Uf, (x) — решения однотипных
краевых задач и легко вычисляются в возмущений
теории.
Совсем иная ситуация имеет место, напр., для кра-
краевой задачи
т. к. при в—0 порядок уравнения понижается. Пре-
Предельная задача имеет вид
^^^=ia/(x)g-/+b(x)u = t(r), \ C)
«1ао = фСт) J
и, вообше говоря, неразрешима. Пусть " = 2, харак-
характеристики предельного уравнения имеют вид, указан-
указанный на рис., и их ориентация индуцирована векторным
полем {clj (х)}. Если ре-
шение предельного урав-
нения известно в нек-
некрой точке, то оно изве-
известно вдоль всей харак-
характеристики, проходящей
через эту точку; поэтому
краевая задача C) не-
неразрешима для любых
ср(х). При в —>- 0 реше-
решение задачи B) стремит-
стремится к решению и0 (х)
предельного уравнения
Louo=f, к-рое равно
(р(х) на участках А В и CD. На остальной части гра-
границы происходит потеря граничных условий. В ок-
окрестности каждого из участков AD и ВС, имеющих
характерную ширину е2 и называемую пограничным
слоем, решение задачи B) близко к сумме
ий (хL-г0 (ре~2, х').
Здесь х' — координата вдоль границы AD(BC), р —
расстояние до границы по нормали, а ре— т. н. внут-
внутренняя переменная. Решение задачи B)
разлагается в асимптотич. ряд вида A) всюду, кроме
пограничного слоя и нек-рых особых характеристик
(на рис. 1 — это СС). Частичные суммы асимптотич.
ряда равномерно приближают решение задачи B) в
области, полученной из G выбрасыванием любых
фиксированных окрестностей линий AD, ВС и СС.
В пограничном слое, вне окрестностей точек А, В, С, D,
С, к асимптотич. ряду A) добавляется асимптотич. ряд
Функции y2fc(i> x>) экспоненциально убывают при
|—> со. Первый асимптотич. ряд обычно наз. вне ш-
н и м асимптотическим рядом, а вто-
второй — внутренним асимптотическим
рядом, а функции v2k (|, х) — функциями
пограничного слоя. Эта терминология, как
и сами задачи, происходят из проблем обтекания тел
жидкостью с малой вязкостью (см. Гидродинамики
математические задачи, а также [1] — [4]). Указанный
способ наз. методом пограничного слоя,
и он но существу не отличается от такого же метода
для обыкновенных дифференциальных уравнений.
В окрестностях точек А, В, С, D, в к-рых характе-
характеристики оператора Lo касаются границы, и вблизи
линии СС асимптотика решения носит более сложный
характер. Усложнения возникают и в случае, когда
граница не всюду гладкая (имеются угловые точки, а
при п>2 — ребра). В нек-рых простых случаях можно
построить асимптотику добавлением дополнительных
функции пограничного слоя, зависящих уже от боль-
большего числа переменных, но по-прежнему экспоненци-
экспоненциально стремящихся к нулю на бесконечности. Но,
как правило, картина сложнее: как коэффициенты
ик(х) внешнего разложения, так и коэффициенты г>/&(|,
х') внутреннего разложения имеют сильные особен-
особенности в особых точках (на рис.— это точки А , В, С, D).
Асимптотика решения, равномерная в замкнутой об-
области G, может быть построена методом многих мае-
штабов (методом согласования асимптотич. рядов,
методом сращивания асимптотич. рядов [5]). Нек-рые
задачи для уравнений с частными производными могут
быть исследованы другим вариантом метода многих
масштабов (метод подъема): решение рассматривается
как функция основных независимых переменных и
вспомогательных «быстрых» переменных. В резуль-
результате повышается размерность исходной задачи, но
упрощается зависимость от параметров (см. [6]).
Если поле характеристик предельного оператора Lo
имеет стационарные точки, то задача сильно услож-
усложняется. Напр., если /(ж)зЫ_), Ь(.г)=0 и все характери-
характеристики направлены внутрь области, то решение задачи
B) при е —>- 0 стремится к постоянной. Нахождение
этой постоянной и построение асимптотич. ряда реше-
решения — трудная, лишь частично решенная задача (см.
[7]). Уравнение B) описывает случайные возмущения
динамич. системы х=а(х). Проблемы в этой области
также были одним из первоисточников развития М. п. м.
в теории уравнений с частными производными (см.
[8]).
Если ау(ж)=0 в уравнении B), а Ь(х)<С0, то асимпто-
асимптотич. ряд легко находится: всюду вдали от границы
асимптотич. ряд имеет вид A), а в пограничном слое
вблизи границы добавляется асимптотич. ряд
где теперь ^--ре.
Задача резко усложняется, если a.j(x)^0, 6(.r)>0
В этом случае решения сильно осциллируют; асимпто-
асимптотич. методы — ВКБ-метод, квазиклассическое прибли-
приближение, параболического уравнения метод и др.
Имеется класс задач, в к-рых вырождается граница
области при е —>- 0. Для определенности ниже рас-
рассмотрена задача
(Д+*2)«И=0, X?GB, u\dGe = cp(x), D)
где GE — внешность ограниченной области D? в R." и
/с>0; на бесконечности ставятся излучения условия.
Пусть, напр., DE=eD, D —фиксированная область,
содержащая точку х=0; тогда Dz стягивается в точку
х=0 и задача D) не имеет предельной. Величина >,=
=--2nlk имеет смысл длины волны; в данном случае
X^>rfe , где de — диаметр области Ог , и в этом случае
говорят о рассеянии длинных волн на препятствии
Z)E (или гидродинамическое приближение, или рэлеев-
ское приближение). Имеются две перекрывающиеся
зоны: ближняя, содержащая dGB , ее размеры стремятся
к нулю при е ->¦ 0, и дальняя — внешность области,
к-рая стягивается в точку ж=0 при е —>- 0. Асимптотич.
ряд решения имеет различный вид в этих зонах. Наи-
Наиболее трудной оказывается первая краевая задача
при п=2; внутреннее асимптотич. разложение имеет
вид
где Ъ,=е~1х, (I— (lne+a) и а — нек-рая постоянная
(см. [9]). Длинноволновое приближение исследовано
в основном для уравнения Гельмгольца и для системы
Максвелла (см. [10], [11]).
Другой вариант возникает, когда Z)E стягивается
к отрезку L при е —>¦ 0; в этом случае предельная
задача имеется при п=2 и отсутствует при га>2. Та-
Такого типа задачи (в том числе и для уравнения Лапласа,
и для линейных гиперболнч. уравнений, и для нели-
нелинейных уравнений с частными производными) возни-
возникают в гидродинамике и аэродинамике, в теории ди-
дифракции волн (обтекание тонкого тела потоком жид-
жидкости или газа). Задача D) исследована при н = 2 (см.
[12]); при и—-3 она исследована, если fc=0 и D? есть
тело вращения (см. [13]).
Уравнения с частными производными, содержащие
малый параметр, естественно возникают при излу-
излучении нелинейных колебаний, когда возмущение имеет
порядок s, но решение исследуется на большом отрезке
времени порядка s — 1. Если вместо системы материаль-
материальных точек рассматривается непрерывная среда, то
возникают уравнения с частными производными, к
к-рым применяются обобщения метода усреднения (см.
[14]).
Лит.: L1] Шлихтпнг Г., Теория пограничного слоя,
пер. с нем., М., 1969; [2] В а н - Д а й к М., Методы возмущений
в механике жидкости, пер. с англ., М.,1967;[3]Вишик М. И.,
Люстерник Л. А., «Успехи матем. наук», 1957, т. 12, в. 5,
\ 3 —122; [4] Т р е н о г и и В. А., там же, 1970, т. 25, в. 4,
. 12,'i—56; ['•) Н а и ф э А. X., Методы возмущений, пер. с англ.,
№.. 197В: [')] Л омов С. А.. «Изв. АН СССР. Сер. матем.»,
1972, т. ЗН, Л'з 3, с. 635— 51; [7] В е н т ц е п ь Л. Д., Фрейд-
л и н М. И., Флуктуации в динамических системах под дейст-
действием малых случайных возмущений, М., 1979; [8] П о н т р я-
г и н Л., Андронов А., В и т т А., «Ж. эксперимент, и
теоретич. физики», 1933, т. :). ,\5 3, с. 165—80; [9] II л ь и н А. М.,
«Матем. сб.», 1977, т. 103, ,М-2, с. 265—84: [10] Хенл X.,
Mays А., В е с т п ф а л ь К., Теория дифракции, пер. с
нем., М., 1964; [11] М о р с Ф.М.,Фешбах Г., Методы теоре-
теоретической физики, пер. с англ., т. 2, М., 1960; [12] Ильин А. М.,
«Матем. сп.», 1976, т. 99, Л» 4, с. 514—37; [13] Ко у л Д. Д.,
Методы возмущений в прикладной математике, пер. с англ., М.,
1972; [14] Митропольский Ю. А., М о с е е н-
ков Б. И., Асимптотические решения уравнений в частных
производных, К., 1970. А, М. Ильин, М. В. Федорюп.
МАЛЫЕ ЗНАМЕНАТЕЛИ — делители вида
появляющиеся у коэффициентов рядов при интегри-
интегрировании дифференциальных уравнений посредством
рядов Тейлора, Фурье или Пуассона; здесь Р= (рх,
¦ • •, Рт), <?={Яи • • ¦> Яп) — целочисленные, Q= (щ,
. . ., тт) — действительный и Л= (Лъ . . ., )ьп) — ком-
комплексный векторы, а <•,¦> — скалярное произведение.
При этом существование решения и такие его каче-
качества, как аналитичность, гладкость и т. п., сущест-
существенно зависят от арифметич. природы чисел coy, Xf.
и таких же качеств (аналитичность, гладкость и т. п.)
дифференциальных уравнений. Ниже указаны ус-
условия на векторы Q и Л, к-рые обеспечивают аналитич-
аналитичность решения соответствующей аналитич. задачи.
Эти условия различны для задач линейных н нели-
нелинейных.
1. Линейные задачи, а) Р я д Тейлора. Решение
5 уравнения
= 2j<Q, Л> Ф 0, qk > 0 Ф
|де Х= (х1, . . ., ,гп), а функция ф аналптична в точке
Х = 0 (причем ф@) = 0) и разлагается в указанный
ряд Тейлора, дается рядом Тейлора
ряд сходится в пек-рой окрестности нуля, если
гуществугот такие числа е, v>0, что
КО, ЛМ^е^'КЧ |Q| = |9i[+...+|gB|, B)
для всех целочисленных Q^O, <(?, Л>=^0. Это условие
неулучшаемо в классе всех аналитнч. функций ф;
оно необходимо для сходимости ряда |.
б) Ряд Фурье. Решение т| уравнения
где У= (.Vi, ¦ ¦ ., ym)i правая часть к-рого разложена
в ряд Фурье, дается рядом Фурье
к-рый сходится в нек-рой полосе |1тУ1<е0, если
функция тр аналитпчна и
lim ln'<J;Q>l5a0, D)
| Р | -* оо ' Р
где предел берется по всем целочисленным Р, <Р, Q>=^=0.
Это условие неулучшаемо в классе всех аналитич.
функций г)) вида C).
Уравнение C) встречается в задаче приведения си-
системы обыкновенных дифференциальных уравнений
на торе (см. [1], там вместо условия D) ошибочно
дано B)). Аналогично обстоит дело при интегрировании
по t условно периодич. функции г|з (fit). Подобные
линейные задачи возникают в каждом приближении
при итерационном решении нелинейных задач (в
теории возмущений).
Если условия B) или D) не выполнены, то неформаль-
неформальное решение соответствующей задачи может не быть
аналитическим, гладким или даже не существует вовсе
(в зависимости от арифметпч. природы векторов Л
и fi), хотя формальные решения — ряды g и т| всегда
существуют (см. [1]).
2. Нелинейные задачи. В таких задачах М. з. A)
появляются не поодиночке, а в виде произведений.
а) Ряды Тейлора. Рассмотрим систему вблизи
неподвижной точки Х=0:
где фу — сходящиеся ряды Тейлора без свободных
членов. Пусть «2, АуфО для целочисленных Q^O,
Q^=0. Тогда существует формальная обратимая замена
координат
где |/ — также ряды Тейлора без свободных членов,
к-рая приводит систему E) к нормальной форме
«/• = *•/"/' ' = 1> •••>"• E')
Ряды |у сходятся в нек-рой окрестности нуля, если
In р,
где p, = min|«^, Л>| по \Q\<21, «?
(см. [2]).
Впервые нелинейную задачу такого тина решил
К. Зигель (С. Siegel, 1942; см. [2], [3]) при более жест-
жестком условии:
|«?, Л>| =з=8 |Q |-v. G)
При этом условии P^lne — ^v In2 и ряд F) сходится.
Условие B) эквивалентно ограниченности членов ряда
F); оно необходимо для сходимости рядов \j при про-
произвольных аналитических фу. Но пока A982) неиз-
неизвестно, что происходит в «щели» между условиями B;
и F) (см. более сложные резонансные ситуации в [2]).
Если условие B) не выполнено, то между решениями
системы E) и ее нормальной формы E') может не быть
аналитического, гладкого и даже топологич. соответ-
соответствия.
б) Ряды Пуассона. Пусть аналитич. система
Ilk = «л- -г 2 VkpQXQ схр i <Р, У>, [ C)
XQ =л' .. . xl", у = 1, ..., п; fe = l, ...,m, j
правые части к-рой разложены в ряды Пуассона вблизи
инвариантного тора Х = 0 (т. е. в ряды Тейлора по X
и ряды Фурье по У), имеет формальное интегральное
многообразие
х,- = ц/ (хг +1, ..., хп, У), / = 1, ...,г, (9)
где т)у — также ряды Пуассона. Спрашивается, когда
это многообразие будет аналитическим (т. с. когда
ряды т)у будут абсолютно сходиться для достаточно
малых \Х\ и |ImY|). При этом среди координат xj
могут быть и малые параметры, для них Х/ = 0. Впервые
такая задача решена А. Н. Колмогоровым [4] для га-
мильтоновой системы (8) с т степенями свободы и
одним малым параметром хп (т. е. т-\-1 = п и Л = 0):
при условии
\<Р, Q>|Sse|P|-v (Ю,
была доказана аналитичность многообразия (9) с г—»?,
состоящего из инвариантных торов. Там же для до-
доказательства сходимости рядов Пуассона т|у был впер-
впервые предложен «метод Ньютона*, ставший основным
в исследовании нелинейных задач. Условие A0) и
его аналог
использовались затем в задздах такого же типа (см.
[5] — [7]). Условия B) и D) здесь также необходимы
для сходимости рядов (9) (см. более сложные вырож-
вырожденные ситуации в [7]). Если эти условия не вы-
выполнены, то может не быть аналитического (и даже
непрерывного) инвариантного многообразия вида (9).
Самое жесткое из ограничений B), F), G) — усло-
условие G) — при v>n—1 выполнено для почти всех (по
мере Лебега) векторов Л. Свойства типа B), F), G1
для векторов Л изучаются в теории диофантовых
приближений. Достаточно хорошо изучен двумерный
случай. Пусть qi — знаменатель Z-й подходящей дроби
цепной дроби числа Л=Л2Л1<0. Тогда условие F)
эквивалентно сходимости ряда
а условие B) — ограниченности его членов.
Рассматривались М. з. A) с переменными векто-
векторами Q и Л (см. [6]).
М. з. впервые встретились в задачах небесной ме-
механики, и основные линейные задачи были решены в
1884 Г. Брунсом (Н. Bruns). Вообще в Солнечной
системе имеется много «острых соизмсрпмостой» между
частотами, следствием к-рых являются М. з. A).
Напр., малый знаменатель 2(О]_—5ш2= 0,007..., где coi
и <о2 — частоты движения Юпитера и Сатурна соот-
соответственно, приводит к появлению больших вяаимных
возмущений в движении этих планет. Другой пример:
щели в поясе астероидов и в кольце Сатурна соответ-
соответствуют резонансам с частотой возмущающего тела
(Юпитера и Мимаса соответственно).
Лит.: [1] Колмогоров А. Н., «Докл. АН СССР»,
1953 т. ',13, .№ 5 с. 763 — 66; [2] Б р ю н о А. Д., «Тр. Моск. ма-
тем. об-ва», 1У71, т. 25, с. 110 — 262; >972, т. 26, с. 19!i—239;
[3] 3 и г е л ь К. Л., Лекции по небесной механике, пер. с
нем., М., 1959; [4] Колмогоров А. Н., «Докл. АН СССР»,
1954, т. У8, № 4, с. 527 — 30; [5J ИГ о з е р Ю., Лекции о гамиль-
тоновых системах пер. с англ., М., 1973; [6] А р н о л ь д В. И.,
«Успехи матем. наук», 1963, т. 18, в. 6, с. 91 — 192; [7] Б р ю-
но А. Д., Локальный метод нелинейного анализа дифферен-
дифференциальных уравнений, М., 1979. А. Д. Брюно.
МАЛЫЙ ОБРАЗ множества АаХ при ото-
отображении/: X —>- У — множество f*А всех то-
точек !/?Y, для к-рых f-1ydA. Эквивалентное опреде-
определение: f#A = Y"-J(X\A). Посредством М. о. можно
охарактеризовать замкнутые и неприводимые отобра-
отображения. Непрерывное отображение /: X —>- У замкнуто
тогда и только тогда, когда для всякого открытого
множества UdX его М. о. /* U открыт. Непрерывное
отображение f : X —>- Y на Y замкнуто и неприводимо
тогда и только тогда, когда М. о. всякого непустого
открытого множества UciX является непустым от-
открытым множеством. в- В. Федорчук.
МАЛЫЙ ОБЪЕКТ категории — понятие, вы-
выделяющее такие объекты категории, к-рым присущи
свойства математич. структур с конечным числом
образующих (конечномерных линейных пространств,
конечно порожденных групп и т. д.). Пусть .Й' — ка-
категория с копроизведениями. Объект 67?ObS? наз.
малым, если для любого морфизма
где Uj= U, i?I, О; — вложения копроизведения, най-
найдется конечное подмножество индексов 1, 2, . . ., п
и такой морфизм
что выполнено равенство
в к-ром морфизм а однозначно определяется равен-
равенствами о'(о-—в[, t=l, . . ., п. Иногда дается более
сильное определение, в к-ром не предполагается, что
все множители копроизведения _lXie/f.7/ совпадают
с U.
В многообразиях универсальных алгебр следующие
условия равносильны: а) алгебра А является М. о.
категории; б) алгебра имеет конечное число образу-
образующих; в) основной ковариантный функтор Нд(Х)=
= Н(А, X) перестановочен с копределами (прямыми
пределами) направленных семейств мономорфизмов.
Свойство в) часто принимается за определение конечно
порожденного объекта произвольной категории.
М. Ш. Цаленко.
МАЛЬЦЕВА АЛГЕБРА, м у ф а н г-л и е в а ал-
алгебр а,— линейная алгебра над полем, удовлетво-
удовлетворяющая тождествам
х2^0, J {х, у, xz)=J(x, у, z)x,
где / (.г, у, z)= (ху)г-{- (zx)y-\- (yz)x— якобиан элемен-
элементов х, ц, :.. М. а. представляют собой естественное
обобщение алгебр Ли. Любая М. а. является бинарно
лиевой алгеброй.
М. а. были введены А. И. Мальцевым [1] и названы
им муфанг-лцевыми алгебрами ввиду их связи с ана-
литич. лупами Муфанг. Касательная алгебра локальной
аналитич. лупы Муфанг является М. а. Верно также
и обратное: любая конечномерная М. а. над полным
нормированным полем характеристики 0 является
касательной алгеброй нек-рой локальной аналитич.
лупы Муфанг.
Имеется тесная связь между М. а. и альтернатив-
альтернативными алгебрами (см. Альтернативные кольца и алгеб-
алгебры). Коммутаторная алгебра произвольной альтерна-
альтернативной алгебры, т. е. алгебра, получаемая заменой
основного умножения на операцию коммутирования
[х, у] = ху — ух,
является М. а.
Всякая простая М. а. характеристики рф2 либо
лиева, либо есть 7-мерная алгебра над своим цент-
центроидом. Всякая первичная М. а. (при рф2) либо
лиева, либо вкладывается в качестве подкольца в
подходящую 7-мерную простую алгебру над нек-рым
полем. Произвольная полупервичная М. а. (при рф2)
изоморфно вкладывается в качестве подалгебры в
коммутаторную алгебру нек-рой альтернативной ал-
алгебры. Вопрос о вложении произвольной М. а. в ком-
коммутаторную алгебру альтернативой алгебры открыт
A982).
Пусть Z(A) — лиов центр М. а. А:
2 (А) = {п?А |/ (п, а,Ь)=О для всех а, Ь?А}.
Для любого идеала / произвольной полупервичной
М. а. А (при рф2) Z(I) = Z{A)r\I.
Свойства алгебраич. М. а. аналогичны свойствам
алгобрапч. алгебр Ли. В произвольной алгебраич.
М. а. (при рф2) существует локально конечный ра-
радикал, т. е. максимальный локально конечный идеал,
факторалгебра по к-рому не содержит локально ко-
конечных идеалов. М. а. характеристики р^п или р = 0,
удовлетворяющие ге-му условию Энгеля (см. Энгелева
алгебра), локально нильпотентны. Различие между
М. а. и алгебрами Ли проявляется при переходе от
локальной нильпотентности к глобальной. Имеется
пример М. а. (р = 0), удовлетворяющей 3-му условию
Энгеля. разрешимой индекса 2, но не ннльпотентной.
Для М. а. имеется аналог теоремы Энгеля, играющей
большую роль в структурной теории алгебр Ли: М. а.,
удовлетворяющая условию Энгеля и условию макси-
максимальности для подалгебр, нильпотентна. Этот резуль-
результат справедлив даже в более общем случае — для
бинарно лиевых алгебр.
Во всякой свободной М. а. (при рф2) имеется не-
ненулевой лиев центр. Свободная М. а. (при рф2) с
тремя и более образующими не является первичной
алгеброй. Свободная М. а. (при р = 0) с девятью и
более образующими содержит тривиальные идеалы.
Если Rn — многообразие М. а., порожденное
свободной М. а. от п образующих и р = 0, то цепочка
многообразий
не стабилизируется ни на каком конечном шаге.
Значительно развита теория конечномерных М. а.
и их представлений. Основные результаты этой тео-
теории аналогичны результатам теории алгебр Ли. Име-
Имеются аналоги классич. теорем Ли: если р — расщеп-
расщепляемое представление разрешимой М. а. характери-
характеристики 0, то все матрицы р (х) могут быть приведены
одновременно к треугольному виду; если р — расщеп-
расщепляемое представление нильпотентной М. а. в про-
пространстве V, то V разлагается в прямую сумму весовых
подпространств Fa, и все матрицы ограничений опе-
операторов р(х) на Va могут быть приведены одновре-
одновременно к треугольному виду с числом а (.г) на главной
диагонали.
Следующие результаты аналогичны критериям Кар-
тана разрешимости и полупростоты алгебр Ли: если
р — точнее представление М. а. А (р=0) и билинейная
форма на А, ассоциированная с представлением р,
тривиальна, то алгебра А разрешима; если р — пред-
представление полупростой М. а., то форма следа, ассо-
ассоциированная с р, невырождена. Если киллингова
форма алгебры А невырождена, то А полупроста.
Любое представление полупростой М. а. с р = 0
вполне приводимо. Если 5 — радикал (макси-
(максимальный разрешимый идеал) М. а. А, N — н и л fa-
pa д и к а л (максимальный нильпотентный идеал),
то для любого дифференцирования D алгебры A SD^N.
Произвольная конечномерная М. а. А характери-
характеристики 0 есть прямая сумма (как линейных пространств)
своего радикала 5 и полупростой подалгебры В, изо-
изоморфной факторалгебре алгебры А по радикалу S,
и любые для полупростых фактора сопряжены внут-
внутренним автоморфизмом (аналог теоремы Леви — Маль-
Мальцева — Хариш-Чапдра, известной для алгебр Ли).
Лит.: [1] М а л ь ц е в А. И., «Матем. сб.», 1955, т. 36, № 3,
с. 569 —7G; [2] S a g 1 8 A. A., «Trans. Amer. Math. Soc», 1961,
v. 101, № 3, p. 426—58; [3] К у з ь м и н Е. Н., «Алгебра и ло-
логика», 1968, т. 7, № 2, с. 42—47; [4] его ж е, там же, № 4.
с. 48—69; [5] его же, там же, 1971, т. 10, ЛВ 1, с. 3 — 22; [6J
его же, там же, 1977, т. 1С, № 4, с. 424—31; [71 Фили п-
п о в В. Т., там же, 1976, т. 15, N1 1, с. 89—109; [8] е г о же,
там же, 1977, т. 16, № 1, с. 101 —108; [9] Г р и ш к о в А. Н.,
там же, М» 4. с. 38»—96; [10] Ш е с т а к о в И. П., там же,
Л'5 2. с. 227 — 40. В. Т. (рилиппов.
МАЛЬЦЕВА ЛОКАЛЬНЫЕ ТЕОРЕМЫ — теоремы
о перенесении свойств с локальных частей модели
на всю модель, установленные А. И. Мальцевым. Си-
Система {М i\i^I} подмножеств множества наз. его
локальным покрытием, если каждый элемент из этого
множества содержится в иек-ром М; и любые два под-
подмножества М(, Mj содержатся в нек-ром третьем
подмножестве Mk. Примеры локальных покрытий:
система всех конечных подмножеств данного множе-
множества, система всех конечно порожденных подгрупп
данной группы. Модель М локально обладает свой-
свойством с, если существует локальное покрытие модели
М, состоящее из подмоделей со свойством а. Для
свойства моделей 0 (и соответствующего класса мо-
моделей) справедлива локальная теорема, если всякая
модель, локально обладающая свойством 0, обладает
этим свойством в целом.
Источником самых разнообразных локальных теорем
является следующая основная локальная
теорема (или теорема компактности узкого исчис-
исчисления предикатов) Мальцева 11]: если совместна
каждая конечная подсистема нек-рой бесконечной
системы аксиом узкого исчисления предикатов, то
совместна и вся система. А. И. Мальцев B] указал
общий метод получения конкретных локальных теорем
теории групп с помощью основной локальной теоремы,
положив этим начало моделей теории. Позднее, усо-
усовершенствовав свой метод, он доказал [3] локальную
теорему для любого свойства, записываемого т. я.
квазиуниверсальными аксиомами. Вопрос о справед-
справедливости локальной теоремы для свойства а, к-рый
решался кустарно для каждого п, был тем самым
сведен к общему и чисто «грамматическому» вопросу:
нельзя,ли записать о кпазиуниверсальными аксиомами?
Лит.: [1] М л л ь ц е в А. И., «Матем. сб.», 1936, т. 1, Яг 3,
с. 323—Зй; [2] его ж е. «Уч. записки Ивановского гос. пед.
ии-га». I'.tii, т. 1, в. 1, с. 3—9; [Я] его же, «Изв. АН СССР.
Сер. матом.». 1959; т. 23, № 3, с. 313—36; [4] Каргаполов
М. И.. М е р з л я к о в Ю. И., Основы теории групп, 2 изд.,
М., 1977. Ю. И. Мерзляков.
МАЛЬЦЕВСКОЕ ПРОИЗВЕДЕНИЕ — операция на
классе всех групп (обозначаемая о), наследственная
при переходе к подгруппам сомножителей, т. е. если
и в каждом сомножителе G,- выбрана подгруппа Н/,
то подгруппы Hi, i?I, в G должны порождать под-
подгруппу Н, являющуюся там же произведением Н[
Прямое и свободное произведения групп являются
мальцевскими. Существуют и другие М. п., однако
до сих пор A982) не решена проблема Маль-
Мальцева о существовании (отличного от прямого и сво-
свободного) М. п., удовлетворяющего закону ассоциа-
ассоциативности и нек-рым другим естественным условиям
(термин М. п. возник в связи с этой проблемой).
Лит.: [1] К у р о ш А. Г., Теория групп, 3 изд., М., 1967.
А. Л. Шмелькин.
МАМФОРДА ГИПОТЕЗА — гипотеза о том, что вся-
всякая полупростая алгебраич. группа G геометри-
геометрически р е д у к т и в н а, т. е. обладает следующим
свойством: для любого рационального представления
группы G в конечномерном векторном пространстве V
и любого неподвижного относительно G ненулевого
вектора v?V существует G-инварпантный однородный
многочлен / положительной степени на пространстве
V, для к-рого f(v)=?O.
Гипотеза была сформулирована Д. Мамфордом [1]
(в несколько отличном от предыдущего, но эквива-
эквивалентном ему виде) с целью найти такое свойство полу-
полупростых групп, определенных над алгебраически замк-
замкнутым полем произвольной характеристики, к-рое
могло бы служить равноценной — с точки зрения
геометрия, инвариантов теории — заменой класенч.
свойства полной приводимости рациональных линей-
линейных представлений полулростых групп, определенных
над полем нулевой характеристики (это последнее
свойство не имеет места в случае положительной ха-
характеристики основного поля), и позволило бы снять
ограничение на характеристику основного поля в ряде
центральных результатов геометрия, теории инвари-
инвариантов (в первую очередь, в теореме о конечной порож-
денности алгебры инвариантов редуктпвной группы
автоморфизмов алгебры конечного типа над полем,
см. Гильберта теорема об инвариантах).
Если характеристика основного поля к равна нулю,
то доказательство М. г. дается классич. теоремой
Вейля о полной приводимости рациональных пред-
представлений полупростых групп (см. [2]): в этом случае
к инвариантной прямой L=kv в пространстве V име-
имеется инвариантное дополнение Г (т. е. такая инва-
инвариантная однородная гиперповерхность Г степени
1 в Г, что Lf] Г-—О), и в качестве / можно взять линей-
линейную форму, являющуюся уравнением Г. В случае
поля к положительной характеристики р М. г. обоб-
обобщает этот факт, также утверждая, что существует
инвариантная однородная гиперповерхность Г в V,
для к-рой Z/ПГ —О, но только степень Г не обязательно
равна 1 (в оригинальной постановке М. г. утверждает
также, что эта степень равна р" для нек-poro целого п).
М. г. эквивалентна также утверждению о том, что
для любого регулярного действия полупростой группы
G на аффинном алгебраич. многообразии X и любых
двух замкнутых непересекающихся инвариантных под-
подмножеств X, и X» в X существует инвариантная регу-
регулярная функция h на X, для к-рой h(X1) = 0 u h(X2) = i
(т. о. Хг и X., разделяются регулярными инвариантами,
см. [3]).
Впервые М. г. доказана в [4] (включая и гипотезу
о степени формы); это доказательство распространено
в [5J на общий случай редуктивных групповых схем
над кольцом.
Доказательство М. г. вместе с результатами работ
[6], [10) позволило, во-первых, придать окончатель-
окончательную форму обобщению теоремы Гильберта об инвари-
инвариантах: если R — алгебра конечного типа над полем к,
G — редуктивная рациональная группа ее /с-автомор-
физмов и RO — подалгебра всех С-пнварпаптных эле-
элементов в R, то RG — также алгебра конечного тина
над к; и, во-вторых, позволило установить, что линей-
линейная алгебраич. группа над полем произвольной ха-
характеристики геометрически редуктпвна тогда и только
тогда, когда она редуктнвна. М. г. имеет приложения
в геометрич. теории инвариантов и теории модулей
(см. [7] - [9]).
Лит.: [1] М и m f о г d D., Geometric Invariant Theory, В.
[а. о.], 1965; [2] F о g я r t у .Г.. Invariant theory, N. Y.—
Amsl., liltti); [3] Дьедонне Ж., К е р о л л Д ж., М а ы-
ф о р д Д., Геометрическая теория инвариантов, пер. с англ.,
М. 1U74; [4] Haboush W. J., «Ann. Math.», 1U75, v. 1П2,
u. U7 —83; [5] Sesludri C. S., «Adv. Math.» 1977, At 26,
p. 225—74; [6] Nat'aia M., «J. Math. Kyoto Univ.». 1964,
№ 3, p. 369—77; [7] S e s h a d r i C, S.. вкн.: Algebraic geometry.
Papers presented at the Bombay colloquium. 196S. L., 1909,
p. 347—71: [8] P о р р Н., Moduli theory and classification the-
theory of algebraic varieties, B. [a. o.], 1977; [9J S e s b a A r i C. S.,
«Proc. Symp. Pure Math.». 1975, v. 2'.\ p. 263 — 304; [101 N',i»a-
t a M. Miyata Т., «J. Math. Kyoto Univ.», J!>'4, л» 3,
p. 37»-—82. В. Л. Попов.
МАНГОЛЬДТА ФУНКЦИЯ — арифметическая функ-
функция, определяемая равенствами
{ In р. если п = рт, р— простое, тЗэ1,
Л (и) = <
{ 0, если п ф рт.
Функция Л (и) обладает следующими свойствами:
где сумма берется по всем делителям d числа п. М. ф.
тесно связана с дзета-функциеа Римана 'Q(s), а именно,
производящим рядом для А («) является логарифмыч.
производная ?¦(«):
М. ф. предложена X. Мангольдтом (Н. Mang(vdt)
1894). С. А. Стой
МАННА ТЕОРЕМА — теорема, дающая оценку плот-
плотности суммы двух последовательностей. Пусть А == {0,
alt а2, . . ., а,-, . . .} — возрастающая последователь-
последовательность целых чисел и
А(п)=У\ 1.
Плотностью последовательности А
наз. величина
Арифметической суммой двух последо-
последовательностей А и В наз. последовательность С=А+В,
состоящая из всевозможных сумм с=а-\-Ь, где а?А
и b?B. M. т. утверждает, что
d (А-{-В) Ss min {d (A) + d{B), 1}.
Из М. т. следует, что если А — последовательность
положительной плотности, меньшей I, a JJ — другая
последовательность положительной плотности, то от
сложения А с В плотность увеличивается. Другим
важным следствием М. т. является утверждение: вся-
всякая последовательность положительной плотности есть
базис натурального ряда. М. т. существенно усиливает
аналогичную теорему Шнирелкмана (см. Шнирельмана
метод). Доказана X. Манном [1].
Лит.: [1] Mann Н. В., «Ann. Math.», 1942, v. 43, p. 523—
527; [2] О s t m a n n H.-H., Additive Zahlentheorie, Bd 1—2, В.,
1956; [3] Г е л ъ ф о н д А. О., Л и н н и к Ю. В., Элементарные
методы в аналитической теории чисел, М., 1962.
Б. М. Бредихин.
МАННА — УИТПИ КРИТЕРИИ — критерии для
проверки гипотезы Но об однородности двух выборок
А'ь . . ., Х,г и Уь . . ., Ym, все п-\-т элементов к-рых
взаимно независимы и подчиняются непрерывным рас-
распределениям. Этот критерий, предложенный X. Ман-
Манном и Д. Уитыи [1], построен на статистике
-*-*!= 1 •<-*/= 1 "¦
где W — статистика Вилкоксона критерия, предна-
предназначенного для проверки этой же гипотезы Но, чис-
численно равная сумме рангов элементов второй выборки
в общем вариационном ряду, а
( 1, если X,- < Y,-,
о,-,= <
\ 0, в противном случае.
Таким образом, статистика U считает общее число тех
случаев, в к-рых элементы второй выборки превосхо-
:ят элементы первой выборки. Из определения стати-
стпьи U следует, что если гипотеза Но верна, то
ii, кроме того, эта статистика обладает всеми свойст-
свойствами статистики Вилкоксона W, в том числе асимп-
ютической нормальностью с параметрами (*), чем я
следует пользоваться при использовании М.— У. к.
на практике, если только min{n, m}>25.
Лит.: Mann Н. В., W h i t n е у D. R., «Ann. Math. Sta-
listics», 1947, v. 18, p. 50 — 60. M. С. Никулин.
МАРГИНАЛЬНОЕ РАСПРЕДЕЛЕНИЕ, частное
распределение,— распределение случайной ве-
лнчины или множества случайных величин, рассмат-
рассматриваемых в качестве компоненты или множества ком-
компонент нек-рого случайного вектора (см. Многомерное
распределение) с заданным распределением. Иначе,
М. р. является проекцией распределения случайного
вектора Х= (Xl7 . . ., Хп) на любую ось хх или под-
подпространство, определяемое переменными х;±, . . . ,
x;k, и полностью определяется по распределению
этого вектора. Напр., если F(хх, х2) — функция рас-
распределения X—-(A'i, X3) в R2, то функция распреде-
распределения Хг равна F1(xl)= F(xt, +co); если двумерное
распределение абсолютно непрерывно и р(х1, х2) —
его плотность, то плотность М. р. Х1 равна
Pi (л-i) =
Аналогично вычисляется М. р. для любой компоненты
или множества компонент вектора Х= (Х1г . . ., Х„)
при любом п. Если распределение X нормально, то
все М. р. также нормальны. В том случае, когда ве-
величины Xj, . . ., Х,г взаимно независимы, по М. р-
компонент Xl5 . . . , Хп вектора X однозначно
определяется его распределение:
Аналогично определяется М. р. по. отношению к
распределению вероятностей, заданному на произве-
произведении пространств, более общих, чем числовая прямая.
Лит.: [1] Лоэв М., Теория вероятностей, пер. с англ.,
№., НN2; [2] К р а м е р Г., Математические методы статистики,
пер. с англ., [2 изд.], М., 1975. А. В. Прохоров.
МАРКОВА КВАДРАТУРНАЯ ФОРМУЛА — см.
Наивысшей алгебраической степени точности квадра-
квадратурная формула.
МАРКОВА КРИТЕРИИ наилучшего инте-
интегрального приближения — теорема, по-
позволяющая в нек-рых случаях эффективно указать
многочлен и величину наилучшего интегрального при-
приближения функции f(x). Установлен А. А. Марковым
в 1898 {см. [1]). Пусть {(pk(x)}, А=1, 2, . . ., л,— си-
система непрерывных на отрезке [а, Ь] линейно незави-
независимых функций, а непрерывная функция г|з (х) меняет
знак в точках хг О2 <. . . Ог интервала (а, Ъ) и та-
такова, что
\ fk (x) sign т|? (х) dx=0, A=l, 2, . .., п.
Если для многочлена
разность f(x)—Рц(х) меняет знак в точках д-д, 4=1,
2, . . ., г, и только в них, то Рп(х) является многочле-
ном наилучшего интегрального приближения функции
f(x) и
dx =
= \ / (х) — Рп (х) | dx = \ / (х) sign ор> (ж) J.r
Для системы функций 1, cos х, . . ., cos пх, рассмат-
рассматриваемых на отрезке [0, it], в качестве функции яр(-х)
можно взять cos(n+l)x; для системы sin x, sin2 x, . . .,
sin nx, 0<:х<:я,— функцию sin(ft-|-l).r, а для системы
1, х, . . ., я", —1<г<1, можно положить г|;(х) =
=sin (re+2)arccos x.
Лит.: [1] М а р к о в А. А., Избр. труды,*»!.— Л., 1948;
[2J А х и е з е р Н. И., Лекции по теории аппроксимации, 2 изд.,
М., 1965; [3] Даугавет II. К., Введение в теорию при-
приближения функций, Л., 1977.
Н. П. Корнейчук, В. П. Моторный.
МАРКОВА НЕРАВЕНСТВО для производ-
производной от алгебраического многочле-
многочлена — неравенство, дающее оценку максимального зна-
значения этой производной через наибольшее значение
самого многочлена. Пусть Рп(х) — алгебраич. много-
многочлен степени не выше п и
М ~ max | Рп (х) .
а < х < ъ
Тогда для любого х из отрезка [а, Ь] выполняется
неравенство
Неравенство (*) получено А. А. Марковым в 1889 (см.
[1]). М. н. является точным. Так, если а=—1, 6 = 1,
Рп (х) = cos n arccos х,
то
и в неравенстве (*) достигается знак равенства.
Для производной любого порядка г<ге из М. н.
следует соотношение
к-рое при т^2 уже не является точным. Точное не-
неравенство для р{,п (х) получено В. А. Марковым [2]:
Лит.: [1] Марков А. А., Избр. труды, Ж.— Л.. 1948;
[2] М а р к о в В. А., О. функциях, наименее уклоняющихся
от нуля в данном промежутке, СПБ, 1S92; [3] Натансон
И. П., Конструктивная теория функций, М.— Л., 1949.
Н. П. Корнейчук, В. П. Моторный.
МАРКОВА ПРОБЛЕМА СПЕКТРА — проблема тео-
теории чисел, возникшая в связи с задачей о распреде-
распределении нормированных значений ариф.метич. минимумов
неопределенных бинарных квадратичных форм. Пусть
/ = /(*, f/) = ax2+Pxy + 7y2, a, P
m(/) = ini|/(z, у)\, х, у?1,*, (х, у) ф @, 0)
— однородный арифметич. минимум формы /. Число
наз. постоя н пой Маркова формы /. Множе-
Множество М— {\i (/)}, когда / пробегает все действительные
неопределенные квадратичные формы, наз. спект-
спектром ,М а р к о в а. Постоянную и спектр Маркова
определяют по-разному, в частности А. А. Марков в
[1] рассматривал множество B/ц.(/)}. Известно, что
|я (/) — инвариант луча F классов форм, т. е. множества
F-^{f'\f'=s.Tf(z), t6R, t> 0},
т.к. u.(/')=u (/)=u (F). Каждому лучу классов F
взаимно однозначно сопоставляется двоякобесконеч-
ная (бесконечная в обе стороны) последовательность
IF={..., а_!, а 0, аъ ...
так, что если обозначить
{знак [; . . .] — обозначение цепной дроби), то
(-1 (F)= sup
Проблему Маркова можно сформулировать следу-
следующим образом: 1) описать спектр Маркова М, 2) для
каждого ц?М описать множество форм /=/(х, у)
(или лучей классов F), для к-рых ц.(/)=ц. (F) = и.
Проблема решена А. А. Марковым для начальной
части спектра М, определяемой условием ц.(/)<3.
Эта часть спектра является дискретным множеством
Л/Г)[О. 3.)={|
= 3тпр, т, п, p?n) = {V~1> lr'8 ^
с единственной предельной точкой 3 (точка конден-
конденсации множества М); т, п, р пробегают все целые
положительные решения диофантова урав-
уравнения Маркова
При этом кан;дон точке этой части спектра отвечает
ровно один луч классов Fт, задаваемый формой Мар-
Маркова fm=fm(.r, у), с условием
Решение (т, п, р) диофантова уравнения (*) наз. т р о й-
к о й Маркова; число т — ч и с л о м Маркова.
Форма Маркова fm следующим образом сопоставляется
числу Маркова m = niax(m, п, р): пусть г, sgZ опре-
определены условиями
nr = p (mod т), 0< г < т,
тогда, по определению,
s ~ у".
Множество М — замкнуто, и имеется такое число
ц,<,= 4,5278..., что [ц,, +оо]с:М, и к и„ примыкает
интервал смежности множества М.
Проблема Маркова тесно связана с проблемой Л а г-
ранжа — Гурвица рациональных приближе-
приближений к действительному числу 9. Величина
Х = Х (9) = sup т, >.<+<»,
где точная верхняя граница берется по всем t?R,
т>0, для к-рых неравенство
имеет бесконечное множество решений р, q?Z, 5>,
наз. постоянной Лагранжа. Множество
L={X(9I9?IR} наз. спектром Лагранжа.
Первым результатом в теории спектра Лагранжа ес-
естественно считать теорему Лагранжа: все
подходящие дроби разложения числа 9 в цепную дробь
удовлетворяют неравенству
е—
Если 8'~6, т. е. если
^ ~пг
то Л(9') = Ме)=Чв), гДе в={9'|9'~9} —класс эк-
эквивалентных чисел. Если 6 разложено в цепную
дробь 9=[а0; аи а2, . . .], то
+ [<**¦> ак^, ..., а^, fr = l, 2, ...
Таким образом, проблему Лагранжа — Гурвица мож-
можно сформулировать так: 1) описать спектр Лагранжа L;
2) для каждого K?L описать множество чисел 9 (или
классов в), для к-рых Х(9) = Х,(в) = Х,.
Для Л(9)<3 ота задача сводится к проблеме Мар-
Маркова, причем
Zfl[O, 3) = МП[0, 3),
и каждому Х?Л, Я,<3, отвечает ровно один класс
чисел 6, описываемых формой Маркова fm. Доказано,
что L, как и М,— замкнутое множество, что LaM,
но ЬфМ, что
+°°] = [Цо, +оо],
причем к [х0 примыкает интервал смежности множе-
множества L. Исследования по структуре L и по связи L и М
описаны в [6]. Об обобщениях и аналогах пробле-
проблемы спектра Маркова и о «явлении изоляции» см. [2],
[3], [7]. ,
Лит.: [1] М а р к о в А. А., «Успехи матем. наук», 1948,
т. 3, в. 5, с. 7—51; [2] К а с с е л с Д ж. В. С, Введение в те-
теорию диофантовых приближений, пер. с англ., М., 1961; [3]
Делоне Б. Н., Петербургская школа теории чисел, М.— Л.,
1947: [4] Г о р ш к о в Д. С, «Зап. научн. семинаров Ленпнгр.
отд. Матем. ин-та АН СССР», 1977, т. 67, с. 39—85; [5] Ф р е й-
м ан Г. А., Диофантовы приближения и геометрия чисел. (За-
(Задача Маркова), Калинин, 1975; [6] Малышев А. В., «Зап.
научн. семинаров Ленингр. отд. Матем. ин-та АН СССР», 1977,
т. 67, с. 5—38; [71 В е н к о в Б. А., «Изв. АН СССР. Сер. ма-
матем.», 1945, т. 9, с. 429—94. А. В. Малышев.
МАРКОВА СИСТЕМА ФУНКЦИИ — система линей-
линейно независимых действительных непрерывных функций
{<fv(x)}, v = l, 2, . . ., ге(п«:оо), заданных на конечном
отрезке [а, Ь] и удовлетворяющих условию: для лю-
любого конечного fc<:n функции ц>1{х), Ф2(^), • • -, Фл(з')
о&разуют на интервале (а, Ь) Чебышева систему.
Примеры М. с. ф.:
а) 1, х, х2, . . .— относительно любого отрезка [а, Ь[\
б) 1, cos a-, cos 2х, . . .— относительно отрезка [0, я];
в) sin х, sin 2т, . . .— относительно отрезка [0, я].
Лит.: [1]Ахиезер Н. И., Лекции по теории аппрокси-
аппроксимации, 2 изд., М., 1965. Н. П. Корнейчук, В. П. Моторный.
МАРКОВА СПЕКТР — см. Маркова проблема
спектра.
МАРКОВА ФОРМА — неопределенная бинарная
квадратичная форма f=f(x, у), для к-рой постоянная
Маркова ^i(/)<3 (см. Маркова проблема спектра).
А. В. Малышев.
МАРКОВА ЦЕПИ НУЛЕВОЙ КЛАСС СОСТОЯ-
СОСТОЯНИЙ — множество К состояний однородной цепи
Маркова \ (t) с множеством состояний S такое, что:
Р{3«> О:6(О = /|6(О) = г} = 1
для любых г, j ? К,
для любых i?K, l?S\K, t>0 и
Е Хц= со
для любого i?K, где Хц — время возвращения в
состояние г:
для цепей Маркова с дискретным временем и
Tl7 = inf{i >O:E(O = J(E(O)=t, Е @ +) 56 0}
для цепей Маркова с непрерывным временем.
Как и в случае положительного класса состояний
(когда (*) заменено условием Ет,-;<оо), состояния,
принадлежащие одному нулевому классу, обладают
рядом общих свойств; напр., для любых состояний
i, / из нулевого класса К
Примером цепн Маркова, множество состояний к-рой
образует один нулевой класс, является симметричное
случайное блуждание на множестве целых чисел:
ё @) = 0, l(t)=l(t-l) + 4(t), г = 1, 2, ...,
где т)A), г|B), . . .— независимые случайные вели-
величины,
Р{т1@=1} = Р{г1@ = -1} = 1/2, »=1, 2, ...
Лит.: [1]Чжун Кай-лай, Однородные цепи Маркова,
пер. с англ., М,, 1964. А. М. Зубков.
МАРКОВА ЦЕПИ ПОЛОЖИТЕЛЬНЫЙ КЛАСС СО-
СОСТОЯНИЙ — такое множество К состояний однород-
однородной цепи Маркова %(t) с множеством состояний S,
что для переходных вероятностей
цепи 5 (г) выполняются условия:
ьирр,-у (t) > 0 при любых j, j?K,
Р«@ = 0 ПРИ любых i?K, l?S\K, i>0 и
ЕТц < оо при любом i?K,
где т./ — время возвращения в состояние п
т„- = тщ{< > в:? @ = (A@)=*)}
для цепей Маркова с дискретным временем и
T,-,= ini {/ >0:l(t) = i(l@) = i, 1@+) ф i)}
для цепей Маркова с непрерывным временем. В слу-
случае Ет,-,= оо класс К наз. нулевым классом состояний.
Состояния, принадлежащие одному и тому же поло-
положительному классу К, обладают рядом общих свойств.
Напр., в случае дискретного времени при любых
i, J'^K существует
lim и-12?_1/>,7@ = Р/ > °;
если
d, = max {d:P {хц делится на d} = i)
— период состояния i, те d,-=dy=d для любых г, )?К
и d наз. периодом класса!; для любого i g К
существует
lim pu(td) = dp*. > 0.
t —> 00
Цепь Маркова с дискретным временем, все состояния
к-рон образуют один положительный класс периода 1,
является примером Маркова цепи эргодической.
Лит.: [1] Ч ж у н К а й - л а й, Однородные цепи Маркова,
пер. с англ., М., 196-4; [2] Д у б Д ж., Вероятностные процессы,
пер. с англ., М., 1956. А. М. Зубков.
МАРКОВА ЦЕПЬ — марковский процесс с конеч-
конечным или счетным множеством состояний. Теория М. ц.
возникла на основе исследований А. А. Маркова,
к-рый в 1907 положил начало изучению последова-
последовательностей зависимых испытаний и связанных с ними
сумм случайных величин [1].
Пусть пространство состояний — множество нату-
натуральных чисел N или его конечное подмножество.
Пусть ?,{t) —состояние М. ц. в момент времени i.
Основным для М. ц. является марковское свойство,
к-рое для М. ц. с дискретным временем (т. е. в случае,
когда время t принимает лишь целые неотрицательные
значения) определяется следующим образом: для лю-
любых t, j?N, любых целых неотрицательных <1<t2<C
<. . .<??<? и любых натуральных iu i.2, . . ., ifc
имеет место равенство
Р{Е(О = ЛЕ(<1) = *1, ..., Е ('*) = **} =
= р {& (О = Ш ('*) = **}¦ «)
Марковское .свойство A) можно переформулировать-
следующим образом. Момент времени t и связанные
с ним события вида {?(*)=./} назовем «настоящим»
процесса; события, определяемые значениями |(и)
с к<?,— «прошлым» процесса; события, определя-
определяемые значениями ?(м) с u^>t,— «будущим» процесса.
Тогда свойство A) равносильно следующему: для лю-
любого t?N при фиксированном «настоящем» |(t)=/
любые «прошлое» А и «будущее» В события условно
независимы, т. е.
Для вероятностного описания М. ц. |(?) большую
роль играют переходные вероятности
В случае, когда переходные вероятности B) не зави-
зависят от /, М. ц. наз. однородной (во времени);
в противном случае — неоднородной. Далее
рассматриваются лишь однородные М. ц. Пусть
Матрица Р= ||jB/yll с элементами р,-у наз. матрицей
переходных вероятностей. Вероятность
любой траектории ?(AO~?jt, k = 0, I, . . ., t, выражается
через переходные вероятности р,у и начальное распре-
распределение Р{|(О)=г} следующим образом:
' P{l(k) = ik, /c = 0, 1, ..., t} =
Наряду с переходными вероятностями р,-у в М. ц.
рассматриваются также переходные вероятности pi/{t)
за t шагов:
Pi/ @ = Р {I (*о + Ц = ] \l (to) = О-
Эти переходные вероятности удовлетворяют
— Чепмена уравнению
Pi/ (h+h) = ^kPik (h)pkj(t2).
С помощью переходных вероятностей можно произ-
произвести следующую классификацию состояний. Два
состояния i и ) наз. сообщающимися, если
найдутся такие ti>0, «3>0, что p;j(t1)>0 и py,-(i.,)>0.
Состояние к наз. несущественным, если най-
найдется такое состояние I, что Pki(ti)>^ Для нек~рого
гх^1 и pift(t)s=0 для всех t?N. Все остальные состоя-
состояния наз. существенными. Таким образом,
все множество состояний М. ц. разбивается на несу-
несущественные и существенные состояния. Множество
всех существенных состояний разбивается на непере-
непересекающиеся классы сообщающихся состояний так,
что любые два состояния из одного класса сообщаются
между собой, а для любых двух состояний i и / из
разных классов р,-/(/)=(), р/(- (О^О. М. ц., все состоя-
состояния к-рой составляют один класс сообщающихся
состояний, наз. неразложимой (см. Маркова
цепь неразложимая); в противном случае М. ц. наз.
разложимой (см. Маркова цепь разложимая).
Если множество состояний конечно, то разбиение его
на эти классы и значительной степени определяет
аснмптотич. свойства М. ц. Напр., для конечной не-
неразложимой М. ц. всегда существует предел
C)
причем ^j/P/ = l- Если, кроме того, М. ц. неперио-
непериодическая, т. е. при нек-ром t0 для всех t~^tB и
всех состояний i и / />,-y(i)>0 (см. также Маркова
цепь периодическая), то имеет место более сильное
утверждение
lim pij (t) = р,- D)
t -> OO
(см. также Маркова цепь эргодическая).
Если множество состояний М. Ц. счетно, то ее аеимп-
тотнч. свойства зависят от более тонких свойств клас-
классов сообщающихся состояний. Ряд
расходится или сходится сразу для всех состояний
данного класса. Класс состояний наз. возврат-
н ы м, если для любого состояния i этого класса ряд E)
расходится, и невозвратным, если ряд E) сходится.
В возвратном классе с вероятностью 1 М. ц. возвра-
возвращается в любое свое состояние, в невозвратном классе
вероятность возвращения меньше 1. Если среднее
время возвращения в возвратном классе конечно, то
класс наз. положительным; в противном слу-
случае класс наз. нулевым (см. Маркова цепи поло-
положительный класс состояний, Маркова цепи нулевой
класс состояний). Если i и ;' принадлежат одному
положительному классу состояний, то существует
предел C), а в непериодическом случае и предел D).
Если ./ принадлежит нулевому классу состояний или
несущественно, то p,-y(i)-»-O, ?—>-oo.
Пусть /(¦) —действительная функция, определен-
определенная на состояниях М. ц. ?(?)¦ Если М. ц. неразложима
и ее состояния образуют положительный класс, то
для сумм
^" и — 0
справедлива центральная предельная
теорема:
1 Bt j I2i J-.
при нек-рых А и i?>0. Для выполнения F) достаточно
дополнительно потребовать Di\f — Bt, f —>- со, В>0.
Если время t принимает любые значения из [0, оо),
то М. ц. является М. ц. с непрерывным временем,
к-рая определяется аналогично с помощью марков-
марковского свойства A). Обычно для М. ц. с непрерывным
временем требуют дополнительно, чтобы существовали
конечные правые производные
у
dp. . (t)
к-рые наз. плотностями вероятностей
перехода. Для конечной М. ц. с непрерывным
временем из уравнения Колмогорова — Чепмена можно
получить две системы дифференциальных
уравнений Колмогорова:
dp,- ¦ (О
(It ~-ik
к к-рым присоединяются начальные условия pij(O}=
= 6,у, где 6,7 — символ Кронекера. При нек-рых до-
дополнительных предположениях системы уравнений G)
и (8) справедливы и для счетных М. ц.
Если М. Ц. с непрерывным временем имеет стацио-
стационарное распределение P{%(t)=i}=Pi (T- е- распреде-
распределение |@i H0 зависящее от времени t), то это распре-
распределение {/>,} удовлетворяет следующей системе ли-
линейных уравнений:
2.^17 = 0, /=1, 2, ... j
М. ц. широко используются при решении различных
прикладных задач. Напр., в теории массового обслу-
обслуживания для расчета распределения вероятностей
числа занятых приборов в системе М\М\п с отказами
(т. е. в системе, состоящей из п приборов с пуассонов-
ским потоком требований и показательным законом
времени обслуживания) используется конечная М. ц.
с непрерывным временем, состояниями 0, 1, . . ., п
и со следующими плотностями вероятностей перехода:
если |?—/|>1 (здесь к — интенсивность пуассонов-
ского потока требований, ц — среднее время обслу-
обслуживания). С помощью (9) в этом случае определяется
следующее стационарное распределение числа занятых
приборов:
р,- = 0, г > п,
к-рое наз. распределением Эрланга.
См. также Маркова цепь сложная, Маркова цепь
возвратная, Поглощающее состояние, Стохастическая
матрица, Переход с запрещениями.
Лит.: ft] Марков А. А., «Изв. Петерб. АН» F), 1907,
т. 1, № 3, с. 61—80; [2] Дуб Д ж., Вероятностные процессы,
пер. с англ., М., 1956; М Чжув К а й - л а й, Однородные
цепи Маркова, пер. о англ., М., 1964; [4] Ф е л л е р В., Вве-
Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд.
т. 1, М., 1967. Б. А. Севастьянов.
МАРКОВА ЦЕПЬ ВОЗВРАТНАЯ — цепь Маркова,
в к-рой случайная траектория %(t), выходящая из
любого состояния 5 @) — i, с вероятностью 1 возвра-
возвращается когда-нибудь в это же состояние. В терминах
переходных вероятностей р,у(?) возвратность цепи
Маркова с дискретным временем эквивалентна расхо-
расходимости при любом i ряда
2Г=„ >»<'>¦
В М. ц. в. траектория ?(<), 0<*<оо, 5@)=;', с веро-
вероятностью 1 возвращается в состояние i бесконечное
число раз. В М. ц. в. нет несущественных состояний,
а все существенные состояния разбиваются на воз-
возвратные классы. Примером М. ц. в. может служить
симметричное случайное блуждание по целочисленной
решетке прямой или плоскости. В симметричном блуж-
блуждании по прямой частица из положения х переходит
в положения rile вероятностями 1/2; в симметричном
блуждании по плоскости частица из точки (х, у) с
вероятностями 1/i переходит в одну из четырех сосед-
соседних точек (х± 1, у), (х, у—1). В этих примерах ча-
частица, начавшая блуждание из какой-либо точки, с
вероятностью 1 возвращается в эту точку. Симметрия-
нею блуждание по целочисленной решетке трехмерного
пространства, когда вероятности перехода из (.г, у, z)
в соседние точки (,т±1, у, z), (.r, y—i, z), (.г, у, z—l)
равны 1/6, невозвратно. В этом случае вероятность
возвращения частицы в начальную точку равна при-
приближенно 0,35.
Лит.: [1] Ф е л л е р В., Введение в теорию вероятностей и
ее приложения, пер. с англ., 2 изд., т. 1, М., 1907.
Б. А. Савостьянов.
МАРКОВА ЦЕПЬ НЕРАЗЛОЖИМАЯ — цепь Мар-
Маркова, переходные вероятности р;/A) к-poir обладают
следующим свойством: для любых состояний i и /
существует такой момент времени ?/у, что /),/(?//)>0.
Неразложимость цепи Маркова равносильна неразло-
неразложимости матрицы переходных вероятностен Р—1!/>;_/Н
для цепей Маркова с дискретным временем и матрицы
плотностей вероятностей перехода Q—Wqj/W, Qii==
dpu (t)
= j-t t_ для цепей Маркова с непрерывным
временем. Множество состояний неразложимой цепи
Маркова состоит из одного класса сообщающихся со-
состояний. Б. -^- Севастьянов.
МАРКОВА ЦЕПЬ ПЕРИОДИЧЕСКАЯ — неразло-
неразложимая цепь Маркова |(;<), " — "I, 2, . . ., однородная во
времени, в к-рой каждое состояние i имеет период,
больший единицы, т. е.
d, = Н. а. д. {п:Р {I (и) = Ч ? @) = Ц > 0} > 1.
В Маркова цепи неразложимой все состояния имеют
одинаковые периоды. Если <2=1, то цепь Маркова
наз. непериодической. В. П. Чистяков.
МАРКОВА ЦЕПЬ РАЗЛОЖИМАЯ — цепь Марко-
Маркова, переходные вероятности pij(t) к-рой обладают сле-
следующим свойством: существуют такие состояния 1ф],
что pij{t)=O для всех <>0. Разложимость цепи Мар-
Маркова равносильна разложимости матрицы переходных
вероятностей Р=1!/>,-/1| для цепей Маркова с дискрет-
дискретным временем и матрицы плотностей вероятностей
dpи (t)
перехода Q=\\q;j\\, q/j= j-t— f_0, для цепей Мар-
Маркова с непрерывным временем. Множество состояний
М. ц. р. либо содержит несущественные состояния,
либо состоит более чем из одного класса сообщаю-
сообщающихся СОСТОЯНИЙ. Б. А. Севастьянов.
МАРКОВА ЦЕПЬ СЛОЖНАЯ — последовательность
случайных величин ?,п обладающая следующими свой-
свойствами:
1) множество значений ?„ конечно или счетно,
2) при любом п и любых значениях i0, iu . . ., in
f {?л= hi I So= io, Si = ii, •••? ?«-.$= b*-.s> ¦••> In-i =
Сложная цепь Маркова, удовлетворяющая (*), наз.
s-c ложно ii. При s~-l условие (*) является обычным
марковским ceoitcmeoM. Изучение «-сложных цепей
Маркова можно свести к изучению обычных цепей
Маркова. Для этого рассматривается последователь-
последовательность случайных величин т|„, значения к-рых нахо-
находятся во взаимно однозначном соответствии со зна-
значениями вектора
(ёл-j + l. Sn-i + 2' •••> Sn-I) ?л)-
Последовательность случайных величин х\п образует
обычную Маркова цепь.
Лит.: [1] Дуб Д ж., Вероятностные процессы, пер. с
англ., М., 1956. В. П. Чистяков.
МАРКОВА ЦЕПЬ ЭРГОДИЧЕСКАЯ — однородная
по времени цепь Маркова !(?), обладающая следующим
свойством: существуют (не зависящие от г) величины
Pj = Inn Vij (О- 2/ PJ = i> A)
где
— переходные вероятности. Распределение {pj} на
множестве состояний цепи ? (г) наз. стационар-
стационарным распределением: если Р {?@) =/}=/>у
при всех ;, то P{%(t)—j}—pj при всех г^О и /. Вместе
с основным свойством цепи Маркова
это позволяет находить {ру},не вычисляя пределов в A).
Пусть
T,7 = min {«5э 1:1 @ = / (? @) = /)}
— момент первого возвращения в состояние ;' (для
цепи Маркова с дискретным временем), тогда
аналогичное (более сложное) соотношение имеет место
для цепи Маркова с непрерывным временем.
Траектории М. ц. э. удовлетворяют эргодич. тео-
'реме: если /(¦) — функция на множестве состояний
цепи 1(?), т0 в случае дискретного времени
в случае непрерывного времени первая сумма в левой
части заменяется интегралом.
Цепь Маркова, для к-рой существуют такие р<1
и С/у<оо, что при всех г, /, t
\Plj{t)-Pj\<Cupi, B)
наз. геометрически эргод и ческой. До-
Достаточным условием для геометрич. эргодичности
М. ц. э. является условие Дёблина (см.,
напр., [1]), к-рое в рассматриваемом здесь случае
дискретных (конечных или счетных) цепей Маркова
может быть сформулировано так: существуют такие
п<оо и состояние ;', что inf p,-y (гс) = 6>0. Если выпол-
выполнено условие Дёблина, то для констант в B) справед-
справедливо соотношение sup С,- ,= С<оо.
I, i
Необходимым и достаточным условием геометрич.
эргодичности счетной цепи Маркова с дискретным вре-
временем является следующее (см. [3]): существуют такие
числа /(/), </<1 и конечное множество В состояний
цепи, что
{/(())||() }
16В
Лит.: [1] Дуб Д ж., Вероятностные процессы, пер. с
англ., М., 1956; [2] Ч ш у н К а й - л а й, Однородные цепи
Маркова, пер. с англ., М., 1964- [3] П о п о в Н. Н.,«Докл.
АН СССР», 1977, т. 234, J* 2, с. 316 — 19. А. М. Зубков.
МАРКОВСКИЙ МОМЕНТ — понятие, используемое
в теории вероятностен для случайных величин, обла-
обладающих свойством независимости от «будущего». Точ-
Точнее, пусть (Й, Jp) — нек-рое измеримое пространство
с выделенным на нем неубывающим семейством (JF/),
t?T, о-подалгебр §г(Т=\0, оо] в случае непрерывного
времени и Т= {0,1,. . . } в случае дискретного времени).
Случайная величина т=т(ш) со значениями в f[| {+oo }
наз. марковским моментом (относительно
семейства (,-fFf), t?T), если при каждом t?T событие
{т(ш)<:г} принадлежит JFf. В случае дискретного
времени это эквивалентно тому, что для любого п? {0,
1, . . .} событие {т(ш)=п} принадлежит (frre.
Примеры. 1) Пусть X(t), t?-T,— действитель-
действительный случайный процесс, заданный на (Q, JF), и
§rt=a{(o:X (s), s<?t}. Тогда случайные величины
x (ш) = iiif {t 5эО:
и
c(eo) = mf {t > 0:.Y
т. е. моменты (первого и первого после -f-0) достижения
(борелевского) множества В, являются М. м. (в слу-
случае {¦}= 0 полагают inf0 —со).
2) Если W(t), t^O,— стандартный винеровский
процесс, то М. м.
x=inf {tSsO:W (t) Saa}, a > О,
имеет плотность распределения вероятностей
При этом Р{т<ео}=1, но ет=оо.
3) Случайная величина
являющаяся первым моментом, после к-рого процесс
Xf остается в множестве В, является примером не-
немарковского момента (случайной величины, зависящей
от «будущего»).
С помощью понятия М. м. формулируется строго
марковское свойство марковских процессов. М. м. и
моменты остановки (т. е. конечные М. м.)
играют важную роль в общей теории случайных про-
процессов и статистическом последовательном анализе.
Лит.: [1] Г и х м а н 11. И., Скороход А. В., Теория
случайных процессов, Т. 2, М., 1973. .4. Н. Ширяев.
МАРКОВСКИЙ ПРОЦЕСС, процесс без по-
следействи я,— случайный процесс, эволюция
к-рого после любого заданного значения временного
параметра t не зависит от эволюции, предшествовав-
предшествовавшей t, при условии, что значение процесса в этот мо-
момент фиксировано (короче: «будущее» н «прошлое»
процесса не зависят друг от друга при известном «па-
стоящем»).
Определяющее М. п. свойство принято наз. м а р-
к о в с к и м; впервые оно было сформулировано
А. А. Марковым [1]. Однако уже в работе Л. Башелье
[2] можно усмотреть попытку трактовать броуновское
движение как М. п., попытку, получившую обосно-
обоснование после исследований Н. Винера (N. Wiener,
1923). Основы общей теории М. п. с непрерывным
временем были заложены А. Н. Колмогоровым [3].
Марковское свойство. Имеются существенно отли-
отличающиеся друг от друга определения М. п. Одним из
наиболее распространенных является следующее. Пусть
на вероятностном пространстве (Q, F, Р) задан слу-
случайный процесс X (t), t^T, со значениями из изме-
измеримого пространства (Е, Si), где Т — подмножество
действительной оси R. Пусть JVt (соответственно .V')
есть a-алгебра в Q, порожденная величинами X (s)
при s^.t (s^l), где s?T. Другими словами, jVr (соот-
(соответственно jV'j — это совокупность событии, связан-
связанных с эволюцией процесса до момента t (начиная с t).
Процесс X (t) наз. марковским процессом,
если (почти наверное) для всех t? T, Ai^iV't и A., ?Nl
выполняется марковское свойство:
Р {AXA2 | X («)} = Р {Ах | X (()} Р {А2 | X (t)} A)
или, что то же самое, если для любых t?T и
Р {Л |ЛГ,} = Р{Л| *(')}• B)
М. п., для к-роио Т содержится в множестве натураль-
натуральных чисел, наз. Маркова цепью (впрочем, последний
термин чаще всего ассоциируется со случаем не более
чем счетного Е). Если Т является интервалом в R,
a E но более чем счетно, М. п. наз. цепью Мар-
кова с непрерывным временем. При-
Примеры М. п. с непрерывным временем доставляются
диффузионными процессами и процессами с незави-
независимыми приращениями, в том числе пуассоновским л
винеровским.
В дальнейшем для определенности речь будет идти
только о случае Г= [0, оо). Формулы A) и B) дают
ясную интерпретацию принципа независимости «прош-
«прошлого» и «будущего» при известном «настоящем», но
основанное на них определение М. п. оказалось не-
недостаточно гибким в тех многочисленных ситуациях,
когда приходится рассматривать не одно, а набор ус-
условий типа A) или B), отвечающих различным, хоти
и согласованным определенным образом, мерам Р.
Такого рода соображения привели к принятию сле-
следующего определения (см. [9], [И]).
Пусть заданы:
а) измеримое пространство (Е, гЗ), где о-алгебра <®
содержит все одноточечные множества в Е;
б) измеримое пространство (Й, F), снабженное се-
семейством о-алгебр FtCZF, 0<$<г<оо, таких, что FstCF%,
если [s, t\a[u, v]\
в) функция («траектория») xf=xt((u), определяю-
определяющая при любых г?[0, оо) и eg [0, t] измеримое ото-
отображение (Й, Fvt) в (Е, <$В);
г) для каждых s~^0 и х?Е вероятностная мера Psx
на о-алгебре Fs&, такая, что функция P(s, . ; t, B)=
= PS {rf6^} измерима относительно гЗ, если s?[0, t]
и B?Si.
Набор X (t)= (xt, Ft, Ps, x) наз- (необрыва ю-
щ и м с я) марковским процессом, задан-
заданным в (Е, Si), если PSt x-H04T)i наверное
каковы бы ни были 0<j<« и A?NT. Здесь Q — про-
пространство элементарных событий, (Е, Si) — фазовое
пространство или пространство состояний, Р (s, x, t,
В) — переходная функция или вероятность перехода
процесса X(t). Если Е наделено топологией, а ей —
совокупность борелевскнх множеств в Е, то принято
говорить, что М. п. задан в Е. Обычно в определение
М. п. включают требование, чтобы P(s, x; s, {х})=1,
и тогда Pj v {Л} с Л ? F'L истолковывается как веро-
вероятность Л при условии, что xs=x.
Возникает вопрос: всякую ли марковскую переход-
переходную функцию Р (s, x\ I, В), заданную в измеримом
пространстве (?, Si), можно рассматривать как пере-
переходную функцию нек-рого М. п. Ответ положителен,
если, напр., Е является сепарабельпым локально
компактным пространством, a Si — совокупностью
борелевских множеств в Е. Более того, пусть Е —
полное метрич. пространство и пусть
limag (h) — О
для любого е>0, где
a.?{h) — sup{P (s, x; it Vt{r):x?E, 0 < t — s < h],
a V? (x) — дополнение е-окрестности точки .г. Тогда
соответствующий М. п. можно считать непрерывным
справа и имеющим пределы слева (т. е. таковыми
можно выбрать его траектории). Существование же
непрерывного М. п. обеспечивается условием аЕ (Л)=
= o(h) при й|0 (см. [9], |11]).
В теории М. п. основное внимание уделяется одно-
однородным (по времени) процессам. Соответствующее
определение предполагает заданной систему объектов
а) — г) с той разницей, что для фигурировавших в
ее описании параметров s и и теперь допускается
лишь значение 0. Упрощаются и обозначения:
РХ=Р«Х, Ft = Fat, Р (/, х, В) = Р @, х; t, В),
х?Е, /3=0,
'{•ллвс, постулируется однородность пространства Q,
л. е. требуется, чтобы для любых й^й и sjsO сущест-
существовало такое co'gQ, что xf (a>') = xf + s (со) при г^О.
Благодаря этому на о-алгебре N, наименьшей из о-
алгебр в Q, содержащих любое событие вида {со: xs?B},
задаются операторы временного сдвига 9/, к-рые
сохраняют операции объединения, пересечения и вы-
вычитания множеств и для к-рых
где s, >, ?
Набор X [t)=- (?), Ft, Px) наз. (н е о б р ы в а ю-
ш, и м с я) о д н о р о д н ы м марковским про-
процессом, заданным в (?', Si), если Р^-почти наве]>ное
Р*{в*Л|/-,} = РЖ({Л} D)
-чя z?E, i>0 и Л?Л\ Переходной функцией про-
провеса X (t) считается Р (t. r, В), причем, если нет
(кециальных оговорок, дополнительно требуют, чтобы
Р @, т. {.i-}1^1. Полезно иметь в виду, что при про-
проверке D) достаточно рассматривать лишь множества
Л вида .\ = {(i):yjgB}, где s>0, B?31, и что в D)
всегда Ft можно заменить о-алгеброй Ft, равной пересе-
пересечению пополнений Ft по всевозможным мерам Рх{х?Е}.
Нередко в аЗ фиксируют вероятностную меру и («на-
(«начальное распределение» и рассматривают марков-
марковскую случайную функцию (xt. Ft, Рц), где Рд —
мора на Foo, заданная равенством
М. п. X (t)= (x-f, Ft, Px) наз. прогрессивно
измеримы и, если при каждом t >0 функция
j(s, g)) = .ts (w) индуцирует измеримое отображение
([0, t]X й, 'SSfX Ft) в (Е, &}), где <Sit есть о-алгебра
борелевекпх подмножеств в [0, t]. Непрерывные справа
М. п. прогрессивно измеримы. Существует способ сво-
сводить неоднородный случай к однородному (см. [11]),
и в дальнейшем речь будет идти об однородных М. п.
Строго марковское свойство. Пусть в измеримом про-
пространстве (Е, SB) задан М. п. X (t)— {x*, Ft, Px).
Функция т : Q —>- [0, оо ] наз. марковским моментом,
если {со:т«:?}(;/\ для всех i^0. При этом множество
AcOi --{at: т<оо} относят к семейству FT, если
ЛП{Ы : т<0€ Ft иРи i^0 (чаще всего Fx интерпрети-
интерпретируют как совокупность событий, связанных с эволю-
эволюцией X (t) до момента т). Для Л?ЛГ полагают
Прогрессивно измеримый М. п. X наз. строго
марковским п р о ц е с с о м (с. м. п.), если для
любого марковского момента т и всех <J>0, x?E и
Л ? Лг с оотношение
Px{QxA\Fx} = PXx{A} E)
(строго марковское свойство) выпол-
выполняется РЛ-почти наверное на множестве QT. При
проверке E) достаточно рассматривать лишь множе-
множества вида A = {co:;rj?B}, где s^0, B?<$3; в этом случае
8ТЛ— {(о : xs+x?B}. С. м. п. является, напр., любой
непрерывный справа феллеровскип М. п. в топологич.
пространстве Е. М. п. наз. феллеровским
марковским процессом, если функция
Pff(-)= [f(y)P(t, •;
непрерывна всякий раз, когда / непрерывна и ограни-
ограничена.
В классе с. м. п. выделяются те или иные подклассы.
Пусть марковская переходная функция P(t, х, В),
заданная в метрическом локально компактном про-
пространстве Е, стохастически непрерывна:
limP (t, х, U) = i
для любой окрестности U каждой точки х?Е. Тогда
если операторы Р1 переводят в себя класс непрерывных
и обращающихся в 0 в бесконечности функций, то
функции Р (t, х, В) отвечает стандартный М. п.
X, т. е. непрерывный справа с. м. п., для к-рого
1) Ft = Ft при t?[0, оо) и Ft=r\s>tFs при *g[0, оо)
и 2) lim xx =хх Рд-почти наверное на множестве {ш:т<
п-*т п
<оо }, где т = lim т„, а т„(га^1) — неубывающие
с ростом п марковские моменты.
Обрывающийся марковский процесс. Нередко физия.
системы целесообразно описывать с помощью необры-
вашщегося М. п., но лишь на временном интервале
случайной длины. Кроме того, даже простые преоб-
преобразования М. п. могут привести к процессу с траек-
траекториями, заданными на случайном интервале (см.
Функционал от марковского процесса). Руководствуясь
этими соображениями, вводят понятие обрывающегося
М. п.
Пусть X(t)—(xt, Ft, Px) — однородный М. п. в
фазовом пространстве (Е, В), имеющий переходную
функцию Р (t, х, В), it пусть существуют точка е?Е
- и функция ?:Q—>-10, оо] такие, что xt (<») = <; при ?((о)<г
и х^{(л)-фе в противном случае (если нет специальных
оговорок, считают ?>0). Новая траектория xt((a)
задается лишь для ?<¦; [0, ?(ш)) посредством равенства
xt((a)~Xf(to), a Ft определяется как след Ft в множе-
множестве {(o:j>i}.
Набор X{t)=(xt, Z, Ft, Рх), где х?Е = Е\{е}, наз.
обрывающимся марковским процес-
процессом (о. м. п.), полученным из X A) с помощью обрыва
(или убивания) в момент ?. Величина ?, наз. момен-
моментом обрыва, или временем ж и з н и, о. ы. п.
Фазовым пространством нового процесса служит (Е, <33),
где Si есть след ст-алгебры ей) в Е. Переходная функция
о. м. п.— это сужение P(t, x, В) на множество f^O,
х?Е, В?$). Процесс X (t) наз. строго марков-
марковским процессом, или стандартным
марковским процессом, если соответст-
соответствующим свойством обладает X (t). Нсобрывающийся
М. п. можно рассматривать как о. м. п. с моментом
обрыва ?=°°- Неоднородный о. м. п. определяется
аналогичным образом. м. г. Шур.
Марковские процессы и дифференциальные уравне-
уравнения. М. п. типа броуновского движения тесно связаны
с дифференциальными уравнениями параболич. типа.
Переходная плотность р (s, x, t, у) диффузионного
процесса удовлетворяет при нек-рых дополнительных
предположениях обратному и прямому дифференци-
дифференциальным уравнениям Колмогорова:
Эр
F)
Функция р (s, х, t, у) есть функция Грина уравнений
F) — G), и первые известные способы построения
диффузионных процессов были основаны на теоремах
существования этой функции для диффергнциальных
уравнений F) — G). Для однородного но времени
процесса оператор L (s, x) — L(x) на гладких функциях
совпадает с характеристич. оператором М. п. (см.
Переходных операторов полугруппа).
Математич. ожидания различных функционалов от
диффузионных процессов служат решениями соответ-
соответствующих краевых задач для дифференциального
уравнения A). Пусть Bs х(-) — математич. ожидание
по мере Ps,x. Тогда функция Е^, хц(Х [Т))=иг (s, х)
удовлетворяет при $<Г уравнению F) и условию
ih(T, х) = у(х).
Аналогично, функцхтя
u2(s, x) = Esx ^ f(t, X(t))dt
удовлетворяет при s<.T уравнению
и условию iin(T, х) = 0.
Пусть т — момент первого достижения границы 0D
области OczR" траекторией процесса X (t), тлТ~
= min(T, T). Тогда при нек-рых условиях функция
ua(s, z)=Es-xys" f(t, X(t))dt +
+ E5, x(P (тлГ, X (ГАГ))
удовлетворяет уравнению
ди \ т t \ 1
—^ у- L (S, X) U — J
и принимает значения ф на множестве
Г={х < Т, x?dD}(j{s=T, x?D}.
Решение 1-й краевой задачи для общего линейного
параболич. уравнения 2-го порядка
-|т- + ? («, х) и + с (s, x) u = — / (s, x), \
«|г=Ф / ()
при довольно общих предположениях может быть
записано в виде
Xf(v, X(v))dv + ?s,x{exv{^XsATc(t, X (t)) dt} X
Хф(тлГ, Л-(тлГ))]- (9)
В случае, когда оператор L и функции с, / не зависят
от s, аналогичное (9) представление возможно и для
решения линейного эллиптич. уравнения. Точнее,
функция
и (х) = Ея J J ехр { 5° с (X (t)) dt}f(X И) dv +
+ Ех { ехр { J^ с (X (t)) dt} <р (X (т))} A0)
при нек-рых предположениях есть решение задачи
L (х) и + с (х) и=— f (x), u\dD----q>. A1)
В случае, когда оператор L вырождается (dot b(s, x) = 0)
или граница <)D недостаточно «хорошая», граничные
значения могут н не приниматься функциями (9), A0)
в отдельных точках или на целых множествах. По-
Понятие регулярной граничной точки для оператора L
имеет вероятностную интерпретацию. В регулярных
точках границы граничные значения достигаются
функциями (9), A0). Решение задач (8), A1) позволяет
изучать свойства соответствующих диффузионных про-
процессов и функционалов от них.
Существуют методы построения М. п., не опираю-
опирающиеся на построение решении уравнений (В), G),
напр, метод стохастических дифференциальных урав-
уравнений, абсолютно непрерывная замена меры и др. Это
обстоятельство вместе с формулами (9), A0) позволяет
вероятностным путем строить и изучать свойства кра-
краевых задач для уравнения (8), а также свойства ре-
решений соответствующего эллпптнч. уравнения.
Так как решение стохастического дифференциаль-
дифференциального уравнения нечувствительно к вырождению мат-
матрицы b(s, x), то вероятностные методы применялись
для построения решений вырождающихся эллипти-
эллиптических и параболических дифференциальных уравне-
уравнений. Распространение принципа усреднения Н. М. Кры-
Крылова и Н. Н. Боголюбова на стохастические диффе-
дифференциальные уравнения позволило с помощью (9)
получить соответствующие результаты для эллипти-
эллиптических и параболических дифференциальных уравне-
уравнений. Нек-рые трудные задачи исследования свойств
решений уравнений такого типа с малым параметром
при старшей производной оказалось возможным решить
с помощью вероятностных соображений. Вероятност-
Вероятностный смысл имеет и решение 2-й краевой задачи для
уравнения (ti). Постановка краевых задач для неог-
неограниченной области тесно связана с возвратностью
соответствующего диффузионного процесса.
В случае однородного по времени процесса (L не
зависит от s) положительное решение уравнения L*q~Q
с точностью до мультипликативной постоянной сов-
совпадает при нек-рых предположениях со стационарной
плотностью распределения JVI. п. Вероятностные со-
соображения оказываются полезными и при рассмотре-
рассмотрении краевых задач для нелинейных параболич. урав-
уравнений. Р- 3. Хасъминский.
Лит-: [1] Марков А. А., «Изв. физ.-мат. об-ва Казан.
ун-та», 1 РОИ, т. 15, №4, с. 135—5*5; [2] В а с h e I i e г L.,
«Ann. scient. Ecole norm, super.», 1900, v. 17, p. 21—86; [3]
Колмогоров А. Н., «Math. Ann.», 1931, Bd 104, S. 415—
458; рус. пер.— «Успехи матеи. наук», 1938, в. 5, с. 5—41; [4]
Ч ж у н К а й - л а и, Однородные цсшг Маркова, пер. с англ.,
М., 1964; [5] F е 1 1 е г W., «Ann. Math.), 1954, v. «0, p. 417—36;
hi] Д ы н к и н В. Б., 10 ш к е в и ч А. А., «Теория вероятн. и
ее примсн.», 1956, т. 1, в. 1, с. 149—55; [7] X а н т Д ж.-А.,
Марковские процессы и потенциалы, пер. с англ., М., 19;
[8] Д е л л а ш е р и К., Емкости п случайные процессы, пер.
с франц., М., 1975; [9J Д ы н к и н Е. Б., Основания теория
марковских процессов, М., 1959; [10] его же, Марковские
процессы, М., 1963; [11] Г и х м а н И. И., Скороход А. В.,
Теория случайных процессов, т. 2, М., 1973; [12] Фрейд-
л и н М. П., в кн.: Итоги науки. Теория вероятностей, матема-
математическая статистика.— Теоретическая кибернетика. 1966, М.,
1967, с. 7 — 58; 113] X а с ь м и н с к и й Р. 3., «Теория вероятн.
и ее прнмеп.)), 1У(>3, т. 8, в. 1, с. 3—25; [14] Вент цель А. Д.,
Фрейд лиц М. И., Флуктуации в динамических системах
под действием малых случайных возмущений, М., 1979; [15]
Blumenthal R. M., Getoor К. К., Markov processes
and potential theory, N.Y.— L., 19(i8; [161 Getoor R. K.,
Markov processes: Ray processes and right processes, В., 1975;
?17] Кузнецов С. К., «Теория вероятн. и ее примен.»,
1980, т. 25, в. 2, с. 389—93.
МАРКОВСКИЙ СТАЦИОНАРНЫЙ ПРОЦЕСС -
марковский процесс, являющийся стационарным слу-
случайным процессом. М. с. п., отвечающий однородной
марковской nepextitiiii'ii функции, существует тогда и
только тогда, когда существует стационарное началь-
начальное .распределение у (А), отвечающее этой функции,
т. е. \х(А) удовлетворяет уравнению
\i(A)=\jXP(x, t, А) у. (их).
Если фазовое пространство процесса X — конечное
множество, то стационарное начальное распределение
существует всегда, независимо от того, рассматрива-
рассматривается процесс с дискретным (t=0, 1,2,...) или непре-
непрерывным временем. Для процесса с дискретным време-
временем и счетным множеством X условие существования
стационарного распределения найдено А. Н. Колмо-
Колмогоровым [1]: для этого необходимо и достаточно, чтобы
нашелся такой класс сообщающихся состояний Ус Л',
что математнч. ожидание времени попадания из ?/х ? Y
в i/2^K было конечно для любых у,? Y. Этот критерий
обобщается на строго марковские процессы с произ-
произвольным фазовым пространством X: для существования
Стационарного процесса достаточно, чтобы существовал
компакт А"сХ такой, что математпч. ожидание вре-
времени достижения К из х конечно для всех г?Х. Спра-
Справедливо следующее достаточное условие существования
М. с. п. в терминах Ляпунова стохастических функций:
если существует функция F(x)>0, для к-рой LV(x)^.— 1
при х (^ К, то М. с. н., отвечающий марковской пере-
переходной функции Р (.г, /, /1), существует.
R случае, когда стационарное начальное распреде-
распределение ц единственно, соответствующий стационарный
процесс аргоднчен. В этом случае среднее по Чезаро
переходных вероятностей слабо сходится к |Л. При
нек-рых дополнительных условиях
lim P (x, t, A) = [i{A) (слабо).
Стационарное начальное распределение удовлетво-
удовлетворяет уравнению Фоккера — Планка — Колмогорова
Л*ц=-(), где L* — оператор, сопряженный к инфини-
тезимальному оператору процесса. Напр., для диф-
диффузионных процессов L* — сопряженный оператор
к производящему дифференциальному оператору про-
процесса. В атом случае ц имеет плотность р, относи-
относительно лебеговой меры, удовлетворяющую уравнению
L*[i—0. Для одномерного случая это уравнение ре-
решается в квадратурах.
Лит.: [1] К о л м о г о р о в А. Н., Цепи Маркова со счет-
счетным числом возможных состояний, М., 1937; [2] Дуб Д т.,
Вероятностные процессы, пер. с англ., М., 1956; [3] Севасть-
Севастьянов Б. А., «Теория вероятн. и ее примен.», 1957, т. 2, в. 1,
с. 106 —16. Р. 3. Хасъминскип.
МАРКОВСКОЕ СВОЙСТВО для действительного слу-
случайного процесса А~(/), t?TczR,— свойство, заклю-
заключающееся в том, что для любого набора г1<<2<. . .<
<Лп + \ моментов времени из Т и любого борелевского
множества В с вероятностью 1
т. е. условное распределение вероятностен для X(tn + i)
относительно величин X (tn), . . ., X (ij) совпадает
(почти наверное) с условным распределением Х(?„ + 1)
относительно X(tn). Это свойство интерпретируется
как независимость «будущего» X(tn + 1) от «прошлого»
(X (?„_]), . . ., X (t^) при фиксированном «настоящем»
X(tn). Случайные процессы, удовлетворяющие свой-
свойству (¦¦ \ паз. марковскими процессами. М. с. допускает
(при нек-рых дополнительных предположениях) уси-
усиление, известное под названием «строго марковского
свойства». В случае дискретного времени Т={1, 2, . . .}
строго марковское свойство, спра-
справедливое всегда для. (марковских) последовательно-
последовательностей, удовлетворяющих свойству (*), означает, что для
всякого момента остановки т (относительно семей-
семейства (Fn), п>1, с Fn=a{m:X(l). . . ., Х(п)} с вероят-
вероятностью единица
Лит.: [1] Г и х ма н И. И., Скороход А. В., Теория
случайных процессов, т. 2, М., 1973. А. Н. Ширяев.
МАРТИНА ГРАНИЦА в теории марков-
марковских процессов — граница фазового прост-
пространства марковского процесса или его образа в нек-ром
компакте, строящемся по схеме, подобной схеме Мар-
Мартина (см. [1]).
Впервые вероятностное истолкование конструкции
Мартина было предложено Дж. Дубом (см. [4]), рас-
рассмотревшим случай дискретных цепей Маркова.
Пусть Р (t, х, В) — переходная функция однород-
однородного марковского процесса Х = (xf, t, Ft, Px), задан-
заданного в сепарабельном локально компактном простран-
пространстве Е, где i^O, х?Е, В?&3, a Si — семейство бо-
релевских множеств в Е. Функция ga(x, y)^0, опре-
определенная для ос^О, x?E, у?Е я являющаяся (й8Х со-
соизмеримой при фиксированном а, наз. функцией
Грина, если для каждого В ?
Sa (х, У) т (dy) ^ ^e-cct p (t, x, В) dt,
где т — нек-рая мера на S3. Чтобы избежать неодно-
неоднозначности в определении функции Грина, в нем до-
дополнительно требуют, напр., чтобы при любом выборе
непрерывной функции f(x) с компактным носителем
функция
8а (')=$?/(*)?«(*, -)m(dx)
была Л-непрерывной (последнее означает существо-
существование непрерывной слева по t функции F(t, со) такой,
что
Px{F(t, со) ??ga(xt((o))}^0, х?Е, t>0).
Фиксируя меру у на S3 и постулируя наличие функции
Грина, определяют ядро Мартина
где
о (ж, у) у (dx)
(при этом приходится ввести нек-рые ограничения,
обеспечивающие, в частности, положительность и
Л-непрерывность q(y)). Если у — единичная мора,
сосредоточенная в нек-рой точке, а X — винеровский
процесс, обрываемый в момент первого выхода из
нек-рой области, то определение К°у(х) сводится к
своему аналогу из [1]. При широких условиях уста-
устанавливается существование компакта (§ («компакта
Мартина»), мер К^ (dx) на S3 (сх>0, у?(§) и отобра-
отображения i:E-*-(§, для к-рых a) i(E) плотно в (§\ б)
функции
разделяют точки и непрерывны в (§, если / пробегает
Совокупность непрерывных в Е функций с компакт-
компактными носителями, и в) мера Kfiyi (dx) совпадает с
K^(x)m(dx), если у?Е. Граница множества i(E)
в $ наз. Мартина границей или гран п-
цей-вы ходом (при изучении разложений экс-
цессивных мер возникает двойственный объект — гра-
граница-вход, см. 13], [4]).
Для описания свойств компакта (§ удобно привлечь
fe-процессы в смысле Дуба: каждой эксцессивной функции
h можно соотнести переходную функцию
Ph(t,x, B) = h~1 (x) С h(y) P (t,x,dy)
в (Eh, S3h), где ?/г= {х ? Е : 0 <h (х) < оо }, а сЗЛ= {А ? S3 :
Aczi-'1}; соответствующий ей марковский процесс и есть
Л-процесс. Все Л-процессы вместе с X реализуются на
одном и том же пространстве элементарных событий,
так что они различаются лишь семействами мер {Р*}.
В $ строится модификация xt — непрерывный слева
процесс Zf(O<?<?), для к-poro ?Нк{цфг (?f)}==0, если
h^L1 (у). В топологии компакта ? предел z? = lim zt
существует почти наверное.
Существует множество U<ZL(§ («пространство вы-
выходов») такое, что, во-первых, PX{ZX, 6 U}=1 для всех
h(x) указанного вида, во-вторых, мера А" при y?U
имеет плотность fcy(-) по мере ia(a^0), причем в ка-
качестве ку(-) можно взять эксцессивную функцию со
спектральной мерой, совпадающей с сосредоточенной
в у единичной мерой, и, в-третьих, h(.f) допускает
единственное интегральное разложение вида
Мера (х из этого разложения наз. спектральной
мерой функции 'i; она дается формулой
где В — борелевское множество в ?.
В теории марковских процессов применяются и
компактификацип иных типов, особенно такие, в к-рых
любая функция вида
f (у) Р (t, х, dy), а>0, x?E,
допускает непрерывное продолжение для достаточно
обширного набора функций /.
Лит.: [llMartin В. S., «Trans. Amer. Math. Soc», 1941,
v. 49, p. 137—72; [2] M о t о о М., в кн.: Proceedings of the fifth
Berkeley Symposium on Mathematical Statistics and Probability,
v. 2, pt 2, Berk.—Los Ang., 1967, p. 75—110; [3] К u n i t a H.,
Watanabe Т., там же, p. 131 —t>4; [4j D о о b J. L., «J.
Math, and Mech.», 1959, v. 8, Л» 3, 433—58; [5] Watanabe
Т., «Mem. Coll. Sci. Univ. Kyoto. Ser. А», 19B0, v. 33, № 1, p. 39—
108; МХант Д ж. А., «Математика», iii61, т. 5, J* 5, с. 121 —
? 49; [7] Хеннекен П. Л., Т о р т р а А., Теория вероятно-
¦ j ей и некоторые ее приложения, пер. с франц., М., 1974: [81
Knnita H., Watanabe Т., «111. J. Math.», 19е.">, v. 9,
Ye 3, p. 485—52E; [9] Ш у р М. Г., «Тр. Моск. нн-та электронного
машиностроения», 1970, в. 5, с. 192—251; 110] J е и 1 i n Т.,
«Z. Wahrscheinlichkeitstheorie undverw. Geb.», 1978, Bd 42, ,V 3,
S. 229—ВО; [И] Д ы н к и н Е. Б., «Успехи матем. паук», 1909,
т. 24, в. 4, с. 89—152. М.Г.Шур.
МАРТИНА ГРАНИЦА в теории потенци-
потенциала — идеальная граница Грина пространства Q
(см. также Кольцевая граница), позволяющая постро-
построить характеристич. представление положительных гар-
монич. функций на Q. Пусть Q — локально компакт-
компактное, но не компактное топологнч. пространство, Ф —
семейство непрерывных функций /:Q->-[—со, -!-оо].
Теорема Констант инеску — Корня
[2] утверждает, что существует единственное с точно-
точностью до гомеоморфизма компактное пространство Q
со следующими свойствами: 1) Я есть подпространство
Q, всюду плотное в Q; 2) каждая функция /?Ф не-
непрерывно продолжается на Q до функции /, разделя-
разделяющей точки идеальной границы Д—- QN Q пространства
Q относительно семейства Ф; 3) Q есть открытое множе-
множество в Q.
Пусть теперь Q — ограниченная область евклидова
пространства R", п~^2, пли, вообще, пространство
Грина; G=G(x, у) — Грина функция Q с полюсом
j/^Q, точка Уо^О, фиксирована. Пространство
Мартина, или к о м п а к т и ф и к а ц и я Мар-
Мартина, Q области Q получается по теореме Константн-
неску — Корня в том случае, если в качестве семей-
семейства Ф принимается
причем, по определению, К(,r0, j/0)~ 1. М. г.— это
соответствующая идеальная граница Д=?2\Й.
Топология Мартина Т — это топология про-
пространства Мартина ii. Пространства Мартина Q',
Q", соответствующие выбору различных точек г/о, !/о?й,
гомеоморфны между собой. Функция К(|, (/):ДХЙ~>
—>* [О, -f-oo], являющаяся продолжением К (.г, у),—
гармоническая по у и непрерывная но совокупности
переменных (§,' у); Q — метризуемое пространство.
Основная теорема Мартина [1] утверждает:
класс всех положительных гармонич. функций и(;/)^0
на Q характеризуется представлением Мар-
Мартина:
где ,и — нек-рая положительная мера Радона на Д.
В представлении (*) мера [х определяется по функции и
неоднозначно. Гармония, функция v^O наз. м и н н-
м а л ь н о й в Q, если каждая гармонич. функция
w такая, что 0<?Wt?v в Q, пропорциональна г. Мини-
Минимальные гармонич. функции у?=0 пропорциональны
К (i, у), соответствующие точки ?сД наз. минималь-
минимальными, множество всех минимальных точек ДхсА
наз. минимальной границе й Мартин а.
Подчиняя меру и, в (*) дополнительному условию,
чтобы она была сосредоточена на Дь получают кано-
каноническое представление Мартина:
в к-ром мера (Xj^O определяется по и однозначно.
Пример ы. 1) Если G= {x?R": \x\ <R} — шар
радиуса R в пространстве R", п^2, то
есть ядро Пуассона, U совпадаете евклидовым замыка-
замыканием, й=й, М. г. Д есть сфера {??IR'!: |g] = i;}, всо
точки к-рой минимальные. Представление (*) в этом
случае сводится к формуле Пуассона —
Герглотца (см. Интегральное представление ана-
аналитической функции, Пуассона интеграл).
2) М. г. Д совпадает с евклидовой границей F=Q\Q
всякий раз, когда Г есть достаточно гладкая гиперпо-
гиперповерхность в R", ге^2.
3) Если Q — односвязная плоская область, то М. г.
Д совпадает с множеством граничных элементов, nJiii
простых концов по Каратеодори. Таким образом, эле-
элементы М. г. | ? Д можно рассматривать как обобщение
понятия простых концов для размерностей п^2.
Лит.: [1] М а г t i n R. S., «Trans. Атет. Math. See», 19J1.
v. 4«, p. 137—72; ElConstan tijescu С, С о г n e a A.,
Ideale Kander Riemannscher Flachen, B. [«. a.J, 1963; [3] Б ре-
л о М., О топологиях и границах в теории потенциала, пер.
С англ., М., 1974. Е. Д. Соломенцев.
МАРТИНГАЛ — стохастическая последовательность
X=(Xf, Ff), t?T<=[0, оо), заданная на вероятностном
пространстве (Q, F, Р) с выделенным на нем неубы-
неубывающим семейством о-алгебр (Fi)tiT, Fs'~Ft~F, s<?t,
такая, что Е|Х/|<оо, Xf являются /"'[-измеримыми л
E(Xt\Fs) = Xs A)
(с вероятностью 1, или почти наверное). В случае
дискретного времени Т={1, 2, ...}, в случае непре-
непрерывного времени Т=-[0, оо). Родственными понятиями
являются стохастич. последовательности, образующие
суб мартингал, для к-рых
Е (Xt | Fs) S& Xs,
и с у п е р м а р т и н г а л, для к-рых
Е (Xt \ Fs) <; Xs.
Пример 1. Если ?-,, \г, . . .— последовательность
независимых случайных величин с Е|,- —0, то X —
= (Хп, Fn) с Хп=^+. . .-i-ln, Fn=a{(u:l1, . . ., |„}
является М., л>1.
Пример 2: Пусть У= (Уп, fn) — М- (субмартин-
(субмартингал), F=(Vn, /*„) — нек-рая предсказуемая последо-
последовательность (т. е. Vn являются не только /"„-измери-
чымп, но и /"„-г-измеримыми, п>1, F0=[2Z, О} и
Тогда если величины (ГУ)„ интегрируемы, то стоха-
стич. последовательность ((VY)n, Fn) образует М. (суб-
(субмартингал). В частности, если \и ?2, . . .— последо-
последовательность независимых случайных величин, соот-
соответствующих схеме Бернулли
2;осли Si=--.=g*-i = i; Bj
0, в остальных случаях,
то ((Р"У)„, fn) образует М. Эта стохастич. последова-
последовательность служит математич. моделью игры, в к-рой
игрок выигрывает единицу капитала, если ?ft=4-l,
и проигрывает единицу, если g^=—1, а \\ — вели-
величина его ставки в к-й партии. Игровой смысл функции
Т'&, определяемой равенством B), состоит в том, что
игрок увеличивает ставку вдвое при проигрыше и
прекращает игру при первом выигрыше. Такая си-
система игры в игровой практике носит название М.,
что п послужило причиной возникновения математич.
термина «мартингал».
Один из основных фактов теории М. состоит в том,
то структура М. (субмартингалов) Х= {Xf, Ff) со-
сохраняется при случайной замене времени. Точная
формулировка этого факта (называемого теоремой
о преобразовании свободного выбора)
состоит в следующем: если тл и т2 — два конечных
марковских момента, Р{т!<:т2}=1 и
Х% 1 < оо, liminf \, ,,|Xf |dP = O, C)
то Е (Ху | Fx Y>. = XX (с вероятностью 1, или почти
наверное), где
В качестве частного случая отсюда следует Вальда
тождество:
К числу основных результатов теории М. относятся
неравенства Дуба: если X— (Х„, Fn) — не-
неотрицательный субмартингал,
Хп= max X/,
1 < / < я
Ыр={Ь\Хп\РI'Р, pSsl, n&l,
то
Р{х:^е}<:Ц1, D)
\\XJip<:\\Xn\\p<:JL-\\Xn\\p, р>1, E)
Если Х=(ХП1 Fn) — М., то для случая р>{ спра-
справедливы неравенства Буркхольдера
(обобщающие неравенства Хпнчина и Марцннкевича —
Зигмунда для сумм независимых случайных величин):
Чр < II х„ \\р <: вр | VWYn \Р, (?)
где Ар -л Вр — нек-рые универсальные константы (не
зависящие от X и от п), в качестве к-рых можно взять
С учетом E) из G) следует, что
АР1 viWn ip < li *¦«
где
На случай р =1 обобщаются неравенства (8). Именно,
имеют место неравенства Дэви с а: сущест-
существуют такие универсальные постоянные А и В, что
а ' VixTn lit «= |! х'пHi <s || VJxTn Ik.
Для доказательства разного рода теорем о сходи-
сходимости субмартингалов с вероятностью единица клю-
ключевую роль играет неравенство Дуба для
математического ожидания EEn (а, Ь)
числа пересечении Р„(а, Ь) субмартингалов X— (Хп,
Fn) интервала [я, Ъ] снизу вверх за п шагов
Ер„(а, Ь)<Е|Л6"_';|П'- (9)
OcnoBHoii pesj-льтат о сходимости субмартингалоп
содержится в т о о р е м о Дуба: если Х= (Хп, Fn) -
Субмартингал и sup ?|Х,г|<оо, то с вероятностью
единица существует limA(=^XO0) и EU^Kj,. Если
субмартингал А* равномерно интегрируемый, то помимо
сходимости с вероятностью единица имеет место и
сходимость в смысле Ь1г т. е.
Е 1 А'„ — А'„ |—>(), п—-оо.
Следствием этого результата является теорема
Лев и о непрерывности условных ма-
математических ожиданий: если Е11| <оо,
то
Е(||^„)—E(g|^.)t
где F-^F^z... и F»=ff(U/J.
Естественным обобщением М. является понятие л о-
к а л ь н о г о мартингала, т. е. такой стоха-
стнч. последовательности Х= (Xf, F-f), для к-рой най-
найдется последовательность {хт)т> j конечных марков-
марковских моментов, т,яжоо (с вероятностью 1 или почти
наверное4!, m^l, таких, что для каждого nC^l «оста-
«остановленные» последовательности
XT'"=(Xt/XXmI(xm >0), Ft)
являются М. В случае дискретного времени каждый
локальный М. Х= (Хп, Fn) есть м а р т и н г а л ь-
н о е преобразование, т. е. представим в
виде А"„= (VY)n, где V — нск-рая предсказуемая
последовательность, а У — нек-рый М.
Каждый субмартингал Х= {Xf, Ff) допускает и
притом единственное разложение Дуба — Мейера Xf- =
= Mt-\-Au где M=(MU Ft) — М.," а А== (At, Ft) —
предсказуемый процесс. В частности, если m= (mt,
F-t) — квадратично-интегрируемый Л1., то его квадрат
m2= (m~i, Ft) является субмартннгалом, для к-рого
в его разложении Дуба — Мейера m?= JV/^-{-<m>^ про-
процесс <ш>= «m>f, F't) наз. к в а д р а т и ч е с к о й
характеристикой мартингала т. Для
каждого квадратично-интегрируемого М. т и предска-
зуемого процесса F= (Vf, F^) таких, что
\ V\d <,mys < оо (с вероятностью 1, или почти
J О
наверное), t > О,
можно определить стохастич. интеграл
Г* t
(Vm)t= ^ Vsdms,
к-рый является локальным М. В случае внперовского
процесса W==(Wi, F-t), являющегося квадратично-
интегрируемым М., {jnyt=t и стохастпм. интеграл
(VW)t есть не что иное, как стохастич. интеграл Ито
по винеровскому процессу.
В случае непрерывного времени неравенства Дуба,
Буркхольдера и Дэвиса также остаются в силе (для
процессов непрерывных справа и имеющих пределы
слева).
Лит.: [11 Д у б Д ж., Вероятностные процессы, пер. с англ.,
М., 1956; [2] Г и х м а н И. И., Скороход А. В., Теория
случайных процессов, т. 1, М., 1971. А. Н. Ширяев.
МАРЦИНКЕВИЧА ПРОСТРАНСТВО — банахово
пространство М$ всех измеримых на полуоси @, оо)
функций (классов) с конечной нормой
1М1м,= SUP [ipih)]-1^ x*(s)ds, A)
где x* (s) — перестановка функции x(t), т. е. невоз-
растающая непрерывная слева функция, равноизме-
рпмая с \x(t)\, a ty(t) — нек-рая положительная не-
неубывающая на @, оо) функция, для к-рой ty(t)/t не
возрастает (в частности, т|) (t) — неубывающая вогну-
вогнутая функция); введено И. Марцинкевичем [1].
Если т|)(?) ограничена снизу и сверху положитель-
положительными константами, то пространство М-ц, изоморфно L1.
Во всех других случаях оно не сепарабельно. Про-
Пространство М$ является интерполяционным люжду
L' и L°° с интерполяционной константой 1.
На пространстве Л/ф определен функционал
F(x)= sup t[^(t)]-ix*(t),
О < ( < ™
к-рый всегда не превосходит IklUi^. Функционал F (х)
не обладает свойствами нормы; он эквивалентен норме
М тогда и только тогда, когда при l
(в частности, для ty(t)=ta при 0<а<1).
Пространство М$ возникло впервые в интерполя-
интерполяционной теореме Марцинкевича (с функционалом
F(х)) и связано с интерполированием операторов сла-
слабого типа. Оно обладает экстремальным свойством:
является наиболее широким среди всех симметричных
пространств Е, для к-рых фундаментальная функция
совпадает с hi^(h), т. е. \\%@. h)\\F=h/ty{h), где %iOi h) —
характеристич. функция интервала (О, К). Если
ф(+0)=0, ip(oo) = oo, B)
то Mty изоморфно (изометрично, если ф вогнута) со-
сопряженному пространству к пространству Лоренца с
нормой
где 'ф(з) — наименьшая вогнутая мажоранта -ф (s).
При условиях B) в Мф выделяется подпространство
М\:, состоящее пз всех функций из М^,, для к-рых
lim [У(К)]-Х [h x*(t)dt = O.
h->¦ 0, ~ •) °
Если, кроме того, lim ib (*)/*= оо то подпространство
М\ совпадает с замыканием в ЛГф множества всех
финитных ограниченных функций. При этом сопряжен-
сопряженное к пространству М\ изоморфно пространстпу Ло-
Лоренца и, следовательно, Л/ij, изоморфно второму со-
сопряженному пространству к М^.
Если Щ} — пространство, на оалгебре измеримых
множеств к-рого определена о-конечная мера |л, то
для каждой измеримой функции х(т) определена ее
перестановка х* (s), 0<s<oo, так что можно ввести
М. п. Л/ф(ЗД1, и.) с нормой (IV
Лит.: [ll.Marcinkiewicz J., «С. г. Acad. sci.», 193!),
t. 208, p. 1272 — 73; [2] К р е й н С. Г., П е т у н и н Ю. П.,
Семенов Е. М., Интерполяция линейных операторов, М.,
1978; [31 С т е й н И., В е й с Г., Введение в гармонический ана-
анализ на евклидовых пространствах, пер. с англ., М., 1Р74.
С. Г. Ирейн.
МАССА — физическая величина, определяющая
инертные и гравитационные свойства материи. В клас-
снч. механике инертная масса — постоянный
для данного тела коэффициент пропорциональности
между силой и ускорением во втором законе Нью-
Ньютона. Гравитационная масса определяет-
определяется как коэффициент пропорциональности в законе
всемирного тяготения. Согласно принципу эквивалент-
эквивалентности инертная и гравитационная М. пропорциональны
друг другу, а при обычном выборе систем единиц —
равны. В классич. физике М. аддитивна — М. системы
равна сумме М. ее частей. В специальной теории от-
относительности М. (т. н. м а с с а покоя) может быть
определена как коэффициент пропорциональности в
формуле, связывающей импульс тела р и его скорость у
где с — скорость света в вакууме. Иногда вводят
величину
т
т
наз. массой движения тела. Можно считать,
что в теории относительности импульс и скорость свя-
связаны классич. формулой р-=тлк. v, но М. завмспт от
скорости. М. тела связана с его анергией Е соотно-
соотношением Е=тс2. В относительности теории М. не ад-
аддитивна: М. устойчивой системы меньше суммы М.
ее частей на величину Ат^= АЕ/с2, где АЕ — энергия
связи системы, равная той энергии, к-рая выделилась
при образовании системы. Величина Am наз. дефек-
дефектом массы. М. покоя всех известных фияич. тел
неотрицательна (равна нулю, напр. М. покоя фотона),
однако иногда телам приписывается отрицательная
масса. Д- Л- Соколов.
МАССА И КОМАССА — сопряженные нормы в
нек-рых двойственных друг другу векторных прост-
пространствах.
1) Масса г-векторасх — число
| a |0=inf \2j. I a,i |:a = 2 aii а,-—простые г-векторы}.
Ко масса r-ковектора со — число
со |o = snp {| со-сх |, а — простые r-векторы, | а [ = 1}.
а
Здесь | -| — стандартная норма r-вектора, со.а — ска-
скалярное произведение вектора и ковектора.
Масса |а|0 и комасса | со|0 — сопряженные нормы
соответственно в пространствах r-векторов 1\, и
r-ковекторов F^, при этом:
а) |w|0 = sup{|6>-a |:| а|0 = 1},
а
a |0 = sup{| и-а|:| со |0 = 1};
ш
б) | a 'oSsa, | со |0 :з со,
и равенства имеют место в том и только в том случае,
когда а (со) — простой г-(ко)вектор;
в) |avP|ofi=|a|o|P|o, I w V t |„ =s? В | со ]0 | t, |„
для внешних произведений v, причем для простого
поликовектора со (или \) .6=1, а в общем случае B=Crr+s,
.ели сое^[Г], 1$*™;
г) | сола |0< В | со |0 \а |0
для внутренних произведений Л, причем В=1 при
r^s и B=Cs при r<:s, co^f'-'^ , aG^rsv
Ути определения позволяют определить М. и к. для
• оченин соответствующих расслоений, стандартными
>лоями к-рых являются F^ и Frrn. Напр., к о м а с-
>¦ а формы со в области GcEn равна
|со |0=-sup {|со (р) |0, p?G}.
2) Масса полиэдральной цели А =
— ^,ai°? равна
mi==2kiKI'
где | о;| — объем клетки аГ{. Для произвольной цепи
массу (коночную или бесконечную) можно определить
несколькими способами, к-рые для бемольной цепи (см.
Бемольная норма) и диезной цепи (см. Диезная норма)
дают одно и то же значение массы.
3) К о м а с с а (бемольной, в частности диезной)
коцепи X определяется стандартным образом:
*1=
где А — полиэдральная цепь, X -А — значение коце-
коцепи X на цепи А.
Лит. см. при ст. Бемольная по-рма. М. И. Войцехоеский.
МАССИВНОЕ МНОЖЕСТВО — множество М топо-
юглч. пространства X, являющееся пересечением
четного числа открытых плотных в X подмножеств.
Ксли каждое М. м. плотно в X, то X оказывается Бэра
пространством. М. И. Бойцехявский.
МАССОВАЯ ПРОБЛЕМА, алгоритмическая
проблема,— проблема нахождения алгоритма для
решения бесконечной серии однотипных задач, зави-
зависящих от нек-рого параметра. Простейшие примеры
\\. п.: сложить два данных десятичных числа, умно-
умножить два данных числа, проверить, является дан-
данное целое число простым или нет, найти производ-
производную данной функции, разложить данную функцию
в степенной ряд и т. д. Если искомый алгоритм не
существует, то говорят, что рассматриваемая М. п.
неразрешима.
Проблему нахождения алгоритма, решающего дан-
данную М. п., иногда называют проблемой р а з-
решимост и. Этот несколько неудачный термин
исторически впервые появился в связи с проблемой
распознавания выводимости формул в классическом
исчислении предикатов. Вообще же говоря, под про-
олемой разрешимости данной М. п. естественно счи-
считать вопрос о том, разрешима или нет эта М. п., т. е.
существует или нет искомый алгоритм.
См. также Алгоритмическая проблема. с И Адян
МАССОВОГО ОБСЛУЖИВАНИЯ СИСТЕМА — поня-
понятие, к-рое включает в себя случайный «входящий»
ноток требований (вызовов, клиентов), нуждающихся
в «обслуживании», и механизм (алгоритм), осуществ-
осуществляющий это «обслуживание».
Типичным примером М. о. с. являются автоматич.
телефонные станции, на к-рые случайным образом
поступают требования — вызовы абонентов (входящий
поток вызовов), а механизм обслуживания состоит из
фиксированного числа п каналов (линий) связи, каж-
каждый из к-рых остается занятым под обслуживание
очередного вызова случайное время, равное длитель-
длительности разговора. Если все л каналов заняты, то вызов
получает «отказ». Механизм (алгоритм) обслуживания
может включать в себя также указания, на какую из
свободных линий следует направлять очередной вызов,
предложение ждать, если требуемый абонент занят,
и др.
Существуют и системы другого тина, когда каждое
требование непременно должно быть обслужено, как
это имеет место, напр., в потоке самолетов, прибы-
прибывающих в аэропорт для посадки, или в потоке задач
(программ), к-рые должны быть реализованы на элект-
электронно-вычислительной машине.
«Случайную» часть М. о. с. удобно описывать с
помощью случайных последовательностей или процес-
процессов. Наиболее простые М. о. с. можно описывать дву-
двумерными управляющими случайными последователь-
последовательностями
неотрицательных случайных величин. Последователь-
Последовательность {т/} определяет поток вызовов е: она указывает
случайные моменты времени
Р Р- Р Р (* Р
То, To + Tl, To + Ti + T-i, ...,
в к~рые в систему поступают требования, подлежащие
обслуживанию. Эквивалентным образом входной поток
можно характеризовать случайным процессом {e(t);
f^O}; значение e(t) указывает число вызовов, посту-
поступивших в систему к моменту времени t. Вторая по-
последовательность {ту} описывает процесс обслужи-
обслуживания s: случайная величина т/ означает время, к-рое
тратится на обслуживание вызова с номером ;. Об-
Обслуженные вызовы выбывают из рассмотрения.
Весьма распространено описание управляющих по-
последовательностей с помощью маркированных точеч-
точечных процессов, в к-рых т/ представляют собой интер-
интервалы между точками, а т/ — марки этих точек.
Задание управляющей последовательности не оп-
определяет однозначно поведение системы. Необходимо
задать еще алгоритм обслуживания — правило, кото-
которое определяет моменты начала обслуживания и пове-
поведение вызовов в зависимости от состояния системы.
Многообразие алгоритмов обслуживания порождает
чрезвычайно много различных видов систем обслужи-
обслуживания. Ниже приведена классификация простейших
из них.
I. С и с т е м ы с ожиданием (или системы
с очередь го). Вызовы, поступившие в систему
и не принятые немедленно к обслуживанию, накапли-
накапливаются, образуя «очередь», ожидающую обслужи-
обслуживания. В дальнейшем вызовы обслуживаются в порядке
поступления. Система занята в момент вре-
времени t, если в этот момент есть очередь или происходит
обслуживание очередного вызова. В противном случае
система наз. свободной в момент времени t.
Различают два типа систем с очередью.
1Х. Обычные систем ы. Если система сво-
свободна, то она начинает действовать (обслуживать оче-
очередной вызов) немедленно при поступлении вызова.
Если система занята, то обслуживание очередного
вызова начинается после окончания обслуживания
предыдущего. Такие системы наз. также п о л н о д о-
с т у п н ы м и.
12. С и с т е м ы с автономным обслужи-
обслуживанием. Здесь обслуживание начинается только в
моменты времени 0, ti, T1+T2, . . .
II. Системы с ограниченной оче-
очередью. Считают, что длина q(t) очереди в момент t
равна re^sl, если один вызов в этот момент находится
на обслуживании ил — 1 вызовов ждут обслуживания.
Пусть qn=q(to-\-. . .-\-Tn-i) длина очереди в момент
прихода я-го вызова (без учета этого вызова). В си-
системах с ограниченной очередью вызов с номером п
«получает отказ» и выбывает из рассмотрения, если
в момент его прихода длина qn очереди оказывается
равной максимальному допустимому значению JV^l.
Число .V является существенной характеристикой си-
системы. Если iV=oo, то получаются обычные системы
с неограниченной очередью.
Рассматривают также системы со случайной ограни-
ограниченной очередью и системы со случайным ограничен-
ограниченным временем ожидания.
III. Системы с ограниченной очередью в случае JV=1
наз. системами с отказами. Для систем
с отказами автономное обслуживание обычно не рас-
рассматривается.
В каждом из рассмотренных простейших видов
систем задание управляющей последовательности пол-
полностью определяет эволюцию системы. Другими сло-
словами, для каждого элементарного события со и любого t
однозначно определено состояние системы к моменту
времени t.
Помимо перечисленных выше типов систем обслужи-
обслуживания, возможны и другие, более сложные системы.
Они связаны с более сложными управляющими по-
последовательностями и алгоритмами обслуживания.
IV. Групповой входной поток и
групповое обслуживание. Управление
такими системами может происходить с помощью че-
четырехмерных управляющих последовательностей
{tJ. vj, т?, vj; /=sO},
где v/ и V/ — неотрицательны и целочисленны. Смысл
новых переменных следующий: вызовы поступают груп-
группами объемов \'о, vf, . . . (соответственно в моменты
времени То, To+ti, . . .); обслуживание также про-
происходит группами: в первой партии обслуживается
Vo вызовов, во второй vi вызовов и т. д. (объемы
этих групп могут быть и меньше, если в очереди не
окажется достаточного количества вызовов). При
этом на обслуживание k-ii партии тратится вре-
время т|.
Для систем с групповым входом и обслуживанием
возможны те же алгоритмы обслуживания, к-рые
были описаны выше.
V. Многоканальные системы. В таких
системах обслуживание может вестись одновременно
в m^sl каналах, так что обслуживание очередного
вызова (или партии вызовов при групповом обслужи-
обслуживании) может начаться прежде, чем закончится об-
обслуживание предыдущей. Алгоритмы обслуживания
многоканальных систем выглядят аналогично для всех
рассмотренных типов обслуживания (каждый канал
действует как самостоятельное обслуживающее уст-
устройство). Надо лишь дополнить эти алгоритмы ука-
указаниями, в какой канал должны направляться вызовы,
если свободными оказались одновременно несколько
каналов. При этом по-прежнему на обслуживание i-ii
партии (объема <:v?) тратится время т^.
Многоканальная система наз. системой с о т-
к а з а м и, если вызовы, в момент прихода к-рых все
каналы оказались занятыми, получают отказ н выбы-
выбывают из рассмотрения.
Иногда для того чтобы упростить природу управ-
управляющих последовательностей для многоканальных
систем, удобно задавать не две, а т+1 управляющих
двумерных последовательностей
(т?, v?), (xf, vf), ...,(тГ, vD,
так что &-й канал обслуживания управляется последо-
последовательностью (г* , Vf ), &=1, . . ., т. Напр., т* есть
время обслуживания партии вызовов, к-рая является
г-й в к-м канале.
Приведенная классификация охватывает далеко не
все виды систем обслуживания. Широкое распростра-
распространение имеют, напр., системы, у к-рых вызовы подраз-
подразделяются на два или более типов и одни типы имеют
приоритет в обслуживании перед другими (такая
ситуация возникает, когда стоимость простоя одних
вызовов выше, чем у других). Характеризация таких
систем требует введения в рассмотрение нескольких
входящих потоков вызовов — по числу типов требо-
требований. К системам с приоритетным обслуживанием
можно отнести также системы, у к-рых обслуживающее
устройство требует перерывов в работе. Закон появ-
появления и длительности перерывов можно характеризо-
характеризовать специальным входным потоком.
В литературе по массового обслуживания теории
рассмотрены и др. специальные виды систем обслужи-
обслуживания. Однако при этом следует иметь в виду, что:
1) основные и наиболее распространенные типы
М. о. с. находятся в рамках приведенной выше клас-
классификации;
2) методы исследования М. о. с. для различных си-
систем, как правило, отличаются мало и в достаточной
степени иллюстрируются методами изучения «основ-
«основных» систем; в основе этих методов лежит аппарат
теории вероятностей, как общие его разделы, так и
специально разработанные.
Основной целью изучения является исследование
распределений различных параметров, характеризу-
характеризующих состояние системы (напр., длины очереди, вре-
времени ожидания начала обслуживания, вероятности
данному вызову получить отказ и т. д.). Главный
интерес при этом представляют эргодич. теоремы,
описывающие поведение указанных характеристик че-
через большой промежуток времени. Напр., одной из
характеристик эффективности работы автоматической
телефонной станции является доля вызовов, получив-
получивших отказ, т. е. предел р при t —>- оо (если он сущест-
существует) отношения r(t)le(t) числа r(t) вызовов, потерян-
потерянных за время t, к общему числу e(t) вызовов, поступив-
поступивших за это время. Этот предел можно с достаточными
на то основаниями называть вероятностью
отказа. Показателями, характеризующими системы
с ожиданием, являются предельные при п —*¦ оо рас-
распределения вероятностей P{wn<Cx} и Р{<7„<а:} для
времени wnj к-рое п-й вызов ожидал начала обслужи-
обслуживания с момента прихода, и для длины qn очереди в
момент появления в системе п-то вызова.
Метод исследования часто состоит в отыскании мар-
марковских процессов или последовательностей, харак-
характеризующих состояние системы. Если, напр., случай-
случайные величины т; и т/ показательно распределены и
при разных индексах независимы, то «процесс оче-
очереди» q(t) будет марковским и допускает описание с
помощью простых дифференциальных уравнений для
стационарного распределения. В других случаях обыч-
обычно пытаются построить случайные моменты времени
<!, ?2i • • - такие, что q(tn) или значения других ха-
характеристик (напр., времени ожидания), взятые в
моменты ij, i2, . . ., образовывали бы цепь Маркова.
Это т. н. метод вложенной цепи Маркова. Этот метод
часто используется в модифицированном виде, когда
строятся полумарковские процессы, описывающие ин-
интересующие нас состояния системы.
В более сложных случаях приходится использовать
асимптотич. методы (см. Массового обслуживания тео-
теория) или прибегать к моделированию случайных
процессов, описывающих поведение М. о. с, по Мон-
Монте-Карло методу.
В статьях Массового обслуживания система с ожи-
ожиданием и одним каналом обслуживания, Массового
обслуживания система с ожиданием многоканальная,
Массового обслуживания система с отказами, Массо-
¦пго обслуживания система (входящий поток вызовов)
ьолее подробно рассматриваются основные виды си-
i гем обслуживания и входные потоки. В этих стать-
статьях приняты следующие обозначения.
Е — класс последовательностей независимых слу-
случайных величин с показательным распределением.
Запись {т:е/}?Е означает, что
р{т/> х} = е~ах, а>0.
Запись {I/}?G/ означает, что случайные величины
с,- независимы и одинаково распределены (само рас-
распределение может быть произвольным). Соотношения
вида {т/}^?" или {ту}?С/ обычно предполагают
также, что управляющая последовательность {ту}
не зависит от остальных управляющих последователь-
последовательностей.
Класс стационарных в узком смысле последователь-
костей обозначен G$.
Приведенные обозначения могут применяться и к
многомерным последовательностям. Напр., {ту, Tyj^G/
означает, что двумерная последовательность стацио-
стационарна и составлена из независимых векторов.
Для простоты изложения, как правило, ограничи-
ограничиваются рассмотрением «ординарных» входных и выход-
выходных процессов, когда v/=v/=l (вызовы поступают
и обслуживаются по одному). Возможности обобще-
обобщений на «неординарный» случай (вызовы поступают
и обслуживаются группами: vy^l или v/^1) огова-
оговаривают отдельно.
Кроме того, природа управляющих последовательно-
гей будет простой и однородной, если выделять из
них начальные условия. Именно, рассматривают уп-
управляющие последовательности {ту, ту} при 1</<оо
и считают, что q@) = 0, а первый вызов пришел в си-
систему в момент То=О. Если управление задается вход-
входным процессом e(t), то фиксация То не производится.
Лит. см. при ст. Массового обслуживания теория.
А. А. Боров-ков.
МАССОВОГО ОБСЛУЖИВАНИЯ СИСТЕМА; вхо-
входящий поток вызовов — случайный про-
провес, заданный тем или иным образом и описывающий
поступление вызовов в систему обслуживания. Вхо-
Входящий поток определяется обычно случайной последо-
последовательностью {ту, v/}, где ту, /=1, 2, . . ., указывают
интервалы между поступлениями в систему групп
требований объемов соответственно vf^l, \>2*3=1, • • •
Если vy=l, то поток наз. ординарным. Экви-
Эквивалентным образом входящий поток можно задавать
с помощью точечного процесса или процесса {e(t)\
г^0}< указывающего количество вызовов, поступивших
в систему к моменту времени t. Можно считать для
определенности, что e(t) = e(t—0).
Наиболее распространенное требование, к-рое обычно
предъявляется к входному потоку, состоит в его ста-
стационарности. Это условие может быть двояким: либо
требуется стационарность в узком смысле последо-
последовательности {ту, vy} (обозначается {ту, "V/JG^s)»
либо требуется, чтобы процесс e(t) был процессом со
стационарными в узком смысле приращениями (обо-
значается {e(t)}?G/s). Эти два требования, вообще
говоря, не совпадают.
Интенсивностью стационарного потока наз.
число
Если {e(t))€G/s, то
M.= E(e(t + lj — e(t)) = ? (e(i) — e@)),
так что (х равно среднему числу вызовов, поступивших
в систему за единицу времени. Если последователь-
последовательность {т/} стационарна и эргодична и {v/}?Gy, то
7
В остальных случаях связь ji с распределением после-
последовательности {т./, v/} ? Gg может быть более сложной.
Пусть дан процесс {e(t)}?Gjs с интенсивностью (х
и с начальным значением е@)=0. С числом (.t tccijo
связан другой параметр входного потока, определя-
определяемый равенством
„— и™ р !«(*)> 1}
Этот предел всегда существует и a<gp.. Если |х<оо,
то a=u тогда и только тогда, когда входной поток
ординарен.
При изучении свойств входного потока часто ис-
используются т. н. функции Пальма
А = 0, 1, ...
(здесь е@) = 0), к-рые имеют смысл условных вероят-
вероятностей того, что на интервале @, t) появится к вызовов
при условии, что в момент времени 0 пришел вызов.
С распределением e(t) функции <Ps @ связаны равен-
равенствами
Если {Tej)?G,, то
фо
Значительную роль в теории массового обслужива-
обслуживания играют т. н. простейшие, или пуассоно в-
ские, входные потоки — стационарные вход-
входные потоки, для к-рых vy=l, {iCj}?E. Чтобы опре-
определить простейший поток в терминах процесса e(t),
требуют, чтобы процесс {e(t)} был пуассоновскпм. При-
Приращения этого процесса на непересекающихся интер-
интервалах времени независимы н имеют распределение-
Пуассона с параметрами, пропорциональными длинам
интервалов.
Находят широкое применение (особенно в телефо-
телефонии) также и неоднородные пуассоновские потоки,,
к-рые характеризуются процессами e{t) с независимыми
приращениями, распределенными по закону Пуассона
) — e{t) = k} =
))
(A (t + u)-A (t))*,
где A (t) — ведущая функция процесса (в однородном
случае A(i)=at).
Особая роль пуассоновских процессов в теории
массового обслуживания во многом объясняется ос-
основной предельной теоремой для входящих потоков,
к-рая устаиавлпнает, что в широких предположениях
сумма большого числа произвольных независимых
стационарных входных потоков малой интенсивности
сходится к пуассоновскому процессу. Частое исполь-
использование предположения о том, что входной поток
пуассоновский, обусловливается тем, что во многих
прилолсенттях реальные входные потоки образуются
именно таким способом (напр., поток вызовов, посту-
поступающих на телефонную станцию, представляет собой
сумму слабых потоков, исходящих от отдельных або-
абонентов).
Ниже приведена основная предельная теорема в
двух формах. Первая относится к суммам произволь-
произвольных (нестационарных) входных потоков.
Пусть даны возрастающие вместе с п совокупности
независимых процессов е^ n(t), . . ., еп_ n(t), n=l, 2, . . .,
зависящих от параметра л (т. е. рассматривается схема
серий), и введены следующие обозначения
А„ (t, и) = 2" = 1 Р К. п (*) — ег, „ (и) Гё= 1},
Bn(t, и) = 2" = х Р {«,. „ @ -«г. п (и) 3= 2}.
Пусть, кроме того, при любом фиксированном ?>0
выполнено условие
щт п -> со равномерно по г (это и есть условие малой
интенсивности иотоков ег, „(<)). Тогда, для того чтобы
конечномерные распределения процесса
сходились к распределениям пуассоновского процесса
с ведущей функцией A (t), необходимо м достаточно,
чтобы при п —*¦ оо
An(t, u)-^A(t) — A(u), Bn{t, u)~^0.
Если в рассматриваемой схеме серий, процессы
er + n(*)€G/s п ординарны, то имеет место также
следующее утверждение. Пусть цг,п — интенсивность
еГ, п Ъ) и ПРИ п —*¦ °°
Тогда для сходимости конечномерных распределений
процессов еп (t) к распределениям пуассоновского
процесса e(t) с параметром а необходимо и достаточно,
чтобы при каждом t
S'4T (»)<*«-* at, B)
где фХ (и) — функция Пальма для процесса er,n(t),
определенная равенством A). Если при п —>- оо
A_ф<;>@) — о
равномерно по г, то условие B) очевидно будет выпол-
выполнено.
Лит. Си. при ст. Массового обслуживания теория.
МАССОВОГО ОБСЛУЖИВАНИЯ СИСТЕМА с "онГи-
давнем и одним каналом обслужи-
обслуживания — система массового обслуживания, алгоритм
к-рой предусматривает, что вызовы, не принятые не-
немедленно к обслуживанию (заставшие систему занятой),
накапливаются в очереди; при этом обслуживание
следующего вызова (пли партии вызовов) может на-
начаться лишь после того, как окончится обслуживание
предыдущего (или предыдущей партии, если вызовы
обслуживаются группами). Основные определения и
обозначения см. в ст. Массового обслуживания система.
Наиболее естественными характеристиками состоя-
состояния систем с очередью являются следующие: а) время
wn ожидания начала обслуживания требования с но-
номером п и виртуальное время w{t) ожидания, к-рое
определяется как время, необходимое для освобож-
освобождения системы от вызовов, пришедших до момента
времени t; б) длина qn очереди в момент прихода п-то
вызова и длина q{!) очереди в момент времени t.
1) В «ординарном» случае (v/=l) значения шп свя-
связаны рекуррентным соотношением
и>„ + 1 = тах @, wn-\-c,n), %„ = %% —теп- A)
Такого же типа уравнениями (для времени ожиданпя
или для длины очереди) могут описываться системы
с ожиданием и в «неординарном» случае, когда v/,
vSj отличны от единицы. Напр., для длины qn очереди
справедливы соотношения
, qn+ven — $n), B)
где Р„ — число вызовов, к-рое может быть обслужено
за время Тл при бесперебойной работе системы. Если
, {vSj}?Gi, то распределение Р„ можно наптп
из соотношении
Ехе еЛР«= exp ITena 2™_ (еЛк — l) Р {v/ —
где а — показатель распределения т./.
Если обозначить Х0 = 0, -Уп=Ед+. . . + Е_,., то реше-
решение уравнения A) имеет вид
wn + \ = Xn — min (—wu Xu ..., Хп)*=
= max (*„+">!, Хд-A'i, ..., Хп-Х,^1, 0). C)
Отсюда следует, что если {it,}?.Gs и Р{Х„?Д}->-0
при любом фиксированном интервале Д и п -^ оо, то
существует предельное распределение времени ожи-
ожидания:
lira P {w.n > .т} = Р {У > х},
П ~> оо
где
У= sup У^, У* = l-s+• • •+i_i, Уо = 0.
Здесь величины 5—а — элементы последовательности
{|„}^=_сс, являющейся расширением {|,;}^=i до по-
последовательности, стационарной на всей оси. В даль-
дальнейшем будет предполагаться что такое расширение
произведено над всеми управляющими последователь-
последовательностями.
Значения
if*--sup@, Еь, ?ь+?ь_1, ЕьЧ-Еь_1 + Еь_о, ...)
удовлетворяют уравнению A) и имеют распределение-,
совпадающее с предельным распределением wn. Это —
стационарный процесс времени ожидания.
Пусть последовательность {mJ^Gs и эргодпчна
(Х„/п —>- Eli с вероятностью 1). Тогда
Р{У<оо} = Р {««;*< оо} = 1,
если Е|А<0 или если Е|А=0 и g*=r|fc + i—rjft, где
{^fcJ^^s- В остальных случаях
Р {У = оо} = Р {«'*= оо} = 1.
Если {с,,,} ?G/, то
Р {У < 00} = 1
тогда и только тогда, когда ЕЕ^<0 (тривиальный случай
1^ = 0 исключается).
2) Как уже отмечалось, другой возможной харак-
характеристикой состояния системы является виртуальное
время w(t) ожидания. Грубо говоря, это — время,
к-рое прождал бы начала своего обслуживания вызов,
пришедший в момент t. Пусть S (t) есть сумма времен
обслуживания вызовов, поступивших в систему до
момента времени t, X(t)=S(t)—t. Аналогом равен-
равенства C) здесь является соотношение
wit)=X{t)—^iDi<t(Q,X{u)). D)
Пусть Gjg — класс процессов со стационарными
в узком смысле приращениями и Gjr — класс про-
процессов с независимыми приращениями (fin и Gf$ здесь
можно понимать и более узко; напр., можно считать,
что Gj] — класс обобщенных пуассоновских про-
процессов с положительными скачками и сносом —1).
Если процесс {X (t); t^O}?G/s, то он может быть
расширен до процесса {X (t); — оо<г<оо}, заданного
на всей оси п также принадлежащего G/s. В этом
случае существует
lim P{w(t) > я} = Р {У > х},
где
Y= sup Y(t), Y(t) = X@) — X(—t).
Если, кроме того,
Е (.Y A) — X @))=Е (У A) —У @)) = а < О,
то распределение процесса
Wf (U) ={
сходится при t —»- оо к распределению процесса
z^(u)=sup (X(u) — X(v)),
о< и
к-рый является собственным стационарным процессом
виртуального времени ожидания. Сходимость здесь
имеет место в сильной форме:
для любого измеримого В.
Далее, если {X(i)}?G/s и а<0, то существует
условная функция восстановления Н0(х) процесса
X(t):
Н0(х)=^ Р{0<Х(и)-Х@) <х\Х(О) =
= inf X (v) \ du < оо;
о< О I
при этом
Приведенные формулы сохраняются и в случае v/=?l.
Для систем, у к-рых {т./—t/}?G/, существуют
простые связи между распределениями wk и ws (t).
3) Эргедические теоремы для длины очереди могут
быть получены с помощью соответствующих теорем
для времени ожидания. Пусть, напр., последователь-
последовательность {т/, t/J^Gs эргодична (метрически транзи-
тивна). Если, кроме того, Е(т./-—т/)<0, то сущест-
существует предельное (стационарное) распределение qn
такое, что
lim P{gn> fe} = P{^°
Если же {x/}?G/, {x/}?G/ и распределение т/ нере-
нерешетчато, то существует
lim P{q(t) > k+l} = P{w« > xf+.-.+Tfe + v}, к^гО,
X —*¦ со
lim P {g («) = 0} = —a/Exe,
т -<- О
где все компоненты под знаком вероятности в правой
части независимы, у имеет плотность, равную
Р {т./ > 4/ЕтЛ
w° = sup@, 10, io+g-i, ...). ?/ = х/ —X/.
Если {x/}?.E, то предельные распределения qn и
q(t) совпадают.
4) Если {х;}??, {f/JGG/ (допускается также,
что v/^1, {v/}?G/), то можно получить точные фор-
формулы и для допредельного распределения w(t):
+ ± ^ Е (У («)/«; У (и) < 0) Р {У (t-u) < х} da,
p{w(t) = O) = -E{Y(t)/t, Y(t)<0).
При а<0 и f —>- оо имеет место формула Хин-
чин а для стационарного распределения:
с .(Яш* (ы) _ 1-аЕ8 ,. . _ р ав
где 0 — величина скачка процесса X(t) (9=т/, если
v/^1), а — показатель распределения т/.
Пусть Tj, /=1, 2, . . .,— периоды занято-
занятости системы (т. е. длины интервалов времени
в течение к-рых w(t)~>0). Тогда для рассматриваемых
систем
±X(u) 6 @, da)}.
u+du)} P{X(
5) Для систем, у к-рых {т/, x/}?G7 (допускается,
также v/^1, {x/, x/, v/}^G/) распределение ш* совпа-
совпадает с распределением величины
y=sup(o, ix, ii+g2, ...)•
По известному распределению \j распределение
У может быть найдено следующим образом. Если
Р{У<оо}=1 (это всегда при Eiy<0), то справедливо
следующее факторизационное тождество
где р=Р{У>0}, %<:0 — величина первой неположи-
неположительной суммы среди |lt ii+iai . . . Это соотношение
позволяет отождествить с Bei^Y отношение w+ (k)/w+ @)
в любом тождестве
1 _ Ее'я5 = w_ (ЩШ+ (Я), 1тЯ, = 0, E)
в к-ром функции ш±(Я) допускают представление
.w-jr
(F± — функции ограниченной вариации). Равенство
E) осуществляет т. н. F-факторизацию функции 1—Ее'^6.
Оно позволяет указать следующие случаи, когда воз-
возможно отыскание Ее'^ в явном виде.
Предполагают, что —оо<Е?<0, и обозначают
так что f(X)=f+ (Я,)/_ (Я).
А) Если /+—рациональная функция: 1+ = PmlQn,
где Рт ш Qn — многочлены степеней тип соответст-
венно, то функция A—f)Qn B области 1иЛ<0 имеет
ровно п нулей Х1, . . ., Хп и
EeaY=w + (X)/w+ @).
Это означает, что если распределение Xs представимо
в виде
гДр Рк (х) — многочлены, то такого же вида представ-
представление (при других а/; и Рц, определяемых нулями
Я], . . ., Хп) будет иметь место и для Р{У>ж}.
В) Если f- = Pm/Qn — рациональная функция, то
функция A—f)Qn в области 1гдЯ>0 имеет п—1 нулей
Ях, . . ., Х„_! и
w+ (X) = ^ПГ1. (X-Xk)/Qn (Я) A-/(Я)).
Кроме этих формул, дающих явное выражение для
распределения У, можно также в широком классе
случаев описать асимптотич. поведение Р{У>#} при
х-*- оо. Именно, если
Y=sup (\i:te^ < оо) > О
и EeVl>l, то определен единственный корень д>0
уравнения Еей=1. В этом случае при х —*- оо
P{Y > a:} = cie-«*
Если же у=0, —оо<Е|<0, то
Постоянные сх и с2 найдены в явном виде.
Результаты, аналогичные изложенным в пп. 2) — 5),
справедливы и для систем с дискретным временем, '
когда время t и случайные величины управляющих
последовательностей принимают лишь целочисленные
значения.
6) Теоремы устойчивости выясняют условия, при
к-рых малое изменение конечномерных распределений
управляющих последовательностей влечет за собой
малое изменение стационарного распределения вре-
времени ожидания или длины очереди. Важность во-
вопроса об устойчивости систем обслуживания объяс-
объясняется тем, что обычно в реальных задачах пользу-
пользуются теми или иными предположениями о природе
управляющей последовательности (напр., предпола-
предполагается, что |у независимы или что т/ распределены но
показательному закону), в то время как на самом деле
эти предположения выполняются лишь приближенно.
Спрашивается, будет ли решение таких «идеализиро-
«идеализированных» задач близко к решению истинной задачи.
Чтобы получить точную постановку проблемы рас-
рассматривают схему серий, когда уравнением A) управ-
управляют стационарные последовательности (серия после-
последовательностей) |(га)= {!/"', —оо</<оо}, п=1,2, . . .
Кроме того, рассматривают стационарную последова-
последовательность g= {|y-; — оо</<оо} и обозначают
У<»>= supY(kn\Ykn)=yn li'f.
Ответ на поставленный выше вопрос дает следующее
утверждение.
Пусть конечномерные распределения |("» слабо
сходятся к соответствующим распределениям после-
последовательности 5, относительно к-рой предполагается,
что она эргодична и Е|у<0. Тогда для слабой схо-
сходимости
Р {У<"> < t} => Р {У < t} F)
(т. е. для сходимости распределений стационарных
времен ожидания) достаточно, чтобы
Сформулированное условие сходимости близко к не-
необходимому.
Если управляющие последовательности {т'/1', x/")s}
и {т/, т|} таковы, что т'")е и T/")s независимы, а
. распределения {т'/1^, x/"'s} слабо сходятся к рас-
распределениям {т/, ty}, то для выполнения F) доста-
достаточно, чтобы
Аналогично обстоит дело со стационарным распре-
распределением виртуального времени ws (t) ожидания. Если
конечномерные распределения процессов У(п) @ G^/s
сходятся к распределениям Y(t)?G/s и последова-
последовательность {т)?=У(/с+1) — Y(к)} эргодична, Er|?=a<0,
то для сходимости распределений
sup У<"> («) и sup У (i)
* >о <> о
достаточно, чтобы
7) Асимптотич. методы исследования одноканальных
систем (они включают в себя и теоремы устойчивости)
дают приближенные формулы для случая больших и
малых нагрузок. Пусть {Y{t)}?G}s- Тогда говорят,
что система имеет большую нагрузку, если
а-^Е (У (* 4-1) — У @) < °
близко к 0, и малую нагрузку, если а близко к —1.
Точная постановка задачи связана здесь как и в
п. 6) с введением схемы серий. Именно, для случая
больших нагрузок рассматривают процессы Xa(t),
зависящие от параметра а -+ 0. Пусть X" (t) удовле-
удовлетворяют условиям слабой зависимости, обеспечива-
обеспечивающим при t -> оо выполнение условий
Е A X" (О —А'" @) —at f + Ч/А) < Ы1 + Ч/о~ ,
lim p lx°m-x*_V»-at < x lA\ = Г* e- u^du
равномерно по а, где
у > 0, с > 0, а > О, А= I Ха @)= inf Xa (v)\ .
\ и<0 /
Тогда для стационарного виртуального времени ws(t)
при о —у 0 справедливо
P{u>-"-@ > x[\ a\}^e-2XJo\
Аналогичный результат будет иметь место и для ста-
стационарного распределения wk.
Если условия большой нагрузки наложить на по-
последовательности {g(")==T/")e—t)n)e}^.G/ (также в схеме
серий по параметру п), потребовав, чтобы
О > «„= E^n> _0, Dl)m _* о2 > 0, G)
то весьма полно можно описать также и распределение
допредельного времени wn ожидания, включая т. н.
переходные явления. Именно, пусть в дополнение к G)
lim Е[(|}-">)8; U}]
П -> со
при любом е>0. Тогда если а=а,г —>. О при ;г —>- оо
не меняя знака, так что па? -+¦ и2, то
Р {wn < .r/| а |} — >
—>- Р {(У (м) < (г — MSignna)/O; 0 =s; u < г.'2}, (8)
где w(u) — стандартный винеровский процесс. Зна-
Значение правой части (8) вычислено в явном виде. Если
па2 —у 0, то
Если 7га2 —у со, а<0, то
Р К > xl\ а |} -
Если па2 —у оо, а>0, то
Р {wn < ап + х}Ш)=-±= [
V 2jt J — °
8) Системы с О1раниченной очередью характеризу-
характеризуются тем, что вызовы, пришедшие в систему и застав-
заставшие очередь объема iC^N, получают отказ и выбывают
из рассмотрения. В этом случае qn*cN, а вероятность
P{qn=N} будет также вероятностью того, что ге-й
вызов получил отказ.
Уравнения B) здесь следует заменить на уравнение
вида
Gf« + i = min (Лг, max @, д„ + т)„)), reSsO.
Пусть b"\n}?Gs и последовательность {т|я} мет-
метрически транзитивна. Пусть, кроме того, выполнено
следующее условие: или Er)j=^O или ЕтI=О, но во
втором случае г\п не представимы в виде т)„--=7и—Y«-i,
где {yn}?Gs- При выполнении этих условий сущест-
существует предельное распределение qn при п —у со.
Если, кроме того, {r]n}?G/ (это имеет место, напр.,
в случае, когда {t}}?E, а остальные управляющие
последовательности принадлежат G,), то можно найти
явный вид стационарного распределения для qn при
п —>- оо, поскольку в этом случае qn связаны в простую
однородную цепь Маркова с конечным числом со-
состояний.
Существует также следующее представление для
стационарного распределения:
-i-P {X(k — N, k) = k — N}P {x(—l, N)^sN), (9)
где %( — l, m) — положение частицы, вышедшей из О
и блуждающей со скачками r]ft, &=1, 2, . . ., в момент
ее первого выхода за пределы интервала (—I, т).
Если Vn=l (т. е. если Р{т|л<:1}=1), то вероятности
(9) могут быть явным образом выражены через рас-
распределения т; и vy.
9) В системах с автономным обслуживанием обслу-
обслуживание вызовов в отличие от обычных систем с ожи-
ожиданием может начинаться лишь в моменты времени О,
х*, ti4-t2, . ¦ -, где ту — элементы управляющей по-
следовртельности. Таким образом, вызов, заставший
систему свободной, должен ждать до начала очеред-
очередного этапа обслуживания.
Наряду с процессом {e(t)}, описывающим входящий
поток, рассматривают процесс {$(?)}, где s(t) опреде-
определяется как число вызовов, к-рое приняла бы на об-
обслуживание система к моменту t при бесконечной
очереди. Обозначив через q(t) длину очереди в момент
t, не считая вызовов уже находящихся па обслужи-
обслуживании, и положив X(t) = e(t)—s(t), получают
q(t) = q @) + A" (t) - inf @, А (и) + q @)) =
0< и< t
= sup {q@) + X (t), X(t) — X(u)).
0< u< t
Это равенство аналогично соотношению D) и приводит
к следующему результату. Если процесс {X(t)}?G/s
и эргодичен,
то распределение процессов {Х^ (и)= X {t-\-и);
сходится при t —>- оо к распределзнию стационарного
процесса
Х(м)= sup (X (и) — Х (v)).
V ^ U
Если {х/}?? или {т/}^?, а остальные управляющие
подпоследовательности принадлежат G/, то можно
указать явные формулы для распределения Х(и).
Лит. см. при ст. Массового обслуживания теория.
А. А. Боровков.
МАССОВОГО ОБСЛУЖИВАНИЯ СИСТЕМА с о ж и-
данием многоканальная — система мас-
массового обслуживания, алгоритм к-рой предусматри-
предусматривает накапливание вызовов в очереди, если в момент
их прихода система оказалась занятой; при этом об-
обслуживание вызовов ведется в нескольких каналах
одновременно. Основные определения и обозначения
см. в Ст. Массового обслуживания система.
Функционирование многоканальных систем с оче-
очередью, управляемых последовательностью {х/, х/},
происходит следующим образом. Вызовы прибывают
в моменты времени 0, xf, xf+xf, .... На обслужи-
обслуживание вызова с номером / тратится время х/, в каком
б i б
р р р /,
бы из m^ssi каналов ни обслуживался этот вызов.
Пришедшие вызовы тут же направляются (в порядке
поступления) в любой свободный канал, если каналы
не все заняты, или ждут, когда освободится какой-
нибудь из каналов, куда и поступают на обслужива-
обслуживание. Пусть для простоты в момент времени i=0 система
свободна.
1) Для наглядности изложения использованы следу-
следующие обозначения: wn= (w,lt ь . . ., и)п>т) — вектор
времени ожидания re-го вызова, где w,u ,¦ — время,
к-рое должен ждать этот вызов до освобождения i
каналов от вызовов, пришедших раньше, чем он; так
что шПу ! — «истинное» время ожидания. Пусть, кроме
того, ж+=тах@, х),
05+= D, ..., *т), е=A, О, ...,0), *=A, 1, ..., 1),
а вектор В (аз) получен из ж упорядочиванием по воз-
возрастанию его координат (так что первая координата
В (ж) равна min(x1, . . ., хт)). Тогда имеет место следу-
следующее рекуррентное соотношение для wn, обобщаю-
обобщающее свой одномерный аналог
и>п+1=[-В (м>»+х^е)— xeni]+. A)
Если последовательность {х/, x/}?Gs и Е(х?—
—тах«)<0, то существует собственная последователь-
последовательность {">*}? G\s, удовлетворяющая A) и такая, что
функция распределения гюп при п —>- оо монотонно
сходится к функции распределения w°. Это утверж-
утверждение допускает обобщение на случай v/^1 и распро-
распространяется также на длину qn очереди в момент при-
прихода re-го вызова (под qn понимают очередь, включая
вызовы, находящиеся на обслуживании). Существуют
формулы, связывающие предельные распределения для
'ivп и дп.
Если {t/}?G,, {x/}?G,, to A) позволяет записать
интегральное уравнение для стационарного распре-
распределения iva. В этом случае можно указать также про-
простые связи между стационарными распределениями
длины очереди и времени ожидания. Именно, если wi
означает k-ю координату вектора w°, то при к^т—1
существуют
lim P {д„ {f |}
Если т>к^0, то
lim P{q
Здесь все случайные величины, стоящие под знаком
вероятности, независимы.
Если, кроме того, распределение ту нерешетчато,
то аналогичные формулы верны и для предельного
распределения q(t). Если {%}}?Е, то
lim Р{?л=й} = lim P{q(t) = k}.
2) Если {t/}?G7, {isj}?E, то можно указать явные
формулы для предельных распределений qn, q(t), tvn.
Пусть а — показатель распределения ту и атЕтг>1.
Тогда числа
pfe= lim P {qn=k}
описываются как известного вида рациональные функ-
функции от значений ц и г|)(—/a), j = l, . . ., т, где |х —
единственный корень в области |[х|<1 уравнения
Если к~>т, то
причем А от Л не зависит. Для предельного распре-
распределения времени ожидания
W {х) = lim Р {ш„, J > х]
П —> оо
имеет место равенство
Если ту — нерешетчатая случайная величина, то
существуют
lim P {q (t) = k} = Pft,
где
~ ~ при 1 </с < т,
при
В случае {ij}?E, {y}?E
Pft = 2— Я* При 1 sg
him"
ръ = —-— X при
где
К=[атВте]-1 < 1.
3) Теоремы устойчивости (о непрерывной зависимо-
зависимости стационарного распределения w° от распределений
т/ и т/) получены в менее общей форме, чем для одно-
канальных систем, и связаны с условием о сущест-
существовании т. н. обновляющих событий. Однако в случае
{т/}€<?/, Ы}€<?/. Е(т?—т%%)<0 это условие с
необходимостью выполнено. Если для таких систем в
схеме серий распределения %)п)е и x/")s слабо схо-
сходятся соответственно к распределениям ту и ту и,
кроме того, Exy")s —>- Ету, то распределение м>(">° будет
слабо сходится к распределению w°.
4) Асимптотич. методы исследования многоканаль-
многоканальных систем для больших нагрузок дают результаты,
аналогичные соответствующим результатам для одно-
канальных систем.
Пусть в схеме серий для управляющих последова-
последовательностей {ty}?G/, {ту}?б/ выполнено условие
8 = 1/Ете — то/Ет*—<-0
(б равно разности между средним количеством вызо-
вызовов, поступивших в систему, и средним количеством
вызовов, к-рое система может обслужить за единицу
времени; если v/^1, v/^1, то в качестве параметра S
можно выбрать число Eve/Exe—mE\slETs, имеющее тот
же смысл). Тогда если
и Е|те|2+?, Е It:-5 [2-не равномерно ограничены при
нек-ром е>0, то для длины q(t) очереди в момент
времени t справедливы при t —>- оо, б —>- 0 следующие
соотношения:
при б Y~t —>- v, i>> — оо,
lim ?{q(t) < х/\Ь ]}=---¦
= P {w (и) < (x— Msign5)/o; 0<M<va},
где w(u) — стандартный винеровский процесс;
при ЬУТ—^0
Дт ?{q(t)<x\r~t} = У± $ f е ~ «V* da;
при &y~t —э- оо, б > О,
lim P {q («)
t У2л
Аналогичные соотношения верны для длины qn очс
реди и для времени tvn ожидания.
Другое возможное направление асимптотич. иссле-
исследований для многоканальных систем состоит в изу-
изучении систем с интенсивным входным потоком и не-
неограниченно возрастающим (вместе с Е (еA)—«@)))
числом каналов обслуживания.
5) Поведение многоканальных систем с бесконечным
числом каналов обслуживания, управляемых после-
последовательностью {т/, т/}, описывается так же, как
поведение многоканальных систем с очередью, с той
лишь разницей, что здесь всегда есть свободные каналы
и, следовательно, время ожидания для любого вызова
равно 0. В качестве характеристики состояния системы
рассматривают число qn занятых линий в момент
прихода гс-го вызова или число q(t) занятых линий в
момент времени t (как и везде выше qn и q(t) — длины
очереди и ^=0).
Пусть {ту, т/} ? Gs и, кроме того, последователь-
последовательность {т/} метрически транзитивна. Тогда если Ет/<
<оо, то распределение последовательности {qn + k\
к~^0} при п —> оо монотонно сходится к распределению
собственной стационарной последовательности
2ir=o , B)
где I{А} индикатор события А. Условие Ету<оо
близко к необходимому условию для конечности B).
6) Для систем, у к-рых то=оо, {Ty}?G/, {x/}?G/,
распределение стационарной длины qk очереди можно
описать с помощью уравнений. Для этого следует
ввести величины
Число q° (х) указывает, сколько вызовов осталось в
системе, работающей в стационарном режиме, спустя
время х после прихода нек-рого вызова, но без учета
данного вызова и всех вызовов, поступающих после
него.
Ооозначив
Pj(x) = P{q° (*) = /}, / = 0, 1, ...,
Р(х) = Р{т* > х), F (х) = Р{%* <х),
получают
Р{?* = /} = Р{до@) = /} = Р/@);
система функций Pj{x) удовлетворяет уравнениям
, Л=1, 2, ...
Здесь Р _1(х) следует положить, равной 0. Каждые
из первых &-}-1 уравнений этой системы относительно
Р0(х), ..., Pk(x) имеют единственное решение в классе
функций ограниченной вариации, обладающих свой-
свойствами
РоП—* 1, Р,-(х)—>0 при г S&1, х—<-оо.
Аналогичные утверждения справедливы для рас-
распределения процесса q(t).
Если {•$??, {%*}?G;, то
lim P{g(t) = *}= lim Р {д„ = Л} =-^
где а=?т/, а — показатель распределения
Если {x/}^G/t {т?}^, то
Pk= ^ р{9„=Л} =2;=А (-1У-
где
с-
a — показатель распределения т/. Если, кроме того,
т/ — нерешетчатые случайные величины, то
lim P {q(t) = k} = pk-ilkaExe, k=l, 2, ...
t —> оо
7) Теоремы устойчивости в случае т=оо, как и в
предыдущих разделах, выясняют условия, при к-рых
малое изменение управляющих последовательностей
влечет за собой малое изменение стационарного рас-
распределения числа дк занятых линий.
Для схемы серий, когда система управляется ста-
стационарными последовательностями {т(">', т(л)*}, за-
зависящими от параметра ге=1, 2, . . ., пусть выполнены
следующие условия.
(A) Существует последовательность {т/, x/}^G5
такая, что {т/} метрически транзитивна, Ет/<оо и
конечномерные распределения {х)п)е, x}")s} сходятся
при п —>- оо к распределениям {ту, т/}.
(B) Et/")s^Et/ при ге-»-оо.
(C) Распределения т!/—2*=—Л* ПРИ всех 7^=0
непрерывны в точке 0.
Теорема устойчивости утверждает тогда, что при
выполнении условий (А), (В), (С) распределения по-
последовательностей {д<">*} длин очередей (к-рые оп-
определяются равенством B) с управляющими последо-
последовательностями {т}")е, Ty-")s}) сходятся при п -»- оо
к распределениям {<?*}.
Все три условия (А), (В), (С), присутствующие в
этом утверждении, существенны; отказ хотя бы от
одного из них сразу позволяет строить примеры, где
сходимость распределений {д(л)*} отсутствует.
8) Асимптотич. анализ систем с бесконечным числом
каналов обслуживания становится естественным и
эффективным при изучении т. н. нагруженных систем,
когда велика интенсивность входного потока. Несом-
Несомненным преимуществом асимптотич. подхода является
большая общность и универсальность установленных
закономерностей.
Пусть входной поток e{t)=er(t), означающий число
вызовов, поступавших в систему к моменту времени t,
зависит от параметра Т —>- оо (схема серий), так что
er(t) —*¦ оо при Т —>- оо для каждого фиксированного
?>0, и, кроме того, существуют неубывающая функция
m(t), функция В (Т) —>- оо при Г->- оо и непрерывный
случайный процесс |(i), заданный на [0, t0], такие,
что распределения /(?г№). гДе
sr y' в (о
слабо сходятся при Т —> оо к распределению /(?())
для любого измеримого и непрерывного относительно
равномерной метрики функционала /.
Если, напр., {tj}?Gj и управление системой про-
происходит с помощью последовательности x^—ijlT, to
сформулированные условия будут выполнены при
любом t0, при этом
m (t) = t/Ey, В* (Т) = 2-Dt,-/(Et,-K,
I (t) — стандартный винеровский процесс.
Относительно обслуживающего устройства предпо-
предполагают, что {t/}?G/. Тогда:
1) Если В (ТI У Т—*¦ оо, то конечномерные распре-
распределения нормированного процесса очереди
, . _ qJty-TQJt)
Z^>ВЦ
Q(t)=\[ G(t — u)dm(u),
слабо сходятся при Т —>- оо к распределениям про-
процесса
@=5^ G(t-u)dl{u).
2) Если В (T)l YT-+a^sO, to конечномерные рас-
распределения процесса
2 w Vt
слабо сходятся к конечномерным распределениям
процесса
J' G{t-u)dl(u),
где 0(<) —центрированный гауссовский процесс, не
зависящий от ?(/), с ковариационной функцией
Ев (t) в (* + ц)= V G (t + u — v) (I — G (t — v)) dm (v).
Если потребовать от функций m(t) или G(t) нек-рой
гладкости, то сходимость процессов z,- (t) к прецессам
?i№> J=l> 2, будет иметь место и в более сильном
смысле (напр., сходимость распределений /(z,-(i)) к
/(?;(i)) при Г —>- оо для всех функционалов, непрерыв-
непрерывных относительно равномерной метрики).
Лит. см. при ст. Массового обслуживания теория.
А. А. Боровпов.
МАССОВОГО ОБСЛУЖИВАНИЯ СИСТЕМА с о т-
к а з а м и — система массового обслуживания, ал-
алгоритм к-рой предусматривает выбывание вызовое, в
момент прихода к-рых все каналы оказались занятыми.
Основные определения и обозначения см. в ст. Массо-
Массового обслуживания система.
1) Естественными характеристиками состояния М. о. с.
с отказами являются число qn (или q{t)) занятых линий
в момент прихода n-го вызова (в момент времени t).
Однако, в отличие от систем с бесконечным числом
каналов обслуживания, здесь всегда q:l<:m, где т —
число каналов в системе. Если в момент прихода ге-го
вызова оказывается qn= m, то этот вызов получает
отказ н выбывает из рассмотрения. Если же qn<Cm,
то вызов направляется на обслуживание в один из
свободных каналов.
Предположив, что управляющая последовательность
{Tj> T/}€^S метрически транзитивна, Ету<оо, можно
сформулировать эргодич. теорему для систем с отка-
отказами, используя систему с бесконечным числом кана-
каналов обслуживания, управляемую той же последова-
последовательностью. Для такой системы существует собствен-
собственная стационарная последовательность {Qk} длины
очереди. Величину Q0 можно представлять как число
занятых линий стационарной системы в момент при-
прихода нек-рого вызова. Обозначив условно номер этого
вызова через 7, определяют Qi как число линий, за-
занятых вызовами, пришедшими до вызова 7о> в момент
прихода вызова с номером 7+'> так чт0 (?о=(?0, Q°i<-Q°-
Тогда если вероятность события
положительна, то распределения последовательностей
{Яп+k'i &>0} длин очереди для систем с отказами
будут сходиться при п —>- оо к распределению нек-рой
стационарной последовательности \qk\ к~^0]. Смысл
события А весьма прост: оно состоит в «обновлении»
системы: после него в системе будут находиться лишь
вызовы с номерами 7 и выше.
Приведенная теорема есть частный случай более
общего утверждения, использующего т. н. метод
обновлений. Если{т/}?С, {Ty}?G7, то для выполнения
сформулированных условий достаточно, чтобы
Р {т/< miej\ > 0, Ету < оо.
Утверждение, аналогичное сформулированному выше,
будет иметь место и относительно сходимости при
t —у оо процессов {q(t~ru); и 5=0} к стационарному
процессу {qs (и); и^О} длины очереди. При этом по-
помимо приведенных условий дополнительно требуется,
чтобы входной процесс е (t) (число поступивших вызо-
вызовов к моменту времени t) был процессом со стацио-
стационарными приращениями.
2) Если {%)}?Е, {т/}?С , то справедливы фор-
формулы Э р л а н г а
р {qk= /} = р {qs (и) = /} = с i2L°2L ,
где а— Ету, а — показатель распределения ту,
Если {x/}?G/, {t/}??, то последовательность qn
связана в простую однородную цепь Маркова с конеч-
конечным числом (пг+1) состояний. В этом случае вероят-
вероятности
Р/-=Р{<7° = /}= Пт Р {<?„ = /}
/ —> оо
также можно найти в явном виде. Если, кроме того,
распределение ту нерешетч^то и Ету<оо, то
Р {cf @) = /} = Дгп^ Р {.7 (*)=/} = ^~ ,
где а — показатель распределения ту.
Эти утверждения указывают условия существования
и явный вид для стационарной вероятности отказа,
равной
P{?° = m}= lim ?{qn = m).
3) Теоремы устойчивости для систем с отказами
вполне аналогичны теоремам устойчивости для систем
с бесконечным числом каналов. Пусть даны последо-
последовательности {х)п)е, x/")s}, п—1, 2, . . ., управляющие
системами с отказами и удовлетворяющие следующему
условию:
(А) существует последовательность {%), т/}, к рас-
распределениям к-рой сходятся при п —*¦ оо конечномер-
конечномерные распределения {тс/"е, x5">s}. Кроме того, все
названные последовательности удовлетворяют усло-
условиям (см., напр., п. 1), обеспечивающим существо-
существование стационарных последовательностей длины оче-
очереди. Чтобы имела место сходимость распределений
этих стационарных последовательностей длины оче-
очереди, к-рые обозначены {q{n)k', к^О} и {qk; к^О},
следует ввести еще два условия:
(B) Ет(л)^—*Ет* при га—>оо;
(C) распределения
при всех у'^0 непрерывны в точке 0.
При выполнении условий (А), (В), (С) конечномер-
конечномерные распределения последовательностей {q{n)k; к^О}
слабо сходятся к распределениям {<?*; к^О).
4) Асимптотич. методы исследования систем с от-
отказами могут быть эффективными также при изучении
систем с интенсивным входным потоком или с боль-
большим числом каналов обслуживания.
Исследование систем с интенсивным входом свя-
связано с получением результатов в предположениях,
близких к тем, к-рые рассматриваются при асимптотич.
анализе систем с бесконечным числом каналов обслу-
обслуживания. Изучение систем с большим числом каналов
проводится как путем асимптотич. анализа явных
формул, к-рые становятся малоэффективными при
больших т, так и с помощью изучения близости рас-
распределения qk к распределению числа занятых линий
в аналогичной системе, но с бесконечным числом ка-
каналов обслуживания.
Напр., для систем с последовательностями {
стационарная вероятность отказа равна
где
0 ' J \ j J *-*¦k=1 Ф (h/m) ' Ф w i
a — показатель распределения т/. Эти соотношения
при больших т становятся малоп])игодными для оты-
отыскания числовых значений рт. В то же время оказывает-
оказывается, что при т. —>- оо действуют достаточно простые фор-
формулы, к-рые устанавливают аёимитотич. поведение рт
и к-рые, следовательно, можно использовать для при-
приближенных вычислений вероятности отказа. При этом
определяющую роль играет параметр р— Emax/, ха-
характеризующий отношение среднего числа 1/Ет/ вы-
вызовов, поступивших в систему, к среднему числу вызо-
вызовов ?ra/Ex/=ma, к-рое может обслужить система за
единицу времени. Если р<1, то система обычно пол-
полностью загружена, если р>1, то система недогружена.
Если р<1—е при m-^-ми нек-ром е>0, то рт/A—р)-*-
—>- 1. Если Е (татф2<е<оо при т —>- оо, то при-
веденное соотношение для рт сохраняется и при р—>- 1,
если только A—р)|^т—>-оо. Если же A — p)Y~m—у
->• const, то рт ведет себя асимптотически как Ы У~т,
где постоянная Ь найдена в явном виде. Найдено также
асимптотич. поведение рт и в случае A—р)У~т—>- —оо.
5) Несколько более полно могут быть изучены одно-
канальные системы с отказами (когда т=1). Пусть,
напр., {т./, т/}^С/. Случайную величину т) определяют
равенством
т| = max (Л: Xfe Ss xl),
где Xft=xf+. • .+т|. Тогда, для того чтобы при любом
начальном условии существовал предел
необходимо и достаточно, чтобы наибольший общий де-
делитель возможных значений т) равнялся 1. При этом
Pi=l—1/Ет). Если хе нерешетчата, то всегда существует
lim P (q (t) = 1} = _!lf_ .
При более широком понимании вероятности отказа
как предела отношения пп=гп1п, где гп — число необ-
служенных вызовов среди первых п поступивших, усло-
условия существования lim л„ будут более широкими.
Напр., для случая {т/, T/}?G/ предел п„ существует
всегда и равен 1 — 1/Ет].
Лит. см. при ст. Массового обслуживания теория.
А. А. Боровков.
МАССОВОГО ОБСЛУЖИВАНИЯ ТЕОРИЯ, тео-
теория очередей,— раздел теории вероятностей,
изучающий математич. модели разного рода реальных
массового обслуживания систем. Эти модели представ-
представляют собой случайные процессы специального вида,
к-рые наз. иногда процессами обслуживания. Чаще
всего используется описательное определение этих
процессов, поскольку формальное их построение ока-
оказывается весьма сложным и не всегда эффективным.
М. о. т. использует главным образом аппарат теории
вероятностей. Основные задачи М. о. т. обычно состоят
в том, чтобы на основании «локальных» свойств рас-
рассматриваемых случайных процессов изучить их стацио-
стационарные характеристики (если таковые существуют) или
поведение этих характеристик за большой промежуток
времени. Одна из главных конечных целей исследова-
исследований в этой области состоит в выборе наиболее разумной
организации систем массового обслуживания.
Напр., для такого типичного объекта М. о. т., как
автоматические телефонные станпии (см. Массового об-
обслуживания система с отказами), одной из основных ха-
характеристик является доля вызовов получивших отказ,
т. е. предел р при t —>- оо (если он существует) отноше-
отношения r(t)/e(t) числа r(t) вызовов, получивших отказ за
время t, к общему числу е (t) вызовов, поступивших за
это время. При этом предполагаются известными рас-
распределение интервалов времени xf, x%, ... между
поступлениями вызовов и распределение времени об-
обслуживания xi, x|, ... этих вызовов. Задание рас-
распределения случайной (управляющей) последова-
последовательности {х/, х); /^1, ...} вместе с описанием алго-
алгоритма, по к-рому происходит эволюция системы мас-
массового обслуживания, и составляют исходные данные,
характеризующие «локальные свойства» процесса об-
обслуживания.
Аналогичным образом для массового обслуживания
систем с ожиданием многоканальных изучаются пре-
предельные при п —ь- оо распределения вероятностей
P{wn<x} и P{qn<x} для времени wn, к-рое ге-й по
счету вызов, поступивший в систему, ожидал начала
своего обслуживания с момента прихода, и для длины
qn очереди в момент появления в системе га-го вызова.
Рассматриваются также предельные распределения
lira P{q(t)<Lx} для длины очереди в момент времени t
t-*a>
и др. При этом исходным опять является задание управ-
управляющей последовательности случайных величин (рас-
(распределение интервалов и времени обслуживания) и
алгоритм, определяющий работу системы массового
обслуживания.
Для сравнительно простых систем массового обслу-
обслуживания и при нек-рых предположениях относительно
управляющей последовательности случайных величин
удается найти требуемые характеристики аналитич.
методами. Однако число таких систем не велико. Ха-
Характер условий, накладываемых на управляющие по-
последовательности, можно продемонстрировать на при-
примере системы массового обслуживания с отказами (ав-
(автоматические телефонные станции). Пусть: 1) случайные
величины т/ показательно распределены:
РН> x}=e~ax, a>0,
т. е. входящий поток является пуассоновским; 2) ве-
величины т/ независимы, одинаково распределены и не
зависят от {т/}. Тогда определенная выше вероятность
отказа р существует и равна
где р равно отношению математич. ожиданий
Для рассматриваемой системы отказ от одного из усло-
условий 1) — 2) значительно усложняет или делает невоз-
невозможным отыскание явных формул для числа р.
В основе аналитич. подхода в поисках явных выра-
выражений для искомых характеристик лежит прием, свя-
связанный с построением марковских процессов, описы-
описывающих состояние системы. Этот тип процессов доста-
достаточно хорошо изучен, и решение задачи в этом случае
сводится к составлению и решению соответствующих
уравнений для стационарных распределений (инвари-
(инвариантной меры). Такой подход часто используется в мо-
модифицированном виде, когда строятся полумарковские
процессы или вложенные марковские процессы (свойст-
(свойство марковости выполняется лишь в пек-рые случайные
моменты времени).
Для более сложных систем массового обслуживания
точные аналитич. методы, как правило, не эффективны и
приходится использовать асимптотич. методы исследо-
исследования или моделировать соответствующие случайные
процессы с помощью Монте-Карло метода. Асимпто-
Асимптотич. методы уместны в тех случаях, когда рассматривае-
рассматриваемая система близка (в смысле ее локальных свойств)
к другой системе, к-рая либо достаточно хорошо изу-
изучена и допускает вычисление нужных характеристик,
либо эта система является в каком-то смысле критиче-
критической. Направление асимптотич. исследований в первом
случае описывается теоремами устойчивости (или не-
непрерывности). Во втором случае стационарные характе-
характеристики часто не существуют, но для них удается уста-
устанавливать «собирательные» предельные теоремы, т. е.
такие, в к-рых предельное поведение определяется не
индивидуальными свойствами управляющих последо-
последовательностей, а лишь несколькими их числовыми пара-
параметрами. Примером второго типа асимптотич. резуль-
результатов могут служить т. н. теоремы о нагруженных одно-
канальных системах с ожиданием. Они устанавливают
следующее. Пусть интервалы т/, 7=1, 2, ... , между
поступлениями вызовов и временем обслуживания %),
/=1, 2, ... , образуют независимые друг от друга
последовательности независимых одинаково распреде-
распределенных величин и пусть математич. ожидание
а=Е {%)-%))
разности случайных величин т/ и т/ положительно. Тог-
Тогда существует невырожденное предельное распределе-
распределение
w (х) = lim P {wn ^ х}
для времени wn ожидания га-го вызова. Кроме того,
пусть случайные величины т/, т/ меняются так, что
а —>- 0, оставаясь положительным, дисперсия D (т/—т/)
сходится к положительному пределу о2<оо, а матема-
математич. ожидание Е[т/—T/]2+v равномерно ограничено
при нек-ром 7>0. Тогда при каждом фиксированном z
w (z/a) ~+е-*г/а'. (*)
Это соотношение дает возможность приближенно вычис-
вычислять w(x) при малых значениях а. Предельная система,
соответствующая значению а=0, является критической
в том смысле, что для нее не существует невырожден-
невырожденного предельного распределения w(x), и для каждого
я>0 выполняется w(х) = 1 (время ожидания re-го кли-
клиента неограниченно растет с ростом га). Соотношение
(*) может быть распространено на широкий класс
систем обслуживания с ожиданием при очень общих
предположениях на управляющие последовательности.
Возникновение М. о. т. было вызвано интересом к
новым математич. задачам, возникающим в организации
телефонных сетей. Первые публикации по этому поводу
принадлежат А. Эрлангу (A. Erlang) и относятся
к 20-м гг. 20 в. Дальнейшее развитие М. о. т. получила
в 40—50-е гг. в работах К. Пальма (С. Palm), Ф. Пол-
лачека (F. Pollaczek), А. Я. Хинчина и др. Последнему
принадлежит и термин «массового обслуживания тео-
теория». В СССР эти работы по М. о. т. были продолжены
Б. В. Гнеденко с группой его учеников и др.
Развитие М. о. т. стимулируется как расширением
круга ее приложений, так и математич. содержатель-
содержательностью возникающих при этом задач. Являясь фор-
формально частью теории случайных процессов, М. о. т.
выделилась в самостоятельную область исследований
со своим кругом проблем и своими подходами к их ре-
решению.
Лит.: [1] X и н ч и н А. Я., Работы по математической те-
теории массового обслуживания, М., 1963; [2] Г н е д е н к о Б. В.,
Коваленко И. Н., Введение в теорию массового обслу-
обслуживания, М., 1966; [3J Б о р о в к о в А. А., Вероятностные
процессы в теории массового обслуживания, М., 1972; [41 его
ж е, Асимптотические методы в теории массового обслуживания,
М.. 1980. А. Л. Боровков,
МАССОВЫЙ ОПЕРАТОР, оператор масс ы,—
оператор, учитывающий взаимодействие частицы с ее
собственным полем и другими полями. Пусть состояние
системы описывается величиной
где г)з (х) — оператор поля, действующий на волновую
функцию Ч*^ (вектор состояния), х — четырехмерная
координата. Если W (х) удовлетворяет уравнению
где оператор L (х) соответствует свободной частице,
а М (х) учитывает ее взаимодействие с собственным по-
полем и др. полями, то оператор М (х) наз. массовым
оператором. М. о. является интегральным опе-
оператором с ядром М(х, х'):
М (х) ? (а:)= С М (х, х') Ч (х1) dx'.
М. о. тесно связан с одночастичной Грина функцией
G(x, x'), к-рая является решением уравнения, подоб-
ного (*), но с б-образным источником в правой части
[L(x)+M(x)]G(z, x')=6(x-x'),
где 6(х—х') —четырехмерная дельта-функция.
Лит.: [1] Б о г о л ю б о в Н. Н., Ш и р к о в Д. В., Вве-
Введение в теорию квантованных полей, М., 1957; [2] А б р и к о-
с о в А. А., Г о р ь к о в Л. П., Дзялошинский И. В.,
Методы квантовой теории поля в статистической физике, М.,
1962. А. Б. Иванов.
МАСШТАБНЫЙ ПАРАМЕТР — один из т. н. пара-
параметров расположения, многообразием значений к-рых
описывается семейство распределений вероятностей
одного типа. Если распределение в R с функцией рас-
распределения F (х) принадлежит тому же типу, что и фик-
фиксированное распределение с функцией распределения
F0(x), то F(x) = F0(^-). Здесь а>0 - М. п., а Ь —
параметр сдвига (или центрирующий параметр). Смысл
М. п. разъясняется следующим образом: если Fo и F —
функции распределения случайных величин Хо и X
соответственно, то переход от Хо к Х=аХ0 (при Ь=0)
представляет собой изменение единицы измерения.
А. В. Прохоров.
МАТЕМАТИКА — наука о количественных отно-
отношениях и пространственных формах действительного
мира. В неразрывной связи с запросами техники и ес-
естествознания запас количественных отношений и прост-
пространственных форм, изучаемых М., непрерывно расши-
расширяется, так что это общее определение М. наполняется
все более богатым содержанием.
Ясное понимание самостоятельного положения М.
как особой науки стало возможным только после на-
накопления достаточно большого фактич. материала и воз-
возникло впервые в Др. Греции в 6—5 вв. до н. э. Разви-
Развитие М. до этого времени естественно отнести к пери-
периоду зарождения математики, а к 6—•
5 вв. до н. э. приурочить начало периода эле-
элементарной математики. В течение этих
двух первых периодов математич. исследования имеют
дело почти исключительно с весьма ограниченным запа-
запасом основных понятий, возникших еще на очень ранних
ступенях историч. развития в связи с самыми простыми
запросами хозяйственной жизни. Первые задачи меха-
механики и физики могли еще удовлетворяться этим же за-
запасом основных математич. понятий.
В 17 в. новые запросы естествознания и техники за-
заставляют математиков сосредоточить свое внимание
на создании методов, позволяющих математически изу-
изучать движение, процессы изменения величин, преобра-
преобразования геометрич. фигур. С употребления переменных
величин в аналитич. геометрии и создания дифференци-
дифференциального и интегрального исчисления начинается п е-
риод математики переменных вели-
величин.
Дальнейшее расширение круга количественных от-
отношений и пространственных форм, изучаемых М.,
привело в нач. 19 в. к необходимости отнестись к про-
процессу расширения предмета математич. исследований
сознательно, поставив перед собой задачу систематич.
изучения с достаточно общей точки зрения возможных
типов количественных отношений и пространственных
форм. Создание «воображаемой геометрии» Лобачевско-
Лобачевского было первым значительным шагом в атом направле-
направлении. Развитие подобного рода исследований внесло в
М. столь важные новые черты, что М. 19 и 20 вв. ес-
естественно отнести к особому периоду совре-
современной математики.
1. Зарождение математики. Счет предметов на самых
ранних ступенях развития культуры привел к созда-
созданию простейших понятий арифметики натуральных чи-
чисел. Только на основе разработанной системы устного
счисления возникают письменные системы счисления и
постепенно вырабатываются приемы выполнения над
натуральными числами четырех арифметич. действии.
Потребности измерения (количества зерна, длины доро-
дороги и т. п.) приводят к появлению названий и обозначе-
обозначений простейших дробных чисел и к разработке приемов
выполнения арифметич. действий над дробями. Таким
образом накапливается материал, складывающийся
постепенно в древнейшую математич. науку — ариф-
арифметику. Измерение площадей и объемов, потребности
строительной техники, а несколько позднее астрономии
вызывают развитие начатков геометрии. Эти процессы
шли у многих народов в значительной степени незави-
независимо и параллельно. Особенное значение для дальней-
дальнейшего развития науки имело накопление арифметич. и
геометрич. знаний в Египте и Вавилонии. В Вавилонии
на основе развитой техники арифметич. вычислений
появились также начатки алгебры, а в связи с запроса-
запросами астрономии — начатки тригонометрии.
2. Период элементарной математики. Только после
накопления большого конкретного материала в виде
разрозненных приемов арифметич. вычислений, спосо-
способов определения площадей и объемов и т. п. возникает
М. как самостоятельная наука с ясным пониманием свое-
своеобразия ее метода и необходимости систематич. разви-
развития ее основных понятий и предложений в достаточно
общей форме. В применении к арифметике и алгебре
указанный процесс начался уже в Вавилонии. Однако
вполне определилось это новое течение, заключавшееся
в систематическом и логически последовательном по-
построении основ математич. науки, в Др. Греции. Соз-
Созданная древними греками система изложения элемен-
элементарной геометрии на два тысячелетия вперед сделалась
образцом дедуктивного построения математич. теории.
Из арифметики постепенно вырастает чисел теория.
Создается систематич. учение о величинах и измерении.
Процесс формирования (в связи с задачей измерения
величин) понятия действительного числа (см. Число)
оказывается весьма длительным. Дело в том, что поня-
понятия иррационального и отрицательного чисел относятся
к более сложным математич. абстракциям, к-рые, в
отличие от понятий натурального числа, дроби или
геометрич. фигуры, не имеют достаточно прочной
опоры в донаучном общечеловеческом опыте. Создание
алгебры как буквенного исчисления завершается лишь
в конце рассматриваемого периода. Период элементар-
элементарной математики заканчивается (в Зап. Европе в нач.
17 в.), когда центр тяжести математич. интересов пере-
переносится в область М. переменных величин.
3. Период создания математики переменных величин.
С 17 в. начинается существенно новый период развития
М. Круг количественных отношений и пространствен-
пространственных форм, изучаемых теперь М., уже не исчерпывается
числами, величинами и геометрич. фигурами. В основ-
основном это было обусловлено явным введением в М. идей
движения и изменения. Уже в алгебре в скрытом виде
содержится идея зависимости между величинами (зна-
(значение суммы зависит от значений слагаемых и т. д.).
Однако чтобы охватить количественные отношения в
процессе их изменения, надо было самые зависимости
между величинами сделать самостоятельным объектом
изучения. Поэтому на первый план выдвигается поня-
понятие функции, играющее в дальнейшем такую же роль
основного и самостоятельного предмета изучения, как
ранее понятия величины или числа. Изучение перемен-
переменных величин и функциональных зависимостей приводит
далее к основным понятиям математич. анализа, вво-
вводящим в М. в явном виде идею бесконечного, к поняти-
понятиям предела, производной, дифференциала и интеграла.
Создается анализ бесконечно малых, в первую очередь
в виде дифференциального исчисления и интегрального
исчисления, позволяющий связывать конечные изме-
изменения переменных величин с их поведением в непосред-
непосредственной близости отдельных принимаемых ими зна-
чений. Основные законы механики и физики записы-
записываются в форме дифференциальных уравнений, и задача
интегрирования этих уравнений выдвигается в качестве
одной из важнейших задач М. Разыскание неизвестных
функций, определенных условиями другого рода (ус-
(условиями минимума или максимума нек-рых связанных
с ними величин), составляет предмет вариационного
исчисления. Таким образом, наряду с уравнениями, в
к-рых неизвестными являются числа, появляются урав-
уравнения, в к-рых неизвестны и подлежат определению
функции.
Предмет изучения геометрии также существенно рас-
расширяется с проникновением в геометрию идей движе-
движения и преобразования фигур. Геометрия начинает изу-
изучать движения и преобразования сами по себе. Напр.,
в проективной геометрии одним из основных объектов
изучения являются сами проективные преобразования
плоскости или пространства. Впрочем, сознательное
развитие этих идей относится лишь к кон. 18 и нач.
19 вв. Гораздо раньше, с созданием в 17 в. аналитиче-
аналитической геометрии, принципиально изменилось отношение
геометрии к остальной М.: был найден универсальный
способ перевода вопросов геометрии на язык алгебры и
анализа и решения их чисто алгебраич. и аналитич.
методами, а с другой стороны, открылась широкая воз-
возможность изображения (иллюстрирования) алгебраич.
и аналитич. фактов геометрически, напр, при графич.
изображении функциональных зависимостей.
4. Современная математика. Все созданные в 17
и 18 вв. разделы математич. анализа продолжали
с большой интенсивностью развиваться в 19 и 20 вв.
Чрезвычайно расширился за это время и круг их
применения к задачам, выдвигаемым естествознани-
естествознанием и техникой. Однако помимо этого количественного
роста с кон. 18 и в нач. 19 вв. в развитии М. наблюдает-
наблюдается и ряд существенно новых черт.
Накопленный в 17 и 18 вв. огромный фактич. матери-
материал привел к необходимости углубленного логич. ана-
анализа и объединения его с новых точек зрения. Связь
М. с естествознанием, оставаясь по существу не менее
тесной, приобретает теперь более сложные формы. Боль-
Большие новые теории возникают не только в результате не-
непосредственных запросов естествознания и техники, но
также из внутренних потребностей самой М. Таково
в основном было развитие функций комплексного пере-
переменного теории, занявшей в нач. и сер. 19 в. централь-
центральное положение во всем математич. анализе. Другим
замечательным примером теории, возникшей в резуль-
результате внутреннего развития самой М., явилась Лоба-
Лобачевского геометрия.
В более непосредственной и непрерывной зависимо-
зависимости от запросов механики и физики происходило фор-
формирование векторного и тензорного исчислений. Пере-
Перенесение векторных и тензорных представлений на бес-
бесконечномерные величины происходит в рамках функ-
функционального анализа и тесно связывается с потребнос-
потребностями современной физики.
Таким образом, в результате как внутренних пот-
потребностей М., так и новых запросов естествознания круг
количественных отношений и пространственных форм,
изучаемых М., чрезвычайно расширяется; в него вхо-
входят отношения, существующие между элементами про-
произвольной группы, векторами, операторами в функцио-
функциональных пространствах, все разнообразие форм прост-
пространств любого числа измерений и т. п.
Существенная новизна начавшегося в 19 в. этапа
развития М. состоит в том, что вопросы необходимого
расширения круга подлежащих изучению количествен-
количественных отношений и пространственных форм становятся
предметом сознательного и активного интереса матема-
математиков. Если прежде, напр., введение в употребление от-
отрицательных и комплексных чисел и точная формули-
ровка правил действий с ними требовали длительной
работы, то теперь развитие М. потребовало выработки
приемов сознательного и планомерного создания новых
геометрия, и алгебраич. систем.
Чрезвычайное расширение предмета М. привлекло в
19 в. усиленное внимание к вопросам ее «обоснования»,
т. е. критич. пересмотру ее исходных положений (ак-
(аксиом), построению строгой системы определений и до-
доказательств, а также критич. рассмотрению логич.
приемов, употребляемых при этих доказательствах.
Стандарт требований к логич. строгости, предъявляе-
предъявляемых к практич. работе математиков над развитием
отдельных математич. теорий, сложился только к кон.
19 в. Глубокий и тщательный анализ требований к ло-
логич. строгости доказательств, строения математич. тео-
теорий, вопросов алгоритмич. разрешимости и неразреши-
неразрешимости математич. проблем составляет предмет матема-
математической логики.
В нач. 19 в. прот."ходит новое значит, расширение
области приложений математич. анализа. Если до этого
времени основными отделами физики, требовавшими
большого математич. аппарата, оставались механика я
оптика, то теперь к нттм присоединяются электродина-
электродинамика, теория магнетизма и термодинамика. Получают
широкое развитие важнейшие разделы механики не-
непрерывных сред. Быстро растут и математич. запросы
техники. В качестве основного аппарата новых облас-
областей механики и математич. физики усиленно разрабаты-
разрабатывается теория дифференциальных уравнений обыкно-
обыкновенных, дифференциальных уравнений с частными про-
производными и математической физики уравнений.
Теория дифференциальных уравнений послужила
отправным пунктом исследований по топологии много-
многообразий. Здесь получили свое начало «комбинаторные»,
«гомологические» и «гомотопические» методы алгебраи-
алгебраической топологии. Другое направление в топологии
возникло на почве множеств теории и функционально-
функционального анализа и привело к систематич. построению теории
общих топологических пространств.
Существенным дополнением к методам дифференци-
дифференциальных уравнений при изучении природы и решении
технич. задач являются методы вероятностей теории.
Если в нач. 19 в. главными потребителями вероятност-
вероятностных методов были теория артиллерийской стрельбы и
теория ошибок, то в кон. 19 и в нач. 20 вв. теория ве-
вероятностей получает много новых применений благо-
благодаря созданию теории случайных процессов и развитию
аппарата математической статистики.
Теория чисел, представлявшая собрание отдельных
результатов и идей, с 19 в. развивалась в различных
направлениях как стройная теория (см. Алгебраическая
теория чисел, Аналитическая теория чисел, Диофанто-
вы приближения).
Центр тяжести алгебраич. исследований переносится
в новые области алгебры: теорию групп, полей, колец,
общих алгебраич. систем. На границе между алгеброй
и геометрией возникает теория непрерывных групп,
методы к-рой позднее проникают во все новые области
М. и естествознания.
Элементарная и проективная геометрия привлекают
внимание математиков гл. образом под углом зрения
изучения их логич. и аксиоматич. основ. Но основными
отделами геометрии, где сосредоточиваются наиболее
значительные научные силы, становятся дифферен-
дифференциальная геометрия, алгебраическая геометрия, ри-
манова геометрия.
В результате систематич. построения математич. ана-
анализа на основе строгой арифметич. теории иррацио-
иррациональных чисел и теории множеств возникла функций
действительного переменного теория.
Практич. использование результатов теоретического
математич. исследования требует получения ответа на
поставленную задачу в числовой форме. Между тем
даже после исчерпывающего теоретич. разбора задачи
это часто оказывается весьма трудным делом. Зародив-
Зародившиеся в кон. 19 и в нач. 20 вв. численные методьГана-
лиза и алгебры выросли в связи с созданием и исполь-
использованием ЭВМ в самостоятельную ветвь М.— вычисли-
вычислительную математику.
Отмеченные основные особенности современной М. и
перечисленные основные направления исследований
М. по разделам сложились в нач. 20 в. В значительной
мере это деление на разделы сохраняется, несмотря на
стремительное развитие М. в 20 в. Однако потребности
развития самой М., «математизация» различных облас-
областей науки, проникновение математич. методов во мно-
многие сферы практич. деятельности, быстрый прогресс
вычислит, техники привели к перемещению основных
усилий математиков внутри сложившихся разделов М.
и к появлению целого ряда новых математич. дисциплин
(см., напр., Автоматов теория, Информации теория,
Игр теория, Исследование операций, а также Киберне-
Кибернетика, Математическая экономика). На основе задач
теории управляющих систем, комбинаторного анализа,
теории графов, теории кодирования возник дискретный
анализ. Вопросы о наилучшем (в том или ином смысле)
управлении физич. или механич. системами, описывае-
описываемыми дифференциальными ур-ниями, привели к созда-
созданию оптимального управления математической теории.
Исследования в области общих проблем управления
и связанных с ними областях М. в соединении с про-
прогрессом вычислит, техники дают основу для автомати-
автоматизации новых сфер человеческой деятельности.
По материалам статьи А. Н. Колмогорова [1].
Лит.: [1] Колмогоров А. Н., Математика, в кн.:
Большая Советская Энциклопедия, 2 изд., т. 26, М-, 1954; [2]
Виноградов И. М., Математика и научный прогресс, в кн.:
Ленин и современная наука, кн. 2, М., 1970; [3] Гил ь бе р т Д.,
Бернайс П., Основания математики. Логические исчисле-
исчисления и формализация арифметики, пер. с нем., М., 1979; [4]
Математика, ее содержание, методы и значение, т. 1—3, М.,1956;
[5] История математики с древнейших времен до начала XIX
столетия, т. 1—3, М., 1970—72; [6] Математика XIX века.
Математическая логика. Алгебра. Теория чисел. Теория веро-
вероятностей, М., 1978; [7] Математика XIX века. Геометрия. Тео-
Теория аналитических функций, М., 1981; [8] С т Р о й к Д. Я.,
Краткий очерк истории математики, пер. с нем., 3 изд., М.,
1978; [9] Марджанишвили К. К., Математика в
Академии наук СССР, «Вестн. АН СССР», 1974, J\fi 6; [10]
W е у 1 Н., A Half-century of mathematies, «Amer. Math. Mon-
Monthly», 1951, v. 58, J\T« 8.
МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ — метод дока-
доказательства математич. утверждений, основанный на
принципе математической индук-
индукции: утверждение А (х), зависящее от натурального
параметра х, считается доказанным, если доказано А A)
и для любого натурального п из предположения, что
верно А (га), выведено, что верно также А (га+1).
Доказательство утверждения А A) составляет пер-
первый шаг (или базис) и н д у к ц и и, а доказа-
доказательство А (ге+1) в предположении, что верно А (га),
наз. индукционным переходом. При этом
х наз. параметром индукции, а предполо-
предположение А (п) при доказательстве А (ге+1) наз. индук-
индуктивным предположением. Принцип М. и.
является также основанием для индуктивных опреде-
определений. Простейшим примером такого определения яв-
является определение свойства: «быть словом длины п
в данном алфавите
Базис индукции: каждая буква алфавита (*) есть слово
длины 1. Индукционный переход: если Е — слово дли-
длины п, то каждое слово Еа/, где 1 ¦</<:&, есть слово дли-
длины ге+1. Индукция может начинаться с нулевого шага.
Часто бывает так, что А A) к А (га+1) доказываются
аналогичными рассуждениями. В таких случаях удоб-
удобно пользоваться следующей эквивалентной формой
принципа М. и. Если для всякого га из предположения:
А (х) верно при любом натуральном я<га — следует,
что А (х) верно также при х—-п, то утверждение А (х)
верно при любом натуральном х. В такой форме прин-
принцип М. и. может быть применен для доказательства
утверждений А (х), в к-рых параметр х пробегает то
пли иное множество, вполне упорядоченное по нек-ро-
му трансфинитному типу (трансфинитная индукция).
В качестве простых примеров трансфинитной индукции
отметим индукцию по параметру, пробегающему мно-
множество всех слов в данном алфавите, упорядоченное
лексикографически, и индукцию по построению формул
в данном логико-математич. исчислении.
Иногда для доказательства нек-рого утверждения А (п)
индукцией по п приходится одновременно с А (га)
доказывать индукцией по п ряд других утверждений,
без к-рых индукцию для А (п) не удается провести.
В формальной арифметике можно указать такие утверж-
утверждения А (п), для к-рых в рамках рассматриваемого ис-
исчисления индукция не может быть проведена без до-
добавления новых вспомогательных утверждений, зави-
зависящих от га (см. [3]). В таких случаях мы имеем дело
с доказательством ряда утверждений совместной
математической индукцией. Все эти
утверждения формально можно объединить в одну конъ-
конъюнкцию, однако практически такое объединение только
усложнило бы рассмотрение, т. к. при этом исчезла бы
возможность неформальных осмысленных ссылок на
определенные индуктивные предположения.
В нек-рых конкретных математич. исследованиях
число понятий и утверждений, определяемых и доказы-
доказываемых сложной совместной индукцией, исчисляется
трехзначной цифрой (см. [4]). В этом случае ввиду на-
наличия в индуктивном доказательстве большого числа
перекрестных ссылок на индуктивные предположения,
для содержательного (неформального) понимания лю-
любого (даже самого простого) определения или утвержде-
утверждения при. данном достаточно большом значении парамет-
параметра индукции читатель должен быть знаком с содержа-
содержанием всех вводимых совместной индукцией понятий
и многих свойств этих понятий для меньших значений
параметра индукции. По-видимому, единственным кор-
корректным с логич. точки зрения выходом из возникаю-
возникающего здесь логич. круга является аксиоматич. изложе-
изложение всей рассматриваемой системы понятий. Таким
образом, большое число понятий, определяемых сов-
совместной индукцией, приводит к необходимости приме-
применения аксиоматического метода в индуктивном опре-
определении и доказательстве. Это — наглядный нример
необходимости аксиоматич. метода для решения кон-
конкретных математич. задач, а не только вопросов, отно-
относящихся к основаниям математики.
Лит.: [1] Гильберт Д., Б е р н а й с П., Основания
математики. Логические исчисления и формализация арифме-
арифметики, пер. с нем., М., 1979; [2J К л и н и С. К., Введение в ме-
метаматематику, пер. с англ., М., 1957; [3] Ц и н м а н Л. Л.,
«Матем. сб.», 1968, т. 77, №1, с. 71—104; [4] А д я н С. И.,
Проблема Бернсайда и тождества в группах, М., 1975.
С. И. Адян.
МАТЕМАТИЧЕСКАЯ ЛИНГВИСТИКА — математи-
математическая дисциплина, предметом к-рой является разра-
разработка и изучение понятий, образующих основу фор-
формального аппарата для описания строения естественных
языков (т. е. метаязыка лингвистики). Возникнове-
Возникновение М. л. можно отнести приблизительно к 50-м гг.
20 в.; она была вызвана к жизни прежде всего внутрен-
внутренними потребностями теоретич. лингвистики, в к-рой
к этому времени назрела необходимость уточнения ос-
основных понятий, а также задачами, связанными с авто-
автоматизацией переработки языковой информации (см.
Автоматический перевод). В М. л. широко используют-
используются методы теории алгоритмов, теории автоматов и ал-
алгебры. Сохраняя свое прикладное значение, М. л. по-
постоянно эволюционирует по пути превращения в тео-
ретическую математич. дисциплину, являющуюся по
сути дела одним из ответвлений математич. логики.
В то же время круг приложений М. л. расширился —
ее методы нашли применение в теории программи-
программирования.
Лингвистич. концепции, лежащие в основе формаль-
формальных методов описания строения языка, принадлежат
структурной лингвистике. Главнейшая из этих кон-
концепций — представление о языке как о «системе чистых
отношений», сближающее язык с абстрактными систе-
системами, изучаемыми в математике. Это представление
конкретизируется в концепции функционирования язы-
языка как преобразования нек-рых абстрактных объек-
объектов — «смыслов» — в объекты другой природы —
«тексты» и обратно. Такая концепция приводит к мысли
об изучении указанного преобразования (после уточне-
уточнения понятий «смысла» и «текста») математпч. средства-
средствами. Использование этого подхода затруднительно, если
пытаться рассматривать преобразование «в целом»,
ввиду его чрезвычайной сложности, а также ввиду
трудности формализации понятия «смысла». Однако
содержательные соображения подсказывают расчлене-
расчленение преобразования на этапы. Напр., при одном из
наиболее грубых членений нек-рый этап может состоять
в переходе от «смыслов» предложений к «синтаксиче-
«синтаксическим структурам без линейного порядка» — наборам
элементов предложений, соединенных «синтаксически-
«синтаксическими связями», но еще не расположенных в линейные по-
последовательности; на следующем этапе получаются
линейные последовательности слов, потом они превра-
превращаются в цепочки звуков. При более тонких членениях
вводятся синтаксич. структуры нескольких уровней, все
более отдаляющиеся от «смыслового» и приближаю-
приближающиеся к «текстовому»; «послесинтаксические» этапы так-
также подвергаются дальнейшему расчленению. Такие
этапы уже легче описывать математически, уточняя
представления об объектах промежуточных уровней и
моделируя переходы от одних уровней к другим эффек-
эффективными отображениями. Правда, рассматриваемое
преобразование неоднозначно, и таковы же все или поч-
почти все (в зависимости от способа членения) промежуточ-
промежуточные этапы; это связано с одной из важнейших особен-
особенностей языка — наличием в нем явления синонимии,
т. е. возможности выражать одно и то же содержание
разными способами. Поэтому приходится строить не
детерминированные эффективные системы (алгоритмы),
а недетерминированные (исчисления), позволяющие
либо для данного объекта нек-рого уровня перечислять
отвечающие ему объекты соседнего уровня или объекты
(того же уровня), ему синонимичные, либо перечислять
множество «правильных» объектов заданного уровня
(т. е. таких, к-рые известным регулярным способом
сопоставляются объектам предыдущего уровня), либо
перечислять множество пар отвечающих друг другу
объектов двух заданных соседних уровней (напр.,
«предложение + его синтаксическая структура») и т. п.
Такого рода исчисления известны как грамматики фор-
формальные. Одновременно с формальными грамматиками,
моделирующими преобразования языковых объектов,
возникают конструкции, предназначенные для фор-
формального описания самих этих объектов. Кроме того,
на множествах объектов одного уровня возникают клас-
классификации и отношения, во многом сходные с катего-
категориями традиционной грамматики (такими, как часть
речи, род, падеж и т. п.) и в ряде случаев совпадающие
с ними; без введения таких классификации и отноше-
отношений реальное построение формальных грамматик для
естественных языков фактически невозможно.
Таким образом, можно выделить три аспекта фор-
формального описания языка: описание строения языковых
объектов различных уровней, описание нек-рых специ-
специальных отношений и классификаций на множествах
этих объектов и описание преобразований одних объек-
объектов в другие, а также строения множеств «правильных»
объектов. Этим аспектам отвечают три основных раз-
раздела М. л.: 1) разработка и изучение способов описа-
описания строения отрезков речи; 2) изучение лингвисти-
лингвистически значимых отношений и классификаций на мно-
множествах языковых объектов (построенные для этой
цели формальные системы обычно называют аналити-
аналитическими моделями языка); 3) теория формальных грам-
грамматик.
Для описания строения отрезков речи используются
синтаксич. структуры, представляющие собой графы
или биграфы специального вида, обычно с помеченными
вершинами и/или дугами. Лучше всего разработана
теория описания «поверхностных» уровней (т. е. наибо-
наиболее далеких от «смыслового»); на этих уровнях структу-
структуры обычно являются деревьями. Интенсивно разра-
разрабатываются способы описания более «глубинных»
уровней. Для этого, в частности, предложен аппарат
т. н. лексических функций, играющих
при описании смысловой сочетаемости слов роль, сход-
сходную с той, к-рую традиционные категории рода, паде-
падежа, числа и т. п. играют при описании синтаксич. со-
сочетаемости. Средств строгого описания «смыслового»
уровня пока нет, но многим исследователям представ-
представляется вероятным, что на таком пути «последователь-
«последовательного приближения» можно надеяться выработать под-
подход к формальному описанию смысла. Это не исключает
и иных подходов; в частности, много исследований по-
посвящено способам выражения в естественных языках
предикатов, пропозициональных связок, кванторов,
«переводу» с формально-логич. языков на естественные
и обратно. Сюда же примыкают работы по конструи-
конструированию так наз. семантических языков,
в к-рых смыслы сопоставляются текстам простыми и
строго формальными способами.
Аналитич. модели языка важны, в частности, ввиду
того, что они позволяют уточнить логич. природу
многих понятий и категорий традиционного языкове-
языковедения. Эти модели не всегда носят характер эффектив-
эффективных процедур, поскольку в них могут входить такие
понятия, как (бесконечное) множество грамматически
правильных предложений нек-рого языка, считающееся
заданным. Однако в ряде моделей все исходные данные
представляют собой конечные множества и финитные
отношения; в этих случаях входящие в модель про-
процедуры эффективны. К теории аналитич. моделей языка
примыкает теория лингвистической де-
ш и ф.р о в к и: ее предметом является построение
процедур, применяемых, подобно аналитич. моделям,
к «неупорядоченным» эмпирич. данным о языке, но
всегда эффективных и позволяющих получать не
только абстрактные определения, но и конкретные све-
сведения о строении конкретных языков (напр., алгорит-
алгоритмы, осуществляющие автоматич. разбиение множества
фоном языка на классы гласных и согласных без ис-
использования каких-либо сведений о языке, кроме
нек-рого достаточно длинного текста).
Теория формальных грамматик занимает в М. л. цен-
центральное место, т. к. она позволяет моделировать наи-
наиболее существенный аспект функционирования языка —
переработку смыслов в тексты и обратно — и благодаря
этому служит связующим звеном между остальными
разделами М. л. По характеру своего аппарата теория
формальных грамматик во многом близка к теории ал-
алгоритмов н теории автоматов. Более других разработа-
разработаны те типы формальных грамматик, к-рые служат для
харяктеризации множества грамматически правильных
предложений языка и приписывания этим предложе-
предложениям синтаксич. структур. Предложения при этом
моделируются цепочками (словами) в конечном алфа-
алфавите, элементы к-рого интерпретируются как слова ее-
тественного языка (поэтому в М. л. термин «цепочка»
предпочитают термину «слово», а алфавит часто назы-
называют также словарем), и моделью множества грам-
грамматически правильных предложений служит нек-рый
формальный язык. К этому типу относятся, в частно-
частности, грамматики порождающие. Порождающая грам-
грамматика представляет собой по существу частный случай
исчисления Поста: она состоит из конечного алфавита,
разделенного на две части — основной и вспомогатель-
вспомогательный алфавиты, конечного множества правил вы-
вывода, представляющих собой правила подстановки
вида ф —>- \р (ф, г|) — цепочки) и одной аксиомы (обычно
состоящей из одного вспомогательного символа, назы-
называемого начальным). (Формальный) язык, по-
порождаемый такой грамматикой,— это множество цепо-
цепочек в основном алфавите, выводимых из аксиомы. Наи-
Наиболее важный для лингвистич. приложений класс по-
порождающих грамматик — грамматики составляющих,
у к-рых каждое правило имеет вид ЪцА ?2 —>¦ ii^^i гДе
li, 1г> 9 — цепочки в объединении основного и вспомо-
вспомогательного алфавитов, А — вспомогательный символ и
G непуста. Грамматика составляющих позволяет естест-
естественным образом сопоставлять цепочкам порождаемого
ею языка размеченные системы составляющих. Этот
класс грамматик наиболее важен и в чисто математич.
отношении, т. к. языки, порождаемые грамматиками
составляющих, представляют собой простой и весьма
важный подкласс класса примитивно рекурсивных
множеств. Среди грамматик составляющих в свою оче-
очередь особенно важны как в теоретическом, так и в при-
прикладном аспектах грамматики бесконтекстные, у
к-рых правила имеют вид А —>- 6, где А — вспомога-
вспомогательный символ. К бесконтекстным грамматикам близ-
близки грамматики доминационные, также порождающие
формальные языки, но сопоставляющие цепочкам этих
языков деревья подчинения, и грамматики категори-
категориальные, характеризующиеся особым способом задания
информации о синтаксич. свойствах слов. Принципи-
Принципиально иной тип формальных грамматик представляют
собой грамматики трансформационные; они служат для
осуществления преобразований синтаксич. структур, не
«привязанных», вообще говоря, к цепочкам; эти грам-
грамматики представляются наиболее перспективными для
описания строения естественных языков, т. к. позволя-
позволяют рассматривать синтаксические и линейные отноше-
отношения между словами раздельно, что лучше отражает язы-
языковую реальность.
Теория формальных грамматик наряду с «традицион-
«традиционными» для нее лингвистич. приложениями нашла при-
применение в теории программирования для описания
языков программирования и трансляторов. Особенно
широко применяются для этих целей бесконтекстные
грамматики, но используются и грамматики более об-
общего вида.
Лит.: [1] X омский Н., в кн.: Новое в лингвистике,
в. 2, М., 1962, с. 412—527; [2] Гладкий А. В., Мель-
Мельчук И. А., Элементы математической лингвистики, М., 1969.
А. В. Гладкий.
МАТЕМАТИЧЕСКАЯ ЛОГИКА, теоретиче-
теоретическая логика, символическая логи-
логика,— раздел математики, посвященный изучению ма-
математич. доказательств и вопросов оснований матема-
математики.
Исторический очерк. Идея построения универсаль-
универсального языка для всей математики и формализации на
базе такого языка математич. доказательств выдвига-
выдвигалась в 17 в. Г. Лейбницем (G. Leibniz). Но только в
сер. 19 в. появились первые научные работы по алгеб-
раизации аристотелевой логики [Дж. Буль (G. Boole,
1847) и О. де Морган (A. de Morgan, 1858)]. После того
как Г. Фреге (G. Frege, 1879) и Ч. Пирс (С. Peirce,
1885) ввели в язык алгебры логики предикаты, пред-
предметные переменные и кванторы, возникла реальная
возможность применить этот язык к вопросам основа-
оснований математики.
С другой стороны, создание в 19 в. неевклидовой
геометрии сильно поколебало уверенность математиков
в абсолютной надежности геометрич. интуиции, на
к-рой была основана евклидова геометрия. Сомнениям
в надежности геометрич. интуиции способствовало так-
также то, что в результате развития исчисления бесконечно
малых математики натолкнулись на неожиданные при-
примеры всюду непрерывных функций без производных.
Появилась потребность отделить понятие действитель-
действительного числа от неясного понятия «величины», к-рое было
основано на геометрич. интуиции. Эта задача была ре-
решена разными путями в работах К. Вейерштрасса
(К. Weierstrap"), Р. Дедекинда (R. Dedekind) и Г. Кан-
Кантора (G. Cantor). Они показали возможность «арифме-
тизации» анализа и теории функций, в результате чего
в качестве фундамента всей классич. математики стала
рассматриваться арифметика целых чисел. Затем была
предпринята аксиоматизация арифметики [Р. Дедекинд
A888) и Дж. Пеано (G. Реапо, 1891)]. При этом Дж.
Пеано создал более удобную символику для логич.
языка. Позже этот язык был усовершенствован в сов-
совместном труде Б. Рассела (В. Russell) и А. Уайтхеда
(A. Whitehead) «Принципы математики» A910), где бы-
была предпринята попытка сведения всей математики к
логике. Но эта попытка не увенчалась успехом, т. к.
оказалось невозможным вывести из чисто логич. аксиом
существввание бесконечных множеств. Хотя логистич.
программа Фреге — Рассела в основаниях математики
так и не достигла своей главной цели •— сведения
математики к логике, в их работах был создан богатый
логич. аппарат, без к-рого оформление М. л. как полно-
полноценной математич. дисциплины было бы невозможно.
На ,рубеже 19 — 20 вв. были обнаружены антиномии,
связанные с основными понятиями теории множеств.
Наиболее сильное впечатление на современников про-
произвела опубликованная в 1903 антиномия Рассела.
Пусть М есть множество всех таких множеств, каждое
из к-рых не является своим собственным элементом.
Легко убедиться, что М является своим элементом тог-
тогда и только тогда, когда М не является своим элемен-
элементом. Конечно, можно пытаться выйти из создавшегося
противоречия, сделав заключение, что такого множест-
множества М не бывает. Однако, если не может существовать
множество, состоящее в точности из всех элементов,
удовлетворяющих такому четко определенному усло-
условию, к-рое мы имеем в приведенном выше определении
множества М, то где гарантия того, что в нашей повсе-
повседневной работе мы не столкнемся с множествами, к-рые
также не могут существовать? И каким, вообще, усло-
условиям должно удовлетворять определение множества
для того, чтобы оно существовало? Ясно было одно:
нужно как-то ограничить канторовскую теорию мно-
множеств.
Л. Брауэр (L. Brouwer, 1908) выступил против при-
применения правил классич. логики к бесконечным мно-
множествам. В выдвинутой им интуиционистской про-
программе предлагалось отказаться от рассмотрения
абстракции актуальной бесконечности, т. е. бесконеч-
бесконечных множеств как завершенных совокупностей. Допус-
Допуская существование сколь угодно больших натуральных
чисел, интуиционисты выступают против рассмотрения
натурального ряда как завершенного множества. Они
считают, что в математике всякое доказательство суще-
существования того или иного объекта должно быть конст-
конструктивным, т. е. должно сопровождаться построением
этого объекта. Если предположение о том, что искомый
объект не существует, приведено к противоречию, то
это, по мнению интуиционпстов, не может рассматривать-
рассматриваться как доказательство существования. Особой критике
со стороны интуиционистов подвергся исключенного
третьего закон. Ввиду того, что этот закон первона-
первоначально рассматривался применительно к конечным
множествам и, учитывая, что многие свойства конечных
множеств не выполняются для бесконечных множеств
(напр., что всякая собственная часть меньше целого),
интуиционисты считают неправомерным применение
этого закона к бесконечным множествам. Так, напр,,
чтобы утверждать, что проблема Ферма имеет положи-
положительное решение или имеет отрицательное решение,
интуиционист должен указать соответствующее реше-
решение этой проблемы. А пока проблема Ферма не решена,
эта дизъюнкция считается неправомерной. Такое же
требование предъявляется к пониманию всякой дизъ-
дизъюнкции. Это требование интуиционистов может создать
затруднения и в случае рассмотрения задач, связанных
с конечными множествами. Представим себе, что кто-то,
закрыв глаза, достает шар из урны, в к-рой имеются
три черных и три белых шара, и тут же бросает этот
шар обратно. Если никто не видел этот шар, то мы не
имеем возможности узнать, какого он был цвета. Од-
Однако вряд ли можно всерьез оспаривать достоверность
утверждения, что этот шар был либо черного, либо бе-
белого цвета.
Интуиционисты построили свою математику, имею-
имеющую интересные своеобразные особенности. Но она
оказалась более сложной и громоздкой, чем классич.
математика. Положительный вклад интуиционистов в
исследование вопросов оснований математики выразил-
выразился в том, что они еще раз решительным образом подчерк-
подчеркнули различие между конструктивным и неконструк-
неконструктивным в математике, они провели тщательный анализ
многих трудностей, с к-рыми столкнулась математика
в своем развитии, и тем самым способствовали их пре-
преодолению.
Д. Гильберт (D. Hilbert, см. добавления VII—X в
[9]) наметил другой путь преодоления трудностей, воз-
возникших в основаниях математики на рубеже 19—20 вв.
Этот путь, основанный на применении аксиоматич. ме-
метода рассмотрения формальных моделей содержатель-
содержательной математики и на исследовании вопросов непротиво-
непротиворечивости таких моделей надежными финитными сред-
средствами, получил в математике название ф и н и т и з-
ма Гильберта. Признавая ненадежность гео-
метрич. интуиции, Д. Гильберт прежде всего предпри-
предпринимает тщательный пересмотр евклидовой геометрии,
освобождая ее от обращения к интуиции. Результатом
такой переработки явились его «Основания геометрии»
A899).
Вопросы непротиворечивости различных теорий по
существу рассматривались и до Д. Гильберта. Так, по-
построенная Ф. Клейном (F. Klein, 1871) проективная
модель неевклидовой геометрии Лобачевского сводит
вопрос о непротиворечивости геометрии Лобачевского
к непротиворечивости евклидовой геометрии. Непро-
Непротиворечивость евклидовой геометрии аналогично можно
свести к непротиворечивости анализа, т. е. теории
действительных чисел. Однако не видно было, какими
средствами можно строить модели анализа и арифмети-
арифметики для доказательства их непротиворечивости. Заслуга
Д. Гильберта состоит в том, что он указал прямой путь
для исследования этого вопроса. Непротиворечивость
данной теории означает, что в ней не может быть по-
получено противоречие, т. е. не может быть до-
доказано нек-рое утверждение А и его отрицание ~\А.
Д. Гильберт предложил представить рассматриваемую
теорию в виде формальной аксиоматич. системы, и
к-рой будут выводимы все те и только те утверждения,
к-рые являются теоремами нашей теории. Тогда для
доказательства непротиворечивости достаточно устано-
установить невыводимость в рассматриваемой теории нск-рых
утверждений. Таким образом, математич. теория, не-
непротиворечивость к-рой мы хотим доказать, становится
предметом изучения нек-рой математич. науки, к-рую
Д. Гильберт назвал метаматематикой, или
теорией доказательств.
Д. Гильберт писал, что парадоксы теории множеств
вызваны не законом исключенного третьего, а «скорее
тем, что математики пользуются недопустимыми и бес-
бессмысленными образованиями понятий, к-рые в моей тео-
теории доказательств исключаются сами собой. ...Отнять
у математиков закон исключенного третьего — это то
же, что забрать у астрономов телескоп или запретить
боксерам использовать кулаки» (см. [9] с. 383). Д. Гиль-
Гильберт предлагает различать «действительные» и «идеаль-
«идеальные» предложения классич. математики. Первые имеют
содержательный смысл, а вторые не обязаны иметь
содержательный смысл. Предложения, соответствующие
употреблению актуальной бесконечности, идеальны.
Идеальные предложения присоединяются к действи-
действительным для того, чтобы простые правила логики
были применимы и к рассуждениям о бесконечных мно-
множествах. Это существенно упрощает структуру всей
теории подобно тому, как при рассмотрении проектив-
проективной геометрии на плоскости добавляется бесконечно
удаленная прямая, пересекающая любые две параллель-
параллельные прямые в нек-рой точке.
Выдвинутая Д. Гильбертом программа обоснования
математики и его энтузиазм вдохновили современников
на интенсивную разработку аксиоматического метода.
Именно с предпринятой в начале 20 в. Д. Гильбертом
и его последователями разработкой теории доказа-
доказательств на базе развитого в работах Г. Фреге, Дж. Пеа-
но и Б. Рассела логич. языка следует связывать станов-
становление М. л. как самостоятельной математич. дисцип-
дисциплины.
Предмет и основные разделы математической логики,
связь с другими областями математики. Предмет совре-
современной М. л. разнообразен. Прежде всего следует
отметить исследование логич. и логико-математич. ис-
исчислений, из к-рых основным является классич. исчис-
исчисление предикатов. Еще в 1930 К. Гёдель (К. Godel)
доказал теорему о полноте исчисления предикатов, со-
согласно к-рой множество всех чисто логич. утверждений
математики совпадает с множеством всех выводимых в
исчислении предикатов формул (см. Гёделя теорема о
полноте). Эта теорема покавала, что исчисление пре-
предикатов является той логич. системой, на базе к-рой
можно формализовать математику. На базе исчисления
предикатов строятся различные логико-математич. тео-
теории (см. Логико-математические исчисления), представ-
представляющие собой формализацию содержательных матема-
математич. теорий — арифметики, анализа, теории множеств,
теории групп и др. Наряду с элементарными теориями
рассматриваются также теории высших порядков, в
к-рых допускаются также кванторы по предикатам,
предикаты от предикатов и т. д. Традиционными во-
вопросами, к-рые исследуются для тех или иных формаль-
формальных логич. систем, являются исследования структуры
выводов в этих системах, выводимость тех или иных
формул, вопросы непротиворечивости и полноты рас-
рассматриваемых систем.
Доказанная в 1931 Гёделя теорема о неполноте ариф-
арифметики поколебала оптимистич. надежды Д. Гильберта
на полное решение вопросов оснований математики
на указанном пути. Согласно этой теореме, если фор-
формальная система, содержащая арифметику, непротиво-
непротиворечива, то утверждение о ее непротиворечивости, выра-
выразимое в этой системе, не может быть доказано средства-
средствами, формализуемыми в ней. Это означает, что с вопро-
вопросами оснований математики дело обстоит не так просто,
как хотелось или казалось Д. Гильберту вначале. Но
уже К. Гёдель заметил, что непротиворечивость ариф-
арифметики можно доказывать, пользуясь достаточно надеж-
надежными конструктивными средствами, хотя и выходящими
за рамки средств, формализуемых в арифметике. Ана-
Аналогичные доказательства непротиворечивости арифме-
арифметики были получены Г. Генценом (G. Gentzen, 1936)
и П. С. Новиковым A943).
В результате анализа канторовской теории множеств
и связанных с ней парадоксов были построены различ-
различные системы аксиоматической теории множеств, в
к-рых принимается то или иное ограничение на обра-
образование множеств, чтобы исключить возникновение из-
известных антипомин. В этих аксиоматич. системах могут
быть развиты довольно обширные разделы математики.
Вопрос о непротиворечивостп достаточно богатых аксио-
аксиоматич. систем теории множеств остается открытым. Из
наиболее значительных результатов, полученных в
аксиоматич. теории множеств, следует отметить ре-
результат К. Гёделя о непротиворечивости континуум-
гипотезы и выбора аксиомы в системе Борнайса — Гё-
Гёделя 2 A939) и результат П. Коэна (P. Cohen, 1963)
о независимости этих аксиом от аксиом системы Церме-
ло—Френкеля ZF. Отметил, что эти две системы акси-
аксиом 2 и ZF равнонепротиворечивы. Для доказательства
своих результатов К. Гёдель ввел важное понятие кон-
конструктивного множества (см. Конструктивное по Гё-
делю множество) и показал существование модели сис-
системы 2, состоящей из таких множеств. Метод К. Гёделя
был использован П. С. Новиковым для доказательства
непротиворечивости нек-рых других утверждений де-
дескриптивной теории множеств A951). Для построения
моделей теории множеств ZF, в к-рых выполняются
отрицания континуум-гипотезы или аксиомы выбора,
П. Коэн ввел так наз. вынуждения метод, к-рый впо-
впоследствии был усовершенствован и стал основным ме-
методом построения моделей теории множеств, удовлетво-
удовлетворяющих тем или иным свойствам.
Одним из наиболее замечательных достижений М. л.
явилась разработка понятия общерекурсивной функции
и формулировка Чёрча тезиса, утверждающего, что по-
понятие общерекурсивной функции является уточнением
интуитивного понятия алгоритма. Из других эквива-
эквивалентных уточнений понятия алгоритма наибольшее рас-
распространение получили понятия Тьюринга машины и
нормального алгорифма Маркова. По существу вся ма-
математика связана с теми или иными алгоритмами. Но
только после уточнения понятия алгоритма появилась
возможность обнаружить существование неразрешимых
алгоритмических проблем в математике. Неразрешимые
алгоритмич. проблемы были обнаружены во многих
разделах математики (алгебра, теория чисел, тополо-
топология, теория вероятностей и др.), причем оказалось, что
они могут быть связаны с очень распространенными и
фундаментальными понятиями математики. Исследова-
Исследование алгоритмич. проблем в той или иной области мате-
математики, как правило, сопровождается проникновением
идей и методов М. л. в эту область, что приводит к ре-
решению также и других проблем, уже не имеющих алго-
алгоритмич. характера.
Разработка точного понятия алгоритма дала возмож-
возможность уточнить понятие эффективности и развивать на
базе такого уточнения конструктивное направление в
математике (см. Конструктивная математика), вопло-
воплотившее в себе нек-рыо черты интуиционистского направ-
направления, но существенно отличающееся от последнего.
Выли созданы основы конструктивного анализа, кон-
конструктивной топологии, конструктивной теории веро-
вероятностей и др.
В самой теории алгоритмов можно выделить исследо-
исследования в, области рекурсивной арифметики, куда входят
различные классификации рекурсивных и рекуренвно-
перечислимых множеств, степени неразрешимости ре-
рекурсивно-перечислимых множеств, исследования слож-
сложности записи алгоритмов и сложности алгоритмич. вы-
вычислений (по времени и по зоне, см. Алгоритма слож-
ность). Обширным развивающимся разделом теории
алгоритмов является теория нумераций.
Как отмечалось выше, аксиоматич. метод оказал
большое влияние на развитие многих разделов мате-
математики. Особенно значительным было проникновение
этого метода в алгебру. Так, на стыке М. л. и алгебры
возникла общая теория алгебраических систем, или
моделей теория. Это направление было заложено в ра-
работах А. И. Мальцева, А. Тарского (A. Tarski) и их
учеников. Здесь можно отметить исследования по эле-
элементарным теориям классов моделей, в частности воп-
вопросы разрешимости этих теорий, аксиоматизируемость
классов моделей, изоморфизм моделей, вопросы кате-
категоричности и полноты классов моделей.
Важное место в теории моделей занимает исследова-
исследование нестандартных моделей арифметики и анализа.
Еще на заре развития дифференциального исчисления
в работах Г. Лейбница (G. Leibniz) и И. Ньютона
(I. Newton) бесконечно малые и бесконечно большие
величины рассматривались как числа. Позже появи-
появилось понятие переменной величины, и математики от-
отказались от употребления бесконечпо малых чисел,
модуль к-рых отличен от нуля и меньше любого поло-
положительного действительного числа, т. к. их употреб-
употребление потребовало бы отказа от аксиомы Архимеда.
И только через три столетия в результате развития
методов М. л. удалось установить, что (нестандартный)
анализ с бесконечно малыми и бесконечно большими
числами непротиворечив относительно обычного (стан-
(стандартного) анализа действительных чисел.
Не обошлась без влияния аксиоматич. метода и инту-
интуиционистская математика. Так, еще в 1930 А. Гейтинг
(A. Heyting) ввел в рассмотрение формальные системы
интуиционистской логики высказываний и предикатов
(конструктивные исчисления высказываний и предика-
предикатов). Позже были введены формальные системы интуи-
интуиционистского анализа (см., напр., [8]). Многие иссле-
исследования по интуиционистской логике и математике
имеют дело с формальными системами. Подвергались
специальному изучению также так наз. промежуточ-
промежуточные логики (или суперинтущцэднистские), т. е. логики,
лежащие между классической и интуиционистской ло-
логиками. Понятие реализуемости формул по Клини пред-
представляет одну из попыток интерпретировать понятие
интуиционистской истинности с точки зрения классич.
математики. Однако оказалось, что не всякая реализуе-
реализуемая формула исчисления высказываний выводима в ин-
интуиционистском (конструктивном) исчислении выска-
высказываний.
Подверглась формализации также и модальная логи-
логика. Однако, несмотря на наличие большого числа работ
по формальным системам модальной логики и по их
семантике (Крипке модели), можно сказать, что здесь
происходит процесс накопления пока еще разрозненных
фактов.
М. л. имеет большое прикладное значение; с каждым
годом растет глубокое проникновение идей и методов
М. л. в кибернетику, в вычислительную математику,
в структурную лингвистику.
Лит.: [1] Гильберт Д., Б е р н а й с П., Основания
математики. Логические исчисления и формализация арифмети-
арифметики, пер. с нем., М., 1979; [2] К л и н и С. К., Введение в мета-
метаматематику, пер. с англ., М., 1957; [3] М е н д е л ь с о н Э.,
Введение в математическую логику, пер. с англ., 2 изд., М., 1976;
[4] Новиков П. С, Элементы математической логики, 2 изд.,
М., 1973; [5] Е р ш о в Ю. Л., Палютин Е. А., Математиче-
Математическая логика, М., 1979; [6] Ш е н ф и л д Д. Р., Математическая
логика, пер. с англ., М., 1975; [7] H о в и к о в П. С, Конструк-
Конструктивная математическая логика с точки зрения классической, М.,
1977; [8] К л и н и С. К., В е о л и Р., Основания интуициони-
интуиционистской математики с точки зрения теории рекурсивных функций,
пер. с англ., М., 1978; Е9] Г и л ь б е р т Д., Основания геоме-
геометрик, пер. с нем., М., 1948; [10] Френкель А.-А., Б а р-
X и л л с л И., Основания теории множеств, пер. с англ., М.,
1966; [11] Математика XIX века. Математическая логика. Ал-
Алгебра. Теория чисел. Теория вероятностей, м., 1978;
H2I Mostowski A., Thirty years of foundational studies,
Hels., 1965.
См. также лит. при статьях об отдельных разделах М. л.
С. И. Авян.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ — приближенное
описание какого-либо класса явлений внешнего мира,
выраженное с помощью математич. символики. М. м.—
мощный метод познания внешнего мира, а также про-
прогнозирования и управления. Анализ М. м. позволяет
проникнуть в сущность изучаемых явлений. Процесс
математического моделирования,
т. е. изучения явления с помощью М. м., можно под-
подразделить на 4 этапа.
Первый этап — формулирование законов, связываю-
связывающих основные объекты модели. Этот этап требует широ-
широкого знания фактов, относящихся к изучаемым явлени-
явлениям, и глубокого проникновения в их взаимосвязи. Эта
стадия завершается записью в математич. терминах
сформулированных качественных представлений о свя-
связях между объектами модели.
Второй этап — исследование математич. задач, к
к-рым приводят М. м. Основным вопросом здесь яв-
является решение прямой задачи, т. е. получение
в результате анализа модели выходных данных (теоре-
тич. следствий) для дальнейшего их сопоставления с
результатами наблюдений изучаемых явлений. На этом
этапе важную роль приобретают математич. аппарат,
необходимый для анализа М. м., и вычислительная
техника — мощное средство для получения количест-
количественной выходной информации как результата решения
сложных математич. задач. Часто математич. задачи,
возникающие на основе различных М. м. явлений, бы-
бывают одинаковыми (напр., основная задача линейного
программирования отражает ситуации различной при-
природы). Это дает основание рассматривать такие типич-
типичные математич. задачи, как самостоятельный объект,
абстрагируясь от изучаемых явлений.
Третий этап — выяснение того, удовлетворяет ли
принятая (гипотетическая) модель критерию практики,
т. е. выяснение вопроса о том, согласуются ли резуль-
результаты наблюдений с теоретич. следствиями модели в
пределах точности наблюдений. Если модель была впол-
вполне определена — все параметры ее были заданы, то оп-
определение уклонений теоретич. следствий от наблюде-
наблюдений дает решение прямой задачи с последующей оцен-
оценкой уклонений. Если уклонения выходят за пределы
точности наблюдений, то модель не может быть приня-
принята. Часто при построении модели нек-рые ее характери-
характеристики остаются неопределенными.' Задачи, в к-рых
определяются характеристики модели (параметриче-
(параметрические, функциональные) таким образом, чтобы выходная
информация была сопоставима,в пределах точности на-
наблюдений с результатами наблюдений изучаемых яв-
явлений, наз. обратными задачами. ЕслиМ. м.
такова, что ни при каком выборе характеристик этим
условиям нельзя удовлетворить, то модель непригодна
для исследования рассматриваемых явлений. Примене-
Применение критерия практики к оценке М. м. позволяет де-
делать вывод о правильности положений, лежащих в ос-
основе подлежащей изучению (гипотетической) модели.
Этот метод является единственным методом изучения
недоступных нам непосредственно явлений макро- и
микромира.
Четвертый этап — последующий анализ модели в
связи с накоплением данных об изучаемых явлениях и
модернизация модели. В процессе развития науки и
техники данные об изучаемых явлениях все более и бо-
более уточняются и наступает момент, когда выводы, по-
получаемые на основании принятой М. м., не соответству-
соответствуют нашим знаниям о явлении. Таким образом, возника-
возникает необходимость построения новой, более совершенной
М. м.
Типичным примером, иллюстрирующим характерные
этапы в построении М. м., является модель Солнечной
системы. Наблюдения звездного неба начались в глу-
глубокой древности. Первичный анализ этих наблюдений
позволил выделить планеты из всего многообразия не-
небесных светил. Таким образом, первым шагом было вы-
выделение объектов изучения. Вторым шагом явилось
определение закономерностей их движений. (Вообще,
определения объектов и их взаимосвязей являются ис-
исходными положениями — «аксиомами» — гипотетич.
модели.) Модели Солнечной системы в процессе своего
развития прошли через ряд последовательных усовер-
усовершенствований. Первой была модель Птолемея B в.
я. э.), исходившая из положения, что планеты и Солнце
совершают движения вокруг Земли (геоцентрич. мо-
модель), и описывавшая эти движения с помощью правил
(формул), многократно усложнявшихся по мере накоп-
накопления наблюдений.
Развитие мореплавания поставило перед астрономией
новые требования к точности наблюдений. Н. Копер-
Коперником (N. Kopernik) в 1543 была предложена принци-
принципиально новая основа законов движения планет, пола-
полагавшая, что планеты вращаются вокруг Солнца по
окружностям (гелиоцентрич. система). Это была качест-
качественно новая (но не математически) модель Солнечной
системы. Однако не существовало параметров системы
(радиусов окружностей и угловых скоростей движения),
приводящих количественные выводы теории в должное
соответствие с наблюдениями, так что Н. Коперник был
вынужден вводить поправки в движения планет по
окружностям (эпициклы).
Следующим шагом в развитии модели Солнечной сис-
системы были исследования И. Кеплера (I. Kepler, нач.
17 в.), к-рый сформулировал законы движения планет.
Положения Н. Коперника и И. Кеплера давали кине-
матич. описание движения каждой планеты обособлен-
обособленно, не затрагивая еще причин, обусловливающих эти
движения.
Принципиально новым шагом были работы И. Нью-
Ньютона (I. Newton), предложившего во 2-й пол. 17 в.
динамич. модель Солнечной системы, основанную на
законе всемирного тяготения. Динамич. модель согла-
согласуется с кинематич. моделью, предложенной И. Кепле-
Кеплером, т. к. из динамич. системы двух тел «Солнце —
планета» следуют законы Кеплера.
К 40-м гг. 19 в. выводы динамич. модели, объектами
к-рой были видимые планеты, вошли в противоречие
с накопленными к тому времени наблюдениями. Имен-
Именно, наблюдаемое движение планеты Уран уклонялось
от теоретически вычисляемого движения. У. Леверье
(TJ. Le Verrier) в 1846 расширил систему наблюдаемых
планет новой гипотетич. планетой, названной им Неп-
Нептуном, и, пользуясь новой моделью Солнечной системы,
определил массу и закон движения новой планеты так,
что в новой системе противоречие в движении Урана
было снято. Планета Нептун была открыта в мес-
месте, указанном У. Леверье. Аналогичным методом, ис-
используя расхождения в теоретической и наблюдаемой
траектории Нептуна, в 1930 была открыта планета
Плутон.
Метод математич. моделирования, сводящий иссле-
исследование явлений внешнего мира к математич. задачам,
занимает ведущее место среди других методов исследо-
исследования, особенно в связи с появлением ЭВМ. Он позво-
позволяет проектировать новые технич. средства, работаю-
работающие в оптимальных режимах, для решения сложных
задач науки и техники; проектировать новые явления.
М. м. проявили себя как важное средство управления.
Они применяются в самых различных областях знания,
стали необходимым аппаратом в области экономич.
планирования и являются важным элементом автома-
автоматизированных систем управления. А. Н. Тихонов.
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА — раздел мате-
математики, посвященный математич. методам системати-
систематизации, обработки и использования статистич. данных
для научных и практич. выводов. При этом статистич.
данными наз. сведения о числе объектов в какой-либо
более или менее обширной совокупности, обладающих
теми или иными признаками.
Предмет и метод математической статистики. Ста-
Статистич. описание совокупности объектов занимает про-
промежуточное положение между индивидуальным описа-
описанием каждого из объектов совокупности, с одной сто-
стороны, и описанием совокупности по ее общим свойст-
свойствам, совсем не требующим ее расчленения на отдельные
объекты, с другой. По сравнению с первым способом
статистич. данные всегда в большей или меньшей сте-
степени обезличены и имеют лишь ограниченную ценность
в случаях, когда существенны именно индивидуальные
данные (напр., учитель, знакомясь с классом, получит
лишь весьма предварительную ориентировку о поло-
положении дела из одной статистики числа выставленных
его предшественником отличных, хороших, удовлетво-
удовлетворительных и неудовлетворительных оценок). С другой
стороны, по сравнению с данными о наблюдаемых из-
извне суммарных свойствах совокупности статистич.
данные позволяют глубже проникнуть в существо дела.
Напр., данные гранулометрич. анализа породы (т. е.
данные о распределении образующих породу частиц
по размерам) дают ценную дополнит, информацию по
сравнению с испытанием нерасчлененных образов по-
породы, позволяя в нек-рой мере объяснить свойства по-
породы, условия ее образования и пр.
Метод исследования, опирающийся на рассмотрение
статистич. данных о тех или иных совокупностях объек-
объектов, наз. статистическим. Статистич. метод
применяется в самых различных областях знания.
Однако черты статистич. метода в применении к объек-
объектам различной природы столь своеобразны, что было
бы бессмысленно объединять, напр., социально-эконо-
мич. статистику, физич. статистику, звездную стати-
статистику и т. п. в одну науку.
Общие черты статистич. метода в различных областях
знания сводятся к подсчету числа объектов, входящих
в те или иные группы, рассмотрению распределения
количественных признаков, применению выборочного
метода (в случаях, когда детальное исследование всех
объектов обширной совокупности затруднительно), ис-
использованию теории вероятностей при оценке достаточ-
достаточности числа наблюдений для тех или иных выводов и
т. п. Эта формальная математич. сторона статистич.
методов исследования, безразличная к специфич. при-
природе изучаемых объектов, и составляет предмет М. с.
Связь математической статистики с теорией вероят-
вероятностей. Связь М. с. с теорией вероятностей имеет в раз-
разных случаях различный характер. Вероятностей тео-
теория изучает не любые массовые явления, а явления
случайные и именно «вероятностно случайные», т. е.
такие, для к-рых имеет смысл говорить о соответствую-
соответствующих им распределениях вероятностей. Тем не менее
теория вероятностей играет определенную роль и при
статистич. изучении массовых явлений любой-природы,
к-рые могут не относиться к категории вероятностно
случайных. Это осуществляется через основанные на
теории вероятностей теорию выборочного метвда и оши-
ошибок теорию. В этих случаях вероятностным закономер-
закономерностям подчинены не сами изучаемые явления, а приемы
их исследования.
Более важную роль играет теория вероятностей при
статистич. исследовании вероятностно случайных явле-
явлений. Здесь в полной мере находят применение такие
основанные на теории вероятностей разделы М. с, как
статистических гипотез проверка, статистическое оце-
оценивание распределений вероятностей и входящих в них
параметров и т. д. Область же применения этих более
глубоких статистич. методов значительно уже, т. к.
здесь требуется, чтобы сами изучаемые явления были
подчинены достаточно определенным вероятностным
закономерностям. Напр., статистич. изучение режима
турбулентных водных потоков или флюктуации в радио-
радиоприемных устройствах производится на основе теории
стационарных случайных процессов. Однако примене-
применение той же теории к анализу экономических временных
рядов может привести к грубым ошибкам в виду того,
что входящее в определение стационарного процесса
допущение наличия сохраняющихся в течение длитель-
длительного времени неизменных распределений вероятностей
в этом случае, как правило, совершенно неприемлемо.
Вероятностные закономерности получают статистич.
выражение (вероятности осуществляются приближенно
в виде частот, а математич. ожидания — в виде сред-
средних) в силу закона больших чисел.
Простейшие приемы статистического описания. Из-
Изучаемая совокупность из п объектов может по какому-
либо качественному признаку А разбиваться на классы
Ах, А2, ... , Аг. Соответствующее этому разбиению
статистич. распределение задается при помощи указа-
указания численностей (частот) щ, п2, ... , пг (где 7^ 1";=n)
отдельных классов. Вместо численностей и,- часто ука-
указывают соответствующие относительные частоты (час-
(частости) hj=rij/n (удовлетворяющие, очевидно, соотно-
соотношению ?/i=1hi=l). Если изучению подлежит нек-рый
количественный признак, то его распределение в сово-
совокупности из п объектов можно задать, перечислив непо-
непосредственно наблюденные значения признака: Xj,
хъ ... , хп, напр., в порядке их возрастания. Однако при
больших п такой способ громоздок и в то же время не
выявляет отчетливо существенных свойств распределе-
распределения. При сколько-либо больших п на практике обычно
совсем не составляют полных таблиц наблюденных зна-
значений х{, а исходят во всей дальнейшей работе из таб-
таблиц, содержащих лишь численность классов, получаю-
получающихся при группировке наблюденных значений по над-
надлежаще выбранным интервалам.
Обычно группировка по 10—20 интервалам, в каж-
каждый из к-рых попадает не более 15—20% значений ж,-,
оказывается достаточной для довольно полного выяв-
выявления всех существенных свойств распределения и на-
надежного вычисления по
групповым численностям
основных характеристик
распределения (см. о них
ниже). Составленная по
таким группированным
данным гистограмма на-
13,10 13,30 13,50 13,70 глядно изображает рас-
Диаметр в мм пределение. Гистограмма,
Рис j составленная на основе
группировки с маленькими
интервалами, обычно многовершинная и не отражает
наглядно существенных свойств распределения.
В качестве примера на рис. 1 дана гистограмма рас-
распределения 200 диаметров нек-рой детали (в мм), обна-
обнаруженного при статистич. исследовании массовой про-
продукции при длине интервала группировки 0,05 мм, а на
рис. 2 — гистограмма того же распределения при ин-
интервале 0,01 мм. С другой стороны, группировка по
слишком крупным интервалам может привести к потере
ясного представления о характере распределения и к
грубым ошибкам при вычислении среднего и других
характеристик распределения (см. соответствующую
гистограмму на рис. 3).
В пределах М. с. вопрос об интервалах группировки
может быть рассмотрен только с формальной стороны:
полноты математич. описания распределения, точности
вычисления средних по сгруппированным данным и
т. д.
13,10 13,20 13,30 13,40 13,50 13,60 13,70
Диаметр в мм
Рис. 2.
Простейшими сводными характеристиками распре-
распределения одного количественного признака являются
среднее
— 1
и среднее квадратичное отклонение
где
При вычислении х, S2 и D по группированным данным
пользуются формулами
или
где г — число интервалов группировки, а^ — их се-
середины. Если материал сгруппирован по слишком
то
* 150
13,10
13,30 13,50
Диаметр в мм
Рис. 3.
13,70
крупным интервалам
такой подсчет дает слиш-
ком грубые результаты,
Иногда в таких случаях
полезно прибегать к спе-
циальным поправкам на
группировку. Однако эти
поправки имеет смысл вво-
вводить лишь при условии
выполнения определенных
вероятностных предположений.
О совместных распределениях двух и большего числа
признаков см. статьи Корреляция, Регрессия.
Связь статистических распределений с вероятностны-
вероятностными. Оценка параметров. Проверка вероятностных гипо-
гипотез. Выше были изложены лишь нек-рые избранные
простейшие приемы статистич. описания, представляю-
представляющего собой довольно обширную дисциплину с хорошо
разработанной системой понятий и техникой вычисле-
вычислений. Приемы статистич. описания интересны, однако
не сами по себе, а в качестве средства для получения
из статистич. материала выводов о закономерностях,
к-рым подчиняются изучаемые явления, и о причинах,
приводящих в каждом отдельном случае к тем или иным
наблюденным статистич. распределениям.
Напр., данные, нанесенные на графики на рис. 1, 2,
3, собраны с целью установления точности изготовления
деталей, расчетный диаметр к-рых равен 13,40 мм, при
нормальном ходе производства. Простейшим допуще-
допущением, к-рое может быть в этом случае обосновано не-
к-рыми теоретич. соображениями, является предполо-
предположение, что диаметры отдельных деталей можно рас-
рассматривать как случайные величины А', подчиненные
нормальному распределению вероятностей:
Если это допущение верно, то параметры аист2 —
«реднее и дисперсию вероятностного распределения —
можно с достаточной точностью оценить по соответст-
соответствующим характеристикам статистич. распределения
(т. к. число наблюдений ;г=200 достаточно велико).
В качестве оценки для теоретич. дисперсии ст2 предпо-
предпочитают не статистич. дисперсию
D2=S2/n,
а несмещенную оценку
s2=S2/(re—1).
Для теоретич. среднего квадратичного отклонения ст
не существует общего (пригодного при любом распре-
распределении вероятностей) выражения несмещенной оцен-
оценки. В качестве оценки (вообще говоря, смещенной) для
о чаще всего употребляют s. Точность оценок х и s
для аист указывается соответствующими дисперсиями,
к-рые в случае нормального распределения A) имеют
вид
as ~ a2/2re — s°/2n,
где знак ~ обозначает приближенное равенство при
больших п. Таким образом, уславливаясь прибавлять
к оценкам со знаком — их среднее квадратичное откло-
отклонение, имеем при больших п в предположении нормаль-
нормального распределения A):
а=~х ± s/y~~n, O = s ± siyin. B)
Объем выборки и=200 достаточен для законности поль-
пользования этими формулами теории больших выборок.
Дальнейшие сведения об оценке параметров теоре-
теоретич. распределений вероятностей см. в статьях Стати-
Статистическая оценка, Доверительное оценивание.
Все основанные на теории вероятностей правила
статистич. оценки параметров и проверки гипотез дей-
действуют лишь с определенным значимости уровнем
?0<Г1, т. е. могут приводить к ошибочным результатам
с вероятностью а=1 — <в. Напр., если в предположении
нормального распределения и известной теоретич.
дисперсии а2 производить оценку а по ж по правилу
х— ко/У п < а < х^-ко/У п,
то вероятность ошибки будет равна а, связанному с к
соотношением:
а= . ¦ f °° е~ х2>'° dx.
V2n J
Вопрос о рациональном выборе уровня значимости
в данных конкретных условиях (напр., при разработке
правил статистического контроля качества массовой
продукции) является весьма существенным. При этом
желанию применять правила лишь с высоким (близким
к единице) уровнем значимости противостоит то обстоя-
обстоятельство, что при ограниченном числе наблюдений та-
такие правила позволяют сделать лишь очень бедные вы-
воды (не дают возможности установить неравенство
вероятностей даже при заметном неравенстве частот
и т. д.).
Дальнейшие задачи математической статистики. Упо-
Упоминавшиеся выше способы оценки параметров и про-
проверки гипотез основаны на предположении, что число
наблюдений, необходимых для достижения заданной
точности выводов, определяют заранее (до проведения
испытаний). Однако часто априорное определение чис-
числа наблюдений нецелесообразно, т. к., не фиксируя
число опытов заранее, а определяя ого в ходе экспери-
эксперимента, можно уменьшить его математич. ожидание.
Сначала это обстоятельство было подмечено на приме-
примере выбора одной из двух гипотез по последовательности
независимых испытаний. Соответствующая процедура
(впервые предложенная в связи с задачами приемочного
статистического контроля) состоит в следующем: на
каждом шаге по пезультатам уже проведенных наблю-
наблюдений решают а) провести ли следующее испытание,
или б) прекратить испытания и принять первую гипо-
гипотезу, или в) прекратить испытания и принять вторую
гипотезу. При надлежащем подборе количественных ха-
характеристик подобной процедуры можно добиться (при
той же точности выводов) сокращения числа наблюдений
в среднем почти вдвое по сравнению с процедурой вы-
выборки фиксированного объема (см. Последевателъный
анализ). Развитие методов последовательного анализа
привело, с одной стороны, к изучению управляемых
случайных процессов, с другой — к появлению стати-
статистических решений теории. Эта теория исходит из того,
что результаты последовательно проводимых наблю-
наблюдений служат основой принятия нек-рых решений (про-
(промежуточных — продолжать испытания или нет, и окон-
окончательных — в случае прекращения испытаний). В за-
задачах оценки параметров окончательные решения суть
числа (значение оценок), в задачах проверки гипотез —
принимаемые гипотезы. Цель теории — указать пра-
правила принятия решений, минимизирующих средний
риск или убыток (риск зависит и от вероятностных
распределений результатов наблюдений, и от принимае-
принимаемого окончательного решения, и от расходов на прове-
проведение испытаний и т. п.).
Вопросы целесообразного распределения усилий при
проведении статистич. анализа явлений рассматривают-
рассматриваются в теории планирования эксперимента, ставшей важ-
важной частью современной М. с.
Наряду с развитием и уточнением общих понятий
М. с. развиваются и ее отд. разделы, такие как дис-
дисперсионный анализ, ковариационный анализ, многомер-
многомерный статистический анализ, статистический анализ
случайных процессов, факторный анализ. Появились
новые оценки в регрессионном анализе (см. также Сто-
Стохастическая аппроксимация). Большую роль в задачах
М. с. играет бейесовский подход к статистич. задачам.
Историческая справка. Первые начала М. с. можно
найти уже в сочинениях создателей теории вероятнос-
вероятностей — Я. Бернулли (J. Bernoulli), П. Лапласа (P. La-
Laplace) и С. Пуассона (S. Poisson). В России методы
М. с. в применении к демографии и страховому делу
развивал на основе теории вероятностей В. Я. Буня-
ковский A846). Решающее значение для всего дальней-
дальнейшего развития М. с. имели работы русской классич.
школы теории вероятностей 2-й пол. 19 — нач. 20 вв.
(П. Л. Чебышев, А. А. Марков, А. М. Ляпунов,
С. Н. Бернштейн). Многие вопросы теории статистич.
оценок были по существу разработаны на основе тео-
теории ошибок и метода наименьших квадратов [К. Гаусс
(С. Gauss) и А. А. Марков]. Работы А. Кетле (A. Quete-
let), Ф. Гальтона (F. Galton) и К. Пирсона (К. Pear-
Pearson) имели большое значение, но по уровню использо-
использования достижений теории вероятностей отставали от
работ русской школы. К. Пирсоном была широко раз-
вернута работа по составлению таблиц функции, неоо-
ходимых для применения методов М. с. Эта важная
работа была продолжена во многих научных центрах
(в СССР она велась усилиями Е. Е. Слуцкого,
Н. В. Смирнова и Л. Н. Болынева). В создании теории
малых выборок, общей теории статистич. оценок и про-
проверки гипотез (освобожденной от предположений о на-
наличии априорных распределений), последовательного
анализа весьма значительна роль представителей англо-
англоамериканской школы [Стьюдент (Student, псевд.
У. С. Госсета, W. S. Gosset), P. Фишер (R. Fisher),
3. Пирсон (Е. Pearson), 10. Нейман (J. Neyman)], дея-
деятельность к-рых началась в 20-х гг. 20 в. В СССР значи-
значительные результаты в области М. с. получены В. И. Ро-
Романовским, А. Н. Колмогоровым, Е. Е. Слуцким,
к-рому принадлежат важные работы по статистике свя-
связанных стационарных рядов, Н. В. Смирновым, зало-
заложившим основы теории непараметрич. методов М. с,
Ю. В. Линником, обогатившим аналитич. аппарат М. с.
новыми методами. На основе М. с. особенно интенсивно
разрабатываются статистич. методы исследования и
контроля массового производства, статистич. методы
в области физики, гидрологии, климатологии, звезд-
звездной астрономии, биологии, медицины и др.
Лит.; [1]Смирнов Н. В.,Дунин-БарковскийИ. В.,
Курс теории вероятностей и математической* статистики для тех-
технических приложений, 3 изд., М., 1969; [2] Б о л ь ш е в Л. И.,
Смирнов Н. В. Таблицы математической статистики,
[2 изд.], М., 1968; [3]Ван-дер-Варден Б. Л., Мате-
Математическая статистика, пер. с нем., М., 1960; [4] Крамер Г.,
Математические методы статистик-и, пер. с англ., B изд.), М.,
1975; [5] X а л ь д А., Математическая статистика с технически-
техническими приложениями, пер. с англ., М., 1956; [6] К с н д а л л М.,
С т ь ю а р т А., Теория распределений, пер. с англ., М., 1966;
Е7] и х же, Статистические выводы и связи, пер. с англ., М.,
1973; [8] их же, Многомерный статистический анализ и вре-
временные ряды, пер. с англ., М., 1976.
См. также лит. при статьях о разделах М. с.
А. Н. Колмогоров, Ю. В. Прохоров,
МАТЕМАТИЧЕСКАЯ ФИЗИКА — теория математи-
математических моделей физических явлений; занимает особое
положение и в математике, и в физике, находясь на
стыке этих наук.
М. ф. тесно связана с физикой в той части, к-рая ка-
касается построения математич. модели, и в то же время
М. ф.— раздел математики, поскольку методы исследо-
исследования моделей являются математическими. В понятие
методов М. ф. включаются те математич. методы, к-рые
применяются для построения и изучения математич.
моделей, описывающих большие классы физических
явлений.
Методы М. ф. как теории математич. моделей физики
начали интенсивно разрабатываться в трудах И. Нью-
Ньютона (I. Newton) по созданию основ классич. механики,
всемирного тяготения, теории света. Дальнейшее раз-
развитие методов М. ф. и их успешное применение к изу-
изучению математич. моделей огромного круга различных
физич. явлений связаны с именами Ж. Лагранжа
(J. Lagrange), Л. Эйлера (L. Euler), Ж. Фурье (J. Fou-
Fourier), К. Гаусса (С. Gauss), Б. Римана (В. Ricmann),
М. В. Остроградского и многих др. ученых. Большой
вклад в развитие методов М. ф. внесли А. М. Ляпунов
и В. А. Стеклов.
Начиная со 2-й пол. 19 в. методы М. ф. успешно
применялись для изучения математич. моделей физич.
явлений, связанных с различными физич. полями и
волновыми процессами в электродинамике, акустике,
теории упругости, гидро- и аэродинамике и ряде дру-
других направлений исследования физич. явлений в сплош-
сплошных средах. Математич. модели этого класса явлений
наиболее часто описываются при помощи дифференци-
дифференциальных уравнений с частными производными, получив-
получивших название математической физики уравнений.
Помимо дифференциальных уравнений М. ф., при
описании математич. моделей физики применение на-
ходят интегральные уравнения и интегро-дифференци-
интегро-дифференциальные уравнения, вариационные и теоретико-вероят-
теоретико-вероятностные методы, теория потенциала, методы теории
функций комплексного переменного и ряд других раз-
разделов математики. В связи с бурным развитием вычис-
вычислительной математики особое значение для исследова-
исследования математич. моделей физики приобретают прямые
численные методы, использующие ЭВМ (конечнораз-
ностные методы и др. вычислительные алгоритмы крае~
вых задач), что позволило методами М. ф. эффективна
решать новые задачи газовой динамики, теории пере-
переноса, физики плазмы, в том числе и обратные задачи
этих важнейших направлений физич. исследований.
Теоретич. исследования в области квантовой физики
и теории относительности, широкое использование
ЭВМ в различных областях М. ф., включая и обратные
(некорректно поставленные) задачи, потребовали зна-
значительного расширения используемого М. ф. арсенала
математич. методов. Наряду с традиционными раздела-
разделами математики стали широко применяться теория опе-
операторов, теория обобщенных функций, теория функций
многих комплексных переменных, топология, и алгеб-
раич. методы. Это интенсивное взаимодействие теоре-
теоретич. физики, математики и использования ЭВМ в науч-
научных исследованиях привело к значительному расшире-
расширению тематики, созданию новых классов моделей и
подняло на новый уровень современную М. ф. Все это-
внесло большой вклад в развитие научно-технич. про-
прогресса.
Постановка задач М. ф. заключается в построении
математич. моделей, описывающих основные законо-
закономерности изучаемого класса физич. явлений. Такая по-
постановка состоит в выводе уравнений (дифференциаль-
(дифференциальных, интегральных, интегр о-дифференциальных или
алгебраических), к-рым удовлетворяют величины, ха-
характеризующие физич. процесс. При этом исходят из
основных физич. законов, учитывающих только наибо-
наиболее существенные черты явления, отвлекаясь от ряда
его второстепенных характеристик. Такими законами
являются обычно законы сохранения, напр., количест-
количества движения, энергии, числа частиц и т. д. Это приводит
к тому, что для описания процессов различной физич.
природы, но имеющих общие характерные черты, ока-
оказываются применимыми одни и те же математич. моде-
модели. Напр., математич. задачи для простейшего уравне-
уравнения гиперболич. типа
в2и „ аги
= п^
at2 Эх2 '
полученного первоначально Ж. Д'Аламбером (J.D'Alem-
bert, 1747) для описания свободных колебаний одно-
однородной струны, оказываются применимыми и для опи-
описания широкого круга волновых процессов акустики,
гидродинамики, электродинамики и других областей
физики. Аналогично, уравнение
в2и , в2и в2и „
Их^^ау1' dz2 ~u>
краевые задачи для к-рого первоначально изучались
П. Лапласом (P. Laplace, кон. 18 в.) в связи с построе-
построением теории тяготения, в дальнейшем нашло приме-
применение при решении многих проблем электростатики,
теории упругости, задач установившегося движения
идеальной жидкости и т. д. Каждой математич. модели
физики соответствует целый класс физич. процессов.
Для М. ф. характерно также то, что многие общие
методы, используемые для решения задач М. ф., разви-
развились из частных способов решения конкретных фпзпч.
задач и в своем первоначальном виде пе имели строгого
математич. обоснования и достаточной завершенности.
Это относится к таким известным методам решения за-
задач М. ф., как методы Ритца и Галеркина, к методам
теории возмущений, преобразований Фурье и многим
другим, включая метод разделения переменных. Эф-
Эффективное применение всех этих методов для решения
конкретных задач является одной из причин для их
строгого математич. обоснования и обобщения, приво-
приводящего в ряде случаев к возникновению новых матема-
математич. направлений.
Воздействие М. ф. на различные разделы математики
проявляется в том, что развитие М. ф., отражающее
требования естественных наук и запросы практики,
влечет за собой переориентацию направленности иссле-
исследований в нек-рых уже сложившихся разделах матема-
математики. Постановка задач М. ф., связанная с разработкой
математич. моделей реальных физич. явлений, привела
к изменению основной проблематики теории дифферен-
дифференциальных уравнений с частными производными. Воз-
Возникла теория краевых задач, позволившая впоследствии
связать дифференциальные уравнения с частными про-
производными с интегральными уравнениями и вариацион-
вариационными методами.
Изучение математич. моделей физики математич. ме-
методами не только позволяет получить количественные
характеристики физич. явлений и рассчитать с задан-
заданной степенью точности ход реальных процессов, но и
дает возможность глубокого проникновения в самую
суть физич. явлений, выявления скрытых закономерно-
закономерностей, предсказания новых эффектов. Стремление к бо-
более детальному изучению физич. явлений приводит к
все большему усложнению описывающих эти явления
математич. моделей, что в свою очередь делает не-
невозможным применение аналитич. методов исследова-
исследования этих моделей. Это объясняется, в частности, тем,
что математич. модели реальных физич. процессов яв-
являются, как правило, нелинейными, т. е. описываются
нелинейными уравнениями М. ф. Для детального ис-
исследования таких моделей успешно применяются пря-
прямые численные методы с использованием ЭВМ. Для
типичных задач М. ф. применение численных методов
сводится к замене уравнений М. ф. для функций не-
непрерывного аргумента алгебраич. уравнениями для
сеточных функций, заданных на дискретном множестве
точек (на сетке). Иными словами, вместо непрерывной
модели среды вводится ее дискретный аналог. Приме-
Применение численных методов в ряде случаев позволяет за-
заменить сложный, трудоемкий и дорогостоящий физич.
эксперимент значительно более экономичным математи-
математическим (численным) экспериментом. Достаточно полно
проведенный математич. эксперимент является основой
для выбора оптимальных условий реального физич.
эксперимента, выбора параметров сложных физич. ус-
установок, определения условий проявления новых фи-
физич. эффектов и т. д. Таким образом, численные методы
необычайно расширяют область эффективного исполь-
использования математич. моделей физич. явлений.
Математич. модель физич. явления, как всякая мо-
модель, не может передать всех черт явления. Установить
адекватность принятой модели исследуемому явлению
можно только при помощи критерия практики, сопо-
сопоставляя результаты теоретич. исследований принятой
модели с данными экспериментов.
Во многих случаях об адекватности принятой модели
можно судить на основании решения обратных задач
М. ф., когда о свойствах изучаемых явлений природы,
недоступных для непосредственного наблюдения, де-
делаются заключения по результатам их косвенных фи-
физич. проявлений.
Для М. ф. характерно стремление строить такие ма-
математич. модели, к-рые не только дают описание и объ-
объяснение уже установленных физич. закономерностей
изучаемого круга явлений, но и позволяют предсказать
еще не открытые закономерности. Классич. примером
такой модели является теория всемирного тяготения
F:
Ньютона, позволившая не только объяснить движение
известных к моменту ее создания тел Солнечной систе-
системы, но и предсказать существование новых планет.
С другой стороны, появляющиеся новые эксперимен-
экспериментальные данные не всегда могут быть объяснены в рам-
рамках принятой модели. Для их объяснения требуется
усложнение модели.
Лит.,- [1] Т и х о н о в А. Н., Самарский А. А., Урав-
Уравнения математической физики, 4 изд., М., 1972; [2] В л а д и м и-
) о в В. С, Уравнения математической физики, 4 изд., М., 1981,
_3] Соболев С. Л., Уравнения математической физики,
4 изд., М., 1966; [4] К у р а н т Р., Уравнения с частными про-
производными, пер. с англ., М., 1964; [5] М о р с Ф. М., Ф е ш б а \
Г., Методы теоретической физики, пер. с англ., т. 1, М., 1958
А. Н. Тихонов, А. А. Самарский, А. Г. Свешников.
МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА — математиче-
математическая дисциплина, предметом к-рой являются модели
экономич. объектов и процессов и методы их исследова-
исследования. Однако понятия, результаты, методы М. э. удобно
и принято излагать в тесной связи с их экономич. про-
происхождением, интерпретацией и практич. приложения-
приложениями. Особенно существенна связь с экономич. наукой
и практикой.
М. э. как часть математики начала развиваться толь-
только в 20 в. Ранее были лишь эпизодич. исследования,
к-рые нельзя в строгом смысле отнести к математике.
Особенности экономико-математического моделиро-
моделирования. Особенность экономич. моделирования состоит
в исключительном разнообразии и разнородности пред-
предмета моделирования. В экономике присутствуют эле-
элементы управляемости и стихийности, жесткой опреде-
определенности и существенной неоднозначности и свободы
выбора, процессы технич. характера и социальные про-
процессы, где на первый план выдвигается поведение че-
человека. Разные уровни экономики (напр., цех и народ-
народное хозяйство) требуют существенно различного оии-
сания. Все это приводит к большой разнородности мо-
моделей математич. аппарата. Тонким вопросом является
форма отражения типа социально-экономич. системы,
к-рая моделируется, учет общественного строя. Нередко
оказывается, что абстрактная математич. модель того
или иного экономич. объекта или процесса с успехом
применима и к капиталистической, и к социалистиче-
социалистической экономике. Все дело в способе использования, ин-
интерпретации результатов анализа.
Производство, эффективное производство. Экономи-
Экономика имеет дело с благами, или продуктами, к-рые пони-
понимаются в М. э. чрезвычайно широко. Для них приме-
применяется общий термин ингредиенты. Ингредиен-
Ингредиентами являются услуги, природные ресурсы, отрица-
отрицательно воздействующие на человека факторы окружаю-
окружающей среды, характеристика комфортности от имеющейся
системы безопасности и т. д. Обычно считается, что чис-
число ингредиентов конечно и пространство продуктов
есть R' — евклидово пространство, где I — число ин-
ингредиентов. Точка z из R1 при надлежащих условиях
может рассматриваться как «производственный» спо-
способ, положительные компоненты указывают объемы
выпуска соответствующих ингредиентов, а отрицатель-
отрицательные — затраты. Слово «производственный» взято в ка-
кавычки, поскольку производство понимается в самом
широком смысле. Множество наличных (заданных, су-
существующих) производственных возможностей есть
ZCZ.R'. Способ производства z?Z эффективен,
если не существует z?Z такой, что z^z и хотя бы для
одной компоненты выполняется строгое неравенство.
Задача выявления эффективных способов — одна из
важнейших в экономике. Обычно предполагается, и это
во многих случаях хорошо согласуется с действитель-
действительностью, что Z — выпуклый компакт. С помощью рас-
расширения пространства продуктов задача анализа эф-
эффективных способов при этом может быть сведена к
случаю, когда Z — выпуклый замкнутый конус.
Типичной задачей выявления эффективного способа
является основная задача производст-
производственного планирования. Задано множество
производственных способов ZcR1 и вектор потребно-
потребностей и ресурсных ограничений b^R'. Требуется най-
найти способ z=(b, \x.)^Z такой, что (х^|л для всех (Ь, ц,)?
?Z. Если Z — выпуклый замкнутый конус, то это есть
общая задача выпуклого программирования. Если Z
задан конечным числом образующих (так наз. базисных
способов), то это общая задача линейного программиро-
программирования. Решение z лежит на границе Z. Пусть я — коэф-
коэффициенты опорной гиперплоскости для Z в точке z,
т.е. яг«:0 для всех z?Z и гя=О. Основная теорема
выпуклого программирования находит условия, при
к-рых Я;>0. Напр., достаточно условия: существует
вектор (Ь, u.)?int Z (так наз. условие Слей-
тер а). Коэффициенты я, характеризующие эффектив-
эффективный способ z, имеют важный экономич. смысл. Они ин-
интерпретируются как цены, соизмеряющие эффектив-
эффективность затрат и выпуска отдельных ингредиентов. Способ
эффективен тогда и только тогда, когда стоимость
выпуска равна стоимости затрат. Данная теория эф-
эффективных способов производства и их характеризации
с помощью п оказала революционизирующее влияние
на теорию и практику планирования соцпалистич.
экономики. Она легла в основу объективных количест-
количественных методов определения цен и общественных оце-
оценок ресурсов, дающих возможность выбора наиболее
эффективных экономич. решений в условиях социалп-
стич. хозяйства. Теория естественным образом обоб-
обобщается на бесконечное число ингредиентов. Тогда про-
пространство ингредиентов оказывается подходящим об-
образом выбранным функциональным пространством.
Эффективный рост. Ингредиенты, относящиеся к раз-
разным моментам или интервалам времени, формально мож-
можно считать различными. Поэтому описание производ-
производства в динамике в принципе укладывается в изложенную
выше схему, состоящую из объектов {X, Z, Ь}, где X —
пространство ингредиентов, Z — множество производ-
производственных возможностей, Ь — задания требований и ог-
ограничений на экономику. Однако изучение собственно
динамич. аспекта производства требует более специ-
специальных форм описания производственных возможно-
возможностей.
Производственные возможности достаточно общей
модели экономич. динамики задаются с помощью точеч-
точечно-множественного отображения (многозначной функ-
ции) a:R+-»-2 +. Здесь R+— (фазовое) простран-
пространство экономики, a^R+ интерпретируется как состоя-
состояние экономики в тот или иной момент времени, где х^ —
количество продукта к, имеющегося в наличии в этот
момент. Множество а(х) состоит из всех состояний
экономики, в к-рые она может перейти за единичный
временной интервал из состояния х. Будем называть
графиком отображения а. Точки (х, у) —
допустимые производственные процессы.
Рассматриваются различные варианты задания воз-
возможных траекторий развития экономики. В частности,
потребление населения учитывается либо в самом ото-
отображении о, либо выделяется в явном виде. Напр., во
втором случае допустимой траекторией является после-
последовательность (X, C)=(x(t), c(i+l))?Lo такая, что
x[t+l)+c(tJrl)?a(x{t)), с(г)>0для всех «.Изучаются
различные понятия эффективности траекторий. Траек-
Траектория (X, С) эффективна по потребле-
н п го, если не существует другой допустимой траекто-
рии {X, С), выходящей из того же начального состояния,
для к-рой С~^С. Траектория (X, С) внутренне
эффективна, если не существует другой допус-
допустимой траектории (X, С), выходящей из того же началь-
начального состояния, момента времени t0 и числа Х>1, что
Оптимальность траектории обычно определяется в
зависимости от функции полезности и: R+—>-R+ и
коэффициента приведения полезности во времени (х^1
(о функции полезности см. ниже). Траектория (X, С)
наз. (м, (х)-о птимальноп, если
j Й)) -Т2 < ^
для любой допустимой траектории (X, С), выходящей
из того же начального состояния. Имеется ряд довольно
общих теорем существования для соответствующих
траекторий.
Эффективные в различных смыслах траектории ха-
характеризуются последовательностью цен точно так же,
как эффективный способ z характеризовался ценами
(коэффициентами опорной гиперплоскости) я. Т. е.
если для эффективного способа стоимость затрат равна
стоимости выпуска в оптимальных ценах, то на эффек-
эффективной траектории стоимость состояний постоянна и
максимальна, а на всех других допустимых траекториях
пе может возрастать.
Все приведенные определения легко обобщаются на
случай, когда производственное отображение а, функ-
функция и и коэффициент м, зависят от времени. Само время
может быть непрерывным или вообще параметр t может
пробегать множество довольно произвольного вида.
С экономич. точки зрения интерес представляют тра-
траектории, на к-рых достигается максимально возможный
темп роста экономики, к-рый она может выдержать
сколь угодно долго. Оказывается, что при неизменных
во времени а ж и такие траектории являются ста-
стационарными, т. е. имеют вид
где а — темп роста (расширения) экономики. Стацио-
Стационарные эффективные в том или ином смысле, а также
стационарные оптимальные траектории наз. маги-
магистралями.
При весьма широких предположениях имеют место
теоремы о магистрали, утверждающие, что всякая эф-
эффективная траектория, независимо от начального со-
состояния, с течением времени приближается к магист-
магистрали. Имеется большое число различных теорем о ма-
магистрали, различающихся определением эффективности
или оптимальности, способом измерения расстояния
до магистрали, типом сходимости, наконец, конечным
или бесконечным временным интервалом.
Модель экономич. динамики, у к-рой производст-
производственные возможности задаются многогранным выпуклым
конусом, наз. моделью Неймана. Частным
случаем модели Неймана является замкнутая
модель Леонтьева, или (по другой термино-
терминологии) замкнутый динамический меж-
межотраслевой баланс (термин «замкнутый»
используется здесь как характеристика свойства эко-
экономики, состоящего в отсутствии невоспроизводимых
продуктов), к-рый задается тремя матрицами с неотри-
неотрицательными элементами Ф, А и В порядка 1X1. Процесс
(х, y)?Z тогда и только тогда, когда найдутся векторы
v, w?R+ такие, что выполнены неравенства:
Модель межотраслевого баланса получила большое рас-
распространение из-за удобства получения исходной ин-
информации для ее построения.
Модели экономия, динамики рассматриваются также
в непрерывном времени. Одними из первых стали изу-
изучать как раз модели с непрерывным временем. В част-
частности, ряд работ был посвящен простейшей однопродук-
товой модели, задаваемой уравнением
x—f (г)—с,
где х — объем фондов, приходящихся на единицу тру-
трудовых ресурсов, с — потребление на душу населения,
/ — производственная функция (возрастающая, вогну-
вогнутая). Неотрицательные функции (x(t), c(t))T=o, Удовле-
Удовлетворяющие этому уравнению, характеризуют допусти-
допустимую траекторию. Для заданной функции полезности и
и коэффициента дисконтирования и, определяется опти-
оптимальная траектория. Оптимальные траектории (и
только они) удовлетворяют аналогу уравнения Эйлера
и (с)х= и (с) — и(с),
где с — максимальное число, удовлетворяющее усло-
условию 1 (х)—с=х.
Модель Леонтьева также была сначала сформулиро-
сформулирована в непрерывном времени в виде системы дифферен-
дифференциальных уравнений
Х=АХ+ВХ+С,
где X — потоки продуктов, А и В — матрицы текущих
и капитальных затрат соответственно, С — потоки
конечного потребления.
Эффективные и оптимальные траектории в моделях
с непрерывным временем изучаются с помощью методов
вариационного исчисления, оптимального управления,
математич. программирования в бесконечномерных про-
пространствах. Рассматриваются также модели, допусти-
допустимые траектории в к-рых задаютея дифференциальными
включениями вида х?а(х), где а — производственное
отображение.
Рациональное поведение потребителей. Вкусы и цели
потребителей, к-рые определяют их рациональное
поведение, даются в виде нек-рой системы предпочтений
в пространстве продуктов. А именно, для каждого по-
потребителя г определено точечно-множественное отобра-
отображение Рi : Z —>- 2х, где Z — нек-рое пространство си-
ситуаций, в к-рых может оказаться потребитель в процес-
процессе выбора, X — множество векторов, доступных по-
потребителю, XdR1. В частности, Z может включать в
себя в качестве подпространства RA Содержательно
множество Р i(z\x) состоит из всех векторов х?Х,
к-рые (строго) предпочитаются вектору х в ситуации z.
Напр., отображение j°,- может быть задано в виде
функции полезности и, где и (х) показывает
полезность от потребления набора продуктов х. Тогда
Пусть в описание ситуации : входят цены я на все про-
продукты и денежный доход потребителя d. Тогда В,(z) =
= {x?X\xn<.d} есть множество наборов, к-рые по-
потребитель может приобрести в ситуации г. Это множест-
множество наз. б ю д ж е т н ы м. Рациональность поведения
потребителя заключается в то.м, что он выбирает такие
наборы х из Bj(z), для к-рых P/(z\x)f\Bi(z)=0. Пусть
D (z) — множество наборов продуктов, выбираемых
потребителем i в ситуации z; Di наз. о т о б р а ж е н и-
е м (нлп функцией в случае, когда D ,-(z) состоит
из одной точки) спроса. Имеется ряд исследований,
посвященных выяснению свойств отображений i3,, В;,
D,-. В частности, довольно подробно изучен случай,
когда отображения />,- могут быть заданы в виде функ-
функции. Определены условия, при к-рых отображения
В; и D; являются непрерывными. Особый интерес пред-
представляет изучение свойств функции спроса D,-. Дело
в том, что иногда удобнее считать в качестве первичных
именно функции спроса D,-, а не предпочтения Р,, по-
поскольку их легче построить ио имеющейся информации
о поведении потребителей. Напр., в экономике (торго-
(торговая статистика) могут наблюдаться величины, прибли-
приближенно оценивающие частные производные
dDik (z) dDik (z)
где jtp — цена на продукт р, d — доход.
К теории рационального поведения потребителей
примыкает теория группового выбора, имеющая дело,
как правило, с дискретными вариантами. Обычно пред-
предполагается, что имеется конечное число участников
группы и конечное число, напр., альтернативных ва-
вариантов. Задача состоит в выборе группового решения
о выборе одного из вариантов при заданных отношениях
предпочтения между вариантами для каждого участ-
участника. Групповой выбор обеспечивает различные схемы
голосования, рассматриваются также аксиоматический
и теоретико-игровой подходы.
Согласование интересов. Носителями интересов яв-
являются отдельные части экономич. системы, а также
общество в целом. В качестве таких частей выступают
потребители (группы потребителей): предприятия, ми-
министерства, территориальные органы управления, пла-
плановые и финансовые органы и т. п. Различают два
взаимно переплетающихся подхода к проблеме согла-
согласования интересов — аналитический, или конструк-
конструктивный, и синтетический, или дескриптивный. Соглас-
Согласно первому подходу в качество исходного принима-
принимается глобальный критерий оптимальности (форма-
(формализация интересов всего общества в целом). Задача
состоит в том, чтобы вывести локальные (частные)
критерии из общего, учитывая при этом частные ин-
интересы. При втором подходе исходными являются
как раз частные интересы и задача заключается в объе-
объединении их в единую непротиворечивую систему, функ-
функционирование к-рой приводит к результатам, удовле-
удовлетворительным с точки зрения всего общества в целом.
К первому подходу впрямую относятся декомпозици-
декомпозиционные методы математич. программирования. Пусть,
напр., в экономике имеется т производителей и каждый
производитель / задается множеством производствен-
р / д р
ных возможностей Yj, где YjcR1 и является выпук-
выпуклым компактом. Задана целевая функция V всего об-
общества в целом, где V : R+ —»- R + — вогнутая функ-
функция. Экономика должна быть организована таким об-
образом, чтобы решалась задача выпуклого программиро-
программирования: найти у из условий г/>0, y^^jYj, У (у)—vmax.
По теореме о характеристике эффективных способов про-
производства существуют цены p?R+ (рфО) такие, что
г/(-"/> = max yW>p для всех/, у —У] У^¦
yd) 6 у. -"'
Величина yij)p интерпретируется как прибыль /-го
производителя при ценах р. Отсюда следует, что кри-
критерий максимизации прибыли у каждого из производи-
производителей не противоречит общей цели, если действующие
цены определены соответствующим образом. Схемы, от-
относящиеся ко второму подходу, получили большое раз-
развитие в рамках моделей экономич. равновесия.
Экономическое равновесие. Предполагается, что эко-
экономика состоит из отдельных частей, являющихся
носителями собственных интересов: производителей,
занумерованных индексами 7 = 1, ..., т, и потребите-
потребителей, занумерованных индексами ?=1, ..., п. Произ-
Производитель j описывается множеством производственных
возможностей YjcR.1 и отображением F}- : Z —>- 2Yi.
задающим его систему предпочтений. Здесь Z — мно-
множество возможных состояний экономики, конкретизи-
конкретизируемое ниже. Потребитель i описывается множеством
возможных наборов продуктов, доступных для потре-
потребления, XjCZR1, начальным запасом продуктов w^C-
?R*, предпочтением P,:Z—>-2 ' и, наконец, функ-
функцией а,- : Z —> R распределения доходов, где a,- (z) по-
показывает количество денег, поступающих потребителю
(всостоянии z. Множество возможных цен в экономике
есть Q. Тогда множество возможных состояний есть
Z= JJ ..Х,-Х Д\УуХ(). Бюджетное отображение В;
определяется здесь так:
В; (z) = {г«> ? Xt | х^р s? a; (z) +w">p}.
Состояние равновесия описанной экономики есть z?Z,
удовлетворяющее условиям
(I), г?,, (z)nр,- (z~= 0, yynFy (I)-0.
По существу состояние равновесия экономики совпада-
совпадает с определением решения бескоалиционной игры мно-
многих лиц в смысле Неймана — Нэша с дополнительным
условием, чтобы выполнялся баланс по всем продуктам.
Существование состояния равновесия доказано при
весьма общих условиях для исходной экономики. Го-
Гораздо более жесткие условия необходимо накладывать
для того, чтобы состояние равновесия было оптималь-
оптимальным, т. е. доставляло решение нек-рой глобальной оп-
оптимизационной задаче с целевой функцией, зависящей
от интересов потребителей. Напр., пусть Р,- задано во-
вогнутой непрерывной функцией к,- : R1 —>- R + , a F/
задано функцией py{j),
где Yj, X{— выпуклые компакты, 0?Y/, w^'^ int X,-
Любое подмножество S={i1, ..., ir] индексов потреби-
потребителей образует подэкономику исходной экономики, в
к-рой каждому потребителю is из S соответствует (один
и только один) производитель, множество производст-
производственных возможностей к-рого есть
Функции распределения доходов при этом имеют вид
Состояние z?Z наз. сбалансированным,
если
Говорят, что сбалансированное состояние z исходной
экономики блокируется коалицией потребителей S,
если в подэкономике, определяемой коалицией S, су-
существует такое сбалансированное состояние z(i), что
и; {xiis))^ui (a;(ii)) для s=l, ..., ги хотя бы для одного
индекса имеет место строгое неравенство. Ядром
экономики наз. множество всех сбалансирован-
сбалансированных состояний, к-рые не блокируются никакой коали-
коалицией потребителей. Для экономики с описанными свой-
свойствами имеет место теорема: всякое состояние равнове-
равновесия принадлежит ядру. Обратное неверно, однако най-
ден ряд достаточных условий, при к-рых множество со-
состояний равновесия и ядро близки друг к другу или
вообще совпадают. В частности, если число потребите-
потребителей стремится к бесконечности и влияние каждого по-
потребителя на состояние экономики становится все бо-
более малым, то множество состояний равновесия стре-
стремится к ядру. Совпадение ядра и множества состояний
равновесия имеет место в экономике с бесконечным (кон-
(континуальным) числом потребителей (теорема А у-
м а н а).
Пусть экономика является моделью рынка (т. е. от-
отсутствуют производители), множество участников (по-
(потребителей) к-рой является замкнутым единичным от-
отрезком [0, 1], обозначаемым далее Т. Состояние эко-
экономики есть z= (х, р), где р ? {р ? R+ | 2LikPk= 1 }, х есть
функция, отображающая Т в R|, каждая компонента
к-рой интегрируема по Лебегу на отрезке Т. Начальное
распределение продуктов между участниками задано
г*
функцией w, \ ip>0, таким образом сбалансированное
J Т
состояние z таково, что \x=\w. Коалиция участни-
участников — это измеримое по Лебегу подмножество множе-
множества Т. Если подмножество имеет меру 0, то соответст-
соответствующая коалиция паз. нулевой. Ядро — это множество
всех сбалансированных состояний, к-рые не блокируют-
блокируются ни одной ненулевой коалицией. Состояние z=(x, p)
является равновесием, если для почти каждого участ-
участника t
щ (х (()) = maxMf (x (t)),
x(t)?{x\xp<pw{t)}.
Теорема Аумана утверждает, что в описанной экономи-
экономике ядро и множество состояний равновесия совпадают.
Интерес представляет вопрос о структуре множества
состояний равновесия, в частности когда это множество
конечно или состоит из одной точки. Здесь имеет место
теорема Дебре. Пусть множество моделей рынка VF—
= {(w{i), D,-)?=!}, где u>('>?R+ суть начальные запасы
продуктов у участника i, вектор w=(w{1), ..., win))
является параметром, определяющим конкретную мо-
модель из множества W, w?|R"''. Отображение D; : QX
X М —>- R+ представляет собой функцию спроса для
г'-го участника. Функции Du ..., Dn заданы (не меня-
меняются) для всего множества экономик W. Пусть Wo,
WoczW,— совокупность экономик, у к-рых множество
состояний равновесия бесконечно. Теорема Деб-
р е утверждает, что если функции Diy ... , Dn непре-
непрерывно дифференцируемы и отсутствуют точки насыще-
насыщения хотя бы для одного из участников, то замыкание
множества Wo имеет (лебегову) меру нуль в пространст-
пространстве W.
О численных методах. М. э. имеет тесную связь с вы-
вычислительной математикой. Линейное программирова-
программирование, линейные экономич. модели оказали большое вли-
влияние на вычислительные методы линейной алгебры. По
существу благодаря линейному программированию не-
неравенства в вычислительной математике стали столь жо
употребительны, как и уравнения.
Трудным и многоплановым вопросом является вы-
вычисление экономич. равновесия. Напр., много работ
посвящено условиям сходимости к равновесию системы
дифференциальных уравнений
P=F(p), (*)
где р — вектор цен, F — функция избыточного спроса,
т. е. разность функций спроса и предложения. Равно-
Равновесные цены р, по определению, обеспечивают равен-
равенство спроса и предложения: F(p) = 0. Функция избыточ-
ного спроса F задается либо непосредственно, либо че-
через более первичные понятия соответствующей модели
равновесия. С. Смейлом [8] изучена существенно бо-
более общая динамич. система, чем (*), применительно
к модели рынка; наряду с изменением во времени цен
р рассмотрено изменение состояния х\ при этом допу-
допустимая траектория (p(t), x(t))T=o удовлетворяет нек-
рым дифференциальным включениям вида р?К(р),
х?С(р), где К (р) и С(р) — множества возможных на-
направлений изменения р и х, определенные через мо-
модель рынка.
Экономич. равновесие, решение игры, решение той
или иной экстремальной задачи могут быть определены
как неподвижные точки подходящим образом сформу-
сформулированного точечно-множественного отображения.
В рамках исследований по М. э. разрабатываются чис-
численные методы поиска неподвижных точек разных
классов отображений. Наиболее известен метод Скарфа,
к-рый является комбинацией идей леммы Шпернера и
симплекс-метода решения задач линейного програм-
программирования.
Смежные вопросы. М. э. тесно связана со многими
математич. дисциплинами. Иногда трудно определить,
где границы между М. э. и математич. статистикой или
выпуклым анализом, функциональным анализом, топо-
топологией и т. д. Можно указать, напр., на развитие тео-
теории положительных матриц, положительных линейных
(и однородных) операторов, спектральных свойств су-
суперлинейных точечно-множественных отображений под
влиянием потребностей М. э.
Лит.: [1] Нейман Д ш., Моргенштерн О., Тео-
Теория игр и экономическое поведение, пер. с англ., М., 1970;
L2] Канторович Л. В., Экономический расчет наилучшего
использования ресурсов, М., 1959; [3] Ни к аи до X., Вы-
Выпуклые структуры и математическая экономика, пер. с англ.,
М., 1972; [4] М а к а р о в В. Л., Рубинов А. М., Мате-
Математическая теория экономической динамики и равновесия,
М., 1973; [5] М и р к и н Б. Г., Проблема группового выбора
[информации], М., 1974; [6] Scarf H., The Computation of
Economic Equilibria, L., 1973; [7] Данциг Д ж., Линейное
программирование, его применения и обобщения, пер. с англ.,
М., 1966; [8] Smale S., «J. math. Economics», 1 976, №2,
p. 107—20. Л. В. Канторович, В. Л. Макаров.
МАТЕМАТИЧЕСКИЙ АНАЛИЗ — часть математи-
математики, в к-рой функции и их обобщения изучаются методом
пределов. Понятие предела тесно связано с понятием
бесконечно малой величины, поэтому можно также
сказать, что М. а. изучает функции и их обобщения
методом бесконечно малых.
Название «М. а.» — сокращенное видоизменение ста-
старого названия этой части математики — «Анализ бес-
бесконечно малых»; последнее полнее раскрывает содержа-
содержание, но оно — тоже сокращенное (название «Анализ
посредством бесконечно малых» охарактеризовало бы
предмет более точно). В классическом М. а. объектами
изучения (анализа) являются прежде всего функции.
«Прежде всего» потому, что развитие М. а. привело к
возможности изучения его методами более сложных об-
образований, чем функция,— функционалов, операторов
и т. д.
В природе и технике всюду встречаются движения,
процессы, к-рые описываются функциями; законы яв-
явлений природы также обычно описываются функциями.
Отсюда объективная важность М. а. как средства изу-
изучения функций.
М. а. в широком понимании этого термина охваты-
охватывает весьма большую часть математики. В него входят
дифференциальное исчисление, интегральное исчисление,
функций действительного переменного теория, функ-
функций комплексного переменного теория, приближения
теория, теория дифференциальных уравнений обык-
обыкновенных, теория дифференциальных уравнений с част-
частными производными, теория интегральных уравнений,
дифференциальная геометрия, вариационное исчисление,
функциональный анализ и нек-рые другие математич.
дисциплины. Современные чисел теория и вероятностей
теория применяют и развивают методы М. а.
Все же термин М. а. часто употребляется для наиме-
наименования только основ математического
анализа, объединяющих в себе теорию действи-
действительного числа, теорию пределов, теорию рядов, диф-
дифференциальное и интегральное исчисление и их непо-
непосредственные приложения, такие как теория максиму-
максимумов и минимумов, теория неявных функций, Фурье ряды,
Фурье интегралы.
Функция. В М. а. исходят из определения функции
по Лобачевскому и Дирихле. Если каждому числу х из
нек-рого множества F чисел в силу к.-л. закона приве-
приведено в соответствие число у, то этим определена функ-
функция
от одного переменного х. Аналогично определяется
функция
/ (*)=/ (хи ¦¦¦, хп)
от п переменных, где х=(х1, ..., х„) — точка ге-мерного
пространства; рассматривают также функции
!(x)=f{xx, ж2, ...)
от точек х=(хи х.2, ...) нек-рого бесконечномерного про-
пространства, к-рые, впрочем, чаще называют функцио-
функционалами.
Элементарные функции. Фундаментальное значение
в М. а. играют элементарные функции. На практике
в основном оперируют с элементарными функциями,
ими приближают функции более сложной природы.
Элементарные функции можно рассматривать не толь-
только для действительных, но и комплексных х; тогда пред-
представления об этих функциях становятся в определенном
смысле законченными. В связи с этим возникла важная
ветвь М. а., наз. теорией функций комплексного пере-
переменного, или теорией аналитических функций.
Действительное число. Понятие функции существенно
базируется на понятии действительного (рационально-
(рационального и иррационального) числа. Оно окончательно сфор-
сформировалось только в конце 19 в. В частности, установ-
установлена логически безупречная связь между числами и
точками геометрич. прямой, к-рая привела к формаль-
формальному обоснованию идей Р. Декарта (R. Descartes, сер.
17 в.), к-рын ввел в математику прямоугольные системы
координат и представление в них функций графиками.
Предел. В М. а. методом изучения функций является
предел. Различают предел последовательности и предел
функции. Эти понятия окончательно сфермирова-
лись только в 19 в., хотя представление о них имели
еще др.-греч. ученые. Достаточно сказать, что Архи-
Архимед C в. до н. э.) умел вычислять площадь сегмента
параболы при помощи процесса, к-рый мы назвали бы
предельным переходом (см. Исчерпывания метод).
Непрерывные функции. Важный класс функций,
изучаемых в М. а., образуют непрерывные функции.
Одно из возможных определении этого понятия: функ-
функция y=f(x) от одного переменного х, заданная на ин-
интервале (а, 6), наз. непрерывной в точке х,
если
lim Д(/= lim [f (x + A.r)—f (x)] = 0.
Ах -»• 0 Ах ->¦ О
Функция непрерывна на интервале
(а, Ь), если она непрерывна во всех ого точках; тогда ее
график представляет собой кривую, непрерывную в
житейском понимании этого слова.
Производная и дифференциал. Среди непрерывных
функций следует выделить функции, имеющие произ-
производную. Производная от функции
y=f(x), a<x<b,
в точке х есть скорость изменения ее в этой точке, т. е.
предел
lim -?= lim /(x+^-/fa) = /'(x). A)
Ах -> 0 ' Д* ->• О
Если у есть координата точки, движущейся по оси ор-
ординат в момент времени х, то /' (х) есть мгновенная ско-
скорость точки в момент времени х.
По знаку производной /' (х) судят о характере изме-
изменения f(x): если /'(.т)>0 (/'(т)<0) иа интервале (с, d),
то функция / возрастает (убывает) на этом интервале.
Если же функция / в точке х достигает локального экст-
экстремума (максимума или минимума) и имеет в этой точке
производную, то последняя равна нулю в этой точке
/'(а-„) = 0.
Равенство A) можно заменить эквивалентным равен-
равенством
j!L=f' (х) + е(Ах), е(Д*)-*0, Д*-—О,
или
где г(Ах) есть бесконечно малая, когда Ах —>¦ 0; т. е.
если функция / имеет производную в точке х, то прира-
приращение ее в этой точке разлагается на два слагаемых.
Из них первое
dy=f'(x)Ax B)
есть линейная функция от Ах (пропорциональная Да;),
второе — стремится к нулю быстрее, чем Да:.
Величина B) наз. дифференциалом функции, соот-
соответствующим приращению Ах. При малых Ах можно
считать Дг/, приближенно равным dy:
Ay~dy.
Приведенные рассуждения о дифференциале харак-
характерны для М. а. Они распространяются на функции
многих переменных и на функционалы.
Напр., если функция
z = f (a-j, х2, ..., xn) = f (x)
от п переменных имеет непрерывные частные производ-
производные в точке х=(хг, ... , хп), то ее приращение Дг, соот-
соответствующее приращениям Ахг, Ах2, ... , Ахп незави-
независимых переменных, можно записать в виде
\x), C)
где е(Дх) —>. О при Ах —>- 0, то есть если все Ах% —>- 0.
Здесь первый член в правой части C) есть дифференциал
dz функции /. Он линейно зависит от Ax=(Ati, ... ,
Ахп), а второй член стремится к нулю при Ах —>- 0 быст-
быстрее, чем Ах.
Пусть задан функционал (см. ст. Вариационное
исчисление)
J (х) =
(x)=V1L(t, х, x')dt,
J »о
распространенный на классы Ш1 функций x(t), имею-
имеющих на отрезке [t0, tx] непрерывную производную
и удовлетворяющих граничным условиям x(to) = xo,
x(tl)=x1, где х0, хЛ — данные числа; пусть, далее,
ЭП0 — класс функций h (t), имеющих непрерывную про-
производную на [tg, «J и таких, что h(to)=h(t1)=O. Очевид-
Очевидно, если я(/NЭД1 и h(t)?m0, то x(t)+h(t)?m.
В вариационном исчислении доказывается, что при
известных условиях на L приращение функционала
J (х) может быть записано в виде
J(x+h)-J (*)=J? (|L_ JL(J|l)) h (t) dt+o (\\h\\) D)
при life II -+0, где
||fe||= max | h («)|+ max \h' (t) |,
ta<t<tl to<t<?tl
и, таким образом, второй член правой части D) стре-
стремится к нулю быстрее, чем \\h\\, а первый член линейно
зависит от h?ffi}0. Первый член в D) наз. вариацией
функционала и обозначается б/(х, К).
Интеграл. Наряду с производной интеграл имеет
фундаментальное значение в М. а. Различают неопре-
неопределенный и определенный интегралы.
Неопределенный интеграл тесно связан с первооб-
первообразной функцией. Функцию F(x) наз. первооб-
первообразной от функции f на интервале (д, Ь), если на
этом интервале F'(x)=f(x).
Определенный интеграл (Римана) от функции / на
отрезке [а, Ь] есть предел
lim 2;Л=' / <&/) (*/ + !-*/)
при шах(жу + 1—xj) —»-0; здесь а=а;0<а;1<...
<= b.
Если функция / положительна и непрерывна на от-
отрезке [а, ?>], то интеграл от нее на этом отрезке равен
площади фигуры, ограниченной кривой y=f{x), осью
Ох и прямыми х=а, х—Ъ.
Класс интегрируемых по Риману функций содержит
все непрерывные на [а, 6] функции и нек-рые разрыв-
разрывные функции. Но все они необходимо ограничены. Для
неограниченных функций, растущих не очень быстро, а
также для нек-рых функций, заданных на бесконечных
интервалах, вводят так наз. несобственные интегралы,
требующие для своего определения двойного перехода
к пределу.
Понятие интеграла Римана для функции одного пере-
переменного распространяется на функции многих перемен-
переменных (см. Кратный интеграл).
С другой стороны, потребности М. а. привели к обоб-
обобщению интеграла совсем в другом направлении, имеется
в виду Лебега интеграл или более общий Лебега—
Стилтъеса интеграл. Существенным в определении
этих интегралов является введение для нек-рых мно-
множеств, называемых измеримыми, понятия их меры и на
этом основании — понятия измеримой функции. Для
измеримых функций и вводится интеграл Лебега —
Стнлтьеса. При этом рассматривается широкий диапа-
диапазон разных мер и соответствующих им классов измери-
измеримых множеств и функций. Это дает возможность при-
приспособить тот или иной интеграл к определенной кон-
конкретной задаче.
Формула Ньютона — Лейбница. Между производной
и интегралом имеется связь, выражаемая форму-
формулой (теоремой) Ньютона — Лейбница
С* / (х) dx = F (b) — F (a).
Здесь f(x) непрерывная на [а, Ь] функция, a F(x) — ее
первообразная.
Формула и ряд Тейлора. Наряду с производной и ин-
интегралом важнейшим понятием (орудием исследования)
в М. а. являются Тейлора формула и Тейлора ряд. Если
функция j{x), аО<6, имеет в окрестности точки х0
непрерывные производные до порядка п включительно,
то ее можно приблизить в этой окрестности многочленом
наз. ее многочленом Тейлора (степени га)
по степеням х—z0:
f (х) ~ Рп (х)
(формула Тейлора); при этом ошибка прибли-
приближения
стремится к нулю при х —>• х0 быстрее, чем (х—хо)п:
Rn (х) = о ((х — х0)") при х—>х0.
Таким образом, функция / (х) в окрестности точки
х0 может быть приближена с любой степенью точности
весьма простой функцией (многочленом), требующей
для своего вычисления только арифметич. операций —
сложения, вычитания и умножения.
Особенно важными являются так наз. аналитические
в определенной окрестности х„ функции, имеющие бес-
бесконечное число производных, такие, что для них в этой
окрестности Rn(x) —>- 0 при п—>- оо; они могут быть
представлены в виде бесконечного степенного ряда
Тейлора:
Разложения Тейлора при определенных условиях
возможны н для функций многих переменных, а также
функционалов и операторов.
Историческая справка. До 17 в. М. а. представлял
собой совокупность решений разрозненных частных
задач; напр., в интегральном исчислении — это задачи
на вычисление площадей фигур, объемов тел с кривыми
границами, работы переменной силы и т. д. Каждая
задача или частная группа задач решалась своим мето-
методом, подчас сложным и громоздким (о предыстории
М. а. см. статью Бесконечно малых исчисление). М. а.
как единое и систематич. целое сложился в трудах
И. Ньютона (I. Newton), Г. Лейбница (G. Leibniz),
Л. Эйлера (L. Euler), Ж. Лаграюка (J. Lagrange) и др.
ученых 17—18 вв., а его база — теория пределов —
была разработана О. Коши (A. Cauchy) в нач. 19 в.
Глубокий анализ исходных понятий М. а. был связан
с развитием в 19—20 вв. теории множеств, теории ме-
меры, теории функций действительного переменного и
привел к разнообразным обобщениям.
Лит.: [1.1 Ла В а л л е - П у с с е н Ш.-Ж. д е, Курс ана-
анализа бесконечно малых, пер. с франц., т. 1—2, М., 1933; 12]
Ильин В. А., П о з и я к Э. Г., Основы математического
анализа, 3 изд., ч. 1, М., 1971; 2 изд., ч. 2, М., 1980; [3] И л fa-
fail н В. А., Садовничий В. А., С е н д о в Б. X., Матема-
Математический анализ, М., 1979; [4] К у д р я в ц е в Л. Д., Матема-
Математический анализ, 2 изд., т. 1—2, М., 1973; [5] Николь-
Никольский С. М., Курс математического анализа, 2 изд., т. 1—2,
Ы., 1975; [6] У и т т е к е р Э. Т., В а т с о н Д ж. Н., Курс
современного анализа, пер. с англ., ч. 1—2, 2 изд., М., 1962—63;
[7] Ф и х т е н г о л ь ц Г. М., Курс дифференциального и ин-
интегрального исчисления, 7 изд., т. 1—2, М., 1970; 5 изд., т. 3,
М., 1970. С. М. Никольский.
МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ Э В М,
программное обеспечен и е,— совокуп-
совокупность программ и программных комплексов, посредст-
посредством к-рых происходит преобразование алгоритмов про-
программы пользователя, записанных на алгоритмич.
языках высокого уровня, в последовательность команд,
понимаемых электроникой ЭВМ, организуется автома-
тич. прохождение задач пользователей на ЭВМ, обес-
обеспечивается эффективное использование оборудования
ЭВМ (см. [1] — [4]).
Появление М. о. было вызвано необходимостью повы-
повышения производительности труда программистов и спе-
специалистов, эксплуатирующих ЭВМ. Действительно,
команды вычислительной машины представляют собой с
точки зрения возможности записи алгоритма весьма
элементарные операции, и запись алгоритма (програм-
(программирование) в виде последовательности этих команд яв-
является трудоемкой работой. Это стимулировало созда-
создание средств автоматизации программирования. Проис-
Происходило укрупнение операций, понимаемых электрони-
электроникой машины, но это не решило проблемы. Даже у сов-
ременных ЭВМ команды, как правило, представляют со-
собой элементарные операции. Существенно больший
успех был достигнут на пути создания программных
средств, облегчающих программирование. Первым ша-
шагом было создание М. о., позволяющего программиро-
программировать на автокоде. Программа на автокоде фактически
представляет собой ту же последовательность команд
ЭВМ, но записанных символическими обозначениями —
в мнемоническом виде. Преобразование мнемонич. кода
программы в команды машины осуществляют специаль-
специальные программы — ассемблеры. Затем появились
макроассемблеру, к-рые дали возможность
использовать в текстах программ макрооператоры,
обеспечивающие выполнение группы команд машины.
Следующим этапом автоматизации программирова-
программирования было создание алгоритмических языков высокого
уровня. Имеется свыше тысячи алгоритмич. языков
различного назначения, применение к-рых существен-
существенно сокращает затраты на разработку и создание про-
программ. Первым, получившим широкое распространение,
стал язык фортран. Затем появились языки алгол, ал-
гамс, а в СССР и язык альфа, предназначенные в основ-
основном для проведения научно-технич. расчетов. Для запи-
записи алгоритмов обработки экономия, информации был
создан язык кобол. Алголоподобный язык паскаль имеет
средства для описания структуры данных. Для работы
с текстовой информацией предназначены языки лисп,
снобол, амбит, едл и др. Для описания алгоритмов про-
проведения аналитич. преобразований на ЭВМ получила
широкое распространение система Reduce, а в СССР
и язык аналитик (см. [5]). Как развитие и обобщение
языков фортран, алгол и кобол появились языки ПЛИ
и алгол-68.
Параллельно с развитием языковых средств велись
работы по созданию библиотек стандартных программ.
Имеются тысячи подпрограмм, программ и программ-
программных комплексов, в к-рых реализованы алгоритмы обще-
общего и специального назначения с использованием мето-
методов вычислительной математики. Среди них: вычисле-
вычисление элементарных и специальных функций, линейная
алгебра, счет интегралов, численное решение обыкно-
обыкновенных дифференциальных уравнений и уравнений с
частными производными, метод наименьших квадратов
и др. Стандартные программы организованы в виде биб-
библиотек подпрограмм, записанных на магнитные ленты
или диски, так что они легко доступны. Для вызова под-
подпрограммы достаточно поставить в программе оператор
обращения к ной. Наиболее часто применяемые под-
подпрограммы хранятся в виде стандартных модулей за-
загрузки на языке, весьма близком к кодам ЭВМ. Как
правило, трансляторы с алгоритмич. языков выдают
результат своей работы в виде последовательности от-
отдельных подпрограмм и процедур, к-рые сразу же пос-
после трансляции записываются во временную библиотеку
в виде стандартных модулей загрузки. Последующее
объединение отдельных подпрограмм в рабочую про-
программу в кодах ЭВМ с соответствующей настройкой
осуществляет загрузчик либо перед началом счета (ста-
тич. загрузчик), либо во время счета в момент вызова
конкретной подпрограммы (динампч. загрузчик).
В нек-рых системах объединение отдельных оттрансли-
оттранслированных ранее частей программ в единую программу
осуществляет т. н. редактор связен, а загрузчик только
располагает готовую программу в памяти машины.
Наряду с пополнением библиотеки стандартных под-
подпрограмм все большее распространение получает прак-
практика создания пакетов прикладных программ, рассчи-
рассчитанных на решение не отдельной задачи, а целого
класса задач. Пакет программ представляет собой сово-
совокупность подпрограмм, работающих под управлением
головной программы.' Режим работы пакета задается
посредством специализированного проблемно-ориенти-
ровалного языка, чаще всего являющегося подмножест-
подмножеством обычного профессионального языка или жаргона.
Современные ЭВМ наряду со средствами, облегчаю-
облегчающими написание н отладку программ, оснащаются так-
также программными комплексами, обеспечивающими эф-
эффективное использование самих ЭВМ путем организа-
организации автоматич. прохождения задач (управление зада-
заданиями), управления данными, динамич. распределения
памяти, внешних устройств (управления ресурсами).
Совокупность этих программных средств наз. опера-
операционной системой (ОС) ЭВМ (см. [1] —
14], [6]). ОС стали неотъемлемой частью вычислительных
систем. Без ОС невозможно функционирование ЭВМ,
т. к. управление работой внешних устройств, обмен ин-
информацией, организация взаимодействия отдельных
элементов ЭВМ в значительной мере осуществляются
посредством программ, входящих в ОС. Под управле-
управлением ОС функционируют трансляторы с алгоритмич.
языков, системы программ, облегчающих программи-
программирование и отладку (в том числе и в диалоговом режиме),
а также обеспечивающих работу с графич. информаци-
информацией. ОС предоставляют средства для работы с большими
массивами данных, для ведения файлов (последова-
(последовательность групп данных, как правило, одинаковой
структуры), создания баз данных и различного рода ин-
информационно-поисковых систем. ОС обеспечивает ис-
использование ЭВМ в составе многомашинных комплек-
комплексов, в сетях ЭВМ. Кроме языковых средств, облегчаю-
облегчающих программирование, пользователю также предо-
предоставляется возможность управления работой ОС по-
посредством управляющих операторов (перфокарт),
к-рые вводятся в ЭВМ вместе с программой.
В зависимости от режима работы, к-рый обеспечи-
обеспечивается ОС, различают три типа использования ЭВМ.
1) Пакетная обработка программ за-
заключается в автоматич. прохождении (решении) потоков
задач на ЭВМ, в том числе и в мультипрограммном ре-
режиме. Примерами ОС, обеспечивающих такой режим ра-
работы, являются ОС ЕС и ДОС ЕС для машин единой се-
серии (см. [1], [8]) и машин фирмы ИБМ; системы ОС
ДУБНА и ОС ДИСПАК для БЭСМ-6 (см. [91); систе-
система NOS/BE для машин фирмы Control Data.
2) Режим разделения времени дает
возможность одновременно обслуживать многих поль-
пользователе]!, работающих с терминалов, связанных с
ЭВМ, в том числе находящихся на больших расстояниях
от нее. В качестве примеров ОС, обеспечивающих работу
в таком режиме, можно назвать одну из ранних экспери-
экспериментальных систем MULTICS и систему TSS/360 для
машин ИБМ. В крупных вычислительных системах
режим разделения времени, как правило, обеспечи-
обеспечивается операционными системами, к-рые одновременно
ведут счет и в режиме пакетной обработки. При этом
взаимодействие с ОС происходит посредством специаль-
специальных подсистем, работающих под управлением основ-
основной ОС. В NOS/BE это — система Intercom, в ОС ДУБ-
ДУБНА — мультитайп, в ОС ДИСПАК — система ДИМОН
(см. [10]), в ОС ЕС — ДУУВЗ и СРВ (см. [11]).
При работе с терминалов на ЭВМ, ведущей счет в па-
пакетном режиме, пользователям предоставляются в ре-
режиме разделения времени только средства для набора,
редактирования программ и их запуска на счет. Транс-
Трансляция программ и счет идут в обычном режиме пакет-
пакетной обработки, как правило, с высшим приоритетом.
Пользователи имеют возможность просмотреть резуль-
результат .ирохом-тения задач и, если необходимо, заново их
отредактировать и вновь запустить на счет. Программа
может обращаться к терминалу и в реальном времени,
как к внешнему устройству ЭВМ, для ввода-вывода ин-
информации в режиме диалога.
Системы режима разделения времени часто оснащают-
оснащаются трансляторами, работающими в режиме интерпре-
тации, когда отдельная инструкция (оператор языка)
преобразуется в коды ЭВМ и выполняется сразу же по-
после ее набора на терминале.
3) Операционные системы реаль-
реального времени обеспечивают функционирование
ЭВМ на линии с внешним оборудованием, к-рое в про-
произвольные моменты времени может посылать в ЭВМ
информацию, требующую оперативной обработки в мо-
момент ее поступления. ОС такого типа предназначены
для управления экспериментальными и технологич.
установками, работающими на линии с ЭВМ (см. [12],
[13], [14], [15]). Нередко в роли ОС реального времени
выступают соответствующим образом доработанные ОС
пакетного режима. ЭВМ, предназначенные для работы
на линии с оборудованием (управляющие ЭВМ), имеют
технические и программные средства, облегчающие
создание программ и их функционирование в реальном
времени.
Понятия и терминология в области М. о. п системно-
системного программирования еще не четко установились. Ра-
Ранее в состав ОС включались трансляторы, теперь боль-
большинство исследователей относят их к прикладным
программам, работающим под управлением ОС. Раз-
Разными учеными название компонент ОС, а часто и раз-
разбиение ОС на отдельные компоненты делается по-раз-
по-разному. Это связано главным образом с быстрым разви-
развитием этой области науки н непрерывным появлением
новых понятий.
Кроме рассмотренного выше М. о. ЭВМ общего па-
значения (операционные системы и прикладные паке-
пакеты общего назначения), имеется и продолжает активно
создаваться М. о., нацеленное на решение конкретных
проблем в различных отраслях науки, техники и на-
народного хозяйства. Программные проблемно-ориенти-
проблемно-ориентированные комплексы создаются с использованием
языковых средств и других возможностей, предостав-
предоставляемых ОС ЭВМ. Объем этого М. о. намного превос-
превосходит объем М. о. ЭВМ общего назначения.
В крупных институтах ядерной физики и физики вы-
высоких энергий используются десятки (иногда более'
сотни) ЭВМ разного класса в основном для управле-
управления и съема информации с экспериментальных устано-
установок. Для каждой такой установки созданы специали-
специализированные ОС реального времени или разделении
времени (см. [16]). Специализированные ОС обеспечива-
обеспечивают функционирование не только ЭВМ, но и сложных
электронно-механич. систем. Большие комплексы про-
программ под управлением этих ОС контролируют пра-
правильность работы аппаратуры, съем информации, ее
обработку, сжатие и накопление. Экспериментатору
предоставляются богатые средства диалогового графич.
взаимодействия с системой.
Часть систем работает в режиме автоматич. опозна-
опознавания событий и их изображений. Кроме специализиро-
специализированных ОС, в состав М. о. экспериментов также входят
большие комплексы программ, предназначенные для
обработки экспериментальной информации. Система
программ для обработки фильмовой информации имеет
объем в десятки тысяч операторов фортрана, она соз-
создана в рамках модульной системы программирования
ГИДРА (см. [17]). Система ГИДРА предоставляет поль-
пользователю средства для редактирования, организации
хранения различных версий программ, для создания
версий программ для конкретной трековой камеры, экс-
эксперимента и типа доступной электронной машины.
В системе нашли воплощение все современные достиже-
достижения программирования: модульный принцип, структур-
структурное программирование, самодркумонтированне, дина-
мич. распределение оперативной памяти, удобные сред-
средства генерации. Создание конкретной версии программы
сводится к написанию последовательности строк, ука-
указывающих тип измерительного устройства, этап об-
работки и форму выдачи информации, и к заданию
числовой информации, описывающей параметры тре-
трековой камеры (константы оптич. системы, карта
магнитного поля) и топологию изучаемых событий. Ре-
Результатом работы системы является текст программы на
фортране, сгенерированный из модулей, хранящихся
в системе или введенных пользователем.
Не только для ядерной физики, но и для многих
других отраслей науки и техники созданы большие про-
проблемно-ориентированные комплексы программ (см. [18]).
Среди них комплексы программ для обработки инфор-
информации в молекулярной биологии и кристаллофизике
(см. [19]), электро- (ЭПАК) и сейсморазведке (СЕЙО
ПАК) полезных ископаемых (см. [20]), программные
комплексы для автоматизации проектирования (см.
[21]), для автоматизированных систем управления(АСУ)
в народном хозяйстве и многие др. Как правило, созда-
создание программы для решения той или другой задачи с
использованием проблемно-ориентированных систем
сводится к подготовке ее описания на языке, являю-
являющемся управляющим, входным языком системы и по-
построенным на основе определений и понятий, исполь-
используемых в данной области науки, техники.
Таким образом, М. о. ЭВМ можно представить в виде
двух уровней.
Первый уровень — комплекс программ, входящих в
ОС или работающих под ее непосредственным управ-
управлением, к-рый является общим М. о., поставляемым
вместе с вычислительной системой. Кроме программ
собственно ОС, в общее М. о. входят в первую очередь
трансляторы с машинно-ориентированных и широко
распространенных процедурно-ориентированных алго-
ритмич. языков, а также библиотеки стандартных под-
подпрограмм общего назначения.
Второй уровень представлен проблемно-ориентиро-
проблемно-ориентированными программными комплексами. Они являются,
как правило, надстройкой над общим М. о. первого
уровня и создаются с использованием языковых средств
и др. возможностей, представляемых М. о. первого
уровня. Проблемно-ориентированное М. о. по общей
организации и назначению можно разбить на два типа.
Первый — это программные комплексы, создаваемые
на универсальных ЭВМ общего назначения с исполь-
использованием средств, представляемых М. о. Они предназ-
предназначены для решения определенных классов задач или
обработки данных. С точки зрения связи с ОС ЭВМ эти
комплексы являются обычными прикладными програм-
программами. Второй тип представлен специализированными
ОС реального времени или управляющими програм-
программами, к-рые создаются как с использованием средств,
предоставляемых стандартными ОС ЭВМ, так и без их
использования. Это М. о. управляет сложными элек-
электронными и электромеханич. системами, в к-рых ЭВМ
составляют только часть из всего оборудования систе-
системы.
Лит.: [1] К о р о л е в Л. Н., Структуры ЭВМ и их матема-
математическое обеспечение, 2изд., М., 1978; [2] К риниц ки й Н. А.,
М и р о н о в Г. А., Ф р о л о в Г. Д., Программирование и
алгоритмические языки, 2 изд., М., 1979; [3] Ф л о р е с А.,
Программное обеспечение, пер. с англ., М., 1971; [4] Д о н о-
в а н Д ж., Системное программирование, пер. с англ., М., 1975;
[5] Г л у ш к о в В. М. [и др.], «Кибернетика», 1971, № 3,
с. 102—34; [6] К а т ц а н Г. (мл.), Операционные системы, пер.
с англ., М., 1976; [7] В е л ь б и ц к и й И. В., Технология про-
производства программ на базе Д-метаязыка, в кн.: Системное и те-
теоретическое программирование, т. 1, Киш., 1974; [8] Система
математического обеспечения ЕС ЭВМ, М., 1974; [91 М а з-
ный Г. Л., Программирование на БЭСМ-6 в системе «Дубна»,
М. 1978; [10] Усов С. А., Диалоговый монитор Димон, М.,
1979; [11] П е л е д о в Г. В., Р а й к о в Л. Д., в кн.: Вычис-
Вычислительная техника социалистических стран, в. 2, М., 1977,
с. 78—82; [12] Глушков В. М., Автоматизированные сис-
системы управления, в кн.: Тр. Всесоюзной конференции по про-
программированию «ВКП-2», Новосиб., 1970; [13] В и л е н-
н и н С. Я., Трахтенгерц Э. А., Математическое обеспе-
обеспечение управляющих вычислительных машин, М., 1972; [14]
Мартин Дж., Программирование для вычислительных сис-
1ем реального времени, пер. с англ., М., 1975; [15] Тезисы докла-
дов [1-го Всесоюзного симпозиума по математическому обеспе-
обеспечению вычислительных систем, работающих в реальном мас-
масштабе времени], К., 1972; [16] Говорун Н. Н., Иван-
Иванченко 3. м., «Программированием, 1976, №.4, с. 52—65;
[17] Говорун Н. Н. [и д р.], «Физика элементарных частиц
и атомного ядра», 1975, т. 6^ в. 3, с. 742—75; [18] С е р г и е н-
к о И. В., Парасюк И. Н., Т у к а л е в с к а я Н. И.,
Автоматизированные системы обработки данных, К., 1976; [19]
Рентгеновский структурный анализ, в кн.: БСЭ, 3 изд., т. 22,
с. 23—27; [20] Б е з р у к И. А., Сафонов А. С,в кн.:
Прикладная геофизика, в.98, М. ,1980; [2ЦГ л ушков В. М.,
Капитонова Ю. В., Л я т и ч е в с к и и А. А., «Кибер-
«Кибернетика», 1970, №4, с. 1 — 6. Н. Н. Говорун.
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ, среднее
значение, случайной величины —
числовая характеристика распределения вероятностей
случайной величины. Самым общим образом М. о. слу-
случайной величины Х(ш), co^fi, определяется как ин-
интеграл Лебега по отношению к вероятностной мере Р
в исходном вероятностном пространстве (Q, А, Р):
\=\QX (co)P(a'co). (*)
M. о. может быть вычислено и как интеграл Лебега
от х по распределению вероятностей Рх величины X'.
где ЗЕ — множество всех возможных значений X.
М. о. функции от случайной величины X выражается
через распределение Рх- напр., если X — случайная
величина со значениями в R1 и / (х) — однозначная бо-
релевская функция х, то
Е/ (Х)= JQ/ (X (со)) Р (*¦>)= JRi/ (х) Px(dx).
Если F(x) — функция распределения X, то М. о.
представимо интегралом Лебега — Стилтьеса (или Ри-
мана — Стилтьеса)
при этом интегрируемость X в смысле (*) равносильна
конечности интеграла
+ °° xdF (x).
В частных случаях, если X имеет дискретное распреде-
распределение с возможными значениями х^, к=1, 2, . . ., и
соответствующими вероятностями />ft=P {со : X (w)=
= хь], то
если X имеет абсолютно непрерывное распределение
с плотностью вероятности р{х), то
хр (х) dx;
при этом существование М. о. равносильно абсолют-
абсолютной сходимости соответствующего ряда или интеграла.
Основные свойства М. о.:
а) ЕХ!<ЕХ2, если Хх(«))<:Х2(ш), co?Q;
б) ВС=С для любого действительного С;
в) В(аХ1-\-рх2)=аВХ1-\-рвХ2 для любых действи-
действительных а и Р;
г) Е B°°—1 -^л) = 2 =1 ЕХл> если сходится ряд
2,U
д) g(?X)<Eg(X) для выпуклых функций g(x)\
е) любая ограниченная случайная величина имеет
конечное М. о.
Кроме того,
ж) Е (Д*=1 ^*)=Пй=г E^ft для взаимн0 независи-
независимых случайных величин Хи . . ., Хп.
Естественным образом можно определить понятие
случайной величины с бесконечным М. о. Типичным
примером служат времена возвращения в нек-рых слу-
случайных блужданиях (см., напр., Бернулли блуждание).
С помощью М. о. определяются многие числовые и
функциональные характеристики распределения (как
М. о. соответствующих функций от случайной вели-
величины), напр, производящая функция, характеристиче-
характеристическая функция, моменты любого порядка, в частности
дисперсия, ковариация.
М. о. есть характеристика расположения значений
случайной величины (среднее значение ее распределе-
распределения). В этом качестве М. о. служит нек-рым «типич-
«типичным» параметром распределения и его роль аналогична
роли статич. момента — координаты центра тяжести
распределения массы — в механике. От прочих харак-
характеристик расположения, с помощью к-рых распределе-
распределение описывается в общих чертах,— медиан, мод, М. о.
отличается тем большим значением, к-рое оно и соответ-
соответствующая ему характеристика рассеяния — дисперсия —
имеют в предельных теоремах теории вероятностей. С
наибольшей полнотой смысл М. о. раскрывается боль-
больших чисел законом (см. также Чебышева неравенство) и
больших чисел усиленным законом. В частности, для
последовательности взаимно независимых и одинаково
распределенных случайных величин Х1? . . ., Хп
с конечными М. о. а=ВХ^ при п —>¦ оо для любого е>0
и, более того,
Х,+ . . .+ХГ,
с вероятностью единица.
Понятие М. о. как ожидаемого значения случайной
величины впервые наметилось в 18 в. в связи с теорией
азартных игр. Первоначально термин «М. о.» был вве-
введен как ожидаемый выигрыш игрока, равный /рьпь
для возможных выигрышей х1г . . ., хп и соответствую-
соответствующих вероятностей рх, . . ., р„. Особые заслуги в обоб-
обобщении и использовании понятия М. о. в современном
его значении имеет П. Л. Чебышев.
Лит.: [1] Колмогоров А. Н., Основные понятия тео-
теории вероятностей, 2 изд., М., 197-4; [2] Феллер В., Введение
в теорию вероятностей и ее приложения, пер. с англ., 2 изд.,
тт. 1—2, М., 1967; [3] Л о э в М., Теория вероятностей, пер. с
англ., М., 1962; [4] К р а м е р Г., Математические методы ста-
статистики, пер. с англ., 2 изд., М., 1975. А. В. Прохоров.
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ — ма-
математическая дисциплина, посвященная теории и ме-
методам решения задач о нахождении экстремумов функ-
функций на множествах конечномерного векторного прост-
пространства, определяемых линейными и нелинейными ог-
ограничениями (равенствами и неравенствами). М. п.—
раздел науки об исследовании операций, охватывающий
широкий класс задач управления, математич. моде-
моделями к-рых являются конечномерные экстремальные
задачи. Задачи М. п. находят применение в различных
областях человеческой деятельности, где необходим
выбор одного из возможных образов действий, напр,
при решении многочисленных проблем управления
и планирования производственных процессов, в зада-
задачах проектирования и перспективного планирования.
Наименование «М. п.» связано с тем, что целью реше-
решения задач является выбор программы действий.
Математич. формулировка задачи М. п.: минимизи-
минимизировать скалярную функцию векторного аргумента
Ф (х) на множестве
X={x:q;(x)^0, i=\, 2, ..., k;
hj(x) = Q, /=1, 2, ..., от},
где qi (x) и hj (x) — скалярные функции. Функцию
Ф(х) наз. целевой функцией, функцией
цели, а также критерием качества, множество
X — допустимым множеством, или мно-
множеством планов, решение х* задачи М. п.—
оптимальной точкой (вектором), точкой
глобального минимума, а также опти-
оптимальным планом.
В М. п. принято выделять следующие разделы. Ли-
Линейное программирование', целевая функция ф(ж) и
ограничения д,(х) и hj-(x) линейны; квадратичное про-
программирование: целевая функция квадратична и вы-
выпукла, допустимое множество определяется линейными
равенствами и неравенствами; в ы п у к л.о е про-
программирование: целевая функция и допусти-
допустимое множество выпуклы; дискретное программирова-
программирование: решение ищется лишь в дискретных, напр, цело-
целочисленных, точках множества X; стохастиче-
стохастическое программирование: в отличие от
детерминированных задач здесь входная информация
носит элемент неопределенности. Напр., в стохастич.
задачах о минимизации линейной функции
при линейных ограничениях
2?=i aiJxJ^bi> '=1, 2, ....
либо все величины су, а,у, Ь,-, либо часть из них слу-
случайны. Задачи линейного, квадратичного и выпуклого
программирования обладают общим свойством: всякая
точка локального минимума является оптимальной
точкой. Значительно более сложными и менее изучен-
изученными являются так. наз. многоэкстремальные задачи —
задачи, для к-рых указанное свойство не выполняется.
В основе теории выпуклого программирования, и
в частности линейного и квадратичного, лежит тео-
теорема Куна — Такера о необходимых и доста-
достаточных условиях существования оптимальной точки х*:
для того чтобы точка х* была оптимальной, т. е.
Ф (х*) = mi и ф (х),
лге X
необходимо и достаточно, чтобы существовала такая
точка у*=(у*, yl, . . ., y*k), чтобы пара точек х*, у*
образовывала седло функции Лагранжа
L (х, У) = ф (*) + 2*=, Vifi И ¦
Последнее означает, что
L(x*, y)<L(x*, y*)<L(x, у*)
для любых х и всех у^О. Если ограничения /,-(ж) не-
нелинейны, то теорема справедлива при нек-рых допол-
дополнительных предположениях о допустимом множестве,
напр, в предположении существования такой точки
х? X, что /,- (л:)>0, г=1, 2, . . ., к,— условия ре-
регулярности Слей тер а.
Если функции ф(ж) и fi(x) дифференцируемы, т»
следующие соотношения определяют седловую точку
-^7^0, /=1, 2, ..., п;
<0 г=1'2- •••' *;
i=l,2, ...,*.
Таким образом, задача выпуклого программирования-
сводится к решению системы уравнений и неравенств.
На основе теоремы Куна — Такера разработаны
различные итерационные методы минимизации, сводя-
сводящиеся к поиску седловой точки функции Лагранжа.
В М. п. одно из главных мост принадлежит вычисли-
вычислительным методам решения экстремальных задач. Ши-
Широкое распространение среди этих методов получил
метод возможных направлений.
В этом методе последовательность {хт} точек мно-
множества X строится по формуле xp + 1'-=xp-\-apsp. На каж-
каждой итерации для вычисления точки хр + х решаются
задачи выбора направления (вектора) sp и длины шага
(числа) ар. В качестве sp выбирают то из возможных
направлений (направлений в точке хр, малое перемеще-
перемещение вдоль каждого из к-рых не выводит из множе-
множества X), к-рое составляет острый угол с направлением
g(xp) скорейшего убывания целевой функции (с век-
вектором g{xp= — d<s>d{f | х=х , если ц>(х) — дифференци-
дифференцируемая функция) .Таким образом, вдоль этого направ-
направления функция i|) ^(a)=cp(?p+asp) убывает. Число ар
выбирают так, чтобы выполнялись условия хр + х?Х и
ф (xp + i) <ф (хр)- Для вычисления sp в точке хр опреде-
определяют конус возможных направлении, к-рый задается
системой линейных неравенств, и формулируют за-
задачу (линейного программирования) отыскания такого
возможного направления, по к-рому целевая функция
убывает быстрее всего. Решение атой задачи без труда
получают, напр., по стандартной программе симплекс-
симплексного метода. Величину шага ар вычисляют, решая
задачу минимизации одномерной функции typ(a). При
весьма общих предположениях доказано, что расстоя-
расстояние между точками хр и множеством стационарных то-
точек исходной задачи (т. е. множеством точек, в к-рых
выполняются необходимые условия локального ми-
минимума функции ц>{х) на множестве X) стремится
к нулю при р—>-оо. В случае, если исходная задача
является задачей выпуклого программирования, то хр
при р -> оо стремится к множеству решений (оптималь-
(оптимальных точек) исходной задачи. Метод возможных направ-
направлении допускает приближенное решение указанных
задач определения sp и ар, и в этом смысле он устойчив
по отношению к погрешностям вычислений.
Для допустимых множеств специальной структуры
(с точки зрения простоты решения задачи выбора на-
направления sp) находят применение методы минимиза-
минимизации, отличные от метода возможных направлений. Так,
в методе проекции градиента в ка-
качестве направления спуска в точке хр выбирают sp =
= Ур — хР, где (/^ — проекция точки vp=xp-\-g{xp),
g(xP)= — d<td{xX) x=x , на множество X.
Если множество X задано линейными ограниче-
ограничениями, весьма перспективным является метод ус-
условного градиента: в точке хр линеаризуют
целевую функцию, строя функцию l(x) = q (хр)п <,g(-i'p),
хр—хУ, затем, минимизируя I (х) на множестве X, на-
находят точку ее минимума ур, после чего полагают
*р=УР—ХР-
Успешно разрабатываются методы минимизации не-
негладких функций. Одним из представителей этого
класса методов является метод обобщенного
градиента. Обобщенным градиентом в точке хр
наз. любой вектор g(xp), удовлетворяющий для любой
точки у?Х неравенству <p(y) — <p(xp)^!<g(xp), y—xp>.
Этот метод отличается от метода проекции градиента
тем, что в качество проектируемой точки выбирают
точку vp=xp — g(xp).
Весьма распространены также стохастиче-
стохастические методы минимизации. В простейшем ва-
варианте метода случайного спуска в ка-
качество sp выбирают случайную точку на n-мерной еди-
единичной сфере с центром в начале координат, и если sp
является возможным направлением и, кроме того,
функция ф (х) убывает вдоль этого направления, то
осуществляют шаг, т. е. переходят к точке хр+1. В про-
противном случае процедуру выбора sp повторяют.
Характерной особенностью вычислительной стороны
методов решений задач М. п. является то, что приме-
применение этих методов неразрывно связано с использова-
использованием ЭВМ, в первую очередь потому, что задачи М. п.,
формализующие ситуации управления реальными си-
системами, являются задачами большого объема, недо-
недоступными для ручного счета.
Одним из распространенных методов исследования
задач М. п. является штрафных функций метод. Суть
этого метода состоит в замене исходной задачи М. п.
такой последовательностью парамотрич. задач без-
безусловной минимизации, что при стремлении параметра
к бесконечности (в иных случаях — к нулю) решения
этих задач стремятся к решению исходной задачи М. п.
Заметим, что в задачах безусловной минимизации лю-
любое направление является возможным, вследствие чего
отыскание вектора sp сопряжено с меньшей затратой
усилий по сравнению с аналогичной задачей в методе
возможных направлений (напр., в методе скорейшего
спуска выбирают sp= 'jj х ). То же самое от-
относится и к задаче отыскания числа ар.
Важным направлением исследований в М. п. яв-
являются проблемы устойчивости. Здесь существенное
значение имеет изучение класса устойчивых задач —
задач, для к-рых малые возмущения (погрешности)
в исходной информации влекут за собой малые возму-
возмущения и в решении. В случае неустойчивых задач
большая роль отводится процедуре аппроксимации
неустойчивой задачи последовательностью устойчивых
задач — так наз. процессу регуляриза-
регуляризации.
Наряду с конечномерными задачами М. п. рассмат-
рассматриваются также задачи М. п. в бесконечномерных
пространствах. К этим задачам относятся различные
экстремальные задачи математич. экономики, техники,
задачи оптимизации физич. характеристик ядерных
реакторов и др. В терминах М. п. в соответствующих
функциональных пространствах формулируются за-
задачи вариационного исчисления и оптимального уп-
управления.
М. п. как наука сформировалось в 50—70-х гг. 20 в.
Это в первую очередь связано с развитием ЭВМ, а сле-
следовательно, с возможностью проводить математич.
обработку больших потоков информации и на этой
основе решать задачи управления и планирования, где
применение математич. методов связано в первую оче-
очередь с построением математич. моделей и соответствую-
соответствующих им экстремальных задач, в том числе задач М. п.
Лит.: [1] М о и с е е в Н. Н., Иванилов Ю. П., Сто-
Столярова Е. М., Методы оптимизации, М., 1978; [2] К а р м а-
н о в В. Г., Математическое программирование, М-, 1975; [3]
II о л а к Э., Численные методы оптимизации. Единый подход,
пер. с англ., М., 1974; [4] Ермольев Ю. М., Методы стоха-
стохастического программирования, М., 1976. „ _ „
В. Г. Карманов.
МАТЕМАТИЧЕСКОЙ ФИЗИКИ УРАВНЕНИЯ —
уравнения, описывающие математические модели фи-
физических явлений. М. ф. у.— часть предмета матема-
математической физики. Многие явления физики и механики
(гидро- и газодинамики, упругости, электродинамики,
оптики, теории переноса, физики плазмы, квантовой
физики, теории гравитации и т. д.) описываются крае-
краевыми задачами для дифференциальных уравнений.
Эти задачи составляют весьма широкий класс М. ф. у.
Для полного описания эволюции физич. процесса,
помимо уравнений, необходимо, во-первых, задать
картину процесса в нек-рый фиксированный момент
времени (начальные условия) и, во-вторых,
задать режим на границе той среды, где протекает
этот процесс (граничные условия). Началь-
Начальные и граничные условия образуют краевые усло-
условия, а дифференциальные уравнения вместе с соот-
соответствующими краевыми условиями — краевую задачу
математич. физики.
Ниже приведены нек-рые примеры уравнений и со-
соответствующих краевых задач.
Уравнение колебаний
Р-д?-= div (p grad и) —qu + f (x, t) A)
описывает малые колебания струн, стержней, мем-
мембран, акустические и электромагнитные колебания.
В уравнении A) пространственные переменные х=
= (хи . . ., хп) изменяются в области GdRn, n=
= 1, 2, 3, где развивается рассматриваемый фпзич.
процесс; при этом в соответствии с физич. смыслом
входящих величин должно быть р>0, р>0 и q^O.
Кроме того, полагают р, q?C(G) и p?Cx(G). При этих
условиях уравнение A) — гиперболического типа урав-
уравнение.
При р=1, p=e2=const и q=0 уравнение A) превра-
превращается в волновое уравнение
~?-=a*Au + f(x,t), B)
где Д — оператор Лапласа.
Уравнение диффузии
p-^-=diw(pgtadu) — qu + f(x,t) C)
описывает процессы диффузии частиц и распростра-
распространения тепла в среде. Уравнение C) — параболиче-
параболического типа уравнение. При р=1, p=a2=const и д=0
уравнение C) превращается в теплопроводности урав-
уравнение
^ ,t). D)
Для стационарных процессов, когда отсутствует за-
зависимость от времени t, уравнения колебаний A) л
диффузии C) принимают вид
—div(p grad u)+qu=f(x). E)
Уравнение E) — эллиптического типа уравнение. При
р=1 и q=0 уравнение E) паз. Пуассона уравнением:
hu=-f(x), F)
а при /=0 — Лапласа уравнением
Ди=0. G)
Уравнениям F) и G) удовлетворяют различного рода
потенциалы: ньютонов (кулонов) потенциал, потенциал
течения несжимаемой жидкости и т. д.
Если в волновом уравнении B) внешнее возмущение
/ ¦— периодическое с частотой со,
/ (х, t) = a2f (x) е{<м,
то амплитуда и (х) периодич. решения с той же час-
частотой со
и (х, t) = u (x) е1^*
удовлетворяет Гельмголъца уравнению
Аи + к2и = — / (х), /с2=со2/а2. (8)
К уравнению Гельмгольца приводят задачи на рас-
рассеяние (дифракцию).
Для полного описания процесса колебаний необ-
необходимо задать начальное возмущение и начальную
скорость
и |< = о=«о (х), ¦jf\t = o = u1(x), x?G, (9)
а для процесса диффузии — только начальное возму-
возмущение _
"|t=o="o(*), *GG. A0)
Кроме того, на границе S области G необходимо удов-
удовлетворить заданному режиму. В простейших случаях
физически осмысленные граничные условия для урав-
уравнений A), ^3), E) описываются соотношением
k~ + hu\s^v(x,t), t>0, A1)
где к и h — заданные неотрицательные функции, н&
обращающиеся в нуль одновременно, п — внешняя
нормаль к поверхности S и v — заданная функция.
Напр., для струны условие
означает, что конец струны х0 закреплен, а условие-
— I -0
означает, что конец х0 свободен. Для теплопроводности
условие
и |5=^о (*, t) A2)
означает, что на границе S области G поддерживается
заданный температурный режим, а условие
=M*.O A3).
задает поток тепла через S. В случае неограниченных
областей, напр, внешпости ограниченной области,,
кроме условия на границе задается также условие
на бесконечности. Так, для уравнения Пуассона F)
в пространстве (п=3) таким условием является усло-
условие
и(х) = оA), [ ^ | —^ оо, A4)
а на плоскости (га=2) — условие
и(х) = ОA), \х\—^оо. A5)
Для уравнения Гельмгольца (8) на бесконечности за-
задаются излучения условия Зоммерфельда
A6)
причем знак «—» соответствует расходящимся, а знак
«+»— сходящимся волнам.
Краевая задача, к-рая содержит только начальные
условия (и стало быть, но содержит граничных усло-
условий, так что область G — вес пространство R"), паз.
Коши задачей. Для уравнения колебаний A) задача
Коши A), (9) ставится следующим образом: найти
функцию и(х, t) класса С2(г>0)П С1 (?>0), удовлет-
удовлетворяющую уравнению A) при г>0 п начальным ус-
условиям (9) па плоскости t=0. Аналогично ставится и
задача Коши C), A0) для уравнения диффузии C).
Если в краевой задаче присутствуют и начальные и
граничные условия, то такая задача паз. смешан-
смешанной задачей. Для уравнения колебаний A) сме-
смешанная задача A), (9), A1) ставится так: найти функ-
функцию и (х, t) класса
C2(GX(O, oo))nC1(Gx[0, оо)),
удовлетворяющую уравнению A) в цилиндре GX(O, оо),
начальным условиям (9) на его нижнем основании
GX {0} и граничному условию A1) на его боковой по-
поверхности 5Х[0, оо). Аналогично ставится смешанная
задача C), A0), A1) для уравнения диффузии C).
Существуют и другие постановки краевых задач, напр.
Гурса задача, Трикоми задача.
Для стационарного уравнения E) начальные уело- I
вия отсутствуют и соответствующая краевая задача
ставится так: найти функцию и(х) класса С2(G)Г\ С1 (G),
удовлетворяющую уравнению E) в области G и гранич-
граничному условию на границе S области G:
Для уравнения E) краевая задача с граничным усло-
условием
u|s=M*) A2')
наз. Дирихле задачей, а с граничным условием
= M*) A3')
— Неймана задачей. Различают внешние и внутренние
краевые задачи Дирихле и Неймана. Для внешних
задач кроме граничных условий необходимо задавать
условия на бесконечности типа A4), A5), A6).
К краевым задачам для уравнения E) относятся
также задачи на собственные значения: найти те зна-
значения параметра к (собственные значения), при к-рых
однородное уравнение
Lu = — div (р grad и) -j- qu = Хри A7)
имеет нетривиальные решения (собственные функции),
удовлетворяющие однородному граничному условию
Если G — ограниченная область с достаточно глад-
гладкой границей S, то существует счетное число неотри-
неотрицательных собственных значений Xlt Я2, . . . задачи
A7), A8) @<Я!<:Я2<. . ., Я, -^-оо), каждое Х^ — ко-
конечной кратности, соответствующие собственные функ-
функции и^(х), Lu^ = pukj k=l, 2, . . ., образуют полную ор-
тонормированную систему функций в L2 (G; р); при этом
всякая функция класса С2 (G), удовлетворяющая гра-
граничному условию A8), разлагается в регулярно схо-
сходящийся ряд Фурье по системе собственных функций
{«ft}-
Изложенные постановки краевых задач предпола-
тают достаточную гладкость решения как внутри об-
области, так и вплоть до границы. Такие постановки
краевых задач наз. классическими. Однако во
многих физически интересных задачах приходится
отказываться от таких требований гладкости. Внутри
области решение может быть обобщенной функцией и
удовлетворять уравнению в смысле обобщенных функ-
функций, краевые условия могут удовлетворяться в каком-
либо обобщенном смысле (почти везде, в Ьр, в слабом
смысле и т. д.). Такие постановки краевых задач наз.
обобщенными постановками, а соот-
соответствующие решения — обобщенными реше-
решениям и. Напр., обобщенная задача Коши для вол-
волнового уравнения ставится следующим образом. Пусть
и — классич. решение задачи Коши B), (9). Функции
и и / продолжаются нулем на i<0 и обозначаются через
и и / соответственно. Тогда функция и будет удовлетво-
удовлетворять в смысле обобщенных функций во всем прост-
пространстве R"+1 волновому уравнению
^=а2Дм + и0(.г)х6'(г) + Мг)Хб (*) + />, t). A9)
При этом начальные возмущения м0 и их играют роль
мгновенно действующих внешних источников типа
двойного слоя, ио{х)Хб' (t), и простого слоя, и1(х)Х
X6(t). Сказанное позволяет ввести следующее опреде-
определение. Обобщенной задачей Коши для
волнового уравнения с источником F?D' (Rn + 1),
/¦=0 при i<0, наз. задача об отыскании тех обобщен-
ных решений и(х, t) в R" + 1 волнового уравнения
?±=a*Au + F(x, t), A9'}
к-рые обращаются в нуль при i<0. Аналогично ста-
ставится обобщенная задача Коши и для уравнения тепло-
теплопроводности D).
Поскольку краевые задачи математич. физики опи-
описывают реальные физич. процессы, то они должны удов-
удовлетворять следующим естественным требованиям, сфор-
сформулированным Ж. Адамаром (J. Hadamard).
1) Решение должно существовать в нек-ром
классе функций Мг.
2) Решение должно быть единственным в,
возможно, другом классе функций Мг.
3) Решение должно непрерывно зависеть от
данных задачи (начальных и граничных данных, сво-
свободных членов, коэффициентов уравнения и т. д.).
Требование непрерывной зависимости решения возни-
возникает в связи с тем, что данные физич. задачи, как пра-
правило, определяются из эксперимента приближенно, и
поэтому необходимо быть уверенным в том, что решение
задачи не будет существенно зависеть от погрешностей
измерений этих данных.
Задача, удовлетворяющая перечисленным требова-
требованиям 1)—3), наз. корректно поставлен-
н о й, а множество функций Мх [~1 Мг — классом
корректности. Хотя требования 1)—3) на пер-
первый взгляд кажутся естественными, их, тем не менее,
необходимо доказывать в рамках принятой математич.
модели. Доказательство корректности — это первая
апробация математич. модели,— модель непротиворе-
непротиворечива, не содержит паразитных решений и мало чувст-
чувствительна к погрешностям измерений.
Нахождение корректных постановок краевых задач
математич. физики и методов построения их решений
(точных или приближенных) и составляет одно из глав-
главных содержаний предмета М. ф. у. Известно, что все
перечисленные выше краевые задачи поставлены кор-
корректно.
Пример. Задача Коши г/'=/(ж, у), г/(хо)=г/о по-
поставлена корректно, если /6 С1.
Задача, не удовлетворяющая хотя бы одному пз
условий 1)—3), наз. некорректной задачей. Некоррект-
Некорректные задачи приобретают в современной математич.
физике все возрастающее значение: сюда в первую оче-
очередь относятся обратные задачи, а также задачи, свя-
связанные с обработкой и интерпретацией результатов
наблюдений.
Примером некорректно поставленной задачи может
служить задача Коши для уравнения Лапласа (п р и-
мер Адамара):
. . . _ . „ ди I sin kx
Аи(х,у) = 0, и\у = 0 = 0, ¦^\у=0=—Г--
Решение
и (х, у) = -р- sin kx sh ку =^ 0, к —>- оо,
однако
Для приближенного решения некорректных задач
существует регуляризации метод, использующий до-
дополнительную информацию о решении и сводящийся
к решению ряда корректно поставленных задач.
Важную роль в М. ф. у. играет понятие Грина функ-
функции. Функцией Грина линейного дифференциального
оператора
2a
±- — Л.
бх, ' ' ' ¦' дхп ' at
с заданными (однородными) краевыми условиями на
границе области изменения переменных (.г, t) наз.
функция G(.r, t; |, т), удовлетворяющая при каждом
(?, т) из этой области уравнению
L(r, t; D)G(x, t; g, x) = b(x — \, t — x). B0)
В физпч. ситуациях функция Грина G(x, t\ |, т) опи-
описывает возмущение от точечного (в точке |) мгновен-
мгновенного (в момент т) источника интенсивности 1 (с учетом
неоднородности среды и краевого эффекта). В случае
постоянных коэффициентов и отсутствия границы функ-
функция Грина при |=0 и т=0 наз. фундаменталь-
фундаментальным решением и обозначается Е (х, t),
L (D)E (x, *) = 6 (х, t). B0')
Доказано существование фундаментального решения
из D' и S' для любого оператора L(D)^0.
Примеры фундаментальных реже-
н и и. Волновое уравнение
(х, ') = ?^6+ (a2t"— \ х \2),
где 6 (t) — функция Хевисайда: 6(i) = 0 при «<0;
6@ = 1 при г>0.
Уравнение теплопроводности:
Е (х U- 0(" с-\х\УАаП
Уравнение Лапласа:
Ег(х)=±.\х\, Е2 (.г) = i In |*|, ^з(-~) = -Т7ГТ^-
С помощью фундаментального решения Е (ж, t) ре-
решение u (j;, t) уравнения
L(D)u = F(x,t) B1)
с произвольной правой частью F?D' выражается во
всем пространстве R" + 1 сверткой
u = F*E, B2)
если она существует в D'.
В физпч. ситуациях смысл формулы B2) следующий:
это есть суммарное наложение элементарных возмуще-
возмущений F(|, %)Е (х—|, t—т) от точечных источников
F(%, t)&(x—%, t—x), на к-рые разлагается источник
F(x, t) в силу тождества F=F*b, При этом свертка
F * Е играет роль соответствующего потенциала с ис-
точнико.м (плотностью) /'. В этом состоит сущность
метода точечного источника решения
линейных задач математич. физики.
В частности, решения обобщенной задачи Коши для
волнового уравнения (и уравнения теплопроводности)
выражается волновым (тепловым)потен-
ц и а л о м
и = F * Еп. B2')
Из формулы B2') при надлежащих предположениях
о гладкости источника
F (.г, t) = ua(x)b' @ + И б (*)+/(*> 0
следуют классич. формулы решения задач Коши.
Напр., для волнового уравнения в пространстве —
Кирхгофа формула:
B3)
Для уравнения теплопроводности — Пуассона формула:
Таким же путем, строя функцию Грина для уравнения
Лапласа для шара, получают решение внутренней за-
задачи Дирихле для (трехмерного) шара lz|<i? в виде
Пуассона интеграла:
т*7^"°(|)<^ B5)
Для исследования и приближенного решения сме-
смешанных задач используется Фурье метод (разделения
переменных) при условии, что коэффициенты в урав-
уравнении и в граничном условии не зависят от времени t.
Идея метода, применительно, напр., к задаче C), A0),
A8) состоит в следующем: искомое решение и (х, t) и
правая часть f(x, t) разлагаются в ряд Фурье по собст-
собственным функциям {«ft} краевой задачи A7), A8)
и (х, t) = 2J= j bk (t) uk (x), f (x, t) = 2 ™= j ck (t) uk (x).
B6)
Подставляя формально эти ряды в уравнение C), для
неизвестных функций Ь^A) получают уравнение:
b'k(t)-i-Xkbk(t)^ck(t), fc=l, 2, ... B7)
При этом, чтобы ряд B6) для и удовлетворял началь-
начальному условию A0), необходимо положить
Ък @)= \с9 (х) "° (г) "* {Х) dx = ak- B8)
Решая задачу Коти B7), B8), получают формальное
решение задачи C), A0), A8) в виде ряда:
B9)
Возникает задача обоснования метода Фурье: когда
формальный ряд B9) даст классическое или обобщенное
решение задачи C), A0), A8)?
При обосновании метода Фурье и, вообще, при уста-
установлении корректности смешанной задачи для урав-
уравнения диффузии C) используется максимума принцип.
Аналогично метод Фурье применяется и к смешанной
задаче A), (9), A8) для уравнения колебаний. В этом
случае оказывается полезным метод энергии интеграла.
Метод разделения переменных находит применение
также и для решения краевых задач для уравнения
эллиптич. типа E), в частности для вычисления собст-
собственных функций и собственных значений при условии,
что область G обладает достаточной симметрией.
Для исследования и приближенного решения крае-
краевых задач для уравнения E) широко используются
вариационные методы. Так, напр., для задачи на соб-
собственные значения A7), A8) (при р=1) собственные
значения Х^ удовлетворяют вариационному принципу:
Xft= inf и и г- > C())
(ц, и(.) = 0. г = 1 *-1
где функции сравнения и (х) предполагаются из класса
C2(G) и удовлетворяют граничному условию A8);
при этом inf в C0) реализуется на любой собственной
функции, соответствующей собственному значению Х^,
и только на них.
При исследовании краевых задач для уравнения E)
(в частности, для гармонич. функций) применяется
принцип максимума.
Перечисленные краевые задачи далеко не исчерпы-
исчерпывают все многообразие краевых задач математич, фи-
физики — это есть простейшие классич. примеры краевых
задач. Краевые задачи, описывающие реальные физяч.
"процессы, могут быть весьма сложными: это могут быть
системы уравнений, уравнения высших порядков, не-
нелинейные уравнения. Сюда в первую очередь отно-
относятся: уравнение Шрёдингера, уравнения гидродина-
гидродинамики, переноса, магнитной гидродинамики, уравнения
Максвелла, теории упругости, уравнения Дирака,
уравнения Эйнштейна, уравнения Янга — Мпллса и ДР-
В связи с поисками нетривиальных моделей, описы-
описывающих взаимодействие квантовых нолей, возрос ин-
интерес к классическим нелинейным уравнениям:
Щ — Ъии'х+и'ххх^О C1)
¦— Кортевега — Ое Фриса уравнение;
"i't — "хх — S! ("), g > 0,
— нелинейное волновое уравнение (Лиувилля при
/=е"; Sine-Гордона при /=—sin и);
iu't + uxx-rv I «• I2 "—-О, v > 0.
— нелинейное уравнение Шрёдингера.
Характерной чертой таких уравнений является на-
наличие решений типа «уединенной волны» (солитонов).
Напр., для уравнения C1) таким решением является
и (х, «) = • " , а > 0, х0 — любые.
2 ch2 I —^- (я-at-Ko)
Это решение обладает конечной энергией.
Лит.: [1] Тихонов А. Н., Самарский А. А., Уран-
нения математической физики, 5 изд., М., 1977; [2] Владими-
Владимиров В. С, Уравнения математической физики, 4изд.,М., 1981;
[3] Т и х о н о в А. Н., Арсенин В. Я., Методы решения
некорректных задач, М., 1974; [4] Хермандер Л., Линей-
Линейные дифференциальные операторы с частными производными,
пер. с англ., М., 1965; [5] А д а м а р Ж., Задача Коши для ли-
линейных уравнений с частными производными гиперболического
типа, пер. с франц., М., 1978; [6] У и з е м Д ж., Линейные и
нелинейные волны, пер. с англ., М., 1977; [7] МихайловВ.П.,
Дифференциальные уравнения в частных производных, М-,
1976: [8] Ладыженская О. А., Краевые задачи матема-
математической физики, М., 1973; [9J Курант Р., Гильберт Д.,
Методы математической физики, пер. с нем., 2 изд., т. 2,
М.—Л., 1951; [10] Владимиров B.C., Обобщенные функ-
функции в математической физике, 2 изд., М., 1979. В. С- Владимиров,
МАТРИЦ АЛГЕБРА, матричная алгеб-
алгебра,— подалгебра полной матричной алгебры F,, всех
(пХп)-матриц над полем F. Операции в Fn опреде-
определяются следующим образом:
ab = с = !|
с if ||, c;j = 2V= i °iv* v/
для %?F, a=||a,7||, b= ||6,7|| g Fn. Алгебра Fn изо-
изоморфна алгебре всех эндоморфизмов «-мерного линей-
линейного пространства над F. Размерность Fn над F равна
п2. Любая ассоциативная алгебра с единицей, размер-
размерность к-рой над F не больше п, изоморфна нек-рой
подалгебре в Fn. Ассоциативная алгебра без единицы,
размерности меньше п над F, также изоморфно вкла-
вкладывается в Fn. В силу теоремы Веддербер-
н а алгебра Fn проста, т. е. имеет лишь тривиальные
двусторонние идеалы. Центр алгебры Fn состоит из
всех скалярных (пХп)-матриц над F. Группа обрати-
обратимых элементов алгебры Fn есть полная линейная груп-
группа GL(n, F). Каждый автоморфизм k алгебры Fn яв-
является внутренним:
(n, F).
Неприводимая М. а. проста. Если М. а. А абсолютно
неприводнма (напр., когда поле F алгебраически замк-
замкнуто), то A = Fn при и>1 (теорема Б ё р н с а й-
д а). М. а. полупроста тогда и только тогда, когда она
вполне приводима.
С точностью до сопряженности в Fn имеется единст-
единственная максимальная нилыютентная подалгебра —
алгебра всех верхних треугольных матриц с нулевой
диагональю. В алгебре /'„ тогда и только тогда имеется
коммутативная подалгебра размерности г, когда
(теорема Шура). Для поля комплексных чисел
С множество классов сопряженных максимальных
коммутативных подалгебр алгебры С„ при жО ко-
конечно, а при и>6 бесконечно.
В алгебре Fn выполняется стандартное тождество
степени 2п:
где 52„ — спмметрич. группа, и никакое тождество
меньшей степени не выполняется.
Лит.: 11] В е й л ь Г., Классические группы, их инварианты
и представления, пер. с англ., М., 1947; [2] Джекобеон Н.,
Строение колец, пер. с англ., М.. 1961: [3] Херстейн И.,
Некоммутативные кольца, пер. с англ., М., 1972; [4] Ван д о р
В а р д с н Б. Л., Алгебра, пер. с нем., М., 1976; [5] С у п р у-
н е н к о Д. А., Т ы ш к с в и ч Р. И., Перестановочные матри-
матрицы, Минск, 1966. Д. А. Супруненко.
МАТРИЦ КОЛЬЦО, полное кольцо м а т-
р и ц,— кольцо всех квадратных матриц фиксиро-
фиксированного порядка над кольцом Л. Кольцо (лХ и)-матрпц
над Л обозначается Л„ или Мп(Щ. Всюду ниже Л —
ассоциативное кольцо с единицей 1.
Кольцо Rn изоморфно кольцу End M всех эндомор-
эндоморфизмов свободного правого Л-модуля М, обладающего
и-элементным базисом. Матрица i?,,= diag [1, . . ., 1] —
единица в й„. Ассоциативное кольцо А с единицей 1
тогда и только тогда изоморфно Rni когда в А есть
множество из п2 элементов e,;j, i, /'—1, ¦ ¦ -, ", подчи-
подчиненное следующим условиям:
2) централизатор множества элементов eLj в А изо-
изоморфен кольцу R.
Центр кольца Rn совпадает с Z(R)En, где Z (R) —
центр R; при п>1 кольцо Rn некоммутативно.
Мультипликативная группа кольца Rn (группа всех
обратимых элементов) наз. п о л н о й лине и н о й
группой и обозначается GL(n, Л). Матрица и»
Rn обратима в Rn тогда и только тогда, когда ее столб-
столбцы составляют базис свободного правого модуля всех
(«Х1)-матриц над R. Если R коммутативно, то обра-
обратимость матрицы а в Rn равносильна обратимости ео
определителя det а в Л. Имеет место равенство (/'„,)„=
= Rmn-
Кольцо Rn тогда и только тогда просто, когда просто
R, ибо двусторонние идеалы в Rn имеют вид к,:, где
к — двусторонний идеал в R. Артпново кольцо тогда
и только тогда просто, когда оно изоморфно М. к. над
телом (теорема Веддерберна — Арти-
на). J(Mn(R))=Mn(J(R)), где /(Л) - радикал Дже-
кобсона кольца R. Следовательно, для полупростого
кольца Л М. к. над Л также полупросто.Если Л регу-
регулярно (т. е. для любого a?R в Л есть такое Ь, что
а6а=я), то н Л„ регулярно. Если R — кольцо с ин-
инвариантным базисным числом, т. е. число базисных
элементов каждого свободного Л-модуля не зависит от
выбора базиса, то Л„ также кольцо с инвариантным
базисным числом. Кольца Л и Rn эквивалентны в
смысле Мориты (см. Мориты эквивалентность): кате-
гория Л-модулей эквивалентна категории Л„-модулей.
Однако из того, что проективные Л-модули свободны,
еще не следует, что будут свободны и проективные
Л„-модули. Так, если Л — поле, а ге>1, то сущест-
существуют несвободные конечно порожденные проективные
Л„-модули.
Лит.: [1] Ф е й с К., Алгебра: кольца, модули и категории,
пер. с англ., т. 1, М., 1977; [2] л а м б е к И., Кольца и модули,
пер. с англ., М., 1971; [3] Б о к у т ь Л. А., Ассоциативные коль-
кольца, ч. 1, Новосиб., 1977. Д. А. Супруненко.
МАТРИЦА — прямоугольная таблица
A)
ат1
состоящая из т строк и п столбцов, элементы к-рой
a.[j принадлежат нек-рому множеству К. Таблица A)
наз. также (тХ п)-м атрицей над К, или мат-
матрицей размера тХгенад К. Пусть Мт> п(К) —
совокупность всех (гоХп)-матриц над К. Если т=п,
то A) наз. квадратной матрицей по-
порядка п. Множество Мп(К) — совокупность всех
квадратных М. порядка п над К.
Для М. пользуются также обозначениями
В наиболее важных случаях в качестве К выступают
поле действительных чисел, поле комплексных чисел,
произвольное поле, кольцо многочленов, кольцо целых
чисел, кольцо функций, произвольное ассоциативное
кольцо. Операции сложения и умножения, определен-
определенные на К, естественным образом переносятся на М.
над К и возникает матричное исчисление —
предмет теории М.
Понятие М. впервые появилось в середине 19 в. в ра-
работах У. Гамильтона (W. Hamilton) и А. Кэли (A. Cay-
ley). Фундаментальные результаты в теории М. при-
принадлежат К. Вейерштрассу (К. Weierstrass), К. Жор-
дану (С. Jordan), Г. Фробениусу (G. Frobenius).
И. А. Лаппо-Данилевский развил теорию аналитич.
функций многих матричных переменных и применил
ее к изучению систем линейных дифференциальных
уравнений.
Действия над матрицами. Пусть К — ассоциативное
кольцо, А = \\ац\\, B=\\bij\\?Mmj „(К). Тогда сумма
М. А и В, по определению, равна
При этом 4+Bf Jlfffl] n(K) и сложением, ассоциативно
и коммутативно. Нулевой М. из Мт< „(К) наз.
М. О, все элементы к-рой равны нулю. Для всякой
А+0=0-\-А = А.
Пусть А=\\аи\У€Мт<к(К), В=\\Ьи\\?Мк,п(К). Про-
Произведение М. А и В определяется по правилу
где
fe h
Произведение двух М. из М„(К) всегда определено и
принадлежит М„(К)- Умножение М. ассоциативно:
если AGMn,k{K), В?Мк,„(К), С?Мп,р(К), то
=Л (ВС)
и АВС?Мт „(К). Верен и дистрибутивный закон: для
А?М{К), В, С?Мп,т(К)
(В+С) А = ВА + СА. B)
В частности, B) верно и для А, В, С?М„(К). Следо-
Следовательно, Мп(К) — ассоциативное кольцо. Если К. —
кольцо с единицей 1, то М.
1 ... О II
О ... 1 I
будет единицей кольца Мп(К,)'-
ЕпА= АЕп = А
для всех А?Мп{К). Умножение М. некоммутативно:
при и!>2 для любого ассоциативного кольца К с еди-
единицей найдутся такие М. А и В в Мп(К), что АВфВА.
Пусть а ? К, А = \\аи-\\?Мт<п(К); произведе-
произведение М. А н а элемент (ч и с л о) а, по опреде-
определению, равно аА = ||ао,-у-||. Тогда
Пусть К — кольцо с единицей. М. е,у- определяется
как М. в Mmin(A), единственный ненулевой элемент
к-рой равен 1 и расположен на позиции (г, /), l<i<m,
1</<п. Для любой 4 = ||о(у|| из Мт_п(К)
Если К — поле, то Мт> п(К) — векторное пространство
над К размерности тп, а М. е,-у составляют один из
базисов этого пространства.
Клеточная матрица. Пусть т=т1-\-. . .-\-т^, п—
:=п1-\-. . .-\-щ, где rn.fi и nv— целые положительные
числа. Тогда М. А ?Мт, п(К) можно записать в виде
А=---
Ап ... Аи
4» •'¦'¦ АЫ
C)
где А)лУ?Мт^ „v (ЙГ), ц=1, . . ., k, v—1, . . ., I; M. C)
наз. клеточной. Пусть B?MHi p{K), P=Pi+
+ . . --\-pt, Р;>0 и В записана в виде
Вц\\
• • • , В,-
\В
Тогда
и
Си
Cfr,
... В
а
It It
Сы\
.(К).
ivfj
Напр., если п=Ы, то Мп(К) можно рассматривать
как Мп{1), где 2 = М1{К).
М. А из Мп(К) вида
0,2
о
lft
где а[?М„.(К), а О/у — нулевая М. из Мп.,п/(К),
обозначается diag [Аи . . ., Ak] и наз. клеточно-
дпагональной. Причем
i, ..., Ak]
, ..., AkBk],
если порядки Л,- и В,- совпадают для i=l, . . ., fc.
Квадратные матрицы над полем. Пусть К — поле,
^М(/С), det А — определитель матрицы А. М. А
наз. невырожденной, если det A=?=0. M. А ~г?
?М„(К) наз. обратной к Л, если АА ~1==Л ~гА =
= Еп. Обратимость Л в Мп(К) равносильна невырож-
невырожденности и
А ..
А - г — II с 1 !|, с,-
С'У
det А
где Aji — алгебраическое дополнение
det A~1={det А)-1. Для Л и В из Мп(К)
Совокупность всех обратимых М. из М„ (К) образует
группу относительно умножения, к-рая наз. пол-
полной линейной группой и обозначается
GL(ra, К). Степени М. А определяются следующим об-
образом:
А°=Е„- Ак=А"~1А
для А->0, а если А обратима, то A ~k=(A ~1)k. Для
многочлена
определяется матричный многочлен
/ (Л) = а0Еп + «!Л + ... +а4Л<.
Всякая М. из Мп{К) задает нек-рое линейное пре-
преобразование га-мерного векторного пространства V
над К. Пусть dj, . . ., i;n базис в F, а а : V-+V — ли-
линейное преобразование пространства V. Тогда о одно-
однозначно определяется последовательностью векторов
«1 = о Ю, ..., ип=а (vn).
При этом
о
\ -м- Г Л. Л- -^ I I It »** ¦ |
D)
где aij^K. Матрица Л = ||а,-у|| наз. М. преобра-
преобразования ов базисе Vj., . . ., vn. При фиксирован-
фиксированном базисе М. А-\-В будет М. преобразования а-\-х,
а АВ — М. преобразования от, где В — М. линейного
преобразования т. Равенства D) можно записать в виде
[а(рх),
] = [iI, ..., vn]A.
Пусть wu
wn]=[i'i, .
в базисе w1
, wn — тоже базис в V. Тогда [wlt . . .,
vn]T, T?GL(n, К), а T'^AT — U. a
1, . . ., wn. M. А и В из Мп(К) наз. подоб-
подобными, если в GL(n, ./() найдется такая М. Т, что
В=Т~1АТ. При этом det .4= det Т~ХА Т и ранги мат-
матриц А и В совпадают. Линейное преобразование a
наз. невырожденным, если a(V)= V; о тогда
и только тогда невырождено, когда его М. невырож-
невырождена. Если V трактовать как пространство столбцов
МПу1(К), то линейное преобразование пространства V
представляет собой умножение столбцов v?V на М.
А из Мп(К) слева: a(v)=Av, и М. преобразования а
в базисе
совпадает с А. М. А?Мп(К) тогда и только тогда вы-
вырождена, когда в Мп1(К) существует такой столбец
vфO, что ЛО
Транспонирование и матрицы специального вида.
Пусть А = \\а{/\\?Мт,п(К). Тогда М. АТ=\\аТ.\\?
(К), где aj^a.., наз. транспонирован-
транспонированной к А. Матрица Ат обозначается также tA
Пусть Л=||а,7ИеМт,„(С). Тогда М. А = IK/
aij — число, комплексно-сопряженное с a;j,
комплексно-сопряженной с А.
i А'.
где
наз.
Мат-
Матрица A* = A^i где А?Мп{С), наз. эрмитово-
сопряженной с А. Многие М., используемые
в приложениях, имеют специальные названия.
Название
матрицы
Симметри-
Симметрическая
Кососим-
метриче-
ская
Ортого-
Ортогональная
Эрмитова
Унитар-
Унитарная
Нормаль-
Нормальная
Определяющее
условие
АГ = А.
АГ=-А.
АТ=А-К
А* = А.
А* = A-i.
А* А = АА*.
Название
матрицы
Унипо-
тентная
Стохасти-
Стохастическая
Двояко-
стохасти-
стохастическая
@,1)-мат-
рица
Определяющее
условие
(А-Еп)п = 0.
А=\\а ,..||6М (R),
а >Л.
1J
У" «(-у- = 1.
5=1
1 = 1,. . . , п.
М. А и AT сто-
стохастические.
Каждый эле-
элемент А равен
либо 0, либо 1.
Полиномиальные матрицы. Пусть К — поле, К{х] —
кольцо всех многочленов от х с коэффициентами из К.
М. над К[х\ наз. полиномиальной. Для М.
из кольца Мп(К[х]) вводятся элементарные
операции: 1) умножение строки или столбца М.
на ненулевой элемент поля К, 2) прибавление к строке
(столбцу) другой строки (столбца) М., умноженной
на многочлен из К[х]. М. А и В из Мп(К[х\) наз. э к-
вивалентными (А—В), если В можно получить
из А с помощью конечного числа элементарных опе-
операций.
Пусть
iV=diag[/1H, . . ., fr(x), 0, . . ., 0]?Мп(К[х)),
где: i) 1[(х)фО, 2) jj(x) делится на f,-{x) при ]>i,
3) коэффициенты старших членов многочленов /,¦ (х)
равны 1. Тогда jV наз. канонической поли-
полиномиальной М. В каждом классе эквивалент-
эквивалентных М. кольца Мп(К[х]) содержится единственная ка-
нонич. М. Многочлены
/l(j). ¦ • •» fr(x),
где
iV = diag[/1(x), ..., fr{x), 0, ..., 0]
— каноническая М., а А—.V, наз. инвариант-
инвариантными множителями М.л; число г совпадает
с рангом М. А. Матрица А из Мп(К[х\) тогда и только
тогда имеет обратную в Мп(К\х\), когда А~Еп. В свою
очередь А ~Еп <=> det A g K\0. Матрицы А и В из
Мп(К\х]) тогда и только тогда эквивалентны, когда
B=PAQ,
где Р, Q?Mn(K[x]), P~Q~En.
Пусть А ?М„(К). Матрица
хЕп-А?Мп(К[х\)
наз. характеристической матрицей
матрицы А , a det (хЕп—А) — характеристиче-
характеристическим многочленом М. А. Для любого много-
многочлена вида
в Мп(К) существует М. F,
det (xEn —
для к-рой
) = 1 (x).
Такова, напр., матрица
0 0 ...
1 О ... О —«!
О 1 ... О —а2
О О ... 1 — «„_j
Характеристич. многочлены двух подобных М. совпа-
совпадают. Однако из совпадения характеристич. многочле-
многочленов двух М. еще не вытекает подобие этих М. Крите-
Критерий подобия: Л и В из Мп (К) тогда и только
тогда подобны, когда полиномиальные М. хЕп—А
\ixEn—В эквивалентны. Множество всех М. из Мп(К),
имеющих заданный характеристич. многочлен f(x),
разбивается на конечное число классов подобных М.,
это множество состоит из одного класса тогда и только
тогда, когда f (х) не имеет кратных множителей в К[х].
Пусть А?Мп(К), v?Mnil(K), уфО и Av=Xv, где
/.?/(. Тогда v наз. собственным вектором
М. А, а X — собственным значением.
Элемент X из К тогда и только тогда является собст-
вснпым значением М. А, когда X — корень характе-
характеристич. многочлена М. А. Совокупность всех столбцов
и?МП: \{К) таких, что Аи=Хи, где X — фиксирован-
фиксированное собственное значение М. А, является подпрост-
подпространством пространства Мп1{К). Размерность этого
подпространства равна дефекту d M. ХЕп—А
(d=n—г, где г — ранг М. ХЕп—А). Число d не превы-
превышает кратности корня X, но не обязательно совпадает
с ней. Матрица А из Мп (К) тогда и только тогда по-
подобна нек-рой диагональной М., когда А имеет га ли-
линейно независимых собственных векторов. Если для
и Xj различны, то верно следующее: А тогда и только
тогда подобна диагональной М., когда для каждого
Xj, j—\, . • ., I, дефект М. XjEn—А совпадает с rij.
В частности, М., имеющая п различных собственных
значений, подобна диагональной. Для алгебраически
замкнутого поля любая М. из Мп(К) подобна нек-рой
треугольной М. из Мп(К)- Теорема Гамиль-
Гамильтона — К э л и: пусть f(x) — характеристич. много-
многочлен М. А, тогда f(A) — нулевая М.
Минимальным многочленом М. А^
?Мп(К) наз. многочлен т(х)-?К[х] такой, что: 1)
т{А) = 0, 2) коэффициент старшего члена т(х) равен 1,
3) если Оф\р(х)(^К{х], а степень я|)(ж) меньше степени
т(х), то тр(А)Ф0. Всякая М. обладает единственным
минимальным многочленом. Если g(x)?K[z] и g(A) = O,
то g(x) делится на минимальный многочлен т(х) М.
А. Минимальный многочлен М. А совпадает с послед-
последним инвариантным множителем М. хЕп—А, а характе-
ристпч. многочлен — с произведением всех инвари-
инвариантных множителей. Минимальный многочлен М. равен
det {хЕп-А)
где dn-1(x) — наибольший общий делитель миноров по-
порядка п—1 М. хЕп—А. М. А из Мп(К) тогда и только
тогда подобна диагональной М. над полем К, когда ее
минимальный многочлен есть произведение различных
линейных множителей из кольца К[х].
М. А ?Мп(К) наз. нильпотентной, если
,4*= 0 для нек-рого целого k. M. нильпотентна тогда
и только тогда, когда <\et(xEn—А) = х". Любая ниль-
потентнаяМ. из Мп(К) подобна нек-рой треугольной М.
с нулевой диагональю.
Лит.: [1] В о е в о д и н В. В., Линейная алгебра, М., 1974;
[2] Г а н т м а х е р Ф- 1'., Теория матриц, 3 изд., М., 1967'
[3J Кострикин А. И., Введение в алгебру, М., 1977; [4]
К у рош А. Г., Куре высшей алгебры, 11 изд., М., 1975; [51
Мальцев А. И., Основы линейной алгебры, 3 изд., М., 1970;
[6] Мишина А. П., Проскуряков И. В., Высшая
алгебра, 2 изд., М., 1965; [7] Т ы ш к е в и ч Р. И., Феден-
ко А. С., Линейная алгебра и аналитическая геометрия, 2 изд.,
Минск, 1976; [8] Б е л л м а н Р., Введение в теорию матриц,
пер. с англ., 2 изд., М., 1976; [9] Б у р б а к и Н., Алгебра.
Алгебраические структуры. Линейная и полилинейная алгебра,
пер. с франц., М., 1962; [10] Ланкастер П., Теория матриц,
пер. с англ., М., 1978; [11] М а р к у с М., М и н к X., Обзор
по теории матриц и матричных неравенств, пер. с англ., М.,
1972. Д. А. Супруненко.
МАТРИЦАНТ — фундаментальная матрица X (t) ре-
решений системы обыкновенных дифференциальных урав-
уравнений
x=A(t)x, x?R», (*)
нормированная в точке t0. M. является единственным
непрерывным решением матричной начальной задачи
X=A(t)X, X(to) = I
(/ — единичная матрица), если матричная функция
A (t) локально суммируема на нек-ром интервале
Для любой матрицы М(t), составленной из столбцов-
решений ж,, . . ., хт системы (*), где т — натуральное
число, справедливо представление М (t)=X (t)M (t0).
В частности, любое решение х (t) системы (*) записы-
записывается в виде x(t)=X (t)x(t0).
Для М. справедливы разложение
X («) = /-)-Г A (s) ds+V A (s) V А (г) drds+...,
сходящееся абсолютно для всякого t?J и равномерно
на каждом конечном отрезке из /, и Лиуеилля —
Остроградского формула
det X (t) = exp V sp A (s)ds.
J н
Если матрица A (t) удовлетворяет условию Лап-
по-Данилевского
A(t)-V A (s)ds=V A(s)ds-A(t),
X @ =
V A (s) ds.
В частности, если A (t)=A — постоянная матрица, то
X (t) = eA«-h\
Если ХдA) есть М. системы (*) с матрицей A (t), то
XA + B(t) = XA(t)XD(t),
где
D(t) = [XA(t)]-iB(t)XA(t).
М. позволяет записать любое решение неоднородной
системы
х= A (t) х-\-Ъ (t)
с локально суммируемой на / функцией b (t) по формуле
Коши:
x(t) = X(t)x(to)-\-[' C(t, s)b(s)ds, t?J,
J to
при этом
C(t, s) = X(t)[X(s)]-i
наз. матрицей Коши системы (*). Матрица
Коши С (t, s) непрерывна по совокупности аргументов
на /X/ и для любых t, s, r из / обладает свойствами:
1) C(t, s) = C(t, t0) [C(s, to)]-i;
2) С (t, s) = C(t, r)C{r, s);
3) C(s, t) = [C(t, s)]-i;
4) с (t, «) = /;
5) \C(t, s)|<exp \ J A {,¦) \dr, s*St,
J
где | • | —норма в R";
6) если H (t, s)—матрица Коши сопряженной
системы
х = — A* (t) х,
то
H{t, s) = [C*(t, s)]~i.
Лит.: [1] Б у р О а к и Н., Функции действительного пере-
мешюго. Элементарная теория, пер. с франц., М., 1965; [2] Г а н т-
м а х с ]¦ Ф. Р., Теория матриц, 2 изд., М., 1966; [31 Д е м и д о-
вич Б. л., Лекции по математической теории устойчивости,
М., 1967: [4] Я к у б о в и ч Б. Д., Старшинский В. М.,
Линейные дифференциальные уравнения с периодическими ко-
коэффициентами и их приложения, М. 1972. Ю. В. Комлсако.
МАТРИЧНАЯ ГРУППА — группа квадратных
(геХ н)-матрнц с элементами из ассоциативного кольца
с единицей относительно обычного умножения матриц.
См. Линейная группа.
МАТРИЧНАЯ ИГРА — антагонистическая игра,
в к-рой каждый игрок имеет конечное число чистых
стратегий. Если игрок I имеет т стратегий, а игрок II
имеет и стратегии, то М. и. может быть задана (шХл)-
матрицей А = ||a,y!i, где <г,у, i~i, . . ., т, j=i, . . ., п,
есть выигрыш игрока I, если он выбирает стратегию г,
а игрок II — стратегию ;. Согласно общему принципу
оптимальности в антагоннстич. играх (см. также Мини-
макса принцип), игрок I стремится выбрать такую стра-
стратегию г0, на к-рой достигается
max min a,-y = y;
i i ~~
а игрок II стремится выбрать стратегию /0, на к-рой
достигается
min max a;} — v.
i i
Если v= и, то пара (i0, /0) составляет седловую точку
игры; число а,„у0 есть значение игры, а стратегии го> /о
суть оптимальные чистые стратегии. Если v=f=v (т. е.
решения в чистых стратегиях нет), то всегда у<и.
В этом случае оптимальные стратегии игроков следует
искать среди их смешанных стратегий. Пусть XdRrn
(соответственно УсК") — множество смешанных стра-
стратегий игрока I (соответственно игрока II). Тогда иг-
игрок I будет стремиться к стратегии х*, на к-рой до-
достигается
y*=max min хАу^,
~ хех yeY
а игрок II — к стратегии у*, на к-рой достигается
у*= min max x
yev xeX
(символом т обозначено транспонирование). Основная
теорема теории М. и. (теорема Неймана о
м и н и м а к с е) утверждает, что v*=v*=v, т. е. для
любой М. и. существуют оптимальные смешанные стра-
стратегии а*, у* и значение игры v.
Для численного решения М. и. (т. е.
нахождения оптимальных стратегий и значения игры)
чаще всего используют возможность сведения М. и.
к задаче линейного программирования. Менее эффекти-
эффективен итеративный метод Брауна — Робин-
с о н, к-рып состоит в фиктивном «разыгрывании»
М. и., причем игроки на каждом шаге выбирают наи-
наилучшие чистые стратегии в условиях «накопленной»
смешанной стратегии противника. М. и., в к-рых один
из игроков имеет только две стратегии, просто ре-
решаются графич. методом.
М. и. могут служить математич. моделями многих
простейших конфликтных ситуаций из области эконо-
экономики, математич. статистики, военного дела, биологии.
В приложениях в качестве одного из игроков нередко
рассматривают «природу», иод к-рой понимается вся
совокупность внешних обстоятельств, неизвестных при-
принимающему решение лицу (другому игроку).
Лит.: [1] Матричные игры. Сб. статей, М., 1961; [2] Ней-
Нейман Д ж., Моргенштерн О., Теория игр и экономиче-
экономическое поведение, пер. с англ., М., 1970; [3] Оуэн Г., Теория
игр, пер. с англ., М., 1971; [41 В о р о б ь е в Н. Н., Теория
игр. Лекции для экономистов-кибернетиков, Л., 1974.
А. А. Порбит.
МАТРИЧНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕ-
УРАВНЕНИЕ — уравнение, неизвестной в к-ром является функ-
функциональная матрица, входящая в уравнение вместе со
своей производной.
Пусть рассматривается линейное М. д. у. вида
X' = A(t)X, t?R, A)
где A (t) есть (пХ п)-матрица~функция с локально ин-
интегрируемыми по Лебегу элементами, и пусть X (?) —
абсолютно непрерывное решение уравнения A), удов-
удовлетворяющее условию X(to)=I, I — единичная мат-
матрица. Тогда вектор-функция x(t) = X (t)h, h?R", яв-
является решением линейной системы
x' = A(t)x, B)
удовлетворяющим условию x{to) = h. Обратно, еслп
hu . . ., hn?R" и х{ (t) — решение системы B), удов-
удовлетворяющее условию Х{ (to) = h;, i=i, . . ., и, то функ-
функциональная матрица X (t), столбцами к-рой служат ре-
решения xi(t), является решением М. д. у. A). Если при
этом векторы hu . . ., hn линейно независимы, то
&е%ХA)ф0 при всех t^R.
Уравнение A) является частным случаем следующего
М. д. у. (возникающего в теории устойчивости)
— XB(t)+C{t). C)
Решение М. д. у. C) с начальным условием X(ta)=X$
дается равенством
X(t)--U(t, to)XoV(t, 10)+\* U (t, s)C(s)V(s, t)ds,
где U(t, s) — решение М. д. у. A) с условием X (s, s) =
= J, a V(t, s) — решение М. д. у. X' — В (t)X с усло-
условием X (s, s)=I.
В различных прикладных задачах (теории стабили-
стабилизации, оптимального управления, фильтрации управ-
управляемых систем и др.) большую роль играет т. н. м а т-
ричное дифференциальное уравне-
уравнение Риккати
Х' = А (t)X-~XB(t) + C(t)+XD{t)X.
Напр., если матричное уравнение Риккати
А" = - (F (<) + М)т Х-Х (F (t) + kl) — l +
+ XG(l)GT (t)X,
где т означает транспонирование, имеет при 5l^s=0
ограниченное на прямой R решение X (t) и для всех
h?R", всех i?R и нек-рого е>0 выполнено нера-
неравенство /tTZ(i)A?i-efeTfe, то любое решение управляемой
системы
x' = F (t) x + G (t) и, x?R", !/?R"*,
замкнутой обратной связью u=— ¦—¦ <5Т (t)X (t)x, удов-
удовлетворяет неравенству
\x(t)\<M\x (s) | exp 1-Х (* — «)], s< t,
где | -| — евклидова норма в R", а постоянная М не
зависит от s.
Лит.: [1] Лаппо-Данилсвский И. А., Примене-
Применение функций от матриц к теории линейных систем обыкновенных
дифференциальных уравнений, М., 1957; [2] Далецкий
Ю. Л., Крейн М. Г., Устойчивость решений дифференци-
дифференциальных уравнений в банаховом пространстве, М., 1970; [3] А т-
к и н с о н Ф. В., Дискретные и непрерывные граничные задачи,
пер. с англ., М., 1968; [4] Reid W. Т., Riccati differential equa-
equations, N. Y.—L., 1972 (Math. Sci. and Eng., v. 86); [5] Захар-
И т к и н М. X., «Успехи матем. наук», 1973, т. 28, в. 3, с. 83—
МАТРИЧНОЙ ФАКТОРИЗАЦИИ МЕТОД j *м етТд
матричной прогонки,— метод решения ко-
печиоразностных систем, аппроксимирующих краевые
задачи для систем обыкновенных дифференциальных
уравнений в одномерных задачах и для уравнений эл-
лнптич. типа в двумерных задачах.
Решение трехточечной разностной схемы
AiYi_1 — CiYi-\-BiYi + 1 = -Fi, i=l, 2, ...,Л'-1,
где Y{= {у1 ., у2 ., . . ., у ;.} — искомая сеточная век-
вектор-функция, F[ — вектор правой части, А;, ?,-, С,- —
заданные квадратные матрицы, при краевых условиях
— Co^o + ^o^i — — ^о> ^Л'^ Л'-i —СyYд'= — F N
ищется так же, как в скалярном случае, в виде
Y,^ni + 1Yi + 1 + Qi+1, i = 0, i, ..., IV —1. (*)
Прогоночные коэффициенты, матрица i?, + i и вектор
Qi+i определяются рекуррентными соотношениями
(«прямая прогонка»)
Qi + i(i ii)(iQi\ ;), , ,,
а -Я], Qi — левым краевым условием:
Y; считаются по формуле (*) («обратная прогонка»), а
Устойчивость этого метода по отношению к ошибкам,
округления имеет место при условиях
ЦСо-'Во! < 1, \\CnAnW < 1, IC^Bil + Wc^AiW < 1,
i=1, 2, .. ., Л' —1,
из к-рых следует, что ||Я,-||<1, г=1, 2, . . ., Лг (см. [1]).
Имеется другая форма условий устойчивости (см. [2],
[3]). М. ф. м. применяется и к двухточечным разност^
ным схемам (см. [3]). Используется вариант, в к-ром
обращение матриц заменено ортогонолизациеи (см. [4]).
Лит.: Ll] Самарский А. А., Введение в теорию разно-
разностных схем, М., 1971; [2] О г н е в а В. В., «Ж. вычисл. матем.
и матем. физики», 1967, т. 7, № 4, с. 803 — 12; [3] С а м а р с к и й
Л. А.. Николаев Е. С, Методы решения сеточных уравне-
уравнений, М., 1978; [4] Г о д у н о в С. К., «Ж. вычисл. матем. и ма-
матем. физики», 1962 т. 2, ,"N5 6, с. 972—82. Т. А. Гермогенова.
МАТРИЧНЫЙ МЕТОД СУММИРОВАНИЯ — один
из методов суммирования ряда и последовательности
г помощью бесконечной матрицы. Посредством беско-
бесконечной матрицы ||о„й11, ni к=1, 2, . . ., данная последо-
последовательность {sn} преобразуется в последовательность
Ы
Если ряд справа сходится для всех п=\, 2, ... и по-
последовательность {а„} имеет предел s при п—>-сс:
11 m on=s,
то последовательность {s,,} паз. суммируемой
методом, определенным матрицей
!ianfc!l, или просто суммируемой матрицей
j|an^||, а число s — ее пределом в смысле этого метода.
суммирования. Если {sn} рассматривается как последо-
последовательность частичных сумм ряда
то этот ряд паз. суммируемым к сумме s
матрице й ||anft||.
М. м. с. для ряда может быть также определен и не-
непосредственным преобразованием ряда A) в последо-
последовательность {уп}:
гДе WgnkW — данная матрица. В этом случае ряд A)
наз. суммируемым к с у м м е s, если для
всех п=1, 2, ... сходится ряд справа в B) и
lim yn=s-
П —У оо
Менее распространены М. м. с, определенные прео-
преобразованием ряда A) в ряд
где
и преобразованием последовательности {s,,} в ряд
2Г=1р». D>
где
Ря=2Т=1 P«*s*. "=1. 2, ....
при помощи соответственно матриц l|a,,fcl! и 1!РП^!'.
В этих случаях ряд A) с частичными суммами sn сум-
суммируем к сумме s, если ряд C) сходится к s или соот-
соответственно ряд D) сходится к s.
Матрицу метода суммирования, все элементы к-poft
неотрицательны, наз. положительной мат-
матрицей. К М. м. с. относятся, напр., Вороного .метод
суммирования, Чезаро метод суммирования, Эйлера
метод суммирования, Риса метод суммирования
(Н, рп), Хаусдорфа метод суммирования и другие (см.
Суммирования методы).
Лит.: Ш X а р д и Г., Расходящиеся ряды, пер. с англ.,
М., 1951; [2] Кук Р., Бесконечные матрицы и пространства
последовательностей, пер. с англ., М., 1960; [3] Итоги науки и
техники. Математический анализ, т. 12, М., 1974, с. 5—70: [4]
Барон С, Введение в теорию суммируемости р^дов, 2 изд.,
Таллин, 1977. Л. II. Волков.
МАТРОИД — гиперграф специального вида. М. оп-
определяется заданием множества V элементов и се-
семейства ^= {?*!, Е2, . . .} подмножеств множества У,
называемых независимыми множества-
м и, для к-рых выполняются следующие аксиомы:
1) пустое множество независимо; 2) каждое подмно-
подмножество независимого множества независимо; 3) для
всякого подмножества А^Е все независимые множества
М., содержащиеся в Л и являющиеся максимальными
по включению относительно А, имеют одинаковое
число элементов.
Пример ы. 1) Множество V строк произвольной
прямоугольной матрицы и семейство $ всех подмно-
подмножеств множества V, составленных из линейно незави-
независимых строк, образуют М. 2) Пусть X—{LU ?,, . . .}
— множество всех остовных лесов (см. Дерево) графа G,
а R(L{) — множество ребер леса L,-, г=1, 2, ....
Тогда множество ребер V графа G и семейство $ =
= {R(Li), i=l, 2, . . .} образуют М. 3) Пусть G — граф
двудольный с долями W, W". Подмножество T'czyp'
вершин, для к-рого существует паросочетание Р графа
G такое, что каждая вершина i>? V инцидентна нек-рому
ребру паросочетания Р, наз. трансверсалью.
Множество V и множество всех трансверсалей графа G
образуют т. н. трансверсальный матроид.
М. можно задать также множеством V элементов и
семейством С={Сг, С2, . . .} непустых подмножеств
С,с=7, называемых циклами и удовлетворяющих
следующим аксиомам: никакое собственное подмно-
подмножество цикла не является циклом; если v?Cif)Cj, то
Ci\JC/\{v] содержит цикл. Независимыми множест-
множествами этого М. являются подмножества ?c=F, не со-
содержащие циклов.
Если G — граф, то множество его ребер и семейство
простых циклов образуют т. н. циклический
матроид. Если в качестве циклов М. взять коциклы
(разрезы, см. Графа связность) графа G, то полученный
тажим образом М. наз. коциклическим. М.
двух последних типов наз. графическими. По-
Понятие «М.» используется в теории графов и комбинато-
комбинаторике при доказательстве нек-рых утверждений о по-
покрытиях и упаковках, паросочетаниях.
Лит.: [1] Whitney H., «Amer. J. Math.», 1935, v. 57,
p. 509—33; [2] Tutte W. Т., «J. Res. Nat. Bur. Standards.
Sec. B», 1965, v. 69, № 1—2, p. 1—47; [3] X a p a p и Ф., Теория
графов, пер. с англ., М., 1973. А. А. Сапоженко.
МАТЬЁ ГРУППА — конечная группа, изоморфная
одной из пяти групп, открытых Э. Матьё [1]. Серия
М. г. состоит из групп, обозначаемых
они представимы как группы подстановок на множест-
множествах из И, 12,22, 23, 24 элементов соответственно. Группы
М12 и М24 являются пятикратно транзитивными. Ми
реализуется естественным образом как стабилизатор
в М12 элемента множества, на к-ром действует М1г,
М23 — как стабилизатор элемента в М24, М22 — как
стабилизатор элемента в М23. Порядки М. г. равны
соответственно
7 920, 95 040, 443 520, 10 200 960, 244 823 040.
При рассмотрении М. г. часто пользуются (см. [2])
представлением ее в виде группы автоморфизмов соот-
соответствующей системы Штейнера S (I, т, п),
т. е. множества из и элементов, в к-ром выделена си-
система (™)/(Т) подмножеств, называемых блоками, со-
состоящих из т. элементов множества, причем каждые I
элементов содержатся в одном и только в одном блоке.
Автоморфизмом системы Штейнера наз. под-
подстановка множества ее элементов, переводящая блок
в блок. Группа Мп является группой автоморфизмов
системы Штейнера 5D, 5, 11), группа М12 — системы
5E, 6, 12), группа М22 — системы 5C, 6,-22), группа
М23 — системы 5D, 7, 23), группа Ми — системы
5E, 8, 24).
М. г. были первыми (и на протяжении более 80 лет
единственными) известными спорадическими конеч-
конечными простыми группами.
Лит.: [1] М a t h i e u Ё., «J. math, pures et appl.», 1861,
t. 6, p. 241—323; 1873, t. 18, p. 25—46; [2] W i t t E., «Abhandl.
Math. Semin. Univ. Hamburg», 1938, Bd 12, S. 256—64, 265—75;
[3] Итоги науки и техники. Алгебра. Топология. Геометрия,
т. 14, М.,.1976, с. 5 — 56. С. П. Струнков.
МАТЬЁ УРАВНЕНИЕ — обыкновенное линейное
дифференциальное уравнение
с действительными коэффициентами. Введено Э. Матьё
[1] при исследовании колебаний эллиптич. мембраны;
частный случай Хилла уравнения.
Фундаментальная система решений М. у. имеет вид
Ul (z) = е<**ф (z), u2 (z) = Ml (- z) (*)
при a^ni, n — целое, где cp(z) есть я-периодическая
функция, а Ляпунова характеристический показа-
показатель а либо действительный, либо чисто мнимый. При
Im a=0 одно из решений неограниченно возрастает,
а другое стремится к нулю для z—y-f-oo (зоны неустой-
неустойчивости на плоскости аЬ параметров), при Re a=0
эти решения ограничены (зоны устойчивости). На гра-
границе этих зон (случай, исключенный в (*)) одна из
функций фундаментальной системы решений М. у.
либо я-периодична, либо 2я-периодична (последняя наз.
Матъё функцией), а вторая получается из первой ум-
умножением на z. Зоны неустойчивости имеют вид криво-
криволинейных треугольников с вершинами в точках а=гс2,
Ь=0, и=0, 1,2,... (см. [2], [4]).
М. у. имеет и другую форму (см. [3]).
Лит.: [1] М а t h i e u Ё., Cours de physique mathemalique,
P., 1873; [2] С т р е т т М. Д. О., Функции Ламе, Матье и род-
родственные им в физике и технике, пер. с нем., Хар.—К., 1935; [3]
Камке Э., Справочник по обыкновенным дифференциальным
уравнениям, пер. снем., 5 изд., М., 1976; [4] Я к у б о в и ч В. А.,
С т а р ж и н с к и й В. М., Линейные дифференциальные урав-
уравнения с периодическими коэффициентами и их приложения, М.,
1972. _ В. М. Старжипский.
МАТЬЁ ФУНКЦИИ — 2я-периодические решения
Матъё уравнения
к-рые существуют только тогда, когда точка (a, q)
на плоскости параметров лежит на границе зон устой-
устойчивости. М. ф. четна или нечетна и единственна с точ-
точностью до множителя; второе линейно независимое
решение линейно растет по z при |z|—»-oo, если q-Ф^О.
Четные М. ф.— собственные функции интегрального
уравнения
[ kcoszcostG(t)dt, к=
-я
Аналогичное уравнение имеется для нечетных М. ф.
Обозначения М. ф.:
се0 (z, q), co1(z, q), ...; se, (z, q), se2 (z, q), ...
При g—>-0 эти функции приводятся к тригонометрич.
системе
1, cos z, .. .; sin z, sin 2z, ...
и обладают теми же свойствами ортогональности на
интервале (—я, я). М. ф. разлагаются в ряды Фурье,
к-рые сходятся при малых |<зг]<<г„; коэффициенты ря-
рядов — сходящиеся ряды по степеням q, напр.
ceo(z, 9) = 1 + 2Г=
п Cn+4Jn + 'g" + « (on + i\\ COS 2hz.
((+l)!)« -rL W )]
Лит.: [1] Уиттекер Э.-Т., В а т с о н Д.-Н., Курс
современного анализа, пер. с англ., 2 изд., ч. 2, М., 19ВЗ; [2]
Бейтмен Г.,Эрдейи А., Высшие трансцендентные функ-
функции. Эллиптические и автоморфные функции. Функции Ламе и
Матье, пер. с англ., М., 1967; [3]СансонеД ж., Обыкновен-
Обыкновенные дифференциальные уравнения, пер. с итал., т. 1, М., 1953;
[4] С т р е т т М. Д. О., Функции Ламе, Матье и родственные им
в физике и технике, пер. с нем., Х&р.—К., 1935; [5] М а к- Л а х-
л а н Н. В., Теория и приложения функций Матье, пер. с англ.,
М., 1953. М. В. Федорюк.
МАУРЕРА — К APT АН А ФОРМА — левоинвариант-
ная 1-форма на группе Ли G, т. е. дифференциальная
форма со степени 1 на G, удовлетворяющая условию
1а со= со для любого левого сдвига lg : x^-gx, g, x?G.
M.— К. ф. на G находятся во взаимно однозначном
соответствии с линейными формами на касательном
пространстве Te(G) в точке е; точнее, соответствие,
сопоставляющее каждой М.— К. ф. со ее значение со,,
из TP(G)*, является изоморфизмом пространства
М.— К. ф. на Te{G)*. Дифференциал М.— К. ф. есть
левоинвариантная 2-форма на G, определяемая фор-
формулой
d<o(X, Y) = -(o([X, Y]), A)
где X, Y — любые левоинвариантные векторные поля
на G. Пусть Хг, . . ., Хп — базис в Те (G) и пусть со/,
i=i, ¦ ¦ ., п,— такая М.— К. ф., что
iej) ij = 1, ..., п.
Тогда
dco,- = _ 2"/;= 1 с) k со; Л соА, B)
где cj-fe — структурные константы алгебры Ли g
группы G, состоящей из левопнвариантных векторных
полей на G, в базисе Хг, . . ., Л'„ таком, что
(X;)e=Xh i=l, ..., П.
Равенства B) (или A)) наз. уравнениями М а у-
рера — Картава. Первым их получил (в иной,
но эквивалентной форме) Л. Маурер [1]. Формы со,-
были введены Э. Картаном в 1904 (см. [2]).
Пусть хь . . ., хп — канонич. координаты в окрест-
окрестности точки е на G, определенные базисом Xlt . . ., Хп.
Тогда формы со,- записываются в виде
со,= ^._ Аи (хи ..., хп) dxj,
причем матрица
А (хг, ..., xn) = (Aif (xu ..., хп))
вычисляется по формуле
— айХ
А(хи ...,хп)= ~;dx ,
где Х = ^.=1х/Х;, ad — присоединенное представле-
представление алгебры Ли д.
Далее, пусть 0 есть tj-значная 1-форма на G, сопо-
¦ тавляющая каждому касательному вектору к G един-
единственное левоннвариантное векторное поле, содержа-
содержащее этот вектор (каноническая левая диф-
дифференциальная форма). Тогда
d0+-L[e, 6]=0,
что является еще одной записью уравнений Мауре-
ра — Картана.
Лит.: [1] Maurer L., «Sitzungsber. math, physik. Kl.
Bayerischen Akad. Wiss.» (Munchen), 1899, Bd 18, S. 103—50;
hi С a r t a n E., CEuvres completes, pt. 2, vol. 2, P., 1953, p.
:>71 — И24; [3J Ш е в а л л е К., Теория групп Ли, т. 1, М., 1948;
14] Б у р б а к и Н., Группы и алгебры Ли. Алгебры Ли, свобод-
свободные алгебры Ли и группы Ли, пер. с франц., М., 1976; [5] Н е 1-
t as о 11 S., Differential geometry, Lie groups and symmetric spaces,
.\. Y.— San Pr. — L., 1978. А. Л. Онищик.
МАХА ПРИНЦИП — утверждение, согласно к-рому
инертные свойства каждого физич. тела определяются
всеми остальными физич. телами во Вселенной. В клас-
сич. механике, напротив, считается, что инертные
свойства тела, напр, его масса, не зависят от наличия
или отсутствия других тел. М. п. был сформулирован
0. Махом (Е. Mach, 1896, см. [1]) при критич. анализе
оснований классич. механики, однако им не была при-
приведена точная математич. формулировка этого прин-
принципа. Имеется ряд неэквивалентных математич. фор-
формулировок М.п.
Лит.: [1] М а х Э., Механика, пер. с нем., СПБ, 1909; [2]
Э й н ш т е й н А., Собр. научных трудов, т. 4, М., 1967.
Д. Д. Соколов.
МАХА ЧИСЛО — один из основных критериев аэро-
динамич. подобия, когда нельзя пренебрегать сжимае-
сжимаемостью газа. М. ч. M=vla равно отношению скорости
течения газа v к скорости звз'ка а в той же точке по-
потока (или отношению скорости тела в газе к скорости
звука в этой среде). М. ч. наз. по имени Э. Маха
(Е. Mach). По материалам БСЭ-3.
МАХАЛАНОБИСА РАССТОЯНИЕ — величина
р(Х, Y\A) = {(X-Y)TA(X-Y)}1'\
где X, Y — векторы, А — матрица (т — транспониро-
транспонирование). М. р. используется в многомерном статистнч.
анализе, в частности при проверке гипотез и классифи-
классификации наблюдений. Введено П. Махаланобисом [1J,
к-рый использовал в качестве расстояния между двумя
нормальными распределениями с математич. ожида-
ожиданиями |ix и |л2 и общей ковариационной матрицей 2
величину
Р (Hi. И* I 2-1).
М. р. между двумя выборками (из распределений с оди-
одинаковыми ковариационными матрицами) или между
выборкой и распределением определяется путем за-
замены соответствующих теоретич. моментов выбороч-
выборочными. В качестве оценки М. р. между распределениями
применяется М. р. между извлеченными из них выбор-
выборками, а в случае использования линейной дискрими-
нантной функции — статистика Ф~1(а)+ф-1(Р), где
а — частота правильной классификации в первой
совокупности, Р — во второй, Ф — функция нормаль-
нормального распределения с математическим ожиданием 0 и
дисперсией 1.
Лит.: [1] М a h a I a n о b i s Р. С, «J. Asiatic Soc. of Ben-
Bengal», 1930, v. 26, p. 541—88; [2] e г о ж е, «Ргос. Nat. Inst. Sci
India (Calcutta)», A936), v. 12, p. 49—55; [3] А н д е р с о н Т.,
Введение в многомерный статистический анализ, пер. с англ.
М., 1963; [4J А й в а з я н С. А., Б е ж а е в а 3. И., Старо-
Староверов О. В., Классификация многомерных наблюдений М.
1974. А. И. Орлов.
МАЦУСИМЫ КРИТЕРИЙ: однородное простран-
пространство G/H, где G — аффинная редуктивная алгебраич.
группа, определенная над алгебраически замкнутым
полем к, а // — ее замкнутая подгруппа, является
аффинным алгебраич. многообразием тогда и только
тогда, когда // — редуктивная группа. Впервые най-
найден И. Мацусимой [1] для случая, когда к — поле ком-
комплексных чисел. Позже появились доказательства,
пригодные для любого алгебраически замкнутого поля
нулевой характеристики (см. [2J — [41). В случае, когда
характеристика к положительна, доказательство М. к.
было получено лишь после доказательства Мамфорда
гипотезы (см. [5], [6]).
Лит.; [1] Matsushima Y., «Nagoya Math. J.», 1960,
v. 16, p. 205 — 18; [2] В i a 1 у n i с k i- В i r u 1 a A., «Amer.
J. Math.», 1Й63, v. 85, p. 577—82; [3] Luna D., «Bull. Soc
math. France», 1973, mem. 33, p. 81—105; [4] Bore] A., Ha-
rish-Chandra, «Ann. Math.», 1962, v. 75, p. 485—535; [5] H и c-
н е в и ч Е. А., «Функц. анализ и его прилож.» 1977 т. 11
N5 1, с. 73—74; [6] Richardson R. W., «Bull. London Math.
Soc», 1977, v. 9, p. 38 — 41. В. Л. Попов.
МАШИНА (в математике) — абстрактное устройство,
осуществляющее переработку информации. Употреби-
Употребительны также термины «абстрактная маши-
н а», «а в т о м а т». Абстрактные М. являются частным
случаем управляющих систем. Возникновение их свя-
связано с анализом понятия алгоритма, начавшегося
в середине 30-х гг. 20 в., с развитием ЭВМ и с пост-
построением математич. моделей биологич. систем. Наи-
Наибольшее распространение получили М., перерабаты-
перерабатывающие дискретную информацию, типичными пред-
представителями к-рых являются автомат конечный и
Тьюринга машина. Абстрактные М. обладают боль-
большой наглядностью, возможностью легко осуществлять
различные композиции, элементарностью шагов ра-
работы. Изучение М. проводится в рамках алгоритмов
теории, математич. кибернетики и преследует цели
анализа и формализации понятия алгоритма, матема-
математич. моделирования реальных устройств и процессов.
Существует плодотворная связь между абстрактными
М. и реально существующими ЭВМ. Идеи построения
ЭВМ, программирования на ЭВМ в значительной мере
опираются на соответствующие пдеи из теории алгорит-
алгоритмов, математич. кибернетики. В свою очередь практика
работы с ЭВМ ставит новые задачи, подсказывает мо-
модели М., наиболее удобные для их решения.
Общим для всех абстрактных М. является наличие
конечного управляющего устройства, к-рое может
находиться в одном из состояний qu . . ., gfc. M. имеет
потенциально неограниченную внешнюю память и
устройства для считывания и записывания информа-
информации во внешнюю память. Считывание (записывание)
информации происходит, как правило, локальным об-
образом. Функционирование М. определяется програм-
программой, к-рая состоит из команд вида q;a-+qjb, где q/, qj —
состояния управляющего устройства, а — упорядочен-
упорядоченная информация локального характера из внешней
памяти, Ь — запись изменений содержимого внешней
памяти и положения считывающих устройств в ней.
Работа М. протекает в дискретном времени. На каждом
шаге t работы М. из внешней памяти в управляющее
устройство с помощью считывающего устройства по-
поступает информация а. Если на шаге t управляющее
устройство М. находится в состоянии qi и программа М.
содержит команду q-a-^-qjb, то на следующем шаге
г+1 управляющее устройство будет находиться в со-
состоянии qj, а содержимое внешней памяти и положе-
положение считывающих устройств будет изменено согласно Ь.
Обычно среди состояний управляющего устройства вы-
выделяются одно или несколько начальных и одно или
несколько заключительных. Перед началом работы
управляющее устройство приводится в начальное
состояние, конец работы определяется заключитель-
заключительным состоянием.
Во многих случаях абстрактные М. конструируются
для вычисления числовых (словарных) функций и пре-
предикатов. Вычислимость функции i(xl, . . ., х„) на ма-
машине М понимается следующим образом. Для произ-
произвольного набора аргументов (хг, . . ., хп) указывается
тачальная конфигурация К\ (?ь . . ., хп) машины М,
к-рая представляет собой заполнение внешней памяти
и положение читающих устройств в ней, отвечающие
аргументам хг, . . ., хп. Определяется, какие конфи-
конфигурации машины М считать заключительными, т. е.
соответствующими окончанию процесса вычисления
функции / на машине М. Определяется, как по за-
заключительным конфигурациям получить значения вы-
вычисляемой функции. Процесс вычисления значения
f{xu . . ., хп) состоит в серии переходов в соответст-
соответствии с программой машины М от начальной конфигу-
конфигурации К1(х1, . . ., хп) к непосредственно следующей
K<z,{xi, . . ., хп) и т. д. до тех пор, пока не будет до-
достигнута заключительная конфигурация. Если значе-
значение /(.г!, . . ., х,г) не определено, то машина М, отправ-
отправляясь от начальной конфигурации К\{хг, . . ., хп), ни-
никогда не попадет в заключительную конфигурацию. В
этом случае процесс вычисления может происходить
бесконечно долго.
Часто за основу определяемой абстрактной М. бе-
берется обычная машина Тьюринга, а отличия состоят
в добавлении новых или ограничении имеющихся воз-
возможностей последней. Модификации машины Тьюринга
обычно происходят по следующим трем направле-
направлениям.
1. Организация внешней памяти. Наибольшее рас-
распространение получило введение нескольких лент
(многоленточные машины Тьюринга). Изучаются также
М. с односторонними и многомерными лентами, с внеш-
внешней памятью в виде бесконечного графа (напр., в виде
бесконечного двоичного дерева). Другой подход со-
состоит в замене традиционной ленты регистрами или
счетчиками, способными содержать произвольные
натуральные (целые) числа или слова произвольной
длины. Так обстоит дело с машинами Ш е ф е р д-
с. она — Стургиса [6], машиной Минско-
Минского [3] и машиной с произвольным
доступом к памяти.
2. Хранение, преобразование и получение информа-
информации из внешней памяти. Рассматриваются М., у к-рых
часть информации из внешней памяти, не поступающая
в управляющее устройство в течение нек-рого времени,
зависящего от входа, становится в дальнейшем вообще
недоступной для читающих устройств М. На близкой
идее основано определение машин Тьюринга с лентами
магазинного типа (магазинные автомат ы).
Для М., к-рые воспринимают и преобразуют инфор-
информацию из внешней памяти побуквенно, типичным огра-
ограничением является запрет печатать одни символы вместо
нек-рых других. Таковы, в частности, неетпрающпе
машины Тьюринга и двусторонние автоматы, эквива-
эквивалентные конечным автоматам. Сюда же относят важ-
важный класс абстрактных М.— конечные автоматы. Од-
Однако более распространенными являются ограничения
на объем внешней памяти, время работы и т. п. Напр.,
линейно ограниченные автоматы представляют собой
обычные машины Тьюринга, у к-рых длина используе-
используемой в вычислении ленты ограничена линейной функцией
от длины входа.
Часто получение информации из внешней памяти
происходит с помощью нескольких головок. Более об-
общий подход состоит в том, что на внешней памяти М.
определяются общерекурсивные предикаты. Набор зна-
значений этих предикатов представляет собой информа-
информацию, к-рая поступает в управляющее устройство М.
Нта идея используется в машинах Шефердсона — Стур-
Стургиса, у к-рых вдобавок запись информации во внешнюю
память может осуществляться с помощью произволь-
произвольных общерекурсивных функций.
3. Способ функционирования. Здесь различают детер-
детерминированные, недетерминированные и вероятностные
М. У детерминированных М. каждый
шаг работы однозначно определяется состоянием уп-
управляющего устройства и информацией из внешней
памяти, полученной с помощью читающих устройств.
Программа недетерминированной М. мо-
может содержать различные команды с одинаковыми ле-
левыми частями. Поэтому для недетерминированной М.
при заданном входе рассматривают не одно, а множе-
множество всех вычислений, согласованных с программой.
Вероятностная М. представляет собой М.,
к-рая либо снабжена датчиком случайных чисел, либо
имеет программу, в к-рой переходы от одних команд
к другим осуществляются с заданными вероятностями.
В недетерминированном случае обычно рассматри-
рассматривают вычисления предикатов. Если недетерминирован-
недетерминированная машина М вычисляет предикат р(х1у . . ., х„),
то p(xlt . . ., х„) истинен тогда и только тогда, когда
среди всех возможных вычислений машины М, начи-
начинающихся с конфигурации Ki(xu . . ., хп), существует
вычисление, содержащее заключительную конфигу-
конфигурацию.
В целом вычислительные возможности детермини-
детерминированных, недетерминированных и вероятностных ма-
машин представляются одинаковыми. Однако в отдель-
отдельных узких классах М. недетерминированные и вероят-
вероятностные М. могут оказаться мощнее детерминирован-
детерминированных. Для многих типов абстрактных М. с ограниче-
ограничениями на объем внешней памяти или время работы
проблема «детерминизации» недетерминированных ма-
машин является интересной открытой проблемой A982).
См. также Вычислительная машина абстрактная.
Лит.: [11 Автоматы. Сб. статей под ред. К. Э. Шеннона и
Дж. Маккарти, пер. с англ., М., 1956; [2] Мальцев А. И.,
Алгоритмы и рекурсивные функции, М., 1965; [31 М и н-
с к и й М., Вычисления и автоматы, пер. с англ., М., 1971; [4]
Проблемы математической логики. Сб. переводов, М., 1970: [5]
Сложность вычислений и алгоритмов. Сб. переводов, М., 1974;
!iij Shepherd son J. C, S t u г g i s H. E., «J. Assoc.
Comput. Machinery», 1963, v. 10, № 2, p. 217—55.
С. С. Марченков.
МАШИННО-ОРИЕНТИРОВАННЫЙ ЯЗЫК — язык
программирования, позволяющий при составлении про-
программ учитывать особенности системы команд и пред-
представления информации в объектной вычислительной
машине. М.-о. я., в отличие от универсальных проб-
проблемно-ориентированных языков программирования, осу-
осуществляющих отображение множества Р входных про-
программ во множество М машинных программ, стремятся
отображать Р на М.
Простейшими М.-о. я. являются ассемблеры,
к-рые, полностью сохраняя структуру машинной про-
программы, позволяют использовать символич. обозначе-
обозначения для команд и адресов памяти, а также собирать
программы из нескольких отдельно написанных кус-
кусков. Дополнительные возможности по текстовым под-
подстановкам и другим простым преобразованиям при
сборке программного текста предоставляются макро-
макроассемблерами. М.-о. я. высокого уровня, аналогично
универсальным языкам, имеют фразовую структуру,
допуская составные объекты и определяемые опера-
операции, однако содержат дополнительно средства описа-
описания элементарных объектов и базовых операций в тер-
терминах машинных конструкций.
Лит.: [1] Д ж е р м е й н К., Программирование на IBM/360,
пер. с англ., 2 изд., М., 1973; [2] Браун П., Макропроцессоры
и мобильность программного обеспечения, пер. с англ., М., 1977;
[3] К а т к о в В. Л., Р а р А. Ф., Программирование на языке
ЭПСИЛОН. Новосиб., 1972. А. П. Ершов.
МАЯТНИКА КОЛЕБАНИЙ УРАВНЕНИЕ — обык-
обыкновенное дифференциальное уравнение вида
я= — a sin х, (*)
где а — положительная константа. М. к. у. возникает
при изучении свободных колебаний в поле тяжести
математич. маятника — материальной точки, имею-
имеющей одпу степень свободы и находящейся на конце не-
нерастяжимого и несжимаемого невесомого подвеса, дру-
другой конец к-рого закреплен на шарнире, допускающем
вращение маятника в вертикальной плоскости. Неиз-
Неизвестная функция x(t) — это угол отклонения маят-
маятника в момент t от нижнего положения равновесия,
выраженный в радианах;
a=g/l,
где I — длина подвеса, g — ускорение свободного па-
падения. Уравнение малых колебаний маятника около
нижнего положения равновесия имеет вид:
х = — ах.
Качественное изучение М. к. у. производится с по-
помощью закона сохранения энергии, связывающего
положение и скорость маятника:
где ?=const — полная энергия маятника. Масштаб
времени можно выбрать так, чтобы было я=1. При
этом значению полной энергии ?<1 соответствует
колебательное движение маятника (скорость периоди-
периодически меняет знак), а значению ?>1 соответствует
вращательное движение (скорость сохраняет знак).
Решение x(t) M. к. у. (*) с начальным условием
х@)=0, х@) = а при ?=а2/2<1 удовлетворяет соот-
соотношению
где Якоби эллиптическая функция sn имеет модуль а/2.
Большое прикладное значение имеют уравнения,
близкие к М. к. у. Наличие малого трения, зависящего
от положения и скорости маятника, приводит к урав-
уравнению
х=—a sin ж + е/ (х, х);
малые колебания маятника с трением описываются
уравнением:
х= — ax-\-zf (х, х),
частным случаем к-рого является Ban дер Поля урав-
уравнение. Колебание маятника при периодич. изменении
длины подвеса (движение качелей) описывается Хилла
уравнением, важный частный случай к-рого — Матъё
уравнение.
Лит.: [1] Арнольд В. И., Обыкновенные дифференци-
дифференциальные уравнения, 2 изд., М., 1975; [2] К а м ке Э., Справочник
по обыкновенным дифференциальным уравнениям, пер. с нем.,
5 изд., М., 1976; [3] А н д р о н о в А. А., В и т т А. А., X a Ji-
Jilt и н С. Э., Теория колебаний, 2 изд., М., 1959.
Ю. С. Плъяшенко.
МГНОВЕННОЕ СОСТОЯНИЕ для однородной цепи
Маркова со счетным множеством состояний — состоя-
состояние (напр., i), для к-рого плотность вероятности пере-
перехода
А; О
где pa(h) — вероятность перехода из i в i за время h,
равна —оо. В противном случае состояние i наз. не-
немгновенным, или задерживающим.
Лит.: [1] Г и х м а н И. И., Скороход А. В., Теория
случайных процессов, т. 2, М., 1973. А. Н. Ширяев.
МЁБИУСА ЛИСТ — неориентируемая поверхность,
у к-рой эйлерова характеристика равна нулю, а край
представляет собой
замкнутую линию. М. л.
может быть получен
отождествлением двух д 1с~
противоположных сто-
сторон А В и CD прямо-
прямоугольника А В CD так,
что точки А и В совме-
совмещаются соответственно
с точками С и D (см. рис.). М. л. в евклидовом про-
пространстве Е3 является односторонней поверхностью
(см. Односторонние и двусторонние поверхности).
М. л. был рассмотрен (в 1858—65) независимо друг
от друга А. Мёбиусом (A. Mobius) и И. Листингом
(I. Listing). А. В. Иванов.
МЁБИУСА ПЛОСКОСТЬ, круговая плос-
плоскость, инверсная плоскост ь,— плос-
плоскость, элементы к-рой составляют два непересекаю-
непересекающихся множества — множество точек и множество
окружностей, с симметричным отношением инцидент-
инцидентности (связывающим точку и окружность). Отношение
инцидентности удовлетворяет следующим аксиомам:
1) каждые три различные точки инцидентны одной
и только одной окружности;
2) через точку, не инцидентную окружности, прохо-
проходит одна и только одна окружность, пересекающая
данную окружность в данной точке;
3) существуют по крайней мере четыре различные
точки, не инцидентные одной окружности. Каждая
окружность инцидентна по крайней мере трем раз-
различным точкам.
Из М. п. можно получить аффинную плоскость, если
назвать одну из точек М. п. несобственной, а окруж-
окружности, инцидентные этой точке,— прямыми.
В трехмерном проективном пространстве Р3 точки
овоида о и плоскости, пересекающей овоид в более чем
одной точке, с тем же отношением инцидентности, что
и в Р3, образуют М. п. М (о) (см. [1]). М. п. наз. овало-
подобной, если она изоморфна М (о) для нек-рого ово-
овоида о. Среди овалоподобных М. п. наиболее известна
I модель М (S), где S — сфера в трехмерном евклидовом
пространстве, т.е. плоскость, изоморфная М(с), где
с — нелинейчатая квадрика в трехмерном проектив-
проективном пространстве над полем действительных чисел.
М. п. наз. конечной, если она состоит из конеч-
конечного числа точек и окружностей. На всех окружностях
конечной М. п. лежит одинаковое число точек и через
каждую точку плоскости проходит одинаковое число
окружностей. Число, на единицу меньшее числа точек
па окружности, наз. порядком плоскости.
М. п. порядка п содержит и2+1 точек и п(/?2+1) ок-
окружностей; через каждую точку плоскости проходит
п(п-|-1) окружностей. Наиболее известна следующая
модель М. п. порядка п=р1г. Точками плоскости яв-
являются элементы поля Галуа GF (p2h) и несобственная
точка {оо}, а окружностями — образы множества
K=GF{p/l)[J {оо} относительно группы подстановок
вида
Необходимым условием существования М. п. по-
порядка п является существование конечной аффинной
плоскости того же порядка. Доказана единственность
М. п. порядка п=2, 3, 4, 5, 7, И (см. [5]). Если М. п.
порядка п содержит собственную подплогкость по-
порядка т, то WEsn(mod 2) и m2-\-m<in (см. [2]).
Проводилась классификация М. п. (см. [3], [4]).
М. п. названа по имени А. Мёбиуса (A. Mobius, 1855),
заложившего основы теории окружностей.
Лит.: [I] Derabowski P., Finite geometries, В., 1968;
М Dcmlowski P., Hughes D. R., «J. London Math.
Soc», 19б.г>, v. 40, p. 171—82; [3] He ring С h., «Math. 7..»,
1965. Bd 87, S. 252—62; [4] К r i e r N., в кн.: Proceedings of
International Conference on Projective Planes, Wash., 1973, p.
157—63; [5] Истомина Л. И., в сб.: Кибернетико-матема-
тические методы исследования процессов и структур, Пермь,
197В, с. 81—83. В. В. Афанасьев.
МЁБИУСА РЯД — функциональный ряд вида
М. р. исследован А. Мёбиусом [1], к-рый нашел для
ряда (*) формулу обращения:
где (.1 (s) — Мёбиуса функция. А. Мёбиус рассмотрел
также формулы обращения для конечных
сумм по делителям заданного натурального числа п:
i ^
Другая формула обращения: если Р (п) — вполне
мультипликативная функция, для к-рой Р (i)~ 1,
а /(.г) функция, определенная при всех действительных
х>0, то из
следует
Лит.: L1] Mobius A. F., «J. reine und angew. Math.»,
1832, Bd 9, S. 105 — 23; [2] Виноградов И. М., Основы тео-
теории чисел, 8 изд., М., 1972; [3] П р а х а р К., Распределение
простых чисел, пер. с нем., М., 1967. Б. М. Бредихин.
МЁБИУСА ФУНКЦИЯ — арифметическая функция
натурального аргумента: [лA)=1, u.(n) = 0, если п
делится на квадрат простого числа, в противном слу-
случае \х(п)—(—1)*, где к — количество простых множи-
множителей числа п. Введена А. Мёбиусом (A. Mobius, 1832).
М. ф.— мультипликативная функция; Zj. \i(d) = 0,
если п~>\. М. ф. используется при изучении других
арифметич. функций, она содержится в формуле обра-
обращения (см., напр., Мёбиуса ряд). Для среднего значе-
значения М. ф. известна оценка [2]
-11У
И»)
ехр { — с ln3/l5 х (Inln x)"
где с — постоянная. Из стремления среднего значения
к нулю при х—>-оо следует асимптотич. закон распреде-
распределения простых чисел в натуральном ряде.
Лит.: tlj Виноградов И. М., Основы теории чисел,
9 изд., М., 1981; [2] Waif isz A., Weylsche Exponentialsum-
mcn in der neueren Zahlenthcorie, В., 1963. H. if. Климов.
МЕДИАНА треугольника — прямая (или ев
отрезок внутри треугольника), соединяющая вершину
треугольника с серединой противоположной стороны.
Три М. треугольника пересекаются в одной точке,
к-рая называется центром тяжести треу-
треугольника, центроидом, или барицент-
барицентром. Эта точка делит каждую М. на две части, отноше-
отношение между к-рыми равно 2 : \, считая первый отрезок
ОТ вершины. П. С. Моденов.
МЕДИАНА — одна из числовых характеристик рас-
распределения вероятностей, частный случай квантили.
Для действительной случайной величины X с функцией
распределения F(х) М. наз. число т, к-рое удовлетво-
удовлетворяет условиям F(m)<V2 и ^(ш+0)>х/2. Любая слу-
случайная величина имеет по крайней мере одну М. Если
-/?(х) = 1/2 при всех х из замкнутого интервала, то каж-
каждая точка этого интервала есть М. Если F(х) строго
монотонная функция, то М. единственна. В симмет-
симметричном случае М., если она единственна, совпадает с
математич. ожиданием, если последнее существует.
Тот факт, что М. существует всегда, используется для
центрирования случайных величин (см., напр., Леей
неравенство). В математич. статистике для оценки М.
распределения по независимым результатам наблюде-
наблюдений Xlt . . ., Хп используют т. н. выборочную ме-
медиану — М. соответствующего вариационного ряда
ХAЬ . . ., Х(п): величину Х^ + 1), если п—2к-\-1 — нечет-
нечетное, и — [Х^)-\-ХAг + 1)], если п = 2к — четное.
Лит.: [1] Л о эв М., Теория вероятностей, пер. с англ..
М., 1962; [2] Крамер Г., Математические методы стати-
статистики, пер. с англ., 2 изд., М., 1975. А. В. Прохоров.
МЕДИАНТА двух дробей alb и eld с положитель-
положительными знаменателями — дробь (a-\-c)l(b-\-d). M. двух
дробей заключена между ними, т. е. если (alb)^s(cld),
&>0, d>0, то -g-< ? + с, sg -j- ¦ Конечная последова-
последовательность дробей, каждая промежуточная из к-рых
является М. соседних с ней, наз. рядом Фаре я.
М. двух соседних подходящих дробей разложения
действительного числа а в цепную дробь заключена
между числом а и подходящей дробью меньшего по-
порядка. Таким образом, если PjQn и Pn + ilQn + i —
подходящие дроби порядков п и «-{-1 разложения чи-
числа а. в цепную дробь, то
^2.
Qn
Р„+рп
Qn
Qn+Qn+i Qn
Лит.: [11 X и н ч и н А. Я., Цепные дроби, 4 и?д., М., 1978.
В. И. Нечаев.
МЕЙЕРА ПРЕОБРАЗОВАНИЕ — интегральное пре-
преобразование вида
2, v
@ dt<
где1 Wjx, v(^) — Уиттекера функция. Формула обра-
обращения имеет вид
/@= lim ^т—-rA + 2v) a
А—»- + °°
х S Т-а еХ'/2 (^)^1/2 ми-1/2, v (*0 F (*) dx,
где Мц, v(^) — функция Уиттекера.
При p,= ±v М. п. переходит в Лапласа преобразо-
преобразование; при |х=—V2 в Kv-преобразование:
F(x) = ~ ^ ~ e~xtl- [xt)l'" R\. (xt/2) f (t) dt,
где Kv (x) — Mакдоналъда функция.
К М. п. сводится преобразование В а р-
м а:
F (x) =
J" (xOv/s e-*4*W^ v (xt) f (t) dt.
Мейера ^-преобразование (Мейе-
pa — Бесселя преобразование) — интег-
интегральное преобразование вида
F (х) = |/-1 Jj Kv (xt) VHf (t) dt.
Если функция f(t) локально интегрируема на @, оо),
имеет ограниченное изменение в окрестности точки
t=to'>O и сходится интеграл
I/O \dt, P ;
то имеет место формула обращения
'2 F (х) dx.
При v=±1/2 ^-преобразование Мейера переходит
в преобразование Лапласа.
М. п. введено К. Мейером [1], А'-преобразование
Мейера — им же [2].
Лит.: [1] Meijer С. S., «Proc. Koninkl. Nederl. acad. wet.»,
1941. v. 44, p. 727—37; [2] его же, там же, 1940 т. 43, р. 599—
¦608, 702— И; [3] Б р ы ч к о в Ю. А., П р у д н и к о в А. П.,
Интегральные преобразования обобщенных функций, М., 1977;
[4] Итоги науки. Математический анализ. 1966, М., 1967, с. 7—
S-. Ю. А. Брычпов, А. П. Прудников.
МЕЙЕРА ТЕОРЕМА: пусть f(z) — мероморфная
функция в единичном круге D= {z?C: |z|<l}, тогда
все точки окружности r={z?C: |z| = l}, исключая,
быть может, множество первой категории на Г, яв-
являются либо точками Фату, либо точками Мейера.При
этом точка е'е окружности Г наз. точкой Фату
для f(z), если существует угловое граничное значение
lim/(z)=^ при z—>-e'e по любому некасательному пути.
Точка е1'9 наз. точкой Мейера (или обладает
свойством М с н е р а), если: 1) полное пре-
предельное множество С (е'е ; /) функции f(z) в точке е»е
субтотально, т. е. не совпадает со всей расширенной
комплексной плоскостью С; 2) множество всех пре-
предельных значений вдоль любой хорды круга D, прове-
проведенной в точку е'е , совпадает с С(е'е; /). Теорема была
доказана К. Мейером [1].
М. т. является аналогом в терминах категории мно-
множеств Плеснера теоремы, формулирующейся в тер-
терминах теории меры. Уточнение М. т. см. в [3].
Лит.: [1] Meier К., «Math. Ann.», 1961, Bd 142, S. 328—
344; [2] К о л л и н г в у д Э., Лов ат е р А., Теория предель-
предельных множеств, пер. с англ., М., 1971; [3] Г а в р и л о в В. И.,
Канатников А. Н., «Докл. АН СССР», 1977, т. 233, № 1,
с. 15 —17. Е. Д. Соломенцев.
МЕЛЕРА КВАДРАТУРНАЯ ФОРМУЛА — наивыс-
наивысшей алгебраич. степени точности квадратурная формула
для промежутка [ —1,1] и веса 1/ У 1—х2, имеющая вид
cos
'A)
Узлы — корни многочлена Чебышева
Гдг (х) = cos Лг arccos x,
коэффициенты одинаковы и равны n/N. Алгебраич.
степень точности равна 2N—1. Формула A) установ-
установлена Ф. Мелером [1].
Квадратурная формула наивысшей алгебраич. сте-
степени точности с весом 1/ У\—ж2 и с 2N-\-l узлами,
у к-рой N фиксированных узлов совпадают с узлами
квадратурной формулы A), такова:
(x)dx
Квадратурной формулой B) пользуются для уточне-
уточнения приближенного значения интеграла, полученного
с помощью квадратурной формулы A), при этом зна-
значения подинтегральной функции в узлах формулы A)
уже вычислены, так что необходимо вычислить ее зна-
значения лишь в N-\-1 дополнительных узлах. Квадратур-
Квадратурная формула B) представляет собой также наивысшей
алгебраич. степени точности квадратурную формулу
с весом i/y~i— ж2, у к-рой фиксированными узлами
являются концы промежутка [ — 1, 1] и, следовательно,
остальные узлы суть корни ортогонального относи-
относительно промежутка [—1,1] и веса У~1—х2 многочлена
степени 2N—1 — многочлена Чебышева U2n-i(x) 2-го
рода. Алгебраич. степень точности квадратурной фор-
формулы B) равна 4iV—1.
Иногда формулу A) наз. квадратурной фор-
формулой Эрмита.
Лит.: [1] Mehler F. G., «J. reine und angevc. Math.»,
1864, Bd 63, S. 152—57; [2] Крылов В. И., Приближенное
вычисление интегралов, 2 изд., М. 1967. И. П. Мысовских.
МЕЛЕРА — ФОКА ПРЕОБРАЗОВАНИЕ — интег-
интегральное преобразование вида
F (x)=^ Ph_1/2(x)f(r)dr, 1<*< оо, A)
где Pv (х) — сферич. функция Лежандра 1-го рода.
Если f(x)?L[O, оо), !/'(т)| —локально интегрируема
на [0, оо) и /@)=0, то имеет место формула обращения
/ (т) = т th зтт J ™Pix _ 1/2 (х) F (х) dx. B)
Равенство Парсеваля. Пусть М.—Ф. п.
определено равенствами
G (т) = J ~ yTthl^ Ph_ 1/2 (x) g (х) dx,
-1/2 (*) G (т) dr.
Если gi(x), i=l, 2,— произвольные действительные
функции и выполняются условия
gi(x)x~1/2ln(l+x)€L(i, оо), gi(x)?L2(i, оо),
Gx (т) С2 (т) йт= J ™ gl (x) g2 (x) dx.
Обобщенное М.— Ф. п. и формула его обращения
имеют вид
/1(*)/(T)dT, C)
= -i-Tshnirr (-|~ft+ix) Г (-L-k — ix) x
W^Hdx, D)
где P(v '(rr) — присоединенные функции Лежандра 1-го
рода. При к=0 формулы C), D) переходят в A), B),
при /с=1/2, y=ch а. формулы C), D) приводят к косинус-
преобразованию Фурье, а при к=—V2, i/=ch а к си-
синус-преобразованию Фурье. Преобразования A) и B)
введены Ф. Мелером [1], основные теоремы доказаны
В. А. Фоком [2].
Лит.: [1] Mehler F. G., «Math. Ann.», 1881, Bd 18, S.
161—94; [2] Ф о к В. А., «Докл. АН СССР», 1943, т. 39, с. 279—
283; [3] Итоги науки. Математический анализ. 1966, М., 1967,
с 7—82. Ю. А. Брычков, А. П. Прудников.
МЕЛЛИНА ПРЕОБРАЗОВАНИЕ — одно из интег-
интегральных преобразований. Оно определяется формулой
сводится к Лапласа преобразованию подстановкой
t=e~z. M. п. применяется к решению определенного
класса плоских задач на гармонии, функции в секто-
риальной области, задач теории упругости и пр.
Теорема обращения. Пусть т0/^) €
?L@, oo), причем функция )(%) имеет ограниченное
изменение в окрестности точки %=t. Тогда
Теорема представления. Пусть функ-
функция М (o-\-iu) суммируема по и на (—оо, +оо) и имеет
ограниченное изменение в окрестности точки u=t;
тогда
4- [М (a+i(t + 0)) + M (a-f-i (i—0))] =
= lim ^K f(x)xa+it-1dx,
где
« С о + i oo
=-L\ . М (s)x-sds.
2лг J cj-ioo v '
Лит.: [1] М е 1 1 1 n H., «Acta Soc. sci. (ennica», 1896, v. 21,
№ 1, S. 1—115; [2] e r о же, «Acta math.», 1902, v. 25, S. 139—
164; [3! Тчтчмарш Е. К-, Введение в теорию интегралов
Фурье, пер. с англ., М.—Л., 1948; [4] Д и т к и н В. А., П р у д-
ников А. П., Интегральные преобразования и операционное
исчисление, 2 изд., М., 1974. П. И- Ливоркин.
МЕНГЕРА КРИВАЯ — пример линии, содержащей
топологич. образ любой линии (и, более того, любого
одномерного метризуемого пространства счетного ве-
веса). Поэтому она наз. универсальной кри-
кривой. Построена К. Менгером [1] (конструкцию М. к.
см. в ст. Линия). М. к. топологически характеризуется
[3] как одномерный покадьно свяаныйметризуемый кон-
континуум К, не имеющий локально разбивающих точек
(т. е. для любой связной окрестности О любой точки
х?К множество О\ {х} связно) и не имеющий непустых
открытых и вложимых в плоскость подмножеств.
Лит.: [1] Meager К., Kurventheorie, Lpz., 1932; [2]
Пархоменко А. С, Что такое линия, М., 1954; [3] А п-
derson R., «Ann. Math.», 1958, v. 68, № 1, p. 1 — 16.
Б. А. Пасынков.
МЕНЕЛАЯ ТЕОРЕМА —
теорема о соотношении меж-
между длинами отрезков на
сторонах треугольника, пе-
пересеченного прямой. Имен-
Именно, если прямая пересекает
стороны треугольника А ВС
(или их продолжения) в точ-
точках С", А' и В', то справедливо соотношение
АС В А' СВ __ ,
С В ' А'С ' В'А ~ ¦
М. т. есть частный случай Карно теоремы; она допус-
допускает обобщение на случай многоугольника. Пусть пря-
прямая / пересекает стороны АлАг, A2AS, . . ., Ап^хАп,
АпАг многоугольника АХА2А3 . . . Ап соответственно
в точках alt а2, . . ., я„_1, ап- В таком случае справед-
справедливо соотношение
Atn!i _ А2а2 _ _ An_lan_l ^ Апап .
аА oA ' ' ' UniAn опАи '
где знак минус соответствует случаю нечетного п, а
аыак плюс — четного п.
М. т. была доказана Менелаем A в. н. э. ) и, по-
видимому, была известна Евклиду C в. до н. э.).
Л. С. Моденов.
МЁНЬЕ ТЕОРЕМА: кривизна к кривой у, лежащей
на поверхности, кривизна кд- нормального сечения,
плоскость к-рого проходит через касательную к кри-
кривой у в данной ее точке Р, и угол а между соприка-
соприкасающейся плоскостью кривой у в точке Р и плоскостью
N нормального сечения связаны соотношением
fejv=ft cos a.
В частности, кривизна любого наклонного сечения
поверхности выражается через кривизну нормального
сечения с тон же касательной.
Теорема доказана Ж. Мёнье в 1776 (опубл. в [1]).
Лит.: [UMeusnler J., «Mem. pres. sav. etrangers. Ac.
sci.», 1785, t. 10, p. 477—510. Д. Д. Соколов.
МЕНЬШОВА ПРИМЕР НУЛЬ-РЯДА - первый не-
нетривиальный пример тригонометрич. ряда, сходяще-
сходящегося к нулю всюду вне нек-рого совершенного мно-
множества меры нуль; построен Д. Е. Меньшовым [1].
Ряды такого типа наз. нуль-рядами. С этим
понятием естественно связан вопрос о единственности
разложения функции в тригонометрич. ряд (см. Един-
Единственности множество).
Лит.: [1] М е н ьш о в Д.Е.,«С. г. Acad. sci.», 19I6, t. 163,
p. 433—36; [2] Б а р и Н. К., Тригонометрические ряды, М-,
1961, с. 804—06. М. И. Войцеховский.
МЕНЬШОВА — РАДЕМАХЕРА ТЕОРЕМА — теоре-
теорема о сходимости ортогональных рядов почти всюду:
если система функций {(pn(t)}n=i ортонормирована на
отрезке [а, Ь], то при условии
ряд
сходится почти всюду на [а, Ь\. Эта теорема доказана
независимо Д. Е. Меньшовым [1] и X. Радемахером [2].
Д. Е. Меньшов доказал, что ее утверждение оконча-
окончательно в следующем смысле. Если монотонно возрас-
возрастающая последовательность положительных чисел
со(п) удовлетворяет условию а(п)=о (log2 n), то най-
найдется всюду расходящийся ортогональный ряд (*),
коэффициенты к-рого удовлетворяют условию
У" о^со (п) < оо.
Лит.: [!] Menchoff D., «Fundam. math.», 1923 t. 4,
p. 82—105; [2] Rademacher H., «Math. Ann.», 1922, Bd
87, S. 112—38; 13] А л е к с и ч Г., Проолемы сходимости орто-
ортогональных рядов, пер. с англ., М., 19U3, с. 87, 94.
Б. И. Голубое.
МЕРА, мера множества,— обобщение поня-
понятия длины отрезка, площади фигуры, объема тела, ин-
интуитивно соответствующее массе множества при нек-ром
распределении массы по пространству. Понятие М.
множества возникло в теории функций действитель-
действительного переменного в связи с изучением и усовершенст-
усовершенствованием понятия интеграла.
Определения и общие свойства. Пусть X — нек-рое
множество и $ — нек-рый класс его подмножеств.
Неотрицательная (не обязательно конечная) функция
множеств К, определенная на $, наз. аддитив-
аддитивной, конечно аддитивной или счетно
аддитивной, если
когда
соответственно при л=2, п — любом конечном и п<:оо.
Совокупность 5" подмножеств множества А наз.
полукольцом множеств, если:
1) 0^'\
2) Е-,, E2^3>
3) Е, Е^р,
существует представление Е^ 1)"=1Е{, Eff]Ey = я
при гф], Ei^^p, i=i, . . ., п, п<<х>. Совокупность 5?
подмножеств множества X наз. кольцом мно-
множеств, если:
1 €
)
2) ?&> ^^Р, ^zZM
Пример полукольца: X=Rk, ff> —- совокупность
интервалов вида
{х=(хъ ..., j-j)gR«:a;<i; < bh i=l, ...,k}.
Совокупность всевозможных конечных объединений
таких интервалов является кольцом.
Совокупность <ff подмножеств множества X наз.
сг-к о л ь ц о м, если
1) €У
2) Еъ
Всякое а-кольцо является кольцом; всякое кольцо
является полукольцом.
Конечно аддитивной мерой наз. не-
неотрицательная конечно аддитивная функция множеств
т такая, что т@) = О. Областью определения ?т ко-
конечно аддитивной М. может быть полукольцо, кольцо
или а-кольцо. В определении конечно аддитивной
меры на кольце пли о-кольце условие конечной адди-
аддитивности можно ослабить до аддитивности — при этом
получается то же понятие.
Если т — конечно аддитивная М. множества Е,
Ei, ¦ ¦ ¦, Еп принадлежат области ее определения и
?,., то
Конечно аддитивная М. т2 с областью определения
$т наз. продолжением конечно аддитивной
меры М. т1 с областью определения <§т , если <§т ZD
3<?"т и т2(Е)=т1(Е) при Е(^$т.
Всякая конечно аддитивная М. т, определенная на
полукольце 3s, может быть однозначно продолжена
до конечно аддитивной М. т' на наименьшем кольце
5?СР), содержащем $>. Это продолжение определяется
следующим образом: любое Е?ЗКЗ*) представимо
в виде E=\Jni=lE;, Е;?3>, Ejf)Ej=0, гфу, т' (Е)
полагают равным
Конечно аддитивная М., обладающая свойством
счетной аддитивности, наз. мерой. Пример меры:
пусть X произвольное ненустое множество, <§т—
or-кольцо, кольцо или полукольцо подмножеств X,
{.Tj, х2, . . .} — счетное подмножество X, рь р2> • • • —
неотрицательные числа. Тогда функция
где бх(?)=1 при х?Е и Ьх(Е)=--0 при х(^Е, является
М., определенной на ^ц. Меры бх наз. элементар-
элементарными, пли вырожденными, мерами. Не
всякая конечно аддитивная М. является М. Напр.,
если X есть множество рациональных точек отрезка
[О, 1], 5* — полукольцо пересечений всевозможных
подинтервалов [0, 1] с X и для любых а, Ъ, 0<я<6<1,
m((a,b)f\X) = m([a, Ь)[\Х) = т((а, Ь][)Х) =
= т([а, Ъ][\Х) = Ъ — а,
то т конечна, но не счетно аддитивна на *гР>.
(Конечно аддитивная) М. т с областью определения
<§ т наз- конечной (соответственно а - к о н о ч-
н о и), если т(Е)<С<х> для любого Е^$т (соответст-
(соответственно, если для любого Е?$т существует последова-
последовательность множеств {Е;} из $т такая, что Ecz\J™=1Ei,
т(?/)<оо, i=l, 2, . . .). (Конечно аддитивная) М. т
наз. вполне конечной (вполне а-к о-
н е ч н о й ), если она конечна (соответственно о-ко-
нечна) и Х^_?т.
Пара (X, оУ), где X — множество и ?f есть а-кольцо
его подмножеств такое, что (JEs<yE=X, наз. изме-
измеримым пространством. Тройка (X, ,ff, ц),
где (X, of) — измеримое пространство п |х есть М. на
of, наз. пространством с мерой. Прост-
Пространство с вполне конечной М. |х, нормированной усло-
условием |х (X)= \, наз. вероятностным прост-
пространством. В абстрактной теории М., где исход-
исходным является измеримое пространство (X, $>) или
пространство с М. (X, $>, \i), множества из ?f наз. и з-
меримыми множествам и.
Свойства пространства с мерой. Пусть {и1,-} — про-
произвольная последовательность измеримых множеств,
тогда
1) ц (lim inf Ei) sg: lim inf \x (E(),
2) если ft у. . Ei) < со
для нек-рого iQ, то
(x (lim sup E{\ Э= lim sup (x (E[),
V. t->oo J l->»
3) если lim E[ существует и выполнено условие из 2), то
г-»-со
\l( lim ЕЛ= lim jx (E;).
Определенная на кольце конечно аддитивная М.
является М. тогда и только тогда, когда
т f lim ЕЛ = lim m(Ej)
для любой монотонно возрастающей последователь-
последовательности {?/} множеств из 54 такой, что [)°°=1Е,?Э1-
Пусть (X, ЗРи (Xj) — пространство с М., (Х2, af2) —
измеримое пространство и Г—и змеримое отоб-
отображение Х± в Х2, т. е.
г - * (#) = {^*
для любого E^ofo. Мерой, порожденной
отображением Т (обозначается \iT~x), наз. М.
на of\, определяемая соотношением
Пусть (X, of, fx) — измеримое пространство и
Пусть на множествах Е из о-кольца S'{X
}
цх (Е) = inf
1 ?CF
Тогда (Х1, aff]Xly ЦХ\) есть измеримое пространство;
М. цх, наз. ограничением меры (хна Xj.
Атомом пространства с М. (X, of', и.) (или меры
(х) наз. всякое множество Е(^<У положительной меры
такое, что если FcE, F^_^f', то fx(^)=O либо (x(F)=
= ц(Е). Пространство с М., не содержащее атомов,
наз. н е а т о м и ч е с к и м, или непрерывным
(сама М. при этом тоже наз. неатомической,
или непрерывной). Если (X, ?р, и.)— простран-
пространство с неатомич. а-конечной М. и E^tf', то для любого
aKiniEj) (возможно, равного оо) существует такой эле-
элемент jE2€uf> чт0 E2CZE1 и ц(Е2)=а.
Пространство с М. (X, <ff, \х) (или мера ц.) наз. пол-
полным, если из E?<ff, FcE, ц (Е)= 0 следует, что Е?&>.
Всякое пространство с М. (X, of, ц.) можно пополнить,
если к ?р присоединить множества вида E\JN, где
Ftzof, NczN', N'?df, ii(N') = 0, 11 положив для них
\i(E\J N)=\i(E). Класс множеств указанного вида об-
образует 0-кольцо, при этом ц — полная М. на нем. Мно-
Множества нулевой М. наз. нулевыми множест-
множествами. Если множество точек из X, для к-рых нек-рое
свойство Q не выполняется, является нулевым множест-
множеством, то говорят, что свойство Q выполняется почти
всюду.
Продолжение мер. М. ц2 есть продолжение М. \ily
если fXj есть продолжение мер цг в классе конечно ад-
аддитивных М. (см. выше). Всякую определенную на полу-
полукольце ff3 M. можно однозначно продолжить до М. на
кольце Э1E*), порожденном 1р (продолжение осущест-
осуществляется с помощью той же конструкции, что и в слу-
случае конечно аддитивных М.). Далее, всякую М. ц,
определенную на кольце 5?, можно продолжить до
М. ,и' на порожденном Щ а-кольце of {${)', если \х а-
конечна, то это продолжение единственно и а-конечно.
Значение ц' на множестве Е^$>(Э1) можно задать
формулой
Наследственным классом подмножеств
множества X наз. всякий класс, содержащий вместе
с каждым своим множеством любое его подмножество.
Внешней мерой наз. функция множеств т*,
определенная на наследственном а-кольце ffl (классе
множеств, являющемся одновременно наследственным
классом и 0-кольцом) и обладающая следующими свой-
свойствами:
1) 0 < т* (Е) < оо, т* @) = О,
2) E<=F => т* (Е) < т* (F),
3) т
По М. р, на кольце 5i можно построить внешнюю М. ц*
на наследственном а-кольце 5% (Ж), порожденном
ЭЬ {Ж (Ш) состоит из всех множеств, к-рые могут быть
покрыты объединением счетного числа множеств из 5?),
по формуле
(=1, 2, ..., ?cU^ E{\ .
Внешняя М. и* наз. внешней м о р о и, и н д у-
цированной мерой ц..
Пусть т* — внешняя М. на наследственном а-кольце
ffl подмножеств X. Множество E^ffl наз. то*-и з м е-
р и м ы м, если
то* (А) = т* (А П Е) + т* (А П (Х\Е))
для любого A ?ffl. Совокупность of т*-измеримых
множеств образует о-кольцо, содержащее все множе-
множества нулевой внешней М., а функция множеств т на of,
определяемая равенством т(Е)=т* (Е), является пол-
полной мерой. М. т наз. мерой, индуцирован-
индуцированной внешней мерой т*.
Пусть (х есть М. на кольце 5?, И* — внешняя М. на
Ж (Э1), индуцированная М. р.- Пусть <У — совокуп-
совокупность (х*-измеримых множеств, и. есть М. на of, инду-
индуцированная внешней М. |х*. Тогда М. ц, есть продолже-
продолжение М. (х, и поскольку of (R)<^,ff, то функция |х' на
of (Ж), задаваемая формулой (*), тоже М., продолжаю-
продолжающая (х. Если исходная М. (х на у{ о-конечна, то простран-
пространство (X, ,ff, u) является пополнением пространства
(X, <ff(9l), и.'), см. (*). Если М. (х задана на
0-кольце ?f, то индуцированная ею внешняя М. ц* на
наследственном о-кольце ffl(af), порожденном (У, дает-
дается формулой
Наряду с внешней М. [i* вводится понятие внут-
внутренней меры ц*, индуцирован но"
мерой (х на <ff, именно:
= sup {ц (F) :E^F, Е ?<(?}, ЕGЖ
Для всякого множества Е из Ж (of) определяются его
измеримое ядро Е' н и з м е р и м а я обо-
оболочка ?" как множества из cjf такие, что E'czEc^E"
и (x(F')=(x(/"') = 0 для любых f, F'^df таких, что
F'cE\E', F"dE"\E. Измеримое ядро всегда сущест-
существует, а измеримая оболочка существует всякий раз,
когда Е имеет о-конечную внешнюю М.; при этом
|xN.(?') = (x(?"), |х*(?')=(х(?"). Пусть и, есть М. на коль-
кольце Й и ц' - ее продолжение на порожденное % а-
кольцо of (Oft). Внутреннюю М. и* на подмножествах
множества Е конечной ц-меры можно выразить в тер-
терминах внешней М. (х* (а стало быть, и (х):
V* (А) = (х (Е) - ц* (Е\А), AczE.
Кроме того, множество F из наследственного о-кольца
Ж {Ж) с конечной внешней ц*-мерой |и*-измеримо тогда
и только тогда, когда ц* (i?)=|x*(F). В случае, когда
исходная М. |х на М вполне конечна, справедливо сле-
следующее необходимое и достаточное условие ^-.изме-
^-.измеримости множества ЕсХ
Для вполне конечных мер на 5? это условие нередко
берется в качестве определения (х*-измеримости Е.
Если (X, еУ, ц) — измеримое пространство с о-ко-
нечной М. и AT-!, . . ., Хп — конечное число множеств
из наследственного а-кольца Ж (of), порожденном #", то
на а-кольце qf, порожденном gf и множествами Хл, . . .,
Хп, можно определить М. и, совпадающую на ?f с ц.
Меры Жордана, Лебега и Лебега — Стилтьеса. При-
Примером продолжения М. является мера Лебега в R*.
Интервалы вида
1 = {(хи ..., хп):а{^х1 < bh i=l, . . ., к}
образуют полукольцо у* в Rk. Пусть для каждого та-
такого интервала
совпадает с объемом /]. Функция X о-конечна и
счетно аддитивна на fp и однозначно продолжается
до М. X' на 0-кольце ?f, порожденном J3, к-рое совпа-
совпадает с о-кольцом борелевсиих множеств (или множеств,
измеримых по Борелю) в R*; М. X' впервые была
определена Э. Борелем (Е. Borel, 1898) (см. Бореля
мера). Пополнение X М. X' (определенное на of) наз.
мерой Лебега, введенной в 1902 А. Лебегом
(Н. Lebesgue) (см. Лебега мера). Множества из области
определения ?Р меры X наз. измеримыми по
Лебегу. Ограниченное множество jEcR* принад-
принадлежит ?f тогда и только тогда, когда ХA)=Х* (Е)-\-
-гХ*A\Е), где 1?5> — какой-либо интервал, содержа-
содержащий Е, при этом X (Е) = Х* (Е). Множество
принадлежит ?f тогда и только тогда, когда Е П ?Р r
при всех п для нек-рой последовательности {гп}, г„>0,
п=1, 2, . . ., г„^оо, где^^^еК*, 1|х||<г}. Мощ-
Мощность совокупности всех борелевских множеств в R
есть с (мощность континуума), а мощность совокуп-
совокупности всех множеств, измеримых по Лебегу, есть 2е.
так что включение ofcZaf строгое, т. е. есть множества,
измеримые по Лебегу и неизмеримые по Борелю.
Мера Лебега X инвариантна относительно ортого-
ортогональных линейных преобразований А пространства
R* п относительно сдвигов на x?Rk, т. е. к(АЕ-\-х) =
= Х(Е) для любого E^ff".
Используя аксиому произвольного выбора, можно
доказать, что существуют множества, неизмеримые
по Лебегу. Напр., на прямой таковым является мно-
множество, к-рое получится, если взять по одной точке из
каждого класса смежности R по аддитивной подгруппе
рациональных чисел.
Мерам Бореля и Лебега в R* исторически предшест-
предшествовала М., определенная К. Жорданом (К. Jordan,
1892") (см. Жордана мера). Определение меры 'Джор-
'Джордана идейно весьма близко к классич. определению
площади и объема, восходящему к древним грекам:
множество EdRk наз. измеримым по Жор-
дану, если найдутся множества, являющиеся конеч-
конечными объединениями непересекающихся прямоуголь-
прямоугольников, одно — содержащееся в Е, другое — содержа-
содержащее Е, разность объемов (определяемых очевидным об-
образом) к-рых сколь угодно мала. Мерой Жордана
такого множества Е наз. нижняя грань объемов мно-
множеств — конечных объединений прямоугольников, на-
накрывающих Е. Множество, измеримое по Жордану,
измеримо и по Лебегу, и его мера Жордана совпадает
с его мерой Лебега. Область определения меры Жор-
Жордана является кольцом, но не о-кольцом, и это сильно
сужает границы ее применимости.
Мера Лебега является частным случаем более общей
меры Лебега — Стилтьеса. Последняя определяется
посредством определенной на R* действительной функ-
функции F такой, что
1) — оо < F < оо,
2) Л6,-а, ..- t±bk-akF («и ¦ ... ak)^s0
при я,<Ь,-, г~1, . . ., к, где Аь--а. — разностный опе-
оператор с шагом bj — я,-, взятый в точке а,- применительно
к i-ii координате,
3) F (au ...,ak)\F (Ьг, ...,Ьк) при а,- | Ъ,-, i = 1, ..., к_
По заданной функции F М. цр интервала
/={(*!, .. ., хц):а?*?х; < b; i = l, ..., к]
определяется формулой
оказывается счетно аддитивной на полукольце всех
таких интервалов и продолжается на о-алгебру боре-
левских множеств; пополнение этого продолжения и
есть мера Лебега — Стилтьеса, отвечаю-
отвечающая функции F. В частном случае, когда
F(xu . . ., хк) = хх ... хк,
получается мера Лебега.
Меры в произведениях пространств. Произведе-
Произведением измеримых пространств (Хи еУ^)
и (Х2, сУг) наз- измеримое пространство, образованное
множеством Х1ХХ2={(х1, хг) : х1?Х1, х%?Х.г} (про-
изведенном множеств Х3 и Х2) и о-кольцом <ff1 X of \ его-
подмножеств (произведением о-колец <±f1 и ?f'.,), порож-
порожденным полукольцом 5s множеств вида
Если (Хх, ^fu (Xj), (Х2, с^з, (х2) — пространства сМ.,та
формула
определяет М. на !р; когда М. |хх и jx2 о-конечны. М. р,
однозначно продолжается до М. на ^X^j, обозначае-
обозначаемой р^Хц,. Мера ^Хцз и пространство (Х,Х12>
vfxXofi, Hi X |х2) наз. соответственно произведе-
произведением мер Ц]И(х2ипроизведенпем про-
пространств с мерой (Хи ofx. (Xj) и (I,, с5Рг, ix2).
Пополнение произведения меры Лебега в R* и меры
Лебега в R1 есть мера Лебега в Rk + l. Аналогично'
определяется произведение любого конечного числа
пространств с М.
Пусть (Х[, qf'л (i.,-), i^/,— произвольная совокуп-
совокупность пространств с М. таких, что li,- (X,-)=l. Про-
Пространство-произведение Х= П,- е{Х;, ПО-
определению, есть множество всех функций на /,
принимающих при каждом г?/ значение х^Х,-. И з-
меримым прямоугольником в X наз.
множество вида ГТ1€ jEj, где E^^fi и лишь конеч-
конечное число Я,- отлично от X/. Семейство измеримых
прямоугольников образует полукольцо 53- Порож-
Порожденное fp а-кольцо обозначается П,- 6 1QTi и наз, произ-
произведением о-колец (jP,-. Пусть jx — функция
на 5\ определенная равенством \i(E)= T\i6iP-i(Ei) для
?"=П,6/i?,-. Так, определенная функция [х является
М., к-рая может быть однозначно продолжена до М.,
обозначаемой ГТ16/[х,-, на W^jofi- Пространство
(П[е1Х{, IIie]afi, П,-6/ц,) наз. произведени-
произведением пространств (X,-, ?fi, (x,), i?I.
Произведение пространств с М. в произвольном числе
является частным случаем следующей более общей
схемы, играющей важную роль в теории вероятностей.
Пусть (X/, ofi), i?I,— семейство измеримых прост-
пространств (of i есть а-алгебра) и пусть для каждого ко-
конечного множества I^CZl в измеримом пространстве
(П,^/^;, П^,^.-) задана вероятностная М. (х/;
(произведение М. соответствует тому случаю, когда
(X7l= ГТ( е / (х,- для любого конечного I^CZl). Пусть М.
H/i и М-/а согласованы в том смысле, что если
^С/г и р.п проекция П(-6/2Х,- на П^^Х,-, то
\ЫЛЕ) = \-1пР~г\{Е) для всех EaXX^j^i (по определе-
определению, p2i есть такое отображение ГТ,- s / X/ на П^^-У/,
что (p2i(^)), = x,- при всех t^/i). Существует ли вероят-
вероятностная М. на Wi^iifi такая, что для любого конеч-
конечного I\Cl и любого .Е?;Г14-е/ of'/ справедливо равенст-
равенство |х/, (?")= НР^), гДе р — проекция П/е/Х/ на
П1е/ X,-? Оказывается, что такая М. существует не
всегда! для ее существования нужны дополнительные
условия. Одним из таких условий является совершен-
совершенность М. (х,- (отвечающих одноточечным множествам
i?I). Понятие совершенной М. впервые было введено
Б. В. Гнеденко и А. Н. Колмогоровым 16]. Простран-
Пространство с вполне конечной М. (X, $>, fx) и сама М. [х наз.
совершенными, если для всякой ^-измеримой
действительной функции / найдется такое борелевское
множество Bc:f(X), что (х(/-1(Д)) = (х(Х). В рамках
совершенных М. невозможен целый ряд «патологи-
«патологических» явлений, возникающих в общей теории М.
Меры в топологических пространствах. При изуче-
изучении М. в топологнч. пространствах обычно рассмат-
рассматривают М., определенные на множествах, так или иначе
«вязанных с топологией пространства. Один из типич-
типичных подходов состоит в следующем. Пусть X — произ-
произвольное топологич. пространство и Ц — класс мно-
множеств вида f~1(F), где / — действительная непрерыв-
непрерывная функция на X и F ? R1 — замкнутое множество.
Пусть ЭС — алгебра, порожденная классом %, <SB есть
о-алгеСра, порожденная % {Si наз. а-а л г е б р о й
6 э р о в с-к и х м н о ж е с т в), и пусть 9Л — класс
вполне конечных конечно аддитивных М. т на 31, ре-
регулярных в '; ом смысле, что
т (Е) = sup {m (Z) :Z<^E, Z?%)
для любого Е(^Щ.. В ЯЛ выделяют подмножества ЗД1а,
!Шт , -О!;, образованные (конечно аддитивными) М., об-
обладающими дополнительными свойствами гладкости.
По определению, ц.?Ш}а, если u. (Zn) \ 0 для любой по-
последовательности Zn i 0, Zn^_% (это свойство равно-
равносильно счетной аддитивности и; М. из ЯЛст могут быть
однозначно продолжены на ей?, и в дальнейшем они
считаются заданными на Si), |а?ЭД1т, если цBа)|0 для
любой сети2а j, 0, Za?.g и М'ёф'Ь если для любого
е>0 существует компакт К такой, что (i(i?)<6, когда
Имеют лгесто включения Щ1Г)!Ша ГзЯЛх ЗЯЛ<. М. из
Ш1ст наз. б э р о в с к и м и мерами.
Существует тесная связь между М. из Ш1 и линей-
линейными функционалами на пространстве С (X) ограни-
ограниченных непрерывных функций на X. Именно, формула
устанавливает взаимно однозначное соответствие между
М. m^2Jl и неотрицательными линейными функцио-
функционалами А на С (X) (неотрицательность означает, что
Л@ когда /(з-)^гО, х?Х). Более того, для любого
m (Z) = inf {Л (/) :%2 < / < 1}.
где у.2 — индикатор множества Z. При этом М. из ЭЛСТ
отвечают a-гладкие функционалы Л (т.е.
такие, что Л(/„)-*0, когда /„^0 в С(Х)), М. из ЯЛт отве-
отвечают т - г л а д к и е функционалы Л (т. е.
такие, что Л(/а)—>-0 для любой сети /ajO в С(Х)) и М.
из 931г соответствуют плотные функцио-
функционалы Л (т. е. такие, что Л(/а)—>-0 для любой сети /а
в С(X) такой, что ||/а||<1 при всех а и /а->-0 равно-
равномерно на компактных подмножествах; здесь || • || —
равномерная норма).
В пространстве ЯЛ обычно рассматривается слабая
топология w; в этой топологии базисными окрестно-
окрестностями являются множества вида
U (то, /и ¦ • •> /л. Е) =
fk (dm—dma) < e,
*=1, ..., в, /1; ..., f«6C(X)J.
В топологии w ЗЛ есть вполне регулярное хаусдорфово
пространство. Сходимость в топологии w обычно обо-
обозначается знаком =>. Для сходимости сети то.=>'п не-
необходимо и достаточно, чтобы тпа(Х)—*-т(Х) и lim sup
та B)<mB) для всех Х^^. Другим необходимым и
достаточным условием является та(Е)—*-т(Е) для всех
??2( таких, что существует Zl, Z2?JI, для к-рых
X\EcZu EdZ2 и m(Z1r\Z2) = 0. Если пространство X
.вполне регулярно и хаусдорфопо, то 93JT метризуеио
тогда и только тогда, когда метризуемо X. Если X —
метрпч. пространство, то ЭД!Т метризуемо как сепара-
бельное метрич. пространство тогда и только тогда,
когда X сспарабельно, и Ш2т метризуемо как полное
метрич. пространство тогда и только тогда, когда X
метризурмо как полное метрич. пространство. Когда X
метрнзуемо, Ш!ст метризуемо тогда и только тогда,
когда оно метризуемо Леей — Прохорова метрикой.
Пространство Ша секвенциально замкнуто в *Ш (т е о-
р е м а Александрова). Множество ЛсЗД} наз.
плотным, если sup {т(Х) : т? А }< оо и если для
любого е>0 существует компакт К такой, что т(Е)-СЬ,
когда ЕсХ\К, т?А, ??31. Если iciOio плотно,
то А относительно компактно в Щ}о; обратно, если X
метризуемо и топологически полно, АаШа относи-
относительно компактно и каждая мера из А сосредоточена
на нек-ром сепарабельном подмножестве, то А плотно
(теорема Прохорова).
При определенных условиях М. из ЗЛи могут быть
продолжены до борелевских М., т. е. М., определен-
определенных на а-алгебре борелевских множеств (см. Боре-
левское множество, Бореля мера). Так, если X — нор-
нормальное хаусдорфово счетно паракомпактное прост-
пространство, то каждая М. u.?3J!CT может быть однозначно
продолжена до регулярной борелевскон М. Бели X —
вполне регулярно и хаусдорфово, то всякая т-гладкая
(плотная) бэровская М. может быть однозначно про-
продолжена до регулярной т-гладкой (плотной) борелев-
ской М.
Носителем бэровской (борелевской) М. паз.
наименьшее множество Z из | (наименьшее замкнутое
множество), М. к-рого совпадает с М. всего про-
пространства. У т-гладких М. носители всегда существуют.
Нередко при рассмотрении М. в топологич. прост-
пространствах (особенно — в локально компактных хаусдор-
фовых пространствах) борелевские и бэровские М. счи-
считают заданными на более узких классах множеств —
на 0-кольцах, порожденных соответственно компакт-
компактными множествами и компактными Сб -множествами.
Пусть G — локально компактная хаусдорфова то-
топологич. группа. Левой мерой Хаарав G
наз. М., определенная на а-кольце, .порожденном всеми
компактными множествами, не равная тождественно
нулю и такая, что \x.(xE)=[i(E) для любых x?G и Е
из области определения ц. Правая мера Хаара
определяется аналогично заменой условия \i(xE)=\i(E)
на условие \х(Ех)=:ц(Е). В любой группе рассматри-
рассматриваемого типа существует и единственна (с точностью
до мультипликативной положительной постоянной)
левая мера Хаара. Всякая левая мера Хаара регулярна
в том смысле, что (x(?) = sup {(x(if) : КаЕ}, где К —
компактные множества. Аналогичными свойствами об-
обладает и правая мера Хаара. Мера Лебега в Rft яв-
является частным случаем Хаара меры. См. также ст.
Мера в топологическом векторном пространстве.
Изоморфизм пространств с мерой. Пусть (X, ?f, ц) —
пространство с М. Назовем множества Е, Е' ?<§? р,-
равными (E=E'\\t]), если \i(EAE') = 0 (здесь
Е Д?"—симметрич. разность Е и Е'). Класс множеств ?f
с таким определением равенства обозначим af^. В of\
корректно определены теоретико-множествеиные опе-
операции, проводимые в конечном (или счетном) числе;
напр., если E1=Ei[\i] и Е2=Е'2[{х.], то jE'1U^2=?'iU
U^Iu]. Мера (х переносится очевидным образом на ofsx.
Пусть of д — подмножество ^д, состоящее из множеств
конечной М. Функция р(Е, Е')-ц(ЕАЕ') на (У^Х^ц
является метрикой. Пространство с М. (X, ?р', ц) наа.
сепарабельным, если ЗР\х, с метрикой р сепара-
бельно. Если (X, <ff, ц.) — пространство с о-конечной
М. и гг-кольцо ?Р имеет счетное число образующих (т. е.
существует счетное множество {En)c:ff> такое, что ?f
есть наименьшее содержащее его о-кольцо), то метрич.
пространство ?Ру. сепарабельно.
Два пространства сМ. (Хи <$fx, \ir) и (Х2, &'2, ц.,) наз.
изоморфными, если существует взаимно одно-
однозначное отображение ф из (ofi)^ на (с5рг)д2 такое, что
Ф (E\F) = Ф (?)\ф (F), ф (Я U Л = ф (Я) Uф (Л
и {х1(?') = }х2{ф(Я)) для любых Е, Ffzidfi)^- Пусть
теперь (X, of, ц) — произвольное пространство с впол-
вполне конечной М. Существует разбиение X на непересе-
непересекающиеся множества Хп, ге=1, 2, . . ., из ^ такое, что
ограничение ц на Х„ изоморфно либо М., сосредото-
сосредоточенной в одной точке, либо М., с точностью до поло-
положительного множителя равной прямому произведению
П,-6И*7/, <М/, «,), где ^-={0,1}, u,({0}) = u,-({l})-1/a,
а множество / может иметь произвольную мощность
(теорема Магарам — Колмогорова).
Если пространство (X, <ff, |x) сепарабельно, неатомиче-
неатомическое и и(Х)=1, то оно изоморфно пространству
^i6/(^''i ^ь м')> гДе ^ счвтн0, к-рое в свою очередь
изоморфно единичному интервалу с мерой Лебега.
Наряду с теорией М. как функции подмножеств
нек-рого множества развита также теория М. как
функции элементов булева кольца (или булевой ал-
алгебры); эти теории во многом параллельны. Другая
распространенная конструкция М. восходит к У. Юнгу
(W. Young) и П. Даниел'ю (P. Daniell) (см. [12]). По-
Помимо теории положительных М., имеются также раз-
развитые теории М., значения к-рых действительны, ком-
комплексны или, вообще, принадлежат нек-рым алгебраич.
структурам.
Лит.: ll]Ca к с С, Теория интеграла, пер. с англ., М., 1949:
[2] X а л м о ш П. Р., Теория меры, пер. с англ., М., 1953; [3]
Данфорд Н., Шварц Дж., Линейные операторы. Об-
Общая теория, пер. с англ., М., 1962; [4] Колмогоров А. Н.,
Фомин С. В., Элементы теории функций и функционального
анализа, 5 изд., М., 1981; [5] Н е в ё Ж., Математические осно-
основы теории вероятностей, пер. с франц., М., 1969; [6J Г н е д е н-
к о Б. В., Колмогоров А. Н., Предельные распределе-
распределения для сумм независимых случайных величин, М.—Л., 1949;
[7]Варадарайн В. С, «Матем. сб.», 1961, т. 55, Л"> 1
с. 35—100; [8] Р а г t h a s а г a t h у К. R., Probability me-
measures on metric spaces, N. Y.—L., 1967; [9] Б и л л и н г с л и П.,
Сходимость вероятностных мер, пер. с англ., М., 1977; [10] G и-
к о р с к и й Р., Булевы алгебры, пер. с англ., М., 1969; [11]
Владимиров Д. А., Булевы алгебры, М., 1969; [12] Бур-
баки Н., Интегрирование. Меры на локально компактных
пространствах. Продолжение меры. Интегрирование мер. Меры
на отделимых пространствах, пер. с франц., М., 1977; [J3] D ics-
tel J., U h 1 J., Vector measures, Providence, 1977.
В. В. Сазонов.
МЕРА в топологическом векторном
пространстве — термин, употребляемый при-
применительно к мере, заданной в топологическом вектор-
векторном пространстве, когда хотят подчеркнуть те свойства
атой меры, к-рые связаны с линейной и топологич.
структурой этого пространства. Общей проблемой при
построении М. в топологич. векторном пространстве
является задача продолжения предмеры до М. Пусть
Е — (действительное или комплексное) локально вы-
выпуклое пространство, %(Е) — алгебра его цилиндри-
цилиндрических множеств и на алгебре И(Е) определена пред-
мера. Задача состоит в продолжении атой предме-
предмеры до счетно аддитивной М., определенной на о-ал-
гсбре $8п(Е) — наименьшей о-алгебре, содержащей
алгебру Ш(Е); SS0(E) — самая узкая из всех о-алгебр
(слабоборелевскои, борелевской и т. д.), естественно
связанных с топологией Е; для большого класса про-
пространств Е эти о-алгебры совпадают. В частном, по
наиболее важном случае, когда пространство E=V\
т. е. является сопряженным к нек-рому локально вы-
выпуклому пространству V, рассматриваемому в слабой
«-топологии (так что E'—V), для продолжимости
предмеры (j, в V до М. достаточно, чтобы ее характери-
стич. функционал (преобразование Фурье)
X (ф) = ^v. ехр {гх (ф)} d\x (x), x?V
был непрерывен в т. н. т о п о л о г и и Сазонова
в пространстве V (т. е. топологии, порожденной всеми
непрерывными гильбертовыми полунормами в Г), и в
ряде случаев, напр, когда V — Фреше пространство,
необходимо, чтобы характористич. функционал был не-
непрерывен в исходной топологии V. Так, когда V —
ядерное пространство, топология Сазонова совпадает
с исходной топологией, и любая предмера на V с не-
непрерывным характеристич. функционалом продолжается:
до М. В случае, когда предмера определена в гильбер-
гильбертовом пространстве Н, сформулированное выше до-
достаточное условие ее продолжимости до М. является и
необходимым. Кроме этого общего критерия продолжи-
продолжимости предмеры до М. существуют частные ревультаты
такого рода, приложимые к тому или иному классу М.
(или классу пространств). Напр., гауссова пред-
предмера на V, где V— локально выпуклое пространст-
пространство'(т. е. предмера, сужение к-рой на любую а-алгебру
5>(^)cr2t(F'), LcV, dim L<oo, является гауссовым
распределением с корреляционным функционалом
В(Ч>1, Фг, ), Фь Фгб^), продолжается до М., если су-
существует выпуклая окрестность нуля в V, к-энтропия
к-рой в метрике, порожденной скалярным произведе-
произведением <ф], фг> —Л (ф!, ср2), меньше двух.
Для слабой сходимости последовательности (вероят-
(вероятностных) М. в сопряженном пространстве V достаточны
поточечная сходимость характеристич. функциона-
функционалов этих М. (она же и необходима) и равностепенная
непрерывность их в нуле относительно топологии Са-
Сазонова в V, а необходима равностепенная непрерыв-
непрерывность этих функционалов относительно исходной топо-
топологии V. В случае, когда V — гильбертово пространст-
пространство, известны необходимые и достаточные условия сла-
слабой компактности семейства М. в V, также выражающие-
выражающиеся в терминах их характеристич. функционалов. Во-
Вопрос о квазиинвариантности М. в топологическом век-
векторном пространстве (см. Квазиинвариантная мера)
относительно нек-рой совокупности сдвигов (множества
квазнинвариантности) этого пространства (известие,.
что для ряда бесконечномерных векторных пространств
множество квазиинвариантности ненулевой М. не
может совпадать со всем пространством), а также во-
вопрос о критериях абсолютной непрерывности одной
М. относительно другой исследованы лишь A982) для
гауссовых М. Изучение М. в топологических век-
векторных пространствах связано главным образом с
интегралами по траекториям, а также с теорией обоб-
обобщенных случайных полей и в значительной степени сти-
стимулируется приложениями этих теорий к физике и ме-
механике.
Лит.: [1] Д а н ф о р д Н., Шварц Д т., Линейные опе-
операторы. Общая теория, пер. с англ., М., 1962; [2] Бур-
баки Н., Интегрирование. Меры на локально компактных
пространствах. Продолжение меры. Интегрирование мер. Меры
на отделимых пространствах, пер. с франц., М., 1977; LS] Г и х-
м а н И. И., С к о р о х о д А. В., Теория случайных процес-
процессов, т. 1, М., 1971; [4] Гель фан д И. М., Виленкин
Н. Я., Некоторые применения гармонического анализа. Осна-
Оснащенные гильбертовы пространства, М., 1061; [5] Судаков
В. Н., «Тр. Матем. ин-та АН СССР», 1976, т. 141; [6] Смол я-
н о в О. Г., Фомин С. В., «Успехи матем. наук», 1976, т. 31,
в. 4, с. 3—56. Р. А. Мичлос.
МЕРГЕЛЯНА ТЕОРЕМА — теорема о возможности
равномерной полиномиальной аппроксимации функций
комплексного переменного. Пусть К — компакт СО'
связным дополнением на плоскости С комплексного
переменного z. Тогда всякая фупкция /, непрерывная
на К и голоморфная в его внутренних точках, равно-
мерпо на К приближается многочленами от z.
Эта теорема была доказана С. Н. Мергеляном (см.
[11, [2]); она завершила большой цикл исследований
по теории приближений в комплексной плоскости и
имеет много применении в различных разделах ком-
комплексного анализа.
В случае, когда К ие имеет внутренних точек, это
утверждение было доказано М. А. Лаврентьевым [3];
а для случая, когда К — замкнутая область со связ-
связным дополнением, соответствующая теорема доказана
М. В. Келдышем [4].
Из М. т. вытекает следующее утверждение. Пусть
К — произвольный компакт на плоскости С. Для того
чтобы функция /, непрерывная на if и голоморфная
внутри К, равномерно приближалась многочленами от
z, необходимо и достаточно, чтобы / голоморфно про-
продолжалась во все ограниченные связные компоненты
множества С\К.
Задача о приближении многочленами является част-
частным случаем задачи о приближении рациональными
функциями с полюсами вне К. С. Н. Мергелян доказал
также несколько достаточных условий рациональной
аппроксимации (см. [2]). Полное решение этой задачи
(для компактов КсС) получено в терминах аналити-
аналитических емкостей (см. [5]).
К М. т. примыкает большой цикл работ о полино-
полиномиальных, рациональных и голоморфных приближе-
приближениях в пространстве многих комплексных переменных
С". Здесь получены пока только частные результаты
для специальных типов компактов.
Лит.: [1J М е р г е л я н С. Н., «Докл. АН СССР», 1951.
т. 78, Л1> 3, с. 405—08; [2] е г о же, «Успехи матем. наук», 1952>
т. 7, в. 2, с. 31—122; [3] Л а в р е н т ь е в М. A., Sur les foir
ctions d'une variable complexe representables par des series de
polynoraes. P., 1936; L4] К е л д ы ш М. В., «Матем. сб.», 1945,
т. 16, JV- 3, с. 249—57; [5] В и т у m к и и А. Г., «Успехи матем.
наук», 1967, т. 22, R. 6, с. 141—99; [6] Некоторые вопросы теории
приближений, пер. с англ., М., 1963; [7] Гамелин Т. В.,
Равномерные алгебры, пер. с англ., М., 1973. Е. М. Чирка.
МЕРОМОРФНАЯ ФУНКЦИЯ одного комп-
комплексного переменного в области QcrC
(или на римановой поверхности Я) — голоморфная
функция в области Я\{аь а2, . . .}, к-рая в каждой
особой точке av имеет полюс (т.е. av—изолированная
точка множества {ах, а2, . . .}, не имеющего предель-
предельных точек в Q, и lim |/(z)| = oo). Совокупность Л/(Я)
z^av
всех М. ф. в Q является полем относительно обычных
поточечных операций с последующим доопределением
в устранимых особенностях.
Отношение срЛ|) любых голоморфных в Q функций,
г|з^О, является М. ф. в Я. Обратно, всякая М. ф. в
области ЯсС (и на некомпактной римановой поверх-
поверхности Я) представляется в виде /=фЛ?>, iJj^O, где ср, ty
голоморфны и не имеют общих нулей в Я. Таким обра-
образом, на некомпактной римановой поверхности поло
Jlf(fl) совпадает с полем отношений кольца О (Я) го-
голоморфных функций в Я.
Всякая М. ф. /?Л# (Я) определяет непрерывное ото-
отображение / области Я в сферу Римана CU{<x}, к-рое
является голоморфным отображением относительно
стандартной комплексной структуры С [J {°° J — C-Pi.
Обратно, всякое голоморфное отображение /: Я—>-
-*-CU{oo}, /=Й°э, определяет М. ф. / в Я: множество
полюсов / совпадает с дискретным множеством f~1(ao)
и /(z) = /(z)?C, если г^Я\/-1(оо). Таким образом,
М. ф. одного комплексного переменного можно отож-
отождествлять с голоморфными отображениями (^оо) в
сферу Римана.
Основные задачи теории М. ф.— это вопросы суще-
существования (и построения) М. ф. с данными особенно-
особенностями.
I. Задано замкнутое дискретное подмножество
Й1> а2> ¦ ¦ -}с:Я и в каждой точке av—главная часть
разложения Лорана
требуется найти М. ф. f^M(Q) с этими главными ча-
частями, т. е. такую, что / голоморфна в Q\{ab o2, . . .}
и f—fv голоморфна в окрестности av для каждого v.
Если число точек av конечно, то (в области QcC) зада-
задача решается тривиально функцией 2/v • В общем слу-
случае эту задачу решает теорема Миттаг-
Л е ф ф л е р а: на всякой некомпактной римановой
поверхности существует М. ф. с заданными главными
частями /v , v=l, 2, ... На компактной римановой по-
поверхности (напр., на торе) эта задача в общем нераз-
неразрешима — нужны дополнительные условия согласова-
согласования главных частей.
Вторую основную задачу удобно формулировать в
терминах дивизоров, т. е. отображений D : Q —*¦ Ъ та-
таких, что для всякого компакта KdQ число точек z?Kt
в к-рых D (г)ФО, конечно (число D (z) наз. кратностью D
в точке z). Дивизор наглядно можно записать в виде
формальной суммы ^Jcvav, где av ?Q — точки, в к-рых
D (ov )= '¦ kv фО\ в случае конечного числа слагаемых
число 2^hv = : deg D наз. степенью дивизо-
дивизора D. Для М. ф. / ее дивизор (/) равен 0 во всех точ-
точках, кроме нулей и полюсов /, где его кратность пола-
полагается равной соответственно порядку нуля или по-
полюса (порядки полюсов отрицательны).
II. В точках замкнутого дискретного подмножества
{%, я2, . . .}сй заданы «кратности» — целые числа
ку ФО. Требуется найти М. ф. с нулями и полюсами
данных кратностей, т. е. такую, что / голоморфна в
ff\{ai» я2, . . .} и f(z) (z—a.x)~kv голоморфна и не рав-
равна нулю в окрестности av, v=l, 2, ... В случае ко-
конечного числа точек av (и QcC) такой будет, напр.,
/(z) = II(z—av) v. В общем случае задачу решает те-
теорема Вейерштрасса: на некомпактной ри-
римановой поверхности Q для любого заданного дивизора
D существует М. ф. /, дивизор к-рой (/) совпадает с
D. Для компактной римановой поверхности Q голоморф-
голоморфное отображение в сферу Римана, определяемое не-
непостоянной М. ф. /, является разветвленным накрытием,
и поэтому каждое значение функция / принимает оди-
одинаково часто, в частности число нулей / равно числу ее
полюсов (с учетом кратностей). Таким образом, ус-
условие deg (/) = 0 необходимо для разрешимости задачи
II на компактной римановой поверхности. В общем оно
не достаточно; необходимое и достаточное условие су-
существования М. ф. с данным дивизором дает теорема
Абеля (см. [2]).
Функции /?Af(Q), удовлетворяющие условию
(/)+.?>>О для данного дивизора D на компактной ри-
римановой поверхности Q, образуют конечномерное ли-
линейное пространство Ор (над полем С); если deg D<0,
то Од={0}.
Теорема Римана — Роха утверждает, что
dim О и—dim Ok-d= deg D — g-\-i,
где К — т. н. канонич. дивизор и g — род римановой
поверхности Я. Из этого соотношения получаются
многие теоремы существования (если dim O^-D~\-degD >
>g—2, то dim Од^2 и, значит, в Од имеются непосто-
непостоянные М. Ф-). Напр., на всякой компактной римановой
поверхности Q рода g существует М. ф., осуществляю-
осуществляющая не более чем (#+1)-листное разветвленное накры-
накрытие / : Q-»-CU {oo}.
Большое место в теории М. ф. одного комплексного
переменного занимает распределения значений теория
(теория Неванлинны), изучающая распределение корней
уравнений f(z) = a, a?C{J {со}, при подходе к границе
области.
Мероморфная функция нескольких комплексных пере-
переменных. Пусть Q — область в С" (или комплексное
л-мерное многообразие) и PczQ — (комплексное) ана-
литич. подмножество коразмерности 1 (или пустое).
Голоморфная функция /, определенная в Q\.P, наз.
мероморфной функцией в Q, если для
каждой точки р?Р найдется сколь угодно малая ок-
окрестность U ^р в Q и голоморфные в U функции ф, г|з
без общих необратимых в 0A7) множителей такие, что
/=ф;1|з в U\P. Множество P = Pf наз. полярным мно-
множеством М. ф. /. Его подмножество N=Nf, к-рое ло-
локально определяется условием ср=г|5=О, наз. м в о-
жеством (точек) неопределенности
М. ф. /; это аналитич. подмножество Q (комплексной) ко-
коразмерности ^2. В каждой точке p?N функция / не
определена по существу: предельные значения /(г)
при z-^p, г?Я\Р, заполняют всю сферу Римана
CU {оо}. С другой стороны, в точках множества .Р\ЛА
существует lim / (z)= оо, и после доопределения / (р)= оо
для p"?P\N получается голоморфное отображение
?Г .N в сферу Римана. Обратно, если N — произволь-
произвольное комплексное аналитич. подмножество Q коразмер-
коразмерности ^2 (возможно, пустое), то любое голоморфное
отображение / : О\ЛГ^»С (J {оо } определяет М. ф. в Q,
равную / в ft\.P, где P — N\Jf~1(co) оказывается ана-
аналитич. подмножеством Q коразмерности 1 или пустым.
Таким образом, М. ф. / в Q — это голоморфное отоб-
отображение в сферу Римана, определенное вне аналитич.
подмножества N/CZQ коразмерности ^2.
Третье, полностью локализованное, определение
М. ф. (эквивалентное приведенным выше) формулиру-
формулируется в терминах пучков. Пусть О — пучок ростков го-
голоморфных функций на Q и Мг для каждой точки z?Q
есть поле отношений кольца Oz (слоя пучка О над точ-
точкой: z). Тогда M=\}MZ естественно наделяется струк-
структурой пучка полей, к-рый наз. пучком рост-
ростков М. ф. в Q. М. ф. в Q определяется как глобальное
сечение М, т. е. непрерывное отображение / : z—yfz
такое, что fz(zMz для всех z?Q. Множества Pj и Nj
определяются так: если /г=срг/г|5г, где фг, г|)г^0,,
^/^0, то можно считать, что ф^ и трг взаимно просты,
т. е. не имеют общих необратимых в Oz множителей;
тогда z?P, еслиг|ь(z) = 0, и z?N, если \pz(z) = q>z(z) = O.
Значение так определенной М. ф. / в точке z(?P, по
определению, равно фг(г)/г|5г (z).
Как и в одномерном случае, совокупность всех М. ф.
в Q образует поле М (Я) относительно поточечных ал-
гебраич. операций с последующим доопределением в
устранимых особенностях.
Замыкание Z=Zf множества нулей М. ф. /, т. е.
множества {z ?Q\Pf : f (г)=0}, является аналитич. под-
подмножеством Q коразмерности 1 (или пустым), множество
неопределенности N=Zf\P. На Zf и Pf можно опреде-
определить порядки (кратности) нулей и полюсов М. ф. /.
Если р — регулярная точка аналитич. множества
Z\JP, то в нек-рой окрестности U^p множество
(Z{JP)f\ U связно и задается уравнением g=0, g?O (U),
причем dg-j^O всюду в U. Поэтому существует макси-
максимальное целое 4jreno k(p) такое, что функция fg~k{P>
голоморфно продолжается в U; это число наз. поряд-
порядком (нуля, если p(zz, и полюса, если р?Р)
М. ф. / в точке р. Функция к(р) локально постоянна
на множестве регулярных точек Z\JP. Поэтому каж-
каждой М. ф. / в Q можно сопоставить ее дивизор (/) =
= j?mkvAv, где Av—неприводимые компоненты Z^U-P/
и lcv -ткратность (порядок) / в регулярных точках Z\}P,
принадлежащих Av (другие обозначения: (/)=2)^=Д^и
т. п.). На компактном комплексном многообразии
М. ф. определяется своим дивизором однозначно с точ-
точностью до постоянного множителя.
Задачи, к-рые в одномерном случае решают теоремы
Миттаг-Леффлера и Вейерштрасса, в многомерном слу-
случае наз. соответственно первой (аддитивной) и второй
(мультипликативной) Кузена проблемами. Ввиду слож-
сложности полярного множества Рj понятие главной части
М. ф. / в общем не определено, и проблемы Кузена фор-
формулируются так.
I. Дано открытое покрытие {Uv } многообразия Q
и в каждом Uv задана М. ф. fv ; требуется найти М. ф.
f?M(Q) такую, что f—fv €.O(UV) для всех V.
II. Для данного дивизора D = j>jkvAv на Q найти
М. ф. f?M(Q) такую, что (/)^27.
Условия разрешимости этих задач в многомерном
случае гораздо более жесткие, чем в одномерном.
Задача о представлении М. ф. в виде отношения
двух голоморфных функций наз. проблемой
Пуанкаре. Усиленная проблема Пу-
Пуанкаре — представимость М. ф. в виде отношения
голоморфных функций, ростки к-рых в каждой точке
z?Q взаимно просты в Oz. Проблема Пуанкаре нераз-
неразрешима на связном компактном комплексном многооб-
многообразии, если на нем есть непостоянные М. ф. Однако она
разрешима в любой области QczC", более того, в
любой области на Штейна многообразии (см. [7]).
Разрешимость усиленной проблемы Пуанкаре следует
из разрешимости проблемы II Кузена (обратное не-
неверно).
Функции /i, . . ., fk?M(Q) наз. алгебраиче-
алгебраически зависимыми, если существует многочлен
F^O от к переменных с комплексными коэффициентами
такой, что F(f1(z), . . ., /д, (z))=0 в общей области оп-
определения функций fv ¦ Максимальное число алгебра-
алгебраически независимых М. ф. на Q наз. степенью
трансцендентности поля М(Q). На любом
компактном комплексном многообразии ото число не
превосходит его (комплексной) размерности (теоре-
(теорема 3 и г е л я), более того, это поле имеет конечное
число образующих (см. [6]).
На конкретных комплексных многообразиях М. ф.
могут обладать дополнительными свойствами. Так, в
проективном комплексном пространстве СРп множе-
множество неопределенности любой непостоянной М. ф. не-
непусто. Всякая М. ф. на проективном алгебраич. мно-
многообразии рациональна, т. е. представляется в виде
отношения piq однородных многочленов от однородных
координат. На алгебраич. многообразиях поле М{Q)
достаточно богато. С другой стороны, существуют ком-
комплексные многообразия (напр., нек-рые неалгебраич.
торы), на к-рых всякая М. ф. постоянна. Многомерные
обобщения теоремы Римана — Роха не столь эффек-
эффективны, и теоремы существования различных классов
М. ф. получаются лишь для нек-рых классов комплек-
комплексных многообразий.
См. также Вейерштрасса теорема, Миттаг-Леф-
Миттаг-Леффлера теорема, Римана — Роха теорема.
Лит.: [1] Неванлинна Р., Однозначные аналитиче-
аналитические функции, пер. с нем., М.—Л., 1941; [2] Форстер О.,
Римановы поверхности, пер. с нем., М.. 1980; [Я] Хейман
У.-К., Мероморфные функции, пер. с англ., М., 1966; [4] III а-
б а т Б. В., Введение в комплексный анализ, ч. 1—2, М., 1976;
ШХермандер Л., Введение в теорию функций нескольких
комплексных переменных, пер. с англ., М., 1968; [6] Ш а ф а-
р е в и ч И. Р., Основы алгебраической геометрии, М., 1972;
[7] К a j i w а г a J., S a k a i Е., «Nagoya Math. J.», 1967,
V. 29, р. 75—84. Е. М. Чирпа.
МЕРОМОРФНОЕ ОТОБРАЖЕНИЕ комплекс-
комплексных пространств — обобщение понятия ме-
роморфной функции. Пусть X и У — комплексные
пространства, А — открытое подмножество в X такое,
что .Y\yl — нигде не плотное аналитич. подмножество,
и пусть дано аналитич. отображение / : А—>-У. Отобра-
Отображение / наз. мероморфным отображен и-.
е ы пространства X в У, если замыкание Г^ графика А*
отображения /в XXY является аналитич. подмножест-
подмножеством в XXY, причем проекция я : Г^—>-Х — собственное
отображение. Множество Г^ наз. графиком пе-
перо и о р ф я о г о отображения /. Отобра-
Отображение п : Tj—>-X сюръективно и определяет биектив-
биективное отображение множеств неприводимых компонент.
Если АдСХ — наибольшее открытое подмножество,
на к-рое / можно продолжить в качестве аналитич.
отображения, то If=X\Ao — аналитическое нигде
не плотное подмножество пространства X, наз. м н о-
жеством неопределенности отображе-
отображения /. Множество я~1(Ло) = ^4о открыто и плотно в Г^,
причем А*^Ао* и Гг\А'о* аналитично и нигде не
плотно в Г/. Ограничение я : А'о* —уА0 есть изоморфизм
аналитич. пространств. Если X — нормальное ком-
комплексное пространство, то codim 7/^2 и сНт^л (х)>0
гогда и только тогда, когда :?л~1(х) и x?If. Если X
не нормально, то л~' (х) может состоять из конечного
числа точек даже в случае, когда x^Ij. В случае
У— СР1 понятие М. о. сводится к понятию мероморф-
iioii функции.
Пусть / : X-yY, g : Y^-Z, к : X—>-Z — мероморфные
отображения комплексных пространств. Говорят, что
композиция go/ отображений / и g определена и равна к,
если существует открытое всюду плотное подмножество
U в X такое, что U^Af0, f(U)czA§, UczAo и что k\U=
= g°f\U. Мероморфное отображение /: X—>-У наз.
б и м е р о м о р ф н ы м, если существует мероморфное
отображение g : Y-^-X такое, что f°g=iy n g°f=lx-
Композиция бимероморфных отображений X^-Y и
У—>-2 всегда определена.
Лит.: [1] Andreotti A., S t о 1 1 W., Analytic and
algebraic dependence of meromorphic functions, В. — 1л. о.],
1971; [2] R e m m e г t R., «Math. Ann.», 1957, Bd 133, X» 3,
S. 328 — 70. Д. А. Пономарев-
МЕРСЕННА ЧИСЛО — простое число вида Мп=
= 2" —1, где п~\, 2, 3, ... . М. ч. рассматривались
в 17 в. М. Мерсенном (М. Mersenne). Числа Мп могут
быть простыми только при простых значениях п. При
п=2, 3, 5, 7 получаются соответственно простые числа
Мп='Л, 7, 31, 127. Однако при п=11 число М„ будет
составным. В дальнейшем при простых значениях п
среди чисел Мп встречаются как простые, так п состав-
составные числа. Быстрый рост чисел Мп затрудняет их ис-
исследование. При рассмотрении конкретных чисел Мп
было доказано, напр., что М. ч. являются числа М31
(Л. Эйлер, L. Euler, 1750) и Msl (И. М. Первушин,
1883). С помощью вычислительных машин был най-
найден ряд других весьма больших М. ч., напр, число
MllilB является М. ч. Остается нерешенной A982) про-
проблема о существовании бесконечного множества М. ч.
Эта проблема тесно связана с вопросом о существова-
существовании совершенных чисел.
Лит.: [1] X а с с е Г., Лекция по теории чисел, пер. с нем.,
М., 1953; [2] Б у х ш т а О А. А., Теория чисел, 2 изд., М., 1966.
Б. М. Бредихин.
МЕРСЕРА ТЕОРЕМА: билинейный ряд
эрмитова положительно определенного непрерывного
в DXD ядра К (s, t), где D — замыкание ограниченной
области в евклидовом пространстве Я,., абсолютно и
равномерно сходится в О ХО к ядру K(s, t). Здесь A.m —
характеристич. числа ядра A" (s, t), (fm (s) — соответ-
соответствующие им ортонормированные собственные функции.
Интегральный оператор Т : L2(D)~^L2(D)
с ядром К, удовлетворяющим условиям М. т.,— ядер-
ядерный и его след 2«^« вычисляется по формуле:
«(», *)ds.
М. т. допускает обобщение на случай разрывных огра-
ограниченных ядер.
Теорема доказала Дж. Мерсером [1].
Лит.: [1] Mercer J., «Philos. Trans. Roy. S:>c. London.
Ser. A.», 1909, v. 209, p. 415—46; [2] его же, «Piuu. Koy. Soe.
London. Ser. A», 1910, v. 83, p. 69 — 70: [Si Петровский II. Г.,
Лекции по теории интегральных уравнений, 3 тд., М., 1965;
[4] Три коми Ф., Интегральные уравнения, пер. с англ.,
М., 1960; [5] Красносельский :>1. А. 1и др.], Интеграль-
Интегральные операторы в пространствах суммируемых функций, М., 1966.
В. Б. Короткое.
МЕТАБЕЛЕВА ГРУППА — двуступенно разреши-
разрешимая группа, т. е. группа, коммутант к-рой абелев.
Все М. г. образуют многообразие (см. Групп многооб-
многообразие), определяемое тождеством
[[*, у], [z, t]\ = l.
Особый интерес представляют конечно порожденные
М. г. Все они финитно аппроксимируемы (см. Финит-
Финитно аппроксимируемая группа) и удовлетворяют усло-
условию .максимальности (см. Обрыва цепей условие) для
нормальных подгрупп. Аналогичными свойствами об-
обладают обобщения этих групп — конечно порожден-
порожденные группы, у к-рых факторгруппа по абелевой нор-
нормальной подгруппе полициклическая (см. Полицикли-
Полициклическая группа).
Иногда под М. г. понимают нильпотентную группу
класса нильпотентности 2.
Лит.: [1] К у р о ш А. Г., Теория групп, 3 изд.. М., 1967;
[2] К а р г а п о л о в М. И., Мерзляков Ю. II., основы
теории групп, 2 изд., М., 1977. А. Л. Шм-лькин.
МЕТАЛОГИКА — логика, используемая в рассуж-
рассуждениях о формальной аксиоматич. теории в рамках
нек-рой метатеории. В основаниях математики к ме-
метатеории часто предъявляются спецнфпч. требования,
связанные с отказом от нек-рых употребительных мате-
матич. абстракций с целью повышения философской
убедительности метатеории. Примерами таких подвер-
подвергающихся критике абстракций являются абстракция
актуальной бесконечности, абстракция отчуждения,
ответственная за появление антиномий, и др. Это, как
правило, приводит к тому, что в метатеории использу-
используется логика, отличная от классической, напр. модаль-
модальная логика или интуиционистская логика, если мета-
метатеория строится в рамках интуиционизма.
С другой стороны, в доказательств теории интуи-
интуиционистские и другие некласснческие логпч. теории
часто исследуются и традиционными математич. сред-
средствами без всяких специфич. ограничении, напр, сред-
средствами теории множеств. В этом случае в роли М. вы-
выступает КЛаССИЧ. ЛОГИКа. А. Г. Др-ггалин.
МЕТАМАТЕМАТИКА — совокупность математич.
теорий, используемых при изучении формальных теорий
(исчислений). М., относящаяся к изучению данной
формальной теории, составляет то, что наз. метатеорией
формальной теории.
В близком смысле термин <<М.» используется как
синоним доказательств теории. А. Г. Драгалин.
МЕТАТЕОРЕМА — утверждеш!е об изучаемой фор-
формальной аксноматич. теории, полученное в рамках
определенной метатеории. а. Г. Драгалин.
МЕТАТЕОРИЯ — совокупность математич. средств
и методов, предназначенных для описания и опреде-
определения нек-рой формальной акепоматич. теории, а
также для исследования ее свойств. М. является важ-
важной составной частью метода формализации — одного
из центральных методов математич. логики.
Суть этого метода можно кратко охарактеризовать
следующим образом. Допустим, нас интересует иск-рая
содержательная математич. теория 7\. Это может
быть сложная теория, семантика к-рой недостаточно
интуитивно ясна (напр., это может быть теория мно-
множеств, математич. анализ, арифметика 2-го порядка
и т. п.). Нас интересует, является ли Тх непротиворечи-
непротиворечивой теорией или совместен ли с Тг нек-рый математич.
принцип (напр., выбора аксиома). С целью выяснения
этого вопроса вначале формулируется точный логико-
ыатематич. язык Q такой, что все интересующие нас
утверждения Т1 записываются в виде формул языка Q.
Затем логич. принципы, употреблявшиеся в теории для
получения новых фактов, формализуются в виде ак-
аксиом и чисто формальных правил вывода, позволяю-
позволяющих выводить новые формулы языка Q из аксиом и уже
выведенных формул. Таким образом, возникает фор-
формальная система (или, иначе, формаль-
формальная аксиоматическая теория, исчи-
исчисление) 1\, точно описывающая нек-рый интере-
интересующий нас фрагмент содержательной теории Тг. Су-
Существенно при этом, что формулировка Т1 не требует
исчерпывающего проникновения в, быть может, весь-
весьма сложную семантику Т±. Исчисление Т1 строится по
простым законам как чисто знаковая система и для по-
понимания устройства этой знаковой системы нет нужды
вникать в смысл выводимых в ней формул.
Такой подход открывает, во-первых, возможность
строго математически сформулировать интересующие
нас проблемы, относящиеся к "выводимости нек-рых
формул в Тх и, во-вторых, исследовать Тг средствами
нек-рой содержательной теории Г2- В этой ситуации
Т1 паз. предметной теорией, а 72— ее
метатеорией.
С точки зрения оснований математики важно, чтобы
Т2 была в нек-ром отношении более надежной теорией,
чем 71], так что исследование 7\ средствами Тг можно
было бы рассматривать как действительное разъясне-
разъяснение и обоснование неясных деталей семантики Tt с
помощью более убедительной теории Г2. В этой связи
особенное предпочтение отдается достаточно надеж-
надежным М., отражающим финитные установки в матема-
математике, теориям, построенным в рамках интуиционизма
или конструктивной математики. Впрочем, вне осно-
оснований математики это ограничение не является обяза-
обязательным. Если нас интересует не столько вопрос об
интуитивной ясности Tlt сколько просто факт о выво-
выводимости или невыводимости нек-рых формул в Tlt ес-
естественно исследовать Т1 средствами любой историче-
исторически сложившейся и убедительной для исследователя
математич. теории Т2, не накладывая никаких априор-
априорных ограничений.
Можно далее исследовать аналогичным образом и
метатеорию Т2, построив формальную систему 1\
и изучая уже Тг средствами нек-рой м е т а м е т а-
теории Т3. Такого рода исследования характерны
для доказательств теории.
Лит.: [1] К лин и С. К., Введение в метаматематику, пер.
с англ., М., 1957. А. Г. Драгалип.
МЕТАЦИКЛИЧЕСКАЯ ГРУППА — группа, обла-
обладающая циклической нормальной подгруппой, фактор-
факторгруппа по к-рой также циклическая. Всякая конечная
группа, порядок к-рой свободен от квадратов (т. е.
не делится на квадрат какого-либо числа), является
М. г. Обобщением М. г. являются полициклические
группы. А- Л. Шмелькин.
МЕТАЯЗЫК — логико-математический язык, ис-
используемый для формулировки метатеории. В более
широком смысле, М.— неформализованный язык, на
к-ром формулируются утверждения метаматематики.
А. Г. Драгалин.
МЕТЕОРОЛОГИИ МАТЕМАТИЧЕСКИЕ ЗАДАЧИ —
задачи в области физики, химии и биологии атмосферы,
решаемые с помощью математич. методов. Большинство
М. м. з. метеорологии характеризуются сложностью
и большим объемом перерабатываемой информации,
поэтому для решения этих задач наряду с аналитич.
методами широко используются методы численного мо-
моделирования на ЭВМ.
Математич. задачи фпзики атмосферы — преимуще-
преимущественно задачи гидротермодинамики стратифициро-
стратифицированной жидкости с характерными особенностями, со-
создаваемыми вращением Земли и неоднородностями рель-
рельефа и температуры поверхности Земли. Теоретич. ос-
основой математич. моделей являются законы сохранения
массы, импульса и энергии, к-рые вместе с законами
термодинамики и химии описывают процессы, протека-
протекающие в атмосфере, и взаимодействие атмосферы с океа-
океаном п поверхностью Земли. В математич. выражении —
это системы многомерных нелинейных дифференциаль-
дифференциальных уравнений с частными производными, к-рые реша-
решаются в предположении, что внешним источником энер-
энергии является Солнце. Кроме функций, описывающих
состояние и режим атмосферы (температура, давлепие,
плотность, скорость ветра и др.), оти уравнения содер-
содержат ряд параметров. Под параметрами обычно пони-
понимаются коэффициенты уравнений, в нестационарных
задачах — начальные значения функций, описываю-
описывающих состояние атмосферы, характеристики поверхно-
поверхности Земли, внешние источники и др. Начальные усло-
условия определяются по результатам измерений в реальной
физич. системе «атмосфера — Земля». Процесс мате-
математич. моделирования состоит из нескольких этапов:
качественный анализ математич. модели (коррект-
(корректность постановки задачи, разрешимость ее в физически
разумных классах функций и др.), построение дискрет-
дискретных ее аналогов, разработка вычислительных алгорит-
алгоритмов и программ для реализации дискретных моделей
на ЭВМ, исследование чувствительности модели к ва-
вариациям параметров, оценка параметров по априорной
информации и данным измерений и др. Структура мате-
математич. моделей зависит от пространственно-временных
масштабов исследуемых процессов в атмосфере и спосо-
способов их описания.
Численное моделирование является одним из основ-
основных средств для решения задач прогноза погоды и те-
теории климата. Особенно большое значение приобре-
приобретает проблема численного моделирования при изуче-
изучении вариаций климата под влиянием естественных и
антропогенных факторов и при оценке влияния дея-
деятельности человека на окружающую среду. Выбор и
обоснование физич. моделей для данного класса задач
тесно связаны с исследованием фундаментальных воп-
вопросов устойчивости, предсказуемости и чувствитель-
чувствительности физич. системы, состоящей из атмосферы, оке-
океана, снежного покрова, континентов и биосферы, к-рую
обычно наз. климатич. системой. Предсказуемость
определяет возможности научно-детерминированного
подхода к предсказанию физич. процессов и тем самым
определяет возможности построения математич. моде-
моделей для описания и предсказания поведения климатич.
системы или ее частей. Чувствительность характери-
характеризует степень устойчивости этой системы по отношению
к вариациям внешних воздействий и внутренних па-
параметров. Если воздействия антропогенных факто-
факторов интерпретировать как возмущения, вносимые в
систему, то оценку их влияния можно рассматривать
как один из прикладных аспектов теории чувстви-
чувствительности.
Задачей краткосрочного прогноза погоды (от не-
нескольких часов до нескольких суток) является задача
нахождения нестационарного решения системы нелиней-
нелинейных дифференциальных уравнений гидротермодипамики
атмосферы с заданными краевыми и начальными усло-
условиями. В задачах долгосрочного прогноза погоды опре-
определяются нек-рые обобщенные или осредненные ха-
характеристики поведения атмосферы. Численный эк-
эксперимент но общей циркуляции атмосферы состоит в
интегрировании соответствующих уравнений на дли-
длительный срок при идеализированных начальных дан-
данных. Нахождение стационарного решения или решения
с годовым периодом есть численный эксперимент по
климатич. фону.
Атмосферные процессы имеют волновую структуру.
Построение отдельных типов атмосферных волн осу-
осуществляется методами нелинейной механики с исполь-
использованием асимптотич. разложений в ряды по степеням
малого параметра. Математич. теория атмосферных
волн для линеаризованных моделей хорошо разработа-
разработана. Среди решений уравнений гидродинамики выделе-
выделено несколько классов волн (акустические, гравитаци-
гравитационные, волны Росби). Среди нелинейных волн изучены
лишь отдельные примеры (гравитационные волны Гер-
стнера, нелинейные волны Росбн и др.). Для выясне-
выяснения структуры атмосферных движений широко ис-
используются численные методы решения задач на соб-
собственные значения и собственные функции для опера-
операторов гидротермодинамикн и их дискретных аналогов.
Математич. задачей атмосферной акустики является
изучение распространения волн в слоистых средах.
При этом используются аналитические (метод В КБ и
др.) и численные методы. Важную роль, особенно в
связи с изучением и моделированием динамики цикло-
циклонов и фронтов в атмосфере, имеют исследования гидро-
дннамич. неустойчивости атмосферных волн и взаимо-
взаимодействие волн различных масштабов.
В области атмосферной оптики возникают специ-
специфические обратные задачи нз класса условно-кор-
условно-корректных задач. Типичным примером может быть за-
задача восстановления параметров атм-осферы по дан-
данным дистанционного зондирования со спутников.
Процессы многократного рассеяния света в атмосфере
исследуются различивши асимптотическими и чи-
численными методами. Для решения уравнения пере-
переноса излучения в атмосфере используются численные
методы. Особенно эффективным является метод Мон-
Монте-Карло.
Многие теоретические и прикладные задачи метеоро-
метеорологии связаны с проблемой атмосферной турбулентно-
турбулентности. Спектр масштабов турбулентности в атмосфере
чрезвычайно широк. Турбулентность играет опреде-
определяющую роль во взаимодействии атмосферы с океаном
и с поверхностью Земли, в диффузии атмосферных при-
примесей, в болтанке самолетов и других летательных ап-
аппаратов, в вибрации зданий под напором ветра, флук-
флуктуации световых и радиосигналов от наземных и кос-
мич. источников и т. д. Имеется несколько подходов
к созданию математич. моделей турбулентности и спо-
способов ее параметризации.
При решении задач метеорологии возникает ряд
проблем, характерных для сложных задач математич.
физики. Это прежде всего подготовка входных данных
(объективный анализ, статистич. обработка временных
рядов на сотке измерений, пространственно-временной
анализ и согласование метеорологич. полей), а также
использование методов теории чувствительности и
оптимизации для идентификации параметров моделей
по данным измерений. Математич. модели в метеороло-
метеорологии имеют большое число степеней свободы, и поэтому
возникает проблема их уменьшения (напр., посредст-
посредством параметризации или за счет использования инфор-
информативных обобщенных переменных).
К М. м. з. относятся задачи, связанные с изучением
и оценкой влияния деятельности человека на атмосфе-
атмосферу. Это — задачи моделирования микроклимата горо-
дов и индустриальных районов с учетом антропоген-
антропогенных факторов, оценка загрязнения атмосферы промыш-
промышленными выбросами, оценка влияния изменений по-
поверхности Земли на динамику и термин, режим ат-
атмосферы и др. Проблема выбора эффективной хозяй-
хозяйственной политики формализуется с помощью методов
теории оптимизации, примененной к задачам метеоро-
метеорологии. В частности, задача оптимального размещения
промышленных комплексов с учетом санитарно-допу-
стимых норм загрязнения окружающей среды форму-
формулируется математически как вариационная задача с
ограничениями.
Комплекс математич. задач, включающий практиче-
практически все перечисленные выше, возникает в связи с про-
проблемой мониторинга при реализации режима слежения
за атмосферными процессами локального и глобального
масштабов.
Лит.: [1] Б е л о в П. Н., Практические методы численного
прогноза погоды, 2 изд., Л., 1967; [2.1 Блинова Е. Н., «Докл.
АН СССР», 1943, т. 39, X» 7, с. 284—87; [3] Г а н ди н Л. С,
Объективный анализ метеорологических полей, Л., 1963; [4]
Голицын Г. С, Введение к динамику планетных атмосфер,
Л., 1973; [5] К и б е л ь И. А., Введение в гидродинамические
методы краткосрочного прогноза погоды, М., 1957; [6] Конд-
Кондратьев К. Я., Актинометрия, Л., 1965; [7] Л а й х т м а н
Д. Л., Физика пограничного слоя атмосферы, 2 изд., Л., 1970;
[8] Лоренц Э. Н., Природа и теория общей циркуляции ат-
атмосферы, пер. с англ., Л., 1970; [9] Малкевич М. С, Опти-
Оптические исследования атмосферы со спутников, М., 1973; [10J
М а р ч у к Г. И., Численные методы в прогнозе погоды, Л.,
1967; [И] Матвеев Л. Т., Основы общей метеорологии.
Физика атмосферы. Л., 1965; [12] М о н и н А. С, Я г л о м
A.M., Статистическая гидромеханика, ч. 1—2, М., 1965—67;
[13] Нелинейные системы гидродинамического типа, М., 1974;
[14] Томпсон Ф. Д., Анализ и предсказание погоды числен-
численными методами, пер. с англ., М., 1962; [15] Э к к а р т К., Гид-
Гидродинамика океана и атмосферы, пер. с англ., М., 1963; [16}
Юдин М. И., Новые методы и проблемы краткосрочного прог-
прогноза погоды, Л., 1963. Г. И. Марчук.
МЕТРИЗУЕМОЕ ПРОСТРАНСТВО — пространство,
топология к-рого порождается нек-рой метрикой по
правилу: точка принадлежит замыканию множества
в том и только в том случае, если она лежит на нулевом
расстоянии от этого множества. Если такая метрика су-
существует, то она не единственна —за исключением того
случая, когда пространство пусто или состоит из одной
лишь точки. В частности, топология каждого М. п.
порождается нек-рой ограниченной метрикой. В М. п.
выполняются сильные отделимости аксиомы: они
нормальны и даже коллективно нормальны. Каждое
М. п. паракомпактно. Все М. п. удовлетворяют первой
аксиоме ечетности. Но ни одно из названных условий,
ни их совокупность недостаточны для метризуемости
пространства. Достаточное условие метризуемости было
найдено П. С. Урысоном A923): каждое нормальное
пространство (и даже каждое регулярное пространст-
пространство — А. Н. Тихонов, 1925) со счетной базой мотризуемо.
Первый общий критерий метризуемости пространства
был предложен в 1923 П. С. Александровым и П. С. Уры-
Урысоном (см. [1]). На его основе были выработаны два
следующих более совершенных критерия метризуемо-
метризуемости: 1) пространство метризуемо в том и только в том
случае, когда оно коллективно нормально и обладает
счетным измельчающимся множеством открытых покры-
покрытии; 2) пространство метризуемо, если и только если
оно обладает счетным фундаментальным множеством
открытых покрытий и удовлетворяет ^-аксиоме от-
отделимости (критерий Стоуна — Архан-
Архангельского). При этом множество ? открытых по-
покрытий пространства X наз. фундаменталь-
фундаментальным, если для каждой точки х?Х, каждой ее окрест-
окрестности Ох найдутся покрытие у?§ и окрестность Огх
точки х такие, что каждый элемент покрытия у, пере-
пересекающийся с Огх, содержится в Ох. Указанные кри-
критерии связаны со следующим принципиально важным
свойством неограниченной делимости,
или звездной нормальности, метр из у-
емых пространств. В каждое открытое по-
покрытие у М. п. X можно вписать открытое покрытие у'
такое, что, какова бы ни была точка х?Х, найдется
U?y, для к-рого U {W?y' : x?W}aU.
На другой важной концепции — локальной конечно-
конечности — основаны общие метризационные критерии.
Критерий Нагаты — Смирнова: про-
пространство X метризуемо в том и только в том случае,
если оно регулярно и обладает базой, распадающейся
на счетное множество локально конечных семейств мно-
множеств. Критерий Бинга аналогичен, но в нем
вместо локально конечных фигурируют дискретные
семейства множеств. Удобные варианты приведенных
выше основных критериев метризуемости связаны с
понятиями равномерной базы и регулярной базы. База
<® пространства X наз. регулярной (равно-
(равномерно й), если для всякой точки х?Х и любой ее
окрестности Ох найдется окрестность О±х этой точки
такая, что число элементов базы сйЗ, пересекающих
одновременно О\х и дополнение к Ох, конечно (соот-
(соответственно, если множество {{7?сйЗ : U^x, UC?.Ox}
конечно). Пространство X метризуемо тогда и только
тогда, когда оно коллективно нормально и обладает
равномерной базой. Наконец, для метризуемости 7\-
пространства необходимо н достаточно, чтобы оно обла-
обладало регулярной базой. Регулярные базы удобны тем,
что они вскрывают механизм паракомпактности про-
произвольного М. п.: чтобы вписать в произвольное откры-
открытое покрытие у пространства X, обладающего регуляр-
регулярной базой сЗ, локально конечное открытое покрытие,
достаточно взять совокупность всех максимальных
элементов семейства
cS3Y = {l/?c63: существует ТГ?у такое, что UczW).
Метризационные критерии достигают простоты в
ряде специальных классов пространств. Так, для ме-
метризуемости бикомпакта X любое из следующих че-
четырех условий необходимо и достаточно: а) X обладает
счетной базой; б) X обладает точечно-счетной базой;
в) в X есть счетная сеть; г) диагональ в XXX имеет
тип Gg. Для метризуемости пространства топологич.
группы необходимо и достаточно, чтобы в последнем
выполнялась первая аксиома счетности — причем тог-
тогда пространство метризуемо инвариантной метрикой
(напр., по отношению к умножению слева).
Характерным свойством М. п. является совпадение
для них ряда мощностных характеристик. В частности,
для М. п. совпадают число Суслина, число Линделё-
фа, плотность, протяженность, вес. Несовпадение этих
чисел свидетельствует о неметризуемости соответству-
соответствующих пространств.
Не всякое М. п. метризуемо полной метрикой; та-
таково, напр., пространство рациональных чисел. Про-
Пространство метризуемо полной метрикой в том и только
в том случае, если оно метризуемо и является множе-
множеством типа Gf> в нек-ром содержащем его бикомпакте.
Важным топологич. свойством пространств, метризуе-
мых полной метрикой, является свойство Бэра:
пересечение любого счетного семейства всюду плотных
открытых множеств всюду плотно.
К М. п. наиболее близки по свойствам т. в. м о р о в-
ские пространства — вполне регулярные про-
пространства, обладающие счетным измельчающимся се-
семейством открытых покрытий, и кружевные простран-
пространства.
Широкий спектр обобщений концепции М. п. получа-
получается, если варьировать аксиомы метрики, ослабляя их
в том или ином отношении и рассматривая порожден-
порожденные такими t'-метриками топологии. На этом пути полу-
получаются симметризуемые пространст-
пространства — путем отказа от аксиомы треугольника. В эту
схему укладываются и моровские пространства. Дру-
roe важное обобщение концепции метризуемости свя-
связано с рассмотрением «метрик» со значениями в полу-
полях и других алгебраических образованиях общей
природы.
Лит.: [1] Архангельский А. В., Пономарев
В. И., Основы общей топологии в задачах и упражнениях, М.,
1974; [2] Е n g e I k i n g F., General topology, Warsz.. 1977;
[3] Антоновский М. Я., Болтянский В, Г., С а-
р ы м с а к о в Т. А., Метрические пространства над полуполя-
ми, Таш., 1961. А. В. Архангельский.
МЕТРИКА, расстояние на множестве
X,— определенная на декартовом произведении XXX
функция р с неотрицательными действительными значе-
значениями, удовлетворяющая при любых х, у?Х условиям:
1) р(^, у) = 0 тогда и только тогда, когда х=у (а к-
сиома тождества);
2) р(х, у)+р(у, z)^p(x, z) (аксиома т р е-
угольник а);
3) р(-т, у) = р(у, х) (аксиома с и м м е т р и и).
Множество X, на к-ром может быть введена М., наз.
метризуемым. Множество X, наделенное некото-
некоторой М., наз. метрическим пространен
в о м.
Примеры. 1) На любом множестве имеется д и-
скретная метрика:
р=1 (х = у) ир = 0(т^}).
2) В пространстве IR" возможны разные М., среди
них:
p(x, y)=V Zj(xi — yi>~>
P (x, y)=sup \xi-yt I,
i
P (x, J/) = 2 1 xi~ У1 Ь
здесь {*,-}, {y;}?
3) В римановом пространстве М. определяется мет-
метрическим тензором или дифференциальной квадратичной
формой (в нек-ром смысле это — аналог первой М. из
примера 2)). Обобщение М. этого типа см. в ст. Финс-
лерово пространство.
4) В функциональных пространствах над (би)ком-
пактом X также вводятся разные М., напр, равно-
равномерная метрика
р(/, g) = suj>\f(x)—g(x)\
хех
(аналог второй М., из примера 2)), интеграль-
интегральная метрика
5) В нормированном пространстве над R М. опре-
определяется через норму | •!:
р{х, у)=\х—у\.
В нормированном кольце — более сложная формула:
р(х, у)=\х-\-у\ — \ху\.
6) В метрич. пространстве вводится другая М.— т.
н. внутренняя метрика.
7) В пространстве замкнутых подмножеств метрич.
пространства определяется хаусдорфова метрика.
Следует заметить, что в традиционном определении
М. условие 3) и требование неотрицательности излиш-
излишни, т. е. вытекают уже из достаточности условия 1)
и условия 2).
Если вместо 1) выполняется лишь условие:
1') Р (-г> У)=0> если х—у (так что при р=0 не всегда
х=у), функция р наз. псевдометрикой [2],
[3], или отклонением [4].
М. (и даже псевдометрика) позволяет определить ряд
дополнительных структур на множестве X. Прежде все-
го, это — топология (см. Топологическое пространство),
кроме того — равномерная (см. Равномерное простран-
пространство) или близостная (см. Близости пространство)
структуры. Термин М. используется также и для обо-
обозначения более общих понятий, к-рые не обладают все-
всеми свойствами 1)— 3), таковы, напр., индефинитная
метрика, симметрика и т. д.
Лит.: [1] Александров II. С, Введение в теорию
множеств и общую топологию, М., 1977; [21 К е л л и Д ж.-Л.,
Общая топология, пер. с англ., М., 1968; [3] К у р а т о в с к и й
К., Топология, [пер. с англ.], т. 1, М., 1966; [4] Б у р б а к и [
Н., Общая топология. Использование вещественных чисел в
общей топологии. Функциональные пространства. Сводка ре-
результатов. Словарь, пер. с франц., М., 1975.
AI. И. Войцеховский.
МЕТРИЧЕСКАЯ ПРОЕКЦИЯ, оператор на-
наилучшего приближен и я,— многозначное
отображение Рщ;х—*-Рмх, ставящее в соответствие каж-
каждому элементу х метрич. пространства Х= (X, р)
совокупность
Рмх^{т?М:р(х, т) = р{х, М)}
наилучшего приближения элементов из множества MczX.
Если М — чебышевское множество, то М. п.— однознач-
однозначное отображение. Задачу построения элемента наилуч-
наилучшего приближения часто решают приближенно, т. е.
находят элемент из множества
где ?>0 достаточно мало. По свойствам отображения
Р'м '¦ х-+Р мх иногда можно судить о множестве М.
Так, если для любого элемента х нормированного про-
пространства X существует число t=t(x)^>0 такое, что
Р*МХ выпукло (связно), то множество М выпукло (соот-
(соответственно связно).
С точки зрения приложений полезно знать, облада-
обладает ли М. п. такими свойствами, как линейность, не-
непрерывность, равномерная непрерывность и т. д.
М. п. на чебышевское подпространство нормированного
пространства X, вообще говоря, не линейна. Если М. п.
на каждое подпространство фиксированной размерно- )
сти является однозначной ц линейной, то X линейно
изометрично пространству с внутренним произведе-
произведением. М. п. на непустое аппроксимативно компактное
множество в метрич. пространстве полунепрерывна
сверху, в частности, в нормированном пространстве
М. п. на конечномерное чебышевекое подпространство
непрерывна; полунепрерывности снизу М. п. может не
быть, если это подпространство не чебышевское. Су-
Существует рефлексивное строго выпуклое пространство
и в нем бесконечномерное подпространство, М. п. на
к-рое разрывна. Для М. п. на любое замкнутое выпук-
выпуклое множество М гильбертова пространства выполня-
выполняется условие Липшица
с константой К=1.
Свойство непрерывности М. п. и ее обобщений на-
находит применение в некорректных задачах, задаче о
выпуклости чебышевских множеств, при построении
элементов наилучшего приближения и т. д.
Лит.: [1] S i n g е г I., The theory of best approximation and
functional analysis, Phil., 1974; [2] В л а с о в Л. П., «Успехи
матем. наук», 1973, т. 28, в. 6, с. 3—66; [3] Б е р д ы ш е в В. И.,
в кн.: Теория приближения функций. Тр. Международной конфе-
конференции по теории приближения функций. Калуга. 1975, м.,
1977 с. 37 — 41. В. И. Бердышев.
МЕТРИЧЕСКАЯ РАЗМЕРНОСТЬ — числовая ха-
характеристика компакта, определяемая с помощью по-
покрытия «эталонами меры», число к-рых и определяет
М. р. Пусть F — компакт, Л>(е) — минимальное число
множеств с диаметром, не превосходящим 8, необходи-
необходимое для того, чтобы они покрывали F. Эта зависящая
от метрики F функция принимает целочисленные зна-
значения для всех е>0 и неограниченно возрастает при
е—>-0; она наз. функцией объема /".Метри-
/".Метрическим порядком компакта F наз. число
<е)\
J.
, ,. / lnJV <е)\
к-шпд 1пе J.
Эта величина но является еще топологич. инвариантом.
Так, метрпч. порядок жордановой дуги с евклидовой
метрикой равен 1, а для жордановой дуги, проходящей
через совершенно вполне несвязное множество в IR"
положительной меры, эта величина равна п. Однако
нижняя граница метрич. порядков для всех метрик ком-
компакта /' (наз. метрической размерностью)
равна его Лебега размерности (теоре.ма П о и т р я г и-
н а — Ш н и р е л ь м а н а, 1!K1, см. прил. к [1]).
Лит.: [1] Гурсвич В., В о л м а н Г., Теория размер-
размерности пер с англ., М., 1948. 1\1. П. Вош^хавскип.
МЕТРИЧЕСКАЯ СВЯЗНОСТЬ — линейная связность
в векторном расслоении я : A'—>-i?, снабженном били-
билинейной метрикой в слоях, при к-рой параллельное пе-
перенесение вдоль произвольно кусочно гладкой линии в
В сохраняет метрику, т. е. скалярное произведение век-
векторов остается постоянным при их параллельном перене-
перенесении. Если билинейная метрика задается тензорным
полем gafs, а линейная связность — матрицей 1-форм
о>а, т0 эта связность является метрической, если
В случае невырожденной симметрической билинейной
метрики, когда gap=gpa, det lgap|^=O, M. с. является
евклидовой связностью. В случае невырожденной косо-
симметрич. метрики М. с. наз. с п м п л о к т и ч е-
ской связностью в векторном расслоении.
При проективизации векторного расслоения, когда
симметрическая билинейная метрика порождает
нек-рую проективную метрику в каждом слое (как в
проективном пространстве), роль М. с. играет про-
еКТНВНОМетрИЧ. СВЯЗНОСТЬ. Ю. Г. Лцмисте.
МЕТРИЧЕСКАЯ ТЕОРИЯ ДИНАМИЧЕСКИХ СИ-
СИСТЕМ — то же, что эргодическая теория.
МЕТРИЧЕСКАЯ ТЕОРИЯ ФУНКЦИЙ — раздел те-
теории функций действительного переменного, и к-ром
свойства функций изучаются на основе понятия меры
множества.
Исследованиями многих математиков 19 в. была соз-
создана новая математич. дисциплина — теория функции
действительного переменного. К кон. 19 в. четко вы-
выкристаллизовались нек-рые проблемы, требовавшие
своего решения: проблема меры множества, длин кри-
кривых и площадей поверхностей, представления функций
рядами (в частности, тригонометрическими), прими-
примитивной и интеграла, взаимосвязи интегрирования и
дифференцирования, почленного интегрирования ря-
рядов и др. Решение этих проблем имело общематематпч.
значение; в этом направлении работали крупнейшие
математики, чем, в частности, и объясняется бурное
развитие М. т. ф. в 1-й трети 20 в. Основы М. т. ф.
были заложены 0. Борелем (Е. Borel), P. Бэром (R. Bai-
ге), А. Лебегом (Н. Lebesgue) и др.
В 1902 А. Лебег ввел чрезвычайно важное понятие
меры множеств (Лебега меры). На основе этого поня-
понятия им была создана теория интеграла (Лебега интег-
интеграла). Эти два основных понятия — мера и интеграл —
составляют фундамент М. т. ф., к-рая занимается изу-
изучением свойств функций, производных, интегралов,
функциональных рядов (в частности, трпгонометрич.
рядов и общих ортогональных рядов), площадей поверх-
поверхностей и т. п.
Многие основные свойства меры и интеграла Лебега
были установлены в нач. 20 в. самим А. Лебегом (счет-
(счетная аддитивность меры и интеграла, предельный пере-
переход под знаком интеграла, дифференцирование неопре-
неопределенного интеграла и др.). Кроме того, А. Лебег дал
многочисленные приложения этих исследовании к раз-
различным вопросам математич. анализа (площади по-
поверхностей, разнообразные свойства тригонометрич.
рядов, сингулярных интегралов и др.)- Дж- Витали
(G. Vitali, 1904) независимо открыл меру, тождествен-
тождественную мере Лебега, а несколько позже У. Юнг (W. Young,
1905) также построил интеграл и меру, эквивалентные
интегралу и мере Лебега. Однако они не развили свою
теорию и не дали ей в этот период существенных при-
приложений. Начало развития М. т. ф. в России следует
отнести к нач. 2U в., хотя первые крупные результаты
в этой области были получены русскими математиками
во 2-м десятилетии 20 в. (Д. Ф. Егоров, Н. Н. Лузин),
когда произошло становление нового крупного центра
исследований по М. т. ф. Создателем и руководителем
школы М. т. ф. в СССР был Н. Н. Лузин.
Развитие М. т. ф. можно охарактеризовать двумя
большими направлениями. Первое направление: на
базе меры множества и интеграла Лебега, а также их
обобщений исследуются как общие свойства функций,
интегралов, тригонометрич. рядов, ортогональных ря-
рядов и т. п., так и их более конкретные тонкие свойства,
выявление и изучение к-рых при помощи методов клас-
сич. анализа было труднодоступным. Это направление
и представляет, собственно, М. т. ф. Второе, не менее
важное направление, состоит в проникновении методов
М. т. ф. в другие разделы математики, а также в созда-
создании на базе ее идей других новых областей математи-
математики, к-рые в свою очередь оказывают стимулирующее
влияние на теорию функций.
На базе М. т. ф. началось детальное изучение гра-
граничных свойств аналитических функций; была создана
метрическая теория чисел, методы к-рой неразрывно
связаны с М. т. ф. Велико влияние теории функций на
создание функционального анализа.
Нттже отмечаются нек-рые характерные результаты
по М. т. ф., каждый из к-рых знаменовал собой реше-
решение юго или иного узлового вопроса, повлекшего в
дальнейшем многочисленные исследования. Так, в
1911 Д. Ф. Егоров доказал, что всякая сходящаяся по-
последовательность измеримых функций является равно-
равномерно сходящейся, если пренебречь нек-рым множеством
сколь угодно малой меры (см. Егорова теорема). Н. Н.
Лузин A912) установил, что всякая измеримая функ-
функция становится непрерывной, если пренебречь некото-
некоторым множеством сколь угодно малой меры (см. Лузина
('.-свойство). Эти два результата трудно переоценить,
т.к., с одной стороны, ими устанавливается определен-
определенная взаимосвязь между основными понятиями М. т. ф.
и класчич. анализа, а с другой — они являются фун-
фундаментом, на к-ром очень часто строятся многие иссле-
исследования по теории функций.
II. Н. Лучин доказал A915) существование примитив-
примитивных в классе измеримых функций. Именно, он показал,
что для всякой конечной измеримой функции f (х) су-
существует непрерывная функция F (х) такая, что F' (х) =
=/(z) почти всюду. На основе этого утверждения он
решил задачу Дирихле в классе измеримых функций.
Это послужило началом активного развития москов-
московской школы теории функций комплексного переменного
и, особенно, началом изучения граничных свойств
аналптич. функций.
Интеграл Лебега не разрешает проблемы нахожде-
нахождения примитивной F (х) по точной конечной производной
F' {x) = f(x). Эту проблему решил А. Данжуа (A. Denjoy,
1912) на основе специального интеграла (узкий ин-
интеграл Данжуа), к-рый естественно обобщает интеграл
Лебега п не противоречит ему (см. Данжуа интеграл).
В 191 й Л. Данжуа гг А. Я. Хинчин построили еще более
общий интеграл, к-рый носит название интеграла Дан-
Данжуа в широком смысле и к-рый связан с аппроксима-
аппроксимативной дифференцируем остью.
В начале 3-го десятилетия 20 в. Д. Е. Меньшов и
X. Радемахер (Н. Rademacher) установили, что после-
последовательность log2n является множителем Вейля для
сходимости почти всюду рядов по любым ортонорми-
рованным системам. Кроме того (и это является осо-
особенно важным и принципиальным), Д. Е. Меньшов
доказал A923), что указанное выше утверждение теряет
силу, если последовательность {log2 n} заменить на
любую последовательность {ы(п)} с ш(п) = о (log2 n)
при п—>-оо. Эти результаты стали тем фундаментом, на
к-ром основывались и основываются многочисленные
исследования по теории сходимости и суммируемости
ортогональных рядов.
В 1926 А. Н. Колмогоров построил пример всюду рас-
расходящегося тригонометрич. ряда Фурье от суммируе -
мой функции. В то же время длительный период оста-
оставалась нерешенной проблема сходимости почти всюд\
тригонометрич. рядов Фурье от функций /??2, поста
вленная Н. Н. Лузиным в 1914. Положительное реше-
решение этой проблемы было дано Л. Карлесоном (L. Саг-
lesori) лишь в 1966 (см. Карлесона теорема). П. Дю-
буа-Реймоном (P. du Rois-Reymond), А. Лебегом и
Ш. Валле Пуссеном (Ch. la Vallee Poussin) был решен
вопрос о восстановлении коэффициентов тригонометрич.
рядов, сходящихся к суммируемым функциям. В 40-х гг.
20 в. А. Данжуа построил интеграл, при помощи к-ро-
го им была решена проблема восстановления коэффи-
коэффициентов по сумме произвольных всюду сходящихся три-
тригонометрич. рядов. В это же время Д. Е. Меньшов до-
доказал, что всякая конечная измеримая функция пррд-
ставима нек-рым почти всюду сходящимся тригономет-
тригонометрич. рядом.
Г. Кантором (G. Cantor), У. Юнгом, Н. К. Бари и др.
были заложены основы теории единственности триго-
тригонометрич. рядов.
Лит.: [1J Л е б е г А., Интегрирование и отыскание прими-
примитивных функций, пер. с франц., М.- Л., 1934; [2] Л У з и н Н. Н.,
Интеграл и тригонометрический ряд, М., 1951; [3] Б а р и Н. К.,
Тригонометрические ряды, М., 1961; [4] С а к с С, Теория ш,-
теграла, пер. с англ., М., 1949' [5] X а л м о ш П. Р., Теория
меры, пер. с англ., М., 1953; [б]Паплаускас А. Б., Три-
Тригонометрические ряды от Эйлера до Лебега, М., 1966; [7] П е-
с и н И. Н., Развитие понятия интеграла, М., 1966; [8] Мень-
Меньшов Д. Е., Ульянов П. Л., «Вестн. Моск. ун-та. Матем.,
мех.», 1967, .№ 5, с. 24—36; [9] Колмогоров А. Н., Теория
функций действительного переменного, в кн.: Наука в СССР за
пятнадцать лет. Математика, М.—Л., 1932; [10] Метрическая тео-
теория функций действительного переменного, в кн.: Математика
в СССР за тридцать лет, М.—Л., 1948; [11] Лозинский
СМ., Натансон И. П., Метрическая и конструктивная
теория функций вещественной переменной, в кн.: Математика в
СССР за сорок лет, т. 1, М., 1959; [121 Ульянов П. Л., Мет-
Метрическая теория функций, в кн.: История отечественной мате-
математики, т. 3, К., 1968; [13] Итоги науки. Математический анализ.
1970, М., 1971. П. Л. Ульянов.
МЕТРИЧЕСКАЯ ТЕОРИЯ ЧИСЕЛ — раздел теории
чисел, в к-ром изучаются и метрически (т. е. на основе
теории меры) характеризуются множества чисел, обла-
обладающих определенными арифметич. свойствами. М. т. ч.
тесно связана с теорией вероятностей, что иногда дает
возможность использовать ее методы и результаты
для анализа теоретико-числовых моделей.
Многие задачи, касающиеся арифметич. свойств от-
отдельных чисел, допускают также метрич. постановку;
напр., наряду с вопросом о том, будет ли равномерно
распределена последовательность дробных долей {an},
п=1, 2, . . ., при а= >^2 или In 3, можно ставить
вопрос о том, какова мера Лебега тех а из интервала
@,1), для к-рых эта последовательность равномерно
распределена. Такое метрич. обобщение задачи часто
оказывается весьма полезным и даст возможность пред-
представить явление в целом. Иногда на основе метрич. рас-
рассуждений без особого труда удается доказать существо-
существование чисел с определенными арифметич:. свойствами,
тогда как прямое построение таких чисел бывает слож-
сложным (нормальные числа Бореля, числа с определенными
свойствами аппроксимации и т. п.).
Наиболее значительные достижения М. т. ч. отно-
относятся к диофантовых приближений метрической тео-
теории, к теории равномерного распределения числовых
последовательностей, к теории цепных дробей и др.
областям теории чисел.
Одной из первых теорем М. т. ч. является теоре-
теорема Б о р е л я (Е. Вorcl, 1909): почт» все (в смысле
меры Лебега) действительные числа а интервала @, 1)
нормальны в системе счисления с любым целым основа-
основанием g. В другой равносильной формулировке эта те-
теорема утверждает, что дробные доли \a.gn}, п=1, 2, . . .,
равномерно распределены на интервале @, 1). Теорема
Бореля обобщалась и углублялась многими математи-
математиками. Плодотворной оказалась точка зрения, основан-
основанная на том, что «цифры» 0, 1, . . ., g—1, встречающиеся
в разложении а в системе счисления с основанием g
(g-ичной системе), являются независимыми случай-
случайными величинами. Явно или неявно основываясь на
этом обстоятельстве и применяя методы, разработан-
разработанные в теории вероятностей для отыскания асимптотич.
законов распределения сумм независимых и слабо за-
зависимых случайных величин, были решены основные
вопросы, касающиеся распределения «цифр» 0, 1, . . .,
g—1, и произвольных групп «цифр» в g-ичном разложе-
разложении чисел а, «случайно» выбираемых в интервале @,1).
Напр., полагая
где а; — числа ряда 0, 1, . . ., g—1, находят, что
а,- = а,-(сс) можно рассматривать как независимые слу-
случайные величины, определенные на интервале @, 1)
с мерой Лебега на этом интервале в качестве вероятност-
вероятностной меры. Если а — любое число ряда 0, 1, . . .,
g—1, kn(a) — число тех г<г?г, для к-рых а[(а) = а при
данном а, то
(kn(a)-nlS)glY~n(g—l)
распределяется асимптотически по нормальному зако-
закону, т. о. при любом действительном х мера множества
тех а, для к-рых
*„(«)-»/* <}/»(«-!)
при п—>-оо стремится к пределу
Г. Вейль (Н. Weyl, 1916) доказал, что если ап, п=
= 1, 2, . . ., — произвольная возрастающая последо-
последовательность натуральных чисел, то для почти всех а
дробные доли {<хап} равномерно распределены на ин-
интервале @, 1). В предположении, что ап являются зна-
значениями нек-рой функции, определенной на бесконеч-
бесконечном интервале A, оо) и обладающей специальными ана-
литич. условиями, эта теорема допускает уточнения,
касающиеся «качества» равномерного распределения.
И. Коксма [8] доказал общую теорему о распределении
дробных долей функции двух переменных /(а, п), где
а — действительное переменное, принимающее почти
все значения из интервала A, ее), а /г=1, 2, ... .
Напр., дробные доли {а"} для почти всех а>1 равно-
равномерно распределены на интервале @, 1).
Помимо вопросов, связанных с нормальными числами
Бореля, одним из основных объектов М. т. ч. в начале
ее развития была метрич. теория цепных дробей. Пусть
а — действительное число из интервала @, 1),а=[0,
О], . . .] — его разложение в цепную дробь, гп(а) =
— {ап, ап + \, . . .], qn(oc) — знаменатель ге-й подходя-
подходящей дроби [0, %, . . ., ап]. А. Я. Хннчпн установил
A935), что для почти всех а при ге->оо
. l\lnft/ln2
= 2,68545...,
ц существует такая абсолютная постоянная у, что для
почти всех а будет у qn (а.) —у у при п—уоо. П. Леви
(P. Levy) нашел, что •у=схр(л2/12 In 2). Кроме того,.
А. Я. Хинчин [5] использовал полученные им резуль-
результаты о метрич. свойствах цепных дробей для доказа-
доказательства теоремы о приближении чисел рациональны-
рациональными. Пусть f(x)— положительная непрерывная функция
положительного аргумента .г, причем xf (х) — невозра-
стающая функция. Тогда неравенство
I Ct — p/q | < / (q)lq (*>
имеет для почти всех а бесконечное множество решений
в целых р и q (g>0), если при нек-ром с>0 интеграл
J с
/ (х) dx
расходится; напротив, неравенство (*) имеет для
почти всех а не более конечного числа решений в це-
целых р и q (g>0), если интеграл сходится для всех с>0.
Эта теорема переосмысливалась и обобщалась с раз-
различных точек зрения. Она стала исходным пунктом
интенсивного развития метрич. теории диофантовых
приближений. П. Ордёш [7], завершая серию работ сво-
своих предшественников, получил следующие результаты.
Необходимое и достаточное условие того, что для почти
всех а бесконечное число <ц (а) содержится в произ-
произвольной последовательности п1<??2<. . ., есть
где ф(п) — функция Эйлера. При этом же условии
для почти всех а неравенство
| a — т/п;\ < г/п], (т, и,-) = 1,
где т — целое, е>0 — любое, имеет бесконечное чис-
число решений. Эти результаты близки к гипотезе A982):
если п1<Сп2 < . . . — произвольная последовательность
целых чисел, 5,->0 — любые, то неравенство
|а — т/п; | < б,7п,-, (т, 7г,) = 1,
имеет бесконечное число решений для почти всех а.
тогда и только тогда, когда
у- ^ (".->=«
Р. О. Кузьмин доказал A928), что при любом xg @, 1)
мера тп(х) множества тех а, для к-рых гп(а) — ап<Сх,
равна
где А,>0 — абсолютная постоянная. Асимптотич. соот-
соотношение
тп(л;)~1пA + л;)/1и2 (п—+оо)
было известно К. Гауссу (С. Ganss), но он не опублико-
опубликовал его, а в одном из писем к П. Лапласу (P. Laplace)
указывал, что было бы весьма желательно оценить
разность тп{х) — In (\-\-x)i\n 2. Оценка Кузьмина
0{е~~хУп) была улучшена П. Левп A929) до О(е~>-п).
Метод Кузьмина явился источником многих других
метрич. теорем о цепных дробях.
Современная трактовка метрич. вопросов, связанных
с нормальными числами Бореля и с теорией цепных
дробей, использует идеи оргодич. теории. Это основано
на том, что отображения интервала @, 1) на себя а—у
—*-{<xg} и а—>-{1/а}, тесно связанные с разложением а
в g-ичную дробь и цепную дробь соответственно, явля-
являются сохраняющими меру и эргодическими: первое со-
сохраняет меру Лебега, второе— меру (г(Л), опреде-
ляемую для каждого измеримого множества А из @,1)
формулой
it" их
С этой точки зрения теорема Гаусса — Кузьмина без
оценки остаточного члена непосредственно следует
из индивидуальной эргодич. теоремы Биркгофа. Со-
Соображения эргодич. теории оказываются полезными
и при оценке остатков в нек-рых предельных теоре-
теоремах. Напр., результаты А. Я. Хинчина допускают (см.
[10]) уточнение:
У qn (а) = ехр (л2/12 In 2) + О (л1/2 (In /гJ + Е),
где е>0 — произвольно. Идеи эргодич. теории оказыва-
оказываются полезными и во многихдругих задачах М. т. ч.
(линейные диофантовы приближения, распределение
значений матричной показательной функции, алгоритм
Якоби — Перрона и др.).
В нск-рых случаях метрич. характеристика число-
числовых множеств, основанная на мере Лебега, оказывается
слишком грубой, и тогда применяют более тонкие ха-
характеристики, напр, размерности Хаусдорфа. Такой
подход оказывается особенно полезным в теории дио-
фантовых приближений и теории трансцендентных чи-
чисел. Напр., было установлено [6], что при любых фик-
фиксированных п и ш^гп+1 множество тех действительных
чисел х, для к-рых неравенство
\х-а\< h-™
имеет бесконечное число решений в алгебраич. числах а
степени п н высоты ha, имеет размерность Хаусдорфа,
равную (n-\-i)lw. Если ш<п+1, то соответствующее
неравенство имеет бесконечное число решений для почти
всех х, в то время как предполагается, что это верно
для всех ж (гипотеза Вирзинга). Аналогич-
Аналогичные результаты известны для комплексных чисел. Они
непосредственно связаны с фундаментальными вопро-
вопросами классификации трансцендентных чисел [3].
С метрич. точки зрения анализируются не только
задачи, касающиеся действительных и комплексных
чисел, но также р-адических чисел, аделей, формальных
степенных рядов и т. д. и вообще элементов всех про-
пространств, в к-рых введена мера и в к-рых ставится
«арифметическая» задача. В частности, для р-адических
чисел верны аналоги многих метрич. теорем теории рав-
равномерного распределения и теории диофантовых приб-
приближений действительных чисел, несмотря на то, что
область р-адических чисел отличается своей метрикой
и топологией (см. [3], [9]).
Метрич. подход оказывается эффективным при ре-
решении «некорректно» поставленных задач, когда не-
недостаток информации об объекте исследования компен-
компенсируется допущением «случайного» выбора этого объек-
объекта из нек-рого множества сходных объектов. При этом,
конечно, не удается исследовать первоначальный объ-
объект, что иногда в принципе невозможно из-за недостатка
информации о нем, но получаются выводы, что «почти
все» объекты из рассматриваемого множества обладают
определенными свойствами. Напр., пусть А *= {К
<яГ<а2<. . .} — последовательность натуральных
чисел, возрастающая не быстрее нек-рой степени, т. е.
а,<г'^, (г—const. Ставится вопрос, существует ли такое
число г, что любое натуральное число можно предста-
представить суммой не более чем г слагаемых из А *. Ясно, что
имеющейся информации о последовательности А * не-
недостаточно для решения задачи.
Пусть Ж — множество последовательностей А =
= {1<а1<а2<. . .} целых чисел, где каждое а,- «слу-
чайно» выбирается из отрезка [а,-, a1+i). Ha ЗГ можно оп-
определить меру Лебега и доказать, что для ночти всех А
существует искомое число г<оо (см. [4]).
Весьма содержательной и глубокой является связь
между «глобальными» утверждениями М. т. ч. и их
«индивидуальными» реализациями. Несмотря на то,
что почти все элементы нек-рого множества обладают
определенным свойством, бывает очень трудно устано-
установить, что данный конкретный элемент этого множества
обладает этим же свойством. Напр., Э. Борель высказал
предположение, что такие числа, как Y~2, е, я, In 3
и т. д., нормальны, и хотя почти все числа нормальны,
до сих пор A982) неизвестно, является ли нормальным
хотя бы одно из этих чисел. Во многих случаях дока-
доказать метрич. теорему легче, чем подобную «индивиду-
«индивидуальную». Однако это не означает, что в М. т. ч. нет
глубоких проблем, т. к. многие проблемы М. т. ч.
тесно связаны с нек-рыми «индивидуальными» пробле-
проблемами, что иногда обнаруживается достаточно быстро.
С другой стороны, решение «индивидуальных» проблем
обнаруживает их связь с метрическими.
Идеи М. т. ч. играют фундаментальную роль во мно-
многих разделах аналитич. теории чисел, в особенности
тогда, когда используется интегрирование но нек-рой
мере. В этих случаях вывод какой-либо метрич. теоре-
теоремы не является целью исследования, но метрич. со-
соображения используются как промежуточный этап
рассуждений. Они могут быть одним из главных прин-
принципов, лежащих в основе рассуждения, хотя оконча-
окончательная формулировка результата не будет содержать
никаких мотрич. понятий. Примером систематич. ис-
использования такого рода рассуждений является метод
Харди — Литлвуда — Виноградова, в к-ром сущест-
существенную роль играют метрич. свойства приближения
чисел рациональными дробями («большие» и «малые»
дуги Харди — Литлвуда). Это обстоятельство позволило
И. М. Виноградову формулировать свои новые теоре-
теоремы об оценках сумм Вейля как нек-рые метрич. теоре-
теоремы [1]. Кроме того, метод И. М. Виноградова оценок
сумм Вейля носит ярко выраженный метрич. характер,
где устанавливается связь между «глобальной» оцен-
оценкой интеграла и «индивидуальной» оценкой конкретной
суммы. Примеров такого рода в теории чисел мало.
Лит.: [1] Виноградов И. М., Метод тригонометриче-
тригонометрических сумм в теории чисел, М., 1971; [2] Постников А. Г.,
«Тр. Матем. ин-та АН СССР», 1966, т. 82, с. 3 — 111; [3] С п р и н д-
жук В. Г., Проблема Малера в метрической теории чисел,
Минск, 1967; [41 е г о же, «Известия АН БССР. Сер. Физ.-
матем. наук», 1970, Mi 1, с. 5 —14; [5] X и н ч и н А. Я., Цепные-
дроби, 4 изд., М., 1978; [В] В a k e r A., Schmidt W., «Proc.
London Math. Soc», C), 1970, v. 21, p. 1—11; [7] E r d б s P.,.
«J. Number Theory», 1970, v. 2, p. 425—41; [8] К о к s m a J. P.,
Diophantische Approximationen, В., 1936; [9] L u t z Ё., Sur
les approximations diophantiennes lineaires p-adiques, P., 1955;
[10] Philipp W., «Pacific J. Math.», 1967, v. 20, JV 1, 109—
27; Ц и г л е р И., Хельмберг Г., «Математика», 1963,
т. 7, Ms 3, с. 3—46. В. Г. Сприпджук.
МЕТРИЧЕСКАЯ ТРАНЗИТИВНОСТЬ д и и а ми-
ческой системы {Т^} с ( к в а з и) инва-
инвариантной мерой [I — свойство системы {7\},
состоящее в том, что любое измеримое подмножество А
фазового пространства W, инвариантное относительно
Tf (в том смысле, что оно совпадает со всеми своими
прообразами (Ti)-1A), либо имеет меру нуль, либо с
точностью до множества меры нуль совпадает с W.
Формально более сильный вариант этого свойства полу-
получится, если в определении вместо инвариантных мно-
множеств говорить о множествах, инвариантных по mod О
(такое множество А при любом t может отличаться от
(Tt)~lA на множество меры нуль). Эти два варианта
эквивалентны, если \х является о-конечной и «время» t
пробегает локально компактную группу со счетной ба-
базой (см. доказательство для потоков в [1]), но для произ-
произвольных групп преобразований это не так (см. пример,
приведенный' по другому поводу, в [2]).
Вместо М. т. говорят также о метрической
неразложимости, или эргодичности. Если у
данной системы рассматривается несколько (квази) ин-
инвариантных мер и ц — одна из них, то, вместо того
чтобы говорить о М. т. (эргодичности) системы по от-
отношению к мере |.i, говорят о М. т. (эргодичности) меры р..
Р а з л о ж и м о с т ь нормированной инвари-
инвариантной меры \1 естественно понимать иначе — как
возможность представления ц в виде «^Н+Яг^г, гДе
и,,-— нормированные инвариантные меры, отличные от
и, п а,->0. Неразложимость ц эквивалентна второму
(более сильному) варианту М. т. (см. [2], [3]).
Если в W введена топология, то при естественных
предположениях (ем. обсуждение для потоков в [1]) из
М. т. следует, что для почти всех w?W траектория точ-
точки w всюду плотна (в этом смысле из М. т. следует то-
топологическая транзитивность). Обратное неверно.
Начиная с Дж. Неймана [4|, получен ряд результа-
результатов о разложении неэргодич. систем на эргодич. ком-
компоненты. Традиционный в чисто метрич. теории ва-
вариант (W — Лебега пространство, соответственно речь
идет только об одной (квазн) инвариантной мере) см.
в [5], [6], [И]. Н. М. Крылов, Н. Н. Боголюбов [7]
получили для топологич. потоков и каскадов с ком-
компактным метрическим W более сильные результаты
двоякого рода (см. также [8], [9]): 1) разложение инва-
инвариантных нормированных мер, совместимых с тополо-
топологией, на эргодпч. меры; 2) «геометрическая» реализа-
реализация сразу всех этих разложений посредством эргоди-
ческих множеств. Относительно обобщения этих ре-
результатов на другие группы преобразований извест-
известно, что 1) справедливо в более широких предположе-
предположениях, чем 2) (см. [2], [3].). Имеются также аналогич-
аналогичные результаты для динамич. систем (пока только
каскадов и потоков) в подходящих измеримых простран-
пространствах и (или) для квазшщвариантных мер (см. [9] —
[11]).
М. т. разбиения | пространства с
мер о й (И7, и.) — свойство разбиения |, состоящее
в том, что любое измеримое подмножество AczW, це-
целиком состоящее из элементов ?, либо имеет меру нуль,
либо с точностью до множества меры нуль совпадает
со всем W. Вместо М. т. говорят также об абсолют-
абсолютной неизмеримости ?. М. т. динамич. сис-
системы, образованной группой преобразований, так что
траектории образуют разбиение фазового пространства,
совпадает с М. т. этого разбиения. Если же преобра-
преобразования, образующие динамич. систему, необратимы,
то ее М. т. тоже сводится к М. т. нек-рого разбиения,
хотя оно описывается сложнее: его элемент, содержа-
содержащий нек-рую точку, состоит из всех ее образов и всех
прообразов этих образов.
Лит.: [1] X о п ф Э., «Успехи матем. наук», 1949, т. 4, в. 1,
с. 11J—82; [2] Ф о м и н С. В., «Изв. АН СССР. Сер. матем.»,
1950, т. 14, .\5 3, с. 261 — 74; [3] Б о г о л ю б о в Н. Н., Избр.
труды, т. 1, К., 1969, с. 561—69; [4] Neiimann J., «Ann.
Math..>. 1932, v. 33, Mi 3, p. 587 — 642; Ml 4, p. 789 — 92; [51 P о x-
л и н В. А., «Успехи матем. наук» 1949, т. 4, в. 2 с. 57 —128;
[6] его ж е, «Матем. сб.», 1940, т. 25, Ms 2, с. 235—49; [7] К р ы-
л о в Н. М., Боголюбов Н. Н. в кн.: Боголюбов
Н. Н., Избр. труды, т. 1, К.. 1969, с. 411—63; [8] Н е м ы ц-
кий В. В., Степанов В. В., Качественная теория диф-
дифференциальных уравнений, 2 изд., М.—Л., 1949; [9] О к с т о-
0 и Д ж., «Успехи матем. наук», 1953, т. 8, в. 3, с. 75—97; [10]
К и ф е р Ю. И., Пирогов С. А., там же, 1972, т. 27, в. 1,
с. 77 — 80; [11] и х же, там же, в. 5, с. 239—40. Д. В. Аносов.
МЕТРИЧЕСКИЙ ИЗОМОРФИЗМ пространств
с мерой (Х1, 5УЬ щ) и (Х2, 51^2> Iх г) — биективное
отображение / : j^—>-А%, при к-ром образы и прообразы
измеримых множеств измеримы и имеют ту же меру
(здесь 23/ — нек-рая булева а-алгебра или о-кольцо
подмножеств пространства X,-, называемых измеримы-
измеримыми, а 1л,- — заданная на 5Ц,- мера). Более общее поня-
понятие — (метрический) гомоморфизм этих
пространств, т. е. такое отображение / : Хг—>-Х2, что
прообразы измеримых множеств измеримы и имеют ту
же меру. При (Xlf $bvb (i1) = (Z2, >В2, (г2) вместо изо-
изоморфизма или гомоморфизма говорят о (метриче-
(метрическом) автоморфизме или эндоморфиз-
м е.
В соответствии с обычной в теории меры тенденцией
пренебрегать множествами меры нуль вводятся (и
преимущественно используются) варианты всех этих
понятий «по mod 0». Напр., пусть iVjdX;, ц,(Лг;) = О,
г=1, 2, и / : X1\N1—>-X2\N2— М. и.; тогда говорят,
что / есть изоморфизм исходных пространств с мерой
по mod 0. (Оговорку «по mod 0» часто опускают.)
Для ряда объектов, заданных в ЛГ; (подмножеств,
функций, преобразований, а также их систем), имеет
смысл утверждение, что при М. и. / эти объекты пере-
переходят друг в друга. Тогда говорят, что / есть М. и.
соответствующих объектов. Можно говорить также об
их М. п. по mod 0. При этом подразумевается, что при
нек-рых Ni меры нуль соответствующие объекты О; мо-
могут рассматриваться как нек-рые объекты О\ в Х,\ЛГ,-
(для преобразований это означает, что X{\N[ инва-
инвариантны относительно этих преобразований, а для
подмножеств и функций это имеет смысл при любых
N; — надо взять пересечения рассматриваемых подмно-
подмножеств с Xf\N; и ограничения функций на Х;\Л",-) и
что / есть М. и. объектов О\. Класс всех метрически
изоморфных по mod 0 друг другу объектов называют
(метрическим) типом; говорят, что два объек-
объекта из этого класса имеют одинаковый тип.
С (А',-, 58,-, ц,-) ассоциируются гильбертово простран-
пространство L2(X;, |i(), в к-ром дополнительно к обычной
структуре гильбертова пространства имеется еще опе-
операция обычного перемножения функций (определенная,
правда, не всюду, ибо произведение функций из I?
не всегда принадлежит L2), и булева er-алгебра с мерой
ЯЛ/, получающаяся из 53/ отождествлением множеств,
симметрич. разность к-рых имеет меру нуль (т. е. фак-
факторизацией по идеалу, состоящему из множеств меры
нуль). М. и. mod 0 / индуцирует изоморфизм булевых
о-алгебр с мерой Щ}/ и унитарный изоморфизм гильбер-
гильбертовых пространств L2(Xi, u.,), к-рый мультипли-
мультипликативен, т. е. переводит произведение (когда оно
определено) в произведение образов сомножителей.
Если (X,-, 33,-, (г,-) — Лебега пространство, то верно
и обратное: всякий изоморфизм булевых а-алгебр с
мерой 2Rj или мультипликативный унитарный изомор-
изоморфизм пространств L2(Xj, \ц) индуцируется нек-рым
М. и. по mod 0.
Лит.: [1] Р о х л и н В. А., «Матем. сб.», 1949. т. 25, № 1,
С. 107 — 50. Д. В. Авосов.
МЕТРИЧЕСКИЙ ТЕНЗОР, основной тензор,
фундаментальный тензо р,— поле дважды
ковариантного симметрич. тензора g=g(X, Y) па п-мер-
ном дифференцируемом многообразии Мп, п^2. За-
Задание на Мп М. т. вводит в касательном к М" в точке
р?М" векторном пространстве М^, скалярное произве-
произведение (X, У> контравариантных векторов X, Y?Mp,
определяемое как билинейная функция gp(X, У), где
gp — значение поля g в точке р. В координатной записи:
<Х, Yy = gi/(p)X'Y/, Х = {Х'}, Y = {YJ), 0<i
Метрика пространства М'р с введенным в нем скаляр-
скалярным произведением принимается в бесконечно малом
за метрику многообразия М", что выражается в выборе
дифференциальной квадратичной формы
квадратом дифференциала длины дуги кривой М",
исходящей из р в направлении da-1, . . ., dx". По со
геометрич. смыслу форму (*) наз. метрической,
или первой основной, формой на М",
соответствующей М. т. g. Обратно, если на Мп задана
симметрическая квадратичная форма вида (*), то ей
сопоставляется поле дважды ковариантного тензора
g(X, Y)-=g[jX'(?)YJ, соответствующая метрич. форма
к-рого совпадает с g. Таким образом, задание на Мп
М. т. g равносильно заданию на М" метрики с квадра-
квадратом линейного элемента вида (*). М. т. полностью оп-
определяет внутреннюю геометрию М".
Совокупность М. т. g и определяемых ими метрик
подразделяется на два класса — вырожденные метри-
метрики, когда dot (gi/) = 0, и невырожденные, когда
det(gi/)^=0. Многообразие М" с вырожденной метри-
метрикой (*) паз. изотропным. Среди невырожденных М. т.,
в свою очередь, различаются р и м а н о в М. т., для
к-рого квадратичная форма (*) является положительно
определенной, и п с е в д о р и м а н о в М. т., когда
форма (*) является знакопеременной. Риманова (псев-
дориманова) метрика, вводимая на Мп через риманов
(псевдориманов) М. т., определяет на М" риманову
(соответственно псевдориманову) геометрию.
Обычно под М. т. без специального на то указания
понимается риманов М. т.; но если, рассматривая не-
невырожденный М. т., хотят подчеркнуть, что речь идет
именно о римановом, а не псевдоримановом М. т., то об
этом М. т. говорят как о собственно римановом М. т.
Собственно риманов М. т. может быть введен на любом
паракомпактном дифференцируемом многообразии.
Лит.: [1] Э й з е н х а р т Л. П., Риманова геометрия, пер.
с англ., М., 1948; [2] Р а ш е в с к и й П. К., Риманова гео-
геометрия и тензорный анализ, 3 изд., М., 1967; [31 Г р о м о л Д.,
Клингенберг В., М е й е р В., Риманова .геометрия
в целом, пер. с нем., М., 1971. И. X. Сабитов.
МЕТРИЧЕСКОЕ ПРОСТРАНСТВО — множество
X вместе с нек-рой метрикой р на нем. Теоретико-мно-
Теоретико-множественный подход к изучению фигур (пространств)
основан на исследовании взаимного расположения
составляющих их элементарных частей. Одной из фун-
фундаментальных характеристик взаимного расположения
точек пространства является расстояние между ними.
Этот подход к пространственным отношениям и приво-
приводит к понятию М. п., впервые выделенному М. Фреше [2]
в связи с рассмотрением функциональных пространств.
Оказалось, что естественную метрику несут на себе
множества объектов самой разной природы. Как М.п.
могут рассматриваться множества состояний, функций
и отображений, любые подмножества евклидовых про-
пространств и гильбертова пространства. Рассмотрение
метрик важно при исследовании сходимости (рядов,
функций), при решении вопросов аппроксимации.
Развитие теории М. п. шло по следующим важнейшим
направлениям.
Общая теория М. п. В ней исследуются свой-
свойства М. п., инвариантные относительно изометрий —
взаимно однозначных отображений на, сохраняющих
расстояние. К числу таких свойств относятся полнота,
ограниченность, вполне ограниченность, диаметр. Свой-
Свойства этого типа наз. метрическими.
Топологическая теория М.п. Пред-
Предметом ее являются свойства М. п., сохраняющиеся
при гомеоморфизмах. Среди них — компактность, се-
сепарабельность, связность, свойство Бэра, нульмер-
нульмерность. Свойства атого типа наз. топологиче-
топологическим и.
Теория пространств, на к-рых за-
задана метрика, согласованная с какой-либо до-
дополнительной алгебраич. структурой (напр., век-
векторного пространства или группы). Сюда относятся
евклидовы пространства, предгильбертовы и гильбер-
гильбертовы пространства (любого веса), банаховы простран-
пространства, банаховы алгебры, банаховы решетки, счетно нор-
нормированные пространства. Имеющиеся здесь факты
существенно связаны с рассмотрением важных в идей-
идейном отношении свойств метрик или норм, но по со-
держанию целиком принадлежат соответствующим об-
областям алгебры и функционального анализа.
Рассмотрение специальных метрик играет важную
роль при исследовании неевклидовых геометрiiii, в
дифференциальной геометрии, механике и физике.
Центральное место здесь занимает понятие римановой
метрики риманова пространства (см. Риманоеа геоме-
геометрия). Более широкий подход к изучению поверхно-
поверхностей и фигур, возникающих в дифференциальной гео-
геометрии, связан с концепцией G-пространства, получаю-
получающейся добавлением к аксиомам метрики нек-рых ус-
условий (см. Геодезических геометрия), создающих ос-
основу для рассмотрения геодезических в G-пространстве,
обеспечивая их существование и правильные свойства.
Характерным здесь является отказ от пользования
методами дифференциального исчисления, при этом об-
обнаруживается, что многое в дифференциальной геоме-
геометрии не связано с условиями дифференцируемости, а
определяется только геометрия, аксиомами. Геометрия
геодезических представляет интерес не только как обоб-
обобщение римановой геометрии, но и как попытка заме-
заменить вычисления рассуждеш:ями, сделать исследова-
исследование геометрич. объектов более геометрпчным.
На каждом множестве X может быть определена ме-
метрика рТ по следующему правилу: рт(х, ?/) = <->, если
х=у, и ртЬ', у)~ 1, если хфу. Эта метрика наз. т р и в и-
альной. Каждая метрика р на множестве X позволяет
естественным образом ввести на X топологию ?Гр.
Концепция топология, пространства заключает в себе
аксиоматизацию отношения абсолютной близости точки
к множеству, тогда как концепцией М. п. формализу-
формализуется отношение сравнительной близости между точка-
точками. Расстояние р(х, Л) от точки х до множества
А в М. п. {X, р} определяется как inf {р(х, у) : у?А }.
Точка х объявляется абсолютно близкой ко множеству
А, если р(х, Л) = 0. Замыканием [А] множества А
в {X, р} наи. множество всех точек из X, абсолютно
близких к А. Однозначно отвечающая этой операции
топология на множестве X и наз. топологией,
порожденной на X метрикой р. Триви-
Тривиальной метрике на X отвечает дискретная тополонш —
все множества замкнуты.
В исследовании М. п. (особенно их топологич.
свойств) важная роль принадлежит понятию сходящей-
сходящейся последовательности. Это объясняется тем, что тополо-
топология каждого М. п. может быть полностью описана на
языке последовательностей.
Пусть \={хп, ге=Н, 2, . . ^ — последовательность
точек в М. п. {X, р}. Она наз. сходящейся к
точке х? X, если для каждого s>0 найдется целое число
N такое, что р(ж, хп)<.г при всех n>iV. Последователь-
Последовательность % наз. фундаментальной, если для
каждого е>0 найдется целое число JV такое, что
р(хп, хт)<е при всех т, n>N.
Важным метрич. свойством является полнота — М. п.
{X, р} наз. полным, если каждая фундаментальная
последовательность в нем сходится к нек-рой его точке.
Пространство {X, р7-} полно. Полнота М. п. не явля-
является топологич. свойством: М. п., гомеоморфное иол-
ному М. п., может не быть полным, напр, действитель-
действительная прямая R с обычной метрикой р{х, у)= \х—у\
гомеоморфна интервалу @, 1)={.t?R: 0<.с<1), на-
наделенному той же метрикой, однако первое М. п. полно,
а второе — нет.
Примерами полных М. п. могут служить евклидовы
и банаховы пространства. Важным свойством полных
М. п., сохраняющимся при гомеоморфизмах, является
Бэра свойство, в силу к-рого каждое полное М. п. без
изолированных точек несчетно. Поэтому обычная то-
топология пространства рациональных чисел не порожда-
порождается никакой полной метрикой. Однако каждое М. п.
может быть представлено как часть нек-рого полного
М. п. посредством стандартной конструкции пополне-
пополнения. Две фундаментальные последовательности ?—
= {хп} и г\ = {уп} в М. п. {X, р} наз. эквивале н т-
н ы м и, если
Итр(а;„, уп) = 0.
Пусть X — множество всех возникающих классов
эквивалентности. Метрика р на X вводится правилом:
если а', а"?Х и я'Э1'=К}, О?"=К}, то
р(о', а")= \\тр{х'п, х'п).
«->со
Для .г?Х пусть i(x)= {хп}, где х„=з; при всех п. Тогда
{X, р} — полное М. п. и i: Х->-Х — изометрич. отоб-
отображение пространства X, р на всюду плотное подпро-
подпространство в {X, р} (в связи с чем {X, р} и наз. п о-
полнением пространства {X, р}).
С рассмотрением пополнений связана Лаврентьева
теорема о продолжении гомеоморфизмов. Из нее сле-
следует, что свойство М. п. быть множеством типа Gs в
своем пополнении топологически инвариантно (в отли-
отличие от неинвариантности самой метрич. полноты отно-
относительно гомеоморфизмов).
Метрики Pi и р2 на множестве X наз. тополо-
топологически эквивалентными, если совпада-
совпадают порожденные ими топологии S~Pi и <$~Рг- На ко-
конечном множестве все метрики эквивалентны — они
порождают дискретную топологию. Теорема
Александрова — Хаусдорфа: метрика р
на множестве X топологически эквивалентна нек-рой
полной метрике в том и только в том случае, если X
является множеством типа G& в пополнении М. п. {Х,р}.
В частности, пространство иррациональных чисел с
обычной метрикой (не полное относительно ее) гомео-
морфно полному метрич. пространству Бэра, точками
к-рого являются всевозможные бесконечные последова-
последовательности {п{} натуральных чисел, а расстояние зада-
задается правилом: р({«,-}, {то,})=1//с, где к таково, что
щфтъ и ге,-=т,- при всех i<Jk.
Важен следующий пример полного М. п.: простран-
пространство Cjo.i], составленное из всех непрерывных функ-
функций, определенных на отрезке [0, 1], и несущее на себе
метрику, определенную правилом
р(/, g)=max{\f(x)-g(x)\:x?[O,l]}
для всех/, g€^fo,u- Пространство C[Oiu сепарабельно —
в нем есть счетное всюду плотное множество. Оказы-
Оказывается, каждое сепарабельное М. п. изометрично
нек-рому подпространству C[0,ij (теорема Бана-
Банаха — М а з у р а). Этот результат означает, в частности,
что все метрики, порождающие сепарабельные тополо-
топологии, оправданы (ибо изометричное пространство может
быть получено сужением естественной метрики мно-
множества непрерывных функций).
Подмножество У полного М. п. {X, р}, наделенное
той же метрикой р (точнее, ее сужением на YXY),
является полным М. п., если и только если Y замк-
замкнуто в {.Y, р}.
Существует фундаментальная связь между понятиями
полноты и компактности М. п. Компактность
М. п. X, р равносильна любому из следующих условий:
1) любая последовательность в {X, р} содержит схо-
сходящуюся предпоследовательность; 2) каждое счетное
открытое покрытие пространства {X, р} содержит ко-
конечное подпокрытие; 3) в любом открытом покрытии
пространства {X, р} найдется конечное подпокрытие;
4) каждая убывающая последовательность непустых
замкнутых в {X, р} множеств имеет непустое пересе-
пересечение; 5) каждое замкнутое дискретное подпростран-
подпространство пространства {X, р} конечно.
Простейшие примеры компактных М. п.: конечные
дискретные пространства, любой отрезок (с концами),
квадрат, окружность, сфера. Вообще, подпространство
евклидова пространства Еп, взятое в обычной метрике,
компактно в том и только в том случае, если оно зам-
замкнуто в Еп и ограничено.
Не все из перечисленных условий равносильны за
пределами класса М. п. (см. Бикомпактное прост-
пространство). А. Лебег (Н. Lebesgue, 1911) установил,
что для каждого открытого покрытия у компактного
М. п. {X, р} существует число б>0 такое, что вся-
всякое множество АаХ диаметра <б содержится в неко-
некотором элементе покрытия у. Отсюда следует фунда-
фундаментальное свойство компактных М. п., характеризу-
характеризующее их в классе всех М. п.: всякое непрерывное от-
отображение такого пространства в произвольное М. п.
равномерно непрерывно. Далее, М. п. компактно в
том и только в том случае, если каждая непрерывная
действительная функция на нем ограничена (и достига-
достигает наименьшего и наибольшего значений).
Каждое компактное М. п. полно, но обратное невер-
неверно; простейшим примером служит бесконечное дискрет-
дискретное пространство, наделенное тривиальной метрикой.
Но имеет место следующая характеристика: М. п.
компактно в том и только в том случае, если всякое
гомеоморфное ему М. п. полно.
Интуитивно очевидно, что компактность включает,
помимо полноты, условие типа ограниченности, что
подтверждается рассмотрением компактных подпрост-
подпространств в Еп. В общем случае М. п. {X, р} наз. ограни-
ограниченным, если существует действительное число а
такое, что р(х, г/)<а для всех х, у?Х. Каждое ком-
компактное М. п. ограничено. Пространство {X, pj-} полно
и ограничено, но не компактно, если X бесконечно,
так что полнота и ограниченность в совокупности не-
недостаточны для компактности М. п. Вообще, всякая
метрика на любом множестве топологически эквива-
эквивалентна нек-рой ограниченной метрике — полной, если
заданная метрика полна. В связи с этим получает важ-
важное значение понятие вполне ограниченности. М. п.
{X, р} наз. вполне ограниченным, если
для каждого е>0 существует конечное множество
AECZX такое, чтор(з;, As )<е при всех ,т? X. Множество
.4е наз. при этом е-с е т ь ю в {X, р}. М. п. {X, р}
компактно, если и только если оно полно и вполне огра-
ограничено, и {X, р} вполне ограничено в том и только в
том случае, если оно изометрично подпространству
нек-рого компактного М. п. Точнее, вполне ограничен-
ограниченность М. п. {X, р} равносильна компактности его по-
пополнения {X, р}. Каждое подпространство вполне
ограниченного М. п. вполне ограничено. Все вполне
ограниченные М. п. (в частности, все компактные М. п.)
сепарабельны и обладают счетной базой. Компактность,
вообще говоря, не наследуется подпространствами;
множество AczX компактно в М. п. {X, р}, если за-
замыкание А в {X, р} является компактным М. п. Если
[X, р} полно, то компактность множества AczX в
{X, р} равносильна вполне ограниченности А, наде-
наделенного метрикой р.
Важную роль в функциональном анализе играет кри-
критерий компактности произвольного множества А не-
непрерывных функций, определенных на отрезке [0, 1],
в М. п. Cfo.iji заключенный в следующей теореме
Арцела — Асколи: множество А компактно в
C[o,ij, если и только если выполняются условия: 1) су-
существует число Мтакое, что |/(з;)| <СМ при всех х?[0, 1]
и всех f?A; 2) для каждого е>0 найдется у>0 такое,
что \f(x')-—f(x")\<e для всех /?Л и всех х', х"?[0, 1],
для к-рых \х'—з:"|<6.
Отображение / М. п. {X, р} в себя наз. сжимаю-
сжимающим, если существует действительное число Х
такое, что
Р (/(*), Пу))<Др(*, у)
при всех х, у?Х. Важной теоремой о полных М. п.
является принцип сжимающих (сжатых)
отображений: для каждого такого отображения
(непустого) полного М. п. {X, р} в себя существует
ровно одна неподвижная точка.
Тополоп.ч. теория М. п. значительно проще общей
теории топологнч. пространств. Ниже приводятся
наиболее важные тонологич. свойства М. п. {X, р}—-
имеются ввиду свойства топологии аГр , порожденной
метрикой.
Каждое М. п. нормально и даже коллективно нор-
нормально. Это позволяет продолжать непрерывные дей'
ствительные функции с замкнутых подмножеств М. п.
на все пространство. Более сильное утверждение: для
каждого замкнутого подмножества Y М. п. {X, р}
существует линейное отображение <р пространства
всех непрерывных действительных функций на {Y, р}
в пространство всех непрерывных действительных функ-
функций на {X, р} такое, что (каково бы ни было /) <р(/)
является продолжением функции / и
sup {| / (х) | ;X?Y) = sup {| Ф (/) (*) \:х?X)
(теорема Д у г у н д ж и). Эта теорема связана С
теоремой Ха у сдорфа о продолжений
метрики: если замкнутое подпространство У ме-
тризуемого пространства X уже метризовано метрикой
pt (порождающей на Y топологию подпространства X),
то можно продолжить рх до метрики р на всем X, по-
порождающей исходную топологию на X. Аналогичные
утверждения справедливы для вполне ограниченных
метрик и полных метрик.
Исследование топологич. свойств М. п. в большей
степени основывается на следующей теореме Сто-
Стоуна: М. п. паракомпактно, т. о. в любое его
открытое покрытие у можно вписать локально конечное
открытое покрытие ). (локальная конечность означает
наличие у каждой точки окрестности, задевающей лишь
конечное множество элементов покрытия ).). На тео-
теореме о паракомпактности М. п. основан метризацион-
метризационный критерий Н а г а т ы — Смирнова (см.
Метризуемое пространство).
Для М. п. имеют место важные теоремы об эквива-
эквивалентности топологич. свойств, различаемых в рамках
общей топологии. Так, совпадают следующие карди-
нальнозначные инварианты: плотность, вес, число Сус-
лина, число Лпнделёфа. Для М. п. равносильны: счет-
счетная компактность, псевдокомпактность и бикомпакт-
ность. Для М. п. совпадают размерности dim (в смысле
покрытий) и Ind (большая индуктивная), а для сепа-
рабельных М. п. с dim и Ind совпадает и малая индук-
индуктивная размерность ind (ом. Размерности теория).
Каждое М. п. {Аг, р} звездно нормально: в любое
открытое покрытие у пространства {X, р} можно впи-
вписать открытое покрытие X звездно, т. о. так, что для
каждой точки х?Х найдется U?y, содержащее вся-
всякое Г ? /., для к-рого х ? V. С этой теоремой связан кри-
критерий метризуемости (Стоун а—А р х а н-
г е л ь с к о г о). Критерием метризуемости регуляр-
регулярного пространства вполне ограниченной метрикой явля-
является наличие в этом пространстве счетной базы — но
даже счетное регулярное пространство может быть не
метризуемо. Простейший пример получается присоеди-
присоединением к дискретному натуральному ряду какой-ни-
какой-нибудь одной точки из нароста Стоуна — Чеха биком-
бикомпактного расширения натурального ряда. Неожиданный
характер носит критерий метризуемости метризуемого
пространства X полной метрикой — для этого необхо-
необходимо и достаточно, чтобы X было множеством типа G&
в каком-нибудь (а тогда и в любом) бикомпактном
хаусдорфовом расширении пространства X. Впрочем,
бикомпактные хаусдорфовы расширения М. п. несут
полную информацию о топологии последних, как это
видно из т с о р е м ы Чеха: М. гт. гомеоморфны в
том и только в том случае, если гомеоморфны их расши-
расширения Стоуна — Чеха.
М. п. может не иметь счетной базы, но всегда удов-
удовлетворяет первой аксиоме счетности — имеет счетную
базу в каждой точке. Более того, каждый компакт в
М. п. имеет счетную базу окрестностей. Сверх того, в
каждом М. п. существует такая база, что каждая точ-
точка пространства принадлежит лишь счетному мно-
множеству ее элементов — точечно-счетная база, но это
свойство слабее метризуемости даже в присутствии
паракомпактности и хаусдорфовости. Не обязано быть
метрпзуемым и регулярное сепарабельное пространство
с первой аксиомой счетности.
Просто выглядит условие метризуемости отделимой
топологич. группы — для этого необходимо и до-
достаточно, чтобы пространство группы удовлетворяло
первой аксиоме счетности, причем на группе тогда
существуют как левоинвариантная, так и правоинва-
риантная метрики, порождающие ее топологию.
С каждым М. п. {А', р} стандартным образом свя-
связано другое М. п., а именно пространство F(X) всех
его непустых замкнутых подмножеств, несущее на себе
метрику Ха усдорфа, определяемую следую-
следующей формулой:
рн(А, ?)=max {sup {p (a, B):a?A}, sup {p(h, A):b?/i}}.
Пространство {X, р} изометрично замкнутому подпро-
подпространству полученного М. п. {F(X), р/f}. Если метрика
р полна, то и метрика р/^ полна. Но из топологич. эк-
эквивалентности метрик р' и р", заданных на X, не сле-
следует, вообще говоря, что отвечающие им метрики Ха-
усдорфа ря и рн топологически эквивалентны.
Непрерывный образ М. п. может быть не гомеомор-
фен никакому М. п., даже удовлетворяя аксиоме отде-
отделимости Хаусдорфа. Ото относится и к факторпростран-
ствам М. п. Напр., если на плоскости «склеить» в точ-
точку фиксированную прямую, взяв в качестве отдель-
отдельных элементов разбиения все точки плоскости, не попас-
попасшие на эту прямую, то получится неметрнзуемое нор-
нормальное сепарабельное пространство — в особой его
точке не выполняется первая аксиома счетности. Име-
Имеется общий критерий метризуемости факторпростран-
ства М. п. (см. [6]). В частности, пространство непре-
непрерывного разбиения М. п. на компакты всегда метрнзуемо.
Всякое хаусдорфово пространство, являющееся непре-
непрерывным образом компактного М. п., метрпзуемо и
компактно — это частное проявление общего положе-
положения о неповышении веса топологич. пространства при
непрерывном отображении на бикомпакт. Но и когда
образ У М. п. {X, р} метрнзуем, метрику, осуществля-
осуществляющую метризацию У, не удается получить из метрики
р посредством какой-либо формулы. Вместо метрики
на УХ У по р естественно определяется функция А
посредством правила: d(y',y") для любых у', у"?У
равно расстоянию в смысле р между прообразами точек
у' и у" при рассматриваемом отображении. Часто
(напр., если У — пространство разбиения М. п. на кок-
пакты) d хорошо согласуется с топологией У И явля-
является с и м м е т р и к о и. Последнее означает, что
d(y', y")=d(y", у') для всех у', y"?Y, d(y', y")=0,
если и только если у' = у". Симметрика а, так опреде-
определенная, почти никогда не удовлетворяет аксиоме тре-
треугольника, но если разбиение на компакты непрерыв-
непрерывно, то d обладает топологич. свойствами, с успехом за-
заменяющими аксиому треугольника и гарантирующими
метризуемость образа «настоящей» метрикой. Тополо-
Топологич. пространство, являющееся образом М. п. при
непрерывном, открытом и замкнутом отображении,
само гомеоморфно нек-рому М. п. Однако при непре-
непрерывных открытых отображениях метризуемость сохра-
сохраняется не всегда — все пространства с первой аксио-
аксиомой счетностн и только они представимы как обра-
образы М. п. при непрерывных открытых отображениях.
Среди обобщений М. п. наиболее важны псевдометрич.
пространства, пространства с симметрикой и простран-
пространства с 0-метрикой [7]. Они определяются аксиомати-
аксиоматически посредством естественных ослаблений системы
аксиом М. п. Но расстояние здесь по-прежнему вы-
выражается неотрицательной действительным числом.
Можно рассматривать обобщенные метрики со значе-
значениями в упорядоченных полугруппах, полуполях и
т. д. (см. [8]). На этом пути можно осуществить обоб-
обобщенную метризацию произвольного вполне регулярно-
регулярного пространства.
Фундаментальным обобщением концепции М. п.
является понятие равномерного пространства. Далее
идут чисто топология, расширения класса М. п., среди
к-рых важны классы пространств с равномерной базой,
моровских пространств, перистых и паракомпактных
перистых пространств, кружевных пространств. Класс
паракомпактов является слишком широким обобщением
класса М. п., чтобы считаться таковым: паракомпакт-
паракомпактность не сохраняется даже при возведении в квадрат.
Напротив, класс паракомпактных перистых прост-
пространств является удачным одновременным обобщением
класса пространств, гомеоморфных М. п., и класса би-
бикомпактов. В ином направлении обобщают понятие
метрики х-метрнки и б-метрики [4]. Концепция стати-
стич. М. п., введенная К. Менгером (К. Menger), в то-
пологич. отношении оказалась равноценной понятию
пространства с симметрикой.
Лит.: [1] Александров П. С, Введение в теорию
множеств и общую топологию, М., 1977; [2] Frechet M.,
«Rend. Gircolo mat. Palermo», 1906, v. 22; [3] Архангель-
Архангельский А. В., Пономарев В. И., Основы общей тополо-
топологии в задачах и упражнениях, М., 1974; [41 Щепин Е. В.,
«Успехи матем. наук», 1976, т. 31, в. 5, с. 191—226; [5] Е n g e 1-
k I n g R., General topology, Warsz., 1977; (^Архангель-
(^Архангельск и й А. В., «Докл. АН СССР», 1964, т.155, ЛЬ 2, с. 247 — 50; [7]
Н е д е в С. Й., «Тр. Моск. матем. об-ва», 1971, т. 24, с. 201—36;
[81 Антоновский М. Я., Болтянский В. Г., С а-
рымсаков Т. А., «Успехи матем. наук», 1966, т. 21, в. 4,
с. 185—218; [9] Н е д е в С. Я., Ч о Ран М. М., «Сердикп»,
1975, т. 1,с. 12—28. А. В. Архангельский.
МЕХАНИЧЕСКИХ КВАДРАТУР МЕТОД, м е х а-
нических кубатур метод, — метод реше-
решения интегральных уравнений, основывающийся на за-
замене интеграла суммой при помощи квадратурных (ку-
батурных) формул. Пусть рассматривается уравнение
x(t)=t\jQK(t, s)x(s)ds + y(t), A)
где QczRm — ограниченная открытая область. С ис-
использованием какого-либо квадратурного (кубатурно-
го) процесса
z (s) ds = 2"= j «ynz (sjn) + ф„ (г)
составляют систему линейных уравнений
xln='?^icc/nK (sin, sJn)xJn + y(sin), i = l, ..., n, B)
относительно Xin~x(sin), t=l, . . ., п.
Пусть свободный член у и ядро К непрерывны соот- •
ветственно на Q и fixS (й — замыкание Q) и пусть
уравнение A) имеет единственное решение x(t). Пусть
<pn(z)—>-0 при и->оо для любой непрерывкой на Q функ-
функции z{t). Тогда при достаточно больших п система B)
однозначно разрешима и
max \xin —
где Cj и с2— нек-рые положительные постоянные,
8„= max | ф„ (К (sin, s) x (s)) | —>¦ О
при и—>-оо.
М. к. м. может быть применен для решения нелиней-
нелинейных интегральных уравнений [3] и проблемы собст-
собственных значений для линейных интегральных опера-
операторов. Метод сходится и для нек-рого класса уравнения
с разрывными ядрами [4].
Лит.: [1] Крылов В. И., Бобков В. В., Лона-
стырн ы й П. И., Вычислительные методы, т. 2, М., 1977;
[2] Б е р е з и н И. С., Ж и д к о и II. П., Методы вычислений,
2 изд., т. 2, М., J962; [3] Приближенное решение операторных
уравнений, М., 1909; [4] В а й н и к к о Г. М., «Сиб. матем. ж.»,
1971, т. 12, № 1, с, 40 — 53; [5] П р ё с д о р ф 3., Некоторые
классы сингулярных уравнений, пер. с нем., М., 1979.
Г. М. Вайникко.
МЕШАЮЩИЙ ПАРАМЕТР — любой неизвестный
параметр вероятностного распределения в статистич.
задаче, связанной с изучением других параметров дан-
данного распределения. Точнее, пусть по реализации слу-
случайной величины X, принимающей значения в выбо-
выборочном пространстве (J, 9?, Ре), 6=Fi, ¦ ¦ •> 6ft>
8д. + 1, . . ., Qn),?dczR", необходимо сделать статистич.
выподы о параметрах Bj, . . ., 0^. Тогда 8fc + 1, . . .. Qn
суть М. п. в данной задаче. Напр., пусть Х1? . . .,
Х„ — независимые случайные величины, подчиняющие-
подчиняющиеся нормальному закону Ф / "г'~ц ), параметры к-poro g
и о2 неизвестны, и пусть проверяется гипотеза Но: t= ?0,
где !„— нек-рое фиксированное число. Неизвестная ди-
дисперсия а2 является М. п. в задаче проверки гипотезы
Но. Другой важный пример задачи с М. п. дает Бе-
репса — Фишера проблема. Естественно, что при реше-
решении статистич. задач с М. п. желательно уметь получать
статистич. выводы, не зависящие от этих параметров.
В теории статистич. проверки гипотез этого часто до-
добиваются за счет сужения класса всех критериев,
предназначенных для проверки нек-рой гипотезы На
при наличии М. п., до класса подобных критериев.
Лит.: [1] Л и н н и к Ю. В., Статистические задачи с ме-
мешающими параметрами, М., 196В. М. С. Никулин.
МИКРОРАССЛОЕНИЕ — отображение Р : Е^Х,
являющееся ретракцией (т. о. существует g '. Х—*-Е,
для к-рого pg=ix)i локально тривиальное в том смысле,
что для каждой точки х?Х имеется представление
нек-рой окрестности U точки gx в Е в виде прямого
произведения U=VxR", при к-ром р\ц оказывается
проекцией на сомножитель и. Если для каждой такой
окрестности U на каждом слое (р\г/)~1(х) фиксирована
кусочно линейная структура, причем проекция U
на R" кусочно линейна на каждом слое и для двух
окрестностей Ur и U2 и всякой точки л-^р (U^CiP {U2)
структуры на (р\ц,)~1 (х) и (р!;;.,) (.г) совпадают в нек-
рой окрестности точки gx, то такое М. наз. кусочно
линейны м. Аналогично можно вводить и другие
структуры.
Понятие М. было введено с целью определить аналог
касательного расслоения для топологического или ку-
кусочно линейного многообразия У. Именно, здесь Е=
— NXN, р (х, у) = у, g(x)= (х, .г). Каждое топологич. М.
эквивалентно единственному локально тривиальному
расслоению со слоем R™ соответствующей размерности,
т. е. имеется гомеоморфизм h нек-рой окрестности W
множества gX в ? на окрестность W нулевого сече-
сечения нек-рого расслоения р : Е—>-Х со слоем R". Этот
факт верен и для кусочно линейных М. Несмотря на
то, что в связи с этой теоремой понятие М. потеряло
теоретич. интерес, оно еще используется в конкретных
задачах. л. в. Чернавский.
МИЛНА МЕТОД — конечноразностный метод ре-
тения задачи Коши для системы обыкновенных дпф-
ференцнальных уравнений 1-го порядка:
y' = f(x, У), у(а)=Ь.
В М. м. используется конечноразностная формула:
где
Xi = a + ih, i=0, 1, 2, ...
Для вычисления по этой формуле необходимо каким-
либо иным способом найти дополнительное начальное
значение ;/i~j/(?i). M. м. имеет 2-й порядок точности,
устойчив по Далквисту, т. е. все решения однородного
разностного уравнения у;—1/,_2=0 ограничены равно-
равномерно по h при i=0, 1, . . ., Г —г—I для любого фик-
фиксированного отрезка [а, А]. Для устойчивости по
Далквисту достаточно, чтобы простые корни характерис-
тич. многочлена левой части разностного уравнения не
превосходили по модулю единицы, а кратные —были
по модулю строго меньше единицы. В данном случае
характернстич. многочлен р(Я) = л2 — 1 имеет корни
},= ztzi п, следовательно, удовлетворяет указанному
условию устойчивости. Однако при решении систем
уравнений у' = Ау с матрицей А, имеющей отрицатель-
отрицательные собственные значения, происходит быстрый рост
вычислительной погрешности.
П р е д с к а з ы в а ю in е - и с. п р а в л я ю щ и й
М. м. использует пару копечноразностных формул:
предсказывающую
и исправляющую
i), i=4, 5, ...,
,_i), 1=4,5, ...,
где
/,• = /(*/, Уд, Ъ = /(¦'¦,¦. уд-
В качестве приближенного выражения погрешности
берется величина
^1 = ^(^1— У~д-
Дополнительные начальные значения Vj~y(xj),i~
= ¦1,2, 3, вычисляются каким-либо иным способом,
напр, методом Рунге — Кутта, имеющим четвертый
порядок точности. Метод предложен в [31.
Лит.: Ш Бахвалов Н. С, Численные методы, 2 изд.,
М., 1975; [2] Д е м и д о в и ч Б. П., Марон И. А., Ш у-
в а л о в а Э. 3., Численные методы анализа. Приближение
функций, дифференциальные уравнения, М., 1962; [3] Милн
В. Э., Численное решение дифференциальных уравнений, пер.
с англ., М-, 1955. В. В. Поспелов-
МИЛНЛ ПРОБЛЕМА — проблема теории переноса
излучения о решении односкоростного кинетич. урав-
уравнения переноса квантов пли частиц для полупростран-
полупространства. Впервые интегральное уравнение М. п. с источ-
источником на бесконечности при нулевом потоке падаю-
падающего извне излучения было выведено Э. Милном [1]
для случая изотропного рассеяния квантов, распростра-
распространяющихся без поглощения в звездной атмосфере.
Уравнение Милна имеет вид
B(x)^±'\~B(t)E1(\x-t\)dt. A)
Здесь В (х) — плотность излучения (или частиц),
Л, lxi= \ аи,
1 v jo ц ^
— интегро-показательная функция (/?1(.г) = —Ei (—х)).
В нейтронной физике М. и. используется для по-
постановки приближенных граничных условий при ре-
шении уравнений диффузионного приближения в ог-
ограниченной области; при этом учитываются захват
нейтронов в среде, анизотропия рассеяния и кривизна
границы.
Здесь М. п. состоит в решении интегро-дифференци-
ального уравнения
с Г + 1
с краевым условием на границе полупространства, за-
заполненного веществом, с вакуумом
г|>@, |i) = 0 для 0 <(i<l, B)
где с есть среднее число вторичных нейтронов, прихо-
приходящееся на одно соударение с ядром (с<1 в рассеиваю-
рассеивающем и поглощающем нейтроны веществе), р (и., и/) —
индикатриса рассеяния (р (|л, |х')=1 при изотропном
рассеянии). Аналогично ставится сферическая или
цилиндрическая М. п. о распределении нейтронов в
пространстве вне поглощающей сферы или цилиндра.
Решение М. п. удобно проводить, применяя преобра-
преобразование Лапласа к интегро-дифференциальному урав-
уравнению переноса (см. [3]) и используя для решения
получающихся функциональных уравнений Винера —
Хопфа метод.
Для решения М. п. было предложено использовать
разложений по обобщенным собственным функциям и
методы ретнения сингулярных интегральных уравнений
(см. [4]). Решение М. п. при р (jx, ц')=1, е<1 ищется в
виде
() |() + \ А{){ )d
где
q>vOi) = (cv/2) Р Л- + A, (v) 8 (v-ji)
— собственные функции непрерывного спектра, Р —
символ главного значения по Коши, 8 (v—ц) есть 6-
функция Дирака,
X (v) = l— ve Arthv, i|H± = <p0± (ц)
Дискретные собственные значения =tv0 суть корни
характеристич. уравнения
v с Arth — = 1,
— собственные функции дискретного спектра имеют
вид
iVo-д'
Система собственных функций ф0+ (|л) и cpv (yi), 0<v<l,
оказывается полной в пространстве обобщенных функ-
функций на отрезке 0<(х<1 и ортогональной с весом W(\i),
к-рый находится как решение сингулярного интеграль-
интегрального уравнения (см. [4]).
Граничное условие B) М. п. дает ((л^гО):
Si
A (v) фу(ц) dv,
то есть а0+ и Л (v) определяются как коэффициенты
разложения функции
Асимптотич. плотность нейтронов
обращается в нуль при
х = — jo = (vo/2) (In a0 +— г л).
Для с=1 p(\i, ц')=1, постоянная Хопфа
О71О446
Лит.: ll] М i 1 п е Е- A., «Mon. Notices Roy. .Astron. Soc»,
1921, v. 81, p. 361—75; [2] Hopf E., Mathematical problems
of radiative equilibrium, Camb., 1934: [3] С н е д д о н И., Пре-
Преобразование Фурье, пер. с англ., М., 1955; U] К е й з К.-М.,
Цвайфепь П.-Ф., Линейная теория переноса, пер. с англ.,
М., 1972. В. А. Чуяное.
МИЛНОРА СФЕРА — гладкое многообразие, гомео-
морфное (кусочно линейно изоморфное) сфере S", но
не диффеоморфное ей. Впервые пример такого многооб-
многообразия был построен Дж. Мплнором в 1956 (см. Ш);
этот же пример — первый пример гомеоморфных, но не
диффеоморфных многообразий.
Построение М. с. Любое гладкое замкнутое
многообразие, гомотопически эквивалентное сфере S",
при п'^5 гомеоморфно (и даже кусочно линейно изо-
изоморфно) сфере S" (см. Пуанкаре гипотеза обобщенная,
h-коипрдизм). Сигнатура замкнутого гладкого почти
параллелизуемого многообразия размерности kk де-
делится на число Ofi, экспоненциально растущее с ростом
к. Для любого к имеется иараллелизуемое многообра-
многообразие P4li сигнатуры 8 (именно, древовидное многообразие
Милнора), край к-рого М—дР есть при /с>1 гомото-
гомотопическая сфера (см. [2]). Если бы М было дпффеоморфно
сфере б'4*, то многообразие И'4*, полученное из Pik
добавлением конуса над краем, было бы гладким почги
параллелизуемым замкнутым многообразием сигнатуры
8. Таким образом, М есть М. с.
Имеется и др. пример М. с. (см. [5]).
Классификация М. с. Имеется 28 различных
(не диффеоморфных) 7-мерных М. с. (в эти 28 многообра-
многообразий включена стандартная сфера S7, и в дальнейшем
термин <<М. с.» используется и для обозначения стан-
стандартной сферы Sn).
Множество всех гладкостей на кусочно линейной сфе-
сфере (точнее, сглаживаний, но для сфер это одно и то же)
эквивалентно множеству элементов группы я,- (PL/0).
Последняя группа при г<7 тривиальна, так что лю-
любая М. с. размервбети, меньшей 7, дт1ффеоморфна стан-
стандартной.
Пусть Qn — множество классов fe-кобордантностп п-
мерных гладких многообразий, гомотопически экви-
эквивалентных сфере S". Операция связной суммы превра-
превращает это множество в группу, где нуль — класс h-
кобордантности сферы S". При гс>5 элементы груп-
группы 9.J находятся во взаимно однозначном соответствии
с классами диффеоморфности я-мерных М. с. Для вы-
вычисления групп 6„, п>5, задается (см. [3]) тривпализа-
пия стабильного нормального расслоения (оснащение)
М. с. М". Это возможно, так как Мп стабильно парал-
лелпзуемо. Полученное оснащенное многообразие оп-
определяет элемент стабильной гомотопич. группы ТТ =
= lim л,чпE'). Этот элемент зависит, вообще говоря,
i
от выбора оснащения (8„—>-TJ — «многозначное отоб-
отображение»). Пусть 6„Cя) — подгруппа в вп, состоя-
состоящая из М. с, ограничивающих параллелпзуемые мно-
многообразия. Построенное многозначное отображение
индуцирует гомоморфизм a: dn/Qn(dn)—>-Coker /, где
/ : лпEО)-^- JJ —стационарный Уайтхеда гомомор-
гомоморфизм и а—изоморфизм. Вычисление группы 6„/(дп(дп))
сводится к задаче (нерешенной, 1982) вычисления группы
JJ и вычисления группы вч(дл), что делается посредст-
посредством Морса перестроек пленки (при сохранении края).
Пусть \Мп]?В(дл), то есть Mn=dWn + 1 и Wn + 1 па-
раллелнзуемо. Если W — стягиваемое многообразие,
то после вырезания в W маленького диска многообра-
зне М /г-кобордантно S", то есть [Д/'г] = 0?8л. Если
и четно, то можно так изменить W посредством пере-
перестроек Морса, что новое многообразие W с 0W--M
будет стягнваемым (здесь требуется параллелизуемость
многообразия W и условие н>5). Итак, 62п(дл) = 0.
Случай п+1 = 4&. Если сигнатура а (И7) многообра-
многообразия W есть 0, то W можно перестройками Морса прев-
превратить в стягиваемое многообразие, так что в этом слу-
случае М есть стандартная сфера. Если M=dWn M' = 0W,
то M#(—M')=d(W#(—W))u a(W#(— W'))=o(W)—
— a(W') (здесь A^B — связная сумма многообразий
А и В). Если a(W)=a(W), то \М]=\М'], так что ин-
инвариант a(W) однозначно определяет элемент [М]?9„.
Если [Л/] = 0?в4й_1(йя) и M—dW, то a(W) делится на
0"?. Обратно, для любого ?>1 существует гладкое зам-
замкнутое многообразие Bik с a(Bik)=aji, поэтому если
M=dW п ff(№)=nob то 7l/=d(W#( — nfi4*)), где PFrft
#(—nS4*) параллелизуемо и а(ТУ4}:( — refi4*)) —0.
Элемент [Af]? O^-i (дл) полностью определяется выче-
вычетом a(W) mod afc, и разные вычеты определяют раз-
разные многообразия. Так как a(W) принимает любое зна-
значение, кратное 8, то ord 04ft _i A>л)=о"„д.,'8.
Случай ji=4&-i-l- Пусть M=dWik + -. Если Кервера
инвариант многообразия ТУ есть нуль, то есть ф (ТУ) = О,
то W перестраивается до стягиваемого многообразия,
то есть [М] = 0. Пусть теперь ^(\?)ф0. Так как при
¦4^+2^=2'—2 не существует гладкого замкнутого почти
параллелияуемого (что в размерности 4k-f-2 равносильно
параллелизуемости) многообразия с инвариантом Кер-
Кервера, не равным нулю, то М не диффеоморфно Sik + 1.
В этом случае Qni + i(dn)jc0, то есть Qi!t + 1(dn)-= Z2.
При 4/c-J-2=2' — 2 и тех значениях г, где существует
многообразие с ненулевым инвариантом Кервера,
МxSik + 1, то есть в4? + 1 (дл) = 0, но вопрос об описании
всех таких не решен A982), хотя при г<:6 ответ поло-
положителен. Итак, dik + i(dn) есть %г или 0.
Имеется другое представление М. с. Пусть в простран-
пространстве C" + 1 W — алгебраическое многообразие с урав-
уравнением
и Se есть Bп+1)-мерная сфера радиуса е (малого) с цен-
центром в начале координат. При подходящих значениях
afc M=Wf)Se есть М. с. (см. [4]). Напр., при п = 4 и
at=Qk—1, a2— 3, a3=«4 = a;5=2 и ft=l, 2, . . ., 28 по-
получаются все 28 7-мерных М. с.
Лит.: [1] М и л н о р Д ж., <сМатематика», 1957, т. 1, Л» 3,
с. 35—42; [2] М i 1 п о г J., К е г v а i г е М., в кн.: Procee-
Proceedings of the International Congress of Mathematicians, 1958, Comb.,
1960, p. 454—58; [3] и х ж e, «Ann. Math.», 1963, v. 77, Л» 3, p
504—37; [4] M и л н о р Д ж., Особые точки комплексных ги
перповерхностей, пер. с англ., М., 1971; [5] М и л н о р Д ж.
С та шеф Д ж., Характеристические классы, пер. с англ.
М., 1979. Ю. Б. Рудяк.
МИНЙМАКС — смешанный экстремум
inf sup F (х, у), min max F (x, у)
ytYxeX yeYxeX
и т. тт. (см. также Максимин); может интерпретировать-
интерпретироваться (напр., в теории принятия решений, исследовании
операций или статистике) как наименьшие потери из
тех, к-рые нельзя предотвратить принимающему решения
субъекту в наихудших для него обстоятельствах.
Н. Н. Воробьев.
МИНИМАКСА ПРИНЦИП — принцип оптимально-
оптимальности в антагонистических играх, выражающий стремле-
стремление каждого ля игроков к получению наибольшего га-
гарантированного выигрыша. М. п. реализуем в антаго-
нпстцч. игре Г=<Л, В, Ну, если справедливо равен-
равенство
i? = max inf Н (а, Ь) =min sup//(а, Ь), (*)
т. е. если существуют значение игры, равное и, и оп-
оптимальные стратегии у обоих игроков.
Для матричных игр и нек-рых классов бесконечных
антагонистнч. игр (см. Бесконечная игра) М. п. реа-
реализуем в смешанных стратегиях. Известно, что равен-
равенство (*) равносильно выполнению неравенств (см.
Седлоеая точка):
Н (а, Ь*) ==? Н (а*, Ъ*) s? Н (а*, Ъ)
для всех а?А, Ь?В, где а*, Ь*— стратегии, на к-рых
достигаются внешние экстремумы в (*). Таким обра-
образом, М. п. математически выражает интуитивно пони-
понимаемую идею устойчивости, т. к. ни одному из игроков
невыгодно отклоняться от своих оптимальных страте-
стратегий а* (соответственно Ъ*). Вместе с тем М. п. гаранти-
гарантирует игроку I (II) получение выигрыша (проигрыша),
не меньшего (не большего), чем значение игры. Было
дано аксиоматич. обоснование М. п. для матричных игр
(см. [1]).
Лит.: [1] В и л к а с Э., «Теория вероятн. и ее примен.л,
1963 т. 8, в. 3, с. 324—27. Е. В. Яновская.
МИНИМАКСНАЯ ОЦЕНКА — статистическая оцен-
оценка, к-рая получена в результате конкретизации поня-
понятия минимаксности статистической процедуры в за-
задаче статистич. оценивания.
Пример 1. Пусть случайная величина X подчи-
подчиняется биномиальному закону, параметры к-рого суть
п и в, причем 8, 0<6<1, неизвестен. Статистика
X Уп | 1
~ п 1+Vn ' 2 (i+Vn)
является М. о. для параметра в относительно функции
потерь
Ь(в, *)=(в-03-
Пример 2. Пусть Х1, . . ., Хп—независимые слу-
случайные величины, к-рые подчиняются одному и тому
же вероятностному закону, имеющему непрерывную
плотность вероятности f(x—в), \х\ <оо, |в| <оо. Оцен-
Оценка Пит мена
t = t(Xlt ...,
является М. о. для неизвестного параметра сдвига в
относительно функции потерь L(Q,t)=(Q—tJ, где
X(i) — первый член вариационного ряда, построенного
по выборке Хг, . . ., Хп. В частности, если Xlt . . .,
Xn~N(Q, 1), то t= (Xx+ • • • +Хп)/п.
Лит.: [1] 3 а к с Ш., Теория статистических выводов, пер.
с англ., М., 1975; [2] Кокс Д., Хинкли Д., Теоретиче-
Теоретическая статистика, пер. с англ., М., 1978. М. С. Никулин.
МИНИМАКСНОЕ СВОЙСТВО собственных
значений — специального типа соотношения, свя-
связывающие собственные значения вполне непрерывного
самосопряженного оператора А с максимальным и ми-
минимальным значениями соответствующей ему квадра-
квадратичной формы (Ах, х). Пусть А — самосопряженный
вполне непрерывный оператор в гильбертовом простран-
пространстве Н. Спектр оператора А состоит из конечного или
счетного множества действительных собственных зна-
значений Хп, имеющих единственную предельную точку,
равную нулю. Соответствующие ненулевым собствен-
собственным значениям корневые подпространства состоят из
собственных векторов и конечномерны; собственные под-
подпространства, отвечающие различным собственным зна-
значениям, взаимно ортогональны; оператор А имеет пол-
полную систему собственных векторов. Спектральное раз-
разложение операторам! имеет вид: Л=2Я,/>,-, где X,,- —
различные собственные значения, Р; — проекторы на
соответствующие собственные подпространства, при-
причем ряд сходится по операторной норме. Норма опе-
оператора А совпадает с максимальным по модулю соб-
ственным значением и совпадает с max \(Ax, х)\; при
хен, |лг| = 1
этом максимум достигается на соответствующем соб-
собственном векторе.
Пусть Xi^hi^ ... — положительные собственные
значения оператора А, причем каждое собственное зна-
значение повторяется столько раз, сколько его кратность.
Тогда
х, х) \
W1 |
Л„+1 = mm max ' ' ' , геЗэ1, ( v1'
Ух Уп (х- yj) = °
(=1 П )
где х, г/j, . . ., уп — произвольные ненулевые векторы
пространства //. Аналогичные соотношения справедли-
справедливы для отрицательных собственных значений Xy^z
дгб Н ' ж '
лл+1 = max min ; ^ , п 3
у, Уп (х, !/,•) = о ' *'
»=1 л
Соотношения A) и B) применяются для нахождения
собственных значений интегральных операторов с
симметричным ядром. Если А и В — самосопряженные
вполне непрерывные операторы, А -*сВ (т. е. (Ах, ж)<:
<:(Вх,х )), кп, \in — последовательности их положитель-
положительных собственных значений, занумерованных в порядке
убывания, причем каждое значение повторяется столь-
столько раз, какова его кратность, то Xn<c\in-
Лит.: [11 Д а н ф о р д Н., Шварц Д ж.-Т., Линейные
операторы, пер. с англ., т. 2, М., 1966. А. И. Логинов.
МИНИМАКСНОСТЬ СТАТИСТИЧЕСКОЙ ПРОЦЕ-
ПРОЦЕДУРЫ — один из вариантов оптимальности в матема-
тич. статистике, согласно к-рому статистич. процедура
объявляется оптимальной в минимаксном смысле, если
она минимизирует максимальный риск. В терминах
решающих функций понятие М. с. п. определяется
следующим образом. Пусть случайная величина X
принимает значения в выборочном пространстве ($,
53> ^9 ), 6(:®> п пусть Д= {6} — класс решающих функ-
функций, с помощью к-рых по реализации случайной ве-
величины X надлежит выбрать решение d из простран-
пространства решений D, т. е. S (•) : Ti-^-D, при этом задана нек-
некрая функция потерь L(Q,d), определенная на &XD.
В таком случае статистич. процедура 6*?Д наз. ми-
минимаксной в задаче принятия статистич. решения
относительно функции потерь ?@, d), если при всех
S ? Д выполняется соотношение
sup Ее ? (в, S* (X)) < sup Eg ?(в,
бе в ббв
где
(в, S (Х)) = Л (в, б)= Г L (9, 6 (х)) dPe(x)
— функция риска, отвечающая статистич. процедуре
(решающему правилу) S, при этом решение d*=6* (х),
отвечающее наблюденной реализации х и минимакс-
минимаксной процедуре б*, наз. минимаксны м. Так как
величина
sup Eg L (9, 8 (X))
бее
показывает ожидаемые потери, к-рые можно понести
при использовании процедуры б?Д, то М. с. п. 6*
означает, что если руководствоваться процедурой S*
в задаче выбора решения d из пространства решений D,
то наибольший ожидаемый риск
sup Л F, б*)
9бв
будет настолько малым, насколько это возможно. Прин-
Принцип М. с. п. не всегда приводит к разумным выводам
Я18,8> (см. рис.); в данном случае
следует ориентироваться ва
процедуру &!, а не на 82,
хотя
sup Л (в, 8j) > sup Л (в, аа).
9ев бев
Понятие М. с. п. является
полезным в задачах приня-
принятия статистич. решений в условиях отсутствия априор-
априорной информации относительно параметра 8.
Лит.; [1] Л е м а н Э., Проверка статистических гипотез-
пер. с англ., 2 изд., М., 1979; [2] 3 а к с Ш., Теория статистиче-
статистических выводов, пер. с англ., М., 1975. М. С. Никулин-
МИНИМАЛЬНАЯ ДОСТАТОЧНАЯ СТАТИСТИКА,
необходимая достаточная стати-
с тика,— статистика X, являющаяся достаточной
статистикой для семейства распределений 5^= {^9 >
6?в} и такая, что для любой другой достаточной ста-
статистики Y имеет место X=g(Y), где g — нек-рая изме-
измеримая функция. Достаточная статистика минимальна
тогда и только тогда, когда порождаемая ею достаточ-
достаточная о-алгебра минимальна, т. е. содержится в любой
другой достаточной а-алгебре.
Используется также понятие !?>-м инимальной
достаточной статистики (а-а л г е б-
р ы). Достаточная а-алгебра й„ (и соответствующая ста-
статистика) наз. ^-минимальной, если й0 содержится в
пополнении й любой достаточной а-алгебры с® от-
относительно семейства распределений 5s- Если семей-
семейство ^р домпнировано а-конечной мерой \i, то а-аЯ-
гебра й0, порождаемая семейством плотностей
является достаточной и ^-минимальной.
Общий пример М. д. с. дает направляющая стати-
статистика Т=(ТХ, . . ., Тп) экспоненциального семейства
в предположении точности канонич. параметризации
этого семейства.
Лит.: [11 Барра Ж.-Р., Основные понятия математиче-
математической статистики, пер. с франц., М., 1974; [2] III м е т т е р е р Л-,
Введение в математическую статистику, пер. с нем., М., 1976.
А. С. ХолевЗ.
МИНИМАЛЬНАЯ МОДЕЛЬ — алгебраическое мно-
многообразие с условием минимальности относительно су-
существования бцрациональных морфизмов на неособые
многообразия. Точное, пусть В — класс всех бирацио-
нальпо эквивалентных неособых проективных многооб-
многообразий над алгебраически замкнутым полем /с, поля
функций к-рых изоморфны заданному конечно порож-
порожденному расширению К над к. Многообразия из класса В
наз. проективными моделями этого класса,
или проективными моделями поля К/к. Многообразие
Х?В наз. относительно минимальной
моде л ь ю, если всякий бирациональный морфизх
/: X—уХ', где Х'?В, является изоморфизмом. Иначе
говоря, относительно М. м.— это минимальные эле-
элементы в В относительно частичного порядка, определяе-
определяемого следующим отношением доминирования: X, до-
доминирует Х2, если существует бирациональный морфиэм
h : Х1—уХ2. Если относительно М. м. единственна в В,
то она наз. м и н и м а л ь н о й модель ю.
В каждом классе бирационально эквивалентных кри-
кривых существует единственная (с точностью до изомор-
изоморфизма) неособая проективная кривая. Так что всякая
неособая проективная кривая является М. м. В общем
случае, если класс В не пуст, то в нем существует
хотя бы одна относительно М. м. Непустота класса В
известна (благодаря теоремам о разрешении особенно-
особенностей) для многообразий любой размерности в характе-
характеристике 0 и для многообразий размерности ге<еЗ в ха-
характеристике р>5.
Основные результаты о М. м. алгебраич. поверхно-
поверхностей заключаются в следующих утверждениях.
1) Неособая проективная поверхность X тогда и
только тогда является относительно М. м., когда она
не содержит исключительных кривых первого рода
(см. Исключительное подмногообразие).
2) Всякая неособая полная поверхность обладает
бирациональным морфизмом на относительно М. м.
3) В каждом непустом классе В бирационально эк-
эквивалентных поверхностей, кроме классов рациональ-
рациональных и линейчатых поверхностей, существует (и притом
единственная) М. м.
4) Если В — класс линейчатых поверх?!остей с
кривой С рода g]>0 в качестве базы, то все относительно
М. м. в В исчерпываются геометрически линейчатыми
поверхностями я : X—*-С.
5) Если В — класс рациональных поверхностей,
то все относительно М. м. в В исчерпываются проектив-
проективной плоскостью Р2 и серией минимальных рациональ-
рациональных линейчатых поверхностей Fn=P (Qpl-\-Qpl(n))
для всех целых п^2.
Имеется (см. [6], [7]) обобщение теории М. м. по-
поверхностей на регулярные двумерные схемы. Описаны
(см. [2]) М. м. рациональных поверхностей, опреде-
определенных над произвольным полем.
О М. м. для многообразий размерности ге^З почти
ничего не известно A982).
Лит.: Fl] Алгебраические поверхности, М., 1965 (Тр. Матем.
ин-та АН СССР, т. 75); [2] И с к о в с к и х В. А., «Изв. АН
СССР. Сер. матем.», 1979, т. 43, Л1» 1, с. 19—43; [3] ГД а ф а р е-
вич И. Р., Основы алгебраической геометрии, М., 1972; [4]
Bombicri E., Husemoller D., Classification and
embeddings of surfaces. Proc. symp. pure math., v. 29 — Algebraic
geometry arcata 1974, Rhode Island, 1975, p. 329—420; [5] H a r t-
shorne R., Algebraic geometry N. Y.—Hdlb.—В., 1977; Гб]
Lichtenbaum S., «Amer. J. Math.», 1968, v. 90, № 2,
p. 380—405; [7] Shafarevitch I., Lectures on minimal
models and birational transformations of twodimensional schemes,
Bombey, 1966. В. А. Псковских.
МИНИМАЛЬНАЯ НОРМАЛЬНАЯ ПОДГРУППА -
неединичная нормальная подгруппа Н такая, что между
ней и единичной подгруппой нет других нормальных
подгрупп всей группы. М. н. п. имеются далеко не во
всякой группе. Если группа конечна, то любая ее
М. н. п. является прямым произведением изоморфных
простых групп. Если М. п. п. у группы G существует
и единственна, то она наз. монолитом (иногда
сердцевиной), а сама группа G наз. м о н о л и-
т и ч н о й.
Лит.: [1] К у р о ш А. Г., Теория групп, 3 изд., М., 1967.
А. Л. Шмелъпин.
МИНИМАЛЬНАЯ ПОВЕРХНОСТЬ — поверхность, у
к-рой средняя кривизна Н равна нулю во всех точках.
Первые исследования о М. п. восходят к Ж. Лагран-
жу (J. Lagrange, 1768), к-рый рассмотрел следующую
вариационную задачу: найти поверхность наименьшей
площади, натянутую на данный контур. Предполагая
искомую поверхность задаваемой в виде z=z(x, у),
Ж. Лагранж получил, что z(x, у) необходимо должна
удовлетворять т.н. уравнению Эйлера —¦
Л агранжа
^-2p?0-|^-+(l + Ps)gf = 0, A)
dz dz
Позже Г. Монж (G. Monge, 1776) обнаружил, что ус-
условие минимальности площади приводит к условию
#=0, и поэтому за поверхностями с 11=0 закрепилось
название «минимальные». В действительности, однако,
нужно различать понятия М. п. и поверхности наимень-
наименьшей площади, т. к. условие минимальности Н=0 пред
ставляет собой лишь необходимое условие минимально-
минимальности площади, вытекающее из равенства нулю 1-й ва-
вариации площади поверхности среди всех поверхностей
класса С2 с заданной границей. Для проверки достиже-
достижения в указанном классе хотя бы относительного (ло-
(локального) минимума приходится исследовать 2-ю ва-
вариацию площади поверхности.
Теория М. п. имеет богатую историю — ею занима-
занимались почти все крупные математики 19 — 20 вв. Ее зада-
задачи стимулировали развитие многих смежных областей
математики. Первые общие методы интегрирования
уравнения Эйлера — Лагранжа были предложены
Г. Монжем A784) и А. Лежандром (A. Legendre, 1787)
в виде т. н. ф о р м у л М о н ж а, полученных через
комплексные характеристики уравнения A):
где г и т — комплексные переменные, АA), . . .,
Сх (т)— голоморфные функции, удовлетворяющие ус-
условиям
Однако эти методы в силу недостаточного еще развития
теории функций комплексного переменного долгое
время оставались без применения [в 1832 С. Пуассон
(S. Poisson) писал, что из формул Монжи трудно из-
извлечь какую-либо пользу, т. к. они усложнены введе-
введением комплексных переменных].
Новые результаты о М. п. стали появляться лишь с
начала 30-х гг. 19 в. С. Пуассон анонсировал A832)
решение им вариационной задачи Лагранжа в случае,
когда край поверхности близок к плоской кривой.
Вскоре к известным уже М. п.— катеноиду [Л. Эйлер
(L. Euler, 1774), Ж. Мёнье (J. Meusnier, 1776)] и гели-
геликоиду (Ж. Мёнье, 1776) — была добавлена третья
М. п.— Шерка поверхность (Н. Scherk, 18341. В 1842
Э. Каталан (Е. Catalan) доказал, что геликоид является
единственной линейчатой М. п.; в 1844 была поставлена
и решена Бъёрлинга задача; в 50-х гг. 19 в. в серии ра-
работ О. Бонне (О. Bonnet) были даны новые доказатель-
доказательства известных к тому времени фактов теории М. п.
и найдены другие свойства М. п. (единственность кате-
катеноида как М. п. вращения, конформность сферич. ото-
отображения М. п. и др.).
В 1866 были открыты формулы Вепс р-
ш т р а с с а:
представляющие односвязную М. п. S (х, у, z) через
голоморфные функции /(if) и g(w), определенные в
круге или во всей плоскости изменения внутренних
изотермических координат (и, v), w~-u-'-iv. Эти фор-
формулы эквивалентны или содержат как частные случаи
все другие найденные до этого параметрич. представ-
представления М. п. [Б. Риман (В. Riemann, 1860), А. Эннепер
(А. Епперег, 1864), К. М. Петерсон, 1866, и др.] и дают
регулярную М. п. только в случае, когда / и g ке имеют
общих пулен, а в случае совпадения нулей функций /
и g поверхность является т. н. обобщенной М. п.
с вырождающейся в общих нулях fug метрикой
В этих точках появляются ветвления точки М. п. С по-
помощью формул Вейерщтрасса появилась возмоншость
явного построения и изучения многих конкретных М. п.,
в частности алгебраич. М. п., получаемых при алгебра-
ич. функциях / и g.
В 1874 Г. Шварц (Н. Schwarz) получил представле-
представление М. п. в изотермич. координатах (и, v) в виде
г (w)^r (u + w) = Re [F (w) — i [^ n (w)dF (
где F (w) и n(w) —трехмерные векторы с голоморф-
голоморфными компонентами, совпадающими соответственно
с г(и,0) и единичной нормалью п(и, 0) к М. п. При
Im w~0 эта формула дает решение задачи Бьёрлинга
в явном виде и позволяет распространить па М. п.
принцип симметрии Шварца.
В эти же годы С. Ли (S. Lie, 1878) развил свою интер-
интерпретацию формул Монжа, сопоставив каждой М. п.
с гармонич. радиус-вектором r(w) комплексно-анали-
тич. кривую
, Re Я (w) = \ г (w)
и представив М. п. как поверхность переноса кривой
В (w) и ей комплексно-сопряженной KpiiBoit R(w),
что послужило отправной точкой для установления пло-
плодотворных связей между теорией М. п. и аналитнч.
кривых. Таким образом, труды К. Вейерштрасса, С. Ли,
Б. Римана, Г. Шварца и др. привели к концу 19 в. к
широкому использованию в теории М. п. методов и
результатов теории функций комплексного переменного.
В своих опытах Ж. Плато (J. Plateau, 1849) пришел
к физич. реализации М. п. в виде мыльных пленок,
натянутых на проволочные каркасы различной формы.
Его опыты оживлли интерес к старой проблеме нахож-
нахождения М. п. по ее заданному граничному контуру. Эту
проблему стали называть Плато задачей. Первые ее ре-
решения были получены для различных случаев полиго-
полигональных контуров, при этом, в частности, была откры-
открыта Римана — Шварца поверхность.
В 1816 в теории М. п. появилась новая задача
Ж е р г о н н а: найти М. п., если часть ее границы
задана, а остальная часть должна располагаться на
нек-рои заранее заданной поверхности; эта задача стала
наз. задачей о М. п. с о свободной грани-
ц е й. Первые результаты но ее решению также отно-
относятся к случаям, когда заданная часть границы состоит
из отрезков прямых, а остальная ее часть должна на-
находиться на заданных плоскостях (более подробно см.
в [1], [2]).
С начала 20 в. усилился интерес к изучению М. п.
«в целом». Изучалась задача Дирихле для уравнения
Эйлера — Лагранжа [А. Корн (А. Когп, 1909), С. Н.
Бернштейн, 1900]; была получена Бернштейна теорема
о М. п.; вообще с началом работ С. Н. Бернштейна в те-
теорию М. п. вошли методы теории дифференциальных
уравнений с частными производными. Г. Либмап
(Н. Liebmann, 1919) установил связь между М. п. и
бесконечно малыми изгибаниями сферы. Венцом до-
достижений 1-й пол. 20 в. в теории М. п. было полное ре-
решение задачи Плато, сначала в случае односвязных
поверхностей, а затем и для двумерных поверхностей
произвольного топологич. типа в евклидовом н ри.ма-
новом пространстве (см. [{] — [5]). Результаты о М. п.
были распространены на случай решений более общих
вариационных задач (обобщающих вариационную зада-
задачу для минимума поверхности), более общих дифферен-
дифференциальных уравнений (обобщающих уравнение Эйлера —
Лагранжа для М. п.) и на случай более общего класса
поверхностей (папр., с постоянной средней кривизной)
(см. [3], [6], [7]).
Среди имеющихся розультатов и ведущихся иссле-
исследований по М- п. можно выделить несколько направле-
направлений.
1) Внутренняя геометрия М. п. Не
для всякого риманова многообразия неположительной
кривизны существует изометрич. погружение в ев-
евклидово пространство Е", п^З, в виде нек-рой М. п.
Критерий существования М. п. в Е3 с данной метрикой
заключается в следующей теореме Риччи: для
того чтобы данная метрика ds2 была изометрпчна мет-
метрике нек-рой М. п. в Е3, необходимо и достаточно,
чтобы ее кривизна К была неотрицательна, а в точках,
где К<0, метрика йФ= У—К ds2 была евклидова.
На основании этого критерия удается охарактеризо-
охарактеризовать все изгибания М. п., удовлетворяющей условиям
теоремы Риччи, в классе всех М. п. из Е", п^З. Прежде
всего, имея в Еп М. п. F, заданную в изотермич. коор-
координатах (и, v) гармонич. функциями ?fe("> *>) —
= КеФй(ш), w=u-\-iv, l<fc<rc, Ф/tiw) — голоморфные
функции, строят так наз. ассоциированные
с F и друг с другом М. п. Еа с компонентами радиус-
вектора x!t=--'Re(Oii(w)e-ia), F=F0. Ассоциированные
М. п. Fa, все оказываются изометричными друг другу,
а в случае п^З их изгибания друг в друга при измене-
изменении а обладают следующим характеристич. свойством:
нормали к Fa ъ соответствующих по изометрии точках
параллельны, причем изгибания М. п. F в Е3 в классе
М. п. исчерпываются семейством ассоциированных с
F М. п.; напр., катеноид и геликоид — две ассоцииро-
ассоциированные (а значит, изометричные) М. п. с параметрами
сс=О и сс=я/2. Далее, по данной М. nJe E" можно
построить изометричную ей М. п. GcE2" с радиус-
вектором ~= (хи . . ., тп, У1, . . ., уп), i/fc=Im Фъ
а затем, отправляясь от G, строится нек-рое специаль-
специальное двухпараметрич. семейство изометричных F М. п.
Ga, р?Я2". В итоге оказывается, что если нек-рая
М.'и. М?Е2П удовлетворяет условиям теоремы Риччи,
то существует М. п. FczE3, изометричная М, причем:
1) или MczE3 и тогда она входит в семейство ассоцииро-
ассоциированных с F М. п.; 2) или М?Ее (и не принадлежит Еъ)
и она входит в упомянутое выше семейство fiap.
Однако уже в Е* существуют М. п., метрики к-рых
не удовлетворяют условиям теоремы Риччи. Поэтому
возникает задача описания всех метрик, порождае-
порождаемых двумерными М. п. в Е", ге^4, и изгибаний этих
М. п.; эта задача также решена с достаточной полнотой
в терминах нек-рых классов голоморфных отображе-
отображений. Имеется также ряд результатов о внутренней ха-
характеристике метрик двумерных М. п. в сферах S",
п>3 (см. [81).
Что касается метрик многомерных М. п., то здесь
пока нет сколько-нибудь существенно продвинутых ре-
результатов, а вопросы единственности и изгибаний М. п.
исчерпываются главным образом описанием возможных
видов компактных минимальных подмногообразий
rt-мерной сферы. Изгибания М. п. на поверхности дру-
другого внешнего строения также изучены недостаточно
полно даже для Е3.
Другой круг проблем внутренней геометрии М. п.
составляют изопериметрич. неравенства, к-рые, впро-
впрочем, в наиболее точных и интересных формах зависят
от внешнего строения М. п. (см. [9]).
2) Л о к а л ь н ы е свойства М. гг. Сюда
можно отвести результаты об аналитичности М. п.
(само определение М. п. требует принадлежности ее
лишь классу С2) и решений ряда вариационных задач,
утверждение о том, что достаточно малая область М. п.
реализует абсолютный минимум площади среди всех
поверхностей с той же границей, что и рассматриваемая
область, теоремы об устранимости изолированных или
маломощных особенностей решений уравнения М. п. и
его обобщений, изучение строения обобщенных М. п.
в окрестности их точек ветвления, исследования осо-
особенностей М. п. и решений так наз. эллиптических ва-
вариационных задач в многомерных евклидовых и рима-
новых пространствах (см. [2], [3], [6], [10], [12]).
3) Изучение конкретных М. п. или
М. п. при априори заданных свойствах края, плоских
сечений, сферич. отображения и т. п. Напр., теорема о
выпуклости горизонтальных сечений двусвязной М. п.
с выпуклыми горизонтальными краями; теорема о
совпадении с катеноидом полной М. п., расположенной
между плоскостями z=C1 и z=C2, —оо <:С!<С2<:оо,
и имеющей звездные сечения z= const; детальное изуче-
изучение классич. М. п.— Эннепера, Щерка, Римана —
Шварца и др. Особо нужно отметить исследования ми-
минимальных конусов в R", «^4, приведшие к построе-
построению контрпримера для теоремы Бернштейна в Е",
п^9, и к нахождению примера нерегулярного реше-
решения задачи Плато для гиперповерхностей в Е8. Кон-
Конкретные примеры различных М. п. начались изучаться
также и в многомерных римановых пространствах
(см. [1], [2], [6], [12], [13]).
4) Р а з в и т и е теории М. п. в Е", п^З, по
аналогии с функциями комплексного переменного в
С1. Здесь можно назвать результаты о граничных свой-
свойствах М. п.— теорема об аналитич. продолжении М. п.
через регулярную аналитич. дугу границы, теоремы о
гладкости М. п. в зависимости от гладкости ее границы
(напр., если граница класса Сп- а, rCg^l, 0<«<1, то
М. п. принадлежит тому же классу); работы по построе-
построению для М. п. аналога теории Неванлинны о распре-
распределении значений мероморфных функций (см. [2], [6],
[13]).
5) Р а б о т ы об уравнении Эйлера —
Л а г р а н ж а. Наряду с изучением «в целом» реше-
решений этого уравнения и его обобщения для п-мерных
М. п. (хи . . ., хп, fx(x), . . ., fk{x)) в Е" + 1г, k>i,
У" е"-?!-., B)
*->i, i = i gx' дх'
(где /=(/i, . . ., /ft), g'J—контравариантные компонен-
компоненты метрич. тензора gij), большое количество работ
посвящено локальному поведению решений уравнения
Эйлера — Лагранжа и его обобщения B). Это — во-
вопросы устранимости особенностей при коразмерностях
к=\, существование нерегулярных решений при боль-
больших коразмерностях, и особенно — исследование зада-
задачи Дирихле. Эту задачу можно по-другому трактовать
как задачу Плато по определению М. п. с заданным
контуром и с дополнительным условием однозначной
проектируемости М. п. на ту же плоскость, что и гра-
граничный контур. Такая трактовка позволяет во многих
случаях получать выводы о задаче Дирихле на осно-
основании известных результатов о задаче Плато (напр.,
существование и единственность решения задачи Ди-
Дирихле в Е3 для случая выпуклой области D получается
как следствие одной теоремы Радо о задаче Плато).
В общем случае установлено, что для разрешимости
задачи Дирихле в коразмерности 1 для любой непрерыв-
непрерывной граничной функции необходимо и достаточно,
чтобы вектор средней кривизны края dD был направлен
внутрь области D (при п=2 это означает выпуклость
области D); при этом решение задачи единственно. Что
касается невынуклых областей, то, напр., доказано,
что для любой невыпуклой области D с жордановой
границей dD можно найти такую непрерывную функ-
функцию ф(р), p?dD, что для нее соответствующая задача
Дирихле будет неразрешимой. В больших коразмер-
коразмерностях задача Дприхле может быть неразрешимой
даже для случая, когда область совпадает с шаром в Еп.
Задача Дирихле рассматривалась также во внешности
области D. Здесь получаются новые факты (напр.,
теряется единственность решения, не всегда получает-
получается разрешимость и т. д.). Имеются также результаты в
случае постановки задачи Дирихле с неполными или
частично неограниченными граничными значениями
(см. [2], [6]-[8], A4]).
6) П о л н ы е М. п. Под полными М. п. понимаются
М. п., полные как метрич. пространства относительно
своей внутренней метрики. Полные М. п. бывают ком-
компактные (без границы) и некомпактные, или открытые.
В исследованиях полных М. п. интерес направлен глав-
главным образом на изучение связей, существующих менаду
глобальными метрич., геометрич. и топологич. свойст-
свойствами поверхностей.
Наиболее продвинуто изучение двумерных полных
М. п. в Е'3, ге^З, для к-рых большинство результатов
получается применением методов теории функций ком-
комплексного переменного. В частности, показано суще-
существование в Е3 полной М. п. любого заранее заданного
рода g и связности к; получены теоремы о связях между
интегральной кривизной \ \ KdS и топологическим
]i конформным типами полной М. п. (напр., \ \ KdS^.
<2яE(—к), где % — эйлерова характеристика поверх-
поверхности, к — число компонент ее границы; если
Kds <oo, то поверхность S конформно эквивалент-
на римановои поверхности с конечным числом выколо-
выколотых точек, если полная М. п. S бесконечно связна или
конформно гиперболич. типа, то ее интегральная кри-
кривизна бесконечна, и нормали к S принимают все на-
направления бесконечное число раз, за возможным исклю-
исключением множества направлений нулевой емкости, и
т. д.); изучена структура сферич. отображения (напр.,
полная М. п. в Е3 есть или плоскость, или ее сферич.
образ не содержит, самое большее, множество емкости
нуль, полная М. п. в Е3, п^З, является либо плоско-
плоскостью, либо ее образ при обобщенном сферич. отобра-
отображении пересекается со всюду плотным множеством ги-
гиперплоскостей, для любого ?к:4 в Е3 существуют пол-
полные М. п., сферич. образ к-рых не содержит ровно п
заранее заданных точек, и т. д.); найдены поверхности,
полностью определяемые их интегральной кривизной и
топологич. типом (это катеноид и Эннепера поверхность);
показана внешняя неограниченность в Е", ге^З, пол-
полных М. п. с ограниченной интегральной кривизной.
Результаты о компактных М. гг. относятся в основном
к полным М. п., расположенным в сферах SncEn + 1.
Интерес именно к этим М. п. объясняется, помимо труд-
трудностей случая общего риманова пространства, еще и
наличием важных связей между минимальными кону-
конусами в Еп + Х и М. п. в Sn (каждый гиперконус в Еп + 1,
определяемый своей вершиной О и пересечением со
сферой S" с центром в О, является минимальным тогда
л только тогда, когда его пересечение с Sn будет М. п.
н S"). Исследуемые здесь вопросы в основном те же,
что и для полных М. п. в Е". Напр., показано, что лю-
любое компактное двумерное многообразие, за исключе-
исключением проективной плоскости, может быть реализовано
в виде полной М. п. в S3; в S3 получен аналог теоремы
Берннгтейна: если нормали к полной М. п. лежат в
открытой полусфере, то эта М. п. совпадает с эквато-
экваториальной гиперсферой; найдены и другие признаки сов-
совпадения полной М. п. в S" с гиперсферой, исследованы
возможные виды и вопросы единственности полных М. п.
в S" в зависимости от величины их скалярной кривизны
и т. д. (см. [2], [6], [8], [13]).
7) Построение различного рода обобщений М.
п., а также уравнений и вариационных задач, решения
к-рых сохраняют свойства М. п., здесь к классич. тео-
рии М. п. непосредственно примыкают работы о поверх-
поверхностях с заданной средней кривизной, с квазиконформ-
квазиконформным сферич. отображением, работы о квазилинейных
эллиптич. уравнениях со многими свойствами уравне-
уравнения Эйлера — Лагранжа двух и большего числа пере-
переменных; более далекие обобщения сделаны в теориях,
связывающих М. п. с множествами, минимизирующими
интегральные потоки или различные меры Хаусдор-
фа, и т. п. (см. [2], [6], 17], [10], [И]).
8) Работы о задаче Плато для двумер-
двумерных и многомерных М. п. (см. Плато задача, Плато
многомерная задача).
Из приведенного перечня исследуемых задач и полу-
полученных результатов видно, что диапазон вопросов тео-
теории М. п. весьма велик, соответственно разнообразны
и применяемые в ней методы. Если в классич. исследо-
исследованиях в основном применялись методы дифференци-
дифференциальной геометрии, теории функций комплексного пере-
переменного и дифференциальных уравнений, то сейчас воз-
возрастает роль методов топологии, теории меры и функ-
функционального анализа, особенно в исследованиях М. п.
в многомерных пространствах.
Лит.: [1] Курант Ф., Принцип Дирихле, конформные
отображения и минимальные поверхности, пер. с англ., М., 1953;
[2] N i t s с h e J. С. С, Vorlesungen uber Minimalflachen,
В.—[u. a.], 1975; [3] R a d E Т., On the problem of Plateau, В.,
1933; [41 D о u g 1 a s J., «Trans. Amer. Math. Soc», 1931, v. 33,
p. 263 — 321; [5] M о г г е у С, «Ann. Math.», 1948, v. 49, p. 807 —
851; [6] H и ч е И. С. С, «Математика», 1967, т. 11, № 3, с. 37 —
100; [7] Оссерман Р., «Успехи матем. наук», 1967, т. 22,
в. 4, с. 55 — 136; [8] е г о же, «Математика», 1971, т. 15, № 2,
с. 104—25; [9] е г о же, «Bull. Amer. Math. Soc», 1978, v. 84,
MS 6, p. 1182—1238; [10] F e d e r e r H., Geometric measure-
theory, В.—[u. a.], 1969; [llj Morrey C, Multiple integrals
in the calculus of variations, B.—[u. a.], 1966; [12] Фоменко
А. Т., «Изв. АН СССР. Сер. матем.» 1972, т. 36, MS 5, с. 1049 —
79; [13] L a w s о n H. «Ann. Math.», 1970, v. 92, MS 2, p. 335—74;
[14] L a w s о n H., Osserman R., «Acta math.», 1977,
v. 139, MS 1—2, p. 1 —17; [15] Аминов Ю. А., «Укр. геом. сб.»,
1976, в. 19, с. 3—9. И. X. Сабитов.
МИНИМАЛЬНАЯ ПРОСТАЯ ГРУППА — неабелева
простая группа, все собственные подгруппы к-рой разре-
разрешимы. Полное описание конечных М. п. г. получено
(см. [1], [2]) попутно с классификацией всех конечных
групп, все локальные подгруппы (т. е. нормализаторы
р-подгрупп) к-рых разрешимы. А именно, конечная
М. п. г. изоморфна одной из следующих проективных
специальных линейных групп:
PSLB,2p), p — любое простое;
PSLB,3p), р — любое нечетное;
PSLB, p), рфЪ — простое,
удовлетворяющее сравнению р2+1 = 0 (mod 5);
PSLC,3),
или
Судзуки группе SzBp), p — любое нечетное простое.
В частности, каждая конечная М. п. г. порождается
двумя элементами.
Лит.: [1] Т h о m p s о n J. G., «Bull. Amer. Math. Soc»,
1968, v. 74, p. 383—437; [2] e г о же, «Pacif. J. Math.», 1970,
v. 33, p. 451 — 536; 1971, v. 39, p. 483 — 534; 1973, v. 48, p. 511 — 92;
1974, v. 50, p. 215—97; v. 51, p. 573—630. С. П. Струнцов.
МИНИМАЛЬНОЕ МНОЖЕСТВО—1) М. м. в р и м а-
новом пространстве — обобщение мини-
минимальной поверхности. М. м. есть fc-мерное замкнутое
подмножество Хо в римановом пространстве М", и>А-,
такое, что за исключением подмножества Z fc-мерной
хаусдорфовой меры нуль множество Xe\Z является
дифференцируемой fc-мерной минимальной поверхно-
поверхностью (т. е. экстремалью функционала fc-мерного объема
Л*, определенного на fc-мерных поверхностях, вложен-
вложенных в М"). Понятие «М. м.» объединяет в себе несколько
математич. понятий, призванных обслуживать так наз.
Многомерную Плато задачу. А. Т. Фоменко.
2) М. м. топологической динамиче-
динамической системы {Sf} — такое непустое зам-
замкнутое инвариантное (т. е. целиком состоящее из тра-
траекторий) подмножество F фазового пространства W
системы, к-рое не имеет собственных замкнутых инва-
инвариантных подмножеств. Последнее эквивалентно тому,
что каждая из лежащих в F траекторий всюду плотна в
F. Понятие М. м. ввел Дж. Биркгоф (G. Birkhoff,
см. [1]) применительно к случаю потока («время» t
пробегает действительные числа). Он доказал (см. [1],
[2]), что если F — компактное М. м. и u>(z.F, то для лю-
любой окрестности U точки w множество тех t, для к-рых
Sfw(z U, относительно плотно (т. е. имеется такое I,
что в каждом «отрезке времени» \s, $-\-l] длины I содер-
содержится хоть одно t с Sfw? U); обратно, если W — пол-
полное метрич. пространство и точка w обладает указан-
указанным выше свойством, то замыкание траектории {S^w} —
компактное М. м. (то же самое справедливо и для кас-
каскадов; о более общих группах преобразований см., напр.,
[3] или [4]). Сформулированное свойство точки w (и ее
траектории) Дж. Биркгоф назвал рекуррент-
рекуррентностью этой точки (и траектории), употребителен
также предложенный У. Готшалком и Г. Хедлундом
13] другой вариант терминологии, в к-ром это свойство
наз. почти-периодичностью точки w.
Если F= W, то саму динамич. систему называют м и-
н и м а л ь н о й.
Если нек-рая траектория имеет компактное замыка-
замыкание, то в нем содержится нек-рое М. м. F (для полугрупп
непрерывных преобразований {Sf} с неотрицательны-
неотрицательными действительными или целыми t справедлив аналог
этого результата, причем на F преобразования Sf уже
обратимы [5]). Однако исследование предельного по-
поведения траекторий динамич. системы не сводится к
изучению одних только М. м. последней. Очень просто
устроено М. м. гладкого потока класса С2 на двумер-
двумерной замкнутой поверхности — это либо точка, либо
замкнутая траектория, либо вся поверхность, к-рая
в этом случае является тором (теорема Ш в а р-
ц а, см. [6]). В общем случае строение М. м. может быть
весьма сложным (в связи с этим, дополнительно к ска-
сказанному в [2] — [41, надо указать, что минимальность
динамич. системы не накладывает никаких ограничений
на ее эргодпч. свойства по отношению к имеющимся
у нее инвариантным мерам [7]). М. м. — основной объ-
объект изучения в топологической динамике.
Лит.: [1] Биркгоф Д ж. Д., Динамические системы.
Ji(.'P. с англ., М.—Л., 1941; [21 Н е м ы ц к и й В. В., Степа-
Степанов В. В., Качественная теория дифференциальных уравне-
уравнений, 2 изд., М.—Л., 1949: [3] G о t t s с h a 1 k W. H., H е d-
lund G. A., Topological dynamics, Providence, 1955; [4]Брон-
штейн И. У., Расширения минимальных групп преобразова-
преобразований, Киш., 1975; [5] Левитан Б. М., Ж и к о в В. В., Поч-
Почти-периодические функции и дифференциальные уравнения, М.,
1978; [6] Хартман Ф-, Обыкновенные дифференциальные
уравнения, пер. с англ., М., 1970; [7] Итоги науки и техники.
Математический анализ, т. 13, М., 1975, с. 129—262. Д.В. Аносов.
МИНИМАЛЬНОЕ ПРОПОЗИЦИОНАЛЬНОЕ ИС-
ИСЧИСЛЕНИЕ, минимальное исчисление
высказывай и й,— логическое исчисление, полу-
получающееся из позитивного пропозиционального исчисле-
исчисления П добавлением новой связки ~~| (отрицание) и схе-
схемы аксиом
(А=> В) Z> ((A
к-рая наз. законом приведения к а б-
« У Р Д У-
М. п. и. отличается тем, что в нем не всякая формула
выводима из «лжи», т. е. формулы вида "\А&А. М. п. и.
можно получить из исчисления П и другим способом:
добавлением к языку вместо связки П новой пропози-
пропозициональной константы _|_ (ложь) без добавления новых
схем аксиом. Отрицанием ~]А формулы А здесь служит
формула A Z>_]_.
Лит.: [1] Чёрч А., Введение в математическую логику,
лер. с англ., М., 1960. С. Н. Соболев.
МИНИМАЛЬНОЕ СВОЙСТВО частных сумм
ортогональных разложений: для любой
функции /(.г)?LZ [а, Ь], для любой ортонормированной
на [а, Ь] системы {(fn(x)}^=i и для любого п имеет место
равенство:
{ak}k=i "
= $J/(*)—Sn(/. х)\*ах,
где
— n-я частная сумма разложения / (х) по системе
{ф*(*)}, т. е.
cft (/)=$*/И Фй (*)<**•
Этот минимум достигается только на сумме Sn(f, х),
при этом
Неравенство Бесселя, равенство Парсеваля для полных
систем, а также нек-рые другие основные свойства
ортогональных разложений по существу являются
следствиями этого равенства.
Лит.: [1] Колмогоров А. Н., Фомин С. В., Эле-
Элементы теории функций и функционального анализа, 5 изд., М.,
1981; [2] К а ч м а ж С, Штейнгауз Г., Теория ортого-
ортогональных рядов, пер. с нем., М., 1958. А. А. Талалян.
МИНИМАЛЬНОЕ ФУНКЦИОНАЛЬНОЕ ИСЧИС-
ИСЧИСЛЕНИЕ, минимальное исчислен иепре-
д и к а т о в,— исчисление предикатов, задаваемое все-
всеми схемами аксиом минимального пропозиционального
исчисления и обычными кванторными схемами аксиом
п правилами вывода, т. е.
(t — произвольный терм), модус поненс и
CD А (а) А (а)Р С
CD viA (x) ' 3xA{x)D С
(переменная а не входит в А (х) ш в С).
Лит.: [1] Ч ё р ч А., Введение в математическую логику,
пер. е англ., М., I960. С. Н. Соболев.
МИНИМАЛЬНЫЙ ИДЕАЛ — минимальный эле-
элемент частично упорядоченного множества идеалов опре-
определенного типа нек-рой алгебраич. системы. Поскольку
порядок в множестве идеалов определяется отношением
включения, М. и.— идеал, не содержащий отличных
от себя идеалов того же типа. Для мультиоператорных
групп (в частности, для колец) и для решеток, в отличие
от полугрупп, всегда предполагается, что рассматривае-
рассматриваемое частично упорядоченное множество идеалов не со-
содержит нулевого идеала. Если класс идеалов специаль-
специально не оговорен, то под М. и. понимают минимальный
элемент в множестве всех (ненулевых) двусторонних
идеалов.
Минимальный двусторонний идеал, есл^такоп суще-
существует в полугруппе 5, будет единственным минималь-
минимальным двусторонним идеалом и является наименьшим
двусторонним идеалом; он наз. ядром полугруп-
полугруппы S. Не всякая полугруппа обладает ядром (при-
(пример — бесконечная моногенная полугруппа), но, напр.,
ядро есть у любой конечной полугруппы. Ядро явля-
является идеально простой полугруппой (см. Простая по-
полугруппа). Если ядро полугруппы S есть группа, то
S наз. гомогруппой. Полугруппа S будет го-
гомогруппой тогда и только тогда, когда в S существует
элемент z, делящийся слева и справа на любой элемент
из S (то есть z ? xSf]Sx для любого х ?5); в этом
случае ядро состоит из всех таких элементов. Гомо-
Гомогруппой будет, напр., всякая конечная коммутатив-
коммутативная полугруппа.
Если полугруппа S обладает минимальным левым
идеалом (м. л. и.) L, то для любого х? ? произведение
Lx также будет м. л. и., причем всякий м. л. и. может
быть получен таким образом. Каждый м. л. и. есть
простая слева полугруппа. В полугруппе с м. л. и.
каждый левый идеал содержит нек-рый м. л. и., объ-
объединение всех м. л. и. (к-рые попарно не пересекаются)
является ядром полугруппы. Если полугруппа S
обладает м. л. и. Л и минимальным правым идеалом
(м. п. и.) R, то Rf)L~RL есть подгруппа в S, и L=
= Se, R — eS, где е — единица этой подгруппы, произве-
произведение LR совпадает с ядром полугруппы S, являющим-
являющимся в этом случае вполне простой полугруппой.
Для полугрупп с нулем содержательным является
рассмотрение ненулевых идеалов, и минимальный эле-
элемент в соответствующем частично упорядоченном мно-
множестве идеалов наз. 0-м инпмальным (левым,
правым, двусторонним) идеалом. Свой-
Свойства 0-минимальных идеалов @-м. п.) во многом по-
повторяют свойства М.и., с нек-рыми естественными ого-
оговорками. Напр., 0-минимальный двусторонний идеал
не обязательно единствен и не обязательно будет
0-простой полугруппой; он может быть и полугруппой с
нулевым умножением (см. Нилъпотентная полугруппа).
Объединение всех 0-минимальных левых идеалов (со-
(соответственно 0-минимальных правых идеалов) полу-
полугруппы с нулем наз. ее левым (соответственно
правым) цоколем (по определению, цоколь
равен нулю, если соответствующих 0-м. и. в полугруп-
полугруппе нет). Полугруппа совпадает со своими левым и пра-
правым цоколями тогда и только тогда, когда она есть
0-ирямое объединение вполне 0-простых полугрупп
и полугруппы с нулевым умножением.
Рассмотрение тех или иных М. и. и 0-м. и. играет
существенную роль в структурной теории ряда важных
классов полугрупп (см., напр., Вполне простая полу-
полугруппа, Регулярная полугруппа, а также [1] § 2.5,
2.7, гл. 6, §§ 7.7, 8.2, 8.3; [2] гл. V). л. я. Шеврин.
Кольца (как и полугруппы) не обязаны обладать
М. и. (простейший пример — кольцо целых чисел), и
М. и. в кольце, если он существует, не обязан быть
единственным. Сумма всех (левых, правых, двусто-
двусторонних) М. и. кольца наз. (соответственно левым,
правым, двусторонним) цоколем
кольца. Все артиноеы кольца, очевидно, обладают
ненулевым цоколем. Наличие М. и. в примитивном
кольце делает его близким к матричному в следующем
смысле: примитивное кольцо с ненулевым цоколем
изоморфно нек-рому плотному подкольцу кольца всех
линейных преобразований нек-рого векторного про-
пространства над телом, содержащему все преобразова-
преобразования конечного ранга [3]. в. Е. Говоров.
Лит.: [1] Клиффорд А., Престон Г., Алгебраиче-
Алгебраическая теория полугрупп, пер. с англ., М., 1972; [2] Л я-
п и и Е. С, Полугруппы, М., 1960; [3] Д ж е к о б с о н Н.,
Строение колец, пер. с англ., М., 1961.
МИНИМАЛЬНЫХ ИТЕРАЦИЙ МЕТОД — метод ре-
решения системы линейных алгебраич. уравнений Ах=Ь,
в к-ром решение х представляется в виде линейной ком-
комбинации базисных векторов, ортогональных в нек-рой
метрике, связанной с матрицей системы.
В случае симметричной матрицы А ортогональная
система векторов р0, plt . . ., р„-х строится по трех-
трехчленным рекуррентным формулам
i. fc=l,2, ...,n — 2, A)
px=Ap0—aop, p0— произвольный вектор, где
(Лр^) ...,в_2,
(V Pk) , , 9 9
(pk-V pk-l)
Решение системы Ах=Ъ находится по формулам х=
2ft' a коэффициснты ск дают решение системы
(Ь. Po)
^7J
, ...,n-2, |
(b. Pn-i)
В случае вырождения п алгоритме ортогонализации,
т. е. когда р2=0 при г<л, выбирают новый: начальный
вектор j^o1', ортогональный р0, ps, . . ., /V-i. " достраи-
достраивают систему базисных векторов до полной системы.
Для случая несимметричной матрицы разработан
бнортогональный алгоритм.
Если матрица А симметрична и положительно опре-
определена, то построение Л-ортогопальной системы век-
векторов р„, ри . . ., р„_, по формулам A) с
(Apk, Арк) __ (Арк, рк)
k Pk
позволяет избежать решения вспомогательной системы
B) и получить явное выражение для коэффициентов
(Ь, рь)
съ : Ch= —s —— . При этом методу .4-минимальных
k k (АРк Pk)
(к k)
итераций можно придать итерационную форму
¦причем x—xn-i. Такая модификация метода не требует
повторного использования всех векторов />0, pv ....
Pk — i- M. и. м. используется также для решения полной
проблемы собственных значений и для нахождения
обратной матрицы.
Лит.: [1] L а п с z о s С «J. Res. Nat. Bur. Stand,», 1950,
v. 45, №4, p. 255—88; [2] Ф а д д е е в Д. К., Фаддее-
в а В. Н., Вычислительные методы линейной алгебры, М.,
1960. Е. С. Николаев.
МИНИМАЛЬНЫХ НЕВЯЗОК МЕТОД — итераци-
итерационный метод решения линейного операторного урав-
уравнения
Au=r-j A)
с самосопряженным положительно определенным огра-
ограниченным оператором .4, действующим в гильберто-
гильбертовом пространстве Н, и заданным элементом f?H. Фор-
Формулы М. н. м. имеют вид
uk + i^uk^аи (Аик — /), fc = 0, 1, ..., B)
где параметр
ak={A^, 1*)/(А|*, А%*) C)
выбирается на каждом шаге k^O из условия макси-
максимальной минимизации нормы невязки |*+1=.4и* + 1—/;
т. е. требуется выполнение соотношения
D)
Если спектр оператора А принадлежит отрезку
[то, М] действительной оси, где m<z.M — положитель-
положительные числа, то последовательные приближения {uk}
метода B) — C) сходятся к решению и* уравнения
A) со скоростью геометрич. прогрессии со знамена-
знаменателем </=(Af—m)/(Af+m)<l.
Различные способы определения в Н скалярного
произведения приводят к различным итерационным ме-
методам. В частности, при специальных скалярных про-
произведениях формулы М. н. м. совпадают с формулами
наискорейшего спуска метода и метода минимальных
ошибок (см. [2]).
Условия сходимости М. н. м. могут быть ослаблены
по сравнению с перечисленными выше: если рассматри-
рассматривать на нек-рых подмножествах из Н. Напр., если рас-
рассматривать М. н. м. только в действительных простран-
ствах, то можно отказаться от требования самосопря-
самосопряженности оператора А (см. [3], [4]).
Лит.: [1] К р а с н о с е л ь с к и й М. А., К р е й н С. Г.,
«Матем. сб.», .1952, Л5 31, с. 315—34; [2] Приближенное решение
операторных уравнений, М., 1969; [3] С а м а р с к и й А. А.,
Введение в теорию ралностных схем, М., 1971; [4] М а р-
ч у к Г. И., Кузнецов Ю. А., Итерационные методы и
квадратичные функционалы, Новосиб., 1972. Ю. А. Кузнецов.
МИНИМИЗАЦИЯ ВЫЧИСЛИТЕЛЬНОЙ РАБОТЫ —
раздел современной вычислительной математики, по-
посвященный конструированию и исследованию методов,
позволяющих находить приближенное с заранее ука-
указываемой точностью е>0 решение поставленной задачи
Р из класса {Р } при наименьших затратах вычислитель-
вычислительной работы (при наименьшем объеме вычислений).
Этот раздел вычислительной математики может быть
отнесен к более общему, имеющему дело с задачей оп-
оптимизации методов (см., напр., [1], [2)), в к-ром наряду
с указанной проблемой М. в. р. рассматривается и
двойственная по отношению к ней проблема нахождения
среди приближенных методов, требующих примерно
одинаковой допустимой вычислительной работы, ме-
метода, обладающего максимальной точностью (наи-
(наименьшей погрешностью). Последняя проблема харак-
характерна, напр., для задач численного интегрирования,
в к-рых фиксируется число узлов интегрирования, слу-
служащее мерой совершаемой вычислительной работы.
Пусть е.^0 (обычно е>0, при е;---0 ищется точное ре-
решение Р) — требуемая точность решения задачи Р
из заданного класса {Р} родственных задач, а те — до-
допустимый метод для отыскания решения любой задачи
из {Р}, и множество таких методов обозначено через
{т}. Пусть число Wm(P, е)>0 характеризует затраты
вычислительной работы в методе т, позволяющие най-
найти решение Р с точностью е, а
Wm({P}, e)= sup Wm({P}, е).
Ре{Р)
Тогда задача минимизации состоит в отыскании такого
метода т0, что
Wm ({P}, e)= inf Wm({P}, s),
0 т g {in}
то есть по существу ищется оптимальный метод реше-
решения не одной фиксированной задачи Р, а целого класса
задач (оптимизация на классе). Чаще же всего М. в. р.
производится в асимптотич. смысле при е—>-0, N-+oo,
где Лт — параметр, определяющий «размерность» ре-
решаемой задачи.
Метод т0 наз. оптимальным по порядку,
если затраты вычислительной работы в нем не превы-
превышают более чем в конечное число раз величину
W({P], е) — полученных оценок снизу затрат вы-
вычислительной работы в любом возможном методе; ме-
метод т0 наз. логарифмически опт им ал ь-
н ы м, если
lnWmJ{P}, e) = (l + o(l)) In W({P}, в).
Вычислительная же работа Wm (P, в) обычно характе-
характеризуется числом арифметич. действий, производи-
производимых в методе т для достижения точности е при его ре-
реализации на условной ЭВМ. До какой-то степени это
является оправданным упрощением, поскольку во
многих методах логич. операций на реальных ЭВМ со-
совершается лишь в конечное число раз больше, чем ариф-
арифметических. От допустимых методов, как правило,
требуют их устойчивости по отношению к ошибкам
округления. Важно, чтобы и асимптотич. рост коли-
количества используемых ячеек машинной памяти не был в
этих методах чересчур большим.
При конкретизации указанных задач М. в. р. должно
быть уточнено и описание класса {Р} п указано метрич.
пространство Н, с помощью к-рого определяется точ-
точность решения исходной задачи.
Решение многих таких конкретных проблем мини-
минимизации представляет не только теоретич. интерес, но
и имеет большое прикладное значение, позволяя часто
решать задачи на ЭВМ при сравнительно небольших за-
затратах машинного времени. Особенно это важно или
для задач, требующих большого объема вычислений,
что характерно, напр., для многомерных задач мате-
матич. физики (см. [2]—-[10]), или для задач, подобных
задачам вычисления элементарных функций и нахожде-
нахождения дискретных преобразований Фурье (см. [1], [11]),
являющихся стандартными, и многократно используе-
используемых для решения других, более сложных. Указанные
задачи М. в. р. достаточно сложны и во многих случаях
их решения получены лишь частично или даже пока
A982) совсем не известны.
На практике при решении задач не очень большой
размерности и не с очень большой точностью иногда
метод с худшими асимптотич. характеристиками может
потребовать меньше машинного времени. Часто же если
затраты вычислительной работы приемлемы, то руко-
руководствуются при выборе метода прежде всего сообра-
соображениями его простоты и надежности.
Пусть исходная задача конечномерна и существуют
методы, дающие точное решение за конечное число ариф-
метич. действий, если эти действия совершаются без
ошибок округлония. В качестве примеров можно взять
задачу вычисления значения многочлена рм(х) степени
N при заданном значении х с \х\ <:1, перемножения двух
квадратных матриц порядка N, решения определенной
системы линейных алгебраич. уравнений Ах=Ъ с ква-
квадратной матрицей порядка N и задачу нахождения ди-
дискретного преобразования Фурье (см. [1], [11]):
2 ЯП .
1
где I — мнимая единица, вектор и= (и0, ии . . ., u/v_i)
задан и ищется вектор v=(v0, vu . . ., i?jv_i), ЛГ=2Г,
r=0, 1, 2, ... Никаких конкретных ограничений на
вид рм(х), х?[ —1,1],Л, Ь, число г и вектор и не накла-
накладывается, и поэтому в каждой из этих задач допустимый
класс {Р} состоит из всех задач такого вида. В подоб-
подобных задачах N выступает в роли параметра и особое
внимание уделяется поведению затрат вычислительной
работы Wm{P, 0)ss^Wm(P) при N-+oo. Для первой из
этих задач метод Горнера, записывающий рм(х) в виде
позволяет вычислить рм(х) за N умножений и N сло-
сложений. Доказано (см. [11]), что этот метод является
оптимальным; не существует метода, к-рый требовал
бы меньшего суммарного числа сложений и вычитаний
или меньшего числа умножений и делений; устойчи-
устойчивость его приемлема, если V] |а,-| не велика (см. [1]).
Для второй и третьей задач существует большое
число методов, дающих их решения при ./У—э-оо за
W(N)^N3 арифметич. действий (см. [1]) и реально
применяемых на практике. Наименьшие же затраты
вычислительной работы среди всех пока известных
методов достигаются на методе с оценкой W(N)^Nlog27
(см. [11]). Этот метод достаточно сложен и по ряду
причин интересен пока только с теоретич. точки зре-
зрения. Не известно A982), является ли он даже лога-
логарифмически оптимальным. Имеется гипотеза, что у ло-
логарифмически оптимального метода с числом ариф-
арифметич. действий W(N) должно быть
In W(N) = 2 In N+o(In N).
Для задачи же A), являющейся предметом гармонич.
анализа, простейшие методы требуют ~iV2 арифметич.
действий с комплексными числами. В 1965 был пред-
предложен метод, позволяющий находить вектор за W(N)~zz
— Win W арифметич. действий (см. [1], [11]), получив-
получивший название метода быстрого дискрет-
дискретного преобразования Фурье. Этот ме-
метод является логарифмически оптимальным; он широко
применяется и на практике. Имеется большое число
подобных задач минимизации, решенных и нерешен-
нерешенных (см. [11], [12]); оптимальные по порядку или лога-
логарифмически оптимальные оценки затрат вычислитель-
вычислительной работы для нахождения решения подобных задач
могут рассматриваться как показатель их сложности.
М. в. р. при решении сеточных систем уравнений,
возникающих или в разностных методах, или в проек-
ционно-разностных (методах конечных элементов) для
приближенного решения краевых задач для уравнении
и систем уравнений сильно эллиитич. типа, имеет осо-
особое теоретическое п прикладное значение и обычно
осуществляется асимптотически при Л"—>оо, где N —
число неизвестных в системе, и при е->0. Для решения
простейших разностных аналогов нек-рых краевых
задач для уравнения Пуассона в прямоугольнике или
параллелепипеде успешно применяются нек-рые пря-
прямые методы, являющиеся логарифмически оптималь-
оптимальными и требующие затраты О (N In N) арифметич.
действий (см. [3], [5], [13], [14]). Известен в случае
прямоугольника (см. [15]) и оптимальный по порядку
метод, требующий О (N) действий. Используя же ите-
итерационные методы, удается получить логарифмически
оптимальные оценки типа
W=O{N In N\\n е|),
где в — точность решения системы в той или иной мет-
метрике, для довольно широкого класса дискретных крае-
краевых задач на параллелепипедной сетке для линейных
и нелинейных сильно эллиптич. систем, рассматри-
рассматриваемых в нек-рых идеальных областях (см. [2] — [10],
[16], [17]) (напр., на плоскости Q может быть образо-
образована из конечного числа прямоугольников со сторо-
памп, параллельными осям координат, а в случае трех-
трехмерного пространства Q должна конечным числом плос-
плоских разрезов, параллельных заданной координатной
плоскости, разбиваться на параллелепипеды с гранями,
параллельными координатным плоскостям). Для более
сложных областей Q использование сеток, топологи-
топологически эквивалентных указанным сеткам идеальных об-
областей Q, и нек-рых типов проекционно-разностных
методов позволяет часто получить системы уравнений,
решаемые столь же эффективно, что и в случае идеаль-
идеальных областей (см. [3], [8], [101, [16], [17]). При этом:
правые части этих систем могли быть любыми векто-
векторами; если же учитывать, что они порождались спе-
специальным образом как нек-рые функционалы от доста-
достаточно гладких функций, то удается построить методы
с затратами работы О (X In Лг) и даже O(N) при усло-
условии, что e^N~a, a>0. Методы последнего типа для
решения задачи на заданной сетке используют последо-
последовательность подобных же задач на более редких сет-
сетках.
Существуют методы, позволяющие пайтн с точностью
е младшие собственное значение и соответствующую
собственную функцию для нек-рых сеточных аналогов
эллиптич. задач на собственные значения, при затрате
O(N In N\ln e|) или даже O(NlnN) (при ехЛг"а,
а>0) действий (см. [9]).
Пусть задача Р состоит в решении корректного опе-
операторного уравнения
L(u) = f, B)
оператор L действует из Н в F, где Н и F — беско-
бесконечномерные банаховы пространства. Пусть класс {Р}
состоит из таких задач с различными /, при к-рых ре-
шения уравнения B) принадлежат нек-рому ком-
компакту V. Обычно U задается условием:
\\u\\H'^R, C)
где Н' — нек-рое банахово пространство, вложенное
в Н. Если u(~U ищется с точностью е>0 в норме //, то
часто известны информационные оценки, равномерные
относительно всех u(~U наименьшей размерности
АГ=Л'(е) вектора i>jv= (vu v2, . . ., vN), задание к-рого
позволяет получить элемент
v д. = 2г= 1и^'(z) ? н с [i и—д"||я "^8 D)
(см. [1], [2], [6], [7], [18], [19]). Эти оценки снизу для
N (е) дают и очевидные оценки снизу для необходимых
затрат вычислительной работы в любом допустимом
методе. Для ряда краевых задач сильно эллиптич.
систем построены варианты проекционно-разностньтх
методов, приводящих к алгебраич. системам уравнений
LN(uN) = JN E)
с N неизвестными, для к-рых, во-первых, известны
оптимальные по порядку итерационные методы при-
приближенного решения и, во-вторых, соответствующие
восполнения ujy вектора upj (см. [4]) являются t'-ait-
проксимациями в Н решения уравнения B\ причем
ЛГ<:А-Л'(е), где к — константа, не зависящая от е (см.
[6] — [8], [10], [17]). Если не учитывать работу на фор-
формирование E), то такие методы приводят к оценкам
затраты вычислительной работы, минимальным по
порядку. Напр., для случая эллиптич. уравнения 2-го
порядка H=W\(Q), H'=W'l(Q) {w\(Q) — простран-
пространство С. Л. Соболева [20]), если Q — область на плос-
плоскости, достижимы оценки затрат числа арпфметич.
действии :хе~2. Вычислительную работу на формиро-
формирование E) тоже часто можно оценить как О(АТ In Л'),
если брать информацию о заданных функциях в соот-
соответствующих пространствах. В частности, в упомяну-
упомянутом примере / должна рассматриваться как элемент
F=W^1(Q), но не L2(Q) (см. [8], [17]). Подобного рода
оценки получены и для нек-рых дифференциальных
задач на собственные значения (см. [9]).
Рассматривались нек-рые вопросы М. в. р. при ре-
решении интегральных уравнений, обыкновенных диф-
дифференциальных уравнений и нестационарных уравнений
с частными производными (см., напр., [1] — [4], [21] —
[23]).
Лит.: [1] Б а х в а л о в Н. С, Численные методы, 2 изд.,
М., 1975; [2J его же, в сб.: Международный конгресс матема-
математиков в Ницце, 1970, М., 1972, с. 27—33; [3] М а р ч у к Г. И.,
Методы вычислительной математики, М., 1977; [4] Сама р-
с к и й А. А., Введение е теорию разностных схем, М., 1971;
[5] С а м а р с к и й А. А., Николаев Е. С, Методы реше-
решения сеточных уравнений, М., 1Я78; [6] О г а н е с я н Л. А.,
Р и в к и н д В. Я., Руховец Л. А., в сб.: Дифференциаль-
Дифференциальные уравнения и их применения, Вильнюс, в. 5, 1973; в. 8, 1974;
[7] Дьяконов Е. Г., сЧис.ченные методы механики сплош-
сплошной среды», НовосиО., 197В, т. 7, JV» 5, с. 14—78; [8] е г о ж е,
в кн.: Вариационно-разностные методы в математической физике,
Новосиб., 1978, с. 149—64; [9] Дьяконов Е. Г., О р е-
х о в М. Ю., «Матем. заметки», 1980, т. 27, № 5; [101 Корне-
е в В. Г., Схемы метода конечных элементов высоких порядков
точности, Л., 1977; [11] Borodin A., M u n г о I., The Com-
Computational Complexity of Algebraic and Numeric Problems, N. Y.,
1975; [12] Analytic Computational Complexity, N. Y., 1976; [13]
С о n с и s P., G о 1 и b G., «SIAM J. Numer. Anal.», 1973, v.
10, p. 1103—20; [14] Barker R. J., в кн.: Mathematical mo-
models and numerical methods (Banach Center Publications) Warsz.,
1978, v. 3, p. 255—68; [15] Bank R. E., Rose D. J., «Proc.
Symp. Carnegie-Mellon Univ.», N. Y., 1976, p. 201—49; {18]
Кузнецов Ю. А., в кн.: Вариационно-разностные методы
в математической физике, Новосиб., 1978, с. 178 — 212; [17] Д ь я-
конов Е. Г., в кн.: Численные методы в математической
физике, Новосиб., 1979, с. 45—68; L18] Теоретические основы и
конструирование численных алгоритмов задач математической
физики, М., 1979, с. 45—118; [19] Тихомиров В. М., Не-
Некоторые вопросы теории приближений, М., 1976; [20] С о б о-
л ев С. Л., Некоторые применения функционального анализа
в математической физике, Новосиб., 1962; [21] Емелья-
Емельянов К. В., Ильина. М., «Ж. вычисл. матем. и матем. физ.».
1967, т. 7, N, 4, с. 905 — 10; [22] И в а н о в В. В., в кн.:
Механика сплошной среды и родственные проблемы анализа,
М., 1972, с. 209—19; [231 Акопян Ю. Р., Оганесян
Л. А., «Ж. вычисл. матем. и матем. физ.», 1977, т. 17, № 1, с.
109 — 18. Е. Г. Дьяконов.
МИНИМИЗАЦИЯ ПЛОЩАДИ — задача о минимуме
площади A (F) римановой поверхности, на к-рую дан-
данная область В плоскости z отображается взаимно одно-
однозначно регулярными в ней функциями F данного
класса R, т. е. задача о нахождении
min A
FaR
(F)^min \ \ \F'(z)\*do (*)
(da — элемент площади). Под интегралом в (*), взя-
взятым по области В, понимается предел интегралов, взя-
тых по областям Вп, n—i, 2, ,.., исчерпываю-
исчерпывающим область В, т. е. таким, что BnczB, BncBn+i
и что любое замкнутое множество EdB, начиная с
нек-рого п, лежит в Ви.
В случае, когда Я — класс функций F(z), F@) = 0,
F' @)=1, регулярных в данной одпосвязной области В,
содержащей точку z=0 и имеющей более одной гранич-
граничной точки, минимум А площади A (F) образа области В
в классе R дает единственная функция, однолистно
отображающая область В на полный круг |z|O, где
г — конформный радиус области В в точке z=0, при-
причем А = пг°.
Рассматривалась также задача о минимальной пло-
площади образа многосвязной области (см. [1] с. 225,
594).
Лит.: [1] Г о л у з и н Г. М., Геометрическая теория функ-
функций комплексного переменного, 2 изд., М., 1966.
Е. Г. Голузина.
МИНИМИЗИРУЮЩАЯ ПОСЛЕДОВАТЕЛЬ-
ПОСЛЕДОВАТЕЛЬНОСТЬ — последовательность элементов уп из мно-
множества М, для к-рой соответствующая последователь-
последовательность значений нек-рой функции Ц>(уп) стремится
к точной нижней грани ее значений на М, т. е.
limq>(jin)= inf ф (у).
Л->-со ЦЧМ
Компактность М. п., т. е. существование подпоследо-
подпоследовательности, сходящейся к элементу из М, в сочетании
с лол5'непрерывностыо снизу функции ср обеспечивает
существование оптимального элемента
<р (;/") = min ff (у).
M
В теории приближений М. п. у„?М для данного эле-
элемента из метрич. пространства Х=(Х, р) — последо-
последовательность, для к-рой
Р (х, Уп) ~^ Р (х, М) = inf {p (х, у):у?М}.
См. Аппроксимативно компактное множество.
Ю. Н. Субботин.
МИНИМИЗИРУЮЩАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ—
последовательность элементов {z,,}, zn?Z, минимизи-
минимизирующая непрерывных! функционал /[z], z^Z:
I lzn] —* inf I [z], n —* oo .
zez
Задачи минимизации функционалов принято разде-
разделять на две группы. К первой относят нахождение ми-
минимального значения функционала, при к-ром несу-
несущественно, на каких элементах z достигается искомый
минимум. В этом случае в качестве приближенных ре-
решений можно использовать значения функционала на
любой М. п. Другая группа задач состоит в отыскании
элемента z*, на к-ром функционал /[z] достигает своего
наименьшего значения:
inf /[z] = /[z*]=7*. (!)
Ъ
При этом существуют М. п., не сходящиеся к эле-
элементу z*.
Пусть задача минимизации A) имеет единственное
решение z* и {z,t} — М. п., т. е. такая последователь-
последовательность, что
lim I[zn] = I*. B)
Задача минимизации A) иаз. устойчивой, если
всякая М. п. B) сходится к элементу z*?Z.
При решении устойчивых задач М. п. находится по-
построением последовательности итераций таких, что
по zn (ге-й итерации) находится «направление» уп, а за-
затем выбирается элемент
z»+i=zn —/ (f>n) Уп
из множества элементов zn—/(p)i/,,, минимизирующих
функцию I [zn — / (р) уп\ переменной р.
Методы построения М. п. для устойчивых задач (\)
распадаются на три семейства. В первом производные
не используются; это — прямые методы. Второе се-
семейство использует первые производные функционала;
такие методы обычно наз. .методами спуска. Третью
группу методов составляют алгоритмы с использова-
использованием вторых производных функционала.
В задачах минимизации функционалов, не обладаю-
обладающих свойством устойчивости, для построения последо-
последовательностей {z,,}, сходящихся к элементу z*, приме-
применяют методы регуляризации.
Лит.: [1] Т и х о н о в А. Н., А р с е н и н В. Я., Методы
решения некорректных задач, М., 1974; [2] Се а Ж., Опти-
Оптимизация. Теория и алгоритмы, пер. с франц., М., 1973.
Ю. В. Ракитский-
МИНИМУМ — см. Максимум и минимум функции,
Максимума и минимума точки.
МИНКОВСКОГО ГЕОМЕТРИЯ — геометрия конеч-
конечномерного нормированного пространства, т. е. аф-
аффинного пространства, в к-ром введена метрика
Минковского — инвариантная относительно па-
параллельных переносов метрика, при к-рой роль еди-
единичной сферы играет фиксированное центрально-сим-
центрально-симметричное Выпуклое тело. В. А. Залгаллер.
МИНКОВСКОГО ГИПОТЕЗА — предположение, со-
согласно к-рому для действительных линейных форм
Lj (x) =-= адагх-f- . . . -f ajnxn, К / < п,
от п переменных хг, . . ., хп с отличным от нуля опреде-
определителем Д при любых действительных а,, . . ., а„ су-
существуют целые хи . . ., хп такие, что будет выполнено
неравенство
Эта гипотеза была доказана Г. Минковскнм (Н. Min-
kowski, 1910) в случае п—2. Известны A982) доказа-
доказательства гипотезы для п-<5, а при ге>5 справедливость
неравенства (*) доказана при нек-рых дополнитель-
дополнительных ограничениях (см. [2]).
Лит.: [1] К а С С е л С Д ж. В. С, Введение в геометрию
чисел, пер. с англ., М., 19E5; [23 С к у б е н к о Б. Ф., в кн.:
Исследования по теории чисел. 2, Л., 1973, с. ti—Зи («Записки
научных семинаров ЛОМИ АН СССР», т. 33).
Э. Л. Ковалевская.
МИНКОВСКОГО НЕРАВЕНСТВО—1) Собственно
М. н.: если действительные числа xt, г/,->0 при i=d,
. . ., п и р>1, то
Выведено Г. Минковским [1]. При р<1, рфО нера-
неравенство заменяется на противоположное (для р<0
следует считать х,, у;>0). В каждом из этих случаев
равенство имеет место тогда и только тогда, когда
строки {х[} и {у,} пропорциональны. При р=2 М. и.
наз. неравенством треугольника. М. н.
допускает обобщения в различных направлениях (они
также носят названия неравенств М и н к о в-
с к о г о ). Ниже приводятся нек-рые из них.
2) М. н. д л я сум м. Пусть хц^О для i=l, ...
. . ., л п /=1, . . ., т и р>1, тогда
Знак неравенства меняется на обратный при р,
p=tQ и для р<1 полагается ж(-/>0. В каждом из этих
случаев равенство имеет место тогда и только тогда,
когда строки {хц}, . . ., {х1т} пропорциональны. Су-
Существуют также обобщения неравенств A) на кратные
и бесконечные суммы. Однако при использовании пре-
предельных процессов особого внимания требует форму-
формулировка случаев возможного равенства (см. [2]).
Неравенства A) и B) однородны относительно 5]'
и потому они имеют аналоги для различных средних,
напр., если Му (xi) = <f~l\2j$(xi)}, где cp=ln t, то
Mn
подробнее см. в [2].
3) М. н. для интегралов аналогично нера-
неравенству B) и имеет место опять же вследствие однород-
ности относительно \. Пусть f(x),g(x.) —интегрируе-
—интегрируемые функции в нек-рой области XcR" относительно
элемента объема dV, тогда при 1
Естественно получается обобщение неравенства C)
для большего числа функций. Дальнейшее обобщение:,
если А>1, то
1(xi У) = Ч> (х)'§ {у)-i причем равенство имеет место лишь
в случае f (x, y) = q>(x)ty(y).
4) Другие неравенства типа М. н.:
а) для произведений: если г,-, j//J>0 ,то
б) неравенство Малера: пусть F (х) —
обобщенная норма в Еп, G(y) — ее полярная функция.
Тогда
(.г, y)<.F(x)G(y),
где (•, •) — скалярное произведение;
в) для определителей: если А, Б — неот-
неотрицательные эрмитовы матрицы над С, то
(det (А + В)I/П5э (det A)x'n +(det
5) Наконец, с именем Г. Минковского связываются
п др. неравенства, в особенности в выпуклом анализе
и теории чисел, напр. Брунна — Мипковского тео-
теорема.
Лит.: El] M i n k о w s к i H., Geometrie der Zahlen, 1,
Lpz., 1896, § 115—17; МХарди Г. Г., Литтльвуд Д ж.,
Полна Г., Неравенства, пер. с англ., М., 1948; [3] Беккен-
бах Э. Ф., Беллман Р., Неравенства, пер. с англ., М.,
1965; [4] М а р к у с М., М и н к X., Обзор по теории матриц
и матричных неравенств, пер. с англ., М., 1972.
М. И. Войцеховспий.
МИНКОВСКОГО ПРОБЛЕМА: существует ли замк-
замкнутая выпуклая гиперповерхность F, у к-рой гауссова
кривизна К (?) является заданной функцией единич-
ного вектора внешней нормали \. Поставлена Г. Мин-
ковским [1], к-рому принадлежит обобщенное решение
проблемы в том смысле, что оно не содержит никакой
информации о характере регулярности F, даже если
КA) — аналитич. функция. Он доказал, что если за-
заданная на единичной гиперсфере S непрерывная поло-
положительная функция К (?) удовлетворяет условию
то существует и притом единственная (с точностью до
параллельного переноса) замкнутая выпуклая поверх-
поверхность F, для к-рой К(%) является гауссовой кривиз-
кривизной в точке с внешней нормалью \.
Регулярное решение М. п. дано А. В. Погореловым
в 1971 (см. [2]), им же рассмотрены нек-рые вопросы
геометрии и теории дифференциальных уравнений,
примыкающие к этой проблеме. Именно он доказал, что
если К (?,) принадлежит классу С'л, ттСйЗ, то получае-
получаемая поверхность F принадлежит классу Ст+г- а, а>0,
а в случае аналитичности К (?) поверхность F также
оказывается аналитической.
Естественное обобщение М. п. состоит в решении
вопроса о существовании выпуклой гиперповерхности
с заданной элементарной симметрич. функцией глав-
главных кривизн <pv (|) любого данного порядка V, г^и=
= dim F. В частности, при v=l это — проблема Крис-
тоффеля о восстановлешги поверхности по средней крп-
визне. Необходимое условие разрешимости этой обоб-
обобщенной М. п. аналогично (*) имеет вид
Однако это условие недостаточно (А. Д. Александров,
1938, см. [3]). Вот примеры достаточных условий:
1 — -M max (Ov, t — ЧЧ t) < ®v,i
" /<t>v.t\1/'n
где <?v> < = f
При этом регулярность F та же, что и в М. п. Эти ре-
результаты с помощью аппроксимаций оказываются
справедливыми и для функций Ц>(%), обладающих свой-
свойствами неотрицательности, симметрии и вогнутости.
Лит.: [11 Minkowski H., «Math. Ann.», 1903, Bd 57,
S. 447—95; [2] П о г о р е л о в А. В., Многомерная проблема
Минковского, М., 1971; [3] Буземан Г., Выпуклые поверх-
поверхности, пер. с англ.. М., 1964. М. И. Войцехов'-кий
МИНКОВСКОГО ПРОСТРАНСТВО — четырехмерное
псе вд о евклидово пространство сигнатуры (\, 3), пред-
предложенное Г. Мпнковским (Н. Minkowski, 1908) в ка-
качестве геометрич. интерпретации пространства-вре-
пространства-времени специальной теории относительности (см. \\]).
Каждому событию соответствует точка М. п., три коор-
координаты к-рой представляют собой координаты трех-
трехмерного пространства; четвертая — координата с!, где
с — скорость света, t — время события. Связь между
пространственными расстояниями и промежутками
времени, разделяющими события, характеризуется
квадратом т. н. интервала:
s2=c2(AiJ — (ДяJ — (Дг/J— (AzJ.
Интервал в М. п. играет роль, аналогичную роли рас-
расстояния в геометрии евклидовых пространств. Вектор
с положительным квадратом интервала наз. в р е м е-
ниподобным вектором, с отрицательным
квадратом интервала — пространственно-
подобным вектором. Линия, касательный
вектор к к-рой в каждой ее точке времениподобен, наа.
времениподобной линией. Аналогично
определяются пространственноподоб-
н ы е и изотропные линии. Событие в дан-
данный момент времени в данной точке наз. мировой
т о ч к о и; множество мировых точек, описывающее
развитие какого-либо процесса или явления во вре-
времени, наз. м и р о в о и л и н и е й. Если вектор, со-
соединяющий мировые точки, времешшодобен, то сущест-
существует система отсчета, в к-poii события происходят в од-
одной и той же точке трехмерного пространства. Время,
разделяющее события в этой системе отсчета, равно
Д^=т=х/с, где т — т. и. собственное время.
Ни в какой системе отсчета эти события не могут быть
одновременными (т. е. имеющими равные коорди-
координаты I). Если вектор, соединяющий мировые точки двух
событии, пространственноподобен, то существует си-
система отсчета, в к-рой эти два события происходят
одновременно; они не связаны причинно-следственной
связью; модуль интервала определяет пространствен-
пространственное расстояние между этими точками (событиями)
в этой системе отсчета. Касательный вектор к мировой
линии является времениподобньш вектором. Касатель-
Касательный вектор к световому лучу является изотропным
вектором.
Движениями М. п., т. е. преобразованиями, сохра-
сохраняющими интервал, являются Лоренца преобразова-
преобразования.
Обобщение М. п.— псевдориманово пространство,
к-рое используется при построении теории тяготения.
Лит.: Ш М и н к о в с к и и Г.. Пространство и время,
в кн.: Принцип относительности, М., 1973; [2] Ландау Л. Д.,
Л и ф ш и ц Е. М., Теория поля, 6 изд., М., 1973: .[3] Фок
В. А., Теория пространства, времени и тяготения, 2 изд., М.,
1961; Е4] Рашевский П. К., Риманова геометрия и тен-
тензорный анализ, 3 изд., М., 1967; [5] С и н г Д ж- Л-, Общая
теория относительности, пер. с англ., М., 1963.
Д. Д- Соколов.
МИНКОВСКОГО ТЕОРЕМА — 1) М. т. о в ы п у к-
л о м теле — одна из теорем геометрии чисел, по-
послужившая основой выделения геометрии чисел в раз-
раздел теории чисел. Установлена Г. Мннковским в 1896
(см. [1]). Пусть ft — замкнутое выпуклое тело, симмет-
симметричное относительно начала координат О, имеющее
объем F(ft'). Тогда всякая точечная решетка Л опреде-
определителя d(A), для к-рой
V (ftMs2"d (Л),
имеет в ft точку, отличную от О.
Равносильная формулировка теоремы Минковского
Д (ftKs2-«V (ft),
где Л (ft) — критнч. определитель тела ft. Обобще-
Обобщением теоремы Минковского на невыпуклые множества
является теорема Блихфельдта (см. Геометрия чисел).
Теоремы Минковского и Блихфельдта позволяют оце-
оценивать сверху арнфметнч. минимумы лучевых функций.
Лит.: ll] Mi n kc wsk i If. Geometric der Zahlen, Lpz.,
189h; Lpz.—В., 1910; N. Y., 195.4. А. В. Малышке.
2) M. т. о линейных неравенствах:
система неравенств
',. atjX:\ < с,-, 2<;=SJra,
где ац, с;—действительные числа, имеет целое решение
(х1у . . ., хп)ф0, если сг . . .cn^|det(a,7)|. Установлена
Г. Минковским в 1896 (см. [1|). М. т. является следст-
следствием более общей теоремы Минковского о выпуклом
теле (см. п. 1).
Лит.: [1] Minkowski H., Gcometrie der Zahlen, Lpz.,
1896; Lpz.—В., 1910; N. Y., 1953; [2J его же, Diophantische
Approximationen, Lpz., 1907; [3] К а с с е л с Д ж. В. С, Вве-
Введение в геометрию чисел, пер. с англ., М., 19U5.
Э. И. Ковалевская.
МИНОР порядка к — определитель матрицы,
элементы к-рой стоят в данной прямоугольной матрице
на пересечении к разных столбцов и к разных строк.
Если номера отмеченных строк совпадают с номерами
отмеченных столбцов, то М. наз. главным, а если
отмечены первые к строк и первые к столбцов — уг-
угловым. Базисным минором матрицы наз.
любой ее ненулевой М. максимального порядка. Для
того чтобы М. был базисным, необходимо и достаточно,
чтобы все окаймляющие его М. (т. е. содер-
содержащие его М. на единицу большего порядка) были
равны нулю. Система строк (столбцов) матрицы, свя-
связанных с базисным М., является максимальной линейно
независимой подсистемой системы всех строк (столб-
(столбцов) матрицы. В. Н. Ремесленников.
МИНОРАНТА — см. Мажоранта и миноранта.
МИНУТА — единица измерения плоских углов, рав-
равная 1/60 части градуса, обозначается знаком '. М. де-
делится на 60 секунд F0"). Метрическая М.—
1/10000 часть прямого угла, обозначается знаком с.
Метрическая М. делится на 100 метрических секунд
A00"-).
МИРОВАЯ ЛИНИЯ — линия в пространство-вре-
пространство-времени, являющаяся пространственно-временной траек-
траекторией материальной точки. Пусть в нек-рой области
пространства-времени введена локальная система ко-
координат t, г, (/, z, н пусть точка P(t, r, у, z) лежит на
М. л. у. Точку Р наз. мировой точкой, она
описывает событие, состоящее в том, что мате-
материальная точка в данный момент времени t имеет про-
пространственные координаты х, у, z. Абстракция события
н связанные с ним абстракции мировой точки и М. л.
являются одними из основных понятий теории относи-
относительности, дополняющими абстракцию материальной
точки, заимствованную из классич. механики. Обычно
рассматрпвают гладкие (или кусочно гладкие) мировые
линии. М. л. материальной точки с положительной
массой покоя является времешшодобной кривой. М. л.
материальной точкп с нулевой массой покоя (такая
материальная точка является неквантовой моделью
фотона и др. элементарных частиц нулевой массы
покоя) является изотропной линией. Произвольная точ-
точка пространства-времени рассматривается в качестве
мировой точкп, т. е. (возможного) события, а каждая
временнподобная или изотропная линия — в качестве
М. л. нек-рой материальной точки. М. л. материальной
точки, не испытывающей воздействия негравитацион-
ных сил, является согласно геодезических гипотезе
нек-рой геодезической пространства-времени. Единич-
Единичный касательный вектор у к М. л. у наз. четырехмер-
четырехмерным вектором скорости; в локальных координатах он
имеет вид
i у \
где
dx dy rh
dt' dt ' It
См. также Минковского пространство.
Д. Д. Соколов.
МИРОВАЯ ФУНКЦИЯ — значение интеграла
взятого вдоль геодезической Г , соединяющей две
точки Р' (х1) и Р (х) пространства-времени. При этом Г
задана уравнениями ж'=|'(и), где и — канонич. пара-
параметр, a U'= *t . М. ф. равна с точностью до знака
половине квадрата меры геодезической, соединяющей
Р' и Р, и является двухточечным инвариантом в том
смысле, что ее величина не изменяется, когда незави-
снмо преооразуются координатные системы в окрест-
окрестностях Р' и Р.
В плоском пространстве-времени существует такая
система координат, что
где
g?/=diag(l, I, 1,-1).
Лит.: [1] С и и г Д ж., Общая теория относительности, пер.
¦;англ. ,М., 1963. М. Я. Войцеховский.
МИТТАГ-ЛЕФФЛЕРА ЗВЕЗДА — то же, что
звезда элемента функции.
МИТТАГ-ЛЕФФЛЕРА МЕТОД СУММИРОВАНИЯ —
полунепрерывный метод суммирования числовых и
функциональных рядов, определенный последователь-
ностью функций
**<в> = г7ПЖ)' в>0, * = 0,1,2, ....
Г (х) — гамма-функция. Ряд
I1 у м м и р у е м методом М и т т а г - Л е ф-
Ф л е р а к сумме s, если
lim.i*=c
и ряд под знаком предела сходится. Метод был перво-
первоначально введен Г. Миттаг-Леффлером (G. Mittag-
Lefiler, [1]) для ряда
2°° zk
М.-Л. м. с. является регулярным (см. Регулярные ме-
методы суммирования) и применяется как аппарат для
аналитич. продолжения функций. Если /(z) — главная
ветвь аналитич. функции, регулярной в нуле и пред-
ставнмой рядом
для малых z, то этот ряд суммируем М.-Л. м. с. к f(z)
во всей звезде функции /(z), причем равномерно в лю-
любой замкнутой ограниченной области, содержащейся
внутри звезды.
Из методов суммирования, определенных преобразо-
преобразованием последовательности в последовательность полу-
полунепрерывными матрицами а^ {со) типа
где
— целая функция, Г. Миттаг-Леффлером рассматри-
рассматривался случай, когда
Матрицу ak(a>) с такой целой функцией наз. матри-
матрицей Миттаг-Леффлера.
Лит.: [1] Atti del IV Congresso Internationale, v. 1, Roma
1908, p. 67—85; [2] M i t t a g - L e ( f 1 e r G., «Acta math.»,
1905, v. 29, p. 101—81; [3] X ар ди Г., Расходящиеся ряды,
пер. с англ., М., 1951; [4] Кук Р., Бесконечные матрицы и про-
пространства последовательностей, пер. с англ., М., 1960.
Я. Я. Волков.
МИТТАГ-ЛЕФФЛЕРА ТЕОРЕМА — 1) М.-Л. т. о
разложении мероморфной функции
'см. [1], [2]) — одна из основных теорем теории анали-
аналитических функций, дающая для мероморфных функций
аналог разложения рациональной функции на простей-
простейшие дроби. Пусть {а,, }л=1 — последовательность раз-
различных комплексных чисел
I ai I < I а2 I <• ¦ -, Пта„=оо,
П-у со
11 {gn(z)} — последовательность рациональных функ-
функций вида
Х
так что точка аа является единственным полюсом со-
соответствующей функции gn(z). Тогда существуют меро-
морфные функции /(г) в плоскости С комплексного
переменного z , имеющие полюсы в точках ап и только
в них с заданными главными частями A) Лорана ря-
рядов, соответствующих точкам ап. Все эти функпии / (z)
представимы в виде разложения М п т т а г-
Леффлера:
f{z) = h(z)+ ^l= 1[ga(z)+ Pn B) ], B)
где рп (z) — нек-рые многочлены, подбираемые ио ап
и gn(z) так, чтобы ряд B) равномерно (после вы-
выбрасывания конечного числа членов) сходился на
любом компакте KdC, h(z)— произвольная целая
функция.
Из М.-Л. т. вытекает, что любая наперед заданная
мероморфная функция /(г) в С с полюсами ап н соот-
соответствующими главными частями gn (z) разложении
/(z) в ряды Лорана в окрестности о.п разлагается в ряд
B), где целая функция h(z) определяется по f(z).
Г. Миттаг-Леффлер указал общую конструкцию много-
многочленов pn(z), отыскание же целой функции h(z) по
данной f(z) иногда представляет собой более трудную
задачу. Для получения разложения B) можно приме-
применить методы теории вычетов (см. также [3] — 15]).
Справедливо обобщение приведенной теоремы, так-
также принадлежащее Г. Миттаг-Леффлеру и состоящее
в том, что каковы бы пи были область D расширенной
комплексной плоскости С, последовательность {ап}
точек an(zD, все предельные точки к-рой находятся на
границе 0D, и соответствующие главные части A),
существует мероморфная в D функция f(z), имеющая
полюсы в точках ап и только в них с заданными глав-
главными частями A). В такой форме М.-Л. т. обобщается
и для открытых римановых поверхностей D (см. [7]);
о существовании мероморфных функций с заданными
особенностями на компактных римановых поверхностях
см. А белее дифференциал, Дифференциал на римано-
вой поверхности, Римана—Роха теорема. М.-Л. т. верпа
и для абстрактных мероморфных функции gn, f ¦ ?>—*
->F, DdC, со значениями в банаховом пространстве 1<
(см. [8]).
Другое обобщение М.-Л. т. состоит в том, что для
любых последовательности {an}czC, \a1\^.\a2\<- ¦ .,
lim a,,= oo, и соответствующих функций
=у:
k=.\ B-а„)* '
являющихся целыми функциями относительно пере-
переменного wn=\/(z—а„), существует однозначная ана-
аналитическая функция /(z), имеющая особые точки ап
и только их с главными частями gn(z\ (см. [3]).
Для аналитических функций многих комплексных
переменных обобщением задачи Миттаг-Леффлера о по-
построении функции с заданными особенностями является
первая (аддитивная) Кузена проблема. В связи с этим
часто оказывается полезной следующая равносильная
формулировка М.-Л. т. Пусть Q=(J/^y, me Qy — от-
открытые множества в С, и пусть даны мероморфныо
функции gj соответственно на множествах Qy-, причем
разности gj—gk суть регулярные функции на пересе-
пересечениях QjP\Qk при всех / и к. Тотда на Q существует
мероморфная функция / такая, что разности /—gj
регулярны на Qy для всех / (см. [5], [6]).
2) М.-Л. т. о разложении однознач-
однозначной ветви аналитической функции
в звезде — см. Звезда элемента функции.
Лит.: [1] Mittag-Leffler G., En metod att analy-
tisk framstalla en funktion at rationel karakter...— Ofversigt
Kongl. Vetenskaps-Akad. Forliandh'ngar, 1876, v. 33, № 6, p. 3—
10; [2] e г о ж e, «Aeta math.», 1884, v. 4, p. 1—79; [3] Г у р-
ca Э., Курс математического анализа, пер. с франц., 3 изд.,
т. 2, М.—Л., 1936; [4] М а р к у ш е в и ч А. И., Теория ана-
аналитических функций, 2 изд., т. 2, М., 1968; [5] Ш а б а т Б. В.,
Введение в комплексный анализ, 2 изд., ч. 1—2, М., 1976; [6]
Хёрмандер Л.. Введение в теорию функций нескольких
комплексных переменных, пер. с англ., М., 1968; [7] В е h n k e
Н., Sommer F., Theorie der analytischen Funktionen einer
komplexen Veranderlichen, 3 Aufl., В., 1965; [8] Шварц Л.,
Анализ, пер. с франц., т. 2, М., 1972. Е. Д. Соломенцев.
МИТТАГ-ЛЕФФЛЕРА ФУНКЦИЯ — целая функ-
функция Ер (z) комплексного переменного z, введенная
Г. Миттаг-Леффлером [1] как обобщение показательной
функции:
l
В связи с тем, что М.-Л. ф. и более общая функция
типа Миттаг-Леффлера
EP(z; F) = 2L
широко используются в интегральных представлениях
и преобразованиях аналитпч. функций, их свойства,
в частности асимптотика, изучены весьма подробно
(см. [2], [3]).
Лит.: [1] Mittag-Leffler G., «Acta math.», 1905,
v. 29, p. 101—81; [2] Д ж р б а ш я н М. М., Интегральные
преобразования и представления функций в комплексной обла-
области, М., 1966; [3] Г о л ь д б е р г А. А., Островский
И. В., Распределение значений мероморфных функций, М.,
.1970. Е. Д. Соломенцев.
МИХАЙЛОВА КРИТЕРИЙ: все корни многочлена
Р (z) = z« + a,,_1z«-1+...+a1z + a0
с действительными коэффициентами имеют строго от-
отрицательные действительные части тогда и только
тогда, когда комплекснозначная функция z=P(Jco)
действительного переменного ю?[0, оо) описывает
в комплексной плоскости z кривую (годограф
М и х а й л о в а), начинающуюся на положительной
действительной полуоси, не попадающую в начало ко-
координат и последовательно проходящую против хода
часовой стрелки п квадрантов (эквивалентное условие:
когда радиус-вектор Р (?оо) при возрастании со от 0
до +00 нигде не обращается в нуль и монотонно пово-
поворачивается в положительном направлении на угол
яге/2).
Этот критерий впервые был предложен А. В. Михай-
Михайловым [1]. Он равносилен Рауса — Гурвица критерию,
однако носит геометрич. характер и не требует проверки
детермпнантных неравенств (см. [2], [3]). М. к. дает
необходимое и достаточное условие асимптотич. устой-
устойчивости линейного дифференциального уравнения п-го
порядка
ж<п> + а„_1а:("-1)+ . . . -j-а^'+ аож = 0
с постоянными коэффициентами или линейной системы
х—Ах, x?R",
с постоянной матрицей А, характеристич. многочлен
к-роп совпадает с Р (г) (см. [4]).
М. к.— один из частотных критериев устойчивости
линейных систем автоматич. регулирования (примы-
(примыкающий, напр., к Найквиста критерию). Известны
обобщения М. к. на системы автоматич. регулирования
с запаздыванием, на импульсные системы (см. 15]), а
также аналоги М. к. для нелинейных систем управ-
управления (см. [6]).
Лит.: [1] Михайлов А. В., «Автоматика и телемехани-
телемеханика», 1938, № 3, с. 27 — 81; [2] Ч е б о т а р е в Н. Г., Мей-
май Н. Н., Проблема Рауса — Гурвица для полиномов и це-
целых функций, М.—Л., 1949 («Тр. Матем. ин-та АН СССР», т. 26);
[3] Л а в р е н т ь е в М. А., Ш а б а т Б. В., Методы теории
Функций комплексного переменного, 4 изд., М., 1973; [4] Д е м и-
д о в и ч Б. П., Лекции по математической теории устойчивости,
М., 1967; [а] Г н о с н с к и й Л. С, Каменский Г. А.,
Эльсгольц Л. Э., Математические основы теории управляе-
управляемых систем, М., 1969; [6] Б л а к ь е р О., Анализ нелинейных
систем, пер. с англ., М., 1909. Н- X. Розов.
МНИМАЯ ЕДИНИЦА — комплексное число i, квад-
квадрат к-рого равен минус единице: i2=—1.
МНИМОЕ ЧИСЛО — число вида x-\-iy, где i — мни-
мнимая единица, х и у — действительные числа и уфО, т. е.
комплексное число, не являющееся действительным'
М. ч. вида iy наз. чисто мнимым (иногда только
такие числа наз. М. ч.).
МНОГОГРАННАЯ МЕТРИКА — внутренняя мет-
метрика связного симплициального комплекса из евклидо-
евклидовых симплексов, в к-ром склеиваемые грани изометрич-
ны и склеивание производится по изометрии. Расстоя-
Расстоянием между точками комплекса служит нижняя грань
длин ломаных, соединяющих эти точки, и таких, что
каждое из звеньев умещается в одном нз симплексов.
Примером М. м. служит внутренняя метрика на по-
поверхности выпуклого многогранника в ?3. М. м. может
рассматриваться также на комплексе из симплексов
пространства постоянной кривизны.
М. м. допускают синтетич. приемы исследования.
Обычно М. м. рассматривают для комплексов, являю-
являющихся многообразиями или многообразиями с краем.
В теории выпуклых поверхностей и двумерных многооб-
многообразий ограниченной кривизны приближение посредством
М. м. служит универсальным аппаратом исследования
(см. [1], [2]). Для изучения выпуклых поверхностей ус-
успешно привлекались также трехмерные М. м. (см. [3]).
На М. м. размерности п>2 обобщены нек-рые из ре-
результатов римановой геометрии в целом (см. [4], [5]).
Лит.: [1Г А лександров А. Д., Внутренняя геометрия
выпуклых поверхностей, М.— Л., 1948; [2] Александ-
Александров А. Д., Залгаллер В. А., Двумерные многообразия
ограниченной кривизны, М.— Л., 1962 («Тр. Матем. ин-та АН
СССР» т. 63); [3J Волков Ю. А., «Вестн. Ленингр. ун-та»,
1960, J45 19, с. 75—86; [4] М и л к а А. Д., «Укр. геометр, сб.»,
1968, №5—6, с. 103—14; 1970, Ni 7, с. 68—77; [5] S t о n e D. А.,
«Trans. Amer. Math. Soc», 1976, v. 215, № 488, p. 1—44.
В. А. Залгаллер.
МНОГОГРАННИК — совокупность конечного числа
плоских многоугольников такая, что: 1) каждая сторо-
сторона любого из многоугольников есть одновременно сто-
сторона другого (но только одного), называемого смежным
с первым (по этой стороне); 2) от любого из многоуголь-
многоугольников, составляющих М., можно дойти до любого нз
них, переходя к смежному с ним, а от этого, в свою оче-
очередь, к смежному с ним, и т. д. Эти многоугольники
наз. гранями, их стороны — ребрами, а их
вершины — вершинами М.
Приведенное определение М. получает различный
смысл в зависимости от того, как определить много-
многоугольник. Если под многоугольником понимают плоские
замкнутые ломаные (хотя бы и самопересекающиеся),
то приходят к первому определению М. Основная часть
статьи построена на основе второго определения М.,
при к-ром его грани являются многоугольниками, по-
понимаемыми как части плоскости, ограниченные лома-
ломаными. С этой точки зрения М. есть поверхность, со-
составленная из многоугольных кусков. Если эта поверх-
поверхность сама себя не пересекает, то она есть полная по-
поверхность нек-рого геометрии, тела, к-рое также наз.
М.; отсюда возникает третья точка зрения на М. как
на геометрич. тела, причем допускается также сущест-
существование у этих тел «дырок», ограниченных конечным
числом плоских граней.
Простейшими примерами М. являются призмы и пи-
709
МНОГОГРАННИК
рамиды. М. паз. я-угольной пирамидо й, если он
имеет одной своей гранью (основанием) какой-
либо я-угольник, а остальные грани — треугольникп
с общей вершиной, не лежащей в плоскости основания.
Треугольная пирамида наз. также тетраэдром.
М. наз. n-угольной и р и з м о й, если он имеет двумя
своими грапями (основаниям и) равные п-уголь-
ники (не лежащие в одной плоскости), получающиеся
710
друг из друга параллельным переносом, а остальные
грани — параллелограммы, противоположными сторо-
сторонами к-рых являются соответственные стороны осно-
оснований. Для всякого М. нулевого рода эйлерова харак-
характеристика (число вершин минус число ребер плюс
число граней) равна двум; символически: В—Р-\-Г=2
(теорема Эйлера). Для М. рода р справедливо
соотношение В—Р+/1=2—2р.
21
25
709
МНОГОГРАННИК
рамиды. М. паз. я-угольной пирамидо й, если он
имеет одной своей гранью (основанием) какой-
либо я-угольник, а остальные грани — треугольникп
с общей вершиной, не лежащей в плоскости основания.
Треугольная пирамида наз. также тетраэдром.
М. наз. n-угольной и р и з м о и, если он имеет двумя
своими грапями (основаниям и) равные п-уголь-
ники (не лежащие в одной плоскости), получающиеся
710
друг из друга параллельным переносом, а остальные
грани — параллелограммы, противоположными сторо-
сторонами к-рых являются соответственные стороны осно-
оснований. Для всякого М. нулевого рода эйлерова харак-
характеристика (число вершин минус число ребер плюс
число граней) равна двум; символически: В—Р-\-Г=2
(теорема Эйлера). Для М. рода р справедливо
соотношение В—Р+/1=2—2р.
21
25
Выпуклым многогранником наз. выпуклая оболочка
конечного числа точек, т. е. такой М., к-рый лежит по
одну сторону от плоскости любой его грани. Внутрен-
Внутренняя его часть есть выпуклое тело. Если поверхность вы-
выпуклого тела многогранная, то соответствующий М.—
выпуклый. Наиболее важны следующие выпуклые М.
Правильные многогранники (тела Платона) — такие
выпуклые М., все грани к-рых суть одинаковые пра-
правильные многоугольники и все многогранные углы при
вершинах правильные и равные (см. рис. 1 — 5).
Изогоны и изоэдры — выпуклые М., все многогран-
многогранные углы к-рых равны (изогоны) или равны все грани
(изоэдры); причем группа поворотов (с отражениями)
изогона (изоэдра) вокруг центра тяжести переводит
любую его вершину (грань) в любую другую его вер-
вершину (грань). Каждый из изоэдров может быть реали-
реализован так, что все его грани суть правильные много-
многоугольники. Полученные так М. наз. п о л у п р а-
вильными многогранниками (тела-
(телами Архимеда) (см. рис. 10—25).
Параллелоэдры (выпуклые) — М., рассматриваемые
пак тела, параллельным пересечением к-рых можно
заполнить все бесконечное пространство так, чтобы
они не входили друг в друга и не оставляли пустот меж-
между собой, т. е. образовали разбиение пространства (см.
рис. 26—30).
Основываясь на первом (указанном в начале статьи)
определении М., можно указать еще четыре правиль-
правильных невыпуклых М. (тела Пуансо). В этих М.
либо грани пересекают друг друга, либо сами грани —
самопересекающиеся многоугольники (см. рис. 6—9).
Для изучения вопросов, связанных с площадями по-
поверхностей и объемами таких М., удобно пользоваться
именно первым определением М.
Если у М. можно так ориентировать грани, чтобы
каждое ребро в тех двух гранях, к-рые смежны по
этому ребру, имело бы обратные направления, то его
наз. ориентируемым, в противном случае —
неориентируемым. Для ориентируемого М.
(даже если он — самопересекающийся и его грани —
самопересекающиеся многоугольники) можно ввести
понятия площади поверхности и величины объема.
Площадью ориентируемого М. наз. сумму площадей его
граней. При определении объема следует иметь в виду,
что совокупность внутренних кусков граней М. разде-
разделяет пространство на определенное число связных
кусков, из к-рых один по отношению к М. бесконечный
(внешний), а остальные конечные (внутренние). Если
из внешней по отношению к М. точки провести отрезок
в какую-либо внутреннюю точку внутреннего куска,
то сумму «коэффициентов» тех внутренних кусков гра-
граней М., к-рые пересечет этот отрезок, наз. коэффи-
коэффициентом рассматриваемого внутреннего куска М,
(она не зависит от выбора внешней точки); такой коэф-
коэффициент есть целое положительное, отрицательное чис-
число или нуль. Сумму обычных объемов всех внутренних
кусков М., умноженных на эти их коэффициенты, наз.
объемом М.
Рассматриваются и n-мерныо М. Некоторые из ука-
указанных определений имеют «-мерное обобщение. В част-
частности, найдены все выпуклые правильные М., при ге=4
их оказалось 6, а при всех больших « всего 3: обобщение
тетраэдра, куба и октаэдра. В то же время, напр., не-
неизвестны A982) все 4-мерные изоэдры и изогоны.
Лит.: [1] Энциклопедия элементарной математики, кн. 4 —
Геометрия, М., 1963; [2] Гильберт Д., Кон-Фос-
сен С, Наглядная геометрия, пер. с нем., 3 изд., М.— Л.,
1981; [3] Александров А. Д., Выпуклые многогранники,
М.— Л., 1950; [4] Л ю с т ер н и к Л. А., Выпуклые фигуры и
многогранники, М., 1958; [5] Bruckner M., Vielecke und
Vielflache. Theorie und Geschiehle, Lpz., 1900.
По материалам одноименной статьи из БСЭ-3,
МНОГОГРАННИКА ГРУППА — группа Sym P сим-
симметрии многогранника Р в и-мерном евклидовом про-
странстве En, т. е. группа всех движений пространства
Е", переводящих Р в себя. Многогранник Р наз. пра-
правильным, если группа Sym P транзитнвно дейст-
действует на множестве его «флагов» — наборов
F = {Г(н Гх, ..., Г,,-!},
где Tfc есть /с-мерная замкнутая грань и Tk_1czTk.
Группа симметрии правильного многогранника порож-
порождается отражениями (см. Отражений группа). Ее
фундаментальной областью является симплициальный
конус К, вершина к-рого совпадает с центром много-
многогранника Р, а ребра проходят через центры граней,
составляющих какой-либо флаг F. Тем самым образую-
образующие отражения ги . . ., гп группы Sym P получают ес-
естественную нумерацию: гк есть отражение относитель-
относительно той гиперплоскости, ограничивающей К, к-рая не
проходит через центр грани Г^_х. Образующие ;¦# и г;
при \к—Л5>2 коммутируют, а порядок rkrft + 1 равен р^ —
числу /с-мерных (или (к~ 1)-мерных) граней многогран-
многогранника Tfc + 1, содержащих грань Г^_2 (если считать, что
Тк = Р, а Г_х=0). Последовательность {рг, ... , рп_х}
наз. символом Шлофли многогранника.
Трехмерные правильные многогранники (тела Плато-
Платона) имеют следующие символы Шлефли: тетраэдр —
{3,3}, куб — {4,3}, октаэдр — {3,4}, додекаэдр —
{5,3}, икосаэдр — {3,5}.
Символ Шлефли определяет правильный многогран-
многогранник с точностью до подобия. Обращению символа Шле-
Шлефли соответствует переход к взаимному мно-
многограннику, вершинами к-рого служат центры
(п—1)-мерных граней многогранника Р. Взаимные
многогранники имеют одинаковые группы симметрии.
Все возможные символы Шлефли правильных много-
многогранников можно получить из классификации конеч-
конечных групп отражений, выделив из них те, граф Коксте-
ра к-рых линеен. При njs5 в Еп существует лишь 3 пра-
правильных многогранника: симплекс, куб и многогранник
взаимный кубу (аналог октаэдра). Их символы Шлефли
суть {3, ... , 3}, {4,3, ... , 3} и {3, ... , 3, 4}. В 4-мерном
пространстве имеется 6 правильных многогранпиков;
{3, 3, 3}, {4, 3, 3}, {3, 3, 4}, {3, 4, 3}, {5, 3, 3} и {3, 3, 5}.
.Каждая грань правильного многогранника Р также
является правильным многогранником, причем ее сим-
символ Шлефли есть начальный отрезок символа Шлефли
самого многогранника Р. Напр., 3-мерная грань много-
многогранника {5, 3, 3} имеет символ Шлефли {5, 3}, т. е.
является додекаэдром.
Лит.: Ш С о х е t е г Н. S. М., Begular Polytopes, 2 ed.,
N. Y.— L., 1963; [21 РозенфельдБ. А., Многомерные
пространства, М., 106П. 9. Б. Винбере.
МНОГОГРАННЫЙ УГОЛ — часть пространства,
ограниченная одной полостью многогранной конич. по-
поверхности, направляющая к-рой —
плоский многоугольник без самопере- , i
сечений. Грани этой поверхности наз.
гранями М. у., вершина — вер-
вершиной М. у. Многогранный угол наз.
правильным, если равны все его
линейные углы и все его двугранные
углы. Мерой М. у. является площадь,
ограниченная сферич. многоугольником
(см. рис.), полученным пересечением
граней М. у., сферой с радиусом, рав-
равным единице, и с центром в вершине
М. у.
МНОГОГРУППОВОЕ ПРИБЛИЖЕНИЕ — один из
методов приближенного описания и изучения системы
большого числа взаимодействующих частиц (газ, жид-
жидкость), применяемый в статистич. физике.
Этот метод основан на предположении, что всякая
(или почти всякая) конфигурация частиц разбивается
на конечные группы частиц — кластеры, распо-
расположенные достаточно далеко и почти не взаимодеяст-
вующие друг с другом. Иными словами, система вза-
взаимодействующих частиц представляется в виде газа
кластеров, к-рым запрещено слишком сближаться.
Следующий шаг состоит в пренебрежении этим запре-
запретом, а также в том, что из рассмотрения исключаются
кластеры очень больших размеров или очень сложной
формы (в этом собственно и состоит М. п.).
Основное допущоние о разложении конфигурации на
кластеры, лежащее в основе метода, верно в случае
малой плотности частиц и короткодействующих сил
между ними. Оправдано ли это допущение в других
случаях — неизвестно A982). Применяемые же в М. п.
аппроксимации, по-видимому, дают хорошее приближе-
приближение также лишь при малых значениях плотности и ста-
становятся слишком грубыми в случае фазового перехода,
когда одинаково существенную роль начинают играть
кластеры всех размеров.
Лит.: [lj Band W., «J. Chem. Phys.», 1939, v. 7, p. 324 —
26; [2J Frenkel J., там же, р. 200; [3] M и н л о с Р. А.,
Сина й Я. Г., «Матем. сб.», 1967, т. 73, в. 3, с. 375—448; [4]
X и л л Т., Статистическая механика, пер. с англ., М., 1960.
Р. А. Минлос.
МНОГОЗНАЧНАЯ ЛОГИКА — раздел математи-
математической логики, изучающий математич. модели логики
высказываний. Эти модели отражают две основные
черты последней — множественность значений истин-
истинности высказываний и возможность построения новых
более сложных высказываний из заданных при помощи
логич. операции, к-рые позволяют также по значениям
истинности исходных высказываний устанавливать
значение истинности сложного высказывания. Приме-
Примерами многозначных высказываний являются суждения
с модальным исходом («:ш>>, «нет», «может быть») и суж-
суждения вероятностного характера, а примерами логич.
операций — логич. связки типа «и», «или», «если...,
то». В общем случае модели М. л. представляют собой
обобщения алгебры логики. Важно отметить, что в алгеб-
алгебре логики высказывания принимают только два значе-
значения истинности («да», «нет»), в связи с чем она в общем
случае не может отразить всего многообразия логич.
построений, встречающихся на практике. При доста-
достаточно широком толковании М. л. в нее иногда включают
также логические исчисления.
Исторически первыми моделями М. л. явились дву-
двузначная логика Дж. Буля (G. Boole, сер. 19 в.), назы-
называемая также алгеброй логики, трехзначная логика
Я. Лукасевича (J. tucasiewicz, 1920) и гп-значная ло-
логика Э. Поста (Е. Post, 1921). Изучение этих моделей
составило важный этап в создании теории М. л.
Основные модели многозначной логики. М. л. обла-
обладает определенной спецификой, состоящей в рассмотре-
рассмотрении задач и подходов, возникающих при исследовании
М. л. с позиций математич. логики, математич. кибер-
кибернетики и алгебры. Так, с позиций математич. кибернети-
кибернетики модели М. л. рассматриваются как языки, описы-
описывающие функционирование сложных управляющих
систем, компоненты к-рых могут находиться в нек-ром
числе различных состояний, а с точки зрения алгебры
модели М. л. представляют алгебраические системы,
имеющие наряду с прикладным и теоретич. интерес.
Построение моделей М. л. осуществляется по анало-
аналогии с построением двузначной логики. Так, индиви-
индивидуальные высказывания логики, разбитые на классы с
одним и тем же значением истинности, приводят к по-
понятию множества Е — констант модели, к-рые факти-
фактически отождествляют все индивидуальные высказыва-
высказывания, заменяя их соответствующими значениями истин-
истинности; переменные высказывания приводят к перемен-
переменным величинам хх, х2, ... , которые в качестве значений
принимают элементы из множества Е; логич. связки
приводят к множеству М элементарных функций (опе-
(операций), к-рые, как и их аргументы, принимают значе-
значения из Е. Сложные высказывания, построенные из ин-
дивидуальных и переменных высказываний, а также
логич. связок, приводят к множеству <АГ> формул над
М. Значение истинности из Е сложного высказывания
является функцией от соответствующих значений ис-
истинности высказываний, входящих в данное сложное
высказывание. В модели эта функция приписывается
формуле, соответствующей данному сложному выска-
высказыванию; говорят также, что формула реализует
эту функцию. Функции, отображающие кортежи эле-
элементов из Е в Е, наз. функциями т-з н а ч н о й
л о г и к и, где т обозначает мощность множества Е.
Множество всех функций m-значной логики обозначают
через Рт. Множество формул <АГ> приводит к множе-
множеству [М] функций, реализуемых формулами из <М> и
наз. суперпозициями (или компози-
композициям и) над М. Множество [М\ наз. замыкани-
замыканием множества М. Задание конкретной модели
М. л. Мр считается эквивалентным указанию множеств
Е, At, <Af> и [М], при этом говорят, что модель порож-
порождается множеством М; если М конечно, говорят, что
модель является конечно порожденной.
Эта модель наз. формульной моделью, а
также т-з н а ч н о и логикой.
Своеобразие подхода математич. кибернетики к М. л.
состоит в рассмотрении моделей М. л. как управляю-
управляющих систем. Элементарные функции при этом являются
элементами, производящими определенные операции,
а формулы интерпретируются как схемы, построенные
из элементов и также осуществляющие переработку
входной информации в выходную. Такого рода управ-
управляющие системы, известные в кибернетике как схе-
схемы из функциональных элементов
(без ветвления), широко используются в теоротич. и
практич. вопросах кибернетики.
Вместе с тем существует ряд задач логики и кибер-
кибернетики, к-рый связан с изучением соответствий между
множествами М и [At] и при к-ром роль множества (My
несколько затушевывается, сводясь к способу опреде-
определения второго множества по первому. В этом случае
приходят к другой модели М. л., представляющей
собой алгебру, элементами к-рой являются функции,
принимающие в качестве значений, как и их аргумен-
аргументы, элементы из Е. В качестве операций в этих алгебрах
обычно используется специальный набор операций,
эквивалентный в смысле соответствий М и [At] множе-
множеству формул, построенных из функций множества М,
т. е. получению сложных функций из заданных путем
подстановки одних функций вместо аргументов других.
Эти алгебры наз. алгебрами т-з н а ч н ы х
логик. Конкретно это может быть достигнуто, напр.,
введением следующих унарных операций: ?, т, Д, V
и бинарной операции *. В предположении, что каждая
функция / из Рр с учетом фиктивных переменных за-
зависит от переменных хь х2, ... , х„, где п определяется
функцией /, эти операции могут быть заданы так:
(?/) (xt, ..., xn) = f (х2, х3, ...,х„,хх),
(т/) (хх, хг, ¦¦¦, xn) = f (х2, хх, х3, ..., х„),
Ш) (хг, ..., ж„_!) = / (хх, хх, ха, ..., х„-х),
если п>1, и ?/=т/=Д/=/, если п=\;
(V/) (*i, ¦¦¦, хп, xn + i) = f (xt, х3, ..., хп + х)
и для f(xu ... , х„) и g{xu ... , хт)
(f*g) (ХЪ *2> ¦¦•> xn + m-l) =
~f\8 (xl' • ¦ • i xm)i xm + l< • • ¦ 1 xm+n-l)-
Возникающие алгебры МЬ-=<(М, ?, т, Д, V, *> иногда
наз. алгебрами Поста.
Проблематика многозначной логики. К числу задач,
характерных для формульной модели М. л., относится
задача «об описании», т. е. вопрос об указании для за-
данного множества Micz[M-i\ всех формул из <МХ>,
реализующих функции из М2. Частным случаем такой
задачи является важный вопрос математич. логики об
указании всех формул, реализующих заданную кон-
константу, что, напр., для исчисления высказываний экви-
эквивалентно построению всех тождественно истинных вы-
высказываний.
Пограничным вопросом между математич. логикой
и алгеброй, примыкающим к задаче об описании, яв-
является задача о тождественных преоб-
преобразованиях. В ней при заданном множестве Л/
требуется выделить в нек-ром смысле простейшее под-
подмножество пар равных, т. е. реализующих одну и ту же
функцию, формул из <М> (тождеств), позволяющее
путем подстановки выделенных равных формул одной
вместо другой получить из любой формулы все форму-
формулы, равные ей (полную систему тождеств).
Аналогичное место занимает т.н. проблема
и о л нот ы, состоящая в указании всех таких под-
подмножеств М1 заданного замкнутого, т. е. совпадающего
со своим замыканием, множества М, для к-рых выпол-
выполнено равенство [7lfx] — M, т. е. имеет место свой-
свойство полноты (или свойство функцио-
функциональной полноты) М1 в М. К этой задаче при-
примыкает задача о базисах, состоящая в указа-
НШ1 всех полных в М подмножеств Мх, никакое собст-
собственное подмножество к-рых уже не полно в М (базисы
называют также полными независимыми
системами функций). Выделяют два подхода
к решению задачи о полноте — алгоритмический и ал-
алгебраический. В первом случае ставится вопрос о суще-
существовании алгоритма, устанавливающего полноту или
неполноту систем функций, описанных на нек-ром язы-
языке; во втором — переходят к изучению свойств решетки
подалгебр данной алгебры m-значной логики и решают
задачу о полноте, используя эти свойства. Важным
понятием при алгебраич. подходе является понятие
критериальной системы подалгебр. Система N подал-
подалгебр алгебры М=(М, 'Q, т, А, V* :;:> наз- критери-
критериально й, если любое множество М'с=М является
полным тогда и только тогда, когда оно но является под-
подмножеством ни одной подалгебры из N. Таково, напр.,
множество всех собственных подалгебр алгебры М.
В общем случае последняя критериальная система яв-
является избыточной. Всякая критериальная система
содержит все максимальные подалгебры алгебры М
(или предполные класс ы), и это позволяет
перейти к рассмотрению более экономных критериаль-
критериальных систем, к-рые не содержат подалгебр максималь-
максимальных подалгебр. Таким образом, в задачах о полноте
можно ограничиться использованием критериальных
систем вида iV=S1U22, где St — множество всех мак-
максимальных подалгебр, а множество 22 состоит из
нек-рых таких подалгебр, к-рые не являются подалгеб-
подалгебрами никакой максимальной подалгебры. В случае пус-
пустоты 2 2 задача о полноте сводится к описанию макси-
максимальных подалгебр алгебры N.
Глобальной задачей для М. л. является описание
решетки замкнутых классов данной модели М. л.
Характерный для теории управляющих систем вопрос
о сложности этих систем естественно возникает и по
отношению к формулам и функциям из М. л. Типичной
при таком подходе является следующая задача
о сложности реализации. На множестве
всех элементарных формул нек-рым способом вводится
числовая мера (сложность форму л), к-рая
затем распространяется на множество всех формул,
напр, путем суммирования мер всех тех элементарных
формул, к-рые участвуют в построении заданной фор-
формулы. Требуется для заданной функции указать ту
формулу (простейшую), к-рая реализует эту функцию
и имеет наименьшую сложность, а также выяснить, как
эта сложность зависит от нек-рых свойств рассматри-
рассматриваемой функции. Исследуются различные обобщения
этой задачи.
Широкий круг вопросов связан с реализацией функ-
функций формулами с наперед заданными свойствами. Сюда
относятся задача о реализации функций алгебры логики
дизъюнктивными нормальными формами и связанная
с этим задача минимизации; а также задача о реализа-
реализации функций формулами в нек-ром смысле ограни-
ограниченной глубины (т.е. такими формулами, в
к-рых цепочка подставляемых друг в друга формул
имеет ограниченную длину, такое ограничение связано
с надежностью и скоростью вычислений), задача о д е-
к о м п о з и ц и и, т. е. о реализации функций от
переменных при помощи формул, построенных из эле-
элементарных формул, реализующих функции от меньшего
числа переменных, и ряд других.
Решения всех перечисленных выше задач существен-
существенно зависят от мощности множества Е и множества Л/,
порождающего заданную модель М. л.
Важнейшие примеры многозначных логик. К числу
наиболее важных примеров М. л. относятся конечно-
значные логики (т. е. m-значные логики, для к-рых т
конечно). Для них обычно полагают, что Е = Ет={(),
1, ... , т—1}, а m-значную логику MF обозначают Мт.
Наиболее глубоко исследован случай т~2, при этом
функции двузначной логики паз. также булевыми функ-
функциями. Важнейшим результатом здесь является полное
описание Э. Постом (Е. Post, см. [1]) решетки замкну-
замкнутых классов. Множество их оказалось счетным, а каж-
каждый класс и решетки их по включению строятся эффек-
эффективно. Эти классы паз. классами Поста.
Всякий замкнутый класс имеет конечный базис, и его
мощность но превосходит 4. Из этих результатов полу-
получаются решения задач о выразимости, полноте и бази-
базисах, а также задачи о тождественных преобразованиях.
Относительно полных конечных систем для «почти всех»
функций указано поведение меры сложности простей-
простейших формул, реализующих эти функции, и построен
соответствующий алгоритм синтеза формул (см. B]).
Изучены задачи о построении оптимальных по сложно-
сложности формул, реализующих функции надежно и доста-
достаточно хорошо по быстродействию, а также вопросы
сложности реализации для большого числа специаль-
специальных классов функций и отдельных функций.
Одним из глубоко исследованных вопросов для дву-
двузначной логики является также задача мини-
минимизации. В ней изучается специальный язык зада-
задания функций двузначной логики — язык дизъюнктив-
дизъюнктивных нормальных форм (д. н. ф.). Вводится понятие
сложности д. н. ф.— число букв в ней — и изу-
изучаются задачи поиска, строения и метрич. свойств «про-
«простейших» в смысле этой меры д. н. ф., реализующих
заданную функцию (см. [3]). Задача о декомпозиции для
булевых функций состоит в выяснении условий, при
к-рых заданная функция от п переменных может быть
реализована формулой, построенной из функций от
меньшего числа переменных, причем все функции, под-
подставляемые друг в друга в процессе построения форму-
формулы, не зависят от общих переменных. Такие формулы
наз. бесповторными. Показано, что не су-
существует конечной системы функций такой, что каждая
функция может быть реализована бесповторной форму-
формулой над этой системой, и даже что «почти все» функции
не допускают реализации бесповторными формулами.
В целом двузначные логики, в силу нек-рых их особен-
особенностей, являются главным объектом, на к-ром просмат-
просматриваются общие постановки задач.
Для произвольных конечнозначных логик, к-рые
при т^>2 существенно отличаются от двузначной логи-
логики, имеются эффективные решения задач о выразимости
для конечных систем. Показано, что при т^Л сущест-
вуют m-значные логики с конечным базисом и в то же
время не имеющие конечной полной системы тождеств
(см. [4]), тогда как в двузначной логике каждый замк-
замкнутый класс имеет конечную полную систему тождеств
(см. [5]). Для конечнозначных логик с конечным бази-
базисом имеется эффективное решение задачи о полноте.
Оно достигается следующим путем. Говорят, что функ-
функция f (хи ... , хп) сохраняет множество К= {g\(rl, •¦• ,
•гп), ¦¦¦ , gs(-Tu ¦¦¦ , хп)}, если для любого набора g(j.
Sin ¦¦¦ , Sik, где KijtzK, имеет место f(gh, git, ... , g;n) ?
? А'. Множество К паз. правильным, если се-
селекторная функция gj(xx, ... , xn) = xj содержится в К
при всех /, 1 </<:«, и каждая функция из К
сохраняет Л". Если М=[К], то в М выбирают все
системы К' с такими свойствами: функции в них зави-
зависят только от .Г], ... , т„, добавление к ним всех селек-
селекторных функции делает их правильными, они не со-
содержат в качестве подмножества К. Указанная проце-
процедура выделения всех правильных множеств Кг, ... , А"/,
i<2mn, является эффективной. Критериальной систе-
системой является {?/(А',), U(K2), ¦¦¦ , U(Kt)}, где U(Kj)
{класс сохранения к{) состоит из всех функций из М,
сохраняющих К^, 1 <(<:<. Невключение произвольного
конечного множества Кс^М в каждый из классов
U(К() проверяется также эффективно. Каждый пред-
полный класс является одним из классов сохранения,
а множество всех предполных классов в этом случае
образует критериальную систему. Показано, что при
raj3=3 в Р т имеется континуум замкнутых классов, су-
существуют замкнутые классы с базисами заданной ко-
конечной или счетной мощности, а также такие классы,
к-рые не имеют базисов, при этом сами семейства клас-
классов без базисов или со счетным базисом континуальны.
Примерами классов без базиса или имеющих счетный
базис являются [{/„, /ь ... , /„, ...}] и [{glt g2, ... , gn,
...}], где: /,,ssO при п=0, а при я>0 функция/„ (л-,,
... , хп) равна 0 на всех наборах, кроме B, ... , 2),
на к-ром равна 1; gn(.x,, ... , хп) равна 0 на всех наборах,
кроме наборов вида B, ... , 2,1, 2, ... , 2), на к-рых рав-
равна 1 (см. [61).
Особый интерес представляет задача о полноте в т-
значной логике Рт. В Рт существуют конечные полные
системы, что позволяет из каждой полной системы вы-
выделить конечную полную подсистему и свести задачу
к изучению полноты конечных систем. Существуют так-
также полные системы, состоящие из одной функции, такие
функции наз. ш е ф ф е р о в ы м и. Примером их
может служить функция Вебба max(.r1, л-2)-|-
— l(mod m). В силу конечной порожденности в Рт эф-
эффективно решается задача о полноте.
В Рт явно построены все предполные классы, являю-
являющиеся классами сохранения специальных предикатов.
Указание этих предикатов составляет содержание тео-
теоремы о полноте в конечнозначных логиках (см. [7]).
Говорят, что функция /(х1( ... , хп) сохраняет
предикат R: (i?OT)A -> {0, 1}, если формула
R (zu, z12, . . ., z,A) & ... & Pi (znl, zn2, . . ., znh) —»-
—- R (f (zii, z21, . . . , znl), . . ., / (zih, г2Л, . . ., znh))
тождественно равна 1 при всех зпачениях переменных
z,y, l«:j<:rc, l</<:/i. Класс U(R) всех функций, сохра-
сохраняющих предикат R, наз. классом сохране-
сохранения предиката R. Показано, что для каждого
предполного класса N можно выбрать такой предикат
R, зависящий не более чем от т-\-2 переменных, а при
т!>3 не более чем от т переменных, что N=U (R).
Эти предикаты могут быть разбиты на шесть семейств:
Н, S, E, L, Z, U. Семейства Н, S и Е состоят из
всех двуместных предикатов отношения порядка на Ет,
имеющих по одному максимальному и минимальному
элементу,— в первом случае; задающих подстановки
на Ет, разлагающиеся в циклы одинаковой простой
длины (без инвариантных элементов),— во втором слу-
случае; и задающих нетождественные и неуниверсальные
отношения эквивалентности на Ет — в третьем случае.
Семейство L не пусто при т=рЛ, р — простое, н со-
состоит из всех четырехместных предикатов ftG (yu if.,, ;/.,,
г/4) таких, что Rq (г/х, i/2, г/3, г/4) —1 эквивалентно У\-г
+ г/г=2/з"гг/1, где G — абелева группа, в к-рой каждый
ненулевой элемент имеет порядок р. Предикат R (yi, ¦¦¦
... , .V/,), ls^ftsOn, рефлексивен, если из того, что i;e
все числа аи а.2, ... , ah различны, следует, что R(au
а2, ... , я/,) = 1, и симметричен, если для любой подста-
подстановки s чисел 1, 2, ... , h имеет место В {у1, ... , j/ft1 =
= ^(i/.s(ih ¦¦¦ > У.тСп)- Множество элементов с??т та-
таких, что R{ui, ¦¦¦ , a/z-i, с)=1 для любых аь ... , а/г_ъ
наз. центром симметричного преди-
предиката R. Предикат Я (г/ь ... , у^) является централь-
центральным, если он рефлексивен, симметричен и имеет центр с
такой, что 0dcczEm. Семейство Z состоит из всех h-
местных центральных предикатов таких, что l</i<:m.
Для о из Ehk полагают a—^ffzliali-h1, где [a]t?Ek.
Семейство U состоит из всех предикатов R (г/ь ... , у/,)
таких, что при 3<А<т и hk<.m, fc>l, для нек-poii
сюръекции (р: Ет-*- Ehk равенство Я (а1, ... , а/г)-\
эквивалентно тому, что набор ([<p(ai)](, ¦¦¦ , [ф(О1()
неразнозначен при любом Z=0, 1, ... , к—1. Установ-
Установлено, что предикаты из разных семейств задают разные
предполные классы, и указаны условия, когда преди-
предикаты из одного и того же семейства задают одинаковые
классы. Показано, что число предполных классов аспи-
c[m-l/2]
птотпчески равно 6(m)-ni-2 m~l , где б(то) = 1, если
т четно, и б (то) = 2, если т нечетно (т. е. это число рас-
растет достаточно быстро), что указывает на малую прак-
тич. эффективность критериальных систем (см. [8]).
Рассматриваются различные модификации задачи о пол-
полноте, сводящиеся к исследованию систем с нек-рыми за-
заранее известными свойствами, напр, систем, содержа-
содержащих множество Рт всех одноместных' функций или Ни'
множество Sm всех подстановок. В первом случае сис-
система при то>2, а во втором при т>4 является полно!!
тогда и только тогда, когда она содержит сущее т-
венную функцию, т.е. функцию, зависящую
более чем от одного переменного и принимающую все
т значений (см. [9], [10]). С ними связана задача указа-
указания всех таких подмножеств Т множеств р)п и Sm, каж-
каждое из к-рых вместе с любой существенной функцией об-
образует полную систему. Показано, что подмножеств
Т cr Pxm всех одноместных функций, не принимающих
хотя бы одного значения, является таковым, а подмно-
подмножество Т <=: plm всех одноместных функций, не прини-
принимающих хотя бы двух значений, вообще говоря, тако-
таковым уже не является. При ;ге>4 таковыми являются
те и только те подмножества Т, к-рые 4-тран-
зитивны при m=2ft, 3-транзитивны при m—pk,
р — простое, рФ2, 2-транзитивны при остальных т.
Эти условия после естественного обобщения тран-
транзитивности сохраняются и для произвольных систем
функций, к-рые принимают все т значений (см. [11]).
Для систем, состоящих из одной функции, крите-
критерием полноты является условие 2-транзитивности.
Произвольное множество функций при ттг>2 является
полным тогда и только тогда, когда оно т-транзитпв-
но и степень транзитивности не может быть понижена.
От конечных полных систем путем операции отож-
отождествления можно перейти к рассмотрению более про-
простого класса полных систем, наз. простыми базисами.
Под простым базисом понимается такая ко-
конечная полная система, к-рая теряет свойство полноты
после отождествления любой пары существенных поре-
менных у любой функции этой системы. Существует
лишь конечное число q простых базисов и log q—
~/п"г~1-<п'-1Н [12]. Число переменных у функции из
простых базисов но превосходит тт~х, и существует
функция, входящая в простой базис и существенно за-
зависящая от т переменных. Указаны представления
М. л. Pk в Рт, т. е. гомоморфизмы Рь в Рт [13); по-
построены также нек-рые аналоги теории минимизации для
произвольных конечнозначных логик.
Первыми примерами конечнозначных логик явились
трехзначная логика Лукасевича,
к-рая порождается функциями 1—х, min(l, 1—л^+а^),
где хг, х.2 принимают значения 0, 1/2, 1, и т-з н а ч-
иая логика Поста, к-рая порожда-
порождается функциями хг-\-\ (mod m), max (х1, х.,), где
х1, х2 принимают значения 0, 1, ... , т—1. К конечно-
значным логикам примыкают алгебры многозначных
функций, на которые в значительной мере переносятся
проблематика и методы исследования конечнозначных
логик.
Примерами других М. л. являются счетнозначныо и
континуумзначные логики (т. е. такие m-значные ло-
логики, для к-рых мощность т является соответственно
счетной или континуальной). Эти модели играют важ-
важную роль в математич. логике, теории моделей и в ма-
тематич. анализе. Для счетнозначных логик установле-
установлена гпперконтинуальность множеств предполных (а зна-
значит и множества всех) замкнутых классов н найдено
решение задачи о полноте систем, содержащих множе-
множество PL всех одноместных функций [14]. В отличие от
конечнозначных логик Рт при т>2, где имеется толь-
только один предполный класс, содержащий все одномест-
одноместные функции, в Р^п существуют два таких предпол-
предполных класса и указанная система функций является
полной тогда и только тогда, когда она не содержится
в этих классах. Если обобщить понятие существенной
функции и считать, что таковой является всякая функ-
функция, образующая полную систему вместе с Р$о, то
так же, как и в конечнозначных логиках, возникает
задача описания всех тех подмножеств множества PL ,
к-рыо содержат все множество S» подстановок из
Р^ и вместе с любой существенной функцией образуют
полную систему. Показано, что пересечение всех таких
замкнутых подмножеств само обладает указанным
свойством. Это пересечение, к-рое отлично от S^
эффективно описано в теоретико-множественных тер-
терминах.
В счетнозначных и континуумзначных логиках осо-
особую роль играют различные их подклассы. Таковыми
являются в первом случае предельные логики, а во
втором — М. л. непрерывных функций. Предель-
Предельные логики представляют собой счетные замкну-
замкнутые классы функций М. л. Р^ , содержащие гомоморф-
гомоморфные прообразы всех коночнозначных логик. Существует
континуум различных и даже конечно порожденных
попарно неизоморфных предельных логик. Установле-
Установлено, что в общем случае для предельных логик задача о
полноте но эквивалентна отысканию всех предполных
классов. Мощность множества предполных классов в
предельных логиках может быть равной любому нату-
натуральному числу, а также быть счетной или континуаль-
континуальной (см. [15]). Для М. л. непрерывных функ-
функций показана полнота всех двуместных функций и
получены нек-рые аналоги теоремы о полноте систем,
состоящих из всех одноместных и многоместной функ-
функций. Установлено также, что всякую непрерывную
функцию можно представить в виде суммы специально
выбранных непрерывных одноместных функций. Пока-
Показано, что для к раз дифференцируемых функций от п
переменных, вообще говоря, невозможно представле-
представление их с помощью суперпозиций функций той же глад-
гладкости но зависящих от меньшего числа переменных
(см. [16]).
К М. л. могут быть отнесены также и такие алгебры
функций, в к-рых запас операций несколько отличается
от описанного выше. Таковы алгебры неоднородных
конечнозначных функций (их аргументы принимают
конечное число значений из своих областей), рекурсив-
рекурсивных и частично-рекурсивных функций, алгебры авто-
автоматных отображений и ряд других.
Лит.: [1] Яблонский СВ., Г а в р и л о в Г. П.,
Кудрявцев В. В., Функции алгебры логики и классы
Поста, М., 1966; [2] Л у пан о в О. Б., «Проблемы киберне-
кибернетики», 1965, в. 14, с. 31 —110; [3] Журавлев Ю. И., «Проб-
«Проблемы кибернетики», 1962, в. 8, с. 5—IS; [4] Лин дон P. K-,
«Кибернетич. сб.», 1960, в. 1, с. 234—45; [5] М у р с к и й В. Л-,
«Докл. АН СССР», 1965, т. 163, № 4, с. 815 — 18: [6] Ян он Ю. И.,
Мучник А. А., «Докл. АН СССР), 19М1, т. 127,Л- 1. с. 44 —
46; [7J R о s e n b е г g J., Ober die ftinktionale Vollstandigkeit
mdenmehrwertigen Logiken, Praha, 1У70-. [8]3 a x a p о в а Е. Ю.,
Кудрявцев В. В., Яблонский С. В., «Докл. АН
СССР», 1969, т. 186, № 3, с. 509—12; [(•] Я б л о н с к и й С. В.,
«Тр. Матем. ин-та АН СССР», 1958, т. 51, с. 5—142; [10] С а л о-
м а а А., «КиРернетич. сб. », 1964, в. 8, с. 7—32; [11] Кудряв-
ц е в В Б. «Elektronische Informatkmsverarbeitung und Ку-
bernetik» (EIK), 1973, Bd 9, Hft 1/2, S. «1 — 105; [12] Алек-
Алексеев В. В., «Дискретный анализ», 1971, Л» 19, с. 3—10; [13]
Мальцев А. И., «Алгебра и логика», 1966, т. 5, в. 2, с.
5—24; [14] Г а в р и л о в Г. П., «Проблемы кибернетики», 196»,
в. 15, с. 5—64; [151 Де метров и ч Я., «Проблемы киберне-
кибернетики», 1975, в. 30, с. 5—42; [16] Витушкин А. Г., в кн.:
Тр, Международного конгресса математиков, М., 1968, с. 322—
28. В. Б. Кудрявцев.
МНОГОЗНАЧНАЯ ФУНКЦИЯ — функция f, края
ставит в соответствие каждому элементу х?Х нек-ров
подмножество f (х) множества У : f(x)czYz причем су-
существует хотя бы одно y?Y, состоящее не менее чем
из двух элементов. См. также Многозначное отобра-
отображение. -Т. Д- Кудрявцев.
МНОГОЗНАЧНОЕ ОТОБРАЖЕНИЕ, точечно-
множественное отображение,— отоб-
отображение Г: X —>- У, ставящее в соответствие каждому
элементу х множества X нек-рое подмножество Г (.г)
множества У. Если для каждого х?Х множество Г (.г)
состоит из одного элемента, то отображение Г наз.
однозначным. М. о. Г можно трактовать как
однозначное отображение X в 2Y, т. е. во множество
всех подмножеств множества У.
Для двух М. о. Г; : X -> У, г=1,2, естественным об-
образом определяется включение Г^сГ,, если
Г1(х)сГ2(х) для всех х?Х. Для любого семейства М. о.
Га : X —>- У, а ? А, определяется объединение
и пересечение: Т=1\аеДТа, еслп Т(х)~
= Ua€AVa-(^) Для всех х?Х, иГ=Па6>!Га, если Г(ж) =
= Па€,,}Га (ж) для всех х?Х. Для любого семейства
М. о. Г« : X -> Ya, а ?А , М. о. Г= Ца е А Та : А'-^Га 6
?AYa наз. декартовым произведением
М. о. Га, если Г(ж)= ДаедГа(^). Сечением М. о.
Г наз. такое однозначное отображение / : X —>- У, что
/(жN Г (х) для всех г^Х. Графиком М. о. Г наз.
множество G(T)={(x, у)?ХХ У : у? Г(х)}.
М. о. Г топологич. пространства X в топологич.
пространство У наз. полунепрерывным
сверху, если для всякого открытого множества
U а У множество Г + (м)= {х?Х : Т (х)с: U, Г(х)ф0}
открыто в X, или эквивалентно: для любой точки х?Х
II любой окрестности U множества Г (л:) найдется окрест-
окрестность Ох точки х такая, что T@x)czU, если Г@х) =
= U{^(!/); У^Ох}. М. о. Г топологич. пространства X
в топологнч. пространство У наз. полунепре-
полунепрерывным снизу, если для любого открытого мно-
множества UczY множество T~(U)= {х^Х : Г(х){]иф0)
открыто в X. Если для М. о. Г выполнены оба свойства
одновременно, то оно наз. непрерывным М. о.
Пусть У — топологич. векторное пространство. М. о.
Г : X —у У на;;, выпукло компактнознач-
н ы м, если Г (.г) является выпуклым компактом для
всех х?Х. Для конечного множества М. о. Г; : X —>- У,
??/, определяется алгебранч. С5'мма Г=^.16/Г?С по-
помощью равенства: Г(ж) = ^?б /Т( (х). Пересечение лю-
любого (конечного) семейства полунепрерывных сверху
(непрерывных) М. о. является полунепрерывным свер-
сверху (непрерывным) отображением. Декартово произве-
произведение конечного семейства полунепрерывных сверху
М. о. является полунепрерывным сверху отображени-
отображением. Алгебраич. сумма конечного семейства полунепре-
полунепрерывных сверху (выпукло компактнозначных) отображе-
отображений является полунепрерывным сверху (выпукло ком-
компактнозначным). Пересечение и декартово произведе-
произведение любого семейства выпукло компактнозначиых ото-
отображений является выпукло компактнозначным. Пусть
X — паракомпактное пространство и У — метрич. ли-
линейное локально выпуклое пространство.
Пусть Г: X -> У — М. о., являющееся полунепре-
полунепрерывным сверху и таким, что множество Г (х) замкнуто
в У для каждого х?А'. Тогда М. о. Г допускает непре-
непрерывное сечение. Пусть (X, 21) и (У, ?5) — пространства
с заданными на них а-алгебрами Щ и 5?; М. о. Г:
(X, 2t) —>- (У, 23) наз. измеримы м, если график
G(F) принадлежит наименьшей а-алгебре 2(Х5В произ-
произведения XXY, содержащей все множества вида ЛХВ,
если А ?2С и В ?85. Если Г — измеримое М. о. прост-
пространства (X, 2С) в полное сепарабельное метрич. прост-
пространство (У, **), причем 58 — борелевская сг-алгебра У,
то существует измеримое сечение / М. о. Г.
Лит.: [1] К у р а т о в с к и й К., Топология, пер. с англ.,
т. 1 — 2, М., 196В—69. Б. А. Ефимов.
МНОГОЗНАЧНОЕ ПРЕДСТАВЛЕНИЕ связной
топологической группы G — обычное
представление я такой связной топологич. группы С,
что группа G изоморфна (как топологич. группа) фак-
факторгруппе группы G' по ее дискретному нормальному
делителю N, к-рый не содержится в ядре представления
л. М.- п. наз. и-значным, если я (N) содержит в точ-
точности п элементов. Отождествлением элементов группы
G с элементами группы G'IN получается, что для мно-
множеств я(#), g?G=G' ;X, справедливы соотношения
я(е)Э1, я(?ь ?2)=я(г1)я(г2)> Si, g2??- Существование
М. п. связной локально линейно связной топологич.
группы G возможно лишь у веодносвязных групп. Важ-
Важнейший пример М. п.— спинорное представление ком-
комплексной ортогональной группы SO (и, С), п^&\ это
представление является двузначным представлением
группы SO (n, С) и определяется точным представле-
представлением универсальной накрывающей группы для SO
(", С).
Лит.: L1J Кириллов А. А., Элементы теории представ-
представлений, 2 изд., М., 1978: [2] Н а й м а р к М. А., Теория пред-
представлений групп, М., 1976. А. И. Штерн.
МНОГОЗНАЧНОЙ ЛОГИКИ ФУНКЦИИ — функ-
функции, совокупность к-рых вместе с соответствующими
операциями над ними образует многозначную логику.
М. л. ф., как и их аргументы, принимают в качестве
значений элементы одного и того же множества, состоя-
состоящего из констант многозначной логики.
В. Б. Кудрявцев.
МНОГОКРАТНАЯ РЕКУРСИЯ — вид рекурсии, в
к-рой участвуют сразу несколько переменных. Наборы
значений этих переменных упорядочиваются лексико-
лексикографически. Под это определение подходят многочис-
многочисленные конкретные рекурсивные описания. Если в та-
таком описании искомая функция не подставляется сама
в себя, то оно сводится к примитивной рекурсии. В об-
общем случае М. р. выводит за рамки примитивно рекур-
рекурсивных функций, т. к. посредством двукратной рекур-
рекурсии (ведущейся по двум переменным) можно построить
функцию, универсальную для примитивно рекурсивных
функций (аналогично, для fc-рекурсивиых функций су-
существует (&+1)-кратная универсальная функция). Все-
Всевозможные разновидности fc-кратной рекурсии можно
свести к следующей нормальной форме:
ф (п1, ..., nfc)=0, если «1-п2-...-71^ = 0,
ф (" 1 +1, ••-, »й + 1) = Р(л1, -.., пк, фь ..., щ),
где ф,- = ф((ге1_|_1) ..., nt-i+l, re,-,
y[l\(nu ...,nk, ф(ге1 + 1, ..., nk_1-\-i, nk)),
..., Yft-i («i, •-., nk, ф(лН-1. •••, «fc-i + l> «ft)))-
Лит.: [1] Петер Р., Рекурсивные функции, пер. с нем.,
М., 1954. Н. В. Белякин.
МНОГОКРИТЕРИАЛЬНАЯ ЗАДАЧА — математи-
математическая модель принятия оптимального решения одно-
одновременно по нескольким критериям. Эти критерии могут
отражать оценки различных качеств объекта (или про-
процесса), по поводу к-рых принимается решение, или
оценки одной и топ же его характеристики, но с различ-
различных точек зрения. Теория М. з. относится к числу ма-
тематич. методов исследования операций.
Формально М. з. задается множеством X «допусти-
«допустимых решений» и набором целевых функций fu ... , fn
на X, принимающих действительные значения. Сущ-
Сущность М. з. состоит в нахождении оптимального ее ре-
решения, т. е. такого х?Х, к-рое в том или ином смысле
максимизирует значения всех функций /,-, г=1, ... , п.
Существование решения, буквально максимизирующе-
максимизирующего все целевые функции, является редким исключением.
Поэтому в теории М. з. понятие оптимальности полу-
получает различные и притом нетривиальные истолкования.
Содержание теории М. з. состоит в выработке таких
концепций оптимальности, доказательстве их реали-
реализуемости (т. е. существования оптимальных в соответст-
соответствующем смысле решений) и нахождении этих реализа-
реализаций (т. е. в фактич. решении задачи).
Наиболее прямолинейным подходом к решению М. :i.
является сведенце ее к обычной («однокритериальной»)
задаче математич. программирования путем замены си-
системы целевых функций Д,..., /„ на одну «сводную»
функцию F{f\, ..., /„). В ее роли могут выступать
«взвешенные суммы» 2"=1Л//м ^/^0, «взвешенные мак-
максимумы» max ktfi и др. «свертки» исходных целевых
функций. Такой подход концептуально и технически
представляется самым удобным. Основным его недо-
недостатком является трудно выполнимое требование со-
содержательной сопоставимости значений различных це-
целевых функций, а также неопределенность (и нередко
произвольность) в выборе функции F и, в частности,
«весов» %[. Для их установления нередко рекомендуется
прибегать к экспертным оценкам.
Частный случай описанного подхода состоит в выде-
выделении «решающего критерия», т. е. в том, чтобы все
веса %i, за исключением нек-рого А,,о, полагать равными
нулю. Тогда М. з. перейдет в обычную задачу матема-
математич. программирования, а множество ее оптимальных
решений можно рассматривать как множество допусти-
допустимых решений новой М. з. с целевыми функциями /,,
В качестве решений М. з. можно рассматривать ре-
решения, оптимальные по Парето, т.е.
решения, не поддающиеся улучшению по какому-либо
критерию, иначе как за счет ухудшения по другим кри-
критериям (иначе говоря, такие х ? X, что для любого у ? X
из fi(x)<fi(y) следует f/(y)<f/(x) при нек-ром /). Недо-
Недостатком этого подхода является множественность опти-
оптимальных по Парето решений. Этот недостаток преодо-
преодолевается предложенным Дж. Нэшем (J. Nasli) методом
«арбитражных решений», существенно ограничиваю-
ограничивающим число выбираемых решений среди оптимальных
по Парето. Он состоит в установлении на основании
содержательных соображений нек-рых минимальных
допустимых значений /? и в последующем нахождении до-
допустимого х, максимизирующего JJ" (//(ж) — /?)
(см. также Арбитражная схема).
М. з. можно рассматривать как игру (см. Игр теория)
и подходить к ее решению на основе различных теоре-
теоретико-игровых методов. Напр., если допустимое решение
х выбирается с целью максимизировать одну из целевых
функций /,, ... , /„, но какую именно — для принимаю-
принимающего решение субъекта неизвестно, то можно восполь-
воспользоваться Езвешенной суммой этих функций, взяв в ка-
качестве весов компоненты смешанной стратегии «приро-
«природы». Возможны трактовки М. з. как бескоалиционной
игры, в том числе с позиций кооперативной теории (см.
Кооперативная игра), и применения связанных с этим
принципов оптимальности.
Лит.: [11 Л ь ю с Р. Д,, Р a ft ф ф а X., Игры и решения,
пер. с англ., М., 1961. Н. Н. ВоюоСъев.
МНОГОЛИСТНАЯ ОБЛАСТЬ — область S рйма:ш-
вой поверхности Я, рассматриваемой как накрывающая
поверхность над плоскостью комплексного переменно-
переменного С, такая, что над каждой точкой ее проекции ВсС
расположены не менее двух точек S; ветвления точка Я
порядка к— 1 считается при этом за к точек. Напр.,
аналитнч. функция ш=г2 отображает взаимно одно-
значпо круг J9={z?C : |z|<l} на двулистную область
(двулистный круг) S={w?J{ : !И<1} римановой по-
поверхности Я этой функции; всюду, кроме начала коор-
координат, это отображение конформно.
Для аналнтич. функций многих комплексных пере-
переменных также возникают многолистные римановы об-
области над комплексным пространством С™.
Е. Д. Соломенцев.
МНОГОЛИСТНАЯ ФУНКЦИЯ — понятие, естест-
естественным образом обобщающее понятие однолистной
функции. Функция /(z), регулярная или мероморфная
в области D комплексной плоскости г, наз. р-л и с т-
н о й вй (р=1, 2, ...}, если она принимает в этой об-
области каждое свое значение не более р раз, т. е. если
число корней уравнения f(z) = w в области D при лю-
любом w не превосходит р. Геометрически это означает,
что над каждой точкой плоскости w лежит не более р
точек римановой поверхности, на к-рую функция w=
= /(z) отображает область D. При р=1 функция /(z)
является однолистной в области D.
Наряду с этим простейшим классом р-листных функ-
функций большую роль в теории М. ф. играют функции,
р-лнстные в нек-ром обобщенном смысле, <ф-листные
в среднем». Пусть функция / (z) регулярна или меро-
морфна в области D плоскости z, n(w) — число корней
уравнения f{z)=w в D и р — положительное число.
Функция / (z) наз. р-л и с т н о й в среднем по
окружности в D, если для всех Я >0 выполняет-
выполняется условие:
Геометрически это означает, что линейная мера дуг,
принадлежащих римановой поверхности, на к-рую
функция w=f(z) отображает область D, и проектирую-
проектирующихся в любую окружность \w\-R, не превосходит р
длин таких окружностей. Функция /(z) наз. р-л и с т-
ной в среднем по площади в D, если
для всех Я >0. Геометрически это означает, что площадь
проектирующейся в любой круг \w\<.R части римано-
еой поверхности, на к-рую функция w—f(z) отобража-
отображает область D, не превосходит р площадей таких кругов.
Из ятих определений следует, что функция, р-листная
в нек-рой области, является в ней и р-лнстной в сред-
нем по окружности, а функция, р-листная в среднем
по окружности, является р-листной в среднем по пло-
площади. Функция, р-листная в среднем, может оказаться
бесконечнолистной.
М. ф., как и однолистные, изучаются в различных
направлениях: с точки зрения характеристики искаже-
искажения области при ее отображениях этими функциями,
оценки коэффициентов рядов, представляющих эти
функции, и т. д. Они обладают многими экстремальны-
экстремальными свойствами, аналогичными экстремальным свойст-
свойствам однолистных функций. Напр., имеются следующие
обобщения на случай р-листных функций двух классич.
результатов теории однолистных функций — площадей
принципа и оценки второго коэффициента (см. Бибер-
баха гипотеза).
Если функция
F (?) =.Sl=1 а«?т + 2Г=0 !"" ' аР ^ °- I t I > 1. A)
р-листна и регулярна в области |?|>1, за исключением
полюса в точке ?= оо, то
Если функция
/ (z)^zP + ap + 1zP^+... C)
регулярна п р-листна в круге |;|<1, то
D)
Неравенства B) и D) не могут быть улучшены. Эти
два результата относятся к наиболее ранним основным
результатам теории р-листных функций. Неравенство
B) доказано также для функций вида A), р-листных в
среднем по площади в |?|>1, а неравенство D) — для
функций вида C), р-листных в среднем по площади в
11
Значительно продвинуть исследование класса р-лист-
р-листных функций позволило рассмотрение его как подклас-
подкласса функций, р-листных в среднем. Получены для р-лист-
р-листных функций и точные аналоги основных теорем иска-
искажения и покрытия, известных для однолистных функ-
функций (см. Искажения теоремы, Покрытия теоремы),
именно: для функций /(z) вица C), р-листных в сред-
среднем по окружности в круге \z\ <1, верны точные оценки:
функция f(z) принимает в Ы<1 каждое значение w с
\w\<.i,'ip ровно р раз (прямой аналог теоремы покры-
покрытия Кебе). Этим последним свойством обладают и функ-
функции f(z) вида C), р-листные в среднем по площади в
Ы<1. Для функций, р-листных в среднем по окруж-
окружности, получен ряд неулучшаемых результатов, харак-
характеризующих рост их коэффициентов. Так, для функции
вида
р-листной в среднем по окружности в круге |z|<),
>0 существует, и притом конечный, предел
a= lim (l — r)
при р>1/4. Всякий раз, когда получается оценка для
а, отсюда следует и соответствующая точная оценка
асимптотич. роста коэффициентов. В частности, если
/(z) имеет вид C), то последнее равенство принимает вид
lim _^LLr = _?_)
где а<1, за исключением того случая, когда /(z) =
= zP(i— ze^)~-P (9 — вещественно). Далее, для функ-
функций вида C), р-листных в среднем по окружности в кру-
круге |z|<l, получена точная оценка:
а для подкласса р-листньтх функций такого вида была
указана точная оценка н следующего коэффициента:
Два последних неравенства являются для М. ф. анало-
аналогами оценок |а3|«:3 и |я,|<:4, известных для однолист-
однолистных функций (см. Бибербаха гипотеза). Так как экс-
экстремальными функциями приведенных выше оценок
оказываются р-листные функции, то все эти результаты
не могут быть улучшены и в классе р-листных функций.
Для функций вида E;, р-листных в среднем по пло-
площади в круге Ы<1, известны следующие оценки их ко-
коэффициентов для всех п~^\:
\а„\< A(p)iipn2P-1 (p > 1/4), F)
\а„\ < А\ао\п-%>- log(n + l) (p = l/4), G)
), (8)
K + i !-| *п II < А (р) у,рП?Р-г (Р5з 1) .(9)
и оценка
max|/(z)| < А (р) ц A — г)~*Р @ < г < 1): A0)
здесь А (р) зависит только от р, ц„=тах |av|. Порядок
величин в F), (9) и A0) не может быть улучшен.
Имеется также следующий аналог для М. ф. теоре-
теоремы, известной для однолистных мероморфных функций:
в классе всех функций
^@ ^(i + +
р-листных п регулярных в области |?|>1, за исключе-
исключением полюса в ?=оо, имеющих в фиксированной точке
'С,„фсо этой области разложение
областью значений функционала
w=log[F
является круг
|u;|<-plogfl—
Кроме указанных выше основных классов М. ф.,
значительное место в исследованиях занимают более
специальные классы М. ф., напр, функции типично ве-
вещественные порядка р, р-лпетно звездные, р-лпетно
выпуклые, р-лпетно близкие к выпуклым, ограничен-
ограниченные р-листные н др., являющиеся обобщениями соответ-
соответственно типично вещественных функций, звездообразных
функций, выпуклых функции, близких к выпуклым, ог-
ограниченных однолистных и других функций.
Функция
наз. типично вещественной порядка
р в круге |z|<l, если она регулярна в нем, имеет ве-
вещественные коэффициенты а,, и обладает свойством:
существует такое число 6 = 6 ('/), 0<6<1, что для вся-
всякого г из промежутка 1—б<г<1 мнимая часть Im {/(z)}
меняет своп знак на окружности |z| = r точно 2р раз.
При атом /(z) может быть более чем р-листной в |z|<l.
Для коэффициентов такой функции имеет место точная
оценка:
, . ,р.
(p + h)! (n-p-1)! ' к l? v "'
n > p.
Одним из аналогов гипотезы Бибербаха для функций
вида A1), регулярных и р-листных в круге | z | < 1,
является гипотеза Гуд мена о справедливости
для их коэффициентов а„ неравенства A2). В частности,
эта гипотеза Гудмена верна для р-листных типично ве-
вещественных функций порядка р в \z\ <1. Доказано, что
она верна также для одного из классов р-листных
функций, являющегося обобщением класса однолист-
однолистных функций, выпуклых в направлении мнимой оси.
Другим аналогом гипотезы Бтгбербаха для р-листных
функций является следующая г и п о т с а а Г у д-
м е н а. Пусть функция
регулярна и р-листна, р—1, 2, ... , в круге \z\<Cl, n
пусть она имеет t нулей аь ... , а^ в области 0<|z|<i,
t<.p—q. Гипотеза состоит в том, что |а„|<В„, п></, где
Вп — коэффициенты разложения
Для типично вещественных функций порядка р в |z|<l
это неравенство доказано.
Классы р-л и с т н о звездных и р-л и с т н о
выпуклых функций, соответственно S (р) и С (р),
определяются следующим образом. Функция f(z) при-
принадлежит классу S (р) (р — 1, 2, ...), если она регулярна
в круге \z\ <1, /@) = 0 и если существует такое число р,
0<р<1, что
Re fz-?J^l)
2рп, 0 = arg z
для p<|z|<l. Функция f(z) принадлежит классу С(p^
(р=1, 2, ...), если она регулярна в круге |z|<l, /@) = ()
и если существует такое р, что
=2№ e=argz
для p<|z|<l. Для функций этих двух классов получен
ряд точных оценок.
Классы S (р) и С (р) оказываются подклассами более
широкого класса р-листных функций — функций р-ли-
стно близких к выпуклым. Функция
<*>=!¦„": I-»*"-
регулярная в круге \z\ <i, наз. р-л и с т н о б л и я-
кой к выпуклой, если она удовлетворяет одно-
одному из следующих условий:
(А) существуют функция / (z) ?S(p) и число р, 0<р<1,
такие, что
Re X7W2 } > 0 (р < 1 г I < 1), A3)
(Б) F(z) регулярна на |z| = l и существует функция
f(z)(:S(p), также регулярная на |z| = l, такая, что яа
|z| = l выполняется неравенство A3). Для функций
F(z) этого класса найдены точные оценки снизу и сверху
\F'(z)\ и доказана справедливость неравенства A2) —
при д=р+1 для всех функций этого класса и при всех
"s3=P + l для его функций с вещественными коэффи-
коэффициентами. Точные оценки, обобщающие нек-рые ре-
результаты для ограниченных однолистных функций,
получены и для ограниченных функций, р-листных в
соответствующем обобщенном смысле. Так, был найден
радиус р-л истности в классе регулярных и
ограниченных в круге функций, именно: если функция
f (z) регулярна и ограничена по модулю единицей в
круге |z|<l, нормирована условиями /@) = 0, /'@)=а1,
0<|а1| <1, то радиус р наибольшего круга |z|<p, в
к-ром она р-листна, определяется из уравнения
Эта теорема обобщает на случай р>1 теорему
Ландау о радиусе однолистности
функций, регулярных и ограниченных в круге |z|<l.
Известны различные достаточные условия для того,
чтобы функция, регулярная в области, была в ней
р-лиетной. Напр., если f(z) регулярна в выпуклой
области D и существуют такое вещественное 0 и такое
целое к, 0<&<р—1, что
то f (z) р-листна в D.
М. ф. исследуются также и в многосвязных областях.
Многие оценки здесь выражаются через функции, отоб-
отображающие данную мрогосвязн\ю область на канониче-
канонические римановы поверхности, и через Бергмана керп-
функцию. Первым основным результатом, относящимся
к вопросу существования конформных отображений
многосвязной • области на многолнстные канонич. по-
поверхности, явилась следующая теорема Г р у н-
с к о г о: пусть D — конечносвязная область плоско-
плоскости z с внутренней точкой z= oo и с отличными от точек
граничными компонентами и Qp(z) — любой заданный
полином степени р, р^1; тогда для любого заданного 0,
0<:6<я, существует единственная функция fl>e(z), ре-
регулярная в области D, за исключением полюса в z=<x>,
главная часть к-рой в z= oo (с включением в нее свобод-
свободного члена) совпадает с Qp(z) и к-рая ставит в соответ-
соответствие каждой граничной компоненте области D прямо-
прямолинейный отрезок наклона 8 к вещественной оси. Иначе
говоря, функция и;=Фе (z) отображает область D на
полную р-листную плоскость w с параллельными раз-
разрезами наклона 6. Доказано существование конформ-
конформных отображений данной конечносвязной области и на
другие канонические многолистные поверхности; уста-
установлены экстремальные свойства М. ф., аналогичные
нок-рым. экстремальным свойствам однолистных функ-
функций. Выявлен просто характеризуемый геометрически
наиболее общий класс М. ф., мероморфных в конечно-
конечносвязной области, для к-рых верна теорема площадей.
Основными методами исследования М. ф. являются:
контурного интегрирования метод, симметризации
метод, метод квадратичных дифференциалов.
Вариационный метод в теории М. ф. менее эффекти-
эффективен, чем в теории однолистных функций.
Лит.: [1] Г о л У з и н Г. М., «Матем. сб.», 1940, т. 8, в. 2,
с. 277—83; [2J X е й м а н В. К., Многолистные функции, пер.
с англ., М., 1960; [3] Д ж е н к и н с Дж., Однолистные функции
и конформные отображения, пер. с англ., М., 1962: [41 Pet"
he К., «Bull. Acad. Polon. Sci.», HO2, v. 20, Л° 3, p. 219 — 20;
[5] Livingston A. E., «Trans, Aincr. Math. Soc», 19tio,
v. 115, Ms 3 p. 161— 79; [6] L e а с h R. J., «Pacific J. Math.»,
1978, v. 74, Ms 1 p. 133—42; [7] К г z у z J., «Ann. Univ. Ma-
riae Curie-Sklodowska. Sec. A», 1958, v. 12, M» 2, p. 23—28, MS 3,
p. 29—38; [8] О z a k i S., «Sci. Rep. Tokio Bunrika Daigaku»,
A, 1935, v. 2, Л» 40, p. 167 — 88; [Я] А л е н и ц ы н Ю.Е-,
«Изв. АН СССР. Сер. матем.», 1973, т. 37, № 5, с. 1132 — 54;
[10] S ingh S. К., «Math. Student», 1962, v. 30, JVi 1—2,
p. 79—90; [11] Goodman A. W., «Bull. Amer. Math. Soc»,
1968, v. 74 Л» 6 p. 1035 — 50. Ю. Е. АлеиицыН.
МНОГОМЕРНАЯ ВАРИАЦИОННАЯ ЗАДАЧА, в а-
р и ац ионная задача с частными про-
и з в одним и,— задача вариационного исчисления,
в к-рой требуется определить экстремум функционала,
зависящего от функций многих независимых перемен-
переменных. Обычные вариационные задачи, в к-рых рассмат-
рассматриваются функционалы от функций одной независимой
переменной, можно назвать в этом смысле одномерны-
одномерными вариационными задачами.
Примером двумерной вариационной
задачи может служить задача, в к-рой требуется
определить функцию двух независимых переменных
и(х, у), непрерывную вместе со своими частными про-
производными 1-го порядка, доставляющую экстремум
функционалу
I (и) = \ \ D F (x, у, и, ux, uu) dx dy A)
при граничном условии
u(x, y)U = uo(x, у), B)
где I — замкнутый контур, ограничивающий область D
ио(х, У) — заданная функция, F (.г, у, и, их, иу) — дваж-
дважды непрерывно дифференцируемая функция по совокуп-
совокупности своих аргументов. Пусть и(х, у) есть решение за-
задачи A), B). Подстановка функций сравнения и (х, у)-\-
-\-ал\(х, у), где ц (х, i/)!j=0, a — числовой параметр, в
функционал A), дифференцирование по а и приравни-
приравнивание а=0 позволяет получить следующее выражение
для первой вариации функционала
oJ = \ \ (^иЦ-\-Ри "Пж + ^ы r\1i)^xdy. C)
Если и(х, у) имеет непрерывные производные 2-го по-
порядка, то легко показать, что необходимым условием
равенства нулю первой вариации 61 является выполне-
выполнение условия
FFF 0 <4'
Уравнение D) наз. уравнением Эйлера —
Остроградского (иногда — уравнением
Остроградского). Этому уравнению должна
удовлетворять функция м(.г, у), доставляющая экстре-
экстремум функционалу A) при граничных условиях B).
Уравнение Эйлера — Остроградского является анало-
аналогом уравнения Эйлера для одномерных вариационных
задач. В развернутом виде D) представляет собой урав-
уравнение с частными производными 2-го порядка.
В случае тройного интеграла и функции и (г, у, z),
зависящей от трех независимых переменных, уравнение
Эйлера — Остроградского принимает вид:
Следующее условие является аналогом Лежандра
условия. Для того чтобы функция и (х, у) доставляла
хотя бы слабый экстремум функционалу A), необходи-
необходимо, чтобы в каждой внутренней точке области D выпол-
выполнялось условие
F f F2 >о
Для минимума необходимо Fu u ^0, а для максимума
X X
Рассматриваются также разрывные М. в. з. (см. [4]).
Лит.: [1] К у р а н т Р., Гильберт Д., Методы матема-
математической физики, пер. с нем., 2 изд., т. 2, М.— Л., 1951; [2]
Смирнов В. И., Курс высшей математики, 5 изд., т. 4, М.,
1958; [3] А х и е з е р Н. И., Лекции по вариационному исчис-
исчислению, М., 1955; [4] К е р и м о в М. К., «Тр. Тбилисск. матем.
ин-та АН Груз. ССР», 1951, т. 18, с. 209 — 19.
И. Б. Вап}сярский.
МНОГОМЕРНАЯ ГЕОМЕТРИЯ — геометрия про-
пространств размерности, большей трех; термин приме-
применяется к тем пространствам, геометрия к-рых была пер-
первоначально развита для случая трех измерений и только
потом обобщена на число измерений ге>3, прежде всего
евклидово пространство, а также пространства Лоба-
Лобачевского, Римана, проективное, аффинное, псевдо-
псевдоевклидово. (Общие же римановы и др. пространства
были определены сразу для п измерений.) В настоящее
время разделение трехмерной и многомерной геометрий
имеет главным образом историческое и педагогич. зна-
значение, т. к. задачи ставятся и решаются для любого чис-
числа измерений, когда и поскольку это осмысленно.
Построение геометрии указанных пространств для п
измерений проводится по аналогии со случаем трех из-
измерений. При этом можно исходить из обобщения не-
непосредственно геометрич. оснований трехмерной гео-
геометрии, из той или иной системы ее аксиом или из
обобщения аналитич. геометрии, перенося ее основные
выводы со случая трех координат на произвольное п.
Именно так и начиналось построение re-мерной евкли-
евклидовой геометрии.
Исторически представление о более чем трехмерном
пространстве зарождалось постепенно, первоначально
на почве геометрич. представления степеней: а2 —
«квадрат», а3 — «куб», но а4 и т. д. уже не имеет нагляд-
наглядного представления, и говорили о4 — «биквадрат»,
а" — «кубо-квадрат» и т. д. (еще у Диофанта в 3 в.
и далее у ряда средневековых авторов). Мысль о много-
многомерном пространстве выражал И. Кант (I. Kant, 1746),
а о присоединении к пространству времени в качестве
4-й координаты писал Ж. Д'Аламбер (J. D'Alembert,
1764). Построение же re-мерной геометрии было осущест-
осуществлено А. Кэли (A. Cayley, 1843), Г. Грассманом
(Н. Grassmann, 1844) и Л. Шлефли (L. Schlatli, 1852).
Первоначальные сомнения и мистика, связанные со
смешением этих обобщений с физич. пространством, бы-
были преодолены, и re-мерное пространство как плодот-
плодотворное формально-математич. понятие скоро полностью
укрепилось в математике.
Евклидово пространство произвольного числа из-
измерений ге^З (не исключая случая бесконечномерного)
проще всего определить как такое, в к-ром выделены
подмножества — прямые и плоскости, имеются обыч-
обычные отношения: принадлежности, порядка, конгруэнт-
конгруэнтности (или определены расстояния, или движения) и
выполняются все обычные аксиомы, кроме следующей:
две плоскости, имеющие общую точку, имеют по край-
крайней мере еще одну. Если это выполнено, то пространст-
пространство трехмерно, если же не выполнено, так что есть две
плоскости с единственной общей точкой, то простран-
пространство, как минимум, четырехмерно.
Понятие плоскости обобщается следующим образом:
плоскостью наз. такое множество точек, к-рое вместе
с любыми двумя своими точками содержит и проходя-
проходящую через них прямую. В этом смысле все пространство
тоже является плоскостью. Пересечение всех плоско-
плоскостей, содержащих данное множество точек М, будет
плоскостью, «натянутой на М» (аффинной оболочкой
М). Если плоскость натягивается на то+1 точку, но
не натягивается на меньшее их число, то она наз.
в-мерно й, или, короче, га-плоскостью.
Точка есть 0-плоскость, прямая — 1-плоскость, обыч-
обычная плоскость — 2-плоскость, трехмерное пространст-
пространство — 3-плоскость. Пространство наз. га-мерным, если
оно является re-плоскостью. То есть, для определения
n-мерного евклидова пространства Еп при любом дан-
данном ге^гЗ достаточно добавить аксиому: пространство'
есть re-плоскость. В нем есть m-плоскости с 0<:т<:га—1.
Каждая го-плоскость с т'^2 является го-мерным евкли-
евклидовым пространством Ет. Так как 4 точки всегда содер-
содержатся в 3-плоскости, то и любые две прямые содержат-
содержатся в 3-плоскости, т. е. в Е3.
В Еп через любую точку можно провести п, и не бо-
более, взаимно перпендикулярных прямых и ввести со-
соответственно прямоугольные координаты хг, ... , хп\
в них длина любого отрезка XY выражается формулой
XY=V{x1-y1)*+...-\-(xn-yn)*. (*)
Формулу (*) можно положить в основу координатного
определения Еп, равносильного предыдущему. Именно:
Еп есть такое множество, в к-ром введены координаты
хи ... , хп (принимающие все возможные значения)
и каждой паре точек X (хъ ... , ,г„), Y(yt, ... , уп) со-
сопоставляется число — «расстояние» формулой (*); при
этом к геометрии Еп относятся те и только те определе-
определения и утверждения, к-рые могут быть формулированы
через отношения расстояний. Напр., отрезок А В есть
множество всех точек X, для к-рых АХ+ХВ=АВ, а
прямая АВ — всех тех X, для к-рых ±.4Х±ХВ — АВ.
Векторное исчисление строится в Еп так же, как в Е3
(исходя из геометрических или координатных опреде-
определений); разница лишь в том, что в Еп вектор имеет га
составляющих (соответственно п векторов могут быть,
независимыми). Напр., скалярное произведение:
(а,Ь) = \a\\b\ cosa = 2 aibi-
Только векторное произведение при ге>3 не может
быть определено, т. к. 2-плоскость имеет перпендику-
перпендикуляры разных направлений (проведенные из одной точки
они заполняют (п—2)-плоскость). Вместо векторного
произведения пользуются понятием бивектора. Сочета-
Сочетание непосредственно геометрических, координатных
и векторных методов дает наиболее полный арсенал
средств развития геометрии Еп. Геомстрич. подход
позволяет сразу перенести в Еп планиметрию и стерео-
стереометрию, т. е. геометрию на 2- и 3-илоскостях, и далее
построить стереометрию самого Еп, к-рая естественно
обобщает стереометрию Е3: теорема о перпендикуля-
перпендикулярах, параллельных плоскостях и др. Напр., прямая,
перпендикулярная го прямым в го-плоскости, перпен-
перпендикулярна ко всякой прямой в ней. Многие определе-
определения и доказательства даются для Еп индукцией по п.
Напр., re-мерный многогранник, или ге-многогранник,
есть тело (замкнутая ограниченная область в Еп),
граница к-рого состоит из конечного числа (п — 1)-мно-
гогранников. Простейшие многогранники: призма за-
заполняется равными параллельными отрезками, прове-
проведенными из всех точек (ге—1)-многогранника, пирами-
пирамида — отрезками, проведенными из одной точки во все
точки (и—1)-многогранника; простейшие из них:
ге-куб — прямая призма, грани к-рой суть (га—1)-кубы
B-кубы — квадрат); re-симплекс с (ге—1)-симплексом
в основании B-симплекс — треугольник). Объем опре-
определяется так же, как в Е3, соответственно в Еп имеется
п объемов: 1-объем — длина, 2-объем — площадь и
т. д. У призмы n-объем V=Sh, у пирамиды F= — Sh,
где S есть (га—1)-объем основания, h — высота. Обшир-
Обширную и развитую область геометрии Еп представляет
теория выпуклых тел.
Можно различать три рода фактов М. г.: 1) те, к-рые-
являются прямым обобщением фактов из Е3 (напр.,.
только что приведенные теоремы об объемах); 2) те,.
к-рым соответствуют аналогичные факты для разных
размерностей т^п (напр., выпуклое тело с центром
симметрии однозначно определяется m-объемами своих
m-мерных проекций при любом данном mjsl и т<Сп);
3) те, в к-рых обнаруживаются существенные различия
в разных Еп (напр., число правильных многогранников
в ?'з = 5, в ?4=7, в Еп при nj>5 их всего 3: симплекс,
куб и двойственный кубу аналог октаэдра; другой при-
мер: выпуклый многогранный (не трехгранный) угол в
Е3 изгибаем, в Еп при ;г>3 всегда неизгибаем; сущест-
существенно различаются теории поверхностей в Е3 и в Еп
¦с п>3).
Совершенно аналогично Еп определяются простран-
пространство Лобачевского Ап и аффинное пространство Ап.
В пространстве Ап выполняются все те ?ке аксиомы, что
в Еп, с заменой аксиомы параллельности на противо-
противоположную, а в Ап — все аксиомы Еп за вычетом аксиом
конгруэнтности, вместе с чем исключается и само поня-
понятие конгруэнтности. Аналогично, изменением аксиом
•сочетания можно определить re-мерное проективное,
пространство Рп. Другой способ определения всех этих
пространств состоит в том, что в них вводятся коорди-
координаты, задается группа их преобразований и геометри-
геометрическими считаются те и только те соотношения, к-рые
инвариантны относительно этой группы. В случае Еп —
это группа подобий (сочетания ортогональных преоб-
преобразовании, переносов и умножений всех координат на
число =7^=0); для Ап — это группа всех линейных (неод-
(неоднородных) преобразований; см. также Проективная
геометрия, Лобачевского геометрия.
Псевдоевклидовы пространства можно определить
в координатах: Е'п~т есть множество, в к-ром введены
координаты хх, ... , хп и «интервалы» между точками
X, Y:
(Хх — У\)-+ ¦¦¦ + (^т — УтJ —
— (*/я-1— Ут-lJ— •¦•— (хп — УпJ\
геометрическими считаются определения и утвержде-
утверждения, формулируемые через отношения интервалов;
пначе — те, к-рые инвариантны относительно группы
преобразований, сохраняющих отношения интервалов.
В частной теории относительности пространство-время
определится как Е\: в нем интервалы
где t — время, .г, у, z — пространственные координаты
в данной системе отсчета и c=const — скорость света.
А. Д. Александров,
МНОГОМЕРНОЕ РАСПРЕДЕЛЕНИЕ — распределе-
распределение вероятностей на сг-алгебре борелевских множеств
.s-мерного евклидова пространства Rs. О М. р. обычно
говорят как о распределении многомерной случайной
величины или случайного вектора Х=(Х1, ... , Xs),
понимая под этим совместное распределение действи-
действительных случайных величин Х1(ш), ... , Xs(a>), заданных
на одном и том же пространстве элементарных событий
Q (можно рассматривать Хъ ... ,XS как координатные
величины в пространстве Q=RJ). M. р. однозначно
определяется функцией распределения —•
¦функцией
F (*!, ..., xs) = P{X1<x1, ..., Xs < xs}
действительных переменных хг, ... , xs.
Так же, как и в одномерном случае, наиболее распро-
распространенными М. р. являются дискретные и абсолютно
непрерывные распределения. В дискретном случае
\1. р. сосредоточено на конечном или счетном множест-
ие точек (х; , ... , а;,-,) пространства Rs, так что
(см., напр., Полиномиальное распределение). В абсолют-
абсолютно непрерывном случае почти всюду (по мере Лебега)
в R*
8SF (*. xs) , s
—dXl...dxs =P(-rl' ¦ ¦ ¦' **>'
где р(хи ...,i,)>0-iiioiHOtTb M. p.:
р(х1, ..., xs)dx1 ... dxs,
для любого А из а-алгебры борелевских множеств про-
пространства Rs и
\ р (xu ..., xs) dx1 . . . dxs=l.
Распределение любой случайной величины X,- (а
также при любом m<s распределение величин Х,^, ...,
X ¦ ) по отношению к М. р. наз. ч а с т н ы м,
или маргинальным распределением. Маргинальные рас-
распределения полностью определяются заданным М. р.
В том случае, когда величины Xlt ... , Xs независимы,
то
F (хг, ..., xs) = Fl(x1) ...Fs(xs)
и
р(хи . .., xs) = p1(xl) . .. ps(xs),
где Fj(x) и р;(х) соответственно маргинальные функции
распределения и плотности случайных величин X;.
Математич. ожидание любой функции /(Xj, ... , Xs)
от Xi, ... , Xs определяется интегралом от этой функ-
функции по М. р., в частности в абсолютно непрерывном
случае интегралом
j, . . ., xs) p (xlt ..., xs) dxx ... dxs.
Характеристич. функция М. р. есть функция вектора
t=(tu ... , ts), равная
где tx' = t1x1-j-...-Jrtsxs. Основными характеристиками
М. р. служат моменты: ЕХ[' . . .Xss — смешанные
моменты и Е(Х1—EXj)*1 . . .(Xs—EXs)ks — централь-
центральные смешанные моменты, где fej+. . .-\-ks — порядок
соответствующего момента. Роль математич. ожидания
и дисперсии для М. р. выполняют вектор ЕХ=(ЕХ1,
... , EXS) и совокупность центральных смешанных
моментов 2-го порядка, образующих ковариационную
матрицу. Если Е(Х,-—ЕХ,)(Ху—ЕХу) = О при всех
i, j, ъф], то случайные величины Xj, ... , Xs наз. попар-
попарно некоррелированными (ковариационная матрица диа-
гональна). Если ранг г ковариационной матрицы мень-
меньше s, то М. р. наз. вырожденным распределением', в этом
случае М. р. сосредоточено на нек-ром линейном мно-
многообразии в Rs размерности г.
О методах исследования зависимости между Хг, ...,
Xs см. статьи Корреляция, Регрессия. А. В. Прохоров.
МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ —
раздел математич. статистики, посвященный математич.
методам построения оптимальных планов сбора, систе-
систематизации л обработки многомерных статистич. данных,
направленным на выявление характера и структуры вза-
взаимосвязей между компонентами исследуемого много-
многомерного признака и предназначенным для получения
научных и практич. выводов. Под многомерным
признаком понимается р-мерный вектор ж=(х1,
... , Хр) показателей (признаков, переменных) хи ... , хр,
среди к-рых могут быть: количественные,
т. е. скалярно измеряющие в определенной шкале сте-
степень проявления изучаемого свойства объекта, п о-
рядковые (или о р д и н а л ь н ы е), т. е. позво-
позволяющие упорядочивать анализируемые объекты по
степени проявления в них изучаемого свойства; и
классификационные (или н о м и н а л ь-
н ы е), т. е. позволяющие разбивать исследуемую сово-
совокупность объектов на не поддающиеся упорядочиванию
однородные (по анализируемому свойству) классы. Ре-
Результаты измерения этих показателей
{*.,•}? = {(*i» Ъ:, •.., *pt)'}i A)
на каждом из и объектов исследуемой совокупности
образуют последовательность многомерных наблюде-
наблюдении, пли исходный массив многомерных данных для
проведения М. с. а. Значительная часть М. с. а. об-
обслуживает ситуации, в к-рых исследуемый многомер-
многомерный признак ж интерпретируется как многомерная
случайная величина и соответственно последователь-
последовательность многомерных наблюдений A) — как выборка из
генеральной совокупности. В этом случае выбор мето-
методов обработки исходных статпстич. данных и анализ их
свойств производится на основе тех или иных допуще-
допущении относительно природы многомерного (совместного)
закона распределения вероятностен Р (ж).
По содержанию М. с. а. может быть условно разбит
на три основных подраздела: М. с. а. многомерных рас-
распределений и их основных характеристик; М. с. а.
характера и структуры взаимосвязей между компонен-
компонентами исследуемого многомерного признака; М. с. а.
геометрич. структуры исследуемой совокупности много-
многомерных наблюдений.
Многомерный статистический анализ многомерных
распределений и их основных характеристик охматы-
вает лишь ситуации, в к-рых обрабатываемые наблю-
наблюдения A) имеют вероятностную природу, т. е. интерпре-
интерпретируются как выборка из соответствующей генеральной
совокупности. К основным задачам этого подраздела
относятся: статистич. оценивание исследуемых много-
многомерных распределений, их основных числовых харак-
характеристик и параметров; исследование свойств исполь-
используемых статистич. оценок; исследование распределений
вероятностей для ряда статистик, с помощью к-рых
строятся статистич. критерии проверки различных
гипотез о вероятностной природе анализируемых мно-
многомерных данных. Основные результаты относятся к
частному случаю, когда исследуемый признак ж подчи-
подчинен многомерному нормальному закону распределения
Np(fi% V), функция плотности к-рого /(ж|A, V) задается
соотношением
-X
Хехр /— ~(х — ц)' V-1(ac — ц)\ , B)
где fJi=(|Xi, ¦•¦ , РрУ — вектор математич. ожиданий
компонент случайной величины ж, т. е. \ii=Exh 1=
= 1,2,... , р, a F=(iu/y||^/=i — ковариационная мат-
матрица случайного вектора ж, т.е. i-vy" E (я<—|Д.;)(г/ —
— \ij) — ковариации компонент вектора ж (рассматри-
(рассматривается невырожденный случай, когда ранг V=p; в про-
противном случае, т. й. при ранге У=р' <р, все результаты
остаются справедливыми, но применительно к подпро-
подпространству меньшей размерности р', в к-рои оказывается
сосредоточенным распределение вероятностей исследуе-
исследуемого случайного вектора ас).
Так, если A) — последовательность независимых
наблюдений, образующих случайную выборку из
Лтр(ц, V), то оценками максимального правдоподобия
для параметров ц и V, участвующих в B), являются
соответственно статистики (см. [1], [2])
?=42-=1ж-<- C)
и
причем случайный вектор fx подчиняется р-мерному
нормальному закону Np(}i, — F) и не зависит от V, а
совместное распределение элементов матрицы (j=^nV~
описывается т. н. распределением У и ш а р-
т а (см. [4]), плотность к-рого
2(Л-1)р/2 яр(р-1)/4 , Fi*"-1)''2]^^ Г | 1^[
если Q — положительно определена;
О — в противном случае.
В рамках этой же схемы исследованы распределения
и моменты таких выборочных характеристик многомер-
многомерной случайной величины, как коэффициенты парной,
частной и множественной корреляции, обобщенная дис-
дисперсия (т. е. статистика \V\), обобщенная .^-статистике
Хотеллинга (см. [5]). В частности (см. [1]), если опреде-
определить в качестве выборочной ковариационной матрицы
Sn подправленную «на несмещенность» оценку V, а
именно:
то распределение случайной величины V~n(\Sn\ I \V\ — 1)
стремится к N±@,2p) при л -^ оо, а случайные величи-
величины
-^ . v^ 2 . . _^ и / ¦ ¦ ¦ ¦ t V * / i ¦ ¦¦) /i-il
p(n-l
2-Р~ I у- 2
2)р
С)
подчиняются /^-распределениям с числами степеней
свободы соответственно (р, п—р) и (р, Гс]4-и2—р — 1).
В соотношении G) щ и ге2 — объемы двух независимых
выборок вида A), извлеченных из одной н той же гене-
генеральной совокупности Np(n, У), рп , и Sn— оценки
вида C) и D)—C), построенные по i-й выборке, а
— общая выборочная ковариационная матрица, по-
построенная по оценкам Sni и S,,2.
Многомерный статистический анализ характера н
структуры взаимосвязей компонент исследуемого мно-
многомерного признака объединяет в себе понятия и ре-
результаты, обслуживающие такие методы и модели
М. с. а., как множественная регрессия, многомерный
дисперсионный анализ и ковариационный анализ, фак-
факторный анализ и метод главных компонент, анализ
канонич. корреляции. Результаты, составляющие со-
содержание этого подраздела, могут быть условно раз-
делены на два основных типа.
1) Построение наилучших (в определенном смысле)
статистич. оценок для параметров упомянутых моделей
и анализ их свойств (точности, а в вероятностной по-
постановке — законов их распределения, доверительных
областей и т. д.). Так, пусть исследуемый многомерный
признак ж интерпретируется как векторная случайная
величина, подчиненная р-мерному нормальному рас-
распределению Np(n, V), и расчленен на два подвектора-
столбца ?сA) и Я5B) размерности q и р—(/соответственно.
Это определяет и соответствующее расчленение вектора
математич. ожиданий ц, теоретической и выборочной
ковариационных матриц V и F, а именно:
Тогда (см. [1], [2]) условное распределение подвектора
жA) (при условии, что второй подвектор принял фикси-
фиксированное значение жB)) будет также нормальным
Лг(?(}1.11)-г.В(жB)—fiC)), 2j). При этом оценками макси-
максимального правдоподобия В и 2 для матриц регресси-
регрессионных коэффициентов В и ковариаций 2 этой класси-
классической многомерной модели множественной регрессии
(8)
взаимно независимые статистики соответственно
здесь распределение оценки В подчинено нормальному
закону Nq{p-q) (В, VB), а оценки п 2 — закону Уиншр-
та о параметрами 2 и п—(р—q) (элементы ковариацион-
ковариационной матрицы Vд выражаются в терминах элементов мат-
матрицы V).
Основные результаты по построению оценок пара-
параметров и исследованию их свойств в моделях факторно-
факторного" анализа, главных компонент и канонич. корреляций
относятся к анализу вероятностно-статистич. свойств
собственных (характеристических) значений и векторов
различных выборочных ковариационных матриц.
В схемах, не укладывающихся в рамки классич.
нормальной модели и тем более в рамки какой-либо
вероятностной модели, основные результаты относятся
к построению алгоритмов (и исследованию их свойств)
вычисления оценок параметров, наилучших с точки зре-
зрения нек-рого экзогенно заданного функционала каче-
качества (или адекватности) модели.
2) Построение статистич. критериев для проверки
различных гипотез о структуре исследуемых взаимо-
взаимосвязей. В рамках многомерной нормальной модели (по-
(последовательности наблюдений вида A) интерпретируют-
интерпретируются как случайные выборки из соответствующих много-
многомерных нормальных генеральных совокупностей) по-
построены, напр., статпстич. критерии для проверки
следующих гипотез.
I. Гипотезы fx = ja* о равенстве вектора математич.
ожиданий исследуемых показателей заданному конкрет-
конкретному вектору ц*; проверяется с помощью Г2-статистики
Хотеллинга с подстановкой в формулу F) (x=fi*.
II. Гипотезы fi.A' = fiB) о равенстве векторов матема-
математич. ожиданий в двух генеральных совокупностях (с
одинаковыми, но неизвестными ковариационными мат-
матрицами), представленных двумя выборками; проверя-
проверяется с помощью статистики f2 (см. [7]).
III. Гипотезы fi<1)=fi,<2>=... = fi,(ft>=fi о равенстве
векторов математич. ожиданий в нескольких генераль-
генеральных совокупностях (с одинаковыми, но неизвестными
ковариационными матрицами), представленных своими
^выборками; проверяется с помощью статистики
о, fc-i, n-k —"
в к-рой ж''* есть i-e р-мерное наблюдение в выборке
объема rij, представляющей у-ю генеральную совокуп-
совокупность, a jxU> и Д — оценки вида C), построенные соот-
соответственно отдельно по каждой из выборок и по объеди-
объединенной выборке объема n=n1-j-...-\-nll.
IV. Гипотезы fi<1> = fi*2' = ... = fi>ft) = fi и Vl=... = Vk=
= V об эквивалентности нескольких нормальных гене-
генеральных совокупностей, представленных своими выбор-
выборками {ж(:')}_{, /=1, 2, ... , к; проверяется с помощью
статистики
(п-к)/2
в к-рой V; — оценка вида D), построенная отдельно по
наблюдениям у'-й выборки, /=1, 2, ... , /с.
V. Гипотезы о взаимной независимости подвекторов-
столбцов аз*1), жB), ... , жш) размерностей соответствен-
соответственно Pi, P2, ¦¦¦ 1 Рт, на к-рые расчленен исходный р-мер-
ный вектор исследуемых показателей аг, Pi+P2+---~f"
-j-pm = p; проверяется с помощью статистики
в к-рой F и V; — выборочные ковариационные матри-
матрицы вида D) для всего вектора ж и для его подвектора
as*'* соответственно.
Многомерный статистический анализ геометрической
структуры исследуемой совокупности многомерных на-
наблюдений объединяет в себе понятия и результаты таких
моделей и схем, как дискриминантный анализ, смеси
вероятностных распределений, кластер-анализ и так-
таксономия, многомерное шкалирование. Узловым во
всех этих схемах является понятие расстояния (меры
близости, меры сходства) между анализируемыми эле-
элементами. При этом анализируемыми могут быть как
реальные объекты, на каждом из к-рых фиксируются
значения показателей х,— тогда геометрич. образом
i-ro обследованного объекта будет точка ж,1 = (х1/, ... ,
Хр()' в соответствующем р-мерном пространстве, так и
сами показатели ж(., l=i, 2, ... , р,— тогда геометрич.
образом Z-ro показателя будет точка ж1==(х[1, xi-2, ... ,
xin) в соответствующем и-мерном пространстве.
Методы н результаты дискриминантного анализа (см.
[1], [2], [7]) направлены на решение следующей задачи.
Известно о существовании определенного числа к^2
генеральных совокупностей и у исследователя имеется
по одной выборке из каждой совокупности («обучающие
выборки»). Требуется построить основанное на имею-
имеющихся обучающих выборках наилучшее в определенном
смысле классифицирующее правило, позволяющее при-
приписать нек-рый новый элемент (наблюдение ж) к своей
генеральной совокупности в ситуации, когда исследова-
исследователю заранее не известно, к какой из совокупностей
этот элемент принадлежит. Обычно под классифицирую-
классифицирующим правилом понимается последовательность дейст-
действий: по вычислению скалярной функции от исследуемых
показателей, по значениям к-рой принимается решение
об отнесении элемента к одному из классов (построение
дискриминантной функции); по упорядочению самих
показателей по степени их информативности с точки
зрения правильного отнесения элементов к классам;
по вычислению соответствующих вероятностей ошибоч-
ошибочной классификации.
Задача анализа смесей распределений вероятностей
(см. [7]) чаще всего (но не всегда) возникает такжр
в связи с исследованием «геометрической структуры»
рассматриваемой совокупности. При этом понятие г-го
однородного класса формализуется с помощью гене-
генеральной совокупности, описываемой нек-рым (как пра-
правило, унимодальным] законом распределения Р(л;\вг),
так что распределение общей генеральной совокупнос-
совокупности, из к-рой извлечена выборка A), описывается смесью
распределений вида
*
где пг — априорная вероятность (удельный вес элемен-
элементов) г-го класса в общей генеральной совокупности.
Задача состоит в «хорошем» статистич. оценивании (по
выборке {а?.,}^) неизвестных параметров 9Г, лг, а иног-
иногда и к. Это, в частности, позволяет свести задачу клас-
классификации элементов к схеме дискриминантного анали-
анализа, хотя в данном случае отсутствовали обучающие
выборки.
Методы и результаты кластер-анализа (классифика-
(классификации, таксономии, распознавании образов «без учителя»,
см. [2], [6], [7]) направлены на решение следующей за-
задачи. Геометрич. структура анализируемой совокуп-
совокупности элементов задана либо координатами соответст-
соответствующих точек (т. е. матрицей lk,yll, i=l, •¦• , р\ /=1,
... , п), либо набором геометрич. характеристик их
взаимного расположения, напр, матрицей попарных
расстояний Ilp,yll7,/=i- Требуется разбить исследуемую
совокупность элементов на сравнительно небольшое
(заранее известное или нет) число классов так, чтобы
элементы едного класса находились на небольшом рас-
расстоянии друг от друга, в то время как разные классы
были бы по возможности достаточно взаимоудалены
один от другого и не разбивались бы на столь же уда-
удаленные друг от друга части.
Задача многомерного шкалирования (см. [6]) отно-
относится к ситуации, когда исследуемая совокупность эле-
элементов задана с помощью матрицы попарных расстоя-
расстояний llp,yl!?,/=i и заключается в приписывании каждому
из элементов заданного числа (р) координат таким об-
образом, чтобы структура попарных взаимных расстоя-
расстояний между элементами, измеренных с помощью этих
вспомогательных координат, в среднем наименее отли-
отличались бы от заданной. Следует заметить, что основные
результаты и методы кластер-анализа и многомерного
шкалирования развиваются обычно без каких-либо до-
допущений о вероятностной природе исходных данных.
Прикладное назначение многомерного статистическо-
статистического анализа состоит в основном в обслуживании следую-
следующих трех проблем.
Проблема статистического исследования зависимо-
зависимостей между анализируемыми показателями. Предпола-
Предполагая, что исследуемый набор статистически регистрируе-
регистрируемых показателей -.г разбит, исходя из содержательного
смысла этих показателей и окончательных целей иссле-
исследования, на (jr-мерный подвектор жA> предсказываемых
(зависимых) переменных и (р—<jr)~MePHbln подвектор ,/;B>
предсказывающих (независимых) переменных, можно
сказать, что проблема состоит в определении на основа-
основании выборки A) такой g-мерной векторной функции
f(jc{-)) из класса допустимых решений F, к-рая давала
бы наилучшую, в определенном смысле, аппроксимацию
поведения подвектора показателей жA). В зависимости
от конкретного вида функционала качества аппрокси-
аппроксимации и природы анализируемых показателей приходят
к тем или иным схемам множественной регрессии, дис-
дисперсионного, ковариационного или конфлюентного
анализа.
Проблема классификации элементов (объектов или
показателей) в общей (нестрогой) постановке
заключается в том, чтобы всю анализируемую совокуп-
совокупность элементов, статистически представленную в виде
матрицы ]|х,у||, ('—1, ... , р; /=1, ... , и, пли матрицы
||p,yll, г, /=1, ... , n, разбить на сравнительно неболь-
небольшое число однородных, в определенном смысле, групп
[7]. В зависимости от природы априорной информации
и конкретного вида функционала, задающего критерий
качества классификации, приходят к тем или иным схе-
схемам дискриминантного анализа, кластер-анализа (так-
(таксономии, распознавания образов «без учителя»), рас-
расщепления смесей распределений.
Проблема снижения размерности исследуемого фак-
факторного пространства и отбора наиболее информатив-
информативных показателей заключается в определении такого па-
бора сравнительно небольшого числа т<^.р показателей
s=(z,, z2, ... , zm)', найденного в классе допустимых
преобразований Z(ж) исходных показателей se=(.r,,
х2, ... , хр), на к-ром достигается верхняя грань нек-рой
экзогенно заданной меры информативности то-мерной
системы признаков (см. [7]). Конкретизация функцио-
функционала, задающего меру автоинформатив-
н о с т и (т. е. нацеленное на максимальное сохранение
информации, содержащейся в статистич. массиве A)
относительно самих исходных признаков), приводит,
в частности, к различным схемам факторного анализа
и главных компонент, к методам экстремальной группи-
группировки признаков. Функционалы, задающие меру
внешней информативности, т. с. наце-
нацеленные на извлечение из A) максимальной информации
относительно нек-рых других, не содержащихся непо-
непосредственно в ас, показателей или явлений, приводят к
различным методам отбора наиболее информативных
показателей в схемах статистич. исследования зависи-
зависимостей и дискриминантного анализа.
Основной математический инструментарий М. с. а.
составляют специальные методы теории систем линей-
линейных уравнений и теории матриц (методы решения про-
простой и обобщенной задачи о собственных значениях и
векторах; простое обращение и псевдообращение мат-
матриц; процедуры диагонализации матриц и т. д.) и нек-
рые оптимизационные алгоритмы (методы покоординат-
покоординатного спуска, сопряженных градиентов, ветвей и границ,
различные версии случайного поиска и стохастич. ап-
аппроксимации и т. д.).
Лит.: [1] Андерсон Т., Введение в многомерный статисти-
статистический анализ, пер. с англ., М., 1963; [2] К е н д а л л М. Д ш.,
Стьюарт А., Многомерный статистический анализ и вре-
временные ряды, пер. с англ., М., 1976; [3] Большее Л. Н.
«Bull. Int. Stat. Inst.», 1969, W» 43, p. 425—41; [4] W i sh a r t J.
«Biometrika», 1928, v. 20A, p. 32—52; [5] Hotelling H.
«Ann. Math. Stat.», 1931, v. 2, p. 360 — 78; [6] К г u s k a 1 J. B.
«Psychometrika», 1964, v. 29, p. 1—27; [7] Айвазян С A..
Бежаева З. И., Староверов О. В., Классификация
многомерных наблюдений, М., 1974. С. А. Айвазян.
МНОГОМЕРНЫЙ УЗЕЛ — изотопический класс вло-
вложений сферы в сферу. Более точно, re-мерным узлом
коразмерности q наз. пара K=(Sn + 4,kn), состоящая
из ориентированной сферы Sn + 4 и ее ориентированного
локально плоского подмногообразия к", гомеоморфного
сфере Sn. Два узла K1=(S"^4, к1) и K2=(Sn + 4, к")
наз. эквивалентными, если существует изо-
изотопия сферы Sn + i, переводящая ki на к? с сохра-
сохранением ориентации. В зависимости от того, в какой ка-
категории (Diif, PL или Тор) понимаются термины «под-
«подмногообразие» и «изотопия» в предыдущих определени-
определениях, гопорится о гладких, кусочно линейных или тоно-
логич. М. у. соответственно. В, гладком случае подмно-
подмногообразие к" может иметь и нестандартную дифферен-
дифференцируемую структуру, re-мерный узел коразмерности q,
изотопный стандартному вложению, наз. триви-
тривиальным, или незаузленным, узлом.
Изучение М. у. коразмерности 1 связано с Шёнфлиса
гипотезой. Всякий топологич. узел коразмерности 1
тривиален. Это же верно и для кусочно линейных и
гладких узлов, если пф?,, 4.
Кусочно линейные и топологич. М. у. коразмерности
<^3 тривиальны. В гладком случае ато не так. Множе-
ство изотогшч. классов гладких гс-мерных узлов кораз-
коразмерности о^З совпадает при п^Ъ с множеством 6" + <?> п
классов кобордизмов узлов (два М. у. К1=
= Eп + «, к") и K2=(Sn + 9, hi) наз. кобордантны-
м и, если существует гладкое («+1)-мерное подмного-
подмногообразие WczS" + QXI, трансверсально выходящее на
d(Sn + 9Xl), причем dW=(ki XO)(J(—/с?XI) и W яв-
является h-кобордизмом между /с?ХО и hi Xl). Множество
0и + в>н явлдется абелевой rpynnoii относительно связ-
связного суммирования. В этой группе противоположным
к классу М. у. (Sn + i, kn) является класс кобордизмов
узла (— S" + Q, —k"), где минус означает обращение ори-
ориентации. Имеется естественный гомоморфизм 9" + 0"»—>-
—г- в", где 6" — группа n-мерных гомотопич. сфер; этот
гомоморфизм сопоставляет узлу (?" + <?, к") дифферен-
дифференцируемую структуру сферы к". Ядро этого гомоморфиз-
гомоморфизма, обозначаемое Z" + i'", совпадает с множеством изо-
тогшч. классов стандартной сферы S" в Sn+Cl. Если
2(?>га+3, то группа 2п + 1'п тривиальна. Если 2<7<:
<И-3 и (ге+1)^0 (mod 4), то группы 2" + ''- « и 9" + "' "
конечны. В случае, когда 2<jr<n-[-3 и (пЧ-1)=0 (mod 4),
группы О"?!" и 2п + <?> « являются конечно порожден-
порожденными абелевыми группами ранга 1 (см. [1], [2]). Вычис-
Вычислено также множество классов конкордатных гладких
вложений S" в Sn + 4 при q>2 (см. [3]).
Изучение М. у. коразмерности 2, к-рые в дальней-
дальнейшем будут наз. просто узлами, проходит почти анало-
аналогично во всех трех категориях (Diff, Pi, Top). При п^5
всякий топологпч. узел переводится изотопией в глад-
гладкий. Однако существуют топологич. трехмерные узлы
в 55, не эквивалентные и даже не кобордантные глад-
гладким узлам (см. [4]).
Множество изотопич. классов и-мерных узлов (каж-
(каждой категории) образует абелеву полугруппу от-
относительно связного суммирования. Известно, что
при п -— 1 в этой полугруппе всякий элемент представ-
представляется в виде конечной суммы простых, т. е. нетриви-
нетривиальным образом неразложимых элементов, и такое раз-
разложение единственно.
re-мерный узел К~ (Sn + -, k") тривиален тогда и только
тогда, когда п,-Eп + 2—kn)=n.((S1) при всех (<|^j— [ .
Дана (см. [6]) алгебраич. классификация узлов К,
у к-рых я,-E'! + 2—/с2)— JT^iS1) при всех г<:| Щ— I — 1 и
число п нечетно (узлы типа L): при ге^5 множество изо-
изотопич. классов таких узлов находится во взаимно одно-
однозначном соответствии с множеством ^-эквивалентных
классов Зейферта матриц. Узлы типа L важны с точки
зрения приложений в алгебраич. геометрии, т. к. среди
них находятся все узлы, получаемые с помощью следую-
следующей конструкции (см. [15]). Пусть /(z,, ... , zg + 1) —
комплексный многочлен ненулевой степени, имеющий
О в качестве изолированной особой точки и /@) = 0.
Пересечение к гиперповерхности У=/-1@) с малой сфе-
сферой S2f + 1 с центром в нуле является (q—2)-связным
B<jr—1)-мерным многообразием. Многообразие к гомео-
морфно сфере 52? тогда и только тогда, когда | Д AI =
= 1, где A(f) — полином Александера. В этом случае
возникает узел (S2i + 1, к). Такие узлы наз. алгеб-
алгебраическими, все они являются узлами типа L.
Внешностью гладкого узла K=(Sn + 2, к")
наз. дополнение X открытой трубчатой окрестности к"
в Sn + '1. При ге^2 для всякого re-мерного узла К сущест-
существует такой узел %(К), что всякий узел, внешность к-ро-
го диффеоморфна внешности узла К, эквивалентен либо
К, либо %{К). Если Хи Хг — внешности двух гладких
н-мерных узлов, ге^З, и я1(Х1) = я1(Х2)~ %, то следую-
следующие утверждения равносильны (см. [7]): 1) X, и Х.г диф-
феоморфны, 2) пары (Хи дХг) и (.Y2, дХг) гомотопиче-
ски эквивалентны. Эти результаты сводят проблему
классификации узлов к гомотопич. классификации пар
(X, ОХ) и к решению вопроса о TOif, определяет ли внеш-
внешность тип узла, т. е. верно ли равенство К=т(К)? Из-
Известно, что это равенство справедливо для узлов типа
L (см. [6]), для узлов, получаемых конструкцией
Артина и конструкцией сверхзакручивания (см. [8]).
Однако найдены двумерные узлы в S4, для к-рых Кф
фт(К) (см. [9]).
Изучение гомотоппч. типа внешности X усложняется
из-за ее нсодносвязности. Если G — группа узла (т. е.
G=n1(X)), то G/[G, G]=I,, tf2(G) = 0, вес группы G
(т. е. минимальное число элементов, не содержащихся
ни в одном собственном нормальном делителе) равен 1.
При ;i^3 эти свойства полностью описывают класс
групп 72-мерных узлов (см. [10]). Группы одномерных и
двумерных узлов обладают рядом дополнительных
свойств (см. Узлов теория, Двумерный узел).
Поскольку Н1(Х; %)=-'?, внешность X обладает
единственным бесконечным циклическим накрытием
р: X —у X, к-рос иаз. бесконечным цикличе-
циклическим накрытием узла. Гомологии //*(.?; '?)
являются ZlZl-модулями. Их Аленсандера инвариан-
инварианты являются инвариантами узла. Об алгебраич. свой-
свойствах модулей Нх(Х; Z) см. [10] — [13].
Благодаря тому обстоятельству, что на бесконечном
циклическом накрытии группа g действует без непод-
неподвижных точек, (я+2)-мерное некомпактное многообра-
многообразие X обладает рядом гомологич. свойств компактных
(ге+1)-мерных многообразий. В частности, на гомоло-
гиях многообразия X с коэффициентами в поле F суще-
существует невырожденное спаривание
л л (X \ I) (X) М п + \ _ ? \X'i *J —*~ * 1 "- ^^ *» • • • ? ^т
по свойствам напоминающее спаривание, определяемое
пересечения индексом в (ге-|-1)-мерных компактных мно-
многообразиях. Имеется также спаривание
аналогичное зацепления коэффициентам в (п-|-1)-мер-
ных многообразиях (см. [13]), где JyX = Tors Hj(X; '/>]).
Эти гомологнч. спаривания порождают инварианты
гомотоппч. типа пары (.Y, дХ). Для получения алгебра-
алгебраич. инвариантов используются также конечнолистные
циклические разветвленные накрытия (см. [14]).
Задача классификации узлов коразмерности 2 с точ-
точностью до кобордизма — отношения эквивалентности
более грубого, чем изотопич. тип,— полностью решена
при ге>1 (см. Узлов кобордизм).
Лит.: [1] Haefliger A., «Ann. Math.», 1962, v. 75,
p. 452—66; [2] e г о же, там же, 1966, v. 83, р. 402—36: [3]
Levine J., там же, 1965, v. 82, р. 15—51; [4J С а р р е 1 1 S.
Shaneson J., «Topology», 1973, v. 12, p. 33—40; [а] Со-
Сосинский А. Б., «Матем. сб.», 1970, т. 81, № 1, с. 145—58;
[6] Levine J., «Comm. math, helv.», 1970, v. 45, p. 185 — 98;
[7] L a s h о f П., S h a n e s о n J., «Bull. Amer. Math. Soc»,
1969, v. 75. p. 171—75; [8] С a p p e 1 1 S., в кн.: Topolosry of
Manifolds, Chi., 1971, p. 358 — 83; [9] С а р р с 1 1 S., S h a'n e -
son J., «Ann. Math.», 1976, v. 103, p. 349 — 53- [10] К е г v a i -
re M., «Bull. soc. math. France», 1965, t. 93, p. 225—71: [11]
Levine J., «Ann. Math.», 1966, v. 84, p. 537 — 54: [12) его
ж е, в кн.: Knots, groups and 3-manifolds, Princeton, 1975 p. 25—
34; [13] Ф а р б е р М. Ш., «Изв. АН СССР. Сер. матем.», 1977,
т. 41, с. 794 — 828; [14] Вир о О. Я., там же, 1973, т. 37,
с. 1241 — 58; [15] М и л н о р Д ж., Особые точки комплексных
гиперповерхностей, пер.сангл., М.,1971. М. Ш. Фарбер.
МНОГОМЕСТНЫЙ ФУНКТОР, мультифунк-
т о р,— функция от нескольких аргументов, опреде-
определенная на категориях, принимающая значения в кате-
категории и задающая одноместный функтор по каждому
аргументу. Более точно, пусть даны п категорий S\lt
,й'2, ¦¦¦ , Xtn- Построим декартово произведение катего-
категорий }){=.#! Х.<Г2Х ...Х.#„, где каждая категория .ff,-
либо совпадает с jiit либо с дуальной категорией Я';.
Одноместный ковариантный функтор F из Si со значе-
значениями в категории E наз. га-м е с т н ы м функто-
функтором, заданным на категориях .Ч\, >Г.,, ... , Stn со
значениями в категории E. Функтор F ковариантен по
тем аргументам, к-рые соответствуют множителям SX;
в произведении SX, и контравариантен по остальным
аргументам.
Выпишем явно соотношения, к-рым должно удовле-
удовлетворять отображение F: SX —>¦ С? (для простоты и = 2
и первый аргумент считается контравариантным, а
второй — ковариантным). Функтор F: Si XS2 -*¦ E
сопоставляет каждой паре объектов (Л, В), где А?
? Ob ,ff,, B?Ob ,ft2, объект ^(Л, 5)?0b 6 и каждой
паре морфизмов (а, Р), где
морфизм
F (а, $):F (Аи В)—> F (A, Bj)?Mor g.
При этом выполняются следующие условия:
1) -F(l^! 1д)=1/г(.-1, л> Для любой пары объектов А, В;
2) если а: А -*¦ А,, ах : Лх-> Л2, а, ^М Й
то
Примеры М. ф.
1) Пусть jf — категория с конечными произведе-
произведениями. Тогда произведение п объектов можно рассмат-
рассматривать как ге-меетный ковариантный по всем аргумен-
аргументам ф/нктор, определенный на декартовой степени
$" = ,\iXA'X...X,$f (re раз) и принимающий значения в
Ш- Аналогичные функторы можно построить для ко-
произведений, тензорных произведений и т. д.
2) Пусть ,Н — произвольная категория. Сопоставим
каждой паре объектов А, В из Я множество морфизмов
НS(A , В) и каждой: паре морфизмов a : А -*-Аь Р : В -*
->¦ Вг отображение множеств #(г(сс, Р) : ЯЛ(ЛЬ В) -*
—>-Яя(Л, Si), заданное следующим образом:
если ф: Ах—у В, то Яя (а, Р)(ф)=асрР.
Описанное построение задает двуместный функтор из
Д'*Х.Н1 в категорию множеств, контравариантный по
первому аргументу и ковариантный по второму.
Если ,Н' — аддитивная категория, то можно считать,
что построенный функтор принимает значения в кате-
категории абелевых групп.
3) Пусть ,Н' — категория с конечными произведе-
произведениями. Рассмотрим произведение как двуместный функ-
функтор X: StXSf—>-il. Тогда, комбинируя примеры 1)
и 2), можно построить трехместные функторы Н&(А,
В У, С) и Н$(АХВ, С). Первый функтор естественно эк-
эквивалентен функтору НЯ(А, В)ХНк{А, С). В случае
категории множеств Р второй функтор естественно эк-
эквивалентен функтору Не(А, Н^(В, С)).
4) Пусть ¦& — малая категория п F($, R) — катего-
категория диаграмм над категорией множеств (л со схемой О,
т. е. категория одноместных ковариантпых функторов
и их естественных преобразований. Построим двумест-
двуместный ковариантный по обоим аргументам функтор
Е : Six F(&, (г) —¦* V; если A gOb Я и F?Ob F(&, 15),
то Е(А, F)=F{A); если a : А -*- SgMor St и a : F -»-
—*¦ G— естественное преобразование, то Е (а, а)=
= F (a)aB=a^G(ai. Функтор Е называют функтором
«вычисления значений». Этот функтор естественно экви-
эквивалентен функтору Nat (Яд, F):S\XF(x>, E) —^- (S,
к-рый сопоставляет объекту А ?Я и функтору F : St —*¦
-*¦ (S, множество естественных преобразований основ-
основного функтора IIА в F (лемма Ионед ы).
М. Ш. Цалепгм.
МНОГООБРАЗИЕ — геометрический объект, локаль-
локально имеющий строение (топологическое, гладкое, гомо-
гомологическое или иное) числового пространства R" или
другого векторного пространства. Это фундаменталь-
фундаментальное понятие математики уточняет и обобщает на любое
число измерений понятия линии и поверхности. Введе-
Введение этого понятия вызвано разнообразными потребнос-
потребностями как самой математики, так и др. наук. В матема-
математике М. возникают прежде всего как совокупности
решений невырожденных систем уравнений, а также
как различные совокупности геометрических и др. объ-
объектов, допускающих введение локальной параметриза-
параметризации (см. ниже), напр., совокупность плоскостей раз-
размерности к в R". Они появляются также как решение
многомерных вариационных задач (мыльные пленки),
как интегральные многообразия пфаффовых систем и ди-
динамических систем, как группы геометрических преоб-
преобразований и их однородные пространства и др. В физике
они играют роль моделей пространства-времени, в ме-
механике служат фазовыми пространствами, уровнями
энергии и проч., в экономике поверхностями безразли-
безразличия, в психологии пространством ощущений (напр.,
цветов) и т. д.
Хотя исходная идея, кладущаяся в основу определе-
определения М., относится к их локальному строению («такому
же, как у R"»), эта идея позволяет выделить целый ряд
характерных именно для М. глобальных черт: (не)
ориентируемость, гомологическая Пуанкаре двойствен-
двойственность, возможность определения степени отображения
одного М. на другое той же размерности п проч. Особое
значение имеет введение касательного расслоения и свя-
связанных с ним инвариантов.
Локальное строение М. позволяет также привлечь
к их изучению геометрическую технику: приведение
в общее положение, построение Морса функций и проч.,
к-рая служит для геометрического изучения глобаль-
глобального строения М., oio, грубо говоря, заключается в
представлении возможно более простым образом М.
в виде объединения простых кусков, симплексов или
ручек.
При использовании понятия М. также обычно со-
совершается переход от локального к глобальному. Пер-
Первым шагом является введение параметриза-
ц и и, т. е. представление «пространства состояний»
данной задачи областью числового пространства. Это
дает возможность описать каждое состояние набором
чисел — координатами соответствующей точки (коорди-
(координатный метод). В целом пространство состояний может
не допускать подобного описания, т. е. может не иметь
гомеоморфизма на область в R". Если не прибегать к
параметризации с вырождениями (как в полярных ко-
координатах и их обобщениях), то возможны два пути:
либо введение сначала большего, чем необходимо, чис-
числа параметров, и выделение истинного пространства
неявно системой уравнений («уравнения состояния»),
либо пространство параметризуется по частям локально,
«в малом». Например, множество прямых на плоскости
покрыто двумя подмножествами: Пг, состоящее из пря-
прямых с уравнениями вида y=kx-\-b, иП„, состоящее из
прямых с уравнениями вида x=ky-\-b\ оба они гомео-
морфны R2 с параметризацией парами (к, Ъ) и (к, Ь)
соответственно. Однако в целом это множество гомео-
мтэрфно открытому листу Мёбиуса.
Когда М. естественно появляются в той или иной об-
области, они обязательно несут какую-либо дополнитель-
дополнительную структуру, к-рая и служит предметом изучения в
этой области. Однако важную роль играет и тополо-
гич. строение, к-рое ограничивает априорные возмож-
возможности. Наоборот, в топологии локальные и глобальные
свойства М. изучают, привлекая дополнительные
структуры (напр., гладкую) в качестве инструментов.
Фундаментом общего понятия М. является опреде-
определение топологического многообразия как топологич.
пространства, в к-ром каждая точка имеет окрестность
i 11 гомеоморфизм ф: ? —>¦ U на область в R" или в
полупространстве R"={x?R", xn^0}; гомеоморфизм
Ф наз. локальной параметризацией
или картой, в ЭЁ- Размерность re=dim M является
инвариантом связного М. Для несвязного М. обычно
берут компоненты одной размерности. М. распадается
на внутренность Int M и край дМ: точки
края отвечают в своих картах точкам границы R" в
R™. Край является (п—1)-мсрным М. без края и может
быть пустым. Связное М. без края наз. открытым,
если оно некомпактно, и замкнутым, если оно
компактно. Простейшими примерами четырех возмож-
возможных типов М. служат R", R + , шар В" и его граничная
сфера S"~x. Хотя нехаусдорфовы М. встречаются в не-
некоторых ситуациях (напр., пространства пучков),
обычно принимают, что М. хаусдорфово, паракомпакт-
но, имеет счетную базу, в частности, метризуемо.
Глобальное задание М. осуществляется атла-
атласом — набором карт, покрывающих М. Для исполь-
использования М. в математич. анализе нужно, чтобы пере-
пересчет координат от одной карты к другой был дифферен-
дифференцируемым. Поэтому чаще всего рассматривают диффе-
ренцируемые многообразия. Более общим образом вво-
вводится понятие Г-строения на М., задаваемого атласами
{ф/ : S,—>- Ui), в к-рых координатные переходы h,-j=
^Ф/фГ1 межДУ картами являются гомеоморфизмами,
входящими в систему Г-отображений областей в R",
замкнутую относительно композиций. Если Г состоит
из непрерывно дифференцируемых г раз отображений,
то говорят, что класс гладкости М. есть С. Аналогично
определяются аналитические многообразия, кусочно
линейные, липшицевы и др. типы М. Два Г-атпаса за-
задают одно Г-с троение, если их объединение есть
Г-атлас. Классификация Г-строеннй является важней-
важнейшей проблемой геометрии М. Отображение / : М —>¦ N
одного Г-многообразия в другое наз. Г-о т о б р а ж е-
н и о м, если локально оно имеет «координатное пред-
представление» /,•;•= фу/ф?1, где фу, ф,- — карты в М и .V,
a /,у?Г. В частности, имеется понятие Г-г о м с о-
м о р ф и з м а (С-д и ф ф е о м о р ф и з м а в случае
Т=С'Г).
Поскольку в математич. анализе М. важны как но-
носители дифференцируемых отображений, их иногда оп-
определяют (см. [12]) через запас гладких функций, опре-
определенных в окрестностях точек (см. Росток). Развитие
этой идеи привело к понятию предмногообразия, или
окольцованного пространства (пучка колец), и далее к
понятию схемы. Заменяя R" на другие векторные и
иные пространства, приходят к различным обобщениям
понятия М., таким, как напр, комплексно-аналитиче-
комплексно-аналитические М. Бесконечномерные М. возникают
в математич. анализе и топологии как пространства
отображений и сечений расслоений, как пространства
гомеоморфизмов, замкнутых подмножеств и пр. Их ло-
локальными моделями служат векторные пространства
(банаховы и иные) и такие пространства, как гильбер-
гильбертов кирпич. Понятие гладких и иных строений на бес-
бесконечномерных М. изучено недостаточно. Трудности
здесь возникают из-за отсутствия технических теорем
типа аппроксимаций, существования разбиения единицы
(.мал запас гладких функций), теоремы о неявной функ-
функции и т. п.
М. возникают как подмножества R" при неявном за-
задании их в виде множеств решений систем уравнений
(и неравенств в случае непустого края). Этим М. за-
задается сразу, а не по частям, как в случае задания
атласом. Однако необходимы условия невырожденно-
сти, иначе всякое замкнутое множество можно задать
одним уравнением. Существование локальной парамет-
параметризации обеспечивается по теореме о неявной функции
условием максимальности ранга Якоби матрица дан-
данной системы. Уравнения служат языком для выраже-
выражения средствами математич, анализа свойств М., служа-
служащих для определения М. Наир., свойство ортогонально-
ортогональности (геХ и)-матрицы записывается системой из ";+
уравнений относительно элементов матрицы. Система
оказывается невырожденной, а группа ортогональных
матриц гладким подмногообразием в R.
В механич. системе с уже введенными координатами
меньшие системы выделяются уравнениями или не-
неравенствами, выражающими ограничения или «связи».
Если условие невырожденности системы F;=0 выпол-
выполнено во всех точках М., то градиенты функций F,- обра-
образуют оснащение (ft-репер, ортогональный к
касательной плоскости в точке М. и непрерывно зави-
зависящий от этой точки). М., допускающие оснащение,
образуют довольно узкий класс стабильно па-
р а л л е л и з у е м ы х М. (напр., они имеют ориента-
ориентацию). Но локально любое дифференцируемое М. в
R" может быть задано невырожденной системой, а
с помощью разбиения единицы можно построить
и систему постоянного (а не максимального) ранга, за-
задающую М.
Для М., заданного атласом, возникает задача реали-
реализации его как подмногообразия в R" с учетом того или
иного Г-строения. Любое топологическое, гладкое пли
кусочно линейное М. М вкладывается, т, е.
Г-гомеоморфно подмногообразию, в R2", а в R'2" + x
множество вложений плотно в пространстве всех не-
непрерывных отображений. Для других классов вопрос
существенно сложнее. Интенсивно он изучается, напр.,
для римановых многообразий. Алгебраические много-
многообразия, реализующиеся в комплексном проективном
пространстве (заменяющем здесь R"), составляют
очень специальный класс Ходжа многообразий. Если
допускать вырожденность системы уравнений, то воз-
возникают М. с о с о б е н н о с т я м и. В алгебраич. гео-
геометрии обе идеи комбинируют: алгебраическое прост-
пространство определяется склейкой частей, к-рые локально
задаются полиномиальными системами с вырождения-
вырождениями. В теории кобордизмов в топологии под названием
М. с особенностями рассматривают пространства, уст-
устроенные локально как произведения конусов над М.
Дальнейшие обобщения связаны с рассмотрением не-
непрерывных семейств М. (см. Расслоенное пространство,
Слоение, Стратификация).
Изучение М. чисто топологическими методами чрез-
чрезвычайно сложно и до последнего времени оно ограни-
ограничивалось локальными свойствами М., т. е. в сущности
свойствами R" (непрерывное разбиение, дикое вложение
и пр.). Глобальное изучение М. и по необходимости
требует привлечения или гомологических и других
средств алгебраической топологии, пли гладких, кусоч-
кусочно линейных и иных строений. Основное гомологиче-
гомологическое свойство М.— Пуанкаре двойственность, сохра-
сохраняющаяся и для гомологических многообразий и слу-
служащая для таких обобщений понятия М. как Пуанкаре
комплексы. Гомологическую природу имеет и степень
отображения, фундаментальное понятие, определяемое
также для псевдомногообразий — прост-
пространств (обычно, комплексов), обладающих открытыми
связными плотными подмножествами, являющимися М.
Геометрическое изучение М., основанное на исполь-
использовании различных строений, исходит прежде всего из
локальной эквивалентности М. с R" и из возможности
благодаря этому аппроксимации отображений гладкими
или кусочно линейными, приведения их в общее поло-
положение и пр. Начальной задачей здесь является пред-
ставление М. в виде пространства, склеенного из про-
простых кусков. Первоначальной идеей было понятие
триангуляции М., развившееся в широкое понятие ком-
плекса. Трудные проблемы триангулируемости и экви-
эквивалентности триангуляции были прояснены в 60—
70-х гг. 20 в. (см. Топология многообразий). Более гиб-
гибким инструментом оказалось разбиение М. на ручки,
эквивалентное рассмотрению функций Морса. С по-
помощью техники постепенного упрощения такого разби-
разбиения были доказаны важные теоремы (об /г-кобрдизме,
обобщенная Пуанкаре гипотеза и др.). Эта техника по-
послужила также геометрич. основой для теорем класси-
классификации гладких и кусочно линейных строений на за-
заданном гомотопич. типе М. Эти теоремы потребовали,
однако, привлечения тонких инвариантов, связанных
с касательным расслоением М. (см. ниже)-. Большое
значение имело также открытие новых гомологпч. тео-
теорий: К-теории и особенно теорий кобордизмое. Два М.
кобордантны, если они вместе ограничивают третье М.
При этом учитывается тот или иной тип строения. Это
отношение эквивалентности легло в основу первона-
первоначального определения гомологии, когда циклы рассмат-
рассматривались наивно как кусочно гладкие М. В теории
кобордизмов эта идея восстанавливается, но подмного-
подмногообразия заменяются отображениями М. Особую роль
в вопросах классификации строений на М. играет фун-
фундаментальная группа, благодаря к-рой устанавливает-
устанавливается связь этих вопросов с алгебраической К-теорией.
Важнейший инвариант гладкого М. М — его каса-
касательное расслоение хМ. Предметом анализа на М. слу-
служит изучение сечений хМ и различных ассоциирован-
ассоциированных с ним расслоений. С топологической точки зрения
хМ характеризуется существованием экспоненциального
отображения ехр : хМ -> М, диффеоморфно отобра-
отображающего малые шары в слоях ххМ на окрестности со-
соответствующих точек х?М. Его можно описать как
проекцию трубчатой окрестности диагонали в MX M
на сомножитель. В такой форме определение хМ пере-
переносится на топологический, кусочно линейный и др.
случаи (см. Микрорасслоение).
Различные редукции структурной группы касатель-
касательного расслоения наз. структурами на М. Если
можно подобрать атлас такой, что матрицы Якоби его
координатных переходов принадлежат уменьшенной
структурной группе и определяют тем самым эту ре-
редукцию, то такая структура наз. и н т е г р и р у е-
м о й. Вопросы классификации структур и их интегри-
интегрируемости относятся к основным вопросам дифференци-
дифференциальной геометрии многообразий. В топологии М. вопрос
о классификации гладких, кусочно линейных и иных
строений сводится в основном к классификации соот-
соответствующих структур на касательном расслоении и
приводится тем самым к гомотопич. задачам.
Важная роль касательного расслоения состоит в том,
что с ним инвариантно связываются когомологич.
классы (см. Характеристический класс) в той или иной
гомологической теории, несущие в себе наиболее су-
существенную информацию о глобальном строении М.
и связывающие свойства различных строений и струк-
структур на М. с его топологическими свойствами.
Исследование топологии М. в этом направлении до
70-х гг. было по-существу использованием гладких и ку-
кусочно линейных строений на М. (точнее, на гомото-
пичеа.ом типе М.). Переход к чисто топологическим ре-
результатам стал возможным лишь после доказательства
трудных и глубоких теорем, начиная с доказательства
топологической инвариантности характеристических
(рациональных) классов (см. Топология многообразий),
В конце 70-х г. с этим направлением слилось и упо-
упомянутое выше направление чисто топологического
изучения М. Ярким примером служит доказательство
гипотезы о том, что двойная надстройка над гомологи-
ческой трехмерной сферой есть многообразие (сфера).
Это позволило дать топологическую характеризацпю М.
(известную до этих пор лишь для одномерных многооб-
многообразий и двумерных многообразий), прояснить вопрос о
том, какие полиэдры являются М. (препятствием здесь
служит лишь недоказанная пока A982) Пуанкаре ги-
гипотеза в размерностях 3 и 4) и др., см. Топология много-
многообразий и [19].
Исторический очерк. Начальный период
изучения М. связан с анализом понятия многомерной
параметризации, с исследованиями по геометрии фи-
зич. мира (земной поверхности) и но геометрия, аксио-
аксиоматике. Два способа задания М. в R" (локальная пара-
параметризация и уравнения) были рассмотрены впервые
К. Гауссом (К. Gauss, см. [1] с. 127) для случая по-
поверхностей в R3, а в многомерном случае А. Пуанкаре
(Н. Poincare, см. [3], с. 459). Ю. Плюккер [5] изучал
локальные координаты в М., составленных из кривых,
поверхностей и т. и. Г. Грассман пришел в [6] к общей
идее «многомерной протяженности», к-рая была под
названием «многообразие» введена в математику Б. Ри-
маном (В. Riemann) в его знаменитой лекции «О гипо-
гипотезах, лежащих в основании геометрии» (см. [1| с. 30).
Свойства различных специальных координат изучались
К. Якоби (С. Jacobi), Г. Ламе (G. Lame) и др. (см. [8]).
К. Гаусс (см. [1] с. 123) начал в связи со своими
работами по геодезии систематич. изучение поверхнос-
поверхностей, введя понятие внутренней геометрии и тем самым
о М., не зависящем от объемлющего числового про-
пространства, и фактически понятие структуры на М. Его
идеи были вполне поняты лишь в теории характернстич.
классов, построенной в середине 20 в. В. Риман перенес
идеи К. Гаусса на многомерные М. На основе рпмано-
вой геометрии был создан трудами Риччи, Лени-Чи-
впта, Кристоффеля и др. тензорный анали::, дальней-
дальнейшее развитие к-рого шло в тесной связи с теорией отно-
относительности. Другая геометрическая линия развития
понятия М. берет начало в открытии возможности не-
неевклидовых геометрий и в построении геометрии на ос-
основе понятия движения (Г. Гельмгольц, Н. Helmlioltz,
см. [1] с. 366). Эта идея была превращена в широкую
программу теоретико-группового построения геометрии
Ф. Клейном (К. Klein, см. [1] с. 399 и [8]) и привела к
глубоким работам С. Ли (S. Lie) по теории непрерыв-
непрерывных групп. Линия Гельмгольца — Клейна — Ли дол-
долгое время оставалась в стороне от линии Гаусса — Ри-
мана — Риччи, заимствовав у нее понятие кривизны,
но интересуясь лишь Клейна пространствами. Однако
здесь были поставлены важные вопросы о глобально.м
строении групп Ли и их однородных пространств и тем
самым привлечено внимание к глобальному строению
М. Важным фактом было произведшее глубокое впе-
впечатление открытие Клейном эллиптической геомет-
геометрии, локально эквивалентной сферической, но гло-
глобально имеющей существенно иные свойства, а так-
также открытие Мёбиусом и Клейном явления неориенти-
неориентируемости.
Синтез обоих направлений произошел в работах
Э. Картана (Е. Cartan, см. [1] с. 483). Отправляясь от
исследований Г. Дарбу (G. Darboux) по теории поверх-
поверхностей, он рассмотрел подвижного репера метод для про-
произвольного М. в R" и пришел к теории уравнений
структуры — далекого обобщения теории Дарбу, вклю-
включившего в себя теорию С. Ли. В картановском понятии
G-структуры соединились идеи римановой геометрии
и теории действия групп Ли. По существу Э. Картан
ввел понятие касательного расслоения и его структур-
структурной группы, окончательно оформленного лишь в
40-х гг. 20 в. (см. [13]). Это понятие позволило июне
объединить математич. анализ на М. с топологич. изу-
изучением М. Основой послужил изоморфизм де Рама (см.
Рама теорема) — окончательное оформление принад-
лежащей Пуанкаре идеи (см. [3] с. 472) о связи между
вещественными когомологиями и дифференциальными
формами. Важнейшим следующим шагом было введение
характеристических классов и их выражение как интег-
интегралов от форм, выражающихся через форму кривизны
(примером здесь служит выражение эйлеровой харак-
характеристики в теореме Гаусса — Бонне в форме Дика, см.
[14] с. 186).
Топологическое изучение М. началось с открытия
римановых поверхностей в связи с представлением ком-
комплексно аналитических функций интегралами как по-
попытка избавиться от многозначности этих функций.
«Периоды» интегралов привели R понятию чисел связ-
связности и в конечном счете к гомологиям. Мысль о много-
многомерном обобщении этого понятия и идея о глобальном
гомологическом изучении М. принадлежит Риману
(см. [2j с. 294). Это изученяе было начато А. Пуанкаре,
сделавшим ряд важных открытий и доказавшим Пуанка-
Пуанкаре двойственность. Стимулирующую роль имело по-
последовавшее за открытием Римана изучение двумер-
двумерных многообразий (в первую очередь Мёбиусом и
К. Жорданом, см. [14] с. 244), приведшее к полной их
классификации. Окончательно это оказалось возмож-
возможным проделать лишь после прояснения понятия «чисто-
«чистого» гомеоморфизма (А. Пуанкаре, например, пользо-
пользовался в сущности кусочно гладкими гомеоморфизма-
гомеоморфизмами). Это прояснение явилось одним из итогов анализа
непрерывности числового континуума, предпринятого
в конце 19 в. Наибольшее значение имели в этом на-
направлении постановка 5-й проблемы Гильберта и работы
Л. Брауэра (L. Brouwer, [9]), доказавшего теоремы (ин-
(инвариантность области, инвариантность размерности),
к-рые позволили Г. Вейлю [4] сформулировать приятие
тонологич. М. Однако в высших размерностях тополо-
топологическое изучение М. долгое время велось в рамках
гладких и кусочно линейных строений. Гладкие строе-
строения, введенные в книге [20], были проанализированы в
основном X. Уитни [21], а также Г. Уайтхедом и др.
Кусочно линейные структуры были введены Л. Брауэ-
ром и проанализированы Дж. Александером [22] и
также М. Ньюменом (М. Newman') и Г. Уайтхедом. Дол-
Долгое время они рассматривались лишь как вспомогатель-
вспомогательное средство топологического изучения М. Лишь
в конце 50-х гг. была открыта неединственность
гладких строений уже на сферах и в конце 60-х гг.
возможность неединственности кусочно линейных стро-
строений (например, на торах). После 50-х гг. 20 в. изучение
М. проходило под знаком объединения идей топологии
и анализа, основанного в первую очередь на понятии
характеристич. классов (см. [17]).
Лит.: [1] Обоснованиях геометрии, М., 1956; [2] Р и м а н Б.,
Соч., пер. с нем., М.— Л., 1948; [3] Пуанкаре А., Избр.
тр., пер. с франц. т. 2, М., 1972; [4] W е у 1 Н., Die Idee der
Riemannschen Flache, 3 Aufl., Stuttg., 1955; [5] P 1 u e с k e r J.,
Neue Geometrie des Raumer . . ., Abt. 1—2, Lpz., 1868—69; [6]
Grassmann H., Die Ausdehnungslehre von 1844, Lpz.,
1894; [7] Kronecker L., «Ittonatsber. Preuss. Akad.
Wiss.», 1869, S. 159—226; [8] Клейн Ф., Высшая гео-
геометрия пер. с нем. М.— Л., 1939; [9] В г о u w е г L. E. J.
«Math. Ann.», 1911, Bd 70, S. 161 — 65; 1911, Bd 71, S. 97 — 115;
1912, Bd 72, S. 55—6; [10] Weyl H., Mathematische Analyse
des Raumproblems, В., 1923; [11] Стинрод Н. Е., Топология
косых произведений, пер. с англ., М., 1953; [12] Ш е в а л л е К.,
Теория групп Ли, пер. с англ., т. 1, М., 1948; [13]Лихнеро-
в и ч А., Теория связностей в целом и группы голономий, пер.
с франц., М., 1960: [14] X и р ш М., Дифференциальная топо-
топология, пер. с англ., М., 1979: [15] М а н к р с Д ж., в кн.: М и л -
н о р Д ж., С т а ш е ф Д ж., Характеристические классы,
пер. с англ., М.. 1979, с. 270—358; [16] Ni] ennuis A.,
Theory of the Reometric object, Amst., 1952; [17] Хирцеб-
p у x Ф., Топологические методы в алгебраической геометрии,
пер. с англ., М., 1973; [18] СУлливан Д., Геометрическая
топология, пер. с англ., М., 1975; [19] Cannon J. W., «Bull.
Amer. Math. Soc», 1978, v. 84, X« 5, p. 832—66; [20] В е б л е н О.,
УайтхедДж., Основания диференциальной геометрии,
пер. с англ., М., 1940- [21] Whitney H., «Ann. Math.», 1936,
v. 37, p. 645—80; [22] Alexander J. W., «Trans. Amer.,
Math. Soc.», 1926, v. 28, p. 301—29.
См. также лит. при статьях Дифференциальная гео-
метрия многообразий, Дифференциальная топология,
Дифференцируемое многообразие. А- в- Чернявский.
МНОГООБРАЗИЕ категорий — понятие, ана-
аналогичное понятию многообразия универсальных ал-
алгебр. Пусть Sx — бикатегория с произведениями. Пол-
Полная подкатегория 2J1 категории $ наз. многооб-
многообразием, если она удовлетворяет следующим усло-
условиям: а) если и: А —>- В — допустимый мономорфизм и
В ?ОЬ Щ], то A gOb Щ1; б) если v : А -*- В — допусти-
допустимый эпиморфизм и A gOb Щ), то В g Ob Ш; в) если Л,?
боь an, t?i, то А=Лх(е/А^оът.
Если бикатегория $ локально мала слева, т. е. до-
допустимые подобъекты любого объекта образуют множе-
множество, то всякое М. является рефлективной подкатего-
подкатегорией категории Я. Это значит, что функтор вложения
1с19Л R. : ©I -*¦ Я обладает сопряженным слева функто-
функтором 5 : Я -*- Ш1. Единица этого сопряжения — ес-
естественное преобразование г : Ыя -*- Г=51с19з( ж обла-
обладает тем свойством, что для каждого Л^ОЬЙ' морфизм
ед : А —>¦ Т(А) является допустимым эпиморфизмом.
Во многих важных случаях функтор Т оказывается
точным справа, т. е. он переводит коядро v пары мор-
физмов а, р : А -*- В в коядро пары морфизмов Т(а),
Г(Р), если (а, 6) — ядерная пара морфизма v. Более
того, точность справа и наличие естественного преоб-
преобразования в : Idff-*- Г являются характсристич. свойст-
свойствами функтора Т.
Всякое М. наследует многие свойства объемлющей
категории. Оно снабжается структурой бикатегории и
является биполной категорией, если исходная катего-
категория биполна.
В категориях с нормальными кообразами, как и в
случае многообразий групп, можно определить произве-
произведение М. Строение возникающего при этом группоида
М. изучено только в ряде частных случаев.
Лит.: [1] Ц а л е н к о М. III., Ш у л ь г е й ф е р Е. Г.,
Основы теории категорий, М., 1974: [2] F г б h I i с h A., «Quart.
J. Math.», 1960, v. 11, № 43, p. 211 — 28. M. Ш. Цаленко.
МНОГОСВЯЗНАЯ ОБЛАСТЬ линейно связ-
связного пространства — область D, в к-рой су-
существуют замкнутые пути, не гомотопные нулю, или,
иначе говоря, фундаментальная группа к-рой не три-
тривиальна. Это означает, что в D существуют замкнутые
пути, к-рые нельзя непрерывно деформировать в точку,
оставаясь все время в М. о. D, или, иначе, М. о. D —
это область, не являющаяся односвязной областью.
Порядком связности плоской области D
пространства R2 или С^С1 (или компактификаций
этих пространств R или С) наз. число (гомологически)
независимых одномерных циклов, т. е. одномерное
Бетти число р1 области D. Если число к связных ком-
компонент границы плоской области D, рассматриваемой
как область компактифицированного пространства R2
или С, конечно, то р1 = /с, в противном случае полага-
полагают рх=оо. В случае рх=1 D есть односвязная область,
в случае р1<оо — конечносвязная область
(применяются также термины двусвязная об-
область, трехсвязная область, ..., к-
связная область), в случае рг== оо Д — б е с-
конечносвязная область. Все плоские
конечносвязные области, порядки связности к к-рых
равны, гомеоморфны между собой. Удаляя из такой
области D все точки к—1 разрезов, т. е. жордано-
вых дуг, соединяющих попарно связные компоненты
границы, всегда можно получить односвязную область
D*cz.D. О конформных типах плоских М. о. см. ст.
Римановых поверхностей конформные классы.
Топологич. типы областей пространств R", ге^З, или
Ст, т^2, гораздо более разнообразны и не могут быть
охарактеризованы каким-либо одним числом. При этом
иногда термин «М. о.» (с различными оговорками) упо-
употребляется и в тех случаях, когда фундаментальная
группа тривиальна, но не тривиальна какая-либо из
Групп ГОМОЛОГИИ ВЫСШеЙ размерности. Е. Д. Соломенцев.
МНОГОУГОЛЬНИК — 1) Замкнутая ломаная ли-
линия, именно: если Аг, А2, ... , Ап — различные точки,
никакие последовательные три из к-рых не лежат на
одной прямой, то совокупность отрезков [^!^21, [Л2Л3],
... , [А,,.^] наз. многоугольником (см.
рис. 1). М. могут быть пространственными или плоски-
плоскими (ниже рассматриваются плоские М.).
А,
А,
Рис.
(многосвязная) область, граница к-рой
со тоит из конечного числа отрезков и является замкну-
замкнутой ломаной линией (или состоит из нескольких замк-
замкнутых ломаных, в этом случае М. иногда наз. много-
многоугольной фигурой, см. рис. 2). Многоуголь-
Многоугольник в смысле первого определения наз. одномер-
одномерным М., а в смысле второго определения — дву-
двумерным М.
Вершины ломаной линии (точки А,-) наз. верши-
вершинами М., отрезки [Л,-Л,-+1] — его сторонами.
Две стороны, имеющие общую вершину, наз, с м е ж-
н ы м и, а две вершины ломаной — концы одного от-
отрезка ломаной — наз. смежными вершина-
вершинами М. Если граница М. является простой ломаной
линией, так что несмежные ее стороны не имеют общих
точек (внутренних или концевых), то М. наз. п р о с-
т ы м. Если граница двумерного М. не является про-
простой, то она наз. самопересекающейся
(рис. 3) (самопересекающийся М.в смысле пер-
первого определения). В этом случае М. является объеди-
объединением простых М. Самопересекающаяся ломаная линия
делит плоскость на определенное число кусков, один из
к-рых — бесконечный. Если в качестве границы М.
рассматриваются и лучи, то определяется беско-
бесконечный М., имеющий своей границей конечное чис-
число отрезков и лучей.
Рис. 4.
Рис. 3.
Всякий простой М. (или граница простого М.) делит
плоскость на внутреннюю (конечную) и внешнюю (бес-
(бесконечную) области (теорема Жордана). Про-
Простой М. может иметь весьма сложное строение границы.
Для выяснения принадлежности какой-либо точки
внешней или внутренней области достаточно провести
из этой точки луч, не проходящий через вершины М.:
если число пересечений луча с границей М. четное, то
исследуемая точка лежит во внешней области, если
нечетное — во внутренней.
Угол, образованный лучами, имеющими начало в не-
к-рой вершине М. и содержащими обе смежные стороны
этой вершины, наз. внутренним углом (уг-
лом) М., если этот угол имеет непустое пересечение с
внутренней областью М. и этому пересечению принад-
принадлежит рассматриваемая вершина М. (см. рис. 4). Сумма
внутренних углов простого re-угольника равна 180°
(п—2). Простой М. имеет хотя бы один внутренний угол,
меньший развернутого.
Прямая, проходящая через две несмежные вершины
М., наз. диагональной, а отрезок с концами в
несмежных вершинах М. наз. диагональю М.
М. наз. ориентируемым, если можно ука-
указать порядок обхода его вершин так, что конец одной
стороны является началом следую-
следующей. Границу М. в этом случае наз.
многоугольным (ориен-
(ориентированным) замкнутым
путем на плоскости. Ориенти-
Ориентированный простой двумерный М.
при обходе границы всегда остается
либо только слева от границы, ли-
либо только справа от нее; области
М. с самопересекающейся границей
могут оказаться по разные стороны от
Простой М. наз. правильным
ски правильным), если все его углы конгру-
конгруэнтны между собой как конгруэнтны и все стороны (име-
(имеют равные длины). Около правильного М. можно опи-
описать окружность и можно вписать окружность в пра-
правильный М. Радиус вписанной окружности является
апофемой правильного М. Правильные М. с оди-
одинаковым числом сторон подобны друг другу. В приве-
приведенной таблице указаны радиус описанной окружности,
радиус вписанной окружности и площадь нек-рых пра-
правильных многоугольников (я — длина стороны М.).
Рис. о.
нее.
(м е т р и ч е-
Число
сторон
3
4
5
6
8
10
Радиус описан-
описанной окружности
,3
аУ2
¦Z
-fLVlOE^'5,
а
_fj_j/2B + K2)
^-A + П)
Радиус вписан-
вписанной окружности
Н
а
2
~A+V2)
-J-V о*-2Уъ
Площадь
а2! Т
4
а2
^ilK5E + 2K5)
За2Г,Т
-
2°2 A+>'2)
4- а*У 5т21'5
М. наз. выпуклым, если он располагается по од-
одну сторону относительно прямой, содержащей любую
сторону М. Выпуклый М.— всегда простой. Правиль-
Правильный М. является выпуклым. В выпуклом М. число диа-
диагоналей равно -к-п(п—3) (га — число сторон), из каж-
каждой вершины можно провести п—3 диагоналей, к-рые
делят М. на п—2 треугольников (рис. 5).
Угол, смежный с внутренним углом выпуклого М.,
наз. внешни м. Сумма внешних углов, взятых по
одному при каждой вершине, выпуклого М. составляет
полный угол C60°). Внешний угол наз. поворотом гра-
границы М. в вершине.
Самопересекающийся М., все стороны к-рого конгру-
конгруэнтны и все углы конгруэнтны, наз. звездчатым
(звездчато-правильны м). Звездчатые М-
существуют при числе сторон начиная с пяти, hv можно
рассматривать как определенную совокупность диаго-
диагоналей правильного в-угольника.
Пол у прав ильным наз. М-, у к-рого конгру-
конгруэнтны только все углы или конгруэнтны только все сто-
стороны. Полуправильный М. с четным числом вершин
наз. равноугольно-полуправ ильным,
если у него все углы конгруэнтны, а стороны конгруэнт-
конгруэнтны через одну (простейший пример — прямоугольник).
Всегда существует окружность, проходящая через все
вершины равноугольно-полуправильного М. Существу-
Существуют также две окружности, из к-рых каждая касается
сторон равноугольно-полуправильного М. через одну.
Полуправильный М. с четным числом вершин наз.
равносторонне - полуправильным,
если все его стороны конгруэнтны, а углы конгруэнтны
через один (простейший пример — ромб). В равносто-
равносторонне-полуправильный М. можно вписать окружность
так, что она будет касаться всех его сторон; существуют
две окружности, из к-рых каждая проходит через вер-
вершины этого М., взятые через одну. Построение равно-
равноугольно-полуправильных и равносторонне-полупра-
равносторонне-полуправильных М. осуществляется с помощью правильных М-
Правильный М. может быть построен циркулем и ли-
линейкой в случае, если число его сторон п=2тр1р2...рк,
где р; — целые простые различные числа вида р==
_22G-;-1, о — целое положительное число (теорема
Г а у с с а). Известны пять чисел указанного вида:
3, 5, 17, 257, 65537. Никакие другие правильные М. не
могут быть построены циркулем и линейкой. Таким об-
образом, можно построить циркулем и линейкой правиль-
правильные «-угольники, если » = 3, 4, 5, 6, 8, 10, 12, 15, 16, 17,
20, 24, 32, 34, ... , и нельзя построить циркулем и ли-
линейкой, если п=7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25,
26, 27, 28, 29, 30, 31, 33, ... . Задача построения пра-
правильного ;г-угольника эквивалентна задаче деления
окружности на ?г равных частей.
Построение звездчатых n-угольников осуществ-
осуществляется также с помощью деления окружности на равные
части: если соединить отрезками делящие точки окруж-
окружности через каждые р делений (р — целое число, вза-
взаимно-простое с п, р<гс), то получается звездчатый
п-угольник. Напр., при и=15 существуют 3 различные
звездчатые 15-угольннкн. На рис. 6 изображены пра-
правильные и звездчатые М. для п—3, 4, 5, 6, 7.
/7=6
Рис.
В нек-рых разделах геометрии под сторонами М.
понимают прямые, на к-рых лежат отрезки замкнутой
ломаной линии. В этом случае М. наз. многосто-
ройником. Возможны одновременно вписанные и
описанные М. (вершины одного лежат на стороне дру-
другого) и даже одновременно описанные и вписанные са-
сами в себя многосторонники (см., напр., Конфигурация).
Площадь любого М. может быть вычислена путем раз-
разложения на треугольники, квадраты и т. д. Площади
ориентированного простого М. приписывается знак
плюс, если при обходе границы внутренняя область
остается слева, и минус, если область останется справа.
В случае, когда граница М. является многоугольным
замкнутым самопересекающимся путем, делящим плос-
плоскость на куски, то площадь такого М. может быть опре-
делена •• помощью т. и. коэффициента куска: если из
нек-poii точки во внешней области М. провести отрезок
в точку, лежащую внутри данного куска, и граница
М. пересекает этот отрезок р раз слева направо и q
раз справа налево, то р—q наз. коэффициентом куска.
Этот коэффициент не зависит от выбора указанных двух
точек. Площадью ориентированного М. (площадью
многоугольного пути) в этом случае является сумма
площадей каждого куска, умноженных на соответству-
соответствующий коэффициент куска.
Если на плоскости введена декартова прямоугольная
система координат хОу, то площадь ориентированного
М. вычисляется при помощи интеграла J ydx, где у —
ордината точек границы М., обходимой один раз. В по-
полярных координатах (р, ф) площадь М. вычисляется
при помощи интеграла — ф р2Лр, где р пробегает
один раз границу М.
М. может быть криволинейны м, его граница
состоит из конечного числа кусков кривых. Такие М.
существуют и на кривых поверхностях. Если граница
М. на поверхности состоит из кусков дуг геодезич. ли-
линий этой поверхности, то М. наз. геодезическим.
В случае, когда М. ограничен отрезками асимптотич.
линий поверхности, то М. наз. асимптот и че-
с к и м, и т. д. Для криволинейных М. определяется
внутренний угол при вершине, к-рый связан с поворо-
поворотом границы в вершине и составляет с ним развернутый
угол (поверхности предполагаются регулярными). Про-
Простые М. на поверхности могут иметь всего две стороны
и две вершины (напр., геодезич. двуугольник на сфере).
М. может быть определен и как нек-рый набор век-
векторов, к-рые рассматриваются как радиус-векторы
вершин М. (п — угольника), т. е. точка (вершина) со-
сопоставляется с нек-рым вектором. Свойства п-уголь-
ника переводятся на язык векторной алгебры, что от-
открывает возможность применения алгебраич. методов
в исследовании классов М. Определяется, в частности,
сумма М., произведение М. на нек-рое число из комму-
коммутативного поля (характеристика к-рого взаимно проста
с числом вершин М.), циклич. классы п-угольников,
циклич. отображения и их алгебра и т. п. На этом пути
оказывается возможным устанавливать многие общие
свойства n-угольников (см., напр., [3]).
М. определяется также и с помощью понятия выпук-
выпуклой оболочки, к-рая является выпуклым М. Именно,
фигура Ф наз. М., если ее можно разложить на
выпуклые М.:
J=0 при
где F{ — выпуклые М.
Лит.: [1] Перепелкин Д. II., Курс элементарной
геометрии, ч. 1, М.— Л., 1948; [2] Адамар Ж., Элементар-
Элементарная геометрия, пер. с франц., 4 изд., ч. 1, М., 1957; [33 Б а х -
м а н Ф., Шмидт 3., n-Угольники, пер. с нем., М., 1973; [4]
Энциклопедия элементарной математики, кн. 4 — Геометрия,
М., 1963. Л. А. Сидоров.
МНОГОУГОЛЬНОЕ ЧИСЛО — см. Арифметиче-
Арифметический ряд.
МНОГОЧЛЕН, полином,— выражение вида
f (х, у, ..., w) = Axbyl. . ,wm-\-Bx"yP. . .w9-\- . . .
. . . -\-DxryS. . .u7f)
где .г, у,---, w — переменные, а А, В, . . ., D (коэф-
(коэффициенты М.) и к, I, . . ., t (показатели
степеней — целые неотрицательные числа) — по-
постоянные. Отдельные слагаемые вида
Axkyl. . . wm
наз. ч л е н а м и М. Порядок членов, а также порядок
множителей в каждом члене можно менять произволь-
произвольно; точно так же можно вводить или опускать члены с
нулевыми коэффициентами, а в каждом отдельном
члене — степени с нулевыми показателями. В случае,
когда М. имеет один, два или три члена, его наз. одно-
одночленом, двучленом или трехчленом.
Относительно коэффициентов М. предполагается,
что они принадлежат нек-рому полю, напр, полю ра-
рациональных, действительных или комплексных чисел.
Два члена М. наз. подобными, если в них
показатели степеней при одинаковых переменных
попарно равны. Подобные между собой члены
А'хку1.. .wm, В'хку1.. .wm,...,D'xkyl.. .wm
можно заменить одним
(А' + В' -\- • • • +-D') хку1. ¦ -ют
(приведение подобных членов). Два М. наз.
равными, если после приведения подобных все члены
с отличными от нуля коэффициентами оказываются
попарно одинаковыми (но, может быть, записанными
в разном порядке), а также если все коэффициенты
этих М. оказываются равными нулю. В последнем
случае М. наз. тождественным нулем и
обозначают знаком 0.
Сумму показателей степеней какого-либо члена М.
наз. степенью этого члена. Если М. не тождест-
тождественный нуль, то среди членов с отличными от нуля
коэффициентами (предполагается, что все подобные
члены приведены) имеются один или несколько наи-
наибольшей степени; эту наибольшую степень наз. сте-
степенью М. Тождественный нуль не имеет степени.
М. нулевой степени сводится к одному члену А (по-
(постоянному, не равному нулю).
М. от переменных х^, х2, . . ., хп наз. симметрическим
многочленом, если он не меняется ни при какой пере-
перестановке неизвестных. М., все члены к-рого одина-
одинаковой степени, наз. однородным многочле-
н о м, или формой; формы первой, второй н треть-
третьей степеней наз. линейными, квадратичными, кубиче-
кубическими, а по числу переменных (два, три)—двоичными
(бинарными), тройничными (тернарными) (напр., f(xr,
xii x^) = x\-\-x\-\-x\—хххг—х2х3—ххх3 есть тройничная
квадратичная форма).
Степенью многочлена f(xlt ,т2, х3, . . ., хп) по
отношению к одному из переменных х;, ?—1, 2, . . ., п,
наз. наивысший показатель, с к-рым х; входит в члены
этого М. (эта степень может быть и нулевой). Из двух
членов М. тот считается выше (относительно данной
нумерации переменных), у к-рого показатель при х1
больше, а если эти показатели равны, то тот, у к-рого
показатели при х2 больше, и т. д. Если все члены М.
расположены в таком порядке, что каждый следующий
член ниже предыдущего, то говорят, что члены этого
М. расположены лексикографически. Тот
член, к-рый при этом стоит на первом месте, наз. в ы с-
ш и м членом многочлена. М. от одного
переменного, члены к-рого расположены в лексико-
графич. порядке, имеет вид
/ (х) = аох» + avxn-!+...+ ап _ хх + ап,
где аи, аи . . ., ап — коэффициенты.
Корнем многочлена от одного неизвест-
неизвестного над полем к наз. решение алгебраического урав-
уравнения
f(x) = O.
Корни М. связаны с его коэффициентами формула-
формулами Виета (см. Виета теорема).
Совокупность всевозможных различных М. от п
переменных с коэффициентами из данного поля обра-
образует кольцо относительно естественным образом опре-
определяемых операций сложения и умножения. Рассмат-
Рассматриваются также кольца М. от бесконечного множества
переменных. Многочленов кольца являются ассоциа-
тивно-коммутатнвными кольцами без делителей нуля
(т. е. произведение М., не равных 0, не может дать 0).
Если для двух многочленов Р и Q можно найти
такой многочлен В, что P = QR, то говорят, что Р
делится на Q; Q наз. делителем, a R — частным. Если
Р не делится на Q, но оба Л1. содержат одно и то же
переменное, напр, х, и степень Р по отношению к х
есть п, а степень Q есть т и re^m^l, то можно найти
такие многочлены />, R и S, что pP=QR-\-S, причем р
совсем не содержит х, а в S переменное х содержится
в степени ниже т. В случае, когда х является един-
единственным переменным, можно р считать равным 1;
тогда операцию отыскания R н S по Р и Q наз. деле-
делением с остатком; деление с остатком можно произво-
производить с помощью Горпера схемы.
Посредством повторного применения этой операции
можно находить наибольший общий делитель Р и Q,
т. о. такой делитель Р и Q, к-рый делится на любой
общий делитель этих М. (см. Евклида алгоритм). Два
М., наибольший общий делитель к-рых равен 1, наз.
взаимно простыми.
М., к-рый можно представить в виде произведения
М. низших степеней с коэффициентами пз данного
ноля, наз. приводимым (в данном поле), в про-
противном случае — н е п р и в о д и м ы м. Неприводи-
Неприводимые М. играют в кольце М. роль, сходную с ролью
простых чисел в кольце целых чисел. Напр., верна
теорема: если произведение PQ делится на неприво-
неприводимый многочлен R, а Р на R не делится, то Q должен
делиться на R. Каждый М., степени большей нуля,
разлагается в данном поле в произведение неприво-
неприводимых множителей единственным образом (с точностью
до множителей нулевой степени). Напр., многочлен
х*-\-\, неприводимый в поле рациональных чисел,
разлагается на два множителя в поле действительных
чисел и на четыре множителя в поле комплексных чи-
чисел. Вообще, каждый М. от одного переменного х
разлагается в поле действительных чисел на множи-
множители первой и второй степени, в поле комплексных
чисел — на множители первой степени (алгебры основ-
основная теорема). Для двух и большего числа переменных
этого уже нельзя утверждать. Над любым полем к
для любого rC^'l существуют М. от п переменных,
неприводимые в любом расширении поля к. Такие М.
наз. абсолютно неприводимыми. Напр.,
многочлен x:J-|-j/z'2-f-za неприводим в любом числовом
поле.
Если переменным .г, у, . . ., w придать определен-
определенные числовые значения (напр., действительные или
комплексные), то М. также получит определенное
числовое значение. Таким образом, каждый М. можно
рассматривать как функцию соответствующих перемен-
переменных. Эта функция непрерывна и дифференцируема
при любых значениях переменных; ее можно харак-
характеризовать как целую рациональную функ-
ц и ю, т. е. функцию, получающуюся из переменных
и нек~рых постоянных (коэффициентов) посредствен
выполнения в определенном порядке действий сложе-
сложения, вычитания и умножения. Целые рациональные
функции входят в более широкий класс рацио-
рациональных функций, где к перечисленным дей-
действиям присоединяется деление: любую рациональную
функцию можно представить в виде частного двух М.
Наконец, рациональные функции содержатся в классе
алгебраических функций.
К числу важнейших свойств М. относится то, что
любую непрерывную функцию можно с произвольно
малой ошибкой заменить М. (см. Вейерштрасса тео-
теорема).
Специальные системы М.— ортогональные много-
многочлены — используются в теории приближения как
средство представления функций в виде рядов.
В элементарной алгебре М. иногда наз. такие ал-
гебраич. выражения, в к-рых последним действием
является сложение или вычитание.
Лит.: [1] Мишина А. П., Проскуряков И. В.,
Высшая алгебра. Линейная алгебра, многочлены, общая алгебра,
2 изд., М., 1965; [2] Курош А. Г., Курс высшей алгебры,
11 изд., М., 1975; [3] Б у р б а к и Н., Алгебра. Многочлены и
поля. Упорядоченные группы, пер. с франц., М., 1965.
А. И. Маркушевич.
МНОГОЧЛЕНОВ КОЛЬЦО кольцо, элементами
к-рого являются многочлены с коэффициентами из
нек-рого фиксированного поля к. ' Рассматриваются
также М. к. над произвольным ассоциативно-комму-
ассоциативно-коммутативным кольцом R, напр, над кольцом целых чисел.
М. к. от конечного множества переменных хг, х2, . . .,
,т„ над В принято обозначать через R[xu х2, ¦ ¦ ., хп].
Можно говорить и о М. к. от любого бесконечного
множества переменных, считая, что каждый отдельный
многочлен зависит лишь от нек-рого конечного числа
переменных. М. к. над кольцом В является (комму-
(коммутативной) свободной алгеброй с единицей над R; мно-
множество переменных служит системой свободных об-
образующих этой алгебры.
М. к. над произвольной областью целостности само
является областью целостности. М. к. от любого ко-
конечного числа неремённых над любым факториальным
кольцом R само является факториалышм.
Для М. к. над полем к от конечного числа перемен-
переменных имеет место Гильберта теорема о базисе: всякий
идеал в k[xlt . . ., хп] может быть порожден (как идеал)
конечным числом элементов. Кольцо многочленов от
одного переменного к[х] является главных идеалов
кольцом, т. е. любой его идеал может быть порожден
одним элементом. Более того, к[х] является евклидовым
кольцом. Это свойство к[х] дает возможность исчерпы-
исчерпывающим образом описать конечно порожденные модули
над ним и, в частности, привести к канонич. виду
линейный оператор в конечномерном векторном про-
пространстве (см. Жорданова матрица). При п>1 кольцо
к[хг, . . ., хп] не является кольцом главных идеалов.
Пусть S — нек-рая ассоциативно-коммутативная к-
алгебра с единицей, о= (ах, а2, . . ., ап) — элемент
декартовой степени S", тогда существует единственный
гомоморфизм М. к. от п переменных в S
(fa:k [.rj. хг, ..., xn]—>-S,
при к-ром (fa(xj)=a; для всех i=l, ...,«, а фоA) —
единица S. Образ многочлена f^k[xlt. . -,хп] при
этом гомоморфизме наз. его значением в точ-
точке а. Точка a?Sn наз. нулем системы многочленов
Fakix-L, . . ., .?•„], если значение каждого многочлена
из F в этой точке есть 0?S. Для М. к. имеет ме-
место Гильберта теорема о нулях: пусть 31 — идеал
кольца R=k[x1, . . ., хп], М — множество нулей
идеала 31 в к", где к — алгебраич. замыкание поля к,
g — многочлен из R, обращающийся в нуль во всех
точках из М, тогда существует натуральное число т
такое, что ?m?2I.
Пусть А — произвольный модуль над кольцом
Л — к\хг, . . ., х„]. Тогда существуют свободные Д-мо-
дулп Хо, Хл, . . -,Хп такие, что последовательность
гомоморфизмов
{0} ._ А <— Хо .*— Х1 ч— ... ч— Хп ^- {0}
точна, т. е. ядро предыдущего гомоморфизма является
образом последующего. Это утверждение — одна из
возможных формулировок Гильберта теоремы о сизи-
сизигиях для М. К.
Конечно порожденный проективный модуль над
М. к. от конечного числа переменных с коэффициен-
коэффициентами из кольца главных идеалов свободен (см. [5],
[6]1; это есть решение проблемы Серра.
Лишь в нек-рых частных случаях имеются ответы
на следующие вопросы: 1) не порождается ли группа
автоморфизмов М. к. элементарными автоморфизмами;
2) не порождается ли к[х±, . . ., хп] произвольным
множеством fu . . .,/„ таким, что det\\ д— —ненулевая
константа; 3) если S(^)k[y] изоморфно к[хг, . . ., хп],
не будет ли S изоморфно к[хг, . . ., ж„_]]?
Лит.: [1] Лен г С, Алгебра, пер. с англ., М., 1968; [21
Бурбаки Н., Алгебра. Многочлены и поля. Упорядоченные
группы, пер. с франц., М., 1965; [3] Н i I b е г t D., «Math. Ann.»,
1893, Bd 42, S. 313—73; [4] его же, «Math. Ann.», 1890,
Bd 36, S. 473 — 534; [5] Суслин А. А., «Докл. АН СССР»,
1976, т. 229, с. 1063—66; [б] Quillen D., «Invent, math.»,
1976 v. 30, p. 167 — 71. Ю. А. Бахтурин.
МНОГОЭКСТРЕМАЛЬНАЯ ЗАДАЧА — экстремаль-
экстремальная задача, имеющая несколько или неизвестное число
локальных экстремумов.
Проблема отыскания глобального экстремума f(x),
х= (.г1, • . ., х")?Х (g R", решена для основных классов
унимодальных функции (прежде всего для выпуклых
и родственных им, см. Выпуклое программирование). Для
мультимодальных функций, даже для гладких и мед-
медленно меняющихся, в настоящее время A982) отсутст-
отсутствуют методы достоверного вычисления глобального
экстремума за исключением сканирования по траек-
траекториям, образующим всюду плотное множество в до-
допустимом множестве X. На практике трудоемкое ска-
сканирование комбинируют с алгоритмами поиска ло-
локального экстремума: с помощью сканирования и
априорных сведений об f(x) (оценок производных,
функциональных уравнений и неравенств и др.) окон-
туривается область притяжения каждого
локального экстремума и мертвые зоны, где
конкретный локальный алгоритм теряет эффективность
(напр., для градиентного метода мертвыми зонами
являются окрестность седловой точки и «дно оврага»).
Затем экстремумы оцениваются или ищутся с помощью
локальных методов и сравниваются между собой.
Для функций, удовлетворяющих условию Липшица
(V*. х'?Х)& < ео) |/(*)-/(*') К *!*-*'II.
наиболее универсальным является метод покры-
покрытий (перебор на неравномерной сетке), к-рый к тому
же легко реализуем в многомерном случае.
Для нахождения локальных экстремумов, близких
к глобальному, в приложениях используются эмпи-
эмпирические «эвристические» способы, к-рые можно на-
назвать кваз и глобальным и:
1. Алгоритмы типа тяжелого шарика метода или
овражных методов (см. Овражных функций методы ми-
минимизации), способные «проскакивать» через нек-рые
локальные экстремумы или «огибать» области их
притяжения.
2. Случайный перебор значений / (х) с помощью
Монте-Карло метода.
3. Модификация локальных методов путем введения
стохастич. параметров. Напр., траектория рандоми-
рандомизированного градиентного метода
где 5@ — случайный процесс типа белого шума, при
нек-рых условиях способна попадать из точки локаль-
локального в точку глобального экстремума.
4. «Огрубление» функции путем се аппроксимации
последовательностью унимодальных функций. Аппрок-
Аппроксимация может производиться по значениям / (х) в
нек-рых точках, разложением по параметрам, входящим
в аналитич. выражение функции, мажорантами или
минорантами и т. п.
5. Поиск локального экстремума осредненной функ-
функции f(x) (скользящее среднее)
р(х,
Примеры:
2. Ж-$х«-(х-БI/(&)
Физич. смысл такого усреднения заключается в «сгла-
«сглаживании» исходной функции и «отфильтровании» от
нес колеблющихся слагаемых.
Если /(.r)=const (x) (быстроосциллирующая функция
f{x)), то перед усреднением исходную функцию можно
«продетектпровать» с помощью нелинейного преоб-
преобразования, напр.
P(x, I) \fil)\dl. B)
В качестве взвешивающей при усреднении функции
р (.с, ?) можно взять и
х
| / (х)
и А
vrai sup | / (х) | =lim 1/
а/ ж п->-к r
Ы X n-t-x, У ixdM ix)
Последнее соотношение возможно также использовать
для получения оценок существенных максимума и
минимума.
Формулы A) и B) можно интерпретировать как фор-
формулы математпч. ожиданий для функции случайной
величины Н, распределенной с плотностью вероятно-
вероятностей р (х, |). Поэтому данную М. з. можно трактовать
как задачу стоха-тического программирования и при-
применять к ней его методы.
После нахождения экстремума аппроксимирующей
или усредненной функции (обзорный поиск)
можно произвести в окрестности найденной точки д е-
тальнып поиск экстремума исходной функции
fix).
Глобальную оптимизацию отдельных функций можно
произвести с помощью частных специфич. приемов.
Напр., построить такую динамич. систему, для к-рой
точка глобального экстремума является асимптоти-
асимптотически устойчивой точкой покоя.
Одним из источников идей новых методов (квази)
глобальной оптимизации является моделирование про-
процессов в физических и биологических системах.
Громоздкие вычислительные процессы нелокального
поиска можно оптимизировать по ряду показателен
с учетом ограничений на вычислительные средства,
априорной и последовательно накапливаемой инфор-
информации об исследуемой функции fix), вероятностных
характеристиках случайных факторов и пр. Один из
подходов, к-рые здесь пытаются применить, основан
на теории статистич. решений.
Помимо отыскания глобального экстремума возни-
возникают и иные М. з., напр, определение колебания функ-
функции, перечисление и отыскание всех локальных экст-
экстремумов в заданной области.
Для многочленов разработаны весьма аффективные
правила подсчета и отделения корней производных.
Для точек экстремума трансцендентных функций
здесь могут быть полезны соображения типа Ролля
теоремы или сравнения теорем для решений диффе-
дифференциальных уравнений.
Число стационарных точек аналитич. функции мо-
может быть оценено с помощью аргумента принципа.
Если функция имеет бесконечную последователь-
последовательность экстремумов, то на практике вычисляется непо-
непосредственно несколько из них, а остальные — с по-
помощью асимптотич. разложения (напр., Г-функция).
Квазиклассич. приближение для дифференциальных
уравнений можно рассматривать как асимптотич. раз-
разложение решения уравнения по числу его экстремумов.
О М. з. в бесконечномерном случае см. Вариационное
исчисление в целом. Дискретные аналоги освещены в
ст. Целочисленное программирование и Дискретное
программирование.
Лит. см. при ст. Максимизация и минимизация функций.
Ю. П. Иванилов, В. В. Охримеико.
МНОЖЕСТВ КАТЕГОРИЯ — категория, объектами
к-рой являются всевозможные множества, морфпз-
мами — всевозможные отображения множеств друг в
друга, и умножение морфизмов определяется как
последовательное выполнение отображений а : А —>- В
и Р : В —>- С. Если теоретико-категорные рассмотрения
проводятся внутри фиксированного универсального мно-
множества U, то под М. к. понимают категорию, объек-
объектами к-рой являются всевозможные множества, при-
принадлежащие U, а морфизмы и нх умножение вводятся,
как и выше. М. к. обозначают лиПо (\, либо Ens,
либо St, либо Me.
Пустое множество 0 является левым нулем (ини-
(инициальным объектом), а одноэлементное множество —
правым нулем (терминальным объектом) М. к. Всякое
непустое множество является образующим объектом,
всякое множество, содержащее не менее двух элемен-
элементов,— кообразуклцим (коинтегральным) объектом М. к.
Всякий мономорфизм с непустым началом есть обра-
обратимое справа лнъективное отображение, всякий ,»пи-
морфизм есть обратимое слева сюръективное отобра-
отображение. М. к. обладает единственной бикатегорной
структурой.
М. к. является локально малой биполной катего-
категорией. В частности, произведение семейства множеств
совпадает с декартовым произведением этого семей-
семейства, копроизведение семейства множеств совпадает с
разъединенным объединением этого семейства. Декар-
Декартово произведение, рассматриваемое как бифунктор,
Hom-функтор Н : (?,* х (S —»-($ и одноэлементное мно-
множество снабжают М. к. структурой замкнутой катего-
категории. Всякая категория относительная категория
над М. к. Двухэлементное множество снабжает М. к.
дополнительной структурой (абстрактпого) топоса.
Категория Я тогда и только тогда эквивалентна М. к.,
когда в it имеется формально присоединенный левый
нуль Л, а полная подкатегория Jt\A является кате-
категорией с регулярными кообразами с унарным образу-
образующим объектом, для каждого объекта А к-рой сущест-
существует произведение Ах А и каждое. отношение экви-
эквивалентности
(и,], |х=|ш1 (X) |Ш2:-Я—^Ау.А(л1,Ло)
индуцировано ядерной парой (иль и.л2) нек-рого мор-
физма. Объект U наз. унарным, если существуют
любые копроизведения
n*uluh ui==u,
и если всякий морфизм
a:U -^П*?/ U.i(Oi)
представим в виде сс=с/ а,- для единственного I. О дру-
других характерпзациях М. к. см. [2], "[3].
Категории, изоморфные подкатегориям М. к., наз.
конкретными. О необходимых и достаточных
условиях конкретности категории см. [1].
Л 11} F d P J P d Al
р р []
Лит.: 11} F г е у d P., «J. Pure and Appl. Algebra», 1073;
v. 3, № 2, p. 171—91; [2J L a w v e r n F. W_, «Proc. Nat.
Acad. Sci. USA», 19B4, v. 52, № 6, p. 1506 —11;'[3] Скорня-
СкорняЛ А М б 1969 80 N 4 492502
, , , , p 5 ;[] ор
ков Л. А., «Матем. сб.», 1969, т. 80, .N» 4, с. 492—502.
М. Ш. Дален ко.
МНОЖЕСТВ ТЕОРИЯ наивная — учение о свой-
свойствах множеств, преимущественно бесконечных, э л и-
минирующее св-ойства элементов, составляющих
эти множества. Понятие множества принадлежи! к
числу первоначальных математич. понятий и может
быть пояснено только при помощи примеров. Так,
можно говорить о множестве людей, живущих на нашей
планете в данный момент времени, о множестве точек
данной геометрич. фигуры, о множестве решений
данного дифференциального уравнения. Люди, жи-
живущие на нашей планете в данный момент времени,
точки данной геометрич. фигуры, решение данного
дифференциального уравнения являются элементами
соответствующего множества. Множество А считается
заданным, если указано характеристич. свойство эле-
элементов этого множества, т. е. такое свойство, к-рым
обладают все элементы этого множества и только они.
Одним из основных понятий М. т. является понятие
принадлежности элемента множеству. В качестве обо-
обозначения того, что предмет а принадлежит множеству
А, пишут а?А. (Если а не принадлежит А, то пишут
а?А, афА.) Может случиться, что характеристич.
свойством, определяющим множество А, не обладает
вообще ни один предмет; тогда говорят, что множество
А пустое и пишут А = 0. Напр., множество действи-
действительных решений уравнения ,г'2=—1 пустое. Если
каждый алемент множества А является в то же время
элементом множества В, то множество А наз. под-
подмножеством множества В и пишут АсВ. Если
одновременно выполнено АсВ и ВсА, то говорят,
что множества ЛиВравныи пишут А = В. Объ-
Объединением A U В множеств А а В наз. множе-
множество, состоящее из всех элементов, принадлежащих
хотя бы одному из множеств А и В. Пересече-
Пересечением А [)В множеств А и В наз. множество, состоя-
состоящее из всех элементов, принадлежащих как А, так и В.
Операции объединения и пересечения коммутативны,
ассоциативны и взаимно дистрибутивны. Например,
(А [}В)С\С= (А Г\С)[} (ВПС)- Во многих разделах М. т.
рассматриваются только такие множества, к-рые со-
содержатся в нек-ром фиксированном множестве X.
Если А — подмножество X и Р — свойство, харак-
характеризующее элементы из А, то пишут А — {х?Х:
Р (х) — истина}. Напр., если X — множество всех
действительных чисел, а Л — подмножество положи-
положительных чисел, то А= {.т?Х: ж>0}. Если АаХ, то
множество Х\А= {х?Х:х?А } наз. дополнен и-
е м множества А. Операции объединения, пересечения
и дополнения связаны т. н. з а к о н а м и д е Мор-
Моргана. Напр., Х\(А f\B)= (X\A)\J {X\B). Раздел М.
т., к-рый занимается исследованием операций над мно-
множествами (не только конечных, но и бесконечных опе-
операций), наз. алгеброй множеств. Алгебра
множеств в свою очередь является частным случаем
теории булевых алгебр.
М. т. была создана работами математиков 19 в.,
к-рые ставили себе целью разработку оснований ма-
математич. анализа. Уже в первых работах в этой области
[Б. Больцано (В. Bolzano), П. Дюбуа-Реймон (P. Du
Bois-Reymond), P. Дедекинд (R. Dedekind)], в к-рых
рассматривались числовые множества или множества
функций, ставился вопрос о количественном сравнении
бесконечных множеств. Является ли бесконечность мно-
множества чисто отрицательным свойством, не допуска-
допускающим расчленения, или же существуют различные
ступени математич. бесконечности, бесконечные мно-
множества различной количественной силы, различной
«мощности»? Ответ на ятот вопрос дал Г. Кантор (G. Can-
Cantor, 1871—83), к-рый представил почти современное
изложение теории кардинальных чисел и порядковых
чисел и теории вполне упорядоченных множеств. Воз-
Возможность сравнительной количественной оценки мно-
множеств опирается на понятие взаимно однозначного
соответствия (или биекции) между двумя множест-
множествами. Пусть каждому элементу множества А соответ-
ствует в силу какого бы то ни было правила или закона
нек-рый определенный элемент множества В, если при
этом каждый элемент множества В оказывается по-
поставленным в соответствие одному и только одному
элементу множества А, то говорят, что между множе-
множествами А и В установлено взаимно однознач-
однозначное соответствие (или биективное ото-
отображение, или б лекция). Между двумя ко-
конечными множествами можно установить биекцию
тогда и только тогда, когда оба множества состоят из
одного и того же числа элементов. В обобщении этого
факта Г. Кантор определил количественную
эквивалентность, или равномощность,
как возможность установить между ними взаимно
однозначное соответствие. Если множество А равно-
мощно множеству В, то множества А и В имеют одно
и то же кардинальное число. Ценность понятия мощ-
мощности множества определяется существованием не-
равномощных бесконечных множеств. Напр., множе-
множество всех действительных чисел и множество всех
натуральных чисел имеют разные мощности.
Первое имеет мощность континуума, а второе —
счетное множество. В каждом бесконечном множестве
А имеется собственное подмножество, равномощное
всему А, в то же время как ни в одном конечном мно-
множестве такой правильной части найти нельзя. Поэтому
наличие правильной части, равномощной целому,
можно принять за определение бесконечного множества.
Заслуга Г. Кантора состоит не только в решении
проблемы мощности множества, но и в том решитель-
решительном шаге, к-рый сделал он, рассмотрев множества,
состоящие из элементов произвольной природы. О том,
что шаг к общности был трудным, свидетельствуют,
во-первых, различные противоречия {антиномии), от-
открытые разными учеными к началу 20 в. и приведшие
к созданию аксиоматической теории множеств, и,
во-вторых, то, что естественным образом возникшие
задачи (напр., континуум-гипотеза) оказались нераз-
неразрешимыми.
Дальнейший вклад в М. т. внес Ф. Хаусдорф (F. Haus-
dorff), разработав теорию линейно упорядоченных
множеств и применив М. т. к топологии, он заложил
основы теории топологических пространств (или общей
топологии). Далее, Л-операция, возникшая при ис-
исследовании борелевских множеств, привела к созданию
дескриптивной теории множеств. Из ряда задач ком-
комбинаторной математики и теории графов возникла
комбинаторная теория множеств. Наконец, открытия,
сделанные К. Гёделем (К. Godel) и П. Коэном (P. Co-
Cohen) в аксиоматич. теории множеств существенно
повлияли на методы и развитие М. т.
Лит.: [11 Александров П. С, Введение в общую
теорию множеств и функций, М.— Л-, 1948; [2] Б о л ь ц а-
но Б., Парадоксы бесконечного, пер. с нем., Одесса, 1911; [3]
Учение о множествах Георга Кантора, СПБ, 1914 (Новые идеи в
математике. Сб. № 6); [41 X а у с д о р ф Ф., Теория множеств,
пер. с нем., М.— Л., 1937; [5] Куратовский К., М о с-
т о в. с к и й А., Теория множеств, пер. с англ., М., 1970; [G]
Бур бак и Н., Теория множеств, пер. с франц., М., 1965.
Б. А. Ефимов.
МНОЖЕСТВЕННОЕ СРАВНЕНИЕ — задача проверь
ки гипотезы относительно значений скалярного про-
произведения в-1--с вектора 6= Fl5 . . ., 0ft), координаты
к-рого суть неизвестные параметры, на заданный вектор
с= (cj, . . ., с/;)-1-. В статистич. исследованиях задача
М. с. часто возникает при проведении дисперсионного
анализа, где, как правило, вектор с выбирается таким
образом, что сх+. . . + е? = 0, а само скалярное произ-
произведение в-'--с в таком случае наз. контрастом. В пред-
предположении, что 6-,, . . ., Oft суть неизвестные матема-
тич. ожидания одномерных нормальных законов, Дж.
У. Тьтоки (J. W. Tukey) и Г. Шеффе (Н. Scheffe) пред-
предложили Г-м е т о д и 5-м е т о д соответственно для
оценивания контрастов, к-рые являются основными
методами в задаче построения доверительных интер-
интервалов для контрастов.
Лит.: [1] Шеффе Г., Дисперсионный анализ, пер. с
англ., М., 1963; [2] Кендал л М., С т ь ю а р т А., Много-
Многомерный статистический анализ и временные ряды, пер. с англ.,
М., 1976. М. С. Никулин.
МНОЖЕСТВЕННЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯ-
КОРРЕЛЯЦИИ — мера линейной зависимости между одной и
нек-рой совокупностью случайных величин. Точнее,
если (Хь . . ., Xk) случайный вектор со значениями
в Rk, то М. к. к. между Х1 и Х2, . . ., Х^ определяется
как обычный коэффициент корреляции между Хг и
наилучшим линейным приближением Х± но Xi, . . .,
Xk, т. е. регрессией Е(Х1|Х2, . . ., Х%) величины Хг
по Х2, . . ., Xk. M. к. к. обладает тем свойством, что
если "при ЕХХ=. . .E—Xk--^0
есть регрессия Х1 по X2, . . ., X),, то среди всех линей-
линейных комбинаций величин Х2, . . ., Х% величина Xi
имеет наибольшую корреляцию с Хг; в этом смысле
М. к. к.— частный случай канонич. коэффициента кор-
корреляции. При А-—2 М. к. к. равен обычному коэффи-
коэффициенту корреляции р]2 между Хх и Х2. М. к. к. между
Х1 и Х2, . . ., Хь обозначается Р].(о /г) и выражается
через элементы корреляционной матрицы Д=11р,у!!,
i, /=1, . . ., к, следующим образом
где |Д| — определитель Л, a Rn алгебраич. дополне-
дополнение элемента рц = 1; при этод1 0<:р|.B ^)<1- Если
PlB АI^^' т0 величина Х1 с вероятностью 1 равна
нек-рой линейной комбинации величин Х2, . . ., Х^,
т. е. совместное распределение величин Хг, . . ., Х^
сосредоточено в нек-рой гиперплоскости пространства
Rft. С другой стороны, р].B. k) =0 тогда и только
тогда, когда р12=. . -^Pift = 0, т. е. когда Л\ не корре-
лнрована ни с одной из величин Х2, - . •, Хп. Для
вычисления М. к. к. можно также использовать фор-
формулу
Pi B ...ft)" 1
где CTi — дисперсия Х^, а
2, ..., Хк))*
дисперсия Xj относительно регрессии.
Выборочным аналогом М. к. к. Р[.B k) является
где «^./9 ?v и s] — оценки CFj B k^ и Oj по выборке
объема п. Для проверки гипотезы об отсутствии связи
используются выборочные распределения rl.vi..,k). При
условии, что выборка произведена из многомерной нор-
нормальной совокупности, величина r\,^ k^ имеет бета-
распределение с параметрами [ ~ , —— \ , если
f 1.B . .ft)—0; если р!,B ...й^О, то величина nr\.B k)
при п —>¦ оо имеет в пределе нецентральное «хи-квадрат»-
распределение с к—1 степенями свободы и параметром
нецентральности nr^^2 ky
Лит.: [1] Крамер Г., Математические методы статистики,
пер. с англ., 2 изд., М., 1975: [2] К е н д а л л М., Стыо-
арт А., Статистические выцоды и связи, пер. с англ., М., 1973.
А. В. Прохоров.
МНОЖЕСТВО — набор, совокупность, собрание ка-
каких-либо объектов, наз. его элементами, обла-
обладающих общим для всех их характеристич. свойством.
«Множество есть многое, мыслимое нами как единое»
(Г. Кантор). Это не является в полном смысле логич.
определением понятия М., а всего лишь пояснением
(ибо определить понятие — значит найти такое родо-
родовое понятие, в к-рое данное понятие входит в качестве
вида, но М.— это, пожалуй, самое широкое понятие
математики и логики). При этом можно либо дать
перечень элементов М.— его перечислен и е,
либо дать правило для определения того, принадлежит
или нет данный объект рассматриваемому М.— его
опис ание (впрочем, первое приемлемо, лишь
когда речь идет о конечных М.).
Для содержательного развития «наивной» множеств
теории такого пояснения вполне достаточно, ибо для
математич. теории существенны определенные соот-
соотношения между элементами М. (или между самими
М.), а не их природа. При описании же тех М., к-рые
могут быть элементами других М., во избежание т. н.
антиномий, вводится, напр., термин «класс». И тогда,
говоря более формально, теория М. имеет дело с объ-
объектами, наз. классами, для к-рых определено отноше-
отношение принадлежности, а само М. определяется как
класс, являющийся элементом нек-рого класса.
В последнее время все более вырисовывается объ-
объединяющая роль теории категорий (и, в частности,
понятия универсального множества), построение к-рой
основывается на аксиоматической теории множеств,
позволяющей рассматривать, напр., такие «большие»
совокупности, как категория всех множеств, групп,
топологич. пространств и т. д.
Лит.: [1] Учение о множествах Георга Кантора. СПБ, 1914
(Новые идеи в математике. Сб. Л5 6); L2]III и х а н о в и ч Ю. А.,
Введение в современную математику, М., 1965; [3] Конда-
Кондаков Н. И., Логический словарь-справочник, 2 изд., М., 1У75;
[4] Б у р б а к и Н., Теория множеств, пер. с франц., М., 196Г>
[5] Н о в и к о в П. С, Элементы математической логики, 2 изд.
М., 1973; [6] Кон П., Универсальная алгебра, пер. с англ.
М., 1968; [7] Ш е н ф и л д Д ж., Математическая логика, пер
с англ., М., 1975. М. И. ВойцеховскиЬ
МНОЖЕСТВО ТИПА Fa(G6), Fo-m ножество
(Gg-м ножество),— объединение (пересечение)
счетного числа замкнутых (открытых) множеств. См.
Борелевское множество.
А-МНОЖЕСТВО, аналитическое множе-
множество, в полном сепарабельном метрическом прост-
пространстве — непрерывный образ борелевского множе-
множества. Так как любое борелевское множество является
непрерывным образом множества иррациональных чи-
чисел, то Л-м. можно определить как непрерывный
образ множества иррациональных чисел. Счетное
пересечение и счетное объединение Л-м. является
Л-м. Любое Л-м. измеримо в смысле Лебега. Свойство
быть Л-м. инвариантно относительно измеримых по
Борелю отображений, а также относительно А-опе-
рации. Более того, для того чтобы множество было
А-и., необходимо и достаточно, чтобы оно представ-
представляло собой результат Л-операции, примененной к
нек-рой системе замкнутых множеств. Существуют
примеры Л-м., к-рые не являются борелевскими; так,
в пространстве 27 всех замкнутых подмножеств от-
отрезка / действительных чисел множество замкнутых
несчетных множеств является Л-м., но не является
борелевским. Любое несчетное Л-м. топологически
содержит канторов совершенное множество. Таким
образом, Л-м. «реализует» континуум-гипотезу: их
мощность либо конечна, либо #„, либо 2*'. Для Л-м.
справедливы Лузина принципы отделимости.
Лит.: [1] Куратовский К., Топология, пер. с англ.,
т. 1, М., 1900; [2] Лузин Н. Н., Лекции оО аналитических
множествах и их приложениях, М-, 1953. Б. А. Ефимов.
СЛ -МНОЖЕСТВО —дополнение к А-множеству, ле-
лежащему в полном сепарабельном метрич. пространстве
X, т. е, РаХ есть СА-м., если Х\Р является Л-мно-
жеством или, другими словами, АС-м. есть проектив-
проективное множество класса 2. Существует пример СА-м.,
не являющегося Л-множеством. Любое Л-множество
является взаимно однозначным и непрерывным обра-
образом нек-рого СА-м. (теорема Мазуркевича).
Точка у наз. значением порядка 1 ото-
отображения /, если существует одна и только одна точка
такая, что у—/(.г). Значения порядка 1 В-измеримого
отображения / произвольного борелевского множества
образуют СА-м. (теорема Лузина). Имеет
место и обратная теорема: пусть С — нек-рое СА-м.,
принадлежащее пространству X; тогда существует
непрерывная функция /, определенная на замкнутом
подмножестве пространства иррациональных чисел,
такая, что С есть множество точек порядка 1 функции /.
Теорема Куратовского о редукции:
пусть дана бесконечная последовательность СА-м.
U1, U2, . . ., тогда существует такая последователь-
последовательность непересекающихся СА-м. V1, V2, . . ., что V"czU"
Лит.: [1] К уратовский К., Топология, пер. с англ.,
т. 1, М., 1966. Б. А. Ефимов.
МОДА — одна из числовых характеристик распре-
распределения вероятностей случайной величины. Для слу-
случайной величины, имеющей плотность вероятности
р(.г), М. наз. любая точка Хе, максимума р(х). М. оп-
определяется и для дискретных распределений: если
значения х^ и случайной величины X с распределением
Pi{—P{X~xk} расположены в порядке возрастания,
то точка хт наз. м о д о й, если pm>pm-i и рт>рт + 1.
Распределения с одной, двумя или большим числом
М. наз. соответственно унимодальными (или
одновершинными), бимодальными и
м у л ь т и м о д а л ь н ы м и. Наиболее важными в
теории вероятностей и математич. статистике являются
унимодальные распределения. Наряду с математич.
ожиданием и медианой М. служит характеристикой
расположения значений случайной величины. Для
унимодального и симметричного относительно нек-рон
точки а распределения М. равна а и совпадает с медиа-
медианой и математич. ожиданием, если последнее сущест-
существует. -А- -В. Прохоров.
МОДАЛЬНАЯ ЛОГИКА — область логики, в к-рой
наряду с обычными высказываниями рассматриваются
модальные высказывания, т. е. выска-
высказывания типа «необходимо, что...», «возможно, что...»
и т. п. В математич. логике рассматриваются различ-
различные формальные системы М. л., выявляется взаимо-
взаимосвязь между этими системами, изучаются их интерпре-
интерпретации.
Элементы М. л. имелись по существу еще у Аристо-
Аристотеля D в. до н. э.), а от него перешли в классич. фило-
философию. Впервые М-. л. была формализована К. Льюи-
Льюисом [1], к-рый построил пять пропозициональных
систем М. л., получивших в литературе обозначения
SI — S5 (их формулировки приведены ниже). Затем
были построены и исследованы другие системы М. л.
Большое разнообразие систем М. л. объясняется тем,
что понятия «возможно» и «необходимо» можно уточ-
уточнять различными способами и, кроме того, по-разному
трактовать сложные модальности типа «необходимо
возможно» и «взаимоотношения» модальностей с логич.
связками. Большинство изучавшихся систем М. л.
опирается на классич. логику, однако рассматриваются
и системы, основанные на интуиционистской логике
(см., напр., [6]).
Ниже описывается несколько наиболее хорошо изу-
изученных пропозициональных систем М. л. Язык каждой
из этих систем получается из языка классич. исчис-
ления высказываний Р добавлением новых одномест-
одноместных связок (модальных операторов) П
(необходимо) и <^> (возможно). Поскольку почти во
всех системах имеет место соотношение
то в качестве исходного берется один модальный опе-
оператор, напр. [Н, а другой определяется через него с
помощью соотношения (*).
Система S1. Схемы аксиом:
1) все формулы вида ПИ) где А — выводимая в Р
формула,
2) ОЮА=>А),
3) П(ПИ=>В)&П(В=>С)
Правила вывода:
т, A A ГЭ В , _ ,
I) 7j (модус поненс),
; П(ПАЭПВ)
Система .82: S1+ {? (П^ЗП {А V В))}.
С и с т е м а S3: S2+ {Q (? (А ЗВ)ЗП (П^
Система К. Схемы аксиом:
1) все схемы аксиом исчисления высказываний Р,
2) пИзВ)з(П/1зПЯ).
А —^
Правила вывода: модус поненс и —-г- (П'-введение).
Система Т: К+ {[7И =зЛ }=
S2+{правило [^-введения}.
С и с т е м а В: Т+ {^зОО^ )¦
Система S4: S3+
{}
Система S5: S4+ {? (АГЭПО-4)}•
Среди вышеупомянутых систем важное значение
имеет S4, т. к. в ней интерпретируется интуционист-
ское исчисление высказываний /, т. е. по всякой про-
пропозициональной (немодальной) формуле А можно
построить такую формулу А* модальной логики, что
S4|— Л*.
В связи с этим особый интерес представляет система
Гжегорчика (см. [5]):
для к-рой верна теорема о переводе: для
любого множества схем^ксиом Г и любой формулы А
1 + Г\—А ?=р S4+T*|— Л*<?=ф> G + r*[— A*,
где Г*= {В*\В? Г}, причем G — самая сильная си-
система с таким свойством. Эта теорема позволяет пере-
переносить нек-рые свойства (напр., полноту или разреши-
разрешимость) с расширений системы S4 (или 6) на промежу-
промежуточные логики.
Для каждой пропозициональной системы М. л. S
можно рассмотреть соответствующую предикатную си-
систему, к-рая получается добавлением к языку системы
S предметных переменных, предикатных символов и
кванторов V, 3 (или одного из них). Также добавля-
добавляются обычные схемы аксиом и правила вывода для
кванторов. Кроме того, иногда добавляют и другие
аксиомы, описывающие действие модальных операто-
операторов на кванторы, напр. т. н. ф о р м у л у Баркан:
Алгсбраич. интерпретация систем М. л. задается
нек-рой алгеброй (называемой также матрице й)
%К = <М, D; &*, V*, а*, 1*, [:*>,
где М — множество истинностных значений, D —
множество выделенных истинностных значений,
D(zM, а &*, /*, г)*, *, ?* — операции на М, соот-
соответствующие связкам &, V, ИЭ, , ?• Формула наз.
общезначимой на алгебре Щ!, если при всякой
оценке ее просозициональных переменных элементами
М она принимает выделенное значение. Система М. л.
S наз. полной относительно класса алгебр аТ, если
псякая формула выводима в S тогда и только тогда,
когда она общезначима на всякой алгебре из X. Напр.,
система S4 полна относительно класса конечных т. н.
топологических булевых алгебр (см. [3]). Вообще,
система S наз. финитно аппроксимиру-
аппроксимируемо и, если она полна относительно конечных алгебр.
Если система конечно аксиоматизируема и финитно
аппроксимируема, то она разрешима, т. е. для
нее алгоритмически разрешима проблема распозна-
распознавания выводимости. Матрица Щ! наз. характери-
характеристической, или адекватной, для системы S,
если S полна относительно {ffll}. Никакая из упомя-
упомянутых выше пропозициональных систем М. л. не имеет
конечной адекватной матрицы, но каждая из этих
систем финитно аппроксимируема и поэтому разре-
разрешима. С другой стороны, всякое расширение системы
S5 имеет конечную адекватную матрицу с одним выде-
выделенным значением. Свойством финитной аппроксими-
аппроксимируемости обладают также все расширения системы
]B) V О (OB ^ О А)}.
Важным инструментом изучения М. л. являются
Крипке модели, имеющие вид (W, R, 9), где W — мно-
множество «миров», «ситуаций», R — нек-рое отношение
на W, 9 — оценка пропозициональных переменных
подмножествами W. Для s, t? W отнотенпе sRt можно
трактовать как «мир t возможен в мире s». Пару (W, R)
наз. структурой Крипке, или остовом
(встречается также термин ш кала). Формула А
наз. общезначимой на остове (W, R),
если для всякой оценки 6 формула А истинна в модели
Крипке (W, R, 9). Система S наз. полной по
Крипке, если всякая не выводимая в S формула
опровержима на нек-рой структуре Крипке, на к-рой
общезначимы все выводимые в S формулы. Напр.,
система Т полна относительно структур (W, R), где
R — рефлексивное отношение; S4 полна относительно
структур с рефлексивным и транзитивным отношением.
Среди конечно аксиоматизируемых расширений си-
системы S4 существуют такие, к-рые не полны по Крипке
(см. [7]).
Для предикатных систем М. л. модели Крипке имеют
вид (W, R, D, \|), 9), где D={Ds}s5W, Ds — универсум
мира s, г|з — интерпретация предикатных символов в
D, а Э — оценка, сопоставляющая каждой предметной
переменной нек-рып элемент множества Us^w^s-
Для систем, содержащих формулу Баркан, надо также
потребовать, чтобы
sRt => Dt>=Ds.
Модели Крипке имеют, как правило, более нагляд-
наглядную структуру, чем алгебраич. модели, поэтому часто
они удобнее для изучения различных систем М. л.
Лит.: [1] L e w i s С."I., L an g f о г d С. Н., Symbolic Logic,
2 ей., N. Y., 1959; [2] Фейс Р., Модальная логика, [пер. с
англ.]. М., 1974; [3] Р а с е в а Е., С и к о р с к и и Р., Ма-
темагп.';,а метаматематики, пер. с англ., М., 1972; 14] М н н ц Г.Е.,
«Тр. Матем. ин-та АН СССР», 1968, т. 98, с. 88 — 111; [5] G г г е-
g-orczy.lt Л., «Fundam. niath.», 19fi7, t. во, .\i 2, p. 223—31;
[li] Bull R. A., «Notre Dame J. Form. Loaic», 1965, t. (i,
p. 142—46; [7] F i n e K., «Theoria», 1974, v. 40, pt 1, p. 23 — 29;
[8]Gabbay D. M., «Ann. Math. Log.», 1975, v. 8, № 3,p.237 —
95. С. К. Соболев.
МОДАЛЬНОСТЬ — свойство суждения, характери-
характеризующее степень ого достоверности. Различные М. и
изаимосвязь между ними изучаются модальной логикой.
М. «необходимо» и «возможно» были введены в логику
еще Аристотелем D в. до н. э.), к-рый, однако, 1-е
придавал им точного смысла. Эти М. наз. основ-
н ы м и и обозначаются соответственно символами Г ]
и <*> (иногда L и М). Различные комбинации основных
М. и отрицания ~~| также являются М. Двойствен-
Двойственной к М. Q наз. М. Q, получаемая из Q заменой
каждого вхождения П на <5, и обратно. В подавляющем
большинстве систем модальной логики для М. Q и
двойственной ей М. Q имеет место эквивалентность
В принципе можно образовать бесконечное число
комбинаций из \_^, <0> и ~], однако часто в конкретгшх
системах число попарно не эквивалентных М. оказы-
оказывается ограниченным (ввиду соотношения (*) и на-
наличия аксиом, упрощающих нек-рые М. или сводящих
одни М. к другим). Напр., в системе S3 имеется ровно
40 различных М., а в системе S4 их только 12:
ПА, ПО л, г\ООА, 1ПЛ, -]п<М. 1О0ОА,
а также М., двойственные этим. В системе S5 имеется
всего 4 М.: Г_\А, (~}А, ]ПЛ, ~~|<^>Л. С другой стороны,
в системе Т модальной логики, а также в S1 и S2 число
М. бесконечно и, более того, нет редукций М., т. е.
две положительные (не содержащие знака ~\) М. Qi
и (>2 эквивалентны тогда п только тогда, когда Q-y=Q%-
Иногда к М. относят (формализованные в соответст-
соответствующих теориях) такие понятия, как «истинно», «до-
«доказуемо», «опровержимо», а также связанные ео вре-
временем «будет», «всегда было» и т. п.
Лига. см. при ст. Модальная логика. С. К. Соболев.
МОДЕЛЕЙ ТЕОРИЯ — раздел математической ло-
логики, изучающий математические модели.
Начало М. т. относится к 30-м гг. 20 в., когда были
доказаны следующие две основные теоремы.
Теорема 1 (теорема Гёделя — Мальце-
в а). Если каждая конечная подсовокупность совокуп-
совокупности Т высказываний языка 1-й ступени совместима,
то совместна и вся совокупность Т (см. [1]).
Теорема 2 (теорема Лёвенхейма — С к о-
лема — Мальцева). Если совокупность выска-
высказываний языка 1-й ступени сигнатуры Я имеет беско-
бесконечную модель, то она имеет модель любой бесконеч-
бесконечной мощности, не меньшей мощности сигнатуры Я.
Теорема 1, называемая теоремой компакт-
компактно с т и, получила широкое применение в алгебре.
На основе этой теоремы А. И. Мальцев создал метод
доказательства локальных теорем алгебры (см. Маль-
Мальцева локальные теоремы).
Пусть А — алгебраич. система сигнатуры Я, \А\ —
основное множество системы А, Хд=|Л|, <Й, Х> обо-
обозначает сигнатуру, получаемую из Я добавлением
символов выделенных элементов са для всех а?Х,
а (А, X) обозначает алгебраич. систему сигнатуры
<й, .У>, к-рая является обогащением алгебраич. си-
системы Лив к-рой для каждого а?Х символ са интер-
интерпретируется элементом а. Множество О (А) всех замк-
замкнутых формул сигнатуры <Q, |Л|> языка 1-й ступеки,
истинных в системе (А, \А\), наз. описанием ал-
алгебраической системы А, а множество
D (А) тех формул из О (А), к-рые являются либо атом-
атомными, либо отрицаниями атомных, наз. диаграм-
диаграммой А. Алгебраич. система В наз. элементар-
элементарным расширением алгебраич. системы А,
если |Л|с=|В| и (В, \А\) есть модель для О (А). В этом
случае А наз. элементарной подсисте-
подсистемой В. Напр., множество рациональных чисел вместе
с обычным отношением порядка является элементарной
подсистемой системы действительных чисел с обычным
отношением порядка.
Подсистема А алгсбраич. системы В сигнатуры Q
тогда и только тогда является элементарной подси-
подсистемой системы В, когда для каждой замкнутой фор-
формулы (Зг-')Ф (f) языка 1-й ступени сигнатуры <Q, |Л|>,
истинной в (В, \А\), найдется такой а?|Л|, что Ф (са)
истинна в (В, \А\). Из этого критерия сразу следует,
что объединение возрастающей цепочки элементарных
подсистем является элементарным расширением каж-
каждой из этих систем. Если замкнутая уз~Ф°РмУла
языка 1-й ступени истинна в каждой системе возраста-
возрастающей цепочки систем, то эта формула истинна и в объ-
объединении этой цепочки (см. [lj).
Пусть сигнатура Q содержит символ U одномест-
одноместного отношения. Говорят, что модель А теории Т
сигнатуры Q имеет т и п (а, р1), если мощность А равна
а, а мощность U (А)= {а? \А \ \А (= U{а)} равна р\
Теорема Вот а: если элементарная теория Т
счетной сигнатуры имеет модель типа (а, Р), где а>р\
то Т имеет модель типа (#3, #0) (см. [7], [10]). В пред-
предположении, что справедлива обобщенная гипотеза
континуума, элементарная теория счетной сигнатуры
имеет модель типа (Nct,+-2, Sa+i) для каждого ее,
если она имеет модель типа (jj(\, tf0) (см. [10J). При
этом же предположении теория Th (Л), где сигнатура А
есть <-}-, -, 0, 1, <, Uy, \А\ — множество всех дей-
действительных чисел, U(А) — множество целых чисел,
а +, •, 0, 1, < определены обычным образом, не имеет
модели типа (tf2, Но)-
Пусть (А, Р) обозначает обогащение алгебраич.
системы А при помощи предиката Р, a <Q, P> — сиг-
сигнатуру, полученную из Q присоединением предикат-
предикатного символа Р. Во многих случаях важно понять,
когда в каждой системе из класса К алгебраич. систем
сигнатуры <Q, P> предикат Р задается формулой
языка 1-й ступени сигнатуры Q. Частичный ответ на
этот вопрос дает теорема Бета: тогда и только
тогда существует формула Ф (х) языка 1-й ступени
сигнатуры Q такая, что формула (V^) (Ф (х) ч—> Р (х))
истинна на всех системах аксиоматизируемого класса К
сигнатуры <Q, РУ, когда множество {Р\(А, Р)?К}
содержит не более одного элемента для каждой алге-
алгебраич. системы А сигнатуры Q (см. [2]).
Многие исследования по М. т. связаны с изучением
свойств, сохраняющихся при операциях над алге-
алгебраич. системами. К числу важнейших операций от-
относятся гомоморфизмы, прямые и фильтрованные про-
произведения.
Говорят, что высказывание Ф устойчиво от-
относительно гомоморфизмов, если из истинности ф
в алгебраич. системе А следует истинность ф во всех
эпиморфных образах А. Формула Ф языка 1-й ступени
наз. положительной, если Ф не содержит
знаков отрицания и импликации. Доказано (см. II]),
что высказывание Ф языка 1-й ступени устойчиво
относительно гомоморфиз-мов тогда и только тогда,
когда Ф эквивалентно положительному высказыванию.
Аналогичная теорема верна и для языка Lb>l и.
Формула Ф (х1, . . ., хп) языка 1-й ступени сигна-
сигнатуры Q наз. х о р н о в с к о и, если она может быть
получена конъюнкциями и навешиванием кванторов
из формул вида (Ф,& . . . &Ф^) -+Ф, ~\ {Ф^ . . .&Ф1),
где Фь . . ., Ф^, Ф — атомные формулы языка 1-й
ступени сигнатуры Q. Примерами хорновских формул
являются тождества и квазитождества. Центральной
в теории ультрапроизведений является теорема
Лося (J. -Los): всякая формула языка 1-й ступени
фильтруется по любому ультрафильтру (см. [1]).
Формула языка 1-й ступени условно фильтруется по
любому фильтру тогда и только тогда, когда эта фор-
формула эквивалентна хорновской формуле. Имеет место
теорема (см. [9]): алгебраич. системы А и В сигнатуры
Q тогда и только тогда элементарно эквивалентны,
когда существует такой ультрафильтр D на множе-
множестве /, что A1 ID л В1 ID изоморфны. Мощность фильт-
фильтрованного произведения бесконечна, если для каждого
натурального п число сомножителей мощности п ко-
конечно. Если для каждого натурального п множество
тех индексов, для к-рых соответствующий сомножи-
сомножитель имеет мощность п, не принадлежит D, то мощность
ультрапроизведенпя по неглавному ультрафильтру D
на счетном множестве / равна континууму. Для каж-
каждого бесконечного / мощности а существует такой
фильтр D на /, что для каждого фильтра о1 на /,
содержащего D, и каждого бесконечного множества А
мощность A1 Dx не меньше 2°- (см. [1]).
Много применений находит теорема о су-
существовании моделей с большим
числом автоморфизмов (см. 13]): для лю-
любого линейно упорядоченного множества А" в аксио-
аксиоматизируемом классе К алгебранч. систем, содержащем
бесковечную систему, существует такая система А,
что Х<=\А\ и каждое сохраняющее порядок одно-
однозначное отображение X на X продолжается до
автоморфизма А.
Важными понятиями М. т. являются понятия уни-
универсальной, однородной и насыщенной систем. Пусть
А и В — алгебранч. системы сигнатуры Q. Отобра-
Отображение / множества Х<^\А\ во множество Уя^\В\ наз.
элементарным, если для каждой формулы
Ф (j-t, . . ., хп) языка 1-й ступени сигнатуры Q и любых
аи ¦ ¦ ч аи^.Х имеет место эквивалентность А (=Ф (аь
. . ., а„)<?г=5>.В(=Ф (/аъ . . ,,fan). Система Л на;), а-уни-
в е р с а л ь н о й, если для каждой системы В, эле-
элементарно эквивалентной системе А и имеющей мощ-
мощность, не превосходящую а, существует элементарное
отображение \В\ в \А\. Система А наз. а-о д н о р о д-
н о н, если для любого множества Х?1-4|, мощность
к-рого меньше а, каждое элементарное отображение
X в \А\ продолжается до элементарного отображения
\А\ на \А\ (т. е. до автоморфизма А). Система А сиг-
сигнатуры Q наз. сс-н асыщенноп, если для каждого
множества Хя^\А\, мощность к-рого меньше п., и каж-
каждой совокупности 2 формул яаыка 1-й ступени сигна-
сигнатуры <Q, Х>, не содержащих свободных неременных,
отличных от х0, из конечной выполнимости I в (.4, X)
следует выполнимость 2 в (Л, А'). Система А наз.
универсальной (соответственно о д н о р о д-
н о й и лп насыщенно й), если и А является а-
уннверсальнон (соответственно сс-однородной или а-
насыщенной), где а есть мощность :.4|. Система тогда
и только тогда насыщена, когда она одновременно
универсальна и однородна. Две элементарно эквива-
эквивалентные насыщенные системы одной мощности изо-
изоморфны (см. [3]). Все несчетные модели категоричной
в несчетных мощностях элементарной теории счетной
сигнатуры насыщены (теорема М о р л и, см.
[3], [8]). Большое число примеров а-насыщенных
систем доставляют ультрапроизведення. Напр., если
D — неглавный ультрафильтр на счетном множестве
/, то JTjgj^//^* является ^-насыщенной системой
для любых алгебраич. систем A;(i?l) счетной сигна-
сигнатуры а.
Основными задачами М. т. являются изучение выра-
выразительной возможности формализованного языка и
изучение классов структур, определимых средствами
этого языка. Найдены нек-рые важные свойства ста-
стабильных теорий, еще более детально изучены классы
категоричных и суперстабильных теорий.
Основным аппаратом при изучении стабильных тео-
теории является классификация формул и локально сов-
совместных множеств формул в этих теориях. Такая
классификация осуществляется путем приписывания
формулам рангов. Эти ранги обычно принимают в
качестве значений ординалы, а рангующие функции
задаются с помощью специальных топологий или другим
способом. Изучение рангующих функций и их усовер-
усовершенствование — богатый источник информации о тео-
теориях.
В изучении классов моделей выясняют число раз-
различных с точностью до изоморфизма моделей теории
в рассматриваемой мощности и наличие специальных
моделей, напр, простых, минимальных, насыщенных,
однородных, универсальных, конструктивизируомых
и т. п., и создают способы их построения.
Классич. примерами применения методов М. т. в
математич. анализе являются работы А. Робинсона
(A. Robinson) и его школы, сформировавшиеся в са-
самостоятельную науку — нестандартный анализ; бла-
благодаря работам А. Й. Мальцева и его школы разви-
развивается применение методов М. т. в топологич. алгебре;
новейшие результаты о свойствах стабильных теорий
находят использование при изучении конкретных
алгебраич. вопросов.
Перечисленные выше проблемы встают и при изуче-
изучении различных неэлементарных языков, напр., получа-
получаемых добавлением новых кванторов, введением в рас-
рассмотрение бесконечных выражений, модальностей и
т. п.
Лит.: [1] М а л ь ц е в А. И., Алгебраические системы,
М., 1970; [2] Робинсон А., Введение в теорию моделей и
метаматематику алгебры, пер. с англ., М., 1967; [3] Т а й ц-
л и н М. А., Теория моделей, Новосиб., 1970; [4] Е р-
ш о в Ю. Л., Проблемы разрешимости и конструктивные мо-
модели, М., 1980; [5] Е р ш о в Ю. Л., П а л ю т и н Е. А.,
Математическая логика, М., 1979; [6] Е р ш о в Ю. Л. [и др.],
«Успехи матем. наук», 1965, т. 20, в. 4, с. 37 — 108; [7] Маль-
Мальцев А. И.,Тр. Четвертого Всесоюзного математического съезда,
т. 1, Л., 1963, с. 169—98; [8] К е й с л е р Г., Ч э н Ч. Ч.,
Теория моделей, пер. с англ., М., 1977; [9] С а к с Д ж., Теория
насыщенных моделей, пер. с англ., М., 1976; [10] V a u g h t R.L.,
в сб.: Infinistic methods, N. Y. [а. о.], 1961, p. 303—21; [11]
M о г 1 e у М., V а и g h t R., «Math, scand.», 1962, v. 11, fasc. 1,
p. 37—57; [12] M о r I e у М., «Trans. Amer. Math. Soc», 1965,
v. 114, Л» 2, p. 514—38; [13] S h e 1 a h S., Classification theory
and the number of non-isomorphic models, Amst., 1978; [14]
Bell I. L., S 1 о m s о n А. В., Models and ultraproducts.
An introduction, Amst.— L., 1969.
А. Д. Тайманов, M. А. Таицлип.
МОДЕЛЬ — интерпретация формального языка. Ос-
Основным формальным языком является язык La 1-г о
порядка (или 1-й ступени) данной сигнатуры
Q, включающей предикатные символы Rj, i?I, функ-
функциональные символы /у, /?/, и константы ck, k?K.
Модель языка LQ есть алгебраическая система
сигнатуры Q.
Пусть 2 — нек-рое множество замкнутых формул
языка Z/q. Модель для 2 есть М. языка La, в к-рой
истинны все формулы из 2. Множество 2 наз. с о-
в м е с т н ы м, если оно имеет хотя бы Одну М. Класс
всех М. для 2 обозначается Mod 2. Совместность мно-
множества 2 означает, что Mod 2^=0.
Класс К моделей языка LQ наз. аксиомати-
аксиоматизируемым, если существует такое множество 2
замкнутых формул языка LQ, что X=Mod2. Множе-
Множество Т (К) всех замкнутых формул языка Lq, истинных
в каждой М. из данного класса К моделей языка 1/Й7
наз. элементарной теорией класса К. Таким образом,
класс К моделей языка La аксиоматизируем тогда и
только тогда, когда K=Mod T(K). Если класс К
состоит из М., изоморфных данной М., то его элемен-
элементарная теория наз. элементарной теорией
этой модели.
Пусть А — нек-рая М. языка La, имеющая основ-
основное множество А. Каждому элементу а?А сопостав-
сопоставляют константу са и рассматривают язык Lq ^ 1-го
порядка сигнатуры QA, к-рая получается из Q добав-
лением констант са, а?А. Язык LqA наз. диаграм-
диаграммным языком модели А. Множество О (А)
всех замкнутых формул языка LqA , истинных в А
при замене каждой константы са соответствующим
элементом а из А , наз. описание м (или элемен-
элементарной диаграммой) М. J. Множество D (А)
тех формул из О (А), к-рые являются атомными или
отрицаниями атомных формул, наз. диаграммой
М. А.
Наряду с М. языка 1-го порядка рассматривают так-
также М. других типов (логики с бесконечными форму-
формулами, многосортной логики, логики 2-го порядка,
многозначной логики, интуиционистской логики и
модальной логики).
Лит. см. при ст. Моделей теория. Д. М. Смирнов.
МОДЕЛЬ ВЫЧИСЛИТЕЛЬНАЯ — типовая абстракт-
абстрактная или конкретная задача, соответствующая проблеме
численного решения нек-рого класса математпч. или
прикладных задач. Напр., в теории квадратур рас-
рассматривают задачу вычисления интегралов от функ-
функций, удовлетворяющих нек-рому условию ||/(л)||-<^4.
Отработка методов решения задачи Коши для систем
обыкновенных дифференциальных уравнений истори-
исторически производилась путем исследования свойств
методов на моделях из последовательности усложняю-
усложняющихся моделей (отрезок интегрирования [О, X]):
1) уравнение у'=-0;
2) уравнение у'=т,у, \т\Х — порядка 1 (модели 1)
и 2) соответствуют задаче интегрирования систем с
гладкими решениями на небольших промежутках
времени);
За) уравнение у'= ту, т<0, 1ш|Х^>1; эта модель
соответствует задаче интегрирования на больших про-
промежутках времени систем с устойчивыми решениями;
36) уравнение у' = х ; модель уравнения с особен-
особенностями производных решения;
4) система yi^m1y1, y'i=m.2y.2, 0>m1>m2, |;n2|X^>
^ImjIX, Im-xlX — порядка 1; модель т. н. жесткой
дифференциальной системы, у к-рой одни компоненты
решения меняются относительно медленно, а другие
быстро.
Лит.: [1J Б а х в а л о в Н. С, Численные методы, 2 изд.,
М., 1975. Н. С. Бахвалов.
МОДЕЛЬ МАТЕМАТИЧЕСКАЯ — см. Математи-
Математическая модель.
МОДИФИКАЦИЯ аналитического про-
пространства — аналитическое отображение /: X —>- Y
аналитических пространств такое, что для нек-рых
аналитических множеств SdX и TaY меньших раз-
размерностей выполняются условия:
/: Х\5 —>¦ Y\T — изоморфизм
и
Модификация / наз. также стягиванием анали-
тич. множества S на Т. Примерами М. являются
моноидальные преобразования.
См. также Исключительное аналитическое множе-
множество, Исключительное подмногообразие.
Лит.: [1] В е h n k e H., Stein К., «Math. Ann.», 1951,
Bd 124, Н. IS. 1 — 10. А. Л. Онищип.
МОДУЛЕЙ КАТЕГОРИЯ — категория mod-Я,
объекты к-рой — правые унитарные модули над про-
произвольным ассоциативным кольцом R с единице]!, а
морфизмы — гомоморфизмы Д-модулей. Эта категория
является важнейшим примером абелевой категории.
Более того, для всякой малой абелевой категории су-
существует полное точное вложение в нек-рую М. к.
Если R=WJ — кольцо целых чисел, то mod-й
есть категория абелевых групп, а если R = D-je.4o
(поле), то mod-R есть категория векторных про-
пространств над D.
Свойства М. к. mod-Л отражают ряд важных
свойств кольца R (см. Гомологическая классификация
колец), с этой категорией связан ряд важных гомологич.
инвариантов кольца, в частности его гомологические
размерности. Центр М. к. mod-Л (т. е. множе-
множество естественных преобразований тождественного
функтора категории) изоморфен центру кольца R.
В теории колец, гомологич. алгебре и алгебраич.
А-теории изучаются различные подкатегории М. к.,
л частности подкатегория конечно порожденных про-
проективных Л-модулей и ассоциированные с ней А-функ-
торы (см. Алгебраическая К-теория). По аналогии с
двойственностью Понтрягина изучаются двойствен-
двойственности между полными подкатегориями М. к., в част-
частности между подкатегориями конечно порожденных
модулей. Напр., установлено, что если R и S — нёте-
ровы кольца и имеет место двойственность между ко-
конечно порожденными правыми Я-модулями и конечно
порожденными левыми iS-модулями, то существует би-
модуль $Ur такой, что данная двойственность экви-
эквивалентна двойственности, определяемой функторами
Нот# (-, U) и Нот5 ('-, U),
кольцо эндоморфизмов ЕпсШд изоморфно S, a Endsf/
изоморфно R, бимодуль U — конечно порожденный
инъективный кообразующий (и как Л -модуль, и как
S-модуль), кольцо R полусовершенно. Наиболее важ-
важным классом колец, возникающим при рассмотрении
двойственности модулей, является класс квааифробепи-
усовых колец. Артиново слева кольцо R будет квази-
фробениусовым тогда и только тогда, когда отображение
, R)
определяет двойственность категорий левых и правых
конечно порожденных Я-модулей.
Лит.: [1] Б а с с X., Алгебраическая /<С-теория, пер. с англ.,
М., 1973; [2] Б у к у р И., Деляну А., Введение в теорию
категорий и функторов, пер. с англ., М., 1972; [3] Фейс К.,
Алгебра: кольца, модули и категории, т. 1—2, пер. с англ.,
М., 1977 — 79. . А. В. Михалев,
МОДУЛЕЙ ПРОБЛЕМА — классическая проблема
о рациональности или унирациональности многообра-
многообразия модулей алгебраич. кривых рода g.
Рпмановы поверхности рода g (рассматриваемые
с точностью до изоморфизма) зависят от 3g—3 ком-
комплексных параметров — модулей (см. Модули римано-
вой поверхности). Множество классов неособых про-
проективных кривых рода g над алгебраически замкну-
замкнутым полем к обладает структурой квазипроективного
алгебраич. многообразия Mg (см. [3] — [5]).
Многообразие Mg в случаях g=0 и 1 устроено про-
просто: Мо состоит из одной точки, a Mj изоморфно аф-
аффинной прямой А1. Поэтому М. п. относится к кривым
рода g>2 и формулируется следующим образом;
является ли рациональным или хотя бы унирацио-
нальным многообразие модулей Mg кривых рода g^2?
Рациональность Mg установлена только для g=2
{см. [2], там же явно описано многообразие М2)-
Для доказательства унирациональности многооб-
многообразий Mg построен [6] общий метод, к-рым, в част-
частности, доказана унирациональность Mg для всех g«:10.
Доказана унирациональность М12.
Часто М. п. трактуется более широко (см., напр.,
E]): к ней относят весь комплекс задач, связанных с
существованием пространств модулей тех или иных
алгебраич. объектов (многообразий, векторных рас-
расслоений, эндоморфизмов и т. д.), с изучением их раз-
различных алгебро-геометрич. свойств и с техникой
компактификации пространств модулей (см. Модулей
теория).
Лит.: [lj Hartshorne R., Alprebraic seomeiry, N. Y.,
1977; [21 Igusa J., «Ann. Math.», 1960, v. 72, ,N» 3, p. 612—
49; [Й M ii m I о г d D., Geometric invariant theory, В.— [а.о.],
1965; [4] его же, «L.'enseignement math.», 1977, t, 23,
JN« 1—2, p. 39—110; [5] P о р р Н., Moduli theory and classifica-
classification theory of algebraic varieties, В.— Hdlb.—N.Y., 1977; [G]
S e v e r i F., «Atti della R. Ace. Naz. Lincei Rend.», 1915, v.
24, p. 877—88. В. А. Псковских.
МОДУЛЕЙ ТЕОРИЯ — теория, изучающая непре-
непрерывные семейства объектов алгебраич. геометрии.
Пусть А — класс объектов алгебраич. геометрии
(многообразий, схем, векторных расслоений и т. п.),
на к-ром задано нек-рое отношении эквивалентности
R. Основная задача классификации (описания множе-
множества классов AIR) состоит из следующих двух частей:
1) описание дискретных инвариантов, к-рые обычно
позволяют разбить AIR в счетное число подмножеств,
объекты к-рых уже непрерывно зависят от парамет-
параметров; 2) задание и изучение алгебро-геометрич. структур
на множествах параметров. Вторая часть составляет
содержание М. т.
М. т. возникла при изучении эллиптич. функций:
существует непрерывное семейство различных полей
эллиптич. функций (или их моделей — неизоморфных
эллиптич. кривых над С), параметризованное ком-
комплексными числами. Б. Риман (В. Riomann), к-рому
принадлежит и сам термин «модули», показал, что
поля алгебраич. функций над С (или их моделей —
компактных римановых поверхностей) рода g^2 за-
зависят от 3g—3 непрерывных комплексных парамет-
параметров — модулей.
Основные понятия М. т. Пусть 5 — нек-рая схема
(комплексное или алгебраич. пространство). Семей-
Семейство объектов, параметризованных
схемой S (или, как часто говорят, «н а д S», или
«с б а з о ii S»),— это набор объектов
снабженный дополнительной структурой, согласован-
согласованной со структурой базы S. Эта структура в каждом
конкретном случае задается явно. Функтор се-
семейств — это контравариантный функтор a/fl из
категории схем (или пространств) в категорию мно-
множеств, определяемый следующим образом: o$(S) —
множество классов изоморфных семейств над 5. Каж-
Каждому морфизму /: Т —>- S сопоставляется отображение
f*'-arf/(S) —>- оМ(Т) посредством взятия индуцированного
семейства.
Пусть М — объект в категории схем (комплексных
или алгебраич. пространств) и h-м — функтор точен
в этой категории, т. е. hj^=Hom(S, M). Если функтор
семейств a/ft представим, т. е. аМ=Ьм Для нек-рого М,
то существует универсальное семейство с базой a/ft, и М
наз. тонкой схемой (соответственно тон-
тонким комплексным или алгебраиче-
алгебраическим пространством) модулей. Функ-
Функтор аЖ представим в очень немногих случаях, в связи
с чем было введено также понятие грубой схемы мо-
модулей; М наз. грубой схемой модулей,
если существует морфизм функторов ср: a/ft -у hj^,
обладающий свойствами: а) если S = SpccK=pt —
одна точка (где К — алгебраически замкнутое поле),
то отображение ф: a$(pt) —>- hj^(pt) биективно, иначе
говоря, множество геометрич. точек схемы Ш нахо-
находится в естественном взаимно однозначном соответст-
соответствии с множеством классов эквивалентности парамет-
параметризуемых объектов; б) для каждой схемы N и мор-
физма функторов г|): a/ft —>- h^ существует единственный
морфизм % : км —>- Адг такой, что 1|>=ОС°Ф- Аналогично
определяются грубая схема комплексного и алгебраи-
алгебраического пространств модулей.
Грубая схема модулей хотя и параметризует одно-
однозначно классы изучаемых объектов с заданными диск-
дискретными инвариантами, но естественное семейство над
ней не обладает (в отличие от семейства над тонкой
схемой модулей) сильным свойством универсальности.
Грубая схема (пространство) модулей существует уже
в достаточно большом числе случаев.
Примеры. 1) Модул и алгебраических
кривых. Пусть A/R = ^S\g (соответственно Щ1г) —
множество классов изоморфных проективных неособых
кривых (соответственно стабильных кривых) рода g^2
над алгебраически замкнутым полем А'. Семейство над
5 — это гладкий (плоский) собственный морфизм схем
f:X —*- S, слоями к-рого являются гладкие (стабиль-
(стабильные) кривые рода g. Тогда существует грубая (но не
тонкая) схема модулей Mg (соответственно Mg),
являющаяся квазипроективным (проективным) непри-
неприводимым и нормальным многообразием над А. (см. [3],
[5], [6J).
2) Модули алгебраических кривых
с якобиевой жесткостью. Пусть /: X -*¦ S—
гладкое семейство проективных кривых (соответст-
(соответственно плоское семейство стабильных кривых) рода
g^i, п — целое число, обратимое на S, и R'f* (%1п'?) —
первый прямой образ постоянного пучка ъ'т% в эталь-
ной топологии. Тогда -ff1/* (Z/«Z) локально свободен,
имеет ранг 2g и снабжен локально невырожденной
симплсктпч. формой со значением в %1пЪ,о. точностью
до обратимого элемента из TLlnTL. Якобиева структура
уровня п на X — это задание симплектич. изоморфизма
л1/* (г1п%) ^ {%,
Пусть ojflg, п (соответственно aSg, n) — функтор се-
семейств гладких (стабильных) кривых рода g3&2 с
якобиевой жесткостью уровня п. Тогда при гС^Ъ
(|улктор aSg, п (соответственно oMg, n) представим ква-
зипроективцой (проективной) схемой Mg: n (соответ-
(соответственно Mg!tl) над Spec Ъ [1/п, §„], где \п — первооб-
первообразный корень й-й степени из 1, т. е. существует тон-
тонкая схема модулей Mgr n (соответственно Mg „) для
гладких (стабильных) кривых рода g^2 над полем
характеристики взаимно простой с п, снабженных
якобиевой жесткостью уровня п. Для достаточно боль-
больших п схема М,, „ является гладкой [5].
3) Поляризованные алгебраические
многообразия. Поляризованным семейством наз.
пара (XIS, Sp/5), где X/S — гладкое семейство много-
многообразий, т. е. гладкий собственный морфизм f:X —>- S,
a ?$/S — класс относительно обильного обратимого
пучка Xxis B Нот E, PicX/5) по модулю Hom(S,
Pic°X/iS), где ~P\cXlS — относительная схема Ппкара,
a Pic°X/S — ее связная компонента нулевого сечения.
В этом случае строится функтор поляризованных
семейств а$п с заданным многочленом Гильберта h.
Без дополнительных ограничений этот функтор не
представим. Существование грубого пространства мо-
модулей известно A982) лишь в отдельных случаях.
Для поляризованных алгебраич. многообразий так-
также существует понятие жесткости уровня п.
4) Векторные расслоения. Пусть AIR —
множество классов векторных расслоений ранга п на
алгебраич. многообразии X. Семейство над S — это
векторное расслоение Е на XXS. Грубое пространство
модулей Mdi n существует здесь как нормальное про-
проективное многообразие для полустабильных векторных
расслоений ранга п и степени d на неособой проек-
проективной алгебраич. кривой X над алгебраически замк-
замкнутым нолем К. Стабильные векторные расслоения
в М^_ „ параметризуются открытым гладким подмно-
подмногообразием Jtfjj^jCA/j^' Если d и п взаимно простьг,
то Л/^_ n=Md„. Аналогичные результаты получены и
для стабильных векторных расслоений на алгебраич.
поверхности. Более того, в этом случае существует
тонкая схема модулей (см. [7], [10] — A4J).
Локальная и глобальная теории. Локальная теория
возникла как теория деформаций комплексных струк-
структур (см. Деформация 1) и 2)). Основными методами гло-
глобальной теории являются теория представимых функ-
функторов и геометрич. теория_ инвариантов, теория алге-
брапч. стеков и алгебраизация формальных модулей.
Метод построения глобального пространства модулей
восходит к классической инвариантов теории. Он
заключается в следующем. Строится достаточно боль-
большое семейство X —*- Н, содержащее представителей
всех классов эквивалентности изучаемых объектов,
причем такое, что отношение эквивалентности на Н
сводится к действию алгебраич. группы G. Затем
развивается теория действия алгебраич. групп на
алгебраич. многообразиях (схемах, пространствах) с
целью выяснения условий существования фактора HIG
в соответствующей категории. Основным инструмен-
инструментом построения семейства X —> Н является теория
Гильберта схем. При таком подходе трудности пост-
построения семейства X —>- Н сводятся к проблеме одновре-
одновременного погружения изучаемых объектов в проек-
проективное пространство. Важным результатом о возмож-
возможности такого одновременного погружения является
теорема Мацусаки. Трудной проблемой остается и
проблема существования фактора 1IIG. Имеются по-
понятия категорного и геометрич. факторов. Конструк-
Конструкция грубого пространства модулей сводится к задаче
о существовании геометрич. фактора, при этом исполь-
используется понятие стабильности точек, соответствующее
понятию орбиты общего положения. Результаты о
действиях редуктивных групп на алгебраич. много-
многообразиях над полями характеристики 0 распростра-
распространяются н на случай полей характеристики р>0.
Другой подход к глобальной М. т.— метод алгебра-
алгебраич. стеков, т. е. метод глобализации локальной теория
деформаций. Первый шаг в исследовании представи-
представимости глобального функтора семейств при таком под-
подходе — установление алгебраизуемости формальной
версальной деформации для каждого объекта Хй.
Трудностью для построения глобального пространства
модулей является то, что не всегда факторизация базы
семейства по отношению эквивалентности будет от-
отделимым пространством. В таких случаях заменой
объекта, представляющего функтор &#, служит алге-
алгебраич. стек, изучение свойств к-рого позволяет полу-
получить нек-рую информацию о пространстве модулей.
Один из подходов к глобальной М. т. над С — это
теория отображения периодов. Основным объектом
здесь является классифицирующее пространство D
поляризованных Ходжа структур веса к для заданных
чисел Ходжа. Для семейства X —>- S поляризованных
алгебраич. многообразий над С периоды определяют
отображение S в соответствующее классифицирующее
пространство D структур Ходжа. Проблема модулей
сводится к изучению условий биективности отображе-
отображении периодов. Наличие локальной (глобальной) инъ-
ективности для отображения периодов — это т. н.
локальная (глобальная) проблема
Т о р е л л и. На этом пути существование грубых
пространств модулей доказано для кривых, абелевых
многообразий и ЯЗ-поверхностей.
Задача компактификации многообразия модулей М
заключается в нахождении естественного и полного
(проективного или компактного в теории над полем С)
многообразия М, содержащего М в качестве плотного
открытого подмножества, а также в описании и гео-
геометрич. интерпретации границы М\М. В примере 1) ес-
естественной компактификацией грубого многообразия
модулей Mg кривых рода g^2 служит проективное
многообразие модулей Mg стабильных кривых. В при-
примере 4) многообразие стабильных векторных расслоений
ранга п и степени d на алгебраич. кривой само явля-
является проективным и гладким, если (d, n)=l. Для по-
поляризованных абелевых многообразий над С известны
несколько способов компактификацип многообразий
модулей.
Лит.: [1] Art in M., Algebra)zation of formal moduli
T. Global Analysis, Tokyo, 1969, p. 21—71; [2] e г о ж е, «Invent,
math.». 1974, v. 27, p. 105 — 89; [3] Делинь П., M а м-
ф о р д Д., «Математика», 1972, т. 16, № 3, с. 13—53; [4] Д ь ё-
донне Ж., К е р р о л Дж., Мамфорд Д., Геометри-
Геометрическая теория инвариантов, пер. с англ., М., 1974; [5] Mum-
ford D., Geometric invariant theory, В.— Га.о.], 1965; [В] его
ж е, «L'enseignement math.», 1977, v. 23; [7] Gieseker D..
«invent, math.», 1977, v. 43, p. 233—82; [8J e г о ш е, «Ann. Math.»,
1977, v. 106, p. 45 — 60; [9J M a t s u s a k а Т., «Amer. J. Math.»,
1972, v. 94, JVb 4, p. 1027—77; [10] Newstead P. E., Lectures
on introduction to moduli problems and orbit spaces, B.—Га.о.],
1978; [11] OkonekC, S с h e i d e r M., Spindler H..
Vector budles on complex projective spaces, Boston, 1980; [12]
P о р р Н., Moduli theory and classification theory of algebraic
varieties, В.—[a. o.l, 1977; [13] Seshadri C. S.,"«Ann. Math.»,
1967, v. 85, p. 302—36; [14] Тюрин А. Н., «Успехи матем.
наук», 1974, т. 29, в. 0, с. 59 — 88. В. А. Псковских-
МОДУЛИ РИМАНОВОЙ ПОВЕРХНОСТИ — числен-
численные характеристики (параметры), Одни и те же для
всех конформно эквивалентных римановых поверх-
поверхностен, в своей совокупности характеризующие кон-
конформный класс эквивалентности данной римановой
поверхности. При этом две римановы поверхности
R^ и R., наз. конформно эквивалент н ы-
м v, если существует конформное отображение R^
на R2. Напр., конформные классы компактных рима-
римановых поверхностей топологич. рода g>l характери-
характеризуются 6g—6 действительными М. р. п.; риманова
поверхность типа тора (g=l) характеризуется двумя
модулями; ?г-связная плоская область, рассматрива-
рассматриваемая как риманова поверхность с краем, при га^З
характеризуется Зп—6 модулями. О структуре про-
пространства М. р. п. см. Римановых поверхностей кон-
конформные класса.
Необходимым условием конформной эквивалент-
эквивалентности двух плоских областей является одинаковая
связность этих областей. Согласно Римана теореме
все Одноевязные области с более чем одной граничной
точкой конформно эквивалентны друг другу: каждую
такую область можно конформно отобразить на одну
и ту же канонич. область, в качестве к-рой обычно
рассматривают единичный круг. Для областей связ-
связности п, гС^2, точного эквивалента теоремы Римана
не существует: нельзя указать какую-либо фиксиро-
фиксированную область, на к-рую можно однолистно и кон-
конформно отобразить все области данного порядка связ-
связности. Это привело к более гибкому определению
канонич. ?г-связной области, к-рое указывает общую
геометрич. структуру этой области, но не фиксирует
ее модулей (см. Конформное отображение).
Каждая двусвязная область D плоскости z с невы-
невырожденными граничными континуумами может быть
конформно отображена на нек-рое круговое кольцо
r<C\w\<R, O<r<i?<oo. Отношение Rlr радиусов
граничных окружностей этого кольца является кон-
конформным инвариантом и наз. модулем д в у с в я з-
ной области D. Пусть D — область связности
о, п^З, с невырожденной границей. Область D можно
конфорлшо отобразить на нек-рую гс-свянную круговую
область А, представляющую собой круговое кольцо
г<|1?>|<Я с п—2 выброшенными кругами, ограничен-
ограниченными окружностями Cfc= {w:|w—ifft| = г^}, k=i, . . .,
re—2; окружности С/,, k=i, ¦ . ., n — 2, лежат в кольце
r<IH<i? и попарно не имеют общих точек. При этом
можно считать, что Д=1 и w1^0. Тогда область Д
зависит от Зп — 6 действительных параметров: от п — 1
чисел г, ги . . ., г„_2 и от 2ге—5 действительных пара-
параметров, определяющих центры w^ окружностей С#,
ft=l, . . ., п—2. Эти Зп — 6 действительных параметров
и являются модулями и-с вязной области
D в случае п^З.
В качестве модулей «-связной области D можно
взять и другие (х действительных параметров ([1=1,
если л = 2, и [i=3n—6, если п^З), определяющих
конформное отображение области D на нек-рую кано-
нич. n-связную область другого вида.
Лит.: [1]С п р и н г е р Д ж., Введение в теорию римановых
поверхностей, пер. с англ., М., 1960, с. 74, 325; [2] Б е р с Л.,
«Успехи матем. наук», 1973, т. 28, в. 4, е. 153—98; [3]
Голузин Г. М., Геометрическая теория функций комплекс-
комплексного переменного, 2 изд., М., 1966; [4] К у р а н т Р., Принцип
Дирихле, конформные отображения и минимальные поверхности,
пер. с англ., М., 1953. Г. В. Кузьмина, Е. Д. Соломенцее.
МОДУЛЬ — числовая характеристика какого-либо
математич. объекта. Обычно значение М.— неотрица-
неотрицательное действительное число — элемент R ' , обла-
обладающий нек-рыми характеристич. свойствами, обус-
обусловленными свойствами множества Q рассматриваемых
объектов. Понятие М. фигурирует в различных разде-
разделах математики, хотя иногда и под другими назва-
названиями — абсолютное значение, норма и т. п. Все они,
в сущности, являются обобщениями понятия абсолют-
абсолютной величины действительного или комплексного числа
(но термин М. обычно означает обобщение специального
вида). При этом функция Q —>- R+ оказывается морфиз-
мом нек-рой структуры в Я на одну из (алгебраических)
структур в R+, среди к-рых важнейшие — это порядок,
аддитивность и мультипликативность. При этом не-
необходимо сохранение основных свойств абсолютной
величины (см. ниже а) — е)). В более абстрактных
ситуациях вместо R+ естественно использовать упо-
упорядоченные полукольца (такой концепции М. удов-
удовлетворяют, напр., мера, емкость, масса и т. д.). На-
Наконец, термином М. обозначаются числовые характе-
характеристики и др. объектов: таковы, напр., модуль плоской
области, модуль кольца, модули римановой поверх-
поверхности, непрерывности модуль, гладкости модуль (и
даже — М. в теории упругости (сжатия, сдвига)).
Однако во всех таких случаях можно ввести величины,
функционально зависящие от такого М. и более аде-
адекватно отражающие природу рассматриваемых объ-
объектов (напр., экстремальную длину вместо М. семей-
семейства кривых).
Примеры. 1) М. элемента х полуупорядоченного
пространства Р — число
где х+ (х~) — положительная (отрицательная) часть
х. При этом, как и для действительных чисел,
а) \х\^х, —х; |ж|=| — л-|;
=0 @-нульвР).
2) М. элемента х отделимого предгильбертова про-
пространства Н, в частности конечномерного векторного
пространства,— число
где <•, •> — скалярное произведение в Н. Это — одна
из норм в //, и потому
6) |А,ж1 = |Я,|к|, к — скаляр.
3) М. элемента х локально компактного тела — число
\x\ = \i(.rS)/n(S) (хФО) или 0 (х=0),
где (х — мера Хаара на аддитивной группе К, S —
измеримое множество в ней. При этом, как и для чисел
из R, С, Н,
е) U(/|=|.r||(/|.
Обобщением этого понятия является модуль автомор~
физма.
4) М. эндоморфизма Л векторного пространства V
над полем К (частный случай М. автоморфизма) —
число mod у (Л), оказывающееся равным просто
mod/f (det j4)=|det<4|, где |-| означает М. элемента пз
примера 3). М. И. Войцеховский.
МОДУЛЬ — абелева группа с кольцом операторов.
М. является обобщением (линейного) векторного про-
пространства над полем К для случая, когда К заменяется
нек-рым кольцом.
Пусть задано кольцо А. Аддитивная абелева группа
М наз. левым Л-м о д у л е м, если определено
отображение АхМ -+ М, значение к-рого на паре
(а, т) для а?А, т?М записывается как am, причем
выполняются аксиомы:
A2I2
2) (a1+a2)m=a1m-|-a2m,
3) Й1 (а.,т) = (а1а2)т.
Если кольцо А обладает единицей, то обычно требуют
дополнительно, чтобы для любого т?М выполнялось
равенство lm=m. М. с этим свойством наз. у н и т а р-
н ы м, или унитальным.
Аналогично определяются правые А-м о д у л и;
при этом аксиома 3) заменяется условием (та1)а2=
= m(a1ai). Любой правый Л-модуль можно рассмат-
рассматривать как левый А "-модуль над кольцом Л", анти-
изоморфным кольцу Л, поэтому любому утверждению
о правых Л-мОдулях соответствует нек-рое утверж-
утверждение о левых Л "-модулях и наоборот. В случае, когда
кольцо А коммутативно, любой левый Л-модуль можно
рассматривать как правый Л-модуль, и различие
между левыми и правыми М. исчезает. Ниже будут
рассматриваться только левые Л-модули.
Простейшие примеры М. (конечные абелевы группы,
т.е. 2-м ©дул и) появляются уже у К. Гаусса (C.Gauss)
как группы классов бинарных квадратичных форм.
Общее понятие М. встречается впервые в 60—80-х гг.
19 в. в работах Р. Дедекинда (R. Dedekind) и Л. Кро-
некера (L. Kronecker), посвященных арифметике полей
алгебраич. чисел и алгебраич. функций. Проводив-
Проводившееся примерно в это же время исследование конечно-
конечномерных ассоциативных алгебр, и в частности группо-
групповых алгебр конечных групп (Б. Пирс, В. Peirce, Ф. Фро-
бениуе, F. Frobenius), привело к изучению идеалов
нек-рых некоммутативных колец. Первоначально тео-
теория М. развивалась преимущественно как теория идеа-
идеалов нек-рого кольца. Лишь позднее в работах Э. Нётер
(Е. Noetber) и В. Крулля (W. Krull) было замечено,
что многие результаты удобнее формулировать и до-
доказывать в терминах произвольных М., а не только
идеалов. Последующее развитие теории М. связано с
применением методов и идей теории категорий, в част-
частности метвдев гомологич. алгебры.
Примеры модулей. 1) Любая абелева группа
М является М. над кольцом целых чисел %. Для а?2
и т?М произведение am определяется как результат
сложения т а раз.
2) В случае, когда Л — поле, понятие унитарного
Л-модуля в точности эквивалентно понятию линейного
векторного пространства над Л.
3) Координатное и-мерное векторное пространство V
над полем К можно рассматривать как М. над кольцом
Мп(К) всех (п X и)-матриц с коэффициентами из К.
Для v?V и Х?Мп(К) произведение Xv определяется
как умножение матрицы X на столбец координат век-
вектора V.
4) Ассоциативное кольцо Л является левым Л-мо-
Л-модулем. Умножение элементов кольца на элементы М.
совпадает с обычным умножением в А.
5) Дифференциальные формы на гладком много-
многообразии X снабжены естественной структурой М. над
кольцом всех гладких функций на X.
6) С любой абелевой группой М связано ассоциа-
ассоциативное кольцо с единицей End(M) всех эндоморфизмов
группы М. Группа М снабжена естественной струк-
структурой End (Af )-модуля.
Если на М задана структура Л-модуля для нек-рого
кольца А. то отображение т ->- am является эндомор-
эндоморфизмом М для любого а?М. Сопоставляя элементу
а?А порождаемый им эндоморфизм М, получают го-
гомоморфизм ф кольца А в End (M). Наоборот, любой
гомоморфизм ц>:А —*¦ End (М) определяет на М струк-
структуру Л-модуля. Таким образом, задание структуры
Л-модуля на абелевой группе М равносильно заданию
гомоморфизма <f.A —>-End(Af). Такой гомоморфизм
наз. также представлением кольца А,
а М наз. модулем представления. С лю-
любым представлением ср связан двусторонний идеал
Ann(Af) = Ker ср, состоящий из элементов а?А таких,
что агп = 0 для всех т?М. Этот идеал наз. а н н у л я-
тором модуля М. В случае, когда Ann (Л/) —О,
представление наз. точным, М — точным мо-
модулем.
Очевидно, что модуль М можно рассматривать также
как М. над факторкольцом А/Апп(М). В частности,
хотя определение М. и не предполагает ассоциатил
ности кольца А , кольцо A /Ann (M) всегда ассоциативно.
Поэтому в большинстве случаев достаточно ограни-
ограничиться рассмотрением М. над ассоциативными коль-
кольцами. Ниже, везде, где не оговорено противное,
кольцо А будет предполагаться ассоциативным.
G-модули. Пусть G — нек-рая группа. Аддитивная
абелева группа М наз. левым G-модулем, если
задано отображение GxM -*¦ М, значение к-рого на
паре (g, m), где g?G, т?М, записывается как gm,
причем для любого g?G отображение т —>- gm явля-
является эндоморфизмом группы М, для любых gt, gi^G,
т?М, (gig<L)m== gi(gzm) и ДЛя всех да?М, lm=m,
где 1 — единица группы G. Для любого g?G отобра-
отображение т i—*¦ gm является автоморфизмом группы М.
Аналогично можно определить правые G-модули.
При gm=mg~1 любой правый G-модуль будет левым
G-модулем.
Примеры G-мОдулей. 1) Пусть К — расши-
расширение Галуа нек-рого поля к с группой Галуа G. Тогда
аддитивная и мультипликативная группы поля К
снабжены естественной структурой G-модуля. Если
к — поле алгебраич. чисел, то G-модулями также яв-
являются аддитивная группа кольца целых чисел поля
К, группа единиц поля К, группа дивизоров и группа
классов дивизоров поля К, и т. д. М. над группой
Галуа наз. также модулями Галуа.
2) Пусть задано нек-рое расширение абелевой группы
М, т. е. точная последовательность групп
1 _^Af -» F ->-G-> I,
где М — абелев нормальный делитель группы F и
G — произвольная группа. Тогда группу М можно
снабдить естественной структурой G-модуля, положив
для g?M, m?M, gm=gmg~1, где g — нек-рый про-
прообраз элемента g в группе F.
В тех случаях, когда групповая операция в абелевой
группе М записывается мультипликативно (напр.,
М — мультипликативная группа нек-рого поля), вме-
вместо записи gm используют также запись mS, т. е. опе-
операторы из группы G записывают как показатели.
Пусть задан G-модуль М. Сопоставляя элементу
g?G автоморфизм т \—> цт группы М, получают
гомоморфизм группы G в группу обратимых элемен-
элементов кольца End(M). Наоборот, любой гомоморфизм
группы G в группу обратимых элементов кольца End (M)
задает на М структуру G-модуля.
Понятия М. над кольцом и G-модуля тесно связаны.
Именно, любой G-модуль М можно рассматривать как
М. над групповым кольцом % G, если распространить
действие группы G на М по линейности, т. е. положить
где a;?Z, g(?G, т?М. Наоборот, если на М задана
структура унитарного % G-модуля, то М можно рас-
рассматривать как G-модуль.
В случае, когда М является А'-модулем над нек-рым
коммутативным кольцом К и одновременно G-модулем,
причем действие элементов группы G на М переста-
перестановочно с действием элементов К, М можно снабдить
структурой XG-модуля, распространяя действие с G
на KG по линейности. Напр., если V — линейное
векторное пространство над нолем К, то задание
структуры KG-моцуля на V эквивалентно заданию
представления G в пространстве V.
Используя стандартную инволюцию g —>- g в груп-
группе G, любой левый G-модуль М можно превратить в
правый G-модуль, положив mg-—g~1m для т?Л/, g?G.
Аналогично, любой правый G-модуль можно превра-
превратить в левый G-модуль.
Модуль над алгеброй Ли. Пусть $ — алгебра Ли
над коммутативным кольцом К и М — нек-рый /С-мо-
дуль. Задание структуры д-модуля на М состоит
в задании .йГ-эндоморфизма т i—*¦ gm группы М для
каждого g?Cj, причем требуется выполнение аксиомы
для любых glt #2?д, m(^M. Это определение отли-
отличается от данного ранее определения Л-модуля. За-
Задание на М структуры д-модуля равносильно заданию
^-гомоморфизма д в алгебру Ли кольца End(Af).
Модуль М над алгеброй Ли Д можно рассматривать
также как М. в обычном смысле над универсальной
обертывающей алгеброй алгебры д.
Конструкции в теории модулей. Исходя из заданных
Л-модулей, можно получать новые Л-модули при по-
помощи ряда стандартных построений. Так, с любым
модулем М связана решетка всех его подмодулей.
Напр., если кольцо А рассматривать как левый М.
над собой, то его левые подмодули — это в точности
левые идеалы кольца А. Ряд важных типов М. опре-
определяется в терминах решетки подмодулей. Напр.,
условие обрыва убывающих (возрастающих) цепей
подмодулей определяет артиновы модули (нётеровы
модули). Условие отсутствия нетривиальных подмо-
подмодулей, т. е. подмодулей, отличных от 0 и всего М.,
выделяет неприводимые модули.
Для модуля М и любого его подмодуля N фактор-
факторгруппу MIN ¦ можно снабдить структурой Л-модуля.
Этот модуль наз. фа. ктор модулем М по N.
Гомоморфизм Л-модулей определяется как гомомор-
гомоморфизм абеловых групп f:M —>- N, перестановочный с
умножением на элементы кольца Л, т. е. удовлетво-
удовлетворяющий условию f(am) = af(m) для всех т?М, а?А.
Если заданы два гомоморфизма Д, f.2:M —у N, то их
сумма, определяемая формулой (Д+/2) (m)=/i(m)+
+/2(то), снова будет гомоморфизмом Л-модулей. Это
сложение задает на множестве Нотд(М, jV) всех го-
гомоморфизмов модуля М ъ N строение абелевой группы.
Для любого гомоморфизма f:M —>- JV определены под-
подмодули Кег/ (ядро f) и Im/(образ /), а также фактор-
модули Coker/=JV/Im / (коядро /) и Coim /=Af/Ker/
(кообраз/). М. Im/ и Coim / канонически изоморфны,
поэтому их обычно отождествляют. Напр., для любого
левого идеала / кольца А определен фактормодуль
AlJ. M. AlJ неприводим тогда и только тогда, когда
/ — максимальный левый идеал. Если М — пек-рый
неприводимый Л-модуль, не аннулируемый кольцом
Л, то М изоморфен М. AlJ для нек-рого максималь-
максимального левого идеала /.
Для любого семейства .4-модулей {М:\ где i про-
пробегает нек-рое множество индексов /, в категории
Л-модулей существуют прямая сумма и прямое произ*
ведение семейства {М;}. При этом элементы прямого
произведения ТТ. М; можно ]ттерпретировать как
векторы (. . ., т/, . . .)> компоненты к-рых заиндек-
спрованы множеством /, причем для каждого индек-
индекса i, m,?M;. Сложение таких векторов и умножение
их на элементы кольца определяются покомпонентно.
Прямую сумму ]jjg )М[ семейства {Л/(-} можно ин-
интерпретировать как подмодуль прямого произведения,
состоящий из векторов, у к-рых все компоненты,
кроме конечного числа, равны нулю.
Для проективной (индуктивно]!) системы 4-модулей
проективный (индуктивный) предел этой системы можно
естественным образом снабдить структурой А-модуля.
Прямое произведение и прямая сумма М. могут рас-
рассматриваться как частные случаи понятий проектив-
проективного и индуктивного пределов.
Образующие и соотношения. Пусть X — нек-рое
подмножество Л-модуля М. П о д м о д у л е м, по
рожденным множеством X, наз. пересечение всех под
модулей модуля М, содержащих X. Если этот подмо-
подмодуль совпадает с М, то X наз. семейством (пли
системой) образующих модуля М. М.,
допускающий конечное семейство образующих, наз.
конечно порожденным модулем. Напр.,
в нётеровом кольце любой идеал является конечно
порожденным М., прямая сумма конечного числа ко-
конечно порожденных М. снова конечно порождена.
Любой фактормодуль конечно порожденного М. также
конечно порожден. Для построения системы образу-
образующих модуля М часто оказывается полезной л е м м а
Н а к а я м ы: для любого идеала 31, содержащегося
в радикале кольца Л, из условия 4iM---=M следует
М—0. В частности, в условиях леммы Накаямм эле-
элементы mlt . . ., тг являются системой образующих
для М, если их образы порождают модуль М/Щ.М.
Ото соображение особенно часто используется в слу-
случае, когда А — локальное кольцо и 1 — максималь-
максимальный идеал в А.
Пусть М — модуль с системой образующих {x,}ig j.
Тогда отображение (р:у,- —>- х; определяет эпиморфизм
ф свободного Л-модуля F с образующими {у,}11: j на
М (М. F можно определить как множество формальных
конечных сумм 2а/у,-, а,-?Л, отображение ср распро-
распространяется с образующих на элементы М. F по линей-
линейности). Элементы М. Д = Кег ц> наз. соотношения-
соотношениями между образующими {х;} модуля М.
Если модуль М можно представить как фактормодуль
конечно порожденного свободного М. F так, чтобы М.
соотношений R также был конечно порождён, что М
наз. конечно представ и мым модулем.
Напр., над нётеровым кольцом А любой конечно
порожденный М. конечно представим. В общем случае
конечная представимость не следует из конечной
пор ожденности.
Замена кольца. Существуют стандартные конструк-
конструкции, позволяющие рассматривать Л-модуль М как М.
над нек-рым другим кольцом. Напр., пусть задан
гомоморфизм колец tp:B—>-A. Тогда, полагая Ът=-
= ф(Ь)т, можно рассматривать М как В-модуль.
Если модуль М — унитарный Л-модуль, и гомомор-
гомоморфизм ф переводит единицу в единицу, то М станет
унитарным В-модулем.
Пусть задан нек-рый гомоморфизм колец ф:Л —у В и
Л-модуль М. Тогда В можно снабдить структурой (В,
Л)-мОДуля, полагая Ьа-=Ьц>(а) для Ь?В, а?А, и мож-
можно рассмотреть левый В-модуль В(?)дМ. Говорят, что
этот М. получен из А/ расширением скаляров.
Категория модулей. Класс всех М. над заданным
кольцом А с гомоморфизмами М. в качестве морфиз-
мов образует абелеву категорию, обозначаемую Л =mod.
Из функторов, определенных на этой категории, наи-
наиболее важны функторы Нот (гомоморфизмы) и 0
(тензорное произведение). Функтор Нот принимает
значения в категории абелевых групп и сопоставляет
паре Л-модулей М, N, группу Homj (M, N). Для
f:Ml —>- М и <p:N —>- JVX очевидным образом опреде-
определяются отображения
f:HomA{M, N)—> Нотл (М 1? N)
ф':Нотл (М, N) —+ Нотл (М, Л^),
т. о. функтор Нот контравариантен но первому аргу-
аргументу и ковариантен по второму. В случае, когда М
или Лг несет структуру бимодуля, группа Нотд (М, N)
обладает дополнительной модульной структурой. Если
Л' есть (А ,В)-модуль, то HomA(M,N) — правый В-мо-
дуль, а если М есть {А , В)-бимодуль, то Hom^ (M, N) —
левый В-модуль.
Функтор (g)^ ставит в соответствие nape M, N, где
М — правый Л-модуль, a iV — левый ^4-модуль, тен-
тензорное произведение M(?)AN модулей М и N над коль-
кольцом А. :)тот функтор принимает значения в категории
абелевых групп и коварнантен как по М, так и по N¦
В случае, когда М или N — бимодули, группу MQ)AN
можно снабдить дополнительной структурой. Именно,
если М есть (В, Л)-модуль, то M(/)AN есть В-модуль,
а если N есть (А, В)-бимодуль, то M(/)AN — правый
S-модуль. Изучение функторов Нот и (>?), а также их
производных функторов является одной из основных
задач гомологнч. алгебры.
Многие важные типы М. характеризуются в терми-
терминах функторов Нот и (g). Так, проективный модуль М
определяется требованием, чтобы функтор Нот,} (М, X)
(от X) был точным. Аналогично, инъектиеный модуль N
определяется требованием точности Hovn^fX, N)
(от X). Плоский модуль М определяется требова-
требованием точности функтора М(?)дХ.
М. над данным кольцом А можно рассматривать с
двух точек зрения.
1) Можно изучать М. с точки зрения их внутренней
структуры. Основной задачей здесь является полная
классификация М., т. е. построение для каждого М.
системы инвариантов, характеризующей этот М. с
точностью до изоморфизма, и умение но заданному
набору инвариантов строить М. с этими инвариантами.
Для нек-рых типов колец такое описание возможно.
Напр., если М — конечно порожденный М. над груп-
групповым кольцом KG конечной группы G, где К — нек-рое
поле, характеристика к-рого взаимно проста с по-
порядком G, то М представим в виде конечной прямой
суммы неприводимых подмодулей (модуль М вполне
приводим). Это представление определено однозначно
с точностью до изоморфизма (сами неприводимые под-
подмодули в общем случае не определяются однозначно).
Все неприводимые подмодули также допускают про-
простое описание: все они содержатся в регулярном пред-
представлении группы G и находятся во взаимно однознач-
однозначном соответствии с неприводимыми характерами этой
группы. Также простое описание допускают М. над
кольцом главных идеалов и над дедекиндовым коль-
кольцом. Именно, любой конечно порожденный модуль М
над кольцом главных идеалов А изоморфен конечной
прямой сумме М. вида Л/ЭД/, где 2[,- — нек-рые идеалы
кольца А (возможно, нулевые), причем StiSSla— • • ¦ —
<==ЖтФА и идеалы 21; однозначно определяются по-
последним условием. Таким образом, набор инвариантов
{31,-} полностью определяет модуль М. Если М —
конечно порожденный М. над дедекиндовым кольцом
А, то M-'-M^Mz, где Мг — перподич. М., а Мг —
М. без кручения (выбор модуля Мг не однозначен).
Модуль М2 аннулируется нек-рым идеалом 31 кольца
А и, следовательно, является М. над кольцом главных
идеалов Al% и допускает описание, указанное выше,
а модуль Мх представим в виде ©M(+3i?i, где SJ? —
нек-рый идеал А , a Q3™ — прямая сумма п раз. Мо-
Модуль Мл с точностью до изоморфизма однозначно опре-
определяется двумя инвариантами: числом п и классом
идеала 5J3 в группе классов идеалов.
2) Другой подход к изучению М. состоит в изучении
категории A=mod и данного модуля М как объекта
этой категории. Такое изучение является предметом
гомологич. алгебры и алгебраич. А'-теории. На этом
пути было получено много важных и глубоких резуль-
результатов.
Часто рассматривают М., несущие нек-рую допол-
дополнительную структуру. Так рассматриваются градуи-
градуированные модули, фильтрованные модули, топологи-
топологические модули, модули с полуторалииейной формой
и т. д.
Лит.: [1] Бурбаки Н., Алгебра. Модули, кольца,
формы, пер. с франц., М., 1966; [2] е г о ж е, Коммутативная ал-
алгебра, пер. с франц., М., 1971; [3] е г о ж е, Группы и алгебры
Ли. Алгебры Ли, свободные алгебры Ли и группы Ли, пер. с
Франц., М., 1976. L4] Ленг С., Алгебра, пер. с англ., М., 1968;
[5] Ван дер ВарденБ. Л., Алгебра, лер. с нем., 2 изд.,
М., 1979; [И] Кострикин А. И., Введение в алгебру, М.,
1977; [7] Д ж е к о б с о н Н., Строение колец, пер. с англ.,
М., 1961; [8] X е р с т е й и И., Некоммутативные кольца,
пер. с англ., М., 1972; [9] Ф е й с К., Алгебра: кольца, модули и
категории, пер. с англ., т. 1—2, М., 1977 — 79; [10] К apian A.,
Эйленберг С, Гомологическая алгебра, пер. с англ., М-,
I960; [11] М а к л е й н С, Гомология, пер. с англ., М., 1966;
[12] Басе X., Алгебраическая А'-теория, пер. с англ., М., 1973;
[13] Милнор Д ж., Введение в алгебраическую .ЙГ-теорию,
пер. с англ., М., 1974. Л. В. Кузьмин.
МОДУЛЬ АВТОМОРФИЗМА — действительное по-
положительное число, ставящееся в соответствие авто-
автоморфизму, локально компактной группы. Если G —
такая группа и а — нек-рый автоморфизм группы G
как топологич. группы, то модуль автоморфизма а
определяется формулой
где [г — левоинвариантная мера Хаара на группе G
и S — любое компактное подмножество группы G
положительной меры (причем modo (а) не зависит от
S). Если G компактна или дискретна, то всегда mod<j(a)=
= 1, т. к. для компактной группы можно положить
S=G, а для дискретной S=o, где а — любой элемент G.
Если аир — два автоморфизма группы G, то
modo («•&) = modG (a) modo (p).
Если Г — нек-рая топологич. группа, к-рая непре-
непрерывно действует на группу G автоморфизмами, то
modG (a) определяет непрерывный гомоморфизм Г —>- R+,
где R+ — мультипликативная группа действительных
положительных чисел. В частности, сопоставляя каж-
каждому элементу a?G порождаемый им внутренний ав-
автоморфизм группы G и рассматривая модуль этого
автоморфизма, получают непрерывный гомоморфизм G
в группу R+. Этот гомоморфизм тривиален тогда и
только тогда, когда левоннвариантная мера Хаара
на группе G является' одновременно и правоинвари-
антной. Группы, удовлетворяющие последнему усло-
условию, паз. унимодулярными.
Другой пример — локально компактное тело Kt
каждый ненулевой элемент а к-рого определяет авто-
автоморфизм умножения на а аддитивной группы тела К.
Функция modA-(a) используется при изучении струк-
структуры локально компактных тел.
Лит.: [1] Бурбаки Н., Интегрирование. Векторное
интегрирование. Мера Хаара. Свертка и представления, пер. с
франц., М., 1970; [2] В е й л ь А., Интегрирование в топологи-
чесьих группах и его применения, пер. с франц., М.. 1950; [3]
его же, Основы теории чисел, пер. с англ., М., 1972.
Л. В. Кузьмин.
МОДУЛЬ БЕЗ КРУЧЕНИЯ — модуль М над коль-
кольцом А без делителей нуля такой, что нз равенства
ат=0, где а?А и т(?М, следует а^О или m=0. При-
Примерами таких модулей (левых) являются само кольцо
А, а также все его ненулевые левые идеалы. Подмодуль
М. б. к., а также прямая сумма и прямое произведе-
произведение М. б. к.— также М. б. к. Если кольцо А комму-
коммутативно, то для любого модуля М определен подмодуль
кручения
Т (М) = {т?М\Эа?А, аф 0, am = 0}.
Тогда фактормодуль MlT{M) является М. б. к.
Л. В. Кузьмин,
МОДУЛЬ КОЛЬЦА — величина, обратная экстре-
экстремальной длине семейства замкнутых кривых в кольце
r!<:|z|<:/-2) разделяющих граничные окружности; М. к.
равен
С помощью конформного отображения на соответст-
соответствующее кольцо К получается модуль mG коль-
кольцевой области G. Оказывается, что mG =
=—D (u), где D (и) — Дирихле интеграл От дейст-
действительной части функции и, отображающей G на К:
{|<|и>|<е °}- (Таким образом, данная кольцевая
область отображается на кольцо с определенным от-
отношением радиусов граничных окружностей. Этот
факт может быть принят за другое определение М. к.,
обобщение к-рого ведет к понятию модуля плоской
области.)
Обобщением понятия модуля кольцевой области
является модуль ту граничного элемен-
элемента у открытой римановой поверхности R относительно
его окрестности. В зависимости от того, конечна или
бесконечна величина т , граничный элемент имеет
гипорболич. или параболич. тип, a R обладает или
нет Грина функцией.
Для Односвязной области D гиперболич. типа опре-
определяется т. н. приведенный модуль mZ0
относительно z0 ? D как предел
lira ( т (г) -f- -;— In r
г ->- О ^ '-Я
где т(г) —модуль кольцевой области ?>(r) =
—zo| >;}. Оказывается, что mZo= j^lni?, где R — кон-
конформный радиус D относительно zo??>.
М. П. Войцеховский.
МОДУЛЬ СЕМЕЙСТВА КРИВЫХ — конформно ин-
инвариантная числовая характеристика семейства кри-
кривых; величина, обратная экстремальной длине этого
семейства.
МОДУЛЬ ЭЛЛИПТИЧЕСКОГО ИНТЕГРАЛА — па-
параметр к, входящий в выражение эллиптпч. интеграла
в нормальной форме Лежандра, напр, в неполный
эллиптич. интеграл 1-го рода
dt ()
()
Число к2 иногда наз. л е ж а н д р о в ы м м о д у-
л е м, к'= Y^i—к2 наз. дополнительным мо-
модулем. В приложениях обычно имеет место нор-
нормальный случай, когда 0<&<1; при этом
острый угол 0 такой, что sin6=A-, наз. модуляр-
модулярным у г л о м. Модуль к входит и в выражения
Якоби эллиптических функций, возникающих при
обращении эллиптич. интегралов вида (*).
Е. Д. Соломекцее.
МОДУЛЯРНАЯ ГРУППА — группа Г всех дробно-
линейных преобразований у вида
*-^7(г) = ?±|, ad-bc--=l, A)
где а, Ъ, с, d — целые рациональные числа. М. г. отож-
отождествляется с факторгруппойSL2(Z)l{—E}, где .?= L .
н является дискретной подгруппой в группе Ли
PSL2 (R)=SL2(R)/{rt?}. Здесь SL2(R) (соответственно
SL.2(S)) — группа матриц
2( (
J, a, fr, с, d — действи-
действиJ
тельные (соответственно целые) числа, ad—foc= 1.
М. г. является дискретной группой преобразований
верхней комплексной полуплоскости Н= {z=x-\-iy\y^>Q}
(плоскости Лобачевского) и допускает
представление образующими T:z—»-z+1 и S:z —>- —1/z
и соотношениями 52= (?ГK— 1, т. е. является свобод-
свободным произведением циклич. группы порядка 2, порож-
порожденной 5, и циклич. группы порядка 3, порожденной
SТ (см. [2]).
Интерес к М. г. связан с изучением модулярных функ-
функций, римановой поверхностью к-рых является фактор-
пространство HIT, отождествляемое с фундаментальной
областью G М. г. Компактификация ХГ= (HIT) \J oo
аналитически изоморфна комплексной проективной
прямой, причем изоморфизм задается основной моду-
модулярной функцией /(z). Фундаментальная область О
имеет конечную площадь Лобачевского
±,
т. е. М. г. есть фуксова группа 1-го рода (см. [3]). Для
решетки L=Z + Zz, z?H, решетка Lx= 2 + SV (s1> 7 =
= <a , ^ Г, эквивалентна L, т. е. получается из L
умножением элементов последней на ненулевое ком-
комплексное число X=(cz+d)-1.
Каждой решетке соответствует комплексный тор
C/L, аналитически эквивалентный неособой кубич.
кривой (эллиптич. кривой). Это дает взаимноодно-
взаимнооднозначное соответствие между точками факторпрост-
ранства HIT, классами эквивалентных решеток и
классами (аналитически) эквивалентных эллпптпч.
кривых (см. [3]).
Исследование подгруппы М. г. представляет интерес
в теории модулярных форм и алгебраических кривых.
Главной конгруэнц-подгруппой Г (N)
М. г. уровня JV^l (N — целое число) наз. группа
преобразований у (z) вида A), у к-рых as=-d=l (mod N),
c=b=Q (mod iV). Подгруппа ГсГ наз. конгруэнц-
подгруппой, если ГзГ(Л^) для нек-рого числа
N; наименьшее такое Л^ наз. уровнем Г. Примеры
конгруэнц-подгрупп уровня N: группа Г0(Л) преоб-
преобразований A) с с, делящимся на JV, группа Г\ (Лг) пре-
преобразований A) с a=d=l mod N и с=0 mod Л'. Индекс
подгруппы F(N) в М. г. равен (Л'3/2) IT (l—p~'z),
если JV>2, р — простые числа и 6, если N = 2, по-
поэтому каждая конгруэнц-подгруппа имеет конечный
индекс в М. г.
Каждой подгруппе Г конечного индекса в М. г.
соответствует полная алгебраич. кривая Х~ (модуляр-
(модулярная кривая), полученная из факторпространства HIT,
и накрытие X—у X . Изучение ветвления этого на-
накрытия позволяет найти для конгруэнц-подгрупп Г
образующие и соотношения, род кривой Х~ и доказать,
что существуют подгруппы конечного индекса в М. г.,
не являющиеся конгруэнц-иодгруппами (см. [31, [8],
[7] т. 2). Изучение представлений М. г. началось в
работах (см. [4], [6]) в связи с теорией модулярных
форм. Такие представления интенсивно изучаются в
рамках теории автоморфных форм (см. [7]). Многие
результаты, относящиеся к М. г., переносятся на
случай арифметич. подгрупп в алгебраич. группах Ли.
JIvm.: IlJ Г у р в и ц А., Курант Р., Теория функций,
пер. с нем., М., 1968: [2] С е р р Ж.-П., Курс арифметики, пер.
с франц., М., 1972; [3] Ш и м у р а Г., Введение в арифметиче-
арифметическую теорию автоморфных функций, пер. с англ., М., 1973; [4]
Нес к е Е., Mathematische Werke, 2 Aufl., Gott., 1970, S. 789—
918: [iJKlein F., Fricke R., Vorlesungen (iber die Theorie
der elliptischen Modulfunktionen, Bd 1—2, Lpz., 1890—92; [6]
Kloosterman H. D., «Ann. Math.» 1946, v. 47, p. 317 —
447; [7] Modular functions of one variable, [v.] 1—6, B.— Hdlb.—
N. Y., 1973—77; [8] R a n k i n R., Modular forms and functions,
Camb., 1977. А. А. Папчишпин.
МОДУЛЯРНАЯ КРИВАЯ — полная алгебраич. кри-
кривая X ~, униформизуемая подгруппой Г конечного
индекса модулярной группы Г; точнее, М. к. есть пол-
полная алгебраич. кривая, получаемая из факторпро-
странства Hi Г, где Н — верхняя полуплоскость, при-
присоединением конечного числа параболич. точек (клас-
(классов эквивалентности относительно Г рациональных
точек границы области Н). Наиболее известные при-
примеры подгрупп f конечного индекса в Г — конгруэнц-
подгруппы, содержащие для нек-рого целого N^\
главную конгруэнц-подгруппу Г (N) уровня N, пред-
ставимую матрицами
mod Л
(см. Модулярная группа). Наименьшее такое N наз.
уровнем подгруппы Г. В частности, под-
подгруппа Г0(Л"), представимая матрицами, к-рые срав-
сравнимы с верхними треугольными матрицами по mod N,
имеет уровень N. Каждой подгруппе Г конечного
индекса соответствует накрытие М. к. X >- X , к-рое
разветвлено только над образами точек z=?, z= A +
-М У 3)/2, з=оо. Для конгруэнц-подгрупп Г ветвление
этого накрытия позволяет определить род М. к. Х~,
доказать существование подгрупп Г конечного индекса
в Г, не являющихся конгруэнц-подгруппами (см. [4]
т. 2 и [2]). Род кривой Xt(N) равен 0 для iV<2 и равен
р — простые, при Л>2. М. к. всегда определена над
полем алгебраич. чисел (обычно над Q или его круго-
круговым расширением). Рациональные функции на М. к.
поднимаются до модулярных функций (высшего уров-
уровня) и образуют поле; автоморфизмы этого поля изу-
изучены (см. [2]). Голоморфная дифференциальная форма
на М. к. Х~ задается на Н дифференциалом f(z)dz (где
f(z) — голоморфная функция), инвариантным относи-
относительно преобразований z—yy(z) из Г; при этом f(z)
есть модулярная форма веса 2 относительно Г. Дзета-
функция М. к. есть произведение Меллина преобразо-
преобразований модулярных форм и, следовательно, она имеет
мероморфное продолжение и удовлетворяет функцио-
функциональному уравнению. Этот факт послужил отправной
точкои теории Ленглендса — Вейля о связи модуляр-
модулярных форм и рядов Дирихле (см. [7], [8]). В частности,
есть предположение, что каждая эллиптич. кривая
над нолем Q (кондуктора JV) униформизуется моду-
модулярными функциями уровня N. Гомологии М. к.
связаны с модулярными символами, что позволяет
исследовать арифметику значений дзетафункции М. к.
в центре критич. полосы и построить р-адическую
дзета-функцию М. к. (см. [1]).
М. к. параметризует семейство эллтгатич. кривых,
являясь их многообразием модулей (см. [7] т. 2).
В частности, для Г= Г (N) точки z факторпространства
HlV(N) взаимно однозначно соответствуют парам,
состоящим из :)лл(гнтпч. кривой Ez (аналитически эк-
эквивалентной комплексному тору C/B+Zz)) и точки
порядка N на Ez (образа точки zlN).
Над каждой М. к. Х~ имеется естественное алге-
браич. расслоение Е-. —>- X~ на эллиптич. кривые,
компактифицированное вырожденными кривыми над
параболич. точками М. к. Х~. Его расслоенные сте-
(w)
пени Ef , где w — целое Jsl, наа. многообра-
многообразиями К у г и (см. [3], [5]). Дзета-функции много-
многообразий Е^ связаны с преобразованиями Меллина
модулярных форм, а их гомологии — с периодами
модулярных форм (см. [3], [7]).
Рациональные точки на М. к. соответствуют эллип-
эллиптич. кривым, имеющим рациональные точки конечного
порядка (или рациональные подгруппы точек), их
описание (см. [6]) позволило решить проблему круче-
кручения эллиптич. кривых над Q.
Исследование геометрии и арифметики М. к. осно-
основано на использовании группы автоморфизмов проек-
проективного предела кривых Х- по убывающим Г, к-рая
(по существу) совпадает с группой вЬ2(Л) над кольцом
А рациональных аделей. На каждой М. к. Х~ это
дает нетривиальное кольцо соответствий R~ (кольцо
Гекке), имеющее приложения в теории модулярных
форм (см. [2]).
Лит.: [1] М а н и н Ю. И., «Изв. АН СССР. Сер. матем.»,
1972, т. 36, № 1, с. 19—66; [2] Ш и м у р а Г., Введение в ариф-
арифметическую теорию автоморфных функций, пер. с англ., М., 1973;
[3] Ш о к у р о в В. В., «Матем. сб.», 197В, т. 101 J* 1, с. 131 —
1 57; [4] К 1 е i n P. Fricke К., Vorlesungen iiber die Theorie
der elliptischen Modulfunktionen, Bd 1—2, Lpz., 1890—92; [5]
Kug-a M., ShimuraG., «Ann. Math.», 1965, v. 82, p. 478—
539- [6] M a z u г B. S e г г e J.-P., в кн.: Seminaire Bourbaki,
1974/75, В. — [u. a.], 1976, p. 238—55; [7] Modular functions of
one variable, [v.] 1 — 6 В.— Hdlb.— N. Y., 1973—77; [8]
Weil A., «Math. Ann.», 1967, Bd 168, S. 149 — 56.
А. А. Панчишпин, А. Н- Паршин.
МОДУЛЯРНАЯ РЕШЕТКА, модулярная
структур а,— то же, что дедекиндова решетка.
МОДУЛЯРНАЯ ФОРМА одного комплексного пере-
переменного, эллиптическая модулярная
форм а,— функция / на верхней полуплоскости
Н= {z?C|Im z>0}, удовлетворяющая при нек-ром фик-
фиксированном к условию автоморфности:
для любого элемента
ГРУППЫ SL2(Z) целочис-
ленных матриц с определителем ad—6с=1, и такая,
что
I \zt — /I _n ип4 >
где д—ехрBягг), z?H, <г„?С. Целое число к^О наз.
в е с о м М. ф. /. Если ао = О, то М. ф. / наз. парабо-
параболической модулярной формой. Име-
Имеется также [8] определение М. ф. для всех действи-
действительных значений к.
Пример М. ф. веса fe^4 дает ряд Эйзенштейна (см.
[4])
где звездочка означает, что при суммировании пара
(mi, 'rea)— @, 0) отбрасывается. При этом Ga (z)=0
для нечетных к и
где CFft_1(«) = ^]rf|nd*-1, a, Bk — число Бернулли.
Множество М. ф. веса fe есть комплексное векторное
пространство, обозначаемое М^\ при этом M^MiCzMk + i.
Прямая сумма (JjfeLoM\ образует градуированную
алгебру, к-рая изоморфна кольцу многочленов от
независимых переменных G4 и G6 (см. [3]).
Для каждого z?H комплексный тор C/(Z + Zz)
аналитически изоморфен эллиптич. кривой, задава-
задаваемой уравнением
y* = 4x*-g2(z)x-g3(z), B)
где #2(z)-=60G4(z), gs(z)=li0G&(z). Дискриминант ку-
бич. многочлена в правой части равенства B) есть
параболич. М. ф. веса 12:
= 2-* Bя)]2 V~_i т(п) <?",
где т(ге) — функция Рамануджана (гм. [1]).
Для каждого целого JV^l вводятся модуляр-
модулярные формы высшего уровня N, удов-
удовлетворяющие условию A) лишь для элементов |г Ji
IIе "II
конгруэнц-подгруппы Г уровня N модулярной группы.
В этом случае с М. ф. / связан голоморфный дифферен-
дифференциал /(z) (dz)k/2 на модулярной кривой Х~. Известный
пример М. ф. высшего уровня дают тэта-ряды f(z)
целочисленных положительно определенных квадра-
квадратичных форм F(хг, х2, . . ., хт):
к-рые суть М. ф. высшего уровня веса к~т/2. В этом
примере ап есть целое число, равное числу решений
диофантова уравнения F(xlt x2, ¦ . ., хт)=п.
Теория М. ф. позволяет получать оценки, а иногда
и точные формулы для чисел типа ап (такие, как срав-
сравнение Рамануджана T{n)~^jd[ йитос1691), а также
исследовать их свойства делимости (см. [7]). Получена
наилучшая оценка для чисел типа ап (см. [2]).
Важные арифметич. приложения М. ф. связаны с ря-
рядами Дирихле
2"
преобразований Меллина М. ф. /. Такие ряды Дирихле
поддаются детальному изучению (оценки коэффици-
коэффициентов, свойства аналитичности, функциональное урав-
уравнение, разложения в эилеровские произведения) ввиду
наличия на модулярных кривых нетривиального коль-
кольца соответствий R. Для кривой Хг это кольцо порож-
порождается соответствиями Tn(z)='S\ y(z), где у пробегает
все представители элементов фактормножества
{А?М2 Ш :det A = n}/SL B, %).
Соответствия индуцируют действующие на простран-
пространстве М. ф. линейные операторы (операторы
Г е к к е), к-рые самосопряжены относительно скаляр-
скалярного произведения Петерсона (см. [3], [7]). М. ф.,
являющиеся собственными функциями операторов Гек-
ке, характеризуются тем, что их преобразования Мел-
Меллина разлагаются в эйлеровское произведение.
Другие продвижения в теории М. ф. связаны с изу-
изучением модулярных кривых и ассоциированных с
ними расслоений — многообразий Куги, а также с
теорией бесконечномерных представлений аделъпых
алгебраич. групп. При этом теория М. ф. одного пере-
переменного успешно переносится на случай многих пере-
переменных (см. [6]). Обзор теоретико-числовых прило-
приложений М. ф. дан в [5].
Лит.: [1] ГурвицА., Курант Р., Теория функций,
пер. с нем., М., 1968; [2] Д е л и н ь II., «Успехи ма^см. наук»,
1975, т. 30, в. 5, с. 159—90; [3] Л е н г С, Введение в теорию
модулярных форм, пер. с англ., М., 1979; [4] Серр Ж.-П.,
Курс арифметики, пер. с франц., М., 1972; [51 Итоги науки и
техники, Алгебра. Топология, Геометрия, т. 15, М., 1977; [в]
Modular functions of one variable, [v.] 1—ri, B.— Hdlb.— N. Y.,
1973—77; [7] О g g A., Modular forms and Dirichlet series, N. Y.,
1969; [8] Rankin R., Modular forms and functions, Camb.,
1977. А. А. Панчишкин.
МОДУЛЯРНАЯ ФУНКЦИЯ, эллиптическая
модулярная функция, Одного комплексного
переменного — автоморфная функция комплексного
переменного z—x-\-iy, ассоциированная с группой Г
всех дроби о-линейных преобразований у вида
Z *i W cz+d ' ' * '
где а, Ь, с, d — целые действительные числа (эта группа
наз. модулярной). Преобразования группы Г
переводят действительную ось
в себя, и областью определе-
определения М. ф. можно считать верх-
верхнюю полуплоскость {z:Im z>0}.
Группа Г порождается двумя
образующими z—>-z+1, z-*•
->- —1/z. Фундаментальная об-
область G модулярной группы
изображена на рис. 1; это — /
криволинейный четырехуголь- /
ник ABCDA с вершинами А (оо), —'-
-^D
^, () ( \
-\-iY~3/2), две стороны к-рого Рис. 1.
АВ и DA — отрезки прямых со-
соответственно х=—1/2 и x=il2, a BD — дуга окруж-
окружности |z| = l. Участки границы АВ и ВС включаются в
G, a CD и DA не включаются. Образы области G при
всевозможных отображениях группы Г покрывают
всю полуплоскость Im z>0 без пересечений.
Изучение М. ф. началось в 19 в. в связи с изучением
эллиптич. функций и предшествовало появлению об'
щей теории автоморфных функций. В теории М. ф.
в качестве основных модулярных форм используются
следующие тета-ряды:
A 7 V"^ °° nhh2'1 \
где h=einz, а звездочка означает, что нулевая пара
(ти т.2)= @, 0) отбрасывается. Согласно термино-
терминологии К. Вейерштрасса (К. Weierstrass) это — отно-
относительные инварианты, играющие важ-
важную роль в его теории эллиптич. функций (см. Вейер-
Вейерштрасса эллиптические функции), а <\наз. также диск-
дискриминантом. С точки ярения теории автоморф-
автоморфных функций это — автоморфные формы соответст-
соответственно веса 2, 3 и 6, ассоциированные с модулярной
группой. Основная М. ф. имеет вид
Функция /(z) наз. также абсолютным инва-
инвариант о м. Она регулярна в верхней полуплоскости,
а внутри фундаментальной области G принимает каж-
каждое конечное значение, кроме 0 и 1, в точности один
раз; кроме того, /(—\'2+г ]//2) = 0, J(i)=i.
В теории эллиптич. функций М. ф. J (z) играет важ-
важную роль, позволяя по заданным вейерштрассовым
относительным инвариантам a—g2, b=ga, a3—27&2=И=0,
определить периоды 2а>х, 2со3, а следовательно, и по-
построить все эллиптич. функции Вейерштрасса. Если
т — единственное в фундаментальной области решение
уравнения
то при афО, ЬфО имеем 0)i = a/6, a>3= с^т; при я=0
имеем т=—1/2+г}//2, и щ определяется из урав-
уравнения
1
140
при Ь— 0 имеем т—i, и
4 во V4*
определяется из уравнения
1
Для построения Яиоби эллиптических функций
удобнее, вместо /(г), функция
C)
>!(=>
В(-Н
СЩ
Рис. 2.
так;ке называемая М. ф. На самом деле k(z) является
автоморфной функцией только относительно подгруппы
Г2 модулярной группы Г, причем к Г2 относятся все
те преобразования вида A), у к-рых (в качестве до-
дополнительного условия) and —
нечетные числа, & и с — четные.
Фундаментальная область G2
группы Г2 изображена на рис.
2; это — криволинейный четырех-
четырехугольник A BOCA с вершинами
А (оо), В( — 1), О, СA), две сторо-
стороны к-рого А В и С А — отрезки
прямых соответственно аг=—1 и
. х= 1, а ВО и ОС — дуги окружно-
окружностей соответственно |г+1/2|=^1/2 и
\z—1/21 = 1/2- Участки границы сле-
слева от мнимой оси включаются в
С,, а ОС и СА не включаются.
Функция X (z) также регулярна
и верхней полуплоскости Ira z>0. Внутри области G2
она принимает каждое конечное значение, кроме О
и 1, в точности один раз; кроме того, Цоо)=0 и /Ц0)=1.
При заданном модуле эллиптич. функций Якобп к
для их построения необходима величина т=йK/'а'1
или h=-enir, к-рая однозначно определяется из урав-
уравнения Х{т)—к2. Практически, в нормальном случае
0</с<1 определяют сначала е= A— |/V)/2A+ V~k'),
где к'— |/"l—А-2, а затем строят решение этого урав-
уравнения в виде ряда Л^е+2е5+15е9+150е13+О(е17).
М. ф. ?ь=Х (z) и J (z) связаны формулой
(Z> ~ 27 'к* A-W2 •
М. ф. w=J(z) дает наиболее удобное представление
конформных классов римановых поверхностей эллиптич.
функций, когда род g=l и эйлерова характеристика
%=0. Каждому значению w соответствует решение
т=«3/со1 уравнения J (x)=w, определяющее конформ-
конформный класс и соответствующее поле эллиптич. функций.
Напр., ш=0 соответствует параллелограмм периодов
в виде ромба с углами 120° и 60°, а ш=1 — квадрат.
М. ф. применяются также при изучении конформных
отображений, граничных свойств аналитических функ-
функций и предельных множеств. М. ф. w—J(z) дает кон-
конформное отображение левой половины фундаменталь-
фундаментальной области G (рис. 1), т. е. криволинейного треуголь-
треугольника А ВС А, на верхнюю полуплоскость Im w~>0,
причем точки В, С, А переходят соответственно в 0, 1,
оо. М. ф. 'w=h(z) отображает конформно криволиней-
криволинейный треугольник АВОА (рис. 2) на верхнюю полупло-
полуплоскость, причем точки В, О, А переходят соответст-
соответственно в О, 1, оо.
В геометрнч. вопросах часто удобнее принять за
область определения М. ф. единичный круг. При этом
модулярная группа A) переходит в модулярную группу
автоморфизмов единичного круга. Напр., удобно при-
применить дробно-линейное преобразование
переводящее верхнюю полуплоскость Im z>0 в еди-
единичный круг |?|<1, причем точки О, 1, оо переходят
соответственно в точки А (е~ил/6), В(е~Ы/г>), С(i)
на единичной окружности
1^1 = 1 (рис. 3). Тогда слож-
сложная функция !t>=fx(?)—A(z(?))
есть М. ф., регулярная в еди-
единичном круге и принимающая
в нем все значения, кроме О,
1, оо. Она отображает кон-
конформно криволинейный тре-
треугольник А ВС А (рис. 3) на
верхнюю полуплоскость Imz>
>(). Именно эта М. ф. и.(?) ис-
используется при доказательстве
Пипара теорем и в ряде
других геометрических воиро- Рис.
con.
Лит.: [1] Г у р в и и А., Курант Р., Теория функций,
пор. [с нем.], М., 1968; [2] А х и е з с р Н. И., Элементы теории
эллиптических функций, 2 изд., Й., 1970; [3] Ф о р д Р., Авто-
морфные функции, пер. с англ., М.— Л., 1936; [4] Klein F.,
Fri eke R., Vorlesungen iiber die Theorie der elliptischen Mo
dulfunktionen, Bd 1—2, Lpz., 1890—92. E. Д. Соломеицев.
МОДУЛЯРНЫЙ ИДЕАЛ — правый (левый) идеал
/ кольца R, обладающий следующим свойством: в
кольце Я найдется хотя бы один такой элемент е, что
для всех х из R разность х—ех принадлежит / (соот-
(соответственно х—,ге?/). Элемент е наз. левой (и р а-
в о и) единицей по модулю идеала /.
В кольце с единицей всякий идеал является модуляр-*
ным. Всякий собственный модулярный правый (ле-
(левый) идеал можно вложить в максимальный правый
(левый) идеал, к-рын автоматически будет модуляр-
модулярным. Пересечение всех максимальных модулярных
правых идеалов ассоциативного кольца совпадает с
пересечением всех максимальных левых идеалов моду-
модулярных и является Джекобсона радикалом этого коль-
кольца. М. п. иногда наз. также регулярными идеа-
идеалами.
Лит.: [1] Д ж е к о б с о н Н., Строение колец, пер. с англ.,
М., 1961. ' К. А. Жевлаков.
МОДУС ПОНЕНС (modus ponens), правило от-
отделения,— вывода правило в формальных логич.
системах. Правило М. п. записывается в виде схемы
А А Э В
В '
где А и В — обозначения для формул формальной
логич. системы, аз — логич. связка импликации.
М. п. разрешает выводить В из посылок А (малая
посылка) и AzdB (большая посылка).
Если в нек-рой интерпретации формальной системы
формулы А и A Dfi истинны, то по смыслу импликации
истинна формула В. М. п. вместе с другими правилами
вывода и аксиомами формальной системы определяет
класс формул, выводимых из множества формул М,
как наименьший класс, содержащий формулы из М,
аксиомы и замкнутый относительно правил вывода.
М. п. можно рассматривать как операцию над вы-
выводами данной формальной системы, позволяющую
образовывать вывод формулы В из вывода а формулы
А И вывода Р формулы AZ)B. в. Н. Гришин.
МОМЕНТ — числовая характеристика распределе-
распределения вероятностей. Момент порядка А; (А;>0 —
целое) случайной величины X определяется как мате-
матич. ожидание ЕХ*, если оно существует. Если
F(x) функция распределения случайной величины X,
то
\ "^ x*dF(x). (===)
При определении М. в теории вероятностей использу-
используется прямая аналогия с соответствующим понятием,
играющим важную роль в механике: формулой (*)
определяется М. распределения масс. М. 1-го порядка
(статич. момент в механике) случайной величины X —
математич. ожидание EX. Величина Е(Х— а)* нал.
моментом порядка к относительно а,
Е (X—ЕХ)* — центральным моментом по-
порядка к. Центральный М. 2-го порядка Е(Х — EX'f
наз. дисперсией ОХ (М. инерции в механике). Вели-
Величина Е(Х|* наз. абсолютным моментом порядка к
(абсолютный М. определяется и для нецелых к). Ана-
Аналогично определяется М. совместного распределения
случайных величин Х1, . . ., Хп (см. Многомерное рас-
распределение): для любых целых к^О, &!+. . ,-\-кп=к
математич. ожидание Е(Х]', . . ., Хп") наз. сме-
смешанным моментом порядка к, а
E(Xt — EXj)*i. . . (Х„—ЕХ„)*в — центральным
смешанным моментом порядка к. Сме-
Смешанный М. Е(Х1—ВХ1)(Х2—ЕХ,) наз. ковариацией и
служит одной из основных характеристик зависимости
между случайными величинами (см. Корреляция).
Многие свойства М. (в частности, неравенства для М.)
являются следствием того факта, что для любой
случайной величины X функция g(k) = \ogE\X\k вы-
выпукла по к в каждом конечном интервале, где эта
функция определена; (Е|Х|*)'^* является неубываю-
неубывающей функцией от к. Моменты ЕХ* и Е(Х—а)* сущест-
существуют тогда и только тогда, когда Е|Х|*<оо. Из су-
существования М. Е|Х|*о вытекает существование всех
М. порядка к<?к0. Если Е|Х,-|*<оо при всех i=l, ...,
. . ., re, то существуют смешанные М. ЕХ*1. . -Хпп
для всех целых к{^0, к\-\-. . .-^кп<,к. В нек-рых
случаях для определения М. бывает полезна т. н. п р о-
и з водящая функция моментов — функ-
функция M(t), для к-рой М. распределения служат коэф-
коэффициентами при разложении ее по степеням: для
целочисленных случайных величин эта функция свя-
связана с производящей функцией Р (s) соотношением
Д^(г)=Р(е'). Если Е\Х\к<сс, то характсристнч.
функция / (?) случайной величины X имеет непрерыв-
непрерывные производные до порядка к включительно, при
этом М. порядка к является коэффициентом при {И)к/к\
в разложении f(t) по степеням t
Если существует производная характернстпч. функции
порядка 2/с в нуле, то Е1Х|-*<оо.
О связи М. с семиинвариантами см. ст. Семиинва-
Семиинвариант.
Если известны М. распределения, то можно сделать
нек-рые утверждения о вероятностях отклонения слу-
чайной величины от ее математич. ожидания в терми-
терминах неравенств; наиболее известны Чебышееа неравен-
неравенство
?{\Х — ЬХ\^г}<^Щ, е > О,
и его обобщения.
Задача, состоящая в определении распределения
вероятностей последовательностью его М., носит на-
название моментов проблемы. Впервые эта задача была
рассмотрена П. Л. Чебышевым A874) в связи с иссле-
исследованиями по предельным теоремам. Для того чтобы
распределение вероятностей случайной величины X
однозначно определялось своими М. aft—EX*, до-
достаточно, напр., выполнение условия Карле-
м а н а
Аналогичное утверждение справедливо и для М. слу-
случайных векторов.
Использование М. при доказательстве предельных
теорем основывается на следующем факте. Пусть Fn,
п -1, 2, . . ., последовательность функций распреде-
распределения, все М. к-рых а^(ге) конечны, и пусть при каж-
каждом целом к^1 имеет место сходимость
ак (п) —*¦ ak при га —»- оо ,
где а^ конечны. Тогда существует подпоследователь-
подпоследовательность Fn., слабо сходящаяся к функции распределе-
распределения F, имеющей ак своими М. Если М. определяют F
однозначно, то последовательность Fn слабо сходится
к F. На этом основан т. н. моментов метод, использу-
используемый, в частности, в математич. статистике при изу-
изучении отклонений эмпирич. распределения от теоре-
теоретического и для статистич. оценки параметров распре-
распределения (о выборочных М. как об оценках М. нек-рого
распределения см. Эмпирическое распределение).
Л. В. Прохоров.
МОМЕНТОВ МЕТОД — метод определения распреде-
распределения вероятностей по его моментам. В тооретич.
отношении М. м. основан на единственности решения
моментов проблемы: если ао=1, аь . . ., ап, . . .,—
нек-рые постоянные, то при каких условиях существует
единственное распределение Р такое, что
ап = С xnP {dx)
суть моменты распределения Р при всех н? Сущест-
Существуют различные типы условий, достаточных для того,
чтобы распределение однозначно определялось своими
моментами, напр, условие Карле мана
Использование М. м. при доказательстве предельных
теорем теории вероятностей и математич. статистики
основано на соответствии между сходимостью распре-
распределений и моментов: если J''n(x) — последовательность
функций распределения с конечными моментами a.k (га)
любого порядка /с^1 и cck(n) —>- р^ при п —у оо и
каждом /с, то Рд, — моменты нск-рой функции рас-
распределения F(х); если F(х) однозначно определяется
своими моментами, то при п —>- оо Fn(x) слабо схо-
сходится к F(x). Впервые М. м. для случая сходимости
к нормальному распределению был разработан П. Л. Че-
Чебышевым A887), а доказательство центральной пре-
предельной теоремы М. и. было осуществлено А. А. Мар-
Марковым A898).
М. м. в математич. статистике — один из общих
методов нахождения статистич. оценок для неизвест-
неизвестных параметров распределения вероятностей по ре-
зультатам наблюдений. Впервые в этих целях М. м.
был использован К. Пирсоном (К. Pearson, 1894) при
решении задачи аппроксимации эмпирич. распределе-
распределений с помощью системы распределений Пирсона. Про-
Процедура М. м. такова: определяются моменты эмиирич.
распределения (выборочные моменты) и в количестве,
равном числу оцениваемых параметров, приравнива-
приравниваются к соответствующим моментам распределения
вероятностей, являющимся функциями от неизвест-
неизвестных параметров; полученная система уравнений ре-
решается относительно параметров, и полученные реше-
решения суть искомые оценки. На практике М. м. приводит
часто к весьма простым вычислениям. При нек-рых
довольно общих условиях М. м. позволяет найти
оценки, к-рые асимптотически нормальны, имеют ма-
тематич. ожидание, лишь величиной порядка 1/и
отличающееся от истинного значения параметра, и
стандартное отклонение — порядка i/yn. Однако оцен-
оценки, найденные по М. м., не являются наилучшими из
возможных с точки зрения их эффективности — их
дисперсия не является минимальной. В случае нор-
нормального распределения М. м. приводит к оценкам,
совпадающим с оценками максимального правдоподобия
метода, т. е. к асимптотически несмещенным и асим-
асимптотически эффективным оценкам.
Лит.: [1] Прохоров Ю. В., Розанов Ю. А., Тео-
Теория вероятностей, 2 изд., М., 1973; [2| К р а м е р Г., Матема-
Математические методы статистики, пер. с англ., [2 изд.], М., 1975;
13] К е н д а л л М., С т ь ю а р т А., Теория распределений,
пер. с англ., М., 1966. А. В. Прохоров.
МОМЕНТОВ МЕТОД — то же, что Галеркина метод.
МОМЕНТОВ ПРОБЛЕМА -- одна из интерполяци-
интерполяционных задач в действительной или комплексной об-
области.
Первая четкая постановка начального варианта
М. п. в действительной области принад-
принадлежит Т. Стилтьесу (Т. Stieltjes, 1894). Им в связи с
исследованиями цепных дробей поставлена и факти-
фактически решена следующая задача: дана последователь-
последовательность действительных чисел {цп}, га=0, 1, 2, . . .,
найти ограниченную и неубывающую на [0, Н-оо)
функцию г|)(х) такую, что
x"dy(x)=nn, и = 0,1,2,... A)
Как и в каждой интерполяционной задаче, решение
М. п. A) распадается на два этапа.
Задача А. Пусть 9J) — множество всех последо-
последовательностей действительных чисел {цп}, для каждой
из к-рых бесконечная система уравнений A) имеет
по крайней мере одно решение г|з(х) с указанными выше
свойствами; найти необходимые и достаточные (кон-
(конструктивные) условия, к-рым должны удовлетворять
числа (х„, /г=0, 1, 2, . . ., для того чтобы {ц„}€2^-
Задача В. Найти множество всех решений в
классе ограниченных и неубывающих на [0, + оо)
функций ty(x), удовлетворяющих бесконечной системе
уравнений A) при заданных ц„, га=0, 1, 2, . . .,{цп}€5Ш-
Левые части равенства A) названы Т. Стилтьесом
«моментами». Этот термин заимствован им из механики.
Если интерпретировать di!p(x) как массу, размещенную
А|)@ — масса, разме-
размещенная на [0, X]. И тогда интегралы A) для и=1 и га=2
представляют собой соответственно первый (статиче-
(статический) и второй (инерции) моменты относительно начала
координат #=0 всей массы \ dty(x) (она отвечает
значению и=0 в A)), размещенной на [0, оо). Обобщая
эти понятия, Т. Стилтьес называл интеграл
моментом га-го порядка (относительно х=0}
С *
данной массы \ Л|з(х), распределение к-рой на [0г
+ оо) характеризуется функцией г|)(х).
Т. Стилтьес связал решение М. п. A) следующим об-
образом с «природой» цепной (или непрерывной) дроби,
отвечающей интегралу
а точнее — формальному ряду
Интегралам / (z, г|з) соответствует цепная дробь
а также «тесно примыкающая» к C) цепная дробь
Цепная дробь D) получается из C) в результате «со-
«сокращений» вида
z —
I I I z-V z-(P+v) '
Опираясь на теорию цепных дробей, Т. Стилтьес
доказал, что в определенном смысле необходимым и
достаточным условием разрешимости системы A) (что
эквивалентно {ци}62Л) является положительность
всех ап в формуле C), что, в свою очередь,— следствие
положительности кп и сп в D). В терминах |_1„ эти
условия равносильны положительности определителей
A*,1> = dctBM-i+y + i«?+/=o.
M. п. A) наз. определенной для данной
последовательности {(*„}, {цп}€Ш^> если система A)
имеет единственное решение ty(x). В противном случае
показано, что если при заданных ц„, {ци}?ЭД], система
A) имеет более одного решения, то тогда необходимо-
система A) имеет бесконечное множество решений.
Пример: две функции
' t~lntdt
, 1],
имеют равные моменты
при всех и=0, 1,2, ... .
Т. Стилтьес привел эффективное построение нек-рых
решений М. п. A), к-рые, разумеется, все в известном
смысле совпадают, если М. п. A) является определен-
определенной. В случае же, когда М. п. A) н е о п р е д е л е н-
н а, решения Т. Стилтьеса обладают рядом экстремаль-
экстремальных свойств. Затем Т. Стилтьес показал, что М. п.
A) является определенной или цепной в зависимости
от сходимости или расходимости цепной дроби C) (что
равносильно сходимости или расходимости ряда Е^о^и)-
При этом дробь C) может быть сходящейся к I (z, г|))
в то время, как ряд
л = 0
(-1)" tin
может расходиться для всех z, z?C.
До работы Т. Стилтьеса [1] М. п. в действительной
области рассматривалась в менее общей и менее чет-
четкой постановке; таковы, напр., серия работ П. Л. Че-
бышева [2] и А. А. Маркова [3]. Ими в основном была
исследована следующая задача: дать описание свойств
класса U функций, определенных на (—со, +оо),
такого, что соотношения
+ °°х"р (х) dx= С + °° xne-x*dr; E)
- со J - -х
п = 0, 1, 2, ...,
приводят к тождеству
Другими словами, здесь идет речь о максимально
полной и конструктивной характеристике класса един-
единственности U интерполяционной задачи E). Решение
М. и. E) играет важную роль в теории вероятностей
и математич. статистике. Имеют важное значение также
многочлены ып(х), являющиеся знаменателями по-
последовательных приближений (т. н. аппроксимант)
цепной дроби D). Изучение свойств систем многочленов
{и>п(х)} впоследствии открыло широкое поле иссле-
исследований в теории ортогональных многочленов.
Г. Гамбургером (G. Hamburger, 1920) М. п. A) была
обобщена на случай всей действительной оси R= (— со,
-j-oo), при этом рассмотрение отрицательных значений
х внесло ряд особенностей и не было тривиальным.
Г. Гамбургер, существенно используя принцип выбора
Хелли, исследовал необходимые и достаточные условия
разрешимости системы
\ 1I х" *Р ^ = (*'" « = 0,1.2,..., F)
решив полностью задачу о сходимости цепных дробей
C) и D), порожденных F). Объединение задач А и В,
относящихся к F), называют проблемой мо-
моментов F). Г. Гамбургер нашел критерий сущест-
существования единственного решения М. п. F). При этом
М. п. F) может быть неопределенной в то время, как
соответствующая М. п. A) (с теми же и„) является
определенной (имеет единственное решение). Р. Не-
ванлпнна (R. Nevanlinna, 1922) представил решение
М. п. F) с помощью интегралов
и изучил свойства этих решений. Ему принадлежит
важное замечание о т. н. «экстремальных решениях»
М. п. F).
М. Рисе (М. Riesz, 1921) нашел решение М. п. F),
опираясь на теорию квазиортогональных многочленов,
состоящих из линейных комбинаций вида Апап{х)-{-
+Лп_1(оп_1(а-), где Ak— константы, а со^ (х) — зна-
знаменатель к-п аппроксиманты цепной дроби D), отве-
отвечающей М. п. F). Он заметил тесную связь между ре-
решениями М. п. F) и справедливостью формулы Пар-
севаля для системы ортогональных многочленов{со„ (х)}.
Т. Карлеман (Т. Carleman, 1923 — 26) установил связь
между М. п. F), теорией квазианалитич. функций и
теорией квадратичных форм от счетного множества
переменных. Ему же принадлежит наиболее общий
критерий определенности М. и. F). Ф. Хаусдорф
(V. Hausdorff, 1923) нашел критерий разрешимости
М. п. F) (<$=р{цп]?ЯЛ) при условии, что функция ^()
в F) постоянна вне заданного интервала. Он дал эф-
эффективную конструкцию решения ip(z) М. п. F)(к-рое
при сделанных им предположениях, отмеченных выше,
всегда единственно); это дает возможность найти
критерии того, чтобы ретение г|з(х) М. п. F) дополни-
дополнительно обладало рядом специальных свойств (было
непрерывным, дифференцируемым и т. п.). Т. Карле-
ман, а затем М. Стоун (М. Stone, 1932) провели весьма
полное исследование М. п. F), базируясь на резуль-
результатах теории квадратичных форм Якоби и теории
сингулярных интегральных уравнений. Э. К. Хэви-
ленд (Е. К. Haviland, 1935) и X. Крамер (Н. Cramer,
1937) распространили теорию Рисса М. п. F) на мно-
многомерный случай.
Рассмотрены также многочисленные различные обоб-
обобщения М. п. В основном упомянутые обобщения явля-
являлись вариациями (или комбинациями) следующих
двух направлений:
замена степеней хп в интегралах F) «моментными»
последовательностями функций {ср„(х)} другого вида, и
замена левых частей равенств F) интегралами иной
природы (напр., изучался случай, когда (Щ>(х) заме-
заменено на ц>(х)йх, где Ц>(х)^Ьр, p~S?i) или даже операто-
операторами, действующими в абстрактных пространствах.
Так, в связи с первым направлением находится т. н.
тригонометрическая проблема мо-
моментов, к-рая состоит в следующем: дана беско-
бесконечная числовая последовательность {сп}^=-оо', найти
неубывающую на [—я, л] функцию ty(.r), удовлетво-
удовлетворяющую соотношениям
лр'''^^И = ^> « = 0, ±1, ±2, ..., G)
т. е. решить задачи А и В для системы G).
Точные формулировки нек-рых предложений из
теории М. п. в действительной области таковы. Пусть
R" есть «-мерное евклидово пространство. Функция
множества Ф (е), определенная на семействе (В= {е}
всех борелевских множеств в R", наз. функцией рас-
распределения, если Ф (е)^0 для всех е?[3, и
если e,-De/=0i гф), где е,-?В для всех г, /=1, 2, ....
Спектром сг(Ф) функции распределения Ф наз.
множество всех точек х= {хи х2, . . ., rn)?Rn таких,
что Ф(б)>0 для произвольного открытого множества
С, G?R", содержащего х. Пусть
К 1,...1„Ь '1' г'*' ¦••' '« = 0, 1, 2, ..., (8)
— п-кратная бесконечная последовательность дейст-
действительных чисел. Спрашивается, каковы необходимые
и достаточные условия, к-рым должны удовлетворять
числа (8) для того, чтобы существовала функция рас-
распределения Ф со спектром сг(Ф), содержащемся в
наперед заданном замкнутом множестве F, являющаяся
решением системы
h, н, .. ., in = 0, 1, 2, ...
(задача А для системы (9)). Аналогичным образом фор-
формулируется задача В для системы (9). Объединение
задач А и В для системы (9) наз. F-n роблемой
моментов. F-M. п. (9) определена, если ее решение
в нек-ром смысле единственно. В противном случае
F-M. п. (9) наз. неопределенной.
Теорема. Необходимым и достаточным условием
разрешимости F-M. п. (9) в R2 является выполнение
условия:
2 а
для любого многочлена
Р (и, v) = 2 ajbjU'vf,
принимающего неотрицательные значения при всех
(u, v), (и, v)?F.
Эта теорема является основой получения условий
разрешимости (т. е. решения задачи А) различных
вариаций М. п. (9). Вот нек-рые из них.
Т е о р е м а 1. Для того чтобы М. п. F) (F=R) имела
решение, необходимо, чтобы
A,,--det||(x,- + /||7+/=0Ss0, ге = 0, 1, 2,...
Для существования решения М. п. F) со спектром,
отличным от конечного числа точек, необходимо и
достаточно, чтобы
А„ > 0, п = 0, 1, 2, ...
Для существования решения М. п. F) со спектром,
состоящим в точности из k-\-i различных точек, не-
необходимо и достаточно, чтобы
Ао>0, Д!>0, ..., Д*>0, ДА + 1 = ДА + 8=...=0.
В последнем случае М. п. F) всегда является опреде-
определенной.
Теорема 2. Для того чтобы М. п. A) (Р=[0, оо))
была разрешима, необходимо, чтобы
д = 0, 1, 2, ...
Для существования решения М. п. A) со спектром,
отличным от конечного числа точек, необходимо и
достаточно, чтобы выполнялись неравенства
Д„ >0 и Д^Х)> 0, га = О, 1, 2, ...
Найдены также необходимые и достаточные условия
существования решения М. п. A) со спектром сг(г|з),
состоящем в точности ия fc+1 различных точек, от-
отличных от д-=0. Эти условия подобны приведенным
в заключительной части теоремы 1.
Теорема 3. Необходимым и достаточным усло-
условием разрешимости хаусдорфовой М. п. в R:
= ц„, я = 0, 1, 2, ..., /' = [0, 1],
является выполнение соотношений Акцу^О для всех к,
v=0, 1, 2, ... (здесь через Д* обозначена операция
взятия к-ii разности).
Теорема 4. Необходимым и достаточным усло-
условием разрешимости хаусдорфовой М. п. в R2:
nl7, *, / = 0, 1, 2,...,
F=[0, l]XfO, 1],
является выполнение соотношений
Д?Д"ц,7 5з 0, га, т, i, / = 0, 1, 2, ....
Теорема 5. М. п. F) определенна, если .
Известны (см., напр., [4]) необходимые и достаточ-
достаточные условия, к-рым должны удовлетворять цп для
того, чтобы М. п. F) (М. п. A)) была определенной;
однако они менее обозримы по сравнению с условием
A0), носящим достаточный характер, а их формули-
формулировка несколько громоздка.
М. п. в комплексной области наз. об-
обширный класс интерполяционных задач, описыва-
описываемый следующим образом. Пусть D — открытая одно-
связная область комплексной плоскости С, <x(fcD;
A (D) — пространство функций, аналитических в D.
с топологией, определяемой равномерной сходимостью
на произвольном компакте A', KdD; пусть A* (D) —
пространство всех функций y(z), аналитических в
окрестности V°°=V°°(y) бесконечно удаленной точки,
причем y(oo)~0 и supp ydD для любой -у, yczA* (D)
(последняя запись эквивалентна тому, что множество
особенностей функции у, y?A*(D) лежит в D). То-
Топология в A*(D) определяется равномерной сходимо-
сходимостью на одной из кривых семейства иростых замкну-
замкнутых жордановых кривых {Va}dD, обладающего свой-
свойством: для произвольного компакта К, KdD сущест-
существует Гао=Га„(#)е{Га} такая, что Kcintt ao(D)
(здесь через intFa0 обозначена открытая односвязная
область с границей Гао, являющаяся «внутренней» па
отношению к Гао). Известно, что пространства A (D)
и A* (D) —взаимно сопряженные.
М. п. в комплексной области такова. Пусть заданы
целое число р, р>1; функции 0^As(D)dA (D), s=0, I,
. . ., р— 1, однолистная в D функция W(z)?A (D) и
совокупность из р последовательностей комплексных
чисел
«/>={{«»Л. " = о, *> 2. •••; s=o, 1,.... p-i}.
Спрашивается, существует ли функция у (z)y(z)?A * (D)t
для к-рой имеют место равенства
lW(z)]»PAs(z)y(z)dz = ans, (И)
ге=0, 1, .. .; s = 0, 1, ..., p — i,
где
supp у a int Г с Г <r int Г с D?
Вообще говоря, не для всякой заранее взятой сово-
совокупности &р бесконечная система уравнений A1) имеет
хотя бы одно решение y(z), y(z)?A*(D). Поэтому
совокупность а.р наз. Д-допустимой, если существует
(хотя бы одна) y(z)?A*(D), удовлетворяющая соот-
соотношениям A1).
Задача А. Найти необходимые и достаточные ус-
условия (конструктивного характера) fl-допустнмости
совокупности &р.
3 а д а ч а В. Пусть ар fl-допустима. Спрашивается,
как по числам ans, находящимся в правых частях
равенств A1), отыскать все множество функций y(z)t
y(z)?A*(D), удовлетворяющих соотношениям A1)?
Объединение задач А и В наз. М. п. в комплексной
области. Задача В для случая, когда р=1, а Л0(г)=1,
впервые была рассмотрена в 1937 А. О. Гельфондом
[6]; им было указано на принципиальную возмож-
возможность решения задачи В (при р=1 и A0(z)s^i система
A1) всегда имеет единственное решение при fl-допу-
стимых правых частях ans). Исследованы многочис-
многочисленные частные случаи задач А и В (см. [7] — [10]).
Использование аппарата теории краевых задач позво-
позволило провести (см. [11] — [14]) достаточно полное
исследование М. п. в комплексной области.
Область G, GcC, наз. 2я/р-инвариантной [G?InvBit/
р)], если exp Bnt/p)G=G.
Исчерпывающее решение М. п. в комплексной об-
области D при весьма естественных предположениях
относительно функций As(z), s=0, I, 2, . . ., p — i,
дано [10] для случая W(D)=G?lnv Bя/р), а также
для областей, образы к-рых W(D) погружаемы в
нек-рую область G, G?InvBJt/p). Привлечение теории
краевых задач к решению М. п. в комплексной области
позволило найти в квадратурах полное решение задачи
В для областей указанных типов. В частности, при/?=1
всякая область G принадлежит классу InvBn/p).
Также найдены необходимые и достаточные условия
единственности решения системы A1) для важных
в приложениях областей D, ^-образы к-рых не яв-
являются погружаемыми. Здесь принципиально раз-
различны два случая: 0?W{D) и 0?W(D) (в последней
из отмеченных возможностей вопрос о единственности
решения системы A1) исчерпывающе исследован в
предположении, что ;г = 0, ±1, ± 2, . . .). Возможны
различные вариации М. п. A1), относящиеся к пове-
поведению соответствующих функций на Г.
К М. п. в комплексной области с помощью преобра-
преобразования Бореля и его обобщений (см. Сравнения функ-
функция) сводится ряд широко известных интерполяцион-
интерполяционных задач, напр.:
Л«> (hn) = ап\ Я"> (со") = я„;
? (ып) -= ап; &"? (hn) = а„;
(«s)= ans,
ra = O, 1, ..., s=0, 1, ..., p —1, 0<lj<l;
A2n + ls? (as + 2hn) — a,ns, s = 0, 1; и^О, 1, 2, ...
Кроме того, многие из теорем о целозначных функ-
функциях сводятся к весьма частным случаям задачи А.
Лит.: [1] С т и л т ь е с Т. И., Исследования о непрерыв-
непрерывных дробях, пер. с франц., Хар.— К., 1936; [2] Ч е 0 ы-
шев П. Л., Поли. собр. соч., т. 3, М.—Л., 1948; [3] Мар-
Марков А. А., Избр. труды по теории непрерывных дробей...,
М.— л., 1948; [4] S h о h a t J. A., Tamarkin J. D.,
The Problem of Moments, N. Y., 1950; [5] A x и е з е р Н. И.,
Классическая проблема моментов..., М., 1961; [6] Гель-
фонд А. О., Исчисление конечных разностей, 3 изд., М.,
1967; [7] Buck R. С, «Trans. Amer. Math. Soc», 1948, v. 64,
p. 283 — 98; [8] e г о же, «Duke Math. J.», 1948, v. 15, p. 879 — 91;
[9] e г о ж е, «Comment, math, helv.», 1953, t. 27, p. 75—80;
[10] Лохин И. Ф., «Матем. сб.», 1954, т. 35, № 2, с. 223—
230; [11] Казьмин Ю. А. «Докл. АН СССР», 1970, т. 194,
с. 1251—54; [12] его ж е, там же, 1972, т. 204, А"о в, с. 1309 —
1312; [13] его же, там же, т. 205, №1, с. 19 — 22; [14] Бибер-
б ах Л., Аналитическое продолжение, пер. с нем., М., 1967;
[15] Г а х о в Ф. Д., Краевые задачи, 3 изд., М., 1977; [16]
КрейнМ. Г., Н у д е л ь м а н А. А., Проблема моментов
Маркова и экстремальные задачи, М., 1973. Ю. А. Казьмин.
МОНЖА КОНУС, направляющий конус,—
огибающая касательных плоскостей к интегральной
поверхности в точке (л0, j/0, z0) дифференциального
уравнения
?(х, у, z, р, q)=--0, (*)
где p^dzldx, q=dz/dy. Бели функция ? нелинейна по
р, q, то имеет место общий случай: касательные пло-
плоскости образуют одно-
параметрич. семейство
плоскостей, проходящих
через фиксированную точ-
точку; его огибающей явля-
является конус. Если функ-
функция ? линейна по р, д,
то получается пучок пло-
плоскостей, проходящих че-
через прямую, т. е. М. к.
вырождается в т. и. ось
М о н ж а. Направления
образующих М. к., соот-
соответствующего нек-рой точ-
точке (.г0, и„, z0), наз. харак-
характеристическими направлениями. Ли-
Линия на интегральной поверхности, касающаяся в
каждой своей точке соответствующей образующей
М. к., наз. х а р а к т е р и с т и ч е с к о й л и н и е й,
характеристикой, фокальной к р и-
в о й, или кривой М о и ж а.
Геометрич. трактовку (см. рис.) уравнения (*)
как поля конусов направлений дал Г. Монж (G. Monge,
1807). А. Б. Иванов.
МОНЖА УРАВНЕНИЕ — дифференциальное урав-
уравнение вида
F{x, у, z, dx, dy, dz) = O.
Г. Монж (G. Monge, см. [1]) изучал такие уравнения
в связи с построением геометрия, теории дифференци-
дифференциальных уравнений с частными производными 1-го
порядка. Частным случаем М. у. является Пфаффа
уравнение.
Напр., если рассматривается дифференциальное урав-
уравнение с частными производными 1-го порядка для
неизвестной функции z двух независимых переменных
х, у:
то направления образующих Монжа конуса (характе-
ристич. направления) в нек-рой точке подчиняются
М. у., к-рое можно записать в форме
М(х, у, х, -У-, 4е-) =0.
Vй dx ' dx J
Это соотношение представляет собой одно обыкно-
обыкновенное дифференциальное уравнение с двумя неиз-
неизвестными функциями, т. е. является простейшим слу-
случаем недоопределенной системы. Часто М. у. наз.
произвольная недоопределенная система обыкновен-
обыкновенных дифференциальных уравнений, в к-рой число
уравнений меньше числа неизвестных функций.
Лит.: [1] Монж Г., Приложение анализа к геометрии,
пер. с франц., М.— Л., 1936; [21 Курант Р., Уравнения С
частными производными, пер. с англ., М., 1964; [3] Р а ш е в-
с к и й П. К., Геометрическая теория уравнений с частными
производными, М.— Л., 1947. Н. X. Розов.
МОНЖА — АМПЕРА УРАВНЕНИЕ — дифферен-
дифференциальное уравнение с частными производными 2-го
порядка вида
д2г д2г д"г
г ~ ал:2 1 s — ад: a.v ' ~ эу2 '
коэффициенты к-poro зависят от переменных а-, у,
неизвестной функции z(x, у) и ее первых производных
dz _ дг
Тип М.— А. у. зависит от знака выражения
Л=ср-|- ас—Ь2.
Если Д>0, М. — А. у. есть уравнение эллиптич. типа,
если Д<0.— гиперболического, если Д=0 — парабо-
параболического. М.—А. у. инвариантно относительно пре-
преобразования прикосновения. В частности, преобра-
преобразование
переводит уравнение
rt—s2=op(p, q)
в уравнение
B 1
дх* ду' V дхду J Ф (I, т|) '
Развитие теории М.—А. у. связано главным образом
с решением различных задач геометрии, к-рые в ана-
литнч. постановке сводятся к рассмотрению таких
уравнений. Напр., построение поверхности с данным
линейным элементом сводится к решению уравнения
Дарбу, к-рое является М.—А. у. В случае полугеоде-
зич. параметризации (линейный элемент dst=du2-{-c2dvi)
это уравнение имеет вид
Тип уравнения Дарбу зависит от знака гауссовой кри-
кривизны к=—саа'с. В случае гиперболич. типа урав-
уравнения Дарбу (гауссова кривизна отрицательна) ха-
характеристиками являются асимптотич. линии. Приме-
Применение теоремы Коши — Ковалевской к уравнению
Дарбу дает теорему существования поверхности с
данным линейным элементом, коэффициенты к-рого
являются аналитич. функциями.
Особенно высокого уровня развития теория М.—А. у.
эллиптич. типа получила благодаря введению понятия
обобщенного решения и применению геометрич. ме-
методов его изучения. В простейшем случае уравнения
Tt—s2=<p обобщенное решение определяется как вы-
выпуклая функция z(x, у), удовлетворяющая равенству
где М — произвольное борелевское множество пло-
плоскости ху в области, где рассматривается решение,
а М* — т. н. нормальное изображение множества М,
к-рое состоит из тех точек плоскости pq, для к-рых
р и q являются угловыми коэффициентами опорных
плоскостей поверхности z^z(x, у) в точках (.г, г/, z),
проектирующихся в М. Регулярное (дважды диффе-
дифференцируемое) решение является обобщенным. Обоб-
Обобщенное решение в случае непрерывной положительной
функции <р является гладким, однако вторые произ-
производные могут не существовать. Построение обобщен-
обобщенного решения в своей существенной части сводится
к чисто геометрич. задаче о построении бесконечного
выпуклого многогранника с заданными направлениями
конечных граней и заданной функцией на этих гранях.
В частности, если правая часть <р уравнения зависит
только от х и у, этой функцией является площадь
грани. Предельным переходом от таких многогранни-
многогранников получается график обобщенного решения урав-
уравнения. Для обобщенных решений получаются доста-
достаточно общие теоремы существования и единственности
решения задачи Дирихле. В частности, имеет место
следующая теорема. Задача Дирихле для уравнения
rt—s2=<p(.r, у, z, р, д)
в выпуклой области G разрешима при любых непре-
непрерывных граничных значениях, если кривизна кривой,
ограничивающей область G, положительна, функция <р
непрерывна, положительна, неубывающая но z и при
р2+д2 -*¦ °° имеет порядок роста не более p2~[-q2.
При заданном направлении выпуклости это решение
является единственным.
Существенным результатом теории М. — А. у. эллип-
эллиптич. типа является теорема о регулярно-
регулярности обобщенных решений. Для простей-
простейшего уравнения
rf—s2=y(x, у, z, p, д)
эта теорема гласит: при ср>0, <рг>0 всякое обобщенное
решение с регулярной правой частью (<р) является
регулярным. Именно, если ср есть к раз дифференциру-
дифференцируемая функция (й:>3), то обобщенное решение по край-
крайней мере fc-^-1 раз дифференцируемо. Если ср — анали-
аналитич. функция, то обобщенное решение — аналитиче-
аналитическое.
Среди общих М.—А. у. эллиптич. типа наиболее
изучены сильно эллиптические урав-
уравнения. Это — уравнения, у к-рых <р>0 п квадра-
квадратичная форма
неотрицательна. Основные результаты, приведенные
для простейшего М. — А. у., распространены на слу-
случай сильно эллиптич. уравнений. Для них введено
понятие обобщенного решения, при весьма общих
условиях доказано существование и единственность
решения задачи Дирихле, а также доказана регуляр-
регулярность обобщенного решения в зависимости от регуляр-
регулярности коэффициентов уравнения. Уравнение Дарбу
для линейного элемента с положительной кривизной,
вообще говоря, не является сильно эллиптическим.
Его обобщенное решение определяется как z-коордп-
ната поверхности, реализующей данный линейный
элемент. Уравнение Дарбу имеет обобщенное решение
в любой области, выпуклой в смысле заданной метрики
(геодезич. кривизна края положительна). В любой
такой области при достаточно общих условиях доказы-
доказывается разрешимость задачи Дирихле. Обобщенное
решение является регулярным, если коэффициенты
линейного элемента являются регулярными. Обобщен-
Обобщенное решение — аналитическое, если коэффициенты —
аналитические.
Важные результаты получены для М.—А. у. эллип-
тич. типа на многообразиях, гомеоморфных сфере.
К таким уравнениям приводят, в частности, две клас-
сич. проблемы: Вейля проблема и Мииковского проблема.
Решения этих проблем, полученные предельным пере-
переходом от многогранников, являются обобщенными.
Регулярность этих решений получается из теорем о
регулярности обобщенных решений.
М.—А. у. рассматривались Г. Монжем (G. Mongc,
1784) и А. Ампером (A. Ampere, 1820).
Лит.: [1] Г у р с а Э., Курс математического анализа,
пер. сфранц., т. 3, ч. 1,М.— Л., 1933; [2] П о г о р е л о в А. В.,
Об уравнениях Монжа — Ампера оллиптического типа, Хар..,
1960; [3] его же, Внешняя геометрия выпуклых поверхностей,
М., 1969. А. В. Погорелое.
МОНОГЕННАЯ ПОЛУГРУППА, циклическая
полугрупп а,— полугруппа, порожденная одним
элементом. М. п., поро?кденная элементом а, обозна-
обозначается обычно <а> (иногда [а]) и состоит из всевозмож-
всевозможных степеней ак с натуральными показателями. Если
все эти степени различны, то (а) изоморфна аддитив-
аддитивной полугруппе натуральных чисел. В противном
случае <а> конечна, и тогда число ее элементов наз.
порядком полугруппы <а>, а также п о-
рядком элемента а. Если <а> бесконечна,
то говорят, что элемент а имеет бесконечный
порядок. Для конечной М. п. А = <а> существует
наименьшее число h с тем свойством, что ай=а* при
нек-ром &>/г; число h наз. индексом элемента
а (а также полугруппы А). Если при этом d —
наименьшее число с тем свойством, что aA=a* + d, то d
наз. периодом элемента а (полугруп-
п ы А). Пара (h, d) наз. типом элемента а
(полугруппы А). Для любых натуральных чи-
чисел h и d существует М. п. типа (h, d); две конечные
М. п. изоморфны тогда и только тогда, когда их типы
совпадают. Если (h, d) — тип М. п. А=<а>, то элементы
а, . . ., ah + d-i различны, и, следовательно, порядок А
равен h-\-d—1; множество
G={a", a"+1, ..., a* + d-1}
является в А наибольшей подгруппой и наименьшим
идеалом; единица е группы G будет единственным идем-
нотентом в А, причем e=ald при любом I таком, что
Id^h; группа G — циклическая группа, ее порождаю-
порождающим элементом будет, напр., ае. Идемпотснт конечной
М. п. является в ней единицей (нулем) тогда и только
тогда, когда ее индекс (соответственно период) равен 1;
это эквивалентно тому, что данная М. п. есть группа
(соответственно нилъпотентная полугруппа). Всякая
подполугруппа бесконечной М. п. является конечно
порожденной полугруппой.
Лит.: [1] Клиффорд А., Престон Г., Алгебраи-
Алгебраическая теория полугрупп, пер. с англ., т. 1, М-, 1972; [2] Л я-
пин Е. С, Полугруппы, М., 1960. Л. Н. Шеврин.
МОНОГЕННАЯ ФУНКЦИЯ — функция комплекс-
комплексного переменного, имеющая конечную производную.
Точнее, функция /(z), определенная на множестве Е
комплексной плоскости С, наз. моногенной (от-
(относительно множества Е) в конечной неизолированной
точке ???", если она имеет в этой точке конечную
производную 1'E(t) по переменному z?E:
= lim
Функция, моногенная в каждой неизолированной
точке множества Е. наз. моногенноп на Е.
Если E=G — область плоскости С, то функция,
моногенная на G, наз. аналитической функцией в об-
области G.
Если Е не является областью, то моногенные на Е
функции, вообще говоря, уже не обладают характер-
характерными свойствами аналитич. функций. Однако если
множество Е, не содержащее в своем составе областей,
является достаточно «массивным» вблизи большинства
своих точек (точнее, если дополнение к Ё в плоскости С
является достаточно разреженным вблизи большинства
точек t,?E), то функции, моногенные на Е, обладают
в ослабленном виде многими свойствами аналитич.
функций. В попытках разобраться в глубинных связях
между основными свойствами аналитич. функций поня-
понятие аналитич. функции обобщалось различными пу-
путями: посредством обобщения ее области определения,
обобщения самого понятия производной, ослабления
условий Коши — Рпмана, ослабления условий тео-
теоремы Мореры и т. п. (см. [13] § 6). С этой же целью
для «тощих» множеств Е, напр, для отрезка Е=[а, b]cz
С: (— оо, оо), выделялись т. н. квазианалитические
классы функций. Изучались также функции, опреде-
определенные на нигде не плотных достаточно массивных
компактах Е, близкие к аналитич. функциям в том
смысле, что они могут быть с любой точностью равно-
равномерно на Е приближены аналитич. функциями или,
что то же самое, рациональными функциями перемен-
переменной z.
Ниже приведены нек-рые результаты из перечис-
перечисленных направлений.
1. Функции, моногенные в области. Если f(z)=f(x-\-
+ iy) = u(x, y)+iv{x, у) (при этом и(х, у) и v(x, у) —
действительнозначные функции), то для аналитичности
/ (z) в области G достаточно (и необходимо) выполнения
в каждой точке x-\-iy?G одновременно двух условий:
1) и (х, у) и v(x, у) имеют полные дифференциалы du(x, у)
и dv(x, у) по совокупности действительных переменных
(х, у); 2) выполнены условия Коши — Римана:
ди (х, у) ду (.у, у) да (х, у) _ ду (х, у)
дл ду ' ду дх
Условия этой теоремы ослаблялись и обобщались.
Напр., показано, что требование существования пол-
полных дифференциалов у и и v можно заменить сущест-
существенно более слабым условием ограниченности и и
v в G и, сохранив требование существования первых
частных производных функций и и v всюду в G, по-
потребовать выполнение условий Коши — Римана лишь
почти всюду в G (в смысле плоской меры Лебега) (см.
[6]).
Пусть L (z) — какая-либо пара различных прямых,
пересекающихся в точке z, R (z) — какая-либо тройка
выходящих из z попарно неколлпнеарных лучей а
Е (г) — какое-либо измеримое множество, имеющее z
своей точкой плотности в смысле Лебега. Аналитич-
Аналитичность непрерывной в G функции / (z) обеспечивается
каждым из следующих условий в отдельности (см.
[3] — [5]): а) всюду в G существует f'L(z) (г)^оо; б) всюду
в G существует j'R (z)=^=oo; в) всюду в G существует
¦F <г) (z^°°¦ Здесь каждое из множеств L(z), R(z),
Е (z) — свое для каждой точки. Следует заметить, что
(z) зависит от / и z, но не зависит от Е (z); произ-
производная
наз. асимптотической (аппроксима-
(аппроксимативной) производной, а функция, имеющая
асимптотич. производную в точке z (соответственно в
области G), наз. асимптотически моно-
моногенной в точке z (соответственно в G). Вместо ус-
условия б) достаточно потребовать существования пре-
предела для
arg((/(z>)-/B))/(z'-z)) яри z'-^z, z'?R(z).
2. Функции, моногенные на нигде не плотных мно-
множествах. Э. Борель [8] построил такое совершенное
связное .множество (континуум) Е без внутренних
точек и такую расширяющуюся последовательность
E^czE2cz. . .czE совершенных множеств, что площадь
mes2E множества Е положительна,
и из моногенности / (z) на Е (или хотя бы на каждом
множестве Е„, п=\, 2, . . .) следует бесконечная диф-
ференцируемость /(z) по г?ЕП() при каждом фиксиро-
фиксированном щ. Можно указать нек-рые сравнительно
общие достаточные условия на Е, чтобы Е обладала
этим свойством или более слабым свойством fe-кратной
дифференцируемое™ по z?En, где к — наперед задан-
заданное натуральное число. Найдены также достаточные
условия на нигде не плотный континуум Е для того,
чтобы для функций, моногенных на нем, были спра-
справедливы аналоги интегральной теоремы Коши, раз-
разложения в ряд Тейлора и различные формы теоремы
единственности, напр, такая: если моногенные на Е
функции fi(z) и /2(z) совпадают на нек-рой порции
множества Е (т. е. на непустом пересечении Е с нек-рым
открытым кругом), то /1(z)ss/2(z) на Е (см. [9]).
3. Функции, близкие к аналитическим. Как иавестно,
любая аналитическая в области G функция / (z) явля-
является пределом нек-рой последовательности рациональ-
рациональных функций rn(z), к-рая сходится к /(z) равномерно
на каждом компакте KdG. Рассматривая достаточно
массивный нигде не плотный континуум Е и класс
R (Е) функций /(z), z?E, для каждой из к-рых сущест-
существует последовательность рациональных функций гп (г, /),
равномерно сходящаяся к /(z), получают еще одно
обобщение понятия области и понятия функции f{z),
аналитической на Е. Если Е — нигде не плотное мно-
множество на С, то всегда найдется функция f^B(E),
не имеющая производной f'E (z) ни в одной точке z?E
(см. [10]). Однако для каждого т, 2<Ст<:оо, можно
указать условие на ?", при выполнении к-рого каждая
функция f?R(E) будет иметь производные /Li; (z),
п
где 1«:/с<;», а Еп замкнуто, EnczE, хаевя(Е\Еп)<Ц,'п
(см. [11]). М. В. Келдыш построил пример нигде не
плотного континуума Е, на к-ром для функций /lt
f2?R(E) справедлива теорема единственности в форме,
приведенной в конце п. 2 (см. также [12]). (По поводу
моногенных свойств функций из R (Е) в терминах
функционального анализа см. [12] ч. I, § 17.) Иссле-
Исследовалась также зависимость моногенных свойств функ-
функций f?R(E) от скорости приближения ее посредством
рациональных функций.
Лит.: [1] Федоров В. С, «Успехи матем. наук»,
1952, т. 7 в. 2, с. 7 — 16- [2] В о h r H., «Math. Z.», 1918, Bd I,
S. 403—20; [31 Меньшов Д. Е., «Pundam. math.», 1935,
v. 25, p. 59—97; [4] е г о ж е, Les conditions de monogeneite, P.,
1936; [5J его же, «Матем. сб.», 193d, т. 1, с. 189—210; [6]
Т о л с т о в Г. П., О криволинейном и повторном интеграле,
М.— Л., 1950 (Тр. Матем. ин-та АН СССР, т. 3;>); [7] Трохи м-
чук Ю. Ю., Непрерывные отображения и условия моноген-
моногенности, М., 1У63; [8] В о г е 1 В., Lemons sur les fenctions monoge-
nes uniformes d'une variable complexe, P., 1917; [9] Селез-
Селезнев А. И., «Докл. АН СССР», 1956, т. 108, № 4, с. 591—94;
[10] Д о л ж ен к о Е. П., там же, 1959, т. 125, JVS 5, с. 970—
973; [И] е г о ш е, там же, 1962, т. 143, Л"а 4, с. 771—74; [12]
Итоги пауки и техники. Современные проблемы математики,
т. 4, М., 1975. с. 143 — 250; [13] БермантА. Ф., Марну
ш е н и ч А. И., в кн.: Математика в СССР за тридцать лет.
1917 —1947 М.— Л. 1948, с. 401 — 406. Е. П. Долженко.
МОНОГЕННОСТИ МНОЖЕСТВО — множество всех
производных чисел данной функции комплексного
переменного в данной точке. Точнее, пусть Е — мно-
множество на комплексной плоскости С, ? — неизолиро-
неизолированная его точка, /(z) — комплекснозначная функция
переменного z?E. Комплексное число а (собственное
или равное оо) паз. производным числом
функции / в точке ?, относительно множества ?, если
существует последовательность zn?E со свойствами:
Множество ЩЩ, /, Е) всех производных чисел функции
/ в точке ? относительно Е наз. множеством
моногенности функции / в точке ? относительно
Е (см. [1]). Множество 2Л(?, /, Е) состоит из един-
единственной конечной точки а тогда и только тогда, когда
f(z) — моногепная функция в точке {, относительно Е
и f'E(t,) = a. Множество 2Л(?, /, Е) всегда замкнуто,
и для каждого замкнутого множества А расширенной
комплексной плоскости С, каждого множества EczC
и каждой конечной неизолированной точки ? этого
множества найдется такая функция /(z), z?E, что
2J!(u, /, Е)=А. Если ? — внутренняя точка Е, то для
любой непрерывной в нек-рой окрестности этой точки
функции /(z) множество 9Л(?, /, Е) является замкну-
замкнутым и связным (континуумом) на С, н обратно, для
любого континуума А'сС найдется функция f(z),
непрерывная в нек-рон окрестности ?, для к-рой 2Л(?,
/, Е)=К. Если функция f(z) = f(x-{-iy) = и(х, y)-\-iv(x, у)
дифференцируема по совокупности действительных
переменных (.г, у) во внутренней точке g=g-j- tr) мно-
множества Е, то 2Л(?, /, Е) представляет собой окруж-
окружность у(т, с)={гг:|ы-—с\ = г) (возможно, вырожденную
в точку при г=0) с центром c=df(t)/dz и радиусом
r=\df(t,)ldl\, где
of
от j_ I _d/ aj_ \ _
dz ~~ 2 V dx dy J
— _L (EJLa UJL\ uL ( dv du
2 'ydx ' l dy )~~ 4 \ dx Эу J "+- 2 ^ ax
du \
ву J
— т. н. формальные производные. Верно
и обратное: каждая окружность является М. м. для
нек-рой функции /, дифференцируемой по (х, у) в за-
заданной внутренней точке $ множества Е.
Если / (г) непрерывна в области G, то почти в каждой
точке ??G множество ШA, }, G) есть либо нек-рая
окружность у (г, с), 0<:?-<оо, либо С (см. [2]). В общем
случае произвольного (необязательно измеримого) мно-
множества Е и произвольной (необязательно измеримой)
конечной функции f(z), z?E, почти в каждой точке
??/? имеет место один из следующих трех случаев:
а) ЩЦ?, /, Е) = у(г, с), с?С,0<г<оо; б) ЯП(?,/, Е) = С;
в) Щ1(?, /, E) = y(r, c)|Joo, c^C, 0<г<оо. При этом
почти в каждой точке дифференцируемое™ функции
j(z)—f(x-\-iy) по совокупности (х, у)?Е выполнен
случай а), почти же в каждой точке непрерывности
функции }(z) — один из первых двух случаев. Каждый
из случаев а) — в) в отдельности может реализоваться
почти в каждой точке t?E
Лит.: [1] Федоров В. С, «Успехи матем. наук», 195L.
т. 7, в. 2, с. 7 — 16; [2] Т р о х и м ч у к Ю. Ю., Непрерывны-
отображения и условия моногенности, М., 1963; МДолжен-
к о Е. П., «Изв. АН СССР. Сер. матем.», 1902, т. 26, с. 347—6A.
Е. П. Долженко.
МОНОДРОМИИ ГРУППА обыкновенного линейного
дифференциального уравнения или линейной системы
уравнений — группа (пХ п)-матриц, к-рая отвечает
системе п-то порядка
х=А (t)x (*)
и определяется следующим образом. Пусть матрица
A (t) голоморфна в области GczC, точка to?G и X (t) —
фундаментальная матрица системы (*), заданная и
малой окрестности t0. Если yczG — замкнутая кривая
с началом в точке t0, то при аиалитич. продолжении
вдоль у, X (t) -+¦ X (t)C , где С — постоянная (пХ п >-
матрица. Если кривые уь у2 гомотопны в G, то С =
= С ; если Y=YiY2, то С^=Су^С^. Отображение
у —*¦ С., есть гомоморфизм фундаментальной группы
области G:
Я1(С, t0) ->Oh(n, С),
где GL(», С) — группа (гаХп)-матриц с комплекс-
комплексными элементами; образ этого гомоморфизма наз.
группой м о н о д р о м и и М (t0, G) системы (*).
При этом
M(tu G)=r-M/(f0, G)T,
где Т — постоянная матрица. М. г. вычислена для
уравнений Эйлера, Папиеритца (см. [1], [2]).
Лит.: [1] Голубев В. В., Лекции по аналитической
теории дифференциальных уравнений, 2 изд., М.— Л., 1950;
[2] Айне Э. Л., Обыкновенные дифференциальные уравне-
уравнения, пер. с англ., Хар., 1939. М. В. Федорюк.
МОНОДРОМИИ МАТРИЦА —постоянная («X ^-мат-
^-матрица Х(ю), к-рая является значением в точке ?= си
фундаментальной матрицы X (t), нормированной и
нуле, линейной системы дифференциальных уравнений
х' = А (t) х, t?R, x?R",
с сй-периодической матрицей А (?), суммируемой на
каждом компактном промежутке из R. ю. в. Комленпо.
МОНОДРОМИИ ОПЕРАТОР — линейный ограничен-
ограниченный оператор U(T), ставящий в соответствие началь-
начальному значению х{Ь)=хй решения дифференциального
уравнения х=А (t)x в банаховом пространстве с огра-
ограниченным оператором А (*), непрерывно и периоди-
периодически с периодом Т зависящим от t, его значение в
момент времени Т: х(Т)= U(Т)х0. Для всякого решения
справедливо: x(t-\-T)= (J(T)x(t). В конечномерном
случае оператору U (Т) отвечает монодромии, матрица.
Расположение спектра М. о. влияет на существование
периодич. решений уравнения, на поведение его реше-
решений на бесконечности, на приводимость уравнения к
уравнению с постоянными коэффициентами, на наличие
экспоненциальной дихотомии. В терминах спектра
М. о. решается также вопрос о существовании и един-
единственности периодич. решений неоднородного урав-
уравнения x=A{t)x-\-j(t) с периодическими A (t) и f(t).
См. также Качественная теория дифференциальных
уравнений в банаховом пространство. С Г Нрейп
МОНОДРОМИИ ПРЕОБРАЗОВАНИЕ — преобразо-
преобразование слоев (или их гомотопич. инвариантов) рассло-
расслоенного пространства, соответствующее нек-рому пути
в базе. Более точно, пусть р'.Е —>¦ В — локально три-
тривиальное расслоение п пусть у\[0, 1] —>- В — путь в В
с началом в точке а = у@) и концом в Ь=у(\). Тривиа-
лизация расслоения у*Е определяет гомеоморфизм
Ту слоя р~г(а) на слой р-1(Ь), Ту -.р'1 (а) -»- р~1(Ь).
При изменении трпвиализации у*Е гомеоморфизм
Ту замепяется на гомотопнчески эквивалентный го-
меоморфизм; это же происходит и при замене пути у
гомотопным путем. Гомотопич. тип гомеоморфизма
Ту и наз. преобразованием монодро-
м и и, соответствующим пути у. Когда а=Ь, т. е. когда
путь -у является петлей, М. п. Ту — гомеоморфизм
слоя F= р~г(а,) в себя (определенный, опять-таки, с
точностью до гомотопин). Это отображение, а также
гомоморфизмы, индуцированные им в гомологиях и
когомологиях слоя F, также наз. М. п. Сопоставление
петле у преобразования Ту задает представление фун-
фундаментальной группы я1(^, а) на Н* (F).
Понятие М. п. возникло при изучении многозначных
аналитич. функций (см. Монодромии теорема). Если
S -+ Р1 (С) — риманова поверхность такой функции,
то выбрасыванием из сферы Римана Р1 (С) особых
точек функции получается неразветвленнос накрытие.
М. п. в этом случае наз. также преобразова-
преобразованием наложения или скольжения.
Наиболее часто М. п. возникает в следующей ситуа-
ситуации. Пусть D={z?C, [z|<l} — диск в комплексной
плоскости, X — аналитич. пространство, a f:X —>- D —
собственное голоморфное отображение, Xf — слой
f-l(t), t?D, D*=D~\{0} и X*~f~1(D*). Уменьшая,
если нужно, радиус D, можно добиться, чтобы рас-
расслоение f:X* —>- D* стало локально тривиальным.
М. п. Т, связанное с обходом вокруг О в D, наз. м о н о-
дромией семейства /:Х->1) в точке О ? D;
оно действует в когомологиях (или гомологиях) слоя
X-f, где t?D*. Более других изучен случай, когда
пространство X гладкое, как и все слои Xf, (=^=0.
Действие монодромии Т на пространстве Н* (Xf, Q)
в этом случае квазиунипотентно [4], т. е.
существуют целые положительные числа к и N такие,
что (Tk—1)^=0. В свойствах монодромии проявля-
проявляются многие характерные черты вырождения семей-
семейства / :Х —*¦ D. Монодромия семейства X —*¦ D тесно
связана со смешанной структурой Ходжа в когомоло-
когомологиях Н*(Х0) и H*(Xt) (см. [5] — [7]).
В случае, когда особенности / :Х —>- D изолированы,
М. п. может быть локализовано. Пусть х — особая
точка отображения / (или, что то же, слоя Хо) и пусть
В — шар достаточно малого радиуса в X с центром в
х. Уменьшая, если нужно, радиус D, можно определить
локальную тривиализацию расслоения B(]f~x (-D*)—>-
->fl*, согласованную на границе с тривиализацией
расслоения dBf\f~1(D)-^~D. Это даст диффеоморфизм
Т многообразия «исчезающих циклов» Vt=Bf\Xt
в себя, тождественный на его крае dV-t и называемый
локальной монодромией / в точке х.
Действие М. п. на когомологиях Н* (Ft) отражает
важнейшее свойство особенности отображения / в
точке х (см. [1], [2], [7]). Известно, что многообразие
Vf гомотопически эквивалентно букету ц ге-мерных
сфер, где «+l = dimX, а и. — число Милнора ростка /
в х.
Простейшим является случаи особенности Морса,
когда функция / в окрестности точки х приводится к
виду /=zo-i-z?-r. . .-j-Zn. В этом случае (х=1, а внут-
внутренность Vt многообразия Vt диффеоморфна касатель-
касательному расслоению к я-мерной сфере Sn. Исчезаю-
Исчезающим ц и к л о м б наз. образующая группы когомо-
логий с компактными носителями Нп (F?, Z)—Z, опре-
определенная с точностью до знака. Вообще, если / :Х —>-D —
собственное голоморфное отображение (как выше,
имеющее единственную морсовскую особенность в
точке х), то и с ч е з а ю щ и м в точке х циклом
бх наз. также образ цикла 6?#"(F?) при естественном
отображении Н" (Vt) ->- Н" (Xj). В этом случае гомо-
п mod 4
±
0
-
2
1
-
0
о
+
2
3
+
0
морфизм специализации rt :Н'(Хо) -+ W {Х\) является
изоморфизмом при i-фп, ге+1, и последовательность
О _+ ffn {Хо) _^ цп (Xt) <-^> % _*
—>¦ #" + 1 (Z()) -^ //" + 1 (Xt) —*0
точна. М. п. Т действует на Hl(Xt) тривиально при
1фп, а его действие на 11" (Xt) задается форму-
ламиПикар а—Л е ф-
шеца: для z?H"(Xf)
Tz=z± (z, 8Х)8Х.
Знаки в этой формуле п
значения (8Х, дх) собра-
собраны в таблице.
М. п. Т сохраняет форму пересечения на Hn(Xf).
Исчезающие циклы и М. п. используются в т е о-
рии Пи кара — Лефшеца, сравнивающей ко-
гомологии проективного комплексного многообразия
и его гиперплоского сечения. Пусть Xc:PN— гладкое
многообразие размерности ге+1, a {Xf}, t?Pl,— пучок
гиперплоскнх сечений многообразия X с базисным
множеством (осью пучка) YczX; п пусть выполняются
следующие условия: а) У — гладкое подмногообразие
в X; б) существует такое конечное множество SdP1,
что Xt гладкое при t^P1—S; в) для s?S многообразие
Xs имеет единственную невырожденную квадратичную
особую точку xs, причем xs ^ Y. Пучки с такими свой-
свойствами (пучки Лефшеца) всегда существуют.
Пусть а :Х —>- X — моноидальное преобразование с
центром в оси пучка У, а / :Х —*- Р1 — морфизм, опре-
определяемый пучком {Xt}; при этом f~1(t)^Xf для всех
t^P1. Фиксируется точка о^Р1—S; тогда М. п. за-
задает действие фундаментальной группы % (Р1—S, о)
на Я1 (Хо) (нетривиальное лишь при i=ra). Для опи-
описания действия монодромии на Нп(Х0) выбираются
точки s', расположенные около s?S, и пути y's, веду-
ведущие из о в s'. Пусть ys^^iiP1—$, °) — петля, уст-
устроенная так: сначала она идет по y'Sl затем обходит
один раз вокруг s и, наконец, возвращается по y's в о.
Кроме того, пусть 6S — исчезающий в точке xs цикл
(точнее, нужно взять исчезающий цикл в Нп(Х$,}
и перенести его в Н"(Х0) при помощи М. п., соот-
соответствующего пути y^) Пусть, наконец, Еа:Н"(Х0, Q)—
подпространство, порожденное исчезающими циклами
$s, s(z$ (пространство исчезающих
к о г о м о л о г и й). Тогда имеют место следующие
утверждения:
1) группа л1 (Р1 — S, о) порождается элементами
2) действие ys задается формулой
3) пространство EczH" (Xo) инвариантно относи-
относительно действия группы моиодромии я1(Р1 — S, о);
4) подпространство инвариантных относительно мо-
монодромии элементов Н"(Х0) совпадает с ортогональ-
ортогональным дополнением к Е относительно формы пересече-
пересечения на Нп(Х0), а также с образами естественных го-
гомоморфизмов Н" (X) -+. Нп (Хо) и II" (X) -+ Нп (Хо);
5) исчезающие циклы —8S соиряжены (с точностью
до знака) относительно действия пг (Р1 — S, о);
6) действие я1(-Р1 — S, о) на Е абсолютно неприво-
димо.
Формализм исчезающих циклов, М. п. и теория Пи-
кара — Лефшеца построены также для Z-адических
когомологий алгебранч. многообразий над любым
полем (см. [3]).
Лит.: [1] Арнольд В. И., «Успехи матем. наук», 1974,
т. 29, в. 2, с. 11—49; [2] М и л н о р Д ж., Особые точки комп-
комплексных гиперповерхностей, пер. с англ., М., 1971; [3] Groupes
de monodromie en geometrie algebrique, B.— Hdlb.— N. Y.,
1973 (Lect. Notes Math., J\fi 340); [4] С 1 e m e n s С. Н., «Trans.
Amer. Math. Soc», 1969, v. 136, p. 93—108; S с h m i d W., «In-
«Invent. Math.», 1973, Bd 22, S. 211—319; [6] S t e e n Ь г i n k J.,
«Invent. Math.», 1976, Bd 31, S. 229 — 57; [7] Symposium in
Mathematics, Oslo, 1976, p. 524—63; [8] LefschetzS.,
L'Analysis situs et la geometrie algebrique P., 1924; [9] Л еф-
ш е ц С, «Успехи матем. наук», 1970, т. 25, МЬ 6, с. 193—215.
В. И. Данилов.
МОНОДРОМИИ ТЕОРЕМА — достаточный признак
однозначности ветви аналитической функции. Пусть
D — односвязная область комплексного числового
пространства С", п^\. Тогда, если нек-рый элемент
аналитич. функции 2 (z°; r) с центром z°?D анали-
аналитически продолжаем вдоль любого пути, расположен-
расположенного в О, то возникающая при этом аналитич. продол-
продолжении ветвь аналитич. функции /(z), z= (z-^, . . ., zn)
однозначна в D. Иначе говоря, ветвь аналитич. функ-
функции /(z), определяемая односвязной областью D и
элементом 2 (z°; r) с центром z°?D, обязательно одно-
однозначна. Другая равносильная формулировка: если
элемент 2 (z°; r) аналитически продолжается вдоль
всех путей, принадлежащих произвольной области
Z>cC", то результат этого продолжения в любую
точку z*?D (т. е. элемент аналитич. функции 2 (z*; r*)
с центром z*) один и тот же для всех гомотопных путей
в D, соединяющих точки 2° и z*.
М. т. справедлива и для аналитич. функций /(z),
определенных в областях D на римановых поверхно-
поверхностях или на римановых областях. См. также Полная
аналитическая функция.
Лит.: [1] Маркушевич А. И., Теория аналитических
функций, 2 изд., т. 2, М., 1968; [2] Стой лов С, Теория
функций комплексного переменного, пер. с рум., т. 1, М., 1962;
[3] Владимиров В. С, Методы теории функций многих
комплексных переменных, М., 1964. Е. Д. Соломенцев.
МОНОДРОМНАЯ ФУНКЦИЯ в области D
комплексной плоскости — однозначная и
непрерывная функция в области D (исключая, быть
может, полюсы). Термин «М. ф.» применялся О. Коши
(A. Cauchy) в связи с необходимостью подразделения
класса аналитических функций на М. ф. и многознач-
многозначные аналитич. функции; в настоящее время A982) он
вышел из употребления.
См. также Монодромии теорема. Е. Д. Соломенцев.
МОНОИД — термин, используемый для сокращения
словосочетания «полугруппа с единицей». Таким об-
образом, моноидом наз. множество М, на к-ром
задана бинарная ассоциативная операция, обычно
именуемая умножением, ив к-ром существует
такой элемент е, что ех=х=хе для любого х^М. Эле-
Элемент е наз. единицей и часто обозначается 1.
В любом М. имеется ровно одна единица. Если задан-
заданная в М. операция коммутативна, то ее часто наз.
сложением, а единицу — нулем М. и обо-
обозначают 0.
Примеры М. 1) Множество всех отображений
произвольного множества S в себя является М. от-
относительно операции последовательного выполнения
(суперпозиции) отображений. Единицей служит тож-
тождественное отображение. 2) Множество эндоморфизмов
любой универсальной алгебры А является М. отно-
относительно операции суперпозиции, единица — тождест-
тождественный эндоморфизм. 3) Всякая группа является М.
Всякую полугруппу Р без единицы можно вложить
в М. Для этого достаточно выбрать символ 1, не при-
принадлежащий Р, и на множестве .PU{1} задать умно-
умножение следующим образом: 1-1 = 1, 1 ¦х=х=х-1 для
любого х?Р, на элементах из Р операция остается
прежней. Всякий М. можно представить как М. всех
эндоморфизмов нек-рой универсальной алгебры.
Произвольный М. можно рассматривать также как
категорию с одним объектом. Это позволяет сопоста-
вить моноид М дуальный (двойственный) моноиду М°Р.
Элементы обоих М. совпадают, а произведение х п у
в М°Р полагается равным произведению ух в М.
Развитие теории М. и сопряженных функторов вы-
выявило полезность определения М. в т. н. м о н о и-
дальных категориях. Пусть в категории ЗК
задан бифунктор (g):9Ttx3Jl ->¦ Ш, выделен объект Z
и фиксированы естественные изоморфизмы
А®(В®С),
A,
удовлетворяющие ус- } Р^Ы.
ловиям когерентности. v I '
Объект М наз. М. ка-
тегории Ш, если су-
ществуют такие мор-
физмы ц: М®М^М
и в: Z —>- М, что еле-
дующие диаграммы
коммутативны:
Если в качестве Ш] взять категорию множеств, в ка-
качестве (X) — декартово произведение, в качестве Z —•
любое одноточечное множество, а изоморфизмы а, X
и р выбрать естественным образом (а ((а, Ъ), е)) =
= (а, (Ь, с)), X(z, а) = а=р(а, z), то второе определение М.
оказывается равносильным исходному определению.
Лит.: [1] Клиффорд А., Престон Г., Алгебраичес-
Алгебраическая теория полугрупп, пер. с англ., т. 1—2, М., 1972; [2] М а с
Lane S., Categories for the working mathematician, N. Y.
[a. o.], 1971. M. Ш. Цалепко.
МОНОИДАЛЬНОЕ ПРЕОБРАЗОВАНИЕ, р а з д у-
т и е, 0-п р о ц е с с,— специального вида бирацио-
налъпый морфизм алгебраич. многообразий или биме-
роморфный морфизм аналитич. пространств. Пусть,
напр., X — алгебраич. многообразие (или произволь-
произвольная схема), a DcX — замкнутое подмногообразие,
задаваемое пучком идеалов /. М оно и дальним
преобразованием X с центром в D
наз. Х-схема A" = Proj (фп>0/")—проективный спектр
градуированного пучка Ox-алгебр ф„>0/"- Если /:
X' —>- X — структурный морфизм Х-схемы X', то
пучок идеалов /*(/) = / -Ох' на X' (определяющий
исключительную подсхему f~r(D) в X) обратим. Это
значит, что f~1(D) является дивизором в X''; кроме
того, / индуцирует изоморфизм между X'—f(D) и
X—D. М. п. f:X' —>. X схемы X с центром в D харак-
характеризуется следующим свойством универсальности [1]:
пучок идеалов /* (/) обратим и для любого морфизма
g:X" —>Х, для к-рого g* (J) обратим, существует
единственный морфизм h:X" -*- X' такой, что g=fok.
Аналогично определяется и характеризуется М. п.
алгебраич. или аналитич. пространства X с центром
в замкнутом подпространстве DczX.
Важный класс М. п. составляют допустимые
моноидальные преобразования, к-рые
выделяются тем условием, что центр D таких преоб-
преобразований неособый, а X — нормально пло-
плоская схема вдоль D. Последнее означает,
что все пучки /«//" + 1 являются плоскими (Ox/J)~
модулями. Важность допустимых М. п. объясняется
тем, что они не ухудшают особенности многообразия.
Более того, доказано (см. [1]), что подходящая последо-
последовательность допустимых М. п. улучшает особенности,
что позволило доказать теорему о разрешении особен-
особенностей алгебраич. многообразий над полем нулевой
характеристики.
Особенно просто устроены допустимые М. п. неосо-
неособых многообразий. Если f:X' —>- X М. п. с неособым
центром ВсХ, то X' снова неособое, а исключитель-
исключительное подмногообразие f~1(D) канонически изоморфно
проективизации конормального пучка к D в X. В част-
частном случае, когда D состоит из одной точки, М. п.
заключается в «раздутии» этоп точки в целое проек-
проективное пространство касательных направлений. О по-
поведении различных инвариантов неособых многообра-
многообразий (таких как кольцо Чжоу, когомологии, .К-функтор,
классы Чжэня) при допустимом М. п. см. [2] — [5].
Лит.: [11 Хиронака X., «Математика», 1965, т. 9,
JV» 6, с. 2—70; [2] Theorie des intersections et theoreme de
Riemann-Roch, B.— Hdlb.— L., 1967; [3] Cohomologie i-adique
et fonctions L (SGA-5), B.— Hdlb.— L., 1977; [4] Porteous
I.. «Pme. Cambridge Phil. Soc», 1960, v. 56, As 2. p. 118—24;
[51 M а н и н Ю. И., ('Успехи матем. наук», 1969, т. 24, в. 5, с.
3—86. " В. И. Данилов.
МОНОМИАЛЬНАЯ ГРУППА ПОДСТАНОВОК -
подгруппа группы GL(m, "Z[H\) всех обратимых матриц
порядка т над целочисленным групповым кольцом
%\Н\ (см. Групповая алгебра) нек-рой группы Н, со-
состоящая из всевозможных матриц, содержащих в
каждой строке п каждом столбце точно один ненулевой
элемент из Н. Каждой такой матрице, содержащей
на (;, ;)-м месте ненулевой элемент hjj?H, может
быть поставлена в соответствие нек-рая моном и-
а л ь н а я подстановка, т. е. отображение
г|з:«,- —>- hijuj, где/ = /(г), г=1, 2, . . ., т, а «,• —>- Uj —
подстановка конечного множества S= {мь . . ., ит}.
Произведение таких отображений вычисляется по
формуле
¦4>i4>2:«<—-+(hijhik)uk
(tyi-iii —>- hfjiij, i|Vity —>- hikuk), и ему будет соответ-
соответствовать произведение матриц, сопоставляемых ото-
отображениям ty-t и г|з2. В М. г. п. изоморфно вкладывается
любая группа G, содержащая Н в качестве подгруппы
индекса т. М. г. п. является (прямым) сплетением
группы Н с симметрия, группой S (т) степени то.
Лит.: [1]Каргаполов М. II., Мерзляков Ю. И.,
Основы теории групп, 2 изд., М., 1977; [2] X о л л М., Теория
групп, пер. с англ., М., 1962. Н. Н. Вильяме.
МОНОМИАЛЬНАЯ МАТРИЦА — квадратная мат-
матрица над ассоциативным кольцом с единицей, каждая
строка и каждый столбец к-рой содержат только один
ненулевой элемент. Если ненулевые элементы М. м.
равны 1, то эта матрица наз. м а т р и ц е й - п о д-
становкой. Любая М. м. есть произведение
матрицы-подстановки и диагональной матрицы.
Д. А. Супрунеико.
МОНОМИАЛЬНОЕ ПРЕДСТАВЛЕНИЕ конеч-
конечной группы G — такое представление р группы
G в конечномерном векторном пространстве V, что в
нек-ром базисе (е)= {еь . . ., еп} этого пространства
матрица Afp^g) оператора p(g) для любого элемента
g(^G имеет точно один ненулевой элемент в каждой
строке II в каждом столбце. Иногда М. п. наз. непо-
непосредственно матричное представление g i—> Afp(g>- M. п.
является частным случаем импримитивного представ-
представления (см. Импримитивная группа). А именно, набор
одномерных подпространств в V, порожденных век-
векторами elt . . ., еп, является системой импримитив-
импримитивности для р. Наоборот, если для нек-рого представ-
представления ф группы G в векторном пространстве W сущест-
существует система импримитивности, состоящая из одномер-
одномерных подпространств, то ф — М. п. Пусть Н — какая-
либо подгруппа в G. Примером М. п. может служить
представление G, индуцированное каким-нибудь од-
одномерным представлением подгруппы Н (см. Инду-
Индуцированное представление). Такие представления наз.
также индуцированными М. п. (см. [1]).
Не всякое М. п. р является индуцированным М. п.
(однако, если М. п. р неприводпмо, то оно будет пнду-
цировакным М. п.). Данное выше определение М. п.
возникло в классич. теории представлений конечных
групп. Часто, однако, это определение изменяют,
называя М. п. произвольное представление группы С,
индуцированное одномерным представлением какой-
либо подгруппы // в С. В таком виде определение М. п.
имеет смысл уже не только для конечных групп и их
конечномерных представлений, но и, напр., для групп
Ли и их представлений в гильбертовых пространствах
(подгруппа Н при этом предполагается замкнутой).
Для достаточно широкого класса групп конструкция
М. п. оказывается достаточной для описания всех
унитарных неприводимых представлений. А именно,
группы, все унитарные неприводимые представления
к-рых мономиальны, наз. моном иальными
группами, или М-т р у п п а м и. К их числу
относятся, напр., все конечные нильпотентные группы
и все связные нильпотентные группы Ли. Все конечные
Af-группы, а также все мономиальные группы Ли
разрешимы (см, [2]).
Лит.: [1] К э р т и с Ч., Р а й н е р И., Теория представ-
представлений конечных групп и ассоциативных алгебр, пер. с англ.,
М., 1969; [2] К и р и л л о в А. А., Элементы теории представ-
представлений, 2 изд., М., 1978. В. Л. Попов.
МОНОМОРФИЗМ в категории — морфизм
\i: А —>- В категории $, для к-рого из всякого равен-
равенства ац.= |3|л (а, |3 из Й1) следует, что а=|3 (другими
словами, на [i можно сокращать справа). Другое
эквивалентное определение М.: для любого объекта X
категории Я индуцируемое морфизмом ц отображение
множеств
Нот(Х, А)-*-Кот(Х, В)
должно быть инъективным. Произведение двух М.
является М. Каждый левый делитель М. есть М. Класс
всех объектов и класс всех М. произвольной категории
Я составляют подкатегорию категории Я (обознача-
(обозначаемую обычно Mon if).
В категории множеств роль М. играют инъекции.
Двойственным к понятию М. является понятие эпи-
эпиморфизма.
Лит.: [1] ЦаленкоМ. Ш., Ш у л ь г е й ф е р Е. Г.,
Основы теории категорий, М., 1974; [2] Б у к у р И., Д е л я-
н у А., Введение в теорию категорий и функторов, пер. с англ.,
М., 1972. О. А. Иванова.
МОНОСПЛАЙН — разность между функцией х" и
полиномиальным сплайном Sn_1(x) степени п—1. М.
возникают при изучении квадратурных формул для
дифференцируемых функций. Ю. Н. Субботин.
МОНОТОННАЯ БУЛЕВА ФУНКЦИЯ — булева
функция f(xu х2, . . ., хп), п=0, 1, 2, . . ., обладающая
следующим свойством: если для нек-рых наборов
а= («,, а.2, . . ., а„) и р = (рх, р, р„), а,€ {«, 1}.
|3у? {0, 1}, выполнено условие а,-<:|3,- для всех i (в
этом случае пишут а^р>), то /(а)<:/(|3). Напр., функ-
функция f(xu xi)=x1Q)x2 (сложение по модулю 2) не яв-
является монотонной, т. к. (О, 1)^A, 1), но 1=/@, 1)>
>/A, 1) = 0.
Примеры М. б. ф.: константы 0 и 1, тождественная
функция f(x)=x, дизъюнкция хг\/х2, конъюнкция
хх&.хг и т. д. Примеры немонотонных булевых функций:
отрицание х, импликация х1 —>- хг и т. д. Любая функ-
функция, полученная с помощью операции суперпозиции
из М. б.ф., сама является монотонной. Другими сло-
словами, класс всех М. б. ф. является замкнутым. Более
того, класс всех М. б. ф. является одним из пяти
максимальных (предполных) классов в множестве
всех булевых функций, т. е. не существует замкнутого
класса булевых функций, содержащего все М. б. ф.
п отличного от класса М. б. ф. и класса всех булевых
функций. Сокращенная дизъюнктивная нормальная
форма любой М. б. ф., отличной от констант 0 и 1,
не содержит отрицаний переменных. Множество функ-
функций {0, 1, хх\1 х2, ,т1&.т2} является полной системой
(и, более того, базисом) в классе всех М. б. ф.
Для числа i|)(n) М. б. ф., зависящих от п переменных,
известно, что
С["/2] A + Е(Л))
¦ф (га) = 2 "
где 0<е(ге)<е 0g", с — нек-рая константа (см. [2]).
Для сложности реализации класса М. б. ф. схемами
из функциональных элементов и контактными схемами
получены более низкие значения, чем для сложности
реализации произвольных булевых функций (см. Син-
Синтеза задачи). Нек-рые дискретные экстремальные
задачи сводятся к задаче расшифровки
М. б. ф. В этой задаче требуется, зная, что нек-рая
функция f(x1, ¦ ¦ ., хп) является М. б. ф., выяснить
ее значения на всех наборах, задав как можно меньше
вопросов вида: «Чему равно значение j(аг, . . ., ап)
на нек-ром наборе сс= (а1? . . ., а„)?». Был предложен
[3] алгоритм, к-рый требует для расшифровки произ-
произвольной М. б. ф. задания не более С["/21 + С\?/21+1
вопросов. С другой стороны, не существует алгоритма
расшифровки, к-рый отличал бы функцию
0, если
!, ¦•-, *п)= \
^ 1 если
( 0,
\
^ 1,
от всех остальных М. б. ф. менее чем за С^'2^-\-С^^2^ +
вопросов.
Обобщением понятия М. б. ф. являются монотон-
монотонные функции ?-3 н а ч н о й логики. Если
на множестве Е^= {0, 1, . . ., к—1} задано произволь-
произвольное частичное упорядочение S (пишут <<s), TOi n0
определению, для любых двух наборов а= (а1( . . .,
ап) и р=(рь . . ., Р„), щ?Ек, $j?Ek, запись a<sp
означает, что <x,-«:sP,- для всех i. Функция А-значной
логики f (х1, • • -, хп) (т. е. определенная и принимающая
значение на Е^) наз. монотонной относи-
относительно S, если для любых наборов сс= (al5 . . .,
ап) и Р== (Pi, . . ., Р„) из условия а-<,^> вытекает
/(a)<s/(P)- Класс всех функций, монотонных отно-
относительно нек-рого частичного упорядочения S на Е^,
всегда является замкнутым классом; он является
предполным классом в А-значной логике в том и только
в том случае, если в S имеются ровно один минимальный
и ровно один максимальный элементы. Для числа %(ге)
функций i-значной логики, зависящих от п перемен-
переменных и монотонных относительно S, при п —у оо имеет
место соотношение
где С (S) — константа, эффективно вычисляемая по
данному частичному упорядочению S (см. [5]).
Лит.: [1] Я б л о н с к и й G. В., Введение в дискретную
математику, М., 1979; [2]Клейтмен Д., «Кибернетич. сб.»,
1970, в. 7, с. 43—52; [3] А н с е л Ж., там же, 1968, в. 5, с.47—52,
53—57, 58—63; [4] М а р т ы н ю к В. В., «Проблемы киберне-
кибернетики», 1960, в. 3, с. 49—60; [5] Алексеев В. Б., там же,
1974, в. 28, с. 5—24. В. Б. Алексеев.
МОНОТОННАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ — такая
последовательность хп, что для всех п=1, 2, ... вы-
выполняется
хп<Схп + } (строго возрастающая последовательность),
xn<Zixn + 1 (неубывающая последовательность),
хп>хп + 1 (строго убывающая последовательность),
хп^хп + 1 (невозрастающая последовательность).
МОНОТОННАЯ ФУНКЦИЯ —функция одного пере-
переменного, определенная на нек-ром подмножестве дей-
действительных чисел, приращение к-рой A/ (x) = f (х1)—/ (х)
при Ах=х'—z>0 не меняет знака, т. е. либо всегда
неотрицательно, либо всегда неположительно. Если
А/(х) строго больше (меньше) нуля, когда Д.г>0,
то М. ф. наз. строго монотонной (см. Воз-
Возрастающая функция, Убывающая функция). Различные
типы М. ф. представлены в таблице.
Если функция / в каждой точке нек-рого промежутка
имеет производную, к-рая не меняет знака (соответ-
ственяо сохраняет постоянный знак), то функция /
монотонна (строго монотонна) на этом
пр о межутке.
Понятие М. ф. действительного переменного обоб-
обобщается на функции различных классов.Напр.,функция
А1(х)>0
Af(x)^O
Af(z)>0
Af(x)<0
Возрастающая
(неубывающая)
Убывающая
(неубывающая)
Строго
возрастающая
Строго
убывающая
^ '
f{x1, . . ., xn), определенная на R", паз. м о н о т о н-
н о й, если из условия хг<.х1, . . ., хп<.х'п следует, что
всегда f (хи . . ., xn)<.f{x[, . . ., х'п) или всегда / (х[,
. . ., xn)^j(x[, . . ., х'п). Подобным же образом опреде-
определяется М. ф. алгебры логики.
М. ф. многих переменных, возрастающие или убыва-
убывающие относительно нек-рой точки, определяются сле-
следующим образом. Пусть функция / определена на п~
мерном замкнутом кубе Q", xo?Q", Et= {x:f(x)=t,
X?Q") — множество уровня функции /. Функция /
наз. возрастающей (соответственно убыва-
убывающей) относительно точки х0, если для любого числа
t и любой точки х' ?Qn\Ef, не отделенной в кубе Q"
множеством Ef от х0, имеет место f(x')<Ct (соответст-
(соответственно/(ж') >f), а для любой точки x"?Q"\Ef, отделен-
отделенной в кубе Q" множеством Et от х0, имеет место J(x")y-t
(соответственно f(x")<Ct). Функции, возрастающие или
убывающие относительно нек-рой точки, наз. моно-
монотонными о т н о с и т е л i о э т о 5 точки.
МОНОТОННОЕ ОТОБРАЖЕНИЕ — то же, """что
изотопное отображение.
МОНОТОННЫЙ ОПЕРАТОР — одно из понятий не-
нелинейного функционального анализа.
Пусть Е — банахово пространство, Е* — его сопря-
сопряженное, (у, х) — значение линейного функционала
у?Е* на элементе х?Е. Оператор А, вообще говоря,
нелинейный и действующий из Е в Е*, наз. моно-
монотонным, если
для любых хи х2?Е. Оператор А нал. полуне-
полунепрерывным, если для любых м, v, w?E числовая
функция (A (u-{-tv), w) непрерывна по t. Примером
полунепрерывного М. о. является градиент выпуклого
дифференцируемого в смысле Гато функционала. Мно-
Многие функционалы вариационного исчисления выпуклы
и потому порождают М. о.; они полезны при решении
нелинейных интегральных уравнений и именно к ним
впервые применялись.
Различные приложения М. о. к вопросам разреши-
разрешимости нелинейных уравнений основаны на следующей
теореме (см. [1], [2]). Пусть Е — рефлексивное банахово
пространство и А — полунепрерывный М. о., облада-
обладающий свойством коэрцитивное™,
lim
Be (Аи, и) _ 00_
Тогда для любого f?E уравнение Au=f имеет хотя
бы одно решение.
Определенный на множестве DcE оператор А со
значениями в Е* наз. монотонным на D, если
неравенство A) имеет место для любых хи x2?D,
и максимальным монотонным, если он
монотонный на D и не имеет строгого монотонного
расширения.
Исследование уравнений с М. о. во многом стимули-
стимулировалось задачами теории квазилинейных эллиптич.
и параболич. уравнений. Так, напр., краевые задачи
для квазилинейных параболич. уравнений приводят к
уравнению вида
Ax-\-Ax=f B)
в подходящем банаховом пространстве Е. Такое же
уравнение естественным образом возникает и при
исследовании задачи Коши для абстрактных эволюци-
эволюционных уравнений с нелинейными операторами в бана-
банаховых пространствах. Если пространство Е рефлек-
рефлексивно, А — ограниченный, полунепрерывный и коэр-
коэрцитивный М. о., а Л — линейный максимальный М. о.
с плотной в Е областью определения, то уравнение B)
разрешимо при любом /?/?*. Идеи монотонности
применялись также в задаче о почти периодических
решениях нелинейных параболич. уравнений.
Лит.: [1] В г о w d е г F., «Bull. Amer. Math. Soc», 1963,
v. 69, p. 858—61; [2] MintyG. J., «Proc. Nat. Acad. Sci.
USA», 1963, v. 50, p. 1038—41; [3] В а й н б е р г М. М., Ка-
ч у р о в с к и й Р. И., «Докл. АН СССР», 1959, т. 129, М 6,
с. 1199—1202; [41 В а й н б е р г М. М., Вариационный метод и
метод монотонных операторов в теории нелинейных уравнений,
М., 1972; [о] Лионе Ж.-Л., Некоторые методы решения не-
нелинейных краевых задач, пер. о франц., М., 1972; [6] Леви-
Левитан Б. М., Ж и к о в В. В., Почти-периодические функции и
дифференциальные уравнения, М., 1978; [71 Качуровс-
ки й Р. И., «Успехи матем. наук», 1968, т. 23, в. 2, с. 121 —
168. В. В. Жиков.
МОНТЕ-КАРЛО МЕТОД, метод статистиче-
статистических испытани й,— численный метод, основан-
основанный на моделировании случайных величин и построе-
построении статистпч. оценок для искомых величин. Принято
считать, что М.-К. м. возник в 1949 (см. [1]), когда
в связи с работами по созданию атомных реакторов
Дж. Нейман (J. Neumann) и С. Улам (S. Ulam) пред-
предложили использовать аппарат теории вероятностей для
решения прикладных задач с помощью ЭВМ. М.-К. м.
получил свое название по имени города Монте-Карло,
известного своими игорными заведениями.
Моделирование случайных вели-
величин с заданными распределениями.
Как правило, такое моделирование осуществляется
путем преобразования одного или нескольких неза-
независимых значений случайного числа а, распределенного
равномерно в интервале @, 1). Последовательности
«выборочных» значений а обычно получают на ЭВМ
с помощью теоретико-числовых алгоритмов, среди
к-рых наибольшее распространение получил т. н.
метод вычетов, напр, в таком виде:
ио=1, и„ = ип_1-5-Р + 1 (mod2m), ап=и„-2~т.
Здесь т — число разрядов мантиссы ЭВМ, а
p = max{g:52<' + 1 < 2"'}.
Числа такого типа наз. псевдослучайными
числами; они проверяются статистич. тестами и
решением типовых задач (см. [21 — [6]). Длина периода
для указанного варианта метода вычетов равна 2т~2.
В М.-К. м. используются также фнзич. генераторы и
таблицы случайных чисел, а также квазислучайные
числа. Существуют М.-К. м. с малым числом разыгры-
разыгрываемых параметров (см. [7]).
Стандартный метод моделирования дискретной слу-
случайной величины | с распределением Р{^— хь)=рк,
k=0, \, . . ., состоит в следующем: полагают \=хт,
если для выбранного значения а выполняется соотно-
соотношение
Стандартный метод моделирования непрерывной слу-
случайной величины (иногда наз. методом обрат-
обратной функции) состоит в использовании легко
проверяемого представления: |— F~1(a), где F — функ-
ция распределения с заданной плотностью f{x). Иногда
полезна рандомизация моделирования (иначе — ме-
метод суперпозиции) на основе выражения
при этом сначала выбирают номер т с распределением
Р{т=к}=р^, а затем получают выборочное значение
| из распределения с плотностью fm(x). При других
способах рандомизации нек-рые параметры детерми-
детерминированного способа решения задачи рассматривают
как случайные величины (см. [7] — [9]).
Другим общим методом моделирования непрерывной
случайной величины является метод исключе-
исключения (метод отбора), в основе к-рого лежит
утверждение: если точка (?, г\) распределена равномерно
в области G={(x, у): 0<г/<^(^)}, то f^(x) = g{x)/G.
В методе исключения выбирают точку (|0, т|) равно-
равномерно по области G^G и полагают |=|0)если (sci^^G;
в противном случае повторяют выбор (|0) т|) и т. д.
Напр., если а<|<Ь и g(x) = cf(z)<-R, то можно по-
полагать g0— a-\- (Ь—a)alt т|==Да2. Среднее число опе-
операций в методе исключения пропорционально вели-
величине GJG.
Для многих случайных величин получены специаль-
специальные представления вида %=tP(aii • • ч ап)- Напр.,
случайные величины
У — 2 lnaj -cos2na2 и У — 2 In a2 -sin 2ла2
имеют стандартное нормальное распределение и неза-
независимы; случайная величина In (a^. . .а.„) имеет
гамма-распределение с параметром п; случайная ве-
величина тах(ах, . . ., <хп) распределена с плотностью
пхп~1, 0<:з;<:1; случайная величина ехр( У, —г-5- )
имеет бета-распределение с параметрами р, п (см. [3] —
[6]).
Стандартный алгоритм моделирования непрерывного
случайного вектора ?= (Si, . . ., in) состоит в после-
последовательном выборе значений его компонент из услов-
условных распределений соответственно представлению
Метод исключения переносится на многомерный случай
без изменений, надо лишь в его формулировке рас-
рассматривать |, ?0 и х как векторы. Многомерный нор-
нормальный вектор можно моделировать с помощью спе-
специального линейного преобразования вектора незави-
независимых стандартных нормальных случайных величин.
Разработаны также специальные приемы приближен-
приближенного моделирования стационарных гауссовских про-
процессов (см., напр., [3], [6]).
Если в расчете но М.-К. м. моделируются случай-
случайные величины, определяемые реальным содержанием
явления, то расчет представляет собой прямое модели-
моделирование (имитацию) этого явления. Разработано мо-
моделирование на ЭВМ процессов переноса, рассеяния
и размножения частиц: нейтронов, гамма-квантов,
фотонов, электронов и др. (см., напр., [11J — [18]);
моделирование эволюции ансамблей молекул для ре-
решения различных задач классической и квантовой
статистич. физики (см., напр., [10], [18]); моделиро-
моделирование массового обслуживания и производственных
процессов (см., напр., [2], [6], [18]); моделирование
различных случайных процессов в технике, гидроло-
гидрологии, метеорологии, геологии, химии, биологии и т. д.
(см. [18]). Алгоритмы моделирования обычно тща-
тщательно обрабатывают, напр, табулируют сложные
функции, изменяют стандартные процедуры и т. д.
Тем не менее часто прямое моделирование не может
обеспечить требуемой точности оценок искомых ве-
личин. Разработано много способов повышения эф-
эффективности моделирования.
Алгоритмы М.-К. м. для оценки мно-
многократных интегралов. Пусть необходимо
оценить интеграл /= \ h (x)dx по мере Лебега в евкли-
евклидовом s-мерном пространстве X и/е(ж) — плотность ве-
вероятности такая, что / можно записать в виде мате-
матич. ожидания следующим образом:
где S=A(iV/g(l)- Моделируя % на ЭВМ, можно полу-
получить N выборочных значений хи . . ., хдг. В смысле
закона больших чисел
Одновременно можно оценить среднеквадратичную по-
погрешность JN, т. е. величину 0уу= (Dg/iVI''2, и при-
приближенно построить подходящий доверительный ин-
интервал для /. Выбором плотности / можно распоря-
распорядиться для получения оценки с возможно меньшей
дисперсией. Напр., если О<т1«:/г//<:т2<-Ь00, то
D?<:(m2—m-^flk, и если /=/г//, то D?=0. Соответст-
Соответствующие алгоритмы наз. существенной вы-
выборкой (выборкой по важности). Дру-
Другая общая модификация — метод выделения
главной части — строится в тех случаях, когда
определена функция ho^h с известным значением ин-
интеграла. Иногда полезны сочетания М.-К. м. с классич.
квадратурами — т. н. случайные квадра-
квадратурные формулы, основная идея к-рых со-
состоит в том, что узлы и коэффициенты какой-либо
квадратурной суммы (напр., интерполяционной) вы-
выбираются случайно из распределения, обеспечивающего
несмещенность получаемой оценки интеграла [3].
Частными случаями этих формул являются: т. н. м е-
тод слоистой выборки, в к-ром узлы выби-
выбираются по одному в каждой части фиксированного
разбиения области интегрирования, а коэффициенты
пропорциональны соответствующим объемам; так наз.
метод симметричной выборки, к-рый
в случае интегрирования по интервалу @, 1) опреде-
определяется выражением (см. [10])
При этом порядок скорости сходимости М.-К. м. по-
повышается и в нек-рых случаях становится максимально
возможным на рассматриваемом классе задач.
В общем случае область интегрирования разбивается
на параллелепипеды. В каждом параллелепипеде зна-
значение интеграла вычисляется через среднее значение
в случайной точке и точке, симметричной ей относи-
относительно центра параллелепипеда.
Ряд модификаций М.-К. м. основан на (может быть,
формальном) представлении искомой величины в виде
двукратного интеграла:
J=)X)yf(X> У) k(X' ¦
где t,=h(\, r|), а вектор (|, г|) распределен с плотностью
f(x, у). Известно, что е?=ЕЕ(?11) и
A)
где Е (S15) — условное математич. ожидание, a D(?l!)
условная дисперсия ? для фиксированного значения |.
Формула A) широко используется в М.-К. м. В част-
частности, она показывает, что DE(?|?)<D?, т. е. ана-
литич. осреднение по какой-либо переменной увели-
чивает точность М.-К. м. Однако при этом может
значительно возрасти объем вычислений. Для ЭВМ
время, необходимое для достижения заданной по-
погрешности, пропорционально величине tDt,, где t —
среднее время получения одного значения С. По этому
критерию оптимизируется метод расщепле-
расщепления, простейший вариант к-рого состоит в исполь-
использовании несмещенной оценки:
где T|i> • • •> Лп — условие независимы и распределены
как т] при фиксированном значении |. С помощью A)
можно получить оптимальное значение
п=[(А2/А1) (/i,^)]1/2,
где tt, t2 — средние времена ЭВМ, соответствующие
выборкам %, т] (см., нгшр., [4]).
Если подинтегральная функция зависит от пара-
параметра, то целесообразно использовать метод за-
зависимых и с п ы т а н и й, т. е. оценивать инте-
интегралы для различных значений параметра по одним и
тем же случайным узлам [20]. Важным свойством
М.-К. м. является сравнительно относительно слабая
зависимость среднеквадратич. погрешности о"дг от
числа измерений, причем порядок сходимости по числу
узлов N всегда один и тот же: JV~ '*. Это позволяет
оценивать (после предварительных преобразований
задачи) интегралы очень высокой и даже бесконечной
кратности. Напр., разработана методика оценки ин-
интегралов Винера [19].
Алгоритмы М.-К. м. д л я решений ин-
интегральных уравнений 2-го рода.
Пусть необходимо оценить линейный функционал
Jh= (ф> h), гДе ф~А'ф+/, причем для интегрального
оператора К с ядром к(х', х) выполняется условие,
обеспечивающее сходимость ряда Неймана: ||Х"о|]<1.
Цепь Маркова {хп} определяется начальной плотностью
л(х) и переходной плотностью р(х', х) = р (х'—^ х);
вероятность обрыва цепи в точке х' равна
р (х,' х) dx;
N — случайный номер последнего состояния. Далее
определяется функционал от траектории цепи, мате-
матич. ожидание к-рого равно /д. Чаще всего исполь-
используется т. н. оценка по столкновениям
где
п — t <х°^ П — П ft (жп_1, хп)
Vo^ Я Ceo) ' Vn-Vn-1 р(х„_и Хп) ¦
Если р{х', х)фО при к(х', х)фО и л(х)фО при f(x)=?O,
то при нек-ром дополнительном условии
(см. [3] — [5]). Возможность достижения малой диспер-
дисперсии в знакопостоянном случае показывает следующее
утверждение: если
( }~ (/, Ф*> Р{ ' >~ [К*ф*](л:') '
где ф*^=Х*ср* + Д, то Dg^O, a E|=/ft (см. [4]). Моде-
Моделируя подходящую цепь Маркова на ЭВМ, получают
статистич. оценки линейных функционалов от решения
интегрального уравнения 2-го рода. Это дает возмож-
возможность и локальной оценки решения на основе представ-
представления: ф(ж)=(ф, kx)+f(x), где hx(x') = k{x', x). В ряде
случаев при решении таких задач наряду с М.-К. м.
применяются теоретико-числовые методы (см. [21]).
М.-К. м. оценка 1-го собственного значения инте-
трального оператора осуществляется итерационным
методом на основе соотношения [22]:
Е[<?nh(rn)] =(Knf, h).
Все рассмотренные результаты почти автоматически
распространяются на системы линейных алгебраич.
уравнений вида x-\-Hx=h (см. [23]).
М о д и ф и к а ц и и М.-К. м. в теории переноса
излучения (см. [И] —[17]). Для плотности сред-
среднего числа столкновений частиц в фазовом пространстве
координат г и скоростей w справедливо интегральное
уравнение 2-го рода, ядро к-рого в односкоростном слу-
случае имеет вид
Q"s ('•') g (Д) ехр (-т (»•'¦ ¦>¦)) о ('•)
б ю--
¦—¦¦\
Здесь os(r) — коэффициент (сечение) рассеяния, а (г) —
коэффициент ослабления, g(\i) — индикатриса рассея-
рассеяния, т(г', г) — оптич. длина пути от г' дог (см. [3], [4]).
Для построения оценок с малой дисперсией исполь'
зуются, напр., асимптотич. решения сопряженного
уравнения переноса [4]; простейший алгоритм такого
типа представляет собой т. н. экспоненциальное пре-
преобразование (см. [4], [11]). Разработаны модификации
локальной оценки потока частиц (см. [3], [4], [И] —
[13], [17], [18]). С помощью моделирования одной цепи
Маркова (напр., физич. процесса переноса в нек-роп
среде) можно одновременно получать зависимые оценки
функционалов для различных значений параметров;
дифференцируя «веса» Qn, иногда можно строить несме-
несмещенные оценки соответствующих производных (см. [4],
[12]). Это дает возможность использовать М.-К. м. при
решении нек-рых обратных задач [12]. Для решения
ряда задач теории переноса эффективно используется
«расщепление» траекторий и аналитич. осреднение [11].
Моделирование траекторий частиц в сложных средах
иногда существенно упрощается методом максимального
сечения (см. [3] — [5]).
Алгоритмы М.- К. м. для решения
уравнений эллиптического типа
строятся на основе соответствующих интегральных со-
соотношении. Напр., стандартная пятиточечная разност-
разностная аппроксимация для уравнения Лапласа имеет вид
формулы полного математич. ожидания, соответствую-
соответствующей симметричному блужданию по сетке с поглощением
на границе (см., напр., [2], [3]). Непрерывным аналогом
этой формулы является соотношение
- B)
где интеграл берется по поверхности сферы, целиком
лежащей в заданной области, с центром в точке Р. Фор-
Формула B) и другие аналогичные соотношения дают воз-
возможность использовать процесс изотропного «блужда-
«блуждания по сферам» для решения эллиптич. и параболич.
уравнений (см. [24], [4]). М.-К. м. эффективен, напр.,
для оценки решения многомерной краевой задачи в од-
одной точке.
Моделирование марковских ветвящихся процессов
позволяет строить оценки решения нек-рых нелинейных
уравнений, напр, уравнения Больцмана в теории
разреженных газов [3].
Лит.: [1] Neumann J., «NBS Appl. Math, series», 1951,
Mb 12, p. 36—38; [2] Бусленко Н. П. [и др.], Метод ста-
статистических испытаний (метод Монте-Карло), М., 1962; [З]
Ермаков С. М., Метод Монте-Карло и смежные вопросы,
М., 1971; [4] М и х а й лов Г. А., Некоторые иопросы теории
методов Монте-Карло, Новосиб., 1971; [5] Соболь И. М.,
Численные методы Монте-Карло, М., 1973; [6] П о л л я к Ю. Г.,
Вероятностное моделирование на электронных вычислительных
машинах, М., 197!; [7] Б а х в а л о в Н. С, в ей.: Численные
методы решения дифференциальных и интегральных уравнений и
квадратурные формулы, М., 1964, с. 5—63; [8] е г о же, «Ж.
вычисл. матем. и матем. физики», 1961, т. 1, № 1, с. 64—77;
[9] его же, «вестник МГУ. Сер. матем., механики, астроно-
астрономии, физ., хим.», 1959, № 4, с. 3 — 18; [10] Hammeri-
1 е у J. М., Н a n d s с о m b D. С, Monte Carlo methods, L.—
N. Y., 1964; [11] Метод Монте-Карло в проблеме переноса из-
излучений, М., 1967; [12J М а р ч у к Г. И. |и др.], Метод Монте-
Карло в атмосферной оптике, Новосиб., 1976; [13]Спа-
н ь е Д ж., Г е л 0 а р д Э., Метод Монте-Карло и задачи перено-
переноса нейтронов, пер. с англ., М-, 1972; [14] Ч а в чан идз е В. В.,
«Изв. АН СССР. Сер. физ.», 1955, т. 19, № 6, с. 629—38; [15]
Прохождение излучений через неоднородности в защите,
М., 1968; [16] Франк-Каменецкий А. Д., «Атомная
энергия», 1964, т. 16, № 2, с. 119—22; [17] Kalos М. Н.,
«Nuclear Sci. and Eng.», 1968, v. 33, p. 284—90; [18] Методы
Монте-Карло и их применения. Тезисы докл. на III Всесоюзн.
конф. по методам Монте-Карло, Новосиб., 1971; [19] Гель»
ф а н д И. М., Ф р о л о в А. С, Ч е н по в Н. Н., «Изв.
вузов. Сер. матем.», 1Я58, Х° 5, с. 32 — 45; [20] Фролов А. С,
Ченцов Н. Н., «Ж. вычисл. матем. и матем. физ.», 1962,
т. 2, № 4, с. 714—17; [21] Коробов Н. М., Теоретикочисло-
вые методы в приближенном анализе, М., 1963; [22] Влади-
Владимиров В. С-, «Теория вероятн. и ее примен.», 1956, т. 1, в. 1,
с. 113—30- [23] Curtiss J. H., «J. Math. Phys.», 1954, v. 32,
№ 4, p. 209—32; [24] M u 1 1 e г M. E., «Ann. Math. Stat.»,
1956, v. 27, Ni 3, p. 560—89. Г. А. Михайлов,
МОНТЕЛЯ ПРОСТРАНСТВО — бочечное простран-
пространство (в частности, Фреше пространство), в к-ром каждое
замкнутое ограниченное множество компактно. Прост-
Пространство Н (G) всех голоморфных функций в области G
с топологией равномерной сходимости на компактах
является пространством Фреше и в силу Монтеля тео-
теорема 2 всякая ограниченная последовательность голо-
голоморфных функций компактна в H(G), так что Н(G) —
М. п. Пространство C°°(Q)=^ (Q) всех бесконечно диф-
дифференцируемых в области Q? Rn функций, пространство
D (О.) финитных функций, пространство 5(Rn) быстро
убывающих бесконечно дифференцируемых функций —
также М. п. в естественных топологиях.
М. п. рефлексивно. Сильно сопряженное простран-
пространство к М. п. является М. п., в частности пространства
обобщенных функций $'(&), D'(Q), S'(Q) — М. п.
Нормированное пространство является М. п. в том
и только в том случае, когда оно конечномерно.
Лит.: [1] Б у р б а к и Н., Топологические векторные
пространства, пер. с франц., М., 1959; [2] Роберт-
сон А.-П., Робертсон В.-Дж., Топологические век-
векторные пространства, пер. с англ., М., 1967; [3] Э дв а р д с Р.-Э.,
Функциональный анализ. Теория и приложения, пер. с англ.,
М. 1969. С. Г. Крейн.
МОНТЕЛЯ ТЕОРЕМА— 1) Ы. т. о приближе-
приближении аналитических функций много-
многочленами: если D —открытое множество точек комп-
комплексной плоскости z, не содержащее точку z=oo, a
f(z) —однозначная функция, аналитическая в каждой
точке zGD, то существует последовательность много-
многочленов {Pn(z)}, сходящаяся к /(z) в каждой точке
z?D. Эта теорема является одной из основных в тео-
теории приближения функций комплексного переменно-
переменного; получена П. Мотелем [1].
2) М. т. об условиях компактности
семейства голоморфных функций
(принцип компактности, см. [2]): пусть
ср= {/ (г)} — бесконечное семейство голоморфных функ-
функций в области D комплексной плоскости z; тогда для
того чтобы семейство ср было компактным, т. е. чтобы из
любой последовательности {/&(г)}сср можно было вы-
выделить подпоследовательность, равномерно сходящуюся
внутри D, необходимо и достаточно, чтобы ср было рав-
равномерно ограничено внутри D. Эта М. т. обобщается
на области D в пространстве С", п~^1 (см. Компактно-
Компактности принцип).
3) М. т. об условиях нормальности
семейства голоморфных функций
(принцип нормальности, см. [2]): пусть
cp={/(z)} — бесконечное семейство голоморфных функ-
функций в области D комплексной плоскости z. Если сущест-
существуют два различных значения а и Ь, к-рые не прини-
принимаются ни одной функцией /(z)?cp, то ср — нормальное
семейство, т. е. из любой последовательности {/fc(z)}c:<p
можно выделить подпоследовательность, равномерно
сходящуюся внутри D к голоморфной функции или к со.
Условие этой М. т. можно несколько ослабить: доста-
достаточно потребовать, чтобы все функции/(г)^ф не прини-
принимали одного из значений, напр, а, а другое значение b
принимали не более т раз, 1<:т<оо. Эта М. т. обоб-
щается на случай областей D в пространстве С, п~^\.
Лит.: [1] М о п t е 1 P., Lemons sur les series de polynomes &
une variable, P., 1910; [2] M о н т е л ь П., Нормальные семей-
семейства аналитических функций, пер. с франц., М.— Л., llJ3(i,
Е. Д. Соломепцчв,
МОПЕРТЮИ ПРИНЦИП — принцип наименьшего
действия, первая словесная формулировка к-рого дана
П. Мопертюи (P. Maupertuis). Первоначально A744)
П. Мопертюи вывел из М. п. законы отражения и пре-
преломления света, согласующиеся, по его словам, «с важ-
важным принципом, по к-рому природа при осуществлении
своих действий идет всегда наиболее простыми путями»
(см. [1]), а затем A746) объявил его универсальным за-
законом движения и равновесия: «Общий принцип. Когда
в природе происходит нек-рое изменение, количество
действия, необходимое для этого изменения, является
наименьшим возможным. Количество действия есть
произведение массы тел на их скорость и на расстояние,
к-рое они пробегают» (см. [2j). Универсальность М. п.
обосновывалась П. Мопертюи туманными рассуждени-
рассуждениями метафизич. характера с помощью телеологич. и те-
ологич. аргументов, к-рые в последовавшей затем дис-
дискуссии о М. п. вызвали резкие возражения со стороны
ряда его современников. Кроме законов распростране-
распространения света П. Мопертюи вывел из М. п. лишь известные
законы удара тел и равновесия рычага. По мнению
Ж. Лагранжа (J. Lagrange), «указанные применения
носят слишком специальный характер, чтобы на них
можно было построить доказательство общего принци-
принципа; кроме того, они несколько неопределенны и произ-
произвольны, что придает некоторую ненадежность и выво-
выводам, которые можно было бы сделать на основании их
о точности самого принципа» (см. [3]).
Первая математич. идея принципа наименьшего
действия для частного случая изолированных тел при-
принадлежит Л. Эйлеру (L. Euler). Он показал A744), что
под действием центральных сил тела описывают траек-
траектории, для к-рых интеграл \ vds достигает минимума
или максимума (см. [4]); здесь о — скорость, us — эле-
элемент кривой.
Для общего случая движения любой системы тел,
действующих одно на другое каким угодно образом так,
что полная механич. энергия системы сохраняется,
принцип наименьшего действия установил Ж. Ла-
гранж A760). Исходя из законов механики, он доказал,
что сумма произведений масс на интегралы скоростей,
умноженных на элементы пройденных путей, является
всегда максимумом или минимумом (см. [5]), т. е.
i\ Vi
«Этот принцип, будучи соединен с принципом живых
сил и развит по правилам вариационного исчисления,
дает тотчас же все уравнения, необходимые для разре-
разрешения каждой проблемы; отсюда возникает столь же
простой, как и общий, метод разрешения проблем, ка-
касающихся движения тел» (см. [3]).
Принцип наименьшего действия в форме Лагранжа
(Лагранжа принцип) принято математически записы-
записывать в форме равенства A4) (см. Вариационные прин-
принципы классической механики). Исключением времени из
A4) с помощью интеграла энергии A3) К. Якобй
(С. Jacobi, 1837) представил принцип наименьшего дей-
действия в форме A6) (см. также Якоби принцип).
Лит.: [1] М о п е р т ю и П., в кн.: Вариационные принципы
механики, М., 1959, с. 23—30; Негоже, там же, с. 41 — 55;
[3] Л а гран ж Ж., Аналитическая механика, пер. с франц.,
т. 1, М.— Л., 1950- [4] Э й л е р Л., в кн.: Вариационные прин-
принципы механики М. 1059, с. 31—40; [5] L a g r a n g e J., (Euv-
res, t. 1, P., 1867, p. 335 — 62; [6] Jacob! C, «C. r. Acad. sci.»,
1837, t. 5, p. 61 — 67. В. В. Румянце».
МОРДЕЛЛА ГИПОТЕЗА — гипотеза о конечности
множества рациональных точек на алгебраич. кривой
рода g>l. Выдвинута Л. Морделлом [1] для случая,
когда основное ноле К — ноле рациональных чисел.
В настоящее вре.мя под М. г. понимается утверждение
о конечности множества рациональных точек X (L)
неприводимой алгебраич. кривой X рода ?>1, опреде-
определенной над полем К конечного типа над полем рацио-
рациональных чисел Q, в любом конечном расширении Li К.
В такой форме М. г. не доказана A982) ни для одной
кривой. Получека редукция М. г. к наиболее трудному
случаю, когда К — поло алгебранч. чисел (см. [3]).
Известен ряд частных результатов, относящихся к М. г.
Так, доказано [2J, что множество X (К) конечно, если
ранг группы /i-шоморфизмов из X в эллиптич. кривую
Y больше ранга группы Y{К). Установлена [7] конеч-
конечность X (К) для широкого класса модулярных кривых
и их поля определения К. Найдена [8] оценка роста вы-
высот
h (xn) ^ exp (an + b)
рациональных точек хп?Х (К), показывающая, что они
расположены гораздо «реже», чем на кривых рода g<l.
Доказано также, что М. г. является следствием гипоте-
гипотезы Шафаревича о конечности числа алгебраич. кривых,
имеющих заданный род g>l, поле определения (конеч-
(конечное расширение Q) и множество точек плохой редук-
редукции (см. [4], а также Зигеля теорема о целых точках).
Геометрич. аналогом М. г. является утверждение
о конечности числа сечений у расслоения
где V — неособая проективная поверхность, В — кри-
кривая, а общий слой отображения / — неприводимая кри-
кривая рода g>l. Это утверждение верно, если расслоение
непостоянно, т. е. не является прямым произведением
после нек-рого накрытия базы В, и характеристика ос-
основного поля к равна 0 (см. [3], [6]). Для постоянных
расслоений можно утверждать лишь конечность числа
классов, состоящих из сечений, алгебраически эквива-
эквивалентных как кривые на V. Если же характеристика поля
к положительна, то геометрич. аналог М. г. для посто-
постоянных расслоений неверен [4].
Лит.: [1] М о г d е 1 1 L. J., «Proc. Camb. Phil. Soc.» 1922,
v. 21, p. 179—92; [2] Д е м ь я н е н к о В. А., «Изв. АН СССР.
Сер. матем.», 1966, т. 30, Л» 6, с. 1373—96; [3] М а н и н Ю. И.,
там же, 1963, т. 27. Л"8 6, с. 1395 — 1440; [4] Pare in A. N..
в кн.: Actes du Congres International des mathematiciens. 1970,
t. 1, P., 1971, p. 467—71; [5] Grauert H., «Publ. Math.
IHES», 1965, X° 25, p. 131 — 50; [6] L a n g S., Diophantine geo-
geometry, N. Y.— L., 1962; [7]M a z u г В., в кн.: Modular functions
of one variable, [v. 5], В.— Hdlb.— N. Y., 1977, p. 107—48;
[8] M u m f о r d D., «Amer. J. Math.», 1965, v. 87, Ni 4, p. 1007 —
16. A. H* Паршин.
МОРЕРЫ ТЕОРЕМА: если (однозначная) функция
/(z) комплексного переменного z в области D непрерыв-
непрерывна и интеграл от нее по любому замкнутому спрямляе-
спрямляемому контуру TC.D равен нулю, т. е.
f(z)dz = O, YdD, (*)
то /(z) — аналитич. функция в D. Эта теорема была по-
получена Дж. Морерой [1].
Условие сформулированной М. т. можно ослабить,
ограничившись требованием, чтобы обращались в нуль
интегралы (*), взятые по границе Г=<ЭА любого тре-
треугольника Д, компактно принадлежащего области D,
т. е. такого, что АсДсО. М. т. представляет собой (не-
(неполное) обращение Коши интегральной теоремы и
является одной из основных теорем теории аналитич.
функций.
М. т. обобщается на случай функций многих комп-
комплексных переменных. Пусть функция /(z) = /(z1; . . ., zn)
комплексных переменных z1( . . ., г„, rej^l, непрерывна
в области D комплексного пространства С" и такова,
что обращается в нуль интеграл от нее, взятый по гра-
границе dTv любой компактно принадлежащей D призма-
тич. области вида
Tv=[a1, zjx.. . X[av-i, zV-i]XAvX
X[ov+i, zv+1]X . ..Х[а„, zn], v=l, 2,..., re,
где [ац, z^], [1ф\\ [х=1, . - ¦, n,— прямолинейные от-
отрезки в плоскостях СBц) с концами ац и гц, a Av —
треугольник в плоскости C(zv). Тогда /(z) — голоморф-
голоморфная функция в D.
Лит.: [1] More r a G., «Rend. 1st. Lomb.», 1886, t. 19,
p. 304—308; [2J M a p к у ш е в и ч А. И., Теория аналитиче-
аналитических функций, 2 изд., т. 1,'М., 1Я67; [3]Ш а б а т Б .В., Введение
в комплексный анализ, 2 изд., ч. 1—2, М., 1976; [4] В л а ди-
миров В. С, Методы теории функций многих комплексных
переменных, М., 1964, Е. Д. Соло.менуео.
МОРИТЫ ЭКВИВАЛЕНТНОСТЬ — отношение экви-
эквивалентности на классе всех колец, определяемое сле-
следующим образом: кольца Я и S наз. Морита-эк-
Бивалентными, если категории левых (правых)
Я- и 5-модулей эквивалентны. Важнейший пример
М. э. колец: кольцо Я и кольцо всех (пХ ге)-матриц над
ним. Для существования М. э. между кольцами Я и S
необходимо и достаточно, чтобы в категории левых R-
модулей существовал такой конечно порожденный про-
проективный образующий V, что его кольцо эндоморфиз-
эндоморфизмов изоморфно кольцу S. При этом левому Л-модулю А
ставится в соответствие левый 5-модуль Hom# (U,A).
Среди свойств, сохраняющихся при переходе к кольцу,
эквивалентному в смысле Мориты: артиновость, нёте-
ровость, первичность, простота, классич. полупросто-
полупростота, регулярность, самоинъективность, наследствен-
наследственность, примитивность.
Наряду с М. э. рассматривается двойствен-
двойственность в смысле Мориты, связывающая
нек-рые подкатегории категорий левых Д-модулей
и правых 5-модулей (чаще всего подкатегории конечно
порожденных модулей). Однако само существование
такой двойственности накладывает определенные огра-
ограничения на кольца Я и S. В частности, при Я = Я это
ведет к тому, что Я — кеазифробениусово кольцо.
Общая концепция М. э. была разработана К. Мори-
той [1].
Лит.: [1] Morita К., «Sci. Repts Tokyo Kyoiku Dajgaku
A», 1958, v. 6, p. 83—142; [2] Б а с с Х., Алгебраическая К-тео-
рия, пер. с англ., М., 1973; [3] Ф е й с К., Алгебра: кольца,
модули и категории, пер. с англ., т. 1—2, М., 1977—79; [4]
Colin P., Morita equivalence and duality, L., 1976.
Л. А. Скорняпов.
МОРСА ИНДЕКС — число, сопоставляемое критиче-
критической точке гладкой функции на многообразии или гео-
геодезической на римановом (или финслеровом) многооб-
многообразии.
1) М. и. критической точки р гладкой функции / на
многообразии М равен, по определению, отрицательно-
отрицательному индексу инерции гессиана функции / в точке р, т. е.
размерности максимального из подпространств каса-
касательного пространства ТМр многообразия М в точке р,
на к-ром гессиан отрицательно определен. Это определе-
определение имеет смысл и для дважды дифференцируемой (по
Фреше) функции на бесконечномерном банаховом мно-
тообразии. Отличие состоит лишь в том, что для индек-
индекса допускается значение +оо. В этом случае целесооб-
целесообразно ввести понятие коиндекса критич. точки р
функции / как положительного индекса инерции гес-
гессиана B-го дифференциала Фреше) функции / в точке р.
2) Пусть Vo и \\ — два гладких подмногообразия
полного риманова пространства М. Для кусочно глад-
гладкого пути со : [0, 1] —>. М с a>{i)^V,-, г'=0, 1, трансвер-
сального к Vo и \\ на своих концах со(О) и соA), анало-
аналогом касательного пространства является векторное
пространство Та— Та_ vo,Vt всех таких кусочно гладких
векторных полей W вдоль со, что W(a>{i))?(TV;)mi)t
г=0, 1. Для любой геодезической у : [0, 1] —у М с
y(i)?V;, ортогональной в своих концах 7@) и yA) к
Vo и V-i соответственно, 2-я вариация 62Е функционала
действия (см. Морса теория) определяет симметричный
билинейный функционал Е** на Ту (аналог гессиана).
М. и. геодезической равен., по определению, отрица-
отрицательному индексу инерации этого функционала. Нуле-
Нулевое пространство Ny гессиана Я** на Ту (множество
Х?Ту, для к-рого Е**(Х, У) = 0 для всех Y?Ty) в
точности состоит из Якоби полей J? Ту . При Ny Ф0 гео-
геодезическая наз. (Fo, F1)-b ы рожденной, и dim Ny
наз. степенью вырождения геодезической.
Геометрич. интерпретация М. и. в общем случае
весьма тяжеловесна и, по-видимому A982), не оконча-
окончательна [2]. Поэтому здесь рассматривается случай,
когда Vx является точкой q?M. Пусть v — нормальное
расслоение к многообразию V= Vo в многообразии М,
a v(p) — его слой над точкой p?V. Сужение экспонен-
экспоненциального отображения ТМ —>- М определяет отобра-
отображение охр : v —>. М. Геодезическая у (f) = exp (i^M
i€v(p)> 0<:i<:l, тогда и только тогда (V, ехр ?)-вырож-
дена, когда ядро дифференциала d| ехр : 7\>| ->¦ ТМехр |
отображения ехр в точке ? отлично от нуля; при этом
размерность этого ядра равна степени вырождения
геодезической у. Точка s=y(t0), 0<Z0«1, наз. ф о-
кальвой точкой многообразия V вдоль геоде-
геодезической у, если геодезическая у': t—>y(tlt0) (V, s)-
вырождена; степень вырождения геодезической у' наз.
кратностью фокальной точки s. По
Сарда теореме множество фокальных точек имеет меру
нуль, так что типичная геодезическая невырождена.
Если V тоже состоит из одной точки р?М (случай p = q
не исключается), то фокальная точка наз. сопря-
сопряженной ср вдоль геодезической у. Теорема
Морса об индексе [1] утверждает, что М. и.
геодезической конечен и равен числу сосчитанных с
учетом кратности фокальных точек y(t) многообразия
V, 0<«1.
Лит.: [1] М о г s e M., The calculus of variations in the large,
N. Y., 1934; [2] Ambrose W., «Ann. Math.», 1961, v. 73,
p. 49—86. M. M. Постников, Ю. Б. Рудяк.
МОРСА ЛЕММА — утверждение, описывающее стро-
строение ростка дважды непрерывно дифференцируемой
функции. Пусть / : R" —>- R1 — функция класса С2,
имеющая точку OgR" своей невырожденной критиче-
критической точкой. Тогда в нек-рой окрестности U точки О
существует такая система локальных координат (кар-
(карта) х1, . . ., хп с центром в О, что для всех х? U имеет
место равенство
/(*) = / @)-^-...-4+4+i+•¦•+**¦
При этом число X, 0<Л<:п, является Морса индексом
критич. точки О функции /. Справедлив также аналог
М. л. для функций / : С" -*- С1, именно: если / голо-
голоморфна в нек-рой окрестности своей невырожденной
критич. точки (в другой терминологии — точки пере-
перевала, см. Перевала метод) 0?С", то в нек-рой окрест-
окрестности U точки О существует такая система локальных
координат zlt . . ., zn, что
М. л. справедлива и для функций / : Е —>- R на се-
парабельном (бесконечномерном) гильбертовом прост-
пространстве Е. Пусть / дважды дифференцируема (по Фре-
ше) в нек-рой окрестности своей невырожденной кри-
критич. точки 0?Е. Тогда существуют такая выпуклая ок-
окрестность нуля VcE, такая окрестность нуля U(Z.E и
такой диффеоморфизм (карта) 0 : t/->-Fc Q@)=0, что
для всех x?U имеет место равенство
/ (х) = || Р (9 (х)) |Р -1 (/ - Р) (9 (*)) |Р,
где Р -*¦ Е : Е — непрерывный ортогональный проек-
тор, а 7 — тождественный оператор. При этом размер-
размерность dim Im (/—Р) совпадает с индексом Морса критич.
точки 0 ? Е функции /, а размерность dim im P — с ее
коиндексом.
Лит.: Ш М о г s e M., The calculus of variations in the large,
N. Y., 1934. M. M. Постников, Ю- Б. Рудяк.
МОРСА НЕРАВЕНСТВА — вытекающие из теории
Морса неравенства, связывающие число критических
точек функции Морса на многообразии с его гомологич.
инвариантами.
Пусть / — Морса функция на гладком re-мерном мно-
многообразии (без края) М, имеющая конечное число кри-
критич. точек. Тогда гомологии группы Н^{М) конечно
порождены и потому определены их ранги »\ =
= rk {H% (М)) и периодич. ранги \ = t (H^ (M)) (перио-
(периодический ранг абелевой группы А
с конечным числом образующих — минимальное число
циклич. групп, в прямую сумму к-рых может быть раз-
разложена максимальная периодич. подгруппа группы
А). М. н. связывают число т^ критич. точек функции /',
имеющих Морса индекс л, с этими рангами, и имеют вид:
При Х=га последнее М. н. всегда является равенством,
так что
где Z(Af) — эйлерова характеристика многообразия М.
М. н. имеют место и для функций Морса триад (W,
Vo, V,-), достаточно заменить группы Н%(М) группами
относительных гомологии Н% (W, Vo).
Согласно М. н. многообразие, имеющее «большие»
группы гомологии, не допускает функций Морса с
малым числом критич. точек. Замечательно, что давае-
даваемые М. н. оценки точны: на замкнутом односвязном
многообразии размерности ^5=6 существует функция
Морса, для к-рой М. н. являются равенствами (С м е й-
ла теорема, см. [2]). В частности, на любом замк-
замкнутом многообразии, гомотопически эквивалентном
сфере S" с ге^б, существует функция Морса с двумя
критич. точками, откуда непосредственно следует (см.
Морса теория), что многообразие М гомеоморфно сфе-
сфере S" (см. Пуанкаре гипотеза). Аналогичное применение
теоремы Смейла позволяет доказать и теоремы об h-
и s-кобордизмах.
Аналоги М. н. имеют место также для функций Морса
/ : X —>- R на бесконечномерных гильбертовых много-
многообразиях и связывают (для любых регулярных значе-
значений a, b?R, а<Ь, функции /) числа т^(а, Ь) лежащих в
f~1[a, b] критич. точек конечного индекса % с рангом
г%(а, Ь) и периодич. рангом (}. (а, Ь) группы Н% (Mb, M"),
где Mc=j~1( — оо, с]. Именно,
гх(а,
% = 0, 1,...,
При достаточно больших К последнее неравенство ста-
становится равенством.
Лит.: ll] Morse M., The calculus of variations in the
large N. Y., 1934; [2] С м е й л С, «Математика», 1964, т. 8,
№ 4, с. 95 — 108. М. М. Постников, Ю. Б. Рудяк.
МОРСА ПЕРЕСТРОЙКА, хирургия,— преобра-
преобразование гладких многообразий, к-рому подвергается
многообразие уровня гладкой функции при переходе
через невырожденную критическую точку; важнейшая
конструкция в топологии многообразий.
Пусть V — гладкое п-мерное многообразие (без края),
в к-рое (гладко) вложена (к—1)-мерная сфера iS^-1.
Предположим, что нормальное расслоение сферы S*--1
в многообразии V тривиально, т. е. что замкнутая труб-
трубчатая окрестность Т сферы S^^1 в V разлагается в
прямое произведение T=S>-~1XDn-^+1, где D"-^1 —
диск размерности re—X+1. Выбрав такое разложение,
вырежем из V внутренность окрестности Т. Получится
многообразие, край к-рого разложен в произведение
5^-1X»?n~^ сфер. Но точно такой же край имеет
многообразие D*- X Sn~^. Отождествив края многооб-
многообразий F\int T и D^ XSn-^ по диффеоморфизму, сохра-
сохраняющему структуру прямого произведения S^-~1X
XSn~b, снова получим многообразие V' без края, к-рое
и наз. результатом перестройки Мор-
с а многообразия V вдоль сферы S^-1.
Для осуществления М. п. необходимо задать разло-
разложение окрестности Т сферы S^-1 в прямое произведе-
произведение, т. е. т р и в и а л и з а ц и ю нормального рас-
расслоения сферы S*--1 в многообразии V, при этом разные
тривиализации (оснащения) могут давать существенно
различные (даже гомотопически) многообразия V.
Число X наз. индексом М. п.,а пара (X, п—Х-\-\)
ее т и п о м. Если V' получается из V М. п. типа (X,
п—Я+1), то V получается из V М. п. типа (п—Я+1, X).
При Х=0 многообразие V является дизъюнктным объ-
объединением многообразия V (к-рое может быть в этом слу-
случае пустым) и сферы Sn. Конструкция М. п. может быть
проведена также для кусочно линейных и топология,
многообразий.
Пример. При V=S2 и Х=2 в результате М. п.
получается дизъюнктное объединение двух сфер, а при
X=i — тор. При F=53 и Я=2 получается произведение
SXXS2. Случай V=S3 и Я=1 сложнее: если сфера 5^-1 =
= Sl вложена в S3 стандартным образом (большая ок-
окружность), то в зависимости от выбора ее тривиализа-
тривиализации нормального расслоения получаются всевозможные
линзовые пространства; если же допустить заузливавис
сферы S1, то получается еще больший набор трехмер-
трехмерных многообразий.
Если V является краем (ге+1)-мерного многообразия
М, то V1 будет краем многообразия М', полученного
из М приклеиванием ручки индекса М'. В частности,
если / — гладкая функция на многообразии М и а<_Ъ —
такие числа, что множество f~4a, b] компактно и со-
содержит единственную критич. точку р, к-рая невырож-
невырождена, то многообразие Vb=f~1(b) получается из много-
многообразия Va = f-1(a) M. п. индекса X, где X — Морса
индекс критич. точки р. Более общим образом, любая
перестройка V' многообразия V индекса X определяет
нек-рый бордизм (W; V, V) (получающийся из произве-
произведения FX[O, 1] приклеиванием ручки индекса X к его
«правому краю» FX {1}), и на триаде (W; V, V) сущест-
существует Морса функция, обладающая единственной кри-
критич. точкой индекса X, причем любой бордизм (W;
V, V'), на к-ром существует такого рода функция Мор-
Морса, получается этим способом. Отсюда (и из существо-
существования на триадах функций Морса) следует, что два мно-
многообразия тогда и только тогда бордантны, когда одно
из них получается из другого конечной последователь-
последовательностью М. п.
При известных предосторожностях в обращении с
ориентациями результат М. п. ориентированного мно-
многообразия будет снова ориентированным многообрази-
многообразием. Вообще, для любой структурной серии (В, ср) (см.
(В, (р)-структуры) можно определить понятие (В, <р)-
перестройки Морса; при этом два многооб-
многообразия тогда и только тогда (В, ср)-бордаптны, когда они
связаны друг с другом конечпой последовательностью
(В, ф)-М. п.
Важная роль М. п. в топологии многообразий объяс-
объясняется тем, что они позволяют «деликатно» (не нарушая
тех или иных свойств многообразия) уничтожать «лиш-
«лишние» гомотопич. группы (обычно используемая с этой
целью в теории гомотопий операция «приклеивания
клетки» мгновенно выводит из класса многообразий).
Практически все теоремы классификации структур на
многообразиях основываются на изучении вопроса,
когда для отображения / : М —>- X замкнутого много-
многообразия М в клеточное пространство X существуют та-
такой бордизм (W\ М, Л') и такое отображение F : W —>- X,
что .Fl;n=/, a FljV '• -V -> X является гомотопнч. эквива-
эквивалентностью. Естественный путь решения этой задачи
состоит в том, чтобы последовательностью М. п. унич-
уничтожить ядра гомоморфизмов /^ : лДЛ/) ->- Л;(Х) (где
я,- — гомотопич. группы). Если это удается, то резуль-
результирующее отображение будет гомотопич. эквивалент-
эквивалентностью. Изучение соответствующих препятствий (ле-
(лежащих в т. я. группах Уолла, см. [4]) явилось одним из
главнейших стимулов в развитии алгебраической К-тео-
рии.
Лит-: [1] М о г s e M. The calculus of variations in the large,
N. Y., 1934; [2] H о в и к о в С. И., «Изв. АН СССР. Сер. ма-
тем.», 1964, т. 28, Л» 2, с. 365—474; [3] К е г v a i г е М. А.,
М i 1 п о г J. W., «Ann. Math.», 1963, v. 77, p. 504—37; [4]
Мищенко А. С, «Успехи матем. наук», 1976, т. 31, в. 2,
с. 69—134. М. Ы. Постников, Ю. Б. Рудяк,
МОРСА ТЕОРИЯ — общее название для трех различ-
различных теории, основывающихся на идеях М. Морса [1]
и описывающих связь алгебро-топологич. свойств
топологич. пространства с экстремальными свойствами
функций (функционалов) на нем. М. т. является раз-
разделом вариационного исчисления е целом; Однако пос-
последнее шире: напр., оно включает в себя теорию кате-
категорий в смысле Люстерника — Шнирельмана.
1) М. т. критических /почек гладких функций / на
гладком многообразии М (сокращенно — М. т. 1) раз-
разбивается на две части: локальную и глобальную.
К локальной части относятся понятия крптич. точки
гладкой функции, гессиана функции в ее крптич. точке,
Морса индекса крптич. точки и т. п. Основным резуль-
результатом ее является Морса лемма, описывающая строение
гладкой функции в окрестности невырожденной кри-
тич. точки.
Изучение гладких функций в окрестностях вырож-
вырожденных точек не относится собственно к М. т. и выде-
выделяется в отдельную теорию особенностей дифференци-
дифференцируемых отображений.
Основными утверждениями глобальной М. т. явля-
являются следующие. Пусть / — функция на гладком мно-
многообразии М. Если множество f~1(a) не содержит кри-
тич. точек функции / и не пересекается с краем много-
многообразия М, то Ma=f~1(—со, а) является гладким мно-
многообразием с краем f~1(a). Если множество f~x[a, Ь]
компактно, не пересекается с краем многообразия М
и не содержит критич. точек функции /, то существует
такая гладкая изотопия йу : М —>- М, 0<s<<:1 (осущест-
(осуществляемая сдвигом по траекториям градиента функции
/), что ho=id^i и /»i диффеоморфно отображает А1Ь на
Ма. В частности, Ма диффеоморфно М° и включение
МасМь является гомотопнч. эквивалентностью.
Если множество f~1[a, b] компактно, не пересекается
с краем многообразия М и содержит ровно одну кри-
критич. точку p(zf~1(a> Ь), имеющую индекс Морса X, то
Мь диффеоморфно многообразию, полученному из Ма
приклеиванием ручки индекса К. В частности, если р —
единственная точка глобального минимума функции /,
то при малом е>0 множество Д/?'Р)+Е диффеоморфно
диску D", где re=dim М. Отсюда следует, что если М —•
замкнутое гладкое многообразие, обладающее функцией
с ровно двумя критич. точками (причем обе невырож-
невырожденные), то М получается склепкой двух гладких дис-
дисков по их общей границе и потому гомеоморфно (но,
вообще говоря, не диффеоморфно) сфере S".
Поскольку приклеивание ручки индекса К гомотопи-
чески эквивалентно приклеиванию клетки размерности
Я, отсюда непосредственно вытекает следующая о с-
новная теорема М. т. 1: каждой Морса функ-
функции f на гладком многообразии М (без края) отвечает
гомотопнчески эквивалентное многообразию М клеточ-
клеточное пространство, клетки к-рого находятся в биектив-
биективном соответствии с критич. точками функции /, причем
размерность клетки равна индексу соответствующей
критич. точки. Морса неравенства являются непосред-
непосредственным следствием этой теоремы. Аналогичная теоре-
теорема справедлива и для функций Морса триад (W,V0, V\).
2) М. т. геодезических на римаповом многообразии
(сокращенно — М. т. 2) описывает гомотопич. тип пе-
петель пространства QM гладкого многообразия М с. ри-
мановон метрикой g,y. Ее цель — перенести на случай
этого пространства (вернее, его подходящей модели)
результаты М. т. 1. Роль функции / играет при :>том
определенный на пространстве PS (ЛЛ кусочно гладких
путей со : t —>- co(t), 0<:?<:1; функционал действия Е
(иногда неправильно наз. функционалом энергии |5]),
значения к-рого на пути o)?PS(M) определяются в ло-
локальных координатах х1, . . ., xh формулой
Е (ш) = Г gu ахЧхК
В первоначальном построении М. т. рассматривался
функционал длины
L (ш) = \ у gij dx' dxi ,
но по многим технич. причинам функционал Е оказы-
оказывается предпочтительнее. Вместе с тем экстремали функ-
функционала Е (т. е. пути w?PS(Af), для к-рых определен-
определенный вариацией ЬЕ функционала Е линейный функцио-
функционал Е^ на пространстве Та равен нулю) совпадают с гео-
геодезическими метрики giy (экстремалями функционала
длины L) в их натуральной параметризации.
Пусть р, q — две (не обязательно различные) точки
из М и QPs(JV/; pi g)czPS(M) — пространство кусочно
гладких путей, соединяющих р с q. Для каждого l?R
полагается
PS —1 PS
й^ = й/ (М; р, д) = ? [О, ']П" (М; р, q).
Если риманово многообразие М полно, то пространство
Q^jE-MO, l)f]Qt (внутренность множества Qt) дефор-
деформационно ретрагпруется на нек-рое гладкое многооб-
многообразие Б, точками к-рого являются «ломаные геодезиче-
геодезические» с фиксированным числом звеньев, соединяющие
р с q (так что, в частности, В содержит все геодезиче-
геодезические из Й[). При этом функция Е' = Е\д\ 2?—yR гладкая;
для любого а<1 множество Ба—(Е')-1 [0, а] компакт-
компактно и является деформационным ретрактом множества
Qa; критич. точки функции Е' совпадают с экстремаля-
экстремалями функционала Е : Qt —*- R п представляют собой гео-
геодезические, соединяющие р с q и имеющие длину < УI;
индекс Морса критич. точки функции ?" равен индексу
Морса соответствующей геодезической; нулевое прост-
пространство Ny функционала Е## на геодезической у ? Qt
конечномерно и изоморфно нулевому пространству
гессиана функции Е' в соответствующей критич. точке;
в частности, если р и q не сопряжены ни на одной соеди-
соединяющей их геодезической у, то Е' — функция Морса.
Применяя М. т. 1 и переходя к пределу при I —>- оо.
и замечая, что пространство QpS{M; p, q) гомотопически
эквивалентно пространству Q.{M; p, q) всех непрерыв-
непрерывных путей, соединяющих р с q, получаем следующую
основную теорему М. т. 2: пусть М — пол-
полное риманово многообразие и р, q — две его точки, не
сопряженные ни на какой соединяющей их геодезиче-
геодезической. Пространство Q(M; p, q) всех путей, соединяю-
соединяющих р с д, гомотоппчески эквивалентно клеточному про-
пространству, клетки размерности К к-рого нахедятся в
биективном соответствии с геодезическими индекса %,
соединяющими р с q. Так как гомотоиич. тип простран-
ства п{М\ р, q) не зависит от выбора точек р и q, то
теорема даст, в частности, описание гомотопич. типа
пространства петель QM.
Известно [10], что для нестягиваемого многообразия
М пространство QM имеет нетривиальные группы го-
гомологии в сколь угодно больших размерностях. В силу
основной теоремы М. т. 2 отсюда следует, что несопря-
несопряженные точки в полном римановом нестягпваемом мно-
многообразии соединены бесконечным числом геодезиче-
геодезических (на примере сферы видно, что, вообще говоря, эти
геодезические могут быть отрезками одной периодиче-
периодической геодезической).
В даваемом основной теоремой описании гомотопич.
тшы фигурируют (хотя и неявно) поля Якобгг, поэтому
М. т. устанавливает связь между кривизной многооб-
многообразия и его топологией. Напр., если М — полное одно-
связное риманово многообразие, кривизна к-рого по
всем двумерным направлениям неположительна, то лю-
любое поле Якоби, обращающееся в нуль в двух точках
геодезической, является тождественно нулевым. По-
Поэтому пространство петель QM такого многообразия
имеет тип нульмерного клеточного пространства и, сле-
следовательно (ввиду односвязности М), стягиваемо.
Поэтому М также стягиваемо, т. е. гомотопически эк-
эквивалентно пространству R". Более тонкое использо-
использование соображений М. т. показывает, что М даже диф-
феоморфно пространству R" (см. [31, [5]).
Весьма эффективным оказалось применение М. т. к
топологии групп Ли [3]. Напр., для любой односвяз-
ной группы Ли G пространство QG имеет гомотопич. тип
клеточного пространства без нечетномерных клеток.
Апофеозом здесь является теорема Ботта о периодич-
периодичности, играющая основополагающую роль в .йГ-теории
и, следовательно, во всей дифференциальной тополо-
топологии. Пусть U — предел последовательности вложенных
унитарных групп ...UndUn + 1d... , а О — предел по-
последовательности вложенных ортогональных групп
...0nd0n + 1d... .Теорема периодичности
Ботта утверждает, что имеют место гомотопич.
эквивалентности Q2U~U, QSO~O, где Q" есть п-крат-
п-кратная итерация функтора перехода к пространству пе-
петель. Эта теорема позволяет вычислить гомотопич. груп-
группы Л:U и я,0 и, следовательно, гомотопич. группы n,-Un
и TijOn при i<2?;, /<п.
М. т. 2 обобщается также на случай, когда вместо
точек р, q рассматриваются гладкие подмногообразия
Vo, \\ многообразия М. Изучается функционал дейст-
действия на пространство fips(Af; Vo, \\) всех кусочно глад-
гладких путей со : t ->- co(i), 0<i<l, ы{1)?У[, i=0, 1,
трансверсальных на концах к Vo и Fb и устанавливает-
устанавливается связь экстремалей этого функционала с гомотопич.
типом пространства fi {М; Vo, Fx). Соответствующая ос-
основная теорема аналогична сформулированной выше ос-
основной теореме М. т. 2; трудность состоит в геометрич.
интерпретации индекса Морса геодезической.
3) Естественным развитием М. т. 2 является М. т.
критич. точек гладких функций на банаховых (беско-
(бесконечномерных) многообразиях — М. т. 3, представляю-
представляющая собой уже не аналог, а непосредственное обобщение
М. т. 1. К настоящему времени A982) М. т. 3 находится
в стадии становления и построена лишь в весьма пред-
предварительном контексте при очень сильных (и явно не
необходимых) условиях на модельное банахово прост-
пространство (типа сепарабельности и гильбертовости), когда
не возникает специфических функциональио-аналитич.
трудностей [9], хотя имеются и попытки построения М.
т. 3 в довольно общей ситуации. Поэтому в современ-
современном виде М. т. 3 является почти дословным повторением
М. т. 1. Единственное заслуживающее быть отмеченным
отличие состоит в том, что в М. т. 3 условие компактно-
компактности множеств f~l[a, b] заменяется условием С Пале —
Смейла (см. Морса функция), к-рое, впрочем, выпол-
няется не во всех интересных ситуациях. Кроме того,
хотя для банаховых многообразий приходится приклеи-
приклеивать и ручки бесконечного индекса, в силу гомотопич.
тривиальности бесконечномерных сфер эти ручки на
гомотопич. тип не влияют. Поэтому в основной теореме
М. т. 3 участвуют лишь критич. точки конечного ин-
индекса.
Лит.: [1] М о г s e M., The calculus of variations in the large,
N. Y., 1934; [21 M и л н о р Д ж.. Теория Морса, пер. с англ.,
М., 1965; [3] е г о ж е, Теорема ои h-кобордизме, пер. с англ.,
М., 1969; [41 3 е Я ф е р т Г., Т р е л ь ф а л л ь В., Вариацион-
Вариационное исчисление в целом, пер. с нем., М., 1947; [5] Г р о м о1л Д.,
К л и н г е н б е р г В., М е й е р В., Риманова геометрия в
целом, пер. с нем., М., 1971; [6] Бишоп Р.-Л., К р и т т е н-
д е н Р.- Д ж., Геометрия многообразий, пер. с англ., М., 1967;
[7] Постников М. М., Введение в теорию Морса, М., 1971;
[8] его iK е, Вариационная теория геодезических, М., 1965;
[9] И л л с Д ж., «Успехи матем. наук», 1969, т. 24, в. 3, с. 157 —
210; [10] С е р р Ж.-П., Сингулярные гомологии расслоенных
пространств, в кн.: Расслоенные пространства и их приложения,
пер. с франц., М., 1958, с. 9—98.
М. М. Постников, Ю. Б. Рудяк.
МОРСА ФУНКЦИЯ — гладкая функция, обладаю-
обладающая нек-рыми специальными свойствами. М. ф. возни-
возникают и используются в Морса теории.
Пусть W — гладкое гильбертово полное (относитель-
(относительно нек-рой римановой метрики) многообразие (напр.,
конечномерное), край к-рого dW является несвязным
объединением (возможно, пустых) многообразий Vo и
Vx. М. ф. триады {W\ Vo, \\) — такая гладкая (класса
С2 по Фреше) функция / : W —*¦ [а, Ь), —оо <а, 6<+оо
(пли / : JF—>- [а, оо]) при \\=0, что:
1) /-V)=V0, /-i(b)=Fx;
2) все критические точки функции / лежат в W\dW—
=f~1[a, b] и невырождены;
3) условие С Пале — Смейла (см. [2],
[3]): на любом замкнутом множестве SdW, где функция
/ ограничена, а нижняя грань функции х —>- \\df (x)\\
равна нулю, существует критич. точка функции /.
Напр., если функция / собственная, т. е. все множест-
множества /~х[с, d], —оо <с, d<oo, компактны (что возможно
только при dim JF<oo), то/ удовлетворяет условию С.
М. ф. достигает минимума (глобального) на каждой ком-
компоненте связности многообразия W. Если многообразие
V конечномерно, то для к~^2 множество М. ф. класса
Ck является множеством 2-й категории (а если W ком-
компактно, то даже плотным открытым множеством) в
пространстве всех функций
/ : (W; v'o, Ft) -» ([а, Ь], а, Ь)
в С*-топологии.
Лит.: [lj M о г s e M., The calculus of variations in the large,
N. Y., 1934: [2] P a 1 a i s R., «Topology» 1963, v. 2, p. 299—340;
[3] Smale S., «Ann. Math.», 1964, v. 80, p. 382—96.
M. M. Постников, Ю. Б. Рудяк.
МОРСА — СМЕЙЛА СИСТЕМА динамичес-
динамическая — гладкий поток {Sf} или каскад {Sn} (порож-
(порожденный диффеоморфизмом S, к-рый в этом случае наз.
диффеоморфизмом Морса — Смейла)
на компактном, (обычно замкнутом) дифференцируемом
т- мерном многообразии Мт, имеющий следующие
свойства.
1) Система имеет конечное число периодич. траекто-
траекторий (включая сюда в случае каскада и неподвижные
точки) и (в случае потока) положений равновесия.
2) Каждая траектория из перечисленных в 1) обла-
обладает локальной грубостью (обычно в определении фи-
фигурируют эквивалентные этому свойства соответствую-
соответствующих линеаризованных систем). Это гарантирует сущест-
существование у траектории устойчивого и неустойчивого ин-
инвариантных многообразий IVs и Wu (если траектория
устойчива или вполне неустойчива, то считается, что
W", соответственно XVs, сводится к ней самой); размер-
размерность W" наз. ее индексом. Индекс обобщает по-
понятие Морса индекса невырожденной критической (ста-
(стационарной) точки w0 гладкой функции / : М —>- R, ибо
последний совпадает с индексом w0 как положения рав-
равновесия градиентной динамической системы
ш-=—grad/(u7), A)
где градиент берется по отношению к какой-нибудь ри-
мановой метрике на М.
3) Инвариантные многообразия траекторий из пере-
перечисленных в 1) пересекаются трансверсально (т. е. если
w ?Wlf\W", то касательные пространства TwWl~\-
+ TWW%=TWM).
4) Все остальные траектории при t ^- ±<х> или при
п —»- ± оо стремятся к траекториям из перечисленных
в 1).
5) Если М имеет край, то нужны еще нек-рые усло-
условия о поведении системы вблизи края. Для потоков (до
сих пор в этом случае только они и рассматривались)
обычно требуют, чтобы вектор фазовой скорости был
всюду трансверсалсн к краю.
М.— С. с. являются грубыми системами [1]. Имен-
Именно в связи с изучением последних впервые рассматри-
рассматривались частные случаи М.— С. с.— потоки в плоских
областях (см. более позднее подробное изложение в [2])
и каскады на окружности (см. [4] — [6]). В общем слу-
случае М.— С. с. введены С. Смейлом [7], ограничившимся
тогда М. — С. с. на замкнутом М, для к-рых были до-
доказаны следующие неравенства Морса —
С м е й л а. Пусть т; для каскада — число периодич.
точек индекса г, а в случае потока — сумма числа
положений равновесия индекса г и числа периодич.
траекторий индексов i и i-\-i; тогда при i = 0, 1,
где Ъ; есть г-е Бетти число многообразия М (если среди
Wl, Ws, введенных в 2), имеются неориентируемые, то
числа Бетти надо брать над полем характеристики два).
При г=т неравенство B) обращается в равенство.
Неравенства B) обобщают обычные Морса неравенст-
неравенства для гладкой функции / : М -+- R с невырожденными
критич. точками. Именно, неравенства Морса можно
получить применением B) к системе A) (к-рая, правда,
не обязательно является М.— С. с, так что требуется
небольшое дополнительное рассуждение, см. [7],[8]).
Исследовался вопрос, когда в данном классе изотопии
диффеоморфизмов существует диффеоморфизм Морса —
Смейла (см. [9], [10]), а для Мт с нулевой эйлеровой ха-
характеристикой — и аналогичный вопрос о гомотопич.
классе неособых векторных полей (здесь при т^4 ответ
всегда положительный, см. [11]). Для потоков при т=2
(см. [12], [13]) и нек-рых специальных типов потоков
при т^З (см. [14], [15]) выяснено, какие топологич.
инварианты определяют топологич. эквивалентность
двух М.— С. с. [В двумерном случае этот вопрос ре-
решен для более широкого класса потоков (см. [3], [16]),
а случай т=1 тривиален.]
Лит.: [1] П э й л и с Д ж., С м е й л С, «Математика»,
1969, т. 13, М 2, с. 145—55; [2] Андронов А. А., Ле-
онтович Е. А., ГордонИ. И.,МайерА. Г., Теория
бифуркаций динамических систем на плоскости, М., 1967; [3]
их же, Качественная теория динамических систем второго
порядка, М., 1966; [4] Майер А. Г., «Уч. зап. Горьк. гос.
ун-та», 1939, в. 12, с. 215—29: [5] Плисе В. А., «Вести.
Ленингр. ун-та. Сер. матем.», 1960, № 13, в. 3, с. 15—23; [6]
Арнольд В. И., «Изв. АН СССР. Сер. матем.», 1961, т. 25,
№ 1, с. 21—86; 1964, т. 28, №2, с. 479—480; [7] С м е й л С.
«Математика», 1967, т. 11, JM4 4, с. 79—87; [8] Smale S.,
«Ann. Math.», 1961, v. 74, № 1, p. 199—206; [9] Ш у б М.,
в кн.; Гладкие динамические системы, М., 1977, с. 118—39;
[10] Шуб М., Сулливан Д., там же, с. 140—180; [11]
Asimov D., «Ann. Math.», 1975, v. 102, Js6 1, p. 55—65; [12]
P e i x о t о М-, «С. г. Acad. sci.», 1971, t. 272, № 3, p. A 262—
265; [13] e г о ж е, в кн.: Dynamical systems, N. Y.—L., 1973,
p. 389—419; [14] Ума некий Я. Л., «Докл. АН СССР»
1976, т. 230, Nt 6, с. 1286—89; [15] Пилюгин С. Ю., «Диф-
«Дифференциальные уравнения», 1978, т. 14, М 2, с. 245—54; [16]
Neumann D., O'Brien Th., «J. differentia] equations»,
1976, v. 22, № 1, p. 89 — 110. Д. В. Аносов.
МОРФИЗМ категории — термин, используе-
используемый для обозначения элементов произвольной катего-
категории, играющих роль отображений множеств друг в
друга, гомоморфизмов групп, колец, алгебр, непрерыв-
непрерывных отображении топологич. пространств и т. п. М.
категории — неопределяемое понятие. Каждая катего-
категория состоит из элементов двух классов, наз. клас-
классом объектов и классом морфизмов
соответственно. Класс М. категории Я обычно обозна-
обозначается Мог Я'.
Любой М. а категории Я имеет однозначно опреде-
определенное начало — объект А и однозначно определенный
конец — объект В. Все М. с общими началом А и кон-
концом В образуют подмножество Н§1 {А, В) класса
Мог Я- Тот факт, что М. а имеет начало А и конец В,
можно записать обычным образом: a?ff$(A, В),
пли с помощью стрелок: а : А —>- В, А ^ В и т. п.
Деление элементов категории на М. и объекты имеет
смысл только в пределах фиксированной категории,
т. к. М. одной категории могут быть объектами другой
и наоборот. М. любой категории образуют систему,
замкнутую относительно частичной бинарной опера-
операции — умножения. В зависимости от свойств М. по
отношению к этой операции выделяются специальные
классы М., напр, мономорфизм, эпиморфизм, биморфизм,
изоморфизм, нулевой морфизм, нормальный мономор-
мономорфизм, нормальный эпиморфизм и т. д. м. ЯГ. Цаленко.
МОТИВОВ ТЕОРИЯ — обобщение различных тео-
теорий когомологий алгебраич. многообразий. М. т. систе-
систематически обобщает идею использования якобиана ал-
алгебраич. кривой X в качестве замены когомологий
Я1 (X, Q) в классич. теории соответствий и использова-
использовании этой теории для изучения дзета-функции кривой X
над конечным полем. М. т. универсальна в том смысле,
что всякая геометрич. теория когомблогийтипа классич.
сингулярных когомологий алгебраич. многообразий над
полем С с постоянными коэффициентами, Z-адических
когомологий для различных простых чисел I, отличных
от характеристики основного поля, кристаллич. кого-
когомологий и т. п. (см. Вейля когомологий) является функ-
функтором на категории мотивов.
Пусть V (к) — категория гладких проективных мно-
многообразий над нолем к и X ->- С (X) — контравариант-
ный функтор глобальной теории пересечений из V(k)
в категорию коммутативных Л-алгебр, где Л — нек-рое
фиксированное кольцо. Напр., С(X) — кольцо Чжоу
классов алгебраич. циклов на X по модулю подходя-
подходящего (рационального, алгебраического, численного и
т. п.) отношения эквивалентности, или С(Х)=К(Х) —
кольцо Гротендика, или С (Х)=Hev (X) — кольцо клас-
классов когомологий четной размерности и т. д. Категория
V(k) и функтор X ->- С (X) позволяют определить новую
категорию — категорию соответствий CV(k), объекта-
объектами к-рой являются многообразия X?V(k), обозначае-
обозначаемые через X, а морфизмы определяются формулой
J, Y) = C (XxY)
с обычным законом композиции соответствий (см. [1]).
Пусть функтор С принимает значения в категории
коммутативных градуированных Л-алгебр А (Л), тогда
категория CV(к) будет Л-аддитивной категорией граду-
градуированных соответствий. Более того, CV(k) будет обла-
обладать прямыми суммами и тензорными произведениями.
Категория, объектами к-рой являются многообразия
из V(k), а морфизмами — соответствия степени 0, обоз-
обозначается CVa(k). Из V(k) определен естественный функ-
функтор в CV°(k), и функтор С продолжается до функтора Т
из CV°(k) в А (А). Категория CV°(k), как и CV(k), не
является абелевой. Рассматривается ее псевдоабелево
пополнение — категория Мс(к), к-рая получается из
CV°(k) формальным добавлением образов всех проекто-
ров р. Точнее, объектами Мс(к) являются пары (X, р),
где X?CV°(k) и р?Нот(Х, X), р2=р, a Hom_((Z, p),
(У, q)) — это множество соответствий / : X —> У таких,
что /ор=?с/, по модулю соответствий g с g°p=pcg=0.
Категория CF°(fe) вкладывается в Мс(к) посредством
функтора X —*- (X, id). Естественный функтор h : V (к)-~>-
—*¦ Мс(к) наз. функтором мотивных кого-
мологий, а Мс(к) — категорией эффек-
эффективных мотивов.
Пусть р=AХе), где е — класс любой рациональной
точки на проективной прямой Р1, a L=(P1, р). Тогда
Если Х=Р(Е) — проективизация локально свобод-
свободного пучка Е ранга г на Y, то
Вычислены также мотивы моноидального преобразова-
преобразования с неособым центром и мотивы кривых (см. [1]),
мотивы абелева многообразия (см. [2]) и мотивы гипер-
гиперповерхностей Вейля.
Категория мотивов Мс(к) получается из
Мс(к) формальным добавлением отрицательных сте-
степеней мотива L. По аналогии с Z-адическими когомоло-
(X)-i
гиями, T=L наз. мотивом Т е й т а. Операция
тензорного умножения на мотив Т наз. скручива-
скручиванием с помощью мотива Тейта. Скру-
Скручивание позволяет определить понятие уровня мотива,
как в Z-адических когомологиях. Любой функтор кого-
мологий Вейля пропускается через функтор h : V (к) —>•
—у- Мс(к). Имеется гипотеза, что Мс(к) в нек-ром смысле
не зависит от теории пересечений С и что сам функтор
X->-h(X) является (универсальной) теорией когомо-
логий Вейля. Эта гипотеза тесно связана со стандарт-
стандартными гипотезами Гротендика (см. [5]) об алгебраич.
циклах (также пока, 1982, не доказанными).
Лит.: [1] М а н и н Ю. И., «Матем. сб.», 1968, т. 77, N5 4,
с. 475—507; [2j Ш е р м е н ё в А. М., «Успехи матем. наук»,
1971, т. 26, № 3, с. 215—16; [3] D о m a z и г е М., Motives des
varietes algebrique, Sem. Bourbaki, 365, P., 1069; [4] К 1 e i-
m a n S. L., Motives, «Proceeding of the 5-th Nordic Summer-
School in Math. Algebraic geometry», Oslo, 1970, p. 52—82;
15] его же, Algebraic cycles and the Weil conjectures, в кн.:
Dix exposes sur la eohomologie des schemas, Amst. — P., 1968.
В. А. Псковских.
МОЩНОСТИ КРИТЕРИЯ ФУНКЦИЯ — функция,
характеризующая качество статистического критерия.
Пусть по реализации х случайного вектора X, прини-
принимающего значения в выборочном пространстве (J, S3,
Ре), 6?в, надлежит проверить гипотезу Но, согласно
к-рой распределение вероятностей Ре случайного век-
вектора X принадлежит подмножеству Но= {Ре , 60
Св}, против альтернативы Н1, согласно к-рой
и пусть ф(-) — критич. функция статистич. критерия,
предназначенного для проверки Но против Нг. Тогда
наз. функцией мощности статистиче-
статистического критерия, имеющего критич. функцию
ф. Из (*) следует, что М. к. ф. РF) показывает, с ка-
какими вероятностями статистич. критерий, предназна-
предназначенный для проверки Но против Н1, отклоняет прове-
проверяемую гипотезу Но, если X подчиняется закону Ре
е^в
В теории проверки статистических гипотез, основан-
основанной Ю. Нейманом (J. Neyman) и Э. Пирсоном (Е. Pear-
Pearson), задача проверки сложной гипотезы Нй против
сложной альтернативы ffl формулируется в терминах
М. к. ф. и заключается в построении статистич. крите-
критерия максимизирующего М. к. ф. РF), когда б^в! прл
условии, что РF)<а для всех 6?в0, где число а @<
<а<1), наз. уровнем значимости крите-
критерия,— заданная допустимая вероятность ошибочного
отклонения гипотезы Но, когда она в действительности
верна.
Лит.; [1] Леман Э. Л., Проверка статистических гипо-
гипотез, пер. с англ., 2 изд., М., 1979; [21 Крамер Г., Математи-
Математические методы статистики, пер. с англ., 2 изд., М., 1975; Lai
Ван-дер-Варден Б. Л., Математическая статистика,
пер. с нем., М., 1960. М. С. Никулин.
МОЩНОСТНАЯ ХАРАКТЕРИСТИКА топологи
ческого пространства — функция, сопо-
сопоставляющая этому пространству бесконечное карди-
кардинальное число и принимающая одинаковые значения ш
гомеоморфных пространствах. М. х. наз. также кар-
кардинальными инвариантами. Областью
определения М. х. может служить класс всех тополо-
гич. пространств или нек-рый его подкласс. Следующие
М. х. были выделены уже на первом атапе развития
общей топологии. Пусть X — произвольное топологич.
пространство. Его мощность |Х| есть мощность
множества всех его точек — тривиальный инвариант.
Вес w (X) — минимум мощностей всевозможных баз
пространства X. Плотность d(X) — минимум
мощностей всюду плотных в X множеств. Число
С у с л и н а с(Х) — наименьший бесконечный карди-
кардинал т такой, что мощность всякого семейства попарно не
пересекающихся непустых открытых множеств в X не
превосходит т. Число Линделёфа I (X) — наи-
наименьший бесконечный кардинал т такой, что из всякого
открытого покрытия пространства X можно выделить
подпокрытие мощности <:т. Эти простые понятия сразу
доказали свою важность, войдя решающим образом в
формулировки фундаментальных теорем и проблем.
Примеры: регулярное пространство счетного веса мет-
ризуемо (теорема У р ы с о н а — Тихонов»,
1925), бикомпакт метризуем в том; и только в том слу-
случае, если вес его счетен; для пространства X любой би-
бикомпактной группы число Суслина счетно; число Лип-
делёфа I (X) счетно (т. е. равно Af0) для всякого прост-
пространства X счетного веса. Проблема Суслина:
верно ли, что всякий связный упорядоченный биком-
бикомпакт X такой, что c(X) = tf0 гомеоморфен обычному от-
отрезку [0, 1], сводится к вопросу о соотношении между
двумя М. х.: плотностью и числом Суслина. Для поло-
положительного решения проблемы Суслина достаточно
в указанных выше предположениях установить, что
d(X)<c(X). Вопрос о сравнении М. х. между собой —
решение к-рого, как видно из приведенного примера,
может иметь ключевое значение для окончательного
заключения о строении пространства — занимает цент
ральное место в теории М. х. Причина этому находится
в самой природе понятия М. х.: значениями М. х. яв-
являются кардинальные числа, совокупность к-рых впол-
вполне упорядочена по величине. Следовательно, любые
две М. х. фх и ф2 можно пытаться сравнить по величине.
Возникает серия взаимосвязанных вопросов. Верно ли,
что для любого X фг(Х)-<ф2(Х), для каких X у^Х)^
<Ф2(Х), когда ф1(Х) = ф2(Х), и т. д.
С кардинальными числами можно производить вы-
вычисления: перемножать их, складывать, возводить в
степень. Соответственно, можно производить вычисле-
вычисления и с кардинальными инвариантами — перемножать
и складывать их как функции и т. д. Это открывает но-
новые возможности для сравнения М. х.— с помощью вы-
вычислений. Всегда
— т. е. число Суслина не превосходит плотности, плот-
плотность не превосходит веса и число Линделёфа не пре-
восходит веса. Но плотность и число Линделёфа в этом
смысле не сравнимы: существуют пространства X, Y,
Z, для к-рых
) = d(Z) = c(Z).
Неожиданной на первый взгляд представляется несрав-
несравнимость мощности и веса: существуют нормальные счет-
счетные ^-пространства несчетного веса. Но всегда d(X)«:
<:|Х| и 1(Х)-^.\Х\. Для всякого ^-пространства X,
\Х\ <:ехр (w (X)) (пишут ехр т вместо 2х). Для всякого
хаусдорфова пространства X, \Х\ <:ехр (ехр (d(X))).
Всегда w (Х)<ехр| А'|.
В задачу сравнения могут быть естественно вовлече-
вовлечены не два, а большее число М. х. На этом пути получа-
получаются особенно тонкие, красивые и часто неожиданные
результаты, поражающие своей общностью: для каждого
хаусдорфова пространства X, \Х\ <ехр (с(Х) -%(Х)),
где %(Х) — наименьший бесконечный кардинал т та-
такой, что в каждой точке пространства X имеется
база мощности <:т (см. [1], [2]). Исследования в теории
М. х. стимулировала проблема оценки мощности биком-
бикомпакта с первой аксиомой счетности, остававшаяся не-
нерешенной с 1923 по 1969. Оказалось: для каждого хаус-
хаусдорфова пространства X, \Х\ <ехр {1(Х) ¦%(Х)) (тео-
(теорема Архангельского, см. [2], [4]).
Вычисления М. х. возникают во всех разделах общей
топологии в силу теоретико-множественной природы
последней. Поэтому и применения теория М. х. находит
практически во всех областях общей топологии и при
любых подходах к исследованию пространств.
В частности, при изучении пространств методом по-
покрытий на первый план выступают число Линделёфа,
плотность и число Суслина. При исследовании и клас-
классификации пространств методом непрерывных отоб-
отображений (в частности, при построении теории диадич.
бикомпактов и теории абсолютов) возникли и сыграли
ключевую роль новые М. х.: спрэд и я-вес. С п р э д
s(X) пространства X есть точная верхняя грань мощно-
мощностей дискретных подпространств пространства X, а
я-вес nw(X) этого пространства — минимум мощ-
мощностей всевозможных семейств у (наз. я-базами)
непустых открытых в X множеств таких, что для каж-
каждого непустого открытого в X множества U найдется
V(zY такое, что VczU. При исследовании пространств
методом обратных спектров важную роль играют число
Суслина, характер, вес. Но имеется подход к общей то-
топологии, при к-ром М. х. выступают и как главное
средство исследования строения пространств, и как
основной язык, на к-ром выражаются свойства прост-
пространств из тех или иных классов и, наконец, как средство
классификации и выделения новых естественных клас-
классов тополегич. пространств. В основе и здесь лежит за-
задача сравнениям, х. Основной вопрос ставится следую-
следующим образом. Дан класс ^ тоиологич. пространств,
к-рым ограничивается область определения М. х. Как
выглядят основные соотношения между кардинальными
инвариантами в этих условиях? Развивая теорию М. х.
для класса 53, мы как бы получаем «кардинальный пор-
портрет» класса !р. Сравнение кардинальных портретов
каких-либо классов ^i и ^>2 Дает возможность судить
о соотношениях между этими классами, а также достав-
доставляет эффективные средства доказательства для конкрет-
конкретных пространств принадлежности их тому или иному
классу.
Этот подход демонстрируется на примере класса
метризуемых пространств. Характерной чертой здесь
является совпадение для этого класса ряда основных
М. х.: число Суслина равно плотности, весу и числу
Линделёфа. Этот факт часто применяется, напр, чтобы
доказать, что нек-рое пространство неметризуемо, дос-
достаточно показать, что на нем различаются хотя бы два
из названных выше инвариантов.
Если в классе метризуемых пространств теория М. х.
отличается главным образом упрощениями, то в классе
бикомпактов она совершенно и нетривиальным обра-
образом меняет свой вид. Ответственны за это фундамен-
фундаментальные положения этой теории — совпадение для би-
бикомпактов характера и псевдохарактера, веса и сетево-
сетевого веса. При этом псевдохарактером г|з (х, X)
пространства X в точке х наз. наименьшее число от-
открытых множеств, дающих эту точку в пересечении, а
характером х (х,: X) пространства X в точке х
наз. минимум мощностей баз пространства в этой точке.
Сетевым весом nw(X) наз. минимум мощностей
семейств S множеств в X, удовлетворяющих условию',
если х?Х и i? UczX, где U открыто в X, то найдется
Р ?S, для к-рого igPc U (такие семейства наз. с е т я-
м и в X). Для всякого бикомпакта X верно следующее:
1) -ф (.т, Х)=х(х, X) для всех х?Х; 2) nw(X) = w{X).
Поэтому при непрерывном отображении на бикомпакт
вес не может возрастать, и если бикомпакт X представ-
представлен в виде объединения двух своих подпространств Хх и
Х2, то вес Хг{}Хг не превосходит максимума весов Хх
и Х2 (а дд и ц ионная теорема для вес а).
По той же причине вес бикомпакта всегда не превосхо-
превосходит его мощности — в частности, всякий счетный би-
бикомпакт метризуем. Ни одно из перечисленных выше
положений теории М. х. в классе бикомпактов не рас-
распространяется на класс всех вполне регулярных прост-
пространств. Важным специфич. результатом является сле-
следующий: если X ¦— бикомпакт, т — кардинал, x^ttn и
%(х, Х)>т для всех х?Х, то |Х|>ехр т (теорема
Чеха — П о с п и ш и л а). Почти все критерии мет-
метризуемости бикомпактов также являются теоремами
о М. х. Так, метризуемость бикомпакта X равносильна
любому из следующих условий: a) w (X)=tf0;
б) nw(X)=if0; в) диагональ в XXX является множест-
множеством типа бб; г) X обладает точечно-счетной базой.
В исследовании строения бикомпактов важная роль
принадлежит тесноте. Теснотой t(X) (см. [2],
[4]) пространства X наз. наименьший кардинал i^So
такой, что если х? X, АсХ и х? [А], то найдется ВсА,
для к-рого х?[В] и |5|<т. Теснота не возрастает при
возведении бикомпакта в любую конечную степень (в
классе вполне регулярных пространств это — не так).
Если теснота бикомпакта X не превосходит т, то для
каждой точки х?Х найдется семейство у непустых от-
открытых в X множеств такое, что \у\ <:т и каждая окрест-
окрестность Ох точки х содержит элемент семейства у. Поэтому
я-вес каждого сепарабельного бикомпакта счетной тес-
тесноты равен Цо. Спрэд бикомпакта мажорирует его
тесноту.
Особыми свойствами диадич. бикомпактов также в
большой степени управляют теоремы о М. х. Так, для
всякого диадич. бикомпакта его вес совпадает со спрэ-
дом и с теснотой. К числу диадич. бикомпактов относят-
относятся пространства любых бикомпактных групп, так что, в
частности, каждая бикомпактная группа счетной тесно-
тесноты метризуема.
Для теории диадич. бикомпактов и других разделов
теории М. х. важное значение имеет вопрос о поведении
последних при операции умножения. Существенную
роль играют здесь следующие две теоремы, первая из
к-рых влечет вторую. Если F — семейство пространства
такое, что й(Х)«:т для каждого X?F и |/"|<ехр т, то
плотность произведения всех пространств из F не пре-
превосходит т (см. [1] —[4]). Если X — произведение ка-
какого-нибудь множества пространств, плотность каждо-
каждого из к-рых не превосходит т, то е(Х)<:т. В последнем
утверждении нет никаких ограничений на число сомно-
сомножителей. В частности, получается, что число Суслина
любого тихоновского куба (произведения произвольно-
произвольного множества отрезков) счетно. Таким образом, условие
c(X) = tf0 не несет в себе ограничения на мощность
пространства.
Многие просто формулируемые вопросы о поведе-
поведении М. х. при операции умножения оказываются весь-
весьма деликатными. Например, верно ли, что всегда
с{ХХ Х) = с(Х) оказывается связанным с гипотезой Сус-
лина и континуум-гипотезой?
Напротив, поведение М. х. при переходе от простран-
пространства X к его образу У при непрерывном отображении
/ : X —> У, где f(X)=Y, подчиняется в основном про-
простым общим правилам.
Напр., всегда c(Y)^c(X), d(Y)<.d{X), геш(У)<
<inw(X), l(Y)<?.l(X). Если / факторно, то г(У)<*(Х).
То обстоятельство, что основу теории М. х. составляет
система простых универсальных правил этого рода,
'также можно рассматривать как одну из причин, обес-
обеспечивающих широкую применимость этой теории.
Значительная информация о строении пространств
получается при рассмотрении вопроса: как ведут себя
М. х. при переходе к подпространству. То М. х. ср, для
к-рых из YczX всегда следует, что ф(У)«:ф(Х), наз.
монотонными. К ним относятся: вес, сетевой вес,
теснота, характер, спрэд. Немонотонны число Суслина,
плотность, число Линделёфа. Возникают следующие во-
вопросы: каковы те пространства X, для к-рых с(У)<т
для всех YczX; каковы те X, для к-рых й(У)<:т для
всех YczX; как отражается на топологии пространства
X требование: ^(У)<:т для всех YaX. Ответ на первый
вопрос прост: сформулированное условие означает, что
спрэд X не превосходит т. Но двумя последующими
требованиями выделяются новые классы пространств.
Исследование их оказалось зависящим от специальных
гипотез теории множеств — в частности, от аксиомы
Мартина.
Своеобразный характер приобретает теория М. х.
на пространствах топологич. групп. Так, критерий
метризуемости сводится здесь просто к требованию счет-
ности характера. На языке М. х. формулируются важ-
важные свойства линейных топологич. пространств, в част-
частности пространств С (X) непрерывных действительных
функций на пространстве X. Сюда относятся теоремы
о бикомпактах Эберлейна (каждый бикомпакт Эберлей-
Эберлейна является пространством Фреше — Урысона, вес
бикомпакта Эберлейна равен его числу Суслина), тео-
теорема: если X — бикомпакт, то теснота пространства
С (X) в ^топологии поточечной сходимости счетна.
Между рядом М. х. пространств X и С (X) имеет ме-
место соответствие типа двойственности.
Лит.: [1] J u h a s z I., Cardinal functions in topology, Amst.,
1971; [2] Архангельский А. В..Пономарев В. И.,
Основы общей топологии в задачах и упражнениях, М., 1974;
[3] EngelkingR., General topology, Warsz., 1977; [4]
Архангельский А. В., «Успехи матем. наук», 1978,
т. 33, в. 6, с. 29—84; [5] Е n g e I k i n g R., General topology,
Warsz., 1977. А. В. Архангельский.
МОЩНОСТЬ, кардинальное число, мно-
множества А — такое свойство этого множества, к-рое при-
присуще любому множеству В, эквивалентному А. При
этом два множества наз. эквивалентными
(или равно мощным и), если между ними воз-
возможно установить взаимно однозначное соответствие.
Таким образом, «определяя через абстракцию», можно
сказать, что М.— это то, что есть общего у всех эквива-
эквивалентных множеств. Так как у всех эквивалентных меж-
между собою конечных множеств этим общим является ко-
количество элементов, или одинаковое число, из к-рых они
состоят, то в применении к бесконечным множествам
понятие М. является аналогом понятия количества. М.
есть фундаментальное понятие теории множеств, при-
принадлежащее Г. Кантору (G. Cantor). Множества, экви-
эквивалентные множеству всех натуральных чисел, наз.
счетными. Соответствующая М. обозначается ft0
(алеф-нуль). М. множеств, эквивалентных множеству
всех действительных чисел, наз. М. континуума
и обозначается с или 2 "°. Напр., счетную М. имеет
множество всех алгебраич. чисел, а М. континуума
имеет множество всех замкнутых подмножеств д-мср-
ного евклидова пространства. Теорема Канто-
Кантора — Бернштейна: если из двух множеств А ж В
каждое эквивалентно части другого, то эти два мно-
множества эквивалентны. В этом случае говорят, что
множества А и В имеют одинаковую М. Если множе-
множество А эквивалентно части множества В, тогда как
множество В не эквивалентно никакой части множе-
множества А, то говорят, что М. множества В больше М.
множества А. Теорема Кантора: М. множества
всех подмножеств любого непустого множества А боль-
больше М. множества А. Эта теорема дает возможность
построить иерархию М. (см. Кардинальное число).
Лит.: [1] Александров П. С, Введение в теорию
множеств и общую топологию, М., 1977. Б. А. Ефимов.
МОЩНОСТЬ СТАТИСТИЧЕСКОГО КРИТЕРИЯ —
вероятность, с к-рой статистический критерий, пред-
предназначенный для проверки простой гипотезы Но против
сложной альтернативы Hlt отклоняет Но, когда в дейст-
действительности верна гипотеза Их. В случае, когда гипоте-
гипотеза II и конкурирующая с проверяемой гипотезой Но,
является сложной (при этом сама гипотеза Но может
быть как простой, так и сложной, что символически
записывают следующим образом: На : 6?©0С©,
Нг: 6?в!=в\ви), М. с. к., предназначенного для про-
проверки Во против Hi, определяется как сужение функ-
функции мощности Р F), 6рв = вои01, этого статистич.
критерия на множество &±.
Кроме этого определения широко распространено
следующее: М. с. к., предназначенного для проверки
гипотезы Но : 6?в0Св против сложной альтернативы
Hi : 6ge1=e\0o, есть inf Р(в), где EF) — функция
е е е,
мощности этого статистич. критерия (см. Мощности
критерия функция).
Лит.: [1] Л е м а н Э. Л., Проверка статистических гипо-
гипотез, пер. с англ., 2 изд., М., 1979; [2] Гаек Я., Ш и д а к 3.,
Теория ранговых критериев, пер. с англ., М., 1971; [3J В ан-
дер-Варден Б. Л., Математическая статистика, пер. с
нем., М., 1960; [4] Крамер Г., Математические методы ста-
статистики, пер. с англ., 2 изд., М., 1975. М. С. Никулин.
МУАВРА ФОРМУЛА — формула, выражающая пра-
правило для возведения в степень га комплексного числа,
представленного в тригонометрич. форме
2=p(cos ф+г sin ф).
Согласно М. ф. модуль р комплексного числа возводит-
возводится в эту степень, а аргумент ф умножается на показа-
показатель степени
z™= [p (созф+ i sin ф)]« = р« (cos иф+ i sin пф).
М. ф. была найдена А. Муавром (A. Moivre, 1707),
современная ее запись предложена Л. Эйлером (L. Eu-
1ег, 1748).
М. ф. может быть использована для выражения cos гаф
и sin гсф через степени cos ф и sin ф:
sin гаф = Сп cos" фвтф — C^cos""
Обращение М. ф. приводит к формуле для извлечения
корня из комплексного числа:
у р (cos ф + i sin ф) =
л/~~/ ш + 2яй , . . ф + 2яй \ , „ .
= j/ P (cos -^ Hsm-i—-—) , k=0, 1, ...,
к-рую также иногда наз. М. ф. БСЭ-з.
МУАВРА— ЛАПЛАСА ТЕОРЕМА — см. Лапласа
теорема.
МУЛЬТИАЛГЕБРА — множество, на к-ром задана
система (вообще говоря, частичных) мультиопераций.
Частичной мультиоперацией на мно-
множестве А наз. частичное отображение f : А" —*-А
декартовых степеней множества А, где n, т^О. При
этом под А0 понимается одноэлементное множество. Го-
Гомоморфизмом g : А —> В мультиалгебр с одной и той же
системой мультиопераций наз. такое отображение g,
что если / — мультпоперация, отображающая ге-ю де-
картову степень в т-ю, то
g"» (f (xu ..., xn)) = f(g(x1), ..., g(xn))
для всех Х[?А. Понятие М. является обобщением по-
понятия универсальной алгебры. В то же время М. являет-
является частным случаем алгебраической системы, поскольку
отображение / : Ап ^>-А можно отождествить с (га+
-г-т)-арным отношением (.г, f (х)) на А, х?Ап. Наибо-
Наиболее естественно М. возникают в связи с функторным по-
пониманием универсальных алгебр (см. [1]). Именно,
пусть С — категория, объектами к-рой являются нату-
натуральные числа и нуль, причем объект та+n есть прямое
произведение объектов т и п. Тогда функтор F из С
в категорию множеств, перестановочный с прямыми про-
произведениями, есть М. на множестве F{i)=A с системой
мультиопераций F (f) '¦ А" —> Ат, где / : га^ та в С.
Гомоморфизмами в этом случае будут служить в точ-
точности естественные преобразования функторов.
Лит.: [1] Lawvere F. W., «Proc. Nat. Acad. Sci. USA»,
1963, v. 50, № 5, p. 869—72; [2] Б е л о у с о в В. Д., Алгебраи-
Алгебраические сети и квазигруппы, Киш., 1971. В. А. Артамонов.
МУЛЬТИГРАФ — граф, в к-ром допускаются крат-
кратные ребра.
МУЛЬТИМОДАЛЬНОЕ РАСПРЕДЕЛЕНИЕ, м н о-
говершинное распределени е,— распре-
распределение вероятностей с несколькими модами или, что
то же самое, с несколькими относительными максиму-
максимумами, соответствующими этим модам. В отличие от
унимодальных распределений М. р. встречаются сравни-
сравнительно редко и, как правило, представляют собой смеси
распределений вероятностей. а. В. Прохоров.
МУЛЬТИОПЕРАТОРНАЯ ГРУППА, fi-г р у п-
п а,— универсальная алгебра, являющаяся группой
относительно операции сложения -f- (не обязательно
коммутативной), в которой задана система операций
Q-арностей 5г1. Предполагается, что нулевой эле-
элемент 0 аддитивной группы является подалгеброй, т. е.
0...0@=0 для всех m?fi. Таким образом, М. г.
объединяет понятия группы, линейной алгебры и коль-
кольца. Идеалом fi-r р у п п ы наз. такой нормальный
делитель N в аддитивной группе А, что
для всех a?N, х;?А, ш?Й, 1<:?<:п. Конгруэнции на
М. г. описываются разложениями на смежные классы
по идеалам.
Пусть А, В, С суть fi-подгруппы в Й-группе G (т. е.
подалгебры универсальной алгебры G), причем С по-
порождена А ж В. Взаимным коммутантом
[А, В] подгрупп А и В наз. идеал в С, порожден-
порожденный всеми элементами вида
— а — Ь-\-а-\-Ь,
— (О!.. ¦«„(?>) — (Ь1.. .Ъпш) + {а1 + Ь1). . .(а„ + Ь„) ш,
где а, а,?А, b, b;?B, w?fi. Пусть G'= \G, G]. М. г.
наз. а б е л е в о й, если G' = 0. Индуктивно определя-
определяются идеалы G,- + 1=[G,-, G], где Gl=G', и G<'+I> = [G<'\
G(/)], где GA) = G'. М. г. G наз. н и л ь и о т е н т н о и,
если G,-=0, и разрешимой, если G(() = 0 для
нек-рого г. На эти классы М. г. переносятся многие
свойства соответствующих классов групп и колец.
М. г. А наз. мультиоператорной (линей-
н о й) fi-a л г е б р о й над коммутативно-ассоциатив-
коммутативно-ассоциативным кольцом к с единицей, если сложение в А коммута-
тивно, ?1^=1$. и все операции из Q полилинейны над к
(см. 12] -16]).
Лит.: [1] Higgins Ph. J., «Proc. London Math. Soc»,
1956, v. 6, p. 366 — 416; [2] К у р о ш А. Г., «Сиб. матем. ж.»,
1060, т. 1, № 1, с. 62—70; [3] е г о ж е, Лекции по общей алгебре,
2 изд., М., 1973; [4] е г о ж е, Общая алгебра. Лекции 1969—
1970 учебного года М., 1974; [5] е г о ж е, «Успехи матем. наук»,
1969, т. 24, в. 1 с. 3—15- [6J Б а р а н о в и ч Т. М., Б у р-
г и н М. С, там же, 1975, т. 30, в. 4, с. 61—106; [7] Итоги науки
и техники. Алгебра. Топология. Геометрия, т. 14, М., 1976,
с. 191—248; [8] Кольца, [т. 1], Новосиб., 1973, с. 41 — 45.
В. А. Артамонов.
МУЛЬТИПЛИКАТИВНАЯ АРИФМЕТИЧЕСКАЯ
ФУНКЦИЯ — арифметическая функция одного аргу-
аргумента /(т), удовлетворяющая условию
= f{m)-f(n) (*)
для любой пары взаимно простых чисел т, п. Обычно
предполагается, что / (т) не равна тождественно нулю
(что равносильно условию /A)=1). М. а. ф. наз.
сильно мультипликативной, если / (ра) = / (р)
для всех простых р и всех натуральных а. Если усло-
условие (*) выполняется для произвольных двух чисел т, п,
а не обязательно взаимно простых, то /(т) паз. впол-
вполне мультипликативной; в этом случае
) [(\
f(P) [f(p)\
Примеры М. а. ф.: функция %(т) — число нату-
натуральных делителей натурального т, функция а(т) —
сумма натуральных делителей натурального та; Эйлера
функция ср(та), Мёбиуса функция \i(m). Функция 'f™
является сильно М. а. ф., степенная функция /(те) =
= ms — вполне М. а. ф. й. П. Кубилюс.
МУЛЬТИПЛИКАТИВНАЯ ГРУППА тела — груп-
группа, элементами к-рой являются все ненулевые элементы
данного тела, а операция совпадает с операцией умно-
умножения в теле. М. г. поля — абелева группа.
О. А. Иванова.
МУЛЬТИПЛИКАТИВНАЯ ПОЛУГРУППА ассо-
ассоциативного кольца — полугруппа, образуе-
образуемая всеми элементами данного ассоциативного кольца
относительно умножения. Неассоциативное кольцо по
умножению является лишь группоидом, называемым
мультипликативным группоидом
КОЛЬЦа. О. А. Иванова.
МУЛЬТИПЛИКАТИВНАЯ РЕШЕТКА — полная ре-
решетка L=(L, v, Л> с дополнительной бинарной ком-
коммутативной и ассоциативной операцией, наз. умноже-
умножением (и обозначаемой •), такой, что наибольший эле-
элемент решетки играет роль мультипликативной единицы
и
для любых Ь, i)af ti произвольного множества индек-
индексов /. Теория М. р. возникла как результат применения
теоретико-структурных методов к изучению решеток
идеалов коммутативных колец (см. [2]), и поэтому
большинство понятий и результатов имеет аналоги
(или приложения) в коммутативных кольцах (см. [1]).
Пусть L — М. р. и a, b?L, тогда a:b= V {x \x?L,
x-b<^a}. Элемент e^L паз. V-главным (соответствен-
(соответственно Д-главным), если (а V (Ь-е)):е=(а:е) v Ъ (соответ-
(соответственно (аЛ(Ь : е))-e=(a-e)Ab) для любых a, b?L;
V-главный и д-главный одновременно элемент наз.
главным. Нётеровой решеткой наз. мо-
модулярная и удовлетворяющая условию обрыва возра-
возрастающих цепей М. р., в к-рой каждый элемент является
объединением нек-рых главных элементов. Полная
решетка М наз. модулем над мультипли-
мультипликативной решеткой L, если для любых X?L
?М определено произведение Ха?М, причем
la=a, 0La = 0M,
(здесь >.ь Х.2, ha?L, а, а„ ?М, 1 —наибольший элемент
L в и Oi, Од; — нули решеток L и М соответственно).
Наиболее изученный класс М. р.— нётеровы решет-
решетки. Здесь можно выделить следующие направления.
1) Вопросы представления нётеровой решетки как ре-
решетки идеалов подходящего нётерова кольца (известно,
что решетка идеалов любого нётерова кольца — нё-
нётерова, однако существуют нётеровы решетки, к-рые
нэ могут быть даже вложены в решетку идеалов нёте-
нётерова кольца [3]). 2) Изучение нётеровых модулей над
М. р. 3) Изучение понятий и свойств, к-рые переносят-
переносятся на нётеровы решетки из теории идеалов нётеровых
колец (понятия простого и примарного элементов, раз-
размерности, собственного максимального элемента, полу-
полулокальной и локальной решетки). Описаны [4] дист-
дистрибутивные регулярные локальные нётеровы М. р. По-
Построена теория локализации и ассоциированных про-
простых элементов для гораздо более широкого, чем нёте-
нётеровы, класса М. р., включающего в себя решетки иде-
идеалов произвольных коммутативных колец.
Лит.: [1] Б у р б а к и Н., Коммутативная алгебра, пер.
с франц., М., 1971; [2] D i I w о г t h R. P., «Pacific J. Math,»,
1962, v. 12, p. 481—98; [3] В о gar t K., «Proc. Amer. Math.
Soc», 1969, v. 22, Mi 1, p. 129—33; [4] e г о ж е, «Mich. Math.
J.», 1968, v. 15, № 2, p. 167 — 76; 1969, v. 16, № 3, p. 215—23;
[5] Фофанова Т. С, в сб.: Упорядоченные множества и
решетки, в. 3, Саратов, 1975, с. 22 — 40. Т. С. Фофанова.
МУЛЬТИПЛИКАТИВНАЯ СИСТЕМА — ортонорми-
рованная на [а, Ь] система функций {ф,,0г)), удовлетво-
удовлетворяющая условиям:
1) вместе с двумя функциями q>k(x) и q>i(x) система
{фп(ж)} содержит и их произведение q>n(x) = <fk(x)q>i(x);
2) вместе с каждой функцией фд.(г) система {<fn(x)}
содержит и функцию <pm(x)=l/<pf,(x).
Примеры М. с: показательная система
{ег2Япх\п=-оо, ортогональная на отрезке [0, 1], Уолта,
система функций.
Лит.: [1] К а ч м а ж С, Штейн гауз Г., Теория орто-
ортогональных рядов, пер. с нем., М., 1958, с. 459—74; [2J Наг-
muth H., Transmission of information by orthogonal functions,
2 ed., В.— N. Y., 1972; [3] Applications of'Walsh functions. 1971.
Proc. of the symposium [National technical information service],
Wash., 1971. А. В. Ефимов.
МУЛЬТИПЛИКАТИВНЫЙ ИНТЕГРАЛ — предел
произведений вида
П =/ (Sn)(sn-Sn-l)eA(sn-l)(sn-l-Sn~2)^eA{s1)(s1-s0)t
где A (s) — непрерывная на отрезке \а, Ь] функция со
значениями в пространстве ограниченных операторов
в банаховом пространстве Е, Л — разбиение отрезка
[а, Ь] точками so=a, sb ... , sn=-b. Предел берется, когда
диаметр разбиения |Л|—>-0 и обозначается
\ exp A (s) ds.
J a
Если операторы A (t) коммутируют при различных t, то
7б
\ exp A (s) ds=e
М. и. является удобной формой представления эволю-
эволюционного оператора U(t, г) для дифференциального
уравнения Х=А (t)X (см. [1]). При этом
U (t, т)=^ A(s)ds. A)
Произведение, пределом к-рого является последний
М. и., также является эволюционным оператором для
уравнения с кусочно постоянным оператором A (t)=
= 4 (sk) при sft<
Если A (s) и В (s) — две непрерывные оператор-функ-
оператор-функции, то справедлива формула
--= lim п" /(s*Ms*-s*-i)eB(s*)(s*-s*-i) {2)
I Л|0 *=1
где знак ^ над произведением означает, что множители
с меньшими номерами пишутся правее множителей с
большими.
Формулы A), B) допускают обобщения на нек-рые
классы дифференциальных уравнений с неограничен-
неограниченными оператор-функциями, откуда получаются пред-
представления решений дифференциальных уравнений с ча-
частными производными параболического и шрёдингерова
типов в виде интегралов по траекториям (континуаль-
(континуальных интегралов) (см. [2]).
Формулы типа B) лежат также в основе нек-рых чис-
численных методов решения уравнений.
Если / B) — скалярная непрерывная функция, а
F (t) операторнозначная непрерывная функция ограни-
ограниченной вариации, то существует предел
lim ПП ef<s*> С М-" (**->» = \bexV <f (t)dF(t)),
наз. мультипликативным интегралом
Стилтьеса. Эти интегралы нашли применение в
теории /-нерастягивающих матриц и операторов (см.
[3], [4]).
Лит.: [1] Далецкий 10. Л., Крейн М. Г., Устой-
Устойчивость решений дифференциальных уравнений в банаховом
пространстве, М., 1970; [2] Далецкий 10. Л., «Успехи
матсм. наук», 1962, т. 17, в. 5, с. 3—115; [31 П о т а п о в В. П.,
«Тр. Моск. матем. оС-ва», 1955, т. 4, с. 125—236; [4] Г и н з-
бург Ю. П., «Матем. исследования», (Ниш.), 1967, т. 2, № 2,
с. 52—83. С. Г. Крейн.
МУЛЬТИПЛИКАТОР ГРУППЫ, представлен-
представленной в виде факторгруппы FlR свобод-
свободной группы F,— факторгруппа
где F' — коммутант группы F, a [R, F] — взаимный
коммутант R и F. Мультипликатор группы не зависит
от способа представления группы в виде факторгруппы
свободной группы. Он совпадает со второй группой го-
гомологии группы FlR с целочисленными коэффициен-
коэффициентами. При изучении М. г. важным является вопрос о
его нетривиальное™. А. Л. Шмелъкин.
МУЛЬТИПЛИКАТОРЫ первого и второго
рода — собственные значения монодромии оператора
канонич. уравнений.
В комплексном гильбертовом пространстве уравне-
,ния вида x~iJH{t)x, где / и Н(?) — самосопряженные
операторы, /2=/ и Н(t) периодичен, наз. канони-
каноническими. В конечномерном случае собственные
числа оператора монодромии U(Т) для этого уравнения
наз. мультипликаторами. Если все решения
канонич. уравнения являются ограниченными на всей
оси (уравнение устойчиво), то М. лежат на единичной
окружности. Если рассмотреть канонич. уравнение ж—
= ikJH (t)x с действительным параметром, то все М.
делятся на две группы: М. 1-го B-го) рода, к-рые дви-
движутся против (по) часовой стрелке при увеличении па-
параметра X.
Канонич. уравнение наз. сильно устойчи-
в ы м, если оно устойчиво и остается устойчивым при
достаточно малых вариациях оператора Н (t). Для силь-
сильной устойчивости необходимо и достаточно, чтобы все М.
лежали на единичной окружности и чтобы не было сов-
совпадающих М. разного рода.
Теория М. 1-го н 2-го родов позволила получить
ряд тонких признаков устойчивости и оценок зон устой-
устойчивости д.* канонич. уравнений. В терминах М.
проведена гоиотопич. классификация устойчивых и не-
неустойчивых канонич. уравнений.
Лит.: [1] Д а л е ц к и й 10. Л., К р е й н М. Г., Устой-
Устойчивость решений дифференциальных уравнений в банаховом
пространстве, М., 1970; [2] Я к у б о в и ч В. А., Стар-
жив с в и й В. М., Линейные дифференциальные уравнения с
периодическими коэффициентами и их приложения, М., 1У72.
МУЛЬТИПОЛЯ ПОТЕНЦИАЛ — гармоническая
функция в области R"\{0} пространства R", п^2,
являющаяся частной производной какого-либо поряд-
порядка |т|^1 от главного фундаментального решения
уравнения Лапласа, т. е. функция вида
т\
In— при п = 2,
Пусть для краткости и=3; при ]т| = 1 потенци-
потенциалы диполей имеют вид
ж, cos a x2 cos В х3 cosv
где cos a, cos E, cos у — направляющие косинусы ра-
радиус-вектора точки наблюдения (а^, х2, х3). Функция
—xl/ri1 напр., истолковывается как потенциал диполя с
моментом 1 и осью Охг, то есть как предел при а —»- 0+
суммы ньютоновых потенциалов массы —1/2я, поме-
помещенной в точке (а, 0, 0), и массы 1/2а, помещенной в точ-
точке (— а, 0, 0); иначе эту функцию можно представить
себе как магнитный потенциал маленького магнита,
расположенного вдоль оси Охх в начале координат.
Аналогично, функции —xjr3 и —х3/г3 суть потенциалы
диполей с осями соответственно Охг и Ох3. Составляя
линейные комбинации этих функций, можно получить
потенциал произвольно ориентированного диполя с
любым моментам и.. При |т| = 2 имеют место к в а д-
руполей потенциалы, получаемые предель-
предельным переходом для определенных систем четырех
точечных масс, сумма которых всегда равна нулю,
и т. д.
Ньютонов потенциал U (хг, х2, х3) ограниченного тела
G плотности p=pEi Ц, ?)i расположенного так, что 0?G
можно разложить в ряд по М. п.
U(xu
X 2 JL , A)
где
— общая масса тела G, а коэффициенты
наз. при |m\ = 1 дипольными моментами,
при |m| = 2 — квадрупольнымп момен-
моментами и, вообще, при всех Iml^l — ы у л ь т и-
п о л ь н ы м и моментами. Ряд A) отличается от
разложения потенциала U(xit х2, х3) по сферич. функ-
функциям
и (г, в, *)=-4L
перегруппировкой членов, п члены ряда B) можно
также истолковывать как потенциалы специальным об-
образом ориентированных мультиполеи (см. [1]). Поэтому
коэффициенты qmi также часто наз. соответственно д и-
п о л ь н ы м и, к в а д р у п о л ь н ы м и и, вообще,
м у л ь т и п о л ь н ы м и моментами.
Разложения типа A) и B) применяются для описа-
описания и приближенного представления скалярных или
векторных потенциалов не только в связи с фундамен-
фундаментальным решением уравнения Лапласа, но и уравнения
Гельмгольца (см. [2]).
В гидродинамике плоских течений идеальной несжи-
несжимаемой жидкости находят также применение комплекс-
комплексные М. п. вида
где z — комплексное переменное, ц. и а — соответст-
соответственно момент и угол ориентации мультиполя. Получаю-
Получающийся при т=\, ц.= 1 и а=0 днпольный потенциал ис-
истолковывается как предел при а —>- О-j- суммы комплекс-
комплексных потенциалов источника мощности 1 в точке z=
= а>0 и стока мощности 1 в точке z=—а. Разложению
A) здесь соответствует разложение комплексного по-
потенциала скоростей потока, обтекающего плоское тело
G, в окрестности бесконечно удаленной точки:
тл °° .. Jam
При этом действие обтекаемого тела G заменяется сум-
суммарным действием М. п., помещенных в начале коорди-
координат (см. [3]).
Лит.: [1] М о р с Ф. М., Ф е ш б а х Г., Методы теорети-
теоретической физики, пер. с англ., т. 2, М., 1960; [2] Д ж е к с о н Д ж.,
Классическая электродинамика, пер. с англ., М., 1965; [31 Мил н-
Т о м с о н Л.-М., Теоретическая гидродинамика, пер. с англ.,
М., 1964. Е. Д. Солпменцев.
МУРА ПРОСТРАНСТВО — топологическое простран-
пространство М с единственной нетривиальной приведенной
группой гомологии
Hk(M) = G, Н;(М)= 0, гфк.
Если К (Ж, п) — Эйленберга — Маклейна пространст-
пространство группы Ъ целых чисел, а Мk(G) — М. п. с
Hk(Mk(G))=G, то
lim \y\N + kX, K(Z, N + n)AMk(G)~\=H"{X, G),
т. е. {К(%, n)aM^G)} — спектр теории когомологий
//*( , G). Это позволяет распространить понятие кого-
когомологий с произвольными коэффициентами на обобщен-
обобщенные теории когомологий. Для любого спектра Е спектр
EaM)i(G) определяет теорию когомологий (Е AMk(G))*,
наз. теорией Е*-к ого молот и й с груп-
группой коэффициентов G. Для определения
обобщенных теорий гомологии с коэффициентами в
группе G используется т. н. к о - М у р а простран-
пространство Mk(G), характеризуемое равенствами
Напр., группа л,-(Х; G) = [Mk(G), X] наз. гомото-
гомотопической группой пространства X
с коэффициентами bG. Однако пространство
Mk(G) существует-не для всех пар (G, к). Если группа G
конечно порождена, то Mk(G) существует.
Лит.: [1] М о о г е J. С, «Ann. Math.», 1934, v. 59, MS 3,
p. 549 — 57. А. Ф. Ха-ршиладзе.
МУФАНГ ЛУПА — лупа, в к-рой выполняются сле-
следующие (эквивалентные между собой) тождества:
x(y-xz) = (xy -x)z,
(zx-y)x=z{x-yx),
ху •zx=x (yz -x).
.(in .ivnbi были введены и изучены Р. Муфанг [1]. Она,
в частности, доказала следующую теорему, показываю-
показывающую близость этого класса луп к группам: если три
элемента а, Ь, с М. л. связаны ассоциативным соотно-
соотношением ab-c=a-bc, то они порождают ассоциативную
подлупу, т. е. группу (теорема Муфанг). След-
Следствием этой теоремы является диассоциатив-
н о с т ь М. л., т. е. любые два элемента лупы порож-
порождают ассоциативную подлупу.
Для коммутативных М. л., к-рые определяются
одним тождеством
i2 -yz=xy-xz,
верна следующая теорема: всякая коммутативная М. л.
с п образующими центрально нильпотентна класса
нильпотентности не более п—1 (см. [2]). Центральная
нильпотентность определяется аналогично нильпотент-
нильпотентности в группах.
Если нек-рая лупа изотопна М. л., то она сама есть
М. л., т. е. свойство быть М. л. универсально. Более
того, изотопные коммутативные М. л. изоморфны.
Лит.: [1] М о u f a n к R., «Math. Ann.», 1935, Bd 110,
S. 416—30; [2] В г и с k R. H., A survey of binary systems,
В.— Hdlb.— Gott., 1958. ' В. Д~. Белоусов.
МЮНЦА ТЕОРЕМА, теорема о полноте
системы степеней {х к} на отрезке
[а, Ь], 0<а<6<оо: пусть 0<\1<\2<... ; для того чтобы
для любой функции f{x), непрерывной на [а, Ь], и лю-
любого е>0 нашлась линейная комбинация
такая, что
||/ — р\\ = max \f(x) — P(x)\<e,
ъ а< х < b
необходимо и достаточно, чтобы выполнялось условие
В случае отрезка [а, Ь], а,—0, к системе {х *} при-
присоединяют единицу и для полноты пополненной системы
условие (*) остается по-прежнему необходимым и дос-
достаточным. Условие а~^0 существенно: так, система
fz2*}?¦=(, (для нее выполняется условие (*)) не полна на
[ — 1, 1] (нечетную функцию нельзя приблизить с любой
точностью комбинацией четных степеней).
Условие (*) необходимо и достаточно для полноты
{х *}, —1/р<).1<Я2<...,на[а, Ь], о>0, в метрике Lp,
р>1, т. е. чтобы для каждой функции f(x)?Lp(a, Ъ)
и любого е>0 пашлась линейная комбинация Р (х) та-
такая, что
1/р
\f-Ph =
p
< г.
Теорема получена X. Мюнцем [1].
Лит.: [1] Miintz H., Approximationssatz von Weierstrass
[Festschrift H. A. Schwarz], [В.], 1914; Г2] A x и е з е р Н. И.,
Лекции по теории аппроксимации, 2 изд., М., 1965.
А. Ф. Леонтьев.
МЯГКИЙ ПУЧОК — пучок множеств ff" на тополо-
гич. пространстве X, любое сечение к-рого над нек-рым
замкнутым подмножеством в X может быть продолжено
до сечения пучка JT над всем X. Напр., М. п. являются:
пучок ростков разрывных сечений произвольного пучка
множеств на X; любой вялый пучок ?f~ на паракомпакт-
ном пространстве X; любой тонкий пучок §~ абелевых
групп на паракомпактном пространстве X. Свойство
мягкости пучка ff" на паракомпактном пространстве X
локально: пучок JT является М. п. тогда и только тогда,
когда любая точка х ?Х обладает такой открытой ок-
окрестностью U, что ,f | U — М. п. на U. М. п. на параком-
паракомпактном пространстве индуцирует М. п. на любом замк-
замкнутом (а если X метризуемо, то и на любом локально
замкнутом) подпространстве. Пучок модулей над М. п.
колец является М. п.
Если
— точная последовательность М. п. абелевых групп на
паракомпактном пространстве X, то соответствующая
последовательность групп сечений
тоже точна. Когомологии НР(Х, <|р) любого М. п. Jp
абелевых групп на паракомпактном пространстве X
тривиальны при р>0.
Лит.: [1] Г о д е м а н Р., Алгебраическая топология и тео-
теория пучков, пер. с франц., М., 1961: [2] У э л л с Р., Дифферен-
Дифференциальное исчисление на комплексных многообразиях, пер. с
англ., М., 1976. А. Л. Онищик.
НАБЛЮДЕНИЙ ОБРАБОТКА — применение к ре-
результатам наблюдений математич. потопов для построе-
построения выводов об истинных значениях искомых величин.
Всякий результат наблюдении, связанных с измерения-
измерениями, содержит ошибки (погрешности) различного проис-
происхождения. По своему характеру ошибки делятся на три
группы: грубые, систематические и случайные (о гру-
грубых ошибках см. ст. Ошибок теория; в дальнейшем бу-
будет предполагаться, что наблюдения не содержат гру-
грубых ошибок). Обычно результат измерения У нек-рой
величины ц. считают случайной величиной; тогда ошиб-
ошибка измерения б = У—[х будет также случайной величи-
величиной. Пусть Ъ~ Еб —математич. ожидание ошибки.
Тогда
Величина Ь наз. систематической о ш и б-
к о й, а б— Ь — случайной о ш н б к о й; мате-
математич. ожидание б — Ъ равно нулю. Снстематич. ошибка
Ь часто бывает известна заранее л в этом случае легко
устраняется. Напр., в астрономии при измерении вели-
величины угла между направлением на светило и плоскостью
горизонта систематич. ошибка является суммой двух
ошибок: систематич. ошибки, к-рую дает прибор при
отсчете данного угла (инструментальная ошибка) и
систематич. ошибки, обусловленной рефракцией, т. е.
преломлением лучей света в атмосфере. Инструмен-
Инструментальная ошибка определяется с помощью таблицы или
графика поправок для данного прибора; ошибку, свя-
связанную с рефракцией (для зенитных расстояний мень-
меньших 80°), достаточно точно можно вычислить теорети-
теоретически.
Влияние случайных ошибок оценивается с помощью
методов теории ошибок. Если У15 У2, ... , У„ — ре-
результаты п независимых измерений величины ц, про-
произведенных в одинаковых условиях и одинаковыми
средствами, то обычно полагают
ll~Y-b=[(Y1 + Y2+...+Yn)/n]-b, A)
где b — систематич. ошибка.
В том случае, когда требуется вычислить значение
нек-рой функции f(y) в точке j/=u, причем величина и.
оценивается по п независимым наблюдениям У1? У2, ...
... , У„, приближенно полагают
Ь). B)
Пусть В — математич. ожидание величины
Д = /(У_Ь)-/(A).
тогда _
Поэтому В — систематич. ошибка и (А—В) — случай-
случайная ошибка приближенного равенства B). Если слу-
случайные ошибки независимых наблюдений Уг, У2, ...
... , У„ подчиняются одному н тому же распределению
и функция / (у) в окрестности точки у = ц мало отличает-
отличается от линейной, то В~0 и
Аи/' (ц) F-Ь),
Где (§—ь) — арифметич. среднее случайных ошибок
исходных наблюдений. Это означает, что если
Ё(б,- — bJ = a2, i=l. 2, .... к.
то
Е (Д — By ~ ЕД2 я; [/' (|л)]2 о^/п —>- О
при п —*¦ оо.
В случае нескольких неизвестных параметров Н. о.
часто осуществляется с помощью метода наименьших
квадратов.
Если изучается зависимость между случайными ве-
величинами X и У на основе совокупности п независимых
наблюдений, каждое из к-рых есть вектор (X;, У,), г=
= 1, 2, ... , п, подчиняющийся исследуемому совмест-
совместному распределению величин X и У, то соответствую-
соответствующая Н. о. выполняется с помощью теории корреляции.
При Н. о. приходится делать нек-рые предположения
и допущения о характере функциональной зависимости,
о распределении случайных ошибок и т. д., поэтому
Н. о. должна включать в себя проверку согласия сде-
сделанных допущений с результатами использованных и
др. наблюдений. См. Статистических гипотез проверка.
Лит.; [1] Уиттекер Э., Робинсон Г., Математи-
Математическая обработка результатов наблюдений, пер. с англ., 2 изд.,
Л.— М., 1935; [2] Л и н н и к Ю. В., Метод наименьших квад-
квадратов и основы математико-статистической теории обработки
наблюдений, 2 изд., М., 1962. Л. Н. Большее.
НАВЬЕ — СТОКСА УРАВНЕНИЯ — основные урав-
уравнения движения вязкой жидкости, представляющие
математическое выражение законов сохранения импуль-
импульса и массы. Для неустановившегося течения сжимаемой
жидкости Н.— С. у. в декартовой системе координат
могут быть записаны в виде
du ~r dp . а Г /о da 2 ,.
р-т^-= X —g^~+~air I I1 ( 2-g^ 3~ diviv
du , dv \ . Э Г ( dw . Эи
dv v dp , д Г /„ dv 2 ,. \ 1
dv , dw \\ , a j f du_ j^_
dll < dx J I ' I \V
_9p_ , э (pu> , a (pp) , a (pw) „ I
dt "¦" dx ~*~ dy ' dz ~~ ' )
где w — вектор скорости с проекциями и, и, w на cooi
ветствующие оси координат х, у, %\ р — давление, р —
плотность, [г — коэффициент вязкости; X, У, Z — про-
проекции вектора массовой силы К на координатные оси;
-tj' =rj~\-iv grad w — субстанциональная производ-
производная. При выводе уравнений A) использован обобщенный
закон трения Ньютона, предполагающий, что для дви-
движущихся жидкостей и газов напряжения пропорцио-
пропорциональны скоростям деформаций. Для исследования сжи-
сжимаемых течений к уравнениям A) необходимо добавить
уравнение состояния, связывающее между собой дав-
давление, плотность и температуру, и уравнение энергии.
Уравнения A), составляющие основу гидродинамики,
впервые были получены Л. Навье [1] и С. Пуассоном [2]
на основе соображений о действии межмолекулярных
сил. Б. Сен-Венан [3] иДж. Г. Стоке [4] вывели эти урав-
уравнения, допуская только, что нормальные и касательные
напряжения линейно связаны со скоростями деформа-
деформаций.
Для течений несжимаемой изотермич. жидкости
(p=const) уравнения A) в векторной форме могут быть
представлены в виде
= K—grad/j + uAtt», I
При анализе Н.— С. у., как правило, рассматриваются
в безразмерной форме, к-рая получается путем отнесе-
отнесения всех величин, входящих в уравнения, к соответст-
соответствующим характерным величинам. Так, в случае стацио-
стационарных течений несжимаемой жидкости при отсутствия
массовых сил в Н.— С. у. появляется один определяю-
определяющий безразмерный параметр, наз. Рейнолъдса числом'
Re=pFJ/u=F//v,
где V и I — характерные скорости и линейный размер,
v — кинематическая вязкость.
Для исследования двумерных несжимаемых течений
часто используются Н.— С. у. в форме Гельмгольца:
as д-ф э| et at
A t
at "f" ду дх дх ду Re ^fc
где г|з — функция тока и Ъ, — вихрь связаны с проек-
проекциями скорости и и v следующим образом:
Основные краевые задачи для стационарных Н.— С-
у. связаны с исследованием течепий в замкнутых по-
полостях, каналах, течений со спободными поверхностя-
поверхностями, с обтеканием тел, течений в струях и следах за те-
телами. При этом интегрирование Н.— С. у. проводится
в областях (конечных или бесконечных), на границе
к-рых ставятся условия из соображений физич. харак-
характера (условия прилипания или скольжения на поверх-
поверхности тел, вдува или отсоса на проницаемых поверхно-
поверхностях, условия внешнего потока вдали от обтекаемого
тела, условия на свободной границе и др.). Для неста-
нестационарных задач помимо граничных условий должны
задаваться начальные условия.
Строгий математич. анализ разрешимости краевых
задач гидроаэромеханики для Н.— С. у. сжимаемого
газа отсутствует A982). Имеются нек-рые результаты
в математич. теории динамики вязкой несжимаемой жид-
жидкости (см. Гидродинамики математические задачи).
Первоначально усилия исследователей были направ-
направлены на отыскание точных решений. Напр., для несжи-
несжимаемой жидкости имеются точные решения для устано-
установившихся течений: в плоском канале при заданном
постоянном перепаде давления (течение П у а-
з ё и л я); между двумя параллельными плоскими стен-
стенками, одна из к-рых покоится, а другая движется в
своей плоскости с постоянной скоростью (течение
К у э т т а); в прямолинейной трубе с круглым попереч-
поперечным сечением при постоянном перепаде давления (т е-
чение Хагена — Пуазёйля). Найдены так-
также нек-рые автомодельные решения, среди них: плоско-
плоскопараллельное (и осеснмметричное) течение вблизи кри-
критической точки (течение X о у а р т а); течения в
суживающемся и расширяющемся каналах (течение
Г а м е л я).
Приближенные решения Н. — Су. ос-
основаны на упрощающих предположениях. Здесь еле-
дует отметить решения при очень малых числах Рей-
нольдса (Re<;l), соответствующие так наз. ползущим
движениям, среди к-рых наиболее известно течение
С т о к с а около шара. Предельный случай очень боль-
больших чисел Рейнольдса приводит к теории гидродинами-
гидродинамического пограничного слоя. Уравнения пограничного
слоя позволили решить большой круг практически важ-
важных задач на основе широко разработанных приближен
ных и численных методов.
Для решения нек-рых классов задач динамики вязких
жидкостей и газов разработаны достаточно эффектив-
эффективные алгоритмы, основанные на использовании разност-
разностных схем. Напр., для задачи расчета ламинарных те-
течений вязких несжимаемых жидкостей в областях про-
простой формы (или около тел простой формы). Наиболь-
Наибольшее распространение здесь получили разностные мето-
методы для уравнений в форме C), хотя для этой системы
и имеются трудности, связанные с определением гра-
граничных условий для ?. Первые результаты по решению
стационарного варианта системы C) были получены с
помощью простейших явных пятиточечных схем и ите-
итерационных методов (см. [6]). Решение стационарных
задач динамики вязкой несжимаемой жидкости большей
частью основано на использовании метода установления
и применении явных и неявных схем для системы C).
Среди явных схем используются двухслойные по време-
времени схемы с симметричной аппроксимацией первых про-
производных центральными разностями и решением второ-
второго уравнения из C) на каждом временном слое с по-
помощью метода Зейделя, а также трехслойная схема,
в к-рой конвективные члены аппроксимируются по
схеме «крест», а диффузионные — по схеме Дюфорта —
Френкеля. С помощью уже этих схем были получены
нек-рые результаты при решении стационарных задач
о ламинарных двумерных течениях в суживающемся и
расширяющемся каналах, в прямоугольной выемке с
движущейся крышкой, а также нестационарной задаче
обтекания в канале плоской пластины, расположенной
перпендикулярно к направлению потока.
Неявные схемы, как правило, основаны на примене-
применении метода дробных шагов (см. [8]). Общая структура
таких схем для уравнения C) может быть представлена,
напр., в виде
0,5a
0,5a
'
где Ai|, Lag, Li$, L2^ — разностные одномерные опе-
операторы:
¦¦s — б.г-2 бг/ бх ' L'2s — ев* т" их бу '
В этих формулах т — временной шаг, а — итерацион-
итерационный параметр, s, s-r1/^, s+1 — итерационные индексы
при решении уравнения Пуассона из C) на (ге+1)-
6" б2 6
временном слое итерационным методом; т-^ , т-; , т- ,
в
т разностные операторы, аппроксимирующие со-
соответствующие вторые и первые производные. Первое
уравнение из C) используется для нахождения значе-
ний |, а второе — значений тр на последующем времен-
временном слое. Аппроксимация вторых производных, как
правило, симметричная, а аппроксимация первых про-
производных в уравнении для | проводится или симмет-
симметричными разностями, или односторонними разностями
против потока с учетом знака скорости. Хорошо заре-
зарекомендовала себя схема в [9] с применением монотонной
аппроксимации (см. [10]). Эта схема для первого урав-
уравнения C) имеет вид
и-\и\ F1 у
\ D)
~ Re | , . \u\h6x* ' ' . \v\l 6j/2 1 ' j
/
где h и I — шаги сетки по х и г/,
tfi +1 _
v 6jc У ~~ i
Разностные уравнения D) обычно приводятся к трех-
диагональному виду и совместно с соотношениями,
аппроксимирующими граничные условия, решаются
методом прогонки. При решении стационарных задач
методом установления может применяться либо пооче-
поочередное решение уравнений D) (без внутренних итераций
для определения г|з), либо одновременное решение соот-
соответствующих уравнений из D) для совместного нахож-
нахождения \ ия|з с помощью векторной прогонки. Трудности,
связанные с постановкой граничных условий для урав-
уравнений C), заключаются в том, что обычные граничные
условия прилипания на твердых стенках для Н.— С. у.
дают условия только для г|з. Для численного решения
уравнения для Ъ, формально требуют граничные усло-
условия для вихря. Эти условия могут быть получены на
каждом временном слое либо приближенно на границе
области, либо путем интегрирования уравнения для |
только в области, расположенной внутри основной об-
области интегрирования [9].
Для исследования двумерных течений уравнения в
форме B) используются реже и, как правило, с некото-
некоторой регуляризацией уравнения неразрывности. Вариа-
Вариационно-сеточные методы, и в частности метод конечных
элементов, нашли свое применение для решения уравне-
уравнений динамики вязкой жидкости в форме B) и C).
С помощью разностных методов исследовались разно-
разнообразные задачи течения вязких несжимаемых жидкос-
жидкостей. Среди них задачи обтекания эллиптического и кру-
кругового цилиндра (в том числе вращающегося), пластины
конечной толщины (в том числе под углом атаки), ци-
линдрич. торца, капли, плоской ступени п др. Изуча-
Изучались также течения в каверне, в плоском и цилпндрич.
канале, в канале с препятствиями на стенках, течения
со свободной поверхностью, течения естественной, вы-
вынужденной и смешанной конвекции.
Применение разностных методов для расчета течений
вязкого сжимаемого газа на основе полных Н.— С. у.
сопряжено с нек-рыми дополнительными трудностями
по сравнению с расчетами течений несжимаемой вязкой
жидкости. Это связано с тем, что в течениях сжимаемого
газа существуют не только области пограничных слоев,
но и другие области больших градиентов искомых функ-
функций, к-рые соответствуют ударным волнам и волнам
разрежения в невязких течениях газа. Сложность самой
системы Н.— С. у. для сжимаемого вязкого газа предъ-
являет повышенные требования к быстродействию и
памяти ЭВМ. Использование явных схем в этом случав
приводит к более простым алгоритмам. Примером явной
схемы, хорошо зарекомендовавшей себя для расчета
стационарных течений методом установления, является
схема, к-рая для простого модельного уравнения с по-
постоянными коэффициентами
может быть записана в виде
11+ 1 II 11 11+ X
т+ 1 т т+\ т—1 ,
' Т. =а 2Й И h> - ~ ¦
Эта схема аппроксимирует E) на гладком установив-
установившемся решении с порядком O(h-) и устойчива при т<
<Jila. Условие устойчивости не зависит от v. Это озна-
означает, что при применении этой схемы к Н.— С. у. усло-
условие устойчивости не зависит от числа Рейнольдса. Тем
не менее ограничение на итерационный шаг по времени
для явных схем является существенным. Неявные схе-
схемы, как правило, не обладают такими ограничениями
и абсолютно устойчивы для соответствующих линейных
уравнений с постоянными коэффициентами. Неявные
схемы для расчета двумерных течений вязкого газа
используются в сочетании с методом дробных шагов.
Построены A982) различные разностные схемы метода
переменных направлений: с полной и неполной аппрок-
аппроксимацией на промежуточных слоях, дивергентные и не-
недивергентные (см. [11]), схемы повышенного порядка
точности (выше второго) относительно шагов сетки по
пространству (см. [12]). Численное моделирование те-
течений вязкого газа на основе Н.— С. у. связано с рас-
расчетом течений сложной структуры и с использованием
достаточно подробных сеток, что невозможно в силу ог-
ограниченности памяти ЭВМ без применения метода вза-
взаимно перекрывающихся областей (см. [13]). Разностные
методы решения Н.— С. у. применялись для исследова-
исследования большого числа задач динамики вязкого газа. Сре-
Среди них задачи — сверхзвукового обтекания затуплен-
затупленных тел (сферы, торца кругового цилиндра), составных
тел (сфера — конус, сфера — цилиндр), клина, перед-
передней кромки плоской пластины. Рассмотрены также те-
течения в следах за телами конечных размеров, течения
в соплах и воздухозаборниках, течения в полости при
внешнем до- и сверхзвуковом потоке, исследовалось
взаимодействие пограничного слоя с ударной волной,
структура ударной волны в плазме и др. задачи. Пере-
Перечисленные течения предполагались, как правило, лами-
ламинарными.
Лит.: [1] N а v i е г, «Mem. Acad., sci.», 1827, t. 7, p. 375—94;
[2] Poisson S. D.,«J. Ecole polytechn.», 1831, t, 13, p. 1—174;
[3] Saint-V e n a n t, «C. r. Acad. sci.», 1843, t. 17; [4] S t о k e s
G. G., «Trans. Carabr. Phil. Soc», 1849, v. 8, p. 287 — 319; [5]
Шлихтинг Г., Теория пограничного слоя, пер. с нем., М.,
1974; [6] Т о м А., Э й п л т К., Числовые расчеты полей в тех-
технике и физике, пер. с англ., М.— Д., 1964; [7] Б р а и л о в-
с к а я И. Ю., Кускова Т. В., Чудов Л. А., в кн.:
Вычислительные методы и программирование, в. 11, М., 19C8,
с. 3—18; [8] Я н е н к о Н. Н., Методы дробных шагов решения
многомерных задач математической физики, Новоеиб., 1967;
[9] Л о л е ж а е в В. И., Г р я з н о в В. Л., «Докл. АН СССР»,
1974, т. 2J9, Л"» 2, с. 301—04; [10] Самарский А. А., «Ж.
вычисл. матем. и матем. физики», 1965, т. 5, с. 548—51; [11]
КовеняВ. М., ЯненкоН. Н., Метод расщепления в за-
задачах газовой динамики, Новоеиб., 1981; [12] Толстых А. II.,
«Ж. вычисл. матем. и матем. физики», 1978, т. 18, № 1, с.
139—53; [13] Ко.кошинскаяН. С, Павлов Б. М.,
Пасконов В. М., Численное исследование сверхзвукового
обтекания тел вязким газом, М., 1980: [14] Темам Р., Урав-
Уравнения Навье — Стокса. Теория и численный анализ, пер. с
англ., М., 1981; [15] Численное исследование современных за-
задач газовой динамики, М., 1974; [16] Роуч П. Д ж.. Вычи-
Вычислительная гидродинамика, пер. с англ., М., 1980; [17]
Beyret В., Tiviand H., «Lect. Notes Comput. Sci.»,
1974., Л"» 11, p. 160—84; [18.1 Burggraf О. R., «Lect.
Notes Phys.», 1976, [Л*« 59], p. 52—64. В. М. Пасконов.
НАГЕЛЯ ТОЧКА — точ-
точка пересечения прямых (см.
рис.), соединяющих вершины
треугольника с точками каса-
касания противоположных сторон
с внеописанными окружностя-
ми. Названа по имени X. На-
геля (Ch. Nagel, 1336). —^
А. Б. Иванов.
НАГРУЖЕННОЕ ИНТЕГ-
ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ —
интегральное уравнение, ко- /'
торое в одномерном случае имеет вид
Ф (х)—Х \ЬК-(х, s)ф (s) ds —
J О.
\21 i А** (x>$^ "p {sj]=f(x)> A)
где <p — искомая, / — заданная в [а, Ъ] непрерывные
функции, Sj?\a, b], /=1, ... , т,— заданные фиксиро-
фиксированные точки, К, К1 — заданные непрерывные в квад-
квадрате [a, b]X[a, Ь] функции. В том случае, когда
Ki (*, Sj) = afK (х, sj),
где а/—положительные постоянные, уравнение A)
можно представить в виде
К (х, s)<f(s) ds = f(x), х?[а, Ь], B)
где новый символ интегрирования от произвольной ко-
конечной интегрируемой функции г|з определяется по фор-
формуле (см. [1]):
= 5
Для уравнения B) остается в силе теория Фредголъма
уравнений, а также в случае симметричного ядра тео-
теория интегральных уравнений с симметричным ядром.
В случае многомерных Н. и. у. искомая функция мо-
может участвовать под интегралами, к-рые распростра-
распространены на многообразиях различных размерностей.
Напр., в двумерном случае Н. и. у. может иметь вид
г/)ф (у) Лгу + А^ГА (ж,
где D — нек-рая область на плоскости, Г — ее грани-
граница, у j — фиксированные точки, принадлежащие замк-
замкнутой области D U Г Это уравнение также можно за-
записать в обычной форме
Ф (*)—*. $$DUrA" (х' У) Ф (У) rfwy = / (*).
если соответствующим образом определить функцию К
и элемент объема duty (см [4]), причем и в этом случае
остается в силе теория интегральных уравнений Фред-
гольма.
Лит.: [1] К n e s e г A., «Rend. Circolo mat. Palermo», 1914,
t. 37, p. 1«9—97; [2] Lichtenstein L., «Studia math.»,
1931, t. 3, p. 212—25; [3] Г ю н т е р Н. М., там же, 193.S, t. 4,
р. 8—14; [4] Смирнов В. И., Курс высшей математики,
6 изд., т. 4, ч. 1, М., 1974. Б. В. Хвсделидзе.
НАДГРАФИК функции — подмножество в де-
декартовом произведении RXX, состоящее из точек (а,
х), лежащих «над» графиком функции / : X —>- R, опре-
определенной на нек-ром множестве X и принимающей зна-
значения в расширенной прямой R=R(j{—ooJLKt0};
Н. иногда наз. эпиграфом и обозначается epi /:
epi/ = {(«, x)?RxX\ }
Проекция Н. функции / на X наз. эффективной
областью /и обозначается dom /:
domf = {z?X\f(x) < + oo}.
Функция / наз. собственной, если
/ (х) > — оо, ух, и dom / =? 0.
Выпуклые функции f : X —>- R, определен-
определенные на векторном пространстве X, характеризуются
тем, что epi / — выпуклое подмножество в RXX;
замкнутые функции f : X —*¦ R, определен-
определенные на топологич. пространстве X, характеризуются
тем, что epi / — замкнутое множество.
И. М. Тихомиров.
НАДЕЖНОСТИ ТЕОРИЯ — инженерное направление
применений математич. методов, в к-ром разрабаты-
разрабатываются: а) приемы расчета надежности технпч. систем,
б) методы оценки надежности изготовленных изделий,
в) способы оптимизации и повышения эффективности
функционирования сложных технич. систем и состав-
составляющих их элементов в процессе эксплуатации (вклю-
(включая в это понятие также хранение и перевозку). В Н. т.
вводятся количественные показатели надежности на
основе построения соответствующих математич. моде-
моделей. При этом учитываются такие факторы, как назна-
назначение технич. системы, условия, в к-рых ей придется
работать, а также экономич. факторы. В Н. т. исполь-
используются разнообразные математич. методы, но особое
место среди них занимают теория вероятностей и мате-
математич. статистика. Это обусловлено тем, что события,
описывающие количественные и качественные показа-
показатели надежности (отказ, длительность безотказной ра-
работы, длительность ремонта, стоимость восстановления
и т. п.), случайны. Широкое применение находят также
методы теории оптимизации, математич. логики и др.
Понятие надежности включает в себя: 1) без-
безотказность, 2) долговечность, 3) приспособленность к
ремонту. Нередко, однако, решающее значение имеет
лишь первая характеристика. Так, для всех технич.
устройств одноразового использования третье свойство
не требуется совсем.
Основным понятием Н. т. является понятие о т к а-
з а, т. е. постепенной или внезапной потерн устройст-
устройством работоспособности. Формализованное описание это-
этого понятия базируется на следующей общей схеме по-
построения математич. моделей Н. т. Предполагается, что
состояние технич. системы определяется точкой х в
фазовом пространстве Х= {х} состояний. Эволюция
состояний этой системы во времени описывается процес-
процессом x(t), вообще говоря, случайным. В X выделяется
подмножество Хо состояний, соответствующих наступ-
наступлению отказа. Безотказность — свойство сис-
системы непрерывно сохранять работоспособность. Коли-
Количественно безотказность измеряется временем от данно-
данного момента до момента попадания в Хо. Долговеч-
Долговечность — свойство технпч. системы сохранять рабо-
работоспособность с необходимыми перерывами для ремон-
ремонтов и технич. обслуживания при условии экономич. це-
целесообразности дальнейшей эксплуатации. Р е м о н-
топриспособленность технич. системы оп-
определяется удобством ее технич. обслуживания и про-
проведения ремонтных работ; количественно измеряется
затратами или же временем на поддержание технич.
системы в работоспособном состоянии.
Важнейшим количественным показателем надежности
является вероятность безотказной ра-
работы R (t) технич. системы в течение времени t, т. е.
вероятность того, что за время t процесс x(t) не достиг-
достигнет подмножества Хо. Функция распределения наступ-
наступления отказа до момента t равна /"(/)—1—R(t). Если
существует плотность распределения / (t)=F'(t), то
функция X(t) = f(t)lR (t) наз. функцией и н т е н-
сив и ост и отказа. Вероятностный смысл k(t)
состоит в том, что это есть условная плотность распре-
распределения отказа при условии, что техннч. система про-
проработала безотказно время t. Таким образом, k{t)dt
является вероятностью того, что система откажет в
промежутке времени (t, t-'rdt) при условии, что она не
отказала до момента t.
В Н. т. используются различные классы функций
R (t). Если —In R (t) есть выпуклая функция, то функ-
функция распределения наступления отказов наз. функцией
распределения с возрастающей интенсив-
интенсивностью отказа; класс таких функций распреде-
распределения обозначается ВФИ. Если же — In R (t) ость
вогнутая функция, то функция распределения наступ-
наступления отказа наз. функцией распределения с убы-
убывающей интенсивностью отказа; со-
соответствующий класс функций распределения обозна-
обозначается УФИ. В Н. т. используются и другие непара-
метрич. классы функций распределения, напр, класс
ВФИС (возрастающая функция интенсивности отказа
в среднем): для распределений этого класса функция
— Г' "
возрастает; класс НЛС (новое лучше старого): функции
распределения этого класса удовлетворяют условию
для любых t, s>0, т. е. распределение отказов при ус-
условии, что технич. система уже проработала время t
выше, чем безусловное. Это и означает, что для прора-
проработавшей технич. системы отказы поступают чаще, чем
для новой. Для нек-рых классов функций распределе-
распределения доказаны теоремы об инвариантности функции рас-
распределения наступления отказов при образовании опре-
определенных структур (последовательного или параллель-
параллельного соединения элементов и т. д.). Широкое примене-
применение в Н. т. находят модели, в к-рых функция R (/)
задается параметрически. В качестве функций распре-
распределения внезапных отказов часто используется экспо-
экспоненциальное распределение
F(t)=i — e-M, t > 0, F(t)=O, *<0,
распределение Вейбулла
F (t)=i — exp [— (at)P], t > 0, F @=0, t < 0,
и др.
Для увеличения надежности технич. систем исполь-
используются различные приемы: резервирование, профилак-
тич. осмотры и ремонты, эксплуатация при пониженных
нагрузках. Под резервированием понимает-
понимается метод повышения надежности путем введения избы-
избыточности того или иного рода — дополнительных эле-
элементом, узлов, устройств, к-рые не требуются для функ-
функционирования техннч. системы, дополнительного вре-
времени на выполнение работы, использование избыточной
информации и пр. В связи с этим рассматриваются
следующие типы резервирования: структурное (допол-
(дополнительные элементы), временное (дополнительное вре-
время), информационное, функциональное (использующее
способность элементов технич. системы выполнять до-
дополнительные функции), нагрузочное. Структурный
резерв может находиться в трех следующих состояниях:
а) ненагруженном, б) нагруженном, в) облегченном.
В нагруженном резерве резервный эле-
элемент несет такую же нагрузку, как и основной (рабо-
(рабочий), и интенсивность отказов резервного элемента та
же, что у основного. В ненагруженном ре-
резерве элемент совсем не несет нагрузки, что соответ-
соответствует отсутствию отказов. В облегченном ре-
резерве элемент несет нагрузку меньшую, чем основ-
основной, поэтому для него интенсивность отказов меньше,
чем для основного. Значительное увеличение надежно-
надежности дает восстановление отказавших элементов — ре-
резервирование с восстановлением.
Если элемент имеет один резервный, находящийся в не-
нагружепном состоянии, функция распределения дли-
длительности безотказной работы каждого из элементов
есть F(t), функция распределения длительности восста-
восстановления есть G(t), переключатели абсолютно надежны
и переключение на работу, на восстановление н в резерв
происходит мгновенно, то для длительности безотказной
работы дублированной системы (т. е. от начала работы
до момента, когда оба элемента окажутся в состоянии
отказа) имеет место формула
где
a=^xdF(x), y=^G(x)dF (x).
Исследование резервированных систем явилось источ-
источником ряда чисто математич. исследований — развитие
теории линейчатых и полумарковских процессов, пре-
предельных теорем для сумм случайного числа случайных
величин и др.
Профилактическое обслуживание
применяется в моменты, когда технич. система еще ра-
работоспособна, но имеется основание считать, что появи-
появилась повышенная вероятность отказа. Обычно задачи
профилактики связаны с решением вопросов оптими-
оптимизации: как выбрать моменты начала профилактич. об-
обслуживания, чтобы суммарные потери на проведение
профилактики и на ущерб от возможного отказа до мо-
моментов профилактик за данный промежуток времени Т
были минимальны; как организовать профилактич.
обслуживание, чтобы вероятность безотказной работы
за данный промежуток времени была максимальной
и т. д. Для нек-рых функций распределения длитель-
длительностей безотказной работы системы, в том числе для
всех распределений класса УФИ, профилактика не уве-
увеличивает среднего времени безотказной работы. У функ-
функций распределения класса УФИ X (t) является невоз-
растающей функцией. К ним, в частности, относится
функция распределения
F (x) = l — e-te, х > О, F (x)=0, z<0,
при любом постоянном А,>0. Ряд оптимизационных
задач возникает в связи с поиском неисправностей в
сложной системе: как производить поиск неисправно-
неисправности, чтобы затратить на ее обнаружение в среднем наи-
наименьшее время; в какой последовательности для этой
цели следует проверять работоспособность составляю-
составляющих систему узлов и элементов и т. д.
Существенное место в Н. т. занимают задачи получе-
получения статистич. выводов о функции распределения нас-
наступления отказа на основе данных о результатах стен-
стендовых испытаний. Простейшие математич. модели
стендовых испытаний следующие. Пусть
N — число ячеек для испытаний изделий. В процессе
испытаний отказавшие изделия не заменяются новыми
(класс испытаний Б) или заменяются новыми (класс
испытаний В). Продолжительность испытаний опреде-
определяется правилом остановки, напр, заданием предельно-
предельного времени испытаний Т, предельного числа г наблю-
наблюдаемых отказов и др. Существенной характеристикой
испытаний является суммарная наработка
S(t), т. е. сумма времен безотказной работы всех испы-
испытываемых изделий на интервале @, t). При испытаниях
по плану [МБ (г)] испытывают N изделий, к-рые
при отказах не заменяются новыми. Наблюдения про-
продолжаются до r-го отказа. По плану [NB(N)\ ис-
испытания продолжаются до отказа всех Лг испытывае-
испытываемых изделий, при использовании плана [NE (г, Т)]
Лг изделий иеиытываются до момента t=min(tr, T), где
tr — момент отказа r-го отказавшего объекта. По мо-
моментам отказов ti, ... , tr требуется проверить гипотезы
о виде функции распределения наступления отказа,
напр, о ее принадлежности классу ВФИ или УФИ и
др.; требуется оценить ее параметры. Для оценки функ-
функции интенсивности отказа используются методы полу-
получения изотонных оценок. При испытаниях по плану
[NE (г)] точечная несмещенная оценка параметра X
экспоненциального распределения имеет вид
где суммарная наработка
S (tr) = t1 + ... + tr+(N — r)tr.
Статистич. задачи стендовых испытаний разнообразны
и требуют привлечения таких разделов математич.
статистики, как теория оценивания и теория проверки
статистич. гипотез.
Осложняющим обстоятельством является зависи-
зависимость вероятности безотказной работы от режима е
проведения испытаний:
R(t)=R{t, г).
Более тяжелый режим (повышение температуры, ам-
амплитуды вибраций и т. п.) как бы приближает моменты
наступления отказов. Проблема пересчета показателей
надежности с одних режимов s на другие е* является
одной из актуальных задач Н. т. Применяются планы
испытаний, в к-рых режимы меняются с течением вре-
времени (примерами могут служить планы со ступенчатым
нагружением). Разрабатываются математич. модели
пересчета результатов ускоренных испытаний на нор-
нормальные режимы. Один из подходов к пересчету осно-
основан на гипотезе, согласно к-рой испытания в течение
времени tx в режиме sx эквивалентны испытаниям в ре-
режиме е,, если время t2 выбрано из условия R (гь 6])=
= Д(*2,"е2).
В Н. т. проводится расчет показателей функциони-
функционирования систем, составленных из компонент, не являю-
являющихся абсолютно надежными. Одна из задач — оценка
надежности системы по результатам стендовых ис-
испытаний компонент. Пусть система представлена в виде
последовательной цепочки компонент разных типов
(резервирования нет). Тогда нижняя 7"ДовеРительная
граница вероятности безотказной работы системы R{t),
все компоненты к-рой испытывались время t и отказы
не наблюдались, совпадает с нижней 7~Д°веРительной
границей вероятности безотказной работы компонент
того типа, к-рые испытывались в наименьшем числе.
Одним из примеров оптимизации в Н. т. являются
задачи оптимального резервирования.
Пусть Rj(t) — вероятности безотказной работы элемен-
элементов i-го типа, x-t — их число. Вероятность безотказной
работы системы
Требуется подобрать такие числа xiy 2=1, 2, .-.. , m,
чтобы R (t) было максимальным и были выполнены не-
неравенства
к-рые трактуются как ограничения на суммарный вес,
объем, общую стоимость элементов и т. п.
Расчет количественных показателей надежности сис-
систем с учетом возможности восстановления отказавших
компонент во многом аналогичен расчету систем в мас-
массового обслуживания теории. Моментам поступления
заявок в систему соответствуют моменты отказов, а
длительностям обслуживания — длительности восста-
новления. Простейшая математич. модель соответствует
процессу восстановления (см. Восстановления теория).
Поскольку основные математич. модели Н. т., учиты-
учитывающие восстановление отказавших элементов, не до-
допускают явных аналитич. решений, в Н. т. интенсивно-
развивается направление, связанное с использованием
асимптотич. методов. При этом предполагается, что-
восстановление является «быстрым», т. е. заданные по-
показатели восстановления (напр., среднее время) стано-
становятся бесконечно малыми по отношению к аналогичным
показателям интервалов безотказной работы.
Лит.: [1] Б а р 3 и л о в и ч Е. Ю., Каштанов В. А.,
Некоторые математические вопросы теории обслужипания
сложных систем, М., 1971: [2] Б а р л о у Р., ПрошанФ.,
Математическая теория надежности, пер. с англ., М., 1969:
[3] Barlow R. В., Pros chan P., Statistical theory of
reliability and lifetesting: Probability models., N. Y., 1975;
[4] Г н е д е н к о Б. В., Беляев Ю. К., Соловь-
Соловьев А. Д., Математические методы в теории надежности, М.,
1965; L5] Коваленко И. Н., Исследования по анализу на-
надежности сложных систем, К., 1975; [6] К о з л о в Б. А.,
Ушаков И. А., Справочник по расчету надежности аппа-
аппаратуры радиоэлектроники и автоматики, М., 1975; [7]
Шор Я. Б., Статистические методы анализа и контроля каче-
качества и надежности, М., 1962. Ю. Н. Беляев, Б. В. Гневенко.
НАДЕЖНОСТЬ И КОНТРОЛЬ УПРАВЛЯЮЩИХ
СИСТЕМ, проблемы надежности управ-
управляющих систе м,— одно из направлений теории
управляющих систем, к-рое изучает управляющие сис-
системы, подверженные помехам.
Пусть U={C/} — нек-рый класс управляющих сис-
систем (у. с.) и пусть имеется источник помех, или источ-
источник неисправностей, к-рый, воздействуя на у. с. U,
переводит ее в у. с. Ult . . ., Ur из нек-рого класса 11'.
Если допустить, что источник помех может также сох-
сохранять у. с. неизменной, напр. U1=U, то Ш=1Г.
Пусть каждая у. с. из Ц' вполне определяется своей
схемой 2, тогда воздействие источника помех сводится
к воздействию на ее схему 2. Источник неисправностей
преобразует схему, что может проявляться: а) путем
нарушения работы элементов, т. е. изменением элемен-
элементов; б) путем изменения соединений элементов и т. п.
В результате действия источника неисправностей исход-
исходная схема 2 у. с. U переходит в «неисправные» состоя-
состояния Sj, ... , 2Г, где 2Х=2, определяющие соответст-
соответственно у. с. U1, ..., Uг. Пусть этим схемам соответствуют
функции Ф1т . . . , Фг, наз. также функциями
неисправностей (здесь Ф^Ф характеризует
функционирование у. с. U). Обычно источник неисправ-
неисправностей дополнительно характеризуется либо распреде-
распределением вероятностей ошибок, либо ограничениями на
возможное число элементарных неисправностей.
Проблемы надежности рассматриваются
в основном для трех классов у. с: схем из функцио-
функциональных элементов, контактных схем и автоматов.
Пусть U — класс схем из функциональных элемен-
элементов, принадлежащих данному базису Б, где Б = Б!иБ2
и Bt= {Flt ... , Fs}. В случае, если источник неисправ-
неисправностей воздействует только на элементы схемы, то он
преобразует элементы F; из Б3, г=1, ... , s, в элементы
с таким же числом входов, как н F,-, но, быть может, с
иным функционированием, а элементы из Б., оставляет
неизменными. Таким образом, В1 состоит из ненадеж-
ненадежных, а Б2 — из надежных элементов. В этом случае
источник можно характеризовать вероятностями pt, ...
..., ps выхода из строя соответственно элементов Flt ...
... , Fs. Напр., Б1 состоит из инверторов, конъюнкторов
и дизъюнкторов, а Б2 — из элементов голосования,
реализующих соответственно функции х, ж1&^2, хг\/х2-
и h(xj, хг, х3) = хгх%Vxjx3\yx2x3. При этом можно по-
положить, что Р1=Р2=7=Рз~Р — вероятность выхода из
строя элементов из Бг.
В случае, когда Д — класс контактных схем, рас-
рассматривают источник неисправностей, к-рый в каче-
качестве элементарных неисправностей дает либо короткое
замыкание контакта, либо разрыв контакта. При этом
дополнительно предполагают, что для контактных схем,
реализующих функции от п переменных, возможно
не более т(п) элементарных повреждений.
В проблематике Н. и к. у. с. можно выделить три
направления.
I. Построение надежных схем из ненадежных элемен-
элементов. Это направление развито для двух классов у. с:
контактных схем н схем из функциональных элементов.
В случае схем из функциональных элементов схема 2
характеризуется пек-рой вероятностью р тех случаев,
когда она функционирует неправильно. Здесь рассмат-
рассматривают два основных вопроса.
1) Какими свойствами должен обладать базис Б,
чтобы для любой булевой функции f(xlt ... , хп) и любо-
любого s>0 можно было построить схему 2, реализующую /
и такую, что вероятность р ее неправильной работы бьь
ла бы меньше е, т. е. каждая булева функция допускала
бы сколь угодно надежную реализацию.
Установлено, что существуют базисы, в к-рых для
любой функции возможна сколь угодно надежная реа-
реализация. Примером такого базиса является базис В
(см. выше): Б1 состоит из инверторов, конъюнкторов и
дизъюнкторов с вероятностью ошибки p<V3, а Б2 со-
состоит из абсолютно надежного элемента голосования.
Найдены необходимые и достаточные условия на базис
Б, при к-рых возможно построение сколь угодно надеж-
надежных схем для всех булевых функций.
2) Построение метода синтеза минимальных (или в
том или ином смысле близких к минимальным) схем,
реализующих булевы функции, ненадежность к-рых не
превосходит заданной величины 8. Оказывается (напр.,
для предыдущего базиса с p<V9), что можно построить
метод синтеза схем, к-рый для большинства булевых
функций и данного е дает асимптотически (по п) мини-
минимальные схемы. В частности, для функции Шен-
Шеннона L{n, г), выражающей минимальное число
элементов из Б (см. пример выше), достаточное для ре-
реализации любой булевой функции от п переменных с
ненадежностью, не большей е, получена асимптотика
\ on
L (п, е)~— "— .
II. Построение самокорректирующихся схем. Это на-
направление наиболее полно изучено для двух классов
у. с.— контактных схем и схем из функциональных эле-
элементов. Здесь источник неисправностей характеризует-
характеризуется ограничениями на число элементарных повреждений.
Считается, что в пределах рассмотрений дальнейших
изменении в схеме не происходит. Схема 2, роализую-
Xri щая функцию Ф, наз. само-
самокорректирующейся от-
относительно данного источника не-
неисправностей, если Ф, = Ф, г=1,
'. . ., г. Другими словами, само-
самокорректирующаяся схема функ-
функционирует правильно, несмотря
на воздействие источника неис-
неисправностей. Напр., контактная
схема на рис. 1, реализующая функцию Xjx2\/ x^gV х2х3,
является самокорректирующейся относительно источ-
источника, вызывающего не более одного разрыва контакта.
Основными задачами этого направления являются:
1) выяснение условий, при к-рых существуют самокор-
самокорректирующиеся схемы, и 2) разработка методов синтеза
минимальных (пли в том или ином смысле близких к
минимальным) самокорректирующихся схем. Ниже
показано решение этих задач на примере контактных
схем с источником неисправностей, вызывающим не
более т(п) замыканий и разрывов.
Оказывается, что для любой булевой функции / (а^, ...
... , хп) можно построить самокорректирующуюся от-
носительно этого источника неисправностей схему. Для
этого достаточно взять любую контактную схему 2,
реализующую /, и в ней каждый контакт ха заменить
на подсхему, состоящую из т+1 последовательно сое-
соединенных одинаковых блоков, каждый из к-рых яв-
является параллельным соединением т-\-1 экземпляров
данного контакта ха . Такую схему наз. тривиаль-
тривиальной самокорректирующейся схемой.
Построенная самокорректирующаяся схема будет в
(т+1J раз сложнее исходной. Предыдущий пример
(рис. 1) показывает, что существуют и нетривиальные
самокорректирующиеся схемы.
Задача построения самокорректирующихся схем —
специальная задача синтеза у. с. с дополнительными
требованиями. Главный результат здесь состоит в том,
что для большинства булевых функций /(хх, ... , хп)
можно построить самокорректирующуюся схему (отно-
(относительно нек-рого класса источников), сложность к-рон
асимптотически (при п->оо) равна сложности мини-
минимальной схемы, реализующей / без требования само-
самокоррекции. Здесь показано, что при нек-рых ограниче-
ограничениях на порядок роста т(п) имеет место следующая
асимптотика для функции Шеннона
Lm (n) ~ IT ¦
III. Контроль управляющих систем. Это направление
наиболее полно изучено для трех классов у. с: контакт-
контактных схем, схем из функциональных элементов и авто-
автоматов. Рассмотрение проблем контроля у. с. предпола-
предполагает: 1) наличие источника неисправностей, к-рый, со-
совершив воздействие на у. с, в течение нек-рого проме-
промежутка удерживает неисправное состояние исходной
у. с. и не производит других повреждений; 2) задание
цели контроля. Последняя определяется как распозна-
распознавание нек-рого свойства данной у. с. Напр., выяснение,
является ли данная у. с. исправной или нет (задача о
проверке), или, в случае, если у. с. неисправна, на-
нахождение неисправности (задача о диагностике); 3) фик-
фиксацию средств контроля. Контроль может происходить
либо без вмешательства в схему, либо допускается воз-
возможность вмешательства. Напр., замена элементов на
эталонные, перестановка однотипных блоков, исполь-
использование дополнительных контрольных точек в схеме
и т. п. Средства контроля включают в себя также про-
процедуру получения информации о контролируемом объ-
объекте. Ими являются эксперименты, к-рые делятся на
безусловные и условные. В безусловных экс-
экспериментах последовательности, подаваемые на
вход контролирующего устройства, определяются зара-
заранее и не зависят от последовательности на его вы-
выходе. В условных экспериментах каж-
каждый последующий символ входной последовательно-
последовательности может выбираться в зависимости от символов, по-
появившихся на выходе в предшествующие моменты
времени.
Совокупность экспериментов, позволяющая распо-
распознать данное свойство, наз. тестом. Так как обычно
существует много различных тестов, распознающих тре-
требуемое свойство, то на множестве тестов вводят меру
сложности и ищут тест, имеющий минимальную слож-
сложность. Основная задача состоит здесь в том, чтобы для
каждого свойства уметь строить минимальные или близ-
близкие к ним тосты. Эта задача является частью более общей
проблемы — построения компактных алгоритмов рас-
распознавания тех или иных свойств.
Проследим решение этих задач на примере контакт-
контактных схем и схем из функциональных элементов для слу-
случая, когда нет вмешательства в схему. Исходным пунк-
пунктом здесь являются функции неисправностей фь ... , Фг
схемы 2, реализующей ф, причем Ф1=Ф. При этом воз-
возможен случай Ф,'=Фу для нек-рых пар (г, /), что означа-
ет неразличимость i-й и /-й неисправностей. Таким об-
образом, множество функций {Ф,} разбивается на классы
эквивалентности фь ... . фг такие, что Ф,- и Фу принадле-
принадлежат одному классу тогда п только тогда, когда ф,=фу,
причем Фг принадлежит классу (pt. Неисправности,
приводящие к функциям из одного класса, неразличи-
неразличимы. Классы ф!, ... , ф; приводят к таблице функций
неисправностей.
При м е р. Контактная схема (рис. 2) реализует
функцию
источник помех вызывает не более одного разрыва.
Здесь Ф!=Ф2, Ф;)=Ф4., Ф5=Фб, Ф7=Фв, Фэ=Фю " Фц=
=Ф12. Таким образом, имеем семь классов: ф1={Ф},
= {Фц, ®iz}, к-рые дают
таблицу функций неис-
неисправностей (см. табли-
таблицу). Свойство, подлежа-
подлежащее распознаванию,
обычно задают через под-
подмножество ЧЯ пар (i, /) но-
номеров классов функций
неисправностей, к-рые требуется отличать. Если, напр.,
91= {A, i)}, *=2, ... , /, то свойство выражает отличи-
отличимость исправной схемы от любого неисправного состоя-
состояния (задача проверки). Если ЭД= {(;, /)}, 1Ф), 1<?г, \<Х,
то требуется уметь отличать каждое состояние схемы от
любого другого (задача о диагностике). Наконец, если
9J={(i, /')} и 1<j<Z0</<:Z, то имеют дело с задачей о
диагностике «блока», т. е. с задачей выяснения, в какой
части схемы находится поврежденный элемент.
Рис.
Наборы
e-i
е
е
е
е
е
е
е8
001
011
010
no
100
101
000
111
1
1
1
1
1
1
0
0
Фг
0
0
1
1
1
1
0
0
фа
1
0
0
1
1
1
0
0
1
1
0
0
1
1
0
0
ф5
1
1
1
0
0
1
0
0
ф8
1
1
i
1
0
0
0
0
'¦Р;
0
1
1
1
1
0
0
0
Пусть {е1, ... , efc} — множество наборов, на к-рых
определены функции (plt ... , ф(. Совокупность наборов
Т= {е} из {еи ... , ek} наз. тестом для данной таб-
таблицы функций неисправностей отно-
относительно подмножества 5R, если для любой пары (i, j)
из 91 существует набор е из Т такой, что Ф;(е)=»^<Р/(е).
Тест Т наз. минимальным, если он содержит
наименьшее число наборов. Тест Т наз. т у и и к о-
в ы м, если при удалении любого набора е из Т полу-
получается подмножество наборов, не являющееся тестом.
Множество {е1, ... , е^} является тестом (тривиальным
тестом). Минимальный тест является тупиковым. Про-
Проблема нахождения минимального теста связана с необ-
необходимостью сокращения времени контроля.
Существует алгоритм для нахождения всех тупико-
тупиковых (значит и Минимальных) тестов. Пусть {е[',... ,
ev(i, ;')}— множество всех наборов, на к-рых отличают-
отличаются ф,- и фу. Если в выражении
/
совершить умножение по правилам булевой алгебры ir
затем удалить «поглощаемые» члены, пользуясь соот-
соотношением А&В\/А =А, то оставшиеся произведения
будут соответствовать тупиковым тестам. Так, если для
рассмотренного выше примера взять задачу проверки
«Я = {A,2), A, 3), ..., A, 7)},
то указанный алгоритм дает:
{e1we2) (e2ve3) (e3Ve4) (f4Ve5)'((-svc6!
V е2еяеьей.
Имеется пять тупиковых тестов: 7\= {eu е3, е5}, Т.г=
— \et, ei, ее}, ^з= {«1, е2, «4, «5}, ^4={еь ез, г4, г6}, ^5=
= {ег, е3, e5i еа}> пз к-рых Т1 и Г3 являются минималь-
минимальными. Описанный алгоритм может быть применен для
обнаружения ошибок при монтаже в соединениях эле-
элементов. Данный алгоритм с небольшими модификация-
модификациями годится также для построения тупиковых кратных
экспериментов для автоматов. Эффективность алгорит-
алгоритма построения тупиковых тестов резко падает с увели-
увеличением размеров таблицы функций неисправностей. По-
Повышение эффективности связано с учетом строения таб-
таблицы, а также с учетом информации о структуре схемы.
В этом направлении построена серпя[методов. Другие ас-
аспекты Н. и к. у. с. развиваются в рамках теории веро-
вероятностей.
Лит.: [1] Ч е г и с И. А., Я б л о н с к и й С. В., «Тр. Ма-
тем. ин-та АН СССР», 1958, т. 51, с. 270—360; [2] Соловь-
Соловьева А., Тесты, Новосиб., 1978; [3] ПотапевЮ. Г.,
Яблонский С. В., <.Докл. АН СССР», 1960, т. 134, J* 3,
с. 544—47; [4] Нейман Дж., в кн.: Автоматы, М-, 1956. с.
Ь8—139; |5] Мур Э. Ф., Шеннон К. Э., Кибернетический
сборник, в. 1, М., 1960, с. 109 — 48. С, В. Яблонский.
НАДСТРОЙКА над топологическим
пространством (клеточным разбиением) X —
пространство (клеточное разбиение)
[(Хх[0,
где [0, 1] — единичный отрезок, а косая черта обозна-
обозначает операцию отождествления подпространства с одной
точкой. Надстройкой над пунктированным про-
пространством (X, х0) наз. пунктированное пространство
= (ХХ[0,
Оно наз. также приведенной, или стяну-
стянутой, надстройкой. Н. обозначается символом
SX (а иногда 2Х). Соответствие X —>- SX определяет
функтор из категории топологических (пунктирован-
(пунктированных) пространств в себя.
Функториальность Н. позволяет определить гомо-
гомоморфизм пп(Х) —>- n.n + 1(SX), к-рый также наз. над-
надстройкой. Этот гомоморфизм совпадает с компози-
композицией гомоморфизма, индуцированного вложением X -+¦
-+QSX и изоморфизма Гуревича nn(QSX)—nn+ i(SX)
(здесь Q — операция взятия петель пространства).
Для любой гомологии теории hn (когомологип h*) имеет
место изоморфизм
б: 1гп {X) ss Л'! + 1 EХ) = ЛП + 1 (СХ, X),
совпадающий со связывающим гомоморфизмом точной
последовательности пары (СХ, X), где СХ — конус
над X. Образ класса x?h"(X) при этом изоморфизме
наз. надстройкой над х и обозначается 6*
(или Sx).
Надстройкой над когомологической операцией
а наз. когомологич. операция, действие к-рой на h*
совпадает с 8~1а8, а на h*(pt) — с а. а. Ф. Харшиладзг.
НАИБОЛЕЕ МОЩНЫЙ КРИТЕРИЙ — статистиче-
статистический критерий, имеющий наибольшую мощность среди
всех критериев с заданным значимости уровнем. Пусть
по результатам наблюдений надлежит проверить про-
простую гипотезу Яо против простой альтернативы) //}
и пусть задана допустимая вероятность а ошибки
первого рода, к-рую можно совершить в результате от-
клонения проверяемой гипотезы Но по статистич. кри-
критерию, построенному для проверки Яо против Hi,
когда в действительности гипотеза Но справедлива.
В теории проверки статистич. гипотез наилучшим
критерием среди всех статистич. критериев, предназ-
предназначенных для проверки Но против Нг и имеющих одну
it ту же вероятность ошибки первого рода или, что то же
самое, один и тот же уровень значимости а, является
тот критерий, к-рый имеет наибольшую мощность; т. е.
наилучший критерий с наибольшей вероятностью от-
отклоняет проверяемую гипотезу Но, когда справедлива
конкурирующая гипотеза Н1. Именно этот наилучший
критерий наз. Н. ы. к. уровня а среди всех статистич.
критериев уровня ос, предназначенных для проверки
простой гипотезы Но против простой альтернативы Н1.
Так как мощность етатистнч. критерия равна дополне-
дополнению до единицы вероятности ошибки второго рода,
к-рую можно совершить, принимая Нй, когда она в дей-
действительности неверна, то понятие Н. м. к. часто фор-
формулируют в терминах вероятностей ошибок первого и
второго рода: Н. м. к.— статпстич. критерий, предназ-
предназначенный для проверки простой гипотезы против про-
простой альтернативы и к-рый имеет наименьшую вероят-
вероятность ошибки второго рода среди всех статистич. кри-
критериев с заданной вероятностью ошибки первого рода.
Решение задачи о построении Н. м. к. в случае простых
гипотез дается Неймана — Пирсона леммой, согласно
к-рой отношения правдоподобия критерий является
Н. м. к.
В случае, когда конкурирующие гипотезы Но и Нг
являются сложными, задача построения Н. м. к. фор-
формулируется в терминах равномерно наиболее мощного
критерия, если таковой существует.
Лит.: [1] Леман Э. Л., Проверка статистических гипо-
гипотез, пер. с англ., 2 изд., М., 1979; [2] N е у m a n J., Pear-
s о n E., «Phil. Trans. Roy. Soc. London. A», 1933, v. 231, p. 289—
337. M. С. Никулин.
НАИБОЛЬШЕГО ГАРАНТИРОВАННОГО РЕЗУЛЬ-
РЕЗУЛЬТАТА ПРИНЦИП — один из основных принципов
принятия решения, используемый в исследовании one-
раций и игр теории. Н. г. р. п. реализуется в стремле-
стремлении выбрать такую стратегию, чтобы минимальный вы-
выигрыш, получаемый в результате ее применения, был
максимальным (см. Максимин). В ряде случаев Н. г.
р. п. может быть получен как следствие в нек-рой си-
системе аксиом, отдельные аксиомы к-рой указывают на
те естественные свойства, к-рыми должен обладать вся-
всякий «разумный» принцип оптимального поведения (см,
[5]). Конкретизация Н. г. р. п. в различных ситуациях
приводит к постановке целого ряда задач на максимин.
Исследование операций, т. е. совокупности дейст-
действий, ведущих к достижению поставленной цели, прово-
проводится исследователем операции в интересах оперирую-
оперирующей стороны, к-рая стремится к достижению цели, ма-
математически выражаемой желанием увеличить к р и-
терий эффективности'— функцию f(x, у),
где х — выбор оперирующей стороны, у — неконтро-
неконтролируемый оперирующей стороной фактор. Выбор конк-
конкретных значений х?Х ъ зависимости от информирован-
информированности оперирующей стороны и исследователя операции
о значениях у определяет стратегию х=х(у) оперирую-
оперирующей стороны.
Исходя из информированности исследователя о зна-
чениях у, неконтролируемые факторы у подразделяются
на три группы: фиксированные факторы, значения
к-рых известны; случайные факторы, т. е. случайные
процессы с известными законами распределения; неоп-
неопределенные факторы, для к-рьгх известна только об-
область Y, к-рой они принадлежат, или область, к-рой
принадлежат их законы распределения.
Оценка эффективности стратегий и выбор из них осу-
осуществляются исследователем операций на основе полу-
получения максимально гарантированной величины кри-
критерия эффективности при предполагающейся информи-
рованности оперирующей стороны о неконтролируемых
факторах. Если х — стратегия оперирующей стороны,
то ее оценкой, когда известно лишь, что y?Y, наз. ве-
величина
inf / (x, у).
ye Y
Наибольший гарантированный ре-
результат (н. г. р.) определяется как величина
sup inf / {х, у); (*)
х veY
стратегия х*, для к-рой
inf / (х*, у) = sup inf / (х, у),
Y ? Y
является оптимальной в рассматриваемой операции.
В случае, когда оперирующая сторона не ожидает
информации о конкретных значениях y?Y, т. е. х(у) =
= х, н. г. р. определяется величиной
sup inf / (x, у)
х е X у ? Y
(см. Минимакса принцип).
Если значение у известно точно, то для (*) выпол-
выполняется равенство
sup inf f{x(y), i/) = inf sup f (x, y).
x(y) ye Y yeY xsX
Если значения у формируются активным противником,
исследователь операции и оперирующая сторона инфор-
информированы о критерии эффективности противника Ц>{х, у),
y?Y, и при этом у выбирается противником из усло-
вияmax ц>(х(у), у),то н. г. р. определяется величиной
Y
sup inf _ / (х, у),
где
у(х(у), г/)=тахф(ж(г/), у)).
V6Y
Конкретизация Н. г. р. п. в играх с фиксированной
последовательностью ходов игроков и в операциях,
когда информация о неопределенных факторах уточ-
уточняется во времени, приводит к решению весьма слож-
сложных минимаксных задач (напр., дифференциальных игр).
Пусть в операции, наряду с неопределенным факто-
фактором y,y?Y, есть случайный фактор z, z?Z, с известным
законом распределения Р, и оперирующая сторона про-
производит осреднение по случайностям. В этом случае
критерием эффективности является математич. ожида-
ожидание — — (* —
f(x, y) = \zf(x. У, z)dP(z),
что означает для оперирующей стороны согласие с оп-
определенным риском. Как правило, введение / приме-
применяется в многократно повторяющихся операциях.
Если у при повторениях не меняет своего значения и
х=х(у), то н. г. р. равен
sup inf / (x, у).
Y
Если же от повторения к повторению у меняется про-
произвольным образом, то н. г. р. имеет вид
sup \ inf / (х, у, z) dP (z).
х JZyeY
В других случаях (а также в других классах страте-
стратегий, напр, вида х=х(у, z)) н. г. р. выражается иными
комбинациями операций взятия экстремума и интегри-
интегрирования (см. [1], [3]).
Смешанной стратегией паз. вероятност-
вероятностная мера V на X. Если, как выше, оперирующая сто-
сторона согласна на осреднение критерия эффективности
^xf(x, у) dV(x),
то е. г. р. равен
sup inf / C?, у).
V yeY
Большое значение имеет задача вычисления оптимальн.
смешанных стратегий (см. Антагонистическая игра).
В многошаговых операциях с конечным числом п
шагов критерий эффективности имеет вид
f(*i, г/1, ..-, х„, уп),
где Х[?Х; — выбор оперирующей стороны, a у/?У,- —
значение неконтролируемого фактора на г-м шаге.
Н. г. р. в многошаговых операциях записывается, как
правило, е виде кратного (последовательного) макси-
мина. Так, в антагонистич. игре с полной информацией
н. г. р. равен
sup inf ... sup inf / (xi, yu ..., xn, yn).
x^XiViSY,. xnt=XnyneYn
К подобным минимаксным задачам приводят и нек-рые
проблемы теории дифференциальных игр.
Для нечетко формулируемой цели оперирующей сто-
стороны, когда, напр., имеется набор критериев эффектив-
эффективности /^.г), /.,(¦?), ... , fn(x) и неопределенным фактором
для исследователя операций является номер г, данный
принцип приводит к свертке критериев, и н. г. р. ранен
max min (/,- (х) — /Ч),
х г
где /9 — уровень, к-рый желательно обеспечить по i-ii
компоненте. Если величина н. г. р. неотрицательна,
желательные уровни достижимы.
Последовательное применение Н. г. р. п. в разных
условиях информированности оперирующей стороны
позволяет единым образом оцепить эффективность стра-
стратегий и построить полную теорию принятия решения в
условиях неопределенности.
Лит.: [1] Гермейер Ю. Б., Введение в теорию иссле-
исследования операций, М., 1971; [2] Воробьев Н. Н., «Успехи
матем. наук», 1970, т. 25, в. 2, с. 81 —140; [3] Г ершейер Ю.Б.,
Игры с непротивоположными интересами, М., 1976; [4] В е н т-
ц е л ь Б. С, Исследование операций, М., 1972; [5] Вил-
Вилка с Э., «Теория вероятн. и ее примен.», 1963, т. 8, № 3, с. 324—
327. Ф. И. Ерешко, В. В. Федоров.
НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ — наиболь-
наибольший из общих делителей целых, в частности натураль-
натуральных, чисел ах, ... , ап. Если данные числа но все равны
нулю, то такой делитель существует. Н. о. д. чисел
%, ... , ап обычно обозначают символом (аь ... , ап).
Свойства Н. о. д.:
1) Н. о. д. чисел аь ... , ап делится на любой общий
делитель этих чисел;
2) (аи ... , ап, о„ + 1)=((о1, ... , ап), ап + 1);
3) если целые числа at, ... , ап представлены в виде
где р1, ... , ps — различные простые,
i=l, ... , s, и 6'1-=min(a/, ... , v,-), то
H. о. д. двух натуральных чисел можно найти при
помощи Евклида алгоритма. Число шагов, необходимых
для отыскания Н. о. д. двух чисел, превосходит не бо-
более чем в пять раз число цифр наименьшего из них, за-
записанного в десятичной системе счисления.
Н. о. д. элементов области целостности наз. тот из
общих делителей данных элементов, к-рый делится на
любой из их оСмцих делителей. Так, Н. о. д. двух мно-
многочленов над данным полем — тот их общий делитель,
к-рьш делится на любой из их общих делителей. Если
Н. о. д. двух элементов области целостности существу-
существует, то он единствен с точностью до обратимого множите-
множителя. Н. о. д. идеалов а и b данного кольца наз. идеал
(а, Ь), порожденный объединением множеств а и Ь
(см. Факториалыюе кольцо).
Лит.: [1] Виноградов И. М., Основы теории чисел,
9 изд., М., 1981; [2] Б у хш т а б А. А., Теория чисел, 2 изд.,
М.? 1966; [3] М а р к у ш е в и ч А. И., Деление с остатком в
арифметике и алгебре, М.— Л., 1949; [4] Фор Р., К о ф-
м а н А., Дени-Иапен М., Современная математика, пер.
сфранц., М., 1966; [5] Л е н г С, Алгебра, пер. с англ., М., 1908.
А. А. Бцхштпб, В. И. Нечсев.
НАИВЫСШЕЙ АЛГЕБРАИЧЕСКОЙ СТЕПЕНИ
ТОЧНОСТИ КВАДРАТУРНАЯ ФОРМУЛА — формула
вида
'* р (х) f (х) dx и 2*1 jCjf (xj), A)
где весовая функция р(х) предполагается неотрицатель-
неотрицательной на [а, 6] и такой, что существуют интегралы
Vk = \baP(x)xkdx, A = 0, 1, 2...,
при этом Цо>О. Узлами ху квадратурной формулы A)
являются корни ортогонального на [я, Ъ] с весом р(х)
многочлена степени Л", а коэффициенты определяются
тем, что квадратурная формула является интерполяци-
интерполяционной. Такая квадратурная формула имеет алгебраич.
степень точности 2ЛГ — 1, т. е. она является точной для
всех алгебраич. многочленов f(x) степени не выше 2N—
— 1 и не точна для 3.--Л", и наз. квадратурной
формулой гауссова типа.
Имеется следующее обобщение квадратурных формул
наивысшей алгебраич. степени точности. Пусть в квад-
квадратурной формуле
* р (x)f (х) dx « 27= гAjf («/) + 2"= i Cjf (*/> B>
с числом узлов N—m-\-n узлы %, ... , ат заданы зара-
заранее (фиксированные узлы), а узлы хи ... , хп выбира-
выбираются так, чтобы квадратурная формула имела наивыс-
наивысшую алгебраич. степень точности. Пусть
а (х) ™ Jl"=1(x-*j), ш (х) ^ Л"=1(х-ху).
Чтобы квадратурная формула B) была точна для всех,
многочленов степени не выше т-\-2п—1, необходимо
и достаточно, чтобы она была интерполяционной и мно-
многочлен а{х) был ортогонален на [а, Ь] с весом а{х)р(х)
ко всем многочленам степени не выше п — 1. Это приво-
приводит вопрос о существовании квадратурной формулы,
точной для всех многочленов степени не выше т-\-2п—1,
к нахождению многочлена со (г) степени п, ортогональ-
ортогонального на [а, Ь] с весом а(х)р(х), и выяснению свойств
его корней. Если корпи со (х) действительные, простые,
принадлежат [а, Ь] и их совокупность имеет пустое
пересечение с совокупностью фиксированных узлов, то
требуемая квадратурная формула существует. Если,
кроме того,
{''р (х)о- (.г) ш2 (х) dx ф 0,
Jo
то ее алгебраич. степень точности равна т-\-2п—1.
При указанных выше предположениях о весовой
функции р (х) ортогональный на [а, Ь] с весом а (х) р(х)
многочлен со (г) степени п определяется однозначно (с
точностью до отличного от нуля постоянного множи-
множителя) в следующих частных случаях.
1) го=1, п — любое. Берется один фиксированный
узел, совпадающий с концом промежутка [а, Ь], при этом
выбранный конец промежутка должен быть конечным
числом.
2) то=2, n — любое. В качестве фиксированных уз-
узлов берутся оба конца промежутка [а, Ь], к-рый считает-
считается конечным.
3) т — любое, п=т-\-1, В качестве фиксированных
узлов берутся корни ортогонального на [а, Ь] с весом
р(х) многочлена Рт(х).
В случаях 1) и 2) многочлен ч>(х) является ортого-
ортогональным относительно веса в(х)р(х), сохраняющего
знак на промежутке интегрирования [а, Ь], поэтому
его корни действительные, простые, лежат внутри (а, Ь)
и, следовательно, не совпадают с а и Ь. Квадратурная
формула B) существует, ее коэффициенты положитель-
положительны и алгебраич. степень точности равна т-\-2п—1.
Квадратурные формулы, соответствующие случаям
1) и 2),наз. формулами Маркова.
В случае 3) вес а(х)р(х) меняет знак на [а, Ь], и это
осложняет исследование корней (о(х). Если [а, Ь] =
= [—1,1] и р(х)=A— х2)а, где — 1/2<сс<3/2, то корни
ш (г) лежат внутри (—1, 1) и разделяются корнями
Рт(х): между любыми двумя соседними корнями а>(х)
лежит точно один корень многочлена Рт(х) (см. [2]).
Для рассматриваемого веса квадратурная формула B)
существует и точна для всех многочленов степени не
выше Зт-j-l; однако нельзя утверждать, что алгебраич.
степень точности равна Зто+1. При а=—1/2 и а=1/2
узлы и коэффициенты квадратурной формулы можно
указать явно (см. [3]), при этом алгебраич. степень точ-
точности в первом случае повышается до 4т—1, а во вто-
втором — до 4m-j-l. Для р(х)=1 и промежутка [0, 1] вы-
вычислены (см. [4]) узлы и коэффициенты квадратурной
формулы B) (с фиксированными узлами типа 3)) при
т= 1AL0 (т меняется от 1 до 40 с интервалом 1); ал-
алгебраич. степень точности равна Зт+1 при т четном и
равна Зт-\-2 при т нечетном. Квадратурная формула
B) с фиксированными узлами типа 3) существует также
для промежутка [—1, 1] и веса A—х)а A + х)~а при
а=±1/2, при этом узлы и коэффициенты можно ука-
указать явно (см. [3]).
Лит.: [1] К р ы л о в В. И., Приближенное вычисление
интегралов, 2 изд.,М., 1967; [2] S z e g о G., «Math. Ann.», 1934,
Bd 110, Н. 4, S. 501—13; [3] М ы с о в с к и х И. П., «Изв.
АН БССР. Сер. ф!з.-тэхшч. навук», 1964, № 4, с. 125—27;
[4] К р о н р о д А. С, Узлы и веса квадратурных формул.
Шестнадцатизначные таблицы, М., 1964. И. П. Мысовских.
НАИЛУЧШАЯ КВАДРАТУРНАЯ ФОРМУЛА, оп-
оптимальная квадратурная форму-
л а,— формула приближенного интегрирования, обес-
обеспечивающая на заданном классе функций минимальную
погрешность среди всех формул определенного типа.
Пусть рассматривается квадратурная формула
(х) / (х) dx = ^nk=i j?=0Pklfil> {Zk) + R (/), (*)
где р(х) — весовая функция. Остаток (погрешность)
R(f) = R(f, Хп, Рпт) зависит как от функции f(x),
так и от вектора (Хп, Рпт) узлов х^ (обычно предпола-
предполагается, что xk?[a, b)) и коэффициентов pk/, k=l, 2,
... , п, i=0, 1, ... , т. При фиксированных гС^\ и C
через А обозначим нек-рое множество векторов (Хп,
Рпт) (и, следовательно, квадратурных формул), опре-
определяемое теми или иными ограничениями на узлы и ко-
коэффициенты (в частности, можно рассматривать множе-
множество А=А (Хп) коэффициентов p^i при фиксированном
векторе узлов Хп). Пусть 9Л — нек-рый класс функций
f{x), причем предполагается, что для /?ЭД1 интеграл и
сумма в (*) имеют смысл. Н. к. ф. вида (*) для класса Щ}
относительно множества А определяется вектором
(Х*п,Рпт), ДЛЯ К-рОГО
sup | Д (/, Хп, Рпт)\ =
/6 т
inf sup | R (f, Xn, Pnm)\.
(Xn,pnm ca /em
Задача отыскания Н. к. ф. тесно связана с нек-рыми
задачами сплайн-аппроксимации; в ряде случаев она
сводится к минимизации нормы моносплайна (см. [1]).
Известны Н. к. ф. и соответствующие точные оценки
остатка для многих важных классов непрерывных и
дифференцируемых функций. С более общей точки зре-
зрения отыскание Н. к. ф. и доставляемой ею на классе ЭД}
погрешности можно рассматривать как задачу опти-
оптимального восстановления функционала
J(t)=\b p(x)i(x)dx,
где /?!Ш, по информации {/<'"> (xk)}, fc=l, 2, ... , п,
?=0, 1, ... , т. Понятие Н. к. ф. естественным образом
обобщается на случай функций многих переменных,
т. е. на кубатурные формулы.
Лит.: [1] Н и к о л ь с к и й С. М., Квадратурные формулы,
3 изд., М., 1979; [2] Крылов В. И., Приближенное вычисле-
вычисление интегралов, 2 изд., М., 1967; [3] Л о р а н П. Ж., Аппрок-
Аппроксимация и оптимизация, пер. с франц., М., 1975; [4] Ж е н с ы к-
6 ае в А. А., «Успехи матем. наук», 1981, т. 36, в. 4, с. 10 7—59.
Н. П. Иориейчук, В. П. Моторный.
НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ МНОГОЧЛЕН,
наилучшего приближения поли-
полином,— многочлен, осуществляющий наилучшее при-
приближение функции x(t) в той или иной метрике среди
всех многочленов, построенных по той же (конечной)
системе функций. Если X — линейное нормированное
пространство функций (напр., С [а, Ь] или Lp(a, Ь),
Р>1),
и„={щA), ..., un{t)}
— система линейно независимых функций из X, то
для любой х?Х (обобщенный) Н. п. м.
определяемый соотношением
flz — u|| = min \x —
{ck}
существует. Единственность Н. п. м. для всех х?Х име-
имеет место, во всяком случае, если X — пространство со
строго выпуклой нормой (т. е. из ||г||=
= Иг/11 и хфу следует, что ||;г+2/11<1ЫН-|Ы1)- Таким яв-
является пространство Lp(a, b) при 1<р<оо. В простран-
пространстве С [а, Ь], норма к-poro не является строго выпуклой,
Н. п. м. для любой х?С [а, Ь] единствен, если система
Un является чебышевской на [а, Ь], т. е. каждый много-
многочлен
имеет на отрезке [а, Ъ] не более чем п—1 нулей. В част-
частности, единственность имеет место для алгебраич. мно-
многочленов в С [а, Ь], а также для тригонометрич. поли-
полиномов в пространстве С2Л непрерывных на всей оси 2я-
периодических функций с равномерной метрикой. Если
Н. п. м. существует и единствен для любой х?Х, то он
непрерывно зависит от х.
Известны критерии, указывающие необходимые и до-
достаточные признаки Н. п. м. в пространствах С и Lp.
Справедлива, напр., теорема Чебышева:
если система Uп является чебышевской, то для того, что-
чтобы многочлен (*) являлся для функции х? С[а,Ъ\ Н. п. м,
в метрике пространства С [а, Ъ], необходимо и достаточ-
достаточно, чтобы нашлась система из д+1 точек i,F,-: <
<f2<... <?„ + 1<:Ь, в к-рых разность
Д (t)=z(*) — u(t)
принимает значения
± max | Д (*) |,
причем
Д (</ + i)= —A (*.'). »=*. 2, ..., п.
Многочлен (*) является Н. п. м. для функции х (t) ?
?Lp[a, b], р>1, в метрике этого пространства тогда я
только тогда, когда
uk (t) | х (О-в (О IP-1 sign [x (t) — u @] Л =0,
A=l, 2, ... , п. В случае р=1, т. е. в пространстве
L\[a, Ь], условия
"*(*) sign [*(<) — u(«)]di=O, A = l, 2, ..., л,
достаточны, а если мера множества тех точек t из (а, Ь),
где я (<)=«(?), равна нулю, то и необходимы, чтобы u(t)
был Н. п. м. для z^ija, &]; см. также Маркова крите-
критерий.
Существуют алгоритмы приближенного построения
многочленов наилучшего равномерного приближения
(см., напр., [3], [5]).
Лит.: [1] Ахиезер Н. И., Лекции по теории аппрок-
аппроксимации, 2 изд., М., 1965; [2] К о р н е й ч у к Н. П., Экстре-
Экстремальные задачи теории приближения, М., 1976; [3] Д з я-
д ы к В. К., Введение в теорию равномерного приближения
функций полиномами, М., 1977; [4] Тихомиров В. М.,
Некоторые вопросы теории приближений, М., 1976; [о] Л о-
ран И. Ж., Аппроксимация и оптимизация, пер. с франи.,
М., 1975; [6] Р е м е з Е. Я., Основы численных методов чебы-
шевского приближения, К., 1969.
Н. Л. Корнейчук, В. П. Моторный.
НАИЛУЧШЕГО ПРИБЛИЖЕНИЯ ЭЛЕМЕНТ —
элемент Uo данного множества F, доставляющий задан-
заданному элементу х метрич. пространства X наилучшее
приближение, т. е. такой, что
р (х, uo)=inf {p (х, и): u?F].
Понятие Н. п. э. обобщает классич. понятие наилуч-
наилучшего приближения многочлена. Основные вопросы, ка-
касающиеся Н. п. э.: существование и единственность
Н. п. э., характернстич. свойства Н. п. э. (см. Чебыше-
ва теорема), свойства оператора, сопоставляющего
каждому х?Х множество Н. п. э. (см. Метричес-
Метрическая проекция, Аппроксимативно компактное мно-
множество), численные методы построения Н. п. э.
Ю. н. Субботин-
НАИЛУЧШЕЕ ПОЛНОЕ ПРИБЛИЖЕНИЕ — наи-
наилучшее приближение функции f(x1} x%, ... , xk) к пере-
переменных (к^2) алгебраическими или тригонометрич.
многочленами. Пусть X — пространство С или Lp
2я-периодических по каждому переменному функций
f(xlt x2, ... , х%), непрерывных либо суммируемых со
степенью р (р^1) на /с-мерном кубе периодов.
Н. п. п. функции f(xu х2, ... , хк) ? X тригонометрич.
полиномами есть величина
En1,nt,...,nJf)x= mf Wf-Tni,n3, ...,Bft||x,
Tnlr n2, ..., nи
где точная нижняя грань берется по всевозможным три-
гонометрич. полиномам порядка л,- от переменных
лг,-A <:?<:/i;). Наряду с Н.п.п. функции / рассматриваются
частные наилучшие приближения этой функции.
Наилучшее частное приближение
функции/(^i, x2, ...,xk)?X—есть наилучшее приближе-
приближение функциями TnVi< „Vz, ..., „Vr(xu х.г, ... , xk)?X, яв-
являющимися трнгонометрич. полиномами степени ?iv
nv , ... , nv A<:г<А-) соответственно от фиксированных
переменных xv , ху , ... , ху с коэффициентами, завися-
зависящими от остальных к—г переменных, т. е. величина
EnVl, «v2, .... nvr,»(/)x= inf \\f—TnVl,nV2,...,nvrl\x-
"V,. «V,. —. «V
Очевидно, что
Ещ, п2 пг пк (f)x ^= ЕПи nj „г> «, (f)x-
Для непрерывных функций двух переменных
С. Н. Бернштейн [1] доказал неравенство
Eni. n, (f)c<A In B+min {щ, n2}) (Enu«,(f)c+En,^(f)c),
A)
где А — абсолютная константа. Установлено [31, что в
неравенстве A) (и в аналогичном соотношении для прост-
пространства Ly) нельзя заменить In B+min {щ, п2}) на мно-
множитель, растущий при min {ль л2}—>-оо медленнее.
В пространстве Lp (р>1) имеет место неравенство
Епи п, пк (/)!,< Ар, ft^Li E«r°° (/) V B)
где постоянная Ар< k зависит только от р и к.
Аналогично определяются Н. п. п. и наилучшее част-
частное приближение функций, заданных в замкнутой огра-
ограниченной области QcRfc алгебраическими многочлена-
многочленами, и в этом случае известны неравенства вида A), B).
Лит.: [1] Бернштейн С. Н., Собр. соч., т. 2, М.,
1954; [2] Т и м а н А. Ф., Теория приближения функций дей-
действительного переменного, М., I960; [3] Темляков В. Н.,
«Докл. АН СССР», 1975, т. 223, № 5, с. 1079—82.
Н. П. Корнейчук, В. П. Моторный.
НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ функции
х (t) функциями и (t) из фиксированного множества F —
величина
Е (х, F) = inf ц (х, и),
us F
где ц(ж, и) — погрешность приближения (см. Прибли-
Приближения функций мера). Можно говорить о Н. п. в про-
произвольном метрич. пространстве X, когда \i(x, и) опре-
определяется расстоянием между элементами ж и и, в этом
случае Е (х, F) — расстояние от элемента х до множест-
множества F. Если X — линейное нормированное пространство,
то при фиксированном FdX H. п.
Е (х, F)= inf || ж —u || ж
можно рассматривать как заданный на X функционал
(функционал наилучшего приближе-
приближения).
Функционал Н. п. непрерывен, каково бы ни было
множество F. Если F — подпространство, то функцио-
функционал Н. п. является полунормой, т. е.
Е(Х1+хг, F)<zE(xlt F)+E(x2, F)
Е(Хх, F)=\X\E(x, F)
для любого JvgR1. В случае, когда F — конечномерное
подпространство, в F для любого х ? X существует эле-
элемент и0 (элемент наилучшего прибли-
приближен и я), на к-ром в A) реализуется нижняя грань:
Е(х, F)=\\x—ua\\.
В пространстве X со строго выпуклой нормой элемент
Н. п. единствен.
С помощью теорем двойственности Н. п. в линейном
нормированном пространстве X может быть выражено
через верхнюю грань значений нск-рых функционалов
из сопряженного пространства X* (см., напр., [5], [81).
Если F — замкнутое выпуклое множество в X, то для
любого х?Х
Е (х, F) = sup [/ (x) -sup / (и)]; B)
в частности, когда F — подпространство, то
E(x,F)= sup f (x), C)
где F^— множество функционалов / из X* таких, что
f(u)=O для любого u?F. В функциональных простран-
пространствах С и Lp правые части B) и C) конкретизируются с
учетом формы линейного функционала. В гильбертовом
пространстве Н Н. п. элемента х?Н и-мерным подпро-
подпространством Fn реализуется оператором ортогонального
проектирования на Рп и может быть вычислено:
_,/ G (x, и„ ..., un)
G (и,, .... и„)
где ult ... , и„ — базис Fn, a G (щ, ... , и„) — опреде-
определитель Грама, составленный из скалярных произведе-
произведений (и;, itj), i, j=i, ... , п. Если базис {«&} ортонорми-
рован, то
Е* (х, Fn)=\\xf-^nk=i(x, uk)\
В пространстве С=С \а, Ь] для величины наилучшего
равномерного приближения функции x(t)?C>и-мерным
чебышевским подпространством Fnd С справедлива
оценка (теорема Балле Пуссена): если для
нек-рой функции u(t)?Fn существует ге-j-l точек tf.,
C<C b в к-рых разность
принимает значения с последовательно чередующимися
знаками, то
\A(tk)\.
О Н. п. в пространстве L^(a, b) см. Маркова критерий.
В ряде важных случаев Н. п. функций конечномерным
подпространством можно оценить сверху через диффе-
дифференциально-разностные характеристики (напр., модуль
непрерывности) приближаемой функции или ее произ-
производных.
Понятие наилучшего равномерного приближения не-
непрерывных функций многочленами ввел П. Л. Чебышев
A854), к-рый разработал теоретич. основы Н. п. и
установил критерий многочлена Н. п. в метрике прост-
пространства С (см. Наилучшего приближения многочлен).
Наилучшее приближение класса
функций — верхняя грань Н. п. функций /(?) из
заданного класса <Ш фиксированным множеством функ-
функций F, т. е. величина
Е Ш, F) = sup Е (/, F) = sup inf (i (/, Я>).
/ е ж / е т (f е f
Величина ?(!Ш, F) характеризует максимальное откло-
отклонение (относительно выбранной метрики) класса ЭД1 от
приближающего множества F и показывает, на какую
минимально возможную погрешность можно рассчиты-
рассчитывать, приближая произвольную функцию /(г)?Щ1 функ-
функциями из F.
Пусть [ffi принадлежит функциональному линейному
нормированному пространству X, U= {u^t), u2(t), ...}—
линейно независимая система функций из X и Fn, n=
= 1, 2, ... ,— подпространства, порожденные первыми
п элементами этой системы. Исследование числовой
последовательности Е(ЙЛ, Fn), n=l, 2, ... , позволяет
судить как о структурных и гладкостных' характеристи-
характеристиках функций класса Щ], так и об аппроксимативных
свойствах системы U относительно класса 2Л. Если X —
банахово пространство функций и система U замкнута
в X, т. е. у Fn=X, то Е (Ш\, Fn) ->• 0 при п ->• со тогда
и только тогда, когда !Ш является компактным в X
множеством.
В ряде важных случаев, напр, когда Fn — подпро-
подпространства тригонометрич. полиномов или периодич.
сплайнов, а класс 2R задается ограничениями на норму
или модуль непрерывности нек-рой производной f{r*(t),
величины ?@Л, Fn) точно вычислены [5]. В непериодич.
случае имеются результаты, дающие точную асимпто-
асимптотику Е(Ш, Fn) при п->- со.
Лит.: [1] Чебышев П. Л., Полн. собр. соч., т. 2, М.—
Л., 1947; [2] А х и е з е р Н. И., Лекции по теории аппрокси-
аппроксимации, 2 изд., М., 1965; [3] Д з я д ы к В. К., Введение в тео-
теорию равномерного приближения функций полиномами, М., 1977;
[4] Гончаров В. Л., Теория интерполирования и прибли-
приближения функций, 2 изд., М., 1954; [5.1 Корнейчук Н. П.,
Экстремальные задачи теории приближения, М., 1976; [6] Ни-
Никольский С. М., Приближение функций многих переменных
и теоремы вложения, 2 изд., М., 1977; [7J Тиман А. Ф.,
Теория приближения функций действительного переменного,
М., 1960; [8] Тихомиров В. М., Некоторые вопросы
теории приближений, М., 1976: [9] Лоран П. Ж., Аппрок-
Аппроксимация и оптимизация, пер. с франц., М., 1975.
И. П. Корнейчук, В. П. Моторный.
НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ В СРЕДНЕМ —
наилучшее приближение функции x(t) функциями u(t)
из фиксированного множества F, когда мера (погреш-
(погрешность) приближения выражается с помощью интеграль-
интегральной метрики (см. Наилучшее приближение, Приближе-
Приближение в среднем). Н. П. Корнейчук, В. П. Моторный.
НАИЛУЧШИЙ ЛИНЕЙНЫЙ МЕТОД — линейный
метод приближения, обеспечивающий на заданном мно-
множестве Ш1 приближаемых элементов наименьшую, по
сравнению с другими линейными методами, погреш-
погрешность. В линейном нормированном пространстве А' ли-
линейный метод приближения элементов х ?WdX элемен-
элементами фиксированного подпространства FdX задается
линейным оператором, отображающим все пространст-
пространство X или нек-рое, содержащее Ш!, линейное многооб-
многообразие в F. Если X — совокупность всех таких опера-
операторов, то Н. л. м. для множества [ДО (если он сущест-
существует) определяется оператором Л?<5?, для к-рого
sup || х — Лж]|= inf sup J| х — АгИ.
Метод, определяемый оператором А из <5?, заведомо яв-
является Н. л. м. для ЙЛ относительно приближающего
множества F, если для всех х?Ш1
||х — Ar||< sup Е (х, F)
хеШ
(Е(х, F) — наилучшее приближение элемента х множест-
множеством F) и, тем более, если для всех х?Х
\\х-Ах\\ = Е(х, F).
Последний факт имеет место, когда X — гильбертово
пространство, F=Fn есть re-мерное (га=1, 2, ...) его под-
подпространство, А — линейный оператор ортогонального
проектирования на Fn, т. е.
гДе (еь е-г, ¦¦¦ > еп) — ортонормированный базис в Fn.
Пусть X — банахово пространство заданных на всей
действительной оси функций с нормой, инвариантной
относительно сдвига: \\х( -+1I1= \\х( -)|| (этому условию
удовлетворяет, напр., норма пространств С=С[0, 2л]
и Lp=Lp(Q, 2л), lsgp^co, 2я-периодических функций),
F= Тп — подпространство тригонометрия, полиномов
порядка п. Для класса QDt функций x(t) из X, содержа-
содержащего вместе с x(t) также и x(t-\-a) при любом agR1,
существуют Н. л. м. (относительно Тп), в частности
Н. л. м. вида
А {х- Ц (х, v)=H?l2 +
+ ^ {llk (uf-coskt -\-bks\nkt) + v/j (a^sinkt—bkcoskt)},
(*)
где ak и bfr — коэффициенты Фурье функции x(t) по
тригонометрии, системе, [х^ и vj. — нек-рые числа.
На классах W^M (и W\M), г=1,2, ... , 2я-псриоди-
ческих функций x(t), у к-рых производная л;1/'~1)(г)
локально абсолютно непрерывна, а x(r)(t) по норме в
L<x, (соответственно в Ьг) ограничена числом М, Н. л. м.
вида (*) дает в метрике пространства С (соответственно
Ьх) ту же погрешность (на всем классе), что и наилучшее
приближение подпространством Тп; аналогичный факт
имеет место для таких классов при любом дробном г>0
(производная x{r){t) понимается в смысле Веиля). При
целых г=1, 2, ... Н. л. м. вида (*) строится только
с помощью коэффициентов \ik (все Vfc = 0).
Если F=Sn — подпространство 2л-периодических
полиномиальных сплайнов порядка г дефекта 1 по раз-
разбиению knln, к = 0, ±1, ... , то для классов WrJxM (и
W[+1M), r^i, 2, ... , Н. л. м. в Ьр, 1<р<со (соответ-
(соответственно в Ьх), доставляют сплайны из Srn, интерполи-
интерполирующие функцию x(t) в точках knln-\-\i-{- (— 1)г]л/4л.
Лит.: [1] А х и е з е р Н. И., Лекции по теории аппрок-
аппроксимации, 2 изд., М., 1965; [2] Корнейчук Н. П., Экстре-
Экстремальные задачи теории приближения, М., 1976; [31 Т и х о м и-
р о в В. М., Некоторые вопросы теории приближений, М., 1Э7В-
Н. П. Норнейчук В. П. Моторный-
НАИЛУЧШИХ ПРИБЛИЖЕНИИ ПОСЛЕДОВА-
ПОСЛЕДОВАТЕЛЬНОСТЬ—числовая последовательность {Е(г, Fn)},
n=i, 2, ... , где Е (х, Fn) — наилучшее приближение
элемента х линейного нормированного пространства
X элементами л-мерного подпространства FndX, при-
причем f,crF2cr..., так что Е(х, F1)'^E(x, F2)^i... .
Обычно Fn есть линейная оболочка первых п элементов
нек-рой фиксированной системы {щ, и2, ...} линейно
независимых элементов из X.
В случае, когда Х=С [а, &], Fn=Fn— подпрост-
подпространство алгебраич. многочленов степени п—1, Н. п. п.
впервые рассматривалась в 50-х гг. 19 в. П. Л. Чебы-
шевым; тот факт, что
Е (х, Fn) —*- 0 при п —>¦ со
для любой функции x(t)?C [a, b], установлен в 1885
К. Вейерштрассом (К. V\ eierstrass). В общем случае
соотношение
lim E (x, Fn) для всех х?Х
выполняется всегда, когда объединение подпространств
Fn, л=1, 2, ... , всюду плотно в X, т. е.
(по существу это эквивалентные утверждения). Однако
последовательность Е (х, Fn) может стремиться к нулю
как угодно медленно. Это вытекает из теоремы
Берпштейпа: если {Fn} — последовательность
подпространств размерности л=1, 2, ... линейного нор-
нормированного пространства X, причем F1dFid... и
U Fn= X, то какова бы ни была монотонно стремящаяся
к нулю числовая последовательность {,и„}, [г„^0, су-
существует элемент х?Х такой, что Е(х, Fn)==llm n=l,
2, ... . В функциональных пространствах С и Ьр ско-
скорость стремления к нулю Н. п. п. зависит как от сис-
системы подпространств Fn, так и оттладкостных характе-
характеристик приближаемой функции х (модуля непрерывно-
непрерывности, существования производных до определенного по-
порядка и пр.) и может быть оценена через эти характери-
характеристики. Обратно, зная скорость стремления к нулю по-
последовательности Е(х, Fn), можно судить о гладкости
функции х (t) (см. Приближение функций; прямые и об-
обратные теоремы).
Лит.: [1] Б е р н ш т е й н С. Н., Собр. соч., т. 2, М., 1954;
[2] Г о н ч а п о в В. Л., Теория интерполирования и прибли-
приближения функций, 2 изд., М., 1954; [3] Т и м а н А. Ф., Теория
приближения функций действительного переменного, М., I960.
Н. П. Кор-иейчук, В. П. Моторный.
НАИМЕНЕЕ БЛАГОПРИЯТНОЕ РАСПРЕДЕЛЕ-
РАСПРЕДЕЛЕНИЕ — априорное распределение, максимизирующее
функцию риска в статистич. задаче принятия решения.
Пусть по реализации случайной величины X, при-
принимающей значения в выборочном пространстве (ЭЕ,
Sj, Рв), G?0, надлежит принять решение йиз прост-
пространства решений Bs, ЗЗф), при этом предполагается, что
неизвестный параметр 8 является случайной величиной,
принимающей значения в выборочном пространстве (в,
iBe , Щ), t? Т. Пусть функция Л (8, d) выражает потери,
к-рые возникают при принятии решепия d, если истин-
истинное значение параметра есть 8. Априорное распределе-
распределение щ* из семейства {щ, t? T} наз. наименее
благоприятным для решения d в статисти-
статистической задаче принятия решения при бейесовском под-
подходе, если
sup p (щ, d) =p (я*«, d)\
где
р (щ, d) = $e$/ F, d {х)) dPQ (x) dnt (8)
— функция риска, выражающая средние потери от
принятия решения d. H. б. р. щ* позволяет вычислить
самые «тяжелые» (в среднем) потери р(я/*, d), возни-
возникающие при принятии решения d. В практич. деятель-
деятельности ориентируются, как правило, не на Н. б. р., а
наоборот, стараются принять такое решение, к-рое
предохранило бы от максимальных потерь при измене-
изменении параметра 0, что приводит к поиску минимакс-
минимаксного решения d*, минимизирующего максимальный
риск, т. е.
inf sup p (щ, d) = sup p {щ, d*).
В задаче проверки сложной статистич. гипотезы про-
против простой альтернативы при бейесовском подходе
Н. б. р. определяется с помощью редукции
В а л ь д а, к-рая заключается в следующем. Пусть по
реализации случайной величины X надлежит прове-
проверить сложную гипотезу Яо, согласно к-рой закон рас-
распределения X принадлежит семейству Но= {Рв , Э?в},
против простой альтернативы Н1г согласно к-рой слу-
случайная величина X подчиняется закону Q, и пусть
dPa (X) j/-» /лЛ
где ц.(.) — нек-рая а-конечная мера на ($, 33Ж),
{щ, t?T} — семейство априорных распределений на
(©, 9?е)- Тогда для любого г? Т сложной гипотезе Но
можно сопоставить простую гипотезу Ht, согласно
к-рой случайная величина X подчиняется вероятност-
вероятностному закону, имеющему плотность вероятности
Согласно Неймана — Пирсона лемме для проверки про-
простой гипотезы Hf против простой альтернативы Н^
существует наиболее мощный критерий, построенный на
отношении правдоподобия. Пусть р( — мощность этого
критерия, тогда Н. б. р. есть то априорное распределе-
распределение щ* из семейства{щ, *? Г}, для к-рого выполняется
неравенство fV<pf для всех «? Т. Н. б. р. обладает тем
свойстволт, что плотность вероятности ft*{x) случайной
величины X при гипотезе Ht* «наименее удалена» от
альтернативной плотности q(x), т. е. гипотеза Ht*
является самой «близкой» из семейства {Hf, t?T}
к конкурирующей гипотезе Ht. См. Бейесовский подход.
Лит.- [1] Л е м а н Э., Проверка статистических гипотез,
пер. с англ., 2 изд., М., 1979; [2] 3 а к с Ш., Теория статисти-
статистических выводов, пер. с англ., М., 1075. М. С. Никулин.
НАИМЕНЕЕ УКЛОНЯЮЩИЙСЯ ОТ НУЛЯ МНО-
МНОГОЧЛЕН — алгебраический многочлен степени п со
старшим коэффициентом, равным единице, имеющий
минимальную норму в пространстве С [а, Ъ\ или Lp[a, Ъ\.
П. Л. Чебышев [1] установил, что среди всех много
членов вида
минимальную норму в пространстве С [а, Ь] имеет един-
единственный многочлен
/Ь~а\п 2х-а—Ь
Т„ (х) — 2{ ~4~ J cos n arc cos ь_а ,
причем
и 1 л Не [а, Ь] — * у~Г~) "
Многочлен
2х-а-Ь
sin(n+l) arc cos :
—r
Ь-а
V(b-x)(x-a)
является единственным Н. у. от н. м. в пространстве
Lx[a, Ь] среди всех многочленов вида A), при этом
В пространстве Lp[a, Ь], 1<р<оо, Н. у. от н. м. сущест-
существует ц единствен, известен ряд его свойств (см. [2], [5]).
На множестве многочленов вида A) интеграл
Ql(x)(,(x)dx, p(*)>0, B)
будет минимальным тогда и только тогда, когда Qn(x)
ортогонален с весом р {х) на интервале (а, Ъ) всем много-
многочленам степени п — 1. Если
о=—1, Ь=1, p(x) = (i — x)^(l+xf,
где а, р> — 1, то интеграл B) минимизируется Якоби
многочленом (при <x=f>=0 Лежандра многочленом) степе-
степени п со старшим коэффициентом, равным единице.
Среди тригонометрич. полиномов вида
a cos пх-\-Ь sin пх-\-^ _ (а^ cos кх-\-Ь^ sin kx),
где а и Ь фиксированы, минимальную норму в простран-
пространствах С [0, 2л] и Lp[0, 2я] при любом р^1 имеет поли-
полином
a cos nx-{-b sin nx.
Лит.: [[] Чебышев П. Л., Полн. собр. соч., т. 2,
М.— Л-, 1947; [2] Тихомиров В. М., Некоторые вопросы
теории приближений, М., 1976; [3] Т и м а п А. Ф., Теория
приближения функций действительного переменного, М., 1960;
[4] С е г б Г., Ортогональные многочлены, пер. с англ.. М.,
1962; [5] Никольский С. М., Квадратурные формулы,
3 изд., М-, 1979; [6] С у е т и н П. К., Классические ортогональ-
ортогональные многочлены, 2 изд., М., 1976.
Н. П. Корнейчук, В. П. Моторный.
НАИМЕНЬШЕГО ЧИСЛА ОПЕРАТОР, |л-о п е р а-
тор, оператор минимизаци и,— способ
построения новых функций из других функций, со-
состоящий в следующем. Пусть g есть («+1)-местная
арифметич. функция, т. е. функция, аргументы к-рой
так же, как и она сама, принимают значения в множест-
множестве натуральных чисел. Функция g предполагается час-
частичной функцией, т. е. определенной не обя-
обязательно для всех значений аргументов. Говорят, что
re-местная арифметич. функция / получается из функции
g с помощью Н. ч. о., если выполнено условие: для лю-
любых натуральных чисел &х, ... , кп, к
f (А-ь ..., кп) = к
тогда и только тогда, когда для всех 1<_к значения
g(kt, ... , кп, I) определены и отличны от нуля, а значе-
значение g(kt, ... , кп, к) определено и равно нулю. Если /
получается из функции g с помощью Н. ч. о., то пишут:
/ (хи . .., хп) = цу [g (xlt ..., хп, у)=0].
Важным свойством Н. ч. о. является то, что с его
помощью из вычислимой функции g всегда получается
частичная вычислимая функция /. Именно, если имеет-
имеется алгоритм для вычисления g, то значение f(x1, ... , хп)
может вычисляться следующим образом. Вычисляем
g (#1, ... , хп, 0). Если процесс вычисления закончится,
т. е. значение g(xj, ... , хп, 0) определено, и g(zi, ... , хп,
0)=0, то полагаем f(xu ... , хп) = 0, а если g(x1, ... , хп,
0)=^0, то начинаем вычислять g{x1, ... , хп, 1). Если
процесс закончится и g{x1} ... , хп, 1) = 0, то полагаем
f\xu ... , хп)=1, а если g(xx, ... , хп, 1)^=0, то перехо-
переходим к вычислению g(xiy ... , хп, 2) и т. д. Процесс вы-
вычисления закончится, если найдется такое у, что для
всех z<i/ значение g(x1, ... , х„, z) определено и отлично
от нуля, a g(xlt ... , хп, у) определено и равно нулю-
Тогда f(xu . . ., хп) = у.
Н. ч. о. играет важную роль в определении класса
частично рекурсивных функций. В. Е. Плиско.
НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ — наименьшее
положительное из общих кратных целых, в частности
натуральных, чисел аи ... , ап. Н. о. к. чисел аи ... , ап
существует, если аг ... апф1). Н. о. к. чисел аи ... , ап
обычно обозначают символом [аь ... , ап].
Свойства Н. о. к.:
1) Н. о. к. чисел аи ... , ап — делитель любого об-
общего кратного этих чисел;
2) [аи ... , а„, an + 1l = [[fli, ... , а„], ап + 1];
3) если целые числа аи ... , ап представлены в виде
где рх, ... , ps — различные простые, а,-^0, ... , v,-^0,
г=1, ... , s, и (х,-=тах(а,-, ... , v,-), to
[alt ..., а„] = р^...р^;
4) если аЬ>0, то [a, b]-(a, b) = a-b, где (а, Ь) — наи-
наибольший общий делитель для а и Ь.
Последнее свойство позволяет находить II. о. к. двух
чисел при помощи Евклида алгоритма. Понятие Н. о. к.
может быть введено для элементов области целостно-
целостности, а также для идеалов коммутативного кольца.
Лит.: [1] Виноградов И. М., Основы теории чисел,
9 изд., М., 1981; [2] Б у х ш т а б А. А., Теория чисел, 2 изд.,
М., 1966; [3] Фор Р., К о ф м а н А., Дени-Папен М.,
Современная математика, пер. с франц., М., 1966.
В. И. Нечаев, А. А. Бухштаб.
НАИМЕНЬШИХ КВАДРАТОВ МЕТОД — один из
методов ошибок теории для оценки неизвестных вели-
величин по результатам измерений, содержащим случайные
ошибки. Н. к. м. применяется также для приближенно-
приближенного представления заданной функции другими (более
простыми) функциями и часто оказывается полезным
при обработке наблюдений. Н. к. м. предложен К. Га-
Гауссом (С. Gauss, 1794—95) и А. Лежандром (A. Le-
gendre, 1805—06). Строгое обоснование и установление
границ содержательной применимости Н. к. м. даны
А. А. Марковым и А. Н. Колмогоровым. В простейшем
случае линейных связей (см. ниже) и наблюдений, не
содержащих систематич. ошибок, а подверженных лишь
случайным ошибкам, оценки неизвестных величин, по-
полученные с помощью Н. к. м., являются линейными
функциями от наблюденных значений. Эти оценки не
имеют систематич. ошибок, т. е. являются несмещенны-
несмещенными (см. Несмещенная оценка). Если случайные ошибки
наблюдений независимы и подчиняются нормальному
распределению, то Н. к. м. дает оценки неизвестных с
наименьшей дисперсией, т. е. эти оценки являются эф-
эффективными (см. Статистическое оценивание). В этом
смысле Н. к. м. является наилучшим среди всех ос-
остальных методов, позволяющих находить несмещенные
оценки. Однако если распределение случайных ошибок
существенно отличается от нормального, то Н. к. м.
может и не быть наилучшим.
При обосновании Н. к. м. (по Гауссу) предполагает-
предполагается, что «убыток» от замены точного (неизвестного) зна-
значения нек-poii величины ц ее приближенным значением
X, вычисленным по результатам наблюдений, пропор-
пропорционален квадрату ошибки (X— цJ; оптимальной
оценкой считается такая лишенная систеыатич. ошибки
величина X, для к-рой среднее значение Е (X—fiJ
«убытка» минимально. Именно это требование и состав-
составляет основу Н. к. м. В общем случае отыскание опти-
оптимальной в смысле Н. к. м. оценки X — задача весьма
сложная, поэтому практически эту задачу сужают и в
качестве X выбирают линейную функцию от результа-
результатов наблюдений, лишенную систематич. ошибки, и та-
такую, для к-рой среднее значение убытка минимально в
классе всех линейных функций. Если случайные ошиб-
ошибки наблюдений подчиняются нормальному распределе-
распределению и оцениваемая величина ц зависит от средних зна-
значений результатов наблюдений линейно (случай, весьма
часто встречающийся в приложениях Н. к. м.), то ре-
решение этой задачи будет одновременно являться и ре-
решением общей задачи. При этом оптимальная оценка X
также подчиняется нормальному распределению со
средним значением ц и, следовательно, плотность веро-
вероятности случайной величины X
достигает максимума в точке х=ц (это свойство и вы-
выражает точное содержание распространенного в теории
ошибок утверждения: «оценка X, вычисленная согласно
Н. к. м.,— наиболее вероятное значение неизвестного
параметра р>).
Случай одного неизвестного. Пусть
для оценки значения неизвестной величины \i произве-
произведено п независимых наблюдений, давших результаты
Yu У2, ... , У„, т. е. Y^p+би Y2=y,+82, ... , У„=
= и.+6„, где 8], 82, ... , 8„ — случайные ошибки (по
определению, принятому в классич. теории ошибок,
случайные ошибки — независимые случай-
случайные величины с нулевым математич. ожиданием: Еб,=
= 0; если же Еб,=т^О, то Ев,- наз. систематиче-
систематическими ошибками). Согласно Н. к. м. в качестве
оценки величины ц принимают такое X, для к-рого бу-
будет наименьшей сумма квадратов (отсюда и само назва-
название метода):
где
= kla\ и o-2=D8,- =
(коэффициент &>0 можно выбирать произвольно).
Величину pi наз. весом, а а, — квадратичным
отклонением измерения с номером i. В частно-
частности, если все измерения равноточны, то а1=аа=... = а„,
и в этом случае можно положить р1=р2=... = р„=1;
если же каждое У,- — арифметич. среднее из /г,- равно-
равноточных измерений, то полагают р, = я,-.
Сумма S (X) будет наименьшей, если в качестве X
выбрать взвешенное среднее:
X = Y=jr^PiYh где Р = 2>/.
Оценка У величины fi лишена систематич. ошибки, име-
имеет вес Р и дисперсию DY=k/P. В частности, если все
измерения равноточны, то У — арифметич. среднее
результатов измерений:
При нек-рых общих предположениях можно пока-
показать, что если количество наблюдений п достаточно
велико, то распределение оценки У мало отличается от
нормального с математич. ожиданием [г и дисперсией
к/Р. В этом случае абсолютная погрешность прибли-
приближенного равенства \i^Yменьше tVklP с вероятностью,
близкой к значению интеграла
ia J о
Via
е~иг1Чи
A)
(напр., /A,96) = 0,950; /B,58) = 0,990; / C,00) = 0,997).
Если веса измерений р,- заданы, а множитель к до
наблюдений остается неопределенным, то этот множи-
множитель и дисперсия оценки У могут быть оценены по фор-
формулам:
и
DY=k/P « s2=S (Y)/[(n — 1) Р]
(обе оценки лишены систематич. ошибок).
В том практически важном случае, когда ошибки 8,-
подчиняются нормальному распределению, можно най-
найти точное значение вероятности, с к-рой абсолютная
погрешность приближенного равенства ^«У окажется
меньше ts (t — произвольное положительное число):
где постоянная Cn-i выбрана таким образом, чтобы
выполнялось условие /„ _х(оо)== 1 (Стъюдента распре-
распределение с п—1 степенями свободы). При больших п
формулу B) можно заменить формулой A). Однако при-
применение формулы A) при небольших п привело бы к
грубым ошибкам. Так, нанр., согласно A) значению /=
= 0,99 соответствует ?=2,58; истинные значения t, оп-
определяемые при малых п как решения соответствующих
уравнений /n_i(i)=0,99, приведены в таблице:
п . . . .
t . . . .
2
63,
66
3
9,92
4
5,84
5
4,60
10
3,25
20
2,86
30
2,76
Пример. Для определения массы нек-рого тела
произведено 10 независимых равноточных взвешива-
взвешиваний, давших результаты У,- (в г):
Y
i
п1
18 ,41
1
18 42
3
18,43
3
18 44
1
18 45
1
18 _ЛВ
1
(здесь ге,- — число случаев, в к-рых наблюдалась масса
У,-; л=2п,-=10). Так как все взвешивания равноточные,
то следует положить р,= п; и в качестве оценки для не-
неизвестного веса [д, выбрать величину У=2л;У,72щ=
= 18,431. Задавая, напр., /9=0,95, по таблицам распре-
распределения Стьюдента с девятью степенями свободы мож-
можно найти, что (= 2,262, и поэтому в качестве предельной
абсолютной погрешности приближенного равенства
\i~ 18,431 следует принять величину
2ii(Yi — УJ/90 = 2,262-0,0048 = 0,011.
Таким образом, 18,420 <(х<18,422.
Случай нескольких неизвестных
(линейные связи). Пусть п результатов изме-
измерений Ух, У2, ... , У„ связаны с т неизвестными вели-
вели( й
чинами хг, х2, ..
соотношениями
(т<^п) независимыми линейными
'' '=1. 2, .... и,
C)
где аи — известные коэффициенты, а 8,-— независимые
случайные ошибки измерений. Требуется оценить неиз»
вестные величины ху (эту задачу можно рассматривать
как обобщение предыдущей, в к-рой
ц = х1 и т=ац=1; г=1, 2, ..., п.
Так как Еб,-=О, то средние значения результатов из-
измерений !/,=ЕУ,- связаны с неизвестными величинами
хх, х2, ... , хт линейными уравнениями (линейные свя-
связи):
Следовательно, искомые величины х[ представляют со-
6oit решение системы D), уравнения к-рой предполага-
предполагаются совместными. Точные значения измеряемых вели-
величин г/,- и случайные ошибки б/ обычно неизвестны, по-
поэтому вместо систем C) и D) принято записывать так
наз. условные уравнения
Согласно Н. к. м. в качестве оценок для неизвест-
неизвестных х j применяют такие величины Ху, для к-рых сумма
квадратов отклонении
2
будет наименьшей (как и в предыдущем случае, р,- —
вес измерения, Y,- — величина, обратно пропорциональ-
пропорциональная дисперсии случайной ошибки б,). Условные урав-
уравнения, как правило, несовместны, т. е. при любых
значениях Ху разности
не могут, вообще говоря, все обратиться в пуль. Н. к. м.
предписывает в качестве оценок выбрать такие значения
Ху, к-рые минимизируют сумму S. В тех исключитель-
исключительных случаях, когда условные уравнения совместны и,
значит, обладают решением, это решение совпадает с
оценками, полученными согласно Н. к. м.
Сумма квадратов S представляет собой квадратичный
многочлен относительно переменных Ху, этот многочлен
достигает минимума при таких значениях Х1; Х2, ... ,
Хт, ПРИ к-рых обращаются в нуль все первые частные
производные:
ir=-2Y." PiA«- = 0, / = 1, 2, ..., m.
Отсюда следует, что оценки Ху, полученные согласно
Н. к. м.~ должны удовлетворять системе т. н. н о р-
м а л ь н ы х уравнений, к-рая в обозначениях,
предложенных К. Гауссом, имеет вид
2Г [Р*/в/]*/ = [/>^Ь 1 = 1,2, ...,т, E)
где
Оценки, получающиеся в результате решения систе-
системы нормальных уравнений, лишены систематич. ошибок
(EXj=Xj); дисперсии DXj величин Ху равны kdyyld,
где d — определитель системы E), a dyy — минор, со-
соответствующий диагональному элементу [paj<ij] (иными
словами, dyyld — вес оценки X,-). Если множитель про-
пропорциональности к (к наз. дисперсией на еди-
единицу веса) заранее неизвестен, то для его оценки,
а также для оценки дисперсии DXy служат формулы
kxSf(n-m) и DXyXS^Sdyy/d (n — т)
(S — минимальное значение исходной суммы квадра-
тов). При нек-рых общих предположениях можно пока-
показать, что если количество наблюдений п достаточно
велико, то абсолютная погрешность приближенного ра-
равенства Xj^Xj меньше tsj с вероятностью, близкой к
значению интеграла A). Если случайные ошибки на-
наблюдений б,- подчиняются нормальному распределению,
то все отношения (X j—xj)Isj распределены по закону
Стьюдента с н—т степенями свободы (точная оценка аб-
абсолютной погрешности приближенного равенства про-
производится здесь с помощью интеграла B) так же, как
в случае одного неизвестного). Кроме того, минималь-
минимальное значение суммы S в вероятностном смысле не зави-
зависит от Хи Х2, ... , Хгп, и потому приближенные значения
дисперсий оценок DXj-asj не зависят от самих оценок
Один из наиболее типичных случаев применения
Н. к. м.— «выравнивание» таких результатов наблю-
наблюдений Yj, для к-рых в уравнениях C) я,-/—ау(г;), где
aj(t) — известные функции нек-рого параметра t (если
t — время, то t\, t2, ... — те моменты времени, в к-рые
производились наблюдения). Особенно часто встречает-
встречается в приложениях случай т. н. параболической
интерполяции, когда aj(t) — многочлены (напр.,
°i@ —!. ai(t) = t, а3{1) = Р, ...); если t2—h=t3—12 —
= ... = <„—<n_i, а наблюдения равноточные, то для вы-
вычисления оценок Xj можно воспользоваться таблицами
ортогональных многочленов. Другой важный для при-
приложений случай — т. н. гармоническая ин-
интерполяция, когда в качестве a.j(t) выбирают три-
гонометрич. функции (напр., a,-(i) = cos(/— \)t, /=1,
2, ... , т).
II р и м е р. Для оценки точности одного из методов
химич. анализа этим методом определялась концентра-
концентрация СаО в десяти эталонных пробах заранее известного
состава. Результаты наблюдений указаны в таблице
(г — номер эксперимента, t,- — истинная концентрация
СаО, Тi — концентрация СаО, определенная в резуль-
результате химич. анализа, У/= 71,-—t, — ошибка химич.
анализа):
1
4
—о,
3
2
8
-0.2
3
12,
-0,
5
4
4
16
—0,
4
5
20
-0,2
6
25
—0,
5
7
31
+ 0,
1
8
30
—0,
5
9
40
—0,
6
10
40
-0,5
Если результаты химич. анализа не имеют система-
тич. ошибок, то ЕУ,-=0. Если же такие ошибки име-
имеются, то в первом приближении их можно представить
в виде: ЕУ,-=а+р?,- (а наз. постоянной ошиб-
ошибкой, а Р<,- — методической ошибкой)
или, что то же самое,
где
Для отыскания оценок а и ft достаточно оценить вели-
величины хх=а+р( и ?2=р. Условные уравнения в данном
случае имеют вид
Yi = x1 + x2(ti—l), i = l, 2, ..., 10,
поэтому a,i=l, а,-2=*(-—t (согласно предположению о
равноточности наблюдений все р,= 1). Так как [ага2]^
= [a2aJ = S (ti—1) = 0, то система нормальных уравне-
уравнений записывается особенно просто:
[a2a2] X2 = [Ya,],
где
= 10, [ага2\=^ (f,—7J = 1569,
2г,-(*/-<)=-8,225.
Дисперсии компонент решения этой системы суть
h k k h
DX И DX
где /с — неизвестная дисперсия на единицу веса (в
данном случае к — дисперсия любой из величин У,).
Так как в этом примере компоненты решения принима-
принимают значения Х1=— 0,35, и Х2=—0,00524, то
к ~ Sj(n — т) =
= Т SL°i [у/-Х1-Х2('<—012 = 0,0427,
DXj и sj = 0,00427, DX2 я 4 = 0,000272,
¦г1 = 0,065, s2 = 0,00522.
Если случайные ошибки наблюдений подчиняются
нормальному распределению, то отношения \Xj—xj\Isj,
j=i, 2, распределены по закону Стьюдента. В частно-
частности, если результаты наблюдений лишены систематич.
ошибок, то ж1=ж1=0, и, значит, закону Стыодента
должны подчиняться отношения IXJ/sj и |X2|/s2. С по-
помощью таблиц распределения Стьюдента с н—пг=8 сте-
степенями свободы можно убедиться, что если действитель-
действительно х1=х2=0, то с вероятностью 0,999 каждое из этих
отношений не должно превосходить 5,04 и с вероят-
вероятностью 0,95 не должно превосходить 2,31. В данном слу-
случае |X1|/s1=5,38>5,04, поэтому гипотезу отсутствия
систематич. ошибок целесообразно отвергнуть; в то же
время следует признать, что гипотеза об отсутствии ме-
тодич. ошибки (х2=0) не противоречит результатам
наблюдений, т. к. |X2|/s2=l,004<2,31. Таким образом,
можно заключить, что для определения t по результату
наблюдения Т целесообразно пользоваться приближен-
приближенной формулой t= Г+0,35.
Случай нескольких неизвестных
(нелинейные связи). Пусть п результатов из-
измерений У,- связаны с m неизвестными Xj (то<п) функ-
функциональной зависимостью Yi=f((x-L, хг, ... , хт)-\~Ь/;
i=l, 2, ... , п, где 8,-— независимые случайные ошибки,
а функции /,- (в общем случае нелинейные) дифференци-
дифференцируемы. Согласно Н. к. м. в качестве оценок для xj при-
принимают такие величины Xj, для к-рых сумма квадратов
будет наименьшей. Так как функции /,• нелинейные, то
решение нормальных уравнений dS/dXj=Q в этом слу-
случае может представлять значительные трудности. Иног-
Иногда нелинейные связи каким-либо преобразованием мо-
могут быть приведены к линейным.
Напр., при намагничивании железа напряженность
магнитного поля Н связана с магнитной индукцией В
эмпирич. формулой В = Н/(х1-\-Нх2) (коэффициенты х1 и
х.г определяются по измеренным значениям В,- при за-
заданных Н{). Индукция В — нелинейная функция от ху
и хг. Одпако обратная величина индукции зависит от
х1 и х2 линейно. Применение II. к. м. к исходному и
преобразованному равенствам дает, вообще говоря,
различные оценки для неизвестных хх и х2, по если дис-
дисперсия случайных ошибок измерения индукции значи-
значительно меньше измеряемых величин В;, то D(l/B)x:
тВ~*. Поэтому величинам i/B; следует приписать веса
A/.В,-L; естественно ожидать, что при этих условиях
различие оценок в нелинейном и линейном случаях бу-
будет практически несущественным.
В тех случаях, когда не удается тождественными
преобразованиями заменить нелинейные уравнения ли-
линейными, пользуются другим способом линеаризации.
Из заданных п уравнений отбирают какие-либо т урав-
уравнений, решение к-рых X?, Х\, ... , Хт принимают за
нулевое приближение для неизвестных xj. Если поло-
положить \j=Xj—X'j, то систему условных уравнений мож-
можно записать в виде:
y,-=//(^J + Si, -Y2° + g2, .-., Xm + ?m), 1 = 1,2, .... и.
Разлагая правые части в ряд по степеням %j и ограни-
ограничиваясь линейными членами, получают
где (/,¦)„ и [ —— J — значение функции/,- и ее производ-
производных по xj при x3 = .Yj, ж2 = Х2, ... , хт=Хт. Эта система
уравнений линейна, и поэтому для оценки неизвестных
\j легко может быть применен Н. к. м. Оценив Ну, полу-
получают первое приближение для неизвестных X1j= Xaj-\-\j.
Величины X) берут за исходное приближение, и всю
операцию повторяют, пока с заданной точностью не сов-
совпадут два последовательных приближения. Если дис-
дисперсии ошибок 6,- уменьшаются, то процесс сходится.
Очень часто при малых D6,- оказывается вполне до-
достаточным уже первое приближение: не имеет смысла
требовать нахождения Xj с точностью, значительно
превышающей Y^DXj.
Во многих практически важных случаях (и в част-
частности, при оценке сложных нелинейных связей) коли-
количество неизвестных параметров бывает весьма большим,
и поэтому реализация Н. к. м. оказывается эффектив-
эффективной лишь при использовании современной вычислитель-
вычислительной техники.
Лит.: Ш Марков А. А., Нечисление вероятностей,
4 изд., М., 1924; [2] Колмогоров А. Н., «Успехи матем.
наук», 1946, т. 1, в. 1, с. 57—70; L;J] Л и н н и к Ю. В., Метод
наименьших квадратов и основы математико-статистической
теории обработки наблюдений, 2 изд., М., 1962; [4] Нали-
Налимов В. В., Применение математической статистики при ана-
анализе вещества, М., 1960; [5] Helmert F. R., Die Ausglci-
chungsreclmung nach der Mcthode (ler kleinsten Quadrate, 3 Aull.,
Lpz.— В., 1924. Л. Н. Большее.
НАИМЕНЬШИХ РЕАКЦИЙ ПРИНЦИП — след-
следствие из Гаусса принципа, получаемое из последнего
с помощью уравнений, выражающих второй закон Нью-
Ньютона для точек несвободной системы (см. [1]). Согласно
Н. р. п. для действительного движения системы веди-
чина
Zmd 2m
есть минимум в классе мыслимых по Гауссу движений:
Здесь Rv — реакции связей, mv — массы точек системы.
Лит.: [1] Четаев Н. Г.,Устойчивость движения. Ра-
Работы по аналитической механике, М., 1962, с. 493.
В. В. Румянцев.
НАИСКОРЕЙШЕГО СПУСКА МЕТОД — частный
случай .метода спуска, когда направление gk, указываю-
указывающее спуск, выбирается противоположным grad f(xk).
Формулы Н. с. м. имеют вид
^+1 = ** —«ft/' (Ж*), fc = 0, 1, ...,
где параметры {сс^} выбираются из условия максималь-
максимального убывания на каждом шаге функции f(x). Если
функция / дважды непрерывно дифференцируема и
матрица /" ее вторых производных удовлетворяет при
любых х, у неравенству
с константами Л/^т>0, то (см. [2], [4]) последователь-
последовательность {хк} сходится к решению х* задачи минимизации
функции / со скоростью геометрич. прогрессии со зна-
знаменателем д<1.
Широкое применение Н. с. м. нашел при решении
систем линейных алгебраич. уравнений Ax=f с эр-
эрмитовой и положительно определенной матрицей А.
В действительном случае задача решения этой системы
эквивалентна нахождению вектора х*, минимизирую-
минимизирующего в пространстве тг-мерных векторов функционал
f(x) = (Ax,x)-2(x,f). (*)
Применительно к (*) формулы Н. с. м. принимают вид
причем значение р.к определяется из условия минимума
функционала (*) по формуле
Если спектр матрицы А принадлежит отрезку дейст-
действительной оси [т, М], где М^то>0, то последователь-
последовательность {х*} сходится к решению х* со скоростью геомет-
геометрич. прогрессии со знаменателем q=(M—m)/(MJrm).
Н. с. м. может быть применен для решения оператор-
операторного уравнения Au=f с самосопряженным положитель-
положительно определенным ограниченным оператором А. Если
оператор А не удовлетворяет наложенным условиям,
задачу можно симметрировать, сведя к задаче
A*Au = A*f,
и уже затем применить Н. с. м. (см. также Минималь-
Минимальных невязок метод).
Лит.: [1] К а н т о р о в и ч Л. В., «Докл. АН СССР», 1947,
т. 56, К, 3, с. 233—36; [2] К а н т о р о в и ч Л. В., Ави-
Авилов Г. П., Функциональный анализ, 2 изд., М., 1977; 13]
Фаддеев Д. К., Фаддеева В. Н., Вычислительные
методы линейной алгебры, 2 изд., М.— Л., 1963; МПшеиич-
ный Б. Н., Данилин Ю. М., Численные методы в экст-
экстремальных задачах, М., 1975; [5] Бахвалов Н. С, Числен-
Численные методы, 2 изд., т. 1, М., 1975. Ю. А. Кузнецов.
НАЙКВИСТА КРИТЕРИИ — необходимое и доста-
достаточное условие устойчивости замкнутой линейной сис-
системы автоматич. регулирования (системы с обратной
связью), формулируемое в терминах свойств разомкну-
разомкнутой системы (системы с разомкнутой цепью обратной
связи).
Пусть рассматривается нек-рая линейная система
автоматич. регулирования с обратной связью и пусть
W УР> — N (р)
— передаточная функция соответствующей разомкну-
разомкнутой системы, причем степень многочлена М (z) не выше
степени многочлена N (z). Комплекснозначная функция
z=W(iw) действительного переменного ш?[0, со) (а м-
плнтудно-фазовая характеристика
разомкнутой системы) описывает в комплексной пло-
плоскости z кривую, наз. диаграммой Найкви-
с т а. Пусть характеристич. многочлен N (z) разомк-
разомкнутой системы имеет к, 0<:&<:«, корней с положитель-
положительными и н—к корней с отрицательными действительными
частями. Н. к. гласит: замкнутая система автоматич.
регулирования асимптотически устойчива тогда и толь-
только тогда, когда диаграмма Найквиста охватывает точку
z=—1 против хода часовой стрелки к/2 раз (эквивалент-
(эквивалентное условие: когда вектор с началом —1 и концом W(ia)
при возрастании со от 0 до -\- сю поворачивается в
положительном направлении на угол лк).
Этот критерий впервые был предложен X. Найквис-
том [1] для усилителей с обратной связью; он представ-
представляет собой один из частотных критериев устойчивости
линейных систем автоматич. регулирования (примы-
(примыкающий, напр., к Михайлова критерию, см. [2], [3]).
Важно отметить, что если уравнения нек-рых элементов
системы неизвестны, то диаграмму Найквиста можно по-
построить экспериментально, подавая гармонич. сигнал с
изменяющейся частотой на вход при разомкнутой цепи
обратной связи [4]. Известны обобщения Н. к. на систе-
системы автоматич. регулирования с запаздыванием и на
импульсные системы (см. [5]).
Лит.: [1] Nyquist H., «Bell System Techn. J.», 1932,
v. 11, № l,j. 126—47; [2] Булгаков Б. В., Колебания,
М., 1954; [3] Лаврентьев М. А., Ш а б а т Б. В., Методы
теории функций комплексного переменного, 4 изд., М., 1973;
[4] Р о й т е н б е р г Я. Н., Автоматическое управление, 2 изд.,
М., 1978; [5] Г н о е н с к и й Л. С, К а м е н с к и й Г. А.,
ЭльсгольцЛ. Э., Математические основы теории управ-
управляемых систем, М., 1969. Н. X. Розов.
НАКЛОННАЯ к прямой / — прямая, пересе-
пересекающая прямую I под углом, отличным от прямого.
Н. к плоскости — прямая, пересекающая эту
плоскость под углом, отличным от прямого. БСЭ-з.
НАКОПЛЕНИЕ ПОГРЕШНОСТИ при числен-
численном решении алгебраических урав-
уравнений — суммарное влияние округлений, сделан-
сделанных на отдельных шагах вычислительного процесса,
на точность полученного решения линейной алгебраич.
системы. Наиболее распространенным способом априор-
априорной оценки суммарного влияния ошибок округления в
численных методах линейной алгебры является схема
т. н. обратного анализа. В применении к решению сис-
системы линейных алгебраич. уравнений
Ах=Ъ A)
схема обратного анализа заключается в
следующем. Вычисленное прямым методом М решение
хм не удовлетворяет A), но может быть представлено
как точное решение возмущенной системы
Качество прямого метода оценивается по наилучшей
априорной оценке, к-рую можно дать для норм матрицы
Fм и вектора км- Такие «наилучшие» Fm и км наз. соот-
соответственно матрицей и вектором эквивалентного воз-
возмущения для метода М.
Если оценки для Fm и км имеются, то теоретически
ошибка приближенного решения хм может быть оцене-
оценена неравенством
cond(A) f\\FM\\ . \\hM\\\
ТъТ) ¦ (д}
Здесь cond (А) = [\А \\\\А ~1|| — число обусловленности
матрицы А, а матричная норма в C) предполагается
подчиненной векторной норме || ||.
В действительности оценка для 11^4 —х [| редко бывает
известна, и основной смысл B) состоит в возможности
сравнения качества различных методов. Ниже приво-
приводится вид нек-рых типичных оценок для матрицы Fm-
Для методов с ортогональными преобразованиями
и арифметики с плавающей запятой (в системе A) А
и Ь считаются действительными)
В этой оценке е — относительная точность арифметич.
операций в ЭВМ, \\А ||?=Bа|/I/'2 — евклидова матрич-
матричная норма, /(и) — функция вида Спк, где п — порядок
системы. Точные значения константы С и показателя
к определяются такими деталями вычислительного
процесса, как способ округления, использование опе-
операции накопления скалярных произведений и т. д. Наи-
Наиболее часто &=1 или 3/2.
В случае методов чипа Гаусса в правую часть оценки
D) входит еще множитель g(A), отражающий возмож-
возможность роста элементов матрицы А на промежуточных
шагах метода по сравнению с первоначальным уровнем
(такой рост отсутствует в ортогональных методах).
Чтобы уменьшить значение g(A), применяют различные
способы выбора ведущего элемента, препятствующие
возрастанию элементов матрицы.
Для квадратного корня метода, к-рый применяется
обычно в случае положительно определенной матрицы
А, получена наиболее сильная оценка
\\Рм\\Е<С\\А\\Е-г.
Существуют прямые методы (Жордана, окаймления,
сопряженных градиентов), для к-рых непосредствен-
непосредственное применение схемы обратного анализа не приводит
к эффективным оценкам. В этих случаях при исследо-
исследовании Н. п. применяются и иные соображения (см. [6] —
[9]).
Лит.: [1] Givens W., «TJ. S. Atomic Energy Commiss.
Repts. Ser. OR NL», 1954, JMi 1574; [21 W 1 1 k i n s о n J. H.,
Rounding errors in algebraic processes, L., 1963; [3] У и л к и н-
с о н Д ж.-Х., Алгебраическая проблема собственных значений,
пер. с англ., М., 1970; [4] Воеводин В. В., Ошибки округ-
округления и устойчивость в прямых методах линейной алгеб-
алгебры, М., 1969; [5] его же, Вычислительные основы
линейной алгебры, М., 1977; [6] Peters G., W i I k i n-
s о n J. H., «Communs Assoc. Comput. Math.», 1975, v. 18,
№ 1, p. 20—24; [7] В г о у d e n С. G., «J. Inst. Math, and
Appl.», 1974, v. 14, № 2, p. 131—40; [8J R e i d J. К., в кн.:
Large Sparse Sets of Linear Equations, L.— N. Y., 1971, p. 231 —
254; [9] И к р а м о в X. Д., «Ж. вычисл. матем. и матем. фи-
физики», 1978, т. 18, Кг 3, с. 531—45. X. Д. Икрамов.
Н. п. округления или погрешности
метода возникает при решении задач, где решение
является результатом большого числа последовательно
выполняемых арифметич. операций.
Значительная часть таких задач связана с решением
алгебраич. задач, линейных или нелинейных (см. вы-
выше). В свою очередь среди алгебраич. задач наиболее
распространены задачи, возникающие при аппроксима-
аппроксимации дифференциальных уравнений. Этим задачам свой-
свойственны нек-рые специфич. особенности.
Н. п. метода решения задачи происходит по тем же
или по более простым законам, что и Н. п. вычислитель-
вычислительной погрешности; Н. п. метода исследуется при оценке
метода решения задачи.
При исследовании накопления вычислительной по-
погрешности различают два подхода. В первом случае счи-
считают, что вычислительные погрешности на каждом шаге
вносятся самым неблагоприятным образом и получают
мажорантную оценку погрешности.
Во втором случае считают, что эти погрешности случай-
случайны с определенным законом распределения.
Характер Н. п. зависит от решаемой задачи, метода
решения и ряда других факторов, на первый взгляд
могущих показаться несущественными; сюда относятся
форма записи чисел в ЭВМ (с фиксированной запятой
или с плавающей запятой), порядок выполнения ариф-
арифметич. операций и т. д. Напр., в задаче вычисления
суммы N чисел
A
существенен порядок выполнения операций. Пусть
вычисления производятся на машине с плавающей за-
запятой с t двоичными разрядами и все числа лежат в
пределах 1/2<!а„| <:1. При непосредственном вычисле-
вычислении Лдг с помощью рекуррентной формулы
А,г + 1 = Ап + ап, П = 1, ..., N— 1,
мажорантная оценка погрешности имеет порядок 2~fN.
Можно поступить иначе (см. [1]). При вычислении по-
попарных сумм ^4^=a2fc_1+a2fc (если iV=2Z+l нечетно)
полагают A}+i=a2i + 1. Далее вычисляются их попарные
суммы Л| = Alk-i+Alk и т. д. При 2m~1<N<2OT после
т шагов образования попарных сумм по формулам
получают А\ =Лдг; мажорантная оценка погрешности
порядка 2~4og2N.
В типичных задачах величины ат вычисляются по
формулам, в частности рекуррентным, или поступают
последовательно в оперативную память ЭВМ; в этих
случаях применение описанного приема приводит к
увеличению загрузки памяти ЭВМ. Однако можно орга-
организовать последовательность вычислений так, что за-
загрузка оперативной памяти не будет превосходить
—log2N ячеек.
При численном решении дифференциальных уравне-
уравнений возможны следующие случаи. При стремлении ша-
h~~ Я
га сетки h к нулю погрешность растет как (а (К)) , где
g>0, a lim |а(АI>1. Такие методы решения задач
относят к классу неустойчивых. Их применение
носит эпизодич. характер.
Для устойчивых методов характерен рост по-
погрешности как A (h)h~4, где lim |Л(/г)|<оо. Оценка
ft-0
погрешности таких методов обычно производится следу-
следующим образом. Строится уравнение относительно воз-
возмущения, вносимого или округлением, или погрешно-
погрешностями метода и затем исследуется решение этого уравне-
уравнения (см. [2], [3]).
В более сложных случаях применяется метод
эквивалентных возмущений (см. [1J,
[4]), развитый в отношении задачи исследования на-
накопления вычислительной погрешности при решении
дифференциальных уравнений (см. [3], [5], [6]). Вычис-
Вычисления по нек-рой расчетной схеме с округлениями рас-
рассматриваются как вычисления без округлений, но для
уравнения с возмущенными коэффициентами. Сравнивая
решение исходного сеточного уравнения с решением
уравнения с возмущенными коэффициентами получают
оценку погрешности.
Уделяется существенное внимание выбору метода по
возможности с меньшими значениями q и А [К). При
фиксированном методе решения задачи расчетные фор-
формулы обычно удается преобразовать к виду, где q<.\
(см. [3], [5]). Это особенно существенно в случае обык-
обыкновенных дифференциальных уравнений, где число ша-
шагов в отдельных случаях оказывается очень большим.
Величина А (К) может сильно расти с ростом проме-
промежутка интегрирования. Поэтому стараются применять
методы по возможности с меньшим значением A (h).
В случае задачи Коши ошибка округления на каждом
конкретном шаге по отношению к последующим шагам
может рассматриваться как ошибка в начальном усло-
условии. Поэтому нижняя грань A (h) зависит от характери-
характеристики расхождения близких решений дифференциаль-
дифференциального уравнения, определяемого уравнением в вариа-
вариациях.
В случае численного решения обыкновенного диф-
дифференциального уравнения y' = f{x, у) уравнение в
вариациях имеет вид
и потому при решении задачи на отрезке (х0, X) нельзя
рассчитывать на константу A (h) в мажорантной оценке
вычислительной погрешности существенно лучшую, чем
гх № fy(t,y(t))dt
\ eJX dx.
Поэтому при решении этой задачи наиболее употреби-
употребительны одношаговые методы типа Рунге — Кутта или
методы типа Адамса (см. [3], [7]), где Н. п. в основном
определяется решением уравнения в вариациях.
Для ряда методов главный член погрешности метода
накапливается по подобному закону, в то время как
вычислительная погрешность накапливается существен-
существенно быстрее (см. [3]). Область практич. применимости
таких методов оказывается существенно уже.
Накопление вычислительной погрешности существен-
существенно зависит от метода, применяемого для решения сеточ-
сеточной задачи. Напр., при решении сеточных краевых за-
дач, соответствующих обыкновенным дифференциаль-
дифференциальным уравнениям, методами стрельбы и прогонки Н. п.
имеет характер A (h)h~9, где q одно и то же. Значения
A (h) у этих методов могут отличаться настолько, что в
определенной ситуации один из методов становится не-
неприменимым. При решении методом пристрелки сеточ-
сеточной краевой задачи для уравнения Лапласа Н. п. имеет
характер с 'h, с>1, а в случае метода прогонки Ah~9.
При вероятностном подходе к исследованию Н. п.
в одних случаях априорно предполагают какой-то закон
распределения погрешности (см. [2]), в других случаях
вводят меру на пространстве рассматриваемых задач и,
исходя из этой меры, получают закон распределения
погрешностей округления (см. [8], [9]).
При умеренной точности решения задачи мажорант-
мажорантные и вероятностные подходы к оценке накопления вы-
вычислительной погрешности обычно дают качественно
одинаковые результаты: или в обоих случаях Н. п.
происходит в допустимых пределах, или в обоих слу-
случаях Н. п. превосходит такие пределы.
Лит.: [1] Воеводин В. В., Вычислительные основы
линейной алгебры, М., 1977; [2] Шура-Бура М. Р., «Прикл.
матем. и механ.», 1952, т. 16, № 5, с. 575—88; [3] Б а х в а-
л о в Н. С, Численные методы, 2 изд., М., 1975; [4] У и л-
кинсон Д ж. X., Алгебраическая проблема собственных
значений, пер. с англ., М., 1970; [5] Б а х в а л о в Н. С. в кн.:
Вычислительные методы и программирование, в. 1, М., 1962,
с. 69—78; [6] Годунов С. К., Рябенький В. С, Раз-
Разностные схемы, 2 изд., М., 1977; [7] Бахвалов Н. С,
«Доил. АН СССР», 1955, т. 104, JM1 5, с. 683—86; [8] е г о же,
«Ж. вычислит, матем. и матем. физики», 1964; т. 4, JMS 3, с. 399—
404; [9] Л а п ш и н Е. А., там же, 1971, т. 11, Л! 6, с.1425—36.
Н. С. Бахвалов.
НАКОПЛЕНИЯ ТОЧКА множества А — точка х то-
пологич. пространства X такая, что в любой ее окрест-
окрестности есть отличная от х точка множества А. У множест-
множества Л в пространстве может быть много Н. т., но может
не быть ни одной. Напр., любое.действительное число
является Н. т. для множества всех рациональных чи-
чисел по отношению к обычной топологии. В дискретном
пространстве ни у одного множества нет ни одной Ы. т.
Множество всех Н. т. множества А в пространстве X
наз. производным множеством (от А).
В ^-пространстве любая окрестность Н. т. множества
содержит бесконечно много точек этого множества.
Следует отличать понятие Н. т. от понятий прикос-
прикосновения точки и полного накопления точки. В частности,
всякая точка множества является его точкой прикосно-
прикосновения, точкой же накопления его ока может и не быть
(пример — дискретное пространство).
Л. В. Архангельский.
НАКРЫВАЮЩАЯ ГОМОТОПИЯ. для гомотопии
Ff отображения Fo : Zf-*- Y при заданном отображении
р : X —>- У — гомотопия Gf : Z —*- X такая, что pGf—
= Ff. При этом, если накрывающее отображение Go для
отображения Fo было задано заранее, то Gf продол-
продолжает Go- Аксиома накрывающей гомо-
гомотопии в сильной форме требует, чтобы для данного
отображения р : X —>- Y любой гомотопии F-f : Z —>- У
с паракомпактным Z и любого G0(pG0= Fo) имелось бы
продолжение Go до Н. г. G<. В этом случае р наз. рас-
расслоением Гуревича. Наиболее важным при-
примером их служат локально тривиальные расслоения.
Если в этом определении требовать лить, чтобы Z
было конечным полиэдром, то р наз. расслоени-
расслоением С е р р а.
Пусть X и Y линейно связны и рд — пространство
путей в А (т. е. непрерывных отображений q : [0, 1] —>-
—>- А). Пусть задано непрерывное отображение
где
D = {(z,q)\x?X
и такое, что |х (х, q) начинается в точке х и накрывает q.
Тогда формула Gf(.r)=|x (G0(x), Ft(x)) дает продолжение
накрывающего отображения Go до Н. г. Gf. В частности,
такое отображение М единственным образом определя-
определяется для накрытий, а также для гладкого векторного
расслоения с фиксированной связностью. Выполнение
аксиомы Н. г. в форме Серра позволяет построить точ-
точную гомотопич. последовательность расслоения (см. Го-
Гомотопическая группа). А. В. Чернавский.
НАКРЫВАЮЩАЯ ПОВЕРХНОСТЬ — то же, что
двумерное накрытие.
НАКРЫТИЕ — отображение р : X ^- Y простран-
пространства X на пространство У, при к-ром прообраз нек-рой
окрестности U(у) каждой точки y?Y распадается на
открытые подмножества, гомеоморфно отображающие-
отображающиеся посредством р на U (у).Эквивалентно: р — локально
тривиальное расслоение с дискретным слоем.
Обычно Н. рассматривается в предположении связ-
связности X и Y и также локальной связности и локальной
односвязности Y. При этих предположениях устанавли-
устанавливается связь между фундаментальными группами п^Х,
х0) и ^\{Y, у0): если р (хо)=уо, то индуцированный гомо-
гомоморфизм р% отображает Лх(Х, ха) изоморфно на под-
подгруппу в л1(У, !/0) и, меняя точку ха в р~1(у), можно
получить в точности все подгруппы из нек-рого клас-
класса сопряженных подгрупп. Если этот класс состо-
состоит из одной подгруппы Н (т. е. Н — нормальный дели-
делитель), то Н. наз. регулярным. В этом случае
возникает свободное действие группы G=nx(Y, уоIП на
А", причем р оказывается факторотображением на про-
пространство орбит Y. Это действие порождается подняти-
поднятием петель: если петле q : [О, 1] —*¦ Y, q(O)=q(l)=yo, со-
сопоставить единственный путь q : [0, 1] —»- X, для к-рого
q@) — x0 и pq=q, то точка q(\) будет зависеть только от
класса этой петли в G и от точки ха. Таким образом, эле-
элементу из G отвечает перестановка точек в р~1(у0). Эта
перестановка по имеет неподвижных точек, если у=тИ,
и непрерывно зависит от точки у0. Возникает гомео-
гомеоморфизм X.
В общем случае эта конструкция определяет лишь
перестановку в р~1(у), т. е. имеется действие яг(У, yQ)
на р~'(у), наз. монодромией накрытия.
Частным случаем регулярного Н. является универсаль-
универсальное накрытие, для к-рого G—n\(Y, y0). Вообще, по каж-
каждой группе Hani(Y, у0) однозначно строится Н. р : X,
хо-+- У, !/„, для к-рого рн.(я1(Х, хо)) = Н. В качестве то-
точек X берутся классы путей q : [0, 1] —>- У, q@)=xo:
два пути qi и д2 отождествляются, если g1(l)^g2(l) и
петля q-iq^1 лежит в элементе из Н. Точка q(l) для пу-
путей из одного класса считается образом этого класса,
что определяет р. Топология в X однозначно задается
требованием, чтобы р оказалось Н.: при этом существен-
существенна локальная односвязность Y. Для любого отображе-
отображения / линейно связного пространства Z, z0 в Y, i/0
поднятие его до отображения / : Z, z0 —*¦ X, х0 сущест-
существует тогда и только тогда, когда f^n-^Z, zo))CZH. Между
накрытиями У имеется отношение частичного порядка
(накрытие накрытия есть накрытие), двойственное
включению подгрупп в Я](У, у0). В частности, универ-
универсальное Н. является единственным максимальным
элементом.
Пример ы. Параметризация окружности (cos cp,
sin ф) задает ее Н. числовой прямой <p?R, к-рое часто
записывают в комплексной форме e»<P и наз. экспо-
экспоненциальным. Аналогично, тор накрывается
плоскостью. При отождествлении диаметрально проти-
противоположных точек сферы возникает Н. сферой проектив-
проективного пространства соответствующей размерности. Во-
Вообще, свободные действия дискретных групп — обыч-
обычный источник регулярных Н. (над пространством ор-
орбит, хотя и не всякое такое действие задает Н. (про-
(пространство орбит может оказаться неотделимым)), но
ЭТО так ДЛЯ КОнеЧНЫХ Групп. А. В. ЧеънавсКич.
НАЛОЖЕНИЯ ОБЛАСТЬ, область над
С",— пара (X, я), где X — линейно связное хаусдор-
фово пространство, я : X —*¦ С" — локальный гомео-
гомеоморфизм, наз. проекцией. Н. о. возникают при
аналитич. продолжении голоморфных функций. Каж-
Каждой аналитической (вообще говоря, многозначной) в
области DczCn функции / отвечает ее Н. о. D с проек-
проекцией я : D -»- D точно так же, как каждой аналитич.
функции одного комплексного переменного соответ-
соответствует риманова поверхность; на Ъ функция / одно-
однозначна. Н. о. наз. также римановой обла-
областью.
Лит.: El] Щ а б а т Б. В., Введение в комплексный анализ,
2 изд., ч. 2, М., 1976. В. В. Жаринов.
НАПРАВЛЕНИЕ — бинарное отношение «? на мно-
множестве А такое, что 1) если х<.у, i/<:z, то кг для лю-
любых х, у, z(~A\ 2) для любого х?А всегда х<^х; 3) каковы
бы ни были ос, у?А, существует z?A такое, что кг,
i/<z (свойство Мура — Смита).
В. И. Пономарев.
НАПРАВЛЕНИЙ ПОЛЕ — геометрическая интер-
интерпретация множества линейных элементов, соответству-
соответствующих системе обыкновенных дифференциальных урав-
уравнений
i,-=/,-(«,*!, ...,хп), * = 1, ..., п. A)
Линейным элементом наз. набор чисел
t, хг, ..., х„, /х(*, хъ ...,хп), ..., fn(t, хи ..., хп), B)
где (t, xlt ... , хп) — точка области GaRn + 1, в к-рой
определены правые части системы A). Линейный эле-
элемент B) можно представить себе как совокупность точки
(t, xx, ... , xn)?G и соответствующего ей направления
с направляющими косинусами
C)
к-рое изображается отрезком малой длины, проходя-
проходящим через эту точку параллельно вектору
A.Ы*, хи ..., хп), ..., /„(«, хи ..., хп)).
Для системы в симметричной форме
dt (faj dxn
fa ((, я,, . . ., х„) ~~ fx (t, x,, . . ., хп)~" ' fn(t,xi, . . .,х„) '
в отличие от системы A), среди направлений поля воз-
возможны и ортогональные оси t.
Любая интегральная кривая системы A) в каждой
своей точке касается отвечающего этой точке направле-
направления поля; всякая кривая, обладающая таким свойст-
свойством, является интегральной кривой системы A). Таким
образом, задание Н. п. эквивалентно заданию системы
A), а задача интегрирования системы A) состоит в оты-
отыскании таких кривых в (ге+1)-мерном пространстве
Rn + 1, касательные к к-рым в каждой точке имеют на-
направление, определяемое формулами C), т. е. имеют
направление, совпадающее с направлением поля в этой
точке.
Особенно наглядной геометрич. картина становится
при п=1. В этом случае через каждую точку (t, x) об-
области определения GaR2 правой части уравнения 1-го
порядка
-?- = /(',*) D)
можно провести отрезок малой длины с угловым коэф-
коэффициентом f(t, x), так что (ориентированный) угол
между осью t и этим отрезком равен arctg/(?, x) (см.
рис.). Часто дифференциальное уравнение D) рассмат-
рассматривается в совокупности с дифференциальным уравне-
уравнением
?=F(t,x), E)
где F(t, x)—i!f(t, x) для то-
чек (t, x)?G, в к-рых f(t,x)?=
ФО, и F{t, x)=0 для то-
точек (t, x)?R2\G, в к-рых
функцию F(t, x) можно доопре-
доопределить этим значением по не-
непрерывности. Тем самым для
пары уравнений D), E) об-
область G расширяется до обла-
области Go за счет пополнения точ-
точками, в к-рых направление параллельно оси х, а интег-
интегральным кривым разрешается иметь и точки с верти-
вертикальной касательной.
Если в области G для уравнения D) (или в области Со
для пары уравнений D), E.)") изобразить Н. п. достаточ-
достаточно подробно, то по построенным отрезкам можно соста-
составить примерное качественное представление о картине
поведения интегральных кривых. Это соображение ле-
лежит в основе приближенного графич. метода решения
уравнения D) — метода изоклин, в к-ром
построение Н. п. осуществляется с помощью изоклин.
На использовании геометрич. связи Н. п. и интеграль-
интегральных кривых базируется приближенный численный ме-
метод решения уравнения D) — Эйлера метод.
Для автономных систем обыкновенных дифференци-
дифференциальных уравнений более удобна и наглядна геометрич.
интерпретация в виде векторного поля — поля фазовых
скоростей в фазовом пространстве системы.
Лит.: И] П о н т р я г и к Л. С, Обыкновенные диффе-
дифференциальные уравнения, 4 изд., М., 1974; [2] Камке Э.,
Справочник по обыкновенным дифференциальным уравнениям,
пер. с нем., 5 изд., М., 197В; [3] С а н с о н с Д ж., Обыкновен-
Обыкновенные дифференциальные уравнения, пер. с итал., т. 1—2, М.,
1953—54. И. X. Розов.
НАПРАВЛЕННОЕ МНОЖЕСТВО — множество А,
наделенное направлением. Всякое (частично) упорядо-
упорядоченное множество, каждой конечное подмножество к-ро-
го имеет верхнюю (нижнюю) грань, является Н. м.
и тогда А наз. направленным вверх (вниз)
множеством. Напр., множество всех открытых покры-
покрытий {у} топологич. пространства является Н. м., в нем
у'<:у", если у' вписано в у"; другой пример Н. м.—
предфильтр, т. е. семейство б непустых мно-
множеств такое, что если U, F?8, то существует W?8,
для к-рого WdU[\V. Основное назначение Н. м. (рав-
(равно как и фильтров) — служить множеством номеров
при определении обобщенных последовательностей то-
точек, или направленностей, в топологич. пространствах,
СХОДИМОСТИ ИХ и Т. д. А. В. Архангельский.
НАПРАВЛЕННОСТЬ, обобщенная после-
последовательность, — отображение направленного
множества А (в топологическое) пространство X, т. е.
соответствие, по к-рому каждому а?А сопоставляется
нек-рое х<х.?Х. В терминах «Н.» характеризуются отде-
отделимости аксиомы, свойства типа компактности, осу-
осуществляются различные построения (напр., бикомпакт-
бикомпактные расширения) и т. д. Так, Н. {ха : <х?А,*?} тополо-
топологич. пространства X сходится (иногда добавляется: по
направлению <:) к точке ж ?Х в пространстве X, если
для каждой окрестности Ох найдется $?А такое, что
ха G Ох ПРИ Р <а 6^4. Это — сходимость по Му-
Муру — Смиту [3] (она представляется более отвечаю-
отвечающей интуитивным представлениям, чем теория сходи-
сходимости, построенная на понятии фильтра).
Обычная последовательность — частный случай Н.,
когда множество А состоит из всех натуральных чисел.
Лит.: II] Келли Д ж., Общая топология, пер. с англ.,
М., 1968; [2] Рид М., Саймон Б., Методы современной
математической физики, т. 1— Функциональный анализ, пер.
с англ., М., 1977; [3] М о о re E., Smith H-, «Amer.
J. Math.», 1922, V. 44, p. 102—21. В. И. Пономарев.
НАПРАВЛЯЮЩИХ ФУНКЦИОНАЛОВ МЕТОД —
специальный метод для вывода теоремы о разложении
по собственным функциям самосопряженного диффе-
ренциальвого оператора. В частном случае сингуляр-
сингулярного дифференциального оператора второго порядка на
полуоси соответствующая теорема была впервые полу-
получена Г. Вейлем [1]. Общая теорема для случая диффе-
дифференциального оператора порядка 2ге была доказана
М. Г. Крейном [2] методом, получившим название Н.
ф. м. Соответствующий результат формулируется сле-
следующим образом (см. [3]). Пусть 1(у) — самосопряжен-
самосопряженное дифференциальное выражение порядка 2ге на интер-
интервале (а, Ь), щ{х, X), ... , и2п{х, к) — система решений
уравнения
удовлетворяющая начальным условиям:
uj W - \ 0 при j ф к,
где х0 — фиксированная точка интервала (а, Ь), а
ulk—l] есть (к—1)-я квазипроизводная функции uj. Тог-
Тогда для всякого самосопряженного расширения L опе-
оператора, порожденного выражением 1(у), существует
матричная функция распределения
такая, что для любой функции f(x)?L2(a, b) справедли-
справедливы формулы:
f(x)u/(x,k)dX, A)
и=S! 12)Г*=1 *'{к) Uk (x'k) dcJk (k)' B)
причем интегралы в формулах A) и B) сходятся в смысле
метрик в La и L2(a, b) соответственно. При этом имеет
место аналог равенства Парсеваля
5 j
Функционалы ср (X), заданные на финитных функциях
из L2(a, 6), наз. направляющими функци-
функционалами дифференциального выражения 1(у).
Обобщение и развитие Н. ф. м. привело к понятию
оснащенного гильбертова пространства и разложения по
обобщенным собственным элементам (см. [4], [5], [6]).
Лит.: [1] W е у 1 Н., «Math. Ann.», 1910, Bd 68, S. 220—
269: [2] К р е й н М., «Докл. АН СССР», 1946, т. 53, JSffi 1, с. 3—
6; [3] НаймаркМ. А., Линейные дифференциальные опе-
операторы, 2 изд., М., 1969; [4] Березанский Ю. М., Раз-
Разложение по собственным функциям самосопряженных операто-
операторов, К., 1965; [5] Гельфанд И. М., III и л о в Г. Е.,
Некоторые вопросы дифференциальных уравнений, М., 1958;
[6] Гельфанд И. М., ВиленкинН. Я., Некоторые
вопросы гармонического анализа. Оснащенные гильбертовы
пространства, М., 1961; [7] Л е в и т а н Б. М., Разложение по
собственным функциям дифференциальных уравнений второго
порядка, М.— Л., 1950. А. И. Логинов.
НАПРЯЖЕНИЙ ТЕНЗОР — тензор, определяющий
распределение внутренних напряжений в деформируе-
деформируемом теле. Н. т.— симметричный тензор 2-го ранга а,у.
Компонента о,^ Ы. т. есть ?-я компонента силы, дейст-
действующей на единицу поверхности, перпендикулярную
к оси г;,. Так, на единичную площадку, перпендикуляр-
перпендикулярную к оси х, действуют нормальная к ней (направлен-
(направленная вдоль оси х) сила <зхх и тангенциальные (направлен-
(направленные по осям у и г) силы аух и агх. Напряженное состоя-
состояние, заданное компонентами Н. т., может быть разло-
разложено на два напряженных состояния. Первое из них
характеризуется компонентами т. н. сферическо-
сферического (шарового) тензора напряжений:
Второе напряженное состояние характеризуется компо-
нентами девиатора тензора напряже-
напряжений:
а. =°i7 з б<7°"«-
Лит.: [1] Л а н д а у Л. Д., Л и ф ш и ц Е. М., Теория
упругости, 3 изд., М-, 1965. А. Б. Иванов.
НАРОСТ пространства X— множество
Y\X, где Y — бикомпактное расширение X. Свойства
Н. связаны со свойствами X: бикомпактность Н. экви-
эквивалентна локальной бикомпактности X, нульмерность
Н. в нек-рых расширениях связана обычно со свойст-
свойством периферич. бикомпактности X, существование
компактного метризуемого расширения с Н. размерно-
размерности <7с обеспечивает наличие в X открытой базы, в
к-рой компактно пересечение границ любых &-J-1 раз-
различных множеств, и т. п. Если всякий связный биком-
бикомпакт в Y\X состоит из одной точки (напр., ind (Y\X) =
= 0), Н. наз. пунктиформным. Если сущест-
существует хотя бы одно бикомпактное расширение с пункти-
пунктиформным Н., то среди таких расширений найдется мак-
максимальное [iX, причем оно является минимальным
совершенным расширением. е. г. Спляренко.
НАСЛЕДСТВЕННО НЕРАЗЛОЖИМЫЙ КОНТИ-
КОНТИНУУМ, континуум Кнастера,— неразложи-
неразложимый континуум, в к-ром неразложим и каждый соб-
собственный ПОДКОНТИНУУМ. А. А. Мальцев.
НАТУРАЛЬНОЕ УРАВНЕНИЕ кривой — систе-
система равенств
задающих кривизну к± и кручение кг кривой как функ-
функции натурального параметра s на кривой. Для любых
регулярных функций ф(*)^0 иг|)(«) существует единст-
единственная с точностью до движения в пространстве кривая
с кривизной cp(s) и кручением t|3(s). Необходимым и до-
достаточным условием того, что кривая является плоской,
служит тождественное обращение в нуль кручения.
Необходимым и достаточным условием совпадения кри-
кривой с прямой или ее отрезком является тождественное
обращение кривизны в нуль. д. д. соколов.
НАТУРАЛЬНОЕ ЧИСЛО — одно из основных поня-
понятий математики. Н. ч. может быть истолковано как
кардинальное число непустого конечного множества.
Множество N= {1, 2, ...} всех Н. ч. и операции над ни-
ними: сложение (-J-) и умножение (¦) образуют систему
Н. ч. <jV, -f, •, 1>. В этой системе обе бинарные опера-
операции ассоциативны, коммутативны и связаны законом
дистрибутивности; 1 — нейтральный элемент умноже-
умножения, т. е. а-\ = а для любого Н. ч. а; сложение не имеет
нейтральных элементов и более того а-\-Ьфа для любых
Н. ч. а и Ь. При этом выполняется условие (а к с и о-
м а и и д у к ц и и): любое подмножество множества
N, содержащее 1 и вместе с каждым элементом а сумму
a-j-1, совпадает с N. См. Натуральный ряд, Арифмети-
Арифметика формальная.
Лит.: [1] История математики с древнейших времен до
начала XIX столетия, т. 1, М., 1970; [2] Нечаев В. И.,
Числовые системы, М., 1975. А. А. Бухштаб, В. И. Нечаев.
НАТУРАЛЬНЫЙ ПАРАМЕТР на с п р я м л я е-
м о й кривой — такой параметр s на кривой у с
параметрнч. уравнением r=r(s), для к-рого длина дуги
кривой между точками Г {s±) и r{s2) равна \st—s2\. Пара-
Параметризация кривой с помощью Н. п. наз. естест-
естественной параметризацией. Естественная
параметризация к раз дифференцируемой (аналитиче-
(аналитической) кривой без особых точек является также к раз
дифференцируемой (аналитической). д. д. Соколов
НАТУРАЛЬНЫЙ РЕПЕР, трехгранник
(или репер) Френе, естественный
трехгранни к,— фигура, составленная из каса-
касательной, главной нормали, бинормали и трех плоско-
плоскостей, попарно содержащих эти прямые. Если ребра
Н. р. в данной точке кривой принять за оси прямоуголь-
ной декартовой системы координат, то уравнение кри-
кривой в естественной параметризации (см. Натуральный
параметр) имеет в окрестности этой точки вид:
где kY и к2 — кривизна и кручение кривой в указанной
точке. А. В. Иванов.
НАТУРАЛЬНЫЙ РЯД — непустое множество
N= {1, ... }, в к-ром определена унарная опера-
операция S (т. е. S — однозначное отображение N в N),
удовлетворяющая условиям (Пеано аксиом ы):
1) для любого а из Л':
2) для любых а и 6 из N: если
Sa=Sb,
то
а=Ъ;
3) любое подмножество N, к-рое содержит 1 и вместе
с каждым элементом а элемент Sa, совпадает с N.
Элемент Sa множества N обычно наз. элемен-
элементом, непосредственно следующим
за а. Н. р. представляет собой вполне упорядоченное
множество. Можно доказать, что следующие условия:
a+i=Sa, a + Sb=S (а-\-Ъ),
а>1=а, a-Sb = а6 -\-а,
где а и b — любые элементы из N, определяют во
множестве N бинарные операции (+) и (¦). Система
<ЛГ, +, •, 1> является системой натуральных чисел.
Лит.: [1]Ван дорВарденБ. Л., Алгебра, пер. с
нем., 2 изд., М., 1979. А. А. Бухштаб, В. II. Нечаев.
«НАЧАЛА» ЕВКЛИДА (Zxoixeia) — научное произ-
произведение, написанное в 3 в. до н. э., содержащее основы
античной математики: элементарной геометрии, теории ¦
чисел, алгебры, общей теории отношений и метода опре-
определения площадей и объемов, включавшего элементы
теории пределов. «Н.» Е.— образец дедуктивной сис-
системы, содержащей исходные предложения геометрии
и других разделов математики, на основе к-рых все
теории развиваются строго логически.
«Н.» Е. составлены по определенной схеме, сложив-
сложившейся еще до Евклида и кратко изложенной в сочине-
сочинениях Аристотеля: сначала приводятся определения, по- |
стулаты и аксиомы, затем формулировки теорем и их
доказательства. Помимо теорем в «Н.» Е. имеются и
проблемы, решаемые построением или с помощью ариф-
метич. алгоритмов. Вслед яа определением основных
геометрич. понятий и объектов Евклид доказывает су-
существование остальных объектов геометрии (напр., рав-
равностороннего треугольника) путем их построения,
к-рое выполняется на основании пяти постулатов. В
постулатах утверждается возможность выполнения сле-
следующих элементарных построений: 1) через две точки
можно провести прямую; 2) отрезок прямой можно не-
неограниченно продолжить; 3) данным радиусом из дан-
данной точки можно провести окружность; 4) все прямые
углы равны между собой (этим обеспечивается единст-
единственность продолжения прямой); 5) если две прямые,
лежащие в одной плоскости, пересечены третьей и если
сумма внутренних односторонних углов меньше суммы
двух прямых, то прямые пересекутся при неограничен-
неограниченном их продолжении с той стороны, с к-рой эта сумма
меньше. Все постулаты (кроме 4-го, к-рый заменяется
требованием, чтобы через две точки проходила единст-
единственная прямая) вошли в качестве аксиом в современные
курсы оснований геометрии. Особенно интересна судьба
5-го постулата. Еще в древности математики пытались
его доказать. Аналогичные попытки продолжались
вплоть до работ Н. И. Лобачевского (см. Лобачевского
геометрия), построившего первую систему неевклидо-
неевклидовой геометрии, в к-рой этот постулат не имеет места. За
постулатами в «Н.» Е. приводятся аксиомы — предло-
предложения о свойствах отношений равенства и неравенства
между величинами: 1) равные одному и тому же равны
между собой, 2) если к равным прибавляются равные,
то и целые будут равны, 3) если от равных отнимаются
равные, то остатки будут равны, 4) совмещающиеся
друг с другом равны между собой, 5) целое больше части
(в нек-рых списках «Н.» Е. к этому добавляют еще
четыре аксиомы).
«Н.» Е. состоят из тринадцати книг (отделов или час-
частей). В книге I рассматриваются основные свойства тре-
треугольников, прямоугольников, параллелограммов и
производится сравнение их площадей. Заканчивается
книга теоремой Пифагора. В книге II излагается т. н.
геометрич. алгебра, т. е. строится геометрич. аппарат
для решения задач, сводящихся к квадратным уравне-
уравнениям. При этом величины изображаются отрезками, а
произведение двух величин — площадями. Алгебраич.
символика в «Н.» Е. отсутствует. В книге III рассмат-
рассматриваются свойства круга, его касательных и хорд
(эти проблемы были исследованы Гиппократом Хиос-
Хиосским во 2-й лол. 5 в. до н. э.), в книге IV — правильные
многоугольники. В книге V дается общая теория отно-
отношений величин, созданная Евдоксом Книдским D в.
до н. э.); она отличается особенной логич. завершен-
завершенностью и в основном эквивалентна теории дедекпндовых
сечений, являющейся одним из обоснований учения о
действительных числах. Общая теория отношений яв-
является основой учения о подобии (книга VI) и метода
исчерпывания (книга XII), также восходящих к Ев-
доксу. В книгах VII—IX изложены начала теории чи-
чисел, основанные на алгоритме нахождения наибольшего
общего делителя. В эти книги входит теория делимости,
включая теоремы об однозначности разложения целого
числа на простые множители и бесконечности числа
простых чисел, а также строится учение об отношении
целых чисел, эквивалентное по существу теории рацио-
рациональных чисел. В книге X на этой основе дается класси-
классификация квадратичных и биквадратичных иррацио-
нальностей и обосновываются нек-рые правила их пре-
преобразования. Результаты книги X применяются в кни-
книге XIII для определения ребер пяти правильных
многогранников. Значительная часть книг X и XIII
(а вероятно, и VII) принадлежит Теэтету (начало 4 в.
до н. э.). В книге XI излагаются начала стереометрии.
В книге XII определяются с помощью метода исчерпы-
исчерпывания отношение площадей двух кругов и отношений
объемов пирамиды и призмы, конуса и цилиндра. Эти
теоремы были впервые доказаны Евдоксом. Наконец, в
книге XIII определяется отношение объемов двух
шаров, строятся пять правильных многогранников и
доказывается, что иных правильных тел не существует.
Последующими греч. математиками к «Н.» Е. были
присоединены книги XIV и XV, не принадлежащие
Евклиду. Они часто и теперь издаются совместно с ос-
основным текстом «Н.» Е. Содержание их не представляет
большого научного интереса.
«Н.» Е. получили широкую известность уже в древ-
древности. Архимед, Аполлоний Пергский и другие ученые
опирались на них при своих исследованиях в области
математики и механики. В кон. 8 — нач. 9 вв. появля-
появляются переводы «Н.» Е. на арабский язык. Первый пере-
перевод на латинский язык был сделан с арабского в 1-й
четверти 12 в. Старинные списки «Н.» Е. отличаются су-
существенными разночтениями; подлинный текст их точно
не восстановлен. Первое печатное издание «Н.» Е. в
переводе на латинский язык появилось в 1482 с черте-
чертежами на полях книги. Наилучшим считается издание
Й. Хейберга E тт., 1883—88), в к-ром приводится как
греческий текст, так и его латинский перевод. На рус-
русском языке имеются следующие переводы: И. Астаро-
ва — «Евклидовы елементы», сокращенные проф.
А. Фархварсоном (8 кн., 1739, пер. слатин.), Н. Курга-
Курганова — «Евклидовы елементы геометрии» (8 кн., 1769,
пер. с франц.), П. Суворова и В. Никитина — «Евкли-
«Евклидовы стихии» (осьм книг, 1 — 6, 11, 12; 1784, пер. с греч.),
Ф. Петрушевского — «Эвклидовых начал восемь книг,
а именно: первые шесть, одиннадцатая и двенадцатая,
содержащие в себе основания геометрии» A819, пер.
с греч.), Ф. Петрушевского — «Эвклидовых начал три
книги, а именно: седьмая, осьмая п девятая, содержа-
содержащие общую теорию чисел древних геометров» A835,
пер. с греч.), М. Е. Ващенко-Захарченко — «Начала
Евклида» A880), Д. Д. Мордухай-Болтовского — «На-
«Начала Евклида» C тт., 1948—50, пер. с греч.).
По материалам одноименной статьи И. Т. Башмаковой
и А. И. Марпушевича ив БСЭ-2.
НАЧАЛЬНЫЕ УСЛОВИЯ — условия при постанов-
постановке задачи Коган для дифференциальных уравнений.
Для обыкновенного дифференциального уравнения, раз-
разрешенного относительно старшей производной:
uim) = f (?j Uj „', ...)U<m-l>), A)
H. у. состоят в задании производных (данных
Кош и)
u(to) = uo, u'(to) = u'o, ...,«(«-!> (*0) = uim-1>, B)
где (t0, u0, u'o, ... , иот~1у) — произвольная фиксиро-
фиксированная точка области определения функции F; эта точ-
точка наз. начальной точкой искомого решения.
Задачу Коши A), B) часто наз. также начальной
задачей.
Для дифференциального уравнения с частными про-
производными, записанного в нормальной форме относи-
относительно выделенной переменной V.
da+ku
| < го, х =(хг, ...,хп),
Н. у. состоят в задании производных (данные К о-
ш и):
01"
= 0
от искомого решения и(х, t) этого уравнения на гипер-
гиперплоскости t=0 (носителя начальных ус-
условий). А. Л. Солдатвв.
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ — раздел гео-
геометрии, в к-ром пространственные фигуры, а также ме-
методы решения и исследования пространственных задач
изучаются при помощи по-
"|/7р строения их изображений на
плоскости. Построение изо-
изображений осуществляется
при помощи центрального
или параллельного проекти-
проектирования фигуры (натуры,
объекта, оригинала) на пло-
плоскость проекций. Наибо-
Наиболее распространенным видом
Риг j техннч. чертежа является
комплексный ч е р-
; с ж, к-рый строится с помощью ортогональной про-
проекции. Сущность этого способа заключается в следую-
следующем: выбирают две взаимно перпендикулярные плоско-
cvii проекций Д, и П„. Плоскость Пх наз. горизон-
горизонтально й и л о с к о с т ь ю проекций, а плоскость
П2 — фронтальной плоскостью проек-
проекций. Произвольную точку А пространства ортогональ-
ортогонально проектируют на эти плоскости (см. рис. 1); получают
Аг
Л\
\
¦4гз
р,и
*3
Л 13
Агг
Лгз
горизонтальную проекцию Аг ж фрон-
фронтальную проекцию Аг. Часто бывает полез-
полезным добавить третью — профильную проек-
проекцию ^4 з — на профильную плоскость
Я3, перпендикулярную к плоскостям П^ и Я2. Для по-
получения комплексного чертежа, состоящего из трех
указанных проекций, плоскости Л1 д,3
и П3 совмещают с плоскостью Я3
(«главной» плоскостью) путем вра-
вращения их вокруг линий р12 и р23
пересечения этих плоскостей с пло-
плоскостью Я2 (см. рис. 2). Обычно Лг
на практике не указывается поло-
положение осей проекций р1г н р13,
т. е. положение проекций опреде-
определяется с точностью до параллель- 1<ис_ 2
ного переноса.
Для построения более наглядных изображений в
Н. г. применяется аксонометрия. Для изображения
объектов, обладающих большой протяженностью, при-
применяют изображения, выполненные в центральной
проекции — перспективе.
Лит.: И] Монж Г., Начертательная геометрия, пер. с
[франц.]. М., 1947; [2] Г л а г о л е в Н. А., Начертательная
геометрия, 3 изд., М., 1953; [3] Курс начертательной гестаетрии,
М., 1956. А. Б. Иванов.
НЕАБЕЛЕВО ЧИСЛОВОЕ ПОЛЕ — поле алгебраич.
чисел, имеющее неабелеву Галуа группу над полем ра-
рациональных чисел Q, или же поле, не являющееся нор-
нормальным над Q. Иногда вместо Q рассматривается
нек-рое другое основное поле к алгебраич. чисел и тер-
термин «неабелевость» понимается как неабелевость (в оп-
определенном выше смысле) над к. Л. В. Кузьмин.
НЕАБЕЛЕВЫ КОГОМОЛОГИИ — когомологии со
значениями в неабелевой группе, пучке неабелевых
групп и т. д. Наиболее известные примеры Н. к.— это
когомологии групп, топологич. пространств и, более
общо, топологизированных категорий в размерностях
О, 1. Единый подход к Н. к. дает следующее понятие.
Пусть С0, С1 — группы, С2 — множество с отмеченной
точкой е, Aff С1 — голоморф группы С1, Aut С2 — груп-
группа преобразований множества С2, сохраняющих е.
Тогда неабелев коцепноы комплекс —
это набор
где р : С" ->- Aff С1, о : С0 -+ Aut С2 — гомоморфизмы,
а б : С1 —>- С2 — такое отображение, что
б(е)=е и 6 (р (я) Ь) = а (а) 6 (Ь), а^С°,
Определяются 0-мерная группа когомологии
и 1-мерное множество (с отмеченной точкой) когомоло-
когомологии
где Z1 = 6~1(e)?=C1, а факторизация проводится при по-
помощи действия р группы С0.
Примеры. 1) Пусть X — топологич. пространст-
пространство с пучком групп if, U — его покрытие; тогда имеется
комплекс Чеха
с* A1, Ю = (С° (U, Ю' с1 (И, Ю, с2 (и, §¦)),
где С' (И, йР) определяются так же, как в абелевом слу-
случае (см. Когомологии),
{a (a) (c))ijb = aicijkaT1,
Когомологии Я'(C*(U, |П)> i=0, 1, при переходе к
пределу по покрытиям дают когомологии
IP {X, JF), ?--=0, 1, пространства X со зна-
чениями в ,f. При этом Н°(Х, <F) = dF (X). Если ff"—
пучок ростков непрерывных отображений со значения-
значениями в топологич. группе G, то Hx{X,^f) интерпретирует-
интерпретируется как множество классов изоморфных топологических
главных расслоений над X со структурной группой G.
В аналогичных терминах получается классификация
гладких и голоморфных главных расслоений. Таким же
способом определяются Н. к. топологизированной ка-
категории; по поводу их интерпретации см. Главный
G-объект.
2) Пусть G — нек-рая группа и А — (не обязательно
абелева) G-rpymia, т. е. операторная группа с группой
операторов G. Пусть результат действия оператора
g?G на элемент а?А обозначается aS. Комплекс
C*(G, А) определяется формулами:
C* = Map(G*, А), А = 0, 1, 2,
(p(a){b))(g)=ab(g)(aS)-\
Группа B°(G, A)=H°(C*(G, А)) совпадает с подгруппой
A ° неподвижных точек в А относительно G, а множество
#*((?, A)=H1(C*(G, А)) есть множество классов эквива-
эквивалентных скрещенных гомоморфизмов G —у А и интер-
интерпретируется как множество классов изоморфных глав-
главных однородных пространств над А. По поводу прило-
приложений и конкретных вычислений Н. к. групп см. Галуа
когомологии. Аналогично определяются Н. к. катего-
категорий и полугрупп.
3) Пусть X — гладкое многообразие, G — группа
Ли, (( — ее алгебра Ли. Не а белев комплекс
д е Рама Rq(X) определяется следующим образом:
Rq(X) — группа всех гладких функций X -^- С;
RkG(X), * = 1, 2,
—пространство внешних А-форм на X со значениями в $.
(/)(P) = (Ad/)P,
= da — [a, a],
Множество H1(Ra(X)) есть множество классов вполне
интегрируемых уравнений вида d/-/~1=a, а=Де,
относительно калибровочных преобразований. Аналог
теоремы де Рама дает интерпретацию этого множества
как нек-рого подмножества в множестве Я1 (п^М), G)
классов сопряженных гомоморфизмов пг(М) -^- G. В слу-
случае комплексного многообразия М и комплексной груп-
группы Ли G определяются также неабелевы голоморфный
комплекс де Рама и комплекс Дольбо, тесно связанные
с задачей классификации голоморфных расслоений [3].
Неабелевы комплексы дифференциальных форм яв-
являются также важным аппаратом в теории псевдогруп-
псевдогрупповых структур на многообразиях [7].
С каждым подкомплексом неабелева коцепного ком-
комплекса связана точная последовательность когомоло-
когомологии. Напр., для комплекса C*(G, А) из примера 2) и его
подкомплекса C*(G, В), где В есть G-инвариантная
подгруппа в А, она имеет вид
е —>¦ Я° (G, В) —>¦ Н° (G, А) —>¦ (А/ВH ^ Я1 (G, В) —*
— #i(G, A).
Если В — нормальный делитель в А, то последователь-
последовательность можно продолжить до члена HX(G, А/В), а если В
лежит в центре, то — и до H2(G, А). Эта последователь-
последовательность точна в категории множеств с отмеченными точ-
ками. Кроме того, существует аппарат («подкручивание»
или «скручивание» коцепного комплекса), позволяю-
позволяющий описывать прообразы всех, а не только отмеченных
элементов (см. [1], [6], [3]). Можно построить также
спектральную последовательность, связанную с двой-
двойным неабелевым комплексом, и соответствующую крае-
краевую точную последовательность [4].
Кроме описанных выше 0-мерных и 1-мерных, суще-
существуют также 2-мерные Н. к. Классич. примером яв-
являются 2-мерные когомологии группы G со значениями
в нек-рой группе А, к-рые определяются следующим
образом. Через jg2(G, А) обозначается множество всех
нар (т, ф), где m:GxG—>¦ A, y.G—>- Aut A — такие
отображения, что
Ф (gi) Ф (Ы ф (gigi)~1 = Int m (ёи Ы>
т (gi, gi) т (gigs, g3) =ф (el) (т (i?a> Вз)) ™ (gi, S-г. ёз)\
здесь Int a — внутренний автоморфизм, порожденный
элементом а?А. В jg2(G, А) определяется отношение
эквивалентности: (то, ф)—(то', ф'), если существует та-
такое отображение h : G —>- А, что
Ф' (g) = (Int h (g)) Ф (g)
Классы этой эквивалентности и составляют множество
когомологии ffl2(G, А). Они находятся во взаимно одно-
однозначном соответствии с классами эквивалентных рас-
расширений группы А при помощи G (см. Расширение
группы).
Соответствие (то, ф) —>- ф дает отображение 6 множе-
множества $%2{G, А) в множество всех гомоморфизмов
G —j- Out A = Aut A/lnt A;
пусть H%(G, A)=Q-X (а) для agOut А. Если фикси-
фиксировать a?Out А, то на центре Z(A) группы А будет
задана структура G-модуля и тем самым определены
группы когомологии Hk (G, Z(A)). Оказывается, что
непустота множества H%(G, А) равносильна тривиаль-
тривиальности нек-рого класса из H3(G, Z(A)). Далее, при этом
условии группа H2(G, Z(A)) просто транзитивно дей-
действует на множестве //«(G, A).
Это определение двумерных коголшлогии можно обоб-
обобщить, перенеся его на топологпзированные категории
(см. [2], где даны также приложения этого понятия).
Общая алгебраич. схема, приводящая к двумерным
когомологиям, указана в [4]; так же, как и в описанном
выше частном случае, их вычисление сводится к вычис-
вычислению одномерных неабелевых и обычных абелевых ко-
когомологии.
Лит.: [1] Серр Ж.-П., Когомологии Галуа, пер. а
франц., М., 1968; [2] Giraud J., Cohomologie non abelienne,
В.— Hdlb.— N. Y., 1971; [3] О н и щ и к А. Л., «Тр. Моск.
матем. об-ва», 19С7, т. 17, с. 45—88; [4] Т о л пыг о А. К., в сб.:
Вопросы теории групп и гомологической алгебры, в. 1, Ярос-
Ярославль, 1977, с. 156—97; [5] р е d е с к е г Р., в кн.: Category
theory, homology theory and their applications, v. 2, B.— Hdlb.—
N. Y.. 1969, p. 32 — 64; [6] Frenkel J.,«Bull. Son. math.
France», 1957, t. 85, MS 2, p. 135—220; [7] G о 1 d s с h m i d t H.,
«Bull. Amer. Math. Soc», 1978, v. 84, Ni 4, p. 531—46; [8]
Springer Т. А., в кн.: Proceudings of Symposia in pure
mathematics, Providence, v. 9, 1966. p. 164—82.
А. Л. Онищик, А. Н. Толпыго
НЕАРХИМЕДОВА ГЕОМЕТРИЯ — совокупность гео-
метрич. предложений, вытекающих из групп аксиом:
инцидентности, порядка, конгруэнтности и параллель-
параллельности системы Гильберта аксиом евклидовой геометрии,
и не связанных с аксиомами непрерывности (с аксиома-
аксиомами Архимеда и полноты). В узком смысле Н. г. описы-
описывает геометрич. свойства прямой, на к-poii не верна ак-
аксиома Архимеда (н е а р х и м е д о в а прямая).
Для исследования геометрич. соотношений в Н. г.
вводится исчисление отрезков — неархимедова число-
числовая система, рассматриваемая как специальная комп-
лексная числовая система. Определяются понятия от-
отрезка, отношения отрезков, сложение и умножение от-
отрезков. В частности, вводится дезаргова числовая сис-
система — неархимедова система, в к-рой умножение от-
отрезков некоммутативно. С помощью этих числовых сис-
систем в Н. г. строится теория подобия фигур, теория
площадей и т. д. Теория площадей многоугольников, ле-
лежащая в основе теории измерения площадей фигур на
неархимедовой плоскости, опирается на понятие равно-
великости многоугольников по дополнению, к-рое в
Н. г. является более общим по отношению к понятию
равносоставленности (равновеликое™ по разложению
на пары конгруэнтных треугольников).
В II. г. существуют треугольники, имеющие соответ-
соответственно равные меры высот и оснований, равновеликие
по дополнению, но не равносоставленные. Равновели-
Равновеликие но дополнению многоугольники в Н. г. имеют оди-
одинаковую меру площади, и два многоугольника с одина-
одинаковой мерой площади всегда равновелики по дополне-
дополнению. Для мрямоугольных треугольников в Н. г. имеет
место теорема Пифагора.
С помощью исчисления отрезков в неархимедовом про-
пространстве вводится система аффинных (или проективных)
координат. Напр., на плоскости выбираются две пря-
прямые — оси координат, проходящие через фиксирован-
фиксированную точку, на каждой из осей отмечаются единичные
отрезки. В этой системе аффинных координат уравнение
прямой является линейным, т. е. имеет вид ах-\-Ьу-]-с=
= 0, где х, у — числа (отрезки), определяют координаты
точек на прямой, а, Ь, с — фиксированные числа (от-
(отрезки), причем умножение фиксированных отрезков
на отрезки хну производится всегда слева, и, вообще
говоря, уравнение xa-\-yb-\-c=0 в этой системе коорди-
координат не представляет прямую.
Система геометрич. предложений, составляющих Н.
г., может быть реализована на модели из конечного
набора основных объектов: «точек», «прямых» и т. д.
(здесь на каждой «прямой» не предполагается сущест-
существование бесконечного множества «точек»). Построение
числовых моделей Н. г. приводит к т. н. транс-
трансфинитным (н е а р х и м е д о в ы м) прост-
пространствам Гильберта. Такое числовое прост-
пространство на прямой наз. линейным простран-
пространством Веронезе.
Числовая реализация Н. г., в к-рой коммутативный
закон умножения не является необходимым, играет так-
также важную роль в построении непаскалевой геометрии
(см. также Недезаргова геометрия).
Значение Н. г. определяется ее ролью в исследова-
исследовании независимости и непротиворечивости системы Гиль-
Гильберта аксиом евклидова пространства. Реализация на
числовой модели групп аксиом инцидентности, порядка,
конгруэнтности и параллельности доказывает как их
независимость от аксиом полноты, так и непротиворечи-
непротиворечивость самой Н. г. С другой стороны, выясняется и роль
аксиом непрерывности в построении евклидовой гео-
геометрии на основе аксиом Гильберта. В частности, без
аксиом непрерывности невозможно доказать эквива-
эквивалентность евклидовой аксиомы параллельности предло-
предложению о равенстве суммы внутренних углов любого
треугольника двум прямым углам.
Геометрич. построения на неархимедовой плоскости
всегда осуществимы с помощью линейки с отмеченным
эталоном длины (отмеченным отрезком).
Лит.: [1] Гильберт Д., Основания геометрии, пер.
с нем., М.—Л., 1948. Л. А. Сидоров.
НЕАССОЦИАТИВНЫЕ КОЛЬЦА И АЛГЕБРЫ —
множества с двумя бинарными операциями -j- и ., удов-
удовлетворяющими всем аксиомам ассоциативных колец и
алгебр, кроме, быть может, аксиомы ассоциативности ум-
умножения. Первые примеры неассоциативных колец
(Н. к.) и неассоциативных алгебр (Н. а.), не являю-
щихся ассоциативными, появились в сер. 19 в. (Кэли
числа и вообще гиперкомплексные числа). Если в ассоци-
ассоциативном кольце (алгебре) рассматривается (вместо
обычного) умножение [а, Ь] = аЬ—Ьа, то получается
Н. к. (Н. а.), являющееся кольцом Ли (алгеброй Ли).
Еще один важный класс Н. к. (Н. а.) — нордановы
кольца (алгебры): если в ассоциативной алгебре над
полем характеристики Ф2 (или над коммутативным
кольцом операторов с 1 и 1/2) ввести операцию а-Ъ=
= а * а, то полученное кольцо является йордановым.
Теория Н. к. и а. развилась в самостоятельное направ-
направление алгебры, имеющее много точек соприкосновения
с другими частями математики, а также с физикой, ме-
механикой, биологией и др. Центральная часть теории
Н. к. и а.— это теория т. н. колец и алгебр,
близких к ассоциативным: лиевых, аль-
альтернативных, йордановых, мальцевских колец и ал-
алгебр и нек-рых их обобщений (см. Ли алгебра, Альтер-
Альтернативные кольца и алгебры, Йорданова алгебра, Маль-
Мальцева алгебра).
Один из важнейших вопросов, к-рый ставится при
изучении того пли иного класса Н. а.,— это вопрос об
описании простых алгебр как конечномерных, так и бес-
бесконечномерных. При этом описание понимается по мо-
модулю какого-то «классического» класса, содержащегося
в данном (так, для альтернативных колец описание про-
простых алгебр дается по модулю ассоциативных колец,
для мальцевских — по модулю лиевых, для йордано-
йордановых — по модулю специальных йордановых и т. д.).
С этой точки зрения различные классы Н. а. можно
разделить на те, в к-рых «много» простых алгебр, и те,
в к-рых их «мало». Типичными классами алгебр, в
к-рых много простых алгебр, являются классы ассо-
ассоциативных, лиевых и специальных йордановых алгебр.
Именно, в этих классах справедлива следующая теоре-
теорема вложения: любая ассоциативная (лиева, специаль-
специальная йорданова) алгебра над нолем вложима в простую
алгебру того же типа. Много простых алгебр в нек-рых
классах алгебр, далеких от ассоциативных,— в клас-
классах всех алгебр, коммутативных (антикоммутатпвных)
алгебр. В них также справедлива теорема вложения,
аналогичная предыдущей.
Задача описания конечномерных простых ассоциатив-
ассоциативных, лиевых, альтернативных и йордановых алгебр —
предмет класспч. части теории этих алгебр. В дальней-
дальнейшем основные результаты о строении простых конечно-
конечномерных ассоциативных (альтернативных, йордановых)
алгебр были перенесены на артиновы кольца того же
типа, т. е. на кольца с условием минимальности для
односторонних идеалов; в случае йордановых колец
под односторонним идеалом понимается квадратичный
идеал (см. Йорданова алгебра).
Вызывают интерес классы алгебр, в к-рых «мало» про-
простых алгебр. Типичные примеры таких классов — клас-
классы альтернативных, мальцевских и йордановых алгебр.
В классе альтернативных алгебр, но модулю ассоциа-
ассоциативных, простыми являются только (восьмнмерные)
алгебры Кэли — Диксона над ассоциативно-коммута-
ассоциативно-коммутативным центром. В классе мальцевских алгебр, по моду-
модулю лиевых, простыми являются только (семимерные)
(относительно операции коммутирования [а, Ь}) ал-
алгебры, присоединенные к алгебрам Кэли — Диксона.
В классе йордановых алгебр, по модулю специальных,
простыми являются (двадцатисемимерные) алгеб-
алгебры Алберта над своим ассоциативным центром
(алгебры серии Е) (см. Йорданова алгебра). В более
широких классах, таких, как правоальтернативные и
бинарно лиевы алгебры, описание простых алгебр еще
A982) не закончено. Известно, что не существует конеч-
конечномерных простых бинарно лиевых алгебр над полем
характеристики 0, отличных от мальцевских, однако
неизвестно, справедлив ли этот результат в бесконечно-
бесконечномерном случае. В классе правоальтернативных алгебр
известно, что хотя все конечномерные простые алгебры
из этого класса альтернативны, существуют бесконеч-
бесконечномерные простые правоальтернативные алгебры, не
являющиеся альтернативными. Все простые алгебры
ассоциативны для т. н. (у, б)-алгебр (при (у, д)фA, 1));
эти алгебры естественно возникают из условия, что
квадрат идеала есть идеал. Известно описание всех йор-
дановых алгебр с двумя порождающими: любая йорда-
нова алгебра с двумя порождающими является специ-
специальной (теорема Ширшова). Описаны (по мо-
модулю ассоциативных алгебр с делением) все йордановы
алгебры с делением.
В классах альтернативных, мальцевских и йордано-
вых алгебр описаны все первичные кольца
(т. е. алгебры, группоид двусторонних идеалов к-рых не
содержит делителей нуля). Именно, первичное альтер-
альтернативное кольцо (с 1/6 в коммутативном кольце опера-
операторов) либо ассоциативно, либо есть кольцо Кэли —
Диксона. Первичное мальцевское кольцо либо является
лиевым, либо его центральное замыкание есть (семи-
(семимерная) алгебра, присоединенная к алгебре Кэли —
Диксона. Первичная невырожденная йорданова алгеб-
алгебра либо специальна, либо является кольцом Алберта
(йорданово кольцо А наз. кольцом Алберта,
если его ассоциативный центр Z состоит из регулярных
элементов и алгебра Z~lA — (двадцатисемимерная)
алгебра Алберта над своим центром Z~1Z).
В нек-ром смысле противоположными к простым и
первичным алгебрам являются нильалгебр ы.
В случае алгебр с ассоциативными степенями, не яв-
являющихся антикоммутативными (таких, как ассоциа-
ассоциативные, альтернативные, йордановы и др.), нильалгеб-
ры определяются как алгебры, в к-рых каждый элемент
в нек-рой степени равен нулю; в случае антикоммута-
антикоммутативных алгебр (т. е. алгебр с тождеством х2=0, напр,
лиевых, мальцевских и бинарно лиевых алгебр) ниль-
алгебры — это то же, что иэнгелевы алгеб-
р ы, т. е. алгебры с условием
п
V*, уЗп((ху)...у) = 0.
В альтернативных (в частности, ассоциативных) алгеб-
алгебрах любая нильалгебра ограниченного индекса (т. е. с
тождеством х"=0) является локально нильпотентной,
а если в ней нет m-кручения (т. е. тх=0 => х=0) при
т<:;г, то она разрешима (для ассоциативных — нильпо-
тентна). Проблема Ширшова о локальной
нильпотентности нордановых нильалгебр ограниченно-
ограниченного индекса решена положительно. Неизвестно A982),
существует ли простое ассоциативное нилькольцо.
В случае алгебр Ли вопрос о локальной нильпотент-
нильпотентности энгелевых алгебр Ли решается теоремой
Кострикина: любая алгебра Ли с тождеством
[...[ху]...у] = О над полем характеристики р>п является
п
локально нильпотентной. Из этой теоремы следует по-
положительное решение ослабленной проблемы Бёрн-
сайда для групп показателя р. Вообще, круг проблем,
связанный с локальной нильпотентностью нильалгебр,
наз. проблемами бёрнсайдовского
типа. К проблемам бёрнсайдовского типа относится
также проблема Кур оша о локальной конеч-
конечности алгебраич. алгебр. Альтернативная (в частности,
ассоциативная) алгебраич. алгебра А ограниченной
степени (т. е. степени многочленов, к-рым удовлетворя-
удовлетворяют элементы алгебры А, ограничены в совокупности)
локально конечна. В общем случае проблемы бёрнсай-
бёрнсайдовского типа (такие, как проблема локальной нильпо-
нильпотентности ассоциативных нильколец и др.) имеют отри-
отрицательное решение.
Изучались свободные алгебры и свободные произве-
произведения алгебр в различных многообразиях. В многооб-
многообразии всех Н. а. любая подалгебра свободной алгебры
сама свободна, а любая подалгебра свободного произ-
произведения алгебр есть свободное произведение своих
пересечений с сомножителями и нек-рой свободной ал-
алгебры (теоремы К у р о ш а). Теоремы этого типа
справедливы также в многообразиях коммутативных
(антикоммутативных) алгебр. Наиболее интересны эти
вопросы в случае алгебр Ли. Любая подалгебра сво-
свободной алгебры Ли является свободной алгеброй Ли
(теорема Ширшова). Вместе с тем для под-
подалгебр свободного произведения алгебр Ли теорема
типа теоремы Куроша уже не верна, однако эти подал-
подалгебры тем не менее могут быть описаны в терминах по-
порождающих элементов идеала, по к-рому дополнитель-
дополнительно нужно профакторизовать свободное произведение
пересечений и свободной подалгебры. Изучены свобод-
свободные альтернативные алгебры — их радикал Жевлакова
(квазирегулярный радикал), центры (ассоциативные и
коммутативные) этих алгебр, факторалгебры по ради-
радикалу Жевлакова и др. В отличие от свободных ассоциа-
ассоциативных алгебр, свободные альтернативные алгебры с
ге^4 порождающими имеют делители нуля и, более
того, тривиальные идеалы (ненулевые идеалы, квадрат
к-рых равен нулю). Известны также тривиальные иде-
идеалы в свободных мальцевских алгебрах с ге^5 порож-
порождающими, а напр., о свободных йордановых алгебрах с
ге^З порождающими известно только, что они содержат
делители нуля.
Изучение свободных алгебр тесно связано с вопроса-
вопросами о тождествах в различных классах алгебр. Сюда от-
относится также и вопрос о базисном ранге многообразия
(базисный ранг — наименьшее натуральное
число п такое, что данное многообразие порождается
свободной алгеброй с п порождающими; если такого п
не существует, то базисный ранг, по определению, ра-
равен бесконечности). Базисный ранг многообразий ас-
ассоциативных и лиевых алгебр равен двум, а для аль-
альтернативных и мальцевских — бесконечности.
Общая теория многообразий и классов Н. а. изучает
классы алгебр, лежащие за пределами классических, и
их различные взаимосвязи. Характерным является,
напр., следующий результат: оказалось, что введенные
в разное время и разными исследователями многооб-
многообразия достижимых, обобщенно достижимых и обобщен-
обобщенно стандартных алгебр на самом деле входят в восьми-
элементную подрешетку решетки всех многообразий
Н. а., к-рая складывается также из многообразий йор-
йордановых, коммутативных, ассоциативных, ассоциатив-
ассоциативно-коммутативных и альтернативных алгебр. Многооб-
Многообразие, порожденное конечным ассоциативным (альтер-
(альтернативным, лиевым, мальцевским и йордановым) коль-
кольцом, является конечно базируемым, в то же время
существует конечное Н. к. (алгебра над конечным по-
полем), порождающее не конечно базируемое многооб-
многообразие. Существует алгебра Ли над бесконечным полем
с этим свойством. Вместе с тем неизвестно A982) ни
одного не конечно базируемого многообразия ассоциа-
ассоциативных алгебр (проблема Шпехта), а также
многообразия алгебр Ли над полем характеристики
нуль.
Алгоритмич. проблемы теории Н. к. и Н. а. возникли
под влиянием математич. логики. Оказалась разреши-
разрешимой проблема равенства в многообразии всех Н. а.
(теорема Жукова). Аналогичный результат
справедлив и для коммутативных (антикоммутативных)
алгебр. Известно, что алгебры Ли с одним соотношением
имеют разрешимую проблему равенства. Вместе с этим
существуют конечно определенные алгебры Ли с нераз-
неразрешимой проблемой равенства. Изучалась проблема
равенства в многообразии разрешимых алгебр Ли дан-
нои ступени разрешимости п. Для ге=2 эта проблема
разрешима, а для «^3 — не разрешима. Доказано,
что любую рекурсивно определенную алгебру Ли (ассо-
(ассоциативную алгебру) над простым полем можно вложить
в конечно определенную алгебру Ли (ассоциативную ал-
алгебру).
Лит.: II] Ширшов А. И., «Успехи матем. наук», 1958»
т. 13, в. 6, с. 3—20; [2] Ж е в л а к о в К. А., С л и н ь к о А. м.,
Шестаков И. П., Ширшов А. И., Кольца, близкие к
ассоциативным, М., 1У78; 13] Кострикин А. И., «Изв
АН СССР. Сер. матем.», 1959, т. 23, N» 1, с. 3—34; [41 В о-
кутьЛ. A., «Colloq. math.», 1966, v. 14, p. 349—53; [5] его
ж е, «Сердика», 1У77, т. 3, с. 299—308; [6] Кузьмин Е. Н.,
«Алгебра и логика», 1968, т. 7, № 4, с. 48—69; [7] Ф и л и п -
п о в В. Т., там же, 1И76, т. 15, jvfi 2, с. 235—42; [8] е г о ж е,
там же, 1977. т. 16, Mj 1, с. 101—08; [9] К у к и н Г. П., там же,
1978, т. 17, № 4, с. 402—15; [10] его же, там же, 1972, т. 11,
JM5 1, с. 59—86: [11] Львов И. В., там же, 1973, т. 12, № 3,
с. 269—97; [121 Дорофеев Г. В., там же, 1976, т. 15, М« 3,
с. 267—91; [13] Голод Е. С, «Изв. АН СССР. Сер. матем.»,
1964, т. 28, с. 273—76; [14] К у р о ш А. Г., «Матем. сб.», 1955,
т. 37, с. 251—64; [15] Ширшов А. И., там же, 1953, т. 33,
с. 441—52; [16] Jacob son N., Structure and representations
of Jordan algebras. Providence, 1968; [17] Зельманов Е. И.,
«Докл. АН СССР», 1979, т. 249, № 1, с. 30 — 33. Л. А. Бокутъ.
НЕАТОМИЧЕСКАЯ ИГРА — игра, в к-рой на мно-
множестве всех игроков / задана а-алгебра подмножеств %
и на % существует такая неатомическая мера, что мно-
множества игроков C??j\ имеющие нулевую меру, не ока-
оказывают влияния на исход игры. Н. и. служат моделя-
моделями ситуаций, в к-рых имеются большие количества очень
«малых» индивидуумов, подобных потребителям в
экономич. системе, и развитие теории Н. и. было тесно
связано с изучением моделей экономик с большим чис-
числом участников (см. [1]). Н. и. подчиняются общей
классификации, принятой в игр теории, и основные
теоретико-игровые принципы оптимальности (см. Ядро
в теории игр, Шепли вектор) естественным образом на
них распространяются. При этом стратегич. принципы
¦оптимальности в Н. и. реализуются, как правило, без
обычных предположений о выпуклости (см. [2]), и раз-
различные принципы оптимальности в Н. и. оказываются
более тесно связанными между собой; напр., для ши-
широкого класса неатомич. моделей типа рынков множе-
множество конкурентных равновесий совпадает с с-ядром,
к-рое состоит из единственного элемента, совпадающего
со значением игры (аналогом вектора Шепли для Н. и.,
•см. [1]). Разрабатываются два направления — коопе-
кооперативная теория Н. и. (см. [1], [3], [4]) и теория бескоа-
бескоалиционных Н. и. (см. [2]).
Кооперативная неатомическая иг-
р а, по аналогии с обычной кооперативной игрой, за-
задается в виде тройки </, v, Ну, где /=(/, %) — изме-
измеримое пространство игроков, элементы C=g наз. коа-
коалициями, v — действительнозначная функция на
%, наз. характеристической функци-
е й, а Н — нек-рос подмножество множества FA всех
конечно аддитивных мер ограниченной вариации на %
(обычно предполагается, что u.(/) = i;(/) для всех и.?Я). \
В простейшем случае v является функцией от неатомич.
меры на %. Предполагается, что пространство / стан-
стандартно, а функция множества v имеет ограниченную ва-
вариацию (т. е. представима в виде разности двух моно-
монотонных функций). Описаны [1] различные подпрост-
подпространства пространства BV всех функций ограниченной
вариации на %>, для к-рых можно построить аналог век-
вектора Шепли (как положительных"! линейный оператор со
значениями в FA).
Понятия сбалансированной игры, игры рынка, игры
без побочных платежей (см. Кооперативная игра) и
связанные с ними результаты переносятся на коопера-
кооперативные Н. и. (см. [3], [4]).
Определение бескоалиционной неато-
м н ч е с к о й игры аналогично определению
клаесич. понятия бескоалиционной игры. Для бескоали-
бескоалиционных Н. и. известны аналог Нэша теоремы, а также
общие результаты о существовании ситуаций равнове-
равновесия без предположений о выпуклости, к-рые не имеют
места для игр с конечным числом участников (см. [2]).
Лит.: [1] А у м а н Р., Ш е п л и Л., Значения для неато-
неатомических игр, пер. с англ., М., 1977; [2] К и р у т а А. Я., в кн.:
Математические методы в социальных науках, в. 6, Вильнюс,
1975, с. 18—71- [3] Розенмюллер И., Кооперативные
игры и рынки, пер. с нем., М., 1974; [4] R о s е п го и 1 1 е г J.,
«Operat. Res. Verfahren», 1975, Bd 20, S. 107—28.
А. Я.. Кирута, Е. 3. Яновская.
НЕАТОМИЧЕСКАЯ МЕРА — мера и. на измеримом
пространстве <Х, аР>, для к-рой нет атомов положи-
положительной меры, т. е. множеств A(~df с и.(^4)>0, а при
ВаА из [х(?)>0 следует В = А. Н. Н. Воробьев.
НЕБЛУЖДАЮЩАЯ ТОЧКА динамической
системы — точка фазового пространства этой сис-
системы, не являющаяся блуждающей точкой.
НЕВАНЛИННЫ ТЕОРЕМЫ — две основные теоре-
теоремы, доказанные Р. Неванлинной (см. [1], [2]) и лежащие
в основе теории распределения значений мероморфных
функций (см. Распределения значений теория). Пусть
f(z) — мероморфная функция в круге
KR = {z:\z\ < Д«оо},
при этом случай i?=oo означает, что функция f(z) ме-
роморфна во всей открытой комплексной плоскости.
Для каждого г, 0<г<Д, функция приближения /(г)
к числу а определяется так:
то (г, oo,/)=-J_
т (г, a, f) = m (г, со,-L-j , а ф оо,
а считающая функция числа а-точек f(z) определяется
формулой
N (г, а, /)= \ п {t'a' ^>-"<0' a'f> dt-\-n @, а, /) In г,
где n(t, а, /) означает число а-точек f(z), с учетом их
кратностей, попавших в круг {z : |z|<t}.
Функция Т (г, f)=m(r, оо, f)~\-N(r, oo, /) наз. н е-
ванлинновской характеристикой
функции f(z).
Первая теорема Неванлинны. Для
произвольной мероморфной в круге К# функции
/(z), для каждого г, 0.<г<Л, и для любого комплекс-
комплексного числа а выполняется соотношение
m(r, a, f) + N(r, a, f) = T (г, /) + Ф(г, а), A)
где
|ф(г, а)|<1п+ |а| + |1п
а с означает первый отличный от нуля коэффициент в
ряде Лорана в окрестности нуля функции f(z)~—a, если
/(О) = а=#=сзо, и функции/(z), если /@)=оо. Таким об-
образом, для функций с неограниченно растущей при
г —>- R характеристикой Т (г, /) сумма то (г, а, /) +
-j-N(r, a, /) для различных значений а, с точностью
до ограниченного слагаемого ср(г, а), сохраняет значе-
значение Т (г, /). В этом смысле все значения а для произ-
произвольной мероморфной в круге Кц функции /(z) являют-
являются равноправными значениями. По этой причине в тео-
теории распределения значений мероморфных функций ин-
интересуются вопросами асимптотич. поведения одного
слагаемого то (г, а, /) или N (г, а, /) в инвариантной сум-
сумме A).
Вторая теорема Неванлинны пока-
показывает, что в сумме A) для почти всех точек а основную
роль играет функция N (г, а, /). Эта теорема утверждает
следующее.
Для произвольной мероморфной в круге Kg= {z:\z\ <
<Л<оо} функции /(z) и для каждых q, g>3, различ-
ных чисел {<zft}fc=1 из расширенной комплексной плос-
плоскости имеет место соотношение
S*=i m<r' «к, /)<2Г (r,/)-^i(r, /) + 5(r, /), B)
где
iVi(r, t)=2N(r, оо, /)-iV(r, oo, /'),
а величина S (г, /) обладает следующими свойствами.
1) Если i?=oo, т. о. /(г) мероморфна во всей открытой
комплексной плоскости, то при г —>- оо
S (г, П = О(\п(г-Г(г, /)))
для всех значений г, за возможным исключением неко-
некоторого множества Е такого, что
2) Если Д<оо, то при г
для всех значении г, за возможным исключением не-
некоторого множества Е такого, что
Функция N^r, f) не убывает с ростом г, поэтому правая
часть в соотношении B) при г —>- R вне нек-рого исклю-
исключительного множества Е не может возрастать быстрее,
чем 2 Г (г, /).
Лига.: [1] Нева н л инна Р., Однозначные аналитичес-
аналитические функции, пер. с нем., М.—Л., 1941; [2] Nevanlinna R.,
Le TlH'oreme de Picard—Borel et la tneorie des functions meromor-
phes, P., 1929; [3] W e у 1 H., W e у 1 .1 Meromorphic functions
and analytic curves, Princeton, 1943; [4] AhlforsL., «Acta
Soc. scient. fennica. Nova ser. A», 1941, v. 3, J4» 4, p. 1—31;
[5] Cart an H., «Mathematica» (Cluj), 1933, v. 7, p. 5 — 31;
[6] Гриффите Ф., К и н г Д ж., Теория Неванлинны и
голоморфные отображения алгебраических многообразий, пер.
с англ., М., 1970; [7] Петренко В. II., Рост мероморфных
функций, Хар., 1978. В. П. Петренко.
НЕВАНЛИННЫ — ПИКА ПРОБЛЕМА — проблема
для класса ф аналитич. функций в области G комплек-
комплексной плоскости (или, более общо, римановой поверх-
поверхности), заключающаяся в нахождении условий, не-
необходимых н достаточных для разрешимости в классе
функций § интерполяционной задачи
= wa, A)
где {za} — подмножество точек области С, {wa} —
нек-рое множество комплексных чисел, а а, как пра-
правило, пробегает счетное (иногда конечное или даже
несчетное) множество индексов. Классич. результат
Г. Пика [1] и Р. Неванлинны [2] (соответственно для
конечных н счетных подмножеств {za}ciG) дает ре-
решение Н.—П. п., напр., для класса Вх аналитич. функ-
функций в единичном круге, ограниченных по модулю едини-
единицей, в виде условия неотрицательности квадратичных
форм
——щП \—W-Wb
Si,*iTrrr
Первоначальное доказательство этого, а также вполне
аналогичных и сводящихся к нему результатов для
ряда других классов функций § (см. [3]) проводилось
алгебраическими и теоретико-функциональными мето-
методами. Более поздние доказательства, основывающиеся,
напр., на сведении Н. — П. п. к нек-рой проблеме мо-
моментов (см. [4]) пли же полученные с точки зрения
теории гильбертовых пространств (см. [5]), позволили
охватить случай несчетных подмножеств {za}aG и
наметить пути возможных обобщений.
Естественным развитием Н. — П. п., потребовавшим
привлечения функционально-аналитич. методов иссле-
довапия, явился вопрос о разрешимости интерполяцион-
интерполяционной задачи A) на классе W правых частей {wa}; в
этом случае, как правило, {z<x} является счетным мно-
множеством (последовательностью) точек области G, а в
качестве W выступают различные пространства после-
последовательностей комплексных чисел. Применительно
к классу Я™ ограниченных аналитич. функций в еди-
единичном круге и пространству 1°° ограниченных последо-
последовательностей полное описание соответствующих по-
последовательностей точек {za} (т. н. универсаль-
универсальные интерполяционные последова-
последовательности) было получено (см. [6]) в виде условия
п;
= 1,
B)
Этот результат сыграл важную роль в описании струк-
структуры пространства максимальных идеалов алгебры Я™
(см. [7]) и одновременно явился отправным моментом
для многочисленных исследований Н. — П. п. (в ука-
указанной обобщенной постановке) для классов Харди НЧ и
пространств IP (включая весовые пространства). Оказа-
Оказалось, что при q=<x решение Н.— П. п. не зависит от
р и дается условием B), а при д<оо необходимо ме-
меняется при изменении q и р (см. [8]). Другое обобщение
Н.— П. п. связано с интерполяционной задачей сра (/)"=
= «-'а, где {фа}—нек-рая система функционалов в
классе jV Возникающую при этом задачу описания
множества {{<ра (/)} : / ? $3 } можно рассматривать так-
также как обобщение известной коэффициентов проблемы
для классов аналитич. функций.
Лит.: [1] Pick G., «Math. Ann.», 1916, Bd 77, S. 7—23;
[2] Nevanlinna R.. «Ann. Acad. sci. fenn. Ser. A», 1929,
v. 32, № 7, p. 1 — 15; [3] К p е й н М. Г., Н у д е л ь м а н А. А.,
Проблема моментов Маркова и экстремальные задачи, М.,
14O3; [4] К р е й н М. Г., Р е х т м а н П. Г., «Тр. Одесского
гос. ун-та», 1938, т. 2, с. 63—68- [5] S z - N a g у В., К о г а-
п у i A., «Acta math. Acad. sci. hung.», 1956, v. 7. p. 295—303;
[6] С а г 1 e s о n L., «Amer. J. Math.» 1958, v. 80, № 4, p. 921 —
30; 17] e г о ж e, «Ann. Math.», 1962, v. 76, p. 547—59; [8] HI в е -
д e ii к о С. В., «Матем. заметки», 1977, т. 21, JMi 4, с. 503—08.
С. В Шведеппо.
НЕВОЗМОЖНОЕ СОБЫТИЕ — событие, крое и
рамках данных условий не осуществляется ни при каких
обстоятельствах. Если (Q, <Д, Р) — вероятностное
пространство, то Н. с.— это событие 0?с/?, не на-
наступающее ни с одним из элементарных исходов <»?Й
(пустое множество). Н. с. является дополнением к
достоверному событию Q в рассматриваемой вероят-
вероятностной модели и поэтому Н. с. приписывают вероят-
вероятность нуль: Р@) = О. А.В.Прохоров.
НЕВЫРОЖДЕННАЯ МАТРИЦА, неособенная
матриц а,— квадратная матрица, определитель
к-рой отличен от нуля. Для квадратной матрицы А
над полем невырожденность эквивалентна каждому из
следующих условий: I) A — обратима; 2) строки (столб-
(столбцы) матрицы А линейно независимы; 3) элементарными
преобразованиями строк (столбцов) матрицу А можно
привести к единичной матрице. О. А. Иванова.
НЕВЫРОЖДЕННОЕ ПРЕДСТАВЛЕНИЕ — линей-
линейное представление я группы (кольца, алгебры, полу-
полугруппы) X в векторном пространстве Е такое, что из
равенства я(а:)|=0 для нек-рого 5?Я и всех х?Х сле-
следует |—0. А. И. Штерн.
НЕВЫЧЕТ степени гепо модулю т. — чис-
число а, для к-рого сравнение х"^а (mod m) не имеет ре-
решения; см. Вычет.
НЕВЯЗКА приближенного решения —•
одна из характеристик качества приближенного реше-
решения и операторного уравнения Р (и)—0 (напр., линей-
линейной алгебраич. системы, дифференциального уравне-
уравнения). Невязкой наз. величину Р (и) или нек-рую
ее норму ЦР(ц)||2. Если известна оценка
II »i-и» Hi < С || P(Ml)-i> (и,) Ц,,
то погрешность решения можно оценить через Н.
Если такой оценки нет, то Н. является косвенной
характеристикой качества приближенного решения.
Лит.: [1] Б е р е з и н И. С, Ж и д к о в Н. П., Методы
вычислений, 3 изд., т. 1, М., 196R; 2 изд., т. 2, М., 1962;
[2] Б а х в а л о в Н. С, Численные методы, 2 изд., М., 1975.
Н. С. Бахвалов.
НЕГОЛОНОМНЫЕ СИСТЕМЫ — системы материаль-
материальных точек, стесненные связями, среди к-рых имеются
кинематич. связи, накладывающие ограничения на ско-
скорости (но не на положения) точек системы в ее возмож-
возможных положениях (см. Голономная система), задава-
задаваемые неинтегрируемыми дифференциальными соотно-
соотношениями вида
, t)=Q, A)
* = 1, ..., го, <ps(x,
к-рые не могут быть заменены эквивалентными конеч-
конечными соотношениями между координатами. Здесь xv —
декартовы координаты точек, t — время, .V — число
точек системы. В большинстве случаев рассматриваются
линейные относительно скоростей х,- связи A) вида
Si^i t=0- As.(x, t), As(x,
Связи A) наз. стационарными, если ^=0. Связи A)
налагают ограничения также на ускорения wv точек
системы вида
Эф ^4iV
Z
Следуя Н. Г. Четаеву [2], принимают, что возможные
перемещения систем, стесненных нелинейными связя-
связями A), удовлетворяют условиям вида
3JV _^s_6xv = Qt ,- = 1,...,га. B)
v=l dxv
В случае линейных связей отсюда следуют общеприня-
общепринятые соотношения
Z
В отличие от голономныд систем перемещение между со-
соседними бесконечно близкими возможными положения-
положениями Н. с. может быть невозможным (см. [1]).
В обобщенных лагранжевых координатах уравне-
уравнения A) и B) записываются в виде
._
Для Н. с. число п—т ее степеней свободы меньше числа
п независимых координат щ на число т неинтегрируе-
мых уравнений связей.
Выведено много различных видов дифференциальных
уравнений движения Н. с, напр. Лагранжа уравнения
первого рода, А ппеля уравнения в лагранжевых коор-
координатах и квазикоординатах, уравнения Чаплыгина и
Воронца в лагранжевых координатах, Болъцмана урав-
уравнения и уравнения Гамеля в квазикоординатах и др.
(см. [3]).
Для Н. с. характерно, что в число дифференциальных
уравнений их движения в общем случае входят урав-
уравнения связей.
Лит.: [1] Hertz H., Gesammelte Werke, Bel 3 — Die
Prinzipien der Mechanik, Lpz., 1894; в рус. пер.— Принципы
механики, изложенные в новой связи, М., 105 9; [2] Ч е т а-
е в Н., «Изв. Физ.-матем. об-ва при Казан, ун-те»,C), 1932,
т. 6, с. 68—71; [3] Н е й м а р к Ю. И., Ф у ф а е в Н. А.,
Динамика неголономных систем, М., 1967. В. В. Румянцев.
НЕДЕЗАРГОВА ГЕОМЕТРИЯ — геометрия на плос-
плоскости, в к-рой Дезарга предложение может не иметь ме-
места. В этом случае плоскость наз. недезарговой
плоскостью. Теорема Дезарга не может быть
доказана в плоскости на основе лишь проективных ак-
аксиом плоскости без привлечения аксиом конгруэнт-
конгруэнтности (метрических аксиом) или без привлечения про-
пространственных аксиом. Напр., в геометрии плоскости,
построенной на основе всех плоскостных аксиом сис-
системы Гильберта, за исключением аксиомы конгруэнт-
конгруэнтности треугольников, теорема Дезарга не может быть
получена как их следствие. Геометрия этой плоскости
является недезарговой, она не может рассматриваться
как часть пространственной геометрии, в которой
выполняются все аксиомы системы Гильберта, кро-
кроме указанной аксиомы конгруэнтности. Недезаргова
проективная 2-плоскость не вкладывается в проек-
проективные пространства высших размерностей (см. [1]
[4], [5]).
Возможность построения Н. г. плоскости позволяет
выяснить независимость различных групп аксиом сис-
системы Гильберта, а также выяснить роль теоремы Де-
Дезарга как независимой дополнительной аксиомы пло-
плоской проективной геометрии (см. [2]).
Рассматриваются и так наз. недезарговы
системы, в к-рых теорема Дезарга не выполняется
как конфигурационное предложение (см. Конфигура-
Конфигурация). Недезарговы системы существуют, в частности,
на нек-рых поверхностях и вообще на нек-рых римано-
вых многообразиях, являющихся прямыми простран-
пространствами. Простой пример дает параболоид z=xy, на
к-ром недезаргову систему образуют точки и соединяю-
соединяющие их кратчайшие. Другой пример дает тор: суще-
существуют его метризации без сопряженных точек, в
к-рых геодезические универсального накрывающего
пространства образуют недезаргову систему (см. также
[5], [6]).
Лит.: [1] Гильберт Д., Основания геометрии, пер. с
нем., М.— Л., 1948; [21 Скорняков Л. А., «Успехи матем.
наук», 1951, т. 6, в. 6, с. 112—54; [3] Б у з е м а н Г., Геометрия
геодезических, пер. с англ., М., 1962; [4] Mohrmann H.,
Festschrift D. Hilbert, В., 1922; [5] В i e b е г Ь а с h L., Ein-
leitung in die hohere Geometrie, Lpz.— В., 1933; [в] N a r а у а-
n a R а о М. L., Kuppuswamy Rao K., «J. Combin. Theory,
Ser. A», 1975, v. 19, p. 247 — 55. Л. А. Сидоров.
НЕДЕЛИМЫХ МЕТОД — возникшее в кон. 10 в.
наименование совокупности довольно разнородных
приемов определения отношений площадей или объемов
фигур. В основе Н. м. лежит сравнение «неделимых»
элементов (или же совокупностей элементов), так или
иначе образующих фигуры, отношение размеров к-рых
требуется найти. Само понятие «о неделимых» в разные
времена различные ученые понимали по-разному.
Н. м. ведет начало от древнегреч. науки. Демокрит
D в. до н. э.), по-видимому, рассматривал тела как
«суммы» чрезвычайно большого числа чрезвычайно
малых «неделимых» атомов; Архимед C в. до н. э.)
нашел площади и объемы многих фигур, сочетая прин-
принципы учения о рычаге с представлением, что плоская
фигура состоит из бесчисленного количества параллель-
параллельных отрезков прямых, а геометрич. тело — из бесчис-
бесчисленного количества параллельных плоских сечений.
Однако в древности же подобные представления и ме-
методы подверглись серьезной критике. Архимед, напр.,
считал обязательным передоказывать результаты, полу-
полученные с помощью Н. м., методом исчерпывания (см.
Исчерпывания метод). Идеи Н. м. были возрождены
в математич. исследованиях на рубеже 16—17 вв.
И. Кеплером (I. Kepler) и особенно Б. Кавальери
(В. Cavalieri), с именем к-рого и связывают чаще всего
Н. м. Развитый Б. Кавальери Н. м. был затем суще-
ственно преобразован и послужил одним из этапов в
создании интегрального исчисления. См. Бесконечно
малых исчисление. БСЭ-3
НЕДИФФЕРЕНЦИРУЕМАЯ ФУНКЦИЯ — функ-
функция, не имеющая дифференциала. В случае функций
одного переменного Н. ф.— это функция, не имеющая
производной. Напр., функция /(х)=|х| не дифферен-
дифференцируема в точке х=0, вместе с тем она дифференцируема
в этой точке как слева, так и справа, т. е. имеет в этой
точке левую и правую производные. Непрерывная
функция f(x)=x sin— при хфО и /@)=0 не только не
дифференцируема в точке х=0, но и не имеет в этой
точке производной (ни конечной, ни бесконечной) ни
справа, ни слева.
Первые примеры непрерывных на всей числовой оси
функций, во всех точках, не имеющих конечных про-
производных, были указаны Б. Больцано (В. Bolzano) в
1830 (опубл. в 1930) и К. Вейерштрассом (К. Weier-
strass) в 1860 (опубл. в 1872). Функция Вейерштрасса
задается рядом
где 0О<1, Ъ — нечетное натуральное число, <zb>l-f-
-f-3jt/2. Более простой пример, основанный на той же
идее, в к-ром периодич. функции типа cos со х замене-
заменены периодич. ломаными, был построен Б. Л. Ван дер
Варденом (В. L. Van der Waerden). Пусть ио(х) —
функция, равная для каждого действительного числа х
абсолютной величине разности между числом х и бли-
ближайшим к нему целым числом. Эта функция линейна
на каждом отрезке вида [п/2, (п+1)/2], где п — целое;
она непрерывна и имеет период, равный единице. Пусть
Bft(z) = MoD**)/4*, k = i, 2, ...,
тогда функция Ван дер Вардена задается равенством
Эта функция непрерывна на всей числовой оси и ни в
одной точке не имеет конечной производной. Первые три
частные суммы полученного ряда изображены на ри-
рисунке.
Для функций более одного переменного дифферен-
цируемость в точке не эквивалентна существованию в
этой точке частных производных; существуют недиф-
ференцируемые функции, имеющие частные производ-
производные. Напр., функция
0
пр. *Ч-У>
при х = у = 0
во всех точках плоскости непрерывна и имеет частные
производные, однако в точке @, 0) не дифференцируема.
Л. Д. Кудрявцев.
НЕДООПРЕДЕЛЕННАЯ СИСТЕМА — система диф-
дифференциальных уравнений, число уравнений к-рой
меньше числа неизвестных. См. также Переопределенная
система. А. П. Солдатов.
НЕЕВКЛИДОВО ПРОСТРАНСТВО — пространство,
свойства к-рого базируются на системе аксиом, отличной
от евклидовой. Геометрия Н. п. является неевклидовой
геометрией. В зависимости от аксиоматики, на основе
к-рой развертываются неевклидовы геометрии II. п.,
можно классифицировать Н. п. по различным призна-
признакам. С одной стороны, Н. п. может являться конечно-
конечномерным векторным пространство?" со скалярным про-
произведением, к-рое выражается в декартовых координа-
координатах по формуле
(а, 6) = 2*=, *iVi-2Г=Л+1 *'¦"'•
В этом случае Н. п. представляет собой псевдоевклидово
пространство. С другой стороны, Н. п. может быть оха-
охарактеризовано как нек-рое и-мерное многообразие с
определенной структурой, описываемой системой ак-
аксиом, отличной от евклидовой.
Н. п. могут классифицироваться и с точки зрения
дифференциально-геометрических свойств как римано-
вы пространства с постоянной кривизной (в том числе
нулевой кривизны, но топологически отличные от ев-
евклидовых пространств). Л. А. Сидоров.
НЕЕВКЛИДОВЫ ГЕОМЕТРИИ — в буквальном по-
понимании — все геометрич. системы, отличные от гео-
геометрии Евклида; однако обычно термин «Н. г.» при-
применяется лишь к геометрич. системам (отличным от
геометрии Евклида), в к-рых определено движение
фигур, причем с той же степенью свободы, что и в гео-
геометрии Евклида. Степень свободы движения фигур в
евклидовой плоскости характеризуется тем, что каждая
фигура без изменения расстояний между ее точками
может быть перемещена так, чтобы любая выбранная
ее точка заняла любое заранее назначенное положение;
кроме того, каждая фигура может вращаться вокруг
любой своей точки. В евклидовом трехмерном простран-
пространстве каждая фигура может быть перемещена так, что-
чтобы любая выбранная ее точка заняла любое заранее на-
назначенное положение; кроме того, каждая фигура мо-
может вращаться вокруг любой оси, проходящей через
любую ее точку.
Среди Н. г. особое значение имеют Лобачевского гео-
геометрия и Римана геометрия, к-рые чаще всего и под-
подразумеваются, когда говорят о Н. г. Геометрия Лоба-
Лобачевского — первая геометрич. система, отличная от
геометрии Евклида, и первая более общая теория
(включающая евклидову геометрию как предельный
случай). Геометрия Римана, открытая позднее, в
нек-рых отношениях противоположна геометрии Лоба-
Лобачевского, но вместе с тем служит ей необходимым до-
дополнением. Совместное исследование геометрий Евкли-
Евклида, Лобачевского и Римана позволило в должной мере
выяснить особенности каждой из них, а также их связи
друг с другом и с другими геометрич. системами. Ниже
обе Н. г. и геометрия Евклида сопоставляются, как
синтетич. теории, затем в плане дифференциальной
геометрии и, наконец, в плане теории групп.
Неевклидовы геометрии как син-
синтетические теории. Геометрия Лобачевского
строится на основе тех же аксиом, что и евклидова,
за исключением только одной аксиомы о параллельных.
Именно, согласно аксиоме о параллельных евклидовой
геометрии через точку, не лежащую на данной прямой а,
проходит точно одна прямая, к-рая лежит в одной пло-
плоскости с прямой а и не пересекает эту прямую; в геоме-
геометрии Лобачевского принимается, что таких прямых
более одной (затем доказывается, что их бесконечно
много).
В геометрии Римана принимается аксиома: каждая
прямая, лежащая в одной плоскости с данной прямой,
пересекает эту прямую. Эта аксиома противоречит сис-
системе аксиом евклидовой геометрии с исключением аксио-
аксиомы о параллельных. Таким образом, система аксиом,
лежащая в основе геометрии Римана, необходимо долж-
должна отличаться от системы аксиом евклидовой геометрии
не только заменой одной аксиомы о параллельных дру-
другим утверждением, но и части остальных аксиом. Раз-
Различными в этих геометриях являются аксиомы, к-рые
служат для обоснования т. н. отношений порядка гео-
метрич. элементов. Сущность дела в следующем: в
евклидовой геометрии и в геометрии Лобачевского по-
порядок точек на прямой является линейным, т. е. по-
подобным порядку во множестве действительных чисел;
в геометрии Римана порядок точек на прямой является
циклическим, т. е. подобным порядку во множестве
точек окружности. Кроме того, в геометриях Евклида
и Лобачевского каждая прямая, лежащая в данной
плоскости, разделяет эту плоскость на две части; в
геометрии Римана прямая не разделяет плоскость на
две части, т. е. любые две точки плоскости, не лежащие
на данной прямой, можно соединить в этой плоскости
непрерывной дугой, не пересекая данную прямую (то-
пологич. моделью плоскости Римана служит проектив-
проективная плоскость).
Требования аксиом, определяющих движение фигур,
для всех трех геометрий одинаковы.
Примеры теорем Н. г.
1) В геометрии Лобачевского сумма внутренних
углов любого треугольника меньше двух прямых; в
геометрии Римана эта сумма больше двух прямых (в ев-
евклидовой геометрии она равна двум прямым).
2) В геометрии Лобачевского площадь треугольника
выражается формулой
5=Д2(л-а-Р-7), A)
где а, Р, у — внутренние углы треугольника, R — по-
постоянная, к-рая определяется выбором единицы изме-
измерения площадей. В геометрии Римана имеет место
формула
S = R2(u+$-\-y-n) B)
при аналогичном значении символов (в евклидовой гео-
геометрии зависимости между площадью треугольника и
суммой его углов нет).
3) В геометрии Лобачевского между сторонами и
углами треугольника существует ряд зависимостей,
напр.:
ch-?-= ch A-ch-<L—Sh ±- sh -?¦ cos o, C)
где sh, ch — гиперболические синус и косинус, a, b, с —
стороны треугольника, а, р\ у — противолежащие им
углы, R — постоянная, определяемая выбором масшта-
масштаба; для прямоугольного треугольника (с гипотенузой с
и прямым углом у) имеет место, напр., равенство
ch-|- = ctg a ctg р\ D)
При нек-ром согласовании линейного масштаба и еди-
единицы измерения площадей постоянная R в формулах
A), C), D) будет одинаковой. Число Я наз. радиу-
радиусом кривизны плоскости (или прост-
пространства) Лобачевского. Число R при дан-
данном масштабе выражает определенный отрезок в пло-
плоскости (пространстве) Лобачевского, к-рый также на-
называют радиусом кривизны. Если масштаб меняется,
то меняется число R, но радиус кривизны, как отрезок,
остается неизменным. Если радиус кривизны принять
за масштабный отрезок, то R=i. В геометрии Римана
существуют сходные равенства:
а Ъ с ¦ b . с /Ц\
cos -к- = cos -=-cos----)-sm -=- sin -g-coso \°)
rt ri H ri ri
(для произвольного треугольника) и
cos ~ = ctg о ctg р F)
(для прямоугольного) при аналогичном значении сим-
символов. Число R наз. радиусом кривизны
плоскости (или пространств а) Риман а.
Как видно из формул D) и F), в каждой из Н. г. ги-
гипотенуза прямоугольного треугольника определяется
его углами; более того, в Н. г. стороны любого треуголь-
треугольника определяются его углами, т. е. не существует
подобных треугольников, кроме равных (в евклидовой
геометрии нет формул, аналогичных формулам D) и
F), и нет никаких других формул, выражающих ли-
линейные величины через угловые). При замене R на
iR формулы A), C), D) превращаются в формулы B),
E), F); вообще, при замене R на iR все метрпч. формулы
геометрии Лобачевского (сохраняющие при этой за-
замене геометрич. смысл) переходят в соответствующие
формулы геометрии Римана. При Д—>-оо п те и другие
дают в пределе формулы евклидовой геометрии (либо
теряют смысл). Стремление к бесконечности величины
R означает, что масштабный отрезок является беско-
бесконечно малым по сравнению с радиусом кривизны (как
с отрезком). То обстоятельство, что при этом фор-
формулы Н. г. переходят в пределе в формулы евклидо-
евклидовой геометрии, означает, что для малых (по сравне-
сравнению с радиусом кривизны) неевклидовых фигур со-
соотношения между их элементами мало отличаются от
евклидовых.
Неевклидовы геометрии в плане
дифференциальной геометрии. В каж-
каждой из Н. г. дифференциальные свойства плоскости ана-
аналогичны дифференциальным свойствам поверхностей
евклидова пространства; именно: в неевклидовой пло-
плоскости могут быть введены внутренние координаты и, v
так, что дифференциал ds дуги кривой,соответствующей
дифференциалам du, dv координат, определяется ра-
равенством:
ds2^Edu2-Jr2 F dudv+Gdi-2. G)
Пусть, в частности, в качестве координаты и про-
произвольной точки М берется длина перпендикуляра,
опущенного из М на фиксированную прямую, а в ка-
качестве координаты I? — расстояние от фиксированной
точки О этой прямой до основания указанного перпен-
перпендикуляра; величины и, v следует брать со знаком, по-
подобно обычным декартовым координатам. Тогда формула
G) для плоскости Лобачевского будет иметь вид
ds2 = du2 + ch2 (~\ dv2, (8)
а для плоскости Римана
ds2 = du*-{-cos2 ( ~\ dv2, (9)
R — та же постоянная, к-рая входит в формулы пре-
предыдущего раздела (радиус кривизны). Правые части
(8) и (9) суть метрич. формы поверхностей евклидова
пространства, имеющих соответственно постоянную от-
отрицательную кривизну К=—\IR2 (как, напр., псевдо-
псевдосфера) и постоянную положительную кривизну К —
= \IR2 (как, напр., сфера). Поэтому внутренняя геоме-
геометрия достаточно малой части плоскости Лобачевского
совпадает с внутренней геометрией на соответствующей
части поверхности постоянной отрицательной кривизны.
Аналогично, внутренняя геометрия достаточно малых
частей плоскости Римана реализуется на поверхностях
постоянной положительной кривизны (поверхностей,
к-рые реализуют геометрию всей плоскости Лобачев-
Лобачевского, в евклидовом пространстве нет). При замене Я
на iR метрическая форма (8) переходит в метрическую
форму (9).
Так как метрич. форма определяет внутреннюю гео-
геометрию поверхности, то при такой замене и другие ме-
метрич. соотношения геометрии Лобачевского переходят
в метрич. соотношения геометрии Римана (что уже было
отмечено выше). При i?=oo каждое из равенств (8) и
(9) дает
cZs2 = tfa2 + cfo2,
т. е. метрич. форму евклидовой плоскости.
Трехмерные неевклидовы пространства по своим
дифференциальным свойствам относятся к числу ри-
мановых пространств в широком смысле и выделяются
среди них прежде всего тем, что имеют постоянную ри-
манову кривизну. Как в двумерном, так и в трехмерном
случае постоянство кривизны обеспечивает однород-
однородность пространства, т. е. возможность движения фигур
в нем, причем с той же степенью свободы, как (соответ-
(соответственно) на евклидовой плоскости или в евклидовом
пространстве. Пространство Лобачевского имеет отри-
отрицательную кривизну, равную — 1/R2, пространство
Римана — положительную кривизну, равную 1/Д2 (R —
радиус кривизны). Евклидово пространство занимает
промежуточное положение и является пространством
нулевой кривизны.
Пространства постоянной рпмановой кривизны могут
иметь весьма разнообразное строение в смысле тополо-
топологии. Среди всех пространств постоянпой отрицательной
кривизны пространство Лобачевского однозначно выде-
выделяется двумя своими свойствами: оно полно (в смысле
полноты метрич. пространства) и топологически
эквивалентно обычному евклидову пространству. Про-
Пространство Рпмана среди всех пространств положитель-
положительной кривизны однозначно выделяется свойством то-
пологич. эквивалентности проективному пространству.
Аналогичными условиями выделяются многомерные
пространства Лобачевского п Рпмана среди многомер-
многомерных пространств постоянной рнмановой кривизны.
Неевклидовы геометрии в плане
теории г р у п п. Пусть на проективной плоскости
введены проективные однородные координаты (art, х2, ,г3)
и задана нек-рая опальная линия 2-го порядка, обоз-
обозначаемая дальше буквой к, напр.
Каждое проективное отображение проективной плоско-
плоскости на себя, к-рое оставляет на месте линию /г, наз.
автоморфизмом относительно к. Каждый автоморфизм
отображает внутренние точки линии к также во внут-
внутренние ее точки. Множество всех автоморфизмов от-
относительно линии к составляет группу. Условимся рас-
рассматривать только точки проектив-
проективной плоскости, лежащие внутри к;
хорды линии к будем называть «пря-
«прямыми». Две фигуры будем считать
равными, если одна из них перево-
переводится в другую нек-рым автоморфиз-
автоморфизмом. Так как автоморфизмы составля-
составляют группу, то имеют место основные
свойства равенства фигур: 1) если фи-
фигура А равна фигуре В, то В рав-
равна А; 2) если фигура .4 равна фигуре В, а В равна
фигуре С, то А равна С. В получаемой таким обра-
образом геометрической теории будут соблюдены требо-
требования всех аксиом евклидовой геометрии, кроме акси-
аксиомы о параллельных; вместо этой последней аксиомы
соблюдается аксиома о параллельных Лобачевского
(см. рис., где показано, что через точку Р проходит
бесконечно много «прямых-), не пересекающих «пря-
«прямой» а). Тем самым получается истолкование (двумер-
(двумерной) геометрии Лобачевского при помощи проектив-
проективной плоскости или, как говорят, проективная мо-
модель геометрии Лобачевского; линия к паз. а б с о л го-
готом этой модели. Автоморфизмы относительно к
играют роль движений. Поэтому геометрию Лобачев-
Лобачевского можно рассматривать как теорию, изучающую
свойства фигур и связанные с фигурами величины,
к-рые остаются неизменными при автоморфизмах; ко-
роче говоря, геометрию Лобачевского можно рассма-
рассматривать как теорию инвариантов группы автоморфизмов
относительно овального абсолюта.
Геометрия Римана (двумерная) допускает сходное ис-
истолкование; именно, она является теорией инвариантов
относительно нулевого абсолюта
4 + 4+4 = 0. (Ю)
При этом в качестве точек и прямых модели берутся
все точки и прямые проективной плоскости, автоморфиз-
автоморфизмы определяются чисто алгебраически, как линейные
преобразования, к-рые переводят уравнение A0) is
уравнение того же вида.
Евклидову геометрию также можно рассматривать
как теорию инвариантов пек-рой группы проективных
преобразований, именно, группы автоморфизмов от-
относительно вырожденного абсолюта
т. е. относительно мнимых точек A, г, 0), A, — г, 0);
эти точки наз. круговыми точками. Предме-
Предметом модели являются все точки проективной плоскости,
кроме точек прямой х3—0, и все прямые проективной
плоскости, кроме прямой х3=0. В последнем случае
автоморфизмы играют роль подобных преобразований,
а не движений, как в случае Н. г.
Рассмотренные модели относятся к двумерным гео-
геометриям; проективные модели высших размерностей
строятся аналогично.
Соответственно характеру уравнений абсолютов гео-
геометрия Лобачевского наз. г и и е р б о л и ч е с к о и,
геометрия Римана — эллиптической, геометрия
Евклида — параболической.
Лит.: [1] Александров П. С, Что такое неэвклидона
геометрия, М., 1950; [2] К л е й н Ф., Неевклидова геометрия,
пер. с нем., М.— Л., 1936; [3] Е ф и м о в Н. В., Высшая
геометрия, 0 изд., М., 1978. Н. В. Ефимов.
НЕЗАВИСИМОСТЬ в теории вероятно-
вероятностей — одно из важнейших понятий этой теории.
Иногда используют термины статистическая
независимость, стохастическая не-
независимость. Предположение о Н. рассматри-
рассматриваемых событий, испытаний п случайных величин было
обычной предпосылкой в задачах, к-рые рассматрива-
рассматривались в математической вероятностей теории со вре-
времени ее возникновения.
Для двух случайных событий понятие Н. вводится
следующим образом. Пусть А и В — два случайных
события, Р(А) и Р (В) — их вероятности. Услов-
Условную вероятность события В при условии осу-
осуществления события А определяют формулой
где Р(Л П^) — вероятность совместного осуществле-
осуществления событий А и В. События А и В наз. н с з а в и с и-
м ы м л, если
?(А[\В)=?(А)?(В). A)
При Р(Л)>0 это равносильно соотношению
?(В1А) = ?(В). B)
Смысл данного определения Н. можно пояснить следую-
следующим образом. Предполагая, что производится большое
число N испытаний, и переходя в B) от вероятностей
к частотам, можно заключить, что между частотой со-
события В во всех N испытаниях и частотой его появле-
появления в тех испытаниях, в к-рых наступает А, должно
иметь место приближенное равенство. Н. событий ука-
указывает такпм образом либо на отсутствие связи между
наступлением одного из этих событий и наступлением
другого, либо на несущественный характер этой связи.
Так, событие, заключающееся в том, что наудачу выб-
ранное лицо имеет фамилию, начинающуюся, напр.,
с буквы «А», и событие, заключающееся в том, что этому
лицу достанется выигрыш в очередном тираже лоте-
лотереи,— независимы.
Определение Н. п случайных событий Аг, А2, . . .,
Ап, гс>2, может быть дано в нескольких равносиль-
равносильных вариантах. Согласно одному из них эти события
наз. независимыми, если для любого т, 2<:т<;
¦<гс, и для произвольных попарно различных нату-
натуральных чисел кг, к,, . . ., кт<^:п вероятность совмест-
совместного осуществления событий Akl, . . ., Ahm равна
произведению их вероятностей
Р (Ак1 П ... П AkJ = P (Ак1).. . Р (Акт). C)
Отсюда, как и ранее, можно вывести, что условная ве-
вероятность каждого из рассматриваемых событий при
условии, что какие-либо из остальных наступили, равна
его «безусловной» вероятности.
Иногда наряду с Н. (взаимной Н.) событий А1, А2,
. . ., Ап рассматривают так наз. попарную Н.,
означающую, что любые два из этих событий A-t и
Aj, 1ф], независимы. Н. событий влечет их попарную
Н., а обратное, вообще говоря, неверно.
В период, предшествовавший аксиоматич. построе-
построению теории вероятностей, содержание понятия Н. не
воспринималось достаточно отчетливо. «Понятие о не-
независимых событиях можно считать вполне ясным в из-
известных теоретических вопросах; в других же вопросах
это понятие, конечно, может совершенно затемняться
вместе с затемнением основного понятия о вероятно-
вероятности»,— писал А. А. Марков (см. [1] с. 24).
В рамках аксиоматич. подхода понятие Н. наиболее
естественно вводится следующим образом. Пусть (Я,
Л, P) — какое-либо вероятностное пространство, где
Q — множество элементарных событий, Л — а-алгебра
событий, Р — определенная на Л вероятностная мера.
Сначала определяют Н. классов событий (здесь будут
рассмотрены только классы 53, являющиеся
ст-подалгебрами ст-алгебры Л)- Классы fBi, ЗЗ2, • • •,
SBn наз. независимыми (относительно Р), если
любые события .41?58i, . . ., Ап?ЗЗп независимы в
смысле равенства C); классы S3t (t?T, где Т — про-
произвольное множество индексов) наз. независ и-
м ы м и, если при любом целом п^2 и любых попарно
различных tu . . ., tn?T классы SBu, ¦ ¦ ¦, 93tn не-
независимы. Н. событий Afr, 1<:/с«:гс, равносильна Н.
классов
93k = {0, 4,4- Щ-
Для испытаний Н.— это Н. порождаемых ими а-ал-
гебр.
Для случайных величин Xf, t?T, H. определяют
как Н. ст-подалгебр S3(Xf), где .38(Xt) — прообраз
относительно отображения Xf а-алгебры борелевских
множеств на числовой прямой. Н. случайных событий
Alt . . ., Ап равносильна Н. их индикаторов Ia^, т. е.
случайных величин, определяемых формулами
/ЛА(?°) = 1 Для в>€4
/Лй(ш)=0 для (й^Ак.
Для Н. случайных величин Хг, . . ., Хп не-
необходимы и достаточны следующие условия.
1) Для любых действительных чисел ах, а2, . . ., ап
функция распределения
Рхх-- Х„(. ...,а„) = Р{ш:Х1(ю) < аь ..., Хп(а)<ап}
равна произведению соответствующих функций рас-
распределения:
FX>- ¦ -Хп («l. ...,an) = FXi (ях).. .FXn (an).
2) При наличии плотностей Pxlw xn (ai> • ¦ •> ап)
плотность для почти всех по лебеговой мере в R"
значений (а1? а2, . . ., ап) равна произведению
рх (ах) . . . рх (а„) соответствующих плотностей.
3) Характеристич. функция
для всех действительных чисел иь и2, . . ., м„ равна
произведению /x,("i) • • • fxn{un), fxk(uk)=EelukXl1,
соответствующих характеристич. функций.
На гипотезе Н. тех или иных событий и случайных
величин основаны важнейшие схемы теории вероятно-
вероятностей: последовательности независимых случайных ве-
величин (см., напр., Вернулли блуждание^ Больших чисел
закон, Предельные теоремы теории вероятностей), слу-
случайные процессы с независимыми приращениями (см.,
напр., Винеровспий процесс, Случайный процесс) и т. д.
(см. также Нуль-единица закон).
Общие замечания к понятию независимости.
1) Независимость функций от не-
независимых случайных величин. Из
данной Н. случайных величин Хь . . ., Хп можно
вывести довольно очевидные (и вполне соответствую-
соответствующие интуитивно ожидаемым от понятия Н.) следствия;
напр., функции от Х1( . . ., Хк и от Xfe + 1, . . ., Хп,
1 <:&<«, будут независимыми случайными величинами.
Н. другого типа функций может иметь место только
при специальных дополнительных предположениях и
может служить для характеризации определенных клас-
классов распределений. Напр., если Хг, . . ., Хп незави-
независимы, одинаково распределены и имеют нормальное
распределение, то функции
(статистич. оценки математич. ожидания и дисперсии
Xfc соответственно) являются независилшми случай-
случайными величинами. Верно и обратное утверждение: из
Н. функций D) и E) вытекает нормальность распреде-
распределений Хк. Точно так же, если известно, что две ли-
линейные формы
являются независимыми случайными величинами и
ни один из коэффициентов ау и bj не равен нулю, то все
Xj имеют нормальное распределение (из подобного
рода теорем может быть при минимальных допущениях
выведен, напр., закон Максвелла для распределения
скоростей молекул). Приведенные утверждения служат
примерами т. н. характеризационных теорем, наибо-
наиболее полно изученных Ю. В. Линником и его школой.
2) Существование независимых
случайных величин на заданном ве-
вероятностном пространстве. Если мно-
множество элементарных событий Q состоит из трех эле-
элементов, каждому из к-рых приписана вероятность, рав-
равная 1/3, то на Q не существует независимых случайных
величин, отличных от констант. Если в качестве веро-
вероятностного пространства взят отрезок [0, 1] с мерой Ле-
Лебега т, то для любой последовательности функций рас-
распределения .Fi(z), F^(x), ... найдутся определенные
на [0, 1] измеримые функции Хк(а>), являющиеся по
отношению к то независимыми случайными величинами
и такие, что
Хк (со) < x} = Fk (x).
Простейшим примером такого рода статистически неза-
висимых функций на [О, 1] служат знаки двоичного
разложения со, 0<ш<1, или связанные с ними функ-
функции Радемахера
mBn-2*-1(o)) k = l, 2, ...
Следует отметить, что существование какого-ни-
какого-нибудь вероятностного пространства, на к-ром опре-
определены независимые случайные величины с заданными
распределениями, вытекает из теоремы Колмогорова о
вероятностях в бесконечномерных пространствах (см.
[3] гл. III, § 4).
3) Независимые случайные вели-
величины как источник других схем.
Пусть Уо, ylt Y2, - . ., Yn, . . .— последовательность
независимых случайных величин и h(x, у) — (борелев-
ская) функция двух переменных. Полагая
Х„ = A (*B-i. Ya), ....
получают последовательность случайных величин, об-
образующих Маркова цепь. Подобным же образом можно
получать марковские процессы, напр, из винеровского
процесса при полощи стохастических дифференциаль-
дифференциальных уравнений. Из гауссовских случайных мер с не-
независимыми значениями можно, используя преобразова-
преобразование Фурье, построить гауссовскпе стационарные слу-
случайные процессы и т. д.
4) Слабая зависимость. Асимптотич. за-
законы теории вероятностей, установленные для после-
последовательностей независимых случайных величин, обыч-
обычно могут быть распространены и на последовательности
т. н. слабо зависимых величин, т. е. на последователь-
последовательности Хг, Х2, ..., ХП1 ..., где надлежащим образом из-
измеренная зависимость между «удаленными» друг от
друга отрезками последовательности «мала» (в простей-
простейших случаях это могут быть последовательности
m-зависимых величин, где Х^ п Xt при \к—1\ >го неза-
независимы, или последовательности величин, образую-
образующих Маркова цепь эргодическую, п т. п.). Один из ос-
основных приемов доказательства соответствующих тео-
теорем — сведение рассматриваемого случая к случаю Н.
5) Н е з а в и с и м о с т ь в теории чисел.
Пусть р^2 и q^s2 — два взаимно простых натуральных
числа. Пусть Л* — натуральное число, и пусть наудачу
выбирают одно из чисел от 1 до N (вероятность для
каждого считают равной \IN). Пусть Ар (соответствен-
(соответственно Aq) событие, состоящее в том, что выбранное число
делится нацело на р (соответственно q). Тогда
^>=4-
и при Л'—>-оо события Ар и Aq становятся «почти неза-
независимыми». Значительно более глубокий факт, состоя-
состоящий в том, что при N-+oo можно выбрать S=Sjy—>-oo
так, что события А2, As, . . ., A (A j есть ;-е простое
число) в совокупности «почти независимы», служит
основой для исследования распределения значений
арифметич. функций, см. Чисел теория; вероятност-
вероятностные методы. Имеются и другие разделы теории чисел,
где идея Н. явно или неявно присутствует.
6) О проверке гипотезы Н. по результатам наблю-
депнй см. Статистических гипотез проверка.
Лит.: [1] М а р к о в А. А., Исчисление вероятностей,
4 над., М., 1924; [2] Колмогоров А. Н., Основные
понятия теории вероятностей, 2 изд., М., 1974; [3] е г о же,
Теория вероятностей, в кн.: Математика, ее содержание, методы
и значения, М., 1956; Ш К а ц М., Статистическая независимость
в теории вероятностей, анализе и теории чисел, пер. с англ., М.,
1963; [5] Ф е л л е р В., Введение в теорию вероятностей и ее
приложения, пер. с англ., 2 изд., М., 1967. Ю. В. Прохоров.
НЕЗАВИСИМОСТЬ СИСТЕМЫ АКСИОМ — свойст-
свойство системы аксиом данной аксиоматич. теории, состоя-
состоящее в том, что каждая аксиома является незави-
независимой,!, е. не является логическим следствием
из множества остальных аксиом этой теории. Система
аксиом, обладающая этим свойством, наз. незави-
независимой.
Независимость той или иной аксиомы данной аксио-
аксиоматич. теории означает, что эту аксиому можно без
противоречия заменить ее отрицанием. Иными словами,
аксиома независима в том и только в том случае, если
имеется интерпретация, при к-рой эта аксиома ложна,
а все остальные аксиомы данной теории истинны. По-
Построение такой интерпретации является классич. ме-
методом доказательства независимости.
При построении аксиоматич. теории в виде формаль-
формальной системы, где отношение логич. следования форма-
формализуется в виде понятия выводимости, аксиома счита-
считается независимой, если она не может быть выведена
из других аксиом с помощью правил вывода данной
формальной системы. Для широкого класса формальных
систем (т. н. теорий 1-го порядка) независимость от-
относительно выводимости совпадает с независимостью от-
относительно логич. следования.
По отношению к формальным системам и вообще
исчислениям имеет смысл говорить о независимости пра-
правил вывода. Правило вывода наз. независимым,
если существует теорема данного исчисления, которая
не может быть выведена без использования этого пра-
правила.
Н. с. а. сама по себе не является обязательным свой-
свойством аксиоматич. теории. Она лишь свидетельствует
о том, что совокупность исходных положений теории не
является избыточной, и представляет нек-рые технич.
удобства. Однако исследования, посвященные Н. с. а.,
и доказательства независимости способствуют лучшему
пониманию изучаемой теории. Достаточно вспомнить,
какое влияние на развитие математики оказал вопрос о
независимости пятого постулата Евклида в системе
аксиом геометрии.
Лит.: [1] Н о в и К о в П. С, Элементы математической
логики, 2 изд., М., 1973; [2] Гильберт Д., Берна й с П.,
Основания математики. Логические исчисления и формализация
арифметики, пер. с нем., М., 1979; [3] Френкель А.,
Бар-Хил л ел И., Основания теории множеств, пер. с
англ., М., 1966. В. Е. Плиско.
НЕЗАВИСИМЫЕ ИЗМЕРИМЫЕ РАЗБИЕНИЯ про-
пространства с нормированной мерой
ц — такие два измеримых разбиения \ п т), что если
В(\) и В (х\) — булевы ст-алгебры измеримых множеств,
целиком состоящие из элементов разбиений \ и т| соот-
соответственно, то элементы одной из них независимы от
элементов другой в том смысле, как это понимается в
теории вероятностей: \i(A{\B)=\i(A) \i{B) при
А ?В (?), В ?В (г\). Если при этом измеримое разбиение,
являющееся подразбиением обоих разбиений ? и г\,
совпадает по mod 0 с разбиением на отдельные точки,
то ? и г\ наз. независимыми дополнения-
м и друг друга. Известны условия того, чтобы изме-
измеримое разбиение Лебега пространства имело независи-
независимое дополнение.
Лит.: [1] Рохлин В. А., «Матем. сб.», 1949, т. 25, JN» 1,
с. 107—50; [2] Е р ш о в М. П., «Успехи матем. наук», 1977,
т. 32, в. 1, с. 187—88. Д. В. Аносов.
НЕЗАВИСИМЫЕ МЕРЫ — меры [г и v, определен-
ые на локально компактном пространстве Т такие,
то inf (u, v) = 0.
Для того чтобы две меры \i и v были независимы,
еобходнмо и достаточно, чтобы в Т существовали та-
ие непересекающиеся множества М и N, что \i сосре-
сосредоточена на М, a v на N.
Лит.: [1] Б у р б а к и Н., Интегрирование. Меры, инте-
интегрирование мер, пер. с франц., М., 1967. М. И. Войцехоеский.
НЕЗАВИСИМЫХ ФУНКЦИЙ СИСТЕМА — последо-
последовательность измеримых функций {/,¦ (х)} таких, что
ц {x:fi (х) < «!, ... , /„ (х) < «„}-= JJ"= } ц, {х:/,. (г) < а,}
для любого п и любых аь ..., а„. Наиболее простой
пример Н. ф. с. — Радемахера система.
Критерий (Колмогорова) сходимости почти
всюду ряда Н. ф. с: для того чтобы ряд \j™ /,• (х)
сходился почти всюду, необходимо и достаточно, что-
чтобы для нек-рого С > 0 сходились три ряда:
2,
(J
где
? i-л - i i-
0, I /,• (x) | < С
fi (*) = |
Е. М.
НЕИЗМЕРИМОЕ МНОЖЕСТВО — множество, не яв-
являющееся измеримым множеством. Подробнее: мно-
множество X, принадлежащее наследственному о-кольду
H(S), неизмеримо, если
ц*(Х) > Ц* (А');
здесь S есть а-кольцо, на к-ром задана мера ц, а р,*
и ц* — внешняя и внутренняя меры соответственно
(см. Мера).
Для интуитивного овладения понятием Н. м. полезно
следующее «эффективное построение» его.
Пример 1. Пусть
— единичный квадрат,
— множество, соответствующее измеримому по Лебегу
множеству Е меры т(Е), и пусть ^(Ё)^1т(Е). Тогда
множество
Х = {(х, 0):О<а:<1, у = 1/2}
будет Н. м., причем u*(Z)=l, цН!(Х)=0.
Наиболее ранняя л простейшая конструкция Н. м.
принадлежит Дж. Витали (G. Vitali, 1905).
Пример 2. Пусть Q — множество всех рацио-
рациональных чисел. Тогда множество X (множество
В и т а л и), имеющее согласно аксиоме выбора с каж-
каждым из множеств вида Q-j-a, где а — любое действи-
действительное число, ровно по одному общему элементу, яв-
является Н. м. Ни одно из множеств Витали не обладает
Бэра свойством.
Пример 3. Пусть В, (С) — множество чисел ви-
вида д+то!;, ? — иррациональное число, то, п — целые,
с четным п (с нечетным п), а Хо— множество, получен-
полученное также с помощью аксиомы выбора из классов эк-
эквивалентности множества действительных чисел по
отношению:
х~у, если i—y?A = B\jC.
Пусть Х=Х0-\-В. Тогда для всякого измеримого мно-
множества Е имеют место равенства:
На возможности ввести полное упорядочение во мно-
множестве мощности континуума основана еще одна конст-
конструкция Н. м.
Пример 4. Существует множество SczR. такое,
что В и R\B пересекаются с каждым несчетным зам-
замкнутым множеством. Любое такое множество (м н о-
жество Бернштейна) неизмеримо (и не об-
ладает свойством Бэра). В частности, любое множество
положительной внешней меры содержит Н. м.
Помимо инвариантности относительно сдвига (пример
2) и топологич. свойств (пример 3) есть причины и тео-
теоретико-множественной природы, по к-рым невозможно
определить нетривиальную меру для всех подмножеств
данного множества, в этом, напр., состоит теорема
У л а м а (см. [2]) для множеств ограниченной мощ-
мощности.
Неизвестен A982) ни один конкретный пример Н. м.,
для построения к-рого не использовалась бы аксиома
выбора.
Лит.: [1] Халмош П., Теория меры, пер. с англ., М.,
1953; [2] О к с т о б и Д ж., Мера и категория, пер. с англ., М.,
1974; [3J Г е л б а у м В., О л м с т е д Д ж., Контрпримеры в
анализе, пер. с англ., М., 1967. М. И. Вопцеховский.
НЕИВИРТА УЗЕЛ — полигональный узел E3, к1),
группа к-рого обладает конечно порожденным комму-
коммутантом. Дополнение S3\fc1 H. у. есть пространство рас-
расслоения над окружностью, причем слой F является
связной поверхностью, род к-рой равен роду узла.
Коммутант G' группы G— лг Eя\кх) Н. у. является сво-
свободной группой ранга 2g, где g — род узла. Коэффи-
Коэффициент при старшем члене полинома Александера И. у.
равен 1, а степень этого многочлена равна 2g. Все то-
рические узлы являются Н. у. Всякий альтернирую-
альтернирующий узел, старший коэффициент полинома Алексан-
Александера к-рого равен ±1, также Н. у.
Н. у. введены Л. Нейвиртом (см. [1]).
Лит.: [1] Neuwirth L., Knot groups, Princenton (N. Y.),
1965. M. Ш. Фарбер.
НЕЙЛЯ ПАРАБОЛА — название полукубической па-
параболы по имени У. Нейла (W. Neil), к-рый нашел в
1657 длину ее дуги.
НЕЙМАНА АЛГЕБРА — подалгебра А алгебры
93 (Н) ограниченных линейных операторов в гильбер-
гильбертовом пространстве Н, самосопряженная (т. е. со-
содержащая вместе с каждым оператором Т сопряженный
к нему оператор Т*) и совпадающая со своим бикомму-
тантом (т. е. содержащая те и только те операторы
Та9В(Н), к-рые перестановочны с каждым оператором,
перестановочным со всеми операторами из А). Эти ал-
алгебры были введены Дж. Нейманом [1]. Согласно т е-
ореме Неймана самосопряженная алгебра
Acz38(H) тогда и только тогда является Н. а., когда
алгебра А (или ее единичный шар) замкнута в слабой,
сильной, ультраслабой или ультрасильной, но не рав-
равномерной операторной топологии. Данная симметричная
банахова алгебра В тогда и только тогда изометрически
изоморфна нек-рой Н. а., когда В есть С*-алгебра,
изометричная нек-рому сопряженному пространству;
банахово пространство Е, удовлетворяющее условию
Е*=В, определено однозначно с точностью до изоме-
трич. изоморфизма и может быть отождествлено с
пространством ультраслабоненрерывных линейных
форм на изометрически изоморфной В Н. а., это про-
пространство обозначается В„. и паз. преддвойст-
венным пространством для В. Такие
симметричные банаховы алгебры наз. ТУ*-а л г е б р а-
м и. Пусть А Н. а. в гильбертовом пространстве //,
А'— ее коммутант, Z=A f)A' — центр алгебры, Р —
проектор в А, Р'—проектор в А'. Подпространство
Р'Н инвариантно относительно А, и семейство ограни-
ограничений операторов из А на подпространство Р'Н обра-
образует Н. а. в пространстве Р'Н; эта алгебра обозначается
Ар' и наз. индуцированной, а отображение
Т—>-Т\р,н наз. индукцией А на Ар; семейство
ограничений операторов вида РТР, Т?А, на подпро-
подпространство РН образует Н. а. Ар в пространстве РН,
эта алгебра наз. редуцированной. Если Р=
= Р' ?Z, то редуцированная и индуцированная Н. а.
совпадают. Изометрический изоморфизм Н. а. наз. а л-
г с б р а и ч е с к и м; Н. а. в гильбертовом прострап-
стве Н наз. пространственно изоморф-
изоморфной Н. а. В в пространстве К, если существует уни-
тарный-оператор U, отображающий Н на К и удовлетво-
удовлетворяющий условию В= UAU~X. Пересечение любого
семейства Н. а. в данном гильбертовом пространстве
есть Н. а.; наименьшая Н. а., содержащая данное мно-
множество М, наз. Н. а., порожденной множе-
множеством М. Пусть Hh i?I,— гильбертовы простран-
пространства, H=2J®H; — их прямая сумма, А; —И. а. в //,-,
А — Н. а. в пространстве Н, порожденная такими опе-
операторами Т из 35 {Н), что каждое подпространство //,-
инвариантно относительно Т и ограничение Т на Ht
принадлежит Af, H. а. наз. прямым произве-
произведением Н. a. Ai и обозначается А= хА;. Для Н. а.
ig J
определены также операции тензорного произведения
и бесконечного тензорного произведения. Н. а. наз.
фактором, если ее центр состоит из операторов, крат-
кратных единичному.
Пусть А — Н. а., А+ — множество положительных
операторов из А. Весом на А наз. аддитивное отоб-
отображение ф множества А в [0, оо], однородное относи-
относительно умножений на положительные числа. Вес ср
наз. следом, если (f(UTU-1)=(f(T) для всех Т?А +
и всех унитарных операторов U из А. След наз. к о-
н е ч н ы м, если ср (Т) < оо для всех Т ?А; полуко-
полуконечным, если для любого S?A+ величина <p(S)
есть верхняя грань чисел вида <р(Т), где ср(Г)<оо и
0<Г<5'; точным, если из условия ср(Г) = О, Т?А +,
следует Т=0; нормальным, если для любого
возрастающего семейства Та элементов из А + с точной
верхней границей Т величина Ц>{Т) является верхней
гранью чисел <р(Та). H. а. А наз. конечной, если
на А существует семейство нормальных конечных сле-
следов, разделяющее точки Л;собственно беско-
бесконечной, если на А не существует ненулевых конеч-
конечных следов; полуконечной, если на А сущест-
существует точный нормальный полуконечный след, и ч и с т о
бесконечной, или алгеброй типа III,
если на ; А не существует ненулевых нормальных
полуконечных следов. Н. а. наз. дискретной,
или алгеброй типа I, если она алгебраиче-
алгебраически изоморфна Н. а., коммутант к-рой коммутативен;
такая алгебра полуконечна. Н. а. наз. непре-
непрерывной, если для любого ненулевого центрального
проектора Р Н. а. Ар не является дискретной. Непре-
Непрерывная полуконечная алгебра наз. алгеброй т и-
п а II. Конечная алгебра типа II наз. Н. а. типа Ид;
собственно бесконечная алгебра типа II наз. Н. а. ти-
типа П.». Принадлежность Н. а. к определенному типу
равносильна принадлежности ее коммутанта тому же
типу, но коммутант конечной Н. а. не обязательно яв-
является конечной Н. а.
Пусть А — Н. а., Р, Q — проекторы в А, Р и Q наз.
эквивалентными, Р—Q, если существует та-
такой элемент U?A, что P=U*U, Q=UU*. Пусть
P-K.Q, если существует такой проектор Рх ?А, что
Р—Рг и Pj <<2> отношение •< есть отношение частичного
порядка. Классификация Н. а. по типам I и т. д. мо-
может быть проведена в терминах этого отношения, в ча-
частности: проектор Р?А наз. конечным, если из
условий Pi?A, Рг~Р, Рх^Р следует, что Р1=Р;
Н. а. конечна тогда и только тогда, когда единичный
проектор конечен, и полуконечна, если и только если
точная верхняя граница семейства конечных проекторов
есть единичный проектор.
Н. а. А полуконечна тогда и только тогда, когда она
может быть реализована как левая Н. а. нек-рои совер-
совершенной гильбертовой алгебры; элементами соответ-
соответствующей гильбертовой алгебры являются такие эле-
элементы х?А, что ф(х*х)<оо, где ф — точный нормаль-
нормальный полуконечный след на А. Для алгебр типа III
соответствующая реализация может быть получена с
помощью обобщенных гильбертовых алгебр и весов на
Н. а.
Пусть Нр — фиксированное гильбертово простран-
пространство размерности р, р=1, 2, . . ., #0,? — борелевское
пространство, ц — положительная мера на Z, Z=
= U *LxZp — разбиение Z на непересекающиеся изме-
измеримые подмножества, L2{Zp, u, Н р)— гильбертово
пространство суммируемых с квадратом jx-измерпмых
отображений пространства Zp в IIр,
Пусть H(t,) = Hp при t,?Zp; если /?#, то f=^pfp, где-
1p?L2(Zp, u, Нр); пусть f(i)=fp(%) при t?Zp; отобра-
отображение Z,-+T(t,), где Т (t,) — непрерывный линейный опе-
оператор в гильбертовом пространстве H(t,), наз. изме-
измеримым полем операторов, если для любого-
f?H функция ?—>-Г(?)/(?) измерима на каждом мно-
множестве Zp. Если ?—>Т (Z,) — измеримое поле операторов
п функция ?—*-11У(?I1 существенно ограничена на Z,
то для любого f^H существует единственный вектор
g?H такой, что g{?)—T(Z) f(t) ц-почти всюду. Отоб-
Отображение Т : Н^-Н, определенное формулой 77= g
для всех f?H, является ограниченным линейным опе-
оператором в Н, и
|| Т || = ess sup || Т (I) |].
Такой оператор Т в // наз. разложимым. Пусть
для любого L?Z определена Н. а. А (?) в простран-
пространстве Н {t,); отображение Z,—*-А (Z) наз. измеримы м
полем Н. а., если существует такая последова-
последовательность {?—>-?",,(?)} измеримых операторных полей,
что при любом t^Z H. a. A (Z) порождается операто-
операторами Tn(Q. Множество всех таких разложимых опе-
операторов Т в //, что Т E) ? А (?) при каждом ? ? Z, есть.
Н. а. в Н, обозначаемая
она наз. прямым интегралом Н. а. А (?) ш*
мере и,. Любая Н. а. в сепарабельном гильбертовом
пространстве изоморфна нек-рому прямому интегралу"
факторов. Произвольная Н. а. может быть подвергну-
подвергнута алгебраич. разложению, в связи с чем теория фак-
факторов и представляет интерес для общей теории Н. а.
Н. а. естественно возникают в задачах, связанных
с операторами в гильбертовом пространстве, и имеют
многочисленные приложения как в самой теории опе-
операторов и теории представлений групп п алгебр, так
и в теории динамич. систем, статистич. физике и кван-
квантовой теории поля.
Лит.: [1] Murray F., Neumann J., «Ann. Math,»,.
1936 v. 37 p. 1 IB—229; «Trans. Amer. Math. Soc», 1937, v. 41,
p. 208—48; [2] Neumann J. , «Ann. Math.», 1943, v. 44, p.
716—808; [3] Dixmier J., Les alpehres d'operateurs dans,
l'espace hilbertien, 2 6d., P., 1969; [4] Д и ксыье Ж., С*-ал-
гебры и их представления, пер. с франц., М., 1974; [5J S а-
kai S., C*-algebras and W*-algebras, В., 1971; [6] Neu-
Neumann J., «Сотр. math.», 1938, v. 6, p. 1—77; «Ann. Math.»,
1940, v. 41, p. 94—161; [7] G u i с h a r d e t A., «Ann. scient.
Ecole norm, super.», 1966, t. 83, p. 1—52; [8] T а к е с а к u M.,
«Математика», 1974, т. 18, № 3, с. 84—120, № 4, с. 34—63; [91
Z s i d 6 L., Topological decompositions of operator algebras,
Vienna, 1974; [Ю1Наймарк М. А., Нормированные коль-
кольца, 2 изд., М., 1968. А. И. Штерн.
НЕЙМАНА ЗАДАЧА — то же, что вторая краевая
задача. Названа по имени К. Неймана (К. Neumann,
1877), к-рый впервые систематически исследовал ее.
НЕЙМАНА МЕТОД ДОВЕРИТЕЛЬНЫХ ИНТЕРВА-
ИНТЕРВАЛОВ — один из методов доверительного оценивания,
позволяющий получать интервальные оценки для не-
неизвестных параметров вероятностных законов по ре-
результатам наблюдений. Предложен и развит Ю. Ней-
маном (см. [1], [2]). Суть метода заключается в следую-
следующем. Пусть Х1, . . ., Хп — случайные величины, сов-
совместная функция распределения к-рых F(x, 9) зависит
от параметра B^GcR1, x=(xx, . . ., xn)?Rn. Далее,
пусть в качестве точечной оценки параметра Э исполь-
используется статистика Т^Т(Х1, . . ., Хп), функция распре-
распределения к-рой есть G(t, 6), 9?в. Тогда для любого
числа Р из интервала 0,5<Р<1 можно определить
систему из двух уравнений относительно переменной Э:
При определенных условиях регулярности функции
F(x, G), к-рые выполняются почти во всех интересных
для практики случаях, система (*) имеет единственное
решение
е = 0(Г), е = е(Г), ё, ege,
такое, что
р{е <е <е|е}э=2/>—1.
Множество @, 0)св наз. доверительным
интервалом (доверительной оцен-
к о и) для неизвестного параметра Э с доверительной
вероятностью 2Р—1. Статистики 0 и 0 наз. нижним
п верхним доверительными преде-
пределам и, отвечающими выбранному коэффициенту до-
доверия Р. В свою очередь, число
р= inf Р{9 < 6 < G | в>
Оев ~
наз. коэффициентом доверия доверитель-
доверительного интервала F, 9). Таким образом, Н. м. д. п. при-
приводит к интервальным оценкам, коэффициент доверия
к-рых р^2Р — 1.
Пример 1. Пусть независимые случайные ве-
величины Х1у . . ., Хп подчиняются одному и тому же
нормальному закону Ф (х—9), математич. ожидание
к-рого G неизвестно. В этом случае наилучшей оценкой
для б является достаточная статистика Х = —^?=1Х,-,
к-рая распределена по нормальному закопу
Ф \Уп(х — ®)]. Фиксируя Р из интервала 0,5<Р<1 и
решая уравнения
находят нижний и верхний доверительные пределы
отвечающие выбранному коэффициенту доверия Р.
Так как
Ф-1(г/)+ф-1A_г/)^о, у€[о, 1],
то доверительный интервал для неизвестного мате-
математич. ожидания 9 нормального закона Ф (х—9) имеет
вид
причем коэффициент доверия его в точности равен
2Р — \.
Пример 2. Пусть \i — случайная величина, под-
подчиняющаяся биномиальному закону с параметрами
п и 9, т. е. для любого целого пг=0, 1,2,.. ., п
, 0 < 9
где
— неполная бета-функция @<х<1, а>0, Ь>0). Если
параметр «успеха» 0 неизвестен, то для определения
доверительных пределов нужно согласно Н. м. д. и. ре-
решить уравнения
/i-е (га —ц, М-+1) =
Г'
Ь-р,
где 0,5<Р<1. По таблицам математич. статистики
определяют корни Э и G этих уравнений, являющиеся
соответственно верхним и нижним доверительными
пределами с коэффициентом доверия Р. Полученный
таким образом доверительный интервал F, Э) имеет
коэффициент, в точности равный 2Р—1. Очевидно, что
если в эксперименте получают ц=0, то в этом случае
9=0, если же ц=и, то 6=1.
Н. м. д. и. существенно отличается от бейесовского
метода и метода, основанного на фидуциальном под-
подходе Фишера. В Н. м. д. п. неизвестный параметр Э
функщш распределения F(x, 9) трактуется как посто-
постоянная величина, а сам доверительный интервал (в(У),
9(Г)) строится до эксперимента, в ходе к-рого вычис-
вычисляется значение статистики Т. Следовательно, согласно
Н. м. д. и. вероятность одновременного выполнения
неравенств 9<0<6 есть априорная вероятность того,
что доверительный интервал (9, 9) «накрывает» не-
неизвестное истинное значение параметра 6. Очевидно,
что на самом деле доверительный метод Неймана оста-
остается в силе, если 9 является случайной величиной, так
как в Н. м. д. и. интервальная оценка строится до
проведения эксперимента и, следовательно, не зависит
от априорного распределения параметра. Н. м. д. и.
выгодно отличается от бейесовского и фидуциального
подходов своей независимостью от априорной инфор-
информации о параметре 6, и при этом, в отличие от метода
Фишера, логически безупречен. В общем случае
Н. м. д. и. приводит к целой системе доверительных
интервалов для неизвестного параметра, в связи с чем
возникает задача построения оптимальной интерваль-
интервальной оценки, обладающей, напр., свойствами несме-
несмещенности, селективности или подобия, к-рая находит
свое решение в рамках теории проверки статистич.
гипотез.
Лит.: [1] Neyman J., «Ann. Math. Statistics», 1935,
v. 6, p. Ill —16; [2] e г о же, «Philos. Trans. Roy. Soc. London.
Ser. A.», 1937, v. 236, p. 333—80; [3] Б о л ь ш е в Л. Н., Смир-
Смирнов Н. В., Таблицы математической статистики, 2 изд., М.,
1968; [4] Б о л ь ш е. в Л. Н., «Теория вероятн. и ее примен.»
1965, т. 10, ЛК 1, с. 187—92; [5] Леман Э., Проверка ста-
статистических гипотез, пер. сангл., 2 изд., М., 1979. М. С. Никулин
НЕЙМАНА РЯД — ряд вида
где JVt-n — Бесселя функции (цилиндрич. функции 1-го
рода), v — нек-рое число (действительное или комплек-
комплексное). К. Нейман [1] рассмотрел частный случай,
когда v — целое число. Он показал, что если f(z) — ана-
литич. функция в замкнутом круге с центром в начале
координат, z — внутренняя точка круга, С — граница
круга, то имеет место равенство
где
«о = /(О), an=4f
On— многочлен степени га-j-l относительно i/t:
O0(t)=l/t,
он обычно наз. многочленом Неймана n-го
порядка (сам К. Нейман эту функцию называл бесселе-
бесселевой функцией 2-го порядка, ныне этим термином поль-
пользуются для обозначения одного из решений уравнения
Бесселя).
Примеры представления функций с помощью Н. р.:
cos (z sin ф) = /0(г) + 2 2°°_ ^2« B) cos ^"Ф>
sin(z cos <р) =^ 2 2]J= ] /2„_! (г) sinBre — 1) ф,
где |х — любое не целое отрицательное число, Г —
гамма-функция.
В теории интегральных уравнений Фредгольма
*, «)<P(s) <*« = /(*), *€[*. Ь]. С1)
рядом Неймана наз. разложение резольвенты
R (х, s; Я) ядра К:
R (х, s; Я) = 2J= ! Я"АГ„ (*, *), B)
где Кп — интерированные ядра (ядра К), определяе-
определяемые рекуррентными формулами
Кг(х, s) = K(x, s),
bKn_l(x, t)K(t, s)dt, п=з2.
С помощью формулы B) решение уравнения A) при
малых Я представляется равенством
ф (¦*) = /() +2Г Х" S
Последний ряд также наз. рядом Неймана.
Ряд C) был рассмотрен К. Нейманом [2] в случае урав-
уравнения A), к к-рому сводится задача Дирихле в теории
потенциала.
Пусть А ¦— ограниченный линейный оператор, ото-
отображающий банахово пространство X в себя, и пусть
норма |И||<1. Тогда оператор /—А, где / — тождест-
тождественный оператор, имеет единственный обратный огра-
ограниченный линейный оператор (/—Л), допускающий
разложение
к-рое в теории линейных операторов наз. рядом
Неймана. Ряд C) можно рассматривать как част-
частный случай ряда D).
Лит.: [1] Neumann К., Theorie der Besselschen Functio-
nen, Lpz., 1867; [21 его же, Untersuchungen iiber das logarith-
mische und Newtonsche Potential, Lpz., 1877; [3] В а т с о н Г. Н.,
Теория бесселевых функций, пер. с англ., ч. 1, М., 1949; [4]
Кузьмин Р. О., Бесселевы функции, 2 изд., Л.— М., 1935;
[5] И о си да К., Функциональный анализ, пер. о англ., М.,
1967; [6] Т р и к о м и Ф., Интегральные уравнения, пер. с
англ., М., 1960. Б. В. Хведелидзе.
НЕЙМАНА СТРУКТУРА — структура, определяе-
определяемая статистикой, не зависящей от достаточной статисти-
статистики. Понятие Н. с. введено 10. Нейманом (J. Neyman,
см. [1]) в связи с задачей построения подобных кри-
критериев в теории проверки статистич. гипотез, при этом
сам термин «Н. с.» употребляют по отношению к струк-
структуре статистич. критерия, если его критич. функция
имеет Н. с. Пусть по реализации случайной величины X,
принимающей значения в выборочном пространстве
(ЭЁ, SP, Pq), 9?в, надлежит проверить сложную ги-
гипотезу Но : 9?восв, причем для семейства {Ре,
96®о) существует достаточная статистика Т с распре-
распределением из семейства {Ре, 6€®о}- В этом случае
любой статистпч. критерий уровня а, предназначенный
для проверки гипотезы Но, имеет Н. с, если его кри-
тич. функция ф удовлетворяет условию:
Е {ф (X) | Т = t} = a почти всюду по мере Ре, 6^в0. A)
Очевидно, что если статистич. критерий имеет Н. с,
то он является подобным по отношению к семейству
{Рв, 9?G0}, так как
для всех 6?в0.
Выполнение условия A) по существу сводит задачу
проверки сложной гипотезы Но к задаче проверки про-
простой гипотезы Ло при каждом фиксированном значении
t достаточной статистики Т.
Пример. Пусть независимые случайные величины
Х± и Хг подчиняются законам Пуассона, параметры
к-рых Яг и Я2 неизвестны, и пусть проверяется гипотеза
Но : Xj=X2 против альтернативы Н1 : 'к1Ф'кг. В силу
независимости Х1 и Хг статистика Т=Х1-\-Х2 подчиня-
подчиняется закону Пуассона с параметром A^+^i а условные
распределения случайных величин Хг и Х2 при ус-
условии T=t суть биномиальные распределения с пара-
параметрами t, Xj/ (Ях+^г) и (, Я2/ (К1-\-Х2) соответственно,т. е,
у \ / Я- \/г / Я. \t-ti
, (_i—) (i—5—4-)
Я/ V Xi + Хг J \ А1 + Я2 /
к = 0, 1 t. B)
При справедливости гипотезы На статистика Т явля-
является достаточной для неизвестного общего значения
Я=Л1=Х2, а из B) следует, что если гипотеза Но имеет
место, то условное распределение случайной величины
Хг при фиксированном значении достаточной статисти-
статистики T=t является биномиальным с параметрами t и 1/2)
т. е. при На
(i)(±)t ft=0, I t.
Таким образом, в этом случае задача проверки слож-
сложной гипотезы Но свелась к задаче проверки простой
гипотезы Но, согласно к-рой условное распределение
случайной величины Х1 (при фиксированной сумме
Хг-\-Х2=^ является биномиальным с параметрами t
и 1/2. Для проверки гипотезы Н{, можно воспользо-
воспользоваться, напр., знаков критерием.
Понятие Н. с. имеет большое значение в задаче
проверки сложных статистич. гипотез, т. к. именно
среди критериев, имеющих Н. с, часто находится
наиболее мощный критерий. Э. Леман (Е. Lehmann)
н Г. Шеффе (Н. Scheffe) показали, что статистич. кри-
критерий для проверки сложной гипотезы Но : 9^в0
имеет Н. с. по отношению к достаточной статистике Т
тогда и только тогда, когда семейство {Pq-, 0?в0},
индуцированное статистикой Т, является ограниченно
полным. На основе понятия Н. с. разработаны общие
методы построения подобных критериев. См. Распреде-
Распределений полное семейство, Подобный критерий.
Лит.: [1] Нейман Дш., Текущие задачи математичес-
математической статистики, [пер. с англ.]. Международный математический
конгресс в Амстердаме. 1954,М., 1961; [2J Леман Э.,Проверка
статистических гипотез, пер. с англ., 2 изд., М., 1979; [3] Л и н-
н и к Ю. В., Статистические задачи с мешающими парамет-
параметрами, М., 1966. М. С. Никулин.
НЕЙМАНА ТЕОРЕМА эргодическая: для
изометрич. оператора U в гильбертовом пространстве
Н и любого h?H существует предел
lim 4"V" ~
(понимаемый в смысле сходимости по норме в //). Для
непрерывной однопараметрич. группы унитарных пре-
преобразований {Uf} в Н и любого h?H существует предел
lim 4f [I Uthdt=li
(понимаемый в том же смысле). При этом h есть орто-
ортогональная проекция h на пространство инвариантных
относительно U (или {?/;}) элементов //.
Н. т. сформулирована и доказана Дж. Нейманом [1],
имевшим в виду в первую очередь ее применения в
эргодич. теории, когда в пространстве с мерой (X, \i)
задан эндоморфизм Т (или измеримый поток {Tf}),
II—L- (X, \i) и U есть оператор сдвига:
Uh (х) = h (Тх) или Uth (х) = h (Tt (x)).
В этом случае Н. т. означает, что временные средние
функции h{x), т. е. средние значения h(Tkx) пли h(Ttx)
на отрезке времени 0<А <п или 0<?КТ, при удлинении
этого отрезка сходятся к h (х) в среднем квадратичном
по х (что часто подчеркивается термином mean ergodic
theorem). В частности, при достаточной длине интервала
осреднения временное среднее функции h (x) для боль-
большинства х близко к h(x). Поэтому Н. т. (и ее обобще-
обобщения) часто (в особенности применительно к данному слу-
случаю) наз. статистической эргод и ческой
т е о р е м о и, в отличие от индивидуальной
эргоди ческой т е о р е м ы, т. е. Биркгофа эр-
годической теоремы (и ее обобщений). Из последней
(и — при ц(Х)=т — из используемых при ее дока-
доказательстве рассуждений) в данном случае можно вы-
вывести Н. т. Однако в общем случае, когда // не реализо-
реализовано как L2 (X, jj,) п оператор U или Uf не связан с ка-
какими-то преобразованиями в X, Н. т. не следует из
теоремы Биркгофа.
Первоначальное доказательство Н. т. опиралось на
спектральное разложение унитарных операторов.
Позднее появился ряд других доказательств (прос-
(простейшее из них принадлежит Ф. Риссу, V. Riesz, см.
[2]) и обобщений для более широких классов групп и
полугрупп операторов в банаховых пространствах
(см. [3], [4]).
Н. т. и ее обобщения принадлежат к числу опера-
операторных эргодических теорем.
Лит.: [1] Neumann J., «Ргос. Nat. Acad. Sci. USA»,
1932, v. 18, p. 70—82: L2J X а л м о ш П. Р., Лекции по эргоди-
ческой теории, пер. с англ., М., 1959; [3] Вершин А. М.,
Юз вине кий С. А., в кн.: Итоги науки. Математический
анализ. 1967, М., 1909, с. 133—87; [4] Каток А. Б., С и-
н а й Я. Г., Степан А. М., в кн.: Итоги науки и техники.
Математический анализ, т. 13, М., 1975, с. 129—282.
Д. В. Аносов.
НЕЙМАНА ФУНКЦИИ — цилиндрические функции
2-го рода. Н. ф. Хр(х) [иногда применяется обозначе-
обозначение Yр (х)] могут быть определены через Бесселя функ-
функции Jp (х) следующим образом:
Jk(x)coskn-J _k(x)
N,Ax)= lim —г ^— =—.
1 k ~* p SIn я
H. ф. действительны при действительном положитель-
положительном х и стремятся к нулю при х—юо. При больших х
справедливо асимптотпч. представление
sm x—— ря— •
Н. ф. связаны рекуррентными формулами
Np _ J (х) + Np + 1(x) = Bp/x) Np (x),
( 2
При р = п целых:
для малых х:
где In у=С= 0,5772 . . .— постоянная Эйлера.
0,5
1
/
/
1
\
it-
If
L
1/
/
l\
h
/
7
7.
s
i
/
"'
\
u
^
\
No
\
/
t
7] /L/-I--
/
f
/
/ 1
Vr
/
-
-
-\
/
\
)
--
U
/
i,
N
—-
X
X
r,.
3"
>
-Hi
л
0^
V
/K
s\/
л
1
\
^*
1
^*-
71
J
•¦0 5 -
-1.0
"'0 1 23456789 10 II 12
X
Графики функций НеМмана.
H. ф. для «полуцелого» порядка р^=п-\-11а выражают-
выражаются через тригонометрия, функции, в частности
¦— cos x, Я ,„ (ж) = I/ -^- sin ;
ях - l/i ч ' У лх
H. ф. предложепы К. Нейманом (К. Neumann, 1867).
Лит. см. при ст. Цилиндрические функции. В. И. Битюцков.
НЕЙМАНА — ПИРСОНА ЛЕММА —лемма, утверж-
утверждающая, что в задаче статистич. проверки простой
гипотезы ffg против простой альтернативы Н1 отноше-
отношения правдоподобия критерий является наиболее мощ-
мощным критерием среди всех статистич. критериев,
имеющих один и тот же заданный значимости уровень.
Н.— П. л. доказана Ю. Нейманом и Э. Пирсоном [1].
Н.— П. л. часто наз. фундаментальной лем-
леммой математической статистики. См.
также Статистических гипотез проверка.
Лит.: [1] N е и га a n J., Р е а г s о n E. S., «Philos. Trans
Roy. Soc. London. Scr. A», 1933, v. 231, p. 289—337; [2] Jle-
м а н Э. Л., Проверка статистических гипотез, пер. с англ.
2 изд., М., 1979. м. С. Никулин.
НЕЙТРАЛЬНОГО ТИПА УРАВНЕНИЕ — диффе-
дифференциальное уравнение с отклоняющимся аргументом,
в к-рое старшая производная входит при более чем одной
значении аргумента, в том числе при основном (непре-
образовапном), н это последнее значение является на-
наибольшим из присутствующих в уравнении. Напр.,
уравнение
х' (t) = f (t, x(a(t)), x' (P (*))) (*)
есть Н. т. у. при <x(i)<i, |5(i)<i.
Для Н. т. у. разрешима начальная задача; так,
если для Н. т. у. (*) с возрастающей р (i) задать
то при
, т, гс^эО, p^sl,
существует (при ге>1 — единственное) кусочно глад-
гладкое решение, к-рое при выполнении /c=l + min {m, п,
р—1} условий согласования, т. о. усло-
условий типа
ф ( Ф((о)ф(Р(о))),
принадлежит Ck. H. т. у.— один из наиболее изучен-
изученных классов уравнений с отклоняющимся аргументом.
Н. т. у. естественно появляются в прикладных задачах,
в постановку к-рых входит то или иное свойство пов-
повторяемости. А, д. мышкис.
НЕКЛАССИЧЕСКАЯ ТЕОРИЯ МОДЕЛЕЙ — теория
моделей, отличающаяся от классической тем, что либо
формальный язык, с к-рым она имеет дело, отличен от
языка первого порядка Ьа№, либо логика, лежащая в
ее основе, отлична от классической (двузначной). В
дальнейшем, если не оговорено противное, логика счи-
считается двузначной.
В теории моделей языка L наиболее важными явля-
являются следующие проблемы.
а) Аксиоматизируемость множества тождественно
истинных формул. Если существует эффективная ну-
нумерация формул языка L натуральными числами, то
проблема уточняется: будет ли множество номеров тож-
тождественно истинных формул рекурсивно перечпслимым?
б) Язык L наз. (а, [})-к о м п а к т н ы м, если для
любого множества 2 высказываний языка L мощности
<:а из выполнимости каждого подмножества 2 '?2
мощности <fi следует выполнимость 2. Проблема ком-
компактности состоит в описании пар кардиналов <а, {5>,
для к-рых L является (а, Р)-компактным.
в) Если формулы языка L образуют множество
(несобственный класс), то существует такой кардинал
а, что всякое множество высказываний языка L, име-
имеющее модель мощности Р^а, имеет модели сколь угод-
угодно больших мощностей. Наименьший такой кардинал
наз. числом X а н ф а языка L. Для Ьша оно
равно счетной мощности ы. Проблема заключается в
вычислении числа Ханфа для L и в установлении ус-
условий существования моделей малых мощностей.
Ниже перечислены наиболее изученные неклассич.
языки и для каждого из них отмечены нек-рые решения
проблем а) — в).
1) Язык L2 логики второй ступени.
Он получается пз Ьшш добавлением переменных для
предикатов и разрешением навешивания на них кван-
кванторов. Высказывание Ф языка L2 наз. истинным
в системе <Л, _Fl7 . . ., /<'„, . . .> (где А — модель сиг-
сигнатуры Ф, a Fn, n~^\,— множества и-местных преди-
предикатов на А), если Ф истинно в А при ограничении кван-
кванторов по и-местным предикатам множествами Fn.
Если при этом Fm n^l, совпадают с множествами всех
и-местных предикатов на А, то говорят, что Ф истинно
в модели А. Существует высказывание языка L2, ха-
характеризующее арифметику натуральных чисел с точ-
точностью до изоморфизма. Из Гёделя теоремы о неполноте
арифметики следует, что множество высказываний
языка L2, истинных во всех моделях, не аксиоматизи-
аксиоматизируемо. Однако существует естественное обобщение 22
аксиоматики исчисления предикатов первой ступени,
для к-рого справедлива теорема Хенкина
о полноте: из Х2 выводимы те и только те выска-
высказывания языка Z,2, к-рые истинны во всех системах
<А, Fu . . ., Fn . . .>, удовлетворяющих аксиомам 2?.
В этом случае имеется аналог теоремы Л ё-
венхейма — Сколем а для Ь^ы'. если вы-
высказывание Ф языка L2 истинно вместе с аксиомами
2 2 в нек-рой системе, то Ф и 22 истинны в системе
<Л, Fl, . . ., Fn, . . .>, где А и Fn, га>1, не более чем
счетные. Нек-рые вопросы теории моделей языка L2 свя-
связаны с проблемами теории множеств и неразрешимы в
аксиоматике теории множеств Цермело — Френкеля.
2) Язык Z,ap (а, [} — кардиналы). Формулы этого
языка строятся из формул языка 1-го порядка с по-
помощью конъюнкций и дизъюнкций множеств формул
мощности <а, отрицания и кванторной приставки по
предметным переменным длины <C. Истинность фор-
формулы в модели определяется, аналогично языку 1-го
порядка, индукцией по построению формулы. Кардинал
а наз. компактным, если для любого кардинала у
язык Laa является (у, а)-компактным. Среди языков
Lafi после Law наиболее изучен Z/оыо. Всякую счет-
счетную модель счетной сигнатуры можно охарактеризо-
охарактеризовать высказыванием языка La^ с точностью до изо-
изоморфизма. Язык Z,coro) для любого а является (a, Wi)-
компактным. Число Ханфа для Lalb) равно 2е0' И1, где
2a'v определяется индукцией по ординалу v : 2a> =a,
2a, 6+1 = 2«, 6 и 2а'6=2ц<б2а' *\ если 6 — предельный
ординал.
3) Язык =S?a с квантором «существует
по крайней мере a>a». Язык J?a получается
из //щи добавлением нового квантора Qa. Истинность
формулы определяется индукцией по длине формулы.
При этом формула (QtxxL> (х) истинна в модели А, если
мощность множества {а\а?А, Ф (а) истинна в А} не
меньше о>а. Пусть Va обозначает множество формул
языка J?a, истинных во всех моделях мощности ^ша-
Множество Vo не аксиоматизируемо, Fx аксиоматизируе-
аксиоматизируемо. Язык <5?0 не (со, со)-компактен. Однако нек-рая ком-
компактность имеет место в языках Ха- Пусть C«
означает, что из Х,<ш„ и Y,<u>o(i?K) следуетД. jY
<Q)a- Если Шо-<<(о)а, то Ха будет (со», со)-компакт-
ным. Число Ханфа для J?x равно 20)'м.
До сих пор рассматривались модели, в к-рых лю-
любое высказывание языка L сигнатуры а было либо ис-
истинным, либо ложным. Рассмотрим теперь модель А
сигнатуры ст, в к-рой «-местные предикаты понимаются
не как подмножества А", а как отображения Ап в
множество X. Если на X определены операции, соот-
соответствующие логич. связкам языка L и кванторам
(понимаемым как бесконечноместные операции), то
можно определить значение истинности ||Ф|И^^(Г лю-
любого высказывания Ф языка L в модели А. Таким обра-
образом, получается теория моделей с множеством значений
истинности X. Наиболее плодотворной оказывается
теория, когда X — компактное хаусдорфоно тополо-
гич. пространство или полная булева алгебра. В этих
случаях работают многие методы класснч. теории моде-
моделей. В случае, когда X — полная булева алгебру,
конъюнкция, дизъюнкция и отрицание определяются
как пересечение, объединение и дополнение соответ-
соответственно. Значение ||(Уя)Ф(яIИ определяется как пере-
пересечение всех элементов вида ||Ф(аIИ, а?А. Булево-
значные модели нашли широкое применение в дока-
доказательствах совместности различных предложений тео-
теории множеств с основными аксиомами аксноматич. тео-
теории множеств.
Лит.: [1] Чёрч А., Введение в математическую логи-
логику, пер. с англ., т. 1, М., 1960: [2) К е й с л е р Г. Д., Ч э н
Че н ь-ч у н ь, Теория непрерывных моделей, пер. с англ., М.,
1971. Е. А. Палютин, А. Д. Таймапив.
НЕКОРРЕКТНЫЕ ЗАДАЧИ, точнее — некор-
некорректно поставленные задач и,— задачи,
для к-рых не удовлетворяется хотя бы одно из приво-
приводимых ниже условий, характеризующих коррект-
корректно поставленные задачи [короче — кор-
корректные задачи (к. з.)]. Задача определения
решения z=R(U) из метрпч. пространства Z (с расстоя-
расстоянием pz( 1 }) по «исходным данным» и из метрич. про-
пространства U (с расстоянием рц( , ) ) наз. коррект-
корректно поставленной на паре пространств (Z, U),
если: а) для всякого и?U существует решение z?Z;
б) решение определяется однозначно; в) задача устой-
устойчива на пространствах (Z, U), что означает: для вся-
всякого е>0 существует такое 6(е)>0, что для любых
ui> U2^.U из неравенства ри(щ, и2)<6(е) следует не-
неравенство pz(h, Z2)<e> гДе zi=-ff ("ih z2=i?(u2).
Понятие к. з. принадлежит Ж. Адамару (J. Hada-
mard, 1923), высказавшему точку зрения, что всякая
математич. задача, соответствующая какой-либо физич,
или технич. задаче, должна быть корректной. В самом
деле, какую физич. интерпретацию может иметь реше-
решение, если как угодно малым изменениям исходных дан-
данных могут соответствовать большие изменения решения?
К таким задачам затруднительно применять прибли-
приближенные методы решения. Это поставило под сомнение
целесообразность изучения Н. з.
Однако такая точка зрения, естественная в примене-
применении к нек-рым явлениям, развивающимся во времени,
не может быть перенесена на все задачи. В самом деле,
неустойчивыми в метрике С, а следовательно и Н. з.,
являются задачи: решения интегральных уравнений
1-го рода; дифференцирования функций, известных
приближенно; численного суммирования рядов Фурье,
когда их коэффициенты известны приближенно в ме-
метрике 1.2; задача Коши для уравнения Лапласа; задача
аналитич. продолжения функций; обратные задачи
гравиметрии. Некорректными являются также задачи
решения систем линейных алгебрапч. уравнений в
условиях равного нулю определителя системы (а также
плохо обусловленные системы); минимизации функцио-
функционалов, имеющих несходящиеся минимизирующие по-
последовательности; нек-рые задачи линейного програм-
программирования и оптимального управления; проектирова-
проектирования оптимальных систем, конструкций (синтез антенн и
других фпзнч. систем); задачи об управлении объекта-
объектами, описываемые дифференциальными уравнениями
(вчастности, дифференциальные игры). К перечисленным
задачам приводят самые различные фнзнч. и техннч.
проблемы (см. [71).
К Н. з. относится широкий класс т. н. обратных задач,
возникающих в физике, технике и других отраслях
знаний, в частности — задачи обработки результатов
физич. экспериментов. Пусть z — количественная ха-
характеристика изучаемого явления (объекта). В физич.
эксперименте часто величина z недоступна непосред-
непосредственному измерению, а измеряется нек-рое ее проявле-
проявление Az=u. Для интерпретации результатов измерений
необходимо определять z по и, т. е. решать уравнение
вида
Az=u. A)
Задачи решения уравнений A) часто наз. задачами
распознавания образов. Задачи, при-
приводящие к задачам минимизации функционалов (зада-
(задачи синтеза антенн и других систем и конструкций,
задачи оптимального управления и многие др.), наз.
также задачами синтеза.
Пусть в задаче обработки результатов физич. экспе-
экспериментов изучаемый объект (явление) характеризуется
элементом z (функцией, вектором), принадлежащим
множеству возможных решений Z метрпч. пространства
Z. Пусть Zj недоступен для прямого измерения и изме-
измеряется его проявление AzT=uT, uT?AZ, где AZ —
образ Z при его отображении с помощью оператора А.
Очевидно, zy=^А ~гит, где^4-1— оператор, обратный
оператору А. Так как элемент uj получают путем изме-
измерений, то он бывает известен лишь приближенно. Пусть
и — это приближенное значение. В этих условиях речь
может идти лишь о нахождении приближенного (к
zy) «решения» уравнения
Az = п. B)
Оператор А во многих случаях таков, что обратный
ему оператор А не является непрерывным, напр,
когда А — вполне непрерывный оператор в гильберто-
гильбертовом пространстве, в частности интегральный оператор
вида
\ЬК(х, s)z(s)ds.
В этих условиях нельзя, следуя классич. концепциям,
брать в качестве приближенного к jf «решения» точ-
точное решение уравнения B), т. °. элемент z=A~1u, так
как: а) такого решения может не существовать на Z,
поскольку и может не принадлежать множеству AZ;
б) такое решение, если даже оно существует, не будет
обладать свойством устойчивости к малым изменениям
и (поскольку обратный оператор А*1 не является не-
прерывным) и, следовательно, пе может быть физически
интерпретируемым. Задача B) является Н. з.
Численные методы решения некорректных задач.
Для Н. з. вида A) возникает вопрос: что понимается
под приближенным решением таких задач? При этом
необходимо так определить приближенное решение,
чтобы оно было устойчивым к малым изменениям ис-
исходной информации. Второй вопрос: каковы алгоритмы
построения таких решений. Исчерпывающие ответы на
эти основные вопросы впервые даны А. Н. Тихоновым
(см. [1], [2]).
Метод подбора. В нек-рых случаях прибли-
приближенные решения уравнений A) находятся методом под-
подбора. Он состоит в том, что из класса возможных реше-
решений MaZ подбирают элемент z, для к-рого A z прибли-
приближает правую часть уравнения A) с требуемой точно-
точностью. В качестве искомого приближенного решения бе-
берут элемент z. Возникает вопрос: когда этот метод при-
применим, т. е. когда из неравенства
v
следует, что
Pz(z, 2г) «?e (S),
где е (б)—уО при S—>-0. Это имеет место при условии од"
нозначной разрешимости уравнения A) и при условии»
что множество М — компакт (см. [3]). На основе этих
соображений сформулировано понятие коррект-
корректности но Тихонову, наз. также услов-
условной корректностью (см. [4]). В применении к
уравнению A) задача наз. корректной по Ти-
Тихонову, если известно, что для точного значения
правой части и—ит существует единственное решение
zr уравнения A), принадлежащее заданному компакту
М. В этом случае А~г непрерывен на множестве М,
и если вместо элемента ит известен элемент и б такой,
что ри(иь, иг)«:6 и ив ?АМ, то в качестве приближен-
приближенного решения уравнения A) с правой частью и=и(,
можно брать элемент гб^А~ги(,. При S—>-0 zj будет
стремиться к Zj.
Во -многих случаях приближенно известная правая
часть и не принадлежит множеству AM. В этих усло-
условиях уравнение A) не имеет классич. решения. В ка-
качестве приближенного решения берется обобщенное
решение, называемое квазирешенпем (см. [5]). Элемент
z?M, минимизирующий при данном и функционал
Pu(Az, и) на множестве М, наз. к в а з и р е га е н и е м
уравнения A) на М (см. [6]). Если М — компакт, то ква-
знрешенне существует для любого u?V, и если, кроме
того, и?АМ, то квазирепшнне z совпадает с классиче-
классическим (точным) решением уравнения A). Существование
квазнрешенпя гарантируется лишь при условии ком-
компактности множества возможных решений М.
Метод регуляризации. Для ряда при-
прикладных задач, приводящих к уравнению A), харак-
характерна ситуация, когда множество возможных реше-
решений Z не является компактом, оператор А~х ке явля-
является непрерывным на AZ и изменения правой части
уравнения A), связанные с ее приближенным характе-
характером, могут выводить ее за пределы множества AZ. Та-
Такие задачи наз. существенно некоррект-
некорректными задачами. Разработан подход к решению
Н. з., позволяющий строить с помощью ЭВМ прибли-
приближенные решения существенно Н. з. вида A), устойчи-
устойчивые к малым изменениям исходных данных. К исход-
исходным данным задач вида A) относится как правая часть
и, так и оператор А.
В дальнейшем для простоты изложения предполага-
предполагается, как правило, что оператор А известен точно. В
основе подхода лежит понятие регуляризирующего опе-
оператора (см. [2], [7]). Оператор R(u, 6) из U в Z наз.
регулярпзирующим оператором для
уравнения Az=u (в окрестности и=и?), если он об-
обладает свойствами: 1) существует такое бх>0, что опе-
оператор R(u, б) определен для всякого б, 0<S<Si, и
любого u(,?U такого, что Ри(иь, их)<.Ь; 2) для вся-
вся0 б0—бо( )&
(,? , Ри(, х д
кого ?>0 существует б0—бо(е, ит)^.&1 такое, что из
неравенства Рц(и&, U7-)<s:S<6o следует неравенство
Pz(z6, z7xe, где гб=^Д(«6, б).
Иногда удобнее пользоваться другим определением
регулярпзпрующего оператора, в к-ром содержится при-
приведенное определение. Оператор R(u, а) из U в Z,
зависящий от параметра а, наз. регулярпзиру-
регулярпзирующим оператором для уравнения Az—u (в
окрестности и=ит), если он обладает свойствами: 1) су-
существует такое число Oj>0, что оператор R{u, а) оп-
определен для всякого а>0 и любого ив ? V, для к-рого
Ри(и&, uT)<C8<&i', 2) существует такая функция от б,
а—а (б), что для любого е>0 найдется число б(е)<:б1
такое, что если ив ? ^ и Ри(иб , ит)<?.д (е), то Pz(z6 > zr) <
<е, где Z5=i?(u6, «.(б)). В этом определении не пред-
предполагается однозначность оператора R (и, а (б)).
Если p(j(u(,, ит)^6, то в качестве приближенного ре-
решения уравнения A) с цриближенно известной правой
частью uq можно брать элемент za= R (ug , а), получен-
полученный с помощью регулярнзпрующего оператора R (и, а),
где а=ос(б) согласовано с погрешностью исходных дан-
данных «6 (см. [1], [2], [7]). Это решение наз. р е г у л я р н-
з о в а н н ы м решением уравнения A). Чис-
Числовой параметр а наз. параметром регул я-
р и з а ц н и. При 6—>-0 регуляризнрованное прибли-
приближенное решение za((,y—R (ив , а (б)) стремится (в метри-
метрике Z) к точному решению zT.
Таким образом, задача нахождения приближенных
решений уравнения A), устойчивых к малым изме-
изменениям правой части, сводится: а) к нахождению регу-
ляризирующего оператора; б) к определению параметра
регуляризации а по дополнительной информации о за-
задаче, напр, по величине погрешности, с к-рой задается
правая часть и.
Построение регуляризирующпх
операторов. Предполагается, что уравнение
Az=uT имеет единственное решение zT. Пусть вместо
уравнения Az—uT решается уравнение Az=u(,, причем
Ри(«б, ит)<с6. Так как рц(Агт, ue)<6, то приближен-
приближенное решение уравнения Лг=«в ищется в классе Ze эле-
элементов z(, таких, что pu(Az, мв)-<б. Множество Z& есть
множество возможных решений. В качестве приближен-
приближенного решения нельзя брать произвольный элемент zg
из Ze , т. к. такое «решение» не единственно и оно не
будет, вообще говоря, непрерывным по б. В качестве
принципа отбора возможных решений, обеспечивающе-
обеспечивающего получение такого элемента (или элементов) из Zg,
к-рый непрерывно зависел бы от б и при б—>-0 стремил-
стремился бы к zT, используется т. н. в а р и а ц и о н н ы й
принцип (см. [1]). Пусть Q [z] — непрерывный неот-
неотрицательный функционал, определенный на всюду
плотном на Z подмножестве Fx множества Z и такой,
что: a) zj-g/1,; б) для всякого d>0 множество элемен-
элементов z из Flt для к-рых Q [z]<d, является компактным
на F. Функционалы Q [z], обладающие такими св-вами,
наз. стабилизирующими функционал а-
м и для задачи A). Пусть Q [z] — стабилизирующий
функционал, определенный на подмножестве F1 мно-
множества Z (F± может совпадать с Z). Среди элементов
множества Fit 6= ^i П ^6 ищется такой (такие), к-рый
минимизирует функционал Q [z] на Fi, §. Доказывается
существование такого элемента ze (см. [7]). Его можно
рассматривать как результат применения нек-рого
оператора R1{ii(), б) к правой части уравнения A z=u§ ,
то есть ze =i?! (ив . о). Оператор Л, (и, б) является регу-
ляризирующим для уравнения A). Фактич. отыскание
элемента ze можно осуществлять следующим образом:
при незначительных дополнительных ограничениях
на Q [z] (при условии квазимонотошюсти У [z], см. [7])
доказывается, что inf Q [z] достигается на элементах ze,
для к-рых P(j{Aze, и&) = 6. Элемент zg является решением
задачи на минимум функционала Q[z] при условии
(>(/(Лг, мб) = 6, т. е. решением задачи на условный
экстремум, к-рую можно решать методом неопределен-
неопределенных множителей Лагранжа и сводящейся к миними-
минимизации функционала
M*[z, u6]--=p*(Az, u6) + ai2[z].
При любом а>0 доказывается существование элемента
za, минимизирующего Ma[z, иё\. Параметр а определя-
определяется из условия pu(Aza, U5)=8. Если существует та-
такое а, что pu(Aza, u(,)—b, то исходная вариационная
задача эквивалентна задаче минимизации функцио-
функционала Afa[z, ив], к-рая может быть решена различными
способами на ЭВМ (напр., путем решения соответству-
соответствующего уравнения Эйлера для Ma[z, иь\). Элемент za>
минимизирующий функционал Afa[z, ив], можно рас-
рассматривать как результат применения к правой части
уравнения Лг = мв нек-рого оператора i?2(, a), завися-
зависящего от параметра а, т. е. га=Я2(иб, &), в к-ром а оп-
определяется но невязке из соотношения р^(Дга, ий)=6\
Оператор Я2[», а] является регуляризирующнм опе-
оператором для уравнения A). Эквивалентность исходной
вариационной задачи на нахождение минимума функци-
функционала Ma[z, ив] имеет место, напр., для линейных
операторов А. Для нелинейных операторов А это может
быть и не так (см. [8]).
Функционал Af«[z, и$], наз. сглаживающим
функционалом, можно ввести в рассмотрение
формально, не связывая его с задачей на условный эк-
экстремум функционала Q [z], и искать элемент za, ми-
минимизирующий его на множестве f\y g- При этом возни-
возникает задача нахождения параметра регуляризации a
как такой функции от §, a=aF), для к-рой оператор
Я2(и, аF)), определяющий элемент za—-i?2(«6, а(^)),
был бы регуляризирующим для уравнения A). При
определенных условиях (напр., если известно, что
(>и(ив, ит)^8 и А — линейный оператор) такая функ-
функция существует и может быть найдена из соотношения
pu(Az0L, ыв)=б. Возможны и другие способы нахожде-
нахождения а F).
Пусть Tg — класс неотрицательных неубывающих и
непрерывных на отрезке [0, 6j] функций; zT есть реше-
решение уравнения A) с правой частью и=ит и А — не-
непрерывный оператор из Z в U. Тогда, каковы бы ии
были положительное число е>0 и функции ВгF), В2F)
из класса Уб такие, что В2@)=0 и 62/В1(а)<:В2F)>
существует такое 60----б0(е, В1т В2), что для us?U и
6«:60 из неравенства (>„("б, иг)<^ следует неравенство
pz(za, zr)<e, где га=Д2(иб, а), для всех а, удовлет-
удовлетворяющих неравенствам 62/В1(б)<:а<:В2(б).
Способы нахождения параметра регуляризации оп-
определяются характером имеющейся дополнительной
информации о задаче. Если известна погрешность пра-
правой части уравнения и§, т. е. ри(и&, ит)^.б, то согласно
предыдущему естественно определять а по невязке, т. е.
из соотношения py(Az^, и^)^=(р(гх)=Ь.
Функция ф (а) является монотонной и полунепре-
полунепрерывной справа и слева при каждом а>0. Если опе-
оператор А линейный, Z — гильбертово пространство и
Q [z] — строго выпуклый функционал (напр., квадра-
квадратичный), то элемент za единственный и ф(а) однозначная
функция. В этих условиях для всякого положитель-
положительного числа 6<P[j(Aza, ue), где zo? {z; Q [z] = inf Q [(/]},
ye Ft
существует aF) такое, что Pu(AzaF), "б) = б (см. [7]).
Для нелинейного оператора А уравнение ф(а) = б
может не иметь решения (см. [8]).
Метод регуляризации тесно связан с построением
сплайнов. Так, напр., задача нахождения функции z(x)
с кусочно непрерывной на [а, Ь] производной 2-го по-
порядка, минимизирующей функционал Q [z]= \ (z"J dx и
J а
принимающей заданные значения {z,} на сетке {х[}, эк-
эквивалентна построению сплайна 2-го порядка.
Регуляризирующий оператор можно строить с помо-
помощью интеграла по спектральной мере оператора (см. [7],
[9]), для уравнений типа свертки — с помощью клас-
сич. интегральных преобразований (см. [10], [7]), ме-
методом квазиобращений (см. [И]), с помощью метода
итераций (см. [12]). Указаны (см. [13]) необходимые и
достаточные условия существования регуляризирующе-
го оператора.
Пусть приближенно задана не только правая часть
уравнения A), но и оператор А, таким образом вместо
точных исходных данных (А, ит) имеются D/j, ий), где
р.. (-4.2, Az)
h = sup " ' " L <
5 1/2
В этих условиях процедура получения приближенного
решения будет той же, только вместо функционала
Ma[z, ug] надо рассматривать функционал
M*[z, и6, Ah] = pl (Abz, u6)+aQ[z],
а параметр а определять, напр., из соотношения (см. [7]):
Если уравнение A) имеет бесконечное множество
решений, то вводится понятие нормального pe-
pern е н и я. Пусть пространство Z нормировано, тогда в
качестве такового можно брать, напр., решение z,
норма уклонения к-рого от заданного элемента zo?Z
минимальна, т. е.
Приближение к нормальному решению, устойчивое к
малым изменениям исходных данных уравнения A),
находится описанным выше методом регуляризации.
К числу таких задач с бесконечным числом решений
относятся вырожденные системы линейных алгебраич.
уравнений. Так наз. плохо обусловленные системы
линейных алгебраич. уравнений можно рассматривать
как системы, полученные из вырожденных путем за-
замены оператора А его приближением А/,. В качестве
нормального решения совместной вырожденной систе-
системы можно брать решение системы z с минимальной нор-
нормой ||z||. В сглаживающем функционале в качестве
Q [z] можно брать функционал Q [z]=||z||2. Приближен-
Приближенные решения плохо обусловленных систем также на-
находятся методом регуляризации с Q [z]=||z2|] (см. [7]).
Аналогично решается задача нахождения решения
интегрального уравнения Фредгольма 2-го рода на
спектре, т. е. в случае, когда параметр к уравнения
равен одному из собственных значений ядра.
Неустойчивые задачи минимиза-
минимизации функционалов. Ряд практически важных
задач приводится к задачам лшнимизации функционалов
/[z]. Различается два типа таких задач. К первому от-
относятся те из них, в к-рых надо находить минимальное
(или максимальное) значение функционала. К этому
типу относятся многие задачи проектирования опти-
оптимальных систем, конструкций. Для этих задач несуще-
несущественно, на каких элементах достигается искомый ми-
нимум. Поэтому в качестве приближенных решений
таких задач можно брать значения функционала /[z]
на любой минимизирующей последовательности {zn}.
Ко второму типу относятся задачи, в к-рых надо най-
найти элементы z, на к-рых достигается минимум функцио-
функционала / [z]. Их называют задачами минимиза-
минимизации по аргументу. Среди них встречаются
такие, в к-рых минимизирующие последовательности
могут быть несходящимися. В этих задачах нельзя
брать в качестве приближенных решений элементы ми-
минимизирующих последовательностей. Такие задачи наз.
неустойчивыми, или некорректно по-
поставленными. К ним относятся, напр., задачи
оптимального управления, в к-рых оптимизируемый
(целевой) функционал зависит только от фазовых пере-
переменных.
Пусть на метрпч. пространстве Z задан непрерывный
функционал /[z] и существует элемент zo?Z, миними-
минимизирующий /[г]. Минимизирующую последовательность
{zn} функционала /[z] наз. регуляризован-
н о й, если существует компактное в Z множество Z,
содержащее {zn}. Если задача минимизации функцио-
функционала / [z] имеет единственное решение z0, то регуляри-
зованная минимизирующая последовательность схо-
сходится к z0, и в этих условиях для решения неустойчивой
задачи минимизации функционала достаточно указать
алгоритмы построения регуляризованных минимизи-
минимизирующих последовательностей. Это можно сделать путем
использования стабилизирующих функционалов Q [z].
Пусть Q [z] — стабилизирующий функционал, опре-
определенный на множестве F1aZ; inf / [z]=f (z0] и zo? F-y.
zeZ
Часто вместо / [z] имеется его 6-приближение /e[z] no
отношению к Q [z], т. е. такой функционал, что для
всякого г?/\:
При любом а>0 задача минимизации функционала
M*[z, /6] = /6[z] + aQ[z]
по аргументу устойчива.
Пусть {6„} и {а„} — сходящиеся к нулю последо-
последовательности такие, что б„/а„<д<1 для всякого п и
{zan 5} — последовательность элементов, минимизи-
минимизирующих функционалы Ma"[z, /б ]. Эта последователь-
последовательность является регуляризованной минимизирующей
последовательностью для функционала /°[z] (см. [7])
и, следовательно, сходится к элементу z0 при гс—>-оо.
В качестве приближенных решений задачи можно брать
элементы г„ л .
Аналогично строятся приближенные решения Н. з.
оптимального управления.
В прикладных Н. з. исходные данные часто содержат
случайные погрешности. Для построения приближен-
приближенных- решений таких задач возможен- как детерминиро-
детерминированный, так и вероятностный подходы (см. [7], [15]).
Лит.: [1] Т и х о н о в А. Н., «Докл. АН СССР», 1963,
т. 151, № 3, с. 501—04; [2] е г о ж е, там те, т. 153,.№ I.e. 49—
52; [3] е г о же, там же, 1943, т. 39, М 5, с. 195—98; [44 Л а в-
рентьев М. М., О некоторых некорректных задачах матема-
математической физики, Новосиб., 1962; [51 Иванов В. К., «Ма-
тем. сб.», 1963, т. 61, М» 2, с. 211—23; [6] е г о ж е, «Докл. АН
СССР», 1962, т. 145, JV» 2, с. 270—72; R] Тихонов А, Н„
Арсенин В. Я., Методы решения некорректных задач,
2 изд., М., 1979; [8] Гончарский А. В., Л е о н о в А. С,
Я г о л а А. Г., «Докл. АН СССР», 1974, т. 214, № 3, с. 499—
500; [9] Б а к у ш и н с к и й А. В., «Ж. вычисл. матем. и матем.
физики», 1967, т. 7, № 3, с. 672—77; [10] Арсенин В. Я.,
«Тр. Матем. ин-та АН СССР», 1973, т. 133, с. 33—51; [11] Л а т-
т е с Р., Лионе Ж.-Л., Метод квазиобращения и его прило-
приложения, пер. с франц., М., 1970; [12] К р я н е в А. В., «Докл.
АН СССР», 1973, т. 210, J\ft 1, с. 20—22; [13] В и н о к у-
р о в В. А., «Ж. вычислит, матем. и матем. физ.», 1971, т. 11,
№ 5, с. 1097—112; [14] Тихонов А. Н., там же, 1966, т. 6,
№ 4, с. 631—34; [15] Лаврентьев М. М., Василь-
Васильев В. Г., «Сиб. матем. ж.», 1966; т. 7, № 3, с. 559—76.
В. Я. Арсенин, А. Н. Тихонов.
НЕКОРРЕКТНЫЕ ЗАДАЧИ теории функ-
функций комплексного переменного —
первоначально (Н. з. п о А д а м а р у) задачи для диф-
дифференциальных уравнений с характером неустойчи-
неустойчивости, аналогичным неустойчивости задачи Коши для
уравнения Лапласа. Для задач этого типа строится
пример Ада мара — вариации данных, сколь
угодно малые вместе с любым конечным числом своих
производных, к-рым соответствуют конечные вариации
решений (см. [21, [51). Ныне термин «Н. з.» понимается
значительно шире (см. [1], [6]).
Задачи аналитич. продолжения теории функций
комплексного переменного (одного) являются Н. з.
но Адамару. Такую задачу для функций одного комп-
комплексного переменного в общем виде можно сформули-
сформулировать следующим образом. Задана область D комп-
комплексной плоскости и заданы два множества А, В, при-
принадлежащие замыканию D : AaBaD. На множестве А
задана аналитич. функцияДг), регулярная в области D.
Требуется определить функцию f(z) на множестве В.
Относительно функции /(z), кроме регулярности в D,
может быть задана дополнительная информация, напр.
|/(z) |< С, z?D, (*)
где С — заданная константа.
Классич. задачами аналитич. продолжения явля-
являются следующие: 1) А — подобласть области D; 2)
А — часть границы Г области D; предполагается, что
Г — непрерывно (кусочно) дифференцируемая замкну-
замкнутая кривая, Г=Г1(_|Г2, А—Гг; 3) А —множество,
имеющее предельную точку внутри D.
Теоремы единственности отмеченных задач были
доказаны в 19 в. (они приводятся в учебниках по теории
функций комплексного переменного). Задача 2 экви-
эквивалентна задаче Коши для уравнения Лапласа.
Оценки условной устойчивости задач аналитич.
продолжения типа 1), 2) наз. теоремами о трех
константах (оценка изменения решения задачи че-
через изменение данных при условии типа (*)). Задачи ана-
аналитич. продолжения являются линейными, и к ним при-
применимы универсальные методы регуляризации линейных
Н. з. (см. [3], [6]). Для задачи 2) разработаны спе-
специальные методы регуляризации, основанные на по-
построении функций Карлемана (см. [3]).
Задачи аналитич. продолжения связаны с широким
кругом прикладных проблем. Часто из физич. зако-
законов следует, что различные физич. поля являются
аналитич. функциями по нек-рым переменным. Требу-
Требуется по значениям поля на нек-ром множестве (на к-ром
производятся измерения) определить поле на более
широком множестве. Нек-рые из этих прикладных
задач следующие.
1. Задача определения гравитационного и магнит-
магнитного поля над поверхностью Земли по значениям поля
на поверхности. Эта задача используется при разведке
месторождений полезных ископаемых.
2. Задача определения потенциала течения идеаль-
идеальной жидкости, фильтрации постоянного электрпч. тока
внутри нек-рого тела по значениям потенциала и потока
на части поверхности (см. [4]).
3. Задача определения финитной функции по зна-
значениям преобразования Фурье этой функции, извест-
известным на конечном отрезке.
С точки зрения приложений значит, интерес пред-
представляет задача определения аналитич. функции по ее
значениям на конечных множествах. Решение этой зада-
задачи не единственно. Однако если множество в нек-ром
смысле близко к множеству единственности, возможно
приближенное решение с малой погрешностью.
Для функций нескольких комплексных переменных
существуют как корректные, так и некорректные за-
дачи аналнтпч. продолжения. Для задач аналитич.
продолжения с множеств внутри области регулярности
известен следующий общий результат: для того чтобы
множество было множеством единственности, необхо-
необходимо и достаточно, чтобы это множество не являлось
объединением конечного числа аналитич. многообразий.
Лит.: [1] Иванов В. К., Васин В. В., Тана-
на В. П., Теория линейных некорректных задач и ее приложе-
приложения, М., 1978; [2] К у р а н т Р., Уравнения с частными произ-
производными, пер. с англ., М., 1964; [3] Лаврентьев М. М. О
некоторых некорректных задачах математической физики, Но-
восиб., 1962; L4] Лаврентьев М. А., Ш а б а т Б. В.
Методы теории функций комплексного переменного, 2 изд., М.
1958; [5] С о б о л е в с. Л., Уравнения математической физики
h изд., М., 1966; [6] Тихонов А. Н., А р с е н и н В. Я.
Методы решения некорректных задач, М., 1974; [7] Фукс Б. А.
Теория аналитических функций многих комплексных перемен-
переменных, 2 изд., ч. 1, М., 1962. М. М. Лаврентьев.
НЕКРАСОВА ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ — не-
нелинейное интегральное уравнение вида
, у, ф(у))]К(х, y)dy, (*)
где Я, К — известные функции, причем К — сим-
симметричная функция, ф — искомая функция, X — чис-
числовой параметр. Интегральные уравнения такого типа
были получены А. И. Некрасовым (см. [1]) при решении
задач, возникающих в теории волн на поверхности
жидкости. А. И. Некрасов в определенных условиях
строит решение уравнения (*) в виде ряда по степеням
малого параметра, сходимость к-poro доказывается
методом мажорант.
Иногда уравнения типа (*) наз. Гаммерштейна
уравнением, хотя А. И. Некрасов [2] свои исследования
опубликовал раньше А. Гаммерштейна [3].
Лит.: [1] Некрасов А. И., Собр. соч., Т. 1, М., 1961;
[2] е г о же, «Изв. Иваново-Возн. политехи, ин-та», 1922, № 6,
с. 155—71; [31 Hammerstein A., «Acta math.», 1930
Bd 54, S. 117—76. Б. В. Хведелидзе.
НЕЛИНЕЙНАЯ КРАЕВАЯ ЗАДАЧА — определе-
определение в нек-рой области D переменных х= (,гх, . . ., хп)
решения и (х) дифференциального уравнения
(Lu)(x)=f(x), x?D,
по заданным краевым условиям на границе S этой об-
области (или ее части)
где, по крайней мере, один из операторов L или В
является нелинейным.
См. также Краевая задача. а. п. Солватов.
НЕЛИНЕЙНАЯ КРАЕВАЯ ЗАДАЧА; числен-
численные методы решения — методы, заменяю-
заменяющие решение краевой задачи решением дискретной
задачи (см. Линейная краевая задача; численные ме-
методы решения и Нелинейное уравнение; численные
методы решения). Во многих случаях, особенно при
рассмотрении краевых задач для систем обыкновенных
дифференциальных уравнений, описание численных
методов обычно проводится без указания дискретиза-
дискретизации исходной задачи, но такая дискретизация неявно
все же подразумевается и осуществляется по относи-
относительно известным образцам.
Пусть, напр., рассматривается двухточечная краевая
задача для системы обыкновенных дифференциальных
уравнений
y' = f(x, у) при 0 < х < X, A)
Я B/@)) = 0, D(y(X)) = 0, B)
где
»=(и. •••, т)Т, i = (h fl)T,B=(B1,..., д,_г)г,
D =(?>ъ ..., Dr)T, 0<r<i.
Пусть вектор G(y)s^(G1(y), . . ., Gr(y)) таков, что
система уравнений
В(у) = 0, G{y) = g C)
однозначно определяет вектор y = a(g) при каждом
векторе g=(gi, • . ., gr)T', напр., часто целесообразно
взять
Gi(y) = yi-r + i, • ••, Gr(y)^syl.
Тогда задача {1), B) может быть сведена к системе
(операторному уравнению)
0, D)
где ty(g)=D(a>(g)), со (g) — значение при х—X ре-
решения уравнения A) при начальном условии г/@) =
= a(g). При этом для получения значений ty(g) не-
необходимо численно решать (см. [1], [2]) соответствую-
соответствующие системы дифференциальных уравнений, что и бу-
будет означать дискретизацию исходной задачи. Для ре-
решения системы D) можно применять различные итера-
итерационные методы решения нелинейных уравнений. Най-
Найдя решение g* уравнения D), можно определить век-
вектор г/* = а(#*) из системы C) и, решая уравнение A)
при начальном условии у(О) = у*, получить решение
задачи A), B). В ряде методов наряду со значениями
функции гр используются и значения ее производной,
отыскиваемые либо путем интегрирования уравнения
(уравнения в вариациях для A)), либо с помощью каких-
либо формул численного дифференцирования. Указан-
Указанный способ редукции краевой задачи к уравнению D),
наз. методом пристрелки, применим к зада-
задачам более общего вида
y'--^f(x, у, g) при 0<х<Х,
у(О) = а(у), D(y(X(g),g)) = 0,
явно содержащим векторный параметр g, в частности
к задачам на собственные значения; здесь функция
a (g) считается заданной. Однако если решения урав-
уравнения E) сильно растут вместе с х, то погрешность
численного интегрирования приводит к большим ошиб-
ошибкам в значениях функции ty(g) и ее производной и в
конечном счете к большой погрешности получаемого
решения.
В методе линеаризации (см., напр., [1], [3]) прибли-
приближения к решению задачи A), B) определяются как ре-
решения последовательности линейных уравнений
y'n+i= А„ (х) (yn + 1 — yn) + f (х, уп) при 0 < х < X F)
с линейными краевыми условиями
0, \
где Ап(х) — квадратная функциональная матрица по-
порядка I, Вп и Dn— числовые матрицы размеров (I—г) X п
и гХ/, п = 0, 1, .... Начальное приближение уп(х)
считается известным. В случае метода Ньютона — Кан-
Канторовича уравнения F), G) приобретают вид
^ , (8)
4?- (уп (А')) (уп + л (X) ~ уп (X))+D (уп (X)) = 0. j
Если f(x,y), B(y), D (у) дважды непрерывно диффе-
дифференцируемы но у, задачи (8), (9) корректны и уо(х) до-
достаточно близко к искомому решению у(х), то
где К>0 — постоянная, ||г/||с=тах \у{х)\ (см. [1]).
о<х<Х
Упомянутые методы обобщаются и на случай более
общих условий вида
А(у(Хв), !/(*!) У(Хт))=0,
где
^D ..., AL)T, 0=Х0 < Х± <...< Хт^Х.
Многие важные теоретические и прикладные задачи
приводят к необходимости решать Н. к. з. (и родствен-
родственные к ним проблемы) для уравнений и систем уравне
ний эллиптич. типа (см., напр., [4J — [8]). Для такого
класса задач основными численными методами являются
проекционные методы (проекцнонно-разностные, ва-
вариационно-разностные, конечных элементов) и раз-
разностные методы (см. [7] — [14]). Их конструкции во
многом аналогичны конструкциям соответствующих .ме-
.методов для линейных краевых задач (см. Лапласа урав-
уравнение; численные методы решения; Пуассона уравнение;
численные методы решения), но получаемые в этих ме-
методах дискретные (сеточные) аналоги краевых задач,
являющиеся системами нелинейных уравнений
LN (mn) -= Tn, A°)
где_ _
uNs=(u1, иг, ..., uN)T и /jv=(/i. /2. •¦•> /iv)r,
часто вызывают дополнительные значительные труд-
трудности как в плане анализа самих систем и близости в
том или ином смысле их решений к решению исходной
задачи, так и в плане затрат вычислительной работы
на формирование самих систем A0) и отыскание их ре-
решений. Специфика нелинейности краевой задачи застав-
заставляет особое внимание уделять выбору банаховых прост-
пространств п их сеточных аналогов, в к-рых и сама зада-
задача и ее конечномерные аппроксимации поддаются ана-
анализу (см., напр., [5] — [12], [15]). Но наиболее подроб-
подробно изучены особенно в алгоритмич. плане лишь числен-
численные методы для классов нелинейных задач, родствен-
родственных в нек-ром смысле линейным задачам (слабонелнней-
ные уравнения, уравнения с ограниченной нелиней-
нелинейностью) и позволяющих обойтись использованием гиль-
гильбертовых пространств п их конечномерных аналогов
(евклидовых пространств).
Пусть Л]у^гН — евклидово пространство вектор-
функций цд'=м со скалярным произведением (г;, у)=
^2Li=,iuivii a 1(Н) — пространство линейных самосо-
самосопряженных положительно определенных операторов,
отображающих Н в Н; наряду с Н будет использо-
использоваться и евклидово пространство Ид, В?1(Н), отли-
отличающееся от Н лишь видом скалярного произведения:
Пусть, далее,
Бели оператор Ljy непрерывен на 5д(г) и таков, что
для любого и с ||м||д ^=г справедливо неравенство
(LNu)-JN, и) 5s 0, (И)
то система A0) имеет по крайней мере одно решение
из Sв(г). Это утверждение (см., напр., [8], [9]) является
одним из следствий класепч. теорем существования ре-
решений у нелинейных операторных уравнений, основан-
основанных на топологич. принципах (см., напр., [14]) и на
монотонности операторов (см., напр., [6], [11], [14]).
В частности, если Ьц непрерывен всюду и
(LN(u),u)^b\\ufB, б > 0, A2)
для любого и, то система A0) всегда имеет решение и
любое ее решение принадлежит SB(r) с r=6~1|| /jvllB-i.
Если же для любых и, v, w справедливы неравенства
(LN(u) — LN(v), и — v) 5s б0 ||и — v ||, б0 > 0, A3)
\(LN{u)~LN(v), w)\<b1iu — v\\B\\w\\B, A4)
означающие сильную монотонность и Липшиц-непре-
Липшиц-непрерывность оператора Л^у, то система A0) и ее единствен-
единственное решение может быть найдено с помощью итераци-
итерационного метода
Аи" + 1= Аи" — у (LN(un) — JN), A5)
где A ?L(H) и итерационный параметр 1>>0 определя-
определяется константами типа 60 и 6%, получаемыми при замене
в A3) и A4) оператора В на А (см., напр., [8], [9]).
Поэтому для разностных методов оценки погрешности
получаются как следствие корректности системы A0)
и наличия аппроксимации исходной краевой задачи
разностной краевой задачей A0). Часто весьма целе-
целесообразен такой выбор оператора В, что пространство
Нв становится дискретным (сеточным) аналогом соот-
соответствующего пространства Соболева (напр., Wa(Q)
для уравнений 2-го порядка) и тем самым делается
возможным использование или самих теорем вложения
(в случае проекционных аппроксимаций), или их се-
сеточных аналогов (см., напр., [5] — [9]) для проверки
неравенств типа A2) — A4). Проекционные методы и,
в частности, проекционно-разностные (вариационно-
разностные) методы обладают тем достоинством, что
неравенства A2) — A4) следуют из соответствующих
неравенств для дифференциальных операторов, а за-
задача оценки погрешности метода легко сводится к зада-
задаче аппроксимации решения исходной задачи элемен-
элементами выбранного конечномерного подпространства (см.
[0] — [91, [11]). Вместо справедливости неравенств
A3), A4) во всем пространстве достаточно их справед-
справедливости, напр., в нек-ром шаре из Нв, окружающед!
искомое решение. Иногда полезны неравенства, полу-
получаемые из A2) — A4) заменой скалярных произведе-
произведений в левых частях на скалярные произведения в //в,
а норм |)г||д в правых частях на \\Bz\\. Для ряда задач
на основе априорных оценок их решения возможна за-
замена их эквивалентными краевыми задачами, для к-рых
неравенства типа A2) — A4) будут выполнены (см.
[15]).
При выполнении неравенств A3), A4) итерацион-
итерационный метод A5) с А=В сходится при любом начальном
приближении, и если константы б0 и бх не зависят от JV,
то он позволяет получить решение системы A0) с точ-
точностью е за О(|1п е|) итераций (обычно еХ7Уа, а<0).
За счет удачной конструкции сеточного метода иногда
удается так выбрать оператор В, что решение системы
A0) с точностью №- при помощи итерационного метода
типа A5) осуществляется при затрате лишь O(N liAV)
или даже O{N In N) арифметпч. действий (см. Миними-
Минимизация вычислительной работы). Использование после-
последовательности сгущающихся сеток позволяет довести
эти оценки до O(N In N) и O(N) действий и тем самым
получить асимптотически оптимальные по трудоемко-
трудоемкости численные методы решения нек-рых нелинейных
эллиптических краевых задач. При этом предполага-
предполагалось, что само вычисление невязки L(un)—/7у требует
не больше KN действий. Все же для нек-рых задач
(при больших /4") целесообразно уменьшить частоту
таких вычислений. Этого можно добиться за счет на-
нахождения более точного начального приближения,
использования той или иной линеаризации L^ и ме-
методов типа продолжения по параметру (см. Нелинейное
уравнение; численные методы решения). Чаще же всего
линеаризации методы в сочетании с методами продол-
жения по параметру попользуются в наиболее трудных
ситуациях, когда, напр., условие A3) может не вы-
выполняться. К нелинейным краевым задачам эллиптич.
типа могут быть отнесены и нек-рые задачи на собствен-
собственные значения (см., напр., [8], [12], [14]); конструкция
соответствующих численных методов во многом анало-
аналогична уже упомянутым.
Нек-рые стационарные краевые задачи могут быть
приближенно заменены краевыми задачами для силь-
сильно эллиптич. систем с малым параметром (см., напр.,
[17]). Численные же методы для нестационарных
Н. к. з., включающих в себя задачи для уравнений и
систем параболич. типа, гнперболпч. типа, смешанного
типа и др., хотя и используют дискретные аналоги
эллиптич. операторов, подобные выше рассмотренным.
но для них наиболее характерно расслоение прибли-
приближенного метода по отдельным временным слоям.
Лит.: [1] Б а х в а л о в Н. С, Численные методы, 2 изд..
М., 1975; [2] Ш а м а н с к и й В. Е., Методы численного реше-
решения краевых задач на ЭЦВМ, ч. 2, К., 1966; 13] Б е л л м а н Р..
К а л а б а Р., Квазилинеаризация и нелинейные краевые зада-
задачи, пер. с англ., М., 1968; [4J Б е р е з о в с к и й А. А., Лек-
Лекции по нелинейным краевым задачам математической физики.
2 изд., ч. 1, К., 1976; 15] Ладыженская О. А., У р а л ь ц <-
в а Н. Н., Линейные и квазилинейные уравнения эллиптиче-
эллиптического типа, М., 1964; Lb] Лионе Ж.-Л., Некоторые методь
?ешения нелинейных краевых задач, пер. с франц., М., 1972
7] Гловински Р., Лионе Ж.-Л., Тремольер Р..
Численное исследование вариационных неравенств, пер. с франц..
М., 1979; 18] Д ь я к о н о в Е. Г., в кн.: Численные методы ме-
механики сплошной среды, т. 7, в. 5, Новосиб., 1976, с. 14—78
[9] его же, в кн.: Разностные методы решения краевых за-
задач, в. I — Стационарные задачи, М., 1971; Г10] К а р ч с и-
с к и й М. М., Л я ш к о А. Д., Разностные схемы дл.-i нели-
нелинейных задач математической физики, ч. 1, Казань, 1976: [11]
Варга Р., Функциональный анализ и теория аппроксимации
в численном анализе, пер. с англ., М., 1974; [12] Стренг Г.,
Фикс Д ж.. Теория метода конечных элементов, пер. с англ.,
М., 1977; [13] О д е н Д ж., Конечные элементы в нелинейной
механике сплошных сред, пер. с англ., М., 1976; [14] Крас-
Красносельский М. А. [и др.]. Приближенное решение опера-
операторных уравнений, М., 1969; [1 5] Р и в к и н д В. Я., У р а л ь-
цева Н. Н., в кн.: Проблемы математического анализа, в. 3,
Л., 1972, с. 69 —111; [16] А м о с о в А. А., Б а х в а л о в Н. С,
О с и п и к Ю. И., «Ж. вычисл. матем. и матем. физики», 198A.
т. 20, .№ 1, с. 104—11; [17] Соболевский П. Е., Васи-
Васильев В. В., в кн.: Численные методы механики сплошной среды.
т. 9, в. 5, Новосиб., 1978, с. 115 — 39.
Е. Г. Дьяконов, А. Ф. Шппкип
НЕЛИНЕЙНАЯ СВЯЗНОСТЬ — дифференциально-
геометрическая структура, задаваемая на категории
гладких расслоенных пространств, ассоциированных
с нек-рым главным G-расслоенпем, к-рая фиксирует
определенный для данной Н. с. изоморфизм слоев
(параллельный перенос) вдоль каждой кусочно глад-
гладкой кривой базы расслоения данной категории, согла-
согласованный с изоморфизмом соответствующих слоев глав-
главного G-расслоения. При этом предполагается, что ука-
указанная структура не тождественна ставшему класси-
классическим понятию линейной связности, к-рое определя-
определяется тем или иным G-пнвариантным горизонтальным рас-
распределением. Иной смысл [5] имеет термин Н. с, состоя-
состоящий в том, что определяемый горизонтальным распреде-
распределением перенос векторных слоев расслоения теряет
линейный характер, т. е. не является изоморфизмом этих
слоев.
Необходимость введения и исследование Н. с. дик-
диктовалась потребностями изучения различных дпфферен-
циально-геометрич. структур высших порядков (таких,
как напр. Кавагути пространства). Основы общей
теории Н. с. достаточно развиты, исследованы и полу-
получили приложения нек-рые специальные типы Н. с.
(см. [2J - [4]).
Пусть я : X (В, G)—>-B гладкое главное G-расслс-
ение со структурной группой Ли G и канонич. проек-
проекцией л на базу В, а К(X) — категория всех ассоцииро-
ассоциированных с X расслоений. Изоморфизмом слоя Gx=
= л~1(х) на слой Gg=n~1(y), x, у?В, наз. отображе-
отображение i : G^-^Gy, коммутирующее с действием группы в
на X. Любой изоморфизм i может быть задан формулой
4log)=i(lo) g, ?o€X, g?G, и, следовательно, является
диффеоморфизмом слоев Gx и Gy. Множество Г(Х) всех
изоморфизмов между всевозможными слоями главного
расслоения X является гладким расслоением со струк-
структурой группоида над базой ВХВ (группоид — катего-
категория с обратимыми элементами). Изоморфизм г?Г(Х)
порождает соответствующий изоморфизм слоев над
точками х, у?В любого ассоциированного расслоения
Y?K(X) и тем самым группоид Т(Х) обслуживает
всю категорию К(Х).
Пусть Л (В) — категория всех кусочно гладких кри-
кривых базового многообразия В. Связностью в
категории К(Х) гладких расслоений в самом об-
общем смысле наз. любой функтор
у : Л (Я)-* Г(Х),
тождественный по базе ВХВ. Пусть aXfi: Г(Х)->
-*-ВхВ — канонич. проекция группоида Г(Х) на свою
базу ВХВ, определяемая тем условием, что если
Г(Х)Э* : Gx->- Gy, то а (г) = х, $(i) = y. Тем самым
многообразие В отождествляется с подмногообразием
ВаГ(Х) всех левых и правых единиц группоида
Г(Х). Пусть П(Х) — векторное расслоение над B^s=B,
образованное слоями вида Те[а-1(е)], е?В, а Тр(В) —
расслоенное над В пространство /^-скоростей многообра-
многообразия В (элементами ТР(В) являются регулярные р-струн
всевозможных гладких отображений R—*-В с источни-
источником o?R). Расслоения П(Х) и Тр (В) обладают ка-
канонич. проекциями на касательное расслоение Т (В)
я':П(Х)—+Т (В), пР;Тр (В)—>¦ Т (В).
Связность у наз. нелинейной связностью
порядка р=1, 2, 3, . . ., если р— наименьшее
число, для к-рого функтор у определяет гладкое ото-
отображение
уР:Тр (В)—>П(Х)
такое, что я' -уР=пР. Функтор у в свою очередь опре-
определяется соответствующим ему отображением уР.
В случае, когда р = \ и отображение Т(В)-^-П(Х) по-
послойно линейное, связность вырождается в линейную
связность на категории К(Х). В изучении свойств
Н. с. п в их классификации фундаментальную роль иг-
играют структурные уравнения отображений уР : Тр (В) —>¦
—»-ЩХ), записанные в форме уравнений Пфаффа,
связывающих дифференциалы относительных коор-
координат геометрич. объектов, описывающих расслое-
расслоения Тр(В) и П(Х). В терминах коэффициентов струк-
структурных уравнений с помощью операций их дифферен-
дифференциального продолжения и охватов установлено [2],
что Н. с. уР в X (В, G) порождает линейную связность
специальной структуры в главном G-расслоении
Х(В, G)@BTP(B) над базой ТР(В), и этой линейной
связностью полностью характеризуется. Найдены фор-
формы указанной линейной связности и их структурные
уравнения. Доказан нелинейный аналог теоремы о
группе голономин, в определении к-рой участвуют не
только кривизна, но и линейная оболочка распределе-
распределения горизонтальных конусов, заменяющих в нелиней-
нелинейном случае подпространства горизонтального распре-
распределения линейной связности.
. Лит.: [1] Вагнер В. В., «Тр. семинара по векторному
и тензорному анализу», 1950, в. 8, с. 11—72; 12J Б в т у-
щ и к Л. Е., «Изв. ВУЗов. Математика», 1969, № 2, с. 32—44;
[3J е г о же, «Сиб. матем. т.», 1973, т. 14, .№3, с. 536—48;
[4] Е в т у ш и к Л. Е., Третьяков В. В., «Тр. геометр,
семинара», 1974, т, 6, с. 243—55; [5] К а w а g у с h i A., «Ten-
«Tensor. New ser.», 1952, v. 2, p. 123 — 42. Л. Е. Евтушик.
НЕЛИНЕЙНОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕ-
УРАВНЕНИЕ — дифференциальное уравнение (обыкновенное
или с частными производными), в к-рое по крайней
мере одна из производных неизвестной функции (вклю-
(включая и производную нулевого порядка — саму неизвест-
ную функцию) входит нелинейно. Этот термин обычно
употребляют, когда хотят специально подчеркнуть,
что рассматриваемое дифференциальное уравнение
Н=0 не является линейным, т. е. его левая часть Н не
представляет собой линейную форму от производных
неизвестной функции с коэффициентами, зависящими
только от независимых переменных.
Иногда под Н. д. у. понимается наиболее общее
уравнение определенного вида. Напр., нелиней-
нелинейным обыкновенным дифференци-
дифференциальным уравнением 1-го порядка
наз. уравнение
с произвольной функцией f(x, у, и); при этом линейное
обыкновенное дифференциальное уравнение 1-го по-
порядка соответствует частному случаю
f(x, у, и) = а(х)и+Ъ(х)у.
Н. д. у. с частными производными 1-го
порядка для неизвестной функции z от п не-
независимых переменных х\, . . ., хп имеет вид
dz dz \_q
где F — произвольная функция своих аргументов;
в случае
г. V" л / ч dz
такое уравнение наз. квазилинейным, ав слу-
случае
т" (-тъ • • •> хп) z-+- ь (xlt . .., хп)
— линейным. н- х- Розов,
НЕЛИНЕЙНОЕ ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ —
интегральное уравнение, содержащее неизвестную функ-
функцию нелинейно. Ниже приведены основные классы
Н. и. у., к-рые часто встречаются при исследовании
различных прикладных задач и теория к-рых в опреде-
определенной постановке достаточно хорошо разработана.
Важным примером Н. и. у. является Урысона урав-
уравнение
т(х) = Х\ К[х, s, ф (s)] ds, x?Q, A)
где Q — замкнутое ограниченное множество конечно-
конечномерного евклидова пространства, К[х, s, t] — заданная
функция, наз. ядром, определенная при х, s, ? Q,
— оо-О< оо, X — числовой параметр, ф — искомая
функция.
П. С. Урысон (см. [2]) при определенных предполо-
предположениях дал полное исследование спектра собственных
значений уравнения A), допускающих положительные
собственные функции. Было показано, что положи-
положительные собственные функции <р(х, X) соответствуют
значениям X только из нек-рого интервала (а, |3),
причем ф (х, X) является монотонно возрастающей функ-
функцией X н (f(x, а) = 0, ф(ж, E)=оо.
Частным случаем уравнения Урысона является
Гаммерштейна уравнение:
где К(х, s), /(s, t) — известные функции. Теоремы су-
существования и единственности впервые были установ-
установлены А. Гаммерштейном (см. [9]). Он исследовал урав-
уравнение B) в предположении, что действительная функ-
функция f(s, t) непрерывна по совокупности аргументов и
что самосопряженный в L2(Q) линейный интегральный
оператор, порожденный ядром К, является положи-
положительным и действует вполне непрерывно из L.2(Q)
в пространство непрерывных функций.
Другим примером II. и. у. является Ляпунова —
Шмидта уравнение:
Xv^°(x)v(il(s1)...vPi (si)ds1...dsi--=O, x?Q, C)
в к-рых функции Ка, р и v — заданные, <р — искомая,
число i фиксировано, и суммирование распростра-
распространено на всевозможные векторы a(a0, a:, . . ., a,),
Р(Ро> Pi, • • ¦> Pi) c неотрицательными целочисленными
компонентами. Левая часть равенства C) наз. и н т е-
гро-степенным рядом от двух функцио-
функциональных аргументов v, <p.
Уравнение типа C) впервые рассмотрел А. М. Ля-
Ляпунов (см. [1]), а позднее, в более общем виде, Э. Шмидт
(см. [8]). В их исследованиях были заложены основы
теории ветвления Н. и. у., целью к-рой является ре-
решение следующей задачи. Пусть ищется решение не-
нелинейной задачи, зависящее от некоторых парамет-
параметров, причем для некоторых их значений решение мо-
может разветвляться. Возникают вопросы о нахожде-
нахождении самого решения и тех значений параметров,
при которых оно разветвляется, о числе ветвей и о пред-
представлении каждой ветви как функции параметров
(см. [6]).
Теория Н. и. у. является частью общей теории не-
нелинейных операторных уравнений. Именно, интеграль-
интегральные уравнения рассматриваются как конкретные иллю-
иллюстрации соответствующих операторных уравнений.
Для этого требуется выяснение общих свойств (непре-
(непрерывность, полная непрерывность и т. д.) конкретных
интегральных операторов, входящих в уравнение
(см. [3] - [7]).
Лит.: [1] Л я п у н о в А. М., «Записки Академии Наук»,
СПБ, 1906, с. 1—225; [2] У р ы с о н П. С, «Матем. сб.», 1923,
т. 31, с. 236—55; [3] В а й н б е р г М. М., Вариационные мето-
методы исследования нелинейных операторов, М., 1956; [4] Крас-
Красносельский М. А., Топологические методы в теории не-
нелинейных интегральных уравнений, М., 1950; f5] Красно-
Красносельский М. А. [и др.]. Интегральные операторы в про-
пространствах суммируемых функций, М., 1966; [6] Вайнберг
М. М., Треногий В. А., Теория ветвления решений нели-
нелинейных уравнений, М., 1969; 17] В а й н б е р г М. М., Вариа-
Вариационный метод и метод монотонных операторов в теории нелиней-
нелинейных уравнений, М., 1972; [8J Schmidt E., «Math. Ann.»
1908, Bd 65, S. 370—99; 19] H a m m e г s t e i n A., «Acta
math.», 1930, v. 54, p. 117 — 76. Б. В. Хведелидзс.
НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ — раздел
математического программирования, посвященный те-
теории и методам решения задач оптимизации нелиней-
нелинейных функций на множествах, задаваемых нелинейными
ограничениями (равенствами и неравенствами).
Основная трудность решения задач Н. п. состоит
в том, что эти задачи являются многоэкстремальными,
и известные численные методы их решения гарантируют
в общем случае сходимость минимизирующих последо-
последовательностей лишь к точкам локальных экстремумов.
Наиболее изученным разделом Н. п. является вы-
пуклое программирование, задачи к-рого характеризу-
характеризуются тем, что любая точка локального минимума яв-
является точкой глобального минимума.
Лит.: [1] 3 а н г в и л л У. И., Нелинейное программиро-
программирование. Единый подход, пер. с англ., М., 1973; [2] Карма-
Карманов В. Г., Математическое программирование, М., 1975; [3]
II о л а к Э., Численные методы оптимияации. Единый подход,
пер. с англ., М., 1974. В. Г. Карманов.
НЕЛИНЕЙНОЕ УРАВНЕНИЕ; численные ме-
методы решения — итерационные методы решения
нелинейных уравнений.
Под нелинейными уравнениями понимаются (см.
[1] — [3]) алгебраические и трансцендентные уравне-
уравнения вида
Ф(*)=0, A)
где х — действительное число, ф (х) — нелинейная функ-
функция, а под системой нелинейных уравнений — система
вида
ф1 (*i, х2, ..., xN) = О,
не являющаяся системой линейных алгебрапч. уравне-
уравнений; решением системы B) является iV-мерный вектор
х~(х!, х2, . . ., x^i). Уравнение A) и система B) мо-
могут трактоваться как нелинейное операторное уравне-
уравнение
L(u)=j C)
с нелинейным оператором L, действующим из вектор-
векторного конечномерного пространства Н^ в Ндг.
Численными методами решения Н. у. C) наз.
итерационные методы, определяемые переходом от
уже известного приближения ип на гс-й итерации
к новому приближению ип + 1 и позволяющие при до-
достаточно большом числе итераций найти решение урав-
уравнения C) с нужной точностью 8. Важнейшие итераци-
итерационные методы приближенного решения уравнения C)
как относительно общего вида, так и специального вида,
характерного для дискретных (сеточных) методов ре-
решения краевых задач для уравнений и систем уравне-
уравнений с частными производными сильно эллиптич. типа,
п являются предметом рассмотрения настоящей статьи.
Нелинейные операторные уравнения, связанные с рас-
рассмотрением бесконечномерных пространств (см., напр.,
[4] — 18]), являются весьма широким математич. по-
понятием, содержащим в себе как частные случаи, напр.,
нелинейные интегральные уравнения и нелинейные
краевые задачи. Численные методы нх приближенного
решения включают в себя также методы их аппрокси-
аппроксимации конечномерными уравнениями; эти методы рас-
рассматриваются отдельно.
Одним из важнейших методов решения уравнения
C) является метод простой итерации,
предполагающий возможность замены уравнения C)
эквивалентной системой
и=Р(и), D)
где u=(ult и2, . . ., ujy) — элемент конечномерного нор-
нормированного пространства Ядг, а оператор Р, отобра-
отображающий Ну в Hjy, является оператором сжатия:
39<1, Vu, v\\P(u) — P(v)\Kq\\u — v\\. E)
Тогда в силу общего принципа сжатых отображений
(см. [1] — [4]) уравнение A) имеет единственное реше-
решение, итерационный метод простой итерации
и« + 1=Р(И«), ге = 0, 1, ..., F)
сходится при любом начальном приближении и0, и
для погрешности z"Ha ге-й итерации справедлива оценка
||z»||«Cg»(l — д)-1||ц« — И1||.
Пусть нек-рое решение и системы C) удается окружить
шаром S(и, Д)езе{р; \\v—и||«:Л}, и система C), рассма-
рассматриваемая вместе с дополнительным условием
u?S(u, R), G)
эквивалентна системе D), рассматриваемой вместе с
условием G), причем неравенство E) справедливо для
и=и и любого y=u+z c||z||<:i?. Тогда при выборе на-
начального приближения и0 из S {и, R) в методе F) тоже
гарантируется сходимость ип к и с оценкой погрешности
Для дважды непрерывно дифференцируемых функ-
функций ср,- при наличии хорошего начального приближения
к решению системы B) часто эффективным методом
повышения точности является метод Ньютон а—
Канторовича. В этом методе уравнение ф,(х],
х2, . . . , xjv) = 0 из B), определяющее нек-рую поверх-
поверхность />,¦, заменяется уравнением касательной плоскости
к ]';, проводимой через точку хп, где хп— ранее полу-
полученное приближение к решению B) (см. [1] — [5]). При
нек-рых дополнительных условиях метод Ньютона —
Канторовича приводит к оценке погрешности типа
где с± и с — нек-рые константы. На каждой итерации
этого метода необходимо решать систему линейных
алгебрапч. уравнений с матрицей А 1"> при неизвестных
-"-.,,
х=х"
Иногда эту матрицу сохраняют на нескольких итера-
итерациях, иногда производные <9(p,7ctey заменяют разност-
разностными аппроксимациями.
Метод Ньютона — Канторовича относится к группе
методов линеаризации C). Другим методом из этой
группы является метод секущих (см. [3]).
Большое число итерационных методов (так наз.
методов с п у с к а) (см. [1] — [3], [9], [10]) ос-
основано на замене задачи решения уравнения C) зада-
задачей минимизации нек-рого функционала 1(и). Напр.,
в качестве /(») можно взять
I(u)=e\\L{u)-ff. (8)
В ряде случаев, когда исходные Н. у. сами являлись
уравнениями Эйлера для задачи минимизации нек-рого
функционала 1(и), такая вариационная формулировка
задачи является еще более естественной; операторы L
в подобных ситуациях являются градиентами функцио-
функционалов I (и) и наз. потенциальными опера-
операторами (см. [5], [6]). Среди различных вариантов
методов спуска можно назвать метод покоординатного
спуска, различные градиентные методы и, в частности,
метод наискорейшего спуска, метод сопряженных гра-
градиентов и др., а также и их модификации (см. [21, [9],
flO] » др.). Ряд итерационных методов для решения
уравнений C), описывающих нек-рое стационарное со-
состояние, можно трактовать как дискретизации соответ-
соответствующих нестационарных задач. Поэтому методы из
этого класса называют установления методами (см.,
напр., [2]). Примером таких нестационарных задач яв-
являются задачи, описываемые системой обыкновенных
дифференциальных уравнений:
A+ А
Введение дополнительной независимой переменной ха-
характерно и для метода дифференцирова-
дифференцирования по параметру (см. [51, [11]). Его суть
состоит во введении вспомогательного параметра
^€№> 1]> выборе непрерывно дифференцируемых функ-
функций Fj(x, Я) и замене системы B) на систему
F((x, X)=0, i=--i, 2, ..., N, 0<Х<1, (9)
при >,= 0 система (9) должна легко решаться, а функции
F{(r, 1) должны совпадать с ср,(х), г = 1, 2, . . ., N.
Система (9), вообще говоря, определяет
х (к) = (*!(%), х2(к), ..., .rN(X))
как функцию от к, и искомое решение системы B) со-
совпадает с хA). Если систему (9) продифференцировать
по }., то получится система обыкновенных дифференци-
дифференциальных уравнений
дг dF. dx. dF{
-df +
= 0' *=1, 2, ...,ЛГ. A0)
Если на отрезке 0<:^«:1 решить для нее задачу Коти
с начальным условием, являющимся решением системы
1<\(х, 0) = 0, i^i, 2, ..., N,
то будет найдено и нек-рое решение системы B). Ди-
Дискретизация A0) но X и приводит к численному методу
для решения системы B).
Вметоде продолжения по парамет-
р у система (9) решается при К=х, 2т, . . ., тгет, тт=1,
причем при каждом указанном значении X применяется
нек-рый итерационный метод с начальным приближе-
приближением, совпадающим с приближенно полученным реше-
решением системы при предыдущем значении X. Оба назван-
названных метода по сути дела являются итерационными ме-
методами решения системы B) со специальной процедурой
нахождения хорошего начального приближения.
Для случая систем большую трудность представляет
задача локализации решения. Так как большинство
итерационных методов сходится лишь при наличии
достаточно хорошего приближения к решению, описан-
описанные выше два метода часто позволяют избавиться от
необходимости непосредственной локализации решения.
Для локализации также часто используются теоремы,
основанные на топология, принципах и монотонности
операторов (см. [4] — [8]).
Для решения уравнений A), являющихся простейши-
простейшими частными случаями C), число известных и применя-
применяемых на практике итерационных методов очень велико
(см., напр., [1] — [3], 112]). Помимо уже рассмотренных
можно указать, напр., итерационные мето-
методы высших порядков (см. [1]), включаю-
включающие в себя метод Ньютона как частный случай, н боль-
большое число итерационных методов, специально ориенти-
ориентированных на нахождение действительных или комплек-
комплексных корней многочленов
рп (z) ^ а^» + ап_12»-1+ ... +«о,
где а,-— действительные или комплексные числа (см.
[1], [12]).
Проблема локализации решения уравнения A) сво-
сводится к отысканию интервала, на концах к-рого не-
непрерывная функция ср принимает значения разных зна-
знаков. Для случая, когда ф является многочленом, она
теряет свою остроту, т. к. известны теоретич. оценки
(см. [1]) и имеются методы нахождения всех корней с
нужной точностью без задания хороших приближений
к ним (см. [12]).
Итерационные методы для решения уравнений C),
возникающих в сеточных аналогах нелинейных крае-
краевых задач для уравнений с частными производными,
являются частными случаями методов решения сеточ-
сеточных систем (см., напр., [3], [13] — [181). Одним из на-
наиболее интенсивно применяемых методов решения урав-
уравнения C), вероятно, является модифицированный метод
простой итерации, записываемый в виде
Bu" + 1 = Bun — y(L(un) — f), A1)
где уравнение C) рассматривается как операторное
уравнение в TV-мерном евклидовом пространстве Hjv=Il;
B?S, где S — обозначение множества линейных сим-
симметричных и положительных операторов, отображаю-
отображающих Н в Н. Целесообразно изучение таких методов
проводить не в пространстве Я, а в пространстве Нв с
новым скалярным произведением:
(". ")но^(в«, v)> II" II =(Я". и),
а
где (w, v) — скалярное произведение в //.
Если оператор L таков, что для него выполнены ус-
условия строгой монотонности и Липшиц-непрерывности
\/и, v (L(u)— L{v), и — г>)гзбо||и — vfB, б„ > 0, A2)
V«, v \\L(u)-L(v)fB-,<ibz\\u-vfB, A3)
то уравнение C) имеет единственное решение, метод
A1) при подходящем выборе у сходится при любом и"
с оценкой погрешности:
\\z"l\B<qn\\zo\\B, A4)
где q=qF0, б2, у) < 1 (см. [13], [15]).
В более общем варианте этой теоремы достаточно
требовать выполнения A2), A3) для решения и и всех
г, принадлежащих шару SB(u, R)s^{v; \\v—u\\B<s?R),
и принадлежности u° этому шару (см. [13]). В этом слу-
случае и константы 60, 62 могут зависеть от П. Для про-
проверки таких условий достаточно, напр., с помощью ап-
априорных оценок локализовать и, получая ||и|!в</?0>
а затем, если A2) и A3) выполнены для любых и и v из
SB@, RJ, «!>/?„, взять SB(u, R)^SB{u, i?,-i?0).
В A4) константу q можно уменьшить, если оператор L
дифференцируем и для его производной Lv, представ-
представленной в виде суммы симметрия, части Lv, с и кососим-
метрич. части L'v a известны неравенства
yv?SB(u,R) аой<^ц, c<OiB, о0 > 0;
Vw\\L'v, аш|в-><а2И";1]в-
Тогда q=q(y, a0, a2, a2) (см. [11], [13], [15]). Иногда
при рассмотрении некоторых типов нелинейностей вме-
вместо A2) и A3) целесообразно использовать неравенства
типа
(L(u)—L(v), В (и — и)) S* б || Я (и — v)f, 6\, > 0;
\\L (u)-L (v)f<i6'2\\B(u-v)f
(см. [13]). В качестве операторов В в A1) используются,
напр., расщепляющиеся разностные операторы (.метод
переменных направлений) и факторизуемые разностные
операторы (попеременно-треугольный метод, метод не-
неполной матричной факторизации) и др. Наиболее при-
привлекательно с асимптотич. точки зрения использование
операторов В таких, что константы б/ или б,- не зависят
от размерности пространства Нм (см. [13]), а сами опе-
операторы В достаточно просты. На этом пути удалось в
ряде случаев строить итерационные методы, позволя-
позволяющие находить решение уравнения C) с точностью е
при затрате всего O(N In JV|ln el) (или даже O(N In JV))
арифметнч. действий при eXJV-a, a>0 (см. [13], [14]),
если затраты вычислительной работы на вычисление
L(u") при заданном и" можно оценить как O(N). При
проверке указанных условий типа A2), A3) во многих
случаях большую помощь оказывают сеточные (раз-
(разностные) аналоги теорем вложения С. Л. Соболева
(см. [19]). Важно учитывать и специфику нелинейности.
Так, напр., для случая, когда L (и) = Ли-\-Ри, где Л —
линейный положительный оператор, а Р — квадрати-
чески нелинейный, обладающий свойством «кососнм-
метрии» (уи(Р(и),и) = 0), удается часто получить кон-
константу 62(Й) в любом шаре SB@, R), а б0— зависящую
только от ||и||д; тогда сходимость A1) имеет место для
любого и0 (см. [20]). В ряде случаев на основе априор-
априорных оценок можно заменить исходную задачу ей эк-
эквивалентной, для к-рой нужные условия уже выполня-
выполняются во всем пространстве (см. [21]).
Лит.: [1] Б е р е з и н И. С, Жидков Н. П., Ме-
Методы вычислений, 3 изд., т. 1, М., 1966; [2J Бахвалов Н. С,
Численные методы, 2 изд., М., 1975; [3] О рте г а Д ж.,
Рейнболдт В., Итерационные методы решения нелиней-
нелинейных систем уравнений со многими неизвестными, пер. с англ.,
М., 1975; [4] Красносельский М. А. [и д рЛ. При-
Приближенное решение операторных сравнений, М., 1969; [5]
М и х л-и н П. Г., Численная реализация вариационных ме-
методов, М., 1966; [6] Вайнберг М. М., Вариационный ис-
истод и метод монотонных операторов, М., 1972; [71 Гас в-
с к и й X., Г р ё г с р К., 3 а х а р и а с К., Нелинейные
операторные уравнения и операторные дифференциальные
уравнения, пер. с нем., М., 1978; 18] Лионе Ж,- Л., Неко-
Некоторые методы решения нелинейных краевых задач, пер. с франц.,
М., 1972; [9] Васильев Ф. П. Лекции по методам реше-
решения экстремальных задач, М., 1974; [10] Пшеничный Б. Н.,
Данилин Ю. М-, Численные методы в экстремальных
задачах, М., 1975; [11] Яковлев М. Н., «Тр. Матем. ин-та
АН СССР», 1965, т. 84, с. 8 — 40; [12] Воеводин В. В.,
Численные методы алгебры. Теория и алгорифмы, М., 1966;
[13] Дьяконов Е. Г., в кн.; Численные методы меха-
механики сплошной среды, т. 7, № 5, Новосиб., 1976, с. 14—78;
?14] его же, в кн.: Вариационно-разностные методы в мате-
математической физике. Материалы Всесоюзной конференции, Но-
яосиб., 1978, с. 149—64; [15] Самарский А. А., Нико-
Николаев Е. С. Методы решения сеточных уравнений, М.,
1978; [16] Гловински Р., Лионе Ж.-Л, Т р е-
м о л ь е р Р., Численное исследование вариационных нера-
неравенств, пер. с франц., М., 1979; [17] Келлер Г., в кн.:
Газностные и вариационно-разностные методы, НовосиО., 1977,
с. 8—36; [18] Кобельков Г. М., «Докл. АН СССР»,
1978, т. 243, Mi 4, с. 843—46; [19] Дьяконов Е. Г., в
кн.: Применение функциональных методов к краевым задачам
математической физики, Новосиб., 1972, с. 55—62; [201 его
ж е, «Acta Univ. Carolinae. Math, et Phys.», 1974, v. 15, A» 1—2,
p. 11 — 15; [21] P и в к и н д В. Я., У р а л ь ц е в а Н. Н.,
в кн.: Проблемы математического анализа, в. 3, Л., 1972, с. 69—
111. Е. Г. Дьяконов.
НЕЛИНЕЙНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРО-
ПРОИЗВОДНЫМИ — уравнение вида
F (х, и, ..., ?><*г/) = О, A)
где x=(Xl,...,xn)€Rn, u=(uu...,um)?R'», F=
~(Fi, ¦ ¦ ¦, Fft)G"^*' a=(aii • • ¦> an) есть мультииндекс
с целыми неотрицательными ос-,, . . ., ос„ и Da=Dc*1. . .
?>"" , где Z),-=g^-, i—i, . . ., п. Аналогично определя-
определяется Н. у. с ч. п. в случае комплекснозначных функций.
Если /с>1, то векторное Н. у. с ч. п. обычно наз.
системой Н. у. с ч. п. Порядком уравнения A)
наз. наивысший порядок производной, входящей в
это уравнение.
Из существенно нелинейных уравнений наиболее из-
известным является Монжа — Ампера уравнение
det
д2и
¦х:,.,
x, и, Du)X
здесь и ниже Du=-(l>\ и, . . ., Dnu).
Если к=т и функция F дифференцируема относи-
относительно своих «старших» переменных, соответствующих
старшим производным, то тип уравнения B) определя-
определяется типом главной линейной относительно старших
производных частью функции F (см. Дифференциальное
уравнение с частными производными). При этом произ-
производным по соответствующим переменным, либо соот-
соответствующим дифференциальным операциям, в общем
случае, присваивается соответствующий определенный
вес. Напр., в нелинейном уравнении теплопроводности
ди 1 I _ ди в2 и
ах, -' у" -" "' ах2 ' дх2
df - вЫ ди
¦г—- > 0, р22*~*—5 1 производная -— имеет вес рав-
ный двум.
Так как линеаризация уравнения A) относительно
етарших производных проводится в окрестности фикси-
фиксированного решения, то в отличие от линейного урав-
уравнения тип уравнения A) (даже в фиксированной точк»
х) может зависеть от этого фиксируемого решения.
Напр., уравнение
является уравнением эллиптич. типа на решениях с
|^- >0 и уравнением гиперболич. типа на решениях
Тип уравнения определяет постановку корректных
краевых (смешанных) задач для этого уравнения и
методы их исследования.
Если функция F является линейной относительно
старших производных, то уравнение A) наз. квази-
квазилинейным уравнением. Напр., уравнение
C) является квазилинейным уравнением. В противном
случае уравнение наз. существенно нели-
нелинейным уравнением. Напр., уравнение Мон-
жа — Ампера B) является существенно нелинейным.
Если коэффициенты квазилинейного уравнения при
старших производных не зависят от искомого решения
(и его производных), то это уравнение наз. слабо
нелинейным уравнением. Напр., уравне-
уравнение
Дв=/(*. и, Du) D)
является слабо нелинейным уравнением.
Разделение Н. у. с ч. п. на квазилинейные и
слабо нелинейные носит условный характер и не отра-
отражает внутреннего существа самих уравнений. Слабо
нелинейное уравнение может обладать более сильными
нелинейными свойствами, нежели квазилинейное и да-
даже существенно нелинейное уравнение. Напр., суще-
существуют слабо нелинейные уравнения вида D), к-рые
при заданном граничном условии Дирихле в ограни-
ограниченной области обладают счетным множеством разных
решений.
Уравнения вида A) могут рассматриваться во всем
пространстве R" либо в нек-рой области этого про-
пространства. В первом случае функциональный класс
решений включает условия поведения решений на бес-
бесконечности. В случае области на границе этой области
либо на части ее ставятся определенные граничные ус-
условия либо одно граничное условие. Эти граничные
условия также могут содержать нелинейные операторы.
Н. у. с ч. п. вместе с граничным условием (условия-
(условиями) порождает нелинейную задачу. Эта нелинейная
задача рассматривается в соответствующем простран-
пространстве функций. Выбор этого функционального прост-
пространства решений определяется структурой нелинейного
дифференциального оператора F, задаваемого в обла-
области, и структурой граничных операторов. Выбор функ-
функционального пространства для нелинейной задачи
является существенным моментом при исследовании
этой задачи. Напр., нелинейной задаче
V
_ (—1I« I ?>а (| ?>au|p-isgn ?>ац) = / (х) с р > 1
в ограниченной области QcR" и
DPu = 0, | р | <; т — 1 на границе дп
соответствует пространство Соболева W™(Q). Эта за-
задача при любой функции / из сопряженного простран-
пространства Wp™(Q)=(W%(Q)) *, ^г + — = 1, имеет единст-
единственное решение и из W™(Q). Здесь и ниже W%(Q)
есть замыкание множества всех бесконечнодифферен-
цируемых финитных в Q функций в пространстве Со-
Соболева W%(Q).
При исследовании задач для Н. у. с ч. п. рассма-
рассматриваются вопросы о существовании решения, о числе
решений, об отсутствии решения, о разрушении реше-
решения, о бифуркации (ветвлении) решения, об асимптотике
решения при аргументе, стремящемся к границе, в
частности к бесконечности, в случае неограниченных
областей. Теория таких задач имеет два аспекта: ло-
локальный и глобальный.
Локальная теория относительно полно развита для
общих нелинейных задач, принадлежащих либо к эл-
липтич. типу, либо к параболнч. типу, либо к гипербо-
лич. типу. Эта теория основана на теореме о неявной
функции из нелинейного функционального анализа
и общей теории линейных задач соответствующего типа.
В случае краевых (смешанных) задач для нелиней-
нелинейных параболич. либо гиперболич. уравнений эта ло-
локальная теория позволяет установить разрешимость
задачи либо на достаточно малом временном проме-
промежутке, либо на фиксированном временном промежутке
при условии достаточно малого отклонения (в соот-
соответствующей метрике) данных задачи от данных извест-
известного решения (как правило нулевого решения) близкой
задачи.
Глобальная теория нелинейных задач развита менее
полно и только для отдельных классов уравнений.
Нелинейные уравнения с частными производными
первого порядка. Для широкого класса квазилинейных
скалярных уравнений первого порядка вида
Ж + ^]_ ^Гф'(*' *' ") + *('• х' ") = ° E)
установлена теорема существования и единственности
решения задачи Коши с начальным условием при t=0
для всех i>0.
Для более узкого класса уравнений вида E) рассмо-
рассмотрены также вопросы асимптотики решений таких задач
при *—>-+ оо и краевые задачи.
Теория систем квазилинейных уравнений с частны-
частными производными первого порядка развита менее полно
(см. Квазилинейные гиперболические уравнения и сис-
системы).
Нелинейные уравнения с частными производными
второго порядка.
Уравнения эллиптич. типа и пара-
парабол и ч. т и п а. Относительно полно развита теория
разрешимости в целом краевых задач для широкого
класса квазилинейных скалярных уравнений эллип-
тпч. типа второго порядка, имеющих вид
У" -?-а;(х, и, Du) + a(x, и, Du) = 0, F)
либо
?" _ аи(х, и, Du) axa'ox.+«(*. и, Ви) = 0 G)
при условии существования априорной оценки
тах|«(х)|. При этом коэффициенты уравнений удов-
X
летворяют определенным условиям.
Аналогично положение и с теорией разрешимости
в целом краевых (смешанных) задач для широкого
класса квазилинейных скалярных уравнений парабо-
параболич. типа второго порядка, имеющих вид
§ГУ ?n (8)
либо
ди
--У" аи(х, и, Du) а'^ + а(х, и, Du). (9)
J-~i, /= l ' ;
Эта теория разрешимости основана на теории априор-
априорных оценок и методе Лере — Шаудера.
Получение априорной исходной оценки тах\и(х)\
X
для определенных классов нелинейных уравнений F) —
(9) основано либо на максимума принципе, либо на спе-
специальных интегральных неравенствах и соответствую-
соответствующих вложения теоремах функциональных пространств.
Теория разрешимости в целом краевых задач для
существенно нелинейных скалярных уравнений эллип-
тич. типа развита для узкого класса таких уравне-
уравнений в случае двух независимых переменных.
Разрешимость в целом краевой (смешанной) задачи
для существенно нелинейных скалярных уравнений
нараболич. типа установлена для широкого класса
уравнений параболич. типа вида
х, и,
ди_ дги \
вх ' дхг )
в случае одной пространственной переменной x?R.
Вопросы разрешимости в целом задач для систем
квазилинейных уравнений эллиптич. типа либо пара-
параболич. типа рассмотрены для отдельных узких классов
таких систем.
Одним из эффективных методов в исследовании
Н. у. с ч. п. второго порядка, принадлежащих либо
к эллиптич., либо к параболич. типу, является метод
верхних и нижних решений. Напр., пусть поставлена
краевая задача
—Au = f(x, и, Du) в ограниченной области QczR",
и = 0 на границе dQ класса С2 ' '
с непрерывной функцией /, определенной на QX RX R"
и такой, что выполнено условие Бернштейна
\f(x, и, Б)|<л/(|ы|)-A + |Е|*)
при всех (.г, и, §)?QxRXR" с возрастающей функ-
функцией М : R + —>-R + = {??RU;>0}. Тогда если сущест-
существуют функции г; + , и~ ?Wp(Q) с р>?г такие, что
Д + /( + D + ) Q + >0 дп
фу ?p
Дв + >/(.г, u + , Du + ) почти всюду в Q, it + >0 на дп,
— Д«-«:/(;г, «-, Du~) почти всюду в Q, »-<0 на дп
(« + — верхнее решение задачи A0), и~— нижнее ре-
решение задачи A0)), и и + (х)^и- (х) в Q, то существует
решение u?Wp(Q) задачи A0) и и~ (х)^.и (х)<.и+ (х) в
й. Правильный выбор верхних и нижних решений
исходных нелинейных задач, основанный на решениях
модельных задач, дает возможность устанавливать не
только разрешимость и нижнее число решений, но и
получать тонкие априорные оценки и асимптотику для
этих решений исходных нелинейных задач.
Исследование поведения в целом решений краевых
(смешанных) задач для нелинейных параболич. урав-
уравнений, как и в случае обыкновенных дифференциаль-
дифференциальных уравнений, связано с исследованием стационар-
стационарных решений краевых задач для соответствующих не-
нелинейных эллиптич. уравнений.
В связи с тем, что краевые задачи для нелинейных
эллнптич. уравнений не всегда имеют решение и для
краевых (смешанных) задач для нелинейных парабо-
параболич. и гиперболич. уравнений не при всех г>0 суще-
существует решение, развивается теория отсутствия реше-
решений задач для Н. у. с ч. п.
Уравнения гиперболич. типа. Эти
уравнения занимают особое место среди Н. у. с ч. п.
второго порядка. «Потеря одной производной» при обра-
обращении гиперболич. оператора второго порядка при-
приводит к принципиальным трудностям при исследовании
нелинейных гиперболич. уравнений. Даже для созда-
создания локальной теории нелинейных гиперболич. уравне-
уравнений и систем потребовалось развитие специальной тео-
теории о неявных функциях в нелинейном функциональ-
функциональном анализе, так как классич. теорема о неявной
функции из функционального анализа оказалась здесь
неприменимой.
Для (существенно) квазилинейных гиперСолнч. урав-
уравнений второго порядка с числом независимых пере-
переменных больше двух вопрос о разрешимости в целом
даже задачи Кошм не исследован.
В случае двух независимых переменных (t?R1,
R) разрешимость задачи Коши в целом установлена
для отдельных уравнений вида
un — a2(ux)uxx=f(t, х, ии их),
сводимых к специальным квазилинейным гиперболич.
системам — законам сохранения (см. Квазилинейные
гиперболические уравнения и системы).
В случае квазилинейных гиперболич. уравнений вида
Au = f(t, х) в QX [О, Т]
установлена разрешимость в целом (для любого 7">0)
смешанной задачи с условиями: ы = 0 на ЗЯХ[0, Т]
и н —<р, к1=г|; при ?--0, x?Q в определенном классе
бесконечно гладких по х функций. Здесь Q — ограни-
ограниченная область из R" с границей д Q класса С°° и
Разрешимость в целом задачи Коши, а также крае-
краевой (смешанной) задачи установлена для широкого
класса слабо нелинейных гиперболич. уравнений вида
utt — \u = f{t, х, и, щ, Du), t > 0, i^QcR».
Особое место в теории нелинейных гиперболич.
уравнений занимает вопрос о существовании периодиче-
периодических по t решений краевых задач для этих уравнений.
Даже для слабо нелинейных уравнений этот вопрос
рассмотрен только для уравнений вида
в случае двух переменных t?R и х?\а, 6]cR. Слож-
Сложность этого вопроса обусловлена бесконечномерностыо
ядра соответствующей линейной задачи.
Слабо нелинейные и квазилинейные гиперболич.
уравнения, содержащие диссипативные слагаемые, ис-
исследованы более полно.
Нелинейные уравнения с частными производными
высшего порядка. Разрешимость краевых (смешанных)
задач исследована для широкого класса квазилиней-
квазилинейных уравнений дивергентного вида
= /(*), |Р1<1и, (И)
= f(t, 2-), IP Km.
При этом относительно фУнкЦии Аа предполагается
выполненным ряд условий, к-рые обеспечивают, что
нелинейные операторы будут определены в соответству-
соответствующих функциональных пространствах и обладать ря-
рядом свойств. Напр., для разрешимости краевой задачи
в ограниченной области QczRn с условиями
D<»u = 0, |и|<т — 1 на границе д& A2)
для уравнения A1) достаточно выполнение условий:
1) Функции Аа(х, ?„, . . ., |р), gp<->DPu, являются
измеримыми по х при всех |0, . . ., ?р, непрерывными
по Eо, • ¦ -, !р) почти при всех igt! и удовлетворяют
неравенству
\ Y I "^ '' *
с р>1 и А'>0, |а|<т.
2) Выполнено следующее условие коэрцитивности:
для любой функции и из пространства Соболева W™(Q.)
справедливо неравенство
3) Выполнено условие монотонности: для любых
функций it и у из Wpl(Q) справедливо неравенство
V „ \п(Аа(.г, и, ..., DPu) —
*—ь\ а | < т J Q
— Аа (х, v, ..., Dfiu) (/;«» — ?>«<;)) dx За 0.
Тогда при выполнении условий 1) —3) краевая зада-
задача A2) для уравнения A1) при любой функции / из
сопряженного пространства (Wp"(Q)) * имеет решение
и из W%(Q).
Все эти условия можно существенно расширить.
Напр., для дифференциальных операторов вида A1) с
граничными условиями A2), к-рые являются нечетными
и однородными в главном при нек-рых условиях, но без
условия коэрцитивное™, справедлива альтернатива
Фредгольма: если соответствующая краевая задача с
пулевыми граничными условиями A2) для уравнения
(И) с /—0 имеет только тривиальное решение, то зга
задача разрешима при любой функции / из соответ-
соответствующего сопряженного пространства.
Для широкого класса краевых (смешанных) задач
для Н. у. с ч. п. развита теория нормальной разреши-
разрешимости, к-рая обобщает теорию нормальной разрешимо-
разрешимости (по Хаусдорфу) линейных операторных уравнений
на нелинейный случай. Ута теория дает достаточные
условия разрешимости краевых (смешанных) задач для
нелинейных уравнений И систем уравнений нарабо-
лич. типа и для слабо нелинейных уравнений и систем
гиперболич. типа.
В теории краевых задач для нелинейных уравнений
эллиптич. типа особое место занимает вопрос о суще-
существовании собственных функций. Теория собственных
функций краевых задач для квазилинейных уравнений
эллиптич. тпиа развита для достаточно широкого клас-
класса задач. В частности, на широкий класс задач перене-
перенесена абстрактная теория Люстерника — Шнирельмана
о существовании счетного множества собственных функ-
функций.
Особое место в теории нелинейных уравнений эллип-
эллиптич. типа высшего порядка и в теории систем нелиней-
нелинейных уравнений уллинтич. типа с числом независимых
переменных, большим двух, занимает вопрос о регуляр-
регулярности решений этих уравнений и систем.
В случае скалярного квазилинейного равномерно
эллиптич. уравнения второго порядка с достаточно
гладкими коэффициентами, удовлетворяющими вме-
вместе со своими первыми производными определенным ус-
условиям роста, решение обладает гладкостью внутри
области на две производные, превышающие гладкость
правой части из соответствующего пространства.
В случае квазилинейных уравнений эллиптич. типа
порядка выше двух и систем квазилинейных уравнений
эллнцтич. тина второго либо более высокого порядка
с числом независимых переменных, большим двух,
соответствующая гладкость решений имеет место не
всюду внутри области, а почти всюду. При дополни-
дополнительных условиях удается уточнить размерность этой
нулевой (хаусдорфовой) меры, на множествах к-рой,
вообще говоря, гладкость решений теряется. Для спе-
специального класса квазилинейных эллинтич. систем с
ограниченными нелинейностями установлена регуляр-
регулярность решений всюду в области.
Развита теория краевых задач для широкого клас-
класса квазилинейных уравнений дивергентного вида беско-
бесконечного порядка.
Теория точных решений. К методам точных решений
относятся: метод, основанный на групповом анализе
Н. у. с ч. п.; метод, основанный на преобразованиях
Ли — Беклунда; метод, «снованный на обратной задаче
теории рассеяния, и нек-рые др.
Метод обратной задачи рассеяния позволил иссле-
исследовать ряд физически важных уравнений, таких, как
нелинейные уравнения Кортевега — де Фриса:
нелинейное уравнение синус-Гордона:
"и — i'xx + sin " = 0;
нелинейное уравнение Шредингера:
и ряд других с одной пространственной переменной
x?R. С помощью этого .метода удалось рассмотреть
отдельные нелинейные уравнения типа уравнения
Кортевега — де Фрпса с двумя пространственными пе-
переменными.
Лит.: [1] Курант Р., Уравнения с частными произ-
производными, пер. с англ., М., 1964; [2] Ладыженская О. А.,
У р а л ь ц е в а Н. Н., Линейные и квазилинейные уравне-
уравнения эллиптического типа, 2 изд., М., 1973; [3] G i 1 1) а г g D.,
Trudingcr N. S., Elliptic Partial Differential Equations of
Second Order, B.— N. Y., 1977; [4] Ладыженская О. А.,
С о л о н н и к о в В. А., Уральцева Н. Н., Линейные
и квазилинейные уравнения параболического типа, М., 1967;
[5] Фридман А., Уравнения с частными производными
параболического типа, пер. с англ., М., 19И8; [6] Н и р е н-
берг Л., Лекции по нелинейному функциональному анали-
анализу, пер. с англ., М., 1977; [7] Лионе, Ж.-Л., Некоторые
методы решения нелинейных краевых задач, прр. с франц., М.,
1972; [8] Рождественский Б. Л., Я н е н к о Н. Н.,
Системы квазилинейных уравнений..., М., 1978; [9] С к р ы п-
н и к И. В., Нелинейные эллиптические уравнения высшего
порядка, К., 1973: [101 F u с i k S., N е с a s J., S о и с е к J.,
Sou сек V., Spectral Analysis of Nonlinear Operators, В.,
1973; [llj Овсянников Л. В., Групповой анализ диффе-
дифференциальных уравнений, М., 1978; [12] Захаров В. Е.,
Манаков С. В., Новиков С. П., П и т а е в с-
кий Л. П., Теория солитонов. Метод обратной задачи, М.,
1980; [13] В и шик М. И., «Тр. Моск. матем. об-ва», 1963,
т. 12, с. 125—64; [141 Giaquinta M., Modica G.,
«Manuscripta math.», 1979, v. 28, J4« 1—3, p. 109—58; [15]
Дуби некий Ю. А., «Матем. сб.», 1975, т. 98, .V» 2, с.
163—84; [16] Kazdan J. L., Kramer R., «Comm. pure
and appl. Math.», 1978, v. 31, №5, p. 619—45; [17] Ко-
шел ев А. И., «Успехи матем. наук», 1978, т. 33, в. 4, с.
3 — 49; [18] Кружков С. Н., «Матем. сб.», 1970, т. 81,
№ 2, с. 228—55: [19] его же, «Тр. Моск. матем. об-ва»,
1967, т. 16, с. 329—46; [20] Олейник О. А., «Успехи ма-
матем. наук», 1959, т. 14, в. 2, с. 165—70; [21] П о х 0-
ж а е в С. П., «Матем. сб.», 1970, т. 82, N> 2 с. 192—212;
[22] его же, «Матем. сб.», 1975, т. 9й, № 1, с. 152—66; [23]
его же, «Матем. сб.», 1980, т. 113, № 2, с. 324—38.
С. И, Похожаев.
НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ — колебания в фи-
зич. системах, описываемые нелинейными системами
обыкновенных дифференциальных уравнений
<с=А (t)x+nX(t, ж, ц)+/(*), A)
где scgR", X содержит члены не ниже 2-й степени
по компонентам вектора ж, f{l) — вектор-функция
времени t, u,>0 — малый параметр (либо ц,= 1 и Х=
= JC(t, ж)). Возможные обобщения связаны с рассмо-
рассмотрением разрывных систем, воздействий с разрывными
характеристиками (напр., типа гистерезиса), запазды-
запаздывания и случайных воздействий, интегро-дифференцп-
альных п дифференциально-операторных уравнений,
колебательных систем с распределенными параметра-
параметрами, описываемыми дифференциальными уравнениями
с частными производными, а также с использованием
методов оптимального управления нелинейными коле-
колебательными системами. Основные общие задачи II. к.:
отыскание положений равновесия, стационарных режи-
режимов., в частности периодич. движений, автоколебаний и
исследование их устойчивости, проблемы синхрониза-
синхронизации и стабилизации Н. к.
Все физич. системы, строго говоря, являются нели-
нелинейными. Одна из наиболее характерных особенно-
особенностей Н. к.— это нарушение в них принципа суперпо-
суперпозиции колебаний: результат каждого из воздействий
в присутствии другого оказывается иным, чем в случае
отсутствия другого воздействия.
Квазилинейные системы — системы A)
при а>0. Основным методом исследования является
малого параметра метод. Прежде всего это метод
Пуанкаре — Лнндштедта определения не-
риодич. решений квазилинейных систем, аналитиче-
аналитических по парадгетру при его достаточно малых значениях,
либо в виде рядов по степеням fi (см. [1] гл. IX), либо
в виде рядов по степеням ц и Рь . . ., р",,— добавок к
начальным значениям компонент вектора ж (см. [1]
гл. III). О дальнейшем развитии этого метода см.,
напр., в [2] — [4].
Другим из методов малого параметра является метод
осреднения. Вместе с тем в исследование квазилиней-
квазилинейных систем проникали и новые методы: аспмптотпч.
методы (см. [5], F]), метод ^-функций (см. [7]), бази-
базирующийся на фундаментальных результатах А. М. Ля-
Ляпунова — Н. Г. Четаева, и др.
Существенно нелинейные системы,
в к-рых отсутствует заранее предписываемый малый
параметр (ц = 1 и X=X(t, ж) в A)). Для систем Ляпу-
Ляпунова
ж = Аж-{-Х(ж) B)
ГДе _ 110-1
— 2 + - . 2 ~~ I 1 0
причем среди собственных чисел (&ХА-)-матрицы Р нет
кратных корню ±Xi, Х(ж) — аналптнч. вектор-функ-
вектор-функция яг., разложение к-рой начинается с членов не ниже
2-го порядка, и 1шеет mqcto аналитический первый ин-
интеграл специального вида, А. М. Ляпунов (см. [8] § 42)
предложил метод отыскания периодич. решений в виде
ряда по степеням произвольной постоянной с (за к-рую
может быть принято начальное значение одной из двух
крнтич. переменных хг либо х2).
Для систем, близких к системам Ляпунова,
где А и Х(ж) того же вида, что и в B), V — аналитпч.
вектор-функция ж и малого параметра и, непрерывная
и 2л-периоднческая no t, также предложен метод опре-
определения периодич. решений (см. [4] гл. VIII). Системы
тина Ляпунова B), в к-рых матрица А имеет I нулевых
собственных значений с простыми элементарными дели-
делителями, два — чисто мнимых собственных значения
±Xi и не имеет собственных значений, кратных
±Xi, Х(ж) — такая же, как и в B), могут быть сведены
к системам Ляпунова (см. [9] § IV. 2). Исследовались
также Н. к. в системах Ляпунова и в т. н. с и с т е-
мах Ляпунова с демпфированием, а
также решалась общая задача о перекачке энергии в
них (см. [9] гл. I, III, IV).
Пусть существенно нелинейная автономная система
приведена к жорданову виду ее линейной части
—j— Xy) / ш. _ ,ir\ / VO^l * * • *^»J J *V ~— J-7 ...1 If. О»? —— {) 5 VI
где вектор A=(Xj, . . ., Xn) по предположению имеет
хотя бы одну ненулевую компоненту; 6lt . . ., 6n_t
равны нулю или единице соответственно при отсут-
отсутствии или наличии непростых элементарных делите-
делителей матрицы линейной части, /vO — коэффициенты;
множество 5Jiv значений вектора (?=(<2i, • • •, чп) с
целочисленными компонентами таково:
Тогда существует нормализующее преобразование:
iv=Jv+Jv2s e%\hvQyQil---yn"' v = l, ..., re, D)
приводящее C) к нормальной форме дифференциальных
уравнений
У\ = h/ Уу + 6v Уч+1 +
+ »v2fi€S (л. Q)=o gvoyV-.-yf^^i, ...,«; 6=0,
E)
и такое, что gv(y-0, если (Л, О)ф0. Таким образом,
нормальная форма E) содержит лишь резонансные
члены, т. е. коэффгщиевты gvg в E) могут быть отличны
от нуля лишь для тех Q, для к-рых выполнено резо-
резонансное уравнение
играющее существенную роль в теории колебаний. Схо-
Сходимость и расходимость нормализующего преобразова-
преобразования D) исследована (см. [10] ч. I, гл. II, III); дано
вычисление коэффициентов hvn, gvQ (посредством их
симметризации) (см. [9] § 5.3). В ряде задач о Н. к.
существенно нелинейных автономных систем оказался
эффективным метод нормальных форм (см. [10], [9]
гл. VI—VIII).
Из других методов исследования существенно нели-
нелинейных систем применяются метод точечных отобра-
отображений (см. [2], [11]), стробоскопии, метод [12] и функ-
ционально-аналптлч. методы [13].
Качественные методы Н. к. Исходными
здесь являются исследования вида интегральных кри-
кривых нелинейных обыкновенных дифференциальных
уравнений, проведенные А. Пуанкаре (Н. Poincare,
см. [14]). Приложения для задач Н. к., описываемых ав-
автономными системами 2-го порядка см. в [2], [15].
Изучены [16] вопросы существования периодич. ре-
решений и их устойчивости в большом для многомерных
систем; рассмотрены [13] почти периодические Н. к.
Приложения теории обыкновенных дифференциальных
уравнений с малым параметром при нек-рых производ-
производных к задачам релаксационных Н. к. см. в [17].
Важные аспекты Н. к. и лит. см. в статьях Возму-
Возмущений теория, Колебаний теория.
Лит.: [11 Пуанкаре А., Избр. труды, пер. с франц.,
т. 1, М., 1971; [21 Андронов А. А., В и т т А. А., X а й-
кин С. Э., Теория колебаний, 2 изд., М., 1959; [3] Бул-
Булгаков Б. В., Колебания, М., 1054; [4] М а л к и н И. Г.,
Некоторые задачи теории нелинейных колебаниа, М., 1956*
[5] .Боголюбов Н. Н., Шбр. труды, т. 1, К., 196У;
[а] Б о г о л ю б о и Н. Н., М и т р о п о л ь с к и й 10. А.,
Асимптотические методы в теории нелинейных колебаний, 4 изд.,
М., 1974; L7J Каме н к о в Г. В., Избр. труды, т. 1 — 2, М.,
1971 — 72; [8i Ляпунов А. М., Собр. соч., т. 2, М.— Л.,
1950, с. 7—263; [9] С т а р ж и н с к и й В. М., Прикладные
методы нелинейных колебаний, М., 1977; [10] Б р ю н о А. Д.,
«Тр. Моск. матем. оО-иа», 1971, т. 25, с. 119—262; 1972, т. 28,
с. 199 — 239; [11] II е it м а р к 10. И., Метод точечных отобра-
отображений в теории нелинейных колебаний, М., 1П72; [12] М i-
norsky N., Introduction to non-linear mechanics, Ann Arbor,
1947; ll.il Красносельский М. А., Б у р д В. III.,
Колосов Ю. С, Нелинейные почти периодические коле-
колебания, М., 1970; [141 Пуанкаре А., О кривых, определяе-
определяемых дифференциальными уравнениями, пер. с франц., М. —Л.
1947; [151 В у т с н и н Н. В., Н е им а р к Ю. И., Ф у ф п-
е в II. А., Введение в теорию нелинейных колебаний, М., 1976;
[16] Плисе В. А., Нелокальные проблемы теории колебаний,
М. —Л., 1964; [17] М и щ* н к о Е- Ф., Розов Н. X.,
Дифференциальные уравнения с малым параметром и релакса-
релаксационные колебания, М., 1975. В. М. Старжинскш'/..
НЕЛИНЕЙНЫЙ ОПЕРАТОР — отображение А век-
векторного (как правило) пространства X в векторное
пространство Y над общим полем скаляров, не облада-
обладающее свойством линейности, т. е. такое, что, вообще
говоря,
А (а1х1 -f а2.г2) т= аг Ах^а.^ Ах„.
Если Y есть множество действительных чисел R или
комплексных чисел С, то Н. о. наз. нелинейным функ-
функционалом. Простейшим примером Н. о. (нелинейного
функционала) служит действительная функция действи-
действительного аргумента, отличная от линейной функции.
Одним из важных источников возникновения II. о. явля-
являются задачи ыатематич. физики. Если при составлении
локального математнч. описания процесса учитываются
малые не только первого, но и высших порядков, то
возникают уравнения с Н. о. К нелинейным оператор-
операторным уравнениям приводят также нек-рые задачи мате-
матич. экономики, авторегулнрования, теории управ-
управления и т. д.
Примеры нелинейных операторов.
1) Ах=[ЬаК (t, s, x(s))ds,
где K(t, s, и), а<:/, s<:6, —оо<м<оо,— такая функ-
K(t, s, x{s)) ds есть непрерывная на
а
[а, Ь\ функция для любой функции x(s)?C(а, Ь)
(напр., K(t, s, и) непрерывна на я-<<, s<:6, —оо<и<
<оо). Если K(t, s, и) нелинейна по и, то А — нелиней-
нелинейный оператор Урысона, отображающий
С\а, Ь] в С[а, Ь]. При других ограничениях на K(t, s, и)
оператор Урысона действует в других пространствах,
напр, в L-zla, b], или отображает одно пространство
Орлича Ьли[а, Ь] в другое LMl[a, Ъ].
2) Bx=\ibaK(t, s)g(s, x(s))ds,
где g(t, и) — нелинейная по и функция, определенная
на a-*g.t-*g.b, —оо<и<оо. При соответствующих огра-
ограничениях на g(t, и) оператор В действует из одного
функционального пространства в другое и наз. нели-
нелинейным оператором Гаммерштейна.
3) F(x)=f(t,x(t))
— оператор суперпозиции, наз. также
оператором Немыцкого, преобразующий
при соответствующих ограничениях на нелинейную по
2-му аргументу функцию пространство измеримых функ-
функций x(t) в себя.
4) Я H = 2lfcl<m ?>*(«*(*, х, Dx, ...
— нелинейный дифференциальный опе-
оператор порядка 2т дивергентного
в и д а, действующий в пространстве Соболева Wpm(G)
при соответствующих ограничениях на нелинейные
функции а^(г, и0, »!, . . ., ит). Здесь к — мультииндекс
(ftlf . . ., кп), | к |=Ы-. . . + *„, Д*= ь kdW — И
G — ограниченная область пространства R".
5) J (х) = f * К (г, s, х (s), х' (*)) ds
— нелинейный интегро-дифференциаль-
ный оператор, действующий при соответствую-
соответствующих ограничениях на функцию K(t, s, м0, их) в про-
пространстве СЦа, Ъ\ непрерывно дифференцируемых
функций.
На Н. о., действующие из одного топологического
векторного пространства X в другое топологическое
векторное пространство Y, переносятся многие поня-
понятия и операции математнч. анализа действительных
функций действительного переменного. Так, Н. о.
А : М —>- У, MczX наз. ограниченным, если
А(В(~\М) — ограниченное множество в Y для любого
ограниченного множества BczX; H. о. А непрерывен в
точке х?М, если прообраз А ~1(иуцх) окрестности U^x
точки Ах содержит M[~\UX для нек-рой окрестности
точки х. Как и для функций, Н. о., непрерывный в
каждой точке компактного множества М, ограничен
на этом множестве. В отличие от линейных операто-
операторов, для Н. о., действующих в нормированных про-
пространствах, из ограниченности оператора .4 на нек-
ром шаре не следует непрерывность А на этом шаре.
Однако в нек-рых случаях из непрерывности (ограни-
(ограниченности) Н. о. на шаре следует непрерывность (огра-
(ограниченность) оператора во всей области его определения.
Среди Н. о., действующих из X в У, можно выделить
нек-рые важные классы.
1) П о л и л п н е й н ы е операторы А :
: XX XX . . . X X—yY, линейные по каждому аргументу.
Пространство Ln{X, Y) (I) всех n-лннейных операторов
изоморфно пространству L{X\...L (X, У), . . .]} (II),
где L(X, У) — пространство всех линейных операторов
из X в У. Если X и Y — нормированные пространства,
то пространства (I) и (II) изометричны. Если А симмет-
симметричен по всем аргументам, то А (х, х, . . ., х) обознача-
обозначается Ахп и наз. однородным оператором
п-й степени.
2) В пространствах, наделенных частичной упоря-
упорядоченностью,— изотонные операторы А и
ант и тонные операторы А, характеризу-
характеризующиеся соответственно условиями х<.у=^>Ах^.Ау и
у^у
3) В гильбертовом пространстве // — монотон-
монотонные операторы М, определяемые условием
(Мх—My, х—i/>JsO для любых х, у?Н.
4) Компактные операторы, преобразую-
преобразующие ограниченные подмножества своей области опре-
определения в предкомпактные множества, в том числе
вполне непрерывные операторы, яв-
являющиеся одновременно компактными и непрерывными.
Для Н. о. нетривиальными и полезными являются по-
понятия дифференциала и производной. Оператор А,
действующий из открытого множества G нормированного
векторного пространства X в нормированное вектор-
векторное пространство У, наз. дифференцируемым
по Фреше в точке x?G, если существует линейный
непрерывный оператор А (х) : X—>Y такой, что для
любого h?X, для к-рого x-\-h?G, имеет место
А {х+Ю—А (х) = А'(х)к+ю,
где ш/№||—>-0 при h—>-0. В этом случае линейная по h
часть A'(x)k приращения A (x-\-h)—А (х) наз. диф-
дифференциалом Фреше оператора А в точке х
и обозначается dA (x, h), а ш=ш(Л, х, h) наз. остат-
остатком приращения. Линейный ограниченный
оператор А' (х) . наз. производной Фреше
оператора А в точке х. Помимо дифференцируемое™
по Фреше вводится дифференцпруемость по Гато. Имен-
Именно, оператор А наз. дифференцируемым
но Гато в точке х, если существует
}A<x) = DA(x, h),
t -* о
наз. дифференциалом Гато оператора А
в точке х. Дифференциал Гато однороден по h, т. е.
DA (x, Xh) = IDA (x, h). Если DA (x, h) линеен по k
п DA (x, h) = A '0(x)h, то линейный оператор А(,(х) наз.
производной Гато оператора А. Из диффе-
ренцпруемостн по Фреше следует дифференцируемость
по Гато и равенство А'д(х) = А (х). Из дифференцируе-
мостп по Гато не следует в общем случае дифференци-
дифференцируемость по Фреше, но если DA (х, К) существует
в окрестности точки х, непрерывен по А и равномерно
непрерывен по х, то А дифференцируем по Фреше в
точке х. Для нелинейных функционалов / : G—>-R. диф-
дифференциалы и производные Фреше и Гато определяются
аналогично. При этом производная Гато /<j наз. гра-
градиентом функционала / и является опе-
оператором из G в X* . Если ^i=grad f(x) для нек-рого
нелинейного функционала /, то оператор А наз. и о-
тенциальным.
Для операторов, действующих в отделимых тополо-
топологических векторных пространствах, возможно несколько
определений дифференцпруемости. Пусть 5Ш — нек-рая
совокупность ограниченных множеств топологического
векторного пространства X. Отображение ш : GXX^>-Y
наз. *Ш-м алым, если для любого М?9)} имеет место
со (ж, th)/i—>-0 при t—y-О равномерно по /г?9Л. Отобра-
Отображение А : G-+Y (GczX н открыто) наз. 2R - д и ф ф е-
ренцируемым в точке x?G, если
A (x+h)~Ax=A' (x)h-\-a>(A, x, h),
где ш есть SCR-малое отображение. Чаще всего в каче-
качестве 9Л берется либо совокупность всех ограниченных
множеств, либо совокупность всех компактных мно-
множеств, либо совокупность всех конечных множеств
пространства X. Для Н. о. в нормированных простран-
пространствах первый случай приводит к дифференцируемостн
по Фреше, третий — к дифференцируемостп по Гато.
Обычным образом, как производные от производ-
производных, определяются производные высших порядков
А{п)(х) и А о"' (х) оператора А. Это — полилинейные
симметрич. отображения. Дифференциалом re-го по-
порядка будет при этом однородная форма п-й степени
Aw(x)hn. Возможны иные определения высших про-
производных. Пусть, напр., X и Y — нормированные
векторные пространства, GcX — открыто, x?G. Если
для любого h такого, что x-{-h?G,
A (x + h) — A (*) = a0 (*) + «! (х) *+...+«„ (z)h»-\-a>, (*)
где ш=о(\\h||"), то полилинейная форма к\аь(х) наз.
производной fc-ro порядка. Выражение (*)
наз. при этом ограниченным разложени-
разложением re-го порядка разности A (x-^rh) — А (х).
При выполнении соответствующих ограничений раз-
различные определения высших производных эквивалент-
эквивалентны.
Если в пространстве X задана скалярная счетно ад-
аддитивная мера, то Н. о. можно интегрировать, понимая
\ A (x)dx в смысле Бохнера интеграла.
Для Н. о. А : M-+Y, как и в случае линейного,
значения параметра К такие, что (/—Х.4) существует
и непрерывен на А (М), естественно назвать регу-
регулярными, а остальные точки X отнести к с п е к т-
р у. По своим свойствам спектр Н. о. А может резко
отличаться от спектров линейных операторов. Так,
спектр вполне непрерывного Н. о. может иметь непре-
непрерывные участки; из собственного элемента хй оператора
А, т. е. такого, что хо=ХаАхо, могут выходить ветви
собственных элементов, и т. п.
Лит.: [1] Л ю стер ни к Л. А., Соболев В. И.,
Элементы функционального анализа, 2 изд., М., 1965; [2] Кан-
Канторович Л. В., А к и л о в Г. П., Функциональный ана-
анализ, 2 изд., М., 1977; [3] В а й н б е р г М. М., Вариационные
методы исследования нелинейных операторов, М., 1956; [41
Красносельский М. А., 3 а б р е й к о П. П., Гео-
Геометрические методы нелинейного анализа, М., 1975; [5] Г а е в-
ский X., Грёгер К., Захариас К., Нелинейные
операторные уравнения и операторные дифференциальные урав-
уравнения, пер. с нем., М., 1978. В. И. Соболев.
НЕЛИНЕЙНЫЙ ПОТЕНЦИАЛ — порожденная ра-
доновской мерой и. функция Г/ц, (х) точки т евклидова
пространства R^, N~^z2, нелинейно зависящая от по-
порождающей меры.
Напр., при исследовании свойств решений диффе-
дифференциальных уравнений с частными производными Я
граничных свойств аналитич. функций оказываются
полезными Н. п. следующего вида:
р, 1) =
= еге **у
где |.r—y\ — расстояние между точками х и у, р.
радоновская мера с компактным носителем, р и I
действительные числа, 1<р<оо, 0<7<оо.
При р = 2 Н. п. (*) обращаются в линейные Рисса
потенциалы, при р = 2 и 1=1 — в классический нью-
ньютонов потенциал. Для Н. п. (*) строятся понятия
емкости и энергии, доказываются аналоги нек-рых ос-
основных теорем потенциала теории (см. [I]).
Лит.: [1] М а э ь я В. Г., X а в и н В. П., «Успехи ма-
тем. наук», 1972, т. 27, в. й, с. 67 —138. Е. Д. Соломснцев.
НЕЛИНЕЙНЫЙ ФУНКЦИОНАЛ — частный случай
нелинейного оператора, определенного на действитель-
действительном (комплексном) векторном пространстве X, зна-
значениями к-рого являются действительные (комплекс-
(комплексные) числа. Примерами Н. ф. могут служить функцио-
функционалы вариационного исчисления
/(*)=$*/"(*, x(t), x' (t))dt;
выпуклые функционалы, определяемые условием
где х, у?Х, 0<:А,<:1, напр. /(#)= ||ж|| — норма элемента
нормированного пространства. в- И. Соболев.
НЕЛИНЕЙНЫЙ ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ—
один из разделов функционального анализа, изучаю-
изучающий нелинейные отображения (нелинейные операторы)
бесконечномерных векторных пространств, а также нек-
рые классы нелинейных пространств и их отображения.
Основными разделами Н. ф. а. являются следующие.
1) Дифференциальное исчисление нелинейных отоб-
отображений банаховых, топологических векторных, и
нек-рых других более общих пространств, включая
теоремы о локальном обращении дифференцируемого
отображения и теорему о неявной функции.
2) Нахождение условий действия, непрерывности,
компактности нелинейного оператора, действующего
из одного бесконечномерного конкретного простран-
пространства в другое.
3) Принципы неподвижной точки для различных
классов нелинейных операторов (сжимающих, компакт-
компактных, уплотняющих, монотонных и др.); применение
этих принципов для доказательства существования
решений различных нелинейных уравнений.
4) Изучение нелинейных монотонных, вогнутых,
выпуклых, имеющих монотонную миноранту и др. опе-
операторов в пространствах, наделенных структурой упо-
упорядоченного векторного пространства.
5) Исследование спектральных свойств нелинейных
операторов (точки бифуркации, непрерывные ветви
собственных элементов и пр.) в бесконечномерных век-
векторных пространствах.
6) Приближенное решение нелинейных операторных
уравнений.
7) Изучение пространств, линейных в малом, и ба-
банаховых многообразий — глобальный ана-
л и з.
8) Исследование на экстремум нелинейных функцио-
функционалов и вариационные методы изучения нелинейных
операторов.
Лит.: [1] В а й н б е р г М. М-, Вариационный метод и
метод монотонных операторов в теории нелинейных уравнении,
М., 1972; [2J Гаевский X., Грёгер К., 3 а х а р и-
а с К., Нелинейные операторные уравнения и операторные диф-
дифференциальные уравнения, пер. с нем., М., 1978; [3] И л л г
Д ж., «Успехи матем. наук», 1969, т. 24, в. 3, с. 157—210; [4]
Красносельский М. А., Положительные решения
операторных уравнений, М., 1962; [5] Красносель-
Красносельский М. А., Забрейко П. П., Геометрические методы
нелинейного анализа, М., 1975; [6] Л е н г С, Введение в тео-
теорию дифференцируемых многообразий, пер. с англ., т. 1, М..
1967; [7] Л ю стер ни к Л. А., С о б о л е в В. И., Эле-
Элементы функционального анализа, 2 изд., М., 1965; [8l H и-
ренберг Л., Лекции по нелинейному функциональному
анализу, пер. с англ., М., 1977; [9] X и л"л е Э., Фи л-
липс Р., Функциональный анализ и полугруппы, пер. с
англ., 2 изд., М., 1962. В. И. Соболев.
НЕОБХОДИМАЯ ДОСТАТОЧНАЯ СТАТИСТИКА —
см. Минимальная достаточная статистика.
НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ —
условия правильности утверждения А, без выполне-
выполнения к-рых утверждение Л заведомо не может быть вер-
верным (необходимые условия), п, соответственно, при
выполнении к-рых утверждение А заведомо верно (до-
(достаточные условия). Часто выражение «необходимо и
достаточно» заменяется выражением «тогда и только
тогда» или же выражением «в том и только в том слу-
случае». Н. и д. у. обладают большой познавательной
ценностью. В сложных математпч. проблемах разыска-
разыскание удобных для пользования Н. ид. у. бывает иногда
чрезвычайно трудным. В таких случаях достаточные
условия стараются сделать возможно более широкими,
т. е. охватывающими возможно большее число случаев,
в к-рых интересующий нас факт все еще имеет место, а
необходимые условия — возможно более узкими, т. е.
охватывающими возможно меньше лишних случаев,
в к-рых изучаемый факт уже не имеет места. Таким
образом, достаточные условия постепенно сближаются
с необходимыми. бсэ-з.
НЕОГРАНИЧЕННЫЙ ОПЕРАТОР — отображение А
множества М топологического векторного пространства
X в топологическое векторное пространство У такое,
что существует ограниченное множество NczM, об-
образ к-рого A (N) есть неограниченное множество в У.
Простейшим примером Н. о. является оператор дпф-
ференцпрованпя -п-, определенный на множестве
Сх\а, Ъ] всех непрерывно дифференцируемых функций
пространства С[а, Ь] всех функций, непрерывных на
так как оператор ^- переводит ограниченное
множество {sin nt} в неограниченное множество
{п cos nl}. H. о. А необходимо разрывен в нек-рых (а
если А линеен, то и во всех) точках своей области опре-
определения. Поэтому важным классом Н. о. являются
замкнутые операторы, обладающие свойством, в
нек-рой степени заменяющим свойство непрерывности.
Пусть А и В — П. о. с областями определения D ^
и DB. Если D &[\D ВФ0, то на этом пересечении
определен оператор (aA-\-f>B)x=aAxJrf>Bx, a, f>? R
{или С), и аналогично, если DA[)A~1(DB)^0, то
определен оператор (ВА)х=В(Ах). В частности, таким
образом определяются степени Ak, к=\, 2, . . ., Н. о.
А. Оператор В наз. расширением оператора
А, В>А, если DAc^DB и Вх=Ах для x?DA. Так,
В (А±-\-А2)^>BAi~\-BA2. Перестановочность двух опе-
операторов обычно рассматривается для того случая,
когда один пя операторов ограничен: Н. о. А переста-
перестановочен с ограниченным оператором В, если BAczAB.
Для линейных Н. о- определяется понятие сопряжен-
сопряженного оператора. Пусть Н. о. А, заданный на множестве
D А, плотном в топологическом векторном пространстве
X, действует в топологическое векторное пространство
У. Если X* и У*— пространства, сильно сопряженные
соответственно с X п У, и DA*— совокупность линей-
линейных функционалов ф?У*, для к-рых существует ли-
линейный функционал f?X* такой, что (Ах, <р>=-<.т, />
при всех x?DA, то соответствие ф«->/ определяет на DA*
(к-рое, впрочем, может состоять лишь из нулевого
элемента) пространства У* оператор А*, наз.операто-
наз.оператором, сопряженным с А.
Лит.: [1] II о си да К., Функциональный анализ, пер. с
англ., М., 1967; [21 Д а н ф о р д Н., Шварц Д ж., Линей-
Линейные операторы. Общая теория, пер. с англ., М., 1962; L3]
Рисе Ф., Секефальви-Надь Б., Лекции по функ-
функциональному анализу, 2 изд., пер. с франц.. М., 1979; [4] Л ю-
стерник Л. А., Соболев В. И., Элементы функцио-
функционального анализа, 2 изд., М., 1965; [5] Нейман Д ж.,
Математические основы квантовой механики, пер. с нем., М.,
1964. В. И. Соболев.
НЕОПРЕДЕЛЕННОЕ УРАВНЕНИЕ — уравнение,
содержащее более одного неизвестного. Систему урав-
нений, в к-рой число неизвестных больше числа урав-
уравнений, наз. неопределенной системой
уравнений. Н. у. и неопределенные системы
уравнений имеют, как правило, бесконечное число ре-
решений. Термин «Н. у.» употребляется в теории чисел,
где интересуются решениями Н. у., удовлетворяющих
тем или иным арпфметпч. условиям (обычно ищут ре-
решения Н. у. в целых или рациональных числах).
Изучение таких решений составляет предмет теории
диофантовых уравнений. БСЭ-з.
НЕОПРЕДЕЛЕННОСТЕЙ РАСКРЫТИЕ — методы
вычисления пределов функций, заданных формулами,
к-рые в результате формальной подстановки в них пре-
предельных значений аргумента теряют смысл:, т. е. пере-
переходят в выражения типа
¦?, ~, 0-00, 00 — 00, 0°, 00°, 1°°,
по к-рым нельзя судить о том, существуют пли нет иско-
искомые пределы, не говоря уже о нахождении их значений,
если они существуют. Основным инструментом для
раскрытия неопределеЕШОстей служит Тейлора формула,
с помощью к-рой выделяется главная часть функции.
Так, в случае неопределенности типа 0/Q, для того
чтобы найти предел
где
lim f(x)= lim g(x) = 0,
X _> Х„ X -* Xa
функции / и g представляют но формуле Тейлора в
окрестности точки х0 (если это возможно) до первого
не равного нулю члена:
в результате получается, что
( 0, если п > т,
Нт ^Ш=-у lim (* — жо)«-m = <| ° если n = m,
\ оо, если п < т.
В случае неопределенности типа оо/оо для нахожде-
нахождения предела
lim —~ ,
где
lim / (.с) = lim #(ж)=оо,
X ->- Ха X -у Х„
применяют преобразование
f (х)= g(x)
g(x) ^_ '
/(Ж)
сводящее задачу к раскрытию неопределенности типа
О/О.
Неопределенности типа О-оо и оо — оо также Е;елесо-
образно приводить к виду О/О следующими преобразо-
преобразованиями:
_1 1_
f (X)
_
8 (*) / (х) 1 (х) g (x)
с оответственно.
Для раскрытия неопределенностей типа 0", оо°, 1 °°
целесообразно первоначально прологарифмировать
выражения, предел к-рых требуется найти.
Другим общим методом раскрытия неопределенно-
неопределенностей тина — и -2- и сводимых к ним является Допита-
ля правило. л- Д- Кудрявцев.
НЕОПРЕДЕЛЕННОСТИ ПРИНЦИП, принцип
Гейзенберг а,— один из важнейших принципов
квантовой механики, утверждающий, что дисперсии
значений двух физпч. величин а и Ъ, описываемых не-
коммутирующими операторами а и Ь, коммутатор [а, Ь]
к-рых отделен от нуля, в любом состоянии физнч. сис-
системы не могут одновременно быть очень малыми.
Точнее, пусть (р?П, 11ф1!=1,— состояние физпч.
системы (// — гильбертово пространство таких состоя-
состояний, (•, •) — скалярное произведение в Н) и Аф^=
= [(оАр, <т>)—(аф, фJ]'^2 — дисперсия величины а в со-
состоянии ф; а
неравенство
стоянии ф; аналогично определяется Дф. Всегда верно
ДфАф 3* 4" I <!«• ?1Ф. ФI-
В частности, координаты х, у, % квантовой частицы и
составляющие ее импульса рх, ру, pz при всех стандарт-
стандартных способах квантования (что означает выбор про-
пространства Н и правила сопоставления физич. величинам
самосопряженных операторов, действующих в Л) пред-
представляются операторами х, у, z и рх, ру, рг такими, что
[Рх, *\=[Ру, У]=[Рг, z]=dE,
где Е — единичный оператор в Я, a ft — т. н. постоян-
постоянная Планка. Таким образом, для любого ф?#
-— Лр~Лг> —
^ 2 ' аф аф^ 2 '
Лит.: [1] Ландау Л. Д., Л и ф ш и ц Е. М., Кванто-
Квантовая механика, 3 изд., М., 1974. Р. А. Минлос.
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ — интеграл
от заданной функции одного переменного, определен-
определенной на нек-ром промежутке — совокупность всех пер-
первообразных данной функции на этом промежутке.
Если функция / определена на нек-ром промежутке Д
числовой осп и F — нек-рая ее первообразная на Л,
т. е. F' (x)--j(x) для всех х?А, то всякая другая пер-
первообразная функция / на А имеет вид F-\-C, где С —
нек-рая постоянная. Следовательно, Н. и. (*) состоит
из всевозможных функций вида Р-\-С.
Неопределенным интегралом Ле-
Лебега от суммируемой на отрезке [а, Ъ] функции /
наз. совокупность всех функций вида
В этом случае равенство F' (х)=}(х) выполняется,
вообще говоря, лишь почти всюду на отрезке [а, Ь].
Неопределенным интегралом Лебега (в широком
смысле) от суммируемой функции /, определенной на
измеримом пространстве X с мерой ц,, наз. функция
множеств
определенная на множестве всех измеримых множеств
Е пространства X.
Лит.: [1] К о л м о г о р о в А. Н., Фомин С. В., Эле-
Элементы теории функций и функционального анализа, 5 изд., М.,
1981; [2] Никольский СМ., Курс математического
анализа, 2 изд., т. 1—2, М., 1975; [з] Ильин В. А., II о з-
н я к Э. Г., Основы математического анализа, 3 изд., ч, 1, М.,
1971. Л. Д. Кудрявцев.
НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ МЕ-
МЕТОД — нахождение искомой функции в виде точной
или приближенной линейной комбинации (конечной
или бесконечной) известных функций. Указанная ли-
линейная комбинация берется с неизвестными коэффициен-
коэффициентами, к-рые определяются тем или иным способом из
условий рассматриваемой задачи. Обычно для них полу-
получается система алгебраич. уравнений.
Классич. примером Н. к. м. является его использо-
использование для разложения правильной рациональной дроби
в комплексной или действительной области на элемен-
элементарные дроби. Пусть Р (z) и Q (z) алгебраич. многочле-
многочлены с комплексными коэффициентами, причем степень
п многочлена Р (z) меньше степени т .многочлена Q(z),
коэффициент при старшем члене многочлена Q (z) ра-
равен 1, z,-—корень многочлена Q(z) кратности ait
г—1, 2, . . ., к, ах+. . .-4-а?—л и, следовательно,
Правильная рациональная дробь Р (z)!Q (z) представи-
ма и притом единственным образом в виде
Q(z)
((=i4i-iv=1
где A (v— неизвестные пока комплексные числа (их
всего т). Для их отыскания обе части равенства при-
приводят к общему знаменателю. После его отбрасывания
и приведения в правой части подобных членов полу-
получается равенство, в каждой частп к-рого стоят много-
многочлены степени не выше чем т — 1: в левой части с изве-
известными коэффициентами, в правой — в виде линейных
комбинаций неизвестных чисел A ,-v. Приравниванием
коэффициентов у одинаковых степеней переменного z
получается система т линейных уравнений относитель-
относительно А (V, к-рая в силу существования и единственности
разложения A) имеет и притом единственное решение.
Иногда бывает удобно использовать несколько иные
приемы нахождения коэффициентов A iv. Напр., пусть
все корни многочлена 0(z) простые и, следовательно,
разложение A) имеет вид
Р (z) VI Ai
Q (z) = 2*i= ! z-z( ¦
После приведения к общему знаменателю обеих час-
частей и его отбрасывания получается равенство
P(z) = ym AiT\m (z~zk).
Полагая в нем последовательно z=zh i=i, 2, . . ., т,
сразу получают
В общем случае бывает полезно комбинировать об::
указанных приема нахождения коэффициентов A ,-v.
Пусть Р (х) н Q (х) — многочлены с действительны-
действительными коэффициентами,
где хг, . . ., хК— действительные корни многочлена
Q (х) соответственно кратностей ах, ¦ . ., а^, а
квадратный трехчлен xS-j-py.z-f-g^ с действительны-
действительными коэффициентами pj, q;- является произведением
(х—zj) (х—zj), где zy — существенно комплексный ко-
корень кратности р"у, / = 1, 2, . . ., I, многочлена Q (z) и
fvX
Тогда для правильной рациональной дроби Р (x)iQ (x)
существует и притом единственное разложение вида
Р (х) учи уча,- А;ц
-^/=1 <"v=l
где коэффициенты Л,ц, ц=1, 2, . . ., а,-, г=1, 2, . . ., /с,
J/yv и .V/v, v = l,'2, . . ., Ру, /=1, 2, . . ., /, суть
действительные числа. Метод их отыскания тот же,
что и в описанном выше комплексном случае: равен-
равенство B) приводится к общему знаменателю, после от-
отбрасывания к-рого приравниваются коэффициенты у
одинаковых степеней переменной х в обеих частях ра-
равенства. В результате получается система т уравне-
уравнении с т неизвестными А щ, MjV и Njv, имеющая един-
единственное решение.
Разложение правильных рациональных дробей на
элементарные применяется, напр., для разложения ра-
рациональных дробей в ряд Лорана (в частности, в ряд
Тейлора), для интегрирования рациональных дробей.
Н. к. м. используется также при интегрировании ра-
рациональных дробей с помощью Остроградского метода,
при интегрировании функций вида Р (х) Y~ax2-\-bx-\-c.
В этом случае интеграл имеет вид
= Q (.г) УаГ* + Ъх + с+ X Г dx C)
J ' ах2+Ьх + с
где степень многочлена Q (х) на единицу меньше степе-
степени многочлена Р(х). Для нахождения коэффициентов
многочлена Q (х) и числа X равенство C) дифференциру-
дифференцируется. После приведения к общему знаменателю н его
отбрасывания приравниваются коэффициенты у одина-
одинаковых степеней переменной х. В результате снова полу-
получается система линейных уравнений с единственным ре-
решением. Подобные методы интегрирования могут быть
применены и в нек-рых других случаях.
Н. к. м. применяется при отыскании решений диф-
дифференциальных уравнений (обыкновенных и с частны-
частными производными) в виде степенных рядов. Для этого
в окрестности рассматриваемой точки степенной ряд
с неопределенными коэффициентами подставляется в
данное уравнение. Иногда в результате для коэффици-
коэффициентов ряда получаются соотношения, из к-рых с по-
помощью заданных начальных или граничных условий
удается найти эти коэффициенты, а следовательно, и
решение уравнения в виде ряда. Напр., решая таким об-
образом гипергеометрическое уравнение, можно получить
разложение в ряд гипергеометрической функ11.ии.
Н. к. м. применяется и в др. способах решения диф-
дифференциальных уравнений, напр. Галеркина методе,
Ритца методе, Треффца методе; используется в чис-
численных методах: в методе Крылова получения коэффи-
коэффициентов векового уравнения, при приближенном ре-
решении интегральных уравнений. Л. Д. Кудрявцев.
НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ МЕТОД
построения численных алгорит-
алгоритмов — специальный метод построения алгоритмов,
основанный на требовании, чтобы алгоритм был точен
или имел погрешность определенного порядка точности
на нек-ром множестве задач.
Типичным примером задач, к-рые наряду с другими
методами могут решаться Н. к. м., являются следую-
следующие (см. [1], [2]). Известны значения функции /(Pi), . . .,
HPn)- Требуется построить формулу для приближе-
приближения функции:
P);
формулу для вычисления производной:
Df*gD(f(Pd, ..-, f(PN), P);
формулу для вычисления интеграла:
/ (/) = $Q / (Р) Р (Р) dP ~ g, (/ (Рг), ..., 1 (PN)).
Для решения последней из этих задач задаются нек-рой
формой приближенного решения, напр, линейной
и определяют коэффициенты Сп из требования, чтобы
приближенная формула /(/)ss^ была точной для функ-
функций из нек-рой совокупности, напр, вида
где wm (Р) фиксированы, ат произвольны. Как пра-
правило, берут M=N. Чтобы равенство
выполнялось при все.х ат, достаточно выполнения соот-
соотношений
Отсюда определяют (если это возможно) искомые С„.
Иногда задаются более сложной формой зависимости.
Напр., при приближении функций часто известно, что
рассматриваемая функция хорошо приближается функ-
функциями вида
g(au ..., од1, Р),
где ат неизвестны. Параметры ап подбирают из системы
уравнений
?(«!, ..., ам, Pn)=f(Pn), n = i, ..., N.
В случае формул численного интегрирования в ка-
качестве неизвестных параметров часто выступают и
координаты узлов интегрирования. Напр., в квадра-
квадратурных формулах Гаусса вида
рассматриваются как свободные параметры координаты
узлов Рп\ благодаря этому удается построить квадра-
квадратуры, точные для многочленов степени 2;V—1. При
конструировании аппроксимаций дифференциальных
уравнений с помощью Н. к. м. требуют, чтобы при под-
подстановке в конечноразностную схему решения задачи
получалась величина рассогласования (невязка) требуе-
требуемого порядка малости по отношению к шагу сетки. Та-
Такой прием положен в основу способов построения мето-
методов Рунге — Кутта и конечноразностных методов
(см. [11, [2]).
Особенно широко Н. к. м. используется при построе-
построении аппроксимаций уравнений с частными производ-
производными (см. [3]).
Лит.: [1] Б е р е з и н И. С, Жидков Н. П., Методы
вычислений, 3 изд., т. 1, М., 1966; 2 изд., т. 2, М., 1962; [2] Бах-
Бахвалов Н. С, Численные методы, 2 изд., М., 1975; [3] Го-
Годунов С. К., Рябенький В. С, Разностные схемы.
Введение в теорию, 2 изд., М., 1977. Н. С. Бахвалов.
НЕОРИЕНТИРУЕМОЕ МНОГООБРАЗИЕ — много-
многообразие, не допускающее ориентации. Таковы, напр.,
Мёбиуса лист, Клейна поверхность, проективное про-
пространство ИРп четной размерности, м. и. Войцеховский.
НЕОСОБАЯ ГРАНИЧНАЯ ТОЧКА, правиль-
правильная граничная точка,— достижимая гра-
граничная точка ? области определения D однозначной
аналитич. функции /(z) комплексного переменного z
такая, что /(z) аналитически продолжается в ? вдоль
любого пути, ведущего из D в С. Иначе говоря,
Н. г. т.— это достижимая граничная точка, не явля-
являющаяся особой граничной точкой. См. также Особая
точка аналитической функции. Е. Д. Соломенцев.
НЕОСЦИЛЛЯЦИИ ПРОМЕЖУТОК, промежу-
промежуток несопряженност и,— связный промежу-
промежуток / числовой оси R такой, что любое нетривиальное
решение x=x{t) линейного обыкновенного дифферен-
дифференциального уравнения n-го порядка с действительными
коэффициентами
xW + a,. (t) *<"-!>+... +а„ @ х = 0, (*)
имеет на нем самое большее п—1 нулей, считая т-
кратный нуль за т нулей. Свойства решений уравнения
(*) на Н. п. хорошо изучены (см., напр., [1] — [31).
Имеются различные обобщения понятия Н. п. для ли-
линейных систем дифференциальных уравнений, для не-
нелинейных дифференциальных уравнений, а также для
других типов уравнений (разностных, с отклоняющимся
аргументом).
Лит.: [1] X а р т м а н Ф., Обыкновенные дифференциаль-
дифференциальные уравнения, пер. с англ., М., 1970; [2] Левин А. Ю.,
«Успехи матем. наук», 1969, т. 24, в. 2, с. 43—96; [3] Cop-
pel W. A., Disconjuffacy, В.—N. Y., 1971.
Ю. В. Комленко.
НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ СТАТИСТИ-
СТАТИСТИКИ — методы математич. статистики, не предполага-
предполагающие знания функционального вида генеральных рас-
распределений. Название «непараметрические методы»
подчеркивает их отличие от классических — парамет-
параметрических — методов, в к-рых предполагается, что ге-
генеральное распределение известно с точностью до
конечного числа параметров, и к-рые позволяют по
результатам наблюдений оценивать неизвестные зна-
значения этих параметров и проверять гипотезы относи-
относительно их значений.
Пример. Пусть Xj, . . ., Хт и Yu . . ., Yn—
две независимые выборки, извлеченные из совокуп-
совокупностей с непрерывными генеральными функциями рас-
распределения F и G; и пусть проверяется гипотеза Но о
равенстве распределений F и G против альтернативы
сдвига, т. е. гипотезы
//j : G(t)=F(t—в)
для всех t и нек-рого 0=^=0. В классич. варианте этой
задачи предполагается, что функции распределения F
и G нормальны, и для проверки рассматриваемой ги-
гипотезы используется Стъюдента критерий. При не-
параметрич. постановке задачи о виде F и G не делается
никаких предположений, кроме непрерывности. Ти-
Типичным непараметрич. критерием для проверки ги-
гипотезы Но против Н^ является Вилкоксона критерий,
основанный на сумме рангов элементов первой выборки
в общем вариационном ряду. Гипотезу о равенстве рас-
распределений отвергают, если вычисленная по наблюде-
наблюдениям статистика критерия оказывается слишком боль-
большой или слишком малой. Статистика критерия Вил-
Вилкоксона проста для вычислений, а ее распределение
при Нп не зависит от F. Критич. значения, отвечающие
заданному значимости уровню при небольших значе-
значениях т и п, находят по таблицам (см., напр., [1]);
при больших т л п пользуются нормальной аппрокси-
аппроксимацией.
В ряде случаев важно не столько проверить гипотезу
об отсутствии сдвига, сколько оценить этот сдвиг 0,
к-рый может интерпретироваться, напр., как измене-
изменение урожайности при смене способа обработки почвы
или дополнительное время сна при применении снот-
снотворного. Оценка параметра 0 посредством величины
Y—X, к-рая вполне удовлетворительна в нормальном
случае, является очень неустойчивой к отклонениям
от нормальности и может даже не быть состоятельной.
Гораздо лучшими свойствами в этом отношении обла-
дает непараметрич. оценка 9 (см. [2]): медиана набора
тп чисел Yj—X,-, г = 1, . . ., т, /=1, . . ., га. Эта оценка
тесно связана с критерием Вплкоксона. Можно ска-
сказать, что она находится в том же отношении к оценке
У—X, в каком критерий Вилкоксона находится к
критерию Стьюдента.
Несмотря на многообразие задач, решаемых с помо-
помощью негнараметрич. методов, эти задачи можно условно
разделить на две большие части: задачи проверки гипо-
гипотез и задачи оценки неизвестных распределений и пара-
параметров, к-рые понимаются как нек-рые функционалы
от этих распределений.
Непараметрич. проверка статистич. гипотез — наи-
наиболее развитая часть Н. м. с. Требуется построить про-
процедуру (критерий), позволяющую принять или отверг-
отвергнуть проверяемую гипотезу при заданной альтернативе.
Типичным примером является проверка согласия, дру-
другими важными для приложений примерами являются
проверка симметрии, независимости и случайности.
Задача проверки согласия состоит в
том, что по выборке из совокупности с генеральной
функцией распределения G требуется проверить ги-
гипотезу о том, что G=F, где F — заданная непрерывная
функция распределения. Непараметрич. характер за-
задачи проявляется здесь в непараметричностп альтерна-
альтернативы, к-рая может быть сформулирована, напр., в
одностороннем варианте: F<CG или F>G, либо в дву-
двустороннем: РФ-G.
Задача проверки симметрии заклю-
заключается в проверке симметрии генеральной функции
распределения G относительно заданной точки ха, т. е.
равенства
G(xo+t)+G(xo-t)=i.
В качестве альтернатив могут выступать односторонние
условия
со строгим неравенством хотя бы для одного t либо
двустороннее условие того же типа.
Задача проверки независимости
возникает в тех случаях, когда необходимо проверить,
являются ли независимыми два признака, наблюдае-
наблюдаемые у одного и того же объекта, по независимым на-
наблюдениям над такими объектами. Сходным образом
формулируется п гипотеза случайности, когда предпо-
предполагается, что элементы выборки — независимые и
одинаково распределенные величины. Наряду с аль-
альтернативами общего вида встречаются случаи, когда
оказывается возможным указать, чем именно буду;
отличаться распределения элементов выборки при аль-
альтернативе; так возникают, напр., альтернативы тренда
и регрессии.
Способы алгоритмич. построения непараметрич. про-
процедур с заданными свойствами разработаны пока недо-
недостаточно, и большую роль в выборе подходящей проце-
процедуры играют обычно интуиция и эвристич. соображения.
На этом пути накоплено большое количество способов и
приемов решения часто встречающихся непараметрич.
задач (см. C1).
Большая группа непараметрич. критериев основан;/
на использовании эмпирпч. функции распределения.
Пусть Fn— эмппрпч. функция распределения, постро-
построенная по выборке объема п из совокупности с генераль-
генеральной функцией распределения F. В силу теоремы Гли-
венко — Кантеллп
sup | Fn (t) — F (t) |—i-O при re —> oo
с вероятностью 1. Таким образом, эмпирическая и
истинная функции распределения с вероятностью 1
неограниченно сближаются, и на мере их близости
можно основывать критерии согласия с гипотезой об
истинной функции распределения.
Первыми критериями этого типа были Колмогорова
критерий и Крамера — Мизеса критерий, предложен-
предложенные в начале 30-х гг. 20 в. и основанные соответственно
на статистиках
Следует отметить, что обе эти статистики имеют рас-
распределения, не зависящие от генеральной функции рас-
распределения F, если только последняя непрерывна.
Их предельные распределения, найденные в середине
30-х гг. А. Н. Колмогоровым и II. В. Смирновым, табу-
табулированы, что позволяет приближенно найти границу
критич. области, отвечающей заданному уровню зна-
значимости (см. [1]).
Предложено и изучено много вариантов критериев со-
согласия, основанных на разности Fn и F, напр. Рснъи
критерий, критерии Андерсона — Дарлинга, Ватсона
и др. (см. [4]). Для успешного их применения в случае
больших выборок необходимо в первую очередь знать
соответствующие предельные распределения. Послед-
Последние могут быть найдены с помощью подхода, в соответ-
соответствии с к-ры.м статистика критерия представляется в
виде непрерывного функционала от эмпирич. процесса
где Gn(t) — эмпирическая функция распределения, по-
построенная по выборке объема п из равномерного рас-
распределения на [0, 1]. Процесс !„(*) слабо сходится в
пространстве D [0,1] к нек-рому гауссовскому процессу,
т. н. броуновскому мосту (см. [6]). Поэтому предельное
распределение изучаемой статистики совпадает с рас-
распределением соответствующего функционала от бро-
броуновского моста, к-рое вычисляется с помощью стан-
стандартных методов.
Существуют модификации статистик Dn и ш%, пред-
предназначенные для проверки гипотез о распределении
в многомерном случае, а также для проверки гипотез
независимости и симметрии. В этих случаях возникает
ряд дополнительных трудностей. Напр., в многомерном
случае все рассмотренные статистики теряют свойство
универсальности (независимости от исходного распре-
распределения). Наиболее важен случай равномерного рас-
распределения на единичном кубе, поскольку выборку из
многомерного распределения можно тем или иным спо-
способом превратить в выборку из равномерного распре-
распределения. Однако ни точное, ни предельное распре-
распределения статистики Колмогорова неизвестны A982)
даже в этом простом случае. Сходные затруднения
появляются и в том случае, когда проверяется не
простая, а сложная гипотеза о распределении, т. е.
если предполагается, что генеральная функция рас-
распределения имеет вид F(t, в), где 6 — неизвестный
параметр, одномерный или многомерный. В этом слу-
случае естественно оценить 6 по выборке, напр, посред-
посредством оценки максимального правдоподобия 0„, и срав-
сравнивать Fn(t) с F(t, ёп). Статистики />„, ы„ и их раз-
разновидности можно построить, как и в случае простой
гипотезы. Однако распределения этих статистик —
как точные, так и предельные — оказываются снова
зависящими от вида F, а во многих случаях — и от не-
неизвестного истинного значения 8. Задача вычисления
этих распределений трудна и точный вид, их неизвестен,
хотя для статистик типа соя в ряде случаев удается
составить таблицы предельного распределения (см. [5]).
Для нек-рых других статистик известны процентные
точки, вычисленные экспериментальным путем.
Наряду с рассмотренными выше критериями согла-
согласия строятся их двухвыборочные и многовыборочные
аналоги, к-рые могут использоваться как для проверки
согласия, так и для проверки однородности нескольких
выборок (см. Смирнова критерий).
Общим свойством критериев согласия и однороднос-
однородности, основанных на эмшгрич. функции распределения,
является состоятельность против любых альтернатив.
Однако выбор той илп иной статистики в практпч. за-
задаче затруднен недостаточной изученностью их мощ-
ностных свойств. При больших объемах выборок мож-
можно опираться на значения асимптотич. относительной
эффективности (АОЭ) по Питмену, вычисленные для
ряда наиболее простых статистик (см. [7]).
Другую группу непараметрич. критериев образуют
ранговые критерии. Наиболее раннее использование ран-
рангового критерия знаков встречается у Дж. Арбетнот-
та (J. Arbuthnott, 1710), к-рый использовал его при
анализе статпетпч. данных о рождаемости мальчиков
и девочек для получения «аргументов в пользу боже-
божественного провидения». Однако современный период
развития ранговых критериев начинается в кон. 30-х гг.
20 в. После опубликования в 1945 работы Ф. Вилкок-
сона (F. Wilcoxon), в к-рой был предложен ранговый
критерий, носящий его имя, ранговые методы вступают
в период интенсивного развития.
Использование ранговых процедур основано на сле-
следующем соображении. Поскольку вектор рангов вместе
с вектором порядковых статистик содержит всю инфор-
информацию, содержащуюся в выборке, то нек-рая доля этой
информации содержится только в ранговом векторе. По-
Поэтому можно строить статнетич. процедуры, основыва-
основываясь только на рангах и не используя знание самих вы-
выборочных значений. Преимуществом таких процедур
является вычислительная простота, вытекающая из
целочисленное™ рангов. Другой важной особенностью
ранговых тгроцедур является их применимость и в тех
случаях, когда наблюдения носят не количественный, а
качественный характер, лишь бы они допускали упоря-
упорядочение, что особенно важно в исследованиях по соци-
социологии, психологии и медицине. Наконец, распределе-
распределения ранговых статистик при основной гипотезе не за-
зависят от генерального распределения, что позволяет
раз и навсегда вычислить эти распределения.
По мере развития ранговых методов выяснилось, что
доля информации, содержащаяся в векторе рангов, мо-
может оказаться значительной, что обеспечивает этим
процедурам высокую эффективность. В рассмотренном
выше примере, связанном с проверкой однородности
двух выборок, расширение области применимости крите-
критерия приводит к потере в мощности, и в нормальном
случае критерий Стьюдента имеет большую мощность,
нежели любой ранговый критерий. Однако при боль-
большом числе наблюдений критерий Вплкоксона мало про-
проигрывает критерию Стьюдента. Оказывается, что в
нормальном случае АОЭ критерия Вилкоксона по от-
отношению к критерию Стьюдента равна 3/я = 0,955.
Если же генеральное распределение отлично от нор-
нормального, то указанная АОЭ может быть сколь угодно
большой, но никогда не опускается ниже значения
0,864 (см. [4]). Более того, существует ранговый кри-
критерий ("т. н. критерий нормальных м е-
т о к), АОЭ к-рого по отношению к критерию Стьюден-
Стьюдента равна 1 в нормальном случае и превосходит 1 при
любом отклонении от нормальности. Таким образом,
этот критерий асимптотически оказывается предпочти-
предпочтительнее критерия Стьюдента.
Другой пример связан с проверкой гипотезы симмет-
симметрии. Пусть выборка Хг, . . ., Хп извлечена из совокуп-
совокупности с генеральной плотностью / и проверяется ги-
потеза о симметричности / относительно нуля снова при
альтернативе сдвига. Наиболее простым критерием в
этой задаче является знаков критерий, основанный на
числе положительных значений среди X,-. Знаково-
анговый критерий Вилкоксона основан на статистике
х >о^' гДе ^ — ранг элемента X,- в вариационном
ряду для \Хи\, . . ., \Хп\. Статистика этого критерия
использует не только информацию о знаках наблюде-
наблюдений, но и информацию о их величине. Поэтому можно
рассчитывать, что критерий Вилкоксона окажется
более эффективным, чем критерий знаков. Действи-
Действительно, АОЭ этих критериев по отношению к критерию
Стьюдента равна соответственно 3/я — 0,955 и 2/я=
= 0,637 (в нормальном случае). Таким образом, крите-
критерий Вплкоксона в 1,5 раза превосходит критерий зна-
знаков п мало уступает критерию Стьюдента.
Еще один пример связан с проверкой гипотезы не-
независимости. Пусть имеется ряд объектов, каждый из
к-рых обладает двумя признаками, количественными
или качественными (математические и музыкальные
способности учащегося, цвет и спелость ягоды, и т. д..).
Предполагается, что наблюдения над качественными
признаками могут быть упорядочены. Требуется по п
независимым наблюдениям над объектами проверить
гипотезу о независимости признаков против, напр.,
альтернативы их положительной зависимости. Пусть
R,- и S,- ранги признаков, соответствующие i-му на-
наблюдению. Естественный критерий для проверки неза-
независимости основан на коэффициенте ранговой корре-
корреляции Сппрмена rs, к-рый может быть вычислен но
формуле
Г о = 1 — .
J п3 — п
Гипотеза независимости отвергается при больших, т. е.
близких к 1, значениях rs. Крптич. значения при малых
п находят по таблицам, при больших п пользуются
нормальной аппроксимацией. АОЭ критерия, осно-
основанного на rs, по отношению к критерию, основанному
на выборочном коэффициенте корреляции, снова до-
довольно высока и равна 9/л2-=0,912 (см. [9]).
Поскольку для проверки каждой непараметрич. ги-
гипотезы существует много ранговых критериев, пред-
предложенных часто из эврисгич. соображений, выбор кри-
критерия следует основывать на каких-либо соображениях
оптимальности. Как известно, равномерно наиболее
мощные критерии в классе всех возможных альтерна-
альтернатив редко существуют даже в иараметрпч. случае.
Поэтому роль оптимальных ранговых критериев для
конечных объемов выборок выполняют локально наи-
наиболее мощные критерии. Так, напр., критерий Внлкок-
сона является локально наиболее мощным в двухвыбо-
рочной задаче проверки однородности против альтерна-
альтернативы сдвига для логистич. распределения с плотностью
ех{1-\-ех)~2, а критерий нормальных меток— в той
же задаче для нормального распределения. В асимпто-
тнч. теории для отражения свойства оптимальности
используются те или иные понятия аспмптотич. эф-
эффективности, причем локально наиболее мощные кри-
критерии обычно оказываются и асимптотически оптималь-
оптимальными (см. [8]).
В теории ранговых критериев предполагают, что рас-
распределения наблюдений непрерывны, так что наблюде-
наблюдения могут быть упорядочены без совпадений, и ранго-
ранговые статистики определяются однозначно. Однако на
практике наблюдения всегда округляются, п поэтому
совпадения будут иногда появляться. Наиболее употре-
употребительны следующие два способа преодоления этой труд-
трудности. Первый состоит в том, чтобы упорядочить сов-
совпавшие наблюдения случайным образом. При втором ме-
методе каждому из группы совпавших наблюдений припи-
сывается средний ранг этой группы. Достоинства обоих
методов исследованы пока недостаточно.
Непараметрич. оценивание представляет собой раз-
раздел ненараметрич. статистики, имеющий дело с зада-
задачами оценки неизвестных распределений или функцио-
функционалов от них таких, как квантили, моменты, мода, эн-
энтропия, информация ио Фишеру и т. д.
Общепринятой оценкой неизвестной функции распре-
распределения является эмпирия, функция распределения.
Сильная равномерная состоятельность ее как оценки не-
неизвестной функции распределения следует из теоремы
Гливенко — Кантелли, а минимаксный характер уста-
установлен в [10]. Состоятельное же оценивание неизвест-
неизвестной плотности распределения представляет собой более
сложную задачу. Для корректной постановки задачи
оценивания необходима дополнительная априорная ин-
информация о классе плотностей F, к к-рому принадле-
принадлежит оцениваемая плотность /. В класенч. постановке
априорное семейство плотностей задается в нараме-
трич. форме и определяется конечномерным вектором не-
неизвестных параметров. При непараметрич. постановке
задача приобретает бесконечномерный характер, и
точность оценивания неизвестной плотности существен-
существенно зависит (см. [11]) от геометрнч. характеристик «мас-
«массивности» класса F. В качестве последних использу-
используются, напр., ?г-яорный поперечник н «-мерный внутрен-
внутренний радиус класса F.
Наиболее распространенными оценками неизвестной
плотности / являются оценки
где Xj— наблюдения, функция К абсолютно интегри-
интегрируема и удовлетворяет условию
а последовательность hn такова, что Д„—>-0, ий„—коз.
В нек-рых случаях используются другие ненараметрич.
оценки плотности: более простые (гистограмма, поли-
полигон частот) или более сложные, напр, проекционные
оценки Ченцова. Вопрос о точности приближения
этими оценками неизвестной плотности в зависимости
от свойств класса F хорошо изучен (см. [11], [12]).
Эмпирич. функцию распределения и непараметрнч.
оценку плотности можно использовать для оценки функ-
функционалов от неизвестных генеральных распределений;
для этого достаточно подставить в выражение для оце-
оцениваемого функционала вместо неизвестного распреде-
распределения его оценку. Сама идея и начало ее реализации
восходит к работам Р. Мизеса (R. Mises) 30—40-х гг.
20 в. Доказано, что при нек-рых ограничениях на класг
оцениваемых функционалов и на непараметрич. класс
распределений существует минимаксная граница снизу
качества непараметрич. оценок (см. [12]). Непараметрпч.
оценивание тесно связано с проблемой построения роба-
стных оценок.
Лит.: [1] К'ныпев Л. Н., Смирнов Н. В., Таблицы
математической статистики, 2 изд., М., 1968; [2] Н о d g e s J.,
Lelira a n n E., с Ann. Math. Stat.», 19(!3, v. 34, №2, p. 598 —
611; [31 Walsh J. E., Handbook of nonparametric statistics,
v. 1—3, Princeton, 19E2, 19A5, 1968; [4] Кен да л л М.,
Стьюарт А., Статистические выводы и связи, пер. с англ.,
М., 1973; [5] М а р т ы н о в Г. В., Критерии омега — квад-
квадрат, М., 1978; [6J Б и л л и н г с л и П., Сходимость вероят-
вероятностных мер, пер. с англ., М., 1977; [7] W i e a n d H., «Ann.
Stat.», 1976, v. 4, № 5, р. 1003—11; [8] Г ае к Я.,Шидак 3..
Теория ранговых критериев, пер. с англ., М., 1971; [9] К е п-
дэл М., Ранговые корреляции, пер. с англ., М., 1975; [101
Dvoretzky A., Kiefer J., Wolfowjtz J., «Ann.
Math. Stat.», 1956, v. 27, JV. 3, p. 642—69; [111 Ч е н ц о в Н. Н.,
Статистические решающие правила и оптимальные выводы, М.,
1972; [12] Ибрагимов И. А., X а с ь м и н с к и й Р. 3.,
Асимптотическая теория оценивания, М., 1979; [13] Ван дер
Варден Б. Л., Математическая статистика, пер. с нем., М.,
1960; [14] Л е м а п Э., Проверка статистических гипотез, пер.
с англ., 2 изд., М., 1979; [151 Шметтерер Л., Введение в
математическую статистику, пер. с нем., М,, 1976; [16] L e li-
lima nn Е., Nonparametrics: statistical methods based on ranks,
S. F.— N. Y., 1975. Я. Ю. Никитин-
НЕПАРАМЕТРИЧЕСКИЙ КРИТЕРИЙ — стати-
статистический критерий для проверки гипотезы На : 0?
?вос6 против альтернативы Н1 : 9?в1=в\в„,
когда сама задача статистич. проверки Яо против Н%
является непараметрпческой, т. е., по крайней мере,
одно из двух параметрич. множеств 60 и в1 не является
топологически эквивалентным подмножеству евклидова
пространства. Наряду с этим определением широко рас-
распространено другое, согласно к-рому статистнч. кри'
терий наз. непараметр пческпм, если статп-
стич. выводы, получаемые с помощью этого критерия,
не зависят от распределений вероятностей случайных
величин, по результатам наблюдений к-рых проверяют
Но против Н\. В этом случае вместо термина Н. к,
часто употребляют термин «критерий, свободный от
распределения». Колмогорова критерий является клас
снч. примером Н. к. Ом. также Непараметрические ме-
методы статистики, Колмогорова — Смирнова критерий.
Лит.: 11J Р а о СР., Линейные статистические методы и
их применения, пер. с англ., М., 1968; [2] Б о л ь ш е в Л. Н.,
Смирнов Н. В., Таблицы математической статистики,
[2 изд.], М., 1968; [3] И б р а г и м о в И. Л., X а с ь м и н-
с к и й Р. 3., Асимптотическая теория оценивания, М., 1979;
[4] К е н д а л л М., С т ь ю а р т А., Статистические пыводы
и связи, пер. с англ., М., 1973. М. С. Никулин.
НЕПАСКАЛЕВА ГЕОМЕТРИЯ — геометрия с не-
некоммутативным умножением. Вследствие того, что в
аффинной геометрии свойство коммутативности умноже-
умножения эквивалентно Паскаля теореме, то неыаскалевой
обычно наз. геометрию, в к-рой не имеет места предло-
предложение: иусть на каждой из двух пересекающихся пря-
прямых даны три точки А, В, С и соответственно Alf
В\, С\, отличные от точки пересечения данных прямых;
если СВг параллельна ВСг и СА1 параллельна АСг, то
В А х будет параллельна ABt; эту теорему иногда наз.
теоремой Папиа, она является частным слу-
случаем теоремы Паппа — Паскаля из теории конич. се-
сечений.
Возможность построения Н. г. вытекает из того,
что указанная теорема Паскаля не является следствием
аксиом инцидентности, порядка, параллельности при
условии исключения метрнч. аксиом в системе аксиом
Гильберта. С другой стороны, существование Н. г,
связано также с возможностью построения геометрия
над некоммутативным телом, то есть Н. г. является в
то же время и неархимедовой геометрией.
Значение Н. г. определяется ролью теоремы Паскаля
в исследованиях, связанных с установлением незави-
независимости системы аксиом, логич. связи между предло-
предложениями.
Лит.: [1] Гильберт Д., Основания геометрии, пер. с
нем., М.— Л., 1948; [2] В i e b е г b а с h L., Einleitung in
die hohere Geometrie, Lpz.— В., 1933; [3] С к о р н я к о в Л.
А., «Успехи матем. наук», 1951, т. 6, в. 6, с. 112—54.
Л. А. Сидоров.
НЕПЕРОВО ЧИСЛО — см. е (число).
НЕПОДВИЖНАЯ ОСОБАЯ ТОЧКА — общая осо-
особая точка z0 всех решений дифференциального урав-
уравнения F(z, w, w')=0 (F — аналнтич. функция), рас-
рассматриваемых как функции w(z) комплексного пере-
переменного z, начальные условия к-рых пробегают
нек-рую область в пространстве (z, w).
Лит.: [1] Голубев В. В., Лекции по аналитической
теории дифференциальных уравнений, 2 изд., М.— Л., 1950.
Ю. С. Ллъяшеико t
НЕПОДВИЖНАЯ ТОЧКА — 1) Н. т. отобра-
отображения F множества X — такая точка х? X,
что F(x)=--x. Доказательства существования Н. т. н
методы нахождения Н. т.— важные задачи математики,
т. к. решение всякого уравнения f(x)=0 путем преобра-
преобразования его к виду z±j(х) = х сводится к нахождению
Н. т. отображения F= I±{, где / — тождественный опе-
оператор. В зависимости от того, какой структурой наделе-
но множество X и каковы свойства отображения F,
возникают те или иные принципы неподвиж-
неподвижной точки. Наибольший интерес представляют
случаи, когда X — топологпч. пространство и F —
непрерывный в том или ином смысле оператор.
Простейшим из таких принципов является прин-
принцип сжимающих о т о б р а ж е н п й. Пусть
X — полное метрнч. пространство и оператор F : Х-+Х
таков, что
p(F(x), F(y))<q[>{x, у), 0<q<i. A)
Тогда оператор F имеет в точности одну Н. т. х, к-рая
может быть получена как предел последовательных
приближений xn=F(xn_1), n=l, 2, . . ., где хо?Х про-
произвольно. Этим принципом не только устанавливается
существование Н. т., но и указывается способ ее на-
нахождения, причем довольно просто оценивается быстро-
быстрота сходимости последовательности {хп} к х. В общем
случае условие A) нельзя заменить условием
p(F(x), F(y))<p(x,y), B)
но если X компактно, то условие B) по-прежнему обе-
обеспечивает наличие у оператора F единственной Н. т.
Более общим является принцип обобщен-
обобщенного сжатия. Пусть, как и выше, X — полное
метрпч. пространство, F : Х-+Х и
p(F(x), F{y))<g(a, p, )p(.r, ?/) C)
при a«p(r, у)<Р, где ?(а, Р)<1 для 0<a<f?<oo.
Тогда F имеет единственную Н. т. Если X — банахово
пространство, то условие A) есть не что иное, как ус-
условие Липшица для оператора F с константой, мень-
меньшей единицы. Принцип сжимающих отображений ши-
широко используется для доказательства существова-
существования и единственности решений алгебраических, диф-
дифференциальных, интегральных и других уравнений и
для приближенного нахождения решений этих урав-
уравнений.
Существуют другие условия тонологич. характера,
обеспечивающие существование Н. т. у оператора F.
Наиболее известным из них является принцип
Шаудера. Пусть X — банахово пространство и
F — вполне непрерывный оператор, отображающий
ограниченное выпуклое замкнутое множество CczX на
свою часть. Тогда F имеет в С хотя бы одну Н. т. Однако
в этом случае вопрос о числе Н. т. остается открытым,
и нет указаний о способе их нахождения.
Пример (теорема Пеан о). Пусть функция
f(t, x) непрерывна по совокупности переменных в обла-
области \t—<0|<о, \х—хо|<6 и P=max | }{t,x)\ в этой об-
области. Если h=min {а, 6/р}, то на отрезке [t0—h,
tu-\-h] существует хотя бы одно решение уравнения
x'(t) = f(t,x) D)
такое, что
хD) = хо- E)
Уравнение D) вместе с условием E) эквивалентно ин-
интегральному уравнению
x(t)=xo+\' /(т, x(T))di.
J 'о
Оператор
F(x)=xo+V /(т, х{%))йт
J * о
в условиях теоремы отображает шар |]х—ro]|<:b про-
пространства t'Uo—^> tg-\-h] в себя и вполне непрерывен на
этом шаре. Поэтому в силу принципа Шаудера сущест-
существует Н. т. оператора F, к-рая и является решением
задачи Коши (см. [4], E1).
Обобщением принципа Шаудера является п р и н ц и п
Тихонова. Пусть X — отделимое локально вы-
пуклое пространство и F — непрерывный оператор,
отображающий выпуклое компактное множество СсХ
в себя. Тогда F имеет на С хотя бы одну Н. т. Существу-
Существуют и другие обобщения принципа Шаудера, в том числе
на многозначные отображения, однако во всех случаях
необходимо предполагать выпуклость множества С,
без чего теорема Шаудера и ее обобщения становятся
неверными. Возможно комбинирование принципа Ша-
Шаудера и принципа сжимающих отображений. Пусть
оператор F, преобразующий ограниченное замкнутое
выпуклое множество С банахова пространства X в себя,
можно представить в виде F=F1-{-Fi, где 1\— вполне
непрерывный и F2— сжимающий операторы. Тогда F
имеет в С хотя бы одну Н. т.
Принципы шаудеровского типа могут быть следую-
следующим образом распространены на некомпактные опера-
операторы. Пусть М — ограниченное множество полного
метрич. пространства X. Мерой некомпактно-
с т п %(М) этого множества наз. точная нижняя гра-
граница значений тех е>0, при к-рых существует конечная
е-сетъ для М. Для компактных множеств %(Л1)=0.
Оператор F : Х-^-Х наз. уплотняющим, если
%(F(Л/))</(Л/) для любого некомпактного ограничен-
ограниченного множества МсХ. Пусть уплотняющий оператор F
преобразует ограниченное выпуклое замкнутое мно-
множество СсХ в себя. Тогда F имеет в С хотя бы одну Н. т.
I? банаховых пространствах можно вводить и другие
меры некомпактности, варьируя к-рые, можно полу-
получать разные варианты теоремы, позволяющие доказы-
доказывать существование решений различных дифференци-
дифференциальных, интегральных п иных уравнений с не вполне
непрерывными операторами.
Привлечение более тонких топологнч. понятий поз-
позволяет сформулировать более сильные признаки сущест-
существования Н. т. Пусть на границе дМ ограниченной
области М банахова пространства X задано невырожден-
невырожденное векторное поле Ф, т. е. каждой точке х?дМ постав-
поставлен в соответствие ненулевой вектор Ф (х). Такому полю
при выполнении нек-рых условий можно соотнести це-
целое число, наз. вращением у(Ф, дМ) поля Ф на
дМ. Пусть сначала X конечномерно и Ф непрерывно
на дМ. Тогда у(Ф, дМ) определяется как топология.
степень отображения г|1(ж)=ф (хI\\Ф (х)\\ множества дМ
на единичную сферу ||г||=1. Пусть теперь X — бана-
банахово бесконечномерное пространство и Ф(х) = х—F(x),
где F — вполне непрерывный на М оператор. Такие
поля наз. вполне непрерывными.
Пусть конечномерное подпространство ХпаХ дос-
достаточно хорошо аппроксимирует F (М) и Рп— оператор
проектирования F{M) на Xп. Если \\PnF(х) — F(х)\\
достаточно мало для х?дМ, то поле Фп=1д—PnF
также невырождено на дМ(]Хп и его вращение уп
не зависит от выбора аппроксимирующих подпрост-
подпространств Хп и оператора Рп. Это число уп наз. враще-
вращением вполне непрерывного вектор-
векторного поля Ф на границе дМ и обозначается
¦у-(Ф, дМ). Важным свойством вращения является то,
что оно не меняется при гомотопных преобразовани-
преобразованиях поля Ф.
Принцип Лере — Шаудера. Пусть на за-
замыкании М ограниченной области М банахова про-
пространства X задано вполне непрерывное векторное
иоле Ф, невырожденное на дМ, и пусть у(Ф) дМ)фО.
Тогда Ф обращается в пуль по крайней мере в одной
точке х?М, т. е. оператор F имеет в М хотя бы одну
II. т. Инвариантность вращения при гомотопных пре-
преобразованиях позволяет вычислять вращение следую-
следующим образом. По заданному полю Ф (х) строится кон-
континуум полей Ф1.г, к\ а«Л«{5, так, что все эти поля
гомотопны друг другу и Ф(х, Я0)=Ф (х) при нек-ром
^GI PI- Если при другом Я?[а, E] вращение поля
Ф (х, X) легко вычисляется и равно к, то также
•у(Ф, дМ) = к. Этим приемом, использовавшим степень
отображения для установления наличия Н. т. у вполне
непрерывных операторов, получено доказательство су-
существования решений ряда довольно сложных диффе-
дифференциальных уравнений с частными производными выс-
высших порядков.
Усиливая требования, предъявляемые к простран-
пространству, можно ослабить ограничения, налагаемые на опе-
оператор. Напр., оператор F наз. нерастягиваю-
щ к м, если р (F(x), F(y))^.p(x, у). Пусть банахово
пространство равномерно выпукло (напр., гильбертово)
и F — нерастягивающий оператор, преобразующий
ограниченное замкнутое выпуклое множество СсХ
в себя. Тогда F имеет на С хотя бы одну Н. т.
Все предыдущие принципы Н. т. предполагали не-
непрерывность оператора F. Если наделить X структурой
частично упорядоченного множества, то в нек-рых слу-
случаях требование непрерывности можно опустить.
Принцип Биркгофа — Т а р с к о г о.
Пусть X — полная решетка и F — изотонный оператор
из X в X. Тогда F имеет по крайней мере одну Н. т.
Имеет место следующий вариант этого принципа. Пусть
X — условно полная решетка, т. е. всякое ограничен-
ограниченное подмножество множества X имеет в X точную верх-
верхнюю и нижнюю границы. Если F — изотонный опера-
оператор, отображающий порядковый интервал [я, Ь] =
= {x\a^ixiCb}ciX в себя, то F имеет на [я, Ь] по край-
крайней мере одну Н. т.
Комбинирование топологич. условий с порядковыми
приводит к новым принципам Н. т. Напр., пусть X —
частично упорядоченное банахово пространство и F —
непрерывный пзотонный оператор, отображающий по-
порядковый интервал [а, Ъ\ в себя. Если полуупорядочи-
полуупорядочивание пространства X правильное, т. е. всякая моно-
монотонно возрастающая порядково ограниченная после-
последовательность {хп}аХ сходится по норме простран-
пространства X, то оператор F имеет на [я, Ь] хотя бы одну.Н. т.
При этом условия теоремы не требуют решеточной упо-
упорядоченности пространства X, т. е. не для всяких двух
элементов х, у ? X должен в X существовать их sup и
inf. Наконец, Н. т. линейного оператора F есть соб-
собственный элемент этого оператора, соответствующий
собственному значению, равному единице.
Лит.: [1] Люстерник Л. А., Соболев В. И.,
Элементы функционального анализа, 2 изд., М., 1965; [2] К р а с-
носельский М. А., Топологические методы в теории
нелинейных интегральных уравнений, М., 1956; [3] К р а с-
носельский М. А., Забрейко П. П., Геометриче-
Геометрические методы нелинейного анализа. М., 1975; [4] Н е м ы ц-
кий В. В., «Успехи матем. наук», 1936, в. 1, с. 141—74;
[5] Л е р э й Ж., Ш а у д е р Ю., там же, 1946, т. 1, в. 3—4,
с. 71—95; [51 Садовский Б. Н., там же, 1972, т. 27,
в. 1, с. 81 — 146. В. И. Соболев.
2) Н. т. д р о б н о - л и н е й н о г о преобра-
преобразования А замкнутой комплексной плоскости
С — точка р?С, удовлетворяющая уравнению
ар_+_Ь
где
аг
Л:С—>-С, г —>- w = A (z) =
cz +d
есть дробно-линейное преобразование, я, Ъ, с,
и ad—ЪсфО, "C*=C(J {oo}. Если Аф1 (/ — тождест-
тождественное преобразование w=z), то А имеет одну или две
Н. т. С помощью Н. т. можно классифицировать
дробно-линейные отображения (I из рассмотрения ис-
исключается). О. М. Фоменко.
3) Н. т. системы обыкновенных диф-
дифференциальных уравнений или дина-
динамической системы — см. Равновесия положение.
НЕПОЛНАЯ БЕТА-ФУНКЦИЯ — функция, опре-
определяемая формулой
0<Ж 1, а > О, Ь > О,
где
Если а — целое, то
Представление в виде ряда:
Jxla' °'~ aB (о, Ь) \J ' Х-<„ = 0 В (а + Ь, n + 1) |
О < ж < 1;
в виде непрерывной дроби:
/ (а м
где
t (а + т) (а + Ъ + т) х , т (Ъ-т) х
a2m + l (o+2m) (а +2т+1) ' 2т (о + 2т-1) (n +
Аспмптотич. представление при больших а п Ь
(а, Ъ) = ф 1 3 )
I. У [аA-10]2/3/а+(Ь.х:J/3/Ь
min (а, Ь)
где
Аспмптотич. представление при больших Ь и огра-
ограниченных а:
где
Связь с пшергеометрич. функцией:
Рекуррентные соотношения:
Ix{a, 6) = l-/i_,(b, я),
У, (в, Ь)=а-/,(в-1
Лит.: [1] Справочник по специальным функциям, пер. с
англ., М., 1979; [2J Пирсон К., Таблицы неполной йета-
функции, пер. с англ., М., 1974. В. И. Пагурова.
НЕПОЛНАЯ ГАММА-ФУНКЦИЯ — функция, оп-
определяемая формулой
где
Г (т)= \ е~Чт~1 dt—гамма-функция.
J О
Если 7?^0 — целое, то
I (х, и + 1) = 1 — е-* У -^-.
Представление в виде ряда:
, . е-Ххт I , у°° х*
1 (х, т) — г (m+1) \1"r^/i_] (m + l) ... (т + й)/'
в виде непрерывной дроби:
. ._. х^е-х \ 1 1 -т 1 2-т 2 )
У (ж, т) —1 — Г(т) ^— -j^- — -j-p x+ . . . j".
Асимптотич. представление при больших х:
/ (г, т) =
Г (m) \-*-^i=0 ж'ГA-т) J
Асимптотич. представление при больших т:
I (х, т)=--Ф B У~с~ ym—l)+O (m~lf"),
/(х, т) =
где
фB) ^ еЛ_
!¦ 2Я J -о»
Связь с вырожденной гппергеометрич. функцией:
Связь с многочленами Лагерра Л^ (ж):
Рекуррентное соотношение
ml (х, т-\-1)-\-х1 (х, т—\.)={х-\-т) I (х, т).
Лит.: [1] Справочник по специальным функциям, пер. с
англ., М., 1979; [2j П а г у р о в а В. И., Таблицы неполной
гамма-функции, М., 1963. В. И. Пагурова.
НЕПРАВИЛЬНОСТИ КОЭФФИЦИЕНТЫ л и н е й-
и о ii системы обыкновенных д и ф ф е-
ренциальных уравнений — неотрицатель-
неотрицательные функции о (А), равные нулю в том и только в том
случае, если система
x = A(t) х, (*)
где А (¦) — суммируемое на каждом отрезке отобра-
отображение R + ->Hom (R", R") (пли R+-*Hom (С", С")),—
правильная линейная система. Наиболее известны (и
наиболее просто определяются) следующие Н. к.
1) Коэффициент неправильности
Ляпунова [1]
X; (A)— lim ~
*~ t —*¦ 4- с
где Я/ (А) —Ляпунова характеристические показа-
показатели системы (*), занумерованные в порядке невозра-
невозрастания, a tr A (t) — след отображения A (t).
2) Коэффициент неправильности
Пер р.о н а [2]
ап(А)= max (А,,- D) + А,п + 1_,- (— А*}),
1 ^С i <; «
где А* (I) — отображение, сопряженное к A(t).
Если система (*) есть система уравнений в вариаци-
вариациях гамильтоновой системы
ОН
то ге=2А- и
Xi(~A*)=k;(A), i = l, ..., и;
поэтому для правильности системы уравнений в вариа-
циях гамильтоновой системы необходимо и достаточно,
чтобы
ki(A) = -Xn + 1_;(A), i = l, ..., к
(теорема Персидского)
Имеются также другие Н. к. (см. [4] — [61).
Лит.: [1] Ляпунов А. М., Собр. соч., т. 2, М., 1956;
[2] Р е г г о п О., «Math. Z.», 1929/1930, Bd 31, S. 748—66;
[3] М а л к и н И. Г., Теория устойчивости движения, 2 изд.,
М., 1966, §79; [4] Былов Б. Ф., Виноград Р. Э.,
Г р о б м а н Д. М., Н е м ы ц к и й Б. В., Теория пока-
показателей Ляпунова..., М., 1966; [5] И зобов II. А., в кн.:
Итоги науки и техники. Математический анализ, т. 12, М.,
1974, с. 71 — J46; [6J Прохорова Р. А., «Дифференц.
уравнения», 1976, т. 12, JM» 3, с. 475 — 83; .N1 4, с. 766—69.
В. М. Миллионщиков.
НЕПРЕДИКАТИВНОЕ ОПРЕДЕЛЕНИЕ — опреде-
определение, осмысленность к-рого предполагает наличие
определяемого объекта.
Образование множества всех множеств неиредикатпв-
но. Определение наименьшей верхней грани произволь-
произвольного множества действительных чисел также непредпка-
тивно. Любое Н. о. можно рассматривать как свойство,
выделяющее нужный объект из нек-рой заданной сово-
совокупности. Так как при этом остается проблема су-
существования выделяемого объекта, то вместо Н. о.
можно говорить о непредпкативных свойствах. Если
фиксирован язык, на к-ром выражаются свойства, то
понятие непредикативности уточняется следующим
образом. Свойство (точнее, языковое выражение, вы-
выражающее это свойство) наз. н е п р е д и к а т и в-
н ы м, если оно содержит связанную переменную, в
область изменения к-рой попадает определяемый объект.
Свойство наз. предикативным, если оно не
содержит таких связанных переменных.
Понятие непредикативности возникло в связи с об-
обнаружением теоретико-множественных парадоксов, а
сам термин принадлежит А. Пуанкаре (Н. Poincare,
1906), впервые выдвинувшему возражения против Н. о.
Обнаруженные в начале 20 в. антиномии содержат
непредикативность. Напр., в парадоксе Рассела мно-
множество R всех множеств, не содержащих себя в каче-
качестве элемента, определяется формулой:
где х — переменная, пробегающая все множества.
В этой формуле R является возможным значением пе-
переменной х. В математике Н. о. широко распростране-
распространены. Напр., объединение S всех множеств натурального
ряда, удовлетворяющих условию ср, задается формулой
где п — переменная по натуральному ряду, М — пере-
переменная по подмножествам натурального ряда. В при-
приведенной формуле S является возможным значением
связанной переменной М. Непредикативный способ
задания объекта часто удается заменить предикатив-
предикативным. Напр., если в качестве свойства ц>(М) взять фор-
формулу ЛТ=А\/М=В, где А и В — некоторые фиксиро-
фиксированные множества, то формула (*) эквивалентна пре-
предикативной формуле
(? ?А V
выражающей, что S есть объединение множеств А н В.
Б. Рассел (В. Russell) предпринял попытку построе-
построения математики на предикативной основе. В его раз-
разветвленной теории TiiiioB множества выстраиваются в
иерархию, в соответствии с определяющими пх выра-
выражениями. Напр., множество S из формулы («) должно
относиться к более высокому уровню в иерархии, чем
уровень переменной М и уровни переменных, содержа-
содержащихся в формуле ф. На предикативной основе не уда-
удается построить анализ в полном объеме. Приходится
снабжать формулировки оговорками об уровнях рас-
рассматриваемых объектов. Б. Рассел был вынужден вве-
сти аксиому сводимости, стирающую фактически раз-
различие между уровнями. Однако предикативная теория
при наличии арифмотич. аксиом позволяет строить
анализ, достаточный для многих приложений (см. [4]).
Феномен не предикативности существенно основан
на абсолютном характере понимания слова «все» (нее
без каких-либо ограничений, решительно все). Распре-
Распределение множеств по уровням представляет собой
попытку ограничить этот абсолютный характер. Наи-
Наиболее радикальная ревизия способа мышления, осно-
основанного на абсолютном понимании понятия «все», пред-
предпринимается интуиционистским и конструктивным нап-
направлениями в математике.
Лит.: [1] Чёрч А., Введение в математическую логику,
пер. с пнгл., М., 1960; [2] Ф р е н к е л ь А,- А., Б а р - X и л-
лел И., Основания теории множеств, пер. с англ., М., 1906;
[3] Гильберт Д., Аккерман В., Основы теоретиче-
теоретической логики, пер. с нем., М., 1947; [4] Takenti G., Two
applications of logic to mathematics, Tokyo, 1978. В. Н. Гришин.
НЕПРЕРЫВНАЯ ГРУППА — в работах основопо-
основоположников теории групп Ли (С. Ли, S. Lie; А. Пуанкаре,
Н. Poincare; Э. Картан, Е. Cartan; Г. Вейль, Н. Weyl,
и др.)—группа гладких пли аналитических локальных
преобразований пространства R" или С", гладко или
аналитически зависящих от параметров. В случае ко-
конечного числа числовых параметров Н. г. называлась
конечной, что соответствует современному понятию ко-
конечномерной Ли группы. При наличии функциональных
параметров говорили о бесконечной Н. г., что соответ-
соответствует современному понятию псевдогруппы преобра-
преобразований. В настоящее время A982) термин «Н. г.»
часто обозначает топологическую группу [21.
Лит.: [1] Lie S., Scheffers G., Vorlesungen iiber
continuierliche Gruppen..., Lpz., 1893; [2] Понтрягин Л.
С, Непрерывные группы, 3 изд., М., 1973; [3] Б у р б а к и Н.,
Группы и алгебры Ли. Алгебры Ли, свободные алгебры Ли и
группы Ли, пер. с франц., М., 1970. А. Л. Онищик.
НЕПРЕРЫВНАЯ ДРОБЬ — то же, что цепная
дробь, т. е. выражение вида
где
— конечные или бесконечные последовательности комп-
комплексных чисел. Для Н. д. употребляется обозначение
й++ + +
Обычно предполагается, что последовательности {я„}
и {Ьп} таковы, что для всех п, 0<:/г<(ц-}-1,
(Qn определяются рекуррентно, причем (>_ 2=1, Q_j=O).
О. А. Иванова.
НЕПРЕРЫВНАЯ СЕРИЯ ПРЕДСТАВЛЕНИЙ, о с-
новная серия представлений,— семей-
семейство неприводимых унитарных представлений локально
компактной группы G, входящих в разложение регу-
регулярного представления группы G, но не принадлежащих
дискретной серии представлений этой группы. Если
G — действительная нолупростая группа Ли, G=
= КА N — ее Ивасавы разложение, М — централизатор
группы А в А, то основной невырожден-
невырожденной Н. с. п. группы G наз. семейство непрерывных
унитарных представлений группы G, индуцированных
конечномерными неприводимыми унитарными пред-
представлениями группы B = MAN, тривиальными на N.
Дополнительной (соответственно вырож-
вырожденной) Н. с. п. такой группы G наз. семейство
неприводимых унитарных представлений группы G,
входящих в дополнительную серию представлений (со-
(соответственно в вырожденную серию представлений)
группы G и не являющихся изолированными точками
этой серии (как подмножества двойственного простран-
пространства группы G). Аналитпч. продолжение основной не-
невырожденной Н. с. п. есть семейство (вообще говоря,
неунитарных) представлений группы G, индуцирован-
индуцированных всевозможными конечномерными неприводимыми
представлениями группы В, тривиальными на Л'; это
семейство играет решающую роль в теории представле-
представлений действительных полупростых групп Ли и гармо-
гармония, анализе на этих группах; в частности, любое впол-
вполне неприводимое представление группы G в гильбер-
гильбертовом пространстве инфпнитезимально эквивалентно
подпредставлению нек-рого факторпредставления одно-
одного из представлений аналитич. продолжения основной
невырожденной Н. с. п. См. также Бесконечномерное
представление групп Ли.
Лит.; [1] Гель фан д И. М., Наймарк М. А.,
Унитарные представления классических групп, М.— Л., 1950;
12] Кириллов А. А., Элементы теории представлений,
2 изд., М., 1978; [3] W а г n e r G., Harmonic analysis on semi-
simple Lie groups, v. 1—2, B.— [a. O.I, 1972. А. И. Штерн.
НЕПРЕРЫВНАЯ ФУНКЦИЯ — одно из основных
понятий математического анализа.
Пусть действительная функция / определена на нек-
ром подмножестве Е действительных чисел R, т. е.
/ : E-+R. Функция / наз. непрерывной в точ-
точке хо?Е (или, подробнее, непрерывной в точке х0
по множеству Е), если для любого числа е>0 существу-
существует такое число б>0, что для всех точек х?Е, удовлетво-
удовлетворяющих условию
k-:rol<6,
выполняется неравенство
1/(-г)-/(-*о)Ке.
Если обозначить
U(x0, 6) = (хо-8, хо+б)
V(f(xo),z)=(f(xo)-e, /(хо)+е)
соответственно б- и е-окрестностн точек х0 и /(х0),
то данное определение можно перефразировать следу-
следующим образом: функция / наз. непрерывной
в точке хо?Е, если для любой е-окрестности
F=F(/(.ro),e) точки f(xQ) существует такая б-окрест-
ность U=U{xo,8) точки х0, что f(Uf]E)czV.
Используя понятие предела, можно сказать, что функ-
функция / непрерывна в точке х0, если в этой
точке существует ее предел по множеству Е и этот пре-
предел равен f{x0):
lim /(*)=/(*„).
х->-х„, хеЕ
Это равносильно тому, что
lim Дг/=О,
Лдг->-о, х е Я
где Ах=х—х0, х?Е, Ay=f(x)—f(x0), т. е. бесконечно
малому приращению аргумента в точке х0 соответствует
бесконечно малое приращение функции.
В терминах предела последовательности определение
II. ф. в точке х0: функция /непрерывна в точ-
к е х0, если для любой последовательности точек
хп?Е, п=1, 2, . . ., lim zn=x0) имеет место
П->оо
lim /(*„) = /(*„).
Все приведенные определения Н. ф. в точке эквивалент-
эквивалентны между собой.
Если функция / непрерывна в точке х0 по множе-
множеству Ef] {х : x^Xff) (соответственно но множеству
Е{\ {х : я<г0}), то функция/ наз. непрерывной
справа (слева) в точке х0.
Все основные элементарные функции являются непре-
непрерывными во всех точках их областей определения. Важ-
Важным свойством Н. ф. является замкнутость класса не-
непрерывных функций относительно арпфметич. опера-
операций и операции композиции функций. Более точно,
если действительные функции / : Е—>R и g : E—+-R,
EciR, непрерывны в точке хи?Е, то их сумма f-\-g и
произведение fg, а при g(xo)^O и частное fig (заведомо
определенное в пересечении нек-рой окрестности точки
х0 с множеством Е) непрерывны в точке х0. Если, как
и выше, функция / : Е—>R непрерывна в точке
хо?Е, а функция ср : D-+-R, DczR, такова, что cp(D)dE
и, следовательно, имеет смысл композиция /оф, причем
существует такое to?D, что <p(to)=xo и функция ц.
непрерывна в точке t0, то композиция /оср также непре-
непрерывна в точке t0. Таким образом, в этом случае
Шп/[ф (*)]=/[ НтФ (<)] = /[ф (t0)],
t-*ta t-*t,
т. е. в этом смысле операция предельного перехода
перестановочна с операцией взятия Н. ф. Из перечис-
перечисленных свойств Н. ф. следует, что не только основ-
основные, но и любые элементарные функции непрерывны в
области их определения. Сохраняется свойство непре-
непрерывности и при равномерном предельном переходе:
если последовательность функций {/„} равномерно
сходится на множестве Е и каждая функция /„ непре-
непрерывна в точке хо?Е, п=\, 2, . . ., то и предельная
функция
/=Нш/я
непрерывна в этой точке.
Если функция / : E—+R непрерывна в каждой точке
множества Е, то она наз. непрерывной на
множестве Е. Если хо?Е'сЕ и функция / не-
непрерывна в точке х„, то сужение функции / на мно-
множестве Е' также непрерывно при х=х0. Обратное,
вообще говоря, неверно. Напр., сужение Дирихле функ-
функции как на множестве рациональных, так и иррацио-
иррациональных точек непрерывно, а сама функция Дирихле
разрывна во всех точках.
Важный класс действительных Н. ф. одного перемен-
переменного образуют функции, непрерывные на отрезках.
Они обладают следующими свойствами.
Первая теорема Вейерштрасса:
функция, непрерывная на отрезке, ограничена на нем.
Вторая теорема Вейерштрасса:
функция, непрерывная на отрезке, принимает на нем
наибольшее и наименьшее значения.
Теорема Коши о промежуточных
значениях: функция, непрерывная на отрезке,
принимает на нем любое значение, заключенное между
значениями, к-рые она принимает на концах отрезка.
Теорема об обратной функции: если
функция непрерывна и строго монотонна на отрезке,
то у нее существует однозначная обратная функция,
к-рая также определена на нек-ром отрезке, строго мо-
монотонна и непрерывна на нем.
Теорема Кантора о равномерной
непрерывности: функция, непрерывная на от-
отрезке, равномерно непрерывна на нем.
Всякая функция, непрерывная на отрезке, может
быть равномерно сколь угодно точно приближена алге-
браич. многочленом, а всякая функция /, непрерывная
на отрезке [0, 2л] и такая, что /@)=/Bя), может быть
равномерно сколь угодно точно приближена тригоно-
метрич. полиномами (см. Вейерштрасса теорема о при-
приближении функций).
Понятие Н. ф. обобщается на более общие виды функ-
функций, прежде всего на функции многих переменных.
Сформулированное выше определение Н. ф. формаль-
формально сохраняется, если под Е понимать подмножество
и-мерного евклидова пространства R", под \х—хо\ —
расстояние в этом пространстве между точками х?Е и
хо?Е, под U(x0, б) — б-окрестность в R" точки х0, а
под
lim х„ = х0
понимать предел последовательности точек в простран-
пространстве R". Функция / : E-+R, EdRn, многих переменных
xl7 . . ., хп, непрерывная в точке хо=(х[\ . . ., х'пу)?Е,
наз. также непрерывной в этой точке по
совокупности переменных xlf . . ., хп,
в отличие от функций многих переменных, непрерывных
по отдельным переменным. Функция / : E-*-R, EciR",
наз. непрерывной в точке х0, напр., п о
@)
переменной х1, если в точке х\ непрерывно
сужение функции / на множестве
т. е. в точке хТ непрерывна функция f(x1, хB0>, . . ., х^)
одного переменного хх. Функция / : Е—>-R, EcR",
п^2, может быть непрерывной в точке х по каждому
переменному хи х2, . ¦ ., хп, но может не быть непре-
непрерывной в этой точке по совокупности переменных.
Определение Н. ф. непосредственно переносится на
комплекснозначные функции. Следует лишь в данном
выше определении под 1/(х) — f(xo)\ понимать абсо-
абсолютную величину комплексного числа f(x)—f(x0), а под
lim f (xn)=f(x0)
— предел в комплексной плоскости.
Все эти определения являются частным случаем бо-
более общего понятия Н. ф. /, областью определения
которой является некоторое топологическое простран-
пространство X и значения которой принадлежат некоторому
топологическому пространству Y (см. Непрерывное
отображение).
На непрерывные отображения топологич. пространств
переносятся многие свойства действительных Н. ф.
одного переменного. Обобщение упомянутых выше тео-
теорем Вейерштрасса: непрерывный образ бикомпактного
топологич. пространства в хаусдорфовом топологич.
пространстве является бикомпактом. Обобщение теоре-
теоремы Коши о промежуточных значениях непрерывной на
отрезке функции: непрерывный образ в топологич.
пространстве связного топологич. пространства также
связен. Обобщение теоремы о функции, обратной к не-
непрерывной строго монотонной функции: взаимно одноз-
однозначное непрерывное отображение бикомпакта на топо-
топологич. хаусдорфово пространство есть гомеоморфизм.
Обобщение теоремы о пределе равномерно сходящей-
сходящейся последовательности непрерывных функций: если
/„ : X—>-У—равномерно сходящаяся последовательность
непрерывных в точке хь ? X отображений топологич.
пространства X в метрич. пространство У, то предель-
предельное отображение /=lim /„ также непрерывно в точке хв.
Обобщением теоремы Вейерштрасса о приближении
функций непрерывных на отрезке многочленами явля-
является Вейерштрасса — Стоуна теорема.
Лит.; [1] Александров П. С, Введение в теорию
множеств и общую топологию, М., 1977; [2] Колмого-
Колмогоров А. Н., Фомин С. В., Элементы теории функций и
функционального анализа, 5 изд., М., 1981; [3] Николь-
Никольский С. М., Курс математического анализа, 2 изд., т. 1—2,
М., 1975; Е4] И л ь и н В. А., П о з н я к Э. Г., Основы мате-
математического анализа, 3 изд., ч. 1, М., 1971. Л. Д. Кудрявцев.
НЕПРЕРЫВНОЕ МНОЖЕСТВО — (линейно) упо-
упорядоченное множество X, все собственные сечения
к-рого являются дедекиндовыми сечения-
м и, т. е. при любом разбиении X на два непустых
подмножества X' и X" таком, что каждый элемент из
X' предшествует каждому элементу из X", либо в X'
есть наибольший элемент, но в X" нет наименьшего
элемента, либо в X' нет наибольшего элемента, но в X"
есть наименьший элемент. м. И. Войцеховский.
НЕПРЕРЫВНОЕ ОТОБРАЖЕНИЕ — отображение
/ : X—^-Y топологич. пространства X в топологич. про-
пространство Y такое, что для всякой точки хо?Х и для
всякой окрестности V=V(f(x0)) ее образа f(xb) суще-
существует такая окрестность ?7= U(xa) точки х0, что / (U)cz V.
Это определение является перефразировкой окрестное^
ного определения непрерывности функций действитель-
действительного переменного (см. Непрерывная функция). Суще-
Существует много эквивалентных определений непрерыв-
непрерывности. Так, для непрерывности отображения / : X—>-Y
необходимо и достаточно, чтобы выполнялось любое
из следующих условий:
а) прообраз /~XG всякого открытого в Y множества
G открыт в X;
б) прообраз j-^F всякого замкнутого в Y множества
F замкнут в X;
в) f[A]d[fA] для всякого множества АсХ (образ
замыкания содержится в замыкании образа).
Понятие непрерывной функции, корректно сформу-
сформулированное еще Б. Больцано (В. Bolzano) и О. Коши
(A. Cauchy), сыграло большую роль в математике 19 в.
Функция Вейерштрасса, не дифференцируемая ни в
одной точке, «канторовская лестница», кривая Пеано
указали на необходимость рассмотрения более частных
случаев непрерывности. Необходимость выделения спе-
специальных классов Н. о. еще более возросла, когда ста-
стали рассматривать Н. о. более общих объектов — топо-
топологич. пространств. Можно отметить следующие важ-
важнейшие типы Н. о.: топологич. отображения или го-
гомеоморфизмы, совершенные отображения, замкнутые
отображения, открытые отображения, факторные
отображения.
Если даны два Н. о. / : X-+Y и g : Y-+-Z, то их ком-
композиция g°f: X-+-Z, т. е. сквозное отображение
X^U-^-Z, непрерывна. Очевидно непрерывно и всякое
тождественное отображение Ix '¦ Х—>-Х. Поэтому то-
топологич. пространства и Н. о. образуют категорию.
Одним из методов топологии является метод взаим-
взаимной классификации пространств и отображений. Его
сущность состоит в следующем: выделяются три основ-
основные, тесно связанные между собой задачи. 1) В каком
случае каждое пространство нек-рого фиксированного
класса Л может быть отображено на нек-рое простран-
пространство класса S3 посредством Н. о., принадлежащего
классу XI 2) Какими внутренними свойствами харак-
характеризуются пространства, принадлежащие классам
МС, являющимся образами пространств из класса С
при Н. о. из класса Ml 3) Пусть Hom(^, S3) — обоз-
обозначение множества Н. о., областью определения к-рых
служат пространства из класса Л, а областью значе-
значений — пространства из класса SB, пХ — нек-рый дру-
другой класс отображений. Каковы свойства отображений
из класса Horn (J,, ЭЗ)Г\Х?
Эти общие формулировки охватывают, в частности,
следующий вопрос: какие топологич. свойства сохра-
сохраняются теми или иными отображениями при переходе
от пространства к его образу или прообразу. 1) Вся-
Всякое га-мерное в смысле dim пространство может быть
существенно отображено (см. Существенное отобра-
отображение) на re-мерный куб. 2) Точечно-счетная база сохра-
сохраняется при совершенных (даже при бифакторных) отоб-
отображениях. 3) Всякое замкнутое отображение / из класса
Horn (ut, S3), где Л — класс я-мерных пространств со
счетной базой, 53 — класс нульмерных пространств
со счетной базой, по крайней мере (я+1)-кратно.
Первые конкретные задачи этого рода были решены
более полувека назад. Таковы, напр., представление
произвольного компакта в виде непрерывного образа
канторова совершенного множества (теорема
Александрова); характеристика метрнч. про-
пространств со счетной базой как открытых непрерывных
образов подпространств пространства иррациональных
чисел (теорема Хаусдорфа); описание ло-
локально связных континуумов как непрерывных обра-
образов отрезка. Решение этих задач не только позволило
ответить на вопросы о взаимоотношениях между раз-
различными известными ранее классами пространств, но
п вызвало появление новых интересных классов про-
пространств. Таковы, напр., диадические бикомиакты,
наракомпактные р-пространства, совершенно п-мерные
пространства, псевдокомпактные пространства.
Понятие действительной непрерывной функции, т. е.
Н. о. топология, пространства в R, лежащее в основа-
основании теории функций, играет большую роль и в общей
топологии. Здесь прежде всего стоит отметить. Урысона
лемму, теорему Брауэра — Урысона о продолжении
непрерывных функций с замкнутых подмножеств нор-
нормальных пространств, определение А. Н. Тихоновым
вполне регулярных пространств, Вейерштрасса —
Стоуна теорему. Эти п другие исследования привели к
созданию теории колец непрерывных функций, методы
к-рой оказались достаточно плодотворными в общей
топологии.
Существенную часть теории размерности составляет
изучение поведения размерностных характеристик
пространств при переходе к образу или прообразу от-
относительно отображений тех или иных классов. Боль-
Большую роль здесь играют е-сдвпгн, е-отображения и
w-отображения, существенные отображения, конечно-
кратные отображения, счетнократные отображения,
нульмерные отображения, n-мерные отображения п др.
При этом метод Н. о. приводит к взаимному обогащению
и проникновению друг в друга таких совершенно
различных по своему происхождению областей общей
топологии, как имеющая наглядно-геометрич. смысл
теория размерности и абстрактная по характеру тео-
теория кардинальнозначных инвариантов.
Одной из характеристик размерности является воз-
возможность продолжения с замкнутого подмножества
Н. о. в «-мерную сферу. Эта теорема является одним из
вариантов теоремы о продолжении отображений, ко-
которая, как и тесно связанная с ней теорема о непод-
неподвижной точке, имеет кардинальное значение для таких
разделов современной математики, как топология, ал-
алгебра, теория функций и функциональный анализ,
дифференциальные уравнения.
Одним из наиболее изученных классов Н. о. являет-
является класс совершенных неприводимых отображений. Тео-
Теорема об абсолюте регулярного пространства породила
целый ряд исследований в этой области. В частности,
понятие абсолюта было распространено на класс всех
хаусдорфовых пространств. С понятием Н. о. ока-
оказалось тесно связанным понятие 0-блпзостп, к-рое дало
возможность внутреннего описания всех совершенных
неприводимых прообразов произвольного бикомпакта.
Распространение теории неприводимых Н. о. на класс
всех хаусдорфовых пространств показало, что Н. о.
не хватает для изучения нерегулярных пространств
и что более естественно здесь рассматривать 8-непре-
рывные отображения.
Выделение равномерно непрерывных функций из
класса всех числовых функций одной пли нескольких
действительных переменных стало одной пз отправных
точек исследований, приведших к созданию равномер-
равномерной топологии.
Н. о. того или иного типа лежат в основе теории
ретрактов, спайнов, гомологии. Большую роль в сов-
современной математике играют различные аспекты теорий
многозначных отображений. Интересны богатством
идейною содержания вопросы Н. о. евклидовых про-
пространств.
Лит.: [1J Александров И. С, Введение в теорию
множеств и общую топологию, М., 1977; [2] Б у р б а к и Н.,
Общая топология. Осношше структуры, пер. с франц., М., 1968;
[3] К е л л и Д ж., Общая топология, пер. с англ., 2 изд., М.,
1981; [4] Архангельский А. В., Пономарев В. И.,
Основы общей топологии в задачах и упражнениях, М., 1974;
[5] А л е к с а н д р я н Р. А., М и р з а х а н я н Э. А., Об-
Общая топология, М., 1979. В. В. Федорчук-
НЕПРЕРЫВНОЕ ПРЕДСТАВЛЕНИЕ — линейное
представление я тоцологпч. группы (полугруппы, алгеб-
алгебры) X в топология, векторном пространстве Е такое,
что отображение ш пространства ЕхХ в Е, определяе-
определяемое формулой ф(ё, х) = я(.г)|, Ъ,^Е, х?Х, непрерывно.
Если отображение ср непрерывно по каждому ар-
аргументу, то в нек-рых случаях (напр., если X — ло-
локально компактная группа, а ? — банахово простран-
пространство) ф автоматически непрерывно по совокупности
переменных, т. е. я — Н. п. А- И- Штерн-
НЕПРЕРЫВНОЕ РАЗБИЕНИЕ топологиче-
топологического пространствах — покрытие у про-
пространства X попарно непересекающимися непустыми
множествами, удовлетворяющее условию: каковы бы
ни были F ?у н окрестность U множества F в X, най-
найдется окрестность V множества F в X, содержащаяся
в U и являющаяся объединением нек-рого множества
элементов семейства у. Разбиение непрерывно в том И
только в том случае, если отвечающее ему факторное
отображение пространства X на пространство этого
разбиения замкнуто. Непрерывное отображение / : X—г
—>У пространства X на пространство Y замкнуто в том
итолько втом случае, если разбиение y/={f~1(y), y?Y)
пространства X непрерывно.
Н. р. часто встречаются в теории бикомпактных
пространств. Каждое непрерывное отображение биком'
пактного пространства на хаусдорфово пространство
замкнуто. Поэтому каждое непрерывное отображение
бикомпактного пространства X на хаусдорфово про-
пространство Y порождает Н. р. пространства X на про-
прообразы точек. По той же причине для непрерывности
разбиения бикомпакта достаточно (и необходимо), что-
чтобы пространство этого разбиения удовлетворяло аксиоме
отделимости Хаусдорфа. Достоинством Н. р. простран-
пространства на замкнутые множества является сохранение та-
такими разбиениями нормальности и паракомпактности.
Напротив, пространство Н. р. метрнзуемого простран-
пространства может быть не метризуемо. Простейший пример
такой ситуации — пространство разбиения плоскости,
единственный нетривиальный элемент к-рого — фикси-
фиксированная прямая.
Как и вообще разбиения, Н. р. служат важным сред-
средством построения новых топологич. пространств из
уже имеющихся, а также представления более сложных
тоиологич. пространств в виде пространств Н. р. более
простых или более стандартных пространств. Так, вся-
всякий метрнзуемый бикомпакт является пространством
Н. р. канторова множества. Каждый локально связ-
связный связный метризуемый бикомпакт можно предста-
представить как пространство Н. р. отрезка. Н. р. естествен-
естественным образом входят в нек-рые конкретные конструк-
конструкции; так, напр., проективная плоскость, рассматривае-
рассматриваемая как толологич. пространство, является простран-
пространством Н. р. обычной сферы па пары диаметрально
противоположных точек. Аналогично, «-мерное проек-
проективное пространство с топологич. точки зрения является
пространством Н. р. re-мерной сферы, лежащей в
(п-|-1)-мерном евклидовом пространстве, на пары диа-
диаметрально противоположных точек. На этом языке,
как пространство нек-рого II. р. прямоугольника, ак-
аккуратно определяется лист Мёбиуса » строятся другие
гсометрнч. объекты.
Лит.: [11 Архангельский А. В., Понома-
Пономарев В. И., Основы общей топологии в задачах и упражнени-
упражнениях, М., 1974. А. В. Архангельский.
НЕПРЕРЫВНОЕ РАСПРЕДЕЛЕНИЕ — распределе-
распределение вероятностей, не имеющее атомов. Если атомы суть
отдельные точки, то Н. р. противоположно дискретному
распределению (см. также Атомическое распределе-
распределение). Вместе с дискретным распределением Н. р. обра-
образует основные типы распределений. По теореме Жор-
дана любое распределение вероятностей есть смесь дис-
дискретного распределения и Н. р. Напр., пусть F (х) —
функция распределения, соответствующая нек-рому
распределению на прямой, тогда F=pF1-\-(l—p)F2,
гдеО<р<1, а 1<\(х) и F.2(x) — функции распределения,
отвечающие дискретному и непрерывному типу. Н. р.
соответствует непрерывная функция распределения.
Значительный вес среди II. р. имеют абсолютно
непрерывные распределения. К этому
типу распределении относятся распределения Р на
измеримом пространстве (Q, -А), иредставнмые при лю-
любом А ?</? в виде
где p(x)~^sO, \ f р (х)ц.(сЬ;)=1. Функция р (х) наз. и л о т-
ностью распределения относительно ме-
меры [г (обычно (х — мера Лебега). На прямой для соот-
соответствующей функции распределения F(x) имеет место
представление
F(x) = \' p(u)du,
J — оо
при этом почти всюду (по мере Лебега) F' (х) = р(х)-
Распределение абсолютно непрерывно тогда и только
тогда, когда соответствующая функция распределения
абсолютно непрерывна (как функция действительного
переменного). Противоположность абсолютно непре-
непрерывным распределениям составляют Н. р., сосредото-
сосредоточенные на множествах, имеющих меру нуль. Такие рас-
распределения наз. сингулярными распределениями по
отношению к нек-рой мере. По теореме Лебега о разло-
разложении любое Н. р. является смесью двух распределе-
распределении, из к-рых одно абсолютно непрерывно, а другое
сингулярно по отношению к заданной мере.
Наиболее важны следующие Н. р.: арксинуса распре-
распределение, бета-распределение, гамма-распределение, Ко-
ши [>асг.]>еделепие, нормальное распределение, равномер-
равномерное распределение, показательное распределение, Стью-
дента распределение, чхи-квадрат» распределение.
Лит.: [11 Л о о в М., Теория вероятностей, пер. с англ.,
М., 1962; [21 Ф е л л е р В., Введение в теорию вероятностей
и ее приложения, пер. с англ., 2 изд., т. 2, М., 1967.
А. В. Прохоров.
НЕПРЕРЫВНОЕ СЕЧЕНИЕ — непрерывное отобра-
отображение h : f(X)-yX образа f{X) непрерывного отобра-
отображения / : X->Y топологич. пространств X, Y такое,
что /о/г — тождественное отображение f(X).
М. II. Войцеховский.
НЕПРЕРЫВНОСТИ АКСИОМА — аксиома, выра-
выражающая тем или иным образом непрерывность множе-
множества действительных чисел. Н. а. действительных чисел
может быть сформулирована, напр., в терминах сечений
действительных чисел: всякое сечение действительных
чисел определяется нек-рым числом (аксиома Д е-
д е к п н д а): в терминах вложенных отрезков: всякое
семейство вложенных отрезков имеет непустое пересе-
пересечение (аксиома Кантора); в терминах верх-
верхней или нижней грани множеств: всякое непустое огра-
ограниченное сверху множество имеет конечную верхнюю
грань, а всякое ограниченное снизу — нижнюю грань
(аксиома В е и е р ш т р а с с а), л. д. Кудрявцев.
НЕПРЕРЫВНОСТИ МОДУЛЬ — одна из основных
характеристик непрерывных функций. Н. м. непрерыв-
непрерывной на отрезке функции f(x) определяется как
w(°. /)= max max | / (x-j-й)—/ (х) \.
|hK6 х
Определение Н. м. введено А. Лебегом (A. Lebesgue)
в 1910, хотя по существу понятие было известно и ра-
ранее. Если Н. м. функции f(x) удовлетворяет условию
@F, /)<A#6a,
где 0<а<:1, то говорят, что функция f(x) удовлетворя-
удовлетворяет Липшица условию порядка а.
Для того чтобы неотрицательная функция со (о) была
Н. м. нек-рой непрерывной функции, необходимо и
достаточно, чтобы она обладала следующими свойст-
свойствами: со(О) = О, шF) не убывает, юF) непрерывна,
coF4r|)<wF)+oj(ri), б, т)>0.
Рассматриваются также Н. м. высших порядков
F, /)= max max I Л*/(х) |,
I h|< 6 x
где
— конечная разность к-то порядка функции /(.г), и
Н. м. в произвольных пространствах функций, напр,
интегральный Н. м. функции f(x), интегрируемой на
отрезке [а, Ь] со степенью 1
+ h)-f(z)\Pdx}
p {\\f(x + h)-f(z)\Pdx}1"'
o<h<6 УJ I
Для 2я-периодической функции интеграл в выраже-
выражении (*) берется по отрезку [0, 2я].
Лит.: [1] Зигмунд А., Тригонометрические ряды, пер.
с англ., [2 изд.], т. 1, М., 1965; [2J А х и е з е р Н. И., Лекции
по теории аппроксимации, 2 изд., М., 1965; [3] Д з я д ы к В. К.,
Вьеление в теорию равномерного приближения функций
полиномами, М., 1977. А. В. Ефимов.
НЕПРЕРЫВНОСТИ ТЕОРЕМА, и р и п ц и п н е-
прерывности: пусть G — голоморфности область
в С", п>2, и Sk(^_G и Tk<SG, A-=l, 2', . . ., — любые
последовательности множеств, для к-рых имеет место
принцип максимума относительно
модулей функции /, голоморфной в G, т. е.
|/(s)|<;max |/(Z)|, z?Sk, fc=l, 2, ...;
T
тогда если S^ сходятся к нек-рому ограниченному мно-
множеству S, а У ft— к множеству Т и T<iiS, то S<SG. Если
в качестве S% взять аналитич. гиперповерхности и в
качестве Т^— их границы dSk, то получают т е о р е-
му Беенке — Зоммера (см. [1]). Отсюда сле-
следует, что всякая область голоморфности псевдовыпук-
ла. Применительно к конкретной функции нек-рые
модификации Н. т. известны как теоремы о «диске».
Напр., т. н. сильная теорема о «диске»
утверждает следующее. Пусть в С" задана жорданова
кривая вида
z (l) = lo-\-bX(t), 0<г<1, Ь"?С"-\ z~=(z2, ...,zn).
Пусть D (t), 0<;<:l, — семейство областей в плоскости
z]? обладающее тем свойством, что для любого ком-
компакта KczD@) найдется число т| = т|(А'), для к-рого
KczD(t) при всех 0<i<r). Тогда если /(z) голоморфна
в точках «дисков»
), z=~z(t), 0 < i
и в одной точке предельного «диска»
[z-=(zb z): z^D(O), z~=z(O)],
то /(z) голоморфна и во всех точках предельного «дис-
«диска». Теоремы о «диске» весьма полезны при голоморф-
голоморфном расширении областей и при построении голоморф-
голоморфности оболочек, напр, при доказательстве теоремы
Бохнера об оболочке голоморфности трубчатой обла-
области, при доказательстве теорем Осгуда — Брауна, «о
вложенном ребре», «об острие клина», «о С-выпуклой
оболочке» и др.
Лит.: [1] Behnke H., Thullen P., Theorie der
Funktionen mehrerer komplexer Veranderlichen, В., 1934; [2]
Владимиров В. С, Методы теории функций многих ком-
комплексных переменных, М., 1964; [3] Шабат Б. В., Введе-
Введение в комплексный анализ, 2 изд., ч. 2, М., 1976.
В. С. Владимиров.
НЕПРЕРЫВНОСТЬ — одно из важнейших матема-
математических понятий, обычно употребляемое применитель-
применительно к понятию отображения (см. Непрерывная функция,
Непрерывное отображение,. Непрерывный оператор).
В частности, можно изучать Н. нек-рой алгебраич. опе-
операции в заданном множестве относительно имеющейся
в нем топологии. При наличии Н. рассматриваемой
операции термин «Н.» применяется и к самому множе-
множеству (напр., Непрерывная группа). Термин «Н.» упо-
употребляется также в смысле невозможности «пополне-
«пополнения по непрерывности» нек-рого математпч. объекта,
напр, метрич. пространства; в этом смысле говорят о
Н. множества действительных чисел. л. Д. Кудрявцев.
НЕПРЕРЫВНЫЕ АНАЛОГИ ИТЕРАЦИОННЫХ
МЕТОДОВ — непрерывные модели, позволяющие ис-
исследовать вопросы существования решений нелиней-
нелинейных уравнений, проводить с помощью развитого аппа-
аппарата непрерывного анализа предварительные иссле-
исследования сходимости и оптимальности итерационных
методов, получать новые классы итерационных мето-
методов.
Можно установить соответствие между методами ре-
решения стационарных задач путем установления (см.
Установления метод) и нек-рыми итерационными ме-
методами (см. [1], [2]). Напр., для решения линейного
уравнения
Au=f A)
с положительно определенным самосопряженным опера-
оператором А известны сходящиеся при достаточно малых
Т/.>0 двучленные итерационные методы вида
Если ввести непрерывное время t, а величины uk рас-
рассматривать как значение нек-рой функции u(t) при
t=lk, где
если положить Tj=p(i^) (tk—'s-i), где непрерывная
функция p(i)>0 при t^O, то при переходе к преде-
пределу в B) при Atk=tk + 1—1/,-^-0 получают Н. а. и. м. B):
| = -p(!)(Ai-/), b(O)=d, C)
И если
при t—>-oo, то u(t) стремится к и(ао) — решению урав-
уравнения A).
Двучленным градиентным итерационным методам
минимизации функции F(и):
иы 1 = ufc — rkgradF (uk), u° = v, D)
аналогичным образом можно сопоставить Н. а. и. м.
вида
•ПГ = -Р С) grad F(«), u@) = ». E)
Здесь функция р (t) влияет лишь на параметризацию
линии наискорейшего спуска. Для решения уравнения
A) можно взять F(u)=(Au, u)—2(f, и), тогда формулы
D) примут вид B), а уравнение E) — вид C).
Трехчленные итерационные методы:
ub + i = uk_ak(Ault — t) — $k(ub — ub-1) F)
с помощью преобразований можно записать в виде
(и* —M*
G)
где величины yk, Ц/j, pj., tk определяются (неоднозначно)
по параметрам ак, Pft метода F). Переход в G) к преде-
пределу при Д*д->-0 приводит к Н. а. и. м. вида
+ Y(O + l*(O«=-p(')(^-/). (8)
Метод установления с использованием уравнения типа
(8) носит название метода тяжелого шар и-
к а (см. [2]). Существуют итерационные методы, для
к-рых Н. а. и. м. содержат дифференциальные опера-
операторы более высоких порядков (см. C]).
Источником получения дифференциальных уравне-
уравнений, играющих роль Н. а. и. м., может быть метод
продолже ни я по параметру (см. [4], [5]).
В этом методе для нахождения решения уравнения
<р(м) = О (9)
строят уравнение
Ф(и,К)=0, A0)
зависящее от параметра Я и такое, что при к=0. ре-
решение A0) известно: г((О) = и°, а прпЯ=1 решения урав-
уравнений (9), A0) совпадают. Напр., можно взять
Ф(и, Я)=ф(м) — A — к) у (и0). A1)
Дифференцируя уравнение A0) по параметру и счи-
считая и=^и{Х), получают дифференциальное уравнение
для и(Х); оно для случая A1) примет вид
^ = -ф'(и)-1ф(«0)- A2)
Разбивая отрезок [0, 1] на п частей точками Яо=
=0<Х1< . . . <Xn-1<Xrt=l и применяя к уравнению
A2) одну из формул численного интегрирования по
точкам Хд (метод Эйлера, Рунге — Кутта и т. п.),
получают рекуррентные соотношения между величинами
uk=u(Xjl), к-рые используют для построения формул
итерационного метода. Так, после применения метода
Эйлера уравнение A2) заменится соотношениями
и* = и*-1_ДЯАф' (и*-1)-1ф(м»). A3)
где Д>.Л=Х^—Я,А_!, к-рые определяют следующий дву-
ступенчатый итерационный метод, содержащий вну-
внутренний и внешний циклы итераций:
/с=1, 2, ..., п; и[ = у''~\ i = l, 2,. .., и%=и». A4)
При ДЯ!=1, п=\ этот метод превращается в классич.
метод Ньютона. Н. а. и. м. Ньютона может быть полу-
получен и другим путем: в формуле A1) заменяется перемен-
переменная Я= 1—е~*. Тогда дифференциальное уравнение
A2) принимает вид
|Н. = -ф'(и)-1ф(«), и@) = и». A5)
Численное интегрирование уравнения A5) методом Эй-
Эйлера но точкам t/i приводит к итерационному методу
совпадающему при Д^_х=1 с классич. методом Нью-
Ньютона.
Н. а. и. м. решения краевых задач для дифференци-
дифференциальных уравнений математич. физики являются, как
правило, смешанными задачами для уравнений с ча-
частными производными специального вида (напр., с
быстро осциллирующими коэффициентами или с ма-
малыми коэффициентами при старших производных).
См. также ст. Замыкание вычислительного алгоритма.
Лит.: [1] Г а в у р и н М. К., «Изв. ВУЗов. Математика»,
1958, Л» 5F), с. 18—31; [2] Б а х в а л о в Н. С, Численные
методы, 2 изд., т. 1, М., 1975; [3] М а р ч у к Г. И., Лебе-
Лебеде в В. И., Численные методы в теории переноса нейтронов,
М., 1971; [4] О р т е г а Д ж., Рейнболдт В., Итераци-
Итерационные методы решения нелинейных систем уравнений со многи-
многими неизвестными, пер. с англ., М., 1975; [5] Д а в и д е н-
к о Д. Ф., «Ж. вычисл. матем. и матем. физ.», 1975, т. 15,
J\° 1, с. 30 — 47. В. И. Лебедев.
НЕПРЕРЫВНЫЙ ОПЕРАТОР — непрерывное отоб-
отображение А множества М топологического и, как пра-
правило, векторного пространства X в такое же простран-
пространство Y, а именно: 1) отображение А : M—*-Y, MczX,
непрерывно в точке хо?М, если для любой окрест-
окрестности VczY точки Ах0 найдется окрестность UczX точ-
точки т0 такая, что А {Мf) U)aV; 2) отображение
А : M-+Y непрерывно на множестве М, если оно не-
непрерывно в каждой точке этого множества.
Для того чтобы оператор А : M-+Y был непрерывен
на М, необходимо и достаточно, чтобы для любого от-
открытого (замкнутого) множества HczY полный прооб-
прообраз А~1(Н) был следом на М открытого (замкнутого)
множества в X, т. е. Л ~ 1(Н)=MQG, где G открыто
(замкнуто! в X. Для Н. о. справедливо цепное правило:
пусть A: M—>~Y, MczX, и А непрерывно на М (в точке
хо?М), а В : N-*-Z, AczY, и В непрерывно на N (в
точке уо?Х); если Q=M[\A~1(N) непусто (уо=Ах0),
то В о А непрерывно на Q (в точке х0).
В случае, когда X и Y — топологические векторные
пространства, и А — линейный Н. о. на линейном под-
подмногообразии LczX со значениями в Y, то из непрерыв-
непрерывности А в любой точке L, напр, в нуле, следует непре-
непрерывность А на всем L. Непрерывный на многообразии L
топологического векторного пространства X оператор
ограничен на этом множестве, т. е. образ любого
ограниченного подмножества NczL есть ограниченное
множество в Y. Если X и Y отделимы, то из ком-
компактности .V следует компактность A (N).
Оператор А равномерно непрерывен
на М, если для любой окрестности нуля VczY суще-
существует окрестность нуля UczzX такая, что из х—y?U
следует Ах—Ay?V. Оператор линейный и непрерыв-
непрерывный на линейном многообразии топологического век-
векторного пространства автоматически равномерно непре-
непрерывен на этом многообразии.
Помимо непрерывности вводится понятие счетной
непрерывности оператора. Оператор А : М—*-Y счет-
счетно непрерывен в точке х0 ? М, если для любой
последовательности хп—>-г0, {xn}czM, имеет место
Ахп-+Ах0. Для случая метризуемых пространств по-
понятия счетной непрерывности и непрерывности совпа-
совпадают.
Лит.: [11 К о л м о г о р о в А. Н., Фомин СВ., Эле-
Элементы теории функций и функционального анализа, 5 изд., М.,
1981; [2] К а н т о р о в и ч Л. В., А к и л о в Г. П., Функ-
Функциональный анализ, 2 изд., М., 1977. В. И- Соболев.
НЕПРЕРЫВНЫЙ ПОТОК — 1) Н. п. в эргодической
теории — такое семейство {Г*} (t пробегает действи-
действительную ось R) автоморфизмов по mod 0 пространства
с .мерой (М, и), что: а) при любых t, s?R равенство
TlTs(x)= Tt+S (x) имеет место для всех х?М, кроме,
быть может, тех х, к-рые принадлежат нек-рому исклю-
исключительному множеству меры нуль (оно может зависеть
от t, s); иначе говоря, Tl7's= Tt + S mod 0; б) для любого
измеримого AczM мера симметрии, разности \i(A AT1 A)
непрерывно зависит от t. Пусть 21 — совокупность всех
автоморфизмов mod 0 пространства (М, ix) с обычным
отождествлением: если Т и S совпадают почти всюду,
то они определяют один и тот же элемент из Ш. Если
3t снабдить слабой топологией (см. [1]), то условие
б) означает непрерывность отображения R—»-31, пе-
переводящего t в Т'.
Если (М, (х) — Лебега пространство, то понятие
Н. п. практически совпадает с понятием измеримого
потока: последний всегда есть Н. п. (см. [2]), а для
любого Н. п. {Т*} существует такой измеримый поток
{St}, что Г(^5* mod 0 при всех t (см. [3]; родственный
результат доказан в [4], см. также исправление в [5]).
Обращение к тому или иному из этих понятий зависит
от характера рассматриваемого вопроса и используе-
используемых приемов.
2) В другом смысле термин «Н. п.» может употреб-
употребляться с целью подчеркнуть, что рассматриваемый по-
поток относится к топологической динамике. В этом смыс-
смысле Н. и. есть такая совокупность гомеоморфизмов {Т<}
топологич. пространства М, что Т*(Т$ (х)) = Tt + S(x)
для всех t, s?R, z?M; отображение MxR^M,
переводящее (х, t) в Ttx, непрерывно.
Во избежание смешения с п. 1) лучше в данном слу-
случае говорить о топологическом потоке;
а в п. 1)— о метрической непрерывно-
непрерывности.
Лит.: ШХалмош II. Р., Лекции по эргодической тео-
теории, пер. с англ., М., 1959; [2] Хопф Э., «Успехи матем.
наук», 1949 т. 4, в. 1, с. 113—82; [3] В е р ш и к А. М., «Изн.
АН СССР. Сер. матем.», 1965, т. 29, № 1, с. 127—36; [4j M а-
с к е у G. W., «Illinois J. Math.», 1962, v. 6, N° 2, p. 327—35;
[5J Ramsay A., «Advances Math.», 1971, v. C, Mi 3, p. 253—
322. Д. В. Аносов.
НЕПРЕРЫВНЫЙ ФУНКТОР — синоним понятия
«функтор, перестановочный с пределами». Пусть Ж и
© — категории с пределами. Одноместный ковариант-
ный функтор F : 9t—>-(? наз. непрерывным, если
для любой диаграммы / : 3)—>9t с произвольной малой
схемой 3) выполнено равенство F (lim /) = lim J F.
Более подробно последнее равенство означает следую-
следующее: если (А; р,д, Z)?3)) — предел диаграммы J, при-
причем р,д: A->J(D), Z)?Ob3),— морфизмы, входящие в
определение предела, то (F(A); F(\iD), D ?ОЬЗЗ)
предел диаграммы JF : 3)—>-E.
Функтор F : Sft->E непрерывен тогда и только тогда,
когда он перестановочен с произведениями любых
семейств объектов и ядрами пар морфизмов. Всякий
основной функтор Иа(Х)~Н%(А, X) из категории 91
в категорию множеств непрерывен. М. Ш. Цаленко.
НЕПРЕРЫВНЫЙ ФУНКЦИОНАЛ — непрерывный
оператор, отображающий топологическое и, как пра-
правило, векторное пространство X в R или С. Поэтому
определение и признаки непрерывности произвольного
оператора сохраняются с соответствующей специфи-
спецификацией и для функционалов. Так, напр.:
1) для того чтобы функционал / : М-+С, где М —
подмножество топологического пространства X, был
непрерывен в точке хп?М, для любого е>0 должна
существовать окрестность U точки х0 такая, что
|/(х) — /(хо)|<8 при x?U (определение непрерывно-
непрерывности функционала);
2) функционал, непрерывный на компактном мно-
множестве отделимого топологического векторного про-
пространства, ограничен на этом множестве и достигает
на нем своих точных границ (теорема Вейер-
ш т р а с с а);
3) так как всякий ненулевой линейный функционал
отображает банахово пространство X на все R (или С),
то он осуществляет открытое отображение, т. е. образ
любого открытого множества GcX есть открытое мно-
множество В R (ИЛИ С). В. И. Соболев.
НЕПРЕРЫВНЫХ ФУНКЦИЙ ПРОСТРАНСТВО —
нормированное пространство С (X) ограниченных не-
непрерывных на топологич. пространстве X функций
/ : Х->С с нормой ||/Ц=sup |/(z)|. Сходимость последо-
хех
вательности /„ в пространстве С (X) означает равномер-
равномерную сходимость. Пространство С (X) является комму-
коммутативной банаховой алгеброй с единицей. Если X — би-
бикомпакт, то всякая непрерывная на нем функция
/: Х—*С ограничена и, следовательно, пространство
С(Х) совпадает с пространством всех непрерывных на
X функций.
В случае, когда Х=[а, Ь] — отрезок действительных
чисел, пространство С (X) обозначается С [я, 6]. Множе-
Множество всех целых неотрицательных степеней 1, х, х2, ... ,
х", ... образует согласно Вейерштрасса теореме о
приближении непрерывных функций многочленами пол-
полную систему в пространстве С [а, Ь] (это означает, что
множество линейных комбинаций указанных степеней,
т. е. многочлены, образует в С [а, Ь] всюду плотное мно-
множество), следовательно, пространство С [а, Ь] сепара-
бельно. В пространстве С [а, Ь] существует базис, напр.
Фабера — Шаудера система функций образует базис
в пространстве С [О, 1]. Критерий компактности в про-
пространстве С [а, Ь] дается соответствующей теоремой
А р ц е л а: для того чтобы нек-рое семейство функций
fGC\a, Ь] было компактным относительно пространства
С [а, Ь], необходимо и достаточно, чтобы это семейство
было равномерно ограничено и равностепенно непре-
непрерывно. Этот критерий обобщается на случай метрич.
пространства С(Х, Y) непрерывных отображений мет-
метрич. компакта X в метрич. компакт Y. Для компакт-
компактности замкнутого подмножества А пространства
С (X, У) необходимо и достаточно, чтобы входящие
в А отображения были равностепенно непрерывны. Рас-
Расстояние между отображениями / и g из пространст-
пространства С(Х, Y) задается формулой
р(/, g)= sup р (/(*), g(x)).
Лит.: [1] Александров П. С, Введение в теорию
множеств и общую топологию, М., 1977; [21 Колмогоров
А. Н., ФоминС. В., Элементы теории функций и функцио-
функционального анализа, 5 изд., М., 1981. Л.Д.Кудрявцев,
НЕПРИВОДИМАЯ МАТРИЧНАЯ ГРУППА — груп-
группа G матриц размера пХп над полем к, к-рую нельзя
привести путем одновременного сопряжения в общей
линейной группе GLn(k) к полураспавшемуся виду
]А ¦*
||0 В '
где А, В — квадратные клетки фиксированных разме-
размеров. Более точно, G наз. неприводимой над
полем к. На языке преобразований: группа G ли-
линейных преобразований конечномерного векторного
пространства V наз. неприводимой, если V— минималь-
минимальное G-инвариантное подпространство (отличное от ну-
нуля). Неприводимые абелевы группы матриц над алгеб-
алгебраически замкнутым полем одномерны. Группа матриц
над полем, неприводимая над любым его расширением,
наз. абсолютно неприводимой. Если
поле к алгебраически замкнуто, то для всякой группы
G<=GLn(k) следующие условия равносильны: 1) G не-
приводима над к, 2) G содержит п2 матриц, линейно не-
независимых над к, 3) G абсолютно неприводима. Таким
образом, абсолютная неприводимость над полем равно-
равносильна неприводимости над его алгебраическим замы-
замыканием.
Лит.: [1] Ван дер Варден Б. Л., Алгебра, пер. с
нем., М., 197fi; [2] Мерзляков Ю. И., Рациональные
группы, М., 1980. Ю. И. Мерзляков.
НЕПРИВОДИМОЕ АНАЛИТИЧЕСКОЕ ПРОСТРАН-
ПРОСТРАНСТВО — аналитическое пространство, к-рое нельзя
представить в виде объединения локально конечного
семейства его аналитич. подпространств. Н. а. п. яв-
является обобщением понятия неприводимого аналитиче-
аналитического множества. Всякое аналитич. пространство мож-
можно единственным образом представить в виде несократи-
мого объединения локально конечного семейства его
неприводимых аналитич. подпространств, называемых
его неприводимыми компонентами
(разложение пространства на неприводимые компо-
компоненты). Комплексное аналитич. многообразие непрпво-
димо тогда и только тогда, когда оно связно; неприво-
неприводимые компоненты многообразия — это его компоненты
связности. Росток аналитич. пространства в данной
его точке наз. неприводимым, если его нельзя
представить в виде объединения конечного числа рост-
ростков аналитич. подпространства в этой же точке. Всякий
росток аналитич. пространства в точке единственным
образом представляется в виде объединения конечного
числа своих неприводимых подростков. Росток приве-
приведенного комплексного пространства (X, Q) в точке
х?Х непрпводим тогда и только тогда, когда локаль-
локальное кольцо Qx не имеет делителей нуля. Комплексное
пространство, ростки к-рого во всех его точках непри-
водимы, является неприводимым тогда и только тогда,
когда оно связно; неприводимые компоненты такого
пространства суть его компоненты связности.
Лит.: [1] Ганнинг Р., Росси X., Аналитические
функции многих комплексных переменных, пер. с англ., М.,
1969; [2] Э р в е М., Функции многих комплексных перемен-
переменных. Локальная теория, пер. с англ., М., 1965.
Д. А. Пономарев.
НЕПРИВОДИМОЕ МНОГООБРАЗИЕ — алгебраиче-
алгебраическое многообразие, являющееся неприводимым тополо-
топологическим пространством в топологии Зариского- Ина-
Иначе говоря, Н. м.— алгебраич. многообразие, к-рое
нельзя представить в виде объединения двух собствен-
собственных замкнутых алгебрапч. подмногообразий. Анало-
Аналогично определяется неприводимость схемы. Для глад-
гладкого (и даже нормального) многообразия понятия не-
неприводимости и связности совпадают. Каждое непри-
неприводимое многообразие обладает единственной общей
точкой.
По аналогии с разложением топологич. пространства
на неприводимые компоненты любое алгебраич. много-
многообразие является объединением конечного числа не-
неприводимых замкнутых подмногообразий. Алгебраи-
Алгебраическим фундаментом такого представления (доставляю-
(доставляющим заодно и более точную формулировку) является
примарное разложение в коммутативных не'теровых
кольцах.
Произведение Н. м. над алгебраически замкнутым
полем также неприводимо. Для произвольного основ-
основного поля этот факт уже не верен. Полезен также сле-
следующий вариант понятия Н. м.: многообразие А' над
полем к наз. геометрически неприво-
д и м ы м, если для любого расширения к' поля к
неприводимым остается многообразие Х^^к', полу-
полученное ИЗ X заменой базы. В. II. Данилов.
НЕПРИВОДИМОЕ ОТОБРАЖЕНИЕ — непрерывное
отображение топологич. пространства X на топологич.
пространство У такое, что образ всякого замкнутого
в X множества, отличного от X, отличен от У. Бели
/ : X —V У — непрерывное отображение, причем /(Х) =
= У и все прообразы точек при / бикомпактны, то су-
существует замкнутое в X подпространство Хг такое, что
/(Xj) У и сужение / на Хг является Н. о. Яркий эффект
дает соединение требований неприводимости отображе-
отображения и его замкнутости. Пространства, соединенные та-
таким отображением, не отличимы по ряду важных ха-
характеристик: в частности, по числу Суслпна и я-весу.
Но главное значение замкнутым Н. о. дает централь-
центральная роль, к-рую они играют в теории абсолютов.
Лит.: [1] Архангельский А. В., Понома-
Пономарев В. И., Основы общей топологии в задачах и упражнени-
упражнениях, М.,1974. А. В. Архангельский.
НЕПРИВОДИМОЕ ПРЕДСТАВЛЕНИЕ — (линей-
(линейное) представление я группы (алгебры, кольца, полу-
полугруппы) X в векторном пространстве (или топологиче-
топологическом векторном пространстве) Е, единственными (замк-
нутыми) инвариантными подпространствами к-рого
являются (О) и Е. Часто Н. п. в топологическом вектор-
векторном пространстве наз. топологически непри-
неприводимым представлением; если я —
представление в топологическом векторном пространст-
пространстве Е. являющееся Н. п. как представление в векторном
пространстве Еу то представление я наз. алгебраи-
алгебраически неприводимым представлен и-
е м. Алгебраически Н. п. является топологически
Н. п.; обратное, вообще говоря, неверно. Есть ряд по-
понятий, близких к понятию Н. п., в том числе — опе-
раторно неприводимое представление, вполне непри-
неприводимое представление (представление, семейство опе-
операторов к-рого образует вполне неприводимое множест-
множество). Вполне Н. п. является (топологически) Н. п. и
операторно Н. п.; обратные утверждения, вообще гово-
говоря, неверны. А. И. Штерн
НЕПРИВОДИМОЕ ТОПОЛОГИЧЕСКОЕ ПРОСТ-
ПРОСТРАНСТВО — топологическое пространство, к-рое нельзя
представить как объединение двух собственных замкну-
замкнутых подпространств. Эквивалентным образом Н. т. п.
можно определить, потребовав, чтобы любое его откры-
открытое подмножество было связным или чтобы любое от-
открытое непустое подмножество было всюду плотным.
Образ Н. т. п. при непрерывном отображении является
Н. т. п. Произведение Н. т. п. снова Н. т. п. Понятие
неприводимости представляет интерес лишь для неот-
неотделимых топологич. пространств; оно постоянно исполь-
используется в алгебраич. геометрии, имеющей дело с неотде-
неотделимой топологией Зариского.
Неприводимой компонентой тополо-
топологич. пространства X наз. любое максимальное неприво-
неприводимое подмножество в X. Неприводимые компоненты
замкнуты и их объединение дает все X. в. и. Данилов
НЕПРИВОДИМЫЙ КОНТИНУУМ — невырожден-
невырожденный континуум, неприводимый между нек-рой парой
своих точек, т. е. не содержащий никакого собственного
подконтинуума, содержащего эти точки.
А. Л. Мальцев.
НЕПРИВОДИМЫЙ МНОГОЧЛЕН — многочлен
f(x1, ... , ?„) = / от п переменных надполем к, являющий-
являющийся простым элементом кольца к [х±, ... , хг1], т. е. не-
непредставимый в виде произведения f=gh, где g и h —
многочлены с коэффициентами из к, отличные от кон-
константы (неприводимость над к). Многочлен
наз. абсолютно неприводимым, если он
ненриводим над алгебраич. замыканием поля коэффи-
коэффициентов. Абсолютно Н. м. одной переменной — это
многочлены 1-й степени и только они. В случае несколь-
нескольких переменных существуют абсолютно Н. м. сколь
угодно высокой степени, напр, любой многочлен вида
}{х1, ... , тп_1)-\-хп абсолютно неприводим.
Кольцо многочленов к [хг, ... , хп] факторнально:
любой многочлен разлагается в произведение Н. м.,
причем это разложение определено однозначно с точ-
точностью до постоянных множителей. Над полем действи-
действительных чисел любой Н. м. одной переменной имеет
степень 1 или 2, причем многочлен 2-й степени непри-
неприводим тогда и только тогда, когда он имеет отрицатель-
отрицательный дискриминант. Над любым полем алгебраич. чисел
существуют Н. м. сколь угодно высокой степени;
напр., многочлен хп^-рх-\-р, где ге>1 и р — нек-рое
простое число, неприводим в силу критерия Эйзен-
Эйзенштейна (см. Алгебраическое уравнение).
Пусть А — целозамкнутое кольцо с полем частных к
и f(x)?A \х] — многочлен одной переменной со стар-
старшим коэффициентом 1. Если f(x) — g{x)h(x) в к [х],
причем g(x) и h(x) имеют старший коэффициент 1, то
g(x), h(x)?A\x].
Редукционный критерий неприво-
неприводим о с т и. Пусть задан гомоморфизм областей це-
целостности а : А -> В. Если степень многочлена o(j(x))
совпадает со степенью многочлена f(x) и a(f(x)) непри-
неприводим над полем частных области В, то не существует
разложения f(x)~g(x)h{x), где g(x) и h(x)?A [x] и
g(x), h(x) отличны от константы. Напр., многочлен
/(z)?Z [х] со старшим коэффициентом 1 прост в Z [х]
(и, следовательно, неприводим в Q [х]), если для
нек-рого простого р неприводим многочлен a(f(x)), по-
полученный из f(x) редукцией коэффициентов по мо-
модулю р.
Лит.: 11J Ван дер Варден Б. Л., Алгебра, пер. с
нем., М., 1976; [2] Л енг С, Алгебра, пер. с англ., М., 1968;
[3]3арисский О., Самюэль П., Коммутативная ал-
алгебра, пер. с англ., т. 1—2, М., 1963. Л. В. Кузьмин.
НЕПРИВОДИМЫЙ МОДУЛЬ, простой мо-
модуль,— ненулевой унитарный модуль М над кольцом
Л с единицей, содержащий лишь два подмодуля — ну-
нулевой и сам М.
Примеры: 1) если R=% — кольцо целых чисел,
то неприводимые Д-модули — это абелевы группы
простого порядка; 2) если Л — тело, то неприводимые
Л-модули — это одномерные векторные пространства
над Л; 3) если D — тело, V — левое векторное про-
пространство над D, R = Eadj) V — кольцо Линейных пре-
преобразований пространства V (или плотное подкольцо
этого кольца), то правый Л-модуль неприводим; 4) если
G — группа, к — поле, то неприводимые представле-
представления группы G над к — это в точности Н. м. над группо-
групповой алгеброй kG.
Правый Л-модуль М неприводим тогда и только тог-
тогда, когда он изоморфен R/I, где / — нек-рый макси-
максимальный правый идеал в Л. Если А, В — неприводимые
Л-модули, f?Hom.fi(A, В), то либо /=0, либо / — изо-
изоморфизм (откуда следует, что кольцо эндоморфизмов
Н. м. является телом). Если же Л — алгебра над ал-
алгебраически замкнутым полем к, А ж В — Н. м. над R,
то (л е м м а Шура)
, . т \ *> если А=В,
Нощр (А, В) = < frv.
К ' \ {0} в противном случае.
Понятие Н. м. является одним из основных в теории
колец и теории представлений групп. С его помощью
определяются композиционный ряд и цоколь модуля,
Джекобсона радикал модуля и кольца, вполне приводи-
приводимый модуль. Н. м. участвуют в определении ряда важ-
важных классов колец: классически полупростых колец,
примитивных колец и др.
Лит.: [1] Д ж е к о б с о н Н., Строение колец, пер. с
англ., М., 1961; [21 Кар тис Ч., Р айн ер И., Теория
представлений конечных групп и ассоциативных алгебр, пер.
сангл., М., 1969; [3] Лам бек И., Кольца и модули, пер.
с англ., М., 1971; [4] Фейс К., Алгебра: кольца, модули и
категории, пер. с англ., т. 1—2, М., 1977—79. А. В. Михалев.
НЕПРОТИВОРЕЧИВОСТЬ — свойство формальной
системы, состоящее в том, что не каждая формула этой
системы доказуема в ней. Формальные системы, обла-
обладающие этим свойством, наз. непротиворечи-
непротиворечивыми, или формально непротиворечи-
непротиворечивыми. В противном случае формальная система наз.
противоречивой, или несовместной.
Для широкого класса формальных систем, язык к-рых
содержит знак отрицания ~], Н. эквивалентна свойству:
«не существует такой формулы ср, что ф и ~]ф обе дока-
доказуемы». Класс формул данной формальной системы наз.
непротиворечивым, если не всякая формула этой сис-
системы выводима из данного класса. Формальная система
наз. содержательно непротиворечи-
непротиворечивой, если существует модель, в к-рой истинны все
теоремы этой системы. Если формальная система со-
содержательно непротиворечива, то она формально не-
непротиворечива. Для формальных систем, основанных
на классическом исчислении предикатов, справедливо
и обратное утверждение: в силу Геделя теоремы о пол-
полноте классического исчисления предикатов, всякая
такая непротиворечивая система имеет модель. Таким
образом, один из способов доказательства Н. формаль-
формальной системы состоит в построении модели. Другой (ме-
(метаматематический) метод доказательства Н., предло-
предложенный в начале 20 в. Д. Гильбертом (D. Hilbert), со-
состоит в том, что утверждение о Н. нек-рой формальной
системы рассматривается как высказывание о доказа-
доказательствах, возможных в этой системе. Теория, объек-
объектами к-рой являются произвольные математич. доказа-
доказательства, наз. доказательств теорией, или метаматема-
метаматематикой. Примером применения метаматематич. метода
может служить предложенное Г. Генценом (G. Gentzen)
доказательство Н. формальной системы арифметики
(см. Генцена формальная система).
Любое доказательство Н. использует средства той
или иной математич. теории, а потому лишь сводит
вопрос о Н. одной теории к вопросу о Н. другой теории.
При этом говорят также, что первая теория непро-
непротиворечива относительно второй теории. Боль-
Большое значение имеет вторая теорема Гёделя, к-рая ут-
утверждает, что Н. формальной теории, содержащей ариф-
арифметику, невозможно доказать с помощью средств самой
рассматриваемой теории (при условии, что эта теория
действительно непротиворечива).
Лит.: [1] Гильберт Д., Б е р н а й с П., Основания
математики. Логические исчисления и формализация арифмети-
арифметики, пер. с нем., М., 1979; [2] Н о в и к о в П. С, Элементы ма-
математической логики, 2 изд., М., 1973; [3] Френкель А.,
Бар-Хиллел И., Основания теории множеств, пер. с
англ., М., 1966; [4] Г е н ц е н Г., в кн.: Математическая тео-
теория логического вывода, М., 1967, с. 77—153; [5] Минц Г. Е.,
в кн.: Итоги науки и техники. Алгебра. Топология. Геометрия,
т. 13, М., 1975, с. 5—49; [6] G б d e 1 К., «Monatsch. Math, und
Physik», 1930, Bd 37, S. 349—60. В. Е. Плиско.
НЕРАВЕНСТВО — отношение, связывающее два чис-
числа ах и я2 посредством одного из знаков: < (мень-
(меньше), < (меньше или равно), > (больше), ^ (больше или
равно), ф (неравно), то есть
a2, а1>а2, я^я-г, а1фа2.
Иногда несколько Н. записываются вместе, напр.
а<Ь<с.
Н. обладают многими свойствами, общими с равенст-
равенствами. Так, Н. остается справедливым, если к обеим
частям его прибавить (или от обеих частей отнять)
одно и то же число. Точно так же можно умножить обе
части Н. на одно и то же положительное число. Однако
если обе части Н. умножить на отрицательное число,
то смысл Н. изменится на противоположный (т. е.
знак > заменяется на <, а < на ». Из неравенств
А <В и C<D следует A + C<B+D uA—D<B — C, т. е.
одноименные Н. (А <В и C<.D) можно почленно скла-
складывать, а разноименные Н. (А <В и D>C) — почленно
вычитать. Если числа А, В, С и D положительны, то из
неравенств А<$ и C<.D следует также AC-CBD и
¦^ < -?- , т. е. одноименные Н. (между положительными
числами) можно почленно перемножать, а разноимен-
разноименные — почленно делить.
Н., в к-рые входят величины, принимающие различ-
различные числовые значения, могут быть верны для одних
значений этих величин и неверны для других. Так, не-
неравенство х2—4x+3>0 верно при х—А и неверно при
j-=2. Для Н. этого типа возникает вопрос об их реше-
решении, т. е. об определении границ, в к-рых следует брать
входящие в Н. величины для того, чтобы Н. были спра-
справедливы. Так, переписывая неравенство х2—4a;-f-3>0
в виде: (х—1)(х—3)>0, замечают, что оно будет верно
для всех х, удовлетворяющих одному из следующих не-
неравенств: ж<1, ?>3, к-рые и являются решением дан-
данного Н.
Ниже приводятся нек-рые Н., выполняющиеся тож-
тождественно в той или иной области изменения входящих
в них переменных.
1) Неравенство для модулей. Для
любых действительных или комплексных чисел ах, я2,
... , ап справедливо Н.
+•••+«„ Kl«il + ] «2 I+.-. + I аи|-
2) Неравенство для средних. Наибо-
Наиболее известны Н., связывающие гармоническое, геомет-
геометрическое, арифметическое и квадратичное средние:
здесь все числа а1( а2, ..., ап — положительны.
3) Неравенства для сумм и их инте-
интегральные аналоги. Таковы, напр., Буняков-
ского неравенство, Гелъдера неравенство, Гильберта
неравенство, Кохии неравенство.
4) Неравенства для степеней чисел.
Наиболее известно здесь Минковского неравенство и его
обобщения на случай рядов и интегралов.
5) Неравенства для некоторых клас-
классов последовательностей и функ-
ц и й. Примерами могут служить Чебышева неравенство
для монотонных последовательностей и Иенсена нера-
неравенство для выпуклых функций.
6) Неравенство для определителей.
Напр., неравенство Ада мара — см. А дама-
ра теорема об определителях.
7) Линейные неравенства. Рассматри-
Рассматривается система Н. вида
«/А+Я/2;Г2+ • • • +e/;AlSs*G 1 = 1, 2 П.
Совокупность решений этой системы Н. представляет
собой нек-рый выпуклый многогранник в н-мерном про-
пространстве (a-j, х2, ... , хп); задача теории линейных не-
неравенств состоит в том, чтобы изучить свойства этого
многогранника.
Н. имеют существенное значение для всех разделов
математики. В теории чисел целый раздел этой дисци-
дисциплины — диофантовы приближения — полностью ос-
основан на Н.; аналитич. теория чисел тоже часто опери-
оперирует с Н. (см., напр., Виноградова оценки). В геометрии
Н. постоянно встречаются в теории выпуклых тел и в
изопериметрич. задаче (см. Изопериметрическое нера-
неравенство, Изопериметрическое неравенство классическое).
В теории вероятностей многие законы формулируются
с помощью Н. (см., напр., Чебышева неравенство и его
обобщение Колмогорова неравенство). В теории диффе-
дифференциальных уравнений используются т. п. дифферен-
дифференциальные неравенства. В теории функций постоянно
употребляются различные Н. для производных от мно-
многочленов и тригонометрич. полиномов (см., напр.,
Верншгпейна неравенство, Джексона неравенство); о Н.,
связанных с вложением классов дифференцируемых
функций, см. Колмогорова неравенство, Вложения тео-
теоремы. В функциональном анализе при определении нор-
нормы в функциональном пространстве требуется, чтобы она
удовлетворяла Н. треугольника 1!-?+;/1!<:|И|-Н|г/||. Мно-
Многие классич. Н. в сущности определяют значения нормы
линейного функционала или линейного оператора в том
или ином пространстве или дают оценки для них
(см., напр., Бесселя неравенство, Минковского неравен-
неравенство). В вычислительной математике Н. применяются
для оценки погрешности приближенного решения за-
задачи.
Лит.: X а р д и Г. Г., Литтльвуд Дж. Е., П о-
пиа Г., Неравенства, пер. с англ., М., 1948; Б с к к е н-
б а х Э., Б е л л м а н Р., Неравенства, пер. с англ., М., 1965.
По материалам одноименной
статьи из БСЭ-3.
НЕРАЗВЕТВЛЕННЫЙ ИДЕАЛ — простой идеал $
поля алгебраич. чисел К, лежащий над таким простым
числом р, что главный идеал (р) имеет в поле К разло-
разложение в произведение простых идеалов вида
где
$,=$ и $„ ...,Щ,*ф,
причем е1=1. Точнее этот идеал наз. абсолютно
неразветвленным. В общем случае, пусть
А — дедекиндово кольцо с полем частных к, К — ко-
конечное расширение поля к и В — целое замыкание А
в К. Простои идеал Щ, кольца В, лежащий над идеалом
3} кольца А, наз. неразветвленным в рас-
расширении К/к, если
где $рх, , tys — попарно различные простые идеалы
кольца В, 5pi=$ и«!=1. Если все идеалы^, , ?$s
не разветвлены, то иногда говорят, что идеал J} остает-
остается неразветвленным в К/к. Для расширения Галуа
К/к неразветвленность идеала ф кольца В эквивалент-
эквивалентна тому, что подгруппа разложения ф в группе Галуа
G(Klk) совпадает с группой Галуа расширения полей
вычетов E/5р)/(Л/§)). В любых конечных расширениях
полей алгебраич. чисел все идеалы, кроме конечного
числа, не разветвлены.
Лит.: [1] Боревич 3. И., Ш а ф а р е в и ч И. Р.,
Теория чисел, 2 изд., М., 1972; [2] Л е н г С, Алгебраические
числа, пер. с англ., М., 1966; [3] Алгебраическая теория чисел,
пер. с англ., М., 1969. Л. В. Кузьмин.
НЕРАЗВЕТВЛЕННЫЙ ХАРАКТЕР — характер
группы Галуа G(K/k) расширения Галуа локальных
полей К/к, тривиальный на подгруппе инерции. Любой
Н. х. можно рассматривать как характер группы Галуа
расширения Кцр/к, где К^р — максимальное нераз-
ветвленное подполе в расширении Klk. H. х. образуют
подгруппу в группе всех характеров. Неразвет-
Неразветвленным характером наз. также характер
мультипликативной группы к* локального поля к,
тривиальный на группе единиц поля к. Это определение
согласовано с предыдущим, т. к. согласно основной тео-
теореме локальной теории полей классов для любого абе-
лева расширения локальных полей К/к определен ка-
нонич. гомоморфизм взаимности 8 : к* —»- G(K/k), по-
позволяющий отождествить характеры группы G(Klk)
с нек-рой подгруппой в группе характеров группы к*.
Для расширения Галуа глобальных полей К/к ха-
характер % группы Галуа G(K/k) наз. неразветв-
неразветвленным в точке й поля к, если он остается не-
неразветвленным в указанном выше смысле и при огра-
ограничении на подгруппу разложения любой точки 5K поля
К, лежащей над 3i. Аналогично, характер х группы
классов иделей С (к) поля к наз. неразветвлен-
неразветвленным в 3?, если его ограничение на подгруппу единиц
пополнения к^ поля к относительно J} тривиально,
где группа кЙ вложена стандартным образом в С (к).
Из глобальной теории полей классов следует, что оба
эти определения неразветвленностп в точке 3} согла-
согласованы, как и в локальном случае.
Лит.: [1] В е й л ь А., Основы теории чисел, пер. с англ.,
М., 1972. Л. В. Кузьмин.
НЕРАЗЛОЖИМОЕ ПРЕДСТАВЛЕНИЕ — представ-
представление группы (или алгебры, кольца, полугруппы и
т. д.), неэквивалентное прямой сумме ненулевых пред-
представлений той же группы (соответственно алгебры и
т. д.). Таким образом, Н. п. образуют класс представ-
представлений, к-рые должны рассматриваться как простейшие
представления соответствующей алгебраич. системы
и являются тем классом представлений, с помощью
к-рого следует изучать структуру алгебраич. системы,
ее теорию представлений и гармонич. анализ на этой
системе. Представление топологич. группы (соответст-
(соответственно алгебры и т. д.) в топологическом векторном про-
пространстве наз. Н. п., если оно не эквивалентно тополо-
топологической прямой сумме ненулевых представлений той
же алгебраич. системы.
Всякое неприводимое представление есть Н. п. Класс
конечномерных Н. п. группы R и разложение данного
конечномерного представления группы R на Н. п. не-
непосредственно связаны с жордановой нормальной фор-
формой матрицы и с теорией линейных обыкновенных диф-
дифференциальных уравнений с постоянными коэффициен-
коэффициентами. Классификация Н. п. даже таких групп, как R"
и %п, ге>1, далека A982) от завершения. Н. п. полу-
полупрямых произведений групп — в частности Н. п. раз-
разрешимых групп Ли — могут быть приводимы (даже в
конечномерном случае). С другой стороны, конечномер-
конечномерные Н. п. действительных полупростых групп Ли не-
приводимы, но эти группы пмеют приводимые бесконеч-
бесконечномерные Н. п., принадлежащие, в частности, аналп-
тич. продолжению основной непрерывной серии пред-
представлений таких групп.
Лит.: [1] Кириллов А. А., Элементы теории пред-
представлений, 2 изд., М., 1978; [2] Ж е л о б е н К о Д. П., Ком-
Компактные группы Ли и их представления, М., 1970; [3] Н а й-
марк М. А., Теория представлений групп, М., 1976; L4]
Гельфанд И. М., Пономарев В. А., «Успехи ма-
тем. наук», 1968, т. 23, в. 2, с. 3—60. А. И. Штерн.
НЕРАЗЛОЖИМОЕ РАСПРЕДЕЛЕНИЕ — невырож-
невырожденное распределение вероятностей, не представимое
в виде свертки невырожденных распределений. Случай-
Случайную величину, распределение к-рой неразложимо, не-
невозможно представить в виде суммы независимых не-
непостоянных случайных величин.
Примерами Н. р. могут служить арксинуса распре-
распределение, бета-распределение при условии ге+т<2,
Уишарта распределение, любое распределение в Rk,
k^2, сосредоточенное на строго выпуклой замкнутой
гиперповерхности. Множество Н. р. достаточно богато
и является плотным во множестве всех распределений
в топологии слабой сходимости.
В сверточной полугруппе распределений вероятно-
вероятностей Н. р. играют роль, в нек-рой степени аналогичную
роли простых чисел в арифметике (см. Хинчина теорема
о факторизации распределений), но не каждое распре-
распределение имеет делитель, являющийся Н. р.
Лит.: [1] Л и н н и к Ю. В., Островский И. В.,
Разложения случайных величин и векторов, М., 1972; [2]
Лившиц Л. 3., Островский И. В., Чистя-
Чистяков Г. П., в кн.: Итоги науки и техники. Теория вероятно-
вероятностей. Математическая статистика. Теоретическая кибернетика,
т. 12, М., 1975, с. 5—42; [3] Р а г t h a s a r a t h у К. R.,
Rao R. R., Varadhan S. R. S., «Trans. Amer. Math.
Soc», 1962, v. 102, p. 200 —17. И. В. Островский.
НЕРАЗЛОЖИМЫЙ КОНТИНУУМ — невырожден-
невырожденный континуум, к-рый нельзя представить в виде объе-
объединения двух собственных подконтинуумов.
А. А. Мальцев.
НЕРАЗРЕШИМОСТИ СТЕПЕНЬ — класс эквива-
эквивалентности =7'i индуцированной отношением <:г тью-
ринговой сводимости на подмножествах натурального
ряда (А=ТВ, если 4<Г2? и В*?ТА). Иначе говоря, два
множества принадлежат одной Н. с, если для каждого
из них существует эффективная разрешающая проце-
процедура при возможности время от времени получать
от «оракула» ответы на возникающие до ходу вычи-
вычислений вопросы о принадлежности того или иного чис-
числа другому нз рассматриваемых множеств (см. так-
также Алгоритмическая сводимость). Н. с. определяют
также как класс эквивалентности на множестве всюду
определенных функций (отображающих натуральный
ряд в себя), индуцированной отношением ¦<# относи-
относительной рекурсивное™ (функция / рекурсивна
относительно функции g, если для / существует
рекурсивное определение, в к-ром в число исходных
функций, помимо обычных, входит g); в этом случае
Н. с. данной функции наз. также ее степенью
н е в ы ч и с л и м о с т и. Н. с. наз. также т ь ю-
ринговыми степенями, или Т - с т е п е-
н я м и. Множество всех Н. с при обоих подходах
оказывается верхней полурешеткой (полуструктурой),
причем получающиеся полурешетки Н. с. множеств и
функций изоморфны, и в этом смысле приведенные оп-
определения эквивалентны.
Строение полурешетки Н. с. изучено довольно под-
подробно (см. [1] — [3]). Элементарная теория полуре-
полурешетки Н. с. неразрешима [6].
На множестве Н. с. определена операция ска-
скачка, сопоставляющая степени неразрешимости а
Н. с. я', наибольшую среди Н. с, рекурсивно перечнс-
лимых относительно я (множество В рекурсивно
перечислимо относительно множе-
множества А, если В есть проекция рекурсивного относи-
относительно А множества, а Н. с. b наз. рекурсивно
перечислимой относительно Н. с. а,
если Ь содержит множество В, рекурсивно неречпслимое
относительно нек-рого А?а). Операция скачка моно-
монотонна: из о<:Ь следует я'«:6' (но не обратно). Для вся-
всякой Н. с. а^О' существует такая Н. с. Ь, что а=Ь'.
Н. с. 0(п> являются наибольшими, достижимыми в
классах 2„ и П„ арпфметпч. множеств.
Особый интерес представляют рекурсивно перечнс-
лимые Н. с. (Н. с. рекурсивно перечислимых множеств),
образующие цодполурешетку в полурешетке всех Н. с.
Наибольшей среди рекурсивно перечислимых Н. с.
является О' (Н. с. полного множества). Вопрос о су-
существовании рекурсивно яеречислимых Н. с, отлич-
отличных от 0 и 0' (т. н. проблема Поста), решен
положительно (см. [4], [5]). При решении этой про-
проблемы был развит приоритета метод. Полурешетка
рекурсивно перечислимых Н. с. (в отличие от полу-
полурешетки всех Н. с.) плотна, причем в нее может быть
вложено произвольное счетное частично упорядо-
упорядоченное множество. Для многих типов массовых
проблем, возникающих в математике и состоя-
состоящих в отыскании разрешающего алгоритма для неко-
некоторого множества (таких, как проблема тождества в
теории групп, проблема разрешения конечно аксиома-
аксиоматизируемой элементарной теории и др.), доказано су-
существование неразрешимых проблем соответствующего
типа, имеющих произвольную рекурсивно перечисли-
мую Н. с.
Исследовались Н. с. важнейших типов рекурсивно
перечислимых множеств (так, все креативные множест-
множества имеют Н. с. О', простые множества могут иметь лю-
любую ненулевую рекурсивно перечислимую Н. с, мак-
максимальные — любую рекурсивно перечислимую Н. с.
я, для к-рой я'=0").
Понятие степени вводится и для других типов алго-
ритмич. сводимости, отличных от тыорннговой (в част-
частности, 1-, т-, «-степени и др.), причем исследовался
вопрос о распадении Н. с. на эти, «более мелкие», сте-
степени. Нек-рые из этих промежуточных типов сводимо-
сводимости оказываются связанными с оценкой сложности ра-
работы и задания алгоритмов (см. также Алгоритмическая
теория информации).
Лит.: [1] Роджерс X., Теория рекурсивных функций
и эффективная вычислимость, пер. с англ., М., 1972; [2] Ш е н-
ф и л д Д ж., Степени неразрешимости, пер. с англ., М., 1977;
[3] S а с k s G. E., Degrees of unsolvability, Princeton (N. Y.),
1963; [4] M у ч н и К А. А., «Докл. АН СССР», 1956, т. 108,
№ 2, с. 194—97; [5] Friedberg R. M., «Proc. Nat. Acad.
Sci. USA» 1957, v. 43, p. 236 — 38; [6] Lachlao A. H.,
«Z. math. Log. und Grundl. Math.», 1968, Bd 14, S. 457—72.
В. Л. Душский.
НЕРАЗРЕШИМОСТЬ — невозможность решения
данной задачи точно очерченными средствами. Ниже
рассмотрены важнейшие примеры Н. в математике.
Алгоритмическая неразрешимость.
В различных областях математики возникают проблемы,
в к-рых требуется найти единую механич. процедуру
(алгоритм), с помощью к-рой можно было бы решить
любую задачу из данного бесконечного класса однотип-
однотипных задач. Такие проблемы наз. массовыми
проблемами. Примером может служить 10-я
проблема Гильберта, состоящая в построении алгорит-
алгоритма, к-рый позволил бы для любого заданного многочле-
многочлена с целыми коэффициентами узнать, существуют ли
целые значения переменных, обращающие этот много-
многочлен в нуль. Многие массовые проблемы долгое время
не поддавались решению; впоследствии оказалось, что
трудность их решения имеет принципиальный харак-
характер. Это удалось установить лишь после того, как в
30-х гг. 20 в. в математич. логике было выработано точ-
точное понятие алгоритма и для нек-рых массовых проблем
было доказано, что искомые в них алгоритмы не сущест-
существуют. Такие массовые проблемы наз. неразреши-
м ы м и, или алгоритмически неразре-
ш и м ы м и. Неразрешимыми оказались многие другие
алгорнтмич. проблемы из различных областей матема-
математики, в частности 10-я проблема Гильберта (см. также
Алгоритмическая проблема).
Установление алгоритмической Н. данной массовой
проблемы показывает, что для решения каждой кон-
конкретной задачи из рассматриваемого класса требуется
свой специфический для этой задачи метод, т. к. еди-
единого метода решения всех этих задач не существует.
Неразрешимые предложения. Одним
из способов построения математич. теории является
аксиоматический метод. При аксиоматич. построении
теории ряд ее положений принимается в качестве ис-
исходных, или аксиом, а другие получаются как их след-
следствия. В работах Д. Гильберта (D. Hilbert) и его школы
понятие аксиоматич. теории было уточнено в виде по-
понятия формальной системы. Намеченная Д. Гильбер-
Гильбертом программа обоснования математики предусматри-
предусматривала, в частности, формализацию основных разделов
математики — арифметики, анализа, теории множеств,
т. е. построение формальной системы, из аксиом к-рой
можно было бы вывести практически все математич.
теоремы. Однако в 1931 К. Гёдель (К. Godel) показал,
что всякая формальная система арифметики неполна
в том смысле, что можно указать предложение, к-рое
в этой системе нельзя ни доказать, ни опровергнуть
(т. е. доказать его отрицание). Такие предложения наз.
неразрешимыми, пли формально не-
неразрешимыми, в данной системе. В частности,
для всякой непротиворечивой формальной системы,
содержащей достаточно богатую часть арифметики, ут-
утверждение о непротиворечивости этой системы оказы-
оказывается неразрешимым в ней (см. Гёделя теорема о не-
неполноте).
Н. предложения в данной формальной системе озна-
означает, что невозможно убедиться в его истинности
пли ложности на основании лишь тех представлений
об исследуемом объекте, к-рые выражены в аксиомах
и правилах вывода. Часто оказывается возможным рас-
расширить формальную систему за счет новых аксиом та-
таким образом, чтобы нек-рое конкретное неразрешимое
в ней предложение можно было доказать или опровер-
опровергнуть в получившейся системе. Обнаружение в аксио-
аксиоматич. теории неразрешимых предложений имеет важ-
важное значение для развития этой теории, т. к. стимули-
стимулирует поиск новых фундаментальных положении, к-рые
можно было бы принять в качестве аксиом.
Примером Н. в элементарной математике является
Н. таких геометрич. задач на построение, как трисек-
трисекция угла п квадратура круга при помощи циркуля и
линейки.
Лит.: [1J Гильберт Д., Бернайс П., Основания ма-
математики. Логические исчисления и формализация арифмети-
арифметики, пер. с нем., М., 1979. В. Е. Плиспо.
НЕРАЗРЫВНОСТИ УРАВНЕНИЕ — одно из основ-
основных уравнений гидродинамики, выражающее закон
сохранения массы для любого объема движущейся жид-
жидкости (газа). В переменных Эйлера Н. у. имеет вид
где р — плотность жидкости, v — ее скорость в данной
точке, vx, vy, vz — проекции скорости на координат-
координатные оси. Если жидкость несжимаема (р=const), H. у.
принимает вид:
divt> = 0 или _г + —+ _' = 0.
Для установившегося одномерного течения в трубе,
канале и т. п. с площадью поперечного сечения Н. у.
дает закон постоянства расхода pSv= const. БСЭ-з.
НЕРВ семейства множеств а — симп-
лициалъный комплекс К (ex.), симплексами к-рого явля-
являются конечные непустые подмножества из а, пересече-
пересечение к-рых непусто. В частности, вершины К (а) суть
элементы из а, не являющиеся пустыми множествами.
М. И. Войцеховский.
НЕРОНА МОДЕЛЬ абелева многообра-
многообразия — групповая схема, сопоставляемая абелеву мно-
многообразию и обладающая нек-рым свойством минималь-
минимальности. Если R — локальное гензелево кольцо дискрет-
дискретного нормирования с полем вычетов к и полем частных
К, А — абелево многообразие размерности d над полем
А, то моделью Нерона многообразия А наз.
гладкая коммутативная групповая схема 21 над коль-
кольцом R, общий слой к-рой 3t/j — изоморфен многообразию
А, а канонич. гомоморфизм 21(й) —*- 9tfc (К) является
изоморфизмом. Это понятие было введено А. Нероном
[1] в случае совершенного поля к. В локальном случае
Н. м. существует и определена однозначно с точностью
до -R-изоморфизма. Н. м. обладает следующим свойст-
свойством минимальности: для любой гладкой Д-схемы ¦?
и любого морфнзма ф : 91^ —*- Э? общих слоев существу-
существует однозначно определенный морфпзм ф : 91 —*- ¦? R-
схем, индуцирующий морфпзм ф.
Если S — одномерная регулярная нётерова схема,
¦ц — ее общая точка, i : г\—*¦ S — ее канонич. вложение,
А — абелево многообразие над к(г\), то Н. м. многооб-
многообразия А определяется как гладкая квазипроектпвная
групповая схема 21 над S, представляющая пучок i%A
относительно плоской топологии Гротендика на S
(см. [4]).
Об обобщении понятия Н. м. на произвольные схемы
см. [3].
Лит.: [1] Neron A., Modules minimaux des varietes
absliennes sur les corps locaux et globaux, P., 1964 (Publ. Math.
INES, N 21); [21 M а з у р Б., «Математика», 1973, т. 17, Л» 2,
с. 3—57; [3] R а у n a u d M., «С. г. Acad. sci., Ser. A.», 11N6,
t. 262, p. 345—47; [4] его же, в кн.: Dix exposes sur la coho-
moloprie des schemas, Amst.— P., 1968, p. 12—30; [5] Groupes
de monodromie en geometric algebrique, v. 1, В., 1972.
НЕРОНА—СЕВЕРИ ГРУППА — группа классов ди-
дивизоров по отношению алгебраич. эквивалентности на
неособом проективном многообразии.
Пусть X — неособое проективное многообразие раз-
размерности ^2, определенное над алгебраически замкну-
замкнутым полем к, D (X) — группа дивизоров многообразия
.Y, a Da(X) — подгруппа алгебраически эквивалент-
эквивалентных нулю дивизоров. Факторгруппа D(X)lDa(X)
наз. группой Нерона — Север и многооб-
многообразия X и обозначается NS (X). Теорема
Нерона — Север и утверждает, что абелева
группа NS(X) имеет конечное число образующих.
В случае к—С Ф. Северп в цикле статей о теории
базы (см., напр., [1]) предложил доказательство этой
теоремы, использующее топологические и трансцен-
трансцендентные средства. Первое абстрактное доказательство
(годное для ноля к любой характеристики) принадлежит
А. Нерону (см. [21, [3], а также [4]).
Ранг группы NS(X) совпадает с алгебраич. числом
Бетти группы дивизоров на X, т. е. с алгебраич. ран-
рангом многообразия X. Это число наз. также числом
Пи кара многообразия X. Элементы конеч-
конечной периоднч. подгруппы NStors(^) наз- делите-
делителями С е в е р и, а порядок этой подгруппы —
числом С е в е р и; группа NStors(^Q является би-
рациональным инвариантом (см. [6]).
Имеются обобщения теоремы Нерона — Северн на
другие группы классов алгебраических циклов (см.
[1] (классическая теория) и [7] (современная тео-
рня)).
Лит.: [Ц Sever i F., «Mem. Accad. Ital.», 1934, t. 5,
p. 239—83; [21 Neron A., «Bull. Soc. math. France», 1952, t. SO,
p. 101—66; [3] его же, «Coll G6om. algebric. Liege», 1952,
p. 119—2Й; [4j Lang S., Neron A., «Amer. J. Math.»,
1959. v. 81. N 1, 95—118; [5] H a r t s h о r n e R., Algebraic geo-
geometry, N. Y., 1977; [6] Бальдассарри М., Алгебраиче-
Алгебраические многообразия, пер. с англ., М., (961; [7] Итоги науки и
техники. Алгебра. Топология. Геометрия, т. 12, М., 1974,
с. 77—170. В. А. Псковских.
НЕСАМОСОПРЯЖЕННЫЙ ОПЕРАТОР — линей-
линейный оператор в гильбертовом пространстве, спектраль-
спектральный анализ которого не укладывается в рамки теории
самосопряженных операторов и ее простейших обобще-
обобщений: теории унитарных операторов и теории нормаль-
нормальных операторов. Н. о. возникают при рассмотрении
процессов, протекающих без сохранения энергии: в за-
задачах с трением, в теории открытых резонаторов, в за-
задачах неупругого рассеяния и др. К исследованию Н. о.
приводят и нек-рые самосопряженные задачи, в к-рых
при разделении переменных возникает операторно-
значная функция Ж (Я), нелинейно зависящая от спек-
спектрального параметра Я. Многие из предложений, отно-
относящиеся к теории Н. о., справедливы и для операторов,
действующих в произвольных банаховых пространст-
пространствах, F-пространствах, топологических векторных про-
пространствах и т. д.
Наиболее распространенным методом изучения Н. о.
является метод оценки резольвенты, использующий тео-
теорию аналитич. функций, теорию асимптотич. разложе-
разложений и др.
Первыми работами, относящимися к теории Н. о.,
были работы Г. Биркгофа (G. Birkhof), Я. Д. Тамар-
кина, В. А. Стеклова и др. по исследованию задач для
обыкновенных дифференциальных уравнений. Эти уче-
ученые применяли метод Коши контурного интегрирова-
интегрирования резольвенты.
Для дифференциальных Н. о. с частными производ-
производными долгое время отсутствовали эффективные методы
изучения. Объясняется это сложным строением резоль-
резольвенты оператора, как аналитич. функции.
В развитии общей теории Н. о. (и, в частности, опе-
операторов с частными производными) большую роль сыг-
сыграла работа М. В. Келдыша [1] (см. также [2]). В ней
изучено уравнение
у = Х(Х)у, A)
где у — элемент некоторого гильбертова пространства
II, а оператор X (Я) допускает представление
Здесь Яо — вполне непрерывный обратимый самосопря-
самосопряженный оператор конечного порядка, Bj, 0 <:/<:«—1,
— произвольные вполне непрерывные операторы.
(Вполне непрерывный оператор А , действующий в гиль-
гильбертовом пространстве, называется оператором
конечного порядка, если 2jS^(A)<i<x при
нек-ром 0<р<оо; через s^(A) обозначены сингулярные
числа А, т. е. собственные значения оператора (А А *)'/'2.)
Собственные значения уравнения A) —
те значения Я, при к-рых это уравнение имеет нетриви-
альные решения у; эти решения наз. собственны-
собственными векторами.
При сделанных выше предположениях спектр урав-
уравнения A) дискретен. Вследствие несамосопряженности
оператора Ж (Я), наряду с собственными векторами,
естественно, возникают (при наличии кратного спектра)
присоединенные векторы. В работе [1] строится цепочка
присоединенных векторов ylt y2, ... , ук, отвечающих
собственному значению Я и собственному вектору у по
правилу
У.
v = l, 2, ..., к.
Система собственных и присоединенных векторов опе-
оператора X (Я) наз. re-кратно полной, если лю-
любые п векторов фо, Фх, ¦•• , ф„_1 пространства Н можно
аппроксимировать по норме Н с любой точностью ко-
конечными линейными комбинациями вида
RfLo
с одними и теми же коэффициентами ck. Здесь vk(t)
вектор-функция вида
Определение н-кратной полноты, естественно, связано
с решением задачи Коши для соответствующего уравне-
уравнению A) нестационарного уравнения.
Согласно теореме М- В. Келдыша, при сделанных
предположениях относительно коэффициентов <5?(Я)
система всех собственных и присоединенных векторов
оператора X (Я) n-кратно полна в if. В работе [1] было
также показано, что собственные значения X (Я)
асимптотически приближаются к лучам arg Я= Уп/п.
При доказательстве полноты М. В. Келдыш развил
новый метод оценки резольвенты абстрактного вполне
непрерывного Н. о. конечного порядка. При этом вы-
выявилась особая роль, к-рую играют в проблеме полноты
вольте рровы операторы — вполне непре-
непрерывные операторы с единственной точкой спектра в
нуле. Для доказательства асимптотич. поведения соб-
собственных значений М. В. Келдыш [3] использовал уста-
установленную им новую тауберову теорему.
Исследования М. В. Келдыша были продолжены мно-
многими учеными. Его теорема распространена [4] на слу-
случай, когда в уравнении A) оператор =5Р(Я) рационально
зависит от Я.
Было рассмотрено (см. [5] — [7]) уравнение М(Х)у=0
с М (Я) = /+ЯВ-гЯ2С, где С — вполне непрерывный по-
положительно определенный оператор, а В — ограничен-
ограниченный самосопряженный оператор. Обобщение теоремы
Понтрягина (см. [8]) о существовании у /-самосопря-
/-самосопряженного оператора А максимального /-неотрицатель-
/-неотрицательного инвариантного подпространства позволило (см.
[6] и [7]) установить, в важных для приложений ситуа-
ситуациях, двухкратную полноту всех собственных и при-
присоединенных векторов М(к), а также однократную пол-
полноту подсистемы, соответствующую спектру, располо-
расположенному в левой (правой) полуплоскости. Эти резуль-
результаты получили дальнейшее развитие.
Установлена (см. 19]) суммируемость рядов Фурье
по собственным и присоединенным векторам вполне
непрерывного оператора А конечного порядка р, у
к-рого значения квадратичной формы (Ах, х) лежат в
секторе комплексной плоскости, раствора меньшего
я/р (по поводу приложений этой теоремы и ее дальней-
дальнейших обобщений см. [10] и библиографию там).
Вопрос о том, когда система собственных и присоеди-
присоединенных векторов образует базис в гильбертовом прост-
ранстве, изучался в ряде работ (см. [11]). Наиболее
общие условия, при к-рых система собственных и при-
присоединенных векторов диссипативного вполне непре-
непрерывного оператора образует базис, найдена в [12].
В случае сингулярных дифференциальных операто-
операторов с дискретным спектром получен (см. в [11] и [13])
ряд тонких результатов о полноте собственных и при-
присоединенных функций оператора Штурма—Лиувилля с
комплексным потенциалом. Важные результаты полу-
получены в случае эллиптич. операторов (см. [14]). Дано
обобщение теоремы Келдыша на случай обобщенных
собственных и присоединенных функций несамосопря-
несамосопряженных эллиптич. операторов (см. [15], [16]).
Попытка перенести теорему о приведении конечно-
конечномерного оператора к жордановой форме на бесконечно-
бесконечномерный случай привела к построению треугольного
интегрального представления. Для вполне непрерывных
операторов В=Вц-\-гВ/, где В% и Вг — самосопряжен-
самосопряженные и В1 имеет конечный порядок, получен аналог тео-
теоремы Шура об унитарной эквивалентности оператора В
треугольному (см. [17]). Особое место в проблеме тре-
треугольного представления заняли вольтерровы опера-
операторы.
В проблеме треугольного представления существен-
существенную роль сыграла теорема Неймана о существовании
у линейного вполне непрерывного оператора в гильбер-
гильбертовом пространстве нетривиального инвариантного
подпространства; у произвольного ограниченного ли-
линейного оператора в банаховом пространстве нетриви-
нетривиального инвариантного подпространства может не
быть; соответствующий вопрос для случая гильбертова
пространства остается открытым A982). Волыерров
оператор наз. одноклеточным, если из каж-
каждых двух его инвариантных подпространств Ql it Q.,.
либо Q^aQz. либо Q^d Qx. Найдено [18] необходимое
и достаточное условие однолистности оператора В в
предположении, что Bf — ядерный неотрицательно
определенный: это условие формулируется в терминах
роста резольвенты оператора В при X —*¦ 0. Указано [19]
простое достаточное условие одноклеточности.
Н. о. с непрерывным спектром впервые были иссле-
исследованы М. А. Наймарком (см. [20], [21]), к-рый получил
разложение в интеграл Фурье, связанное с несамосопря-
несамосопряженной задачей
<оо, C)
у'(О)-ву(О)=О, D)
где р (х) — комплекснозначная функция, удовлетворяю-
удовлетворяющая условию
$"(l + *»)|p(*)|<fa<oo. E)
8 — комплексное число. Из результатов работы [20],
в частности, следует, что в окрестности точек действи-
действительной оси, обращающих функцию 4(s)=-td*@, .?)—
— 9со@, s) в нуль (s= Ух), спектральные проекторы опе-
оператора C)—D) яеограничены (через <л(х, s) обозначено
решение уравнения C), удовлетворяющее условию
<и(х, s\e~ixs—*- 1 при х —*¦ -\-'св — решение И о с-
т а); действительные нули функции А (ь) названы в [20]
спектральными особенностями. По-
Получено (см. [22]) обобщение результатов работы [20] на
случай уравнения Шредпнгера в трехмерном простран-
пространстве. В развитие работы [20] было показано (см. [23]),
что в общем случае (без ограничения типа E)) спект-
спектральная функция дифференциального оператора долж-
должна рассматриваться как линейный непрерывный функ-
функционал, заданный на некотором топологическом прост-
пространстве.
Исследовалась (см. [24]) система несамосопряженных
уравнений с. особыми точками, положение к-рых зави-
сит от спектрального параметра. Эти системы встреча-
встречаются в безмоментной теории оболочек. Для таких сис-
систем установлены асимптотич. свойства решений, а также
доказаны теоремы разрешимости типа теоремы Коши.
Установлены теоремы полноты системы собственных и
присоединенных функций несамосопряженных интегро-
дифференциальных операторов, порождающих нерегу-
нерегулярную задачу.
Важной задачей теории дифференциальных Н. о.
является задача о разложении ядра оператора Грина
в биортогональный ряд по собственным п присоединен-
присоединенным функциям, а также проблема их базясности.
Я. Д. Тамаркин [25] исследовал разложения суммируе-
суммируемой функции в ряд по собственным п присоединенным
функциям регулярной задачи, а также вопросы равно-
равносходимости с тригонометрии, рядом Фурье. Позже было
показано (см. [26], [27]), что для нерегулярных задач
равносходимость с тригонометрическим рядом не имеет
места.
Для усиленно регулярных условий система собствен-
собственных и присоединенных функций образует базис в L2.
Показано (см. [28], [29]), что указанная система образу-
образует не только базис, но и так наз. базис Рисса.
Развит в (см. [30]) важный метод изучения условий
базисностп и равномерной сходимости разложений по
собственным и присоединенным функциям обыкновен-
обыкновенного Н. о. Этот метод является дальнейшим развитием
идей, примененных при исследовании самосопряженных
задач. Предложена новая трактовка собственных и при-
присоединенных функций, что позволило отказаться от
конкретного вида граничных условий; рассмотрены
общие обыкновенные дифференциальные операторы или
пучки таких операторов и установлены необходимые и
достаточные условия базисности собственных и присо-
присоединенных функций таких операторов, а также крите-
критерии равносходимости. Метод основан лишь на формуле
среднего значения для собственных и присоединен-
присоединенных функций (см. также [31]). Оказалось также, что
если у оператора число присоединенных функций бес-
бесконечно, то свойство базисности зависит от выбора
последних (см. [32]).
Для несамосопряженных эллиптич. операторов имеет
место (см. [33]) сходимость некоторой последовательно-
последовательности средних типа Пуассона частичных сумм биортого-
нального ряда, т. е. предложен способ суммирования.
Разложения по собственным и присоединенным функ-
функциям нерегулярных задач впервые получены для задачи
вида y"'=ky,y(O)=y'{O)=y(i)=O. Доказано (см. [26]),
что в равномерно сходящиеся ряды такого вида могут
быть разложены функции, удовлетворяющие нек-рым
условиям аналитичности.
К числу фундаментальных относятся исследования
(см. [34]), в к-рых изучается вопрос о возмущении спек-
спектра оператора Лапласа при изменении области. При этом
впервые была выявлена роль емкости варьируемого
множества на спектр оператора. Эти методы с успехом
применяются при исследовании несамосопряженных
задач.
В теории Н. о. успешно применяются методы регуля-
регуляризации, основы к-рых были заложены в [35]. Пример —
вопрос регуляризованных следов Н. о. Первой работой
по теории следов была статья [36], где был вычислен
регуляризованный след оператора Штурма — Лиувилля.
Наиболее общие результаты в теории следов операто-
операторов получены в статьях [37], [38]. Оказалось, что фор-
формулы следов обыкновенных несамосопряженных диффе-
дифференциальных операторов, зависящих сложным образом
от спектрального параметра, могут быть получены как
следствия из формул регуляризованных сумм корней
некоторого класса целых функций. (По поводу следов
для сингулярных операторов и операторов с частными
производными см. [38], [39].)
К числу важных работ, в к-рых развиты новые методы
и идеи теории Н. о., относится также обзорный доклад
[40].
Построение окончательной теории Н. о. далеко от
завершения A982). С одной стороны, в самой этой тео-
теории формируются новые направления исследования,
напр, теория рассеяния [41], построение теории опера-
операторов сжатия [42], метод канонического оператора Мас-
лова [43], теория спектральных операторов [44] и др.,
а с другой стороны — исследования прикладных задач,
механики, математической физики подсказывают новые
пути развития этой теории.
Лит.: [1] Келдыш М. В., «Докл. АН СССР», 1951,
т. 77, № 1, с. И —14; [2] е г о же, «Успехи матем. наук», 1971,
т. 26, в. 4, с. 15—41; [3] его же, «Тр. Матем. ин-та АН СССР»,
1951, т. 38, с. 77—86; [4] Аллахвердиев Д ж. Э.,
«Докл. АН СССР», 1957, т. 115, № 2, с. 207—10; [5]Лангер Г.,
«Докл. АН СССР», 1960, т. 134, JMi 2, с. 263—66; [6] К р е й и М.
Г., там же, 1964 т. 154, № 5, с. 1023 — 26; L7] К р е й н М. Г.,
Лангер Г. К., в кн.: Приложения теории функций в ме-
механике сплошной среды, М., 1965 (Тр. Международного симпо-
симпозиума, т. 2); [8] П о н тр я г и н Л. С, «Изв. АН СССР. Сер.
матем.», 1944 т. 8, с. 243—80; [9] Л и д с к и й В. В., «Докл.
АН СССР», 1956, т. 110, № 2, с. 172—75; [10] Агранович
М. С, «Функц. анализ и его приложения», 1976, т. 10, .N» 3,
с. 1—12; [11] Гохберг И. Ц., К р е й н М. Г., Введение
в теорию линейных несамосопряженных операторов в гильбер-
гильбертовом пространстве, М., 1965; [12] Кацнельсон В. Э.,
«Функц. анализ и его приложения», 1967, т. 1 Л? 2, с, 39 — 51;
[13] Л и деки й В. В., «Докл. АН СССР», 1957, т. ИЗ, № 1,
с. 28—31; [14] КостюченкоА. Г., там же, 1964, т. 158,
JV» 1 с. 41—44; [15] П о н о м a D е в С. М., «Дифф. уравнения»,
1974, т. 10, X» 12, с. 2294—96; [16] Круковский Н. М.,
там же, 1976, т. 12, № 10, с. 1832—51; [17] Гохберг И. Ц.,
К р е й н М. Г., Теория вольтерровых операторов в гильберто-
гильбертовом пространстве и ее приложения, М., 1967; [18] Бродский
М. С, К и с и л е в с к и й Г. Э., «Изв. АН СССР. Сер. матем.»,
1966, т. 30, .№ 6, с. 1213—28; [19] Никольский Н. К.,
«Докл. АН СССР», 1967, т. 172, № 2, с. 287 — 90; [20] Н а й-
марк М. А., «Тр. Моск. матем. об-ва», 1954, т. 3, с. 181 —-
270; [21] его же, Линейные дифференциальные операторы,
2 изд., М., 1969; [22] Гаеымов М. Г., «Докл. АН АзССР»,
1966, т. 22, Хя 10, с. 9—12; [23] Марченко В. А., «Матем.
сб.», 1960, т. 52, с. 739—88; [24] Садовничий В. А., «Тр.
Семинара им. И. Г. Петровского», 1976, в. 2, с. 211—21; [25]
Тамаркин Я. Д., О некоторых общих задачах теории
обыкновенных линейных дифференциальных уравнений..., Пг.,
1917; [26] Ward L. E., «Ann. Math.», 1925, v. 26, p. 21—36;
его же, «Trans. Amer. Math. Soc», 1932, v. 34, p. 417—34;
[27] Хромов А. П., «Тр. Второй науч. конференции мате-
матич. кафедр педагогич. вузов Поволжья» (Куйбышев), 1962,
в. 1, с. 109—13; [28] Михайлов В. П., «Докл. АН СССР»,
1962, т. 144, № 5, с. 981—84; [29] Кессельман Г. М.,
«Изв. ВУЗов. Математика», 1964, J\ft 2, с. 82—93; [30] И л ь-
ин В. А., «Докл. АН СССР», 1976, т. 230, Л» 1, с. 30 — 33;
[31] Моисеев Е. И., там же, 1977, т. 233, № 6, с. 1042—45;
[32] Тихомиров В. В., «Матем. сб.», 1977, т. 102 № 1,
с. 33 — 55; [33] Ли деки й В. В., «Матем. сб.», 1962, т. 57,
М5 2, с. 137—50; [34] Самарский А. А., «Успехи матем.
наук», 1950, т. 5, в. 3, с. 133—34; [35] Тихонов А. Н.,
«Докл. АН СССР», 1963 т. 153, № 1, с. 49—52; 1943, т. 39 Я» 5,
с. 195—98; [36] Гельфанд И. М., Левитан Б. М.,
там же, 1953, т. 88, № 4, с. 593—96; [37] Л и д с к и й В. В.,
Садовничий В. А., там же, 1967, т. 176, № 2, с. 259—62;
[38] Садовничий В. А., «Дифф. уравнения», 1974, т. 10,
№ 7, с. 1276—85; [39] Садовничий В. А., Любят-
кин В. А., «Докл. АН СССР», 1981, Т. 261, № 2, с. 290 — 93; [40]
Келдыш М. В., Л и д с к и й В. В., в кн.: Тр. Четвертого
Всесоюзного математического съезда, т. 1, Л., 1963, с. 101—20;
[41] Лаке П. Д., Фи л липе Р. С, Теория рассеяния
для автоморфных функций, пер. с англ., М., 1979; [42] С е к е-
фальви-Надь Б., Фояш Ч., Гармонический анализ
операторов в гильбертовом пространстве, пер. с франц., М.,
1970; [43] Мае лов В. П., Операторные методы, М., 1973;
[44] Данфорд Н., Шварц Д ж., Линейные операторы,
пер. С англ., ч. 3, М., 1974. В. А. Садовничий.
НЕСГЛАЖИВАЕМОЕ МНОГООБРАЗИЕ — кусочно
линейное или топологическое многообразие, не допу-
допускающее гладкой структуры.
Сглаживанием кусочно линейного многообразия X
наз. кусочно линейный изоморфизм /:Af->-,Y, где
М — гладкое многообразие. Многообразие, не допус-
допускающее сглаживания, и наз. н е с г л а ж и в а е м ы м
многообразием. Сказанное с нек-рыми изме-
изменениями применимо и к топологическим многообразиям.
Пример Н. м. Пусть Wik, /с>1, — 4/с-мерное
многообразие Мшшора (см. Древовидное многообразие).
В частности, Wi^ параллелнзуемо, его сигнатура рав-
на 8, и его край M—dWik гомотопически эквивалентен
сфере S4*-1. Подклейка к W конуса СМ над dW при-
приводит к пространству Pik. При этом, так как М есть
кусочно линейная сфера (см. обобщенная Пуанкаре
гипотеза), то СМ кусочно линейный диск, так что Р —
кусочно линейное многообразие. С другой стороны, Р
есть Н. м., так как его сигнатура равна 8, а сигнатура
гладкого почти параллелизуемого (т. е. параллелизуе-
мого после выкалывания точки) 4-х мерного многооб-
многообразия кратна числу ак, экспоненциально растущему
с ростом к. Многообразие М не диффеоморфно сфере
Sk~x, т. е. М — Милнора сфера.
Критерий сглаживаемостп кусочно линейного много-
многообразия. Пусть Оп — ортогональная группа, a PLn —
группа сохраняющих начало кусочно линейных гомео-
гомеоморфизмов R" (см. Кусочно линейная топология).
Включение Оп —>- PLn индуцирует расслоение ВОп -*¦
—>- BPL, где BG — классифицирующее пространство
группы G. При п —*¦ оо получается расслоение р : ВО —>.
—>- BPL, слой к-рого обозначается через MlO. Кусочно
линейное многообразие X обладает линейным стабиль-
стабильным нормальным расслоением v, классифицируемым
отображением v : X —>- BPL. Если же X является глад-
гладким (сглаживаемым) многообразием, то оно обладает
векторным стабильным нормальным расслоением v,
классифицируемым отображением v : X —>- ВО, причем
ро v=v. Это условие также и достаточно, т. е. замкну-
замкнутое кусочно линейное многообразие X сглаживаемо тог-
тогда и только тогда, когда его кусочно линейное стабиль-
стабильное нормальное расслоение допускает векторную редук-
редукцию, т. е. когда отображение v : X —>- BPL «поднимает-
«поднимается» в ВО (существует такое v : X —*- ВО, что ро v=v).
Два сглаживания / : М —у X н g : N —>- X наз. экви-
эквивалентными, если существует диффеоморфизм h : М —>.
—>- N с f—gh (см. Структура на многообразии). Множе-
Множество ts(X) классов эквивалентности сглаживаний нахо-
находится в естественном взаимно однозначном соответствии
с классами послойной гомотопности поднятий v : X —*¦
—>- ВО отображения v : X -+ ВО. Иными словами, для
сглаживаемого X множество ts(Z) = [X, PLlO].
Лит.: [1] Kerva ire M., «Comment, math, helv.», 1960,
t. 34, p. 257—70; [2] Милнор Д ж., Сташеф Д ж.,
Характеристические классы, пер. с англ., М., 1979.
Ю. И. Рудяк.
НЕСМЕШАННЫЙ ИДЕАЛ — идеал m области це-
целостности Л (конечно порожденной над нек-рым полем
к), обладающий следующим свойством: все простые иде-
идеалы $р1? ... , §р^, ассоциированные с примарными иде-
идеалами Qj, ... , JQj из примарного разложения
имеют одну и ту же размерность, т. е. факторкольца
Л/§Р,- имеют одну и ту же размерность Крулля для
всех г. Эта общая размерность наз. размерностью
несмешанного идеала т.
Если R — кольцо регулярных функций на нек-ром
аффинном многообразии X, то его идеал m — Н. и,
тогда и только тогда, когда все неприводимые компо-
компоненты подмногообразия YcX, определяемого идеалом
ГП, имеют одну И ту же размерность. Л. В. Кузьмин.
НЕСМЕЩЕННАЯ ОЦЕНКА — статистическая оцен-
оценка, математич. ожидание к-рой совпадает с оцениваемой
величиной. Пусть по реализации случайной величины
X, принимающей значения в выборочном пространстве
C:, 5Й, Ре), 9?в, надлежит оценить функцию/ : в —>-
—*¦ Q, отображающую параметрич. множество в в не-
к-рое множество Q, и пусть в качестве оценки функции
/(в) выбрана статистика Т—Т(Х). Если статистич,
оценка Т такова, что равенство
е {Г} = ^7 (*)<№„ (*) = / (в)
выполняется для всех в?в, то Т наз. несмещен-
несмещенной оценкой функции /(в). Про Н. о. часто го-
говорят, что она лишена систематич. ошибки.
Пример 1. Пусть Xlt ... , Хп — случайные ве-
величины, имеющие одно и то же математич. ожидание в,
Е{Х1} = Е{Х,}=...=Е{Х„} = в.
В таком случае статистика
T=e1X1 + eiXi + . . . +е„Хп, П + С.+ . . . +сп = 1
является Н. о. математич. ожидания в. В частности,
среднее арифметическое наблюдений Х=(Х1-\~Х2-\-----\~
-\-Х,.Iп является Н. о. для в. В данном примере /F)=
=в.
Пример 2. Пусть Хи Х2, ... , Хп — независи-
независимые случайные величины, подчиняющиеся одному и
тому же вероятностному закону, функция распределе-
распределения к-рого есть F(x), т. е.
Р{Х{ < x] = F (х), \x\ <oo, j = l, 2, . .., п.
В таком случае функция эмпирич. распределения
F,,(x), построенная по наблюдениям X-j, Х2, ¦¦¦, Хп,
является Н. о. функции распределения F(x), т. е.
?{Fn(x)}=F(x). M<oo.
Пример 3. Пусть Т= Т(Х) — Н. о. параметра
9, т. е. Б {Т}=в, и пусть /(Э) = ав+6 — линейная
функция. В таком случае статистика аТ-{- Ь является
Н. о. для /F).
Следующий пример показывает, что имеются такие
случаи, в к-рых Н. о. существуют и даже единственны,
но при этом они могут оказаться бессмысленными.
Пример 4. Пусть X — случайная величина, под-
подчиняющаяся геометрич. распределению, параметр ус-
успеха к-рого есть в, т. е. для любого натурального чис-
числа к
P{X=k\G} = Q(l — в)*-1, 0<в<1.
Если Т=Т(Х) — Н. о. параметра Э, то она должна удо-
удовлетворять уравнению несмещенности Е {Г}=в или,
что то же самое, уравнению
единственное решение к-рого есть
Очевидно, что статистика Т является хорошей только,
если в очень близко к 1 либо к 0, в противном случае Т
не несет никакой полезной информации о параметре в.
Пример 5. Пусть случайная величина X подчи-
подчиняется биномиальному закону с параметрами п и Э,
т. е. для любого к=0, 1, п
*(i—в)«-*, о < е < 1.
Известно, что наилучшей Н. о. (в смысле минимума
квадратичного риска) параметра успеха в является
статистика T=Xln. Тем не менее, если в — иррацио-
иррациональное число, то Р {77=в}=0. Этот пример отражает
одно общее свойство случайных величин, заключающее-
заключающееся в том, что случайная величина, вообще говоря, не
обязана принимать значение, совпадающее с ее матема-
математич. ожиданием. И наконец, возможны случаи, когда
Н. о. вообще не существуют. Так, если в условиях
примера 5 в качестве оцениваемой функции выбрать
/(в)=1/0, то (см. пример 6) не существует Н. о. Т(X)
для 1/е.
Приведенные примеры демонстрируют, что само по
себе понятие Н. о., при всей своей естественности,
не помогает экспериментатору избавиться от всех ос-
ложнений, к-рые могут ждать его при построении ста-
тистич. оценок, так как Н. о. может оказаться как
очень хорошей, так и совершенно бессмысленной, она
может быть неединственной, а может вовсе не существо-
существовать. Кроме того, Н. о., как и всякая точечная оценка,
обладает еще следующим недостатком: она дает лишь
нек-рое приближенное значение для истинного значе-
значения оцениваемой величины, к-рое как было неизвест-
неизвестным до эксперимента, таковым ц остается после его
проведения. Вообще, в задаче построения точечных ста-
тпстич. оценок нет серьезных обоснований к тому, что-
чтобы во всех случаях стремиться к получению Н. о., если
не считать того, что при изучении Н. о. возникает про-
простая и стройная теория. Так, напр., Рао — Крамера
неравенство имеет простой вид для Н. о. Именно, если
Т=Т(Х) — Н. о. для функции /(в), то при довольно
широких условиях регулярности семейства {Ре } и
функции /(в) из неравенства Рао — Крамера следует,
что
0{Г}=Е{[7'-/(в)П^7^г/'(в), A)
где /(в) — информационное количество Фишера. Та-
Таким образом, существует нижняя граница для диспер-
дисперсий Н. о. функции /(9), и этой границей служит
/'(в)//(в). В частности, если /(9)=в, то из A) следует,
что
D {Т} ё= 1/7 (9).
Статистич. оценка, для к-рой в неравенстве Рао —
Крамера достигается равенство, наз. эффектив-
н о й. Так, статистика Т—Х/п, рассмотренная в при-
примере 5, является эффективной Н. о. параметра успеха 9
биномиального закона, т. к.
D {Т} = ^-8A -в)
т. е. Т—Х/п является наилучшей точечной оценкой
параметра в смысле минимума квадратичного риска в
классе всех Н. о.
Естественно, что для экспериментатора представляет
интерес тот случай, когда класс Н. о. достаточно богат,
чтобы иметь возможность выбора наилучшей в каком-
то смысле Н. о. В этой связи большую роль играет
Рао — Блэкуэлла — Колмогорова теорема, позволяю-
позволяющая строить Н. о. с наименьшей дисперсией. Эта тео-
теорема утверждает, что если семейство {Ре } имеет дос-
достаточную статистику ЧГ = Ч('(Х), а Т=Т(Х) — произ-
произвольная Н. о. функции /(в), то статистика Т*=
= Ев {T\V}, получающаяся в результате осреднения Т
при фиксированной достаточной статистике х?, имеет
риск, не превосходящий риска статистики Т относитель-
относительно произвольной выпуклой функции потерь при всех
в ?в. F.wra при этом семейство {Ре } является полным,
то статистика Т* определяется единственным образом.
То есть из теоремы Рао — Блэкуэлла — Колмогорова
следует, что Н. о. нужно искать лишь в терминах дос-
достаточных статистик, если они существуют. Практич.
ценность теоремы Рао — Блэкуэлла — Колмогорова
заключается в том, что она дает рецепт построения наи-
наилучших Н. о., а именно: нужно построить произволь-
произвольную Н. о. для/(9), а затем осреднить ее по достаточной
статистике.
Пример 6. Пусть случайная величина X имеет
распределение Паскаля (отрицательное биномиальное
распределение) с параметрами г и 9 (т\>2, 0<:9<:1), т. е.
В этом случае статистика Т=(г—i)/(X—1) является
Н. о. параметра 9. Так как статистика Т выражена в
терминах достаточной статистики X, а система функций
1, х, х2, ... является полной на отрезке [0, 1], то Т яв-
является единственной Н. о., а следовательно, наилуч-
наилучшей оценкой для в.
Пример 7. Пусть X —• случайная величина, под-
подчиняющаяся биномиальному закону с параметрами п и
9. Производящая функция Q(z) этого биномиального
закона выражается формулой
откуда следует, что для любого целого числа к={, 2,
... , п
С другой стороны,
<?<*>A) = Е {X (Х-1). . .(*-* + 1)} = Е {ХМ},
откуда следует, что
т. е. статистика
т^Х) = ^ГхШ B)
является Н. о. для в*, причем в силу того, что Тк(Х)
выражена в терминах достаточной статистики X, а
также в силу полноты системы функций 1, х, .г3, ... на
отрезке [0, 1] следует, что Тк(Х) —• единственная, а
значит, и наилучшая Н. о. для в*.
В связи с этим примером возникает следующий воп-
вопрос: какие функции /(8) от параметра в допускают не-
несмещенное оценивание. А. Н. Колмогоров показал [1],
что только для многочленов степени т<:« существуют
Н. о. Так, если
то из B) следует, что статистика
является единственной Н. о. для /(в). Из этого резуль-
результата, в частности, следует, что для функции /(в) = 1/6
не существует Н. о.
Пример 8. Пусть X — случайная величина, под-
подчиняющаяся закону Пуассона с параметром 9, т. е. для
любого целого числа к=0, 1, 2, ...
В силу того, что Е{Х}==9, само наблюдение X являет-
является Н. о. своего математич. ожидания в. В свою очередь,
напр., Н. о. функции /(В)=62 является Х{Х—1).
Вообще, статистика
XM = X{X — \){X — 2)...(X — r + i), г = 1, 2, ...,
является Н. о. функции /(в)=вг. Из этого факта, в
частности, следует, что статистика
является Н. о. функции /(в) = A + в)-1, 0<в<1. Вооб-
Вообще, если функция /(в) допускает несмещенное оценива-
оценивание, то для нее должно выполняться уравнение несме-
несмещенности Е{77(Х)}=/(в), к-рое равносильно следую-
следующему:
!?
-*=„г^<
откуда получается, что Н. о. существует для любой
функции /F), допускающей разложение в степенной
ряд в своей области определения QcFtt.
Пример 9. Пусть независимые случайные ве-
величины Xlt X2, ... , Хп подчиняются одному и тому же
закону Пуассона с параметром 9, в>0. Производящая
функция этого закона, выражающаяся формулой
*,(е)=ехр{в(*-1)},
является целой аналитич. функцией, и, следовательно,
для нее существует единственная Н. о. Достаточной
статистикой в этом случае является Х=Х1-\-...-\-Х„,
к-рая подчиняется закону Пуассона с параметром п&.
Если Т(Х) — Н. о. для gz(Q), то она должна удовлетво-
удовлетворять уравнению несмещенности
откуда следует, что
{
0, в противном случае,
т. е. Н. о. для производящей функции закона Пуассона
является производящая функция биномиального зако-
закона с параметрами X и 1/ге.
Примеры 6—9 демонстрируют, что в нек-рых случаях,
довольно часто встречающихся на практике, именно
благодаря понятию Н. о. задача построения наилучших
оценок оказывается легко разрешимой, если ограни-
ограничиться классом Н. о. А. Н. Колмогоров [1] рассмотрел
вопрос построения Н. о., в частности задачу построе-
построения Н. о. функции распределения нормального закона,
параметры к-рого неизвестны. Э. Леману (Е. Lehmann)
принадлежит более общее определение Н. о. Согласно
определению Э. Лемана (см. [2]) статистич. оценка
Т=- Т(Х) параметра в наз. несмещенной отно-
относительно функции потерь L(Q, T), если
Ее{/,(в', Т (Z))} S& Ев {L (в, Т (X))} для всех в, в'?6.
Имеется модификация этого определения (см. [3]).
Ю. В. Линником и его учениками (см. [4]) была уста-
установлена независимость наилучшей Н. о. от функции
потерь при довольно широких предположениях.
Лит.: [1] Колмогоров А. Н., «Изв. АН СССР. Сер.
матем.», 1950, т. 14, №4, с. 303—26; [2] Л е м а н Э., Про-
Проверка статистических гипотез, пер. с англ., 2 изд., М., 1979;
{31 Клебанов Л. Б., «Теория всроятн. и ее применения»,
1976, т. 21, JV. 3, с. 584—98; [4] К л е б а н о в Л. Б., Л и н-
ник Ю. В., Рухин А. Л., «Докл. АН СССР», 1971,
т. 200, № 5, с. 1024—25; [5] 3 а к с Ш., Теория статистических
выводов, пер. с англ., М., 1975. М. С. Никулин.
НЕСМЕЩЕННЫЙ КРИТЕРИЙ — статистический
критерий размера а, 0<а<1, для проверки сложной
гипотезы Но : в?вис:в против сложной альтернативы
Н1 : e^e1=e\0o, функция мощности к-рого Р(-)
удовлетворяет неравенствам:
РF)«а, если 8?60,
PF)Saa, если
Во многих задачах статистич. проверки гипотез не суще-
существуют равномерно наиболее мощные критерии, но если
ограничиться классом Н. к., то задача построения рав-
равномерно наиболее мощного критерия может иметь по-
положительное решение. Если в задаче проверки гипоте-
гипотезы Но против альтернативы Н1 существует равномерно
наиболее мощный критерий, то он является Н. к., так
как мощность такого критерия не может быть меньше
мощности т. н. бесполезного критерия, критич. функция
к-рого ф (•) постоянна и равна размеру критерия а,
т. е. ф(Х)=а, где X — случайная величина, по реали-
реализации к-рой проверяют гипотезу Но против альтернати-
альтернативы Нг.
Пример. Знаков критерий является равномерно
наиболее мощным Н. к. в задаче проверки гипотезы
Но, согласно к-рой неизвестное истинное значение пара-
параметра р биномиального распределения равно ]/2,
против альтернативы Нх: рфх1„.
Лит.: [1] Леман Э., Проверка"статистических гипотез,
пер. с англ., 2 изд., М., 1979. М. С. Никулин.
НЕСОБСТВЕННОЕ РАСПРЕДЕЛЕНИЕ — то же, что
вырожденное распределение.
НЕСОБСТВЕННЫЙ ИНТЕГРАЛ — интеграл от не-
неограниченной функции или от функции по неограни-
неограниченному множеству. Пусть функция / определена на
конечном или бесконечном полуинтервале la, b),
— оо <а<6<:-|-оо, и для любого т]?[а, Ь) функция/ ин-
интегрируема но Риману (по Лебегу) на отрезке [а, г\].
Тогда предел
lim \^f(x)dx A)
Tl_»6_o •> а
(в случае Ъ=-\-оо условие т| —>- Ъ—0 понимается как
г| —*¦ + оо) наз. несобственным интегра-
интегралом
Если предел A) существует, то говорят, что Н. и. схо-
сходится, если не существует — расходится. Напр.,
Н. и.
— , а > О,
а ха
при а>1 сходится, а при а<:1 расходится. Если же
6<+оо, то
ГЬ dx
)а (Ь-х)а
сходится при а<1 и расходится при a^l.
Если 6<+°о и функция / интегрируема по Риману
(по Лебегу) на отрезке [а, Ь], то Н. и. A) совпадает с
определенным интегралом.
Аналогично при соответствующих предположениях
определяют Н. и. по промежутку (а, 6], —оо<:а<Ь<
< +°°,
[Ь f(x)dx= lim \bJ{x)dx. B)
Если функция / интегрируема по Риману (по Лебегу)
на каждом отрезке [?, п]с:(а, b), cf(a, b) и существуют
Н. и.
то Н. и.
J* / (*) dx
определяется как сумма
/ (х) dx = [° f (x) dx + [b f (x) dx
и не зависит от выбора точки с.
Если на интервале (а, Ъ) имеется конечное число точек
хк (к=0, 1, 2, ... , и): a=xo<x1<...<xk_1<xk<...<
<Сг„= Ъ таких, что функция / интегрируема по Риману
(по Лебегу) на каждом отрезке [\, г\], не содержащем
ни одной точки xk, и для каждого к=1, 2, ..., п сущест-
существуют Н. и.
\ f(x)dx,
«хк-1
то Н. и.
Это определение не зависит от выбора точек
На Н. и. переносятся общие свойства интегралов:
линейность, аддитивность относительно промежутков,
по к-рым производится интегрирование, правило интег-
интегрирования неравенств, теоремы о среднем, интегриро-
интегрирование по частям и замены переменного, формула Нью-
Ньютона — Лейбница. Напр., если функция / почти всюду
на [а, Ь) совпадает с производной функции F, к-рая аб-
абсолютно непрерывна на каждом отрезке [а, ц], а<т)<6,
то
Для выяснения сходимости Н. и. от знакопостоянных
функций применяется признак сравнения:
напр., для Н. и. вида A) при выполнении условия
х~>- Ь—0, f{x)^O, g(x)^O, x?[a, 6), из сходимости Н. и.
() dx
5*,<*).
следует сходимость Н. и.
/ (х) dx;
функция g(x) наз. в этом случае функцией срав-
сравнения. В качестве функции сравнения для интегра-
интегралов A) в случае конечного предела интегрирования Ъ
часто используются функции 1/F—х)а; для интегралов
вида B) в случае конечности предела интегрирования
а — функции i/(x—а)а, при наличии одного или двух
бесконечных пределов интегрирования — функции
i/\x\a. Из признака сравнения следует, напр., если для
неотрицательной функции /, определенной при х^а,
существует предел
lim .т« / (х) = к,
то при а>1 и 0<А-< + ?» Н. п.
вида A) сходится, а при а<:1 и 0<fc<:+oo H. и. рас-
расходится.
Необходимое и достаточное условие сходимости Н. и.
дает критерий Коши. Так, Н. и. вида A) сходится тогда
и только тогда, когда для любого е>0 существует такое
Т)?[а, Ь), что для всех т)'^(т), Ь), Т]"?(ть &) выполняется
неравенство
is:
Н. и.
наз. абсолютно сходящимся, если сходится
Н. и.
\ba\f{x)\dx.
Если Н. и. абсолютно сходится, то он сходится и совпа-
совпадает с интегралом Лебега. Существуют Н. и. сходящие-
сходящиеся, но не абсолютно. Напр., для конечного проме-
промежутка Н. и.:
Si I i
0 Т sm Т х'
а для бесконечного:
X
Существуют различные признаки для установления
сходимости Н. и. Так, если функции fug определены
для х~^а, функция / имеет на полуоси х~^а ограничен-
ограниченную первообразную, a g — монотонная функция, стре-
стремящаяся к нулю при х—>¦ +оо, то Н. и.
/ (x) g (x) dx
сходится. Другой признак: если Н. и.
°° / (х) dx
сходится, а функция g монотонна и ограничена при
х~^а, то Н. и.
[1°° f (x) g (х) **
сходится.
Сходимость Н. и. можно выразить в терминах сходя-
сходящихся рядов: напр., для того чтобы Н. и. A) сходился,
необходимо и достаточно, чтобы для любой последова-
последовательности Ьп ->- Ь, а<*„<6, ге=0, 1, 2, , сходился
РЯД
причем в случае его сходимости сумма ряда совпадает
с Н. и. A).
Понятие Н. и. обобщается для функций многих пере-
переменных. Пусть функция / определена на открытом (ог-
(ограниченном или неограниченном! множестве G п-мер-
ного евклидова пространства R" и интегрируема по
Риману на любом измеримом по Жордану множестве
Е, EczG. Функцию / наз. интегрируемой в
несобственном смысле по множеству G,
если для любой последовательности измеримых по Жор-
Жордану множеств Ек таких, что E^cG, EkdE/t+1, k=l,
2, ..., и (Jft~i^'ft==G, существует предел
к
lim \ / (х) dx,
-v+oo JEk
не зависящий от выбора указанной последовательности
Ек. Этот предел, если он существует, наз. Н. и.
Jff / (*) dx
и, как в одномерном случае, говорят, что этот интеграл
сходится. Он существует тогда и только тогда, когда
существует интеграл
\f(x)\ dx.
В этом случае Н. и.
совпадает с интегралом Лебега. Это обстоятельство свя-
связано с тем, что при ге=1 и данном выше определения
Н. и. переход к пределу осуществлялся по весьма
специальному классу измеримых по Жордану множеств,
а именно по отрезкам. В качестве же Ек были взяты
произвольные измеримые по Жордану множества.
Впрочем, при п>2 сделанное утверждение остается в
силе и в том случае, когда в качестве множеств Ек взя-
взяты только измеримые ио Жордану области. Таким обра-
образом, в этом случае понятие Н. и. не приводит к ново-
новому понятию по сравнению с интегралом Лебега.
Для Н. и. от функции многих переменных справедлив
признак сравнения, аналогичный одномерному случаю.
В качестве интегралов сравнения берут
dx Г dx
где
хп), г = У х\-\-х\-\- . .. 4-х%
Первый сходится при а<п и расходится при
второй сходится при а>ге и расходится при
К Н. и. относятся интегралы в смысле главного зна-
значения. Пусть функция / определена на открытом мно-
множестве GczR", кроме, быть может, точки x?G, и пусть
для любого е>0 функция / интегрируема (по Риману
или по Лебегу) на множестве G\U(x, е), где U(x, e)
есть е-окрестность точки х. Тогда если существует пре-
предел
lim [ f (х) dx,
то его наз. интегралом в смысле главно-
главного значения и обозначают
v. p. \Qf(x)dx. ,
Если интеграл
г»
/ (х) dx
существует как Н. и., то он существует и в смысле глав-
главного значения. Обратное, вообще говоря, неверно.
Напр., Н. и.
5+1 dx
расходится, а
d
v-P-
Аналогично определяют интегралы в смысле главного
значения в бесконечно удаленной точке.
Лит.: [1] Ильин В. А., П о з н я к Э. Г., Основы ма-
математического анализа, т. 2, М., 1973; [2] Кудрявцев Л.
Д., Курс математического анализа, т. 2. М., 1981; [3] Ни-
Никольский С. М., Курс математического анализа, 2 изд.,
т. 2, М., 1975. Л. Д. Кудрявцев.
НЕСОВМЕСТИМОСТЬ — свойство формальной си-
системы, противоположное свойству непротиворечиво-
непротиворечивости: формальная система наз. несовместимой,
или несовместной, если она не является не-
непротиворечивой. Если нек-рый класс формул в языке
данной формальной системы не является непротиворе-
непротиворечивым, то говорят, что он несовместим с данной фор-
формальной системой. В частности, если класс, состоящий
из одной формулы, несовместим с формальной системой,
эта формула наз. несовместимой с данной сис-
системой. Н. формулы означает, что если ее включить в
множество аксиом, то получится несовместимая фор-
формальная система.
Несовместимые формальные системы не имеют со-
содержательной интерпретации.
Обнаружение Н. отрицания нек-рой формулы с дан-
данной формальной системой составляет т. н. метод д о-
казательства от противного: для ши-
широкого класса формальных систем из Н. формулы ф
следует выводимость ее отрицания. В. Е. Плиспо.
НЕСОИЗМЕРИМЫЕ ВЕЛИЧИНЫ — см. Соизмери-
Соизмеримые и несоизмеримые величины.
НЕСТАНДАРТНЫЙ АНАЛИЗ — раздел математич.
логики, посвященный приложению теории нестандарт-
нестандартных моделей к исследованиям в традиционных обла-
областях математики: математич. анализе, теории функций,
теории дифференциальных уравнений, топологии и др. В
общих чертах основной метод Н. а. можно описать сле-
следующим образом. Рассматривается нек-рая математич.
структура М и строится логико-математич. язык 1-го
порядка, отражающий аспекты этой структуры, ин-
интересующие исследователя. Затем методами теории мо-
моделей строится нестандартная модель
теории структуры М, являющаяся собственным расши-
расширением М. При надлежащем построении новые, не-
нестандартные, элементы модели могут быть истолкованы
как предельные, «идеальные» элементы первоначальной
структуры. Напр., если первоначально рассматрива-
рассматривалось упорядоченное поле действительных чисел, то
нестандартные элементы модели естественно рассмат-
рассматривать как «инфинитезимальные», т. е. бесконечно
большие или бесконечно малые, но отличные от нуля
действительные числа. При этом все обычные отношения
между действительными числами автоматически пере-
переносятся и на нестандартные элементы с сохранением
всех их свойств, выразимых в логико-математич. языке.
Подобным образом в теории фильтров на данном мно-
множестве нестандартный элемент определяет непустое
пересечение всех элементов фильтра; в топологии воз-
возникает семейство нестандартных точек, расположенных
«бесконечно близко» к данной точке. Истолкование не-
нестандартных элементов модели часто позволяет дать
удобные критерии для обычных понятий в терминах
нестандартных элементов. Напр., можно доказать, что
стандартная действительная функция f{x) непрерывна
в стандартной точке х0 тогда и только тогда, когда j(x)
бесконечно близка к /(%,) для всех (и нестандартных)
точек .г, бесконечно близких к х0. Полученные критерии
могут быть с успехом применены к доказательству обыч-
обычных математич. результатов.
Результаты, полученные методами Н. а., могут
быть естественно передоказаны и обычным образом,
но рассмотрение нестандартной модели имеет то значи-
значительное преимущество, что позволяет актуально вво-
вводить в рассуждение «идеальные» элементы, что позво-
позволяет давать прозрачные формулировки для многих
понятий, связанных с предельными переходами от
конечного к бесконечному. В Н. а. на строгой матема-
математической основе реализуется до некоторой степени
идея Г. Лейбница (G. Leibniz) и его последователей о
существовании бесконечно малых величин, отличных
от нуля,— идея, к-рая в последующем развитии мате-
матич. анализа была заменена точным понятием пре-
предела переменной величины.
С помощью Н. а. был обнаружен ряд новых фактов.
Многие классич. доказательства заметно выигрывают
в наглядности при изложении их методами нестандарт-
нестандартного анализа. Н. а. был с успехом использован для по-
построения точной теории нек-рых полуэмпирич. методов
механики и физики.
Лит.: [11 Robinson A., Non-standard analysis, Amst.,
1966; [2] Денис М., Прикладной нестандартный анализ,
пер. с англ., М., 1980. А. Г. Драгалин.
НЕСУЩЕСТВЕННОЕ ОТОБРАЖЕНИЕ — непрерыв-
непрерывное отображение f : X —>-(?" топологич. пространства X
в n-мерный шар Q" такое, что существует непрерывное
отображение g : X —>- Qn, совпадающее с / на прообразе
f-igti-i ГранПцы 5" шара Q" и переводящее X в
Sn~l (т. е. gXs^S"~1). Для нормального хаусдорфова
пространства X тогда и только тогда dim X<n, когда
любое непрерывное отображение /: X—^Q", re-—1,
2, ... , есть Н. о. (теорема Александрова).
Непрерывное отображение топологич. пространства
в n-мерную сферу наз. несущественным, если
оно гомотопно постоянному отображению.
Б. А. Пасынков.
НЕСЧЕТНОЕ МНОЖЕСТВО — бесконечное множе-
множество, не являющееся счетным множеством, т. е. неэкви-
неэквивалентное множеству натуральных чисел. Напр., мно-
множество действительных чисел, в отличие от множества
раЦИОНаЛЬНЫХ, ЯВЛЯетСЯ Н. М. М. И. Войцехевский.
НЕ ТЕР ПРОБЛЕМА — вопрос о рациональности
поля инвариантов конечной группы, действующей авто-
автоморфизмами поля рациональных функций. Подробнее,
пусть K=Q(xlt ... , хп) — поле рациональных функций.
от п переменных с коэффициентами в поле рациональ-
рациональных чисел Q, т. е. К — чисто трансцендентное расши-
расширение поля Q степени трансцендентности п. И пусть
G — конечная группа, действующая автоморфизмами
поля К посредством перестановок переменных х1, ... ,
хп. Будет ли подполе Ка в К, состоящее из всех непо-
неподвижных относительно G элементов, само полем рацио-
рациональных функций от п (других) переменных с коэффи-
коэффициентами в Q? Эта проблема была поставлена Э. Нётер
[1] в связи с рассмотрением Галуа теории обратной
задачи. В случае положительного решения Н. п. можно
было бы построить расширение Галуа поля Q с задан-
заданной конечной группой Галуа G (см. [5]). Н. п. также тес-
тесно связана с Люрота проблемой.
Н. п. в общем случае решается отрицательно. Первый
пример нерационального поля К0 был построен в [2],
причем в этом примере группа G порождена циклич.
перестановкой переменных. В [3] было установлено,
что необходимое условие рациональности поля Ка,
найденное в [21, является и достаточным. Вопрос о ра-
рациональности поля К° в случае абелевой группы G
тесно связан с теорией алгебраических торов (см. [4]).
Часто под Н. п. понимают более общую проблему,
получающуюся заменой в оригинальной Н. п. поля Q
произвольным полем к. Эта проблема решена положи-
положительно, напр., в случае, когда к алгебраически замк-
замкнуто, a G абелева.
'Лит.: [1] N о е t h е г Е., «Math. Ann.», 1917/1918, Bd 78,
S. 221—29; [2] Swan R. G., «Invent, math.», 1969, v. 7,
fasc. 2, p. 148; [3] Воскресенский В. Е., «Изв. АН
СССР. Сер. матем.», 1971 т. 35, с. 1037; [4] его же, Алгебраи-
Алгебраические торы, М., 1977; [5] Ч е б о т а р е в Н. Г., Теория Га-
Галуа, М.— Л., 1936, с. 18 — 32 и 90—94. В. Л. Попов.
НЁТЕР ТЕОРЕМА — 1) Первая теорема
Нётер — теорема, устанавливающая связь между
инфинитезимальными симметриями функционала вида
А (и (х)) = <\jL(x,u (x), u,j (x)) d"x,
где х=(х1, ... , х") — независимые переменные, u(z)=
= (ul(x), ... , uN(.r)) — функции, определенные в
нек-рой области Dc:Rn, и,/ — —j u{x) — их частные
dxJ
производные, L — нек-рая функция (функция Лагран-
жа), и законами сохранения для соответствующей си-
системы уравнепий Эйлера — Лагранжа
Шг — Ща — —idua. ~ U'
дающей необходимые условия экстремума функциона-
функционала А. Именно, инфинитезнмальной симметрии Z, т. е.
векторному полю
Z = X' (x) d/dx' + U0 (х, и) д/диа,
к-рое порождает однопараметрич. группу преобразова-
преобразований, сохраняющую функционал А, соответствует закон
сохранения
j^ 1
Adx'A .. .dx"
(где значок ~ означает пропуск соответствующего
множителя), т. е. зависящая от функции и (х) (п—1)-
форма, к-рая замкнута, если и (х) удовлетворяет урав-
уравнениям Эйлера — Лагранжа.
В теории поля и=4 координаты х интерпретируются
как координаты пространства-времени, функционал А
наз. действием, а функция и(х) — полем. Поля и(х),
доставляющие экстремум функционалу действия, соот-
соответствуют физически реализуемым полям с данной
функцией Лагранжа. Если такое поле и(х) обращается
в нуль на границе области D, то в силу теоремы Стокса
интеграл от закона сохранения v по гиперповерхности
D f] {х' = с} не зависит от выбора числа с. В частности,
если х1 — координата времени, то этот интеграл дает
величину, сохраняющуюся с течением времени.
Инвариантность функций Лагранжа различных фи-
зич. полей относительно параллельных переносов и
преобразований Лоренца (являющаяся следствием од-
однородности и изотропности пространства-времени Мин-
ковского) приводит но Н. т. к тензору энергии-импуль-
энергии-импульса и тензору момента количества движения поля и к
соответствующим им закопан сохранения энергии, им-
импульса и момента количества движения. Инвариант-
Инвариантность функционала действия электромагнитного поля
относительно градиентных преобразований приводит к
закону сохранения электрич. заряда. Аналогично из
инвариантности лагранжиана того или иного поля отно-
относительно калибровочных преобразований получаются
законы сохранения различных зарядов.
В классич. механике и=1 и координата х1 интерпре-
интерпретируется как время. Если функция Лагранжа не зави-
зависит явно от х1, то векторное поле д/дх1 является симмет-
симметрией и Н. т. приводит к закону сохранения энергии.
Для механич. системы, движение к-рой описывается
движением по геодезическим нек-рой римановой мет-
метрики, симметриями соответствующего функционала
действия будут киллинговы поля. В этом случае закон
сохранения, даваемый Н. т., геометрически означает,
что величина проекции киллингова поля на направле-
направление геодезической постоянна вдоль этой геодезической.
Общая современная формулировка Н. т. на языке рас-
расслоенных пространств состоит в следующем. Пусть
я : Е —>- М — расслоение над и-мерным многообразием
М с фиксированной и-формой объема ю?Ап(М), а
пк : JkE -+-М — расслоение й-струй сечений расслоения
я. Если х1 — локальные координаты в М, в к-рых форма
(о имеет вид @=Лг:хл... Adx", а ж1', иа — локальные ко-
координаты в Е, то в JkE возникают локальные коорди-
координаты х!, иа, иаа, где а=((Х], ..., а„) — мультииндекс,
1а| = а1+...-г(х,,<:?- Значение координаты и%, на А^струе
/'? u(x) сечения и (х) расслоения я равно
) (
Гладкая функция L : JkE —>- R определяет функцио-
функционал действия А, сопоставляющий сечению s : х —*- и (х)
число
\L(x, u(x), u_a(x))w.
Экстремальные для этого функционала сечения и (х)
(в задаче с закрепленными концами) удовлетворяют
уравнениям Эйлера — Лагранжа
i?==V , 1Jg| d" dL _0
6ua Д=(а„ ...,«„), |a|<fcl ' dxad
где
— = (
dxa {dx. \
— полные производные. Инфинитезимальный автомор-
автоморфизм расслоения я, т. е. векторное поле Z на Е вида
Z = Х{ (х) д/дх' + Ua (х, и) д/диа,
наз. инфинитезимальной симметрией функционала А,
если производная Ли от re-формы Лагранжа ?(й?
?An(JkE) по направлению векторного поля Z(fc), яв-
являющегося продолжением поля Z на JkE, равна нулю:
Для производной Ли справедлива следующая фунда-
фундаментальная формула Нётер:
dx
где
a F' — компоненты нек-рого векторного поля, завися-
зависящие от Ua, L и их производных. В частности, F' =
_ dL
= Ua диа при k=i. Если поле Z является инфинитези-
мальной симметрией, то
т. е. нек-рая линейная комбинация вариационных про-
производных bLlbua функции Лагранжа L является дивер-
дивергенцией векторного поля J=J'd/dxl. В таком виде Н. т.
впервые была сформулирована Э. Нётер (Е. Noether).
Дивергенция поля / (наз. током Нётер) обра-
обращается в нуль на экстремалях функционала действия,
а двойственная к нему (п—1)-форма л>г=-^ __1<а, полу-
получающаяся из ш внутренним умножением на /, замкну-
замкнута, т. е. является законом сохранения.
Имеются важные обобщения Н. т. (см., напр., [5]—
[7]). Они основаны на расширении понятия инфините-
зимальной симметрии. Вместо векторных полей на Е,
к-рым отвечают однопараметрич. группы преобразова-
преобразований, рассматриваются векторные поля на Е, коэффици-
коэффициенты к-рых зависят от сечений и(х\ и их сколь угодно
высоких производных. Такие поля Y уже не определяют
никаких однопараметрич. групп преобразований, одна-
однако и для них можно чисто алгебраически определить
понятие производной Ли. Поле Y наз. алгебраи-
алгебраической инфинитезимальной симмет-
симметрией, если производная Ли от формы Лагранжа по
направлению этого поля равна нулю или, более общо,
обращается в нуль на экстремалях функционала дей-
действия. Обобщенная теорема Нётер сопоставляет каждой
алгебраич. симметрии закон сохранения. В примене-
применении к различным уравнениям математич. физики таким
образом получается большое число новых важных
законов сохранения.
2) Вторая теорема Нётер утверждает,
что если функционал действия допускает бесконечно-
бесконечномерную алгебру Ли инфинитезимальных симметрии,
коэффициенты к-рых линейно зависят от р произволь-
произвольных функций (р1^), ..., (рР(х) и их производных до nO-
рядка т, то вариационные производные v-д функции
Лагранжа L удовлетворяют системе из р дифференци-
дифференциальных уравнений порядка т. Именно, если
Z = (f"U?d/dua + ф!<т (х) U4a д/ди«,
где
0 = (а1, ..., а„), |а|=0!+ . ..+а„< к
есть инфинитезимальная симметрия при любых гладких
функциях (pJ(i), s=l, ..., р, то справедливы тождества
Эта теорема находит применения, напр., в теории ка-
калибровочных полей.
Первая и вторая Н. т. доказаны Э. Нётер (Е. Noether,
1918, см. [1]).
Лит.: [1] Н е т е р 3., в кн.: Вариационные принципы ме-
механики, М., 1959, с. 611—3A; [2] Боголюбов Н. Н.,
Ш и р к о в Д. В., Введение в теорию квантованных полей,
2 изд., М., 1973: [3] Г е л ь ф а н д И. М., Фомин С. В.,
Вариационное исчисление, М., 1961; L4] Арнольд В. И.,
Математические методы классической механики, М., 1974;
[5] Овсянников Л. В., Групповой анализ дифференци-
дифференциальных уравнений, М., 1978; [6] Манин Ю. И., в кн.:
Итоги науки и техники, Современные проблемы математики,
т. 11. М., 1978, с. 5—152; [7] Виноградов А. М., «Докл.
АН СССР», 1977, т. 236, № 2, с. 284—87; [8] Л ы ч а г и н В. В.,
«Успехи матем. наук», 1979, т. 34, в. 1, с. 137—65.
Д. В. Алексеевский.
3)Н. т. о нормализации: в любой конечно
порожденной коммутативной целостной А-алгебре А,
имеющей над полем к степень трансцендентности d,
найдутся такие d элементов х1; ..., х^, что А цела над
подалгеброй В, порожденной этими элементами. Если
fc-алгебра А обладает градуировкой вида Л=ф|>0Л,-,
А0~к, то элементы хи ..., х^ могут быть выбраны одно-
однородными.
Эта теорема (иногда называемая также леммой
Нётер о нормализации) доказана Э. Нётер
[11; в градуированном случае она была сформулирована
еще Д. Гильбертом [2].
Элементы хх, ..., хд алгебраически независимы над
А-, так что В — алгебра многочленов от переменных с
коэффициентами из к. Если поле к бесконечно, то эле-
элементы хи ..., хд можно выбрать из линейных комбина-
комбинаций образующих алгебры А над к. В случае алгебраи-
алгебраически замкнутого поля к Н. т. допускает следующую
геометрич. формулировку: любое неприводимое аффин-
аффинное d-мерное алгебраич. многообразие X является ко-
нечнолистным (разветвленным) накрытием аффинного
d-мерного пространства Аа, точнее, обладает конечным
морфизмом на Аа. Более того, если X — замкнутое
подмножество в кп, то указанный морфизм может быть
реализован как сужение на X нек-рого линейного от-
отображения пространства к" на его d-мерное линейное
подпространство.
Алгебра А, как 5-модуль, конечно порождена. Под-
Подалгебра В выбирается неоднозначно, однако ряд свойств
.б-модуля А не зависят от ее выбора. Напр., если А
градуирована, как выше в условиях теоремы, а элемен-
элементы л:], ..., х& однородны (так что В тоже градуирована),
то свойство алгебры А быть свободным В-модулем не
зависит от выбора В.
Лит.: [1] N о е t h e r E., «Math. Ann.», 1927, Bd 96, S. 26—
61; [2] Hilbert D., «Math. Ann», 1893, Bd 42, S. 313—73;
[3] Атья М., Макдональд И., Введение в коммута-
коммутативную алгебру, пер. с англ., М., 1972; [4] Б у р б а к и Н.,
Коммутативная алгебра, пер. с франц., М., 1971; [5J 3 а р и с-
ский О., Самюэль П., Коммутативная алгебра, пер.
с англ., т. 1—2, М., 1963; [6] Л е н г С, Алгебра, пер. с англ.,
М., 1968. В. Л. Попов.
НЁТЕРА — ЭНРИКЕСА ТЕОРЕМА о канони-
канонических кривых — теорема о проективной нор-
нормальности канонической кривой и об определяемости ее
квадратичными уравнениями.
Пусть ХсР?~1 — гладкая канонич. кривая (неги-
перэллиптическая) рода g^3 над алгебраически зам-
замкнутым полем к и 1х — однородный идеал в кольце
к [ха, ..., Xg-i), определяющий X в Ре~1. Теорема
Нётера — Энрикеса (наз. иногда также тео-
теоремой Нётера — Энрикеса — Петри)
утверждает, что:
1) X проективно нормальна в Pg~ ;
2) если ?=3, то X — плоская кривая степени 4, а
если g^i, то градуированный идеал I x порождается
компонентами степени 2 и 3 (и это означает, что кривая
X является пересеченяем квадрик и кубик в PS-1, че-
через нее проходящих);
3) идеал 1х порождается компонентами степени 2 во
всех случаях, кроме следующих: а) X — тригональная
кривая, т. е. обладает линейным рядом (системой) #з
размерности 1 и степени 3, б) X — кривая рода 6,
изоморфная плоской кривой степени 5;
4) в исключительных случаях а) п б) квадрики, про-
проходящие через X, высекают поверхность F, являющую-
являющуюся соответственно: а) неособой рациональной линейча-
линейчатой поверхностью степени g—2 в РВ'1, #5=5, причем
ряд g3 на X высекается линейной системой прямых на F,
а при ?=-4 — квадрикой в Р3 (возможно конусом),
б) поверхностью Веронезе У4 в Ръ.
Эта теорема (в несколько иной, алгебрапч. формули-
формулировке) была установлена М. Нётером [1]. Геометрич.
изложение было дано Ф. Энрикесом (F. Enriques, о его
результатах см. [2]; современное изложение в [3], [4],
обобщение в [5]).
Лит.: [1] N other M., «Math. Ann.», 1880, Bd 17,
S. 263—84; [2] В a b b a g e D. W., «J. London Math. Soc»,
1939, v. 14, J* 4, p. 310 — 14; [3] S a i n t - D о n a t В., «Math.
Ann.», 1973, Bd 206, S. 157 — 75; [4] III о куров В. В.,
«Матем. сб.», 1971, т. 86, JM« 3, с. 367—408; [5] А г b а г е 1-
1 о Е.., S е г n e s i E., «Invent, math.», 1978, v. 49, p. 99—
119. В. А. Исковских.
НЁТЕРОВ МОДУЛЬ — модуль, любой подмодуль
к-рого обладает конечной системой образующих. Экви-
Эквивалентные условия: любая строго возрастающая цепоч-
цепочка подмодулей обрывается на конечном номере; любое
непустое множество подмодулей, упорядоченное отно-
относительно включения, содержит максимальный элемент.
Подмодуль и фактормодуль Н. м. также нётеровы. Если
в точной последовательности модулей
0 _>. М' ->- М ->- М" -> 0
модули М' и М" нётеровы, то М также нётеров. Модуль
над нётеровым кольцом нётеров тогда и только тогда,
когда он имеет конечное число образующих.
Лит.: [1] Лен г С, Алгебра, пер. с англ., М., 1968.
Л. В. Кузьмин.
НЁТЕРОВ ОПЕРАТОР — линейный оператор, од-
одновременно п- нормальный и <2-нормальнып (см. Нор-
Нормально разрешимый оператор). Иначе говоря, Н. о.
А — это нормально разрешимый оператор с конечной
^-характеристикой (п(А)<.-\-<х, й(Л)<-(-оо). Индекс
%{А) Н. о. А также является конечным числом. Про-
Простейший пример Н. о.— линейный оператор действую-
действующий из R* в R'. Название по имени Ф. Нётера [1],
с работ к-рого теория Н. о. развивается параллельно
теории сингулярных интегральных уравнений. Ли-
Линейные операторы, порождаемые общими краевыми за-
задачами для эллиптич. уравнений, часто являются
Н. о.
На практике обычно удается проверить справедли-
справедливость следующих предложений (теоремы Нёте-
р а):
1) либо уравнение Ах=0 не имеет нетривиальных
решений, либо оно имеет конечное число п линейно
независимых решений;
2) либо неоднородное уравнение Ах=у разрешимо
при любой правой части у, либо для его разрешимости
необходимо и достаточно, чтобы <г/, 1|з,>=0, г~1, ..., т,
где {%} т— полная система линейно независимых ре-
решений союзного однородного уравнения или формаль-
формально сопряженной однородной задачи.
Из 1), 2) следует, что А — Н. о.
Свойство нётеровости устойчиво: если А — Н. о.,
аВ — линейный оператор достаточно малой нормы или
вполне непрерывный, то А-{-В — также Н. о., при этом
Х(А+В)=х(А).
Пусть A ?L(X, Y), где L(X, Y) — пространство ли-
линейных операторов из X в У, и является Н. о. Тогда
имеют место прямые разложения
X = N(A)+X, Y = Z + R(A),
где N {А) — подпространство нулей A, R (А) — область
значений A, dim Z=d(A). Общее решение уравнения
Ах=у, y?R(A), имеет вид х=А~ y-\-v, где A = L(X,
R(A)), А=А на X (сужение .4), a v?N{A) — произ-
произвольно. Если А -- Н. о. с ^-характеристикой (п, т),
то Л* Н. о. с ^-характеристикой (т, п).
Лит.: [11 Noether F., «Math.' Ann.», 1921, Bd 82,
S. 42—63; [2| К р е й н С. Г., Линейные уравнения в банаховом
пространстве, М., 1971; [3] В а й н б е р г М. М., Трено-
Треногий В. А., Теория ветвления решений нелинейных уравне-
уравнений, М., 1969. В. А. Треногий.
НЁТЕРОВА ГРУППА, группа с условием
максимальности для подгруп и,—
группа, в к-рой любая строго возрастающая цепочка
подгрупп обрывается на конечном номере. Названа в
честь Э. Нётер (Е. Noether), к-рая изучала кольца с ус-
условием максимальности для идеалов — мётеровы коль-
кольца. Подгруппа и факторгруппа Н. г. также обладают
этим свойством. Построены примеры Н. г., не являю-
являющихся конечными расширениями полициклических
групп [1].
Лит.: [1] Ольшанский А. Ю., «Докл. АН СССР»,
1979, т. 245, № 4, С. 785—87. В. Н. Ремесленников.
НЁТЕРОВА ИНДУКЦИЯ — принцип рассуждений,
применимый к частично упорядоченному множеству, в
к-ром любое непустое подмножество содержит мини-
минимальный элемент, напр, к множеству замкнутых под-
подмножеств в нек-ром нётеровом пространстве. Пусть
М — такое множество и F — его подмножество, обла-
обладающее тем свойством, что для любого а ? F найдется
строго меньший элемент b?F. Тогда F пусто. Напр.,
пусть М — множество всех замкнутых подмножеств
нек-рого нётерова пространства и F — множество тех
замкнутых подмножеств, к-рые нельзя представить в
виде конечного объединения неприводимых компонент.
Если YdF, to У приводимо, т. е. Y=Y1[)Y2, где У1;
У2 замкнуты, оба строго содержатся в У и хоть одно
из них принадлежит F. Следовательно F пусто.
Обращение порядка позволяет применять Н. и. так-
также к частично упорядоченным множествам, любое не-
непустое подмножество которых содержит максималь-
максимальный элемент, например к решетке идеалов в нётеровом
кольце.
Лит.: [1] Бур баки Н., Коммутативная алгебра, пер.
с Франц., М., 1971. л. в. Кузьмин.
НЁТЕРОВА СХЕМА — схема, допускающая конеч-
конечное открытое покрытие спектрами нётеровых колец.
Аффинная Н. с.— в точности спектр нётерова кольца.
Топологпч. пространство Н. с. X является нётеровым
топология, пространством, а все локальные кольца
6х, х нётеровы. Если каждая точка схемы обладает
открытой аффинной нётеровой окрестностью, схема
наз. локально нётеровой. Квазикомпактная
локально Н. с. есть Н. с. Примером Н. с. является схе-
схема конечного типа над полем (алгебраич. многообразие)
ИЛИ над любым нётеровым КОЛЬЦОМ. -В. И. Данилов.
НЁТЕРОВО ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ — ин-
интегральное уравнение, для к-рого справедливы теоремы
Нстера (см. ниже). Пусть X — банахово пространство,
А — линейный ограниченный оператор (отображение),
отображающий X в себя: А : X —*¦ X, А* — сопряжен-
сопряженный с А оператор,
Ах=у A)
— линейное уравнение, где х — искомый, а у — за-
заданный элементы пространства X. Пусть, далее, R (А)—
совокупность всех у?Х, для к-рых уравнение A)
разрешимо (область значений операто-
оператора А), и N {А) — совокупность всех решений соответ-
соответствующего однородного уравнения
Ах=0 B)
(нуль-пространство, или ядро опера-
оператора А). Отображение А (уравнение A)) наз. нёте-
нётеровым, оператором (нётеровым уравнен и-
е м), если выполняются следующие условия.
1) Определенный на всем банаховом пространстве
оператор А (уравнение A)) является нормально
разрешимым, т. е. уравнение A) разрешимо тог-
тогда и только тогда, когда правая часть у ортогональна
всем решениям сопряженного однородного уравнения
C)
т. е. (ф, у)=0 для любого <p?N(A*).
2) Однородные уравнения B) п C) могут иметь лишь
конечное число линейно независимых решений; число
xA=--k—k*,
тде k=dim N(A), A*=dim N (А*), наз. индексом
оператора А (индексом уравнения
(I))-
Нётеров оператор с нулевым индексом наз. фред-
фредгольмовым оператором (абстрактным), а
соответствующее уравнение A) — фредгольмо-
фредгольмовым уравнением. Напр., если V — вполне не-
непрерывный оператор У : X —*¦ X, то уравнение
x—Vx=y D)
будет фредгольмовым. Его наз. каноническим
уравнением Фредгольма. Если в уравне-
уравнении D) вполне непрерывное отображение в нек-ром
функциональном пространстве являемся интегральным
оператором
(Fa;)(s)=f K(s, t)x(t)dt,
то уравнение наз. интегральным уравне-
уравнением Ф р р д г о л ь м а. Аналогично, если в урав-
уравнении Нётера A) линейное отображение задается с по-
помощью интегральных операторов, то его наз. нёте-
нётеров ы м интегральным уравнением.
Ф. Нётер [1] рассмотрел интегральные уравнения с
Гильберта ядром
) =а («) Ф (*)+*?* 5"яс1«Цг <Р W dt +
ifK(s,t)(p(t)dt=f(t), E)
тде несобственный интеграл понимается в смысле глав-
главного значения. Для уравнения E) он установил спра-
справедливость трех теорем, называемых ныне теорема-
теоремами Нётера (предполагается, что заданные и иско-
искомая функции действительны, непрерывны в смысле
Гёльдера и a2(s)-j-fc2(s)=?t0):
1) уравнение нормально разрешимо;
2) уравнение имеет конечный индекс;
3) индекс вычисляется по формуле:
тде [ ]"я обозначает приращение функции, заключен-
заключенной в скобки.
Теорема 3) впервые указала на существование таких
линейных сопряженных интегральных уравнений, к-рые
могут иметь различное число линейно независимых ре-
решений. Кроме того, из этой теоремы вытекает, что ин-
индекс уравнения E) не зависит от его вполне непрерыв-
непрерывной части.
Оператор Нётера иногда наз. фредгольмо-
фредгольмовым, обобщенно фредгольмовым,
Ф-оператором, F-оператором.
Лит.: [1] Noether F., «Math. Ann.», 1921, Bd 82,
S. 42—63; [2] H и к о л ь с к и й С. М., «Изв. АН СССР. Сер.
матем.», 1943, т. 7, № 3, с. 147—66; [3] А т к и н с о н Ф. В.,
«Матем. сб.», 1951, т. 28, JV. 1, с. 3—14; [4] К р е й н С. Г.,
Линейные уравнения в банаховом пространстве, М., 1971;
[5] Крачковский С. Н., Ди-канский А. С,в кн.;
Итоги науки. Математический анализ. 1968, М., 1969, с. 39—71;
[6] Д а н и л ю к И. И., Нерегулярные граничные задачи На
плоскости, М., 1975; [7] Прёсдорф 3., Некоторые классы
сингулярных уравнений, пер. с нем., М., 1979. В. В. Хведелидза.
НЁТЕРОВО КОЛЬЦО левое (правое)— коль-
кольцо А, удовлетворяющее одному из следующих эквива-
эквивалентных условий:
1) Л — левый (правый) нётеров модуль над собой;
2) любой левый (правый) идеал в А имеет конечный
базис;
3) любая строго возрастающая цепочка левых (пра-
(правых) идеалов в А обрывается на конечном номере.
Примером Н. к. моя;ет служить любое кольцо глав-
главных идеалов, в к-рых любой идеал имеет одну образую-
образующую.
Н. к. названы по имени Э. Нётер (Е. Noether), сис-
систематически исследовавшей такие кольца и перенес-
перенесшей на них ряд результатов, известных ранее только
при более жестких ограничениях (напр., теорию при-
марного разложения Ласкера).
Кольцо нётерово справа не обязано быть нётеровым
слева и наоборот. Напр., пусть А — кольцо матриц ви-
вида q ц , где а — целое рациональное число и а, Р —
рациональные числа с обычным сложением и умноже-
умножением. Тогда А нётерово справа, но не нётерово слева,
О а
т. к. левый идеал элементов вида
О О
не имеет конеч-
конечного базиса.
Факторкольцо и конечная прямая сумма Н. к. снова
нётеровы, но подкольцо Н. к. может не быть нётеровым.
Напр., кольцо многочленов над нек-рым полем от бес-
бесконечного числа переменных не является нётеровым,
хотя оно содержится в своем поле частных, к-рое нё-
нётерово.
Если А — нётерово слева кольцо, то кольцо много-
многочленов А [х] также нётерово слева. Аналогичное свой-
свойство справедливо и для кольца формальных степенных
рядов над Н. к. В частности, кольца многочленов ви-
вида К[Хи ..., Хп] или % [Хи ..., Х„], где К — нек-рое
поле, a Z — кольцо целых чисел, а также любые их
факторкольца являются нётеровыми. Любое артино-
во кольцо нётероио. Локализация коммутативного Н. к.
А относительно нек-рой мультипликативной системы S
снова является Н. к. В коммутативном Н. к. А для
любого идеала m такого, что все элементы вида \-\-m,
где m?m, не являются делителями нуля, выполняется
соотношение П*=1!Я*=0. Это соотношение означает,
что любой такой идеал nt определяет на А отделимую
щ-адическую топологию. В коммутативном Н. к. лю-
любой идеал представим в виде несократимого пересечения
конечного числа примарных идеалов. Хотя такое пред-
представление не однозначно, но однозначно определены
число идеалов в представлении и множество простых
идеалов, ассоциированных с данными примарными
идеалами.
Лит.: [1] Ван дер Варден Б. Л., Алгебра, пер. с
нем., 2 изд., М., 1979; [2] Лен г С, Алгебра, пер. с англ.,
М., 1968; [3] Ф е й с К., Алгебра: кольца, модули и категории,
пер. с англ., т. 1, М., 1977. Л. В. Кузьмин.
НЁТЕРОВО ПРОСТРАНСТВО — топологическое про-
пространство X, удовлетворяющее условию обрыва убываю-
убывающих цепочек замкнутых подмножеств. Эквивалентное
условие: любое непустое семейство замкнутых подмно-
подмножеств в X, упорядоченное относительно включения,
имеет минимальный элемент. Любое подпространство
Н. п. снова нётерово. Если пространство X допускает
конечное покрытие нётеровыми подпространствами, то
X само нётерово. Пространство X нётерово тогда и толь-
только тогда, когда любое открытое подмножество в X ква-
знкомпактно. Н. п. X является объединением конечно-
конечного числа своих неприводимых компонент.
Примеры Н. п. доставляют спектры коммутативных
колец. Для кольца А пространство Spec (А) (спектр А)
нётерово тогда и только тогда, когда А — нётерово
кольцо.
Лит.: [1] Б у р б а к и Н., Коммутативная алгебра, пер.
с франц., М., 1971. Л. В. Кузьмин.
НЕФОРМАЛЬНЫЙ АКСИОМАТИЧЕСКИЙ МЕ-
МЕТОД — аксиоматический метод, не фиксирующий жест-
жестко применяемого языка и тем самым не фиксирующий
границы содержательного понимания предмета, но
требующий аксиоматич. определения всех специальных
для данного предмета исследования понятий. Этот тер-
термин не имеет общепринятого толкования.
История развития аксиоматич. метода характеризует-
характеризуется все возрастающей степенью формализации. Н. а. м.—
определенная ступень в этом процессе.
Первоначальное, дапное Евклидом, аксиоматич. по-
построение геометрии отличалось дедуктивным характе-
характером изложения, при к-ром в основу клались определе-
определения (пояснения) и аксиомы (очевидные утверждения).
Из них, опираясь на здравый смысл и очевидность, вы-
выводились следствия. При этом в выводе неявно иногда
использовались не зафиксированные в аксиомах пред-
предположения геометрич. характера, особенно относящие-
относящиеся к движению в пространстве и взаимному располо-
расположению прямых и точек. Впоследствии были выявлены
геометрич. понятия и регламентирующие их употреб-
употребление аксиомы, неявно используемые Евклидом и его
последователями. При этом возникал вопрос: действи-
действительно ли выявлены все аксиомы. Руководящий прин-
принцип для решения этого вопроса сформулировал Д. Гиль-
Гильберт (D. Hilbert): «Следует добиться того, чтобы с рав-
равным успехом можно было говорить вместо точек, пря-
прямых и плоскостей о столах, стульях и пивных кружках».
Если доказательство не теряет доказательной силы
после такой замены, то действительно все используемые
в этом доказательстве специальные предположения
зафиксированы в аксиомах. Достигаемая при таком под-
подходе степень формализации представляет собой уро-
уровень формализации, характерный для Н. а. м. Эталоном
здесь может служить классич. труд Д. Гильберта
«Основания геометрии» [1].
Н. а. м. применяется не только для придапия опре-
определенной завершенности аксиоматически излагаемой
конкретной теории. Он представляет собой действенное
орудие математич. исследования. Поскольку при изу-
изучении системы объектов по этому методу не использует-
используется их специфика, или «природа», то доказанные утверж-
утверждения переносятся на любую систему объектов, удовле-
удовлетворяющую рассматриваемым аксиомам. Согласно Н. а.
м., аксиомы — это неявные определения первоначаль-
первоначальных понятий (а не очевидные истины). Что представля-
представляют собой изучаемые объекты — неважно. Все, что нуж-
нужно о них знать, сформулировано в аксиомах. Предметом
изучения аксиоматич. теории служит любая ее интер-
интерпретация.
Н. а. м., кроме непременного аксиоматич. определе-
определения всех специальных понятий, имеет и другую харак-
характерную особенность. Это свободное, неконтролируемое
аксиомами, основанное на содержательном понимании
использование идей и понятий, к-рые можно применить
к любой мыслимой интерпретации, независимо от ее
содержания. В частности, широко используются теоре-
теоретико-множественные и логич. понятия и принципы, а
также понятия, связанные с идеей счета, и др. Проник-
Проникновение в аксиоматич. метод рассуждений, основанных
на содержательном понимании и здравом смысле, а не
на аксиомах, объясняется нефиксированностью языка,
на к-ром формулируются и доказываются свойства ак-
аксиоматически заданной системы объектов. Фиксирова-
Фиксирование языка ведет к понятию формальной аксиоматич.
системы (см. Аксиоматический метод) и создает мате-
материальную основу для выявления и четкого описания
допустимых логич. принципов, для контролируемого
употребления теоретико-множественных и других об-
общих или не специальных для исследуемой области
понятий. Если в языке нет средств (слов) для передачи
теоретико-множественных понятий, то этим отсеивают-
отсеиваются все доказательства, основанные на использовании
таких средств. Если в языке есть средства для выраже-
выражения нек-рых теоретико-множественных понятий, то их
применение в доказательствах можно ограничить опре-
определенными правилами или аксиомами.
Фиксируя различным образом язык, получают раз-
различные теории основного объекта рассмотрения. Напр.,
рассматривая язык узкого исчисления предикатов для
теории групп, получают элементарную теорию групп,
в к-рой нельзя сформулировать какого-либо утвержде-
ния о подгруппах. Если перейти к языку исчисления
предикатов второй ступени, то появляется возможность
рассматривать свойства, в к-рых фигурирует понятие
подгруппы. Формализацией Н. а. м. в теории групп
служит переход к языку системы Цермело — Френкеля
с ее аксиоматикой.
Лит.: [1] Гильберт Д., Основания геометрии, пер.
с нем., М.— Л., 1948; [2] Гильберт Д., Б е р н а й с П.,
Основания математики. Логические исчисления и формализация
арифметики, пер. с нем., [т. 1], М., 1979. В. Н. Гришин.
НЕФРЕДГОЛЬМОВО ИНТЕГРАЛЬНОЕ УРАВНЕ-
УРАВНЕНИЕ — интегральное уравнение, для к-рого неверны
те или иные Фредголъма теоремы. Иногда Н. и. у. наз.
особым интегральным уравнением.
Так, напр., интегральное уравнение
Фурье
ф(г) — У -^-\« sinlxs)w(s)ds = l
имеет решение
фо W = у — '
где а — произвольное положительное число; собствен-
собственному значению У~2/л уравнения A) соответствует бес-
бесконечное множество линейно независимых решений,
т. е. для уравнения A) перестает быть справедливой
теорема Фредгольма о том, что однородное уравнение
имеет конечное число линейно независимых решений.
В случае интегрального уравнения
Лалеско — Пикара
ф (s) ds = 0 B)
любое ^?@, -)-оо) является собственным значением,
а именно, любому положительному числу J. соответст-
соответствуют два линейно независимых решения:
Следовательно, для уравнения B) перестает быть спра-
справедливой теорема Фредгольма о том, что множество
собственных значений уравнения но более чем счетно.
Подробно разработаны теории двух классов Н. и. у.:
уравнений, в к-рых искомая функция содержится под
знаком несобственного интеграла в смысле главного
значения (сингулярные интегральные уравнения); урав-
уравнения, в к-рых искомая функция содержится под зна-
знаком интегрального преобразования свертки (интеграль-
(интегральные уравнения типа свертки). Для таких уравненш':,
вообще говоря, нарушается равенство чисел линешк
независимых решений однородных союзных (сопряжен-
(сопряженных) уравнений, а также альтернатива Фредгольмл.
Лит.: [1] П р и в а л о в И. И., Интегральные уравнения,
2 изд., М.— Л., 1937; [2] П е т р о в с к и й И. Г., Лекции
по теории интегральных уравнений, 2 изд., М.— Л., 1951. См.
также лит. при статьях Интегральное уравнение типа свертки.
и Сингулярные интегральные уравнения. Б. В. Хвевеливзе.
НЕХОПФОВА ГРУППА — группа, допускающая
эндоморфизм на себя с нетривиальным ядром, т. е. изо-
изоморфная иек-рой своей собственной факторгруппе (в
противном случае группа наз. х о п ф о в о й). Термин
происходит от проблемы X о п ф а (Н. Hopf,
1932) о существовании таких групп с конечным множе-
множеством порождающих. Оказалось, что существуют даже
конечно определенные Н. г. Примером конечно порож-
порожденной Н. г. является группа с порождающими х, у и
одним определяющим соотношением
Бесконечно порожденные Н. г. строятся совсем просто,
таково, напр., прямое произведение бесконечного числа
изоморфных между собой групп.
Лит.: [1] К у р о ш А. Г., Теория групп, 3 изд., М., 1967;
[2] Магнус В., К а р р а с А., С о л и т э р Д., Комби-
Комбинаторная теория групп, пер. с англ., М., 1974.
А. Л. Шмелькин.
НЕЦЕНТРАЛЬНОЕ «ХИ-КВАДРАТ» РАСПРЕДЕ-
РАСПРЕДЕЛЕНИЕ, нецентральное %2- распределе-
н и е,— непрерывное, сосредоточенное на положитель-
положительной полуоси 0<z<oo распределение вероятностей с
плотностью
Х + Х П—1 , j
где п — число степеней свободы, а Я — параметр не"
центральности. При к=0 эта плотность совпадает с
плотностью обычного (центрального) «хи-квадрат» рас-
распределения. Характеристич. функция Н. «х.-к.» р.
выражается формулой
математич. ожидание и дисперсия равны соответственно
п+Я, и 2(п-\-2Х). Н. «х.-к.» р. принадлежит классу без-
безгранично делимых распределений.
Обычно Н. «х.-к.» р. появляется как распределение
суммы квадратов независимых случайных величин
Xlt ..., Хп, имеющих нормальное распределение с от-
отличными от нуля средними т,- и единичными диспер-
дисперсиями, точнее, сумма х1-\-...-\-Х2п имеет Н. «х.-к.» р. с
п степенями свободы и параметром нецентральности
X=^j. тп2[. Сумма нескольких взаимно независимых
случайных величин с Н. «х.-к.» р. имеет распределение
этого же типа, и его параметры суть суммы соответст-
соответствующих параметров слагаемых.
Если число п четное, то функция распределения Н.
«х.-к.» p. Fn(x; К) (всегда равная нулю при х^.0) при
х>0 равна
Я,
Эта формула устанавливает связь между Н. «х.-к.» р.
и Пуассона распределением. Именно, если X и У имеют
распределения Пуассона с параметрами -|- и -g- соответ-
соответственно, то для любого целого ,«>0
Н. «х.-к.» р. часто возникает в задачах математич.
статистики, посвященных исследованию мощности кри-
критериев типа «хи-ксадрат». Так как существующие таб-
таблицы Н. «х.-к.» р. недостаточно полны, то в статистич.
приложениях широко используют различные прибли-
приближения с помощью «хи-квадрат» распределения и нор-
нормального распределения.
Лит.: [1] Б о л ь ш е в Л. Н., Смирнов Н. В., Таб-
Таблицы математической статистики, 2 изд., М., 1968; [2] Кен-
далл М., Стьюарт А., Статистические выводы и связи,
пер. с англ., М., 1973; [3] Р a t л a i k Р. В., «Biometrika»,
1949, v. 36, р. 202. А. В. Прохоров.
НЕЧЕТНАЯ ФУНКЦИЯ — функция, меняющая
знак при изменении знака независимого переменного,
т. е. функция, удовлетворяющая условию /(—х)=
= —f(x). График Н. ф. симметричен относительно нача-
начала координат.
НЕЧЕТНОЕ ЧИСЛО — целое число, не делящееся
(без остатка) на 2.
НЕЭФФЕКТИВНАЯ СТАТИСТИКА — статистиче-
статистическая оценка, дисперсия к-рой больше дисперсии эффек-
эффективной оценки. Иначе говоря, для Н. с. в Рао — Кра-
Крамера неравенстве равепство не достигается хотя бы
при одном значении оцениваемого параметра. Мерой ка-
качества Н. с. служит величина е, наз. ее эффектив-
эффективностью и равная отношению дисперсии эффектив-
ной оценки к дисперсии Н. с. Эффективность е неотри-
неотрицательна и не превосходит 1. Величина 1/е показывает,
во сколько раз нужно увеличить число наблюдений при
использовании Н. с. но сравнению с эффективной ста-
статистикой, чтобы считать эквивалентными результаты
применения этих двух статистик. Напр., медиана рп
эмпирия, распределения, построенного по п независи-
независимым нормально jV (9, о2) распределенным случайным
величинам Ху, ..., Хп, асимптотически нормально рас-
распределена с параметрами 9 и ст2л/2п и является неэф-
неэффективной порядковой статистикой для математич.
ожидания 0. Эффективной статистикой в данном слу-
случае является оценка Х=(Х1-\-... + ХпIп, к-рая рас-
распределена по нормальному закону с N(Q, o2!n). Эффек-
Эффективность е статистики ип равна
Следовательно, при использовании статистики ц„ в
среднем необходимо в я/2 «1,57 раза больше наблюде-
наблюдений по сравнению со статистикой X, чтобы получить
одну и ту же точность в оценке неизвестного математич.
ожидания 9.
Лит.: [1] К р а м е р Г., Математические методы статисти-
статистики, пер. с англ., 2 изд., М., 1975; [21 Больше! Л. Н.,
Смирнов Н. В., Таблицы математической статистики,
2 изд., М., 1968. М. С. Никулин.
НЕЯВНАЯ ФУНКЦИЯ — функция / : Е -> У, за-
заданная уравнением F(x, y)=z0, где F : XXY -v Z,
х?Х, y?Y, ЕсХ, X, Y и Z — нек-рые множества, т. е.
такая функция /, что при любом х?Е имеет место
F (x, f{x))=z0. Если X, Y и Z — топологич. пространст-
пространства и для нек-рой точки (х0, yo)?XxY выполняется ус-
условие F(x0, i/0)=z0, то при определенных условиях в
нек-рой окрестности точки (х0, у0) уравнение F(x, г/) = г0
одноаначно разрешимо относительно одной из перемен-
переменных. Свойства решения этого уравнения описываются
теоремами о Н. ф.
Простейшая теорема о Н. ф. состоит в следующем.
Пусть X и Y — подмножества числовой прямой R,
•zo?X, yo?Y, (x0, уй) — внутренняя точка множества
X X Y на плоскости; тогда если функция F непрерывна
в нек-рой окрестности точки (х0, у0), F(x0, yo)=O п су-
существуют такие 6>0 и е>0, что при любом фиксиро-
фиксированном х?(х0—6, хв-\-8) функция F(x, у) как функция
переменного у строго монотонна на интервале
0
1
_ 1
^\
' т
1
1
$
Т
t
i
i л
ха-г
N4
.—"Тч-Уъ) \
I
—v
\)
I/
/нх,У)'О
X
(;/o—е) 2/o+8)i то найдется такое 60>0, что существует
и притом единственная функция
f:(x0 — о0, хо-\-Ьо)—"(уо — 8, Уо+е)
такая, что F(x, /(х))==0 для всех х?(ха—60, хо-\-8о),
причем функция / (х) непрерывна и f{xo) = yo. Условия
этой теоремы выполняются, если функция F (х, у)
непрерывна в окрестности точки (х0, у0), существует
частная производная Fu, непрерывная в точке (ж0, г/0),
F(xo, Уо)~О, a Fy{xa, yo)=^O. Если, кроме того, сущест-
существует и частная производная Fx, также непрерывная
в точке {.Го. г/о)» то Н. ф. / дифференцируема в точке х0,
причем
df (х„) _ _ Fx (ж„ у„)
dx Fy (х0, у„)
Эта теорема обобщается на случай системы уравне-
уравнений, т. е. когда F является векторной функцией. Пусть
R" и Rm суть п- и m-мерные евклидовы пространства
с фиксированными системами координат, точки к-рых
соответственно х=(хи ..., х„) и y—(yi, ¦¦¦, ут). Пусть F
отображает нек-рую окрестность W точки (хй, г/о)€
?R"XRm, .xo?R", i/0?Rm, в пространство Rm it Ft,
г=1, 2, ..., m,— координатные функции (от п-\~т пере-
переменных .Г], ..., хп, г/1, ..., ут) отображения F, т. е. F=
= (FU ..., Fm). Если отображение F дифференцируемо на
W, F{xc, уо)=О, а якобиан
djF,, Fm) , „
д (У1, . . ., Ут) (Хо. У о) '
то существуют окрестности U и V точек х0 и г/0 соответ-
соответственно в пространствах R" и Rm, UX Fc W и единст-
единственное отображение / : U —*- V такие, что для всех
x?U выполняется условие F(x, /(a))=0?IRm. При
этом f{xo)=yo, отображение/ дифференцируемо на U, а
если f=(fi, ..., fm), T0 явное выражение дл-я частных
производных dfjldx[, t—1, 2, ..., n, /=1, 2, ..., то, нахо-
находится из системы т линейных относительно этих про-
производных уравнений
9Fh
к—\, 2, ..., m, i фиксировано (i=i, 2, ..., ;г). Иногда
основное утверждение теоремы формулируется следую-
следующим образом: существуют окрестности U и Wa точек х9
и {х0, уь) в пространствах R." и R"XRm, WoclC,
и единственное отображение f : U —*¦ Rm такие, что
для всех x^U выполняются условия (х, f(x))?W0,
F(x, /(x)) = 0. Иначе говоря, условия
F(x, j/)=0
равносильны условиям з:^ {7, y=i(x). В этом случае
гояорят, что уравнение F (х, г/) = 0 однозначно разреши-
разрешимо в окрестности Wo точки (ж0, г/0).
Сформулированная классич. теорема о Н. ф. обобща-
обобщается на случай более обших пространств следующим об-
образом. Пусть X — топологич. пространство, Y и Z —
аффинные нормированные пространства над полем
действительных или комплексных чисел, т. е. аффин-
аффинные пространства над указанными полями, к-рым со-
сопоставлены соответственно нормированные векторные
пространства Т и Z, причем Т — полное пространство,
X (Y, Z) — множество линейных непрерывных отобра-
отображений пространства Y я пространство Z, W — откры-
открытое множество в произведении пространств XX Y и
( )&У ?Х ?У
(о, Уо& о? ?
Пусть F : W —*- Z — непрерывное отображение W в
Z и F (x0, j/0) = z0. Если при каждом фиксированном х и
(х, у) С W отображение F имеет частную Фреше произ-
производную Fy?Je(Y, Z), причем Fy(x,y) : W-+X(Y, Z)
является непрерывным отображением W в JC (Y, Z), а
линейное отображение Fy{x0, у0) : Y—yZ имеет непре-
непрерывное обратное линейное отображение (т. е. является
обратимым элементом пространства ?{Y, Z)), то су-
существуют такие открытые соответственно в пространст-
пространствах X п Y множества UcX и VcY, xo?U, ya?V, что
для любого х? U существует и притом единственный
элемент y?V, обозначаемый y=f(x) и удовлетворяющий
условиям:
При этом так определенная функция y=f(x) является
непрерывным отображением U в V и yo=f(xo).
Если А' также является аффинным нормированным
пространством, то при определенных условиях Н. ф.
f : х н- у, удовлетворяющая уравнению
F(x, y) = z0, A)
также дифференцируема. Именно, пусть X, Y, Z —
аффинные нормированные пространства, W — откры-
открытое множество из XXY, F: W—r-Z, F(x0, </0)=z0,
хо?Х, Do?Y, и пусть/ — неявное отображение, задава-
задаваемое уравнением A) и отобраясающее нек-рую окрест-
окрестность U точки х0 в открытое подмножество V простран-
пространства Y, UXVcW. Таким образом, для всех x?U
имеет место
F(x,f(x))=z0. B)
Пусть, кроме тою, отображение / непрерывно в точке х0
11 Кха)—Уо- Тогда если отображение F дифференциру-
дифференцируемо в точке (х0, у0) н его частные производные Фреше
Fx (хо, ?'о) и Fy (xui Уо) являются линейными непре-
непрерывными операторами, отображающими соответственно
векторные пространства X и Y, сопоставленные аф-
аффинным пространствам X и Y, в векторное простран-
пространство Z, сопоставленное аффинному пространству Z,
причем оператор Fy(x0, у0) является обратимым эле-
элементом пространства X(Y, Z), то отображение / диффе-
дифференцируемо в точке х0 и его производная Фреше задает-
задается формулой
/' (*о) = — Fy1 (х0, y0)oFx (х0, у0).
Эта формула получается в результате формального
дифференцирования функции B):
Fx(-r0, Уо) + Ру(х<>, y0)of'(x0)=0^je(X, Y)
и умножения слева этого равенства на FyX(x0, у0).
Если, кроме того, отображение F : W -> Z непрерыв-
непрерывно дифференцируемо на W, Н. ф. / : U —*¦ V непрерывна
на U, UX VcW и для любого х? U частная производ-
производная Фреше Fy(x, f(x)) является обратимым элементом
пространства X(Y, Z), то отображение / — непрерывно
дифференцируемое отображение U в V.
Можно указать и в общем случае условия существо-
существования и единственности Н. ф. в терминах непрерывно-
непрерывности производной Фреше: если пространство Z полно,
отображение F : W -»- Z непрерывно дифференцируемо
на W, F(x0, #o)=zo и частная производная Фреше
Fy(x0, г/0) является обратимым элементом иространстпа
.&(Y, Z), то уравнение A) однозначно разрешимо в до-
достаточно малой окрестности точки (х0, г/0), т. е. сущест-
существуют окрестности U и V точек х0 и у„ соответственно
в пространствах X н Y, UX КсИ' и единственная Н. ф.
/ : U -> V, удовлетворяющая условиям B). При этом
отображение / непрерывно дифференцируемо на U.
В таком виде теорема о Н. ф. для нормированных про-
пространств представляет собой прямое обобщение соответ-
соответствующей классич. теоремы о Н. ф. для одного скаляр-
скалярного уравнения с двумя переменными.
Если, кроме того, функция F : W—>-Z непрерывно
дифференцируема в окрестности W точки (.г0, уи) к раз
(к=1, 2, ...), то Н. ф. / : U -> V также к раз непрерывно
дифференцируема.
Более далекие обобщения классич. теоремы о Н. ф.
на случай дифференциальных операторов даны Дж.
Нашем (.1. Nash) (см. Нэша теорема).
Лит.: [1] Колмогоров А. Н., Фомин С. В., Эле-
Элементы теории функций и функционального анализа, 5 изд., М.,
1981; [2] Л ю с т е р н и к Л. А., Соболев В. И., Эле-
Элементы функционального анализа, 2 изд., М., 1965; [3] Ни-
Никольский С. М., Курс математического анализа, 2 изд.,
т. 1—2, М., 1975; [4] Шварц Л., Анализ, пер. с франц., т. 1,
М., 1972; [5] И л ь и н В. А., II о з н я к Э. Г., Основы
математического анализа, 3 изд., ч. 1, М., 1971.
Л. Д. Кудрявцев.
НЕЯВНАЯ ФУНКЦИЯ в алгебраической
геометрии — функция, задаваемая алгебраич.
уравнением. Пусть F(XU ..., X п, Y) — многочлен от
Хи , Хп, Y (напр., с комплексными коэффициента-
коэффициентами). Тогда многообразие F(.F)cC" + 1 нулей этого мно-
многочлена можно рассматривать как график нек-рого со-
соответствия у : С" —*- С. Это соответствие и называют,
допуская известную неточность, функцией, неявно за-
заданной уравнением F(x, y)=0. Вообще говоря, соответ-
соответствие у многозначное и не всюду определенное и поэтому
не является функцией в обычном смысле. Имеется два
способа превратить это соответствие в функцию. Пер-
Первый, восходящий к В. Риману (В. Riemann), заключа-
заключается в том, что областью определения Н. ф. у считают
не С", а многообразие V(F), конечнолистно накрываю-
накрывающее С". Этот прием приводит к очень содержательному
понятию римановой поверхности. При таком подходе
понятие Н. ф. смыкается с понятием алгебраической
функции.
Другой способ состоит в том, чтобы представить
V(F) локально как график однозначной функции. Раз-
Различные теоремы о Н. ф. утверждают существование
открытых t/crC" и WCzC, для к-рых (UXW)r\V(F)
является графиком гладкой в том или ином смысле
функции у : U —у W (см. Неявная функция). Однако
открытые подмножества U и W, как правило, не яв-
являются открытыми в топологии Зариского и лишены
смысла в абстрактной алгебраич. геометрии. Поэтому
указанный способ модифицируется следующим образом.
Формальным р о с т к о r.i (или в е т в ь ю) в точ-
точке ас С" Н. ф., заданной уравнением F(X, У)=0, наз.
формальный степенной ряд y^Cff^x—аа, ..., Хп—«„]]
такой, что F(X, p)=-0. Вообще, степенной ряд у, удо-
удовлетворяющий полиномиальному уравнению F(X,Y) = 0,
наз. алгебраическим степенным ря-
д о м. Алгебраический степенной ряд сходится в некото-
некоторой окрестности точки а.
Пусть А — локальное нётерово кольцо с максималь-
максимальным идеалом lit. Элемент у из пополнения А локального
кольца А наз. алгебраическим над А, если
F(y) — O для нек-рого многочлена F(Y)?A [У]. Множе-
Множество алгебраических над А элементов А образует коль-
кольцо А. Следующий вариант теоремы о Н. ф. показывает,
что алгебраич. функций достаточно много. Пусть
f(Y) = (fl(Y1, ..., Ym), ..., fm<yu ..., Ym)) _
— набор т многочленов из A [Yu ..., Ym] и пусть г/°=
= (l/i, ••¦) Ут) — элементы поля вычетов А/т такие, что:
"П /(!/°)=0 (черта сверху означает редукцию по
модулю lit);
2)
det (ft
Тогда существуют алгебраические над А элементы
у=(уЛ, .... ут) такие, что /(г/)=-0 и у~=--у°. Другими сло-
словами, А — гензе.гево кольцо.
Другой результат того же типа — теорема Артина
об аппроксимации (см. [2]). Пусть А — локальное
кольтю, являющееся локализацией алгебры конечного
типа над нолем. Пусть, далее, задана система f(Y)=O
полиномиальных уравнений с коэффициентами из А
(или из А) и у — вектор с коэффициентами из попол-
пополнения А такой, что /(г/)—0. Тогда найдется вектор у
с коэффициентами из А, сколь угодно близкий к у и
такой, что /(i/) = 0. Вариант этой теоремы верен 13] и для
систем аналптич. уравнений.
Лит.: Ш Ар тин М., «Успехи матем. наук», 1971, т. 26,
в. 1, с. 181 — 205; [2] Art in M., «Publ. Math. IHES», 1969,
№36, р. 23—58; [3] е г о же, «Invent, math.», 1968, v. 5,
p. 277—91. В. И. Данилов.
НЕЯВНЫЙ ОПЕРАТОР — решение y=f(x) нели-
нелинейного операторного уравнения F(x, г/)=0, в к-ром х
играет роль параметра, а у — неизвестного. Пусть X,
Y, Z — банаховы пространства, F(x, у) — нелинейный
оператор, непрерывный в окрестности Q точки (х0, г/0)?
? X-f- Y и отображающий Q в окрестность нуля в Z.
Если Фреше производная Fy(x, у) непрерывна в Q, су-
существует и ограничен оператор [Fy(x0, г/о)!» а F(xa
Уо) — О, то найдутся числа е>0 и б>0 такие, что при
\\х—хо\\<6 в шаре |1у—гд>!1<е уравнение F(x, y) = 0
имеет единственное решение у=/(я). При этом Н. о.
f(x) непрерывен по' х и f(xo)=yo. Если дополнительно
F(x, у) п раз дифференцируем в Q, то и f(x) n раз диф-
дифференцируем. Если Fix, у) — аналитический оператор
в Q, то и f(x) — аналитический. Эти утверждения обоб-
обобщают известные предложения о неявных функциях.
О вырожденных случаях см. Ветвление решений нели-
нелинейных уравнений.
Лит.: [1] Hildebrandt Т. Н., Graves L. М.,
«Trans. Amer. Math. Soc», 1927, v. 29, p.127—53; [2] Л ю c-
т е р н и к Л. А., Соболев В. И., Элементы функпис-
нального анализа, 2 изд., М., 1965; [3] Вайнберг М. М.,
Треногий В. А., Теория ветвления решений нелинейных
уравнений, М., 1969; [41 Ниренберг Л., Лекции по не-
нелинейному функциональному анализу, пер. с англ., М., 1977.
В. А. Треногий.
НИГДЕ НЕ ПЛОТНОЕ МНОЖЕСТВО топологи-
топологического пространства X — множество А г
определяемое следующим свойством: каждое непустое
открытое множество FczX содержит непустое открытое
множество ГосГ такое, что А{]Тп— 0. Другими сло-
словами, А — Н. не п. м., если оно не плотно ни в каком
непустом открытом множестве. м. И. Войцеховский.
НИЖНИЙ ПРЕДЕЛ последовательности
множеств А1у А2, ..., Ап, ... в топологиче-
топологическом пространстве X — совокупность точек
р?Х, любая окрестность к-рых пересекается со всеми
элементами последовательности, начиная с нек-рого N.
Н. п. числовой последовательности
см. в ст. Верхний и нижний пределы. А- А- Мальцев.
НИЖНЯЯ ГРАНЬ м н о ж е с т в а — см. Верх-
Верхняя и нижняя грани.
НИЖНЯЯ ГРАНЬ семейства топологий
/¦(заданных на одном множестве X) —
теоретико-множественное пересечение этого семейства
топологий, т. е. П^"- Обозначается f\F. Всегда AF —
топология на X. Если топологии $\ и ?Гг заданы на
множестве X и ?Г\ содержится в ^ (как множество),
ТО пишут саГ1<аГ2-
Топология AF обладает свойством: если $" — то-
топология на X и $" <^Г для всех J^"^ F, то #" < л F.
Свободная сумма пространств, получающихся при на-
наделении множества X всеми отдельно взятыми тополо-
топологиями из семейства F, канонически отображается на
пространство X, A F. Важным свойством этого отобра-
отображения является его факторность. На этой основе дока-
доказываются общие теоремы о сохранении ряда свойств при
операции пересечения топологий.
Лит.: [1] Архангельский А. В., Понома-
Пономарев В. И., Основы общей топологии в задачах и упражне-
упражнениях, М., 1974. А. В. Архангельский.
НИКОЛЬСКОГО ПРОСТРАНСТВО — банахово про-
пространство Нр(И), состоящее из функций, определенных
на открытом множестве Q 7г-мерного евклидова прост-
пространства R" и обладающих определенными разностно-
дифференциальными свойствами, характеризующимися
вектором г=(ги ..., гп), г,->0, г—\, 2, ..., п, в метрике
Ьр, 1<р<+оо. Введены С. М. Никольским.
Н. п. Hp(ii) можно описать в терминах свойств разно-
разностей от частных производных порядка п по переменной
xh где /¦(-==г<* + а/. п — целое, 0<а,-<:1, г=1, 2, ..., п;
если через &sh.f обозначить разность порядка s=l, 2, ...
с шагом hi по переменной х,- функции /, то
f€K(Mi> -,М„; Q),M;>0,
тогда и только тогда, когда функция / имеет в Q обоб-
обобщенные частные производные
1хг1> =дга/дхГс,
i=l, 2, ..., п, и при 0<а,- <1 имеет место неравенство
а при а=1 — неравенство
где Qr\ — множество точек х?Q, удаленных от границы
множества Q больше чем на т]>0, a h,- — произвольно.
Пространство Hrp{Q) = Hrp" •¦¦• r"(Q) определяется как
объединение всех Нп(Мх, ..., Мп\ Q) при всевозможных
М;>0, г=1, 2, ..., п.
Если ?1Ф0, то при любых г,->0, г=1, 2, .... п,
1 <р <-f сю Н. п. Яр1' ¦••• r"(Q) не пусто и в нем
существуют функции, не принадлежащие Н. п.
нп, ..., г,-_„ n+e, r,- + i, .... г„, ... яи при каком е>о
и ни при каком г=1, 2, ..., п.
В случае р=сс, не целых г,- и непрерывности рассмат-
рассматриваемых производных Н. п. является гёлъдеровым
пространством. Понятие Н. п. обобщается на случай
функций, определенных на достаточно гладких много-
многообразиях (см. [2]).
Имеется описание Н. п. Я^" ¦••• rk(Q) в терминах
свойств разностей от частных производных, меньших
чем г\ порядков, в частности в терминах свойств разно-
разностей достаточно высокого порядка от самой функции.
Пусть Hp(Q) — изотропное пространство, т. е. гг =
= ... = г„=г. Если область Q такова, что любую функцию
/ класса Нгр@) можно продолжить с сохранением клас-
класса на все пространство R", т. е. так, что продолженная
функция будет принадлежать классу Hp(Rn) (это всег-
всегда имеет место, если граница области достаточно глад-
гладкая), то для того, чтобы f?Hp(Q), необходимо и доста-
достаточно, чтобы для любых целых неотрицательных к и s
таких, что 0<г—«<А-, у функции / существовали все
частные производные /li) порядка s и существовала по-
постоянная Л/>0, для к-рой выполнялись неравенства
В ДЙ/"> ||ья »*(*>> <ЛПЛ1'~'' A)
тде ^=(/1!, ..., hn), Aft/(J) — разность fc-ro порядка с
векторным шагом к от функции /<*>. Условие A) эквива-
эквивалентно аналогичному условию для модуля непрерывно-
непрерывности производной /(*': существует такое Л/>0, что
Q*(/<», 6)<М6'-*, б > О,
где
, 6)def sup Sap ri
Если для функции f?Hp(Q) через Mf обозначить
нижнюю грань всех М, для к-рых выполняется условие
A) для всех h?R" и всех частных производных допус-
допустимого порядка s, то
является нормой в Н. п. Hp(ii), причем нормы, полу-
получающиеся при различных допустимых парах к, s, экви-
эквивалентны между собой.
Н. п., состоящее из функций, определенных на всем
пространстве R", можно охарактеризовать в терминах
наилучших приближений функций из этого простран-
пространства с помощью целых функций экспоненциального
типа. Пусть JEvi, ..., vn(f)p — наилучшее приближение в
метрике Lp{Rn) функции f?LJRn^ при помощи целых
функций qVl ...vn(*i> ¦••> xn)^Lp(R") экспоненциаль-
экспоненциального типа степеней Vj, ..., vn соответственно по перемен-
переменным xlt .. , хп. Для Н. п. справедливы следующие пря-
прямая и обратная теоремы типа теорем Бернштейна,
Джексона, Зигмунда.
Если функция /€#р г"(Мг, ..., М„; R"), то
для любых v,->0 выполняется неравенство
г
(постоянная с>0 не зависит от функции /).
Наоборот, если для функции f?Lp(R") выполняется
неравенство B) для v,-=a*, &=0, 1, ..., a,->l, i==l,
2, ..., п, и у является целой функцией степени единица,
по каждой из переменных хи ..., хп, для к-рой
(она существует в силу B) при к=0), то
f-g?Hp" ¦¦¦•r»(Af'1 M'n;R"),
где
причем постоянные с>0 в B) и с,->0 в C) не зависят от
Л/,', г=1, 2, ..., я.
В случае периодической по всем переменным функций
/ аналогичное описание Н. п. делается посредством наи-
наилучших приближений функций через тригонометрич,
полиномы вместо целых функций акспоненциального
типа (см. llj, [4]).
Н. п. могут быть описаны с помощью оператора Бес-
Бесселя — Макдональда, применяемого к нек-рому классу
обо5щенных функций (см. Вложения теоремы).
Для пространств Нгри ¦¦•• r"(Q) С. М. Никольским
доказаны транзитивные теоремы вложения для разных
размерностей и метрик (см. [3] и Вложения теоремы),
перенесенные в дальнейшем на более общие классы
функций. Эти теоремы показывают, что Н. п. образуют
замкнутую систему относительно граничных значений
входящих в них функций: следы функций из Н. п. на
гладких многообразиях в определенном смысле полно-
полностью описываются в терминах Н. п.
Свойства Н. п. дали возможность получить необхо^
димые и достаточные условия разрешимости Дирихле
задачи в соответствующих Н. п. в терминах принад-
принадлежности граничной функции также к нек-рому Н. п.;
для того чтобы гармония, функция и принадлежала
классу Hp(Q), r>l/p, где Q — ограниченная область
в R" с достаточно гладкой границей 0Q, необходимо
и достаточно, чтобы граничные значения к|а?2 принад-
принадлежали к классу #p~1//p(dQ). Отсюда при jb = 2 следу-
следует, в частности, что если и\да?Н%{д0,), р>1/2, то
Дирихле интеграл D (и) от функции и по области Q ко-
конечен и потому задачу Дирихле можно решить пря-
прямым вариационным методом. Из теорем вложения для
Н. п. следует, что если для функции и ее интеграл
Дирихле по области Q конечен, то uIqq? H}J2(dii)
(см. [6]).
Обобщением Н. п. является пространство Бесова
Лит.: [1] Никольский С. М., «Тр. Матем. ин-та
АН СССР», 1951, т. 38, с. 244—78; [2] е г о ж е, «Матем. сб »,
1953, т. 33, № 2, с. 261—326; [3] е г о же, «Докл. АН СССР»,
1958, т. 118, JM» 1, с. 35—37; [4] е г о же, Приближение функ-
функций многих переменных и теоремы вложения, 2 изд., М. 1977-
[5] Б е с о в О. В., Ильин В. П., Никольский
С. М., Интегральные представления функций и теоремы вло-
вложения, М., 1975; [6] Н и к о л ь с к и й С. М., «Докл. АН
СССР», 1953, т. 88, в. 3, с. 409—11. Л. Д. Кудрявцев.
НИКОМЕДА КОНХОИДА — плоская алгебраич.
кривая 4-го порядка, уравнение к-рой в декартовых
прямоугольных ко-
координатах имеет
вид
У) (?/)
-гу=о;
в полярных
ординатах:
ко-
I.
a) t<a
в) L-a
а
sinip
Внешняя
ветвь (см. рис.).
Асимптота х=а. Две точки перегиба В и С.
Внутренняя ветвь. Асимптота х=а. Нача-
Начало координат — двойная точка, характер к-рой зави-
зависит от величин а и I: при 1<Са — изолированная точка,
кривая имеет еще две точки перегиба Е, F; при />а —
узловая точка; при 1=а — возврата точка. Н. к.—
конгоида прямой х=а.
Н. к. названа по имени Никомеда C в. до н. э.),
к-рый применял ее для решения задачи о трисекции
угла.
Лит.: [1] С а в е л о в А. А., Плоские кривые, М., 1960.
Д. Д. Соколов.
НИЛЬАЛГЕБРА — алгебра с ассоциативными сте-
степенями (в частности, ассоциативная), в к-рой всякий
элемент нильпотентен. Частным случаем Н. являются
нильпотентная и локально нильпотентная алгебра.
В ассоциативном случае построение Н.,не являющихся
локально нильпотентными, представляет собой трудную
задачу; по существу известен лишь один пример такой
алгебры (см. [5]).
Класс Н. замкнут относительно взятия гомоморфных
образов и перехода к подалгебрам. Кроме того, расши-
расширение Н. с помощью Н. снова оказывается Н. Поэтому
во всякой алгебре сумма всех нильидеалов является на-
наибольшим нильидеалом, содержащим всякий ниль-
идеал. Он наз. верхним нильрадикалом
алгебры, факторалгебра по нему не содержит не-
ненулевых нильидеалов. Вопрос о том, будет ли сумма
односторонних нильидеалов односторонним нильидеа-
нильидеалом, составляет содержание проблемы Кёте.
Неизвестно также A982), существуют ли простые ниль-
нилькольца. Выполнение условий «бернсайдовского типа»
для Н. часто влечет ее нильпотентность или локальную
нильпотентность; нётерова Н. нильпотентна; артинова
Н. (в частности, конечномерная) нильпотентна; Н. огра-
ограниченного индекса (индексы нильпотентности элемен-
элементов ограничены в совокупности) над полем нулевой ха-
характеристики нпльпотентна (теорема X и г м е-
н а); Н., удовлетворяющая полиномиальному тождест-
тождеству, локально нильпотенша. Не выяснено A982), будет
ли нилыготентной конечно определенная нильалгебра.
Особый интерес представляют условия, при к-рых
радикал Джекобсона Rad А алгебры А над полем к
совпадает с нильрадикалом. Вот нек-рые из них: А
артинова, в частности конечномерная, алгебра (Rad A
даже нильпотентен); card k^dim^A, в частности если
А конечно порождена над к и к несчетно; алгебраич.
алгебра А; А конечно порожденная над к алгебра с по-
линомиальным тождеством и к бесконечно. Радикал
конечно порожденной алгебры с полиномиальным тож-
тождеством над полем нулевой характеристики нильпотен-
тен. Этот факт эквивалентен условию выполнимости в
такой алгебре нек-рого стандартного тождества.
Некоторые из сформулированных утверждений име-
имеют аналоги в неассоциативных алгебрах. Так, в альтер-
альтернативном кольце с условием максимальности для пра-
правых идеалов, не имеющем элементов порядка 2 и 3 в ад-
аддитивной группе, всякий односторонний ннльпдеал
нильпотентен. В йордановой алгебре А над полем к
радикал Джекобсона Rad А является нильидеалом,
если выполнено одно из следующих условий: card /c>
>2-rdimyl; A — алгебраич. алгебра. Всякое альтер-
альтернативное или специальное йорданово нилькольцо огра-
ограниченного индекса без элементов 2-го порядка в адди-
аддитивной группе локально нильпотентно (теорема
Ширшова). Конечномерная обобщенно стандарт-
стандартная Н. нильпотентна.
Всякая антикоммутативная алгебра является Н. В
определенном выше смысле, поэтому в классе антиком-
антикоммутативных колец понятие Н. бессодержательно. Одна-
Однако полезными оказываются различные аналоги этого
понятия. Так, в классе колец Ли аналогом Н. являются
энтелевы алгебры, т. е. алгебры, в к-рых внутренние
дифференцирования элементов нилыготентны. Энгелева
алгебра не обязана быть локально нпльпотентной, од-
однако если индексы нильпотентности внутренних диф-
дифференцирований ограничены в совокупности и основное
поле имеет нулевую характеристику, то энгелева алгеб-
алгебра локально нильпотентна. Неизвестно A982), будет ля
она при этих ограничениях ннльпотентной (проблема
Хигигаса).
Лит.: [1] Д ж е к о б с о н Н., Строение колец, пер. с
англ., М., 1961; [2] Херстейн И., Некоммутативные коль-
кольца, пер. с англ., М., 1972; [3] К о с т р и к и н А. И., «Изв.
АН СССР. Сер. матем.», 1957, т. 21, № 4, с. 515—40; [4] Шир-
Ширшов А. II., «Матем. сС», 1957, т. 41, Mi 3, с. 381—94; [5]
Голод Е. С, «Изв. АН СССР. Сер. матем.», 1964, т. 28,
J4» 2, с. 273—76; Ш Н i g m a n G., «Proc. Cambr. Phil. Soc»,
1956, v. 52, p. 1—4; [7] H i g g i n s P., там же, 1954, v. 50,
p. 8—15; [8] Ж е в л а к о в К. А., «Алгебра и логика» 1967,
т. 6, М4 с. 11 — 17; [9] McGrimmon К., «Proc. Nat.
Acad. Sci. USA»), 1969, v. 62, № 3, p. 671 — 78. В. Н. Латышев.
НИЛЬГРУППА — группа, в к-рой любые два эле-
элемента х, у связаны соотношением
[[...[[*, у] у], ...]у] = 1,
где квадратные скобки обозначают коммутатор
[а, Ь]=а~1Ь-1аЬ,
причем в определении число коммутирований п зависит,
вообще говоря, от пары х, у. В случае, если число га
ограничено для всех х, у из данной группы, группа наз.
энгелевой. Всякая локально нилъпо пентная
группа является Н. Обратное в общем случае неверно,
но верно при нек-рых дополнительных предположени-
предположениях, напр, при условии локальной разрешимости груп-
группы. Вопрос о локальной нильпотентности энгелевой
группы открыт A981).
Термин «Н.» иногда употребляется в ином смысле.
А именно, нильгруппой наз. группу, в к-рой
всякая циклич. подгруппа субнормальна, т. е. вклю-
включается в нек-рып субнормальный ряд группы (см. Нор-
Нормальный ряд группы).
Лит.: [1] К у р"о ш А. Г., Теория групп, 3 изд., М., 1967.
Л. Л. Шмелъкин.
НИЛЬМНОГООБРАЗИЕ — компактное факторпро-
странство связной нпльпотентной группы Ли (иногда,
впрочем, компактности не требуется).
Лит.: [1] М а л ь ц е в А. И., «Изв. АН СССР. Сер. матем.»,
1949, т. 13, Лг 1, с. 9—32. Д. В. Аносов.
НИЛЬПОЛУГРУППА — полугруппа с нулем, неко-
некоторая степень каждого элемента к-рой равна нулю. Н.
составляют один из важнейших классов периодических
полугрупп: это в точности периодич. полугруппы с един-
единственным идемпотентом, являющимся нулем. Более
узкий класс составляют локально нильпо-
нильпотентные полугруппы (л. н. п., то есть полу-
полугруппы, каждая конечно порожденная подполугруппа
к-рых нильпотентна, см. Нилъпотентная полугруппа).
Для любого ге>1 существует полугруппа с тождеством
х"=0, не являющаяся л. н. п. (см., напр., [1] гл. VIII,
§ 4). Конечная Н. нильпотентна, и л. н. п.— это в точ-
точности локально конечные Н. (см. Локально конечная
полугруппа). Еще более узкий класс составляют полу-
полугруппы с возрастающим аннулятор-
н ы м рядом (в. а. р.). Полугруппа 5 наз. полугруп-
полугруппой с в. а. р., если она обладает начинающимся с нуля
возрастающим идеальным рядом (см. Идеальный ряд
полугруппы!, для любых двух соседних членов Аа,
Aa+i к-рого имеет место
Н- будет полугруппой с в. а. р. тогда и только тогда,
когда она обладает возрастающим рядом идеалов, все
факторы к-рого конечны. Всякая полугруппа с в. а. р.
имеет единственное неприводимое порождающее мно-
множество, состоящее из ее неразложимых элементов. Про-
Произвольная же л. н п. может совпадать со своим квад-
квадратом. Наложение на Н. многих условий конечности
(см. Полугруппа с условием конечности) влечет конеч-
конечность полугруппы; таковы, напр., условие минималь-
минимальности для идеалов, условие максимальности для пра-
правых (левых) идеалов. Если все нильпотентные подполу-
подполугруппы Н. S конечны, то и S конечна.
Лит.: [1] Дшекобсон Н., Строение колец, пер. с
англ., М., 1961; [2] Ш е в р и н Л. Н., «Матем. сб.», 1961,
т. 53, № 3, с. 367—86; [3] е г о же, там же, т. 55, № 4, с. 473—
480. Л. Я. Шеврин.
НИЛЫ1ОТЕНТНАЯ АЛГЕБРА — алгебра, для
к-рой существует такое натуральное число п. что любое
произведение п элементов алгебры равно нулю. Если
при этом существует произведение п — 1 элементов, не
равное нулю, то п наз. индексом нильпотент-
нильпотентности Н. а.
Примерами Н. а. являются: алгебры с нулевым ум-
умножением, алгебра строго верхнетреугольных матриц,
прямые суммы Н. а., индексы нильпотентности к-рых
ограничены в совокупности, тензорное произведение
двух алгебр, из к-рых одна нильпотентна.
Класс Н. а. замкнут относительно взятия гомоморф-
гомоморфных образов и перехода к подалгебрам. В ассоциатив-
ассоциативной алгебре сумма конечного числа нильпотентных иде-
идеалов является нильпотентным идеалом, а сумма произ-
произвольного множества нпльпотентных идеалов является,
вообще говоря, локально нильпотентным идеалом.
Конечномерная алгебра над полем нулевой характери-
характеристики, обладающая базисом, состоящим из нильпотент-
нильпотентных элементов, нильпотентна. Если алгебра удовлетво-
удовлетворяет полиномиальному тождеству степени d, то всякое
ее нпльпотентное подкольцо в степени [d/2] принадле-
принадлежит сумме нильпотентных идеалов. Производная алгеб-
алгебра конечномерной алгебры Ли над полем нулевой ха-
характеристики нильпотентна. Нильпотентные подалгеб-
подалгебры, совпадающие со своим нормализатором (п о д-
алгебры Картана), играют существенную
роль в классификации простых алгебр Ли конечной
размерности. Н. а. Ли обладает внешним автомор-
автоморфизмом. Алгебра Ли с регулярным автоморфизмом
(т. е. автоморфизмом, не имеющим неподвижных
элементов, кроме нулевого) простого периода ниль-
нильпотентна.
Лит.: [1] Д ж е к о б с о н Н., Строение колец, пер. с
англ., М., 1961; [2] его же, Алгебры Ли, пер. с англ., М.,
1964; [3] А 1 b e r t A. A., Structure of algebras, [3 ed.], Pro-
Providence, [19681; [4] Jacobson N., «Proc. Amer. Math. Soc»,
1955, v. 6, № 2, p. 281—83; [SlHigman G., «J. Lond. Math.
Soc», 1957, v. 32, JVj 3, p. 321 — 34. B. II. Латышев.
НИЛЬПОТЕНТНАЯ ГРУППА — группа, облада-
обладающая нормальным рядом
таким, что каждый его фактор Л,/Л, + 1 лежит в центре
факторгруппы GlAi + 1 (такой ряд наз. централь-
центральным). Длипа наиболее короткого центрального ряда
Н. г. наз. ее классом (или ступенью) ниль-
нильпотентности. В любой Н. г. нижний (а также
верхний) центральный ряд (см. Подгрупп ряд) обрывает-
обрывается на единичной подгруппе и имеет длину, равную клас-
классу нильпотентности группы.
Конечные Н. г. исчерпываются прямыми произведе-
произведениями р-групп, т. е. групп порядков рк, где р — про-
простое число. В любой Н. г. элементы конечных порядков
образуют подгруппу, факторгруппа по к-рой не имеет
кручения. Конечно порожденные Н. г. без кручения
исчерпываются группами целочисленных треугольных
матриц с единицами на главной диагонали и их под-
подгруппами. Любая конечно порожденная Н. г. без кру-
кручения аппроксимируется конечными р-группами для
любого простого р. Конечно порожденные Н. г. явля-
являются полициклическими группами, более того, они
имеют центральный ряд с циклич. факторами.
Все Н. г. класса нильпотентности не больше с обра-
образуют многообразие (см. Групп многообразие), определяе-
определяемое тождеством
[[...[[Xj, Ж2] Х3], .. .] Xc + 1]=i.
Свободные группы этого многообразия наз. свобод-
свободными ннльпотентными группами.
О пополнении Н- г. без кручения см. Локально ниль-
потентная группа.
Лит.: [1] Курош А. Г., Теория групп, 3 изд., М.,
1967; [2] К а р г а п о л о в М. И., Мерзляков Ю. И.,
Основы теории групп, 2 изд., М., 1977. А. Л. Шмелъкин.
НИЛЬПОТЕНТНАЯ ПОЛУГРУППА — полугруппа
S с нулем, для к-рой существует такое п, что Sn=0;
это эквивалентно выполнению в S тождества
хх.. .хп = у1...Уп.
Наименьшее для данной полугруппы число п с указан-
указанным свойством наз. ступенью (иногда классом)
нильпотентности Н. п. Если 52=0, то S наз.
полугруппой с нулевым умножен и-
е м. Следующие условия для полугруппы S эквива-
эквивалентны: 1) S есть Н. п., 2) 5 обладает конечным анну-
ляторным рядом (т. е. возрастающим аннуляторным
рядом конечной длины, см. Нильполугруппа), 3) су-
существует такое к, что любая подполугруппа из S мо-
может быть включена в идеальный ряд длины <А полу-
полугруппы S.
Более широким является понятие н и л ь п о т е н т-
ной полугруппы в смысле Мальцева
[2]. Так называется полугруппа, удовлетворяющая для
нек-рого н тождеству
где слова Хп, Уп определяются по индукции следую-
следующим образом: А'0=т, Y0=y, Хп=Хп^1и„У„_1, У„=
= Уп_1ыпАГ„_1, х, у, иг, ..., ип — переменные. Группа
будет Н. п. в смысле Мальцева тогда и только тогда,
когда она нильпотентна в обычном теоретико-групповом
смысле (см. Нильпотентная группа), причем выполне-
выполнение тождества Х"„— Yп эквивалентно тому, что ступень
ее нильпотентности <ж Всякая полугруппа с законом
сокращения, удовлетворяющая тождеству Хп= Уп,
вложима в группу, удовлетворяющую тому же тож-
тождеству.
Лит.: [1] Л я пин Е. С, Полугруппы, М., 1960; [2]
Мальцев А. И., «Уч. зап. Ивановского гос. пед. ин-та»,
1953, т. 4, с. 107 — 11; [31 Ш е в р и н Л. Н., «Матем. сб.»,
1961, т. 53, № 3, с. 367—86; [4] е г о же, там же, 1963, т. 61,
№ 2, с. 253—56. Л. Н. Шеврин.
НИЛЬ ПОТЕНТНЫЙ ИДЕАЛ — односторонний или
двусторонний идеал М кольца или полугруппы с нулем
А такой, что для нек-рого натурального п выполняется
Мп= {0}, т. е. произведение любых п элементов идеала
М равно нулю. Напр., в кольце Zlp"Z вычетов по мо-
модулю рп, где р — нек-рое простое число, все идеалы,
отличные от самого кольца, нильпотентны. В групповом
кольце Fp[G] конечной р-грунпы G над полем из р эле-
элементов идеал, порожденный элементами вида а—1,
где a?G, нильпотентен. В кольце верхних треугольных
матриц над нек-рым полем матрицы, у к-рых на главной
диагонали стоят нули, образуют Н. и.
Любой элемент Н. и. нильпотентен. Любой Н. и. яв-
является одновременно нильидеалом и содержится в ради-
радикале Джекобсона кольца. В артпновых кольцах радикал
Джекобсона нильпотентен, и понятия Н. и. и ниль-
идеала совпадают. Последнее свойство справедливо
и для нётеровых колец. В нётеровом слева кольце любой
левый (правый) нильидеал нплыштентен.
Все Н. и. коммутативного кольца содержатся в ниль-
нильрадикале, к-рый в общем случае может быть не ниль-
потентным, а лишь нильидеалом. Простой пример такой
ситуации доставляет прямая сумма колец Zlp"Z по
всем натуральным п. В коммутативном кольце любой
нилъпотентный элемент а содержится в нек-ром Н. и.,
напр, в главном идеале, порожденном а. В некомму-
некоммутативном кольце могут существовать нильпотентные
элементы, к-рые не содержатся ни в одном Н. п. (и даже
нильидеале). Напр., в полном кольце матриц над полем
имеются нильпотентные элементы, в частности нпльпо-
тентны упоминавшиеся выше матрицы, у к-рых нену-
ненулевые элементы стоят только над главной диагональю,
но это кольцо просто и, следовательно, не имеет ненуле-
ненулевых Н. и.
В конечномерной алгебре Ли G существует макси-
максимальный Н. и., состоящий из элементов х?<3, для
к-рых эндоморфизм у —>- [т, ,(/] для y?G нплыютентен.
Лит.: [1] Лен г С., Алгебра, пер. с англ., М., 1968;
[2] д ж е к о б с о н Н., Строение колец, пер. с англ., М.,
1961; [3] Фей с К., Алгебра: кольца, модули и категории,
пер. с англ., т. 1, М., 1977; [4] Херстейн И., Некомму-
Некоммутативные кольца, пер. с англ., М., 1972; [5] Б у р б а к и Н.,
Группы и алгебры Ли. Алгебры Ли, свободные алгебры Ли и
группы Ли, пер. с франц., М., 197й. Л. В. Кузьмин.
НИЛЫ1ОТЕНТНЫЙ ЭЛЕМЕНТ, н и л ь п о-
т е н т,— элемент а кольца или полугруппы с нулем А,
удовлетворяющий равенству аКг=0 для нек-рого нату-
натурального га. Минимальное значение п, для к-рого спра-
справедливо это равенство, наз. индексом нильпо-
нильпотентности элемента а. Напр., в кольце вычетов
по модулю рп, где р — нек-рое простое число, класс
вычетов числа р — нилыготент индекса п, матрица
0 1
X г. является нильпотентом индекса 2 в кольце
BХ2)-матриц с коэффициентами в нек-ром поле К, в
групповой алгебре Fp[G], где F р —- поле из р элементов,
a G — циклнч. группа порядка р с образующей а, эле-
элемент 1 — а является нильпотентом индекса р.
Если а — Н. э. индекса п, то справедливо равенство
1 = A — а) A + а + я2+... Н-а''-1),
т. е. элемент A —а) обратим в кольце А и обратный к
нему элемент записывается в виде многочлена от а.
В коммутативном кольце А элемент а нильпотентен
тогда и только тогда, когда он содержится во всех про-
простых идеалах кольца. Все Н. э. образуют идеал /, наз.
нильрадикалом кольца и совпадающий с пере-
пересечением всех простых идеалов кольца А. Кольцо A/J
уже не имеет Н. э., отличных от нуля.
При интерпретации коммутативного кольца А как
кольца функций на пространстве Spec А (спектре А)
нильпотентам соответствуют функции, тождественно
рапные нулю. Тем не менее рассмотрение нильпотентов
часто оказывается полезным в алгебрапч. геометрии,
т. к. они позволяют получить чисто алгебраич. аналог
ряда понятий, типичных для анализа и дифференциаль-
дифференциальной геометрии (бесконечно малые деформации и т. п.).
Лит.: [1] Лен г С, Алгебра, пер. с англ., М., 1968; [2]
Херстейн И., Некоммутативные кольца, пер. с англ.,
М., 1972; [3] Ш а ф а р е в и ч И. Р., Основы алгебраической
геометрии, М., 1972. Л. В. Кузьмин.
НИЛЬПОТОК — поток на нильмногообразии
M=GIH, определяемый действием на М какой-нибудь
однопарамстрич. подгруппы gt нильпотентной группы
Лп G: если М состоит из смежных классов gH, то под
действием Н. такой класс аа время t переходит в класс
H
Лит.: ШАуслендер Л., Грин Л., Хан Ф., По-
Потоки на однородных пространствах, пер. с англ., М., 19(i6.
Д. В. Аносов,
НИТЬ обратного спектра {Ха, «%; а ?91} топологи-
топологических пространств Ха — такая система х={ха} точек
^а€^а (по одной точке из каждого Ха), т. е. такая точ-
точка произведенияЦа€^Ха .множеств Ха, что <ча.{ха)=^^а
ВСЯКИЙ раз, КОГДа р>а. Б. А. Пасынков.
НОМОГРАФИЯ — раздел математики, в к-ром изу-
изучаются способы графич. представления функциональ-
функциональных зависимостей. Получающиеся при этом чертежи
наз. номограммами. Каждая номограмма стро-
строится для определенной функциональной зависимости
в заданных пределах изменения неременных. На номо-
номограммах вычислительная работа заменяется выполнени-
выполнением простейших геометрич. операций, указанных в клю-
ключе пользования номограммой, и считыванием ответов.
Точность получения ответов по номограммам зависит
от вида номографированной зависимости, пределов из-
изменения переменных, размеров чертежа и выбранного
типа номограммы. В среднем номограммы могут обеспе-
обеспечить получение ответов с 2—3 верными значащими циф-
цифрами. Когда точность номограмм недостаточна, их мож-
можно использовать для прнкндочных расчетов, для на-
нахождения нулевых приближений, для контроля вычис-
вычислений с целью обнаружения грубых ошибок.
Номограммы можно применять и для исследования
функциональных зависимостей, положенных в их осно-
основу. Часто такое исследование выполняется на номо-
номограммах значительно проще и нагляднее, чем иными
способами. С помощью номограмм можно исследовать
влияние различных переменных на искомую перемен-
переменную, дать наглядную геометрнч. интерпретацию каким-
либо ранее известным свойствам данной зависимости,
установить ранее неизвестные ее особенности. Номо-
Номографические методы исследования можно, напр., при-
применять в задачах на подбор параметров эмпирич. фор-
формул по результатам наблюдений, на аппроксимацию од-
одной функции другой, на нахождение экстремальных
значений функции.
Значения переменных изображаются на номограммах
помеченными точками и помеченными линиями. Множе-
Множество помеченных точек, зависящее от одной переменной,
наз. шкалой. Уравнения шкалы переменной <хх
в прямоугольной системе координат хОу записываются
в виде
где fx и gx — функции f(ax) и g(cci). Схема шкалы <xt
приведена на рис. 1.
Множество помеченных точек, зависящее от двух
неременных, наз. бинарным полем. Бинарное
поле обычно оформляется в виде сетки, состоящей из
двух семейств помеченных линий. Точка в бинарно.м
поле определяется как точка пересечения линий с за-
заданными пометками. В системе прямоугольных коорди-
координат хОц бинарное поле переменных аг и а2 задается
уравнениями
где /]2 и g12 — функции
/12@4, аг) и ?i2(°4. <*2)- Пред-
Предполагается, что функции /х,
и g12 таковы, что в заданной
области изменения перемен-
переменных каждой паре значений
Рис j Рис о ai и а2 отвечает только одна
пара значений х и </. Схема
бинарного поля (al7 <х2) приведена на рис. 2.
Шкалы, семейства помеченных линий и бинарные но-
ноля в номограммах оформляются так, чтобы было удоб-
удобно находить точки и линии с заданными пометками и оп-
определять пометки ответных точек и линий.
Элементарными номограммами наз.
номограммы, в к-рых ответ или ответы находятся в ре-
результате выполнения одной геометрич. операции (опре-
(определение точки на шкале или в бинарном поле; проведе-
проведение прямой через две точки; построение окружности по
известному центру и радиусу; деление отрезка в задан-
заданном отношении; проведение прямой, параллельной
данной; откладывание отрезка, длина к-рого равна дли-
длине данного отрезка; построение параллелограмма по
трем его известным вершинам; наложение одной плос-
плоскости на другую).
К элементарным номограммам относятся: график
функции; сдвоенная шкала; сетчатая: из выравнен-
выравненных точек; из равноудаленных точек; циркульная;
с параллельным индексом; барицентрическая; ром-
ромбоидальная, с ориентированным транспарантом и
с транспарантом общего
0.001 х
а 20 i 0,010.05 Ь
0.3-, ,. гю^ц t5L°Vm
"" -Г"
0,6-
0,5-
вида.
На
рис. 3 приведена
элементарная номограм-
номограмма из выравненных точек
для определения величи-
величины х из уравнения
ха -1 _ j 1п(с-ж)
с-х-1 '
применяющегося при
Рис. з. термическом расчете
вентиляторных проти-
воточных градирен. Номограмма построена в пределах:
0,3<а<0.8; 0,1<6<20; 0,1<с<20; 0,001 <ж<0,5. Пе-
Переменные а и 6 представлены на номограмме шкалами;
переменные сих — бинарным полем. На номограмме
показано решение числового примера (дано: а=0,75;
й—7; с=10; ответ: ,т=0,1).
Элементарные номограммы имеют простое геометрич.
обоснование: номографич. интерпретация условия рас-
расположения трех точек на одной прямой приводит к но-
номограмме из выравненных точек; формулы расстояния
между двумя точками — к номограмме из равноудален-
равноудаленных точек и к циркульной; формул для координат
точки, делящей отрезок в заданном отношении,— к
барицентрич. номограмме; условия параллельности
двух прямых — к номограмме с параллельным индек-
индексом; формул, определяющих координаты четвертой вер-
вершины параллелограмма по трем его заданным верши-
вершинам,— к ромбоидальной номограмме; формул преобра-
преобразования прямоугольных координат без поворота и с по-
поворотом осей — к номограммам на двух плоскостях (с
ориентированным транспарантом и с транспарантом
общего вида).
Каждому виду элементарной номограммы соответст-
соответствует своя канонич. форма зависимости, к-рую можно
изобразить номограммой. Нек-рые канонич. формы до-
допускают построение элементарных номограмм различ-
различного типа.
Наиболее общая канонич. форма, представимая эле-
элементарной номограммой из выравненных точек, имеет
вид
/34 ~ /12
gli— gl2
Соответствующая номограмма состоит из трех бинарных
полей (ctj, a2), (а3, а4) и (а5> ав), связанных одним вы-
выравниванием.
Ниже приведены часто встречающиеся на практике
канонич. формы для отдельных уравнений и систем
уравнений, цредставимые номограммами того или иного
типа.
Канонич. формы для отдельных уравнений: а) с тре-
тремя переменными:
= 0,
б) с четырьмя переменными:
= 0, /l2 =
в) с пятью переменными:
г) с шестью перемеЕШЫми:
/12 +/13 = /45 +/46, /
д) с семью переменными:
каноиич. формы для систем уравнений:
/3 = /l2, 1 /l2 + /34 = /56, ^ /l2 /56=/з4 /78,
gl=gl2', ) gl2 + gu=he', J ?12 ?56=?34 gis't
— /7 =/34 — fs = fbs — /9, 1
2 ?7 = ?34 ga=g5S g<>- )
Составными номограммами наз. номо-
номограммы, состоящие из элементарных номограмм одного
или разных типов. Введение составных номограмм зна-
значительно расширяет класс номографируемых зависимо-
зависимостей. Сводку канонич. форм, представимых элементар-
элементарными и составными номограммами, см. в [3]. f4].
Всегда номографируемы зависимости с тремя перемен-
переменными. Зависимости с четырьмя и большим числом пере-
переменных допускают построе-
построение номограмм лишь в част-
частных случаях.
Для расширения круга
номографируемых зависи-
зависимостей применяют прибли-
приближенное номографирование.
Оно основано на замене с
нек-роы допустимой погреш-
погрешностью данной зависимости
номографируемой. ^
На рис. 4 приведена при-
приближенная номограмма из
равноудаленных точек для
определения величин г) и v (или Q и v) из системы
уравнений:
0,»3/сек т)
0.1 05 1 5,- „10.5 0.3 0,1
1 , , ,Г \уХ T^fi ?
Рис. 4.
применяющейся при гидравлнч. расчете прямоуголь-
прямоугольных лотков. Эта система для возможности номографи-
номографирования была приближенно заменена системой:
с относительной погрешностью в величинах Q и v, не
превышающей 2,5%. Штриховая окружность на номо-
номограмме соответствует решению числового примера (да-
(дано: г=0,0005; Ь=2 м; <?=2,2 м3/сек; ответы: т) = С,5 и
u=l,l м/сек).
В нек-рых случаях методы приближенного номогра-
номографирования дают возможность представлять номограм-
номограммами таблицы с несколькими входами.
Для номографирования данной зависимости ее при-
приводят точно или приближенно к номографируемому виду
и записывают уравнения элементов номограммы в пря-
прямоугольной системе координат. Входящие в эти уравне-
уравнения параметры преобразования (а иногда и произволь-
произвольные функции) подбирают так, чтобы придать номограм-
номограмме удобный для пользования вид. Далее рассчитыва-
рассчитывают таблпцы координат отдельных элементов номограм-
номограммы, а затем вычерчивают номограмму.
Получила развитие машинная номогра-
номография (см. [4]): разработаны системы процедур и стан-
стандартных программ для автоматич. расчета и построения
элементов номограмм с помощью ЭВМ и графопострои-
графопостроителя, а также стандартные программы для автоматич.
конструирования, расчета и вычерчивания номограмм
различных типов.
Основными проблемами теоретич. Н. являются проб-
проблемы представимости и единственности. Суть первой
проблемы состоит в том, чтобы выяснить, можно ли за-
заданное уравнение или систему уравнений привести к
той или иной канонич. форме, и если возможно, то ука-
указать алгоритм такого приведения. Получены решения
этой проблемы для нек-рых канонич. форм. Они сложны
и на практике не применяются. Суть второй проблемы
заключается в том, чтобы выяснить, единственным ля
способом приводится данная зависимость к канонич.
форме, и если не единственным, то указать вес возмож-
возможные способы п установить возможности преобразования
номограмм в каждом пз них.
Лит.: [1] Пентковский М. В., Номография, М-—Л.,
1949; [2] Невский Б. А., Справочная книга по номогра-
номографии, М.—Л., 1951; [3] Хованский Г. С, Основы номо-
номографии, М., 1976; [4] его же, Номография и ее возможно-
возможности. М., 1977. Г. С. Хованский.
НОРМА — 1) Отображение х -*- ||,г|| векторного
пространства X над полем действительных или ком-
комплексных чисел в совокупность действительных чисел,
подчиненное условиям:
|| х [| 5= 0, причем || х || = 0 только при х = 0;
||Ях|| = | X \-\\x\\ для каждого скаляра %;
\х + 1/Ц<|1^|| + || у\ для всех х, у?Х (аксиома
треугольника). При этом число ||х|| и наз. нор-
нормой элемента х.
Векторное пространство X с отмеченной Н. паз. нор-
нормированным пространством. Н. инду-
индуцирует на X метрику но формуле dist(x, г/1= ||х—у\\,
а следовательно и топологию, совместимую с этой
метрикой. Тем самым нормированное пространство
наделяется естественной структурой топологического
векторного пространства. Нормированное пространство,
полное относительно указанной метрики, наз. бана-
банаховым пространством. Каждое нормиро-
нормированное пространство обладает банаховым пополнением.
Отделимое (хаусдорфово) топологическое векторное
пространство наз. нормируемы м, если его топо-
топология совместима с нек-рой Н. Нормируемость равно-
равносильна существованию выпуклой ограниченной окрест-
окрестности нуля (теорема Колмогорова, 1934).
Н. в нормированном векторном пространстве X тогда
и только тогда порождается скалярным произведенном
(т. е. пространство X изометрически пяоморфно пред-
предгильбертову пространству), когда для всех х, ?Х
\\х+ у !!2+ ||i- у !12= 2 (\\х\?+ \\у II2).
Две Н. !i-Pi н |]-||2, заданные на одном и том же век-
векторном пространстве X, наз. эквивалентными,
если они индуцируют одну и ту же топологию. Это рав-
равносильно существованию таких констант Ct и Сг, что
||.г|!1<С1|!.г||.21 ||а;||2<:С2||.-с!|1 для всех х?Х.
Если пространство X полно относительно обеих Н., то
их эквивалентность является следствием согласован-
согласованности. При этом согласованность означает, что выполне-
выполнение предельных соотношений
U*B-a||, -v 0, \\хп-Ъ\ -> О
влечет за собой равенство а=Ь.
Не на каждом топологическом векторном простран-
пространстве, даже в предположении локальной выпуклости,
существует непрерывная Н. Напр., непрерывной Н. нет
на бесконечном произведении прямых с топологией по-
покоординатной сходимости. Отсутствие непрерывной
Н. может служить очевидным препятствием к непре-
непрерывному погружению одних топологич. пространств
в другие.
Если Y — замкнутое подпространство в нормирован-
нормированном пространстве X, то факториространство Х'.У клас-
классов смежности no Y наделяется Н.
\\х\\=М{\\х\\:х^х},
относительно к-рой оно становится нормированным
пространством. Н. образа элемента х относительно
естественной проекции X —> XlY наз. факторно р-
м о й элемента ж по подпространству У.
Совокупность X* непрерывных линейных функцио-
функционалов ty на нормированном пространстве X образует
банахово пространство относительно Н.
Н- всех функционалов достигаются в подходящих точ-
точках единичного шара исходного пространства тогда
и только тогда, когда пространство рефлексивно.
Совокупность L(X, Y) линейных непрерывных (ог-
(ограниченных^ операторов А из нормированного прост-
пространства X в нормированное пространство Y превраща-
превращается в нормированное пространство путем введения
операторной нормы:
Относительно этой Н. пространство L(X, Y) полно,
если полно Y. При полном X=Y пространство L(X)=
= L(X, X) с умножением (суперпозицией) операторов
становится банаховой алгеброй, поскольку операторная
Н. удовлетворяет условию
где / — тождественный оператор (единица алгебры).
Интересны п другие эквивалентные Н. на L(X), под-
подчиненные тому же условию. Такие Н. наз. алгебра-
алгебраическим и, или кольцевыми. Алгебраич.
Н. можно получить, эквивалентно перенормируя X и
беря соответствующую операторную Н., однако даже
при dim X = 2 на этом пути получаются не все плгебра-
ич. Н. на L(X).
Преднормой, или полунормой, на век-
векторном пространстве X паз. отображение р со свойст-
свойствами Н., кроме свойства невырожденности: равенство
р (х)=0 не исключает хфО. Если dim X<oo, то нену-
ненулевая преднорма р на L(X), подчиненная условию
p(AB)*s.p(A)p(B), фактически оказывается Н. (т.к.
в этом случае L (X) не имеет нетривиальных двусторон-
двусторонних идеалов). С другой стороны, для бесконечномер-
бесконечномерных нормированных пространств это уже не так. Если
X — банахова алгебра над С, то спектральный радиус
| х | = lim j) х" |р '"
является полунормой тогда и только тогда, когда он
равномерно непрерывен на X, и это условие равносиль-
равносильно коммутативности факторалгебры по радикалу.
Лит.: [1] Колмогоров А. Н., Фомин С. В., Эле-
Элементы теории функций и функционального анализа, 5 изд., М.,
1981; [2] Л ю с т е р н и к Л. А., С о б о л е в В. И., Эле-
Элементы функционального анализа, 2 изд., М., 1965; [3] Ш и-
л о в Г. Е., Математический анализ. (Специальный курс),
2 изд., М., 1961; [4] К а н т о р о в и ч Л. В., А к и л о в Г. П.,
Функциональный анализ, 2 изд., М., 1977; [5] Рудин У.,
Функциональный анализ, пер. с англ., М., 1975; 16] Д э й М. М.,
Нормированные линейные пространства, пер. с англ., М., 1961;
[7] Г л а з м а н И. М., Л ю б и ч Ю. И., Конечномерный
линейный анализ в задачах, М., 1969; [Sj A u p e t i t В., Pro-
prietes Spectrales desAlgebres de Banach, В.—Hdlb.—N. Y., 1979;
[!)] Кириллов А. А., Гвишиани А. Д., Теоремы
и задачи функционального анализа, М-, 1979. Е. А. Горин.
2) Н.— то же, что абсолютное значение на теле или
кольце (см. также Нормирование).
3) Н. группы — совокупность элементов группы,
перестановочных со всеми подгруппами, т. е. пересече-
пересечение нормализаторов всех подгрупп. Н. содержит центр
группы и содержится во втором гиперцентре Z.2. Для
группы бея центра Н. равна единичной подгруппе Е.
Лит.: [1] К у р о ш А. Г., Теория групп, 3 изд., М., 1967.
О. А. Иванова.
НОРМАЛИЗАТОР подмножества М груп-
группы G в подгруппе Н той же группы G — множество
Nh (M) = {
т. е. множество всех таких элементов h подгруппы Н,
для к-рых при любом т^М элемент h~ 1mh (сопряжен-
(сопряженный с т посредством h) также принадлежит М. При
любых М и Н нормализатор Nfj(M) является подгруп-
подгруппой в Н. Чаще всего рассматриваются Н. подгрупп
группы G во всей группе G. Подгруппа А группы G тогда
и только тогда инвариантна в G, когда Nq(A)=G. H.
множества, состоящего из одного элемента, совпадает
с его централизатором. При любых Н и М мощность
класса подмножества, сопряженных с М элементами из
Н (т. е. подмножеств вида h~1Mh, h?H), равна индексу
\Н:МИ(М)\.
Лит.: ШКаргаполов М. И., Мерзляков Ю. И.,
Основы теории групп, 2 изд., М., 1977. Н. Н. Вильяме.
НОРМАЛИЗАТОРНОЕ УСЛОВИЕ для под-
подгрупп — условие на группу, заключающееся в том,
что всякая ее собственная подгруппа строго содержится
в своем нормализаторе. Всякая группа, удовлетворяю-
удовлетворяющая Н. у.,— локально нильпотентная группа. С другой
стороны, Н. у. удовлетворяют все нильпотентные груп-
группы и даже группы, обладающие возрастающим цент-
центральным рядом (ZA-r p у п п ы). Однако существуют
группы с Н. у., имеющие тривиальный центр. Таким
образом, класс групп с Н. у. является строго промежу-
промежуточным между классами ZA-групп и локально нпльпо-
тентных групп.
Лит.: [1] Курош А. Г., Теория групп, 3 изд., М.,
1967. А. Л. Шмелъкин.
НОРМАЛИЗАЦИИ ПРИНЦИП — см. Нормальный
алгорифм.
НОРМАЛЬ к кривой линии (поверхно-
(поверхности) в данной ее точке — прямая, проходящая через
эту точку и перпендикулярная к касательной прямой
(касательной плоскости) в этой точке кривой (поверх-
(поверхности). Плоская гладкая кривая имеет в каждой точке
единственную Н., расположенную в плоскости кривой.
Если кривая на плоскости в прямоугольных координа-
координатах определяется уравнением y=f(x), то уравнение Н.
к кривой в точке (х0, у0) имеет вид:
Пространственная кривая имеет в каждой своей точ-
точке бесконечное множество Н., заполняющих нек-рую
плоскость (нормальную плоскость). Н., лежащая в
соприкасающейся плоскости, наз. главной нормалью',
Н., перпендикулярная к соприкасающейся плоскости,
наз. бинормалью.
Н. к поверхности, заданной уравнением z=f(x, у),
в точке (х0, г/0, z0) определяется уравнением
Если уравнение поверхности имеет вид r=r(u, v),
то векторное уравнение Н.:
Б С9-3.
НОРМАЛЬНАЯ ДИНАМИЧЕСКАЯ СИСТЕМА —
1) То же, что стационарный (в узком смысле) гауссов-
ский процесс, рассматриваемый как динамич. система.
2) В 40—50-х гг. 20 в. так иногда называли динамич.
системы (измеримые потоки и каскады) в Лебега прост-
пространстве (последнее в то время называли нормаль-
нормальным пространством с мерой).
НОРМАЛЬНАЯ КРИВИЗНА регулярно й"по-
й"поверхности — величина, характеризующая откло-
отклонение поверхности в направлении I от своей касатель-
касательной плоскости в точке Р, совпадающая по абсолютной
величине с кривизной соответствующего нормального
сечения. Н. к. в направлении I равна
kt = (п, Лт) к,
где к — кривизна нормального сечения в направлении
I, n — единичный вектор главной нормали нормаль-
нормального сечения, N — единичный вектор нормали поверх-
поверхности. Н. к. поверхности в данном направлении совпа-
совпадает с Н. к. соприкасающегося параболоида в том же
направлении. Н. к. поверхности, параметризованной
параметрами и, v, может быть выражена через значения
первой и второй квадратичных форм поверхности, вы-
вычисленных для значений (du : dv), соответствующих на-
направлению I по формуле
_ II ___L du* + 2M du dv + N dv2
kt~ 1 ~ E du* + 2F du dv+G dv* '
Кривизна регулярной кривой, лежащей на поверхно-
поверхности, связана с Н. к. поверхности в направлении I. ка-
касательном к кривой, и с геодезич. кривизной kg этой
кривой соотношением
kn = kg [n, 1]+к^
(см. также Мёнъе теорема^. С помощью Н. к. констру-
конструируется Дюпена индикатриса, гауссова л средняя кри-
кривизны поверхности и многие другие понятия локальной
геометрии поверхности. Д. Д. Соколов.
НОРМАЛЬНАЯ МАТРИЦА — квадратная матри-
матрица А, перестановочная со своей сопряженной (т. е.
АА*=А*А).
НОРМАЛЬНАЯ ПЛОСКОСТЬ пространст-
пространственной кривой в данной ее точке М —
плоскость, проходящая через М перпендикулярно к
касательной прямой в той же точке. Н. и. содержит все
нормали к кривой, проходящие через данную точку.
Если кривая задана в прямоугольных координатах
уравнениями
*=/('), V=g(t), z=h(t),
то уравнение Н. п. в точке М(х0, у,„ z0), соответствую-
соответствующей значению *0 параметра t, может быть записано
в виде
Если уравнение кривой имеет вид r=r(t), то уравнение
Н. п.:
БС9-3.
НОРМАЛЬНАЯ ПОДГРУППА — то же, что нор-
нормальный делитель.
НОРМАЛЬНАЯ ПОДПОЛУГРУППА полу-
полугруппы S — подполугруппа Н, удовлетворяющая
¦следующему условию: для любых х, y^S1 (по поводу
обозначения 51 см. Нормальный комплекс) таких, что
xy?S, и любого h ? Я включения xhy ^Яи ху^Н эк-
эквивалентны. Подмножество полугруппы S будет
Н. п. тогда н только тогда, когда оно является полным
прообразом единицы при нек-ром гомоморфизме полу-
полугруппы S на полугруппу с единицей.
Лит.: [1] Л я пин Е. С., Полугруппы, М., 1960.
Л. Н. Шеврин.
НОРМАЛЬНАЯ ПРОИЗВОДНАЯ — производная
функции в направлении нормали к заданному многооб-
многообразию. Л. Д.* Кудрявцев.
НОРМАЛЬНАЯ РАЗРЕШИМОСТЬ интеграль-
интегральных уравнений — свойство линейного интег-
интегрального уравнения быть разрешимым тогда и только
тогда, когда его правая часть ортогональна всем реше-
решениям соответствующего сопряженного однородного
уравнения. При соответствующих условиях Н. р. об-
обладают Фредгольма уравнения, сингулярные интеграль-
интегральные уравнения, интегральные уравнения типа свертки.
Б. В. Хведелидзе.
НОРМАЛЬНАЯ СХЕМА — схема, все локальные
кольца к-рой являются нормальными коль-
кольцами (т. е. приведенными и целозамкнутыми в пол-
полном кольце частных). Н. с. локально неприводима;
для такой схемы понятия связной и неприводимой ком-
компоненты совпадают. Множество особых точек нётеровой
Н. с. имеет коразмерность, большую 1. Имеется сле-
следующий критерий нормальности [1 ]:
нётерова схема X нормальна тогда и только тогда, когда
выполняются два условия: 1) для любой точки х?Х
коразмерности <<1 локальное кольцо Ох, х регулярно;
2) для любой точки х?Х коразмерности >1 глубина
~кольца Ох, х больше 1. Для любой приведенной схемы
X существует канонически связанная с ней Н. с. Х^
<н о р м а л и з а ц и я). Х-схема Xя является целой,
хотя и не всегда конечной над X. Однако если схема X
превосходная (см. Лревосходное кольцо), напр, если X —•
схема конечного типа над полем, то Хн является конеч-
конечной над X.
Лит.: [1] Серр Ж.-П., «Математика», 1963, т. 7, №5,
с. 3—93. В. И. Данилов.
НОРМАЛЬНАЯ СХОДИМОСТЬ — сходимость ряда
составленного из ограниченных отображений и# : X —»-
—>- Y множества X в нормированное пространство У,
такая, что сходится ряд с положительными членами
^Ift==1||uft!;, составленный из норм отображении
Из Н. с. ряда A) вытекает абсолютная и равномерная
сходимость ряда /?jii=1uk(x)i состоящего из элементов
пространства У; обратное заключение неверно. Напр.,
если uk : R -> R есть действительная функция, опре-
определяемая равенствами: u/;(x)=sin nxlk при ^<+
н uk(x) — 0 при .г?К.\[А-, А+Я, то ряд 2 ик(х)
сходится абсолютно п равномерно, а ряд ^V°° ||мй]|=
\/к расходится.
Пусть, в частности, ик : R —>- У — кусочно непре-
непрерывные функции на нек-ром некомпактном интервале
/cR и имеет место Н. с. ряда A), тогда возможпо по-
почленное интегрирование на интервале /:
Несобственный интеграл
B)
наз. нормально сходящимся на множестве
А, если существует кусочно непрерывная положитель-
положительная функция g : R —*¦ R такая, что для любого х?/ и
любого Х?А выполняется неравенство \\f(x\ X)\]<^.g(x)
и интеграл \ g(t)dt сходится. Из Н. с. интеграла B'
следует его абсолютная и равномерная сходимость;
обратное заключение неверно.
Лит.: [1] Б у р б а к и Н., Общая топология, пер. с франц.,
М., 1975; [2] е г о же, Функции действительного переменного.
Элементарная теория, пер. с франц., М., 1965; [3] III в а р ц Л.,
Анализ, пер. с франц., т. 1, М., 1972. Е. Д. Соломенцев.
НОРМАЛЬНАЯ ФОРМА — 1) Н. ф. матри-
матрицы jI — матрица N заранее определенного специаль-
специального вида, получаемая из А с помощью преобразований
определенного типа. В зависимости от рассматриваемо-
рассматриваемого типа преобразований, от области А', к к-рой принад-
принадлежат коэффициенты А , от вида А и, наконец, от специ-
специфики решаемой задачи (напр., от желания расширять
или не расширять К при переходе от А к N, от необхо-
необходимости определить N по А однозначно пли, наоборот,
с нек-рым произволом) рассматриваются и различные
Н. ф. Часто вместо термина «Н. ф.» употребляют тер-
термины «каноническая форма», «канони-
«канонический в и д». К числу классических Н. ф. отно-
относятся следующие (ниже через Мтхп (К) обозначается
множество всех матриц из т строк и п столбцов с коэф-
коэффициентами из К).
Нормальная форма Смита. Пусть К — либо кольцо Ж
целых рациональных чисел, либо кольцо F [к] много-
многочленов от Я с коэффициентами нз поля F. Матрица
В ? Мтул {К) наз. эквивалентной матрице
А ?Мтхп (К), если найдутся такие обратимые матрицы
С?Мтхт(К) и D?MnXn(K), что B = CAD. Матрица
В эквивалентна А тогда и только тогда, когда В может
быть получена из А с помощью последовательности
элементарных строчных и столбцо-
столбцовых преобразований, т. е. преобразований
следующих трех типов: а) перестановка строк (столб-
(столбцов): б) прибавление к одной строке (столбцу) другой
строки (столбца) с множителем из К; в) умножение
строки (столбца) на обратимый элемент кольца К.
Для преобразований этого типа справедливо следующее
утверждение: всякая матрица А ?Мтхп (К) эквива-
эквивалентна матрице N?MmXn(K) вида
о
О
где A;фО при всех г, d
и если К=%, то все
делит di + l при г=1, ..., г— 1,
положительны, а если /l =
и если К—Z, то все d,- положительны, а если /l =
= F [?Л, то старшие коэффициенты всех многочленов
di равны 1. Указанная матрица Л' наз. нормаль-
нормальной формой Смита матрицы А. Элементы
d,- няя. и н п я X) и я н т л ы м и множителями
¦,- наз. инвариантными
матрицы А, а число г
.., с множителями
матрицы А, а число г — ее рангом. Нормаль-
Нормальная форма Смита определена по А однозначно и может
быть найдена следующим образом. Ранг А равен по-
порядку наименьшего ненулевого минора матрицы А.
Пусть с'<:/<:г; тогда среди всех миноров порядка j
матрицы А имеется хоть один ненулевой. Пусть Д7-,
7 = 1, ..., г.— наибольший общий делитель всех нену-
ненулевых миноров порядка / матрицы А (нормированный
условием, что Ду>0 при К=% и что старший коэффи-
коэффициент многочлена Ду равен 1 при K=F[X]) и пусть До=
= 1. Тогда dy= Ду/Ду-!, 7 = 1, ..., г. Инвариантные мно-
множители являются полным набором инвариантов клас-
классов эквивалентных матриц: две матрицы из Мтхп (К)
эквивалентны тогда и только тогда, когда у них совпа-
совпадают ранги и инвариантные множители с равными но-
номерами.
Инвариантные множители du ..., dr раскладываются
(единственным способом с точностью до порядка со-
сомножителей) в произведение степеней неприводимых
в кольце К элементов elt ..., es (являющихся нек-рыми
целыми положительными числами, большими 1, если
К= %, и нек-рымп многочленами положительной сте-
степени со старшим коэффициентом 1, если K=F [Я]),
где nij — целые неотрицательные числа. Каждый мно-
множитель e"i/, Для к-рого п,-у>0, наз. элементар-
элементарным делителем матрицы А (над К). Каж-
Каждый элементарный делитель входит в совокупность
$а, к всех элементарных делителей матрицы А столько
раз, в разложении скольких инварпантных множителей
он встречается. Элементарные делители, в отличие от
инвариантных множителей, зависну от того, над каким
кольцом К рассматривается А: если К= F [X], a F—
нек-рое расширение поля F и K=F [X], то матрица
А?Мтхп (К)аМтУ<п (К) имеет, вообще говоря, раз-
различные элементарные делители (но одинаковые инвари-
инвариантные множители) в зависимости от того, рассматри-
рассматривается ли А как элемент Мтхп (К) или как элемент
Мтхп (К). Инвариантные множители восстанавлива-
восстанавливаются по полному набору элементарных делителей и
наоборот.
Практический способ нахождения нормальной формы
Смита см., напр., в [1].
Указанный основной результат о нормальной форме
Смита получен для К=Х (см. [7]), для K=F[X] (см.
[8]). Практически без изменений теория нормальных
форм Смита переносится на случай, когда К — любое
кольцо главных идеалов (см. [3], [6]). Нормальная фор-
форма Смита имеет важные приложения, напр, на ней по
существу основывается структурная теория конечно
порожденных модулей над кольцами главных идеалов
(см. [3], [6]) и, в частности, теория конечно порожден-
порожденных абелевых групп и теория жордановой Н. ф. (см.
ниже).
Естественная нормальная форма. Пусть К — поле.
Две квадратные матрицы А и В ?М„хп{К) наз. по-
подобными над К, если найдется такая невырожден-
невырожденная матрица С?Мпхп(К), что В^САС'1. И.меется тос-
ная связь между подобием и эквивалентностью: матри-
матрицы А и В^Мпхп (К) подобны тогда и только тогда, ког-
когда матрицы }.Е—А и ХЕ—В, где Е — единичная мат-
матрица, эквивалентны. Таким образом, для подобия А и
В необходимо и достаточно совпадения инвариантных
множителей или, что то же,— наборов элементарных
делителей над К [Я] у матриц ХЕ—А и ХЕ—В. Практи-
Практический способ нахождения матрицы С для подобных ма-
матриц А и В см. в [1], [4].
Матрица ХЕ—.4 наз. характеристической
матрицей матрицы А ?Мпхп (К), а инвариантные
множители ХЕ—А наз. инвариантами подо-
подобия матрицы А; их п штук. Пусть rfj, ..., dn — инва-
инварианты подобия матрицы А. Многочлен dn равен опре-
определителю матрицы ХЕ—А и наз. характеристи-
характеристическим многочленом матрицы А. Пусть
d1=... = dq=l, а степень dj при /Jsg+l больше 1.
Тогда справедливо утверждение: матрица А подобна
над К блочнодиагональной матрице Nj^^Mn^niK) вида
L(dq+1) О
L {d )
'(dn)
О
где через L (/) для многочлена
обозначена т. н. сопровождающая матри-
матрица многочлена
L(f) =
О
1
^ w ^- » — 1 ^ о — 2
Матрица JV1 определена по А однозначно и наз. пер-
первой естественной Н. ф. матрицы А (см. [1 ],
12]).
Пусть теперь $А щ^л — набор всех элементарных
делителей матрицы ХЕ—А. Тогда справедливо следую-
следующее основное утверждение: матрица А подобна над К
блочнодиагональной матрице Л\2, блоки к-рой — это
сопровождающие матрицы всевозможных элементарных
делителей e™U(z<?>A к [Я] ыатРиДЫ ХЕ—А:
О
О
Матрица Л'„ определена по А лишь с точностью до по-
порядка следования клеток по главной диагонали; она
наз. второй естественной Н. ф. матрицы А
(см. [1], [2]), а также ее ф р о б е н и у с о в о и, ра-
рациональной, канонической и квази-
квазиестественной Н. ф. (см. [4]). В отличие от пер-
первой естественной Н. ф., вторая естественная Н. ф.,
вообще говоря, меняется при переходе от поля К к его
расширению.
Жорданова нормальная форма. Пусть К — поле,
А ?мпхп(К) и ?А 2qx]={e™<7} — набор всех элемен-
элементарных делителей матрицы ХЕ—А над К[Х]. Пусть К
обладает тем свойством, что характеристлч. многочлен
dn матрицы А раскладывается в К [X] на линейные мно-
множители (так будет, напр., если К — поле комплексных
чисел или, более общо, любое алгебраически замкнутое
поле). Тогда каждый из многочленов е,- имеет вид X—а,-
для нек-рого п[?К, а элементарный делитель e"ij соот-
соответственно имеет вид (X—а,) '/. Матрица J (/) иа
Msxs{K) вида
а 1
О
о •;
где f=(X—a)s, а?К, наз. гиперсопровождаю-
щей матрицей многочлена / (см. [1]),
или жордановой клеткой порядка у
с собственным числом а. Справедливо сле-
следующее фундаментальное утверждение: матрица А по-
подобна над К блочнодиагональной матрице J ^ МпХп (К)г
блоки к-рой — это гиперсопровождающие матрицы все-
всевозможных элементарных делителей матрицы %Е—А:
О
"К")
О
Матрица / определена лишь с точностью до порядка
следования клеток на главной диагонали; она является
жордановой матрицей н наз. жордановой Н. ф.
матрицы А. Если К не обладает указанным выше свой-
свойством, то А нельзя привести над К к жордановой Н. ф.
(но можно над нек-рым конечным расширением К).
О так наз. обобщенной жордановой Н. ф., приведение
к к-рой возможно уже над любым полем К, см. [4].
Помимо различных теорий Н. ф. для произвольных
матриц возможны соответствующие теории и для мат-
матриц какого-либо специального вида. Классическими
примерами являются теории Н. ф. симметрич. и косо-
симметрич. матриц. А именно, пусть К — поле. Две
матрицы А, В ? Мпхп (К) наз. конгруэнтными
(см. [1]), если найдется такая невырожденная матри-
матрица С?МпХп (К), что В~САСТ. Н. ф. относительно
отношения конгруэнтности наиболее исследованы
для классов симметрич. и кососимметрич. матриц.
Пусть Char КФ2 и А — кососимметрич. матрица, т. е.
АТ=—А. Тогда А конгруэнтна однозначно определен-
определенной матрице Н вида
О 1
-1 О
Н =
О 1
—1 О
О 1
-1 О
о
к-рая может рассматриваться как Н. ф. А относительно
отношения конгруэнтности. Если же А — симметрич.
матрица, т. е. АТ=А, то она конгруэнтна матрице D
вида
О
D =
о
о
где е,=^=0 при всех г. Число г равно рангу А и опреде-
определено однозначно, а дальнейшее уточнение выбора эле-
элементов 8,- зависит от свойств поля К. Так, если К алге-
алгебраически замкнуто, то можно считать, что г1=...=
= ег—1; если К — поле действительных чисел, то мож-
можно считать, что вг=... = ер=1 и гр +1=.-. — гг=—1 для
нек-poro р. Этими свойствами D уже определена одно-
вначно и может рассматриваться как Н. ф. А относи-
тельно отношения конгруэнтности. О Н. ф. симметрмч.
матриц для ряда других полей, а также об эрмитовых
аналогах этой теории см. [6], [10] и ст. Квадратичная
форма.
Объединяющим обстоятельством в рассмотренных (а
также и других) теориях Н. ф. является то, что допус-
допустимые преобразования над рассматриваемым множест-
множеством матриц определяются действием нек-рой группы,
так что классы матриц, переводимых друг в друга с
помощью этих преобразований,— орбиты этой группы,
а указание И. ф. есть выделение в каждой орбите
нек-рого канонич. представителя. Так, классы эквива-
эквивалентных матриц — орбиты группы G-- GLm(K) X GLn(K)
(где GLS(K) — группы обратимых квадратных ма-
матриц порядка s с коэффициентами из К), действую-
действующей на Мтхп (К) по правилу А —v САГ)-1, где
(CD)?G. Классы подобных матриц — это орбиты груп-
группы GLn(K) на Мтхп (К), действующей по правилу:
4-+CiC-', где C(^GLn(K). Классы конгруэнтных
симметрич. или кососимметрич. матриц — это орбиты
группы GLn(K) на множестве всех симметрич. или косо-
симметрпч. матриц порядка п, действующей по правилу
A -v САСТ, где C?GLn(K). С этой точки зрения каж-
каждая теория Н. ф. является конкретным примером реше-
решения части общей задачи орбитального разложения для
действия нек-рой группы преобразований.
Лит.: [1] Маркус М., М и н к X., Обзор по теории
матриц и матричных неравенств, пер. с англ., М., 1972; [2]
Ланкастер П., Теория матриц, пер. с англ., М., 1978;
[3] Лен г С, Алгебра, пер. с англ., М., 1968; [4] Маль-
Мальцев А. И., Основы линейной алгебры, 4 изд., М., 1975;
[5] Б у р б а к и Н., Алгебра. Алгебраические структуры.
Линейная и полилинейная алгебра, пер. с франц., М., 1962;
[6] Б у р б а к и Н., АлгеРра. Модули, кольца, формы, пер.
с франц., М., 1966; [7] S m i t h H. J., The Collected Mathema-
Mathematical Paper, v. 1, Oxf., 1894, p. 367—409; [8] F г о b e n i u s G.,
«J. reine und angew. Math.», 1879, Bd 86, S. 146—208; [91
Гантмахер Ф. Р., Теория матриц, 2 изд., М., 1966; [10]
Серр Ж.-П., Курс арифметики, пер. с франц., М., 1972.
В. Л. Попов.
2) Н. ф. оператора — представление с точ-
точностью до изоморфизма самосопряженного оператора А,
действующего в гильбертовом пространстве ffl, в виде
ортогональной суммы операторов умножения на неза-
независимую переменную.
Пусть, сначала, А — циклический опера-
т о р; это означав!, что существует элемент ho?ffl та-
такой, что любой элемент h ?S% однозначно представим в
виде F(A)h0, где F(Q — нек-рая функция такая, что
l\F a)\*d(Eth0, h0) < оо,
здесь Ер, —оо<|<оо,— спектральная функция опера-
оператора А. Пусть 3?р — пространство функций, суммируе-
суммируемых с квадратом на (—оо, +оо)с весом р(|) = (?У@, h0),
и KpF=?F(%) — оператор умножения на независимую
переменную с областью определения
Тогда операторы А и К изоморфны, .4~ЛТ, т. е. суще-
существует изоморфное и изометрпч. отображение U : ffl —>¦
-> J?2p такое, что UDA = -DKp и A = U~1KpU.
Пусть, теперь, А — произвольный самосопряженный
оператор. Тогда Н можно разложить в ортогональную
сумму инвариантных подпространств На, на каждом
из к-рых А индуцирует циклич. операторы Аа- так что
Н=--^фНа, Л=2©Ла п Аа~КРа,. Если на Х*=
= 2©-2>Ра задать оператор #=2®#ра, то А~К.
Оператор К наа. нормальной формой, или
каноническим представлением, опе-
оператора А. Теорема о канонич. представлении рас-
пространяется на случай произвольных нормальных
операторов.
Лит.: [1] П л е с н е р А. И., Спектральная теория ли-
линейных операторов, М., 1965; [2] А х и е з е р Н. И., Г л а з-
ман И. М., Теория линейных операторов в гильбертовом
пространстве, 2 изд., М., 1966. В. И. Соболев.
3) Н. ф. оператора — представление операто-
оператора А, действующего в Фока пространстве, построенном
над нек-рым пространством L2(M, а), где (М, а) —
пространство с мерой, в виде суммы
Ха* (Xl)... а* (хп) а Ы... а (ут) JJ"= l da (xt) X
где {а(х), а*(х), х?М} — операторнозначные обобщен-
обобщенные функции, порождающие семейства операторов
уничтожения {a(f), f?L2(M, а)} и рождения {a*(f),
f?L2(M, а)}:
а {х) f (х) da {х)' а* (/) = 1ма* {х) *{х) da {x)-
В выражении A) в каждом слагаемом множители а (уу),
/=1, ..., т, стоят правее всех множителей а*(х,), г=1,
..., га, функции (возможно обобщенные) Кп_ m (xt,
..., хп; уг, ..., ут) от двух наборов переменных (хи
..., хп)?М", (уъ ..., ут)?Мт, п, т=0, \, 2, ..., в случае
симметричного (бозонного) пространства Фока сим-
симметричны по переменным каждого из наборов в от-
отдельности, а в случае антисимметричного (фермионного)
пространства Фока — антисимметричны по этим пере-
переменным.
Для любого ограниченного оператора А нормальная
форма существует п единственна.
Представление A) можно переписать в виде, непо-
непосредственно содержащем операторы уничтожения и рож-
рождения:
A = 2jm,nZj{il, .... in}' 'I' ¦•¦' ]"» C4...inh--.imX
Ха* (//,).. -a* (fin)a (/,,).. .a (fjj, B)
где {fi, i = 1, 2, . . .} — нек-рый ортонормирован-
ный базис в L2 (M, о), и суммирование в B) происходит
по всем парам конечных наборов {/,,.. . ., /j }, {//,,- • •,
/• } элементов этого базиса.
В случае произвольного (сепарабельного) гильберто-
гильбертова пространства Н Н. ф. оператора А. действующего
в пространстве Фока Г (II), построенном над Н, опреде-
определяется при фиксированном базисе {/,-, i = 1, 2, . . . } в
Н с помощью выражения B), где a(f), a*(f), f?H, —
семейства операторов уничтожения и рождения, дей-
действующих в Г (Я).
Лит.: [1] Б е р е з и н Ф. А., Метод вторичного квантова-
квантования, М-, 1965. Р. А. Минлос.
4) Н. ф. рекурсивной функции — спо-
способ задания n-местной рекурсивной функции ф в виде
Ф (*i, • • •, Хп) = S (f*z (/ (хг, ..., хп, z) =0)), (*)
где / есть (ге+1)-местная примитивно рекурсивная функ-
функция, g — одноместная примитивно рекурсивная функ-
функция, \x,z(f(x1, . . ., хп, z) —¦ 0)— результат применения
наименьшего числа оператора к функции /. Теорема
К л и н и о Н. ф. утверждает: существует такая при-
примитивно рекурсивная функция ?, что каждая рекурсив-
рекурсивная функпия ф представнма в виде (*) с подходящей
функцией /, зависящей от q>, т. е.
Ш (Уф) C/) (V.rlt ..., х„) [ф (хи ..., хп) =
= g(Hz(f(x1, ..., хп, z)=0))].
Теорема о Н. ф. является одной из важнейших теорем
в теории рекурсивных функций.
А. А. Марков [2] получил характеристику тех функ-
функций g, к-рые могут использоваться в теореме о Н. ф. в
представлении (*). Функция g тогда и только тогда мо-
может использоваться в качестве функции, существова-
существование к-рой утверждается в теореме о Н. ф., когда урав-
уравнение g(x) = п при любом п имеет бесконечно много
решений. Такие функции наз. функциями боль-
большого размаха.
Лит.: [1] Мальцев А. И., Алгоритмы и рекурсивные
функции, М., 1965; [2] М а р к о в А. А., «Изв. АН^СССР.
Сер. матем.», 1949, т. 13, № 5, с. 417—24. В. Е. Плиско.
5) Н. ф. системы дифференциальных
уравнений
37 = Ф,- (хи ..., xn), i = l, ...,п, A)
вблизи инвариантного многообразия М — такая фор-
формальная система
Vi = $i(Vi> ••¦> 2/п). « = 1, .".., ге," B)
к-рая получается из A) обратимой формальной заменой
координат
xi = li (УЬ •••> Уп)> i = i,..-,n, C)
и в к-рой ряды Тейлора — Фурье % содержат только
резонансные члены. Впервые Н. ф. для одного случая
встречается в диссертации А. Пуанкаре (Н. Poincare,
см. [1]). Посредством Н. ф. B) нек-рые системы A)
интегрируются, многие исследуются на устойчивость
и интегрируются приближенно, для систем A) отыски-
отыскиваются периодич. решения и семейства условно перио-
дич. решений, изучаются их бифуркации.
Н. ф. в окрестности неподвижной точки. Пусть М —
неподвижная точка X s (хи . . ., хп) = 0 системы A)
(т. е. ф,@) = 0), функции ф,- аналитичны в ней и Х1;
. . ., Я„ — собственные значения матрицы ||5ф,/Eху||
при X = 0. Пусть А = (Я,!, . . ., %п) ф 0. Тогда в пол-
полной окрестности точки X = 0 система A) имеет следую-
следующую Н. ф. B): матрица ЦсН^/дг/уН при У = (у1у . . .,
уп) = 0 имеет Н. ф. (напр., жордапову), а ряды Тей-
Тейлора
4>l = yi'^jQ^Ni 8iQYQ' г = 1, ••.,«, D)
содержат только резонансные члены, для к-рых
(<?.Л) = д1Я1+...+д„Я„ = О. ' E)
Здесь Q = (ди. . ., «?„), У«= »«'... »«»,
#,- = {?>:целые ?у-^0, g/S&—I, gx+ •.. + qn5= 0}.
Если уравнение E) не имеет в N = A^U- • •UA'n ре-
решений Q Ф 0, то Н. ф. B) является линейной:
Всякая система A) с Л Ф 0 в окрестности неподвижной
точки приводится к своей Н. ф. B) нек-рым формаль-
формальным преобразованием C), где |,- — (.-тененные ряды (воз-
(возможно, расходящиеся), |;@) = 0 и det|td?,7di//!| ф 0
при У = 0.
Вообще говоря, нормализующее преобразование C)и
Н. ф. B) (т. е. коэффициенты g;Q в D)) неоднозначно
определяются исходной системой A). Н. ф. B) сохра-
сохраняет многие свойства системы A): вещественность,
симметричность, гамильтоновость и др. (см. [2], [3]).
Если в исходной системе имеются малые параметры,
то их можно включить в число координат Xj, тогда xj=Q.
При нормализующем преобразовании такие координаты
не меняются (см. [3]).
Если к — число линейно независимых решений Q ? N
уравнения EJ, то с помощью преобразования
гдеа,-;- — целые и det||a,-y!|=±l, H. ф. B) переводится
в систему вида
(см. [2], [3]). Решение этой системы сводится к решению
подсистемы из первых к уравнений и к п—к квадрату-
квадратурам. Подсистему надо исследовать в окрестности слож-
сложной особой точки zx = . . . = Z?=0, ибо /j, . . ., fk
ве содержат линейных членов. Это можно сделать с
помощью локального метода (см. [3D.
Рассматривался вопрос (см. [2]): при каких условиях
на Н. ф. B) сходится (аналптично) нормализующее пре-
преобразование аналитической системы A)? Пусть
сй& = тт| (Q, Л) |
по таким Q?N, для к-рых
(Q, Л) 5* 0, ?!+...+?„< 2*.
Условие ш : 2fe_! 2 ~ * In сод г < оо.
Условие to : lini 2 ~ * In Wk * < °° при к —>- оо.
Условие со слабее условия со. Оба они выполнены
для почти всех Л (по мере Лебега) и являются очень
слабыми арифметич. ограничениями на Л.
Условие Ав случае ReA=0 (общий случай см. в
[21): существует такой степенной ряд a(Y), что в D)
%—^i2/i«i i = 1, • • -, п.
Если у аналптич. системы A) А удовлетворяет усло-
условию со и Н. ф. B) удовлетворяет условию А, то существу-
существует аналитпч. преобразование системы A) к нек-рой
Н. ф. Если Н. ф. B) получается из нек-рой аналптич.
системы и не удовлетворяет хотя бы одному из условий
со и А, то существует такая аналптич. система A),
к-рая имеет B) своей Н. ф. и всякое преобразование
к-рой к Н. ф. расходится (не аналптично).
Таким образом, поставленный выше вопрос решен для
всех Н. ф., кроме тех, у к-рых А удовлетворяет усло-
условию со и не удовлетворяет условию со, а остальные
коэффициенты Н. ф. удовлетворяют условию А. Усло-
Условие А является очень жестким ограничением на коэф-
коэффициенты Н. ф., и для больших п оно выполнено, вооб-
вообще говоря, только в вырожденных случаях. Т. е. ос-
основная причина расходимости преобразований к Н. ф.—
это не малые знаменатели, а невырожденность Н. ф.
Но и в случаях расходимости нормализующего пре-
преобразования C) по Н. ф. B) можно изучить свойства
решений системы A). Так, для вещественной системы
A) гладкое преобразование к Н. ф. B) существует ив
тех случаях, когда нет аналитического. Большинство
результатов о гладкой нормализации получено при
условии, что все ReXj-фО. При этом условии с помощью
замены X —>- V конечного класса гладкости систему A)
можно привести к укороченной Н. ф.
ii = ^c(V), i = i, ...* п, F)
где % — многочлены степени т (см. [4] — [6]). Если
в нормализующем преобразовании C) отбросить все
члены степени выше т, то получится преобразование
Xi=li(U), i = U...,n G)
(f;- — многочлены), к-рое приводит A) к виду
=Ф;(?О + Ф,-(?О, ^ = 1, ..., в, (8)
гДе % — многочлены, содержащие только резонансные
члены, ф,- — сходящиеся степенные ряды, содержащие
только члены степени выше т. Решения укороченной
Н. ф. F) служат приближениями для решений системы
(8) и после преобразования G) дают приближения ре-
решений исходной системы A). Во многих случаях для
F) удается построить такую Ляпунова функцию (или
Четаева функцию) i{V), что
m 0/ -
и
F |
где сх и с2 — положительные постоянные. Тогда f(U)
будет функцией Ляпунова (Четаева1) для системы (8),
т. е. точка X = 0 будет устойчивой (неустойчивой).
Напр., если все ReA,,- < 0, то можно взять т = 1,
/ = 2,_i '? п получится теорема Ляпунова об устой-
устойчивости по линейному приближению (см. [7]; другие
примеры см. в обзоре [8]).
По Н. ф. B) можно находить инвариантные аналити-
аналитические множества системы A). В дальнейшем для просто-
простоты изложения предполагается, что ReA = 0. По Н. ф.
B) выделяется формальное множество
где а — свободный параметр. На множестве и€ выпол-
выполняется условие А. Пусть К — объединение таких под-
подпространств вида {У : i/, = 0, i=i\, ¦ ¦ ., н), чт0
соответствующие собственные значения ?.у-, ^Фц, ¦ ¦ .,
ii, 1 <:/ <: п, попарно соизмеримы. Формальное множе-
множество Л — ЛГ\К аналитично в системе A). Из Л выде-
выделяется под.множество SB, к-рое аналитично в системе A),
если выполнено условие ш (см. [3]). На множествах
Л и 33 лежат периодпч. решения и семейства условно
пернодич. решений системы A). Рассматривая множе-
множества Л и 3& в системах с малыми параметрами, можно
изучить все аналитич. возмущения и бифуркации таких
решений (см. [9]).
Обобщения. Если систему A) приводить не к Н. ф.
B), а к системе, правые части к-рой содержат нек-рые
нерезонансные члены, то упрощение получается менее
значительным, зато можно улучшить качество преобра-
преобразования. Так, приведение к «полунормальной форме»
будет аналитическим при ослабленном условии А (см.
[2]). Другой вариант — преобразование, нормализую-
нормализующее систему A) лишь на нек-рых подмногообразиях
(напр., на нек-рых координатных подпространствах;
см. [2]). Комбинации этих подходов позволяют доказать
для системы A) существование инвариантных подмного-
подмногообразий и решений определенного вида (см. 19]).
Пусть система A) определена и аналитична в окрест-
окрестности инвариантного многообразия М размерности
k~\-l, к-рое расслаивается на Z-мерные инвариантные
торы. Тогда вблизи М можно ввести такие локальные
координаты
S = (su ..., sk), Y=(yu ..., Vl), Z = {z1, . .., zm),
k-\-l-\-m = n,
что Z = 0 на M, yj имеют период 2 я, S пробегает
нек-рую область Н, и система A) принимает вид
, У, Z),
Y = Q(S, У) + ФB)E\ У, Z), (9)
Z = A(S, y)Z + OW(S, Y,Z),
где фФ = О(\г\), j= 1,2, O«) = 0(iZ|2), А — матрица.
Если Q=const и матрица А треугольна с постоянной
главной диагональю А= (}п, . . ., Хп), то (при слабом
ограничении на малые знаменатели) существует фор-
формальное преобразование локальных координат S, У,
Z —v U, V, W, к-рое приводит систему (9) к Н. ф.
(U)WQ ехр (Р, V), / = 1, ...,т,
где Р?Ъ1, Q?Nm, U?H и i(P, Q) + (Q,A)=0.
Если среди координат Z есть малый параметр, то
систему (9) можно осреднить Крылова — Боголюбова
методом усреднения (см. [10]), и осредненная система бу-
будет Н. ф. Вообще, теорию возмущений можно рассмат-
рассматривать как частный случай теории Н. ф., когда одна из
координат является малым параметром (см. [11]).
На системы (9) и A0) переносятся теоремы о сходи-
сходимости нормализующей замены, теоремы о существова-
существовании аналитических инвариантных множеств и т. д.
Здесь наиболее изучен случай, когда М — периодич.
решение, т. е. к = 0, I = 1. В этом случае теория Н. ф.
во многом идентична случаю, когда М — неподвижная
точка. А. Пуанкаре предложил рассматривать точечное
преобразование нормального сечения за период. В
связи с этим возникла теория Н. ф. точечных отображе-
отображений, к-рая параллельна соответствующей теории для
систем A). Другие обобщения Н. ф. см. в [31, [6]. [121,
[13].
Лит.: [1] П у а н к а р е А., Избр. труды, пер. с франц.,
т. 3, М., 1974; ЫБрюно А. Д., «Тр. Моск. матем. об-ва»,
1971, т. 25, с. 119—262; 1972, т. .26, с. 199—239; [3] е г о же,
Локальный метод нелинейного анализа дифференциальных урав-
уравнений, М., 1979; [4] Хартман Ф., Обыкновенные диффе-
дифференциальные уравнения, пер. с англ., М., 1970; [5] С а м о-
в о л В. С, «Докл. АН СССР», 1972, т. 206, № 3, с. 545 — 48;
[6] Б е л и ц к и й Г. Р., Нормальные формы, инварианты и
локальные отображения, К., 1979; [7] Ляпунов А. М.,
Общая задача об устойчивости движения, 2 изд., М.— Л., 1935;
[8] К у н и ц ы н А. Л., М а р к е е в А. П., Итоги науки
и техники. Сер. Общая механика, т. 4, М., 1979, с. 58—139;
[9] Bibi'kov J. N., Local theory of nonlinear analytic ordi-
ordinary differential equations, В. [а. о.], 1979; [10] Боголю-
Боголюбов H. H., Митропольский Ю. А., Асимптотиче-
Асимптотические методы в теории нелинейных колебаний, 4 изд., М., 1974;
[11] Брюно А. Д., «Ргос. VIII Intern. Conf. on Nonlinear
Oscillations», Prague, 1979, v. 1, p. 177—82; [12] К о с т i н В. В.,
Ле Д1нь Т х ю i, «Доповда АН УРСР. Сер. А», 1975, Л"« 11,
с. 982—85; [13] Zehnder E. J., «Manus. math.», 1978, v. 23,
p. 363—71. А. Д. Брюно.
НОРМАЛЬНАЯ ФУНДАМЕНТАЛЬНАЯ СИСТЕМА
РЕШЕНИЙ линейной однородной си-
системы обыкновенных дифференци-
дифференциальных уравнений — такая фундаментальная
система решений жг(г), . . ., xn(t)aTo& системы уравне-
уравнений, что для любой другой фундаментальной системы
решений хл (t), . . ., xn(t) той же системы уравнений
имеет место неравенство
здесь
)= lim ±\n\y(t)\
t -*+ oo
•— Ляпунова характеристический показатель решения
y(t). Н. ф. с. р. введены A.M. Ляпуновым II], к-рый
доказал, что они существуют у всякой линейной си-
системы
х = А (t)x,
где А (¦) — суммируемое на каждом отрезке отоб-
отображение
R + —> Нот (Rn, Rn) (или R+ —> Нот (С, С")),
удовлетворяющее дополнительному условию
115
t
u
Лит.: [1] Ляпунов А. М., Собр. соч., т. 2, М., 1956.
В. М. Миллионщиков.
НОРМАЛЬНО РАЗРЕШИМЫЙ ОПЕРАТОР — ли-
линейный оператор с замкнутой областью значений.
Пусть А — линейный оператор с плотной в банаховом
пространстве X областью определения и с областью
значений R (А) в банаховом пространстве Y. Тогда А —
Н. р. о., если R(A) = R(A), т. е. если R(A) является
замкнутым подпространством в У. Пусть А * — опера-
тор, сопряженный к Л. Для того чтобы А был Н. р. о.,
необходимо и достаточно, чтобы R (A)=^-N(А *;, т. е.
чтобы область значений А являлась ортогональным до-
дополнением к подпространству нулей оператора А *.
Пусть дано уравнение с Н. р. о.
Ах = у (*)
(нормально разрешимое уравнение).
Если N (А *) = {0}, т. е. однородное сопряженное урав-
уравнение A*t\i = 0 имеет только тривиальное решение, то
R(A)=Y. Если же N (А*) Ф {0}, то для разрешимости
(*) необходимо и достаточно, чтобы (у, г|;> = 0 для
всех решений уравнения А *ф = 0.
Пусть ниже А — замкнутый оператор. Н. р. о. А
наз. га-н ормальны м, если его подпространство
нулей N (А) конечномерно (ra(^4) = dimAr(^4)<+oo).
Н. р. о. А наз. d-и о р м а л ь н ы м, если его дефект-
дефектное подпространство конечномерно (d(A) =
=dim-Li? (A) <+ оо). re-нормальные и d-нормальные опе-
операторы наз. иногда полуфредголь новыми.
Для того чтобы оператор А был re-нормальным, необ-
необходимо и достаточно, чтобы прообраз каждого ком-
компактного множества из R{A) был локально компакт-
компактным.
Пусть X компактно вложено в банахово простран-
пространство Хс. Для га-нормальности А необходимо и доста-
достаточно наличие априорной оценки
Оказывается, оператор А rf-нормален тогда и только
тогда, когда А* га-нормален. При этом n(A) — d(A*).
Следовательно, если X* компактно вложено в банахово
пространство Z, то для d-нормальности А необходимо
и достаточно наличие априорной оценки
Пара чисел (л (A), d(A)) наз. d-x арактеристи-
к о й оператора А. Если Н. р. о. А га-нормален или
d-нормален, то число
Х(А) = п(А) - d(A)
наз. индексом оператора А. Свойства п-
нормальности п d-нормальности устойчивы: если А —
га-нормален (d-нормален), а В — линейный оператор
малой нормы или вполне непрерывный, то А-\-В га-
нормален (rf-нормален).
Лит.: [1] X а у с д о р ф Ф., Теория множеств, пер. с нем.,
М.— Л., 1937, с. 266 — 90; [2] Аткинсон Ф., «Матем. сб.»,
1951, т. 28, Хз 1, с. 3—14; [3] К р е й н С. Г., Линейные диф-
дифференциальные уравнения в банаховом пространстве, М., 1971.
В. А. Треногин.
НОРМАЛЬНО РАСПОЛОЖЕННОЕ ПОДПРОСТ-
ПОДПРОСТРАНСТВО — такое подпространство А в пространст-
пространстве X, что для каждой его открытой окрестности U
в X существует множество Н, являющееся объедине-
объединением счетного семейства замкнутых в X множеств и
удовлетворяющее условию А аНа U. Если А нор-
нормально расположено в пространстве X, а пространство
X является Н. р. п. в пространстве У, то А нормально
расположено в Y. Н. р. п. в нормальном пространстве
само является нормальным пространством в индуци-
индуцированной топологии — этим и объясняется название.
Финальная компактность пространства равносильна
его нормальной расположенности в каком-нибудь
(а тогда н в любом) бикомпактном расширении этого
пространства. Вообще, Н. р. п. в финально компакт-
компактном пространстве само финально компактно.
Лит.; [1] Смирнов Ю. М., «Матем. сб.», 1951, т. 29,
с. 173—76. А. В. Архангельский.
НОРМАЛЬНОГО ПРИТЯЖЕНИЯ ЗОНА — область
вида 0 < х <i|j(n), для к-рой
Р {У > х} — 1 ИЛИ Р{У<-*}—-1
при п —»- оо, где г|;(ге)|оо, {Zn} — последовательность
случайных величин, У — случайная величина, имею-
имеющая нормальное распределение. Изучены Н. п. з. в
случае, когда
где {Хп} — последовательность независимых одина-
одинаково распределенных случайных величин с математич.
ожиданием а и конечной положительной дисперсией а2.
Лит.: [1] Ибрагимов И. А., Линии к Ю. В.,
Независимые и стационарно связанные величины, М., 1965.
В. В. Петров.
НОРМАЛЬНОЕ АНАЛИТИЧЕСКОЕ ПРОСТРАН-
ПРОСТРАНСТВО — аналитическое пространство, локальные коль-
кольца всех точек к-рого нормальны, т. е. являются цело-
замкнутымп областями целостности. Точка х анали-
тич. пространства X наз. нормальной (говорят
также, что Анормально в точке х), если ло-
катьное кольцо 0„ нормально. В окрестности такой
точки пространство обладает приведенной и неприво-
неприводимой локальной моделью. Любая простая (неособая)
точка является нормальной. Простейший пример
Н. а. п. — аналитическое многообразие.
В дальнейшем основное (полное недискретно норми-
нормированное) поле к предполагается алгебраически зам-
замкнутым. В этом случае получены наиболее полные ре-
результаты о Н. а. п. (см. [1]1 п построена теория норма-
нормализации [2], к-рая естественным образом связывает
с произвольным приведенным аналитическим простран-
пространством некоторое Н. а. п. Пусть N (X) — множество
точек аналитич. пространства X, не являющихся нор-
нормальными, a S (X) — множество особых точек в X.
Тогда:
1) N (X) и S (X) — замкнутые аналитич. подмноже-
подмножества в X, причем N(X)aS (X);
2) для x?X\N{X) выполняется неравенство
dimxS (X) Щ &\тх X — 2
(т. е. Н. а. п. гладко в коразмерности 1);
3) если X является полным пересечением в точке х
и выполнено предыдущее неравенство, то X нормально
в этой точке.
Нормализацией приведенного аналитич.
пространства X наз. пара (X, v), где X — Н. а. п., а
v.X—f-X — конечное сюръективное аналитич. отображе-
отображение, индуцирующее изоморфизм открытых множеств
X\v-1(N (X))
Нормализация определена од
нозначно с точностью до изо-
морфнзма, т. е. если (Х1} vj
п (Х2, v2) — две нормализа-
нормализации, то существует единст-
единственный аналитич. изоморфизм
{(•.Xi-^Xv такой, что диаграмма
коммутативна. Нормализация существует и обладает
следующими свойствами. Для каждой точки х?Х
множество неприводимых компонент пространства X
в точке х находится во взаимно однозначном соответ-
соответствии с v~1(^). Слой прямого образа v* (Q~) структур-
Л.
ного пучка б- в точке х?Х естественно изоморфен
целому замыканию кольца Qx в его полном кольце
частных. ' *
Понятие Н. а. п. над С может быть введено в
терминах аналитич. продолжения голоморфных функ-
функций [3]. Именно, приведенное комплексное простран-
пространство нормально тогда и только тогда, когда для не-
него справедлива первая теорема Римана
об устранении особенностей: если UdX — открытое
подмножество, a AczU— замкнутое аналитич. под-
подмножество, не содержащее неприводимых компонент
множества U, то любая функция, голоморфная на
U\A и локально ограниченная на U, допускает един-
единственное аналитпч. продолжение до голоморфной функ-
функции на U. Для нормальных комплексных пространств
верна также ивторая теорема Римана об
устранении особенностей: если соА\тхА^з2 в каждой
точке х?А, то упомянутое аналитич. продолжение
возможно без требования ограниченности функции.
Приведенное комплексное пространство X нормально
тогда и только тогда, когда для любого открытого мно-
множества UcX отображение ограничения голоморфных
функций
r(U,Qx)-^T(U\S(X),6x)
биективно. Свойство нормальности можно сформули-
сформулировать также на языке локальных когомологий — оно
равносильно равенству ffl^^fix—® (см- №])• Для лю~
бого приведенного комплексного пространства X мож-
можно определить пучок колец Q% ростков слабо го-
голоморфных функций, т. е. функций, удов-
удовлетворяющих условиям первой теоремы Римана. Ока-
Оказывается, что кольцо Qx, х конечно как Qx. лгм°ДУль и
равно целому замыканию кольца Qx, х в его полном
кольце частных. Иными словами, (9y="-v.,.(C~), гДе
х.
v : Х—>-Х — отображение нормализации.
Нормальное комплексное пространство можно оха-
охарактеризовать также следующим образом: комплексное
пространство нормально тогда и только тогда, когда
каждая его точка обладает окрестностью, допускаю-
допускающей аналитич. наложение на область пространства С"
(см. [31, [8]).
Приведенное комплексное пространство X является
Штейна пространством тогда и только тогда, когда
этим свойством обладает его нормализация X (см. [4]).
На нормальные комплексные пространства может быть
распространено понятие метрики Ходжа (см. Кэлера
метрика). На компактные нормальные пространства с
такой метрикой переносится теорема Кодапры о проек-
проективном вложении [6].
В алгебраич. геометрии рассматриваются аналоги
Н. а. п.— нормальные алгебрапч. многообразия (см.
Нормальная схема). Для алгебрапч. многообразий над
полным недискретным нормированным полем оба по-
понятия совпадают (см. [7], [1]).
Лит.: [1] A b h у a n k a r S. S., Local analytic geometry,
N. Y.— L., 1964; [2] H о u z e 1 С, в кн.: Semmaire H. Cartan,
13 annee. 1960/61, t. 2, P., 1963, exp. 18—21; fflGrauert H..
Remmert R., «Math. Ann.», 1958, Bd 136, S. 245—318;
[4]Narasimhan R., «Ann. Scuola Norm. Sup. Pisa», 1962,
v. 16, p. 327—33; [5] Sin Y. Т., Trautmann G., Gap-
sheaves and extension of coherent analytic subsheaves, B.—Hdlb.—
N. Y., 1971; [6] Г р а у э р т Г., в кн.: Комплексные простран-
пространства. Сб. пер., М., 1965, с. 45—104; [7] Зарисский О.,
Самюэль П., Коммутативная алгебра, пер. с англ., т. 2,
М., 1963; [8] Фукс Ё. А., Введение в теорию аналитиче-
аналитических функций многих комплексных переменных, М.,ч. 1, 1962.
НОРМАЛЬНОЕ />-ДОПОЛНЕНИЕ к о н е чТсГй
группы G — нормальный делитель А группы G
такой, что G=AS и А ГM= 4, где S — нек-рая снлов-
ская р-нодгруппа в G (см. Силоеская подгруппа). Груп-
Группа G обладает нормальным р-дополнением, если нек-рая
силовская р-подгруппа S группы G лежит в центре
своего нормализатора (теорема Бёрнсайда).
Необходимое и достаточное условие существования нор-
нормального р-дополнения в группе G дается теоремой
Фробениуса: группа G обладает нормальным
р-дополнением тогда и только тогда, когда либо для
любой неединичной р-подгруппы Н группы G фактор-
факторгруппа Nq{H)[Cg(H) есть р-группа (где NG(H) —
аормализатор Н в G, а Са(Н) — централизатор Н в G),
либо подгруппа Nq (Н) для любой неединичной р-
подгруппы Н группы G обладает нормальным р-долол-
нением.
Лит.: [1] Gorenstein D., Finite groups, N. Y., 1968.
H. H. Вильяме.
НОРМАЛЬНОЕ ПРОСТРАНСТВО — топологическое
пространство, удовлетворяющее аксиоме Т4 (см. Отде-
Отделимости аксиома), т. е. такое топологич. простран-
пространство, в к-ром одноточечные множества замкнуты и
любые два дизъюнктные замкнутые множества отде-
отделимы окрестностями (т. е. содержатся в дизъюнктных
открытых множествах). Н. п. образуют частный случай
вполне регулярных пространств (тихоновских), особенно
важный для размерности теории. Всякое замкнутое
подпространство Н. п. нормально (нормальность на-
наследуется по замкнутым множествам). Пространства,
все подпространства к-рых нормальны, наз. наслед-
наследственно нормальными. Для наследственной
нормальности достаточно, чтобы все его открытые под-
подпространства были Н. п. Для наследственной нормаль-
нормальности пространства необходимо и достаточно, чтобы
были отделимы окрестностями всякие два множества,
из к-рых ни одно не содержит точек соприкосновения
другого. Н. п. наз. совершенно нормаль-
н ы м, если в нем каждое замкнутое множество являегся
пересечением счетного числа открытых множеств.
Всякое совершенно Н. п. есть наследственно Н. п.
Произведение двух Н. п. не обязано быть Н. п., п
даже произведение Н. п. на отрезок может быть не нор-
нормальным.
Существуют важные классы пространств, более общие,
чем нормальные, и менее общие, чем вполне регулярные.
Среди этих пространств, близких к нормальным, первы-
первыми [2] были т. н. к в а з и н о р м а л ь н ы е, или я-
нормальпые, пространства. Это — тихоновские
пространства, в к-рых отделимы окрестностями всякие
два дизъюнктные п-м н о ж е с т в а, т. е. множества,
являющиеся пересечением конечного числа замкнутых
канонических множеств. Тихоновские пространства, в
к-рых отделимы окрестностями всякие два дизъюнкт-
дизъюнктные замкнутые канонич. множества, наз. х-н ормаль-
выми [3]; х-нормальные пространства, в к-рых каждое
замкнутое канонич. множество является пересечением
счетного числа открытых канонич. множеств, наз. с о-
вершенно х-н о р м а л ь н ы м и. Классы тихо-
тихоновских х-нормальных, квазинормальных и, наконец,
совершенно х-нормальных пространств идут последова-
последовательно убывая, причем никакие два из этих классов не
совпадают между собою.
Лит.: [1] Александров П. С, Введение в теорию
множеств и общую топологию, М., 1977; [2] Зайцев В. И.,
«Вести. Моск. ун-та. Матем., механ.», 1В67, jvft 3, с. 48—57;
[3] Щ е п и н Е. В., «Сиб. матем. ж.», 1972, т. 13, J* 5, с.
1182 — 1196. П. С. Александров.
НОРМАЛЬНОЕ ПРОСТРАНСТВО в нек-рой точке Р
к поверхности Fm пространства V"— ортогональное до-
дополнение iV^F к касательному пространству Т pF
(см. Аналитическое пространство) в точке Р поверх-
поверхности F. Размерность Н. п. равна п—т (коразмер-
(коразмерность поверхности F). Любое его одномерное подпро-
подпространство наз. нормалью к поверхности F в точке Р.
Если F — гладкая гиперповерхность, то в каждой
точке F существует единственная нормаль.
А. В. Иванов.
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ — одно из важ-
важнейших распределений вероятностей. Термин «Н. р.»,
принадлежащий К. Пирсону (К. Pearson) (более ста-
старые названия Гаусса яапон, Гаусса — Лапласа распре-
распределение), применяют как по отношению к распределе-
распределениям вероятностей случайных величин, так и по отно-
отношению к совместным распределениям вероятностей
нескольких случайных величин (т. е. к распределениям
конечномерных случайных векторов), а также случай-
ных элементов и случайных процессов. Общее определе-
определение Н. р. сводится к одномерному случаю.
Распределение вероятностей случайной величины X
наз. нормальным, если оно имеет плотность
вероятности
Семейство Н. р. (*) зависит, т. о., от двух параметров
а и о">0. При этом математич. ожидание X равно а, ди-
дисперсия X равна а2, а характеристич. функция имеет вид
Кривая Н. р. у=р(х\ а, а) симметрична относительно
ординаты, проходящей через точку х=-а, ц имеет в
этой точке единственный максимум, равный 1.']/Л2ла.
С уменьшением а кривая Н. р. становится все более
островершинной. Изменение а при постоянном а не
меняет форму кривой, а вызывает лишь ее смещение по
оси абсцисс. Площадь, заключенная под кривой Н. р.,
всегда равна единице. При а=0, а=1 соответствующая
функция распределения равна
е ' du.
В общем случае функция распределения Н. р. (*)
F(x; а, а) может быть вычислена по формуле F (х; а, а) =
=Ф (t), где t=(x—а)!в. Для функцииФ (t) (и нескольких
ее производных) составлены обширные таблицы (см.,
напр., [1] , [2] и ст. Интеграл вероятности). Для Н. р.
вероятность неравенства \Х — а\ >А:о>, равная 1—Ф (/с) +
+Ф (—А), убывает весьма быстро с ростом к (см. табл.).
h
1
2
Вероятность h
0,31731
0,45500-10-'
3
4
Вероятность
0,26998-Ю-2
0,63342-10-*
Во многих практич. вопросах при рассмотрении Н. р.
пренебрегают поэтому возможностью отклонений от а,
превышающих За,— т. н. правило трех сигма
(соответствующая вероятность, как видно из табл.,
меньше 0,003). Вероятное отклонение для Н. р. равно
0,67449а.
Н. р. встречается в большом числе приложений. Из-
Издавна известны попытки объяснения этого обстоятель-
обстоятельства. Теоретич. обоснование исключительной роли
Н. р. дают предельные теоремы теории вероятностей
(см. также Лапласа теорема, Ляпунова теорема). Ка-
Качественно соответствующий результат может быть
объяснен следующим образом: Н. р. служит хорошим
приближением каждый раз, когда рассматриваемая
случайная величина представляет собой сумму боль-
большого числа независимых случайных величин, макси-
максимальная из к-рых мала по сравнению со всей суммой
(см. Центральная предельная теорема).
Н. р. может появляться также как точное решение
нек-рых задач (в рамках принятой математич. модели
явления). Так обстоит дело в теории случайных про-
процессов (в одной из основных моделей броуновского
движения). Классич. примеры возникновения Н. р. как
точного принадлежат К. Гауссу (С. Gauss, закон рас-
распределения ошибок наблюдения) и Дж. Максвеллу
(J.Maxwell, закон распределения скоростон молекул) (см.
также Независимость, Характеризационная теорема).
Распределение случайного вектора Х~(Х-,, Х2,
. . ., Хп) в Rn или совместное распределение случайных
величин Xlt Хг, . . ., Хп наз. Н. р. (м н о г о м е р-
н ы м нормальны м), если при любом фиксиро-
фиксированном t?Rn скалярное произведение (?, А') имеет
или Н. р., или равно константе (как иногда говорят,
имеет Н. р. с дисперсией, равной нулю). Для случай-
случайных элементов со значениями из какого-либо вектор-
векторного пространства Е это определение сохраняется
с заменой t на любой элемент I сопряженного прост-
пространства Е* и скалярного произведения (t, X) на
линейный функционал 1{Х). Совместное распределение
нескольких случайных величин Xlt Х2, ¦ • ¦, Хп имеет
характеристическую функцию
t = (h, t
где
E(t, X) = t
— линейная форма,
— неотрицательно определенная квадратичная форма
" 11<7*г!1 — ковариационная матрица вектора X. В слу-
случае положительной определенности соответствующее
Н. р. имеет плотность вероятности
р(хъ х2, ..., xn) = Cexp{—Q-1(x1 — al, х2—гаг, ...,
где Q~l — квадратичная форма, обратная Q, параметры
а,, а2, . . ., ап равны математич. ожиданиям Xlt X2,
. . ., Хп соответственно, а постоянная
С
Общее количество параметров, задающих Н. р., равно
и быстро растет с ростом п (оно равно 2 при я=1,
20 при ге=5 и 65 при ге=10). Многомерное Н. р. служит
основной моделью многомерного статистического ана-
анализа. Оно используется также в теории случайных про-
процессов (где рассматриваются Н. р. в бесконечномерных
пространствах, см. Случайный элемент, а также Винера
мера, Винеровский процесс, Гауссовский процесс).
Из важных свойств Н. р. необходимо отметить сле-
следующие. Сумма X независимых случайных величин
Хг и Х.2, имеющих Н. р., имеет Н. р.; обратно, если
Х=Х1—Х2 имеет Н. р. и Х1 и X» независимы, то
Хх и Х% имеют Н. р. (теорема Крамера). Это
свойство обладает определенной «устойчивостью»: если
распределение X «близко» к Н. р., то и распределения
Хх и Х« «близки» к Н. р. С Н. р. связаны нек-рые дру-
другие важные распределения (см. Логарифмически нормаль-
нормальное распределение, Нецентральное «хи-квадрать распре-
распределение, Стъюдепта распределение, Уишарта распреде-
распределение, Фишера z-распределение, Хотеллинга Т2-распре~
деление, «Хи-квадрат» распределение). Для приближен-
приближенного представления распределений, близких к Н. р.,
широко применяются ряды типа Эджворта рядов и
Грама — Шарлье рядов.
О вопросах, связанных с оценкой параметров Н. р.
по результатам наблюдений, см. ст. Несмещенная оцен-
оценка. О проверке гипотезы нормальности см. Непарамет-
Непараметрические методы статистики. См. также Вероятност-
Вероятностная бумага.
Лит.: [1] Б о л ь ш е в Л. Н., Смирнов Н. В., Таб-
Таблицы математической статистики, 2 изд., М., 1968; [2] Таблицы
нормального интеграла вероятностей, нормальной плотности и
ее нормированных производных, М., 1960; [3] Гнеденко
Б. В., Курс теории вероятностей, 5 изд., М., 1969; [4] Кра-
Крамер Г., Математические методы статистики, пер. с англ.,
2 изд., М., 1975; [5] К е н д а л л М. Д ж., С т ь ю а р т А.,
Теория распределений, пер. с англ., М., 1966; [6] И х ж е, Ста-
Статистические выводы и связи, пер. с англ., М., 1973.
Ю. -В. Прохоров.
НОРМАЛЬНОЕ РАССЛОЕНИЕ подмногооб-
подмногообразия — расслоение, состоящее из касательных век-
торов к объемлющему многообразию, нормальных к
подмногообразию. Если X — риманово многообразие,
У — его (погруженное) подмногообразие, Тх и Ту —
касательные расслоения над X и У, то Н. p. ^'YiX
подмногообразия У есть подрасслоение в Т%\ У, сос-
составленное векторами и?Тх ц, У^У, ортогональными
к TY, у
С помощью Н. р. строятся, напр., трубчатые окрес-
окрестности подмногообразий. Н. р. над У, рассматривае-
рассматриваемое с точностью до эквивалентности, не зависит от
выбора римановой метрики на X, поскольку может
быть определено без помощи метрики как фактор-
расслоение Tx\Y/Ty. Несколько более общей является
конструкция Н. р. произвольного погружения / : У—>-Х
дифференцируемых многообразий:
NYix = f*TxITY.
Аналогично определяется Н. p. ^yix н.еос°бого
алгебраич. подмногообразия У в неособом алгебраич.
многообразии X или Н. р. аналитич. подмногообразия
У в аналитич. многообразии X; оно является алгебраиче-
алгебраическим (соответственно аналитическим) векторным рас-
расслоением над У, ранг к-рого есть codim У. Если, в
частности, codim У=1, то расслоение Nyix изоморфно
ограничению на У расслоения над X, определяемого
дивизором У.
В случае, когда У — аналитич. подпространство
аналитич. пространства (X, Ох), Н. р. подпространст-
подпространства У иногда называют аналитич. семейство векторных
пространств JVyix—f-Y, двойственное к конормальному
пучку Л'у ,j? (см. Нормальный пучок). О приложениях
Н. р. к вопросу о стягиваемости подмногообразий см.
Исключительное аналитическое множество, Исключи-
Исключительное подмногообразие.
Лит.: [1] Итоги науки и техники. Алгебра. Топология. Гео-
Геометрия, т. 15, М., 1977, с. 132 — 56; [2] М и л н о р Д ж., Ста-
шеф Дик., Характеристические классы, пер. с англ., М.,
1979; [3] Р о х л и н В. А., Фукс Д. Б., Начальный курс
топологии. Геометрические главы, М., 1977; [4] X и р ш М.,
Дифференциальная топология, пер. с англ., М., 1979; [5]Ш а-
фаревич И. Р., Основы алгебраической геометрии, М.,
1972. А. Л. Онищик.
НОРМАЛЬНОЕ РАСШИРЕНИЕ поля — алгебраи-
алгебраическое расширение L поля К, удовлетворяющее одному
из следующих эквивалентных условий;
\) любое вложение поля L в алгебраич. замыкание
К поля К является автоморфизмом поля L;
2) L — поле разложения нек-рого семейства мно-
многочленов с коэффициентами из К;
3) любой неприводимый над К многочлен f(x) с
коэффициентами из К, имеющий корень в L, распада-
распадается в L на линейные множители.
Для любого алгебраич. расширения Fl К существует
максимальное промежуточное подполе L, нормальное
над К, причем ?= По Fa, где а — всевозможные вло-
вложения поля F в К. Существует также однозначно оп-
определенное минимальное Н. р. поля К, содержащее F.
Это поле является композитом всех полей F°. Оно
наз. нормальным замыканием поля F
относительно К. Если L1 и L2— нормальные расшире-
расширения поля К, то пересечение ЬгГ\Ь2 и композит Ьг-Ь2
снова нормальны над К. Однако даже если расширения
LIК' и К'!К нормальны, расширение ЫК может и
не быть нормальным.
Для полей характеристики 0 любое нормальное рас-
расширение является расширением Галуа. В общем случае
Н. р. является расширением Галуа тогда и только тогда,
когда оно сепарабельно.
Лит.: [1] Ван дер Варден Б. Л., Алгебра, пер.
с нем., М., 1976; [2] Ленг С, Алгебра, пер. с англ., М.,
1968; [3] Постников М. М., Теория Галуа, М., 1963.
Л. В. Кузьмин.
НОРМАЛЬНОЕ СЕМЕЙСТВО аналитических
функций в области — такое семейство S од-
нозначных аналитич. функций f(z) комплексных пере-
переменных 2=B1, . . ., zn) в области D пространства С",
п^И, что из любой последовательности функций из S
можно выделить подпоследовательность (Л>(г)}, рав-
равномерно сходящуюся внутри D к аналитич. функции
или к бесконечности. При этом, по определению, под-
подпоследовательность {/v (z)} равномерно внутри D схо-
сходится к бесконечности, если для любых компакта KcD
и числа М~>0 можно указать такой номер N= N (К, М),
что !/v (z)|>Af для всех v>Af, z?K.
Семейство S наз. нормальным с е м е й с т-
в о м в точке z°?D, если S нормально в нек-ром шаре
с центром z°. Семейство .9 нормально в области D
тогда и только тогда, когда оно нормально в каждой
точке z° ?Z). Всякое компактное семейство голоморфных
функций является Н. с; обратное заключение неверно
(см. Компактности принцип). Если семейство S го-
голоморфных функций в области DaC" таково, что
ни одна из функций f(z)?S Tie принимает двух опреде-
определенных значений, то S есть Н. с. в D (теорема
М о н т е л я). Этот признак Н. с. значительно упроща-
упрощает исследование аналитич. функций в окрестности су-
существенно особой точки (см. также Пикара теорема).
Нормальное семейство мероморф-
ных функций в области DczC = Cx определя-
определяется аналогично: S есть Н. с. мероморфных функций в
D, если из любой последовательности функций из S
можно выделить подпоследовательность {fv(z)}, рав-
равномерно внутри D сходящуюся к мероморфной функции
/(г) пли к бесконечности. При этом, по определению,
{/v (z)} равномерно внутри D сходится к / (z) (случай
/(г)=со включается), если для любых компакта KczD
и числа е>0 существуют номер N=N(e, К) и круг
B = B(z°, г) радиуса г=г(е. К) с центром в любой точке
z°?K такие, что при v>N выполняется
|/v(z)—/(z)| < е,
когда /(z°) т^оо, или
1 I
/v (z) / (z)
когда /(z°)=oo. Если семейство S мероморфных функ-
функций в области DczC таково, что ни одна из функций
j(z)?S не принимает трех определенных значений, то
S есть Н. с. (т е о р е м а М о н т е л я). Семейство S
мероморфных функций есть Н. с. в области DczC
тогда и только тогда, когда
sup{p(/(z)):/B)eS} < со
на каждом компакте KczD, где
— т. н. сферическая производная
функции /(z).
Начиная с 30-х гг. 20 в. Н. с. приобрели большое
значение в исследованиях граничных свойств аналити-
аналитических функций (см. также Предельное множество,
[31, [4]). Мероморфная функция f(z) в односвязной об-
области DcC наз. нормальной функцией в
области D, если семейство {/(y(z))} есть Н. с. в
D\ здесь y(z) пробегает семейство всех конформных ав-
автоморфизмов области D. Функция/(z) наз. нормаль-
нормальной в многосвязной области D, если
она нормальна на универсальной накрывающей поверх-
поверхности D. Если мероморфная в D функция /(z) опускает
три значения, то f(z) — нормальная функция. Для того
чтобы /(z), /(г)Фconst, была нормальной в единичном
круге G={z?C : |z|<l}, необходимо и достаточно,
чтобы выполнялось условие
= с(/)=сопй.
Для нормальной мероморфной функции j(z) в еди-
единичном круге G из существования асимптотического
значения а в граничной точке ??Г={??С: | ?| = 1}
следует, что ее — угловое граничное значение f(z) в L.
Однако мероморфная нормальная функция в круге G
может и не иметь вовср асимптотич. значений. Напро-
Напротив, если f(z) — голоморфная нормальная функция в
б, то даже угловые граничные значения существуют
на множестве точек единичной окружности Г, плотном
на Г.
Лит.: [1] Мотель П., Нормальные семейства анали-
аналитических функций, пер. с франц., М.— Л., 1936; [2] М а р к у-
шевич А. И., Теория аналитических функций, 2 изд.,
т. 1—2, М., 1967—68; [3] К о л л и н г в у д Э., Л о в а т е р А.,
Теория предельных множеств, пер. с англ., М., 1971; [4] Л о в а-
т е р А., в кн.: Итоги науки и техники. Математический ана-
анализ, т. 10, М., 1973, с. 99 — 259. Е. Д. Соломенцев.
НОРМАЛЬНОЕ СЕЧЕНИЕ гладкой поверх-
поверхности Фв точке Р в направлении! —
сечение поверхности Ф плоскостью, проходящей через
нормаль к поверхности в точке Р и через направление I
в касательной плоскости к Ф в точке Р. Задачу об изу-
изучении локальной структуры поверхности можно свести
к задаче об изучении локальной структуры семейства
кривых — Н. с. поверхности в данной точке и в раз-
различных направлениях (см. Kpueusyia, Нормальная кри-
кривизна). Метод исследования локальной структуры по-
поверхности с помощью Н. с. допускает обобщения на
случай поверхностей произвольной размерности и с
произвольной коразмерностью. Д- Д- Соколов.
НОРМАЛЬНОЕ УРАВНЕНИЕ, нормирован-
нормированное уравнение, прямой на плоскости — уравне-
уравнение вида
х cos a-f г/ sin а—р = 0,
гДе х, У — декартовы прямоугольные координаты плос-
плоскости; cos а и sin a — координаты единичного век-
вектора {cos a, sin а}, перпендикулярного к прямой;
р>0 — расстояние от начала координат до прямой.
К Н. у. уравнение прямой вида
Ах+Ву+С=0
приводится умножением на нормирующий мно-
множитель Я, модуль к-рого есть I/ Уа*-\-В2, а знак
противоположен знаку С (при С=0 знак Я можно выби-
выбирать произвольно).
Аналогично случаю прямой, уравнение плоскости
Ax-\-By+Cz+D=0
приводится к Н. у.
х cos a+j/ cos Р+2 cos "у—р=0,
где cos a, cos E, cos у — направляющие косинусы век-
вектора, перпендикулярного к плоскости, умножением на
нормирующий множитель Я, модуль к-рого есть
1/ ]Ал2-|-?2-|-С2, а знак X противоположен знаку D.
А. Б. Иванов.
НОРМАЛЬНОЕ ЧИСЛО — действительное число а,
0<:а«:1, обладающее следующим свойством: для каж-
каждого натурального s любая заданная s-членная скобка
6=Fi, б2, . . ., 6j), состоящая из знаков 0, 1, . . .,
g—1, появляется в последовательности
«ц «2, «з, •.., «„, ..., A)
получающейся при разложении числа а в бесконечную
g-ичную дробь
"="' I '"I I "¦' I ¦" I "' I '"I
с асимптотич. частотой i'gs.
Подробнее, пусть g>l — натуральное число и
(<*!> «2, ¦ ¦ • > <Ь) Ы, «3, • • • , Us + l) («3, • • • , &S + 2) ¦¦¦ B)
— бесконечная последовательность s-членных скобок,
соответствующая последовательности A). Через N(n, б)
обозначается число появлений скобки б= (б,, б2, . . ., б^)
среди первых га скобок последовательности B). Число
наз. нормальным, если для любого натурального s
и любой заданной s-членной скобки б, состоящей из
знаков 0, 1, . . ., g—i,
lim ^<"'6> =-L.
П -*¦ со U gS
Понятие Н. ч. для п=10 было введено Э. Борелем
(см. [11, [21 с. 197). Э. Борель называл действительное
число а слабо нормальным к основа-
основанию е, если
lim
JV (п, 6) _ 1
Л->-оо П g
где N (я, б) — число появлений знака б, 0<:6<:g—1,
среди первых га членов последовательности (Xj, а2,
а3, . . ., и называл а нормальным, если числа
a, go., g-a, . . . слабо нормальны к основаниям g, g2,
g3, ... Он установил также, что для Н. ч.
lim ^<"'б> =J_
Я->-оо П gS
при любом s и любой заданной s-членной скобке б =
= (&i, .... 8S)- Позднее было показано (см. [3], [4], а
также [8jl, что выполнимость последнего соотношения
эквивалентна борелевскому определению Н. ч.
Число а наз. абсолютно нормальным,
если оно нормально по отношению ко всякому натураль-
натуральному основанию g>l. Существование нормальных и аб-
абсолютно Н. ч. было установлено Э. Борелем на основе
теории меры. Построение Н. ч. в явном виде впервые бы-
было осуществлено в [5]. Ранее (см. [6], [7]) был указан
эффективный процесс построения абсолютно Н. ч.
О других способах построения Н. ч. и о связи понятия
Н. ч. с понятием случайности см. [81.
Равномерное распределение дробных долей {agx},
x=i, 2, 3, . . ., на отрезке [0, 1] эквивалентно тому,
что а — нормальное число.
Лит.: [1] В orel E., «Rend. circ. math. Palermo», 1909,
t. 27, p. 247—71; [2] e г о же, Legons sur la thgorie des foncti-
ons, 3 ed., P., 1928; [3] P i 1 1 a i S., «Proc. Indian Acad. Sci.
Sec. A», 1940, v. 12, p. 179—84; [4] Niven I., Zucker-
m a n H., «Pacific J. Math.», 1951, v. 1, p. 103—09; 15] С h a m-
pernowne D. G., «J London Math. Soc», 1933, v. 8,
p. 254—60; [6] S i e r p i n s k i W., «Bull. Soc. math. France»,
1917, t. 45, p. 127—32; [7] L e b e s q u e H., там же, р. 132—
44; [8] П о с т н и к о в А. Г., Арифметическое моделирование
случайных процессов, М., 1960 («Тр. Матем. ин-та АН СССР»,
т. 57). С. А. Степанов.
НОРМАЛЬНОЙ КРИВИЗНЫ ЭЛЛИПС — геометри-
геометрическая конструкция, к-рая характеризует распределе-
распределение кривизн в нек-рой точке регулярной поверхности
М2 в ^'-мерном евклидовом пространстве Е". Пусть
Р — точка поверхности М2 и Nh есть (га—1)-мерное под-
подпространство, содержащее нормальное дополнение N
и М2 в Р и касательное к М2 в точке Р направление I. Се-
Сечение М2 подпространством Nt наз. нормальным
сечением yt в точке Р. Вектор —- , лежащий в N,
где s — натуральный параметр на сечении у(, наз.
вектором нормальной кривизны М2
в направлении I. Концы векторов нормальной кривиз-
кривизны образуют эллипс нормальной кри-
кривизны.
Для того чтобы двумерная поверхность М2 с нену-
ненулевой гауссовой кривизной в Еп лежала в нек-ром трех-
трехмерном подпространстве Е3, необходимо и достаточно,
чтобы ео Н. к. э. во всех точках Р вырождался в отре-
отрезок, проходящий через Р (см. [2]).
Аналогично определяется индикатриса кривизны для
подмногообразия Мт произвольной размерности т.
Она является (т.—1)-мерной алгебраич. поверхностью
степени 2-1. Векторы нормальной кривизны образу-
образуют конус, к-рый вместо с касательным пространством
к Мт определяет подпространство Ет', наз. обла-
областью кривизны Мг в точке Р. Размерность тх
удовлетворяет условиям
_ т (т + 3) _
т1 < 5 -, т^^п.
Точки, для к-рых т1 = т-{-1, наз. аксиальными
точками, mL= m-\-2—п ланарными точка-
м и, тх=т-\-Ъ — специальны ми точками.
Иногда для подмногообразий с большой коразмерно-
коразмерностью рассматривают Дюпена индикатрису, построе-
построение к-рой вполне аналогично построению индикатрисы
Дюпена для поверхности в трехмерном пространстве.
Лит.: [1] С х о у т е н И. А., С т р о й к Д. Д ж., Вве-
Введение в новые методы дифференциальной геометрии, пер. с нем.,
т. 2, М.— Л., 1948; [2] А м и н о в Ю. А., «Укр. геометр, сб.»,
1975, в. 17, с. 3—22. Д. Д. Соколов.
НОРМАЛЬНЫЙ АЛГОРИФМ — название, закрепив
шееся за алгоритмами некоторого точно охарактеризо-
охарактеризованного типа. Наряду с рекурсивными функциями п Тью-
Тьюринга машинами Н. а. получили известность в каче-
качестве одного из наиболее удобных уточнений общего
интуитивного представления об алгоритме. Понятие
Н. а. было выработано в 1947 А. А. Марковым в ходе
его исследований по проблеме тождества для ассоциа-
ассоциативных систем (см. Ассоциативное исчисление). Деталь-
Детально определение и общая теория Н. а. изложены в
[1] (гл. I-V).
Всякий Н. а. Ж, являясь алгоритмом в нек-ром ал-
алфавите А , порождает в нем детерминированный процесс
переработки слов. Указание этого алфавита входит в
определение Н. а. Ш. в качестве обязательной состав-
составной части, и в рассматриваемой ситуации про Н. а. 31
говорят, что он является Н. а. в алфавите А. Любой
Н. а. в фиксированном алфавите А вполне определяет-
определяется указанием его схемы — упорядоченного конечного
списка формул подстановки в А. Каждая такая форму-
формула но существу представляет собой упорядоченную па-
пару (U, V) слов в А. Слово U наз. левой частью этой
формулы, а V — ее правой частью. Среди формул
дайной схемы нек-рые выделяются специально и объяв-
объявляются заключительными. Обычно в схеме
Н. а. заключительная формула записывается в виде
U—*-'V, а неяаключительная — в виде U—*-V.
Н. а. 31 в алфавите А есть предписание
строить, исходя из произвольного слова Р в А,
последовательность слов />,¦ согласно следующему
правилу. Слово Р берется в качестве начального
члена Ро этой последовательности, и процесс ее по-
построения продолжается далее. Пусть для нек-рого
s^O слово Р{ построено и процесс построения рассма-
рассматриваемой последовательности еще не завершился.
Если в схоме Н. a. 3f нет формул, левые части к-рых
входили бы в Pi, то Я; + 1 полагают равным />,-, и про-
процесс построения последовательности на этом считается
закончившимся. Если же в схеме 31 имеются формулы
с левыми частями, входящими в />,-, то в качестве P; + i
берется результат подстановки правой части первой
из таких формул вместо первого вхождения ее левой
части в слово />,-; при этом процесс построения последо-
последовательности считается завершившимся, если применен-
примененная на этом шаго формула подстановки была заключи-
заключительной, и продолжающимся в противном случае. Если
процесс построения упомянутой последовательности
обрывается, то говорят, что рассматриваемый Н. а. 31
применим к слову Р. Последпий член Q этой
последовательности считается результатом при-
применения Н. а. 91 к слову Р и обозначается симво-
символом 91 (Р). При этом говорят, что Ш. перераба-
перерабатывает Р ъ Q, и пишут tyi(P) — Q. H. а. в каком-
либо расширении алфавита А наз. Н. а. н а д этим ал-
алфавитом.
Имеются веские основания считать, что уточнение
общего представления об алгоритме в алфавите, про-
произведенное с помощью понятия Н. а., является адек-
адекватным. Именно, считается, что для всякого алгорит-
алгоритма 2[ в каком-либо алфавите А может быть построен
Н. а. S3 над этим алфавитом, перерабатывающий про-
произвольное слово Р в А в тот же самый результат, в
к-рый перерабатывает его исходный алгоритм 31. Это
соглашение известно в теории алгоритмов под назва-
названием принципа нормализации. Уточне-
Уточнение понятия алгоритма, осуществленное на основе по-
понятия Н. а., оказывается эквивалентным другим изве-
известным уточнениям (см., напр., [2]). Вследствие этого
принцип нормализации оказывается равносильным
Чёрча тезису, предлагающему считать понятие частично
рекурсивной функции адекватным уточнением понятия
вычислимой арифметич. функции.
Возникшие первоначально в связи с алгебраич. про-
проблематикой И. а. оказались удобным рабочим аппара-
аппаратом во многих исследованиях, требующих точного по-
понятия алгоритма.— особенно тогда, когда основные
объекты рассмотрения имеют неарифметпч. природу и
допускают удобное представление в виде слов в
нек-рых алфавитах (такова, напр., ситуация в конструк-
конструктивном анализе).
Лит.: [1] М а р к о в А. А., Теория алгорифмов, М., 1954
(Тр. Матем. ин-та АН СССР, т. 42); [2] Мендельсон Э.,
Введение в математическую логику, пер. с англ., М., 1971.
Н. М. Нагорный.
НОРМАЛЬНЫЙ ДЕЛИТЕЛЬ, нормальная
подгруппа, инвариантная подгруп-
п а,— подгруппа Н группы G, для к-рой левостороннее
разложение группы С по подгруппе Н совпадает с пра-
правосторонним, т. е. такая подгруппа, что для любого
элемента a?G смежные классы all и На равны (в смы-
смысле совпадения этих множеств). Если подгруппа Н яв-
является Н. д. группы G, то говорят также, что Н нор-
нормальна в G, и пишут H^iG. Если H^iG и Нфй, то пи-
пишут Я<1С Подгруппа Н нормальна в группе G тогда
и только тогда, когда вместе с каждым своим элементом
h она содержит все с ним сопряженные в группе G (см.
Сопряженный элемент), т. е. Над^Н. Н. д. может быть
определен также как подгруппа, к-рая совпадает со
всеми своими сопряженными подгруппами, вследствие
чего он наз. также самосопряженной под-
подгрупп о й.
При любом гомоморфизме ср : G-+-G' множество Т
элементов группы G, отображающихся в единицу груп-
группы G' (ядро гомоморфизма ср), является
Н. д. группы С; и обратно, всякий Н. д. группы G
есть ядро нек-рого гомоморфизма, в частности Н. д. Т
служит ядром канонич. гомоморфизма на факторгруппу
G/T.
Пересечение любого множества Н. д., а также под-
подгруппа, порожденная любой системой Н. д. группы G,
сами ЯВЛЯЮТСЯ Н. Д. группы С. О. А. Иванова.
НОРМАЛЬНЫЙ КОМПЛЕКС полугруппы
S — непустое подмножество .?<=,?, удовлетворяющее
следующему условию: для любых х, y^S1 (здесь
S1^=S, если S содержит единицу, и S1 есть полугруппа,
получаемая пз S присоединением единицы, если S
не содержит единицу) и любых a, b?N из xay?N сле-
следует xby^N. Подмножество N будет Н. к. полугруп-
полугруппы 5 тогда и только тогда, когда N является классом
нек-рой конгруэнции на S.
Лит.: [1] Л я пин Е. С, Полугруппы, М., 1960.
Л. Н. Шеерин.
НОРМАЛЬНЫЙ МОНОМОРФИЗМ — морфизм, об-
обладающий характеристическим свойством вложения
группы (кольца) в группу (кольцо) в качестве нормаль-
нормального делителя (идеала). Пусть й — категория с нулевыми
морфизмамп. Морфизм ц : U-+A наз. нормаль-
нормальным мономорфизмом, если всякий морфизм
Ф : X—*-А, для которого из иа=0, а : Д->У, всегда
следует сра=О, однозначно представим в виде <р-=ф'[х.
Ядро любого морфизма является Н. м. Обратное в об-
общем случае неверно, однако при существовании в ка-
категории коядер морфизмов всякий Н. м. оказывается
ядром своего коядра. В любой абелевой категории
всякий мономорфизм нормален. Понятие Н. м. двой-
двойственно понятию нормального эпиморфизма.
М. Ш. Цаленко.
НОРМАЛЬНЫЙ НУЛЬМЕРНЫЙ ЦИКЛ, цикл
индекса н у л ь,— цикл z=2,-=1«;i? такой, что
^l-=1ai = 0. Гомологичный нулю цикл всегда нормален;
факторгруппа группы нормальных циклов ио подгруппе
циклов, гомологичных нулю, наз. приведенной
нульмерной группой гомологии. Для
связного комплекса приведенная группа — нулевая,
что удобно во всякого рода определениях ацикличности.
Истинный ииклг° = {г?, . . ., г", . . .} ваз. нормаль-
н ы м, если нормален каждый из циклов z%.
А. А. Мальцев.
НОРМАЛЬНЫЙ ОПЕРАТОР — замкнутый линей-
линейный оператор А, определенный на плотном в гильбер-
гильбертовом пространстве Я линейном многообразии D д, та-
кой, что А*А=АА*, где А* — оператор, сопряженный
с А. Если А — Н. о., то Од«=Вди ||4*||=1U1|. Обрат-
Обратно, выполнение этих условий обеспечивает нормаль-
нормальность А. Если А—Н. о., то: А* также нормален;
aA-{-f>I — Н. о. при любых а, Р^С; А-1 нормален
в случае, когда этот оператор существует; если АВ=
— ВА, где В — ограниченный линейный оператор, то
также А*В = ВА*.
Для Н. о. А имеют место:
1) мультипликативное разложение
A = U}fA*A=}rA*AU, А*=и-1
где U — унитарный оператор, однозначно определяе-
определяемый на ортогональном дополнении подпространства
нулей операторов А и Л*;
2) аддитивное разложение
где Дг и А 2— однозначно определяемые самосопряжен-
самосопряженные операторы, перестановочные между собой.
Из аддитивного разложения следует, что для упоря-
упорядоченной пары (А, А*) существует единственная дву-
двумерная спектральная функция Е(АИ, где Ар — дву-
двумерный интервал А.= А|ХД , ?=|4-'ть такая, что
Из этого разложения следует также, что Н. о. А яв-
является функцией нек-рого самосопряженного опера-
оператора С, A = F(C). Обратно, всякая функция любого
самосопряженного оператора есть Н. о.
Важным свойством Н. о. является равенство ||Л"||=
= \\А ||л, из к-рого следует, что спектральный радиус
Н. о. А совпадает с его нормой \\А |1. Собственные эле-
элементы Н. о., соответствующие различным собственным
значениям, ортогональны.
Лит.: [1] Плеснер А. И., Спектральная теория ли-
линейных операторов, М., 1965; [2J Рудин У., Функциональ-
Функциональный анализ, пер. с англ., М., 1975. В. И. Соболев.
НОРМАЛЬНЫЙ ПУЧОК — аналог нормального
расслоения в теории пучков. Пусть
(/, f#)--(Y, Qy) - (X, Qx)
— морфизм окольцованных пространств такой, что го-
гомоморфизм /# '• J*Qx~^*-Qy сюръективен, и пусть
J = Ker/#. Тогда 313г есть пучок идеалов в j*Qxl3&z
=Qy и воэтому является (Зу-модулем. Пучок 0АГу/х5=
=--3/?2°наз. конормальным пучком мор-
морфизм а /, а двойственный (З^модуль оАГу/л:=
= Нот0к(сДГУ/.А-1 Qy) — нормальным пучком
морфизм а /. Эги пучки обычно рассматриваются
в следующих частных случаях.
1) X, У— дифференцируемые (напр., класса С°°) мно-
многообразия, / : Y-+X — погружение. Имеется точная
последовательность (З^модулей
О - M'yix -^ Ых - Qy - О,
где Qx, &Y — пучки ростков гладких 1-форм на X и
У, а 6 определяется дифференцированием функций.
Двойственная точная последовательность
где J7^., gTY — касательные пучки на X, У, показывает,
что оАГу/х изоморфен пучку ростков гладких сечений
нормального расслоения погружения/. Если У — погру-
погруженное подмногообразие, то Jf Y/x и Jfy/x наз- н ° Р"
и а л ь н ы я и конормальным пучками
подмногообразия У.
2) (X, Qx) — неприводимая отделимая схема конеч-
конечного типа над алгебраически замкнутым полем к,
(Y, Qy) ~~ ее замкнутая подсхема, / : Y->X — вло-
жение. Тогда гЖу/х и dfy/X наз' нормальным
иконормальным пучками подсхемы
У. Имеется также последовательность (Зу-модулей
где Qx, QY — пучки дифференциалов на X, У. Пучки
oJVy/x и oJVy/x квазикогерентны, а если X — нётеро-
ва схема, то они когерентны. Если X — неособое много-
многообразие над к, то У является неособым многообразием
тогда и только тогда, когда пучок ofCy/x локально сео-
бодеы или когда в (*) гомоморфизм б инъективен. В этом
случае получается двойстпенная точная последователь-
последовательность
так что Н. п. оЛГу/х — локально свободный пучок ранга
r--codim У, отвечающий нормальному расслоению над
У. В частности, если г=1, то offy/X— обратимый пучок,
отвечающий дивизору У.
В терминах Н. п. выражается самопересечение Y-Y
ноособого подмногообразия YczX. А именно, У -Y=
—f*criolf Y/х)' гДе сг есть г-ж Чжэня класс, /„. : А (У)—>-
—>А (X) — гомоморфизм Чжоу колец, отвечающих! вло-
вложению / : Y-+-X.
3) (X, Qy) — комплексное пространство, (У, Qy) —
его замкнутое аналитич. подпространство, / — вло-
вложение. Пучки JPy/x и oWy/x наз- нормальным
и конормальным пучками подпрост-
подпространства У; они когерентны. Если X — аналитич.
многообразие, а У — его аналитич. подмногообразие,
тОсДГу/х есть пучок ростков голоморфных сечений нор-
нормального расслоения над У.
Лит.: |1] Ш а ф а р е в и ч И. Р., Основы алгебраической
геометрии, М., 1972; [2] TTartshorne R., Algebraic geo-
geometry, N. Y. — Hdlb. — В., 1977. А. Л. ОнищиК.
НОРМАЛЬНЫЙ РЯД группы— ряд нормаль-
нормальных подгрупп
группы G (см. Подгрупп ряд). Если каждый член ря-
ряда нормален не во всей группе, а только в предыд>
щем члене, то такой ряд наз. субнормальным.
Кроме коночных рассматриваются также бесконечные
убывающие и бесконечные возрастающие нормальные и
субнормальные ряды — их члены нумеруются уже по-
порядковыми числами (трансфинитами). Рассматриваются
и более общие нормальные и субнормальные системы,
члены которых нумеруются элементами упорядоченного
множества.
Фактором ряда наз. факторгруппа нек-рого
члена ряда по следующему (или предыдущему, если ряд
записан в порядке возрастания членов) члену. Дли-
Длиной ряда наз. количество его факторов, отличных
от единицы. Неуплотняемый далее Н. р. наз. глав-
главным, а субнормальный — композиционным.
Факторы этих рядов наз. соответственно главными
и композиционными факторами. Два
нормальных (субнормальных) ряда наз. изоморф-
изоморфными, если можду их факторами можно установить
такое взаимно однозначное соответствие, что соответ-
соответствующие друг другу факторы изоморфны. Любые
два нормальных (субнормальных) ряда обладают изо-
изоморфными уплотнениями. В частности, любые два глав-
главных (композиционных) ряда изоморфны (Жор дан а —
Гёлъдера теорема).
Параллельно существует и другая терминология, а
именно: нормальным рядом наз. то, что выше
названо субнормальным, а для приведенного здесь
понятия «нормальный ряд» используется термин —
«инвариантный ряд». а. л. Шмелъкип
НОРМАЛЬНЫЙ ЭПИМОРФИЗМ — морфизм, овла
дающий характеристич. свойством естественного отоб-
отображения группы на факторгруппу или кольца на фак-
торкольцо. Пусть Я категория с нулевыми морфизмами.
Морфизм v : A-+-V наз. нормальным эпимор-
эпиморфизмом, если всякий морфизм ф : Л->У, для к-рого
из av=0, а: Х->А, всегда следует аф=0, однозначно
представим в виде cp=vcp'. Коядро любого морфизма
является Н.э. Обратное утверждение в общем случае
неверно, однако при существовании в категории ядер
морфизмов всякий Н. э. оказывается коядром. В абе-
левой категории всякий эпиморфизм нормален. Двой-
Двойственным к понятию Н. э. является понятие нормально-
нормального мономорфизма. м Ш Цаленко
НОРМЕННОЕ ОТОБРАЖЕНИЕ — отображение NKik
поля К в поле к, где К — конечное расширение поля к,
ставящее в соответствие элементу а^К элемент А7А7^(а),
являющийся определителем матрицы к-линейного ото-
отображения К-^-К, переводящего х?К в ах. Элемент
^Kik (°0 наз- нормой элемента а.
Равенство iVA-/fc (<*) = <) выполняется тогда и только
тогда, когда а=0. Для любых а, $?К
г. е. N[<ik индуцирует гомоморфизм мультипликатив-
ных групп К*-^~к*, к-рый также наз. норменным
отображением. Для любого а?&
NKlk{a)=<zn, где га = [AT:*:].
Группа NKik{K*) наз. норменной подгруп-
подгруппой в к*, или группой норм (из поля К в
поле к). Если f(x) = xnJ^an_1xn~1-\- . . . + a0— харак-
характеристич. многочлен элемента а.?К относительно поля
к, то
Пусть расширение К/к сепарабельно. Тогда для любого
а из К
где а,-— все ^--изоморфизмы поля К в алгебраич. за-
замыкание к поля к.
Н. о. обладает свойством транзитивности. Если Li К и
Kik — конечные расширения, то
JVl/ь (a)=NK/k (Nl/k (а))
для любого а из L,
Лит.: [1] Ленг С, Алгебра, пер. с англ., М., 1968; [2]
Боревич 3. И., Шафаревич И. Р., Теория чисел,
2 изд., М., 1972. Л. В. Кузьмин.
НОРМЕННЫЙ ВЫЧЕТ, символ норме н-
ного вычета, символ Гильберта,—
функция, сопоставляющая упорядоченной паре эле-
.иеятов х, у мультипликативной группы К* нек-рого
локального поля К элемент (х, у)?К*, являющийся кор-
корнем из единицы. Эта функция может быть определена
следующим образом. Пусть t.n?K — нек-рый первооб-
первообразный корень степени п из единицы. Максимальное абе-
лево расширение L поля К с группой Галуа G(L/K) по-
показателя п получается присоединением к К корней у а
для всех а?К*. С другой стороны, существует кано-
нич. изоморфизм (основной изоморфизм локальной
полей классов теории)
Q-.K/K*" ->G (L/K).
Норм е'н ный вычет для пары х, у определяется
из соотношения
в(у)(\/~~х) = (х, у)У~х.
В частном случае, для квадратичных полей, понятие
символа Н. в. было введено Д. Гильбертом (D. Hilbert).
Существует явное п использующее только локчльную
теорию полей классов определение Н. в. [4].
Свойства символа (.г, у):
1) билинейность: (х1 х2, y)=(Xl, y)(x2, у), (х, у1 г/2) =
= (я. У\) (х> г/2);
2) кососимметричность: (х, у) (у, я)=1;
3) невырожденность: из (х, j/)=l для всех
следует, что у?К*"; из (х, у) = 1 для всех
следует, что х?К*п;
4) если х-ту=1, то (х, г/) = 1;
5) если 0 — автоморфизм поля К, то
(ах, ау) = а(х, у);
6) пусть К' — конечное расширение поля К, а?К'*
и Ъ?К*. Тогда
(a, b) = (NK,IK(a),b),
где в левой части формулы символ Н. в. рассматривает-
рассматривается для поля К', в правой части — для поля К,
а Nк'/к —норменное отображение из К' в К\
7) из (х, у^~ 1 следует, что у является нормой из
расширения К(у х) (это свойство дало название сим-
символу).
Функция (,т, у) индуцирует невырожденное билиней-
билинейное спаривание
К*1К*п X К*1К*п ->¦ ц (")>
где ц(п) — группа корней из единицы, порожденная
?„. Пусть задано отображение ? : К*хК*-+А в неко-
некоторую абелеву группу А, удовлетворяющее условиям
]),4)и условию непрерывности: для любо-
любого у?К* множество {х^К*\^?(х, г/)=1} замкнуто в
К*. Символ Н. в. обладает следующим свойством
универсальности [3]: существует гомомор-
гомоморфизм (р:ц(п)-+А такой, что для любых х, у?К*
Это свойство служит основой аксиоматич. определе-
определения Н. в.
Если F — глобальное поле, а К — пополнение поля F
относительно нек-рой точки v, то символом Н. в. на-
называют также функцию (х, y)v, определенную на
F*XF*, получающуюся композицией (локального)
символа Н. в. (х, v) с естественным вложением F*-^>-K*.
Иногда символом Н. в. наз. автоморфизм 6(,^ мак-
максимального абелева расширения поля К, соответствую-
соответствующий элементу х?К* в силу локальной теории полей
классов.
Лит.: [1] Алгебраическая теория чисел, пер. с англ., М.,
1969; [2] Кох X., Теория Галуа р-расширений, пер. с нем.,
М., 1973; [3] Ми л нор Д ж., Введение в алгебраическую
К-теорию, пер. с англ., М., 1974; [4] Шафарсвич И. Р.,
«Матем. сб.», 1950, т. 26, Л'г 1, с. 113—46. Л. В. Кузьмин.
НОРМИРОВАНИЕ, логарифмическое
нормирование, оценка поля,— отобра-
отображение v : К—>-Г„, поля К в Гсе= F(J {оо }, где Г — линей-
линейно упорядоченная абелева группа, а присоединяемый
элемент оо считается больше любого элемента из груп-
группы Г и ж+оо = оо+а:= оо для любого ж?Г. При этом
Н. должно удовлетворять следующим условиям:
1) v @) = оо, v (х) < оо при х Ф 0;
2) v(a-b)=v(a)-\-v(b);
3) v(a — b)Samin(i; (a), v(b)).
Образ К*—К—{0} при отображении г; является под-
подгруппой группы Г и называется группой значе-
значений нормирования v. Всюду в дальнейшем
будет предполагаться, что v(K*) совпадает с Г.
Теми же аксиомами определяется логарифми-
логарифмическое нормирование колец. Всякое
кольцо с неархимедовым абсолютным значением может
быть превращено в логарифмически нормированное
кольцо, если в группоиде значений перейти от мульти-
мультипликативной записи к аддитивной и заменить упорядо-
упорядоченность на инверсную. Элемент 0 при этом естественно
обозначить символом оо. Обратный переход от кольца
с логарифмическим Н. к кольцу с неархимедовым аб-
абсолютным значением также возможен. Если в лольце
было задано неархимедово вещественное нормирование,
то соответствующий переход можно получить, заменяя
любое положительное действительное число ее числом
— lg а. Получающееся при этом логарифмическое Н.
также принято называть вещественным.
Нормирования l>x : К-^-Г1^ и v2 : ЛГ->Г^> наз. экви-
эквивалентными, если существует такой изоморфизм
ф : ГХ->Г2 упорядоченных групп, что для всех ненуле-
ненулевых элементов ?К
Множество таких элементов х поля К, что (
является подкольцом А поля К и наз. кольцом
нормирования v в поле К. Кольцо Н. всегда
является локальным кольцом. Элементы поля К, для
которых v(x)~>0, образуют максимальный идеал mv
кольца А; он наз. идеалом нормирования
v. Факторкольцо Aim, являющееся полем, наз. и о-
л е м вычетов нормирования v.
Пусть в поле К заданы Н. г>, и ч2. Кольца этих Н.,
рассматриваемые как подкольца поля К, тогда и только
тогда совпадают, когда эти Н. эквивалентны. Таким
образом, обозрение всех (с точностью до эквивалент-
эквивалентности) Н. поля К сводится к обозрению всех таких
подколец, которые могут служить для этого поля
кольцами Н. Описание таких подколец дает следующая
теорема: подкольцо А поля К тогда и только тогда
может служить для этого поля кольцом Н., когда для
всякого ненулевого элемента х^К, хотя бы один яз
элементов х, х-1 принадлежит к А. Кольцо Н., таким
образом, может быть абстрактно определено как це-
лостное кольцо (область целостности), удовлетворяю-
удовлетворяющее условию сформулированной выше теоремы по отно-
отношению к своему полю частных. Всякое такое кольцо
служит кольцом т. н. к а н о н и ч е с к о г о норми-
нормирования для своего поля частных, группой зна-
значений канонического Н. является группа K*/U, где
U—мультипликативная группа обратимых элементов
кольца А, упорядоченная отношением делимости.
Кольца Н. можно определить еще одним способом.
Если AczBc^K — два локальных кольца с максималь-
максимальными идеалами т. и п соответственно, то говорят, что В
доминирует А, если mczn. Отношение домини-
доминирования является отношением частичного порядка на
множестве подколец поля К. Максимальные элементы
этого множества и только они являются кольцами Н-
поля А". Если А — кольцо Н., а В^>А — кольцо с тем
же полем частных, что и А, то В также кольцо Н. и В
является локализацией кольца А по нек-рому про-
простому идеалу.
Примеры нормирований.
1) Нормирование поля, определяемое формулой:
v С )= i ®' если х ^ О'
( ' \ оо, если х = 0,
наз. несобственным, или тривиальным,
Н. Таково любое Н. конечного поля. Ему соответствует
точка id ¦ К-+К (тождественное отображение К).
2\ Пусть /; — нек-рое поле и K=-k((t)) — поле фор-
формальных степенных рядов над к. Сопоставление ряду
antn^ran_-ltn + 1-lr. . ., где ап-фЬ, его порядка п (а нуле-
нулевому ряду —оо) продолжается до Н. с группой значе-
значений 2 (аддитивная группа целых чисел) и кольцом
Н. &[[*]1. Ассоциированная точка сопоставляет ряду
ao+a1Z+a?if2-j-. . . из k[[t]] свободный член а0.
Н. со значениями в группе % яаз. дискретным; о их
кольцах Н. см. Дискретного нормирования кольцо.
Описание всех Н. поля рациональных чисел см. в [4].
Для любой линейно упорядоченной абелевой группы
Г существует Н. некоторого поля, группа значений
к-рого изоморфна Г.
Идеалы колец нормирования. Множество идеалов
кольца Н. линейно упорядочено относительно включе-
включения, любой идеал конечного типа— главный, т. е.
кольцо Н. является Безу кольцом. Более полно описа-
описание строения идеалов кольца Н. можно дать в терми-
терминах группы значений Н.
Подмножество М линейно упорядоченного множества
наз. мажорным (или мажором), если пз соотноше-
соотношений х?М и у >ж следует, что у?М. Пусть А — коль-
кольцо Н. о поля К с группой значений Г, Г+ — подполу-
подполугруппа положительных элементов Г и М — мажорное
множество в Г + . Отображение М—*а(М)= {х\х?К,
v(x)?M(J {оо }} является биективным (взаимно одно-
однозначным) отображением множества мажсфных подмно-
подмножеств из Г + на множество идеалов кольца А. При
этом главным идеалам соответствуют мажоры, облада-
обладающие минимальным элементом. Простым идеалам тоже
соответствуют мажоры специального вида, а именно:
мажоры вида Mff=T +—Н + , где Н + — положительная
часть нек-рой выпуклой подгруппы Н группы Г. Та-
Таким образом, устанавливается взаимно однозначное со-
соответствие между простыми идеалами А и выпуклыми
подгруппами группы значений Г.
Пусть р — простой идеал, соответствующий выпук-
выпуклой подгруппе Н, тогда композиция отображений
K->-T-+TlН будет Н. поля К с кольцом Н. Ар и идеа-
идеалом Н. рАр; кроме того, на поле Ар1рАр индуцируется
Н. со значениями в группе Н и кольцом Н. Alp. Тем
самым Н. расщепляется на более простые. Пусть А —
кольпо Н., тогда простой спектр А без нуля (Spec А—@))
является линейно упорядоченным множеством и его
тип наз. высотой, или рангом, соответствую-
соответствующего Н. Если Spec А конечен, то высота Н. есть число
элементов в Spec A—@), и это число совпадает с числом
выпуклых подгрупп группы Г, отличных от самой Г.
Н. конечного ранга сводятся к Н. ранга 1. Последние
характеризуются тем, что их группа значений — ар-
архимедова группа, т. е. изоморфна нек-рой подгруппе
аддитивной группы R действительных чисел. В этом
случае отображение х—>-ехр(-ч(х)) является ультрамет-
ультраметрическим абсолютным значением поля К.
Важное свойство колец Н.— целозамкнутость. Более
того, для произвольного целостного кольца А его це-
целое замыкание равно пересечению всех колец Н., со-
содержащих А. Кольцо Н. вполне целозамкнуто тогда и
только тогда, когда его Н. вещественное, т. е. имеет
ранг 1. Кольцо Н. нётерово тогда и только тогда, когда
Н. дискретно.
Связь нормирования и топологии. Пусть v : К^-Т^
Н. поля К и V —{х\х?К, v(x)>y}, где у?Т, Сово-
Совокупность всех V , у?Г, образует фундаментальную
систему окрестностей нуля топологии tv поля К, на-
называемой топологией, определяемой нор-
нормированием v. Топология iv отделима и несвязна.
Топология, индуцируемая %v на кольце А, как правило,
отлична от топологии локального кольца. Для нетриви-
нетривиального Н. поля К топология tv локально компактна
тогда и только тогда, когда Н. v дискретно, кольцо Н.
полное, а поле вычетов Н. v конечно; кольцо А при
этом будет компактно. Пополнение К поля К относи-
относительно топологии tv является полем; Н. v продолжает-
продолжается по непрерывности до Н. v : .?—>-Г«,, и топология К
совпадает с т~. Кольцо А нормирования г; является
пополнением кольца А нормирования v.
Нормирования v± и у2 поля К наз. независи-
независимыми, если топологии tVi и тУг различны; это экви-
эквивалентно тому, что кольца нормирований AVl и AVi
порождают поле К. Неэквивалентные нормирования
высоты 1 всегда независимы. Имеет место теорема
аппроксимации для нормирований:
пусть v/ : K—^rL, 1<:г'<:ге,— независимые нормирова-
нормирования, а;?К, а,?Г', тогда найдется такой элемент х
поля К, что v/(x—o,-)^a; для всех i.
Продолжения нормирований. Если v' : L ->- FL —
Н. поля L, а К — подполе L, то ограничение v=v'\K
нормирования v' на поле К является Н. поля К, а
его группа значений Г — подгруппой группы Г'; v'
наз. при этом продолжениям Н. v. Обратно,
если v — Н., a L расширение поля К, то всегда сущест-
существует Н. поля L, продолжающее v. Индекс [Г' : Г]
подгруппы Г в группе Г' наз. индексом ветвле-
ветвления Н. г/ относительно v и обозначается e(i'/v).
Поле вычетов kv нормирования г; отождествляется с
подполем поля вычетов kv>, степень расширения [fro> : &г,]
обозначается f(v'lv) и наз. степенью выче-
вычетов Н. i/ относительно о. Продолжение v' норми-
нормирования v наз. непосредственным, еслц
e{v'!v)=f(u'!v) = i.
Пусть L — расширение поля К, а {г;,- [ г?/} — множе-
множество всех продолжений Н. v на L. Если L — конечное
расширение поля К степени п, то множество всех
продолжений v конечно, и
В ряде случаев это неравенство можно заменить на
равенство, напр, когда v дискретно и либо К полно,
либо L сепарабрльно над К. Если L — нормальное
расширение К, то продолжения vb.hL переводятся
друг в друга .k-автоморфизмами L, в частности если
L — радикальное расширение К, то v имеет единствен-
ное продолжение. В случае произвольного бесконечного
расширения KczL или продолжения v' нормирования v
степень трансцендентности L над К больше или равна
сумме
S{v'lv)+r(v'!v),
где S(v'fv) —степень трансцендентности расширения
поля вычетов г/ над полем вычетов v, а г (и> /v) — раз-
размерность пространства (Tv,/Tv)(g)Q.
Понятие «Н.» ввел и изучил В. Крулль [1]. Это поня-
понятие широко используется также в алгебраич. геомет-
геометрии. Так, в терминах «колец Н.» строится абстрактная
риманова поверхность поля (см. [3]).
Лит.: [1] Krull W., «J. reine und angew. Math.», 1932,
Bd 167, S. 160—96; L2] Б у р б а к и Н., Коммутативная алгеб-
алгебра, пер. с франц., М., 1971; [3]3арисский О., Самю-
Самюэль П., Коммутативная алгебра, пер. с англ., т. 2, М., 1963;
[41 К у р о m А. Г., Лекции по общей алгебре, 2 изд., М.,
1973. В. И. Данилов.
НОРМИРОВАННАЯ АЛГЕБРА — алгебра над по-
полем действительных или комплексных чисел, являю-
являющаяся одновременно нормированным пространством,
умножение в к-рой подчиняется определенным условиям
непрерывности. Простейшее из таких условий — раз-
раздельная непрерывность. Раздельная непрерывность,
вообще говоря, слабее непрерывности по совокупности
сомножителей. Если, напр., на множестве всех фи-
финитных последовательностей ж=^(Ei, • • •» \ni 0> • • •) ал~
гебрапч. операции задать покоординатно, а норму —
формулой !W|=2ft=ii?fclA~2> To возникает алгебра, в
к-рой умножение раздельно непрерывно, но не непре-
непрерывно по совокупности. Непрерывность умножения
в Н. а. по совокупности сомножителей равносильна
существованию такой константы С, что ||я#||-<С||г||[|г/||.
В этом и только в этом случае пополнение обладает
структурой Н. а., расширяющей исходную, и является
банаховой алгеброй. Е. А. Горин.
НОРМИРОВАННАЯ СИСТЕМА — система \х;\ эле-
элементов банахова пространства В, нормы к-рых равны
единице, т. е. ||ж,-||в=1. В частности, система {/,• (¦?¦)}
функций, принадлежащих пространству L2[a, b], наз.
Н. с, если
Нормирование в банаховом пространстве В системы
{#,-} отличных от нуля элементов этого пространства
означает определение нормированной в В системы вида
{А.;ж,-}, где ?.,¦ — отличные от нуля числа, наз. норми-
нормирующими множителями. В качестве пос-
последовательности нормирующих множителей можно
взять Я,-=1/||г,-||в.
Лит.: [1] К а ч м а ж С, Ш т е й н г а у з Г., Теория
ортогональных рядов, пер. с нем., М., 1958; 12] Д а н ф о р д Н.,
Шварц Д ж. Линейные операторы. Общая теория, пер. с
англ., М., 1962; [3] К а н т о р о в и ч Л. В., А к и л о в Г. П.,
Функциональный анализ, 2 изд., М., 1977. А. А. Талаляп.
НОРМИРОВАННОЕ КОЛЬЦО — 1) то же, что нор-
нормированная или банахова алгебра.
2) Кольцо с заданным на нем нормированием.
НОРМИРОВАННОЕ ПОЛЕ — поле, на к-ром задано
нормирование (см. также Абсолютное значение на теле).
НОРМИРОВАННОЕ ПРОСТРАНСТВО — векторное
пространство над полрм действительных и комплексных
чисел с отмеченной нормой. &• А. Горин.
НОСИТЕЛЬ МЕРЫ jx— множество S(jj,) = G\G0(n),
где G — локально (би) компактное пространство, на
к-ром определена мера fi, G0(u) — наибольшее от-
открытое множество, для к-рого (x(Go) = O. Другими слова-
словами, S (\х) — наименьшее замкнутое множество, на
к-ром сосредоточена мера \х (при этом \i сосредоточена
на Е, если ji(G\i?)=O). Если S (а) компакт, то мера ft
наз. финитной. М. II. Войцеховский.
НОСИТЕЛЬ МОДУЛЯ М над коммутатив-
коммутативным кольцом/1 — множество всех простых идеа-
лов g кольца А, для к-рых локализованные модули М
ненулевые. Это множество обозначается Supp (М).
Оно является подмножеством спектра кольца. Напр.,
для конечной абелевой группы М, рассматриваемой
как модуль над кольцом целых чисел, Supp (M) состоит
из всех простых идеалов (р), где р делит порядок М¦
Для произвольного модуля М множество Supp (M)
пусто тогда и только тогда, когда М=0.
Лит.: 11] Б у р б а к и Н., Коммутативная алгебра, пер.
с франц., М., 1971. Л. В. Кузьмин.
НОСИТЕЛЬ ФУНКЦИИ / — наименьшее замкнутое
множество 5=supp /с! такое, что значения числовой
функции /, определенной на тонологич. пространстве
X, равны нулю всюду на дополнении CS=X\S. Иначе,
S есть замыкание множества всех точек х?Х, в к-рых
?(х)фО. Е. Д. Соломенцев.
НУЛЕВОЙ ОБЪЕКТ категории — такой объ-
объект (обозначаемый обычно 0), что для каждого объекта X
этой категории множества Н(Х, 0) и /7@, X) одноэле-
одноэлементны. Н. о., если он существует в данной категории,
определен однозначно с точностью до изоморфизма. В
категории множеств с отмеченной точкой Н. о. является
одноэлементное множество, в категории групп — еди-
единичная группа, в категории модулей — нулевой модуль
и т. д. Не всякая категория содержит Н. о., но его всег-
всегда можно формально присоединить к любой заданной
категории. Всякая категория с Н. о. есть категория с
нулевыми морфизмами. М. Ш. Цаленпо.
НУЛЬ — 1) Число, обладающее тем свойством, что
любое (действительное или комплексное) число при
сложении с ним не меняется. Обозначается символом
0. Произведение любого числа на Н. равно Н.:
Если произведение двух чисел равно Н., то один из
сомножителей равен Н. (т. е. из а6=0 следует, что или
а=0, или &=0). Деление на Н. не определено. Непосред-
Непосредственным обобщением этою понятия является понятие
Н. абелевой группы.
2) Н. абелевой группы — элемент абелевой
группы А (в аддитивной записи), также обозначаемый
символом 0 и удовлетворяющий аксиоме O-j-a—а для
всех а?А. Н. абелевой группы определен однозначно.
3) Н. кольца (в частности, тела, поля) —
Н. его аддитивной группы. Н. кольца (как и число 0)
относительно операции умножения обладает свойством
поглощения: а-0=(Ьа=0. Однако в произвольном
кольце произведение двух ненулевых элементов может
быть равно Н. Такие элементы наз. делителями нуля.
Поля, тела и области целостности делителей Н. не
имеют.
4) Левый Н. полугруппы А (в мультипликативной
записи) — элемент 0?Л, удовлетворяющий аксиоме
0-а—0 для всех а?А. Правый Н. определяется
двойственной аксиомой. Двусторонний Н.
(т. е. левый и правый одновременно) в полугруппе может
быть только один. Н. кольца является также Ы. муль-
мультипликативной полугруппы этого кольца.
5) Н. решетки — наименьший элемент этой ре-
решетки. Полная решетка всегда обладает Н., он — пере-
пересечение всех ее элементов.
6) Н. алгебраической системы — эле-
элемент, отмечаемый нульарной операцией (см. Алгебра-
Алгебраическая операция, Алгебраическая система). В боль-
большинстве рассмотренных выше примеров Н. является
единственным в данной системе и даже образует нуле
вую подсистему.
Н. наз. также нулевым элементом.
7)Н. категории — см. в ст. Нулевой объект
категории.
8) Н. функции f(xu . . ., хп), принимающей зна-
значения в нек-рой абелевой группе (кольце, поле, теле)
A,— набор значений переменных (х1. . . ., хп), при
К-ром f(xlt . . .. д-„) = 0. о. А. Иванова, Л. В. Кузьмин.
НУЛЬ — ЕДИНИЦА ЗАКОН — утверждение в тео-
теории вероятностей о том, что всякое событие (т. н. «ос-
«остаточное событие»), наступление к-рого определяется
лишь сколь угодно удаленными элементами последова-
последовательности независимых случайных событий или слу-
случайных величин, имеет вероятность нуль или единица.
Этот закон распространяется на системы случайных
воличин, зависящих от непрерывного параметра (см.
ниже).
Для отдельных остаточных событий равенство их
вероятностей нулю или единице было установлено в
нач. 20 в. Так, если Л,, А2, . . ., А„, . . . — нек-рая
последовательность независимых событий, то Для оста-
остаточного события А, состоящего в том, что наступает
бесконечно много событий А^\
обязательность одного из равенств
Р(А) = 0 или Р(А)=--Л
была отмечена Э. Борелем [1]. Простым подсчетом
было показано, что
Р(А)=0, если]?" Р(Ап)<оо
И
P(A) = i, если 2"=1'РИВ) = '»
(см. Бореля — Кантелли лемма).
Далее, если Хг, Хг, . . ., Хп, . . .—последовательность
независимых случайных величин, то вероятность схо-
димости ряда 2^к=хХ^ может быть равна только нулю
или единице; этот факт (одновременно с критерием,
позволяющим различать эти два случая) был установ-
установлен А. Н. Колмогоровым A928, см. [2J, [5]).
Изучались и остаточные события, связанные с ана-
литич. свойствами сумм функциональных рядов, напр,
степенных рядов со случайными членами. Так, расплыв-
расплывчатому утверждению Э. Бореля A896> о том, что при
«произвольных коэффициентах» граница круга схо-
сходимости степенного ряда является естественной гра-
границей представляемой им аналитич. функции, была
придана X. Шгейнхаузом [3] следующая точная форма.
Пусть Хь Х.;, . . ., Хп, ... — независимые равномер-
равномерно распределенные на @, 1) случайные величины, ak—
заданные числа и пусть ряд
/(*; Хъ Х2, ..., Х„, ...) = 2Г=1«
имеет радиус сходимости Л>0; тогда (остаточное)
событие, состоящее в том, что функция / не продолжима
через границу круга |г|<Л, имеет вероятность, равную
единице. Б. Йессен [4] доказал, что любое остаточное
событие, связанное с последовательностью независи-
независимых равномерно распределенных на @, 1) случайных
величин, имеет вероятность, равную нулю или единице.
Общая теорема о вероятностях, равных нулю или
единице, была сформулирована А. Н. Колмогоровым
(см. [5J) следующим образом. Пусть Хг, Х2, . . .,
Хп, ... — какая-либо последовательность случайных
величин, а /(Хц Х2, . . ., Хп, . . .) — бэровская функ-
функция переменных Xlt Х2, . . ., Хп, . . . такая, что
условная вероятность
Р {/ (Xlt Х2, .. ., Х„, ...) =0 | Хи Х2, ..., X,,}
соотношения
/ (Xii Х2, . .., Хп, . . .) =0
при известных п первых величинах Х-у, Х2, . . ., Хп
остается равной абсолютной (безусловной) вероятности
Р {/(*!, Х2, ..., Х„, ...) = 0} (*)
для каждого п. При этих условиях вероятность (*)
равна нулю или единице. Для независимых Xt, X2: . . .,
Хп, . . . отсюда вытекает Н.—е. з., как он сформулиро-
сформулирован в начале статьи.
Указанная теорема Колмогорова вытекает, как по-
показал П. Леви A937, см. [6]), из более общего свойства
условных вероятностей, состоящего в том, что
ШпР {/(*!, X,, ..., Хп, ...) = 0\Х1, Х2, ..., X,,}
почти наверное равен или единице или нулю (в соот-
соответствии с тем, будет ли f(Xi, Х%, . . ., Хп, . . .) —О
или нет). В свою очередь, это утверждение вытекает из
теорем о мартингалах (см. [7] гл. III, § 1; гл. VII,
§§ 4,5,7 п комментарии к ним; в § 11 имеется аналог
Н.— е. з. для случайных процессов с независимыми
приращениями; из него вытекает, в частности, что выбо-
выборочные функции сепарабельного гауссовского процес-
процесса с непрерывной корреляционной функцией с вероят-
вероятностью 1 непрерывны в каждой точке либо с вероят-
вероятностью 1 имеют разрыв второго рода в каждой точке,
см. [81).
Для специального случая последовательности
Хг, Х$, . . ., Х„, . . . независимых и одинаково распре-
распределенных случайных величин было показано (см. [9]),
что вероятность по только любого остаточного, но и лю-
любого инвариантного относительно перестановок конеч-
конечного числа членов последовательности события равна
нулю или единице.
Лит.: [1] В о г е 1 Е., «Rend. Circolo mat. Palermo», 1909,
v. 27, p. 247—71; [2] Колмогоров А. Н., «Math. Ann.»,
1928, Bd 99, S. 309 — 19; [3] Steinhaus H., «Math. Z.»,
1929, Bd 31, S. 408—16; [4] J e s s e n В., «Acta math.», 1934,
v. «3, p. 249—323; [5] К о л м о г о р о в А. Н., Основные
понятия теории вероятностей, 2 изд., М., 1974; [6] Levy P.,
Theorie de l'addition des variable aleatoires, 2 ed., P., 1954;
[7] Дуб Дж., Вероятностные процессы, пер. с англ., М.,
1956; [8] Д о б р у ш и н Р. Д., «Теория вероятн. и ее приме-
применения», 1960, т. 5, № 1, с. 132—34; [91 Н е w i t t E., Savage
L. J., «Trans. Amer. Math. Soc», 1955, v. 80, JV« 2, p. 470 — 501.
А. В. Прохоров, Ю. В. Прохоров.
НУЛЬМЕРНОЕ ОТОБРАЖЕНИЕ — непрерывное
отображение / : X-^-Y (X, Y — топологич. пространст-
пространства) такое, что /(г/) — нульмерное множество (в смы-
смысле ind) для всякого у?У. Применение Н. о. и близких
к ним позволяет свести исследование данного простран-
пространства к изучению другого, более простого. Так, многие
размерностные свойства и другие кардинальнозначные
инварианты переходят от X к Y (или, чаще, от У к X).
П р п м е р 1. Всякое метрич. пространство X с
dim Х<л допускает вполне Н. о. в пространство Y со
счетной базой, причем dim У</г (теорема Кате-
то в а). При этом полная нульмерность означает, что
для любого s>0 и любого y(zf(X) существует окрест-
окрестность UydY, прообраз f-1(Uy) к-рой распадается в дис-
дискретную в X систему открытых в X множеств диаметра
<е.
П р и м е р 2. Если Н. о. f : X-+Y, где X — нор-
нормальное локально связное пространство, является совер-
совершенным отображением, то вес X совпадает с весом Y.
Лит.: [1] Александров П. С, Пасынков Б. А.,
Введение в теорию размерности, М., 1973.
М. И. Войцеховский.
НУЛЬМЕРНОЕ ПРОСТРАНСТВО в смысле
ind — пространство, обладающее базой из множеств
одновременно открытых и замкнутых в нем. Каждое
дискретное пространство нульмерно, однако Н. п.
может не иметь изолированных точек (пример — про-
пространство рациональных чисел Q). Все нульмерные
пространства вполне регулярны. Нульмерность про-
пространства наследуется его подпространствами и влечет
сильную несвязность пространства: единственными
связными множествами в Н. п. являются одноточечное
и пустое. Однако последнее свойство, наз. вполне
несвязностью, не равносильно нульмерности.
Существуют ненульмерные пространства, в к^рых каж-
каждая точка представима в виде пересечения нек-рого се-
семейства открыто-замкнутых множеств, но среди таких
пространств нет бикомпактов.
Иногда нульмерность пространства понимается более
узко. Пространство наз. нульмерным в смыс-
л е dim, если во всякое его конечное открытое покры-
покрытие можно вписать открытое покрытие, элементы к-рого
не пересекаются. Пространство наз. н у л ь м ер н ы м
в смысле Ind, если любая окрестность любого его
замкнутого подмножества содержит открыто-замкнутую
окрестность этого подмножества. В классе ^-прост-
^-пространств нульмерность в смысле ind вытекает как из нуль-
нульмерности в смысле dim, так и из нульмерности в смысле
Ind. В классе метризуемых пространств со счетной ба-
базой, а также в классе бикомпактов указанные три опре-
определения нульмерности равносильны. Для всех метри-
метризуемых пространств нульмерность в смысле dim равно-
равносильна нульмерности в смысле Ind, однако известен
пример нульмерного в смысле ind метризуемого про-
пространства, к-рое не нульмерно в смысле Ind. Ни нуль-
нульмерность в смысле dim, ни нульмерность в смысле Ind
не наследуется, вообще говоря, подпространствами.
Среди /^-пространств Н. п. в смысле ind характеризу-
характеризуются с точностью до гомеоморфизма как подпростран-
подпространства обобщенных канторовых дисконтинуумов DT —
произведений двоеточий. Любые вполне регулярные
пространства можно получить как образы Н. п. при
достаточно хороших отображениях, напр, при со-
совершенных отображениях и при непрерывных открытых
отображениях с бикомпактными прообразами точек.
Однако непрерывные отображения, открытые и замкну-
замкнутые одновременно, сохраняют нульмерность в смысле
ind и в смысле Ind. Неизвестно A981), каждое ли вполне
регулярнее пространство содержит всюду плотное
нульмерное подпространство.
Лит.: [1] А л е к с а н д р о в П. С, Пасынков Б. А.,
Введение в теорию размерности..., М., 1973.
А. В. Архангельский.
НУЛЬ-СИСТЕМА — инволюционная корреляция
7г-мерного проективного пространства, оператор к-рой
является антисимметричным. Пусть Н.-с. имеет вид
'и=Ах,
тогда скалярное произведение 'их, равное
(х, Ах)-=—(х, Ах),
обращается в нуль.
Лит.: [1] Розенфельд Б. А., Многомерные про-
пространства, М., 1966. Д. Д. Соколов.
НУМЕРАЦИЯ — основное понятие раздела теории
алгоритмов — теории нумераций, изучаю-
изучающей общие свойства классов объектов, занумерованных
с помощью каких-либо конструктивных объектов.
В роли конструктивных объектов, служащих номерами
элементев рассматриваемых классов, чаще всего вы-
выступают натуральные числа.
Идея Н. объектов нечисловой природы (напр., ло-
гич. фврмул) натуральными числами и перенесение
содержательных утверждений об этих объектах в об-
область формальной арифметики натуральных чисел впер-
впервые были использованы К. Гёделем (К. Godel) при до-
доказательстве Гёделя теоремы о неполноте арифметики
Пеано. В дальнейшем эти идеи были использованы
для Н. фундаментальных объектов теории алгоритмов
таких, как Тьюринга машин, частично рекурсивных
функций и рекурсивно перечислимых множеств. На-
Наделение этих классов объектов подходящими Н. позво-
позволило во многих случаях выяснить более отчетливо при-
природу этих объектов, выявить ряд их важных п новых
свойств. Так возникла идея о системами, изучении Н.
произвольных множеств. При реализации этой идеи
было замечено, что многие известные результаты теории
алгоритмов оказываются следствиями общих закономер-
закономерностей теории Н. (о построении теории Н., создании
ее специфич. понятий и методов, о формировании пер-
перспективных направлений в теории Н. см. il] — [4]).
В частности, был плодотворно использован язык теории
категорий, позволивший взглянуть на проблематику
теории II. с новой точки зрения (см. [4]).
Нумерованным множеством наз. па-
пара Щ.=(A, \>>, где А — нек-рое счетное множество, а
v — некоторое отображение множества натуральных
чисел N на Л. Отображение v наз. нумерацией
множества А. Если v(n) = a, то п наз. номе-
номером объекта а при нумерации v. H. Vj множества
Л сводится к Н. v2 множества А (отношение
сводимости Н. обозначается ¦<), если существует
одноместная общерекурсивная функция / такая, что
v1(re) = v2(/(/i)) для всех n?N- Нумерации \\ и v2 мно-
множества А наз. эквивалентными, если \\<.\'2
и VjOv С точки зрения теории Н. эквивалентные Н.
одного и того же множества неразличимы. По этой при-
причине объектом исследования обычно является мно-
множество L{A)—множество классов эквивалентных Н.
множества А, частично упорядоченное отношением
сводимости Н. <:. Часто рассматривается и лгножество
L(A, v) — множество классов эквивалентных Н. мно-
множества А, сводящихся к Н. v. Множества L(A) и
L(A,v) во многих случаях служат нек-рой. «мерой
сложности» множества А.
При сравнении Н. двух множеств А и В основным по-
понятием является понятие морфнзма. М орфизмом
из нумерованного множества 31—<^4,v1> в нумерован-
нумерованное .множество 33 = <.В, v2> наз. всякое отображение ц
из А в В, для к-рого существует одноместная общере-
общерекурсивная функция / такая, что u.Vj («) = v2(/(n)) для
всех n?[\j. Через Мог Ct, SB) обозначают множество
всевозможных морфпзмов из Ж в 93- С изучением мно-
множеств Мог, в частности с выяснением возможности на-
наделения этого множества «хорошими» Н., тесно свя-
связаны многие вопросы общей теории алгоритмов.
Категория Щ. нумерованных множеств состоит из
нумерованных множеств и морфизмов. Исследование
свойств этой категории 9? является основной задачей
теории Н. Исходным пунктом такого исследования
часто является изучение связей нумерованных мно-
множеств с важнейшими конкретными Н.— нумерацией
К л пни ц> всех одноместных частично рекурсивных функ-
функций и нумераций Поста л всех рекурсивно перечисли-
перечислимых множеств. В теории алгоритмов доказано сущест-
существование двуместной частично рекурсивной функции
U(х, у), универсальной для класса всех одноместных
частично рекурсивных функций, т. е. такой, что для
любой частично рекурсивной функции f{x) можно най-
найти число а такое, что f(x)= U(a, x). Нумерация
К л и н и ф задается тогда следующим образом:
фд. (у) = U(х, у). Если Яд. обозначает область значений
функции <рх, то получаем нумерацию Поста я
всех рекурсивно перечнелимых множеств.
Фундаментальную роль при исследовании категории
9? играет введенное А. И. Мальцевым понятие полной
Н., к-рое в самвй общей форме синтезировало глав-
главные свойства нумераций Клини ср и Поста it. H. v
множества А наз. полной, если среди элементов мно-
множества А имеется такой выделенный элемент а, что
для любой одноместной частично рекурсивной функции /
существует одноместная общерекурсивная функция h
такая, что
, , , / v/ (х), если значение / (х) определено,
\х) \ а в противном случае.
Полные Н. играют роль «ппъектпвпых» элементов кате-
категории 9? и наличие у А полных Н. свидетельствует
о значительной универсальности и важности класса
объектов А. В частности, и нумерация Клини ср час-
частично рекурсивных функции, и нумерация Поста я ре-
рекурсивно перечислимых множеств суть полные Н.
(в первом случае выделенным элементом а является
нигде не определенная функция, а во втором — пустое
множество). Важным направлением в исследовании кате-
категории 9J является также выделение и изучение различ-
различных видов подобъектов нумерованных множеств (см. [4]).
Часть теории Н., связанная с изучением нумераций
Клини и Поста, а также их подобъектов, наиболее раз-
разработана, т. к. в этих случаях использование методов
теории алгоритмов наиболее эффективно. Здесь в пер-
первую очередь изучаются т. н. вычислимые Н. Если мно-
множество А, напр., является семейством рекурсивно пере-
перечислимых множеств, то Н. v этого семейства наз. вы-
вычислимой, если отношение x?v(y) само является
рекурсивно перечислимым. Множество классов экви-
эквивалентных вычислимых Н. семейства А обозначают
L°(A). Это множество, как и L(А), частично упорядо-
упорядочивается отношением сводимости Н. <:. Максимальный
элемент множества L°(A), если он существует, наз.
главной вычислимой нумерацией се-
семейства А. В частности, нумерации Клини и Поста
являются главными вычислимыми Н. для соответству-
соответствующих семейств Ф (всех одноместных частично рекур-
рекурсивных функций) и Р (всех рекурсивно перечислимых
множеств). Большое число работ в теории Н. посвяще-
посвящено изучению множеств Ь°(Ф) и Ь°(Р). При этом нужно
учесть, что многие свойства частично рекурсивных
функций и рекурсивно перечислимых множеств, вы-
выявленные в теории алгоритмов, по существу являются
отражениями алгебраич. свойств множеств Ь° (Ф) и
L°(P). Так, напр., легко укладываются в схему теории
Н. изучаемые в теории алгоритмов и играющие там
важную роль так наз. то-степени множеств. Если рас-
рассматривать семейство А, состоящее всего из двух мно-
множеств 0 и {0}, то то-с тепени множеств есть
не что иное, как L (А), а т-с тепени рекурсив-
рекурсивно перечислимых множеств суть L° (A).
Имеется полное алгебраич. описание устройства мно-
множеств L(A) и L°(A) (см. [4]).
Пусть А — нек-рое семейство рекурсивно перечис-
перечислимых множеств (для частично рекурсивных функций
рассматриваемые понятия вводятся аналогично). И н-
д е к с н ы м (или номерным) множеством
семейства А наз. множество
номеров рекурсивно перечислимых множеств семейства
А в нумерации Поста. В теории Н. изучаются индексные
множества QA для различных семейств А. Так, георема
Раиса — Шапиро дает описание тех семейств А, для
к-рых множество QA рекурсивно перечислимо. Такие
семейства в теории Н. носят название вполне пе-
перечислимых классов. Даны также описания
других видов подобъектов нумерации Поста — специаль-
специальных стандартных классов, факторизации и ретрактов.
Большую роль играют т. н. стандартные классы.
Семейство S рекурсивно перечислимых множеств
наз. стандартным классом, если существует
общерекурсивная функция / такая, что: S= {я(/@)),
л(/A)), . . .}; при этом, если tc(x)?S, to n(x)=n{f(x)).
Стандартные классы тесно связаны с полными Н. В
настоящее время A982) нет удовлетворительного описа-
описания стандартных классов. Такое описание могло бы
пролить свет на многие вопросы теории алгоритмов.
В теории Н. также рассматривались главные, эффектив-
эффективно-главные и другие виды подобъектов нумерации Пос-
Поста (см. [4]).
Алгоритмич. аналогом понятия алгебраической сис-
системы, т. о. множества с заданными на нем функциями
и предикатами, является понятие нумерованной,
или конструктивной, алгебраиче-
алгебраической системы. Идея состоит в следующем. Рас-
Рассматриваемое множество А наделяется Н. Вместо функ-
функций и предикатов, заданных на объектах множества А,
рассматриваются «переводы» этих функций и предика-
предикатов, оперирующие соответствующим образом с нату-
натуральными числами как с номерами объектов множест-
множества А. Если при этом можно добиться того, чтобы эти
«переводы» функций и предикатов были общерекурсив-
общерекурсивными, то говорят, что данная алгебраич. система к о н-
структивизируема. Первое систематич. изу-
изучение теории конструктивных алгебраич. систем было
предпринято А. И. Мальцевым [31.
Следует отметить два наиболее ярких применения
теории Н. к задачам теории алгоритмов: завершение
построения теоргси Майхилла об универсальных объек-
объектах и построение теории вычислимых функционалов
конечных типов (см. [4]). Методы и результаты теории
Н. могут быть использованы в смежных к математич.
логике и теории алгоритмов науках, в частностп в
программировании. Так, с помощью теории Н. могут
быть решены нек-рые вопросы семантики языков про-
программирования.
Лит.: [1] М а л ь ц е в А. И., Алгоритмы и рекурсивные
функции, М., 1965; [2] е г о же, «Успехи матем. наук», 1961,
т. 16, в. 3, с. 3—60; [3] У с п е н с к и й В. А.. Лекции о вы-
вычислимых функциях, М., 1960; [4] Ершов Ю. Л., Теория
нумераций, М., 1977. И. А. Лавров.
НУМЕРИЧЕСКИ ВЫРАЗИМЫЙ ПРЕДИКАТ —
арифметический предикат Р (хг, . . ., хп), обладающий
по отношению к данной формальной системе S арифме-
арифметики следующим свойством: существует такая формула
F(xi, . . ., хп) в языке арифметики формальной, что
для любых натуральных чисел кг, . , ., кп
1) если P(ki, . . ., кп) истинно, то |—sF(ki, • • •> ^ПК
2) если Р(кг, . . ., кп) ложно, то f—s~\F(ki, ¦ • •> Аи)>
где |—5 означает выводимость в системе S, а Р(кл,
. . ., кп) — результат подстановки в формулу F(x1, . . .,
хп) вместо переменных хи . . ., хп— термов, изобража-
изображающих числа &i, - . ., кп. В этом случае говорят, что
формула F(xlt . . ., х„) н у м е р и ч е с к и выра-
выражает предикат Р (хг, . . ., хп). Для формаль-
формальной системы S арифметики имеет место утверждение:
в S нумерически выразимы все рекурсивные преди-
предикаты и только они.
и-местная арифметич. функция / наз. нумери-
нумерически пррдставимой в формальной систе-
системе S арифметики, если существует такая арифметич.
формула F(xu . . ., хп, у), что для любых натуральных
чисел А], . . ., кп, I
1) если /(*!, . . ., кп) = 1, то \-SF(ku . . ., кп, I),
2)[~sByF(k1, . . ., кп, y)&VxVy(F(ku . . ., кп,
x)&F(k1, . . ., кп, у) Г)ж=у).
В обычных формальных системах арифметики нуме-
нумерически представимы все общекурсивные функции и
только они.
Лит.: [1] К лини С. К., Введение в метаматематику,
пер. с англ., М., 1957. В. Е. Плиско.
НУМЕРОВАННАЯ МОДЕЛЬ — пара (Щ?, v), где
2Л — модель нек-рой фиксированной сигнатуры а0 и
v — нумерация основного множества М модели >Ш-
Наиболее развитым направлением в изучении Н. м.
является конструктивных моделей теория. Другим
надравлением в теории Н. м. является исследование
проблемы сложности Н. м., под к-рой понимается
сложность множеств натуральных чисел у (ThBJ}, v)),
либо множества y-](Th0(QJ!, v)). В качестве у здесь
берется нек-рая гёделева нумерация всех формул сиг-
сигнатуры (T^a0U{c0, . . ., с„, . . .}, где константы сп
не принадлежат сигнатуре а0, a Th (Щ|, v) — это мно-
множество всех замкнутых формул сигнатуры а истинных
на системе 2Jlv, к-рая получается из системы Щ} обо-
гащением сигнатуры аа до а, причем значение константы
сп полагает равным элементу v(n), a Тпо(Щ}, v) озна-
означает соответственно, множество всех бескванторных
предложений, истинных на системе ffl?v.
Различные специальные модели элементарных теорий
играют важную роль в математич. логике и алгебре.
Один из важных вопросов — проблема их сложности.
Получены следующие результаты. Пусть ИА, ПА, АА
и 2 л, П)г'Л, А]{А обозначают соответственно арифме-
арифметическую и аналитическую иерархии относительно
множества А.
Если теория Т рекурсивна относительно А и имеет
простую модель Щ}, то существует нумерация v мо-
модели Щ] такая, что v~1(ThBJ}, v))?AA, то есть
Y-1(Th (Ш1, v)) рекурсивно относительно множества
А' всех гёделевых номеров х таких вычислимых отно-
относительно А функций (рА, для к-рых уА (х) определено.
Если теория Т рекурсивна относительно А и имеет
счетную насыщенную модель Щ}, то существует нумера-
нумерация v модели <Ш такая, что у-1 (Th (<Ш, 0)) ? А\' а, то
есть Y~1(ThBJ}, v)) есть гиперарифметич. множество от-
относительной; эти оценки сложности являются в нек-ром
смысле точными.
С нахождением точной оценки связан также следую-
следующий результат. Известно, что любая непротиворечи-
непротиворечивая формула имеет Н. м. (?Ш, v) сложности Д°, т. е.
Иерархия ЕршоЕа дает более тонкую классификацию
множеств из Д°. Доказана теорема: для любого п су-
существует непротиворечивая формула ф„, не имеющая
Н. м. (Ш1, v) с предикатами из 2 л1, то есть v-1(P,)^2^1
и Щ}|—ф„, где ао=<Р1, Р2, Р3, Р4>. В конструктивной
безатомной булевой алгебре (ЭД}, v) построен рекурсивно
перечислимый идеал / (т. е. множество v-1 (/) рекурсив-
рекурсивно перечислимо1 такой, что булева алгебра 2J}// не
конструктивизируема. Это позволило доказать нере-
нерекурсивную представимость решетки рекурсивно пере-
перечислимых множеств.
Исследование нумерованных линейных порядков поз-
позволило опровергнуть гипотезу сильной однородности
для тьюринговых степеней.
Лит.: [1] Гончаров С. С, Дроботун Б. Н.,
«Сиб. матем. ж.», 1980, т. 21, № 2, с. 25—41; [2] Денисов
С. Д., «Алгебра и логика», 1972, т. 11, №6, с. 648—55; [3]
Дроботун Б. Н., «Сиб. матем. ж.», 1977, т. 18, №5, с.
1002—14; [4] Ершов Ю. Л., Теория нумераций, М., 1977;
[5] Роджерс X., Теория рекурсивных функций и эффектив-
эффективная вычислимость, пер. с англ., М., 1972; [6] FeinerL.,
«J. Symbol. Logic», 1970, v. 35, p. 365—74; [7] e г о ж е, там
же, р. 375 — 77. С. С. Гончаров
НУССЕЛЬТА ЧИСЛО — безразмерный параметр,
характеризующий интенсивность конвективного тепло-
теплообмена между поверхностью тела и потоком газа (жид-
(жидкости): Nu—al/X, где a^Q/ATS — коэффициент тепло-
теплообмена, Q — количество тепла, отдаваемого (или по-
получаемого) поверхностью тела в единицу времени,
ГД>0 — разница между температурой поверхности
тела и температурой газа (жидкости) вне пограничного
слоя, S — площадь поверхности, I — характерный
размер, % — коэффициент теплопроводности газа.
Н. ч. наз. по имени В. Нуссельта (W. Nusselt).
БСЭ-З.
НЬЮТОНА БИНОМ — формула разложения произ-
произвольной натуральной степени двучлена в многочлен,
расположенный по степеням одного из слагаемых дву-
двучлена:
n—k k
Z2>
где Cm=m\lk\(m—к)\— биномиальные коэффициенты.
Для 7г слагаемых формула (*) принимает вид
-2j&14-ftz + ... + fen = m fct! ft.' ...ftnl Zl *2 ¦¦¦Zn •
При произвольном показателе от, действительном или
даже комплексном, в правой части (*) получается,
вообще говоря, биномиальный ряд.
Постепенное освоение формулы Н. б., начинавшееся
с ее простейших частных случаев (формул «квадрата
суммы» и «куба суммы»), прослеживается уже с 11 в.
Заслуга И. Ньютона (I. Newton), собственно говоря,
состоит в открытии биномиального ряда.
Е. Д. Соломенцев.
НЬЮТОНА ДИАГРАММА, многоугольник
Ньютон а,— выпуклая ломаная, введенная И. Нью-
Ньютоном (I. Newton) в 1669 (см. [1]) для определения по-
показателей главных членов алгебраич. функций. Про-
Процесс последовательного нахождения членов разложе-
разложения алгебраич. функции с помощью Н. д. носит назва-
название метода диаграммы Ньютона. Более
подробно метод Н. д. был разработан В. Пюизё [2], ив
математич. литературе Н. д. иногда няз. диаграм-
диаграммой Пюизё. Алгебраич. вариант Н. д. задолго до
В. Пюизё был исследован Ж. Лагранжем [3].
Пусть F(x, у) — псевдомногочлен относительно у, т. е.
F(x, У)=2"=о *",(*) У*,
где
х, у — комплексные переменные, Frs — комплексные
числа, р — натуральное число, р^ — неотрицательные
рациональные числа, Fn(x)^0, F0(x)^=D. Обычно счи-
считается, что если Fs (x) =?0, то F0S=?0, а значит Fo0^O,
Fonj=O. Решения у—у(х) уравнения
F(x, y)=0 A)
ищутся в виде ряда
У = Уе хе. + уг.хг' + уе»хе" + . . ., B)
где е<е'<е"<. . . или, короче, y=yExs-\~z, где z—
= 0 (хе) при х—>0. Для определения возможных значений
еи}? подставляется B) в A), собираются члены с оди-
одинаковыми степенями х и приравниваются нулю коэф-
коэффициенты при этих степенях.
Процесс начинается с члена наинизшей степени.
Пока показатель 8 не определен, нельзя сказать, какие
из полученных членов будут наинизшими по х. Однако
члены наинизшего порядка содержатся среди следую-
следующих:
. FooxP°, FokyEkxPk + ket F^fiaPn+n*, C)
где к пробегает те из значений 1,2, . . ., для к-рых
Рк(х)ф0. Для уничтожения членов наинизшего по-
порядка необходимо подобрать 8 так, чтобы по меньшей
мере два из показателей р0, p^+ftg, pn-f пг совпали, а
остальные были не меньше их. Это соображение и при-
приводит к Н. д.
На плоскости выбирается прямоугольная декарто-
декартова система координат и строятся точки @, р0), (к, р^),
(п, р„), где к пробегает те же значения, что и в C).
Через точку @, р0) проводится прямая, совпадающая
с осью ординат, к-рая затем вращается вокруг точки
@, ро) против часовой стрелки до тех пор, пока она не
попадет на какую-либо из нанесенных точек, напр.
(I, pi). Тангенс угла, составленного прямой L, проходя-
проходящей через точки @, р0) и G,, р?), с отрицательным на-
направлением оси абсцисс, равен одному из значений 8,
так как po=p(+'6, a Pft+^s > Pz+te, если (к, pk)?
Пусть (s, ps) — точка на L с наибольшей абсциссой и
пусть теперь L вращается против часовой стрелки во-
вокруг точки (s, ps), пока она не попадет на другую из
нанесенных точек, ска-
скажем (t, pf) С t > S.
Пусть L' — прямая, про-
проходящая через (s, p^) и
(t, pt). Тангенс угла,
образованного L' с от-
отрицательным направле-
направлением оси абсцисс, даст
еще одно из возможных
значений 8. Продолжени-
Продолжением этих построений получается выпуклая ломаная,
к-рая п наз. диаграммой Ньютона.
Определение значений коэффициента уе таково.
Пусть (i, pj), (j, pj) — крайние точки отрезка Н. д.,
определяющего одно из возможных значений 8. Для
того чтобы при подстановке B) в A) уничтожились
члены наинизшего порядка, необходимо и достаточно,
чтобы
рп
Po
Pi
Ps
ft
N.
1 1 ^^^M
t- -+ ^
! 1
1 1 1
>t
/i
/ {
/ !
' 1
1
!
где штрих суммы означает, что суммирование проводит-
проводится по р, удовлетворяющим соотношению p^-pse = р,--Ь
+ 1Б. Уравнение D) имеет / — i отличных от нуля
корней (с учетом их кратности), т. е. столько корней,
какова длина проекции взятого отрезка Н. д. Отсюда
видно, что методом Н. д. получаются все п значений
главного члена у?хг в формуле B). Этим же методом оп-
определяется следующий член в разложении B), и т. д.
В результате все п решений уравнения A) имеют вид B)
т. н. рядов Пюизё (см. Алгебраическая функция).
Метод Н. д. применяется также и при решении диффе-
дифференциальных уравнений.
Лит.: [1] Ньютон И., Математические работы, пер.
с латин., М.— Л., 1937, с. 33 — 34; [2] Р u i s е и х V., «J. math,
pure et appl.», 1850, t. 15, p. 365 — 480; [3] L a g г a n g e J.,
«Nouv. Mem. Acad. Roy. Sci.», 1776; [4] В а Й н б е р г М. М.,
Треноги н В. А., Теория ветвления решений нелинейных
уравнений, М., 1969; [5] Исаак Ньютон. 1643—1727.
Сб. статей к трехсотлетию со дня рождения, М.— Л., 1943;
[6] Б р ю н о А. Д., Локальный метод нелинейного анализа
дифференциальных уравнений, М., 1979. В. А. Треногий.
НЬЮТОНА ЗАКОНЫ МЕХАНИКИ — три основных
закона, описывающие движения материальных тел под
действием приложенных к ним сил.
Первый закон: если на материальную точку не
действуют никакие силы (или если приложенные к ней
силы взаимно уравновешиваются), то по отношению к
инерциальной отсчета системе материальная точка бу-
будет находиться в состоянии покоя или равномерного
прямолинейного движения.
Второй закон: если на материальную точку
действует сила F, то точка получает по отношению к
инерциальной системе отсчета такое ускорение w, что
произведение массы т точки на это ускорение равно
силе F:
Третий закон: две материальные точки дей-
действуют друг на друга с силами, равными по абсолютной
величине и направленными в противоположные стороны
вдоль прямой, соединяющей эти точки.
Н. з. м. перестают быть справедливыми для дви-
движения объектов очень малых размеров (элементарных
частиц) и при движениях со скоростями, близкими к
скорости света.
Законы сформулированы И. Ньютоном (I. Newton,
1687). С. М. Таре.
НЬЮТОНА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА —
форма записи Лаграижа интерполяционной формулы.
использующая разделенные разности:
Ln (х) = / (х0) + (х~х0) f (х0; Xl) +
+ (х — х0) (x — xjfixo; хг; хг)+ .. .+(х — х0) (x — xj...
...(x — xn_1)f(xo;x1;...;xn), A)
где f(x0; xi, . . .; xk) — разделенные разности к-то поряд-
порядка; рассматривалась И. Ньютоном (I. Newton, 1687).
Формула A) наз. Н. и. ф. для неравных проме-
промежутков. В случае, когда значения х,- являются
равноотстоящими, т. е.
Xi Хо —Х2 Xi = . . . =Хп Хп_1 — П,
введя обозначение (х — xo)/h—t и выразив разделенные
разности f(x0; . . .; xk) через конечные разности /^2
по формуле
/(*„; хг; ...\xh)=jtnlh4\, к = 0, 1, ..., п,
получают запись многочлена Ln (,x) в форме
L/i+'—2! /1-Г--Н ^i /n/a . B)
которая наз. Н. и. ф. для интерполирова-
интерполирования вперед. Если такая же замена переменных в
интерполяционном многочлене Ln производится по
узлам х0, я_1, . . ., х_„, где x_k = x0 — kh,
Ln (x)=f (xo) + (x~xo) / (х0; х_г) +
+ (х — х0) (x—xx)f (x0; x_i\ ж_2) + ...
... + {х — х0) ... (x — x_n + i)f(x0; ...; хп),
то получается Н. и. ф. для интерполиро-
интерполирования назад:
i 2! /-i + • • • T и] /-л/2. (о)
Формулы B), C) удобны при вычислении таблиц за-
заданной функции f(x), если точка х находится в начале
или конце таблицы, поскольку в этом случае добавление
одного или нескольких узлов, вызванное стремлением
повысить точность приближения, не приводит к пов-
повторению всей проделанной работы заново, как при вы-
вычислениях по формуле Лагранжа.
Лит.: [1] Б е р е з и н И. С, Жидков Н. П., Методы
вычислений, 3 изд., т. 1, М., 1966; [2] Б а х в а л о в Н. С,
Численные методы, 2 изд., М., 1975. М. И. Самарин.
НЬЮТОНА МЕТОД, метод касательны х,—
метод приближенного нахождения корней действитель-
действительного уравнения
/(х)=0, A)
где / — дифференцируемая функция. Последовательные
приближения Н. м. вычисляются по формулам
г* + 1=лгА —[/' (ж*)]-1/(а:*), * = 0, 1, 2, ... B)
Если функция / дважды непрерывно дифференцируема,
х* — простой корень уравнения A) и начальное при-
приближение Xй лежит достаточно близко к х*, то Н. м.
обладает квадратичной сходимостью, т. е.
где с — константа, зависящая только от функции
/ и начального приближения .то.
Часто вместо B) для решения задачи A) применяется
т. н. модифицированный метод Нью-
Ньютона:
ж**1 = ** — [/' (z°)]-i/(z*). C)
При тех же предположениях, при к-рых Н. м. имеет
квадратичную сходимость, метод C) имеет линейную
сходимость, т. е. сходится со скоростью геометрич.
прогрессии со знаменателем меньше единицы.
Применительно к решению нелинейного оператор-
операторного уравнения А (и) = 0 с оператором А : Вх —>¦ В%,
где Вх и В2 — нек-рые банаховы пространства, обоб-
обобщение B) наз. методом Ньютон а—К а н т о -
р о в и ч а. Формулы этого метода имеют вид
uk + i = uk_[A> (м*)]-1 А (и*), к = 0, 1,
где A' (uk) — производная Фреше оператора А в точке
и*, являющаяся обратимым оператором, действующим
из Вг в В2. При специальных предположениях метод
Ньютона — Канторовича обладает квадратичной схо-
сходимостью, а соответствующий модифицированный ме-
метод — линейной сходимостью.
Н. м. разработан И. Ньютоном (I. Newton, 1669).
Лит.: [1] Канторович Л. В., «Успехи матем. наук»,
1948, т. 3, в. 6, с. 89—185; [2] К а н т о р о в и ч Л. В., А к и-
л о в Г. П., Функциональный анализ, 2 изд., М., 1977; [3]
К о л л а т ц Л., Функциональный анализ и вычислительная
математика, пер. с нем., М., 1969; [4] Приближенное решение
операторных уравнений, М., 1969; [5] Б а х в а л о в Н. С,
Численные методы, 2 изд., М., 1975. Ю. А. Кузнецов.
НЬЮТОНА ЧИСЛО — один из критериев подобия
механич. движения, к-рый получается из уравнения,
выражающего второй закон Ньютона: Ne = 2.P/pi>2,
где Р — характерное давление, р — плотность и v —
характерная скорость.
НЬЮТОНА—КОТЕС А КВАДРАТУРНАЯ ФОРМУ-
ФОРМУЛА — интерполяционная квадратурная формула
для вычисления интеграла по конечному промежутку
[а, Ь], узлы к-рой выбираются следующим образом:
х <iP) = a-Jrkh, к = 0, 1,2, ..., п, где п — натуральное
число и h= (b — аIп, число узлов N=n-\-l. Коэффициен-
Коэффициенты определяются тем, что квадратурная формула ин-
интерполяционная, т. е.
д(л)_ (~i)n~k Сп t(t-l)(t-2) ... (t-n) j,.
При n=l, 2, 3, 4, 5, 6, 7, 9 все коэффициенты по-
положительны, при д=8 и тг 5s 10 среди них имеются
как положительные, так и отрицательные. Алгебраич.
степень точности Н.—К. к. ф. (число d такое, что
формула точна для всех многочленов степени но
выше d и не точна для xd + 1) равна п при п нечетном
и равна тг+1 при п четном. Простейшие частные слу-
случаи Н.— К. к. ф\: ?г=1, h=b—a, N=2
f(x)dx5~±?-[f(a) + f (Ь)]
o
— трапеций формула; тг=2, 7г= (Ь—а)/2, 7V=3
— Симпсона формула; тг=3, fe= (Ь—а)/3, JV=4
/ (x) dx a. ~^f (а) + 3/ (a + h) + 3f (a + 2h)+f F)]
— квадратурная формула «трех вось-
м ы х». При больших тг Н.—К. к. ф. применяются редко
(из-за упомянутого выше свойства коэффициентов при
п ^ 10). Предпочитают пользоваться составными Н.—
К. к. ф. при небольших п. Таковы составные квадра-
квадратурная формула трапеций и квадратурная формула
Симпсона.
Коэффициенты Н.—К. к. ф. при тг=1AJ0 приведе-
приведены в [3].
Н.—К. к. ф. впервые появились в письме И. Нью-
Ньютона (I. Newton) к Г. Лейбницу (G. Leibniz) в 1676 (см.
[1]), а затем в книге Р. Котеса [2], где указаны коэф-
коэффициенты формул при тг=1 A) 10.
Лит.: El] Ньютон И., Математические начала натураль-
натуральной философии, пер. с латин., в кн.: Крылов А. Н., Собр.
трудов, т. 7, М.— Л., 1936; [2] Cotes R., Harmonia Mensura-
rum, pt 1—2, L., 1722; [3] К р ы л о в В. И., Шульги-
Шульгина Л. Т., Справочная книга по численному интегрированию,
М., 1966; [4] Б а х в а л о в Н. С, Численные методы, 2 изд.,
М., 1975. И. П. Мысоеских.
НЬЮТОНА — ЛЕЙБНИЦА ФОРМУЛА — форму-
формула, выражающая значение определенного интеграла от
заданной функции / по отрезку в виде разности значе-
значений на концах отрезка любой первообразной F этой
функции
Названа именами И. Ньютона (I. Newton) и Г. Лейб-
Лейбница (G. Leibniz), т. к. правило, выражаемое форму-
формулой (*), было известно им обоим, но опубликовано
позже.
Эта формула справедлива, если функция / интегри-
интегрируема по Лебегу на отрезке [а, Ь], в частности если
функция / непрерывна на этом отрезке и
где С — нек-рая постоянная. В этом случае функция F
абсолютно непрерывна и почти всюду на отрезке [а, Ь]
(всюду, если / непрерывна на [а, Ь]) справедливо ра-
равенство F' (х) = f(x).
Обобщением Н.— Л. ф. является Стокса формула
для ориентированных многообразий с краем.
Л. Д. Кудрявцев.
НЬЮТОНОВ ПОТЕНЦИАЛ в широком смыс-
смысле— потенциал с ньютоновым ядром И\х — г/1л~2,
где \х—у\ — расстояние между точками х и у евкли-
евклидова пространства R-^, Л^З, т. е. интеграл вида
и (х)
= JT^
где интегрирование производится по нек-рой мере
Радона ц на RN с компактным носителем S. В случае
неотрицательной меры ц Н. п. A) есть супергармонич.
функция во всем пространстве RN (см. Субгармоничес-
Субгармоническая функция).
Вне носителя S меры \х Н. п. A) имеет производные
всех порядков по координатам точки х и является
регулярным решением уравнения Лапласа Ди(ж)~0,
т. е. и(х) — гармоническая функция на открытом мно-
множестве CS, регулярная и на бесконечности, и(<х)=0.
В случае абсолютно непрерывной меры \i Н. п. и(х)
имеет вид
где dco — элемент объема в R-W, D — нек-рая конечная
область. Если при этом плотность/ (у) непрерыв-
непрерывна по Гёльдеру в замкнутой области D и граница д!>
состоит из конечного числа замкнутых гиперповерх-
гиперповерхностей Ляпунова, то и (х) имеет непрерывные производ-
производные 2-го порядка внутри D и удовлетворяет уравнению
Пуассона Аи (х) = — (N — 2) 2я^/2 / (х)/Г (N/2).
В работах И. Ньютона (I. Newton) понятие «по-
«потенциала» еще не встречается. Впервые существование
силовой функции ньютоновых сил тяготения доказал
Ж. Лагранж (J. Lagrange, 1773). Термины «потенциа-
«потенциальная функция» и «потенциал», применительно к ин-
интегралам вида B) при 7V=3, впервые встречаются
соответственно у Дж. Грина (G. Green, 1828) и у
К. Гаусса (С. Gauss, 1840). Термин «Н. п.» иногда
употребляется в узком смысле применительно
только к объемным потенциалам вида B), а иногда —
применительно только к физически реальному случаю
B) потенциала сил тяготения при JV=3, создаваемого
массами, распределенными в области D с плотностью
/(У).
Если интеграл типа B) или A) распространен по
гиперповерхности S(zRN, т. е.
S I х-ь
-—f(y)do(y), C)
TO говорят о ньютоновом потенциале про-
простого слоя, к-рын является регулярной гармонич.
функцией всюду вне S. Если S — замкнутая гиперпо-
гиперповерхность Ляпунова и плотность f(y) непрерывна по
Гёльдеру на S, то Н. п. простого слоя непрерывен
всюду в RN, а его производные непрерывны вне S.
При этом его нормальная производная по направлению
внешней к S нормали щ в точке yo?S имеет различные
пределы при приближении к S изнутри и извне, вы-
выражающиеся соответственно формулами
lim
du
dna
du (!/„) (N-2)
dn°
f Ы.
где
du (t/o) _, v
dn0 ч
— т. н. прямое значение нормальной производной Н. п.
простого слоя, (у—у0, щ) — угол между вектором
у—у0 и нормалью щ; при этом нормальная производная
du{yo)ldno непрерывна на S.
Ньютонов потенциал двойного
слоя имеет вид
где п — внешняя нормаль к S в точке y?S. H. п.
двойного слоя — также гармонич. функция вне S,
но при приближении к 5 он терпит разрыв. При тех
же предположениях на S и f(y) он имеет пределы
изнутри и извне S, выражающиеся соответственно
формулами
lim v (x
lim v (x)
Х^-Уо
где
Г (IV/2)
Г (IV/2)
— т. н. прямое значение Н. п. двойного слоя в точке
г/0?5. При несколько более жестких условиях на S
и f(y) нормальная производная Н. п. двойного слоя,
напротив, непрерывна при переходе через S.
См. также Двойного слоя потенциал, Объемный потен-
потенциал, Потенциала теория, Простого слоя потенциал.
Лит.: [1] Г ю н т е р Н. М., Теория потенциала и ее при-
применение к основным задачам математической физики, М., 1953;
[2] Сретенский Л. Н., Теория ньютоновского потенциа-
потенциала, М.— Л., 1946; [3] Л а н д к о ф Н. С, Основы современной
теории потенциала, М., 1966; [4] Б р е л о М., Основы класси-
классической теории потенциала, пер. с франц., М., 1964; [5] У эр-
мер Д ж-, Теория потенциала, пер. с англ., М., 1980: [6]
Kellogg О. D., Foundations of potential theory, В., 1929.
E. Д. Соломенцев.
НЭША ТЕОРЕМА в теории игр — теорема
о существовании ситуаций равновесия в сметаанном
расширении конечной бескоалиционной игры
Г = </, {Si)teJ, {Hi}isj>,
где /, {Si)ieJ — конечные множества соответственно
игроков и их стратегий, Н[: S= ТТ. 5,- -*¦ R1 — функ-
ция выигрыша игрока i?/ (см. также Игр теория).
Установлена Дж. Нэшем(,1. Nash [1]). Пусть Л/,-, i?J,—
множества всех вероятностных мер, заданных на 5
Н. т. утверждает: существует такая мера |*?Л
= ТТ
. М;, для к-рой выполняются неравенства
г|),(||||,)
для всех n;?Mi, i?J, где через |Л*|||Л,- обозначена мера
из М, полученная заменой ?-й компоненты в векторе
и.* на |Л,-, a Hi(\i) = Е(Н/, |л). Известные доказательст-
доказательства Н. т. опираются на теоремы о неподвижной точке.
Лит.: [1] Нэш Д т., в кн.: Матричные игры, М., 1961;
[2] В о р о б ь е в Н. Н., Теория игр. Лекции для экономи-
экономистов-кибернетиков, Л., 1974. Е. Б. Яновская.
НЭША ТЕОРЕМЫ в дифференциальной
геометрии — две группы теорем об изометрич.
вложениях и погружениях римановых многообразий в
евклидовы пространства, и первоначальные варианты
к-рых принадлежат Дж. Нэшу (J. Nash).
1) Н. т. о С1-в ложен и ях и С1-и о г р у ж е-
н и я х. Погружение класса С1 (вложение) / : V" ->
-+Ет л-мерного риманова пространства V класса С0
с метрикой g в от-мерное евклидово пространство
Ет наз. коротким, если индуцированная им на
V" метрика gf такова, что квадратичная форма gn—gf
положительно определена. Тогда если V" допус-
допускает короткое погружение (вложение) в Ет, т ^ л+1,
то F" допускает и изометрич. погружение (вложение)
класса С1 в Ет. Эта теорема при ограничении т^-
^ге+2 доказана в [1], а в приведенной формулировке
доказана в [2]. Из этой теоремы вытекает, в частности,
что если компактное риманово многообразие V" имеет
С1 вложение (погружение) в Ет, m^n-f-1, то V" до-
допускает и изометрич. ^-вложение (погружение) в Ет.
Другим следствием Н. т. является наличие у каждой
точки V" достаточно малой окрестности, допускающей
изометрич. вложение класса С1 в Еп + 1.
2) Н. т. о регулярных вложениях.
Всякое компактное риманово многообразие V" клас-
класса Сг, 3<:г<:оо, допускает изометрич. С вложение
в Е">, где от=1/2Cп2+11ге). Если V" некомпактно,
то оно допускает изометрич. С вложение в Ет', где
т1 = 1/2(Зга2 + 11п) (ге + 1).
Н. т. о регулярных вложениях получена в результа-
результате применения теоремы об обращении широкого класса
дифференциальных операторов — Н. т. о неявной
функции. Смысл этой теоремы состоит в том, что из
разрешимости нек-рой линейной алгебраич. системы
уравнений, естественно свяванной с дифференциальным
оператором L, и при введении разумной топологии в
образе н прообразе рассматриваемый оператор явля-
является открытым отображением, т. е. оператор L локаль-
локально обратим вблизи любой точки из множества его
значений. Для уравнений вложения риманова простран-
пространства в евклидово эти условия сводятся к тому, что
первые и вторые производные отображения / : V ->
-> Ет по внутренним координатам V" должны быть
линейно независимыми. Такие вложения были впервые
рассмотрены в [4]; они наз. свободными вло-
вложениями. Из Н. т. о неявной функции вытекает,
что компактное риманово многообразие V", достаточно
близкое к компактному рпманову многообразию V",
допускающему свободное вложение в EV, также допус-
допускает свободное вложение в Ет. Этот факт и своеобраз-
своеобразный метод продолжения по параметру привели к Н. т.
о регулярных вложениях (см. [3]). С помощью распро-
распространения методов Нэша на некомпактные многообразия
и аналитич. вложения, а также с помощью кардиналь-
кардинального усовершенствования процесса продолжения по
параметру доказано, что всякое бесконечно дифферен-
дифференцируемое (аналитическое) риманово многообразие V"
допускает изометрическое дифференцируемое (аналити-
(аналитическое) вложение в Ет, где m = 1/2 n (ге + 1) + Зи + 5.
Лит.: [1] Н э ш Д ж., «Математика», 1957, т. 1, № 2,
с. 3—16; [2] К ё й п е р Н., там же, т. 1, №2, с. 17—28;
[3] Н э ш Д т., «Успехи матем. наук», 1971, т. 26, в. 4, с. 173—
216; [4] Б у р с т и н К., «Матем. сб.», 1931, т. 38, № 3—4,
с. 74—85. Д. Д. Соколов.
ОБВЕРТЫВАЮЩИЙ РЯД для числа А — ряд
V, ап (*)
такой, что
.+а„) | < | ап + 1\
при всех ге=0, 1, 2, ... О. р. может сходиться или
расходиться; если он сходится, то его сумма равна А.
Ряд («) обвертывает действительное число А вуз-
ком смысл е, если числа ап действительны и при
всех ге=0, 1,2, ...
А — (ао + а1+... + ап)=в„ап + 1, О < в„ < 1.
В этом случае А заключено между двумя любыми по-
последовательными частичными суммами ряда. Напр.,
при ж>0 функции е~х, rn(l-j-z), (\+х)~Р{р > 0),
sin х, cos x, arctg x, J0(x) обвертываются в узком смыс-
смысле своими рядами Маклорена.
Если ряд
А.=.хп ¦
обвертывает при х >*Я > 0 функцию f(x), принимаю-
принимающую действительные значения, п числа ап действитель-
действительны, то знаки чисел аг, а2, . . . чередуются и ряд явля-
является обвертывающим в узком смысле. Этот ряд явля-
является аспмптотич. разложением функции / (х) при х —>.
—у + оо; если он расходится, то наз. полусходя-
полусходящимся рядом. Такие ряды используются для при-
приближенного вычисления значений функции f(x) при
больших значениях х.
Лит.: [1] Полна Г., С е г е Г., Задачи и теоремы из ана-
анализа, пер. с нем., 3 изд., ч. 1 — 2, М., 1978; [2] X а р д и Г.,
Расходящиеся ряды, пер. с англ., М., 1951. М. В. Федорюк.
ОБИЛЬНОЕ ВЕКТОРНОЕ РАССЛОЕНИЕ — век-
векторное алгебраическое или аналитическое расслоение,
пучок регулярных (соответственно аналитических) се-
сечений которвго обилен (см. Обильный пучок, Положи-
Положительное расслоение). О. А. Иванова.
ОБИЛЬНЫЙ ПУЧОК — обобщение понятия обиль-
обильного обратимого пучка. Пусть X — нётерова схема над
полем к, (§ — локально свободный пучок на X (т. е.
пучок сечений нек-рого векторного алгебраич. расслое-
расслоения Е -> X). Пучок ? наз. обильным, если для
всякого когерентного пучка JF на X существует целое
число ге0, зависящее от JF, такое, что пучок ?F(?)Sn(§
при п ^ п0 порождается своими глобальными сечени-
сечениями (здесь Sn(§ обозначает п-ю симметрическую степень
пучка (§).
Локально свободный пучок $ на X обилен тогда и
только тогда, когда обилен обратимый тавтологич.
пучок X((§) на проективизации Р (Е) расслоения Е.
Другой критерий обильности состоит в том, что для
всякого когерентного пучка JF на X должно существо-
существовать целое число п0, зависящее от <f, такое, что группа
когомологий Н' (X, йГ®»?"^) равна нулю при п^щ
и !>0. Если пучки $ п JF обильны, то и <^>B)ёГ — обиль-
обильный пучок [1]. Если X — неособая комплексная проек-
проективная кривая, то пучок ? на X обилен тогда и только
тогда, когда ? и все его факторпучки имеют по-
положительные степени [2]. Касательный пучок на PN
обилен для любого N (см. [1]). Справедливо и обратное
утверждение: любое неособое ТУ-мерное алгебраич.
многообразие с обильным касательным пучком изоморф-
изоморфно PN (см. [1], [3]).
Лит.: [1] Hartshorne R., «Publ. math. IHES», 1966,
№ 29, p. 319—50; [21 e г о же, «Nagoya Math. J.», 1971, v. 43,
p. 73—89; [3] Demazure M., в кн.: «Semin. Bourbaki»,
1979/80, № 544. В. А. Псковских.
ОБЛАСТЬ—непустое связное открытое множество
точек топологич. пространства X. Замыкание D об-
области D ная. замкнутой областью; замкнутое
множество FtD = D\D наз. границей О. fl. Точки
x?D наз. также внутренними точками О.
D; точки z?Fr D наз. граничными точками
для О. D; точки дополнения СД=Х\В -внеш-
-внешними точками для О. D.
Любые две точки О. D действительного евклидова
пространства R", п ^ 1 (либо комплексного простран-
пространства С, т ^ 1, либо римановой поверхности или ри-
мановой области), можно соединить путем (или дугой),
целиком расположенным в D, а в случае DczR" или
D(zCm — даже ломаной линией с конечным числом
звеньев. Конечные и бесконечные открытые интервалы—
единственные О. на числовой прямой R = RX; их гра-
границы состоят не более чем из двух точек. Область D
на плоскости наз. односвязной, если любой замк-
замкнутый путь в D можно непрерывно деформировать в точ-
точку, оставаясь все время вО. В. Вообще говоря, граница
односвязной О. открытой плоскости R2 или C = CJ
может состоять из любого числа к связных компонент,
0 <: к <: оо. Если же D рассматривается как О. ком-
компактной расширенной плоскости R2 или С и число к
компонент границы конечно, то к наз. порядком
связности плоской О. D; при &>1 О. D наз. м в о-
госвязной. Иначе говоря, порядок связности к
на единицу больше минимального числа разрезов, по-
попарно соединяющих компоненты границы, к-рые нужно
провести, чтобы превратить О. D в односвязную. При
/с=2 О. наз. двусвязной, при к=3 — т р е х-
связной и т. д.; при /с<оо имеем конечно-
связные О., при к=со — бесконечносвяз-
н ы е О. Порядок связности плоской О. характеризует
ее топологический тип. Топологич. типы О. про-
пространств R", «5=3, или Ст, т~^2, нельзя характеризо-
характеризовать каким-либо одним числом.
Даже в случае односвязной плоской О. метрич. строе-
строение ее границы Fr D может быть очень сложным (см.
Граничные элементы). В частности, точки границы
делятся на достижимые точки х0?FrD, для
к-рых существует путь ж(i), 0 < t < 1, x@)?D, x(l) =
=х0, соединяющий х0 в D с любой точкой x@)?D, и
недостижимые точки, для к-рых такого
пути не существует. Множество достижимых точек
границы Fr D любой плоской односвязной О. всюду
плотно на Fr D.
Область D пространства R" или Ст наз. ограни-
ограниченной, или конечной, если
sup { \x\:x?D] < оо;
в противном случае О. D наз неограниченной,
или бесконечной. Замкнутая жорданова плоская
кривая разделяет плоскость R2 или С на две ж о р-
д а н о в ы О.: конечную D+ и бесконечную D~. Все
граничные точки жордановых О. достижимы.
Е. Д. Соломеицев.
ОБЛАСТЬ ЗНАЧЕНИИ функции, м н о ж е-
ство значений функц и и,— множество всех
элементов, к-рые заданной функцией поставлены в
соответствие элементам из ее области определения,
т. е. если / : X -> У, то множеством значений функции/
наз. множество Yf всех таких элементов г/?У, для
каждого из к-рых существует такой элемент х?Х,
что f(x)=y. Таким образом, О. з. функции является
образом ее области определения. л. Д. Кудрявцев.
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ функции — множе-
множество, на к-ром задана рассматриваемая функция, т. е.
совокупность X всех тех элементов х, каждому из
к-рых данная функция / ставит в соответствие эле-
элемент у из нек-рого множества У; таким образом, если
/ : X—)-У, ТО X наз. О. О. функции. Л. Д. Кудрявцев.
ОБЛАСТЬ ЦЕЛОСТНОСТИ, целостное коль-
кольцо,— коммутативное кольцо с единицей и без делителей
нуля. Любое поле, а также любое кольцо с единицей,
содержащееся в пек-ром поле, является О. ц. Обратно,
любая О. ц. может быть вложена в нек-рое поле. Такое
вложение дает конструкция поля частных (см. Част-
Частных кольцо).
Если А — О. ц., то кольцо многочленов А[Х] и
кольцо формальных степенных рядов Л[[Х]] над А
также будут О. ц. Если А —коммутативное кольцо с
единицей и / — нек-рый идеал в А, то кольцо А/1
является О. ц. тогда и только тогда, когда идеал /
прост. Кольцо А будет О. ц. тогда и только тогда,
когда спектр кольца А — неприводимое топологич.
пространство.
Иногда в определении О. ц. не требуют коммутатив-
коммутативности кольца А. Примерами некоммутатив-
некоммутативных областей целостности являются тела,
а также подкольца тел, содержащие единицу. Однако,
вообще говоря, неверно, что любая некоммутативная
О. ц. может быть вложена в нек-рое тело (см. [2], а
также Вложение кольца).
Лит.: [1] Лен г С, Алгебра, пер. с англ., М., 1968;
[2] К о и П., Свободные кольца и их связи, пер. с англ., М.,
1975; [3] Фей с К., Алгебра; кольца, модули и категории,
пер. с англ., т. 1, М., 1977. Л. В. Кузьмин.
ОБЛОЖЕНИЕ — вес do(x) системы ортогональных
многочленов {Рп(х)}. Если а (ж) есть неубывающая,
ограниченная на сегменте [а, Ь] функция с бесконечным
множеством точек роста, то мера da(x), называемая
обложением, однозначно определяет систему мно-
многочленов {Рп(х)}, имеющих положительный старший
коэффициент и удовлетворяющих условию ортонорми-
рованности.
Функция распределения, пли интег-
интегральный вес, а(х) представляется в виде
а(х)=а1(х)+а2{х)+а3(х),
где о(х) — абсолютно непрерывная функция, назы-
называемая ядром, а2 (х) — сингулярная компонента и
°"з (х) — функция скачков. Если a2 (х)^а3 (z)s^O, то
под знаком интеграла можно сделать замену da(x)=
= a[(x)dx; при этом производная o[(x)=h(x) наз.
дифференциальным весом системы мно-
многочленов.
Из трех компонент функции распределения на асимп-
тотич. свойства ортогональных многочленов влияет
лишь ядро аг (х).
Лит. см. при ст. Ортогональные многочлены. П. К. Суетин.
ОБОБЩЕННАЯ АНАЛИТИЧЕСКАЯ ФУНКЦИЯ —
функция w(z)=u(x, y)-\-iv(x, у), удовлетворяющая
сиетеме
ди dv . , , п ди , dv . . 1 л ...
с действительными коэффициентами а, Ь, с, d, являю-
являющимися функциями действительных переменных х и у.
В обозначениях
а _ э , . д
2 г- — г-1 ,
dz дх ду
AA = a + b-i-i(c — b), kB = a — d-f i
исходная система записывается в виде
Если коэффициенты А и В системы A) на всей плоско-
плоскости Е комплексного переменного z принадлежат клас-
СУ Lp 2, р > 2, то в любой области D этой плоскости
каждая О. а. ф. w{z), удовлетворяющая уравнению A),
представляется в виде
w (z) = Ф (г) е«> <z>, B)
где
И)
1 С С А 1Г\+ R ГМ i
to (z)=—
а Ф (г) — вполне определенная аналитическая в об-
области D функция переменного г.
Связь между О. а. ф. и аналитич. функциями, осу-
осуществляемая формулой B), является нелинейной, если
В Ф 0. По заданной аналитич. функции из нелинейного
интегрального уравнения B) единственным образом
определяется О. а. ф. w(z).
Существует линейный оператор
w (z) =Ф (z)~-
C)
устанавливающий взаимно однозначное соответствие
между множествами аналитических в ограниченной
области D и непрерывных в замкнутой области D [) S
функций Ф (z) п обобщенных аналитических в D функ-
функций w(z), причем Pi (z, Z) и Г2(г, X) — вполне опреде-
определенные функции, к-рые выражаются через коэффициен-
коэффициенты А и В системы A).
Из формулы C) получаются различные интегральные
представления О. а. ф., обобщающие интегральное пред-
представление Коши для аналитич. функций. Представление
О. ф. в виде C) оказалось полезным при исследовании
краевых задач для О. а. ф.
Если А и В — аналитич. функции действитель-
действительных переменных х, у, то для О. а. ф. в односвязной
области имеет место представление
A(z, T)
+ \z F2(z, z, t)(S(t)dt\ , D)
в к-ром Гг и Г2 — аналитич. функции своих аргумен-
аргументов, выражающиеся через А и В, а Ф (z) •— произ-
произвольная аналитич. функция переменного z. (Формула
D) не является частным случаем формулы C).)
В случае, когда А и В — целые функции перемен-
переменных х и у, представление D) годится для любой од-
носвязной области плоскости комплексного переменно-
переменного z.
Проблема приведения общего эллиптич. уравнения
2-го порядка
в2и , д2и , , ди , ди , , п /сгч
к виду
в'и . дги . . ди , „ ди
эквивалентна задаче редукции к канонич. виду положи-
положительной квадратичной формы adx2^-2bdxdy+cdy'2. По-
Последняя проблема, в свою очередь, сводится к отыска-
отысканию гомеоморфизмов уравнения Бельтрамн
—= — q (z) =0, w = uJriv, F)
dz dz
где
A = ac — b", \q(z)\ < 1.
Если E) — равномерно эллиптич. уравнение
>.A0=const > 0), то |g(z)!<g0=const < 1.
При изучении уравнения Бельтрами основным вопро-
вопросом является построение нок-рого его гомеоморфизма
для данной области D. Это вытекает из следующего
утверждения: если co(zi — гомеоморфизм уравнения
Бельтраып, реализующий топологич. отображение об-
области D на область соШ), то всякое другое его реше-
решение в D имеет вид
w(z) = Ф[ш(г)], G)
где Ф — произвольная аналнтнч. функция в области
соф).
Когда q(z) измерима, q(z)=O вне D и l5(z)«:?o<l>
однолистным решением уравнения Бельтрами F) яв-
является функция
±M^L, (8)
где р удовлетворяет сингулярному интегральному
уравнению (интеграл понимается в смысле главЕюго
значения по Коши)
Это уравнение имеет единственное решение в нек-ром
классе Lp(E), p > 2; его можно получить, напр.,
методом последовательных приближений. Функция (8)
принадлежит классу Са(Е), а=(р—2)/2, реализует
топологич. отображение плоскости на себя, причем
!«(оо)=оо, z-V -^. 1 при z—>-оо. Если q^C'a(E), 0<
, >, то u,(z)€C"?+1-
Равномерно элдиптич. система двух уравнений 1-го
порядка общего вида в комплексной записи имеет вид
°?-qi(z)toL-qAt)te.+ Aw + B-=0w. A0)
С помощью гомеоморфизма нек-рого уравнения вида F)
систему A0) можно привести к виду A). Но ее можно
изучить также непосредственно, что позволяет избе-
избежать нек-рых дополнительных ограничений.
Пусть уравнение A0) рассматривается в нек-рой ог-
ограниченней области при условии, что A, B?Lp(D),
р>2. Тогда всякое решение уравнения A0) предста-
вимо в виде
ir(z)=<D [ш (z)] e<P<z), A1)
где со (z) — нек-рый гомеоморфизм уравнения Бельтра-
Бельтрами (б) с коэффициентом
dw/dz
Ф(со) — аналитич. функция в области a>(D), функция
<f(z)?Ca(E), а=(р—2)/2, голоморфна вне D(jS и
исчезает на бесконечности. Представление A1) имеет
место и тогда, когда коэффициенты в левой части урав-
нения A0) зависят от w и от ее производных любого
порядка, лишь бы на рассматриваемых решениях
выполнялись указанные выше условия. Как и B),
формула A1) допускает обращение.
Формула A1) позволяет перенести целый ряд свойств
класспч. теории аналитич. функций на решения урав-
уравнения A0): теорему единственности, принцип аргумен-
аргумента, принцип максимума и др.
Общее (^-квазиконформное отображение является
решением нек-рой равномерно эллиптич. системы вида
A0) (при А=В=0). Справедливо п обратное утвержде-
утверждение. Поэтому указанные выше результаты позволяют
решить чисто аналитич. путем основные проблемы ква-
квазиконформных отображений.
Теория О. а. ф. позволила исчерпывающим образом
исследовать обобщенную задачуРпман а—
Гильберт а: найти решение уравнения A), непре-
непрерывное в D\JS, по краевому условию
Re[X(S)ir(z)]=ow + Pi; = Y, z?S, A2)
где а, р", у — заданные действительные функции из
класса Ca(S), 0 < а < 1, причем а?-{-$2=1. Область
D, вообще говоря, многосвязна.
Задачу A2) можно редуцировать к эквивалентному
сингулярному интегральному уравнению и получить
полный качественный анализ краевой задачи A2).
Пусть граница S области D состоит из конечного чис-
числа простых замкнутых кривых 50, . . ., Sт, удовлетво-
удовлетворяющих условиям Ляпунова. Так как при конформных
отображениях вид уравнения и краевого условия
сохраняются, то без ущерба общности можно считать,
что So — единичная окружность с центром в. точке
z=0, принадлежащая рассматриваемой области D, а
517 . . ., Sm — окружности, лежащие внутри So.
Индексом задачи A2) наз. целое число п, рав-
равное приращению
-4-arg [а (?) + #(?)],
когда точка ? один раз обойдет S в положительном
направлении. Краевое условие можно привести к
более простому виду
Re [z-"e'C <z>w(z)] = y, z?S,
где C(z) = Cj на Sj, причем C0=0, a Cu . .-,Cm —
некоторые действительные параметры, к-рые однознач-
однозначно выражаются через а и р.
Для сопряженной задачи:
а^1 Aw* — 5ш* = 0, z?D,
)
Индекс вычисляется по формуле ?г' = 7« — п — 1.
Основные результаты по задаче A2) можно сформули-
сформулировать в виде следующих утверждений.
1) Задача A2) имеет решение тогда н только тогда,
когда
где w* — производное решение сопряженной задачи.
2) Пусть I и V — числа линейно независимых ре-
решений однородных задач A2) и A3) соответственно.
Тогда I—1' = п—п' = 2п—т-[-1.
3) Если и<0, то однородная задача A2) не имеет
нетривиальных решений.
4) Если n>m—1, то однородная задача A2) имеет
ровно ?=2n-j-m—1 линейно независимых решений, а
неоднородная задача A2) всегда разрешима. Если ге<0,
то неоднородная задача A2) имеет решение (единствен-
ное) тогда и только тогда, когда \ (а+ф)ю/ yds=O,
7=1,. . ., I', l' = m—2л+1, где Wj — полная система
решений однородной задачи A3).
5) Если т—0 и л=0, то 1=1 и все решения однород-
однородной задачи имеют вид w(z) = ice<a^z\ где с — действи-
действительная постоянная, а а>0 — непрерывная в D (J S
функция.
Приведенные результаты полностью характеризуют
задачу A2) в односвязном (т=0) и многосвязном (га<0,
п>от—1) случаях. Особого рассмотрения требует слу-
случай 0<:п«:то—1.
Лит.: [1] В е к у а И. Н., Обобщенные аналитические
функции, М., 1959. А. В. Вицадзе.
ОБОБЩЕННАЯ ГРУППА — то же, что инверсная
полугруппа.
ОБОБЩЕННАЯ ПРОИЗВОДНАЯ типа функ-
функции — распространение понятия производной на не-
некоторые классы недифференцируемых функций. Первое
определение принадлежит С. Л. Соболеву (см. [1],
[2]), к-рый подошел к определению О. п. с точки зрения
идеи введенного им понятия обобщенной функции.
Пусть /=/(х)=/(хт, . ., хп) и ф=ф(.т) = ср(гх, . . .,
хп) — локально интегрируемые функции на открытом
множестве Q л-мерного пространства Rn, т. е. интег-
интегрируемые по Лебегу на любом замкнутом ограниченном
множестве FczQ. Тогда (р есть обобщенная ч а-
стная производная от/по жу на Q и пишут
ф= df/dxj, если для любой бесконечно дифференцируемой
функции г|), финитной в Q (см. Финитная функция),
Второе эквивалентное определение О. п. df/dxj =ф
заключается в следующем. Если / можно видоизменить
на множестве re-мерной меры нуль так, что видоизменен-
видоизмененная функция (к-рая снова обозначается через /) будет
локально абсолютно непрерывной по xj почти для всех
(в смысле (и—1)-мерной меры) xi=(x1,. . ., ху_х,
Xj + 1, . . ., хп), принадлежащих к проекции Q-' обла-
области Q на плоскость ху=0, то / имеет частную (в обычном
смысле этого слова) производную dl/dxj почти всюду
на Q. Если функция ф= д^- почти всюду на Q, то ф есть
О. п. от / по Xj на Q. Таким образом, О. п. определена
на Q почти всюду; если f непрерывна и имеет на Q
непрерывную обычную производную djldxj, то послед-
последняя есть в то же время О. п. от / по xj на Q.
О. п. d2fldxidxj, d3f/dxid2Xj, . . ., высшего порядка
определяются по индукции. Они не зависят (почти всю-
всюду) от порядка дифференцирования.
Имеется третье эквивалентное определение О. п.
Пусть для всякого замкнутого ограниченного F (z Q
функции / и ф, заданные на Q, обладают свойствами:
lim \F\fv—f\dx = (
V->-oo •> f
lim
-Ф
dx=0,
где функции /v, x=l, 2, . . ., непрерывны на Q вместе со
своими частными производными dfjdxj; тогда ф есть
О. п. по х/ от / на Q (ф=д//дгу) (см. также Соболева
пространство).
С точки зрения теории обобщенных функций О. п.
определяется следующим образом. Пусть задана функ-
функция f{x), локально суммируемая на Q, рассматривае-
рассматриваемая как обобщенная функция, и пусть df/dxj=q> —
частная производная в смысле теории обобщенных
функций. Если окажется, что ф представляет ло-
локально суммируемую на Q функцию, то тогда (по пер-
первому (исходному) определению) ф есть О. п.
Понятие О. п. вводилось и ранее (см., напр., [3],
где рассматривались О. п. с интегрируемым квадратом
на Q). В дальнейшем многие исследователи приходили
к этому понятию независимо от своих предшественников
(см. по этому вопросу [4]).
Лит.: [1] Соболев С. Л., «Докл. АН СССР», 1935,
т. 8, с. 291 — 94- [21 е г о же «Матем. сб.», 1936, т. 1, с. 39—72;
[3] Levi В., «Rend. Circolo mat. Palermo», 1906, v. 2-2,
p. 293 — 359; [41 Никольский С. М., Приближение функ-
функций многих переменных и теоремы вложения, М., 1969.
С. М. Никольский.
ОБОБЩЕННАЯ ФУНКЦИЯ — математическое по-
понятие, обобщающее классич. понятие функции. Потреб-
Потребность в таком обобщении возникает во многих технич.,
физич. и математич. задачах. Понятие О. ф. дает возмож-
возможность выразить в математически корректной форме
такие идеализированные понятия, как плотность мате-
материальной точки, точечного заряда, точечного диполя,
(пространственную) плотность простого или двойного
слоя, интенсивность мгновенного источника и т. д.
С другой стороны, в понятии О. ф. находит отражение
тот факт, что реально нельзя измерить значение физич.
величины в точке, а можно измерять лишь ее средние
значения в достаточно малых окрестностях данной точ-
точки. Таким образом, техника О. ф. служит удобным и
адекватным аппаратом для описания распределений
различных физич. величин. Поэтому иначе О. ф. наз.
распределениями (distributions).
О. ф. были введены впервые в кон. 20-х гг. 20 в.
П. Дираком (P. Dirac, см. [1]) в его исследованиях по
квантовой механике, где он систематически использует
понятие б-функции и ее производных (см. Дельта-функ-
Дельта-функция). Основы математич. теории О. ф. были заложены
С. Л. Соболевым [2] в 1936 при решении задачи Коши
для гиперболич. уравнений, а в 50-х гг. Л. Шварц (см.
[3]) дал систематич. изложение теории О. ф. и указал
многие применения. В дальнейшем теория О. ф. ин-
интенсивно развивалась многими математиками и физи-
физиками-теоретиками, главным образом в связи с потреб-
потребностями теоретич. и математич. физики и теории диф-
дифференциальных уравнений (см. [4] — [71). Теория
О. ф. далеко продвинута, имеет многочисленные приме-
применения и широко вошла в обиход математика, физика
и ттнженера.
Формально О. ф. / определяется как линейный
непрерывный функционал над тем или иным векторным
пространством достаточно «хороших» (основных) функ-
функций ф(х); / : ф -> (/, ф). Важным примером основного
пространства является пространство D (О) — совокуп-
совокупность финитных С°° (О)-функций в открытом множестве
Oc;R", снабженная топологией строгого индуктивного
предела (объединения) пространств 0^@^), Ок<^О/г + 1,
UkOk=O. Пространство С^(Ok) есть совокупность
С" (К«)-функций с носителем в О&, снабженная топо-
топологией счетного числа норм
|| (р | р = max | Ваф (х) |, р = 0, 1, ...
Примером основной функции из D (R") служит «ша-
«шапочка»:
0, |*| > 8, \ ae(x)dx = l.
Сопряженное к D (О) пространство есть про-
пространство О. ф. D'(О); D=D(R"), D' = D'(R").
Сходимость последовательности О. ф. из D' (О) опре-
определяется как слабая сходимость функцио-
функционалов из D'(О), т. е. /fe—vO, к—voo, в D' (О) означает,
что (//;, ф)->0, А—>-оо, для всех <$?D(O).
Для того чтобы линейный функционал / на D (О)
был О. ф. в О, т. е. f?D' (О), необходимо и достаточно,
чтобы для любого открытого множества O'(gO существо-
существовали числа К и от такие, что
@,,, <p?D(O'). A)
Если в неравенстве A) целое число от можно выбрать
независящим от О', то О. ф. / имеет конечный
порядок; наименьшее такое от наз. порядком
/ в О. Таким образом, в силу A), всякая О. ф. / из
D' (О) имеет конечный порядок в любом O'tgzO.
Пространство D' (О) — полное: если последователь-
последовательность О. ф. fk, к=\, 2, . . ., из D' (О) такова, что для
любой функции q>?D(O) числовая последовательность
(fk, ф) сходится, то функционал
(/, ф)= lim (/fe, ф)
принадлежит D' (О).
Простейшими примерами О. ф. являются функцио-
функционалы, порождаемые локально суммируемыми в О
функциями
Ф ->(/, ф) = $ f(x)<p(x)dx, ф??>@). B)
О. ф., определяемые локально суммируемыми в О
функциями f(x) по формуле B), наз. регуляр-
регулярными О. ф. в О; остальные О. ф. наз. сингуляр-
сингулярными. Между локально суммируемыми в О функция-
функциями и регулярными О. ф. в О существует взаимно одно-
однозначное соответствие. В этом смысле «обычные», т. е.
локально суммируемые в О, функции являются (регу-
(регулярными) О. ф. из D' (О).
Примером сингулярной О. ф. в R" служит б-ф у н к -
ция Дирака
(б, ф)=Ф@), Ф??>.
Она описывает плотность массы 1, сосредоточенной в
точке х=0. При этом «шапочка» сое(ж) (слабо) аппрок-
аппроксимирует б-функцию
соЕ -* б, 8 -» + 0 в D'.
Пусть f?D' (О) и <ве (•*) — «шапочка». Тогда функция
из С°° @?) наз. регуляризацией /, и/е—>-
->/, е^—]\-0 в D' (О). Более того, всякая / из D' (О) есть
слабый предел функций из D@). Последнее свойство
иногда берется в качестве исходного для определения
О. ф., что вместе с теоремой о полноте пространства О. ф.
приводит к эквивалентному определению О. ф. [8].
О. ф., вообще говоря, не имеют значений в отдельных
точках. Тем не менее можно говорить о совпадении О. ф.
с локально суммируемой функцией на открытом множе-
множестве: О. ф. / из D' (О) совпадает в O'czO с локально
суммируемой в О' функцией fo(x), если ее сужение на
О' есть /с, т. е. в соответствии с B)
(/, ф) = \ /о (*) ф (х) dx
для всех <(>?D@'), при этом считается f=fo(x), x?O'.
В частности, при /0=0 получается определение того,
что О. ф. / обращается в нуль в О'. Множество точек
О, ни в какой окрестности к-рых О. ф. не обращается в
нуль, наз. носителем О. ф. / и обозначается supp /.
Если supp /(gO, то О. ф. f наз. финитной в О.
Справедлива теорема окусочном склеи-
склеивании обобщенной функции: пусть в
окрестности Uy<s=:O каждой точки у?О задана О. ф. /у
из D' (Uy), причем элементы fy согласованы, т. е. fyi =
=/j,, в иух[\иу2ф0; тогда существует О. ф. / из
D' (О), совпадающая с fy в Uy при всех
Примеры обобщенных функций.
1) 6-функция Дирака: supp 8= {0}.
2) О. ф. 9i(~^j, определяемая равенством
наз. конечной частью, или главным значением, инте-
интеграла от функции — ; supp 5* (if ) = R1. 0. ф.
сингулярна в R1, однако на открытом множестве х
она регулярна и совпадает с —.
3) Поверхностная 6-функция. Пусть S — кусочно
гладкая поверхность и и. — непрерывная функция
на S. О. ф. \i8s определяется равенством
При этом u.6s(z)=0, x?S, \i&s — сингулярная О. ф.
Эта О. ф. описывает пространственную плотность
масс или зарядов, сосредоточенных на поверхности
S с поверхностной плотностью и. (плотность про-
простого слоя).
Линейные операции над О. ф. вводятся как расшире-
расширение соответствующих операций над основными функ-
функциями.
а) Замена переменных. Пусть /??>' (О) и
х=Ау^Ъ — неособенное линейное преобразование О
на Ov О. ф. f(A y-{-b) из D' (OjJ определяется равенством
Ф) = (/ ф [^(ГЬ)
Так как операция ф(г/)—>ц>[А ~х(х—Ь)] — изоморфизм
D (О) на D(Oy), то операция /{x)—>-i(Ау-\-Ь) — изомор-
изоморфизм D' (О) на D' {Ог). В частности, если А=Х1, Ф
фО, 6=0 (х=ку — подобие (с отражением при А<
если А=1 (х=у-\-Ъ—сдвиг на Ь), то
Формула C) позволяет определить трансляционно инва-
инвариантные, сферически симметричные, центрально сим-
симметричные, однородные, периодические, лоренц-ин-
вариантные и т. д. О. ф.
Пусть функция a^C1(Rl) имеет только простые нули
х1, х2, ... на оси R.1. Функция б(а(х)) определяется
равенством
Пример ы. 4) 8(—х)=8(х).
5) (&(х—х0), ф) = ф(х0).
6) б(х2-а2)= ~[6(х-а) + 6(х+а)], а>0.
7) 6(sin x) = ^k=^(x—кк).
б) Произведение. Пусть f?D' (О) па?С°° (О).
Произведение af—fa определяется равенством
(af, ф) = (/, аф), ф?Д (О).
Оказывается, что af^D' (О) и для обычных локально
суммируемых функций произведение af совпадает с
обычным умножением функций f(x) и а(х).
Примеры. 8) а(х)8{х) = а@N(х).
Однако эта операция произведения не допускает
распространения на любые О. ф. так, чтобы она была
ассоциативной и коммутативной. Действительно, в про-
противном случае получилось бы противоречие:
(±) = (б
=6
В нек-рых классах О. ф. такое произведение можно
определить, однако оно может оказаться неоднознач-
неоднозначным.
в) Дифференцирование. Пусть f?D' (О).
Обобщенная (слабая) производная
О. ф. /
а ' а ¦ / (х)
D*t(x)=—5; -^ , |а|=а1+. ..+«„,
Э*1 •• • йл-„
порядка а= («!, . . ., а„) определяется равенством
(?>«/, Ф)= (-l)i <* ! (/,Д»(р), фбД(О). D)
Так как операция ф->(—1Iа|Ваф линейна ннепрерыв-
ннепрерывна из D (О) в D(O), то функционал/H1/, определяемый
правой частью равенства D), есть О. ф. из D' (О). Если
(,/?(р,
Имеют место следующие свойства: операция //
линейна и непрерывна из D' (О) в D' (О), любая О. ф.
из D' (О) бесконечно дифференцируема (в обобщенном
смысле); дифференцирование не зависит от порядка;
справедлива формула Лейбница для дифференцирова-
дифференцирования произведения а/, где а ?С°° (О); дифференцирование
не увеличивает носителя; всякая О. ф. / из D' (О) во
всяком открытом множестве O'lgO есть нек-рая произ-
производная от непрерывной функции в О'; любое дифферен-
дифференциальное уравнение Lu=f, f?D'(О), с постоянными
коэффициентами разрешимо в D'(О), если О — выпук-
выпуклая область; любая О. ф. / порядка N с носителем в
точке 0 единственным образом представляется в виде
Примеры. 10) 6'(х)=б(х),
где 0 — функция Хевисайда (функция вклю-
включения):
в(х)=1, х>0, в(х) = 0, х<0.
И) (б', ф)=-ф'(О);
—6' (х) описывает плотность зарядов, соответствую-
соответствующих диполю момента +1 в точке х=0 и ориентирован-
ориентированного вдоль положительного направления оси х.
12) Обобщением б' (х) является нормальная произ-
производная от плотности простого слоя на ориентируемой
поверхности S:
О. ф.— — (цб^) описывает пространственную плот-
плотность зарядов, соответствующую распределению дипо-
диполей на поверхности S с поверхностной плотностью
момента (х и ориентированных вдоль заданного направ-
направления нормали п на S (плотность двойного
ело я).
13) Общее решение уравнения и' = 0 в классе D' (R1)
есть и(х) = С, где С — произвольная постоянная.
14) Общее решение уравнения хи=0 в классе D' (R1)
есть и (х) — Сё (х).
15) z«6tft>(z) = 0, k=0, I, . . ., т—1.
16) Тригонометрический ряд
сходится в D' и его можно дифференцировать в D'
почленно бесконечное число раз.
г) Прямое произведение. Пусть /?С (х)
и g?D' (O.z). Прямое произведение определяется по
формуле
(/ (*) Xg (у), ф) = (/ (х), (g (у), Ф)), E)
<р(х, y)?D@1x02).
Так как операция 9->(g(*/), ф(-»', у)) линейна и не-
непрерывна из D(O1XO2) в DfOj), то функционал
/(х)Х g(y), определяемый формулой E}, есть О. ф. из
D' (OjXOo). Прямое произведение — коммутативная
и ассоциативная операция, причем
supp (/X?) = supp/Xsuppg.
О. ф. / (х, у) из D' (О1X О,) не зависит от переменной у,
если она представима в виде
f(x, y)=fo(z)XUy), /oG^'(Oi);
в этом случае пишется /(.г, y)=fo(x).
Примеры. 18) 8(х)'=6(х1)Х. . . Хб(х„).
19) Общее решение в D' (R2) уравнения колебаний
однородной струны иц=ихх задается формулой
и(х, t)=f(x+t) + g(x-t),
где /(§) и ^(л) •— произвольные О. ф. из D' (R1).
д) Свертка. Пусть О. ф. / п g из D' (Rn) обладают
тем свойством, что их прямое произведение 1 (x)X,g(y)
допускает расширение на функции вида ф(г+г/), где ф
пробегает D(Rn), в следующем смысле: для всякой
последовательности функций гц. (х, у), к—у<х, из D (R-n)
со свойствами
\D<*r\k(x, y)|<Ca, щ(х, у) -^1,
В«т)А (х, у) —> 0, | а | s* 1, к -> оо,
(на любом компакте), числовая последовательность
(f(x)Xg(y), r\k(x, у)ц)(х+у)) имеет предел, не зави-
зависящий от последовательности {%}. Этот предел паз.
сверткой О. ф. / и g п обозначается f*g, так что
(f*g, ф)= lim(/(г)х^(у), Ли (^ J/) Ф (X + J/)).
"*°° ф^?>(К"). F)
Из полноты пространства D' следует, что f*g?D' (R").
Как показывают элементарные примеры, свертка суще-
существует не для любых пар / и g. Она заведомо сущест-
существует, если одна из О. ф. финитна. Если свертка суще-
существует в С, то она коммутативна i-r-g=g*f и справедливы
формулы дифференцирования свертки
/*?>ag = ?><* (f*g) = D<*/*g. G)
Далее,
/*6 = 6*/ = /, (8)
откуда из G) получается
Наконец,
supp (/*g) с supp /-f-supp g.
Как показывает пример:
(i*6')*9 = i'*e=o*e=o,
1«(б'«0) = 1*0'= 1*6 = 1,
свертка — неассоциатпвная операция. Однако сущест-
существуют ассоциативные (и коммутативные) сверточные
алгебры. Единицей в них, в силу (8), служит 6-функ-
ция. Сверточную алгебру образует, напр., множество
D' (Г), состоящее из О. ф. из D' с носителями в выпук-
лом остром и замкнутом конусе Г с вершиной в 0.
Обозначение:
D+ = D' ([0, оо)), л = 1.
О. ф. <?¦ из D' наз. фундаментальным
решением (функцией точечного ис-
источника) дифференциального оператора L(D) с
постоянными коэффициентами, если она удовлетворяет
уравнению
Зная фундаментальное решение <§ оператора L(D),
можно построить решение уравнения L(D)u=f для тех /
из D', для к-рых свертка /*^ существует, п это решение
дается формулой u=f*$.
Примеры. 20) Ядро оператора дробного диффе-
дифференцирования и дробного интегрирования fa,(x),—аз <
<а<оо:
W4= г(«> '-
*¦ fa+N (х) • а + N > 0, N — целое.
При этом /а*/р=/а+р, /о=б, /i=6, /_fc=6<*>, А: — целое.
Если /?D+, то /*/а=/<а> есть первообразная порядка
а при а > 0 (производная порядка —а при а<0).
21) Д<? = 6(.т),
<^(х) = ^1п|х|, п=2. ^(.г) = --ЙГ1гг, « = 3.
22) <^t - й"** = б (х, о, <? (х, О = -J=- ^"/4f-
23) ^«-^л-х = б(х, о,
е) Преобразование Фурье. Оно опре-
определяется для класса О. ф. S' = S'\Rn) медленного ро-
роста. Пространство основных функций S=S (Rn) состоит
из С°° (И?п)-функц11Й, убывающих на бесконечности
вместе со всеми производными быстрее любой степени
\i-\~1. Топология в S задается счетным числом норм
11ф||я= sup* (l + \x\*)P'-\D<*y(x)\, cp?S, р = 0,1, ...
| а |< р
При этом DcS и S'czD', где указанные вложения
непрерывны. Локально суммируемые в R" функции
медленного роста содержатся в 5', определяя по фор-
формуле B) регулярные функционалы на S.
Всякая О. ф. из S' есть нек-рая производная от
непрерывной функции медленного роста и, стало быть,
имеет конечный порядок в R".
Преобразование Фурье F[f] О. ф. / из S'
определяется равенством
(*"[/]. Ф) = (/. F [ф]),
где
f? — классич. преобразование Фурье. Так как опе-
операция q>^-F [ф] — изоморфизм S на 5, то и операция
f-^.F[f] — изоморфизм S' на S', причем обратной опе-
операцией к F служит операция
Имеют место основные формулы для
DaF [f] = F [(ix)a /], xa=x^
если g финитна. Если О. ф. / — периодическая с п-
пер подом Т—(ТЪ . . ., Т„), Tj > 0, то/??' и ее можно
разложить в тригонометрич. ряд
сходящийся к / в S'; здесь
/2л 2я \ , / 2nfti 2яЬп Л
Примеры. 24) F [x«] = Bn)n(—г) |a|jDa6(|), в
частности F [1] = Bп)"б A).
25) F[jDa6] = ( — фа, в частности F [6] = 1
26) F [8]=T-bn=n6
()
ж) Преобразование Лапласа. Пусть
О. ф. g?S' (Г)=5" П-D' (Г), где Г — замкнутый выпук-
выпуклый острый конус. Пусть C=int Г, где Г*={г/ : (у*,
|)^0, V§ 6 Г} — сопряженный конус к Г. Преобра-
Преобразованием Лапласа О. ф. / наз. выражение
L[g]z = F[g(t)e-iy,t>] (x), z = x + iy. (9)
Операция g-*-L[g] осуществляет изоморфизм сверточ-
ной алгебры S'(Г) на алгебру Н(С), состоящую из
функций f(z), голоморфных в трубчатой области Тс~
= Rn-~iC и удовлетворяющих условию роста: сущест-
существуют числа а=а(/);5гО и Р=Р(/)^О такие, что для лю-
любого конуса С'(Щ:С (т. е. C'cCU {0}) существует число
Mj(C') такое, что
Обратное преобразование к преобразованию Лапласа
L задается равенством
g(l)=e<y.bFx[1(x + ly)\ (I), (Ю)
причем правая часть A0) не зависит от у?С.
Взаимно однозначное соответствие между gE) и
/(z), задаваемое равенствами (9) и A0), удобно изобра-
изображать в виде следующей схемы:
г (S) <->/(*),
причем / наз. изображением g, а g — спект-
спектральной функцией функции /.
Всякая f(z). из алгебры Н(С) имеет граничное зна-
значение /(^+/0) при г/-н»О, z/?C, в S', связанное со
спектральной функцией g функции / формулой f(x-\-
-i-i0)=F \g] согласно (9). Справедливы следующие ос-
основные формулы для преобразования Лапласа:
(Фа 8 A) <-> Daf (=),
l] (x)L[g2] (z), gl, g2?S' (Г).
Пример. 27) /a (t) <r-> (—!-)~a, в частности
6<ft>@<-M—iz)ft, G (i) <_>. -1-.
Лит.: [1] Д и р а к П. А. М., Основы квантовой механики,
пер. с англ., '1 изд., М.— Л., 1937; [2] Соболев С. Л.,
«Матем. сб.», 1936, т. 1, с. 39—72; [3] S с h w а г t z L., Theore
des distributions, t. 1—2, P., 1950—51; [4] Боголюбов
H. H., Логунов А. А., Т о д о р о в И. Т., Основы
аксиоматического подхода в квантовой теории поля, М., 1969;
[5] Гельфаня И. М., Шилов Г. Е., Обобщенные
функции, в. 1—3, М., 1958; [6] Владимиров Й. С,
Уравнения математической физики, 4 изд., М., 1981; [7] его
ж е, Обобщенные функции в математической физике, 2 изд.,
М., 1979; [8] А н т о с и к П., Минусинский Я., С и-
к о р с к я й Р., Теория обобщенных функций. Секвенциаль-
Секвенциальный подход, пер. с англ., М., 1976. В. С. Владимиров.
ОБОБЩЕННО НИЛЫ1ОТЕНТНАЯ ГРУППА —
группа одного из обобщенно нилытотентных классов
групп. Класс групп наз. обобщенно ннльпо-
т е н т н ы м, если он содержит все нильпотентные
группы и пересекается с классом конечных групп по
классу всех конечных нпльпотентных групп. Рассмат-
Рассматривалось довольно много классов О. н. г., причем в ос-
основном изучались связи между этими классами. Важ-
Важнейшие классы О. н. г.— класс локально нильпотент-
ных групп, классы нильгрупп и энгеяевых групп,
группы с нормализаторным условием. Большинство
классов О. н. г. введено при рассмотрении тех или иных
свойств центральных или нормальных рядов и систем
подгрупп (см. [11, [2]).
Лит.: [1] К у р о ш А. Г., Теория групп, 3 изд., М., 1967;
[2] К у р о ш А. Г., Черников С. Н., «Успехи матем.
наук», 1947, т. 2, в. 3, с. 18—59. А. Л. Шмелъпин.
ОБОБЩЕННО РАЗРЕШИМАЯ ГРУППА — группа
одного из обобщенно разрешимых классов групп. Класс
групп наз. обобщенно разрешимым, если
он содержит все разрешимые группы и пересекается с
классом конечных групп по классу всех конечных раз-
разрешимых групп. Рассматривалось довольно много
классов О. р. г., причем в основном изучались связи
между различными такими классами. Важнейшим клас-
классом О. р. г. является класс локально разрешимых групп.
Другие классы, как правило, вводились при рассмотре-
рассмотрении тех или иных свойств нормальных и субнормальных
рядов (см. [1], [2]).
Лит.: [1] К у Р о ш А. Г., Теория групп, 3 изд., М.,
1967; [2] К у р о ш А. Г., Черников С. Н., «Успехи
матем. наук», 1947, т. 2, в. 3, с. 18—59. А. Л. Шмелъкин.
ОБОБЩЕННОГО СДВИГА ОПЕРАТОРЫ, г и п е р-
г р у п па,— понятие, возникшее в результате аксиома-
аксиоматизации нек-рых свойств операторов сдвига в прост-
пространствах функций на группе. В терминах операторов
группового сдвига можно сформулировать такие важ-
важные математич. понятия как свертка, групповая алгеб-
алгебра, положительно определенная функция, почти перио-
периодическая функция и др. В рамках теории О. с. о. уда-
удается получить далеко идущие обобщения фундаменталь-
фундаментальных принципов и результатов, связанных с указанными
понятиями. В частности, теория О. с. о. имеет сущест-
существенные приложения к гармоническому анализу абстрак-
абстрактному.
Термины «О. с. о.» п «гипергруппа» принадлежат Ж.
Дельсарту (см. [1] — [3]). Ему же принадлежат важные
идеи и ряд^первоначальных результатов в данной об-
области. Систематич. построение теории О. с. о. дано
главным образом в работах Б. М. Левитана (см., напр.,
[4] - [7]).
Основные понятия. Пусть Н — произволь-
произвольное множество, Ф — нек-рое векторное пространство
комплекснозначных функций, определенных на Н.
Пусть каждому элементу х?Н сопоставлен линейный
оператор Rx в Ф, причем при любом фиксированном
h?H функция i|)(.z) = Rxq>(h) содержится в Ф для всех
ф^Ф. Линейный оператор ф(х) _>. г|)(х) = Д*ф(/г) в Ф
обозначается Lh (т. е. Lh ф (х) = Дхц> (h)). Линейные
операторы Rх наз. операторами обобщенно-
обобщенного сдвига, если выполнены следующие условия
(аксиомы) : 1) ЛХЬУ= ЬУЯх для любых х, у^Н (акси-
(аксиома ассоциативности), 2) существует в // такой элемент
е, наз. нейтральным, что Re—I, где / — тож-
тождественный оператор. В таком случае множество Н наз.
гипергруппой, так что понятия «О. с. о.» и
«гипергруппа» равносильны. Операторы Rx часто наз.
операторами правого сдвига, тогда как
Lx наз. операторами левого сдвига.
О. с. о. очевидным образом возникают в любом инва-
инвариантном относительно сдвигов векторном простран-
пространстве функций на произвольной полугруппе с единицей,
напр, на группе. Пусть Rx : ф(/г) —>- q>(h-x), где h-x —
произведение элементов h, х в полугруппе, a Lx :
(p(h)~>-<f.(x-h); тогда аксиома ассоциативности сводится
к ассоциативности умножения в полугруппе, а нейтраль-
ним элементом является единица полугруппы, так что
операторы Rx образуют семейство О. с. о. Нетривиаль-
Нетривиальные примеры приводятся ниже.
В общем случае Lx не образуют О. с. о., так как
оператор Le не обязан быть тождественным. Однако
Le является проектором, и его образ Ф наз. основ-
основным подпространством в Ф. В пространст-
пространстве Ф операторы Lx образуют семейство О. с. о., и
симметрия между операторами левого и правого сдвига
восстанавливается. Часто вторую из аксиом О. с. о.
усиливают требованием, чтобы Le=^I, т. е. Ф=Ф.
Условия 1) и 2) являются наиболее общими аксиомами
О. с. о. Накладывая дополнительные условия, можно
выделять более узкие классы О. с. о. Если RxRy=
= RyRx для всех х, у?Н, то О. с. о. Rx наз. ком-
коммутативными; в этсм случае п гипергруппа //
наз. коммутативной. Если относительно // делаются
дальнейшие предположения, то для О. с. о. естествен-
естественным образом возникают новые условия. Напр., если //—
локально бикомпактное пространство с мерой т, то
обычно требуется, чтобы операторы Rx и Lx согласо-
согласованно действовали в пространстве С (Н) непрерывных
функций на Нив пространствах Lp(ff, m), p^i,
причем на Rx и Lx накладываются дополнительные
условия типа непрерывности; если Н — гладкое много-
многообразие, то накладываются условия типа дифференци-
руемости, и т. п. Различные варианты аксиоматики
даны в [1], [3] - [6], [8], [15] - [20].
ПримерыО. с. о., связанных с груп-
группами. Операторы обобщенного сдви-
сдвига Дельсарта. Пусть G — топологич. группа,
К — нек-рая бикомпактная группа автоморфизмов
группы G, dk — мера Хаара на К и \dk=l. В про-
пространстве Ф=СFГ) непрерывных функций на G О. с. о.
Rx определяются с помощью равенства
где ср?Ф, к(х) — образ элемента x?G при автоморфиз-
автоморфизме к?К, g-k(x)— произведение элементов g и к(х)- в
G. Нейтральным элементом является единица группы.
Обе аксиомы О. с. о. выполняются; если G коммута-
коммутативна, то коммутативны и О. с. о. Дельсарта. Основ-
Основное подпространство Ф состоит из всех функций, по-
постоянных на орбитах относительно действия группы К,
а операторы Rx и Ry совпадают в Ф, если х и у лежат
на одной орбите. Поэтому пространство орбит Н также
можно наделить структурой гппергруппы, отождеств-
отождествляя Ф с пространством непрерывных функций на Н
и полагая 7?Л = Д*, где х — произвольный элемент
орбиты h. Если G совпадаете R, а группа автоморфиз-
мол состоит из двух элементов (отражение относитель-
относительно нуля и тождественное отображение), то Rxq>(t)=
= (<$(t-{-x)-\r<p(t—х)I2. В этом случае основное подпро-
подпространство состоит из четных функций, а пространство
орбит отождествляется с полуосью 0<:?<оо. Другой
частный случай О. с. о. Дельсарта получается при G= К
и к(х) = к~1хк\ при этом основное подпространство
состоит из центральных функций на К, а
гипергруппа, образованная орбитами, т. е. классами
сопряженных элементов, коммутативна.
Двойные классы смежности по би-
бикомпактной подгруппе. Пусть G — ло-
локально бикомпактная группа, К — ее бикомпактная
подгруппа, Н — пространство двойных классов смеж-
смежности по подгруппе К (такой класс вместе с элементом
g?G содержит и все элементы вида k-igk2, где /сь к.2?К).
Если К — нормальный делитель в G, то Н совпадает
с факторгруппой G)К. Пусть Ф — пространство, со-
состоящее из всех таких непрерывных функций на G,
что (р(k-Lgk2) = <p(g) для любых элементов
?G О. с. о. определяется формулой
Пространство Ф можно отождествить с пространством
С(Н) непрерывных функций на Я и так же, как для
О. с. о. Дельсарта, можно наделить Н структурой
гипергруппы. Если G — линейная полупростая группа
Ли, К — ее максимальная бикомпактная подгруппа, то
гипергруппа Н коммутативна и тесно связана со сфе-
рич. функциями на G (в частности, все сферич. функции
лежат в Ф).
В описанных выше примерах наряду с пространст-
пространствами непрерывных функций можно рассматривать я
другие функциональные пространства (см. [8], [13],
[15] - [19]).
Гиперкомплексные системы. Пусть
Ф — конечная гиперкомплексная система, т. е. конеч-
конечномерная ассоциативная алгебра с фиксированным
базисом H={h1, . ¦ ., hn}. Алгебра Ф отождествляется
с пространством функций на конечном множестве Н,
причем функции ф№ соответствует элемент
2?=1ф(А,-)Л,-еФ. Пусть
Д*ср (h)= > ф (h{) hi*x, ¦
где hj*x — произведение элементов ft.,- и ж в алгебре Ф.
Операторы Дх образуют семейство О. с. о. тогда и
только тогда, когда один из элементов базиса Н яв-
является правой единицей в алгебре Ф; указанным спо-
способом устанавливается соответствие между любыми
О. с. о. в пространстве функций на конечном множестве
и конечными гиперкомплексными системами. Таким
образом, понятие О. с. о. можно рассматривать как
далеко идущее обобщение классич. понятия гиперкомп-
гиперкомплексной системы. Важные примеры О. с. о., к-рые есте-
естественно трактовать как гиперкомплексные системы
со счетным или континуальным базисом, рассмотрены,
напр., в [4], [5], [8].
Генераторы и теоремы Ли для О. с. о.
Пусть гипергруппа Н является дифференцируемым
(или комплексно-аналитическим) многообразием и и (х,
у) = Rx(p(y) — дифференцируемая (соответственно го-
голоморфная) функция на ЯХЯ при всех ф?Ф. Пусть
(Ах, . . ., hn) — локальные координаты точки h^H,
причем система координат выбрана так, что нейтраль-
нейтральный элемент имеет координаты @, . . ., 0). Генера-
Генераторами (инфинитезимальными опера-
операторами) правого сдвига k-то порядка для
О. с. о. Rx наз. линейные операторы вида
где и(х, h)=Rx(p(h), k=k1Jr. . .-{-kn. Аналогично ге-
генераторы левого сдвига определяются равенством
Из аксиомы ассоциативности можно вывести, что любой
генератор левого сдвига коммутирует со всеми генера-
генераторами правого сдвига (равно как и с операторами Rx).
Дифференцирование условия! ассоциативности
ДхЬУц> (h) = ЬУRxq> (h) по переменным hu . . ., hn соот-
соответствующее число раз дает при h=0 систему урав-
уравнений
?»,, ..., kn- х {u)=Rkl kn- у (и), (*)
где и(.т, y) = Rx(p(y). Эту систему следует рассматри-
рассматривать как обобщение на случай О. с. о. первой прямой
теоремы Ли (см. [3] для О. с. о. Дельсарта и [5] для
общего случая). Не обязательно привлекать все урав-
нения системы (*), чтобы определить и(х, у). Напр.,
для сдвига на группе Ли уже генераторы 1-го порядка
однозначно определяют функцию и (т. е. групповое
умножение). В общем случае нек-рые генераторы низ-
низших порядков могут вырождаться, напр, в умножение
на константу, так что соответствующие уравнения сис-
системы (*) не содержат полезной информации. Поэтому
возникает задача: отобрать минимальное число уравне-
уравнений из системы (*), однозначно определяющих О. с. о.
При этом вырождающиеся генераторы пополняют число
начальных условий. Если конечная система вида (*)
при нек-рых начальных условиях, среди к-рых содер-
содержится условие и|д;=о=ф(?'), однозначно определяет
решение и(х, y) = Rx(f(y), причем операторы, стоящие в
левых частях системы, коммутируют со всеми операто-
операторами, стоящими в правых частях, то операторы Rx суть
О. с. о. Это утверждение является аналогом первой
обратной теоремы Ли [5]. Для нек-рого класса О. с. о.
доказаны (см. [5]) аналоги второй и третьей (прямой и
обратной) теорем Ли. В частности, в пространстве
бесконечно дифференцируемых функций от п перемен-
переменных построены О. с. о., для к-рых генераторы правого
(левого) сдвига порождают любую заданную «-мерную
алгебру Ли. Получено явное описание этих генераторов
в виде интегро-дифференциалъных операторов 2-го
порядка [10]. С помощью аналогичной техники построе-
построены [11] генераторы любого порядка, действующие в
пространстве целых аналитич. функций (от п перемен-
переменных) и порождающие любую n-мерную вещественную
алгебру Ли; по этим генераторам восстанавливаются
О. с. о. Можно строить О. с. о., исходя не только из
алгебр Ли, но и из коммутационных соотношений более
общего вида (см. [7], [12]). Так, напр., уже в [1] О. с. о.
на прямой строились исходя из явно заданного гене-
генератора 2-го порядка с помощью ряда, аналогичного
ряду Тейлора, к-рый дает разложение обычного сдвига
по степеням оператора дифференцирования. Подробно
описаны коммутативные О. с. о. на прямой с генерато-
^юм 2-го порядка типа Штурма — Лиувилля (см. [4],
5]) и указаны приложения к операторам и уравнениям
Штурма — Лиувилля. Дана [14] полная классификация
О. с. о. с генератором типа Штурма — Лиувилля (в
том числе некоммутативных) в пространстве дифферен-
дифференцируемых функций на прямой.
Представления О. с. о. и гипергруп-
гипергрупповые алгебры. Теория представлений для О. с. о.
не столь хорошо разработана, как в случае групп, но
строится аналогичным образом. Эта аналогия прости-
простирается довольно далеко, напр, с помощью понятия
генератора можно изучать представления О. с. о. ин-
финитезимальным методом так же, как это делается
для групп Ли (см. [3], [5], [11]). Представления О. с. о.
удобно трактовать как представления ассоциативных
гипергрупповых алгебр, аналогичных
групповым алгебрам; так же, как и в случае групп,
различным типам гипергрупповых алгебр соответствуют
различные варианты теории представлений и гармония,
анализа (см. Бесконечномерное представление). Если
гипергруппа Н локально бикомпактна, то пространство
М(Н) комплексных мер Радона с бикомпактными
носителями на Н приобретает структуру гипергруппо-
гипергрупповой алгебры относительно обобщенной свертки f*g
элементов /, g^M(H), определяемой равенством
cpd (/*g) = J J Ry<?(x)df(x)dg(y),
где ф — любая непрерывная функция на Н. Аналогич-
Аналогично определяется структура гипергрупповой алгебры в
пространстве D (Н) финитных обобщенных функций на
(или в пространстве А (Н) аналитич. функционалов
на Н), если гипергруппа Н является дифференцируемым
(комплексно-аналитичоским) многообразием. Относи-
Относительно естественных топологий М(Н), D{H), A (It)
являются топологич. алгебрами; 6-функция, сосредото-
сосредоточенная в нейтральном элементе е?Л, является правой
единицей в каждой из этих алгебр. Справедливо и об-
обратное утверждение: если в пространстве М(Л) (соот-
(соответственно ?>(Н), А(Н)), наделенном естественной то-
топологией, задана структура топологической ассоциа-
ассоциативной алгебры с правой единицей, являющейся 8-
функцией, то существует такая (единственная) структу-
структура глпергруппы на Л, что обобщенная свертка совпадает
с умножением в М{Н) (соответственно в D(H) или А{Н)).
Непрерывные представления алгебры М (Л) (D(H),
А (Л)} интерпретируются как непрерывные (беско-
(бесконечно дифференцируемые, голоморфные) представления
соответствующих О. с. о. [20].
Аналогом теории унитарных представлений групп
является теория симметричных представлений гипер-
груиповых банаховых алгебр с инволюцией. Наиболее
полные результаты (см. [4] — [6]) получены для пред-
представлений коммутативных и бикомпактных О. с. о.
При нек-рых условиях структурой гипергрупповой
банаховой алгебры с инволюцией наделяется простран-
пространство L1 (Л, т) суммируемых по положительной мере т
функций на гипергруппе Л. Одно из этих условий
состоит в том, чтобы мера т была инвариантна относи-
относительно обобщенных сдвигов (различные варианты точ-
точных определений см. в [4] — [6], [15] —[19]). При естест-
вепных предположениях доказана единственность (с
точностью до скалярного множителя) меры, инвариант-
инвариантной относительно правых или левых обобщенных сдви-
сдвигов; имеются и достаточные условия существования та-
такой меры (условия типа компактности, коммутативнос-
коммутативности или дискретности гипергруппы, см. [8], [16] — [18]).
Однако вопрос о существовании инвариантной меры для
О. с. о. общего вида остается открытым A982). Наряду
с V- (Л, т) важную роль играют гипергрупповая бана-
банахова алгебра мер ограниченной вариации и гипергруп-
гипергрупповая С*-алгебра.
Гипергрупповые банаховы алгебры и их симметрич-
симметричные представления изучались в [4], [6], [8], [15] — [19].
Алгебры аналитич. функционалов, связанные с нек-рыми
О. с. о. на прямой, описаны в [9]. Для О. с. о. общего
типа топологические гипергрупповые алгебры и их
представления рассмотрены в [20], при этом задачи
спектрального анализа и синтеза трактовались как
задачи изучения идеалов гипергрупповых алгебр.
Техника гипергрупповых алгебр применена [12] для
решения задач математич. физики в рамках оператор-
операторного метода В. П. Маслова.
Гармонический анализ. Следующая мо-
модель вскрывает структуру коммутативных О. с. о.
(см. [4], [5]). Пусть положительные меры т1 и т2 за-
заданы на пространствах Н1 и Л2 соответственно и с
помощью функции %(х,у), определенной на ЛХХЛ2,
задано обобщенное преобразование
Фурье
<Р (х) -+ / (у) = J ф (х) % (х, у) dmx (x),
к-рое определяет изоморфизм гильбертовых пространств
?2(tfi, mj) и L2(ff2> тг)- Пусть справедлива форму-
формула обращения
ф (х) = ^ / (у) х (х> у) dm2 (у);
если мера т2 дискретна, то эта формула дает разложение
функции (р(х) в обобщенный ряд Фурье.
Оказывается, что Л1 имеет структуру гипергруппы,
если для нек-рой точки e?#j; и для всех j/g//2 справед-
ливо равенство %{е, у)=1. В этом случае О. с. о. опре-
определяются формулой
ЛЛФ (*) = $/ (у) X (*. у) % (х, у) dm2 (у).
Поэтому О. с. о. естественно возникают в задачах,
связанных с разложениями по ортогональным системам
функций, спектральной теорией операторов и т. п.,
что обеспечивает широкий круг приложений теории
О. с. о. (см., напр., [4], [5], [8], [15]— [19]). На случай
коммутативных О. с. о. обобщены теорема Бохнера
о представлении положительно определенных функций
и закон двойственности Повтрягина, определено обоб-
обобщенное преобразование Фурье и доказан аналог План-
шереля теоремы [6] (различные варианты этих резуль-
результатов см. в [15] — [17]). С помощью теории представле-
представлений можно строить гармонич. анализ и для некоммута-
некоммутативных О. с. о. Напр., для О. с. о. получены неком-
некоммутативные аналоги теоремы Планшереля и формулы
обращения, включающие в качестве частного случая
соответствующие результаты для локально компакт-
компактных групп; для бикомпактных О. с. о. справедлив
аналог теоремы Петера— Вейля. Для О. с. о. рассматри-
рассматривались варианты гармонич. анализа в духе теорий почти
периодических и средне периодических функций (см. [1],
[2], [4], [8], [9], [14], [20]). Для коммутативных О. с. о.
получен аналог Винера глауберовой теоремы и рассмот-
рассмотрены вопросы спектрального синтеза (см. [21], [22]).
О приложениях О. с. о. к гармонич. анализу на груп-
группах см. [8], [13], [16], [19].
Лит.: [1] D е 1 s a r t e J., «J. math, pures et appl.», 1938,
t. 17, p. 213—31; [2] его же, «Acta math.», 1939, v. 69,
p. 259—317; [3] e г о же, «Colloq. internet. CNRS», 1956,
JMi 71, p. 29—45; ?4] Л е в и т а н Б. М., «Успехи матем. наук»,
1949, т. 4, в. 1, с. 3—112; [5] е г о же, Теория операторов обоб-
обобщенного сдвига, М., 1973; [6] е г о же, «Докл. АН СССР»,
1945, т. 47, с. 3—6, 163—65, 323—26, 401—03; [7] е г о же,
там же, 1958, т. 123, с. 243—45; [8] Б е р е з а н с к и й Ю. М.,
К р е й н С. Г., «Успехи матем. наук», 1957, т. 12, в. 1, с.147 —
52; [9] К р а с и ч к о в И. Ф., «Изв. АН СССР. Сер. матем.»,
1967, т. 31, ЛЬ 1,с. 37—60; 1968, т. 32, ЛЬ 5, с. 1024—32; [10]
Грабовская Р. Я., Крейн С. Г., «Math. Nachr.»
1976, Bd 75, p. 9—29; ?11] Грабовская Р. Я., К о н о-
ненко В. И., Осипов В. Б., «Изв. АН СССР. Сер/
матем.», 1977, т. 41, ЛЬ 4, с. 912—36; [12] Масло в В. П.,
«Теорет. и матем. физика», 1977, т. 33, с. 185—209; 113] Р а-
шевский П. К., «Тр. Моск. матем. об-ва», 1979, т. 38,
с. 139—85; [14] Гуревич Д. И., «Матем. заметки», 1979,
т. 25, ЛЬ 3, с. 393—408; El5] D u n k 1 С h., «Trans. Amer. Math.
Soc», 1973, v. 179,- p. 331—48; [16] J e w e t t R., «Adv. Math.»
1975, v. 18, ЛЬ 1, p. 1—101; [17] Spec tor R., «Lectures
Notes in Math.», 1975, v. 497, p. 643—73; El8] его же, «Trans.
Amer. Math. Soc», 1978, v. 239, p. 147—65; [19] Ross K.,
«Symposia Math.», 1977, v. 22, p. 189—203; [20] Литви-
Литвинов Г. Л., «Тр. Семинара по вект. и тенз. анализу», 1978,
в. 18, с. 345—71; [21] Chilana A., Ross К., «Pacific J.
Math.», 1978, v. 76, p. 313—28; [22] Chilana A., Ku-
Kumar A., «Pacif. J. Math.», 1979, v. 80, ЛЬ 1, p. 59—76.
Б. М. Левитан, Г. Л. Литвинов.
ОБОБЩЕННОЕ РЕШЕНИЕ — обобщение понятия
классич. решений дифференциальных (псевдодифферен-
(псевдодифференциальных) уравнений. Это понятие возникло в связи с
многими задачами математич. физики, когда под реше-
решениями дифференциальных уравнений потребовалось
понимать функции, не имеющие достаточного числа
производных, и даже вовсе недифференцируемые функ-
функции, а также более общие объекты — обобщенные функ-
функции, гиперфункции и т. д. Поэтому понятие О. р. тесно
связано с понятием обобщенной производной и вообще
обобщенной функции.
Под обобщенным решением дифференци-
дифференциального уравнения
L(x, D) (и) = ^а1<таа&*и (x)=f (х), f?D' (О), A)
(О),
в классе D' (О) понимается всякая обобщенная функция
и из D' (О), удовлетворяющая уравнению A) в О, т. е.
для любой основной функции (p?D (О) должно быть вы-
полнено равенство (и, L*cp) = (/, ср), где L* — сопря-
сопряженный оператор к L в смысле Лагранжа:
О. р. краевых задач для дифференциальных уравне-
уравнений удовлетворяют краевым условиям в надлежащем
обобщенном смысле (в Ьр(дО) или D' (дО) и т. д.),
напр.: и (rs) -> и (s), г -> 1— 0, в L2(\s \ = 1), и (х, ')""*"
-+ио(х), t-> + 0 в D'.
О. р. краевых задач для дифференциальных уравне-
уравнений возникают при решении их вариационными мето-
методами, при применении разностных методов, а также как
слабые пределы классич. решений при применении Фу-
Фурье метода, предельного поглощения принципа, предель-
предельной амплитуды принципа, методов, связанных с вве-
введением вязкости, и т. д.
Примеры. 1) Общее решение уравнения х2и' = 0
в классе D' (R) дается формулой
где 0 — функция Хевнсайда: 6(ж)=1, х^О, ;8(:г)=0,
x<fi; б — дельта-функция Дирака, С1г С2, ... —
здесь и далее произвольные постоянные.
2) Уравнение хги'-\-и=0 имеет одно решение в клас-
классе C°°(R), равное 0(—x)e1lx, а в классе гиперфункций
общее решение его дается формулой и (x) = Ciell(-x + г0)_(-
+ Съ ei/(x-i0) + Се 6 (—х) ег'х.
3) Общее решение волнового уравнения иц=а2ихх
в классе С(R2) дается формулой и(х, t)=f{x-\-at)-\-
-\-g(x—at), где fag — произвольные функции класса
C'(R).
4) Всякое решение и из D' @) уравнения Лапласа
Аи=0 — (вещественно) аналитическое в О.
5) Всякое решение в из/)' уравнения теплопровод-
теплопроводности щ=а2Аи — бесконечно дифференцируемое.
6) Всякий дифференциальный оператор Л^=0 с по-
постоянными коэффициентами имеет фундаментальное
решение (медленного роста) из класса S'.
7) Всякое уравнение L(D)u=f, гдеЛ(-О)^0 — диф-
дифференциальный оператор с постоянными коэффициен-
коэффициентами, имеет при любом / из L2(O) О. р. и из Ьг(О),
если О — ограниченная область.
8) О. р. и краевой задачи
Дм=/, "!ао = 0, f?L2(O) B)
в классе Соболева И7™ (О) возникает как решение клас-
классической вариационной задачи о минимуме квадра-
квадратичного функционала
в классе W^iO). Решение этой вариационной задачи
при любом / из L2 (О) существует и единственно в классе
Wiv(O). Таким образом, О. р. краевой задачи B) при
всех f(zL2(O) дают самосопряженное расширение
оператора А (жесткое расширение, или расширение по
Фридрихсу). О. р. краевой задачи B), как и все их
производные,— регулярные в О (т. е. типа локально
интегрируемых функций в О), вторые их производные,
вообще говоря,— сингулярные обобщенные функции.
Лит.: [1] Соболев С. Л., «Матем. сб.», 1936, т. 1,
№ 1, с. 39—72; [2] е г о же, Некоторые применения функцио-
функционального анализа в математической физике, Новосиб., 1962;
[3] S с h w а г t z L., Theorie des distributions, t. 1—2,
P., 1950—51; [4] Г е л ь ф а н д И. М., Шилов Г. Е., Нико-
Никоторые вопросы дифференциальных уравнений, М., 1958; [5]
Хёрмандер Л., Линейные дифференциальные операторы с
частными производными, пер. с англ., М., 1965; [6] Hyperfunc-
tions and pseudo-differential eduations, В.— [u. a.], 1973; [7]
Владимиров В. С, Уравнения математической физики,
4 изд., М., 1981; [8] е г о же, Обобщенные функции в матема-
математической физике, М., 2 изд., 1979. В. С. Владимиров.
ОБОБЩЕННОЙ ФУНКЦИИ НОСИТЕЛЬ — множе-
множество тех и только тех точек, ни в какой окрестности
к-рых обобщенная функция не обращается в нуль,
Обобщенная функция / из D' (О) обращается в нуль
в открытом множестве О'сО, если (/, q>)=0 для
всех cp?jD(O'). С помощью разложения единицы
показано, что если обобщенная функция / из D' (О)
обращается в нуль в нек-рой окрестности Uya0 каждой"
точки у?О, то / обращается в нуль в О. Объединение
всех окрестностей, где / обращается в нуль, наз. нуле-
нулевым множеством обобщенной функции / и
обозначается Of. Носитель /, обозначаемый supp /,
есть дополнение к О/до О, так что supp/=O\O^~ это
замкнутое множество в О. Если supp /(?0, то обобщен-
обобщенная функция / наз. финитной в О. Если функция
f(x) непрерывна в О, то эквивалентное определение1
носителя / таково: supp / есть замыкание в О множества
тех точек, где / (х) обращается в нуль. Напр., supp x= R1,
supp 6= {0}.
Сингулярный носитель (sing supp)
обобщенной функции — множество тех и только тех
точек, ни в какой окрестности к-рых обобщенная функ-
функция не совпадает с С00-функцией. Напр., sing supp x= 0r
sing SUpp 6={0}. -В. С. Владимиров.
ОБОБЩЕННОЙ ФУНКЦИИ ПРОИЗВОДНАЯ —
слабое расширение операции обычного дифференциро-
дифференцирования. Пусть обобщенная функция f?D' (О). Обобщен-
Обобщенная (слабая) производная
д\ « I/
1++
порядка а= (аь . . ., ап) определяется равенством
Так как операция ф —>- (—l)ia|jDa(p линейна и непре-
непрерывна из D (О) в D (О), то функционал Daf, определяе-
определяемый правой частью равенства (*), есть обобщенная
функция из D' (О). Если f?CP(O), то D"-f?Cp~m(O)
при всех а таких, что |а| ¦< р.
Имеют место следующие свойства О. ф. п.: операция
/->Z)a/ линейна и непрерывна из D' (О) в D' (О); любая
обобщенная функция из D' (О) бесконечно дифференци-
дифференцируема (в обобщенном смысле); дифференцирование не-
независит от порядка; справедлива формула Лейбница
для дифференцирования произведения о/, гдеа?С°°@);
supp jDa/crsupp /.
Пусть f?L]0c{0). Может случиться, что нек-рая
обобщенная производная Daf может быть отождествле-
отождествлена с нек-рой l}oc (О)-функцией. В этом случае Daf(x) —
обобщенная производная типа функции.
Примеры. 1) 6' = б, где 6 — функция Хевисайда
и б — функция Дирака.
2) Общее решение уравнения и' = 0 в классе D' есть
произвольная постоянная.
3) Тригонометрический ряд
сходится в В' и его можно дифференцировать в D' по-
почленно бесконечное число раз.
Лит.: [1] Schwartz L., Theorie des distributions, v. 1,
P., 1950; 121 С о б о л е в С. Л., Некоторые применения функ-
функционального анализа в математической физике, Новосиб., 1962,
В. С. Владимиров.
ОБОБЩЕННЫЕ ПОЧТИ ПЕРИОДИЧЕСКИЕ
ФУНКЦИИ — классы функций, являющиеся различ-
различными обобщениями почти периодич. функций. Каждый:
из них обобщает какую-то из сторон в определениях
Бора почти периодических функций и Бохнера почти
периодических функций. В этих определениях встре-
встречаются следующие математич. понятия (структуры):
1) пространство функций, определенных на всей прямой.
как метрич. пространство с метрикой (расстоянием):
р{/, g}= sup \f(x)—g(x)\; (*)
2) отображение прямой R1 в комплексную плоскость
С1 (функция); 3) прямая линия R1 как группа; 4) пря-
прямая линия как топология, пространство.
Имеющиеся обобщения почти периодич. функций
удобно классифицировать в согласии с этими структу-
структурами.
1) Если вместо непрерывности требовать от функции
i(x), z^R1, измеримость и суммируемость с р-й сте-
степенью в каждом конечном промежутке, то в качестве
расстояния можно принять одно из следующих трех
выражений:
расстояние Степанова:
^'1 / (*)-* И \р d*
расстояние Вейля:
расстояние Безиковича:
pdx\l/p.
Этим расстояниям соответствуют обобщенные Степа-
Степанова почти периодические функции, Вейля почти перио-
периодические функции и Безиковича почти периодические
функции.
2) Пусть прямая R1 отображается не в С1, а в бана-
банахово пространство В. Такое отображение наз. абст-
абстрактной функцией. Пусть абстрактные функ-
функции непрерывны н расстояние между нимп определя-
определяется по формуле (*), в к-рой модуль заменен нормой.
Тогда определения Бора и Бохнера обобщаются и при-
приводят к т. н. абстрактным почти перио-
периодическим функциям.
Дальнейшее обобщение получается заменой банахова
пространства на топологическое векторное пространст-
пространство. В этом случае почти период т=т8 опреде-
определяется так: для всякого е > 0 существует такая
окрестность нуля Ue, что f(x-\-%)—f{x)?U?.
Если топологию, определяемую нормой, заменить сла-
слабой топологией, то получаются т. н. слабо почти
периодические функции: функция 1 (х),
i^R1, f(x)?B, наз. слабо почти периодической, если
для любого функционала ср?В*, (p(f(x)) есть числовая
почти пернодич. функция.
3) Пусть вместо прямой R1 рассматривается произ-
произвольная группа G (не обязательно топологическая)
и отображение f(x), x?G, группы Gb топологическое
векторное пространство (в частности, в С1). В качестве
определения почти периодич. функций удобней принять
определение Бохнера: f(х) наз. почти периоди-
периодической функцией на группе, если семейство
функций flxh), h?G (или, что эквивалентно, семейство
f(hx)), условно компактно.
3) В определении почти периодич. функции на груп-
группе важна не сама групповая операция, а операция
сдвига на функциях: T/lf(x)^=f(xh) (или/(Лд-)), х, h?G.
Поэтому дальнейшее обобщение почти перподич. функ-
функций получается обобщением операции сдвига. Пусть Q —
абстрактное пространство (не обязательно группа) и
f{x), x?Q, — функция, определенная на Q. Семейство
линейных операторов Th, fe?Q, наз. обобщенного сдвига
операторами, если выполняются следующие аксиомы:
1) ассоциативность: rjjrj/(r) = TgTxf(ж);
2) существование нейтрального элемента, т. е. такого
элемента ho?Q, что Т/го=1, где / — единичный опе-
оператор.
Функция f(x), x?Q, наз. почти периоди-
периодической относительно семейства
операторов обобщенного сдвига Th,
если семейство функций Tllf(x) (x — параметр) условно
компактно относительно равномерной сходимости на
Q. Следует отметить, что теория таких функций отно-
относительно даже конкретных семейств операторов обоб-
обобщенного сдвига еще слабо разработана (см. [1], [5]).
4) Пусть Xj, X2l. . ., %п, ... — произвольное конеч-
конечное или счетное множество действительных чисел.
Пусть прямая R1 превращена в топологическое вектор-
векторное пространство заданием окрестности нуля как мно-
множества действительных чисел х, удовлетворяющих
неравенствам \еЛпХ—1\<г, к=\, . . ., N (числа г и N
выбираются произвольно и определяют окрестность
нуля). Оказывается, что почти периодич. функции Бора
совпадают с функциями, равномерно непрерывными в
этой топологии (в качестве чисел {Х^} можно взять
показатели Фурье функции или их целый базис). Функ-
Функции, непрерывные в указанной топологии, дают еще
одно обобщение почти периодич. функций. Это — так
наз. N-n очти периодические функции
Левитана. Определение iV-почти периодич. функ-
функций очевидным образом переносится на функции, опре-
определенные на абелевой группе (и менее очевидно — на
некоммутативные группы).
В указанную здесь классификацию О. п. п. ф. не сов-
совсем хорошо укладываются т. н. асимптотические почти
периодич. функции, введенные М. Фреше (см. [9], [10])
в связи с нек-рыми проблемами эргодич. теории. Функ-
Функция / : R1 _> С1 наз. асимптотической поч-
почти периодической функцией, если для
всех а ? R1 и произвольной последовательности дейст-
действительных чисел {/»„}, hn —>- оо существует подпосле-
подпоследовательность {к'^} последовательности {^п}> Для
к-рой /(ж+/с^а>) сходится равномерно для всех х>а.
Лит.: [1]Левитан Б. М. Почти-периодические функ-
функции, М., 1953; [2] Besicovitch A., Almost periodic
functions, Camb., 1932; [3] A m e г i о L., P г о u s e G., Almost-
periodic functions and functional equations, N. Y., 1971; [4]
В о с h n e r S., «Acta math.», 1933, v. 61, p. 149—84; [5] Мар-
Марченко В. А., в кн.: Тр. Моск. матем. об-ва, т. 2, М., 1953,
с. 3—83; [6] Левин Б. Я., «Укр. матем. ж.», 1949, т.' 1,
с. 49—101; [7] Besicovitch A., Bohr H., «Acta math.»,
1931, v. 57, p. 203—92; [8] Л е в и т а н Б. М., Ж и к о в В. В.,
Почти-периодические функции и дифференциальные уравнения,
М., 1978; [9] Frechet М., «С. г. Acad. sci», 1941, t. 213,
p. 520—22; [10] его же, «Proc. Roy. Soc. Edinburgh (A>,
1950, v. 63, p. 61—68. Б. М. Левитан.
ОБОБЩЕННЫЕ ТЕОРИИ КОГОМОЛОГИЙ, экст-
экстраординарные теории когомоло-
гий,— класс специальных функторов из категории
пар пространств в категорию градуированных абелевых
групп.
О. т. к. есть пара (h*, 6), где h* — функтор из кате-
категории Р пар топологич. пространств в категорию GA
градуированных абелевых групп (т. е. каждой паре
пространств (X, А) отвечает градуированная абелева
группа h*(X, A) = Q)n=-ochn(X, А) и каждому непре-
непрерывному отображению f(X, Л1_>-(ф, В) — набор го-
гомоморфизмов {/»"(/): h"(У, B)-+h"(X, A)}n=-oo),
б — заданный для каждой пары (X, А) набор гомомор-
гомоморфизмов
{6?x,A):h"(A)-+hn + i(X, A)},
естественных в том смысле, что для любого непрерыв-
непрерывного fi(X, A) -> (У, В) имеет место
причем должны выполняться следующие три аксиомы.
1) Аксиома гомотопии. Если два отобра-
отображения /, g : (X, А) -> (Y, В) гомотопны, то гомомор-
гомоморфизмы hn(f) и hn(g) совпадают для всех п.
2) Аксиома точности. Для любой пары
(А', А) последовательность
... - hn (А, А) ПЛ А» (X) П° А» (Л) 5^>
точна; здесь i : А ->- X и / : А = (A, 0)d(A, A) ~
очевидные включения.
3) Аксиома вырезания. Пусть (X, А) —
пара пространств п ттусть UaA таково, что UdA.
Тогда включение г : (X\U, AX U) -> (А, А) для всех
п индуцирует изоморфизмы
hn(X, A) -+hn(X\U, A\U).
Для корасслоения (А, А) пз аксиом следует, что
проекция (X, А) —>- (XlA, pt), где pt — пространство,
состоящее из одной точки, индуцирует изоморфизм
h"(X, A) ^h"(X'\U, A\.,U).
Часто вместо h" (f) пишут просто /*, а вместо б"х. А) —
просто б. Группу 1ь"(Х, А) наз. группой и-мерных
(обобщенных) когомологпй нары (X, А), а градуирован-
градуированную группу h* (pt) — группой коэффициентов О. т. к.
В определении О. т. к. можно вместо категории р
брать категорию пар корасслоений или категорию <?>
пар клеточных пространств, или категорию <Sf пар
конечных клеточных пространств (при этом в аксиоме
вырезания надо потребовать, чтобы пара (X\U, A\U)
была изоморфна объекту соответствующей категории.
В этих случаях говорят, что О. т. к. (h, б) определена
на категории <3 (соответственно <&р).
Выбор термина О. т. к. мотивируется следующим об-
обстоятельством. Доказано [2], что любой функтор @f-^-
—>-GA., удовлетворяющий аксиомам \ —3 и т. п. ак-
аксиоме размерности (состоящей в том, что Ы (pt) = O при
i ф 0), есть обычная теория когомологпй Н* с коэф-
коэффициентами в h° (pt). Позже было замечено, что многие
полезные конструкции алгебраич. топологии (напр.,
кобордизмы, К-теория) удовлетворяют аксиомам 1—3 и
что эффективность этих конструкций в значительной
степени обусловлена свойствами, формально вытекаю-
вытекающими из этих аксиом. Эти обстоятельства и привели к
формированию понятия О. т. к.
Пусть X — пунктированное пространство и в: pt-*-X —
пунктированное отображение. Группу приведенных
обобщенных когомологий hn(X) пространства X опре-
определяют, полагая
hn (A) =ker (hn (e)-hn (X) -> hn (pt)).
Имеется очевидное расщепление
и его можно сделать каноническим, считая, что вложе-
вложение hn(pt)Chn(X) индуцировано отображением X—>-pt.
Ясно, что hn{X)Kihn(X, pt). Кроме того, для корас-
корасслоения (А, А) из аксиом 1—3 следует изоморфизм
hn(X, A)^hn(X!A, pt) (см. [2], [3]), так что/i"(А, А)**
mhn(XlА). Здесь, как обычно, X/A = X(Jpt=Xt при
Л = 0.
Если (X, А) — корасслоение, то из аксиом следует
точность последовательности (естественной на катего-
категории корасслоений)
...h" (XI А) И,. hn (X) -il hn (A) JL hn + 1 (XlA) ->¦... (*)
Здесь i : A ->- А и / : X-*XlA — очевидные отображе-
отображения, а б есть композиция
h" (A)dhn (A) -^h" + 1 (X, A) x h" +
В частности, если А' есть конус С А над А , то h* (Х)^=0
(аксиома гомотопии), а XIА есть надстройка SA над Л , и
точность последовательности (*) влечет и з о м о р ф и з-
м ы надстройки Од : h' (A) ~ hl + l (SA), есте-
естественные по А. При этом изоморфизмы о позволяют
восстановить гомоморфизмы б (см. [2], [31); это делается
с использованием т. н. последовательности Пуппе. При-
Применение к последней функтора 1гл', У —у ос, дает точ-
точную последовательность (*"). Таким образом, по приве-
приведенной О. т. к. (h*, а) полностью восстанавливается
О. т. к. (h*. б).
О. т. к. h* наз. мультипликативно й, если
для любых пар пространств (X. А), (У, В) из Р задано
естественное спаривание
hP(X, A)®hV(Y, В) ^hP + 9(XxY, XxB\JAxY),
удовлетворяющее условиям коммутативности и ассо-
ассоциативности (см. [41, [51). В этом случае для (X, А)?Р
группа h*(X, А) является градуированным (коммута-
(коммутативным, ассоциативным) кольцом относительно умно-
умножения
Д*
hP(X, i)®M(X, A) -+hP + 9(XxX, XxA[)AxX) ->¦
, A),
где
Д:(Х, А)-* (XXX, AxA)d(XxX, XxA[)AXX)
диагональ, и индуцированные отображения
f*:h* (У, B)-*-h*(X, А) суть кольцевые гомоморфизмы.
Более общим образом можно определить спаривание
двух О. т. к. в третьей [5].
Обычные когомологии II"(X; G) можно определить
как группу [X, K(G, п)] го.чотонпч. классов непрерыв-
непрерывных отображений из X в Эилеиберга — Маплейиа про-
пространство K(G, n). Это обобщается и на О. т. к. сле-
следующим образом. Спектром пространств
наз. последовательность пространств {Мп}п=-е° и
непрерывных отображений sn: SMn~+ M,l + i, где
SMn — надстройка над Мп. Для пространства X
определяется группа h"(X) равенством
h«(X)=lim [SkX, Mn+k].
Здесь отображения
определяются композицией
Очевггдным образом строятся изоморфизмы надстройки
а'х '¦ It" (X) ~ hn + 1 (SX). Таким образом, каждый спектр
пространств задает нек-рую О. т. к. (h*, о) и, значит,
неприведенную О. т. к. (/?, б).
Если для О. т. к. (h*, б) существует спектр, из к-рого
она получается описанным выше способом, то говорят,
что этот спектр представляет О. т. к. (h'~, 6)
или что теория (А*, б) п р е д с т а в и м а этим спект-
спектром. Известно, что любая О. т. к. на категории ©^ прег-
ставима спектром, единственным с точностью до слабой
гомотоппч. эквивалентности.
Если О. т. к (h*, б) представима кольцевым спект-
спектром пространств, то она мультипликативна [5]. Для
О. т. к., заданной на категории (?¦, верно и обратное.
Пусть /<¦—> Е —>- В — расслоение в смысле Серра.
Для любой О. т. к. h* и любого п группы h" (F) обра-
образуют локальную систему групп на пространстве В.
Существует спектральная последовательность Дольда—
Атыг — Хирцебруха {Epr' Q}, начальный член к-рой
есть E%-q = Hp(B; {h4(F)}). Если В — конечное .кле-
.клеточное пространство, то эта спектральная последова-
последовательность сходится и ее предельный член присоединен к
группе h* (Е) (см. [1]). В частности, еслп F=pt, то полу-
получается спектральная последовательность Hp(X,hi(pt))=i>
=>/г"(Х), позволяющая (иногда) вычислять группу
h*(X) по группам Н* (X) и h*(pt).
С каждой О. т. к. h* можно связать двойственную
обобщенную теорию гомологии h*,
аксиоматика к-рой аналогична аксиоматике О. т. к.
с учетом того, что гомологии — ковариантный функтор
[4]. При этом если пространства X п Y (ге+1)-двойст-
венны (см. S-двойственность), то %'(X) ~ /г„_,-(У).
Кроме того, если О. т. к. h* представима спектром
{мт sn), то
ht(X)= lim ni + k (X л Мк).
При этом для мультипликативной О. т. к. h* имеется
спаривание высечения П:
hliX, X,) -hn_g{X, X2).
Важнейшими примерами О. т. к. является /("-теория
и различные кобордизмы. Двойственные к кобордизмам
обобщенные теории гомологии суть бордизмы.
Пусть | есть n-мерное векторное расслоение над -Y,
ориентируемое в О. т. к. /г*, и ТЬ, — его Тома простран-
пространство. В этом случае имеет место обобщенный Тома изо-
изоморфизм h'(X) « hi + n(T%) (см. ([1]). Отсюда (и из
теоремы двойственности Атьи [7]) следует обобщенная
Пуанкаре двойственность: пусть Р — Пуанкаре про-
пространство формальной размерности п (напр., замкнутое
n-мерное многообразие), нормальное расслоение к-рого
ориентируемо в О. т. к. h*. Тогда для любого целого i
имеет место h' (P) та h"~'(P). Пусть Av есть iV-мерное
нормальное расслоение над Р и Tv — его пространст-
пространство Тома. Пространства Р + — Р \jpt и Tv (N-\~n)-двойст-
(N-\~n)-двойственны (отношение, названное в статье S-двойственность
(/(-(-¦^-двойственностью, часто наз. п-двойственность).
Поэтому
ht (P)mhi (P + ) х hN+n-i (T\) к h"-' (P).
Элемент z группы hn(P), отвечающий при этом изомор-
изоморфизме единице i?ho(P), наз. фундаментальным клас-
классом пространства Р в О. т. к. /г*, это понятие обобщает
классич. понятие фундаментального класса. Доказано,
что изоморфизм h' (P)^hn^i(P) задается «высечением на
фундаментальном классе», т. е. имеет вид x_>z f| х%
(см. [4]).
Пусть F — одно из полей к, С или тело кватерни-
кватернионов Н. Мультипликативная О. т. к. h* наз. F-ори-
ентируемой, если все F-векторные расслоения ори-
ориентируемы в h*. Оказывается, что для любой F-
ориентируемой О- т. к. h* и любого F-векторного рас-
расслоения над X можно определить обобщенные характе-
характеристические классы расслоения ? со значениями в груп-
группе k* {X), при этом для F, соответственно равного R, С
или Н, и обычной теории когомологий Н* (или Д*B2)
для F=R.) получаются соответственно классы Штпфеля,
Чжэня или Бореля. При этом (см. Кобордизм) универ-
универсальной /"-ориентированной О. т. к. является теория
GF-кобордизмов. Это проявляется также в существо-
существовании спектральных последовательностей, связывающих
h* (X) с GFl (X) и h*(pt), где Fo — одно из полей R, С.
Кроме того, с каждой С-ориентированной О. т. к. h*
можно ассоциировать формальную группу над кольцом
h*(pt), и универсальность кобордизмов отражается и в
тем факте, что формальная группа теории унитарных
кобордизмов универсальна (чисто алгебраически) в
классе всех формальных групп. При этом формальная
группа О. т. к. h* несет с последней довольно много
информации.
Часто бывает необходимо продолжать О. т. к. с иод-
категории на всю категорию. Напр., надо продолжить
О. т. к. /г*, заданную на категории (?/?, на всю катего-
категорию @.
Первый способ: берется спектр, представляю-
представляющий (на ©/г) О. т. к. h*, и с его помощью строится
О. т. к. на всем ©.
Второйспособ: пусть О. т. к. h* задана на 3/г
и Хс®, {Ха} — семейство конечных клеточных под-
подпространств пространства X и
\(X)=limk*(X).
Тогда h* — функтор на (?, удовлетворяющий всем ак-
аксиомам О. т. к., кроме аксиомы точности (функтор lim
не сохраняет точность). При этом для любого X ¦*— 3
и любой О. т. к. h* ; <B-*SA, продолжающей О. т. к.
h* : <Sp—®А, естественный гомоморфизм
A*(X)-*-h*(X)
зпиморфен.
В общем случае должны, видимо, возникать спект-
спектральные последовательности, использующие высшие
производные функторы lim^ и вычисляющие h* (X) но
limph*(Xa.) и h*(X) (эти спектральные последова-
последовательности известны A982) лишь для II*).
Для обобщенной теории гомологии h%, заданной
на <&р, функтор
удовлетворяет аксиоме точности и, следовательно,
всегда является продолжением h.% с <Вр на (?.
Третий способ является аналогом способа
Александрова — Чеха и основывается на использова-
использовании конструкции нерва.
О. т. к. можно продолжить и на категорию спектров:
пусть Мп={Мп, sn} — спектр пространств. Группа
h* (M) определяется соотношением
отображения
hi+n(Mn)^V+« + i(Mn + 1)
имеют вид
Я' + " (М„) xh' + n + 1 (SMn)<- h' + " + 1 (Mn + 1).
Полученный функтор h* на категории спектров удовлет-
удовлетворяет всем аксиомам приведенной О. т. к. (при пра-
правильном их переносе в категории спектров) (см. [5]).
Имеется естественная задача «сравнения» различных
О. т. к., и в частности задача выражения одних О. т. к.
через другие. Решение последней можно рассмат-
рассматривать как далеко идущее обобщение формулы уни-
универсальных коэффициентов. Наиболее мощный аппарат
здесь представляют спектральные последовательности
адамсовского типа. Один такой пример уже приводился:
это спектральные последовательности «от кобордизмов
к ориентированной О. т. к.». Другой пример: пусть h*
и к* — две О. т. к. Пусть, далее, А/г — кольцо когомо-
когомологических операций теории h*, Y — спектр, представ-
представляющий теорию к*, и X — нек-рый спектр (в част-
частности, пространство). Тогда (при «хороших X, Y и h*t>,
см. [6]) существует спектральная последовательность,
начальный член к-рой есть Ext'4' (h*(Y), k*(X)), a
предельный член присоединен к к*(Х). Есть и другие
спектральные последовательности (см. [8], [9]), свя-
связывающие одни О. т. к. с другими.
Полезно было бы научиться трактовать О. т. к. как
когомологический функтор, т. е. разлагать h* : Р —>- GA
в композицию Р ->¦ А —>. GA, где I — канонический (не
зависящий от h*) функтор в абелеву категорию А. Один
из путей реализации этого намечен в [8].
Лит.: [1] Дольд А., «Математика», 1965, т. 9, Jvfi 2,
с. 8—14; [2] С т и н р о д Н., Э й л е н б е р г С, Основания
алгебраической топологии, пер. с англ., М., 1958; [3] К о н-
н е р П., Ф л о й д Э., Гладкие периодические отображения,
пер. с англ., М., 1969; [4] У а й т х е д Д ж., Новейшие дости-
достижения в теории гомотопий, пер. с англ., М., 1974; [5] S w i t-
zer R., Algebraic topology-homotopy and homology, В., 1975;
[6] H о в и к о в С. П., «Изв. АН СССР, Сер. матем.», 1967,
т. 31, №4, с. 455—951; [7] Атья М., «Математика», 1966,
т. II), Х° 5, с. 48—69; [8] Adams J., Stable homotopy
and generalised homology, Chi.—[a. o.], 1974; [9] D у е г Е.,
Kahn D., «Trans. Amer. Math. Soc», 1969, v. 145, p. 397 —
437; [10] Milnor J., «Pacific J. Math.», 1962, v. 12, № 1,
p. 337—41' [11] Dyer E., Cohomology theories, N. Y.—Amst.,
19B9. Ю. Б. Рудяк.
ОБОБЩЕННЫХ ФУНКЦИЙ ПРОИЗВЕДЕНИЕ —
произведение af = fa обобщенной функции f из D' (О)
с функцией а?С°° (О), определяемое равенством
(af, <р) = (/, аф), фб-О(О);
при этом af?D' (О) и для (обычных) функций f(x) из
1аос(О) произведение af совпадает с обычным умно-
умножением функций f(x) и а(х).
Примеры. 1) а(х)Ь(х) = а@)Ь(х); 2)х9>±-=\.
Однако эта операция произведения не допускает рас-
распространения на любые обобщенные функции так, чтобы
она была ассоциативной и коммутативной, иначе было
бы противоречие:
> ~ = F (X) X) р ^ = б (X) (х? ± ) = б {X).
Чтобы определить произведение двух обобщенных
функций / и g, достаточно, чтобы они обладали,
грубо говоря, свойствами: насколько / «нерегулярна»
в окрестности произвольной точки, настолько g должна
быть «регулярной» в этой окрестности и наоборот, напр,
если sing supp / f| sing supp g=0 (см. Обобщенной
функции носитель). В нек-рых классах обобщенных
функций их произведение можно определить, однако
оно может оказаться неоднозначным.
Пример ы: 3) Граничные значения из алгебры
голоморфных функций Н (С) (одночастотные обобщенные
функции):
f(x+iO)g(x + iO)= lim f(x+iy)g(x + iy) в S'.
1/-+0, С
Они образуют алгебру, ассоциативную и коммутативную
с единицей [2].
41 б2(г) = сб (х), где с — произвольная постоянная.
Действительно,
6 И,
Но на основных функциях ц>(х) таких, что ср(О) = О,
Поэтому естественно положить (б2, ф) = 0, если p?,
Ф @) = 0. Расширяя этот функционал на все основные
функции ф из .D, получают 4).
5) Определить произведение -^. Функция ^~ не
принадлежит к Ь\ж (R1), однако она определяет регу-
регулярные обобщенные функции: 0 ия D', х < 0, и — иа
D', х > 0. Их можно согласованно продолжить до обоб-
обобщенных функций из D', напр., взяв конечную часть
по Адамару расходящегося интеграла (п е р е н о р м и-
ровав его)
x J M У Jo x JM
Ф
Обобщенная функция ( —— J (перенормированный
в (х) \
функционал для —— ) зависит от произвольного
параметра М > 0. Произвол в перенормировке таков:
м, м w
Эти идеи привели к процедуре перенормировки ампли-
амплитуд Фейнмана в квантовой теории поля. Перенормиро-
Перенормировочные константы (напр., массы и заряды) выступают
как произвольные постоянные, аналогичные ln-rr1 ;
наиболее общее определение О. ф. п. дается в терминах
волновых фронтов.
Лит.: [1] Schwartz L., Theorie des distributions,
t. 1—2, P., 1950—51; [2] В л а д и м и р о в В. С, Обобщен-
Обобщенные функции в математической физике, М., 1976; [3] Бого-
Боголюбов Н. Н., П а р а с ю к О. С, «Acta Math.», 1957, v. 97,
p. 227—66; [4] Хепп К., Теория перенормировок, пер. с
франц., М., 1974. В. С. Владимиров.
ОБОБЩЕННЫХ ФУНКЦИЙ ПРОСТРАНСТВО —
пространство, сопряженное к пространству
основных (достаточно хороших) ф у н к ц и й.
Важную роль здесь играют Фреше пространства
(типа FS) и сильно сопряженные к ним (типа DFS).
Пространство типа FS есть проективный предел ком-
компактной последовательности банаховых пространств и
его сопряженное ость пространство типа DFS. Прост-
Пространство типа DFS есть индуктивный предел компакт-
компактной последовательности банаховых пространств и его
сопряженное есть пространство типа FS. Пространства
типов FS и DFS — полные, сепарабельные, рефлек-
рефлексивные и монтелевские. В пространствах типов FS п
DFS слабая и сильная сходимости совпадают.
Примеры пространств основных и
обобщенных функций.
1) Пространства S и S'. Пространство основных
(быстро убывающих) функций 5=5 (R") со-
состоит из С" (К")-функций, убывающих на бесконечно-
бесконечности вместе со всеми производными быстрее любой сте-
степени Ы. Это пространство есть проективный предел
последовательности банаховых пространств Sp, р=0,
1, . . ., состоящих из О(К")-функций, с нормой
ф - || ф ||= SUp* A + [ X Р)Р/2 | ХХХф {х) |,
|а кр
причем вложение Sp + lcSp компактно; S типа FS.
Сопряженное пространство S' = S' (Rn) (пространство
обобщенных функций медленного роста) есть
индуктивный предел последовательности банаховых
пространств Sp, причем вложение SpCS'p+i компактно,
так что S' типа DFS. Из (слабой) сходимости последо-
последовательности обобщенных функций в S следует сходи-
сходимость по норме функционалов в нек-ром S'p. В про-
пространствах S и S' операция преобразования Фурье
есть изоморфизм.
2) Пространства D (О) и D' (О) (О — открытое мно-
множество в R"). Пространство основных функций состоит
из финитных в О С™ (О)-функций (см. Обобщенной
функции носитель). Оно снабжается топологией стро-
строгого индуктивного предела (возрастающей) последова-
последовательности пространств C^(Ok), k—l, 2, . . ., типа FS,
где {Ok} — строго возрастающая последовательность
открытых множеств, исчерпывающая О : 0?<g0fc + ],
= О. Пространство С„ (О^) есть проективный
предел (убывающей) последовательности банаховых
пространств Cp0(Ok), р~0, 1, ..., состоящих из Ср (Rn)-
функцнй с носителем в Ok, с нормой
ф-*1М1р = max,.jD<*(p(.T)|,
I а |<р
причем вложение Co+1(Ok)aCo (Ok) компактно. Пусть
D' (О) — пространство, (сильно) сопряженное с D (О);
D=D (R") и D'=D' (Rn). Последовательность основ-
основных функций из D (О) сходится в D (О), если она сходит-
сходится в каком-либо пространстве Со° (О^). Последователь-
Последовательность обобщенных функций из D' (О) сходится в D' (О),
если она сходится на каждом элементе us D (О) (слабая
сходимость). Для того чтобы линейный функционал на
D (О) был обобщенной функцией из D' (О), необходимо
и достаточно, чтобы для любого открытого множества
О'О существовали числа К и т такие, что
Пространство D' (О) — (слабо) полное: если после-
последовательность обобщенных функций fu^z®' (О), к=
= 1, 2, . . ., такова, что для любой (р из D (О) числовая
последовательность (/^, ср) сходится, то функционал
(/, ф)= lim (}k, ф)
принадлежит D' (О). Обобщенная функция из D' (О)
имеет произвольный «рост» в окрестности границы дО,
в частности любая функция 1?ь\ос(О) определяет
обобщенную функцию из D' (О) по формуле
3) Пространства Ф и Ф'. Пусть Фр — банахово
пространство, состоящее из всех функций ф(г), z=x-\-
-{-iy, голоморфных в трубчатой области Ы<р, x^R",
с нормой
Ф-М1ф||р= SUP еР ' * ' I Ф (x+iy) I;
| У | < р, Х? R"
вложение Фрс:Фр', р>р', компактно. Пусть Ф —
индуктивный предел (возрастающей) последователь-
последовательности пространств Фг,п, »->оо. Пространство Ф типа
DFS, а его сопряженное Ф' типа FS. Элементы Ф
являются Фурье-гиперфункциями; Ф'
изоморфно также пространству S{.
Лит.: [1] Schwartz L., Theoric des distributions,
t. 1—2, P., 1950—51; [2] Бур баки Н., Топологические
векторные пространства, пер. с франц., М.. 1959; [3] Д ь ё д о н-
н е Ж., Шварц Л., «Математика», 1958, т. 2, JMi 2, с. 77—
107; [4] Г р о т е н д и к А., там же, Л» 3, с. 8!—127; [5] Г е л ь-
ф а и д И. М., Шилов Г. Е., Пространства основных и
обобщенных функций, М., 1958: LfilYoshinaga К., «J. Sci.
Hiroshima Univ. Ser. A», 1957, v. 21, p. 89 — 98; [7] К a w a i Т.,
«J. Fac. Sci. Univ. Tokyo Sec. 1A», 1970, v. 17, p. 467 — 517;
[8] Владимиров В. С, Обобщенные функции в мате-
математической физике, 2 изд., М., 1979. В. С. Владимиров.
ОБОЛОЧЕК ТЕОРИЯ — направление в теории уп-
упругости и строительной механике, основная цель к-рого
состоит в описании напряжений и деформаций, возни-
возникающих под действием внешних нагрузок в оболочке.
Оболочка — твердое тело, ограниченное двумя поверх-
поверхностями, к-рое обладает малой по сравнению с другими
характерными размерами толщиной. В О. т. рассматри-
рассматриваются и другие внешние воздействия, напр, тепловые.
В О. т. вводится гладкая поверхность g, наз. сре-
среди н н о й, по обе стороны к-рой на расстоянии h (x)
вдоль нормали к g расположены точки ограничивающих
оболочку повеБхностей. В большинстве случаев тол-
толщина постоянна: h(x)-=^h. Наиболее распространенный
вариант О. т. использует т. н. г и п о т е з у Кирх-
Кирхгофа — Лява, согласно к-рой всякое нормальное к
g волокно (отрезок прямой, перпендикулярный к сре-
срединной поверхности) сохраняет после деформации свою
прямолинейность, длину и нормальное положение к
срединной поверхности. При этом предположении систе-
систему уравнений трехмерной теории упругости, описыва-
описывающей перемещения точек оболочки как упругого твер-
твердого тела, сводят к системе трех дифференциальных
уравнений с двумя независимыми переменными х1 и
хг — криволинейными координатами точкп х недефор-
мированной срединной поверхности g. В общем случае
эта система нелинейна. При дополнительных предполо-
предположениях о малости деформаций и внешних нагрузок
нелинейные члены могут быть отброшены. Задача сво-
сводится к решению линейной системы (см. [3], [4])
о
2- = i mijuJ=4i' * = 1' 2> 3' М
в к-рой qj — компоненты внешней нагрузки, то,-у —
линейные дифференциальные операторы с коэффициен-
коэффициентами, зависящими от геометрич. характеристик поверх-
поверхности g, a uj(x) — искомые компоненты вектора пере-
перемещения точки срединной поверхности. Система A)
решается при четырех граничных условиях, к-рые за-
зависят от характера закрепления края g. Операторы
mij в A) имеют специальный вид:
малый параметр /г,2 стоит при старших производных.
Система A) является эллиптической в смысле Дугли-
са—Ниренберга (см. [5]) и формально самосопряженной
(см. 17J). При естественно возникающих граничных
условиях система A) порождает эллиптич. краевую за-
задачу. Систему A) принято наз. системой уравнений
м о м е н т н о й О. т., поскольку при ее получении
учитываются члены, содержащие изгибающие и крутя-
крутящие моменты. При дополнительных предположениях
указанным» членами пренебрегают, что приводит к
безмоментной (мембранной) О. т. Фор-
Формально этот переход сводится к отбрасыванию в A)
членов, содержащих малый параметр К1. Безмоментная
система
2,3 = ,1.7й/= ««• 1 = 1- 2' 3> <2>
существенно проще, чем система A). Все операторы
в B) не выше 2-го порядка. Порядок определителя
главного символа (характеристич. полинома) в случае
системы B) равен 4, а в случае A) равен 8.
Наличие малого параметра в A) позволяет восполь-
воспользоваться процедурой аснмптотич. интегрирования (см.
[41). Если гауссова кривизна К срединной поверхности
g положительна, то система B) эллиптична и при усло-
условиях полного или частичного закрепления края вырож-
вырождение моментной задачи в безмоментную при /г-*-0
регулярно. Заметное расхождение решений возможно
лишь в малой окрестности края g (краевой эффект).
При К <; 0 картина вырождения моментной системы
при h —>- О существенно сложнее; переход от системы
A) к B) может привести к значительным погрешностям
не только у края g, но и всюду внутри. Используемая
в О. т. процедура асимптотпч. интегрирования при
нерегулярном вырождении еще A982) не нашла мате-
матич. обоснования.
Безмоментная О. т. тесно связана с проблемой бес-
бесконечно малых изгибаний поверхностей. Существенный
вклад в безмоментную О. т. и одновременно в теорию
бесконечно малых изгибаний был внесен благодаря
привлечению аппарата обобщенных аналитических функ-
функций (см. [2]).
Важной задачей О. т. является исследование устой-
устойчивости форм равновесия, с к-рой связана проблема оп-
определения критич. нагрузки. Эти задачи рассматрпва-
ются в линейной (точнее, использующей линеаризацию)
и нелинейной постановках. Один из методов их реше-
решения в нелинейной постановке существенно использует
теорию изгибаний (см. [8]).
В задачах статики эффективен метод комплексного
представления уравнений О. т., позволяющий путем
введения вспомогательных функций свести систему A)
к эквивалентной системе с характеристич. многочленом
4-го порядка (см. [7]).
Среди вопросов динамики, подвергшихся интенсивно-
интенсивному математич. анализу, находится проблема свободных
и вынужденных колебаний, совершаемых оболочкой.
Методами асимптотич. интегрирования и спектральной
теории операторов найдена структура спектра собствен-
собственных частот и строение соответствующих форм свобод-
свободных колебаний (см. [5], [9]).
В О. т. широко используются методы вычислительной
математики. В случае разделяющихся переменных в
статич. и динамич. задачах особенно эффективен метод
прогонки, в случае оболочек произвольного очертания—
метод конечных элементов.
Лит.: [1] Алумяэ Н. А., Теория упругих оболочек и
пластинок, в кн.: Механика в СССР за 50 лет, т. 3, М., 1972,
с. 227—66; [2] В е к у а И. Н., Обобщрнные аналитические
функции, М., 1959; [3] В л а с о в В. Э., Общая теория оболо-
оболочек и ее приложение в технике, М.— Л., 1949; [4] Г о л ь д е н-
в е й з е р А. Л., Теория упругих тонких оболочек, 2 изд.,
М., 1976; [5] Г о л ь д е н в е й з е р А. Л., Лидс кий В. Б.,
Товстик П. Е., Свободные колебания тонких упругих
оболочек, М., 1979; [6] Муштари X. М., Г а л и-
м о в К. 3., Нелинейная теория упругих оболочек, Казань,
1957; [7] Н о в о ж и л о в В. В., Теория тонких оболочек,
2 изд., Л., 1962; [8] П о г о р е л о в А. В., Геометрические
методы в нелинейной теории упругих оболочек, М., 1967; [9]
Прочность. Устойчивость. Колебания. Справочник, т. 3, М.,
1968. В. Б. Лидский.
ОБРАЗ МОРФИЗМА категории — понятие,
аналогичное понятию образа отображения одного мно-
множества в другое. Однако в теории категорий существует
несколько подходов к определению этого понятия.
Наиболее простой подход тесно связан с понятием би-
категории. Пусть в категории Я1 существует бикатегорная
структура Я= (Я, (?, Ш1), где Й — класс допустимых
эпиморфизмов, Щ1 — класс допустимых мономорфизмов.
Если а : А -^- В — произвольный морфизм из Я н а=
= v|i — допустимое разложение а, т. е. v?(v, ц?Ш!,
то подобъект (ц] объекта 5, определяемый мономорфиз-
мономорфизмом f*, наз. (допустимым) образом м о р ф и з -
м а а (относительно заданной бикатегорной структуры).
Если в Я' имеется единственная бпкатегорная структу-
структура, то можно говорить об О. м. а. В частности, в кате-
категориях множеств, групп, векторных пространств над
нек-рым полем сформулированное определенно приво-
приводит к обычному понятию образа отображения или гомо-
гомоморфизма.
С другой стороны, если в категории St существует
несколько бикатегорных структур, то один и тот же
морфпзм может иметь разные образы относительно раз-
различных бикатегорных структур. Подобная ситуация
имеет место, напр., в категориях топологич. пространств
и ассоциативных колец.
Другой подход к определению О. м. состоит в следую-
следующем. Говорят, что морфизм а : А —*¦ В проходит через
подобъект (ц) объекта 5, если а можно представить в
виде а = а'ц,. Наименьший подобъект объекта В, через
к-рый проходит а, наз. образом а. Если категория Я
локально мала слева и в Я существуют пределы се-
семейств мономорфизмов с общим концом, то каждый мор-
морфизм из Я имеет образ.
Если в Я имеется бикатегорная структура, в к-рой
все мономорфизмы допустимы, то второе определение
О. м. эквивалентно определению О. м. относительно
указанной бикатегорной структуры.
О. м. обычно обозначается Lm а; через im а обозна-
обозначается любой представитель подобъекта Im а.
М. Ш. Паленка.
ОБРАЗУЮЩИЙ ОБЪЕКТ категории, обра-
образующий категории,— понятие, позволяющее распознать
различные морфизмы категории и, как правило, «моде-
«моделировать» все объекты категории с помощью копроизве-
дений одного и того же объекта. Объект U категории Ж
паз. образующим, если для любого объекта А из
Si, не являющегося левым нулем, множество Hg (U, А)
непусто и для любого необратимого мономорфизма
и, : А —>- В существует такой морфизм у : U ->¦ В, к-рый
не представим в виде у = y'\i. Если в категории Ы
каждая пара морфизмов обладает ядром, то для любой
пары морфизмов а, Р : Л —>¦ В, а =т^ Р, найдется такой
морфизм у : U ->¦ А, что уа, ф у$. Следовательно, если
множество Н.«¦ (U, А) непусто для любого A^Ob.ft',
то О. о. Ui оказывается интегральным объектом. По-
этому иногда О. о. определяется как интегральный объ-
объект. В случае абелевых категорий понятия образующе-
образующего и интегрального объектов эквивалентны.
В категории множеств каждое непустое множество
есть О. о. В категориях, порождаемых многообразиями
универсальных алгебр, каждая свободная алгебра есть
О. о. В категории топологич. пространств каждое не-
непустое пространство с дискретной топологией является
О. о.
В бикатегориях обычно рассматриваются допустимые
О. о., т. е. такие объекты, к-рые обладают всеми свой-
свойствами образующих только по отношению к допустимым
МОНОМОрфпЗМаМ. JVT- Ш. Цпленко.
ОБРАТИМЫЙ МОДУЛЬ — модуль М над комму-
коммутативным кольцом А , для к-рого существует Л-модуль N
такой, что M(?)N изоморфно А (изоморфизм А-моду-
А-модулей). Модуль М обратим тогда п только тогда, когда он
конечно порожден, проектнвен и имеет ранг 1 над
каждым простым идеалом кольца А. Классы изоморфных
О. м. образуют группу Пи кара кольца Л;
операция в этой группе индуцирована тензорным про-
произведением модулей, а единичным элементом является
класс модуля А. В некоммутативном случае (A, By
бимодуль, где А ц В — ассоциативные кольца, наз.
обратимы м, если существует такой (В, Л (-би-
(-бимодуль N, что
М (g)B TV ~ А и Лг ®А М ~ В. ¦
Лит.: [1] Бур баки Н., Коммутативная алгебра, пер.
с франц., М,, 1971; [2] Ф е й с К., Алгебра: кольца, модули и
категории, пер. г англ., т. 1, М., 1977. Л. В. Кузьмин.
ОБРАТИМЫЙ ПУЧОК — локально свободный пу-
пучок (9у-модулей ранга 1 на окольцованном простран-
пространстве (X, fix)- Эквивалентное определен-ие О. п.: пучок
C^-модулей, локально изоморфный пучку Q%- О. п.
на X, рассматриваемые с точностью до изоморфизма,
образуют абелеву группу относительно операции тен-
тензорного умножения над Qx- Зта группа наз. Ликара
группой пространства X и обозначается Pic X. Обратным
к пучку X будет в ней пучок jf-1=55fo»t(Jf, (^),
двойственный к X. В случае, когда (X, Qx) — схема
(в частности, алгебрапч. многообразие) или аналитпч.
пространство, пучок (Зх~м()ДУлей обратим тогда и только
тогда, когда он изоморфен пучку регулярных (соответ-
(соответственно аналитических) сечений нек-рого линейного
алгебраического (соответственно аналитического) рас-
расслоения над X.
О. п. на схемах тесно связаны с дивизорами. Каждому
дивизору Картье D на X сопоставляется О. и. Qx(D),
чем определяется инъективный гомоморфизм С1Х -»-
-+PicX, где С1Х — группа классов дивизоров Картье
на X. Для целых схем X этот гомоморфизм является
изоморфизмом.
На проективной схеме X определяется подкручи-
подкручивающий обратимый пучок С е р р а
6x(i) = 0(l)- А именно, если задано вложение схемы X
в проективное пространство Р^, то Qx(i) соответствует
классу гиперплоского сечения. В частности, если X —
= РЛ (к) — проективное пространство над полем к, то
пучок CA) есть прямой образ пучка линейных функций
на к^^1 при естественном отображении АЛ' + 1\{0} ->
-+Рл'(к). Систему однородных координат х0, хх, . . ., х^
в PN (к) можно отождествить с базисом пространства
сечений V(PN, 6A)).
О. п. на схеме X над полем к связаны с рациональны-
рациональными отображениями схемы X в проективные простран-
пространства. Пусть X — О. п. на схеме X, s0, . . .,sj^— сече-
сечения пучка X, значения к-рых в любой точке х?Х
порождают слой X х над 0Х. Тогда существует единст-
единственный морфизм ф : X —>- Р-^(к) такой, что ер*C(\)=Х
и cp*.r,-=s,-, где .т0, хг, . . ., ждг— однородные координаты
в PN(\). О. п. X на X наз. очень обильным,
если существует такое вложение ц> : X -+¦ Р^ (к), что
Ф*CA) = X. О. п. X па X наз. обильным, если
существует такое целое положительное п, что Хп очень
обилен. На нётеровой схеме X над к обратимый пучок X
обилен тогда и только тогда, когда для каждого коге-
когерентного пучка JF на X существует такое целое по>О,
что пучок JT(X)j?'! порождается при п~^п0 своими гло-
глобальными сечениями.
Если X — обильный О. п. на X, соответствующий
дивизору D, то D наз. обильным дивизором.
Дивизор Картье D на схеме X, собственной над алгеб-
алгебраически замкнутым полем к, обилен тогда и только
тогда, когда для каждой замкнутой целой подсхемы
Yc^X индекс пересечения Dr-Y положителен, где г=
= dim Y. По поводу других критериев обильности см.
[5]. Существует также обобщение понятия обильного
дивизора на подмногообразия большей коразмерности
[2].
Понятия очень обильного и обильного О. п. перено-
переносятся также на случай аналптич. пространств (по поводу
крптериев обильности в этой ситуации см. Положитель-
Положительное расслоение).
Лит.: [1] Hartshorne R., Algebraic geometry, N. Y.,
1977; [21 его же, Ample subvarieties ot algebraic varieties,
N. Y. — В., 1970; [3] Мамфор д Д., Лекции о кривых
на алгебраической поверхности, пер. с англ., М., 1968;
Ul ill а ф а р е в и ч И. Р., Основы алгебраической геомет-
геометрии, М., 1972; [5] Итоги науки и техники. Алгебра. Топология.
Геометрия, т. 10. М., 1972, с. 47 —112. В. А. Псковских.
ОБРАТИМЫЙ ЭЛЕМЕНТ полугруппы с
единицей — элемент х, для к-рого существует та-
такой элемент у, что xy=i (правая обрати-
обратимость) или ух=1 (левая обратимость).
Если элемент обратим и справа и слева, то он наз.
двусторонне обратимым (часто просто
обратимым). Множество G(S) всех двусторонне
О. э. полугруппы S с единицей является наибольшей
подгруппой из S, содержащей единицу. Бициклическая
полугруппа доставляет пример существования элемен-
элементов, обратимых только справа и только слева; более
того, существование таких элементов в полугруппе S
влечет наличие в S бициклич. подполугруппы, единица
к-рой совпадает с единицей полугруппы S. Другой аль-
альтернативой является ситуация, когда всякий односто-
односторонне О. э. полугруппы S будет двусторонне обратим—
это имеет место тогда и только тогда, когда либо S=
— G(S), лу.бо S\G(S) есть подполугруппа (являющаяся,
очевидно, наибольшим идеалом в S); такая полугруппа
наз. полугруппой с отделяющейся груп-
групповой частью. Полугруппами с отделяющейся
групповой частью будут, напр., всякая конечная полу-
полугруппа с единицей, всякая коммутативная полугруппа с
единицей, всякая полугруппа с двусторонним сокраще-
сокращением и единицей, всякая мультипликативная полугруп-
полугруппа комплексных матриц, содержащая единичную мат-
матрицу.
Лит.: [1] Клиффорд А., Престон Г., Алгебраи-
Алгебраическая теория полугрупп, т. 1, пер. с англ., М., 1972; [2]
Л я пи н Е. С, Полугруппы, М., 1960. Л. Н. Шеврин.
ОБРАТНАЯ МАТРИЦА к квадратной мат-
матрице Л над полем К — матрица А -1, для к-рой
АА~1=А~1А = Е —единичная матрица. Обратимость
матрицы равносильна ее невырожденности (см. Невы-
Невырожденная матрица). Для матрицы Л = ||а,-у|| обратной
является матрица Л~1=||у,у||, где
A ji — алгебраическое дополнение элемента осу,-. О ме-
методах вычисления О. м. см. Обращение матрицы.
ОБРАТНАЯ ТЕОРЕМА — теорема, условием к-рой
служит заключение теоремы исходной (прямой), а заклю-
заключением — условие. Обратной к О. т. будет исходная
(прямая) теорема, так что прямая и О. т. взаимно
обратны.
О. т. равносильна теореме, противоположной к пря-
прямой, т. е. теореме, в к-рой условие и заключение пря-
прямой теоремы заменены их отрицаниями. Поэтому прямая
теорема равносильна противоположной к обратной, т. е.
теореме, утверждающей, что если неверно заключение
прямой теоремы, то неверно и ее условие. Известный
способ «доказательства от противного» как раз и пред-
представляет собой замену доказательства прямой теоремы
доказательством теоремы, противоположной к обратной.
Справедливость обеих взаимно обратных теорем озна-
означает, что выполнение условия любой из них не только
достаточно, но и необходимо для справедливости зак-
заключения. См. также Теорема, Необходимые и достаточ-
достаточные условия. БСЭ-з.
ОБРАТНАЯ ФУНКЦИЯ — функция, определенная
на множестве значений заданной функции и ставящая в
соответствие каждому его элементу множество всех тех
элементов из области определения рассматриваемой фун-
функции, к-рые в него отображаются, т. е. его полный про-
прообраз. Если данная функция обозначена символом /, то
О. ф. обозначается символом f~1. Таким образом, если
/ : X -> У и Уу — множество значений функции /,
YtCzY, то для любого yGY, справедливо равенство
f-1(y)={x:f(x) = y).
Если для любого элемента y^Yf его полный про-
прообраз состоит в точности из одного элемента х?Х,
т. е. отображение / : X -+ Yу является биекцией, то
О. ф. является однозначной, в противном слу-
случае — многозначной.
Если множества X и Y являются подмножествами чис-
числовой прямой (или вообще нек-рых упорядоченных
множеств), то условие строгой монотонности функ-
функции / необходимо и достаточно для существования
обратной однозначной функции.
По ряду свойств функции / можно судить о соответ-
соответствующих свойствах О. ф. Так, напр., если функция /
строго монотонна и непрерывна на нек-ром промежутке
числовой оси, то ее О. ф. также монотонна и ненрерывна
на соответствующем промежутке. Если взаимно одно-
однозначное отображение бикомпакта на топологическое
ха5'сдорфово пространство непрерывно, то и обратное
отображение непрерывно, т. е. рассматриваемое от-
отображение является гомеоморфизмом. Когда отобра-
отображение / является биективным линейным ограниченным
оператором, отображающим банахово пространство X
на банахово пространство Y, то обратный оператор
/-1 также является линейным и ограниченным.
Пусть / — непрерывное отображение замыкания G
ограниченной области GczR" с достаточно хорошей
границей в R", / — дифференцируемо в G и отобража-
отображает границу G на границу /(G) и множество нулей
его якобиана образует изолированное множество; тог-
тогда если отображение / взаимно однозначно на грани-
границе области G, то оно взаимно однозначно и на G. Для
существования локального обратного отображения в
окрестности данной точки достаточно необращения в
нуль якобиана отображения в нек-рой окрестности
этой точки. Если / : G -+ R", GczR", f — дифферен-
дифференцируемое отображение с якобианом, неравным нулю
во всех точках х ? G, то для любой точки х0 ? G су-
существует такая ее окрестность U=U(x0), что сужение
j\u отображения / на окрестности U взаимно однозначно
отображает множество U на нек-рую окрестность]/— V(y0)
точки г/о==/(-го) u обратное отображение f~l также диф-
дифференцируемо (на V). Эта теорема обобщается и на беско-
бесконечномерный случай: пусть X и У — полные норми-
нормированные пространства, GdX — открытое множество,
/ : G —v У — непрерывно дифференцируемое отображе-
отображение. Если /' (х0) — обратимый элемент пространства
линейных ограниченных операторов X (X, У) (/' —
производная Фреше), xo?G, то существуют такие окре-
окрестности U=U(x0) и V—V(y0) соответственно точек х0 и
!/„= / (х0) в пространствах X и У, что отображение
/ : (/->¦ V является непрерывно дифференцируемым гоме-
гомеоморфизмом вдгесте со своим обратным отображением.
Лит.: [1] Колмогоров \. Н., Фомин С. В.,
Элементы теории функций и функционального анализа, 5 изд.,
М.. 1981; [2] Шварц Л., Анализ, пер. с франц., т. 1, М.,
1972. Л. Д. Кудрявцев.
ОБРАТНО ПАРАБОЛИЧЕСКОЕ УРАВНЕНИЕ —
уравнение вида
— а(х, t)u = f(x, t), (*)
где форма 2а;-Д/|у положительно определена. Перемен-
Переменная t играет роль «обратного» времени. При подстанов-
подстановке i=—t' уравнение (*) приводится к обычному пара-
болич. виду. Встречаются параболич. уравнения «сме-
«смешанного» типа, напр, уравнение Uf=xuxx является
прямым параболическим при х> 0, обратно параболи-
параболическим при х<.0 с вырождением порядка при х=0.
А. П. Солдатов.
ОБРАТНОЕ ОТОБРАЖЕНИЕ (обратный опе-
оператор) к однозначному отображению
(оператору)
на
¦— однозначное отображение g такое, что
g°f=Ix на М, A)
fog = Iy на f(M), B)
где MczX1 f(M)czY, X, Y — нек-рые множества.
Если g удовлетворяет лишь условию A), то оно
наз. правым обратным отображением
к /, если лишь B) — левым обратным отоб-
отображением к /. О. о. /-1 существует тогда и только
тогда, когда для любого y^f(M) полный прообраз/ (у)
состоит из единственного элемента х?М. Если отобра-
отображение / имеет обратное отображение /~\ то уравнение
1{х) = У C)
однозначно разрешимо при любом y^f(M). Если суще-
существует только правое О. о. /п\ то существует и решение
уравнения C), но вопрос об однозначности решения
остается открытым. Наличие же лишь левого О. о.
/jj обеспечивает единственность решения в предполо-
предположении, что оно существует. Если X и У — векторные
пространства, и А — линейный оператор из X в У,
то А~г, если он существует, тоже линеен. Вообще, в
случае наделения X и У той пли иной структурой,
случается, что нек-рые свойства оператора А сохраня-
сохраняются и при переходе к А-1 в предположении, что он
существует. Так, если X и У — банаховы простран-
пространства и А : X —»- У — замкнутый оператор, то А -1
также замкнут; если Н — гильбертово пространство и
А : Н -> Н самосопряжен, то А -г также самосопря-
самосопряженный оператор; если / : R —>- R — нечетная функция,
то /-1 — также нечетная, и т. д. Непрерывность А не
всегда сохраняется при переходе к А-1 для многих
важных классов линейных операторов, напр, вполне
непрерывных. Важными признаками непрерывности
операторов, обратных к линейным, являются следую-
следующие.
Пусть X — конечномерное векторное пространство
с нек-рым базисом и А : X —v X задается в этом базисе
матрицей Ца^-Ц. Для существования А ~х необходимо и
достаточно, чтобы det||a,-y|| Ф О (операторы А и А~х
в этом случае автоматически непрерывны).
Пусть X и Y — банаховы пространства и А —
линейный непрерывный оператор из X в Y.
1) Если ||Ai||^mi|a;||, где щ>0, то А~х существует
и непрерывен.
2) Если X=Y, |U|1<1, то (/ — А)-1 существует и
непрерывен, причем
где ряд справа сходится по норме в пространстве X (X).
3) Оператор А ~г существует и непрерывен на всем Y
тогда и только тогда, когда его сопряженный А * имеет
обратный, определенный я непрерывный на всем X*.
При этом (A-J)* = (A*)~1.
4) Если оператор А'1 существует и непрерывен и
\\А—B||<:i|A ||-1, то оператор В также существует
и непрерывен, причем
Таким образом, множество обратимых операторов
открыто в Х(Х, Y) в равномерной топологии этого
пространства.
5) Теорема Банаха об изоморфиз-
м е: если А взаимно однозначно отображает X на У,
те О. о., к-рое существует, непрерывно. Эта теорема
допускает обобщение: взаимно однозначное линейное
непрерывное отображение совершенно полного простран-
пространства X на отделимое бочечное пространство Y явля-
является топологич. изоморфизмом.
Ряд утверждений о существовании и непрерывности
оператора, обратного к линейному непрерывному, со-
содержится в спектральной теории линейных операторов,
действующих в гильбертовом пространстве. Так, если А
самосопряжен и X не действительно, то (А—Х1)~1
существует и непрерывен.
Лит.: [1] Данфорд Н., Шварц Дж., Линейные
операторы. Общая теория, пер. с англ., М., 1962; [2] Канто-
Канторович Л. В., Авилов Г. П., Функциональный ана-
анализ, 2 изд., М., 1977; [3] РуДин У., Функциональный ана-
анализ, пер. с англ., М., 1975; [4] Робертсон А.-П., Р о-
б е р т с о н В.-Д ж., Топологические векторные пространства,
пер. с англ., М., 1967. В. И. Соболев,
ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ —
функции, обратные гиперболическим функциям. О. г. ф.
наз. ареа-синус гиперболический, ареа-косинус гипер-
гиперболический, ареа-тангенс гиперболический: Аг sli x,
Аг eh х, Аг th х\ другие обозначения: аг sh х, аг ch x,
аг th x\ sh;):, ch^, \Xi~xx.
О. г. ф. действительного переменного х определяют-
определяются формулами
Arshz --=In (я-f |Лг2+1), —оо <я< + оо,
АгсЬл;= ±1п(х+ Ух2 — 1), яЗэ1,
ATthx=±ln — , \x\<i.
О. г. ф. однозначны и непрерывны в каждой точке
своей области определения за исключением О. г. ф.
Arch х, к-рая двузначна. При изучении свойств О. г. ф.
для Аг ch х выбирается одна из ее непрерывных ветвей,
т. е. в формуле для Аг ch x выбирается только один
знак (обычно — плюс).
Графики О. г. ф. см. на рисунке. О. г. ф. связаны
между собой рядом соотношений. Напр.,
1
Ar sh х = Аг th
Аг th х --= Ar sh ¦
X' + 1
У 1-х'
Производные О. г. ф. нахо-
находятся по формулам
1
(Ar ch х)' = ± ¦
(Ar sh x)' =
(Arthi)' = -г-
О. г. ф. комплексного переменного z определяются
по таким же формулам, что и для действительного
переменного х, причем под In z понимается многознач-
многозначная логарифмич. функция. О. г. ф. комплексного пере-
переменного являются аналитич. продолжениями соответ-
соответствующих О. г. ф. действительного переменного в ком-
комплексную плоскость.
О. г. ф. выражаются через обратные тригонометрич.
функции по формулам
Ar sh z= — г' arc sin iz,
Ar ch z= i arc cos z,
Ar th z=— i arc tg iz.
Ю. В. Сидоров.
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНК-
ФУНКЦИИ, а р к ф у н к ц и и, круговые ф у н к-
ции,— функции, обратные тригонометрическим функ-
функциям. Шести основным тригонометрич. функциям со-
соответствуют тесть О. т. ф.: арксинус, арккосинус,
арктангенс, арккотангенс, арксеканс, арккосеканс;
обозначаются соответственно Arc sin x, Arc cos x,
Arc tg x, Arc ctg x, Arc sec x, Arc cosec x. Функции
Arc sin x и Arc cos x определены (в действительной об-
области) для !ж|<:1, функции Arc tg ж и Arc ctg ж — для
всех действительных х, а функции Arc sec x я
Arc cosec x — для \х\^ 1; две последние функции мало-
малоупотребительны. Другие обозначения: sin-'rr, cos^
и т. п.
Так как тригонометрич. функции периодические, то
обратные к ним функции являются многозначны-
м и функциями. Определенные однозначные ветви
(главные ветви) этих функций обозначаются так:
arc sin х, arc cos x, , . . Именно, arc sin x есть та ветвь
функции Arc sin x, для к-рой— я/2<:агс sin к я/2.
Аналогично, функции arc cos х, arc tg x и arc ctg x
определяются из условий: 0<g:arc cos x •< я,
— я/2 < arc tgx < я/2, 0 <
< are ctg x < п.
На рисунке изображены
графики функций у=
= Arc sin .r, y= Arc cos, x, у =
—Arc tg x, y= Arc ctg x; глав-
главные ветви этих функций вы-
выделены жирной линией.
О. т. ф. Arc sin x, ... лег-
легко выражаются через
arc sin x, . . ., напр.:
Arc sin ?= (—1)" arcsina-l-яп,
Arc cos x— ± arc cos x-\-2nn.
Arc tg x = arc tg x -\- nn,
Arc ctg x = arc ctg x-\-nn,
n=0, ±1, ±2, ...
О. т. ф. связаны соотношениями
arc sin x-\-arc cosx = я/2, —1<г<1,
arc tg x-\- arc ctg x = я/2, — oo < x < -f- oo.
Поэтому функции arc cos х и arc ctg x в нижеследую-
нижеследующих формулах не фигурируют.
О. т. ф. бесконечно дифференцируемы и в окрестности
каждой внутренней точки своей области определения
могут быть разложены в ряды Тейлора. Производные,
интегралы и разложения в ряды О. т. ф. :
(arc sin x)' = у== , (arc tg х)' = j^-2 ,
\ arc sin x dx~x arc sin x-\- УI — x2~\-C,
arc tg x dx=xarc tg x—— In A -j-*2) + C,
О. т. ф. комплексного переменного определяются
как аналитические продолжения соответствующих
О. т. ф. действительного переменного в комплексную
плоскость.
О. т. ф. выражаются через логарифмическую функ-
функцию:
arc sin z = —г In (iz+ j/4 — z2),
arc cos z = —г In (z-f- \ z"- — 1),
arc tg z .= у In ¦ +_^z ,
arc ctg z = \-\nlz~-¦¦¦¦ .
6 2 iz +1
Ю. В. Сидоров.
ОБРАЩЕНИЕ МАТРИЦЫ — алгоритм, применяе-
применяемый при численном нахождении обратной матрицы.
Как и в задаче решения линейных систем, методы
численного обращения подразделяются на прямые и
итерационные; однако итерационные методы вследствие
их трудоемкости играют здесь существенно меньшую
роль.
Большинство прямых методов О. м. основано на идее
разложения заданной матрицы в произведение легко об-
обращаемых сомножителей.
Если
A =L\Li. . .Lfc
— такое разложение, то
Типичным (и одним из наиболее употребительных)
прямых методов О. м. является метод Жордана
(см. [1]).
Пусть А — невырожденная матрица порядка п.
Построение обратной матрицы А~1 происходит в п.
шагов; результатом к-то шага будет матрица Af,, первые
к столбцов к-рой совпадают с одноименными столбцами
единичной матрицы. Переход от Ак (пусть А = А0) к
-4ft + i с матричной точки зрения эквивалентен умноже-
умножению А/, слева на матрицу Lk + ^, к-рая отличается от
единичной лишь (А-}-1)-м столбцом. Элементы этого
столбца выбираются так, чтобы привести (A:—f-l)-ii стол-
столбец А ? к единичному, и имеют вид
„(к) „(к)
1, ft+l k, k+i
ak+l, k+l "ft + l, k + l
1 _ ° n, к + 1
,<*> '"¦' „(ft)
lk + \, k+l a k+l, k+l
Из соотношений
вытекает
k, Ап = Е
A)
Получение факторнзованного представления A) для
обратной матрицы А-1 требует примерно n"U опера-
операций умножения и примерно п'1г операций сложе-
сложения. Приблизительно такое же члсло дополнительных
операций необходимо для того, чтобы перемножить
матрицы в A) и получить явный вид А~1. Во многих
приложениях операции О. м. использование фактори-
зованной формы A) столь же удовлетворительно, что и
явного вида. Напр., вычисление произведения А ~~'Ь,
где Ь — вектор-столбец, требует одинаковой арнфметич.
работы в обоих случаях. Одинаковы и требования к
памяти при реализации на ЭВМ.
В приведенном описании метода Жордана предпола-
предполагалось для простоты, что все элементы eft+i, k+i (на-
(называемые ведущими элементами) отличны от
нуля. В действительности метод Жордана, как и методы
типа Гаусса для решения линейных систем, как правило,
применяется с той или иной схемой выбора ведущих
элементов. Использование такой схемы равносильно
введению в A) дополнительных множителей, учитываю-
учитывающих перестановки строк и столбцов обратной матрицы.
Точность вычисленного решения, как и в случае линей-
линейных систем, зависит от степени роста матричных эле-
элементов на промежуточных шагах метода. Такой рост
л, следовательно, ухудшение точности вычисляемого
решения в методе Жордана, даже при выборе ведуще-
ведущего элемента, более вероятны, чем в методах типа
Гаусса.
Н е в я з к о й, соответствующей приближенной обрат-
обратной матрице X для А, наз. матрица R = E—АХ. Имеет
место оценка
1 А ~' - X I
R\
Таким образом, норма невязки является оценкой отно-
относительной точности приближенной обратной матрицы X.
В этом состоит важное отличие задачи численного О. м.
от задачи решения линейных систем, где (напр., в ор-
ортогональных методах или методах типа Гаусса) невязка
обычно мала, а качество полученного решения зависит
от обусловленности системы.
Обращение ряда важных классов матриц может быть
достигнуто значительно более экономичными, чем в об-
общем случае, методами. Таковы теплицевы, ганкелевы,
ленточные (и, в частности, трехдиагональные) матрицы,
блочные матрицы, имеющие теплпцеву структуру или
структуру кронекерова произведения, и т. д. Напр.,
пусть Т — теплицева матрица порядка п-|-1 с элемен-
элементами из Н или С:
Т =
*0
t-1
t-2
t-n t-r.
t-,,
Предполагается, что не только Т, но и ее главная под-
подматрица порядка п невырождены. Тогда для матри-
цы Т-1, уже, вообще говоря, не являющейся тепли-
цевой, справедливо представление (см. [2]):
1
Рп
о
о
ап О
в1
О
о ъ„
0
ьпO
0
«1 iJ
При этом векторы
суть соответственно первый и последний столбцы Т~1.
Таким образом, Т полностью определяется заданием
первого и последнего столбцов. При необходимости па
B) могут быть последовательно вычислены все элементы
Т-1:
{}i + i,j+i{T}iw/ + {bi + 1aj + 1an-in_j)
Это вычисление требует О (я2) арифметич. операций.
В экономичных алгоритмах обращения теплицевых:
матриц (см., напр., [3]) вычисление a,-, bj и рп прово-
проводится по рекуррентным формулам и также требует-
О(п2) операций. Условие невырожденности главных
подматриц может быть ослаблено с сохранением поряд-
порядка О (п-) необходимой арифметич. работы.
Иногда операцию О. м. используют с тем, чтобы ре-
решать линейные системы Ах=Ь по формуле х=А~1Ь.
В случае матрицы общего вида такой образ действии
имеет мало смысла, т. к. сопровождается проигрышем
и в арифметич. работе, и в численной устойчивости по-
сравнению с прямым решением линейной системы.
Для теплицевых (и родственных им) матриц ситуация
иная. Как показывает представление B), вычисление
Т~гЬ сводится к выполнению четырех умножений
теплицевых матриц на векторы и вычитанию векторов.
Существуют экономичные алгоритмы умножения теп-
лицевой матрицы на вектор, требующие (для порядка п)
О(п log га) операций. Для задачи решения теплицевых
систем такая асимптотика арифметич. работы пока не-
недостигнута. Поэтому при многократном решении линей-
линейных систем Тх=Ъ с одной л той же теплицовой матрицей
Т и различными правыми частями b предварительное-
обращение Т, по-видимому, целесообразно.
Предварительное О. м. может быть оправданным л
в случае многократного решения линейных систем с од-
одной и той же матрицей общего вида на ЭВМ с большим
числом параллельно работающих процессоров. Причина-
в том, что по сравнению с операцией умножения мат-
матрицы на вектор прямые методы решения линейных сис-
систем не имеют столь же удобного распараллеливания.
Во многих случаях (напр., в квазиньютоновых мето-
методах математич. программирования) требуется обратпть-
матрицу А, отличающуюся от матрицы В с известной
обратной В~1 матрицей ранга 1 или (в случае сим-
симметричной матрицы В) симметричной матрицей ранга 2.
Такая перестройка обратной матрицы может быть выпол-
выполнена для матриц порядка п за О (га2) арифметич. опера-
операций. Примером может служить следующая формула
(см. [4]): если и и v — векторы-столбцы, то
уг)-1 В-1 B-hTB-1
где y = i-\-vTB~1u считается отличным от нуля.
С точки зрения теории вычислительной сложности
задача О. м. общего вида имеет (на последовательной
машине) сложность того же порядка, что и задача ре-
решения линейной системы (при выполнении нек-рых
естественных условий на скорость роста сложности
•обеих задаче увеличением их порядка [5]). Эта слож-
сложность имеет порядок, не превышающий nlog2 7.
Лит.: [1] Воеводин В. В., Численные методы алгео-
ры, М., 1966; [2] Гохберг И. Д., Фельдман И. А.,
Уравнения в свертках и проекционные методы их решения, М.,
1971: [3] Т г е п с h W., «SIAM J. Contr.», 1964, v. 12, p. 512 —
S22; [4] Ф а д д е е в Д. К., Ф а д д е е в а В. Н., Вычисли-
Вычислительные методы линейной алгебры, 2 изд., М.— Л., 1963; [5]
Ахо А., Хопкрофт Дж., Улъман Дж., Построе-
Построение и анализ вычислительных алгоритмов, пер. с англ., М.,
1979. С. Д. Ипрамов.
ОБРАЩЕНИЕ РЯДА — получение по известному
¦степенному ряду
»=/(*) =2"=0Ьу(*-а)Л bi*0, A)
ряда для обратной функции z=<p(w) в виде
z = 4>(w)=^k=oak(w-b)b, B)
где &=/(а)=Ь0. ао = а,
Ряд B) наз. также О. р. A), или рядом Л а г р а н-
ж а. Более общая задача о получении разложения про-
произвольной сложной аналитич. функции F[q>(w)] реша-
решается Бюрмана — Лагранжа рядом. Если круг сходи-
сходимости ряда A) есть \z—a\ <р, то ряд B) сходится в круге
\w—b\ <б, где б есть расстояние от точки Ь до образа
окружности ]z—а|=р при отображении w=f(z).
Если функция w=f(z) разлагается в ряд вида
if = /(z)=i + 2];™=OT*/(z — аУ' ™Ss2, Ътф0, C)
т. е. если а —критическая точка для /(z), то обратная
¦функция z=q>(w) имеет в b алгебраическую точку
ветвления порядка т—1 и О. р. C) возможно только
в виде ряда Пюизё:
г=ф (w) =a+2°°-i аЬ (w—t>)k"n,
Аналогично решается задача обращения Лорана ряда
по целым отрицательным и положительным степеням
z—а в том случае, когда в таком ряде имеется лишь
конечное число отрицательных (пли положительных)
степеней (см. [1]).
Для аналптич. функций многих комплексных пере-
переменных z= (zb . . ., zn), и>1, вопросы обращения ста-
ставятся по-разному. Напр., если / : С"—*-С" — невырож-
невырожденное (т. е. такое, что ранг матрицы Якоби l|3//3zft||
равен п) голоморфное отображение окрестности нуля
С" в С", /@)=0, то существует в нек-рой окрестности
нуля и голоморфное обратное отображение <р, к-рое
ложно записать в виде многомерного ряда Бюрмана —
Лагранжа (см. [3]).
Slum.: [1] М а р к у ш е в и ч А. И., Теория аналитических
•функций, 2 изд., т. 1, М., 1967; [2]Гурвиц А.,Курант Р.,
Теория функций, пер. с нем., М., 1968; [3] С о л т а н Б. Е.,
и кн.: Голоморфные функции многих комплексных переменных,
^Красноярск, 1972, с. 129 — 37. Е. Д. Соломенцее.
ОБРАЩЕНИЕ ЭЛЛИПТИЧЕСКОГО ИНТЕГРА-
ИНТЕГРАЛА — проблема, состоящая в построении функции и
как функции от z или однозначных сложных функций
вида f(u(z)) в случае эллиптического интеграла
z=[" R (z, w) dz,
где R — рациональная функция от переменных z, w,
связанных уравнением w2—F(z), F(z) — многочлен
Н-н Т1ли 4-й степени без кратных корней. Полное реше-
решение этой проблемы дали почти одновременно в 1827 — 29
Н. Абель (N. Abel) и К. Якоби (С. Jacobi), показав, что
ее решение приводит к новым трансцендентным эллип-
эллиптическим функциям.
Существенно иной подход к теории эллиптич. функ-
функций принадлежит К. Вейерштрассу (К. Weierstrass).
Для эллиптич. интеграла I рода в нормальной форме
Вейорштрасса
Z= \ i
оказывается ^-функцией Вейерштрасса с ин-
инвариантами ?2, g3 (см. Вейерштрасса эллиптические
функции). Для эллиптич. интеграла I рода в нормаль-
нормальной форме Лежандра
Гф dt
) 0 Vi-ft2 sin2 t
z=\ -r
обращение приводит к Якоби эллиптическим функциям.
Лит.: [1] А х и е з е р Н. И., Элементы теории эллипти-
эллиптических функций, 2 изд., М., 1970; [2] Г у р в и ц А., Ку-
Курант Р., Теория функций, пер. с нем., М., 1968.
ОБРЫВА ЦЕПЕЙ УСЛОВИЕ — условие "конечно-
"конечности возрастающих или убывающих цепей в частично
упорядоченном множестве. Условие обрыва
убывающих цепей: для всякой цени а^^а^^...'^
~^ak~^z... элементов частично упорядоченного множества
Р найдется такой номер п, что ап=ап + 1=. . . Выполне-
Выполнение этого условия эквивалентно каждому из следующих
спойств частично упорядоченного множества Р:
1) всякое непустое подмножество М<^Р имеет хотя
бы один минимальный (в М) элемент (условие
м и н и м а л ь н о с т и);
2) все элементы из Р обладают нек-рым свойством
е, если этим свойством обладают все минимальные
элементы множества Р и если справедливость свойства
г для любого а?Р можно вывести из того, что в справед-
справедливо для всех х<Са, х?Р (условие индук-
индуктивности).
Условие индуктивности позволяет для множеств с
условием обрыва убывающих цепей проводить по индук-
индукции доказательства и построения. При этом если Р
вполне упорядочегго,— получается трансфинитная
индукция, а если Р изоморфно множеству всех неотри-
неотрицательных целых чисел,— обычная математич. индук-
индукция (см. Индукции аксиома).
Условие обрыва возрастающих
ц с н е й (и эквивалентные ему утверждения) формули-
формулируется двойственным образом (см. Двойственности
принцип в частично упорядоченных множествах).
В решетке с условпем обрыва возрастающих цепей каж-
каждый идеал — главный. Всякое конечное множество
очевидно удовлетворяет обоим О. ц. у., однако обрат-
обратное утверждение (конечность множества, удовлетворяю-
удовлетворяющего этим двум условиям) неверно. Решетка с условиями
обрыва убывающих и возрастающих цепей полна.
О. ц. у. используются в алгебре, в основном в при-
применении к упорядоченному по включению множеству
подсистем различных алгебраич. систем (см., напр.,
Артинов модуль, Артинова группа, Артиново кольцо,
Композиционный ряд, Нётеров модуль, Нётерова груп-
группа, Не'терово кольцо).
Лит./ [1] Б и р к г о ф Г., Теория структур, пер. с англ.,
М., 1952; [21 К у i> о ш А. Г., Лекции по общей алгебре,
2 изд., М., 1973; [31 С к о р н я к о в Л. А., Элементы теории
структур, М., 1970. Т. С. Фофанова.
ОВЩАЯ АЛГЕБРА — часть алгебры, занимающая-
занимающаяся изучением тех или иных алгебраич. систем, включаю-
включающая в себя теории групп, колец, модулей, полугрупп,
решеток (структур) и т. п. Вне рамок О. а. остаются
такие направления, как изучение матриц и линейных
уравнений, алгебраич. геометрия и алгебраич. теория
чисел, полилинейная алгебра и т. п. Выделение О. а.
как части алгебры довольно условно, и граница ее рас-
расплывчата. Напр., трудно сказать, относятся ли к О. а.
теоригт полей, конечных групп пли конечномерных ал-
алгебр Ли.
Если универсальная алгебра снабжена порядком пли
топологией, согласованными с операциями, то возникает
частично упорядоченная или топологич. алгебра соот-
соответственно. Исследование этих объектов также отно-
относится к О. а. Наиболее развиты теории частично упо-
упорядоченных и топологич. групп и колец.
Начало развития О. а. относится к 19 в., когда были
исследованы нек-рые конечные группы и конечномер-
конечномерные алгебры. Однако современная О. а. связана с
проникновением в алгебру теоретико-множественного
мышления и является продуктом 20 в. Так, первая
монография (О. Ю. Шмидта, см. [1]), где группа не пред-
предполагается конечной, по определению, появилась лишь
в 1916. В первую очередь эта перестройка коснулась
теории групп, а затем теории колец. Результаты этой
перестройки отражены в монографии Б. Ван дер Варде-
на (В. L. Van der Waerden), вышедшей в 1930—31.
Выявление общих моментов, содержащихся в теориях
групп и колец, привело к рассмотрению решеток (струк-
(структур), универсальных алгебр и категорий. Появление
теории моделей и алгебраич. систем связано с вскры-
вскрытием связей алгебры и математич. логики. Желание
выяснить, в какой мере те или иные факты теории групп
зависят от наличия обратных элементов и ассоциатив-
ассоциативности, породило полугруппы и квазигруппы. Все эти
вновь появившиеся разделы О. а. через нек-рое время
обрели собственную проблематику, нашли собственные
пути развития и собственные области приложения
(напр., полугруппы оказались чрезвычайно важными
для алгебранч. теории автоматов). Более того, оти на-
направления в свою очередь начали оказывать влияние на
породившие их классич. разделы О. а. Так, напр.,
понятие многообразия алгебр, выкристаллизовавшееся
в теории универсальных алгебр, играет важную роль в
современной теории групп и колец. В качестве другого
примера можно назвать изучение классов групп и ко-
колец, определяемых свойствами решетки их подгрупп и
нормальных подгрупп, идеалов и подколец, а также
вопросов, связанных с решеточными изоморфизмами.
См. также Универсальная, алгебра.
Лит.: [1] Шмидр О. Ю., Абстрактная теория групп,
2 изд., М.— Л., 1933; [2] В а н дер Варден Б. Л., Ал-
Алгебра, пер. с нем., 2 изд., М., 2979; [3] К у р о ш А. Г., Лек-
Лекции по общей алгебре, 2 изд., М., 1973; [4J е г о же. Общая ал-
алгебра. Лекции 1969/1970 учебного года, М., 1974; [5] Маль-
Мальцев А. И., Алгебраические системы, М., 1970; [6] С у д з у-
ки М., Строение группы и строение структуры ее подгрупп,
пер. с англ., М., 1960. Л. А. Скорняков.
ОБЩАЯ ТОПОЛОГИЯ — ветвь геометрии, посвя-
посвященная исследованию непрерывности и предельного
перехода на том естественном уровне общности, к-рый
определяется природой этих понятий. Исходными поня-
понятиями О. т. являются понятия топологического прост-
пространства и непрерывного отображения, выделенные в
1914 Ф. Хаусдорфом (F. Hansdorf).
Частным случаем непрерывных отображений явля-
являются гомеоморфизмы— непрерывные взаимно однознач-
однозначные отображения топологич. пространств, обладающие
непрерывным обратным отображением. Пространства,
к-рые можно отобразить друг на друга посредством
гомеоморфизма (т. е. гомеоморфные пространства), счи-
считаются в О. т. одинаковыми. Одной из основных задач
О. т. является выделение и исследование естествен-
естественных топологич. инвариантов — свойство пространств,
сохраняющихся гомеоморфизмами. Разумеется, каждое
свойство пространства, к-рое формулируется исключи-
тельно в терминах его топологии, автоматически явля-
является топологии, инвариантом. Доказательство топо-
логич. инвариантности свойства пространства требу-
требуется лишь тогда, когда оно формулируется с привле-
привлечением каких-либо дополнительных структур, опреде-
определенных на множестве точек пространства и так или
иначе связанных с его топологией. Примером может
служить топологич. инвариантность групп гомологии.
Топологич. инвариант не обязательно выражается
числом; напр., связность, бикомпакгность, метризу-
метризуемость — топологич. инварианты. Среди числовых ин-
инвариантов (принимающих числовые значения на конк-
конкретных топологич. пространствах) важнейшими явля-
являются размерностные инварианты: малая индуктивная
размерность ind, большая индуктивная размерность
Ind и размерность Лебега dim (размерность в смысле
покрытий).
Важную роль играют топологич. инварианты ипой
природы, значениями к-рых служат кардинальные чис-
числа. Среди них: вес, характер.
В связи с системой топологич. инвариантов возникают
классы топологич. пространств — каждый класс опре-
определяется ограничением на тот или иной топологич. ин-
инвариант. Наиболее важны классы метризуемых прост-
пространств, бикомпактных пространств, тихоновских про-
пространств, паракомпактных пространств, перистых
пространств.
Основные «внутренние» задачи О. т. таковы; 1) вы-
выделение новых важных классов топологич. пространств;
2) сравнение различных классов топологич. прост-
пространств; 3) изучение пространств в пределах того или
иного класса и категорных свойств этого класса в це-
целом. Центральной в этой группе, безусловно, является
задача 2), направленная на обеспечение внутреннего
единства О. т.
Выделение новых важных классов топологич. прост-
пространств (т. е. новых топологич. инвариантов) часто
связано с рассмотрением дополнительных структур на
пространстве (числовых, алгебраических, порядковых),
естественно согласованных с его топологией. Так,
выделяются метризуемые пространства, упорядоченные
пространства, пространства топологических групп,
симметризуемые пространства и др. Важную роль
при решении задач 1), 2), 3) играет метод покрытий.
На языке покрытий и соотношений между покрытиями,
важнейшими из к-рых являются отношения вписан-
вписанности и звездной вписанности, выделяются фундамен-
фундаментальные классы бикомпактных и паракомпактных про-
пространств, формулируются топологич. свойства типа ком-
компактности. Метод покрытий играет важную роль в раз-
размерности теории.
Для решения центральной задачи 2) особенно важен
метод взаимной классификации пространств и отобра-
отображений. Он направлен на установление связей между
различными классами топологич. пространств посред-
посредством непрерывных отображений, подчиненных тем или
иным простым ограничениям. Пространства весьма об-
общей природы удается при этом описать как образы более
простых пространств при «хороших» отображени-
отображениях. Напр., пространства с первой аксиомой счетности
характеризуются как образы метрич. пространств при
непрерывных открытых отображениях. Связи такого
рода составляют эффективную систему ориентиров при
рассмотрении классов тонологич. пространств.
Метод обратных спектров, тесно связанный с ме-
методом покрытий и методом отображений, позволяет
сводить изучение сложных топологич. пространств к
рассмотрению систем отображений пространств более
простых.
Наконец, в решении задачи 2) существенно участву-
участвует метод кардинальнозначных топологяч. инвариантов,
или мощностных характеристик. Инварианты такого
рода наиболее созвучны теоретико-множественной при-
природе О. т. В связи с этим система кардинальнозначных
инвариантов обладает большой разветвленностыо и
оказывает влияние практически на все остальные топо-
логич. свойства. Другая важная особенность карди-
пальнозначных инвариантов — их тесная взаимосвязь,
в основе к-рой лежит возможность осуществлять над
такими инвариантами арифметнч. операции и сравни-
сравнивать их по величине. Благодаря указанным чертам
теория кардинальнозначных инвариантов играет унифи-
унифицирующую роль в О. т. и дает подход к любому из ее
разделов.
Среди внешних задач О. т. выделяется, прежде
всего, следующая задача общего характера: как свя-
связаны и взаимодействуют свойства топологии и др.
структур, согласованных с этой топологией. Конкрет-
Конкретные задачи этого рода относятся к топологическим
группам, к топологическим векторным пространствам
и к мерам на топологических пространствах. Каждому
бикомпакту отвечает банахова алгебра всех непрерывных
действительных функций на этом бикомпакте. Этим
теория топологич. пространств ставится в тесную связь
с теорией банаховых алгебр. Большую роль в функцио-
функциональном анализе играют слабые топологии на банаховых
пространствах. Это — важный для приложений класс
неметризуемых топологии. Каждое тихоновское про-
пространство характеризуется однозначно кольцом всех
непрерывных действительных функций на нем в тоио-
логии поточечной сходимости. Результаты этого рода
соединяют О. т. и топологическую алгебру.
Понятие бикомпактного расширения нашло приложе-
приложение в теории потенциала (Кольцевая граница, Мартина
граница).
О. т. важна в методич. отношении ири обучении мате-
математике. Только в рамках ее понятий и конструкций
вполне выясняются и становятся прозрачными фунда-
фундаментальные концепции непрерывности, сходимости,
параллельного перехода. Трудно назвать области мате-
математики, в к-рых понятия и язык О. т. совсем бы не ис-
использовались. В этом, в частности, проявляется ее
объединяющая роль в математике. Положение О. т.
в математике определяется и тем, что целый ряд прин-
принципов и теорем, имеющих общематематич. значение,
получает свою естественную (т. е. отвечающую природе
этих принципов, теорем) формулировку только в рамках
О. т. Примерами могут служить понятие бикомпактно-
сти — абстракции от леммы Гейне — Бороля о выборе
конечного шэдпокрытия отрезка, теорема о бикомиакт-
ности произведения бикомпактных пространств (за к-рой
стоит, в качестве прообраза, утверждение о бикомпакт-
ности конечномерного куба), теорема о том, что непре-
непрерывная действительная функция на бикомпакте огра-
ограничена и достигает наибольшего и наименьшего значе-
значений. Этот ряд примеров можно продолжить: понятие
множества второй категории, понятие полноты, понятие
расширения (сам характер этих понятий и относящихся
к ним результатов, важных для математики в целом,
делает наиболее естественным и прозрачным их иссле-
исследование в рамках О. т.).
Лит.: [1] Александров II. С, Теория функций дей-
действительного переменного и теория топологических пространств,
М. 1978, с. 280—358; [2] е г о же, «Успехи матем. наук»,
I960 т. 15 в. 2, с. 25 — 95; [3] его же, там же, 1964, т. 19,
в. 6, с. 3 — 46; 1965, т. 20, в. 1, с. 253 — 54; [4] А л е к с а н д-
р о в П. С, Ф е д о р ч у к В. В., там же, 1978, т. 33, в. 3, с. 3—
48' [5] А р х а н г е л ь с к и й А. В., там же, 1966, т. 21, в. 4,
с. 133—84; [6j e г о же, там же, 1978, т. 33, в. 6, с. 29—84.
А. В. Архангельский.
ОБЩАЯ ТОЧКА — точка топологич. пространства,
замыкание к-рой совпадает со всем пространством.
Тоиологич. пространство, имеющее О. т., является не-
неприводимым топологическим пространством', однако
неприводимое пространство может как вообще не иметь
ни одной О. т., так и иметь много О. т. Впрочем, если
пространство удовлетворяет Колмогорова аксиоме, то
оно может иметь не более одной О. т. Любое неприводи-
неприводимое алгебраич. многообразие пли неприводимая схема
обладают н притом единственной О. т. В этом случае
О. т. есть не что иное, как спектр поля рациональных
функций многообразия.
Термин «О. т.» употребляется иногда также для обо-
обозначения общего положения точки. в- 1L Данилов.
ОБЩЕГО ПОЛОЖЕНИЯ ТОЧКА — точка, принад-
принадлежащая нек-рому открытому плотному в топологии
Зариского подмножеству алгебраич. многообразия.
В алгебраич. геометрии О. п. т. часто наз. просто о 5-
Щ е Й Т о Ч К о Й. °- А- Иванова.
ОБЩЕЕ ПОЛОЖЕНИЕ — словосочетание, употреб-
употребляющееся в оборотах типа: «объекты С в О. п. имеют
свойство S (или свойства ?,-)», «S есть свойство О. п.»,
«приведение в О. п.», точный смысл к-рых зависит от
контекста. Обычно совокупность ?) всех рассматрива-
рассматриваемых объектов снабжается структурой, позволяющей
считать нек-рые подмножества ^tcST1 «малыми», «пре-
небрежимыми» или, наоборот, «большими», «массивны-
«массивными»; тогда S считается «свойством: О. п.», если обладаю-
обладающие им объекты образуют в О «большое» подмножество.
?) обычно имеет одну из следующих структур: а) ал-
алгебраического многообразия, б) дифференцируемого мно-
многообразия (возможного, бесконечномерного), в) тоиоло-
гич. пространства, чаще всего Лора пространства
в нервом значении этого термина, г) пространства с
мерой. «Малыми» считаются соответственно: алгебраич.
подмногообразия (меньшей размерности), дифференци-
дифференцируемые подмногообразия и конечные или счетные объ-
объединения таковых, нигде не плотные множества или мно-
множества первой категории, множества меры нуль. Мно-
Множество ЗГоС* считается «большим», если дополнение к
нему — «малое». Тогда говорят также, что % содержит
«большинство» объектов из О или «почти все» эти объ-
объекты, а свойство S, выполняющееся для почти всех
объектов, наз. «типичным», или свойством О. п. Не-
Нередко говорят о «типичном» объекте, объекте общего по-
положения или объекте, находящемся в О. п., подразу-
подразумевая (иногда молчаливо), что имеется одно или несколь-
несколько «типичных» свойств (каких именно — должно быть
ясно из контекста) и что речь идет об объекте, обладаю-
обладающем этими свойствами.
В более слабом смыеле «большое» подшаджееъво
в случаях в) и г) может означать подмножество вто-
второй категории в непустом открытом подмножестве про-
пространства ?) или подмножество положительной
меры. Тогда говорят, что «этим множеством объектов
нельзя пренебрегать» (но уже не говорят о «типич-
«типичности») .
В случаях а) п б) «малое» множество ЭГсО имеет
положительную коразмерность codim 3t. Естественно
считать, что 2t тем меньше, чем больше codim 31.
Близкой к б) (и более общей) является ситуация, когда
можно говорить об м-нараметрич. семействах объектов
О (Xi, . . ., А,„), достаточно гладко зависящих от п (скаляр-
(скалярных) параметров, и всевозможные такие семейства обра-
образуют пространство Бэра. Если почти все (в смысле в))
эти семейства не содержат объектов из 3(, то говорят,
что codim 3f>«, а если это так при любом «, то пола-
полагают codim 2C= оо. Соображения коразмерности играют
значительную роль в теории бифуркаций и теории
особенностей, дифференцируемых отображений (см.
также [8]).
На объекты могут действовать нек-рые операции g;
их совокупность G обычно является группой или хо-
хотя бы полугруппой с единицей е. О «приведении объек-
объекта 6> в О. п. посредством операции g» говорят, когда
из контекста ясно, что рассматриваются определен-
определенные свойства; «приведение» означает, что gO обла-
обладает этими свойствами. Как и С1, G обычно снабжается
структурой, позволяющей говорить о «большом» мно-
множестве операций или о том, что операцию g, переводя-
переводящую О в объект gO с нужными свойствами, можно
выбрать сколь угодно близкой к е («приведение в О. п.
посредством малого шевеления»).
Напр., на плоскости прямая и окружность в О. п.
либо не пересекаются, либо пересекаются в двух точках.
В. данном случае объект есть пара (а, 6), где а — пря-
прямая, Ь—окружность, а в качестве операций можно взять
евклидовы движения (либо одни только параллельные
переносы),, действующие на а при фиксированном Ь.
Совокупность всевозможных объектов С и группа G
естественно снабжаются всеми названными выше струк-
структурами, и О. н. можно понимать согласно любому из
описанных вариантов. Первоначально об О. п. говорили
именно в подобных геометрич. вопросах, поэтому дан-
данный термин употребляется в разделах математики.
являющихся геометрическими но своему характеру или
по крайней мере испытавших значительное геометрич.
влияние (хотя соображения, связанные с множествами
второй категории или полной меры, используются и за
их пределами). По сей день термин «О. п.» часто приме-
применяется к ситуации, непосредственно обобщающей при-
приведенный пример, когда речь идет о трансверсальности
двух подмногообразий в нек-ром объемлющем многооб-
многообразии (или к роде т ней ной ситуации с трансверсальными
самопересечениями иммерсированного подмногообра-
подмногообразия). В частности, в геометрич. топологии (рассматри-
(рассматривающей кусочно линейные или топологич. многообразия
и соответствующие классы отображений) термин «О. н.»
употребляется почти исключительно как синоним транс-
трансверсальности.
В алгебраич. геометрии простые примеры (вроде при-
приведенного) легко разбираются с помощью теории ис-
исключения, причем основное ноле может быть довольно
произвольным (обычно алгебраически замкнутым). Име-
Имеются теоремы, связанные с О. п. в более сложных си-
ситуациях (напр., Вертини теоремы, Лефшеца теорема о
гиперплоском сечении); при изучении действия алгеб-
алгебраич. группы на алгебраич. многообразии большую
роль играют общего положения точки [1].
В дифференциальной топологии и теории особенно-
особенностей дифференцируемых отображений О.п. используется
очень широко. Доказательства обычно проводятся с
помощью теоремы Сарда или ее следствий — теорем
Абрахама и Тома о трансверсальности (см. [2], [3]),
более удобных для непосредственного применения. В
бесконечномерном случае теорема Сарда не верна,
однако можно получить более слабые результаты, к-рых
иногда бывает достаточно (см. [4], [5]).
В теории гладких динамич. систем имеется ряд ре-
результатов о «типичных» свойствах. Большинство из
них (особенно в локальной теории бифуркаций [3])
доказывается с использованием редукции к теореме
Сарда; положительные результаты, не связанные с такой
редукцией, немногочисленны (см. [6], [7], [9], [10], а
также лит. при ст. Грубая система). Для теории глад-
гладких динамич. систем характерно наличие существенного
различии между О. п. в топологич. ц метрич. смысле [в)
и г) см. выше] [11].
Об О. п. в дифференциальной геометрии многообра-
многообразий см. [12], [13].
,'lum.: ll] M u m f о г d D., Geometric invariant theory,
В.— Hdll),— X. Y., ПКы; 121 Л енг С, Введение в теорию
диффсрешшр>емых мпогоооралий, пер. с англ., М., 1967, при-
приложение Ш: 13] Арнольд В. И., Дополнительные главы
теории обыкновенных дифференциальных уравнений, М., 1978;
[4] Eeils J., McAlpin J., «J. Math. ,and Meeh.», 1968,
V. 17, Ms 11, p. 1055 — 154; Г5] Q u i n n F., в кн.: Global analysis,
Providence, 1970, p. 213—22; [ti] Gutierrez C, «Trans.
Amer. Math. Soc.», 1978, v. 241, p. 311—20; [7] e г о же,
oJ. Ditl. Equations», 1978, v. 29, ЛЬ 3, p. 388—95; [8] К u r-
1 a ii d H., R о b b i n J., в кн.: Dynamical Systems — War-
Warwick, 1974, В.— Hdlb.— N. Y., 1975, p. 135 — 50; [9] T a-
k e n s F., там же, р. 293—304; [10] Добрынский В. А.,
Ill а р к о в с к и й А. Н., «Докл. АН СССР», 1973, т. 211,
.№ 2, с. 273—76; [11] Арнольд В. И., «Изв. АН СССР.
Сер. матсм.», 1Я61, т. 2э, № 1, с. 21 — 86; 1964, т. 28, № 2,
с. 479 — 80; [12] Wall С, в кн.: Geometry and topology,
В.— Hdlb,— N. Y., 1977, p. 707 — 74; [13] К 1 i n g e n Ъ е г jW,,
Lectures on closed geodesies, B.— Hdlb.— N. Y., 1978.
Д. В. Аносов.
ОБЩЕЕ РЕШЕНИЕ системы обыкновенных диффе-
дифференциальных уравнений n-го порядка
x'=^f(t, .г), х = (хи ..., xn)?R», A)
в области О — гладкое по t и непрерывное по совокуп-
совокупности параметров «-параметрическое семейство вектор-
функций
x----q>(t, С1? ..., С„), (Си ..., Cn)^CdR", B)
откуда при соответствующем выборе значений пара-
параметров получается любое решение системы, график
к-рого проходит в области GczD; здесь DdRn + 1 —
область, где выполнены условия теоремы существова-
существования и единственности для системы A). (Иногда условли-
условливаются, что параметры могут принимать и значения
±оо.) Геометрически О. р. системы A) в области G
представляет собой семейство непересекающихся интег-
интегральных кривых этой системы, полностью заметающих
всю область.
О. р. системы A) в области G позволяет найти реше-
решение задачи Коши для этой системы с начальным усло-
условием х (to)=x°, (t0, jr°) ?G: нужно из системы п равенств
?0=<р ((„, Сх, ¦ ¦ ., Сп) определить значения п параметров
Сг, . . ., Сп и подставить эти значения в B). Если ,г=
— \\ (t, t0, x") — решение системы A), удовлетворяю-
удовлетворяющее условию x(t(l) = x", (*„, x°)?D, то ге-парамстриче-
ское семейство
где tu — фиксированное число, a ,rj, . . . п
риваются как параметры, является О. р. системы A)
в нек-рой области GcD и наз. О. р, в форме Ho-
Horn и. Знание О. р. позволяет однозначно восстановить
систему дифференциальных уравнений." для этого надо-
из п. соотношений B) и из п соотношений, получаю-
получающихся дифференцированием соотношений B) по t,
исключить п параметров С\, .... Сп.
В случае обыкновенного дифференциального уравне-
уравнения п-то порядка
y^ = t(x, у, у' j/"-]>) C)
О. р. в области G имеет вид п-параметрического семей-
семейства функций
1/-<р(.т, Си ..., С„), (Си ..., Cn)?Cd<R", D)
из к-рого при соответствующем выборе значений па-
параметров получается решение уравнения C) с любыми
начальными условиями
о
(*о, У о, г/о, ..-, y»n
здесь DczR" + l — область, где выполнены условия тео-
теоремы существования и единственности для уравнения
C).
Функция, получающаяся из О. р. при конкретных
значениях параметров, наз. частным решением.
Семейство функций, содержащее все решения данной
системы (уравнения) в нек-рой области, не всегда уда-
удается выразить в виде явной функции независимой пере-
переменной. Это семейство может оказаться записанным в
виде неявной функции — и тогда оно наз. общим интег-
интегралом — или в параметрич. виде.
Если конкретное обыкновенное дифференциальное
уравнение C) допускает интегрирование в замкнутой
форме (см. Интегрирование дифференциальных уравне-
ний в замкнутой форме), то часто удается получить
соотношение типа D), где параметры возникают как по-
постоянные интегрирования и оказываются произвольны-
произвольными постоянными. (Именно поэтому часто говорят, что
О. р. уравнения n-го порядка содержит п произвольных
постоянных.) Однако такое соотношение далеко не
всегда является О. р. во всей области существования и
единственности решения задачи Коши для исходного
уравнения.
Лит.: [1] Степанов Б. В., Куре дифференциальных
уравнений, 8 изд., М., 1959; [2] Еругин Н. П., Книга
для чтения по общему курсу дифференциальных уравнений,
3 изд., Минск, 1979. Я. X. Розов.
ОБЩЕЗНАЧИМОСТЬ — свойство логической фор-
формулы, состоящее в том, что эта формула истинна при лю-
любой интерпретации входящих в нее нелогич. символов,
т. е. предикатных и пропозициональных переменных.
Логич. формулы, обладающие этим свойством, наз. о б-
щ е з н а ч и м ы м и, или тождественно ис-
истинными, или тавтологиями. Всякая обще-
общезначимая формула выражает логический закон. Вместо
слов «формула А общезначима» часто пишут: «\^А».
Важнейшими видами логич. формул являются пропо-
пропозициональные и предикатные формулы. При классич.
понимании логических операций О. пропозицио-
пропозициональных формул проверяется путем построе-
построения истинностных таблиц: формула общезначима тогда
и только тогда, когда при любых истинностных значе-
значениях пропозициональных переменных она принимает
значение И («истина»). О. предикатной фор-
формулы означает истинность в любой модели. Множе-
Множество общезначимых предикатных формул неразрешимо,
т. е. не существует алгоритма, позволяющего для произ-
произвольной предикатной формулы выяснить, общезначи-
общезначима ли она. Из Гёделя теоремы о полноте следует, что
все общезначимые предикатные формулы и только они
выводимы в классич. исчислении предикатов.
Лит.: [1] К л и н и С. К., Математическая логика, пер.
с англ., М., 1973. В. Е. Плиско.
ОБЩЕРЕКУРСИВНАЯ ФУНКЦИЯ — частично ре-
рекурсивная функция, определенная для всех значений ар-
аргументов. Понятие О. ф. может быть определено и неза-
независимо от понятия частично рекурсивной функции сле-
следующим образом. Класс всех О. ф.— это наименьший
класс функций, содержащий все примитивно рекурсив-
рекурсивные функции и замкнутый относительно композиции
функций и наименьшего числа оператора при условии,
что последний применяется к функции g (хх, . . ., хп, у)
лишь тогда, когда
Va, ..., xn3yg (xu ..., хп, г/)=0.
Однако изучение О. ф. обычно ведется в классе всех
частично рекурсивных функций. Это связано, в частно-
частности, с тем, что ни при каком натуральном и>0 не су-
существует О. ф., универсальной для класса всех и-мест-
ных О. ф.
Все О. ф. нумерически представимы
в арифметике формальной, так что для любой такой
функции f{xlt . . ., хп) можно построить арифметич.
формулу F (я,, . . ., л-п, у), обладающую следующим
свойством: каковы бы ни были натуральные числа < . . .,
kn, к, если }(кг, . . ., kn) = k, то \—F(ki, . ._., kn, #); если
же f(ku . . ., кп)Фк, то \—~\F(ku . . ., кп, *), где А1?
• • ¦> km * — термы, изображающие числа къ, . . .,
к„, к, символ |— означает выводимость в арифметич.
исчислении.
Лит.: [1] Новиков П. С, Элементы математической
логики, 2 изд., М., 1073; [2] Мендельсон Э., Введение
в математическую логику, пер. с англ., М., 1971.
ОБЩЕРЕКУРСИВНЫЙ ОПЕРАТОР — частично^ре-
частично^рекурсивный оператор, к-рый определен на всех всюду
определенных функциях и переводит всюду определен-
определенные функции во всюду определенные. в. Ж. Плиско.
ОБЩИЙ ИНТЕГРАЛ системы обыкновенных диф-
дифференциальных уравнений re-го порядка
Ч = /;(*, *i. ¦¦•, *и)> г = 1, ..., п, A)
в области G — совокупность п соотношений
Ф;{1, Хи ..., Хп)=С(, i = l, ..., П, B)
содержащая ге параметров (Сг, . . ., Cn)?C<pR" и
в неявном виде описывающая семейство функций, соста-
составляющих общее решение этой системы в области G.
Часто О. и. системы A) наз. не соотношения B), а сово-
совокупность функций
Ф,-(*, хх, ..., .?„), i = 1, ..., п. C)
Каждое из соотношений B) [или каждая из функций C)]
наз. первым интегралом системы A). Иногда под О. и.
системы A) понимают совокупность более общих,
чем B), соотношений
Ф,-(г, хи ..., х„, Съ ..., Сп)=0, г = 1, ..., и.
В случае обыкновенного дифференциального уравне-
уравнения n-го порядка
yin> = f(x, у, у', ..., j/*»-1')
О. и. в области G представляет собой одно соотношение
с га параметрами
Ф(*. у, Clt ..., С„)-0,
в виде неявно!! функции описывающее общее решение
этого уравнения в области G-
О. и. дифференциального уравнения с частными про-
производными 1-го порядка наз. соотношение между вхо-
входящими в уравнение переменными, содержащее одну
произвольную функцию и определяющее при каждом
выборе этой функции решение уравнения.
См. также Интеграл дифференциального уравнения.
Лит. см. при ст. Общее решение. Н. X. Розов.
ОБЩИХ ПРЕДСТАВИТЕЛЕЙ СИСТЕМА — множе-
множество R мощности т, являющееся различных представи-
представителей системой для каждого из t семейств подмножеств
Flt F2, . . ., Ff заданного множества S, каждое из к-рых
состоит из т членов. Пусть t=2, m конечно, t\ = {F',
F'r ¦ ¦ - О- *¦*={*¦,". Fl> ¦ ¦ •' F'mh 5=U?Li F't =
= U?Li F"c О- п- с- Для Fiи ^г существует тогда и
только тогда, когда никакие к из множеств семейства Ft
не содержатся менее чем в к множествах из 1\ для каж-
каждого А=1, 2, . • ., т. Эта теорема справедлива также
при бесконечном т, если только все подмножества се-
семейств F1 и F2 кон8чны. Известны условия существо-
существования О. п. с. при t>2, к-рые формулируются более
сложно.
Лит.: [1] Холл М., Комбинаторика, пер. с англ., М.,
1970. В. Е. Тараканов.
ОБЩНОСТИ КВАНТОР — то же, что всеобщности
квантор.
ОБЪЕДИНЕНИЕ (сумма, соединение) множеств —
одна из основных операций над множествами. Пусть
имеется нек-рая (конечная или бесконечная) совокуп-
совокупность множества Аа (индексы а служат для раяличения
элементов данной совокупности). Тогда множество тех
элементов, к-рые принадлежат хотя бы одному из
множеств, входящих в эту совокупность, наз. объ-
объединением множеств, образующих данную совокуп-
совокупность.
О. множеств Аа обозначается \J)Aa, иногда 1Аа.
М. И. Воицеховский.
ОБЪЕКТ геометрический — см. Геометри-
Геометрических объектов теория.
ОБЪЕКТ категории — термин, используемый
для обозначения элементов произвольной категории,
играющих роль множеств, групп, тоиологич. прост-
пространств и т. п. О. категории — неопределяемое понятие.
Каждая категория состоит из элементов двух классов,
наз. классом объектов и классом м о р-
ф и з м о в соответственно. Класс О. категории ,$ обыч-
обычно обозначается ОЬ,Н'. Любому объекту А категории Ж
однозначно соответствует единичный морфпзм 1^,
причем разным О. отвечают разные единичные морфиз-
мы. Поэтому формально можно определить понятие
категории только с помощью морфизмов. Однако тер-
термин «объект категории» является удобным языковым
средством, к-рое практически всегда используется. Де-
Деление элементов категории на О. и морфнзмы имеет
смысл только в пределах фиксированной категории, так
как О. одной категории могут быть морфизмамн дру-
другой и наоборот. Благодаря наличию морфизмов между
О. категории устанавливаются определенные взаимо-
взаимосвязи, что позволяет выделить специальные классы О.:
интегральные объекты, нулевые объекты, малые объекты,
проективные объекты, инъетпивные объекты и т. д.
М. Ш. Цаленко.
ОБЪЕМ т р е х м е р и о г о т е л а — числовая
характеристика тела, равная в простейшем случае, когда
тело можно разбить на конечное множество единичных
кубов (т. е. кубов с ребрами длины единица), числу
этих кубов. О. трехмерных тел (т. е. множеств трехмер-
трехмерного евклидова пространства), для к-рых они опреде-
определены, обладают свойствами, аналогичными свойствам
площадей плоских фигур: 1) О. неотрицательны; 2) О.
аддитивны: если для двух тел Р и Q, не имеющих об-
общих внутренних точек, определены О. v(P) и v(Q), то О.
их объединения равен сумме их О. о \P\JQ\ — v(P)-\-
-\-v (Q)', 3) О. инвариантны относительно перемещений:
если для тел Р и Q определены О. и они конгруентны,
то v(P) = v(Q); 4) О. единичного куба равен единице.
Из этих свойств следуют монотонность О.: если для тел
Р и Q определены О. v(P), v(Q) п PczQ, то выполня-
выполняется неравенство v(P) < v(Q), и равенство отношения
О. подобных тел кубу коэффициента подобия.
На множестве всех многогранников существует и
притом единственная неотрицательная функция, удов-
удовлетворяющая свойствам 1) — 4). Однако если на пло-
плоскости два любых равновеликих (имеющих одинаковую
площадь) многоугольника равносоставлены, т. е. каж-
каждый из них допускает разбиение на многоугольники,
из к-рых можно составить другой, то в пространстве
аналогичное свойство уже не имеет места: существуют
равновеликие (имеющие равные О.), но не равносостав-
ленные многогранники (см. Равновеликие и равносостав-
ленные фигуры).
Понятие О. распространяется с сохранением свойств
1) — 4) при помощи предельного перехода с множества
многогранников на более широкие классы тел, напр.
на тела с кусочно гладкой границей, в частности на
шары, шаровые слои, шаровые сегменты и секторы, ци-
цилиндры, конусы и т. п. Если граница ограниченного те-
тела G является кусочно гладкой поверхностью, то его
О. v(G) определяется следующим образом. Рассматри-
Рассматриваются всевозможные многогранники Р, лежащие в те-
теле G, и всевозможные многогранники Q, содержащие
в себе тело G: PczGczQ. Тогда справедливо равенство
sup v(P)= irif v(O).
P CQ QZ> G
Это общее значение указанных нижней и верхней граней
и наз. объемом v(G) тела G. Аналогично случаю
вычисления площадей плоских фигур для вычисления
О. тел также применяется метод разбиения тела на
части, для к-рых О. либо уже известен, либо может
быть найден более простым путем. При этом для О.
справедлив принцип Кавальер и: если два
тела, для к-рых определен О., пересекаются каждой
плоскостью, параллельной нек-рой заданной, по кон-
конгруэнтным плоским фигурам, то они равновелики. Об-
щий метод вычисления О. дает интегральное исчисление:
вычисление О. сводится к вычислению соответствующих
кратных интегралов. Интегральное исчисление дает
возлгожность обосновать и принцип Кавальери.
Расширенно понятия О. на еще более широкий класс
подмножеств трехмерного евклидова пространства при-
приводит к понятию трехмерной Жордана меры и понятию
кубируемого множества. Все упоминавшиеся выше тела
являются кубнруемыдш множествами и потому для
них определена мера Жордана.
Если М3 — трехмерное непрерывно дифференцируе-
дифференцируемое многообразие с римановой метрикой
и g = det | gij\, то объемом множества Е,
лежащего в .многообразии М3, наз. величина интеграла
ш
\g\dx4x4x3.
Так определенный О. множества инвариантен относи-
относительно выбора локальных координат на рассматривае-
рассматриваемом многообразии.
Определение О. трехмерного тела обобщается на слу-
случай подмножества произвольного «-мерного евклидова
пространств R"; и-м ерным объемом также-
наз. функция множества, удовлетворяющая условиям
1) — 4), если только под кубом понимать ге-мерный
куб. Вычисление О. множеств га-мерного пространства
сводится к вычислению n-кратных интегралов.
Если Е есть я-мерный параллелепипед, натянутый
на радиус-векторы аи . . ., ап, то
v (E) = У | det IK-, О/|||
(под корнем стоит абсолютная величина определителя
Грама векторов а,, . . ., ап).
О. подмножества Е «-мерного риманова многообразия
с метрикой
наз. величина интеграла
S I dx1 . .. dx»,
где g = <let||g,7||.
Обобщением понятия О. является понятие меры..
Иногда термины «О», п «мера» употребляются как сино-
синонимы.
Понятие О. рассматривается не только в евклидовых,
но и в аффинных пространствах. Пусть Е — подмно-
подмножество «-мерного аффинного пространства R" и пусть,
и R" задана аффинная система координат (х1, . . ., хп).
Пусть
Если (у1, . . ., у") — другая система координат и у' =
— al.x}-\-bl, то
Vj,(?) = |det||a'yH \VX(E),
т. е. интеграл Vx (E) является знакопостоянным отно-
относительным инвариантом веса — 1. Относительный ин-
инвариант V'v (E) наз. аффинным О. множества Е.
Аффинный О. не меняется при параллельном переносе.
п если E=-Et\JE2, Ег[)Е^0 и \'Х (?,). Vx(E2)
определены, то Vx (E) = VX (?1])+VX (Ег). Аффинный
О. обладает следующими свойствами, инвариантными
относительно аффинного преобразовании координат:
1) если О. двух тел равны в одной системе координат,
то они равны и в другой; 2) если О. нек-poro множе-
ства равен сумме О. двух множеств в одной координат-
координатной системе, го это равенство верно и в другой; 3) от-
отношение О. двух множеств является инвариантом аф-
аффинного преобразования координат.
Пусть еь ...,«>„ — координатные векторы системы
координат хг, . ¦ ., хп в пространстве К." и пусть их
начала находятся в нек-рой фиксированной точке 0 ? R".
Если (ii = a{ej, i — 1, 2, . . ., re,— нек-рая. система век-
векторов с началом r точке О и Е есть и-мерный параллеле-
параллелепипед, натянутый на векторы к1; . . ., а-„, то
Vx (?) = | det || a
Величина del||a{-|| наз. ориентированным
о б ъ е м о м параллелепипеда Е относительно выбран-
выбранного базиса ел, . . ., е„.
Лит.: II] Н и к,о л ь с к и й С. М., Курс математического
анализа, 2 изд., т. 1 — 2, М., 1975; [2] К о л м о г о р о в А. Н.,
Фомин С. В., Элементы теории функций и функционального
анализа, 5 изд., М., 1981; L3! Р а ш е в с к и й II. К., Риманива
геометрия и тензорный анализ, 3 изд.. М., 1967; [41 Ильин
В. А., П о з н я к Э. Г., Основы математического анализа,
3 изд. ч. 1, М., 1971. Л. Д. Кудрявцев.
ОБЪЕМНОСТИ АКСИОМА — одна из аксиом тео-
теории множеств, утверждающая равенство двух мно-
множеств, если они содержат одни и те же элементы:
В языке, не содержащем символа равенства и имеющем
только один предикатный символ ?, О. а. имеет вид
V!' W (V-c (.г?»<—>*€") => V2 (m?z =>y?z)).
Для формализации математики в системе Цермело —
Френкеля ZF О. а. не имеет существенного значения.
Все, что может быть построено в рамках системы ZF,
может быть формализовано в системе без О. а. Пусть
ZV~ — система ZK, получающаяся из ZF удалением
О. а. п заменой в остальных аксиомах формул вида и = v
на формулу
Тогда можно показать, что существует интерпретация
системы ZF в ZF~. Аналогичное утверждение справед-
справедливо п для теории типов.
Для системы NF Куайна, получающейся из теории
типов «стиранием» типовых индексов, положение ме-
меняется: в системе NF~ невозможно интерпретировать
систему NF. Система NF~ (NF без О. а.) довольно
«лабая теория, ее непротиворечивость доказуема в фор-
формальной арифметике. В то время как система NF не
слабее теории типов с аксиомой бесконечности.
Лит.: [1] Handbook of Mathematical Logic, Amst.—N. Y.—
Oxf., 1977; [2] В of fa M.. «J. Symbol. Logic», 1977, v. 42,
-\« 2, p. 215 — 20. В. Н. Гришин.
ОБЪЕМНЫЙ ПОТЕНЦИАЛ — выражение вида
u(x)=\iDh(\x~y\)f(y)dv(y), (*)
где D — конечная область евклидова пространства
RN, А'5э2, ограниченная замкнутой поверхностью (при
N — 2 — кривой) Ляпунова S, h(\x—у\) — фундамен-
фундаментальное решение оператора Лапласа,
1
»j\i= 2nN/2/T(N/2) — площадь единичной сферы в
R-^, \х—у\ — расстояние между точками х и у,
dp (у) — элемент объема D.
Если f(y)?C(ll{JJ), то О. п. определен для всех
x^R-N и и(х) ?С<Х> (RN). При этом в дополнительной
¦области CD функция и (х) имеет производные всех по-
рядков и удовлетворяет Лапласа уравнению Аи(х) = 0,
т. е. является гармонической функцией; при N Sj 3 эта
функция регулярна на бесконечности, г«(со) = 0. В об-
области D О. п. и (.г) принадлежит классу C'2>(Z)) и удов-
удовлетворяет Пуассона уравнению Дм (х)=—f{x).
Эти свойства обобщаются п различных напиавлениях.
Напр., если f (у) ?И°°Ц1У), то u{x)?C(RX), и(х)?
gC(°°)(CZ)), Ди(ж) = 0 в CD, в jD существуют обобщен-
обобщенные производные 2-го порядка от и(х) и почти всюду в
D удовлетворяется уравнение Пуассона Ди(ж) =—/(я).
Изучены также свойства О. п. произвольной меры [х
Радона, сосредоточенной на Лт-мерной области D:
Здесь также и (.г) ?С<~>(СХМ и Лг<(.г)-=0 в СО, Дц(ж)=
= — а' (ж) почти всюду в /J, где и/ (ж) — производная
меры |Л но мере Лебега в RiV. В определении (*) фунда-
фундаментальное решение оператора Лапласа можно заменить
на произвольную функцию Левп для общего эллиптич.
оператора 2-го порядка L с переменными коэффициен-
коэффициентами класса С<0- *•> (О); при этом перечисленные вы-
выше свойства, остаются в силе с заменой Дм на Lu (см.
[2]-[4]).
О. п. применяется при решении краевых задач для
эллиптич. уравнений с частными производными (см.
[2] - [5]).
При решении краевых задач для параболич. уравне-
уравнений используется также понятие объемного теп-
теплового потенциала вида
G (r' Ц y' T) f (г/' т) dv {yh
где G(x, t; у, х) — фундаментальное решение уравне-
уравнения теплопроводности в R-^:
G(x, t; у, т) =
/(;/, т) — плотность. Функция v(x, t) и ее обобщения на
случай произвольного параболич. уравнения 2-го поряд-
порядка имеют свойства, близкие к указанным выше для и (;с)
(см. [3] - [6]).
Лит.: [1] Г ю н т е р Н. М., Теория потенциала и ее при-
применение к основным задачам математической физики, М., 1953;
[2] Миранда К., Уравнения с частными производными
эллиптического типа, пер. с итал., М., 1957; [31 Тихонов
А. Н., Самарский А. а., Уравнения математической
физики, 5 изд., М., 1977; U] С м и р н о в В. И.. Курс высшей
математики, 5 изд., т. 4, М., 1958; [5] Фридман А., Урав-
Уравнения с частными производными параболического типа, пер.
с англ., М., 1968; [6] Б и ц а д з е А. в., Краевые задачи для
эллиптических уравнений второго порядка, М., 1-961J.
Е. Д. Соломенцег,^
ОВАЛ — замкнутая выпуклая С2-гладкая линия
в R'2. Точки О., в к-рых кривизна достигает экстрему-
экстремума, наз. вершинами О. Число вершин О. не менее
четырех.
Пусть Е—О., пробегаемый против часовой стрелки, в
плоскости с декартовыми прямоугольными координата-
координатами х, у; h — расстояние ориентированной касательной
к ? от начала О (h > 0, если вращение касательной
вокруг О происходит против часовой стрелки). Тогда
уравнение касательной
х cos х + у sin х = h(x),
где х — угол касательной с осью Ох. Величина h (т)
наз. опорной ф у н к ц и е й О. Радиус кривизны
О.:
длина О. (ф о р м у л а Ко ш и):
L=[n h(x)dx.
J -я
Между длиной L и площадью F области внутри О. вы-
выполняется соотношение
L2 —
(уточнение см. в ст. Боннезена неравенство).
А. Б. Иванов.
ОВОИД, о в а л о и д,— множество О точек нек-рого
пространства, к-рое произвольная прямая пересекает
не более чем в двух точках, а прямые, касательные
к О в каждой его точке, лежат в гиперплоскости.
В проективном пространстве нелинейчатая квадрика
является О. Этот термин используется в основном для
конечных геометрий.
В конечных проективных пространствах размер-
размерности большей трех О. не существует. В трехмерных
пространствах порядка q > 2 О. является максималь-
максимальной fe-шапкой и состоит из q2-\-i точек, для нечетного q
каждый О. является эллиптич. квадрикой (см. [1]).
В плоскости порядка q О. наз. овалом и содержит
9+1 точек. В дезарговой плоскости нечетного порядка
любой овал однозначно представим невырожденной
коникой над полем Галуа (см. [2]).
Лит.: [1] Segre В., Introduction to Galois geometries,
Roma, 1967; [2] e г о же, «Canad. J. Math.», 1955, v. 7, J* 3,
p. 414—16; [3] T i t s J., «Rend. mat. e applic», 1962, v. 21,
p. 37—59. В. В. Афанасьев.
ОВРАЖНЫХ ФУНКЦИЙ МЕТОДЫ МИНИМИЗА-
МИНИМИЗАЦИИ — численные методы отыскания минимумов функ-
функций многих переменных. Пусть задана ограниченная
снизу дважды непрерывно дифференцируемая по своим
аргументам функция
J(x)=J(Xl, ...,хт ),
для к-роп известно, что при нек-ром векторе х* =
= {xi, ¦ ¦ ., хт)Т(Т — знак транспонирования) она прини-
принимает наименьшее значение. Требуется построить по-
последовательность векторов {#„}, хп= (х1п, . . ., хтп)т,
такую, что
lim/(*„)=/(*•).
Существует мпого методов, позволяющих получить ука-
указанную последовательность векторов. Однако общим
недостатком большинства алгоритмов является резкое
ухудшение их свойств в случаях, когда поверхности
уровня минимизируемой функции /(#)=const имеют
структуру, сильно отличающуюся от сферической.
В этом случае нек-рую область Q, в к-рой норма век-
вектора-градиента
^'-[дх, дхт)
существенно меньше, чем в остальной части простран-
пространства, наз. дном оврага, а саму функцию — ов-
овражной функцией. Если размерность простран-
пространства аргументов минимизируемой функции больше двух,
то структура поверхностей уровня овражных функций
может оказаться весьма сложной. Появляются (т—к)-
мерные овраги, где число к изменяется от 1 до m—1.
В трехмерном пространстве, напр., возможны одномер-
одномерные и двумерные овраги.
Функции овражного типа локально характеризуются
плохой обусловленностью матриц двух производных
(матриц Гессе)
что приводит к сильному изменению функции J(x)
вдоль направлений, совпадающих с собственными векто-
векторами матрицы Гессе для больших собственных чисел, и
к слабому изменению вдоль других направлений, отве-
отвечающих малым собственным значениям матрицы Гессе.
Большинство известных методов оптимизации позво-
позволяет достаточно быстро попадать на дно оврага, при-
водя иногда к существенному уменьшению значения
функции / (х) по сравнению с его значением в начальной
точке (спуск на дно оврага). Однако далее нроцесс
резко замедляется и практически останавливается в
нек-рой точке из Q, к-рая может быть расположена очень
далеко от истинной точки минимума.
Дважды непрерывно дифференцируемая по своим ар-
аргументам функция / (х) наз. овражной функци-
е й (см. [1]), если существует нек-рая область GczR,
где собственные значения матрицы Гессе J" (х), упоря-
упорядоченные в любой точке x?G по убыванию модулей,
удовлетворяют неравенствам
О < IminX,- (x) <?кг (х). A)
I «'
Степень овражности характеризуется числом
S = кг1 min к; I B)
к. ф о I"
Если собственные значения J"(x) в области G удовлет-
удовлетворяют неравенствам
I ля> W )*».••*» |лт - г +1 \х) I ^ Ат - г W ®* • • • ^> Л1 \х) i
то число г наз. размерностью оврага
функции J(x) при x?G (см. [1]).
Системы дифференциальных уравнений, описывающие
траекторию спуска овражной функции J(x),
-гг=—J {х), х@)=х0, C)
являются жесткими дифференциальными системами.
В частности, когда функция J (х) сильно выпуклая
и матрица Гессе положительно определена (все ее соб-
собственные значения строго больше нуля), неравенства
A) совпадают с известным требованием плохой обус-
обусловленности матрицы Гессе
к (/" (х)) =тах к; (z)/'min X,- (х) ^> 1.
В этом случае спектральное число обусловленности
совпадает со степенью овражности.
Метод покоординатного спуска (см. [2])
•* (¦cii ft + i1 • • •' xi-i, k + Ъ xi, ft + it xi + l, hi • • • i xm, ft) =
= min/ (a-i, ft + i, .. ., z,--i,ft + i, y, xi + ljk, ...,хтшк),
Л = 0, 1, 2, ..., D)
несмотря на простоту и универсальность, в овражной
ситуации эффективен лишь в редких случаях ориента-
ориентации оврагов вдоль координатных осей.
Предложена (см. [2]) модернизация метода D), сос-
состоящая в использовании процедуры вращения осей ко-
координат так, чтобы одна из осей была направлена вдоль
хк — xk-\i после чего начинается поиск на (к-\-\)-ж
шаге. Такой подход приводит к тому, что одна из осей
имеет тенденцию выстраиваться вдоль образующей дна
оврага, позволяя в ряде случаев весьма успешно про-
проводить минимизацию функций с одномерными оврагами.
В случае многомерных оврагов метод непригоден.
Схема метода наискорейшего спуска задается разно-
разностным уравнением
= xk — hkJ'k, J'k=J' (xk)i *5)
где hfr выбирается из условия
/ (xk+i) =min/ (xk — hJ'k).
h>0
Для сильно выпуклой овражной функции, в частности
квадратичной
J(x)=± xTDz-ЬТх, F)
последовательность {х^}, построенная алгоритмом E),
сходится к точке минимума функции х* по закону геО-
метрич. прогрессии (см. [3])
где С=const,
9 = [Л (/" (*•)) -1]/[к (J" (х*)) +1].
Так как для овражной функции k(J" (х*))^>1, то
и сходимость практически отсутствует.
Аналогичная картина наблюдается и для простой гра-
градиентной схемы (см. [4])
Ускорение ее сходимости основано на использовании
результатов предыдущих итераций для уточнения дна
оврага. Может быть использован (см. [4] [5]) градиент-
градиентный метод G) с вычислением на каждой итерации отно-
отношения q= ||/^|!,'|| ^"^ ill - Когда оно устанавливается
около нек-рого постоянного значения д=1, делается
большой ускоряющий шаг согласно выражению
h Tr
xk + l = 4 J-Г^ Jk-
Далее из точки Xf, + l продолжается спуск градиентным
методом до следующего ускоряющего шага.
Различные версии метода параллельных касательных
(см. [4] — [6]) основаны на выполнении ускоряющего
шага вдоль направления ?? + 2—х^ задаваемого точ-
точками x/i, x/i + 2 в градиентном методе. В методе «тяже-
«тяжелого шарика» (см. [4]) очередное приближение имеет вид
+ $ D — xk-i)-
В методе оврагов (см. [7]) предлагается про-
провести локальные спуски градиентным методом G) из
двух случайно выбранных исходных точек, а затем
выполнить ускоряющий шаг по направлению, задавае-
задаваемому двумя полученными на дне оврага точками.
Все эти методы немногим сложнее градиентного ме-
метода G) и построены на его основе. Ускорение сходи-
сходимости получается для одномерных оврагов. В более
общих случаях многомерных оврагов, где сходимость
этих схем резко замедляется, приходится обращаться
к более мощным методам квадратичной аппроксимации,
в основе к-рых лежит метод Ньютона
4 + 1 = хк~ Wk)~X J'k, J"k=J"(xk)- (8)
Точка минимума функции F) удовлетворяет системе
линейных уравнений
Dx = b, (9)
и при условии абсолютной точности всех вычислений
для квадратичной функции метод Ньютона независимо
от степени овражности B) и размерности оврагов при-
приводит к минимуму за один шаг. На самом деле, при
больших числах обусловленности к (D) при ограничен-
ограниченной разрядности вычислений задача получения решения
(9) может быть некорректной, и небольшие деформации
элементов матрицы D и вектора Ь могут приводить
к большим вариациям х*.
При умеренных степенях овражности в выпуклой си-
ситуации метод Ньютона часто оказывается более пред-
предпочтительным по скорости сходимости, чем другие,
напр, градиентные, методы.
Большой класс квадратичных (квазиньютоновских)
методов основан на использовании сопряженных на-
направлений (см. [2], [31, [8]). Эти алгоритмы для случая
минимизации выпуклой функции оказываются весьма
эффективными, ибо, имея квадратичное окончание, они
не требуют вычисления матрицы двух производных.
Иногда (см. [8]) итерации строятся по схеме
где Е — единичная матрица. Скаляр рд подбирается
так, чтобы матрица J"k-\-$kE была положительно оп-
определенной и чтобы
Существует ряд аналогичных подходов (см. [8]),
основанных на получении строго положительно опре-
определенных аппроксимаций матрицы Гессе. При миними-
минимизации овражных функций такие алгоритмы оказываются
малоэффективными из-за трудностей в подборе пара-
параметров P/j, Efe и т. д. Выбор этих параметров основан на
информации о величине наименьших по модулю соб-
собственных значений матрицы Гессе, а при реальных
вычислениях и большой степени овражности эта инфор-
информация сильно искажена.
Более целесообразно обобщение метода Ньютона на
случай минимизации овражных функций проводится на
базе непрерывного принципа оптимизации. Функции
/ (х) ставится в соответствие дифференциальная система
C), интегрируемая системным методом (см. Жесткая
дифференциальная система). Алгоритм минимизации
принимает вид
N
D1)
Ф B*+ Jfc?) = Ф BJ/i?) [2? — „
» = 0, 1, ..., ЛГ—1. j
Предложен [1] алгоритм минимизации овражной функ-
функции, основанный на использовании свойств жестких
систем. Пусть функция J (х) в окрестности х0 аппрок-
аппроксимируется квадратичной функцией F). Матрица D
и вектор Ь вычисляются, напр., с помощью конечно-
разностной аппроксимации. Из представления элемен-
элементов матрицы
где us= (uls, . . ., ums)T , s=l, . . ., m,—ортонормиро-
ванный базис собственных векторов D, следует, что
неточное измерение этих элементов искажает информа-
информацию о малых собственных значениях плохо обусловлен-
обусловленной матрицы, а следовательно, приводит к некоррект-
некорректности задачи минимизации функции F).
Вместе с тем система дифференциальных уравнений
спуска для овражной функции F)
¦§- = -Dx + b, x@)=xo
имеет решение, в к-ром в силу условия A) слагаемые
с сомножителями ехр (—Хх?) оказывают влияние лишь
на малом начальном отрезке длиной Tnc=O(X-J).
Другими словами, компоненты вектора х (t) удовлет-
удовлетворяют равенству
хТ (t)u1~KT1bTu1 = (xoU1 — 'ki1bTu1) ехр (—М),
быстро переходящему в стационарную связь
где xj — компоненты вектора, удовлетворяющие ра-
равенству A2). Это свойство используется в алгоритме.
Выражая jf-ю компоненту вектора х, к-рой соответст-
соответствует максимальная компонента вектора щ, через осталь-
остальные компоненты, вместо функции / (х) получают
новую функцию с аргументом размерности (т—1):
= J (Xi, ..., J.7-1, J/+i, -.., xm). A3)
По функции A3) с помощью конечноразностной аппрок-
аппроксимации находится новая матрица D порядка (т—1)
и вектор Ь. Здесь важно не только и не столько пони-
понижение размерности пространства поиска, сколько умень-
уменьшение степени овражности, т. к. при минимизации но-
новой функции в подпространстве, ортогональном вектору
щ, большое собственное значение уже не оказывает
влияния на вычислительный процесс. Самым суще-
существенным моментом здесь является требование получе-
получения D и Ь по функции A3), а не по матрице D и вектору
Ь. Коэффициенты связи A2) находят степенным мето-
методом, как коэффициенты любого уравнения системы
Если степень овражности не понижается или понижает-
понижается незначительно, то процесс исключения координат
вектора х продолжается рекурсивно до необходимого
ее уменьшения.
Лит.: [1] Ракитский Ю. В., Устинов С. М.,
Ч е р и о р у ц к и й И. Г., Численные методы решения жест-
жестких систем, М., 1979; [2] С е а Ж., Оптимизация. Теория и
алгоритмы, пер. с франц., М., 1973; [3] Пшеничный Б. Н.,
Данилин Ю. М., Численные методы в экстремальных за-
задачах, М., 1975; [4] П о л я к Б. Т. «Экономика и математич.
методы», 1967, т. 3, N, 6, с. 881—902; [5] Ф а д д е е в Д. К.,
Фаддеева В. Н., Вычислительные методы линейной ал-
алгебры, 2 изд., М., 1963; [6] У а й л д Д.- Д ж., Методы поиска
экстремума, пер. с англ., М., 1967; [7] Г е л ь ф а н д И. М.,
Цетлин М. Л., «Докл. АН СССР», 1961, т. 137, № 2,
с. 295—98; [8] Численные методы условной оптимизации, пер.
с англ., М., 1977. Ю. В. Ракитский.
ОГИБАЮЩАЯ семейства кривых на
плоскости — кривая, к-рая в каждой точке каса-
касается одной из кривых семейства, причем касания вдоль
О. переходит от одной кривой семейства к другой.
Напр., для семейства окружностей одинакового радиу-
радиуса с центрами на прямой О. состоит из двух параллель-
параллельных прямых. Если С — параметр семейства, t — пара-
параметр вдоль О., С(t) — значение С для одной из кривых
семейства, касающихся О. в точке с параметром t, то
предполагается возможность выбора C{t) так, что функ-
функция С (t) ни на каком участке изменения t не постоянна.
Для семейства кривых, заданного уравнением
f(x, у, z) = 0, где /gC1 и \fx\-\-\fy\ фО, необходимым
признаком существования О. является выполнение при
г(')> !/(*)» <-•(*) условий
/--0, /с = 0. A)
Система A) служит для нахождения точек О., но A)
могут удовлетворять и другие особые точки семейства.
Достаточным признаком точек О. является /?С2 ц
выполнение, кроме A), условия
fee * °- тЙЙг * 0- B)
Для семейства плоских кривых, заданных С1-гладкой
функцией
Г (и, С) = {х(и, С), у (и, С)},
где С — параметр семейства, и — параметр вдоль
его кривых, необходимым признаком точек О. является
ги\\гс или, что то же,
C)
и выполне-
выполнеD)
V- D(u, С) -"•
Достаточным признаком является г?С2
ние, кроме C), условия
ГиУС^ Гс<Ри Ф 0.
Нарушение условий B), D) чаще всего связано с появ-
появлением на О. точки возврата.
Для зависящего от одного параметра Ссемеыства
поверхностей в пространстве О. есть поверх-
поверхность, к-рая в каждой ее точке с внутренними парамет-
параметрами (и, v) касается поверхности семейства с парамет-
параметром С (и, и), причем функция С (и, v) ни в какой обла-
области изменения (u, v) не постоянна. Напр., для сфер
одинакового радиуса с центрами на прямой О. является
цилиндром. Для семейства, заданного уравнением
f(x, у, z, С) = 0, где /gC1 и |/^| +1/^1+ 1/г1 Ф 0,
необходимым признаком О. является система равенств
/=0, /с = 0, E)
а достаточным: /?С2 и выполнение, кроме E), условий
fee Ф 0,
Д (A
D (ж, у)
D (/, f'c)
(у, г)
D (/, /с)
D (z, =с)
Ф 0. F)
Для семейства г (и, v, С), где г^С1 и ГиХгьф0, не-
необходимым признаком О. служит равенство
<P = (rurvrc)=0, G)
а достаточным:
и выполнение, кроме G), условий
Уи фс фС
Г%
rvrc
Ф 0, i фи | + 1 Ф" I Ф О-
(8)
С нарушением первых из условий F), (8) чаще всего
связано появление на О. ребра возврата. Линию ка-
касания О. с одной поверхностью семейства наз. харак-
характеристикой. Ребро возврата на О. в свою очередь
обычно является О. характеристик.
Для зависящего от двух параметров А, В
семейства поверхностей в пространстве О. есть поверх-
поверхность, касающаяся в каждой своей точке (и, и) поверх-
поверхности семейства с параметрами А (и, и), В (и, v), при-
причем ни в какой области изменения (и, v) не существует
такой функции Ф?СХ, что А(и, v) = Ф(В(и, v)).
Для семейства, заданного уравнением/(г, у, z, А, В) =
= 0, где /?СХ и |/xl+l/^|-f |/г1 ф 0, необходимым при-
признаком О. является система
/ = 0,/л=0,/Ь=0, (9)
а достаточным: /^С2 и выполнение, кроме (9), условий
" (Л fA, f'B)
¦D (х, V, 2)
и>
D (А, В)
Для семейства г (и, v, А, В), где г?Сг и ГцХг^^О,
необходимым признаком О. служит система
q> = (rar0o)=0, г|) = (гаг„Гд)=О, A0)
а достаточным: г?С2 и выполнение, кроме A0), условий
фи
ty'u
rl
фс;
^а
ГаГу
Го
Фл
Ч>А
гигА
rvrA
фв
ГиГв
rvrB
Более сложное понятие О. для зависящего от к пара-
параметров семейства то-мерных подмногообразий в ге-мерном
многообразии вводится (см. [1]) на основе теории осо-
бенностей дифференцируемых отображений как спе-
специальный вид особенности семейства.
Лит.: [1] Залгаллер В. А., Теория огибающих, М.,
1975; [2] Ф а в а р Ж., Курс локальной дифференциальной
геометрии, пер. с франц., М., 1960; [3] Толстов Г. П.,
«Успехи матем. наук», 1952, т. 7, в. 4, с. 173—79.
В. А. Залгаллер.
ОГРАНИЧЕННО КОМПАКТНОЕ МНОЖЕСТВО в
линейном топологическом прост-
пространстве X — такое множество М, что замыкание
N всякого ограниченного подмножества NczM компакт-
компактно и содержится в М (для нормированного простран-
пространства в сильной, соответственно слабой, топологии это
равносильно компактности, соответственно слабой
компактности, пересечений М с шарами). Выпуклое
замкнутое множество в нормированном пространстве
является О. к. м. в том и только в том случае, когда
оно локально компактно. О. к. м. находят применение в
теории приближения в банаховых пространствах; они
обладают свойством существования наилучшего при-
приближения элемента. Бочечное линейное топологич. про-
пространство, являющееся (в самом себе) О. к. м. в сла-
слабой, соответственно сильной, топологии есть реф-
рефлексивное пространство, соответственно монтелево про-
пространство. Нормированное пространство, являющееся
О. к. м., конечномерно.
Лит.: [1] К lee V. L., «Trans. Amer. Math. Soc», 1953,
v. 74, p. 10—43; [2] Э д в а р д с Р., Функциональный анализ,
пер. с англ., М., 1969. Л. П. Власов.
ОГРАНИЧЕННОГО ВИДА ФУНКЦИЯ в обла-
области D комплексно и плоскости С —
мероморфная функция /(г) в облавти D, представимая в
D в виде отношения двух ограниченных аналитич.
функций:
Наиболее изучен класс N (А) О. в. ф. в единичном кру-
круге A = {z?C: | z\ <1}. Для того чтобы мероморфная в
А функция f(z)?N (А), необходимо и достаточно, чтобы
ее характеристика Т (г; /) была ограниченной
(теорема Н е в а н л и н н ы):
Т (г; /)=-2^5Г I \
B)
Здесь сумма в правой части составлена по всем полюсам
bv функции f(z) таким, что 0<|6v|<r, причем каж-
каждый полюс берется столько раз, каков его порядок;
A,S=0 — порядок полюса в начале координат. Поэтому
О. в. ф. класса N (А) наз. также функциями с
ограниченной характеристикой.
Представляет интерес также следующее достаточное
условие: если мероморфная функция / (z) в А не прини-
принимает множества значений Е положительной емкости,
cap ?>0, то f(z)?N(A).
Функции f (z) класса iV(A) обладают следующими
свойствами: 1) почти всюду на единичной окружности
r={z?C : \z\ =1} функция f(z) имеет угловые гра-
граничные значения f(eie), причем In | / (е'е) | ^Л1(Г);
2) если /(е'е) = 0 на множестве точек Г положительной
меры, то /(z)eeeO; 3) функции /(z)giV(A) характери-
характеризуются интегральным представлением вида
, В (г; а,.)
(ак4
где т — целое число такое, что / (z)=zm<p (г), ф()^
оо; Я — действительное число; B1(z; а^) и Д2 (z; 6V) —
Бляшке произведения, составленные по всем нулям
ац=?О и полюсам fcv =?0 функции /(z) внутри А с
учетом их кратности; Ф (8) — сингулярная функция
ограниченной вариации на [0, 2л] с производной, рав-
равной нулю почти всюду.
Важное значение имеет также подкласс N* (А) класса
N (А), состоящий из всех голоморфных О. в. ф. /(z) в Д.
Для того чтобы голоморфная функция /(z)?JV*(A),
необходимо и достаточно, чтобы выполнялось вытекаю-
вытекающее из B) условие
С (/) < оо, 0<г<1. D)
Для функций f (z)?N* (А) в характеристич. представ-
представлении C) В2 (z; bv)=l, т^зО.
Условие D) равносильно требованию, чтобы суб-
гармонич. функция ln+ | / (z) | имела гармонич. мажоран-
мажоранту во всем круге Д. В такой форме это условие употреб-
употребляется обычно для определения класса N* (D) голо-
голоморфных функций /(z) в произвольных областях DczC:
f(z)?N*(D) тогда и только тогда, когда ln+|/(z)|
имеет гармонич. мажоранту во всей области D.
Пусть функция w=w(z) реализует конформное уни-
универсальное накрывающее отображение Д—kD; это —
однозначная аналитич. функция в Д, автоморфная
относительно соответствующей области D группы
G дробно-линейных отображений круга А на себя.
Для того чтобы /(w)?N* (D), необходимо и достаточно,
чтобы суперпозиция / (w (z)) была автоморфной относи-
относительно G и / (w (z))?N* (А). Если область D конечно-
связная и ее граница dD спрямляемая, то угловые
граничные значения /(?), ??5?>, функции f(z)?N*{D)
существуют почти всюду на dD, причем In | /(?) | сумми-
суммируем по гармонич. мере на 3D (подробнее см. обзор [4]).
Пусть теперь /(z), z= (zb . . ., zn), n>l,— голо-
голоморфная функция многих переменных в единичном
поликруге Ara={z?C" : |z/| <1, /=1, • • ., п},
Тп— остов поликруга Д", Tn={z?Crl : | zj\ =1, ;=1,
. . ., п). Класс N* (А") функций с ограничен-
ограниченной характеристикой определяют условием,
обобщающим условие D):
< С (/) < оо, 0 < г < 1,
где ? = (?i , ...,?„ )?Тп, т„(& — нормированная
мера Хаара на Тп, тп (Тп) = 1. Голоморфная функция
/ (z) класса N* (Ап) почти всюду на Т" по мере Хаара
тпп имеет радиальные граничные значения lim/(r?) =
= /(?)> ?6^"' причем ln|/(Q | суммируем на Т". Остав-
Оставляя для О. в. ф. в D = A" первоначальное определение
A), получают, что О. в. ф. /(z) является функцией с
ограниченной характеристикой, N (A")czN* (А"). Од-
Однако при и>1 имеются функции g(z)?N* (An), заве-
заведомо не представимые в виде отношения двух ограни-
ограниченных голоморфных функций (см. [5]).
Лит.: [1] Неванлинна Р., Однозначные аналитиче-
аналитические функции, пер. с нем., М.— л., 1941; [2] М а р к у ш е-
в и ч А. И., Теория аналитических функций, 2 изд., т. 2, М.,
1968; [3] Привалов И. И., Граничные свойства анали-
аналитических функций, 2 изд., М.— л., 1950; [4] Итоги науки.
Математический анализ. 1963, М., 1965, с. 5—80; [5] Р у д и н У.,
Теория функций в поликруге, пер. с англ., М., 1974.
Е. Д. Соломенг{ев.
ОГРАНИЧЕННО-ДЕТЕРМИНИРОВАННАЯ ФУНК-
ФУНКЦИЯ — словарная функция, характеризующая пове-
поведение автомата конечного. (Функция наз. словар-
словарной, если областью определения и областью значений
ее являются множества слов или сверхслов.)
Если А — какой-либо алфавит, то пусть А * обозна-
обозначает множество всех слов, а А" — множество всех слов
или множество всех сверхслов в алфавите А . Функция /,
отображающая А° в В°, где А и В — произвольные
конечные алфавиты, наз. детерминированной
функцией, если выполняются следующие два ус-
условия:
1) для любого ос из А" длина /(ос) равна длине а
и
2) если а — слово длины I и а^аа', а2=аа", где
а', а"?Л°, то значения /(ах) и /(а2) имеют одинаковые
начала длины I.
Если детерминированная функция / определена на
множестве А °° всех сверхслов в алфавите А, то в силу
условий 1) и 2) она однозначно распространяется на
множество А *: для произвольного слова ос длины I
значение / (а) совпадает с началом длины I значения
/(оф), где р — произвольное сверхслово в алфавите А.
Таким образом, всякая детерминированная функция /
удовлетворяет условию:
3) для любого слова а из А* и любого Р из А°
справедливо равенство /(оф)=/(а)/а (р), где /а —
нек-рая детерминированная функция на множестве
А°, однозначно определяемая словом а.
Функция /а наз. остаточной функцией
для /. Из условия 3) следует, что всякая детерминиро-
детерминированная функция / определяет на множестве А * отноше-
отношение эквивалентности R : ccfffS тогда и только тогда, когда
/а=/р- Ранг этого отношения, или, что то же, мак-
максимальное число попарно различных остаточных функ-
функций, наз. весом детерминированной
функции /. Если вес детерминированной функции
конечен, то она наз. ограниченно-детерми-
ограниченно-детерминированной функцией. Это понятие рас-
распространяется и на функции от m переменных, где
тоЗг2, если наборы из т. слов одинаковой длины (или
сверхслов) в алфавитах Ах, . . ., Ат соответственно
рассматривать как слова (сверхслова) в алфавите
А-уХ. . .ХАт, являющемся декартовым произведением
алфавитов Ах, . . ., Ат. Таким же образом можно
рассматривать О.-д. ф. с несколькими выходами, т. е.
значениями к-рых являются наборы из к слов или сверх-
сверхслов соответственно в алфавитах Вх, . . ., В^. Класс
всех О.-д. ф. совпадает с классом функций, вычисли-
вычислимых конечными автоматами. Поэтому для задания
О.-д. ф. могут быть использованы те же средства, что
и для задания конечных автоматов, напр, канонич.
уравнения (см. Автомат конечный, Автоматов способы
задания). Отсюда следует, в частности, что класс
О.-д. ф. с совпадающими алфавитами Ах=. . . = Ат = В
замкнут относительно суперпозиций. Минимальный
(по числу состояний) автомат 31 (А, S, В, ф, г|), sx),
вычисляющий О.-д. ф. / веса т, содержит п состояний
и может быть построен следующим образом. Пусть
oti, . . ., а„ — произвольные представители всех клас-
классов эквивалентности отношения R. Каждому классу
Л (а,), г=1, . . ., п, ставится в соответствие нек-рое
состояние s,- автомата 31. Функция переходов ф и функ-
функция выходов г|) определяются следующими условиями:
если а?А и 1<;г<и, то ф (s,-, a) = Sj, где состояние sj
соответствует классу Я (ос,- а); -ф(s/, a) = fa.(a). В каче-
качестве начального берется состояние, соответствующее
классу R (е), где е — пустое слово.
Лит.: [1] Кудрявцев В. Б., Лекции по теории ко-
конечных автоматов, М., 1976; [2] Я б л о н с к и й С. В., Введе-
Введение в дискретную математику, М., 1979. Ю. И. Янов.
ОГРАНИЧЕННОЕ МНОЖЕСТВО — 1) О. м. в мет-
метрическом пространстве X (с метрикой р (.,.)) —мно-
—множество А, диаметр к-рого
б (Л)= sup p(x, у)
х, у?А
конечен.
2) О. м. в топологич. векторном пространстве Е
(над полем к) — множество В, к-рое поглощается
каждой окрестностью нуля U (т. о. существует такое
ОСрк, ЧТО BdaU). М. И. Войцеховспий.
ОГРАНИЧЕННОЙ ВАРИАЦИИ ФУНКЦИЯ —
функция, имеющая ограниченную вариацию (см. Ва-
Вариация функции). Для функций одного действительного
переменного понятие О. в. ф. введено К. Жорданом [1]
в связи с обобщением Дирихле теоремы о сходимости
рядов Фурье кусочно монотонных функций (см. Жор-
дана признак сходимости ряда Фурье). Функция f(x),
заданная на отрезке [а, 6], является О. в. ф. тогда и
только тогда, когда она может быть представлена в
виде /(ж) = /1(г)— /2(ж), где f1(x) и /2 (х) — возрастаю-
возрастающие (убывающие) на [а, Ь] функции (см. Жордаиа раз-
разложение О. в. ф.). Всякая О. в. ф. ограничена и может
иметь не более чем счетное множество точек разрыва,
причем все 1-го рода. О. в. ф. может быть представлена
в виде суммы абсолютно непрерывной функции (см.
Абсолютная непрерывность), сингулярной функции и
скачков функции (см. Лебега разложение О. в. ф.).
В случае нескольких, переменных понятие О. в. ф.
не является однозначным, т. к. в этом случае сущест-
существует несколько определений вариации функции (см.
Арцела вариация, Витали вариация, Пъерпонта вариа-
вариация, Тонелли плоская вариация, Фреше вариация, Хар-
ди вариация).
Лит.: [1] Jordan С, «С. г. Acad. sci.», 1881, t. 92,
p. 228—30; [2] Натансон И. И., Теория функций вещест-
вещественной переменной, 3 изд., М., 1974. Б. И. Голубое.
ОГРАНИЧЕННЫЙ КВАНТОР — квантор, исполь-
используемый для характеризации предикатов не на всей
области изменения данной предметной переменной, а
на ее части, выделяемой нек-рым предикатом R (х).
При использовании в качестве О. к. всеобщности кван-
квантор (Чх) и существования квантор C#) обычно обо-
обозначаются {ух)ц(х) и (Эж)яи-)- Если Р (х) — нек-рый
предикат, то {4x)R(x) Р (х) означает
Vx(R(x)ZDP(x)),
т. е. что предикат Р (х) истинен при всех значениях
переменной х, удовлетворяющих предикату R(x).
Высказывание (Зх)д(Х)Р (х) означает
3x(R(x)&P(x)),
т. е. что пересечение областей истинности предикатов
R (х) и Р (х) непусто.
В арифметике формальной важную роль играют
О. к. вида Dx)x<t и Cx)x<t, где t — терм, не содер-
содержащий переменной х. При применении таких кванто-
кванторов к разрешимым предикатам получаются также раз-
разрешимые предикаты. в. е. Плиско.
ОГРАНИЧЕННЫЙ ОПЕРАТОР — отображение А
топологического векторного пространства X в тополо-
топологическое векторное пространство Y такое, что А (М) —
ограниченное подмножество в Y для любого ограничен-
ограниченного подмножества М пространства X. Всякий оператор
А : X -+ У, непрерывный на X, является О. о. Если
А : X -* Y — линейный оператор, то для ограничен-
ограниченности А достаточно, чтобы существовала окрестность
нуля UczX такая, что A (U) ограничено в Y. Пусть X,
Y — векторные нормированные пространства и линей-
линейный оператор А : X —>¦ Y ограничен. Тогда
у= sup |1 Ах '| < со.
II * II < 1
Это число наз. нормой оператора Ли обозна-
обозначается ||А ||. При этом
и ||Л|| есть наименьшая из констант С таких, что
|| Ля || < С || я ||
для любого х?Х. Обратно, выполнение этого неравен-
неравенства означает, что А ограничен. Для линейных опера-
торов, отображающих нормированное пространство X
в нормированное пространство У, понятия ограничен-
ограниченности и непрерывности эквивалентны. Для случая
произвольных топологических векторных пространств
X и У это не так, но если X — борнологическое, У —
локально выпуклое пространство, то из ограниченно-
ограниченности линейного оператора А : X —»- Y следует его непре-
непрерывность. Если Н — гильбертово пространство и
А : Н —»- Н —¦ ограниченный симметрич. оператор, то
квадратичная форма <САх, #> ограничена на еди-
единичном шаре Кг = {х : \\х\{ < 1}. Числа
Р= sup <.Ax, х> и а= inf <.Ax, х>
II * ||< 1 11*11 < 1
наз. верхней и нижней границами опе-
оператора А. Точки а н Р принадлежат спектру А ,
и весь спектр лежит на отрезке [a, fl]. Примеры О. о.:
оператор проектирования (проектор) на дополняемое
подпространство банахова пространства и изометриче-
изометрический оператор, действующий в гильбертовом простран-
пространстве.
Если пространства X и Y наделены структурой ча-
частично упорядоченного множества, напр, являются
векторными решетками, то помимо рассмотренной выше
топологич. ограниченности вводится понятие порядко-
порядковой ограниченности оператора. Именно, оператор
А : X -> У наз. порядково ограниченным, если А (М)
есть порядково ограниченное множество
пространства Y для любого порядково ограниченного
множества М пространства X. Пример: изотонный
оператор, т. е. такой оператор, что из х < у
следует А х <: А у.
Лит.: [1] Люстерник Л. А., Соболев В. И.,
Элементы функционального анализа, 2 изд., М., 196 5; [2] Р у-
дин У., Функциональный анализ, пер. с англ., М., 1975;
[3] Б и р к г о ф Г., Теория структур, пер. с англ., М., 1952.
В. И. Соболев.
ОДНОЛИСТНАЯ ФУНКЦИЯ — функция /, регуляр-
регулярная или мероморфная в области В расширенной ком-
комплексной плоскости С и такая, что для всяких z1,
z2?B, 2\фг?., выполняется соотношение /(z1)?fe/(za),
то есть / отображает В в С взаимно однозначно. При
этом обратная функция z=f~1(w) также однолистна.
Обобщением О. ф. являются многолистные функции,
в частности р-листные функции.
При изучении О. ф. одним из основных является
вопрос о возможности однолистного отображения за-
заданной области В на заданную область В' (т. е. ото-
отображения с помощью О. ф.). Необходимым условием
существования такого отображения является равен-
равенство порядков связности областей В ж В' (см., напр.,
[1] с. 28). Если В и В' — односвязные области, гра-
границы к-рых содержат более одной точки, то это ус-
условие является и достаточным (см. Римана теорема)
и задача сводится к отображению заданной области на
круг. В связи с этим особую роль в теории О. ф.
в односвязных областях играет класс S функций /,
регулярных и однолистных в круге Д= {z?C: |z!<l},
нормированных условиями /@) = 0, /' @)=1 п имеющих
разложение
...-ircnz"+..., z?A. A)
В случае многосвязных областей изучают отобра-
отображение заданной многосвязной области на т. н. канонич.
области (см. Конформное отображение). Пусть S (В) —
класс функций F, мероморфных и однолистных в об-
области В, содержащей точку оо, и имеющих в окрест-
окрестности точки оо разложение
F(z)=z + a0+alz-1Jr...+oinz-"+... B)
Если В=- {z?C : \г\ >1 }== А', то этот класс обозна-
обозначают S.
Основные задачи теории О. ф. следующие: 1) изу-
изучение соответствия границ при конформном отобра-
отображении (см. Соответствия границ принцип, Граничные
элементы, Достижимая граничная точка)', 2) получение
однолистности условий; 3) решение различных экст-
экстремальных задач теории функций, в частности полу-
получение оценок различных функционалов и областей
значений функционалов (см. ниже) и их систем в том
или другом классе.
Пусть имеется нек-рый класс (множество) К регуляр-
регулярных или мероморфных функций и пусть на К задан
комплексный функционал и>=Ф(/) (или система функ-
функционалов {(Dft (/) }k=.i)- Областью значений
функционала Ф (/) (или системы функциона-
функционалов {©ft(/)}*=i) на классе К наз. множество D точек
!?>=Ф(/) комплексного пространства С (соответственно
множество точек (Фх(/), • • ., Фп(/)) га-мерного ком-
комплексного пространства С") таких, что f?K. Рас-
Рассматриваются также действительные функционалы.
Всякое множество D', содержащее D, наз. мажо-
мажорантной областью функционала (или
системы функционалов). Знание области значений
функционала позволяет свести решение ряда экстре-
экстремальных задач к более простым задачам анализа.
Напр., если известна область D значений функционала
tUo), f?K (z0 фиксировано), то задача оценки |/(zo)|
сверху и снизу сводится к нахождению самой далекой
и самой близкой точек из D по отношению к точке w=Q.
Первые существенные результаты в теории О. ф.
получены использованием площадей принципа. С по-
помощью внешней теоремы площадей Л. Бибербах (L. Bie-
berbach, 1916) получил точные оценки |/(z)| и |/' (z)|
сверху и снизу для f?S (см. Искажения теоремы),
дал оценку |с2|<:2 для f?S и высказал гипотезу, что
|сп|<:п для f?S (см. Бибербаха гипотеза, Коэффици-
Коэффициентов проблема). Им же было найдено точное значение
постоянной Кёбе. Были также получены оценки мо-
модуля функции, модуля ее производной и другие оценки
в классах выпуклых функций, звездообразных функций,
типично вещественных функций и др. В ряде классов
были найдены выпуклости радиус и радиус звездооб-
разностя (см. Звездообразности граница).
Ниже приведены основные методы теории О. ф.
и нек-рые результаты, полученные с их помощью.
1. Метод интегральных представлений дает возмож-
возможность достаточно просто решать многие задачи теории
функций, в частности экстремальные задачи в классах
функций, имеющих представление с помощью интегра-
интегралов Стилтьеса: выпуклых функций, почти выпуклых
функций, звездообразных функций, типично вещест-
вещественных функций, функций с положительной действи-
действительной частью (см. Каратеодори класс). Для классов
функций, представимых посредством интеграла Стил-
Стилтьеса, был разработан нек-рый вариационный метод
(см. [1] с. 504—19), с помощью к-рого решен ряд экс-
экстремальных задач. Для таких классов разработан вну-
внутренних вариаций метод.
Найдены выпуклые оболочки нек-рых подклассов
класса S (см. [3]). Здесь, в частности, доказано, что
для всякой звездообразной функции / существует
неубывающая на [0,2я] функция ц, такая, что |хBге) —
_"ц.@)=1 и
См. также Интегральное представление аналитиче-
аналитической функции, Параметрическое представление, Пара-
Параметрических представлений метод.
2. Метод контурного интегрирования. С помощью
этого метода было, в частности, доказано, что для f?S
справедливо неравенство (см. Ц] с. 135—39)
где Е и К—полные эллиптические интегралы. Если
z фиксировано @<|z|<l), то это неравенство опреде-
определяет область значений функционала ~ +с2г в клас-
классе S. Получены усиления теорем искажения и доказаны
теоремы об искажении хорд в классах S и 2 (В) (см.
Искажения теоремы и [1] с. 118—35).
См. также Контурного интегрирования метод, Пло-
Площадей принцип.
3. Метод площадей. Пусть Ш (а1; . . . , а„) — класс
систем функций {fk(z)}k=i, конформно и однолистно
отображающих круг Д={|г|<1} на области В*Эа*>
попарно не имеющие общих точек (неналегающие
области), и нормированных условиями /^@)=о^. С по-
помощью теоремы площадей в классе Щ}(оо, аг, . . ., ап),
в частности, получены следующие результаты: 1) если
{fkik=i €ЯП(аь •¦-, ап), ak ? оо,
то
n:
<*;</
« I в*-в'Г2Ве<7*>:?4 C)
это неравенство обобщает на случай комплексных
известное ранее неравенство для действительных у
2) если {/0, AJgOJKO, о»), то
Для Бибербаха — Эйленберга функций
отсюда следует неравенство
выяснены условия, при выполнении к-рых в D) и
D') имеет место знак равенства.
С помощью теоремы площадей для неналегающих
областей получена оценка приближения функции,
регулярной на замкнутой многосвязной области, ра-
рациональной функцией, интерполирующей заданную
функцию в узлах, равнорасположенных на границе
области (см. [4] с. 143—54). Получена область зна-
значений шварциана
для F ? 2 (В) п ряд других областей значений в клас-
классах функций, заданных в многосвязных областях (см.
[4], [5]).
4. Метод Лёвнера. Сам К. Лёвнер (К. Lowner, 1923)
получил точную оценку |c3l<:3 для функций f?S
и точные оценки коэффициентов разложения функции,
обратной к /, в окрестности точки w=0. В частности,
этим методом получена точная форма теоремы вращения
в классе S (см. Вращения теоремы). Доказана теорема:
для /?S при заданных z?A n |/(z)| справедливо не-
неравенство
где х, Ы<|г|, определяется условием
Неравенство E) точное. Из E) следуют точные нера-
неравенства в классе S @<:6<:2ге, 0<:г<1):
Был введен весьма широкий подкласс функций
представпмых в виде
[
где g — звездообразная функция, р — регулярная в
Д функция и такая, что Re{«'Vp (z)}>0 для нек-рого
¦у?[—я/2, я/2], р@) = 1, а>0, —оо<р<+а> (см.
[6] с. 47).
С помощью теорем искажения было установлено, что
функция Кёбе
(ос — действительное) реализует максимум линейной
меры покрытия окружности |м>| = р образом В (г) круга
Дг= {\z\ <г<1} при отображении функциями класса
S, когда р>ея^ег. Из этого свойства функций класса
S следуют оценки площади а(г) области В (г), оценки
среднего модуля функции и другие оценки в классе S,
асимптотически точные при г -> 1 (см. [1] с. 561).
Была предложена нек-рая удобная редукция эк-
экстремальных задач на классе S и нек-рых его подклас-
подклассах к определенным экстремальным задачам на более
простом классе (см. Каратеодори класс), оказавшаяся
применимой к решению ряда экстремальных задач,
в частности к нахождению области значений системы
функционалов {In-^ , In/' (z)} (здесь z, 0<|z|<l,
фиксировано) для/gS (см. [6] с. 115—58).
Метод Лёвнера успешно применялся к исследованию
свойств линий уровня и к решению экстремальных
задач на подклассе S^ ограниченных функций f?S:
|/(г)|<Л/, г?Д (см. [6] с. 150—77).
См. также Лёвнера уравнение, Лёвнера метод, Пара-
Параметрических представлений метод.
5. Вариационные методы. Граничные и внутренние
вариации при решении экстремальных задач приводят
к дифференциальным уравнениям для границ экстре-
экстремальных областей и, соответственно, для экстремаль-
экстремальных функций. Левая часть этих уравнений, как пра-
правило, есть нек-рый квадратичный дифференциал. Раз-
Различные качественные характеристики функций, реали-
реализующих экстремум, получаются при исследовании
свойств соответствующих квадратичных дифференциа-
дифференциалов. В частности, для большого числа экстремальных
задач в классе ? (ив других классах) оказывается, что
экстремальная функция отображает круг Д на всю
плоскость с конечным числом аналитич. разрезов.
Иногда дифференциальное уравнение для экстремаль-
экстремальной функции удается проинтегрировать и тем самым
получить величину экстремума в исследуемой задаче
и все экстремальные функции. Чаще удается лишь
получить одно или несколько конечных уравнений
для величины экстремума. Нек-рые результаты, по-
полученные вариационным методом, перечислены ниже.
Пусть F?2, Wfc, k=\, . . ., п, ri^-1, не принадлежат
образу области Д'={|г|>1} при отображении w=F(z)
и пусть
Доказано, что
^з (F) = I (w1—w2) (w2-w3) (wa-W!) | < 12 ]/
и знак равенства имеет место только для
где а — действительное (см. [1] с. 140—46).
Доказано (см. [1] с. 127 — 35), что область значений
функционала
для ^?2, где yv — заданные числа, не равные одно-
одновременно нулю, ?v — заданные точки из области Д',
является кругом
| w\ <-Re 2" v. = 1 YvV In A-S-1^1).
Исследована задача об экстремуме \сп\, п>1, в классе
Sa функций f(z)=^c1z+c2z2Jr. . . , регулярных и одно-
однолистных в круге Д и не принимающих в нем заданных
значений аи . . ., ап (см. [1] с. 151 — 56). Частный
случай и=1 является задачей определения континуума
наименьшей емкости (рассмотрение этой задачи и ее
обобщений см. в [7]).
С помощью вариационного метода исследовались
различные задачи для неналегающих областей. Так,
рассматривалась задача о максимуме произведения
в классе 3J}(ai, . . ., ап) (см. [1] с. 156 — 65). Получена
точная оценка произведения
где ak — любые заданные положительные числа при
и=2 и 3 (см. [1] с. 550-51).
Эта задача равносильна задаче нахождения области
D системы функционалов (|/i@)|, . . ., |/„@)|) в классе
0ЛК, • • ., ап).
См. также Вариационные принципы, Вариация од-
однолистной функции, Внутренних вариаций метод,
Граничных вариаций метод, Вариационно-параметри-
Вариационно-параметрический метод.
6. Метод экстремальной метрики. При решении
экстремальных задач методом экстремальной метрики
основную роль, как правило, играет метрика, порож-
порожденная нек-рым квадратичным дифференциалом Q (z)dz2.
Это тот же квадратичный дифференциал, к-рый возни-
возникает при решении задачи вариационным методом.
Ниже для примера указаны два результата, получен-
полученные этим методом (см. [1] с. 532 — 611, 17] — [9]).
При помощи общей теоремы коэффициентов (о. т. к.)
Дж. Дженкинс (J. Jenkins, 1960) получил решение
задачи об области значений функционала f(z) при фик-
фиксированном z из круга Д= {\z <1} на классе Sr функ-
функций из S с действительными коэффициентами сг, ся,
.... В классах 2 и М, где М — класс функций /,
/@) = 0, /'@)=1, мероморфных и однолистных в круге
Д, он выяснил влияние обращения в нуль нек-рого
числа из начальных коэффициентов на рост после-
последующих.
Было дано добавление к о. т. к. в случае, когда
дифференциал Q (z)dz2 не имеет полюсов порядка,
большего единицы; кроме того, с помощью экстремаль-
экстремально-метрического подхода были установлены весьма
общие теоремы покрытия линий при однолистном кон-
конформном отображении односвязных и двусвязных
областей, в частности уточнен результат о покрытии
отрезков для функций, мероморфных и однолистных
в круге, п аналогичный результат для кругового
кольца (см. [1] с. 559, 560, 564).
См. также Грётша принцип, Грётша теоремы, По-
Полос метод, Квадратичный дифференциал, Бибербаха —
Эйленберга функции, Экстремальной метрики метод.
7. Метод симметризации. С помощью этого метода,
часто в сочетании с другими, решен ряд сложных экс-
экстремальных задач, не поддающихся решению иными
методами. Таковы, напр., следующие задачи (см. [1]
с. 536—611, [7] — [10]). В классе S функций / была
получена точная оценка сверху меры множества точек
окружности \w\ = R, 1/4<:Д<1, не принадлежащих
образу круга Д при отображении w=f{z) (?/(Л)).
В сочетании с методом экстремальных метрик найдена
точная оценка сверху l/(z)| при фиксированном |z| = r,
0<г<1, для
с заданным c2=c=const, 0<:c<:2; обобщены и распро-
распространены неравенства F) на класс р-листных в среднем
по окружности функций
(см. Многолистная функция).
С использованием метода симметризации было до-
доказано, что если Ф — выпуклая неубывающая на
(—оо, + оо) функция, то для /?? при 0<г<1
Ф (In | / (re») \)dt<L $* л Ф (In | К (relt) \ ) dt,
где К(z) = z(l — z)~2 (см. [11]). Если имеет место знак
равенства при нек-ром г, 0<г<1, и при нек-рой строго
выпуклой функции Ф, то
где а действительно.
О приложениях метода симметризации к многосвяз-
многосвязным областям см. в [12], [13]. См. также Симметриза-
Симметризации метод.
Лит,: [1] Г о л у з и н Г.М., Геометрическая теория функ-
функций комплексного переменного, 2 изд., М., 1966; [2] Але к-
сандров И. А., Лебедев Н. А. «Тр. Матем. ин-та
АН СССР», 1968, т. 94, с. 79—89; [3] В г i с k m a n L., М а с-
G г е g о г Т. Н., Wilken D. R., «Trans. Amer. Math. Soc»,
1971, v. 156, p. 91—107: [4] Л е б е д е в Н. А., Принцип пло-
площадей в теории однолистных функций, М., 1975; [5] Ми лин
И. М., Однолистные функции и ортонормированные системы.М.,
1971; [6] Александров И. А., Параметрические продол-
продолжения в теории однолистных функций, М., 1976; [7] К у з ь м и-
на Г. В., «Тр. Матем. ин-та АН СССР», 1980, т. 139, с. 1—241;
[8] Дженкинс Дж., Однолистные функции и конформные
отображения, пер. с англ., М., 1962' [9] PommerenkeC h.,
Univalent Functions, Gott., 1975; [10] ХейманВ. К., Мно-
голистные функции, пер. с англ., М., 1960; till Baernstein
A., «Acta math.», 1974, v. 133, p. 139—69; [12] M и т ю к И. П.,
«Укр. матем. ж.», 1965, т. 17, № 4, с. 46—54; [13] его же,
«Сиб. матем. ж.», 1965, т. 6, № 6, с. 1282—91. Н. А. Лебедев.
ОДНОЛИСТНОСТИ РАДИУС — радиус р(М) наи-
наибольшего круга |z| <p, в к-ром однолистны все функции
семейства регулярных в круге \г\ <1 функций
таких, что \]{z)\<.M при |г|<1. Оказывается, что
р(М)=М— УМ2 — 1, Afrsl,
причем функция
/0 (z) = Mz (I — Mz)l(M — z)
однолистна в круге |г|<Ср(Л^), но не в большем круге
(имеющем центр в начале). Для функций, регулярных
в круге \z\<R и таких, что /@) = 0, /' @) = с, с^=0,
и |/(г)|«Л/, О. р. р*{М) определяется аналогично,
и его значение легко получается из р(М).
Г. К. Антонкж.
ОДНОЛИСТНОСТИ УСЛОВИЯ — необходимые и
достаточные условия, при к-рых регулярная (или ме-
роморфная) функция /(z) однолистна в нек-рой области
комплексной плоскости С. Необходимым и достаточным
условием однолистности /(z) в достаточно малой ок-
окрестности точки а является /' (а)ф0. Такая (локальная)
однолистность во всех точках области еще не гаран-
гарантирует однолистности в области. Напр., функция ez
неоднолистна в круге |г|<:Л, где Л>л, хотя для нее
выполняется условие локальной однолистности в каж-
каждой точке плоскости. Необходимым условием одно-
листности является всякое свойство однолистной функ-
функции, в частности всякое неравенство, к-рому удов-
удовлетворяет однолистная функция. Справедливы следу-
следующие необходимые и достаточные О. у.
Теорема 1. Пусть функция /(г) в окрестности
г=0 разлагается в ряд
...-|-a,1Z»+.>, A)
и пусть
Х-г "*"—V, (?=1 г ч
с постоянными коэффициентами ak и со^_ q. Для того
чтобы /(г) была регулярной и однолистной в Е = {г: |г| <
<1} функцией, необходимо и достаточно, чтобы при
всяком натуральном N и для всяких хр, р=1, . . ., TV,
выполнялось неравенство Грунского
Аналогичные условия имеют место для класса 2 E)
(класс функций F(Q = t,-\-co-\-c1/t,-\-. . ., мероморфных
и однолистных в области fi^oo) (см. [2] с. 599—602,
а также Площадей принцип).
Теорема 2. Пусть граница I конечной области
D есть жорданова кривая. Для того чтобы регулярная
в D и непрерывная в замкнутой области D функция
f(z) была однолистной в D, необходимо и достаточно,
чтобы/(г) взаимно однозначно отображала I на нек-рую
замкнутую жорданову кривую.
Необходимые и достаточные условия однолистного
отображения на области выпуклые, звездообразные
или спиралеобразные относительно начала для функции
A) в круге Е связаны с теоремой 2 и записываются
соответственно в виде
Многие достаточные О. у. описываются с помощью
обыкновенных дифференциальных уравнений (теорема
3) и уравнений с частными производными (теорема 4).
Теорема 3. Мероморфная в круге Е функция
/(г) будет однолистной в Е, если шварциан
{/, *} = [/"(*)//' (z)]'-2-1 [/" (z)/f (z)]2
подчиняется неравенству
|{/, *}|<2Я(|«|), |*|< 1,
причем мажоранта S (г) является непрерывной неотри-
неотрицательной функцией и удовлетворяет условиям: а)
5(г)A — г2J не возрастает по г при 0<г<1, б) диффе-
дифференциальное уравнение y"-{-S(\t\)y=O при —l<i<l
имеет решение г/0(г)>0.
Частными случаями теоремы 3 являются условия
однолистности Нехари — Покорно-
где (ц) ( \ ц
Теорема 4. Пусть /(г, t) есть функция, регуляр-
регулярная в круге Е, непрерывно дифференцируемая по t,
0<:?<оо, /@, i)=0, и удовлетворяющая уравнению
Лёвнера — Куфарева
!? = **(*, t) |f, 0 <t < oo, z?E,
где h (г, t) — функция, регулярная в Е, непрерывная
по t, 0«i<oo, и Reft(z, i)>0. Если
где limao(()= oo, 0A) — конечная величина при 1-ю
для каждого z?E и /(z) — непостоянная регулярная
функция в Е с разложением A), то все функции f(z, t)
однолистны, в том числе однолистными являются,
функции /(z, 0) и /(z).
Теорема 4 приводит к следующим конкретным 0. у.:
. Г B)
' /' B)
где а, Р, у ~ действительные постоянные, а>0, lyl <
<я/2, ф(г) — регулярная функция, отображающая
круг Е на выпуклую область.
Однолистность функции
w = f(z) B)
равносильна однозначной разрешимости уравнения B)
относительно г. В таком понимании достаточные О. у.
распространяются на широкий класс операторных
уравнений. Для этих уравнений, в частности, обоб-
обобщено условие Re[e'V/' (г)]^0 на класс действительных
преобразований выпуклых и невыпуклых областей
я-мерного евклидова пространства.
Лит.: ?11 Лебедев Н. А., Принцип площадей в теории
однолистных функций, М., 1975; [2] Го л узин Г. М., Гео-
Геометрическая теория функций комплексного переменного, 2 изд.,
М., 1966; [3]Маркушевич А. И., Теория аналитических
функций, 2 изд., т. 2, М., 1968; E4J А в х а д и е в Ф. Г., А к—
сентьев Л. А., «Успехи матем. наук», 1975, т. 30, в. 4, с. 3—
60; [5] Г а х о в Ф. Д., Краевые задачи, 3 изд., М., 1977; [6]
Тумашев Г. Г., НужинМ. Т., Обратные краевые зада-
задачи и их приложения, 2 изд., Казань, 1965. Л. А. Апсентъев.
ОДНОМЕРНОЕ МНОГООБРАЗИЕ — топологическое
пространство X, каждая точка к-рого обладает окрест-
окрестностью, гомеоморфной прямой (внутренняя точ-
к а ) или полупрямой (граничная точка). Связ-
Связное паракомпактное хаусдорфово О. м. X без граничных
точек гомеоморфно окружности, если оно компактно,
и прямой, если оно некомпактно; при наличии одной
или двух граничных точек X гомеоморфно соответст-
соответственно полуоткрытому или замкнутому конечному ин-
интервалу. Любое такое О. м. сглаживаемо, так что в
вышеприведенном утверждении гомеоморфность можно-
заменить диффеоморфностыо.
Континуум (связное (би)-компактное хаусдорфово
пространство) К, каждая точка к-рого, за исключением
двух, разделяет его, гомеоморфен замкнутому интер-
интервалу. Если же каждая точка является разделяющей,
то К гомеоморфен окружности. При этом х ? К разде-
разделяет К, если существуют два непустых непересекаю-
непересекающихся открытых множества А и В таких, что К\х=
= А [)В. Другими словами, нек-рые линии являются
О. м.
Лит.: [1] М и л н о р Д т., Уоллес А., Дифференциаль-
Дифференциальная топология. Начальный курс, пер. с англ., М., 1972; [2]
Рохлин В. А., Ф у к с Д. Б., Начальный курс топологии.
Геометрические главы, М., 1977; [3] X и р шМ., Дифференциаль-
Дифференциальная топология, пер. с англ., М., 1979. М. И. Войцеховспий.
ОДНОПАРАМЕТРИЧЕСКАЯ ГРУППА ПРЕОБРА-
ПРЕОБРАЗОВАНИЙ, поток,— действие аддитивной группы
действительных чисел R на многообразии М.
Таким образом, однопараметрическое семейство
{фл 'G^} преобразований многообразия М является
О. г. п., если выполнены следующие условия:
Если многообразие М гладкое, то обычно предпола-
предполагается, что О. г. п. тоже гладкая, т. е. соответствующее-
отображение
>-М, (t, x) —>ццх
является дифференцируемым отображением дифферен-
дифференцируемых многообразий.
Более общим, чем понятие О. г. п., является понятие
локальной о д нопара метрической
группы преобразований многообразия М. Оно
определяется как отображение <p:U —>- М нек-рого
¦открытого подмногообразия UdRXM вида U—
О&~ (^)> е+(х)[, г), где е+ (х)>0, е_ (х)<0 для
удовлетворяющее условиям (*) при всех t, s?R,
Q, для к-рых обе части равенств определены.
С каждой гладкой локальной О. г. п. {ф^} многооб-
многообразия М связывается векторное поле
наз. полем скоростей, или и н ф и н и т е-
з и м а л ь н о й образующей, О. г. п. {q>j}. Об-
Обратно, любое гладкое векторное поле Л" порождает
локальную О. г. п. ф/, имеющую полем скоростей
поле Л". В локальных координатах х' на М эта О. г. п.
задается как решение системы обыкновенных диффе-
дифференциальных уравнений
J = x{xJ)
с начальными условиями <р' @, xJ) = x', где X —
•"' Ох1
Если локальная О. г. п., порождаемая векторным
полем X, продолжается до глобальной О. г. п., то
поле X наз. полным. На компактном многообразии
любое векторное поло является полным, и, таким
образом, существует взаимно однозначное соответствие
между О. г. п. и векторными полями. На некомпакт-
некомпактном многообразии это уже не так, причем множество
полных векторных полей даже не замкнуто относи-
относительно сложения.
Лит.: [1] Арнольд В. II., Обыкновенные дифферен-
дифференциальные -уравнения, М., 1971; [2] Р а 1 a i s R., A global for-
formulation of the Lie theory of transformation groups, Providence,
1957. Д- В. Алексеевспий,
ОДНОПАРАМЕТРИЧЕСКАЯ ПОДГРУППА груп-
группы Ли G над нормированным полем
К — аналитический гомоморфизм аддитивной группы
поля К в С, т. е. такое аналитическое отображение
а: К ->¦ G, что
= a(s)a(t), s, t?K.
О. п. наз. также образ этого гомоморфизма, к-рый, соб-
собственно, и является подгруппой группы G. Если K=R,
то уже из непрерывности гомоморфизма а: К —*¦ G сле-
следует его аналитичность. Если K=R или С, то для
любого касательного вектора X ? TeG к группе G в точ-
точке е существует единственная О. п. а : К —>- G, имею-
имеющая X своим касательным вектором в точке t=0.
При этом a(t) = exj)tX, t?K, где exp: TeG —v G — экс-
экспоненциальное отображение. В частности, любая О. п.
в полной линейной группе G=GL(n, К) имеет вид
oc(*)=exp*A' = V, —t"X".
Если G — вещественная группа Ли, снабженная дву-
сторонне инвариантной псевдоримановой метрикой или
аффинной связностью, то О. п. группы G — это гео-
геодезические, проходящие через единицу е.
Лит.: [1] П о н т р я г и н Л. С, Непрерывные группы,
3 изд., М., 1973; [2] С е р р Ж.-П., Алгебры Ли и группы Ли,
пер. с англ. и франц., М., 1969; [3]Хелгасон С, Дифферен-
Дифференциальная геометрия и симметрические пространства, пер. с англ.,
М., 1964. А. Л. Онищик.
ОДНОПАРАМЕТРИЧЕСКАЯ ПОЛУГРУППА — се-
семейство операторов T(t), t>0, действующих в банахо-
вом или топологическом векторном пространстве X,
обладающее свойством
Т (t-\-T)x = T (t) [Т (т)ж], *, т > 0, х?Х.
Если операторы T(t) линейны, ограничены и дейст-
действуют в банаховом пространстве Л", то из измеримости
всех функций T(t)x, х?Х, следует их непрерывность.
Функция ||У(*)|! растет на бесконечности не быстрее
экспоненты. Классификация О. п. основана на их
различном поведении при t —>- 0. В простейшем случае
Т (t) сильно стремится к единичному оператору при
t —>- 0 (см. Полугруппа операторов).
Важной характеристикой О. п. является произво-
производящий оператор полугруппы. Основной проблематикой
теории О. п. является установление связи между свой-
свойствами полугрупп и их производящих операторов.
Достаточно полно изучены О. п. линейных непрерывных
операторов в локально выпуклых пространствах.
О. п. нелинейных операторов в банаховом простран-
пространстве исследованы в том случае, когда операторы T(t)
сжимающие. Здесь имеются глубокие связи с теорией
диссипативных операторов.
Лит.: [1] Иосида К., Функциональный анализ, пер. с
англ., М., 1967; 12] К р е йн С. Г., Линейные дифференциаль-
дифференциальные уравнения в банаховом пространстве, М., 1967; [3] X и л л е
Э., Фи л липе Р., Функциональный анализ и полугруппы,
пер. с англ., М., 1962; [4]ButzerP., BerensH., Semi-
Semigroups of operators and approximation, В., 1967; [5] В а г b u V.,
Nonlinear semigroups and differential equations in Banach spaces,
Buc—Leyden, 1976. С. Г. Крейн.
ОДНОПЕРИОДИЧЕСКАЯ ФУНКЦИЯ, просто-
периодическая функция,— периодическая
функция /(z) комплексного переменного г, все периоды
р к-рой суть целые кратные одного единственного
основного, или примитивного, периода
2<афО, р = 2п(й. Напр., целой О. ф. является показа-
показательная функция ez с основным периодом 2ш=2лг,
мероморфными О. ф.— тригонометрич. функции tg z
И Ctg Z С ОСНОВНЫМ Периодом 2СО=Я. Е. Д. Соломенцев.
ОДНОПОЛОСТНЫЙ ГИПЕРБОЛОИД — см. Ги-
Гиперболоид.
ОДНОРОДНАЯ ОГРАНИЧЕННАЯ ОБЛАСТЬ —
однородное комплексное многообразие, изоморфное ог-
ограниченной области в С". Примером О. о. о. является
«комплексный шар»
в к-ром транзитивно действует псевдоунитарная группа
SUn>1, представленная проективными преобразова-
преобразованиями пространства С".
Если D — любая ограниченная область в С", то эр-
эрмитова дифференциальная форма
где К — Бергмана кернфункция области D, опреде-
определяет в D кэлерову метрику, наз. метрикой Берг-
Бергмана и инвариантную относительно всех автомор-
автоморфизмов области D (см. [1], [2]). Группа G(D) всех ав-
автоморфизмов области D является вещественной груп-
группой Ли, не содержащей нетривиальных связных ком-
комплексных подгрупп. Если D — однородна, то метрика
Бергмана полна.
Среди О. о. о. выделяются симметрич. области. Ог-
Ограниченная область D наз. симметрической,
если для любой точки z??> существует инволютивный
автоморфизм области D, имеющий z изолированной
неподвижной точкой. Всякая симметрич. область од-
однородна и является эрмитовым симметрич. простран-
пространством относительно метрики Бергмана. Получена [3]
классификация симметрич. областей. Имеются 4 серии
неприводимых симметрич. областей, связанных с клас-
спч. простыми группами Ли, и две особые области раз-
мерностей 16 и 27. К числу классических симметрия,
областей относятся, в частности, комплексный шар и
верхняя полуплоскость Зигеля (см. Зигеля область).
Всякая симметрич. область изоморфна прямому про-
произведению неприводимых симметрич. областей [1].
Всякая О. о. о. размерности <:3 является симмет-
симметрической [3]. Начиная с размерности 4, существуют
и несимметрические О. о. о. (см. [4]). Более того, при
п^Ч имеется континуум га-мерных О. о. о., среди
к-рых лишь конечное число симметрических. Каждая
О. о. о. гомеоморфна клетке и аналитически изоморфна
аффинно однородной области Зигеля, определенной
однозначно с точностью до аффинного изоморфизма.
Классификация О. о. о. производится алгебраич. сред-
средствами [5].
С О. о. о. связаны многомерные обобщения эйлеро-
эйлеровых интегралов (интегралы Зигеля 1-го п 2-го рода),
а также гипергеометрич. функции [6].
Лит.: [1] Хелгасон С, Дифференциальная геометрия
и симметрические пространства, пер. с англ., М., 1964; [21
Фукс Б. А., Специальные главы теории аналитических функ-
функций многих комплексных переменных, М., 1963; [3] С а г t a n E-,
«Abh. Math. Sem. Hamb. Univ.», 1936, Bd 11, S. 116—62; [4]
Пятецкий-Шапиро И. И., Геометрия классических
областей и теория автоморфных функций, М., 1961; [5] В и н-
б е р г Э. Б., Гиндикин С. Г., Пятецкий-Ш а-
п и р о И. И., «Тр. Моск. матем. об-ва», 1963, т. 12, с. 359—88;
[6] Гиндикин С. Г., «Успехи матем. наук», 1964, т. 19,
в. 4, с. 3—92. Э. Б. Винбе-рг.
ОДНОРОДНАЯ ФУНКЦИЯ степени X — чи-
числовая функция /(ж,, . . ., хп) такая, что для всех то-
точек (x-i, . - ., хп) из области ее определения и всех дей-
действительных ?>0 выполняется равенство
/ (txu ..., txn)=thf (Xl, ..., хп),
где X — действительное число; при этом предпола-
предполагается, что вместе с каждой точкой (xt, . . ., хп) из
области определения функции / при любом t>0 к
этой области определения принадлежит и точка (txlt
¦ . ., txn). Если функция
т. е. является многочленом степени не выше чем те, то
она будет О. ф. степени т в том и только в том случае,
когда все коэффициенты ak k при кг-\-. . .-\-кп<т
равны нулю. Понятие О. ф. может быть расширено
на многочлены от п переменных над любым коммута-
коммутативным кольцом с единицей.
Пусть область определения Е функции / лежит в
первом квадранте: хг>0, . . ., хп>0 и вместе с любой
точкой (х1у . . ., хп) содержит и весь луч (txlf . . ., txn),
«>0. Для того чтобы функция / была однородной
степени К, необходимо и достаточно, чтобы существо-
существовала такая функция <р от п — 1 переменных, определен-
ная на множестве точек вида ( — , . . .,— ), где
\ Xi Xi /
(л-j, . . ., хп)?Е, что для всех (xt, . . ., хп)?Е выполня-
выполняется равенство
f (x x ) = x ш —— —
Если область определения Е функции / открытое
множество и функция / непрерывно дифференцируема
на Е, то функция является О. ф. степени X в том и
только в том случае, когда она при всех (хг, . . ., хп)
из ее области определения удовлетворяет равенству
(формула Эйлера)
J xi 57: — hf \xii ¦¦ • i xn>-
Л. Д. Кудрявцев-
ОДНОРОДНОЕ КОМПЛЕКСНОЕ МНОГООБРАЗИЕ —
комплексное многообразие М, группа автоморфизмов
к-рого транзитивно действует на М. Все односвязные
одномерные комплексные многообразия — сфера Ри-
мана, комплексная плоскость и верхняя комплексная
полуплоскость — однородны. Многообразие GlH смеж-
смежных классов комплексной группы Ли G по замкнутой
комплексной подгруппе // является О. к. м.
Среди компактных О. к. м. выделяются комплекс-
комплексные флаговые многообразия, к числу к-рых относятся
все компактные эрмитовы симметрические пространст-
пространства [8]. Комплексные флаговые многообразия могут быть
охарактеризованы как односвязные компактные одно-
однородные кэлеровы многообразия [4], а также как много-
многообразия G/ U, где G — полупростая комплексная группа
Ли, U — ее параболич. подгруппа. Всякое компактное
О. к. м. допускает однородное коломорфное расслоение
над флаговым многообразием со слоем, изоморфным
многообразию смежных классов комплексной группы
Ли по дискретной подгруппе (см. Титса расслоение,
а также [6], [9]).
Другой важный класс О. к. м. составляют однород-
однородные ограниченные области (о. о. о.), к числу к-рых
относятся, в частности, симметрич. области, двойст-
двойственные компактным эрмитовым симметрич. простран-
пространствам.
Флаговые многообразия и о. о. о. представляют со-
собой частные случаи однородных кэлеро-
кэлеровы: многообразий (т. е. кэлеровых много-
многообразий, на к-рых транзитивно действует группа
аналитпч. автоморфизмов, сохраняющих кэлерову мет-
метрику). Существует гипотеза [2], что всякое однородное
кэлерово многообразие допускает однородное голоморф-
голоморфное расслоение, базой к-рого служит о. о. о., а слоем —
прямое произведение флагового многообразия и мно-
многообразия смежных классов комплексного векторного
пространства по дискретной подгруппе. Эта гипотеза
доказана для однородных кэлеровых многообразий,
допускающих полупростую [1] или вполне разрешимую
[2] транзитивную группу автоморфизмов, а также для
компактных однородных кэлеровых многообразий, ко-
которые, таким образом, изоморфны прямым произведени-
произведениям флаговых многообразий и комплексных торов [10].
В теории О. к. м. важную роль играет канониче-
каноническая эрмитова форма fop,. По любой глад-
гладкой мере ц на комплексном многообразии М, задава-
задаваемой внешней дифференциальной формой
i"Kdz1A. . . AdznAdz1A. . . Adzn,
может быть построена эрмитова дифференциальная
форма
(вообще говоря, вырожденная), не зависящая от вы-
выбора системы координат и не меняющаяся при умно-
умножении меры (х на константу. Если мера jx определена
стандартным образом по какой-либо кэлеровой мет-
метрике на М, то форма (—Лц) совпадает с формой Риччи
этой метрики [7]. Если потребовать, чтобы мера ц
была инвариантна относительно какой-либо транзи-
транзитивной группе автоморфизмов многообразия М, то
она будет определена этой группой однозначно с точ-
точностью до умножения на константу, а форма fojj, — впол-
вполне однозначно. В случае, когда М — о. о. о., опреде-
определенная таким образом эрмитова форма fop, положи-
положительно определена и совпадает с метрикой Бергмана.
Для флаговых многообразий форма fop отрицательно
определена.
Каноннч. эрмитова форма О. к. м. может быть вы-
вычислена в терминах соответствующей алгебры Ли [3].
Это служит основой для алгебраизации теории о. о. о.
и других О. к. м.
Одно из направлений в теории О. к. м. состоит в
изучении голоморфных функций на них при помощи
аппарата линейных представлений групп Ли. Напр.
этим способом доказано [5], что многообразие GIH
смежных классов полупростой комплексной группы
Ли б по связной замкнутой комплексной подгруппе Н
является многообразием Штейна тогда и только тогда,
когда подгруппа Н редуктивна.
Существуют О. к. м., не допускающие транзитивной
группы Ли автоморфизмов [11].
Лит.: [1] В о re I A., «Proc. Nath. Acad. Sci. USA», 1954,
v. 40, p. 1147—51; [2] В и в б е р г Э. Б., Г и н д и к и н С. Г.,
«Матем. сб.», 1967, т. 74, Я» 3, с. 357—77; [3] К о s г u I J. L.,
«Canad. J. Math.», 1955, v. 7, № 4, p. 652—76; [4] L i с h n e-
l¦ о w i с z А., в кн.: Geometrie differentielle, P., 1953, p. 171 —
84; [5] Онищик А. Л.,«Докл. АН СССР», 1960, т. 130, с. 726 —
29; [6] T i t s J., «Comm. math, helv.», 1962/1963, t. 37, p. Ill —
20; [7] Фукс Б. А., Специальные главы теории аналитиче-
аналитических функций многих комплексных переменных, М., 1963; [8]
Хелгасон С, Дифференциальная геометрия и симметриче-
симметрические пространства, пер. с англ., М., 1964; [9] Wang Н.-С,
«Amer. J. Math.», 1954, v. 76, № 1, p. 1 — 32; [10] В о re 1 А.,
Bemmert R., «Math. Ann.», 1962, Bd 145, № 5, p. 429—39;
[11] Каир W., «Invent, math.», 1967, v. 3, X« 1, p. 43—70.
Э. Б. Винберг.
ОДНОРОДНОЕ ПРОСТРАНСТВО — множество вме-
вместе с заданным на нем транзитивным действием нек-рой
группы. Точнее, М есть однородное прост-
пространство группы G, если задано отображение
(g, х) —+ gx
множества GXM в М такое, что:
1) (gh)x = g(hx);
2) ех--=х;
3) для любых х, у?М существует такой g?G, что
gx = y.
Элементы множества М наз. точками О. п., группа
б — группой движений, или основной
(фундаментальной) группой, О. п.
Любая точка х О. п. М определяет подгруппу
основной группы G. Она наз. изотропии группой, или
стационарной подгруппой, или стабилизато-
стабилизатором точки х. Стабилизаторы разных точек сопря-
сопряжены в группе б с помощью внутренних автоморфиз-
автоморфизмов.
С произвольной подгруппой Н группы G связано
нек-рое О. п. группы G — множество M=GlH левых
классов смежности группы б по подгруппе Н, на к-ром
G действует по формуле
g(aH) = (ga)H; g, a?G.
Это О. п. наз. факторпространством груп-
группы б по подгруппе Н, а подгруппа Н оказы-
оказывается стабилизатором точки еН=Н этого пространства
(е — единица группы G). Любое О. п. М группы б
можно отождествить с факторпространством группы б
по подгруппе H=GX, являющейся стабилизатором
фиксированной точки х?М, с помощью биекции
где g — любой элемент из G, для к-рого gx—y.
Если группа б является топологич. группой, а Н —
ее подгруппой (соответственно G — группа Ли, а Н —
замкнутая подгруппа в G), то факторпространство
M=GlH канонич. образом снабжается структурой
топологич. пространства (соответственно структурой
аналитич. многообразия), относительно к-рой действие
группы б на М является непрерывным (соответственно
аналитическим). Если группа Ли б транзитивно и
аналитически действует на аналитич. многообразии М,
то для любой точки хо?М подгруппа H=GXl) замкнута
и указанная выше биекция gH —> gx0 аналитична;
если при этом число связных компонент группы б
не более чем счетно, то эта биекция является диффео-
диффеоморфизмом.
Изучаются также случай, когда б — алгебраич.
группа, а М — алгебраич. многообразие (см. Однород-
ное пространство алгебраической группы), и случай,
когда М — комплексное многообразие, a G — вещест-
вещественная (или комплексная) группа Ли (см. Однородное
комплексное многообразие).
В дальнейшем всюду М — аналитич. многообразие,
a G — группа Ли.
Геометрия однородных пространств. Согласно Эр-
лангенской программе Ф. Клейна (F. Klein), предмет
геометрии О. п. есть изучение инвариантов группы
движений О. п. Классич. направлением исследований
здесь является классификация тех или иных подмно-
подмножеств О. п., прежде всего подмногообразий и их объ-
объединений, семейств подмногообразий и т. п. с точностью
до движений из группы G. Такая классификация
может быть получена при помощи построения полной
системы инвариантов подмножества данного типа (при-
(примерами таких систем инвариантов служат длины сторон
треугольника, а также кривизна и кручение гладкой
кривой в трехмерном евклидовом пространстве). Об-
Общий метод построения полной системы локальных
инвариантов {подвижного репера метод) для гладкого
подмногообразия в произвольном О. п. группы Ли
разработан Э. Картаном (см. [61, [16]).
Другое направление исследований состоит в оты-
отыскании и изучении инвариантных геометрич. объектов
на О. п. (см. Инвариантный объект на однородном
пространстве). Действие основной группы Ли G в
О. п. М индуцирует действие группы G в пространстве
различных геометрич. объектов на М (функций, век-
векторных и тензорных полей, связностей, дифференци-
дифференциальных операторов и т. п.). Геометрич. объекты, не-
неподвижные относительно этого действия, наз. инва-
инвариантными объектами. Примерами таких
объектов являются евклидова метрика в евклидовом
пространстве, рассматриваемом как О. п. группы
евклидовых движений, и конформная метрика, зада-
задающая угол между кривыми в конформном пространстве.
С этим же направлением тесно связана задача описания
и изучения О. п., обладающих тем или иным инвари-
инвариантом. Напр., рассматриваются римановы и
псевдоримановы, аффинной связно-
связности, симплектические О. п., однород-
однородные комплексные многообразия, то
есть О. п., обладающие инвариантной метрикой (ри-
мановой или псевдоримановой), аффинной связностью,
симплектич. структурой, комплексной структурой соот-
соответственно. См. Риманово пространство однородное,
Симплектическое пространство однородное, Однород-
Однородное комплексное многообразие.
Важным классом О. п. является класс р е д у к-
т и в н ы х О. п., т. е. таких О. п. GlH, что алгебра
Ли g группы Ли G допускает разложение
8=f + m, fnm={0}, (*)
где \ — алгебра Ли группы Н, а т — подпростран-
подпространство, инвариантное относительно присоединенного
представления подгруппы Я в д. Такое разложение
определяет в О. п. GIH геодезически полную линейную
связность с ковариантно постоянными тензорами кри-
кривизны и кручения. Обратно, односвязное многооб-
многообразие с полной линейной связностью, имеющей кова-
ковариантно постоянные тензоры кривизны и кручения,
является редуктивным О. п. относительно группы
автоморфизмов этой связности (см. [5]). Частным
случаем редуктивного О. п. является спмметрич. про-
пространство, для к-рого разложение (*) удовлетворяет
дополнительно условию [in, mfef. Геометрически
это условие означает, что соответствующая связность
имеет нулевое кручение. Примерами симметрич. про-
пространств являются глобально симметрические римановы
пространства, а также пространство произвольной
группы Ли, на к-ром группа движений порождается
левыми и правыми сдвигами.
Однородные расслоения и теория представлений.
Действие основной группы G продолжается не только
на расслоения геометрич. объектов, но и на более
широкий класс т. н. однородных расслое-
расслоений. Однородное расслоение я над О. п. G/II за-
задается левым действием подгруппы Н на произвольном
многообразии F (типовом слое) и определяется как
естественная проекция
n:GXHF —>¦ G/H,
где GX fjF—расслоенное произведение, получаемое
факторизацией прямого произведения GXF по отно-
отношению эквивалентности
(В, /) ~(gh-\ hf),
Если P — векторное пространство, на к-ром группа Н
действует линейно, то соответствующее однородное
расслоение я является векторным, а в пространстве
Г (л) его сечений возникает линейное представление
группы б, индуцированное представлением подгруппы
И в F. Изучение индуцированных представлений (свой-
(свойства к-рых оказываются тесно связанными с геомет-
геометрией соответствующего О. п.) и их обобщений играет
важную роль в теории представлений групп Ли (см.
[7]).
Анализ на однородных пространствах. К числу наи-
наиболее разработанных разделов относятся: 1) изучение
различных функциональных пространств на О. п.
(пространств функций, пространств сечений однород-
однородных векторных расслоений, пространств когомологий
со значением в соответствующих пучках), 2) изучение
инвариантных дифференциальных операторов, дейст-
действующих на этих пространствах, 3) изучение различных
динамич. систем, связанных с О. п.
К первому разделу относится теория сферич. функ-
функций (и, более общо, сферич. сечений), изучающая
конечномерные инвариантные относительно основной
группы пространства функций на О. п. (см. Представ-
Представляющая функция). Многие специальные функции ма~
тематич. физики интерпретируются как сферич. функ-
функции на том или ином О. п., и изучение представлений
основной группы в пространствах таких функций
позволяет единым образом получить основные резуль-
результаты теории специальных функций (интегральные
представления, рекуррентные формулы, теоремы сло-
сложения и т. п., см. [2]). Естественным обобщением
теории рядов и интегралов Фурье является гармони-
гармонический анализ абстрактный на О. п., одна из основных
задач к-рого состоит в описании разложения про-
пространства квадратично интегрируемых функций на
О. п. в сумму подпространств, неприводимых относи-
относительно действия основной группы. Большинство по-
полученных здесь результатов относится к случаю,
когда О. п. есть пространство полупростой группы
Ли (см. [4]).
Теория автоморфных функций приводит к более об-
общей задаче о разложении на неприводимые компоненты
пространства квадратично интегрируемых сечений од-
однородного векторного расслоения над О. п. G/H,
инвариантных относительно нек-рой дискретной под-
подгруппы Геб.
Кроме пространств функций, изучаются также и
различные пространства мер на О. п., напр, в связи
с приложениями в теории вероятностей (см. [3], [9]).
Ко второму разделу относятся вопросы описания
инвариантных дифференциальных операторов на О. п.,
изучение их свойств, нахождение спектра и фунда-
фундаментального решения, исследование решений соот-
соответствующих дифференциальных уравнений с част-
частными производными (см. [8], [15]).
К третьему разделу относится изучение различных
динамических систем, связанных с О. п., напр, потока,
порожденного однопараметрич. подгруппой основной
группы, потока, порожденного канонич. связностью
группы Ли, геодезического потока однородного рима-
нова пространства и т. п. Исследуются условия
эргодичности потоков, дается описание их первых
интегралов (см. [1]).
К анализу на О. п. примыкает также интегральная
геометрия, представляющая собой теорию инвариант-
инвариантных мер на О. п. и на связанных с ними многообразиях,
точками к-рых являются подмногообразия того или
иного типа.
Топология однородных пространств. Методы алгеб-
раич. топологии позволяют в широком классе случаев
свести задачу о вычислении основных топологич.
инвариантов О. п. (кольцо когомологий, характери-
стич. классы, ff-функтор, гомотопич. группы и т. д.)
к нек-рым алгебраич. задачам, связанным с алгебраич.
строением основной группы и группы изотропии О. п.
Для ряда классов О. п. получены явные результаты в
этом направлении. Напр., теорема А. Картана (Н. Car-
tan) дает алгоритм для вычисления алгебры вещест-
вещественных когомологий H*{GlH; R), где G и II — связ-
связные компактные группы Ли, в терминах инвариантов
групп Вейля для G и Н (см. [10]). В частности, если
GlH имеет ненулевую эйлерову характеристику (это
равносильно совпадению рангов групп G и //), то
многочлен Пуанкаре многообразия GlH имеет вид
где kt, . . ., kr и 1Ъ . . ., lr — степени базисных ин-
инвариантных многочленов групп Вейля для G и II со-
соответственно (формула Хирша).
Наиболее детально изучено топологич. строение
О. п. компактных групп Ли, симметрич. пространств
и солвмногообразий (однородных пространств раз-
разрешимых группы Ли). Теорема М остова —
Карпелевича, утверждающая, что любое О. п.
группы Ли, имеющее конечную фундаментальную
группу, диффеоморфно векторному расслоению над
О. п. компактной группы Ли, в значительной мере
сводит изучение топологии О. п. к случаю, когда основ-
основная группа компактна.
Классификация однородных пространств. Основные
задачи этого направления состоят в определении тех
многообразий, к-рые являются О. п. связных групп
Ли, и в перечислении всех транзитивных действий
связных групп Ли на этих многообразиях. Напр.,
единственными О. п. размерности 2 являются пло-
плоскость, цилиндр, сфера, тор, лист Мёбиуса, проектив-
проективная плоскость и бутылка Клейна. К настоящему време-
времени A982) проведена также классификация всех трех-
трехмерных О. п. и (с точностью до конечнолистных накры-
накрытий) всех компактных О. п. размерностей <:6 (см. [11]).
Для ряда важных классов О. п. М высших размер-
размерностей известна классификация всех транзитивных
действий групп Ли на М (см. [12]). Напр., классифи-
классификация всех транзитивных действий компактных групп
Ли на сферах выглядит следующим образом. Любое
непрерывное транзитивное и эффективное действие
связной компактной группы Ли на S" переводится
нек-рым гомеоморфизмом сферы S" в стандартное
линейное действие группы SO(n+l) или одной из
следующих ее подгрупп:
G=SU(/c) или U (к), если п = 2к — 1;
G = Sp(/t), Sp(/c)X*7(l) или Sp (fc)XSp(l),
если n = ik — 1;
G = Spin G) или Spin (9), если п = 7,15;
G = Giy если п = 6
(теорема Монтгомери — Самельсон а —
Б о р е л я, см. [10]). Что касается транзитивных дей-
действий некомпактных групп Ли на сфере S", то для
четного п единственными такими действиями по су-
существу являются проективное действие группы SL (и+1)
и конформное действие группы SOA, n+1). Для
нечетного п результат выглядит сложнее: здесь могут
существовать транзитивные и эффективные действия
групп Ли с радикалом сколь угодно большой размер-
размерности.
Лит.: [1] Ауслендер Л., Грин Л., Хан Ф-, По-
Потоки на однородных пространствах, пер. с англ., М., 196В; [2]
Вилевкин Н. Я., Специальные функции и теория пред-
представлений групп, М., 1965; [3]Гренандер У., Вероятности
на алгебраических структурах, пер. с англ., М., 1965; [41 Ж е-
лобенко Д. П., Гармонический анализ на полупростых
комплексных группах Ли, М., 1974; [5] К а р т а н Э., Геомет-
Геометрия групп Ли и симметрические пространства, пер. с франц.,
М., 1949; [6] е г о же, Теория конечных непрерывных групп и
дифференциальная геометрия, изложенные методом подвижного
репера, пер. с франц., М., 1963; [7] К и р и л л о в А. А., Эле-
Элементы теории представлений, 2 изд., М., 1978; [8] X е л г а-
сон С, Дифференциальная геометрия и симметрические про-
пространства, пер. с англ., М., 1964; [9] X е н н а н Э., Представле-
Представления групп и прикладная теория вероятностей, пер. с англ., М.,
1970; [10] Б о р е л ь А., в кн.: Расслоенные пространства и их
приложения, М., 1958; [11] Горба цевич В. В., в сб.:
Геометрические методы в задачах алгебры и анализа, Яро-
Ярославль, 1980, с. 37—60; [12] О нищи к А. Л., «Матем. сб.»,
1963, т. 60, Кч 4, с. 447—85; 1968, т. 75, MS 2, с. 255—63; [13]
Итоги науки. Алгебра. Топология, 1963, М., 1964; [14] Итоги
науки и техники. Алгебра. Топология. Геометрия, т. 11, М.,1974;
[15] Helgason S., Analisis on Lie groups and homogeneous
spaces, Providence, 1972; [16] Jensen G., Higher order con-
contact ot submanifolds of homogeneous spaces, B.-[u. a.], 1977; [17]
Кобаяси Ш., Номидзу К., Основы дифференциальной
геометрии, пер. с англ., т. 2, М., 1981; [18] Wolf J. А.,
Spaces of constant curvature, N. У., 1967. Д. В. Алепсеевспий.
ОДНОРОДНОЕ ПРОСТРАНСТВО АЛГЕБРАИЧЕ-
АЛГЕБРАИЧЕСКОЙ ГРУППЫ — алгебраическое многообразие
М вместе с заданным на нем регулярным и транзи-
транзитивным действием алгебраич. группы G. Если х?М,
то изотропии группа Gx замкнута в G. Обратно, если
Я — замкнутая подгруппа нек-рой алгебраич. группы
G, то на множестве левых смежных классов GlH су-
существует структура алгебраич. многообразия, превра-
превращающая его в О. п. а. г. б, причем естественное ото-
отображение я: G —>- GlН регулярно, сепарабельно и
обладает следующим универсальным свойством: для
любого морфизма <р: G—^X, постоянного на смежных
классах, существует такой морфизм <р: GlH —»- X, что
г|)я=ф. Если М — любое О. п. a. r. G и H=GX для
какого-либо х?М, то естественное биективное отобра-
отображение г|): GlH -> М регулярно, а если основное по-
поле К имеет характеристику 0, то г|з бирегулярно (см.
[1], [3]).
Пусть связная группа G, однородное пространство М
и действие группы G на М определены над нек-рым
подполем каК. Тогда группа ^-рациональных точек
G (к) переводит М (к) в себя и G (k)x= Gx (к) для х ? М (к).
Если к конечно, то М{к)Фф, а если при этом подгруп-
подгруппа изотропии Gx связна, то G(k) транзитивно действу-
действует на М(к). В общем случае изучение ^-рациональных
точек в М сводится к задачам теории Галуа когомологий
(см. [2]).
О. п. а. г. G всегда является гладким квазипроек-
квазипроективным многообразием (см. [5]). Если G — аффинная
алгебраич. группа, то многообразие GlH проективно
тогда и только тогда, когда Н — параболическая под-
подгруппа в G (см. [3]). Если G редуктивна, то многооб-
многообразие GlH аффинно тогда и только тогда, когда под-
подгруппа Н редуктивна (см. Мацусимы критерий).
Известно также описание замкнутых подгрупп Н
линейной алгебраич. группы G над алгебраически
замкнутым полем характеристики 0, для к-рых GlH
квазиаффинно (см. [4], [6]).
Лит.: ШБорень А., Линейные алгебраические группы,
пер. с англ., М., 1972; [2] С е р р Ж.-П., Когомологий Галуа, пер.
с франц., М., 1968; [3] Хамфри Д т.. Линейные алгебраи-
ческие группы, пер. с англ., М., 1980; [4] С у хан о в А. А.,
«Успехи матем. наук», 1978, т. 33, в. 2, с. 182—83; [5] С h о w W.,
в кн.: Algebraic geometry and topology. Symp. in Honour of S.
Lefschetz, Princeton, 1957,p. 122—28; [61 Hochschild G. P.,
Basic theory of algebraic groups and Lie alg-ebras, N. Y.—
Hdld.— В., 1981. А. Л. Онищик.
ОДНОРОДНЫЕ КООРДИНАТЫ — координаты, об-
обладающие тем свойством, что определяемый ими объ-
объект не меняется при умножении всех координат на
одно и то же число. Таковы, напр., проективные коор-
координаты, плюккеровы координаты, пентасферические
координаты. Д. Д. Соколов.
ОДНОРОДНЫЙ ВЫПУКЛЫЙ КОНУС — открытый
строго выпуклый конус V в векторном пространстве
R", однородный относительно группы линейных пре-
преобразований <x?GLn(IR) таких, что aV=V (автомор-
(автоморфизмов конуса V). О. в. к. \>\ и У.г наз. изоморфными,
если существует изоморфизм объемлющих векторных
пространств, переводящий Fj в V2.
Примеры. 1) Шаровой конус
Группа автоморфизмов конуса Кп есть прямое произ-
произведение подгруппы индекса 2 группы Лоренца Оп_ t(R)
(изоморфной группе движений я-мерного пространства
Лобачевского) и группы R+ гомотетий с положитель-
положительными коэффициентами.
2) Конус Рп(Щ положительно определенных сим-
симметрических действительных матриц порядка п. Группа
автоморфизмов этого конуса состоит из преобразо-
преобразований вида
3) Конус Рп{С) положительно определенных эрми-
эрмитовых комплексных матриц порядка п.
4) Конус Рп(Н) положительно определенных эр-
эрмитовых кватернионных матриц порядка п.
Выпуклый конус V, сопряженный О. в. к. V (т. е.
конус в сопряженном пространстве, состоящий из всех
линейных форм, положительных на V), также одно-
однороден. О. в. к. V наз. самосопряженным,
если в объемлющем векторном пространстве R" су-
существует такая евклидова метрика, что V=V' при
отождествлении пространства R" со своим сопряжен-
сопряженным с помощью этой метрики. Все приведенные выше
О. в. к. являются самосопряженными.
Классификация самосопряженных О. в. к. основана
на их связи с компактными йордановыми алгебрами
(см, [11, [21). Действительная йорданова алгебра А
наз. компактной, если ТгГ(аJ>0 для любого
а?А, афО, где Т(а) — оператор умножения на а в
алгебре А. Комплексификация устанавливает взаимно
однозначное соответствие между классами изоморф-
изоморфных компактных йордановых алгебр и классами изо-
изоморфных полупростых комплексных йордановых ал-
алгебр. Множество квадратов обратимых элементов ком-
компактной йордановой алгебры является самосопряжен-
самосопряженным О. в. к., и все самосопряженные О. в. к. получа-
получаются таким способом. Отсюда выводится, что всякий
самосопряженный О. в. к. изоморфен прямому произ-
произведению конусов описанных выше четырех типов и
27-мерных конусов, связанных с особой простой йор-
йордановой алгеброй.
Произвольные О. в. к. могут быть представлены в
виде конуса положительно определенных эрмитовых
матриц в нек-рых обобщенных матричных алгебрах
[3]. Простейшим примером несамосопряженного О. в. к.
является 5-мерный конус положительно определенных
симметрических действительных матриц х=[хц\ 3-го
порядка, удовлетворяющих условию ж2з=;Ез2=0. На-
Начиная с п=11 в R" имеется континуум неизоморфных
О. в. к.
Во всяком О. в. к. нек-рым канонич. образом может
быть определена полная риманова метрика, инвариант-
инвариантная относительно всех его автоморфизмов. Самосопря-
Самосопряженные О. в. к. характеризуются тем, что они явля-
являются симметрическими пространствами относительно
этой метрики. Стационарная подгруппа любой точки
О. в. к. является максимальной компактной подгруп-
подгруппой в группе его автоморфизмов. Стационарная под-
подгруппа единицы компактной йордановой алгебры А в
группе автоморфизмов О. в. к., ассоциированного с А,
совпадает с группой автоморфизмов алгебры А. Вся-
Всякий О. в. к. допускает просто транзитивную группу
автоморфизмов, приводящуюся в нек-ром базисе к
треугольному виду.
О. в. к. представляют особый интерес для теории
однородных ограниченных областей в связи с тем, что
указанные области реализуются в виде Зигеля обла-
областей, а для однородности области Зигеля 1-го или 2-го
рода необходимо, чтобы был однороден ассоцииро-
ассоциированный с ней выпуклый конус. О. в. к. и связанные
с ними области Зигеля являются естественными носи-
носителями нек-рых аналитич. конструкций, в частности
обобщения эйлеровых интегралов и гипергеометрич.
функций [8]. С каждым О. в. к. связывается многопа-
раметрич. группа интегралов Римана — Лиувилля,
включающая нек-рые гиперболические дифференциаль-
дифференциальные операторы (напр., в случае шарового конуса таким
образом получается волновой оператор). Для этих
операторов может иметь место усиленный принцип
Гюйгенса [9].
Исследование дискретных групп автоморфизмов са-
самосопряженных О. в. к. важно для компактификации
и разрешения особенностей локально симметрич. про-
пространств [4]. Многие результаты классич. теории при-
приведения, полученные для группы SLn(W1), действую-
действующей в конусе Pn(R), могут быть обобщены на произ-
произвольные самосопряженные О. в. к. (см. [5], [6]).
Лит.: [1] К о е с h е г М., «Math. Ann.», 1958, Bd 135, № 3,
S. 192—202; [2] Винберг Э. Б., «Докл. АН СССР», 1960,
т. 133, № 1, с. 9—12; [3] его же, «Тр. Моск. матем. об-ва»,
1963, т. 12, с. 303—58; 1965, т. 13, с. 56—83; [4] A s h А. [а. р.],
Smoth compactifications of locally symmetric varieties, Brookline,
1975; [5] H e 1 w i g K.-H., «Math. Z.», 1966, Bd 91, S. 152—78,
355—62; [6] Ash A., «Canad. J. Math.», 1977, v. 29, №5,
p. 1040 — 54; [7] R о t h a u s O. S., «Ann. Math.», 1966, v. 83,
№2, p. 358—76; [8] Гиндикин С. Г., «Успехи матем.
наук», 1964, т. 19, в. 4, с. 3—92; [9] В а й н б е р г Б. Р.,
Гиндикин С. Г., «Тр. Моск. матем. об-ва», 1967, т. 16,
с. 151—80. Э. Б. Винберг.
ОДНОРОДНЫЙ ОПЕРАТОР — отображение А век-
векторного пространства X в векторное пространство У
такое, что существует симметрическое полилинейное
отображение
В:ХХ...ХХ —>-У,
п раз
причем В(х, . . ., х)=А (х). Число п наз. степенью
О. о. А. Однородным оператором степени 1 (обычно
говорят, просто однородным) является линейный опе-
оператор L : X -> У. Вместо (х, . . ., х) пишут для сокра-
сокращения хп, понимая под этим элемент пространства
XX. . .XX, у к-рого все координаты равны, но не
степень элемента, к-рая в произвольном векторном
пространстве не определена. Если А есть О. о. степе-
степени и, то
A (tx) = tnA (x).
Более общо:
dnt + . . . +пь-п, л.> 0 "ll.-.n*! l
¦ ¦ ¦ lk a \x\ . • • ¦. xk )¦
В случае, когда X и У — векторные нормированные
пространства, непрерывность О. о. А эквивалентна
его ограниченности п из непрерывности А в нуле
следует непрерывность его на всем X.
Лит.: [1] Л ю с т е р н и к Л. А., Соболев В. И..Эле-
И..Элементы функционального анализа, 2 изд., М., 1965; [2] К а р-
т а н А., Дифференциальное исчисление. Дифференциальные-
формы, пер. с франц., М., 1971. В. И. Соболев.
ОДНОРЯДНОЕ КОЛЬЦО — кольцо, все неразложи-
неразложимые односторонние идеалы к-рого обладают единст-
единственным композиционным рядом и к-рое разлагается
в прямую сумму примарных колец. Отказ от послед-
последнего требования приводит к определению обоб-
обобщенно однорядного кольца, наз. также
рядным кольцом. Всякое обобщенно О. к.
является полуцепным как слева, так п справа (см.
Полуцепной модуль, Полуцепное кольцо). Всякий мо-
модуль над обобщенно О. к. разлагается в прямую сумму
циклич. подмодулей. Кольцо является обобщенно
однорядным тогда и только тогда, когда все левые
модули над ним полуцепные. Примером О. к. может'
служить кольцо верхних треугольных матриц над
телом. Л. А. Скорняков.
ОДНОСВЯЗНАЯ ГРУППА — топологическая группа
(группа Ли, в частности), топологич. пространство
к-рой односвязно. Значение О. г. в теории групп Ли
объясняется следующими теоремами:
1) всякая связная группа Ли G изоморфна фактор-
факторгруппе нек-рой О. г. (называемой универсаль-
универсальной накрывающей группы G) по диск-
дискретной центральной подгруппе, изоморфной яг(б);
2) две О. г. Ли изоморфны тогда и только тогда,,
когда изоморфны их алгебры Ли; более того, всякий
гомоморфизм алгебры Ли О. г. бх в алгебру Ли про-
произвольной группы Ли G2 является дифференциалом
(однозначно определенного) гомоморфизма G± в G2.
Центр Z односвязной полупростой компактной пли
комплексной группы Ли G конечен. Для различных
типов простых групп Ли он приведен в таблице:
1 ВС D D 1 Е Е Е F G<>-
Jlt + l ?j2 iki.
В теории алгебраических групп О. г. наз. связную
алгебраич. группу G, не допускающую нетривиальных
изогений ф: G -+ G, где G — также связная алгебрапч.
группа. Для полупростых алгебраич. групп над полем
комплексных чисел это определение равносильно дан-
данному выше. 9. Б. Винберг..
ОДНОСВЯЗНАЯ ОБЛАСТЬ линейно связ-
связного пространства — область D, в к-рой
все замкнутые пути гомотопны нулю или, иначе говоря,
фундаментальная группа к-рой тривиальна. Это оз-
означает, что любой замкнутый путь в D можно непре-
непрерывно деформировать в точку, оставаясь все время в.
О. о. D. Граница О. о. D, вообще говоря, может со-
состоять из любого числа к, 0 <:&<:<», связных компо-
компонент, даже в случае О. о. евклидовых пространств
Rn, njs2, или Ст, mjsl. Граница конечной плоской
О. о. состоит из одной связной компоненты; все пло-
плоские О. о. гомеоморфны между собой.
См. также Граничные элементы. Е- Д. Соломенце».
ОДНОСТОРОННИЕ И ДВУСТОРОННИЕ ПОВЕРХ-
ПОВЕРХНОСТИ — два типа поверхностей, различающихся no-
способу их расположения в объемлющем пространстве
(одностороннее расположение и
двустороннее расположение). Напр. г
цилиндр представляет собой двустороннюю поверх-
поверхность (д. п.), а Мёбиуса лист — одностороннюю по-
поверхность (о. п.). Характерное отличие этих поверх-
поверхностей — граница цилиндра состоит из двух кривых,
а граница листа Мёбиуса — из одной кривой. Среди
замкнутых поверхностей двусторонней является сфера
и тор, а односторонней — Клейна поверхность. При-
Примерами двустороннего и одностороннего расположения
кривой могут служить вложения окружности в лист
Мёбиуса. Так, цикл а (см, рис.) является односторон-
односторонней кривой, а цикл Р — двусторонней (и вообще, любой
дезориентирующий путь лежит в поверхности одно-
односторонне).
Более точно О. и д. п.— два типа многообразий,
различающихся способом вложения их в объемлющее
пространство (на единицу большей размерности). Дву-
сторонность и односторонность связаны с ориентиру-
ориентируемостью и неориентируемостью (см. Ориентация),
но в отличие от последних не являются внутренними
свойствами поверхности и зависят от объемлющего
пространства. Так, напр., существуют ориентируемые
д. п.: S2aS3, T2dR3; неориентируемые д. п.: RP2X
X0aRP2XSx; ориентируемые о. п.: T2=SXX S1dRP2X
XS1; неориентируемые о. п.: RP2aRP3 (здесь S2 —
сфера, Т2 — тор, RP2 — проективная плоскость,
RP3 — проективное пространство, S1 — дезориенти-
дезориентирующий путь на RP2).
В ориентируемом пространстве (напр., в R") ги-
гиперповерхность является ориентируемой в том и
только в том случае, когда она является д. п.
Пусть вдоль замкнутой кривой на гладкой поверх-
поверхности, погруженной в нек-рое пространство, обно-
обносится нормальный вектор так, чтобы он оставался
нормальным. Если при возвращении в исходную точку
направление нормали совпадает с исходным незави-
независимо от выбора кривой, то поверхность наз. двусто-
двусторонней; в противном случае (когда нормаль ока-
окажется противонаправленной исходной) — односто-
односторонней. Более общо, двусторонность расположения
поверхности П равносильна тривиальности ее нор-
нормального расслоения (в таком расслоении существует
ненулевое сечение). Наоборот, нормальное расслоение
о. п. нетривиально: существует кривая на П, над к-рой
расслоение является листом Мёбиуса.
Локально всякая (гипер)поверхность Мп~1 в про-
пространстве N" разбивает его на две части, т. е. для
точки х?Mn~1aNn имеется такая окрестность UaN,
что U состоит из двух компонент U' и U" и иГ\Мп~х
принадлежит пх общей границе. С другой стороны,
достаточно тесная окрестность М"~1 в N" (если М
замкнуто в N) имеет либо одну, либо две компоненты,
границы к-рых содержат М. В первом случае (гипер)
поверхность Мп~1 также наз. односторонней,
а во втором — двусторонней. Таким образом,
хотя поверхность локально и имеет две стороны,
глобально она может быть о. п. и в противоположность
д. п. не разбивать свою окрестность в пространстве.
Для д. п. М", лежащей в Nn + 1, пересечения индекс
в Nn + 1 для любой замкнутой кривой а на Мп удовле-
удовлетворяет равенству (а, М")=0 mod 2. Если же М"—
о. п., то (а, М")т=0 для нек-рой кривой а?М". Этот
факт также можно принять за определение одно- и
двусторонности (наряду с обносом нормального век-
вектора и разбиением окрестности).
Лит.: [1] Гильберт Д., Кон-Фоссен С, Нагляд-
Наглядная геометрия, пер. с нем., 3 изд., М., 1981; [2] 3 е й ф е р т Г.,
Трельфалль В., Топология, пер. с нем., М.—Л., 1938; [3]
Фукс Д. Б..Фоменко А. Т., Гутенмах«рВ.Л., Го-
Гомотопическая топология, 2 изд., [М., 1969]. М. И. Войцеховский.
ОДНОСТОРОННИЙ ПРЕДЕЛ — предел функции в
нек-рой точке справа или слева. Пусть / — отображе-
ние упорядоченного множества X (напр., множества,
лежащего на числовой прямой), рассматриваемого как
топологич. пространство с топологией, порожденной
отношением порядка, в топологич. пространство Y и
хо?Х. Предел отображения / по любому интервалу
(а, хо)={х: х? X а<х<х0} наз. пределом слева
отображения / и обозначают
lim / (х)
(он не зависит от выбора аО0), а предел по интервалу
(х0, Ь)= {х:х?Х хо<х<Ь} наз. пределом спра-
справа и обозначают
lim / (х)
х-*х„ + 0
(он не зависит от выбора 6>г0). Если точка х0 явля-
является предельной как слева, так и справа для множе-
множества определения функции /, то обычный предел
lim / (х)
*-»• х„
по проколотой окрестности точки хд (в этом случае его
наз. также двусторонним, в отличие от односторонних
пределов) существует тогда и только тогда, когда в
точке х0 существуют пределы слева и справа и они
равны между собой. л- Я- Кудрявцев.
ОДНОСТОРОННЯЯ ПРОИЗВОДНАЯ — обобщение
понятия производной, в к-рой обычный предел заме-
заменяется односторонним пределом. Если для функции
f(x) действительного переменного существует
,. f(x)-f(x0) ( /(*)-/ (.".
lim —та— I lim —пг~
то этот предел наз. правой (левой) произ-
производной функции f(x) в точке х0. В случае равенства
этих О. п. функция имеет в точке хй обычную произ-
производную. См. также Дифференциальное исчисление.
Г. П. Толстое.
ОДНОЧЛЕН — простейший вид алгебраич. выраже-
выражений — многочлен, состоящий из одного члена.
Как и многочлены (см. Многочленов кольцо), О. могут
рассматриваться не только над полем, но и над коль-
кольцом. О. над коммутативным кольцом А от множества
переменных {х,}, где i пробегает нек-рое множество
индексов /, наз. пара (a, v), где а?А, a v — отобра-
отображение из множества / в множество неотрицательных
целых чисел, причем v(i') = 0 для всех i кроме конечного
числа. О. принято записывать в виде
где гь . . ., г„ — все те индексы, для к-рых v(i)>0.
Число v(?) наз. степенью одночлена от-
относительно переменной г,-, а сумма
У. у(?)наз. полной степенью одночле-
н а. Элементы кольца можно рассматривать как О.
степени 0. Одночлен с а= 1 наз. примитивным.
Любой О. с а—0 отождествляется с элементом 0?А.
Множество О. над А от переменных {х,}, i?I, об-
образует коммутативную полугруппу с единицей. При
этом произведение О. (a, v) и F, и) определяется как
(ab, v+x).
Пусть В — нек-рая коммутативная Л»алгебра. Тог-
Тогда О. ахУ'-1^ . . .хУ^1") определяет отображение из В"
в В по формуле (blt ...,Ьп)—+ аЪ\ (Ч . .bvn <'">.
Иногда рассматривают О. от некоммутирующих пере-
переменных. Такие О. определяются как выражения вида
ахУ ^ .. .хУ «п\
где последовательность индексов in, . . ., in фиксиро-
фиксирована, причем не обязательно все эти индексы различны.
Лит.: [1] Л ен г С, Алгебра, пер. с англ., М., 1968.
Л. В. Кузьмин.