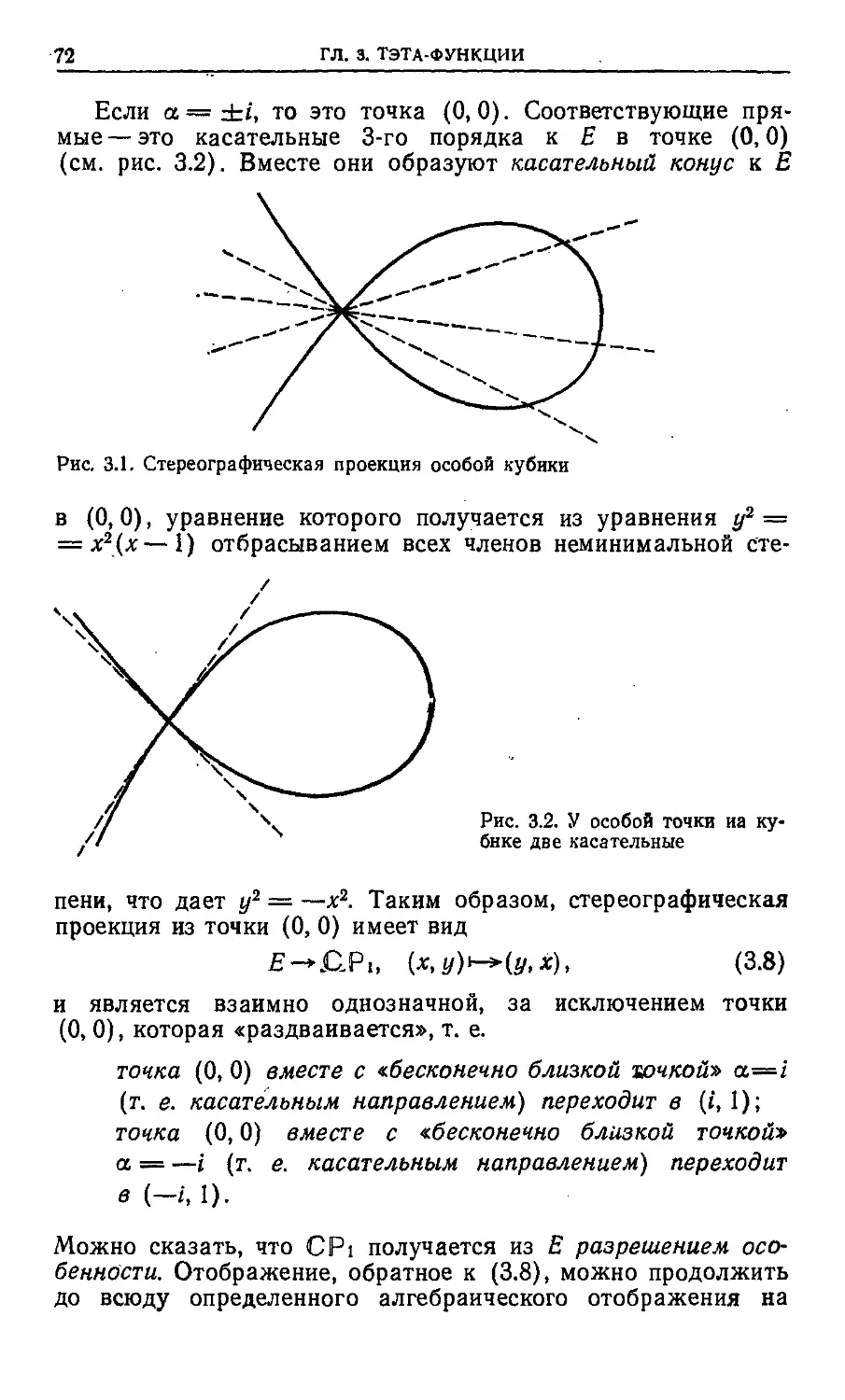
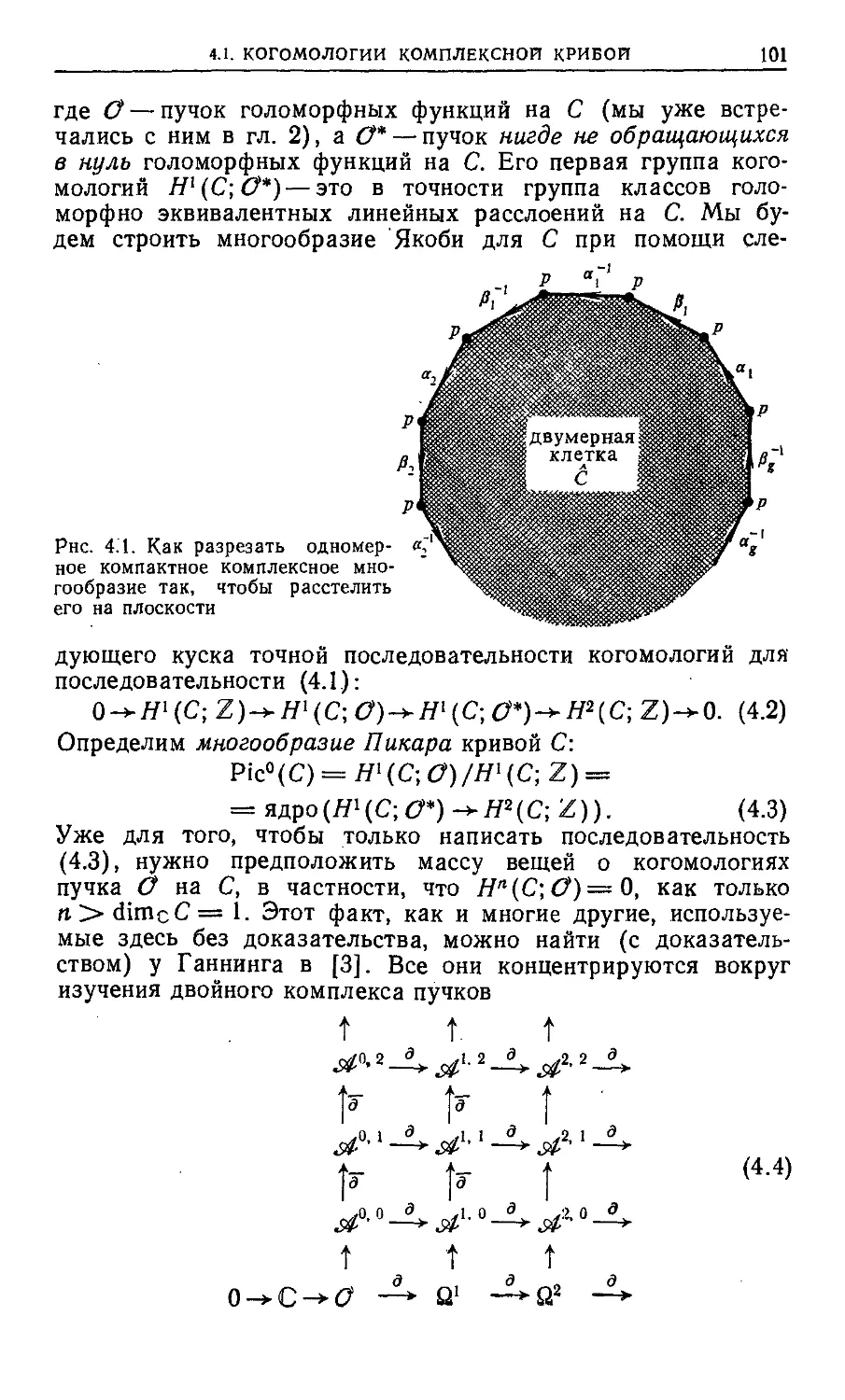
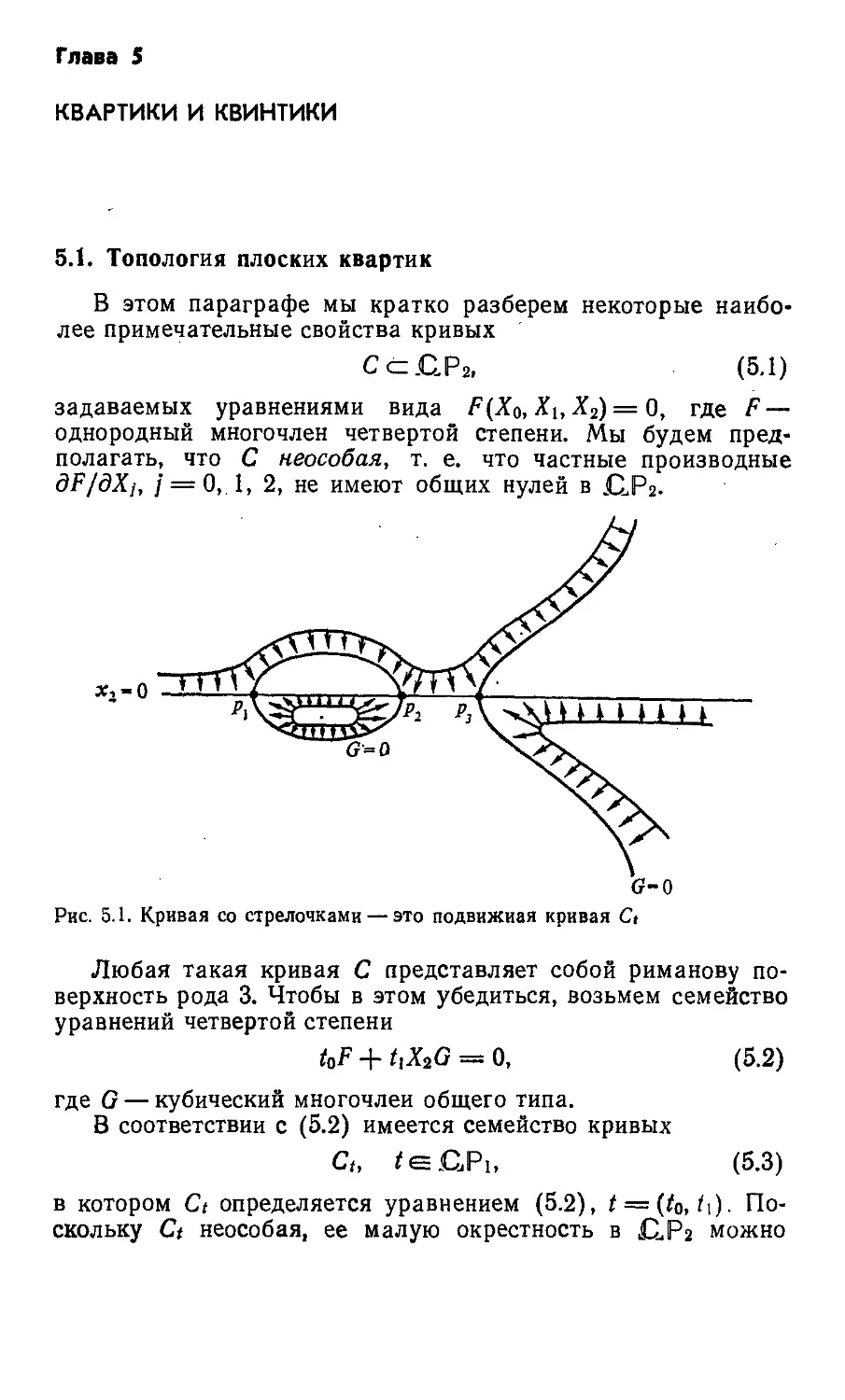
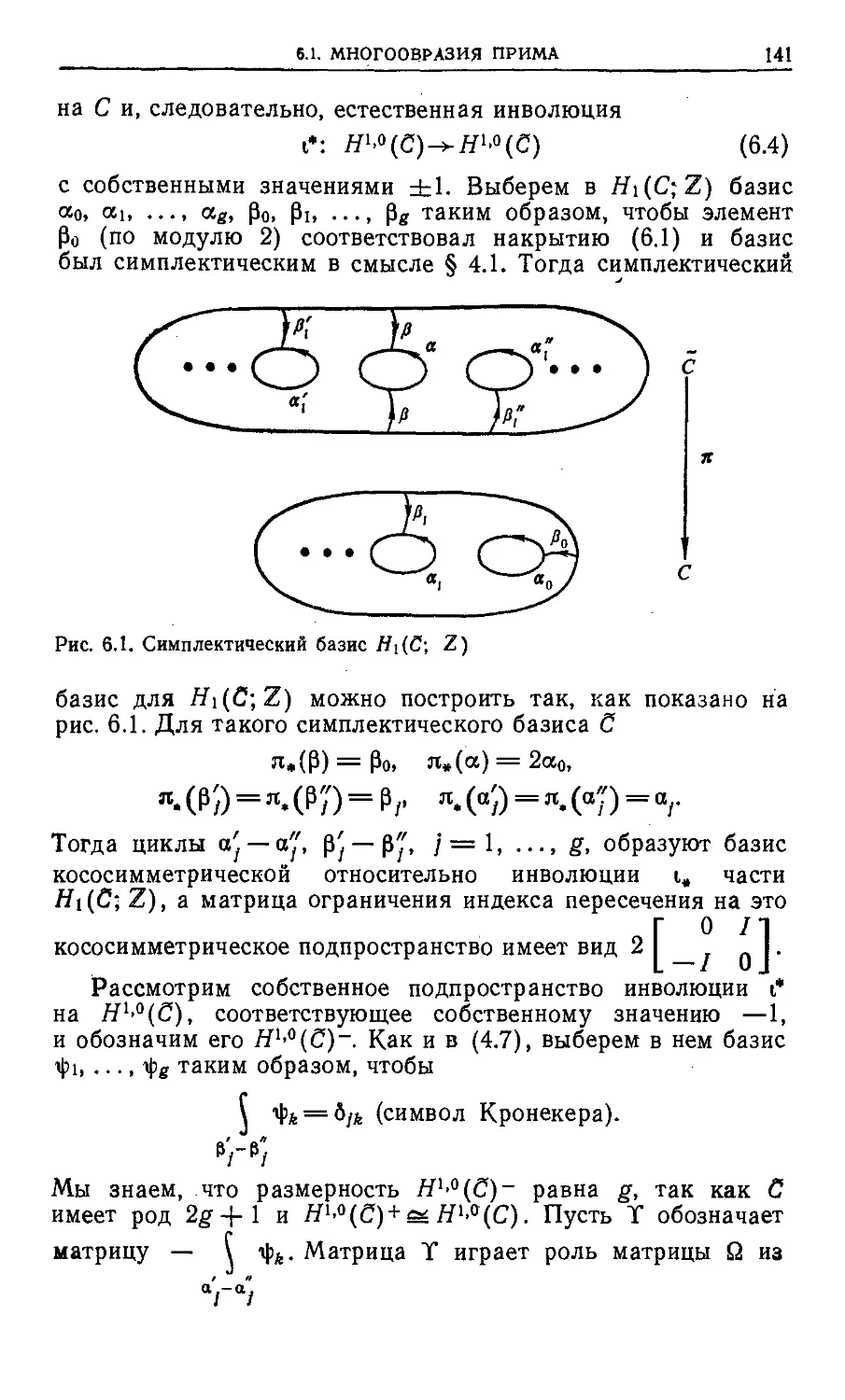
Текст
The University Series in
iVVatliematics
A SCRAPBOOK OF
COMPLEX CURVE THEORY
С HERBERT CLEMENS
University of Utah
Salt Lake City. Utali
Plenum Press ■ New York and London
1980
СОвРВКЕННАЯ МА1ЕМАТИКД
ВВОДНЫЕ КУРСЫ
Г. КЛЕМЕНС
МОЗАИКА
ТЕОРИИ
КОМПЛЕКСНЫХ
КРИВЫХ
Перевод с английского
И. В. АРТАМКИНА
под редакцией
А. Н. ТЮРИНА
МОСКВА «МИР»
1984
ВВК 22.14
К 48
УДК 518.6
Клеменс Г.
К 48 Мозаика теории комплексных кривых: Пер. с англ.—
М.: Мир, 1984. 160 с, ил.
Книга американского математика охватывает многочисленные
результаты теории алгебраических кривых. Это своеобразный синтез
дифференциальной геометрт, алгебры, комплексного анализа н теории чисел. Материал
изложен в серьезной н вместе с тем занимательной форме, что стимулирует
читателя обратиться к специальной литературе.
Для математиков различных специальностей, аспирантов и студентов
уииверептетов.
., 1702040000—444 ,. „. , ББК 22.14
'^ 041(00-84 '^-^^'■''' 517.8
Редакция литературы по математическим наукам
Герберт Клеменс
МОЗАИКА ТЕОРИИ КОМПЛЕКСНЫХ КРИВЫХ
Ст. научный редактор Н. И. Плужиикова. Мл. научный редактор И. В. Герасимова.
Художник А. В. Шипов. Художественный редактор В, И, Шаповалов. Технический
редактор Н. И. Манохина. Корректор В. И. Постиова.
ИБ № 3863
Сдано в набор 29.02.84. Подписано к печати 19.07.84. Формат бОХЭО'/и. Объем 5,00 б. л.
Бумага типографская № 2. Гарнитура литературная. Печать высокая. Усл. печ. л. 10,00.
Усл. кр.-отт. 10,25. Уч.-иад. л. 8,43. Изд. № 1/2912. Тираж 7000 экз. Зак. 107. Цена 85 коп.
ИЗДАТЕЛЬСТВО <МИР»
129820, ГСП, Москва, И-110, 1-й Рижский пер., 2.
Ленинградская типография Jft 2 головное предприятие ордена Трудового Красного
Знамени Ленинградского объединения <Техиическая книга» им. Евгении Соколовой
Союзполиграфпрома при Государственном комитете СССР по делам издательств,
полиграфии и книжной торговли. 198052. г. Ленинград, Л-52, Измайловский проспект, 29.
© 1980 Plenum Press, New York
(g) Перевод на русский язык, «Мир», 1984
ПРЕДИСЛОВИЕ РЕДАКТОРА
ПЕРЕВОДА
Книга Г. Клеменса — уникальная попытка провести
читателя через лабиринт результатов теории алгебраических
кривых, через колоссальное нагромождение полугоравековой
продукции лучших математиков — синтез дифференциальной
геометрии, алгебры, комплексного анализа и теории чисел.
Как ни странно, эта попытка автору удалась: отправляясь от
античной теории конических сечений, он выводит читателя
на передовой край математических исследований, которые
в последнее время привлекли внимание математиков своими
приложениями к трехмерной бирациональной геометрии
и физике.
Весьма необычно и подкупающе отношение автора книги
к читателю. Он как бы предлагает ему вместе пережить,
выразить и закрепить суть предмета, но и по праву требует от
него ответственного и упорного труда. Чтение и понимание
книги требуют неторопливости, внимания и активного
размышления. Геометрические образы очень трудно передаются
стандартными математическими текстами. Общепринятые
методы изложения приводят к многотомным трудам, в
которых нагромождение частностей в конце концов закрывает
горизонт. Впечатление неспециалиста по прочтении такого
текста точно выражает старинная формула: «начало мы
забыли, а конец не поняли, потому что забыли начало». Можно
с уверенностью сказать, что начало этой книги — ее первую
и вторую главы — прочитавший не забудет никогда!
Своеобразие книги заключается в том, что автор
пересыпает изложение загадками — прием, не обычный для
взрослой литературы. Например, при доказательстве
ассоциативности сложения точек на эллиптической кривой (см. рис. 2.6)
читатель должен сам догадаться, что обозначают символы
qr, p{q + r), и т. д. Конечно, в этом случае конфигурация
хитроумного Тэйта (рис. 2.6) подсказывает ответ, но тем не
менее пассивно мыслящий человек с полным правом может
утверждать, что «доказательство отсутствует». Мы не
приводим отгадок и не комментируем их, ибо цель автора
книги — не наполнение памяти читателя [не повторение
понятого] и не техническое упражнение его мысли, а попытка
с первых же шагов выработать у него силу самостоятельного
суждения и умение ориентироваться в еще не исследованном
в ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
И неизвестном. Поэтому, когда какое-то место в книге
непонятно, нужно остановиться и попытаться самому его
истолковать или доказать (как, например, утверждения о делимости
перед формулой (3.7)), а если это не удалось, то обсудить
его с товарищами; если же и этого мало, то нужно обратиться
к специалисту.
Следует твердо помнить, что каждое понятие, вычисление
или факт в теории кривых произвольного рода имеет точный
аналог для случая эллиптической кривой, поэтому ядро
книги — главы 2 и 3 — необходимо понять так, чтобы при
последующем обобщении эллиптические прообразы угадыт
вались.
В заключение заметим, что недавно классическая
проблема Шоттки была наконец решена Игусой (Igusa I. On the
irreducibility of Schottky's divisor. — J. Fac. Science Tokyo
28 (1983), p. 531-545).
A. H. Тюрин
ПРЕДИСЛОВИЕ
Эта книга — записки «впечатлений» о путешествии по
теории комплексных алгебраических кривых. Не следует искать
в ней ни замкнутости, ни целостности, ни особенной строгости
изложения. Как и в любых путевых заметках, взгляду
читателя предстает в основном то, что более всего поразило
воображение автора. Некоторые темы появляется лишь
вследствие своей неотразимой внутренней прелести. Другие, при
всей их важности, вовсе опущены, так как путешественник
счел их скучными или не отдал им должное просто потому,
что оказался слишком ленив или бестолков.
Оглядываясь назад в конце пути, видишь, как это часто
бывает, что из нагромождения впечатлений вырисовывается
главная тема путешествия. Здесь это теория тэта-функций.
На самом деле значительная часть изложенного в этой книге
представляет собой подготовку к изучению заключительной
темы — так называемой проблемы Шоттки. Не раз нам
придется скрепя сердце отрываться от увлекательных сюжетов,
которые могут увести нас в сторону, и возвращаться на
основной маршрут.
Многие наши наблюдения совершенно элементарны. Так,
мы начинаем с прогулок и размышлений в окрестностях
школьной алгебры. Потом вдруг мы без всякого
предупреждения неожиданно ныряем в самую глубину. При этом мы
стараемся обращаться с некоторыми весьма серьезными
и глубокими понятиями так, как с ними стал бы обращаться
всякий новичок, используя все средства подряд — доступные
или те, до которых можно хотя бы «дотянуться». Временами
мы не предполагаем никаких дополнительных знаний и
делаем все подробно, иногда же привлекаем кое-что из
современной «тяжелой артиллерии». Мы надеемся побудить
читателя к дальнейшему изучению предмета или, еще лучше,
к беседам со знающими людьми. Короче говоря, мы
стремились стимулировать математическую активность читателей,
а не познакомить их с какими-то законченными результатами,
и наш подход скорее романтический, чем строгий.
Излагаемый здесь материал был впервые собран воедино
для курса лекций в летней школе, устроенной итальянским
Национальным исследовательским советом в Кортоне,
Италия, в 1976 г. Этот материал происходит из стольких
ПРЕДИСЛОВИЕ
различных источников, что перечислить их все вряд ли
возможно. Исследование вещественных двумерных геометрий
постоянной кривизны взято из классического труда Картана
по римановой геометрии; несколько мест, касающихся
арифметики алгебраических кривых, заимствовано из чудесной
книги Серра «Курс арифметики»; приведенный во второй
главе замечательный результат Манина о рациональных
точках на эллиптических кривых автору объяснил А. Бовилль;
некоторые тождества с тэта-функциями взяты из известного
учебника по анализу Уиттекера и Ватсона; построение
пространства модулей второй ступени для эллиптических
кривых вызвано подходом Дэвида Мамфорда к пространствам
модулей кривых заданного рода. Обсуждение многообразия
Якоби в четвертой главе существенно основывается на работе
Джозефа Левиттеса, а изучение проблемы Шоттки опирается
на работы Акколы, Фаркаша, Игусы и Рауха. Но, пожалуй,
более всего автор обязан Филлипу Гриффитсу, научившему
его любить эту науку.
Автор хотел бы поблагодарить сотрудников
математического факультета Университета штата Юта Сильвию М.
Моррис, подготовившую рукопись к печати, и Тони У. Байкера,
выполнившего рисунки.
ОБОЗНАЧЕНИЯ
Большинство используемых в этой книге обозначений
вполне стандартны, например
Z = кольцо целых чисел,
Q = поле рациональных чисел,
R = поле вещественных чисел,
С = поле комплексных чисел.
Каждая из шести глав подразделяется на параграфы;
например, в гл. 3 имеются параграфы 3.1, 3.2 и т. д. Внутри
каждой главы принята сквозная нумерация формул: (3.1),
(3.2) и т. д. То же относится и к рисункам.
Квадратные скобки используются для обозначения
матриц, а также тэта-функций с характеристиками, например
е[;](ы; т).
В случае сложных показателей для экспоненты
используется символ ехр в соответствии с соглашением ехр{л;} = е-*.
Глава 1
КОНИКИ
1.1. Тени гиперболы
Кривые, с которых мы начнем эту книгу, знакомы всем
еще со школы. Попробуем, тем не менее, работать с ними
так, как будто мы встретили их впервые. Столь элементарное
начало поможет нам выработать правильный тон, который
мы постараемся сохранить и для гораздо более трудных тем.
Всякому математику еще в студенческие годы, конечно,
приходилось изучать множество решений уравнения
Ax^ + Bxy + Cy^ + Dx + Ey + F = 6, (1.1)
где А, В, С, D, Е я F — заданные константы. Если эти
константы вещественны, множество решений уравнения (1.1) на
вещественной плоскости R X R может представлять собой:
эллипс, пару параллельных точку,
прямых,
гиперболу, пару пересекающихся пустое ,. „,
прямых, множество,
параболу, одну «двойную» всю
прямую, плоскость.
Понятия эллипса, гиперболы и параболы можно объединить.
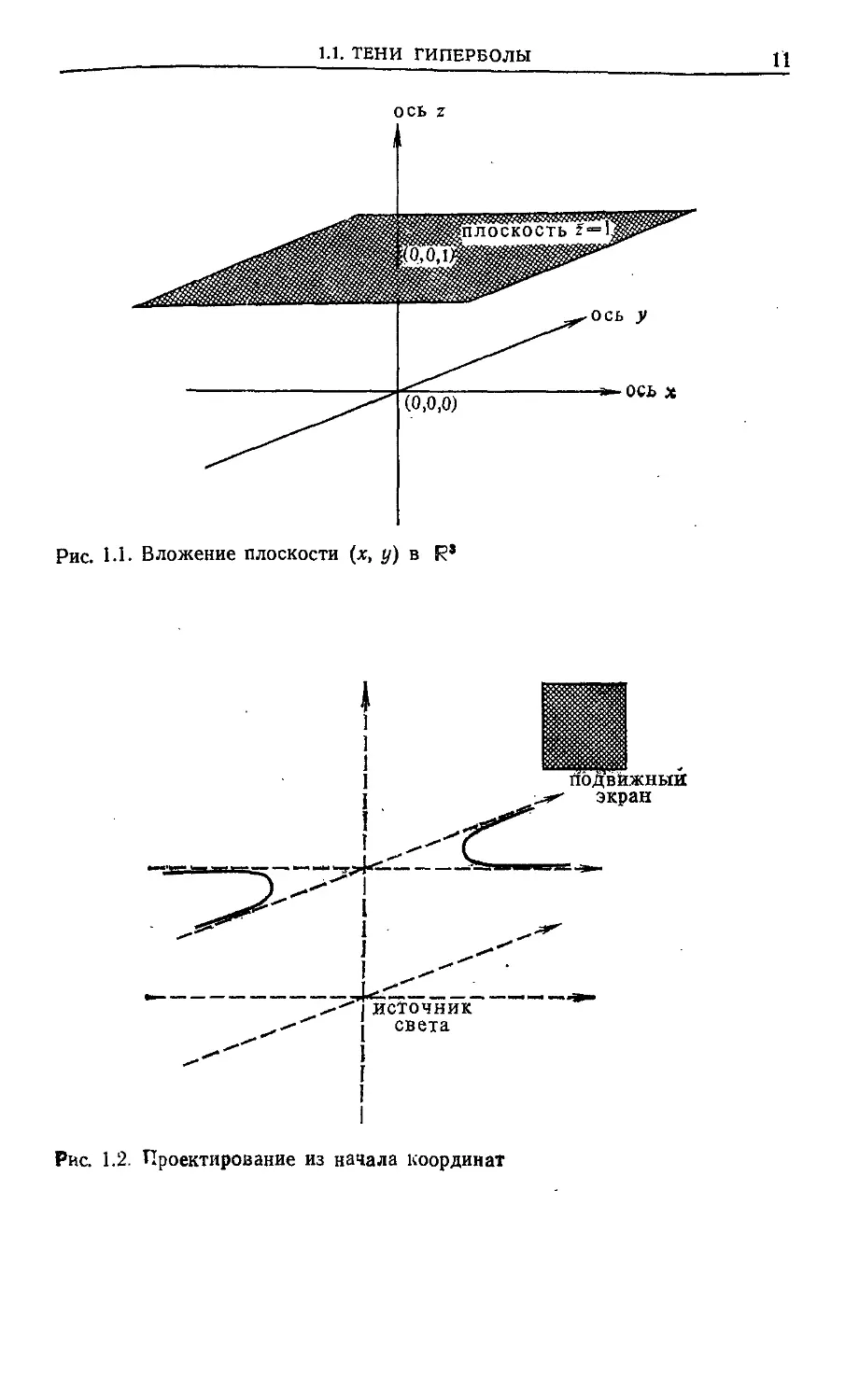
Для этого поместим плоскость {х, у) в трехмерное
пространство, рассматривая ее как множество точек {{x,y,z): 2=1}
в R^ (рис. 1.1). Возьмем, к примеру, гиперболу
ху=1 2=1 (1.3)
и поместим источник света в точку (0,0,0) (рис. 1.2). Чтобы
наблюдать тень от нашей гиперболы, возьмем подвижную
плоскость, которую назовем экраном, и будем располагать
ее в пространстве различными способами. На ней получатся
тени, отбрасываемые гиперболой под разными углами. Если
экран лежит в плоскости 2 = 2, то тень будет просто
большей гиперболой, но если поместить экран в плоскость х = 2,
то вместо гиперболы мы увидим кусок параболы (рис. 1.3).
Проверим это вычислением. Любая точка тени на экране
X = 2 должна лежать на прямой, проходящей через точку
1.1. ТЕНИ ГИПЕРБОЛЫ
11
ifc-OCb X
Рис. 1.1. Вложение плоскости (д;, у) в R'
Z^-
юдвижныи
экран
J
.4^<Г-
■^ I источник
j света
1
f
Рис. 1.2. Проектирование из начала координат
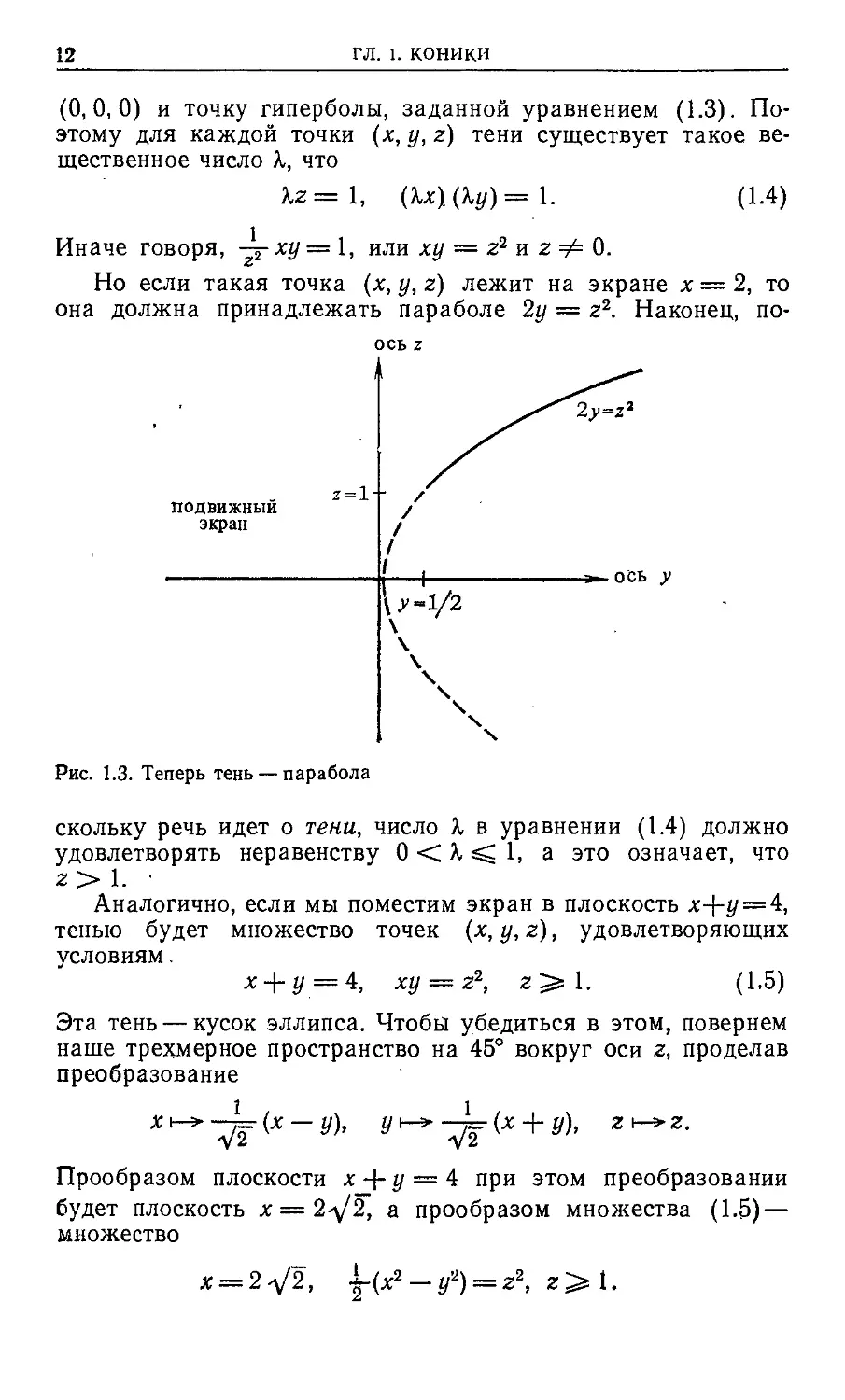
12
ГЛ. 1. коники
(0,0,0) и точку гиперболы, заданной уравнением (1.3).
Поэтому для каждой точки {х, у, z) тени существует такое
вещественное число к, что
Xz=l, {Хх).{Ху)=1. (1.4)
Иначе говоря, ■^ху = 1, или ху ^= z^ и гф 0.
Но если такая точка {х, у, z) лежит на экране х = 2, то
она должна принадлежать параболе 2г/ = z^. Наконец, по-
*-ось у
Рис. 1.3. Теперь тень — парабола
скольку речь идет о тени, число X в уравнении (1.4) должно
удовлетворять неравенству О < Я. ^ 1, а это означает, что
2>1. ■
Аналогично, если мы поместим экран в плоскость х-\-у=А,
тенью будет множество точек {х, у, z), удовлетворяющих
условиям.
х -f г/ = 4, ху = z^,
1.
(1.5)
Эта тень — кусок эллипса. Чтобы убедиться в этом, повернем
наше трехмерное пространство на 45° вокруг оси z, проделав
преобразование
:^(^-у),
V2
=-(х + у),
■Z.
прообразом плоскости х -^ у = А при этом преобразовании
будет плоскость х = 2-у'2, а прообразом множества (1.5) —
множество
2V2, M-y') = z\ z>l.
1.2. ВЕЩЕСТВЕННОЕ ПРОЕКТИВНОЕ ПРОСТРАНСТВО
13
•-ОСЬ у
Рис. 1.4. А теперь получилась эллиптическая тень
Иными словами, в нашем «повернутом мире» ваша
повернутая гипербола отбрасывает на наш повернутый экран
(л; = 2-\/2) тень
Таким образом, тень является частью эллипса (рис. 1.4).
1.2. Вещественное проективное пространство —
«Упроститель Классификаций»
Теперь, по-видимому, уже ясно, что нам будет легче
разобраться в поведении различных проекций нашего множества
решений на подвижный экран, если мы отвлечемся от
«излишних» физических свойств нашей модели.
В частности, нам будет легче уловить суть дела, если мы
будем считать, что «тень» состоит из всех точек пересечения
конуса решений л;г/ = z^ с подвижным экраном
ах -f йг/ -f CZ -1- d = 0.
Действительно, поскольку ход наших рассуждений
подсказывает не делать различия между двумя множествами решений,
если
(a) они являются сечениями одного и того же конуса и
(b) исходный конус может быть по ним восстановлен,
то можно вообще не проводить никаких сечений, а заняться
самими конусами. Другими словами, вместо множества
решений уравнения (1.1) в R^ мы будем рассматривать
множество решений однородного уравнения
Ах^ + Вху + Су^ + Dxz + Eyz + Fz^ — Q
(1.6)
14
ГЛ. 1. коники
в R^. Записанное в (симметрической) матричной форме это
уравнение имеет вид
А S/2 D/2-1
S/2 С EI2
.D/2 Е/2 F
[х у Z]
X -\
У
Z
= 0,
или просто
v.M-*v = 0,
(1.7)
где v^{x,y,z) — вектор в R^, а М — симметрическая 3X3-
матрица.
Предположим теперь, что делается линейная замена
координат {х,у, z). Тогда R^ отображается на себя при помощи
преобразования
Х1-^(/11Х + /12У +/l3Z),
г/ Н-» (/21 х + /22i/ + /232), (1.8)
Z1-» (/31J: -f l^y + /332),
где L^{lij)—обратимая ЗХЗ-матрица. Прообразом конуса
(1.7) при этом отображении является конус
u-('LAfL)-'u = 0.
Чтобы провести классификацию конусов в духе (1.2),
назовем два конуса эквивалентными, если какое-либо уравнение
одного из них получается из какого-либо уравнения другого
линейной заменой координат (1.8).
Положим теперь
(Ul,U2)= Ul-Af-'U2,
(1.9)
где Vi = {Xi, yi, Zi) e R^. Либо Л = В= ... ^f = 0, либо
существует такой вектор ui е R^, что {v\,V\)^ ±1. При
помощи линейной замены координат можно найти
эквивалентный конус, для которого Ui^ (1,0,0), а множество
векторов, «перпендикулярных» v\, т. е. {ueR^: {v,v\)=-Qi),
совпадает с плоскостью {y,z). Уравнение (1.7) для этого нового
конуса будет иметь вид
[х у z]
±1 0
0 с
0 £/2
0 -1
£•/2
F J
• X -
У
_z _
= 0.
(1.10)
и опять либо С = £ ^ F ^ О, либо в плоскости {у, z)
найдется такой вектор иг, что (иг, f2)=±l для конуса (1.10).
1.3. КОМПЛЕКСНОЕ ПРОЕКТИВНОЕ ПРОСТРАНСТВО
15
в результате еще одной замены координат получается
эквивалентный конус, уравнение которого имеет вид
[х у Z]
psi
0
Lo
0
Sj
0
0 -1
0
Бз-
- X
у
.Z
= 0,
(1.11)
где si ^ S2 ^ О, S2 ^ 8з и ы е {О, ±1}. Как видно из табл. А,
классификация конусов (1.2) значительно упростилась.
Таблица А
Описание
1 1
1 1
1 1
1 0
1 0
0 0
1
0
—1
0
-1
0
точка
прямая
«обычный» конус
двойная плоскость
пара пересекающихся плоскостей
1.3. Комплексное проективное пространство —
«Великий Упроститель»
Предположим теперь, что мы начали все сначала. Пусть
А, В, ..., FeC — комплексные числа, множество решений
лежит в С^ и т. д. Переходим опять к конусам, теперь уже
комплексным; к в уравнениях (1.4) становится комплексным
числом и т. д. Как и раньше, мы отождествляем конусы, если
их можно перевести друг в друга обратимым линейным
преобразованием пространства С^. Классификация,
подытоженная табл. В, теперь еще более упростилась (поскольку любое
уравнение второй степени имеет комплексные решения).
ei
1
1
1
0
в!
1
I
0
0 -
е»
1
0
0
0
Таблица В
Описание
«обычный» коиус
пара пересекающихся плоскостей
двойная плоскость
С»
le гл. 1. коники
Будем называть множество комплексных прямых,
проходящих через начало координат в С^,
комплексной проективной плоскостью
и обозначать ее .СРг- Можно представлять себе СРг просто
как обычную комплексную плоскость с добавлением
«идеальных точек» на бесконечности, по одной идеальной точке на
каждую прямую, проходящую через начало координат.
Соотношение между обычными (аффинными) координатами
{х, у) на плоскости С^ и (однородными) координатами
{x,y,z) в пространстве прямых, проходящих через начало
координат в .С.^, выглядит так: если аффинное множество
точек задается уравнением
S A;„„xV = 0, (1.12)
ТО проективное множество комплексных прямых задается
уравнением
S Лшп*'"г/''2(Л'-('»+«)) = 0. (1.13)
т, п ^ N
Мы можем свободно переходить от аффинного объекта к его
проективизации, которая определена, если только найдется
некоторое Лтп ф О при m-\-n^N. Тогда все элементы
(прямые) проективного объекта, кроме конечного числа (^Л^),
соответствуют элементам (точкам) аффинного объекта.
Обратно, мы переходим от проективного объекта (1.13) к
аффинному объекту (1.12), полагая z ^ 1, т. е. рассекая «конус»
(1.13) комплексной плоскостью z^l в С^ Далее будет
удобнее называть элементы С Рг «точками», а не «прямыми».
Посмотрим теперь на множество решений однородного
уравнения (1.6) в СРг. Прежде всего мы всегда
предполагаем, что среди чисел Л, S, ..., f найдутся не равные 0.
Заметим, кроме того, что при умножении этих шести чисел на
одно и то же ненулевое комплексное число множество
решений не изменяется. Поэтому множество «коник» в С.Р2> т. е.
множество решений уравнений вида (1.6), имеет не больше
пяти параметров; коника определяется прямой в C^
проходящей через О и (Л, S f).
1.4. Линейные системы коиик
Перейдем теперь к менее элементарному сюжету. Мы
хотим рассмотреть множество всех коник и поразмышлять
над некоторыми его геометрическими свойствами. Для этого
Н9М понадобится одно важное понятие из алгебры—та5{ на-
1.4. ЛИНЕЙНЫЕ СИСТЕМЫ КОНИК
17
зываемый результант двух многочленов. Это своего рода
средство, позволяющее узнать, когда два уравнения имеют общее
решение.
Предположим, что мы рассматриваем два однородных
полиномиальных уравнения
F(x, у, z)=Y, riix, y)z' = 0,
1-0
п
G {х, y,z)='Z Si {x, у) z^ = 0,
(1.14)
i-O
det
= 0.
где n и Si ^однородные многочлены от {x,y) степени (m — г)
и {п — г) соответственно. Согласно теории исключения (Ван
дер Варден [И], т. 1, с. 127—129')), при фиксированных
значениях х и г/ получающиеся полиномиальные уравнения
относительно z имеют общее решение тогда и только тогда,
когда
I'm ''m-l ••• ''о
''ш ''m-l • • • ''о
{п раз)
''ш ''ш-1 • • • ''о
Sn S„_i ... 5о
S„ S„_i ... So
{m раз)
Sn ^n-l • • • ^0
Это — однородное уравнение относительно {х,у) степени тп.
По теории исключения, если этот результант тождественно
равен О, то многочлены F и G (рассматриваемые как
элементы кольца многочленов от z с коэффициентами в поле
рациональных функций от {х,у)) имеют общий делитель. Из
леммы Гаусса (Ван дер Варден [И], т. 1, с. 116—118)
следует, что тогда они имеют общий делитель и в кольце
однородных многочленов от {x,y,z). Поэтому если два
однородных многочлена F и G степени 2 имеют одинаковое
множество решений, то
F='KG, Хф^.
Таким образом, множество «коник», т. е. множество
множеств решений уравнений вида (1.6), параметризуется пяти-
мерным комплексным проективным пространством (т. е. мно-
') Здесь и далее при ссылках на работы, переведенные на русский
язык, страницы указаны по русскому изданию,— Прим. ред.
18 гл. 1. коники
жеством всех комплексных прямых, проходящих через начало
координат в .С/) с однородными координатами
{A,B,C,D,E,F). (1.15)
Займемся теперь геометрией множества коник,
удовлетворяющих некоторым специальным условиям. Например,
множество коник, проходящих через точку (1,0,0), задается
уравнением
Л = 0,
так что эти коники образуют четырехмерное комплексное
проективное пространство. А что будет, если мы рассмотрим
коники, проходящие через две или более точек? Каждая
новая точка налагает новое линейное условие на (А, В, С, D,
E,F). Правда, надо еще проверить независимость этих
условий. Быть может, некоторые из них лишние? Легко
проверить, что при достаточно общем выборе точек каждая новая
точка налагает независимое условие, по крайней мере до тех
пор, пока через эти точки проходит хоть одна коника.
Приведем, однако, такое доказательство этого факта, которое
годилось бы для проективных плоскостей рРг над многими
полями F и для однородных форм различной степени.
Начнем с множества мономов
x'y'z", (1.16)
где (г -{- j -\- k) равняется некоторому фиксированному числу
Л'^. Если мы подставим у ^ х'', z = х^ при подходящих г и s,
то числа
i + jr -h ks и i' -j- j'r -j- k's
будут всегда различны для различных мономов x'yiz'' и
x^'yi'z^' вида (1.16). Вспоминая теорию определителя Ван-
дермонда (Ленг [5], с. 179), получаем, что если М =
= тах{г -f rj -{- sk: г -f- / -j- fe = Л/^}, то матрица
[(л;,)'+^/+^*], i + j + k = N, /=0 М,
имеет максимальный ранг, когда числа хо, ..., хм попарно
различны. Поэтому если положить г/,=х^, z^^x^, то из
(Af-fl) точек {xi, yi,zi)^СР2 можно выбрать такое
подмножество, равномощное множеству (1.16), что квадратная
матрица
[(Xj'z/^zf)], i -\- j-\- k^ N, I соответствуют подмножеству,
(1.17)
имеет ненулевой определитель. Применяя эти рассуждения
к множеству мономов х^, ху, у^, xz, yz, z^, получаем, что при
подходящем выборе шести точек в jQP? через них не npoxQ-
1.5. ЧУДЕСНЫЙ ШЕСТИУГОЛЬНИК id
дит НИ одна коника, а при подходящем выборе пяти точек
все они лежат на единственной конике. Более того,
поскольку условие того, что шесть точек лежат на конике, есть
полиномиальное условие обращения в нуль определителя
матрицы (1-17), множество шестерок точек, не лежащих на
конике, открыто и плотно в (СРг)^. Аналогично, множество
пятерок точек, которые определяют единственную конику,
открыто и плотно в (С.Рг)^-
1.5. Чудесный шестиугольник
С обсуждавшимися здесь фактами связаны прекрасные
образцы классической геометрии, например восходящая к
античности задача о проведении коники через пять заданных
Рис. 1.5. Точка Р вычерчивает конику, проходящую через точки А, В, С,
D. Е
точек. Наиболее изящное решение, вероятно, получается при
помощи «чудесного шестиугольника» Паскаля. Предположим,
что задано пять точек А, В, С, D, Е. Проделаем следующее
геометрическое построение (см. рис. 1.5):
• Проведем прямые АВ и DE и найдем их точку
пересечения Pi.
• Проведем произвольную прямую через точку А и
обозначим через Рг точку ее пересечения с прямой CD.
• Тогда, если Рг — точка пересечения прямой ВС с
прямой PiPi, точка Р пересечения прямых ЛРг и ЕРг будет
лежать на конике ABCDE. Это произойдет потому, что точки
пересечения противоположных сторон вписанного в конику
шестиугольника лежат на одной прямой.
Чтобы убедиться в правильности последнего предложения,
обозначим конику ABCDE через Q и рассмотрим следующие
три кубики (т. е. множества нулей однородных многочленов
20 ГЛ. 1. КОНИКИ
третьей степени от переменных {х, у, z)):
QUP1P2, ABUCDUEP, PA[jBC[jDE. (1.18)
Все три кубики содержат следующие восемь точек:
А, В, С, D, Е, Ри Р,, Рз. (i:i9)
Как мы уже видели, «в общем случае» следует ожидать, что
множество кубик, проходящих через восемь точек,
представляет собой .С.Рь т. е. множество однородных многочленов
степени 3 от переменных {x,y,z), обращающихся в нуль
в восьми точках общего положения, составляет двумерное
векторное пространство. Можно проверить, что если А, В, С,
D, Е выбраны так, что коника определена однозначно и не-
вырожденна (т. е. все Si=^0 в (1.11)), то восемь точек
(1.19) являются достаточно общими, и потому уравнения
трех кубик из (1.18) должны быть линейно зависимы
(см. Гриффите и Харрис [1], с. 514—516). Поэтому общее
решение любых двух из них будет и решением третьего.
Поскольку Р — общее решение двух последних уравнений, эта
точка принадлежит также и конике Q.
Кроме того, попутно мы коснулись еще одного важного
принципа, который следует напомнить, — теоремы Безу,
утверждающей, что если Ci — плоская кривая степени т
(множество нулей однородного многочлена степени m от
переменных (х, y,z)), а Сг — плоская кривая степени п, то либо
Ci и Сг содержат общую компоненту, либо они имеют не
более тп общих точек. Это ясно из вычисления результанта
системы уравнений (1.14). Результант является однородным
многочленом от {х, у) степени тп.
1.6. Двойное отношение
Другая интересная тема, возникающая при изучении
коник, связана с понятием двойного отношения. Мы введем его
таким же образом, как это понятие, скорее всего, и
появилось в математике впервые. Из рис. 1.6 и тождества sinp =
= sin (л — р) сразу видно, что (sina)//l = (sinP)/S. Из этих
двух равенств и рис. 1.7 следует, что
Л/fi sin a/sin р sin а
A'jB' ~ sin a'/sin р' ~ sin а' '
и, таким образом, получается отношение
АС/ВС _ sin g/sin (Р + у)
Ш/Ш ~ sin (а + P)/sin у
(см. рис. 1.8). Это выражение и называется двойным
отношением (Л, В, С, D) точек А, В, С, D; очевидно, что оно не
1,6, ДВОЙНОЕ ОТНОШЕНИЕ
21
меняется при движении прямой L. Это приводит нас к
утверждению (которое легко проверяется прямым вычислением).
Рис. 1.6. Теорема синусов
Рис. 1.7. Отношение синусов углов а и а', имеющих общую вершину
прямая ][,
Рис. 1.8. Двойное отношение
ЧТО если {x\,yi), {Х2,у2), {хз,уз),- (л;4, г/4) — четыре точки
СРь а
{х,у)^-^{ах + by, cx + dy). (1.201
I—линейное преобразование С}^д на себя, то выражение
(Х\Уз — У1Хз)1{Х}Уз — УзХз)
l(Xiyi — У\Х^)1{Х2У4 — УгХ*)
22
гл. 1. коники
коника
заданные
вершины
Рис. 1.9. Проектирование коники из различных точек
Рис. 1.10. Лучи, пересекающие окружность; первый вариант
Рис. 1.11. Лучи, пересекающие окружность; второй вариант
1.6. ДВОЙНОЕ ОТНОШЕНИЕ 23
является (ненулевым) инвариантом преобразований вида
(1.20). Оно, естественно, и называется двойным отношением
(Pi, Pi, J°3, J°4) точек Pi, где Pi^{Xi,yi). Заметим также, что
можно определить двойное отношение четырех точек на
конике, так как преобразование f пространства C.Pi,
показанное на рис. 1.9, линейно. Поскольку все невырожденные
коники эквивалентны, достаточно проверить последнее
утверждение в случае, когда коника задана в аффинных координатах
Рис. 1.12. Проектирование окружности на прямую из точек (а, 6) и
(а, -Ь)
уравнением х^ -^^у"^ = \, вершины {а,Ь) и {а,—Ь)
фиксированы, а .C.Pi совпадает с осью х, как на рис. 1.12. В этом
конкретном случае наше утверждение опять превращается
в красивый факт из геометрии на плоскости, который мы
сейчас рассмотрим.
Заметим сначала, что на рис. 1.10
2а -f Я. = л, 2р -j- jA = л, 2у -f V = л,
так что
а-ЬР-Ьу = л.
Отсюда следует, что треугольники ACS и DBS подобны
и, значит.
Таким образом, произведение SA-SB не зависит от прямой,
проходящей через S, так что треугольники SAC и SDB на
рис. 1.11 подобны, откуда а ^ б.
Предположим далее, что на рис. 1.11 мы устроили все
так, что 00 ± SC. Тогда а = б = s/2,
24 ГЛ. 1. коники
Теперь мы уже можем объяснить, почему отображение,
показанное на рис. 1.9, является линейным автоморфизмом
пространства £).Pi, т. е. преобразованием вида (1.20).
Рассмотрим рис. 1.12. Из предыдущего мы знаем, что б =
^(2а)/2^а, поэтому р ^ у ^ б + s. Значит, треугольники
ORB и OBS подобны, откуда следует, что
0R-6S = 0B^.
Эта формула и устанавливает линейность отображения f,
поскольку в частном случае, когда коника является единичной
окружностью, это отображение есть просто xt—^l/x.
1.7. Построение геометрий постоянной кривизны:
метод Кэли
Обратимся теперь к увлекательному постороннему
сюжету, связанному с кониками, но уводящему совсем в другую
сторону, к римановой геометрии. Риманова геометрия
возникла из попыток доказать независимость пятого постулата
Евклида, который утверждает, что через точку вне прямой
проходит единственная прямая, не пересекающая данную.
Однако в конце концов были построены двумерные
пространства, удовлетворяющие всем постулатам Евклида, кроме
пятого, причем их «геометрии» оказались однородными
в том смысле, что независимо от того, в какой точке
соответствующего двумерного пространства мы находимся, оно
выглядит одинаково. Английский математик Кэли нашел
замечательный способ изучать все эти геометрии сразу, причем
главными его орудиями были двойное отношение и теория
коник. В следующих пяти параграфах мы коротко
расскажем о высших достижениях теории Кэли. Отправной точкой
служит множество решений уравнения
л;2-f г/2-f 22 = 0. (1.21)
Эта коника в СРг называется абсолютом.
Пусть даны две точки на единичной сфере S:
Ри P,^S= {{x,y,z)eR^: х2 + г/2 + 22=1};
расстояние между ними на 5—это то же самое, что угол б
между прямыми OPi и ОР2, выраженный в радианах.
Положим Pi = {xi, yt, zi) и обозначим комплексную проективную
прямую
через L. Пусть {У?1,/?2} = L[\Q, где Q —стандартный конус
(1,21). Эти две точки R\ и У?? соответствуют значениям "кх
1.7. ПОСТРОЕНИЕ ГЕОМЕТРИЙ ПОСТОЯННОЙ КРИВИЗНЫ 26
И Ji-2 параметра X, являющимся корнями уравнения
{XI + ХХ2) '+(У1 + ХУ2) ^ + (21 + XZ2) 2 = о,
т. е. 1 + (cos б)2Ji, + Я^ = о, и по стандартным формулам для
решения квадратных уравнений получаем
Л] cos б ± (cos^ б — 1)^ COS б ± J sin б ^ gjs
Я,2 cos 6 Т (cos^ б — 1)^'^ сов б Т f sin б
С другой стороны, можно вычислить двойное отношение
{Ри Р2, /?1, ^?2) = W^2.
Таким образом, мы получаем прекрасную формулу для
расстояния на двумерной сфере S:
6 = ±-gj-log(Pi, Р2, Ru R2),
где /?1 и /?2 — две точки, в которых прямая, соединяющая Pi
и Р2, пересекает стандартную конику (1.21), т. е. абсолют.
Конечно, можно спроектировать половинку сферы 5 на
плоскость
x,y^R, 2=1 (1.22)
из центра. Это соответствие позволяет измерять расстояния
между точками на плоскости величиной угла между
соответствующими точками на S. Но поскольку двойное отношение
проективно инвариантно, можно вычислять это расстояние,
не выходя за аределы комплексной плоскости 2=1.
А именно, положим pi, p2^R^, и пусть ri и Г2 — две точки
пересечения комплексной прямой, проходящей через pi и р2,
с коникой
х^ + у' = -1 (1.23)
в С^. Тогда (сферическое) расстояние между pi и р2 задается
формулой
±-^log{pi, р2, г и Г2). (1.24)
Причина этого состоит в том, что двойное отношение
сохраняется при центральном проектировании. Из инвариантности
двойного отношения следует также, что это расстояние
сохраняется при вещественных преобразованиях пространства
С^ вида
йих + ацу + азз ' .
^ аг|Л: + аггУ + агз ' ■'
У ацх + аз2у + азз
26 Гл. I, КОНИКИ
(т. е. таких, что ai/sR), сохраняющих конику (1.23).
Конечно, это просто перефразировка условия ортогональности
матрицы [ац].
Заменим теперь сферу 5 поверхностью Sk, задаваемой
уравнением
K{x^+y') + z^ = l.
Предположим, что мы измеряем расстояние между двумя
точками {хи г/1, Zi) и (хг, г/2, ^г) на 5^ расстоянием между
точками {хи Уи K'^^^Zi) и (хг, г/2, K-^^^Z2) на сфере радиуса
/(■-1/2 Другими словами, если обозначить исходные точки
через Pi и Р2, то расстояние задается формулой
J (d/ -{-dy^+K~' dzy\ ■ (1.26)
где путь интегрирования проходит по пересечению Sk. с
плоскостью OPiPi. При центральном проектировании каждая
такая метрика индуцирует метрику на плоскости z = \.
Поскольку сфера радиуса К~^'^ становится при стремлении К
к нулю все более и более плоской, геометрически очевидно,
что метрика на плоскости 2=1 приближается при этом
к евклидовой. Как и раньше, имеем формулу для расстояния
dist(P„ Р2) = ^^Ьд((дг1, Уи К~"%), (х2, У2, К~"%1 Ri. R2),
где Ri и У?2 — точки пересечения комплексной прямой,
проходящей через точки {xi, у и K~^'^zi) и [х^, у 2, K'^^^z^) с
абсолютом x^ -j- г/^ -j- 2^ = 0.
Далее, корнями уравнения
(XI + %Х2) 2 + (г/1 + Яг/2) ^ + {K-"^zi + IK-^'^z^) 2 = 0
являются просто те Я, для которых Р\ + '^Pt лежит на
комплексном конусе К (х^-j-г/^)-j-2^ = 0. Следовательно, для
метрики, индуцированной на плоскости z = ] при помощи
центрального проектирования, получается формула
dist(p„ p2) = -^^^log(pi, Р2. ri. Гг). (1-27)
где Г\ и Г2 — точки пересечения прямой, проходящей через
Pi и р2, с коникой
А:(х^ + г/^)+1=0.
Поскольку метрика (1.27) индуцирована стандартной
метрикой на сфере радиуса К~^'^, она имеет постоянную
кривизну К.
1.8. В ЗАЗЕРКАЛЬЕ 27
1.8. В Зазеркалье
Мы видели, что сужение метрики (1.26) на Sk. ограничено
при стремлении /С к О, так что на самом деле можно
сделать К отрицательным, причем формула (1.26) будет по-
прежнему определять вполне хорошую метрику на Sk. (или
по крайней мере на верхнем листе гиперболоида, которым
теперь является Зщ). По «принципу аналитического
продолжения» естественно ожидать, что снова получилась метрика
постоянной кривизны К, а геодезическими являются
пересечения Sm с плоскостями, проходящими через 0. Это и на
окружность
радиусаУгС
Рис. 1.13. Гиперболическая геометрия в круге радиуса у — К
самом деле так. При центральном проектировании
индуцируется метрика на части плоскости 2=1, которая является
внутренностью круга
По тому же принципу аналитического продолжения метрика
по-прежнему задается формулой (1.27), где теперь все
четыре точки pi, pi, Ги Гг лежат в вещественной плоскости
2=1, как это видно на рис. 1.13. Далее, любое линейное
преобразование R^, переводящее S^ в себя, индуцирует изо-
метрию, поскольку оно сохраняет вещественную
симметрическую билинейную форму
K{x^ + y^) + z\ (1.28)
Для изучения группы преобразований, сохраняющих (1.28),
достаточно рассмотреть случаи К=\ и А'=—1, так как
единственной важной характеристикой вещественной
симметрической билинейной формы (1.28) является число поло-
28
гл. I. коники
жительных и отрицательных собственных значений. Случай
/С = 1 уже рассмотрен. В случае К = —1 эта группа изо-
метрий называется группой Лоренца ввиду ее важности для
теории относительности. Чтобы представить себе наглядно
ее действие, заметим, что она содержит все вращения вокруг
оси Z, а также преобразования, которые оставляют у на месте
и переводят
(1, у, 0)b^(Xi, у, Zi) , (О, у, l)l-»(X2, у, 22) ,
где
iCi { } """^ 1.) ^о "О '"*~~ i) ^ |"ч ЛI Л[^ __^ \j t
'Г2
"1^2 ■
Как все это выглядит на плоскости {x,z), показано на
рис. 1.14. Поскольку инволюция, меняющая местами оси х
Рис. 1.14. Действие преобразования Лоренца вдоль системы гипербол
И 2, должна менять местами точки {Xi,zi) и (X2, Зг), они
взаимно «эквидистантны» вдоль своих гипербол. Отсюда
немедленно следует, что группа Лоренца транзитивна на
гиперболоиде Sk и на множестве направлений в любой
фиксированной точке Sk. Поэтому наша метрика действительно
имеет постоянную (отрицательную) кривизну.
1.9. Полярная кривая
Существует еще одно важное общее понятие, которое
можно использовать в наших рассуждениях, — это понятие
кривой, полярной к данной плоской кривой. А именно, если
плоская кривая С в СР2 задается однородным уравнением
Fix, y,z) = Zri{x,y)z'^0,
1.9. ПОЛЯРНАЯ КРИВАЯ 29
ТО условие того, что прямая 2 = 0 касается С в точке (1,0,0),
состоит просто в том, что уравнение Го{х,у) = О имеет
двукратный корень в точке (1, 0), т. е.
rod, 0)-0, ^(1,0) = 0.
При помощи формулы Эйлера, утверждающей, что
последнее условие можно переписать в виде
1^(1, 0) = 0. ^(1,0)=0,
и условие касания можно теперь переписать просто как
1^(1,0, 0) = f (1,0, 0) = 0.
Но любую точку .С.Р2 можно линейным преобразованием
перевести в точку (1,0,0), причем так, что заданная прямая,
проходящая через эту точку, перейдет в прямую 2 = 0.
Поэтому в общем случае прямая ах -^ by -{- cz = Q касается
кривой F{x,y,z) = b в точке (хо, г/о, 2о) тогда и только тогда,
когда (хо, у о, 2о) е С и
( дР дР дР \\ л I и X /1 оп\
llF' ~д7' 1Г)[ ^ = ^(а, Ь, с) (1.29)
при некотором Х^:С:. [Если левая тройка чисел нулевая,
будем говорить, что любая прямая, проходящая через
{хо, уо, 2о), касается С в этой точке. Если же левая тройка
чисел ненулевая, равенство ахо -\- Ьуо -j- с2о == О
обеспечивается формулой Эйлера.] Отображение
^с: СРг-^СРг,
i^:c„y,,z,)^(^,^, 4^)1 (1-30)
называется полярным отображением, связанным с плоской
кривой С. Кривая 3)с{С) называется двойственной к С
и обозначается С. Если С — невырожденная коника, то 3)с,
конечно, линейный изоморфизм, так что С тоже
невырожденная коника. Чтобы получить ее уравнение, заметим, что если
С задается матричным уравнением vA'v = 0, то С задается
такой матрицей М, что AM А = А. (Вспомним, что А
симметрична.) Поэтому М = Л-' и
С = С. (1.31)
30
гл. 1. коники
Теперь предположим, что С — невырожденная плоская
кривая произвольной степени. (Невырожденность означает,
что все три частные производные от определяющего ее
однородного уравнения не обращаются в О одновременно.) Если
2)с локально является отображением максимального ранга,
то уравнение G = О двойственной кривой С локально
определяется формулой
f^t дР дР дР\ , р, ,
Дифференцируя, получаем, что если матрица вторых
производных
д^Р
д^Р
д^Р
дхду
д^Р
дхду
ду'
д^Р
д^Р
дхдг
д'Р
ду дг
д'Р
дг^
(1.32)
дх дг ду дг
имеет максимальный ранг в точке (хо, г/о, Zo) е С, то точка
^ (дР дР дР \
Ю^ \-т-, -Т-. -д-] зависит только от значении первых
и вторых производных F в точке .{хо, уо, 2о). Поскольку
существует коника, уравнение которой имеет то же значение
(а итленно 0) и те же первые и вторые производные в точке
{xo,yo,Zo), что и F, из формулы (1.31) для коник следует
такая же формула для произвольных плоских кривых.
Точнее, если отображение S!>c имеет максимальный ранг в
некоторой точке Р е.С.Рг, то в окрестности точки Р на С
2)q °^с = тождественное отображение.
Благодаря линейности полярного отображения в случае
коник, каждому утверждению о кониках отвечает
соответствующее «двойственное утверждение». Для начала пусть
А — симметрическая матрица, связанная с невырожденной
коникой С. Система двух уравнений
X 1
[х у z]A
[х у z]A
У
Z
Хл
Уо
L2o
= 0.
= 0
(1.33)
(1.34)
при фиксированной точке {хо, уо, zo) е СРг имеет два
решения;
iXuyuZl) и iX2,y2,Z2),
1.9. ПОЛЯРНАЯ КРИВАЯ
31
Мы видели, что уравнение касательной прямой к С в точке
(Xi, уи Zi) имеет вид
X -л
[^1 У1 Z,-] А
У
L2
0.
поэтому точка (хо, г/о, 2о) должна находиться на пересечений
касательных к С в точках {xi,yx,z{) и (хг, г/2, ^г) (рис. 1.15).
ix.,y„z,)
i^ а, у а. 2а)
(^i.^.z,)
Рис. 1.15. Построение поляры точки (х^, уо, 2о)
Следовательно, полярное отображение 3)с можно
представлять себе как сопоставление точке {хо, уо, zo) е .С.Рг прямой
(1.34), пересекающей С в двух точках, касательные к С
Рис. 1.16. Стереографическая проекция коняки на проективную прямую
В которых проходят через (хо, г/о, zo). Отсюда ясно, что
получилась прекрасная биекция между СРг и С'^) — множеством
пар точек С (которое называют обычно симметрическим
квадратом С). Стереографическая проекция осуществляет
изоморфизм между С и C.Pi (рис. 1.16), так что имеется
биекция
CP2^(<QPl)(2).
Это согласуется с тем, что мы заметили раньще: если
(хо, ^0, Zo) е С, то ее поляра касается С в точке {хо,уо,го).
32 ГЛ. 1 КОНИКИ
Таким образом, наше сопоставление прямых точкам (или
точек прямым) при помощи полярного изоморфизма
геометрически весьма содержательно. Предложения
точка р принадлежит С,
две прямые, проходящие через точку,
полярны, или двойственны, предложениям
касательная прямая к С в точке р,
две точки, соединенные прямой.
Так, например, при переводе на двойственный язык
рассмотренной ранее теоремы Паскаля о «чудесном шестиугольнике»
получается такая двойственная теорема:
Прямые, соединяющие противоположные вершины
шестиугольника, описанного около коники, пересекаются
в одной точке.
1.10. Перпендикуляры в гиперболическом пространстве
Рассмотрим теперь приложение полярного отображения
к описанным нами раньше плоским геометриям постоянной
кривизны — так называемым сферической и гиперболической
геометриям. Такие геометрии состояли из множества точек
и функции расстояния. Функция расстояния выбиралась
некоторым специальным образом, с тем чтобы каждая такая
геометрия имела максимально возможную группу изометрий,
а именно, чтобы для любой точки и любого направления
в ней существовала (единственная) изометрия, переводящая
их в любую другую точку с произвольным направлением
в ней. С помощью центрального проектирования мы
получили плоское представление каждой такой геометрии (или,
при /С < О, по крайней мере плоское представление большого
ее куска). Одной из трудностей, связанной с этим
представлением, является понятие угла. Скажем, в случае /С < О
обычное плоское евклидово понятие угла между двумя
прямыми не годится, так как, например, правило косинусов не
выполняется даже инфинитезимально, а изометрий не
сохраняют евклидовых углов. Поэтому нам следует попытаться
найти какой-то геометрический способ представления углов
в этой геометрии, а если это не получится, то хотя бы найти
какие-то геометрические соображения, позволяющие
установить, когда две прямые перпендикулярны. Начнем со сферы
радиуса К~^^^ с центром в начале координат в R^.
Рассмотрим две геодезические на этой сфере, проходящие через точку
P = {xo,yo,zo) (рис. 1.17). Пусть М и М' — точки
пересечения этих геодезических с геодезической
хох + уоу + zoz = О (1.35)
1.10. ПЕРПЕНДИКУЛЯРЫ В ГИПЕРБОЛИЧЕСКОМ ПРОСТРАНСТВЕ
33
на этой же сфере. Если б — угол между двумя первыми
геодезическими, то, как мы уже видели.
К-""б-
где N и Л^' — точки пересечения комплексной прямой (1.35)
с абсолютом
л;2 + г/2 + 22 = О, (1.36)
т. е. N а N' — это две точки коники (1.36), касательные в
которых проходят через Р. Если, как и раньше, перевести это
в утверждение о /С-геомет-
рии на плоскости 2=1,
то получится, что /С-угол
между прямыми L и L',
проходящими через точку
р = {х, у), задается
формулой -gflog (L, V, ], ]'),
где J я J' — две
касательные к Л:(л;2 + г/2)+1 =0,
проходящие через точку
р. (Двойное отношение
четырех прямых,
проходящих через точку р, —
это просто двойное
отношение четырех точек их
пересечения с прямой, не
проходящей через р). По
«принципу аналитического продолжения» следует ожидать,
что та же формула верна и для отрицательного К, что и
соответствует действительности. Мы не можем «увидеть»
прямые У и У ни в случае положительного, ни в случае
отрицательного К (т. е. прямые J и Г не вещественны). Тем не менее
можно понять, что означает перпендикулярность двух
геодезических.
Займемся теперь перпендикулярностью в случае К <.0.
Имеем две геодезические L и L', пересекающиеся в точке ро,
лежащей внутри круга, ограниченного окружностью
Рис. 1.17. Угол между геодезическими в
сферической геометрии
К{х^+у')+1^0
(1.37)
(рис. 1.18). Как мы видели, каждой прямой соответствует
полярная ей точка относительно коники (1.37); обозначим их
р и р'. Например, р — это просто точка пересечения
касательных к (1.37), проведенных в точках пересечения ее с L.
Прямые L и L' перпендикулярны, если log(Z,, L', У, У) = го',
2 Зак. 107
34
ГЛ. I. коники
т. е. если {L, L',J,J') = —1. Пусть, как и в § 1.9, Л
—матрица нашей коники; тогда соотношение рА^ро = О означает,
что р принадлежит полярной прямой точки ро, которую мы
Я
точка
точка
точка
точка
точка
Р
Р'
Ро
п
п'
Рис. 1.18. Углы в гиперболической геометрии
обозначим Н. Аналогично, р'^.Н. При полярном
отображении получаем
-прямая L,
'Прямая L',
►прямая Н,
'Прямая /,
''прямая /',
где п и п' — точки пересечения / и У с коникой (1.37). Но
п и п' должны лежать на Н, поскольку У и У проходят через
Ро. Полярное отображение линейно, поэтому оно сохраняет
двойное отношение. Следовательно, {L, L', J, )') = (р, р', п, п').
Предположим теперь, что р е L\ Тогда рА'р' = О, откуда
р' ^L. В этом случае (L, L', J, J') = (р', р, п, п'), так как
двойное отношение четырех прямых, проходящих через ро,
можно вычислять как двойное отношение их точек
пересечения с Н. Поэтому если p^L' (или, эквивалентно, f/^L),
то (р', р, п, п') = (р, р', п, п'). Поскольку р, р', п, п' все
различны, это возможно лишь в случае, когда (р, р', ПуП') = —1.
Обратно, так как (L, L\J, Г) есть инъективная функция
£,', ясно, что если {L, L', ]^]')=—1, то p^L' (а значит,
и р' ^:L). Таким образом,
L и и ангармоничны относительно J и Г (г. е.
{L, L',J,J')=—1) тогда и только тогда, когда L и L'
перпендикулярны в К-геометрии.
1.11. ОКРУЖНОСТИ в Л-ГЕОМЕТРИИ 35
Или на чисто геометрическом языке:
Перпендикуляром к L, проходящим через точку ро,
является прямая pop, где р — полярная точка к L.
1.11. Окружности в /С-геометрии
Задача. Найтн множество точек, равноудаленных от
заданной точки Ро.
Для решения этой задачи достаточно найти кривую,
которая переходит в себя при всех изометриях, сохраняющих ро.
Пусть L, поляра точки ро, пересекает конику (1.37) в
(мнимых) точках п и п'. Если J(x,y,z) = Q, J'{x,y,z)= О —
уравнения двух касательных к (1.37) в точках п и п'
соответственно, то мы имеем семейство коник
tolKix^ + y^)+ 1] + tj{x, у, z)J'{x, у, z) = О,
параметризованное однородными координатами (/о. ^i)-
Будем обозначать это семейство
С(,.. ,,). (^0, /i)eCPi. (1.38)
Аналогично тому как в общем случае существует лишь С Pi
коник, проходящих через четыре фиксированные точки,
существует лишь .CPi коник, проходящих через две точки
и имеющих в этих точках фиксированные направления
касательных. Поэтому семейство (1.38) должно содержать
вырожденную конику, представляющую собой двойную прямую
L = пп'. Далее, изометриями в нашей геометрии являются
линейные преобразования, сохраняющие конику (1.37).
В частности, имеется однопараметрическое (с вещественным
параметром) семейство изометрий, сохраняющих ро (а
следовательно, пи п'), которое транзитивно действует на
множестве вещественных прямых, проходящих через ро- Эта
группа изометрий линейно действует на семействе (1.38),
причем на самом деле она оставляет на месте три коники
(2-L, конику (1.37) и (Ро«) + (ро"')) • Следовательно, эта
группа тривиально действует на множестве коник (1.38). От-
сюда сразу следует, что семейство
to{K{x^ + y^)+n+U
[хуЦ
гК 0
0 к
.0 0
От п^
О
■1
'л
= 0, (1.39)
где Iq, /i^R, высекает семейство «окружностей» в
/С-геометрии, т. е. каждая коника из (1.39), задевающая множество
X, у вещественны, /C(jc'^-f г/'^)+1 >■ О,
2*
36
гл. I. коники
пересекает его по множеству точек, равноудаленных от /зь.
Двойственная переформулировка задачи, исходящая из
прямой L в /С-геометрии и ее полярной точки /7о, лежащей вне
круга точек этой геометрии, приводит к заключению, что
семейство (1.39) состоит из множеств точек, равноудаленных
от прямой L (рис. 1.19).
В любой геометрии всякой кривой в каждой ее точке
сопоставляется некоторое число, называемое геодезической
кривизной в этой точке, которое зависит только от функции
расстояния в этой геометрии (О'Нейл [7], с. 329—330).
L
Рис. 1.19. Множество точек, равноудаленных от заданной прямой, в
гиперболической геометрии
В геометрии с таким большим количеством изометрий, как
/*С-геометрия при /С < О, окружности должны иметь одну и ту
же геодезическую кривизну в каждой своей точке. Чтобы
понять, как ведет себя эта кривизна^ взглянем на рис. 1.20.
Рассмотрим /С-окружность с центром в (а, 0), проходящую
через (0,0). Когда а стремится к (—К)~^'^, эта окружность
приближается к конике, все четыре точки пересечения
которой с К{х^ + У^)-\-\ =^^ слипаются в точку {{—К)~^'^, 0).
(Чтобы в этом убедиться, достаточно рассмотреть
геометрическую конструкцию семейства (1.38) или рис. 1.20.) Будем
говорить, что предельная коника и К{х^ -\- У^) Л- ^ =■ ^ имеют
касание 4-го порядка в точке ((—K)~^'^,Q)- Порядок касания
так велик (^3), что обычная евклидова кривизна этих двух
кривых в этой точке должна быть одинаковой. Это общее
значение, следовательно, равно (—К) ^'^. В силу симметрии,,
предельная коника имеет евклидову кривизну (—К.)^^^
в (О, 0). Но можно показать, что i^C-метрика и обычная
евклидова метрика [ (dx'^-\-dy^f'^ совпадают в точке (О, 0) с точ-.
1.12. РАЦИОНАЛЬНЫЕ ТОЧКИ НА КОНИКАХ 37
ностью ДО малых второго порядка. В дифференциальной
геометрии доказывается, что в таком случае геодезические
кривизны в точке (О, 0) относительно этих метрик тоже должны
совпадать. Следовательно, в /С-геометрии не существует
окружностей, геодезическая кривизна которых меньше
(—/С)"^^ а все значения кривизны, большие (—/С)'''^
реализуются!
К(х^+у^)+1=0
Рис. 1.20. Предельная окружность, проходящая через заданную точку, в
гиперболической геометрии
Пришло время двигаться дальше, но прежде чем мы
расстанемся с кониками, необходимо затронуть еш,е один
сюжет').
1.12. Рациональные точки на кониках
Скажем теперь несколько слов об арифметике коник.
Пусть дано уравнение
Ах' + Вху + Ct/2 + Dxz + Eyz + Fz^ — 0, (1.40)
где коэффициенты А, В, ..., р принадлежат полю
рациональных чисел Q. Спрашивается: когда уравнение (1.40) имеет
решение в Qp2 — множестве одномерных подпространств
векторного пространства Qs? Если существует одно такое
решение (хо, уо, Zo). то можно построить много других при
помощи стереографической проекции (рис. 1.21), если только
множество комплексных решений, т. е. решений в .CjP2,
представляет собой настоящую невырожденную конику.
Действительно, предположим, что уоФ О, и зададимся произвольной
') Читатель, который хотел бы глубже познакомиться с римановой
геометрией, не найдет, пожалуй, источника прекраснее классических
лекций Эли Картана (Cartan Е. Lemons sur U Geometrie des Espaces de Rie-
mann, —Paris; Gauthier-VUUrs, 1963).
38 гл. I. коники
точкой (xi, о, zi)eQP2 на прямой у= 0; тогда уравнение
Л {X, + tx,J + Б (^0 + ^^0 У, + Су1 + о (Хо + /д;,) (z„ + tz,) +
+ £t/o(Zo + /Zi) + /^(Zo + iZif=0 (1.41)
имеет решение i = О, а следовательно, и второе рациональное
решение. Поэтому задача отыскания множества решений
(1.40) в QP2 сводится к ответу на единственный вопрос:
имеет ли (1.40) вообще какие-нибудь рациональные
решения? Приводя все к общему знаменателю, можно считать
А, В, С, ..., F целыми и задать эквивалентный вопрос: имеет
ли (1.40) г^ель^е решения?
(^о.^о.^о)
ось у "О
Рис. 1.21, Опять стереографическая проекция
Замечательно, что этот последний вопрос можно
эффективно разрешить для любого заданного уравнения (1.40).
Во-первых, описанный ранее процесс отыскания линейного
преобразования RP2, приводящего уравнение (1.40) к виду
eiX2+ 621/2 — 22 = О, (1.42)
на самом деле может быть весь осуществлен над Q, т. е. при
помощи ЗХЗ-матриц с рациональными элементами, которые
задают автоморфизм QP2, правда, при условии, что мы
откажемся от требования |8,|=1. Поэтому можно считать, что
наше уравнение имеет вид (1.42). Для существования
рациональных решений (1.42) необходимо по крайней мере
наличие вещественных решений, так что хотя бы одно zi должно
быть положительным. Можно также предположить, что
J8ij^J82]. Более того, заменяя при необходимости х на ах,
а у на by, можно считать, что J8,j есть произведение
различных простых чисел в первой степени каждое.
Рассмотрим два примера:
3x2 + 2j/2-z2 = 0, (1.43)
3X2 + (/2 _ 22 ^ 0. (144)
1.12. РАЦИОНАЛЬНЫЕ ТОЧКИ НА КОНИКАХ 39
Предположим, что (1.43) имеет целое решение {хо,уо,го) без
общих делителей. Если З-^г/о (3 не делит г/о), то,
рассматривая (1.43) как уравнение с коэффициентами в поле 1Рз =
= Z/3Z вычетов по модулю 3, мы приходим к противоречию.
Если же 3|г/о, то 3|zo, поэтому З'^|3х^, так что 3\xq.
Поскольку хо, г/о. и Zo не имеют общих делителей, (1.43) не имеет
рациональных решений. С другой стороны, уравнение (1.44)
имеет решение (1,1,2). Заметим, что ег в (1.44) является
квадратом по модулю 8i.
Подобные рассуждения приводят к общему
заключению, что если (1.42) имеет целые решения, то
82 является квадратом по модулю р
для любого простого числа р, делящего 8i. Тогда по
китайской теореме об остатках')
82 является квадратом по модулю 8i.
Это означает, что существуют числа с и е{, для которых
|cK|8i|/2h
с =82 -f- 8j8[,
8,8; = С2 - 82 = (с + el/2) (с - 8l/2).
Таким образом, суш,ествование рациональных чисел а, Ь, для
которых
8,=(a + 6ef)(a-68f),
эквивалентно суш,ествованию таких рациональных чисел а',
Ь', что
г[^{а' + Ь'в1^){а' - Ь'гУ^).
Другими словами, уравнение 8ix^ + 82J/^ — 2^=0 имеет
рациональное решение тогда и только тогда, когда его имеет
уравнение г[х^ + ЦУ^ — z^ = 0. При | е, | > 1
■|^|<¥+'<1м.
так что (если исключить квадраты, встречающиеся в
разложении [e^l на простые сомножители) наша задача сводится
к такой же задаче с меньшей суммой |8i|4-|e2|. Это
рассуждение можно повторять до тех пор, пока |82| не перестанет
быть квадратом по модулю |8i| или же пока мы не
достигнем случая |8i| = |82|=l, в котором решение существует
тогда и только тогда, когда 8i или 82 положительно.
') См Ленг С. Алгебра. Пер. с англ. — М.; Мир, 1968, с. 82.~ Прим.
перев.
Глава 2
КУБИКИ
2.1. Точки перегиба
Приступим теперь к изучению множества решений Е cz
CZ С.Рг уравнения
F{x,y,z)==0, (2.1)
где F — однородный многочлен степени 3. Будем, как и
раньше, предполагать, что частные производные
dF/дх, дР/ду, дР/дг (2.2)
не обращаются в нуль одновременно. В отличие от
квадратичного случая каждый кубический многочлен с
вещественными коэффициентами имеет по крайней мере один
вещественный корень, поэтому если коэффициенты F вещественны,
то множество решений (2.1) в КРг всегда будет гладкой
кривой. Вопрос о существовании решения в QP^ в случае
рациональных коэффициентов многочлена (2.1) чрезвычайно
сложен, и алгоритм для выяснения этого в общем случае до
сих пор не известен.
Для начала рассмотрим полярное отображение
3>е: С,Р2-^СР2,
введенное в гл. 1. Когда степень Е равна трем, это
отображение уже не является изоморфизмом. Действительно, оно
вырожденно в тех точках р, где
det
J1L
дхду
дх дг
ip)
ip)
ip)
дхду
£F
ду
d^F
ду dz
{?)
rip)
d^F
дхдг
d^F
iP)
ду dz
d^F
dz^
ip)
ip)
ip)
0.
(2.3)
Поскольку это детерминантное уравнение однородно сте»:
пени 3, можно ожидать, что найдутся 3X3 = 9 точек из,Я,
в которых наше отображение вырожденно. А как обстоит делО;
с ограничением 3)ё е"? Возьмем точку р S £, для которой
выполняется (2.3). Если бы S>e\e имело в точке р
максимальный ранг, то ядро S^E в точке р не могло бы лежать
8 касательном пространстве к Е в р. Отсюда следовало Щ
2.1. ТОЧКИ ПЕРЕГИБА 41
существование такой строки [х у z\, что
но
(^ у z]-ж = (0,0,0),
где М —матрица из (2.3). Тогда, умножая это последнее
уравнение справа на '/?, мы придем к противоречию с
формулой Эйлера. Поскольку отображение 2)е\е, очевидно, не
всюду вырожденно, мы видим, что оно вырожденно не более
чем в девяти точках. Сделаем теперь замену координат так,
чтобы одна из этих точек стала точкой ро = (О, 1,0), причем
в точке ро
(дР/дх, дР/ду, дР/dz) = (О, О, 1).-
Тогда уравнение Е принимает вид
уЧ + yQ {X, z) + C (X, z) = О, (2.4)
где Q и С — однородные формы степеней соответственно 2
и 3. Положим
Q [х, Z) = j [ах^ + 26jcz + cz%
Вырожденность 3!)е в точке /7о—это просто вырожденность
матрицы
(2.5)
^У+ дх^
ax + bz
\-^У+дхдг
ax + bz
2z
2у-\- bx-\- cz
''У^- дхЬг
2у + bx + cz
'У + дг^
В точке (0,1,0). Таким образом, ро тогда и только тогда
является точкой перегиба, когда а = 0.
Далее, продифференцируем
д (определитель (2.5)) I „ д^С
дх Ip^ — дх^ •
Но д^С/дх^ ф О, так как иначе в уравнении (2.4) не будет
члена с х^ и кривая будет содержать прямую z = О, т. е.
будет особой. Следовательно, множество нулей определителя
матрицы (2.5) и Е пересекаются в точке ро трансверсально.
Отсюда вытекает, что ЗЬе вырожденно в девяти различных
точках Е. Ясно также, что ограничение уравнения (2.4) на
прямую Z = О имеет вид ех^ = 0; в таком случае будем
говорить, что эта прямая и Е имеют касание третьего порядка
в точке ро- Последнее эквивалентно вырожденности 3!)е
в точке Ро, причем, как легко видеть, эта эквивалентность
42 гл. 2. КУБИКИ
имеет место и для уравнений и кривых степени выше третьей.
Однако в последнем случае нельзя утверждать, что кривая
Гессе, задаваемая детерминантом матрицы [d^F/dXidxj],
пересекает Е трансверсально во всех точках пересечения. Эти
точки пересечения называются точками перегиба кривой, и их
число (с учетом кратностей) равно п[3{п — 2)], где л —
степень кривой.
2.2. Нормальный вид уравнения кубики
Пусть теперь имеется невырожденная (или, как мы иногда
будем говорить, неособая) кривая Е степени 3, и
предположим, что мы подгадали так, чтобы одной из девяти точек
перегиба Е стала точка роо = (О, 1,0), а касательная к Е
в этой точке — прямая z = О, т. е. бесконечно удаленная
прямая относительно аффинных координат {х,у).
Рассмотрим теперь семейство прямых
X = ez, е е С. (2.6)
Согласно нашему предположению о точке р<х> е Е, уравнение
Е должно иметь вид
y^z + yQ{x,z)+C{x,z), 1
так что можно найти те значения е, при которых прямая
(2.6) касается Е. Для этого надо вычислить дискриминант
уравнения
y' + Qie,l)y + C{e,l) = 0,
т. е. определитель матрицы
•1 Q(e, 1) С(е, 1)-,
2 Q(e, 1) О
.0 2 Q(e, 1)
или просто найти множество решений уравнения
-Q(e,l)24-4C(e,l)==0. (U.7)
Поскольку, как мы видели, д^С/дх^ =5^ О и d^Q/dx^ = О, это
уравнение имеет три корня (учитывая временно и
возможные кратные корни). Предположим, что один из этих корней
соответствует точке (0,0, 1). Тогда прямая х = 0 касается Е
в этой точке, так что д^С/дг? = d^Q/dz^ = 0. Если
е—кратный корень уравнения (2.7), то получается, что d^C/dxdz^=
= 0. Но тогда все частные производные уравнения,
определяющего Е, обращаются в нуль в точке (0,0, 1), что
противоречит гладкости Е. Таким образом, все корни уравнения
2.2. нормальный ВИД УРАВНЕНИЯ КУБИКИ
43
(2.7) различны и соответствуют трем различным точкам рь
Ръ Рг в СРг. Это показано на рис. 2.1.
Рассмотрим теперь три кубические кривые:
Е,
(прямая М) + (прямая N) + (прямая р<х,р),
(прямая /,)') + 2(прямая pipi),
где р — третья точка пересечения Е с прямой, проходящей
через pi и р2. Эти три кубики имеют восемь общих точек,
а именно
Зроо, 2pi, 2р2, р.
Но, как мы уже видели в гл. 1, занимаясь чудесным
шестиугольником Паскаля, отсюда следует, что уравнения, опре-
к точке в
к точке п
К точке п
К точке р
z = 0
Р
Рис. 2.1. Проектирование кубики из точки перегиба р»
деляющие эти три кубики, линейно зависимы, а это означает,
что у данных трех кубик есть девятая общая точка. Этой
точкой должна быть точка р, так что прямая ро^р двукратно
пересекает Е в точке р, т.^ е. р = рз и три точки pi, рг, Рз
лежат на одной прямой.
Подходящей линейной заменой координат можно, ничего
не нарушая в наших построениях, сделать так, чтобы
р, = (0,0,1), Р2 = (1,0,1), рз = (Х,0, 1).
') Бесконечно удаленная прямая, касающаяся Е в роо. — Прим. ред.
44 гл. 2. КУВИКИ
Поскольку тогда Q(e, 1) должно обратиться в нуль tipn
е = О, 1, Я, мы заключаем, что Q{x, z) ^ О, и наше уравнение
для Е принимает вид
y'^z — x{x — z){x — \z) = 0. (2.8)
2.3. Кубики как топологические группы
При изучении коник в первой главе мы почти не
обсуждали их топологию в jC.P2. поскольку все и так было очень
просто. А именно стереографическая проекция (рис. 2.2)
устанавливает диффеоморфизм между нашей коникой и
проективной прямой L, которая в свою очередь диффеоморфна
Рис. 2.2. Проектирование коники из точки р» на ней
стандартной двумерной сфере в R^. Однако, когда мы
попытаемся построить стереографическую проекцию
эллиптической кривой, дело несколько усложнится (см. рис. 2.1). Если
центром проекции рсо выбрана точка перегиба, то уравнение
(2.7) имеет степень 3, а если нет, то степень 4. При этом
стереографическая проекция представляет Е как двулистное
накрытие jC.Pi, разветвленное в четырех точках (одна из
которых находится на бесконечности, если роо — точка
перегиба). Слово «разветвленное» означает, что вокруг данной
точки отображение проектирования устроено так же, как
проекция
(кривая г/2 = д;)->-(ось х), {х,у)^->х
вблизи (О, 0). Исходя из этого, легко построить
топологическую модель Е. Возьмем две сферы, сделаем на каждой из
2.3. КУБИКИ КАК ТОПОЛОГИЧЕСКИЕ ГРУППЫ 45
Рис. 2.3. Как разрезать кубику пополам
Рис. 2.4 Как вновь склеить кубику
НИХ по два одинаковых надреза (рис. 2.3), раскроем
получившиеся дырки, а затем перевернем нижнюю сферу и склеим
ее с верхней по краям разрезов в соответствии с разметкой
(рис. 2.4). Таким образом, топологически Е — это тор, т. е.
факторпространство (RXR)/(ZXZ). Это означает, что Е
на самом деле является топологической группой.
Но, конечно, групповая структура на Е гораздо более
тесно связана с ее комплексной геометрией. Исследуем эту
связь. Чтобы хорошо представлять себе, что происходит,
удобно считать X вещественным и рассматривать множество
решений (2.8) в КРг или просто на (х, у)-плоскости R'^
(рис. 2.5). Определим бинарную операцию на Е, полагая
Pi + Р2 = {х, —у),
если точки р1, р2 и (х, у) лежат на одной прямой.
Коммутативность этой бинарной операции и существование обратного
для каждого элемента очевидны; за нулевой элемент
принимается точка р<х,. Интерес представляет проверка
ассоциативности. Основная идея — что кубики, проходящие через восемь
точек, имеют и девя-^ую общую точку — уже дважды исполь-
46
ГЛ. 2. КУБИКИ
зована нами. Чтобы понять, как она работает в данном
случае, рассмотрим рис. 2.6, взятый из замечательных лекций
Джона Тэйта по арифметике кубических кривых,
прочитанных в Haverford College в апреле 1961 г. Чтобы доказать
,-:v)
(х.у)
Рис. 2.5. Приведенная к нормальному виду вещественная кубика,
рассеченная прямой
ассоциативность, необходимо показать, что точки {р-{- q)r
и p(q-\-r) совпадают. Для этого мы должны найти две ку-
Рис. 2.6. Ассоциативность сложения на кубике
бические кривые (кроме Е), которые проходят через восемь
точек
рсо, р, q, г, qr, pq, {q + r), {р + Я)-
Тогда если одна из этих кубик проходит через точку (p-{-q)r
на Е, а другая через p{q \- г) на Е, то эти две точки совпа-
2.4. ГРУППА РАЦИОНАЛЬНЫХ ТОЧЕК НА КУБИКЕ 47
дают. Вот эти две кубики:
(прямая через р и 9) +(прямая через qr я {д-\-г))-\-
+ (прямая через г и (p-^-q)-).
и
(прямая через q и г) + (Прямая через pq и (p-\-q)) +
-{-(прямая через р и {q-\-r)).
2.4. Группа рациональных точек на кубике
Итак, мы выяснили, что множество комплексных решений
невырожденного кубического уравнения
P{x,y,z) = 0 (2.9)
образует группу, причем в качестве единичного элемента
можно выбрать любую из точек перегиба, а групповая
операция задается простой геометрической конструкцией. Теперь
предположим, что коэффициенты в (2.9) вещественны или
рациональны и что у нас есть некоторое решение р е R Рг
или peQP2- Точка р может быть или не быть точкой
перегиба, и никакая линейная замена координат не изменит этого
положения. Тем не менее, существует бирациональное
преобразование RP2 или QP2 (а также, конечно, и СРг),
которое взаимно однозначно переводит Е в невырожденную
кубическую кривую, а точку р — в точку перегиба этой- кривой.
Чтобы в этом убедиться, обратимся опять к лекциям Тэйта
и предположим, что заданная точка р не является точкой
перегиба. Выберем координаты так, чтобы р = (1,0,0),
касательная прямая к £ в точке р задавалась уравнением
Z = О, а касательная прямая к Е в третьей точке
пересечения прямой 2 = О с Е — уравнением х = 0. Тогда уравнение
Е может быть записано в виде
x2z + xQ(j/,z)+C(j/,z)=0, (2.10)
где Q (у, г) = ау^ + 26г/2 + cz^ и С {и, г) = syz^ -\- It?.
Переведем QPz (и одновременно RPj и С.Рг) в себя по правилу
(X, г/, z)k-»(xz,xj/, z2). (2.11)
Остановимся на минуту и повнимательнее рассмотрим это
преобразование QP2. Во-первых, оно имеет «обратное»:
{х, у, г)^-^{ху, у^/х, yz) (2.12)
II
{х\ yz, xz)
Это означает, что ограничение преобразования (2.11) на
(QPz—{xyz = 0}) есть автоморфизм. Поведение
отображения (2.11) на множестве xyz = 0 изображено на рис. 2.7.
48
ГЛ. 2. КУБИКИ
Чтобы точнее описать происходящее, рассмотрим операцию
«раздутия точки».
Предположим, что мы хотим раздуть точку х = г/ = О на
декартовой плоскости {х,у). Для этого мы просто заменим
эта точка «раздувается»
в прямую z»0
эта прямая стягивается
в точку (О, Г,О)
«раздутая» из этой точки
прямая стягивается в точку;
(0,1,0;^ в то время как точка
на ней. соответствующая
направлению прямой х—О,
«раздувается» в прямую х—О
Рис. 2.7. Действие бирационального преобразования (2.11) во всех
подробностях
ПЛОСКОСТЬ (х,у) замкнутым графиком в Q'^XQPi
отображения
Q^^QPi, ix,y)^{x,y).
Теперь можно показать, что отображение (2.11) строится
поэтапно следующим образом:
Шаг 1. Раздуваем точки (1,0,0) и (0,1,0) в QP2, так
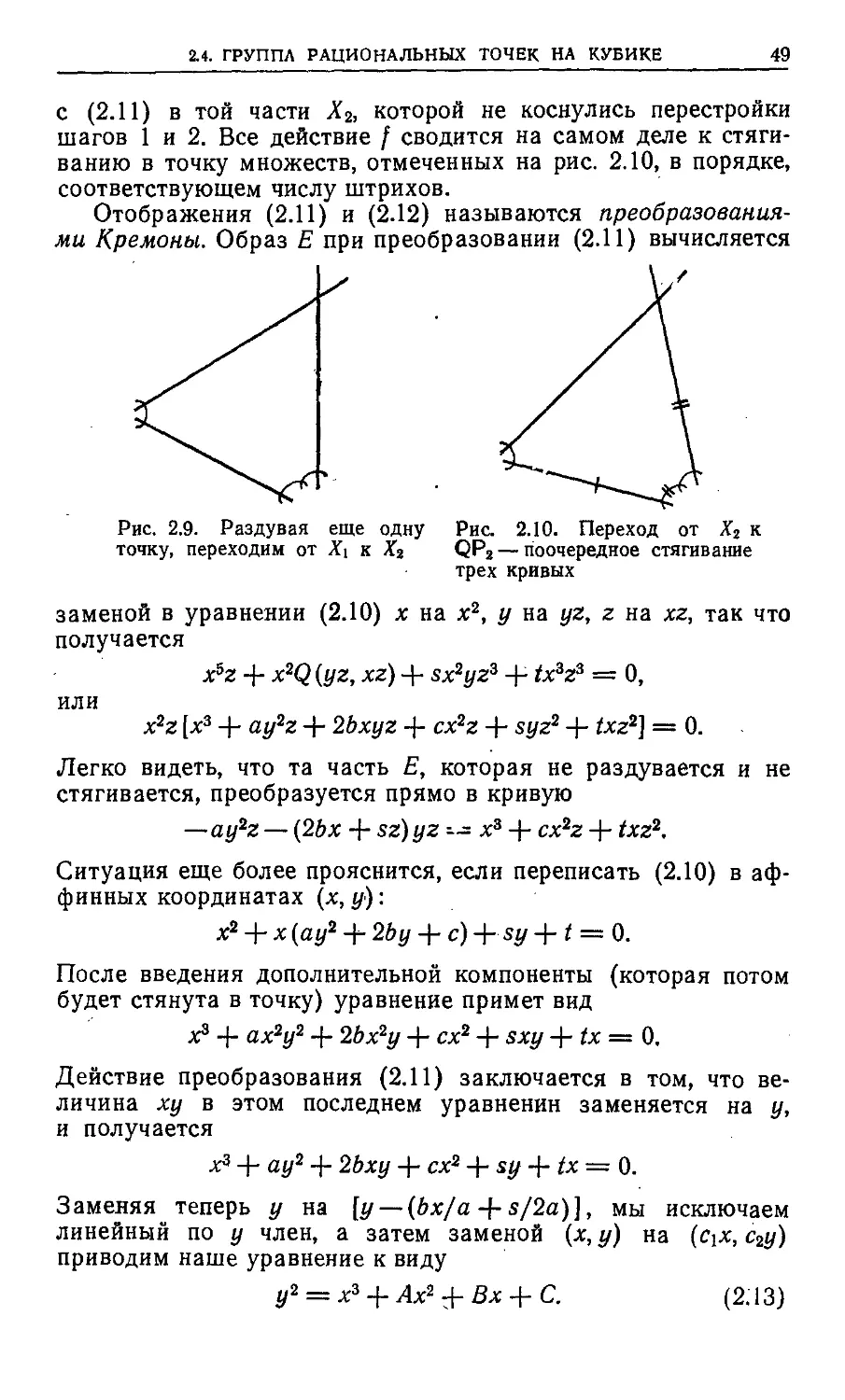
что получается новое «многообразие» Хх (рис. 2.8).
х=0
Рис. 2.8. Раздувая две точки, переходим от QPj к Xi
Шаг 2. Раздуваем точку р в Xi я получаем новое
многообразие ^2 (рис. 2.9).
Можно показать, что существует всюду определенное
«алгебраическое» отображение f: Xs^-QPi, которое совпадает
2.4. ГРУППА РАЦИОНАЛЬНЫХ ТОЧЕК НА КУБИКЕ 49
С (2.11) В ТОЙ части Х2, которой не коснулись перестройки
шагов 1 и 2. Все действие / сводится на самом деле к
стягиванию в точку множеств, отмеченных на рис. 2.10, в порядке,
соответствующем числу штрихов.
Отображения (2.11) и (2.12) называются
преобразованиями Кремоны. Образ Е при преобразовании (2.11) вычисляется
у
Рис. 2.9. Раздувая еще одну Рис. 2.10. Переход от Хг к
точку, переходим от Х[ к Хг QP2 — поочередное стягивание
трех кривых
заменой в уравнении (2.10) х на х^, у на yz, z на xz, так что
получается
x^z -f x^Q {yz, xz) + sx'^yz^ 4- txh^ = 0,
или
x^z [x^ + «^/^2 + 2bxyz -f cx^z + syz^ + txz^ = 0.
Легко видеть, что та часть Е, которая не раздувается и не
стягивается, преобразуется прямо в кривую
—ауН — (2Ьх -f sz)yz --- х^ + сх^г + ixz'^'
Ситуация еще более прояснится, если переписать (2.10) в
аффинных координатах (х, у):
х2 + х(а«/2 + 2Ьу + с) + sy +t = 0.
После введения дополнительной компоненты (которая потом
будет стянута в точку) уравнение примет вид
х^ -f ax2j/2 + 2bx^y + сх2 + sxy +tx=0.
Действие преобразования (2.11) заключается в том, что
величина ху в этом последнем уравнении заменяется на у,
и получается
хз + аг/2 -f 2bxy + сх^ + st/ + tx=0.
Заменяя теперь у на [у — {Ьх/а + з/2а)], мы исключаем
линейный по у член, а затем заменой (х, у) на (cix, Сгу)
приводим наше уравнение к виду
г/2 = хз + Лх2 ^ Бх 4-С (2.13)
50 ГЛ. 2. КУБИКИ
Наблюдая метаморфозы точки р = (1,0,0) при всех этих
преобразованиях, мы видим, что при (2.11) она раздувается,
поэтому для того, чтобы вычислить, какой точке
кубики-образа она соответствует, необходимо рассмотреть
квадратичную часть уравнения Е в точке р, или, другими словами,
проследить, что происходит с прямой 2=0, касательной
к £ в точке р, под действием преобразования (2.11). Тот
факт, что вся эта прямая стягивается в точку (0,1,0),
позволяет заключить, что образом р является точка (0,1,0).
Поскольку остальные замены координат оставляют
бесконечно удаленную точку (О, 1,0) неподвижной, наша точка р
соответствует единственной бесконечно удаленной точке
кривой (2.13). Таким образом, точка р переходит в точку
перегиба. Если,же р с самого начала.была точкой перегиба, то
преобразование (2.11) при приведении уравнения к
нормальному виду производить не нужно.
В любом случае, если наше исходное уравнение (2.9)
имело коэффициенты в Q (или R), то это верно и для
конечного уравнения (2.13), причем существует точное взаимно
однозначное соответствие между (2.9) и (2.13), задающееся
в обе стороны рациональными функциями с рациональными
коэффициентами. Таким образом, Q (или R)-точки кривой
(2.9) находятся по рациональным (вещественным) решениям
уравнения (2.13). Еще вспомним, что в случае уравнений
второй степени с рациональными (вещественными)
коэффициентами, если одно из двух решений ограничения этого
уравнения на рациональную (вещественную) прямую
рационально (вещественно), то же верно и для второго. Точно так
же, если два решения ограничения кубического уравнения на
рациональную (вещественную) прямую рациональны
(вещественны), таково же и третье. Отсюда следует, что наш
геометрический групповой закон корректно определен для кубик
в QP2 и RPj. Одно из высших достижений арифметики
кубик— теорема Морделла — утверждает, что множество
рациональных точек рациональной кубической кривой является
конечно порожденной абелевой группой.
2.5. Размышление о комплексном сопряжении
Множество решений для невырожденной вещественной
кубической кривой топологически представляет собой один
или два овала, в зависимости от числа (один или три)
вещественных корней кубического многочлена от д; в (2.13).
Чтобы представить себе расположение этого множества
решений относительно множества комплексных решений, будем
рассматривать последнее как двулистное накрытие
(комплексной) прямой X, разветвленное в трех точках pi, рг. Рг
2.6. НЕКОТОРЫЕ МЕРОМОРФНЫЕ ФУНКЦИИ НА КУБИКАХ
51
И на оо, причем мы можем считать, что по крайней мере
точка рз вещественна (рис. 2.11). Предположим теперь, что
р1 и р2 не вещественны; тогда множество вещественных
решений (2.13) проектируется на полупрямую, соединяющую
точку рз с бесконечностью. Если же вырезать из Е
множество вещественных решений, то останется цилиндр.
Комплексное сопряжение (х,у)ь—>{х, у) тождественно на множе-
^j
Рис. 2.11. Точки ветвления при проектировании вещественной кубики
стве вещественных решений. Если pi и рг вещественны, то
вырезание обоих вещественных овалов разбивает Е на две
части, которые меняются местами при комплексном
сопряжении. Это же происходит и в случае невырожденных
кривых большей степени л, если только множество
(вещественных) решений содержит максимальное возможное число
овалов [(л—1) (л—2)/2+1].
2.6. Некоторые мероморфные функции на кубиках
Остановимся еще немного на стереографической проекции
из точки р^Е. Эта проекция задает отображение Е-*-СРи
Рис. 2.12. Стереографическая проекция из точки рз дает мероморфную
функцию с множеством нулей {ри рг}
или, что то же самое, мероморфную функцию на Е. Пусть
заданы pi, р2^Е и рз — третья точка пересечения прямой pipz
с Е. Тогда с помощью стереографической проекции из центра
Рз можно построить такую мероморфную функцию / на Е, что
52 ГЛ. 2. КУБИКИ
ее единственными нулями будут pi и рг, а одним из полюсов —
любая наперед заданная точка ро (см. рис. 2.12). Пусть g —
какая-нибудь мероморфная функция с полюсом в точке ро,
нулями которой являются pi и р2. Тогда отношение f/g
обращается в нуль только в одной точке (другом полюсе g)
и имеет лишь один простой полюс (другой полюс /). Иначе
говоря, при отображении
Е^.аРи p^if{p),gip))
точки о и оо имеют единственные прообразы, так что это
отображение есть либо изоморфизм (что топологически
невозможно), либо константа. Следовательно, все мероморф-
ные функции степени 2 на £ получаются с помощью
стереографической проекции.
2.7. Пространство модулей кубик.
Снова двойное отношение
Мы уже видели, что для любой стереографической
проекции все точки ветвления, т. е. точки на C.Pi, над которыми
это отображение разветвлено, различны. Сопоставим точке
р^Е комплексное число {pi, р2, рз, Р*) — двойное отношение
(см. § 1.6) четырех точек ветвления стереографической
проекции с центром р. Поскольку двойное отношение зависит
от порядка, в котором взяты эти четыре точки, мы не
получим таким образом корректно определенную функцию на Е.
Чтобы навести необходимую строгость, через £'('■) обозначим
г-ю симметрическую степень Е, т. е. фактор декартова
произведения f по отношению эквивалентности, индуцированному
перестановками порядка сомножителей. Тогда корректно
определено отображение из £ в четвертую симметрическую
степень £■<*>, которое не задевает диагонали в £■<*>.
Рассмотрим теперь расслоенное произведение, т. е. множество X
таких пар (р, (рь р2, Рз, Рл)), что (рь Р2, Рз, Рл) есть одно из
двойных отношений, возникающих при проектировании из
точки р;
X-->-£*
{ I разветвленное накрытие
I степени 41
+ \
Ш Ш
P'-^iPb Р2, РЗ, Pi)
Тогда отображение двойного отношения корректно
определено как отображение из X в .С.. Эта функция голоморфна,
и, поскольку четыре точки ветвления всегда различны, она не
2.8. АБЕЛЕВ ДИФФЕРЕНЦИАЛ НА КУБИКЕ 53
принимает значений О, 1 и оо. Следовательно, по принципу
максимума, это константа. Как мы уже видели, эти
множества точек ветвления суть в точности множества точек
ветвления мероморфных функций второй степени на Е, что
позволяет сделать такой вывод;
Если кубические кривые Е и Е' изоморфны как
комплексно аналитические многообразия, то множества
двойных отношений точек ветвления для Е и Е'
совпадают.
На самом деле, если какое-нибудь двойное отношение для Е
совпадает с каким-нибудь двойным отношением для Е', то,
как показывают элементарные алгебраические выкладки,
и остальные двойные отношения тоже должны совпадать, ибо
если X — одно из этих двойных отношений, то других
различных значений может быть не более пяти:
1А, 1-Х, 1/{\-Х), {Х-1)/Х, Х/{Х-1).
Обратно, если кривые Е и Е' имеют какое-нибудь общее
двойное отношение X, то несложное рассуждение «по
принципу аналитического продолжения» показывает, что каждая
из них изоморфна кривой
у^ = х{х—1){х — Х).
Итак, мы построили пространство модулей, т. е.
топологическое пространство, точки которого находятся во взаимно
однозначном соответствии с множеством классов изоморфных
кубических кривых. Это пространство представляет собой
(С;— {О, 1, оо})/отношение эквивалентности,
где X ~ X', если X' —одно из чисел \/Х, 1—Я,, 1/(1—Я,),
{Х--1)/Х,Х/{Х — 1).
2.8. Абелев дифференциал на кубике
Существует глубокая связь между анализом, геометрией
и арифметикой кубических кривых. Пусть наша кривая
задана в нормальной форме
F{x,y) = y'^ — x{x — l){x — X) = 0, XeQ, R или С'. (2.14)
Дифференцируя, получаем
в точках (0,0), (1,0) и {Х,0) имеем дР/дхфО, откуда по
теореме о неявной функции следует, что у можно выбрать
54 гл. 2. КУБИКИ
В качестве локальной координаты на £ в окрестности этих
точек. Это означает, что если / — голоморфная функция
в окрестности одной из этих точек в jC.P2, то /jg можно
разложить в степенной ряд по у. Во всех остальных (конечных)
точках Е в качестве локальной координаты можно
использовать функцию
X — X (данная точка).
Поэтому dy^^^^^ —^dx не обращается в нуль в трех
точках (0,0), (1,0) и (X, 0), а следовательно, то же верно
и для
dx/y. (2.15)
Нас также интересует поведение дифференциала (2.15) на
бесконечности, т. е. в точке (О, 1, 0) пространства СРг, в
которое плоскость (х, у) вкладывается как открытое плотное
подмножество. Перепишем сначала (2.14) в однородном виде:
yh — x{x — z){x — Xz)^0.
Аффинное уравнение Е в плоскости (х, г) (окрестности
(0,1,0) в .С.Рг) получится отсюда подстановкой у = 1.
Имеем
G{x,z) = z — x{x — z){x—Xz)=0. (2.16)
Поскольку dG/дгФО в точке (0,0), теорема о неявной
функции позволяет использовать х в качестве локальной
координаты на £■ в этой точке. В частности, на нашей кривой
2=2 fln-*^". и подстановка в (2.16) дает
йо ^ fli ^ 02 = О, 03=^1.
Займемся теперь дифференциалом (2.15). Перепишем его
в однородном виде:
d (х/г) xdz~ zdx
y/z "yz
И далее, полагая у = I, приведем дифференциал (2.15) на
плоскости (х, z) к виду
(x/z)dz — dx ^{2 + положительные степени x)dx. (2.17)
Итак, этот дифференциал в бесконечно удаленной точке
кривой Е конечен и не равен нулю, или, на языке современной
дифференциальной геометрии, сечение (2.15) голоморфного
кокасательного расслоения Е не имеет нулей и полюсов.
Следовательно, кокасательное расслоение Е тривиально (так
что топологическая эйлерова характеристика равна нулю).
Подробнее об этом см., например, [10, § 41].
2.9. ЭЛЛИПТИЧЕСКИЙ ИНТЕГРАЛ 55
2.9. Эллиптический интеграл
Выберем в качестве начальной точки точку (О, 1,0)е£'
и обозначим ее ро. а дифференциал (2.15) обозначим ю.
Рассмотрим отображение
Р х(р)
£•->€, p^-^ (ю= [ — П5. (2.18)
Конечно, это отображение еще не определено как следует,
поскольку мы не уточнили путь интегрирования. Напомним,
/ 0 1
/
дУуХХХ^^ХУУХХ^^^
я А
/ /
/ .0 1
Я А
верхний
лист
нижний
лист
Рис. 2.13. Поэтажный план кубики
ЧТО Е представляется в виде двулистного накрытия оси х,
склеенного крест-накрест вдоль разрезов (см. рис. 2.13).
Выражение
ш = {х{х — 1) (х — Щ-^'Чх
также имеет два значения, в зависимости от знака, с которым
берется квадратный корень. Чтобы получить дифференциал
(В на £■, нужно взять одно из этих двух значений, например
©1, на верхнем листе, а другое ©2 — на нижнем. Тогда по
интегральной формуле Коши отображение (2.18) определено
корректно с точностью до чисел вида тп\ + яя2, т, n^'Z,
где
1 к
Я1 = 2\(В1, я;2 = 2\са1.
о I
Полагая х = и-\- iv, где ия v — вещественные переменные,
получаем
Ч m л л _ Ч ('^Ц + ldv)A {du - i dv)
-\j7l7^rjYir=l^dudv, (2.19)
56 гл. 2. КУБИКИ
ИЛИ, переписывая это в окрестности О в полярных
координатах,
[ 1 гп гг drdQ.
i \х~\\\х—Х\
Действуя подобным образом в окрестностях точек 1, А,
и ро, мы убеждаемся, что этот двойной интеграл по всей
комплексной плоскости конечен и положителен. С другой
стороны, полагая ©i =: |г -|- 1Ц1, i= I, 2, где g; и Ц1 имеют вид
[вещественнозначная функция (и, w) ] da-|-[вещественно-
значная функция {u,v)]dv,
получаем
5 i •"" ^'^i"" S ^" ^ '^' -^ '^- ^^-^^^
Сведем теперь этот поверхностный интеграл к
криволинейному. Сделав разрез на оси х, как показано на рис. 2.14, на
о 1
Рис. 2.14. Разрезание кубики на две надрезанные комплексные прямые
остальной части комплексной прямой можно (по теореме
Грина) найти такую функцию /, что df = h и lim/(p) = 0.
Снова по теореме Грина получаем
о 1 >,
о 1 X
где /+ есть значение / на верхнем берегу разреза, а f~ — на
нижнем, и т. д.
Итак, f+ = —f- вдоль разреза Хоо, на разрезе Тк
со 1
Г = Г-25 lt = r+2\lt=r+^en,
к о
и / ^ — f~ +Яеп1 на 01. Кроме того, ч,'*' = —т]" на Хоо,
Ti,^ = ili" на U и !!,■*■ = — Tj~ на 01.
2.9. ЭЛЛИПТИЧЕСКИЙ ИНТЕГРАЛ 57
Все это означает, что интеграл (2.20) можно вычислять
по Teopeirfe Грина:
00 оо 1 я,
0 0 0 1
= у(Нея1)[1тЯ| +1тя2].
Повторяя эти же рассуждения для dg = щ и Vim g{p) = 0,
получаем
SiiAri, (1тя,)Г5|+ + 5|Л = ^(1тя,)(Нея,+Нея2).
Складывая, получаем
(Кея1)(1тя2) —(1тя1)(Кея2)>0. (2.21)
Это означает, что комплексные числа Я1 и яг линейно
независимы над К, поэтому Е = C/{Zni + /яг) представляет
собой компактный комплексный тор. Соотношение (2.21)
называется вторым соотношением Римана.
Итак, (2.18) задает корректно определенную
голоморфную иммерсию')
Е-^Ё. (2.22)
Поскольку Е компактно, это отображение должно быть ко-
нечнолистным накрытием. На самом деле сразу видно, что
отображение (2.22) индуцирует изоморфизм
Hi(E;Z)^Hi(E;Z),
или, что то же самое, изоморфизм фундаментальных групп.
Поэтому, согласно теории накрытий, отображение (2.22)
само является изоморфизмом
£-^ С/(7я,-f 2я2). . (2.23)
В дальнейшем нам встретитсяизоморфизм, обратный к (2.23).
В частности, композиция этого обратного с координатной
функцией X па Е (см. (2.18)) особенно важна для развития
всей теории, так как у нее есть чрезвычайно удобное явное
выражение. Она называется f-функцией Вейерштрасса.
') Отображение с нигде не вырожденным дифференциалом. — Прим.
ред.
58 ГЛ. 2. КУБИКИ
2.10. Уравнение Пикара — Фукса
Дифференциал ©=:—^ = — г^, определяю-
у [х (х — \) (х — %)у'^
щий отображение (2.18), имеет еще один удивительный
ракурс, а именно, числа
1 я.
щ(%)==2^(а, Я2(Я) = 2 5ю, (2.24)
о 1
называемые периодами Е, зависят от %. Легко видеть, что на
самом деле это голоморфные функции Я,. Например, Я2(Я,)
у
Рис. 2.15. Один из многих эквивалентных путей интегрирования для
определения функции Я2(А.)
можно получить также интегрированием ю по пути у,
изображенному на рис. 2.15. Тогда при малом изменении Я, путь
Рис. 2.16. Один из многих
эквивалентных путей
интегрирования для определения
функции я (Я)
интегрирования не меняется, так что дифференцировать
Я2(Я,) можно просто под знаком интеграла. Положим
к
я (Я,) = щ (Я,) -f Я2 (Я,) = 2 \ ю.
о
функция я (Я,) получается интегрированием ю по пути,
изображенному на рис. 2.16. Когда Я, стремится к О, этот
интеграл стремится к
\ " ■ ,„ = Вычетп U9- — 2я1 (— i) = 2я.
Y
Следовательно, я(Я,)/2я разлагается около точки Я, = О в
степенной ряд. Хотелось бы явно вычислить это разложение.
2.10. УРАВНЕНИЕ ПИКАРА — ФУКСА 59
Для ЭТОГО необходимо изучить дифференциальное уравнение,
которому удовлетворяют я,-(Я,), — так называемое уравнение
Пикара — Фукса.
Попутно нам придется вычислять производные я» (Я,) по к,
т. е. дифференцировать подынтегральные выражения,
поэтому нужно найти
-g, [х-^'Чх- 1Г^'\х - Х)-'^]=^х-'^{х - ly^'^x - Х)-'^
Читатель, знакомый с теорией когомологий де Рама, сразу
заметит, что дифференциалы ю, д(о/дХ, д^(о/дХ^ должны быть
связаны некоторым соотношением, т. е. некоторая их
линейная комбинация (с функциями от Я, в качестве
коэффициентов) должна быть точным дифференциалом. Тогда
соответствующая линейная комбинация дифференциалов т, dni/dX,
(Pnt/dX^ должна равняться нулю.
Однако давайте повычисляем. Если фиксировать X и
дифференцировать по переменной х, то получим
+ ^х^''(х-1Г'^{х-ХГ"'-^х'"{х-1Г(х-Х)-"^]ёх =
=.(х-1)^ + х^-2х{х-1)^ =
= [(х-Х) + {Х-1)]^ + [{х-Х) + Х]^-
-2[{х-Х) + X] [{х-Х) + {Х-1)]^=
--U + ix-D^ + U + x^-
-2[(х-Х) + Х](Л^+(Х-1)^) =
= со + (2Я-1)||-|а>-3(Я-1)-|^-
Интегрируя обе части вдоль наших циклов, получим
уравнение Пикара — Фукса:
1 dn, d^n,
-щ + {2Х-\)-^ + Х{Х-1)-^ = 0. (2.25)
60 гл. 2. КУБИКИ
Теперь нам потребуются некоторые элементарные
сведения из теории обыкновенных дифференциальных уравнений
с регулярными особенностями'). Определяющий многочлен
для (2.25) имеет вид
<7(/-) = /■(/■-!) + /■ = Л
Это означает, что векторное пространство решений
уравнения (2.25) около точки i=0 порождается функциями ai(X)
и (ko2{X)-\-{\ogX)ai{X)), где cti и стг голоморфны и не равны
нулю в точке 0.
При помощи нормировки CTi(0)= 1 получим
ai{X) = n{X)/2n.
л"
Найдем теперь явное разложение cti в степенной ряд 2 о^к'
п-О
Во-первых,
п>0
Поэтому из (2.25) получаем
Zh{}^- !)(« + 2){п+ 1)а„+2 + (2Я -1){п+ 1)а„+, -f
Переписывая, находим, что
„§Д(« + т)^ ««-(«+l)^«/.+i] А." = 0.
Зная, что 00=1, а fln+i = [(« + ?)/(«+1)]^ «л» получаем
«™ = (-Г)^ (2.26)
Заметим, что попутно мы установили вблизи Я, ^ О
соотношение Я1 (Я,) ~ log А.
Итак, получился весьма специфический степенной ряд
оо
Yi ("У^У^". представляющий ограниченное вблизи особой
п-О ^ " ^
ТОЧКИ к = о решение уравнения Пикара — Фукса. Как мы
вскоре увидим, не случайно, что коэффициенты этого ряда
рациональны.
I) Подробности см. в книге: Коддингтон Э, А„ Левинсон Н. Теория
обыкновенных дифференциальных уравнений. Пер. с англ. — М.: ИЛ, 1958,
гл. 4.
a.II. РАЦИОНАЛЬНЫЕ точки НА КУБИКАХ НАД Г^ 61
2.11. Рациональные точки на кубиках над fp
Все, что мы до сих пор делали с дифференциалом ю
и функцией'я(Я,), относилось к области анализа или
геометрии. Удивительно, что эти вычисления имеют и
арифметические приложения. Чтобы убедиться в этом, нужно
рассмотреть кубические кривые над конечными полями Fp = Z/pZ,
где р—^^нечетное простое число. Пусть задано A,eZ;
возьмем его вычет по модулю р и обозначим через Cj, множество
решений уравнения у^^х{х—1)(л; — Я) в FpX Fp.
Зададимся вопросом:
Какова мощность Сх?
Или,эквивалентно:
Для скольких JCе Fp выполняется х{х—\){х — Я,)е Fp?
Поскольку мультипликативная группа (Fp—{0})
циклическая, х(х — 1){х— X)^fI тогда и только тогда, когда
[jc(jc—l)(jc —А)](''-")/2 = 1 или х = 0, 1, Я,.
В остальных Случаях [х{х—\) {х — Я,)]*"-')^^—1. Все это
можно свести к одному изящному сравнению по модулю р:
(число точек в CJ= Z {1+[-«:(* —1) (л:— Я,)]*"-"Z^}. (2,27)
X Ш It р
Упростим теперь правую часть (2.27). Воспользуемся для
этого формулами характеров:
Е дс* ^ О, если {р — 1) 'Г k,
»шГр
v^ ь 2.28)
Е**^-1, если {p-l)\k. '
хшГр
Они легко доказываются, если только заметить, что
2]л;* ^у* 2-*^* при любом у ФО. Распишем теперь
{jc(jc-l)(jc —Я,)](''-')/2 (2.29)
как многочлен по степеням х. Тогда, согласно (2.28),
единственный одночлен в (2.29), дающий ненулевой вклад в
&[л;(л;—1)(дс —Я,)]*"""^,— это одночлен, содержащий
р
л;""'. Коэффициент при этом члене равен коэффициенту при
xip-^)/2 в полиномиальном разложении выражения [(;i;—1)Х
'Х{х — Я,)](''-')/2 ПО степеням х. Но здесь уже можно непо-
62 ГЛ, 2, КУБИКИ
средственно умножить
L ft-0 J L /-0 J
и коэффициент при jc*'^')''^ равен сумме
А+г=(р-1)/2
Последнее сравнение требует некоторых разъяснений. Целое
число
1 р — 1 р —3 р — (2г — 1)
г1 2 ' 2 • ■ • 2
представляет тот же элемент Fp, что и
а(р-1)(р-3) ... [р-(2/--1)], (2.30)
где а — любое такое целое число, что аг\2'' ^ 1 (mod р). Но
тогда (2.30) = а-(—1)(—3) ... [—(2г—1)] (modp), что
и дает требуемое сравнение.
Далее, если г ^ (р + 1)/2, то
/-1/2Л_ (-1)(-3) ... (-р) ... _»
так что формула для мощности С^ по модулю р имеет вид
Это та же самая формула, что и для функции периодов я (Я,)
голоморфного в нуле решения уравнения Пикара — Фукса!
Конечно, это совпадение не случайно и имеет достаточно
глубокие причины, вскрытые сравнительно недавно
Ю. И. Мининым. В заключение этой главы мы постараемся
дать некоторое представление об этом результате Манина.
2.12. Результат Манина: единство математики
Основной составляющей всех наших рассуждений будет
алгебро-геометрический вариант топологической теоремы
Лефшеца о неподвижных точках. Топологическая теорема
такова: если / — дифференцируемое отображение /: М-^М,
где М — компактное дифференцируемое многообразие,
причем график / трансверсально пересекает диагональ в М'Х.М,
2,12. РЕЗУЛЬТАТ МАНИНА; ЕДИНСТВО МАТЕМАТИКИ 63
ТО ЧИСЛО Лефшеца (число неподвижных точек) равно
L{f)= Е ар(/)=Е(-1)''Тг[Г: Н'ЧМ; С)-* Н'ЧМ; С)],
где Стр ^ О, если f{p)¥=p, и cfp=\ (соответственно —1),
если график / пересекает диагональ с положительной
(соответственно отрицательной) ориентацией'). Трансверсальность
в точке р (в локальных координатах) означает, что
отображение (тождественное — /) имеет максимальный ранг в
точке р. Поэтому
a(p)=sgndet[/-/p(/)],
где Jp{f) — матрица Якоби отображения / в точке р. Пусть
А — комплекснозначная треугольная матрица
тогда
det[I-A] = Z{-W Е а/, ••• а/^=Е(-1)'Тг(ЛМ),
где Л'Л обозначает линейный эндоморфизм, который А
индуцирует на г-й внешней степени £).". Формулу Лефшеца
для числа неподвижных точек можно теперь переписать
в виде
. let [1 - Jp (/)..
г, р п=0
^(f)=Z(-^yiJJn-ilu =Z(-^r'^r(r\н'^ш^ (2-31)
Обратим внимание на то, что у нас получились две формулы
для L{f): одна выражена через локальные инварианты,
а другая — через глобальные.
Пусть теперь М — компактное комплексное многообразие,
Г — функтор глобальных сечений и
Г^о,о Л^ YsP'^ -^ Г^о-2 -^ ... (2.32)
^ комплекс Дольбо на М, так что
.5^0. q _ пучок (О, q) -фарм класса С°° на М.
(Подробнее об этом см. Ганнинг и Росси [2].) Группы кого-
мологий этого комплекса обозначаются
НЦМ-а) или Н^''>{М).
') См„ например, Спеньер Э. Алгебраическая топология. Пер, с англ.—
М.: Мир, 1971 гл, IV, § 7.
64 ГЛ. 2, КУВИКИ
Если М — кэлерово многообразие, то H'i{M;0) является
прямым слагаемым в комплекснозначных когомологиях де Рама.
Предположим теперь, что наше отображение F\ М-^М
голоморфно. Тогда / индуцирует соответствующий морфизм на
последовательности (2.32), так что формула (2.31) остается
верной при замене комплекса де Рама на комплекс (2.32).
При этом формула (2.31) принимает вид
г, р п-0
где /"(/)— ограничение отображения Jo{f) на подпростран-
стйо кокасательного пространства, состоящее из ковекторов
типа (О, 1). Но, как и раньше,
i:(-l)^TrA7;(/) = det[l-/';(/)].
Обозначая (1, 0)-компоненту /р(/) через /р(/), имеем
det[l-/^(/)] = det[l-/;(/)].detfl-/;(/)].
Итак, получилась формула
Е(-1ГТг(Г|.'.<л,...)= Е det [!-/(/)]• ^2-33)
р неподв. ^ I' 'P^''i
Замечательно, что формула (2.33) остается верной и в
чисто алгебраическом контексте. Читателя, незнакомого с ко-
гомологиями пучков в алгебраической геометрии над п^)оиз-
вольным алгебраически замкнутым полем k, мы призываем
не смущаться и продолжать чтение. Все используемые
результаты являются формальными аналогами соответствующих
теорем над ,С, и мы надеемся, что эта формальная аналогия
поможет читателю добраться до конца. Во всяком случае,
прелесть полученных результатов должна побудить
заинтересовавшихся читателей к дальнейшему изучению этих
разделов.
Предположим, например, что k — алгебраическое
замыкание поля Fp из р элементов, Xe(Fp—{0,1}), а Af
—множество решений уравнения
y^z = х{х — г) {х — %г)
в k?2 (одномерные подпространства в k^). Другими словами,
М — множество решений уравнения у^ = х{х — 1) (jc — Я,)
в ^2 с добавленной бесконечно удаленной точкой. Пусть / —
отображение Фробениуса:
/: М-*М, {х,у,г)н-^(хР,у'>,гР).
г.12. РЕЗУЛЬТАТ МАНИНА; ЕДКНСТВО МАТЕМАТИКИ 65
Тогда d{xP)/dx = рх"-^ = 0 и H'^{M\0)=Q при л > 1 =
= dimAiW для пучка О регулярных алгебраических функций
на М. Следовательно, по формуле (2.33) имеем
1 — Tr(/*|^f,i^: ^j)=: число неподвижных точек /. (2.34)
Но число неподвижных точек / — это не что иное, как число
точек М, представленных тройками (л, у, г) элементов рр,
поскольку
х=^ хР тогда и только тогда, когда л;е рр-
Так как бесконечно удаленная точка является одной из
неподвижных точек /, формула (2.34) принимает вид
—Тг Г 1я1 ш; 3, = число точек в С,,.
Теперь для объяснения связи между формулой для
мощности Gx и функцией периодов я (Я,) вычислим в явном виде
след /* на Н^{М;(У). При этом нам придется воспользоваться
тем, что если q, q' е М, то
НЦМ\ О)^
^^ (алгебраические функции с полюсами в д к д') ,„ пс\
(функции с полюсами в д) ■+■ (функции с полюсами в д')' ^ ' '
Это получается из точной последовательности пучков
Q-^0-^0{oo.q) + 0{oo.q')-^0{oo-q + oo.q')-^Q,
где "^
С(п •<?) = пучок алгебраических функций на М, имеющих
q единственным полюсом порядка не выше п,
(:?(схз •q)= lim Oiji-q).
n-»oo
Кроме того, при помощи формальных степенных рядов можно
определить дифференциалы на М, и, как и в комплексном
случае, fe-векторное пространство всюду регулярных
дифференциалов одномерно, а образующая локально записывается
в точке q в виде
(й = йх+ ^аг(%)[х — х {q)Y dx. (2.36)
Так же как и раньше, 1 + У^ агЩ[х — x{q)Y удовлетво-
г>1
ряет уравнению Пикара — Фукса, т. е.
= -5j (^разложение ^—(Г^ф ■—в ряд^. (2.37)
66 гл. 2. КУБЙКЙ
Более того, снова используя (2.35), Мы Видим, что
спаривание
j^ (M,u) А 1^ ддффцрц^^ц^^зд^^ J «, (2.38)
Л X ® •—*■ res,(A(u)
невырожденно, поэтому, в частности, dim* Я'(Л/; С) =: 1. Мы
получили алгебраический вариант теоремы двойственности
Серра.
Теперь можно вычислить Тг[/*: W{M;G)-^W(M;G)].
А именно, алгебраическая теорема Римана—Роха (см. гл. 3)
всегда гарантирует нам существование алгебраической
функции Л, имеющей полосы только в q и q', причем полюс в q
простой. Напишем h в виде
1
-f Y,b,[x-xiq)f.
х — х{д)
Тогда отображение / переводит h (х) в
поскольку q выбрано на С^. Поэтому след /* равен
коэффициенту цри \/[х — x{q)] в степенном разложении Л(л;'')©.
Таким образом, согласно (2.36),
Тг/* = ар_1(Я). (2.39)
Но, в силу (2.37),
(я(А-1)^ + (2Я-1)-|^ + 1)а,_,(Я)[;е-^(<7)Г' =
= ^{с(Я)[;с-;е(?)П = 0,
так что ар-\(%) удовлетворяет уравнению Пикара — Фукса\
Кроме того, flp-i (Я,) однозначна в окрестности Я, =: О, поэтому
для вычисления ее степенного разложения можно просто
проделать все формальные выкладки, которые привели нас
к (2.26), что дает
г—о
Для вычисления с нужно только найти число точек на С%
для какого-нибудь одного значения X (что уже сделано).
Итак,
'^^ f \tP Ш; в) = — мощность Cj, =
г.13. ЗАМЕЧАНИЯ о ДВОЙСТВЕННОСТИ СЕРРА 67
2.13. Замечания о двойственности Серра
Обычно в теории комплексных многообразий применяют
другую форму двойственности Серра, а не ту, которая
использована в предшествующих вычислениях. Мы пользовались
невырожденностью спаривания
Н'{М; Qi)'S>H>'{M; ^')-^Н"ЧМ; Й»»), (2.40)
где (t + fe) = (/ + /) = m = комплексная размерность
комплексного многообразия М, а
й' =: пучок голоморфных /-форм нз М.
Когомологии H*(M;Q') вычисляются из точной
последовательности
обобщающей (2.32). Спаривание (2.40) задается формулой
, (©, Ti) (-S. ^ © л Т1,
м
где © есть ^-замкнутая (/,/)-форма, а ц есть ^-замкнутая
(/,fe)-форма. Поэтому в интересующем нас случае обычная
комплексная версия выглядит так:
Н'(М; О) (g) Н''Ш; Q^) ^ С, (tj, ©)^Ua©. (2.41)
Чтобы убедиться, что в комплексном случае это совпадает
со спариванием (2.38), рассмотрим открытое покрытие М
множествами
Ui={M-q), U2 = iM-q').
Тогда если функция / имеет простой полюс в точке q и
единственный полюс q', отличный от q, то соответствующая
1-коцепь Чеха с коэффициентами в (У задается элементом
/1у,ПУ,еС'(М; С-). (2.42)
Построим теперь двойной комплекс групп коцепей Чеха:
0-*&Ш; 0)-*сЧМ; s^'-') -^ &(М; бФ''') -^
У б (г. Л) [в ^g.ag)\f>
^-^с\М', 0)-^с\м: бФ''')-~* с\м; ^•'•') -^
f f ~'А
t t t
в Q Q
68 ГЛ. 2. КУБИКИ
И найдем для коцепи (2.42) представитель dg в Г(.я^''''^.
Для этого возьмем
( гл;
п =
( гладкое в q,
П=(-
гладкое в q ,
(1/2)/ вне некоторой окрестности q',
1/2)/ вне некоторой окрестности <?,
так_что g — Л = / всюду, кроме точек q я q'. Тогда dg =
= dh, и эквивалентность спариваний (2.38) и (2.41) следует
из равенств
\ /со ^ lim \ gf© == \ © л rfgf = \ со л dg.
Дело в том, что (эквивалентная) формулировка спаривания
(2.38) легко распространяется на общий алгебраический
контекст, в то время как формулировка (2.41) имеет смысл
только над полем комплексных чисел.
Глава 3
ТЭТА-ФУНКЦИИ
3.1. Снова групповой закон на кубиках
В этой главе мы займемся введением хорошей структуры
на множестве классов изоморфных кубик и на множестве
кубик с «жесткостью». При этом мы существенно опираемся
на аналитический аппарат тэта-функций и модулярных форм.
Введение здесь этих понятий подготовит также почву для
применения их в более общей постановке в последующих
главах'). '
Как мы видели в § 2.9, если Е — неособая кубика в .СРг,
VI и V2 образуют базис в Я] (£; Z) и Л/ ^ \ ©, то существует
изоморфизм аналитических множеств
р
со.
р^ \
(3.1)
Коль скоро Е я Ё являются группами, хотелось бы, чтобы
это отображение было гомоморфизмом групп. Покажем, что
это действительно так. Для этого обозначим через СРг
множество прямых в .СРг и определим отображение
CPl^E, 1н-> Х; /(р). (3.2)
Легко видеть, что это отображение голоморфно и всюду
определено. Поскольку CPj односвязно, отображение (3.2)
поднимается до отображения СРг-^С, так как С] есть
универсальная накрывающая для Е. Согласно принципу максимума,
последнее отображение должно быть постоянным, и,
поскольку мы нормализовали Е так, что прямая г^О прохо-
') Алгебраическую версию материала этой главы, распространяющую
многие изложенные здесь результаты на кубикн в характеристике р,
можно найти в статье Джона Тэйта (Tate J. Algebraic Formulas in Arbitrary
Characteristic), опубликованной в качестве приложения 1 к книге; LangS.
Elliptic Functions. — Reading, Mass,: Addison-Wesley, 1973.
70 ГЛ. 3, ТЭТА-ФУНКЦИИ
дит через О е £, имеем
Pi + Р2 + Рз = 0 в Е тогда и только тогда, когда
{рр р2' рз}=•^ п £ для L S ср;,
откуда вытекает, что
/(р1) + /(р2) + /(рз) = 0 в Е.
Следовательно, (3.1) еще и изоморфизм групп.
Тут следует добавить пару замечаний. Во-первых, пусть
задано комплексно аналитическое отображение
/: C/(n,Z+n2Z)-*C/(n{Z + n^Z). (3.3)
Тогда функция df/dz двоякопериодическая и, следовательно,
постоянная. Это означает, что если поднять композицию /
с подходящим сдвигом до некоторого преобразования С-*-С,
то полученное отображение будет просто умножением z^—*cz
на некоторую постоянную с. Итак,
С точностью до сдвига, f автоматически является
гомоморфизмом групп.
Во-вторых, возникает естественный вопрос: все ли
комплексные многообразия вида С/{п\Х -{-щ!) — так
называемые эллиптические кривые — возникают из кубических
кривых описанным выше способом. Мы скоро увидим, что это
действительно так. Давайте, однако, разрешим сначала
другой вопрос, уже затронутый нами в гл. 1 и 2.
3.2. Гладкую кубику нельзя параметризовать
алгебраически
Мы- сумели «параметризовать» коники при помощи
отображения, обратного к стереографической проекции, и
получили отображение
С,->• (коника). (3.4)
Сейчас мы воспользовались «обратным» к многозначному
отображению
£->С, рь-*\
0)
о
и получили параметризацию
С^Е. (3.5)
Далее мы опишем отображение (3.5) подробнее, а сейчас
давайте сравним его с (3.4).
, Отображение (3.4), несомненно, алгебраическое
(задаваемое рациональными функциями), в то время как (3.5)—нет.
3,2. КУБИКУ НЕЛЬЗЯ ПАРАМЕТРИЗОВАТЬ АЛГЕБРАИЧЕСКИ ?1
На самом деле не существует таких отношений многочленов
/(2)=р1(2)/р2(г), g(2)=<7l(2)/<72(2),
что
g' = f{f-l){f-X), (3.6)
если только / и g не постоянные функции. Действительно,
если выполнено (3.6), то
Р^? = 4lPi (Pi - Рг) (Р| - ^Р2).
Тогда, поскольку можно предположить (и мы, конечно, это
сделаем), что pi и рг — взаимно простые элементы кольца
многочленов £L[2], а qi и q2 тоже взаимно простые, имеем
pi\ql и <7||р|.
Далее, умножая qi на подходящую константу, получаем
<?? = Pi (Pi - Р2) (Pi - ^Рг). (3-7)
Кроме того, поскольку р|=; (const) (7|, Р2 —полный квадрат.
Рассмотрим теперь семейство многочленов:
Согласно (3.7), четыре многочлена этого семейства являются
полными квадратами, а именно при
(fi.4) = (l,0), (1,-1), (1,-Я), (0,1).
Но если arf— 6г| = квадрат, crj—drf^ квадрат для
некоторых взаимно простых многочленов п и Гг, то
а}1^Гх — 6"^2 = квадрат, c'^V, — ^"^Гг ^квадрат,
а}1^Г\ + 6"V2 = квадрат, с'/^г, + d'/Vj ^ квадрат,
так что многочлены семейства Ur\ + titi тоже становятся
полными квадратами при четырех различных значениях (fi, ^2)
в С Pi. Повторяя это рассуждение и замечая, что степени
многочленов на каждом шаге уменьшаются вдвое, приходим
к противоречию.
Заметим, ато предыдущее рассуждение опиралось на то,
что ХфО, \. Если же, например, % = О, го рациональная
параметризация особой кривой £", несомненно, существует.
Она получается при помощи стереографической проекции
с центром в особой точке (0,0), поскольку каждая прямая,
проходящая, через (0,0), пересекает Е еще только в одной
точке, точь-в-точь как и в случае гладкой коники (см. рис. 3.1).
Если прямая задается уравнением у = ах, а в качестве
параметра на ней выбирается х, то третья точка пересечения
задается соотношением а^х^ =: х^{х—\), т. е. х = а?-\-\.
Итак, третья точка пересечения есть просто (a^-j-1, а^ф'а^,
72 гл. 3. ТЭТА-ФУНКЦИИ
Если а = ±t, то это точка (О, 0). Соответствующие
прямые — это касательные 3-го порядка к £ в точке (0,0)
(см. рис. 3.2). Вместе они образуют касательный конус к Е
Рис. 3.1. Стереографическая проекция особой кубики
В (О, 0), уравнение которого получается из уравнения у'^ =
= х^(,х—1) отбрасыванием всех членов неминимальной сте-
Рис. 3.2. У особой точки на
кубике две касательные
пени, что дает у^ = —х^. Таким образом, стереографическая
проекция из точки (О, 0) имеет вид
£-*£lPi, {х,у)^-*{у,х), (3.8)
и является взаимно однозначной, за исключением точки
(О, 0), которая «раздваивается», т. е.
точка (О, 0) вместе с <сбесконечно близкой хочкой» а=/
(г. е. касательным направлением) переходит в (t, 1);
точка (0,0) вместе с «.бесконечно близкой точкой»
а = —i (г. е. касательным направлением) переходит
в (-1,1).
Можно сказать, что CPi получается из В разрешением
особенности. Отображение, обратное к (3.8), можно продолжить
до всюду определенного алгебраического отображения на
3.3. МЕРОМОРФНЫЕ ФУНКЦИИ НА ЭЛЛИПТИЧЕСКИХ КРИВЫХ 73
все Е, взаимно однозначного всюду, кроме точки (0,0),
которая имеет два прообраза:
- ix, у) ^ (ix/yf + 1, (х/у) {(x/yf + 1)).
3.3. Мероморфные функции на эллиптических кривых
Изучим теперь поле мероморфных функций на неособой
кубической кривой.
Мы хотим научиться строить такие функции на Е или,
что то же самое, двоякопериодические функции на ,Cj с
периодами Я1 и Л2 (линейно независимыми над R). Заменяя
(О = dx/y на С(л с подходящей константой с, можно считать,
что
Л1 = 1. (3.9)
Тогда из второго соотношения Римана, приведенного в § 2.9,
следует, что
(1тл2)>0. (3.10)
Далее мы всюду вместо Лг будем писать т. Если
/—периодическая и голоморфная функция с периодом 1, она
разлагается в ряд Фурье
/(«)= Z а,ё^"^.
П—00
Но если /(и + т)=/(и), то сразу получаем противоречие,
так как тогда
апе^'"^ = ап. (3.11)
Ослабим чуть-чуть соотношение периодичности, так чтобы
вместо (3.11) оно привело к некоторому соотношению между
On и On+i. Множество таких функций будет тогда составлять
не более чем одномерное векторное пространство. Потребуем,
чтобы
/(и + т) = е-2«'(«+«)/(ы).
Это приводит к равенству
т. е. а„е2"'(''*+") = Яп+ь Поэтому, если начать с Оо = 1 и
положить а = (т/2), то получится
а„ = ехр \ 2л1 ( J] (* ~ "г)] т \= ехр {ninh).
так что
/(«)= Z ехр{ш-(л'^т + 2пи)}. (3.12)
f}-._0O ■ ■
74 гл. 3. ТЭТА-ФУНКЦИИ
Согласно (3.10), если и лежит в компактном подмножестве '£],
то при достаточно большом |п(
|ехр{п/(лЧ + 2пи)}( = ехр(—п(/гя1гат + 21гаи)} ^
^ ехр{—п(л/2)л Irax}.
Следовательно, ряд (3.12) сходится абсолютно и равномерно
на компактных подмножествах, и голоморфная функция
(3.12) обозначается
в[о](и; т), (3.13)
или пока что просто В (и). Заметим, что функция 9 (и) четна.
Итак, то, что мы построили, с точки зрения теории рядов
Фурье больше всего похоже на голоморфную функцию на
£ = C/(Z + Zt). Начнем теперь с другого конца.
Вспомним, как строились все мероморфные функции на римановой
сфере .CPi. Этот процесс можно свести к следующим шагам.
1. Отыскиваем однородную форму (сечение некоторого
линейного расслоения) на CPi с единственным простым
нулем; обозначим ее через X
в + Т, тй+Т+1
Рис. 3.3. Фундаментальная область
эллиптической кривой с периодами 1
и X
в+1
2. Действуем на эту форму группой автоморфизмов .C.Pi
и получаем весь набор линейных форм 0^+ ЬУ, где а, b ^С
3. Строим все мероморфные функции на £XPi, взяв
отношения произведений:
(аД + б,/) ... (аД + ЬгП
/=■
{c,X + d,Y) ... {CrX + drY)
Мы проделаем аналогичную процедуру на Е, где функция
9(и) будет играть роль однородной формы X
Для начала рассмотрим область в С, изображенную на
рис. 3.3. Она называется фундаментальной областью для Е,
поскольку при отображении (3.5) эта область однократно
покрывает Е, за исключением того, что противоположные
стороны параллелограмма на рис. 3.3 на Е отождествляются.
Чтобы сосчитать число нулей 8 на рис. 3.3, вычислим контург
ный интеграл:
а+т
^~ 5 rflog9 = -^ 5 (-2ni)du^l,
3 ipac 3J3i »+t+J
8,8. МЕРОМОРФНЫЕ ФУНКЦИИ НА ЭЛЛИПТИЧЕСКИХ КРИВЫХ 75
поскольку
9(и+1)=9(«), е(н_Ьх) = е-"'С+2«)9(и). (3.14)
Чтобы установить местоположение этого единственного нуля,
вычислим
■a+t+l
[СЧ-Т+1
S dlogQ +
а+т -|
+ \ [xd log 6 + И (—2m') du + r {—2ni) du] ==
a+t+l J
= 2^ {(- ni) [(x + 2a + 2) + 2 • (целое число)] +
■+ [(целое число) • (2ш'х)]'+ (л/) (2а + 2х + 1) rf 2ntx} =
= (1/2 + х/2) + от + лх, т, neZ. (3.16)
Таким образом, нуль 6 расположен в центре
фундаментальной области, как и показано на рис. 3.4.
с+1
нуль в
Рис. 3.4. Нуль 9 (и) в фундаментальной
области
0. 1
Пусть теперь pi, ..., рг а qi, ..., qr — такие точки Е, что
5]р/^Х9/> или, если их рассматривать как точки £,.,
^Pj — ^qj = m-{- пх при от, neZ. Построим функцию
Пв(«-Р/-(1/2 + т/2))
f(u) = -4f -.
П 9 («-<?>-(1/2+ -С/2))
Ясно, что f (и + 1) =: /(и), а согласно (3.14),
/ (« + х)// (и) = ехр {2ni ( Ер/ - Е 9/)} = ехр {2лтх}.
Это означает, что функция g{u)=' e-^"^'^"f{u) двоякопериоди'
ческая, т. е.
g{u+l) = g{u), g{u + x)^g{u).
Таким образом, g задает корректно определенную мероморф'
ную функцию на £ с множеством нулей pi, ..., рг и
множеством полюсов qi, ..., qr.
76 гл. 3. tstA-oyMKUHM
Обратно, если g(u)—мероморфная функция на Я с
множеством нулей pi, ..., рг и множеством полюсов ^ь •••, Яг,
то вычисление, аналогичное (3.15), дает
1
2ni
д (рис. 3.3)
\ «d log g = m + пх
при некоторых от, п е Z. Итак, доказана следующая
Теорема Абеля об эллиптических кривых. Мероморфная
функция с множеством нулей {р\, ..., рг} и множеством
полюсов {ди • •., Яг} существует тогда и только тогда, когда
^Рг
E<7/e(Z + ZT).
3.4. Мероморфные функции на плоских кубиках
Мероморфные функции на CPi можно записывать в виде
р{х,у)/д{х,у), где р и 9 однородны одинаковой степени.
Мероморфные функции на неособой кубической кривой
EczJu.Pi, конечно, включают в себя и ограничения на Е
частных
p{x,y,z)/q{x,y,2), (3.16)
где р и q опять однородны одинаковой степени. По теореме
Чжоу (Ганнинг и Росси [2], с. 214), все мероморфные
функции на .СРг имеют вид (3.16), а при помощи теоремы Ко-
даиры об обращении в О (Хирцебрух [4], с. 140) можно
показать, что любая мероморфная функция на Е есть
ограничение на Е функции вида (3.16). Мы, однако, покажем, что
все мероморфные функции на Е получаются ограничением
функций вида (3.16), заданных на С.Рг, более элементарным
способом. Вспомним, что групповую структуру на Е можно
задавать и чисто геометрически (см. гл. 2). Уравнение
Pi+P2 = gi + qz в Е
означает, что прямая L, проходящая через точки pi и рг на
Е, пересекает Е в той же точке, что и прямая М, проходящая
через qi и qz (рис. 3.5). Если /(;c,t/, 2)=: О —уравнение
прямой L, а т{х,у,г)^ О — уравнение прямой М, то
ограничение функции
g {х, y,z)= 1{х,у,г)/т{х,у,г)
на Е есть мероморфная функция с нулями в точках р\ и ps
и полюсами в 9i и ^г- Предположим теперь, что мы знаем,
что при г <. Го любую функцию с множеством нулей (рь ...
..., Рг} и полюсов {^1, ..., qr} можно записать в виде
f{x,y,z)/h{x,y,z), где f и Л — однородные многочлены от
3.4. МЕРОМОРФНЫЕ ФУНКЦИИ НА ПЛОСКИХ КУБИКАХ 77
{х, у, г) одинаковой степени. Если
р1+'--+Рг, = Я1+-'-+Яг,' в Е,
выберем такие р' а q' в Е, что
Р,+ ■■■+Рг,-1 = Я,+ ■'■+Яг,-2+Я'
и Р' + Рг. = Яг,-1 + Яг,.
Складывая эти два уравнения, получаем р' = q'. Кроме того,
по предположению индукции, найдется функция fi/Ai с мно-
Рис. 3.5. Точка пересечения прямых I. и Af лежит иа кубике
жеством нулей {р, Рго-i} ^ полюсов {9,, ..., 9^.-2' ?'}
и функция /2/Л2 с множеством нулей \р', p^J и полюсов
{9го-1' 9г,}. 'Го'^Дз функция hh/hihi имеет нули в {р,, .... p^J
и полюса в [9р • • • > Яг}. Итак, всякая мероморфная
функция на Е может быть записана в виде (3.16).
Существует и другое простое следствие этих теорем. Если
мероморфная функция f па Е имеет ровно один простой нуль
в точке р и ровно один простой полюс в точке 9. то р = q,
так что эта функция вовсе не имеет нулей и полюсов. Пусть
/ — мероморфная функция на Е; напишем формальную
сумму
(/)= 2] (порядок / в точке р)р, (3.17)
называемую дивизором /. При заданном q^E есть много
способов выбрать р\ и рг так, чтобы рх-{- р^^ 2q, т. е.
существует много мероморфных функций с единственным полюсом
порядка ^2 в точке q. Если, однако, / и g —две такие
функции, то существуют константы а и 6, при которых функция
а/ + bg имеет в точке q полюс порядка не выше первого
78 гл. 3. ТЗТА-ФУНКЦИИ
и, следовательно, является постоянной. Продолжая
рассуждать таким образом, получаем следующую теорему.
Теорема Римана — Роха для эллиптических кривых. Если
S
Yjfi^^ " <зс^ /■/ ^ 0. ^0 векторное пространство мероморф-
ных функций, имеющих в точках qj, j ^ I, ..., s, полюсы
порядка не выше ri, имеет (комплексную) размерность
S
3.5. jp-функция Вейерштрасса
Предположим, что мы рассматриваем тригонометричеокую
функцию синус как обратную функцию к функции
=(^>=Sor
Имея это в виду, можно надеяться, что и обратная
функция к
ЬЩ= \ — i ^dx
J (х^ + ах^ + bx + с)^'^
окажется достаточно естественной функцией с хорошими
свойствами. Это и в самом деле так. Решение этой задачи
после подходящей нормировки называется jp-функцией
Вейерштрасса, о которой мы уже упоминали в гл. 2.
Мы начнем построение р-функции с помощью только что
доказанной теоремы Римана — Роха. Из этой теоремы
следует существование мероморфной функции на £ с
единственным полюсом порядка 2 в нуле. Построим эту функцию явно.
Сначала положим
в[;](«;х)= 1 ехр{ш-[(п + -^)\ + 2(п + ^)(« + 4)]}.
Этот ряд сходится по тем же причинам, что и ряд,
определяющий 6[о](и; 'х)- Кроме того,
е[;](«+1; т) = -е[;](«; t). (3.18)
Функция в [ I ] является нечетной и, следовательно, имеет
нуль в 0; далее,
в[',](ы + г, т) = (-1)ехр{-л/(т + 2ы)}в[;](ы; т), (3.19)
3.5. р-ФУНКЦИЯ ВЕЙЕРШТРАССА 79
так что, как и в (3.14) —(3.16), б[,'](ы; т) имеет нули
только в точках (Z +tZ), причем все эти нули простые.
Далее, функция сР log в [ J ] (ы; T)/d«'^ двоякопериодическая,
согласно (3.18) и (3.19), и имеет двойной полюс в нуле,
поскольку б[ ,J имеет там простой нуль.
Исследуем теперь свойства периодичности 6 [ j ] (ы; т)
по т. Во-первых, прямо из определения в[|](и; т) имеем
е[1](«;т+1) = е"'/^[,'](«; т),
а обе функции б[,'](т«; т) и 6[j](«; — 1/т) имеют (Z+
+ (—1/t)Z) в качестве множества нулей, обе нечетные и обе
обладают следующим свойством: если мы применим к ним
оператор —d^ log/du^, то получим двоякопериодическне
функции, разложение которых в ряд Лорана имеет вид
1/и^ +константа+ (четнб£е положительные степени ы).
Поэтому, согласно теореме Римана — Роха,
rfnog 9 Г ! 1 (ти; т) rf2 log 9 Г 11 (и; -1/т)
Распишем теперь разложение в ряд Лорана
rf4og9[i](«;T) J
du- ■ = -;^ + Со(х) + С2(т)«2+...; (3.21)
отсюда сразу следует, что при п > О
С2Г.(Т+ 1) = С2™(Т), С2„(—1/т) = Т2<''+')С2„(Т). (3.22)
Заметим, наконец, что
lim е-^'^Ч [ \ ] (ы; т) = ехр {я1 (" + i) } +
+ ехр { — Я1 (ы + -J-) } = — 2 sin (яи),
откуда lim (3.21)=:л'^со5ес'^(яы). Следовательно, все С2п(х)
остаются ограниченными при стремлении т к бесконечности
вдоль положительной мнимой оси. Вместе с соотношением
(3.22) это говорит о том, что функции С2п(т) являются
модулярными формами (см. Серр [8], с. 128—129). Точнее,
С2„ является модулярной формой веса (п+1) {или
2(п+1), в зависимости от того, каким соглашением
о приписывании веса модулярным формам мы
пользуемся).
80 ГЛ. 3. ТЭТА-ФУНКЦИИ
Далее, очень простое вычисление с вычетами (приведенное
в книге Серра [8]) показывает, что векторное пространство
модулярных форм веса 1 имеет размерность О, а векторные
пространства для весов 2 и 3 имеют размерность 1, причем
их образующие вместе порождают градуированное кольцо
модулярных форм. Таким образом, с точностью до константы
С2(х) = I {1/(т + nxf: (m, п)е ((ZXZ) - {(О, 0)})},
С4(х)=Е1/(т + пт)в,
поскольку сходящиеся ряды в правых частях, называемые
рядами Эйзенштейна, очевидно, являются модулярными
формами подходящего веса. Определим теперь f-функцию Вей-
ерштрасса так:
Р(")= ^^ -Coir),
исключив тем самым сомнительный постоянный член в (3.21).
Чтобы понять, почему эта функция решает задачу,
поставленную в начале параграфа, начнем опять с теоремы Ри-
мана — Роха. А именно, если мы рассмотрим функции
где f'=:df/du, TO получим семь функций на C/(Z-f xZ),
каждая из которых имеет полюс только в точке О, причем
это полюс порядка соответственно О, 2, 3, 4, 5, 6, 6. По
теореме Римана — Роха, все эти функции лежат в шестимерном
векторном пространстве, так что существует соотношение
A + Bf + Cf' + Df + Eff + Ff' + G iff = 0.
Разложим левую часть в ряд Лорана около ы = 0:
{p'(«) = -^ + 2c2-f2c4«=+...,
f{u)f(u) = ^ + au+...,
f(u)^-i, + ^ + 3c,+ ...,
[f'iu)P = ^-^-l&c,+ ... .
Следовательно^ С ==£)=:£'=: 0. Нормализуем уравнение,
полагая G = — 1; получим
iff = 4f - 2ОС2Р - 28С4. (3.24)
3.6. ТЭТА-КОНСТАНТЫ ЗАДАЮТ МОДУЛИ ЭЛЛИПТИЧЕСКИХ КРИВЫХ 81
Отсюда видно, что получилось корректно определенное
отображение
f:C/(Z + TZ)-*£,
в кубическую кривую у^ = ix^ — 20с2 (х)л; — 28сл (т). Если
расширить его до отображения
C/(Z + xZ) -* СР2, и ь-> (F. f, 1).
получится всюду определенное отображение, переводящее
точку О, как и следовало ожидать, в (О, 1,0). Это
отображение всюду имеет максимальный ранг, поскольку р'
обращается в О только в четырех точках ветвления двулистного
накрытия
C/(Z + tZ)-*CP„ u^if(u),l)
и имеет в каждой из них простые нули, так что(р" там в нуль
не обращается. Отображение (3.25) тоже инъективно,
поскольку оно максимального ранга и собственное, а
следовательно, является накрытием, но точка (О, 1, 0) имеет только
один прообраз. Итак:
Всякое многообразие вида C/(Z-fTZ) изоморфно
некоторой кубической кривой.
Если мы теперь возьмем дифференциал dx/y на £ и
поднимем его при помощи отображения (3.25), то получим
дифференциал du в нашей области. Поэтому
Х{ро)
Следовательно, (3.25) является обратным отображением к
Х{Я)
3.6. Тэта-константы задают модули эллиптических кривых
Соотношение (3.20) позволяет заключить, что
е [ ; ] (и; - 1/т)=а (т) ехр {р (т) и'+у (т) и} 6 [ j ] («т; т).
Знаменитая формула суммирования Пуассона из теории
рядов Фурье позволит нам впоследствии вычислить а(т), Р(т),
у (т) явно. Это интересное вычисление мы проделаем в конце
главы.
82 ГЛ. 3. ТЭТА-ФУНКЦИИ
А сейчас заметим, что функции (в[',](«; т))*^ и (в[о] («;
т))'^ удовлетворяют одним и тем же соотношениям
периодичности, а именно
f (и + т) = ехр {- 2я1 (т + 2ы)} / (ы). ^^'^^^
Как и раньше, первое соотношение означает, что f
разлагается в ряд Фурье, а второе —что п-й коэффициент Фурье
определяет (п + 2)-й. Поэтому векторное пространство
функций, удовлетворяющих (3.26), не более чем двумерно.
Поскольку (в[. i](«; т))^ и (в[о](«; т))'^ линейно независимы,
они составляют базис пространства голоморфных функций
на iC:, удовлетворяющих (3.26). Кроме того, получаем
отображение
Л: е -* СРь «ь-> (е [ ° ] [Щ х)\ 6 [; ] (а; т)^). (3.27)
Далее, согласно (3.15), Л(1/2 + т/2) ^ (О, 1) и Л имеет там
простое ветвление, так же как и в Л(0)=:(1,0). Поскольку
Л-'((1.0))== (0}> заключаем, что Л является двулистным
накрытием, разветвленным еще над двумя другими точками
СРь Вычислим проективные координаты этих двух точек.
Для начала заметим, что
СР,-*£, <7ь->Ер, реЛ-'(<7).
поднимается до целой функции на СРь а значит, является
константой. Следовательно, две другие точки ветвления pi
и Р2^ Е, в которых разветвлено А, удовлетворяют условию
2р/= 2-0 = 2-(1/2 +т/2) = 0. ;
Поэтому значения Л в этих точках равны
(е[°](1/2; xf, е[;](1/2; т)^), (е[°](т/2; т)^ в[;](т/2; т)^).
Однако по причинам, которые выяснятся позднее,
предпочтительно выразить значения (3.27) точек ветвления Л в
терминах тэта-констант, т. е. четырех чисел
в[о](0; X), е[°](о;т), e[i](0; т), в[;](0; т)
(два из которых нам еще предстоит определить).
Чтобы это сделать, определим сначала четную функцию
Q[°]{u;x)^Q[l]{u+ 1/2; т) = S ехр (ш [nh + 2п(« + 1/2)]},
которая преобразуется по следующим законам:
е[;](« + 1; т) = е[°](«;т),
е[°](ы + т; т) = -ехр{-ш(х + 2ы)}е[^](ы; т),.
3.7. ПРОСТРАНСТВО МОДУЛЕЙ 83
И четную функцию
e[l]{u;x) = Q[\]{u-l/2; т) = Z ехр{ш [(«+1/2)4+
+ 2 («+1/2) и]}
СО следующими законами преобразования:
e[i](« + l;T) = -e[J](«;T),
в[о](« + т; т) = ехр{-яг(т + 2ы)}е['](ы; т).
Это означает, что для любых б, е е (Q, 1}
6 [ е ] (« + т^> т^) = (-1)" ехр {- ш (т + 2ы)} е [ f ] {и; т).
Кроме того, нетрудно показать прямым вычислением, что
е [ ° ] (т/2; т) = ехр {- nix/4} 6 [ ^ ] (0; т),
е [ I ] (т/2; т) = ехр {-яг (т + 2)/4} 6 [ ° ] (0; т).
Таким образом, мы выразили две остальные точки ветвления
отображения h из (3.27) через тэта-константы. А именно, это
точки
(e[:r.e[jn. (-e[ir.e[?n.
где б[*]=б[*](0; т). Следовательно, наша кривая Е
изоморфна кривой у'^ = х{х — 1) (;с — к), где
^--^[1]>П- (3.28)
В самом деле, тогда все шесть двойных отношений Я, 1/к,
1—Я, 1/(1—Я), Я/(Я—1), (Я —1)Д, которые однозначно
определяют Е, заданы через тэта-константы.
3.7. Пространство модулей «структур второй ступени»
на эллиптических кривых
Обозначим кривую у^ = х{х—1){х — к), или, точнее, ее
замыкание в .С.Рг, через Е{к). В гл. 2 мы интегрировали
дифференциальную форму dx/y вдоль базиса группы
гомологии Hi{E{k); 2), состоящего из циклов
уЛ'к) и угЩ. (3.29)
Циклы (3.29) задавались прообразами разрезов на С Pi,
показанных на рис. 3.6 и 3.7. Когда Я меняется, меняются
и 1-циклы (3.29). Ясно, что если % совершит полный оборот
84 ГЛ. 3. ТЭТА-ФУНКЦИИ
и вернется в прежнее положение, то получится
преобразование гомологии
или
Yi(^)b-^Yi(M+2Y2(^), Y2(^)b-*Y2W.
Первое_ преобразование получается движением к вокруг
разреза 01 на один оборот, а второе — движением к через этот
Рис. 3.6. Разрез СР,, над ко- Рис. 3.7. Разрез CPi, над
которым лежит Yi(^) торым лежит У2(^)
разрез. Эти два преобразования, задаваемые матрицами
[о i] « [2 i]'
порождают группу
^^ = {[с rf]^Sp.(Z):[^ ^]-[J ^]mod2}
преобразований плоскости X, задаваемых целочисленными
матрицами, где
Sp.(Z) = |[" ^]: ad-6c=lj.
Мы убедимся в этом, если умножим | 1 справа на 1 1,
LC dj 12/- 1J
Г 1 25 1
чтобы получить 1а|<|6|, на1 - . I,чтобы получить |&1<
<:|а|, и т. д., пока не придем к b = 0. С другой стороны,
ясно, что, как бы мы ни крутили к (возвращая его в
начальное положение), преобразование гомологии будет
тождественным по модулю 2. В такой ситуации говорят, что
группа монодромии семейства {Е{к)} есть Гг.
Как мы видели.
Поэтому X не соответствует однозначно классу изоморфизма
кривой у'^ = х{х — 1)(;с — X). А чему же тогда соответствует
Я,? Если задано X, то задана не только Е{Х), но и
специальный выбор единичного элемента группы Е{Х) (а именно
бесконечно удаленная точка), а также некоторое специальное
37. ПРОСТРАНСТВО МОДУЛЕЙ 85
упорядочение точек второго порядка на Е{К), а именно
(0,0) (1,0), {1.0). (3.30)
Чтобы получить двойное отношение ^^ ~^' : ^^~ ' , ко-
торое даст нам значение к, нужно упорядочить точки
ветвления следующим образом:
21 = ОО, 22 = 0, 2з=1, Z4 = X.
Чтобы получить 1/К воспользуемся упорядочением
21 = ОО, 22 = О, 2з = Х, 24 = 1",
а для (1 — Я,) — упорядочением
21 = ОО, 22=1, 2з = О, Zi—%.
Поэтому при изоморфизме Е{Х)^ Е{1/Х) первая точка
порядка 2 переходит в первую, а вторая и третья меняются
местами. Аналогично, при изоморфизме £'(Я,)^ £(1—Я,)
первые две точки второго порядка меняются местами.
Поскольку изоморфизмы с остальными кривыми £'(1/(1 —Я)),
Е{К/{Х—1)), Е{{к—1)/к) получаются композицией
предыдущих изоморфизмов, заключаем, что шесть различных
двойных отношений, соответствующих одной и той же
эллиптической кривой, отвечают шести возможным упорядочениям
точек второго порядка, или, что то же самое, шести
различным способам выбора упорядоченного базиса в Hi{E{k); fi).
Назовем выбор упорядоченного базиса в Hi{E{k); F2)
жесткостью. Тогда можно сказать, что к задает кривую Е{к)
вместе с жесткостью на Hi{E{%); IP2). Обратно, для
заданной кубической кривой Е с жесткостью на Hi {Е; F2)
существует единственное такое к, что определяемая им жесткость
совпадает с заданной. Но нам еще следует проявить
некоторую осторожность, поскольку существуют два случая, когда
числа
- 1 , - 1' А. 1-1
л, -7-, 1 Л,
д, > ' '"> 1 _ д, > X, - 1 • А,
не все различны. Во-первых, этими шестью числами могут
быть —I, —1, 2, 1/2, 1/2, 2, что соответствует кривой
у^ = х{х2-1). (3.31)
Во-вторых, мо^ет случиться, что эти шесть чисел составляют
множество р, р, р, р, р, р, где р — первообразный кубический
корень из —1. Это множество двойных отношений отвечает
кривой
1/2 = л^—1. (3.32)
Но кривая (3.31), очевидно, допускает автоморфизм
{x,y)^i-x,iy), (3.33)
гл. 3. ТЭТА-ФУНКЦИИ
который индуцирует нетождественное отображение на
^i(£; Рг)- Этот автоморфизм переводит разные жесткости
на Hi{E; IF2) в разные. Поскольку автоморфизм (3.33)
индуцирован поднятием дробно-линейного преобразования СРь
двойное отношение сохраняется. Аналогично, кривая (3.32)
допускает автоморфизмы {х,у)у->{ах,—у), где а —один из
первообразных кубических корней из единицы. Эти
автоморфизмы тоже нетривиально действуют на все жесткости и
сохраняют двойные отношения.
Предположим теперь, что у нас есть произвольный
изоморфизм а: Е{Хо)^Е{'ко), переводящий О, выбранный на
Е, в 0. Тогда имеет место диаграмма
ЕЦо)^
i<f-"
CPi
Eih)
|(М)
CPi
где / — двулистное накрытие, разветвленное над оо, с /(0) =
= оо. По теореме Римана — Роха f-a = cf-\- d при
некоторых константах с м d, поэтому предыдущую диаграмму
можно дополнить до
Е Но) -^ Е{г^
I' i'
CPi -^ СР,
где преобразование р дробно-линейно. Если а меняет
жесткость на Н\{Е{ко); ^2), то, поскольку р сохраняет двойные
отношения, множество шести двойных отношений должно
содержать повторяющиеся числа. Поэтому Е{ко) должна
быть одной из кривых (3.31) или (3.3,2). Все это можно
подытожить таким образом:
Существует взаимно однозначное соответствие между
множеством классов комплексно аналитически
изоморфных пар
(Е, Г) (3.34)
{где Е — кубическая кривая, а Г — жесткость на
Hi {Е; fi)) и множеством С — (О, 1}.
3.8. Автоморфизмы эллиптических кривых
На самом деле можно перечислить все автоморфизмы
эллиптических кривых. Пусть а: Е-*-Е—автоморфизм
некоторой эллиптической кривой Е. Соединяя а с подходящим
сдвигом, можно считать, что а(0)=0. Если а тривиально
3.9. ПРОСТРАНСТВО МОДУЛЕЙ ЭЛЛИПТИЧЕСКИХ КРИВЫХ 87
действует на Hi(E; fi), то точки Е, имеющие на
фундаментальной области Е координаты 1/2, т/2, 1/2-|-х/2 и О
Рис. 3.8. Фундаментальная область для
эллиптической кривой Е с отмеченными точками
второго порядка
(рис. 3.8), неподвижны на Е под действием а. Поэтому а
действует на прямолинейных отрезках так:
(О, 1/2)^->(0, 1/2) или (1, 1/2),
(О, т/2) h-> (О, т/2) или (т, т/2).
(Напомним, что а линейно.) Поскольку а сохраняет
ориентацию, это возможно только при
а == ±(тождественное отображение).
Это наблюдение позволяет составить полный список
комплексно аналитических автоморфизмов кубических кривых;
(a) сдвиги,
(b) ±(тождественное отображение),
(c) на кривой у'^ = х{х'^—1)—автоморфизм, квадрат
которого есть —(тождественное отображение),
(d) на кривой у'^ = х^—1 — автоморфизм, куб которого
равен —(тождественное отображение).
Все другие автоморфизмы получаются композицией
автоморфизмов, приведенных в нашем списке.
3.9. Пространство модулей эллиптических кривых
Пусть <3^ = {т е С: Im т > 0} — верхняя полуплоскость.
Тогда имеется естественное отображение
5^-* С-{О, 1},
-->(-е[П7в[?Г) ^'-''^
[см. (3.28)]. Напишем £т = C/(Z+ tZ). Как мы уже
видели в (3.3), Ех^Ех' тогда и только тогда, когда существует
такая комплексная константа е, что e(Z+Zt) = (Z+Zt').
Это имеет .место тогда и только тогда, когда можно решить
уравнения
^ (d + сх) =1, е{Ь-\-ах) = т', (3.36)
88 ГЛ. 3. ТЭТА-ФУНКЦИИ
Га 61
где, как и в § 3.7, I , eSpi(Z). Это возможно тогда
и только тогда, когда т' = (ат +6)/(cT + d). Поэтому
определим действие Spi(Z) на Ж по правилу
С :]-=
(ат + 6)(ст+^Г\ (3.37)
Тогда множество орбит этого действия находится во взаимно
однозначном соответствии с множеством классов изоморфных
эллиптических кривых, т. е.
Л (jH^ (классы изоморфных эллиптических кривых) ^
^Spi(A^- (3.38)
Объединяем отображения в диаграмму
v^C-{0,l}
Мы устроили все таким образом, что сплошные стрелки
являются голоморфными отображениями. Изучим теперь
строение отображения, заданного пунктирной стрелкой.
ЗЛО. А кстати, попутно получилась теорема Пикара
Пусть
т: S-^36 (3.39)
— естественное расслоение со слоем Е-^ над каждым теЖ
Можно определить действие Spi(Z) на S, согласованное
с действием (3.37), а именно определим изоморфизм
Ех-^Ех', иу->еи, (3.40)
где, как и в (3.36), е = 1/ (ст + d).
Если Я,(т) то же, что и в (3.28), а т =5^ т', но Я,(т) = Я,(т'),
то существует такой элемент А е Spi (Z), что А-г = х'.
Кроме того, мы устроили все таким образом, что при изоморфизме
Ех-^Е{%{%)), полученном нормировкой отображения (3.27),
Он^оо, 1/2(->1, 1/2 + т/2н^0, т/21-»Я,(т).
Следовательно, отображение (3.40) сохраняет точки
порядка 2. Из (3.36) получается, что
1/2ь-^(—cr'-f а)/2 = 1/2, x/2^->{dx'~b)l2 = x'l2,
зло. А КСТАТИ. ПОПУТНО ПОЛУЧИЛАСЬ ТЕОРЕМА ПИКАРА 89
Следовательно,
Л =/(mod2), т. е. Л еГг. (3.41)
С другой стороны, если выполнено (3.41), то композиция
изоморфизмов
Е{Х{х))^Е,^Е'^'^Е{Х{х'))
сохраняет порядок точек второго порядка, так что Х{х) =
= i{x'). Поэтому имеем инъективное отображение
(вложение)
К: T2\3&-^£i—{0, 1}. (3.42)
Чтобы убедиться в том, что отображение (3.42) на самом
деле и сюръективно, будем рассуждать следующим образом.
Для любого ^о^С—(О, 1} существует такое те5^, что
Ех = Е{ко). Поэтому Е{к{т:))^ Е{Хо), откуда мы заключаем,
что Я,(т) принадлежит множеству из шести двойных
отношений, определяемых Xq. Далее, группа шестого порядка
Spi(Z)/r2 эффективно, т. е. без ядра, действует на шести
упорядочениях точек порядка 2, поэтому существует такое
/leSpi(Z), что если г'— А-г, то изоморфизм £(Я,(т'))^
^Е{ко) сохраняет выделенное упорядочение точек второго
порядка. Поэтому ко = X {%').
Предположим теперь, что существует такое /leSpi(Z),
для которого Л-т = т при некотором теЖ Тогда, согласно
(3.36), изоморфизм
Ех -^ Ех, и t—> ей
есть ± (тождественный изоморфизм) только тогда, когда
с =6 = О, а = d= ±1. Поэтому либо Л = ±
(тождественный изоморфизм), либо кривая Ех допускает нетривиальный
автоморфизм. В последнем случае, согласно § 3.8,
X = i или р.
На самом деле из § 3.7 можно получить еще больше. Всякий
нетривиальный автоморфизм Ei и Ер дает нетривиальную
перестановку точек порядка 2, так что А ф Гг. Поэтому наше
последнее утверждение состоит в том, что Гг действует на 3^
без неподвижных точек и, значит, X: 3&-^{Ci—(0,1})
является накрытием. Таким образом, мы можем отождествить
верхнюю полуплоскость с универсальной накрывающей
комплексной прямой без двух точек.
Реплика в сторону: тривиальным следствием этого
последнего утверждения является теорема Пикара, утверждающая,
что целая функция, которая не принимает по крайней мере
двух значений, есть константа. Дело в том, что этими двумя
исключительными значениями можно считать О и 1, и тогда,
по теореме о накрывающих пространствах, задаваемое этой
90 гл. 3. ТЭТА-ФУНКЦИИ
функцией отображение поднимается до аналитического
отображения в универсальную накрывающую С—(0,1}, т. е.
в Зё. Но З'ё аналитически эквивалентна единичному кругу,
так что эта функция должна быть константой.
3.11. Комплексная структура на Л
В § 3.10 мы убедились, что имеется единственное
отображение
/: (С-{О, 1})-*Л,
(3 43)
Я,|—>[класс изоморфизма Е{К)].
Это просто естественное факторотображение ГгХ^^-^
-^Spi{Z)\3&, индуцированное действием группы Spi(Z)\r2.
Поскольку это отображение «в общей точке» шестилистно,
факторпространство относительно действия этой группы
представляет собой одномерное комплексное многообразие
Jl, топологическая эйлерова характеристика которого
удовлетворяет соотношению
6х-7=-1.
Поэтому X = 1, так что это многообразие односвязно. Точки
многообразия J! находятся во взаимно однозначном
соответствии с классами изоморфных кубических кривых, поэтому
оно называется пространством модулей. По теореме об уни-
формизацин для римановых поверхностей (Спрингер [9],
с. 253), Л есть либо С, либо единичный круг. Поскольку на
(С — (0,1}) нет ограниченных аналитических функций,
J? ^ С. На самом деле в этом можно убедиться и без
теоремы об униформизации. Проверим непосредственно, что
рациональная функция
фЩ=^1^Г/-У ^3.44)
инвариантна относительно подстановок Х^—>\/Х и ^i—» 1—К,
а также относительно подстановок, которые переводят %
в 1/{1—к), к/{к—\) и {к—1)/к соответственно. Поскольку
Ф шестилистно, получается, что Л изоморфно образу
отображения
ф: (С-{0, 1})-^0.
Но так как ф — непостоянная алгебраическая функция,
в этом образе не лежит самое большее конечное множество
точек, а поскольку образ односвязан, он должен совпадать
со всем 'С. Заметим также, что, согласно формуле (3.28),
точка в Л, соответствующая кубической кривой Е,
определяется ее тэта-константами.
3.12. /ИНВАРИАНТ ЭЛЛИПТИЧЕСКОЙ КРИВОЙ 91
Далее, если у нас есть алгебраическое (аналитическое)
семейство кубических кривых в .СРг, т. е. семейство {Et}
кубических кривых
где ai/ft(/)—алгебраические (аналитические) функции
некоторого комплексного параметра /, то по теореме о неявной
функции получаем следующее:
1. Существует такая алгебраическая') (аналитическая)
функция
Р: (прямая с параметром t)-^SlP2,
что Р(/) есть всегда одна из девяти точек перегиба кривой
Et (см. гл. 2).
2. Используя р(/) как центр проектирования, получаем,
что функция
/ь-> Я, (/) = (двойное отношение точек ветвления Et)
является алгебраической (аналитической) функцией, так как
множество точек ветвления есть множество нулей дискрими-
нантного многочлена, коэффициенты которого —
алгебраические (аналитические) функции от /.
3. Индуцированное отображение
(прямая с параметром t)-^Jl
является алгебраическим (аналитическим).
Именно последнее свойство и делает Ж «хорошим»
пространством модулей, причем это свойство характеризует Л
однозначно. Заметим также, что если имеется аналитическое
семейство C/{Z -\-x{t)Z), где т(/)—аналитическая
функция, то из формул (3.28) и (3.44) следует, что отображение
прямой t в JI является аналитическим.
3.12. /-инвариант эллиптической кривой
Вернемся теперь к теме, затронутой в § 3.5 и
предшествующих. Пусть Е — кубическая (или эллиптическая)
кривая; выберем симплектический базис в Hi{E;Z), т. е. пару
таких циклов ул м Y2, что Yi'V2 = +l. При другом выборе,
скажем 6i и бг, получим
6i = ау\ — су2, бг = {—Ъ)у1 + dy2,
где а, Ь, с, dsZ и 6r62 = (ad — bc)=-\-\. Группа таких
') Это «неявная> функция, поэтому она может быть многозначной
алгебраической функцией.
92
ГЛ. 3. ТЭТА-ФУНКЦИИ
матриц
[::]
обозначается Spi(Z) или SL2(Z). Она яв-
b
с d,
ляется группой автоморфизмов
{Hi{E;Z), (спаривание, заданное пересечением циклов)).
Число т, при помощи которого Е представлялось в виде
C/(Z +tZ),,получалось у нас как
т = 5 »/ S «. (3-45)
Yi Vi
где со — всюду голоморфный дифференциал на Е. Поскольку
© не имеет нулей, он, согласно принципу максимума,
единствен с точностью до постоянного
множителя. Следовательно, т
полностью определяется самой кривой
Е по модулю действия
Ь \а) + а \ (й
-. - _Vi yi
ar + b
■Г
Рис. 3.9. Фундаментальная
область действия Spi(Z) иа
верхней полуплоскости
сг + d
группы Spi(Z). Кроме того, в
формуле (3.45) может стоять любое
число, принадлежащее верхней
полуплоскости, так как при любом
заданном т можно положить Е =
DJ{Z +tZ), a = du (стандартный
дифференциал на .С), а vi и ^2 —
стороны фундаментальной области.
Следовательно, существует
взаимно однозначное соответствие между множеством j? классов
изоморфных эллиптических кривых и множеством
Spi(Z)\5^, (3.46)
где Ж — верхняя полуплоскость.
В книге Серра [8], на с. 124—125 показано, что Spi(Z)
действует собственно разрывно, а фундаментальная область
изображена на рис. 3.9. Там показано также, что фактор-
Группа Spl(Z)/(rfcтoждecтвeнный изоморфизм} порождена
элементами
I
[J J] " [I W
т. е. преобразованиями
11—>—1/т, 11—^T-t-l.
(3.47)
3.12. /-ИНВАРИАНТ ЭЛЛИПТИЧЕСКОЙ КРИВОЙ 93
Полученная информация позволяет построить другое
вложение Spi(Z)\5^ = j? в проективное пространство.
Напомним, что в (3.22) мы нашли такие функции С2п: 3^-^£к,
что
С2„(-1/х) = т2<»+»С2„(т),
С2„(Т+ 1) = С2„(Т).
Поэтому, раз преобразования (3.47) порождают действие
Spi(Z) на sag,
/ ат-f 6 \ , I j\2 (n+i) / ч
Га bl
для всех 1 , jeSpi(Z). Поскольку С2п ограничены при
т-^г-оо, говорят, что С2п является автоморфной формой веса
(/г+1)- Ясно, что множество автоморфных форм порождает
градуированную,алгебру, и если /о, •••, fn — однородные
элементы этой алгебры одного и того же веса, то
S^-^CFn, ть-^(/о(т), ..., fn{x))
спускается до отображения Spi(Z)\5^-^CPn.
На самом деле несложное вычисление с вычетами,
приведенное в книге Серра [8], показывает, что если
Ма (3.48)
— векторное пространство модулярных форм веса k, а / —
ненулевой элемент Mk, то
ord„ f + j ordj / + 4 ordp / +
+ [сумма порядков /во всех остальных точках 5^/Spi {Z)]=k/6.
(Для вычисления ordo» нужно воспользоваться униформизую-
щим параметром q = e'^"^'^.) Следовательно, сг имеет
единственный нуль в точке р, причем этот нуль простой; d имеет
единственный и простой нуль в точке i, а некоторая линейная
комбинация
Д(т) = Лс2(т)з + Лс4(т)2 (3.49)
является единственной (с точностью до постоянного
множителя) модулярной формой веса 6 с нулем на бесконечности,
причем этот нуль простой.
Теперь мы можем построить отображение
Spi(Z)\5^-^.G"Pi, ть^(с2(тЗ), А(т)). (3.50)
Итак:
1. Если, следуя книге Серра [8], добавить точку оо к
Spi(Z)\5^, считая, что оо есть точка «7 = О в круге с коорди-
94 ^- гл. 3. ТЭТА-ФУНКЦИИ
натой q, а q ^ e^'^^'^, то получится компактное комплексное
многообразие размерности 1.
2. Отображение (3.50) продолжается до всюду
определенного морфизма /: Л-^СРи так что точка (С2(оо)з, О) имеет
только один прообраз.
Поэтому / является изоморфизмом. Итак, мы еще одним
способом показали, что (Spi(Z) \5^)^,С, а именно при
помощи отображения тi—»с|(т)/Д(т). Эта функция т
называется j-инвариантом эллиптической кривой,
соответствующей т. Она является полным инвариантом этой кривой.
Чтобы найти значения Л и S в (3.49), вспомним, что,
в силу вычисления после (3.22), С2{оо)/л,^ и С4(оо)/я^
задаются соответственно членами второго и четвертого порядка
в разложении со5ес^(яы) в ряд Лорана. Следовательно,
С2(оо) = я715, С4(оо) = 2я7189. (3.51)
Поэтому можно взять
А (т) = (22.53) С2 (т) ^- (3^ • 72) а (т) 2.
Заметим, что А(т) — это не что иное, как дискриминант
кубического многочлена Ал^ — 20с2Х — 28с4. Как мы видели
в (3.24), эллиптическая кривая, соответствующая периоду
т, — это просто кривая С, заданная уравнением
у2 = 4л:3 — 20с2Х — 28с4,
поэтому при т-^г-оо две из четырех точек ветвления (С над
осью х) сливаются в одну. Впрочем, нетрудно и
непосредственно убедиться в том, что, например, при Х-^0
■ X.
f dx
J [х (X - X) (X - \)]^'^
становится, как ему и положено, бесконечным.
3.13. Тэта-константы как модулярные формы
Мы закончим эту главу еще несколькими яркими
примерами соотношений между коэффициентами тэта-функций,
которые еще раз укажут на их связь с теорией модулярных
форм. Чтобы понять, в каком смысле коэффициенты тэта-
функций являются модулярными формами, нужно сравнить
в[*](«; т) се[«](«;т + 1) ие[У(«;т)с e[f](«; -^ 1/т).
Давайте просто посчитаем.
Во-первых, соотношение (3.20) позволяет заключить, что
е[I ](«I - 1/т) = а,(т)ехр{р (т)и'^+ у{х)и]в[1](т«; т).
3.13. tSTA-KOhCtAHTH КАк МОДУЛЯРНЫЕ ФОЙМЫ §g
Далее, поскольку функция 6 [ } ] («; т) нечетна по и, член
eY(t)« можно отбросить; тогда получится
е [ I ] («; - 1/т) = ai (т) ехр {Р (т) и^} 6 [ | ] (ты; т).
Ну а Р(т) можно найти благодаря тому, что обе части этого
уравнения имеют одинаковые мультипликаторы, т. е.
одинаково ведут себя при преобразовании
и I—> ы + 1, и 1~> ы + т.
Поэтому, используя (3.18) и (3.19), получим, что
1 = ехр{р(т)(2«+1)}ехр(-ш[т(2«+1)]},
откуда р (т) = nix. Следовательно,
е [} ] (ы; - 1/т) = О) (т)ехр {ягты^} 6 [ f ] (ты; т), (3.52)
и осталось сосчитать лишь ai(T). Оказывается, это самая
интересная часть всего вычисления.
Для начала мы проведем для б[д](ы; т) вычисления,
совершенно аналогичные тем, которые привели нас к (3.52)
в случае б[,' ](ы; т). Получится
б [ о ] ("' ~ Vt) = оо (т) ехр {ягти^} 6 [" ] (т«; т).
Затем найдем ао(т). Положив для простоты ы = О, получим
2 ехр {я/ [«2 (_ 1/т)]} = Оо (т) £ ехр {я/ (nh)}.
Заметим теперь, что ао(т) — аналитическая функция т, так
что достаточно найти ее для значений т = ix, где х
вещественно и >0. Итак, все свелось к уравнению
S ехр {— пп^х) = Оо {ix) J] ехр {— ппЧ}. (3.53)
Найдем теперь преобразование Фурье функции fit)^
= ехр {—лхР}:
оо оо
f (s) = J е-я«'е-2"'*' dt = e-'^'i^ \ ехр {-(я^/^л:^/2(/ + islx)f} dt=
- OO —OO
00
= n-l/2jg-l/2g-ns»/x J e-i'dt =
— OO
tn/2 OO _l/2
96 ГЛ. 3. ТЭТА-ФУНКЦИИ
Здесь-то мы и воспользуемся формулой суммирования
Пуассона, чтобы заключить, что •)
2 ехр {— лхг?} = л;- "2 ^ ехр {— пп?1х).
Сравнивая с (3.53), получаем a,Q{ix)^ x^l^, откуда
е [ ^ ] («; - 1/т) = (т//)"' ехр {тиЧ} 6 [ ° ] (т«; т).
Кроме того,
e[J](«; -1/т)=е[П(«+1/2; -1/т) =
= {xUf^ ехр {я/ыЧ} ехр {яг (ы + 1/4) т} 6 [ ^ ] (ты + т/2; т) =
= (т/гУ^ ехр {я/ыЧ} 6 [ \ ](ты; т).
Далее, замена т на —1/т и ы на ты в последней формуле
дает
е [ ° ] (ты; т) = (//т)'" ехр {— я/ыЧ} 6 [' ] (ы; - 1/т).
Наконец, при помощи этого тождества и определения
тэта-функций вычисляем
е[;](ы; -1/т) = е[^]{ы+1/2; -1/т) =
= (т//)'" ехр {я/ (ы + \l2f т} е [ t ] (т (ы + 1/2); т) =
= (т//)"^ (— i) ехр {я/ыЧ} В [} ] (ты; т).
Итак, собирая все вместе, имеем
6 [ * ] (ы; - 1/т) = (т//)"^ {- it ехр {яшМ 6 [ ^ ] (ыт; т). (3.54)
Еще надо вычислить б[е](ы; т+ 1)- Это делается
непосредственно при помощи определений, а именно
в[; ](ы; т+1)=Х ехр{я1({а+1/2)2(т+1)+2(м+1/2)(ы+е/2)]}=
= е""^[^](ы; т); (3.55)
6 [ в ] («; т^+1)=Е ехр {я/ (tt2(T + 1) + 2tt (ы + е/2)]} =
= Z ехр {я1 («2 (т) + 2tt (ы + (1 - е)/2)]} = в [,! J (ы; т). (3.56)
Из этих формул, например, следует, что
6 [ °о ] (0-. -г)' + е [ i ] (0; т)« + е [ J ] (0; т)« (3.57)
') Ссылка на работу, где впервые появилась эта формула, а также
интересное обсуждение происхождения материала всего этого параграфа
содержится в § 5 гл. 21 классической книги: Уиттекер Э. Т. и Ватсон Дж. Н.
Курс современного анализа. Ч. 2. Пер. с англ.— М.: Физматгиз, 1963.
3.14. ФУНДАМЕНТАЛЬНАЯ ОБЛАСТЬ ПОДГРУППЫ Г, 97
есть модулярная форма веса 2 со значением 2 в
бесконечности; поэтому, согласно (3.51),
(3.57) = ^С2(т).
Аналогично. Н1Г+^[:тм1т+ч1Г)(ч:г'^[оТ)
должно равняться {189/я^)с4{т).
3.14. Фундаментальная область подгруппы Гг
Итак, некоторые многочлены от четвертых степеней
(четных) тэта-констант порождают кольцо модулярных форм.
Ограничимся теперь подгруппой r2c:Spi(Z) матриц,
сравнимых с единичной по модулю 2. Если забыть на
минуту о граничных условиях, то функция с(т) будет
модулярной формой веса k относительно Га при условии, что
с (т + 2) = с (т), с ( 27ЯГт) = (2^ + ^)'* ' (^)-
Напомним, что, как мы показали выше, факторгруппа
Г1 О-]
Г2/{±единичная матрица} имеет образующие 1 и
СП-
Но
поэтому, как легко проверить, 6 [ * ] (0; т)* является
модулярной формой веса 1 относительно Га, если только бе = 0. Но
раньше в этой главе мы показали, что К{т) = — 6[o]V6[i]*
и отображение к: Т2\Зё-^£)1 инъективно. На самом деле
имеет место диаграмма
m m
Гг \ 5^ ^ CPi - {О, 1, оо} (3.58)
i (алгебраическое
^отображение
Jt Ш CPi —{оо}
Область в Зё, изображенная на рис. 3.10, состоит из
шести фундаментальных областей группы Spi(Z), и легко
4 Зак. 107
98
ГЛ. 3. ТЭТА-ФУНКЦИИ
склейка при
помощи
Z-—^Z-b
склеика при помощи
Z
Z—*•
2z-bl
Рис. 3.10. Фундаментальная область Гг, разбитая на шесть
фундаментальных областей Spi(Z)
видеть, что она является фундаментальной областью для
действия Гг. Если б • е ^ О, имеем
6 [ е ] (0; '^) = Z ехр {я/ ((« + 5/2)2 ^ + 2 (tt + 5/2) (е/2)]} =
= X ехр {яг («Ч + S«T + St/4 + е«)}.
Поэтому если л; > О, то получается, что
limer*](0;w) = (l-d),
откуда,согласно (3.54),
lim д;'/2е [ * ] (0; ix) = lim е[ I ] (0; /л;) = (1 - е).
Используя, наконец, (3.55) и (3.56), находим
lim хЩ[1](0; 1 + ix) = е«"*, lim л;'/^[° ](0; 1 + ^) = е.
Из ЭТИХ формул следует, что координатная функция
— 6 [ о ]7э [1У в (3.58) имеет следующие предельные
значения:
/00 -->- О, 10+-^ 00, 1 + /0+-^- 1.
Точно так же функция В[о]7б[?]* имеет предельные зна-
ioo-^l, Ю+ -^00, 1 + гО+-^ 0.
чения
3.16. ТОЖДЕСТВО ЯКОБИ
99
Следовательно, 1 -(-в[J ]7е[?]') = (^[о ]7в[? J}, ДРУ"
гими словами, получилось тэта-соотношение Римана:
б[?г+б[П'=в[:г- (3.59)
3.15. Тождество Якоби
Наконец, все тэта-константы связаны одним очень
красивым соотношением, называемым тождеством Якоби:
5в[,'](и; т)
ди
„., = (-")e[o]e[ne[i]-
(3.60)
Чтобы в этом убедиться, возведем обе части (3.60) в
восьмую степень. Правая часть является автоморфной формой
веса 6 относительно Spi (Z) с нулем в бесконечности (так
называемая параболическая форма). Это немедленно
следует из уравнений (3.54) — (3.56). Уравнение (3.55) дает
дВ[\](и;г+1)\ ^дВ[\](-'-)
ди
= eni/4.
lu-o
ди
U-0
а при помощи (3.54) получаем
дв[,'](и; -1/т)
ди
ди
wo
так что левая часть (3.60) в восьмой степени тоже является
модулярной формой веса 6. Но прямым вычислением
находим, что
Де[}](ц; т)
ди
^_„ = J] я (2л + 1) (-!)"+'ехр (ш-т (tt + 1/2)^},
поэтому, полагая т ^ ix и устремляя х к +оо, получаем, что
левая часть (3.60) тоже имеет нуль в бесконечности. Но, так
как по формуле для порядков нулей модулярных форм
(3.48) — (3.49) существует единственная параболическая
форма веса 6, уравнение (3.60) тоже должно быть верно
с точностью до постоянного множителя. Чтобы найти этот
множитель, сосчитайте коэффициенты при e«'f/'» в обеих
частях уравнения.
4*
Глава 4
МНОГООБРАЗИЕ ЯКОБИ
4.1. Когомологии комплексной кривой
В этой главе мы опять будем предполагать, что читатель
имеет по крайней мере относительное представление о кого-
мологиях пучков и теории линейных расслоений. Этот
материал легко доступен в современной литературе, а к тому же
при знакомстве с когомологиями Чеха топологических
пространств многое можно домыслить самостоятельно. Цель
этой главы — детальное исследование многообразия Якоби
(якобиана), которое внутренним образом сопоставляется
каждому одномерному компактному комплексному
многообразию. Существование этого добавочного многообразия и
придает теории одномерных компактных многообразий
изящество и законченность, недоступные теории комплексных
многообразий большей размерности. Многомерная теория все
еще часто сводится лишь к попыткам в том или ином
частном случае восстановить или чем-то подменить одномерную
теорию.
Для начала пусть С — компактное комплексное
многообразие размерности I. Поскольку оно триангулируемо, С тем
самым является конечным симплициальным комплексом или
конечным клеточным комплексом. Нетрудно показать, что
как клеточный комплекс С представляется в виде букета 2g
одномерных сфер ai, Pi, аг Pg с общей точкой р, к
которым приклеена двумерная клетка С, как показано на
рис. 4.1. Следовательно,
Но (С; Z) = Z- {р}, Я, (С; Z) = Е (Z • {а,} + Z • {р/}),
HiiC; Z)^Z-{C}.
Целое число g называется родом кривой С. Из рис. 4.1 также
ясно, что
a/-Pft==6/ft (символ Кронекера), а/-а^ = 0, p/-Pft=:0.
Ввиду этих формул {а/, р^} называется симплектическим
базисом H\{C,Z).
Для начала возьмем точную последовательность пучков
на С:
ebiH j
0->Z->C' ^0*->Q, (4.1)
4.1. КОГОМОЛОГИИ КОМПЛЕКСНОЙ КРИВОЙ
101
где о — пучок голоморфных функций на С (мы уже
встречались с ним в гл. 2), а О* — пучок нигде не обращающихся
в нуль голоморфных функций на С. Его первая группа кого-
мологий Н^{С;0*) — это в точности группа классов
голоморфно эквивалентных линейных расслоений на С. Мы
будем строить многообразие Якоби для С при помощи сле-
Рнс. 4Л. Как разрезать
одномерное компактное комплексное
многообразие так, чтобы расстелить
его на плоскости
дующего куска точной последовательности когомологий для
последовательности (4.1):
0->ЯЧС;Х)->Я'(С;С')->Я'(С;С*)->Я2(С;2)->0. (4.2)
Определим многообразие Пикара кривой С:
Pic°(C) = Я' (С; а)/Я' (С; Z) =
= ядро(Я1(С;С'*)->Я2(С;/)). (4.3)
Уже для того, чтобы только написать последовательность
(4.3), нужно предположить массу вещей о когомологиях
пучка О на С, в частности, что Я"(С;С)=0, как только
rt > dime С = 1. Этот факт, как и многие другие,
используемые здесь без доказательства, можно найти (с
доказательством) у Ганнинга в [3]. Все они концентрируются вокруг
изучения двойного комплекса пучков
t t. t
^"■2-i>v-
A 2.
/1.1.
■^
2. 1 .
/O.l.
^о.о_£^^..о_а^^;г,о_£.
(4.4)
0->C->C? -^ Q' -^Q?
102 ГЛ. 4. МНОГООБРАЗИЕ ЯКОБИ
где
^'•/=: пучок комплекснозначных дифференциальных
. С°°-форм типа (i, j) на С;
Q' = пучок голоморфных /-форм на С
{(y = Q°). Дело в том, что биградуированный комплекс
(2 -J^''', д-{-д) является конечной резольвентой постоянного
пучка С, поэтому его глобальные сечения можно
использовать для вычисления обычных групп когомологий де Рама
Я*(С; С). Гораздо более глубоким следствием из теории
Ходжа для кэлеровых многообразий является то, что
спектральная последовательность, ассоциированная с
фильтрацией F{p)= 2 j^''' комплекса (4.4), «вырождается в члене
Ei>. Иначе говоря,
Н°(С; С) = НЧС; О),
Я' (С; С) S Я' (С; О) ф Я" (С; Q')-
4.2. Двойственность
Спаривание
Я' (М; С) X Я' (М; С) -> С. (©. л) ^-^ U л л (4.5)
невырожденно и кососимметрично, поскольку оно является
комплекснфикацией w-умножения в целочисленных когомо-
логиях. Базис
{dludy\t},,k.x 8 (*-6)
в Н^{С; Z), такой, что
V V
называется базисом, двойственным по Пуанкаре к базису
{а/, pft} в Hi{C;Z). Далее, если {юь .... щ} — базис
H°{C;Q^), то (О, I)-формы юь ..., ©g тоже замкнуты и
линейно независимы. Точнее, они представляют линейно
независимые элементы Я^(С;С), и поскольку они лежат в
пространстве
J-замкнутые (0. 1)-формы _ „i ,^. ^> ^ „i ,^, р..
3-точные (О, 1)-формы
ТО, ПО соображениям размерности, эти формы должны
составлять в нем базис. Следовательно, группа де Рама есте-
4.3. КЛАСС ЧЖЭНЯ ГОЛОМОРФНОГО ЛИНЕЙНОГО РАССЛОЕНИЯ
103
"(0, -
•
.©gj
= [/Q]
rdh -
•
-d%.
ственным образом распадается в прямую сумму
Я'(С; С) = (подпространство, порожденное {©i, ..., o)g}) +
+ (подпространство, порожденное {©i, .... C0g}) =
а1!Я'-°(С) + ^'(С).
Отсюда легко видеть, что матрица S = \ Ю/ имеет
h
максимальный ранг, поэтому при подходящем выборе ©ь ...
..., (Og получим
S = (единичная матрица).
Далее мы будем считать, что ю/ выбраны именно таким
образом; тогда
(4.7)
где Q — комплекснозначная g X g-матрица максимального
ранга.
Из формул \ (О/ Л ©4 = О следует, что
Q = 'Q (4.8)
(это называется первым соотношением Римана), а из
формул Г/ \ Ю/ Л ю/j > О — что
G = (мнимая часть Q) = положительно определенная
симметричная матрица (4.9)
(это называется вторым соотношением Римана; мы уже
получили его частный случай в гл. 2). Таким образом,
L/ qJl-/ oJl'q 'qJl-/ oJ==^4o gJ-
Отсюда следует, что столбцы матрицы [/ Q] линейно неза-
^ Г/ Q-J
висимы над R, так как иначе матрица 1 _ I не могла
•- / ей J
бы иметь ранг 2g.
4.3. Класс Чжэня голоморфного линейного расслоения
Теперь мы можем начать изучение структуры
многообразия Пикара, которое было определено в начале этой главы.
Из комплекса (4.4) видно, что отображение Я' (С; Z)->-
104 ГЛ. 4. МНОГООБРАЗИЕ ЯКОБИ
-^Н^(С;0) — это просто ограничение естественной проекции
Я'(С; С)-^ Я'(С; С). ^^ ,^^
2_, а/Сй/ + 0/(0/ f-^ Zj t*/®/-
При этом проектировании отображение H^{C;R)-^H^{C;0)
является изоморфизмом вещественных векторных
пространств, поскольку дифференциальная форма вещественна
тогда и только тогда, когда она совпадает со своей
сопряженной, т. е. тогда и только тогда, когда она имеет вид
2j 0/(0/ -{• й/Ю/. Следовательно, определен естественный
изоморфизм
Р1С"(С)^Я'(С;К)/Я'(С;Х), (4.II)
причем комплексная структура на этом 2^-мерном торе
индуцирована отображением (4.10).
Чтобы продвинуться дальше в понимании (4.3), вспомним,
что группа когомологий Я^(С;С*), вычисленная по Чеху,
представляет собой просто группу классов голоморфной
эквивалентности комплексных голоморфных линейных
расслоений на С. Топологически такие линейные расслоения
классифицируются их классом Чжэня, который является
элементом H^{C;Z)^Z. (См., например, Стинрод [10].) Нужно
проверить, что отображение
H\C\0*)^№{C;Z) (4.12)
в последовательности (4.2) — это действительно отображение
в класс Чжэня. Тогда можно будет заключить, что Pic''(C) —
это пространство модулей топологически тривиальных
комплексных голоморфных линейных расслоений на С.
Итак, разберем определение отображения (4.12). При
этом мы воспользуемся следующим результатом из книги
Ганнинга по римановым поверхностям [3]: любое линейное
расслоение на С есть произведение расслоений вида
Lp = голоморфное расслоение, соответствующее дивизору,
состоящему из одной точки р е С
или Lp . Поэтому мы докажем, что при подходящем выборе
знака в (4.12) {Lp}t—^-{-l. Воспользуемся покрытием С
множествами и, Vi, Vi, строение которого возле точки р
показано на рис. 4.2. Если z — аналитическая координата на Ц
с z{p) = о, то
г на и, 1 на Vi и Fj
4.3. КЛАСС чжэня ГОЛОМОРФНОГО линейного расслоения 105
дает нам глобальное сечение Lp, т. е. функция перехода
Фир, склеивающая £/ X С и F/ X LCJ при построении Lp,
имеет вид
а фр^,р^,= !• Первый шаг при вычислении образа
{'Puvr fuv,^ Ф^,,^,,} е Я'(С; О') (4.13)
состоит в выборе I-коцепи Чеха с коэффициентами в О,
которая переходит в (4.13) при отображении
Воспользуемся функциями
где выбраны те ветви Ьдфу^^ и log фур,,, которые совпадают
£/= внутренность
диска
К,=
Рис. 4.2. Покрытие Чеха кривой С тремя открытыми множествами для
вычисления класса Чжэня Lp
на вещественной и отрицательной полуоси г. Далее
вычислим кограницу Чеха от (4.14):
S (4Л4)у^,^^ == -^ (log фур,, - log 4>uvd =
( I ( правой ■)
\ О \ левой j
(правой"
О "^ (левой Г компоненте f/fl 1^1 т^2-
Ясно, что этот элемент представляет образующую группы
когомологий Чеха Н^{С; Z).
106 гл. 4. МНОГООБРАЗИЕ ЯКОВИ
Для Сравнения когомологий Чеха и де Рама
воспользуемся диаграммой комплексов:
ь ь ь
ь ь ь ^
Ь Ь Ь (4.15)
t ft t
ft ft
0 0 0 0
На линейном расслоении {l^g} еЯ'(С; С*) можно ввести
метрику, найдя такие функции г^;. £/«"*■ К+> что
и=Г^\1а^\\ (4.16)
Тогда
{|„р} е Я' (С; С') н-> {log lap} е С (С; С') н->
Этот последний элемент представляет тот же класс в
Я2(С;С), что и {-^(31og|„p}eC4C; ^^), поскольку их
разность является кограницей в двойном комплексе (4.15).
Но, согласно (4.16), (3logi^p = <5bgг^ — (3logгр, так что
тот же класс представляется элементом
Поэтому, например, в случае Lp можно взять
Г1/1гр вблизи границы U,
^ («сглаженная» положительная функция около центра,
Следовательно, \ ^^^^^ ^и = Р ^°^ ^у = J(-^bgz) = 2те,
t/_ дУ ау
так что (2ni)-'{(3c/logra} е Г^!^'' и в самом деле является
представителем де Рама класса Чжэня Lp. ,
4.4. ТЕОРЕМА АБЕЛЯ ДЛЯ КРИВЫХ 107
Из Предшествующих рассмотрений ясно также, что если
линейное расслоение имеет постоянные функции перехода
Фар, то его класс Чжэня равен нулю. Обратно,
коммутативная диаграмма пучков
0->Z-»>C->C'->0
II П П
0->Z->C->C"->0
дает коммутативную когомологическую диаграмму
Я'(С; С)->Я'{С; С')-^ННС; Z)
I' 1 I
ННС; а)-^ННС; (У)->НЧС; Z)
и, поскольку мы доказали сюръективность отображения а,
ясно, что линейное расслоение с нулевым классом Чжэня
можно получить при помощи постоянных функций перехода.
4.4. Теорема Абеля для кривых
Напомним теперь теорему двойственности Лефшеца из
алгебраической топологии, в которой утверждается, что на
любом компактном многообразии М существует
невырожденное спаривание
Я, (М; С) ® Н' (М; С) -> С. (y. ф) ^^ J ф- (4.17)
V
Ограничение этого спаривания на целочисленные гомологии
и когомологии целочисленно и унимодулярно. Положим по
определению
Я,,о{С) = {Я°.'{С))^ Яо,,(С) = (Я1.о(С))^ (4.18)
где индексом X обозначен аннулятор соответствующего
подпространства относительно спаривания (4.17). Тогда имеет
место разложение
Я,(C;C) = Я,.o(C)-fЯo.l(Q
на комплексные подпространства, причем, как и раньше,
проекция
Я,(С;Р)^Я1,о(С) (4.19)
является изоморфизмом. При помощи спаривания (4.17)
также можно отождествить Hi,o{C) с Я''°(С)* —
комплексным векторным пространством, двойственным к Я''°(б).
Положим по определению
A\b{C) = Hi{C;R)/H,{C;Z) (4.20)
108 ГЛ. 4, МНОГООБРАЗИЕ ЯКОБИ
И введем на этом факторпространстве комплексную
структуру при помощи проекции (4.19).
Чуть позже выяснится, что как комплексные торы
Alb{C)^Pic«(C). (4.21)
(Это «двуликое» многообразие и называется многообразием
Якоби.) Изоморфизм (4.21) — это замаскированная форма
классической теоремы Абеля (с которой мы уже
сталкивались в § 3.3 в случае ^==1). Прежде чем мы убедимся, что
все сказанное действительно имеет место, нам потребуются
еще некоторые конструкции.
Во-первых, выбрав отмеченную точку ро е С, можно
задать отображение
к С->А1Ь(С), Р^1 \ ). (4.22)
Это отображение имеет смысл, поскольку выбор пути у из
точки Ро в р однозначно определяет гомоморфизм \ :
V
Я'(С; R)—»R, который благодаря спариванию (4.17)
действительно является элементом Hi{C;R). Выбрав другой путь
из Ро в р, мы, возможно, получим другой элемент Hi{C;R),
но он отличается от прежнего на элемент из H\{C;Z), так
что отображение х определено корректно. Для проверки
комплексной аналитичности заметим, что если (оеЯ''°(С),
р
то \ (О является аналитической функцией р. Ну а проекция
р р
\ в Hi^oiC) есть в точности функционал юн-»-\(о из
ро . Ро
Н^-°{С)*. Легко проверить также (как это делалось в
начале гл. 3 для кубических кривых), что имеют место
изоморфизмы
X.-. Я1(С; Z)-> я, (Alb (С); Z),
к:Я'(Alb(С); Z)->Я'(С; Z). ^ '
Базис в целочисленных гомологиях и когомологиях С у нас
уже выбран. Воспользуемся теми же символами для
обозначения соответствующих базисов в Alb (С).
Теперь мы хотим построить изоморфизм между Alb (С)
и Pic°{C). Если не обращать внимания на комплексную
структуру, то это довольно легко. Например, спаривание —
пересечение циклов задает отображение Пуанкаре
Я,(С; 2)->Я'(С;2), а»-* (a'h-*a-a'). (4.24)
4,4, ТЕОРЕМА АБЕЛЯ ДЛЯ КРИВЫХ
109
[Вспомним, ЧТО благодаря (4.17) Я' двойственно Hi.]
Поскольку (4.24) — изоморфизм, он, очевидно, индуцирует
изоморфизм
Alb (С) == 4;^ ^ l^ff = Р1с° (С). (4.25)
И теперь главное, что нужно проверить, — комплексную
аналитичность этого отображения.
Для этого перепишем отображение (4.25). Форму
Ф=Zdl|Ady], (4.26)
можно рассматривать как 2-форму де Рама на Alb (С) или
как кососимметрнческую билинейную форму на Hi{C;R).
В первой интерпретации ею можно воспользоваться для
определения топологического отображения свертки:
НАС; Р)==Я1(А1Ь(С); Р)->Я'(А1Ь(С); Р)==Я'(С; R),
ан->(а, Ф).
Соответствующее отображение на уровне симплициальных
комплексов есть просто отображение «/^-умножения на Ф»,
но тут мы имеем еще и изоморфизмы колец
Я. (Alb (С); .) = Л-ЯЛА1Ь(С); •)- , „7^
Я* (Alb (С); .) = Л'Я'("Alb (С); •)-
где умножение в Я,(Alb(С); •) есть умножение Понтрягина,
определяемое для любой абелевой группы Ли G следующим
образом:
Если Mj — компактные rj-мерные многообразия и а/:
Mj-^G — непрерывные отображения, то произведение
элементов О/ (М/) е Нг/ (G) есть образ выделенной
образующей группы Ну {ЛМ,) в Ну (G) при отображе-
нии П Af/ -> G, {Xj) I—> П «/ i^i)-
Итак, согласно (4.27), отображение ан-»-<а, Ф> можно
понимать как обычное отображение свертки, которое всегда
определено между внешней алгеброй векторного
пространства и внешней алгеброй его двойственного. Далее,
<«/. S dl, л d^/> = (а/, - S ^Л/ Л £?!/> = - (о/, d^/> dl, = dl,.
по
гл.. 4. МНОГООБРАЗИЕ ЯКОБИ
так что отображение свертки совпадает с отображением
(4.24).
Перепишем дифференциальную форму Ф относительно
базиса {(01, ..., ©g, ©i, ...,%} в Я'(М;С). Согласно (4.7)
и матричной формуле после определения G в (4.9), _
4i
idr^J
J (О, "
— Q Q
I -I
-- n-i
Это уравнение можно рассматривать как в Я'(С; С), так
и в Я'(Alb(С);.С). Поэтому в Я^(Alb(С); С) получается
следующее выражение для Ф:
[4ь
^Ул
1 г
'dy\i
-^Лв_
со„
Л[0-' -G-']
со,
■К
■К
(Og]A[G-'QG-' -G-'QG-']
(О,
.со,
_"'g J
coJaG-'
(О,
-«e-
Тем самым Ф есть 2-форма типа (I, I) на Alb (С). Тот факт,
что G-' положительно определена, а Ф есть целочисленный
цикл типа (I, I), превращает А1Ь(С) в юлерово
многообразие (см., например, Хирцебрух [4], с. 154).
Точно так же, как мы разложили Hi(C;C) и Н^{С;Ц)
на подпространства Hi,o и т. д. в соответствии с типом, можно
4.4. ТЕОРЕМА АБЕЛЯ ДЛЯ КРИВЫХ Щ
разложить и векторное пространство
Ноте (Я, (С; С), H,{C; С))
II
Я' (С; С) (8) Я' (С; С)
II
Я'-" О Я^-" + Я'-" ® я»- Ч- Я"'' (8) Я''" + Я"'' о Я"' ^
Когомологии Alb (С) тоже можно разложить по типам при
помощи (4.27). Оказывается, в результате получается
разложение Ходжа на кэлеровом многообразии Alb (С).
Предположим, что задан элемент
феЯ1.1(А1Ь(С))^Я2(А1Ь{С);2).
Тогда ф = Ф, так что ф == 2 ^/а®/ Л ©а, где матрица [cjk]
косоэрмитова. Но наличие на Alb (С) естественного
изоморфизма
Я'.«(8)Я«''-^Я''', (О/(8) ©Аь->(0/люъ
означает, что ф определяет единственный элемент
ф1. о = X СдЮ/(8) ©А е Я1'«(8) Я"''.
Положим теперь ф"-' = ф^'°; мы утверждаем, что
(ф1.о + фО,1) (а ® р) = <ф, а л р> (4.28)-
при всех а, р еЯ1(А1Ь(С); С). Чтобы проверить, что ф^'°-4-^
1+ ф''° действительно удовлетворяет (4.28), вычисляем
(ф|. о _|. jpO. I) („ (g, р) 3= (;^ Сдю, (8) ©А + Z ё/АЮ/ ® ©А, а (8) р> =
= (Z С/А®/ ® ©А, а ® р — р (8) а).
поскольку [с/а] косоэрмитова. Так как феЯ2(А1Ь(С); Z)',
элемент (ф'-" + ф°'^) на самом деле принадлежит
Я'(А1Ь{С);г)®Я1{А1Ь{С);г),
т. е. соответствует гомоморфизму
Hi{C;Z)^H'{C;Z). (4.29)
Снова используя (4.28), немедленно получаем, что если
Ф == ф из (4.26), то последнее отображение переводит а/
в d|/, р/ в dir\j и, следовательно, совпадает с (4.24). Легко
проверить также, что (4.29) является изоморфизмом тогда
и только тогда, когда форма ф, рассматриваемая как косо-
симметрическая билинейная форма на Я1(А1Ь(С); Z), уни-
модулярна.
112 гл. 4. МНОГООБРАЗИЕ ЯКОБИ
В результате мы теперь можем проверять аналитичность
любого отображения, полученного тензорным умножением
на R отображения (4.29), происходящего из формы ф типа
(I, I). В самом деле, композиция
Я,,о->Я1{С;Р)->Я'(С;Р)->Яо.>
задается элементом ф'^^е Ноте (Я^о, Я"''), а потому
является комплексно лилейной и, следовательно,
аналитической. Таким образом, получаем
Alb(C)^Pic«(C), (4.30)
причем изоморфизм задается (1,1)-формой Ф. Многообразие,
фигурирующее в (4.30), и называется многообразием Якоби
кривой С и обозначается J (С).
4.5. Классический вариант теоремы Абеля
Чтобы понять, как все это связано с классической
теоремой Абеля, заметим, что имеет место диаграмма
(4.31)
где (i(p) — класс эквивалентности линейного расслоения,
заданного дивизором р — ро, а х то же, что и в (4.22). Тогда
обычная форма теоремы Абеля есть просто утверждение
о коммутативности этой диаграммы. Приступим к его
доказательству.
Пусть 2 — голоморфная координатная функция на диске
Uo в С; пусть ^i, ^2 е f/o, а {Uо} [} {Uа.}a=i m —такое
конечное покрытие С, что (/^ при а =5^ О не задевает некоторой
окрестности простого пути, соединяющего <7i и ^2 в Uo
(рис. 4.3). Используя результаты § 4.3, легко видеть, что
линейное расслоение L^_ 0 L^^' представлено в Н^{С;С)
коциклом {фар}, где
(4.32)
Фар = 0, если афО, ^ фО.
Согласно теореме Римана — Роха (см. (4.48)), на С
существует
мероморфный дифференциал if) (4.33)
с полюсами только в точках ^i и <72. причем эти полюсы
простые и имеют вычеты соответственно ^\ и —1. Поэтому
«5. КЛАССИЧЕСКИЙ ВАРИАНТ ТЕОРЕМЫ АБЕЛЯ 113
МОЖНО выбрать г так, что
i|2m5il5[ =
"^?^^^^^WШ^Ш
Далее, можно считать, что элементы выбранного нами базиса
dli, i/tift в H^ {С; Z) тождественно равны нулю в некоторой
Чг
Рнс. 4.3. Это не змея; это просто путь нз точки дг в точку (/i
окрестности замыкания (7о на С и что гомологические циклы
а/ и Pft также не задевают Оо. Положим
Тогда вне пути, изображенного на рис. 4.3, (i]) — il)') = da
р
для некоторой С"-функции а. Далее, функция е/ (р) == \ со/
р«
определена в некоторой окрестности Оо.
Имеем векторные уравнения
= -М (О/О^^Аш/Л'фЛ^АелшЛ. (4.34)
где е =—(О, I)-компонента il)^. С другой стороны, е
представляет класс (4.32) в Я' (С; О')^^ поскольку если положить
G^ = o\ug^ при а ф О, Од = О, то д{(з^ = е и б{аа}=—{фар}
114 гл. 4. МНОГООБРАЗИЕ ЯКОБИ
[см. (4.32)]. Но отображение двойственности Пуанкаре
(4.24) переводит \ в такую дифференциальную форму р, что
в>
41
J т] = J р Л л.
в»
Поэтому, согласно формуле (4.34), отображение (4.24) пере-
водит \ в (е-j-e). Следовательно, отображение
Ф:А1Ь(С)->Р1с''(С)
переводит \ в класс расслоения L (8) L~^, что и завершает
доказательство теоремы Абеля.
Согласно этой теореме, если У!\ =^^ ^ Alb (С), то су-
ществует рациональная функция / на С с дивизором
(/) == X Рг ~ И Яг- Чтобы представить такую функцию явно,
положим if == 2 'Фг с полюсами ровно в {рг} и {qr} и
вычетами ^1 в Рг, —I в 9г и т. д., как в (4.33). Тогда
I = ехр \ 2ni \ if) ?
f(p) = exp J2n/Jil)> (4.35)
*. р, J
может, однако, не быть еще корректно определенной
функцией, поскольку
\^, \^ (4.36)
могут оказаться не целыми числами. Тем не менее можно
уточнить if) при помощи суммы 2 О/®/ так, чтобы \ il) = 0
Для всякого /'. Поэтому, как и раньше, полагаем
*'==-Z(S^)^^*
4.6. ТЕОРЕМА ОБРАЩЕНИЯ ЯКОБИ
116
И заключаем, что существуют г^елые числа mi, ,,,, nig, ni,
.,., tig, для которых
[IQ]
mg
n,
= [Sco,A^'j==
Заменим теперь ifi на if — 2 fi/®/- Эта новая мероморфная
функция имеет целые периоды, так что функция (4.35)
определена теперь корректно.
4.6. Теорема обращения Якоби
Повозимся еще немного с отображением х: С
самом деле следует писать Хр^,
/(С). На
поскольку оно зависит от
отмеченной точки ро. Во всяком случае, J {С) является абе-
левой комплексной группой Ли, так что можно ввести
аналитические отображения
х: СХ ••• ХС;-» J {С).
г
Но это отображение не зависит от порядка компонент в
/--наборе, поэтому имеет место коммутативная диаграмма
СХ--Х С-
(4.37)
где С''''^ есть г-я симметрическая степень С. Она является
гладким г-мерным комплексным многообразием, локальные
координаты которого — элементарные симметрические
функции локальных координат на СХ ... X С-
Заметим,что,как вытекает из теоремы Абеля, х: С->/(С)
является вложением при g'$il, поскольку на кривой
положительного рода нет мероморфных функций с единственным
полюсом порядка I. Гомологический класс х(С) в J (С) есть
21 «/ХР/, /=1 g
116
гл. 4. МНОГООБРАЗИЕ ЯКОБИ
(где X — умножение Понтрягина), поскольку
5 d%,hd%,=^\^d%iMi%, = 0,
х(С)
\ d|/Л drift = 6/4 (символ Кронекера),
(С)
J dy],hdr]i, = 0.
х(С)
х(С)
Следовательно, отображение гомологии
М*: H2g{C(su,Z)^H2g{J{C);Z)
является изоморфизмом, поскольку
Итак, из топологических соображений следует, что xg сюръ-
ективно и число листов равно 1. Согласно элементарным
свойствам комплексно аналитических морфизмов, это может
быть только в том случае, если Kg инъективно в общей
точке, т. е. если Kg является изоморфизмом открытых
плотных подмножеств в С<*> и J (С). Это утверждение обычно
называется теоремой обращения Якоби.
Итак, для любой точки La J {С) теорема Абеля
утверждает, что xr'(L) является полной линейной системой
дивизоров степени ^ на С (т. е. максимальным множеством
дивизоров, каждый из которых дает одно и то же линейное
расслоение L). Поэтому хг'(L) естественно изоморфно
проективному пространству Р(Я''(С; ОЩ)), где 0{L)—пучок
сечений L. Следовательно, теорема обращения Якоби
утверждает, что «большинство» линейных расслоений степени g
имеют одномерное пространство сечений. Согласно теореме
Римана — Роха (4.48), это есть просто утверждение о том,
что в общем случае g точек на кривой не лежат в множестве
нулей никакого нетривиального голоморфного дифференциала.
4.7. Снова тэта-функции
Введем теперь понятие тэта-функции для рода g. Пусть
б/, eft е {О, 1}, \,k=l, ..., g; определим
6 =
"S,"
.
.
-6в-
, е =
8l
.
.
-8г-
4,7. СНОВА ТЭТА-ФУНКЦИИ цу
e[«](«;Q)==
== Z exp{ni[V + S/2)Q{ni + 6/2) + 2'(m + S/2){«+e/2)]},
(4.38)
где u^lC/. Из утверждения (4.9) о том, что ImQ>0,
следует абсолютная и равномерная сходимость этого ряда,
совершенно аналогично одномерному случаю, разобранному
в гл. 3. Как и раньше, прямые вычисления дают
0[е](«+^/; £2) = ехр{-шб/}е[*](ы; Q),
(4.39)
e[*](« + Q/; Q)=-exp{-n/(2«/ + e/ + (D//)}e[*](«; Q),
где Е,; Qj обозначают /-й столбец соответственно единичной
матрицы / и матрицы Q. Перед нами опять стоит задача
нахождения множества нулей функций (4.39). Мы проделаем
это совершенно классическим способом, восходящим к Ри-
ману. Материал, излагаемый в остальной части этой главы,
содержится в последней работе Римана, опубликованной еще
при его жизни '). Прежде всего вычислим
е[*](-ы; Q)=5]exp{Kj['(»t + 6/2)Q(m-f 6/2)-f
-f 2'(m-f 6/2)(-«-fe/2)]} =
= 5]exp {ni [H—m - 6/2) Q (-m-6/2)-f 2 '(-т-б/2)(ы-8/2)]}=
= £ехр{ш['(—/n —6/2)Q( —m —6/2) +
+ 2*{-m- 6/2)(ы -f e/2) - 2'( - m - 6/2)e]} =
= ехр{ш-'бе}е[*].
Следовательно, функции (4.38) четны, или нечетны в
зависимости от того, четно или нечетно 'б-е. По причинам, которые
выяснятся в дальнейшем, мы хотим переформулировать это
следующим причудливым образом. Положим
[в]=SS/a/-fe/P/eЯ, (С; F^).
где р2 — поле из двух элементов, а а/, Р/ — симплектический
базис в гомологиях, который мы уже использовали выше.
1Гогда
a([e]) = 'S-8(mod2) (4.40)
') Эта статья Римана («Об обращении в нуль тэта-функций»)
напечатана в Borchardt's Journal fur reine und angewandte Matematik, B.65,
в 1865 г., за год до смерти Римана.
118 ГЛ. 4. МНОГООБРАЗИЕ ЯКОБИ
является квадратичной формой на векторном пространстве
Hi{C; F2) над полем Рг, причем ассоциированная с ней
билинейная форма —это индекс пересечения. Отображение С->
-^1{С) поднимается до иммерсии универсальных
накрывающих С-^Н^'^{С)*. На рис. 4.1 изображена фундаментальная
область CczC относительно действия группы накрытия
ni(C,ро). Используя базис Pi, ..., ^g^H^'^(C)*,
двойственный базису coi, ..., dig, получаем явный изоморфизм
Я1.0(С)*^.Сг, при котором проекция Hi{C;Z) в Я'.''(С)«
соответствует решетке, порожденной столбцами £/, Q/
матрицы [/, Q]. Следовательно,
/ (С) ^ CV( S Z£/ -f Е ЩУ (4.41)
Поэтому, согласно (4.39), множество нулей функции
9 [ * ] (ы; Q) является настоящей хорошей гиперповерхностью
в J (С). Ниже будет показано, что с точностью до сдвига
(множество нулей 9[*](ы; 0)) = И(г_1)(С<г-')).
Прежде чем идти дальше, отметим, что при более
современном подходе тэта-функции рассматриваются как сечения
положительных линейных расслоений на абелевых
многообразиях. Формулы (4.39) появляются тогда как «соотношения
переклейки» или возникают естественно при интерпретации
когомологий некоторых групп, связанных с абелевыми
многообразиями. Читатель, желающий продвинуться в этом
направлении, может обратиться к книге Мамфорда [6].
4.8. Основное вычисление
Мы уже видели, что в случае рода 1, когда C = J{C),
\а)=:1 и \(й=— т, имеет место соотношение
(множество нулей 9[*](ы; т)) + [е/]^
^(множество нулей 9[*/+!]("! ''^))> (4.42)
где [g] рассматривается как точка /(С) в соответствии с
соотношениями
HdC; Р2)=|Я,(С; 2)/Я, (С; Z) с= Н^С; Р)/Я, (С; Z) = /(C).
(4.43)
Покажем, что (4.43) верно и в общем случае. Это
утверждение, равно как и утверждение, приведенное в конце § 4.7, мы
докажем с помощью следующего важного вычисления.
4.8. ОСНОВНОЕ ВЫЧИСЛЕНИЕ jjg
Фиксируем постоянный вектор ее 1С/. Тогда имеет смысл
ограничить 9[*](ы+ е; й) на С и посмотреть на множество
ее нулей там. Простое вычисление, совершенно аналогичное
уже проделанному для случая ^ ^ 1 в § 3.3, показывает, что
это ограничение имеет g нулей (если только 9 [ * ] (ы + е; Q) \с
не равно тождественно 0). Ниже приводится более
содержательное вычисление того же типа.
Заметим, что, согласно рис. 4.1, векторнозначная функция и
(координатная функция в jC/) удовлетворяет условиям
(ы вдоль aj^^ = (u вдоль а^^ + Е^,
(4.44)
(ы вдоль Р7')^(" ^Доль р^) + й^.
Поэтому, обозначая через 9 ограничение на С какой-нибудь
функции (4.38), быть может, еще сдвинутой на постоянный
вектор, при малом е имеем:
ы[нули9(ы(- ) + е)] — «[нули 9(ы(- ))] =
- W Z S ^"+^/) ^'^ ^°^ ^ {u+e+E,)~d log 9 (u+Ei)] -
(4.39) ^^
(4.3Э)
LVpi fe(«</>-a/ + e) . e(«</>-Q/)\
(i;i9, 2m-Z.^/'°SV e(«</> + e) • e(«</>) ^Тэ» ^* ^ ^ ^
Если e необязательно мало, имеется некоторая
неопределенность в выборе ветви логарифма на четвертом шаге в (4.45),
но ответ остается таким же по модулю элементов вида
120 ГЛ. 4. МНОГООБРАЗИЕ ЯКОБИ ,
^/П/£/ + «А, /И/, «/eZ. Если 0[е]^"^(^) обозначает
множество нулей в[г](«; й), то 0[е] + б представляет
множество нулей 0[е](и — е; Q). Это значит, что,
отождествляя С с х(С)с=/(С), можно написать
(сумма g точек из ((в [ * ] + ^) ' ^)) ~
— (сумма g точек из (©[е])'^)^^- (4-46)
Конечно, эта формула не имеет смысла, если
Сс(0[*] + е). (4.47)
Вспомним, однако, что функции в[*](ы; Q) задаются
рядами Фурье и поэтому не могут тождественно обращаться
в нуль на £)/, так как не все коэффициенты Фурье равны
нулю. Следовательно, (4.47) может быть выполнено только
для е, лежащих в некотором собственном аналитическом
подмногообразии в J (С). Значение этого подмногообразия
выяснится чуть позже.
Отметим сначала важность формулы (4.46). Она
означает, что отображение
/(С)-*№), ен->((0[*] + е).с)
является (с точностью до сдвига на константу) обратньш
к отображению х^: С^^'>~^1{С). Это, конечно, другой способ
получения теоремы обращения Якоби.
4.9. Теорема Римаиа
Перед тем как двигаться дальше, сформулируем наконец
теорему Римана — Роха для кривых. Доказательство можно
найти в книге Ганнинга по римановым поверхностям ([3],
с. 111). Теорема утверждает, что
/(Z))-j(Z3)=degZ)-f 1-^, (4.48)
где D = Y,mkPk, Pk^C, degZ3 = E'"fc и
/(Z3)^(размерность векторного пространства мероморфных
функций с полюсами в точках pk порядка не выше щ)=^
= dim Я" (С; С? ((^L^^*)).
/(/))•= (размерность пространства мероморфных
дифференциалов с нулями в точках Pk порядка не меньше /и*)^
= dim Я" (С; С' (К ® (^ Z.;J"*)) =
^ = dim Н'(С; а (ig) L'"k^).
двойственность \^ Ч^ * //
4.9. ТЕОРЕМА РИМАНА JJI
Мы уже видели, что для pi + • • • + Ря> лежащих в
открытом плотном подмножестве в С^^^
1{Р1+ ... +pg)=l.
Это есть просто другая формулировка теоремы обращения
Якоби. Положим 6(ы) = 9[о](«; й). Согласно (4.46),
определим в J (С) константу Римана Кр„ формулой
Е {«(Р): Р е [нули 9 (ы (•) - (е + /Ср.))]} = е. (4.49)
Константа Кр„, очевидно, зависит от выбора отмеченной
точки ро, которой мы пользовались при определении
вложения
х: С-*1{С), Р->(0-
Возьмем теперь pi-f ... + pg так, что /(pi+ ••• Ч-Рг)=1.
и так, что если «(pi) -f ... + «(Рг) = е, то
е(ы(-)-(е + /Ср„)) (4.50)
не обращается тождественно в О на С. По формуле (4.49)
и благодаря тому, что никакой другой дивизор ^i + • • • + <7g
не удовлетворяет условию «(<7i)+ ... +ы(<7г)=е, функция
(4.50) обращается в О в точках pi, ..., pg, и только в них.
Отсюда мы заключаем, что
е(-ы(Р2)- ... -«(pff)-Kpo)=o.
Поскольку р2 -Ь ... -Ь Pg может меняться внутри открытого
плотного подмножества в C^^-i)^ а функция 9 четна,
получаем, что •
(«,^_„(№-'))-fKJce[S].
То же самое рассуждение (с другими значениями Кр„) можно
было бы провести и для любой другой в[^].
Обратно, предположим теперь, что О (е -{- Кр„) = 0; тогда
множество таких е, что 9(ы( •) — е —/CpJ^O, имеет
коразмерность ^2 в /(С). В противном случае 9(ы(-) —е —
—/Сро) имеет нули рь ..., р^ с «(pi)+ ... +u{pg) = e. Но
если /(pi-Ь ... -\-pg)= 1, то все точки pk определены
однозначно, поэтому одна из них должна быть отмеченной
точкой Ро, так как 9 (ы (ро) — е —/<Гр„) = 9 (е-f/Ср,) = 0. А если
l(pi+ ... +Рг)>1, всегда можно найти такой дивизор
Ро4-<72+ ... +qg, что ы(ро) + и(<72)+ ... +u(qg) — e.
Поэтому в любом случае eex(g_i)(C<ff-''). Итак, мы получили
теорему Римана:
(«(^_„(С(г-'))+Кр„) = в["о]. (4.51)
122 гл. 4. МНОГООБРАЗИЕ ЯКОБИ
4.10. Линейные системы степени g
Заметим теперь, что если /(pi + ... +рг)>1, то для
любого заданного q еС существуют такие qi, ..., qg, что
«'(9)+«(92)+ ... +«(9г)=«(Р1)+ ... +ы(рг) = е.
Следовательно, в силу (4.51), Q{u{-) — e — Kp^ обращается
в О в точке q. Поэтому 9(ы( •) —е —/Ср,)^0 на С. С другой
стороны, если 9 (ы (.) — е — Кр„) ^ О, то пусть г —
максимальное целое число, для которого
е(ы(-)-(ы(р,)+ ... +ы(р,))-е-/Ср„) = 0
при всех значениях pi, ..., рг. Тогда при общем выборе
р,. ...,рг+1 функция 9(«(•) —(«(Pi)— ... — "(Pr+i)) —^ —
—/CpJ имеет нули рь ..., pr+i, qi, ..., qg-r-u Поэтому,
согласно (4.49),
« (Pl) -f. . .. -f « (Pr+l) -f Ы (9i) -f ... -f Ы (9g-r-l) =
= u{pi)+ ... -f «(pr+i)-f e,
так что eex(g_r-i)(C(*-^-''). Поскольку r^O, мы показали,
что
l{pi -{-... '+ Рг) ^ 1 тогда и только тогда, когда
(e[o] + S«(Pi)+^J^'*(C)' (4.52)
причем в этом случае пересечение есть в точности pi Ч" ...
... + pg. Интуитивно ясно тогда, что можно получить весь
линейный ряд Ipi-1- ... +pg\, взяв всевозможными
способами
lim{x(C)n[e[:]-fS«(p,) + e + Kj}.
4.11. Константа Римана
Положим теперь
Pic*" (С) = пространство классов эквивалентности линейных
расслоений на С степени г (класс Чжэня равен г).
Соответствие
Pic" (С) -> Pic' (С), {Ц н-> {L ® Lp} (4.53)
взаимно однозначно и, следовательно, превращает Pic''(С)
в комплексный тор. В Pic<*-''(C) имеются два внутренним
образом заданных подмногообразия:
(i) в = {L е Pi68-')(С): dim Я" (С; О (Ц) > 0} =
= образ С<«-'> в Pic^8~'^ при отображении х(г-1):
С(в-1)-^Р1с(г-')(С), (pi + ... + Pe-i) н-^ Lp, ®... ® L,
'Pg-i'
4.11. КОНСТАНТА РИМАНА 123
(ii) S == {LеPid-s-"(С): L® Ь^Ж — кокасательное
расслоение на С}.
S называется множеством тэта-характеристик С. При
отображении (4.53) X(g_i)(C<*-'>)4->-в. Кроме того, по
теореме Римана — Роха
l(pi+ ... +pg_,)=/(/C-(pi-f ... +pg-i)
где К — канонический дивизор, т. е. дивизор,
соответствующий линейному расслоению Ж. Поэтому отображение
«(Pi+ ■•■ +Pg-i)>~>u{K)—u{pi+ ... +pg-i)
переводит X(g_i)(C<«-'') в себя, т. е.
Но функция 9[о](и; й) четна, так что
х,г_ 1, (С(«- ») + Кр, = - Кр, - Х(г-1) (С<г- 0).
Из этих двух уравнений заключаем, что ы(/С) = —2/Ср,,
другими словами, что (—Кр„) соответствует в Pic<*-'>(C)
линейному расслоению, квадрат которого есть кокасательное,
или каноническое, расслоение Ж, т. е. соответствует
элементу S.
Положим теперь
/(„) = ^[']("--^)
е[^](кЧ-/.8/2-fQ-6/2)
Из (4.39) сразу выводится, что
f(u + El) = exp{n/a/}/(«), /(ы -f- Q/) = exp{m'a/fi)//}/(u).
Следовательно, мероморфная функция g(«)=exp{—лг X
X 2 "/*/}■/(") корректно определена на /(С). Посмотрим
теперь на
g{u + e)\c (4.54)
при общем выборе константы е. Эта функция либо
постоянна, либо имеет дивизор (pi-f ... ■\-Pg) — (91+ •••
• •• -^-^g)' где l{qi-\- ... ■\-qg)^l. Поэтому единственная
возможность состоит в том, что (4.54) является константой
при каждом фиксированном е и, следовательно, g{u)
постоянна. Мы заключаем отсюда, что
124 ГЛ. 4. МНОГООБРАЗИЕ ЯКОБИ
Чтобы собрать все воедино, нарисуем диаграмму
/(C)-*/(C)^-^Pic(«-'>(C)
и^-^и — К
Рч
в["о]- ^е (^-^^^
(?)ч- >2
Выясним, что надо поставить вместо (?). Для этого
вспомним, что в (4.43) мы отождествили {[g]} с множеством
точек второго порядка на Alb (С). Но, поскольку
2{-Kp, + [lY) = -2Kp, = u{K)
и (—Кр) соответствует в Pic<*-4(C) элементу из S, то же
верно и для каждого элемента (—•^Ро+[е])- Поэтому
в (4.56) {[1]}^^.
Следует еще заметить, что если/(ы)^9[*](ы; Q)/9[o](«;Q),
то /(«+£■/) = ехр{ш'б/}/(ы), /(ы+й/)=ехр{тое/}/(ы). Это
говорит, например, о том, что линейное расслоение на С,
задаваемое дивизором (©[о]+ '2'^/) ~ (®[о])' тривиально
на множестве, полученном удалением из С простого
замкнутого пути а/, а расслоение (®[о]+'о"'^/)~(®[о])
становится тривиальным при выбрасывании цикла Р/.
Следовательно, линейное расслоение порядка 2 в Pic"(С),
соответствующее [*] при двойственности Пуанкаре, — это просто
то расслоение, которое становится тривиальным при
удалении гладкого представителя (по модулю 2) цикла 2 б/О/ + в/Р/.
4.12. Теорема Римана об особеииостях
Множество в[*] нулей функции 9[*](ы; Q) неприво-
димо, поскольку оно является сдвигом X(г_l)(C(г-^>). Кроме
того, оно имеет кратность 1, так как мы видели, что в общем
случае 9[*](ы-1-е; Q) |^ имеет g различных простых нулей.
Оказывается, кратность точки на тэта-дивизоре имеет
прекрасную геометрическую интерпретацию. Она дается
теоремой Римана об особенностях, которая утверждает, что если
LePic(e-i)(C), то
кратностьг.в = dim Я»(С; (У(1)). (4.57)
4.12. ТЕОРЕМА РИМАНА ОБ ОСОБЕННОСТЯХ 125
Тогда, согласно (4.55) и (4.56),
multi в = multfe е [ f ] (ы; Q), (4.58)
где A = (L®Z,;/«"'4^:p„ + /-8/2 + 0-6/2). Из (4.55),
(4.58) и того факта, что 9[*](ы; Q) четна (нечетна) тогда
и только тогда, когда четно (нечетно) число 'б-е, следует,
что если
LeS (множество тэта-характеристик),
то 5'(L)= (1!тЯ''(С; O'(L)) (mod2) является инвариантом
при непрерывной деформации кривой С). Простое
упражнение по комбинаторике — показать, что 'б-е бывает
четным ровно 2«-'(2* + 1) раз и нечетным ровно 2*-'(2^—1)
раз.
Дальше мы постараемся дать некоторое представление
о том, почему верна теорема Римана об особенностях.
Предположим, что /(pi + ... +pg_i)>s. Тогда, если даны qi, ...
..., Qs, существует такое дополнительное множество qs+i, ...
..., qg-x, что
g-i г-1
Z «(Pfc) = Z иЫ = е.
fc-i fc-i
Для любых р\, ..., pg-i и qu ..., qg-u удовлетворяющих
последнему уравнению,
e(t «(Pi)-S «Ы-е-0 =
\ft-i ft-i /
= 9 (- g и (qk) - ^ S^i«{Qk) - Кр^ = О,
так что
9(х, (О*») - X, (С(*)) - е - Кр,) ^ 0. (4.59)
Обратно, если (4.59) выполнено для s, но не выполнено для
s-fl, то при общем выборе pi, ..., ps, qu ..., qs+\ функция
9(«(-)+t«(P/)-g«(9/)-e-Kp„)
имеет нули ^i, ..., qs+u q^+i, ..., Qg- Поэтому, согласно
(4.49),
a s+1 s
£ и (q,) = e + 2 Ы (q,) - |]^ «(p/),
') Алгебраическое доказательство этого факта дано недавно Дэвидом
Мамфордом (Mumford D. Theta Characteristics of an Algebraic Curve. —
Ann. sci. de i'Ecole Normaie Superieure, v. 4, 1971, pp. 181—192.
126 ГЛ. 4. МНОГООБРАЗИЕ ЯКОБИ
•Л '
Т. е. 2j"(P/)+ 2j «(?/) = е. Поскольку р/ выбирались
/=-1 /=-s+2
произвольно,
/(Р1+ ••• +Ps + qs+2+' ... Ч-9г)>«-
СледоБательно, /(pi + ... 4-Pe-i)>s тогда и только тогда,
когда
9 (х, (С(*)) - X, (С(*)) - Е «(Pi) - Kpj ^ 0. (4.60)
Далее, если z — локальная координата б точке р^С,
а Q{y.{C) — к{С) — е — Кр,) = 0, то
0= lim —^ r-^ г-\ ^ = / -3— (— е — /СрЛ -г-^ (р).
q-*p
ПроБОдя ЭТО рассуждение для каждой точки р^ С,
получим, что
^ ' .e-/CJcD/=0,
до
откуда -^j-(—е —/Ср,) = 0, /=1, .... g.
Повторяя это рассуждение, получим первую половину
теоремы Римана об особ1енностях, а именно: если
9 (хЛС<^') - «ЛС<^') - е - Д-J ^ О,
то все частные производные 9 порядка ^s в точке
— е — /Ср„ равны нулю. В другую сторону доказательство
несколько сложнее, но общая идея, наБерное, ясна').
При помощи теоремы Римана об особенностях можно,
например, охарактеризовать множестБО особых точек в,
которое мы обозначим Osg, как множество линейных
расслоений степени {g—1), имеющих по крайней мере ДБа
линейно независимых сечения. Чтобы прикинуть, какоБа
размерность этого множества, Боспользуемся следующим Бесьма
приближенным рассуждением. Касательное пространство к
пространстБу модулей криБЫХ рода g в точке С есть
Н^{С\0{3~)), где 0' — комплексное касательное расслоение
к С^). В силу двойственности Серра, о которой говорилось
в конце гл. 2, кокасательное пространство тогда есть
Я''(С; J5f(^>), а его размерность по теореме Римана — Роха
раБна
2(2g-2)-f 1-^ = 3^-3.
') См. Lewittes J. Riemann Surfaces and the Theta Function. — Acta
Math., V. Ill, 1964, pp. 51-55.
^) Cm. введение к статье: Kodaira К., Spencer D. On Deformation» of
Complex Analytic Structures. — Ann. Math., v. 67, 1958, p. 328 ff.
4.(2. ТЕОРЕМА РИМАНА ОБ ОСОБЕННОСТЯХ 127
(Роды О И 1 ЯВЛЯЮТСЯ исключениями, так как криБые б этих
случаях имеют группы аБТОморфизмов положительной
размерности.) С другой стороны, сколькими способами можно
устроить (g—1)-листное накрытие jQPi, имеющее род g?
Предполагая, что Бсе точки ветБления простые, можно
сосчитать число N точек БвТБления по формуле для эйлероБой
характеристики: получится
(^—1)-2 —iV = 2 —2^, М = 4д — 4.
Предположим, что три из этих точек 2C.Pi суть О, 1, оо;
тогда остальные (4^ — 7) можно свободно БарьироБать.
Поскольку имеется Бсего «сх)3г-з» различных кривых рода g,
можно ожидать, что фиксироБанной общей криБой С рода g
отвечают oo<.*s-7)-<.3g-3) -- oois-*) накрытий. Другими словами,
для рода g предположительно
dim esg = (g-4), (4.61)
что и действительно оказывается так в случае, когда С не
гиперэллиптическая').
') Доказательство этого факта см. в работе: Andereotti А., Mayer А.
On Period Relations for Abelian Integrals on Algebraic Curves. — Ann.
Scuola Norm. Sup., Pisa v. 21, 1967, p. 209.
Глава 5
КВАРТИКИ И КВИНТИКИ
5.1. Топология плоских квартик
В этом параграфе мы кратко разберем некоторые
наиболее примечательные свойства кривых
CCZ.CP2, (5.1)
задаваемых уравнениями вида F{Xo,Xi,X2)^0, где F —
однородный многочлен четвертой степени. Мы будем
предполагать, что С неособая, т. е. что частные производные
dF/dXj, / = 0,1, 2, не имеют общих нулей в ilPa.
X-.'-Q
G-0
Рис. 5.1. Кривая со стрелочками — это подвижная кривая Ct
Любая такая кривая С аредставляет собой риманову
поверхность рода 3. Чтобы в этом убедиться, возьмем семейство
уравнений четвертой степени
toF + UXiG = О, (5.2)
где G — кубический многочлен общего типа.
В соответствии с (5.2) имеется семейство кривых
Ct, t^aPi, (5.3)
в котором Ct определяется уравнением (5.2), t = {to,t\).
Поскольку Ct неособая, ее малую окрестность в ilLPa можно
S.I. топология плоских КВАРТИК
129
представить в виде расслоения на диски над Ct.
Рассматривая пересечения нормальных дисков с близкой Ct,
получаем, что все Ct в (5.3) диффеоморфны, за исключением
конечного числа значений /, для которых Ct особая.
Рис. 5.2. В вещественно четырехмер- Рис. 5.3. Экземпляр S' X (О, 1),
ном пространстве два вещественно вложенный в вещественно четы-
двумерных диска трансверсально пе- рехмерное пространство
ресекаются по одной точке
Одним из особых значений / является, конечно, / ^ (О, 1).
Когда / приближается к (0,1), можно следить за Ct, рисуя
на вещественной проективной
плоскости R Рг
соответствующую подвижную картинку
(рис. 5.1).
Основной смысл
изображенного на рис. 5.1 состоит в том,
что всюду, кроме малых
окрестностей точек р/
самопересечения кривой С(о,1), близкая к
С(о,1) кривая Ct топологически
устроена так же, как С^ол)-
Вблизи точек р; кривая C(o,i)
выглядит как множество
решений уравнения х-у ^ О, а Ct —
как множество решений х-у^
= е при некотором постоянном Рис. 5.4. Вот почему кривая чет-
ефО. Поэтому в комплексном вертой степени имеет род 3
случае можно восстановить
топологическую модель для неособой Ct, отправляясь от
С(о,1) с тремя особыми точками pi, рг, рз. вырезая из C(o,i)
окрестность каждой из них и вставляя вместо каждой такой
окрестности трубку. Так, возле каждой р/ кривая СфЛ)
выглядела как на рис. 5.2, а близкая к ней Ct изображена на
рис. 5.3.
зс,-0
S Зак. 107
130 гл. 5, КВАРТИКИ И КВИНТИКИ
Как же получается топологическая модель нашей
неособой кривой Ct? Берется множество {G ^0}, представляющее
собой тор (см. гл. 2), и множество {Хг^О}, являющееся
двумерной сферой, в каждом из них вырезаются окрестности
тдчек ри рг и рз, а к границе приклеиваются трубки.
Получается рис. 5.4.
Тем же способом легко убедиться, что род кривой
степени п задается формулой
[род кривой степени (п — 1)]-|-(« — 2),
/1-2
или просто у А = (п — 1) (п — 2)/2.
5.2. Двадцать восемь бикасательных
Вспомним теперь отображение
х: C^J{C), (5.4)
описанное в (4.22). По теореме Абеля х инъективно. На
самом деле отображение х всегда является вложением,
поскольку, согласно теореме Римана — Роха, для всякого
р^С имеется такой голоморфный дифференциал со е
еЯ'>''(С), что со|р^О. Поэтому каждому р^С можно
сопоставить одномерное подпространство касательного
пространства к /(С) в точке х(р): Лрс= Гу(С),х(р). которое является
касательным к х(С) в х(р). Структура коммутативной
группы на J (С) однозначно задает единственный
естественный изоморфизм касательных пространств ф: Tj(C), х(р)—>■
-^Т'/(С), о-Таким образом, получается корректно определенное
голоморфное отображение
З: С^Р(Гу(С).о), Р^{Ф(Л)}. (5.5)
называемое отображением Гаусса. Здесь
Р (векторное пространство V) = (множество всех
одномерных подпространств векторного пространства V).
Нетрудно проверить, что отображение g совпадает с
каноническим отображением
С-^Р(Я1.в(С)*), рь->{{соеЯ'.'>(С): (о|р = 0}}.
Таким образом, отображение g инъективно, если не
существует такой пары различных точек р и ^ на С, что любой
дифференциал со, обращающийся в О в точке р, обращается
в О и в ^. Существование такой пары, согласно теореме
Римана — Роха из § 4.9, означает, что f(/> + ?)=i(p) =
5.2. ДВАДЦАТЬ ВОСЕМЬ БИКАСАТЕЛЬНЫХ 131
■■i(^—1). Поэтому, ОПЯТЬ согласно теореме Римана — Роха,
так что кривая С должна быть гиперэллиптической, т. е.
существует мероморфная функция / на С, задающая
двулистное накрытие /: C^-.CPi. Заменяя р + ? на 2р и
рассуждая аналогичным образом, получаем, что если кривая С
не гиперэллиптическая, g является на самом деле вложением
С в {g—1)-мерное проективное пространство. Степень д(С)
равна степени канонического кокасательного расслоения на
С, т. е. (2^ — 2). В случае ^^3 получается, что любая не-
гиперэллиптическая кривая рода 3 (канонически)
вкладывается в Рг как неособая квартика.
Обратно, если С — неособая плоская квартика, то
векторное пространство однородных форм степени 1 на Рг лежит
в пространстве сечений линейного расслоения на С,
ассоциированного с дивизором пересечения прямой Lb Рг с С. Опять
по теореме Римана — Роха
3</(C-L) = i(C-L)-f 4-f 1—3,
так что i(C-L)^l. Но, поскольку каждый голоморфный
дифференциал имеет всего четыре нуля, эти неравенства на
самом деле являются равенствами, а гиперплоское сечение
С — каноническим дивизором, т. е. множеством нулей
голоморфного дифференциала. Поэтому с точностью до
линейного автоморфизма Рг включение С с ^j есть просто
отображение Гаусса д. Следовательно, все неособые плоские
квартики вложены канонически. Значит, негиперэллиптиче-
ские кривые рода 3 существуют, и на самом деле никакая
плоская квартика не гиперэллиптична.
Итак, вся подготовительная работа проделана, и можно
непосредственно заняться знаменитой старинной теоремой
о том, что для данной неособой плоской квартики С имеется
ровно 28 прямых в Рг, касающихся С во всех своих точках
пересечения с С. Давайте начнем с грубого подсчета кон-
стант,чтобы понять, почему получается именно число 28.
Напомним, что в § 1.9 обсуждалось отображение
двойственности:
^: С->Р2 = (множество прямых в Рг).
В случае плоской квартики степень этого отображения равна
^(С)-(прямая в Р2) = С'Гмножество нулей У\^1-дх~)~^'^-
Поскольку, как мы видели, 2) бирационально отображает
кривую на ее образ, можно ожидать, что род ^(С) равен
11-10/2 = 55. Однако g(C) = 3, и единственное объяснение
б*
132
гл. 5. КВАРТИКИ И КВИНТИКИ
этого состоит в том, что 2) (С) особое. В самом деле, можно
даже проанализировать природу этих особенностей.
Во-первых, 3) имеет максимальный ранг всюду, кроме точек
пересечения С с кривой Гессе:
det
dxl
d^F
6X2 SXq
d^F
dXo dX^
dXi
= 0.
Следовательно, имеются 4-6^24 такие точки, и в общем
случае каждая из них добавляет к 2) {С) одну точку
заострения, т. е. особенность, локально аналитически эквивалентную
f/^ = J^.
прямая в
Параметром у
прямая с
параметром z
Рис. б.б. Локальиыо координаты грассмаиова многообразия прямых в
Pj в точке L
Далее, пусть есть две различные точки р и q на С, такие
что 2){р) = 3) (<7) • Это означает, что касательная прямая L
к С в точке р совпадает с касательной к С в точке q.
Поскольку deg С = 4, порядок касания L с С в каждой из этих
точек равен 2, так что 2) имеет в них максимальный ранг.
Покажем, что ^ (р) = ^ {q) является простой точкой
самопересечения 2)(С). Для этого заметим, что локальными
координатами в Рг в точке L могут служить у и z (рис. 5.5).
Поэтому малая вариация касательной в окрестности точки р
выглядит так, как показано на рис. 6.6. Но на рис. 5.6
= 0,
Ит dist (р. р")
так что матрица Якоби отображения 2) в точке р в
локальных координатах у, г имеет вид (О, а) при некотором а-ф^.
Аналогично Matpnna Якоби SD в точке q имеет вид (6,0),
5.2. ДВАДЦАТЬ ВОСЕМЬ ВИКАСАТЕЛЬНЫХ
183
прямая у
Рис. 5.6. Вот как касательная
к С варьируется возле точки р
Следовательно, 2)(С) имеет нормальное пересечение, т. е.
простую двойную точку 2>{р)^ k>{q).
Напишем теперь точную последовательность пучков
0->С'д(с,->^.(9'с->а->0, (6.6)
где, по определению, SD^Pc на открытом множестве V — это
то же самое, что Ос на открытом множестве 3^-^(11). Из
наших вычислений сразу видно, что Q равен нулю всюду,
кроме двойных точек и точек заострения S){C), а в каждой
из этих точек слоем является
одномерное комплексное
векторное пространство. Далее,
точность последовательности пучков
означает, что эйлерова
характеристика
г iPa> (С)) = dim Я" {Ф (С); Oat (о).
-ШтЯ'(^(С); Оацо)
зависит . только от степени
2)(С). Поэтому %{Оа)(С)} должна
равняться (1—55) = —54, поскольку этому числу она равна
для неособых плоских кривых 12-й степени. Возвращаясь
к (5.6), мы получаем тогда, что
= [число двойных точек 3) (С)] -f
+ [число точек заострения ^(C)]-f (1 — бб) =
= [число двойных точек 3) (С)] — 30.
Итак, число бикасательных к С должно равняться 28.
Существует и другой подход к изучению бикасательных
к плоским квартикам. Если L — такая бикасательная, то
(L'C)^2p-f2^ (в некоторых частных случаях, возможно,
p^q). Следовательно, 2p-\-2q является каноническим
дивизором на С, так что линейное расслоение Lp ® Lq,
ассоциированное с дивизором p-\-q, является тэта-характеристикой
(см. § 4.11). Более того, это расслоение имеет по крайней
мере одно сечение, а если
dimЯ<'(C;C'(Lp®L,))>l,
то С должна быть гиперэллиптической, что, как мы знаем,
не так. Следовательно, Lp® Lq — нечетная
тэта-характеристика. Обратно, любая .нечетная тэта-характеристика имеет
184 гл. 5. КВАРТИКИ и КВИНТИКИ
некоторое сечение. Если (р + ?) — множество нулей этого
сечения, то 2р -\-2q — канонический дивизор, т. е. дивизор
пересечения L с некоторой прямой С. Следовательно, имеется
взаимно однозначное соответствие между бикасательными
и нечетными тэта-характеристиками.
Но в (4.57) и последующих рассуждениях было показано,
как сосчитать число нечетных тэта-характеристик. Оно
просто равно числу решений б, ее {0,1}^ уравнения 'б-е^
'^ 1 (mod 2). Прямой подсчет показывает, что это число
равно 2(3-'). (23—1) = 28.
б.З. Где живут гиперэллиптические кривые рода 3?
Заметим, что при обсуждении неособых плоских квартик
в § 5.1—5.2 мы на самом деле занимались просто негипер-
эллиптическими римановыми поверхностями рода 3. Поэтому
естественно спросить: а какое место в наших рассуждениях
могли бы занять гиперэллиптические кривые рода 3? Ключ
к ответу на этот вопрос дает изучение отображения Гаусса
д: С^:-(Я'.''(С)*) (5.7)
в случае гиперэллиптической кривой С (см. (5.5) и
последующие рассуждения). Легко проверить, что точно так же,
как любая эллиптическая кривая записывается в виде
у^ = (кубический многочлен от х)
и имеет голоморфный дифференциал dx/y, так и любая
гиперэллиптическая кривая рода 3 записывается в виде
у"^ = (многочлен степени 7 от х)
и имеет голоморфные дифференциалы dx/y, xdx/y, x'dx/y.
Поэтому отображение Гаусса (5.7) — это просто отображение
с->е«. р^{1,х{р),х^{р)),
так что оно представляет С как разветвленное двулистное
накрытие гладкой коники в Рг.
, Фиксируем теперь гладкую конику А в .СРг, задаваемую
уравнением G (Хо, Xi, Хг) ^ О, и возьмем какую-нибудь
гладкую (неособую) квартику С, задаваемую уравнением
F{Xu,X\,X^^Q, так чтобы С пересекала А трансверсально
в восьми различных точках. Рассмотрим далее семейство
квартик {Ct), задаваемое уравнением
tF-\-G^=Q, (6.8)
где / е Ае — открытому диску в с радиуса е с центром в 0.
Это семейство изображено на рис. 5,7,
5.3. ГДЕ ЖИВУТ ГИПЕРЭЛЛИПТИЧЕСКИЕ КРИВЫЕ РОДА 3? 135
Затем возьмем семейство
{(S, X) е Д^-Х С Рг: s2f (;с) + П^^ = 0},
которое можно представлять себе примерно так, как
показано на рис. 5.8.
э
Ct
Рис. 6.7. Семейство квартнк, двукратно облегающих конику
Наконец, растянем в разные стороны и разделим рис. 5.8
по множеству точек его самопересечения. Это действительно
можно проделать алгебраически (соответствующий процесс
называется нормализацией), и в результате получается
картинка вроде изображенной на рис. 5.9 ').
') Попытаемся объяснить эти построения чуть-чуть более формально.
Семейство, изображенное на рис. 5.7, — это такая поверхность X в
Рг X Де> что слоями ограничения проекции я: Рг X Дг -^ Де на X
являются неособые квартики при / =И= О и двойная коника А при / = 0.
Возведение параметра в квадрат дает двулистное накрытие Д^— -^ ^g, нли б:
Pj X ^j— ->■ Pj X Ag. Семейство У = б-' (X) — это семейство,
изображенное на рис. 5.8. При отображении б: У ^>-Х прообразом квартнкн Ct
семейства X является пара изоморфных квартнк Cs и C-s, где «^ =
= (—s^) = /, что и показано на рис. 5.8. Слоем же при s = О по-преж-
иему является двойная коника А. Легко проверить, что поверхность X
неособая, за исключением восьми точек Л П С в нулевом слое, а на
поверхности У весь нулевой слой является особым (X и У — поверхности в
P^X^g н Р^ X Д^—, заданные одним уравнением: (5.8) для X и s^f-f-
+ G^ = О для У, так что особые точки — это о15щне нули функций djds
(нли djdt), д/дх и д/ду).
Далее, требование нормальности алгебраического многообразия (см.
любой курс алгебраической геометрии) — это некоторое ослабление
требования гладкости; в частности, множество особых точек при этом имеет
коразмерность по крайней мере 2, так что У не нормально. В курсах
алгебраической геометрии (см., например, Шафаревич И. Р. £)сновы
алгебраической геометрии. — М.: Наука, 1972, с. 353—354) доказывается, что
для каждого многообразия У существуют нормальное многообразие Р и
сюръектнвное отображение v: 7->- У, являющееся изоморфизмом на
множестве всех неособых точек У. При этом Р называется нормализацией У.
Семейство, изображенное на рис. 5.9, — это и есть нормализация Р
поверхности У. В нашем случае Р оказывается даже гладким; Р
изоморфно У всюду, кроме нулевого слоя, а ограничение V на нулевой слой — это
отображение (5.9). Еще короче можно сказать, что Р — это нормализация
л в поле С(^)(л/1Г) (см. указанную выше книгу И. Р. Шафаревича,
с. 353). —Прим. перев.
136 гл. 5. КВАРТИКИ И КВИНТИКИ
Далее, можно показать, что семейство кривых {Cs} с
добавленной при 5^0 кривой Со является на самом деле
гладким, откуда следует диффеоморфность Со и Cs при s ф 0.
Поэтому наш конечный вывод /аков: когда / стремится
к нулю, Ct стремится к гиперэллиптической кривой рода 3,
Рис. 5.8. Над Ct (/ Ф 0) лежат две изоморфные кривые: С» и С_»
которая является двулистным накрытием коники Со,
разветвленным в восьми точках Ct П Со. Здесь мы стремимся не
столько к точности, сколько к геометрической наглядности
в описании поведения кривых рода 3. В духе такого подхода
1€^
:/=
Г»
Рис. 5.9. Построение Со — двулистного разветвленного накрытия Со
МОЖНО сказать, что все гиперэллиптические кривые рода 3
сосредоточены на различных направлениях подхода к
двойной конике G^ по семействам типа (5.8).
Интересное упражнение — понять, что происходит с 28'би-
касательными к Ct при /^-0. Ответ, который можно угадать,
исходя и из геометрических, и из • числовых соображений,
состоит в том, что эти 28 бикасательных переходят в
(2) = 28 хорд множества С<ПСо, т. е. множества точек
ветвления отображения
Со^Со. (5.9)
Это означает, что нечетными тэта-характеристиками гипер-
эллиптической кривой (5.9) являются просто линейные
расслоения Lp <8> Lq на Со, где р v. q — различные точки
ветвления отображения (5.9).
6.4. КВИНТИКИ 137
5.4. Квинтики
Мы закончим эту главу некоторыми наблюдениями над
плоскими кривыми степени 5. Тут мы сталкиваемся с одним
новым явлением. «Общая» кривая рода 6 не является
плоской квинтикой, хотя неособые плоские квинтики и
составляют хороший класс кривых рода 6. Это видно уже из счета
констант. Как было отмечено в § 4.12, семейство кривых
рода g имеет (3^ — 3) параметров, тогда как плоские
квинтики имеют не более 21 —9 ^ 12 параметров, поскольку
векторное пространство однородных форм степени 5 имеет
размерность ( '^^)^21, в то время как размерность группы
GL(3; .С), действующей на Рг, а следовательно, и на плоских
квинтиках, равна 9.
Замечательным свойством квинтик является то, что их
каноническое расслоение получается ограничением с СРг
расслоения 0(2). Следовательно, множество канонических
дивизоров на квинтике С получается пересечением С со
всевозможными кониками в СР'г- Быстрее всего в этом можно
убедиться, заметив, что если А — некоторая коника, то по
теореме Римана — Роха
1(С-Л)^6 —10 —l-f6= 1.
Это то же самое рассуждение, с помощью которого мы
доказали, что на квартике ограничение 0(1) дает каноническое
расслоение.
Значит, квинтика С имеет выделенную
тэта-характеристику, а именно (7(1) | с. Из точной последовательности пучков
и теоремы Кодаиры об обращении в нуль (см. Гриффите
и Харрис [1], с. 170) легко получить, что 0{1)\с является
нечетной тэта-характеристикой, причем
dim Я''(С; (7(1)1 с) = 3.
Теорема Римана об особенностях утверждает, что это
происходит в точности тогда, когда тэта-дивизор /(С) имеет
тройную точку.
Кроме того, плоские квинтики обладают еще одним
замечательным свойством — они тесно связаны с кривыми рода 5.
Впервые это заметил русский математик А. Н. Тюрин. При
описании этой связи мы опустим обсуждение любых
патологий, которые могут встретиться в различных частных
случаях. Все наши утверждения будут относиться лишь к связи
между общей плоской квинтикой и общей кривой рода 5.
138 гл. 5. КВАРТИКИ II КВИНТИКИ
(Заметим, что и те и другие образуют 12-мерные
семейства.)')
Первое наше утверждение, верное только «в общем»,
состоит в том, что кривая рода 5 является полным пересечением
трех квадрик Qo, Qu Q2 в С Р4, т. е. базисным (или
неподвижным) множеством семейства
^Qo + liQi -f VQ2 = О (5.10)
однородных форм степени 2 в СР4. Далее, каждая Q/
задается симметричной 5Х5-матрицей (<7/^), а множество
особых квадрик (5.10) выделяется в СРг с однородными
координатами А,, ц, и v уравнением пятой степени
det(kq^^+ix.qf + vqf) = 0. (5.11)
Но на самом деле связь между кривыми степени 5 и
кривыми рода 5 имеет гораздо более тонкое объяснение. Кривая
рода 5, обозначим ее В, возникающая в С Р4 в качестве
базисного множества семейства (5.10), вложена канонически
(доказательство такое же, как и для квадрик). Поэтому, как
и раньше, можно представлять себе, что В лежит в Р {Tj(b), 0)
и там же лежит наше семейство квадрик (5.10). Это есть
просто семейство всех квадрик, содержащих канонически
вложенную кривую рода 5. Существует и другой способ
получать квадрики, содержащие В в ' {Тцв),о), а именно при
помощи тэта-функции 6(ы) = б[° ](ы; Q) на J {В).
Предположим, что для некоторого «0^/(6)
где и = («1, ..., Us)- Тогда мы знаем, что «о является особой
точкой тэта-дивизора ы(5<''>). Согласно теореме Римана об
особенностях из § 4.12 и (4.60),
Q{u{p) — u{q) — Uo — Kp,) = 0
для всех р, q^B. Дифференцируя при р ^ р\, получаем
2] -^ («iPi) -u{q)-Uo- Кр,) а>1 {pi)-= О,
где СО/ — это /-Й элемент базиса Н^'°{В). Продифференцируем
теперь по q при q = pi', получим, что при всех р^ В
/ «
') Используемый ниже подход был применен в основополагающей
работе Андреотти и Майера: Andreotti А., Mayer А. On Period Relations for
Abelian Integrals on Algebraic Curves. — Ann. Scuola Norm. Sup., Pisa,
V. 21, 1967, pp. 189—238.
6.4. КВИНТИКИ _ 139
Поскольку 6 четна, можно заменить (—«о—АГро) на (ыо + ^ро)
и заключить, что касательный конус
К «(fit*)) В точке uq содержит В. Следовательно, каждая точка
подмногообразия особенностей
eseCZu{B(*)) (5.13)
имеет в качестве касательного конуса квадрику семейства
(5.10). Согласно (4.61), dimesg= 1. На самом деле можно
показать, что (опять-таки «в общем случае») Qsg —
неприводимая гладкая кривая.
Кроме того, конус (5.12) особый просто потому, что ыо
не является изолированной особой точкой и{В^*^), как это
было бы, если бы (5.12) было невырожденным. Отсюда
видно, что существует
n:@sg-^C, ыо^-^квадрика (5.12), (5.14)
где С — плоская квинтика, определенная уравнением (5.11).
Это отображение сопоставляет каждому uq то значение
(А,, |д,, v), которое дает касательный конус к и{В'^*'>) в этой
точке. Можно показать, опять-таки «в общем», что (5.14)
есть гладкое неразветвленное двулистное накрытие. То, что
это накрытие по крайней мере двулистно, ясно уже из того,
что ио и (— «о — 2/Cpo) переходят в одну и ту же точку.
Глава б
СООТНОШЕНИЕ ШОТТКИ
6.1. Многообразия Прима
В этой последней главе мы обсудим самый знаменитый
классический результат, полученный на пути к решению
следующего вопроса: какие симметричные матрицы Q с
положительно определенной мнимой частью получаются из кривых
тем способом, который описан в гл. 4? Это так называемая
проблема Шоттки; при ее изучении мы будем довольно
близко следовать работе Фаркаша ').
В конце гл. 5 мы уже рассматривали частный случай
следующего явления. Пусть
л: С^С (6.1)
— неразветвленное неприводимое двулистное накрытие
кривой С рода (^ + 1). Если выбрать отмеченную точку ро^С,
то (6.1) соответствует подгруппе индекса 2 в
фундаментальной группе П1{С,ро). Поскольку эта подгруппа содержит
коммутатор группы ni{C,po) и подгруппу квадратов из
ni{C,po), множество двулистных накрытий (6.1) данной
кривой С находится во.взаимно однозначном соответствии с
множеством подпространств индекса 2 в
Я,(С; Рг). (6.2)
Но так как спаривание, задаваемое индексом пересечения,
невырожденно на (6.2), каждый ненулевой элемент группы
(6.2) однозначно соответствует подпространству индекса 2 —
своему ортогональному дополнению относительно индекса
пересечения. Таким образом, существует естественное
взаимно однозначное соответствие между множеством двойных
накрытий (6.1) и множеством ненулевых элементов Я} (С; fi)-
Если у — простая замкнутая кривая, представляющая
ненулевой элемент Hi {С; fi), то накрытие вида (6.1)
соответствует у тогда и только тогда, когда яг-'(7) разбивает С на
две компоненты связности.
Имеется естественная инволюция
V. С^С (6.3)
') Farkas Н. Оп the Schottky Relation and Its Generalization to
Arbitrary Genus. — Ann. Math., v. 92, 1970, pp. 56—81.
6.1. МНОГООБРАЗИЯ ПРИМА
141
на С и, следовательно, естественная инволюция
I*: Н''°{С)^Н''0{С) (6.4)
с собственными значениями ±1. Выберем в Hi{C;Z) базис
ао, аь ..., ag, Ро. Рь • • •, Ре таким образом, чтобы элемент
Ро (по модулю 2) соответствовал накрытию (6.1) и базис
был симплектическим в смысле § 4.1. Тогда симплектический
Рис. 6.1. Симплектический базис Hi{C; Z)
базис для Hi{C;Z) можно построить так, как показано на
рис. 6.1. Для такого симплектического базиса С
л,(Р) = Ро, я.(а) = 2ао,
«. (р'/)=". (р/)=р/' ". К)=". («;•)=«/•
Тогда циклы а^ —а^', p^ —p^', /=1, .... ^, образуют базис
кососимметрической относительно инволюции i, части
Hi{C', Z), а матрица ограничения индекса пересечения на это
кососимметрическое подпространство имеет вид 2 1 1.
Рассмотрим собственное подпространство инволюции i*
на Н^-°{С), соответствующее собственному значению —1,
и обозначим его Н^'^{С)-. Как и в (4.7), выберем в нем базис
ifii ifig таким образом, чтобы
\ i^A^d/A (символ Кронекера).
Мы знаем, что размерность Н^-°{С)- равна g, так как С
имеет род 2^+1 и Н^'°{С) + ^ Н^-°{С). Пусть Т обозначает
матрицу — \ 'Фа. Матрица Т играет роль матрицы Q из
а;-а;
142 Гл. 6. СООТНОШЕНИЕ ШОТТКИ
§ 4.2, а дифференциалы у^к, называемые дифференциалами
Прима, заменяют со* из гл. 4. Как и в § 4.2, получаются
соотношения Римана Т ^ *Т и 1тТ>0. Следовательно,
вполне аналогично конструкции Pic°(C)^ J (С) в гл. 4 можно
построить комплексный тор
Р(„)^(я'-°(ггГ^ с« , (6.5)
^ ' я, (С; Z)- 2] z£^+ 2] zr^ '
называемый многообразием Прима (примианом) для я.
Кроме того, поскольку для построения тэта-функций нужны
были только соотношения Римана, можно построить
аналогичные функции и в нашей новой ситуации. Так как мы
собираемся сравнивать их с тэта-функциями на /(С), будем
обозначать новые функции буквой ц, а не 6. Итак,
+ 2'(т + |б)(« + 4-8)]}. (6.6)
ZS
Упомянем еще, что если я: Qsg^-C — двойное накрытие
плоской квинтики, связанное с кривой В рода 5 (см. § 5.4),
то Р(я)=/(В)').
Далее, как мы видели, задание симметричной ^Х
^-матрицы А с условием Im Л > О сразу приводит в движение весь
аппарат, связанный с комплексным тором
C«/(ZZ£/+ZZ^/>,
тэта-функциями и т. д. Будем называть такую матрицу А
матрицей периодов. Из счета констант видно, что при g'^ 4
не любая такая матрица А является «матрицей периодов» Q
для какой-нибудь кривой, как это описано в гл. 4. В
частности, при ^ ^ 4 множество матриц периодов является
десятимерным аналитическим множеством, в то время как
множество кривых рода 4 имеет всего лишь 3^ — 3^9
параметров. Следовательно, должно существовать нетривиальное
(аналитическое) соотношение между компонентами тех
матриц Л, которые происходят из некоторой кривой. Одним
таким соотношением, называемым соотношением Шоттки, мы
и будем заниматься в остальной части этой главы.
') Подробнее об этом и о последних достижениях в теории
многообразий Прима см. в работе Beauville А. Prym Varieties and the Schottky
Problem. — Invent. Math., v. 41, 1977, pp. 149—196.
6.2. ТЭТА-СООТНОШЕНИЕ РИМАНА , ,»
148
6.2. Тэта-соотношение Римана
Для получения соотношения Шоттки необходимы два
основных ингредиента. Первый из них — это только что
описанная конструкция многообразия Прима, а второй — это
красивый фокус с использованием формулы характеров для
конечных групп, приводящий к самому «плодоносному»
тождеству для тэта-функций — тэта-соотношению Римана. Мы
уже вывели его для случая ^ ^ .1 другим способом в § 3.14.
Для начала передокажем тэта-соотношение Римана в
случае ^^1. Пусть 61 64 ^—стандартный базис в R*.
Введем стандартное скалярное произведение в R* так, чтобы эти
векторы составляли ортогональный базис. Рассмотрим Две
решетки в R^:
Li = Z6, ф Z62 + 7бз + Z64,
L2 = [подмодуль в "2-^1, порожденный векторами e/ + efe,
1 < /, k^4:, и вектором -j {ei -f «2 + ^з + 64)]-
Тогда {Li{]L2) имеет индекс 2 как в Li, так и в Li, поэтому
скалярное произведение унимодулярно в Li, т. е. матрица,
задающая это скалярное произведение в любом базисе Li,
имеет определитель 1. Как пространства со скалярным
произведением, Li и Li изоморфны. Более того, ортонормиро-
ванный базис Li задается явно:
Л =Т (^1 + 62 + ез -f 64). ^2 = т (^1 + «2 — ез — 64).
^3 = т(б1 — ^2 + ез - е^), ^4 = т (^1 - ^2 - «з -f 64).
Заметим, что если б и f поменять местами, формулы (6.7)
останутся верными. Поэтому матрица М, задающая
изоморфизм между Li и Li, удовлетворяет соотношению
Af^ ^ (единичная матрица). (6.8)
Положим, наконец,
L = Li + Li, (6.9)
так что [L ; Li] = 2, причем расширение порождается любым
из е/, / = 1, ..., 4, и [L:Li] = 2, а это расширение
порождается 4" (^1 + • • • + ^4).
Предположим теперь, что комплексное число А
удовлетворяет соотношению Римана Irii Л > 0; напишем тогда
произведение четырех тэта-функций:
е[«;](«,; Л)е[«;](«2; А)в[Ц]{и,; Л)е[«:](«4; А). (е.Ю)
Здесь gj и hj могут быть любыми элементами R^ —нет
никакой необходимости ограничиваться наборами из g нулей
144
ГЛ. 6. СООТНОШЕНИЕ ШОТТКИ
И единиц. То же самое определение тэта-функций (4.38)
годится и в этой чуть более общей ситуации. Перемножим
теперь ряды Фурье тэта-функций из (6.10). Получится
ехр{2т"(-)}, где в скобках должно стоять выражение
VA
где
т =
т.
-ГП4 .
и т. д., J^^
АЛ
Поэтому (6.10) можно переписать в виде
JZ^exp {2ni [4- Xm+^g) ^ (m + 4- g)+Xm+^ g) (u+^h)] } =
= 4-1 Z l-exp{2m-[4-'(m + 4-^)j!^(m + 4-^) +
+ '('" + тг)(« + 4-Л)]}+ Z ехр{2я/(т-е,)}Х
Xexp {2яг[4 '(m ^\g)s4{m-^\g)-Y \m-^\g)(u+^ h)]}}.
(6.11)
где через (m-ei) обозначено стандартное скалярнре
произведение, упомянутое раньше.
Разобьем теперь каждую из двух сумм (6.11) на две части
в соответствии с тем, лежит ли индекс суммирования в
подгруппе L2 или в ее дополнении в L. Получится
ехр{2ш- [4 Х'п+Тё) ^ ('«+Т S)+' (m+4 g) (и+4 Л)]}+
+ exp{2ni[4'(m + e,+ 4^)^(m + e,+4г) +
+'(/7г+e,+4г)(и+4л)]}+
+ exp {2яг {-jg- е^)} exp {2ni[4 '(m + 4 ^) X
X^(/n. + 4^) + '(m + 4^)(«+4/i+e,)]} +
+ exp {2ni (—Jg- ei)} exp {2ni [jXm+^g+ ei) X
X ^(m + 4^ + e,) + '(m + 4^ + e,)(u+^h+e,)]}.
iZ
6.2. ТЭТА-СООТНОШЕНИЕ РИМАНА ,,.
. 145
-У
Воспользуемся тем, что Af —изометрия на R*, и получим
окончательный вид функции (6.10):
ехр {2я1 [4 \т -V\Mg)si-(m +4Mg) +
+ \т + yAf^) {Ми + '^МЩ +
+ ехр {2я1 [4 \т + j М^ + (j)) j=^ (m +4 Mg + (4)) +
+ '(m + 4 М^ + (4)) (Af« + 4 Ж)]} +
+ ехр {— nig^ ехр {2nt [j '(m + i iW^) ^ (m + ^ M^) +
+ '(m + \Mg) {Mu +\Mh + (4))]} +
+ exp {- nig,} exp {2m [i '(m + ^Mg + {\)) X
X^(m + 4Af^ + (4)) +
+ '(т+4л/^ + (4))(л/«+4ш+(4))]},
где (т) = (т' Т» Т- т)- Следовательно,
ПбК!](«/М)=тЕ «хрЬпаа"-г,]}Пе['Л](«;; Л).
где и'^ Ми, g'^Mg и h'^ Mh, а индекс (^1) пробегает
все элементы ZX Z, компонентами которых являются только
нули и единицы. Частным случаем последней формулы
является тождество
вКГ=4(вГоГ + е[:]Че[;Г),
уже полученное нами в конце гл. 3.
Доказательство соответствующей общей формулы в
размерности g отличается от одномерного доказательства только
обозначениями. Вместо матрицы М берется матрица
размером 4^X4^. получающаяся из М заменой каждой единицы
на единичную матрицу размером g'X.g. Теперь gj, hj, u/
являются векторами, а на шаге (6.11) имеются 2в сумм,
соответствующих 2в характерам группы Z^ со значениями
в группе {±1}. Таким образом, окончательная общая форма
тэта-соотношения Римана выглядит так:
4 4 / ^
П 6 [ f; ] {иг, Л) = -^ Х; ехр {- ш [а" . ^,]} П 4 1ч1" 1 ("'• ^^'
(а-; (6.12)
146 ГЛ. 6. СООТНОШЕНИЕ ШОТТКИ
где и', g', h' — те же, что и выше, а индекс (^„) пробегает
все элементы Х^У\Х^, компоненты которых принимают
только значения О или 1.
6.3. Произведения пар тэта-функций
Чтобы добраться наконец до соотношения Шоттки, нам
потребуется еще одно предварительное соотношение для
тэта-функций, которое получается несложным изменением
рассуждений, использованных для вывода тэта-соотношения
Римана. Начнем опять со случая ^ ^ 1. На этот раз мы
воспользуемся матрицей Л^ = i _, . '^^'^ '^^ М^ = 2
(единичная матрица). Пусть Li^Zei+Ze2 — стандартная
решетка в R^, а Li^ M-^Lu Заметим, что Li'^Li, и,
например, Y (^1 + е2)порождает L2/L1. Кроме того, ^-^ {е^ + е^) • -jX
X (ei+б2)) = Т''''^'^ что стандартное скалярное произведение
принимает на L2 полуцелые значения.
Далее, как и в § 6.2, напишем
/П € L|
= Z ехр {2ni [^ Хт + ^ g') 2^{т + ^ g') -f
+ Xrn + -^g')(u' + ^h')]], (6.13)
где g' = M-^g, h' = Mh и u' = Mu. Теперь разбиваем
последнюю сумму в (6.13) на две в соответствии с классами
смежности Li в L2 и получаем
^[1]^Щ т{1]]^Щ; А) =
= ^;еГ«>'"]«- 2Л)eГ4+<^'|(«^ 2Л), (e.U)
где а' принимает значения О и 1. Как и в § 6.2, аналогичная
(6.14) формула верна в любой размерности. Единственная
разница состоит в том, что а' может быть любым элементом
iZe, состоящим из нулей и единиц,
6.4. ТЕОРЕМА ПРОПОРЦИОНАЛЬНОСТИ
147
6.4. Теорема пропорциональности, связывающая якобианы и
примианы
Теперь мы уже готовы объединить идеи первых трех
параграфов этой главы. Пусть я: С^-С то же, что и в § 6.1.
Имеем матрицы периодов
Q =
(Boo • •
•
-fflgo ...
(Oog-
•
«ee-
ДЛЯ /(C), r =
T[i .
•
_Tgi .
. . Xig'
•
• • '^ge -^
для P (я).
Нетрудно вычислить матрицу периодов для J {С)
относительно базиса в гомологиях С, приведенного в § 6.1. Она
равна
Q =
"2сй,
'00
(В,
'01
Щ-е
(On
(й„
CU01 ... "Jflg
®go i (fflgi+tgi).. • T Ke+T^gg) T (®gi—tgi) • •. T Kg—^gg)
■ • « • •
• ■ • • •
• - • • • •
Пусть / — единичная ^Хё'-матрица; положим, как и в
§ 6.3,
1 О 01
м= о / /
.0 / -/.
Матрица М имеет размеры (2^+1)Х(2^+1). и обратная
к ней матрица есть
П О
о
о ^1 ^1
о -1/ -|/
148
ГЛ. е. СООТНОШЕНИЕ ШОТТКИ
Г2Й ОТ ^
Заметим также, что MQM ^ 1 « ov ■ ^^о^да можно
написать
е[
в е 8
в" 8" е'
]{w; Q)= Z е2"П-1, (6.15)
(mo, m, n) е Z X Z* X Z*
где В квадратных скобках должно стоять выражение
±[то-\-±е', '[т + 4-8'], '[« + 4-8']]Q
1 ^/-1
mo + Y е
m + 4-8'
L «+4-«' J
+ [mo + 4-e'. [m + 4-8']. t« + 4-«']]
te) +
+
e72 -j -
872
L872.
(Вместо 6[g„ g„ gl ] следовало бы писать 6
но это
обозначение слишком громоздко.)
Дальше можно проделать с решеткой индексов тот же
самый фокус, который мы уже несколько раз делали,
а именно можно суммировать по L2 = М-'(Z X Z*'X Z*').
Таким способом получится следующее выражение для (6.15):
2] ехр J 2ni
ms и
1 '" +
ре72
872
О
+ \т +
)[: :л[-^
■е'12 -J
872
. О .
Mw +
Г е72 -1
872
о .
е'72 -
&"
О
+
которое можно переписать в виде
= Z X Z« X ze а'
(6.16)
e.4. ТЕОРЕМА ПРОПОРЦИОНАЛЬНОСТИ
149
где в квадратных скобках должно стоять
< ^ г е'12
872 + а'12
а'12
т +
т +
+ т +
е'12 ■
872 + а'12
а'12
При суммировании, как обычно, а' пробегают те элементы
Z^, компоненты которых равны О и 1. Но сумму (6.16) можно
записать и проще. Положим
Ы^ FO) ^i+ZTg^l, ..., 2g + Z2g],
t»= \Zi 2g+i, .... Zg — Z2gJ'
Тогда (6,16) — это просто
«|:(_1)'^'+<^')-"е[::^'Г'](«; 2й)л[?](«;2Т). (e.i?)
Мы используем здесь букву ■х\ вместо 6, чтобы подчеркнуть,
что эта тэта-функция построена при помощи матрицы
периодов многообразия Прима.
Это довольно сложное вычисление мы провели потому,
что из (6.17) уже проглядывает соотношение между тэта-
функциями, соответствующими матрице периодов Q кривой
С, и тэта-функциями, связанными с матрицей периодов Т
многообразия Прима Р(я). Но при аккуратном выборе
значений для некоторых переменных можно добиться такой
ситуации, когда выражение (6.17) равно нулю. Такой выбор
основывается на следующих соображениях. Пусть выбрана
нечетная тэта-характеристика L на С. Тогда
(11тЯ"(С;0'(1))^1.
Но nf (L) — тэта-характеристика на С, поэтому
dim Я"(С; О*(л* (L)))^ 1.
Если при этом :rt*(L) окажется четной тэта-характеристикой,
то будет
(11тЯ0(С;О'(я*(1)))^2.
Если же, сверх того, б[^, I, l,.^{w', Q) является
тэта-функцией на J{C), соответствующей jf(L) в смысле (4.57), (4.58)
и следующих за этими формулами рассуждений, то из (4.60)
150 гл. е. СООТНОШЕНИЕ ШОТТКИ
можно будет заключить, что
б[:^ 1г "^]{\dw; Q^^O (6.18)
при всех р, q ^С. Такие тэта-характеристики и в самом деле
можно найти. Основной момент здесь состоит в том, чтобы,
проследив за всеми отождествлениями в гл. 4, убедиться,
что изоморфизм (4.56) относительно выбранного в § 6.1 сим-
плектического базиса гомологии действует следующим
образом:
(точки второго порядка на /(C)) ч->-S,
П'Л] + ^['Л]--Ш' (6.19)
S -
(точки второго порядка на /(C))*->S,
1/2 1 ~ г в'/2 •
г 1/2 Т ~ г « /2 1
е'/2 + Q е'/2 ч-^ {пЧ}.
L е''/2 J L е'/2 J
Следовательно, L нечетна, если
е'е" + г'е" = 1 (mod 2), (6.20)
а я*(1) можно сделать четной, просто полагая
е' = 0. (6.21)
Да и соответствие (6.19) не так уж трудно проверить.
Поскольку его истинность (или ложность) инвариантна при
деформации С, достаточно проверить ее для вырожденного
Рис. 6.2. Вырождение С, удобное для проверки равенств Прима
случая, когда С выглядит так, как на рис. 6.2. (Сравните
рис. 6.1 и 6.2!) Понятно, что левая компонента рис. 6.2 ничего
к нашей проверке не добавляет, а вся трудность состоит в том,
чтобы непосредственно, вручную, проверить (6.19) в случае,
когда С, а значит, а С — эллиптические кривые.
Начиная с этого места, будем предполагать, что (6.20)
и (6.21) выполнены. Тогда из уравнения (6.17) следует, что
0^2(-1^^"'''"б[: T'](\du; 2Q\[^\dv; 2tY
о' ^р / \р /
6.5. ТЕОРЕМА ПРОПОРЦИОНАЛЬНОСТИ ШОТГКИ - ЮНГА
ISt
как только г'-г" = 1. Чтобы получить еще лучшее
соотношение, просуммируем (6.22) по всем таким значениям &", что
8'-8"= 1. Чтобы понять, что получится, нужно просто
вычислить
у /_iye'+<»')-(e''+p)
р
где суммирование производится по всем таким р, что p-8i = 0.
Эта сумма равна
2*^"', если а'=8',
— 2^~ , если а' = О,
О в остальных случаях.
Таким образом, получается соотношение
= в[? 'o](\du; 2Q\[l]Udv; 2tY (6.23)
Но оно должно выполняться при всех ъ' Ф О, поскольку
всегда можно найти такое г", что &'•&"= 1. Следовательно,
векторы
пропорциональны при всех р, q^C.
6.5. Теорема пропорциональности Шоттки — Юнга
Полученная в конце предыдущего параграфа теорема
пропорциональности — это еще не совсем то, что нам нужно,
поскольку в нее входят матрицы периодов 2Q и 2Y вместо
Q и Т. Однако это можно исправить при помощи соотношения
(6.14), полученного в § 6.2. Положим
«i=\cf«, М2==0> V\ = \dv, t»2 = 0
и напишем
е["о ::](«,; й)в[? *;](«2;Q) =
= 5(-1)<^'+<^'>-''е[? ^'YWv 22)в[? о']К; Щ~
(6.14) °-
152 гл. 6. СООТНОШЕНИЕ ШОТТКИ
в то время как
= IK-if+<^'>-^"е[: ^'Г'](«;; 2Q)e[: ^]{и'^, 2Q) +
(6.14) "
+ Z (-ir+<^'>-^"e[| ^'Г'](«;; 2Q)e[; ;'](«^; 2Q).
Хитрость тут в том, что, согласно (4.39),
е[_; f](«^;2Q) = -e[; o"'](«2:2Q),
в[:: ^»](«'; 2Q) = (-if-"e[:: П(«'; 2Q).
Теперь сложим
в[^ ::](«,; й)в[? ::](«2; й) + е[^ ::](«,; Q)e[o" ::](«2; Q) =
= 2 Z(-lf'+"'^""e[: *'Г'](«;; 2Q)e[: ;'](«^; 2Q) =
= (константа)1:(-1Г+<^'>-^"л[Т'](«;; 2Т)л["J'](«^; 2Т)=
= (константа) ^ л[8»]("1; Лл[е"]("2; Т^).
(6.14) "
причем существенно, что константа не зависит от выбора &'
и &". Тем самым получилась теорема Шоттки — Юнга,
утверждающая, что векторы
Ш\ Я)(в[: ^A{V^^))+^?[l Я)(е[; S](W)L,)
пропорциональны, где для сокращения записи мы опустили
символы Q и Т и положили «2 = «2 =?= 0. в следующем
параграфе мы воспользуемся этой теоремой для получения
соотношения Шоттки.
6.6. Соотношение Шоттки
Теперь все готово для получения аналитических условий,
которым должна удовлетворять матрица периодов А для
того, чтобы быть матрицей периодов некоторой кривой.
Поскольку можно показать, что (аналитическое) множество
матриц периодов кривых рода g имеет размерность (3^ — 3)
(если g>_^), сначала нужно попробовать найти нетривиаль-
6.6. СООТНОШЕНИЕ ШОТТКИ 163
ное аналитическое соотношение между коэффициентами А
в случае g = 4:. При наличии тэта-соотношения Римана
и пропорциональности Шоттки — Юнга такое соотношение
строится совсем просто.
Начнем с какого-нибудь равенства между
тэта-константами, например тождества Риманаб[о]'' = б[д ]*+ в[° ]*.
Используя тождество ^[о ^^^[о ]* +^[^ ]* и
пропорциональность Шоттки — Юнга, получаем соотношение
которое должно выполняться тождественно, поскольку общая
2 X 2-матрица периодов происходит из кривой. Снова заменяя
6 на Ti и применяя теорему Шоттки — Юнга, получаем
соотношение
дго о опдго о отдго о отдго о оп_
= в[о о o]6[i о о]б[о 1 o]6[i 1 о] +
+ в[ГоПб[ГоПе[::ПеП:П'
которое тоже должно выполняться тождественно. Наконец,
еще раз заменяя в последнем тождестве 6 на ti и подставляя
(^[о e'l^L" е''])''^ вместо 'п[^]. получаем
тэта-соотношение в размерности 4, которое заведомо выполнено по крайней
мере в случае, когда при построении тэта-функции
использовалась матрица периодов, происходящих из кривой
(рода 4).
Итак, осталось проверить, что соотношение Шоттки не
является просто еще одним тождеством, которому
удовлетворяют все абелевы многообразия размерности 4. Для этого
мы приведем набросок рассуждения, принадлежащего Р. Ак-
коле. Начнем с эллиптической кривой Е. Легко проверить,
что для любых восьми различных точек ри ..., /58 на Я
существует риманова поверхность С и двулистное накрытие
Л: С^Е, (6.24)
разветвленное в точках р].
Как и в (5.5), построим каноническое отображение
д: C-*-'Vi. Гиперплоские сечения С в Р4 находятся во взаимно
однозначном соответствии с каноническими дивизорами на С.
На двулистном накрытии (6.24) определена естественная
инволюция i: С-^С, так что hoi = h. Это просто
перестановка листов, поэтому ясно, что I о I = тождественное
отображение. Далее, i индуцирует инволюцию i*: Н^-ЦС)-^
->-Я''''(С), поэтому, как известно из линейной алгебры,
154
Гл. 6. СООТНОШЕНИЕ ШОТТКИ
^'•"(Q разлагается в прямую сумму подпространств
я'' ° (С)+ = {со е я'' ° (С): i* (со) = со},
я'- ° (С)" = (со е я'' ° (С): i* (со) = - со}.
Поскольку все элементы Н^-°{С)+ получаются из
голоморфных дифференциалов на Е, (1'1тЯ''"(С)+= 1, так что
(11тЯ'.о(С)- = 4.
Это дает важную информацию о каноническом
отображении 9 в нашем случае. А именно существует такая точка q
в Р4, что при проекции я: Р4->-Рз с центром в точке q образ
9(C) переходит в эллиптическую кривую. Точнее, имеет
место коммутативная диаграмма
С-^Р4
(6.25)
Легко проверить, что на самом деле 5^ вкладывает Е как
кривую четвертой степени в Рз.
Далее мы только наметим основные шаги. Подробно
провести все рассуждения было бы не слишком трудно, но уж
очень это долгая история. Заинтересовавшиеся читатели
могут при некотором терпении и прилежании заполнить все
пропуски самостоятельно или, что предпочтительнее,
обсудить это со знающим геометром.
Во-первых, в связи с (6.25) следует отметить, что, хотя
множества квадрик в Рз девятимерно, по теореме Римана —
Роха (4.9) они высекают на 5^ (Я) семимерную линейную
систему дивизоров. Следовательно, существует одномерное
семейство квадрик, содержащее 9^{Е). Но пересечение двух
квадрик имеет, как и Ж{Е), степень 4, поэтому а^{Е)
является пересечением любых двух квадрик этого семейства.
При этом говорят, что а^{Е) является базисным множеством
пучка квадрик {Q(X«: w}(x,, ад s р.> где Q(^o;x,) задается
уравнением
^0*700 + ^1^00 • • • Моз + '^i'?o31 Г ^0'
[ло ... Аз]
^0^30 + ^i'?3o • • • КЯзз + ^1'7зз .
X.
3 J
= 0. (6.26)
Имеются четыре значения (Яо, >.i)e Pi, при которых
определитель матрицы (6.26) равен нулю.
Для каждого из этих четырех зна_чений уравнение (6.26)
определяет квадратичный конус в Рз, содержащий Ж{Е).
e.e. СООТНОШЕНИЕ ШОТТКИ
166
Один такой конус изображен на рис. 6.3. Каждая
образующая L этого конуса пересекает 9^{Е) дважды, а если L
и L' —две образующие, то {L +L')[\9^{E) есть
гиперплоское сечение 5^ (Я) в Рз.
Все это означает, что для любого дивизора вида pi Ч-Р2 =
■=1{\9^{Е) дивизор 2A-'(pi) + 2/i-'(p2) является
каноническим дивизором на С, т. е. линейное расслоение на С,
ассоциированное с дивизором /i-'(/5i) +
+ Л~' {р2), является
тэта-характеристикой (см. § 4.11). Более того,
проективная размерность полного
линейного ряда, содержащего этот
дивизор, не меньше единицы, так
как образующую L можно двигать
по конусу. Если бы проективная
размерность этой линейной системы
была бы больше единицы, кривая
С была бы гиперэллиптической
(чего не может быть, так как тогда
кривая 9(C) была бы
рациональной). Следовательно, каждая из
четырех полученных нами
тэта-характеристик четна.
Итак, для каждого из четырех
линейных расслоений L^■^\ U^\ L<'),
LC) имеем Aim Н°{С; 1Щ = 2. При
соответствии (4.56) линейные
расслоения L(^) отвечают четырем
точкам второго порядка: [*|j|]s/(C). Поэтому, согласно
теореме Римана об особенностях (4.67), существуют четыре
такие четные тэта-функции
e[*<;>](«;Q). (6.27)
что в[е|л](0; Й) = 0, Мы пропустим проверку того, что если
е[*](0;Й) = 0 и б-*8 S 0(mod2), то касательный конус
к б[*](м; Q) в нуле дает в точности такой конус, как на
рис. 6.3. Поскольку таких конусов всего четыре, только
функции (6.27) являются четными тэта-функциями,
обращающимися в нуль при ы = 0. И еще одно место требует некоторой
дополнительной работы (которую мы не станем делать). Дело
в том, что можно так выбрать симплектический базис
Bffi(C;Z),4T0
гб(1)1 го о о о от гв(2)1 ГО о о о от
Le(l)J Lo о о о oJ> Le(2)J Ll о о О oj'
Рис. 6.3. Один из четырех
квадратичных конусов,
содержащих д>в(Е)
Гб(3)-1 ГОООООТ Гб(4)-1 го
Le^3)J —Lo О О о ij> L8(4)J='Ll
о о о о on
о о о ij'
/, ft. /-0, 1
156 гл. 6. СООТНОШЕНИЕ ШОТТКИ
Предположим теперь, что мы выбрали двулистное
накрытие кривой С в (6.24), для которого выполнена теорема
пропорциональности Шоттки — Юнга:
Тогда для соответствующего многообразия Прима имеет
место тождество
л[ГоГо]=о=л[Го::]- (6.28)
Напомним, наконец, что соотношение Шоттки имеет вид
Если бы соотношение (6.29) выполнялось для
рассматриваемого многообразия Прима, то из (6.28) мы бы заключили,
что некоторая л [ у ^ " о ] рзвна нулю. Но, опять-таки в силу
пропорциональности Шоттки — Юнга, это означает, что
некоторая другая, т. е. не принадлежащая списку (6.27), четная
тэта-функция 6 [ ^ ] (ы; Q), соответствующая (якобиану)
кривой С, обращается в нуль при ы = 0. Но мы уже упоминали,
что для большинства кривых С, получающихся в (6.24), нш
какая другая четная тзта-функция не обращается в О при
ы = 0. Из этого можно заключить, что соотношение (6.29)
выполнено не для всех 4Х4-матриц периодов, что и
требовалось.
Это, конечно, еще далеко не все, даже для 4Х4-матриц
периодов. Со времен Шоттки в задаче характеризации матриц
периодов, происходящих из кривых, достигнут значительный
прогресс, но задача еще далека от полного решения.
ЛИТЕРАТУРА
1. Griffiths P., Hants J. Principles of Algebraic Geometry.— New York:
John Wiley and Sons, 1978. [Имеется перевод: Гриффите Ф., Хар-
рис Дж. Принципы алгебраической геометрии. — М.: Мир, 1982.]
2. Gunning R. С, Rossi Н. Analytic Functions of Several Complex
Variables.— Englewood Cliffs, N.'J.:! Prentice-Hall, Inc., 1965. [Имеется
перевод: Ганнинг P., Росси X. Аналитические функции многих
комплексных переменных. — М.: Мир, 1969 ]
3. Gunning R. С. Lectures on Riemann Surfaces. — Princeton, N. J.:
Princeton University Press, 1966.
4. Hirzebruch F. Tupological- Methods in Algebraic Geometry. — New
York: Springer-Verlag, 1766. ТИмеется перевод: Хирцебрух Ф.
Топологические, методы в алгебраической геометрии.'—М.: Мир, 1973.]
5. Lang S. Linear Algebra. — Reading, Mass. Addison-Wesley Publishing
Co., 1971.
6. Mumford D. Abelian Varieties. — Tata Institute of Fundamental
Research, Bombay: Oxford University Press, 1970. [Имеется перевод: Мам-
форд Д. А15елевы многообразия. — М.: Мир, 1971.]
7. O'Neill В. Elementary Differential Geometry. — New York: Academic
Press, 1966.
8. Serre J.-P. A Course in Arithmetic. — New York: Springer-Verlag, 1973.
[Имеется перевод: Cepp Ж.-П. Курс арифметики. — М: Мир, 1972.]
9. Springer G. Introduction to Riemann Surfaces. — Reading, Mass.: Addi-
son-WesIey Publishing Co., 1957. [Имеется перевод: Спрингер Дж.
Введение в теорию римановых поверхностей. — М.: ИЛ, I960.]
10. Steenrod N. The Topology of Fibre Bundles. — Princeton, New Jersey:
Princeton University Press, 1951. [Имеется перевод: Стиирод Н.
Топология косых произведений. — М.: ИЛ, 1953.]
11. Van der Waerden В. L. Algebra.— New York: Fredrick Ungar
Publishing Co., 1970. [Имеется перевод; Ваи дер Варден Б. Л. Алгебра.—M,i
Наука, 1976.]
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абеля теорема 76, 108, 112
Абсолют 24
Автоморфиая форма 93
Альбанезе многообразие 107
Аффинное множество, аффинные
объекты 16
Безу теорема 20
Вейерштрасса ^-функция 57, 78.
Гаусса — отображение 130. 134
Геодезическая кривизна 36
Гессе кривая 132
Гипербола 10
Гиперболическая геометрия 32
Гнперэллиптическая кривая 131, 134
Группа моиодромии 84
Двойное отношение 20
Двойственная кривая 29
Двойственность по Пуанкаре 102
Двоякопернодическая функция 7Ь
Де Рама когомологин 106
Дивизор 77
Дольбо комплекс 63
Пикара многообразие 101
— теорема 89
— Фукса уравнение 59, 66
Полярная кривая 28
Полярное отображение 29. 31
Понтрягина умножение 109
Прима дифференциалы, многообразие
(примнан) 142
Проективное множество, проективнаа-
ция 16
Пространство модулей 90
Пуанкаре отображение 108
Пуассона формула суммирования 81,
96
Раздутие точки 48
Разрешение особенности 72
Расслоенное произведение 52
Рациональные точки 37, 47, 61
Результант двух многочленов 17
Римана константа 12U 122
— соотношение второе 57, 103
первое 103
— Роха теорема 66, 78, 80, 120
— теорема 121
об особенностях 124
— тэта-соотношение 99. 143, 145
Риманова геометрия 24, 37
Род кривой 100
Евклида пятый постулат 24
Жесткость 85
Канонический дивизор 123
Каноническое о|то(^ражение 130
Касание третьего порядка 41
Касательный конус 72
Квартики 128
Квинтики 137
Комплексная проектнвиая плоскость 16
Коиики 16
Конус 13-^15
Кремоны преобразование 49
Кубики 40
Кэли теория 24
Серра теорема Двойственности 66. 67
Симметрическая степень 52, 115
Симплектический базис 91, 100
Стереографическая проекция 31
Сферическая геометрия W,
Точки перегиба 42
Тэта-константы 82
Тэта-функции 78, 116, 118
Тэта-характеристики 123
Фровениуса отображение 64
Фундаментальная область 74
Ходжа рааложеиие 111
Лефшеца теорема двойственности 107
о неподвижных точках 62—83
Лоренца группа 28
Чеха когомологни 106
Чисэня класс 104
Манина результат 62
Матрица периодов 142
Мероморфные функции 51, 73, 76
Модулярные формы 79
Шоттки проблема 140
— соотношение 142, 152, 153, 166
■» Юнга теорема пропорциональности
152
Нормализация 135
Нормальный вид
ки 44
уравнения кубн-
Эйзенштейна ряды 80
Эйлера формула 29
Эллипс 10
аллиптические кривые 70
Парабола 10
Параболическая форма 99
Паскаля чудесный шестиугельнах 18
Периоды 58
Якоби многообразие (якобиан) 100,
— теорема обращения Пй, 120. 121
— тождество 99
ОГЛАВЛЕНИЕ
Предисловие редактора перевода 5
Предисловие 7
Обозначения 9
Глава 1. Коники 10
1.1. Тени гиперболы 10
1.2. Вещественное проективное пространство — «Упроститель
Классификаций» 13
1.3. Комплексное проективное пространство—«Великий
Упроститель» 15
1.4. Линейные системы коник 16
1.5. Чудесный шестиугольник 19
1.6. Двойное отношение 20
1.7. Построение геометрий постоянной кривизны: метод Кэли . . 24
1.8. В Зазеркалье . . 27
1.9. Полярная кривая 28
1.10. Перпендикуляры в гиперболическом пространстве . . . . 32
1.11. Окружности в К-геометрни 35
1.12. Рациональные точки на кониках 37
Глава 2. Кубики 40
2.1. Точки перегиба 40
2.2. Нормальный вид уравнения кубики 42
2.3 Кубики как топологические группы 44
2.4. Группа рациональных точек аа кубике 47
2.5. Размышление о комплексном сопряжении ' . . 50
2.6. Некоторые мероморфные функции на кубиках ...... 51
2.7. Пространство модулей кубик. Снова двойное отношение . . 52
2.8. Абелев дифференциал на кубике 53
2.9. Эллиптический интеграл 55
2.10. Уравнение Пикара — Фукса 58
2.11. Рациональные точки на кубнках над Fp .61
2.12. Результат Маннна: единство математики 62
2.13. Замечания о двойственностн Серра .67
Глава 3. Тэта-функции 69
3.1. Снова групповой закон на кубнках 69
3.2. Гладкую кубнку нельзя параметризовать алгебраически . . 70
3.3. Мероморфные функции на эллиптических кривых 73
3.4. Мероморфные функции на плоских кубиках 76
3.5. Р-функция Вейерштрасса . . ' 78
3.6. Тэта-константы задают модули эллиптических кривых . . .81
3.7. Пространство модулей «структур второй ступени» на
эллиптических кривых 83
3.8. Автоморфизмы эллиптических кривых ......... 86
160 ОГЛАВЛЕНИЕ
3.9. Пространство модулей эллиптических кривых 87
3.10. А кстати, попутно получилась теорема Пикара 88
3.11. Комплексная структура на Jf 90
3.12. /-инвариант эллиптической кривой 91
3.13. Тэта-константы как модулярные формы 94
3.14. Фундаментальная область подгруппы Fj 97
3.15. Тождество Якоби , 99
Глава 4. Многообразие Якоби 100
4.1. Когомологни комплексной кривой 100
4.2. Двойственность 102
4.3. Класс Чжэня голоморфного линейного расслоения .... ЮЗ
4.4. Теорема Абеля для кривых 107
4.5. Классический вариант теоремы Абеля 112
4.6. Теорема обращения Якоби 115
4.7. Снова тэта-функции' 116
4.8. Основное вычисление 118
4.9. Теорема Римана 120
4.10. Линейные системы степени g .122
4.11. Константа Римана 122
4.12. Теорема Римана об особенностях ' 124
Глава 5. Квартики и квинтики 128
5.1. Топология плоских квартик 128
6.2. Двадцать восемь бикасательных 130
5.3. Где живут гиперэллиптические кривые рода 3? 134
5.4. Квинтики , . 137
Глава 6. Соотношение Шоттки 140
6.1. Многообразия Прима 140
6.2. Тэта-соотношение Римана 143
6.3. Произведения пар тэта-функций . 146
6.4. Теорема пропорциональности, связывающая якобианы и при-
мианы 147
6.5. Теорема пропорциональности Шоттки — Юнга. ......" 151
6.6. Соотношение Шоттки .... 152
Литература 156
Предметный указатель 158