Міністерство освіти і науки України
Львівський національний університет імені Івана Франка
Я.Г. САВУЛА
ЧИСЛОВИЙ АНАЛІЗ ЗАДАЧ
МАТЕМАТИЧНОЇ ФІЗИКИ
ВАРІАЦІЙНИМИ МЕТОДАМИ
Львів
Видавничий центр ЛНУ ім. Івана Франка
2004

ББК В193я73-1
С- 13
УДК 517.951:519.6(075.8)
Рецензенти:
д-р фіз.-мат. наук, член кореспондент НАНУ Я,Й, Бурак (Центр
математичного моделювання при ШПММ НАН України ім. Я.С. Підстригача), д-р
фіз.-мат. наук, проф. Р.В. Слоньовський (Національний університет
"Львівська політехніка").
Рекомендовано Міністерством освіти і науки України
як навчальний посібник для студентів вищих навчальних закладів.
Лист №/11 - 2971 від 15.07.2003.
Савула Я.Г.
Числовий аналіз задач математичної фізики варіаційними методами. - Львів:
видавничий центр ЛНУ імені Івана Франка, 2004. — 221 с.
ISBN 966-613-017-3
У посібнику викладено основи варіаційних методів у зв'язку з числовим аналізом
задач математичної фізики методом скінченних елементів. Метод скінченних
елементів посідає особливе місце серед числових методів прикладної математики, які мають
застосування в комп'ютерному моделюванні. В посібнику описано методи побудови
найбільш поширених варіаційних формулювань крайових задач та методи
знаходження їхніх наближених розв'язків. Наведено допоміжні поняття і означення, які є
властивими для теорії варіаційних методів. Подано найбільш вживані в методі
скінченних елементів апроксимації. Розглянуто крайові задачі та задачі на власні
значення для диференціальних операторів. Викладено основи застосувань методу
скінченних елементів до параболічних задач. Описано способи приведення задач лінійної
алгебри "великих" розмірів, що виникають у разі застосування методу скінченних
елементів до задач лінійної алгебри звичайних розмірів.
Підручник розрахований на студентів, аспірантів і молодих наукових працівників
у галузі прикладної та обчислювальної математики.
ББК В193я73-1
ISBN 966-613-017-3 © Савула Я.Г., 2004

Зміст
Вступ 7
Розділ 1. Варіаційні методи 9
1.1. Додатні та додатно визначені оператори .... 9
1.2. Варіаційна задача про мінімум квадратичного
функціонала 15
1.3. Існування розв'язку задачі про мінімум
функціонала енергії 18
1.4. Головні та природні граничні умови 22
1.5. Задачі з неоднорідними граничними умовами . . 24
1.6. Метод Рітца 27
1.7. Метод скінченних елементів ЗО
1.8. Слабкий розв'язок крайової задачі 36
1.9. Абстрактна варіаційна задача 38
1.10. Метод Бубнова—Гальоркіна 43
1.11. Вправи для самостійного виконання 45
Розділ 2. Апроксимація на скінченних елементах 49
2.1. Похибки апроксимації кусково-лінійними
функціями 50
2.2. Одновимірні скінченні елементи лагражового типу, 53
2.3. Ермітові одновимірні апроксимації на скінченних
елементах 55

2.4. Одновимірні апроксимації функціями—бульбашками . 56
2.5. Апроксимації на трикутних скінченних елементах . . 58
2.6. Лагранжові апроксимації на прямокутних
скінченних елементах 63
2.7. Ермітові апроксимації на прямокутних
скінченних елементах 64
2.8. Двовимірні ізопараметричні апроксимації 66
2.9. Апроксимації на тетраедрах 70
2.10. Тривимірні ізопараметричні апроксимації .... 73
2.11. Вправи для самостійного виконання 75
Розділ 3. Крайові задачі 77
3.1. Крайова задача для рівняння парного порядку ... 77
3.2. Апріорна оцінка точності МСЕ 79
3.3. Апріорна оцінка точності за Нітше 81
3.4. Схема МСЕ для рівняння четвертого порядку ... 82
3.5. Крайова задача для системи диференціальних рівнянь . 85
3.6. Задача про циліндричний згин пластини 89
3.7. Крайові задачі для рівняння Пуассона 96
3.8. Схема МСЕ для рівняння Пуассона 101
3.9. Схема МСЕ, побудована на ізопараметричних
апроксимаціях 105
3.10. Рівняння стаціонарної адвекції—дифузії 107
3.11. Бігармонічне рівняння 112
3.12. Крайові задачі для рівняння еліптичного типу . . . 117
3.13. Вправи для самостійного виконання 120
Розділ 4. Задачі на власні значення 123
4.1. Математичні моделі, які приводять до задач на
власні значення 123
4.1.1. Коливання струни 123
4.1.2. Згинні коливання стрижня 125
4.1.3. Коливання мембрани 125
4.1.4. Коливання пластини 126

4.2. Властивості спектра оператора 127
4.3. Енергетичні теореми в проблемі власних чисел . . . 130
4.4. Дискретний спектр оператора Штурма—Ліувілля . . 137
4.5. Мінімаксимальний принцип Куранта 140
4.6. Теорема про порівняння власних чисел 142
4.7. Метод Рітца в задачах на власні значення .... 144
4.8. Слабке формулювання задачі на власні значення
і метод Гальоркіна 150
4.9. Числовий аналіз спектральної задачі для
оператора Штурма—Ліувілля 151
4.10. Спектр оператора задачі про згин пластини . . . . 155
4.11. Похибки власних чисел і власних функцій . . . . 157
4.12. Вправи для самостійного виконання 166
Розділ 5. Початково ^крайові задачі 169
5.1. Параболічна задача 169
5.2. Варіаційне формулювання параболічної задачі . . . 171
5.3. Напівдискретні апроксимації Гальоркіна 174
5.4. Енергетичне рівняння 175
5.5. Стійкість напівдискретних апроксимацій 176
5.5.1. Перша оцінка норми напівдискретного роз'язку . 177
5.5.2. Друга оцінка норми напівдискретного роз'язку . 178
5.6. Існування розв'язку варіаційної задачі 180
5.7. Збіжність напівдискретних апроксимацій 182
5.8. Дискретизація варіаційної задачі за часом 187
5.8.1. Кусково-лінійна апроксимація за часом .... 187
5.8.2. Однокрокова рекурентна схема 188
5.9. Стійкість рекурентних схем 190
5.10. Збіжність рекурентних схем 193
5.11. Вправи для самостійного виконання 197
Розділ 6. Проблема " великих" задач лінійної алгебри . 199
6.1. Редукція параметрів внутрішніх вузлових точок .
199

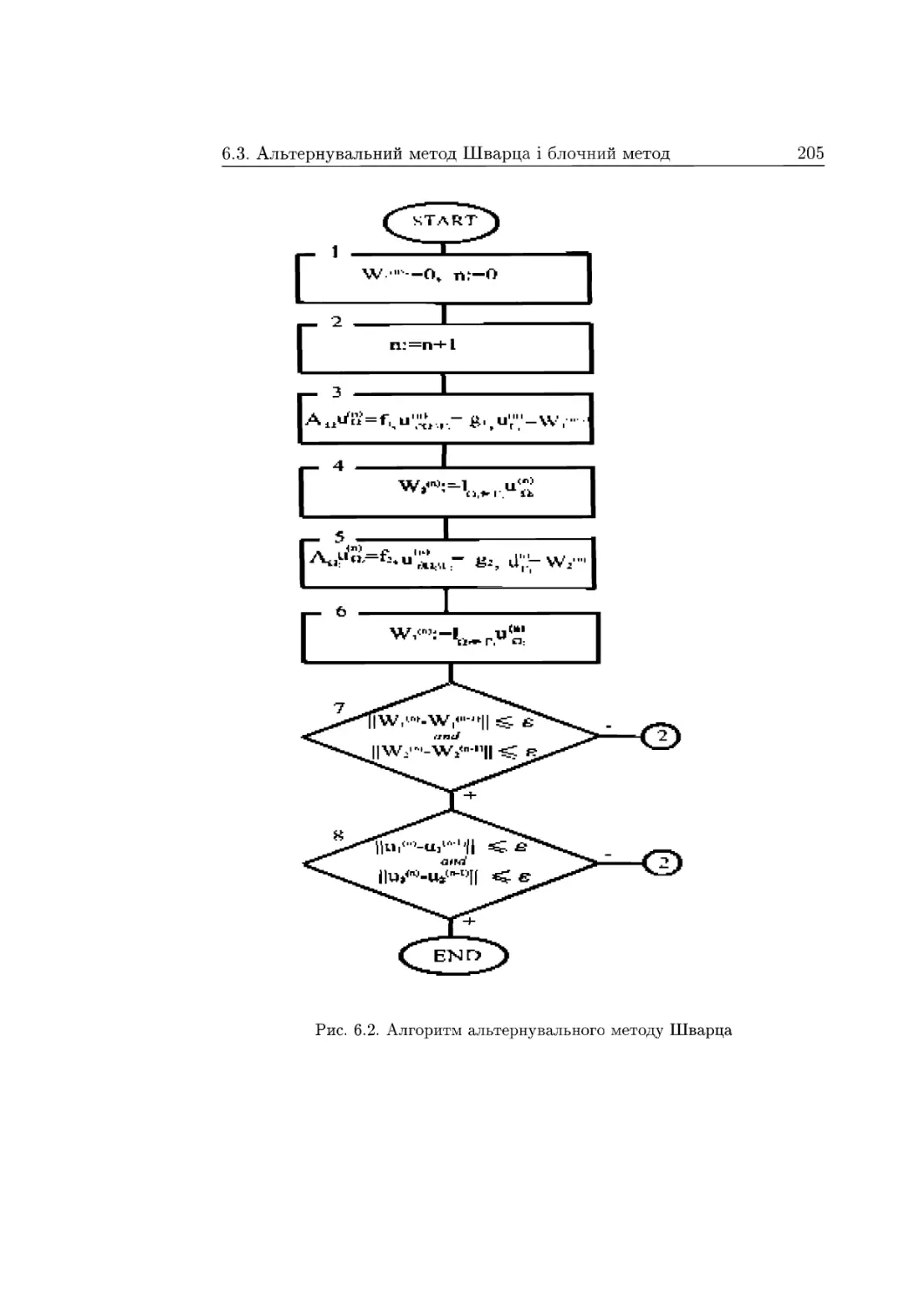
6.2. Класичний альтернувальний метод Шварца .... 202
6.3. Альтернувальний метод Шварца і блочний метод
Гауса—Зейделя 204
6.4. Мультиплікативний метод Шварца 207
6.5. Адитивний метод Шварца 210
6.6. Випадок багатьох підобластей 213
6.7. Вправи для самостійного виконання 213
Додаток 215
Список рекомендованої літератури 221

Вступ
У сучасному інформаційному суспільстві важливу роль відіграє
технологія комп'ютерного моделювання (обчислювального експерименту),
яку можна розглядати як циклічне повторення трьох умовно виділених
етапів: математична модель - алгоритм - програма.
На першому етапі формується математична модель явища, яка
відображає всі його головні властивості. Математичні моделі — це
здебільшого задачі математичної фізики, 3 використанням добре
розвинених методів математичної фізики теоретично вивчають
математичні моделі, що є одним із способів перевірки їхньої адекватності.
Другий етап — вибір алгоритму для реалізації математичної моделі
на комп'ютері, Математичну модель подають у вигляді, зручному для
застосування числових методів, Визначають послідовність операцій,
яка дає змогу з заданою точністю отримувати числові значення
шуканих величин. Обчислювальні алгоритми повинні бути такими,
щоб не спотворювати головні властивості математичної моделі та бути
економними в сенсі кількості виконуваних операцій,
На третьому етапі створюють програми, які є таким записом
алгоритму, який дає змогу реалізувати його на комп'ютері,
Ефективність процесу комп'ютерного моделювання залежить від
багатьох факторів, Зокрема, зростання потужностей комп'ютерів, що
простежується сьогодні, безумовно, приводить до розширення сфер
застосування і можливостей технології комп'ютерного моделювання.
Проте успіхи комп'ютерного моделювання значно залежать і від вдалого
вибору математичних моделей та числових методів їхнього аналізу,
Зазначимо, що серед числових методів, які широко застосовують у
комп'ютерному моделюванні, пріоритетне значення мають варіаційні,
Засобами варіаційних методів можна ефективно виконати як теоретичне

8
дослідження математичних моделей, так і конструювання числових
методів їхнього аналізу
У посібнику викладено основи варіаційних методів у зв'язку з
числовим аналізом задач математичної фізики методом скінченних
елементів. Його матеріал був частиною курсів, які прочитано студентам
факультету прикладної математики та інформатики Львівського
національного університету імені Івана Франка.
Метод скінченних елементів посідає особливе місце серед числових
методів прикладної математики, які застосовують у комп'ютерному
моделюванні, Це зумовлене як його ефективністю в дослідженні задач,
що виникають у різних галузях науки і технології, так і його придатністю
для використання у комп'ютерних програмних комплексах, Теоретичною
базою методу скінченних елементів є варіаційні методи математичної
фізики, які беруть початок від праць відомих учених Бубнова,
Гальоркіна та Рітца (1905—1915). Ці методи отримали новий поштовх для
розвитку завдяки виникненненню електронно-обчислювальних машин у
середині XX ст,
У перших п'яти розділах посібника описано методи варіаційних
формулювань задач математичної фізики та методи знаходження
їхніх наближених ров'язків, наведено різні способи побудови
скінченноелементних апроксимацій шуканих розв'язків задач,
Розглянуто найважливіші крайові задачі, задачі на власні значення та
початково—крайові задачі,
Обчислювальні схеми варіаційних методів зумовлюють потребу
розв'язування великих систем лінійних алгебричних рівнянь, Для цього
розвинено арсенал методів та алгоритмів обчислювальної алгебри,
Водночас є методи, які на рівні формування систем лінійних алгебричних
рівнянь дають змогу зменшити їхні розміри і звести початкову задачу
лінійної алгебри великого розміру до розв'язування послідовності задач
менших розмірів, Найпоширеніші з цих методів описані у шостому
розділі підручника,
Автор висловлює вдячність своїм колегам, колишнім студентам,
аспірантам та співробітникам кафедри прикладної математики доц.
II. Диякові та ст. наук, співроб, М.Ф. Копитко за допомогу і корисні
зауваження в підготовці рукопису книги.

Розділ 1
Варіаційні методи
Описано методи побудови найпоширеніших варіаційних
формулювань крайових задач та методи побудови їхніх наближених розв'язків,
Значна частина матеріалу присвячена задачам з так званими додатно
визначеними операторами. Поряд з цим розглянуто також задачі зі
слабшими обмеженнями на їхні оператори, Наведено допоміжні поняття й
означення, які є властивими теорії варіаційних методів,
1.1. Додатні та додатно визначені оператори
Розглядатимемо задачі вигляду
An = /, (1.1)
де А — лінійний оператор, що відображає деяку множину Da (область
визначення оператора А), яка належить гільбертовому простору Н, на
множину Ra С Н (область значень оператора А).
Приклад 1. Для крайової задачі
-«"(яг) = /, хє(а,Ь); (1.2)
и(а) = 0, и'(Ь) = 0, (1.3)
припускаючи, що / Є С [а, 6], схарактеризуємо область визначення Da її
оператора так:
DA = {и(х) : «(яг) Є С(2) [а, Ь], «(а) = 0, и'(Ь) = 0} . (1.4)

10
Варіаційні методи
Отже, оператор крайової задачі (1.2), (1.3) характеризований
диференціальним рівнянням (1.2) та областю визначення (1.4).
Приклад 2. Розглянемо крайову задачу Діріхле для рівняння Пуас-
сона у двовимірній області Q з границею Г:
-Аи = f (x]
и = 0,
L,Z2),
Жі,Ж2 Є 0;
Хі,х2 Є Г.
(1.5)
(1.6)
Тут
д2и д2и
дх\ дх\'
/ Є С (П) . Очевидно, що область визначення оператора задачі (1.5),
(1.6) можна схарактеризувати так:
DA = {и(хих2) : и(хих2) Є С{2] (П) ; и = 0, хих2 Є Г} . (1.7)
Означення. Оператор А називають симетричним, якщо його область
визначення Da С Н є щільною множиною у просторі Н, і виконується
співвідношення
{Au,v) = {u,Av), \/u,veDA. (1.8)
Приклад 3. Доведемо, що оператор задачі (1.2), (1.3) симетричний.
Перш за все зазначимо, що множина DA (1.4) щільна в L2 (0,1). Цей
висновок ґрунтується на очевидному співвідношенні Cq C Da і
тому факті, що Cq утворює щільну множину у просторі L2 (0,1) [5,10].
Розглянемо скалярний добуток
ь
(Au,v) = - u"vdx: Vu,v Є DA. (1.9)
а
Зінтегруємо праву частину попереднього виразу частинами і візьмемо до
уваги граничні умови (1.3). Отримаємо
ь
(Ащу) = / u'v'dx. (1.10)

1.1. Додатні та додатно визначені оператори
11
Оскільки права частина цього виразу є симетричною відносно функцій
w та v, то можна записати
(Au7v) = (Av,u). (1.11)
З огляду на симетрію скалярного добутку остаточно одержимо
(Au7v) = (u,Av). (1.12)
Означення. Оператор А називають додатним, якщо він
симетричний, і виконуються співвідношення
(Ащи) > 0, \/uGDA; (1.13)
(Аиуи) = 0^и = 0. (1.14)
Якщо в цьому разі існує стала 7 > 0 така, що виконується нерівність
(Ащи) >72\\и\\2Н: (1.15)
то оператор А називають додатно визначеним.
Приклад 4. Доведемо додатність оператора крайової задачі Дірі-
хле для рівняння Пуассона (1.5), (1.6). Область визначення Da цього
оператора є щільною множиною в просторі L2 (П) (див, приклад 1).
Розглянемо вираз
(Аи, и) = — І Аи udQ,.
п
Щоб його перетворити, отримаємо формулу Гріна для оператора Лапла-
са. З цією метою використаємо формулу Остроградського [8ДО]
о г
де іі = cos (і/, Хі)) і = 1, 2; v — зовнішня нормаль до границі Г області СІ.
Приймемо у формулі (1.16) (р = uv, гр = 0. Знайдемо
[v^dQ = - [u^dn+ [uvhdT. (1.17)
J дхг J дхг J

12
Варіаційні методи
Аналогічно матимемо
fv^dn = - fu^dn+ fuvl2dT. (1.18)
о о
Підставивши у формули (1.17), (1.18) замість функції и її похідні ди/дх\
та ди/дх2 і додаючи їх, отримаємо формулу Гріна
— / AuvdQ= / gv&dugmdvdQ — / —vdT, (1*19)
п п г
де
gratk = J —, — І — = —/х + —/2- (1.20
[ от; і дх2} up дхг дх2
Отже, для скалярного добутку {Аи1 и) з урахуванням формули Гріна та
граничних умов (1.6) запишемо
(Ащи) = / {gY&dufdn. (1.21)
о
Очевидно, що (Аи} и) > 0. Припустимо тепер, що
(Ащи) = 0. (1.22)
Звідси, враховуючи (1.21), матимемо
gradw = 0 => и = const. (1.23)
Якщо взяти до уваги граничну умову (1.6), то отримаємо потрібний
результат и = 0.
Зауваження, Для можливості застосування формули Остроград-
ського вважатимемо, що область Q — обмежена зв'язна множина ев-
клідового простору R2 з ліпшицевою границею Г.
Приклад 5. Доведемо додатну визначеність оператора задачі (1.2),
(1.3). Для цього запишемо и{х) у вигляді
х
и{х) = [ ^dt. (1.24)

1.1. Додатні та додатно визначені оператори
13
b
0
Xj
а
Рис. 1.1. Двовимірна область
Звідси, враховуючи нерівність Коші^Буняковського, отримаємо
\а І а а а
Зінтегрувавши ліву та праву частини ланцюжка нерівностей (1.25),
знайдемо
h-v^fiSf*-
(1.26)
Отриману нерівність (1.26) називають нерівністю Фрідріхса.
Використовуючи її, можна довести додатну визначеність оператора задачі (1.2),
(1.3). Справді, враховуючи співвідношення (1.26), матимемо
(Аи, и) >
Отже,
(Ь - а)2
2
\и\
(1*27)
7
{Ь-а)г
Приклад 6. Доведемо додатну визначеність оператора задачі (1.5),
(1.6). Припустимо, не зменшуючи загальності, що однозв'язна область Q
з лшшицевою границею Г розташована у першому квадранті декартової
системи координат (рис, 1.1). Помістимо область Q усередині прямокут-

14
Варіаційні методи
ника П і довизначимо функцію и(хі,х2) на П\0, прийнявши, що в U\Q
вона дорівнює нулю, Запишемо далі очевидне співвідношення
du{t,x2)
и
{хі,х2) = І
dt
-dt.
(1.28)
Звідси, враховуючи нерівність Коші^Буняковського, знайдемо
(аналогічно як у формулі (1.25))
и
а
'(хих2) = хі І (-Q—J dxi-
Зінтегруемо цю нерівність на прямокутнику П
Ju2(xux2)dQ<c2 J U^-
+
ди
дхо
Де
п п
с =тшІТ'ТГ
Урахувавши (1.21) та (1.32), отримаємо
u2dVt.
dQ,
(Au,u)>^J-
(1.29)
/a2 f ( ди\2
u2(xi,x2)dx1dx2 < — J f -— J dxxdx2. (1.30)
n n
Подібним способом отримаємо і таку нерівність:
u2(xi,x2)dx1dx2 < — І І -— 1 dxxdx2. (1-31)
п п
Додаючи нерівності (1.30) та (1.31) і враховуючи, що в U\Q
/ \ г, ди Л ди
и(хи ^2) = °> ^Г = °> ^Г = °'
одержимо нерівність, яку теж називають нерівністю Фрідріхса,
(1.32)
п
Отже, оператор задачі Діріхле для рівняння Пуассона додатно
визначений.

1.2. Варіаційна задача про мінімум квадратичного функціонала 15
1.2. Варіаційна задача про мінімум
квадратичного функціонала
Уважатимемо тут, що задача
Au = f, / Є Я, (1.33)
має додатний оператор, який відображає область його визначення Da у
гільбертів простір Н.
Зазначимо перш за все, що властивість додатності оператора задачі
(1.33) пов'язана з єдиністю її розв'язку. Виконується така теорема:
Теорема 1. Нехай А — додатний оператор. Тоді, якщо задача (1.33)
має розв 'язок, то він єдиний.
Доведення. Припустимо, що існують два розв'язки задачі (1.33) щ
та и2) причому и\ не дорівнює тотожно и2. Розглянемо скалярний добуток
(А (щ — и2), щ — и2). Оскільки А (щ — и2) — Ащ — Аи2 = / — / = 0, то
(А(щ - и2) ,щ - и2) = 0.
Звідси, враховуючи, що А — додатний оператор, робимо висновок,
що^і — и2 = 0. Це суперечить початковому припущенню, а отже,
доводить теорему, ■
Наведена нижче теорема, яка встановлює зв'язок крайової задачі
(1.33) з певною варіаційною задачею, надзвичайно важлива для
конструювання методів побудови наближених розв'язків,
Теорема 2 (теорема про мінімум функціонала енергії). Нехай А
— додатний оператор. Якщо задача (1.33) має розв'язок, то він надає
мінімуму функціоналу
F (и) = (Ащ и) - 2 («, /), иє DA. (1.34)
Навпаки, функція, яка надає мінімального значення функціоналу (1.34),
є одночасно розв'язком задачі (1.33).

16
Варіаційні методи
Доведення. 1. Нехай функція щ є розв'язком задачі (1.33). Візьмемо
довільну функцію 7] G Da - Очевидно, що щ + r\ G Da- Розглянемо
F(uq-\-t]), Враховуючи симетрію оператора А та симетрію скалярного
добутку, отримаємо
F(uQ + ri) = F (щ) + 2 (Ащ -/,//) + (Art, v) ■ (1*35)
Зауважимо, що другий доданок у формулі (1.35) дорівнює нулю,
оскільки Ащ — / = 0. Отже, для довільної функції щ + т/ справджується
співвідношення
F(uQ + ri) = F (щ) + (Агі, rj). (1.36)
Оскільки останній доданок у правій частині формули (1.36) задовольняє
нерівність (Аг), rj) > 0 (А — додатний оператор), то функціонал F досягає
свого мінімального значення на функції щ.
2. Доведемо тепер обернене твердження. Припустимо, що функція
щ G Da надає мінімального значення функціоналу (1.34). Це означає,
що для довільної функції 7] Є Da і довільного дійсного числа t
F(uG + t7])>F(u0). (1.37)
Використавши знову симетрію оператора та симетрію скалярного
добутку, отримаємо
F (щ + trj) = (Ащ, щ) - 2 (/, щ) -
-2t (/, rj) + 2t (Ащ, г]) + t2 (Аг,, т]). (1.38)
Для вибраних функцій щ, /, т\ F (щ + trj) є квадратичною функцією
змінної t. З умови теореми випливає існування у цієї функції мінімуму
при t — 0. Це означає, що виконується рівність
-F(uQ + t7]) U=o= 0 (1.39)
або, згідно з (1.38),
2(Au(hr})-2(f,V) = 0,
тобто
(Ащ-/,ті) = 0. (1.40)
Оскільки 7] — довільна функція, a Da — щільна множина, то звідси
випливає [8]
Ащ - / = 0. ■

1.2. Варіаційна задача про мінімум квадратичного функціонала 17
Нехай А — додатно визначений оператор. Уведемо на множині Da Є
Н новий скалярний добуток
(u,v)A = (Au,v). (1.41)
Можна довести, що добуток (1.41) задовольняє всі аксіоми гільбертового
простору. Розглянемо на множині Da новий гільбертів простір На- У
випадку, якщо цей простір не є повним, доповнимо його граничними (у
сенсі метрики (1.41)) елементами Г^. Отже, для повного простору На
маємо
HA = DAU ГА. (1.42)
У монографії [8] доведено, що НА С Н.
Зауваження, Скалярний добуток (1.41) називають енергетичним
добутком додатно визначеного оператора, Відповідну йому норму \\и\\А —
(иу и)д — енергетичною нормою, простір На — енергетичним простором,
Для довільного и G На виконується нерівність [8]
ІМІ4>7ІМІ, (L43)
яка є наслідком нерівності (1.15). Звідси випливає лема.
Лема 3. Нехай А — додатно визначений оператор і якщо послідовність
{(рп} збіжна за енергетичною нормою (1-41)> то 60па збіжна і за
нормою вихідного простору Н.
Доведення. Очевидне. ■
Функціонал (1.34), який визначений на множині D^ У випадку
додатно визначеного оператора А може бути поширений на енергетичний
простір На- Справді, його можна навести у вигляді
F(u) = (u,u)A-2(uJ), иєНА-
Приклад 7. Запишемо функціонал енергії, що відповідає задачі
-и" (х) = / (х), х Є (а, Ь),
и (а) = 0, и (Ь) = 0.
Беручи до уваги перетворення, виконані під час дослідження прикладу
З, запишемо
ь
F(u)= І (и12 - 2uf) dx, u є ЯА, (1.44)

18
Варіаційні методи
ЯА = {и О) :и' ЄЬ2 (0,1), и (а) = 0, и (Ь) = 0} .
Приклад 8. Запишемо функціонал енергії, що відповідає задачі
— Аи — /, Хі?#2 £ fij
И = 0 Хі?Х2 Є Г.
Урахувавши перетворення, виконані під час дослідження прикладу 4,
отримаємо
2 / о \ 2"
'«-/(£)+(£) К2/
dft-2 fudQ, u G НА.
п
{Я Я Л
u (хІ7х2) : —, — Є L2(Q);u = Q хь х2 Є Г L
1.3. Існування розв'язку задачі про мінімум
функціонала енергії
Розглянемо функціонал
F (u) = (Ащ и) - 2 (и, /), «G £>А. (1.45)
Згідно з теоремою про функціонал енергії, якщо А — додатний оператор,
то задача мінімізації цього функціонала еквівалентна задачі Аи — / за
умови, що існує її розв'язок, Якщо оператор А — додатно визначений,
то функціонал (1.45) можна розглядати в енергетичному просторі
F (и) = {щ и)А - 2 («, /), и Є НА. (1.46)
Тоді ж можна довести, що існує розв'язок задачі про мінімум
функціонала.
Теорема 4. Нехай А — додатно визначений оператор. Тоді варіаційна
задача про мінімум функціонала енергії (1-46) має єдиний розв'язок щ Є

1.3. Існування розв'язку задачі про мінімум функціонала енергії 19
Доведення. Розглянемо лінійний функціонал
l(u) = (uj), uGHA. (1.47)
Доведемо, що він обмежений у просторі На- Використовуючи нерівність
Коші^Буняковського, матимемо
|і(«)і = к«,/)і<іі«і
Запишемо далі, враховуючи (1.43),
\1(и)\ < \\и\\А .
7
Звідси випливає обмеженість лінійного функціонала / (и) в
енергетичному просторі На- Тоді на підставі теореми Pica [5,8,10] існує єдина функція
щ Є На така, що функціонал / (и) можна записати у вигляді скалярного
добутку
І (и) = (и, щ)А , т Є НА- (1.48)
Врахувавши (1.48), перепишемо функціонал (1.46) так:
F(u) = (u,u)A-2(u,Uo)A. (1.49)
Додамо і віднімемо у правій частині формули (1.49) скалярний добуток
(щ7щ)А, Отримаємо
F (и) = («, и)А - 2 (и, щ)А + («о, Щ)А ~ (ио, щ)л =
= \\и - щ\\л - \\uo\\a- (1.50)
З попередньої формули випливає, що мінімум функціонала досягається
тоді і лише тоді, коли и — щ. ш
Означення. Функцію щ: яка надає мінімуму функціоналу енергії на
множині функцій з простору На, називають узагальненим розв'язком
рівняння Аи — /.
Цей термін зумовлений тим, що розв'язок щ Є На і, отже, може не
належати області визначення оператора Da-
Уважатимемо, що простір Н — сепарабельний; тоді, як зазначено у
[8], простір На теж сепарабельний, Отже, у ньому можна знайти повну

20
Варіаційні методи
ортонормовану систему функцій {fin} . Розвинемо узагальнений
розв'язок щ У ряд Фур'є за цією системою функцій
оо
п=1
Прийнявши у формулі (1.48) и — fin, отримаємо
(и0у(рп)А = (/,<?„). (1-52)
Це приводить до такого запису щ У вигляді ряду Фур'є:
оо
^о = ^Ui4>n)<Pn- (1-53)
п=1
Приклад 9. Розвинемо у ряд Фур'є розв'язок задачі
-и"(х) = 1, яє(0,тг),
и (0) = и (тг) = 0.
Виберемо повну ортогональну систему функцій у вигляді (рп — sin nx.
Зауважимо, що згідно з перетвореннями, виконаними під час дослідження
прикладу 3, для енергетичного скалярного добутку маємо вираз
7Г
(u, v)A — \ ufvfdx.
о
Розглянемо скалярний добуток
{fim, fin)А = тП І C0S mX C0S Uxdx = \ пґЧг_ '
0
Отже, якщо взяти послідовність ортогональних функцій у вигляді
{фп} = \ Sinn£,
V тгп
то вона буде ще й нормованою, Обчислимо тепер скалярний добуток
0, m ф щ
m = п.
(fin) 1) = \ — / sinnxdx = —у — — (cosn7r — 1)
о
7Г П2

1.3. Існування розв'язку задачі про мінімум функціонала енергії 21
0, п = 2г;
44=, п = 2і- 1, г = 1,2,....
Тому з урахуванням попередньої формули ряд Фур'є для узагальненого
розв'язку матиме вигляд
4
^о = — > —ї sinnrr.
п=1,3,6
Приклад 10. Розвинемо у ряд Фур'є узагальнений розв'язок задачі
Діріхле для рівняння Пуассона
—Аи — 1, #і, а?2 Є Ф
и = 0, #і, х2 Є Г,
де Г2 — прямокутна область
П = {х\, х2 : 0 < х\ < а, 0 < х2 < Ь] ,
обмежена границею Г. Виберемо повну ортонормовану систему функцій
{Pmn} У ВИГЛЯДІ
<ртп — С sin sin—-—; m, n = 1, 2,...,
c " ' ab
it V 62m2 + a2n2
Ці функції нескінченно диференційовні і дорівнюють нулю на границі
Г області $7. Отже, вони належать множині Da — області визначення
оператора, Легко довести, що вони утворюють ортонормовану систему в
енергетичній метриці оператора задачі Діріхле для рівняння Пуассона,
яка визначена скалярними добутком
ди dv ди dv
f ч f \ ди dv
дх2 дх2
<т.
Обчислимо коефіцієнти ряду Фур'є за формулою (1.52):
2аЬ і ab
\Х>фтп) =
тг2тп V Ь2т2 + а2п2)
1,3,5,....

22
Варіаційні методи
Для парних значень індексів коефіцієнти ряду дорівнюють нулю, Отже,
остаточно ряд Фур'є для узагальненого розв'язку матиме вигляд
_ 16а2Ь2 у, sin gggi sin ^p
7г4 ^гі тп(Ь2т2 + а2п2)'
1.4. Головні та природні граничні умови
У параграфі 1.2 на множині Da — області визначення оператора,
побудовано повний енергетичний простір На- Елементами цього простору
є елементи множини Dai а також деякі граничні елементи, які
утворюють множину Г^. Функції, що належать області визначення оператора
Da, очевидно, задовольняють усі граничні умови, які ставлять у задачі.
Виявляється, що функції з множини Гд: які доповнюють Da до
повного простору, задовольняють тільки деякі граничні умови, Ці граничні
умови називають головними граничними умовами, Наведемо формальну
ознаку поділу граничних умов на головні та природні.
Означення. Нехай диференціальне рівняння має порядок 2к. Тоді
граничні умови, що містять похідні до порядку к — 1 включно, є
головними. Граничні ж умови, що містять похідні порядку к та вище, є
природними граничними умовами,
У варіаційному формулюванні крайової задачі, як задачі мінімізації
квадратичного функціонала, природні граничні умови та
диференціальне рівняння становлять необхідні умови мінімуму функціонала (рівняння
Ейлера),
Приклад 11. Розглянемо мішану крайову задачу для рівняння Пу-
ассона
—Au = f: х1ух2ЄІЇ; (1-54)
и = 0, хіУх2 Є Гі; (1,55)
^ = 0, яьЯаЄГа, Г = І\ U Г2, (1,56)
де v — зовнішня нормаль до границі Г. Нескладно довести, що ця
задача має додатний оператор. Отже, вона еквівалентна задачі про мінімум

1.4. Головні та природні граничні умови
23
функціонала енергії
F(u) = І І ( ^ ) + ( ^Ч \dQ-2 І fudQ. (1.57)
Оскільки диференціальне рівняння є рівнянням другого порядку, то
к = 1. Отже, гранична умова (1.55) є головною умовою, а гранична
умова (1.56) — природною, Шукатимемо розв'язок задачі про мінімум
функціонала (1.57) на множині функцій
М = {и{хих2) : и Є С{2)\и = 0,жі,ж2 Є Гі} .
Ми намагатимемось довести, що функція, яка надає мінімального
значення функціоналу, задовольняє рівняння (1.54). Тому в попередньому
визначенні множини М є завищеними (и Є С^), ніж звичайно,
вимоги щодо гладкості функцій, Доведемо, що необхідними умовами
мінімуму функціонала (1.57) є рівняння (1.54) та граничні умови (1.56). Нехай
F(uq) —> min; візьмемо довільну функцію г\ Є М. Розглянемо v = щ+tr/,
де t Є R. Запишемо необхідну умову мінімуму
dF(v) ,
-^ !<=»= О- (1-88)
Отримаємо
/(£&+s&)"-/"«-* ™
п п
Перетворимо (1.59), використовуючи формулу Гріна (1.19), до вигляду
j (-А«0 - /) Vdn + f ^фТ = 0. (1.60)
о г2
Оскільки 7] — довільний елемент із щільної множини, то з (1.60)
-Ащ = f в ft; (1.61)
^ = 0 на Г2. (1.62)
OV
Отже, рівняннями Ейлера для функціонала (1.57) є диференціальне
рівняння (1.54) та природна гранична умова (1.56).

24
Варіаційні методи
1.5. Задачі з неоднорідними граничними
умовами
Теорема про функціонал енергії та пов'язані з нею результати
виконуються для лінійних операторів, описуваних лінійними рівняннями та
однорідними граничними умовами, Зазначимо, що коли граничні умови
є неоднорідними, то область визначення оператора не є лінійною
множиною і, відповідно, оператор задачі не є лінійним. Тому для побудови
варіаційного формулювання задачі вже неможливо використати
згадану теорему, Проте шляхом заміни шуканої функції можна перетворити
задачу до задачі з однорідними граничними умовами і для цієї задачі
використати теорему про функціонал енергії.
Приклад 12. Проілюструємо це прикладом задачі Діріхле для
рівняння Пуассона
— Au = f: Xi,X2^^l] (L63)
и = д, Х\,Х2 Є Г. (1.64)
Область визначення цієї задачі
DA = {и (хих2) : и Є С(2) (U) ; и = д, хи х2 Є Г}
не є лінійною множиною, бо для довільних u,v Є Da сума и + v ^ Da,
оскільки (и + v) = 2<7, ХіУх2 Є Г. Для задачі (1.63), (1.64) виконаємо
заміну шуканої функції
и = z + w, (1.65)
де z (#1, х2) — нова шукана функція; w — деяка відома функція, що має
певний запас гладкості, наприклад, w Є С^ (О) і w = д, Х\,х2 Є Г. З
(1.65) випливає, що функція z повинна задовольняти на границі Г умову
2 = 0, хих2 Є Г. (1.66)
Підставимо (1.65) в (1.63), отримаємо диференціальне рівняння для
визначення функції z
-Az = f + Aw. (1.67)
Отже, шляхом заміни шуканої функції ми отримали крайову задачу
(1.67) з однорідною граничною умовою (1.66). Запишемо для неї
варіаційний функціонал, Згідно з теоремою про мінімум функціонала енергії

1.5. Задачі з неоднорідними граничними умовами
25
отримаємо
F= {gicidzfdn - 2 / fzdQ - 2 / Awzdil. (1.68)
о
З використанням формули Гріна та граничної умови (1.66) перетворимо
у формулі (1.68) останній доданок:
F = (gvsidzfdn - 2 / fzdVt + 2 / gradw gradzdQ.
Додамо до останньої формули сталу величину
[gradw)2dn - 2 / fwdto,
яка не змінює розв'язку задачі про мінімум функціонала, і перепишемо
його у вигляді
F = [(grad)2udQ - 2 f fudQ. (1.69)
п п
Отже, видно, що функціонал має вигляд такий, як і для однорідних
граничних умов, Проте в разі його мінімізації потрібно враховувати
заміну (1.65)
Приклад 13. Розглянемо тут неоднорідну природну граничну умову
Ньютона
Ои
——Ь сги = а, хіУ Х2 Є Г, о — const, о > 0; (1.70)
OV
для рівняня Пуассона
-Аи = /, х1ух2 Є Q. (1.71)
Як і в попередньому прикладі, виконаємо заміну
и = z + w, (1.72)
де z — нова шукана функція; w — деяка відома функція, що має певний
запас гладкості, наприклад w Є с<2) (о), і

26
Варіаційні методи
dw „.
— + aw = д, хи х2 Є Г. (1.73)
З (1.73) випливає, що функція z повинна задовольняти на границі Г
умову
-^ + az = 0: хих2 Є Г. (1.74)
Знову для визначення функції z отримаємо рівняння
-Az = f + Aw. (1.75)
Оскільки крайова задача (1.75), (1.74) є задачею з однорідними
граничними умовами, то її варіаційне формулювання можна отримати з
теореми про функціонал енергії, Згідно з цією теоремою задача зводиться до
задачі мінімізації функціонала
F = f(grsdz)2dn -2 і fzdSl -2 і AwzdQ + а Г z2dT.
п п п г
Перетворимо цей функціонал за аналогією з попереднім:
F = / (giSidzfdQ -2 fzdQ + 2 / gradw gradzdJH
+a / z2dT -2a gzdY + 2a wzdT.
Г Г Г
Додамо до останньої формули сталу величину
/ (grsdw)2dn - 2 / fwdft — 2a gwdT + a / w2dT,
Q Q Г Г
яка не змінює розв'язку задачі про мінімум функціонала, і перепишемо
його у вигляді
F = f{gicidu)2dn -2 ї fudQ -2 ї gudT + a f u2dY. (1,76)
о о г г
Отже, для задачі, яка має природну граничну умову (1.70), функціонал
енергії вже змінює свій вигляд.

1.6. Метод Рітца
27
Висновок. Для задачі з неоднорідними умовами головного типу
достатньо врахувати заміну вигляду (1.65) і далі чинити так, як і для
однорідних граничних умов, На випадок неоднорідних граничних умов
природного типу потрібно врахувати відповідні зміни у записі функціонала
енергії,
Цей висновок дуже важливий для конструювання числових методів
побудови розв'язків крайових задач,
1.6. Метод Рітца
Для побудови наближеного розв'язку задачі про мінімум
квадратичного функціонала можна скористатися методом Рітца.
Нехай А — додатно визначений оператор. Тоді крайова задача Аи = /
еквівалентна (згідно з теоремою про функціонал енергії) задачі
мінімізації функціонала
F(u) = (u,u)A-2(uJ), uGHA. (1.77)
Виберемо послідовність {(рп}, кожна функція якої задовольняє вимоги
1° <рп Є НА,
2° detG^O,
3° \/щ Є НА, \/є>0 37V, он :
Щ-Yl аг^Рг
г=1
< Є.
А
Тут G = {(<ри ^і)а) — матриця Грамма послідовності функцій {tpn} .
Зазначимо, що умова 2° є умовою лінійної незалежності, а умова 3° —
умовою повноти.
Наближений розв'язок ип задачі про мінімум функціонала (1.77)
запишемо у вигляді
п
ип = 5^<W, (1.78)
г=1
де щ — невідомі коефіцієнти, Для їхнього знаходження використаємо
необхідні умови екстремуму функціонала (1.77) в підпросторі 5П,
побудованому на базисі {(fi} 5
^>=0, .= 1 п. (1.79)
баї

28
Варіаційні методи
Виконавши операцію диференціювання в (1.79), отримаємо
п
Рівняння (1.80) утворюють систему лінійних алгебричних рівнянь для
відшукання невідомих коефіцієнтів а у
Визначник системи лінійних алгебричних рівнянь (1.80) відмінний від
нуля за умовою 2°. Отже, система рівнянь (1.80) має єдиний розв'язок,
Зауваження, Поширеною є також схема методу Рітца, у якому
наближений розв'язок наводять шляхом використання послідовностей
базисних функцій
У цьому разі система лінійних алгебричних рівнянь для визначення
невідомих коефіцієнтів зберігає свій вигляд. Проте для кожного значення
п вона утворюється на основі іншої послідовності базисних функцій,
Теорема 5. Послідовність наблиснсених розв'язків {ип}методу Рітца
(1.78) збігається до узагальненого розв'язку як за енергією, так і за
нормою вихідного простору Н.
Доведення. Використаємо для доведення запис функціонала енергії
(1*50)
F(u) = \\и - щ\\2А - \\и0\\2А , (1-81)
де г^о — узагальнений розв'язок, 3 того, що ип надає мінімального
значення функціоналу (1.81), випливає, що різниця \\ип — щ\\Л набуває
мінімального значення на підпросторі Sn. Отже, згідно з умовою 3°
fan - Щ\\л ^
г=1
< є. (1,82)
А
Це й означає збіжність за енергією, Використаємо далі нерівність
11 11 -^ \ 2 11 11 ^ / і о о \
\\u\\a > 7 НІ , (1*83)
яка випливає з означення додатно визначеного оператора, Ця нерівність,
як зазначено, виконується для довільної функції и Є На- Отже, з (1,82)
та (1,83) випливає, що
\№п - щ\\ < є, (1*84)

1.6. Метод Рітца
29
тобто що послідовність наближених розв'язків збігається також і за
нормою вихідного простору, ■
Теорема 6. Послідовність наближених розв'язків методу Рітца
прямує знизу за енергією до узагальненого розв }язку.
Доведення. Розглядатимемо тут для спрощення викладок, що
послідовність функцій {<рп} є ортонормованою за енергією, тобто виконується
співвідношення
(<Ри<Рі)А = 6ц = { І \Уі (1.85)
Розвинемо узагальнений розв'язок щ у ряд Фур'е
ос
и* = ^2(fyVi)A(Pi' (1-86)
г=1
З (1.86) маємо
оо
ІІ«оІІІ = £(/.^)ї- (1-87)
г=1
Якщо система функцій {<рп} ортонормована, то система рівнянь Рітца
(1.80) спрощується, Вона набуває вигляду
«і = (/>¥><)> г = І,»-,™. (1.88)
Підставимо (1.88) у формулу для ип (1.78) і обчислимо
п
ІКІІл = К, ип)А = Y^ (/, <Рі)2 ■ (1*89)
г=1
Порівнюючи (1.89) з (1.87), можемо записати нерівність
КІІІ<ІІ«оІІІ, (1-90)
яка доводить теорему Якщо ж функції {tpn} не є ортонормовани-
ми, то їх можна ортонормувати шляхом використання процедури
Грамма^Шмідта [5], яка передбачає перерахунок ортонормованих
функцій через неортонормовані за скінченну кількість кроків. У цьому разі
нерівність (1.90) знову виконуватиметься, ■

зо
Варіаційні методи
Зауваження, Нехай ип — наближений за Рітцом розв'язок задачі про
мінімум функціонала енергії, 3 умов мінімуму функціонала випливає, що
(Aun-f,ri) = 0, V?,G5n. (1.91)
Узагальнений розв'язок г^о задовольняє рівність
(А«0-/,г/) = 0. (1.92)
Віднімемо від (1.91) формулу (1.92):
{Аип - Ащ,г)) = 0,
або
(А(ип-щ),гі) = 0. (1.93)
З (1.93) випливає, що наближений розв'язок ип є ортогональною
проекцією узагальненого розв'язку на підпростір 5П, утворений на базисі
1.7. Метод скінченних елементів
Опишемо варіант методу Рітца розв'язування крайових задач для
звичайного диференціального рівняння другого порядку, Його
алгоритм будують з використанням спеціальних кусково-аналітичних
базових функцій, Цей метод відомий у науковій літературі як метод
скінченних елементів.
Для запису одновимірних кусково-лінійних базисних функцій методу
скінченних елементів розділимо проміжок [а, Ь] на відрізки — скінченні
елементи, точками х^ і = 0,1, ...,га, xq = а, хп = Ь. Задамо базисну
функцію if!? (х) співвідношенням
{0, х0 < х < х^г]
_Л±1 т<т<т ■ (L94)
0, ^г+1 Si % < Хп,
де hi = Хі — Хі-\. Графік функції (р^ (х) зображений на рис, 1.2.

1.7, Метод скінченних елементів
31
&
Рис. 1.2. Кусково-аналітичні базисні функції
Функції вигляду (1.94), які відмінні від нуля тільки в певній частині
області визначення, називають функціями з компактним носієм.
З огляду на специфіку побудови функції (р^ (х) мають такі
властивості:
rtf(x)eC[a,b];
2° (<Рг, 4%) = 0, якщо \r-s\> 2;
3° <рї (Xj) = 6ц.
З властивості 3° випливає: якщо
п
uh = J2aWi(x), (1*95)
г=1
то щ = Uh (хі) (позначимо щ (хі) = v.%). На скінченному елементі [^_і, Хі]
функцію Uh можна записати у вигляді
uh = ullV>l1(x) + u№(x). (1.96)
Використаємо кусково-поліноміальні функції (1.94) для побудови на-
ближеного розв'язку задачі Штурма^Ліувіля
~^Р(Х)^ + q(x)u = f(x), хЄ (а, Ь); (1.97)

32
Варіаційні методи
u(a) = 0, u'(b) = Q. (1.98)
Якщо коефіцієнти р(#), д(ж) рівняння (1.97) задовольняють умови
р(я) > Ро > 0, д(ж) > 0, то оператор задачі (1.97), (1.98) є додатно
визначений (параграф 1.1). Крайову задачу (1.97), (1.98) можна
сформулювати як варіаційну, її узагальнений розв'язок існує і єдиний.
Застосувавши метод Рітца до побудови наближеного розв'язку, отримаємо
систему лінійних алгебричних рівнянь
п
Х>,-(р?,$Ь= (/,¥>?), г = 1,...,п, (1.99)
г=1
ь ь
a a
Позначимо тут для зручності скалярний добуток (<р^(р^)л на проміжку
[хк-ихк] через [(pi,<Pj]k, тобто
#fc-i
Врахувавши властивості кусково-поліноміальних функцій, знайдемо, що
(<р£,<РЇ)а = 0, \i~j\>2. (1.101)
Для \і — j\ < 2 матимемо
п
(tf,$b = X>i, ¥>,-]*. (1.Ю2)
Обчислимо г'-й елемент стовпця вільних членів системи лінійних
алгебричних рівнянь (1.99). Запишемо
n **
(/>**) = £ / to***- (і-103)

1.7, Метод скінченних елементів
33
Позначимо тут значення скалярного добутку (/, <pfy на проміжку
[хк-ихк] через (f,<Pi)k, тобто
UM)k= J №<ь-
Хк-1
У формулах (1.102), (1.103) для довільного фіксованого і відмінними від
нуля є тільки два доданки, тобто
(<РІ, $)А = [рі $]. + [рі $]і+1; (1.104)
(fM) = (f,rt)i + №)i+1- (1-Ю5)
У цьому разі, якщо врахувати (1.101), індекс j у (1.104) може набувати
значення і — 1, г, і + 1. Якщо j = г, то у формулі (1.104) є два доданки,
Якщо j = і — 1 або j = і + 1, то у цій формулі залишається тільки один,
відповідно, перший або другий доданок,
Якщо поставити собі за мету обчислити всі можливі значення
((р^(р^)л на проміжку [хі^і^Хі] (скінченному елементі О^), то їх можна
розмістити у матриці
Аг~{ ММ-і]* №М]< J' (1'106)
Аналогічно стосовно скалярного добутку (/, <£>f), Всі можливі його
значення на £іі можна розмістити у матриці-стовпці
В, = ( (^?)). ) . (П07)
Зазначимо, що, враховуючи вигляд скалярного добутку (1.102),
матрицю Аі молена описати сумою двох матриць
А^Кі + Мі, (1.108)
Де
Кг-\ нм^іф мм]* г (1Л09)

34
Варіаційні методи
м_ , [fLnVi-i]^ №-іМ]іл , Г11101
Хі Хі
Матриці Кі і М{ називають матрицями жорсткості та мас. Ця
термінологія перейнята з інженерних наук, зокрема, з комп'ютерної механіки
деформування інженерних конструкцій, Для побудови матриць К^, М^
Вг можна скористатись формалізмом матричних перетворень, а також
матричним записом наближеного розв'язку (1.96) на Г^
uh = Ni(x)Qii (1.111)
Де
Х ~ хі х — хг-1 \ q _ (nth n.h\T
hi ' hi ) '
Легко бачити, що виконуються співвідношення
N, (х) = ( --^, ^—^ ) , Q, = K_1>U?)J
і= J (£N<(x)) P^^d^dx; (1.112)
к.
Хі
М< = f Ni(x)Tq(x)Ni(x)dx] (1.113)
Хі
в
[ Ni(x)Tf(x)dx. (1.114)
%і~1
Зазначимо, що для довільних коефіцієнтів р (х), q (х) з метою
обчислення інтегралів у формулах (1.112) —(1.114) використовують квадратурні
формули, зокрема, формули Гаусса. Якщо коефіцієнти ру q та права
частина / — сталі, то інтеграли в формулах (1.112), (1.113), (1.114) можна
обчислити у явному вигляді
к--*-( l -1
1 нЛ -і і

1.7. Метод скінченних елементів
35
А:
Ь/А
V.
А
Z
А
А.,
ш.
X
ul I
h 1
г2 1
h 1
І3
kJ
|u її |
Г'
^
&|
7^
'/4
В,
>
в,
а.,
7а
Рис. 1.3, Схема формування системи лінійних алгебричних рівнянь
Мі = hi
-1/2
З V -1/2
1 2 \ 1
Остаточно, враховуючи попередні зауваги, систему лінійних
алгебричних рівнянь (1.99) можна зобразити схемою, показаною на рис 1.3.
Матриця системи є тридіагональною та симетричною, Коефіцієнти в
заштрихованих частинах додають, Головна гранична умова и (а) = 0
врахована, оскільки індекс j у формулі (1.95) змінюється від значення 1 (не
від нуля), Штрихом на рис, 1.3 зображені матриці А і і Ві, які
формуються з урахуванням того, що індекс у формулі (1.95) починають
відраховувати від одиниці, 3 кожної з цих матриць використовують тільки один
елемент.

36
Варіаційні методи
1.8. Слабкий розв'язок крайової задачі
Теорему про функціонал енергії можна використати для запису ва-
ріаційнних формулювань задач, оператори яких є принаймні додатними.
Проте існує чимало крайових задач, які є важливими з погляду їх
застосування в комп'ютерному моделюванні, оператори яких не є додатними
і не є навіть симетричними, Наведемо приклад такої задачі, яка моделює
одновимірний процес перенесення забруднень.
Приклад 14. Задачу описує диференціальне рівняння
"^ + РеІ+^/'же(а'ь) (1115)
та граничні умови
и(а) = 0, *ій = о. (1.116)
ах
Тут Ре — безрозмірна стала, число Пекле; / Є L2 (a, b). Область
визначення Da оператора цієї задачі можна описати таким співвідношенням:
DA = іи 0) :и(х)& W!?\ и (а) = 0, ^-^ = ОІ .
Тут W2 простір Соболева функцій, які інтегровні на проміжку [а, 6]
разом з узагальненими похідними до другого порядку включно (див,
додаток),
Запишемо вираз для скалярного добутку (Au^v), що відповідає
операторові задачі (1.115), (1.116). Використавши формулу інтегрування
частинами, отримаємо
ь
f fdudv n du . т , _..
dx dx dx
Видно, що скалярний добуток (1.117) не є симетричним,
З огляду на формулу (1.117) уведемо до розгляду простір
V = {и(х) : и(х) Є W^\ и(а) = о} , (1.118)
де W2 —простір Соболева функцій, які інтегровні на проміжку [а, 6]
разом з узагальненими похідними до першого порядку включно; гранична

1.8. Слабкий розв'язок крайової задачі
37
умова v(a) = 0 для функцій простору W2 виконується в сенсі слідів
(див, додаток),
Означення, Назвемо слабким розв'язком крайової задачі (1.115),
(1.116) функцію и (х) Є V, яка задовольняє варіаційне рівняння
(Ащу) = (і», Уь є V. (1.119)
Виконується включення
DACV.
Тому, очевидно, якщо функція и(х) Є Da є розв'язком задачі ((1.115),
(1.П6))
Au = f,
вона є і слабким розв'язком, тобто задовольняє варіаційне рівняння
(1.119).
Припустимо, що функція и (х) Є V є слабким розв'язком, Тоді вона
задовольняє варіаційне рівняння
ь ь
/(dudv du \ f
— -—h Pe—v + uv \ ax = / jvax.
\dx dx dx J J
a a
Застосувавши до першого доданка у лівій частині формулу інтегрування
частинами і врахувавши запис (1.118), перепишемо це рівняння
ь
ЯсРи п du \ du(b) /тЧ
dx2 dx ) dx
Оскільки v[x) — довільна функція, то звідси випливають рівності
d2u _ du p
dx1 ax
du (b) _ Q
dx
Отже, и{х) є розв'язком задачі (1.115), (1.116), але таким, який
належить ширшій, ніж область визначення D^ множині V. Власне тому
цей розв'язок і називають слабким розв'язком крайової задачі (1.115),
(1.П6).

38
Варіаційні методи
1.9. Абстрактна варіаційна задача
Запишемо варіаційну задачу (1.119) у загальному вигляді, Знайдемо
и Є V таке, що
a(u,v) = l(v)z Vv Є V,
де a (w, v), l(v) — деякі задані білінійна та лінійна форми. Питання
існування і єдиності слабкого розв'язку цієї варіаційної задачі розглянуто у
такій теоремі,
Теорема 7 (Лакса—Мільграма). Нехай V — гільбертів простір, у
якому задана білінійна форма a(u,v) : V х V —> R та лінійна форма
l(v) : V —> R. Уважатимемо, що білінійна форма неперервна та V-
елгптична, тобто виконуються нерівності
\a(u,v)\ < M||u||v|H|v; (1.120)
а{и1 и) > a \\u\\v , (1.121)
де М, а — сталі, М > 0, а > 0 а лінійна форма l(v) неперервна, тобто
задовольняє нерівність
\l{v)\<K\\v\\v, (1.122)
де К — стала К > 0. Тоді така варіаційна задача: знайти таку функцію
и Є V, що
a(u,v) = l(y) \fv^V, (1.123)
має єдиний розв 'язок, і виконується нерівність
\\u\\v < -. (1.124)
а
Доведення. Виберемо деяку функцію и Є V. Білінійну форму
a(u,v) при фіксованій функції и можна розглядати як лінійний
функціонал від змінної v. Позначимо його L(u)(v) = a(u,v). Під записом
L(u)(v) тут треба розуміти лінійний функціонал L(u) від функції v.
Лінійний функціонал L(u)(v) обмежений, оскільки обмежена білінійна
форма а (и} v). Нехай V*—простір, спряжений до V. Позначимо черезЦ-Ц^
норму в просторі К- 3 означення норми обмеженого лінійного функціонала
маємо
\\Т( \< Ml \L(U)(V)\
\\L(U)(V)\\* = SUP —[Пі *
veV \\v\\v

1.9. Абстрактна варіаційна задача
39
Враховуючи далі, що L(u)(v) = а{и,у) та нерівність (1.120), отримаємо
\\L(u)(v)\l<M^Vllv=MMv-
\\v\\v
Отже, лінійний функціонал L(u) : V —> V* теж обмежений. Нехай т :
К —> V відображення Pica, для якого за означенням виконується
твердження, Довільний лінійний, обмежений функціонал можна записати у
вигляді скалярного добутку Візьмемо l(v) Є V. Тоді для довільної
функції v Є V правильний запис
l{v) = {rl,v)y.
З іншого боку, згідно з (1.123) маємо
l(v) = a (w, v) = L(u)(v).
Праву частину останнього ланцюжка рівностей згідно з відображенням
Pica можна записати у вигляді
L(u)(v) = (tL(u)}v)v.
З урахуванням трьох останніх рівностей, матимемо
(tI,v)v = (tL(u),v)v. (1.125)
Отже, розв'язування задачі (1.123) можна звести до знаходження
розв'язку такої задачі:
тЬ(и) = ті (1.126)
Рівняння (1.126) має єдиний розв'язок, якщо існують значення
параметра р > 0, за яких афінне відображення
и £ V ^> и — р(тЬ(и) — ті)
є стискним. Для дослідження цього питання розглянемо вираз
\\и- prL(u)\\2v.
Врахувавши властивості норми, отримаємо співвідношення
||« - prL(u)\\2v = \\u\\2v - 2р(тВД, u)v + р2 \\tL(u)\\2v . (1.127)

40
Варіаційні методи
Перетворимо окремо вирази в другому і третьому доданках
(tL(u), u)v = L(u)(u) = а{и1 и) > a \\u\\v , (1.128)
||rLtt||v = (tLu,tLu)v = Lu(tLu) = a(u,rLu) <
<M\\u\\v\\tLu\\v.
Зазначимо, що з останнього співвідношення випливає
\\tL(u)\\v<M\\u\\v. (1.129)
Урахувавши нерівності (1.128) та (1.129) в разі оцінювання зверху виразу
(1.127), отримаємо
\\и - prL(u)\\2v < (і - 2ра + р2М2) \\и\\2у .
Вимагатимемо, щоб вираз у круглих дужках був менший від одиниці,
Тоді повинна виконуватись нерівність
-2ра + р2М2 < 0.
Очевидно, що цю нерівність задовольняють р Є (0,2а/М2). Для
таких значень р відображення є стискним, і, отже, існування розв'язку
доведене, На завершення доведемо, що виконується нерівність (1.124),
Прийнявши у формулі (1.123) v = и, отримаємо
ol \\u\\v < а(иуи) = І (и) < К \\и||у .
Звідси, поділивши цю нерівність на \\и\\у , знайдемо
и и к
\\и\\у<-Ш
Приклад 15, Розглянемо приклад 14. Маємо простір
V = {« (х) : и (х) Є W^1] (а, Ь); и (а) = о} ,
білінійну форму
ь
ґ \ f a \ f (dudv du \
a (w, v) = (Аи, v) = І І —-—h Pe—v + uv ax,
J \dxdx ах J

1.9. Абстрактна варіаційна задача
41
та лінійну форму
ь
а
Доведемо, що білінійна та лінійна форми задовольняють умови теореми
Лакса—Мільграма, якщо Ре = 1:
(.(.,.))•=(/(£
ь
dv du .
-—h — v + uv I dx
dx dx
Застосувавши очевидну нерівність
2cd< c2 + d2,\Jc,d£ R,
отримаємо
2 / ь ч 2 , , ч 2
<•<»•«»'*3 (/££*) «(/?*) +»(/««*) .(мас)
Оцінимо зверху кожен доданок у правій частині, використовуючи
нерівність Шварца
'ІттА * І (т)'<* І (*)'**•
J dxdx I J \dxJ J \dxJ
a
2
v b 2 b
tvdx) -I{t) dxIv2dx>
Ka J a a
b \ 2 b b
Imdx) */«,*/ль-
Отже, для (a(u,v)Y матимемо оцінку

42
Варіаційні методи
ь ь
+/Л/А
а а
Підсилимо цю нерівність, додавши у правій частині невід'ємний доданок
u2dx.
І(&4
Остаточно перепишемо нерівність (1.130) у вигляді
(a(u,v))2 < 2||«||J||w||J,
де
\u\£=[((^V + u*\dx.
° /
dx
Отже, ми довели неперервність білінійної форми, а саме: доведено
нерівність
\а {и) v)\ < 2 \\и\\г \\v\\x.
Аналогічно можна довести, що лінійна форма 1{у) є теж неперервною,
Доведемо тепер, що білінійна форма є У™еліптичною, тобто доведемо,
що виконується нерівність
Запишемо
ь ,
а(и,и) = І І
а (и, и) > а Ци^ ,
du\ du o
— + ~ru + и \ ах
dx J dx
а
2
2
4- и dx.
Відкинувши перший невід'ємний доданок у правій частині попередньої
формули, отримаємо
a(u7v) > -\\и\\\.
Отже, білінійна форма a (w, v) є V-еліптичною та а = 1.2.

ЇЛО. Метод Бубнова—Гальоркіна
43
ЇЛО. Метод Бубнова—Гальоркіна
Для побудови наближеного роз'язку варіаційної задачі
a(u,v) = l(y), \/v£V (1.131)
застосуємо метод Бубнова—Гальоркіна (у науковій літературі цей метод
називають також методом Гальоркіна), який полягає у такому, Виберемо
у просторі V послідовність функцій {ірі] , які задовольняють такі умови:
1° <Рі Є V;
2° {(fi} — лінійно незалежна система;
3° {<ft} — повна система.
Позначимо через Sn скінченновимірний підпростір простору V,
натягнений на базисні функції ері, ...,<рп. Наближений розв'язок варіаційної
задачі (1.123) шукатимемо у підпросторі Sn. Запишемо його у вигляді
п
ип = 5^а*¥>», (1.132)
і=1
де сіі Є R — невідомі коефіцієнти. Для їхнього знаходження підставимо
(1.132) у варіаційне рівняння (1.131) замість функції и і приймемо v = <pj
(j = 1, ...п). Отримаємо систему лінійних алгебричних рівнянь
п
^2 а (^«' ^') аз = l fa)' і = 1>'"' п' (1.133)
З умов 1°, 2°, накладених на базисні функції, випливає, що система
рівнянь (1.133) має єдиний розв'язок, Справді, наслідком цих умов є те, що
Sn — повний підпростір простору V, і, отже, в Sn справджується теорема
Лакса—Мільграма, яка забезпечує існування в Sn розв'язку,
Для дослідження проблеми збіжності послідовності наближених
розв'язків розглянемо лему
Лема 8 (Сеа). Існує стала С>0, яка не залежить від вимірностг під-
простору Sn така, що виконується нерівність
\\щ ~ ип\\у < С \\щ - vn\\v , (1.134)
де щ — розв'язок варіаційної задачі (1.131); ип — наближений розв'язок
(1.132); vn — довільна функція з підпростору Sn.

44
Варіаційні методи
Доведення. Очевидно, що щ задовольняє співвідношення
a(u0}vn) = l(vn), Vvn Є Sn.
З (1.133) випливає, що для ип виконується формула
a{univn) = l(vn), ^vn Є Sn.
Віднімемо почленно від попереднього співвідношення останнє.
Отримаємо
а(щ - un,vn) = 0, Vvn G 5n. (1.135)
Використавши нерівність (1.121), запишемо
a||u0 - un||v < а(щ — ип,щ — ип) =
а (щ - ип, Щ - vn + vn - ип) = а(щ- unj щ - vn) + а (щ - иП7 vn - ип).
Згідно з формулою (1.135)
а(щ - un,vn - ип) = 0.
Матимемо
а \\щ - un\\v <а(щ- ип, щ - vn).
Використаємо далі нерівність (1.120) для оцінки зверху правої частини
попередньої формули. Отримаємо
а \\щ - ип\\у <а(щ- ип,щ - vn) < М \\щ - ип\\у \\щ - vn\\v .
Звідси легко записати
\\Щ - ип\\у < — \\щ - vn\\v ,
що й потрібно було довести, ■
На підставі леми Сеа доведемо теорему про збіжність послідовності
наближених розв'язків (1.132) до узагальненого розв'язку,
Теорема 9. Нехай послідовність функцій {<рі} задовольняє умови 1°,
2°, 3°. Тоді послідовність наближених розв'язків (1.132) методу
Бубнова— Гальоркіна варіаційної задачі (L123) збіжна за нормою
простору V до слабкого розв'язку; тобто
\\Щ -ип\\у -^ 0.
Доведення. Випливає з нерівності (1.134) (див, теорему про
збіжність послідовності наближених розв'язків методу Рітца), ■

1.11. Вправи для самостійного виконання
45
1.11. Вправи для самостійного виконання
Вправа 1« Довести додатність і додатну визначеність операторів
таких задач:
і-1) -& = /. и'(а) = 0, «(b) = 0;
!-2) "& = /] «'(а) = 0, «'(Ь) = 0;
1.3) — Au + au = f, и\т — 0, о"(жі,Ж2) > 0;
!-4) -Й = /. «(«) = и'(«) = 0, «(b) = «'(Ь) = 0.
Вправа 2. Визначити обмеження на коефіцієнти диференціального
рівняння, за яких оператор задачі
буде додатно визначений.
Вправа 3. Визначити обмеження на коефіцієнти в граничних умовах
задачі
сРи
J1
а$и{а) + aiu'(a) = 0, Pou(b) + f3iu'(b) = 0,
за яких оператор задачі додатно визначений.
Вправа 4. Довести додатну визначеність оператора задачі
аои(а) — а.\и'{а) = 0,
/S0u(b) + /?!«'(Ь) = 0,
a0«i > 0, Д,А > 0, а20 + /302 > 0,
р(х) >р0>0, д(х) > 0.

46
Варіаційні методи
Вправа 5. Записати функціонали, що еквівалентні крайовим
задачам:
5.1) -и" (х) = f (х), и'(а) = и(Ь) = 0;
5.2) -и" О) = / (ж), «'(а) = и'{Ь) = 0;
5.3) -Аи + аи = /, а > 0, и |г= 0;
5.4) -u</v> (ж) - /, «(о) - и'(о) = 0, «(b) = и'(Ь) = 0;
5-5) -±Р(*)Й+ *(*)« = /(*),
u(a) =0, u'(6) = 0, р (ж) > р0 > 0, g (ж) > 0;
5-6) -ІР(«)Й + *(*)« = /(*),
О!о«(а) — ссім'(а) = 0,
A,u(b)+/?iu'(b) = 0,
а0о;і > 0, АА > 0, а§ + /^ > 0,
р(х) > ро > 0, д(ж) > 0.
Вправа 6. Визначити тип граничних умов і довести, що з умов
мінімуму функціонала енергії випливають диференціальне рівняння та
природні граничні умови для таких задач:
6.1) -u"(x) = f(x), хє(а,Ь),
и (а) = 0, и (Ь) = 0;
dx^ \ / ах
6.2) -j-p{x)f + q{x)u = f{x), ж Є (а,6),

1.11. Вправи для самостійного виконання
47
и (а) = 0, и (Ь) = 0, р (х) >ро>0, q (х) > 0;
6.3) wW (х) = / (х), х Є (а, 6),
ги (а) = ги (6) = 0, w" (а) = w" (6) = 0;
6.4) -зЬО*) £ + 9 0*0 « = / 0е)' я Є (а, 6),
а0« (а) — аіУ (а) = 0, и (6) = 0,
р(х) >ро>0, q(x) > 0.
Вправа 7. Побудувати методом Рітца наближений розв'язок задач:
7.1) -и" (х)+и = 1, хє (0, тг), и(0) = и(тг) = 0,
(вибрати систему функцій </?n = sinner);
7.2) -Д« + « = 1,
П = {хі>х2 : 0 < х\ < а, 0 < х2 < Ь} , «|г = 0,
(вибрати систему функцій {рш} = sin ^^^ sin
П7ГЖ2 s
b ,
Вправа 8. Записати слабкі варіаційні формулювання і дослідити бі-
лінійні та лінійні форми, що еквівалентні крайовим задачам:
8.1) -и" (х) = / (х), «'(а) = «(b) = 0;
8.2) -и" (х) = f(x), u'(a) = и\Ь) = 0;
8.3) -Аи + аи = f, а>0, и |Г= 0;
8.4) -«(/v^ (re) = /, «(а) = «'(а) = 0, и{Ь) = и'(Ь) = 0;

48
Варіаційні методи
8-5) -£p(x)fx+q(x)u = f(x),
и(а) = 0, u'(b) = 0, р(х)>ро>0, q(x)>0;
8.6) -ІР(х)І + д(х)и = /(х),
otoii(a) — aiu'(a) = 0,
/30u(b) + /3lU'(b) = 0,
а0аг > 0, #,& > 0, a20 + ffi > 0,
p(x) >Po>0, q(x) > 0.

Розділ 2
Апроксимація на скінченних
елементах
Один із числових методів, який має широке застосування,— метод
скінченних елементів, здебільшого можна розглядати як варіаційний зі
спеціальним вибором базисних функцій, У першому розділі найпростіші,
кусково-лінійні базисні функції на одновимірних скінченних елементах
використано для побудови схеми методу скінченних елементів. Тут
описано інші, найуживаніші в методі скінченних елементів, базисні функції,
Є різні означення скінченних елементів, які з погляду застосування
однакові. Наведемо тут означення Сьярле [15],
Означення, Нехай
1° Qe C Rn — область n-вимірного евклідового простору (область
скінченного елемента);
2° N — fc-вимірний простір функцій на Qe (функції форми);
3° Q — набір лінійно незалежних функціоналів Qi : Qi —^ R (і =
1, 2,..., п) (вузлові параметри). Тоді трійку (fle, JV, Q) називають
скінченним елементом.
Означення. Нехай (fie,iV, Q) — скінченний елемент і нехай
{^1^2) •■•» ^к} ~ базис простору 7V, причому
Qi (rf) = 8ц.
Тоді базис {<Рі, <р%і..., ¥>к} називають вузловим.
У практиці застосування методу скінченних елементів дуже часто
асоціюють термін скінченний елемент з областю скінченного елемента

50
Апроксимація на скінченних елементах
П€. Такий підхід є звичним і обґрунтованим, оскільки область П€ із
вибраними вузловими точками справді визначає все інше, що пов'язане зі
скінченним елементом.
2.1. Похибки апроксимації кусково-
лінійними функціями
Найпростіші кусково-лінійні одновимірні базисні функції, які
використовують у методі скінченних елементів, наведені в 1.7, Похибку
апроксимації цими базисними функціями визначає така теорема.
Теорема 1. Нехай функція и (х) Є W2 {а->Ь). Тоді для їїінтерполянта
п
Uh О) = ^2 Щ{рНі № ' Ui = U (Хі) , (2.1)
г=0
побудованого шляхом використання кусково-лінійних базисних функцій
на сітці
і
Хі = а + У, hj: і — 0,1,..., п
зі змінним кроком hj виконуються оцінки
\\и (х) - uh (x)\\L2 < dh2 \\u\\wi2) , (2.2)
\\u (x) - uh (x)\\w(i} < C2h \\u\\w(2) , (2.3)
deh — max/i^, Сі, Сі — сталі, які не залежать від h.
Доведення* Розглянемо
b
\и - uh\\2Lu = / (« - uhfdx = ^2 / {u-uhfdx,
(2.4)

2.1. Похибки апроксимації кусково-лінійними функціями
51
о
Wu~uh\\2ww = {(u'~ u'hf + (и ~ uhfj dx = (2.5)
а
п 1
= Y1 / \(U' ~ U'hf + (U ~ Uh)) dx-
На коленому проміжку [xj-i^Xj] виконаємо заміну
х = Xj-i -fa, 0 < а < hj (hj = х3 — #j_i). (2.6)
З урахуванням заміни (2.6) введемо позначення
е(а) = и (а) - uh (a). (2.7)
Тут і далі індекс j при h будемо опускати, Оскільки Uh інтерполянт ад,
то є (0) = є (h) = 0. Розвинемо є (а) у ряд Фур'є
еУа) = Z^a^sm_^' (2*8)
к=1
Звідси
Г h °°
J є2 (a) da =-^4- (2.9)
о к~1
Диференціюючи ряд (2.8), отримаємо такі співвідношення:
к=1
j{e'{a))4a = \j^(^al- (2.11)
0 kz=zl
«•«»)=-і: (т)г
&7га;
ajbSin—^—;
f{e^a))4a=\±{^al (2.12)

52
Апроксимація на скінченних елементах
Зазначимо, що для к > 1 виконуються нерівності
"Цх)4"^' (2дз)
З (2.9), замінивши доданки у правій частині згідно з нерівністю (2.13),
знайдемо
h . h
je\a)da = \^Y. (т) < = £ /(А")2 (а) ^ (2Л5)
о kz=:1 о
Врахуємо в (2.15), що згідно з (2.7)
є = и .
оскільки гг/г (а) — лінійний інтерполянт Підставимо (2.15) у праву
частину формули (2.4), отримаємо
«*ііі<£^ У («")»**• (2Л6)
Нехай h = max/ij, тоді, підсилюючи нерівність (2.16), одержимо
нерівність
j v
ь
\и
uh\\2L2<^J((u"Y + (u>f + u>)dx. (2.17)
Нерівність (2.17) можна переписати у вигляді
\и~ин\\ь2 < Cih2 \\u\\w(2)
Отже, нерівність (2.2) доведена.
Для доведення нерівності (2.3) використаємо співвідношення
(2.11) та нерівність (2.14). Отримаємо
h . h
|(е')2 (a) da < ~ J] (^) al = £ J (є")2 (a) da. (2.18)

2.2. Одновимірні скінченні елементи лагранжового типу
53
За аналогією з попередніми викладом із (2.18)
IW-KWl^^lH2^. (2.19)
Додамо нерівності (2.17) та (2.19):
II ' / II2 і II ||2 ^ а || ц2 . п її ц2 /0 огЛ
ІІ« - Ч\\ь> + \\U~ Uh\\b, < —2 ll«llWW + ^4 Mw™ ■ ^2'2°)
Нерівність (2.20) перепишемо у вигляді
||е||'(„<ф2И|'(Ч, (2.21)
де
Очевидно, що
cl=[-^h
7Г2 7Г2
<9і<С|=(і + ^). (2.22)
Тому матимемо нерівність
ІІЄС2(1) - С^ І|«Са(2) ,
де стала С2 не залежить від h та від функції и. З останнього
співвідношення випливає нерівність (2.3). ■
Зазначимо, що сталі Сі, С2 у нерівностях (2.2), (2.3) не залежать від
кроку h та функції и.
2.2. Одновимірні скінченні елементи
лагранжового типу
За аналогією з 1.7 можна побудувати кусково-поліноміальні функції
вищих, аніж перший, порядків, Наведемо тут матричний запис апрок-
СИМуЮЧОЇ фуНКЦІЇ На СКІНЧеННОМу елементі Пі = {Хі_і,Хі)
uh = Ni(x)qi,
(2.23)

54
Апроксимація на скінченних елементах
Рис. 2.1. Кусково-поліноміальна апроксимуюча функція
Де
N.
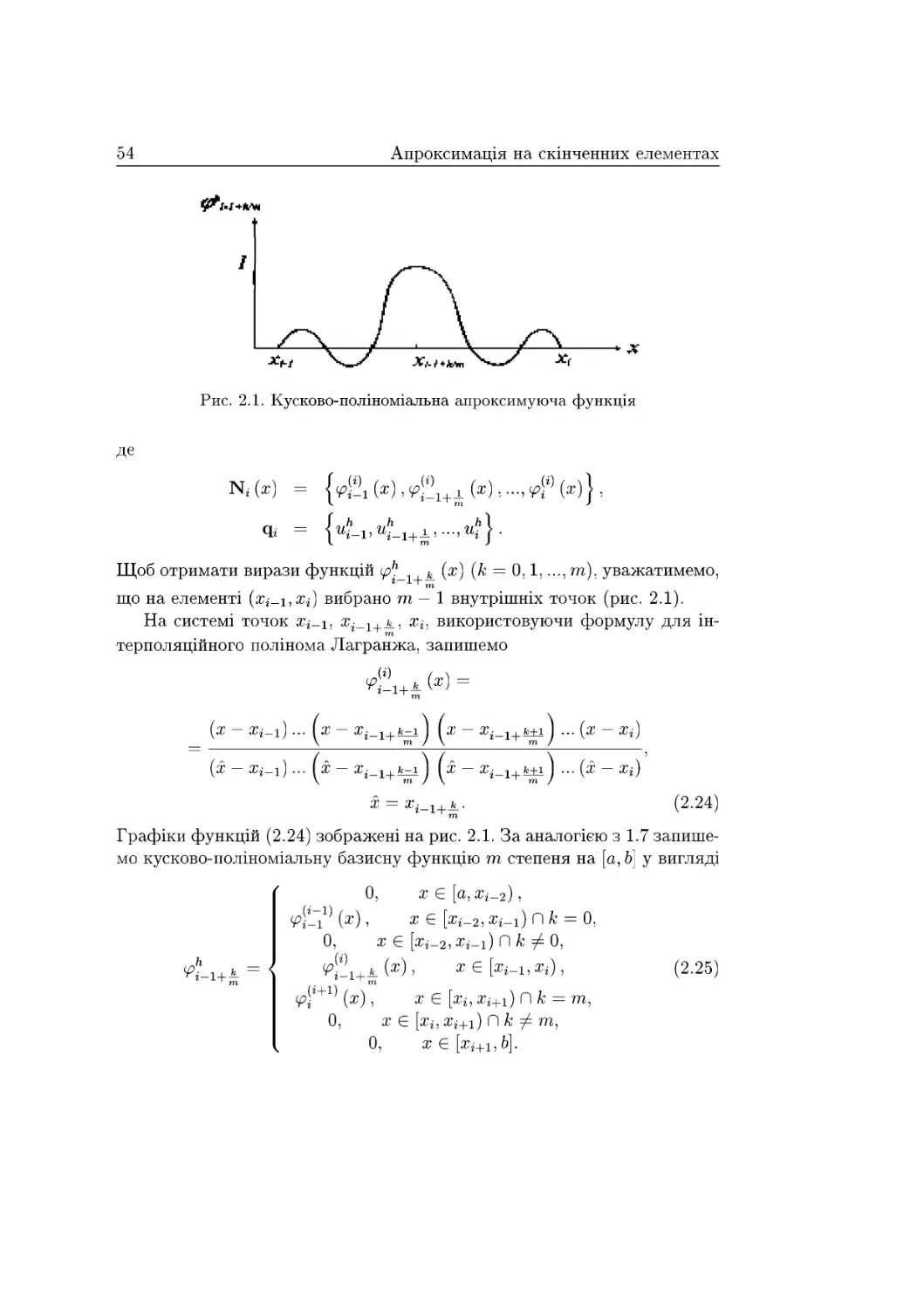
Щоб отримати вирази функцій <£>*,_*_ (ж) (А; = 0,1,..., т), уважатимемо,
що на елементі (з^-ь^і) вибрано m — 1 внутрішніх точок (рис, 2.1),
На системі точок х^-і, хі__1,к_^ х^ використовуючи формулу для ін-
т
терполяційного полінома Лагранжа, запишемо
1 т
(х - Хі-і) ... fa; - ^_1+^і J їх - х{_1+к±іJ ... (х - Хі)
{х - хі-х) ... (х - ^_1+^і j у.
X ^_1+fe+i
(х - Хі)
X — Х^_1+А-
(2.24)
Графіки функцій (2.24) зображені на рис, 2.1. За аналогією з 1.7
запишемо кусково-поліноміальну базисну функцію т степеня на [а, Ь] у вигляді
0, х Є [а,Жі_2),
(р^ (х), £ Є [ягі_2, a?j_i) П fc = 0,
0, х Є [жі_2,:сі-і) ПА: ^ 0,
^-1+А
¥>■
г г
(і)
-1+
(ж), Ж Є [яГі-і.ЯГі)
(2.25)
(ж), ж Є [жі, хі+і) Пк = т,
0, ж Є [ж,, хі+і) П /г ^ т,
0, жє[жт,Ь].

2.3. Ермітові одновимірні апроксимації на скінченних елементах 55
Зазначимо, що функції вигляду (2.25) належать до класу С [а, 6]. Похідні
від них мають розриви першого роду на границях скінченних елементів.
У праці [13] з'ясовано, що для скінченноелементних апроксимацій
степені fc, тобто таких, за допомогою яких довільний повний поліном
багатьох змінних Хі,Х2, ...,Яп степені, що не перевершує fc, може бути
поданий на скінченному елементі за допомогою лінійної комбінації базисних
функцій, виконується оцінка похибки апроксимації
\u-uh\
W.
00
< слк+1-*
m\ww)
(2.26)
2.3. Ермітові одновимірні апроксимації на
скінченних елементах
Для отримання наближених розв'язків задач, описуваних
диференціальними рівняннями порядків, вищих, аніж другий, потрібно мати
базисні функції, які задовольняють підвищені умови щодо їхньої гладкості.
Такі функції можна будувати з використанням інтерполяційних
поліномів Ерміта [15],
Проілюструємо це прикладом кубічного полінома Ерміта, Розглянемо
скінченний елемент Qi = {х : х%-\ < х < Хі}. Виберемо за вузлові
параметри значення функції та її першої похідної
н duhixj)
Uh (Xj)
u*
dx
.h
U4<
M.
Запишемо на Q*
uh = Nj (x) qi:
(2.27)
де
Hi-ito (x
Hi-i,i (x
Ніл (x
Hi-i (x
= {Hi-i,o (x), Яі-ід (x), Hifi (x), Ніл (x)} ;
= H*_1(x)(l + 2Hi(x))-t
= Я? (x) (1 + 2Я,_Х (х));
= hHl1(x)Hi(x);
= -hH?(x)Hi-X(x)\
X ~~ 3^—1
Xi
h
Нг(х)
h

56
Апроксимація на скінченних елементах
ЇЙ*
х±,
*А
Xt*-1
— X
Рис. 2.2. Ермітова базисна функція першого виду
* JC
Рис. 2.3, Ермітова базисна функція другого виду
Отже, формула для наведення апроксимованої функції (2.27)
отримана, шляхом використання двох видів базисних функцій (р^ (х) та ф^ (#),
графічно зображених на рис, 2.2, 2.3. Як бачимо з рисунків, ці базисні
функції неперервні на проміжку [а, Ь] разом з похідними першого
порядку.
2.4. Одновимірні апроксимації функціями»
бульбашками
Є багато задач, для числового аналізу яких необхідно
використовувати спеціальні апроксимації високих порядків, утворені так
званими функціями-бульбашками, Опишемо тут апроксимації функціями-
бульбашками на одновимірних скінченних елементах.
Нехай проміжок [а, Ь] розділений точками
Хі, і = 0,1, ...n, (xq = а, хп = Ь)

2.4. Одновимірні апроксимації функціями-бульбашками
57
на скінченні елементи
Q = {х : Xk-і < х < Xk] , к = 1, 2,..., п. (2.28)
Відобразимо кожен елемент (2.28) на "стандартний" скінченний елемент
Q,* вигляду
П# = {£ : -К £ < 1} (2.29)
за допомогою співвідношення
х = -^—хк-г + ~^хк, £ Є Q*. (2.30)
На елементі Q* побудуємо послідовність базисних функцій
*>і = Ц-^ ^2 = ^, ^ = Ф^_і(0, j = 3,4,...,p+l. (2.31)
Тут <£;(£) визначені через поліноми Лежандра Pj-\ за формулою [7, 20]
г—, І
*і(0 = у2^ Jр^(*)^ і = 2>^■•■■ (2*32)
-1
Наведемо тут вирази для чотирьох перших поліномів Лежандра:
Р0 = 1, Рх = t;
P2 = ^(3t2-1)] (2.33)
P3 = i(5*3-3t).
Зазначимо, що виконується рекурентна формула [7, 20]
{п + 1) Pn+1 (t) = (2n + 1) tPn (t) - пРп-г (t), (2.34)
яка дає змогу знайти вираз для Рп+і через вирази для Рп та Рп_і. Тому,
якщо відомі перші два поліноми Лежандра, за формулою (2.34) можна
знайти вирази для всіх інших.
Відомо, що поліноми Лежандра є ортогональними на проміжку [-1,1],
тобто виконується співвідношення
1
fpi(t)Pj(t)dt={ Jl'fA- (2-35)
1 І 2*4-1' ~ J'
І
-1

58
Апроксимація на скінченних елементах
Базисні функції <£>ь </?2 називають вузловими, У випадку запису апро-
ксимованої функції у вигляді суми за базисними функціями
и = щ-гірг (£) + икір2 (£) + ^2 а№з (£) (2.36)
їм відповідають вузлові значення щ~\, щ- Базисні функції <pj (£), j =
3,4,...,р+1, називають функціями-бульбашками, Ця назва зумовлена
їхньою властивістю
4>і (£) = 0, Є = ±1, З = 3,4, ...,р+ 1. (2.37)
У записі (2,36) коефіцієнти aj не є вузловими значеннями.
Властивість (2,37) зумовлена таким. При £ = — 1 базисні функції
пропорційні (2,32) інтегралові з однаковими верхньою та нижньою
границею. Те, що базисні функції при £ = 1 дорівнюють нулю, зумовлене тим,
що цей інтеграл теж дорівнює нулю, це випливає з властивості ортого-
нальності поліномів Лежандра Pj (j > 1) до одиниці, 3 формули
(2п + 1) Рп (х) = Р'п+1 (х) - Р'п_х (яг), п = 1, 2,..., (2.38)
яку задовольняють поліноми Лежандра [7, 20], випливає таке важливе
співвідношення:
W ® = М, о1 -п ^ (Є) " Р'"2 (^ ' ' = 3' 4' ■"' (2'39)
V2 (23 - !)
яким можна користуватися для обчислення інтегралів від добутків
базисних функцій, 3 (2,32) та (2,35) випливає також:, що для базисних
функцій-бульбашок виконується формула
-1
2.5. Апроксимації на трикутних скінченних
елементах
Припустимо, що двовимірна область Q розділена на скінченні
елементи Qe трикутної форми (рис, 2,4),

2.5. Апроксимації на трикутних скінченних елементах
59
Рис. 2.4. Скінченний елемент трикутної форми
Позначимо літерами г, j, m вершини трикутника з координатами,
відповідно, х\1хг2\ х{,х2; х™,х™, літерою р — біжучу внутрішню точку
трикутника з координатами #і, х2. Побудуємо на трикутнику Qe функції
(р£ (хі, х2), к = г, jf, m за формулою
<р\е] (хих2)
dpjm
Jijm
(2.41)
площі трикутників pjm та ijm.
» (J*) Jti\ _ і : ,M
ДЄ 5p_
Очевидно, що (pf] ix(\x2 J = 1 і tpf] {xi,x2) = 0 на лінії jm.
Використовуючи відомі співвідношення для обчислення площі
трикутника через координати його вершин
Хі
х2
X
dpjm — g U-ЄТ
X
X
(з) Лі)
1 х2
("*) Лш)
З ijm q СІЄ!
X
(0
1
U)
r(0
x2
#
("0 ~(ш
знайдемо
у.
(є)
(a;^, 4j = т (а« + ьіхі + c*s2)
1 '~l '~z ' «5
ЛІ)Л™) ЛІ)Лт) l _ Лі) Лт) _ Лт) Лт) (j)
(2.42)
ир п. — Л1)ТКт) _ і}) {т) , _ VJ) _ ym) _ imj _ imj _ іл гоо
ОТЖЄ, iff Є ЛІНІЙНОЮ фуНКЦІЄЮ ЗМІННИХ Х\,Х2-
Нехай Q = UOe. За ідеями, викладеними в 1.7, побудуємо на об'єд-
є
нанні трикутників Qe кусково-лінійні базові функції
0, і І Ое.
rf(^b^)
{
(2.43)

60
Апроксимація на скінченних елементах
Рис. 2.5, Базисна функція на множині трикутних скінченних елементів
Графічне зображення функції (р\ показано на рис, 2.5.
Функції if!? вигляду (2.43) відмінні від нуля тільки в певній частині
області Q (заштрихована частина на рис, 2.5) на сукупності трикутників,
що містять точку і. Вони мають такі властивості:
Ґ\^ЄС(П);
2°. {(Ргу^) = 0, якщо точки г та 5 не належать одному трикутному
скінченному елементу СІе.
З використанням лінійних функцій (р^ (жі,^) запишемо апроксиму-
ючу функцію Uh на Qe у вигляді
uh = «tV!e) (xi, x2) + utyf (Xl, x2) + uhm4>$ (xu x2). (2.44)
Приклад 1, Розглянемо одну особливість апроксимації функції
хз = х\ лінійною комбінацією (2.44) (рис, 2.6). Нехай
eh = uh- х\, (2.45)
Де
Обчислимо
Згідно з формулою (2.45)
deh _ дщг_
дх2 дх2
М
ь2
Т^ + Tvi
(є)
deh
дхо

2.5. Апроксимації на трикутних скінченних елементах
61
■х?
Рис. 2.6, Апроксимація функції на трикутнику
З геометричних побудов видно, що
duh
hcosO
дхо
2 sin в
Отже, значення похідної від похибки єн наближення функції х\ зростає
зі зменшенням кута в трикутного скінченного елемента. Звідси випливає
висновок, що якість наближення похідних деякої функції на множині
трикутників погіршується, якщо у цій множині є трикутники з гострими
кутами.
У загальному випадку апроксимаційні властивості функцій (2.43)
описує така [18] теорема,
(2)
Теорема 2. Якщо и (х) Є Wf> (Q) і інтерполянт цієї функції Uh{x) =
Yl4^ ixiix2)^ то справджуються оцінки
\и~ин\\ь2 < C^h2 ЇМ
w<
(2)
\и - uh\
W.
(1)
sn h її її
де Сі ^ С2 = const, h — максимальне значення серед сторін трикутників
(діаметр розбиття на скінченні елементи), в — мінімальне значення
серед кутів трикутників.

62 Апроксимація на скінченних елементах
Рис. 2.7. Трикутний скінченний елемент з шістьма вузлами
Доведення. Наведене в монографії [18]. ■
Опишемо один спосіб побудови квадратичних апроксимацій на
трикутних скінченних елементах. Для цього на серединах сторін трикутного
скінченного елемента виберемо додаткові вузлові точки fc, /, n, (рис, 2.7).
Використаємо функції (2.41) і запишемо формулу вигляду (2.44) для
квадратичних апроксимацій на трикутнику
uh = 4Є) (хі, х2)«? + ... + ф(:] (xltx2) uhn, (2.46)
де wf, ...,wj} — вузлові значення апроксимованої функції;
W = *>?' (^і" -1);
*}" = $> (*,!? -1);
<Й' = vt] W -1);
4е) = M'V'e); ФЇ] = *■??№, Й" = iffvtf.
Молена переконатися, враховуючи властивості функцій щ■ , що
Vv (#ь#2) задовольняють умову
^e)(45),4S))=^- (2-47)

2.6. Лагранжові апроксимації на прямокутних скінченних елементах 63
х/т* л:/*
x^kf
Рис. 2.8, Прямокутний скінченний елемент з множиною вузлів
2.6. Лагранжові апроксимації на
прямокутних скінченних елементах
Уважатимемо, що двовимірна область розділена на прямокутні
скінченні елементи Q€ (рис, 2.8).
На кожному елементі виберемо множину вузлових точок на перетині
ліній Х2 — const, x\ = const. Кожна вузлова точка однозначно
характеризована парою чисел %,з і має координати \х\
(«)
%1 , #2
X
U)
Для побудови базисних функцій на вибраному прямокутному
скінченному елементі використаємо спосіб побудови інтерполяційного
полінома Лагранжа у прямокутній області, згідно з яким
Де
,(т)
іГМ =
і1Г]М =
^)(xi,xi)=lim)(x1)l^(xal (2.48)
(Xl - X?) ... (Х1 - Х^) (*1 ~ 4+1)) - (*1 ~ 4т))
(х? - 41}) - (х? - xt1]) (х? - 4т))... (4° - 4т));
(*2-<)•••(
(і-1)
х2 - х$
(z2-4j+1))...(*2-4n))
(4Л - х?) ... (х? - xt1]) (х? - *?+1)) ... (х? - 4П)) '
Оскільки функції і\ (хі) та 1^ (х2) мають властивості

64
Апроксимація на скінченних елементах
то подібну властивість має і функція (p\j (a?i, х2)\
„g> (»<*>, 4") = Г» («!") <Г (4") = ад*. (2.49)
де 5jfc — символ Кронекера.
Враховуючи (2.49), запишемо апроксимуючу функцію ин на
прямокутному скінченному елементі у вигляді
т п
uh (xu x2) = YsY. u*Mf 0*ь х2) • (2.50)
Тут Utj — значення апроксимованої функції у вузловій точці ij.
Базисні функції (ff- {х\, х2) визначені на одному скінченному
елементі. Як і в попередньому, вони можуть бути неперервно поширені на всю
область. У цьому разі базисні функції, які відповідають внутрішнім
вузловим точкам, локалізовані тільки на одному скінченному елементі
(дорівнюють нулю на всіх інших скінченних елементах), Базисні функції,
які відповідають граничним вузловим точкам, локалізовані на
елементах, які містять ці вузлові точки.
2.7. Ермітові апроксимації на прямокутних
скінченних елементах
Побудова на скінченних елементах базисних функцій двох і більше
змінних, які задовольняють більш сильні, ніж неперервність вимоги, є
дуже складною, Задача побудови таких функцій є відкритою, оскільки
відомі її розв'язки лише в деяких часткових випадках, Одним із них
є біку бічна апрокимація на прямокутному скінченному елементі, яку
отримують як узагальнення одновимірної апроксимації Ерміта
(параграф 2.3). Розглянемо прямокутний скінченний елемент Qe (рис, 2.9).
Використовуючи ермітові кубічні поліноми (див, 2.3), запишемо на Qe
таке подання для апроксимованої функції и^
uh (хи х2) = Hi-lfi (хг) /і_і (х2) + Ні_1л (хг) і£і М + (2.51)
+Hifi(x1)fi(x2) + Hiil(xl)fi1)(x2),

2,7, Ермітові апроксимації на прямокутних скінченних елементах 65
&■>
tf-J*
К
-»
ч
г Чр
д:^-м —
.ґї-jj
Рис. 2,9, Прямокутний скінченний елемент
де fr (#2), г = г — 1, і — значення функції гг/г (#і,#2) на лінії а;і = х( ]
Лі) / ч * .... (г)
/г (^2J — значення першої похідної за змінною х\ на лінії х\ = х\ ,
Наблизимо функції fr (х2): /г (#2)5 (г = г — 1,г) ермітовими
кубічними поліномами за їхніми значеннями та значеннями їхніх перших
похідних за змінною х2 у вузлових точках. Отримаємо
fr (>2) = Hj-ifl (х2) и^_г + Hj-iyl (х2)
uarJ-l
дх2
+Hjfi(x2)u^j + Hjil(x2)
ди
г>3 ,
\3
диї.
дх2
(2,52)
rj—1
^W^hiW^^W^
+ЯЛ0 (*2) -^ + Яід (rc2) rj
0ЯГ1
дх\дх2
1,г,
(2,53)
де через
«.
du£, 0«*
(2»,Л
<92гг;
г'5' 9^і ' cb2 ' дх\дх2
і -. . (г) (в)
позначені значення функції Uh та п похідних у вузловій точці я^ х2
(г = і- 1,і , s = j - 1J).
Підставляючи співвідношення (2,52), (2,53) у формулу (2,51),
отримаємо вираз для апроксимації функції Uh на прямокутному скінченному
елементі Пе. Запишемо його у матричному вигляді
uh = Ne(xux2)qe
(2,54)

66
Апроксимація на скінченних елементах
де
N (хл ХЛ ~ llD{m Jh0) J°'1] J1A) Jhl) \
ГЧе {Xi,X2) — ^Vi-lJ-U <Pi-lj-l, (fi-lj-1, fi-lj-i, -.., fij-lf
dT -
*0) =
«1] =
= Hrfi (xi) Hsfi (x2)
= HrA (xi) Hsfi (x2)
= Hrfi (xi) Hs>1 (x2)
tff = НГі1(х1)Н8і1(х2)
r = i-l,i;s = j- 1, j;
т=Ь ^ duU^-i duti^-i ^2Ц?-і„і-і d2uthJ^ d2ul^
j t-i„j-ii ^^ і ^2 і 9o:i9x2 ' дх\дх2 ' ""' дх\дх2
Вигляд функцій Д"Г]о, і?г,і наведено у 2.2.
Отже, для бікубічної апроксимації ермітового типу у кожній вузловій
точці маємо чотири вузлові параметри.
Базисні функції ^ О^ь^г) побудовані на одному скінченному
елементі. Як і у попереднньому, вони можуть бути поширені на всю область.
При цьому розширенні зберігається неперервність до перших похідних
включно в разі переходу через спільні сторони прямокутників,
2.8. Двовимірні ізопараметричні апроксима»
...
ції
Характерною особливістю апроксимацій, які вже розглянуто в
цьому розділі, було те, що двовимірну область у площині Х\,Х2 вважали
полігональною, або в процесі побудови скінченних елементів вона апро-
ксимувалась полігональною областю. Опишемо тут спосіб побудови
таких апроксимацій, які вільні від зазначених обмежень. Питання точності
подання областей з криволінійними границями в рамках цього підходу
детально описано у монографії [18].
Розглянемо квадрат Q>* у системі координат £, г\

2.8. Двовимірні ізопараметричні апроксимації
67
4
1
-L
Л
1 '
0 L
3
1
Рис. 2.10. Скінченний елемент у вигляді квадрата з чотирма вузлами
На квадраті виберемо три сукупності вузлових точок. На вибраних
сукупностях вузлових точок побудуємо такі три системи базисних функцій:
1° білінійну (рис. 2.10)
<Рі (£, V) = 7 С1 + &S) С1 + ViVl г = 1,..., 4;
(2.55)
£j77, — координати г'-ї вузлової точки;
2е біквадратичну (рис. 2.11)
1
<Рі (£, г]) = - (1 + &Є) (1 + w) (££ + 1*77 - 1),
г = 1,3,5,7;
^(£,г/) = ^(і-£2)(1 + г/^),г = 2,6;
Vi (Є, г?) = ^ (1 + 60 (1 - г?2) , * = 4, 8;
3° бікубічну (рис, 2.12)
Mt,v) = ^(l + te)(l + rkri)U2 + ri1-™
г = 1,4, 7,10;
г = 2,3,8,9;
(2.56)
Vi ^v)=і ^"е^(і+^ (І+зб4 (2-57)

68
Апроксимація на скінченних елементах
7
1
Й
1
ї
6
-1
2"
Л
Ч
ft.
0 і'
,5
*
'4'
і
Рис. 2.11. Скінченний елемент у вигляді квадрата з вісьмома вузлами
. 1
то
пі
12.
4
1
f
і
1-1
Р
^^^^_
9
2
£
її '
4
0 1
■і
■і.
3
7
*
[£
> 5
4
Рис. 2.12. Скінченний елемент у вигляді квадрата з дванадцятьма вузлами
^(^) = §(1 + &£)(і + ?72) Q +3^,і = 5, 6,11,12.
Не становить труднощів переконатися у тому, що всі побудовані
базисні функції задовольняють умову
Viiij^j) = $
IJ)
(2.58)
тобто складають вузловий базис.
Відобразимо квадрат £1* на деякий криволінійний чотирикутник Qe

2.8. Двовимірні ізопараметричні апроксимації
69
за допомогою перетворення
Xl = 5>?W£^); (2-59)
і
%2 = ^2^2)(Pi(^V\
(і) (і)
де х\*, х\ — координата г-і точки чотирикутника в площині Х\Х^-
Для того, щоб перетворення координат (2.59) здійснювало взаємно
однозначне відображення області £7* на область Пе, будемо домагатися,
щоб якобіан перетворення (2.59) був відмінним від нуля в О*, тобто
det Ц £ /0' (2*60)
{ dv dv J
Від базисних функцій щ (£,г)) можна за аналогією з 1.7 перейти до
функцій $ (хі,х2)) заданих у всій області. У цьому випадку ці функції
належатимуть класу С (£7), де Q = иОє.
є
Опишемо на Qe апроксимовану функцію Uh співвідношенням
uh
£>u?, (2.61)
яке можна навести у матричному вигляді
Uh = N (£, rj) qe,
Де
qj = K,«5,...}.
Зазначимо, що ці апроксимації називають ізопараметричними, Цей
термін означає, що для подання апроксимованої функції і відображення
$7* на Qe використовують одні й ті ж вузлові точки та базисні функції, В
літературі [14,17,18] відомі й інші типи апроксимацій, в основі побудови
яких є ідея відображення областей, — це суперпараметричні та субпара-
метричні апроксимації,

70
Апроксимація на скінченних елементах
Рис. 2.13. Скінченний елемент у вигляді тетраедра
2.9. Апроксимації на тетраедрах
Припустимо, що деяка тривимірна область Q розділена на скінченні
елементи Q€ у вигляді тетраедрів (рис, 2.13),
Побудуємо на тетраедрі Qe лінійні апроксимаційні функції за
аналогією зі способом побудови апроксимаційних функцій на трикутному
елементі, викладеним у 2.5. Для цього виберемо в Qe деяку внутрішню
точку Р (xi,x2jXs)- Введемо функцію
<р{ке] (хих2,хз)
к
ргут
vk
(2.62)
ijm
де Vpijm, Vkijm — об'єми тетраедрів pijm та kijm. Для їхнього обчислення
використаємо відому формулу з аналітичної геометрії. Отримаємо
Vpijm
det <
Vk,
1
1
1
1
:jm
Xi X2
Лі) Лі)
Лі) Лі)
X\ X2
Лт) Лт^
■і*
Xz
(і)
X
X
U)
X
(то)
>;
(2.63)
(2.64)

2.9. Апроксимації на тетраедрах
71
де
det <
х
(і) Лі)
Хп
X
(Л ЛЛ
X п
.(0
З
(І)
X
(т) (т) (т)
X
х.
Х^
(к)
Розкриваючи визначник у формулі (2.63) за елементами першого рядка,
знайдемо
(є)
7 (ак + Ькх\ + скх2 + dkx3)
о
(2.65)
Де
х
(0 Ji)
Хо
ак = det
х
(і) Ji)
X о
.(0
з
(і)
X
(т) (т) (т)
Ьь = — det <
X.
JL><2
лл
х2
х2
Хо
X
X
(0
з
U)
X
(т)
Ск
Усі інші функції iff отримують аналогічно.
Функції ерг мають властивість (вона є наслідком геометричної
побудови)
(2.66)
<рг ( х± у х2 , х% І — дг
За аналогією з 1.7 запишемо вираз для кусково-аналітичних базисних
функцій, заданих у всій області $7:
<Рі(хих2,х3)
^
.W
0,
і Є Ое
(2.67)

72
Апроксимація на скінченних елементах
J
Рис. 2.14. Скінченний елемент у вигляді тетраедра з шістьма вузлами
Як і раніше (див, 2.5), для запису апроксимованої функції на
скінченному елементі Qe матимемо формулу
uh = u^f + uh^f + «^ W + <^] • (2-68)
Використовуючи функції iff на тетраедрі, можна побудувати апро-
ксимаційні формули вищих порядків, зокрема другого, Для цього на
тетраедрі виберемо систему вузлових точок, зображених на рис, 2.14, де
точки 1, ...,б розміщені на серединах ребер тетраедра.
Система базисних функцій щ на тетраедрі Qe має вигляд
№ = ^е)(2^іе)-і); (2.69)
Усі решта функції фг отримують аналогічно. Можна переконатися, що
ці функції задовольняють умови
№=(x[s\4s\xis))=5rs. (2.70)
Для запису апроксимованої функції на скінченному елементі Qe
матимемо формулу
uh = и№] + uh24e) + - + 44Є) + <Й'. (2.71)

2.10. Тривимірні ізопараметричні апроксимації
73
Рис. 2.15. Скінченний елемент у вигляді куба з вісьмома вузлами,
Зазначимо, що наведені тут апроксимаційні формули на тетраедрі
утворюють у разі розширення їх на область Q функції класу С^ (П).
2.10- Тривимірні ізопараметричні
апроксимації
Криволінійні ізопараметричні апроксимації, запропоновані у 2.8,
можна поширити на тривимірний випадок,
Розглянемо куб
а = {£,?7,С:-1 <<£<!, -1 <»?<!, -1 < С < 1}
у декартовій системі координат £, //, £. На кубі виберемо дві сукупності
координатних вузлів (рис. 2.15, 2.16).
На вибраних системах вузлових точок запишемо такі сукупності
базисних функцій:
1° полілінійну
Уі (£, V, 0 = g (1 + U) (1 + ViV) (1 + GO, г = 1,..., 8; (2.72)
Де &j Wh & — координати г-ї вузлової точки;
2° поліквадратичну

74
Апроксимація на скінченних елементах
19
21L
ІЯ
ІЗ.
94
16,
14 15
12* У
*-'
Ф
^
О,
10
4п
1 2 J
Рис. 2.16. Скінченний елемент у вигляді куба з двадцятьма вузлами,
<Рі (0 V, О = g (1 + 60 (1 + »м) (1 + CO (&£ + W + ОС - 2), (2.73)
« = 1,3,5,7,13,15,17,19;
<^(0?7,0 = ^(1-«Є2)(1 + ^)(1 + 0С), г = 8, 4,16, 20;
<л(0?7,0 ^ J (1 + ^) (1-^(1 + 00, 2 = 2,6,14,18;
¥>і (0 Ї7, 0
(1 + 60 (1 + »м) О " С2) , г = 9,10,11,12.
Зазначимо, що всі вибрані функції (рг (£, т/, £) задовольняють умову
y>r=(4*\4'\4e)) = <W (2.74)
Пропонуємо перевірити її шляхом безпосередніх обчислень.
За допомогою вибраних функцій виконаємо взаємно однозначне
відображення куба на криволінійний шестигранник
%к
E4'W^o, л = і,2,з5
а також на ft* апроксимуємо деяку функцію и (£, /;, 0
«а (0 ^, 0 = 5^ «!Vi (0 »7> 0 ,
(2.75)
(2.76)
де и\ — вузлові значення апроксимованої функції.

2.11. Вправи для самостійного виконання
75
2.11. Вправи для самостійного виконання
Вправа 1. Довести, що квадратичні базисні функції (2.46) є
неперервними в разі переходу через спільну сторону двох суміжних трикутників,
Вправа 2. Зобразити графіки кубічних базисних функцій лагранжо-
вого типу на сукупності одновимірних скінченних елементів.
Вправа 3. Зобразити графіки апроксимованих функцій кубічними
базисними функціями лагранжового типу та кубічними базисними
функціями ермітового типу на сукупності одновимірних скінченних
елементів. Яка між ними суттєва відмінність?
Вправа 4. Зобразити графіки квадратичних базисних функцій (2.46)
на сукупності трикутних скінченних елементів (за аналогією з рис, 2.5).
Вправа 5. Нехай задано два скінченні елементи прямокутної
форми, що мають спільну сторону вздовж лінії х\ = const. На елементах
побудовані апроксимаційні формули вигляду (2.50). Довести, що функції
Uh{x\,X2) є неперервними в разі переходу через спільну границю
елементів.
Вправа 6. Нехай задано два скінченні елементи прямокутної
форми, що мають спільну сторону вздовж лінії Х2 = const. На елементах
побудовані апроксимаційні формули ермітового типу (2.54), Довести, що
функції Uh(xi,x2) і їхні похідні до першого порядку є неперервними в
разі переходу через спільну границю елементів.
Вправа 7. Записати вирази для базисних функцій 9-вузлового (3x3)
прямокутного скінченного елемента лагранжового типу (2.50).
Порівняти їх з біквадратичним ізопараметричними апроксимаційними
функціями. Які відмінності є між базисними функціми цих двох типів?
Вправа 8. Зобразити графіки білінійних базисних функцій типу
(2.50) у прямокутній області, поділеній на 4x4 прямокутних скінченних
елементів.
Вправа 9. За аналогією з нерівністю (2.17) вивести нерівність (2.19).
Вправа 10. Використовуючи рекурентну формулу (2.34) та вирази

76
Апроксимація на скінченних елементах
для поліномів Лежандра Ро, РІ5 отримати вирази для поліномів Р^ Рз-
Звірити їх з формулами (2.33).
Вправа 11, Використовуючи формулу (2.38), отримати
співвідношення (2.39).
Вправа 12, Знайти образи сторін квадрата при білінійному, біквад-
ратичному та бікубічному ізопараметричних відображеннях (2.59).

Розділ З
Крайові задачі
У розділі наведено дослідження операторів деяких крайових задач
та їхні варіаційні формулювання. Описано схеми методу скінченних
елементів побудови наближених розв'язків крайових задач та досліджено
питання їхньої збіжності.
3.1. Крайова задача для рівняння парного
порядку
Розглянемо крайову задачу
Ьи = І^{-1)к^крк{х)^к=і{х\ хЄ (а, 6); (3.1)
к=0
и(а) = и\а) = ... = «('"^(а) = 0;
и(Ь) = и'{Ь) = ... = «('"^(б) - 0. (3.2)
Стосовно відомих коефіцієнтів рівняння та правої частини припустимо
РнЄСМ[а,Ь], r = 0, ...,s, f(x)eC[a,b].
Лема 1. Оператор задачі (3.1), (3.2) симетричний.
Доведення. Зазначимо, перш за все, що область визначення
оператора цієї задачі
DL = {и(х) : и Є С(2в)[а,6], и(а) = 0, ...^"^(б) = 0}

78
Крайові задачі
є щільною множиною у просторі Н = L2(a1b). Розглянемо скалярний
добуток
ь 8
(Lu,v) = /В-1)^ (W)^) vdx. (3.3)
а к~°
Для перетворення інтеграла у правій частині формули (3.3)
використаємо формулу інтегрування частинами. Врахувавши граничні умови (3.2),
отримаємо
ь
dku dkv
(Lw, v)
k=0 І
dxk dxk
dx.
(3.4)
Права частина формули (3.4) симетрична відносно функцій ад, v. Отже,
звідси випливає, що оператор симетричний. ■
Теорема 2. Нехай ps(x) ^ Р > 0 і Рк{х) ^ 0, к = 0,1,..., s — 1, тоді
оператор задачі (3.1), (3.2) додатно визначений.
Доведення. Використаємо формулу (3.4) для обчислення добутку
ь
(3.5)
(Lu, u) = ^2 pkl
к=0 І ^
хи
dxk
dx.
Врахувавши обмеження, накладені на Pk{x) у формулюванні теореми,
запишемо
(3.6)
J U
и
(Lu,u)^P J (^1 dx.
Щоб оцінити знизу праву частину формули (3.6), використаємо
нерівність Фрідріхса (1.26). Якщо врахувати крайові умови (3.2) для функції
и(х) та її похідних до 5 — 1 порядку включно, отримаємо
du
dx
^ 7 \\Щ
о — а
\dsu
d2u
dxs
>
dx2
b — a
>
V2
b — a
dx3'1
du
dx

3.2. Апріорна оцінка точності МСЕ
79
Підставимо ліву частину першої нерівності у праву частину другої і так
далі до останньої нерівності; тоді
dsu
dxs
>
V2_
b — а
u
(3.7)
З урахуванням нерівності (3.7) у (3.6) запишемо
2s
(Lti, и) ^
V2_
b — а
P\\u\
що й треба було довести, ■
За отриманими результатами сформулюємо задачу (3.1), (3.2) у
такому варіаційному вигляді:
F(u) —> min, u G U,
Де
п
s Ь
и) = J2 / р* (
dk
U
dxk
j «j
dx — 2 / ufdfl
U= {u(x) :u(x) £W^S\ u(a) = 0,...,u{s-1)(b) = o}.
3.2. Апріорна оцінка точності МСЕ
Зазначимо, що частковим випадком задачі, розглянутої у
попередньому параграфі, є задача Штурма—Ліувілля
~~dxVx ^ ~dx + Ро ^ и(х) = f(x)i х є (а> Ь)
(3.8)
и(а) = 0, «(6) = 0. (3.9)
У першому розділі описана схема МСЕ (на основі кусково—лінійних
базисних функцій) числового розв'язування цієї задачі, Тут отримаємо
апріорні оцінки точності послідовності числових розв'язків МСЕ. З
метою оцінки збіжності схеми МСЕ (див, 1.7) для задачі Штурма^Ліувілля

80
Крайові задачі
використаємо лему Сеа (див, 1.10) і оцінки похибки апроксимації
кусково-лінійними базисними функціями (див, 2.1), Доведемо для цього,
що енергетична норма оператора задачі (3.8), (3.9) задовольняє подвійну
нерівність
2 II ||2 ^ІІІ|2^л/г2||||2 ґо іг\\
771 \\u\\ww < \\Щ\а ^ М ІРІІ^2(1)" (3*10)
Справді
ь ь
\\и\\2А = / (рги2 + p0u2)dx ^ Р / u,2dx.
а а
Застосуємо далі нерівність Фрідріхса (1.26). Отримаємо
ь ь
\\u\\1>\p f и>Чх + ^^ f чЧх.
Отже, виконується ліва частина нерівності (3.10), і
2 . fir, Р
т = mm < -P.
2 '{b-af}'
Права частина подвійної нерівності (3.10) випливає з такого
співвідношення:
о о
/ (p\Ul2+p0u2) dx^M2 І (и12 + и2) dx,
де
М — max < max pi(x), max p0{x) > ,
^жЄ[а,Ь] жЄ[а,6] J
Ha підставі леми Сеа, та з урахуванням першої нерівності з теореми 1
розділу 2 для наближеного розв'язку ин отримаємо
М2
lluo - ^лііиИ1) ^ ~^C2h \\щ\\ {2) . (З.П)
2 772 2

3.3. Апріорна оцінка точності за Нітше
81
Оцінку вигляду (3.11) називають апріорною оцінкою похибки
наближеного розв'язку Uh- Вона дає інформацію про швидкість збіжності
наближеного розв'язку, який можна отримати МСЕ. Зокрема, для задачі, яку
розглядаємо, з оцінки (3.11) випливає, що наближений розв'язок Uh
прямує до узагальненого розв'язку щ як 0(h). У цьому разі узагальнений
(2)
розв'язок повинен задовольняти умову щ Є W2 .
3.3. Апріорна оцінка точності за Нітше
У попередньому параграфі отримано оцінку збіжності схеми МСЕ
у нормі простору W2 . З'ясовано, що її порядок є 0(h). Зі збіжності у
нормі цього простору випливає збіжність (див, 1.6) і в нормі простору L2.
Опишемо тут спосіб визначення порядку збіжності у цій нормі, відомий
під назвою способу Нітше.
Позначимо єн = щ — Uh: де щ — узагальнений розв'язок задачі (3.8),
(3.9). Розглянемо допоміжну задачу, яку описує цей же оператор, що й
(3.8), (3.9), однак її права частина дорівнює ед, тобто
Az = eh. (3.12)
Запишемо для (3.12) еквівалентну варіаційну задачу (див, 1.7)
(Az,v) = (eh,v), УьєНА. (3.13)
Приймемо в (3.13) v = eh- Отримаємо
(Az,eh) = (eh,eh). (3.14)
Врахуємо, що наближений розв'язок ин є ортогональною проекцією щ
на підпростір Shi натягнений на базисні функції </?f. Це означає, що (див,
і.б)
(Aeh,vh) = Q, VvheSh. (3.15)
Якщо взяти до уваги, що А — симетричний оператор, то (3.15) можна
переписати у вигляді
(Avh,eh) = 0, Vvh<=Sh.
(3.16)

82
Крайові задачі
Віднімемо (3.16) від (3.14):
(A(z-vh)yeh) = \\eh\\2.
Застосуємо далі нерівність Шварца. Отримаємо нерівність
\\eh\\2 ^ \\z ~ vh\\A \\eh\\A. (3.17)
Для оцінки зверху множників у правій частині формули (3.17)
вважатимемо, що vh є лінійним інтерполянтом розв'язку z і використаємо
нерівності
\\€н\\а ^ Cuh \\v>o\\ww] (3.18)
l^-t/ftlh ^ Czh\\z\\w(2), (3.19)
які випливають з оцінки (3.11) та нерівності (3.10) для вихідної задачі
(3.8), (3.9) і задачі (3.12). Окрім цього, використаємо нерівність [12]
INI^(2) ^ К \\eh\\ і
яка виражає неперервну залежність розв'язку задачі (3.12) від правої
частини. Підставимо (3.18), (3.19) у праву частину (3.17). Отримаємо
||ел||2^СгС„Л2і^ ||«0|U2)||eft||. (3.20)
Скоротимо ліву та праву частини нерівності (3.20) на Це^Ц. Остаточно
запишемо
||ел|| ^ Ch2 \\uq\\w(2), (3.21)
де С = CZCUK.
Нерівність (3.21) означає, що у нормі простору L2 наближений
розв'язок збігається до узагальненого як 0(h2).
3.4. Схема МСЕ для рівняння четвертого
порядку
Одним із часткових випадків задачі, розглянутої у 3.1, є задача про
згин стрижня [6], яку описує рівняння
^(EJ{x)i£)=f{x)' же(а,6)' (3-22)

3.4. Схема МСЕ для рівняння четвертого порядку
83
де w(x) — шукана функція-зміщення точки х осі стрижня під дією
зовнішнього навантаження, яке характеризує функція f(x) Є L2 (а, 6); Е —
модуль Юнга; J(x) — момент інерції поперечного перерізу стрижня, До
рівняння (3.22) необхідно додати крайові умови, Якщо кінці стрижня
защемлені, то ці умови матимуть вигляд
w(a) = wf(a) = 0, w(b) = wf(b) = 0. (3.23)
Для побудови схеми МСЕ наведемо задачу (3.22), (3.23) згідно з
результатами 3.1 у такому варіаційному формулюванні:
F{x) -^ min, w Є W: (3.24)
Де
П«) = /(^(^)'-2«/І<Ь,
W = {w(x) : w(x) Є W2{2)(a,b), w(a) = w\a) = w(b) = w'(b) = o}.
У 2.3 зазначено, що для задач, які описані диференціальними
рівняннями порядку вищого, аніж другий, для побудови наближених розв'язків
можна використати ермітові апроксимації на скінченних елементах.
Отже, для наближення розв'язку задачі на скінченному елементі
Q,i = {х : Хі-і < х < Хі]
використаємо поліноми Ерміта третього степеня. Виберемо як вузлові
параметри значення функції та її першої похідної
, h duh (xj) . h t
uh {Xj) = Uj, — = Uj , з = і - 1, i.
Запишемо на Qi
uh = Ni(x)qi, (3.25)

84
Крайові задачі
144
v?.
л
Kz
V
к3
к„
І
К-.
U4
rub
R
kill, і
к.
Рис. 3.1. Структура системи лінійних алгебричних рівнянь
Де
N< (ж) = {Я<_і,о (ж), Я<_і,і (ж), Яі)0 (ж), Яід (ж)};
tfi-LoOr) = Я^1(ж)(1 + 2Яі(ж));
Яі)0(ж) = Я|(ж)(1 + 2Яі„1(ж));
Я,_1д(ж) = hHl1(x)Hl(x);
НІА(х) = -hHf(x)Hi_1(x);
Ні-! (Ж)
Л
, Нг (ж)
Ж ^і—1
h :
Х{ Х^\.
Систему лінійних алгебричних рівнянь МСЕ формують за аналогією
з задачею Штурма^Ліувілля (див, 1.7) з матриць К« та Qj, які
обчислюють за формулами
EJ^dx;
dxz
Xl~l

3.5. Крайова задача для системи диференціальних рівнянь 85
Qi= / tfffdx.
Xl~l
Структура матриці і правої частини системи алгебричних рівнянь
зображена на рис, 3.1.
3.5. Крайова задача для системи
диференціальних рівнянь
Розглянемо крайову задачу, яку описує система звичайних
диференціальних рівнянь
ик(а) = ик{Ь) = 0; fc, j = 1, 2,..., s. (3.27)
Уведемо позначення для матриць-стовпців невідомих і правих частин та
матриць коефіцієнтів
u = {uj}i f = {fj(x)}]
Р = {Pjk(x)}] Q = {qjk(x)}<
Урахувавши їх, задачу (3.26), (3.27) можна записати у такому вигляді:
-^Р(х)^ + Q(x)u = f(x)] х Є (а, 6); f(x) Є L2(a, 6);
u(a) = 0; u(6) = 0.
Зазначимо, що у гільбертовому просторі L2(a,6) векторних функцій
скалярний добуток та норма визначено співвідношеннями
ь ь л
(u, v) = / uT\dx = / \] v>kVkdx\
І І к=1

86
Крайові задачі
ь
lull2 = / uTudx.
н
а
Область визначення Da оператора цієї задачі можна задати
співвідношенням
DA = J u = {«і,..., «в}т : щ Є wj2)(a,6), ик(а) = ик(Ь) = 0,к = 1,..., ^| .
Виконується така лема.
Лема 3. Нехай Р, Q — симетричні матриці. Тоді оператор задачі
(3.26)} (3.27) симетричний.
Доведення. Розглянемо скалярний добуток
ь е ь в
/J J Г
XI l~Pjk(x)-Tvjdx + / X Qjk(x)ukVjdx. (3.28)
a J.fc=1 а J'.fe=1
Зінтегруємо перший доданок частинами і врахуємо граничні умови
(3.27). Отримаємо
ь Т
(Au'v>=/№) p^+/uTQv^ (з-29)
а а
Якщо врахувати, що область визначення оператора є щільною
множиною (див, 1.1), то з (3.29) випливає, що оператор симетричний, ■
Доведемо теорему, яка визначає умови, за яких оператор задачі
(3,26), (3,27) додатно визначений.
Теорема 4. Нехай Р — додатно визначена матриця
tTPt > 0, Vt = (<i,..., ts)T , U Є R,
a Q — невід'ємна матриця
tTQt ^ 0.
Тоді оператор задачі (3.26), (3.21) додатно визначений.

3.5. Крайова задача для системи диференціальних рівнянь 87
Доведення. Зазначимо, що власні числа додатно визначеної матриці
додатні, Це означає, що
tTPt ^ Хг(х)іті, Лі (ж) > 0,
де Лі (ж) — найменше власне число матриці Р. Вважатимемо, що
елементи матриці Р є неперервними функціями х. Тоді Лі (ж) ^ Л > 0.
Розглянемо скалярний добуток (3.29)
ь ь
(Ли,и) = \J I Pjk(%)ufjiifkdx + 2~2 QjkUjUkdx ^ ^/\, / іик) dx. (3,30)
j,k=i{ j9k=i k=i{
Тут враховано попередні міркування й те, що Q — невід'ємна
матриця. Для оцінки правої частини формули (3,30) використаємо нерівність
Фрідріхса (1.26). Отримаємо
(Аи,и)^ га ||и||Ла.и
(Ь-а)
Оскільки оператор задачі (3.26), (3.27) додатно визначений, то її
молена записати у таких варіаційних формулюваннях:
F(u) -> min, ueU; (3.31)
b Ь
S p S S л
F(u) =^2 Pjkitfu'jUbdx + ^2 QjkUjUkdx - 2 J^ / Ujfjdx]
U = |u = {uu...,u8}T : uk Є W2(1)(a,b), uk(a) = uk(b) = 0, k = 1, sj;
(4u, v) = (f, v), Vv Є U, u є U. (3,32)
Варіаційні формулювання (3,31) та (3,32) є еквівалентними.
Для побудови наближеного розв'язку варіаційної задачі задамо поділ
області
а = xq < Х\ <,..., < хп-і < хп = Ь.
Оскільки система диференціальних рівнянь є другого порядку за
кожною змінною, то для наближеного запису розв'язку можна використати

88
Крайові задачі
А
щ
'/6
А,
... | ...
щ
ninJi.il.
А1
_..4-.._.
—4—
■—І—J
Г ' ^
-+--
AjM
"■"і""!
щ
\
А-п-2 І
0- 1
їй
21
її"
Рис. 3.2, Структура системи лінійних алгебричних рівнянь
кусково-поліноміальні базисні функції, описані в 2.2. Використаємо
найпростіші кусково-лінійні базисні функції (1.96). На скінченному елементі
Qi = [#г-ь#г] наближений розв'язок Uft запишемо у вигляді
де матриця N»(ar) (розміру 5 х 2s) має вигляд
Щх)
<РЇ-і 0 0^00
0 <Д_Х ° 0^0
0 0 <^_і 0 0 ^
Діятимемо далі формально за аналогією з випадками параграфа 1.7,
Використаємо одне з еквівалентних варіаційних формулювань (3.31) або
(3.32). Матриця системи лінійних алгебричних рівнянь МСЕ формується
з матриць
Аі = Кі + Мі,

3.6. Задача про циліндричний згин пластини
89
Де
К
%г гр
•=/(sN'(*>) p£N-w^ <3-33>
X
м
. = /" NfQN^x. (3.34)
Ж,_і
Стовпець правих частин системи рівнянь МСЕ формується з матриць
<&і
"-/
Ві= / N/ (x)f (x)dx. (3.35)
Xl~l
Схема формування системи лінійних алгебричних рівнянь (для 5 = 2)
зображена на рис, 3.2.
3.6. Задача про циліндричний згин пластини
Система звичайних диференціальних рівнянь (3.26), незважаючи на
її досить загальний вигляд, все ж не описує всі існуючі математичні
моделі. Наведемо тут систему двох диференціальних рівнянь другого
порядку, яка описує циліндричний згин пластини в рамках математичної
моделі С.П. Тимошенка [10]
dji cPw
dot\ da\
-G(^- + ^) = /,(«!); (3.36)
Тут 7і,ги — шукані функції, фізичним змістом яких є кут повороту
нормалі до серединної площини пластини в напрямі осі а і та прогин
серединної площини; G,D — сталі, які виражають через фізичні характеристики
матеріалу пластини — модуль Юнга Е) коефіцієнт Пуасона ^, коефіцієнт
зсуву к1 = 5/6 та товщину пластини h за формулами
С- k'Eh о- Eh" f337l

90
Крайові задачі
Для системи рівнянь (3.36) розглянемо крайову задачу, яка відповідає
умовам жорсткого защемлення країв
7і (а) = 0, w (а) = 0, 7і 0) = 0, w (b) = 0. (3.38)
Уважатимемо, що fi Є L2(a, Ь), тоді область визначення оператора задачі
(3.36), (3.38) є такою множиною:
D^ = {u = (7i,«;):ueW^M), u(a) = 0, u(6) = o}.
Виконується така лема.
Лема 5. Оператор задачі (3.36) > (3.38) симетричний.
Доведення. Оскільки Cq (a, Ь) С D^, to область визначення D^ є
щільною множиною у просторі L2 (a, 6), Залишається довести, що
виконується співвідношення
(Au,u) = (u, Au),
З урахуванням лівих частин рівнянь (3.36) обчислимо добуток (Аи,її):
^-/M£+S)e-DSf*+e('ft+S*K
а
Виконавши елементарні перетворення та інтегрування частинами,
отримаємо
(Au,u) -
= [iD*hd£ + G
J І doti aa\
а
Права частина останнього виразу є симетричною відносно функцій 7ь Ті
та й;, w. Отже, оператор задачі є симетричний, ■
Тепер сформулюємо і доведемо таку теорему,
Теорема 6. Оператор задачі (3.36), (3.38) додатно визначений.
dw _ dw
\ dw dw 1 1
/ da\ daA \

3.6. Задача про циліндричний згин пластини
91
Доведення. Для доведення теореми потрібно з'ясувати, що
виконується нерівність
(Au,u)>72||u||2,
де 7 > 0,
ь
||и||2 - / (jl + w2) dav
а
Запишемо (Au, u) у вигляді
dalt (3.39)
Використавши нерівність Фрідріхса
ь
/{%)***<>ЬІ#-
(b - аУ
а а
оцінимо знизу перший доданок, Отримаємо
w І [ї%?*+G fa+<+О')] ** (3-40)
Оцінимо далі добуток 271 -j^r, використовуючи елементарну нерівність
dw / 2 1 /dw
dot\ ~ \ г є \dcti
, Ує > 0.
(3.41)
Запишемо
a L
Використаємо знову нерівність Фрідріхса
ь ь
dai.
[ ( dw
J \dax
2 f
da\ > « / w2dai
(b - a)2 J

92
Крайові задачі
для оцінювання знизу другого доданка у попередній формулі:
(Аи, и) >
ь ь
Ч^+еМ/7>і+сИ)(^?/л<і1'
а а
Позначимо
^4&+G(i-4GN)^}-
Матимемо
.(6-а) / V є/ (6-а)'
(Au,u)>72||u||2,
що й треба було довести, Зазначимо, що з умови j2 > 0 випливає таке
обмеження на параметр є
1 < є < « + 1. ■
G(6-a)2
Дослідимо поведінку сталої 72 при h —> 0. Урахувавши
співвідношення (3.37) для сталих D та G, отримаємо
72 > Л7о, (3-42)
де 7о не залежить від /г.
Припустимо, що для числового розв'язування задачі про
циліндричний згин пластини застосовують МСЕ. Нехай алгоритм МСЕ
побудований з використанням кусково-аналітичних поліномів к-го степеня і нехай
узагальнений розв'язок задачі задовольняє умову Uq Є Wi, (a, 6).
Для оцінки точності схеми МСЕ за аналогією з 3.2 доведемо, що
енергетична норма
\\и\\2А = (Au,u),
яка відповідає задачі про циліндричний згин пластини в рамках моделі
С. П. Тимошенка, задовольняє подвійну нерівність
т2 \\u\\2ww < \Н2А < М2 ||и||^(1), (3.43)

3.6. Задача про циліндричний згин пластини
93
Де
№\ww
/[*w+&)'+0!
dai.
Для отримання лівої частини нерівності (3.43) запишемо формулу (3.39)
у вигляді
+G 7!2 + 27l— +
da\ \ dot\
dw
dot\ I doii.
Оцінимо знизу перший доданок під інегралом у попередній формулі,
використавши нерівність Фрідріхса. Матимемо
(Au,u)> J
(6-а)271 2^U*i
+
„ . ., n dw
+G 7l2 + 27l — +
da.\ \ d<y.\
dw
dai.
Оцінимо далі добуток 27ij^- знизу з використанням нерівності (3.41).
Тоді
(Au,u)> J
D
(b - a)'
+ G(l-e) 7l2
Hffl -И
dw
dot\
dai.
Перепишемо цей вираз у вигляді
ь
(Аи,іі)>У [(
D
(Ь - а)'
+ G(l-e) 7l2
2 Vdtt!
G(l\ (dw_
+ 2 1 є J Idai
dcti.

94
Крайові задачі
Оцінимо знизу останній доданок під знаком інтеграла за нерівністю
Фрідріхса
2 Ь
J \daj ~ (6-а)2 I W dai'
Остаточно отримаємо
(Au,u) > m2||u||^u),
Де
m2 = min(f—° +G(1-A —<Ц Л - іНд £ Л - І
Н(Ь-а)2 V ') ib-af V є)'2 '2 V є
З умови т2 > 0 матимемо таке обмеження на параметр є:
D
1< є< 1 +
G(b~a)2'
Права частина нерівності (3.43) є очевидною, її отримано з формули
(3,39) шляхом використання елементарної нерівності
dw 2 / dwx
dai ~ 1 \dai
Як і для сталої у2, виконується оцінка
т2 > hm\, (3,44)
де ті > 0 і не залежить від h. Тоді за Лемою Сеа (див, 1.10), аналогічно
як і в параграфі 3.2 для апріорної оцінки похибки наближеного роз'язку
її/, отримаємо співвідношення
М2 к
\uo~uh\\ww < —т* lluo||w(^+i) (3,45)
2 771 2 і
де t — крок поділу проміжку [а, 6] на скінченні елементи. Підсилимо
праву частину нерівності (3,45), врахувавши нерівність (3.44). Отримаємо
І II / M\ku II
\Щ ~ uh\\ww < j^t l|uo||^+i)

3.6. Задача про циліндричний згин пластини
95
14
М
12
Ю
а
ші;
І -л, і ' 'і
[ /
Г" /д
1 f
(
ш-£*±
ч, ^
!
і !
і
ї
1
1
р
i^i^i^W^i^i^-^—
l
II
4 & в 10 L2
Рис. 3.3, Графіки енергетичної норми
14
З останнього співідношення випливає, що при достатньо малих
значеннях параметра товщини пластини h для досягнення задовільної точності
наближеного розв'язку потрібно вибрати достатньо малий крок t поділу
проміжку (а, Ь) на скінченні елементи.
Розглянемо, для прикладу, числове дослідження задачі про
циліндричний згин пластини. Уважатимемо, що оц Є (0,1) і навантаження на
пластину вибране таким, що праві частини системи рівнянь (3,36) мають
вигляд
fi=P = const, f2 = 0.
Оскільки система рівнянь (3,36) є системою диференціальних рівнянь
зі сталими коефіцієнтами, то неважко знайти її аналітичний роз'язок,
Він має вигляд
Р ( Р Р
W=2Gai+\24D-2G
ал
Р з Р
12D
24D
а
її
Р Р 2 Р З

96
Крайові задачі
Для числового розв'язування цієї задачі застосуємо метод
скінченних елементів, побудований на основі методу Рітца. За базисні функції
виберемо функції-бульбашки (див, 2,3), На рис, 3.3 показані графіки
зміни енергетичної норми \\и\\л розв'язку цієї задачі (для h = Ю~~3)
залежно від кількості поділів (п) проміжку [0,1] на скінченні елементи.
Пряма 1 відповідає нормі аналітичного розв'язку; лінія 2 — нормі
числового розв'язку отриманого МСЕ з використанням кусково-лінійних
базисних функцій; лінія 3 — нормі числового розв'язку отриманого
МСЕ з використанням функцій-бульбашок другого степеня; лінія 1 —
нормі числового розв'язку отриманого МСЕ з використанням функцій-
бульбашок третього степеня; лінія 5 — нормі числового розв'язку
отриманого МСЕ з використанням функцій-бульбашок четвертого степеня.
З рис, 3.3 видно, що в разі використання кусково-лінійних
апроксимацій енергетична норма наближеного розв'зку не наближається до норми
аналітичного розв'язку зі збільшенням кількості скінченних елементів.
Це явище відоме в літературі під назвою "locking effect". Лише
використання апроксимацій функціями-бульбашками дає змогу отримувати
такі числові розв'язки, енергетичні норми яких збігаються до норми
аналітичного розв'язку, У цьому разі найліпший результат відповідає
використанню апроксимацій функціями-бульбашками четвертого степеня.
3.7. Крайові задачі для рівняння Пуассона
Розглянемо головні крайові задачі для рівняння Пуассона (інша
назва — неоднорідне рівняння Лапласа)
-Аи = f (х): х = (хихи...,хп), х Є О, (3,46)
Де
v-^ дги
г—1 1
и (х) — шукана функція, / (х) Є L2 (Q) — задана права частина,
Q C Rn— обмежена область, з ліпшицевою границею Г. Для рівняння
(3,46) звичайно ставлять три головні крайові задачі, які відповідають
таким трьом крайовим умовам:

3.7. Крайові задачі для рівняння Пуассона
97
1° задача Діріхле
и(х) = 0, х Є Г;
2° задача Неймана
ди (х)
ди
Де
0, х Є Г,
ди (х) ^-^ ди (х)
ди 4-' дх{
— похідна за напрямом зовнішньої нормалі v до границі Г;
3° задача Ньютона
U}X' +а(х)и (х) = 0, х Є Г,
ди
де а (х) > сг0 > 0, <т0 = const.
Позначимо через А^ — оператор к-ї крайової задачі для неоднорідного
рівняння Лапласа, а через DAk — його область визначення.
Нехай і — вектор, координатами якого є невід'ємні цілі числа і*.
Уведемо позначення
D'u = . 7V ; . , (3.47)
0І*Іад (ж)
дх[1дх%...дх%
де |г = г'і + іг + »■ + in- 3 використанням уведеного позначення (3.47)
усі похідні до другого порядку включно від функції и можна записати
формулою
D{u(x), \i\ < 2.
Використавши цей факт, наведемо такі описи для множин областей
визначення операторів А^ :
DAl = {и (х) : Вги (х) Є L2 (О), |г| < 2; и (х) = 0, х Є Г};
DA2 = іи (х) : D*u (х) Є L2 (fi), |г| < 2; ^^ = 0,^Г
І ди(х] І
£>Аз = <и(х) : Dlu(x) Є Ь2(П),|і| < 2; v ; + g- (х) и (х) = 0, х Є Г J-.

98
Крайові задачі
Дослідимо властивості оператора А*. Доведемо, що оператори А^ є
симетричними, Для цього розглянемо скалярні добутки {А^и, v).
Використавши формули Гріна та врахувавши граничні умови 1° — 3°, одержимо
Ц«,г;) = /
(Акщ v) = / VuVvdQ, k = 1, 2; (3.48)
Q
{Azu,v) = / VuVvdQ + / auvdT. (3.49)
Q Г
„ т , ди (x) du (x) du (x)
Тут
дх1 ' 5ж2 ' ' cbn
Оскільки, окрім цього, виконуються включення Co C Да*.і T0
оператори трьох головних крайових задач є симетричними,
З метою дослідити додатну визначеність операторів головних
крайових задач для неоднорідного рівняння Лапласа використаємо нерівності
Фрідріхса і Пуанкаре. Позначимо через М лінеал функцій и{х), інте-
гровних разом із частинними похідними першого порядку в Q. Наведемо
нерівності Фрідріхса і Пуанкаре у вигляді теорем,
Теорема 7 (Нерівність Фрідріхса). Нехай Q — обмежена область з ліп-
шицевою границею Г. Тодг існують невід'ємні сталі Сі, С2, які залеоюать
від області Q і не залеоюать від функції лінеалу М, такі, що
виконується нерівність
j u2 (х) dn < d f Y, (^Щ dQ + c2 f u2 (x) dT. (3,50)
n n kz=1 r
Див. [10, c.344].
Теорема 8 (Нерівність Пуанкаре). Нехай Q — обмежена область з ліп-
шицевою границею Г. Тоді існують невід'ємні сталі Сз, с^ які залеоюать
від області Q і не залеоюать від функції лінеалу М, такі, що
виконується нерівність
2
fu2(x)dn<cz [^(Ч^) dn + c4\ fu(x)dQ
П П /с=1 Ш
(3.51)

3.7. Крайові задачі для рівняння Пуассона
99
де
Див. [10, с.345].
Зазначимо, що у наведених теоремах значення функції и (х) на
границі потрібно розуміти в сенсі слідів (див, Додаток),
Теорема 9. Оператори трьох головних крайових задач для неоднорідно-
го рівняння Лапласа є додатно визначеними.
Доведення. Для першої крайової задачі (А; = 1) використаємо
формулу (3.48) скалярного добутку (A\U, u)
(А1щи)= f (VufdQ, (3.52)
п
а п /с~1
Для оцінки знизу виразу у правій частині формули (3.52) застосуємо
нерівність Фрідріхса (3.50), врахувавши крайову умову Діріхле 1°.
Отримаємо
(Aiu, и) > — їй2 (х) dx.
сі J
Це й доводить теорему для задачі Діріхле.
Щодо задачі Неймана зазначимо, що не для всіх функцій / (х) правої
частини рівняння Пуассона вона є несуперечною. Справді, розглянемо
f f(x)dQ = - f AudQ.
Застосуємо до правої частини попередньої рівності формулу Гріна,
вважаючи, що другим множником під знаком інтеграла є одиниця,
Отримаємо
П Q Г
Оскільки VI = 0 і виконується умова Неймана 2°, то

100
Крайові задачі
/
/ (х) <т = о. (з.53)
п
Це і є додаткова умова, яку повинна задовольняти функція / (х).
Легко бачити, що задача Неймана (А; = 2) для рівняння Пуассона
не має єдиного розв'язку, Справді, простою перевіркою можна
з'ясувати, що функція щ + const, де щ — розв1 язок задачі Неймана, є теж
її розв'язком, Отже, перш за все введемо у цьому випадку додаткову
умову, яка могла б забезпечити єдиність розв'язку задачі Неймана для
рівняння Пуассона. Виберемо цю умову за аналогією з умовою (3,53) у
вигляді
J u(x)dQ = Q. (3,54)
п
Доведемо тепер, що оператор задачі Неймана для рівняння Пуассона
з додатковою умовою (3,54) є додатно визначеним. Доведення є таким
же, як і попереднє з тією різницею, що використано нерівність Пуанкаре
(3,51), в якій враховано співідношення (3.54). Отже,
і7и)> —
с3 J
(А2и, и) > — / и2 (х) dx.
с3 J
Q
Для задачі Ньютона (А; = 3) скалярний добуток (А^и} и) має вигляд
(3,49)
{Агщи)= J (Vu)2dQ+ J au2dT.
Q Г
Для дослідження додатної визначенності оператора використаємо
очевидну нерівність
(Л3м, и)> І (Vu)2 dQ + aQ / u2dT
Q Г
та нерівність Фрідріхса (3.50). Отримаємо
(А^и, и) > 72 / и2 (х) dx,

3.8. Схема МСЕ для рівняння Пуассона
101
де
Де
72 = min {1,сг0}/max {с3,с4}.
З останньої нерівності випливає, що задача Ньютона для рівняння
Пуассона має теж додатно визначений оператор. ■
Отже, оскільки оператори головних крайових задач для рівняння
Пуассона є додатно визначененими, то ці задачі можна сформулювати як
варіаційні задачі такогого вигляду;
Fu (и) —> min, u Є Нк, (3.55)
рк (и) = J (gracb)2 дП-2 І fudto, к = 1, 2;
Fs (и) = І (gradu)2 dQ-2 J fudQ + f <ju2dT\
n n r
#i = {« (x) :u(x)G W^1] (П), «(ї) = 0,іЄ Г};
tf2= \u{x) :u(x) Є W^iQ), f
#з = {«(ж) :и(х) Є W2(1)(^)}.
Як наслідок з доведеної теореми про додатну визначеність операторів
головних крайових задач для рівняння Пуассона випливає твердження
про існування та єдиність їхніх узагальнених розв'язків,
3.8. Схема МСЕ для рівняння Пуассона
Нехай двовимірна обмежена область Q з ліпшицевою границею Г
розділена на скінченні елементи трикутної форми
П = иПе, Пі П П, = 0.
udn = 0

102
Крайові задачі
На заданому поділі вибиремо базисні функції вигляду (2.42) (див.
параграф 2.4) і наведемо наближений розв'язок варіаційних задач, що
відповідають крайовим задачам для рівняння Пуассона на Г2е, у вигляді
uh = Neqe
(3.56)
^=(^,^,^); чи = («?,«?,«*,) ■
На підставі варіаційних формулювань (3.55), методу Рітца, отримаємо
систему лінійних алгебричних рівнянь
£«"
■}(V.*>J) = (/.*>?), J = 1,2...,
п.
(3.57)
За аналогією з 1.7 ця система (для задач Діріхле і Неймана) формується
з матриць
К.-
= /"(VNe)TVNedQ;
tie
Де
VNe= 51 )(<РЇ, $,<&)■
Виконавши нескладні обчислення у формулі (3.60), отримаємо
Ке~28
Щ + cf bibj + acj bibm + СіСт
hbj + CiCj Щ + c* bjbm + CjC.
v%0m т CiCm OjOrn -\- CjCm ~m
bl + c
2
m
Тут
0{ — Xo
(m) (то)
X
U)
(3.58)
(3.59)
(3.60)
(3.61)
(3.62)
S — подвоєна площа трикутника Г2е. Формули для 6j, 6TO, Cj, cm можна
отримати з (3.62) шляхом циклічного переставляння індексів і, j, m.
Для обчислення інтеграла у формулі (3.59) зінтерполюемо функцію
/ на трикутнику Г2€ виразом
f{xux2) = N€(xux2)fe,
(3.63)

3.8. Схема МСЕ для рівняння Пуассона
103
Де
'є \Jii Jji Jm) і
fr — f (%i , #2 ) ~~ значення функції / (xi, X2) у вузловій точці ж-l , ж!
r = i,j,m. Підставимо формулу (3.63) у вираз (3.59). Отримаємо
(г)
2 )
Тут
М,
■/
Сіє
Qe - Mefe
(є) (є)
¥\- Vi-
Ce) (є) (є) (є)
<Рі Vm ¥>} Vm
(є) (є)
¥>і V}
И2
(є) (є)
<Ю.
Для обчислення інтегралів у попередньому виразі використаємо
формулу [11]
/И>г)'ш°^=г;
а\Ь\с\
(а + б + с + 2)!
(3.64)
де а, 6, с — цілі невід'ємні числа; S — подвоєна площа трикутника,
У результаті отримаємо
М„ =
24
2 11
12 1
1 1 2
Зазначимо, що для задачі Ньютона в разі формування матриці
системи лінійних алгебричних рівнянь необхідно додатково враховувати
інтеграл за границею, який фігурує у варіаційному формулюванні, Для
задачі Діріхле потрібно врахувати головну граничну умову, а для задачі
Неймана — додаткову умову (3.54).
Для отримання апріорної оцінки збіжності схеми МСЕ, як і в
попередньому, використаємо лему Сеа (див, 1.10) і оцінку похибки
апроксимації на трикутних елементах (див, 2,4), Попередньо доведемо, що
енергетична норма задачі Діріхле для рівняння Пуассона
\и\
І
si
grad2udVt

104
Крайові задачі
задовольняє подвійну нерівність
2 її ||2 ^ її ||2 ^ і уг2 п ц2 /0 ґ*г\
т \\u\\w(i) < \\и\\л < м ІМІ^аь (3*65)
Де
ll^ll^d) = / (grad2u + u2) dQ.
Q
Права частина цієї нерівності є очевидною; справді, для М — 1
/ grad2^d£l < / (grad2w + и2) dQ.
п п
Для доведення лівої частини запишемо
\и
\А = - / gra,d2udfl + - / grad2iid^.
Застосувавши далі нерівність Фрідріхса (3.50), отримаємо
II II2 \ 2 п ц2
Де
2 • Г 1 1\
m = mm < —. - > .
\2ci'2J
Отже, подвійна нерівність доведена.
Згідно з лемою Сеа наближений розв'язок гін задовольняє нерівність
М2
\\и - Uh\\wix) < —$■ p-%L(D- (з.бб)
Оцінимо праву частину нерівності (3.66), використовуючи теорему 2.2.
(2)
Припустивши в цьому разі, що розв'язок задачі и Є W2 , отримаємо
М2„ h „ „ ,о .
h-uh\\w^ < ^C2— \\u\\ww. (3.67)
З оцінки (3.67) випливає, що наближений розв'язок гін прямує до
узагальненого розв'язку задачі в нормі простору W2 \ якщо h —> 0. Порядок
збіжності становить О (h).
З оцінки (3.67) випливає, що в разі поділу області на трикутні
скінченні елементи потрібно уникати трикутників з гострими кутами, для
яких sin в є малим.

3.9. Схема МСЕ, побудована на ізопараметричних апроксимаціях 105
3.9. Схема МСЕ, побудована на
ізопараметричних апроксимаціях
Прикладом задачі Діріхле для рівняння Пуассона
-Аи = / О, и = 0 на Г (3.68)
проілюструємо спосіб побудови схеми методу скінченних елементів, яка
використовує ізопараметричні апроксимації (див, 2.7).
Як відомо (див, 3.7) задача (3.68) еквівалентна задачі про мінімум
квадратичного функціонала
F(u) = / (gr&duf gmdudQ - 2 / fudtl, u є #І5
Де
gmdu = f %}_
#1 = {«(ж) :u(x) GW^iCl), и(ж) = 0,їег}.
Уважатимемо, що область Q розділена на скінченні елементи одного з
трьох видів, які розглядали у параграфі 2.7, і кожен скінченний елемент
може бути однозначно відображений на квадрат Г2* у системі координат
П' = {£,гГ.-1<£,гі<1}-
Як і для інших скінченноелементних апроксимацій, систему лінійних
алгебричних рівнянь формують з матриць
Ке= /(gradN)TgradNdn, (3.69)
Q£
І fNT(Kl, (3.70)
Де
Врахуємо у співвідношеннях (3.69), (3.70), що за допомогою формул

106
Крайові задачі
xi = Yl х^і (£> V)> x2 = Ylx^ (£> V) (3-71)
І І
скінченний елемент Qe молена відобразити на квадрат $7*. Матимемо
dVt = det Jdf dr/. (3.72)
Тут J — матриця Якобі вигляду
7 = ) Ч ді
и * дхі дх2
дх\ дх2
Зх\ дх2
д-ц дг}
Крім того, перейдемо у формулах диференціювання gradN до змінних
£, 7]. Для цього запишемо
дг\ / \ дх2
Звідси
¥ ) = j-1 ( f
Беручи до уваги останнє співвідношення, матимемо
gradN = J~1grad*N,
Де
grad* = f
Отже, остаточно формули (3.69), (3.70) молена звести до вигляду
Кв = / (grad*N)T (Г1)7 J™1grad*N det Jd£drn (3.73)
п*
Qe= f /NT det Jdf d?/. (3.74)
n*
Для обчислення інтегралів у формулах (3.73), (3.74) використовують, як
звичайно, квадратурні формули Гаусса.

3.10. Рівняння стаціонарної адвекції—дифузії
107
3.10. Рівняння стаціонарної адвекції—дифу-
311
Розглянемо тут задачу, яка описує стаціонарний процес адвекції—
дифузії, Оператор цієї задачі не є симетричним, а побудова її числового
розв'язку обчислювально складна, Водночас проблема конструювання
ефективних алгоритмів побудови числових розв'язків цієї задачі є
актуальною з огляду на її важливість у комп'ютерному моделюванні, зокрема
процесів забруднення довкілля.
Нехай Q — обмежена зв'язна область евклідового простору Rn з ліп-
шицевою границею Г і нехай v — одиничний вектор зовнішньої нормалі
до границі,
Хі — безрозмірні координати. Вважатимемо заданим в Q безрозмірний
вектор швидкості перенесення субстанції
W = (PeW1} PeW2, PeW3, ..., PeWn),
Де
w* = (и>і,ги2,гиз, ...,ги„)
— одиничний вектор, який характеризує напрям перенесення; Ре — число
Пекле, яке характеризує швидкість перенесення. Окрім того, будемо
вважати, що середовище, в якому відбувається перенесення, є нестисливим,
тобто вектор швидкості задовольняє умову
divw = E^ = °- (з*75)
Відомо [2], що безрозмірна функція и{х), (х = хі, х^ •■-, хп)) яка
характеризує розподіл концентрації певної субстанції у середовищі, задовольняє
рівняння
—Аи + wgradw = / (х), х Є О, (3.76)
де / (х) Є L2 (П) — задана функція, що характеризує інтенсивність
внутрішніх джерел субстанції, До рівняння додамо такі граничні умови:
и(х) = 0: хЄ Г; (3.77)
Тут, як і раніше, через А позначений оператор Лапласа.

108
Крайові задачі
де
Задачу (3.76), (3.77) запишемо у варіаційному формулюванні про
знаходження слабкого розв'язку и варіаційного рівняня
а (и, v) + b (w, v) = l(v),\/v£ V, (3.78)
a(u,v) = / -AuvdSl\ (3.79)
n
b(u,v) = / wgr&duvdQ] (3.80)
n
l(v) = f fvdtt] (3.81)
r(l)
V = {v (x) : v Є WQ1J (П) itii^O,^ Г.}
Перетворимо вирази правих частин білінійних форм a{u^v) та b(u,v).
Застосувавши формулу Гріна для оператора Лапласа, отримаємо для
білінійної форми a(u,v) такий вираз:
/Г £)
gracb gv&dv d£l — / —vdT.
Q Г
Оскільки виконуються граничні умови (3.77), то другий інтеграл у правій
частині попередньої формули дорівнює нулю, Отже, остаточно матимемо
а («,?;)= / grsdugrsdvdCl. (3.82)
п
Вираз (3.80) для білінійної форми b(u,v) перетворимо з урахуванням
співвідношення (3.75). Зазначимо, що виконується формула
div (wu) = wgracb -f ^divw.
Оскільки згідно з (3.75) divw = 0, то
div (ww) = wgradw, (3.83)

3.10. Рівняння стаціонарної адвекції—дифузії
109
Тому
= J div(wu)vdQ. (3.84)
Перетворимо праву частину цього співвідношення, застосовуючи
формулу Петроградського, до вигляду
/ dxv(wu)vdQ = — І wugrsAvdfl. (3.85)
Наведемо далі білінійну форму b(u,v) у вигляді
Ь (w, v) = - / div (wu) vdft -f - / div (w«) vdfl.
Перетворимо другий доданок у цьому виразі, враховуючи (3.85) та (3.83):
b(u,v) = - / div (ww) vdQ — - / div (угу) udil. (3.86)
З формули (3.86) випливає, що білінійна форма b(u,v) є кососиметрич-
ною, тобто задовольняє умову
b(u,v) = -b(v,u). (3.87)
Доведемо такі теореми.
Теорема 10. Білінійна форма
A(u,v) = a(u,v) + b(u,v): (3.88)
що відповідає варіаційному рівнянню (3.78), є неперервною та
V-еліптичною.
Доведення. Неперервність. Для доведення неперервності потрібно
з'ясувати, що білінійна форма (3.88) задовольняє нерівність
\A(u,v)\ < K\\u\\v\\v\\v.
Використавши очевидну нерівність

110
Крайові задачі
2ab < а2 + Ь2,
запишемо
(г V (г V
(A(u,v)) < 2 І / gradu graded!) 42 І / wgr&du vdfl
Vn / \n /
Оцінимо кожен доданок у попередній нерівності, застосувавши нерівність
Шварца. Отримаємо
{A (w, v)f < 2 / (gradu)2 dfi / (gradz;)2 <ЙН
+2 f (gr&dufdn f (wvfdQ.
n n
Перетворимо праву частину, і зведемо її до вигляду
(A (w, v)f < 2 / (gradu)2 <Ю I / ((gradu)2 4 (wu)2) dVt
Підсиливши праву частину попередньої нерівності, остаточно отримаємо
2 / \ 2
Де
| А (щ ь)\<КІ j ((gradu)2 + u2) rfO I / ((gradu)2 4 v2)
К = 2 max 11, max |w|2 > .
rfO
V~ еліптичність. Зазначимо таке: оскільки білінійна форма b(u,v) є ко-
сосиметричною (3.87), то форму А {и) и) можна записати у вигляді
Перепишемо її так:
А(и,и)= / (gradu)2d£l.
А(и,и) = - / (gradu)2 dVt 4 - / (gradu)2 d£l.

ЗЛО. Рівняння стаціонарної адвекції—дифузії
111
Оцінимо другий доданок, використавши нерівність Фрідріхса (3.50).
Отримаємо
А(и,и)> - (gracb)2 dSl + — / u2dQ.
п п
Звідси відразу випливає У-еліптичність білінійної форми А(и,и), тобто
виконання нерівності
А(щи)> a ((gradw)2 + u2) dfi, a > 0. ■
Теорема 11. Лінійна форма І (v) за умови / (х) Є L^ (Г2), накладеної на
функцію у правій частині рівняння (3.76), обмежена.
Доведення. Очевидне. ■
Висновок. Із двох попередніх теорем та теореми Лакса—Мільграма
(див, 1.9) випливає існування та єдиність слабкого розв'язку варіаційної
задачі (3.78).
Розглянемо, для прикладу, числове дослідження одновимірного
рівняння адвекції—дифузії
-и" + Реи = /, / = const, х Є (0,1) (3.89)
з такими крайовими умовами:
и(0) = 0, и(1) = 0.
Оскільки рівняння (3.89) є звичайним диференціальним рівнянням зі
сталими коефіцієнтами, то неважко знайти його аналітичний роз'язок,
При / = const він матиме вигляд
«(*)=£
еРе
1 -{і-еРєх)+х
(3.90)
Для числового розв'язування цієї задачі застосуємо метод скінченних
елементів, побудований на основі методу Гальоркіна. За базисні
функції вибиремо функції-бульбашки (див. 2.3). На рис. 3.4 показані графіки

112
Крайові задачі
u 103
D OJ О А О.б 0Р3 |aoJ
Рис. 3.4. Графіки розв'язків задачі адвекції—дифузії
розв'язків цієї задачі для значення Ре = 103. Штриховою лінією
зображений графік числового розв'язку отриманого з використанням кусково-
лінійних апроксимацій (функції-шапочки). Видно, що для вибраного
значення числа Ре і вибраної кількості поділу на скінченні елементи (180
елементів) числовий розв'язок навіть якісно відрізняється від
аналітичного в околі точки х = 1. Суцільною лінією зображений числовий
розв'язок цієї ж задачі, отриманий з використанням функцій-бульбашок
сьомого степеня. Його графік збігається на рисунку з графіком аналітичного
розв'язку, Зазначимо, що для цього використано поділ проміжку [0,1] на
10 скінченних елементів, причому поділ на елементи був нерівномірий.
Сітка згущена в околі точки х = 1.
3.11. Бігармонічне рівняння
Для бігармонічного рівняння
А2и = f(x1,x2), £Ьх2єП, (3,91)

3.11. Бігармонічне рівняння
113
Де
2 д4и д4и дАи
дх\ дх\дх\ дх\'
Q — обмежена область з ліпшицевою границею Г; f (хі,х2) £ L2 (П) —
задана права частина, розглянемо крайові задачі, які відповідають таким
крайовим умовам:
дії
« = 0, ^ = 0, хих2 ЄГ, (3.92)
« = 0, ^д = 0, хих2 еГ. (3.93)
Розглянемо скалярний добуток
^ J \дх\ дх\дх\ дх\
Використавши формулу Остроградського (1.16), отримаємо
/ л о \ f (дги dv дги dv
J W
дги dv dzu dv \ 7^
+з^а^ + ЩШі) da+
+ / І ^~^VUl + ^ о о VU2 + Т, о о ^1 + ТГТ^^2 I ^Г'
г
Зазначимо, що другий доданок попередньої формули дорівнює нулю,
якщо взяти до уваги граничні умови (3.92), або (3.93). Застосуємо до
першого доданка правої частини повторно формулу Остроградського (1.16)
( 2 х_ f/d2ud2v д2и d2v d2ud2v\
^ J \dx\dx\ dx\dx2dx\dx2 дх\дх\)
/<
д2и dv д2и dv д2и dv д2и dv . ._
Vi + -z—о—~—v2 + -—-—-—щ + тгт^—^2 ^г
дх\ дхі dx\dx2 dx\ dx\dx2 dx2 dx\ dx2
(3.94)

114
Крайові задачі
Перетворимо граничний інтеграл у цій формулі, зважаючи на
співвідношення
dv dv
dv
ov дх\ ох2
dv
dv
-v2 +
dv
-vx.
дхі * ' дх2
Тут т — напрям дотичної до границі Г. З них отримаємо
(3.95)
dv dv
dv
dv
dx\
dv
dxo
v\
dv
v<i\
dv
ov от
(3.96)
Підставимо отримані співвідношення у вираз граничного інтеграла у
формулі (3.94):
к
d2u dv d2u dv d2u dv d2u dv , ._
v\ + n—о—-^—Щ + -7,—о—~—Щ + тг^-^—^2 | dT =
dx\dx\ dx\dx2dxx dx\dx2dx2
dx\ dx2
f\d4(
J [dx\ \
dv dv \ d2u
[dxl \dv dr J dx\dx2 \dv
dv dv
Щ ~ Tj-v2 ] v2+
d2u (dv dv \ d2u (dv
dx\dx2 \dv dr J dx\ \dv
dv
dT
/dv (д2и 9 d2u d2u Л m
+
dv
~frr
d2u d2u , 2 ?ч d2u
—2*^2 + я д [v-l - v2) 4- ^^2
dxl
dx\dx<i
dxl
dT.
(3.97)
Зазначимо, що виконується формула, яку неважко перевірити
d2u d2u
dv2 dxl
ul + 2
д2и
дхідх2
V\Vi +
82u
v~.
dxf2
(3.98)

3.11. Бігармонічне рівняння
115
dT.
Перепишемо остаточно вираз для скалярного добутку (А2и, v):
(А2 \-[(^!^1 д2и d2v d^$^\dn_
^ J \дх\дх\ дх\дх2дх\дх2 дх\дх\)
п
/d2udv f dv Г д2и д2и , 2 2, д2и
dv2 dv J дт [ дх\ 1 дх\дх2 2 дх\
г г
(3.99)
З цього, що функція и набуває на границі Г нульового значення (крайові
умови (3.92), (3.93)), випливає
ди
— = 0, прижь:&2 Є Г. (3.100)
дт
Отже, видно, що для двох типів крайових умов (3.92), (3.93) інтеграли
за границею у формулі (3.99) дорівнюють нулю. Звідси випливають такі
лема та теорема.
Лема 12. Оператори крайових задач (3.91), (3.92) та (3.91), (3.93) є
симетричними.
Доведення. Випливає з такого запису скалярного добутку:
(А2щу) = (3.101)
/fd2ud2v д2и d2v d2ud2v\
\dxl дх\ дх\дх2 дх\дх2 дх\ дх\ J
Теорема 13. Оператори крайових задач (3.91), (3.92) та (3.91), (3.93)
є додатно визначеними.
Доведення. Необхідно довести, що виконується нерівність
(А2и,и) >72 [иЧП.

116
Крайові задачі
Зазначимо, що за умов цієї теореми можна використати нерівність Фрі-
дріхса (3.50) для отримання таких нерівностей:
J \\dxl
д2и
дх\
+
+
д2и
дх\дх2
д2и
дх\дх2
dQ>
— [ (ди V
сі J \дхі)
ди
сі J \дх2
а
dSl;
dSl.
Додавши ці нерівності та врахувавши формулу (3.101), отримаємо
(Л V«) > ^ /
ди
дхі
+
ди
дх2
<Я1
Для оцінювання правої частини попередньої нерівності знову застосуємо
нерівність Фрідріхса (3.50). Остаточно запишемо
(А2и,и) > -2 / u2dQ.
Отже, 72 = 1/сі- ■
Отримані результати дають змогу сформулювати крайові задачі
(3.91), (3.92) та (3.91) (3.92) у вигляді таких варіаційних задач,
Задача, еквівалентна крайовій задачі (3.91), (3.92),
F (и) —> min, u Є НЛі.
Задача, еквівалентна крайовій задачі (3.91), (3.93),
F (и) —> min, u Є Нд2.
Тут
J \дх\дх\ дхі
д2и d2v d2ud2v\ т^ Л . . ,_
дх2 дх\дх2 дх\ дх\
НА
г(2)
и : и Є W2 (Ф ! « = 0, хи %2 Є Г;
<9и
0,а?і,дг2 € Г ^;
#А2 = {и : и Є W2(2) (П); и = 0, жь х2 Є ГІ.

3.12. Крайові задачі для рівняння еліптичного типу
117
3.12. Крайові задачі для рівняння
еліптичного типу
Використаємо введені у параграфі 3.7 поняття мультиіндексу і
диференціальних операторів D% для запису рівняння
Аи = ^ (-1)'" Di {aij(x)DJu) =
\i\,\j\<k
,£-./ ' дхїдх'і...а<- V ""• •'"ІЛЛ"*1 >dxfdx'2\..dxt)
= /(#), Ж = Х\,Х2<> »., #гг Є ^- (3.102)
Тут £1 С Rn — обмежена область з ліпшицевою границею Г.
Означення. Якщо для довільного дійсного ненульового вектора
£ ау(хі,х2,...,а:п)^^05 (3.103)
Де Є = (ff,^...,U")3 £' = (ЄГ,Є^-,Є), то оператор Aw у лівій
частині рівняння (3.102) еліптичний у точці х = #і, х2,..., яп- Якщо ж
існує деяке число С > 0, яке залежить тільки від заданної області Q і
від коефіцієнтів ац оператора, таке що майже для кожної точки області
Q і для довільного дійсного вектора
£ = (£ь£2) •••)&»)
виконується нерівність
Y, агз{хих2,...,хп)ЄЄ>С\ї\2\ (3.104)
Де |£|2 = £>\к + £ffe 4- ... 4- £*fe, то оператор Aw називають рівномірно
еліптичним в області Q.
Якщо к = 1, то для оператора Aw можна поставити такі основні
крайові умови:

118
Крайові задачі
1° умова Діріхле
и = 0 на Г;
2° умова Неймана
Nu = 0 на Г,
Де
Nu = ^^ aijDlu ІИЛ
КІ,ІІІ=і
|i/|J = cos*71 {v,X\) 4- cosJ'2 (г/, а^г), cos (і/, #*),& = 1, 2 — напрямні косинуси
зовнішньої нормалі v до границі Г;
3° умова Ньютона
Nu + а (х) и = 0 на Г,
де а (х) > сто > 0.
Дослідження операторів цих задач можна виконати аналогічно, як у
3.7. Доведемо лему,
Лема 14. Оператори крайових задач Г, 2°, 3° є симетричними.
Доведення. Наведемо тут доведення для задачі Діріхле.
Припускаючи, що
/0*0 є l2(0),
охарактеризуємо область визначення оператора задачі співвідношенням
DA = {и(х) : Dlu(x) Є L2(fi), |г| < 2; и(х) = 0, х Є Г}.
За аналогією з попереднім (див, 3.7) можемо зробити висновок про те, що
область визначення оператора є щільною множиною у просторі L2(fi).
Розглянемо скалярний добуток
(Ащу) = f І ]Г (-1)N^i {^ijDju) vdn.
Застосувавши формулу Остроградського (1.17)
w-—dQ = — І z-—dQ + / zwlkdT
oxk J dxk J
Q Q Г

3.12. Крайові задачі для рівняння еліптичного типу
119
і врахувавши граничну умову Діріхле, отримаємо
(Au,v)= f J2 aijDiu&vdn. (3105)
Звідси видно, що оператор є симетричний. ■
Має місце така теорема:
Теорема 15. Оператор задачі Діріхле, який описується рівномірно
еліптичним диференціальним оператором другого порядку (к = 1), за
умови
а0о > 0
є додатно визначений
Доведення* Використаємо для доведення властивість рівномірної
еліптичності й оцінимо знизу праву частину у формулі (3.105)
(Ащи) = f J2 aniyu&vdn >C JY^ {tfufda + f amu2<m.
(3.106)
Візьмемо до уваги, що
а0о > 0
і перепишемо формулу (3.106) у вигляді
/Е(о'«)
2
(Аи,и)>С І 2^(D%u) <КІ.
а KM
Оцінимо праву частину отриманого співвідношення знизу,
використовуючи нерівність Фрідріхса (3.50)
fu2(x)dn<Cl fit{%^) dQ + c2 fu2(x)dT,
Q П к=1 Г
отримаємо
(Au,u) > 72||«I|^2(D,
де
72 = —, 72 > 0. ■

120
Крайові задачі
Отже, задачу Діріхле для рівномірно еліптичного рівняння другого
порядку (3.102) можна сформулювати як задачу мінімізаціїї
функціоналу енергії, так і задачу про знаходження розв'язку варіаційного рівняння
виду; знайти функцію и Є V таку, яка задовольняє рівняння
(Au,v) = l(v), Уг; є V,
Де
V = lv :v Є^2(1)^ = 0наГІ.
3.13- Вправи для самостійного виконання
Вправа 1. Записати крайову задачу (3.1), (3.2) у вигляді варіаційного
рівняння для знаходження слабкого розв'язку,
Вправа 2. Для задачі про циліндричний згин пластини Тимошенка
побудувати схему МСЕ й обчислити елементи матриць, з яких
формується система лінійних алгебричних рівнянь,
Вправа 3. Довести, що варіаційні формулювання (3,31), (3,32)
еквівалентні.
Вправа 4. За аналогією з параграфом 1.7 довести, що система
лінійних алгебричних рівнянь МСЕ формується з матриць (3,33), (3,34),
(3.35).
Вправа 5. Отримати апріорну оцінку точності схеми МСЕ для
системи звичайних диференціальних рівнянь,
Вправа 6. Для системи рівнянь (3,36) дослідити задачі, які
відповідають таким крайовим умовам:
і)
2)
7і (а) = 0, w(a) = 0, ^}Ж = 0, w(b) = 0;
*W=M(«) = 0, ^ = 0,7і(6) + ^ = 0.
aoL\ aai
Вправа 7. Сформулювати основні крайові задачі для рівняння Пу-
ассона у вигляді варіаційних рівнянь,

3.13. Вправи для самостійного виконання
121
Вправа 8. Дослідити оператор змішаної крайової задачі для
рівняння Пуассона, яка відповідає крайовим умовам
ди
и = 0 Гі, — = 0 на Г2, Гі U Г2 = Г, Гі П Г2 = 0.
ov
Вправа 9. Записати варіаційні формулювання крайових задач для
неоднорідного рівняння Лапласа у вигляді варіаційних рівнянь для
знаходження слабких розв'язків, Дослідити питання існування їхніх
розв'язків.
Вправа 10. Вивести формулу (3.64) шляхом відображення
довільного трикутника на прямокутний, катети якого лежать на координатних
осях, і зведення подвійного інтеграла до повторного.
Вправа 11. У припущенні, що слабкий розв'язок щ одновимірної
задачі адвекції—дифузії задовольняє умову щ Є W2 (0) 1) і Щ° похибка
апроксимації за нормою W2 (0,1) функціями-бульбашками тго степеня
становить 0(/гт), отримати апріорну оцінку наближеного розв'язку
методу скінченних елементів. Дослідити залежність апріорної оцінки від
числа Ре.
Вправа 12. За аналогією з параграфом 1.7 зобразити схему
формування системи лінійних алгебричних рівнянь методу скінченних
елементів, побудованого з використанням апроксимацій на трикутних
скінченних елементах (див, 3.8).
Вправа 13. Записати за допомогою операторів D% та мультиіндексів
крайові задачі для бігармонічного рівняння,
Вправа 14. Дослідити за аналогією з параграфом 3.7 задачу
Ньютона для рівняння еліптичного типу,
Вправа 15. Дослідити за аналогією з параграфом 3.7 задачу Нейма-
на для рівняння еліптичного типу,
Вправа 16. Вивести формули (3.95), (3.96).
Вправа 17. Вивести формулу (3.105).
Вправа 18. 1°. Дослідити оператори крайових задач;
і)
// /2 р / \ f 7Г ЗТЇ
smx и + cosх и — х и = j (ж), х Є І —, —
<)=°.«(т) = °-'<*>є0<,,(ї-т)

122
Крайові задачі
2)
(1 — sinx) и — cosх и + х и = f (х), х Є І —, — І ,
*(*)=<>• «(т)=°''<*>є0<,,(ї'Т>
з)
— (2 — cos х) и" — sin х v! + e^w = / (ж), ж Є ( 0, — ),
«(0) = 0, «(|)=0, / (*) Є С<°> (о, |) ;
4)
—2sin2 — «" — £#£ u' 4- 5и = / (ж), ж Є ( — —, — ),
«'(-ї)=°-«(з)=^м^,0|(-ї'ї)^
5)
// / р / \ /7Г7Г\
—сіра: sin ж и +smx и 4- и = f (х), жЄ ("""Т1 7 J'
^(-ї)=о.«(ї)=о./(«)^(-ї.ї)^
є)
-(еж + 1па:) «"- (еж + -) «ЧЛ = /(4 ж Є (2,3),
и
'(2) = 0, и(3) = 0, /(ї)еС(°)(2,3).
2°. Записати їхні варіаційні формулювання.
3°. Довести збіжність методу скінченних елементів, побудованого на
лінійних апроксимаціях,

Розділ 4
Задачі на власні значення
Задачі на власні значення становлять окремий клас задач
математичної фізики, До них належать задачі про вільні гармонічні коливання
механічних систем (це показано у параграфі 4,1), У розділі
розглянуто задачі на власні значення для операторів у гільбетовому просторі,
Досліджено властивості власних чисел та власних функцій залежно від
властивостей операторів задач, Описано способи варіаційних
формулювань задач на власні значення. Наведено приклади застосувань методу
скінченних елементів до знаходження власних чисел та власних функцій
операторів,
4.1. Математичні моделі, які приводять до
задач на власні значення
4.1.1. Коливання струни
Рух струни, натягненої силою р, описує рівняння
P^ = PW' 0<ж<а' 0<*<г> (4-1)
де z{x1t) — відхилення струни в точці х у момент часу t в напрямі,
перпендикулярному до осі х] р — густина матеріалу струни, Вважатимемо,

124
Задачі на власні значення
що струна закріплена в точках х = 0, а. Тоді до рівняння (4.1) необхідно
додати граничні умови
z(Q,t) = 0, z{a,t) =0. (4.2)
Окрім співвідношень (4.1), (4.2), математична модель руху струни має
ще початкові умови, Однак для розгляду вільних, гармонічних коливань
струни початкові умови несуттєві, 3 огляду на це тут і надалі початкові
умови опущено,
Якщо розглядати вільні, гармонічні коливання, то розв'язок задачі
(4.1), (4.2) треба шукати у вигляді
z(x,t) = w(x)etuJ\ (4.3)
де U) — колова частота (кількість повних коливань за період часу 2тг).
Зазначимо: термін "вільні коливання" означає те, що рух струни
відбувається тільки під дією сил інерції, будь-яких інших зовнішніх силових
впливів нема. Термін "гармонічні коливання" означає таке: рух
відбувається за певним гармонічним законом у часі і, що визначений
формулою (4.3),
Частотою коливань називають величину
1 2тг'
яка дорівнює кількості повних коливань за одиницю часу,
Підставивши (4.3) в (4.1) та (4.2), отримаємо
cPw
——- - Xw = 0, w(Q) = 0 w{a) = 0, (4.4)
ax1
Де
Л = u2р/р.
Задачу (4.4) називають задачею на власні значення для
диференціального оператора
Aw = —-^, DA = \w(x) : w(x) Є С{2] [0, а], w(0) = 0 w(a) = 0} . (4.5)
ахг
Вона полягає у відшуканні значень частотного параметра Л і
відповідних їм функцій w(x)i відмінних від тотожного нуля, які задовольняють
співвідношення (4.4), Значення Л називають власними значеннями
(власними числами) диференціального оператора (4.5), гии(х) — відповідними
їм власними функціями,

4.1. Математичні моделі, які приводять до задач
125
4.1.2, Згинні коливання стрижня
Відомо, що рух пружного стрижня під дією сил інерції описує
рівняння
EJ0 = -рр% °< х <а' ° < * -т- (46)
Тут z{x1t) — зміщення точки серединної лінії стрижня в момент часу і
в напрямі, перпендикулярному до осі х] Е — модуль Юнга; р — густина
матеріалу стрижня; F^J — const — площа та момент інерції поперечного
перерізу стрижня,
У кінцевих точках стрижня х = 0, х — а запишемо умови, що
відповідають жорсткому защемленнню обидвох його країв:
,(0,t) = 0,^ = 0,*OM) = 0,^ = 0. (4.7)
Розв'язок задачі (4.6), (4.7), який відповідає вільним гармонічним
коливанням, шукатимемо у вигляді
z(x,t) =ь)(х)еш. (4.8)
Підставимо (4.8) в (4.6) та (4.7) і отримаємо задачу на власні
значення, яка описує вільні згинні коливання стрижня,
d w
^-A^ = 0,^G (a, 6); (4.9)
л dw(0) л , ч dw(a) л /л „Лч
w(0) = 0, —^ = 0, w(a) = 0, —^ = 0, (4.10)
ах dx
Де
Л = pFu2/EJ.
Задача (4.9), (4.10) полягає у знаходженні власних чисел Л та
відповідних їм власних функцій w(x), відмінних від тотожного нуля,
4.1.3. Коливання мембрани
Рух тонкої мембрани, натягнутої зусиллям інтенсивності р, в полі сил
інерції описують рівнянням

126
Задачі на власні значення
p&z = p^, в Пх(0,Т]. (4.11)
Тут р — густина матеріалу; р — сила натягу мембрани; z(xi1x2,t) —
зміщення точки ХіУх2 двовимірної обмеженої області Q з ліпшицевою
границею Г в момент часу і у напрямі, перпендикулярному до площини
мембрани;
d2z d2z
дх\ дх\
Уважатимемо, що край Г області О, яку займає мембрана, закріплений,
тобто виконуються граничні умови
z(xu х2, t) = 0, хи х2 Є Г. (4.12)
Як і в попередньому розв'язок рівняння (4.11), який описує вільні
гармонічні коливання, шукатимемо у вигляді
z(xu х2, t) = гю(хих2)еш. (4.13)
Підставивши (4.13) в (4.11), (4.12), отримаємо задачу на власні значення,
яка описує вільні гармонічні коливання мембрани
-Aw - Xw = 0, х1ух2єП; (4.14)
w = 0, хих2 Є Г, (4.15)
де Л = рсо2/р — частотний параметр. Як і раніше, вона полягає у
відшуканні власних чисел Л та відповідних їм власних функцій ги, відмінних
від тотожного нуля,
4.1.4, Коливання пластини
Нехай серединна площина пластини займає обмежену область Q у
площині Хі,^2. Прогин z(xiJx2,t) точки Хі,х2 в момент часу t пластини
під дією сил інерції описує рівняння
d2z
DAAz = -ph-Qt в fi x (0,Г]. (4.16)

4.2. Властивості спектра оператора
127
Тут р — густина матеріалу пластини; h — товщина пластини;
D = Eh3 /12;
Е — модуль Юнга;
А . d4z Л d4z d4z
АА2 = —г + 2-
Уважатимемо, що край пластини, який проходить уздовж кривої Г
(вважатимемо її ліпшицевою кривою) з зовнішньою нормаллю т/, жорстко
защемлений, Це означає, що на краю Г виконуються граничні умови
z(xux2,t)=0, в*(*ь*2,*)=0. гьХ2єГі (4Л7)
Вільні, гармонічні коливання пластини розглядатимемо у вигляді
z{x1}x2yt) = ь)(хих2)еш. (4.18)
Підставивши (4.18) в (4.16), (4.17), отримаємо
AAw - Xw = 0; хих2Є О, (4.19)
w = 0] -^ = 0; хих2єТ. (4.20)
Тут А = phoo2 /D — частотний параметр.
Задача (4.19), (4.20) є задачею на власні значення. Якщо знайти її
розв'язок, тобто власні числа А і відповідні їм відмінні від нуля власні
функції w: то можна описати явище вільних гармонічних коливань
пластини.
4.2. Властивості спектра оператора
Розглянемо задачу на власні значення вигляду
Аи - \и = 0, (4.21)
де А — деякий оператор, який діє в гільбертовому просторі Н — L2.

128
Задачі на власні значення
Означення. Значення А, для яких існує відмінний від тотожного
нуля розв'язок задачі (4.21), називають власними значеннями оператора
А (власними числами), а відповідні їм нетривіальні розв'язки и —
власними функціями (власними елементами) оператора А. Сукупність усіх
власних чисел і власних функцій оператора називають його спектром,
Задачу (4.21) називають також спектральною задачею.
Наведені нижче теореми визначають якісні характеристики власних
чисел та власних функцій залежно від властивостей симетрії, додатності
і додатної визначеності оператора А.
Теорема 1. Нехай А — симетричний оператор. Тоді власні числа задачі
(4*21) є дійсними числами.
Доведення. Домножимо (4.21) на власну функцію и:
(Ащи) = \(и7и). (4.22)
Звідси
= (Аи} и)
(щи) '
де (и,и) — дійсне число. Вважаючи Л комплексним числом, запишемо до
нього спряжене
-= (Ащи)
(щи)
За першою аксіомою комплексного гільбертового простору
маємо (Аи, и) = (и, Аи). Згідно з означенням симетричного оператора
(Аи,и) = (щАи). Отже, (Аиуи) = (Аиуи), тобто комплексне число
(Аи, и) дорівнює своєму спряженому. Таке число є дійсним, ■
Теорема 2. Власні числа додатного оператора невід'ємні; власні числа
додатно визначеного оператора додатні.
Доведення. З формули (4.22) випливає, що
А = ^4- (4-23)
(и,и)
Звідси, якщо взяти до уваги означення додатного і додатно визначеного
оператора, отримаємо доведення теореми. ■

4.2. Властивості спектра оператора
129
Теорема 3. Власні функції симетричного оператора, що відповідають
різним власним числам, ортогональні.
Доведення. Нехай Аі, А2 (Лі ф А2) — власні числа, а и\,и2 —
відповідні їм власні функції, Тоді виконуються співвідношення
Аи\ — \\U\ = 0;
Аи2 — Х2щ = 0.
Домножимо скалярно обидва рівняння на функції и2) Wi, відповідно:
{Аиии2) = Ai(«i,w2);
(Аи2,щ) = A2(w2,wi).
Віднімемо від першого рівняння друге і врахуємо властивість симетрії
оператора А та властивість симетрії скалярного добутку в дійсному гіль-
бертовому просторі (перша аксіома), тобто
(Аиии2) = (ииАи2) = (Аи2,щ).
Матимемо
(Аі - Х2)(иии2) = 0.
Звідси, оскільки Аі Ф А2, випливає, що (щ,и2) = 0, тобто власні функції
щ,и2 ортогональні. ■
Якщо власному числу А відповідає кілька лінійно незалежних
власних функцій, то, використовуючи процес ортогоналізації Шмідта [5,6],
ці власні функції можна ортогоналізувати між собою. Водночас згідно з
доведеною теоремою вони є ортогональні до власних функцій, що
відповідають іншим власним числам. Отже, всі власні функції симетричного
оператора можна вважати ортогональними.
Теорема 4. Власні функції додатно визначеного оператора, що
відповідають різним власним числам, ортогональні за енергією.
Доведення. Нехай А$, Xj (Aj ф Xj) — власні числа, &щ,и3 —
відповідні їм власні функції додатно визначеного оператора, 3 (4.21) випливає,
що
Ащ — Хіщ = 0.

130
Задачі на власні значення
Домножимо це рівняння скалярно на власну функцію Uj. Отримаємо
(Ащ,щ) = Xi(uhUj).
Права частина цього співвідошення дорівнює нулю згідно з теоремою 3.
Отже,
(Ащ.щ) = 0, і ф j,
що доводить ортогональність власних функцій за енергією, ■
4.3. Енергетичні теореми в проблемі власних
чисел
Задачі на власні значення, як і крайові задачі, можна наводити у
вигляді певних варіаційних задач, Розглянемо теореми, які необхідні для
формулювання варіаційних задач, еквівалентних задачам на власні
значення.
Теорема 5. Нехай А — додатно визначений оператор
(Ащи) > 72 ІМІ ,
і нехай Лі (Лі > 72) — точна нижня границя значень функціонала
(Аи, и)
{щи)
(4,24)
Якщо існує функція щ Є Da (Da — область визначення оператора А)
така, що
(-р^ = А„ (4.25)
то Лі є найменше власне число оператора А, а щ — відповідна йому
власна функція.
Доведення. Припустимо, що існує щ, для якої виконується
співвідношення (4.25). Візьмемо довільну функцію т\ Є Da- Розглянемо
v = щ + trj, \ft Є R.
(4,26)

4.3, Енергетичні теореми в проблемі власних чисел
131
Очевидно, що v Є Da- Розглянемо на множині функцій (4.26)
функціонал (4.24)
(Mv} = (A(u1 + tVU1 + tV) =
Функція дійсної змінної (p(t) досягає мінімального значення при t = 0.
Тоді виконується співвідношення ^'(0) = 0. Обчисливши похідну від
правої частини формули (4.27), отримаємо
¥>'(()) = 2^ь»іп^/;-^ь«іп»ь^ = 0 (428)
((«і, wi) {Auurj) - (Auly wi) («і, r})
Врахуємо в чисельнику цього виразу, що згідно з (4.25)
(Аиищ) = Лі («i,wi).
Остаточно запишемо
(Ащ -Лі«і,г/) = 0. (4.29)
Звідси, оскільки 7] — функція зі щільної множини Da, випливає
Ащ — Хіщ = 0,
тобто Лі — власне число, a iti, - відповідна йому власна функція, З
того, що Лі — точна нижня границя відношення (4.24), випливає, що Лі
— найменше власне число. ■
Згідно з доведеною теоремою задачу про знаходження найменшого
власного числа додатно визначеного оператора можна звести до задачі
про мінімум функціонала
^, и є DA. (4.30)
Зауваження, Наведемо ще одне формулювання цієї задачі,
Виконавши в (4.30) заміну <ф = и/ \\и\\ , отримаємо ||^|| = 1 і
(-р4 = (Аф,ф).
(и,и)
Отже, варіаційну задачу про відшукання мінімального власного числа
можна сформулювати як задачу про мінімум функціонала
(Аи,и), и Є DA, (4.31)

132
Задачі на власні значення
за додаткової умови
\\и\\ = 1. (4.32)
Розглянемо тепер варіаційну задачу про знаходження інших, окрім
першого, власних чисел.
Теорема 6. Нехай 0 < Аі < А2 < ... < Ап — тг перших власних чисел
додатно визначеного оператора, щ^щ, ...,un — відповідні їм ортонормо-
вані власні функції Нехай існує функція ип+\, яка не дорівнює
тотожному нулю і надає мінімального значення функціоналу
(Аи,и)
(4.33)
(и,и)
за додаткових умов
(щщ) = 0, і = 1,2,...,п. (4.34)
Тоді ип+\ — власна функція, яка відповідає власному числу
Лп+1 = (^'«n+O (4>35)
Доведення* Візьмемо довільну функцію £ Є Da- Приймемо
п
V = t-1%2(t>uk)uk. (4.36)
Можна переконатися, що функція г\ задовольняє умови (4.34). Разом з
функцією 7] умови ( 4.34) задовольняє і функція
ип+1 + ії), Ш є R. (4.37)
Підставимо (4.37) у функціонал (4.33). Отримаємо функцію змінної і
ірії) = (А (ип+1 + trj), ип+1 + trj) I (w„+i + ti\, un+l + trj),
яка досягає мінімального значення при t = 0. Отже, вона задовольняє
умову
ір1 (t) = 0, * = 0. (4.38)

4.3, Енергетичні теореми в проблемі власних чисел
133
Звідси за аналогією з доведенням теореми про варіаційну задачу для
знаходження найменшого власного числа отримаємо
(Аип+1 - Лп+і«п+і, ті) = 0. (4.39)
Підставивши (4.36) в (4.39), після нескладних перетворень знайдемо
{Аип+і - An+i«n+i,C) = 0.
Оскільки £ — довільна функція із щільної множини Da, to
Аип+1 - Лп+і^п+і = 0.
Отже, Лп+і — власне число, а ип+і — відповідна йому власна функція,
Доведемо, що Лп+і — найменше власне число, яке йде після Лп. Нехай А*
— власне число оператора А, більше від Лп, и* — відповідна йому власна
функція, Згідно з 4.2
Л* = т44^ > *п+і, (4.40)
оскільки Лп+і є мінімумом функціонала (4.33) за додаткових умов (4.34).
■
Доведена теорема свідчить, що задачу про відшукання Лп+і можна
звести до задачі про мінімум функціонала такого ж, як і для найменшого
власного числа, але за додаткових умов (4.34).
У наведених теоремах зроблено припущення про існування власних
функцій та власних чисел задачі, Сформулюємо тепер теорему, яка дає
умови існування власних функцій та власних чисел.
Теорема 7. Нехай А — додатно визначений оператор, який діє в гіль-
бертовому просторі Н, і нехай довільна мноснсина функцій, обмежена
за енергетичною нормою, компактна в Н. Тоді справджуються такі
твердження: а) оператор А має нескінченну кількість власних чисел
0 < Лі < Л2 < ... < ЛП...,ЛП -^ оо;
б) відповідні власні функції утворюють систему, повну як у просторі
Н, так і в енергетичному просторі На-

134
Задачі на власні значення
Доведення. Тут доведемо існування найменшого власного числа та
відповідної йому власної функції, 3 повним доведенням теореми можна
ознайомитись у [8], Нехай А — додатно визначений оператор. Тоді
виконується нерівність
\\и\\2А > 72|М|2, и Є НА. (4,41)
Приймемо
<р(и) = \\и\\2А/\\и\\\ uGHA, (4,42)
і позначимо через Лі точну нижню границю функціонала ір(и).
Очевидно, що Лі > 72- Доведемо, що існує функція ui, яка задовольняє рівність
<р(иі) = Лі.
За означенням точної нижньої границі, яке б не було число п G Z, можна
знайти функцію vn) таку, що виконуються нерівності
Лі < (р (vn) < Лі 4- 1/п. (4,43)
Подвійна нерівність (4,43) означає, що
\im(p(vn) = Лі. (4,44)
п~>оо
Зазначимо, що функціонал (4,42) не зміниться в разі домноження
функції и на сталу, Домноживши vn на ||^П|Г і можна вважати, що \\vn\\ = 1.
Тоді <p(vn) — \\уп\\аі * 3 (4.44) випливає
lim \\vnfA = Аь (4.45)
Нехай \/г/ G Ha^ V£ G R. Очевидно, vn + tr\ G На і
Ьі±Щ > Лі. (4.46)
b>n + tri\\
З (4.46) одержимо
t2 (Ml ~ Лі INI') + *((vn,v)A ~ Аі (vn,V)) + (\\vn\\2A - Ах) > 0. (4.47)
Якщо квадратний тричлен задовольняє нерівність (4,47), то його
дискримінант не додатний. Звідси випливає ланцюжок нерівностей

4.3, Енергетичні теореми в проблемі власних чисел 135
<Н\а\/\К\\2а-М- (4.48)
Нехай довільна функція т\ є такою, що \\т]\\А < С = const, 3 (4,45) та
(4,48) випливає, що
K,^-Ai(v„,r/) -> 0. (4,49)
П~>00
Оскільки 11v«11^ —> Лі, то H^nlU < Сь Де Сі — деяка стала. Якщо
прийняти, що 7] = vn — vm, то за нерівністю трикутника отримаємо
NL<lklU + IKIL<2d.
Тоді згідно зі співвідношенням (4,49)
(vn, vn - vm)A - \x{vn, vn - vm) -> 0.
З попередньої формули виведемо іншу шляхом заміни місцями m та п
та додамо до попередньої:
\\vn-vm\\A-X1\\vn-vm\\ ->0 . (4,50)
п,т—ї ос
Нерівність Н^пІІ^ < С\ означає, що послідовність vn обмежена за
енергетичною нормою, За умовою теореми ця послідовність компактна в
просторі Н. Виділимо з неї підпослідовність, збіжну в Н. Позначимо цю
підпослідовність vn. Нехай вона збігається до щ: тобто
\\уп-щ\\ -^0.
п~>оо
Тоді
\\v„ -vm\\ -»• 0 .
n.m—» oo
З (4.50) випливає, що тоді
\\v„ -vm\\A -*0 .
n,m—?>оо
Це означає, що послідовність vn є збіжною і в просторі На, причому
граничним елементом цієї послідовності в На є цей же елемент и\. Оче~
видним є факт, що
||ui|| = lim \\vn\\ = 1,

136
Задачі на власні значення
а також
||ui|L = Hm \\vn\\A = Лі.
Доведемо тепер, що
Ащ — X\U\ = 0.
Перейдемо в (4.49)до границі при п —> оо :
(«і, гі)а ~ Аі(«і, ті) = 0.\/VG Ha. (4.51)
Розглянемо задачу
Аи = Лі«і. (4.52)
Ця задача еквівалентна (згідно з теоремою про функціонал енергії)
задачі про мінімум функціонала
(и, и)А — 2(u, Ai«), u Є НА.
Перепишемо цей функціонал з урахуванням співвідношення (4.51).
Отримаємо
(и,и)А - 2(щщ)А.
Додамо до цього співідношення і віднімемо від нього вираз (щ^щ)А
{и,и)А - 2(и,щ)А = \\и- щ\\А - \\иі\\А.
Звідси ясно, що мінімум цього функціонала досягається при щ. Отже,
розв'язком задачі (4.52) (можливо, узагальненим) є функція щ, тобто
Ащ = \іщ.
Цим ми довели, що Лі, ще власне число та власна функція оператора
А 3 теореми 5 випливає, що Лі — найменше власне число. ■
Зауваження, Як видно з доведеної теореми, тут ідеться про
існування власних функцій в узагальненому сенсі, тобто таких, що належать
простору НА.

4.4. Дискретний спектр оператора Штурма—Ліувілля
137
4.4. Дискретний спектр
Штурма—Ліувілля
оператора
Розглянемо задачу на власні значення для оператора
Штурма—Ліувілля, яку описують диференціальними рівняннями
d ґ du
~гР \х) ~і—\- q(x)u — ли = 0, а < х < о
ах ах
(4.53)
та граничними умовами
и (а) = 0, ди' (6) 4- du (6) = 0. (4.54)
Уважатимемо, що коефіцієнти р (х) та q (х) задовольняють на [а, Ь] умови
ь
-
а сталі д, d є такими, що
dx
(х)
< оо,
(4.55)
5>0, d>0g + d^0.
Доведемо, що за таких умов оператор задачі на власні значення (4.53),
(4.54) є додатно визначений. Для конкретності приймемо d > 0. У цьому
разі вважатимемо, що і д > 0. Якщо д = 0, то матимемо граничну умову
и (Ь) = 0, яка є значно простішою для дослідження.
Розглянемо скалярний добуток (Аиуи), що відповідає задачі (4.53),
(4.54):
(Аи,и)= І
Р О) ( ^ ) +Я(х) и2
dx 4- -р (6) и2 (6).
Оцінивши його знизу, отримаємо
ь
(Ащи) > В
/рМ® * + «"<»>
(4.56)
Де
В = min •{ 1, -р (6) }.

138
Задачі на власні значення
Уважатимемо: функція и (х) є такою, що виконується
ь
Урахувавши елементарну нерівність
(г, + С)2 < 2 (г? + С2)
з (4.57) матимемо
и2 (х) < 2и2 (Ь) + 2 | j ^
2
dt I .
(4.57)
(4.58)
Врахуємо далі таке співвідношення:
2
/
du(t)
dt
dt
X /
Звідси за нерівністю Коші—Буняковського
2
/
du(t)
dt
dt <
!ml>®
du{t)
dt
dt.
Замінюючи межу інтегрування х на а, підсилимо попередню нерівність.
Тоді отримаємо
г о
dujt)
dt
dt <
fmh*
du(t)
dt
dt.
Отже, з урахуванням співвідношення (4.58)
ь Г ь 2
fu2dx<c\fp(t)(^-\ dt + u2(b)
(4.59)

4.4. Дискретний спектр оператора Штурма—Ліувілля
139
де
С = тах{2А (Ь - а), 2 (6 - а)}.
Звідси, якщо врахувати нерівність (4.56), випливає, що оператор — до-
датно визначений,
7
с
Енергетична норма, що відповідає цьому операторові, має вигляд
ь
\и\
і\Р{Х){
р(х) ( ^Ч +q(x)u2
dx + -р (Ь) и2 (6)
9
Якщо д = 0, то останній доданок треба відкинути, 3 цієї формули,
очевидно, випливає така оцінка:
ь 2
lu&-Ip{x){t) dx-
(4.60)
Нехай деяка функція и (х) задовольняє умову и (а) = 0 і є такою, що
виконується
/"'
и(х)= І и' (t) dt.
(4.61)
Прийнявши
можемо переписати рівність (4.61) у вигляді
(4.62)
и
о
(4.63)
Доведемо, що інтеграл
ь ь
ff&frt)
dxdt

140
Задачі на власні значення
є скінченним. Справді, з формули (4.62) видно, що для всіх можливих
значень ж, t з проміжку [а, Ь] ядро К (ж, t) задовольняє нерівність
1
0 < K(x,t) <
VpWY
Тому
ь ь ь ь
К2 О, *) dxdt < / / А~\ = (6 - а) А < оо.
Нехай задано множину функцій, обмежену за енергетичною нормою:
\\и\\А < С = const. (4.64)
Тоді, згідно з нерівністю (4.60)
ь 2
а
Використаємо в подальшому відомий результат з функціонального
аналізу [8], який полягає у тому, що оператор Фредгольма (4.63), ядро якого
є інтегровне з квадратом за двома змінними, цілком неперервне,
Отже, він перетворює обмежену згідно з (4.65) множину в
компактну, Оскільки (4,65) є наслідком нерівності (4,64), то звідси випливає, що
довільна обмежена за енергією оператора Штурма—Ліувілля множина є
компактною. Тобто оператор Штурма—Ліувілля задовольняє умови
теореми 7, Згідно з цією теоремою оператор Штурма^Ліувілля має
дискретний спектр,
4.5. Мінімаксимальний принцип Куранта
Для варіаційного формулювання задачі про визначення власного
числа Ап+і (п > 1) та відповідної йому власної функції ип+і потрібно
знати всі попередні власні функції щ^щ, ...,wn (теорема 7, див. 4,3), Інколи
потрібно мати варіаційне формулювання задачі про визначення власного
числа Ап+і {п > 1) та відповідної йому власної функції ип+\ за умови,
коли невідомі всі попередні власні функції, Тоді можна використати
мінімаксимальний принцип Куранта, який наведемо у вигляді такої теореми,

4.5, Мінімаксимальний принцип Куранта
141
Теорема 8. Нехай А — додатно визначений оператор з дискретним
спектром, що діє в просторі Н. Нехай 0 < Лі ^ Л2 ^ ... ^ An... —
власні числа оператора А і щ^щ, ...^ип... — відповідні їм власні функції.
Виберемо у просторі На довільні функції fi,f2,..., vn- Позначимо через
A(t;i, v2)..., vn) мінімальне значення величини \\и\\А за додаткових умов
\\и\\2 = 1; (4.66)
(и, ьг) = (и, v2) = ... = («, vn) = 0. (4.67)
тоді п + 1 — ше власне число Лп+і оператора А дорівнює максимуму
^(vli v2) ♦*♦> Vn) за довільних ЗМІН фуНКЦІй V\: ..., Vn.
Доведення* За означенням дискретного спектра (див, 4,3)
система власних функцій ип повна й ортонормована у просторі H та
ортогональна у просторі На- 3 огляду на це довільну функцію и Є H
молена розвинути у ряд Фур'е за цими функціями, Розвинемо функцію
Vj, j = 1, 2,..., п у ряд Фур'е за власними функціями Uk-
ос
v3 = ^bjkuk. (4,68)
Виберемо деяку функцію и* у вигляді суми
п+1
и* = Yjxkuk (4,69)
з невідомими коеффіцієнтами а*. Для неї умови (4,66), (4,67) матимуть
вигляд
п+1
ІІ«*Ц2 = 5>* = 1; (4-70)
п+1
(u*, Vj) = J^b^a* = 0, j = 1,..., п. (4,71)
л=і
Співвідношення (4,70), (4,71) можна розглядати як систему рівнянь для
визначення невідомих коефіцієнтів afc. Зазначимо, що для функції и*
виконується формула
п+1
Л=1

142
Задачі на власні значення
Замінимо в (4.72) А& найбільшим значенням Лп+і:
п+1
ІНІІ < An+1J>* = Ап+1. (4.73)
к=1
Отже,
ІІ«1І < А„+і. (4.74)
Однак тоді й нижня межа Л не перевершує Ап+і, Цим доведено, що
A(vbt;2, ...,vn) ^ Лп+і. (4.75)
Знак рівності у формулі (4.75) досягається, якщо як функції v3 вибрати
власні функції и^ j = 1, 2,..., п. Тоді умови (4.67) збігаються з умовами
теореми 7, які визначають власне число Ап+і, ■
Наслідок. Як наслідок з доведеної теореми випливає такий спосіб
визначення п + 1 власного числа:
An+i = max min |Н|л, ||u|| = 1, (u,Vj) = 0. (4.76)
v3 ЄН а иЄНл
4.6. Теорема про порівняння власних чисел
Нехай А і В — додатно визначені оператори, що діють у просторі Н.
Уважатимемо, що А ^ £?, якщо:
1° На С Нв\
2° llwlL ^ llwlL, Уи є НА.
Теорема 9. Нехай А і В — додатно визначені оператори з дискретними
спектрами і такі, що А^ В, тоді для довільного k G N
Xk ^ (лк, (4.77)
де А*. — k-не власне число оператора А і \хк — k-не власне число
оператора В.
Доведення. Згідно з мінімаксимальним принципом
Хк = max min ||гг||^, Wvj Є НА, \\и\\ = 1, (u,vj) = 0, (4.78)
VjGHauGHa

4.6, Теорема про порівняння власних чисел
143
j = l,2,...,A;-l;
fik = max min |Н|Л, \/vj Є Нв, \\и\\ = 1, (w, vj) = 0, (4.79)
УзЄнвиЄНв
j = l,2,...,k-l.
Оскільки А ^> В, то нерівність
min \\и\\л ^ min \\и\\в (4.80)
виконується і за додаткових умов
|Н| = 1, (щ vj) = 0, j = 1, 2,..., А; - 1.
Таке ж міркування справджується і стосовно максимальних значень
величин
X(v1} v2,..., Vk-г) ^ fi(v1} v2,..., vfc_i) (4.81)
Це й означає, що
Розглянемо приклад, який ілюструє можливе застосування доведеної
теореми,
Приклад . Коливання струни, як відомо, (див, 4.1.1) описує задача
d2z
-—г-Л2 = 0, я(0) = 0, я(а) = 0. (4.82)
ах2
Власні функції цієї задачі (4.82) мають вигляд
ктгх
zk = sin . (4.83)
Підставивши (4.83 ) в (4.82), отримаємо значення власних чисел
Розглянемо струни різних довжин ai та а. Нехай а і ^ а. Тоді згідно з
(4.84) власні числа \к струни довжини а і та власні числа А& струни
довжини а задовольняють нерівність
ЛІ1' < А*. (4.85)

144
Задачі на власні значення
Таку ж нерівність можна отримати шляхом застосування теореми про
порівняння власних чисел. Розглянемо дві задачі на власні значення
d2z
- —--Xz = 0: 2(0) = 0, я(а) = 0; (4.86)
ах1
-0-Л(1)^ = О, 2(0) = 0, z(ai) = 0. (4.87)
Оператори цих задач позначимо, відповідно, А та А\. Оскільки а\ ^ а,
то поширимо функції, що становлять область визначення оператора А,
на проміжок [0, ai] , прийнявши, що вони дорівнюють нулю на [a, ai],
Тоді виконується включення
НАсНАі. (4.88)
Енергетичні скалярні добутки, що відповідають а та а\ запишемо у
вигляді
\U\\A
а а\
|2
= fzt2dx, \\и\\2Аі = І z'2dx. (4.89)
о о
Оскільки функції з області визначення оператора А поширені на [0, ai]
нульовими значеннями, то виконується рівність
INL4NU. v^etfA. (4.90)
З (4.89) та (4.90) на основі теореми 10 випливає, що
Отже, отримана ця ж сама, що й у (4.85) оцінка для власних чисел, але
без обчислення самих власних чисел.
4.7. Метод Рітца в задачах на власні
значення
Нехай А — додатно визначений оператор з дискретним спектром, Тоді
задача на власні значення
Аи-Хи = 0 (4.91)

4.7. Метод Рітца в задачах на власні значення
145
має нескінченну кількість власних чисел
0 < Лі < Л2 < Л3 < ... < Хп —> ос
і відповідних їм власних функцій
Як відомо (див, 4.2), задача визначення найменшого власного числа та
відповідної йому власної функції у варіаційному формулюванні
еквівалентна задачі мінімізації функціонала
Al = mm^^, иєНА, (4.92)
(щи)
або
Лі = min {Аи) и)) («, и) = 1, и є На- (4.93)
Зазначимо, що скалярний добуток (Аи, и) для додатно визначеного
оператора можна розуміти у сенсі енергетичного скалярного добутку, Цим
зумовлене включення и Є На-
До розв'язування задач (4.92) або (4.93) застосуємо метод Рітца,
який полягає у такому, Виберемо послідовність базисних (координатних)
функцій {<£>п}і які задовольняють умови
1° <рп Є НА]
2° для довільного п функції (рп лінійно незалежні;
3° послідовність базисних функцій {срп } повна за енергією,
Приймемо
п
ип = ^ак(рк) (4.94)
к=і
де a,k — сталі коефіцієнти, Виберемо а&, враховуючи варіаційне
формулювання задачі на власні значення (4.93), тобто
п
(Аип,ип) = ^2
(А<рк,(рт) ->min, (4.95)
/г,га=1
за додаткової умови
п
(ип,ип)= ^2 акат(<рк,(рт) = 1. (4.96)
к,т=1

146
Задачі на власні значення
Для розв'язування задачі (4.95), (4.96) використаємо метод множників
Лагража. Розглянемо функцію
Ф (аи а2, а3,..., ап) = (Аипу ип) - Х((иш ип) - 1). (4.97)
Необхідні умови її мінімуму можна записати у вигляді
дФ
да<п
0, т = 1,2,..., те. (4.98)
Перепишемо умови (4.98) з урахуванням співвідношення (4.97).
Отримаємо однорідну систему лінійних алгебричних рівнянь відносно невідомих
сік
п
^2 ак [(А<Рк, <Рт) ~ *(¥>*, <Рт)] = 0, т = 1, 2,..., те, (4.99)
к=1
які не можуть всі одночасно дорівнювати нулю, оскільки наближене
значення власної функції не може тотожно дорівнювати нулю, Це можливе
тоді і тільки тоді, коли визначник системи рівнянь (4.99) дорівнює нулю,
тобто
det {[(A<pk, <pm) - \(<рк, ірт)}} = 0, к, т = 1, 2,..., те. (4.100)
Отже, задача зводиться до матричної задачі на власні значення.
Якщо система базисних функцій (р% ортонормована у просторі Д", то
рівняння (4.100) дещо спрощується, Воно матиме вигляд
(А(ри(рг)-Х (А(р1}(р2)
det< (А<р2,<рі) (А<р2,(р2)-Х ... }=0. (4.101)
Теорема 10. Рівняння (4*100) (4*101) є алгебричними рівняннями п-го
степеня щодо невідомої X.
Доведення. Справді, коефіцієнтом при (~~~1)п Хп в обидвох цих
рівняннях є визначник Грамма
det {(А(рк, (pm)l к, т = 1, 2,..., те (4.102)
системи лінійно незалежних функцій, ■
Отже, рівняння (4.100), (4.101) мають по те коренів,

4.7. Метод Рітца в задачах на власні значення
147
Теорема 11. Всі корені рівнянь (4-100), (4ЛОЇ) дійсні.
Доведення. Нехай Xj — довільний корінь рівняння (4.100) і
а!%(k = l,2,...,n) — відповідний йому розв'язок, визначений з
точністю до сталого множника. Виберемо цей множник так, щоб виконувалась
умова нормування (4.96)
п
J2 а®а$(<рк,<рт) = 1. (4.103)
Підставимо в систему рівнянь (4.99) Xj та а^\ домножимо кожне
рівняння на а\і і підсумуємо за індексом т. Отримаємо
п п
к,т=1 к,т=1
Множник при Лі у правій частиш попередньої формули згідно з (4.103)
дорівнює одиниці, Тому
Аі= (A««),tig>). (4.104)
Звідси випливає, якщо врахувати симетрію оператора Д що всі корені
рівняння (4.100) є дійсними, ■
Нехай функція ип надає мінімального значення функціоналу (4.104),
Тоді Хі можна розглядати як наближене значення найменшого власного
числа. Виконується теорема
Теорема 12. Нехай А — додатно визначений оператор з дискретним
спектром і нехай базисні функції) які використовують у методі Рітца,
задовольняють умови 1° — 3 °, тоді послідовність наближених значень
а{ найменшого власного числа Лі, отриманих методом Рітца, є
збіжною
X? -> Ах,
причому
і(п.
АГ > Аь

148
Задачі на власні значення
Доведення. Нехай функція uh, надає мінімального значення
функціоналу (4.93). Візьмемо деяке N > п. Знайдемо з умови мімімуму
функціонала (4.93) uN та обчислимо Л^ \ Очевидно, що
\{N) < л<п).
Звідси випливає, що послідовність значень Aj" є монотонно незроста-
ючою, обмеженою знизу точною нижньою границею функціонала (див.
4.3)
АІП) > Аі.
Така послідовність, як відомо, збіжна. Доведемо, що її границею є
найменше власне число Лі. За означенням точної нижньої границі для
довільного є > 0 існує функція и* Є Da така, що («*,«*) = 1 і
Лі < (Ли*,м*) < Аі + є.
Оскільки послідовність базисних функцій (рп повна за енергією, то можна
знайти таке п* і відповідне йому
п*
Un* = Z^bk(pkl Ьк = const,
для якого виконується умова
Нм* - и
п*\\А
< у/і. (4105)
Звідси, врахувавши очевидне співвідношення
та нерівність трикутника, отримаємо
\\^пМа < \\ип. ~ U*\\a + \\и*\ІА < л/ї +
і + є.
Піднесемо ліву і праву частини отриманої нерівності до квадрата:
(АиПтУиПт) < (v^+ \Лі + є J .
З цього, що оператор А обмежений знизу, випливає
1
\Щп* — ^*| ^ рг— \\ип* ~~ и*\\А '
VM

4.7. Метод Рітца в задачах на власні значення
149
З урахуванням нерівності (4.105) запишемо
и _ п /Z
\\ип* ^*| ^ у \ *
Звідси, узявши до уваги очевидний запис
та нерівність трикутника, отримаємо
\\ип*\\ > ||^*|| — 11^* — WnJ| > 1
Перейдемо тепер до оцінки відношення
(АиПт,иПт)
Аі'
З огляду на отримання нерівності матимемо
А(».) < (^..tO < (^ + VATT7)2 = Лі +
де 7? прямує до нуля разом з є. Оскільки Лі є мінімумом виразу
(Лад, и)
то
л1<л^<Уц""Ця:)<л1 + ^
Якщо п > п*, то Л^ < Л-^п і, отже
Хі<Х^<Х^] <X1 + rh. (4.107)
З останньої нерівності випливає, що
lim ЛІП) = Лі,
тобто послідовність Лі наближених значень власних чисел є збіжною
до найменшого власного числа Лі,
Аналогічно можна довести [8], що такий граничний перехід
виконується і для інших власних чисел. ■

150
Задачі на власні значення
4.8. Слабке формулювання задачі на власні
значення і метод Гальоркіна
Нагадаємо спочатку (див, параграф 1.8), що слабким розв'язком
задачі
Au = f (4108)
називають функцію и Є V, де V — вибраний простір, яка задовольняє
співвідношення
a(u,v) = (J», \/v Є V. (4109)
Тут a(u,v) — білінійна форма, визначена диференціальним оператором
а(и1 v) = (Аи, у)\
(/, у) — скалярний добуток у Н = L2(Q).
Розглянемо задачу на власні значення
Аи - Хи = 0. (4110)
Запишемо для неї за аналогією з (4109) слабке формулювання
а(щ у) - Х(щ у) = 0, \/v Є V. (4.Ш)
Задачу знаходження числа А і функції и(х) такої, що и Є V
задовольняє рівняння (4111) і не дорівнює тотожно нулю, називають слабким
формулюванням задачі на власні значення.
Для побудови наближеного розв'язку задачі (4.111) застосуємо
метод Гальоркіна, який полягає у такому. Виберемо послідовність базисних
функцій {<£>п}і які задовольняють умови
1° ¥>„ Є V;
2° для довільного п функції (рп лінійно незалежні;
3° послідовність базисних функцій {срп } повна у просторі V.
Приймемо
п
ип = ^ак(рк) (4112)
к=1
де а*. — невідомі коефіцієнти. Для знаходження ак підставимо (4112) у
варіаційне рівняння (4111), У цьому разі замість функцій v
підставлятимемо базисні функції <pj, j = 1, 2,..., п. Отримаємо
п п
^ ака(<рк, tpj) - А ^2 ak (<Pk, <pj) = 0. (4.113)
k=i k=i

4.9, Числовий аналіз спектральної задачі
151
Для того, щоб система однорідних рівнянь (4.113) мала розв'язок,
відмінний від тотожного нуля, необхідно і достатньо, щоб її визначник
дорівнював нулю, тобто
det {a{<pk, <pj) - А (<рк, <pj)} = 0. (4.114)
Рівняння (4.114) є алгебричним рівнянням для визначення наближених
за Гальоркіним власних чисел.
4.9. Числовий аналіз спектральної задачі
для оператора Штурма—Ліувілля
Розглянемо задачу на власні значення для оператора
Штурма^ Ліувілля
-—р (х) — + q (х) и - \и = 0, 0 < х < 7г; (4.115)
ах ах
и(0) = 0, и'(тг) = 0. (4.116)
На коефіцієнти рівняння р (х) та q (x) накладемо такі обмеження:
вважатимемо їх неперервними функціями, які задовольняють нерівності
р(х) >ро>0, q(x) >0. (4.117)
Ці умови забезпечують (див, 4.4) існування дискретного спектра
оператора задачі (4.115), (4.116).
Отже, у разі виконання умов (4.117) задача (4.115), (4.116) має
нескінченну послідовність дійсних власних чисел
0 < Лі < Л2 < ... < Л| —> ос
і відповідну їй повну послідовність власних функцій щ {х\
Якщо p^q — const, то власні числа та функції можна знайти у явному
вигляді, Зокрема, легко бачити, що функції вигляду
щ (х) = J- sin(/ - \)х, / = 1,2,... (4.118)
V 7Г І

152
Задачі на власні значення
задовольняють граничні умови (4,116), Підставивши їх у рівняння
(4.115), отримаємо таку формулу для обчислення власних чисел:
\і=р[і
+ Q:
Z = l,2,....
(4,119)
Згідно з теоремою про порівняння (див, 4,6) отримані значення власних
чисел можна використати для одержання двосторонніх оцінок на
випадок змінних коефіцієнтів, Матимемо
Ртіп(1 ~ ")2 + <?min < А/ < pmax(/ - ")2 + <?в
(4,120)
де Ртїт 9тіт Pm&m Ят&х — найменші та найбільші на проміжку [0,7г] зна-
чення коефіцієнтів р (х) та q (аг).
З двосторонньої оцінки випливає, що порядок збіжності А/ —^ ос
А, = О (/2).
(4.121)
Для побудови наближеного розв'язку задачі (4.115), (4.116)
використаємо метод Рітца, описаний у параграфі 1.7 з вибором кусково-лінійних
базисних "функцій-шапочок" методу скінченних елементів (див. 1.7).
Згідно з цим методом задача на власні значення (4.115), (4.116)
зведеться до такої матричної задачі на власні значення:
KhQh - XhMhQh = 0.
(4.122)
Якщо коефіцієнти оператора Штурма—Ліувілля є сталими, то матриці
Kh, Mh, за аналогією з 1.7 можна записати у такому вигляді:
Kh = pEh + qMh,
(4.123)
де
* = £
2
-1
-1
2
-1
-1
2
2 -1
-1 2 -1
-1 1
(4.124)

4.9. Числовий аналіз спектральної задачі
153
Mh
h
6
4 1
14 1
1 4 1
1 4 1
1 4 1
1 2
(4.125)
Qh = [ «1 «2 «З • • МЛГ-1 UN ] ■
У цьому разі наближений розв'язок задачі (4.115), (4.116) можна
записати у вигляді
JV
(4.126)
З урахуванням вигляду матриць (4.124), (4.125) наведемо систему
рівнянь (4.122) у розгорнутому вигляді:
(4.127)
Зазначимо, що для j = 1, iV у рівнянні (4.127) потрібно прийняти,
відповідно, тій = 0 та гід
7V+1
It'
7V-1-
Компонентами власних векторів Qh є вузлові значення наближених
значень власних функцій ин- Нехай и^ — наближена власна функція, яка
відповідає власному числу Af.
Шляхом безпосередньої підстановки у (4.127) можна переконатися,
що її вузлові значення гіу обчислюють за формулою
1И
2
— sin
7Г
l--2)jh
1,2,...,
iV.
(4.128)
З формули (4.128) випливає, що
^2~
sin
sin
г- § ] 0- 1)/г);
0" + і)л ■
(4.129)

154
Задачі на власні значення
Урахувавши (4.128) та (4.129), з рівняння (4.127) отримаємо
А? = ^+^, (4.130)
т
де
2 (і - cos (l-\)h) 2 + cos (l-\)h
k = — Л 2~L-L,rn= 1 V—. (4.131)
Отже, (див, формулу (4.128)) значення у вузлових точках наближених
власних функцій и^ збігаються зі значеннями власних функцій щ (див,
формулу (4.118)). З огляду на це згідно з теоремою про апроксимацію
кусково-лінійними базисними функціями матимемо оцінки
llw'"w?L ^ dfc2|M|w(2); (4132)
її iixv2 vv 2
\\Ul ~ Ul\\w(l) — ^2^||^||w(2).
Якщо врахувати співідношення (4.121), то отримаємо ще й такі оцінки
||^-nf||L2 = 0(/2^2); (4.133)
ll«j-u?IL<u = °(l2}i)-
и и vv2
Отже, можемо зробити висновок, що похибки обчислення власних
функцій у відповідних нормах мають цей же порядок, що й розв'язок крайової
задачі, яку описує цей же оператор.
Розглянемо проблему знаходження похибки наближеного значення
власного числа Af. Для її обчислення розвинемо в степеневі ряди функції
к та т, уведеш в формулі (4.130)
к = Н)2-пН)4+°евл4)<
Підставивши ці співвідношення у вираз (4.130), знайдемо
Af-A, + /.2^(l-iy + 0(W).

4.10. Спектр оператора задачі про згин пластини
155
Нагадаємо, що тут Л/ — точне значення власного числа, яке обчислюють
за формулою
Хі = р(1~ї) +q- (4134)
З (4.134) отримаємо оцінку
|Л,-Л?| =0(/4/і2). (4.135)
Зазначимо, що права частина співвідношення (4.135) пропорційна до
квадрата правої частини другої оцінки у формулі (4.133).
4.10- Спектр оператора задачі про згин
пластини
Розглянемо задачу на власні значення для оператора, який описує
циліндричний згин пластини (див, 3.6)
\ааі аа.\)
~Di^ + G (7l + ^)"Лті = °'аі е (0, а)> (4136)
шарнірно опертої у крайових точках а\ = const
™ (0) = 0, 7І (0) = 0, w (а) = 0, 7І (а) = 0. (4.137)
Зазначимо, що для задачі на власні значення (4.136), (4.137) власні
числа можна знайти у явному вигляді, якщо за власні функції вибрати такі
тригонометричні функції:
Wi = sin , 7іг = cos • (4.138)
а а
Власні функції (4.138) задовольняють граничні умови (4.137).
Підставивши їх у рівняння (4.136), отримаємо значення для власних чисел:
AM = GE(1 + «Y (4.Ш)
а \ а

156
Задачі на власні значення
А.
(2) _
D
гіг
+ G11 +
т
(4.140)
Отже, кожному значенню параметра і відповідають два власні числа
х(1) \(2)
лі > лі ■
Значення власних чисел
Л1
8%
А2
8%
Аз
8%
А4
8%
1
0,086086
-
1,249283
-
5,500831
-
14,78683
-
~2
0,087326
1.44
1,330241
6,48
6,422821
16,8
-
-
3
0,086183
0,11
1,255687
0,51
5,575346
1,35
15,21150
2,87
~4
0,086093
0,0075
1,249716
0,035
5,505946
0,093
14,84307
0,38
~5 f
0,086089
0,0031
1,249462
0,015
5,502955
0,039
1482488
0,26
Значення власних чисел Лг- (г = 1, 2, 3, 4) наведені в таблиці
(стовпець з номером 1). Вони обчислені для таких вхідних даних задачі:
G = 3,2051 1(Г2, D = 9,15751 10"5, а = 1,
які відповідають таким значенням фізичних характеристик пластини:
Е = 1, г> = 0,3, /г = 0,1 .
У стовпцях з номерами 2—5 наведено наближені значення цих же
власних чисел, отриманих методом скінченних елементів з використанням
поділу проміжку [0, а], відповідно, на 4, 8, 16, 20, одновимірних
квадратних елементів лагранжевого типу, Під наближеними значеннями
власних чисел наведені їхні відносні похибки у процентах, Назвемо три
особливості наближених значень, які мають закономірний характер. По-
перше, наближені значення власних чисел обмежують точні зверху; по-
друге, зі збільшенням порядкового номера власного числа (числа г)
точність його наближеного значення погіршується; по-третє, зі
згущенням сітки скінченних елементів точність обчислення наближених
значень власних чисел поліпшується,

4.11. Похибки власних чисел і власних функцій
157
4.11. Похибки власних чисел і власних
функцій
Розглянемо проблему апріорного оцінювання похибок наближених
значень власних чисел і власних функцій задачі
Аи - \и = 0, и Є DA C Я,
які отримані шляхом застосування методу скінченних елементів.
Стосовно оператора А вважатимемо, що виконуються умови
теореми 7, які забезпечують існування для нього дискретного спектра,
З оператором А асоціюватимемо білінійну форму
a (w, v) = (Auy v)% u, v Є V,
де V — заданий гільбертів простір V С W2 . Уважатимемо, що білінійна
форма є симетричною
a (w, v) = a (v, u\
додатно визначеною
a (w, и) > 72 \\u\\v
та неперервною
a (u,v) < М \\u\\v \\v\\v.
Тут 7,М- const, 7 > 0, М > 0.
Позначимо через S/, скінченновимірний підпростір простору У,
утворений на деякому вибраному скінченноелементному базисі ^, через
Щи — оператор ортогонального проектування відносно білінійної форми
a(u,v) функції и Є V на підпростір £/>, тобто
а{и- ПА«,vh) = 0, Vvh Є 5Л. (4141)
Використаємо тут також відомий результат (див, 2.2) про апріорну
похибку апроксимації поліноміальними базисними функціями ір^ к-то
степеня
II-" - ^hu\\w(s) < Cshk+1~s \\u\\wtk+i) , s = 0,1,..., та, (4142)
де /г — діаметр поділу області на скінченні елементи.
Доведемо три леми, необхідні для оцінки похибки наближених
значень власних чисел.

158
Задачі на власні значення
Лема 13. Нехай Е\ — простір, утворений на системі власних функцій
Щ, U2, ...,Wj, І
erf = max \2{u,u — Uhu) — (и — Uhu, u - Uhu) |. (4143)
иЄЕі
Розглянемо функції П^щ, Пдіг2>• *•, Щі^. Позначимо через Si простір,
побудований на цих функціях. Нехай of < 1, тоді простір Si І-вимірний.
Доведення. Достатньо довести, що рівність Uhu* = 0 (Vu* Є Е{)
виконується тоді і тільки тоді, якщо и* = 0. Доведемо від супротивного,
Припустимо, що Щіг* = 0 виконується для it*, відмінного від тотожно-
го нуля, Нормалізуємо функцію it*, тобто вважатимемо, що (и*,и*) = 1.
Розглянемо
<rf > \2(u*,u*-Ilhu*) - (u*-Uhu\u*-Uhu*)\. (4144)
Після нескладних перетворень отримаємо
|2 («*, и* - Tlhu*) - (и* - Uhu\ и* - Uhu*)\ = («*, и*).
Урахувавши (4,144) та умову нормування функції it*, матимемо
нерівність
°ї > і,
яка суперечить умові леми erf < 1. ■
Лема 14. Нехай еі — множина нормованих функцій з Е\ і нехай erf,
(4-144)) визначена на цій множині, є такою, що erf < 1. Тоді наближені
значення власних чисел Af обмежені зверху, тобто
Доведення* Використавши мінімаксимальний принцип, запишемо
Af<max^\n^. (4,146)
Оцінимо зверху чисельник у правій частині попередньої формули.
Запишемо
а (її, и) = а (Щіі, Щи) + 2а (и — Щи, Щіг) + а (и — Щад, it — Щіі). (4,147)

4.11. Похибки власних чисел і власних функцій
159
Оскільки UhU — проекція відносно білінійної форми, то згідно з (4.141)
а (и — Uhu, Uhu) = 0.
Останній доданок у формулі (4.147) невід'ємний, Тому, відкидаючи його,
отримаємо нерівність
а (Щи, Uhu) < а (щ и). (4.148)
Знаменник у правій частині нерівності (4.147) обмежений знизу, Справді
(Щ«, Uhu) = (щ и) - 2(«, и - Uhu) + (u- Uhu, u - Uhu) >
> 1 - af, (4.149)
Урахувавши нерівності (4.148), (4.149), отримаємо
*? < -^Ч- ■
' " 1 - о\
Лема 15. Нехай
і
и = У^^СіЩ,
г=1
де щ — власні функції) Сі — сталі, і нехай и Є Є/. Тоді
і
(«, и — Тій) = \J c%Xjxa (щ — Пщ, и — Тій). (4.150)
г=1
Доведення. Оскільки щ — власна функція, то згідно з (4.22) маємо
(щ, и - Uhu) = \Jxa (uh u - Uhu). (4.151)
Крім того, якщо в означенні проектора (4.141) прийняти Vh = Щг^, то
a(UhUi,u - Uhu) = 0.
Віднявши цей вираз, домножений на А^1, від правої частини формули
(4.151), запишемо
(щ, и - Uhu) = Х^а (щ - Инщ, и - Щм).
Домноживши останню рівність на q і підсумувавши за індексом г,
отримаємо (4.150). ■
Оцінку похибок наближених значень власних чисел дає така теорема.

160
Задачі на власні значення
Теорема 16. Нехай Sh — скінченно-вимірний підпростір методу
скінченних елементів степеня к. Тодг існує така стала 5, що для
достатньо малих значень діаметра поділу області на скінченні елементи
виконується двостороння нерівність
Л, < Л? < Л, 4- 2С""Л,Л2(*+1-т).
(4152)
Доведення. . Для отримання правої частини нерівності (4.152)
використаємо нерівність (4.145). З цією метою оцінимо величину erf. Оскільки
\а (щ V)\ < М \\U\\ (m) \\V\\ (m),
то для першого доданка в erf (4.143) матимемо
2\(u,u-Ilhu)\ = 2
У^ CiX{ Іа (щ - Инщ, и - Uhu) <
г=1
< 2М
Y2ci\ * (иг ~ Пдггг)
г=1
\и - Щгі||и/(т),
wi
W,
(т)
Позначимо
v = ^2сіХі Іщ.
г=1
Використавши оцінки похибки апроксимації (4.142), запишемо
2|(и,«-ПА«)| < C'h^+^WvWwik+i) \\u\\wik+ih
де С — стала. Вважаючи норми
MlvF(fe+1)' INIpHfc+1)
обмеженими, отримаємо
2 \(и,и - Uhu)\ < C"h2(k+1~s\ C" = const.
Для другого доданка в erf згідно з (4.142) матимемо
(и - Uhu,u- Uhu) < Cgfc2(fc+1) ||u||^(fc+i).

4.11. Похибки власних чисел і власних функцій
161
Ця оцінка є вищого порядку, ніж оцінка для першого доданка, За
нерівністю трикутника на підставі отриманих нерівностей для першого та
другого доданків можемо записати
а? < C'"h2ik+1-m).
Уважатимемо h тут достатньо малим, щоб виконувалась умова 2of < 1.
Тоді, врахувавши очевидну нерівність
яка виконується за цієї умови, отримаємо оцінку зверху для наближеного
значення власного числа
Л? < Л, 4- 2С""Л,Л2(*+1-т). (4153)
Згадаємо, що наближення за Рітцом є наближеннями зверху для власних
чисел. Звідси остаточно отримаємо двосторонню нерівність (4.152), ■
Отже, з (4.152) випливає, що послідовності наближених значень
власних чисел збігаються, і похибка наближеного значення власного числа
становить 0(Л,Л2<*+1-го>).
Перейдемо до оцінювання похибок наближених власних функцій,
Використаємо для цього таку лему,
Лема 17. Нехай власні функції щ та їхні наближені значення uf,
отримані методом скінченних елементів, є нормованими у нормі
простору Н, тобто виконуються співвідношення
(щ,щ) = 1, (4,4) = 1. (4.154)
Тоді виконуєтья співвідношення
а(щ -и^щ-и^) = Хі \\щ-иї\\2н + \ї -А,, (4.155)
де А/ — власне число, що відповідає власній функціїщ\ Af — його
наближене значення.
Доведення. Використовуючи властивість лінійності білінійної
форми a(u,v) за кожним аргументом, запишемо
а (щ - 1$, щ -uf) = а (щ, щ) - 2а (uh uf) + а (гг*, и$) .

162
Задачі на власні значення
Урахувавши тут (4.111) та умови нормування (4.154), отримаємо
а (щ - «*, щ - 4) = Aj [2 - 2 (uh u?)] + А? - А,.
Перетворимо величину у квадратних дужках до вигляду
2-2(и,,и?) = (щ}щ)-2(щ}иї) + (иї,иї) = \\щ-иї\\2н.
Урахувавши його, отримаємо потрібне співвідношення (4.155). ■
Доведена лема дає змогу оцінити енергетичну похибку наближеної
власної функції, якщо відомі похибка наближеної власної функції в
нормі вихідного простору 11 щ — и^ 11 та похибка наближеного значення
власного числа Af — Л/, Остання похибка відома за теоремою 16. Для
отримання похибки наближеної власної функції у нормі вихідного простору
доведемо лему,
Лема 18. Для довільних значень j та І виконується тотожність
(А} - A,) (Uhuh и)) = А, (щ - Uhuh u)). (4.156)
Доведення* Оскільки член —A/ (II^,mJ) є в обох частинах
тотожності (4.156), то його можна опустити. Отже, достатньо довести, що
Aj(nft«/)uJ)=Ai(«/,«J). (4.157)
З огляду на те, що щ та и1? — власні функції, маємо
Auhj = Xі-'«£, Ащ = Хіщ.
Тому можемо записати
\) (nfc«,,UJ) = (Щ«ь Аи)) = a [Uhuhu])
та
А/ (ии и)) = (Auh u)) =a(uh wj).
Отже, співвідношення (4.157) можна переписати у вигляді
a(Rhuuu)) =а(иии)).
Урахувавши лінійність бі лінійної форми за кожним аргументом,
запишемо його так:
а (щ - Uhuhu)) = 0.

4.11. Похибки власних чисел і власних функцій
163
Останнє збігається із визначенням проектора (4.141), Звідси випливає
(4.156). ■
Перепишемо (4.156) за аналогією з викладом, наведеним у доведенні
попередньої леми, у такому вигляді:
(АПнщ - Л,ПАи,, wj) =0.
Ліва частина цього виразу є похибкою рівняння на власні значення,
домноженою на и^. Зазначимо, що множина wf, 7/2, ...,?/£ утворює в
Sh ортогональний базис. Тому виконується
п
ПАи, = £(ПА«ь «£)«}. (4.158)
Із (4.156) видно, що скалярний добуток (Щгі/,г^) є малим, якщо Af не
близьке до А/,
Нехай А/ — власне число, відмінне від інших власних чисел (А/ —
некратне власне число). Тоді згідно з оцінками (4.152) існує така стала
р, що для малих h виконується нерівність
1 <рдляУ?є{1,2,...,п}, з = 1. (4.159)
|AJ- Аг
Позначимо через /3 величину
Матимемо
||ПАи,-0и?|£ = Х;(Щи,,и*)2.
Згідно з (4.156) перепишемо праву частину попереднього співвідношення
у вигляді
2
М2
-її-
зФі зФі
Використаємо далі оцінку (4.159)
£ ( л^Ьг) (щ -п*и''«})2 ^ р2И("' -п*«ь«?)!

164
Задачі на власні значення
Звідси отримаємо
Р2 ^2 іи* - П*М'> U1-) < р2 \\Щ - UhUi\\2H.
З наведеного ланцюжка рівностей та нерівностей, урахувавши нерівність
трикутника, одержимо таку оцінку:
\щ - /Зг/?||я < ||^ - Инщ\\н + \\инщ - ри^\\н <
<(1 + р)|К-ПА«,||я. (4160)
Основним результатом отриманого співвідношення (4.160) є те, що
похибку наближеного значення власної функції молена виразити через
похибку апроксимації на вибраній системі базисних функцій, Похибку
апроксимації обчислюють за нерівністю (4,142), Урахувавши її,
запишемо
\\щ - /ЧНя < ^о (! + Р) h2{k+1) IHI„f+»• (4-161)
Використаємо отриману формулу (4,161) для апріорного оцінювання
похибки наближених значень власних функцій,
Теорема 19. Нехай власні функції щ та їхні наближені значення и^,
отримані методом скінченних елементів, є нормованими у нормі
простору Н. Тоді виконуюються оцінки
\\щ - и^\\н < с0/і2(*+1) \\u\\ww\ (4,162)
Ih'-^L < сі/г2{/г+1"ш). (4,163)
Доведення. Нерівність (4,162) випливає з (4,161), Доведемо тільки,
що виконується співвідношення
\\и1-иЧ\\н<2\\и1-^\\н. (4.164)
Запишемо очевидну рівність
НІя=||(иі-К)+К||я-
Застосуємо до її правої частини нерівність трикутника
іі«ііія< lh-0«?L + l|0«i1lH-

4.11. Похибки власних чисел і власних функцій
165
Звідси отримаємо
\\щ\\н-\\щ-^\\н< ІІКІІя- (4-165)
Праву частину цієї нерівності перетворимо подібним способом
||/?и?|Ія= \\щ - (щ -/Зи^
І Я'
До правої частини отриманого співвідношення знову застосуємо
нерівність трикутника
||К||д<КНя+Ь-К||я- (4-166)
Згадаємо, що згідно з умовою теореми ||^||я = 1 та ||^/||я = 1. Оскільки
в цьому разі власні функції u-f та щ визначені з точністю до множника
±1, то виберемо цей множник так, щоб коефіцієнт /З задовольняв умову
/З > 0. Тоді з нерівностей (4.165), (4.166) отримаємо дві нові нерівності
-(/3-1)< \\щ-^\\н)
(/3-1)< Wm-^W^ (4.167)
Вони еквівалентні такій нерівності:
1/3-1 < \\щ-Ри^\\н, (4.168)
Для норми різниці
\\щ-и^\\н
виконаємо перетворення, аналогічні до попередніх, тобто
\\т - иПн = ІКи< - Ю + (К - иШн ^ ІЬ - №h + ІК/3 - іКіія-
Оцінимо останній доданок правої частини
||(/з-іК||я<|/з-і|||^||я.
Урахувавши, що \\uf || = 1, а також (4.168), отримаємо (4.164), 3 (4.164)
та (4.161) випливає нерівність (4.162),
Доведення теореми (нерівність (4.163)) випливає тепер з попередньої
леми. Оцінимо зверху різницю Af — Л/ у правій частині формули (4.155)
за нерівністю (4.153)
А? - А, < 2CtttXlh^k+1-m\

166
Задачі на власні значення
Для оцінювання \\щ — и1} || використаємо формулу (4.162):
||мі-г/?||д < с0/і2(/г+1) ||w||^2(fc+i).
Отже, для похибки в енергетичній нормі матимемо таку оцінку:
\\Щ ~ «?|£ < clh2^ ||и||^+1) + 2C"%h2lk+1-m\ (4.169)
Де
\\щ - и^\\А = а(щ- и^щ - и1}).
З нерівності (4.169) отримаємо
Ilwi-W?IL <сі^+1"ш. (4.170)
де стала с\ не залежить від діаметра поділу області на скінченні
елементи. ■
Зазначимо, що згідно з лемою Сеа подібну оцінку молена отримати і
в нормі простору V. Вона матиме вигляд
\\щ-иЧ\\у<^Сікк+1-т (4.171)
З отриманих апріорних оцінок випливає, що порядок збіжності
наближених власних функцій до точних власних функцій у нормах енергетичного
простору та простору V становить 0(hkJrl~m) Цей порядок збігається з
порядком збіжності наближеного розв'язку крайової задачі (яку описує
оператор А), отриманого МСЕ шляхом використання цих же базисних
функцій,
4.12. Вправи для самостійного виконання
Вправа 1. Знайти власні числа задачі
d2w
dx2
Де
Xw = 0, w(0) = 0 w(tt) = 0,

4.12. Вправи для самостійного виконання
167
яка описує вільні, гармонічні коливання натягнутої струни, Як власні
функції вибрати такі:
wn = smnx.
Проаналізувати вплив змін густини та сили натягу струни на зміни
колової частоти w.
Вправа 2. Знайти власні числа задачі
—■ - Aw = 0, х Є (0,а);
/Лч r, d2w(0) Л , Ч dw2(a)
Де
Л = pFu2/EJ,
яка описує згинні вільні, гармонічні коливання стрижня, Як власні
функції вибрати такі:
П7ГХ
wn = sin .
а
Проаналізувати вплив змін густини та площі поперечного перерізу
стрижня на зміни колової частоти ио згинних коливань.
Вправа 3. Використовуючи теорему про порівняння власних чисел,
з'ясувати яку нерівність можна поставити між: коловими частотами
згинних коливань а;і, ио<2 стрижнів (див, вправу 2), які мають площі
поперечних перерізів F\ > F2.
Вправа 4. Використовуючи теорему про порівняння власних чисел,
з'ясувати яку нерівність можна поставити між коловими частотами
коливань а;і, о;2 мембран (див, 4.1.3), виготовлених з однакового матеріалу,
натягнених однаковою силою натягу і розміщених в областях Г2і та Г^
так, що Г2і С ^2-
Вправа 5. Використовуючи теорему про порівняння власних чисел,
з'ясувати яку нерівність можна поставити між коловими частотами
коливань о>і, CU2 пластин (див, 4.1.4), виготовлених з однакового матеріалу
і розміщених в областях £71 та Г22 так, що £71 с ^2-
Вправа 6. Отримати вираз для параметра т\ у формулі (4.106),
Вправа 7. Використовуючи метод повної математичної індукції,
довести правильність формули (4.102),
Вправа 8. Вивести формули (4.139), (4.140),

168
Задачі на власні значення
Вправа 9. Використовуючи результати 4.11, переконатися, що для
задачі Штурма^Ліувілля можна отримати однакові оцінки похибок для
власних чисел та власних функцій, що і в 4.9,

Розділ 5
Початково-крайові задачі
У розділі наведено схему побудови числових розв'язків початково-
крайових задач для рівняння параболічного типу. Як приклад такої
задачі розглянуто початково-крайову задачу теплопровідності. Описано
спосіб побудови варіаційного формулювання початково-крайової задачі та
напівдискретизації її розв'язку за методом Гальоркіна. Розглянуто
питання стійкості та збіжності напівдискретизованого розв'язку, а також
існування слабкого розв'язку варіаційної задачі, Побудовано рекурентні
схеми дискретизації задачі за часовою змінною, досліджено їхню
стійкість та збіжність.
5.1. Параболічна задача
Розглянемо початково-крайову задачу для рівняння параболічного
типу, яка полягає у знаходженні функції и (#, і) такої, що задовольняє
рівняння
Ои
p0— + Au = f(x,t) в Пх(0,Г] (5.1)
та початкові умови
u{x,t) = щ в О, t = 0. (5.2)
Тут и (х, і) — шукана функція; А — додатно визначений оператор, який
діє у гільбертовому просторі Н (див., наприклад, 3.12); Q — обмежена
область евклідового простору R/\ Уважатимемо, що границя Г області

170
Початково-крайові задачі
Q є ліпшицевою. Через х = хі, Х2і -., %п позначимо точку області Q, а
через t — часову змінну.
Характерним прикладом рівняння параболічного типу (5.1) є
рівняння теплопровідності, Для нього оператор А визначений
співвідношеннями
х~^ д л ди , .
л- = - £ ^-щ- ^
«J = l J
u(x,t) = Q на Гх(0,Г]. (5.4)
Коефіцієнт ро рівняння теплопровідності (5.1) в операторі Аи вигляду
(5.3) такий:
Ро = pcv,
де р(х) — густина середовища; cv(x) — теплоємність середовища за
сталого об'єму. Відомо, що коефіцієнти теплопровідності середовища \ij(x)
мають властивість симетрії
\ij(x) = \ji(x) (5.5)
та додатної визначеності
п п
J2 Х^Ші > ^о Y1 £ Для v (6,6, -, 60 Є R", (5.6)
i)j=l г=1
де А0 = const, A0 > 0.
Уважатимемо також, що функції р{х)) cv{x)) \%j{x) достатньо гладкі:
tt0GL2(n);/(a;,*)GL2(0,T;L2(fi)).
Зазначимо, що гранична умова вигляду (5.4), не є єдино можливою.
Як і раніше (див, розділ 3), можна розглянути також граничні умови
Неймана
Е. аи
*W = °
г,і=1 J
та Ньютона
Ех 9и
дх3
а також неоднорідні граничні умови.

5.2. Варіаційне формулювання параболічної задачі
171
5.2. Варіаційне формулювання параболічної
задачі
Уведемо деякий простір V. Домножимо рівняння (5.1) та початкову
умову (5.2) на довільну функцію v (x) Є V і зінтегруемо в області Q:
І p0-^vdn+ J Auvdn= J fudn: Vv є V; (5.7)
Q
/ ро (« (я, 0) - п0) vdfi = 0. (5.8)
Уведемо позначення
m(u,v)= / pouvdQ] (5.9)
п
a{u,v) = / Лш;<Ю; (5.10)
о
Z(w) = /"/iwto; (5.11)
п
, ди
ді
Наведемо варіаційне формулювання параболічної задачі,
Знайти функцію u(x,t) Є L2(0,T; V) таку, що задовольняє рівняння
т(и\ v) + а(щ v) = l(v), Vv Є V\ (5.12)
т(и(я,0) -u0,v) = 0. (5.13)
Розв'язок варіаційної задачі (5.12) та (5.13) називатимемо слабким
розв'язком початково-крайової задачі (5.1), (5.2),
Зазначимо, що умову (5.13) можна записати також іншим шляхом,
зокрема
(гг(ж,0) - u0,v) = 0,

172
Початково-крайові задачі
де
(«, v) = І uvdQ.
ft
З подальшого буде зрозуміло, чому співвідношення (5.13) вибране саме
у такому вигляді,
Для задачі нестаціонарної теплопровідності білінійна форма a{u^v)
матиме вигляд
'' дх*
ft *Л=1
a(u,v) = - J У] —\ij-vda (5.14)
З використанням формули Гріна (розділ 1) та врахуванням граничних
умов (5.4) перетворимо її до симетричного вигляду
ft ^'=1
Простір V ідентифікуємо співвідношенням
V = {v(x) :v(x) Є W^\ v(x) = 0, xgt}, (5.16)
Сформулюємо властивості білінійних форм т (u, v) та a («, v) у двох
лемах.
Лема 1. Нехай u,v Є Н (Н = L2 (fi)). Біліпійпа форма т («, и) —
симетрична та Н—еліптична.
Доведення* Властивість симетрії є очевидною, Із запису (5.9)
випливає, що виконується нерівність
т (иу и) > сі ||и||0,
де
ІМІо = / u2dQ,
ft
с\ = min{pcv}\ сі > 0.
Це й доводить Н—еліптичність білінійної форми т (u, v). ш
Наслідок 1. Як наслідок з доведеної леми випливає подвійна
нерівність
сі ||и||0 < т(иу и)* < С\ \\u\\Q.

5.2. Варіаційне формулювання параболічної задачі
173
Лема 2. Нехай u,v Є V. Вілінійна форма a(u,v) — симетрична та
V—еліптична.
Доведення. Доведення леми випливає з того, що оператор А є
додатно визначений. Зокрема, оператор задачі теплопровідності
А — \^ ^ \ ^U
^ дхі %3 дхл
з вибраною граничною умовою Діріхле
и = 0 на Г
теж є додатно визначеним. Для задачі теплопровідності наведемо
доведення цієї теореми у повному вигляді, Симетрія форми a (w, v) випливає
з властивості симетрії (5.5) коефіцієнтів теплопровідності А^-, Якщо ж
урахувати властивість додатної визначеності (5.6), то отримаємо
«(„,») >Л./Д£1«П.
а
ди V
І
Далі, використовуючи нерівність Фрідріхса (розділ 3)
/St
о г—\.
С1 > > :' Ю dn ~ MU1]
п
запишемо
а(щи) > с2 \\u\\2w(i) ,
де С2 = А0\сі, Очевидно, що С2 > 0. Це й доводить У—еліптичність білі-
нійної форми a(u,v) ш
Наслідок 2. Як наслідок з доведеної леми випливає подвійна
нерівність
с2 \\u\\w(d < а(и,и)а < С2 \\u\\w(di

174
Початково-крайові задачі
5.3. Напів дискретні апроксимації Гал ьоркіна
Виберемо у просторі V лінійно незалежну, повну послідовність
функцій {^}. Нехай Vh — скінченновимірний підпростір простору У, який
утворюється на базисі <р^ j = 1,..., N.
Для отримання наближеного розв'язку задачі
m(u\v) + a(u,v) = l(v)] \fv £V\ (5.17)
m(w(x,0) -u0,v) = 0 (5.18)
використаємо напівдискретне подання [2,6,14,16]
TV
uh (x, t) = J2 Ui (t) $ (яг); (5.19)
Від задачі (5.17), (5.18) перейдемо до її наближеної форми
m(u'h, vh) 4- a(uh, vh) = l(vh); \/vh Є Vh; (5.20)
m(uh(x,0) -u0,vh) = 0. (5.21)
Підставимо формулу (5.19) замість розв'язку ии у рівняння (5.20) та
(5.21) і згідно з методом Гальоркіна виберемо за функції v базисні
функції ер!?. Отримаємо задачу Коші
N
J2 {тцЩ it) + снМ (t)} = li (*), t e (0, Г], і = 1,..., N; (5.22)
N
J2mijUj (0) = Pi, (5.23)
Де
ті, = m (tf, y>J); аі} = a (<p%, $);
h(t) = l(<fi)\ Рі = т(щ,(р^).
У матричних позначеннях
М = {rriij}; A = {oij}\

5.4. Енергетичне рівняння
175
U(t) = {Ui(t)};L(t) = {h(t)};P = {pi}
(М, А — квадратні матриці, £/, L, Р — матриці-стовпці) задачу (5.22),
(5.23) можна записати у такому вигляді:
MU1 (t) + AU (і) = L (t), * Є (0, Т]; (5.24)
Mt/(0) = P. (5.25)
Зазначимо, що як наслідок попереднього матриці М та, А є
матрицями з відмінними від нуля визначниками (як матриці Грама лінійно
незалежної системи функцій відносно скалярних добутків m (•, •) та a (•, •));
вони є симетричними та додатно визначеними.
Твердження. Наведених властивостей достатньо для того, щоб
розв'язок задачі Коші (5.24), (5.25) існував та був єдиним [2,14,16].
5.4. Енергетичне рівняння
Вивчимо властивості напівдискретних апроксимацій Гальоркіна
Uh (ж, t) Є L2 (0, Т; Vh). Для цього підставимо у варіаційну задачу
m(ufh, vh) + a(uh} vh) = l(vh)\ \fvh GVh\ tG (0, T];
m(uh(x,0) - u0,vh) = 0
замість довільної функції v наближений розв'язок ин (ж, £). Отримаємо
^rn(uh,uh) + a{uhluh) = l(uh)] t Є (0,Т]; (5.26)
m(uh} uh) = m(u0y uh)\ t = 0. (5.27)
З урахуванням позначення
uh (t) = uh (я, t)
та
\\uh\\2M = rn{uh,Uh)\
\\uh\\2A = a{uh)uh)

176
Початково-крайові задачі
перепишемо ці формули у вигляді
W |«fc||L + Klli = U«ft); <Є(0,Т]; (5-28)
2dt
IK (0)||5, = т(«0,«л(0)). (5.29)
Зінтегруємо рівняння (5.28) на проміжку [Q,t], 0 < t < Т, матимемо
* t
l\\uUt)\\2M + J \\uh(r)\\2Adr = ^\\uh(0)\\2M + J l(uh(r))dr. (5.30)
0 0
Отримане рівняння для задачі теплопровідності називають
енергетичним рівнянням температурного поля. Кожний його доданок має таку
фізичну інтерпретацію:
2 H(*)llL
— енергія температурного поля в момент часу і;
і
/'
W(j)fAdr
\А{
0
— дисипація енергії температурного поля, зумовлена дифузійним
розсіянням;
t
l{uh{r))dr
о
енергія внутрішніх джерел теплоти;
/'
К(о)іі:
енергія початкового розподілу температурного поля.
2 ІК(°)ІІм
5.5. Стійкість напівдискретних апроксима-
* і*
цій
Для дослідження стійкості напівдискретних апроксимацій Гальоркі-
на отримаємо оцінки зверху для двох норм напівдискретного розв'язку
Uh- Сформулюємо також відповідні теореми про єдиність,

5.5. Стійкість напівдискретних апроксимацій
177
5.5.1. Перша оцінка норми напівдискретного
розв'язку
Оцінимо праву частину у співвідношенні (5.30). Для цього
використаємо елементарну нерівність
аЬ < єа2 + — Ь2, Va, by є Є R, є > 0, (5.31)
4є
нерівність Шварца
\(u,v)M\ < |Н|М|М|М,
а також нерівність
Н\а ><*\И\мі «>0,
яка випливає з наслідків 1,2; а = С2\Сі.
Запишемо за аналогією з попереднім ланцюжок очевидних
співвідношень
\1 М| = |(/, «Л)оІ < ІІ/ІІо ІКНо < «_1 ІІ/ІІм IKIL •
Згідно з нерівністю (5.31) для
Отрим,
Звідси
аємо
є = 1/2, а --
\іМ\<
одержимо нерівність
1
2
Wh\
IK
\А>
іі2
\\А
ь
+
= а
1
2^
-1 ІІ/ІІм-
II/IIL-
t t t t
fl{uh{r))dT<f\l{uh{T))\dT<\f\\uh\\\dT^^f\\f\\2MdT.
0 0 0 0
Підставивши це у праву частину енергетичного рівняння (5.30) і
виконавши нескладні перетворення, отримаємо
t
\uh(t)\\2M + J\\uh(r)\\2AdT<\\uh(0f
ч2||2
\м
о
t
+а~2 fl(uh(r))dr, t€ [0,T].

178
Початково-крайові задачі
Врахуємо у попередній нерівності наслідки 1, 2. Отримаємо
і
іі«л(*)іі? + /іі«л(т)|іу^<^||«л(0)2
ч2||2
\м
о
t
а
4
Jl(uh(r))dr, ІЄ[0,П (5.32)
о
де
З доведеної нерівності (5.32) випливає обмеженість напівдискретного
за Гальоркіним розв'язку задачі у нормі простору
Ьж(0,Т;Н)ПЬ2(0,Т;У),
яка визначена співвідношенням
vrai max
0<t<T
К(^)ІІя + / \\uh (т)\\у dr
1/2
Отже, доведено таку теорему,
Теорема 3. Нехай задане значення параметра дискретизації h
(вибраний базис (р1!-). Тодг напівдискретизована варіаційна задача (5.17), (5.18),
яка приводить до задачі Коші (5.22), (5.23), має (якщо він існує) єдиний
розв 'язок у просторі L^ (0, Т; Н) П L2 (0, Т; V).
5.5.2, Друга оцінка норми напівдискретного
розв'язку
Розглянемо ще одну оцінку норми напівдискретного розв'язку, 3 цією
метою перепишемо рівняння (5,28) у вигляді
Ik Ш\м jt Ik (Оііаг + Ik (*)lli = і («й (*))•

5.5. Стійкість напівдискретних апроксимацій
179
Використаємо тут нерівність
ІН|^ > а \\и\\м Vw Є V, а — const > 0. (5.33)
Отримаємо
\\uh(t)\\
(t)\\M + a2\\uh(t)\\2M<l(uh(t)).
Оцінимо праву частину цієї нерівності за нерівністю Шварца
ІКМ*))І<ІІ/ІІлІК(*)ІІя.
Знайдемо
IK Шм Jt IK ШМ + ft2 IK Ш\2М < ІІ/ІІЯ IK Шн-
Використаємо ліву частину нерівності із наслідка 1, тобто
сі||«||я< \\u(t)\\M
Поділимо обидві частини цієї нерівності на с\ \\uh (£)ІІя:
jt\\uh{t)\\H + l2\\uh{t)\\H< ||/||я, (5.34)
де 7 = а\сі
Зазначимо, що
dt
{e^(*)}=e^||^(t)+7p(*)}.
Тоді вираз зліва у формулі (5.34) можемо подати у вигляді
е^Н^{е"Н\\ип(і)\\н}. (5.35)
З формули (5.34), врахувавши (5.35), отримаємо
{е72ЧК(*)ІІя}<Н/(*)ІІя,
є 7
dt
або

180
Початково-крайові задачі
Зінтегруємо цю нерівність на проміжку [0, £]:
t
є7'* \\uh {t)\\H - \\uh (0)||я < je* ||/ (т)\\н dr.
о
Остаточно перепишемо попередню нерівність у вигляді
і
ІК (*)ІІя < <Г7>' \\Щ (0)|1я + fe-^^ ||/ (т)\\и dr. (5.36)
о
Отримана оцінка теж визначає стійкість напівдискретного розв'язку, але
в нормі простору Lqq (0, Т]Н). З цієї нерівності випливає висновок про
те, що в разі відсутності внутрішніх джерел тепла (/ = 0) температурне
поле прямує до нульового значення за експоненціальним законом є 7
при t —> оо.
5.6. Існування розв'язку варіаційної задачі
Напівдискретизацію за Гальоркіним можна використовувати також
для теоретичного дослідження початково-крайових задач, Зокрема,
застосувавши напівдискретне подання, доведемо у цьому параграфі
теорему про існування та єдиність розв'язку варіаційної задачі (5.12), (5.13),
що еквівалентна початково-крайовій задачі теплопровідності.
Теорема 4. Нехай задані функції щ Є Н та / Є £2(0,Т;Я), Тодг
варіаційна задача теплопровідності (5.12) > (5.13) має єдиний розв'язок
і/ЄЬоо(0,Т;Я)ПЬ2(0,Т;^).
Доведення. Для доведення теореми використаємо властивість
повноти базисних функцій <р^ (див 5.3), згідно з якою послідовність напів-
дискретних розв'язків є збіжною за нормою простору V, тобто
uh -^ и,
де и — границя послідовності, яка належить простору V.
Використаємо тут властивість додатної визначенності оператора А та наслідки 1,2,
матимемо
uh —> u,uh —> и,
М А

5.6. Існування розв'язку варіаційної задачі
181
де ця ж гранична функція и належить одночасно просторам На та Н
(див, 1.6). Треба тільки довести, що ця гранична функція задовольняє
рівняння варіаційної задачі
m(uhi v) + aiuh, v) = l(v), Vv Є Vh\ (5.37)
m(uh(x, 0) - «o, v) = 0. (5.38)
Уважатимемо для цього, що функція v залежить від часової змінної і, є
неперервною до похідних першого порядку за цією змінною і задовольняє
умову
v(x,T) = 0.
Отже,
vGWh = {vG С& (0,Т; Vh);v(x,T) = 0}.
Зінтегруємо рівняння (5.37) за часом на проміжку [0, Т],
використовуючи у першому доданку спосіб інтегрування частинами. Отримаємо
т
/ {-m(uh,v') + a(uhlv) - l(v)}dt = m(u0lv),
о
Перейдемо в одержаному рівнянні до границі при /г —> 0 і застосуємо до
першого доданка знову спосіб інтегрування частинами. Матимемо
т
/ {m(ur, v) + a(u, v) — l(v)} dt = m(u(x, 0) — щ^ v). (5.39)
о
Далі зазначимо, що з огляду на повноту системи базисних функцій <р^
множина Wh утворює щільну множину у просторі L2 (0, Т; V). З
урахуванням цієї обставини, а також умови (5.38), з рівняння (5.39) одержимо
т(и\ v) + a(u, v) = l(v).
Це означає, що границя и є розв'язком варіаційної задачі (5.37), (5.38), і
виконується енергетичне рівняння
t t
lh(t)\\2M + fh(r)\\2Adr=l\\u(0)\\2M + Jl(n(r))dr.
о о

182
Початково-крайові задачі
Отже, виконується нерівність
t
ll«(*)llL + y'll«(r)||idr<||fi(0)|^ +
+7""2 [ І 0 (т)) dr, * Є [0, Т]. (5.40)
о
Доведемо далі, що задача (5.12), (5.13) має єдиний розв'язок,
Припустимо протилежне: нехай щ та щ — два різні розв'язки цієї задачі,
Внаслідок лінійності функція и = щ — и<і також є розв'язком задачі
(5.12), (5.13) для випадку / = 0, щ = 0. Оцінка (5.40) тоді дає змогу
зробити висновок и = 0, а це суперечить припущенню, що розв'язки є
різними, ■
5.7. Збіжність напівдискретних апроксима»
* і*
цій
Оцінимо поведінку похибки напівдискретних апроксимацій Гальоркі-
на
eh = uh (t) - и (t) (5.41)
при прямуванні величини h —> 0 або, що рівнозначно, величини N —» сю.
Зазначимо, що внаслідок лінійності задач для визначення и/, (t) та
и (t) похибка є/, є розв'язком варіаційної задачі
m(e'h, v) + a(eh, v) = 0; \/v Є Vh, eh Є L2 (0, Г; VJ,); (5.42)
m(eh(0),v) = 0. (5.43)
Запишемо похибку апроксимації у вигляді
eh (t) = eh (t) - Eh (t), (5.44)
де
£h(t) = uh(t) -Ilhu(t);
Eh it) = u(t)- Uhu (t).

5.7, Збіжність напівдискретних апроксимацій
183
Тут Щ : V —> Vh — оператор ортогонального проектування простору V
на Vh відносно скалярного добутку а (•,•), 3 огляду на це виконується
співвідношення (див, 1.6)
а(и- Uhu, v) = 0, \/v є Vh. (5,45)
Відомо, що
\\и — Uhu\\A = inf \\u — v\\A. (5,46)
veVh
На підставі формули (5,44) та нерівності трикутника можемо записати
+ ЦЯаіі*; (5-47)
\\eh\\A<\\€h\\A + \\Eh\\A. (5.48)
Отже, норму похибки е/> можна оцінити, якщо будуть отримані оцінки
для норм величин єн та Eh.
Для оцінки норми похибки Eh використаємо апроксимаційні
властивості базисних функцій <р^. Зокрема, для кусково-аналітичних базисних
функцій методу скінченних елементів можна використати такий
результат (див, 2,2),
Нехай апроксимована функція
u£VnW^1](tt)] &>0,
тоді існує 7V Є R та сталі a^R такі, що виконуються нерівності
N
< Dmhk+1~m \\u\\wik+i), m = 0,..., fc, (5,49)
(m)
1^'
де Dm = const, які не залежать від h. 3 останнього співвідношення для
задачі, яка містить оператор А за просторовими змінними другого
порядку (зокрема задачі теплопровідності) (5,46) та наслідків 1,2, випливає
нерівність
||w - Щи||^ < Dihk \\u\\w(k+i) ,Di = const.
Звідси
іі^лііл < A^*||w||w(fc+i), (5.50)
Аналогічно приходимо ще й до такої нерівності:
\\Eh\\M < D0hk+1 \\и\\ (*+і), 30 = const, (5,51)

184
Початково-крайові задачі
Залишається оцінити величину ||в^||^. Для цього використаємо
варіаційну задачу (5.42), (5.43) та подання (5.44). Підставивши (5.44) у рівняння
(5.42), (5.43), отримаємо
т (4 (*), v) + a (єн (t) ,v) = m (E'h (t), v), Уг; Є Vh\ (5.52)
m(€h(0)yv) = m(Eh(0)yv). (5.53)
Зазначимо, що у формулі (5.52) опущений доданок a (Eh (t), v): оскільки
згідно з (5.45) він дорівнює нулю,
Приймемо у рівняннях (5.52), (5.53) v = Єн (t) і знайдемо вигляд
енергетичного рівняння для складової єн (t) похибки:
1 /7
2jt \\є» Шм + Ik* Ш\м = т (E'h {t)^h (<))•
Використавши оцінки (5.32) та (5.36), отримані в попередньому
параграфі, знайдемо
t t
Ьк (t)\\2M + f\\*h (r)\\2Adr < \\Eh (0)\\2M + a"2 J \\E'h (r)\\2Mdr. (5.54)
0 0
Тут враховано, що
\\eh(0)\\l = \\eh(0)\\2M + \\Eh(0)\\2M,
а також прийнятий запис початкової умови (5.43), згідно з яким
І|еЛ(0)||2м = 0.
Зазначимо, що власне тут використаний цей запис початкової умови, про
який ішлося у 5.2.
Перейдемо тепер до оцінки величини
\\eh(t)\\2M + f\\eh(t)\\2AdT.
о
Підставимо у цю формулу співвідношення
eh (t) = eh (t) - Eh (t)

5.7, Збіжність напівдискретних апроксимацій
185
Отримаємо
t і
¥нШІ + f \\eh{r)\\\dT=\\ehm2M + f \\єн{т)\\\<іт+
t
+ \\Eh(t)\\2M + f\\Eh(T)\\2AdT-
-2 (eh (t),Eh (t))M - 2 J (eh (т), Eh (t))a dr. (5.55)
0
Зазначимо, що згідно з (5,45) останній інтеграл у попередній формулі
дорівнює нулю. Оцінимо зверху добуток — 2 (eh (£), Eh (£))#,
використовуючи елементарну нерівність
-2 (єн (t),Eh (t))M < \\єн (t)\\2M + \\Eh (t)\\2M . (5.56)
Підставимо нерівність (5,56) в (5.55):
t і
Це* Will + J \\eh (r)\\2Adr < 2 \\єк (t)\\2M + J \\єк (т)\\2Аdr+
0 0
і
+2\\Eh(t)\\2M + J\\Eh(r)\\2AdT.
0
Підсилимо останню нерівність, домноживши другий доданок у правій
частині на коефіцієнт 2:
t t
\\eh (t)\\2M + J \\eh (t)\\2adr < 2 ||ей (t)\\2M + 2 J \\єн (т)||Іdr+
0 0
t
+2\\Eh(t)\\2M + J\\Eh(T)\\AdT.
0
Оцінимо перші два доданки за нерівністю (5.54). Остаточно запишемо

186
Початково-крайові задачі
\\ен (t)\\2M + J \\eh (r)\\2Adr < 2 \\Eh (0)||2M + 2 \\Eh (t)\\
2
M
0
t t
+1 \\Eh (r)\\2Adr +2a~21 \\E'h(r)\\2Mdr.
0 0
Використаємо тепер оцінки (5.47) та (5.48), згідно з якими
\\ен\\А - \\Eh\\A < ІклІІл-
Зібравши разом попередні оцінки та (5.54), запишемо
t
¥н Will + У ||ел (Ollidr < \\Eh (0)|Ц + ЦЯ, (t)||L +
0
і
+ f\\Eh(T)\\AdT + (3-2f\\E'h(T)\\AdT.
0 0
Врахуємо далі нерівності (5.50), (5.51). Матимемо
t
\\eh(t)\\2H + J\\eh(t)\\2vdT<C2h2k{\\u0
wk+i + \\u\\wk+i +
о
t
I [||« (r)\\2w,+1 + /Г2 ЦЕІ (т)||^+і] dr і . (5.57)
Звідси випливає така теорема
Теорема 5. Нехай напівдискретизація варіаційної задачі теплопровід-
ності виконана з використанням базисних функцій, що мають апрокси-
маційні властивості (5.49) > і розв'язок варіаційної задачі характеризує
включення
u£VC\W^1]{tt), & >0,

5.8. Дискретизація варіаційної задачі за часом
187
тоді послідовність апроксимацій {и^ (t)} при h —> 0 збігається відносно
норми
и „ Гм ,,2 „ „2 11/2
ІРІЇ - )JPIILoo(0,T;H) "I" IIuIIl2(0,T;V) /
do розв'язку и задачі, і порядок похибки єн {і) характеризує оцінка (5.57)
(вона становить к).
5.8. Дискретизація варіаційної задачі за
часом
5.8.1, Кусково-лінійна апроксимація за часом
Розділимо проміжок часу [0, Т] на Л^ частин — проміжки [£j,£j+i],
j = 0,1,..., Nt — 1. Для спрощення подальшого викладу вважатимемо ці
частини однаковими за довжиною S = tj+\ — tj. Називатимемо величину
5 кроком дискретизації задачі за часом.
На кожному проміжку [tj7tj+i] розв'язок Uh(t) задачі (5.20), (5.21)
будемо апроксимувати лінійною функцією ush (£), яка має вигляд
и{ (t) = (1-щ (t)) uj + ш3 (t) u>+1. (5.58)
Тут
Wj(t) = (t-tj)/6i «Є [ti5tj+i], j = 0,l,...,iVt;
w*7, ui+1 — невідомі функції, які з огляду на вибір ujj (t) , є значеннями
апроксимованої функції ush (t) у вузлах поділу проміжку часу £т, тобто
ush(tm) = um, m = 0,l,...,JV,-l.
Отже, ush (t) на проміжку [0, Т] є неперервною кусково-лінійною
функцією,
Зазначимо, що, окрім запису (5.58) цієї функції на проміжку [tj, ij+i],
можна отримати ще й інші записи. Зокрема, формулу (5.58) можемо
записати у вигляді
и{ (t) = uj + ш3 (t) (uj+1 - uj). (5.59)

188
Початково-крайові задачі
її молена переписати ще й таким способом:
1\ (uj+1-u>)
и\
(і) = \ (и>+1 + «0 + S (с^ (t) - ^
= «>'+* + <5 L, (*) - ^) «І+І. (5.60)
Тут використані позначення
и3^і = - [uJ^ +uJ), u =- -. (5.61)
2 о
5.8.2, Однокрокова рекурентна схема
Виберемо деяку функцію £ (і) таку, що виконується співвідношення
(Є (*),!)= J £(t)dt?0.
Підставимо апроксимації (5.60) у перший доданок та (5.59) у другий
доданок варіаційного рівняння (5.20), домножимо на вибрану функцію
£ (і), зінтегруемо на проміжку [tj7tj+i] і прирівняємо отриманий вираз
до нуля, Іншими словами, домагатимемося, щоб відхил апроксимованого
за часом розв'язку від слабкого розв'язку був мінімальним. Отримаємо
(£, l)m(u+l,v) + ((£, 1) - (£,";)) a (ui,v) +
+ (£, Ші) а (и*+\ ») - & 1) Р+^ (г,). (5.62)
Тут лінійний функціонал у правій частині апроксимований на часовому
проміжку [tj,tj+i] сталою за часом величиною
F+2 (v) = І (v) |._*J+«J4
z+i
2
Домножимо формулу (5.59) на функцію £ (і) і зінтегруемо на
проміжку часу [£j,£j+i]. Увівши позначення
^ду / Є (*) 4 (*) *, (5.63)
иі+в =

5.8. Дискретизація варіаційної задачі за часом
189
отримаємо
uj+e = uj + 9 (uj+1 -uj), (5.64)
Де
8 = (£,«,,)& І)-1.
Можна довести, що
0 < в < 1.
З урахуванням співвідношення (5.64) перепишемо рівняння (5.62) у
вигляді
т (u+\v) + a (uj+°, v) = /''+* (v), Уг; Є Vh, j = 0,1,..., Nu (5.65)
подібному до рівняння (5.20).
До рівнянь (5.65) додамо ще одне співвідношення, яке випливає з
початкової умови (5.18),
т(и*-щ,ь) =0Vv£Vh. (5.66)
Зазначимо, що перетворення, подібне до перетворення формули (5.59)
до вигляду (5.64), можна застосувати і до формули (5.60). Тоді матимемо
ино = ищ +sfe_A rf+\ (5б7)
Використавши рівняння (5.65) та (5.66), можна сформулювати
рекурентні послідовності обчислень для знаходження функцій г^+1, и^+е. Для
цього, застосувавши (5.64) та (5.67), зведемо рівняння (5.65) до одного з
наступних виглядів:
т (uH1, v) + вба (иі+1, v) = (V+2 (v) - (1 - 9)
+m (uj, v),Vve Vh, j = 0,1,..., N; (5.68)
або
m (uj+e, v) + 66a (uj+e, v) = 69li+^ (v) + m (u\ v),
Vv£Vh, j = 0,l,...,N. (5.69)

190
Початково-крайові задачі
5.9. Стійкість рекурентних схем
Дослідимо стійкість побудованих рекурентних схем інтегрування за
часовою змінною. Для цього використаємо запис рекурентної схеми у
вигляді (5.65)
т (u+\v ] + a(ui+9,v) =lj^(v), \/v Є Vh j = 0,1,..., N. (5.70)
Приймемо у цьому рівнянні v = uJ'+2. Виконаємо перетворення першого
доданка
т \ и 2, uJ"+2 I = -т (V+1 — у?) uj+l — v?)
25
j+ill2
и
\uJ
2S VM~ llM H "J*
Аналогічно перетворимо і другий доданок
)•
(5.71)
І) (F+'
1\ -і+\
\и3+2
\ + \{в 2
2 7 + £
W
uy ■
(5.72)
Підставимо отримані співвідношення (5.71), (5.72) у рівняння (5.70):
_L Мі„Я-і||2 _ ц„>
■К'-ї
28 VI|M ІІЛ*
J+1M2
2 \ ,•+! Ґ
глі„, + «J+2 +
W
^111) =/І+" («'+')' i = 0,l,...,JV. (5.73)
Додамо всі рівняння (5.73), які відповідають значенням індексу j
0,1,..., т:
- \\и
2
m+ll
\М
+*Е
J=0
^+2
-u *л І л * 1 lUim+1ll2 — IU/°II2 -l.
-\—о \ и — —| \\и \\ л — — \\и ,, ~т
а 2 V 2 Я1 IU 2 " 11м
+5^1і+'{^)+\б(в-\)\\и0\
j=o ^ '
л, m = 0,l,..,iV.
(5.74)

5.9. Стійкість рекурентних схем
191
Порівнюючи одержані рівняння з енергетичними рівняннями (див, 5.4)
і і
\ К (і)\\1 + / IK (r)\\2Adr = \ |К(0)|Ц + fl{uh (r)) dr,
0 0
бачимо, що використана дискретизація в часі породжує додаткові члени
у випадку в ф §.
В отриманих співвідношеннях (5.73) (5.74) врахуємо оцінку вигляду
і ліву частину нерівності з наслідка 1
гі+\
U3+2
С\
U3+2
<
н
U3+2
м
Одержимо
рЦ (иШ\ < і_
^1
1»\
м
U3+2
м
Використаємо далі нерівність вигляду (5.31)
6 Л і 1^2
аЬ < -а1 + —Ь\ Va, Ь,є єИ.є > 0.
~ 2 2є
(5.75)
Врахуємо нерівність (див, 5.5.1)
а{и1 и) > а \\и\\н
і приймемо в (5.75)
є = асі, а = IIJJ*+* II і Ь =
Запишемо остаточно
м
UJ+2
м
рЦ ^+^ < І
цЗ+2
а 2ас\
р+І
м
Наведемо (5.73) та (5.74) у вигляді нерівностей
Иі
и
і+і|
\м
\UJ
\м t
+
\uJ+2
і2
\А

192
Початково-крайові задачі
+ в
т
и
J+1I
\УҐ
ІА) - ас2
р+і
н
j = 0,l,...,^-l
(5.76)
та
\и
m+ll
Гм+'їЕИІ1+М«-[)ІІ"'"+1"2
<
-п іім ас2^н їй v %)
г*
oil2
т = 0,1,...,^-1. (5.77)
З одержаної нерівності (5.77) випливає, що побудована однокрокова
рекурентна схема є безумовно стійкою за нормами просторів М та Я^,
якщо параметр схеми
(5.78)
•4
Справді, у цьому випадку з нерівності (5.77) випливає, що для довільного
натурального числа т величина
І m+l II2 . ||7/™+1||2
\U \\м^\\и \\А
є обмеженою. Якщо ж
•4
(5.79)
то ліва частина нерівності (5.77) містить невід'ємні доданки за умови,
що
1 + а<$6 (в--)> 0.
Ця нерівність буде виконана, якщо накласти на крок інтегрування в часі
обмеження
У цьому випадку однокрокова схема буде умовно стійкою. її стійкість
забезпечена виконанням додаткової умови (5.80) на крок інтегрування
за часом.
Приведені висновки щодо стійкості однокрокової схеми у нормах
просторів М та На справедливі також для просторів Н та V. Це випливає
з наслідків 1,2 лем 1,2.

5.10. Збіжність рекурентних схем
193
5.10- Збіжність рекурентних схем
Для того, щоб схарактеризувати збіжність рекурентних схем, оцінимо
похибку
є6 (t) = u{ (t) - uh (t) (5.81)
апроксимації наближеного розв'язку ush (£), отриманого шляхом
використання однокрокової рекурентної схеми, відносно нанівдискретного
розв'язку Uh (t) задачі (5.12), (5.13).
Отримаємо рівняння для значень похибки
ei = ss(tj)
у вузлах
th j = 0,l,...,JV,
часового проміжку [0, Г]. Для цього використаємо рівняня (5.70)
т (u+\vj + a(uj+\v) = lj+* (v), Vv Є Vh, j = 0,1,..., N. (5.82)
Врахуємо у ньому, що згідно з (5.81) та (5.61)
є+~2 = и+2~ - 5'1 («Л (*і+і) - uh (tj)), (5.83)
а також, що згідно з (5.64)
Є3+Є = uJ+6 _ Uh ^ _ q (Uh (^.+і) _ Uh ^у (5g4)
Знайдемо, що похибка є3 задовольняє співвідношення
т(Ґ\у) + a(e^\v) =У(г;), Vu Є V*, j = 0,1,..., TV, (5.85)
де лінійні функціонали ^ (v) мають вигляд
-a (0uh (ti+i) + (1-0) uh (tj), v). (5.86)
Перетворимо вирази для лінійних функціоналів (5.86). Для цього
припустимо, що
uh (t) є С<8> [0, Т]

194
Початково-крайові задачі
і розвинемо Uh (t) в ряд Тейлора в околі точки t = tj+i
uh (t) = uh (tj+i) + (t - ti+i) u'h (*i+i) +
+\ (* - h+\f< (*;+*) + \ (' - ^i)3< ®-
Обчислимо за цією формулою вирази
«Л («і+і) = иЛ (*і+і) + -иЛ (ti+i) + -ul (tHi) + -< (Є);
є f 2 гЗ
ИЛ (tj) = uh (ti+|) - -иЛ (*і+і) 4- -< (tj+.) - ^< (Є)-
Звідси отримаємо
Г1 К (*і+і) " «ft {tj)) = v!h (*i+i) + ^2< (Є); (5.87)
„ (<і+і) + (1 - в) uh (tj) = uh (tj+i) +*[в-\)< (*і+і) +
Out
+\P («ft fa) + !*(*" ^) < (O): 6 ^ («,-, *i+1). (5.88)
Підставимо (5.87) та (5.88) у праву частину (5.86):
7J (v) = (І (v) - т К (tj),v) - a (uh (tj),v)) -
s(e-\)a(u'h{tj+,),v)-82Rj(v).
Врахуємо, що сума перших трьох доданків дорівнює згідно з рівнянням
(5.20) нулю, отже,
у („) = -s(e-^a (u'h (tj+i),v) - 52Rj (v), Vv є Vh. (5.89)
Тут лінійні функціонали Rj (v) мають вигляд
Ri{v) = ±{aW(v),v) + \mM(Z),v) +

5.10. Збіжність рекурентних схем
195
+6[6--)a(u%(£),v)}, V. G 7,
(5.90)
З урахуванням виконаних перетвореннь запишемо рівняння для
визначення похибок у вигляді
т\е 2,г? І 4- a (e^°,v)
6 (в " і) а W''+О '") " *2Д»' І = 0,1,.»,І\Г3 V^F,; (5.
91)
т(є°,и) =0.
(5.92)
Звідси випливає, що однокрокова рекурентна схема має перший
порядок апроксимації (0(6)), якщо в Ф 1/2 і другий порядок апроксимації
(О (б2)), якщо Є = 1/2.
Приймемо у формулі (5.91) v = eJ'+2 і виконаємо перетворення
аналогічно, як у попередньому параграфі, Отримаємо
^m+ll
ЇМ
+
*$i|k+f
і=о
2 , 1Л f ^ М II ^гггН-11|2 _
л + Ґ(в~2 ^ L"
(5.93)
і=о
З використанням нерівності (5.31)
1
аЬ < еа2 + —b2, Va, 6, є Є R, є > 0
4е
запишемо
a(<M'£i+l)^f5^4
gi+j
•+
+s їв
< (*і+0
д.
и) * і-
є>'+*
+ 52||i?,-|
(5.94)
(5.95)

196
Початково-крайові задачі
Зазначимо таке: в записі оцінки (5.94) було використано, що в > 1/2. У
випадку, коли в = 1/2, необхідність у цій оцінці відпадає,
З урахуванням (5.94) та (5.95) з рівняння (5.93) одержимо
< 252Т {(*-!) ІКІ|2с(о,т;Ю + ^тю ||Д,||2}. (5.96)
Отже, доведено таку теорему про збіжність однокрокової схеми.
Теорема 6. Нехай розв'язок ин задачі (5.12), (5.13) є таким, що и9Ц Є
С (0, Т; V), ush — його пусково-лінійна апроксимація, обчислена за
допомогою безумовно стійкої однокрокової рекурентної схеми (5.68) з
параметром в > 1/2. Тоді значення ush(tm) збігаються відносно норм \\-\\м
та \\*\\А до значень Uh (tm), т = 1, 2, ...TV, і в цьому разі для похибок
є6 = и{ (tm) - uh (tm)
виконуються апріорні оцінки (5.96).
З формули (5.96) випливає, що оптимальний порядок збіжності
(відповідає апроксимації за часом лінійним законом і дорівнює 2) досягається
при
6 = \ + 0(6).
Виконується також теорема про збіжність відносно норм ||*||я та ||-||у.
Це випливає з еквівалентності (див, леми 1,2) цих і таких норм: ||-||м та
\\'\\а-
5.11. Вправи для самостійного виконання
Вправа 1. Записати одновимірне за просторовою змінною
формулювання задачі теплопровідності (5.1), (5.2) з однорідними граничними
умовами типу Діріхле у крайових точках.
Вправа 2. Записати одновимірне за просторовою змінною
формулювання задачі теплопровідності (5.1), (5.2) з однорідними граничними
умовами типу Ньютона у крайових точках.

5.11. Вправи для самостійного виконання
197
Вправа 3. Записати одновимірне за просторовою змінною
формулювання задачі теплопровідності (5.1), (5.2) зі змішаними однорідними
граничними умовами (в одній крайовій точці задана умова Діріхле, а в
іншій — умова Неймана) крайових точках.
Вправа 4. Навести варіаційне формулювання одновимірної за
просторовою змінною задачі теплопровідності (із вправи 1).
Вправа 5. Навести варіаційне формулювання одновимірної за
просторовою змінною задачі теплопровідності (із вправи 2),
Вправа 6. Навести варіаційне формулювання одновимірної за
просторовою змінною задачі теплопровідності (із вправи 3),
Вправа 7. Дослідити білінійні форми, які містяться у варіаційному
формулюванні одновимірної задачі теплопровідності (із вправи 1).
Вправа 8. Дослідити білінійні форми, які містяться у варіаційному
формулюванні одновимірної задачі теплопровідності (із вправи 2),
Вправа 9. Дослідити білінійні форми, які містяться у варіаційному
формулюванні одновимірної задачі теплопровідності (із вправи 3),
Вправа 10. Записати енергетичне рівняння (5.28) для одновимірної
за просторовими змінними задачі теплопровідності (із вправи 1) у явному
вигляді, замінивши ||ил (t)\\H , ||«h||v та І (щ) їх явними виразами,
Вправа 11. Записати енергетичне рівняння (5.28) для одновимірної
за просторовими змінними задачі теплопровідності (із вправи 2) у явному
вигляді, замінивши \\щ (t)\\H , ||^/г||у та І (v>h) їх явними виразами,
Вправа 12. Записати енергетичне рівняння (5.28) для одновимірної
за просторовими змінними задачі теплопровідності (із вправи 3) у явному
вигляді, замінивши ||ил (t)\\H , ||«h||v та І (щ) їх явними виразами.

Розділ б
Проблема "великих" задач
лінійної алгебри
Обчислювальні схеми варіаційних методів, розглянуті у попередніх
розділах, зумовлюють потребу розв'язування великих систем лінійних
алгебричних рівнянь, Для цього в обчислювальній математиці
розвинений арсенал методів та алгоритмів, Водночас є методи, які на рівні
формування систем лінійних алгебричних рівнянь дають змогу
зменшити їхні розміри і привести початкову задачу лінійної алгебри великого
розміру до розв'язування послідовності задач менших розмірів,
Найпоширеніші з цих методів описані нижче,
6.1. Редукція параметрів внутрішніх
вузлових точок
У випадку використання лагранжевих поліномів на прямокутниках
(див, 2,5) для апроксимації розв'язку виникає ситуація, коли низка
вузлових точок та відповідних їм вузлових параметрів є внутрішніми
(належать тільки одному скінченному елементові). Це означає, що алгебричні
рівняння методів Рітца—Гальоркіна, які відповідають цим параметрам,
формуються на основі інформації тільки з одного скінченного елемента.
Отже, на цьому елементі невідомі вузлові параметри можуть бути
вилученими, Загальну кількість невідомих у цьому разі можна зменшити
(редукувати) і, отже, процес розв'язування великих систем алгебричних
рівнянь методу скінченних елементів можна звести до розв'язування де-

200
Проблема "великих" задач лінійної алгебри
кількох менших за розміром систем. Така ж ситуація виникає в разі
об'єднання групи скінченних елементів в один, так званий суперелемент.
Внутрішні для цього суперелемента вузлові параметри можна вилучити
і задачу лінійної алгебри для матриць великих розмірів можна звести
до послідовності матричних операцій над системами менших розмірів,
Такий підхід відомий під назвою метод суперелементів,
Опишемо головну ідею цього підходу, Припустимо, що для
апроксимації розв'язку певної задачі, зокрема це може бути задача Діріхле для
рівняння Пуассона, використовують лагранжові апроксимації на
прямокутних елементах Г2е. Наведемо шуканий розв'язок на елементі Qe у
вигляді матричного співвідношення
ufc = (Ni,N2)(*), (6.1)
де Ni — матриця рядок, складена з базисних функцій, що відповідають
вузлам, розміщеним на границі скінченного елемента; N2 — матриця
рядок, складена з базисних функцій, що відповідають внутрішнім вузлам
скінченного елемента; qi — матриця—стовпець граничних вузлових
параметрів; q2 — матриця—стовпець внутрішніх вузлових параметрів,
Нехай для знаходження наближеного розв'язку будуємо числову схему на
основі методу Рітца. Запишемо значення функціонала енергії від
наближеного розв'язку (6.1) у вигляді
F(uh) = Y,*e> (6-2)
є
де Фе — значення функціонала на одному скінченному елементі. Його
можна записати у вигляді
Тут

6.1. Редукція параметрів внутрішніх вузлових точок
201
— матриці, з яких формується система рівнянь методу скінченних
елементів, поділені на частини відповідно до поділу вулових параметрів на
граничні та внутрішні,
Для внутрішніх вузлових параметрів виконується співвідношення
dF дФ* п ^
У формулі (6.3) знака суми нема тому, що q2 — внутрішні параметри,
які відповідають скінченному елементу Г2е.
Обчислимо похідну від Фе за внутрішніми вузловими параметрами q2
і прирівняємо її до нуля;
Kf2qi + K22q2 = Q2
Звідси
02 = K^Ch - K^K^qx. (6.4)
Запишемо також вираз для похідної від Фе за граничними вузловими
параметрами qi
дФ
«-i = K11q1 + K12q2-Q1. (6.5)
<9qi
Вилучимо з (6.5) внутрішні вузлові параметри, врахувавши
співвідношення (6.4):
Ц^ = (Кц - К^К^К^) qi - (Qi - K12K^Q2).
Отже, якщо вилучити внутрішні вузлові параметри, ключова система
лінійних алгебричних рівнянь методу Рітца відносно невідомих
параметрів, що відповідають граничним вузловим точкам скінченних елементів,
формується з матриць
К*і = Кіі - Кі2К^2 К12;
Q* = Qi — Кі2К22 Q2,
Після розв'язування системи алгебричних рівнянь значення внутрішніх
вузлових параметрів можна знайти за формулою (6.4),
Як зазначено, процес вилучення внутрішніх вузлових параметрів для
групи скінченних елементів називають методом суперелементів.
Очевидно, що метод суперелементів можна організувати як багаторівневий

202
Проблема "великих" задач лінійної алгебри
процес вилучення внутрішніх вузлових параметрів, На першому рівні
в групи-суперелементи об'єднують елементи; на другому рівні в групи-
суперелементи другого рівня об'єднують суперелементи першого рівня і
т.д.
6.2. Класичний альтернувальний метод
Шварца
Розглянемо двовимірну область Q, зображену на рис.6.1. Нехай 0Q
— границя області Q. Уведемо штучні границі Г* так, що утворюються
дві підобласті £^ з границями дПі і Q = Qx U Г22. Штучна границя Г* є
частиною границі підобласті Г^, яка лежить всередині Q. Решта частина
границі підобласті Г^ дорівнює dQi \IY
А
Рис. 6.L Двовимірна область, поділена на підобласті
В області Q розглянемо задачу
Du = /, хгх2 Є П; (6.6)
де D — заданий лінійний диференціальний оператор; f(xiyx2), g(xix2) —
задані функції,

6.2. Класичний альтернувальний метод Шварца
203
Для побудови наближеного розв'язку задачі (6.6) використаємо
алгоритм альтернувального методу Шварца, який складається з двох пів-
кроків. Виберемо деяке початкове наближення розв'язку щ в підобласті
Г22. Тоді для ті = 1, 2, 3,... розв'яжемо задачі,
Перший півкрок:
(6.7)
DU{?] :
in]
in]
= /, xitx2 Є fix;
= 9г %\%і Є dQi\Ti\
= U2 і #1,#2 ^ 1 1-
Другий півкрок:
Dv£>
in]
Щ
in]
Щ
= /,
= 9г
in)
xxx2 Є Г22;
xi,x2 Є <9П2\Г2
X\X2 Є Г2.
(6.8)
Під час побудови числового розв'язку задачі (6.6), (6.7), наприклад,
методом скінченних елементів, використовують процес дискретизації
підобластей Пі скінченними елементами, У цьому разі можуть виникати
такі ситуації, Перша, коли вузли сіток у підобластях $71 П £72 збігаються
один з одним, та друга, коли вузли сіток в підобластях Пх П £72 не
збігаються один з одним,
Розглянемо першу ситуацію. Позначимо через и^ вектор—стовпець
вузлових значень шуканої функції в підобласті Qj і наведемо його у
вигляді
иг = идадг, , (6.9)
\ иг, /
де uq. — вектор—стовпець внутрішніх вузлових значень шуканої функції
в області fij, и^пдг^; игг — вектори—стовпці вузлових значень шуканої
функції на відповідних частинах границі,
Позначимо також через f^ вектори—стовпці значень, що відповідають
у дискретних варіаційних задачах (6.7), (6.8) правим частинам
диференціальних рівнянь, а також через g^ — вектори вузлових значень заданої
функції на відповідних частинах границі,

204
Проблема "великих" задач лінійної алгебри
Наведемо дискретизовані задачі (наприклад, шляхом використання
методу скінченних елементів) (6.7), (6.8) у вигляді систем рівнянь
(6.10)
Аіи;->
(«)
иЗПі\Гі
(п)
A2u<n)
(п)
идП2\Т2
= fi, в
= gi, в
т (п~
= f2, В
= g2, В
пі;
afii\ri;
Х), в
ft2;
ЩДГ2;
Гі
(6.11)
„W _ Т і/"-1) хто Г
Тут Аі є прямокутними матрицями. їх можна записати у вигляді
Аг= ( АПг Аапдг, АГг ), (6.12)
де Aq. — квадратні матриці, розміри яких відповідають кількості
внутрішніх вузлових точок; А^пдг^ Арг — прямокутні матриці, кількість
рядків яких дорівнює кількості внутрішніх вузлових точок, кількості
стовпців кожної з цих матриць дорівнюють кількості вузлових точок на
відповідній частині границі, Через
/п._>г< : Пі -> Гі (г = 1, J = 2 г = 2, j = 1)
позначено оператор, який виконує інтерполювання вузлових значень з
вузлів всередині області Г2^ на вузли, що розміщені на границі IV
На підставі цих рівнянь можемо записати алгоритм альтернувального
методу Шварца, який зображений у вигляді блок-схеми на рис, 6.2.
Тут знак "+" означає вихід, що відповідає виконанню умови умовного
оператора, а знак "—" — невиконанню цієї умови,
6.3. Альтернувальний метод Шварца і
блочний метод Гаусса—Зейделя
Наведений алгоритм альтернувального методу Шварца збігається з
алгоритмом блочного методу Гаусса—Зейделя для лінійної системи
рівнянь, що відповідає дискретизації двох підобластей і об'єднання
розв'язків уздовж штучних границь, Щоб довести це, перепишемо алгоритм

6.3. Альтернувальний метод Шварца і блочний метод
205
START
W."'--О^ ґіГ-О
п:=п-ь1
і
,JK=f,.u^',,,,-e.,uVV-W,-
І
<«j
і
j я j
V^Mi'^r й., d^W,
I
Wv^-^ru
Рис. 6.2. Алгоритм альтернувального методу Шварца

206
Проблема "великих" задач лінійної алгебри
у матричному формулюванні, Для цього, використавши записи (6.9) та
(6.12), наведемо два півкроки (6.10), (6,11) алгоритму у вигляді
< \
(АПі А^АГі АГі ) | и^дГі =fi; (6.13)
4? )
(п) (п) т (^—1) (г -і л\
"«ідг, = Si' uri = Jn2^riu^ '; (6.14)
( АП2 АвПа\г2 АГ2 ) [ uj$ ,Гз ] = f2; (6.15)
41
U
■да2\г2
g2, Щ2 = 7^і^Г2и^. (6,16)
Перенесемо у цих співвідношеннях відомі величини у праву частину,
Отримаємо
AftiMni = fi ~ Ашдг^і - Arjn^r^^] (6,17)
A^2US = f2- A^n2\r2g2 - Arjn^^n^.
Уведемо позначення
fi = fi - А^дг^, і = 1, 2,
тоді співвідношення (6.17) можна переписати у вигляді
АП2^2 = f2 - АГ2^Пі^Г2иПі .
Ці вирази є формулами блочного методу Гаусса—Зейделя для такої
системи лінійних алгебричних рівнянь:
АПі АГі/п2^Гі \ ґ ufil \ = / її | (6 19)
АГ2Іаі^Г2 АП2 У V и^2 У V f2 у
Зазначимо, що навіть тоді, коли матриці А^ та А^2 є симетричними,
матриця системи лінійних алгебричних рівнянь (6.19) загалом не є
симетричною. Справді, на загал не виконується співвідношення
Агі^гь^Гі — ( АгДи^Гз) .

6.4. Мультиплікативний метод Шварца
207
Домножимо зліва кожне рівняння системи (6.18) на А^1 та додамо і
віднімемо у правих частинах и^~ . Отримаємо
Для розв'язування системи рівнянь (6.20) можна використовувати
звичайні ітераційні методи (не блочного типу), У цьому разі виникає
потреба у виборі початкового наближення. Зокрема, його можна отриманти
в результаті виконання однієї ітерації альтернувального методу Шварца
з нульовим початковим наближенням (и^' = 0). Такий варіант методу
Шварца називають передумовлювачем.
6.4. Мультиплікативний метод Шварца
Розглянемо тут випадок, коли сітки в областях Г2і та Г^2 є такими, що
мають спільні вузлові точки в Г2іП^2- Для нього алгоритм
альтернувального методу Шварца можна покращити з погляду зменшення кількості
арифметичних операцій і вимог до пам'яті обчислювальної машини.
Припустимо, що крайова задача шляхом застосування методу
скінченних елементів зведена до системи лінійних алгебричних рівнянь
Au = f, (6.21)
де и — вектор стовпець невідомих вузлових значень; А — матриця
системи рівнянь; f — вектор стовпець правої частини. Згрупуємо невідомі
вузлові значення у векторі u так:
и=(иїЛа2 < <пп2 < и£лйі )Т
Відповідно до цього наведемо матрицю системи рівнянь (6.21) у
схематичній формі, зображеній на рис, 6.3.
Уведемо позначення для таких груп внутрішніх вузлових параметрів:
(U^l\^2 \
иг2 ;
иПіПІЗз /

208
Проблема "великих" задач лінійної алгебри
Рис. 6.3, Схематичне зображення матриці системи
Ufi2
Uftinn2
u
■П2\Пі
Відповідні їм квадратні матриці у складі матриці А виділені на
рис, 6.3 штрихуванням лініями різного напряму, Частина, у якій
штрихові лінії перетинаються, відповідає внутрішнім вузловим точкам області
ПіГ)ГІ2. Наприклад, для сіткової області, показаної на рис.6.4, ця частина
відповідає одній вузловій точці,
З огляду на зазначене, матрицю А можемо розглядати як таку, що
формується з матриць
А^ Аа\пг
АПі АГі А,
П2\Пі
(6,22)
А^\п2 Ап2
LHi\n2
АГ2 А^2
(6,23)
Повернемось тепер до ітераційних формул (6,20), записаних на випадок,

6.4. Мультиплікативний метод Шварца
209
Рис. 6.4. Приклад сіткової області
коли вузлові точки в Г2і П Г^2 є спільними для сіткових областей Г2і та 0,2'-
(п)
Пі
(«)
U,
(п-1)
«і
(п-1)
+ А- f, - АпХ'Г " АгХ;
.(«-1)
(тг-11 , а —1 ґг а № а (п—1)\
*п2 - и^2 + АПг [ї2 - АГ2иГ2 - АПаі4 >)
Припустимо, що
тоді (див. формули (6.22), (6.23) та рис.6.3)
0,
АГіиГі
Ап\п1ип^Пі ;
AfoU-
ГгиГ2
(п-1) -
= А
її'*
п\п2ип\п2-
Використавши (6.26), перепишемо формули (6.24) у вигляді
u
(п)
u
(п)
п2
U,
U,
Пі
п2
+ Anl (fi - Aftluft Х) - AnxnxU^)
+ А
б; (і
А (")
Ап\п2ип^П2
П\ПіиП\Пі
AfiX2 J-
(6.24)
(6.25)
(6.26)
(6.27)
Отже, ми усунули явну залежність в алгоритмі методу Шварца від
вузлових значень на штучній границі. Звичайно, це виконується в разі ви-

210
Проблема "великих" задач лінійної алгебри
конання умов (6.25) і, звичайно ж, важливим питанням є те, коли такі
умови виконуються.
У другій з ітераційних формул (6.27) не використано всі отримані
на першому кроці значення розв'язку, Справді, перепишемо ітераційні
формули (6.27) у вигляді
< = и[Г > + А- (її - A^uST1' " Ап^іЩ) ; (6.28)
(п) ~(п — 1) . а —1 іС^ Л (п) А ~(п —1)\
un2=un2 +А2 [Ь - Aft\ft2u^\ft2 - An\niun2 J-
У другій з наведених вище формул враховано всі нові значення, отримані
з першої формули. Вони записані скоригованим значенням и^2 . Вирази
fx-A^u^-Аади^; (6.29)
2 - Ап\п2ип^2 - Ап2иПз
згідно з формулами (6.22), (6.23) є відхилами у вузлах, що відповідають
внутрішнім вузловим точкам областей Г2і та Г22.
Зазначимо, що для їхнього обчислення потрібно мати тільки значення
у вузлових точках в ^ та на Г* (оскільки Ап х^ = 0, А^\^2 = 0),
Описаний алгоритм називають мультиплікативним методом Шварца.
Пояснимо цю назву, 3 цією метою перепишемо ітераційні формули (6.27),
врахувавши (6.29), у вигляді
иМ) = иМ+(АЙ ° ) (f - Aug); (6.30)
u(n+i) = uKD+(° A°ftl)(f-AuH)).
На кожному півкроці відхил потрібно підставити в (6.30) і домножити
на відповідну матрицю, Звідси термін мультиплікативний.
6.5. Адитивний метод Шварца
Перетворимо формули (6.30), підставивши першу формулу у другу:
u(n+l) = u(n) + / А^1 М (f _ Au(«) j +

6.5. Адитивний метод Шварца
211
^оліОМ^'Ч^о)^"')))
Зазначимо, що виконується рівність
0 0 WAJiJO
0 АЙ Д 0 0
Отже, остаточно можемо записати
„(..+'> =„<»>+((>' °) + (° ^))(f-A„<">). («•")
Формула (6.31) описує найпростіший алгоритм адитивного методу
Шварца,
Уведемо тут такі позначення. Нехай Rj — прямокутна матриця,
множення якої на вектор невідомих в Q вузлових значень дає вектор
вузлових значень в Г^, тобто
u„,=Rlu=(i0)(u^)
on,=R,a=(0i)('^)
(6.32)
(6.33)
Зазначимо, що
АПі = RiARj. (6.34)
Справді, якщо і = 1, то згідно з формулою (6.22) матимемо
RxARf = ( І 0 ) ( Апі Af^ ) ( J ) =
(І 0)(
АП, , _ д
Аналогічно це молена довести і для і = 2.
З урахуванням формул (6.32) —(6.34) перепишемо співвідношення
альтернувального методу Шварца у вигляді
u(n+i) = uM+BT^AR^R^f-AuW); (6.35)
u(n+i) = u("+i)+R^(R2ARj)"1R2(f-Au("+")).

212
Проблема "великих" задач лінійної алгебри
Насправді, в разі числової реалізації методу декомпозиції матриці Rj
ніколи не формуються, Вони введені тільки для того, щоб записати різні
алгоритми методу декомпозиції однаковим способом. Позначимо
B, = Rf (R;ARf)-1R; (6,36)
Отже, алгоритм, який складається з двох напівкроків, можна переписати
однією формулою
u(n+i) = u(n) + (Вх+Вз-ВзАВі) (?і - Au(n)) . (6,37)
З формули (6,37) випливає, що передумовлювач визначений матрицею
В = В1+В2—В2АВ1.
Отже, якщо навіть матриця А симетрична, то мультиплікативний
передумовлювач Шварца не є симетричним. Проте його можна симетризувати
шляхом застосування трикрокового алгоритму такого вигляду
п(пЦ) = U(n) + Bi ^_Аи(п)); (6,38)
U(»+I) = иМ)+в2(?-Аи(п+з));
u(n+i) = u("+f)+Bl(f~Au^+i)).
Трикроковий алгоритм, описуваний формулами (6,38), можна навести
аналогічно до попереднього у вигляді однокрокового методу
u(n+i) = u(n) + ^Ві + в2 - B2ABi - ВхАВ2+
+B!AB2AB! (f - Au(n)) , (6,39)
який визначає симетричний передумовлювач у вигляді
В = Вх + (і - ВіА) В2 (і - АВі) . (6,40)
З урахуванням позначення (6,36), запишемо формулу (6,39) у вигляді
u(n+l) = u(n) + (Ві + Вз) (J _ Au(n) j
Отримане співвідношення описує адитивний метод Шварца.

6.6. Випадок багатьох підобластей
213
6.6. Випадок багатьох підобластей
Розглянемо область, яка є об'єднанням з перекриттям р підобластей
$7ї, і = 1, ...,р. Уважатимемо для простоти викладу таке: розрахункові
сітки для застосування числових методів є такими, що на перетині f^nfij
вузлові точки збігаються (в термінах сіткової області, що сіткові області
ПіПП^ 0).
Запишемо за аналогією з 6.3 співвідношення мультиплікативного
методу Шварца. Він складається з таких кроків:
u(n+^) = U(«)+Bl(f-Au(n));
>+§) = u(«+±)+B2(f-Au(n+p));
(6.41)
u(n+i) = u(»+1T1)+Bp(f-Au^+(p-1^).
Нагадаємо, що
В, = Rf (RiAKjy1 Rh Аг = RiARj
Матриця Аг є підматрицею матриці А, що відповідає сітковій області Qim
За аналогією з попереднім можна навести р-крокову формулу одним
записом. Підставивши формули (6.41) одна в одну з кінця, отримаємо
u(n+i) = u(n) + (Ві + в2 + + Вр (_ВрАВр_і -
-Вр_іАВ„_2 - ... - В2АВі (f - Au<n>) . (6.42)
6.7. Вправи для самостійного виконання
Вправа 1, Розглянути задачу Діріхле для рівняння Пуассона. Для
знаходження числового розв'язку цієї задачі використати схему МСЕ
з лінійними апроксимаціями на трикутних скінченних елементах (див,
3.8). Зобразити у вигляді блок-схеми алгоритм числового розв'язування
цієї задачі з використанням однорівневого суперелементного вилучення
внутрішніх вузлових точок.

214
Проблема "великих" задач лінійної алгебри
Вправа 2. Розглянути задачу Діріхле для рівняння Пуассона. Для
знаходження числового розв'язку цієї задачі використати схему МСЕ
з лінійними апроксимаціями на трикутних скінченних елементах (див,
3.8). Зобразити у вигляді блок-схеми алгоритм числового розв'язування
цієї задачі з використанням багаторівневого суперелементного вилучення
внутрішніх вузлових точок.
Вправа 3. Для Т-подібної області, задавши її поділ на трикутні
скінченні елементи, записати співвідношення альтернувального методу
Шварца.
Вправа 4. Довести, що матриця В у формулі (6.40) симетрична.

Додаток
Лінійна множина функцій
Позначимо символом Q TV-вимірну область, тобто відкриту
зв'язну множину евклідового простору R^. Координати точки х Є R^
позначатимемо хі, Х2,..., xn- Розглядатимемо тут тільки обмежені області
з границями Ліпшиця. До цього класу областей належать, наприклад,
двовимірні області з кусково-гладкими границями, які не мають точок
звороту; тривимірні області з кусково-гладкими границями, які не
мають ребер звороту, Зазначимо, що такі види областей є характерними
для багатьох задач математичної фізики, які трапляються в іженерній
практиці та науці,
Позначимо символом Г границю області Q. Множину fi = ПиГ
називатимемо замкненою областю.
Нехай М — множина функцій, заданних на області Q.
Означення 1. Множину функцій називають лінійною (лінеалом)^ якщо
разом з функціями щ^щ, із М вона мість їхню лінійну комбінацію
аіщ + а2и2:
де аі — довільні дійсні сталі.
Позначимо через C^(Q) множину функцій и{х\ частинні похідні
яких до fc-ro порядку включно неперервні в області Q. Похідною
порядку нуль вважаємо саму функцію и (х). Неважко перевірити, що множина
С^(ії) є лінійною.

216
Гільбертів простір
Розглянемо деякий лінеал М. Для двох довільних функцій u,v Є М
визначимо число (ад, v) — скалярний добуток, який задовольняє умови
(щу) = {v,u)\
(aiui + a2u2,v) = ai (ui,v) + a2 {u2,v)\
(u, u) > 0;
(u, u) = 0 Ф> u (x) = 0, x Є Q.
Тут число (vy u) є комплексним спряженим числом.
Означення 2. Лінійну множину М разом з уведеним на ній скалярним
добутком називають гільбертовим простором. Позначатимемо його
Н.
Поряд із введеним комплексним гільбертовим простором
розглядають також дійсний гільбертів простір, у якому перша умова, яку
задовольняє скалярний добуток, має вигляд
(щу) = (vyu).
На основі скалярного добутку можна ввести дуже важливе поняття, а
саме: норму функції
Норма у гільбертовому просторі має такі властивості:
1° тотожно нульова і тільки тотожно нульова функція має норму,
яка дорівнює нулю;
2° якщо А — дійсне число, а и елемент простору Н, то
||Aw|| = |А| ||и||;
3° для довільної пари функцій u,v Є Н виконується нерівність
Коші—Буняковського (нерівність Шварца)
\(u,v)\ < \\и\\ \\v\\]
4° для довільної пари функцій u,v Є Н виконується нерівність
трикутника
\\и + v\\ < \\и\\ + \\v\\.

217
Відомо, що множина функцій, визначених майже всюди в області Q
та інтегровних в Q з квадратом, є лінеалом. Визначимо на цій множині
скалярний добуток, прийнявши
(и, v) — uvdQ.
Утворений таким способом гільбертів простір позначають L2 (Q). Норма
у цьому просторі визначена співвідношенням
\Щ\г =
N
/
иЧП.
Означення 3. Функції u,v Є Н називають ортогональними, якщо
(u,v) = 0.
Означення 4. Функцію и Є Н називають нормованою, якщо
\\и\\ = 1.
Означення 5. Функції <pi,(f2i •••,іРп називають лінійно залежними,
якщо можна відшукати сталі аі, а2)..., ап, серед ягсш; не всг
дорівнюють нулю, такі, щоб виконувалось співвідношення
аі<рі + а2(р2 + — + ап(рГі
0.
Ці функції називають лінійно незалежними, якщо остання рівність
виконується тільки за умови
аг = а2
Виконується така теорема:
0.
Теорема 6. Для того, щоб функції </?ь <£>2> •*•:> ^п Є Н були лінійно
залежними, необхідно і достатньо, щоб дорівнював нулю визначник
(визначник Грама)
det
(¥>2,¥>і) (^2,^2) »■ (¥>2,¥>п)

218
Збіжність у гільбертовому просторі
Нехай у гільбертовому просторі Н задана послідовність функцій
{<рп}. Називатимемо цю послідовність збіжною до функції ір, якщо
1°) <Р Є Я;
2°) lim \\<рп - <р\\ = 0.
Функцію (р називатимемо границею послідовності {ірп}. Якщо
послідовність збіжна, то виконується співвідношення
lim \\(рп -(рт\\ = 0.
Проте із виконання цього співвідношення збіжність послідовності {<рп}
випливає тільки тоді, коли простір ^-повний. Тут розглядатимемо
тільки повні гільбертові простори. Для них наведене співвідношення є
необхідною і достатньою умовою збіжності послідовності, Саму ж
послідовність, яка задовольняє цю умову, називають фундаментальною.
Гільбертів простір L2 (П) є повним.
Означення 7. Множину М с Н називатимемо щільною в
гільбертовому просторі Н, якщо довільну функцію (р Є Н можна отримати як
границю деякої послідовності <рп Є М.
Позначимо через Cq (П) множину функцій, які є нескінченну
кількість разів диференційовними в області Q, і такими, що дорівнюють
нулю у деякому околі границі Г області Q,. Відомо, що множина Cq (ft) e
щільною у просторі L2 (Q).
Наведемо одну лему, яку використовують у викладі теорії варіаційних
методів,
Лема 8. Функція, ортогональна до всіх функцій щільної множини,
дорівнює нулю.
Простори Соболева
Нехай неперервна в Q функція / (х) має неперервну в Q похідну fXl.
Тоді для довільної функції g (x) Є С$ (П) виконується формула
/ fgXldVt = - fXlgdQ,

219
яка випливає з формули Остроградського. Цією рівністю визначають
узагальнену похідну,
Означення 9. Якщо у попередній рівності відмовитися від
неперервності функції f та функції fXl, а замість цього домагатися інтегров-
ності лівої та правої частин цієї рівності в сенсі Лебега, то fXl
називають узагальненою похідною функції /.
Позначимо через W2 гільбертів простір функцій, які мають інте-
гровні з квадратом усі узагальнені перші похідні, Скалярний добуток у
цьому просторі визначений формулою
Цей скалярний добуток породжує норму
і
За аналогією з наведеним означенням узагальненої похідної першого
порядку можна дати означення узагальнених похідних вищих порядків і
розглянути простори Соболева W2 *
Загалом відомо, що простір утворений функціями із лінеалу
С(°°) (О) та його поповненням за нормою, яка визначена на цьому
просторі, тобто такими функціями, про похідні яких можна говорити в
узагальненому сенсі.
На границі Г значення функцій и (х) Є С^ (О) однозначно визначені
та інтегровні з квадратом, Значення на границі інших функцій із W2
потрібно розуміти в певному узагальненому сенсі, який називатимемо
слідом функції, Важливе значення в цьому плані має така теорема,
Теорема 10. Нехай Q — область з границею Ліпшиця. Тоді існує єдиний
обмежений, лінійний оператор Т, який відображає простір W\ (fi) в
простір L2 (Г). Якщо и(х) Є С^(П), то Ти{х) — и(Т), тобто слідом
функції и(х) Є C(°°)(Q) є її значення на границі.

220
З наведеної теореми випливає, що для довільної функції и(х) Є
W2 (ft) існує деяка функція и(Г) Є L2 (Г), яка є її слідом,
Якщо деяка функція и(х) Є W2 (ft), (A; > 1), то вона належить також
простору W2 (ft)« Отже, згідно з наведеною теоремою така функція має
слід и(Т) Є L2 (Г).
Якщо деяка функція и{х) Є W2(/° (ft), (A > 1), то D*u(:r) Є W2(1) (ft)
для всіх і = (іі, ♦.♦, ідг) таких, що |г| < & — 1. Тоді згідно з наведеною
теоремою для похідних Dlu(x) існують сліди Оги(Т) Є L2 (Г).

221
Список рекомендованої літератури
1. Григоренко Я.М., Панкратова Н.Д. Обчислювальні методи в
задачах прикладної математики. К.: Либідь, 1995.
2. Варга Р. Функциональньїй анализ и теория аппроксимаций в чис-
ленном анализе. М.: Мир, 1974,
3. Дейнека B.C., Сергиенко И.В. Скопецкий В.В. Модели и методьі
решения задач с условиями сопряжения, Киев: Наук, думка, 1998.
4. Дюео Г., Лиопс Ж.-Л. Неравенства в механике и физике. М.:
Наука, 1980.
5. Колмозоров A.M., Фомін С В. Елементи теорії функцій и
функціонального анализу, К.: Вища школа, 1974,
6. Ладиоюенская О.А. Краевьіе задачи математической физики, М.:
Наука, 1973,
7. Марчук Г.И. Методьі вьічислительной математики. М.: Наука, 1980.
8. Михлин С.Г. Вариационньїе методьі в математической физике. М.:
Наука, 1970.
9. Михлин С.Г. Численная реализация вариационньїх методов, М.:
Наука, 1966.
10. Ректорис К. Вариационньїе методьі в математической физике и
технике. М.: Мир, 1985.
11. Савула Я.Г Метод скінченних елементів. К.: НМК ВО, 1993.
12. Савула Я.Г., Флейшман Н.П. Расчет и оптимизация оболочек
с резньїми срединьїми поверхностями, Львов: Изд-во при Львов. ун-те,
1989.
13. Савула Я.Г., Шинкаренко Г.А. Метод скінченних елементів. Львів:
Вища школа, 1976,
14. Стрет Г.} Фикс Дж. Теория метода конечньїх злементов, М.:
Мир, 1977,
13. Сьярле Ф. Метод конечньїх злементов, М.: Мир, 1985. 1980.
15. Шинкаренко Г.А. Проекційно-сіткові методи розв'язування
початково-крайових задач, К.: НМК ВО, 1991.
16. Brenner S.C., Scott L.R. The mathematical theory of finite element
methods, Springer^Verlag, 1994
17. Kolar V., Kratochvil J., Leitner F., Zenisek A. Vypocet plosnych a
prostorovych konstrukci metodou konecnych prvku. Praha: SNTL, 1979,

222
18. Smith B., Bjorstad P., Gropp W. Domain decompozition, Parallel
multylevel methods for elliptic partial differencial equations. Cambridge
University Press, 1996.
19. Szaho B., Babushka I. Finite element analysis, John Wiley and
Sons.Inc., 1991.