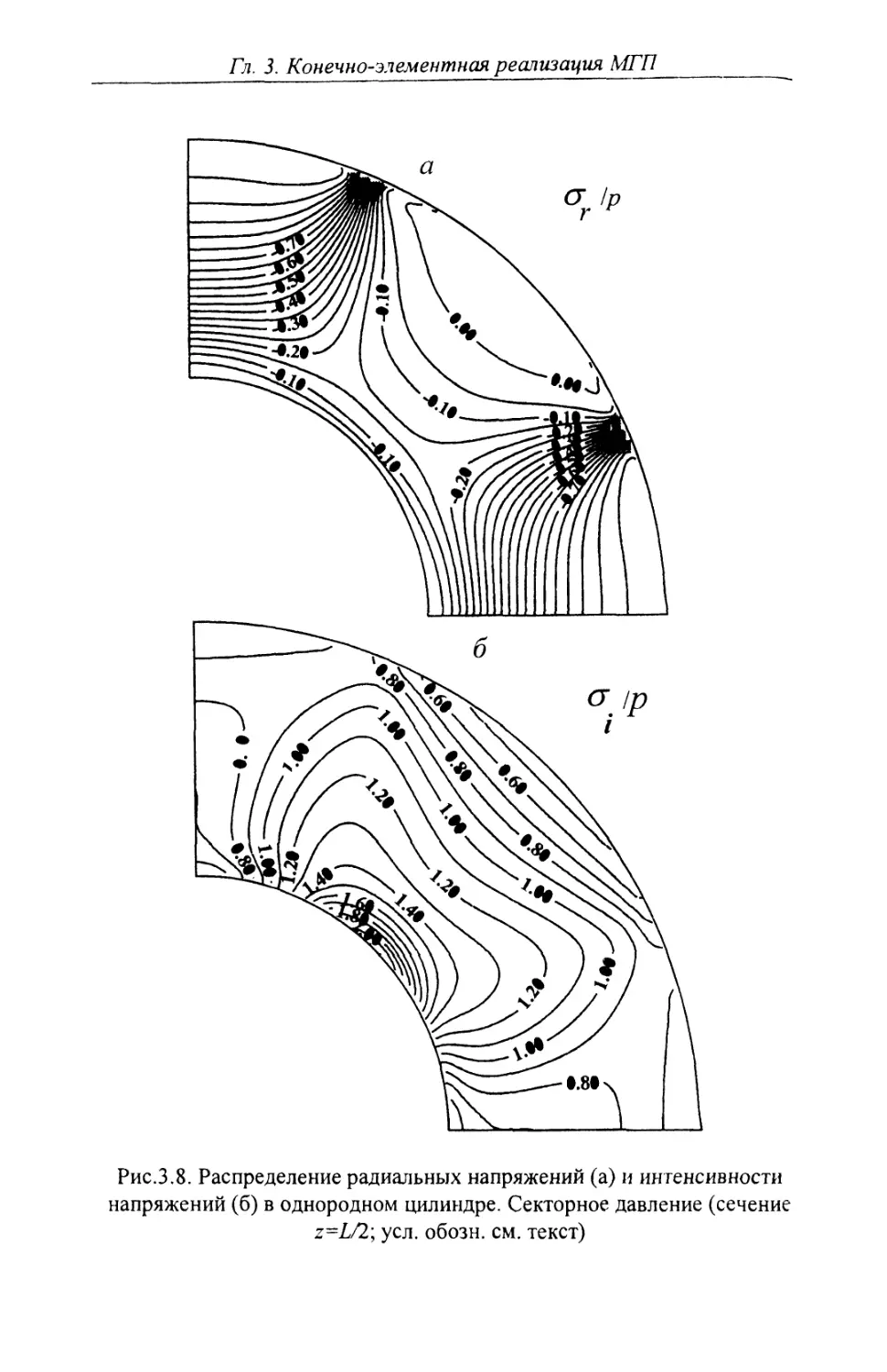
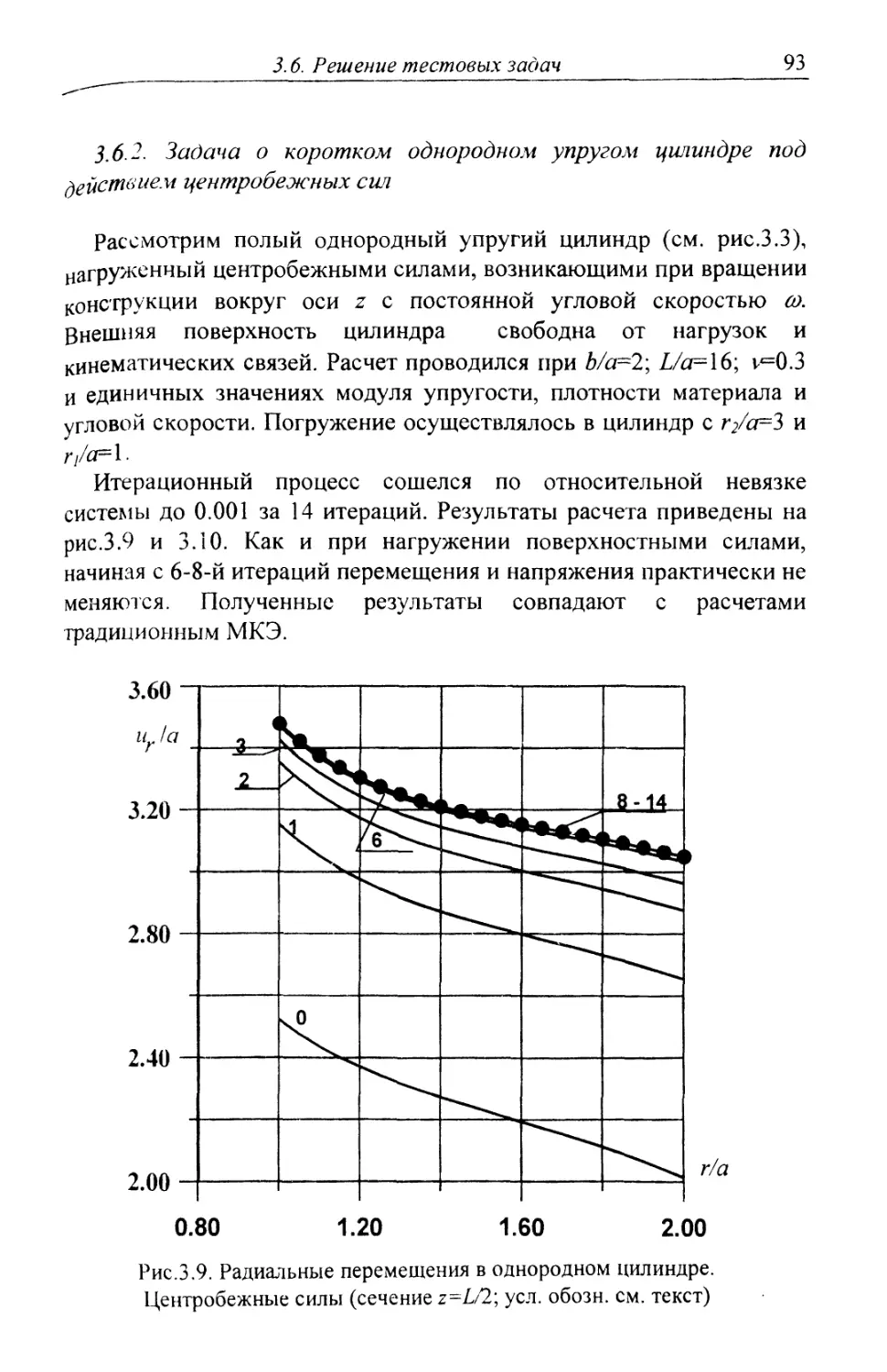
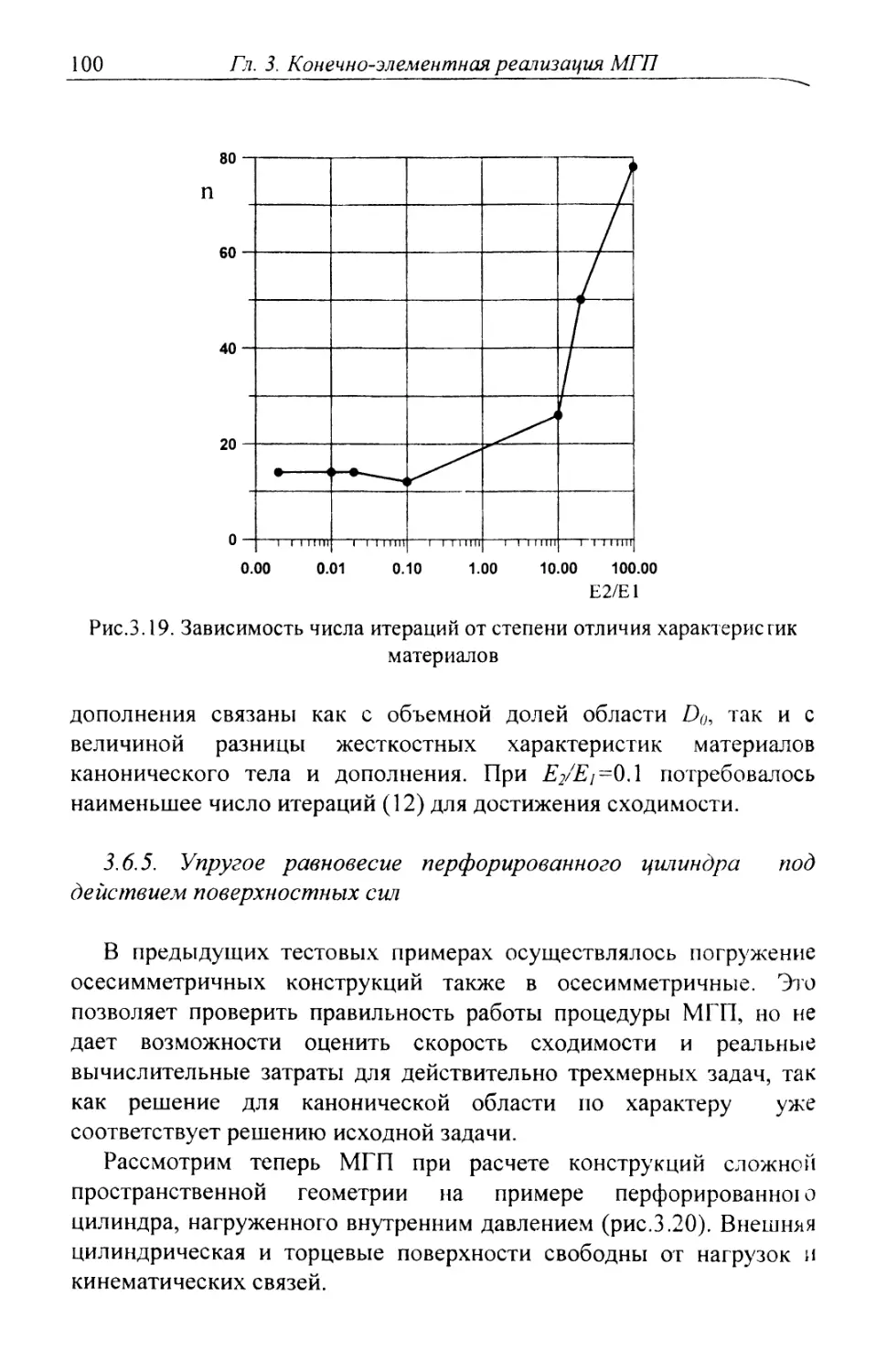
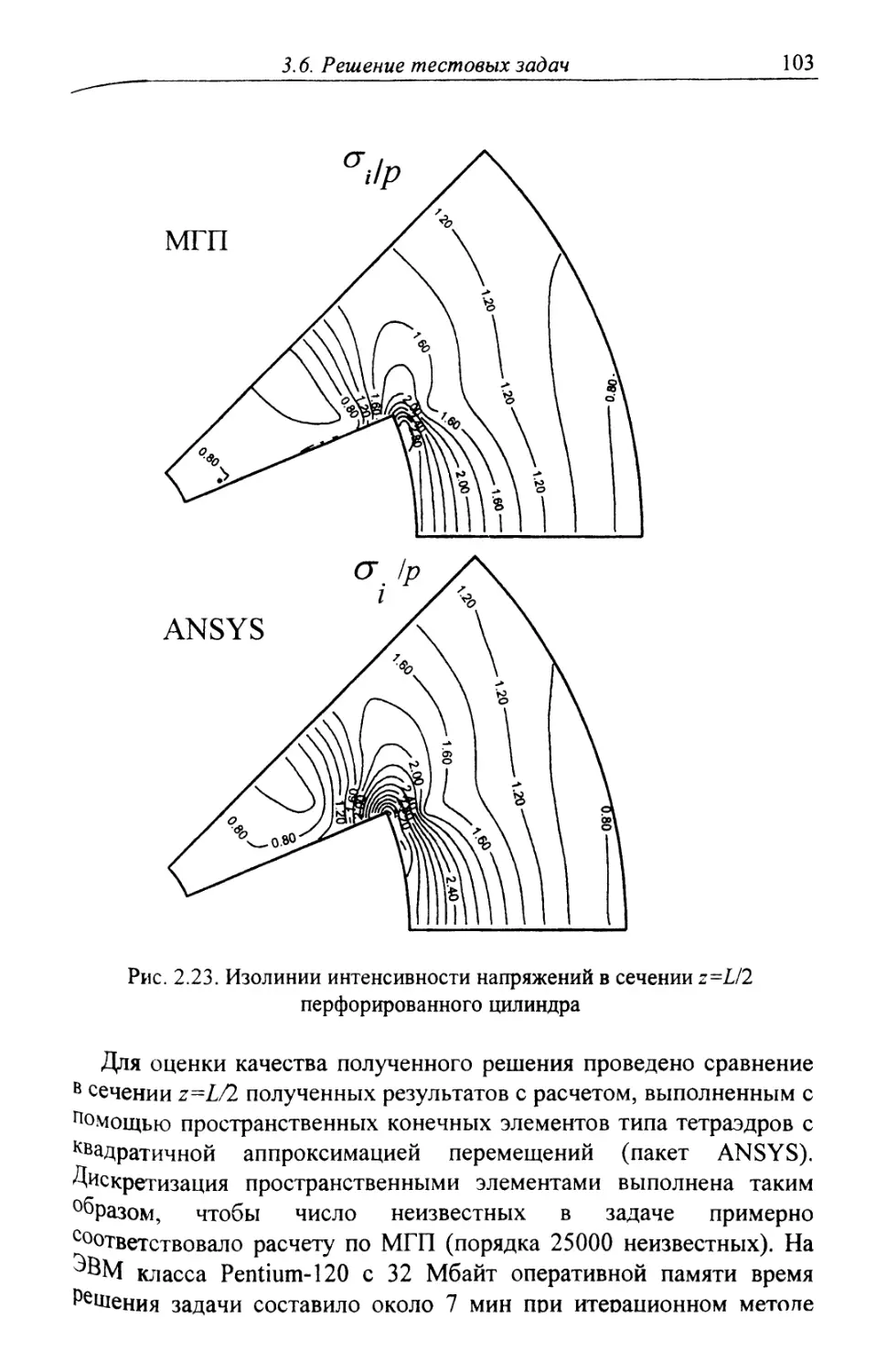
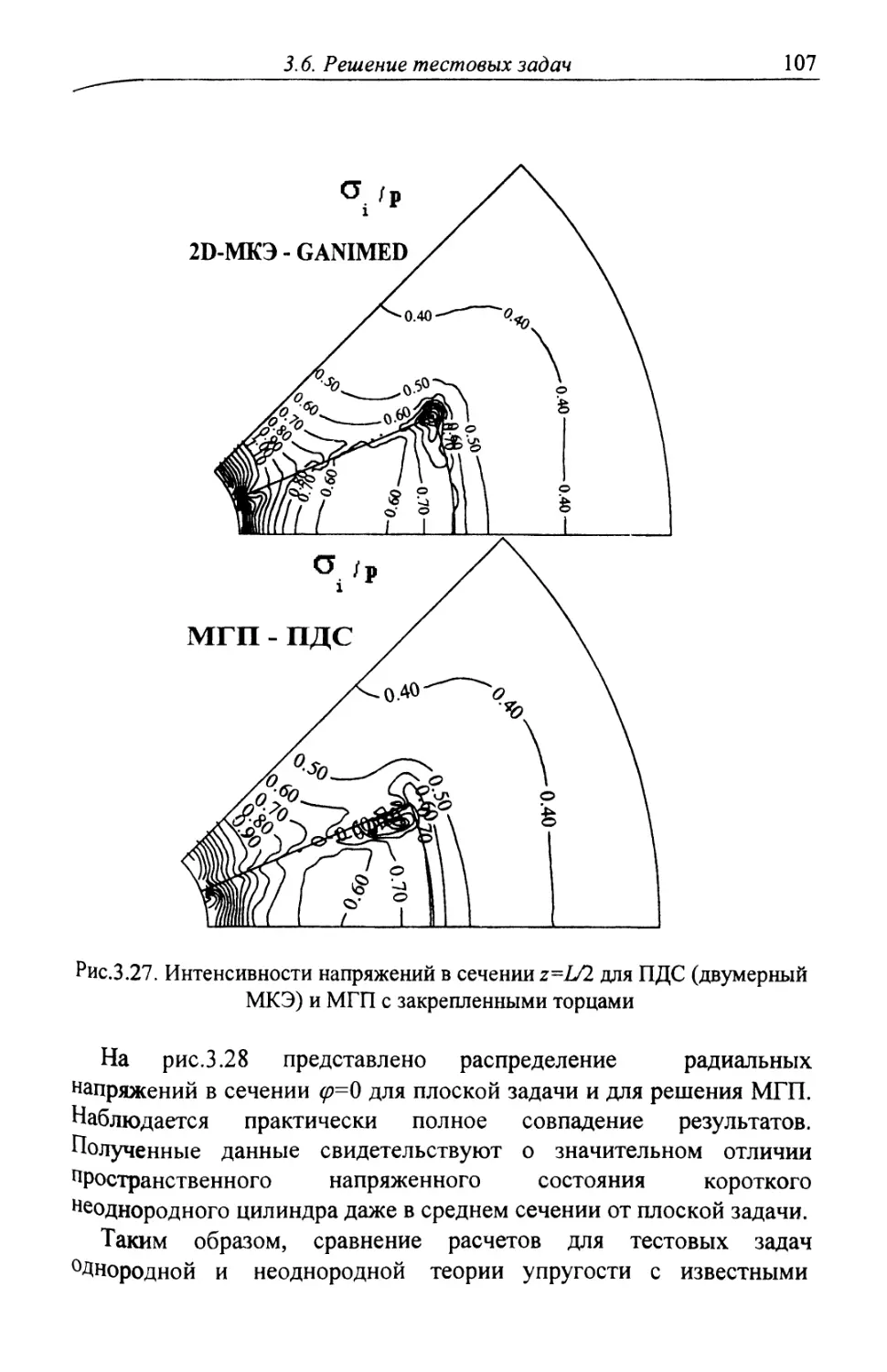
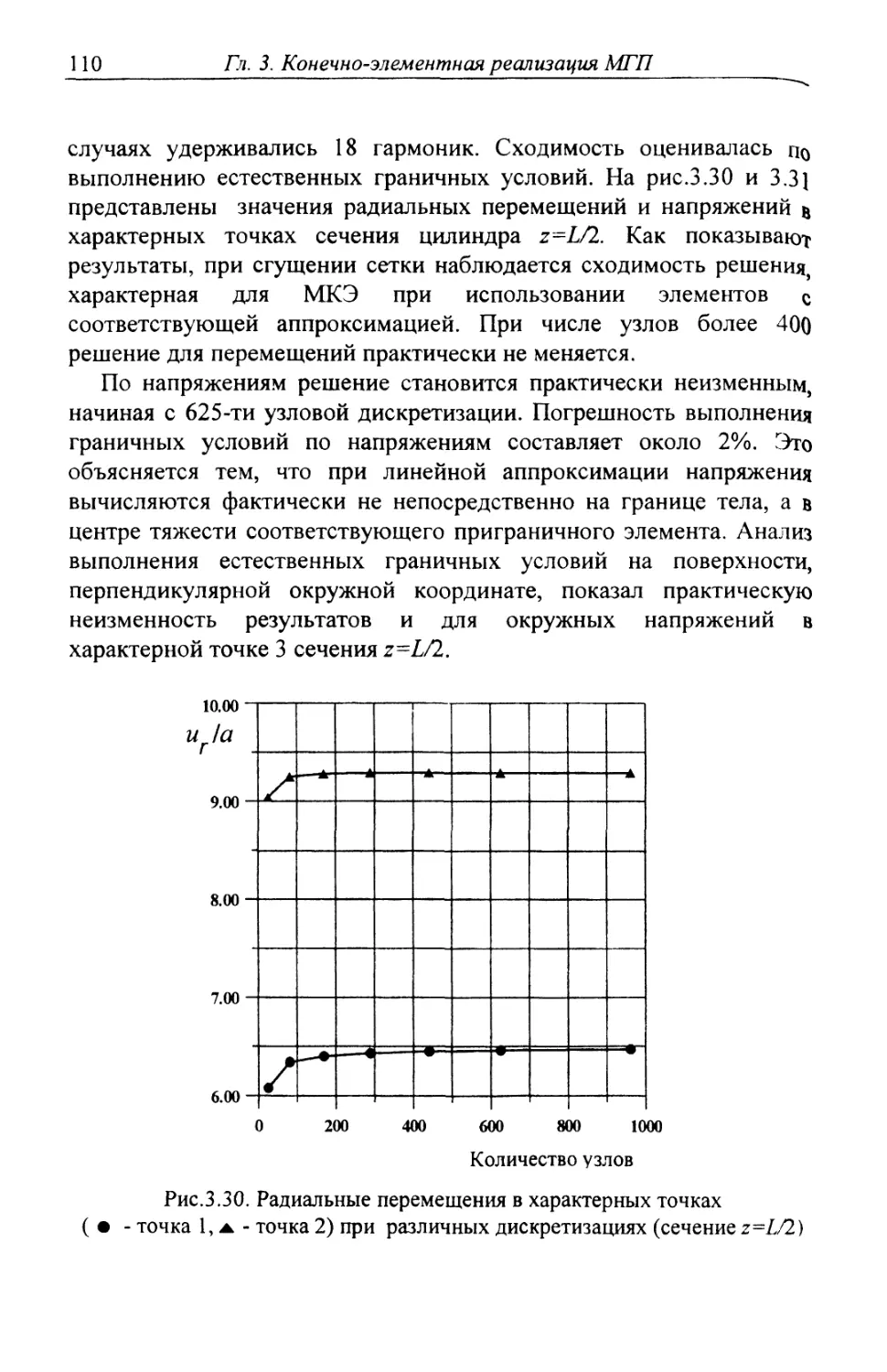
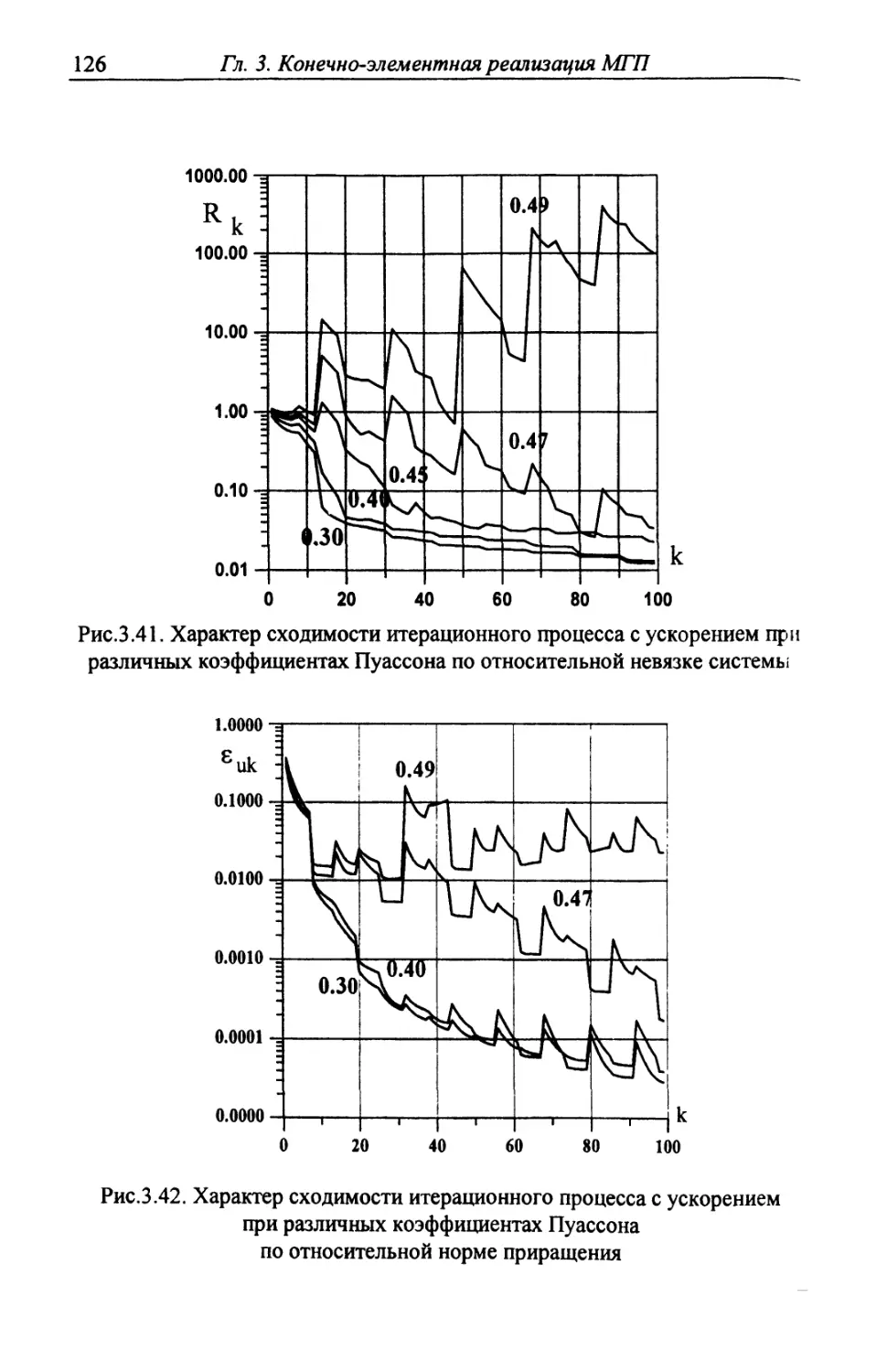
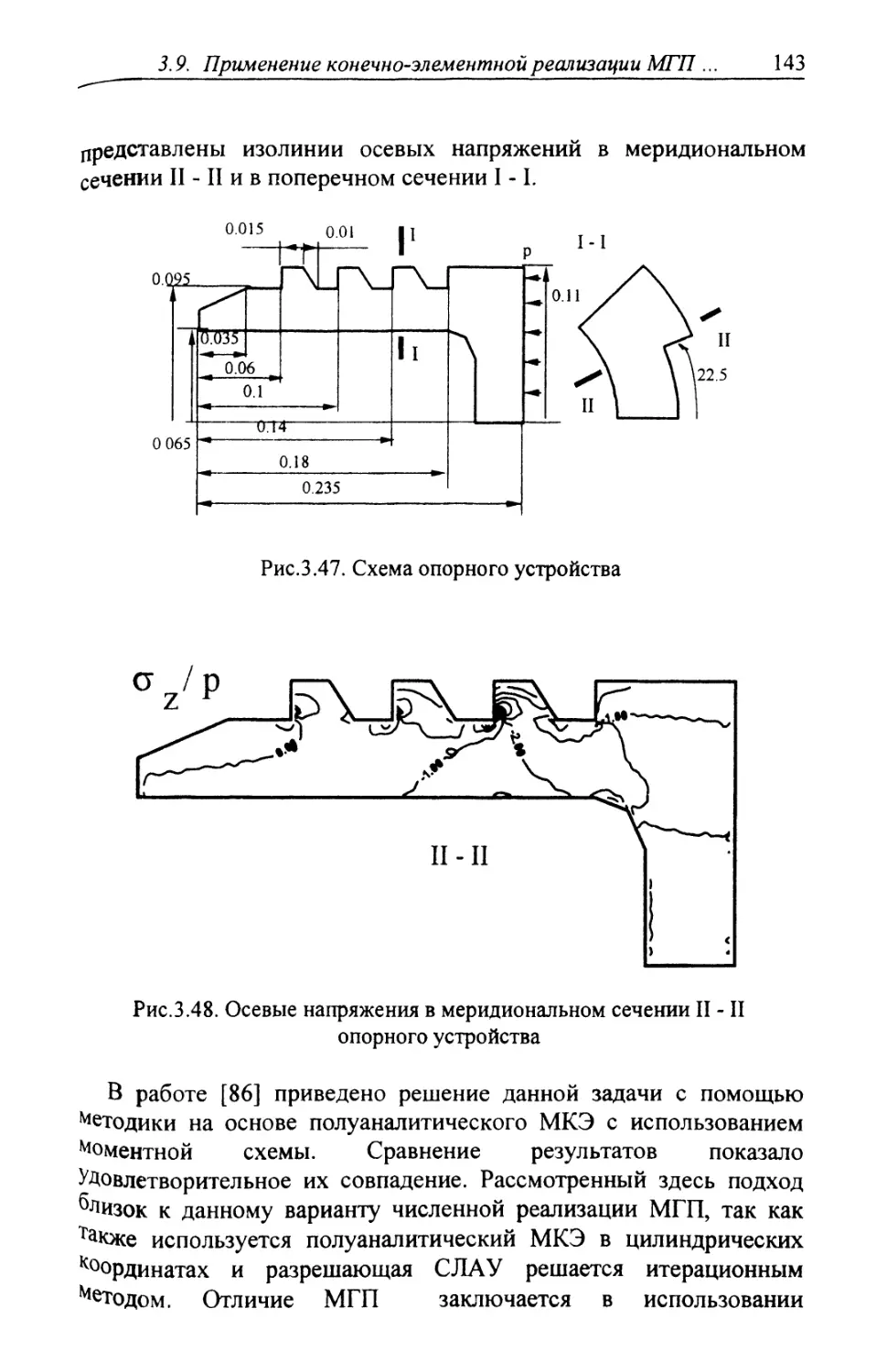
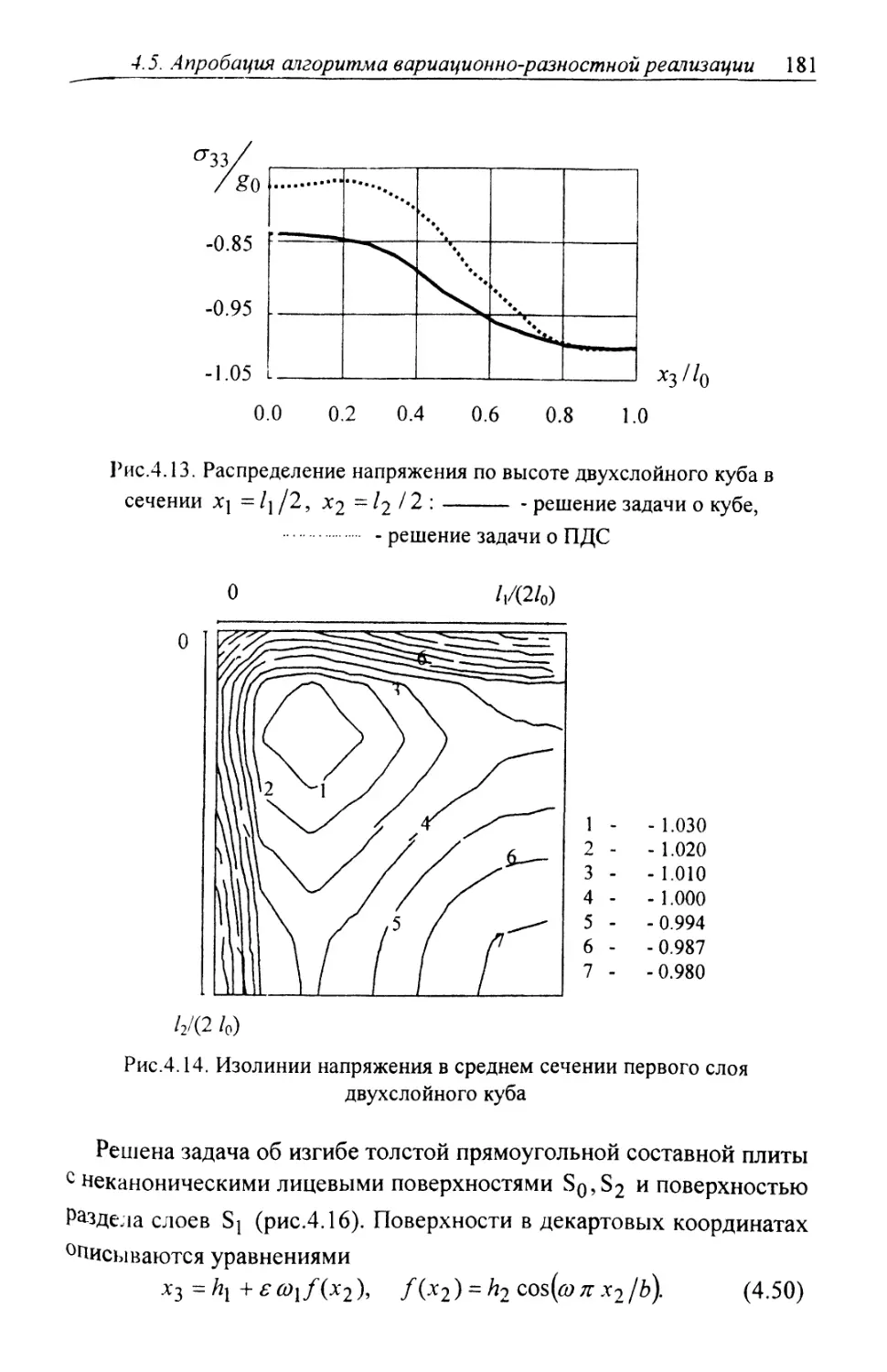
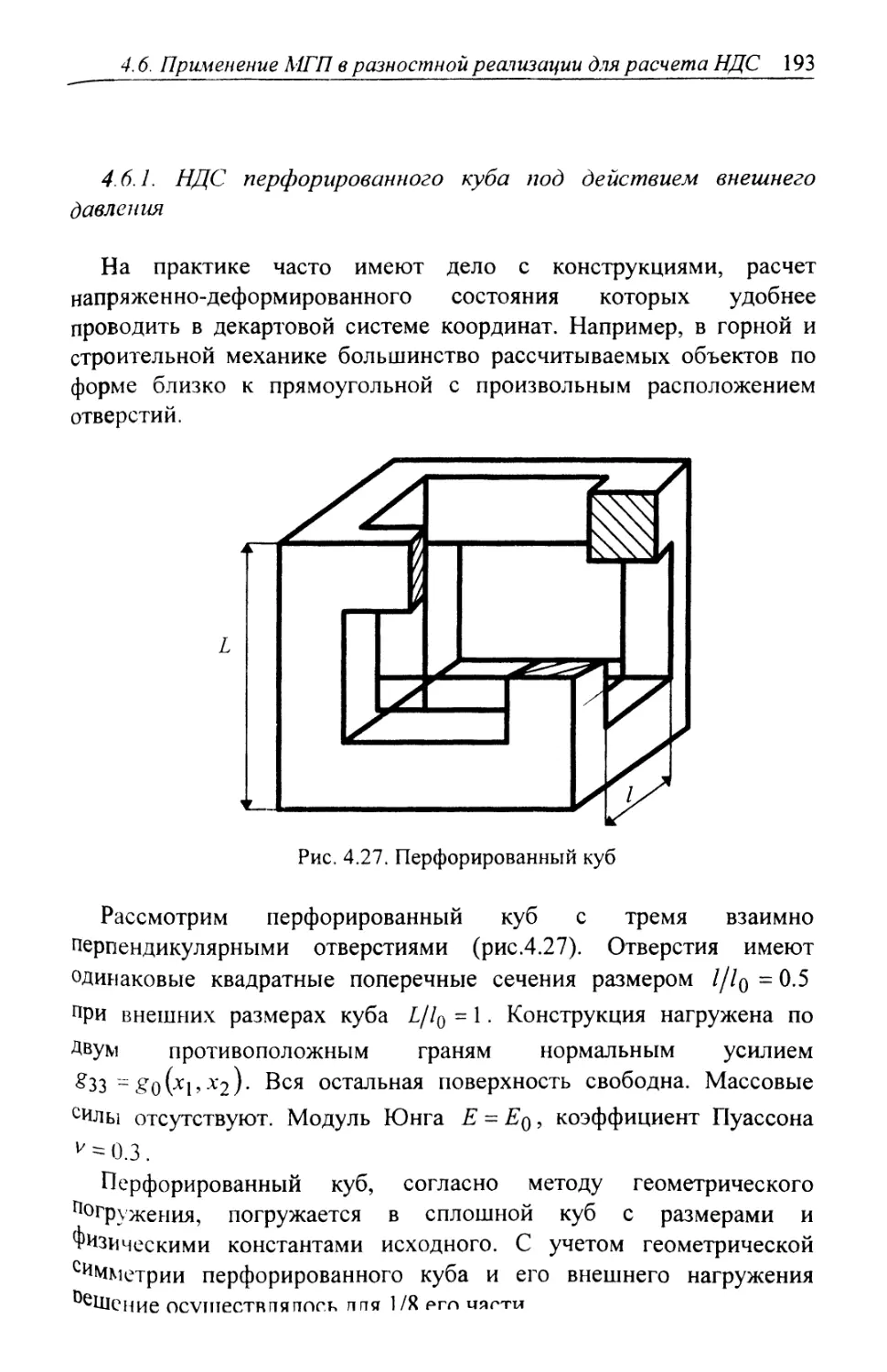
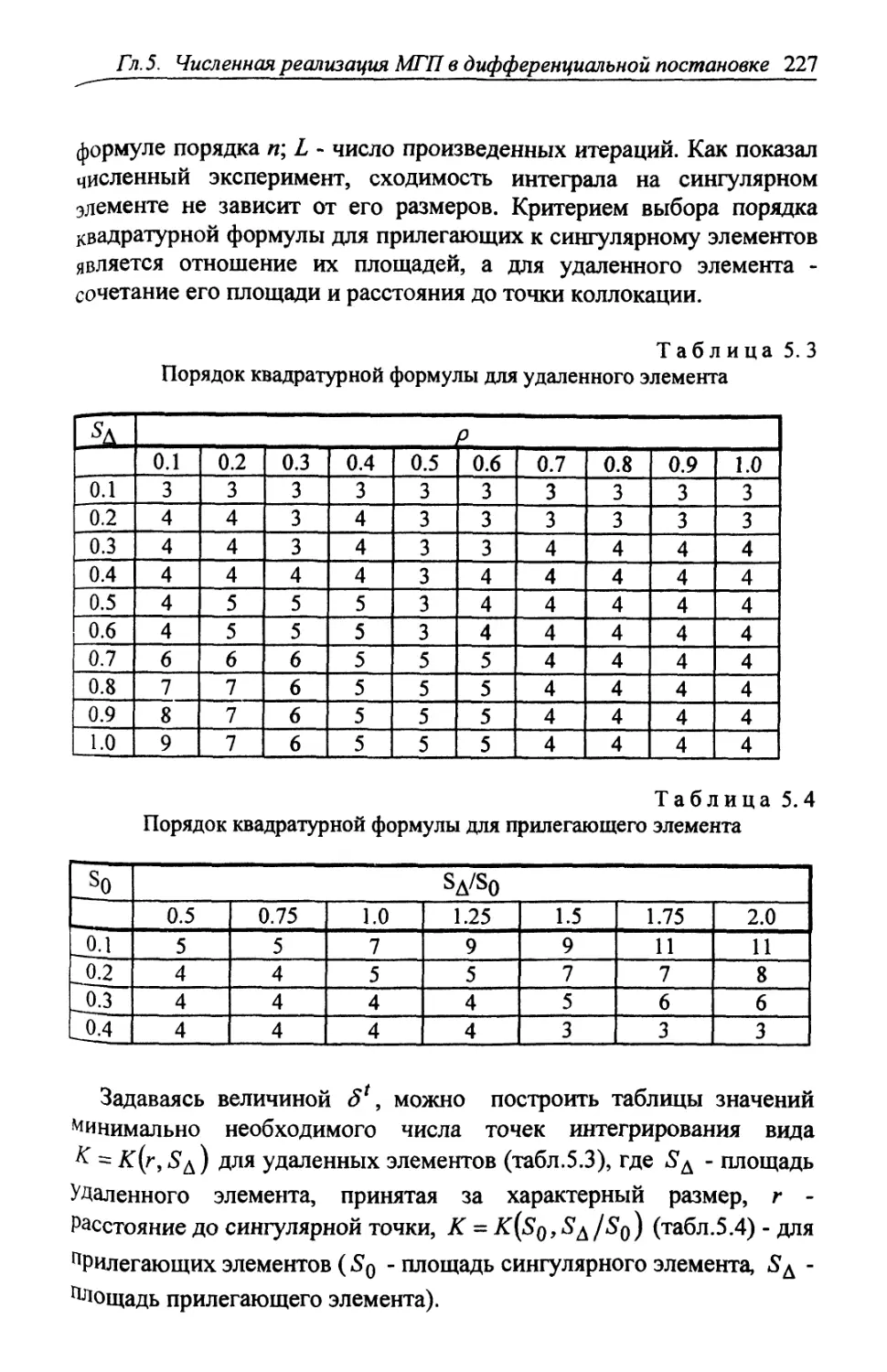
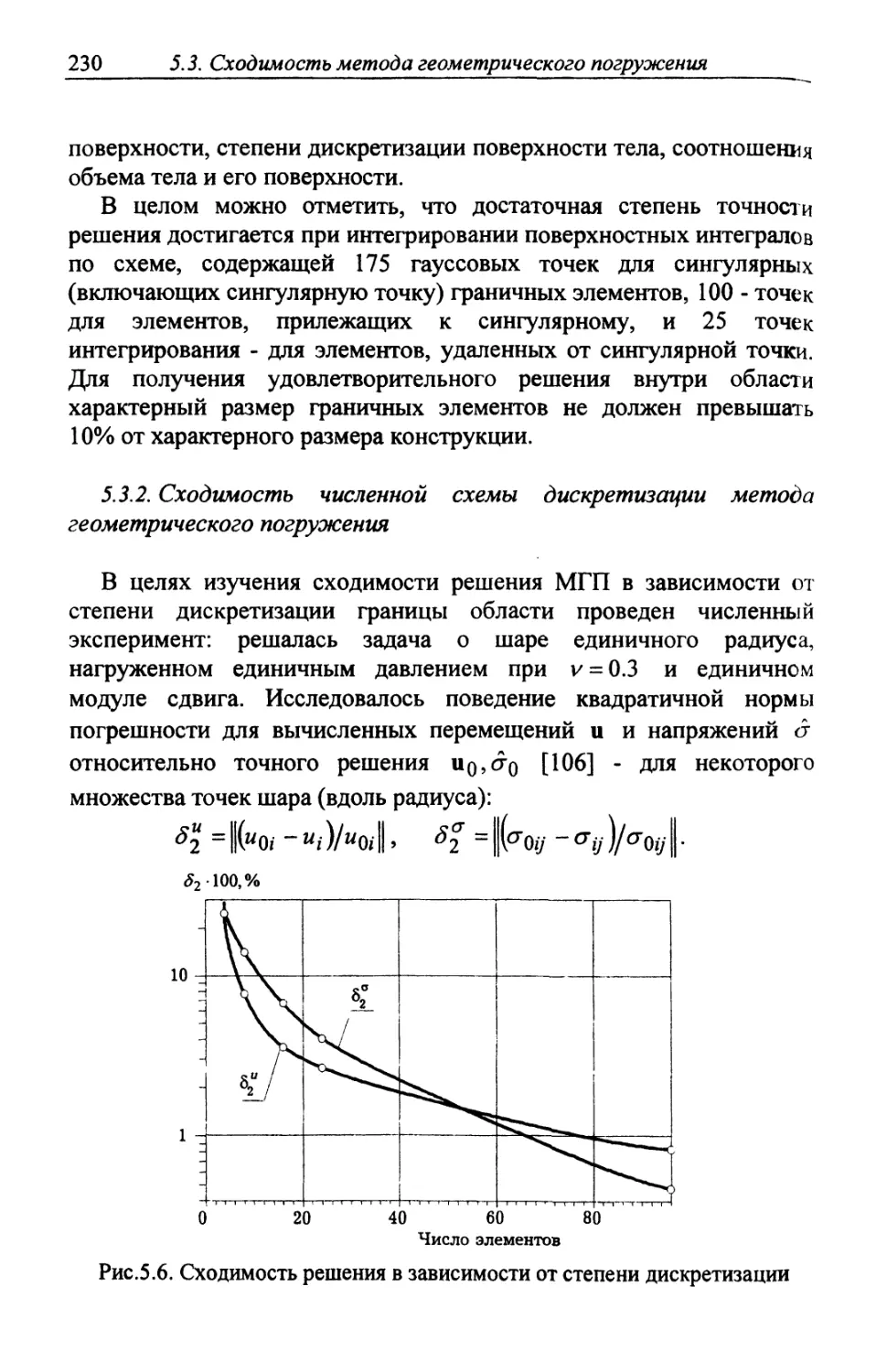
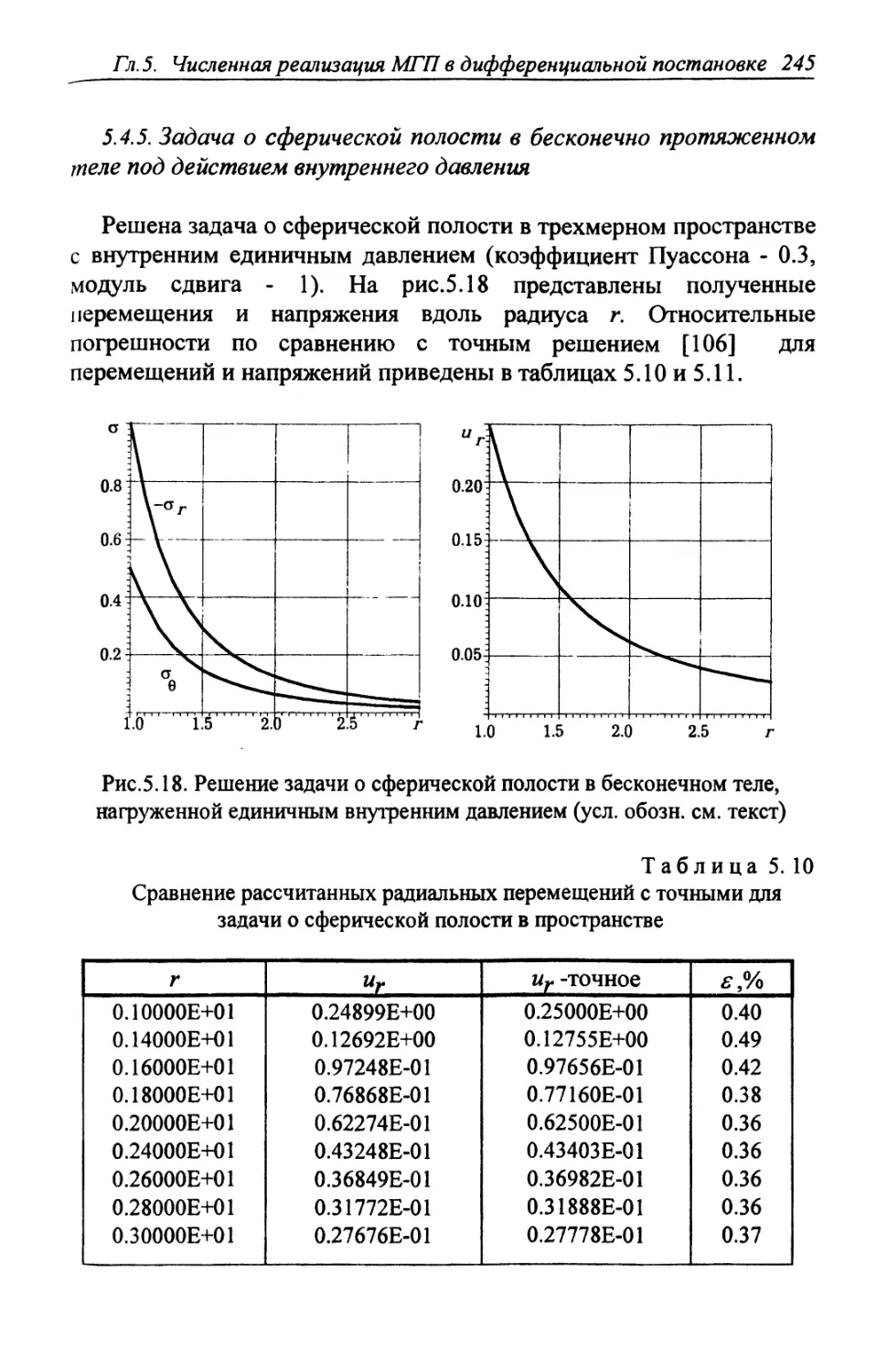
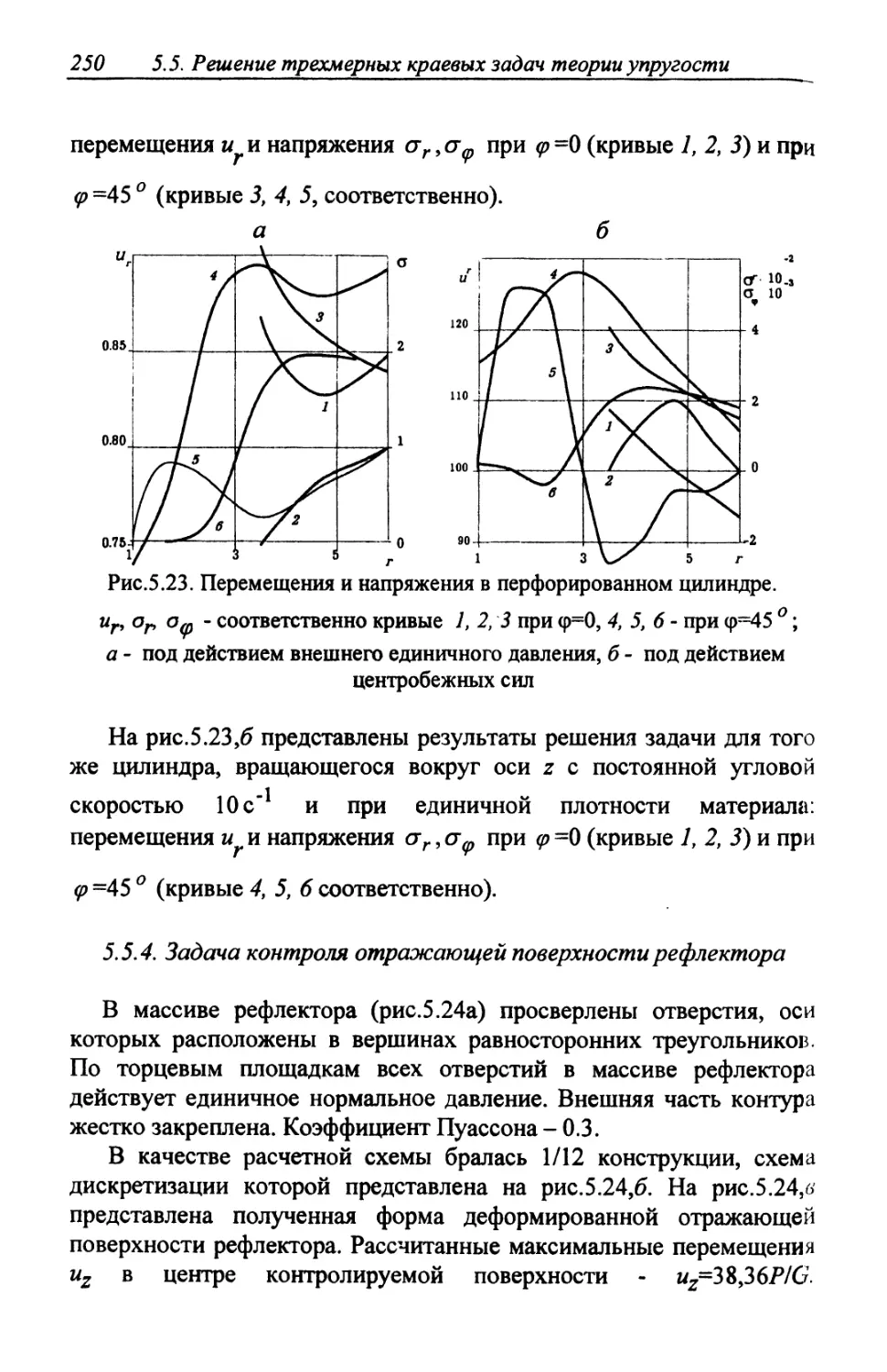
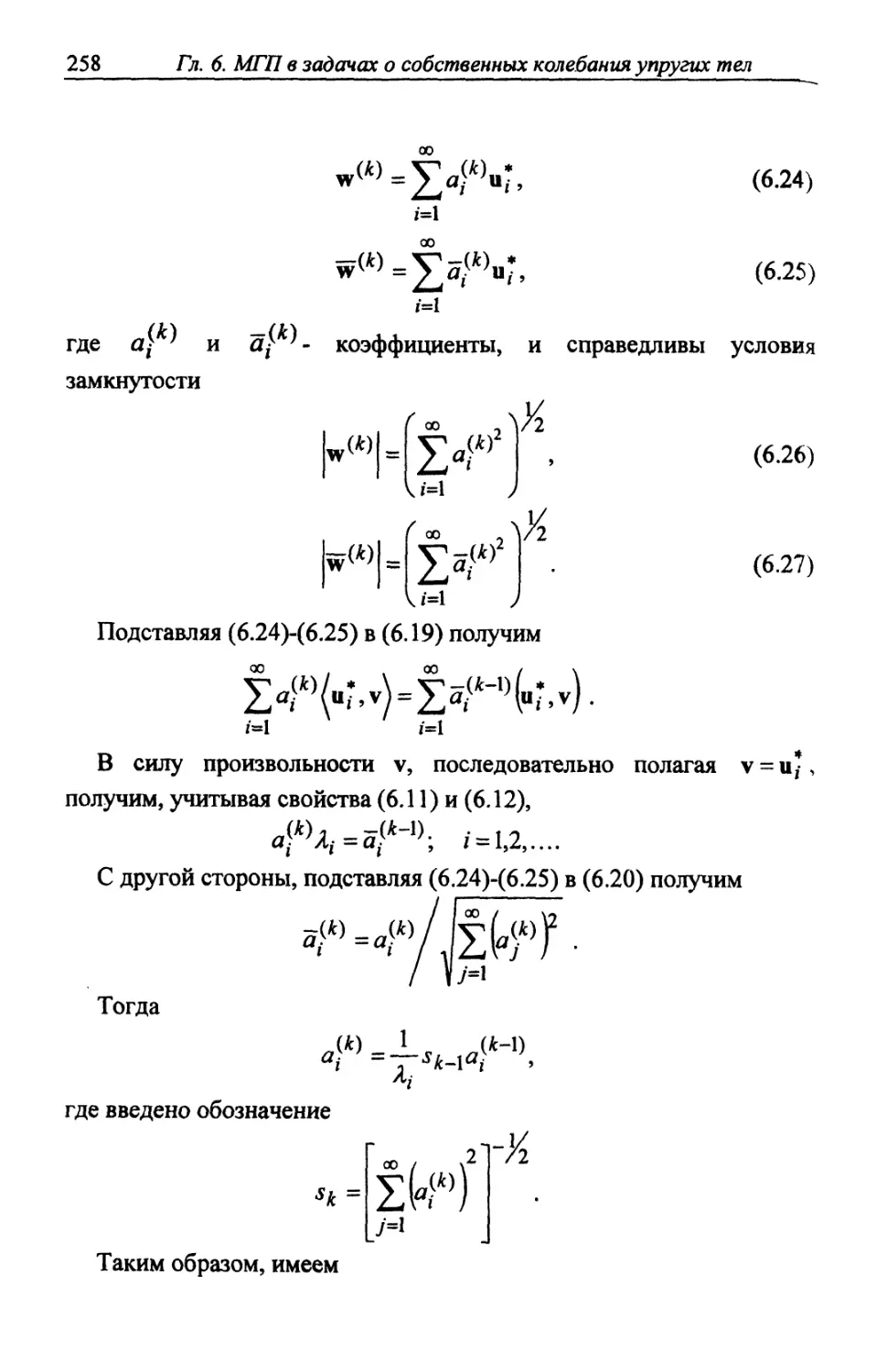
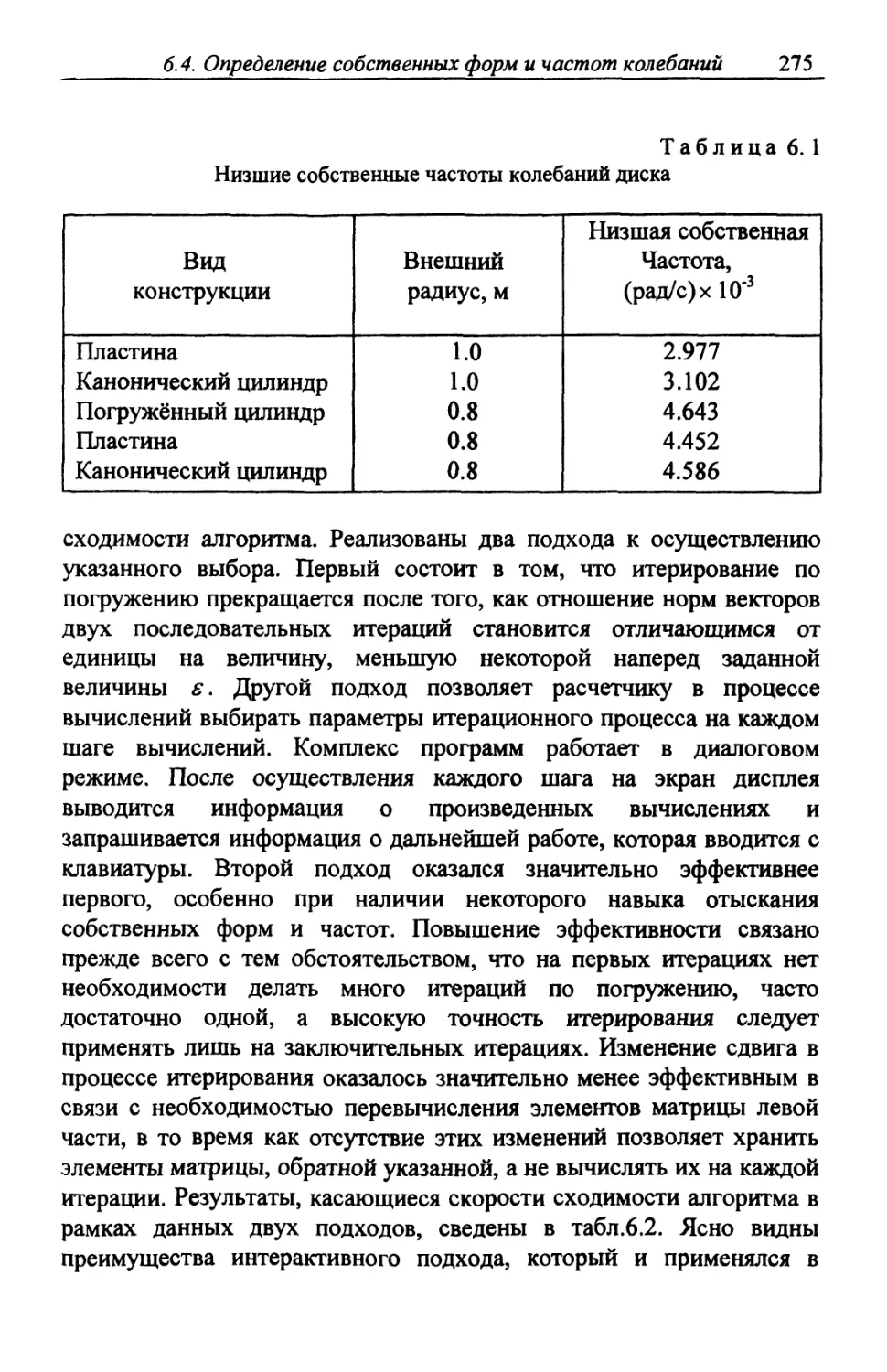
Автор: Шардаков И.Н. Труфанов Н.А. Матвеенко В.П.
Теги: механика деформируемых тел упругость деформация физика механика теория упругости
ISBN: 5-7691-0901-7
Год: 1999
Текст
И. Н. Шардаков
Н. А. Тру фанов
В. П. Матвеенко
МЕТОД
ГЕОМЕТРИЧЕСКОГО
ПОГРУЖЕНИЯ
В ТЕОРИИ УПРУГОСТИ
РОССИЙСКАЯ АКАДЕМИЯ НАУК • УРАЛЬСКОЕ ОТДЕЛЕНИЕ
ИНСТИТУТ МЕХАНИКИ СПЛОШНЫХ СРЕД
И. Н. Шардаков, Н. А. Труфанов,
В. П. Матвеенко
МЕТОД
ГЕОМЕТРИЧЕСКОГО ПОГРУЖЕНИЯ
В ТЕОРИИ УПРУГОСТИ
ЕКАТЕРИНБУРГ • 1999
УДК 539.3
Шардаков И.Н., Труфанов Н.А., Матвеенко В.П. Метод
геометрического погружения в теории упругости. Екатеринбург:
УрО РАН, 1999. 298 с. ISBN 5-7691-0901-7.
Изложены теоретические и вычислительные аспекты метода
геометрического погружения, ориентированного на решение трехмерных
краевых задач теории упругости для тел сложной пространственной
конфигурации. Изначально идея метода иллюстрируется на простых
примерах, а затем дается его строгое математическое обоснование.
Рассмотрены различные варианты численной реализации метода
геометрического погружения, основанные на методе конечных элементов,
методе граничных элементов, конечно-разностных схемах. Приводится
большое число примеров, иллюстрирующих возможности метода.
Книга предназначена для научных и инженерно-технических
работников, а также для аспирантов и студентов старших курсов,
занимающихся численными методами решения краевых задач механики
деформируемого твердого тела.
Рецензент доктор физико-математических наук профессор А.С.Кравчук
Отв. редактор доктор физико-математических наук профессор
И.Н.Шардаков
ISBN 5-7691-0901-7
8ПП6@3I998
И.Н.Шардаков
Н.А.Труфанов
В.П.Матвеенко
ИМСС УрО РАН, 1999 г.
Введение
ВВЕДЕНИЕ
Настоящая книга посвящена разработке теоретических основ и
изложению вычислительных аспектов нового метода решения
краевых задач теории упругости - метода геометрического
погружения. Развиваемый авторами на протяжении последних
пятнадцати лет [3,8,44,45,78,94-100,113-125] метод геометрического
погружения (МГП) ориентирован в основном на численное решение
краевых задач теории упругости, сформулированных на областях
сложной пространственной конфигурации. Традиционные
численные методы, такие как метод конечных элементов (МКЭ) и
метод граничных элементов (МГЭ), имеют в последнее время очень
серьезные достижения в этой области. Использование их в основной
процедуре МГП позволяет получать конечномерные аналоги
краевых задач со многими полезными качествами, зачастую не
присущими обычным формулировкам МКЭ и МГЭ.
Решение краевой задачи теории упругости является основой для
оценки напряженно-деформированного состояния (НДС)
конструкций, сооружений и объектов природного и техногенного
характера. Возникающие при анализе НДС пространственные задачи
являются одними из самых сложных задач механики, что
обусловлено как геометрией области, занимаемой телом, так и
свойствами материалов (нелинейностью, анизотропией и т.д.), а
также сложным пространственным распределением силовых
факторов. Наличие эффективных методов решения таких задач
позволяет оценить характер НДС не только в рамках упругой
постановки. Многие методы решения упругопластических,
вязкоупругих, нелинейных задач основываются на многократном
решении упругой задачи. С многократным решением упругих задач
приходится сталкиваться и в процессе оптимизации параметров
конструкции на стадии проектирования. Поэтому от эффективности
Решения пространственной задачи теории упругости может зависеть
Даже сама возможность расчета НДС конструкций.
Введение
Все используемые для решения пространственных задач методы
можно разделить на аналитические и численные.
Классические аналитические решения полной системы уравнений
трехмерной теории упругости известны прежде всего для объемных
тел относительно простой, канонической, формы, таких как
цилиндр, шар, параллелепипед и т.п. [11,23,31,37,40,41,66], и
преимущественно для изотропных тел. Основными аналитическими
методами являются методы интегральных уравнений (метод
потенциала), метод разделения переменных (метод Фурье и его
различные модификации) в векторной и скалярной формах.
К числу достаточно эффективных и наиболее распространенных
приближенных аналитических методов решения пространственных
задач можно отнести сходные между собой варианты метода
возмущения формы границы, разложения по параметру,
последовательных приближений и асимптотические методы,
которые известны под общим названием методов возмущения
[13,20,39,74]. Для решения пространственных задач с телами,
отличными от канонических, применены различные варианты
метода возмущения, позволяющего с помощью малого параметра
учитывать отклонение формы тела от канонической [12,58-60].
Для большинства реальных пространственных задач решение
приходится отыскивать численными методами, наибольшее
распространение среди которых получили метод конечных
разностей (МКР), вариационно-разностный метод, методы конечных
и граничных элементов и их многочисленные модификации.
МКР является мощным, хорошо разработанным средством
решения пространственных задач [16,24,25,71,80,81,84,85]. Малые
ограничения, накладываемые МКР на размерность задачи и
конфигурацию конструкции, - привлекательные черты этого метода.
С помощью МКР в настоящее время решено огромное количество
важных прикладных задач [4,16,26,55]. Однако трудности, связанные;
с относительно большими [50,105] требованиями к вычислительным)
ресурсам, неизбежным ухудшением сходимости по мере увеличения
различия исходной области от канонической, а также увеличения
размерности задачи [4,14,85], не позволили достичь значительных
успехов в расчетах сложных трехмерных объектов на основе этого
подхода. Возникают трудности и при учете граничных условий,
связанные с необходимостью введения дополнительных фиктивных
узлов и потерей порядка аппроксимации на неравномерной сетке.
Введение
Нередко применение конечно-разностных схем требует введения
граничных условий, дополняющих те, что имеются в
дифференциальной постановке задачи [105]. МКР требует
относительно небольших затрат на программирование, однако
программы, реализующие МКР, нуждаются в практически полной
переработке при переходе от одной задачи к другой.
Получили распространение в практике расчетов и вариационно-
разностные подходы, в которых разностные аппроксимации
используются непосредственно в вариационном уравнении. Для тел
канонической формы получены решения ряда задач в работах
[72,112]. В [73] вариационно-разностный подход был использован
для расчета тел с неканоническими границами. В [77] приведен ряд
решений, полученных вариационно-разностным методом для тел
произвольного меридионального сечения и тел кубообразной формы.
Наибольшее применение в практике расчетов получил метод
конечных элементов [9,17,87]. Наглядность, простота
математического аппарата, гибкость сделали его популярным
инструментом расчетчиков. Обширная библиография по МКЭ
содержится в работах [9,17,79,87]. В последние годы появилось
большое количество универсальных пакетов программ,
реализующих МКЭ. Бурный рост производительности
вычислительной техники сделал возможным решение задач с
помощью пространственного МКЭ даже на ПЭВМ.
Для больших пространственных конструкций сложной формы
получил развитие метод суперэлементов (МСЭ) [32,76,111],
позволяющий выполнить расчет при относительно невысоких
требованиях к оперативной памяти ЭВМ за счет разделения
расчетной области на относительно простые блоки (суперэлементы)
и выполнения расчета для каждого отдельного суперэлеменгга с
учетом их стыковки.
Главный конкурент МКЭ на сегодняшний день - метод граничных
элементов (МГЭ) [6,7,103]. Сложность математического аппарата
задержала его распространение в среде расчетчиков.
Привлекательность МГЭ заключается в снижении на единицу
размерности задачи при сохранении точности. Получаемая при этом
система алгебраических уравнений имеет существенно меньший
порядок, чем в МКЭ. Однако эта система имеет плотнозаполненную
и в общем случае несимметричную матрицу коэффициентов, что
является одним из недостатков метода. К недостаткам можно
Введение
отнести также сложность учета объемных сил, неоднородности
материалов конструкции, анизотропии. Существенны преимущества
МГЭ перед МКЭ при решении задач с бесконечными границами. По
числу публикаций в последние годы МГЭ значительно превосходит
все другие методы. Фактически МГЭ переживает бум, свойственный
МКЭ в 70-80-е годы.
Наличие недостатков МГЭ и МКЭ стимулирует развитие их
совместного использования [7,135], а также появление различных
модификаций, которые стремятся избежать основных недостатков
обоих методов.
Метод геометрического погружения, на наш взгляд, существенно
дополняет перечисленные подходы к решению пространственных
краевых задач теории упругости. Изложение материала в данной
работе организовано следующим образом.
Глава 1 посвящена введению в МГГТ. На простейших
иллюстративных задачах о растяжении однородных и неоднородных
стержней излагаются основные идеи метода, формулируются
вариационный и дифференциальный подходы в МГП, производится
сравнение с точными аналитическими решениями.
Глава 2 содержит математическую теорию МГП. Излагаются
теоретические положения метода геометрического погружения
применительно к краевым статическим задачам теории упругости
изотропных однородных, изотропных неоднородных и
анизотропных однородных тел. Основное внимание уделяется
строгому математическому обоснованию итерационных процедур
метода и доказательству их сходимости. Рассматриваются две
взаимосвязанных формулировки МГП: вариационная и
дифференциальная. Вариационный подход базируется на принципе
минимума общей потенциальной энергии упругого тела и
ориентирован в большинстве случаев на численную реализацию с
применением вариационно-разностного метода или метода конечных
элементов. Дифференциальная формулировка МГП позволяет
построить эффективный гранично-элементный метод численного
решения упругих задач для областей сложной формы.
Как и любой другой численный метод, МГП требует эффективной
численной реализации, а также всестороннего изучения его
сходимости, особенностей, границ применимости и т.д.
В главе 3 построен обобщенный конечномерный аналог
вариационной формулировки МГП на основе полуаналитического
Введение
МКЭ с разложением в ряд Фурье по угловой координате функций
задачи, позволяющий в рамках единого подхода учитывать
сложность геометрии области и неоднородность физико-
механических свойств материалов. На ряде тестовых задач
проиллюстрирована работоспособность программы, реализующей
МГП. Точность и достоверность результатов подтверждены
сравнением с известными аналитическими и численными
решениями. Рассмотрены вопросы практической сходимости
численной реализации МГП в зависимости от степени
дискретизации, а также характеристик материалов конструкции.
Даны рекомендации по критериям остановки итерационного
процесса. Значительное внимание уделено различным
вычислительна аспектам метода, позволяющим существенно
повысить эффективность расчетов: использованию технологии
разреженных матриц, ускорению сходимости итерационного
процесса, использованию нескольких вариантов многошаговых
процедур расчета. Описан один из способов повышения точности
вычисления напряжений и деформаций вблизи границы тела.
Приводятся примеры решений ряда сложных пространственных
задач теории упругости.
Глава 4 посвящена построению и практической реализации
вариационно-разностных схем МГП для задач однородной и
неоднородной теорий упругости в прямоугольных и цилиндрических
координатах. Рассмотрены наиболее эффективные методы решения
системы разностных уравнений. Приведено решение ряда тестовых
задач. Выполнены численные эксперименты по выбору наиболее
эффективного метода решения системы разностных уравнений Й по
определению оптимальных итерационных параметров. Даны
рекомендации по организации итерационного процесса МГП при
решении неоднородных задач. Исследовано напряженно-
Деформированное состояние нескольких конструкций сложной
формы.
В главе 5 описан алгоритм численной реализации
Дифференциальной постановки МГП, обсуждаются вопросы
Дискретизации и численной аппроксимации, вычисления
сингулярных интегралов, адаптивные схемы интегрирования.
Рассматриваются вопросы сходимости итерационной процедуры
МГП, учета симметрии расчетной области в алгоритме, учета
Различных вариантов статических, кинематических граничных
Введение
условий и объемных сил. Демонстрируются достоверность
построенных алгоритмов и эффективность подхода. Решен ряд
классических задач теории упругости. Решения сравниваются с
известными аналитическими и численными, полученными другими
методами. Приведены примеры расчета конструкций со сложной
геометрической конфигурацией.
В главе 6 приведена постановка задачи о собственных колебаниях
трехмерного упругого тела. Предлагается подход к ее решению на
основе использования метода геометрического погружения. Суть
подхода состоит в том, что с помощью метода обратных итераций
задача определения пространственных собственных форм и
собственных частот колебаний сводится к итерационной
последовательности статических задач для этого же тела с
фиктивными массовыми силами. Каждая такая задача решается с
помощью МГП. Обоснована сходимость в случае последовательного
отыскания нескольких низших собственных значений и
соответствующих им пространственных форм. Приведены примеры
построения собственных форм и вычисления соответствующих им
собственных частот колебаний сложных по конфигурации объемных
конструкций. Проведен сравнительный анализ способов организации
вычислений.
Авторы книги выражают глубокую признательность профессору
1 И.Е.Трояновскому|, принимавшему активное обсуждение основных
положений МГП. Также авторы благодарят П.В.Булавина,
С.В.Попова, К.С.Пустовойта, М.А.Труфанову, А.А.Суходоеву и
1 Н.В.Шакировук выполнивших большой объем работ по численной
реализации МГП.
Глава 1
ВВЕДЕНИЕ В МЕТОД ГЕОМЕТРИЧЕСКОГО
ПОГРУЖЕНИЯ
1.1. Введение
Метод геометрического погружения (Mill) представляет собой
процедуру сведения краевой задачи для уравнений в частных
производных эллиптического типа, сформулированной на области
произвольной конфигурации, к задаче на некоторой другой области,
включающей в себя исходную и имеющую "хорошую" форму с
точки зрения более простого построения решения. Идеальным
является случай, когда удается прийти к задаче, имеющей известное
аналитическое решение. Аналитические решения в основном удается
строить для областей, границы которых совпадают с координатными
линиями или поверхностями (круг, прямоугольник, эллипсоид,
сфера, круговой цилиндр и т.п.), такие области в дальнейшем будем
называть каноническими. Стремление перейти к задаче на
канонической области не обязательно может быть связано с
желанием использовать аналитические решения, во многих случаях
для канонической области значительно упрощается построение
конечномерного аналога при использовании численных методов,
улучшаются свойства матрицы коэффициентов разрешающей
системы линейных алгебраических уравнений (СЛАУ), облегчается
выбор базисных функций при применении приближенных методов.
В данной главе, оставив в стороне строгие математические
обоснования МГП, мы на простейших примерах рассмотрим
основные идеи погружения, этапы получения решения и возможные
общие подходы. Отметим, что Mill ориентирован на решение
трехмерных краевых задач теории упругости, теплопроводности,
механики жидкости и т.д. для областей сложной формы и
рассматриваемые здесь задачи носят чисто иллюстративный и
методический характер.
10 Гл.1. Введение в метод геометрического погружения
1.2. Иллюстративная задача: вариационная формулировка
метода геометрического погружения
Рассмотрим одноосное растяжение линейно упругого
однородного стержня, закрепленного на левом конце и
нагруженного силой Р на правом конце (рис. 1.1).
Рис. 1.1. Расчетная схема стержня
Механические свойства стержня характеризуются модулем
упругости Е , геометрия - длиной / и постоянной площадью
поперечного сечения F. Краевая задача теории упругости в этом
случае включает в себя:
уравнение равновесия
^ = 0, *<=(<>,/), A.1)
dx
геометрическое соотношение
е = ^-9 *е@,/), A.2)
dx
физическое соотношение (закон Гука)
ст = Ее9 хе{0,1), A.3)
граничные условия
и(о) = О, A.4)
cr(l)F = P, A.5)
где (j,s, и - напряжение, деформация и перемещение
соответственно.
Из уравнения A.1) следует: <т(х)= const = C, а из граничного
условия A.5) определяется константа С = P/F = а . Тогда, согласно
A.3), деформация постоянна в стержне и равна е ~ РI' EF, а функция
перемещений находится интегрированием уравнения A.2) с
использованием граничного условия A.4). Таким образом, решение
краевой задачи (!.!)-A.5) имеет вид
1.2. Иллюстративная задача: вариационная формулировка
11
s(x) = -L, u(x) = ?. A.6)
Последовательно подставив соотношения A.3) и A.2) в уравнение
равновесия A.1) и граничное условие A.5), получим формулировку
краевой задачи в перемещениях:
и@) = 0,
dx
EF
A.7)
A.8)
A.9)
решение которой, очевидно, имеет вид A.6).
Известно [92,93], что решение краевой задачи A.1)-A.5) или
A.7)-A.9) доставляет минимум квадратичному функционалу общей
потенциальной энергии стержня:
/
Ya*JJ\\2
A.10)
где v(x) - так называемые кинематически возможные функции
перемещений, один раз дифференцируемые и удовлетворяющие
граничному условию A.4), и(х) - та из множества функций v(jc),
которая минимизирует функционал A.10) и является обобщенным
решением [92] краевой задачи A.7)-A.9).
Рис Л .2. Схема погружения рассматриваемого стержня в канонический
Мысленно поместим рассматриваемый стержень в некоторый
Другой, "канонический", имеющий такой же модуль упругости Е,
Площадь поперечного сечения F, но большую длину - /0 > /, и
Скрепленный на обоих концах (рис. 1.2). Заштрихованную область
^У называть дополнением реальной области до канонической.
12 Гл. 1. Введение в метод геометрического погружения
Расширим определение функций v(x) до отрезка [0, /q ] при условии
v(/0) = 0 и выполним тождественное преобразование функционала
A.10):
Щ
dx
о /
Очевидно, что вследствие тождественности выполненного
преобразования минимумы функционалов A.10) и A.11) совпадают.
Из этого факта следует, что функция и(х)9 доставляющая минимум
функционалу A.11) , является обобщенным решением краевой
задачи A.7)-( 1.9) в области [о, /].
Разыскав первую вариацию функционала A.11) и приравняв ее
нулю, получим вариационное уравнение метода геометрического
погружения в виде
ddx
dx dx J dx dx EF
0 /
или, выбрав в качестве v(x) сумму v(*) = u(x) + S м(х), где 8 и -
вариация решения и(х), в виде
/о /о
о о
J dx dx j d
dx dx EF
0 /
Решение вариационного уравнения МГП будем отыскивать
методом итераций:
Cduk dSuk J Cduk~l dSuk J P , к(л , t
i rfx- I c{x + Su (I), A: = 1,2 , A.14)
J dx dx J dx dx EF w
0 /
1.2. Иллюстративная задача: вариационная формулировка 13
причем в дальнейшем будет Доказана гарантированная сходимость
подобных итерационных процедур при любом выборе начального
приближения.
На каждой итерации, в соответствии с уравнением A.14),
решается краевая задача для канонической области. Пусть
отсутствует какая-либо информация о характере решения и(х)в
области [О,/о]. Тогда введем в рассмотрение некоторую систему
{Un}™=i ортогональных функций в канонической области и
используем разложение
при этом функции Un(x) должны удовлетворять кинематическим
граничным условиям. Например, в нашем случае можно
использовать неполный тригонометрический ряд Фурье
00 / \
~г~ >
'о ;
A.15)
причем всегда и@) = m(/q) = 0.
Нетрудно убедиться, что подстановка A.15) в A.14) приводит к
системе линейных алгебраических уравнений относительно
коэффициентов разложения ап A.15):
сп О
О с22
О О
0
О
С33
?
,(*)
Г (Ml
а} >
h
/з
где диагональный характер матрицы коэффициентов вызван
ортогональностью тригонометрических функций sin (я* пх/Iq) на
отрезке [0>/0]. Таким образом, на каждой итерации имеем набор
формул для вычисления коэффициентов разложения A.15), а
количество членов ряда выбирается конечным, исходя из характера
Решения.
Поскольку в случае со стержнем можно заранее предсказать вид
Функции и(х) в канонической области, то это обстоятельство
позволяет достаточно просто проиллюстрировать сходимость
14 Гл. 1. Введение в метод геометрического погружения
вариационного уравнения A.14) метода геометрического
погружения. Выберем искомое решение, удовлетворяющее нулевым
граничным условиям, в виде
a/f^ i***k <u6)
Подстановка выражения A.16) в вариационное уравнение A.14) и
использование основной леммы вариационного исчисления [52]
приводят к итерационному уравнению для отыскания коэффициента
ах\
\х8ах, О < х < I,
8и(х)-\ ,*-//)„
Пусть а\ ' = 0 , тогда из A.17) следует а)' = 1 |.
EF{ lQ)
Выполнение следующих итераций дает результаты:
4]. iD
/02J ?Fl /03
Таким образом, а> ' > , так как / < /n •
1 &»oo ?f u
Получен результат решения задачи по методу геометрического
погружения:
в реальной области х е [о,/]
/ ч Л Р _Р ,
U\X I — , ? , О" п 1
V ; EF EF p F
в дополнении реальной области до канонической х е [/, /q ]
/ ч Р/ *-/<) Р/ 1
V ; EF l-l0 EF l-l0 d F /-/0
Таким образом, полученное для всей канонической области
решение в точках х е [о,/], соответствующих реально исследуемому
1.3. Иллюстративная задача: дифференциальная формулировка 15
стержню, совпадает с точным решением краевой задачи. На границе
реальной и дополнительной областей в точке х = 1 напряжения
(рис.1.3) и деформации меняются скачком, что можно трактовать как
приложение в точке х-l дополнительного сосредоточенного
воздействия величиной R = f{<jр - о*^) = PIq /(/о - /),
направленного вдоль оси д: и обеспечивающего, совместно с силой
Р, такое же деформирование части канонического стержня [О,/]
(см. рис. 1.2), как и деформирование реального стержня под
действием силы Р (см. рис.1.1).
PI/EF
Р I
F/-/0
Рис. 1.3. Эпюра напряжений и перемещения (штриховая линия) в
каноническом стержне.
1-3. Иллюстративная задача: дифференциальная формулировка
метода геометрического погружения
Вернемся к вариационному уравнению МГП A.12) и рассмотрим
Дифференциальную формулировку соответствующей ему краевой
задачи. Проинтегрируем по частям интеграл в левой и правой частях
Уравнения A.12), предполагая существование вторых производных
Функции и(х) на отрезке [0,/0] и выполнение нулевых граничных
Условий и(о) = w(/q ) = 0, в результате получим:
16 Гл. I. Введение в метод геометрического погружения
'W) - 'W)
О о О
Cd2u{x) i ч , [
\^-v{x)dx = -\
A.18)
(du(x)} / ч
где производная —— вычисляется для функции и[х) в
V dx Jx=l
дополнении х е [/, /q j .
Используя понятие обобщенной единичной ступенчатой функции
Хевисайда h(x)n сингулярной обобщенной функции Дирака ^(л)
[21], преобразуем уравнение A.18) к виду
• v(x)dx =
dx2 \ I
x=l
-^1 -v{x)dx, A.19)
из которого, в силу произвольности в интервале @,/q) функций
v(x), следует, что решение вариационной задачи A.12]
соответствует в обобщенном смысле решению краевой задачи:
2 [ \
dx2 [ \ dx Jx=l
Известно [6], что решение краевой задачи на каноническов
области
d2u(x)
dx2
= f(x), xe{0,l0), u{Q) = u{lo)=Q A.21]
можно построить с использованием функции Грина G(x, s) в виде
k
u{x)=\G{x,s)f{s)ds,
1.3. Иллюстративная задача: дифференциальная формулировка 17
—[s-l0), xls,
'0
—( 1 )
'о
A.22)
Если f(x) = CS(x-l), то, учитывая свойства [21] функции
Дирака, получим
/). A.23)
Будем разыскивать решение краевой задачи A.20) итерационным
методом:
EF
dx
dx
,/0), A.24)
Тогда на к- й итерации имеем краевую задачу вида A.21) с
построением решения в виде A.22), A.23). Выберем нулевое
начальное приближение ы'°'(х)=0. Тогда, согласно A.24), A.22) и
A.23):
EF'
dx'
EF
JL.L(x-i0),
Вторая итерация:
dx'
'Жь'
18
Гл. 1. Введение в метод геометрического погружения
Wo
Третья итерация:
7.х=/
Четвертая итерация:
v dx J ,
^ ^ X-l
Продолжая итерации, получаем:
_Р_ 1_
ef'i0
\ dx
V / х=1
'о2
ik-l
' /*Л
V
/
o
p
IF
/ /2
— + — + ... + ¦
h
'о ;
Используя выражение для суммы геометрической прогрессии и
устремляя к -> со, приходим в пределе к точному решению задачи:
Рх
«(*) =
EF'
Р х-10
EF 1-1
о
I 4. Иллюстративная задача: растяжение неоднородного стержня 19
В данном случае нетрудно оценить скорость сходимости МГП.
Определим скачок, в напряжениях в точке х = 1:
R® (к) (к) ^ ' |2
где:
М
Точное значение — =
~ /
Очевидно, что точное значение скачка напряжения
представляется полной суммой S геометрической прогрессии со
знаменателем у* , а приближенное - частичной 5* '.
/10
= л&
F
F
и
1-1
Таким образом, итерационный процесс сходится со скоростью
геометрической прогрессии, знаменатель которой I/Iq всегда
меньше единицы
В дальнейшем будет показано, что в выборе граничного условия
на правой границе х = 10 канонической области имеется
определенный произвол, и можно, например, кроме условия
и Vq ) = 0, использовать условие
ст(/0) = Щ —
=0.
**4. Иллюстративная задача: растяжение неоднородного стержня
При решении неоднородных задач погружение становится
физико-геометрическим. Рассмотрим особенности этой процедуры
На примере деформирования неоднородного стержня (см. рис. 1.1),
20 Гл. 1. Введение в метод геометрического погружения
характеризующегося модулем е(х). Функция Е(х) может быть
кусочно-непрерывной, имеющей конечное число точек разрыва
первого рода. Тогда решение краевой задачи A.1)-A.5) с учетом
зависимости модуля от координаты имеет вид
\гу A25)
v ' F E(x)F x ' F
0
Формулировка краевой задачи в перемещениях в этом случае
имеет вид
-
(О,/) , A.26)
и@)=0, A.27)
Решение краевой задачи A.26)-A.28) доставляет минимум
функционалу общей потенциальной энергии стержня:
/
dx-Pv(l), A.29)
dx
О
l(u) -> min.
Осуществим "погружение" рассматриваемого стержня в
"канонический", имеющий такую же площадь поперечного сечения
F 9 длину Iq > I и закрепленный на обоих концах. Канонический
стержень однороден с модулем упругости Eq = max E(x).
xe[0J]
Расширяя область определения функций v(jc) до отрезка [О, /0 ] при
условии v(/q ) = 0, выполним следующие тождественные
преобразования функционала A.29):
dx
4 Иллюстративная задача: растяжение неоднородного стержня 21
+ —-
A.30)
Выполненные преобразования тождественны, поэтому минимумы
функционалов A.29) и A.30) совпадают, и функция и(дг),
минимизирующая функционал A.30), является обобщенным
решением краевой задачи A.26)-A.28) в области [О,/]. Из A.30)
следует вариационное уравнение Mill:
°Cdu{x) ddujx)^^
J dx dx
0
A.31)
решение которого разыскивается методом итераций:
°Cdu^{x) dSu(%) '°Cdu(k-%) ddi№
J dx ' dx J dx ' dx
'-dx +
причем в дальнейшем будет обоснована сходимость этого процесса.
Решение вариационного уравнения A.32) разыскивается в
однородной канонической области [0,/q] и может быть построено
разложением по системе ортогональных координатных функций, как
и в разделе 1.2.
Рассмотрим дифференциальную формулировку краевой задачи,
соответствующую вариационному уравнению МГП A.31).
роинтегрировав по частям интегралы в A.31) в предположении о
22
Гл. 1. Введение в метод геометрического погружения
существовании вторых производных функции и(х), (w(o)= m(/q) = О),
получим
+ 2 ( \ Гл2 (
J dx J dx
dx
flbc
E0F
A.33)
где производная
du
вычисляется для функции w(jc)b
JC=/
дополнении x e
Ы. а =
- в реальной области х е
[О,']-
Повторяя рассуждения раздела 1.3, получаем, что решение
вариационной задачи A.31) в обобщенном смысле соответствует
решению краевой задачи:
dx'
dx\
dx
dx
x=l
dx
1
u@)=i,(/0) = 0.
^J
-0, xe@,/0),
A.34)
Будем решать краевую задачу A.34) методом итераций:
dx
¦S(x-l)
dx
dx jx=i EQF
xe
@,l0),
= 0,
A.35)
14. Иллюстративная задана: растяжение неоднородного стержня 23
тогда на каждой итерации вновь имеем краевую задачу вида A.21),
решение которой строится через функцию Грина A.22).
Пусть и' '=0, а характер неоднородности задается линейной
зависимостью модуля от координаты:
()
причем в этом случае
а точное решение задачи A.25) имеет вид:
, х Р ( Ъ
"KX' = ~Fb { a
Тогда первая итерация совпадает с задачей в разделе 1.2:
A.36)
dx"
Р J_
EqF'Iq
Вторая итерация:
) {
d_
dx
d2u%)
~~~dxT~
) dx
bP
bP
24 Гл. 1. Введение в метод геометрического погружения
ЬР
E*F
VO
Третья итерация:
ЪР\\-
— \\ds
Р \х_1'
die
2/0
dx
1jc=/
2/0
W
-s(x-D-
Ы f,
— 1
2/п
+ 1 + — + —-
-1 — -
'oj
0 1 /0 J 2/0 /0 /^
1.4 Иллюстративная задача: растяжение неоднородного стержня 25
Ограничимся тремя итерациями и численно сравним результаты с
точным решением A.36). На рис. 1.4 представлены результаты для
следующих исходных данных: а = 1, 6 = 1, P/F = 1, / = 0.4, /0 = 1.
Видно, что наблюдается сходимость итерационного процесса: в
Реальной области *е[0,/] приближенное решение и^ '(х)
стремится к точному решению A.36). После трех итераций (при
^левом начальном приближении) максимальная относительная
погрешность в определении перемещений составляет около 10%.
Отметим, что для однородного стержня с такими же размерами
Реальной и канонической областей относительная погрешность в
определении перемещений после трех итераций не превышала бы
®А%. Таким образом, возможно сочетание процедур
26
Гл. 1. Введение в метод геометрического погружения
геометрического и физического погружения, при этом сохраняется
сходимость итерационной процедуры при снижении ее скорости.
/'0
0.3
0.2
0 1
00 -
А
Т(
А
V/
энное
у/
//
'/
/
X
3
\ N
X
0.0 0.2 0.4 0.6 0.8
х/10
1.0
Рис. 1.4. Перемещения в каноническом стержне при решении неоднородной
задачи A-3 - номера итераций)
Глава 2
ТЕОРИЯ МЕТОДА ГЕОМЕТРИЧЕСКОГО ПОГРУЖЕНИЯ
ДЛЯ РЕШЕНИЯ КРАЕВЫХ ЗАДАЧ ЛИНЕЙНОЙ ТЕОРИИ
УПРУГОСТИ
2.1. Введение
В данной главе излагаются теоретические положения метода
геометрического погружения применительно к краевым статическим
задачам теории упругости изотропных однородных, изотропных
неоднородных и анизотропных однородных тел. Основное внимание
уделяется строгому математическому обоснованию итерационных
процедур метода и доказательству их сходимости. Читатели,
интересующиеся прикладными аспектами МГП, без существенного
ущерба для понимания могут опустить изучение этой главы,
поскольку в следующих главах все необходимые для практических
целей результаты будут изложены в связи с вопросами построения
численных алгоритмов, реализующих МГП.
Рассматриваются две взаимосвязанных формулировки МГП:
вариационная и дифференциальная. Вариационный подход
базируется на принципе минимума общей потенциальной энергии
упругою тела и ориентирован в большинстве случаев на численную
реализацию с применением вариационно-разностного метода или
метода конечных элементов. Дифференциальная формулировка МГП
позволяет построить эффективный гранично-элементный метод
численного решения упругих задач для областей сложной формы.
2«2. Задачи теории упругости для изотропных однородных тел
2.2.1. Постановка задачи
Изложение начнем с краевой задачи теории упругости для
изотропного тела [41J. В «-мерном евклидовом пространстве
^ \я ¦-1,2,3) рассматривается связанное ограниченное открытое
28
Гл. 2. Теория метода геометрического погружения
N
множество D с границей S^JJS, (рис.2.1). Предполагается, чтс
i=l
граница S непрерывна по Липшицу [92], что допускает рассмотрение
всех общеупотребительных видов границ без точек заострения,
Замыкание D = D u S множества D определяет область в Rn,
занятую упругим изотропным телом. Требуется найти вектор
перемещения и(х), являющийся решением краевой задачи
div<r(u) + f = 0, xgD, B.1)
п(х).<т(х) = р(х), xeSa> B.2)
u(x) = 0, xeS,, B.3)
где u, f, p - векторы перемещений, объемных и поверхностных сил;
х - радиус-вектор произвольной точки области, занятой упругим
телом; п - вектор внешней единичной нормали к границе S; о -
тензор напряжений; S^S^ - части границы S, на которых заданы
краевые условия соответственно по напряжениям и перемещениям.
\
Рис.2.1. Область D для исходной краевой задачи
Тензор напряжения связан с тензором деформации е физическим
законом Гука [41]
а = Ш + 2цё, B.4)
где Е - единичный тензор; в - первый инвариант тензора
деформации; Я, ju - упругие параметры Ламе.
Связь линейного тензора деформаций ? с вектором перемещений
определяется геометрическими соотношениями Коши
2.2- Задачи теории упругости для изотропных однородных тел 29
где V - набла-оператор, а верхний индекс "Т" обозначает операцию
транспонирования тензора в B.5).
С учетом соотношений B.4), B.5) краевая задача B.1)-B.3)
относительно вектора перемещения и(х) имеет вид
(Я + /л) grad div u + juV u + f = 0, x e D, B.6)
n-^?divu + /^(Vu)T +/л Vu)=p, xeS^, B.7)
u = 0, xeSw. B.8)
2.2.2. Используемые пространства и нормы, вариационная
формулировка задачи
Введем в рассмотрение функциональное пространство
V(D) = jv е (н1 {D))n; v = 0, х е S Л, B.9)
являющееся полным замкнутым подпространством Соболева
(н1 (D)f [92]. Кроме того, вектор f e (b2(d))" , a p g (l2 (s^))w .
Для используемых пространств вектор-функций определены
скалярные произведения
Vu, v e V(D) (u, v) = ja-(u) • -^(v)dD, B.10)
D
P (u,v)= JuvdD, B.11)
D
(u,v)s= Ju-vdSa. B.12)
Скалярные произведения B.10)-B.12) симметричны, а при v = u
являются положительно определенными квадратичными
Функционалами. Порождаемые ими нормы соответствующих
пространств имеют вид
VveV(d) ||v| = (v,vI/2, B.13)
Vve(L2(D))* |v| = (v,vI/2, B.14)
= (v,vW2. B.15)
J30 Гл. 2. Теория метода геометрического погружения
Рассмотрим обобщенное решение [92] u е V(D) краевой задачи
B.6)-B.8), получаемое из вариационного уравнения
VveV(D) (u,v) = (f,v)+(p,v)s B.16)
и доставляющее минимум квадратичному функционалу общей
потенциальной энергии упругого тела [52]
/(v) = (v,v)-2(f,v)-2(p,v)s, B.17)
определенном на пространстве V(D) B.9). Из условий полноты и
замкнутости пространства V(D), симметричности и V(D)-
эллиптичности биллинейной формы (u,v), а также непрерывности
линейного функционала (f, v)+(p,v)s, из теоремы Лакса-
Мильграмма [52,92] следует существование и единственность
решения и вариационной задачи B.16).
Для осуществления геометрического погружения в рассмотрение
вводится каноническая область Do, представляющая собой
замыкание Do=DquSo ограниченного открытого множества
Dqc:Rw, имеющего непрерывную по Липшицу границу Sq
(рис.2.2). Пусть выполняется условие
DcD0. B.18)
Полагаем также, что
B.19)
\
Рис.2.2. Каноническая область Do, содержащая исходную область D
Рассмотрим соответствие решения уравнения B.16) полному
замкнутому пространству вектор-функций
2.2. Задачи теории упругости для изотропных однородных тел 3J_
s{,=SonSA B.20)
со скалярным произведением
Vu,veV0(D0) (u.vH= J«r(u)--f(v)dDo B.21)
Do
и соответствующей ему нормой
VueVo(Do) H0=(v,v)i/2. B.22)
В B.20): ^(u)- линейный однородный алгебраический оператор,
зависящий от вектора и или только от некоторых его компонент;
Бд - непрерывная по Липшицу граница области Da=D0\D -
дополнения множества D до Dq.
2.2.3. Связь элементов пространств V(D) и V0(D0)
Для установления соответствия элементов пространств V(D) и
Vq (Dо) определим два отображения.
Первое, имеющее место [92], однозначное отображение [35]
у : V0(D0)->V(D); VueV0(D0) 3veV(D);
v = у (u) <-» Vx e D, v = u
утверждает, что каждому элементу и, принадлежащему пространству
V0(Do), соответствует в пространстве V(D) единственный элемент
v = y(u) и это соответствие эквивалентно тому, что при любом
х € D v = u. Или, иначе говоря, это означает сужение области
определения VueVo(D0) до D, при этом справедливо неравенство
VueV0(D0) |u|0>||r(ul, B.24)
которое следует из положительной определенности функционалов
B.13), B.22) и условия B.18).
Также имеет место второе однозначное отображение
у: V(D)->V0(D0); VveV(D) 3ueV0(D0);
u = ^(v)<->VxeD u = v; VxeDA u = v*,
если \ ¦ является решением задачи
div<j(v*) = 0, xeDA B.26)
_32 Гл. 2. Теория метода геометрического погружения
с краевыми условиями
v*=v, xeS^nS, B.27)
а при х е So , как станет ясно из дальнейшего изложения, с одним из
возможных типов:
v*=0, xeSl0; B.28a)
n.<j(v*)=0, xeSjj; B.286)
v»,. =0, nkorjk{v*) = 0, i*j, xeSi, B.28b)
где n = (n\, «2 •> пз) - вектор внешней единичной нормали при
xeSQ; v*,- - компонента вектора v* ; в B.28в) по повторяющимся
индексам осуществляется суммирование. Для такого типа краевых
условий существует единственное решение задачи B.26)-B.28) [41].
Отображение B.25) утверждает, что каждому элементу v,
принадлежащему пространству V(D), соответствует в пространстве
Vq(Dq) единственный элемент и = у/\\) и это соответствие
эквивалентно тому, что при любом х е D u = v, а при любом
х е DA u = v*, где v* - есть решение краевой задачи B.26)-B.28).
Таким образом, отображение у/ осуществляет расширение области
определения VveV(D) до Do, продолжая его однозначно и
непрерывно по значению v при х € Эд n S решением задачи B.26)-
B.28) при VxeDA .
Построенные отображения позволяют утверждать: областью
значений отображения у :Vq(Dq)-> V(D) является все
пространство V(D); решению ueV(D) вариационного уравнения
B.16) будет соответствовать единственный элемент у/(и)е V0(Do),
что следует из однозначности отображения у/ :V(D)-^ V0(Dq). Эти
утверждения позволяют установить соответствие решения u e V(D)
уравнения B.16) пространству Vq(Dq)
Vv е Vo(Do) [у (у/ (u)), y(v)) = (f,у(\)) 4- (р, /(v))s. B.29)
Запись ^(^(и)) обозначает последовательное действие
отображений у/ на элемент ueV(D) и у на элемент ^(u)g V0(Dq).
Отметим, что
Vv€V0(D0) (f,Hv))+(p,r(v))s=(f,v)+(p,v)s. B.30)
2.2- Задачи теории упругости для изотропных однородных тел 33_
Для элементов пространства Vq(D0) имеет место равенство [89]
Vu,veV0(D0) (Hu),Hv)Hu>vH-(u'v>A> B-31^
где билинейная форма
(и,у)д= \&{и)-е (v)dDA, B.32)
Од
симметрична и при v = u является положительным функционалом,
для которого вследствие определения Бд справедливо неравенство
VueV0(D0) (и,иH>(и,и)д. B.33)
Используя B.30), B.31) и B.29), получим
VveV0(D0) (^(u),vH-(Hu),v)A+(f,v) + (p,v)s. B.34)
Из существования и единственности решения u e V(D) исходного
уравнения B.16), из построенных однозначных отображений, а также
из равенства B.31) следуют существование и единственность
решения ^/(u)gV0(D0) вариационного уравнения B.34).
Для метода геометрического погружения в вариационной
формулировке уравнение B.34) будет являться основополагающим.
2.2\4 Дифференциальный аналог вариационного уравнения B.34)
Рассмотрим дифференциальную постановку краевой задачи,
соответствующую вариационному уравнению B.34). Применяя
формул\ Гаусса-Остроградского к скалярным произведениям
W0'( Од вB-34)» получим для ^(u)g Vi(D0) и всех veV0(D0)
-- f (divtr[^(u)])-vdDA+ Jn-(j[^(u)]-vdSJ)+ Jn*-cj*[^(u)
Од
+ jf • vdD + | р • vdSj, + Jp • vdS^, B.35)
D
Где sa ^Sq nSa; S^=SS S^S^S *
S^; n- единичный
ектор внешней нормали для xeS^ по отношению к S^. из
34 Гл. 2. Теория метода геометрического погружения
дополнения D д = D q \ D; пространство вектор-функций V^ (D 0)
определено следующим образом [92]:
u = 0,XeSw|. B.36)
Из B.35) с учетом B.25), B.26) следует, что решение
вариационной задачи B.34) соответствует в обобщенном смысле
решению уравнения
div<r(ii) = -#(D)f -F(S^)(p + n* .<j*(u)) xgDOj B.37)
с краевыми условиями
п<т(и) = р, xeS^; B.38)
u = 0, xgSw, B.39)
где в целях незагромождения записи вместо у/(и) eV{(D0)
использовано обозначение u e Vj (Dq) ; H(p) - обобщенная функция
типа Хевисайда [21], равная 1 при xeD и равная 0 при x?D;
r|sa j- обобщенная функция типа Дирака [21], сосредоточенная на
множестве Sa.
Из анализа B.35) следует возможность потребовать
VveV0(D) n.<j(u)-v = 0, xgSJ>. B.40)
Этому требованию удовлетворяют все типы однородных краевых
условий, записанные в B.28а), B.286), B.28в). Используя этот
произвол, можно выбрать наиболее приемлемый тип краевых
условий для конкретно решаемой задачи и им дополнить краевые
условия B.38), B.39). Следует отметить, что принятый вариант
краевого условия при х е Sq однозначно определит и вид оператора
F(v) в B.20). Например:
1) для краевого условия и = 0 при х е So оператор F(u) = u ;
2) для краевого условия n-<j(u) = 0 при xgSq оператор F(u) как
таковой в B.20) отсутствует, следовательно и отсутствует какое-либо
ограничение на элементы пространства V0(D0) при х е Sq ;
3) для краевого условия ut =0, «^огд(и) = 0, i*j при xgS0
оператор F(u) = W;.
2.2. Задачи теории упругости для изотропных однородных тел 35
2.2.5. Вспомогательное вариационное уравнение
Рассмотрим другое вариационное уравнение
VveV0(D0) (w,vH-(l-^w'v>A+(f'v)+CT
где weVo(Do); ? > 0 - числовой параметр.
Несложно показать, какой краевой задаче в дифференциальной
постановке соответствует обобщенное решение вариационного
уравнения B.41) по аналогии с тем, как это было сделано по
отношению к вариационному уравнению B.34). Соответствующая
краевая задача имеет вид
divff(w) = ^(D)f-r(Sj)(p + (l-f)n*-(j*(w)) xeD0, B.42)
n.<j(w) = p, xGSla, B.43)
w = 0, xeSw, B.44)
а при x e SQ одно из возможных краевых условий типа B.28а),
B.286), B.28в).
Теорема 2.1. Если числовой параметр ? удовлетворяет условию
s > О, B.45)
то разность /(^(u)-w) решений вариационных уравнений B.34) и
B.41) по норме пространства V(D) удовлетворяет неравенству
\\г{у/(и)-^\<Се, B.46)
где постоянная С не зависит от в.
Доказательство. Почленно вычитая из уравнения B.34)
Уравнение B.41), получим соотношение
VveV0(D0) (Hu)-w
которое преобразуется к виду
Vv€V0(D0) (r(Hu)-w),v
Используя произвольность элемента VvgVq(D) , примем его
Равным (i//(u)- w)e Vq(D0) и, подставив его в B.47), получим
(гЫи) -w) > Hv(u)
0ТкУда с учетом положительной определенности скалярных
пРоизведений, помеченных значком "+", следует неравенство
36
Гл. 2. Теория метода геометрического погружения
-^))д • B.48)
К правой части этого неравенства применяем преобразование
Гаусса-Остроградского
Л
B 49)
Из B.26) следует равенство нулю первого интеграла правой части,
а из выражений B.28а)-B.28в), являющихся следствием соотношения
B.40), - равенство нулю второго интеграла правой части в
соотношении B.49). Применим к третьему интегралу неравенство
Коши-Шварца [35], согласно которому
Отметим известное неравенство [92]
u-v
<а u-v
B.50)
B.51)
Vu,veV(D)
где величина а зависит от S.
С учетом того, что S^cS и ^(u)-w)gV(D), соотношение
B.51) позволяет усилить неравенство B.50) и оценить сверху левую
часть равенства B.49)
B.52)
2.2. Задачи теории упругости для изотропных однородных тел 37
Подставляя B.52) в B.48) будем иметь
К
s2
где величина С не зависит от s . Теорема доказана.
Из теоремы 2Л следует, что в интересующей нас исходной
области D решение вариационной задачи B.41) при достаточно
малой величине ? сколь угодно близко к решению исходного
вариационного уравнения B.34) по норме пространства V(D) и
может быть использовано в качестве приближенного решения.
Теорема 2.1 установила степень близости решений краевых задач
B.37)-B.39) и B.42)-B.44) в исходной области D в смысле
соответствующих им обобщенных решений.
2.2.6. Итерационное решение уравнения метода геометрического
погружения
Решение краевой задачи B.42)-B.44) предлагается осуществлять
методом итераций
r(Sj-)(p + (l-?)n* ^*\w* /) хе Do;
n-<r(w*)=p, xgSJ,; B.53)
w*=0, xeSw,
где индекс k последовательно принимает значение 1, 2, 3, ... и
определяет номер итерации, a w = 0.
Как следует из B.53) , на каждой итерации необходимо решать
краевую задачу на канонической области Do, которая содержит в
себе всю исходную область D. Это обстоятельство определило
название метода - метод геометрического погружения. Вид
оператора левой части дифференциального уравнения и краевых
Условий в B.53) не изменяется от итерации к итерации, а правая
часть дифференциального уравнения определяется решением от
пРедыдущей итерации.
38 Гл. 2. Теория метода геометрического погружения
Для обоснования сходимости итерационного процесса B.53) в
смысле обобщенного решения докажем теорему.
Теорема 2.2. Если числовой параметр s удовлетворяет условию
О < s < 1, то последовательность итераций jw | вариационного
уравнения
VveV0(D0) (w*,v) =(l-*)(w*-\v) + (f, v) + (р, v)s,
» '0 \ /Д B.54)
A = 1,2,...; w°=0
сходится по норме пространства Vo(Dq), т. е.
О т,п—>сс
Доказательство. Представим
т
соответственно
k=\
Пусть т>п, тогда
! 1 "О
Переходя в B.55) к неравенству, имеем
B.56)
Из уравнения B.54), почленно вычитая равенство
(w ~ ,v\ =(l —^Yw ~ ,v) + (f,v) + (p,v)g,
получим
VveV0(D0) Uk-wk'\y) -(l-^Vw^-w^5v) . B.57)
При k -1 уравнение B.54) имеет вид
VveV0(D0) (w1,v)o=(f,v)-f(p,v)s.
2.2. Задачи теории упругости для изотропных однородных тел 39
Из непрерывности линейного функционала (f,v) + (p,v)s [92]
на пространстве V0(D0) имеем
Li <Л, B.58)
где величина А зависит от f, p, D и Dq .
Используя произвольность элемента vgVq(Dq) в равенстве
к к—\
B.57) и принимая v = w - w , приходим к соотношению
(w* -w^.w* -w*-1
-w*~2,w* -w*
) (^ , ) B.59)
Применяя неравенство Коши-Буняковского [35] к правой части
B.59), будем иметь
w*_w*-itW*_w*-i
о
-w
С учетом неравенств
справедливость оценки
д
B.33) и B.58) нетрудно
/ д
показать
w'-w*
О
которая позволяет оценить левую часть неравенства B.56)
<А^-^- 9
|ww-w"
НО ?
откуда следует, что если 0 < е < 1 , то
ww-w"
О т,п->оо
что и требовалось доказать.
Из теоремы 2.2 следует, что итерационный процесс B.53) в
смысле соответствующего обобщенного решения сходится всегда
независимо от степени отличия области D от Dq . Геометрическую
конфигурацию области Do можно выбирать достаточно простой с
точки зрения возможности построения решения краевых задач в
итерационном процессе B.53). Произвол выбора однородных
краевых условий при х е Sq следует также использовать с этой же
точки зрения. Уравнение B.54) будем называть вариационным
Уравнением метода геометрического погружения.
40 Гл. 2. Теория метода геометрического погружения
Возможен вариант непосредственной реализации итерационного
процесса B.53), если для канонической области Do известен
обратный оператор (функция Грина) соответствующей краевой
задачи. В этом случае B.53) будет являться итерационным процессом
решения граничного интегрального уравнения
w*(x)=fG(x,y)-f(y)dD(y) +
D
где G(x,y)- функция Грина краевой задачи B.53), являющаяся
тензором второго ранга; Sa =Sa .
Все выше приведенные положения и теоремы останутся
справедливы, если в качестве функции Грина использовать тензор
Кельвина-Сомильяны [30], а область Do распространить на все
евклидово пространство R", так как в этом случае при стремлении
радиуса-вектора х к бесконечности компоненты вектора
а Г1 Г2
перемещения ведут себя как х , а тензора напряжения - как х|
[30], что обеспечивает существование конечной величины
скалярных произведений
Vu5veV0(D0) (u,v)q<oo, (и,у)д<со,
raeVo(Do) = b€HI(Do) ; v - хГ\<т(у)~ |x -z,|x| -> со
2.3. Задачи неоднородной теории упругости
В данном разделе рассматриваются теоретические положения
метода геометрического погружения применительно к решению
краевых задач теории упругости неоднородных материалов.
Отличительная черта этих задач - зависимость упругих констант от
координат, в связи с чем метод имеет ряд особенностей. В частности,
погружение в общем случае будет носить не только геометрический,
но и "физический" характер, вследствие чего каноническая область
будет отличаться от реальной не только удобной для решения
формой границ, но и упругими свойствами.
2.3. Задачи неоднородной теории упругости 41
2.3.1. Постановка задачи
Как и в случае изотропной теории упругости требуется отыскать
вектор перемещения и(х) краевой задачи, включающей в себя
уравнения B.1)-B.3), B.5) и физический закон Гука для
неоднородных материалов
<т = Л(х)б!Е + 2//(х)?, B.61)
в котором физические параметры Ламе Я(х), /л(х) принадлежат
пространству кусочно непрерывных функций, имеющих конечное
число поверхностей разрыва первого рода
А(х)>0, ^(х)>0, xgD.
2.3.2. Используемые пространства и нормы, вариационная
формулировка задачи
Обобщенное решение ueV(D) краевой задачи B.1)-B.3), B.5),
B.61) получаем из вариационного уравнения
Vv € V(D) (u, v) - (f, v) + (p, v)s , B.62)
где V(D)- ранее определенное пространство B.9) вектор-функций.
Скалярное произведение B.10) представим в виде двух
билинейных форм
Vu, v € V(D) (u, v) = (u, v), + (u, vJ , B.63)
где (u,vI = pl(x)divu?-divv?dD, B.64)
D
(u,vJ = j2/i(xMu).^(v)dD, B.65)
D
которые являются симметричными, а при u = v - положительно
определенными квадратичными функционалами. В пространстве
V(D) определим еще две симметричных билинейных формы:
(u, vK = J div и Ё • • div v Ё dD, B.66)
D
(u,vL = J^u)-f(v)dD. B.67)
D
Используя соотношения B.63)-B.67), уравнение B.62) можно
преобразовать к виду
42 Гл. 2. Теория метода геометрического погружения
VveV(D)
где Яо = max (Я(х)); ju0 = max (//(х)). B.69)
xeD xeD
Для скалярных произведений B.64)-B.67) справедливы
неравенства
, B.70)
где u|,|vj - означает, что компоненты тензоров в соотвествующих
скалярных произведениях принимают абсолютные значения;
Хх = min (Я(х)); /лх = min (//(x)), B.71)
xgD xgD
ех =(Я0 -Ai)/A0 <!; ^2 =(/^о -//l)/^0<1- B-72)
Не представляет труда проверить, что решение уравнения B.68)
тождественно равно решению уравнения B.62).
Рассмотрим соответствие решения уравнения B.68) другому
полному замкнутому пространству вектор-функций
Vo(DO) =
B-73)
со скалярным произведением
Vu,veV0(D0)
(u,vH=2yu0 Ji(u)--f(v)dD0+A0 Jdivu-?--diw-?dD0 B-74)
Do Do
и соответствующей нормой
VueV0(D0) ||u|0=(u,u)^. B.75)
Отметим, что
Vu,veV0(D0) (u,vH= f^(u)..^(v)dD0, B.76)
Do
где тензор напряжения <т связан с тензором деформации ё
физическим законом для однородного изотропного материала с
параметрами Ламе Aq , juq .
2.3. Задачи неоднородной теории упругости 43
Как и в разделе 2.2, пусть DqcR" имеет непрерывную по
Липшицу границу So; замыкание D0=DquSq удовлетворяет
условию B.18); SA - непрерывная по Липшицу граница DA = Do \D
- дополнения множества D до Dq.
2.3.3. Связь элементов пространств V(D) и Vq(D0)
Соответствие между элементами пространств V(D) и Vq(Dq)
определяется отображением B.23) и
Z: V(D)-+V0(D0); VveV(D) 3ueV0(D0);
u = ^(v)<->VxeD u = v; VxgD u v
если v* является решением задачи
div(^0#(v* )E + 2//0s(v* ))= О, х € DA B.78)
с краевыми условиями
v*=v, xeSAnS, B.79)
а при х е So , как станет ясно из дальнейшего изложения, с одним из
возможных видов
v*-0, xeSq; B.80a)
п • (Аов{у*)Е + 2jU0e{v* ))= 0, х е Sl0 ; B.806)
v*,- = 0, пк(Лов(у*)Ejk + 2ju0sjk(v*)), i*j9 xeSi>, B.80в)
где Ejk , ?гд - компоненты тензоров соответственно единичного и
деформации.
Отображение B.77) утверждает, что каждому элементу veV(D)
соответствует в пространстве V0(D0) единственный элемент
u = j(v) и это соответствие эквивалентно тому, что при любом
xeD u = v, а при любом xeDA u = v*> где v* есть решение
краевой задачи B.78),B.79) изотропной теории упругости с
параметрами Ламе /lo?/iO. Таким образом, отображение %
°существляет расширение области определения VveV(D) до Do,
пРодолжая его однозначно и непрерывно по значению v при
х е SA nS решением изотропной краевой задачи B.78)-B.80).
44 Гл. 2. Теория метода геометрического погружения
Отображения B.23) и B.77) позволяют утверждать: областью
значений отображения у: V0(D0) -> V(D) является все пространство
V(D) ; решению u е V(D) вариационного уравнения B.68) будет
соответствовать единственный элемент ^(u)e Vq(Dq) , что следует
из однозначности отображения х '• V(D) -> Vq (D o ). Эти
утверждения устанавливают соответствие решения и е V(D)
уравнения B.68) пространству
Vvg V0(D0)
где у{%{и)) обозначает последовательное действие отображений %
на элемент и е V(D) и у на элемент х(и)е Vo (D 0 ).
Для элементов пространства V0(D0) имеет место равенство [88J
Vu, v е Vo Яо (у(и), у(\)) + 2juo (y{u), y(v)) =
I \ I \ B-82)
= (u,vH-(u,v)A,
где билинейная форма
(u,v) =2juq j ^(u)--^(v)dDA + Aq jdivu E-d\v\EdDA B.83)
Од Од
симметрична и при v = u является положительным функционалом,
для которого вследствие определения Од справедливо неравенство
VueV0(D0) <и,иH>(и,и)д. B.84)
Используя B.30) и B.82) применительно к B.81), получим
VveV0(D0) Mu),v)п=Шу)л +ЫхD*)* -(хНу)А +
(f,v) + (p,v)s . B.85)
Из существования и единственности решения u e V(D)
исходного уравнения B.62), из построенных однозначных
отображений B.23), B.77), а также из равенства B.82) следуют
существование и единственность решения ^(u)
вариационного уравнения B.85).
2.3. Задачи неоднородной теории упругости 45
2.3'.4- Дифференциальный аналог вариационного уравнения B.85)
рассмотрим дифференциальную постановку краевой задачи,
соответствующую вариационному уравнению B.85). Применяя
формулу Гаусса-Остроградского к скалярным произведениям
уравнения B.85), получим для #(u) e V^Dq) и всех veV0(D0)
- jdiv (лов{х(и))Е + 2Мое{х(и)))- vdD(
+ f n • [Аг)в(у(и))Ё + 2//oi(y(u))l- vdsi
so
Jf-vdD+ |p-vdSj,.+
D sj, si
div(Ao0(j(u))i + 2/^(z(u)))'VdDA+ B.86)
Од
jn •
D
+ jn ¦ ((Яо -
; S^.=SAnSCT; S^uS^S^; n*-единичный
вектор внешней нормали для xeSa по отношению к DA;
\Aq$ (^(u))? + 2jjq? (/(u))j - тензор напряжения при стремлении х
к S<r из дополнения DA =D0\D; V](Dq)-пространство B.36).
46 Гл. 2. Теория метода геометрического погружения
Из B.86) с учетом B.78)-B.80) следует, что решение
вариационной задачи B.85) соответствует в обобщенном смысле
решению уравнения
div (яов(и)Ё + 2/л0е{и))= ~#(D)f -
()
n • ((Ло - Л)в{и)Ё + 2{Мо - /#(«)
+ Я (D)div ((Яо - Л)в{и)Ё + 2(/i0 - fi)e(u))9
xgD0 B.87)
с краевыми условиями
( xeS^, B.88)
u = 0, xgSw ,
где в целях незагромождения записи вместо /(u)gVj(d0)
использовано обозначение u e V\ (Dq) -
Из анализа B.86) следует возможность потребовать
Vv е Vo (Do) п (лов{и)Ё + 2//0i(u))- v - 0, x e S]Q . B.89)
Этому требованию удовлетворяют все типы однородных краевых
условий B.80а)-B.80в). Используя этот произвол, можно выбрать
наиболее удачный тип краевых условий для конкретно решаемой
задачи и дополнить им краевые условия B.88). Отметим, что
принятый вариант краевых условии при х е Sq однозначно
определит и вид оператора F(u) в B.73). Например, для краевого
условия и = 0 при xgSq оператор F(u) = u ; для краевого условия
п • [Лов(и)Ё + 2jUQe(u))= 0 при х е Sq оператор F(u) как таковой в
B.73) отсутствует, следовательно и отсутствует какое-либо
ограничение на элементы пространства Vq(Dq) при xgSq; для
краевого условия и{ - 0, nk [lQe(u)Ejk + 2/uqSj^ (u))= 0, i' * j,
при x g Sq , оператор F(u) = ut.
2.3. Задачи неоднородной теории упругости 47
2.3.5. Вспомогательное вариационное уравнение
Рассмотрим другое вариационное уравнение
Vv€V0(D0) (w,vH =(l-*Xw,v)A +(f,v) + (p,v)s +
+ (^0(w,vK -(w,v)[)+B//0(w,vL -(w,vJ),
где w e Vo (Do); s > 0 - числовой параметр.
Дифференциальная постановка задачи, соответствующая
вариационному уравнению B.90), имеет вид
div (лоб(ъ)Ё + 2Moe(yv))= -H(D)l - r(s* )x
х [р + (l - еУ ¦ (лов* {уг)Ё + 2/Uqs* (w))+
+ n • ((До - А)в{ъ)Ё + 2(//0 - М)е(w))]+
+ Я(D)div ((Ло - А)в{м)Ё + 2{Мо - ju^w)),
xeD0 B.91)
с краевыми условиями :
п ¦ [V(w)? + 2Moe(v)\= P + n • |(Яо - Щ*г)Е + 2(//0 - //)ff(w)],
xeSla, B.92)
w = 0, xeSu,
а при х е SQ - одно из возможных краевых условий типа B.80а),
B.806), B.80в).
Степень близости решений вариационных уравнений B.85) и
B.90) устанавливается следующей теоремой.
Теорема 2.3. Если числовой параметр s удовлетворяет условию
е > 0, B.93)
то разность f(^(u)-w) решений вариационных уравнений B.85) и
B-Щ по норме пространства V(D) удовлетворяет неравенству
\\r{z{u)-W)\<Ce, B.94)
где постоянная С не зависит от е.
Доказательство. Почленно вычитая из уравнения B.85)
Уравнение B.90), получим соотношение
VveV0(D0)
48 Гл. 2. Теория метода геометрического погружения
(u) - w), v)Q = (Ojt(u) - w), v) д + s{w, v) +
которое, используя A.2.8) - A.2.12), A.2.26), преобразуем к виду
VveV0(D0)
(r(j(") - w), v) = -s(r{z(u) - w), v)A + s(x(u), v)A . B.96J
Принимая произвольный элемент v в B.96) равным (х(и) - w)
получим
(y(x(u) - w), y{x(n) - w)) =
= -?(yix(u)-wlrb:(ll)-JW))A + ?-(^(u>, Of(u) - w)) д
Из условия положительной определенности первых двуя
скалярных произведений в B.97) следует неравенство
. B.98)
К правой части этого неравенства применяем преобразование
Гаусса- Остроградского
Од
r(u) - w)dDA +
Jn • [ло0(ИиР + iMoHxiu))]' Ы«) - w)dsj) + B.99)
Из B.78) следует равенство нулю первого интеграла правой
части, а из B.89) - равенство нулю второго интеграла правой части в
соотношении B.99). К третьему интегралу применяем неравенство
Коши-Шварца [35], согласно которому
2.3. Задачи неоднородной теории упругости 49
JV
B.100)
Отметим известное неравенство [92]
Vu,vgV(d) |u-v|s <a|u-v||, B.101)
чде величина а зависит от S.
С учетом того, что S^czS и ^(u)-w)gV(D), соотношение
2.101) позволяет усилить неравенство B.100) и оценить сверху
1евую часть равенства B.99)
B.102)
Подставляя B.102) в B.98), будем иметь
\)Е + 2Моё*Ш)\-
B.103)
Jn* \ло
гДе величина С не зависит от е, что следует B.103). Теорема
Доказана.
Из теоремы 2.3 следует, что в интересующей нас области D
РеШение вариационной задачи B.90) при достаточно малой величине
? будет сколь угодно близко к решению исходного вариационного
Уравнения B.85) по норме пространства V(d) и может быть
Использовано в качестве приближенного решения. Теорема 2.3
Установила степень близости решений краевых задач B.87)-B.88) и
U.91).B.92) в исходной области D в смысле соответствующих им
°бобщенных решений.
50 Гл. 2. Теория метода геометрического погружения
2.3.6. Итерационное решение уравнения метода геометрического
погружения
Решение краевой задачи B.91)-B.92) предлагается осуществит!
методом итераций
|(* )е + 2//0*(w* )]= -Я (D)f -
с краевыми условиями
[()
= f + П •
g -г жд ^. _v -/-V- y— ¦ -\r-U r/-\ /J ' ^2 1 QTV
а при xgSq - одно из возможных краевых условий типа B.80а)»
B.806), B.80в). Здесь индекс к последовательно принимает значения
1,2,3... и определяет номер итерации, a w =0 . Как следует из
B.104), B.105), на каждой итерации необходимо решать краевую
задачу изотропной теории упругости на области Do , которая
содержит в себе всю исходную область D. Вид оператора левой
части дифференциального уравнения и краевых условий в B.104),
B.105) остается неизменным, а правая часть определяется решением
с предыдущей итерации.
Для обоснования сходимости итерационного процесса B.104),
B.105) в смысле обобщенного решения докажем теорему.
Теорема 2.4. Если числовой параметр ? удовлетворяет условию
O<^<min[(^/Ao),(^i/^o)] > B-106)
то последовательность итераций т \ вариационного уравнения
Vv?V0(D0)
к = 1,2,3,...; w°=0 B.107)
сходится по норме пространства Vo (D), т.е.
2.3. Задачи неоднородной теории упругости
51
ww-w"
q m,n—>cc
->0.
Доказательство. Представим
wm='
соответственно
Пусть т> п , тогда
к=\
,"-i(**-w*-').
Переходя в B.111) к неравенству, имеем
ww-
HO
HO
Из уравнения B.107) , почленно вычитая равенство
= (f'v) + (g> v)sCT +(l~ ?)(™к~2>
получим
При к=\ уравнение B.107) имеет вид
VvgV0(D0) (w'.v) =(f,v) + (g,v)Sff.
Из условия непрерывности линейного
^'v) + (g,v)s [92] на пространстве V0(D0) имеем
Где Величина А зависит от f, g, D и Do.
B.108)
B.109)
B.111)
B.112)
B.113)
B.114)
функционала
B.115)
52 Гл. 2. Теория метода геометрического погружения
Используя произвольность элемента vgVq(Dq) в равенстве
B.113) и принимая v = w* -w^, приходим к соотношению
B.116)
от которого переходим к неравенству
+u
w'-w*-1
w^-w*-1
w*-w*-!
w*-l_w*-2 L*_w*-1
w^-w*
B.117]
Используя соотношения B.70) - B.72) применительно к B.11"),
будем иметь
- w
w -w
:w*-l _W*-2M * _
Л
B.118)
w^-w^1
из чего с учетом условия B.106) и соотношения B.82) следует
2.3. Задачи неоднородной теории упругости
53
B.119)
Применение неравенства Коши-Буняковского к правой части
неравенства B.119) позволяет установить, что
B.120)
W
к-\
С учетом неравенства B.115) нетрудно показать справедливость
оценки
V?>1 w^-w*-1! <A(\-s)k~l , B.121)
которая позволяет оценить левую часть неравенства B.111)
<А{\-е)п1е , B.122)
откуда следует
т,п—>оо
B.123)
что и требовалось доказать.
Отметим, что из B.123) и неравенства B.24), которое имеет
место и для краевой задачи неоднородной теории упругости, следует
сходимость и по норме пространства V(D)
-w")
B.124)
т,п—>оо
Теорема 2.4 утверждает, что итерационный процесс B.104),
B.105) в смысле соответствующего обобщенного решения сходится
всегда независимо от степени отличия исходной области D от Dq и
характера неоднородности физико-механических свойств упругого
материала.
Уравнение B.107) будем называть вариационным уравнением
метода геометрического погружения для краевых задач
Неоднородной теории упругости.
Возможен вариант непосредственной реализации итерационного
пРоцесса B.104), B.105), если для области Do известен обратный
оператор (функция Грина) соответствующей краевой задачи. В этом
случае B.104), B.105) будут являться итерационным процессом
РеШения интегрального уравнения
54 Гл. 2, Теория метода геометрического погружения
rn(x) = JG(x,y)-(f(y)-div[(Ao-.
w()
D
B-125)
(у))] + n(y) ¦ [(До - Л(ур(*п-1 (у)) +
0 -МУ))^И(У))]^(У),
где G(x,y) - функция Грина краевой задачи B.104), B.105);
с2 _ о
Все приведенные в данном параграфе положения и теоремы
останутся справедливыми, если в качестве функции Грина
использовать тензор Кельвина-Сомильяны для изотропного упругого
тела с параметрами Ламе - Яо, /ло, а область Do распространить на
все евклидово пространство Rn, так как в этом случае при
стремлении радиуса-вектора х к бесконечности компоненты
с I Г1
вектора перемещения ведут себя как |х| , а тензора напряжения -
как |х| [42], что обеспечивает существование конечной величины
скалярных произведений
Vu,veV0(D0) |{u,vH|<oo, |(u,v)J<«>, B.126)
где
(Do))"
v~
l
Ixl2
Таким образом, метод геометрического погружения
применительно к решению краевой задачи неоднородной теории
упругости на произвольной области Dq позволил свести ее к
сходящейся последовательности краевых задач изотропной теории
упругости на канонической области Do. Если исходная краевая
задача неоднородной теории упругости изначально поставлена на
канонической области Dq, to изложенный подход позволяет свести
ее к сходящейся последовательности краевых задач изотропной
теории упругости на этой же самой области.
2.4. Задачи анизотропной теории упругости _55
2.4. Задачи анизотропной теории упругости
В данном разделе рассматриваются теоретические положения
метода геометрического погружения применительно к решению
краевых задач анизотропных упругих тел.
2.4.1. Постановка задачи.
Требуется отыскать вектор перемещения и(х) , краевой
задачи, включающей уравнение равновесия
div<r(u)+f = 0, xgD; B.126)
краевые условия
n(x)-d-(u) = g(x), xeSa; B.127)
u(x)=0 , xgSw ;
физический закон Гука для анизотропного упругого тела
<7=4С--?, B.128)
где С= С(х) - тензор четвертого ранга, определяющий
физические свойства анизотропного упругого тела. Компоненты
тензора удовлетворяют условиям симметрии [63]
с учетом которых число независимых компонент в самом общем
случае анизотропии равно 21. Относительно Сщ (х) полагаем, что
°ни принадлежат пространству кусочно-непрерывных функций,
имеющих конечное число поверхностей разрыва первого рода.
Для дальнейшего изложения потребуется запись физического
закона B.128) в матричной форме
{о-} = [(;]{*}, B.130)
гДе {ст }т ={ап,сг 1Ъа ъъ,а 1Ъ,а ъьа 12} - матрица-строка ,
составленная из компонентов тензора напряжения;
\8\ -\е ц,? 22?^ 33>? 23'6" ЪЪ? 12 /" матрица-строка, составленная
Из компонентов тензора деформации; [С] - положительно
°пределенная симметричная матрица [63]
56
Гл. 2. Теория метода геометрического погружения
С1122
С2222
С1133
С2233
С3333
СП23
С2223
С3323
С2323
4131
С2231
С3331
С2331
B.131)
С1112
С2212
С3312
С2Ъ\2
СЪ\\2
симметрично c12i2
составленная из компонентов Сщ тензора физических констант.
Здесь верхний индекс т определяет операцию транспонирования
матриц . Матрицу [с] перепишем в ином виде
с\\ с\2 С13 С14 с\5 с\6
С22 С23 С24 С25 С26
[Ф
С33 С34
с'45
С55
С46
B.132)
симметрично с6
Положительно определенная квадратичная форма {s} [с]{с I
ограничена сверху и снизу
^ГИгфПф^оИ^}, B.133)
где постоянную Gq можно определить, используя теорем}
Гержгорина [102] о распределении собственных значений матрии,
следующим образом:
G п=
B.134)
2.4.2. Используемые пространства и нормы, вариационная
формулировка задачи
Обобщенное решение u(x)e V(d) краевой задачи B.126), B.127)
следует из вариационного уравнения
VveV(D)
(g,u)s
B.135)
2.4. Задачи анизотропной теории упругости 57
где V(D) - ранее определенное пространство B.9) вектор-функций.
Вид скалярного произведения левой части уравнения B.135)
определяется симметричной билинейной формой
Vu,vgV(d) («,v)= Ja(u) -.?(v)dD, B.136)
D
которой соответствует матричная форма записи
(u,v)=j^(u)f[c]^(v)}dD. B.137)
D
При u = v она является положительно определенным
квадратичным функционалом, который порождает норму
пространства V(d)
VugV(d) ||u| = (ii,u) \ B.138)
Для дальнейшего изложения потребуется ранее введенное на про-
пространстве V(d) скалярное произведение B.67)
Vu,veV(d) (u,vL = p(u) .-*(v)dD,
D
которое в матричном представлении имеет вид
(u,vL = j{f(u)}r{f(v)]dD. B.139)
D
Используя соотношения B.134), B.139), уравнение B.135) можно
путем тождественных преобразований привести к виду
VveV(D) (u,vL=(u,vL-
Скалярному произведению (u,v). -\IG q(u,v) соответствует
матричная форма записи
B.141) где Е - единичная, диагональная матрица .
С учетом равенства B.134) и свойств матрицы [с], нетрудно
показать, что для любого х е D модуль величины
ПоДынтегрального выражения в B.141) удовлетворяет неравенству
58 Гл.2. Теория метода геометрического погружения
j, B.142)
где
1=тт[/Щх^, B.I4J)
xeD
Al(x) - наименьшее собственное значение матрицы [с], для
фиксированного значения х. Из B.142) следует, что модуль
величины
где и |, v | означает, что компоненты тензоров в соответствующем
скалярном произведении принимают абсолютные значения.
Рассмотрим соответствие решения уравнения B.140) другому
полному замкнутому пространству вектор-функций
L B.145)
со скалярным произведением
Vu,veV0(D0) (u,vH= p(u)..^(v)dDo ,
Do
которое в матричной форме имеет вид
(u,vH= j{e(u)}T{e{v))dD0. B.146)
Do
Норма пространства Vq(Dq) -
|u|o=(u,uI/2. B.147)
Как и в разделе 2.2, пусть DqcRw имеет непрерывную по
Липшицу границу So; замыкание Dq^DquSq удовлетворяет
условию B.18).
2.4.3. Связь элементов пространств V(d) и Vq(Dq)
Соответствие между элементами пространств V(d)h Vq(Dq)
устанавливается двумя отображениями, первым из которых является
2А. Задачи анизотропной теории упругости 59
У :Vo(Do)-> V(d), определенное соотношением B.23). Аналог
неравенства B.24) - соотношение
VueVo(Do) \\u\\0>yGJr (uj, B.148)
которое следует из B.133) и условия B.18). Также имеет место
второе однозначное отображение
A:V(D)->V0(D0); Vv 3ueV0(d0) ;
()gD,u = v ;VxgDa,u = v*, B.149)
если v* является решением задачи
divs(v*) = 0, xeDA , B.150)
с краевыми условиями
v*=v, xeSAnS, B.151)
а при х е So , как станет ясно из дальнейшего изложения, с одним
из возможных видов:
v, =0, xgSq1; B.152а)
n-s(v,) = 0, xgSq1; B.1526)
*) = 09 i*j, xgSq1. B.152b)
Отображение B.149) утверждает, что каждому элементу v,
принадлежащему пространству V(d) , соответствует в пространстве
V0(Dq) единственный элемент u = h(v), и это соответствие
эквивалентно тому, что при любом х е D u = v, а при любом
хеОд u = v*, где v* есть решение краевой задачи B.150)-
B.152) изотропной теории упругости с параметрами Ламе:
A = 0;/i = 0,5.
Таким образом, отображение h осуществляет расширение
области определения Vv e V(d) до Dq, продолжая его однозначно и
непрерывно по значению v при х е SA n S решением изотропной
краевой задачи B.150)-B.152).
Отображения B.23), B.149) позволяют утверждать, что область
значений отображения у : Vq(Do)-> V(d) - все пространство V(d);
Решению ug V(d) вариационного уравнения B.140) соответствует
еДинственный элемент /г(и)е Vo(Do), что следует из однозначности
°тображения h:V(D)-> V0(D0). Эти утверждения устанавливают
60 Гл.2. Теория метода геометрического погружения
соответствие решения u g V(d) уравнения B.140) пространств!
Vo(do)
VveV0(D0) (У(л(и)),Г(у)L ={у(h(u)),y{^)-
~yGo(r{h{»)lr{v)) + (f,y{v))+{g,r(vha , B-153)
где у Mu)) обозначает последовательное действие отображений k
на элемент u e V(d) и у - на элемент h(u)e Vq(Dq).
Для любых u,vgV0(Dq) имеет место равенство
(r(«Mv)L=(u,vH-(u,v)A , B.154)
где билинейная форма
(u,v)A= p(u).-?(v)dDA= j{^(u)}r{^(v)]dDA B.155)
симметрична и при v = u является положительным функционалом
для которого (вследствие определения для Од) справедлива!
неравенство
VugVo(Do)(u,u)o>(u?u)a. B.156)
Используя B.30) и B.154) применительно к B.153), получим
VvgV0(D0) (Л(и),уH=М+Ы5<7 +
+ (Л(и),г)д +(Л(и),уL -yGQ(h(u),y) . B.157)
Из существования и единственности решения u e V(d)
исходного уравнения B.135), из построенных однозначны*
отображений B.23), B.149), а также из равенства B.154) следую!
существование и единственность решения //(u)gVq(Dq)
вариационного уравнения B.157).
2.4.4. Дифференциальный аналог вариационного уравнения B.157)
Рассмотрим дифференциальную постановку краевой задачи
соответствующую вариационному уравнению B.157). Применяя
формулу Гаусса-Остроградского к скалярным произведениям
уравнения B.157), получим для /2(u)eVi(D0) и всех vgVq(D0)
2.4. Задачи анизотропной теории упругости 61
iv[i(A(u))]} • v dD0 -f Jn • ?(A(u)) • v dSo + Jn • ?(A(u)) • v dSo =
ffvdD + fgvdSl.+ fg-vdS^.- f{div[^(/i(u))]}- vdDA +
J i i J
+ Jn • f(A(u)) • v dSjj- + Jn* ^*(Л(и)) • v dS^. -
+ B.158)
- Jn.^Mu^-l/Go^C-^Cu^.vdS^ +
D Sj,
Sir
J
где 4 = ^0 П Sa; 5^ = 5Д П 5a ; ^ U 5^ = 5CT ; n* - единичный
вектор внешней нормали для xeS^ по отношению к Эд ; ё (Л(и)) -
тензор деформации при стремлении х к Sa из дополнения Бд ;
Vj(Do) - пространство вектор-функций, определенное в B.36) .
Из B.158) с учетом B.150)-B.152) следует, что решение
вариационной задачи B.157) соответствует в обобщенном смысле
решению уравнения
div[e(u)] = -H(D)f - r(Sj)(g + n* ¦ e(u) +
+ n-(f(u)-l/G04C--f(u)))+
X) ° >\ B.159)
+ #(D) div^(u) -1 / Go 4C • ¦? (u)J, x e Do
c краевыми условиями
u = 0, xeSM, B.160)
гДе в целях незагромождения формы записи вместо A(u)e Vj(Dq)
Использовано обозначение и б Vj(D0); H(D) - обобщенная функция
Типа Хевисайда [21], равная единице при xgD и равная нулю при
62 Гл.2. Теория метода геометрического погружения
xgD; F(S^) - обобщенная функция типа Дирака [21],
сосредоточенная на множестве S^-.
Из анализа B.158) следует возможность потребовать
VveV0(D0) v-?(A(u))-v = 0, xgSq. B.161)
Этому требованию удовлетворяют все типы однородных краевых
условий B.152а), B.1526), B.152в). Используя этот произвол,
можно выбрать наиболее удачный тип краевых условий для
конкретно решаемой задачи и дополнить им краевые условия
B.160). Принятый вариант краевых условий при xgSq однозначно
определит вид оператора F(u) в B.145). Например, для краевого
условия и = 0 при xgSq оператор F(n) = u ; для краевого условия
n-?(u) = 0 при xgSq, оператор F(u) как таковой в B.145)
отсутствует, следовательно и отсутствует какое-либо ограничение на
элементы пространства V0(D0) при xgSq; для краевого условия
ui - 0 5 nkejk (u)= 0, i * j 9 ПРИ х g So, оператор F(u) = ut.
2.4.5. Вспомогательное вариационное уравнение
Рассмотрим другое вариационное уравнение
VveV0(D0) (w,vH=(f,v) + (g,v)Sc7 +
+ (l-5)(w,v)A+(w,v>4-l/Go(w,v>, {2A6J)
где wgV0(Dq); б:>0 - числовой параметр .
Дифференциальная постановка задачи, соответствующая
вариационному уравнению B.162), имеет вид
())
+ Нф) div(e(w) -1 /Go 4С • -е (w)), х е Do
с краевыми условиями:
2.4. Задачи анизотропной теории упругости 63
w = 0, xeSu , B.164)
а при xgS0 - один из возможных краевых условий типа B.152а),
B.1526), B.152b).
Степень близости решений вариационных уравнений B.157) и
B.162) устанавливается следующей теоремой.
Теорема 2.5. Если числовой параметр € удовлетворяет условию
?>0, B.165)
то разность у (h(u) - w) решений вариационных уравнений B.157) и
B.162) по норме пространства V(D) удовлетворяет неравенству
\\y(h(u)-w)\<C?, B.166)
где постоянная С не зависит от ?.
Доказательство. Почленно вычитая из уравнения B.157)
уравнение B.162), получим соотношение
VveV0(D0)
которое, используя B.154), преобразуем к виду
VveV0(D0)
l/G0{r(h(u)-yv),\) = -€ ({h(u)-yv),v)A +f(A(u),v)A. B.168)
Принимая произвольный элемент v в B.168) равным (h(u)-w),
получим
(u) - w), (A(u) - w)) д + e(h(u), (A(u) - w)) д. (
Из условия положительной определенности первых двух
скалярных произведений в B.169), следует неравенство
l/Go|r(^u)-w||2 <e (A(u),(A(u)-w))A. B.170)
К правой части этого неравенства применяем преобразование
Гаусса-Остроградского
(Л(и),(А(и) - w))A - - Jdiv(i(A(u)))- (A(u) - w)dDA +
Од
(
64
Гл. 2. Теория метода геометрического погружения
Из B.151) следует равенство нулю первого интеграла право-
части, а из B.152а)-B.152в), которые являются следствие^
соотношения B.161), - равенство нулю второго интеграла право-
части в соотношении B.171). К третьему интегралу применяем
неравенство Коши-Шварца [35], согласно которому
1-2
J
xl/2
B.172)
J(ft(u)-w)-(A(u)-w)dS*
Отметим известное неравенство
Vu,veV(D) |u-v|s<a|u-v| , B.173)
где величина а зависит от S.
С учетом того, что S^-cS и ^(/i(u)-w)gV(D), соотношение
B.173) позволяет усилить неравенство B.172) и оценить сверху
левую часть равенства B.171)
1/2
<а
B.174)
Подставляя B.174) в B.170), будем иметь
Л/2
B.175)
где величина С не зависит от ?, что следует из B.175).
Теорема доказана.
2.4. Задачи анизотропной теории упругости 65
Из теоремы 2.5 следует, что в интересующей нас области D
еШение вариационной задачи B.162) при достаточно малой
величине е будет сколь угодно близко к решению исходного
вариационного уравнения B.157) по норме пространства V(D) и
может быть использовано в качестве приближенного решения.
Теорема 2.5 установила степень близости решения краевых задач
B.159), B.160) и B.163), B.164) в исходной области D в смысле
соответствующих им обобщенных решений.
2.4.6. Итерационное решение уравнения метода геометрического
погружения
Решение краевой задачи B.163), B.164) предлагается
осуществлять методом итерации
i K ч " B.176)
+ #(D) divj^w*) -1 /Go 4C • ^(w*)), x e Do
с краевыми условиями:
w*=0, xeSw; B.177)
а при xg Sq - с одним из возможных краевых типа B.152а), B.1526),
B.152в). Здесь индекс к - последовательно принимает значения
1>2,3,... и определяет номер итерации, a w =0. Как следует из
B.176), BЛ77), на каждой итерации необходимо решать краевую
задачу изотропной теории упругости для области Do, которая
сОДержит в себе всю исходную область D. Вид оператора левой
части дифференциального уравнения краевых условий в B.176),
BЛ 77) остается неизменным, а правая часть определяется решением
от предыдущей итерации.
Для обоснования сходимости итерационного процесса B.176),
ил77) в смысле обобщенного решения докажем теорему.
Теорема 2.6. Если числовой параметр s удовлетворяет условию
<? <Ь\1Ь§, B.1/о)
т° последовательность итераций т \ вариационного уравнения
66 Гл.2. Теория метода геометрического погружения
VveV0(D0)
B.179)
А \ ' /4 ~\ /
к = 1,2,3,--; w°=0
сходится по норме пространства Vq(Dq), т.е.
wm-w'l| -> 0. B.180)
Доказательство. Представим
^ v* -w^) ? B.181)
соответственно
п
w =w +> (w -w ), B.182)
Пусть т> п, тогда
т
w"I-wn = w°+ ^(w^-w^1). B.183)
Переходя в B.183) к неравенству, имеем
< ]Г L* -w*! . B.1X4)
Из уравнения B.179) почленно вычитая равенство
получим
Vv?V0(D0) ((w* -
B.185)
При & = 1 уравнение B.179) имеет вид
VveV0(D0) (w\v) =(f,v) + (g,v)s<y. B.186)
2.4. Задачи анизотропной теории упругости
67
Из условия непрерывности линейного функционала
v) + (g,v)s [107] на пространстве Vq(Dq) имеем
" л
w
о
B.187)
где величина А зависит от f , g и Do.
Используя произвольность элемента veV0(D0) в равенстве
B.185), и принимая v = w* - w*4 , приходим к соотношению
((„* -w*-'),(w* -w') (( )( |
Г4 /^0
от которого переходим к неравенству
w* -
Ь-1
w - w
к-\
^ 2
B.188)
где \|'|?||)д означает, что компоненты тензоров участвующих в
данном скалярном произведении берутся по абсолютной величине.
Используя соотношения B.140), B.145) применительно к B.188),
будем иметь
- w
B.189)
из чего с учетом условия B.178) и соотношения B.154) следует
2
B.190)
- w
о
Применение неравенства Коши-Буняковского к правой части
неравенства B.190) позволяет установить, что
w*-w*-»
I
| ( . B.191)
II о II II о
С учетом неравенства B.187), нетрудно показать справедливость
°Ценки
68 Гл.2. Теория метода геометрического погружения
VJfc»l iw^-w*! ^(l-*)*, B.192)
которая позволяет оценить левую часть неравенства B.184)
wm-wi <A(\-?)n/e, B.193)
Но
откуда следует
и к
->О, B.194)
т,п—>оо
что и требовалось доказать.
Отметим, что из B.194) и неравенства B.148) следует сходимость
по норме пространства V(D)
HwW~wi „.„.„о)Q-
Теорема 2.6 утверждает, что итерационный процесс B.176),
B.177) в смысле соответствующего обобщенного решения сходится
всегда независимо от степени отличия исходной области D от Do и
от характера анизотропии упругих свойств материала.
Уравнение B.179) будем называть вариационным уравнением
метода геометрического погружения для краевых задач
анизотропной теории упругости.
Возможен вариант непосредственной реализации итерационного
процесса B.176), B.177), если для области Do известен обратный
оператор (функция Грина) соответствующей краевой задачи. В этом
случае B.176), B.177) будут соответствовать итерационному
процессу решения интегрального уравнения
•* (х) = fax, у) • (f (у) - div^w* (у)) -
w ()
D
B-195)
+ п(у) • I^w* (у)) -1 /Go 4C(y) • ^(w*-1 (y))])ds2 (у),
где G(\,y) - функция Грина краевой задачи B.176), B.177):
2.4. Задачи анизотропной теории упругости
69
Все приведенные в данном параграфе положения и теоремы
останутся справедливы, если в качестве функции Грина
использовать тензор Кельвина-Сомильяны для изотропного упругого
тела с параметрами Ламе - Я = 0; // = 0.5, а область Dq
распространить на все евклидово пространство Rn, так как в этом
случае при стремлении радиуса-вектора х к бесконечности
компоненты вектора перемещения ведут себя как |х~ , а тензора
напряжения - как |х| [30], что обеспечивает существование
конечной величины скалярных произведений
Vu,veV0(D0)
<оо
B.196)
где
V-r-r, <T(X)~-
2 '
Таким образом, метод геометрического погружения
применительно к решению краевых задач анизотропной теории
упругости на произвольной области D позволил свести их к
сходящейся последовательности краевых задач изотропной теории
упругости на канонической области Do.
Глава 3
КОНЕЧНО-ЭЛЕМЕНТНАЯ РЕАЛИЗАЦИЯ МЕТОДА
ГЕОМЕТРИЧЕСКОГО ПОГРУЖЕНИЯ
3.1. Введение
В соответствие с теоретическими положениями метод
геометрического погружения в вариационной постановке позволяет
перейти от решения вариационного уравнения для тела D сложной
пространственной геометрии к сходящейся итерационной
последовательности вариационных задач B.54) для некоторого
канонического тела Dq :
\<т(и(к)) • s(Sa)dD =(l - e) f <j{xi{k~X)) • -?(&)dV + ff • <5iidDд +
Do DA V
Jp
Jp-&dS, * = 1,2,...; u@)=0, C.1)
So
причем в C.1) в качестве произвольного элемента пространства V
выбран v = u + да . Численные эксперименты позволяют установить,
что итерационная последовательность B.54) сходится и при
значении ? = 0, поэтому в дальнейшем для удобства везде
принимается это значение.
В ряде случаев МГП допускает аналитическую реализацию,
например, используя разложение решения в ряд по каноническим
собственным функциям [120]. Однако в подавляющем большинстве
случаев приходится прибегать к численной реализации.
В работах [99-101,120,123] представлена численная реализация
МГП в цилиндрической системе координат на основе
полуаналитического МКЭ с использованием разложения решения в
тригонометрический ряд Фурье. Погружение в тело вращения в этом
случае позволяет свести задачу для тела сложной пространственной
геометрии к последовательности осесимметричных задач. Такой
подход охватывает широкий класс машиностроительных
конструкций, топологически близких к телам вращения, но
3.2. Основные соотношения для однородных изотропных тел 71
конструкционные и технологические полости и выступы,
нарушающие осевую симметрию.
В настоящей главе представлены основные соотношения
численной реализации МГП на основе полу аналитического МКЭ в
цилиндрических координатах при решении задач линейной теории
упругости для однородных и кусочно-однородных конструкций.
3.2. Основные соотношения конечно-элементной реализации
МГП для однородных изотропных тел
Руководствуясь общей схемой МГП, выберем в качестве
канонического тела Do тело вращения, полностью охватывающее
исходную конструкцию D (рис.3.1).
Для определения перемещений воспользуемся методом Фурье и
представим их в виде тригонометрического ряда по угловой
координате <р. Неизвестные коэффициенты ряда будем определять с
помощью МКЭ. Такой подход по форме напоминает
полуаналитический МКЭ [17], однако, как будет видно в
дальнейшем, имеет ряд специфических для МГП особенностей.
Поскольку погружение осуществляется в тело вращения, то для
дискретизации воспользуемся тороидальными конечными
элементами треугольного поперечного сечения. Использование
треугольного сечения позволяет с достаточно высокой точностью
аппроксимировать геометрию тела со сложной границей.
Рассмотрим процедуру построения конечномерного аналога для
одного конечного элемента De.
Рис.3.1. Исходная (а) и каноническая (б) области (усл. обозн. см. текст)
72
Гл. 3. Конечно-элементная реализация МГП
cos nlcp
0
0
0
cos nlcp
0
0
0
sin nlcp
В матричном виде с учетом разложения в ряд Фурье перемещения
точек тела записываются в виде
C.2)
где {u}={w,w,v} - вектор перемещений тела по осям r,z, ср;
( ) i п /ЛТ
{и п \ - ул%, w%, v% j , p -1,2 - неизвестные коэффициенты
разложения, являющиеся функциями rwz\
sin nlcp О О
О sin nlcp О
О 0 cos nlcp
Целочисленный параметр / характеризует симметрию задачи по
угловой координате и введен в целях исключения из рассмотрения
гармоник, заведомо не дающих вклада в решение.
Такой вид решения наиболее удобен для класса задач, у которых
кинематические граничные условия заданы на поверхности,
описываемой функцией только координат г и z, или, если достаточно
просто получить представление граничных перемещений в виде ряда
Фурье. В разложении для перемещения v функции sin и cos
поменяны местами, так как при симметричном решении для и и w
решение v является кососимметричным. Поэтому такая форма
записи разложения удобнее, в частности, для задач, в которых мы
можем ограничиться разложением в одинарный тригонометрический
ряд.
Согласно общей процедуре МКЭ, представим разыскиваемые
коэффициенты разложения Фурье через их узловые значения и
функции формы конечного элемента :
{u^^I, N2h -.., A^lfx^ /? = 1,2 , C.3)
где Nu - число узлов в элементе; Nt(r,z), i =1, 2, ... , Nu - функции
формы элемента; I - единичная матрица, размером Cx3);
~)ир
w
vnV
nNu
wr
nN1t
вектор
узловых неизвестных п -й гармоники разложения.
Подставив C.3) в C.2), получим:
3.2. Основные соотношения для однородных изотропных тел 73
- kj к
C.4)
/1=0
где
полный
вектор узловых неизвестных элемента для п-й гармоники
разложения.
Подставляя C.4) в соотношения Коши в цилиндрических
координатах [93]
__ ди _ 1 dv __dw
дг' ^ г дф^ * dz'
\ ди v dv dv \ dw du dw
dz r dф " dz dr
получим связь деформаций {s\- \sr,?фЦ?2,yr(p,Ущ,yrz\ в элементе
у р @ — ' '
г dф г dr
с узловыми неизвестными :
00
(з-5)
/i=0
л=0
к,\=
— COS п1ф
~cosnl(p
О
— Nj sin п1ф
г
о
COS П1ф
д z
О
О
—- cos п1ф
О
nl_. .
Nt sin п1ф
г
L COS Ыф
О
— Nj cos п1ф
г
О
dz
д г
74
Гл. 3. Конечно-элементная реализация МГП
а матрица [Bwl получается из [В „Л заменой cos nl(p на sin nlcp,
7 7 nl nl
sin nlcp на cos nl(p и — на .
г г
Физические соотношения для однородного изотропного тела [17]
в матричной форме примут вид
где \а\ =\jr,<jip,crz,тГ(р,т^,тгг\ - вектор напряжений в элементе,
[D] - матрица упругих констант :
1DJ=
A + 2G
Л
Л
0
0
0
л
Л + IG
Л
0
0
0
Е
Л
л
Я + 2в
0
0
0
0
0
0
G
0
0
пяа
0
0
0
0
G
0
0
0
0
0
0
G
я =
соответственно модуль Юнга и коэффициент Пуассона материала
конструкции.
Подставив C.5) в физические соотношения, получим выражение
связи напряжений в элементе с узловыми неизвестными :
J{XJ • C.6)
/i=0 IIх «jJ /i=0
Запишем теперь выражения для вариации энергии упругой
деформации тела в объеме Dq и в объеме D^ , который вырезается
тороидальным элементом из области D& .
Как видно на рис.3.2 , все элементы можно разделить на два типа.
Элементы первого типа не пересекаются с областью Эд и.
следовательно, не дают вклада в вариацию энергии деформации
в объеме D^. Эти элементы фактически аналогичны осесим-
метричным тороидальным элементам. Элементы второго типа
пересекают область DA, причем, возможно, неоднократно.
3.2. Основные соотношения для однородных изотропных тел 75
Зозможность многократного пересечения с областью Б
необходимо учитывать при интегрировании по угловой координате.
Элемент типа 2
Элемент типа 1
Рис.3.2. Конечные элементы типов 1 и 2
С учетом C.5) и C.6) выражение вариации энергии деформации в
объеме Од принимает вид
„ Г
J fB«
Pi
{Xw}.C.7)
Обозначив в C.7)
окончательно получим:
А{Хт}, C.8)
гДе [Ки/Я]д - блок матрицы жесткости для дополнения,
соответствующий гармоникам пит.
Аналогично для вариации энергии деформации в объеме Vq
имеем:
76 Гл. 3. Конечно-элементная реализация МГП
^loJX^}, C.9)
где [К„т]0= J[Bn]T[DjBOT]dD0 - блок матрицы жесткости
J
De n=0
канонического тела.
Подынтегральные выражения в формулах для матриц жесткости
имеют сложную зависимость от координат г и z, что приводит к
необходимости использования методов численного интегрирования.
По угловой координате интегралы легко вычисляются аналитически.
С учетом численного интегрирования по г и z выражение для
[кпт]& примет вид
Nk Vu
I
7=1 k=\ Щк
где Se - площадь поперечного сечения тороидального элемента;
Nti - число точек интегрирования в выбранной схеме (выбор схемы
зависит от степени аппроксимирующих полиномов); Wj - весовой
множитель численного интегрирования; Nj, - число пересечений
тороидального элемента с областью Бд ; (р\к,(Р2к " соответственно
углы входа и выхода при /:-ом пересечении с областью Од ; г,- -
значение г ву'-ой точке интегрирования.
Учитывая ортогональность тригонометрических функций, можно
заметить, что в матрице [К/2т]0 будут отличны от нуля только
диагональные блоки :
Ntl 2*
[К,Д = 5е2^ C.11)
М о
Запишем выражение для матрицы [К^т]д более детально. Из
C.5) следует, что матрица [Кпт ]д имеет блочную структуру вида
3.2. Основные соотношения для однородных изотропных тел 11
N
к=\
k
Пк
Тг
И
Г г if -
N
dcp.
В свою очередь каждый из блоков
состоит из подматриц размером C х 3) :
Пк
кьк
Выполнив умножение матриц в подынтегральном выражении и
вводя обозначения
dr dr r2
r r
дг г dz dz dr
)
r r
«3V/
r
dz dr dr
NrNj 2
r2 '
V; iV,
J J \ 1.
a dNi N;
d z r
ll
r d r r
dz '
d r r dr r dz dz
• smml(pd(p\
<P\k
<P\k
78 Гл. 3. Конечно-элементная реализация МГП
<Р2к <Р2к
Р2к 2к
gj2 = |sin nlcp - cosml(pd(p\ fy2 = (cos a?/#> • sin mlcpd(p\
<P\k <P\k
<P2k <P2k
= [cos nlcp • sin ml(pd(p\ h^ j = J sin nlcp • cos mlcpd(p\
<P\k <P\k
<P2k
Plk 2k
- Г sin nlcp • sin ml(pd(p\ Л22 - cos nl<p' cos mlcpdcp,
получим следующие соотношения для компонент подматриц
||
nmij2\"a\2 %РЯ> Knmij22-a22 8РЯ
Компоненты матрицы [K^m]0 определяются аналогично с учетом
п=т, N^=1, (р\\=0, (р2\=2тг. Все интегралы по угловой
координате легко вычисляются аналитически.
Вариацию работы внешних сил запишем в общем виде
где {fn} - вектор узловых усилий в элементе, определение которых
более подробно будет описано в разделе 3.3.
Подставив C.8), C.9) и C.12) в C.1), получим
3.2. Основные соотношения для однородных изотропных тел 79
и=0 т=0 и=0
Произведя теперь типовую процедуру [87] ансамблирования
конечных элементов и учитывая произвольность вариаций узловых
перемещений, получим итерационную последовательность СЛАУ
относительно неизвестных узловых коэффициентов разложения
Фурье :
я}, ^;
^0 С3-14)
it = 1,2,...; {Хя}<°>-0.
В C.14) [Кял]о и [К„т]д - глобальные матрицы жесткости
ансамбля конечных элементов для канонического тела и дополнения,
а {Х„}и {{п} - глобальные векторы узловых неизвестных и нагрузок
соответственно.
В реальных расчетах число членов ряда ограничено конечным
числом Ng, которое выбирается исходя из специфики задачи так,
чтобы обеспечить удовлетворительное качество решения.
В качестве критерия контроля за сходимостью итерационного
процесса можно использовать, например, относительную невязку
системы
^=|([K]0-[K]AXx}W-{f|2/||{f}||2 C.15)
и/или относительную норму приращения решения на соседних
итерациях:
I{}W{}^)|/|{}(*)|. C.16)
Таким образом, метод геометрического погружения в сочетании с
полуаналитическим МКЭ позволил свести сложную
пространственную задачу к итерационной последовательности
Несимметричных задач для канонического тела. Это позволяет
Использовать весь накопленный арсенал средств решения таких
80 Гл. 3. Конечно-элементная реализация МГП
задач: различные алгоритмы и программы дискретизации плоских
областей, решения систем линейных уравнений и т. п.
Вся сложность решения пространственной задачи сведена к
вычислению на каждой итерации произведения разреженной
матрицы на вектор предыдущего решения в правой части системы и
многократному решению блочно-диагональной системы с разными
правыми частями и постоянной матрицей коэффициентов. Матрица
системы может храниться в факторизованном виде, что сокращает
время решения системы на каждой итерации. Разреженные матрицы
жесткости для дополнения также могут быть собраны один раз и
храниться на внешних носителях.
3.3. Учет различных силовых факторов
При построении разрешающих соотношений конечно-элементной
реализации МГП в разделе 3.2 силовые факторы были записаны в
общем виде как совокупность узловых усилий, эквивалентных
воздействию объемных и поверхностных сил. Рассмотрим теперь
более подробно преобразование действующих на тело нагрузок к
эквивалентным им значениям усилий в узлах конечных элементов.
Следует отметить, что использование разложения в ряд Фурье по
угловой координате для функций задачи несколько сужает круг
силовых факторов, которые достаточно эффективно можно учесть в
расчетах. Например, неблагоприятным для такого подхода является
случай нагружения сосредоточенной силой, который легко
учитывается в классических схемах МКЭ с использованием
пространственных элементов. Описываемый подход целесообразно
использовать для задач, в которых можно получить приемлемые по
точности (качеству) и затратам разложения нагрузок в ряд Фурье по
угловой координате.
3.3.1. Учет действия объемных сил
Пусть конструкция нагружена объемными силами интенсивности
F(r,z,ср) с составляющими по осям Fr(r,z,(p), Fz(r,z,cp) и
F9{r9z,<p).
Из C.12) с учетом C.4) узловые составляющие нагрузки от
действия объемных сил для одного конечного элемента имеют вид :
3.3. Учет различных силовых факторов
81
fob jkf
Dc
dD,
C.17)
где
J nz\ ' Jп
q>\>
fncpNu
г-
вектор узловых нагрузок элемента; [lSn ] - матрица функций формы
элемента из C.4).
Запишем компоненты узловых нагрузок для /-го узла элемента:
te)- Jkf
De
D, /7 =
i = lNu. C.18)
D
Зная выражения для компонент интенсивности объемных сил в
цилиндрических координатах и проинтегрировав по объему
элемента аналитически (если это возможно) или численно, получим
соответствующие приложенным силам значения узловых нагрузок.
Пусть компоненты Fr,Fz иF^ зависят только от координат г и z.
Тогда выражение C.18) с учетом возможного многократного выхода
тороидального элемента в область Эд приобретает вид
ы-
J
cos nlcp
cosnlcp
sin nlcp
где 5е - площадь поперечного сечения тороидального элемента.
Выражение для дш-| получается из C.19) путем замены cosnlp на
sin«/^> и sinnlp - на cosnlcp.
Интеграл по площади сечения тороидального элемента обычно
берется численно по схеме, обеспечивающей заданную точность, а
по угловой координате интегрирование выполняется аналитически.
С учетом этого C.19) принимает вид
82
Гл. 3. Конечно-элементная реализация МГП
nl
- cos
Fz(rj9Zj)
1
-smnl(p2k к
i + cos nlcp2 к J
C.20)
Выражение для лЛ/- J получается из C.20) путем замены cosnl<p на
- sinw/^? и sinnlp на - cosnlp .
Примером такого рода нагружения могут служить центробежные
силы, возникающие при вращении тела с постоянной угловой
скоростью со . В этом случае Fr - рсо г, р - плотность материала
тела, a Fz - F^ = 0 . Эквивалентные узловые нагрузки имеют вид
7=1
,^2 у
nl ?-*
0
0
Выражение для jfm-j получается при замене в ^nij smnlcp на
- cosnlq?.
Другим простым случаем является нагружение объемными
силами постоянной интенсивности вдоль осей декартовой системы
координат. Примером такого рода нагружения может служить
действие собственного веса конструкции. Записав в этом случае с
учетом преобразования координат компоненты Fr,Fz,F(p в виде
Fr - Fx cos (р + Fy sin <p, Fz - F2, F^- -Fx sin (p + Fy cos q>
и подставив их в C.18), получим выражения для узловых нагрузок.
Возникающие при этом интегралы от произведения
тригонометрических функций легко вычисляются аналитически.
3.3. Учет различных силовых факторов
83
3.3.2 Учет действия поверхностных нагрузок
Рассмотрим случай, когда нагрузка распределена по поверхности
тела и известны pr(r, z, (p\ pz{r, z,q>\ p^r.z.cp) - составляющие
интенсивности по осям цилиндрической системы координат. Для
элемента, имеющего выход на поверхность с заданными нагрузками,
аналогично случаю нагружения объемными силами имеем:
Рг
dS,
где
f/2 I ~ \fnr\ >
А А
Jnrb
/2
Jnzb
J
-2 У
п(р\)
C.21)
- вектор
узловых нагрузок элемента; [Nw
элемента из C.4).
Для /-го узла в элементе имеем выражение:
- матрица функций формы
М- ]кГ
Рг
Pz
Pep
¦dS
г Г 1
Sea
Рг
Pz
P<p
dS,
C.22)
Зная выражения компонент интенсивности нагрузки р и вычислив
поверхностный интеграл, получим эквивалентные узловые нагрузки.
При этом возможны два варианта действия нагрузки на поверхность
элемента: 1) на боковую поверхность тороидального элемента; 2) на
поверхность, образующуюся при пересечении элемента с областью
Од при движении по угловой координате - торцевую поверхность
элемента. Рассмотрим случай, когда компоненты интенсивности рг
и Р2 - постоянные, а р^ = 0.
При действии нагрузки на боковую поверхность элемента C.22)
приобретает вид
pr cos nlcp
lAT + l
J
pz cos nlcp
0
C.23)
Проинтегрировав C.23) по <р, получим:
84 Гл. 3. Конечно-элементная реализация МГП
pr{smnl(p2k -i
p.(sinnlq>2к ~sinШщк+х)\, C.24)
0 J
Интеграл /L = ГгЛГ,dL обычно вычисляется численно. Аналогии-
L
но C.24) вычисляются компоненты jfm j при замене sin на - cos .
В случае нагружения торцевой поверхности тороидального
элемента интегрирование по поверхности проводится численно в
естественных координатах криволинейного треугольника [6].
Частным случаем является нагружение плоской торцевой
поверхности элемента, нормаль к которой совпадает с осью ср^ .
При этом рг - р2 =0, ру - /?, а выражение C.22) после выполнения
интегрирования по угловой координате приобретает вид
3.4. Учет кинематических граничных условий
При рассмотрении кинематических граничных условий в
рассматриваемой численной реализации МГП приходится (как и в
случае с силовыми факторами) сталкиваться с рядом ограничений.
Например, практически невозможно учесть закрепление отдельной
точки тела, а также случай, когда перемещения точек заданы на
части отрезка [0,2/г]. Обычно учет кинематических граничных
условий при использовании разложения в ряд Фурье ограничен
случаем, когда перемещения узлов заданы на всем отрезке [0,2я].
Нулевые кинематические граничные условия достаточно просто
учитываются по одной из традиционных для МКЭ схем, например,
путем исключения из разрешающей системы линейных
алгебраических уравнений строк и столбцов, соответствующих
фиксированным узловым перемещениям. Отличие заключается лишь
в том, что в МГП эта процедура должна быть выполнена для матриц
|KmJo и LK/
При учете ненулевых кинематических граничных условий
следует исходить из возможности разложения заданных
3.4. Учет кинематических граничных условии 85^
перемещений в ряд Фурье по угловой координате. Если разложение
Фурье получено, то также используется один из традиционных
приемов учета заданных ненулевых перемещений, принятых в МКЭ.
3.5. Особенности учета разнородных материалов конструкции
Метод геометрического погружения распространен в разделе 2.3
для неоднородных тел. Теперь рассмотрим особенности конечно-
элементной реализации МГП для конструкций, состоящих из разных
материалов. При этом ограничимся случаем, когда каждый из
материалов конструкции однородный и изотропный.
Пусть рассматриваемое тело состоит из Nm материалов с
характеристиками Л\,Л2,...,Лкг и G^G2,...,GN . Согласно общей
процедуре МГП, осуществим погружение в однородное изотропное
тело, геометрически охватывающее исходное и имеющее
характеристики материала Aq и Gq. По теории МГП, для
обеспечения сходимости итерационной процедуры при разнородных
материалах Aq и Go должны удовлетворять следующему условию:
Aq > тах(Я], Л2,..., Ядг ); Gq > max(Gj, G2,..., G^ ),
где Л и С - параметры Ламе.
В роли дополнения Бд здесь выступает объединение
подобластей Dj.b которых характеристики материала отличаются
от Aq и Gq .
Процедура построения конечномерного аналога МГП аналогична
таковой для однородного изотропного тела в разделе 3.2 с той лишь
разницей, что при вычислении матриц жесткости элементов для
области Do используются характеристики материала Aq и Gq, a
Матрицы жесткости для дополнения в объемах Da/ определяются
при Л = Ло~Л; и G = Gq -Gj. С учетом этого C.14) приобретает
вид
т=0
¦V
и - «k~l)
86 Гл. 3. Конечно-элементная реализация МГП
+ {fn}, «-0,оо; к = \,2,...; {Х„}(о)-О, C.25)
где [К^ДЛо ,Go)]q - каноническая матрица жесткости в объеме Dq;
M - матрица жесткости дополнения в объеме
Da/ , вырезаемом тороидальными элементами при движении по
угловой координате в области с характеристиками материала Я.- и
G:, отличными от Aq и Gq .
Соотношение C.25) можно рассматривать как случай
изотропного однородного тела из раздела 3.2 (назовем его
матрицей), у которого области D^ заполнены материалами с
характеристиками Я, и G , (включения). Отличие состоит в том, что
если в качестве материала канонической области будет выбран
материал из Од , то в качестве D м будет выступать область D
J Aj
исходного тела.
Преобразуем соотношение C.25). Пусть Х\ и G]
характеристики матрицы. Учитывая, что
Nm
где Nm - число включений, а также линейную зависимость матриц
жесткости от Я и G , получим:
У=2
-Я,,Go -<ji)]q-/Jk,
У=2
3.5. Особенности учета разнородных материалов конструкции 87
Подставляя C.26) в C.25) и учитывая ортогональность
тригонометрических функций на отрезке [0,2я], окончательно
получим:
m=0 7=2
я_0,оо, Л = 1,2,..., (Xrt)w=0. C.27)
Если Aq = Я], Gq = Gj, Яj ~Gj =0 (вырезы в изотропном
однородном теле), то выражение C.27) в точности соответствует
C.14). Выражение C.27) позволяет единообразно решать задачи как
для кусочно-однородных тел, так и для однородных тел с полостями.
3.6. Решение тестовых задач
Описанный в предыдущих разделах вариант численной
реализации МГП на основе полуаналитического МКЭ реализован в
виде программы на языке FORTRAN для IBM - совместимых ПЭВМ.
Программа предназначена для расчета НДС пространственных
кусочно-однородных конструкций, нагруженных поверхностными
и/или объемными (массовыми) силами, в цилиндрической системе
координат в рамках линейной теории упругости.
Для проверки достоверности получаемых с помощью программы
Результатов был решен ряд тестовых задач, для которых известно
либо аналитическое решение, либо решение, полученное другим
Проверенным численным методом.
88
Гл. 3. Конечно-элементная реализация МГП
3.6.1. Задача о коротком однородном упругом цилиндре под
действием поверхностных нагрузок
В качестве первой тестовой задачи рассмотрим полый
однородный упругий цилиндр длины L с внутренним радиусом а и
внешним Ь, нагруженный по внешней цилиндрической поверхности
равномерно распределенной нагрузкой р (рис.3.3). Остальные
поверхности свободны от нагрузок и кинематических связей.
Рис. 3.3. Расчетная схема цилиндра (усл. обозн. см. текст)
Погружение осуществлялось в цилиндр длины L, но большей
толщины в радиальном направлении. Поскольку реальное тело,
каноническое тело и область дополнения - осесимметричные, то для
получения решения достаточно удержания одного члена в
разложении Фурье.
Расчет проводился при следующих параметрах конструкции:
Ь/а=2; Ь/а=\6;у=03 и единичном модуле Е. Канонический цилиндр
разбит на 4000 тороидальных элементов с линейной аппроксимацией
перемещений B091 узел с 6273 неизвестными), причем половина
элементов приходилась на область, занимаемую реальным телом.
Итерационная процедура МГП выполнялась до тех пор, пока
относительная невязка решения разрешающей системы уравнений Rk
не уменьшалась до 10" . Для выполнения этого условия при
погружении в цилиндр с параметрами г/а=3 и г//я=1 потребовалось
22 итерации обычной процедуры МГП и 14 итераций - при
использовании ускорения сходимости итерационного процесса,
которое будет более подробно рассмотрено в дальнейшем.
3.6. Решение тестовых задач
89
На рис.3.4 и 3.5 приведены соответственно безразмерные
радиальные перемещения и напряжения и динамика их изменения от
итерации к итерации, а также решение задачи традиционным МКЭ
при аналогичной дискретизации тела.
-1.60
-2.40
-2.80
0.80
1.20
1.60
2.00
Рис.3.4. Радиальные перемещения в однородном цилиндре. Внешнее
давление (сечение z = L/2 ; здесь и на рис.3.5, 3.9, 3.10 :
• - осесимметричные КЭ; ост. усл. обозн. см. текст)
Как видно из графиков, начиная с 8-й итерации радиальные
перемещения практически совпадают. Радиальные напряжения
совпадают уже с 5-й итерации. Относительная невязка системы Rk
на 8-й итерации составляет 0.6-10 , тогда как на 1-й итерации она
была 0.96-10 . Незначительное отличие решения на 8-й и 14-й
итерациях (отличия по перемещениям не превосходят 0.03%, а по
Спряжениям - 0.04%), свидетельствует о том, что для практических
расчетов можно ограничиться сходимостью итерационного процесса
по относительной невязке системы до 0.01. Количественный анализ
Результатов в сравнении с традиционным МКЭ показал, что отличия
по перемещениям не превышают 0.02% , а по напряжениям - 0.04%,
т.е. результаты совпадают.
90
Гл. 3. Конечно-элементная реализация МГП
0.00-1
°"Г/Р
-U20-
-0.40-
-аео-
4X80-
-1.00-
г /а
1.00
120
1.40
1.80
200
Рис.3.5. Радиальные напряжения в однородном полом цилиндре.
Внешнее давление (сечениеz - L/2; усл. обозн. см. текст)
Погружение в цилиндр с параметрами гУя=2 и r\/a- 0.5 привело к
тем же результатам, но за 18 итераций ( с ускорением сходимости).
Для определения влияния степени отличия реального и
канонического тел была решена серия задач, в которых погружение
осуществлялось в цилиндры с параметрами г2/а=3...6 и г/я=1.
Степень отличия реального и канонического тел определялась как
Wд =||Кд||2/||Ко||2 • Результаты расчетов, приведенные на рис.3.6,
свидетельствуют о росте числа итераций с увеличением отличия
реального и канонического тел. Поэтому при выборе канонической
области следует стремиться максимально приблизить ее геометрию к
геометрии реального тела, кроме тех случаев, когда выбор
канонического тела с большей степенью отличия дает возможность
более эффективного решения задачи за счет применения
специальных методов.
Рассмотрим теперь цилиндр, нагруженный на четырех секторных
участках внешней боковой поверхности равномерно распределен-
распределенной нагрузкой (рис.3.7).
3,6. Решение тестовых задач
91
4U
3v
in
1U
у
/
0.80
0.85
0.90
0.95
1.00
Рис.3.6. Зависимость числа итераций от степени отличия реального и
канонического цилиндров ( • - с ускорением, А - без ускорения)
r
' \
1 i
C7^ N
b
-r
I \
к ^
._ -._— -.. — . —
I
I
I
1
-J
РисЗ.7. Однородный цилиндр с секторной поверхностной нагрузкой
(усл. обозн. см текст)
В этом случае необходимо удерживать в разложении N гармоник.
^еШение выполнено при параметрах, аналогичных предыдущей
Задаче. Погружение осуществлялось в цилиндр с г2/а=3 и rj/a=\. С
Учетом периодичности задачи расчет проводился для 1/8 части
Инструкции с заданием условий симметрии. В разложении
Удерживалось 20 гармоник. Сходимость итерационной процедуры
^ГТ1 по относительной невязке системы Rn до 0.001 была достигнута
За 15 итераций. На рис.3.8 приведены распределения радиальных
^Пряжений и интенсивности напояжений в сечении 2-1Л.
Гл. 3. Конечно-элементная реализация МГП
Рис.3.8. Распределение радиальных напряжений (а) и интенсивности
напряжений (б) в однородном цилиндре. Секторное давление (сечение
z-L/l\ усл. обозн. см. текст)
3. б. Решение тестовых задач
93
3.6.2. Задача о коротком однородном упругом цилиндре под
центробежных сил
Рассмотрим полый однородный упругий цилиндр (см. рис.3.3),
нагруженный центробежными силами, возникающими при вращении
конструкции вокруг оси z с постоянной угловой скоростью со.
Внешняя поверхность цилиндра свободна от нагрузок и
кинематических связей. Расчет проводился при Ъ/а-2\ L/a=\6\ v=§3
и единичных значениях модуля упругости, плотности материала и
угловой скорости. Погружение осуществлялось в цилиндр с туо=3 и
Итерационный процесс сошелся по относительной невязке
системы до 0.001 за 14 итераций. Результаты расчета приведены на
рис.3.9 и 3.10. Как и при нагружении поверхностными силами,
начиная с 6-8-й итераций перемещения и напряжения практически не
меняются. Полученные результаты совпадают с расчетами
традиционным МКЭ.
3.60
3.20
2.80
2.40
2.00
г/а
0.80
1.20
1.60
2.00
Рис.3.9. Радиальные перемещения в однородном цилиндре.
Центробежные силы (сечение z=L/2; усл. обозн. см. текст)
94
Гл. 3. Конечно-элементная реализация МГП
0.60
0.00
-0.20
-0.40
1.00
1.20
1.40
1.60
1.80
2.00
Рис.3.10. Радиальные напряжения в однородном цилиндре.
Центробежные силы (сечение z=L/2] усл. обозн. см. текст)
3.6.3. Упругое равновесие полой сферы под действием
внутреннего давления
Рассмотрим полую сферу с внутренним радиусом а и внешним к
нагруженную внутренним давлением р (рис.3.11,а). Известно
аналитическое решение этой задачи [106].
Рис.3.11. Задача Ламе для полой однородной сферы (усл. обозн. см. текст)
Погрузим реальную сферу в полую сферу с большим внешни*
радиусом (см. рис.3.11,а). Решение задачи проведено при следуюши!
3.6. Решение тестовых задач
95
параметрах : b/a=2; r2/a=3; v=0.3; p=\ и единичном значении
модуля упругости Е.
Как и в случае с погружением цилиндра в цилиндр, для
получения решения достаточно удержать одну гармонику в
разложении Фурье. Четверть образующего сечения сферы была
разбита на 4000 элементов B000 из них приходилось на реальное
тело). Итерационный процесс МГП сошелся по относительной
невязке системы до 0.001 за 8 итераций. Полученное решение и
динамика его изменения по итерациям приведены на рис.3.12 и 3.13.
Начиная с 4-й итерации, решение практически не меняется.
0.20
0.00
via
0.80
1.20
1.60
2.00
Рис.3.12. Радиальные перемещения. Задача Ламе для сферы.
Погружение в сферу (здесь и на рис.3.13-3.15 :• - решение Ламе, ост. усл.
обозн. см. текст)
Количественное сравнение результатов с аналитическим
РеШением показало, что погрешность по перемещениям не
пРевышает 0.5 % , а по напряжениям 0.8 %.
96
Гл. 3. Конечно-элементная реализация МГП
0.00
-0.20 -
-0.40 ¦
-0.60 -
-0.80
-1.00-
<
/
/
J
V
-
!
]
via
0.80
1.20
1.60
2.00
Рис.3.13. Радиальные напряжения. Задача Ламе для сферы.
Погружение в сферу
Погрузим теперь сферу в цилиндр со сферической полос гью,
совпадающей с внутренней поверхностью сферы (см. рис.3.11,6).
Внешний радиус цилиндра п/а=3 ,а длина L/a=3. И в этом случав
итерационная процедура МГП сошлась до заданной точности по
относительной невязке системы за 8 итераций. Точность
полученного решения аналогична таковой при погружении в сферу.
На рис.3.14 и 3.15. приведены распределения радиальных
перемещений и напряжений по толщине сферы на итерациях МГП.
3.6.4. Упругое равновесие двухслойного кусочно-однородного
цилиндра под действием поверхностных сил
Рассмотренные в предыдущих тестовых примерах конструкций
были однородными и изотропными. Применим теперь процедуру
МГП для расчета кусочно-однородной конструкции. В качестве
примера рассмотрим задачу о равновесии упругого двухслойной
цилиндра, состоящего из материалов с разными модулями упругости
(рис.3.16).
Внешняя цилиндрическая поверхность нагружена равномерно
распределенной нагрузкой р. Остальные поверхности свободны of
нагрузок и кинематических связей. В расчете приняты следующие
3.6. Решение тестовых задач
1.00
и /а
г
0.80-
0.60
0.40
0.20
0.00
0.80
3-8
г/а
1.20
1.60
2.00
Рис.3.14. Радиальные перемещения. Задача Ламе для сферы.
Пофужение в цилиндр (усл. обозн. см. текст)
-0.80
-1.00
0.80
1.20
1.60
2.00
Рис.3.15. Радиальные напряжения. Задача Ламе для сферы
Погружение в цилиндр (усл. обозн. см. текст)
98
Гл. 3. Конечно-элементная реализация МГП
ттт
Материал 1
Материал 2
Рис.3.]6. Двухслойный неоднородный цилиндр
геометрические параметры : b/a=2; c/a=3; L/a=l6. Соотношение
модулей упругости материалов ?/?/ = 10, а коэффициенты Пуассона
v} = v2=03. Погружение осуществлялось в однородный изотропный
цилиндр с внутренним и внешним радиусами а и с соответственно,
Е=тах(Е], Е?) и v=0.3.
Канонический цилиндр разбивался на 4000 тороидальных
элементов с 2091 узлом. С учетом осевой симметрии реального и
канонического тел в разложении Фурье удерживалась одна
гармоника. Итерационная процедура МГП сошлась по
относительной невязке системы R до 0.001 за 26 итераций.
Распределение радиальных перемещений и напряжений в среднем
сечении цилиндра, а также динамика их изменения в ходе
итерационного процесса приведены на рис.3.17 и 3.18.
Как видно из результатов, начиная с 13-й итерации (Rk=0.02),
решение практически не меняется. Количественное сравнение с
результатами, полученными традиционным МКЭ, показывает, что
погрешность по перемещениям не превышает 0.5%, а по
напряжениям - 0.7 % .
Дня анализа влияния степени отличия жесткостных характе-
характеристик материалов конструкции на сходимость процедуры МГП
решена серия задач при различных соотношениях модулей
упругости слоев цилиндра. Результаты расчетов, приведенные на
рис.3 Л 9, показывают, что при более жестком внутреннем слое
требуется существенно больше итераций G6 итераций при ?/?/=100
и 14-при ?/?,=0.01).
Это связано с большей долей дополнения в канонической
матрице жесткости. Величины элементов матрицы жесткости
3.6. Решение тестовых задач
99
-0.20
и 1а
г
-0.40
-0.60
-0.80
-1.00
-1.20
ч
- ^.
1$
V
S
13-21
-и
¦л
— —
\
\
via
1.00 1.50 2.00
2.50
3.00
Рис.3.17. Радиальные перемещения в двухслойном неоднородном цилиндре
(сечение z~LI2\ здесь и нарис.3.18:# - осесимметричные КЭ, ост. усл.
обозн. см. текст)
о.оо
-0.40
-0.80 -
-1.20
1.00
\
0
\
Л
г
L
i
***
— —
,
^^
в
11.
^—
•<
1
о
3
А
10.
rla
1.50
2.00
2.50
3.00
Рис.3.18. Радиальные напряжения в двухслойном неоднородном
цилиндре (сечение z=L/2; ост. усл. обозн. см. текст)
100
Гл. 3. Конечно-элементная реализация МГП
80
60-
40-
20
0.00 0.01 0.10 1.00 10.00 100.00
Е2/Е1
Рис.3.19. Зависимость числа итераций от степени отличия характеристик
материалов
дополнения связаны как с объемной долей области D(h так и с
величиной разницы жесткостных характеристик материалов
канонического тела и дополнения. При E2/Ej=0A потребовалось
наименьшее число итераций A2) для достижения сходимости.
3.6.5. Упругое равновесие перфорированного цилиндра
действием поверхностных сил
под
В предыдущих тестовых примерах осуществлялось погружение
осесимметричных конструкций также в осесимметричные. Это
позволяет проверить правильность работы процедуры МГП, но не
дает возможности оценить скорость сходимости и реальные
вычислительные затраты для действительно трехмерных задач, так
как решение для канонической области по характеру уже
соответствует решению исходной задачи.
Рассмотрим теперь МГП при расчете конструкций сложной
пространственной геометрии на примере перфорированно1 о
цилиндра, нагруженного внутренним давлением (рис.3.20). Внешняя
цилиндрическая и торцевые поверхности свободны от нагрузок и
кинематических связей.
3.6. Решение тестовых задач
101
Рис.3.20. Задача о перфорированном цилиндре (ост. усл. обозн. см. текст)
С конструкциями такого вида приходится сталкиваться,
например, при расчете зарядов твердотопливных ракетных
двигателей [19]. Данная конструкция имеет пространственную
геометрию, существенно отличающуюся от осесимметричной.
Расчет проводился при следующих параметрах : L/a=lO; b/a=3.5;
с/а=6.0;?=100Па; v=03; p=\ Па.
Погружение осуществлялось в цилиндр с внутренним радиусом а
и внешним с. Для дискретизации использовались 800 тороидальных
элементов с линейной аппроксимацией перемещений D41 узел). В
разложении Фурье удерживалось 20 гармоник. Общее число
неизвестных задачи - 26460. Итерационная процедура МГП
выполнялась до относительной невязки системы Rn<0.0\. Для
сходимости по этому критерию потребовалась 101 итерация. Затраты
времени на решение задачи на Pentium-75 составили 34 мин, а на
Pentium-150 12 мин.
На рис.3.21 представлено распределение радиальных напряжений
по радиусу в среднем сечении цилиндра при (р = 0° и #> = 45°.
Наблюдается хорошее выполнение естественных граничных условий
(погрешность составляет 1-2%).
На рис.3.22 приведено распределение напряжений а9 по
Окружной координате в сечении z=Z /2 и г = 2.3 а. Погрешность в
Удовлетворении граничным условиям непосредственно на границе
Связана с особенностями вычисления производных от решения
вблизи точек разрыва, которые будут более подробно рассмотрены в
^ЭДьнейшем. На рис.3.23 представлены изолинии интенсивности
Спряжений в сечении z=L/2.
102
Гл. 3. Конечно-элементная реализация МГП
0.40
о.оо-
-0.40 ¦
-0.80 ¦
-1.20
к*"
ч
1'
Г
/
г/а
1.00 2.00 3.00 4.00 5.00 6.00
Рис.3.21. Радиальные напряжения в перфорированном цилиндре (сечение
z=I/2; • - сечение 0°, ¦ - сечение 45°, А - решение ANSYS @°))
-U.ZU
%'р -
-0.40-
-0.60-
-0.80 -
Л Г\{\
-1.00
-1.20 ~
\
>—•
——ч>
20.00 25.00 30.00 35.00 40.00 45.00
Рис.3.22. Окружные напряжения в перфорированном цилиндре
(сечениеz =1/2, а*/я = 2.3)
3.6. Решение тестовых задач
103
мгп
Рис. 2.23. Изолинии интенсивности напряжений в сечении Z-LI2
перфорированного цилиндра
Для оценки качества полученного решения проведено сравнение
в сечении z=L/l полученных результатов с расчетом, выполненным с
помощью пространственных конечных элементов типа тетраэдров с
Квадратичной аппроксимацией перемещений (пакет ANSYS).
Дискретизация пространственными элементами выполнена таким
°бразом, чтобы число неизвестных в задаче примерно
^ответствовало расчету по МГП (порядка 25000 неизвестных). На
^ВМ класса Pentium-120 с 32 Мбайт оперативной памяти время
РеШения задачи составило около 7 мин пои итерационном метопе
104
Гл. 3. Конечно-элементная реализация МГП
решения СЛАУ. При фронтальном методе время решения задачи
возросло более чем в 2 раза, кроме того, около 8 мин было затрачено
на перенумерацию сетки.
Сравнение результатов, полученных МГП и ANSYS, показало
приемлимое количественное и качественное соответствие
(погрешность 3-5%). Рассматриваемая реализация МГП уступает по
скорости решения задачи пакету ANSYS (при использовании
итерационного метода решения СЛАУ). Этот факт отчасти объясним
тем, что ANSYS - хорошо проработанный промышленный
программный продукт, полностью использующий все ресурсы ЭВМ
(всю область оперативной памяти). Программа, реализующая МГП,
использует минимальное количество оперативной памяти при
решении данной задачи и производит довольно много обменов с
жестким диском, что существенно замедляет процесс решения. При
использовании фронтального метода пакету ANSYS требовалось
значительно большее количество внешней памяти, чем для МГП.
При этом временные затраты сопоставимы.
3.6.6. Упругое равновесие перфорированного ijwnmdpa с
жесткими включениями под действием поверхностных сил
Рассмотрим теперь задачу о равновесии перфорированного
цилиндра со звездообразным вырезом, у которого область вырезов
заполнена более жестким включением (рис.3.24).
f \
L
«^ »
С
b
Рис.3.24. Перфорированный цилиндр с жестким включением (усл. обозн.
см. текст)
Внешняя цилиндрическая поверхость конструкции подвержена
воздействию равномерно распределенной нагрузки единичной
3.6. Решение тестовых задач
105
интенсивности. Остальные поверхности свободны от нагрузок и
К0нематических связей.
Данная конструкция обладает пространственной
неоднородностью, которая существенно отличается от
осесимметричной. Расчет проводился при следующих
геометрических параметрах: L/a=\0; b/a^3.5; c/a=6.0.
Характеристики материалов : Евкл/ЕШТР^Ю0; vMATF=03; vBKJI=03.
Погружение осуществлялось в цилиндр с внутренним радиусом а
и внешним - с из однородного материала с ЕО=ЕВКЛ;; 1^=0.3. Для
дискретизации использовались 1152 тороидальных элемента с
линейной аппроксимацией перемещений F25 узлов). В разложении
Фурье удерживалось 20 гармоник. Общее число неизвестных задачи
37500. Итерационная процедура МГП выполнялась до
относительной невязки системы i?*<0.01. Для сходимости по этому
критерию потребовалось 168 итераций. Высокая степень
неоднородности материалов привела к заметному замедлению
процесса сходимости по сравнению с однородными задачами.
На рис.3.25 представлено распределение радиальных напряжений
по радиусу в сечении z-1/l и <р=0. Как видно из графика,
наблюдается удовлетворительное выполнение естественных
граничных условий.
<Vp
-0.40-
-0.80-
-1.20-
*
\
\
\
ч
г/а
100
2.00
3.00 4.00
5.00
6.00
Рис.3.25. Радиальные напряжения в перфорированним цилиндре с жестким
включением (сечение z=I /2 и (р=0)
106
Гл. 3. Конечно-элементная реализация МГП
На рис.3.26 приведена карта изолиний интенсивности
напряжений в сечении z=L/2. Наблюдается значительная
концентрация напряжений на границе материалов с различными
характеристиками.
СУ. /р
Рис.3.26. Изолинии интенсивности напряжений в сечении z=L/2
перфорированного цилиндра с жестким включением
Произведено сравнение результатов в среднем поперечном
сечении цилиндра с расчетом, выполненным плоскими конечными
элементами с квадратичной аппроксимацией перемещений
(программа GANIMED) для плоско-деформированного состояния.
На рис.3.27,а представлена карта изолиний интенсивности
напряжений, полученная для двумерного МКЭ. Наблюдается
значительное отклонение в значениях, полученных МГП для
короткого цилиндра.
При моделировании условий, близких к плоско-
деформированному состоянию (ПДС), был проведен расчет для
задачи, аналогичной данной, но на торцевых поверхностях
цилиндра был наложен запрет на осевые перемещения. Процедура
МГП для такой задачи сошлась за 87 итераций. Полученные
интенсивности напряжений приведены на рис.3.27,6. При такой
постановке задачи наблюдается хорошее совпадение результатов, за
исключением области, близкой к угловой точке. При этом
необходимо учесть, что расчет плоским КЭ выполнялся на более
мелкой сетке, чем дискретизация соответствующего сечения в МГП.
3.6. Решение тестовых задач
107
О /р
2D-MK3-GANIMED
мгп - пдс
Рис.3.27. Интенсивности напряжений в сечении z=L/2 для ПДС (двумерный
МКЭ) и МГП с закрепленными торцами
На рис.3.28 представлено распределение радиальных
напряжений в сечении <р=0 для плоской задачи и для решения МГП.
Наблюдается практически полное совпадение результатов.
Полученные данные свидетельствуют о значительном отличии
пространственного напряженного состояния короткого
неоднородного цилиндра даже в среднем сечении от плоской задачи.
Таким образом, сравнение расчетов для тестовых задач
°Днородной и неоднородной теории упругости с известными
108
Гл. 3. Конечно-элементная реализация МГП
0.40
°г'Р
0.00
-0.40
-0.80-
-1.20
-1.60 ~
\
\
\
ч
к,
¦ # i
г/а
1.00
2.00
3.00
4.00
5.00
6.00
Рис.3.28. Радиальные напряжения в сечении z=L/2 и #>=0
для: - плоских КЭ, • - МГП
аналитическими решениями и решениями, полученными
проверенным численным методом, свидетельствуют о достоверности
результатов. Сравнение расчетов для тел со сложной геометрией и
состоящих из разных материалов с расчетами пространственными и
плоскими КЭ показывает точность получаемых результатов и
эффективность МГП при расчете однородных и неоднородных
пространственных конструкций сложной геометрии.
3.7. Практическая сходимость конечно-элементной реализации
метода геометрического погружения
Теоретически в главе 2 доказано, что итерационная процедура
метода геометрического погружения сходится к решению задачи
независимо от степени близости реального и канонического тел. При
численной реализации МГП на основе МКЭ необходимо
дополнительное исследование практической сходимости.
Погрешности вычислений на ЭВМ, замена непрерывных функций
задачи их дискретными аналогами и другие параметры могуг
привести к нарушению сходимости конкретного численного
алгоритма.
3.7. Практическая сходимость конечно-элементной реализации 109
В настоящем разделе на ряде задач иллюстрируется практическая
сходимость конечно-элементной реализации МГП в зависимости от
степени дискретизации расчетной области и числа удерживаемых в
разложении гармоник. Рассмотрено влияние механических характе-
характеристик материалов на характер сходимости итерационного процесса.
3.7.1. Сходимость конечно-элементной реализации МГП в
зависимости от степени дискретизации
При проведении расчетов с помощью метода конечных элементов
необходимо проверить сходимость получаемого решения при
увеличении степени дискретизации.
Рис.3.29. Перфорированный цилиндр. Внутреннее давление A-3 -точки,
ост. усл. обозн. см. текст)
Рассмотрим сходимость конечно-элементной реализации МГП на
примере задачи об однородном перфорированном цилиндре под
Действием внутреннего давления (рис.3.29). Особенностью
рассматриваемой численной реализации является тот факт, что по
угловой координате неизвестные функции аппроксимируются
отрезками ряда Фурье, а для коэффициентов разложения,
являющихся функциями г и z, используется традиционная конечно-
элементная аппроксимация на основе тороидальных элементов
треугольного поперечного сечения с линейными функциями формы.
Для оценки сходимости в зависимости от степени дискретизации
проведена серия расчетов на различных сетках. Расчеты
производились при следующих параметрах: L/a=\0; b/a=3.5;
С//а-6.0; ?=100 Па; v^0.3; p=\ Па . В разложении Фурье во всех
по
Гл. 3. Конечно-элементная реализация МГП
случаях удерживались 18 гармоник. Сходимость оценивалась по
выполнению естественных граничных условий. На рис.3.30 и 3.3}
представлены значения радиальных перемещений и напряжений а
характерных точках сечения цилиндра z=L/2. Как показывают
результаты, при сгущении сетки наблюдается сходимость решения,
характерная для МКЭ при использовании элементов с
соответствующей аппроксимацией. При числе узлов более 400
решение для перемещений практически не меняется.
По напряжениям решение становится практически неизменным,
начиная с 625-ти узловой дискретизации. Погрешность выполнения
граничных условий по напряжениям составляет около 2%. Это
объясняется тем, что при линейной аппроксимации напряжения
вычисляются фактически не непосредственно на границе тела, а в
центре тяжести соответствующего приграничного элемента. Анализ
выполнения естественных граничных условий на поверхности,
перпендикулярной окружной координате, показал практическую
неизменность результатов и для окружных напряжений в
характерной точке 3 сечения z-L/1.
10.00
ufla
о гул
/
4
-
О 200 400 600 800 1000
Количество узлов
Рис.3.30. Радиальные перемещения в характерных точках
- точка 1, ^ - точка 2) при различных дискретизациях (сечение z-L/2)
3.7. Практическая сходимость конечно-элементной реализации 111
/ и
-и. /и
Л ОА
-U.oU
-1.00-
\
\
\
\
\
^^
¦—*-.
¦¦—
¦а—
••
— —
—-•
о
200
400
600 800 1000
Количество узлов
Рис.3.31. Радиальные напряжения в характерных точках
( • - точка 1, а - точка 2) при различных дискретизациях (сечение z=U2)
Сравнение коэффициентов разложения, полученных при
различных дискретизациях, в совпадающих узлах сеток показало
аналогичную сходимость.
Рассмотрим сходимость решения в зависимости от числа
гармоник, удерживаемых в разложении. Проведены расчеты для
предыдущей задачи на сетке с 441 узлом с удержанием от 6 до 18
гармоник в разложении. Результаты расчетов в характерной точке 3
(см. рис.3.29) в сечении z=L/2 приведены на рис.3.32,3.33.
Наблюдается сходимость для окружного перемещения на границе
тела. Значения перемещений, полученные при 16 и 18 гармониках,
отличаются на 0.8%. По напряжениям, вычисленным
непосредственно на границе тела в точке 3, наблюдается сходимость
решения, но погрешность выполнения естественных граничных
Условий высока E0%). Это объясняется особенностью поведения
Рядов Фурье в окрестности точек разрыва и влиянием эффекта
Гиббса. Окружные напряжения, вычисленные на некотором
Удалении по угловой координате от границы тела, показали
хорошую сходимость результатов. Значения, полученные при 16 и
*8 гармониках, практически не различаются.
112
Гл. 3. Конечно-элементная реализация МГП
3.68 —
u /a.
Ч 64
Ч ^6
Ч 5?
/
/
/
/
/
4 8 12 16 20
Рис.3.32. Сходимость окружных перемещений в точке 3 от числа гармоник
0.80
0.40-
0.00-
-0.40
-0.80-
-1.20 •
\
\
\
л
S
р*^—1
12
16
20
Рис.3.33. Сходимость окружных напряжений в точке 3 от числа
гармоник(• - 23°,^ - 25°)
Результаты расчетов показали, что сходимость МГП от степени
дискретизации соответствует исследованиям сходимости обычны*
КЭ с соответствующей аппроксимацией перемещений.
3 7. Практическая сходимость конечно-элементной реализации 113
3.7.2. Влияние коэффициента Пуассона на характер сходимости
итерационной процедуры МГП
В настоящей работе конечно-элементный аналог задачи строится
на основе вариационного уравнения типа уравнения Лагранжа. При
коэффициентах Пуассона материала конструкции, близких к 0.5,
резко ухудшается обусловленность матрицы разрешающей СЛАУ.
Это приводит к существенным погрешностям в вычислениях.
Рассмотрим влияние коэффициента Пуассона на сходимость
итерационной процедуры МГП на примере задачи о
перфорированном цилиндре под действием внутреннего давления
(см. рис.3.29). Геометрические параметры задачи аналогичны
принятым в предыдущем разделе. Проведены расчеты для
материалов с коэффициентами Пуассона от 0.3 до 0.49 при
единичном модуле упругости. Во всех случаях было выполнено по
100 итераций. На рис.3.34,3.35 приведены зависимости
относительной невязки системы Rn и относительной нормы
приращения решения gu^ . Как видно из результатов, с увеличением
коэффициента Пуассона сходимость процесса существенно
замедляется. Если при v^O.3 за 100 итераций R^ уменьшилась почти
до 0.02, то при v=0.49 эта величина превышает 0.1. При v>0.45 после
выполнения 100 итераций решение еще претерпевает значительные
10.00
1.00
0.10
0.01
0 20 40 60 80 100
^Ис.3.34. Относительная невязка системы на итерациях МГП при различных
значениях коэффициента Пуассона
114
Гл. 3. Конечно-элементная реализация МГП
изменения на итерации. Поэтому для слабосжимаемых материалов
требуется значительно больше времени для сходимости
итерационного процесса.
0ЛО0-.
0.010 --
0.001-^
и.иии
l\__
1
"^
Л А
^s -—
0.3Q/ N
•
1
1
^^
>_
^^^7*"—
0 20 40 60 80 100
Рис. 3.35. Относительная норма приращения на итерациях МГП
при разных коэффициентах Пуассона
3.7.3. Влияние степени отличия реального и канонического тела
на характер сходимости итерационной процедуры
Уже на тестовых примерах в разделе 3.3 было видно: чем больше
степень отличия реальной и канонической областей, тем больше
итераций требуется для сходимости итерационного процесса до
заданной точности. Важно знать, насколько сильно влияет
геометрическое отличие реальной конструкции от канонического
тела и отличие физико-механических свойств материалов на
сходимость МГП.
Рассмотрим задачу об однородном перфорированном цилиндре
под действием внутреннего давления. Решен ряд задач для
конструкции такого типа, но с различной угловой шириной выреза.
Угловая полуширина выреза принималась равной 15, 20, 22, 22,5,
23, 25 и 30°. Остальные параметры задачи следующие: L/a^lO',
b/a=3.5; c/a=6.0; ?=100 Па; v=0.3; /?=1Па. Использовалась
дискретизация со 129-ю узлами с удержанием 10 гармоник в
3 7. Практическая сходимость конечно-элементной реализации 115
разложении. Итерационный процесс МГП в каждом случае
проводился до достижения точности 0.01 по относительной невязке
системы. Степень отличия реального и канонического тел
оценивалась по отношению норм матриц жесткости
fl^ =[|Кд||2/||Ко|2 . На рис.3.36 представлена зависимость числа
итераций, потребовавшихся для сходимости по заданному критерию,
от степени отличия реального и канонического тел. Результаты
показывают, что прямая зависимость между степенью отличия тел
при различной угловой полуширине выреза нарушается. При
значениях, близких к 22.5°, наблюдается увеличение числа
требуемых итераций. При расчете с большим числом гармоник и
степенью дискретизации характер зависимости сохранялся. Наличие
всплеска можно объяснить ухудшением свойств матрицы системы
при характерных значениях полуширины выреза.
120
к
100
80
60-
40-
20
г—
18
.. '
г>
\
\
/
/
/
1 2
V
2.5
/2i
3
27
зс
0.350 0.400 0.450 0.500 0.550 0.600
Рис.3.36. Зависимость числа итераций от степени геометрического отличия
реального и канонического тел для разной угловой ширины выреза
Рассмотрим, как влияет на сходимость отличие в физико-
механических характеристиках материалов. Для конструкции типа
Перфорированного цилиндра с включениями из другого материала
П°Д действием давления на внешней боковой поверхности (см.
Рис.3.24) проведен ряд расчетов при различном отношении модулей
Упругости материалов включения и основного тела. Степень отличия
116
Гл. 3. Конечно-элементная реализация МГП
также оценивалась по отношению норм матриц жесткости
Жд =|Кд| /||Ко||2 . На рис.3.37 представлена зависимость числа
итераций, потребовавшихся для сходимости по заданному критерию,
от WA. Соотношение модулей Евкл/ЕМАтр принималось равным 10, 50,
100,200.
n
160-
120-
80
40
0 Ч
10
/
50
200
lOOi
/
f
vv,
0.64
Рис.3.37. Зависимость числа итераций от степени неоднородности
материалов
Как показывают результаты расчета, с ростом разницы модулей
упругости материалов наблюдается экспоненциальное увеличение
числа итераций для достижения заданной точности, что, вероятнее
всего, связано с большими градиентами в НДС при большой
неоднородности и ухудшением свойств разрешающей системы
уравнений.
3.7.4. О выборе критерия прекращения итераций
Как показали расчеты, представленные выше, итерационная
процедура конечно-элементной реализации МГП сходится на
практике. При проведении расчетов итерационным методом
необходимо определить момент, когда дальнейшее продолжение
итераций не дает существенного изменения в решении и можно
считать, что процесс сошелся. Опыт проведенных расчетов
показывает, что одним из параметров, позволяющих контролировать
процесс, является величина относительной нормы приращения
. Эта величина характеризует процесс с точки зрения скорости
3.7. Практическая сходимость конечно-элементной реализации 117
изменения решения от итерации к итерации. Требование ?и^ <0.001
в большинстве случаев оказывается достаточным для получения
приемлимого приближения к решению.
Другая величина, характеризующая погрешность решения СЛАУ,
_ относительная невязка системы. При однородных задачах с
коэффициентом Пуассона не более 0.45 достижение точности по
относительной невязке 0.01 оказывается достаточным для того,
чтобы считать процесс сошедшимся. Значение ?и^ составляет
10" -10" . Однако для слабосжимаемых материалов, а также при
большой разнице модулей упругости возникают ситуации, когда при
невязке системы 0.01 решение еще сильно меняется и параметр
?м? составляет значительную величину.
Опыт расчетов показал, что контроль процесса по обоим
параметрам позволяет избежать преждевременного окончания
итераций. Поэтому при решении задач с помощью МГП
используется следующий критерий прекращения итераций: если
относительная невязка системы Rk достигла заданной величины и
при этом относительная норма приращения guk также не
превышает допустимой величины (например 0.001), то процесс
прекращается. В противном случае итерации продолжаются до
выполнения условий по обоим параметрам.
3.8. Повышение эффективности численной реализации метода
геометрического погружения
Теоретически доказанная сходимость МГП к искомому решению
задачи имеет очень важное значение. Однако при практическом
применении может оказаться главным не столько сам факт
сходимости, сколько величина затрат для получения решения. В
вычислительной практике встречаются ситуации, когда тот или иной
метод при реализации на ЭВМ требует использования специальных
приемов для получения решения при разумных вычислительных
затратах. Примером может служить метод Ланцоша для определения
собственных частот и форм [70].
Приведенные тестовые примеры показывают быструю
сходимость итерационной процедуры МГП в случае, когда исходная
118 Гл. 3. Конечно-элементная реализация МГП
и каноническая области топологически подобны. При сложной
пространственной геометрии сходимость замедляется, что ведет к
существенному увеличению вычислительных затрат.
В данном разделе рассмотрены вопросы повышения
эффективности конечно-элементной реализации МГП за счет как
сокращения затрат на каждой итерации, так и модернизации самой
итерационной процедуры, а также некоторые вычислительные
особенности, связанные, например, с определением производных в
окрестностях границы тела.
3.8.1. Выбор метода решения вспомогательных систем
линейных уравнении
Характерная черта рассматриваемого варианта конечно-
элементной реализации МГП - необходимость решения на каждой
итерации ряда независимых систем линейных алгебраических
уравнений (СЛАУ) вида
fti—O
Все разреженные матрицы [K^]q имеют одинаковый портрет
(т.е. структуру расположения ненулевых элементов) и различаются
лишь величинами элементов. Портрет матриц представлен на
рис.3.38. В ходе итерационного процесса приходится многократно
решать системы C.28) для получения очередного приближения.
Сами матрицы [К^]q остаются неизменными, а изменяются лишь
правые части СЛАУ. Общие вычислительные затраты зависят от
того, насколько эффективно решаются системы вида C.28), причем
даже сравнительно небольшое сокращение затрат при решении
СЛАУ приводит при большом числе гармоник и итераций к весьма
существенному сокращению общего времени решения. В работе
[14] представлены различные методы решения разреженных
систем, возникающих, в частности, в методе конечных элементов.
Наибольшее распространение в практике конечно-элементных
расчетов в 80-х годах получили различные варианты ленточного и
профильного методов. Характерные черты этих методов - простота
алгоритма и используемых ctdvktvd данных, соответственно -
3.8. Повышение эффективности численной реализации МГП 119
\
\
Исходная Профильный метод Метод параллельных
сечений
Рис.3.38. Портреты исходной матрицы жесткости и перенумерованной
для профильного метода и метода параллельных сечений.
относительная простота численной реализации, а также
возможность организовать обмен с внешними носителями при
больших системах. В условиях ограниченного объема оперативной
памяти ПЭВМ второй фактор имел до недавнего времени очень
большое (если не решающее) значение.
Кроме ленточного и профильного методов при решении
разреженных положительно определенных СЛАУ используются
методы минимальной степени, древовидного разбиения,
вложенных сечений. Эти методы характеризуются более сложными
структурой хранения информации и алгоритмами решения, но в
них в значительной степени учитывается разреженность матрицы,
что для больших систем приводит к меньшим вычислительным
затратам, чем в профильном методе.
Один наиболее перспективный метод решения разреженных
систем - метод параллельных сечений, предложенный в 1980 г.
А. Джорджем [14,70]. Этот метод сочетает в себе лучшие черты
профильного метода Дженнингса, метода древовидного разбиения
и метода сечений. При этом он имеет достаточно простую
структуру данных и допускает несложную реализацию. Кроме того,
алгоритм метода параллельных сечений может применяться в
зависимости от потребностей для минимизации либо затрат
памяти, либо числа операций при факторизации, либо числа
°пераций при обратной постановке. Возможна даже минимизация
общей стоимости выполнения алгоритма путем учета
сРавнительной стоимости вычислительных ресурсов ЭВМ и
Количества правых частей, для которых требуется решать систему.
По мнению С. Писсанецки [70], метод параллельных сечений
120
Гл. 3. Конечно-элементная реализация МГП
является серьезным претендентом для принятия в качестве
промышленного стандарта математического обеспечения конечно-
элементных расчетов. Для метода характерен и тот факт, что при
неэффективности построения сечений с точки зрения затрат
генерируется структура данных, соответствующая профильной
схеме Дженнингса. Портреты матриц жесткости для профильного
метода и метода параллельных сечений приведены на рис.3.38.
Программы, реализующие профильный метод и метод
параллельных сечений, приведены в работе [14]. Для сравнения
затрат, возникающих при использовании этих методов, проведены
тестовые расчеты для различных дискретизаций прямоугольной
области. При реализации метода параллельных сечений отличие от
программ, представленных в работе [14], заключалось в
использовании представления вещественных чисел с двойной
точностью. Результаты расчетов на регулярных сетках треугольных
линейных элементов с равным числом узлов вдоль сторон
прямоугольника и тремя неизвестными в узле приведены в
табл.3.1-3.3.
Таблица 3.1
Затраты общей памяти для метода параллельных
сечений по отношению к профильного методу
Сетка
13x13
17x17
21x21
25x25
31x31
Число
неизвестных
507
867
1323
1875
2883
Оптимизация по
памяти
0.68
0.64
0.58
0.54
0.49
времени
факторизации
0.74
0.65
0.61
0.56
0.51
времени
решения
0.73
0.68
0.60
0.55
0.50
3.8. Повышение эффективности численной реализации МГП 121
Таблица 3.2
Затраты времени факторизации системы для метода
параллельных сечений по отношению к профильному методу
Сетка
13x13
17x17
21x21
25x25
31x31
Число
Неизвестных
507
867
1323
1875
2883
Оптимизация по
памяти
1.80
1.90
1.20
1.27
1.30
времени
факторизации
1.80
1.90
1.16
1.08
1.29
времени решения
2.50
1.90
1.20
1.10
1.30
Таблица 3.3
Затраты времени решения факторизованной системы для метода
параллельных сечений по отношению к профильного методу
Сетка
13x13
17x17
21x21
25x25
31x31
Число
неизвестных
507
867
1323
1875
2883
Оптимизация по...
памяти
1.40
1.15
1.50
1.40
0.95
времени фактор.
1.40
1.15
1.40
1.30
0.88
времени решения
1.30
1.15
1.30
1.30
0.88
122 Гл. 3. Конечно-элементная реализация МГП
Полученные результаты стали основанием выбора метода
параллельных сечений при решении СЛАУ для каждой гармоники
в итерационной процедуре МГП.
3.7.2. Ускорение сходимости итерационного процесса МГП
Как показывает практика расчетов, сходимость итерационного
процесса МГП на разных стадиях различна. Если на начальном
этапе скорость сходимости достаточно высока, то по мере
приближения к решению задачи она существенно падает, а сам
итерационный процесс становится монотонным. Это приводит к
большим затратам для получения решения с некоторой заданной
точностью. Замедление сходимости итерационного процесса
характерно не только для МГП, но и для большинства
наиболее распространенных итерационных методов решения
СЛАУ.
Сокращения числа итераций при использовании итерационных
методов можно добиться с помощью специальных процедур
ускорения сходимости. В работе [107] подробно рассмотрены
различные способы ускорения сходимости основных
итерационных методов решения СЛАУ: метод сопряженных
градиентов, полиномиальное ускорение и др. Однако описанные
методы требуют, как правило, значительных дополнительных
вычислений, связанных с уточнениями спектральных
характеристик матрицы коэффициентов системы решаемых
уравнений.
В работе [28] предложен более простой способ ускорения
сходимости итерационных процессов, который не требует
значительных вычислительных затрат и хранения большого объема
дополнительной информации.
Пусть
- сходящаяся последовательность приближений к решению
операторного уравнения вида
х*+1=Ах„. C.29)
При п -> оо имеет место соотношение
3.8. Повышение эффективности численной реализации МГП 123
C.30)
где ( • , • ) - скалярное произведение векторов; | • || - квадратичная
норма вектора.
При больших п для векторов решения хп справедливы
приближенные равенства :
ta-xJ; ... C.31)
Но тогда точное решение х можно приближенно записать в
виде
х* = хЛ + (хЛ+1 - хп) + ( хя+2 - хй+1) + ...«
- *п + (x«+i - О+*i(x*+i - хJ+*i2(x^i - xJ+•••;
откуда
xi+\-*n C.32)
1-Ь,
В силу C.30), заменим Ь\ его приближенным значением:
~хп>хп 'хп-\)
Заменив в C.32) t>i на выражение C.33), получим :
*«*п- (**-'«-!»'*-»n-l) . (Хя+1 _ Хл) C 34)
VXW-bl ^Х«+ХА2-ЬХЛ ХП-\)
Формулу C.34) можно использовать для самых общих случаев.
Она дает хорошие приближения х ив некоторых случаях, когда
обычные последовательные приближения расходятся (например,
когда оператор задачи "'слабо линеен"), а весь спектр производной
оператора А лежит внутри единичного круга, кроме одной точки.
Рассчитанное по C.34) приближение х к решению ближе к
Искомому, чем обычное приближение, полученное в итерационном
Процессе.
Методика применения описанного подхода к процедуре МГП
следующая. Выполняется несколько обычных итераций, а затем по
124
Гл. 3. Конечно-элементная реализация МГП
C.32) и C.33) или по C.34) определяется новое приближение к
решению задачи. Далее снова выполняется ряд итераций и
повторяется процедура ускорения. Такой подход требует лишь
хранения, кроме текущего решения, еще двух векторов решения с
предыдущих итераций.
При реализации процедуры ускорения можно в качестве трех
приближений, необходимых для расчета параметров ускорения,
взять решения не с соседних итераций, а с пропуском, например,
через одну итерацию.
Рассмотрим применение процедуры ускорения сходимости на
примере задачи о равновесии короткого перфорированного
цилиндра под действием внутреннего давления (см. рис.3.20).
Проведены тестовые расчеты для 169-узловой дискретизации с
удержанием в разложении Фурье 14 гармоник. На рис.3.39 и 3.40
представлены кривые сходимости итерационного процесса по
относительной норме приращения решения и по относительной
невязке решения системы с ускорением и без ускорения
сходимости.
0.0000
200
400
Рис.3.39. Кривые сходимости по относительной норме приращения
с ускорением A) и без ускорения B)
3.8. Повышение эффективности численной реализации МГП 125
1.00
0.10 -
0.01
0.00
!
I
2
/
1
^
• _
200
400
600
Рис.3.40. Кривые сходимости по относительной невязке системы
с ускорением A) и без ускорения B)
Без ускорения сходимости потребовалось почти в 6 раз больше
итераций для достижения заданной точности, чем при
использовании ускорения.
Как видно из графиков, при использовании ускорения
сходимости наблюдаются осцилляции по относительной норме
приращения по мере приближения к решению. Однако общая
сходимость процесса сохраняется. Практика использования
ускорения сходимости показала, что при расчетах с заданием
высокой точности, а также при некоторых геометрических и
физических параметрах задачи (например при коэффициентах
Пуассона >0.48) наблюдается локальное нарушение сходимости
итерационного процесса при сохранении общей сходимости МГП к
решению задачи. Это связано с приближенностью расчета нового
приближения в процедуре ускорения и, как следствие - с
нарушением структуры решения. Выполнение некоторого числа
обычных итераций, как правило, позволяет восстановить характер
сходимости процесса МГП. Однако, если число обычных итераций
До следующего применения ускорения недостаточно велико, то
новое ускорение может привести к еще большему нарушению
сходимости и даже к расходимости итерационного процесса. На
Рис.3.41 и 3.42 представлен характер сходимости итерационного
Процесса при использовании ускорения соответственно по
126
Гл. 3. Конечно-элементная реализация МГП
0.01
Рис.3.41. Характер сходимости итерационного процесса с ускорением при
различных коэффициентах Пуассона по относительной невязке системы
1.0000 -а
0.0010
0.0001
0.0000
Рис.3.42. Характер сходимости итерационного процесса с ускорением
при различных коэффициентах Пуассона
по относительной норме приращения
3.8. Повышение эффективности численной реализации МГЛ 127
относительной невязке системы и относительной норме
приращения.
На эффективность процедуры ускорения влияет как число
итераций, выполненных от последнего ускорения до первой
итерации, учитываемой в расчете нового ускорения, так и число
итераций между решениями, по которым рассчитывается новое
ускорение. Большое число итераций между ускорениями
неоправданно увеличивает вычислительные затраты, а
недостаточное может привести к локальному нарушению
сходимости, что также требует дополнительных затрат на
восстановление характера сходимости процесса.
Для исследования влияния этих параметров на эффективность
процедуры ускорения была проведена серия расчетов для
упомянутой выше задачи о перфорированном цилиндре.
Итерационный процесс проводился до достижения точности по
относительной невязке системы 0.01. Результаты расчетов сведены
в табл.3.4.
Анализ полученных результатов показывает, что наиболее
эффективно процедура ускорения для данной задачи работает по
следующей схеме: до начала ускорения выполняется 2 или 3
обычные итерации, а затем из последующих итераций для расчета
ускорения выбираются 3 итерации с интервалом 1 или 2 между
ними.
Приведенные результаты получены на 169-узловой
дискретизации. Расчеты при других параметрах сетки подтвердили
характер зависимости от параметров ускорения. Однако для других
задач (например при коэффициенте Пуассона, близком к 0.5)
зависимость эффективности ускорения от параметров может быть
Другой, поскольку нарушения в векторе решения, вызванные
применением процедуры ускорения, могут потребовать большего
числа обычных итераций на восстановление его структуры.
Система же, решаемая на каждой итерации, при слабосжимаемых
телах становится плохо обусловленной и, следовательно,
чувствительной к малым изменениям вектора правой части.
Проведение оптимизации параметров ускорения практически
^возможно, так как для конкретной задачи нельзя заранее
Достаточно точно оценить требуемое число итераций. Поэтому
приходится руководствоваться лишь опытом решения различных
Задач с помощью МГП.
128
Гл. 3. Конечно-элементная реализация МГП
Таблица 3.4
Число итераций для решения задачи о перфорированном цилиндре при
различных параметрах ускорения
Число
итераций до
начала
ускорения
0
1
2
3
4
Число итераций между решениями, участвующими в
расчете ускорения
1
133
116
94
77
104
2
154
87
93
121
138
3
104
121
133
155
158
3.8.3. Использование технологии разреженных матриц в
процедуре МГП при вычислении правой части
Построение конечномерного аналога МГП на основе МКЭ
приводит к итерационной последовательности СЛАУ, матрицы
которых разрежены. Правая часть этих систем имеет зависящую от
текущего приближения к решению составляющую, которая
представляет собой произведение разреженной матрицы с
постоянными коэффициентами на вектор текущего приближения к
решению.
От эффективности выполнения операций с разреженными
матрицами существенно зависят общие затраты на решение задачи,
так как доля затрат на вычисление итерационной составляющей
правой части велика. В настоящее время технология разреженных
матриц, как искусство обращаться с разреженными матрицами,
является устоявшейся научной дисциплиной, представляющей
собой сплав теоретических достижений, численной практики и
здравого смысла [70].
3.8. Повышение эффективности численной реализации МГП 129
При выборе способа решения СЛАУ на итерациях МГП уже
использованы на практике методы технологии разреженных
матриц. Рассмотрим теперь операцию формирования итерационной
составляющей правой части разрешающей системы уравнений
мгп {O^XtK^yxJ^1).
/я=0
Глобальные блоки [Клт]д для каждого пит образуются путем
ансамблирования локальных матриц жесткости элементов типа 2 в
объеме Уд. Матрицы [к„ш]д имеют разреженную структуру,
причем во многих случаях степень их разреженности значительно
выше, чем у блоков канонической матрицы жесткости [K^Jq.
Портреты всех матриц [Клт]д одинаковы и симметричны, однако
сами матрицы (за исключением диагональных блоков [К^д)
несимметричны, что приводит к более высоким затратам памяти,
чем для хранения канонических матриц жесткости. Кроме того, с
ростом числа гармоник в разложении число блоков матрицы
жесткости дополнения и, следовательно, величина затрат на
вычисление итерационной составляющей правой части {fn\'
растут в квадратичной зависимости от числа гармоник. Это
приводит к тому, что вычисление {fn pA ' занимает большую часть
времени, затрачиваемого на получение очередного приближения к
решению, так как доля затрат на решение СЛАУ с
факторизованными матрицами становится очень малой.
Одним из подходов при вычислении {^}д является
формирование всех глобальных блоков [к„т]д до начала
итерационного процесса, а также хранение их на внешних
носителях (жестком диске) с последующим считыванием на
каждой итерации. Учитывая при этом, что [К„т]д = [Кт„]^,
вЬ1числять и хранить необходимо лишь N -(N + 1)/ 2 блоков (N -
число гармоник в разложении). Блоки [Кл/И]д участвуют лишь в
операциях умножения на вектор решения, поэтому для их хранения
^ожно использовать одну из наиболее распространенных схем,
пРинятых для разреженных матриц, - упорядоченный разреженный
130 Гл. 3. Конечно-элементная реализация МГП
строчный формат RR(C)O [70]. При использовании этой схемы
хранятся значения только ненулевых элементов матрицы, а также
столбцовые индексы этих элементов (отсюда и название схемы
хранения) и вектор указателей начала строк в массивах индексов и
значений. Использование специальных процедур вычисления
произведения разреженной матрицы в формате RR(C)O на вектор
позволяет с минимальными затратами вычислять {fw}^'.
Если доля элементов типа 2 в общем числе элементов велика
(например для конструкций с большим нарушением осевой
симметрии по геометрии или по физико-механическим
характеристикам материала в случае кусочно-однородных
конструкций), то хранение матриц [К„т]д может потребовать при
большом числе гармоник в разложении Фурье очень значительных
ресурсов внешних носителей, а затраты на чтение блоков [к^т]д
на каждой итерации - существенно снизить эффективность
применения МГП.
Альтернатива описанному выше подходу - отказ ot
формирования глобальных матриц жесткости дополнения [Кпт]д.
В этом случае на каждой итерации вычисляются вклады в
итерационную составляющую правой части для каждого элемента
типа 2 с последующим суммированием в глобальном векторе
{^}д . Фактически это означает неявное выполнение сборки
глобальных блоков [Кп/„]д на каждой итерации МГП
одновременно с вычислением {^}д • При таком подходе
локальные матрицы жесткости дополнения для элементов типа 2
перевычисляются в ходе итерационного процесса. Общие затраты
памяти (оперативной и на внешних носителях) в этом случае
минимальны и соответствуют затратам на решение задачи для
осесимметричной конструкции при неосесимметричном
нагружении.
И, наконец, третий подход, который занимает промежуточное
положение между первыми двумя, заключается в том, что
глобальные матрицы [к„т]д не формируются, но часть
информации, не меняющейся в ходе итерационного процесса (это
могут быть, например, интегралы от произведения
3.8. Повышение эффективности численной реализации МГП 131
хригонометрических функций, локальные матрицы жесткости
дополнения элементов 2 типа и т.п.), вычисляется до начала
итераций и хранится на внешних носителях, и считывается по мере
необходимости. Это обычно требует существенно меньше памяти
на внешних носителях, чем в случае сборки и хранения глобальных
блоков [Кпт]А .
Для сравнения эффективности применения описанных подходов
проведена серия расчетов на примере задачи о равновесии
перфорированного цилиндра под действием внутреннего давления
(см. рис.3.20). В табл.3.5 приведены относительные затраты
времени на выполнение 1-й итерации МГП для всех описанных
выше подходов в сравнении с результатами, полученными при
ипользовании подхода с формированием глобальных матриц для
дополнения для 169-узловой дискретизации при удержании 10
гармоник в разложении Фурье. Проведены расчеты на IBM-
совместимых ПЭВМ с процессорами 486ЭХ-ЗЗМГц, 486DX4-
100МГц и Реп1шт-75МГц.
Полученные результаты показывают, что при использовании
высокопроизводительного процессора значительно целесообразнее
схема без хранения информации на внешних носителях с
перевычислением локальных матриц жесткости дополнения на
каждой итерации (затраты времени сокращаются более чем в 2
раза). Это связано с низкой скоростью выполнения операций
обмена с внешними носителями в сравнении со скоростью
вычислений процессора. Однако при уменьшении разницы в
скорости обменов и скорости вычислений (в случаях относительно
низкой производительности процессора, использования
высокоскоростных жестких дисков или электронного диска) схема
с хранением глобальных матриц жесткости может оказаться более
эффективной (при условии наличия достаточного количества
памяти на внешних носителях). Для рассмотренной задачи затраты
памяти на жестком диске составили 2000 Кб, с хранением
интегралов от тригонометрических функций - 400 Кб, а для схемы
без хранения - 0 Кб.
Выполнение расчетов при большем числе гармоник и на более
сетках дает приблизительно такие же соотношения.
132
Гл. 3. Конечно-элементная реализация МГП
Таблица з.
Относительные затраты времени на одну итерацию при различных схемах
вычисления
Схема
С формированием глобальных
МЖ дополнения
Без формирования глобальных
МЖ дополнения
Без формирования глобальных
МЖ дополнения с хранением
интегралов от тригонометрических
функций
486DX-33
1.00
1.10
1.08
486DX4-100
1.00
0.77
0.81
Pentium-75
1.00
0.41
0.48
3.8А. Особенности вычисления деформаций и напряжений на
границе перехода тело-дополнение
Компоненты вектора перемещений, вычисленные с помощью
МГП, являются непрерывными функциями координат г, z и ср. Их
аппроксимация по угловой координате отрезком ряда Фурье уже
при сравнительно небольшом числе гармоник обеспечивает
приемлемую точность вычисления перемещений.
Сложнее ситуация при определении деформаций и напряжений.
Компоненты тензоров е и о не являются непрерывными
функциями координат и имеют на границе тело-дополнение разрыв
первого рода. Вне некоторой ^-окрестности от точки разрыва ряд
Фурье для деформаций и напряжений сходится равномерно.
Имеются лишь незначительные периодические колебания решения
относительно истинного значения, что характерно для
аппроксимации функций отрезком ряда Фурье. В ^окрестности
точки разрыва, где значения компонент ? и 6 меняются
скачкообразно, нарушается сходимость по равномерной норме, так
как функции непрерывно переходят от своих значений в точке <р - S
к значениям в точке ср + 8, т.е происходит "размазывание" скачка.
Кроме того, в непосредственной близости от точки разрыва
3.8. Повышение эффективности численной реализации МГП 133
функции начинают осциллировать, причем колебания значений не
имеют тенденции к уменьшению с ростом числа удерживаемых в
разложении гармоник. Предельное значение колебаний частичной
суммы ряда Фурье в окрестности точки разрыва оказывается
больше величины скачка |sj на 0.1405/;г-|? [119]. Такой дефект
сходимости носит название эффекта Гиббса.
Одну из способов борьбы с этим явлением - использование <т-
множителей Ланцоша [108]. При их использовании
быстроколеблющаяся функция частичной суммы ряда Фурье
заменяется сглаженной функцией, усредняющей одно полное
колебание, сосредоточенное около заданной точки ср. В результате
применения сг-множителей эффект Гиббса существенно
уменьшается. Вне ^-окрестности точки разрыва колебания гаснут
практически полностью.
Рассмотрим эффективность использования сг-множителей на
примере задачи о перфорированном цилиндре, нагруженном
внутренним давлением (см. рис.3.20). При движении по угловой
координате в области перфорации напряжения имеют разрыв. На
рис.3.43 приведены графики безразмерных окружных напряжений
в среднем сечении цилиндра z=L/2 и г/а=2.3 (середина области
перфорации). В разложении Фурье удерживалось 20 гармоник. При
дифференцировании по угловой координате использовалось
непосредственное дифференцирование ряда Фурье для
перемещений.
0.40
-1.20
20.00 25.00 30.00 35.00 40.00 45.00
Рис.3.43. Окружные напряжения в однородном перфорированном
цилиндре. Внутреннее давление (сечение z=l/2, г/а = 2.3;
• - с множителями Ланцоша, v - без множителей Ланцоша)
134 Гл. 3. Конечно-элементная реализация МГП
Как видно из графика, при непосредственном
дифференцировании ряда решение сильно осциллирует вблизи
точки разрыва. Величина ^-окрестности, в которой сосредоточены
осцилляции, зависит от числа гармоник в разложении и равна:
S=T/ N,
где TV- число гармоник, а Г- период функции решения.
При удержании 20 гармоник в задаче величина S= 4.5° . Вне S-
окрестности точки разрыва наблюдаются лишь слабые
периодические колебания решения.
Применение сомножителей сглаживает колебания решения. В
точке разрыва естественные граничные условия выполняются с
большой погрешностью. Практически мы можем с приемлимой
точностью вычислить напряжения лишь вблизи от границы
перехода тело-дополнение. Для сокращения ^-окрестности и,
соответственно, приближения области качественного вычисления
напряжений к границе, приходится удерживать большее число
гармоник.
Для более качественного определения производных от Фурье-
разложений функций применяют различные приемы. В работе [56],
например, ряд Фурье дополняется полиномиальными членами, что
позволяет более точно вычислять производные.
Одним из способов определения производных по угловой
координате является использование численного дифференцирова-
дифференцирования. При этом вне ^-окрестности границы тело-дополнение
производные вычисляются с использованием двухточечной
центральной разности :
dF{tp) F{tp + Atp) - F(<p - Atp)
^ — . — ^
dtp 2 • Atp
а вблизи границы - несимметричными разностями, например,
двухточечными, от границы в реальное тело:
dFjtp) ^ F{tp + А(р) - F(tp)
dtp Atp
где Atp - шаг разностной схемы. Возможно применение и
разностных схем более высокого порядка.
Если перемещения определены с высокой точностью, то и
производные от них с использованием разностных схем
вычисляются точнее, чем при непосредственном
дифференцировании ряда Фурье. Шаг разностной схемы
3.8. Повышение эффективности численной реализации МГП 135
необходимо выбирать с учетом числа гармоник в разложении. Для
определения влияния величины Аф на качество решения проведен
ряд расчетов для Аф =T/N, A<p=T/2N и Аф -T/AN. Вне 5-
окрестности границы тело-дополнение (д=Т/ N\ производные по
ф, вычисляются с использованием двухточечной центральной
разности, а вблизи границы - с использованием двух-, трех- и
четырехточечных несимметричных разностных схем [90].
Результаты расчетов приведены на рис.3.44 - 3.46.
-0.80
-1.20
20.00 25.00 30.00 35.00 40.00 45.00
Рис.3.44. Окружные напряжения в однородном перфорированном
цилиндре. Внутреннее давление (сечение z-L/1, г/а = 2.3, А^?= T/N;
несимметричные разности: • - двух-, т - трех-, ? - четырехточечная)
На основании полученных результатов представляется
Целесообразным использование трех-, четырехточечных схем при
k(p=T/2N. При этом сокращается приблизительно в 2 раза зона
"размазывания" скачка в напряжениях по сравнению со схемой
использования непосредственного дифференцирования ряда Фурье.
3.8.5. Использование многошаговых итерационных процедур в
В рассмотренных ранее примерах процедура МГП начиналась с
пРиближения, полученного в результате решения задачи для
Канонического тела, и продолжалась до достижения заданной
точности. Скорость сходимости большинства итерационных
136
Гл. 3. Конечно-элементная реализация МГП
0.40
0.00
-0.40
-0.80
-1.20-
>
I
I
1
1
ф
20.00 25.00 30.00 35.00 40.00 45.00
Рис.3.45. Окружные напряжения в однородном перфорированном
цилиндре. Внутреннее давление (сечение z=Z/2, г/а = 2.3, А<р ~ 7/ N\
несимметричные разности: • - двух-, v - трех-, ? -четырехточечная;
$ - непосредственное дифференцирование ряда Фурье)
0.00-
-0.40-
-0.80-
-1.20-
r
1
1
1
1
\
Ш—1
1—¦
—*-
¦—1
1—¦
1
ф
град
20.00 25.00 30.00 35.00 40.00 45.00
Рис.3.46. Окружные напряжения в однородном перфорированном
цилиндре. Внутреннее давление (сечение z=L/2, г/а = 2.3, А<р=~- Т/N\
несимметричные разности: • - двух-, v - трех-, ? - четырехточечная)
3.8. Повышение эффективности численной реализации МГП 137
методов зависит от выбора начального приближения.
При выполнении расчетов на различных сетках и при разном
числе гармоник в разложении наблюдается сходимость
получаемых решений. Можно предположить, что использование в
качестве начального приближения, например, решения,
полученного с меньшим числом гармоник, позволит сократить
число итераций, необходимых для получения решения с заданным
числом гармоник. Это может привести (за счет меньших затрат на
получение "хорошего" начального приближения) к снижению
общих затрат на решение задачи.
Пошаговое увеличение числа удерживаемых в разложении
гармоник. В качестве первого варианта многошагового МГП
рассмотрим решение некоторых задач с одинаковыми сетками, но
разным числом гармоник в разложении ряда Фурье. При этом
решение, получаемое на каждом шаге, берется в качестве
начального приближения для следующего шага.
Коэффициенты разложения, полученные при расчете с
небольшим числом гармоник, дают хорошее приближение для
первых N гармоник при расчете с большим числом членов ряда.
При реализации основной процедуры МГП общие затраты на
получение решения в значительной мере зависят от времени,
затрачиваемого на вычисление итерационной составляющей
{fn}y = У4клт]д {Xm}'*~^ . При увеличении числа
правой части {y У]д {}
гармоник затраты растут со скоростью N . Поэтому время расчета
при малом числе гармоник значительно меньше, чем при большом
их числе.
Сокращение числа итераций на каждом шаге при использовании
начального приближения, полученного с предыдущего шага для
меньшего числа гармоник, а также сравнительно небольшие
затраты на получения решения с малым числом гармоник в
конечном итоге позволяют существенно сократить общую
стоимость решения задачи. Следует учесть, что на промежуточных
ttJarax решение можно получать с менее высокой точностью, чем
задано для задачи в целом, и лишь на последнем шаге проводить
итерации до требуемой точности.
Одна из проблем, возникающих при таком подходе, - сложность
выбора оптимальной схемы увеличения числа членов ряда от шага
138
Гл. 3. Конечно-элементная реализация МГП
к шагу. Это объясняется невозможностью заранее предсказать
число итераций, которое потребуется до достижения заданной
точности. Медленное наращивание числа гармоник может
привести к затратам, превышающим затраты обычной
одношаговой процедуры МГП.
Для определения эффективности описанного подхода проведен
ряд расчетов при различных схемах увеличения числа гармоник по
шагам. Расчеты проводились для задачи о перфорированном
цилиндре под действием внутреннего давления (см. рис.3.20) при
196-ти узловой дискретизации расчетной области. Общее число
гармоник в задаче - 20. На промежуточных шагах итерации МГП
проводились до достижения точности 0.02, а на последнем шаге до
0.01 по относительной невязке системы. В табл.3.6 приведены
относительные затраты времени на решение задачи в сравнении с
одношаговым вариантом МГП при различном числе шагов.
Таблица 3.6.
Относительные затраты времени на решение задачи о перфорированном
цилиндре в сравнении с одношаговым МГП
Число
шагов
1
6
5
5
4
4
Схема увеличения
числа гармоник
20
4-6-10-14-18-20
4-6-8-12-20
4-6-7-10-20
4-6-10-20
3-5-10-20
Относительное время
решения
1.00
0.72
0.56
0.53
0.55
0.57
Практика расчетов показала, что хорошие результаты дает
следующая схема увеличения числа гармоник по шагам: на каждом
шаге число гармоник берется приблизительно в 2 раза больше, чем
3.8. Повышение эффективности численной реализации МГП 139
на предыдущем шаге. Количественное сравнение результатов,
полученных одношаговым и многошаговыми вариантами,
показало, что решения различаются в пределах 1-2%.
Применение пошаговой процедуры увеличения числа гармоник
в проведенных расчетах позволило сократить время решения
приблизительно в 2 раза. Расчеты на более мелких сетках и с более
высокой точностью показали, что предложенная схема требует
затрат времени в 2-3 раза меньше, чем при одношаговой схеме
МГП.
Многосеточный вариант МГП. В практике конечно-элемент-
конечно-элементных расчетов широкое распространение получили различные
варианты многосеточных методов. Наиболее простой подход
заключается в последовательном решении ряда сеточных задач,
аналогичных исходной, но с более грубой дискретизацией. Процесс
начинается с самой грубой сетки, вычислительные затраты для
которой относительно невелики. Затем полученное решение
интерполируется на более мелкую сетку и используется в
некотором итерационном процессе решения разрешающей СЛАУ
МКЭ. Вследствие общей сходимости решений на сгущающихся
сетках такое начальное приближение, как правило, дает точность,
близкую к удовлетворительной, что приводит к сокращению числа
итераций при решении СЛАУ, а, следовательно, - общих
вычислительных затрат. Более сложные многосеточные схемы
используют для получения очередного приближения к решению
задачи комбинацию решений на двух и более сетках.
Применительно к МГП многосеточный вариант расчета был
реализован по следующей схеме: последовательность сеток
тороидальных элементов треугольного сечения выбирается таким
образом, что каждое более мелкое разбиение получается из
предыдущего путем дробления каждого элемента на четыре. По
полученному для текущей сетки решению вычисляется вектор
коэффициентов разложения в узлах следующей, более мелкой,
сетки. Новый вектор используется в качестве начального
приближения в итерационной процедуре МГП на следующем шаге.
Для оценки эффективности такого подхода были проведены
Расчеты для задачи о перфорированном цилиндре при действии
ВнУтреннего давления (см. рис.3.20) на последовательности из трех
Сеток. Расчет для каждой сетки проводился с удержанием 20
Гармоник, а итерационная процедура МГП выполнялась с
140 Гл. 3. Конечно-элементная реализация МГП
точностью до 0.01 по относительной невязке системы. Результаты
расчета показали, что затраты времени для трехсеточного варианта
на 30% меньше, чем для односеточного, причем количественные
отличия в решениях не превышают 1.7%.
Представляет интерес использование многосеточного варианта
МГП в сочетании с многошаговым увеличением числа гармоник в
разложении для каждой сетки. Проведенный расчет по
трехсеточной схеме с пятью шагами увеличения числа гармоник
потребовал на 45% меньше времени, чем односеточный и
одношаговый вариант МГП.
Как показала практика, при многосеточном расчете не следует
использовать много сеток с незначительным отличием их друг от
друга, так как затраты на переформирование матриц жесткости
могут не только уменьшить выигрыш во времени, полученный при
сокращении числа итераций МГП на каждой сетке, но и привести к
общим затратам на решение задачи больше, чем в односеточном
варианте.
Многошаговый вариант МГП для неоднородных конструкций.
Рассмотренные ранее многошаговые варианты МГП использованы
для решения однородных изотропных задач. Рассмотрим случай,
когда конструкция состоит из нескольких материалов с разными
физико-механическими характеристиками. Скорость и характер
сходимости итерационного процесса МГП в этом случае
значительно зависят от соотношения характеристик материалов
конструкции. Даже для тестовой задачи об осесимметричном
двуслойном цилиндре при отношении модулей упругости, равном
100, число итераций до достижения требуемой точности достигало
78, тогда как при соотношении модулей упругости, равном 10, для
сходимости потребовалось 20 итераций.
Основная идея многошагового расчета по неоднородности
заключается в том, что решается ряд задач, аналогичных данной,
но при меньшей степени отличия в физико-механических
характеристиках материалов. Получаемое на каждом шаге решение
используется в качестве начального приближения на следующем
шаге.
Для исследования эффективности процедуры многошагового
расчета неоднородных конструкций был решен ряд задач для
конструкции типа цилиндра со звездообразным вырезом,
заполненным более жестким включением (см. рис.3.24). Расчеты
3.8. Повышение эффективности численной реализации МГП 141
проводились для 169-ти узловой дискретизации при удержании 20
гармоник в разложении. Соотношение модулей упругости жесткого
включения и основного тела (матрицы) составляло Евкл/ ЕМатр =50.
Для решения такой задачи с помощью обычной процедуры МГП
потребовалось 125 итераций при точности 0.01 по относительной
невязке системы.
При многошаговом расчете возможно два варианта организации
вычислительного процесса. Первый заключается в серии расчетов
при постепенном уменьшении модуля Е^атр от значений, близких к
модулю упругости включения, до требуемой величины при
фиксированном Евкл- Второй вариант, наоборот, предполагает
постепенное увеличение Евкл от величин, близких к Ематр , до
требуемой величины при фиксированном ЕШТр- Расчеты по
каждому варианту выполнялись в пять шагов с одинаковой
степенью неоднородности материалов по шагам. Результаты
расчетов (табл.3.7) показали, что время решения меньше, чем в
одношаговом варианте на 30% и 20% соответственно.
Таблица 3.7
Затраты времени при различных вариантах организации многошаговой
процедуры МГП по неоднородности
Шаг
1
2
3
4
5
Всего
Евкл-50
Ематр
30
20
10
5
1
Число
итераций
4
6
11
16
47
Время,
с
17
24
41
59
170
311
ЕмАтр-1
Евкл
5
10
20
30
50
Число
итераций
12
14
20
20
30
Время,с
45
52
76
73
107
353
142 Гл. 3. Конечно-элементная реализация МГП
Как и в других вариантах многошаговых процедур, в данном
случае трудно определить оптимальную схему организации
многошагового процесса, так как заранее неизвестно, сколько
потребуется выполнить итераций МГП на каждом шаге. Слишком
большое число шагов ведет к увеличению затрат на построение
матриц жесткости, а слишком малое - к большой разнице в
характеристиках материалов и, как следствие, - росту числа
итераций на каждом шаге.
3.9. Применение конечно-элементной реализации метода
геометрического погружения для решения
пространственных задач теории упругости
Конечно-элементный вариант метода геометрического
погружения получил хорошую апробацию при решении ряда
практических задач определении НДС пространственных
конструкций. В данном разделе приведены решения задач для
однородной и кусочно-однородной конструкций.
3.9.1. Напряженно-деформированное состояние опорного
устройства
Рассмотрим задачу об определении НДС опорного устройства,
представляющего собой массивное тело вращения сложного
меридионального сечения, которое имеет три ряда секторных
выступов на наружной цилиндрической части поверхности [86]
(рис.3.47). По торцевой части устройство нагружено
распределенной нагрузкой единичной интенсивности. Материал
конструкции однородный изотропный с единичным модулем
упругости Е и v=0.3. В качестве граничных условий принято
отсутствие смещений на кромках выступов, перпендикулярных
цилиндрической поверхности.
Для расчета НДС такой конструкции использован МГП.
Дискретизация расчетной области производилась с использованием
1824 тороидальных элементов с линейной аппроксимацией
перемещений A032 узла). В разложении удерживалось 20
гармоник. Общее число неизвестных составило 63720. На ПЭВМ
класса Pentium-75 решение задачи заняло 17 мин. На рис.3.48 и 3.49
3.9. Применение конечно-элементной реализации МГП ... 143
представлены изолинии осевых напряжений в меридиональном
сечении II - II и в поперечном сечении I -1.
0.015 0.01 Ц
0.095
0 065
0.035
0.06
0.1
0.18
0.235
0.11
Рис.3.47. Схема опорного устройства
Рис.3.48. Осевые напряжения в меридиональном сечении II - II
опорного устройства
В работе [86] приведено решение данной задачи с помощью
Методики на основе полуаналитического МКЭ с использованием
моментной схемы. Сравнение результатов показало
Удовлетворительное их совпадение. Рассмотренный здесь подход
близок к данному варианту численной реализации МГП, так как
Также используется полуаналитический МКЭ в цилиндрических
координатах и разрешающая СЛАУ решается итерационным
Методом. Отличие МГП заключается в использовании
144
Гл. 3. Конечно-элементная реализация МГП
итерационной процедуры, сходимость которой доказана и которая
не требует подбора каких-либо параметров.
I - I
Рис.3.49. Осевые напряжения в поперечном сечении I-I опорного
устройства
3.9.2. Трехмерное напряженное состояние секции песчано-
полимерной оправки
Песчано-полимерные оправки используются в качестве
формообразующих элементов для изготовления композиционных
оболочек вращения методом силовой намотки. На рис.3.50.
представлена секция оправки с цилиндрической поверхностью.
Воздействие усилий намотки в волокнах заменено распределенным
равномерным давлением р на поверхность оправки. Материал
оправки однороден и изотропен. Каноническая область, в которую
осуществлялось погружение, представляет собой реальную
конструкцию, пространство между ребрами которой заполнено
материалом с такими же механическими свойствами (образуется
3.9. Применение конечно-элементной реализации МГП ... 145
вращением сечения А вокруг оси Ог). Сходимость итерационного
процесса МГП достигалась за 11 итераций на сетке, содержащей
197 узловых окружностей при задании относительной погрешности
отыскания узловых неизвестных 0.001.
А В
Рис.3.50. Расчетная схема секции оправки.
На рис.3.51 показано изменение радиальных напряжений вдоль
радиуса в трех сечениях конструкции А, В и С при z=0.
Максимальные значения достигаются в сечении В, где имеются
концентраторы в месте стыка ребра со сводом и ступицей.
4.0
0.0
0.4
0.6
0.8
1.0
Рис.3.51. Изменение радиальных напряжений вдоль радиуса
в сечениях А, В и С при z=0
146
Гл. 3. Конечно-элементная реализация МГП
Естественные граничные условия в напряжениях выполняются
удовлетворительно, что более наглядно видно на рис.3.52, где
изображены эпюры напряжений &Г/Р' Максимальная
погрешность составляет 12% в сечении В на внешней поверхности
при z=0. Штриховой линией в сечении С показано распределение
радиальных напряжений в области, представляющей собой
дополнение до канонической области. Наблюдается скачок
нормальных напряжений на границе реальной области и
дополнения, что соответствует теории МГП.
-7.01 Г-
-4.98
-1.12
-0.91
-9.26
В
-0.013
0.
с
36
Рис.3.52. Эпюры радиальных напряжений в оправке
J
На рис.3.53 представлены эпюры напряжений <г2/ръ своде
оправки. Здесь величины напряжений определяются сжатием свода
между боковых опор и изгибом полки свода в окрестности ребра.
Так, в сечении С в основном реализуется сжатие, а в сечении А за
счет изгиба появляются положительные величины напряжений,
которым очень слабо сопротивляется материал песчано-
полимерных оправок.
3.9.3. Расчет напряжений в диске с лопатками
Рассматривается задача определения напряженного состояния
авиационного диска с лопатками под действием центробежных сил
{со- угловая скорость вращения) (рис.3.54). В качестве
канонической области вновь выбрано тело вращения,
представляющее исходную конструкцию, у которой пространство
между лопатками заполнено материалом с физико-механическими
3.9. Применение конечно-элементной реализации МГП ... 147
-2.18
-0.9 -1.96
-1.02
В
4-J
Рис.3.53. Эпюры напряжений cz/p в своде оправки
Рис.3.54. Облопаченный диск: а - общий вид, б - дискретизация
конструкции
148
Гл. 3. Конечно-элементная реализация МГП
свойствами материала диска. Численные результаты приведены
для диска с характеристиками ?=1.96 10 Па, v - 0.3 . Лопатки
крепятся по радиусу 0.5536 (Ь - внешний радиус лопатки) и
образуются двумя плоскостями (р =const с углом 0.09 радиан между
ними. Число лопаток - 27.
Рис.3.55 и 3.56 иллюстрируют выполнение естественных
граничных условий в напряжениях (равенство нулю нормальных
напряжений на свободных поверхностях).
аг/
/рсоЧ2
1.0
0.5 -
0.4 -
0.3 -
0.2 -
0.1
0.0
0.4 0.6 0.8 1.0
Рис.3.55. Распределение радиальных напряжений в зоне перехода лопатки
в тело диска в сечении z=Q
(/-р = 0, 2-tp = 0.045 рад, 3- (р = 0.01\рад)
На рис.3.55 представлено изменение безразмерного напряжения
or -Grj\p(o Ъ J вдоль радиуса диска в сечении плоскостью z^0.
Вертикальная штриховая прямая соответствует радиусу крепления
лопатки. Кривая / построена при <р-0, кривая 2 - при
ср = 0.045 рад, кривая 3 - <р = 0.071 рад. Концентрация напряжения
максимальна в точке перехода лопатки в тело диска. На
3.9. Применение конечно-элементной реализации МГП ...
149
поверхности r=b напряжение близко к нулю по сравнению с
напряжениями в других точках конструкции B.5% от о> в центре
диска). В сечении ср- 0.071 рад свободная поверхность г=0.553Ь,
на которой аг практически точно равно нулю. Далее кривая 3 идет
в дополнении DA (пространство между лопатками). Как видно, на
границе областей (в соответствии с теорией МГП) имеется скачок
напряжений, а на границе г=Ъ области Эд величина аг близка к
нулю, поскольку это свободная поверхность канонической области.
На рис.3.56,а показано изменение по углу безразмерного
напряжения а^ -<J^/\рсо2Ь> ) в плоскости 2=0 на поверхностях
r=const. Вертикальная штриховая линия отвечает плоскости
0.4
0.3
0.2
0.1
0.0
0.0 0.02 0.04 0.06 (р,рад
г/Ь = 0.375 У\/
0.546
1,11
/ч
1
/0.719
0.02 0.04 0.06 <р,рад
Рис.3.56. Распределение безразмерных напряжений ог (а) и а^ (б) адоль
угловой координаты (р в сечении z=0
<р - 0.045 рад, образующей боковую поверхность лопатки. При
Г/Ь = 0.719 в лопатке и на боковой поверхности а^ близко к нулю, а
в области DA принимает большие значения. Остальные кривые
Указывают изменение &„ по углу ср в теле диска. На рис.3.56,6
представлены такие же зависимости для аг . Зависимость аг и аф
От <р быстро ослабевает по мере удаления от места крепления
лопатки к телу диска. На рис.3.57 показаны поля безразмерной
интенсивности напряжений gu ~auj\p(o Ъ ] в сечениях
150
Гл. 3. Конечно-элементная реализация МГП
плоскостями ^=const. Видны концентрация напряжений в месте
перехода лопатки в диск и локальный характер пространственного
напряженного состояния, переходящего в осесимметричное на
расстоянии 0.15-0.2й от места крепления лопатки.
ср = 0 рад
<р = 0.045
= 0.071
Рис.3.57. Поля безразмерной интенсивности напряжений в различных
сечениях конструкции
3.9.4. Напряженно-деформированное состояние металло-
композиционного ротора
Рассматривается напряженно-деформированное состояние
вращающегося с угловой скоростью со ротора инерционного
накопителя энергии, состоящего из алюминиевой ступицы с
шестью спицами, на которую последовательно намотаны слои
стекло-, органо- и углепластиков на основе эпоксидного
связующего (рис.3.58). Для сравнения приводятся результаты
расчета аналогичного маховика со сплошной ступицей, полученные
из решения осесимметричной задачи МКЭ. Процедура погружения
аналогична задаче об оправке. При формулировке итерационного
алгоритма МГП упругая энергия анизотропных пластиковых слоев,
осесимметричных по своей геометрии, учитывается в энергии
канонического тела и в итоге оказывает влияние только на
величину матрицы жесткости, стоящей в левой части.
3.9. Применение конечно-элементной реализации МГП
151
В
В
Рис.3.58. Схема металлокомпозиционного маховика
На рис.3.59 изображены деформированные состояния двух
основных сечений А и В обода маховика. На рис.3.60 показаны
перемещения четырех характерных точек обода в зависимости от
окружной координаты. Видно, что в основном деформирование
конструкции в сечении А происходит за счет радиального сжатия
слоев стеклопластика и органопластика, кроме зоны над спицей,
где имеется зона растяжения стеклопластика и частично -
органопластика. В сечении В растяжения практически не
наблюдается.
Г
*"•
Рис.3.59. Деформированное состояние обода маховика в сечениях А и В
152
Гл. 3. Конечно-элементная реализация МГП
1.0
Рис.3.60. Зависимость радиальных перемещений характерных точек
маховика от окружной координаты
Нормальные радиальные и окружные напряжения в маховике
вдоль радиуса изображены на рис.3.61. Здесь же штрих-
пунктирными линиями изображены напряжения, полученные из
решения осесимметричной задачи.
рсоЧЛ
1.0 -
0.5
0.0
0.25
Рис.3.61. Напряжения в роторе при z=0:-
- в сечении А, - в
сечении В (см. рис.3.59), решение в осесимметричной
постановке
3.9. Применение конечно-элементной реализации МГП ... 153
Максимальные значения радиальных напряжений реализуются в
спице, однако более опасны меньшие по величине растягивающие
напряжения в стеклопластике в силу низкой прочности пластика в
направлении поперек волокон. В сечении В уровень радиальных
напряжений незначителен. На рис.3.62 приводятся распределение
радиального напряжения вдоль радиуса в ободе, а также
распределение по углу максимального радиального напряжения в
стеклопластике в месте склейки с металлической ступицей.
Окружные напряжения в ступице (см. рис.3.61, В) не превышают
по величине радиальных напряжений. В ободе окружные
напряжения над ступицей (А) ниже, чем между спицами (В).
0.0
С
0.75 0.80
0.85 0.90 0.95
Рис.3.62. Растягивающие радиальные нормальные напряжения.
а - изменение вдоль радиуса в сечении A (z=0), б - изменение вдоль
угловой координаты в сечении z=0 в месте склейки Al-СП (точкаС)
3.9.5. Определение влияния расположения шарового включения
структурной ячейки зернистого композита на эффективные
характеристики
Полимерные композиты зернистого типа представляют собой
системы, в которых жесткие сфероидальные частицы случайным
°бразом вкраплены в мягкую полимерную матрицу и сохраняют
154
Гл. 3. Конечно-элементная реализация МГП
связность с ней до определенной деформации. Именно такие
системы составляют предмет дальнейшего рассмотрения.
Если через середину промежутков, разделяющих частицы,
провести плоскости, то вокруг каждой частицы появятся случайно
сформированные выпуклые многогранники (полиэдры Вороного).
С известным приближением можно считать, что совокупность
объемных долей частиц внутри соответствующих полиэдров
представляет собой распределение локальных концентраций
наполнителя по элементам структуры.
В,/работе [130] исследуются механические особенности
структурных ячеек особого типа: имеющих форму изометрического
цилиндра (матрицы) со сферическим включением, расположенным
в центре цилиндра.
При замене реальных структурных элементов (частицы
располагаются случайным образом внутри случайно образованных
полиэдров Вороного) геометрически правильными структурными
ячейками с той же объемной концентрацией и с центральным
расположением включения возникает вопрос, в какой мере
смещение включения из его центрального положения изменяет
среднюю жесткость структурной ячейки, ответ на который
позволяет оценить погрешность, вносимую в описание
механического поведения ячейки указанным выше упрощением.
Рис.3.63. Структурная ячейка зернистого композита со смещенным
включением (усл. обозн. см. текст)
3.9. Применение конечно-элементной реализации МГП ... 155
Если включение смещено в радиальном направлении от оси
цилиндра, то задача становится пространственной. Следует также
отметить значительное отличие в модулях упругости матрицы и
включения и их слабую сжимаемость (коэффициент Пуассона
близок к 0.5).
Для решения такой задачи был использован рассматриваемый
вариант МГП. Расчетная схема задачи приведена на рис.3.63.
Ячейка представляет собой изометрический цилиндр радиуса г и
длиной Z,=2r, содержащий смещенное на величину е шаровое
включение из более жесткого материала. Характеристикой ячейки
является коэффициент заполнения kz, представляющий собой
объемную долю включения в общем объеме системы.
Были приняты следующие геометрические параметры ячейки:
r=2, Z=2r=4. Ячейка подвергалась продольному удлинению на 1%
длины. Учет влияния соседних ячеек производился путем
требования сохранения формы цилиндрической поверхности. Это
требование реализовано путем задания в качестве кинематических
граничных условий на цилиндрической поверхности таких
радиальных перемещений, при которых сумма всех нормальных
напряжений на ней обращалась в нуль. Были проведены расчеты
для коэффициентов заполнения 0.2 и 0.3. Расчетная область
разбивалась на 2080 элементов A032 узла). В разложении Фурье
удерживалось 20 гармоник. Общее число неизвестных задачи
составило 63720. Смещение включения задавалось равным
половине расстояния от поверхности центрально расположенного
шара до внешней поверхности цилиндра. Отношение модуля
упругости включения к модулю матрицы принято равным 100.
Расчеты проводились для коэффициентов Пуассона 0.48 и 0.49.
Степень влияния на среднюю жесткость расположения шара
определялась по отношению значений энергии упругого
Деформирования ячейки со смещенным включением и энергии
ячейки с центральным включением. Осредненный модуль
Упругости ячейки рассчитывался как Ес ~WcE^jW^ , где Wc-
эНергия ячейки; W^ - энергия матрицы Ес и Ем - соответственно
Модуль упругости ячейки и матрицы. Рассчитывалась также
^личина Е по эмпирической зависимости Чонга [126] вида
156
Гл. 3. Конечно-элементная реализация МГП
Е =Е
м
1-
0.605
где kz - коэффициент наполнения, а 0.605 - предельный
коэффициент наполнения ячейки данного вида. Для решения
задачи потребовалось порядка 30-40 итераций МГП. При подборе
перемещения на цилиндрической части в процедуре МГП
использовалось начальное приближение от предыдущего пробного
значения. Это позволило практически за 2-3 итерации получать
новое решение при другом значении граничных условий.
Результаты решения данной задачи приведены в табл.3.8.
Таблица 3.8
Результаты расчетов структурной ячейки зернистого композита при
различных коэффициентах заполнения, коэффициентах Пуассона и
смещении включения
к
0.2
0.2
0.3
0.3
0.2
0.2
0.3
0.3
R
1.34
1.34
1.53
1.53
1.34
1.34
1.53
1.53
е
0
0.33
0
0.235
0
0.33
0
0.235
V
0.48
0.48
0.48
0.48
0.49
0.49
0.49
0.49
ИЫООО
4.88
5.68
7.474
8.20
5.014
5.760
7.876
8.780
Ес
1.92
2.23
2.935
3.22
1.98
2.27
3.105
3.47
Е*
1.89
1.89
3.06
3.06
1.89
1.89
3.06
3.06
Полученные результаты показывают, что энергия ячейки со
смещенным включением отличается от энергии ячейки с
3.9, Применение конечно-элементной реализации МГП ... 157
центральным расположением шара на 11-16%. Это позволяет
сделать вывод о допустимости использования цилиндра с
осесимметричным расположением шара в качестве структурной
ячейки зернистого композита. Метод геометрического погружения
позволил решить сложную пространственную задачу теории
упругости для неоднородного тела. При этом многократное
решение задачи при подборе необходимых кинематических
граничных условий потребовало незначительных затрат, так как в
процедуре МГП использовалось решение на предыдущих этапах
подбора, что позволяло выполнять всего несколько итераций для
уточнения начального приближения.
Глава 4
КОНЕЧНО-РАЗНОСТНЫЕ СХЕМЫ МЕТОДА
ГЕОМЕТРИЧЕСКОГО ПОГРУЖЕНИЯ
В главе по методу конечных разностей построен конечномерный
аналог вариационного уравнения метода геометрического
погружения. В качестве канонической области в декартовой системе
координат выбран прямоугольный параллелепипед, в
цилиндрической - короткий круговой цилиндр. Обсуждены вопросы
выбора эффективного метода решения получаемых систем линейных
алгебраических уравнений. Приводятся результаты решения
тестовых задач и примеры расчета конкретных конструкций.
4.1. Дискретный аналог вариационного уравнения метода
геометрического погружения в декартовой системе
координат
Рассмотрим построение вариационно-разностной схемы метода
геометрического погружения. В декартовой системе координат
(;cj,;c2? *з) в качестве канонической области Dq выберем
прямоугольный параллелепипед, так как метод конечных разностей
наиболее эффективен на такой области [72,80]. Поместим начало
координат в одной из вершин параллелепипеда, а оси х\,Х2,хз
направим вдоль его ребер. Выберем равномерную сетку cof2, т. е.
множество точек с координатами (ia - \)ha , /а = 1, 2, ..., Nu ,
а = 1,2,3, где ha - шаг сетки вдоль оси ха . Для аппроксимации на
сетке 0)^ дифференциальных операторов используем семиточечный
шаблон (рис.4.1). На рис.4.1 также показана элементарная ячейка,
окружающая узел с координатами (xj ,X22>J3i)- Ячейка состоит
из восьми подобластей объема (^ь^'^з)^ с указанной
нумерацией.
4.1. Дискретный аначог МГП в декартовой системе координат 159
JL1
АР
Рис.4.1. Элементарная ячейка, окружающая узел с координатами
I jq , *2 , х3 ] в декартовой системе координат (усл. обозн. см. текст)
Запишем вариационное уравнение метода геометрического
погружения B.54) в виде
\a(uk) '?(Suk)dD0= {a(uk~l)--
Щ Da
D
= 1,2,3,....
D.1)
Индекс к в дальнейших записях будем опускать.
Геометрические соотношения B.5) примут вид
ди dv dw I [ ди dv ]
1 f dv dw
— ^ 13 -
\\ dw ди
-_ 1
D.2)
rAe m,v,hw - компоненты вектора перемещений и по осям
-хЬЛ*2Ил*з соответственно.
Физические соотношения B.4) имеют вид
сг 22 =Л\? ц+?• 22+^ 33)+ 2^22»
6* !!+?• 22+^ Зз)+2//?'33'
12 ^ <т 21 — 2/Л? 12? ^13 " ® 31 = 2//611з, о* 32 = ^ 23 = 2/i^ 23
D.3)
160 Гл.4. Конечно-разностные схемы МГП
Поскольку интеграл по области Dq представляет из себя работу
внутренних сил в области Dq, его можно заменить суммой
интегралов по элементарным ячейкам
|<т (и)--* (A) dD0=JT J<r (u)-^ (Л) d(ADj), D.4)
где N = N\x N2* Nj - число узлов сетки со^, ADq - область,
занимаемая л-й элементарной ячейкой.
Интеграл по области ADq заменим суммой по восьми
подобластям ячейки. Поскольку количество подобластей в
элементарной ячейке зависит от расположения узла сетки 57;2Э то
вводим индикаторный множитель кт (т - номер подобласти в n-ii
ячейке). Множитель равен единице, если т-я подобласть
принадлежит области Dq, и нулю, если выходит за ее границы (узлы
на гранях, ребрах и в вершинах параллелепипеда). Интеграл D.4)
примет вид
8
\
о (и) •
ADg
a (u) •
g m
ADo
о V^^o
. D.5)
Интеграл по области ADq m , согласно теореме о среднем, равен
fl. D.6)
Подставляя последовательно D.6) в D.5) и в D.4), получим
N 8 /i h /
;? l^I^]/:m. D.7)
гч П—\ /71=1
ио
Аналогично преобразуется интеграл по области DA
^^? D.8)
N* 8 h h h
о
4.1. Дискретный аналог МГП в декартовой системе координат 161
где N* - число узлов сетки со^, принадлежащих области Эд,а ^ -
равен единице, если т-я подобласть принадлежит D^, и 1гулю, если
не принадлежит.
Изложенные преобразования проводим с интегралом,
представляющим работу объемных сил
где N * - число узлов сетки со^, попадающих в область D .
Интеграл, представляющий работу поверхностных сил,
преобразуем по формуле Остроградского-Гаусса
-AidS^ = JV(p?u)dD. D.10)
Интеграл D.10) примет вид
л/** ft
и и и
5]^-L^-[V(p^u)]/7m^,. D.11)
[} я=1 т-\
Произведем подстановку в D.7), D.8), D.9) и D.11) соотношений
D.3) и D.2). Выражения, полученные в результате подстановки,
содержат первые производные от компонент вектора перемещения
по координатам. Заменим их конечными разностями. Для правой
подобласти элементарной ячейки (/и = 1,4,5,8 - для djdx\,
т - ], 2. 5, 6 - для гI&2 , т - 1, 2,3,4 - для djdx^ ) заменим
производные cjdxa правой разностной производной
ди ua+1-ua
дха ha
D.12)
Для левой подобласти (т - 2,3,6,7 - для ^/^i > w = 3,4, 7, 8 - для
с2 * /;/ - 5,6, 7, 8 - для д\ск-$ ) - левой разностной производной
дха h
'rie or-I. 2,3.
После всех преобразований чапишем левую часть уравнения D. Г)
IJ проекциях на оси. Поскольку получающиеся выражения
162 Гл.4. Конечно-разностные схемы МГП
громоздки, они вынесены в приложение 1 к главе 4 и приведены для
общего случая (для неоднородной задачи теории упругости).
Для упрощения записи введен ряд обозначений D.14),D.15) (см.
приложение 1). Для рассматриваемой задачи в выражениях D.15)
И i\9i2,i3=M и ^ /1,/2,i3= ^ •
Проекция на ось х\ имеет вид D.16), на ось xj - D.17), на ось х3
- D.18) (см. приложение 1).
Интеграл D.8) в правой части уравнения D.1) после всех
подстановок в проекциях на оси х^я^'^З име1°т соответственно
вид D.16), D.17), D.18) (см. приложение 1).
Интегралы D.9) и D.11) правой части уравнения D.1) в проекциях
на ось ха имеют следующий вид:
=/ XMU +KL. ); D.19)
Jxa J xa 8
PXa
4.2. Дискретный аналог вариационного уравнения метода
геометрического погружения в цилиндрической системе
координат
В цилиндрической системе координат (r,cp,z) в качестве
канонической области возьмем круговой цилиндр радиуса R.
Начало координат расположим в центре его нижнего основания.
Введем равномерную сетку ajh, множество точек с координатами
(го+О^ОМ'г-ОМ'з-ОЛз)* гДе О^о ^; /^1,2,...,^;
/*2 =1,2,...,N2; h = 1»2,...,Л^з; N\,N2^Ni> - число узлов на осях
г, ср, z соответственно. Также вводим семиточечный шаблон.
Элементарная ячейка из восьми подобластей объема г;Ahfah^/H,
окружающая узел с координатами [rt , q>t , z, ) показана на рис.4.2.
В вариационном уравнении D.1) компоненты вектора
перемещения равны u~ur,v-u(p nw-uz .
Геометрические соотношения D.5) примут вид
4.2. Дискретный аналог МГП в цилиндрической системе координат 163
Рис. 4.2. Элементарная ячейка, окружающая узел с координатами
yi\ 9 <Pi2 > z/3 ) в Цилиндрической системе координат (усл. обозн. см. текст)
диг
ди-
Г О(р Г
1 ( ди- диг
2i a-
с — _ j j_ 2__
r<p l\rd(p dr r
\{\duz | диЛ
D.21)
21 г дер
Закон Гука в цилиндрической системе координат имеет вид
_ А \
G(p(p - А \?гг + ?фф + 6zz )
crz~r = Я \srr + smcn + е.
D.22)
Здесь ?rr>?w?zz>?r(pi?rzi?(pz " компоненты тензора
Деформации, or r, о^ ^, oz z, or ^, or z, a^ z - компоненты тензора
н^пряжений в цилиндрической системе координат.
Интегралы в D.1) преобразуются по аналогии со случаем
Декартовых координат, только
dD0 =.
D.23)
164 Гл.4. Конечно-разностные схемы МГП
Рассмотрим левую часть уравнения D.1). Обозначения D.14)}
D.15) (см. приложение 1), введенные для декартовой системы
координат, сохраняются. В целях упрощения записи компоненты
вектора перемещения обозначим: ur =u, u^ -v, uz =w.
Получающиеся выражения в проекциях на оси вместе с
дополнительными обозначениями D.24), D.25) вынесем в
приложение 2. Для рассматриваемой задачи в выражениях D.25)
Mibi2,i3 =M и ^ь/2,/3 =Я-
Проекция на ось г имеет вид D.26), на ось ср - D.27), на ось z -
D.28) (см. приложение 2).
Интеграл D.8) в правой части уравнения D.1) после всех
подстановок в проекциях на оси имеет такой же вид: на ось г - D.26),
на ось ср - D.27), на ось z - D.28).
Интегралы D.9) и D.11) правой части уравнения D.1) в проекциях
на ось г имеют следующий вид:
^) («9)
D.30)
Проекции на оси ср и z имеют аналогичный вид.
4.3. Построение дискретного аналога вариационного уравнения
метода геометрического погружения для задач
неоднородной теории упругости
Рассмотрим вариационное уравнение метода геометрического
погружения для неоднородных задач теории упругости B.107).
Запишем уравнение в виде
Jtr (u* ).-
D D D
Ци* [J--?{SuKjdD. D.31)
D D
4.3. Построение дискретного аналога МГП для неоднородных задач 165
Левая часть уравнения и интеграл правой части по области Бд , а
также сумма четвертого и пятого интегралов правой части, имеют в
проекциях на оси вид D.16), D.17) и D.18) (см. приложение 1) или
D.26), D.27) и D.28) (см. приложение 2) в соответствии с выбранной
системой координат. Согласно методу геометрического погружения
физические константы, подставляемые в эти выражения равны
Я 0 = max (Л (х)), /и 0 = max (/у (х)). D.32)
xeV X€V
Для данной задачи в выражениях D.15) (см. приложение 1) или
D.25) (см. приложение 2) Mihi2,i3 = Mo И \i2,b =Я0-
Сумма шестого и седьмого интегралов имеет аналогичный вид,
но физические параметры Ламе зависят от узловых координат.
Интегралы, представляющие собой работу внешних сил, в
проекциях на оси имеют вид D.19) и D.20) в декартовой или D.29) и
D.30) - в цилиндрической системе координат.
4.4. Методы решения системы разностных уравнений
Соотношения D.1), D.31), записанные для всех узловых точек по
объему параллелепипеда или по объему цилиндра, образуют систему
линейных алгебраических уравнений. Запишем систему в матричном
виде
М*)=/$)' D-33)
P(k) = А hh
(k) = ААУAс-\) +fh+Ph "для однородной задачи,
*-о ~
Для неоднородной задачи, где yh - приближенное решение,
полученное на сетке со ^; f ,р¦ - сеточные значения векторов
массовых и поверхностных сил, к - номер итерации по методу
геометрического погружения.
Сходимость приближенного решения у разностной задачи
D.33) к точному решению задачи на канонической области доказана
в [80,81].
На каждой к-й итерации метода геометрического погружения
необходимо решать систему линейных алгебраических уравнений
Вь1сокого порядка и специального вида. Важно отметить, что
166 Гл.4. Конечно-разностные схемы МГП
системы алгебраических уравнений, получаемые в результате
дискретизации линейных задач, как правило, оказываются плохо
обусловленными [73], т.е. отношение минимального и
максимального собственных чисел системы мало. Поэтому важны
устойчивые к ошибкам округления и заданию правой части методы
решения таких систем. Кроме того, матрица Aq системы имеет
разреженную структуру.
Применение прямых методов для такой системы нецелесообразно
из-за необходимости хранения большого объема информации и из-за
большого объема работы. Также в этих методах наблюдается
неустойчивость к ошибкам округления, а обеспечить устойчивость
достаточно трудно ввиду большого числа неизвестных [73].
Широкое распространение в связи с проблемой обеспечения
устойчивости вычислений получили итерационные методы.
Разработаны современные экономичные методы для решения систем
разностных уравнений [15,18,83,84,107,136]. Рассмотрим некоторые
из них. Наиболее эффективны в данном случае методы решения,
записывающиеся в канонической форме [84]
= Р, /=0,1,2,..., D.34)
где Т\9Т2,~- - итерационные параметры, / - номер итерации, >>/ -
итерационное приближение номера /, В - произвольный линейный
оператор. Здесь и в дальнейшем индекс h будем опускать.
Запись итерационных методов в единой форме позволяет
выделить оператор В, ответственный за устойчивость и сходимость
итераций, и сравнить различные методы с различных позиций.
Вообще В = B[+i зависит от /, однако здесь ограничимся случаем,
когда В не зависит от /.
Возникает задача оптимального выбора оператора В из условия
минимизации общего объема вычислительной работы, которая
должна быть выполнена для получения решения с заданной
точностью. Развитие итерационных методов идет по пути
конструирования легко обратимых операторов. К ним (или
экономичным) обычно относят такие операторы, обращение которых
осуществляется за число арифметических действий,
пропорциональное числу неизвестных. Это, например, операторы,
которым соответствуют диагональная, трехдиагональная,
треугольные матрицы и их произведения.
4.4. Методы решения системы разностных уравнений 167
Будем использовать двухслойные неявные итерационные методы,
как наиболее эффективные. Рассмотрим итерационный метод, в
котором оператору В соответствует треугольная матрица. Это метод
последовательной верхней релаксации.
В методе последовательной верхней релаксации матрицу Ао в
D.33) представляем в виде
A0=Aq+D0+A+9 D-35)
где Dq - диагональная матрица; Aq - нижняя треугольная матрица с
нулями на главной диагонали, a~j =tf/y при j<i\ Aq - верхняя
треугольная матрица с нулями на главной диагонали, afj = atJ- при
у>/. Тогда в D.34) B = Dq+coAq, t(i+\)=g> - коэффициент
релаксации.
Расчетная формула метода имеет вид [84]
^) У> D.36)
для /=1, 2, ...,7V найденное у\ + ' размещается на месте у} К
Необходимым условием сходимости такого итерационного
процесса является 1 < со < 2 . При со - 1 будем иметь частный случай,
известный, как метод Зейделя [84].
Оптимальный выбор итерационного параметра со - сложная
самостоятельная задача, особенно при решении задач на областях
произвольной геометрии. С подробным изложением этого вопроса
можно ознакомиться в [107]. На практике параметр со подбирают
путем численного эксперимента. Это особенно удобно, если
решаются однотипные задачи и задачи на канонических областях.
При проведении численного эксперимента не требуется больших
вычислительных затрат, так как величина оптимального со не
зависит от параметров сетки и его можно определить на сетке с
крупным шагом.
Рассмотрим другой вариант двухслойного неявного
итерационного метода. Наибольшая скорость сходимости
итерационного процесса D.34) наблюдается при использовании
Чебышевских итерационных параметров [84]:
168 Гл.4. Конечно-разностные схемы МГП
Mk?MN> k = l,2,-,N. D.37)
Здесь Myv - множество корней полинома Чебышева
^~n, / = 1,2,...,лЛ, D.38)
Константы C\ и С 2 зависят от вида граничных условий, а
у' - от выбора оператора 5.
На сходимость метода также существенно влияет порядок
использования г д. [38]. Необходимо упорядочить множество MN
следующим образом:
MN = |- cos/3 j; /?, = ^ ^/Л), / = 1,2,.... лА, D.39)
используя построенное множество в р по формулам
w = l,2,4,...,2/'-1. D.40)
При построении оператора 5 в D.34) можно исходить из
некоторого оператора 7? - регуляризатора. Оператор В строится из
условия близости по энергии к регуляризатору R. Класс операторов
R существенно более узкий, чем класс, содержащий оператор Aq .
Наиболее распространенный случай факторизованного оператора В
где х > 0 - параметр, Е - единичный оператор.
Для сеточных эллиптических краевых задач оператор Ra обычно
выбирают так, чтобы постоянные С\ и С2 не зависели от параметров
сетки (от числа узлов). Так как Aq соответствует разностному
оператору с переменными коэффициентами, заданному на
равномерной сетке, введенной в параллелепипеде, то в качестве Ra
4.4. Методы решения системы разностных уравнении
169
можно взять оператор, соответствующий разностному оператору
Лапласа
" А„ О О
О -Ла О
О О -Л,
где Аа - вторая разностная производная.
Для такого оператора В известны параметры х>У\ ИУ'2 [84]
1
D.42)
Г\
Xopt
2
\3
\-rj
2/7)
j
I-/3
I-/?
D.43)
где 5 = min Я ^, А = max Я ^ . Здесь Я ^ - собственные значения
оператора Лапласа.
Представление оператора В в виде D.39) позволяет ввести
расщепление или иначе промежуточные переменные
D.44)
{Е + % R\ )УМ/3 = Ву{ - тм (АоУх + /).
Такая система легко решается тремя последовательными
прогонками по направлениям xj, %2 и х$ для компоненты
перемещения по jq; по jc2,л:з и^l Для компоненты по х2; по
Хз,Х] и*2 Для компоненты по хз .
В качестве оператора В можно взять регуляризатор R, тогда
У\=у' =1. В этом случае целесообразно применение дискретного
преобразования Фурье по двум направлениям и прогонки - по
третьему. Особенно эффективен этот подход при равномерной сетке
с числом узлов N ~2п по двум направлениям, так как на такой сетке
можно использовать быстрое дискретное преобразование Фурье или
Маршевый алгоритм. Алгоритмы прогонки и быстрого дискретного
преобразования Фурье подробно изложены в работе [84], маршевый
^горитм - в [133]. В результате чего на каждой итерации метода
170 Гл.4. Конечно-разностные схемы МГП
геометрического погружения будут осуществляться итерации по
решению системы алгебраических уравнений. Получили два
вложенных итерационных процесса, сходимость каждого из которых
гарантирована.
Скорость сходимости итерационного процесса D.34) зависит от
правильности выбора итерационных параметров и оператора В. На
каждой итерации по погружению решается задача на канонической
области типа параллелепипеда или цилиндра, поэтому хорошо
работают все ниже приведенные методы их определения.
Скорость сходимости итераций в D.1) зависит от степени
близости канонической области Do и исходной области D. Для
увеличения сходимости внешнего итерационного процесса D.1)
можно использовать процедуру ускорения [28]:
(М Ы)D.45)
где
4.5. Апробация алгоритма вариационно-разностной
реализации метода геометрического погружения
В данном разделе осуществляется практическая реализация
алгоритма метода геометрического погружения в вариационно-
разностной постановке. Алгоритм решения однородных и
неоднородных пространственных задач изотропной теории
упругости реализован в виде комплекса Фортран-программ на IBM
PC. В целях апробации алгоритма решен ряд тестовых задач. Задачи
выбирались таким образом, чтобы для них существовали
аналитические решения или можно было получить решение с
помощью проверенных алгоритмов, основанных на известных
численных методах.
4.5.1. Равновесие упругого изотропного параллелепипеда
Для тестирования предложенного алгоритма в декартовых
координатах решена задача, имеющая известное аналитическое
решение.
4.5. А пробация алгоритма вариационно-разностной реализации 171
Рассмотрим прямоугольный параллелепипед (рис.4.3) с
размерами /j 2 =1м и /3 = 0.67 м с упругими постоянными v = 0.3,
Е = Е0 под действием нормальной нагрузки G(xi,x2)
интенсивности g0. Остальные грани свободны от нагрузок и
кинематических связей. Граничные условия примут вид
сги=0, сг12=0, сг13=0 при xx =±/i/2;
о21=0, 0-22=0, ^з^О при х2 = ± /2 /2; D.46)
сг31=О, сг32=О, a33=-g0 прих3=±/3/2.
Согласно методу геометрического погружения, погрузим
параллелепипед в куб размерами L\ 2> з = 1м > У которого верхняя и
нижняя грань закреплены по нормальной компоненте (рис.4.4).
\L w у
Рис.4.3. Прямоугольный параллелепипед под действием давления
Для реализации алгоритма, когда для решения системы линейных
алгебраических уравнений выбирается метод последовательной
верхней релаксации, требуется провести ряд численных
экспериментов для определения оптимального итерационного
параметра со . Эксперимент проводился на сетке N\ - N2 = N$ - 1.
t
:t
Л
Рис.4.4. Расчетная схема для параллелепипеда
172
Гл.4. Конечно-разностные схемы МГП
В теории итерационных методов стоит самостоятельный вопрос о
выборе момента окончания итерационного процесса. Наиболее
полно он изложен в работах [54,84,107]. Был выбран наиболее
простой и точный критерий остановки: е* < ?, s~ 0.001, а
?* =
У
С)
D.47)
Результат таких экспериментов отражен на рис.4.5. Когда
канонической областью является куб с граничными условиями
D.46), скорость сходимости итерационного процесса D.34)
максимальна при со = \ .745.
220 |
^итер
180
140
100
60
20
1
\
\
\
к
г
1
/
/
1.00 1.20 1.40 160 1.80 2.00
Рис.4.5. Зависимость необходимого числа итераций по методу
последовательной верхней релаксации от параметра со
При сравнении результатов решений двумя методами в этой
задаче и в последующих будем рассматривать следующую
погрешность 5 :
D.48)
где уп - решение, полученное по вариационно-разностному
алгоритму МГП; упм - решение, полученное аналитическим путем
или известным численным методом.
4.5. Апробация алгоритма вариационно-разностной реализации 173
Таблица 4. 1
Сравнение полученных результатов с аналитическими в параллелепипеде
под действием давления G(xj, х2 )
Результат
Аналитический
Расчетный
Ошибка, %
-0.0575
-0.0574
0.17
w8o/(L3Eo)
-0.1289
-0.1277
0.9
о-зз/so
-1.000
-0.997
0.3
В табл.4.1 приведены результаты сравнения полученного
приближенного решения с точным аналитическим по перемещениям
в точке А (см. рис.4.4). Погрешность S D.48) полученного решения
не превысила 1%. Естественные граничные условия по напряжению
сг3з выполняются с точностью до 0.3% по отношению к заданной
интенсивности.
Решен другой вариант этой задачи с более сложным
нагружением. Параллелепипед с размерами h^h'-lo, h/h~^
сжат по оси *з нагрузкой переменной интенсивности
#3 ~ So 0 ~ cos Bя* х\ )Xl ~ cos Bяг х2 )), (go ~ 0 • Остальные грани
свободны.
Данный параллелепипед погрузим в другой параллелепипед с
размерами L\ = L2 =1\ -12 и L3 //0 = 3 с закрепленными по
нормальной компоненте верхней и нижней гранями (рис.4.6).
Решение задачи проводим с учетом симметрии.
Сравним результаты решения этой задачи с известными
решениями, приведенными в работах [51,72]. Рассмотрим
напряжения сг^з/^о ПРИ хз ~® (табл.4.2). Первая строка таблицы
соответствует решению, полученному М.Мишоновым, вторая -
Б.Е.Победрей и С.В.Шешениным, третья - предложенному решению.
Здесь использованы обозначения
м h
Решение получено на сетке размерностью jVj = N2 = 7, iV3 =15 .
Степень отличия результатов 8 D.48) по обоим решениям не
превышает 1.5%.
174
Гл.4. Конечно-разностные схемы МГП
12=L2
Рис.4.6. Расчетная схема для параллелепипеда под действием
куполообразной нагрузки
Таблица 4. 2
Сравнение напряжений 03 3 /go ПРИ Х3 = ^ с напряжениями, полученными
другими методами, в параллелепипеде с куполообразной нагрузкой
х{ = 0.00
х2 = 0.00
0.920
0.950
0.923
х, = 0.25
х2 = 0.00
0.960
0.964
I, = 0.50
х2 = 0.00
1.010
1.000
1.006
х{ = 0.25
х2 = 0.25
1.000
0.970
0.993
х, = 0.50
х2 = 0.25
1.047
1.030
1.035
х, =0.50
х2=0.50
1.100
1.060
1.083
На рис.4.7 показано распределение перемещения wgo/(/i?o) по
высоте параллелепипеда (х\ - 0.5/j, х2 = 0.5/2) при различных
дискретизациях. Отличие решения на сетке размерностью
Nj = N2 = 9, N3 = 19 от решения на сетке Л^ = Лг2 = 7, jV3 = 15 не
превышает 1%.
4.5. Апробация алгоритма вариационно-разностной реализации 175
-О?
-0.4
-0.6
-0.8
ч>х.
N
Ч
x3/lQ
0.0 0.1
0.2 0.3
0.4
0.5
Рис.4.7. Сходимость результатов решения в зависимости от дискретизации:
- Nx =N2=9, N3 =19; Nx =N2=7, N3 =15;
NX=N2=3, N3=7
В табл.4.3 приведены отклонения cr33/gQ (в процентах) от
#3 /go на поверхности *з = 13 при различных параметрах сетки.
Решение данной задачи подтверждает принцип Сен-Венана: при
*3 - 0 (см. табл.4.2) распределение напряжений почти равномерно,
отличие от среднего напряжения, равного единице, не превышает
10%. Необходимо учесть, что поверхностные силы распределены
существенно неравномерно.
Анализ результатов показал, что удовлетворительная точность
Решения существует уже на сетке размерностью
Л^1 =iV2 = 7,^ =15 и дальнейшее ее измельчение не дает
сУщественного уточнения результатов.
На приведенных выше задачах исследовалась эффективность
Убранных итерационных методов решения системы разностных
Уравнений: метода последовательной верхней релаксации, методов с
Факторизованным оператором В D.39) с применением метода
[1Рогонки по всем направлениям или метода быстрого дискретного
преобразования Фурье по двум направлениям и прогонки по
тРетьему направлению. Скорость сходимости итерационных
процессов сравнивалась при решении задачи на сетках размерностью
176
Гл.4. Конечно-разностные схемы МГП
Таблица 4. 3
Отклонения <з"зз/?о (в процентах) от g^/go на поверхности х3 =/3 при
различных дискретизациях.
хьх2
0.5, 0.5
0.5, 0.0
/V, х N2 х N2
3x3x7
10.8
6.8
5x5x11
6.15
5.40
7x7x15
4.8
4.1
9x9x19
4.15
3.85
2n +1, n = 1,2,3,4 по всем направлениям, поскольку метод
быстрого дискретного преобразования Фурье требует таких сеток
хотя бы по двум направлениям. Итерирование прекращалось после
того, как ?* D.47) становится величиной, меньшей некоторой
наперед заданной величины е.
TW-L ¦ --1
„-У
Г
/
/•
' 3
100
50
°2
Рис.4.8. Время, необходимое для проведения итераций по методу: / -
последовательной верхней релаксации, 2-е факторизованным оператором с
применением прогонки, 3 - с факторизованным оператором с применением
быстрого дискретного преобразования Фурье
На рис.4.8 приведено время в секундах (IBM PC 386/387 - 20
МГц), за которое исследуемые итерационные процессы сходятся при
? = 0.0001 в зависимости от размерности выбранной сетки.
Численный эксперимент показал следующее:
¦ если есть возможность дискретизации области сеткой
размерности 2Р х2п х N, где N - произвольно, то наиболее
4.5. Апробация алгоритма вариационно-разностной реализации 177
эффективен метод с факторизованным оператором В с применением
алгоритма быстрого дискретного преобразования Фурье по двум
координатам и прогонки третьей;
¦ на произвольной сетке хорошо работает метод
последовательной верхней релаксации, хотя из всех рассмотренных
методов с увеличением размерности сетки скорость сходимости
метода падает наиболее быстро;
¦ на произвольных сетках больших размерностей можно
применять метод с факторизованным оператором В с применением
алгоритма прогонки по всем направлениям, такой подход
эффективен при числе неизвестных более 1000.
При последующих расчетах выбор метода решения системы
разностных уравнений осуществлялся с учетом этих выводов.
Поскольку при решении неоднородных задач на каждой итерации
метода геометрического погружения решается задача однородной
теории упругости, сделанные выводы распространяются и на задачи,
которые рассмотрены в следующих главах.
4.5.2. Напряженно-деформированное состояние кусочно-
однородного параллелепипеда с различным типом граничных
поверхностей
Для проверки алгоритма решения неоднородных задач теории
упругости в декартовых координатах решена задача
деформирования двухслойного куба с размерами /1,2,3 = 'о (рис.4.9).
Первый слой имеет физические константы А\ = Л q , // j = ju q ,
второй - Л 2 = Л о • 10, // 2 = /* о ' * 0 ¦ Высота первого слоя
/3//0 = 0.5 , второго - /|//о = 0.5 . Куб нагружен нормальным усилием
G(jcl5A*2) интенсивности gQ по верхней грани. Нижняя грань
закреплена по нормальной компоненте. Остальные грани - свободная
поверхность. Граничные условия имеют вид
°"И =0> СГ12=0' сг13=0 при х{ =±1\/2\
сг21=0, а22=0, ст23=О при*2=±/2/2;
w- 0, oi = 0, <тз2 = 0 при jc3 = 0;
сг31 =0, о-32=0, сг33=-\ прих3=13.
Согласно методу геометрического погружения для неоднородных
3аДач, погрузим куб в однородный параллелепипед с размерами
178
Гл.4. Конечно-разностные схемы МГП
Lx = L2 =/] =/2, ^зЛ) = 1-5 (рис.4.10) и физическими константами,
равными максимальным из заданных: Атах=А2 и //тах = /^ 2,
Параллелепипед закреплен по нормальной компоненте по верхней и
нижней граням.
Рис.4.9. Двухслойный куб (усл. обозн. см. текст)
Х3 ,
1 irl I
^2
Рис.4.10. Расчетная схема двухслойного куба (усл. обозн. см. текст)
4.5. Апробация алгоритма вариационно-разностной реализации 179
Поскольку граничные условия D.49) аналогичны условиям D.46),
то определенный путем численного эксперимента оптимальный
итерационный параметр со = 1.745 (см. раздел 4.6.1) является
оптимальным и для данной задачи.
В качестве тестового решения возьмем решение задачи о
деформировании двухслойной плиты, физические константы
материалов слоев те же, нагружение аналогично. Высота плиты и
размер по оси х\ совпадают с соответствующими размерами куба, а
размер по оси х2 намного превышает два первых. Это позволяет
решать пространственную задачу как задачу о плоском
деформированном состоянии. Решение ее получим методом
конечных элементов. Сравним результаты двух приведенных задач:
о плите с результатами решения двухслойного куба в сечении
х2 = h /2» гДе значения перемещений и напряжений в кубе наиболее
близки к аналогичным при плоскодеформированном состоянии.
При решении методом конечных элементов использовался
шестиузловой элемент, число элементов - 132, общее число
неизвестных - 590. Для сравнения решение по предложенному
алгоритму проводили при дискретизации N\ = N2 = 12, 7V3 =22, что
составило 3168 узлов (9504 неизвестных).
На рис.4.11 приведено распределение компоненты перемещения
H'//o/(/ogo) по высоте куба при х\ =0 и х\ -1\/2. На рис.4.12
показано распределение напряжения сгзз/Яо по высоте куба в
сечении х\ =1\/2, на рис.4.13 - в сечении х\ =0. Погрешность 8
D.48) по перемещениям не превысила 10%, по напряжениям - 12%.
Изолинии напряжений cr^/go B среднем сечении первого слоя
(*3=/з/4) представлены на рис.4.14, в среднем сечении второго
слоя (хз =3/з/4) - на рис.4.15. Погрешность выполнения
естественных граничных условий по 0-33 не превышает 5% по
отношению к заданной интенсивности нагрузки при дискретизации
области, содержащей 250 узлов, а при дискретизации, содержащей
539 узлов, - не выше 3%. Дальнейшее измельчение шага сетки
^Целесообразно.
80
Гл.4. Конечно-разностные схемы МГП
\
2
к
-0.06
-0.12
-0.18
-0.24
0.0 0.2 0.4 0.6 0.8 J u
Рис.4.11. Распределение перемещения по высоте двухслойного куба в
сечении x^-l^ (l ~ х\ - 0> 2 - х\ = 1\ / 2): - решение задачи о
кубе; - решение задачи о ПДС
-1.2
-1.6
-2.0
0.0 0.2 0.4 0.6 0.8 1.0
Рис.4.12. Распределение напряжения по высоте двухслойного куба в
сечении х\ = 0, х^ = /2 / 2 : решение задачи о кубе;
- решение задачи о ПДС
4.5. Апробация алгоритма вариационно-разностной реализации 181
ч^
ч
-II ¦
/80
-0.85
-0.95
-105 l
0.0 0.2 0.4 0.6 0.8 1.0
Рис.4.13. Распределение напряжения по высоте двухслойного куба в
сечении х\ = 1\ /2, х2 = /2 / 2 : решение задачи о кубе,
- решение задачи о ПДС
1 -
2
3 -
4 -
5 -
6 -
7 -
-1.030
-1.020
-1.010
-1.000
- 0.994
- 0.987
- 0.980
/2/B /о)
Рис.4.14. Изолинии напряжения в среднем сечении первого слоя
двухслойного куба
Решена задача об изгибе толстой прямоугольной составной плиты
с неканоническими лицевыми поверхностями Sq,S2 и поверхностью
Раздела слоев Sj (рис.4.16). Поверхности в декартовых координатах
°Писываются уравнениями
х3 =/*! +€щ/(х2\ f(x2) = h2cos(co7rx2/b). D.50)
182
Гл.4. Конечно-разностные схемы МГП
0 - - 1
1 - - 1
2 - - }
3 - - 1
4 - - 1
5 - - 1
6 -
7 - - 1
8 -
9 - - 1
10 -
11 - - (
12 - - (
.500
.450
.400
.350
.300
.250
.200
1.150
1.100
1.050
1.000
).95О
).900
13 - - 0.850
14 - - 0.800
/2//0/2
Рис.4.15. Изолинии напряжения в среднем сечении второго слоя
двухслойного куба
Рис.4.16. Двухслойная плита с неканоническими поверхностями (усл. обозн.
см. текст)
4.5. Апробация алгоритма вариационно-разностной реализации 183
Здесь h\ - константа, равная средней высоте первого слоя плиты;
1; -1<Ш|<1; awb- размеры плиты по осям х\\\Х2
соответственно.
Рассмотрим случай, когда со = 2, коэффициенты Пуассона
Vx -V2 = 0.3 и отношение модулей сдвига М\/М2 = Ю;
? = 0.1; А1/А2=0.5и h2/b = h2/a = l/3; аH=0;щ=бJ=1.
Поперечная нагрузка g2 по направлению оси х$, приложенная к
лицевой поверхности S2 имеет вид
[)^) D.51)
v ^ ; V ь )
На боковых поверхностях выполняются краевые условия:
v = 0, w = 0, <7] i = 0 при xi = 0 и дг| - лг;
D.52)
w rr 0, w = 0, а22 = 0 при х2 = 0 и х2 = й.
Нижняя поверхность 5q свободна, т.е.
(Тзз=О, (Тз1=0, О"з2=0 при *з=0. D-53)
Согласно МГП, погружаем двухслойную плиту в однородный
параллелепипед с физическими константами v = vj = v2 и /i = /л\,
которые максимальны по данным, и с размерами исходной плиты с
плоскими поверхностями, параллельными координатным осям.
Выбираем равномерную сетку TVj = N2 =16, N3 =23 (рис. 4.17).
Рис.4.17. Дискретизация расчетной области
Для граничных условий D.52), D.53) необходимо провести ряд
Пленных экспериментов по определению оптимального
Терационного параметра со. Эксперимент проводился на сетке
1 ^ 6, Лг2 =16, 7V3 = 23 . Итерационный процесс D.34)
184
Гл.4. Конечно-разностные схемы МГП
останавливался, когда величина е* <? , где е* определена в D.47), а
?• = 0.001. Результаты эксперимента отражены на рис.4.18.
Оптимальный параметр со = 1.965.
^итер
400
300
200
100
1.7 1.8 1.9 "V со
\
\
\
\
\
1
/
J
1
Рис.4.18. Зависимость необходимого числа итераций по методу
последовательной верхней релаксации от параметра со для паралленипеда с
граничными условиями D.52), D.53)
Результаты, полученные на сетке Л^ = 7У2 = 16, N3 = 23 по
предложенному алгоритму, сравним с результатами решения этой
задачи приближенным аналитическим методом, приведенными в
работе [61]. Чтобы иметь точность до четырех значащих цифр,
потребовалось около 2200 с на PC 486.
На рис.4.19 дано распределение напряжений <тц/#ц и (Уц/Чи
по толщине в центре плиты с неискривленными поверхностями S\ и
5*2- Величина 5 D.48) не превысила 1%. На рис.4.20 приведены
результаты решения с неканоническими поверхностями. В этом
случае расхождение результатов по напряжениям составило не болев
13%.
В табл.4.4 приведены значения напряжений сгц/^ц ,^22/^11 **
прогиба ^Hilviw^l) B Центре верхнего и нижнего оснований
плиты. Первая строка соответствует предложенному решению»
вторая - решению Ю.Н.Немиша, в третьей приведено расхождение
результатов в процентах.
4.5. Апробация алгоритма вариационно-разностной реализации 185
4.0
2.0
0.0
-2.0
-4.0
\
\
\
\
\
x3/h3
0.0 0.2 0.4 0.6 0.8 1.0
Рис.4.19. Распределение напряжений <j\ \/q\\u cr 22 /я\\ по толщине в
центре плиты с плоскими поверхностями:
приближенным аналитическим методом; ——
— -решение
- решение МГП.
4.0
2.0
0.0
-7 0
\\
'4
0.0 0.2 0.4 0.6 0.S 1.0
Рис.4.20. Распределение напряжений cjj \jq\ \ и cj2llcl\ 1 по толщине в
центре плиты с неканоническими поверхностями: решение
приближенным аналитическим методом; решение МГП.
186
Гл. 4. Конечно-разностные схемы МГП
Таблица 4.4
Значения прогиба и напряжений в центре верхнего и нижнего оснований
для двухслойной плиты
Верхнее основание
<*\\1Я\ 1
-0.957
-1.091
2.3
СТ2 21Я\ 1
-0.717
-0.792
9.5
-0.421
-0.4445
5.3
Нижнее основание
°\ 11Я\ 1
-3.851
СТ2 21Я\ 1
-2.745
иъцг
4\\h2
-0.350
-0.3389
3.3
Погрешность в выполнении естественных граничных условий
определялась следующим образом:
<Г=^п-аг|/?и).100%, D.54)
где ап, аГ - полученное и точное значение напряжения на границе.
Погрешность S* D.54) на боковых поверхностях составила около
8%, на ребре и в точках близких к ребру - не более чем 15%.
Напряжение 0*33 в точках приложения нагрузки отличается от
величины Q\ не более чем на 10%.
4.5.3. Конечный круговой цилиндр под действием внутреннего
давления
Задача решена для тестирования алгоритма в цилиндрических
координатах. Цилиндр размерами го/7?1=О.5, /?2/^1 =^'
L/Ri =10, нагруженный нормальным внутренним давлением
grr - const, согласно МГП, погрузим в цилиндр с внутренним
радиусом и высотой исходного, с большим внешним радиусом
R2/R\=3 (рис.4.21). Физические константы материала
A = Aq и ju = juq. Граничные условия с учетом осевой симметрии И
симметрии относительно среднего сечения по z примут вид
°гг=-ёгг> &r(p=0> CTrz=° ПРИ r = rQ\
7rr = 0, ar(p = 0, Grz =0 при r = i{2;
v = 0, 0-^=0, cr^ =0 при cp-Q w (p-7i I2\
w = 0, azr-Q, <?z(p=0 при z-Z/2.
D.55)
4.5. Апробация алгоритма вариационно-разностной реализации 187
>*0
Рис.4.21. Короткий круговой цилиндр (усл. обозн. см. текст)
При решении задачи, когда для решения системы алгебраических
уравнений используется метод верхней последовательной
релаксации, необходимо путем численного эксперимента определить
оптимальный итерационный параметр со . Эксперимент проводился
аналогично задачам в декартовых координатах. Результат
эксперимента отражен на рис.4.22. Оптимальный итерационный
параметр, когда канонической областью является круговой цилиндр
с граничными условиями D.55), равен со = 1.8 .
итер
200
100
п
Ч^
^ч
*^
ч
/
/
1.0
1.2
1.4
1.6
1.8
со
Рис.4.22. Зависимость необходимого числа итераций по методу
последовательной верхней релаксации от параметра со для цилиндра с
граничными условиями D.55)
Результаты решения данной задачи находятся между
Результатами решенияследующих задач: Ламе (толстостенной
тРубы) и о нагружении кругового кольца. Обе приведенные задачи
иМеют аналитическое решение [84]. Сравнение полученных
188
Гл.4. Конечно-разностные схемы МГП
численных результатов и аналитических решений известных задач
приведено на рис.4.23.
0.6
0.2
0.0
\
s
j
i
j
1
q - КОЛЬЦО
А- труба
— - цилиндр
J
»-— <
i {
mmmmJ
I J
г/г0
1.0
2.0
3.0
4.0
Рис.4.23. Распределение перемещения по радиусу цилиндра
Естественные граничные условия выполняются с точностью S*
D.54) не менее 0.25% при дискретизации N\ = N2 = N3 =-- 7, менее
0.1% - при дискретизации N\-N2~Ni>-9, дальнейшее
уменьшение шага сетки к существенному изменению результатов не
привели.
4.5.4. Задача о деформировании двухслойного конечного кругового
цилиндра
Для тестирования программы расчета неоднородных конструкций
в цилиндрических координатах решена задача о деформировании
двухслойного конечного кругового цилиндра. Материалы слоев
изотропны и имеют физические постоянные: первый слой *
Я] =8.069Я0, /их = 0.89655//0 , второй слой Я2 =104^, ju2 = 104//Q.
Цилиндр с внутренним радиусом го/г1=О.З, внешним радиусом
R2/r\ =\.7 и радиусом раздела слоев R\jr\ =1, высотой Цг\ =1.4
нагружен внутренним нормальным давлением grr - const,
остальные поверхности свободны (рис.4.24).
Согласно методу геометрического погружения для неоднородных
задач, двухслойный цилиндр погружается в однородный изотропный
цилиндр тех же геометрических размеров, что и у исходного, с
4.5. Апробация алгоритма вариационно-разностной реализации 189
физическими константами, которые максимальны из данных. Здесь
Лщах = Л2 и /'max = М2-
Рис.4.24. Двухслойный короткий цилиндр (усл. обозн. см. текст)
Граничные условия с учетом осевой симметрии и симметрии
относительно среднего сечения по z примут вид
агг = ~ёгг > Grcp = °> arz = ° ПРИ г = г0 >
07r=O. сг^-0, crrz=0 при r = R2;
V_Q - „Л
D.56)
я =U при рУи р
w = 0, crzr=0, oZ(p=§ при z = L/2.
Поскольку граничные условия D.56) аналогичны условиям D.55),
то определенный путем численного эксперимента оптимальный
итерационный параметр со-\.% (см. раздел 4.6.3) оптимален для
данной задачи.
В качестве тестового решения возьмем решение этой задачи
классическим методом конечных элементов с квадратичной
аппроксимацией перемещений. Также имеем аналитическое решение
задачи о двухслойном бесконечно длинном цилиндре под действием
внутреннего давления. Его используем для сравнения результатов,
Полученных в среднем сечении цилиндра при z = L/2 .
На рис.4.25 представлена безразмерная величина ujUQ/(grrRi),
Характеризующая радиальное перемещение в среднем сечении
z = /, / 2 . При расчете методом конечных элементов использовалась
Дискретизация 668 элементов, 1405 узлов. Расчеты по
предложенному алгоритму проводились на сетке
190
Гл.4. Конечно-разностные схемы МГП
^1=33,^2=11,^3=15, что составляет 5445 узлов. Различие в
дискретизации связано с тем, что сетка в рассматриваемом случае
пространственная. Значения величины 5 D.48) при сравнении
полученного решения с двумя тестовыми не превысило 8%.
Погрешность S* D.54) в выполнении естественных граничных
условий не выше 6.5%.
На рис.4.26 представлено распределение напряжения crrr/grr по
радиусу в среднем сечении конструкции.
0.12
0.06
0.04
0.00
0.3 0.7 1.1 1.5 Г/Г\
Рис.4.25. Распределение перемещения по толщине цилиндра:
-МКЭ, -МГП, - решение для
бесконечно длинного цилиндра
Err
0.0
-0.5
-1.0
-2.0
У"
7
I
г/г\
0.2
0.6
1.0
1.4
1.
Рис.4.26. Распределение напряжения по толщине цилиндра:
-МКЭ, -МГП, - решение для
бесконечно длинного цилиндра
Проведение итерационного процесса по методу геометрического
погружения при решении неоднородных задач имеет ряД
4.5. Апробация алгоритма вариационно-разностной реализации 191
особенностей. При рассмотрении конструкций, где физические
константы составляющих их материалов отличаются более чем на
один порядок, для более эффективного использования машинного
времени необходимо решение проводить в несколько этапов.
Первый этап - решение вспомогательной задачи. Здесь
максимальные физические константы материала берутся без
изменения, все другие - того же порядка, что и максимальные. Это
видно на примере задачи о двухслойном цилиндре, где
А*СП=А2 и ^cn=/i2> а Л»сп=Ш1 и М™п=\0Мх. Полученные
результаты используются как начальное приближение для
следующего этапа решения. Второй этап - решение задачи с
исходными модулями с ненулевым начальным приближением.
Задачу можно разбивать и на большее количество этапов,
добиваясь постепенного приближения значений физических
констант к заданным. Тем самым получаем значительную экономию
времени. Результаты численного эксперимента по экономии времени
счета для выше приведенной задачи сведены в табл.4.5.
Таблица 4. 5
Время счета вариантов задачи о двухслойном цилиндре
Вариант решения задачи
В один этап (с нулевым начальным
приближением)
В два этапа
_ В три этапа
Затраченное время, с
1140
960
880
Решение задачи проводилось на сетке N\ = N3 -11, N2 = 9.
Итерационная процедура на всех этапах прекращалась, когда
отношение норм векторов двух последовательных итераций D.47)
становилось меньше ? = 0.001. Для последующего сокращения
затрат по времени можно требовать высокую точность итерирования
Лишь на заключительном этапе решения.
• ^ 5. Заключительные замечания
Сравнение решений, полученных методом геометрического
Огружения, с точными аналитическими решениями и решениями,
°лУченными другими приближенными методами, позволило
192 Гл.4. Конечно-разностные схемы МГП
установить, что сходимость МГП при использовании в численной
реализации вариационно-разностного подхода имеет место всегда
независимо от выбора начального приближения и от степени
отличия реальной области от канонической, как по геометрической
конфигурации, так и по физической неоднородности. Эти численные
результаты подтверждают теоретические положения МГП,
изложенные в главе 2.
На приведенных задачах проведено сравнение скоростей
сходимости выбранных итерационных методов решения системы
алгебраических уравнений. Если есть возможность дискретизации
области сеткой размерности 2Р по двум координатам, то наиболее
эффективен метод с факторизованным оператором с применением
алгоритма быстрого дискретного преобразования Фурье по двум
координатам и прогонки - по третьей. При произвольной сетке с
числом неизвестных менее 10000 целесообразно применять метод
последовательной верхней релаксации, а с числом неизвестных
более 10000 - метод с факторизованным оператором с применением
алгоритма прогонки по всем направлениям.
В целях сокращения времени счета при исследовании
неоднородных конструкций, где физические константы
составляющих их материалов отличаются более чем на один
порядок, рекомендуется проводить решение в несколько этапов с
постепенным увеличением различия в константах (решение задачи
на предыдущем этапе используется как начальное приближение для
следующего этапа).
4.6. Применение метода геометрического погружения в
разностной реализации для расчета трехмерного
напряженно-деформированного состояния конструкций
сложной геометрии
В разделе приводятся результаты расчета НДС пространственных
конструкций сложной геометрической конфигурации. Проведены
численные эксперименты по выбору оптимального начального
приближения для однородных и кусочно-однородных задач в целя*
сокращения необходимого времени счета. Даны конкретные
рекомендации по организации вычислений на вложенном D.32) *
внешнем D.1) итерационных процессах.
4.6. Применение МГП в разностной реализации для расчета НДС 193
4.6.1. НДС перфорированного куба под действием внешнего
давления
На практике часто имеют дело с конструкциями, расчет
напряженно-деформированного состояния которых удобнее
проводить в декартовой системе координат. Например, в горной и
строительной механике большинство рассчитываемых объектов по
форме близко к прямоугольной с произвольным расположением
отверстий.
L
у
yZ
i
у
У
У
ш
У
1 JT
Рис. 4.27. Перфорированный куб
Рассмотрим перфорированный куб с тремя взаимно
перпендикулярными отверстиями (рис.4.27). Отверстия имеют
одинаковые квадратные поперечные сечения размером ///0 =0.5
при внешних размерах куба L/l0 = 1. Конструкция нагружена по
Двум противоположным граням нормальным усилием
^33 - ?o(*l'Х2/- ^ся остальная поверхность свободна. Массовые
силы отсутствуют. Модуль Юнга Е = Eq9 коэффициент Пуассона
v - 0.3.
Перфорированный куб, согласно методу геометрического
Г1о^ружения, погружается в сплошной куб с размерами и
Физическими константами исходного. С учетом геометрической
сИмметрии перфорированного куба и его внешнего нагружения
°еШение осуптестигтяпопь ппя 1/8 ргп
194
Гл. 4. Конечно-разностные схемы МГП
g0 = const
Рис. 4.28. Расчетная схема перфорированного куба (усл. обозн. см. текст)
Выберем равномерную сетку (рис.4.28). Систему линейных
алгебраических уравнений будем решать методом последовательной
верхней релаксации. Согласно проведенному численному
эксперименту (см. раздел 4.6.1), параметр со примем равным 1.745.
Для достижения 5% точности выполнения естественных
граничных условий по отношению к заданной интенсивности
нагрузки G (за исключением некоторой малой окрестности точки А
(см. рис.4.28)) потребовалось использовать сетку размерностью
Nx = N2 = W3 = 13 .
При решении задач большой размерности необходимо стремиться
к уменьшению затрат по времени. Время счета можно сократить,
если оптимально выбрать начальное приближение. Использование
ненулевого начального приближения на вложенном (внутреннем)
D.34) и внешнем D.1) итерационных процессах позволяет
значительно уменьшить время счета. На каждой "к + Iм-й итерации
по погружению в качестве начального приближения для
итерационного процесса D.34) используется решение, полученное на
к -ой итерации метода геометрического погружения. Тогда на сетке
размерности N{ = N2 = N3 = 17 внутренний процесс D.34) на первой
итерации (к=^0) процедуры D.1) сходится за 120 итераций, а на
последующих итерациях скорость сходимости вложенного
итерационного процесса возрастает и достигает четырех итераций.
4.6. Применение МГП в разностной реализации для расчета НДС 195
Таблица 4.6
Необходимое число вложенных итераций в ходе внешнего итерационного
процесса
№ итерации
Число внутренних итераций
без ускорения
Число внутренних итераций
с ускорением
1
120
120
2
98
98
3
78
78
4
60
60
5
41
15
6
28
10
7
18
5
8
12
5
9
8
4
Требуемое число вложенных итераций по ходу внешнего
итерационного процесса при дискретизации N\ = N2 = N3 =17
сведено в табл.4.6. В первой строке таблицы - номер итерации по
погружению, во второй - число внутренних итераций, когда внешний
процесс проводился без ускорения сходимости D.43), в третьей -
число внутренних итераций, когда проводилось ускорение
сходимости (первое ускорение проводилось после четвертой
итерации, а последующие после каждой третьей). Итерационный
процесс D.34) останавливался, когда ?* D.47) меньше е = 0.001.
\
Рис.4.29. Элементарная 5*чейка вспомогательной сетки:
• - узлы исходной сетки, \^ - узлы спомогательной сетки
В качестве начального приближения для итерационного процесса
^о методу геометрического погружения берем решение исходной
3аДачи на сетке с более крупным шагом с последующей
Интерполяцией на заданную сетку. Для удобства переноса решения
Используем сетку с вдвое большим шагом (на рис.4.29 показана
196
Гл. 4. Конечно-разностные схемы МГП
элементарная ячейка такой сетки). На рис.4.29 также нанесены узлы
исходной сетки. В выбранном случае решение в узлах исходной
сетки, не совпадающих с узлами вспомогательной, берем как
среднее из полученных. В узлах типа "а" - среднее из двух
имеющихся на стороне, в узлах типа " - из четырех на грани, в
узле типа V - из всех в ячейке. Для получения такого начального
приближения необязательно решать задачу на заданной
конструкции. Также неплохую экономию получим, взяв в качестве
начального приближения решение задачи на канонической области с
заданным нагружением, т.е. проводим только первую итерацию по
погружению (/г=0).
Выбор оптимальной продолжительности итерирования при
решении системы алгебраических уравнений очень существенно
влияет на скорость сходимости предложенного алгоритма.
Численным экспериментом установлено, что на этапе решения
системы уравнений необязательно требовать высокую точность.
Если ограничить точность до двух значащих цифр, то итерационный
процесс по погружению сойдется за то же число итераций, что и при
точности до трех значащих цифр, но при этом экономится время на
внутреннем итерационном процессе.
Таблица 4. 7
Время расчета разных вариантов задачи о перфорированном к>бе
Вариант расчета
Задача с нулевым начальным
приближением
Задача с начальным
приближением, полученным
на сетке с вдвое большим
шагом
Время счета г , с
Точность на
внутреннем
итерационном
процессе до трех
значащих цифр
2630
1405
Точность на
внутреннем
итерационном
процессе до двух
значащих цифр
2120
805
Для наглядности сделанных выводов время счета различны*
вариантов расчета задачи о деформировании перфорированного куба
на сетке Nx = N2 = N3 = 13 свели в табл.4.7. Процесс по погружен***0
4.6. Применение МГП в разностной реализации для расчета НДС 197
прекращался после того, как отношение норм векторов двух
последовательных итераций становилось отличающимся от единицы
на величину с = 0.001. В величину времени г включено время
вычисления начального приближения.
На рис.4.30 показано деформированное состояние конструкции в
масштабе: в 1 см - 0.05125Z, перемещения отложены безразмерные
(перемещения, умноженные на g$ I(LE§)). Напряжения в сечении
х\=0, х2 = L/2 представлены на рис.4.31 при двух различных
дискретизациях. При последующем уменьшении шага сетки
напряжения существенно не изменялись.
Начальное
Деформированное
Рис.4.30. Деформированное состояние 1/8 перфорированного куба
go
0.0
-2.0
-4.0
J
V
/
г
go
^33
xh
0.0
0.25
0.5
Рис.4.31. Распределение напряжений по высоте куба в сечении
Х{ = 0, х2 = L/2 : А - Nx = N2 = N3 = 9 ; - .V, = N2 = Л^3 = 13
198
Гл.4. Конечно-разностные схемы МГП
Анализ картины распределения напряжений показал, что в
окрестности точек В и С (см. рис.4.28) наблюдается концентрация
напряжений. Уровень напряжений а3 в этих зонах в 3-4 раза
превышает уровень давления на поверхности.
4.6.2. Расчет цилиндрического тела со звездообразным каналом
Значительное количество элементов машин и конструкций имеет
базовую цилиндрическую форму в сочетании с
неосесимметричными каналами или произвольно расположенные
отверстия сложной конфигурации. Расчет НДС таких конструкций
удобно проводить в цилиндрической системе координат с
использованием метода геометрического погружения.
Проведен расчет напряженно-деформированного состояния
цилиндрического тела с каналом сложной геометрии (рис.4.32).
Рис.4.32. Цилиндр с каналом звездообразной формы (усл. обозн. см. текст)
Канал во всех сечениях конструкции, перпендикулярных оси oz,
имеет звездообразную форму. Геометрические размеры
исследуемого объекта - К/г$ = 6, гв)гц =3,5, L/r0 =10, (р$ =45° •
Рассчитываются два варианта нагружения: нормальное
распределенное усилие grr единичной интенсивности по внешней
4.6. Применение МГП в разностной реализации для расчета НДС 199
цилиндрической поверхности (остальные поверхности свободны) и
центробежные силы F = рсо г с угловой скоростью со-10рад/с.
Плотность материала конструкции р = 1кг/м . Физические
постоянные - модуль Юнга Е = Е$, коэффициент Пуассона v - 0,3.
Согласно МГП, в качестве канонического тела выберем гладкий
цилиндр, высота и внешний радиус которого исходные, внутренний
радиус равен г0. Для построения решения использована равномерная
цилиндрическая сетка, а для решения системы алгебраических
уравнений - метод последовательной верхней релаксации с
оптимальным параметром а> = 1.8, найденным путем численного
эксперимента (см.раздел 4.6.3).
Все выводы по экономии времени счета (см. раздел 4.7.1),
сделанные при расчете конструкции по алгоритмам, использующим
декартовые координаты, верны и для расчетов в цилиндрических
координатах. Все расчеты данного объекта проводились с
применением ранее разработанных приемов, приводящих к
сокращению машинного времени.
При нагружении внешним давлением погрешность выполнения
естественных граничных условий составила менее 5% по отношению
к заданной интенсивности (при сетке Nx = 7V3 = 11, N2 = 9 ).
Дальнейшее уменьшение шага сетки не приводит к существенному
улучшению результатов.
Рис.4.33. Деформированное состояние цилиндра с каналом G- при
центробежных силах 2 - при внешнем давлении)
На рис.4.33 приведены первоначальное и деформированное
среднее сечения конструкции при обоих типах нагружения.
200 Гл.4. Конечно-разностные схемы МГП
Известны результаты решения такой задачи МГП в конечно-
элементной реализации (см. раздел 3.6.5). При такой постановке
неизвестные перемещения раскладываются в тригонометрический
ряд Фурье по угловой координате и решается ряд двумерных задач
относительно неизвестных коэффициентов ряда Фурье. Для
сравнения полученных результатов взяли следующий вариант
задачи: используется симметричный ряд Фурье с числом его членов,
равным 10, число неизвестных в одной гармонике составляет 243;
берется сетка с треугольными конечными элементами с линейной
аппроксимацией, число элементов - 128, число узлов - 81, общее
число неизвестных - 2430.
Результат сравнения в среднем сечении конструкции z = L/2
отражен на рис.4.34, 4.35. На рис.4.34 приведено распределение
напряжения arr /g$ по радиусу в сечениях ср - 0°, ср = 22.5°, когда
конструкция нагружена внешним давлением. На рис.4.35 дано
распределение напряжения огг /(рсо ) по радиусу в сечении <р = 0°
при центробежной нагрузке. Результаты приведены при двух
дискретизациях. Их расхождение с результатами, полученными по
алгоритму с конечно-элементной реализацией МГП, не превысило
8% при действии на конструкцию внешнего давления и 15% - при
действии центробежных сил. Данные, полученные на сетках
TVj = iV3 =13, N2 =9 и N{ =N2 =N3 = 9 различаются не более чем на
1%, следовательно, дальнейшее измельчение сетки нецелесообразно.
В конструкции при действии центробежных сил в области
3.5>г>4.5 наблюдается концентрация напряжений, особенно в
окрестности угловой точки А (см. рис.4.32).
Таким образом, применение вариационно-разностного метода в
рамках МГП позволяет достаточно эффективно получать решение
существенно трехмерных задач теории упругости.
4.6. Применение МГП в разностной реализации для расчета НДС 201
ч
> = 22,5°
/
/
ло
/go
-0.75
-0.50
-0.25
0.0
1.00 2.67 4.33 r/r0
Piic.4.34. Распределение напряжения по радиусу при внешнем давлении:
—а___ - N{=N2 =N3 -9,—• N{ = N3 =13, N2 = 9;
. конечно-элементная реализация МГП
сгу
ра2г02
1.0
0.0
-1.0
-2.0
"f
j.'/
;
1.00 2.67
4.33
^Ис.4.35. Распределение напряжения по радиусу при центробежных силах:
~--а_._. . ^ =N2 =N3 =9, • N{ =N3=l3, N2=9;
. конечно-элементная реализация МГП
202 Гл.4. Конечно-разностные схемы МГП
4.7. Приложение 1
Для упрощения записи индексы при коэффициентах К\-К\2
опустим, так как они имеют тот же индекс, что и компонента
перемещения, при которой они стоят. Например:
при Un+]J2j3 -^4/l+U2,/3; ПРИ ViM,i2-\J3 ~ KlOiMj2-\j3-
D.14)
D.15)
4.7. Приложение 1 203
D.16)
204 Гл.4. Конечно-разностные схемы МГП
D.17)
4.7. Приложение 1 205
B.18)
206 Гл.4. Конечно-разностные схемы МГП
4.8. Приложение 2
; a\n=biX-hx; a2iX=bn+hx;
Для упрощения записи индексы при коэффициентах К\ - К\7. и
Л/1 - Л/6 опустим, так как они имеют тот же индекс, что и
компонента перемещения, при которой они стоят.
Мл,
D.19)
D.20)
4.8. Пршожение 2 207
D.21)
208 Гл.4. Конечно-разностные схемы МГП
D.22)
4.8. Приложение 2 209
D.23)
Глава 5
ЧИСЛЕННАЯ РЕАЛИЗАЦИЯ МЕТОДА ГЕОМЕТРИЧЕСКОГО
ПОГРУЖЕНИЯ В ДИФФЕРЕНЦИАЛЬНОЙ ПОСТАНОВКЕ
5.1. Введение
Дифференциальная постановка краевой задачи теории упругости
изотропных однородных тел, соответствующая вариационному
уравнению метода геометрического погружения B.34) имеет вид
B.37)-B.39)
W— II л VCQ 1X7 — П V d Q~
— IIQ, A COi/, YY — V, At OQ.
В разделе 2.2.6 также показано, что итерационный процесс
div<r(w*) = -#(D)f - r(Sa)[p + n* •&*(wk~l)], xe Do,
w*=u0, xeSw, w^ =0, X6SO.
сходится по норме пространства Vq(Dq) и, как следствие - по норме
пространства V(Z)), независимо от степени отличия исходной
области D от ?>0.
Если в качестве канонической области Dq выбрать все евклидово
пространство R3 (полагая, что компоненты вектора перемещения
1—2 1—3
ведут себя как х| , а тензора напряжения - как х| , при
стремлении х к бесконечности [41]), то для уравнения E.1) можно
записать [31] соответствующее интегральное уравнение , в котором в
качестве функции Грина выступает тензор Кельвина-Сомильяны [6]:
1
Ga(
г2
'У
где /л и v - модуль сдвига и коэффициент Пуассона средЫ
соответственно, у-х( -?,•, г2 = ухуг, StJ - символ Кронекера, а
интегральное уравнение записывается в виде
5.1. Введение 211
w*(x)= |СУ1х,?Ы(?)сШ(?) +
D
где % - точка рассматриваемой области, по которой ведется
интегрирование. Используя стандартные методы теории потенциала
[6], соотношения Коши и физические соотношения, можно перейти
от E.2) к граничным интегральным уравнениям относительно
усилий на границе рассматриваемой области
t* 00 = |[pOO +**4 Wl + JFM) • [pffi) +1
S E.3)
D
где t(x) = n (х)-ст (х) - вектор искомых фиктивных усилий на
поверхности тела для к-й итерации, действующих со стороны
дополнения DA ; t°(x) = 0; ^(x,^) - сингулярное ядро, являющееся
тензором второго ранга и имеющее вид [6]
-у) г2
U(l-2v^
Г
Соотношение E.3) позволяет непосредственно определять вектор
искомых усилий на границе S для класса задач с заданными
граничными условиями в напряжениях.
Итерационный процесс E.3) эффективно реализуется на ЭВМ.
Уравнение E.3) является базовым для численной реализации
Дифференциальной постановки МГП. Для получения дискретного
аналога уравнения E.3) успешно применяется хорошо
Разработанный аппарат МГЭ [6,7,103]. При этом отпадает
Необходимость в трудоемкой операции обращения плотнозаполнен-
несимметричной матрицы.
212 Гл.5. Численная реализация МГП в дифференциальной постановке
Применяя теоретические положения МГЭ [6], можно получить
уравнения в произвольной точке х области D для перемещений ц
деформаций е и напряжений а, которые используют решение t
уравнения E.3):
Vx б D, u(x) =
D
D
<r(x)=
D
1 1
Для решения исходной краевой задачи E.1) со смешанными
граничными условиями в рамках дифференциальной постановки
МГП используются уравнения E.2)-E.3). Для части границы Sw, на
которой заданы перемещения, записывается уравнение E.2), а Др
части границы области S^., на которой заданы напряжения, - E.3)-
Необходимо отметить также, что недостатком использования E.2) На
этапе численной реализации является увеличение поряД*а
разрешающей системы уравнений (по крайней мере в 4 раза). Э°
связано с необходимостью введения некоторой разностной
вычисления входящих в правую часть E.2) усилий t(x)-n -<x **
границе области через перемещения w на каждой итерации.
Предлагается вместо E.2) использовать уравнение
5.1. Введение 213
D
E.4)
которое получается из E.2) путем несложных преобразований. Здесь
uq(x) - заданные на границе Sw перемещения. В E.4) неизвестной
итерируемой переменной остаются усилия t, что избавляет от
необходимости какого-либо их представления через w.
Следует отметить, что вопросы сходимости такого подхода
остаются открытыми и требуют строгого математического
обоснования. Однако, как показали многочисленные численные
эксперименты, практическая сходимость совместного решения
итерационных уравнений E.3) и E.4) достигается для подавляющего
большинства задач.
В связи с изложенным в данной работе предлагается вместо
уравнения E.2) записать некоторый алгебраический аналог
уравнения E.4) и путем численного эксперимента проверить
практическую сходимость указанного подхода. Как показал
численный анализ, спектр собственных значений интегрального
оператора (для рассмотренных задач) правой части выражения E.4)
находится в интервале [0,1], что обеспечивает сходимость
итерационного процесса. Заменяя уравнение E.2) метода
геометрического погружения на E.4), можно записать постановку
задачи теории упругости со смешанными граничными условиями,
имеющую простую структуру. Такой подход легко программируется.
Вопросы сходимости уравнения E.4) обсуждаются ниже.
Таким образом, строгое математическое обоснование
Дифференциальной постановки метода геометрического погружения
позволяет свести решение краевой задачи теории упругости к
итерационному процессу решения граничных интегральных
Уравнений E.2)-E.3). Дифференциальная постановка метода
Геометрического погружения позволяет, с одной стороны,
Использовать преимущества, присущие методам граничных
Интегральных уравнений, а, с другой стороны - прямое решение
сИстемы линейных алгебраических уравнений некоторого
конечномерного аналога граничных интегральных уравнений
^Меняется гарантированно сходящимся итерационным процессом,
214 Гл.5. Численная реализация МГП в дифференциальной постановке
что, как будет показано ниже, приводит к значительной экономии
вычислительных ресурсов.
Дополнительной привлекательностью дифференциальной
постановки метода геометрического погружения является
возможность непосредственного решения задачи в напряжениях. Для
решения смешанных задач теории упругости предложен
экономичный (с точки зрения численной реализации) подход.
Теоретически он не обоснован, однако позволяет значительно
повысить эффективность метода, а практическая его сходимость
подтверждается численными экспериментами.
5.2. Численная реализация дифференциальной постановки
метода геометрического погружения
При численном решении интегральных уравнений любая ошибка
в итоге получается исключительно из-за дискретизации расчетной
области, способа представления заданных и неизвестных функций и
последующего решения системы алгебраических уравнений. Из
главы 2 следует, что дифференциальная постановка метода
геометрического погружения сводит исходную краевую задачу
теории упругости к итерационному решению двух граничных
интегральных уравнений E.2)-E.3). Вместо уравнения E.2)
использовано уравнение E.4). Систему интегральных уравнений
требуется численно преобразовать к алгебраической системе и
последнюю решить. Построение конечномерного аналога
интегральных уравнений E.3)-E.4) применительно к трехмерным
задачам осуществлялось согласно подходу, изложенному в работе [6]
в три этапа: на первом осуществляется разбиение поверхности тела
на сегменты и покусочное моделирование вектора усилий,
перемещений и самой поверхности; на втором - производится
численное интегрирование для получения алгебраической системы;
на третьем - итерационный процесс решения системы уравнений и
вычисление полей напряжений и перемещений.
5.2.1. Дискретизация границы и объема расчетной области.
Представление неизвестных функций
Для численного представления уравнений E.3)-E.4) геометрия и
поля переменных (граничных перемещений и усилий) должны быть
некоторым образом аппроксимированы. Граница S области D
Гл. 5. Численная реализация МГП в дифференциальной постановке 215
аппроксимировалась ансамблем /^граничных элементов. В качестве
граничных элементов использованы разрывные граничные элементы
[7,129,131], т. е. такие, в которых точки коллокации смещены с
периметра элемента. Число узлов, использующих для коллокации
граничных значений усилий и перемещений в разрывных элементах,
может не совпадать с числом узлов на пе-риметре для описания
геометрии (в отличие от изопараметрических элементов).
Имеются несколько причин для использования разрывных
элементов. Как отмечено в работе [7] , сходимость итерационных
процедур для этих элементов оказывается во многих случаях более
высокой. Дополнительное преимущество такого подхода
возможность легко сочетать элементы различных форм для
представления геометрии тела, поскольку не требуется выполнять
условия совместности аппроксимации между элементами. Кроме
того, наличие вокруг функционального узла некоторой гладкой
окрестности позволяет осуществлять приемы интегрирования
сингулярной функции, описанные ниже. Использование
предложенных схем интегрирования по поверхности разрывных
граничных элементов (как показал численный эксперимент)
позволило точнее вычислять интегралы в E.3)-E.4). Необходимо
отметить, что непрерывность нормали к поверхности в
функциональном узле - существенный фактор, влияющий на
сходимость интегралов. Применение разрывных граничных
элементов значительно упрощает алгоритм сборки глобальной
матрицы разрешающей системы уравнений.
Перечисленные преимущества определили выбор разрывных
граничных элементов, несмотря на известные дополнительные
затраты [129,131] по сравнению с классическими
изопараметрическими элементами. Изначально можно использовать
плоский граничный элемент с точкой коллокации в центре элемента.
Но точность и сходимость такого представления низки. Поэтому
геометрия и переменные представляются полиномиально через
Узловые значения. Декартовы координаты точки р на поверхности
элемента запишутся через значения узловых координат как
9 E.5)
216 5.2. Численная реализация дифференциальной постановки МГП
A,0)
Рис. 5.1 Разрывный граничный элемент A-8 - узловые точки;
• - функциональный узел, О - геометрический узел)
где/=1,2,3 и а =1, 2, ...9А; А - число узловых точек, необходимых
для описания геометрии элемента; Ма - функции формы [6],
определенные в локальной системе координат; rj
локальные координаты элемента. Для представления геометрии
поверхности тела использовались восьмиузловые граничные
элементы с квадратичной аппроксимацией координат а =8. Элемент
площади поверхности запишется как Js-det(Jjj). Матрица якобиана «/у
преобразования декартовой системы координат в локальные
координаты элемента:
Ш" " / = п, У = п, «=п E-6)
а У
~Aia
Функции t, u, p также представляются функциями формы в виде
*i(p) = Np(ri)Zip9 E.7)
где zxp(p) - аппроксимируемая функция; 1ф - узловые значеНИ*
функции; Np - функции формы; /?=1,Я. В случае конформны^
элементов Ма = Np, А =В. Для представления функций t, u, р #*
границе тела использовалась кусочно-линейная аппроксимаШ^
неизвестных при 5=4 с функциями формы
Гл. 5. Численная реализация МГП в дифференциальной постановке 217
E.8)
A,1,1)/
Рис. 5.2 Объемная ячейка (усл. обозн. см. текст)
Наличие объемных сил произвольной природы требует схемы
интегрирования по всему объему тела. Для вычисления объемного
интеграла в E.3)-E.4) внутренняя область D разбивалась на Lv
изопараметрических гексаэдральных ячеек (рис.5.2) с квадратичной
аппроксимацией координат и интегрируемой функции объемных сил
f [6]. Вид аппроксимирующей функции для любой точки q расчетной
области
xi{q) = Hy{r])Xiy, E.9)
где Ну - функции формы [6]; Xiy - узловые координаты объемной
ячейки; 7]-77G71,гJ,7з) " локальные координаты ячейки; /=1, 2, 3;
У = 1,20 . Элемент объема запишется как J =det(J..), где
E.10)
Следует отметить, что, хотя внутренние ячейки имеют такой же
вид, как конечные элементы в схеме дискретизации, используемой в
^КЭ, они представляют лишь удобный способ вычисления влияния
Распределенных по объему сил. Порядок системы линейных
^гебраических уравнений определяется лишь количеством
Использованных граничных элементов и не связан с количеством
218 5.2. Численная реализация дифференциальной постановки МГП
использованных внутренних ячеек. Квадратичная степень
аппроксимации внутренних ячеек выбрана для удобства
согласования разбиения границы и объема тела.
Подставляя E.5)-E.10) в граничные интегральные уравнения
E.3)-E.4), получим для произвольной точки а поверхности тела их
дискретную форму в виде
L*
1 1 1
a (ri)Js G7) d m d
PJa
1 1
111
E.12)
где
- узловые значения функций t, p соответственно.
Помещая точку ха последовательно во все точки коллокации,
использующиеся для определения полей переменных и заданных
функций, и применяя уравнения E.11)-E.12) при соответствующих
граничных условиях (для части границы S^ с заданными
напряжениями - E.11), для части границы Su с заданными
перемещениями - E.12)), получим полную систему уравнений
относительно неизвестных t. В матричном виде система уравнений
запишется
I о
о
\t,
р 1
\
+
F
-G
К
E.13)
Гл. 5. Численная реализация МГП в дифференциальной постановке 219
где
" векторы искомых усилий на поверхностях
и Sw
соответственно; uq, p - векторы заданных перемещений и усилий;
G, F - соответствующие матрицы интегралов по поверхности в
E.11L5.12); fp9fu - соответствующие интегралы от массовых сил. В
более компактной форме это уравнение можно записать
f, E.14)
где
t =
С =
- О
О 1
F
-G
На первом шаге решения итерационного уравнения вычисляются
коэффициенты матрицы А и вектор массовых сил f. Затем
выполняется к итераций с нулевым приближением t = 0.
Сходимость итерационного процесса отслеживается по
относительному среднеквадратичному отклонению двух
последовательных приближений на к-й итерации:
-t^l/pl, E.15)
где ||-|! - квадратичная норма [5].
Полученная система уравнений E.14) - конечномерный аналог
Уравнений E.3)-E.4).
5.2.2. Вычисление интегралов
Известно, что наиболее трудоемкий этап численного решения
граничных интегральных уравнений - вычисление коэффициентов
матрицы влияния, т. е. интегрирование сингулярных функций по
поверхности элемента [1,2,6,7,36,127,128]. В данной работе
предлагается схема вычисления интегралов с сильной особенностью,
°писан алгоритм численного интегрирования с нерегулярным
Распределением множества гауссовых точек по криволинейной
П(>верхности трехмерного тела.
Необходимо отметить, что в подынтегральные выражения
Уравнений E.11)-E.12) входят сингулярные ядра G(c особенностью
220 5.2. Численная реализация дифференциальной постановки МГП
l/r2 ) и F (с особенностью l/r3) (г^Ц> rx^-х^)). В работе [53]
указано, что для интегралов по /w-мерному пространству
особенности порядка l/rC7^) являются слабыми и, следовательно, эти
интегралы существуют в обычном смысле. Интегралы же с
особенностью порядка \1гт существуют в смысле главного значения
по Коши, т. е.
1у =
S
S/e ?
где ? - некоторая окрестность сингулярной точки х.
В работе [6] указано, что при х = ^ поверхностные и объемные
интегралы, содержащие функцию G(x,^), и объемные интегралы,
содержащие функцию /'(х,^), являются интегралами от функций со
слабыми особенностями, и поэтому вычисляются обычным образом
при помощи квадратурных формул Гаусса.
Рис. 5.3. Сингулярный элемент (усл. обозн. см. текст)
Интегрирование сингулярных функций с сильной особенность^
по поверхности элемента требует специальных приемов и схеМ
интегрирования. Когда точка наблюдения ха в подынтегральной
выражении не совпадает с узлом коллокации, произведение ядра Н*
Гл. 5. Численная реализация МГП в дифференциальной постановке 221
базисную функцию и якобиан остается ограниченным и,
следовательно, может быть проинтегрировано численно с помощью
обычных гауссовских квадратурных формул. Когда точка
? стремится к точке х на границе области, поверхностные
интегралы, содержащие функцию F(x^), существуют только в
смысле главного значения по Коши и требуют специальных приемов
вычисления.
В данной работе осуществлены три различные схемы
интегрирования сингулярных интегралов с сильной особенностью.
Основополагающей идеей вычисления сингулярных интегралов
является введение специального сингулярного элемента, т. е. такого
граничного элемента, который содержит точку коллокации, а
именно: х = \а. Сингулярный элемент дополнительно разбивается
на семь подэлементов (рис.5.3). Все реализованные схемы
вычисления сингулярных интегралов базируются на этом типе
граничного элемента. Схемы интегрирования сингулярных ядер
рассмотрим на примере вычисления поверхностного интеграла,
содержащего ядро F(x, {;).
Интеграл по площади элемента для узла а в E.11) имеет
следующий вид:
/?= \{F(jNaJs}dS. E.16)
Sa
1. Полуаналитическое вычисление сингулярного интеграла.
Используем прием, описанный в работе [6]. Выделим на элементе
плоскую ?-окрестность (рис.5.4), касательную к поверхности
элемента, в точке коллокации. Тогда, замечая, что функция формы,
соответствующая а -тому узлу, равна единице в рассматриваемом
Узле, запишем
SA SA/e e
Анализ формулы показывает, что первый интеграл справа
является достаточно гладким в силу того, что (\-Na) обращается в
Куль в особой точке и вычисляется численно по квадратурным
Формулам Гаусса. Второй интеграл также берется численно всюду,
За исключением ?-окрестности. Как показано в работе [6], третий
Интеграл сводится к контурному и вычисляется аналитически.
222 5.2. Численная реализация дифференциальной постановки МГП
Рис. 5.4. Сингулярный элемент
2. Численное вычисление сингулярного интеграла с неявным
выделением ? -окрестности. Интегрирование осуществлялось
численно по квадратурным формулам Гаусса. При этом вокруг
сингулярной точки а в силу расположения подэлементов остается
е -окрестность, в которую не попадают точки интегрирования. Эта
? -окрестность оказывается симметричной относительно
сингулярной точки в локальной системе координат элемента, ее
размер зависит от выбранного числа точек интегрирования. Таким
образом, происходит неявное исключение сингулярной точки.
3. Регулярная схема вычисления сингулярного интеграш.
Регулярное представление сингулярного интеграла можно получить
за счет того, что сингулярная точка выносится за пределы
рассматриваемого тела. В работе [131] исследован вопрос об
оптимальном расположении этой точки, так как ее удаление от
границы области привносит большие погрешности, а ее
приближение к границе затрудняет вычисление интегралов.
Установлено [131], что сингулярную точку следует выносить из
области по нормали к поверхности на удаление, равное
минимальному расстоянию между узлами, в которых отыскиваются
неизвестные величины.
Для исследования сходимости описанных выше схем вычисления
сингулярных интегралов проведен численный эксперимент по
вычислению сингулярного интеграла на модельном искривленном
элементе. В табл.5.1 приведены значения максимальной
относительной погрешности вычисления интеграла E.16) при
выбранном порядке п квадратурной формулы
Гл.5. Численная реализация МГП в дифференциальной постановке 223
E.17)
Таблица 5.1
Сходимость сингулярного интеграла по поверхности
и
2
3
4
5
Число точек
интегрирова-
интегрирования
28
63
112
175
°тах
Схема 1
5.254830Е-01
3.457211Е-01
2.588308Е-01
Схема 2
1.044812Е-01
5.269533Е-02
2.41673 8Е-02
Схема 3
1.438691
9.108319Е-01
3.857455Е-01
На основе проведенного численного эксперимента была выбрана
вторая схема вычисления сингулярного интеграла, так как она
характеризуется наилучшей сходимостью. Указанная схема
применяется и для вычисления интегралов, содержащих ядро G .
Согласно [6], объемный интеграл в E.11) является интегралом от
функции со слабой особенностью, и поэтому вычисляется обычным
образом при помощи квадратурных формул Гаусса. Однако, как
показал численный эксперимент, сходимость объемного интеграла (в
некоторой точке коллокации) достигается только при применении
специального приема интегрирования, который заключается в
неявном исключении сингулярной точки. В зоне, прилегающей к
сингулярному интегралу, выстраиваются объемные ячейки, как
показано на рис.5.5. Тем самым обеспечивается исключение
1
nV
Рис. 5.5. Схема интегрирования объемного интеграла G - сингулярный
элемент, 2 - объемные ячейки)
224 5.2. Численная реализация дифференциальной постановки МГП
сингулярной области из интегрирования. Оставшийся объемный
фрагмент описывается одной объемной ячейкой.
Результаты по исследованию сходимости объемного интеграла от
массовых сил (f=@, 0, -1)) дня куба сведены в табл.5.2. Здесь
приведены значения максимальной относительной погрешности
значений интеграла для двух последовательных квадратурных
приближений (подобно E.17)).
Таблица 5.2
Сходимость объемного интеграла в зависимости от порядка
квадратурной формулы Гаусса п и числа объемных ячеек {L^t?-число точек
интегрирования)
п
2
3
4
5
6
7
8
9
10
Число ячеек Lv
1
V3
8
27
64
125
216
343
512
729
1000
-
8.06907
0.75031
1.98612
6.77721
0.51128
2.05407
5.59079
0.41575
8
V3
64
216
512
1000
1728
2744
4096
5832
8000
^тах
-
0.70025
1.75430
0.65893
1.76561
0.64849
1.77533
0.64558
1.77955
64
V3
512
1728
4096
8000
-
-
-
-
-
^тах
-
2.06071Е-02
1.02566Е-02
6.47436Е-03
-
-
-
-
-
17 (специальная схема)
V3
136
459
1088
2125
-
-
-
-
-
<?тах
-
1.54751Е-02
1.02315Е-02
6.48112Е-03
-
-
-
-
-
Как видно из табл.5.2, при произвольном дроблении объема куба
сходимость появляется лишь при очень большом числе ячеек и
соответственно - точек интегрирования. Применение предложенной
схемы интегрирования по объему позволяет быстро достичь
сходимости интеграла при минимальных затратах.
5.2.3. Построение оптимальной
Адаптивная схема интегрирования
схемы интегрирования.
Как отмечалось выше, интегрирование - самый трудоемкий
вычислительный этап. Поэтому особое внимание уделялось
созданию экономичного и оптимального по вычислительным
Гл. 5. Численная реализация МГП в дифференциальной постановке 225
затратам (при условии достижения заданной точности решения)
алгоритма интегрирования.
Введение расчетной области. Рассматриваемую область D,
занимаемую упругим телом, отобразим на некоторую расчетную
область D таким образом, что
1
VxgD:
X = — X,
а
gD , a= max p(x,y).
Здесь p(x,y) - расстояние между точками х и у области D. Решение
уравнения E.14) ведется в расчетной области D*. Введение
расчетной области позволило разработать алгоритм интегрирования,
нечувствительный к исходным размерам тела.
Адаптивный алгоритм интегрирования. Все множество
граничных элементов в области D разобьем на три подмножества:
1) сингулярные элементы (элементы, содержащие сингулярную
точку); 2) элементы, прилегающие к сингулярным; 3) удаленные или
несингулярные элементы (рис.5.5). Сингулярные интегралы
•
•
•\
/
1
/.
•
•
•
•
•
•
•
•
•
•
/2
•
Рис. 5.5. Типы элементов: 1 - прилегающего, 2 - удаленного, 3 -
сингулярного
вычисляются по схеме, рассмотренной выше. Элементы второго типа
разбиваются дополнительно на четыре подэлемента с последующим
вычислением интегралов по квадратурным формулам Гаусса.
Интегралы по несингулярным элементам также вычисляются по
формулам Гаусса без дополнительного разбиения.
Необходимо отметить, что сходимость интегралов второго и
третьего типов в сильной степени зависит от размеров элементов, а
также от удаленности элемента от сингулярной точки. Для изучения
226 5.2. Численная реализация дифференциальной постановки МГП
характера сходимости используемых схем интегрирования при
различных соотношениях характерных размеров элементов и
расстояний до сингулярной точки рассмотрим множество
последовательных приближений /- значений интегралов E.16)
{Л}
где A,2,..., /) - порядок квадратурной формулы Гаусса. .
В качестве критерия сходимости будем рассматривать величину
E Л 7) максимальной относительной погрешности 8
вычисления интеграла / на w-м приближении.
1.0
0.8
0.6
0.4
0.2
ттттттттт
тттттптт
1
U
12 511
Ж
100 200
Число точек интегрирования
Рис.5.6. Сходимость интегралов для различных типов элементов.
1 - s = 1.0,р = 2.0; 2- s = 4.0,р = 1.0; 5- ^ = 1.0,р = 0.2;
элементы: а - сингулярный, б - прилегающий, в - удаленные
На рис.5.6 представлено поведение функции S^(l) при
интегрировании по различным элементам в зависимости от числа
точек интегрирования для некоторых значений площади элементов и
расстояний до точки коллокации.
Можно показать, что погрешность 6* =
вычисления вектора t в E.14) оценивается неравенством
8* <A + ?(л)(/))?-1, где № - вектор, полученный из E.14) с
матрицей А, коэффициенты которой вычислены по квадратурной
Гл. 5. Численная реализация МГП в дифференциальной постановке 227
формуле порядка п\ L - число произведенных итераций. Как показал
численный эксперимент, сходимость интеграла на сингулярном
элементе не зависит от его размеров. Критерием выбора порядка
квадратурной формулы для прилегающих к сингулярному элементов
является отношение их площадей, а для удаленного элемента -
сочетание его площади и расстояния до точки коллокации.
Таблица 5. 3
Порядок квадратурной формулы для удаленного элемента
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
0.1
3
4
4
4
4
4
6
7
8
9
0.2
3
4
4
4
5
5
6
7
7
7
0.3
3
3
3
4
5
5
6
6
6
6
0.4
3
4
4
4
5
5
5
5
5
5
0.5
3
3
3
3
3
3
5
5
5
5
0
0.6
3
3
3
4
4
4
5
5
5
5
0.7
3
3
4
4
4
4
4
4
4
4
0.8
3
3
4
4
4
4
4
4
4
4
0.9
3
3
4
4
4
4
4
4
4
4
1.0
3
3
4
4
4
4
4
4
4
4
Таблица 5.4
Порядок квадратурной формулы для прилегающего элемента
So
0.1
0.2
0.3
SA/S0
0.5
5
4
4
4
(
).75
5
4
4
4
1.0
7
5
4
4
1.25
9
5
4
4
1.5
9
7
5
3
1.75
11
7
6
3
2.0
11
8
6
3
Задаваясь величиной S*, можно построить таблицы значений
Минимально необходимого числа точек интегрирования вида
К = К(г, 5д) для удаленных элементов (табл.5.3), где ?д - площадь
Удаленного элемента, принятая за характерный размер, г -
Расстояние до сингулярной точки, К = K(Sq, ?д /Sq) (табл.5.4) - для
Прилегающих элементов (Sq - площадь сингулярного элемента, Sд -
> прилегающего элемента).
228 5.2. Численная реализации дифференциальной постановки МГП
Последующий выбор порядка квадратурной формулы Гаусса
производится из построенных таблиц в зависимости от значений гу
5д и Sq для конкретного элемента. Численный эксперимент показал,
что для достижения погрешности вычисления #'"'(/) =0.001 в
сингулярном интеграле достаточно 175 точек интегрирования.
5.2.4. Сборка системы уравнений
В разрывных элементах сборка матрицы А осуществляется
перемещением подматрицы 3x3 локальных коэффициентов,
порожденных узлом коллокации в каждом элементе в глобальную
матрицу, так как каждый узел коллокации принадлежит лишь
одному элементу. Этот факт намного упрощает программирование
формирования глобальной матрицы, а также учета симметрии
задачи.
5.2.5. Учет симметрии расчетной области
Учет симметрии задачи (геометрии области и граничных условий)
позволяет существенно снизить вычислительные затраты на
формирование разрешающей матрицы А и решение уравнения E.14).
Пусть исходная область D получена в результате М симметрич-
симметричных отображений аг некоторой области Dq на D/, /=1,А/, а, -
матрица отображения. Тогда в случае симметрии граничных условий
и отсутствия массовых сил уравнение E.14) запишем в виде:
U
А/
к-\
где t., а., Ь., А.- блоки векторов и матрицы, соответствующие /-му
отображению. Далее, замечая, что
= МЫ*
Гл. 5. Численная реализация МГП в дифференциальной постановке 229
[ф]=
9м.
ОС;
а
i _
где Е - единичная матрица, щ - блочно-диагональные матрицы.
Запишем итерационное уравнение для нулевого блока в виде
ЧЙ4
[п]=[ао1ф].
Здесь [Щ- квадратная матрица, порядок которой в М раз меньше,
чем у исходной матрицы А в уравнении E.14). Дополнительным
преимуществом такого подхода в учете симметрии в отличие от
традиционного состоит в том, что отпадает необходимость в задании
дополнительных граничных условий и введении дополнительных
граничных элементов на плоскостях симметрии.
5.3. Сходимость метода геометрического погружения
Для исследования численной устойчивости [33,48,49] МГП и
оценки достоверности получаемых результатов проведен ряд
численных экспериментов по изучению характера поведения
решения дискретного итерационного уравнения при изменении
таких параметров, как число итераций, степень дискретизации
области, точность интегрирования, коэффициент Пуассона v. При
проведении численных экспериментов анализировалась величина
относительной квадратичной погрешности решений 3% и 3% для
перемещений и напряжений, вычисленных на конкретном множестве
точек тела в зависимости от перечисленных выше параметров.
5.3.1. Сходимость итерационной процедуры МГП
В главе 2 теоретически показано, что итерационная процедура
МГП сходится всегда, независимо от степени отличия исходной
области D от Do.
Численная практика показала, что скорость сходимости решения
Дискретного итерационного уравнения E.14) в значительной степени
зависит от таких факторов, как точность вычисления интегралов по
230
5.3. Сходимость метода геометрического погружения
поверхности, степени дискретизации поверхности тела, соотношения
объема тела и его поверхности.
В целом можно отметить, что достаточная степень точности
решения достигается при интегрировании поверхностных интегралов
по схеме, содержащей 175 гауссовых точек для сингулярных
(включающих сингулярную точку) граничных элементов, 100 - точек
для элементов, прилежащих к сингулярному, и 25 точек
интегрирования - для элементов, удаленных от сингулярной точки.
Для получения удовлетворительного решения внутри области
характерный размер граничных элементов не должен превышать
10% от характерного размера конструкции.
5.3.2. Сходимость численной схемы дискретизации метода
геометрического погружения
В целях изучения сходимости решения МГП в зависимости от
степени дискретизации границы области проведен численный
эксперимент: решалась задача о шаре единичного радиуса,
нагруженном единичным давлением при v = 0.3 и единичном
модуле сдвига. Исследовалось поведение квадратичной нормы
погрешности для вычисленных перемещений и и напряжений 6
относительно точного решения uq,сто [106] - для некоторого
множества точек шара (вдоль радиуса):
*2 =K«w -щ)Ы\, si
52 юо,%
ю
-
\
у"
"- J
1
О 20 40 60 80
Число элементов
Рис.5.6. Сходимость решения в зависимости от степени дискретизации
Гл. 5. Численная реализация МГП в дифференциальной постановке 231
На рис.5.6 показано поведение функций 5%, <5f в зависимости от
числа граничных элементов. Итерационный процесс заканчивался
""
Число
при достижении критерия сходимости E.15) ^(О
итераций для всех вариантов расчета при этом не превышает
двадцати.
1
ю-'
ю-2
10
V
f
V
/
0 10 20 30 N
Рис.5.7 Сходимость итерационного процесса при различной степени
дискретизации A-4 - кривые сходимости)
Следующий численный эксперимент проводился для модельной
задачи о длинном цилиндре, нагруженном единичным внешним
давлением по боковой поверхности (безразмерные радиус цилиндра -
1, длина - 48, модуль сдвига 1, коэффициент Пуассона 0.3). На
рис.5.7 показаны кривые сходимости итерационного процесса МГП
при различной степени дискретизации границы. В качестве
параметра сходимости выбрано относительное изменение величины
E.15)
ек =
где к ' номеР итерации.
Поверхность цилиндра разбивалась на 12, 16, 20, 24 граничных
элемента (кривые 1,2,3,4 соответственно). Как видно из поведения
кривых 1-3, итерационный процесс МГП расходится, начиная с
некоторой итерации, и продолжать решение бессмысленно. МГЭ в
этом случае дает также неверное решение, отличающееся от решения
Ламе для бесконечно длинного цилиндра (в среднем сечении) более
нем на 100%. Но для выяснения этого обстоятельства приходится
полностью завершить процедуры решения СЛАУ и вычисления
232
5.5. Сходимость метода геометрического погружения
решения в точках области. При достаточно хорошем разбиении
поверхности цилиндра (кривые 3, 4) итерации МГП сходятся
хорошо, и получаемое решение при выполненных 40 итерациях
отличается от решения МГЭ в пределах точности ЭВМ, а
погрешность относительно решения Ламе не превышает 2%. Таким
образом, характер сходимости итерационного процесса МГП
является своеобразным критерием качества дискретизации границы
рассчитываемой конструкции.
V
л
/
JA
0.1 0.4 0.7 X
Рис.5.8 Сходимость решения задачи о кубе при различной степени
дискретизации G-5 - кривые сходимости)
4.% tt с
16;
100
300 500 700 900 1100
Число точек интегрирования
Рис.5.9 Сходимость решения задачи о шаре в зависимости от точности
интегрирования (а - оптимальная схема интегрирования)
На рис.5.8 показана сходимость решения (перемещения и по
х) задачи о кубе, нагруженном внешним единичным давлением шо
всей поверхности в зависимости от степени дискретизации границы
Гл. 5. Численная реализация МГП в дифференциальной постановке 233
(начало координат - в центре куба, длина ребра 2, модуль сдвига 1,
коэффициент Пуассона 0.3). Приведены кривые изменения
относительной погрешности ? = \\и° -и)/и0 -100% по оси х (м° -
точное решение): кривые 1,2,3, соответственно - 6, 24 и 54 элемента.
При увеличении числа элементов погрешность решения
уменьшается.
5.3.3. Сходимость МГП в зависимости от точности интегриро-
интегрирования
Для анализа влияния точности интегрирования на сходимость
решения проведен численный эксперимент для задачи о шаре,
описанной выше, при различном числе точек интегрирования. На
рис.5.9 показаны кривые квадратичной нормы погрешности
относительно точного решения задачи в зависимости от числа точек
интегрирования, приходящемся на точку коллокации, и кривая
затрат времени t на формирование матрицы А. Показана точка опти-
оптимальной схемы интегрирования, которая достигается при примене-
применении адаптивного алгоритма интегрирования, описанного выше.
5.3А. Скорость сходимости итерационной процедуры МГП
Для измерения скорости сходимости итерационного уравнения
E.14) определим вектор ошибки на А>й итерации
d<*)-t<*)-t,
где t - решение системы E.14). Качество итерационного процесса
Удобно характеризовать скоростью убывания отношения
погрешности после к итераций к начальной погрешности
Як ни/И! • Eл8)
Для исследования скорости сходимости итерационного процесса
E.14) и поиска факторов, влияющих на скорость сходимости,
проведеи численный эксперимент. Решалась задача о кубе под
воздействием гидростатического давления. Варьировались такие
факторы, как тип граничных условий (статических, кинематических,
смешанных), коэффициент Пуассона, число граничных элементов.
На рис.5.10 представлено поведение функции s, в зависимости от
числа итераций при различных граничных условиях. Кривая 1
234
5.3. Сходимость метода геометрического погружения
соответствует статическим граничным условиям (по всей
поверхности куба задано единичное давление); кривая 2 .
кинематическим граничным условиям (на поверхности куба
задаются перемещения, полученные из аналитического решения
задачи); кривые 3,4,5 соответствуют смешанным граничным
условиям, когда на части поверхности задано давление, на
оставшейся части поверхности (на одной, двух и трех гранях куба.
соответственно) заданы перемещения. Как видно из рис.5.14, тип
граничных условий существенно влияет на скорость сходимости
итерационного процесса.
5 10 15 20
Число итераций
Рис.5.10 Скорость сходимости итерационного процесса при различных
краевых условиях (/-5 - кривые сходимости)
На рис.5.11а показано поведение погрешностей s и еа решения
<т,и, полученного после некоторого числа итераций
относительно решения, получаемого непосредственно при
подстановке вектора t в уравнение E.14): (для перемещений uY'
л
сплошной линией, для напряжений ах - прерывистой линией вдоль
оси х) при задании статических граничных условий для различного
числа итераций. На рис.5.11,в,г показано поведение относительной
погрешности решения при задании кинематических граничны*
условий. На рис.5 Л 1,6 показано изменение квадратичной нормы &
относительной погрешности вычисления напряжений в некотором
множестве точек на оси х при различных типах граничных условий.
Необходимо отметить, что решение для перемещений сходит^
значительно медленнее. Для достижения заданной точности Д#*
Гл. 5. Численная реализация МГП в дифференциальной постановке 235
вычисления перемещений требуется проводить итераций в 4-5 раз
больше, чем для напряжений.
Число
ю-2
ю-4
ю-в-
- — — — -
--^
^ \
\ >
\
Г"'
— 1
2
-—3
9
итераций
~\ КГ1
^3
б
0.1 0.3 0.5 0.7 0.9 х
Iff'
\
¦ II
\\
1
0 10 20 30 40 50
Число итераций
0.1 0.3 0.5 0.7 0.9
0.1 0.3 0.5 0.7 0.9 х
Рис.5.11. Сходимость решения задачи о кубе в зависимости от числа
итераций (граничные условия: / - кинематические, 11 - статические)
В работе [33] указано, что при решении сингулярных
интегральных уравнений итерационными методами на сходимость
значительное влияние оказывает значение коэффициента Пуассона.
Если оно близко к 0.5, то сходимость итерационных методов резко
ухудшается в связи с изменением спектральных свойств матрицы.
236 5.5. Сходимость метода геометрического погружения
Для анализа влияния значения коэффициента Пуассона на скорость
сходимости итерационного процесса МГП проведен численный
эксперимент, результаты которого представлены на рис.5.12 для
задачи со статическими граничными условиями (а, б) и для задачи с
кинематическими граничными условиями (в,г). Коэффициенту
Пуассона задавались значения 0.0, 0.1, 0.2, 0.3, 0.4, 0.45, 0.5 (кривые
1-7, соответственно). Отслеживалось поведение относительной
нормы сходимости ек = {dZW-д'А *U))/dZ{t)\ и
скорости сходимости s^ . Необходимо отметить, что характер
итерационного процесса и скорость сходимости существенно зависят
от коэффициента Пуассона при задании кинематических граничных
условий. Если он равен 0.5, то итерационный процесс расходится.
Влияние числа элементов на скорость сходимости итерационною
процесса показано на рис.5.13. Для задачи о кубе под действием
гидростатического давления увеличение числа элементов более 24 не
приводит к каким-либо изменениям в поведении итерационного
процесса. Влияние степени дискретизации на сходимость МГП
обсуждалось выше.
Для исследования спектральных свойств оператора
дифференциальной постановки МГП в напряжениях проведен
численный эксперимент по определению левой (т) и правой (Л/)
границ спектра при различных значениях коэффициента Пуассона и
видах поверхности: гладкой (сфера) - сплошная линия и кусочно-
гладкой (куб) - пунктирная линия. Результаты эксперимента
приведены на рис.5.14 в сравнении с данными, приведенными в
работе [34] для метода простой итерации с аппроксимацией
оператора некоторым операторным полиномом, структура которого
зависит от расположения границ спектра (на рис.5.14 помечены
звездочкой), и последующим итерационным решением уравнения.
Из рис.5.14 видно, что верхняя граница спектра оператора МГП
имеет большую устойчивость по сравнению с таковой в работе [34]
при изменении коэффициента Пуассона на всем интервале, что
обеспечивает хорошую сходимость процесса [5]. При переходе от
гладкой границы области к кусочно-гладкой наблюдаются
незначительное расширение спектра для МГП и увеличение его
правой границы. Для метода простой итерации такой переход более
выражен.
Гл. 5. Численная реализация МГП в дифференциальной постановке 23 7
о ю 20 зо 40
10
к
ю-
ю~2-
-3
10 -
,о-4"
ю"
in-
б
1\\
\\4\
w\
Л
7
6
10 20 30 40
-1
:
in3"
-4
Iff i
in6-
¦^*^,
-а.
\
0 20 40 60 80 100
Число итераций
-l"
-2
in j
-3
10 :
-4"
10 1
-5
1 n
-6
10 -
T1 1 1 1 '. 1 1 1"
\
Tl' |11'1 1
7
6
5s
0 20 40 60 80 100
Число итераций
^ис.5.12. Сходимость итерационного процесса при значениях коэффициента
Пуассона от 0 до 0.5 A-7 - кривые сходимости)
238
5.3. Сходимость метода геометрического погружения
-1
ю i
10 !
10
10*'
10
10
\
\
V
24
6
0 10 20 30 40 50
Число итераций
Рис.5.13. Влияние степени дискретизации на скорость сходимости
F,24 - элементы)
0.8
0.6
0.4
0.2:
0.0
0.0 0.1 0.2 0.3 0.4 v
Рис.5.14. Границы спектра оператора А (усл. обозн. см. текст)
Следующий пример иллюстрирует эффективность Mill по
сравнению с методом простой итерации [34] и итерационным
методом, использующим информацию о спектре интегрального
оператора. Решалась задача об упругом шаре под действием
единичного гидростатического давления при коэффициенте
Пуассона равном 0.45, радиусе сферы г=0.01 м, модуле Юнга
? = 210 Па. Сравнивались рассчитанные значения радиальных
перемещений в точках на экваторе и на полюсе шара. Известно, что
при коэффициентах Пуассона, близких к 0.5, наблюдается плохая
сходимость метода простой итерации [33,34,65].
:—— Г*
;
———
Гл. 5. Численная реализация МГП в дифференциальной постановке 239
Таблица 5.5
Сравнение сходимости метода простой итерации [34] и МГП
Метод
Простой
итерации
Использо-
Использованный в
работе[46]
МГП
Число
точек
колло-
кации
164
164
96
Точное
значение
-10
хЮ ,М
5
5
5
Приближенное
„Г10
значение хЮ ,м
Полюс
5.36
5.0005
4.9799
Экватор
5.22
4.9599
4.9756
Погреш-
Погрешность, %
7.2...4.4
<0.8
<0.5
Число
итера-
итераций
48
4
4
В табл.5.5 сопоставлена сходимость метода простой итерации,
полинома наилучшего приближения и МГП. В работе [34] отмечено
резкое увеличение скорости сходимости при использовании
информации о границе спектра. МГП дает лучшую сходимость при
гораздо меньшем числе точек коллокации.
5.3.5. Ускорение сходимости итерационного процесса
Рассмотрим три приближения вектора t: t ~ , t , t 9k > 3 .
Согласно [27], t^+^, начиная с некоторой итерации, уточняется по
формуле
Такое уточнение не требует больших вычислительных затрат.
Скорость сходимости итерационного процесса МГП заметно
увеличивается. На рис.5.15 показано поведение итерационного
процесса (кривые зависимости критериев Ъ^ E.17) - пунктирная
линия и $? E.18) - сплошная - от числа итераций) с ускорением
сходимости и без него для задачи о кубе, описанной выше, с
граничными условиями в перемещениях (а) и в напряжениях (б).
5.3.6. Некоторые выводы
Таким образом, построен конечномерный аналог интегральных
уравнений E.3), E.4). Создан высокопроизводительный
240
5.3. Сходимость метода геометрического погружения
автоматический алгоритм генерации сетки граничных элементов и
наполнения объема тела внутренними ячейками. Алгоритм основан
на задании базовых граничных
а б
ю
ю
ю
S
¦A,
\
10 1
Число итераций
%Ъ*к \
10
10
10
/ 0
10 15 20
Число итераций
Рис. 5.15. Поведение итерационного процесса при ускорении сходимости
(/) [27] для задачи о кубе с различными граничными условиями:
а - кинематическими, б - статическими
элементов в декартовой, цилиндрической или сферической системах
координат и последующем автоматическом дроблении сетки в
зависимости от заданных параметров. Информация о сетке
граничных элементов и внутренних ячейках записывается на диск
для многократного использования. Контроль правильное! и
разбиения производится путем визуализации сетки граничных
элементов и внутренних ячеек [132] и сопоставлением значений
площади поверхности и объема расчетной области, полученных в
результате дискретизации, с реальными значениями.
Описанный подход позволил получить эффективную программу
решения трехмерных задач теории упругости:
¦ применены оптимальные по вычислительным затратам и
точности схемы интегрирования;
¦ решение задачи на расчетной области дает возможность
применять описанный алгоритм независимо от исходных размеров
области;
¦ использован алгоритм учета симметрии в исходной задаче, ч\о
такж* приводит к существенному сокращению затрат;
¦ возможно хранение вычисленных значений функций форм и их
производных для различных схем интегрирования на внешних
Гл. 5. Численная реализация МГП в дифференциальной постановке 241
носителях информации и использования их при последующих
расчетах в виде базы данных;
¦ применен алгоритм ускорения итерационного процесса, что
существенно улучшило его сходимость.
В табл.5.6 приведены затраты процессорного времени в
зависимости от степени дискретизации поверхности, иллюстрирую-
иллюстрирующие эффективность дифференциальной постановки МГП по
сравнению с непрямой постановкой МГЭ [6]. В случае МГЭ решение
СЛАУ осуществлялось методом Гаусса с поблочной записью
матрицы коэффициентов влияния на внешний носитель. Тестирова-
Тестирование программы проводилось на задаче о кубе, нагруженном
наружным давлением, при этом погрешность результатов
относительно аналитического решения не превышала 3%.
Таблица 5. 6
Сравнение затрат МГЭ и МГП (для IBM PC AT 486/33)
Число
элемен-
элементов
6
24
54
96
150
Число
степеней
свободы
72
288
648
1152
1800
Время
формирова-
формирования, с
3
31
155
386
1100
Решение системы, с
МГЭ
1
23
330
3948
19269
МГП
1
14
101
270
932
Число
итераций
МГП
7
9
10
11
12
Эф-
Эффект
1
1.6
3.3
14.6
20.7
Всестороннее исследование разработанных алгоритмов и
программ, реализующих дифференциальную постановку Mill,
позволяет утверждать, что построенный конечномерный аналог
обладает высокой степенью устойчивости и сходимости.
5.4. Решение тестовых задач теории упругости
В целях тестирования алгоритмов и программ, а также для
проверки достоверности результатов, полученных при помощи
программы, реализующей дифференциальную постановку МГП,
решен ряд тестовых задач. В качестве их выбраны классические
задачи теории упругости, имеющие аналитическое решение для тел
канонической формы: куба, цилиндра и шара.
242
5.4. Решение тестовых задач теории упругости
5.4.1. Задача об упругом равновесии
действием гидростатического сжатия
куба, находящегося под
На примере этой задачи протестированы различные варианты
учета граничных условий: в напряжениях, когда на поверхности куба
заданы усилия; в перемещениях, когда на поверхности куба заданы
перемещения, соответствующие гидростатическому сжатию куба;
смешанные граничные условия, когда на части поверхности заданы
усилия, а на другой части - перемещения от гидростатического
сжатия.
Таблица 5.7
Перемещения их(х) для задачи о кубе
Аналитическое
решение
0.0
0.2
0.4
0.6
0.8
1.0
-и 0
0.00000
0.03077
0.06154
0.09231
0.12308
0.15385
Граничные условия
Статические
-их
0.00000
0.02996
0.06032
0.09137
0.12315
0.15419
?,%
0.00
2.61
1.97
1.01
0.06
0.22
Кинематические
-их
0.00000
0.03083
0.06167
0.09252
0.12339
0.15385
е,%
0.00
0.20
0.21
0.23
0.25
0.00
Смешанные
-мх
0.00000
0.02956
0.06016
0.09131
0.12307
0.15403
?•,%
0.00
3.95
2.24
1.08
0.01
0.12
Таблица 5. 8
Напряжения охф) для задачи о кубе
Аналитическое
решение
X
0,0
0,2
0,4
0,6
0,8
1,0
1,00000
1,00000
1,00000
1,00000
1,00000
1,00000
Граничные условия
Статические
-crY
0,97172
0,97375
0,97961
0,98811
0,99621
1,00000
е,%
2,83
2,62
2,04
1Д9
0,38
0,00
Кинематические
-<ту
1
1,00201
1,00202
1,00211
1,00243
1,00190
1,00200
е,%
0,20
0,20
0,21
0,24
0,19
0,20
Смешанные __
-ov
0,97732
0,97885
0,98337
0,99010
0,99670
1,00000
2,23
2,12
1,66
0,99
0,33
0,00
Параметры задачи: ребро куба /=1, коэффициент Пуассона v=0.3,
модуль сдвига G=l, давление /?=1, перемещение на поверхности
wf=2/13jc., число граничных элементов - 96. В табл.5.7, 5.8 приведены
результаты теста - перемещения их и напряжения ах вдоль оси х ъ
Гл. 5. Численная реализация МГП в дифференциальной постановке 243
сравнении с аналитическим решением. Начало координат - в центре
куба.
5.4.2. Задача об упругом равновесии полого цилиндра (задача
Ламе)
В целях проверки качества получаемого решения для
цилиндрических тел решена задача об упругом равновесии полого
цилиндра, внешняя поверхность которого нагружена единичным
давлением. Перемещения щ и напряжения а^ и о> вычислялись в
среднем поперечном сечении вдоль радиуса г (рис.5.16, штриховые
линии). Решение сравнивалось с решением Ламе для полого
цилиндра [106], находящегося в плоско-деформированном
состоянии (соответствующие сплошные линии). Параметры задачи:
внешний радиус цилиндра Ъ=6, внутренний радиус а=1, длина
цилиндра /=5, коэффициент Пуассона v=0.3, модуль сдвига G=1,
давление /?=1, число граничных элементов - 96.
1 3 Ъ г
Рис. 5.16. Решение задачи о полом цилиндре в сравнении с решением Ламе
(усл. обозн. см. текст)
5.4.3. Задача о вращающемся цилиндре
Решение задачи о вращающемся диске с теми же
геометрическими и физическими параметрами, что и в предыдущей
задаче (угловая скорость вращения - 1, плотность материала - 1,
число граничных элементов - 56; число обьемных ячеек - 512),
приведено на рис.5.17. Перемещения щ и напряжения <тг, сг^
вычислялись в среднем поперечном сечении вдоль радиуса г
244
5.4. Решение тестовых задач теории упругости
(штриховые линии 1, 2, 3, соответственно). Рассчитанные значения
сравниваются с аналитическим решением для вращающегося диска,
полученным в работе [93] (соответствующие сплошные линии).
ю
3 Ъ г
Рис.5.17. Решение задачи о вращающемся цилиндре в сравнении с [93]
(усл. обозн. см. текст)
5.4.4. Задача об упругом равновесии полой сферы (задача Ламе)
Решена задача о равновесии полой сферы, находящейся под
действием внутреннего и внешнего давлений. В табл.5.9
представлены перемещения и напряжения вдоль радиуса г шара в
сравнении с аналитическим решением [106]. Параметры задачи:
внешний радиус А=1, внутренний радиус я=0.2, коэффициент
Пуассона v=0.3, модуль сдвига G=l, внешнее давление рЛ = 1, внуг-
реннее давление р^ = 1, число граничных элементов -192.
Таблица 5.9
Решение задачи о полой сфере в сравнении с точным
г
0.2
0.4
0.6
0.7
0.8
0.9
1.0
Перемещения
0.03077
0.06154
0.09231
0.10769
0.12308
0.13846
0.15385
-иг
0.03087
0.06170
0.09247
0.10784
0.12322
0.13865
0.15296
€,%
0.33
0.26
0.18
0.14
0.11
0.13
0.57
Напряжения
'СУ?
1.00000
1.00000
1.00000
1.00000
1.00000
1.00000
1.00000
-Gr
0.99907
0.99914
0.99891
0.99875
0.99924
1.00150
1.00000
0.09
0.09
0.11
0.12
0.08
0.15
0.00
Гл. 5. Численная реализация МГП в дифференциальной постановке 245
5.4.5. Задача о сферической полости в бесконечно протяженном
теле под действием внутреннего давления
Решена задача о сферической полости в трехмерном пространстве
с внутренним единичным давлением (коэффициент Пуассона - 0.3,
модуль сдвига - 1). На рис.5.18 представлены полученные
перемещения и напряжения вдоль радиуса г. Относительные
погрешности по сравнению с точным решением [106] для
перемещений и напряжений приведены в таблицах 5.10 и 5.11.
0.201
0.15^
о.ю;
0 05^
\
\
ч
*
1.0
1.5
2.0
2.5
Рис.5.18. Решение задачи о сферической полости в бесконечном теле,
нагруженной единичным внутренним давлением (усл. обозн. см. текст)
Таблица 5. 10
Сравнение рассчитанных радиальных перемещений с точными для
задачи о сферической полости в пространстве
г
О.ЮОООЕ+01
0.14000Е-Ю1
0.16000Е+01
0.18000Е+01
0.20000Е+01
0.24000Е-Ю1
0.26000Е+01
0.28000Е+О1
О.ЗООООЕ+01
иг
0.24899Е+00
0.12692Е+00
0.97248Е-01
0.76868Е-01
0.62274Е-01
0.43248Е-01
0.36849Е-01
0.31772Е-01
0.27676Е-01
иг -точное
0.25000Е+00
0.12755Е+00
0.97656Е-01
0.77160Е-01
0.62500Е-01
0.43403Е-01
0.36982Е-01
0.31888Е-01
0.27778Е-01
?%
0.40
0.49
0.42
0.38
0.36
0.36
0.36
0.36
0.37
246
5.4. Решение тестовых задач теории упругости
Таблица 5. Ц
Сравнение расчитанных напряжений с точными для задачи о
сферической полости с внутренним давлением
г
1.0
1.2
1.4
1.6
1.8
2.0
2.2
2.4
2.6
3.0
1.0000
0.57412
0.36079
0.24232
0.17051
0.12443
0.093536
0.072064
0.056685
0.036899
-О^-точное
1.0000
0.57870
0.36443
0.24414
0.17147
0.12500
0.093914
0.072338
0.056896
0.037037
0.0Q
0.79
1.00
0.74
0.56
0.45
0.40
0.38
0.37
0.37
0.50000
0.29222
0.18185
0.12160
0.085406
0.062279
0.046801
0.036054
0.028359
0.018462
(Тф -точное
0.50000
0.28935
0.18222
0.12207
0.08573
0.062500
0.046957
0.036169
0.028448
0.018519
*,%
0.00
0.99
0.20
0.39
0.38
0.35
0.33
0.32
0.31
0.31
5.4.6. Задача об упругом равновесии полого шара, находящегося
под действием массовых сил
Решена задача о равновесии полого шара, жестко закрепленного
по внешней поверхности и находящегося под действием массовых
сил. Полученные результаты сравнивались с аналитическим
решением, полученным в работе [29]. Максимальные относительные
погрешности составили для перемещений - 4.5%, для напряжений -
9%. На рис.5.19 показано деформированное состояние шара.
Рис.5.19. Деформированное состояние шара (пунктир) под действием
массовых сил (усл. обозн. см. текст)
Гл. 5. Численная реализация МГП в дифференциальной постановке 247
Параметры задачи: внешний радиус 6=1, внутренний радиус
а=0.3, коэффициент Пуассона v=0.3, модуль сдвига G=l, плотность
/7 = 1, число граничных элементов -192, число объемных ячеек - 64.
Как видно из результатов решения тестовых задач, соответствие с
имеющимися аналитическими решениями очень хорошее, что иллю-
иллюстрирует достоверность построенных численных схем.
5.5. Решение трехмерных краевых задач теории упругости
5.5.1.Решение задачи о сжатии параллелепипеда куполообразной
нагрузкой
В работе [72] приведено решение задачи о сжатии
параллелепипеда куполообразной нагрузкой вариационно-
разностным методом (расчетная схема приведена на рис.5.20).
Коэффициент Пуассона v=l/3. На верхней и нижней гранях
параллелепипеда действует сжимающая нагрузка:
Рх = Ру = <>> Pz =[1 - cosB;r(x - 0.5))][1 - cosB*0> - 0.5))], z = 1,
Рх= Ру= °> Pz = 41 - oosBtt(x - 0.5))][1 - cosB/rC, - 0.5))], z = -1.
2
X /
z
/;
/\
i
\
1 Ip
V
/
¦/
У
Рис.5.20. Нагружение параллелепипеда куполообразной нагрузкой
(усл. обозн. см. текст)
Сходимость итерационного процесса [72] решения СЛАУ с
числом неизвестных 4131 достигается при выполненных 48
итерациях. В случае МГП решалась задача для 1/8 параллелепипеда
248 5.5. Решение трехмерных краевых задач теории упругости
с числом элементов - 12 (число неизвестных 144). Для достижения
точности 1% достаточно 13 итераций. В табл.5.12 приведены
напряжения oz в сечении z=0.
Таблица 5. 12
Сравнение напряжений oz для сечения z=0 в параллелепипеде под
действием куполообразной нагрузки (Mill и [72])
X
0.0
0.25
0.5
0.25
0.5
0.5
У
0.0
0.0
0.0
0.25
0.25
0.5
oz,
[72]
0.92
0.96
1.01
1.00
1.047
1.10
г=0
МГП
0.90
0.96
1.00
0.96
0.99
1.03
Из анализа полученных результатов следует, что затраты на
получение решения с сопоставимой точностью для МГП
несоизмеримо меньше, чем в подходе, описанном в работе [72].
5.5.2. Решение задачи о шайбе
В работе [2] приведено решение задачи о шайбе (рис.5.21,
расчетная схема). Шайба изготовлена из материала с упругими
постоянными: ? = 2.16x10 Mna,v = 0.24 и нагружалась давлением
Р = 1 • 105 Мпа (дискретизация 40 элементов со 120 узлами).
4
3.5
А
t-f-гЛ
Щ
Рис.5.21. Расчетная схема, дискретизация поверхности и деформированное
состояние для задачи о шайбе под действием внутреннего давления
Гл. 5. Численная реализация МГП в дифференциальной постановке 249
Решение в работе [2] велось прямым МГЭ при применении
специальных приемов интегрирования. В случае МГП задача
решалась для 1/8 конструкции. На рис.5.21 показаны схема
дискретизации и деформированное состояние конструкции. Отличие
перемещений иг для точек внутренней поверхности относительно
решения в работе [2] составило 15% для среднего сечения.
5.5.3. Решение задачи о перфорированном цилиндре
В качестве иллюстрации, демонстрирующей эффективность
численной реализации дифференциальной постановки МГП при
расчете НДС существенно трехмерных конструкций, решена задача
о цилиндре с внутренним каналом звездообразной формы. На
рис.5.22 представлены расчетная схема и дискретизация границы
рассматриваемой области. В качестве расчетной области бралась 1/8
конструкции. Поверхность разбивалась на 14 граничных элементов, а
внутренняя область для представления объемного интеграла - на 64
объемных ячейки. Исследовалось решение для срединного сечения
цилиндра z=0 вдоль радиуса г в двух сечениях по угловой
координате <р = 0и<р =
Рис.5.22. Расчетная схема задачи о перфорированном цилиндре
(усл. обозн. см. текст)
На рис.5.23,а представлены результаты решения задачи с
заданным внешним единичным давлением по боковой поверхности
цилиндра (модуль упругости - 100 Па, коэффициент Пуассона - 0.3):
250 5.5. Решение трехмерных краевых задач теории упругости
перемещения и и напряжения Сг^ст^ при <р=0 (кривые 1, 2, 3) и при
<р =45 ° (кривые 5, 4, 5, соответственно).
0.85
0.80
0.75:
1
/
а
п
5 !
У-
Рис.5.23. Перемещения и напряжения в перфорированном цилиндре.
ип °г> °<р " соответственно кривые 1, 2, 3 при ф=0, 4, 5, 6 - при ф=45 °;
а - под действием внешнего единичного давления, б - под действием
центробежных сил
На рис.5.23,б представлены результаты решения задачи для того
же цилиндра, вращающегося вокруг оси z с постоянной угловой
скоростью Юс и при единичной плотности материала:
перемещения и и напряжения аг, а^ при <р =0 (кривые 7, 2, 3) и при
<р =45 ° (кривые 4, 5, 6 соответственно).
5.5.4. Задача контроля отражающей поверхности рефлектора
В массиве рефлектора (рис.5.24а) просверлены отверстия, оси
которых расположены в вершинах равносторонних треугольников.
По торцевым площадкам всех отверстий в массиве рефлектора
действует единичное нормальное давление. Внешняя часть контура
жестко закреплена. Коэффициент Пуассона - 0.3.
В качестве расчетной схемы бралась 1/12 конструкции, схема
дискретизации которой представлена на рис.5.24,б. На рис.5.24,6
представлена полученная форма деформированной отражающей
поверхности рефлектора. Рассчитанные максимальные перемещения
uz в центре контролируемой поверхности - wz=3 8,36Р/(/.
Гл. 5. Численная реализация МГП в дифференциальной постановке 251
Поверхность аппроксимировалась 24 элементами. Время
формирования разрешающей матрицы порядка 288 составило 149 с.
Для достижения 3%-й погрешности вычисления перемещений
потребовалось произвести 37 итераций за 16 с. Время вычисления
решения на поверхности - 190 с (данные приведены для ШМ PC AT
486/33).
б
Рис.5.24. Задача о контроле формы отражающей поверхности рефлектора:
а - расчетная схема, б - дискретизация поверхности,
в - деформированное состояние отражающей поверхности
5.5.5. Задача об упругом деформировании опорного устройства
В работе [86] приведено решение задачи об упругом
деформировании опорного устройства (рис.5.25) методом
полуаналитического МКЭ с построением итерационного процесса
решения СЛАУ. Объект исследования представляет собой массивное
тело вращения с четырьмя рядами секторных выступов на наружной
252 5.5. Решение трехмерных краевых задач теории упругости
• lp
0.01
0.015
ч^'УУ/
Л
0.1
0.06
0.035
0.14
0.18
[
22.5
0.235
Рис.5.25. Задача об упругом деформировании опорного устройства
(усл. обозн. см. текст)
поверхности цилиндрической части конструкции. По торцевой части
устройство нагружено равномерно распределенной нагрузкой
единичной интенсивности. В качестве граничных условий принято
Гл.5. Численная реализация МГП в дифференциальной постановке 253
отсутствие вертикальных смещений на нижних кромках выступов.
Расчетная схема конструкции приведена на рис.5.25,я. При решении
этой задачи МГП потребовалось примерно один час на подготовку и
ввод информации о геометрии объекта (объем введенной
информации составил: 60x3 координат геометрических узлов и
27 х 4 - номеров узлов в элементах).
На рис.5.25,6 приведен характер первичной дискретизации
поверхности конструкции на фрагменты, которые затем
использовались для дополнительного измельчения сетки граничных
элементов. Поверхность фрагмента симметрии разбивалась на 49
элементов (узлов коллокации - 196, неизвестных - 588).
Время формирования разрешающей матрицы 1761 с, решение
системы с 3%-й погрешностью F2 итерации) - 282 с, нахождение
вектора перемещений на поверхности - 470 с. На рис.5.25,в,г
показано деформированное состояние цилиндрической части
опорного устройства и пакета секторных выступов.
Глава 6
МЕТОД ГЕОМЕТРИЧЕСКОГО ПОГРУЖЕНИЯ В ЗАДАЧАХ
О СОБСТВЕННЫХ КОЛЕБАНИЯХ УПРУГИХ ТЕЛ
Настоящая глава посвящена решению задач теории упругости о
собственных колебаниях систем. В этих задачах предполагается
отсутствие внешних воздействий: массовых внешних сил, усилий и
перемещений на поверхности. Отыскиваются собственные частоты и
соответствующие им собственные формы колебаний, предлагаемые
алгоритмы ориентированы на решение задач для пространственных
тел сложной формы. Рассматривается использование метода
обратных итераций [64,102] с применением метода геометрического
погружения на каждой итерации. Сформулированы и доказаны
теоремы, гарантирующие сходимость предложенного алгоритма для
рассматриваемого класса задач, предложен один из вариантов
численной реализации метода с применением конечно-элементной
аппроксимации, проведены расчеты собственных форм и частот
нескольких конструкций сложной формы.
6.1. Постановка задачи о собственных колебаниях
Пусть в пространстве R",« = 2,3 упругое тело занимает область
Q с границей Г (рис.6.1). Механическая постановка задачи об
отыскании собственных частот и форм колебаний такого тела
включает в себя, кроме уравнения
-divtj(u) = Au, хеП, F.1)
граничные условия в перемещениях, на части границы Ги
u(x) = 0, хеГи F.2)
и в напряжениях на части границы Г^.
<7(u)n = 0; хеГа. F.3)
Здесь Х-со - собственное значение. Отметим, что Г = Ти иГ(Г
6.2. Алгоритм решения задачи о собственных колебаниях
255
ficR"
Рис.6.1.
Компоненты тензоров напряжений и деформаций связаны (в
рассматриваемом изотропном случае) физическими соотношениями
о = Л§0 Е + 2/jqs . F-4)
Для компонент тензора деформаций и вектора смещений
используют место соотношения Коши:
и)]. F.5)
Для целей настоящего исследования удобно рассматривать
эквивалентную вариационную формулировку задачи. Чтобы записать
вариационное уравнение, введем в рассмотрение гильбертово
пространство:
F.6)
Отметим, что введенное пространство является подпространством
пространства Соболева [92]:
Ус(н1(О$. F.7)
Для произвольных элементов u, v е V определим следующие
скалярные произведения:
(u,v)= J<T(u)--<?(v)dQ , F.8)
Q
(u,v)= fpu vdQ. F.9)
Q
Скалярным произведениям соответствуют нормы
256 Гл. 6. МГП в задачах о собственных колебания упругих тел
F.10)
Известно [52], что собственные пары (Д&»и?/ краевой задачи
F.1)-F.3) удовлетворяют соотношениям
, F.11)
при любых значениях номеров VA:,/gN, а элементы и# образуют
полную ортонормированную систему. Во введенных обозначениях
краевая задача эквивалентна [52] в случае отыскания низшего
собственного значения, задаче минимизации:
F.13)
F.14)
а в случае А:-го собственного значения
\eV
(v,v)
(u*,v)=0; / = 1,...,Л:-1.
Таким образом, если Я^ есть собственное число, а и* -
соответствующий ему собственный элемент, то они удовлетворяют
уравнению
VveV (ul,v) = Ak(u*k,v). F.15)
Для отыскания решения этого уравнения в следующем параграфе
предложен итерационный алгоритм, ориентированный
преимущественно на использование для областей сложной
геометрической формы.
6.2. Алгоритм решения задачи о собственных колебаниях
Для решения вариационного уравнения
A(u,v) F.16)
предлагается следующий итерационный алгоритм, позволяющий
отыскивать произвольное количество собственных значений краевой
задачи F.1)-F.3) в порядке их возрастания, начиная с низшего, и
соответствующие им собственные элементы.
6.2. Алгоритм решения задачи о собственных колебаниях 257
Собственный элемент, соответствующий низшему собственному
значению, предлагается отыскивать как предел последовательности
итераций, осуществляемых следующим образом:
VveF; (wW,v) = (w(^),v), F.16)
F.17)
при этом соответствующее собственное значение определится как
предел
Ях = lim wW , F.18)
где Af=1,2,... - номер итерации.
Сходимость такого итерационного процесса утверждается
следующей теоремой.
Теорема 6.1. Если последовательность итераций jw' Ч
осуществляется таким образом, что
VvgF; (wW,v) = (w(H»,v1 F.19)
:,..., F.20)
то она сходится по норме | • || пространства V к собственному
элементу \х\ , соответствующему наименьшему собственному
значению Я\, при любом начальном приближении - таком, что
>. При этом
limlw^ =/Ц. F.21)
Доказательство. Действительные положительные собственные
значения пронумеруем в порядке их возрастания таким образом,
чтобы
Я\ <Я2 <Я$ <...<Яп <..., F.22)
а соответствующие собственные элементы, образующие в
пространстве V полную ортонормированную систему, обозначим
111 , U 0 9 111,..., 11 и ,... . (O.ZJ)
В силу полноты системы F.23) любой вектор из пространства V
может быть представлен в виде разложения по этой системе, в том
числе имеют место представления
258 Гл. 6. МГП в задачах о собственных колебания упругих тел
w<*>=
F.24)
F.25)
где а\ ' и щ '- коэффициенты, и справедливы условия
замкнутости
\Уг
F.26)
F.27)
,(*)
W=l
Подставляя F.24)-F.25) в F.19) получим
/=i 1=1
В силу произвольности v, последовательно полагая v = u*,
получим, учитывая свойства F.11) и F.12),
а(к)Л -а{к~Х)- 1-12
С другой стороны, подставляя F.24)-F.25) в F.20) получим
Тогда
где введено обозначение
Таким образом, имеем
6.2. Алгоритм решения задачи о собственных колебаниях 259
л=0
и тогда
Подставляя полученное выражение в F.20), найдём
п-
-(»...
<*> / - \к
"|2
где
fk =
7=1
~Уг
Тогда
1А
7=2 ^
260
Гл. 6. МГП в задачах о собственных колебания упругих тел
Далее отметим, что, учитывая F.26)
lim fa = lim
,@)'
окончательно получим
lim Iw^-и* 11 = 0,
что и требовалось доказать.
Отметим, что при w^—ц~*и\ имеем из F.19), что
lim (D) (
т. е. w
(*) 1
щ , и тогда
lim
М)
Итак, сформулирована и доказана теорема о сходимости
итерационного алгоритма нахождения наименьшего собственного
значения и соответствующего ему собственного элемента.
Предположим, что известны п-1 низших собственных значений и
соответствующие им собственные векторы Uj,ii2v5u*_j.
Предлагается находить собственный элемент, соответствующий
следующему по величине собственному значению, как предел
последовательности итерации jw^ j, осуществляемых в
соответствии с формулой
(w?\v) = (*?-»,
при условии, что вектор wKn } принадлежит ортогональному
дополнению линейной оболочки [102] собственных векторов,
соответствующих уже известным п-1 собственным числам. Для
формулировки теоремы, утверждающей сходимость такого
итерационного процесса, введем в рассмотрение некоторые
обозначения. Через Ln__\ обозначим линейную оболочку системы
6.2. Алгоритм решения задачи о собственных колебаниях 261
найденных собственных векторов |и„}. Ортогональное дополнение
к Ln_i обозначим /,„__!.
Теорема 2.2. Если последовательность итераций jw^ 'J
осуществляется следующим образом
W е V /wW, v\ = (w(*~°, v), F.28)
/wo, «pw wv ; =z-(z,uj)ui-...-(z,uw_i)uw_i, она сходится по
норме II пространства V к собственному элементу ип,
соответствующему п-му собственному значению Лп, при условии
Доказательство. Заметим, прежде всего, что vr ' е Ь„_\ . В
самом деле \/k , A: = l,...,/i-l имеем
что и означает принадлежность w^ ' e L^_\ . Таким образом, имеем
представление
^@)_YV°),i*
а, для V^
что отражает тот факт, что вектор нулевого приближения лежит в
пространстве Ln_\ .
(к)
Покажем, что в процессе итерирования вектор wv ; не выходит из
этого подпространства. Воспользуемся принципом математической
индукции. Мы уже показали, что w^ e Ln_\ и w^ e /,„_! ,
теперь необходимо показать, что имеет место следование
262 Гл. 6. МГП в задачах о собственных колебания упругих тел
Отметим прежде всего тот факт, что
так как w' ^ и w^ ' отличаются лишь числовым множителем.
Вследствие полноты ортонормированной системы собственных
векторов ju, j имеем представление
а при предположении
^ ^
g L^\ имеем представление
Подставляя это в F.28), получим
1=1 /=Л
В силу произвольности v, последовательно полагая
= Uy, у = 1,2,..., получим
что и свидетельствует о том, что
справедливы разложения
e L^_x . Таким образом, VA:
Из условия F.29) получим
п=0
где
6.2. Алгоритм решения задачи о собственных колебаниях 263
Тогда
к-\
где
Тогда
00
z
j=n
-1/
2k
л&
Так как
TO
fk = lim
lim
V
= 0,
что и требовалось доказать.
264 Гл. б. МГП в задачах о собственных колебания упругих тел
Отметим, что при такой организации итерационного алгоритма
имеет место соотношение
как и при нахождении первого собственного вектора.
Определенного ускорения сходимости предложенного
итерационного процесса можно достичь, используя сдвиг начала.
Суть этого видоизменения состоит в осуществлении итерационного
процесса в соответствии с формулой
где величина р называется сдвигом. Наложим ограничение на выбор
сдвига так, чтобы выполнялось условие Л\ - р > О.
Сходимость таким образом видоизмененного алгоритма
гарантируется следующей теоремой.
Теорема 6.3. Если последовательность итераций
осуществляется таким образом, что
VvgF /wW,v\-p(wW,v)=(iv(A),v), F.30)
то при р<Я\ она сходится по норме ||| пространства V к
собственному элементу iij, соответствующему наименьшему
собственному значению Х\ при любом начальном приближении -
таком, что (w^, u*) Ф 0.
Доказательство. В силу полноты системы собственных
векторов имеем представления
Подставляя их в F.30), получим
1 = 1
1=1
/=1
ИЛИ
6.2. Алгоритм решения задачи о собственных колебаниях 265
1=1 /=1
Введем обозначение Л, = /I,- - р отметим, что при р < \ имеют
место соотношения
Последовательно полагая v = u,-, получим во введенных
обозначениях
Тогда
где
J=l
Теперь имеем
a(k)-r]aik~l
ai ~Л1 "|
n=0
00
;«"
а так как lim fk = -77^ то
что и требовалось доказать.
При нахождении собственных форм, соответствующих
собственным числам, следующих за первым, итерационная
процедура выглядит точно таким же образом, за исключением
266 Гл. б. МГП в задачах о собственных колебания упругих тел
ограничения, накладываемого на величину сдвига. При нахождении
формы, соответствующей и-му собственному значению, оно
выглядит так
р<Яп.
Сходимость такого итерационного алгоритма определения
собственного элемента, соответствующего и-му собственному
значению (при уже известных пЛ собственных парах), утверждается
следующей теоремой.
Теорема 6.4. Если последовательность итераций jw' 'J
осуществляется таким образом, что
VvgF; /w(*),v\-p(w(*),v)=(w(*),v)f F.31)
{) ,*=tf,..., F.32)
то при р<Яп и w^ ^ =z-(z,Uj)ui-...-(z,uw_i)uw_j она сходится
по норме |-|| пространства V к собственному элементу ип
соответствующему п~му собственному значению Хп , при условии
Доказательство. Как было продемонстрировано выше, при
указанном выборе начального приближения справедливы
представления
00 °°
@) v« @) ¦ —@) V41—@) *
i=n
т.е. w' ' € Zr~*_i и w^ e L^_i . Покажем, что при заданном
способе итерирования векторы w^ ' и w^ ^ не выходят из Ln_\
Воспользуемся принципом математической индукции. Для
доказательства необходимо показать лишь следование:
Вследствие полноты системы собственных векторов ju,-1 имеем
1 = 1
6.2. Алгоритм решения задачи о собственных колебаниях 267
а по предположению w' ' e Ln_
Подставляя это в F.31), получим
)
i=\ /=1 1=1
В силу произвольности v, последовательно полагая
= u*, у = 1,2,..., получим
где Л^ = Я7 ~ /?. Таким образом,
VJfc w
Из F.32) получим
тогда
А-1
Окончательно получим
ik—>
II k-*x>
= o,
что и требовалось доказать.
Увеличение скорости сходимости обеспечивается в этом случае
тем, что
268
Гл. 6. МГП в задачах о собственных колебания упругих тел
причем сходимость тем быстрее, чем меньше величина (Яп - р).
Отметим, что до сих пор речь шла о простых собственных
значениях. При кратных собственных значениях изложенный
алгоритм не претерпевает никаких изменений. Рассмотрим,
например, случай, когда первое собственное значение двукратно:
При итерировании некоторого произвольного вектора начального
приближения w^oh сходится к некоторому вектор},
принадлежащему линейной оболочке первых двух собственных
векторов. К какому именно - зависит от начального приближения.
При отыскании второго собственного вектора с помощью
предложенного итерационного процесса он сходится к некотором)'
вектору, принадлежащему линейной оболочке первых двух
собственных векторов, ортогональному к первому найденному
вектору. Таким образом, линейная оболочка найденных двух
векторов совпадает с линейной оболочкой первых двух собственных
векторов рассматриваемой задачи. Прежде чем сформулировать и
доказать теоремы, гарантирующие сходимость итерационного
процесса в этом случае, введем некоторые обозначения.
Имея в виду существование разложения
00
обозначим
1 _l
1 Т^
\
и
J
3"
-Уг
Ф
Ф
"!0>
1 °1@
= 11*....
J
J>
v2
у
~/2
ф
¦¦ .
U2 з
л.
6.2. Алгоритм решения задачи о собственных колебаниях
269
Видно, что элементы ип образуют, так же как и и„, полную
ортонормированную систему в пространстве V и по ним можно
строить разложения элементов этого пространства
причем имеют место условия замкнутости
Сходимость итерационного процесса для отыскания первого
собственного вектора при кратных корнях утверждается следующей
теоремой.
Теорема 6.5. Если последовательность итераций jvr ^j
осуществляется таким образом, что
VveF;
м
',Ui j^O,
w
(*)
,*=1,2,...
F.33)
F.34)
то
lim
-1
Доказательство. Используя разложения F.24) и F.25), получим
а для векторов w^ ' и w^ ' имеем
п=\
где
270 Гл. 6. МГП в задачах о собственных колебания упругих тел
00 . '
1И
/=1
-Уг
Имеем в нашем случае
lim h=<a
Лк
и тогда
limp» -.М-
:—>ooii И
A:—>oo
= lim
= lim
Л-
1
(оJ (оJ
al +a2
что и требовалось доказать.
~*
Далее, при wv ; -> U] имеем
г (*) 1 @)
hm
X @J @J
^f 4^1 -¦?
@J @J
«2
6.2. Алгоритм решения задачи о собственных колебаниях 271
(к) 1 ~*
при Х\ = A%; wv ' -> —щ и тогда
и теорема доказана.
Сходимость предложенного итерационного алгоритма при
нахождении второго собственного значения, кратного первому, и
соответствующего собственного элемента утверждается следующей
теоремой.
Теорема 6.6. Если последовательность итераций jw' '
осуществляется таким образом, что
VveF;
и w' ' =z-(z,u1 jfii;
w
(к)
Доказательство. Заметим прежде всего, что w^^ e Ь\ и
w^ ^ e if , где L\ - ортогональное дополнение к линейной
оболочке вектора п\ и имеют место представления
Тогда
1=1
1=1
/=2
где
4l
Л.
Имеем
272 Гл. 6. МГП в задачах о собственных колебания упругих тел
= lim
Отметим, что
lim Д
к-*о
М°
= lim •
1 00
7=3
¦ ^^i 2 1 '
Iя;)
(о)
г;
2^
тогда
что и требовалось доказать.
Таким образом, сформулированы и доказаны теоремы,
показывающие, что предложенный итерационный процесс можно без
каких-либо изменений применять как в случае простых собственных
значений, так и при наличии в спектре собственных частот кратных
значений. Это обстоятельство весьма удобно, так как применение
предложенного подхода не требует предварительного знания
кратности отыскиваемых собственных значений.
6.3. Алгоритм решения итерационного уравнения
Предложенный подход к решению задачи об определении
пространственных собственных форм и собственных частот
колебаний упругих тел произвольной геометрической формы
приводит при нахождении однократного низшего собственного
значения и соответствующего ему собственного вектора к
необходимости решения на каждой итерации вариационного
уравнения
((*+l)) (W) F.35)
с нормировкой на каждой итерации
6.3. Алгоритм решения итерационного уравнения 273
Д=1,2,... . F.36)
Здесь w'*' - ненормированный вектор текущей итерации, w* '-
нормированный вектор текущей итерации, w* + '-
ненормированный вектор последующей итерации, v - произвольный
вектор из пространства V.
В случае нахождения высших собственных частот и
соответствующих им собственных форм итерационный процесс
сводится к решению того же вариационного уравнения F.35), будучи
лишь дополненным на каждой итерации процессом ортогонализации,
обеспечивающим принадлежность итерируемого вектора
ортогональному дополнению линейной оболочки уже найденных
собственных векторов.
Если применяется сдвиг и отыскиваются кратные собственные
частоты и соответствующие им собственные формы, то суть дела
остается неизменной - на каждой итерации необходимо решать
вариационное уравнение F.35). Это уравнение представляет собой
вариационную постановку пространственной задачи теории
упругости для тела произвольной формы с некоторыми фиктивными
массовыми силами, так как v - произвольный, wv '- известный, а
w^ ' - отыскиваемый элементы пространства V. Решение этой
задачи предлагается отыскивать методом геометрического
погружения, решая на каждой обратной итерации
последовательность статических задач для канонического тела более
простой геометрической формы, в соответствии с процедурой
Сходимость такой процедуры доказана в главе 2 для статических
задач однородной и неоднородной, изотропной и анизотропной
теории упругости. Факт наличия сходимости имеет место вне
зависимости от степени отличия исходной и канонической областей.
Построение конечномерных аналогов вариационного уравнения,
решаемого на каждой итерации МГП, может производится по
методам, описанным в главах 3-5.
274 Гл. 6. МГП в задачах о собственных колебаниях упругих тел
6.4. Определение собственных форм и частот колебаний упругих
тел сложной формы
Численные расчеты проведены для трех упругих
пространственных конструкций. В качестве канонических
использовались области, имеющие форму различных тел вращения.
Предложенный итерационный алгоритм ориентирован на
использование для областей сложной геометрической формы. Для
проверки его работоспособности проведены расчеты собственных
частот и форм колебаний стального диска, имеющего форму
цилиндра с погружением его в другой цилиндр, такой же толщины ,
но большего диаметра (рис.6.2). Отношение высоты к наружному
диаметру для канонического цилиндра составляло 0.035 .
0.3 м
7777777777
\\\\\\\\\\
0.8м
1.0м
0.035м
Рис.6.2. К расчету собственных частот стального диска
В табл.6.1 представлены результаты расчета низшей собственной
частоты канонического и погруженного в него цилиндра. Здесь же
приведены низшие частоты изгибных колебаний таких же дисков ,
рассчитанные по теории пластин, и частота канонического диска
диаметром 0.8 м при такой же конечно-элементной сетке. Отметим,
что частоты, найденные разными способами, различаются друг от
друга не более чем на 5%.
Итерационный процесс нахождения собственных форм и частот
колебаний упругого тела имеет два иерархических уровня: обратные
итерации и осуществляемые на каждом шаге итерации метода
геометрического погружения. Выбор оптимальной
продолжительности итерирования по погружению на каждом шаге по
обратным итерациям очень существенно влияет на скорость
6.4. Определение собственных форм и частот колебаний 275
Таблица 6. 1
Низшие собственные частоты колебаний диска
Вид
конструкции
Пластина
Канонический цилиндр
Погружённый цилиндр
Пластина
Канонический цилиндр
Внешний
радиус, м
1.0
1.0
0.8
0.8
0.8
Низшая собственная
Частота,
(рад/с) х 10
2.977
3.102
4.643
4.452
4.586
сходимости алгоритма. Реализованы два подхода к осуществлению
указанного выбора. Первый состоит в том, что итерирование по
погружению прекращается после того, как отношение норм векторов
двух последовательных итераций становится отличающимся от
единицы на величину, меньшую некоторой наперед заданной
величины ?. Другой подход позволяет расчетчику в процессе
вычислений выбирать параметры итерационного процесса на каждом
шаге вычислений. Комплекс программ работает в диалоговом
режиме. После осуществления каждого шага на экран дисплея
выводится информация о произведенных вычислениях и
запрашивается информация о дальнейшей работе, которая вводится с
клавиатуры. Второй подход оказался значительно эффективнее
первого, особенно при наличии некоторого навыка отыскания
собственных форм и частот. Повышение эффективности связано
прежде всего с тем обстоятельством, что на первых итерациях нет
необходимости делать много итераций по погружению, часто
достаточно одной, а высокую точность итерирования следует
применять лишь на заключительных итерациях. Изменение сдвига в
процессе итерирования оказалось значительно менее эффективным в
связи с необходимостью перевычисления элементов матрицы левой
части, в то время как отсутствие этих изменений позволяет хранить
элементы матрицы, обратной указанной, а не вычислять их на каждой
итерации. Результаты, касающиеся скорости сходимости алгоритма в
рамках данных двух подходов, сведены в табл.6.2. Ясно видны
преимущества интерактивного подхода, который и применялся в
276 Гл. б. МГП в задачах о собственных колебаниях упругих тел
дальнейшем. Начальное приближение во всех случаях одно и то же,
Таблица 6.2
Сравнительная скорость сходимости алгоритмов
№
обрат-
обратной
итерации
1
2
3
4
5
6
8
Количество
итераций по
погружению
е
ю-3
3
3
3
4
4
4
4
ГО
5
6
6
7
7
Инте-
рактив-
рактивный
подход
1
1
1
1
6
7
10 6
1
х аЛ
1 Ч
рад'-1с"
Б
ю-3
18.050
8.021
7.893
7.812
7.811
7.811
7.810
ю-5
17.230
7.967
7.840
7.808
7.808
-1
>
Интерак-
Интерактивный
подход
19.060
8.222
7.946
7.939
7.808
7.808
Время работы
процессора, с
?
1<Г3
196
248
297
364
432
503
633
ю-5
236
339
442
552
676
Инте-
Интерактив
ный
подход
178
195
212
229
321
432
Изложенный подход использован для получения собственных
форм колебаний, отвечающих низшим собственным частотам для
нескольких тел сложной геометрической формы. Отыскивались
собственные формы и частоты колебаний тела, имеющего форму
диска переменной толщины с расположенными по его периферии
лопатками (рис.6.3).
<Р\
Рис.6.3. Схема диска с лопатками.
6.4. Определение собственных форм и частот колебаний 277
Число лопаток JV=23, Е = 2-\0пПа, v = 0.3, р = 7Я103кг/м3,
<Р\/<Ро =^.1 • Наименьшее полученное собственное значение имеет
величину 6.031 -106рад2 /с2.
Предлагаемый вариант представления результатов основан на
том, что собственный вектор отыскивается в виде
N
w(r, q>, z) = ^Г tfc \(p)wk v 9z) • F.37)
В области D плоскости rOz были выбраны 28 точек,
расположение которых показано на рис.6 А
Рис.6.4. Расположение точек узловых переменных
В выбранных точках линейной интерполяцией узловых
переменных определяются компоненты вектора w в проекции на оси
цилиндрической системы координат. Полученные для каждой
компоненты 28 чисел располагаются в виде таблицы 4x7, в
соответствие с положением точек. Числа каждого такого массива
нормируются делением на максимальное из них, которое перед
нормировкой печатается в качестве масштабного коэффициента.
Печатается также номер элемента t^, причем массивы,
соответствующие первым двум гармоникам, печатаются в одной
таблице, так как cos@ ^) = l, sin@ ^) = 0 и, таким образом, в этой
таблице сведены компоненты, независящие от ср. Такая форма
представления обладает определенной наглядностью и позволяет
получить амплитуду перемещений произвольной точки
рассматриваемого тела с координатами ro,^o»zO' вычислив сумму
по гармоникам разложения.
Часто масштабные коэффициенты отличаются друг от друга
весьма значительно, что позволяет сразу же определить характер
колебаний, например, первая из приведенных ниже форм колебаний
является преимущественно изгибной без узловых диаметров и
узловых окружностей.
278 Гл. 6. МГП в задачах о собственных колебаниях упругих тел
В табл.6.3-6.5 приведены результаты расчёта собственной формы5
отвечающей низшей собственной частоте рассматриваемой
конструкции при <р\/<Ро =0.9. На рис.6.5 эта же форма изображена
графически для сравнения (для наглядности взята одна лопатка).
Таблица 6.3
Результаты расчёта собственной формы, отвечающей низшей собственной
частоте рассматриваемой конструкции
Собственное значение 7.811 • 106, рад2 /с . Гармоника 1,2
Компонента иг,
Коэффициент 5.937-10
Компонента иг
Коэффициент 4.857-10'2
Компонента и^,.
Коэффициент 2.58410
-1.00
-0.31
0.31
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
1.00
-0.98
-0.33
0.33
0.98
0.75
0.75
0.75
0.75
0.85
0.85
0.85
0.85
-0.97
-0.33
0.33
0.97
0.63
0.63
0.63
0.63
0.74
0.74
0.74
0.74
-0.92
-0.30
0.30
0.92
0.51
0.51
0.51
0.51
0.62
0.62
0.62
0.62
-0.85
-0.29
0.29
0.85
0.29
0.28
0.28
0.29
0.44
0.43
0.43
0.44
-0.31
-0.10
0.10
0.31
0.03
0.03
0.03
0.03
0.17
0.17
0.17
0.17
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
Рис.6.5. Собственная форма, отвечающая низшей собственной
частоте колебаний конструкции
6.4. Определение собственных форм и частот колебаний 279
Таблица 6. 4
Результаты расчёта собственной формы, отвечающей низшей собственной
частоте рассматриваемой конструкции
Собственное значение 7.81
Компонента иг
Коэффициент 2.652-100
Компонента и2
Коэффициент 7.59410й
Компонента и^
Коэффициент 1.310100
МО6,
1.00
1.00
1.00
1.00
-1.00
-0.41
0.40
1.00
0.76
0.87
0.87
0.76
рад2
0.71
0.71
0.69
0.69
-1.00
-0.22
0.21
0.99
0.84
0.95
0.95
0.84
1с2.
0.41
0.39
0.38
0.38
-0.40
-0.10
0.11
0.40
-0.25
-0.17
-0.17
-0.25
0.17
0.14
0.14
0.14
-0.09
-0.02
0.02
0.09
-0.19
-0.15
-0.16
-0.20
Гармоника 47
0.01
0.01
0.01
0.01
0.00
0.00
0.00
0.00
-0.02
-0.01
-0.01
-0.01
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
Таблица 6. 5
Результаты расчёта собственной формы, отвечающей низшей собственной
частоте рассматриваемой конструкции
Собственное значение 7.811 • 10б, рад2 /с2. Гармоника 48
Компонента иг
Коэффициент 1.065-10
Компонента uz
Коэффициент 3.134-10
Компонента и^
Коэффициент 2.928-10
-1.00
-0.42
0.42
1.00
0.80
1.00
1.00
0.80
-1.00
-0.40
0.39
1.00
-0.89
-0.31
0.30
0.89
0.48
0.60
0.60
0.48
-0.54
-0.18
0.18
0.54
-0.39
-0.11
0.11
0.39
0.17
0.18
0.18
0.17
-0.16
-0.05
0.05
0.16
-0.14
-0.03
0.04
0.14
0.05
0.05
0.05
0.05
-0.06
-0.01
0.02
0.06
-0.01
0.00
0.00
0.01
0.01
0.01
0.01
0.01
-0.01
0.00
0.00
0.01
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
В табл.6.6-6.8 представлена форма колебаний конструкции,
отвечающая второму по величине собственному значению. Эта форма
280 Гл. 6. МГПв задачах о собственных колебаниях упругих тел
преимущественно изгибная, все
коэффициенты при компоненте
Компоненты амплитуд перемещений
присутствующие в
ит относительно
иг и и7
разложении
невелики.
изменяются
Таблица 6. 6
Результаты расчёта собственной формы, отвечающей второй собственной
частоте рассматриваемой конструкции
Собственное значение 7.963106, рад2 /с2. Гармоника 3
Компонента иг
Коэффициент -6.11710
Компонента «г
Коэффициент 4.532-10'2
Компонента ир
Коэффициент 5.969-10'7
1.00
0.32
-0.32
-1.00
1
]
]
]
1
о о о о
о о о о
о о о о
о о о о
0.95
0.32
-0.32
-0.95
0.70
0.70
0.70
0.70
0.81
0.81
0.81
0.81
0.91
0.30
-0.30
-0.91
0.49
0.49
0.49
0.49
0.64
0.63
0.63
0.64
0.82
0.26
-0.26
-0.83
0.30
0.30
0.30
0.30
0.51
0.51
0.51
0.51
0.59
0.19
-0.19
-0.59
0.18
0.18
0.18
0.18
0.36
0.36
0.36
0.36
0.21
0.07
-0.07
-0.21
0.07
0.07
0.07
0.07
0.12
0.12
0.12
0.12
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
Таблица 6. 7
Результаты расчёта собственной формы, отвечающей второй собственной
частоте рассматриваемой конструкции
Собственное значение 7.963-106 , рад2 /с . Гармоника 4
Компонента иг
Коэффициент-7.924-10"8
Компонента uz
Коэффициент 1.217-10
Компонента uv
Коэффициент 5.486-10
1.00
0.31
-0.31
-1.00
о о о о
о о о о
1.00
1.00
1.00
1.00
0.89
0.30
-0.30
-0.89
0.61
0.61
0.61
0.61
0.93
0.92
0.92
0.92
0.79
0.29
-0.29
-0.79
0.36
0.36
0.36
0.36
0.79
0.79
0.79
0.79
0.70
0.22
-0.22
-0.52
0.21
0.21
0.21
0.21
0.59
• 0.59
0.59
0.58
0.52
0.16
-0.16
-0.16
0.10
0.10
0.09
0.10
0.34
0.34
0.34
0.34
0.16
0.05
-0.05
-0.16
0.04
0.02
0.04
0.04
0.08
0.09
0.09
0.09
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
6.4. Определение собственных форм и частот колебаний 281
приблизительно пропорционально cos 1<р. Это свидетельствует о
том, что вблизи радиусов при <р-п12\ <р = Зя/2 амплитуды близки
к нулю, а вблизи радиусов при <р = 0; <р = л они близки к
максимальным. Таким образом, форма колебаний, отвечающая
второму собственному значению, имеет изгибный характер с узловой
зоной, лежащей вблизи диаметра (р-п12.
Таблица 6. 8
Результаты расчёта собственной формы, отвечающей второй собственной
частоте рассматриваемой конструкции
Собственное значение 7.963-106, рад 1с . Гармоника 45
Компонента иг
Коэффициент 3.672-10
Компонента uz
Коэффициент 6.491 10
Компонента и9
Коэффициент 2.386-10
1.00
0.99
0.99
0.99
-1.00
-0.37
0.37
1.00
0.96
1.00
1.00
0.96
0.56
0.55
0.55
0.55
-0.93
-0.26
0.25
0.92
0.74
0.76
0.77
0.74
0.33
0.31
0.32
0.32
-0.50
-0.11
0.11
0.49
-0.06
-0.07
-0.07
-0.06
0.18
0.17
0.17
0.17
-0.14
-0.01
0.01
0.14
-0.23
-0.25
-0.25
-0.23
0.10
0.10
0.10
0.10
-0.02
0.00
0.00
0.02
-0.21
-0.21
-0.21
-0.21
0.03
0.03
0.03
0.03
0.00
0.00
0.00
0.00
-0.05
-0.05
-0.05
-0.05
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
Формы, отвечающие третьему и четвертому по величине
собственным значениям, имеют преимущественно крутильный
характер, а отвечающие пятому и шестому - преимущественно
изгибный с узловой зоной, лежащей вблизи радиуса 0.52 м .
В табл.6.9-6.11 приведена низшая форма колебаний конструкции,
отличающейся от предыдущей отсутствием одной из лопаток при
(р\/(Ръ =0.5. Виден более сложный характер колебаний по сравнению
с предыдущим случаем: коэффициенты при различных компонентах
амплитуд отличаются друг от друга значительно меньше.
Геометрическая форма второй конструкции, для которой были
проведены расчеты собственных форм и частот изображена на
рис.6.6. Приняты следующие значения характеристик материала:
282 Гл. 6. MTU в задачах о собственных колебаниях упругих тел
= 2
о
10 Па, v = 0.45, /0 = 2-10 кг 1м . Формы, соответствующие
низшим собственным частотам колебаний такой конструкции,
оказались преимущественно крутильными. Первые две формы
представлены на рис.6.7 и 6.8 соответственно. Изображены поля
Таблица 6. 9
Результаты расчёта собственной формы, отвечающей низшей собственной
частоте рассматриваемой конструкции без одной лопатки
Собственное значение (
Компонента щ.
Коэффициент 4.41010
Компонента щ
Коэффициент 3.605-10
Компонента и^.
Коэффициент 8.406-10
5.582106, рад2 /с
-1.00
-0.32
0.32
1.00
1.00
1.00
1.00
1.00
0.78
0.72
0.72
0.78
-0.98
-0.32
0.32
0.31
0.76
0.76
0.76
0.76
1.00
0.76
0.76
1.00
-0.95
-0.31
0.31
0.30
0.64
0.64
0.64
0.64
0.61
0.57
0.56
0.60
2 _
-0.88
-0.29
0.29
0.28
0.52
0.51
0.51
0.52
0.46
0.46
0.44
0.45
—1
Гармоника 1,2
-0.61
-0.19
0.19
0.19
0.29
0.28
0.28
0.29
0.35
0.35
0.35
0.35
-0.26
-0.08
0.08
0.08
0.03
0.03
0.03
0.03
0.10
0.10
0.10
0.10
0.00 1
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
Таблица 6. 10
Результаты расчёта собственной формы, отвечающей низшей собственной
частоте рассматриваемой конструкции без одной лопатки
Собственное значение 6.582-106,
Компонента щ
Коэффициент 3.271-10
Компонента щ
Коэффициент 2.686-1О
Компонента и9
Коэффициент 1.244-10
-1.00
-0.33
0.33
1.00
1.00
1.00
1.00
1.00
1.00
0.33
-0.33
-1.00
рад2
-0.97
-0.32
0.32
0.97
0.75
0.75
0.75
0.75
0.88
0.29
-0.29
-0.88
1с2.
-0.94
-0.31
0.31
0.94
0.63
0.61
0.61
0.61
0.80
0.27
-0.27
-0.79
-0.87
-0.29
0.29
0.86
0.51
0.49
0.50
0.51
0.70
0.24
-0.23
-0.69
Гармоника 3
-0.60
-0.19
0.19
0.60
0.28
0.27
0.27
0.28
0.47
0.14
-0.13
-0.47
-0.26
-0.08
0.08
0.26
0.03
0.03
0.03
0.03
0.13
0.04
-0.04
-0.13
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
6.4. Определение собственных форм и частот колебаний 283
Таблица 6. 11
Результаты расчёта собственной формы, отвечающей низшей собственной
частоте рассматриваемой конструкции без одной лопатки
(\ 9 9
Собственное значение 6.58210 , рад 1 с . Гармоника 4
Компонента иг
Коэффициент 4.695-10
Компонента м2
Коэффициент 3.843-10'2
Компонента и9
Коэффициент 1.780-10
-1.00
-0.33
0.33
1.00
1.00
1.00
1.00
1.00
-1.00
-0.33
0.33
1.00
-0.97
-0.32
0.32
0.97
0.77
0.77
0.77
0.77
-0.87
-0.29
0.28
0.86
-0.92
-0.30
0.30
0.92
0.63
0.62
0.62
0.63
-0.78
-0.26
0.25
0.78
-0.78
-0.27
0.27
0.78
0.50
0.49
0.49
0.48
-0.66
-0.22
0.21
0.66
-0.54
-0.17
0.16
0.54
0.27
0.26
0.26
0.26
-0.42
-0.13
0.13
0.42
-0.20
-0.07
0.07
0.20
0.03
0.03
0.03
0.03
-0.11
-0.03
0.03
0.11
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
А-А
Рис.6.6. Общий вид конструкции (А-А, В-В, С-С, D-D - сечения)
284 Гл. 6. МГП в задачах о собственных колебаниях упругих тел
амплитуд окружных компонент перемещений в четырех (отмеченных
на рис.6.6) характерных сечениях конструкции, тонкими линиями
показана недеформированная конфигурация в каждом из
приведенных сечений. Собственное значение, которому отвечает
собственная форма, изображенная на рис.6.7, составляет 1.176 • 10 , а
форма, изображенная на рис.6.8, отвечает собственному значению
1.190 105. Графическая форма представления информации для
данной конструкции объясняется малостью г и z -компонент
амплитуд, которые на рисунке не изображены.
D-D1
Рис.6.7. Собственные формы,
соответствующие собственному
значению 1.176-10 рад 1с
Рис.6.8. Собственные формы,
соответствующие собственному
значению 1.190 105 рад2 /с2
Список литературы 285
СПИСОК ЛИТЕРАТУРЫ
1. Адлуцкий В.Я. О вычислении напряжений на поверхности упру-
упругого тела // Проблемы прочности. 1983. № 2. С.102-104.
2. Бакин А.Б., Николаев ОЛ., Тарасов М.А. Вычисление сингуляр-
сингулярных интегралов при решении трехмерных задач теории упруго-
упругости прямым методом граничных элементов // Прикладные про-
проблемы прочности и пластичности. Алгоритмизация и автомати-
автоматизация научных исследований по прочности. Горький, 1988.
С.80-87.
3. Барях А. А. Шардаков И.Н., Ковтун В.Я. О влиянии закладки на
распределение напряжений в междукамерных целиках // Разра-
Разработка калийных месторождений. Пермь, ППИ, 1989. С.88-95.
4. Бахвалов КС. Решение первой краевой задачи для системы
уравнений теории упругости методом фиктивных областей.
Препринт. Отделение вычислительной математики АН СССР.
1988. № 191. С.1-14.
5. Бахвалов H.C.t Жидков Н.П., Кобельков Г.М. Численные методы.
М.: Наука, 1987. 600 с.
6. Бенерджи 77., Баттерфилд Р. Методы граничных элементов в
прикладных науках. М.: Мир, 1984.494 с.
7. Бреббия К, Теллес Ж., Вроубел Л. Методы граничных элемен-
элементов. М: Мир, 1987. 524 с.
8. Булавин П.В., Шардаков И.Н. Гранично-элементный подход к
решению трехмерных задач теории упругости методом геомет-
геометрического погружения // ПММ. 1995. Т.59, вып.2. С.252-258.
9. Галлагер Р. Метод конечных элементов: Основы. М.: Мир,
1984.428 с.
10. Гольдштейн Р.В. Дополнение. Метод ГИУ для механики
сплошных сред // Механика. Метод граничных интегральных
уравнений. Сер. Новое в зарубежной науке. М.: Мир, 1978. т. 15.
С. 183-209.
11. Гринченко В. Т. Равновесие и установившиеся колебания упру-
упругих тел конечных размеров. Киев: Наук, думка, 1978. 264 с.
286 Список литературы
12. Гузь А.Н, Немиш Ю.Н. Методы возмущений в пространствен-
пространственных задачах теории упругости. Киев: Вищ. шк., 1982. 352 с.
13. Гузь А.Н. Немиш Ю.Н Методы возмущения формы границы в
механике сплошных сред (Обзор). // Прикладная механика.
1987.№9.С.З-29.
14. Джордж: А., Лю Дж. Численное решение больших разрежен-
разреженных систем уравнений. М.: Мир, 1984. 333 с.
15. Дьяконов КГ. Минимизация вычислительной работы. Асим-
Асимптотически оптимальные алгоритмы для эллиптических задач.
М.: Наука, 1989. 272 с.
16. Дьяконов КГ. Разностные схемы решения краевых задач, (ста-
(стационарные задачи). М.: Изд-во МГУ. 1971. Вып.1.
17. Зенкевич O.K. Метод конечных элементов в технике. М.: Мир,
1975. 541 с.
18. Иванов В.В. Методы вычислений на ЭВМ. Справочное пособие.
Киев: Наук, думка, 1986. 584 с.
19. Илъгамов М. А., Иванов В.А., Гулин Б.В. Расчет оболочек с упру-
упругим заполнителем. М.: Наука, 1987. 260 с.
20. Ионов В.Н., Огибалов П.М. Прочность пространственных эле-
элементов конструкций. М.: Высш. шк. 1972. 752 с.
21. Кеч В., Теодореску П. Введение в теорию обобщенных функций
с приложениями в технике. М.: Мир, 1978. 518 с.
22. Колесникова Н.В., Матвеенко В.П., Юрлова Н.А. Численное мо-
моделирование собственных затухающих колебаний кусочно-
однородных вязкоупругих тел. Приложение к задаче о колеба-
колебаниях двухслойного цилиндра // Расчеты на прочность. М., 1989.
Вып.ЗО.С.166-172.
23. Колтунов М.А., Васильев Ю.Н, Черных В.А. Упругость и проч-
прочность цилиндрических тел. М.: Высш. шк., 1975. 526 с.
24. Коновалов А.Н. Численное решение задач теории упругости.
Новосибирск: Наука, 1968. 211с.
25. Коновалов А.Н., Горский НМ. Метод сеток в задачах теории уп-
упругости // Моделирование в технике. Новосибирск, 1987. Т.1, №
4.С.93-115.
26. Коробицына Ж.Л., Кузнецов СБ. Численная реализация метода
фиктивных областей для осесимметричной статической задачи
теории упругости // Численные методы решения задач теории
упругости: Материалы 10-ой Всесоюзной конференции. Ново-
Новосибирск, 1988. С.141-149.
Список литературы 287
27. Красносельский МЛ. Позитивные линейные системы: Метод
положительных операторов. М.: Наука, 1985. 255 с.
28. Красносельский М. А., Вайникко Г. М, Забрейко Я Я, Рутиц-
кий Я. Б., Стеценко В. Я. Приближенное решение операторных
уравнений. М.: Наука, 1969. 656 с.
29. Кузнецов Г.Б. Упругость, вязкоупругость и длительная проч-
прочность цилиндрических и сферических тел. М.:Наука, 1979. 112с.
30. Купрадзе В.Д. Методы потенциала в теории упругости. М.: Гос.
изд-во физ.-мат. лит., 1963. 472.
31. Купрадзе В. Д., Гегелия Т. Г., Башелейшвили М. О., Бурчуладзе Т.
Трехмерные задачи математической теории упругости и термо-
термоупругости. М.: Наука, 1981. 688 с.
32. Куранов Б.А., Гусев С.С. Применение метода суперэлементов
для расчета сложных машиностроительных конструкций. // Рас-
Расчеты на прочность. М., 1985. Вып. 26. С. 174-182.
33. Кутрунов В.К, Куриленко Е.Ю. Влияние коэффициента Пуас-
Пуассона на сходимость итерационных процессов решения сингу-
сингулярных интегральных уравнений теории упругости // Исследо-
Исследования по механике строительных конструкций и материалов. Л.,
1988.С.76-82.
34. Кутрунов В.Н., Мальцев Л.Е. Усиление сходимости приближен-
приближенного решения интегральных уравнений теории упругости за
счет применения информации о границах спектра // Проблемы
прочности. 1989. № 4. С.53-57.
35. Ладыженская О.А. Краевые задачи математической физики.
М.: Наука, 1973.407 с.
36. Лазарев М.И., Сковорода А.Р. К расчету напряжений при реше-
решении пространственной задачи теории упругости прямым мето-
методом интегральных уравнений // Прикладные проблемы прочно-
прочности и пластичности. Алгоритмизация и автоматизация решения
задач упругости и пластичности. Горький, 1982. С.26-32.
37. Ландау Л. Д, Лифгииц Е. Я. Механика. М.: Наука, 1988. 215 с.
38. Лебедев В.И., Финогенов С.А. Решение проблемы упорядочения
параметров в чебышевских итерационных методах // Журнал
вычислительной математики и математической физики. 1973. №
1.С.18-33.
39. Ломакин В.А. Теория упругости неоднородных тел. М.: Изд-во
МГУ, 1976.367 с.
288 Список литературы
40. Лурье А. И. Пространственные задачи теории упругости. М.:
Наука, 1955. 491 с.
41. Лурье А.И. Теория упругости. М: Наука, 1970. 490 с.
42. Матвеенко В.П. О методе решения задачи сопряжения двух вяз-
коупругих тел в виде ряда по степеням оператора Вольтерра //
Краевые задачи упругих и неупругих систем. Свердловск, 1985.
С.7-13.
43. Матвеенко В.И Численный анализ вынужденных установив-
установившихся колебаний несжимаемых или слабосжимаемых вязкоуп-
ругих тел // Аналитические и численные методы решения крае-
краевых задач пластичности и вязкоупругости. Свердловск, 1986.
С.83-86.
44. Матвеенко В.П., Останов АЛ. Конечно-элементная реализация
метода геометрического погружения применительно к плоской
задаче теории упругости в напряжениях // Модели и методы ис-
исследования упругого и неупругого поведения материалов и кон-
конструкций. Свердловск, 1987. С.11-16.
45. Матвеенко В.И, Трояновский И.Е., Цаплина Г.С. Построение
решений задач теории упругости в виде рядов по степеням уп-
упругих постоянных и их приложения к вязкоупругости // ПММ.
1996. Т.60, вып.4. С.651-659.
46. Матвеенко В.П. Метод численного анализа сингулярности на-
напряжений в угловых точках трехмерных тел // Изв. РАН. Меха-
Механика твердого тела. 1995. № 5. С.71-77.
47. Матвеенко В.П., Борзенков СМ. Полуаналитические сингуляр-
сингулярные элементы для плоских и пространственных задач теории
упругости // Изв. РАН. Механика твердого тела. 1995. № 6.
С.48-61.
48. Машинда К, Якимчук Д.К. Оценка точности решений задач
теории упругости, получаемых в схеме метода граничных инте-
интегральных уравнений. Сообщение 1 // Проблемы прочности.
1983.№12.С.63-65.
49. Машинда И., Якимчук Д.К. Оценка точности решений задач
теории упругости, получаемых в схеме метода граничных инте-
интегральных уравнений. Сообщение 2 // Проблемы прочности.
1986.№6.С.73-77.
50. Мелешонок Е.И., Ожерельев В.А. Некоторые результаты срав-
сравнения МКЭ и МКР на примере задачи изгиба пластин // Тр.
ЦНИИСК им.Кучеренко: Численные методы в исследованиях
строительных конструкций. М., 1986. С.70-76.
Список литературы 289
51. Мишонов М. Общий метод за решение на пространственота
задача на еластичноста за параллелепипеда // Известия техн. ин-
та Бълг. АН, София, 1960. Кн.9-10. С.15.
52. Михлия С. Г. Вариационные методы в математической физике.
М.: Наука, 1970. 512 с.
53. Михлин С.Г. Многомерные сингулярные интегралы и инте-
интегральные уравнения. М.: Физматгиз, 1962. 254 с.
54. Молчанов И.Н., Яковлев М.Ф. Условия окончания итераци-
итерационных процессов, гарантирующие заданную точность // ДАН
УССР. Сер.А. 1980. № 6. С.21-23.
55. Мяченков В.Н., Григорьев КВ. Расчет составных оболочечных
конструкций на ЭВМ. М.: Машиностроение, 1981. 212 с.
56. Наринский В.И. О дифференцируемое™ рядов Фурье при реше-
решении краевых задач // Вопросы прочности тонкостенных конст-
конструкций. М., 1989. С.29-33.
57. Немиш Ю.Н Об одном обобщении метода возмущения формы
границы в механике деформируемого твердого тела // Приклад-
Прикладная механика. 1989. №1. С.5-12.
58. Немиш Ю.Н. К решению пространственных задач для слоистых
некруговых цилиндров // Прикладная механика. 1993. №9. С.69-
76.
59. Немиш Ю.Н. Об одном обобщении метода возмущения формы
границы в механике деформируемого твердого тела // Приклад-
Прикладная механика. 1989. №1. С.5-12.
60. Немиш Ю.Н Элементы механики кусочно-неоднородных тел с
неканоническими поверхностями раздела. Киев: Вищ. шк., 1987.
210 с.
61. Немиш Ю.Н, Маслов В.П., Чернопиский Д.И., Кашталян М.Ю.
О трехмерном напряженно-деформированном состоянии прямо-
прямоугольных двухслойных пластин с неплоскими поверхностями //
Прикладная механика. 1990. Т.26, №11. С.39-44.
62. Николаев О.П., Хуторянский НМ. Метод граничных элементов
для пространственной задачи теории упругости при смешанных
краевых условиях // Прикладные проблемы прочности и пла-
пластичности. Алгоритмизация и автоматизация решения задач уп-
упругости и пластичности. Горький, 1982. С.33-37.
63. Новащий В. Теория упругости. М.: Мир, 1975. 872 с.
64. Парлетт Б. Симметричная проблема собственных значений:
Численные методы. М.: Мир, 1983. 384 с.
290 Список литературы
65. Партой В.З., Перлин П.И Интегральные уравнения теории уп-
упругости. М: Наука, 1977. 312 с.
66. Партой В. 3., Перлин И И Методы математической теории уп-
упругости. М.: Наука, 1981. 668 с.
67. Перлин ИИ. Применение принципа Робена к решению про-
пространственных задач теории упругости // ПММ. 1988. Т.52Г
ВЫП.2.С.337-341.
68. Перлин НИ. Применение регулярного представления сингуляр-
сингулярных интегралов к решению второй основной задачи теории уп-
упругости // ПММ. 1976. Т.40, вып.2. С.366-371.
69. Перлин П.И. Численный метод решения сингулярных инте-
интегральных уравнений основных пространственных задач теории
упругости // Изв. АН СССР. МТТ. 1975. № 3. С.109-111.
70. Писсанецки С Технология разреженных матриц. М.: Мир, 1988
410 с.
71. Победря Б.Е. Численные методы в механике деформируемого
твердого тела. М: Изд-во МГУ, 1995. 366 с.
72. Победря Б.Е., Шешенин СВ. Некоторые задачи о равновесии
упругого параллелепипеда // Изв. АН СССР. Механика твердого
тела. 1981. №1.С.74-86.
73. Победря Б.Е., Шешенин СВ., Холматов Е. Задача в напряжени-
напряжениях. Ташкент : ФАН, 1988.200 с.
74. Подильчук Ю.Н. Трехмерные задачи теории упругости. Киев:
Наук, думка, 1979.240 с.
75. Попов СВ. Многошаговые итерационные процедуры в конечно-
элементной реализации метода геометрического погружения
при решении пространственных задач теории упругости // Вест-
Вестник ПГТУ. Математика и прикладная математика. 1996. № 1.
С.80-85.
76. Постное В.А., Дмитриев С.А., Елтышев Б.К., Родионов Л.А.
Метод суперэлементов в расчете инженерных сооружений. Л.:
Судостроение, 1979. 287 с.
77. Пространственные задачи теории упругости и пластичности.
Киев: Наук, думка, 1986. Т.6. 280 с.
78. Пустовойт КС, Трояновский И.Е., Шардаков ИН. Об одном
подходе к решению трехмерных динамических задач теории уп-
упругости и вязкоупругости для тел сложной формы // ПММ.
1989.Т.53,вып.5.С.856-859.
Список литературы 291
79. Расчеты машиностроительных конструкций методом конечных
элементов:. Справочник. / В.И. Мяченков, В.П. Мальцев, В.П.
Майборода и др., Под ред. Мяченкова В.И. М: Машинострое-
Машиностроение, 1989. 520с.
80. Самарский А.А. Теория разностных схем. М.: Наука, 1983. 616 с.
81. Самарский А.А., Андреев В.Б. Разностные методы для эллипти-
эллиптических уравнений. М.: Наука, 1976. 352 с.
82. Самарский А.А., Гулин А.В. Устойчивость разностных схем. М.:
Наука, 1973.415 с.
83. Самарский А.А, Капорин И.Е., Кучеров А.Б., Николаев Е.С. Не-
Некоторые современные методы решения сеточных уравнений //
Изв. вузов. Математика. 1983. № 7 B54). С.3-12.
84. Самарский А.А., Николаев Е.С. Методы решения сеточных
уравнений. М.: Наука, 1978. 592 с.
85. Самарский A.A.f Назаров Р.Д., Макаров В.Л. Разностные схемы
для дифференциальных уравнений с обобщенными решениями.
М.: Высш. шк., 1987. 296 с.
86. Сахаров А.С., Гуляр А.И., Топор AT. Анализ напряженно-
деформированного состояния тел вращения с вырезами, нару-
нарушающими осевую симметрию // Проблемы прочности. 1986. №
6. С.69-73.
87. Сегерлинд Л. Дж. Применение метода конечных элементов. М.:
Мир, 1979.392 с.
88. Серпик КН., Голоян АЛ. Построение быстросходящегося ите-
итерационного процесса решения краевых задач теории упругости
по методу граничных элементов // Проблемы прочности. 1990.
№ 6. С.73-77.
89. Соболев С. JI. Уравнения математической физики. М.: Гостехиз-
дат, 1947.440 с.
90. Справочник по специальным функциям/ Под ред. Абрамовщ М.,
Стшан К М.: Наука, 1979. 832 с.
91. Суслова Н.Н. Методы решения пространственной задачи теории
упругости для тела в форме параллелепипеда // Итоги науки и
техники / Сер. Механика твердого деформированного тела. М.,
1980.Т.13.С.187.
92. Сьярле Ф. Метод конечных элементов для эллиптических задач.
М.:Мир,1980. 512 с.
292 Список литературы
93. Тимошенко СП., Гудьер Дж. Теория упругости. М: Наука,
1979.560 с.
94. Трояновский И.Е., Шардаков И.Н., Труфанов НА. Обоснование
метода геометрического погружения для краевых задач теории
упругости // Аналитические и численные методы решения крае-
краевых задач пластичности и вязкоупругости. Свердловск, 1986.
С.107-111.
95. Труфанов НА. Пространственная задача вязкоупругости для
конструкции из термонестабильного материала с объемной ре-
релаксацией // Механика и прикладная математика. Тула, 1988.
С.57-61.
96. Труфанов Н.Л., Носиков АА. Пространственное напряженно-
деформированное состояние металло - композиционного ротора
инерционного накопителя энергии // Изв. вузов. Машинострое-
Машиностроение. 1991. № 3-6. С.35-38.
97. Труфанов НА., Полуэктпова АА., Шакирова Н.В. Расчет трех-
трехмерного напряженно-деформированного состояния и оценка
прочности оправок для намотки композиционных оболочек
вращения // Моделирование термомеханического поведения
конструкций из композиционных материалов при их изготовле-
изготовлении. Свердловск, 1990. С.38-44.
98. Труфанов НА., Шакирова Н.В. Расчет пространственного на-
напряженно-деформированного состояния формообразующей
конструкции // Численное моделирование статического и дина-
динамического деформирования. Свердловск, 1990. С.42-45.
99. Труфанов НА., Шардаков КН. МКЭ-реализация метода гео-
геометрического погружения для пространственных задач теории
упругости в цилиндрических координатах. 1. Основные соот-
соотношения // Статические и динамические краевые задачи меха-
механики деформируемых тел. Свердловск, 1989. С.36-45.
100. Труфанов НА., Шардаков КН. МКЭ-реализация метода гео-
геометрического погружения для пространственных задач теории
упругости в цилиндрических координатах. 2. Численный при-
пример // Статические и динамические краевые задачи механики
деформируемых тел. Свердловск, 1989. С.46-50.
101. Труфанов НА., Шардаков КН. Применение метода геометриче-
геометрического погружения для численного расчета пространственных
конструкций // Расчеты на прочность. М., 1990. Вып.31. С. 127-
134.
Список литературы 293
102. Уилкинсон Дж.Х. Алгебраическая проблема собственных значе-
значений. М.: Наука, 1970. 564 с.
103. Угодников А.Г., Хуторянский Н.М. Метод граничных элементов
в механике деформируемого твердого тела. Казань: Изд-во Ка-
Казанского ун-та, 1986. 295 с.
104. Фгатенгольц ГМ. Курс дифференциального и интегрального
исчисления. М.: Наука, 1969. Т.З. 656 с.
105. Флетчер К. Численные методы на основе метода Галеркина. М:
Мир, 1988. 352 с.
106. ХанХ Теория упругости: Основы линейной теории и ее приме-
применения. М.: Мир, 1988. 344с.
107. Хейгеман Л., Янг Д. Прикладные итерационные методы. М.:
Мир, 1986.448 с.
108. Хемминг Р.В. Численные методы. М.: Наука, 1972.400 с.
109. Хуторянский Н.М. Дискретные уравнения с положительно оп-
определенными и симметричными матрицами в методе граничных
элементов для основных краевых задач теорж: упругости //
Прикладные проблемы прочности и пластичности. Алгоритми-
Алгоритмизация и автоматизация научных исследований по прочности.
Горький, 1986,С.35-40.
110. Хуторянский Н.М. Построение экономичных дискретных моде-
моделей интегральных уравнений теории упругости на основе свой-
свойства локальности ядер // Прикладные проблемы прочности и
пластичности. Алгоритмизация и автоматизация решения задач
упругости и пластичности. Горький, 1980. С.36-38.
111. Шабров Н.Н, Заблоцкая КН. Трехмерный суперэлементный
анализ напряжений. // Проблемы прочности. 1991. №6. С.79-89.
112. Шешения С.В., Кузъ КС. Применение вариационно-разностного
метода к осесимметричным задачам теории упругости // Упру-
Упругость и неупругость. М., 1987. С.39-44.
ИЗ.Шардаков КН. Теоретические положения метода геометриче-
геометрического погружения для краевых задач упругогшастического тела
// Общие задачи и методы исследования пластичности и вязко-
упругости материалов и конструкций. Свердловск, 1986. С. 123-
127.
114. Шардаков КН. Метод геометрического погружения в диффе-
дифференциальной постановке для решения краевых задач изотропной
теории упругости // Модели и методы исследования упругого и
неупругого поведения материалов и конструкций. Свердловск,
1987.С.З-6.
294 Список литературы
115. Шардаков КН. Численная реализация дифференциальной по-
постановки метода геометрического для двумерных задач теории
упругости // Модели и методы исследования упругого и неупру-
неупругого поведения материалов и конструкций. Свердловск, 1987.
С.7-11.
116. Шардаков КН Теоретические положения метода геометриче-
геометрического погружения для решения краевых задач анизотропной
теории упругости // Деформирование и разрушение конструк-
конструкций из композиционных материалов. Свердловск, 1987. С.27-33.
117. Шардаков КН. Решение краевых задач теории упругости мето-
методом геометрического погружения в дифференциальной поста-
постановке // Механика и прикладная математика. Тула, 1988. С.61-
64.
118. Шардаков КН. Решение краевых задач теории упругости мето-
методом геометрического погружения в дифференциальной поста-
постановке // Исследования по механике материалов и конструкций.
Свердловск, 1988. С.93-99.
119. Шардаков КН., Барях А. А. Применение одного приближенного
численного метода для оценки напряженно-деформированного
состояния подработанного горного массива // Физико-
технические проблемы разработки полезных ископаемых. 1990.
№1.С.23-27.
120. Шардаков КН., Трояновский И.Е., Труфанов НА. Метод гео-
геометрического погружения для решения краевых задач теории
упругости / Препринт. Свердловск: УНЦ АН СССР, 1984. 66 с.
121. Шардаков КН., Труфанов НА. Обоснование метода геометри-
геометрического погружения и его численная реализация для решения
задач теории упругости // Тез. докл. 8-ой Всесоюз. конф. по
прочности и пластичности. Пермь, 1983. С. 194-195.
122. Шардаков КН., Труфанов НА. Метод геометрического погру-
погружения для двумерных задач теории упругости // Исследование
течений и фазовых превращений в полимерных системах.
Свердловск, 1985. С.110-114.
123. Шардаков КН., Труфанов НА. Конечно-элементная реализация
метода геометрического погружения для двумерных упругих
задач // Напряжения и деформации в конструкциях и материа-
материалах. Свердловск, 1985. С. 19-24.
Список литературы 295
124. Шардаков КН., Труфанов НА. Анализ пространственного на-
напряженно-деформированного состояния вокруг выработки в не-
неоднородном массиве методом геометрического погружения //
Численные методы в исследованиях напряжений и деформаций.
Свердловск, 1987. С.46-51.
125. Шардаков КН., Труфанов НА., Труфанова М.А. Применение
метода геометрического погружения для решения осесиммет-
ричных задач теории упругости // Численные методы в исследо-
исследованиях напряжений и деформаций. Свердловск, 1987. С.51-56.
126. ChongJ. S., Christensen Е. В., Baer A. D. Reology of concentrated
suspension. // J. Appl. Polimer Sci. 1971. V.15. P.2007-2021.
127. Henry Jr. D.P., Banerjee P.K. A new BEM formulation for two- and
three-dimensional elastoplasticity using particular integrals. // Int. J.
Numer. Meth. Eng. 1988. V.26, № 9. P.2079-2096.
128. Henry Jr. D.P., Banerjee P.K. A new boundary element formulation
for two- and three-dimensional thermoelasticity using particular
integrals.// Int. J. Numer. Meth. Eng. 1988. V.26, № 9. P.2061-2077.
129. Manolis G.D., Banerjee P.K. Conforming versus non-conforming
boundary elements in three-dimensional elastostatics. // Int. J.
Numer. Meth. Eng. 1986. V.23, № 10. P.1885-1904.
130. Moshev V. V., Kozhevnikova L.L. Highly predictive structural cell for
particulate polymeric composites // J. Adhesion. 1997. Vol.62.
P.169-186.
131. Patterson C, Elsebai N.A. A regular boudary method using non-
conforming elements for potential problems in three dimensions //
Boudary Element Meth. Eng. Proc. 4th Int. Semin., Southampton,
Sept, 1982. Berlin ets, 1982. P.I 12-126.
132. Perucchio Renato, Ingrajfea Anthony R. Interactiv computer graphic
prepricessing for three-dimensional boudary-integral element
analysis // Comput. and Struct. 1983. V.I6, №. 1 - 4. P. 153-166.
133. Randolph E. Bank, Donald J. Rose. Marching algorithms for elliptic
boundary value problems. 1: The constant coefficient case // SIAM J.
Numer. Anal. 1977. V.14, №.5. P.792-829.
134. Rieder G. Konjugierte Gradienten und die Randelementmethode in
Potential und Elastizitatstheorie // Z. Angew. Math. Und Mech.
199O.V.7O,№6.C.712-713.
296 Список литературы
135. Wearing J. Lt Sheikh M A., Hickson A. J. A combined finite
element boundary element technique for stress analysis // Boundan
elem. x. V.. 1. Math, and Comput. Aspects. Southampton etc., Berlin
etc, 1988. P.493-597.
136. Wilson E.L, Bathe K.-J., Doherty W.P. Direct solution of large sys-
systems of linear equations // Сотр. And Struct. 1974. V.4, № 2. P.363-
372.
Оглавление 297
ОГЛАВЛЕНИЕ
Введение 3
Глава 1. Введение в метод геометрического
погружения 8
1.1. Введение 8
1.2. Иллюстративная задача: вариационная формулировка
метода геометрического погружения 10
1.3. Иллюстративная задача: дифференциальная форму-
формулировка метода геометрического погружения 15
1.4. Иллюстративная задача: растяжение неоднородного
стержня 19
Глава 2. Теория метода геометрического погружения для
решения краевых задач линейной теории упру-
упругости 27
2.1. Введение 27
2.2. Задачи теории упругости для изотропных
однородных тел 27
2.3. Задачи неоднородной теории упругости 40
2.4. Задачи анизотропной теории упругости 55
Глава 3. Конечно-элементная реализация метода геомет-
геометрического погружения 70
3.1. Введение 70
3.2. Основные соотношения конечно-элементной реали-
реализации МГП для однородных изотропных тел 71
3.3.Учет различных силовых факторов 80
3.4. Учет кинематических граничных условий 84
3.5. Особенности учета разнородных материалов конст-
конструкции 85
3.6. Решение тестовых задач 87
3.7. Практическая сходимость конечно-элементной реа-
реализации метода геометрического погружения 108
3.8. Повышение эффективности численной реализации
метода геометрического погружения 117
3.9. Применение конечно-элементной реализации метода
геометрического погружения для решения простран-
пространственных задач теории упругости 142
Глава 4. Конечно-разностные с&емы метода геометри-
геометрического погружения 158
4.1. Дискретный аналог вариационного уравнения метода
298 Оглавление
геометрического погружения в декартовой системе
координат 158
4.2. Дискретный аналог вариационного уравнения метода
геометрического погружения в цилиндрической сис-
системе координат 162
4.3. Построение дискретного аналога вариационного ура-
уравнения метода геометрического погружения для задач
неоднородной теории упругости 164
4.4. Методы решения системы разностных уравнений 165
4.5. Апробация алгоритма вариационно-разностной реа-
реализации метода геометрического погружения 170
4.6. Применение метода геометрического погружения в
разностной реализации для расчета трехмерного на-
напряженно-деформированного состояния конструкций
сложной геометрии 192
4.7. Приложение 1 202
4.8. Приложение 2 206
Глава 5. Численная реализация метода геометрического
погружения в дифференциальной постановке 210
5.1. Введение 210
5.2. Численная реализация дифференциальной постанов-
постановки метода геометрического погружения 214
5.3. Сходимость метода геометрического погружения 229
5.4. Решение тестовых задач теории упругости 241
5.5. Решение трехмерных краевых задач теории упругос-
упругости 247
Глава 6. Метод геометрического погружения в задачах о
собственных колебаниях упругих тел 254
6.1. Постановка задачи о собственных колебаниях 254
6.2. Алгоритм решения задачи о собственных колебаниях... 256
6.3. Алгоритм решения итерационного уравнения 272
6.4. Определение собственных форм и частот колебаний
упругих тел сложной формы 274
Список литературы 285
Научное издание
Игорь Николаевич Шардаков
Николай Александрович Труфанов
Валерий Павлович Матвеенко
МЕТОД ГЕОМЕТРИЧЕСКОГО ПОГРУЖЕНИЯ
В ТЕОРИИ УПРУГОСТИ
Рекомендовано к изданию Ученым советом
Института механики сплошных сред и НИСО УрО РАН
по плану выпуска 1998 г.
Редактор С. С. Гаврилова
Компьютерная верстка Н. А. Труфанова
ЛР № 020764 от 24.04.98
НИСО УрО РАН № 176(98)—166
Подписано в печать 2.03.99. Формат 60 х 90 1/16. Бумага
типографская. Гарнитура Тайме. Усл. печ. л. 18,75 Уч.-изд. л. 20
Тираж 600 экз. Заказ № 34.
614600, г. Пермь, ул. Королева, д. 1. Институт механики сплошных
сред УрО РАН.
620219, г. Екатеринбург, ГСП-169, ул. С. Ковалевской, 18.
Типография УрО РАН.