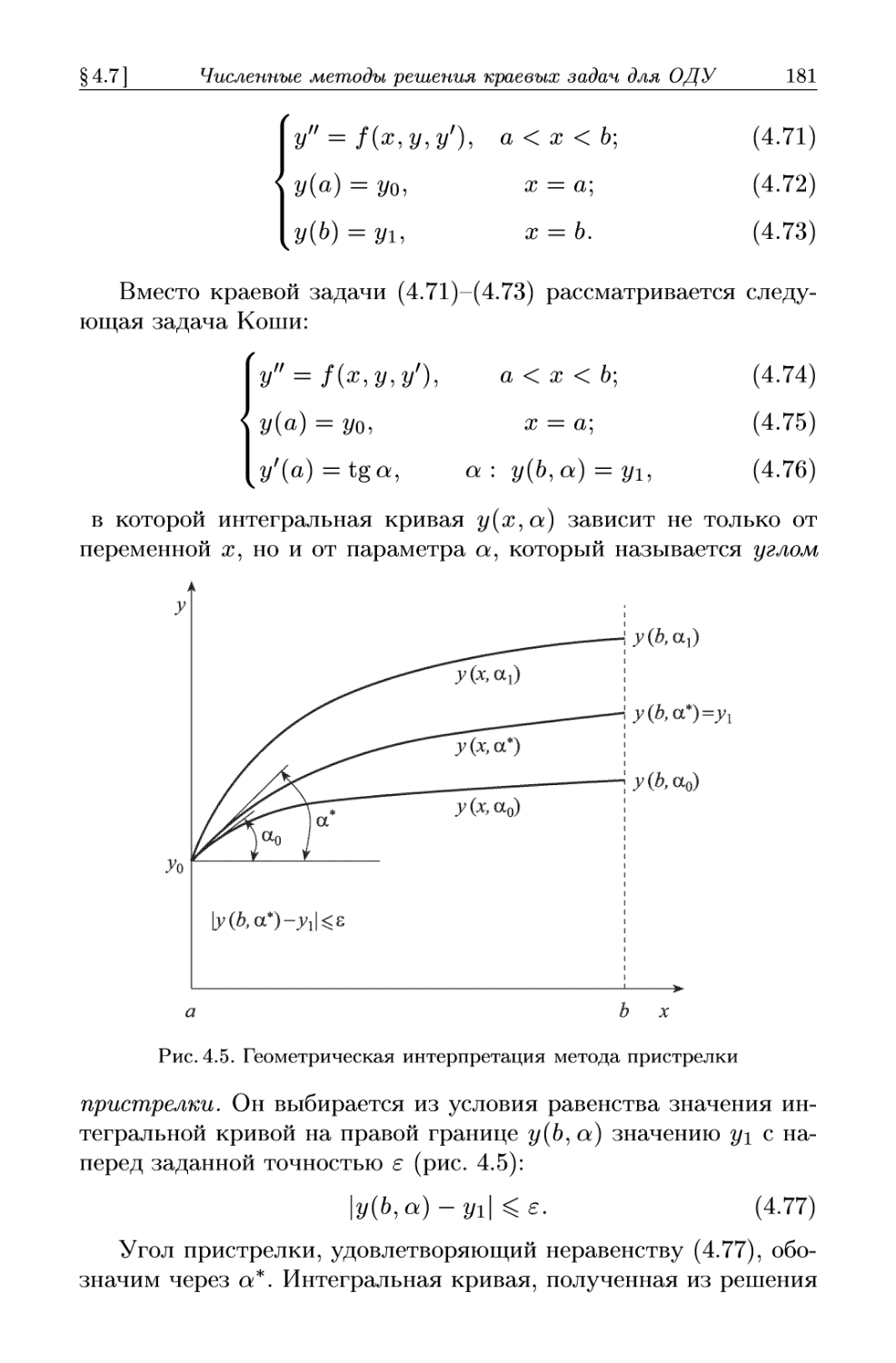
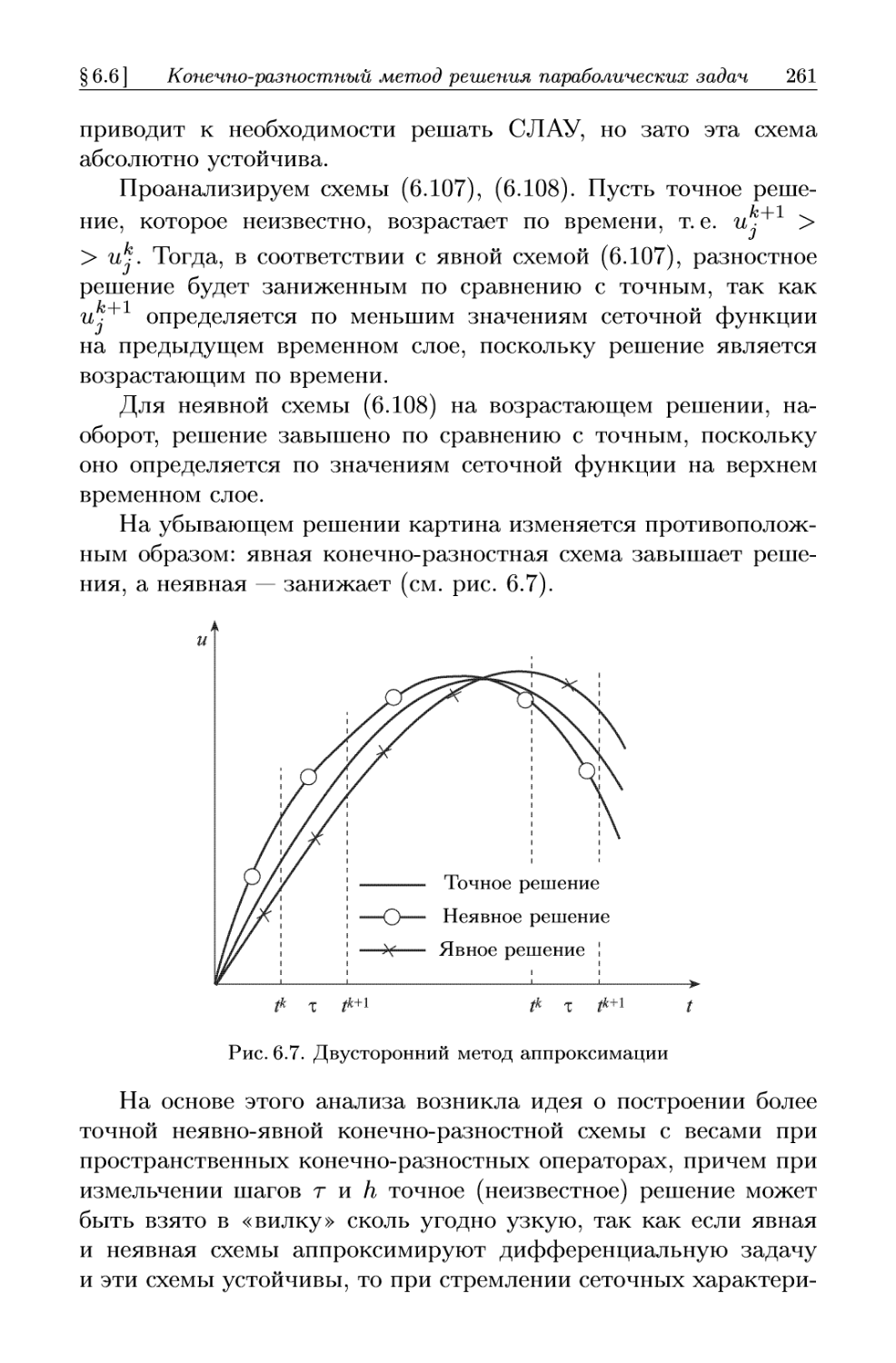
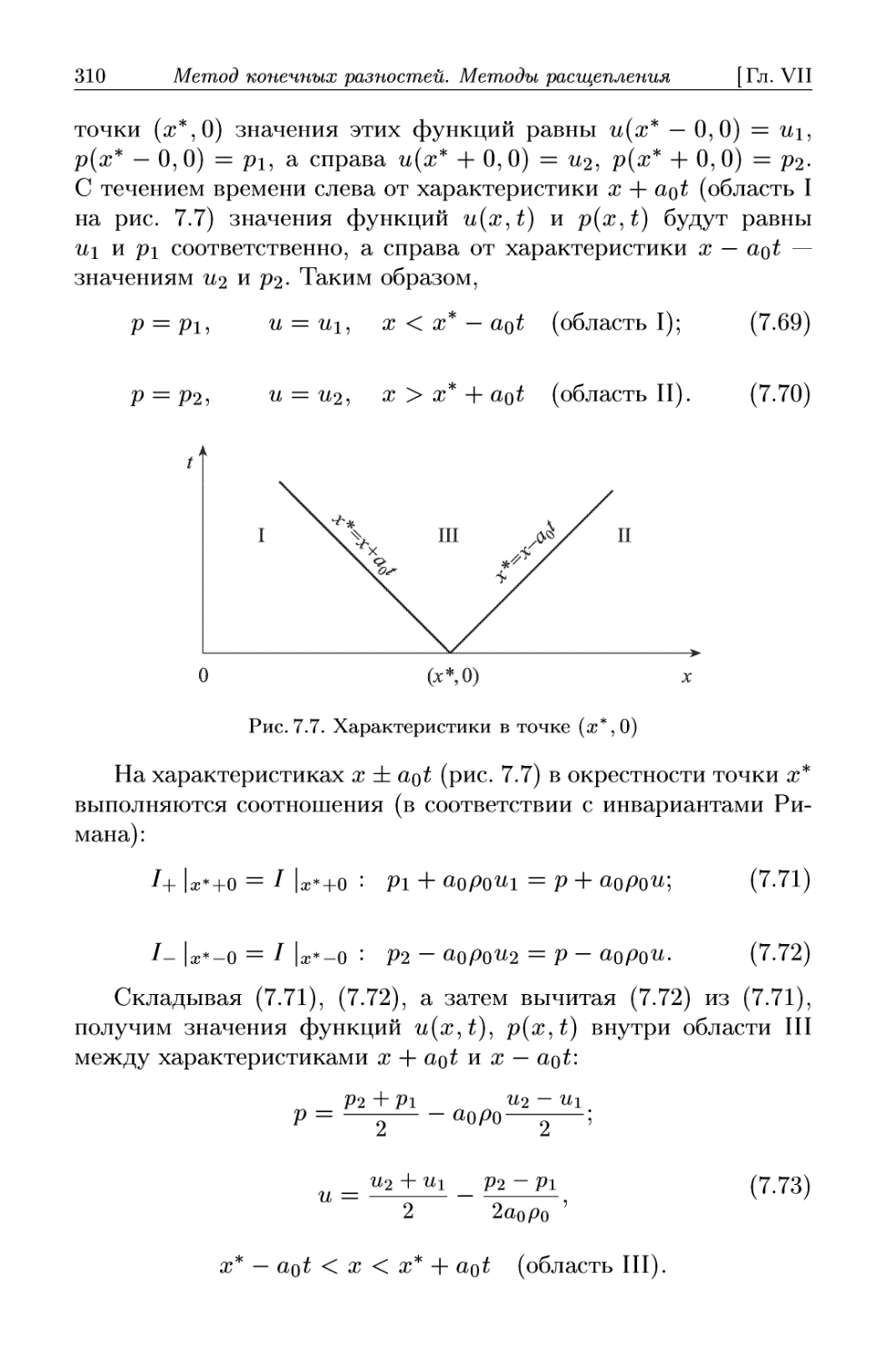
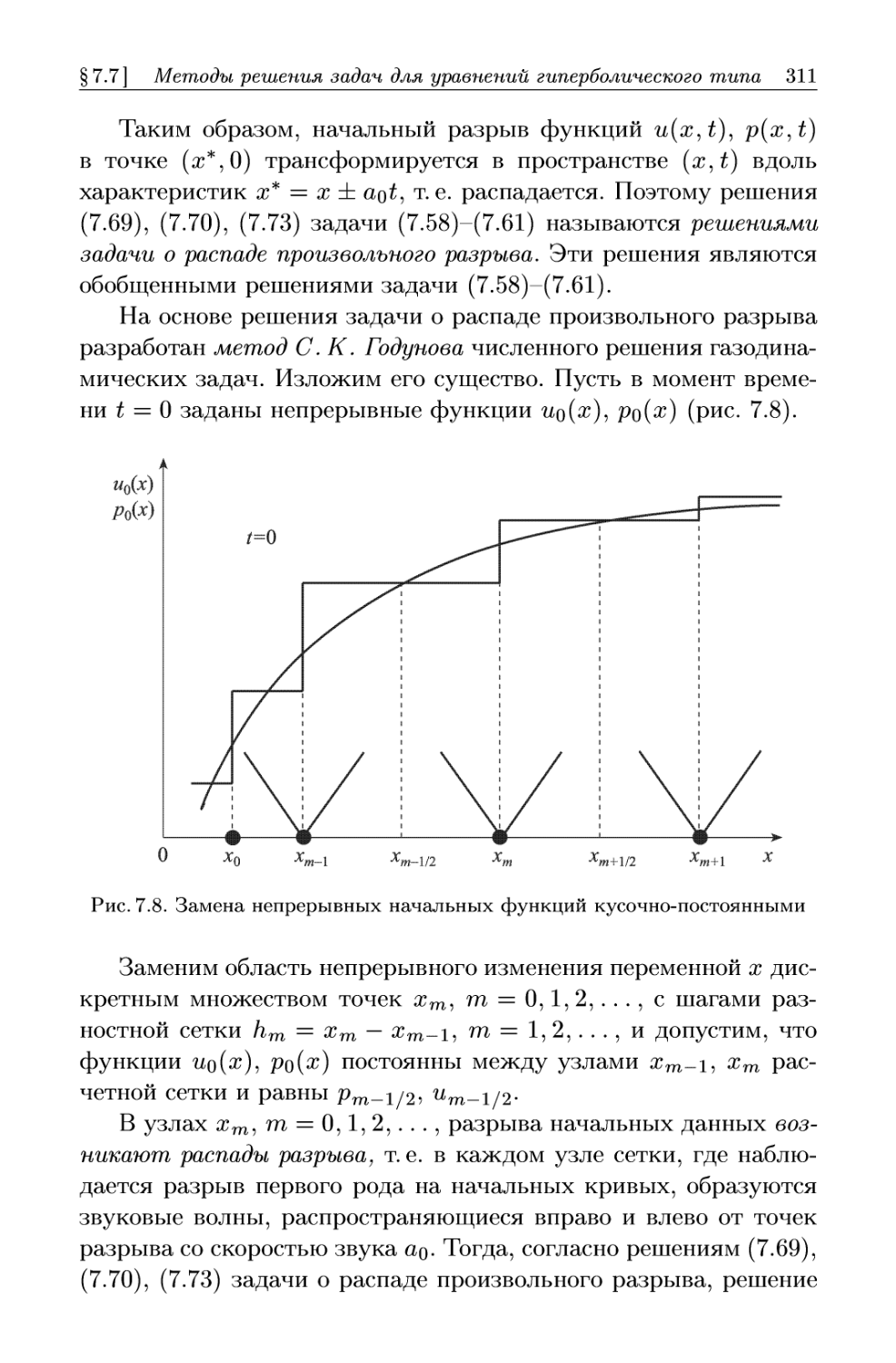
Автор: Формалев В.Ф. Ревизников Д.Л.
Теги: вычислительная математика численный анализ математика
ISBN: 5-9221-0479-9
Год: 2004
Текст
УДК 519.6
ББК 22.19
Ф79
Формалев В. Ф., Ревизников Д. Л. Численные мето-
методы. - М.: ФИЗМАТЛИТ, 2004. - 400 с. - ISBN 5-9221-0479-9.
В учебнике представлены основные численные методы решения
задач алгебры и анализа, теории приближений и оптимизации, за-
задач для обыкновенных дифференциальных уравнений и уравнений
математической физики. Систематически изложены методы конечных
разностей, конечных и граничных элементов, методы исследования
аппроксимации, устойчивости, сходимости, оценок погрешности. Каж-
Каждый метод иллюстрируется подробно разобранным примером, даны
упражнения для самостоятельной проработки.
Для студентов и аспирантов технических университетов, специа-
специализирующихся в области теплотехники, прикладной механики и при-
прикладной математики. Книга ориентирована на двухсеместровый курс
обучения.
© ФИЗМАТЛИТ, 2004
© В. Ф. Формалев, Д. Л. Ревизников,
ISBN 5-9221-0479-9 2004
ПРЕДИСЛОВИЕ
Данный учебник написан на основе двухсеместрового курса
лекций, читавшегося авторами на протяжении пятнадцати лет
студентам математических и механических специальностей Мос-
Московского авиационного института (государственного техническо-
технического университета) (МАИ). Он состоит из двух частей. Первая
часть учебника содержит следующие разделы: элементы теории
погрешностей, численные методы алгебры (как линейной, так
и общей), теорию приближений, численные методы решения за-
задач для обыкновенных дифференциальных уравнений и числен-
численные методы оптимизации.
Вторая часть включает в себя численные методы решения
задач математической физики, исследование аппроксимации,
устойчивости, сходимости и консервативности конечно-разност-
конечно-разностных, конечно-элементных и гранично-элементных методов. Кро-
Кроме этого, во вторую часть учебника вошли разделы по методу ко-
конечных разностей решения многомерных задач математической
физики, среди которых такие методы, как методы расщепления,
установления, прямых, характеристик, метод С. К. Годунова,
а также методы конечных и граничных элементов с анализом
погрешностей.
Отбирая материал для учебника, авторы не загромождали
его изложением всего множества существующих алгоритмов,
а ограничились описанием наиболее широко используемых на
практике и популярных методов, а также изложением новых
эффективных методов.
Вместе с тем изложенные методы вычислений описаны на
таком конструктивном уровне, с использованием решенных при-
примеров и упражнений, что читателю нет необходимости при осво-
освоении материала обращаться к другим источникам по вычис-
вычислительной математике. Правда, он должен обладать знанием
основ линейной алгебры, дифференциального и интегрального
исчислений, обыкновенных дифференциальных уравнений, а для
освоения второй части — основами теории уравнений в частных
производных.
Предисловие
Книга состоит из девяти глав, первые пять из которых состав-
составляют первую часть и содержат материал стандартного односе-
местрового курса численных методов, причем поскольку числен-
численные методы оптимизации читаются, как правило, в отдельном
курсе, то в содержание главы 5 включены только алгоритмы
безусловной минимизации.
В существующих учебниках отсутствует систематическое
изложение метода конечных элементов. Поэтому в данном
учебнике, наряду с систематическим изложением метода
конечных разностей в задачах для обыкновенных дифференци-
дифференциальных уравнений (ОДУ) и уравнений математической физики,
подробно изложены методы конечных и граничных элементов
на основе метода взвешенных невязок Галеркина, а также метод
конечных элементов на основе вариационного принципа.
Кроме этого, в раздел «Методы расщепления численного
решения многомерных задач математической физики» вклю-
включены разработанные авторами новые, экономичные, абсолют-
абсолютно устойчивые методы численного решения многомерных пара-
параболических задач, содержащих смешанные дифференциальные
операторы. Приведено доказательство теорем об аппроксимации
и абсолютной устойчивости.
В отличие от первой части, где для усвоения каждого метода
разбирается соответствующий пример, вторая часть изложена на
основе конкретных задач, обобщающих материал рассматривае-
рассматриваемого раздела.
Таким образом, с позиции содержания материала учебник
носит универсальный характер. В этой связи первую часть
учебника можно рекомендовать студентам, обучающимся по
экономическим и техническим специальностям с односемест-
ровым курсом «Численные методы» или «Численные мето-
методы и алгоритмы». Студентам, обучающимся по специально-
специальностям «Математическая экономика», «Прикладная математика»,
«Прикладная механика» и другим специальностям с углублен-
углубленным изучением математических дисциплин, рекомендуется, на-
наряду с первой частью, и вторая часть учебника, соответствующая
двухсеместровому курсу численных методов.
Кроме студентов, обучающихся по упомянутым выше специ-
специальностям, учебник полезен аспирантам, инженерам, научным
работникам, а также преподавателям вычислительной матема-
Предисловие
тики, которые, кроме всего прочего, могут использовать вторую
часть для чтения специальных курсов.
Значительное влияние на содержание учебника оказал
чл.-корр. РАН, заведующий кафедрой «Вычислительная ма-
математика и программирование» МАИ, профессор У. Г. Пирумов.
Авторы выражают ему свою глубокую благодарность.
Авторы глубоко признательны и аспирантам СВ. Миканеву,
С. А. Колеснику, Т. А. Тихоновой, оказавшим неоценимую по-
помощь при компьютерном наборе рукописи учебника.
ВВЕДЕНИЕ
В настоящее время появилось значительное число различных
программных продуктов (MathCad, Mathlab и т.д.), с помощью
которых, задавая только входные данные и не вникая в сущность
алгоритмов, можно решить значительное число задач, на обуче-
обучение решению которых и направлен данный учебник.
Безусловно, умение пользоваться этими программными про-
продуктами существенно сокращает время и ресурсы по решению
ряда важных задач. Вместе с этим бездумное использование
упомянутых выше программ без тщательного анализа метода,
с помощью которого решается задача, таит в себе следующие
опасности.
Во-первых, все методы имеют ограничения по входным па-
параметрам (например, по размерам матриц при решении систем
линейных алгебраических уравнений), и попытка решить задачу
с входными параметрами за пределами этих ограничений приво-
приводит к неудаче.
Во-вторых, сами методы, в основном численные, имеют су-
существенные ограничения по применению.
В-третьих, незнание метода, с помощью которого решалась
конкретная задача в програмном продукте, приводит к ситуа-
ситуации, когда трудно проанализировать качество решения (напри-
(например, погрешность, скорость сходимости итерационных процессов,
устойчивость и другие важнейшие характеристики численных
методов).
В-четвертых, стандартные программные продукты значи-
значительно ограничены количеством решаемых задач, среди которых
в основном линейные задачи. Вне сферы их применения остается
большинство задач, связанных с уравнениями математической
физики и др.
Поэтому при численном решении задач (а именно с помощью
численных методов решается подавляющее число современных
задач) вычислитель должен четко представлять каждый из сле-
следующих этапов: построение адекватной математической моде-
модели, выбор метода численного решения, разработку алгоритма,
составление программы, формальную, а затем и фактическую
Введение
отладку программы, корректировку и исправление всех этапов,
начиная с математической модели, на основе анализа тестовых
результатов.
Как видно из перечисления этапов решения задач, путь от
постановки до получения результатов не краток. В этой связи
следует заметить, что если неопытный вычислитель после осу-
осуществления первых четырех этапов считает, что задача решена,
то опытный знает, что первый находится в начале сложного пути
с неожиданными результатами и поворотами.
Учебник состоит из девяти глав, неравнозначных по объему.
Самая краткая первая глава содержит элементы теории по-
погрешностей. В ней авторы обращают внимание на тот факт, что
абсолютная погрешность не превышает точности вычислений.
С помощью введенного неравенства легко проясняется существо
фразы: «Решить задачу с точностью ?», хотя всюду имеем дело
с оценкой погрешностей.
Вторая глава посвящена численным методам решения задач
алгебры (как линейной, так и общей). Здесь внимание обраща-
обращается на следующие вопросы, связанные с применением итераци-
итерационных методов:
1. Сходится ли итерационная последовательность, т.е. суще-
существует ли предел итерационной последовательности при стрем-
стремлении количества итераций в бесконечность?
2. Если такое предельное значение существует, то является
ли оно решением задачи?
3. Если получен положительный ответ на первые два вопроса,
то, останавливая итерационный процесс на какой-либо итерации,
необходимо оценить сверху погрешность решения итерационным
методом по сравнению с точным (неизвестным, но существую-
существующим) решением. Если при этом задана точность вычислений, то
из неравенства «погрешность не превышает точность» можно
оценить нижнюю границу числа итераций для достижения за-
заданной точности.
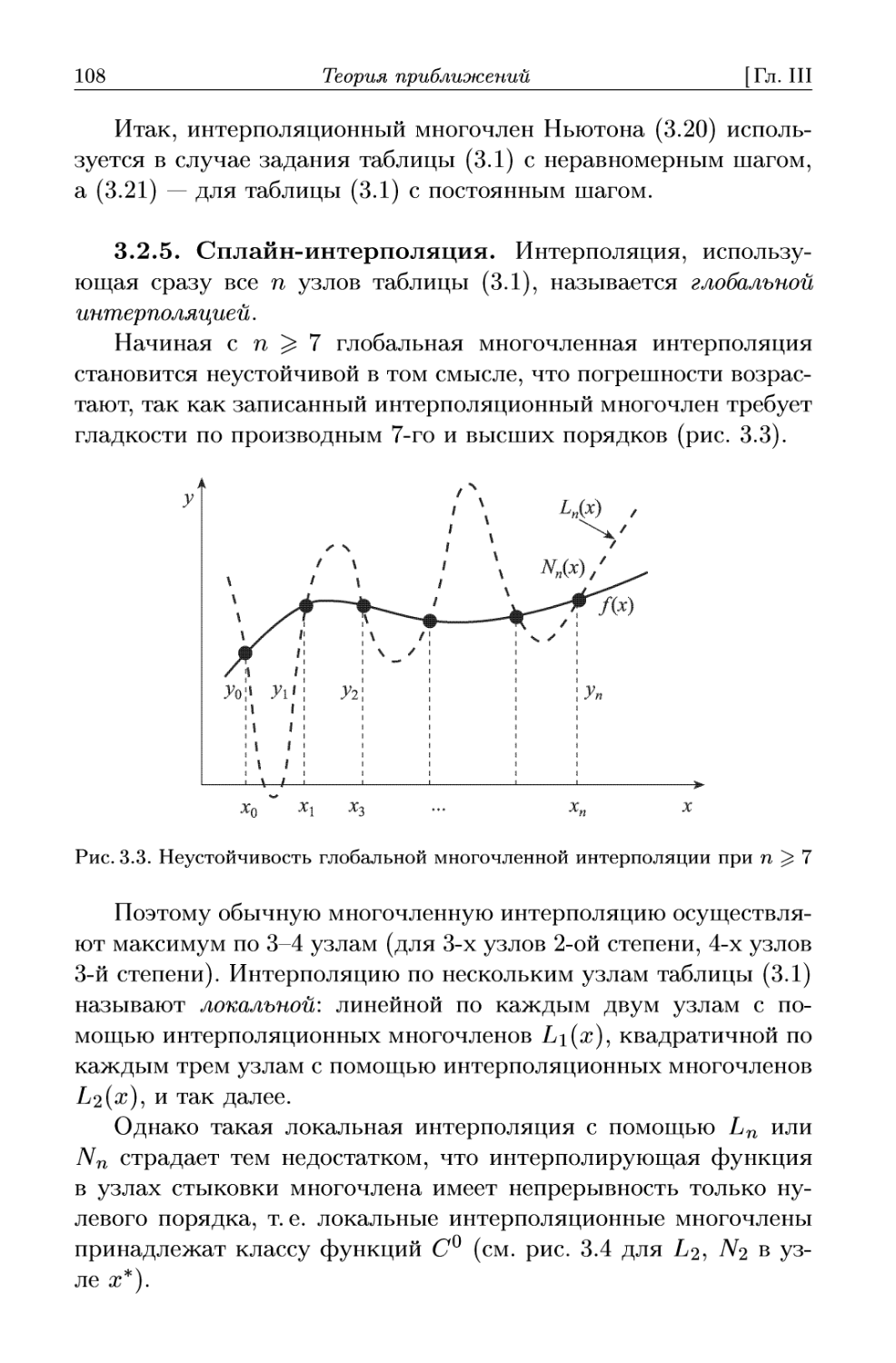
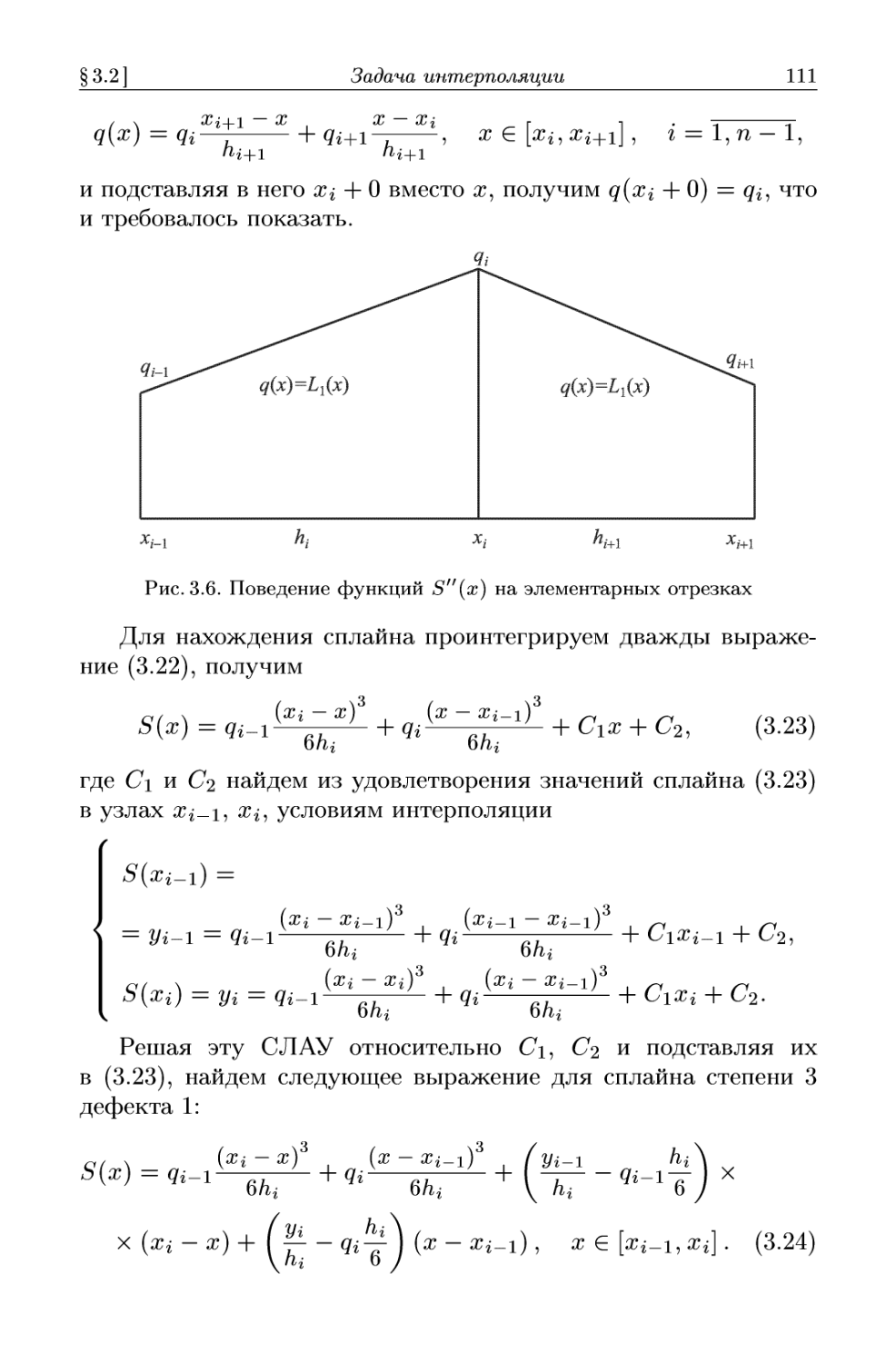
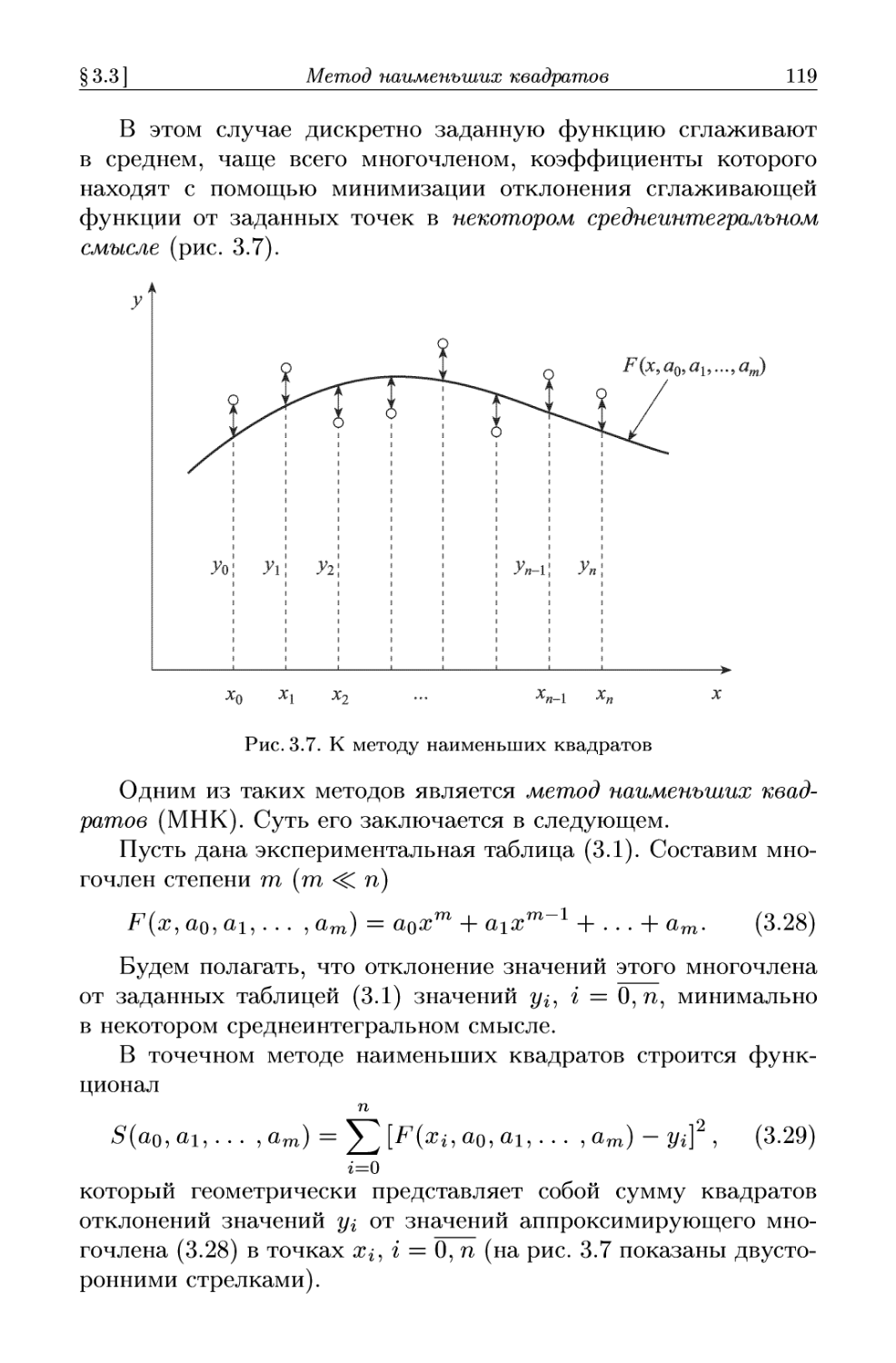
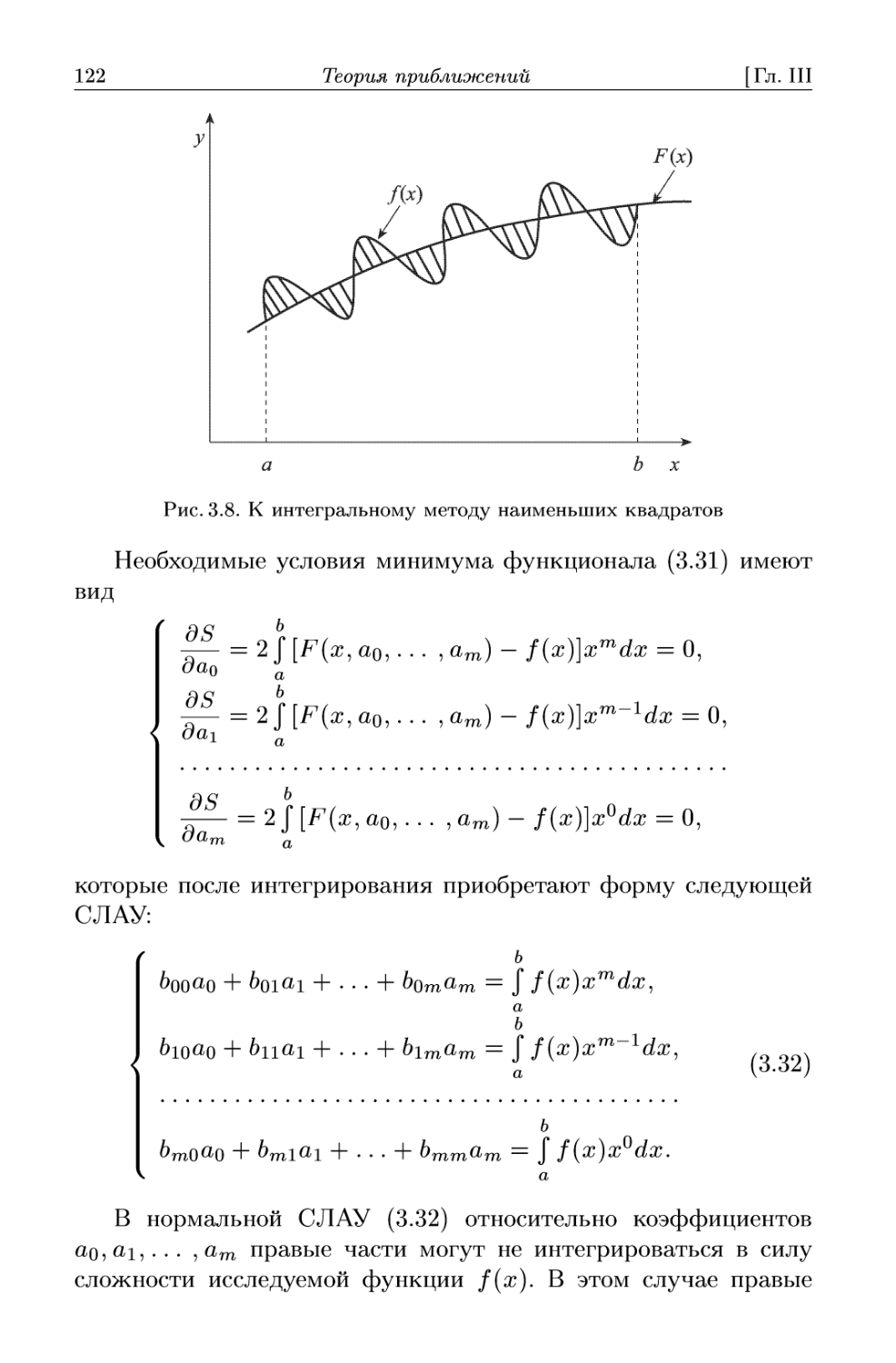
Третья глава содержит основы теории приближений и вклю-
включает следующие разделы: интерполяцию, включая и сплайн-
интерполяцию, аппроксимацию с помощью метода наименьших
квадратов, численное дифференцирование и численное инте-
интегрирование. При этом обращается внимание на то, что метод
численного дифференцирования с помощью отношения конеч-
конечных разностей с оценкой погрешности метода является осно-
Введение
вой конечно-разностного решения задач как для обыкновенных
дифференциальных уравнений, так и для уравнений в частных
производных.
Четвертая глава посвящена численным методам решения
задач для обыкновенных дифференциальных уравнений (задач
Коши и краевых задач). При этом известные и хорошо заре-
зарекомендовавшие себя методы численного решения задач Коши,
такие как методы Эйлера, Эйлера-Коши, Рунге-Кутта, сформу-
сформулированы соответственно на основе квадратурных формул пря-
прямоугольников, трапеций, Симпсона, что позволяет использовать
для оценки погрешности соответствующие оценки для квадра-
квадратурных формул.
Конечно-разностный метод решения краевых задач для ОДУ
с граничными условиями, содержащими производные, описан
так, что порядок аппроксимации дифференциального уравнения
сохранен при аппроксимации краевых условий. Это достигается
допущением о том, что гладкость решений на границах совпа-
совпадает со старшей производной, входящей в дифференциальное
уравнение и дальнейшим использованием дифференциального
уравнения при аппроксимации краевых условий. Ниже, в шестой
главе будет показано, что такой подход не просто выравнивает
порядок аппроксимации краевых условий с порядком аппрок-
аппроксимации дифференциального уравнения, но и делает конечно-
разностную схему консервативной, сохраняющей фундаменталь-
фундаментальные законы, на основе которых выведены дифференциальное
уравнение и краевые условия.
В пятую главу включен материал по численным методам,
безусловной минимизации функций одной и многих переменных,
причем, как отмечалось выше, более сложные аспекты числен-
численных методов математического программирования включаются
в отдельные курсы.
Шестая глава посвящена методам решения задач для
уравнений математической физики. Здесь, кроме конечно-
разностных схем в задачах для уравнений гиперболического, па-
параболического и эллиптического типов и алгоритмов их решения,
сделан акцент на строгое определение понятий аппроксимации,
порядка аппроксимации, устойчивости, сходимости, порядка
сходимости (порядка точности), консервативности, а также на
описание различных методов исследования устойчивости и на-
нахождения порядка аппроксимации. Проанализированы неявно-
Введение 9
явные конечно-разностные схемы, как следствие двусторонних
методов, с исследованием аппроксимации и устойчивости для
схем типа Кранка-Николсона. Идеи, заложенные в этой схеме,
активно используются в методах расщепления для многомерных
задач математической физики. Здесь показано, что конечно-
разностная аппроксимация производных первого порядка в кра-
краевых условиях с помощью отношения односторонних разностей
без использования дифференциального уравнения приводит,
с одной стороны, к схемам пониженного порядка, а с другой —
к схемам, не обладающим свойством консервативности. То есть
приведен пример неконсервативной схемы, пользоваться которой
не рекомендуется, так как численно решается задача, отличная
от дифференциальной задачи.
В главе на основе трудов А. А. Самарского подробно опи-
описан энергетический метод исследования устойчивости конечно-
разностных схем, в котором энергетическое тождество приводит
к достаточным условиям устойчивости вследствие выполнения
принципа максимума. Метод гармонического анализа, также по-
подробно изложенный, дает только необходимые условия устой-
устойчивости.
В седьмой главе приведены численные методы решения мно-
многомерных задач математической физики, такие как методы
расщепления, метод характеристик для квазилинейных гипербо-
гиперболических систем, метод прямых, метод сквозного счета С. К. Го-
Годунова. Наряду с широко известными методами переменных
направлений Писмена-Рэчфорда и дробных шагов Н.Н. Янен-
ко, рассмотрены экономичные абсолютно устойчивые методы
переменных направлений с экстраполяцией и полного расщеп-
расщепления, принадлежащие авторам. В отличие от существующих
методов, предложенные методы применимы к задачам, содер-
содержащим смешанные производные и любую размерность по про-
пространственным переменным с сохранением при этом порядка
аппроксимации и абсолютной устойчивости, что обосновыва-
обосновывается доказательством соответствующих теорем. Для всех мето-
методов расщепления исследованы порядок аппроксимации и устой-
устойчивость.
Восьмая и девятая главы посвящены систематическому из-
изложению методов конечных и граничных элементов соответ-
соответственно. Основное внимание уделено методу взвешенных невязок
Галеркина, поскольку вариационные методы в методе конечных
10 Введение
элементов (МКЭ) существенно ограничивают круг решаемых за-
задач, так как не для всякой задачи математической физики можно
построить вариационный функционал. В главе показано, что ва-
вариационный функционал с использованием метода Релея-Ритца
можно всегда построить для дифференциальных уравнений, со-
содержащих симметрический дифференциальный оператор. Изло-
Изложен метод нахождения погрешности конечно-элементного реше-
решения в классе функций, принадлежащих пространству Соболева
W\. В этот класс, как известно, входят кусочно-линейные базис-
базисные функции, на основе которых строится решение.
Метод граничных элементов изложен для стационарных за-
задач математической физики в многосвязных пространственных
областях, хотя для нестационарных задач можно поступить так
же, как в методе конечных элементов, где дифференциальный
оператор по времени аппроксимирован с помощью отношения
конечных разностей, а пространственные — с помощью метода
конечных элементов.
Часть I
ЧИСЛЕННЫЕ МЕТОДЫ АЛГЕБРЫ
И АНАЛИЗА
В первую часть включены следующие разделы стандартно-
стандартного односеместрового курса «Численные методы»: 1) элементы
теории погрешностей; 2) численные методы алгебры; 3) теория
приближений; 4) численные методы решения задач для обык-
обыкновенных дифференциальных уравнений; 5) численные методы
оптимизации.
ГЛАВА I
ЭЛЕМЕНТЫ ТЕОРИИ ПОГРЕШНОСТЕЙ
Программа
Погрешности, их источники, устранимые и неустранимые погреш-
погрешности. Абсолютная и предельно абсолютная погрешности. Абсолютные
погрешности выражений. Значащие и верные цифры. Точность, соот-
соотношение между погрешностью и точностью. Округление чисел.
Погрешность решения задачи обусловливается следующими
причинами.
1. Математическое описание и исходные данные являются
неточными.
2. Применяемые методы являются чаще всего приближенны-
приближенными, мало того, решение не может быть получено за конечное
число арифметических операций.
3. В процессе вычисления проводятся округления. В соответ-
соответствии с этим погрешности называют:
1) неустранимыми погрешностями;
2) погрешностями метода]
3) вычислительными погрешностями.
12 Элементы теории погрешностей [Гл. I
Пусть а — приближенное число для точного числа А. По-
Погрешностью Аа приближенного числа а называют разность
Аа = А — а.
Абсолютной погрешностью А (а) приближенного числа а на-
называют абсолютную величину погрешности
А(а) = \А - а\ ,
позволяющую отвлечься от знака погрешности.
Поскольку в большинстве случаев точное значение числа А
неизвестно и, следовательно, невозможно вычислить абсолют-
абсолютную погрешность, вводят понятие предельной абсолютной по-
погрешности Аа приближенного числа а, удовлетворяющее сле-
следующему соотношению:
Д(а) = \А-а\ ^ Аа,
или
а- Аа ^ А ^ а + Аа.
При вычислении абсолютных (предельных абсолютных) по-
погрешностей выражений удобно использовать формулы диффе-
дифференцирования, заменяя дифференциалы независимых перемен-
переменных абсолютными (предельными абсолютными) погрешностями.
Пример 1.1.
А(а + Ь) = А(а) + А(Ь) ^Аа + А6;
А(а -Ь) = А(а) - А(Ь) ^ Аа + Аь.
Пример 1.2.
А(а • Ь) = аА(Ь) + ЬА(а) ^ аАъ + ЬАа.
Пример 1.3.
д / " 1 A(a)b - aA(b) aAb + ЬАа
(!) =
Пример 1.4- Вычислить А ( ( —-
Гл. I]
Элементы теории погрешностей
13
Решение. Пусть du(a, 6, с, /)« А I ( ) ) . Тогда
д и
д и
= 2
Д(а) + ^АF) + /JД(с)
Значащими цифрами приближенного числа а называются все
цифры в его записи, начиная с первой ненулевой слева.
Пример 1.5. а = 0,02087, а = 0,0208700 (значащие цифры
подчеркнуты).
Если приближенное число а имеет п значащих цифр , то
за предельную абсолютную погрешность числа а принимают
половину единицы разряда, выражаемого п-й значащей цифрой,
считая слева направо.
Пример 1.6. Пусть даны величины а с предельными абсо-
абсолютными погрешностями Аа:
а
Аа
-2,17
0,005
3,141
0,0005
0,012
0,0005
1795
0,5
Тогда, например, для числа а = —2,17 : —2,175 ^ А ^ —2,165.
Относительной погрешностью 5(а) приближенного числа а
называется отношение в долях единицы:
\А-а\ _ А(а)
5(а) =
Предельной относительной погрешностью да приближенно-
приближенного числа а называют число, не меньшее относительной погреш-
погрешности этого числа:
14 Элементы теории погрешностей [Гл. I
х, , \А - а\ г.
или
8а ^ А ^ а + \а 5а.
8а
5а.
а — \а
Ясно, что
5а =
Значащую цифру приближенного числа а называют верной,
если абсолютная погрешность этого числа не превышает полови-
половины единицы разряда, соответствующего этой цифре (не превы-
превышает предельной абсолютной погрешности числа).
Пример 1.7. Для приближенного числа а = 0,02087 с аб-
абсолютной погрешностью А (а) = 0,4 • 10~5 определить верные
значащие цифры.
Решение. Поскольку данная погрешность числа не превы-
превышает предельной абсолютной погрешности этого числа, равной
Аа = 0,5 • 10, т.е. Д(а) = 0,4 • 10 < Аа = 0,5 • ИГ5, то вер-
верными будут значащие цифры 7, 8, 0, 2, т.е. а = 0,02087 (верные
цифры подчеркнуты).
Вычислить приближенное число а с точностью до е = 10~п
означает необходимость сохранить верной значащую цифру, сто-
стоящую в п-м разряде после запятой.
Пример 1.8. Вычислить л/2 с точностью е = 10~3.
Решение, л/2 = 1,4142; третья цифра после запятой явля-
является верной, т.к. A(v/2) = |1,4142 - 1,414| = 0,0002 < 0,0005 =
= Аа < е = 10~3. Следовательно, все подчеркнутые цифры яв-
являются верными.
Таким образом, из определения абсолютной погрешности
приближенного числа а и точности его вычисления вытекает
очевидная связь:
А(а) < Аа < е,
т. е. абсолютная погрешность и предельная абсолютная погреш-
погрешность не превышают точности.
Относительная погрешность суммы, разности, произведе-
произведения, частного не превышает суммы относительных погрешно-
погрешностей операндов: 5(а ± Ь) ^ 5(а) + S(b); 5(а • b) ^ S(a) + S(b);
S (a/b) ^ S(a) + S(b). Относительная погрешность степени не
Гл. I] Элементы теории погрешностей 15
превышает произведения показателя степени на относительную
погрешность основания: д(ат) ^ тд(а)] д( ш/а) ^ 5{а)/т.
При округлении приближенного числа а до п-й значащей
цифры необходимо к цифре (п + 1)-го разряда прибавить циф-
цифру 5; если полученное число больше или равно 10, то к цифре п-
го разряда добавляется единица, а разряды начиная с (п + 1)-го
отбрасываются; в противном случае разряды начиная с (п + 1)-
го отбрасываются без прибавления единицы к n-му разряду.
Пример 1.9. Округлить число тг = 3,141592: а) до третьей
значащей цифры; б) до четвертой значащей цифры.
Решение, а) 3,14, так как 1,592 + 5 = 6,592 < 10; б) 3,142,
так как 5,92 + 5 = 10,92 > 10.
ГЛАВА II
ЧИСЛЕННЫЕ МЕТОДЫ АЛГЕБРЫ
Программа
Прямые методы решения систем линейных алгебраических уравне-
уравнений (СЛАУ). Метод Гаусса, его применение для обращения и вычисле-
вычисления определителей матриц. Метод прогонки и циклической прогонки,
их обоснование. Матричная прогонка. Нормы векторов и матриц, их
согласование. Итерационные методы решения СЛАУ. Метод простых
итераций и метод Зейделя с обоснованием сходимости. Методы реше-
решения нелинейных уравнений. Методы отделения и уточнения корней,
геометрический смысл, сходимость, погрешность методов: половин-
половинного деления, Ньютона, секущих, простых итераций. Скорость схо-
сходимости, методы ускорения сходимости. Методы простых итераций,
Зейделя и Ньютона решения систем нелинейных уравнений. Числен-
Численные методы решения задач на собственные значения и собственные
векторы матриц. Метод вращения Якоби, степенной метод.
В главе «Численные методы алгебры» рассматриваются чис-
численные методы решения систем линейных алгебраических урав-
уравнений (СЛАУ), численные методы решения нелинейных уравне-
уравнений и систем нелинейных уравнений, численные методы решения
задач на собственные значения и собственные векторы матриц.
Среди численных методов алгебры существуют прямые мето-
методы, в которых решение получается за конечное число операций,
и итерационные методы, в которых результат получается за
бесконечное число операций, но прерывая этот процесс на какой-
либо итерации необходимо сделать следующее:
1) доказать сходимость итерационной последовательности;
2) если итерационная последовательность сходится, необхо-
необходимо определить, является ли предельное значение решением
задачи;
3) при утвердительном ответе на первые два вопроса и оста-
остановке процесса на какой-либо итерации необходимо уметь оце-
оценить погрешность итерационного значения по сравнению с точ-
точным решением, которое неизвестно.
§2.1]
Численные методы решения СЛАУ
17
§2.1. Численные методы решения СЛАУ
Из прямых методов решения СЛАУ рассмотрим методы Гаус-
Гаусса и прогонки [1,2].
2.1.1. Метод Гаусса. В методе Гаусса матрица СЛАУ с по-
помощью элементарных алгебраических операций преобразуется
в верхнюю (нижнюю) треугольную матрицу, получающуюся
в результате прямого хода. В обратном ходе определяются неиз-
неизвестные.
Пусть дана СЛАУ
а\пхп =
«22^2
ап2х2
п = Ьп.
Запишем расширенную матрицу системы с контрольными
суммами:
Ведущая строка
Х\
- • • Хп Ь
|-
«11
«21
«3,
4-
«12 «13-
«22«23-
«32 «33 •
«п2«пЗ-
- Прдти
• -«In
• -«2n
• -«Зп
им
bi
b2
h
Ьп
?3
-6x4
= ь2ч
= bs^
= bn -
n
- 2^ aij
.7=1
n
- E O2j
n
" Z^ a3j
n
ь Е anj
1-й шаг
столбец
На первом шаге алгоритма Гаусса выберем диагональный
элемент ац ф 0 (если он равен 0, то первую строку переставляем
с какой-либо нижележащей строкой) и объявляем его ведущим,
а соответствующую строку и столбец, на пересечении которых
он стоит, — ведущими. Обнулим элементы ведущего столбца,
18
Численные методы алгебры
[Гл. II
находящегося под ведущим элементом. Для этого сформиру-
«21 \ . / _^П \ / «nl
I ' I ) I
ем числа
он
и выпишем их около
ведущей строки. Умножая ведущую строку на число ( —
V аи
складывая со второй и ставя результат на место второй строки,
получим вместо элемента a<i\ нуль, а вместо элементов a^j, j =
соответственно элементы а\- = a2j + a\j ( —
V аи
= 2, n, 62 и
j = 2,n, 6^ =
=
«21
«и
И так
«nl
далее. Умножая ведущую строку на число — , складывая
с n-ой строкой и ставя результат на место n-ой строки, получим
вместо элемента ап\ нуль, а остальные элементы этой строки
будут иметь вид: а1- = anj + «ij ( -— ),b1n = bn + bi[ -— ),
J \ «n/ V an /
Si = Е„ + Si -
«nl
«11
. Сохраняя ведущую строку неизменной,
получим в результате 1-го шага алгоритма Гаусса следующую
матрицу (при этом сумма преобразованных элементов какой-
либо строки и правой части должна быть равна преобразованной
по тому же алгоритму контрольной сумме; если это не так, то
в соответствующей строке сделана ошибка, которую необходимо
устранить):
. . . х
0
0
0
«12
а22
а32
а1г2
4
«13- • -«In
а23* * -а2п
аЗЗ * * * аЗп
а1пЗ'"а1пп
— Rprlimiim,
bi
bl
bl
bi
Si
n
Ведущая строка
2-й шаг
столбец
Ha втором шаге алгоритма Гаусса в качестве ведущего эле-
элемента выбирается элемент а\2 ф 0 (если он равен нулю, то вто-
§2.1]
Численные методы решения СЛАУ
19
рую строку меняем местами с нижележащей строкой). Форми-
Формируются числа I
Х32
а22
а22
, которые ставятся около
а32
ведущей строки. Умножая ведущую строку на число ( ^ I,
а22
складывая с третьей строкой и ставя результат на место третьей
строки, получим вместо элемента а\2 нуль, а вместо элементов
я 3 =
— элементы
22
= b\ + h\ f-ф) , E§ = ?i + Si f-ф ). И так далее.
22
Умножая ведущую строку на число ( у^ ), складывая резуль-
V « У
22
тат с п-ой строкой и ставя полученную сумму на место п-ой
строки, получим вместо элемента а^2 нуль, а вместо элементов
- элементы
a2nj = а\. + а\. ( -°^ ), j = 3~гг, Ь\ =
\ а22 /
= Ь\ + Ь\ (-Ф), ^1 =
V а22
+
ф
-ф). Сохраняя 1-ю и 2-
а22
ю строки матрицы неизменными, получим в результате второго
шага алгоритма Гаусса следующую матрицу (при этом сумма
преобразованных элементов какой-либо строки и правой части
должна быть равна преобразованной контрольной сумме; если
это не так, то в соответствующей строке сделана ошибка):
Х\ Х2
CL\\ Oi\2
0 а\2
0 0
0 0
Хз
а23
2
азз
... хп
¦¦-ain
•••aln
¦¦¦aln
2
• • -а^гп
b
h
bl
bl
bl
Si
S1
3-й шаг
(n — 1)-й шаг
После (n — 1)-го шага алгоритма Гаусса получаем следую-
следующую расширенную матрицу с контрольными суммами, содержа-
20
Численные методы алгебры
[Гл. II
щую верхнюю треугольную матрицу СЛАУ:
х\ Х2 жз . . . хп b
ап
0
0
0
«12
°22
0
0
аи
а23
2
аЗЗ
0
... а1п
... а\п
... а\п
. . . &пп
ъ\
bl
Si
s|
s§
Прямой ход алгоритма Гаусса завершен.
В обратном ходе алгоритма Гаусса из последнего уравнения
сразу определяется жп, из предпоследнего — хп-\ и т.д. Из
первого уравнения определяется х\:
"-'Tl 9
- . . . + ainxn = b\ => Ж1.
Замечание 1. Если элементы какой-либо строки матрицы си-
системы в результате преобразований стали равными нулю, а пра-
правая часть не равна нулю, то СЛАУ несовместна, поскольку не
выполняются условия теоремы Кронекера-Капелли.
Замечание 2. Если элементы какой-либо строки матрицы си-
системы и правая часть в результате преобразований стали равны-
равными нулю, то СЛАУ совместна, но имеет бесконечное множество
решений, получающихся с помощью метода Гаусса для СЛАУ
порядка г, где г — ранг матрицы исходной СЛАУ.
Замечание 3. В результате прямого хода метода Гаусса можно
вычислить определитель матрицы А исходной СЛАУ:
det A =
«
п-1
При этом в случае перестановки строк в процессе прямого
хода необходимо учитывать соответствующие перемены знаков.
Замечание 4- Метод Гаусса можно применить для обращения
невырожденной (det А ф 0) матрицы.
§2.1]
Численные методы решения СЛАУ
21
Действительно, пусть требуется обратить невырожденную
матрицу А = [dij], i,j = 1,п. Тогда, обозначив А~х = X, X =
= [xij], i,j = 1, гг, можно выписать матричное уравнение АХ =
= Е, где Е — единичная матрица
Е =
1 0 ... О
О 1 ... О
О 0 ... 1
на основе которого можно записать цепочку СЛАУ
, ... , А-
г11!
#21
\XnlJ
=
Л
0
W
, А-
Г2)
\Хп2/
=
1
\ 1 /
каждую из которых можно решить методом Гаусса. При этом,
поскольку верхняя треугольная матрица для всех этих СЛАУ
будет одной и той же, то метод Гаусса применяется один раз. Для
этого строится следующая расширенная матрица с контрольны-
контрольными суммами:
Х\п
Х\2
хц
аи
О<21
Х2п
^22
Ж21
^12
^22
аП2
• • • хпп
. . . Хп2
. . . Хп\
.. . а\п
. . . CL2n
• • • &пп
ь1
1
0
0
ъ2 ¦
0 ...
1 ...
0 ...
0
0
1
Si
Sn
22
Численные методы алгебры
[Гл. II
В результате применения (п — 1)-го шага метода Гаусса по-
получаем
xln
XVI
Хц
ОЦ
0
х2п.
Ж22 •
«21 •
«12 ••
а22 ¦ ¦
0 ..
¦ ¦хпп
¦ ¦хп2
. . Хп\
• din
• а2п
п-1
Ьп
Ьп!1
b2 ¦
bl2 ¦
b\2 .
Ьп2г '
.. bn
• • Ь\п
• • ^n1
Si
s1
При этом первый столбец (хц х^\ • • • хп\ )Т обратной матрицы
определяется в обратном ходе метода Гаусса с правой частью б1,
столбец ( ж 12 #22 • • • %п2 )Т — с правой частью б2 и т. д. Столбец
%2n • • • %пп )Т определяется с правой частью Ьп.
Пример 2.1. Методом Гаусса решить СЛАУ
+ Х2 +
Решение.
Прямой ход:
х\ Х2 хз b
= 12,
= 13,
= 14.
10 1 1
2 10 1
V 2 2 10
24 \
26
28
(-2/10); (-2/10)
1-й шаг
1-й шаг
Xl
fio
0
X2
1
9,8
1,8
0
9
хз
1
,8
,8
b
12
10,6
11,6
к
s
24 ^
21
23
2
2/
(-1,8/9,8)
2-й шаг
§2.1]
Численные методы решения СЛАУ
23
2-й шаг
Х\ Х2 Жз
10 1 1
0 9,8 0,8
О 0 9,653
12
10,6
9,653
24 \
21,2
19,31
Обратный ход:
9,653ж3 = 9,653, х3 = 1
= 10,6, х2 = 1
з = 12, Ж1 = 1.
Ответ: жх = х<х = х% = 1.
Пример 2.2. Методом Гаусса вычислить определитель мат-
матрицы и обратить матрицу СЛАУ из примера 2.1
А =
10 1 1 \
2 10 1
\ 2 2 10/
Решение.
det A = 10 • 9,8 • 9,65 = 945,994 (точное значение 946).
Прямой ход:
жзз
Ж12 Ж22 Ж32
Х\\ Ж21 Ж31
10 1 1
2 10 1
2 2 10
1
0
0
0
1
0
0
0
1
13 \
14
15/
(-2/10); (-2/10)
1-й шаг
24
Численные методы алгебры
[Гл. II
#13 #23 Жз3
Ж12 #22 #32
#11 #21 #31
10 1 1
0 9,8 0,8
V 0 1,8 9,8
Ь2 Ь3
10 0
-0,2 1 О
-0,2 О 1
13
11,4
12,4/
(-1,8/9,8)
2-й шаг
#13 #23 Жзз
#12 #22 #32
#11 #21 #31 Ь1
2-й шаг
10 1 1
О 9,8 0,8
О 0 9,653
-0,2
0 О
1 О
-0,163 -0,184 1
13 \ "
11,4
10,31
Обратный ход:
9,653ж31 = -0,163,
0,8ж31 = -0,2,
#2i + #3i = 1;
9,653ж32 = -0,184,
9,8ж22 + 0,8ж32 = 1,
10Ж12 + #22 + #32 = 0;
9,653ж33 = 1,
9,8ж23 + 0,8жзз = 0,
10Ж13 + #23 + #33 = 0.
Отсюда А =
Проверка:
/жцж12#1з\ / 0,104 -0,0085-0,0095^
#21 #22 #23 = -0,019 0,104 -0,0085
V#3i#32#33/ \-0,0169 -0,019 0,104 )
§2.1]
Численные методы решения СЛАУ
25
ю l 1 Л
2 10 1
V 2 2 10 У
/ 0,104 -0,0085-0,0095^
-0,019 0,104 -0,0085
V-0,0169 -0,019 0,104 )
,004 0 0,0005
0,001 1,004 0
\ 0,001 0,001 1,004 /
т. е. с точностью до ошибок округления получена единичная мат-
матрица.
УПРАЖНЕНИЯ.
2.1. Методом Гаусса решить СЛАУ:
-2ж1 + 10ж2 - ж3 = 7,
—х\ — Зж2 + Южз — 6.
2.2. Решить примеры из задания 2.1 методом Гаусса, приведя
матрицы СЛАУ к нижнему треугольному виду.
2.3. Методом Гаусса вычислить определители матриц и обра-
обратить матрицы СЛАУ из задания 2.1.
2.4. Показать с помощью метода Гаусса, что СЛАУ
несовместна.
2.5. Показать с помощью метода Гаусса, что СЛАУ
имеет бесчисленное множество решений. Найти их.
26
Численные методы алгебры
[Гл. II
2.6. Методом Гаусса обратить матрицу
/3 2 Л
А =
2 5 3
2.1.2. Метод прогонки. Метод прогонки является одним
из эффективных методов решения СЛАУ с трехдиагональными
матрицами, возникающих при конечно-разностной аппроксима-
аппроксимации задач для обыкновенных дифференциальных уравнений
(ОДУ) и уравнений в частных производных второго порядка,
и является частным случаем метода Гаусса. Рассмотрим следу-
следующую СЛАУ:
=0
с\х2 =
CL2X\
С3Ж4 =
B.1)
+ Сп-\Хп = rfn_i,
апхп—\ -\- опхп = an, cn = U,
решение которой будем искать в виде
= l,n, B.2)
где Ai, В{,% = 1, n, — прогоночные коэффициенты, подлежащие
определению. Для их определения выразим из первого уравне-
уравнения СЛАУ B.1) х\ через Ж2, получим
откуда
~cl ¦ «1 /1 ,1-»
= -[—Х2 + ~г = А\х2 + Бь
oi »1
A ~Cl
Ь
B.3)
Из второго уравнения СЛАУ B.1) с помощью B.3) выразим
через ж3, получим
-С2
+
= А2хъ
§2.1]
Численные методы решения СЛАУ
27
откуда
л ~с2 п d2-a2B1
и2 -\- GL2J\\ и2 -
Продолжая этот процесс, получим из г-го уравнения СЛАУ
B.1):
JL <i —
следовательно:
+
-Ci
+
j - ajBj-г
i + GLiAi-i '
Из последнего уравнения СЛАУ имеем
dn - апВп.± = Q _
Ьп + апАп_
-жп+1+
Ьп + апЛп_1
т. е.
Ап = 0 (т.к. сп = 0), Вп = f\ anBn-x = хп.
Таким образом, прямой ход метода прогонки по определению
прогоночных коэффициентов Л^, В^, г = 1, п, завершен. В ре-
результате прогоночные коэффициенты вычисляются по следую-
следующим формулам:
Ai = L , ~С\ , В{= I*'"**-1, i = 2,n-l; B.4)
i = —-, B\ = —, так как ai = 0, i = 1;
B.5)
= 0, т.к. cn =
= n.
B.6)
Обратный ход метода прогонки осуществляется в соответ-
соответствии с выражением B.2):
)n — U * ХП-\-\ -\~ Dn — L>ni
B.7)
28
Численные методы алгебры
[Гл. II
Формулы B.4)-B.7) — формулы правой прогонки.
Аналогично, начиная с последнего уравнения СЛАУ B.1)
можно вывести формулы левой прогонки.
Общее число операций в методе прогонки равно 8п + 1,
т. е. пропорционально числу уравнений. Такие методы решения
СЛАУ называют экономичными. Для сравнения метод Гаусса
требует — Bп2 + 9п + 1) операций, т.е. число операций пропор-
6
ционально п3 [1].
Пример 2.3. Методом прогонки решить СЛАУ
= 6,
—х\ + 6ж2 — 2жз = 3,
2х2 + 10ж3 -
— Жз + 6^4 = 5.
Решение.
-с2
6-1-0,25
= 0,3478,
d2-a2B1 C + 1-0,75)
Ъ2
5,75
= 0,374,
= 0,626;
= 1, 0,
= 1, 0,
+ Б2 = 1, 0,
= Aix2 + В\ = 1, 0.
Очень часто приходится решать замкнутые СЛАУ с трехдиа-
гональными матрицами без краевых условий (а\ ф 0, сп ф 0),
§2.1]
Численные методы решения СЛАУ
29
т. е. СЛАУ вида
Ъ\Х\
{-\ + Ъ{Х{ +
= di, г = 2, п — 1, B-8)
сьп'Еп—1 Н~ Ьпхп -\- спх\ —
которые при а\ = 0, сп = 0 совпадают с системой B.1). Такие
СЛАУ решаются с помощью формул циклической прогонки [2]:
X i — ±i X
•) i> — J- 5 77/ _L,
Pn = l,
}n = 0, i = n - 1, 1;
di — aiBi _, —aiCi
B.9)
B.10)
B.11)
6» + а^
6» + а^
г =
Лх = 0, Вг = 0, Ci = 1. B.12)
Сначала по формулам B.12) вычисляются прогоночные ко-
коэффициенты Ai, Bi, d, i = l,n + l, прямого хода. Затем по
формулам B.11) вычисляются прогоночные коэффициенты об-
обратного хода: Pi, Qi, i = n, n — 1, . . . , 1. Наконец, по B.10)
вычисляется жп, а затем по формулам B.9) — ж^, г = 1, п — 1.
Пример 2.4- Методом циклической прогонки решить СЛАУ
= 6,
— Х\ + 6^2 - 2^3 = 3,
10ж3 - 4^4 = 8
— Жз + 6Ж4 + Х\ = 6.
30 Численные методы алгебры [Гл. II
Решение.
1) Аг = 0, В1 = 0, d = 1;
А2 = —^— = 0,3333, В2 =
O + a4 b
C2 = ~°lCl = -0,3333;
Л3 = 0,3529, B3 = 0,7059, C3 = -0,0588;
Л4 = 0,3736, B4 = 0,6154, C4 = 0,01098;
Л5 = -0,777, B5 = 1,1758, C5 = 0,001952.
2) PA = 1,0, Q4 = 0, P3 = Л4Р4 + C4 = 0,3846, Q3 =
+ B4 = 0,6154;
P2 = A3P3 + CZ = 0,07693, Q2 = A3Q3 + BZ = 0,9231,
px = Л2р2 + C2 = -0,3077, Qi = A2Q2 + B2 = 1,3077;
Дб = 1,0, Жз = Pzxa + Qs = 1,0,
Ж2 = Р2Ж4 + Q2 = 1,0, x\ = P1X4 + Qi = 1,0.
Для устойчивости метода прогонки B.4)-B.7) достаточно вы-
выполнения следующих условий [2]:
\bi\ ^ \di\ + \с{\ , г = 1, n, a^ ^ 0, г = 2, п, с^ ^ 0, г = 1, п — 1,
B.13)
причем строгое неравенство имеет место хотя бы при одном г.
Здесь устойчивость понимается в смысле ненакопления погреш-
погрешности вектора неизвестных оператором прогонки при малых по-
погрешностях входных данных (правых частей и элементов мат-
матрицы СЛАУ). Аналогично и для циклической прогонки. При
выполнении B.13) прогоночные коэффициенты А{ (Л^ Сг? Р%
в методе циклической прогонки), г = 1, п, не содержащие правых
частей di СЛАУ, по модулю меньше единицы: |Л.| < 1 в методе
прогонки и \Аг\ < 1, \Вг\ < 1, \Сг\ < 1 в методе циклической
прогонки.
УПРАЖНЕНИЯ.
2.7. Для СЛАУ B.1) составить формулы левой прогонки в на-
направлении от г = п (сп = 0) к г = 1 (а± = 0).
§2.1] Численные методы решения СЛАУ 31
2.8. Для задачи ajXj-i - Ъ{Х{ + c^+i = di, \bi\ ^ \ai\ + \а
а\,
Q>i Ф 0, Ci ф О, г = 1, п - 1; ж0 = cO?i + rf0, « = 0; хп = спхп-\ +
+ dn, г = п, составить формулы правой и левой прогонки. По-
Показать, что прогоночные коэффициенты, не содержащие правых
частей, меньше единицы.
^ 2 1
2.9. Для СЛАУ тъЩ-\ - —^Щ + -^(г^+i + щ) = /г2, г = 1, п,
/б ГЬ ГЬ
щ = ип+\ = 1, /i = 0,1, п = 10 достаточные условия устой-
устойчивости B.13) не выполняются. Является ли метод прогонки
устойчивым?
2.10. Используя метод левой прогонки, выписать форму-
формулы точного решения системы а{Х{-\ — Ъ{Х{ +
\Ь%\ ^ \di\ + \ci\, cti ф 0, С{ ф 0, % — 1, п - 1; жо
г = 0; хп = cnxn-i + dn, г = п, где нулевое уравнение является
нелинейным; а = 10~10.
2.11. Доказать, что метод прогонки для СЛАУ B.1) есть
метод Гаусса.
2.12. Записать формулы циклической прогонки для СЛАУ
п{Щ-\ — Ъ{П{ + С{П{+\ = di, i = 0,n; u-\ = un, ип+\ = щ;
\Ы\ ^ \ai\ + |сг|? ai Ф 0, Ci ф 0 (строгое неравенство имеет место
хотя бы для одного г).
2.13. Найти решение разностной системы Щ—\ — 2ui +
= 0, i = 1, п — 1] щ = 1; ип = 2; п = 6.
2.14. Найти решение разностной системы — Щ-\ + 2ui —
— Ui+i = h2 sin(z/i), i = 1, n — 1; г^о = u\ — h; un = 1; n/i = тт/2.
Определить погрешность путем сравнения с решением задачи
d2u du@) /тг\
—^ + sin ж = 0; —^ = 1; и - ) = 1.
dx dx V 2 /
2.1.3. Обоснование метода прогонки. Метод прогонки
содержит операцию деления и следовательно возможно накоп-
накопление ошибок при увеличении числа уравнений в СЛАУ B.1)
или числа узлов сетки при конечно-разностной аппроксимации
краевых задач.
Поэтому необходимо гарантировать корректность, т.е. вы-
выполнение условия
bi + aiAi-! ф0, г = 1,п, B.14)
и устойчивость, т. е, ненакопление ошибок при увеличении чи-
числа уравнений СЛАУ B.1).
32 Численные методы алгебры [Гл. II
Пусть прогоночные коэффициенты Ai, В{, г = 1, п, вычисле-
вычислены точно, а при вычислении хп допущена ошибка еп\ хп = хп +
+ еп. Тогда из B.7) имеем следующие равенства:
xi = AiXi+i + Bi, i = п — 1, ...,1,
Xi = AiXi+i + Bi, i = n - 1, . . . , 1.
Вычитая из первого равенства второе, получаем
si = AiEi+i, г = п - 1, п - 2, . . . , 1,
т.е., если выполняются условия
|Л|<1, г = 1,п, B.15)
то алгоритм метода прогонки не накапливает ошибок и является
устойчивым.
Для корректности и устойчивости метода прогонки, т. е.
для реализации неравенств B.14), B.15), существует следующая
лемма.
Лемма 2.1 [достаточное условие корректности и устой-
устойчивости метода прогонки):
Пусть коэффициенты СЛАУ B.1) удовлетворяют условиям
О, |6*|>0, |с»|^0, г =
N > Ы + \сг\, г = 2,га-1; B.16)
|6i| ^ |ci| , |ЬП| ^ \ап\ , B-17)
причем хотя бы в одном из неравенств B.16) или B.17) выпол-
выполняется строгое неравенство, т.е. матрица СЛАУ B.1) имеет диа-
диагональное преобладание. Тогда имеют место неравенства B.14)
и B.15), гарантирующие корректность и устойчивость метода
прогонки.
Действительно, из B.17) имеем неравенство |v4i| = j—!-[ ^ 1,
\bi\
а из B.16) — неравенства
г = 2, п- 1.
§2.1] Численные методы решения СЛАУ 33
Кроме этого, из условия B.16) леммы имеем
т.е. Ь{ + а{А{-\ ф О, что и требовалось доказать.
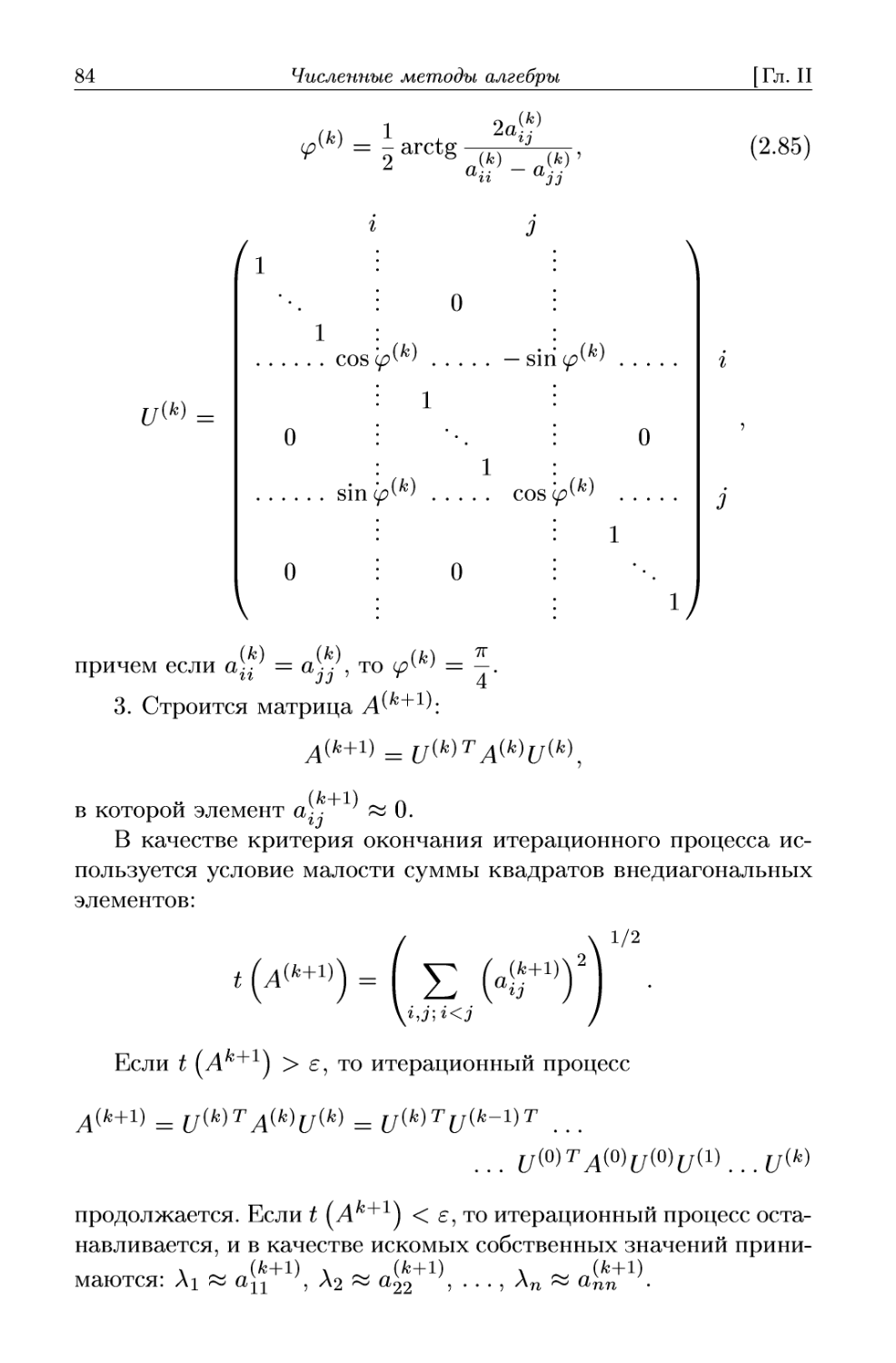
2.1.4. Матричная прогонка. При численном решении
многомерных задач математической физики, например двумер-
двумерных задач для уравнений Лапласа, теплопроводности и т.п.,
результирующая СЛАУ имеет пятидиагональную матрицу,
которую можно представить следующей системой векторно-
матричных уравнений:
+1 = Fii i = 0,N,
B.18)
= 6,
где 0 — нулевая матрица.
Здесь Ai, Bi, Ci, г = О, N, — квадратные матрицы размерно-
размерности М х М; Xi, Fi, г = 0,7V, — соответственно искомые векторы
и векторы правых частей размера М. При этом должно выпол-
выполняться условие
Так же как и в методе скалярной прогонки, решение ищется
в виде
i = 0, N, B.19)
где Pi, Qi, г = О, ЛГ, — соответственно прогоночные матрицы
и прогоночные векторы, подлежащие определению. Для их опре-
определения выразим из нулевого векторно-матричного уравнения
системы B.18) Xq через Х\, получим
Хо = -В^СоХг + B^Fo = РоХг + Qo, B.20)
откуда
Ро = ~Щ Cq, Qo = Bq Fq.
Далее из первого векторно-матричного уравнения системы
B.18) выразим Х\ через X<i с использованием B.20), получим
Xl = -{Вг + А1Ро)~1С1Х2 + {Вг + AlPQ)-\F1 - А^о) =
2 В.Ф. Формалев, Д.Л. Ревизников
34 Численные методы алгебры [Гл. II
откуда
( I
Продолжая этот процесс, получим прогоночные матрицы Pi
и прогоночные векторы Qi в следующем виде:
Pi = -(Bi + AiPi_1)-1Ci,
Qi = (В{ + AiPi-J-^Fi - AiQi-г), г = ОД B.21)
Ло = 0, CN = 0.
Прямой ход метода матричной прогонки завершен. Искомые
векторы Xi определяются из соотношений B.19):
Qn = Qn (Pn
Qn-\->
B.22)
называемых обратным ходом метода матричной прогонки.
Матричная прогонка неэкономична, так как она включает
в себя операцию обращения матриц.
Алгоритм B.21), B.22) устойчив и корректен, если выполне-
выполнены следующие условия:
Q, г = 1,7V;
0, г = 0, N -1;
Здесь норма матрицы может быть выбрана любой (см. сле-
следующий раздел).
2.1.5. Нормы векторов и матриц. Для исследования
сходимости численных методов решения задач линейной алгебры
вводятся понятия нормы векторов и матриц.
§2.1] Численные методы решения СЛАУ 35
Нормой вектора х = (ж1, Ж2, • • • , хп)Т (обозначают ||ж||) в
n-мерном вещественном пространстве векторов х Е Rn называ-
называют неотрицательное число, вычисляемое с помощью компонент
вектора и обладающее следующими свойствами:
а)||ж||^0(||ж||=0 тогда и только тогда, когда х — нулевой
вектор х = #);
б) ||а • ж|| = |а| • ||ж|| для любых чисел а (действительных или
комплексных);
в) ||ж + у|| ^ ||ж|| + ||у||.
Нормой матрицы Апхп (обозначается ||v4||) с вещественными
элементами в пространстве матриц называют неотрицательное
число, вычисляемое с помощью элементов матрицы и обладаю-
обладающее следующими свойствами:
а)||у4||>0(||у4||=0 тогда и только тогда, когда А — нулевая
матрица А = 0);
б) ||а • А\\ = \а\ - \\A\\ для любых действительных и комплекс-
комплексных чисел а;
г) \\А • В\\ ^ \\A\\ • \\B\\ для всех п х n-матриц Аи В рассмат-
рассматриваемого пространства.
Как видно из определения норм векторов и матриц (опреде-
(определения аналогичны, за исключением последнего свойства нормы
матрицы), норма матриц должна быть согласована с нормой
векторов. Это согласование осуществляется связью
Р^НРИЫ. B.23)
Наиболее употребительными являются следующие нормы
векторов:
ЦжЦ-l = max \xi\ , B.24)
ц2-^1^|, B.25)
i=i
\
B.26)
i=i
36
Численные методы алгебры
[Гл. II
= max
г
= max
3
Ъ
n
?
г=1
Clij
")
Согласованными с ними с помощью связи B.23) нормами
матриц будут соответственно:
B.27)
B.28)
B.29)
Можно показать [3], что нормы матриц B.27)—B.29) согла-
согласованы с помощью связи B.23) с соответствующими нормами
векторов B.24)-B.26). Под знаком квадратного корня в норме
матрицы ||v4||3 находится спектральный радиус симметрической
матрицы АТА, для которой, как известно, все собственные зна-
значения являются действительными.
Из линейной алгебры известно, что собственные значения
матриц не превышают их норм. Действительно, из равенства
Ах = Хх и свойств норм векторов и матриц следует: ||Аж|| =
= |Л| \\x\\ = \\Ax\\ ^ \\A\\ \\x\\, |Л| < И|, или р(А) < ||Л||, где
р(А) = max | А^| — максимальное по модулю собственное значение
i
или спектральный радиус матрицы А. Таким образом, за норму
матрицы можно принять ее спектральный радиус.
Пример 2.5. Показать согласованность нормы вектора \\х\\г
B.24) и нормы матрицы \\А\\г B.27).
Решение.
ЦАжЦ-l = тах|т4ж| = max
?«
ij X j
max \
г
aij\ —
3=1
и и V i
= \\х\\л max > \а
ц\
3=1
И 4 II
\\Лх ,
v I
max > \а
j
3=1 3=1
Таким образом, условие согласования B.23) выполнено.
§2.1] Численные методы решения СЛАУ 37
Для исследования погрешностей, возникающих при реше-
решении СЛАУ, вводят понятие числа обусловленности матрицы
cond(A) [4]:
Если в качестве нормы матрицы принять ее спектральный
радиус тах|А^|, то
г
condM) = maxlAJ —:—гт— ^ 1,
г mm | А^
г
поскольку спектральный радиус обратной матрицы А~1 равен
обратной величине минимального собственного значения исход-
исходной матрицы.
Число обусловленности характеризует степень зависимости
относительной погрешности решения СЛАУ от погрешности
входных данных (правых частей и элементов матрицы). Можно
показать, что справедливы следующие неравенства:
Таким образом, чем больше число обусловленности, тем силь-
сильнее влияние погрешности входных данных на конечный резуль-
результат. Матрица считается плохо обусловленной, если cond(/l) ^
^> 1. Чем ближе cond(/l) к 1, тем матрица лучше обусловлена.
Примером может служить ортогональная матрица.
Пример 2.6. Вычислить число обусловленности для мат-
матрицы
А =
1,0 0,99
0,99 0,98
Решение.
Для этой матрицы det А = 10~4 ф 0; А~1 = 104 х
Г 0,98 -0,99] „ 1„
х ; ||A|L =1,99; A L = 1, 99 • 104; cond(^) =
[-0,99 1,0 J
= 39601.
УПРАЖНЕНИЯ.
2.15. Используя неравенство Коши-Буняковского хТу ^
^ ||ж|| ||у||, доказать второе и третье свойства для норм вектора,
определяемых соотношениями B.24)-B.26).
38
Численные методы алгебры
[Гл. II
2.16. Доказать согласованность норм B.25) вектора и B.28)
матрицы [3].
2.17. Согласованы ли нормы B.26) и B.29)?
2.18. Доказать, что для любой (п х п)-матрицы А
max|a^| ^ \\A\\ ^ п • max |а^-|.
2.19. Доказать, что если матрица ортогональна (Л =
то cond(A) = 1.
2.20. Пусть
/
А =
6
13
13 -17\
29 -38
V —17 -38 50 /
( 6 -4 -Л
-4 11 7
V-1 7 5 У
Ai « 0,0588,
Л2 « 0,2007,
Л3 « 84,74.
Найти
!, cond(A).
2.1.6. Итерационные методы решения СЛАУ. Метод
простых итераций. При большом числе уравнений (~ 100
и более) прямые методы решения СЛАУ (за исключением мето-
метода прогонки) становятся труднореализуемыми на ЭВМ, прежде
всего из-за сложности хранения и обработки матриц большой
размерности.
Методы последовательных приближений, в которых при вы-
вычислении последующего приближения решения используются
предыдущие, уже известные приближенные решения, называют-
называются итерационными.
В итерационных методах решение может быть вычислено
за бесконечное число итераций (приближений), а поскольку это
невозможно, то, останавливая процесс вычислений на какой-
либо итерации, необходимо уметь оценивать погрешность метода
итераций.
Рассмотрим СЛАУ
а\пхп =
B.30)
с невырожденной матрицей (det А ф 0).
§2.1]
Численные методы решения СЛАУ
39
Приведем СЛАУ к эквивалентному виду:
х\ =
ol\\X\ + QL12X2
+ QL22X2
B.31)
Xji —
или, в векторно-матричной форме:
х = /3 + olx,
\
annxn,
B.32)
х =
\Хп )
а =
OLr
I
Такое приведение мож:ет быть выполнено различными спо-
способами. Одним из наиболее распространенных является сле-
следующий.
Разрешим систему B.30) относительно подчёркнутых неиз-
неизвестных при ненулевых диагональных элементах ац ф 0, г = 1, п
(если какой-либо коэффициент на главной диагонали равен ну-
нулю, достаточно соответствующее уравнение поменять местами
с любым другим уравнением). Получим следующие выражения
для компонентов вектора /3 и матрицы а эквивалентной системы:
Отметим, что существуют и другие способы приведения
СЛАУ к эквивалентному виду.
В качестве нулевого приближения х^ вектора
неизвестных примем вектор правых частей х^ = /3, или
0) 40) ¦¦¦ Хп]) = (Pi fo ¦¦¦ Рп)Т- Тогда итерационную
последовательность векторов
40 Численные методы алгебры [Гл. II
(°) = /3,
B)=^ + ажA), B.33)
называют методом простых итераций.
При решении СЛАУ B.30) методом простых итераций необ-
необходимо отвечать на следующие вопросы.
1. Сходится ли последовательность ж'0', ж'1', ж'2', . . .
. . . , ж^), . . . , т.е. существует ли lim ж^)? Если предел
к—>-оо
существует ( lim ж' ' = ?), то необходимо ответить на второй
/г—?>оо
вопрос.
2. Является ли предельный вектор ? решением СЛАУ B.31)
или B.32)? Если ? — решение, т.е. B.32) удовлетворяется тож-
тождественно ? = /3 + а?, то необходимо ответить на третий вопрос.
3. Так как бесконечное число итераций осуществить невоз-
невозможно, то, останавливая процесс на к-ой итерации, необходимо
определить: какова погрешность по норме ||? — хк\\? Или из
условия заданной точности ?, определить, каково число итераций
&, удовлетворяющее этой точности?
Для ответа на первые два вопроса существует
Теорема 2.1. (достаточное условие сходимости метода
простых итераций) [1].
Метод простых итераций B.33) сходится к единственному
решению СЛАУ B.32) (а следовательно, и к решению исход-
исходной СЛАУ B.30)) при любом начальном приближении ж0, если
какая-либо норма матрицы а эквивалентной системы меньше
единицы:
\\a\\ < 1 V||a|| и Уж0.
Доказательство.
Запишем последовательность B.33) в виде
XW = /3 + a/3 = (Е + а)/3,
жB) = 13 + а(Е + а)/3 = (Е + а + а2)/3,
§2.1] Численные методы решения СЛАУ 41
жC) = /5 + а(Е + а + a2)f3 = (Е + а + а2 + а3)/?,
B-34)
где Е — единичная матрица с нормой \\E\\ = 1.
Переходя вначале в равенствах B.34) к норме с использова-
использованием свойств норм векторов и матриц:
|U(/c)| = |(# + а + а2 + ... +а*)/з| ^ \\Е + а + а2 + ...
к\ (
... + а
а затем к пределу при /г —> оо, получим
lira ||ж(А;)|| < lim fl + Hall + . . . + llall*)
i II 111т \ Mil Illl/I
k^-oo II II |_/c—>-oo V / J
В квадратных скобках этого неравенства стоит ряд геометри-
геометрической прогрессии со знаменателем ||а||, который легко сумми-
суммируется:
lim У*)| < lim i^
к^-оо 1 —
При ||а|| ^ 1 данный предел не существует, а при ||а|| < 1
сумма бесконечно убывающей геометрической прогрессии равна
-. Таким образом,
1-IHI
lim
|| <
II 1 - ||а||
т. е. предел итерационной последовательности B.33) существует.
Обозначим этот предел через ?: lira x^ = ?.
к—>-оо
Ответим на 2-й вопрос: является ли этот предельный век-
вектор ? решением эквивалентной СЛАУ B.32), а следовательно,
и исходной СЛАУ B.30)? Для этого в равенствах B.34) перейдем
к пределу при к —» оо:
lim х^к) = lim (Е + а + а2 + . . . + ак) • /3. B.35)
42 Численные методы алгебры [Гл. II
В квадратных скобках равенства B.35) стоит матричный ряд,
формально являющийся биномиальным рядом с суммой: S =
= (Е-а)-г.
Следовательно,
)'1
lim xW = ? = (Е-а)'1 -/3,
к—>-оо
откуда получаем следующую цепочку равенств:
(Е -а)? = /3=>f-af = /3, или ? = /3 + а?. B.36)
Сравнивая B.36) и B.32), заключаем, что ? — решение СЛАУ
B.32), а следовательно, и СЛАУ B.30).
Ответим на 3-й вопрос. Покажем, что если процесс итераций
остановить на к-й итерации, то норма погрешности ||? ~ ж ||
будет оцениваться неравенством
м м II llfe+1
1кН B'37)
Действительно, рассмотрим равенства B.33) на двух сосед-
соседних итерациях, получим
yxW = ax(k-V + !3,
откуда
На основе последнего неравенства можно записать следую-
следующую цепочку неравенств:
||ж(*+2) _ ж(*+1)|| <С ||а|| ||ж(*+1) - ж(*0|| ,
|U(^+3) _ ж(Л+2)|| ^ ||а||2 ||ж(Л+1) - х(к)\\ ^
||Ж(&+Р) _ ж(А;Ч-р—1) II < Ц^Ц^ ||ж^+1^ — Ж^^Ц
используя которую в тождестве
§2.1] Численные методы решения СЛАУ 43
получим неравенство
г + ||а|| + ||а||2 + . . .+ \\a\r1
(г
откуда при р —У оо приходим к неравенству B.37) (при ||а|| < 1):
h - x(k)\\ < * IL ||
так как жШ - Ж(°) = (/3 + аж(°)) - /3 = а • /3, ж^0) = /3.
Если задана точность г, то
i-И
откуда получаем априорную нижнюю оценку числа итераций к
при ||а|| < 1:
и , I ^ lgg - lg||/3|| +lg(l - ||а||)
"Т" J- ^^ Г! Г! •
Это неравенство обычно дает завышенное число итераций к.
Как правило, при выполнении достаточного условия сходимо-
сходимости итерационный процесс останавливается при удовлетворении
условию е(к' = —^г~[т \\х^к' — х^к~гЦ\ ^ е (иногда используется
более простое условие ||ж^) — ж^^] ^ е), которое проверяется
начиная с к = 2. После выполнения этого условия принимается
Если используется метод Якоби (выражения B.32) для экви-
эквивалентной СЛАУ), то достаточным условием сходимости являет-
п
ся диагональное преобладание матрицы Л, т. е. \ац\ > ^ \aij I
Vi (для каждой строки матрицы А модули элементов, стоящих
на главной диагонали, больше суммы модулей не диагональных
элементов). Очевидно, что в этом случае \\o-\\i меньше единицы
и, следовательно, итерационный процесс B.33) сходится.
Теорема 2.2 (необходимое и достаточное условие сходи-
сходимости метода простых итераций). Для сходимости итераци-
итерационного процесса B.33) необходимо и достаточно, чтобы спектр
матрицы а эквивалентной системы лежал внутри круга с ра-
радиусом, равным единице.
44
Численные методы алгебры
[Гл. II
Спектр — все собственные значения матрицы на комплексной
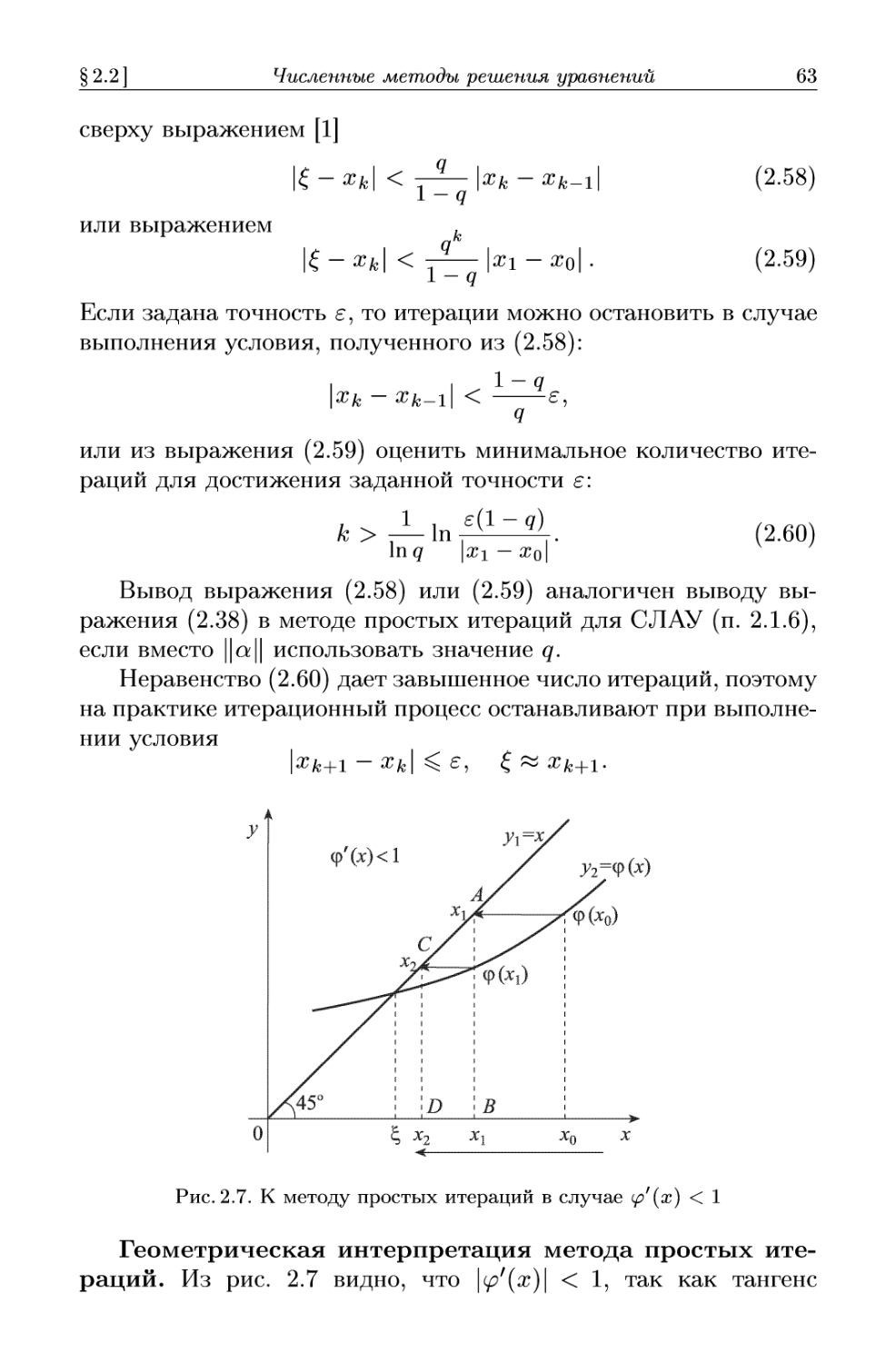
плоскости G, /3) (рис.2.1). Докажем только достаточность: если
спектр матрицы а мень-
меньше единицы, то метод про-
простых итераций B.33) сходит-
сходится к единственному решению
системы B.32).
Доказательство.
Рассмотрим задачу на соб-
собственные значения и собствен-
собственные векторы матрицы а: ау =
Применяя к обеим ча-
частям этого равенства опера-
Рис. 2.1. Спектр матрицы эквива- цию нормы и учитывая, что
тах|Л^| < 1, получим
лентной системы
\Ы\ ,
IMI
откуда, в соответствии с равенством B.23), заключаем:
11«»11 . •¦
\а\\ =
\\y\\
что достаточно для сходимости итерационного процесса B.33)
(см. теорему 2.1).
Пример 2.7. Методом простых итераций с точностью е =
= 0, 01 решить СЛАУ
= 12,
= 13,
= 14.
Решение.
Приведем СЛАУ к эквивалентному виду
— 1,2 - 0,1^2 - 0,
= 1,3 — 0,2^1 — 0,1жз,
= 1,4-0,2ж1 -0,2ж2
§2.1] Численные методы решения СЛАУ 45
О -0,1 -0,1
или х = /3 + ах, где а = | -0,2 0 -0,1 |; /3 =
-0,2-0,2 О
= A,2 1,3 1,4 )Т; IMIi = 0,4 < 1, следовательно, достаточное
условие сходимости метода простых итераций выполнено.
Итерационный процесс выглядит следующим образом:
х(о) = р. x(i) = р + ар = ( 0 93 о,92 0,9 )т;
si1) = 0,333 > е;
жB) =f3 + ax^ = ( 1,018 1,024 1,03 )т;
?B) = 0,0867 > е
ж(з) =р + ажB) = ( о,9946 0,9934 0,9916 )т;
е(з) = 0,0256 > е
жD) = /3 + ах^ = ( 1,0015 1,00192 1,0024 )т;
еD) = 0,0072 < е.
Таким образом, вычислительный процесс завершен за 4 ите-
итерации. Отметим, что точное решение исходной СЛАУ в данном
случае известно: ж* = ( 1 1 1 )Т• Отсюда следует, что задан-
заданной точности е = 0,01 удовлетворяло решение, полученное уже
на третьей итерации. Но в силу использования оценочного вы-
выражения для погрешности процесс останавливается только на
четвертой итерации.
Отметим также, что априорная оценка необходимого коли-
количества итераций в данной задаче дает: к + 1 ^ (—2 + lg 0,6 —
— lg 1,4)/ lg0,4 = 5,95, т.е. для достижения точности е = 0,01,
согласно априорной оценке, необходимо сделать не менее пяти
итераций, что иллюстрирует характерную для априорной оценки
тенденцию к завышению числа итераций.
2.1.7. Метод Зейделя решения СЛАУ. Метод простых
итераций довольно медленно сходится. Для его ускорения суще-
существует метод Зейделя, заключающийся в том, что при вычисле-
вычислении компонента х\ ' вектора неизвестных на (к + 1)-й итера-
46 Численные методы алгебры [Гл. II
(к+1) (к+1) (к+1)
ции используются х\ , #2 , . . . , х\_^ , уже вычисленные
на (к + 1)-й итерации. Значения остальных компонентов х\ ,
(к) (к)
ж^+1, . . . , XnJ берутся из предыдущей итерации. Так же как и в
методе простых итераций, строится эквивалентная СЛАУ B.31)
и за начальное приближение принимается вектор правых частей:
#@) = ( /?i /?2 . . . /?п )Т• Тогда метод Зейделя для известного
( (к) (к) (к) \ 1 /-
вектора I х\ ' х\ . . . х\ ' \ на /с-ои итерации будет иметь вид
(k+i) (к)
OLnn— l%n_i ~Г OLnnXn .
Из этой системы видно, что ж^+1) = /3 + Вх^к+1^ +
где В — нижняя треугольная матрица с диагональными эле-
элементами, равными нулю, а С — верхняя треугольная матрица
с диагональными элементами, отличными от нуля, т. е. а = В +
+ С. Следовательно,
{Е- В)
откуда
x(k+i) = (# _ в)~1Сх^ + {Е- В)'1 /3.
Таким образом, метод Зейделя является методом простых
итераций с матрицей правых частей а = (Е — В)~1С и векто-
вектором правых частей (Е — В)/?, и, следовательно, сходимость
и погрешность метода Зейделя можно исследовать с помощью
формул, выведенных для метода простых итераций, в которых
вместо матрицы а подставлена матрица (Е — Б)-1С, а вместо
вектора правых частей /3 — вектор (Е — В)~1/3. Для практи-
практических вычислений важно, что в качестве достаточных условий
сходимости метода Зейделя могут быть использованы условия,
приведенные выше для метода простых итераций (||ск|| < 1 или,
если используется эквивалентная СЛАУ в форме B.32), — диа-
диагональное преобладание матрицы А). В случае выполнения этих
§2.1]
Численные методы решения СЛАУ
47
условий для оценки погрешности на к-ой итерации можно ис-
использовать выражение
(к) _ IIHI L.W _ ж(Л-1)
Отметим, что, как и метод простых итераций, метод Зейделя
может сходиться и при нарушении условия ||а|| < 1. В этом
г~* ттл/'тт О О С\ / I I /УЪ \ / /УЪ \ /II
wlV ±CJb\D С *
Пример 2.8. Методом Зейделя решить СЛАУ из приме-
примера 2.7.
Решение.
Приведение СЛАУ к эквивалентному виду аналогично при-
примеру B.7). Диагональное преобладание элементов исходной мат-
матрицы СЛАУ гарантирует сходимость метода Зейделя.
Итерационный процесс выглядит следующим образом:
@) = ( 1,2 1,3 1,4 )Т,
х
CW = 1,2 - 0,1 • 1,3 - 0,1 • 1,4 = 0,93,
41} = 1,3 - 0,2 • 0,93 - 0,1 • 1,4 = 0,974,
41} = 1,4 - 0,2 • 0,93 - 0,2 • 0,974 = 1,0192,
xf] = 1,2 - 0,1 • 0,974 - 0,1 • 1,0192 = 1,0007,
42) = 1,3 - 0,2 • 1,0007 - 0,1 • 1,0192 = 0,998,
42) = 1,4 - 0,2 • 1,0007 - 0,2 • 0,998 = 1,0003.
Таким образом, уже на второй итерации погрешность
||жB) — ж*|| < 10~2 = г, т.е. метод Зейделя, в данном случае
сходится быстрее метода простых итераций.
2.1.8. Метод Зейделя для нормальных СЛАУ. Пусть
дана СЛАУ
О<21
\
(
\
XI
Х2
Хп
\
I
=
' Ьг
ь2
[ьп
B.39)
48 Численные методы алгебры [Гл. II
Если СЛАУ имеет диагональное преобладание, т.е. \ац\ >
п
п
> S l&ijl? i — l?^j методы простых итераций и Зейделя схо-
i=i
дятся. Однако единственное решение СЛАУ B.39) существует
и тогда, когда нет диагонального преобладания, но матрица А
является невырожденной (т.е. det А ф 0).
С помощью элементарных преобразований можно из невы-
невырожденной матрицы построить матрицу с диагональным преоб-
преобладанием, для которой рассмотренные итерационные методы бу-
будут сходиться. Однако существует более простой способ, а имен-
именно нормализовать СЛАУ B.39) с невырожденной матрицей А
и применить к ней метод Зейделя.
СЛАУ называется нормальной, если ее матрица симметрична
(А = АТ) и положительно определена. Положительно опреде-
определенная матрица — матрица, для которой квадратичная форма
(Ах, х)>0, или матрица, у которой все собственные значения по-
положительны. По критерию Сильвестра для положительно опре-
определенной матрицы все диагональные миноры матрицы положи-
положительны:
аи а12
аи > 0,
CL22
> 0, ... , det Л > 0.
Из любой невырожденной матрицы можно сделать нормаль-
нормальную, домножив ее на транспонированную слева. Умножим B.39)
слева на АТ, получим
АтАх = АТЬ, или Вх = с,
где В = АтА — нормальная матрица, с + Ат Ь.
Справедлива следующая теорема.
Теорема 2.3. Метод Зейделя всегда сходится для нормаль-
нормальных СЛАУ.
Пример 2.9. Для следующей СЛАУ применить один из
итерационных методов решения:
3 = 13,
= 12,
„ = 14.
Решение.
Эквивалентная СЛАУ и ее матрица имеют вид
§2.1]
Численные методы решения СЛАУ
49
х\ = 6,5 — 5x2 — 0,5жз,
= 12 — 10^1 — Жз,
= 1,4-0,2^1 -0,2ж2,
О -5 -0,5 \
-10 0 -1
-0,2 -0,2 0 )
= 11 ^$> 1, т.е. не выполнено достаточное условие сходимо-
сходимости метода простых итераций. Нормализуем исходную СЛАУ:
АТАх = АТЬ, где
АТА =
108 34 32
34 105 31
32 31 102
АТЬ =
174
170
165
Результирующая СЛАУ имеет симметрическую матрицу и диа-
диагональное преобладание. Следовательно, матрица эквивалент-
эквивалентной системы по норме меньше единицы, что достаточно для
сходимости метода Зейделя.
Отметим, однако, что рассмотренный способ нормализации
существенно ухудшает обусловленность СЛАУ. Кроме того, его
применение к разреженным матрицам может приводить к потере
этого свойства. Поэтому при решении СЛАУ большой размерно-
размерности данный подход используется редко.
УПРАЖНЕНИЯ.
2.21. Методом простых итераций с точностью е = 10~3 ре-
решить СЛАУ, приведя к эквивалентной системе и оценив предва-
предварительно число итераций:
а)
б)
-XI
2х\ — Х2 —
+
Х\ — 5Ж2
= 12,
= -9,
+ 5^4 = 17;
+ Х4 = 0,
+ 2^4 = 4,
4 = 9,
= -7.
50 Численные методы алгебры [Гл. II
2.22. Методом Зейделя с точностью е = 10~3 решить задачи
в задании 2.21 и сравнить по количеству итераций с методом
простых итераций.
2.23. Методом Зейделя с точностью е — 10~3 решить СЛАУ,
приведя их предварительно к виду, удобному для итераций:
= 2,1,
а) \ 3,5жх + 1,7^2 + 2,8жз = 1,7,
5,8ж2 - 1,7ж3 = 0,8;
2,8^2 + 1,9жз — 0,7,
б)
= 2,8.
2.24. Оценить количество итераций к в задачах задания 2.21
для различных значений точности: е\ = 10~2; s<i = 10~3; е% =
= 10~4; 64 = Ю~5. Построить график зависимости к(е).
2.25. Сходится ли метод простых итераций для задач задания
2.23, матрицы которых не имеют диагонального преобладания?
Максимальное собственное значение оценить степенным методом
(см. п. 2.4.3).
§ 2.2. Численные методы решения нелинейных
и трансцендентных уравнений
Рассмотрим уравнение вида
f(x) = 0, B.40)
где f(x) — любая нелинейная или трансцендентная функция,
например f(x) = exp(tgx) — ж3 sin ж.
Для нахождения корней уравнения B.40) различают следу-
следующие два этапа.
1. Отделение корней, т.е. нахождение таких интервалов по
аргументу ж, внутри каждого из которых существует только
один корень уравнения B.40).
2. Уточнение корней заключается в применении некоторого
итерационного метода, в результате которого корень уравнения
B.40) может быть получен с любой наперед заданной точно-
точностью е. При этом, останавливая процесс на какой-либо конечной
§2.2]
Численные методы решения уравнений
51
итерации, необходимо оценить погрешность по сравнению с точ-
точным корнем, который неизвестен.
2.2.1. Способы отделения корней. Наиболее употреби-
употребимыми на практике способами отделения корней являются следу-
следующие.
1. Графический.
2. Метод половинного деления.
В графическом способе строится график функции f(x)
(рис.2.2) и приближенно определяются ее нули (или корни урав-
уравнения f(x) = 0) ?г, г = 1, 2, 3, . . . Заключив эти нули в интервалы
/Фд
У
0
i\ Р2
«2 &i
ЛР2Г
а3
л
/(«з) J
Рз
а4
Ах) 1
у\
^* х
)
Рис. 2.2. Графический метод отделения корней
<!;. ? (а^, /3^), на границах которых выполняются условия /(с^) х
х f(Pi) <0, г = 1, 2, . . . , и знаки производных первого и второго
порядков /'(ж), f"(x) на интервалах (с^,/?г) постоянны, можно
утверждать, что внутри каждого из этих интервалов находится
один корень уравнения B.40).
Если при этом /(&) = /'(&) = 0, a f"{ii) ф 0, то корень & —
двукратный корень (точка ?з на рис.2.2); если /(&) — /'(&) =
— f"(ii) = 0, a f'"{ii) ф 0, то ?г — трехкратный корень (точка
?4 на рис.2.2) и т. д.
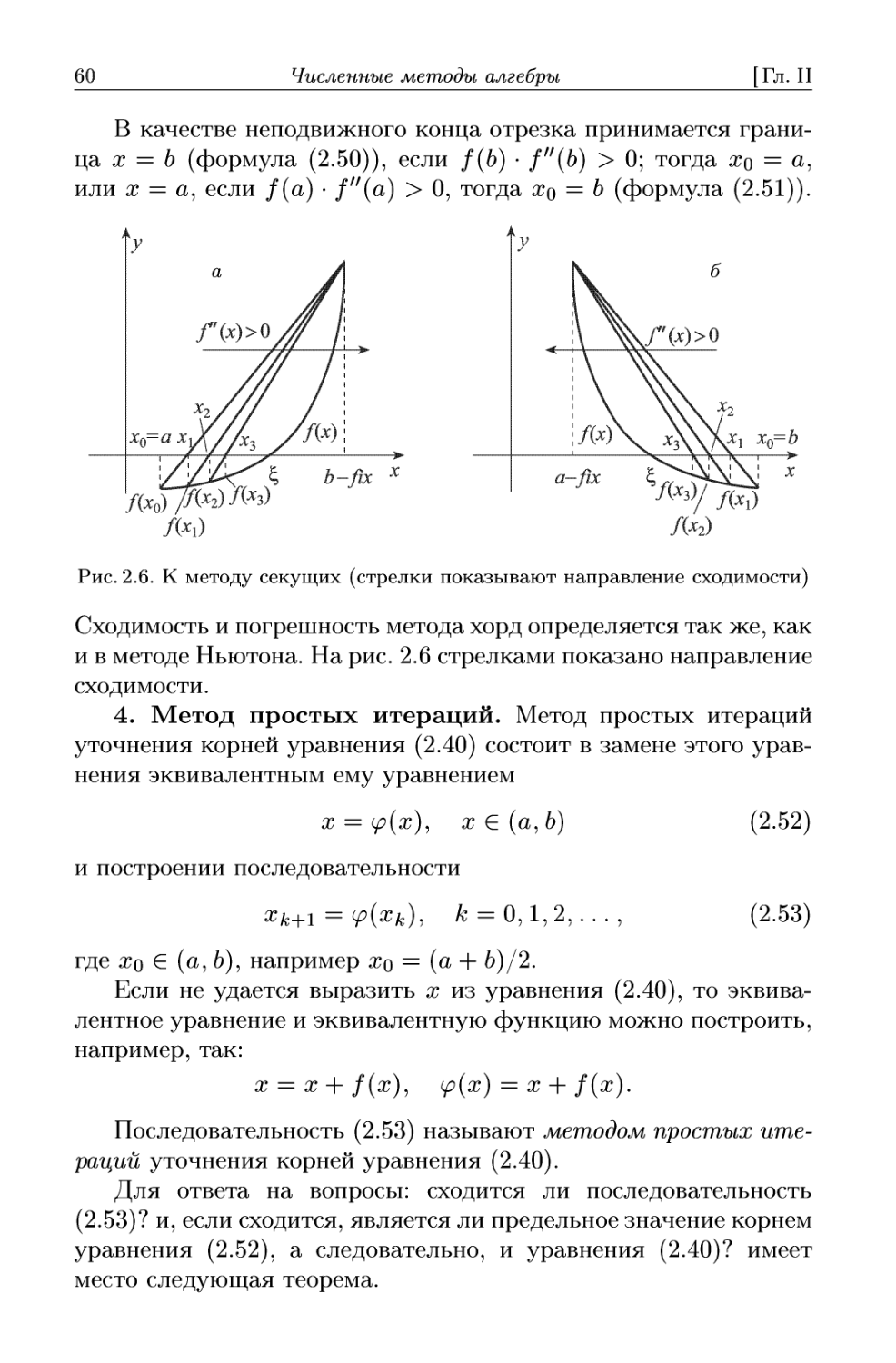
В методе половинного деления область определения функции
/(ж) : х е [а, 6] делят на 2, 4, 8, 16, 32, ... интервала и для каж-
каждого из них анализируют знаки функции на концах интервала;
если они противоположны, то внутри интервала находится не
менее одного корня; если знак первой производной на интерва-
интервале постоянный, т.е. sign//(x)|a,G/a. ^.ч = const (при выполнении
предыдущего условия), то внутри интервала находится точно
52
Численные методы алгебры
[Гл. II
один корень. В данном параграфе рассматриваются однократные
(простые) вещественные корни нелинейных уравнений B.40).
Пример 2.10. Отделить корни уравнения
/ (х) = х2 - е~х/2 = 0, х е [-3; 3] .
Решение.
Уравнению х2 — е~х*2 = 0 соответствует эквивалентное урав-
уравнение х2 = е~х'2. Если построить графики функций у\ = х2
и у2 = е~Ж//2, то абсциссы точек пересечения графиков этих
-2
Рис. 2.3. Отделение корней
функций дадут искомые корни данного уравнения. Из рис. 2.3
видно, что & е (-2; -1); ?2 G @; 1).
2.2.2. Методы уточнения корней. Ниже рассматрива-
рассматриваются следующие итерационные методы уточнения корней нели-
нелинейного уравнения B.40).
1. Метод половинного деления.
2. Метод Ньютона (касательных).
3. Метод секущих (хорд).
4. Метод простых итераций.
Все эти методы являются итерационными.
Предположим, что ~х — приближенное значение корня, ? —
его точное значение. Возникает вопрос, какова погрешность
? — ~х приближенного значения корня ж по сравнению с его точ-
точным значением ?, если последний неизвестен?
§2.2] Численные методы решения уравнений 53
Для этого построим невязку /(?) — /(ж) = —/(ж), т. к. / (?) =
= 0. Применим к невязке теорему Лагранжа о конечных прира-
приращениях:
откуда
/'(о)
Так как точное значение а неизвестно, эту погрешность за-
заменяют верхней оценкой:
к1«
Оценка погрешности B.41) является довольно грубой. Поэто-
Поэтому в каждом итерационном методе уточнения корней, в силу
ограничений применения метода, можно вывести свою оценку
погрешности.
1. Метод половинного деления. Пусть /(ж) = 0 и точное
значение корня ? ? (а, 6).
В методе половинного деления функция /(ж), ж ? [а, Ь], дол-
должна удовлетворять следующим двум условиям:
а) f(a)f(b) < 0;
б) /(ж) непрерывна на отрезке ж ? [а, 6].
Метод половинного деления состоит в построении после-
последовательности вложенных отрезков [ак) bk] С [a&-i, b/c-i] С ...
. . . С [ао, 6о] = [а, 6], на концах которых удовлетворяются усло-
условия / {ak) f {bk) < 0, к = 0, 1, 2, . . . (рис. 2.4).
Опишем один шаг итерационного метода половин-
половинного деления. Пусть на (к — 1)-м шаге найден отрезок
[a&_i, bk-i] С [ао, fro]? Ha котором выполнено условие
/ (ak-i) f (bk-i) < 0. Этот отрезок делится пополам точкой
ж д. = (a&_i + bk-\) /2, и вычисляется / (ж/,). Если / (ж&) = 0,
то ж& = (a/,_i + bk-i) /2 — корень уравнения B.40). Если
f (xk) 7^0? то из ДВУХ половин отрезка выбирается та, на концах
которой функция имеет противоположные знаки, так как корень
находится внутри именно этой половины. Таким образом, а& =
= ськ-ъ ьк = %к, если f (ak-i) f (хк) < 0; ак = хк, Ьк = Ьк-ъ
если / (хк) f F/c-i) < 0.
54
Численные методы алгебры
[Гл. II
Если необходимо найти корень с точностью е, то деление
пополам продолжается до тех пор, пока не выполнится условие
Ьк-ак = {1/2)к(Ь-а)^е. B.42)
Тогда значение ? = (ак + Ьк) /2 приближенно определяет корень
с точностью е.
а=щ
Рис. 2.4. К методу половинного деления
Из B.42) можно оценить число к итераций, необходимых для
достижения заданной точности е: к ^ log2 ((b — а) /е). Отсюда
видно, что для получения трех верных знаков (е = 10~3) необ-
необходимо сделать ~ 10 итераций.
Покажем, что процесс итераций по методу половинного деле-
деления сходится, и сходится к корню уравнения B.40). Для этого на
основании B.42) запишем погрешность, которая получится при
остановке итерационного процесса на к-и итерации:
?-хк = ^(Ь-а). B.43)
Пусть f(ak)f(bk) < 0. Из B.43) видно, что lim (f - хк) =
к—>-оо
= lim —г (Ь — а) = 0, откуда следует lim хк = ?, где ? — точный
к—>-оо 2 /г—)>оо
корень.
Возьмем предел от произведения f(ak) • f(bk) при к —» оо.
Поскольку функция f(x) непрерывна на х ? [а, Ь] по условию
§2.2] Численные методы решения уравнений 55
задачи, то знак предела можно внести под знак функции, т. е.
lim f(ak)f(bk) =
= /(lim ak)f( lim bk) = /@/@ = /2@ < 0, B.44)
?k—)>oo
что невозможно и, следовательно, /2(?) = 0, или /(?) = 0, т.е. ?
является единственным корнем уравнения B.40).
При выводе B.44) были использованы пределы lim а к = ?
к—ь-оо
и lim bk = ?. Действительно, последовательность {а&} является
неубывающей, ограниченной сверху значением ?, а последова-
последовательность {fo&} является невозрастающей, ограниченной снизу
значением ?. Таким образом, пределом слева и справа является
точный корень ?.
Достоинства:
а) метод половинного деления прост в алгоритмизации и про-
программировании;
б) на функцию / (х) не накладывается никаких ограничений,
кроме требования непрерывности.
Недостаток: метод очень медленно сходится, т.е. необ-
необходимо использовать большое число итераций для достижения
заданной точности е.
Априорная оценка количества итераций в соответствии
с неравенством к ^ log2 [(b — а)/е] довольно завышена, поэтому
на практике итерационный процесс останавливается при выпол-
выполнении неравенства
Пример 2.11. Методом половинного деления уточнить наи-
наибольший корень уравнения х2 — е~х = 0 с точностью е = 10~2.
Решение.
Выделим наибольший корень: а = 0,5; b = 1,0. ? ? @,5; 1,0).
1) а0 = а = 0,5; Ьо = b = 1,0; хх = (а0 + Ьо) /2 = 0,75;
f(Xl) = 0,0901 > 0; f(ao)f(xi) = -0,3565 • 0,0901 < 0; ? е
е (а0, х\)\ тогда а\ = а0 = 0,5; Ь\ = х\ = 0,75; |fox -«i| =
= 0,25 > е.
Продолжая этот процесс, получаем на 6-й итерации: clq =
= 0,7032; fo6 = 0,711; |b6 - а6| = 0,0078 < г; ? = (fo6 + а6) /2 =
= 0,7071.
56 Численные методы алгебры [Гл. II
УПРАЖНЕНИЯ.
Методом половинного деления с точностью е = 10~2 уточ-
уточнить корни следующих уравнений:
2.26. tg(l,9z)-2,8ж = 0;
2.27. 1п(8ж) = 9ж-3;
2.28. sinB,2x) - х = 0;
2.29. ехр(-0,8ж) - 4х = 0;
2.30. 0,89ж3 - 2,8ж2 - 3,7ж + 11,2 = 0.
2. Метод Ньютона уточнения корней. Пусть для урав-
уравнения B.40) на интервале х ? (а, Ь) отделен корень ?.
В методе Ньютона функция f(x) должна удовлетворять на
отрезке х Е [а, Ь] следующим условиям:
1) существование производных 1-го и 2-го порядков;
2) Г(х) ф 0;
3) производные 1-го и 2-го порядков знакопостоянны
(signj/^x), fff(x)} = const) на отрезке х ? [а, Ь].
Пусть имеется значение корня на к-й итерации — ж д.. Тогда
значение корня на (к + 1)-й итерации вычисляется следующим
образом:
= %к + hk, B.45)
где hk — шаг, который подлежит определению.
Чтобы определить /i/,, подставим Xk+\ в функцию / (х) и раз-
разложим ее в ряд Тейлора до третьего слагаемого включительно
в окрестности точки Ж&, получим
/ (a*+i) = f(xk + hk) = f (хк) + /' (хк) hk + /" (а) М,
а е (xk,xk+i).
Положим в этом разложении линейную относительно hk
часть равной нулю, в результате чего находим значение шага hk:
h
hk = р(г,
/ (хк)
подставляя которое в B.45), получаем
, к = 0,1,2,... B.46)
§2.2] Численные методы решения уравнений 57
За начальное приближение xq принимается один из концов
отрезка [а, 6], а именно
_ (а, если /(а) • /"(а) > 0;
Ж°-\б, если /(ft) ¦/"(ft) >0.
Выражения B.46), B.47) называют итерационным мето-
методом Ньютона (или касательных) уточнения корней нелинейного
уравнения B.40).
Чтобы не вычислять значение первой производной f (х^) на
каждой итерации, достаточно вычислить ее в точке xq и полу-
полученное значение подставить в выражение B.46), получим
xk+i = xk- ^Nr, к = 0,1, 2,. . . B.48)
Метод B.47), B.48) называют модифицированным методом
Ньютона. Он обладает неоспоримым преимуществом перед ме-
методом B.46), B.47), но сходится медленнее.
Справедлива следующая теорема.
Теорема 2.4. (достаточные условия сходимости метода
Ньютона). Пусть f(x) определена и дважды дифференцируе-
дифференцируема на отрезке х Е [а, 6], причем /(а) • f(b) < 0, производные
f'(x) и f"(x) знакопостоянны и f'(x) ф 0. Тогда исходя из
начального приближения х$ ? [а, 6], удовлетворяющего неравен-
неравенству f(xo) • fff(xo) > 0, можно построить последовательность
B.46), сходящуюся к единственному корню ? уравнения B.40) на
отрезке х Е [а, 6] с погрешностью, оцениваемой неравенством
h2k M2
f
Mo = max \f"(x)\, vn\— min If'(ж) I, жЕ fo.bl.
xe[a,b] xe[a,b]
Действительно, поскольку /(ж) непрерывна, то взяв предел
от B.46) при к —^ ос и поменяв местами знаки предела и функ-
функции, получим
/( lim xk)
lim хь+л = lim ж* — к^°°
/ ( lim Ж/g)
Поскольку последовательность {ж/,} — невозрастающая (не-
(неубывающая) числовая последовательность, ограниченная снизу
58
Численные методы алгебры
[Гл. II
(сверху), то она сходится, т.е. существует предел lim хк = ?.
/г—?>оо
Тогда из последнего равенства (/'(?) ф 0 по условию) имеем
т.е. предельное значение ? является корнем уравнения B.40).
Поскольку невязка равна f{xk+\) — /(?) = /(#&+i), то из
разложения f(xk+i) в ряд Тейлора имеем выражение для невяз-
невязки в виде
f(xk+1) = /"(«)f,
подставляя которое в общую погрешность приближенных мето-
методов B.41) при ж"=жд._|_1, получаем верхнюю оценку погрешности
в виде B.49), где hk = хк+1 - хк.
/(*)
Рис. 2.5. К методу Ньютона
Для случая, приведенного на рис. 2.5, за начальное прибли-
приближение принимается х$ = 6, так как f(b) • f"{b) > 0.
На основе B.49) можно записать, что |? — ж/c+il ^
^ (M2/2rai) |? - ж^|2, и если M2/2mi < 1 и |?-жа.| <
< 10~т,то |? — Xk+i\ < 10~2m, т.е. когда приближение хк
§2.2] Численные методы решения уравнений 59
имеет т верных знаков, Xk+\ будет иметь не менее 2т верных
знаков, т. е. метод Ньютона имеет квадратичную сходимость.
Поскольку верхняя оценка B.49) сложна для вычисления, на
практике итерационный процесс останавливают при выполнении
условия \xk-\-i — Xk\ ^ ?, ? ~ xk+i-> гДе ? ~~ заданная точность.
Метод Ньютона называют еще методом касательных, по-
поскольку в этом методе на каждой итерации к графику функ-
функции f(x) проводится касательная в точке (#&,/(#&)) до пересе-
пересечения с осью абсцисс (рис. 2.5).
Пример 2.12. Методом Ньютона с точностью е = 10~2
уточнить наибольший корень уравнения / (х) = х2 — е~х = О,
х е @,5; 1,0).
Решение.
Начальное приближение х$ = 1,0, так как /A,0) > 0;
/"A,0) > 0. Таким образом ж0 = 1,0; хх = 1 - /A)//'A) =
= 0, 733; х2 = 0, 733 - / @, 733) //' @, 733) = 0, 7038; \х2 — a?i| =
= 0,092 > е; х3 = х2 - f (x2)/f (х2) = 0,7034; \х3 - х2\ =
= 0, 3414 • Ю-3 < е, т. е. f « 0,7034.
УПРАЖНЕНИЯ.
Методом Ньютона с точностью е = 10~3 уточнить корни
следующих уравнений:
2.31. tg A, 262ж) - 1, 84ж = 0;
2.32. 1пC,66ж) =4,12ж-1,5;
2.33. 2,33sinB,86x) = 2ж;
2.34. 0, 7ехр (-0, 59ж) - х = 0;
2.35. 1, 2ж3 - 3, 53ж2 - 1, Збж + 7,11 = 0.
3. Метод секущих (хорд). Заменяя в алгоритме Ньютона
производную f'(xk) приближенно отношением конечных разно-
разностей:
О Хк
получим алгоритм метода хорд с неподвижным правым концом
(рис. 2.6 а):
1(Ьхк) хо = а, B.50)
f(b) -
или с неподвижным левым концом (рис. 2.6 5):
f(x
хк
= Ь'
60
Численные методы алгебры
[Гл. II
В качестве неподвижного конца отрезка принимается грани-
граница х = b (формула B.50)), если f(b) • f"(b) > 0; тогда xq = а,
или х = а, если /(а) • f"{a) > 0, тогда xq = b (формула B.51)).
b-fix
/
f(x2)
Рис. 2.6. К методу секущих (стрелки показывают направление сходимости)
Сходимость и погрешность метода хорд определяется так же, как
и в методе Ньютона. На рис. 2.6 стрелками показано направление
сходимости.
4. Метод простых итераций. Метод простых итераций
уточнения корней уравнения B.40) состоит в замене этого урав-
уравнения эквивалентным ему уравнением
х<Е(а,Ь)
и построении последовательности
к = 0,1,2,...,
B.52)
B.53)
где xq Е (а, 6), например xq = (а + Ь)/2.
Если не удается выразить х из уравнения B.40), то эквива-
эквивалентное уравнение и эквивалентную функцию можно построить,
например, так:
х = х + /(ж), <р(х) = х + /(ж).
Последовательность B.53) называют методом простых ите-
итераций уточнения корней уравнения B.40).
Для ответа на вопросы: сходится ли последовательность
B.53)? и, если сходится, является ли предельное значение корнем
уравнения B.52), а следовательно, и уравнения B.40)? имеет
место следующая теорема.
§2.2] Численные методы решения уравнений 61
Теорема 2.5 (достаточные условия сходимости метода
простых итераций). Пусть функция (р(х) в эквивалентном
уравнении B.52) определена и дифференцируема на отрезке х Е
? [а, Ь]. Тогда, если существует число q такое, что
\<р'{х)\ ^q<l B.54)
на отрезке [а, 6], то последовательность B.53) сходится к един-
единственному корню уравнения B.52) при любом начальном прибли-
приближении xq Е [а, Ь].
Доказательство. Запишем итерационный процесс B.53)
на двух соседних итерациях:
xk =
xk+i = <р(хк).
Вычитая из второго выражения первое, получим
xk+i - хк = ?(хк) - <p(xk-i). B.55)
Применим к правой части выражения B.55) теорему Лагран-
жа о конечных приращениях, поскольку по условию (f(x) —
дифференцируемая функция:
Хк+i ~ хк = (р'(а)(хк - хк-\), а е (xk-i,xk).
Используя условия B.54) теоремы, из последнего равенства
получаем неравенство
\xk+i - хк\ ^ q \xk - xk-i\ ,
на основе которого можно выписать следующую цепочку нера-
неравенств:
\Х2 ~ xi\ ^q\x1- xo\ ,
\xs - x2\ ^ q \x2 - хг\ ^ q2 \x± - xo\ ,
3 I B-56)
q x\ - xo\ v J
\xk+i ~xk\ ^ qk \xi -xo\ .
Тогда на основе тождества
Xk+i = Х0 + (Xi - Хо) + (Х2 - Xi) + . . . + (Xk+1 - Хк)
и неравенства
62 Численные методы алгебры [Гл. II
\xk+i\ ^ \хо\ + \xi - xo\ + \x2-xi\ + ... + \xk+i - хк\
с использованием в нем цепочки B.56), получим следующую
оценку:
( + q + q2 + . . . + qk) \xx - xo\ , B.57)
в круглых скобках которой находится сумма геометрической про-
прогрессии. Взяв предел от B.57) при к —> ос, получим выражение
к
lim \xk+i\ ^ |жо| + \х± - хо\ Hm \^ qn
в котором сумма ряда геометрической прогрессии равна
A — д), поскольку по условию теоремы \q\ < 1.
Таким образом,
lim \хк+1\ ^ ж0 + ] ~ < М < оо.
^ 1 — q
То есть существует конечный предел последовательности
B.53). Обозначим его через ?, т.е.
lim xk+1 = ?.
к—>-оо
Для ответа на 2-й вопрос о том, является ли предельное
значение ? корнем уравнения B.52), перейдем в B.53) к пределу
при к —> оо и, поскольку функция ср(х) дифференцируема и,
следовательно, непрерывна, знаки предела и функции можно
менять местами; получим
lim хкл_1 = if I lim xk
к^оо
откуда следует равенство
то есть ? является единственным корнем уравнения B.52), а сле-
следовательно, и уравнения B.40).
При ответе на 3-й вопрос о погрешности метода можно пока-
показать, что если ? — неизвестный точный корень уравнения B.52)
и итерационный процесс остановлен на к-й итерации, то погреш-
погрешность, которая допускается этим приближением, оценивается
§2.2]
Численные методы решения уравнений
63
сверху выражением [1]
или выражением
B.58)
B.59)
Если задана точность ?, то итерации можно остановить в случае
выполнения условия, полученного из B.58):
i i 1 - Я
| •ь к ^ к — 11 ^ с 1
или из выражения B.59) оценить минимальное количество ите-
итераций для достижения заданной точности е\
т^^- B-60)
Вывод выражения B.58) или B.59) аналогичен выводу вы-
выражения B.38) в методе простых итераций для СЛАУ (п. 2.1.6),
если вместо ||а|| использовать значение q.
Неравенство B.60) дает завышенное число итераций, поэтому
на практике итерационный процесс останавливают при выполне-
выполнении условия
\хк+1 -хк\^е, ? ^ хк+1.
Рис. 2.7. К методу простых итераций в случае у?'(ж) < 1
Геометрическая интерпретация метода простых ите-
итераций. Из рис. 2.7 видно, что |^'(ж)| < 1, так как тангенс
64
Численные методы алгебры
[Гл. II
угла наклона касательной к графику функции у2 = <р(х) мень-
меньше tgD5°) = 1. Следовательно, для произвольного начального
приближения xq в соответствии с 1-й итерацией в B.53) при к =
= 0 определяется (/?(жо), которое равно значению х\ на графике
функции г/1 = ж, а поскольку треугольник ОАВ прямоугольный
и равнобедренный, то ОВ = х\. На второй итерации в B.53) при
к = 1 определяется (p(xi), которое равно значению ж 2 на графике
функции 2/i = ж, а поскольку треугольник ОСD — равнобедрен-
равнобедренный и прямоугольный, то CD = OD = Ж2, т.е. итерационные
значения жо, Ж1, Ж2, ... стремятся в сторону точного корня ?
(указано стрелкой справа налево).
Рис. 2.8. К методу простых итераций в случае у?'(ж) > 1
На рис. 2.8 |(/?'(ж)| > 1. Из рисунка видно, что итерационный
процесс расходится (приближения корня жо, х\, Ж2, . . . стремят-
стремятся от корня ?).
На рис. 2.9 представлен случай |^'(ж)| < 1, (р'(х) < 0. Про-
Процесс итераций сходится с двух сторон, т. е. приближения корня
находятся то слева, то справа от точного корня ?.
Итерационный процесс B.53) можно использовать и в случае,
когда в эквивалентном уравнении |^(ж)| > 1. Для этого вернемся
к исходному уравнению B.40) и построим эквивалентное уравне-
уравнение в виде
X = X ±
max |/'(ж)|'
где берется знак минус, если /'(ж) > 0, и плюс, если /'(ж) < 0.
§2.2]
Численные методы решения уравнений
65
Рис. 2.9. К методу простых итераций в случае |у/(ж)| < 1, (р'(х) < О
Тогда в качестве эквивалентной функции (f(x) можно при-
принять функцию
(f(x) = х =Ь
max |
хЕ[а,Ь]
для которой
<р'(х) = 1 ±
max \f'(x)
хе[а,Ь]
< 1.
Пример 2.13. Методом простых итераций с точностью е =
= 10~2 уточнить наибольший корень уравнения / (ж) = х2 —
-е~х = 0, х е [0,5; 1,0].
Решение.
Эквивалентное уравнение
х = ехр (—ж/2);
<р(х) = ехр (-ж/2); q = max\(pf (х)\ =0,3894 < 1;
же[0,5;1,0]
х0 = @,5 + 1,0) /2 = 0,75; хг = ехр (-0,375) = 0,687;
х2 = ехр (-0,3437) = 0,7091;
\х2 - хг\ = 0,02184 > A - q) • lO~2/q = 0,015;
ж3 = ехр (-0,3546) = 0,7015; |ж3 - ж2| = 0,007646 < 0,015;
f « 0,7015.
3 В.Ф. Формалев, Д.Л. Ревизников
66 Численные методы алгебры [Гл. II
УПРАЖНЕНИЯ.
Методом простых итераций с точностью е = 10~2 уточнить
корни следующих уравнений:
2.36. tgB,2z) -3,2ж = 0;
2.37. 1пD,6ж) = 5,2ж-1,5;
2.38. 5,6sinD,8x)-4,5x = 0;
2.39. 0,8ехр (-0,6ж) - х = 0;
2.40. 0,17ж3 - 0,57ж2 - 1,6ж + 3,7 = 0.
2.2.3. Скорость сходимости. Процедура Эйткена ус-
ускорения сходимости. Скорость сходимости — одна из важ-
важнейших характеристик итерационных методов нахождения кор-
корней уравнения B.40) [5].
Определение 1. Говорят, что итерационный метод схо-
сходится со скоростью геометрической прогрессии, знаменатель
которой q < 1, если справедлива оценка
\^-xk\^coqk, k = 0,1,2,... B.61)
Определение 2. Число р (р ^ 1) называют порядком сходи-
сходимости метода, если в области сходимости имеет место оценка
\?-Xk+i\ ^ с- \?-хк\р , с > 0.
Если р = 1 и с < 1, то метод обладает линейной скоростью
сходимости, при р = 2 — квадратичной, р = 3 — кубичной и т. д.
Имеют место следующие утверждения.
Лемма 2.2. Если итерационный метод обладает линейной
скоростью сходимости [порядок сходимости р = 1), то этот
метод сходится со скоростью геометрической прогрессии со зна-
знаменателем q = cuco = ^ — xq и имеет место оценка погреш-
погрешности |? - Хк\ ^ qk |С - хо •
Лемма 2.3. Если итерационный метод обладает р-м по-
порядком сходимости {сверхлинейная скорость сходимости при
р > 1), то этот метод сходится со скоростью показатель-
показательной функции, имеющей основание q и показатель степени рк,
к
причем справедлива следующая оценка: |? — х^\ ^ с - qp , q =
1/A)
Таким образом, метод половинного деления обладает линей-
линейной скоростью сходимости (р = 1), и, следовательно, сходится со
скоростью геометрической прогрессии со знаменателем q = 1/2
и со = b — а (сравнить B.43) с B.61)).
§2.2] Численные методы решения уравнений 67
Аналогично, метод простых итераций также является ме-
методом первого порядка сходимости и, следовательно, сходится
со скоростью геометрической прогрессии со знаменателем q =
= max ^'(ж)! и со = \х\ — х$\ /A — q) (сравнить B.59) с B.61)).
хе[а,Ь]
В соответствии с леммой 2.3 и оценкой B.49) итерацион-
итерационный метод Ньютона обладает вторым порядком сходимости и,
следовательно, сходится со скоростью показательной функции,
имеющей основание q = с |? — х$\ и показатель степени 2k:
|? - хк\ < с0 • q2k,
где с = M2/2mi, со = 1/с, те. значительно быстрее методов
половинного деления и простых итераций.
Для ускорения медленно сходящихся методов существуют
различные способы ускорения, один из которых, процесс Эйт-
кена, основан на использовании нескольких предыдущих итера-
итерационных значений. Рассмотрим процесс ускорения по Эйткену
применительно к методу простых итераций.
Из выражения B.59) для оценки погрешности в методе про-
простых итераций можно записать: хк — ? = Aqk, где А — константа,
не зависящая от q. Тогда это выражение для трех соседних
итераций можно записать следующим образом:
откуда путем деления 1-го равенства на 2-е и 2-го на 3-е получим
Решая это уравнение относительно ?:
_ xk+1xki -х\
Хк-1 '
получим почти точное значение корня уравнения B.40). Это
значение ? можно принять за уточненное значение корня урав-
уравнения B.40) по методу Эйткена на (к + 1)-й итерации:
(хк+1)ут = **-1**+1-*? , B.62)
^ уУт хк+1 -2хк + хк
68 Численные методы алгебры [Гл. II
Можно показать, что погрешность метода простых итераций
с использованием процедуры Эйткена теперь пропорциональна
не qk, как в B.59), a q2 :
\^-хк\ ^ Aq2\
т. е. процесс итераций сходится со скоростью показательной
функции.
2.2.4. Замечания к методам отделения корней. Если
уравнение f(x) = О является алгебраическим уравнением целой
степени,
аохп + аххп~х + . . . + ап = О, B.63)
то при отделении корней этого уравнения могут использоваться
теоремы общей алгебры [1].
1. Основная теорема алгебры. Число корней уравнения
B.63) (действительных, кратных, комплексных) в точности
равно п — степени уравнения B.63), причем если коэффициенты
ао, &i, . . . , ап все действительные, то возможные комплексные
корни попарно сопряжены.
2. Теорема Декарта. Число положительных действи-
действительных корней уравнения B.63) равно числу перемен знаков
последовательности коэффициентов ао, а\, . . . , ап (не считая
нулевых коэффициентов) или меньше этого числа на четное
число.
Следствие. Число действительных отрицательных корней
уравнения B.63) равно числу постоянства знаков в последова-
последовательности коэффициентов ао, ai, . . . , ап, не считая нулевых,
или меньше этого числа на четное число.
3. Теорема Гюа. Если все корни уравнения B.63) действи-
действительны, то в последовательности коэффициентов ао, а\, . . . ,
ап квадраты некрайних коэффициентов больше произведения со-
соседних, т. е.
l к = 1,2, . . . ,п- 1. B.64)
Следствие. Если хотя бы для одного некрайнего коэффи-
коэффициента условие B.64) не выполняется, т.е. a| ^ a^_ia/g+i, то
имеется хотя бы одна пара комплексных корней.
Пример 2.14' Определить количество действительных и
комплексных корней уравнения
ж4 + 8ж3 - 12ж2 + 104ж - 20 = 0.
§2.3] Численные методы решения систем нелинейных уравнений
69
Решение.
Имеется три перемены знака. Значит, по теореме Декарта
количество положительных корней должно быть равно одному
или трем. Из 4-х корней по следствию из теоремы Гюа имеет-
имеется, по крайней мере, одна пара комплексных корней, так как
(—12J < 8 • 104). Следовательно, среди действительных корней
один положительный и один отрицательный.
§ 2.3. Численные методы решения систем
нелинейных уравнений
При численном решении систем нелинейных уравнений пред-
предполагается существование искомого вектора решений, возмож-
возможность нахождения начального приближения искомого вектора и,
наконец, применение эффективных процедур уточнения реше-
решений. Пусть дана система нелинейных уравнений
0,
0,
B.65)
= 0,
или
где
F = (
X = (
п ) '
0
о
и пусть имеется начальное прибли-
приближение вектора неизвестных:
Ж@) = ( ху Х^ . . . Х^п )Т. B.67)
Рис. 2.10. Начальное прибли-
приближение в случае системы двух
В случае системы двух нелиней- нелинейных уравнений
ных уравнений начальное прибли-
приближение находят графически как точки пересечения графиков
функций Fi(#i, х2) = 0 и F2(xi, х2) = 0 (рис. 2.10).
70 Численные методы алгебры [Гл. II
2.3.1. Метод простых итераций и метод Зейделя ре-
решения систем нелинейных уравнений. Для использования
метода простых итераций или метода Зейделя система B.65)
записывается в следующей эквивалентной форме:
Xi = ФДж1,ж2, • • • ,жп), г = 1,п, B.68)
где Фг(жх, Ж2, • • • , жп) — эквивалентные функции.
Эквивалентные функции могут быть построены, например,
в виде
Фг(ж1, Ж2, ... , Жп) = Жг + ^(жЬ Ж2, . . . , Жп), 1 = 1, П.
Тогда, если известно начальное приближение х° =
= ( х± Х2 • • • %п )Т' можно построить алгоритм метода
простых итераций:
) г=Т^, B.69)
или алгоритм метода Зейделя:
Можно показать, что метод простых итераций (соответствен-
(соответственно метод Зейделя) сходится к решению системы B.65), если
какая-либо норма матрицы Якоби, построенной по правым ча-
частям Ф^ (ж^)), г = 1,п, эквивалентной системы B.68), меньше
единицы на каждой итерации:
B.71)
г, j = l,n, fe = 0, 1, 2, . . .
Метод простых итераций B.69) (или Зейделя B.70)) останав-
останавливается при выполнении условия
|яг(*)|<е. B.72)
Тогда искомый вектор х « ^ +1)
§2.3] Численные методы решения систем нелинейных уравнений 71
Таким образом, методы простых итераций и Зейделя приме-
применяются для дифференцируемых функций Fi(x), г = 1,п, в си-
системе B.65).
Пример 2.15. Методом простых итераций с точностью е =
= 10~2 найти решение нелинейной системы:
sin (ж -0,6) -у- 1,6 = 0,
Зж - cos у - 0,9 = 0.
Соответствующая эквивалентная система имеет вид:
ж = 0,3 + 1/3 cos у = Фх (ж, у) ,
У = -1,6 + Sin (X - 0,6) ЕЕ Ф2 (Ж, у) .
Решение.
1) Начальное приближение ж^°) =0,15, у^ = —2,1 определя-
определяется как точка пересечения графиков эквивалентных функций.
^(ж^),^))^ = 0,31 < 1.
2) ж^1) = 0,1317, yW = -2,035.
Продолжая итерационный процесс, на 6-й и 7-й итерациях по-
получим соответственно жF) = 0,1539; у^ = -2,034; ж^7) = 0,151;
yW = -2,0319; |(жGУ7))Т " (У6У6))Т| = 0,0029 < е.
УПРАЖНЕНИЯ.
2.41. Когда можно применять методы простых итераций
и Зейделя?
Методом простых итераций решить следующие системы
уравнений с точностью е = 10~2:
2 42 { cos(x-1) + 2/ = 0'5'
[ж — cos у = 3;
24з
[ cos (у- 1) + х = 0,7;
2 44 f СОБХ + У = 1'5>
\ 2х - sin (у - 0,5) = 1;
2.45. ( cos(y-2) + x = 0'
1 sin (ж + 0,5) — у = 1;
72 Численные методы алгебры [Гл. II
2у - cos (ж + 1) = О,
2.46. < V J
х + sin у = —0,4;
2 47
s'my — 2x = 1.
2.3.2. Метод Ньютона. Рассмотрим систему нелинейных
уравнений B.65). Метод Ньютона решения систем вида B.65)
сводится к последовательному решению систем линейных алгеб-
алгебраических уравнений, полученных путем линеаризации системы
нелинейных уравнений.
Для к-го приближения вектора неизвестных х^ =
= ( х\' Х2 . . . х\г М будем искать (к + 1)-е приближение
в виде
ж(*+1) = х(к) + Ах(к) ^ B>73)
где вектор приращений Ах^ = (Ах[ ' Ах^ ... Ахп ' J под-
подлежит определению.
Для нахождения этих приращений разложим функцию
F\ (ж^+1^) в ряд Тейлора в окрестности точки х^к' до производ-
производных первого порядка включительно (оставим только линейную
часть относительно Ах) и приравняем это разложение нулю:
^) = 0, получим
Осуществляя те же процедуры для остальных уравнений си-
системы B.65), получим следующую СЛАУ относительно вектора
неизвестных Ах^ = (Ах[к) Ах{2к) . .
§ 2.3 ] Численные методы решения систем нелинейных уравнений 73
dF2
(k
ax fc
dFx
dxn
dF2
dF2
dxr
Ax™ = -F2
OX2
dFn
dxn
ih) = -Fn
B.74)
Для существования единственного решения СЛАУ B.74)
необходимо и достаточно, чтобы матрица этой СЛАУ
J
dF-L
\
дхг
8Fn
8Fn
была невырожденной (det J (ж^^) ^ 0), т. е. существовала обрат-
обратная матрица (J (ж^)) . Матрицу J называют матрицей Якоби
для системы B.65), а ее определитель — якобианом этой системы.
Запишем B.74) в векторно-матричной форме:
J
> = -F
74 Численные методы алгебры [Гл. II
откуда
дя(*) = _ j-i (>)) F (>)) . B.75)
Подставляя B.75) в B.73), получим алгоритм Ньютона решения
систем нелинейных уравнений B.65):
F(x(k)j B76)
(сравнить с методом Ньютона для одного нелинейного уравнения
Итерационный процесс B.76) заканчивается при выполнении
условия
где е — заданная точность, а вектор х «
Таким образом, для применения метода Ньютона B.76) необ-
необходимо выполнение следующих двух условий:
— существование частных производных первого порядка от
функций Fi(xi,X2, . . . ,жп), г = 1,п, по всем переменным х^
3 = !^п;
— матрица Якоби для системы B.65) на каждой итерации к =
= 0,1, 2, ... должна быть невырождена.
Пример 2.16. Методом Ньютона с точностью е = 10~2 ре-
решить систему нелинейных уравнений
F\ (ж1, х2) = xi - 2х\ + 1 = 0,
F2 (xi, х2) = -х\ + 2ж2 - 1 = 0.
Решение.
Графически можно показать, что первое вектор-решение рас-
расположено в прямоугольнике —0,8 < (#i)j < 0,4; 0,5 < (#2I < 1,0,
а второе — в прямоугольнике 0,8 < (#i)n < 1,1; 0,8 < {х<1)ц <
< 1,1. Уточним второе вектор-решение.
1) Начальное приближение х\ ' = @,8 + 1,1) /2 = 0,95; х^ =
= @,8+ 1,1)/2 = 0,95;
§2.3] Численные методы решения систем нелинейных уравнений 75
2) J
1 -3,8
-1,9 2,0
1 / (r\\ (Г\\\ -*
; J-1 (*«•>) = _L
-5,22
2,0 3,8
1,9 1,0
\ /
= A,00374 l,0023)T;
л \ I (^) (^) i
/I | l/7*/7*l
= A,0013 1,0034); ||жB) - хЩ\ = 0,0024 < e.
УПРАЖНЕНИЯ.
2.48. В каких случаях нельзя применять метод Ньютона?
Методом Ньютона с точностью е = 10~3 найти векторы-
решения для следующих нелинейных систем [6]:
2.49.
2.50.
2.51.
2.52.
2.53.
2.54.
sin (ж + 1) — у = 1,
2ж + cos у = 2;
х2 + 2у2 = 1;
2x + tg(xy) = 0,
0,6ж
х
2у = 0,
cosy + 6x = 0;
sin(x + 0,8) + 2y- 1 = 0,
tgx - cos A,5?/) = 0,
2y3 - x2 + 4ж - 3 = 0.
2.55. Сколько итераций требуется в методе Ньютона для
СЛАУ?
76 Численные методы алгебры [Гл. II
§ 2.4. Численные методы решения задач на
собственные значения и собственные векторы
матриц линейных преобразований
2.4.1. Основные определения и спектральные свойст-
свойства матриц. Рассмотрим матрицу Лпхп в n-мерном веществен-
вещественном пространстве Rn векторов
х = (xi х2 ... хп)Т.
1. Собственным вектором х матрицы А называется ненулевой
вектор (ж ^ ^), удовлетворяющий равенству
Ах = Лж, B.77)
где Л — собственное значение матрицы Л, соответствующее рас-
рассматриваемому собственному вектору.
2. Собственные значения матрицы А с действительными эле-
элементами могут быть вещественными различными, вещественны-
вещественными кратными, комплексными попарно сопряженными, комплекс-
комплексными кратными.
3. Классический способ нахождения собственных значений
и собственных векторов известен и заключается в следующем:
— для однородной СЛАУ, полученной из B.77),
(А - ХЕ) х = $, $ = (О 0 ... 0)т , B.78)
ненулевые решения (х ф $, а именно такие решения и находятся)
имеют место при
det(v4- XE) = 0, B.79)
причем уравнение B.79) называют характеристическим уравне-
уравнением, а выражение в левой части — характеристическим мно-
многочленом;
— каким-либо способом находят решения Ai, A2, . . . , Ап алгеб-
алгебраического уравнения B.79) n-й степени (предположим, что они
вещественны и различны);
— решая однородную СЛАУ B.78) для различных собственных
значений Aj, j = 1, n,
(A- XjE)xj = 0, j =
§2.4] Численные методы решения задач на собственные значения 77
получаем линейно независимые собственные векторы х3, j =
= 1, п, соответствующие собственным значениям Aj, j = 1, п.
4. Если количество линейно независимых собственных векто-
векторов матрицы Апхп совпадает с размерностью пространства Rn,
то их можно принять за новый базис, в котором матрица Апхп
примет диагональный вид
Л = U~l • А • U. B.80)
На главной диагонали матрицы Л находятся собственные значе-
значения, а столбцы матрицы преобразования U являются собствен-
собственными векторами матрицы А (матрицы Ли А, удовлетворяющие
равенству B.80), называются подобными).
5. Основные свойства собственных значений и собствен-
собственных векторов:
а) Теорема Перрона. Если все элементы квадратной
матрицы положительны, то наибольшее по модулю
собственное значение ее также положительно, является
простым (не кратным) корнем характеристического уравнения
и ему соответствует собственный вектор с положительными
компонентами;
б) если для собственного значения Л^ найден собственный
вектор х3, то вектор сх3, где с — произвольное число, также
является собственным вектором, соответствующим собственному
значению Aj, при этом векторы х3 и сх3 являются линейно
зависимыми.
в) попарно различным собственным значениям соответству-
соответствуют линейно независимые собственные векторы;
г) /с-кратному корню характеристического уравнения B.79),
построенного для произвольной матрицы Апхп , соответствует
не более к (^ к) линейно независимых собственных векторов;
д) собственные значения подобных матриц Ли Л, удовлетво-
удовлетворяющих равенству B.80), совпадают;
е) симметрическая матрица А (А = АТ) имеет полный
спектр Xj , j = l,n, вещественных собственных значений;
ж) положительно определенная симметрическая матрица
(Л = т4т, (Ах, х) > 0) имеет полный спектр вещественных по-
положительных собственных значений;
з) /с-кратному корню характеристического уравнения B.79)
симметрической матрицы соответствует ровно к линейно неза-
независимых собственных векторов;
78
Численные методы алгебры
[Гл. II
и) симметрическая матрица имеет ровно п ортогональных
собственных векторов (в соответствии со свойством е), при-
приняв которые за новый базис (т. е. построив матрицу преобра-
преобразования ?/, взяв в качестве ее столбцов координатные столбцы
собственных векторов), можно преобразовать симметрическую
матрицу А к диагональному виду с помощью преобразова-
преобразования B.80).
к) для симметрической матрицы А матрица преобразова-
преобразования U в B.80) является ортогональной U~1 = UT, и, следова-
следовательно, преобразование B.80) имеет вид
Л = UT • А • U. B.81)
Покажем, что собственные значения матриц Л и А в соот-
соотношении B.80) (или B.81)) одинаковы, собственные векторы —
различны, а столбцы матрицы U — суть координатные столбцы
собственных векторов матрицы А. Действительно, в соответ-
соответствии с B.80) характеристические многочлены матриц Л и А
одинаковы, поскольку
1
det Л =
• det A • det U = det A
detU
на основе свойства определителя произведения матриц и опреде-
определителя обратной матрицы, т. е. собственные значения матриц Л
и А одинаковы.
Обозначим собственные векторы матрицы Л через у:
Ау = Ху, B.82)
а собственные векторы матрицы А — через ж, тогда
Ау = U^AUy = Л • у, A(Uy) = Л • (?/у), но Ах = Хх,
откуда
Uy = х.
Для первого собственного вектора
ство B.82) имеет вид
0
\
А2
Хг
Vi
„A)
У2
Уп
\
B.83)
матрицы Л равен-
у[^
У?
„A)
у Уп
§2.4] Численные методы решения задач на собственные значения 79
\ (!) \ (!) (!) 1
л\у\ = \iy{ \ откуда у\ = 1,
А2У2 — Aij/2 ? ^2^Ь следовательно у^ = О,
=
Таким образом,
п\ Ап
, следовательно
= 0.
V0/
Из B.83) для у^1' имеем
/
откуда
\ /Л
U21 U22
и
о /
х\
X
A)
Аналогично для всех остальных векторов у^'\ j = 2, п полу-
получаем
Ж1
Х2
=
иц У
U21
\ ип1 )
(п)
X о
\Хп /
=
uln\
U2n
что и требовалось доказать, т. е. столбцы матрицы U суть соб-
собственные векторы матрицы А.
80 Численные методы алгебры [Гл. II
УПРАЖНЕНИЯ.
2.56. Показать, что для любого собственного значе-
значения Л (А) невырожденной матрицы А справедлива оценка
l/ЦЛ!! ^ |Л(Л)| ЦЛ!! ^ \Х(А)\ ^ \\A\\ (использовать опре-
определение cond(v4) в п. 2.1.5).
2.57. Доказать, что для симметрической матрицы А столбцы
матрицы U в равенстве B.80) являются собственными ортого-
ортогональными векторами (столбцы матрицы U ортогональны, если
U — ортогональная матрица, т.е. /У = UT).
2.58. Доказать, что собственные значения симметрической
положительно определенной матрицы А (А = Лт, (Ах, х) > 0)
являются положительными числами.
2.59. Доказать, что у матрицы
А =
2 0,4 0,4
0,3 4 0,4
0,1 0,1 5
все собственные значения вещественны (использовать норму обе-
обеих частей равенства Ах = Хх). Указать интервалы, которым
принадлежат собственные значения.
2.61. Показать, что для экстремальных собственных значений
, Хт[п симметрической матрицы А справедливы оценки
Хт'т(А) ^ тт(ац).
2.62. Показать, что у вещественной трехдиагональной мат-
матрицы А все собственные значения вещественны, если
>0, г = 1, п — 1 (показать, что она подобна трехдиагональной
симметрической матрице). Элементы г-й строки матрицы А —
а*, 6*, с*, г = 1,п.
2.4.2. Метод вращений Якоби численного решения
задач на собственные значения и собственные векторы
матриц. Метод вращений Якоби применим только для симмет-
симметрических матриц Апхп (А = АТ) и решает полную проблему
собственных значений и собственных векторов таких матриц. Он
основан на отыскании с помощью итерационных процедур мат-
матрицы U в преобразовании подобия [5,7] Л = U~1 AU\ а поскольку
§2.4] Численные методы решения задач на собственные значения 81
для симметрических матриц А матрица преобразования подобия
U является ортогональной (U~1 = UT), то
Л = UTAU,
B.84)
где Л — диагональная матрица с собственными значениями на
главной диагонали
Л =
О
\
\
О
\п )
Геометрически метод вращений представляет собой после-
последовательное вращение системы базисных векторов в п-мерном
вещественном пространстве Rn
в плоскости некоторых, спе-
специальным образом выбранных
двух векторов. Такая последова-
последовательность вращений осуществ-
осуществляется до тех пор, пока новые
базисные векторы не совпадут
с собственными векторами, т. е.
в качестве базисных принима-
принимаются собственные векторы мат-
матрицы А. Поскольку симметриче-
симметрическая матрица имеет полный на-
набор ортогональных собственных
векторов (см. п. 2.4.1.), то для
нее можно построить алгоритм
метода вращений на основе преобразования подобия B.84).
Пример 2.17. На плоскости R2 с ортонормированным бази-
базисом (г, j) построить матрицу преобразования вращения U около
начала отсчета на угол ср.
Решение. В соответствии с рис. 2.11 имеем
—i- sin ф О
Рис. 2.11. Геометрическая интер-
интерпретация метода вращения на
плоскости
г' =
jf = —i sin cp + j cos (p,
82
Численные методы алгебры
[Гл. II
COS (f — Sin if
sin (f cos if
т. е. матрица вращения U на плоскости имеет вид
U =
COS (f — Sin (f
sin cp cos (^
Пример 2.18. В пространстве /?3 с ортонормированным
базисом (г, j, /с) построить матрицы вращения на угол (р соот-
соответственно в плоскостях (j, /с), (&, г), (г, j).
Решение. В [8] доказывается, что матрицы вращения
UXI Uy) Uz имеют вид
их =
/ 1 0 0 ^
О cos ip \— sin ip
О sin у? cos ip J
' cos (p 0 sin (p у
0 1 0
— sin ip\ 0 cos ip J
Uz =
costp \— sin cp\ 0 \
sin ip cos cp 0
0
0
i/
из которого видно, что номера базисных векторов в их упорядо-
упорядоченной совокупности (г, j, fc), находящихся в плоскости враще-
вращения, совпадают с номером строки и номером столбца, на пересе-
пересечении которых стоит элемент — sin ср.
Матрица полного вращения U около начала координат на
некоторый угол определяется как преобразование
U = UxUyUz.
Можно показать, что в n-мерном пространстве Rn в плоско-
плоскости вращения, содержащей базисные векторы с номерами г и j,
матрица вращения имеет вид
§2.4] Численные методы решения задач на собственные значения 83
и =
Пусть дана симметрическая матрица А. Требуется вычислить
для нее с точностью е все собственные значения и соответ-
соответствующие им собственные векторы. Алгоритм метода вращений
следующий [5].
Пусть известна матрица А^к\ являющаяся приближением
матрицы Л на к-и итерации, при этом для к = О А^ = А.
1. Выбирается максимальный по модулю недиагональный
(к) (
элемент а-- матрицы А^к' I max
2. Ставится задача найти такую ортогональную матрицу
U^k\ чтобы в результате преобразования подобия Л^+1) =
— ij\k)TAWIJW произошло обнуление элемента а\- матрицы
^(/с+1) g качестве ортогональной матрицы выбирается представ-
представленная ниже матрица вращения U^k\ В ней на пересечении г-й
строки и j-ro столбца находится элемент щ,' = —sin(p(k\ где
ipW _ угол вращения, подлежащий определению. Симметрично
относительно главной диагонали (j-я строка, г-й столбец) рас-
расположен элемент vr-^ = sin(p(k\ Диагональные элементы и\^
r
(k\
и vr-- равны соответственно и\^ = cos(p(k\ uk-- = cosip^] дру-
другие диагональные элементы u\nm = 1, m = 1, п, т ф г, т ф j;
остальные элементы в матрице вращения U^ равны нулю.
Угол вращения ср(к) определяется из условия а\- ' = 0:
84
Численные методы алгебры
[Гл. II
2(k) _ (к) '
1гг ajj
B.85)
COS (fy ' — Sin (fy
1
Sin (f
0
\
0
,(*)
>(*)
1
COS(/?
(к) (к)
\{' — о*)/
3. Строится матрица
(к) (к) (b)
причем если а\{' — о*)/, то (рК) = —.
(к+1) п
в которой элемент а\- « U.
В качестве критерия окончания итерационного процесса ис-
используется условие малости суммы квадратов внедиагональных
элементов:
Если
1) > г, то итерационный процесс
продолжается. Если t (Л +1) < г, то итерационный процесс оста-
останавливается, и в качестве искомых собственных значений прини-
() () ()
маются:
\±
, А2
, . . . , An
§2.4] Численные методы решения задач на собственные значения 85
Координатными столбцами собственных векторов матри-
матрицы А в единичном базисе будут столбцы матрицы U =
• • • ип1) , (ж2) = (и12 и22 ¦ ¦ ¦ ип2), ...
U2n ¦ ¦ ¦ Unn)
гт-1
(ж1) =
причем эти собственные векторы будут ортогональны между
собой, т.е. (жг, хт) « 0, / ф т.
Остановимся подробнее на вычислении угла вращения.
Для определения угла вращения ср( ' на к-ои итерации при-
приравняем нулю внедиагональный элемент а \- ' (стоящий на
(к)
месте максимального по модулю элемента а\-' в матрице
в произведении Д^^1) = JJ\k)TA^U^k\ получим
COSif
— sin
'11
simp
.... cos ip
О
,(*)
,(*)
V
M
{k)
ain
(k)
(k)
•4?
V^nl
nj
86
Численные методы алгебры
[Гл. II
coscpW .... — simp
.... cos lp
После перемножения на месте элемента а^- будет следую-
следующее выражение, которое приравняется нулю:
/
\
г
o(*+i)
aji
3
o(*+l)
aij
)
sin ^(
cos
sin
cos
S-/cos
sin
= 0,
а поскольку А^ — симметрическая матрица (т.е. а\ • = a^),
из последнего равенства следует выражение B.85).
Пример 2.19. С точностью е = 0, 3 вычислить собственные
значения и собственные векторы матрицы
А =
4 2 1
2 5 3
1 3 6
§2.4] Численные методы решения задач на собственные значения 87
Решение.
1) Выбираем максимальный по модулю внедиагональный эле-
элемент матрицы А^\ т. е. находим а- • такой, что
м
=max
@)
Им является элемент а^3 — 3, т. е. г = 2, j = 3.
2) Находим соответствующую этому элементу матрицу вра-
вращения:
1 О
О cos <p
О sin о?
г = 2;
5 — 6
= -0,7033; sinv?@) = -0,65; cosv?@) = 0,76;
1 0 0
0 0,76 0,65
0 -0,65 0,76
3) Вычисляем матрицу
= (/@)
4 0,87 2,06
0,87 2,46 -0,03
2,06 -0,03 8,54
В полученной матрице с точностью до ошибок округления эле-
элемент б43 к 0. Проверяется окончание итерационного процесса:
1/2
следовательно итерационный процесс необходимо продолж:ить.
Численные методы алгебры
[Гл. II
Переходим к следующей итерации (к = 1):
= 2,06;
= max
а%
т.е. i = 1, j = 3;
cos(/?W 0 -sin^W i = l
0 1 0
siny^1) 0 cosy^1)
= ^rCtg4^ = -°'3693;
sin ipW = -0,361; cos (^A) = 0,933;
0,933 0 0,361
0 10
-0,361 0 0,933
3,19 0,819 0,005
0,819 2,46 0,28
0,005 0,28 9,38
1/2
Переходим к следующей итерации (к = 2):
0,005
2I/2
>e.
ag} = 0,819;
= max
гг. р 7—I /,' — О.
§2.4] Численные методы решения задач на собственные значения
1 , 2-0,819
sin v?B' = 0,5445; cos v?B) = 0,8388.
t
0,8388 -0,5445 0 i = 1
0,5445 0,8388 0
0 0 1
3,706 0,0003 0,1565
0,0003 1,929 0,232
0,1565 0,232 9,38
= @,00032 + 0Д5652 + 0,2322)х/2 = 0,078391/2 < e.
Таким образом, в качестве искомых собственных значений
принимаются диагональные элементы матрицы А^:
Ai « 3,706; А2 ~ 1,929; А3 « 9,38.
Собственные векторы определяются из произведения
0,78 -0,5064 0,361
0,2209 0,7625 0,6
-0,58 -0,398 0,7
0,78
0,2209
-0,58
; х =
-0,5064
0,7625
-0,398
0,361
0,6
0,7
90
Численные методы алгебры
[Гл. II
Полученные собственные векторы ортогональны в пределах
заданной точности, т. е.
(ж1, ж2) = -0,00384; (ж1, ж3) = 0,0081; (ж2, ж3) = -0,0039.
УПРАЖНЕНИЯ.
2.63. Показать, что собственные значения матриц Л и Л в пре-
преобразовании подобия B.84) одинаковы, а собственные векто-
векторы — нет.
2.64. Показать, что для симметрической матрицы А матрица
преобразования подобия U в B.84) ортогональна (U~l = UT).
2.65. Для следующих матриц с точностью ? = 10~2 определить
методом вращения собственные значения и собственные векторы:
а)
в)
Д)
ж)
1,0 1,3 1,2
1,3 0,6 1,5
1,2 1,5 0,8
2.2 0,3 0,5
0,3 1,2 0,6
0,5 0,6 1,0
1.3 0,6 0,8
0,6 1,0 1,2
0,8 1,2 1,5
1,2 0,4 2,5
0,4 1,4 0,6
2,5 0,6 0,7
б)
е)
з)
0,6 1,0 2,1
1.0 1,4 0,5
2.1 0,5 1,0
1.2 1,5 0,3
1.5 0,4 2,0
0,3 2,0 1,2
1.6 1,2 0,4
1.2 0,5 1,0
0,4 1,0 0,8
0,7 0,8 1,3
0,8 2,6 1,3
1.3 1,3 0,8
§2.4] Численные методы решения задач на собственные значения 91
и)
1,2 2,0 0,5
2,0 1,4 1,7
0,5 1,7 0,3
2.4.3. Частичная проблема собственных значений
и собственных векторов матрицы. Степенной метод.
Рассмотренный метод вращения решает полную проблему соб-
собственных значений и собственных векторов матриц (симметриче-
(симметрических) в том смысле, что определяются все собственные значения
и собственные векторы.
Зачастую не нужно находить все собственные значения
(спектр) и все собственные векторы, а необходимо найти мак-
максимальное и минимальное из них. Существует степенной метод
определения спектрального радиуса матрицы, т. е. максималь-
максимального собственного значения матрицы, и соответствующего ему
собственного вектора.
Пусть дана матрица Л, и пусть ее собственные значения
упорядочены по абсолютным величинам:
B.86)
,@)
Тогда, выбрав некоторый вектор у*- ', например вектор, ком-
компоненты которого равны единице у(°) = A 1 ... 1)т, можно
построить следующую итерационную последовательность:
уB) = АуA) = А2у@) ^
B.87)
(к) = Ау(к-1) =
92 Численные методы алгебры [Гл. II
Здесь в круглых скобках индексов указаны номера итераций,
а без скобок — показатели степеней.
Покажем, что алгоритм B.87), называемый степенным ме-
методом, можно использовать для получения максимального соб-
собственного значения и соответствующего ему собственного векто-
вектора матрицы А.
Разложим у(°) по собственным векторам матрицы А:
у(°) = aixl + a2xl + . . . + апхп, B.88)
и умножим слева левую и правую части выражения B.88) на
матрицу А , получим
у(к) = Аку@) = a±Akxi + a2Akx2 + ... + апАкхп. B.89)
Рассмотрим в B.89) слагаемое с сомножителем Акх1:
Ах1 = Хгхг; А2хг = А{Ахг) = Л1ЛЖ1 = Xjx1;
А3х1 = Х31х1; ...; Акх1 = Хкх1. B.90)
В соответствии с B.90) выражение B.89) можно записать
следующим образом:
у{к) = Аку@) = aiXkxl
Записав выражение B.91) для j-ro компонента вектора
на к-й и (к + 1)-й итерациях:
yf] = alX)Xk )\ к
y = aiX)Xk+l + a2x)Xk+1 + ... + anx]Xkn+1,
и разделив у. на у-, получим
§2.4] Численные методы решения задач на собственные значения 93
где /3{j = оцх1-^ г = 1,п. Разделим числитель и знаменатель
последнего выражения на
{2т)
V ^
где fii = -1 < 1, г = 2~гг; 7ij = ^-, * = X™
Перейдя в B.92) к пределу при к —» ос,
lim
а затем сняв знак предела, получим для ограниченного к
B-93)
где j — любое из j = 1, п.
С помощью выражения B.93) приближенно вычисляется
максимальное собственное значение Ai матрицы А (ее спектраль-
спектральный радиус).
Точное выражение для Ai может быть записано следующим
образом:
..(*)
где fi2 = т—, j— любое из j = 1, п.
Ai
Для приближенного вычисления собственного вектора, соот-
соответствующего максимальному собственному значению Ai, поло-
положим в выражении B.91) слагаемые, начиная со второго, равными
нулю при большом числе итераций, получим
откуда х1
94 Численные методы алгебры [Гл. II
Поскольку собственные векторы определяются с точностью
до постоянной, то число ol\ можно положить равным 1, тогда
х1 « \у{к)- B.94)
К
Таким образом, определяющими выражениями в степенном
методе являются алгоритм B.87) и выражения B.93) — для
собственного значения и B.94) — для собственного вектора.
При выполнении условий B.86) итерационный процесс сходит-
сходится к искомому собственному значению Ai и соответствующему
собственному вектору, причем скорость сходимости определяет-
определяется отношением |A2|/|Ai| (чем оно меньше, тем выше скорость
сходимости).
В качестве критерия завершения вычислений используется
следующее условие:
Л*) л(*)
Ч ~ Л1
где е — задаваемая вычислителем точность расчета.
С помощью степенного метода можно вычислить и мини-
минимальное собственное значение матрицы А (внутреннего радиуса
спектрального кольца). Для этого достаточно степенной метод
применить к обратной матрице Л, т.е. получить |Атах(Л~1)|
и взять обратную величину:
Соответствующий собственный вектор хп будет
rrn ~ M~1>lfc7/@) \\ • (Л\\к (i№)\ — (ЛЛ Л\
или, с точностью до константы,
Конечно, вычисление минимального собственного значения
матрицы А требует ее обращения, поэтому этот способ вычисле-
вычисления Amin(v4) не распространен широко.
§2.4] Численные методы решения задач на собственные значения
95
Пример 2.20. Вычислить спектральный радиус матрицы
\
А =
5 12
1 4 1
2 13
С ТОЧНОСТЬЮ ? = 0,1.
Решение. В качестве начального приближения собствен-
собственного вектора возьмем г/0' = A 1 1)Т. Реализуем итерационный
процесс B.87), B.93), полагая j = 1:
? =
A)
= (8 6 6f, X? = %у = 8- = 8;
у\ 1
= Ау^ = E8 38 40)т, Ai2) = \ = f = 7,25;
7/ О
Д2)_
л B) Л1)
Л1 ~ Л1
= 0,75 > е;
= ЛуB) = D80 250 274)т, Af} =
= 7,034;
е(з) =
\C) ж B)
Л1 ~ А1
= 0,216 > е;
= B838 1682 1888)т, л{4) = \ =
= 6,9559;
гD)_
kC)
= 0,078 < е.
Таким образом, полученное на 4-ой итерации значение Л^ ^ =
= 6,9559 удовлетворяет заданной точности и может быть взято
в качестве приближенного значения Ai. Искомое значение спек-
спектрального радиуса р(А) = max|A^| = |Ai| = 6,9559.
i
Рассмотренный выше пример наглядно иллюстрирует суще-
существенный недостаток алгоритма B.87), связанный с сильным
возрастанием компонентов итерируемого вектора
в ходе ите-
итерационного процесса. Видно, что
У
(к)
|Ai|. Во избежание
96 Численные методы алгебры [Гл. II
неограниченного возрастания (при |Ai| > 1) или убывания (при
|Ai| < 1) компонентов yW по мере увеличения числа итераций к
обычно при проведении компьютерных расчетов применяется
степенной метод с нормировкой итерируемого вектора. С этой
целью алгоритм B.87) модифицируется следующим образом:
(к) = лЛк-1) Лк) Jj (к)
z — /\у , лг — . л, у —
h(k)\
При этом в качестве начального приближения у(°) берется
вектор с единичной нормой.
Широко распространена также версия степенного метода,
использующая скалярные произведения:
ГЛАВА III
ТЕОРИЯ ПРИБЛИЖЕНИИ
Программа
Исчисление конечных и разделенных разностей. Задача интерпо-
интерполяции, единственность многочленной интерполяции. Интерполяцион-
Интерполяционные многочлены Лагранжа и Ньютона. Погрешность многочленной
интерполяции. Сплайн-интерполяция. Вывод кубического сплайна де-
дефекта один. Метод наименьших квадратов: точечный и интегральный.
Численное дифференцирование с помощью сглаживающих функций
и с помощью отношения конечных разностей. Порядок и уточнение
формул численного дифференцирования. Численное интегрирование.
Методы прямоугольников, трапеций, Симпсона; их геометрическая
интерпретация, погрешность, порядок. Повышение порядка методов
численного интегрирования.
В теории приближений изучаются методы приближения
функций более простыми, хорошо изученными функциями, ме-
методы численного дифференцирования и численного интегриро-
интегрирования. При этом исследуемая приближаемая функция может
быть задана как в аналитическом, так и дискретном виде (в виде
экспериментальной таблицы).
Пусть дана некоторая функция / (х) на отрезке х Е [а, 6], ко-
которая является довольно сложной для исследования. Требуется
заменить эту функцию некоторой простой, но хорошо исследуе-
исследуемой функцией (например, многочленом). Для этого с помощью
/ (х) строят таблицу (ее называют сеточной функцией),
C.1)
которую можно заменить (сгладить) простой функцией с кон-
контролируемой погрешностью.
Рассмотрим два подхода к такой замене.
4 В.Ф. Формалев, Д.Л. Ревизников
х{
Уг
Хо
УО
XI
У1
Уп
98 Теория приближений [Гл. III
1. Пусть приближенная функция, являющаяся многочленом
n-й степени, _
/ (ж) = аохп + сцх71'1 + . . . + ап, C.2)
где п + 1 — число узлов в таблице C.1), с неизвестными пара-
параметрами а^, г = 0, п, так приближает сеточную функцию / (ж),
что _
Уг = f(xi), г = 0, п. C.3)
В этом случае говорят, что функция / (ж) интерполирует
сеточную функцию C.1), а сама задача приближения называется
задачей интерполяции. Точки ж^, г = О, п, называют узлами
интерполяции, а условие C.3) — условием интерполяции. Появ-
Появляется возможность вычислить значения / (х) не только в узлах
интерполяции, но и между ними в точках ? ? (ж^_1, ж^), г = 1, п,
причем /(?) «/(?)•
2. При большом количестве точек ж^, г = 0, п, интерполяция
требует большой гладкости (по п-й производной), что практи-
практически выполнить невозможно. Поэтому сглаживание сеточной
функции C.1) осуществляют путем минимизации некоторого
функционала, построенного с помощью C.1) и многочлена C.2)
степени га, например квадратичного функционала:
п
S (а0, аь . . . , ат) = ^ [yi - f (ж*)] , га < п. C.4)
г=0
Процедуру сглаживания в этом случае называют аппрокси-
аппроксимацией заданной функции функцией C.2), в частности, аппрок-
аппроксимацию с использованием функционала C.4) называют аппрок-
аппроксимацией с помощью точечного метода наименьших квадратов.
Если коэффициенты сглаживающей функции C.2) определя-
определяются путем минимизации функционала,
6
Г — 2
S (а0, аь . . . , ат) = [/ (ж) - / (ж)] dx,
а
сглаживание называют интегральным методом наименьших
квадратов.
Если в качестве сглаживаемой функции задана эксперимен-
экспериментальная таблица C.1), то в методах сглаживания практически
ничего не изменяется. Изменяются методы оценки погрешности
сглаживания.
§3.1] Исчисление конечных разностей 99
При построении методов сглаживания очень часто использу-
используется понятие конечных разностей.
§3.1. Исчисление конечных разностей
Пусть дана сеточная функция C.1) для функции f(x) или
экспериментальная таблица C.1).
В вычислительной математике аналогом понятия дифферен-
дифференциала является понятие конечной разности, которое использу-
используется при построении методов теории приближений, в частности
при построении интерполяционных многочленов.
Определение 1. Конечной разностью первого порядка впе-
вперед (назад) сеточной функции C.1) в узле Х{ называют разность
= Уг+1- У%, Ъ = О, П - 1 (А^ = у{ - Уг-Ъ ^ = 1,п).
Определение 2. Конечной разностью второго порядка впе-
вперед (назад) сеточной функции C.1) в узле Х{ называют разность
первого порядка от разности первого порядка:
А2Уг = А (АУг) = A (yi+1 - Уг) = Ayi+1 - АУг =
= {Уг+2 - Уг+l) - (Уг+1 ~ У г) = Уг+2 ~ ^Уг+\ + У г,
г = 0, п - 2 (Д2У; = уг+1 - 2Уг + Уг-ъ г = 1, п - l) .
Определение 3. Конечной разностью 3-го порядка вперед
(назад) называется разность первого порядка от разности второ-
второго порядка:
i = yi+з - Зуг+2 + 3^+1 ~ Уг, i = О, П - 3
Зуг+1 + Зуг ~ Уг-1, г = 1, П - 2)
И Т.Д.
По аналогии запишем конечную разность k-vo порядка впе-
вперед (назад) в узле Х{\
г = Уг+к ~ Clyi+k-1 +
... + (-1)кУг, г = 0,п- к
г = Уг+k-l ~ С\уг+к-2 + Clyi+k
* ). C.5)
100
Теория приближений
[Гл. III
Здесь С? =
К
*(*-l)(*-2)...(fc-m
га!
Ясно, что конечной разностью сеточной функции C.1) ну-
нулевого порядка в узлах ж^, г = 0,п, являются значения yi этой
функции в этих узлах.
§ 3.2. Задача интерполяции
Пусть на отрезке ж ? [а, Ь] задана функция /(ж), с помощью
которой построена сеточная функция C.1) или задана экспери-
экспериментальная таблица C.1).
При сглаживании функции (или экспериментальной табли-
таблицы) с помощью интерполяции в соответствии с условием интер-
интерполяции C.3) значение интерполирующей функции и значение
заданной функции в узлах сетки должны быть одинаковыми,
следовательно, погрешность интерполяции в узлах ж^, г = 0, п,
равна нулю (рис. 3.1).
У\
Уг
Уп
Xq Xi Х2 ... Хп X
Рис. 3.1. К задаче интерполяции
Задача интерполяции имеет не единственное решение, но
в одном случае, когда интерполирующей функцией является
многочлен п-й степени (п + 1 — число узлов интерполяции)
§3.2]
Задача интерполяции
101
вида C.2), интерполяция имеет единственное решение, т.е. ко-
коэффициенты ао, . . . , ап определяются единственным образом.
Действительно, используя таблицу C.1) и многочлен C.2),
составим СЛАУ относительно неизвестных коэффициентов
ао, . . . , ап:
г = п
q +
п-1
+ . . . + ап =
ап =
C.6)
ап = уп.
Неоднородная СЛАУ C.6) имеет единственное решение для
коэффициентов ао, . . . , ап, так как определитель матрицы этой
СЛАУ не равен нулю:
det
г*П
C0
X
п-1
ХЛ
X
п-1
Т
X
п-1
\ ^n ™n ' ' ' 1 /
поскольку все значения узлов интерполяции различны между
собой и ни одна из строк не является линейной комбинацией дру-
других. Таким образом, задача многочленной интерполяции имеет
единственное решение, так как коэффициенты ао, . . . , ап могут
быть выбраны единственным образом.
3.2.1. Интерполяционный многочлен Лагранжа. Для
многочленной интерполяции можно и не решать СЛАУ C.6),
а многочлен C.2) можно составить следующим образом.
Запишем систему многочленов n-й степени:
(х - xi)(x - х2) • . • (х - хп)
(х0 -
• • • (х0 - хп)
1 X = Xq
(x -xo)(x- x2) ...(x-xn) _ I 1, x =
- xo)(x1 - x2) • • • (zi - xn) \ qx =
i, г — 0, 2, щ
102
Теория приближений
[Гл. III
- хо)(х -
cn - xo)(xn - xx) ... (xn - хп-г)
I 1 X = X
0, ж = Ж?, г = 0, га — 1.
Составим линейную комбинацию этих многочленов (их коли-
количество равно га + 1) с коэффициентами линейной комбинации,
равными значениям yi сеточной функции C.1), получим много-
многочлен n-й степени
Ln (x) =
- Х0) (Х -
- Хп)
i=0
i - Х0) (Xi -
- Xn
C.7)
Многочлен C.7) называют интерполяционным многочленом
Лагранжа п-й степени, так как он, во-первых, удовлетворяет
условию интерполяции
Ln (x{) = yi, г = 0, га,
и, во-вторых, имеет n-ю степень.
Интерполяционный многочлен Лагранжа обладает тем недо-
недостатком, что в случае, когда добавляются новые узлы интерполя-
интерполяции в таблице C.1), все слагаемые в C.7) необходимо пересчиты-
пересчитывать. Но, с другой стороны, он обладает тем достоинством, что
интервалы между узлами могут быть неравномерными: ж^+i —
— Х{ = hi ф const, г = 0, га — 1.
Выпишем наиболее употребляемые многочлены L\(x)
и L,2(x).
1) Для таблицы с двумя узлами интерполяции ж^, #г+1:
Xi
Уг
Жг+1
Уг+1
Li(x) = у,
"^ "^ ъ-\-\
Уг+i
i
2) Для таблицы с тремя узлами интерполяции ж^-i, ж^,
Xi-l
Уг-1
Xi
Уг
%г+1
Уг+1
§3.2] Задача интерполяции 103
) = Уг-1/ _XJ\(X. Х%-х-—) +
(х — Xi-±)(x — Xi+i) (x — X{-i)(x — Х{)
~Г Уг~( w 7 ~г Уг-\-1~/ Г7 V*
3.2.2. Интерполяционный многочлен Ньютона.
Пусть сеточная функция C.1) имеет равномерный шаг между
узлами интерполяции: ж^+i — Х{ = hi = h = const, i = 0, n — 1.
Будем строить интерполяционный многочлен следующим об-
образом:
Nn (х) = ао + а\ (х - хо) + а2 (х - хо) (х - х\) + . . .
. . . + ап (х - х0) • • • {х - xn-i). C.8)
Коэффициенты ао, . . . , ап будем определять из условия
интерполяции Nn(xi) = yi, i = 0, п, с использованием табли-
таблицы C.1):
х = хо : Nn(xo) = уо = а0 ^ а0 = у0; C.9)
х = xi : Nn(xi) = а0 + а\{х\ - ж0) =
Х\ ~
д т / \ . / \
JU JU У . 1 \
2/1-2/0 дУо /о 1Пч
ai = ——; C.10)
h
л 2 л 2
2/2 - 22/i - 2/о А 2/о А 2/о /о 11 \
— 2/2 =^ ^2 — ^ — о"? а2 — о"- (^-И)
2/г2 2!/г2 2!/г2
И так далее,
ап =
Подставляя коэффициенты C.9)-C.12) в многочлен C.8), полу-
получим
{х - х0) {х - ал) + . . .
2\h2
• • • н гт^г (ж - ж0)... (ж - жп_1). C.13)
Многочлен C.13) является интерполяционным многочленом,
поскольку является многочленом n-й степени и удовлетворяет
условию интерполяции C.3). Он называется интерполяционным
многочленом Ньютона. Его достоинство заключается в том, что
104 Теория приближений [Гл. III
он строится проще, чем Ln (ж), и при добавлении новых узлов
интерполяции в таблицу C.1) все предыдущие слагаемые не пе-
ресчитываются, а добавляются новые. К недостаткам многочле-
многочлена Nn(x) по сравнению с Ьп(ж), можно отнести использование
постоянного шага между узлами интерполяции (ниже, в п. 3.2.4,
на основе понятия разделенных разностей строится интерполя-
интерполяционный многочлен Ньютона с переменным шагом).
В силу единственности многочленной интерполяции ясно, что
после раскрытия скобок получим Ln (ж) = Nn (ж).
3.2.3. Погрешность многочленной интерполяции.
Ясно, что в узлах интерполяции погрешность интерполяционно-
интерполяционного многочлена Ln(x) или Nn(x) равна нулю:
l^n \Х{) У%
= 0, г = 0,п.
I
~Уг
Будем искать погрешность Ln(x) — /(ж) в виде разности меж-
между значением интерполяционного многочлена Ьп{х) и значением
функции /(ж) в точке ж, не совпадающей с узлом интерполяции.
Для нахождения погрешности составим следующую вспомо-
вспомогательную функцию:
<p(x) = f (х) -Ьп(х)-а-ш (х), C.14)
где а подлежит определению, а си(х) — многочлен (п + 1)-й
степени:
со (ж) = (ж — жо) (ж — х\) ... (ж — хп). C.15)
Из C.14) и C.15) видно, что [Ln(x)]{n+1) = 0, [и (ж)](п+1) =
= (п + 1!).
Будем искать а из условия, что ср (ж) = 0 в точке, в которой
исследуется погрешность. Обозначим эту точку через ~х\
а = Щ. (з.1б)
Функция ср (ж) имеет (п + 1) корень в узлах интерполяции,
так как там ио (ж) =0 и погрешность / (ж) — Ln (ж) = 0. Но
если добавим еще точку ж", в которой потребуем ср (~х) = 0, то
(р (ж) будет иметь уже (п + 2) корня. Итак ip (ж) имеет (п+2)
корня, (р! (ж) имеет (п+1) корень, ср" (ж) имеет п корней и т.д.,
§3.2]
Задача интерполяции
105
^(n+i) ^ имеет 1 корень. Обозначим этот корень через ? Е
Е (жо,жп).
Покажем, что увеличение порядка производной функции
у (ж) на единицу уменьшает количество корней этой функции на
единицу. Действительно, из теоремы Ролля известно, что если
функция ср (х) на [xi-i^Xi] непрерывна, дифференцируема на
интервале (ж^-ьж^) и имеет на концах одинаковые значения,
то внутри этого интервала найдется хотя бы одна точка, в ко-
которой производная этой функции равна нулю. Функция (р (х)
на каждом отрезке удовлетворяет теореме Ролля (см. рис. 3.2).
Рис. 3.2. Соотношение количества нулей функций (р(х) и <р'(х)
Вычисляя производную (п + 1)-го порядка от C.14) в точке ?
и учитывая, что значение (р(п+1^ (х) = 0, так как (р(х) имеет (п +
+ 2) корня, получим
откуда
a = L( у-. C.17)
Подставляя C.17) в C.16), находим погрешность многочленной
интерполяции в точке ~х Е (ж^-i, ж^), г = 1, п:
106 Теория приближений [Гл. III
_ _ f(n-\-l) (?) _ _ _
f (х) - Ln (х) = \ J(x - хо)(х -xi)...(x- xn),
(п + 1)! (ЗЛ8)
С € (хо,хп) = (а, 6);
~х — точка, в которой ищется погрешность, не совпадает с узлами
интерполяции.
Поскольку точка ? ? (а, Ь) неизвестна, то вместо погрешно-
погрешности C.18) вводится верхняя оценка погрешности в виде
\f{x)-Ln{x)\ <:
max
xe[a,b]
1)!
(х - хо)(х - х\) ... (х - хп) | , C.19)
которая и используется на практике.
В случае, если интерполяционный многочлен строится для
экспериментальной таблицы C.1), функция f(x) отсутствует
и погрешностью в форме C.18) или C.19) воспользоваться не
удается. Тогда, добавляя к таблице C.1) один узел интерполяции,
можно записать верхнюю оценку погрешности C.19) с помощью
отношения конечных разностей (п + 1)-го порядка
Д(П+1)Ы
\у(х) - Ln(x) | ^ | (х - хо)(х - х±). . . (х - хп) \ ,
т. е. с помощью добавочного (п + 1)-го слагаемого в интерполя-
интерполяционном многочлене Ньютона.
3.2.4. Интерполяционный многочлен Ньютона, по-
построенный с помощью разделенных разностей. В вычис-
вычислительной математике аналогом понятия производной является
понятие разделенной разности.
Разделенной разностью сеточной функции C.1) нулевого по-
порядка в узлах Жг, г = 0,п, называются значения этой функции
в этих узлах f(xi) = yi, i = 0, п.
Определение 1. Разделенной разностью функции C.1) пер-
первого порядка в узлах ж^, г = 0, п — 1, называют отношение
§3.2] Задача интерполяции 107
Определение 2. Разделенной разностью функции C.1) вто-
второго порядка в узлах ж^, г = 0, п — 2, называют отношение
f(xitxi+uxi+2) = /(*«+ь*<+а)-/(*„*<+1) =
_ Xj+2 - Xj + 1 Xi+1 - Xj _ Xj+2 - Xi+1 Xi+1 - Xj
Xi+2 - Xi Xi+2 - X{
i = 0, n — 2. И так далее.
Определение 3. Разделенной разностью функции C.1) п-го
порядка в узле xq называют отношение
... ,ЖП) -
Если шаг сетки в таблице C.1) постоянный, т.е. hi = Х{ —
— Xi-i = const, г = 1, п, то разделенные разности совпадают с от-
отношением конечных разностей. Например, разделенные разности
2-го и 3-го порядков в узле х при Х{ — Х{-\ = const имеют вид
_ 2!/г2 2!/г2 _
~" х3 - х0 ~ 3/г ~~ 3!/г3 '
Таким образом, если в интерполяционном многочлене Ньюто-
Ньютона коэффициенты при многочленах в слагаемых заменить разде-
разделенными разностями, т. е. многочлен Ньютона записать в форме
= /(ж0) + /(ж0, xi)(x - ж0) + /(ж0, Ж1, ж2)(ж - жо)(ж -
. . . + /(ж0, Ж1,. . . , жп)(ж - жо)(ж - xi)... (х - жп_1), C.20)
то при /i = const эта форма превращается в обычную выведенную
ранее форму C.13):
? ^-(х - хо)(х -
- хо)(х - хг)... (ж - Хп-г). C.21)
108
Теория приближений
[Гл. III
Итак, интерполяционный многочлен Ньютона C.20) исполь-
используется в случае задания таблицы C.1) с неравномерным шагом,
а C.21) — для таблицы C.1) с постоянным шагом.
3.2.5. Сплайн-интерполяция. Интерполяция, использу-
использующая сразу все п узлов таблицы C.1), называется глобальной
интерполяцией.
Начиная с п ^ 7 глобальная многочленная интерполяция
становится неустойчивой в том смысле, что погрешности возрас-
возрастают, так как записанный интерполяционный многочлен требует
гладкости по производным 7-го и высших порядков (рис. 3.3).
Ln(x) ,
x0 Xi x3 ... xn x
Рис. 3.3. Неустойчивость глобальной многочленной интерполяции при п ^ 7
Поэтому обычную многочленную интерполяцию осуществля-
осуществляют максимум по 3-4 узлам (для 3-х узлов 2-ой степени, 4-х узлов
3-й степени). Интерполяцию по нескольким узлам таблицы C.1)
называют локальной: линейной по каждым двум узлам с по-
помощью интерполяционных многочленов Li(x), квадратичной по
каждым трем узлам с помощью интерполяционных многочленов
L2(x), и так далее.
Однако такая локальная интерполяция с помощью Ln или
Nn страдает тем недостатком, что интерполирующая функция
в узлах стыковки многочлена имеет непрерывность только ну-
нулевого порядка, т. е. локальные интерполяционные многочлены
принадлежат классу функций С0 (см. рис. 3.4 для L^ N2 в уз-
узле ж*).
§3.2]
Задача интерполяции
109
От этих недостатков свободна сплайн-интерполяция, которая
требует непрерывности в узлах стыковки локальных многочле-
многочленов по производным соответственно порядка один, два и т. д.
Определение. Сплайном степени га дефекта г называется
(га — г) раз непрерывно дифференцируемая функция, которая
L2(x)
Рис. 3.4. Локальная интерполяция по каждым трем узлам
на каждом отрезке [жг-ъ#г]? * = ^'п' представляет собой мно-
многочлен степени га.
Наиболее распространенными в науке и технике являются
сплайны 3-й степени дефекта один, т. е.
ТП = 3, I _ _oi_9
г = 1 /
т. е. дважды непрерывно дифференцируемый многочлен 3-й сте-
степени на каждом отрезке [ж^_1,ж^], г = 1,п. Сплайны, удовле-
удовлетворяющие условию интерполяции, называются интерполяцион-
интерполяционными.
Основным достоинством интерполяционного кубического
сплайна S(х) дефекта один является следующее: этот сплайн
обладает минимумом интегральной кривизны на всем заданном
отрезке [а, Ь] по сравнению с другими интерполяционными функ-
функциями /(ж), т.е.
l
[f"(x)Ydx.
Геометрически это означает, что если тяжелую упругую нить
110 Теория приближений [Гл. III
повесить на ряд гвоздей, то она примет форму кубического
сплайна дефекта 1, приведенную на рис. 3.5.
Рис. 3.5. Тяжелая упругая нить, геометрически представляющая собой ку-
кубические сплайны дефекта один
Выведем интерполяционные кубические сплайны Sk(ж), к =
= 1, п, дефекта один в соответствии с таблицей C.1). Кубический
сплайн S(x) на отрезке х ? [жг-ъ хг\ имеет четыре неизвестных
коэффициента. Количество отрезков [жг-ъ жг] в соответствии
с таблицей C.1) равно п. Для определения 4 х п коэффициентов
имеются следующие условия в узлах интерполяции:
— условие интерполяции S(xi) = yi, i = 0, n;
— непрерывность сплайнов S(xi — 0) = S(xi + 0), г = 1, n — 1;
— непрерывность производных 1-го порядка Sf(xi — 0) = Sf(xi +
+ 0), i = l,n-l;
— непрерывность производных 2-го порядка S"(xi — 0) =
= S"(xi + 0), i = l,n-l.
Таким образом, всего имеется (п + 1) + 3(п — 1) = 4п — 2
условий. В качестве двух недостающих условий задают значения
производных 1-го или 2-го порядка в узлах xq и хп. Для вывода
используем значения Sff(xo) = Sff(xn) = 0. В этом случае сплайн
называется естественным.
Пусть Sff(x) = q(x). На отрезке [xi-\,Xi\ рассмотрим пове-
поведение функции q(x) (см. рис. 3.6).
Поскольку сплайн является многочленом 3-й степени, то на
каждом отрезке [ж^_1,ж^] 2-я производная будет линейна. Най-
Найдем ее с помощью интерполяционного многочлена Лагранжа 1-й
степени L\(x)\
q(x) = qi-i— ^— + Яг _ • C.22)
Выражение C.22) уже удовлетворяет условиям непрерыв-
непрерывности производных 2-го порядка. Действительно, подставим
в C.22) х = Xi — 0, получим q(xi — 0) = qi. Затем, выписывая
выражение C.22) для отрезка [x
§3.2]
Задача интерполяции
111
q(x) =
rp . rp
h
rp rp .
e [xi,xi+i] , i = 1, n - 1,
и подставляя в него Xi + 0 вместо ж, получим д(ж^ + 0) = qi, что
и требовалось показать.
Рис. 3.6. Поведение функций S"(x) на элементарных отрезках
Для нахождения сплайна проинтегрируем дважды выраже-
выражение C.22), получим
S(x) = qi-\ ^Xi ~ ^ + q^X~Xi~^ + Cix + С2, C.23)
где С\ и С2 найдем из удовлетворения значений сплайна C.23)
в узлах Xi-i, xi, условиям интерполяции
6/1,-
С2
Решая эту СЛАУ относительно Ci, C2 и подставляя их
в C.23), найдем следующее выражение для сплайна степени 3
дефекта 1:
-х)+1 у±-„-^
' + 1 Л,- Яг 6
. C.24)
112 Теория приближений [Гл. III
В этом сплайне узловые значения для вторых производных
qi пока неизвестны. Будем искать их из условий непрерывности
первых производных в узлах Х{.
Для нахождения производной Sf(xi + 0) запишем C.24) для
отрезка [ж^Жг+х]
- X) + ( |^±I - дг+l^1 ) (^ - Жг), Ж Е [ж*, Ж^+i] . C.25)
\^1 О у
Вычисляя производные первого порядка от C.24) и C.25)
и подставляя в них значение ж = ж^, получим
о О A
Приравняем эти выражения в соответствии с условиями
непрерывности первых производных в узлах интерполяции ж^,
получим
U-lY + Яг ч " +
г = 1, n — 1;
qo = qn = 0. C.27)
Система C.26) с заданными краевыми условиями C.27) —
СЛАУ относительно qi = S"(xi), г = 1, п — 1, имеет трехдиаго-
нальную матрицу, и, следовательно, ее можно решать методом
прогонки. Подставляя найденные д^, г = 0, п, в C.24), полу-
получим кубические сплайны дефекта один на каждом отрезке ж Е
GU. -, ГУ» .1 Л 1 /VI
Таким образом, определяющими выражениями для нахож-
нахождения кубических сплайнов дефекта один являются выражения
C.24), C.26), C.27).
Пример 3.1. Построить интерполяционные многочлены
Лагранжа и Ньютона, совпадающие с функцией / (ж) = Зж, ж Е
Е [—1, 1], в точках жо = — 1, жх = 0, Ж2 = 1. Вычислить значение
§3.2]
Задача интерполяции
113
сеточной функции и оценить погрешность многочленной интер-
интерполяции в точке ж* = 0,5.
Решение. Составим сеточную функцию и занесем ее в таб-
таблицу. Поскольку п = 2, то необходимо построить интерполяци-
интерполяционные многочлены L2 (х) и Л^ (х):
Xi
Уг
х0 = -1
Уо = 1/3
хг=0
2/1 = 1
Х<1 = 1
У2 = 3
(ж - хг) (х - х2)
+
(х-хо)(х-х2)
+ ух
- Х2) (X! ~ Хо) (X! ~ Х2)
+
(х-хо)(х-х1) _ 2 2 4
(Х2 — Хо) (Х2 — Х\) 6 6
—1) = 1/3; L2 @) = 1;
Ь2 [X) =
Проверим условия интерполяции
L2(l) = 3.
Для определения конечных разностей, входящих в интерпо-
интерполяционный многочлен Ньютона, удобно пользоваться таблицей
конечных разностей, в которую конечная разность к-то порядка
в узле Xi определяется как A^yi = A^^yi+i — Д^^, к =
= 1, 2, . . . ; г = 0, п.
Xi
-1
0
1
Уг
1/3
1
3
AVi
1-1/3 = 2/3
3-1 = 2
А*Ш
2 - 2/3 = 4/3
Тогда
Уо / \ . А Уо /
- (ж - ж0)+—-г (ж -
2 +
Здесь использованы конечные разности в узле хо (подчерк-
(подчеркнуты в таблице). Получен результат, подтверждающий теоре-
теорему о единственности многочленной интерполяции, поскольку
L2(x) = N2(x).
114
Теория приближений
[Гл. III
Значение сеточной функции в точке ж* = 0,5 вычислим по
интерполяционному многочлену у @,5) « L<i @,5) = 1,8333.
Верхнюю оценку погрешности интерполяционного многочле-
многочлена определим в соответствии с выражением C.19):
max \f'"(x)\
G[-l,l]
3!
(ж*- ж0) (ж*- xi) (ж*- ж2)|;
max \f"'(x)\= maxit |3Ж • In3 3| = 31 • In3 3 = 3,978;
30'5- (J-0,25 +^-0,5 + 1
^ ^^ 1@,5 + 1) @,5 - 0) @,5 - 1I = 0,249.
6
Поскольку функция /(ж) = Зж известна, то можно вычислить
точное значение абсолютной погрешности в точке ж* = 0,5:
Зж* - L2 (ж*) = З0'5 - (J • 0,25 + 1 . 0,5 + l) | = 0,1012,
т. е. верхняя оценка погрешности примерно в 2,5 раза превышает
абсолютную погрешность в точке ж* = 0,5.
Пример 3.2. Оценить погрешность в точке ж* = 0,5 много-
многочленной интерполяции из примера 3.1 для случая, когда задан-
заданная таблица получена из эксперимента (функция / (ж) отсут-
отсутствует) .
Решение. В этом случае верхнюю оценку погрешности мож-
можно оценить с помощью (п + 1)-го члена формулы C.20)или C.21),
дополнив таблицу еще одним узлом интерполяции со значением
функции, полученным с помощью, например, экстраполяции.
Доп.
узел
Xi
-1
0
1
2
Уг
1/3
1
3
7
2/3
2
4
^2Уг
4/3
2
2/3
(х* -
(х* - Х\) (х* - Х2)\ =
§3.2]
Задача интерполяции
115
= ^\ |@,5 + 1) @,5 - 0) @,5 - 1)| = 0,125,
т. е. получили погрешность, близкую к истинной абсолютной
погрешности, равной 0,1012.
Пример 3.3. Для заданной таблицы
х{
Уг
х0 = -1
Уо = 1/3
хх = 0
2/1 = 1
х2 = 2
2/2 = 9
составить интерполяционный многочлен Ньютона.
Решение. Таблица задана с неравномерным шагом, поэтому
для решения задачи воспользуемся многочленом Ньютона с раз-
разделенными разностями (формула C.20)):
, х2) (х - хо) (х - х\) ,
N2
где
(*) = J
/ы
= 2/о
+
=
/(жо,а
1/3;
ял)(х
- хо)
+ /(
+
Х(
хг-х0 0 + 1 3'
2/2 ~ 2/1 2/1 - 2/о 9-1 1-1/3
10
+ 1
Таким образом, Л^ (х) = —х2 -\ х + 1.
Условия интерполяции соблюдены: А^ (—1) = 1/3; N2 @) = 1;
N2 B) = 9.
Пример 3.4» Для заданной таблицы с h = xi — xi-\ = 1 =
= const выписать интерполяционные кубические сплайны дефек-
дефекта один на каждом отрезке х Е [яЧ-ьяч], г = 1, 4. Проверить
непрерывность сплайнов и их производных до второго порядка
включительно в узле ж* = 2.
г
Xi
2/г
Чг
0
жо = 1
2/о = 1
0
1
х\ = 2
2/1 = 3
18/7
2
ж2 = 3
2/2=6
-30/7
3
хз = 4
2/з = 9
102/7
4
#4 = 5
у4 = 21
0
116
Теория приближений
[Гл. III
Решение. Под заданной таблицей сформируем дополни-
дополнительную строку для вторых производных сплайнов Sff (xi) =
= qi, которая заполняется по мере их вычисления (сразу можно
вписать в нее (/0 — 94 — 0).
Для узлов х\ = 2; х2 = 3; ж3 = 4 с учетом 9о — 94 = 0 состав-
составляется СЛАУ C.26) относительно неизвестных 91, 92•> 9з:
2 1 2/2 — У\ У\ — Уо
— 9i ~Ь ~92 ~~ — ~~
3 6
2 1 Уз~У2
+ oQ2 + -93 =
Vе! ~ У\
1 1
У 4 ~Уз Уз- У2
= 0,
= g
6 3 1 1
Вычисляются прогоночные коэффициенты по формулам
— с,- ' ^
Bi
1
-;
3
-;
4
—;
и значения
<72 =
ь г = 3, 2,
+ ^2 = -
102
15
= Вз = 102/7;
_30
18
Заносим эти значения в дополнительную строку таблицы
и для каждого из четырех интервалов выписываем сплай-
сплайны C.24):
§3.2] Задача интерполяции 117
16[2;3];
- x) + (^ - «4
= ^ E - жK + ^ E - ж) + 21 (я - 4), xe [4, 5].
Проверим правильность построения сплайнов для узла ж* =
= 2. К нему примыкают сплайны S\ (x) и 5п (ж):
ft B - 0) = 3; Sn B + 0) = 3;
51B-0) = ^; 5^B + 0) = ^;
УПРАЖНЕНИЯ.
3.1 Выписать интерполяционные многочлены Лагранжа
и Ньютона для узловых значений у^, заданных функций у =
= / (х) в точках Х{. Вычислить значение многочлена и оценить
погрешность в точке ж*.
а) у = cos ж; жо = 0; х\ — тг/6; Ж2 = тг/3;
^з = тг/2; Ж4 = 2тг/3; ж* = 1.
б) у = tg ж; жо = —тг/3; Ж1 = —тг/6; Ж2 = 0;
^з = тг/6; Ж4 = тг/3; ж* =0, 5.
118 Теория приближений [Гл. III
в) у = In ж; xq = 1; х\ — 1, 5; ж2 — 2;
ж3 = 2,5; ж4 = 3,0; ж* = 2,3.
г) у = еж; ж0 = 0; х\ = 0,1; ж2 = 0, 2;
ж3 = 0,3; ж4 = 0,4; ж* =0,25.
2
д) у = ех ; ж0 = 1; Ж1 = 1,1; ^2 = 1, 2;
Жз = 1, 3; ж4 = 1, 4; ж* = 1, 25.
е) у = ж; жо = 1; жх = 2; ж2 = 3; жз = 4; ж4 = 5; ж* = 2, 5.
ж) у = sin ж; жо = 0; х\ = тг/6; ж2 = тг/3;
жз = тг/2; ж4 = 2тг/3; ж* = 1.
3.2. В заданиях упражнения 3.1 оценить погрешность много-
многочленной интерполяции для случая, когда полученные в них таб-
таблицы считаются экспериментальными (т. е. после формирования
таблицы считать, что / (ж) отсутствует).
3.3. Выписать интерполяционные многочлены Ньютона, ис-
используя разделенные разности.
а) у = sin ж; жо = 0; х\ — тг/6; ж2 = тг/4; жз = тг/2.
б) у — cos ж; жо = 0; х\ — тг/6; ж2 = тг/4; жз = тг/2.
в) у = е~ж; жо = 0; Ж1=0,5; ж2 = 0,8; жз = 1,5.
г) у = tg ж; ж0 = 0; жх = тг/6; ж2 = тг/4; ж3 = тг/3.
3.4. Для заданий упражнения 3.1 выписать интерполяцион-
интерполяционные кубические сплайны дефекта один на каждом отрезке ж Е
? [ж^-1,Жг], г = 1,4. Проверить непрерывность 5(ж2), 5"(ж2),
§ 3.3. Метод наименьших квадратов
При наличии значительного числа экспериментальных точек
сглаживание с помощью многочленной интерполяции не имеет
смысла не только из-за неустойчивости (локальных выбросов)
интерполирующей функции, но и из-за сильного колебания за-
заданных точек. Способы локальной интерполяции, например с по-
помощью сплайнов, также не дают приемлемых результатов.
§3.3]
Метод наименьших квадратов
119
В этом случае дискретно заданную функцию сглаживают
в среднем, чаще всего многочленом, коэффициенты которого
находят с помощью минимизации отклонения сглаживающей
функции от заданных точек в некотором среднеинтегральном
смысле (рис. 3.7).
F(x9aQ9al9...,am)
Уо
У\
У2
Уп
Xq Xi Х2 ... *л_1 Хп X
Рис. 3.7. К методу наименьших квадратов
Одним из таких методов является метод наименьших квад-
квадратов (МНК). Суть его заключается в следующем.
Пусть дана экспериментальная таблица C.1). Составим мно-
многочлен степени га (га <С п)
F(x, а0, аь . . . , аш) = аожт + аххш~х + . . . + аш. C.28)
Будем полагать, что отклонение значений этого многочлена
от заданных таблицей C.1) значений yi, г = 0, п, минимально
в некотором среднеинтегральном смысле.
В точечном методе наименьших квадратов строится функ-
функционал
ь . . . , ат) =
xi, а0, аь . . . , ат) -
C.29)
г=0
который геометрически представляет собой сумму квадратов
отклонений значений yi от значений аппроксимирующего мно-
многочлена C.28) в точках ж^, г = 0, п (на рис. 3.7 показаны двусто-
двусторонними стрелками).
120 Теория приближений [Гл. III
Необходимым условием минимума функции многих перемен-
переменных является равенство нулю ее частных производных первого
порядка по независимым переменным. В функционале C.29)
такими независимыми переменными являются коэффициен-
коэффициенты ао, ai, ... , ат многочлена C.28), которые до их определения
являются не постоянными, а варьируемыми переменными:
2S2[F(xi, а0, аь . . . , аш) - yi] х™ = 0,
да° 7=t
dS П
2S2[F(xi, а0, аь . . . , ат) - yi] х™~1 = 0,
i=o C.30)
dS
2S2[F(i, а0, аь . . . , аш) - уг} х°{ = 0.
1 = 0
Неоднородная СЛАУ C.30) порядка т + 1 относительно
неизвестных ao,ai,... , аш является нормальной, и, следова-
следовательно, ее матрица является симметрической и положитель-
положительно определенной. Решения ao, ai, . . . , аш доставляют минимум
функционалу C.29).
Если представить СЛАУ C.30) в виде
+ boiai + ... + bomam = со,
. . . + bimam = c\,
+ bmiai + . . . + bmrnam = cm,
то можно выписать выражения для коэффициентов
i,j = 0, m, и правых частей с^, г = 0, т:
i=0 i=0
г=0 i=0
i=0 i=0
§3.3] Метод наименьших квадратов 121
п
г
i=0 i=0
г=0 i=0
г=0
Решив эту СЛАУ относительно ао, ах, ... , ат и подставив
их в C.28), получаем многочлен степени mCn, наилучшим
образом сглаживающий дискретную функцию C.1) в средне-
квадратическом смысле.
Для выбора степени многочлена C.28) можно начинать с мно-
многочлена 1-й степени F(x, ао, а\) = clqx + ai, решив задачу о то-
точечном МНК для которого, находят коэффициенты ао, а\.
Определяют максимальную по модулю величину относитель-
относительной погрешности: \5(yi)\m = max \(F(xi) — yi)/yi\, и если она
г
не превышает заданную точность г, то за аппроксимирующий
многочлен принимают F(x) = clqx + a\. В противном случае
увеличивают степень многочлена на единицу и повторяют расчет
и т.д.
Однако на практике заданную таблицу представляют гра-
графически и по заданным точкам приближенно определяют вид
аппроксимирующего по МНК многочлена.
В интегральном методе наименьших квадратов рассматрива-
рассматривается интегрируемая с квадратом функция у = /(ж), х ? [а, 6],
которая трудна для исследования (например, трудно вычислить
производные).
Будем аппроксимировать эту функцию некоторой функцией
с минимизацией заштрихованной площади (см. рис. 3.8), напри-
например с помощью многочлена
F(x, ао, ai, . . . , ат) = х
где ао, ai, . . . , аш находят из условия минимизации следующего
квадратичного функционала:
ъ
S(a0, аь . . . , ат) = [F(x, a0, ab . . . , am) - f(x)]2 dx. C.31)
122
Теория приближений
[Гл. III
F(x)
а Ь х
Рис. 3.8. К интегральному методу наименьших квадратов
Необходимые условия минимума функционала C.31) имеют
вид
8S
да0
= 2 J [F(x, а0, . . . , ат) - f(x)]xmdx = О,
= 2
, а0,. . . , ат) -
= О,
8S
дат
= 2
, а0, . . . , ат) - f(x)]x°dx = О,
которые после интегрирования приобретают форму следующей
СЛАУ:
b10a0
... + bomam = J f(x)xmdx,
a
b
. . . + blmam = J f(x)xm~1dx,
C.32)
b
+ bmidi + ... + bmmam = J f(x)x°dx.
В нормальной СЛАУ C.32) относительно коэффициентов
ao,tti,... , dm, правые части могут не интегрироваться в силу
сложности исследуемой функции f(x). В этом случае правые
§3.3]
Метод наименьших квадратов
123
части вычисляются с помощью методов численного интегриро-
интегрирования, которые рассматриваются ниже, в § 3.5.
Пример 3.5. Используя точечный метод наименьших квад-
квадратов аппроксимировать заданную таблицу линейным и квадра-
квадратичным многочленами.
г
JL <i
Vi
0
0
1
1
6,1
2
2
10,9
3
3
18,1
4
4
27,3
5
5
38
F2
Si
Sii
(xi)
Ы
Ы
-0,4285
2,82
-1,153
0,0071
6,6229
5,9743
0,086
-0,0206
13
11
0
o,
,6743
,0796
,255
0165
20
18
0
o,
,7257
,1287
,145
0016
27,7771
27,1287
0,0174
-0,0063
34,8285
38,078
-0,083
0,0021
Решение. Под заданной таблицей необходимо заготовить
таблицу для значений линейного F\ (xi) и квадратичного F<i (xi)
многочленов, которые будут получены в результате решения
задачи, а также для их относительных погрешностей.
Для линейного многочлена (т = 1) F\ (ж, ао, сц) =
= uqx + а\ составляется функционал (п = 5) S (ао, а\) =
5
= XI [(аохг + O'l) — У г] 5 частные производные от которого по
неизвестным параметрам
as 5
а\ приравниваются нулю:
- Уг] Xi = 0,
г=0
5
г=0
В результате получается СЛАУ 2-го порядка относительно
неизвестных параметров ао, а\\
+
124
Теория приближений
[Гл. III
— V -г2-
Z^ ^i '
г=0
где
5 г=" 5
= ? ж° = 6; d = ? 3
г=0 г=0
г=0
i=0
%\ Ьц =
г=0
Используя табличные значения ж^, yi i = О, 5, получим СЛАУ
= 381,4,
= 103,2.
Решая ее с помощью правила Крамера:
Аап =
_ Аа0<
— * 1 (ЛЛ
д
381,4 15
103,2 6
д =
= 740,4; Асы =
55
15
п -,
1\
15
6
55
15
= 105 ?
381,4
103,2
= -45,
находим а0 = 7,0514; ах = -0,4285; F± (х) = 7,0514ж - 0,4285.
Значения этого многочлена в заданных узлах ж^, г = 0; 5, зано-
заносятся в первую строку дополнительной таблицы, а относитель-
относительные погрешности S\ (yi) = (F\ (xi) — yi)/yi — в третью строку
дополнительной таблицы. Максимальная по модулю относитель-
относительная погрешность max|5i {у%)\ = 1,153, т.е. более 100%, что зна-
г
чительно превышает заданную точность.
Поэтому далее рассматривается квадратичная аппроксими-
аппроксимирующая функция 7*2 (ж, ао, ai, ^2) = «ож2 + а\х + a<i, для кото-
которой функционал и нормальная СЛАУ имеют вид
5
S (а0, аь а2) = ^ [(ao^f + <цхг + а2) - Уг] ,
8S
да0
OS
дах
3S
да2
i=0
= 2
i=0
5
= 2
= 2
= 0,
а2) - уг-] • 1 = 0.
§3.3]
Метод наименьших квадратов
125
Собирая коэффициенты при неизвестных ао,
, получаем
где Ьоо =
|; 601 = Ью =
5
5
i=0
= 6. С0 = Yj УгхЬ Cl =
5 5 5 5
= J] Xi] Ьц = J2 ХЬ Ь
i=0 i=0
5
= Е Уг-
i=0
Тогда в соответствии с табличными значениями Х{, у% имеем
(каждое уравнение разделено на коэффициент при ао)
а0 + 0,2298ai + 0,05618а2 = 1,6337,
а0 + 0,2444ai + 0,06667а2 = 1,6951,
а0 + 0,2727ai + 0,1091а2 = 1,8764,
откуда получаем ао = 0,9743; а\ = 2,18; а2 = 2,82. Таким обра-
образом,
F2 (х) = 0,9743ж2
2,82.
Значения этого многочлена заносятся во вторую строку до-
дополнительной таблицы, а относительные погрешности 6ц (yi) =
= (F2(xi) — Уг)/Уг — в четвертую строку этой таблицы, откуда
видно, что максимальная по модулю погрешность max \6ц (yi)\ —
г
= 0,0206, что меньше заданной точности е = 0,05.
Таким образом, многочлен F<i (x) наилучшим образом в квад-
квадратичном смысле приближает заданную таблицу с точностью
е = 0,05.
УПРАЖНЕНИЯ.
3.5. Точечным методом наименьших квадратов аппроксими-
аппроксимировать линейным и квадратичным многочленами следующие
дискретно заданные функции и определить максимальную по
модулю погрешность аппроксимации:
126
Теория приближений
[Гл. III
х{
Уг
Xi
Уг
Xi
Уг
JL i
Уг
Xi
Уг
0
4,2
0
3,2
0
1,9
0
1,1
0
1,1
Jb i
Уг
0
1,1
1
8,8
1
f ,8
1
5,2
1
3,9
2
16,3
2
15,3
2
9,8
2
9,2
3
24,6
3
23,6
3
17,3
3
16,8
4
36,5
4
35,5
4
25,7
4
25,3
5
48,4
5
47,5
5
37,5
5
35,7
1
4,9
2
11,2
3
18,8
4
29,3
5
40,7
1
5,9
2
13,2
3
21,8
4
33,4
5
45,4
Xi
Уг
0
2,1
1
6,9
2
13,7
3
23,4
4
33,6
5
47,5
Xi
Уг
0
3,1
1
5,8
2
11,2
3
17,7
4
27,4
5
37,5
а)
б)
в)
г)
Д)
е)
ж)
з)
3.6. Показать, что в методе наименьших квадратов решения
ао, &ь ... , аш СЛАУ C.30) доставляют минимум (а не макси-
максимум) функционалу C.29).
3.7. Интегральным методом наименьших квадратов аппрок-
аппроксимировать линейным, квадратичным и кубичным многочлена-
многочленами следующие функции, заданные на отрезках ж G [а; Ь], и опре-
определить относительную погрешность:
а) у = sin (ж), ж е [-тг/4; тг/4];
б) у = tgz, ж е [-тг/4; тг/4];
в) у = еж, х е [-1; 1];
)у ,[;];
д) у = In ж, ж G [0,5; 2];
е) у = cos (ж), ж е [—тг/4; тг/4].
§3.4] Численное дифференцирование 127
§ 3.4. Численное дифференцирование
Этот параграф является основополагающим для численного
интегрирования дифференциальных уравнений, как обыкновен-
обыкновенных, так и в частных производных.
Пусть в некоторой точке ж* требуется вычислить производ-
производные первого, второго и т. д. порядков от дискретно заданной
функции C.1). Могут иметь место следующие два случая: а) точ-
точка ж* Е (ж^-i, ж^), г = 1, п, и б) точка ж* = ж^, г = 1, п — 1, т. е.
совпадает с одним из внутренних узлов заданной таблицы.
Тогда в первом случае заданная таблица сглаживается какой-
либо функцией (р (ж), являющейся глобальным (локальным) ин-
интерполяционным многочленом или многочленом, полученным по
МНК с некоторой погрешностью /?п(ж), в результате чего имеют
место следующие равенства
у{х) = (f(x) + Яп(ж), у(х*) = (р(х*) + Яп(ж*);
у\х) = ^(х) + <(ж), у\х*) = <р'(х*) + <(ж*); C.33)
у"{х) = <р"{х) + <(ж), у" {х-) = <р»(х*) + <(ж*);
Следует отметить, что процедура численного дифференци-
дифференцирования является некорректной в том смысле, что близость
искомой функции у(х) и сглаживающей функции ip (ж) не га-
гарантирует близости их производных (рис. 3.9). Более того, они
могут иметь в одной и той же точке ж* производные различных
знаков. Тем не менее формулы C.33) широко используются на
практике.
Во втором случае (ж* = ж^, г = 1,п — 1) используется ап-
аппарат разложения функций в ряд Тейлора, для чего функция
в точке ж* должна иметь достаточное число производных. С этой
целью предполагается, что заданная таблица C.1) является се-
сеточной функцией для некоторой функции у (ж), имеющей в точ-
точке ж* производные до четвертого порядка включительно, т. е. что
Уг = y(Xi).
Тогда внутренний узел ж* = ж^, г = 1,п — 1, окружают уз-
узлы ж^_1, ж^+1 (рис. 3.10), причем ж^+i — Х{ — Х{ — ж^-i = h.
Тогда, разлагая значения 2/г-ъ Уг+i на точной функции в ряд
Тейлора в окрестности точки Х{ до производной четвертого по-
128
Теория приближений
[Гл. III
Рис. 3.9. К понятию некорректности численного дифференцирования
рядка включительно, получим
Уг-1 =
у"— -
24'
, C.34)
Уг+1 =
. C.35)
Выразим вначале у^ из C.34), а затем из C.35), разделив
предварительно на h и оставляя слагаемые с первой степенью
шага h, получим
У г =
/ =
h
Уг+1 ~ Уг
h
C.36)
C.37)
Вычтем из C.35) выражение C.34), разделим полученное
соотношение на 2/i, получим следующее значение производной
первого порядка в точке Х{ (слагаемые с производными четного
§3.4]
Численное дифференцирование
129
порядка сокращаются за исключением слагаемого с производной
четвертого порядка):
2h
C.38)
Уг
Ум
где А Уг— yi+i — yi-i — центральная разность первого порядка.
Выражение C.36) определяет производную первого порядка
в узле Xi с помощью отношения конечных разностей слева. Она
имеет первый порядок аппроксимации относительно шага h.
Выражение C.37) определя-
определяет производную первого поряд- п
ка в узле Xi с помощью отноше-
отношения конечных разностей справа.
Она также имеет первый поря-
порядок аппроксимации относитель-
относительно шага h.
Выражение C.38) определя-
определяет производную первого поряд-
порядка в узле Xi с помощью отно-
отношения центральных разностей.
Она имеет второй порядок аппроксимации относительно шага h.
Сложим выражения C.34) и C.35), разделим на h2 (слагае-
(слагаемые с производными нечетного порядка сокращаются), получим
I, , ч г/г+1 ~~ ^Уг + Уг-1
h
h
Рис. 3.10. Численное дифферен-
дифференцирование с помощью отношения
конечных разностей
Выражение C.39) определяет производную второго порядка
в узле Xi с помощью отношения центральных разностей второго
порядка. Она имеет второй порядок аппроксимации относитель-
относительно шага h.
Определим порядок точности метода численного дифферен-
дифференцирования с помощью отношения конечных разностей, для чего
рассмотрим, как из выражений C.34), C.35) получаются произ-
производные C.36)-C.38). Например, производная C.36) получена из
C.34) следующим образом:
У г =
Уг ~ Уг-1
h
„h
5 В.Ф. Формалев, Д.Л. Ревизников
130 Теория приближений [Гл. III
Поскольку шаг h является дробной величиной, то главный
член погрешности содержит первую степень h (слагаемое у" — ],
остальные члены погрешности являются членами более высокого
порядка малости (слагаемые, начиная с h2 и далее), поэтому,
отбрасывая их и сохраняя главный член погрешности, следую-
следующий сразу за отношением конечных разностей, получим форму-
формулу C.36). Аналогично получены и остальные формулы.
Порядком точности метода численного дифференцирова-
дифференцирования с помощью отношения конечных разностей называют пока-
показатель степени h в главном члене погрешности. (По поводу связи
погрешности и точности см. гл. I и теорему эквивалентности
в п. 6.3.4).
Таким образом, односторонние производные C.36) и C.37)
имеют 1-й порядок точности и поэтому менее точны, чем
центрально-разностная производная C.38), имеющая второй по-
порядок точности.
3.4.1. Метод Рунге уточнения формул численного
дифференцирования. Из формул C.36)-C.38) видно, что ме-
метод р-го порядка численного дифференцирования совпадает с по-
показателем степени шага h в главном члене погрешности и имеет
вид
f{x) = ip'h{x) + hp . ф(х) + О (hp+1) + О (hp+2) + ... , C.40)
где
а остаточный член имеет вид
Яр = крф(х) + О (hp+1) + О (hp+2) + ...
С целью повышения на единицу порядка точности мето-
метода продифференцируем численно методом р-го порядка функ-
функцию f(xi) = yi, i = 0,n, с шагом /i, получим выражение C.40).
Затем продифференцируем численно функцию тем же методом
р-го порядка, с шагом kh, (к = 1/2; 1/4; 1/16; . . .), получим
f'(x) = <p'kh(x) + (kh)^(x) + О (hp+1) . C.41)
§3.4] Численное дифференцирование 131
Вычитая из C.41) выражение C.40) и определяя из получен-
полученного равенства ф(х), находим
) = +
гъ 1
Выражение C.42) можно использовать для оценки погреш-
погрешности численного дифференцирования.
Подставляя C.42) в C.41), получаем окончательно
/'(*) = <p'hh(x) + k^h{x)k;^fx) + О (h^1) . C.43)
Из C.43) видно, что это уже метод порядка р + 1, т. е. на по-
порядок точнее. В этом и заключается процедура Рунге уточнения
численного дифференцирования.
Пример 3.6. Вычислить производную в точке ж* = 0, 5 от
дискретно заданной функции примера 3.1. Оценить погрешность
производной.
Решение. По заданной таблице составляем интерполяцион-
интерполяционный многочлен
(см. пример 3.1) и погрешность
о Q
^— (X - Х0) (X ~ Xi) (X - Х2) =
3,978
= -^-
Тогда
у (х) = L2 (х) -
у' (х) = L2 (х) + R'2 (х);
у' (х*) = L'2 (х*) + R'2 (х*) = (^х2 + А-х + 1)'ж=а
+ 3,978 г, ^ , 1)у _ D * 44 , 3,978 /о_,2
у'@,5) =Q-0,5 + ^ +^РC-0,52-1) =2-0,166.
То есть
у' @,5) «2; Д? @,5) «-0,166.
132
Теория приближений
[Гл. III
Точное значение производной первого порядка в точке ж* =
= 0,5 будет
у' = {Г)'х=х* = Зж* • 1пЗ = 1,9028.
Аналогично вычисляются и производные 2-го, 3-го и т. д.
порядков. В данном примере производная второго порядка по-
постоянна для всего отрезка [—1; 1] и равна у" « 4/3.
Пример 3.7. Для узла xi заданной таблицы с помощью
отношения конечных разностей слева, справа и отношения цен-
центральных разностей выписать выражения для производной тре-
третьего порядка. Определить порядок аппроксимации во всех трех
случаях.
Решение. Заметим, что из формул численного дифферен-
дифференцирования минимальное количество узлов, необходимое для вы-
вычисления конечных разностей какого-либо порядка, должно быть
на единицу больше этого порядка. Следовательно, для вычисле-
вычисления конечных разностей третьего порядка, входящих в конечно-
разностную производную, необходимо не менее четырех узлов.
В соответствии с этим рассмотрим таблицу с пятью узлами,
отстоящими друг от друга на одинаковом расстоянии h = х^ —
— ж/c-i, к = г — 1, г, г + 1, г + 2.
Xi-2
Уг-2
Xi-1
Уг-\
Xi
Уг
Xi+\
Уг+1
Xi+2
Уг+2
Тогда для вычисления производных 3-го порядка в узле Х{
разложим yi-2, г/г-1, Уг+i, Vi+2, как значения дифференцируе-
дифференцируемой необходимое число раз функции у = / (х), в ряд Тейлора
в окрестности узла Xi до пятой производной включительно, по-
получим
Уг-2 = У (Xi - 2h) =
= Vi-v'i Bh)
-h) = yi- y\h + y'l% - y'l'% + y{v^-
- о И,
О (h5) ,
Vi+l =
y[h + у1'
О
§3.4] Численное дифференцирование 133
Уг+2 = y(Xi
Выпишем различные выражения для производной 3-го по-
порядка с помощью отношений конечных разностей:
_,„ ^ А3у- _ Т/г+1 - 3?/г + ЪУг-1 ~ Vi-2
Vi
h3 ~ h3
Подставляя в эти формулы выше приведенные разложения
в ряды Тейлора, получим
у- = ^^ ——з^-^—-^^- + U \h) ,
п
у- = \ (у? + у'!') + о (h>),
откуда видно, что производные 3-го порядка в узле ж^, вычислен-
вычисленные с помощью отношения конечных разностей слева и справа,
имеют первый порядок аппроксимации, а с помощью отношения
центральных разностей — второй порядок.
УПРАЖНЕНИЯ.
3.8. В заданиях упражнения 3.5 вычислить в точке х = 2, 5
значения производных первого и второго порядков. Оценить их
погрешность.
3.9. В заданиях упражнения 3.5 с помощью отношения конеч-
конечных разностей вычислить в узле Х2 = 2 производные до четверто-
четвертого порядка включительно в виде отношения конечных разностей
слева, справа и отношения центральных разностей. Определить
порядок аппроксимации полученных выражений.
Указание: для производной 4-го порядка использовать сле-
следующее конечно-разностное соотношение:
у{ « A yi/h = [Уг+2 ~ tyi+1 + §Уг ~ ^Уг-1 + Уг-2)/h .
134 Теория приближений [Гл. III
3.10. В заданиях упражнения 3.5 в узле ж 2 = 2 вычислить
значения лево- и правосторонней производных первого порядка
с помощью отношения конечных разностей с шагом h = 1 и h =
= 0,5 и уточнить эти производные с помощью процедуры Рунге.
§ 3.5. Численное интегрирование функций
Известно, что для подавляющего большинства функций не
удается вычислить первообразные, вследствие чего приходится
прибегать к методам приближенного и численного интегрирова-
интегрирования функций. Методы приближенного интегрирования исполь-
используют разложение подынтегральных функций в ряды Тейлора
(Маклорена) и дальнейшего почленного интегрирования членов
ряда. К недостаткам методов приближенного интегрирования
относится требование дифференцируемости подынтегральных
функций до порядка, который требуется при разложении функ-
функций в ряд Тейлора. От этого недостатка свободны методы чис-
численного интегрирования, в которых подынтегральная функция
удовлетворяет только условию непрерывности (для существова-
существования определенного интеграла).
При численном интегрировании по заданной подынтеграль-
подынтегральной функции строится сеточная функция C.1), затем эта
функция с помощью формул локального интерполирования
с контролируемой погрешностью заменяется интерполяционным
многочленом, интеграл от которого хорошо вычисляется и срав-
сравнительно легко оценивается погрешность.
Пусть на отрезке х ? [а, Ь] дана непрерывная функция у =
= /(ж), требуется на ж Е [а, Ь] вычислить определенный интеграл
ь
I = \f(x)dx. C.44)
Заменим данную функцию f(x) на сеточную функцию C.1).
Вместо точного значения интеграла C.44) будем искать его при-
приближенное значение с помощью суммы:
hi = Xi - Xi-i, г = 1,п, ж0 = а, хп = 6,
C.45)
§3.5] Численное интегрирование функций 135
в которой необходимо определить коэффициенты А{ и погреш-
погрешность формулы C.45).
3.5.1. Формула прямоугольников численного инте-
интегрирования. Наиболее простой (и имеющей малую точность)
является формула прямоугольников. Она основана на определе-
определении определенного интеграла как предела последовательности
интегральных сумм:
ь
I I Jb iLLtJU 11111 7
max i=1
о
I
Если в этом определении снять знак предела и положить
• = 1ц, г = 1,п, то появится погрешность Rnp (за ^ можно
принять левый или правый конец отрезка Аж^), т. е.
Г А
f(x)dx = ^ f(xi-i)hi + Rnp) C.46)
a i=1
ИЛИ
(Xi)hi + Rnv. C.47)
Формулы C.46), C.47) — формулы прямоугольников числен-
численного интегрирования.
Рассмотрим погрешность Ri формулы прямоугольников
C.46) на одном шаге [ж^-ьж^] численного интегрирования.
Для этого предположим, что первообразная ^(ж) для подын-
подынтегральной функции /(ж) (она существует, поскольку /(ж)
непрерывна на отрезке ж Е [а, Ь\) непрерывно дифференцируема.
Тогда, разлагая F{xi) в окрестности узла ж^-i в ряд Тейлора
до второй производной включительно и используя равенство
F'(x) = /(ж) = у(ж), получим
Xi
f{x)dx - yi-ih = [F(xi) - F(xi-i)] - yi-\h =
= [Ff(xi_1)h + F"(O^]-yi-ih =
= [Уг-lh + 2/'@y] - Vi-lh = y'@ — , ? € (Xi-ltXi).
136 Теория приближений [Гл. III
На всем отрезке [а, Ь] эту погрешность необходимо просум-
просуммировать п раз (Ь — а = n/г), получим
Я„Р = Я<п = г,'(О*Ц^, ?€(а,Ь). C.48)
Поскольку местоположение точки ? на интервале ж ? [а, 6]
неизвестно, то на основе погрешности C.48) можно выписать
верхнюю оценку абсолютной погрешности метода прямоуголь-
прямоугольников и при заданной точности е метода выписать неравенства
|ЯПР| < ^Ц^М! < е, М1 = max |/'(ar)| .
Последнее неравенство можно использовать для верхней оценки
шага h численного интегрирования по методу прямоугольников:
h ^ U VXT' Ml = mrax,i 1(I
(b - a) Mi xe[a,b]
На всем отрезке х G [a, b] формула прямоугольников C.46)
имеет вид
C.49)
Ее погрешность определяется выражением C.48).
Таким образом, определяющими формулами метода прямо-
прямоугольников являются формула C.49) численного интегрирова-
интегрирования и формула C.48) погрешности.
Из C.48) видно, что на каждом отрезке [жг-ъ жг] форму-
формула прямоугольников имеет погрешность, пропорциональную /г2,
а на всем отрезке х Е [a, b] — шагу численного интегрирования
h. В соответствии с этим метод прямоугольников является ме-
методом первого порядка точности (главный член погрешности
пропорционален шагу в первой степени).
3.5.2. Численное интегрирование с помощью фор-
формулы трапеций. Рассмотрим интеграл C.44) на отрезке х Е
Е [ж^-1, Х{] и будем на этом отрезке вычислять его приближенно,
заменяя подынтегральную функцию интерполяционным много-
§3.5]
Численное интегрирование функций
137
членом Лагранжа первой степени, получим
Xi Xi
Г f(x)dx= I Li{x)dx + Ri, C.50)
где Ri — погрешность, которая подлежит определению (на
рис. 3.11 заштрихована), a L\ — интерполяционный многочлен
?,(*)
0 хг_х h хг h xi+1 x
Рис. 3.11. К выводу формулы трапеций
Лагранжа первой степени, проведенный через два узла интерпо-
интерполяции Xi-i И Xi'.
г / \ % %i X Xi — \
Пусть Xi — Xi-i = h = const, где i = 1, п. Обозначим
X — Xi-
— = t,
тогда
= — = t - 1, dx = hdt,
h h
и многочлен Лагранжа примет вид
Li(x) = L\{xi—\ + hi) = —yi—\(t — 1) + у it.
При х = Xi верхний предел t = 1, при х = Xi-\ нижний предел
t = 0.
138 Теория приближений [Гл. III
Теперь интеграл в C.50) от многочлена L\{x) можно пред-
представить в виде
f(x)dx « L\(x)dx = h \—yi-i{t — 1) + yitldt =
J J J
= ?(l/i-i + I/i). C-51)
Выражение C.51) называют формулой трапеций численного
интегрирования на отрезке ж Е [ж^-i, Х{].
Для всего отрезка [а, Ь] необходимо сложить выраже-
выражение C.51) п раз:
ь / т 1 \
[/(ж) dx*± (yo + Уп + 2^ Vi ) . C.52)
Выражение C.52) называют формулой трапеций численного
интегрирования для всего отрезка [а, Ь].
Перейдем к оценке погрешности Ri формулы трапеций на
отрезке [ж^-ъЖг]. Для этого будем предполагать, что подынте-
подынтегральная функция принадлежит классу С2 (дважды непрерывно
дифференцируема), тогда для первообразной F(x) существует
производная 3-го порядка.
В этом случае погрешность на отрезке [ж^-Ъ хг] определяется
следующим образом:
Xi
Ri= f(x)dx- -(Уг-1 + Уг) =
= [F(Xi) - F(Xi-!)] - ^(Уг-l + Уг). C.53)
Разложим F(xi) в окрестности точки Xi-i в ряд Тейлора до
3-й производной включительно, получим (F(xi) = F(xi-\ + h))
F{xi) - Fixi-г) = -Fixi-г) + F(^_i) +
§3.5] Численное интегрирование функций 139
Тогда
Xi
Г h2 h3
f(x)dx = yi-ih + y'i-iY + /@y5 ? ? fe-i,^).
^-i C.54)
To же самое сделаем и со вторым слагаемым в левой части
равенства C.53), т. е. разложим yi в окрестности точки ж^-i в РЯД
Тейлора до 2-ой производной включительно, получим
Уг-1 + у'г-Ф + /(Оу]
= yi_1h + y'._1^. + y"(^, Zeixi-uXi). C.55)
В соответствии с C.53) вычтем C.55) из C.54), получим
погрешность формулы трапеций на одном шаге h:
(l\) -^y"@i C.56)
где ? Е (xi-i,Xi).
Из рис. 3.11 видно, что если f"{x) < 0, то Щ > 0, что под-
подтверждается выражением C.56); если же f"(x) > 0, то Щ < 0.
На всем отрезке [а, Ь] погрешность C.56) необходимо увели-
увеличить в п раз:
6 — a , 9
12
C.57)
Таким образом, метод трапеций — метод второго порядка
точности относительно шага h (главный член погрешности
пропорционален шагу в квадрате).
Поскольку положение точки ? на интервале (а, Ь) неизвестно,
то, задавая точность е численного интегрирования, можно за-
записать следующие неравенства, используемые для определения
шага h численного интегрирования:
|ЯТРК max |/r)| ^ h2 < s,
xe[a,b] 1^
140
Теория приближений
[Гл. III
откуда
(з-58)
Итак, определяющими формулами метода трапеций являют-
являются выражения C.52), C.57), C.58).
Численное интегрирование по методу трапеций в случае за-
заданной точности е осуществляется следующим образом:
1) по формуле C.58) определяется шаг численного интегри-
интегрирования /г;
2) с помощью этого шага составляется сеточная функция yi =
= f(xi), i = 0,п, для подынтегральной функции f(x) интегра-
интеграла C.44);
3) вычисляется приближенное значение интеграла по фор-
формуле C.52), шаг h в которой гарантирует заданную точность е.
Если точность е не задана, то выбирая шаг h численного инте-
интегрирования, можно по формуле C.57) оценить погрешность RTp
формулы трапеций.
3.5.3. Формула Симпсона численного интегриро-
интегрирования. Разобьем отрезок [а, Ь] на т пар отрезков h = Х{ —
— Xi-i = const, г = 1,п, и через каждые три узла проведем
интерполяционный многочлен /^(ж) (рис. 3.12).
0 хм h xt h xi+l
Рис. 3.12. К методу Симпсона численного интегрирования
§3.5] Численное интегрирование функций 141
Тогда
f(x)dx= L2(x)dx
Xi-l
где
= г/г-1
+ Уг+i:
Сделаем замену
X - Xi-
^- = t, dx = hdt,
h
тогда
h h
x - xi+1 (x - Xj-г) -
h h
Слагаемые в Ь2(х) примут вид
{X - Xj)(x - Xi+1)
-t-2.
\x Xi^){x xi+1) _
— h h ~~ А)Уг1
(X - Xi-!)(X ~ Xi) t(
При x = Xi-\\ t = 0 ; при x = Xi+\\ t = 2.
Тогда
ач+i
J L2(x)dx = h | [^-(t - l)(t - 2) - yit(t - 2) +
+ ^(t ~ l)]dt = ±(yi_1 +
откуда
\ f{x)dx^ \ L2(x)dx = ^(yi-1 + 4yi + yi+1). C.59)
142 Теория приближений [Гл. III
Выражение C.59) называют формулой Симпсона численного ин-
интегрирования на паре шагов от ж^-i ДО #г+1-
На всем отрезке [а, Ь] выражение C.59) необходимо сложить
т раз, поскольку имеется т пар отрезков длиной /г, полу-
получим формулу Симпсона численного интегрирования определен-
определенного интеграла C.44):
г / т m-i \
f{x)dx « - I г/о + Уп + 4 J2 У2*-1 + 2 J^ J/2* ) - C.60)
Погрешность формулы Симпсона на одной паре шагов запи-
записывается следующим образом:
R
Xi+l
= I f(x)dx-^(yi_1+4yi + yi+1). C.61)
Будем вычислять погрешность в предположении, что f(x) E
С4, a F(x) e С5, где F'(x) = f(x).
Перепишем погрешность C.61) в виде
Ri= [ f(x)dx-^(yi-1 + 4yi + yi+1). C.62)
Xi — h
Тогда на основе формулы Ньютона-Лейбница можно записать
f(x)dx = F{xi + h)- F{xi - h). C.63)
I
Разложим значения преобразованных F(xi + /г), F(xi — h)
в ряды Тейлора в окрестности точки Х{ до пятой производной
включительно:
F{xi + h) = F{xi) + F'(xi)h + F"{xi)^- + Fnf{xi)^- +
F(Xi -h) = F(Xi) - F'(xi)h
§3.5] Численное интегрирование функций 143
Тогда, в соответствии с C.63), получим
f(x)dx = 2F'(xi)h + 2F'"(xi)^ + [Fv(^) + FvF)]^-
Для непрерывных на отрезке [ж^-ъ яч+i] функций найдется та-
такое ? Е (?ъ&)> что
т.е.
C.64)
Аналогично, разлож:им у%-\ и y^+i B окрестности точки Х{ в ряд
Тейлора до производных 4-го порядка включительно, получим
i 2 i 3
Уг-1 = У(^г - Л) = у(Жг) ~ У*{xfih + y"(Xi)— - У*"(xi)— +
А О
/г4
i 2 i 3
= у(ж; + /г) = у(Жг) + у1\xi)h + y"(Xi)— + у"'(Хг)— +
А О
^ [yIV(b) + y
IV (
или
-(Уг-1 +4yi + yi+i) =
2fc +
. C.65)
В соответствии с C.62), C.64) и C.65) получим погрешность
формулы Симпсона на двойном шаге, которая пропорциональна
4-ой производной подынтегральной функции и пятой степени
шага h:
144 Теория приближений [Гл. III
Ri=
Для всего отрезка [а, Ь] эту погрешность необходимо умножить
на т пар отрезков:
(a,b), C.66)
т. е. в формуле Симпсона на всем отрезке [а, Ь] погрешность
пропорциональна четвертой степени шага, и, следовательно,
метод Симпсона является методом четвертого порядка точ-
точности (т. е. главный член погрешности пропорционален четвер-
четвертой степени шага h).
Поскольку положение точки ? на отрезке [а, Ь] неизвестно, то
в соответствии с C.66) можно записать верхнюю оценку погреш-
погрешности и при заданной точности е получить
|ЯС| ^ ^ТяУ^ ^ е> М4 = mrax1 UIV(X)\'
loU xe[a,b] ' '
откуда
h < \ГпгЩтг> М4 = max \fIV(x)\ • C-67)
У {b-a)M4 xe[a,b] ' '
Таким образом, определяющими формулами метода Симп-
Симпсона являются выражения C.60), C.66), C.67), в соответствии
с которыми по заданной точности е из C.67) находится шаг h
численного интегрирования, с его помощью составляется сеточ-
сеточная функция Уг = f (xi), % = 0, п, п = 2т, а затем приближен-
приближенно вычисляется интеграл по формуле C.60). Если точность е
неизвестна, то, задаваясь шагом /г, можно по формуле C.66)
вычислить погрешность численного интегрирования.
3.5.4. Процедура Рунге оценки погрешности и уточ-
уточнения формул численного интегрирования. Процедура
Рунге позволяет оценить погрешность и повысить на единицу
порядок метода путем многократного (в простейшем случае дву-
двукратного) просчета с различными шагами.
§3.5] Численное интегрирование функций 145
Пусть используется какой-либо метод численного интегриро-
интегрирования с шагами h и /г/2. И пусть порядок выбранного метода
равен р, тогда
C.68)
C.69)
где / — точное значение интеграла; //>, Ih/2 — вычисленные
значения интеграла с шагом h и h/2 соответственно; вторые
слагаемые справа — главные члены погрешности метода числен-
численного интегрирования порядка р. Для их вычисления вычтем из
выражения C.69) выражение C.68), получим
D/2 - h) + Ф (|У [1 - 2*] + О (/г"+1) = О,
O*=Ij^r+°{hP+1) ¦ (з-7о)
Выражение C.70) позволяет провести апостериорную оцен-
оценку погрешности вычисленного значения определенного интег-
интеграла.
Подставим C.70) в C.69), получим формулу численного ин-
интегрирования уже порядка р+1:
= h/2
Таким образом, формула C.71) — простейшая процедура
Рунге уточнения на один порядок формулы численного интегри-
интегрирования.
Замечание. Если для подынтегральной функции у = f(x)
построена сеточная функция yi = f(xi) с переменным ша-
шагом hi, то погрешность численного интегрирования определя-
определяется как интеграл от погрешности интерполяционного много-
многочлена.
Пример 3.8. Методом трапеций с точностью е — 10~2
и Симпсона с точностью е\ — 10~4 вычислить определенный
интеграл (вычисляемый точно):
146
Теория приближений
[Гл. III
dx
1 + х
= 1п2 = 0,69315.
Решение. 1) Метод трапеций. Исходя из заданной точ-
точности ? = 10~2 вычислим шаг численного интегрирования, для
чего используется формула C.58):
{Ь-а)М2
I /»// / \ I
= max / (ж) = max
хе[0;1] ' ' хе[0;1]
= 2;
Необходимо выбрать такой шаг, который удовлетворяет неравен-
неравенству h ^ 0,2449, и чтобы на отрезке интегрирования х Е [0; 1]
он укладывался целое число раз. Принимаем шаг h = 0,2. Он
удовлетворяет обоим этим требованиям.
Для подынтегральной функции / (ж) = A + х)~ с незави-
независимой переменной ж^, изменяющейся в соответствии с равен-
равенством Xi = xq + ih = 0 + г - 0,2, г = 0, 5, составляем сеточную
функцию с точностью до второго знака после запятой:
г
хг
Уг
0
0
1,0
1
0,2
0,83
2
0,4
0,71
3
0,6
0,63
4
0,8
0,56
5
1,0
0,5
Используется формула трапеций C.52) численного интегри-
интегрирования (п = 5):
= ^ [!?0 + 0,5 + 2 @,83 + 0,71 + 0,63 + 0,56)] = 0,696.
§3.5]
Численное интегрирование функций
147
Сравнивая это значение с точным, видим, что абсо-
абсолютная погрешность не превышает заданной точности е\
|0,69315-0,696| < 0,01.
Таким образом, за приближенное значение определенного
интеграла по методу трапеций с точностью^: = 0,01 принимается
значение
dx
1 + х
0,696.
2) Метод Симпсона. Исходя из заданной точности е\ — 10 4
вычисляется шаг численного интегрирования для метода Симп-
Симпсона по формуле C.67):
h
1806:
(b -a) M±'
же[0;1]
24
= 24;
-4
1 180 • 10
A - 0) • 24
=0,165.
Необходимо выбрать такой шаг, чтобы он удовлетворял нера-
неравенству h ^ 0,165, и чтобы на отрезке интегрирования х Е
? [0; 1] он укладывался четное число раз. Принимаем h = 0,1.
С этим шагом для подынтегральной функции / (х) = A + х)~
формируется сеточная функция с независимой переменной ж^,
изменяющейся по закону Х{ = xq + ih = 0 + i • 0,1, i = 0, 10, n =
= 10, m = 5, причем значения сеточной функции вычисляются
с точностью до четвертого знака после запятой:
г
Xi
Уг
0
0
1,0
1
0,1
0,9091
2
0,2
0,8333
3
0,3
0,7692
4
0,4
0,7143
5
0,5
0,6667
6
0,6
0,625
7
0,7
0,5882
8
0,8
0,5556
9
0,9
0,5263
10
1,0
0,5
Используется формула Симпсона C.60) численного интегри-
интегрирования (п = 10, т = 5)
т га—1 \
г=1 г=1 /
I
L + ж ~ 3"
148 Теория приближений [Гл. III
+0,5 + 4 (ух + уз + Уъ + VI + 2/э) + 2 (у2 + 2/4 + Уб + У%)\ =
= 2il [1,5 + 4 @,9091 + 0,7692 + 0,6667 + 0,5882 + 0,5263) +
о
+2 @,8333 + 0,7143 + 0,625 + 0,5556)] =
= — A,5 + 4 • 3,4595 + 2 • 2,7281) = ^20,7942 = 0,69314.
Сравнение этого значения с точным значением интеграла по-
показывает, что абсолютная погрешность не превышает заданной
точности е\:
|0,69315 - 0,69314| < 0,0001.
Таким образом, за приближенное значение определенного
интеграла по методу Симпсона с точностью е± = 0,0001 прини-
принимается значение
1
dx
0,6931.
о
Замечание. Ясно, что для большинства интегралов от
непрерывных функций первообразная не вычисляется (однако
она существует) и вычисленное приближенное значение сравни-
сравнивать не с чем, однако шаг численного интегрирования, вычис-
вычисленный по заданной точности, гарантирует эту точность вычис-
вычисления.
УПРАЖНЕНИЯ.
3.11. Методом трапеций с точностью е = 10~2 и Симпсона
с точностью е = 10~4 вычислить определенные интегралы:
о
0,5
I
0
1
dx
cos ж'
б)
1-
0
тг/2
б) \cos(x + lJdx; в) [ 2ж^ж;
J J
-1
тг/2
г) ех dx; д) smx2dx; e) cosx2dx;
0 0 о
§3.5] Численное интегрирование функций 149
0,5 1 1
ж) —^Ц-; з) \tg2xdx; и) \esmxdx;
J cosar J J
oo о
li l
к) есо8жо!ж; л) ctg2 x dx; м) tgx2dx.
о од о
Для одного из методов применить процедуру Рунге уточне-
уточнения формулы численного интегрирования.
3.12. Сравнить по трудоемкости методы трапеций и Симпсона
для одной и той же точности е (трудоемкость определяется по
количеству вычислений подынтегральной функции).
ГЛАВА IV
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ
ДЛЯ ОБЫКНОВЕННЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Программа
Постановка задач Коши для обыкновенных дифференциальных
уравнений (ОДУ) и систем ОДУ. Методы Эйлера, Эйлера-Коши,
Рунге—Кутта численного решения задач Коши для ОДУ и систем ОДУ.
Выбор шага численного интегрирования. Порядок метода, процедура
Рунге повышения порядка метода. Постановка краевых задач для
ОДУ. Конечно-разностный метод с использованием метода прогон-
прогонки. Аппроксимация краевых условий, содержащих производные, со
вторым порядком. Метод пристрелки с использованием различных
методов решения нелинейных уравнений.
В этой главе рассматриваются некоторые наиболее употре-
употребительные методы численного решения задач Коши для обык-
обыкновенных дифференциальных уравнений (ОДУ) и систем ОДУ,
а также некоторые численные методы решения краевых задач
для ОДУ.
§4.1. Основные определения и постановка задач
Коши для обыкновенных дифференциальных
уравнений
Определение 1. Уравнение, связывающее одну независи-
независимую переменную ж, искомую функцию у(х) и ее производные
до n-го порядка, называется обыкновенным дифференциальным
уравнением (ОДУ):
F(x,y,y',... ,y^) = 0. D.1)
Определение 2. Порядком ОДУ называется порядок стар-
старшей производной искомой функции у(х). Уравнение D.1) — ОДУ
n-го порядка.
§4.1] Задача Коши для обыкновенных дифференциальных уравнений 151
Определение 3. ОДУ называется линейным, если функ-
функция F линейна относительно искомой функции и ее производ-
производных.
Определение 4- Если искомая функция или ее производные
входят в ОДУ не в 1-й степени или под знаком трансцендентной
функции, то уравнение называется нелинейным.
Определение 5. Общим интегралом ОДУ называется функ-
функция, связывающая независимую переменную ж, искомую функ-
функцию у(х) и п постоянных интегрирования:
Ф(у(ж),ж,С1,с2, ... ,сп) = О,
т.е. у(х) входит в функцию Ф неявным образом.
Определение 6. Общим решением ОДУ называется функ-
функция
у(х) = <р(х,С!,С2, ... ,СП)
независимой переменной х и п постоянных интегрирования, т. е.
у(х) является явной функцией.
Для определения постоянных интегрирования, т. е.
выделения из бесчисленного множества интегральных
кривых единственной, проходящей через заданную точку
М(жо, У о-, Уъ • • • ) Уп-i) в пространстве 7?n+1, необходимо задать
п дополнительных условий в виде значений производных
искомой функции в точке xq до порядка п — 1 включительно.
Эти дополнительные условия называют начальными условиями:
у(п-гНх0) = уп-г.
Задача нахождения решения уравнения D.1), удовлетворяю-
удовлетворяющего п начальным условиям D.2), называется задачей Коши для
ОДУ D.1).
Если старшая производная искомой функции, входящая
в ОДУ, выражается явно через производные меньших порядков
(такие ОДУ называются каноническими), то задача Коши будет
иметь вид (у(х) — искомая функция)
152 Решение задач для обыкновенных дифференциальных уравнений [ Гл. IV
у(х0) = уо,
у'(х0) = уь
D.3)
Определение 7. Система ОДУ называется нормальной,
если каждое уравнение, входящее в систему, слева содержит про-
производную первого порядка от соответствующей искомой функ-
функции, а правая часть зависит от независимой переменной х и п
искомых функций у\{х), У2(ж), . . . , уп(х):
У[{х) =
При формулировке задачи Коши для этой системы ОДУ
к ней необходимо присовокупить п начальных условий (по ко-
количеству неизвестных), задаваемых в одной и той же точке xq:
yi(x0) =
Уп(жо) = Упо-
Порядком нормальной системы называют число уравнений
в этой системе.
Задачу Коши D.3) для ОДУ n-го порядка всегда можно
привести к задаче Коши для нормальной системы ОДУ того же
порядка. Для этого сделаем обозначения:
§4.1] Задача Коши для обыкновенных дифференциальных уравнений 153
у'(
у"
у'"
(»
а)
(х)
— У1
— Zl
[х),
(х)
[ У^)
— z1
= Z2
= z:
№ = za(x).
В соответствии с этими обозначениями дифференциальное
уравнение в задаче D.3) преобразуется в уравнение
Уу
= z'n_x(x) =
Собирая здесь подчеркнутые равенства и приписывая к ним
начальные условия из D.3), получим следующую задачу Коши
для нормальной системы:
у'(х) =
z[(x) =
z'2(x) =
Zn-2(X)
Zn-l(X)
y(x0) =
zi
(x0) =
Zn-i(xo) = Уп-1-
В этой задаче Коши искомыми являются п функций: у(х),
21 (ж), Z2{x), . . . , Zn-i(x).
В соответствии с этим ниже рассматриваются численные ме-
методы решения задач Коши для ОДУ 1-го порядка и задач Коши
для нормальных систем ОДУ.
154 Решение задач для обыкновенных дифференциальных уравнений [Гл. IV
§ 4.2. Метод Эйлера численного решения задач
Коши для ОДУ и систем ОДУ
Пусть дана задача Коши для ОДУ 1-го порядка :
D.4)
D.5)
Заметим, что правая часть ОДУ D.4) /(ж, у) равна произ-
производной у' от искомой функции, и, следовательно, dy = y'dx =
= f(x,y)dy. Для конечно-разностного приращения Ау функции
на шаге Ах в точке Х{ имеет место равенство Ayi = f(xi, yi)Ax.
Ж Ум
0 xt h xi+1 x
Рис. 4.1. Геометрический смысл метода Эйлера
Интегрируя уравнение D.4) на отрезке h = Х{+\ — Х{, полу-
получим
f(x,y(x))dx.
К интегралу в правой части этого выражения применим фор-
формулу прямоугольников:
Уг+i = Vi + hf(xi, yi) + О(/г2), уо = у(ж0), * = 0,1, 2,. . . D.6)
§4.2] Метод Эйлера численного решения задач Коши для ОДУ 155
Формула D.6) — алгоритм метода Эйлера численного инте-
интегрирования задачи Коши D.4), D.5). На каждом шаге численного
интегрирования метод Эйлера имеет второй порядок погреш-
погрешности.
На всем интервале численного интегрирования задачи Коши
метод Эйлера, как и метод прямоугольников, имеет погрешность,
пропорциональную шагу в первой степени и, следовательно, яв-
является методом первого порядка точности.
Геометрический смысл метода Эйлера: если известно ж^, у^,
то можно найти правую часть f(xi,yi) ОДУ D.4), т.е. произ-
производную у[ от искомой функции в точке Х{ (тангенс угла наклона
касательной к интегральной кривой, хотя последняя неизвестна).
Продолжая касательную до пересечения с линией Х{+\ = Х{ +
+ /г, получим Уг+г (рис. 4.1, на котором введено обозначение fi =
4.2.1. Метод Эйлера для нормальных систем ОДУ.
Применительно к нормальным системам ОДУ рассмотрим метод
Эйлера на примере задачи Коши для системы второго порядка:
У[ = fi(x,yi,y2), D.7)
У2 = /2(ж,уьу2), D.8)
yi(xo) = yw, D.9)
У2(х0) = У20- D.10)
Выбирая шаг h численного интегрирования h =
запишем алгоритм D.6) для каждого уравнения системы ОДУ
D.7), D.8) (г = 0,1,2,...):
= Уи + hfi(x{, yu, y2i) + O(h ),г/ю = yi(жо); D-И)
= У21 + hf2{Xi, 2/1г, У2г) + О(/г2),?/20 = 2/2(#()). D-12)
Выражения D.11), D.12) описывают алгоритм метода Эйлера
численного решения задачи Коши для нормальной системы ОДУ
D.7)-D.10).
Если задана задача Коши для ОДУ n-го порядка , то она
сводится к задаче Коши для нормальных систем. Рассмотрим
это на примере задачи Коши для п = 2.
156 Решение задач для обыкновенных дифференциальных уравнений [Гл. IV
У" =
У = z,
z' = f(x,y,z),
У(хо) = Уо,
z(x0) = уг.
D.13)
D.14)
D.15)
D.16)
у(х0) = уо,
у'(х0) = уъ
К задаче D.13)-D.16) можно применить алгоритм D.11),
D.12), если обозначить fi{x,y,z) = z, f2(x,y,z) = f(x,y,z),
причем неизвестными функциями в этой системе являются
функции z(x), y(x).
§ 4.3. Метод Эйлера-Коши (Эйлера с пересчетом)
Пусть дана задача Коши D.4), D.5) для ОДУ 1-го порядка
D.4). Интегрируя D.4) на отрезке h = xi+\ — Xi, г = 0,1,2,...,
получим выражение
Уг+1 = Уг +
f(x,y(x))dx.
Вычислим интеграл в этом выражении с помощью метода
трапеций численного интегрирования с погрешностью на каж-
каждом шаге, пропорциональной /г3:
D.17)
Уг+1 = Уг + ^ [/ (ЖЬ У*) + / (Жг+Ь Уг+l)] + О (/& ) .
Если каким-либо образом вычислено приближение для
то, приняв его за нулевую итерацию и подставив в правую часть
выражения D.17), получим yi+i на 1-й итерации. На этом ос-
основан метод Эйлера-Коши, который выглядит следующим об-
образом. Вычислим вначале у%+\ по обычному алгоритму Эйле-
Эйлера и обозначим это значение через уг+1. Затем это значение
подставим в правую часть выражения D.17), получим для г =
= 0,1,2, . . . , (у0 = у(ж0), #i+i = Xi + h):
Уг+1 = Уг + hf(Xi, уг), D.18)
Уг+1 = Уг + \ [f(Xi,yi) + f (Хг+Ъ yi+i)] + О (/l3) . D.19)
Выражения D.18), D.19) описывают алгоритм метода Эйле-
Эйлера-Коши, называемый еще методом Эйлера с пересчетом. Он яв-
§4.3]
Метод Эйлера-Коши (Эйлера с пересчетом)
157
ляется частным случаем большого класса методов, который на-
называется методами «предиктор-корректор». Например D.18) —
предиктор, D.19) — корректор.
На рис. 4.2 представлена геометрическая интерпретация это-
этого метода. Здесь введены обозначения fi = f(xi,yi), fi+\ =
= /(жг+ъУг+i), /ср = V2 (/г + 7i+i)• Параллельные прямые
указаны двусторонними стрелками.
MCtgfi+
Рис. 4.2. Геометрическая интерпретация метода Эйлера-Коши
Для известных ж^, yi находят значение производной
f(xi,yi) = fiB левом узле шага и yi+1 по D.18). Зная ж^+ъ yi+ij
можно определить значение производной в правом узле шага:
fi+i = f(xi+i, Уг+i), с помощью которого определяется у^+1 по
формуле D.19).
Метод Эйлера-Коши имеет 3-й порядок погрешности на
каждом шаге, а на всем интервале численного интегрирования
погрешность пропорциональна квадрату шага, и поэтому ме-
метод Эйлера-Коши является методом второго порядка. К D.19)
можно применить обычную итерационную обработку, а именно:
полученное значение у^+1 подставить в правую часть вместо y^+i
и получить yi+\ на следующей итерации.
4.3.1. Метод Эйлера—Коши для нормальных систем.
Рассмотрим метод применительно к задаче Коши для нормаль-
нормальных систем ОДУ 2-го порядка D.7)—D.10).
158 Решение задач для обыкновенных дифференциальных уравнений [Гл. IV
Каждый этап алгоритма D.18), D.19) используется сразу для
всех неизвестных (в данном случае yi, 2/2), при этом ую = ух(жо)?
2/20 = У2(х0), Xi+i = Xi + /i, Ъ = 0, 1, 2, . . . :
Уи+1 = Уи + hfi(xi, yu,y2i), и 20)
Шг+1 = У2г + hf2(Xi, Уи,У2г), D.21)
УИ+1 = УН + -j[fl(Xi, УН, y2i) + fl(Xi+l, Уи+1, У2г+1)], D.22)
У2г+1 = У2г + ^LM^i, Шг, У2г) + /2^1, Шг+Ь У2г+1)« ^*2^
Выраж:ения D.20)-D.23) — алгоритм метода Эйлера-Коши
решения задачи Коши D.7)-D.10) для нормальной системы D.7),
D.8) второго порядка.
§ 4.4. Метод Рунге-Кутта
Метод Рунге-Кутта имеет погрешность, пропорциональную
/г5 на каждом шаге численного интегрирования и поэтому яв-
является одним из наиболее употребительных методов численного
решения задач Коши для ОДУ и систем ОДУ. Рассмотрим зада-
задачу Коши D.4), D.5) для ОДУ 1-го порядка D.4). Проинтегрируем
ОДУ D.4) на шаге h = Xi+\ — Xi, i = 0,1, 2, . . . :
Жг+1
Г
Уг+1 = Уг+ f(x,y(x))dx. D.24)
J
Xi
Для вычисления интеграла в D.24) используем формулу
Симпсона численного интегрирования, имеющую на шаге h точ-
точность 5-го порядка. Для формулы Симпсона необходимо три узла
(пара шагов), а в D.24) используются только два узла ж^, яч+ь
Возьмем промежуточную точку ж^+1/2 — xi + h/2 (рис. 4.3),
тогда
жг+i xi+i/2+h/2
Уг+1 = Уг+ f(x,y(x))dx = yi+ f(x,y(x)) dx.
xi+i/2-h/2 D.25)
Теперь для интеграла в выражении D.25) можно использо-
использовать формулу Симпсона с шагом h/2:
§4.4]
Метод Рунге-Кутта
159
Уг+1 = Уг + -у-
4f(xi+1/2, Уг+1/2) +
D.26)
Выражение D.26) является основой для построения различ-
различных методов Рунге-Кутта численного решения задач Коши.
О
Уг
УМ/2
h/2
h/2
Рис. 4.3. Разбиение шага h в методе Рунге-Кутта
Поскольку выражение D.26) является неявным (значения yi+\
и У1+1/2 B правой части неизвестны), то для вычисления второго
и третьего слагаемых в правой части полагаем
= 2/
+ 2/ Ui+l/2, Уг +
+
+
где приращение Ау\ вычисляется по ж^, yi как Ау\ = hf(xi,
т. е. как в методе Эйлера; Ау]1 вычисляется по значениям
Уг + AyJ/2; Ау^ — по значениям а^+ъ Уг + Аугп.
В соответствии с такими вычислениями получаем метод
Рунге-Кутта 4-го порядка точности, который применяется в сле-
следующем виде (уо = у(ж0), xi+1/2 = Xi + h/2, xi+i = xi + h, i =
= 0,1,2,...):
Уг+1 = У г +
D.27)
D.28)
160 Решение задач для обыкновенных дифференциальных уравнений [Гл. IV
К = hf(xi,yi),
kj = hf
kf = hf
D.29)
к'^ D.30)
D.31)
щ + kf) . D.32)
Таким образом, метод Рунге-Кутта является четырехэтап-
ным; в нем к\, &?, &?, kf являются частными приращениями
искомой функции соответственно в левом узле Х{ шага D.29),
в узле Xi + h/2 D.30) и D.31) и в правом узле xi + h шага D.32).
Их линейная комбинация с коэффициентами 1, 2, 2, 1 усредня-
усредняется в соответствии с D.28).
Поскольку метод Симпсона на всем интервале численного ин-
интегрирования является методом четвертого порядка, то и метод
Рунге-Кутта, использующий метод Симпсона, также является
методом четвертого порядка точности.
arctgl+
arctg/cp
0
h/2
t xi+i/2 ^12 xi+1 x
Рис. 4.4. Геометрическая интерпретация метода Рунге—Кутта 4-го порядка
На рис. 4.4. представлена геометрическая интерпретация ме-
метода Рунге-Кутта. Здесь приняты следующие обозначения:
arctg/i =
§4.4]
Метод Рунге-Кутта
161
arctg /cp = - [arctg /* + 2 arctg /*+1/2 + 2 arctg /*+1/2 + arctg
На рисунке параллельные прямые указаны двусторонними
стрелками.
АЛЛ. Метод Рунге—Кутта для нормальных систем
ОДУ. Метод Рунге-Кутта для нормальных систем рассмотрим
на примере задачи Коши для нормальной системы ОДУ второго
порядка D.7)-D.10):
у[ =
2/2 =
= Унь
Будем обозначать частные приращения для искомой функ-
функции у\{х) через k\, kf, &?, к\, а для искомой функции уч{х) —
через Zj, Z|, Zf, Z|. Поскольку правые части системы ОДУ
/х(ж, г/1,2/2)э /2(^,2/1,2/2) зависят от всех искомых функций
(в данном случае от г/i и у2), то приращения для yi(x) и У2{%) ыа
каждом этапе вычисляются одновременно. Тогда метод Рунге-
Кутта четвертого порядка точности для нормальной системы
ОДУ второго порядка примет вид
= У и
= У2г
2/f
D.33)
D.34)
D.35)
D.36)
В.Ф. Формалев, Д.Л. Ревизников
162 Решение задач для обыкновенных дифференциальных уравнений [ Гл. IV
н = hfi(xi,yii,y2i),
к]
УН + у>У2г + у i ,
? = Л/2
УН
2 '
У2г
D.37)
D.38)
D.39)
D.40)
D.41)
D.42)
D.43)
D.44)
где xi+1/2 = Xi + /г/2, Х{+± = X{ + h.
Алгоритм D.33)-D.44) метода Рунге-Кутта для нормальных
систем ОДУ 2-го порядка легко распространяется на нормальные
системы 3-го, 4-го и т. д. порядков. Например, для нормальной
системы 3-го порядка имеются три неизвестные функции yi(#),
У2 (ж), уз (ж), причем для каждой из них вводятся свои частные
приращения, а именно: к], &?, &?, к\ для у\{х)\ l}, /f, /f, /|
для У2(ж); т\, mf, mf, m| для уз(#). Тогда в методе D.33)-
D.44) к каждой паре формул добавляется еще одна для неиз-
неизвестной уз (х).
§ 4.5. Выбор шага численного интегрирования
задач Коши
При численном решении задач Коши для ОДУ и систем ОДУ
шаг численного решения можно выбирать апостериорно и апри-
априорно. В обоих случаях первоначальное значение шага h задается.
При апостериорном выборе шага последний изменяется
в процессе счета на основе получаемой информации о поведении
решения и на основе заданной точности е.
Пусть е — заданная точность численного решения, и пусть
h — первоначально выбранный шаг. Тогда алгоритм дальнейше-
дальнейшего выбора шага следующий.
§4.6] Процедура Рунге оценки погрешности 163
1. Выбранным методом на отрезке х Е [жо,жх], х\ = xq + h
решается задача Коши с шагом h с получением значения y^=h.
2. Тем же методом с шагом h/2 решается задача Коши с по-
h/2 h/2
лучением yJ=h/2 и yj=h.
3. Анализируется неравенство
h h/2
yx=h - yx=h
e. D.45)
Если неравенство D.45) удовлетворяется, то значение шага
численного интегрирования на следующем шаге увеличивается
вдвое по сравнению с первоначально выбранным шагом, т. е.
становится равным 2/г, и алгоритм повторяется начиная с п. 1.
4. Если неравенство D.45) не выполняется, то счет ведется
с шагом /г/4 начиная с отрезка х Е [жо, %о + h/A] и после полу-
/г/4
чения значения yx=h/2 анализируется неравенство
h/2 _ /г/4
yx=h/2 yx=hj
Если оно удовлетворяется, то дальнейший счет ведется с ша-
шагом h/2 и т. д.
При априорном выборе шага расчет ведется с первоначаль-
первоначально выбранным шагом h с получением функции [y(xi)]h, г =
= О, 1, 2, ..., ис шагом h/2 с получением функции
г = 0, 1, 2, ... Затем анализируется неравенство
max
D.46)
Если оно выполнено, то решение [y(#i)]w2, * — 1J,3,...,
принимается за истинное, в противном случае расчет повто-
повторяется с шагом h/A и сравниваются по норме D.46) функ-
функции [y(Xi)]h/2 И [у(ж2*)]Л/4 И Т.Д.
§ 4.6. Процедура Рунге оценки погрешности
и уточнения численного решения задач Коши
У всех рассмотренных методов численного решения задачи
Коши порядок погрешности относительно шага h на всем интер-
интервале решения на единицу ниже порядка погрешности на одном
шаге h.
164 Решение задач для обыкновенных дифференциальных уравнений [ Гл. IV
Определение. Порядком метода назовем показатель р сте-
степени hp в главном члене погрешности метода.
В методе Эйлера главный член погрешности на шаге h про-
пропорционален /г2, а на всем интервале пропорционален шагу h.
Поэтому метод Эйлера — метод 1-го порядка. По той же причине
метод Эйлера-Коши — метод 2-го порядка, метод Рунге-Кутта —
метод 4-го порядка (здесь порядок метода в точности совпадает с
порядком соответствующей квадратурной формулы численного
интегрирования).
Пусть задача Коши решается методом р-го порядка с шагом h
с получением численных значений у^ и главным членом погреш-
погрешности (p(x)hp, пропорциональным hp. Тогда неизвестное точное
решение у(х) можно представить в виде
у(х) = yh + <p(x)hp + О (hp+1) . D.47)
Аналогичное равенство с шагом h/2 представим следующим
образом:
У(х) = yh/2 + <p{x)(h/2Y + О (ЛР+1) . D.48)
h\P
Определим (р(х) I — I вычитанием D.47) из D.48):
V2
D.49)
Выражение D.49) дает апостериорную оценку погрешности
численного решения. Подставляя D.49) в D.48), получим уже
метод (р + 1)-порядка:
так как главный член погрешности в алгоритме D.50) пропорци-
пропорционален степени /ip+1.
Процедура D.50) называется процедурой Рунге уточнения
численного решения задачи Коши. Для ее применения задачу
необходимо решать дважды с шагами h и h/2.
Процесс уточнения с применением формулы D.50) можно
применять и дальше, проводя расчеты с шагами /i/4, h/8 и т.д.,
пока не выполнится условие
max
= l, 2,
§4.6] Процедура Рунге оценки погрешности 165
Пример 1^.1. Методами Эйлера, Эйлера-Коши и Рунге-
Кутта с шагом h = О,1 численно проинтегрировать следующую
задачу Коши для ОДУ 1-го порядка до значения х = О, 2 вклю-
включительно (т.е. два шага):
у' = х + у, у@) = 1, h = 0,1.
Задача допускает аналитическое решение и для анализа точ-
точности численных методов; выпишем его:
у (х) = 2ех - х - 1;
у @) = 1; у @,1) = 1,1103442; у @, 2) = 1,242806.
Метод Эйлера.
Уг+l = Уг + h • (Xi + Уг) , г = 0, 1, 2, . . . ,
уо = 1, 2^ = жо + г Л- = 0 + ih\
г = 0; х0 = 0; у0 = 1 :
У1 = 2/0 + Л • (х0 + у0) = 1 + ОД @ + 1) = 1,1;
г = 1; xi = 0,1; щ = 1,1 :
= yi + h-(xi + yi) = 1,1 + 0,1 @,1 + 1,1) = 1,22;
Поскольку метод Эйлера является методом первого порядка
точности, то только первая цифра после запятой является вер-
верной, а вторая — нет. Это подтверждает сравнение у\ с у @,1) и у2
с у @,2).
Метод Эйлера-Коши.
Уг+1 = У
= Уг + -? [(хг + Уг) +
= 1; h = 0,1; Xi = xq + г/i, i = 0,1, 2, . . . ;
г = 0; ж0 = 0; х\ = 0,1; уо = 1 :
166 Решение задач для обыкновенных дифференциальных уравнений [ Гл. IV
2/1 — УО + h - (xq + уо) — 1 + 0,1 @ + 1) = 1,1,
Уо)
= 1 +^[@
) +@,1 + 1,1)] = 1,11;
j = 1; х\ = 0,1; х2 = 0,2; у\ = 1,11 :
+ yi) = 1,11 + 0,1 @,1 + 1,11) = 1,231;
= 1,11 + ^ [@,1 + 1,11) + @,2 + 1,231)] = 1,24205;
Поскольку метод Эйлера-Коши является методом второго
порядка точности, то первые две цифры после запятой счита-
считаются верными (сравнить у\ с у @,1) и у<х с у @,2)).
Метод Рунге-Кутта.
i+l = У г +
z\ = h-f
•Л —
(Xi + l
h
Xi+ 2
Xi ~r —
= h-f (xi
ft?) = h [(xi + h) + (yi + ft?)]
г = 0; ж0 = 0; ж i = 0,05; х\ = 0,1; уо = 1 :
о+
= уо + Ауо = 1 + 0,11035 = 1,11035,
2ftg + 2ftg + ft*) = I . 0
уо) = 0,1 @ + 1) = 0,1;
Ау0 = 1(к% + 2ftg + 2ftg + ft*) = I . 0,6621 = 0,11035,
§4.6]
Процедура Рунге оценки погрешности
167
)] =0,11,
= 0,1 [0,05 + (l + ^P)l = 0,1105,
к$ = h ¦ [{x0 + h) + (yo + ^o)] =
= 0,1 [0,1 + A + 0,1105)] = 0,1211;
i = 1; xi = 0,1; x i = 0,15; x2 = 0,2; yx = 1,11035 :
i+
у2 = Ш + Ayi = 1,11035 + 0,13247 = 1,24282,
АУ1 = ^ (Л} + 1к\ + 2Af + Af) = ^ • 0,7948 = 0,13247,
к\ = h ¦ (хг + ух) = 0,1 @,1 + 1,11035) и 0,12104;
= 0,1 [@,1 + М) + AД1035 + ^)] = 0,132087,
М) + AД1035
= 0,13264,
h- [{хг + h) + (У1
0,1 [0,2 + A,11035 + 0,13264)] = 0,1443.
Метод Рунге Кутта является методом четвертого порядка
точности, поэтому цифры в первых четырех разрядах после
запятой верны (сравнить у\ с у@,1) и г/2 с у@,2)).
Пример J^.2. Методами Эйлера, Эйлера-Коши и Рунге-
Кутта с шагом h = 0,1 численно проинтегрировать следующую
168 Решение задач для обыкновенных дифференциальных уравнений [ Гл. IV
задачу Коши для нормальной системы второго порядка до зна-
значения х = 0,2 включительно (т.е. два шага):
у[ = x + 2yi + у2,
у'2 = 2x + yi + 2у2,
2/1 @) = 1,
2/2@) = 1.
Задача допускает аналитическое решение, которое имеет вид
= -е6
-ех -х- -;
yi @) = 1; ух @,1) = 1,355583; У1 @,2) = 1,848438;
У2 @) = 1; у2 @,1) = 1,36075; у2 @,2) = 1,86984.
Метод Эйлера.
Уи+1 = Уи + h (xi + 2уц + у2г),
2/2г+1 = V2i + h BXi + уи + 2y2i) ,
?/io = 1, 2/20 = 1;
г = 0; хр = 0; ую = 1; у2р = 1 :
ю + h (х0 + 2ую + У20) = 1 + 0,1 @ + 2 • 1 + 1) = 1,3;
+ h {2x0 + ую + 2у2о) = 1 + 0,1 B • 0 + 1 + 2 • 1) = 1,3;
г = 1; xi = 0,1; уп = 1,3; y2i = 1,3 :
2/12 = 2/11 + h • (ж1 + 2уц + y2i) =
= 1,3 + 0,1 @,1 + 2 • 1,3 + 1,3) = 1,7;
2/22 = 2/21 + Л • B • xi + 2/п + 2y2i) =
= 1,3 + 0,1 B • 0,1 + 1,3 + 2 • 1,3) = 1,71;
§4.6] Процедура Рунге оценки погрешности 169
Метод Эйлера-Коши.
2/1 г+1 = УН + h (Xi + 2уц + У2г) ,
2/2 г+1 = V2i + h BXi + y\i + 2у2г) ,
У\ г+1 = 2/1г + ^ [(^г + tyli + 2/2г) +
2/2 г+1 = У2г + ^ [Bжг' + 2/1г + 22/2г) + B
Ую = 1? У20 = 1;
г = 0; х0 = 0; д?х = ОД; у10 = 1; у20 = 1 :
yn = yio + h (х0 + 22/ю + у2о) = 1 + 0,1 @ + 2 • 1 + 1) = 1,3;
У21 = У20 + h Bх0 + у10 + 2у20) = 1 + 0,1 B • О + 1 + 2 • 1) = 1,3;
У\ 1 = ую + ^ [(ж0 + 2ухо + 2/20) + (жх + 2yi 1 + у21)] =
= 1 + ^ [@ + 2 • 1 + 1) + @,1 + 2 • 1,3 + 1,3)] = 1,35;
У21 = У20 + ^ [Bж0 + ую + 2у2о) + Bж1 + yi 1 + 2y2i)] =
= 1 + ^ [B • 0 + 1 + 2 • 1) + B • 0,1 + 1,3 + 2 • 1,3)] = 1,355;
Zi
г = 1; жх = ОД; х2 = 0,2; yxi = 1,35; g/2i = 1^355 :
= Уи + h (жх + 2yxi + 2/2i) =
= 1,35 + ОД (ОД + 2 • 1,35 + 1,355) = 1,7655;
У22 = У21 + h Bжх + 2/11 + 2y2l) =
= 1,355 + ОД B • ОД + 1,35 + 2 • 1,355) = 1,781;
2/12 = 2/11 + ^ [(Жх + 2УП + 2/2l) + (ж2 + 2^12
= 1,35 + ^[@,1 + 2 • 1,35 + 1,355) +
Zi
+ @,2 + 2 • 1,7655 + 1,781)] = 1,8334;
170 Решение задач для обыкновенных дифференциальных уравнений [Гл. IV
У2 2 = У21 + ^ [BЖ1 + Ун + 2у2\) + BХ2 + У12 + 2у22)] =
= 1,355 + ^[B • 0,1 + 1,35 + 2 • 1,355) +
+ B • 0,2 + 1,7655 + 2 • 1,781)] = 1,8544;
Метод Рунге-Кутта.
Уи+1 = Уи + А Ун,
У2г+1 = У2г
Ay2i = I (I] + Щ + 2/f + ф ,
к} = h- [xi + 2уи + y2i] ,
l} = h- [2xi + уи + 2y2i] ,
i = h [{Xi + I) + 2 (yii + f) + (y2i + I
= Л • [(*< + Л) + 2 (УН + Л?) + (У2г
= h-[2 (Xi + h) + (yu + ft?) + 2 (y2i + If)] ;
г = 0; xo = 0; жо+1/2 = 0,05; x\ = 0,1; ую = 1; У20 = 1
уи = ую + Аую = 1 + 0,35558 = 1,35558;
У21 = Уго + Ау20 = 1 + 0,36073 = 1,36073;
§4.6] Процедура Рунге оценки погрешности 171
Дую = I {Н + Щ + 2kl + kt) =
= - @,3 + 2 • 0,35 + 2 • 0,3578 + 0,4179) = 0,35558;
< 6
6
= - @,3 + 2 • 0,355 + 2 • 0,363 + 0,4284) = 0,36073;
6
kl = h-[xo + 2yio + Шо] = 0,1 @ + 2 • 1 + 1) = 0,3;
ll = h- [2ж0 + ую + 2г/20] = 0,1 B • 0 + 1 + 2 • 1) = 0,3;
= 0,1 [0,05 + 2 (l + ^) + (l + ^)] = 0,35;
= 0,1 [2 • 0,05 + (l + ^) + 2 f1 + -^)] = °'355;
= 0,1 [0,05 + 2 (l + ^) + (l + ^)]= 0,3578;
/g = Л [2 (хо + ^ + (у10 + f) + 2 (У20 + |) ] =
k$ = h- [(хо + h) + 2 (г/ю + Ag) + (y20
= 0,1 [0,1 + 2 A + 0,3578) + A + 0,363)] = 0,4179;
ll = h ¦ [2 (хо + h) + (y10 + feg) + 2 (у20 + /§)] =
= 0,1 [2 • 0,1 + A + 0,3578) + 2 A + 0,363)] = 0,4284;
172 Решение задач для обыкновенных дифференциальных уравнений [Гл. IV
г = 1; xi = 0,1;
0Д5; ж2 = 0,2; уп = 1,35558; у21 = 1,36073 :
У12 = Ун + Ауп = 1,35558 + 0,49283 = 1,8484;
У22 = г/21 + Л г/21 = 1,36073 + 0,5090 = 1,8698;
— _ (]Л _|_ 9^2 -U 9^3 -U ^4>\ —
= ^ @,41719 + 2 • 0,4853 + 2 • 0,4958 + 0,57756) =
= 0,49283;
= - @,4277 + 2 • 0,5013 + 2 • 0,5121 + 0,5997) = 0,5090;
6
k\ = h ¦ [xi + 2уц + 2/21] =
= 0,1 @,1 + 2 • 1,35558 + 1,36073) = 0,41719;
l\ = h- [2<ci + г/11 + 2г/21] =
= 0,1 @,2 + 1,35558 + 2 • 1,36073) = 0,4277;
= 0,1 [0,15 + 2 (l,35558
+ (l,36073 + ^^)] = 0,4853;
= 0,1 [2 • 0,15 + (l,35558 + °'41719) +
+2 (l,36073 + ^^)] = 0,5013;
§4.6]
Процедура Рунге оценки погрешности
173
= 0,1 [о,15 + 2 (l,35558
+ (l,36073 + ^^)] = 0,4958;
/ =
= 0,1 [2 • 0,15 + (l,35558 + —
+2 (l,36073 + ^EH^l = 0,5121;
k\ = h- [(Xl + h) + 2 (yn + kf) + (y21 + If)] =
= 0,1 [0,2 + 2 A,35558 + 0,4958) +
+ A,36073 + 0,5121)] = 0,57756;
If = h ¦ [2 On + h) + (j/n + kf) + 2 (j/21 + /?)] =
= 0,1 [2 • 0,2 + A,35558 + 0,4958) +
+2 A,36073 + 0,5121)] = 0,5997.
Таким образом, метод Эйлера для заданной системы ОДУ
(решение которой растет по экспоненте) дает погрешность уже
в первой цифре после запятой, метод Эйлера-Коши — во вто-
второй, и только метод Рунге-Кутта выдерживает теоретическую
точность, сохраняя верными четыре цифры после запятой.
УПРАЖНЕНИЯ.
4.1. Методом Эйлера, Эйлера-Коши, Рунге-Кутта с шагом
h = 0,1 решить следующие задачи Коши для ОДУ 1-го порядка,
сделав три шага:
6)
у =
3/ A) = 0;
У1 = У2 -
= 0,5;
174 Решение задач для обыкновенных дифференциальных уравнений [Гл. IV
, 2
У +ху2,
е)
у' =
+ х,
1/@) = 1.
4.2. Задачи упражнения 4.1 решить с точностью е = 0,01 для
методов Эйлера и Эйлера Коши и с точностью ei = 10 для
метода Рунге-Кутта, приняв в качестве начального шага h = 0,1.
4.3. Методом Рунге-Кутта с точностью е = 10~4 (ho = 0,1)
решить следующие задачи Коши до значения аргумента хкон =
= 1,0, сведя ОДУ 2-го порядка к нормальной системе ОДУ 2-го
порядка:
а <
у" = - + ху',
б)
= ху'2 - у2,
2/@) = 1,
2/@) = 1;
2/ @) = 1,
у'@) = 1;
г <
у" = е у + жу,
I/ @) = 1, Д)
х + 1
1/@) = 1,
2/@) = 1;
2/@) = 1.
4.4. В заданиях упражнения 4.1 уточнить решения с помо-
помощью процедуры Рунге, просчитав задачи с шагами h = 0,1; h\ =
= 0,05.
4.5. Методами Эйлера, Эйлера-Коши и Рунге-Кутта с ша-
шагом h = 0,1 до хкон = 1 решить следующие задачи Коши для
нормальных систем:
= 1п У1 + У\
х +г
а <
у'2 =
?/2,
б)
У2 @) = 1;
2/1 -22/2,
2/1 @) = 1,
I 2/2 @) = 1;
§4.7] Численные методы решения краевых задач для ОДУ 175
в)
г <
У2 @) = 1;
2/1 @) = 1,
У2 @) = 1;
д)
У2 @) = 1;
Ух @) = 1,
2/2@) = 1.
§ 4.7. Численные методы решения краевых задач
для ОДУ
4.7.1. Постановка краевых задач для ОДУ. Рассмот-
Рассмотрим постановку краевых задач для ОДУ 2-го порядка с гранич-
граничными условиями различных родов.
Пусть на отрезке х ? [а, Ь] определена дважды непрерывно
дифференцируемая функция у (ж), поведение которой описыва-
описывается линейным неоднородным ОДУ 2-го порядка. Принципиаль-
Принципиальным отличием краевой задачи от задачи Коши для ОДУ явля-
является задание дополнительных (краевых или граничных) условий
более чем в одной точке независимой переменной (в задаче Коши
дополнительные условия задаются в одной точке, называемой
начальной).
Если на границах х = а и х = b заданы значения искомой
функции у (а), у(Ь), то такие условия называются граничными
условиями первого рода, а задача
у" + р{х)у' + q(x)y = /(ж), а < х < 6;
у{о) = Уа,
y(b) = yb,
называется первой краевой задачей для ОДУ D.51).
х = а;
x = b
D.51)
D.52)
D.53)
176 Решение задач для обыкновенных дифференциальных уравнений [Гл. IV
Если на границах заданы значения производных искомой
функции, то такие условия называются граничными условиями
2-го рода:
У'{а) = уа; D.54)
У'{Ь) = уь, D.55)
а задача D.51), D.54), D.55) называется второй краевой задачей
для ОДУ D.51).
Если на границах заданы линейные комбинации искомой
функции и ее первой производной:
у'(а) + ау(а) = уа, D.56)
Уь, D.57)
то такие условия называются граничными условиями третьего
рода, а задача D.51), D.56), D.57) называется третьей краевой
задачей для ОДУ D.51).
Чаще всего на разных границах задаются граничные условия
различных родов. Такие задачи называют краевыми задачами со
смешанными краевыми условиями.
4.7.2. Конечно-разностный метод с использованием
метода прогонки решения краевых задач для ОДУ. Рас-
Рассмотрим первую краевую задачу D.51)-D.53) и будем решать
ее конечно-разностным методом, заменяя дифференциальные
операторы отношением конечных разностей с использованием
формул численного дифференцирования (см. §3.4).
Для этого введем конечно-разностную сетку с шагом h:
^h = {xi = ih, i = 0,n} .
Поскольку ОДУ D.51) описывает поведение функции у(х)
внутри расчетной области х ? (а, 6), то производные 1-го и 2-го
порядков можно аппроксимировать с помощью отношения цен-
центральных разностей со 2-м порядком аппроксимации:
У[ = Vi+1~hVi~1 + О (h2) , г = T^T; D.58)
y'l = УШ ~ 2% + "-1 + О (h*) , г = Т^Т; D.59)
= 1, n - 1. D.60)
§4.7] Численные методы решения краевых задач для ОДУ 177
Подставляя D.58)-D.60) в ОДУ D.51), получим следующую
конечно-разностную схему:
Уо = Уа, i = 0;
Уп = Уь, i = ni
которую можно представить в виде следующей СЛАУ с трехдиа-
гональной матрицей:
Q>iVi-i + ЬгУг + сцл+1 = di, i = 1, п - 1, D.61)
где
Pi_. i _ _±_ , n . ^ _ jL j_ ill. Л — f
2 r>L ' °г — ,2 + ^' C^ ~~ 7 2 "^ ог. ' аг — Л •
При г=1 первое слагаемое в левой части D.61) известно и рав-
равно aiyo — агУа] при i = п — 1 последнее слагаемое в левой части
также известно и равно сп-\уп = сп-\уь. Поэтому СЛАУ D.61)
приобретает следующий вид:
ai =0
+ rf* d\ d г = 1,
г-l + ЬгУг + Ciyi+\ = d{, % = 2, П - 2, , ,
г = n — 1,
Cn-1 = 0.
Здесь коэффициенты ai и cn_i полагаются равными нулю
только после вычисления правых частей d\ и d^l_1.
Теперь СЛАУ D.62) пригодна для использования метода про-
прогонки (она имеет трехдиагональную матрицу и а\ = сп-\ = 0).
178 Решение задач для обыкновенных дифференциальных уравнений [Гл. IV
Прогоночные коэффициенты в прямом ходе определяются
с помощью выражений
i = i——-л—; Bi = irz—л—' г = 1>п-1> D-63)
bi + CLiAi_i bi + diAi-i
причем
Ax = -ci/bi, Bi = rfi/6b
так как а\ = 0,
Лп-! = 0,
так как cn_i = 0.
Значения yi, i = n — l,n — 2,... ,1, находятся в обратном
ходе с помощью равенств
Уг = AiVi+i + Bi :
i = n-l: yn-i = An_iyn + B
i = n - 2 : yn-2 = Ап-2Уп-1 +
D.64)
4.7.3. Конечно-разностная схема со вторым поряд-
порядком аппроксимации краевых условий, содержащих про-
производные. В случае решения задачи для ОДУ D.51) с гранич-
граничными условиями 2-го или 3-го родов на границах х = а и х =
= b значения искомой функции у (а) и у(Ь) неизвестны и для
их нахождения должны быть составлены алгебраические урав-
уравнения в граничных узлах. Однако аппроксимацию производных,
входящих в краевые условия, с помощью отношения конечных
разностей справа (в узле х = а) и слева (в узле х = Ь) можно
осуществить только с первым порядком, в то время как диффе-
дифференциальное уравнение аппроксимируется со вторым порядком.
Следовательно, в этом случае вся 2-я (или 3-я) краевая задача
будет аппроксимирована только с первым порядком.
Для повышения на единицу порядка аппроксимации произ-
производных, входящих в краевые условия, предположим, что искомая
функция у(х) дважды дифференцируема не только во внутрен-
внутренних точках расчетной области, но и на границах, т.е. у(х) ? С2,
х Е [а, Ь]. Тогда для решения этой проблемы можно использовать
§4.7] Численные методы решения краевых задач для ОДУ 179
аппарат разложения в ряды Тейлора приграничных значений
сеточной функции на точном решении в окрестности граничных
узлов.
С этой целью разложим на точном решении в ряд Тейлора
до 3-й производной включительно у\ в окрестности узла х = а
для левой границы и уп-1 в окрестности узла х = b для правой
границы.
Затем значения производных 2-го порядка для граничных
узлов в этих разложениях заменяются значениями второй произ-
производной, определенными из ОДУ, после чего из полученных выра-
выражений определяются значения первой производной в граничных
узлах со вторым порядком, которые затем подставляются вместо
производных первого порядка в краевые условия.
Рассмотрим эту процедуру для левой границы xq = a:
У\ = у(хо + К) = Уо + y'oh + уц— + O(hs). D.65)
z
Из D.51) находим у$:
У о = /о - РоУо ~ ЯоУо- D-66)
Подставив D.66) в D.65) и разделив на /i, получим
Уо = 1 h - ^-(/о - РоУо - ЯоУо) + O(h2),
откуда
или
D.67)
Подставляя D.67) в D.56) (или в D.54)), получим
2 »i-yo h {fQ
2-poh h 2-pohyJU
Из D.68) видно, что полученное уравнение для узла х$ =
= а содержит только два неизвестных 2/о и 2/1? а аппроксимация
имеет второй порядок. Следовательно D.68) можно представить
в виде
= d0, D.69)
180 Решение задач для обыкновенных дифференциальных уравнений [ Гл. IV
где
/гB - poh) 2 -
2-poh
Аналогично для правой границы (хп = Ь):
Уп-1 = У(хп -h) = yn- y'nh + у'^ —
Уп = in -РпУп - ЧпУп,
Подставляя это выражение в краевое условие D.57) (или
в D.55)), получим уравнение для правой границы с двумя неиз-
неизвестными Уп-1, Уп и вторым порядком аппоксимации:
2_у^1+ h yn = yb + O{h%
которое можно представить в виде
О"пУп-1 + ЬпУп = 4, D-70)
где
-2 , 2 qnh . Л
Таким образом, результирующая СЛАУ с трехдиагональной
матрицей теперь будет содержать п + 1 уравнение, каждое из
которых получено со вторым порядком точности, а именно:
уравнение D.69) при г = 0, уравнения D.61) для г = 1,п — 1
и уравнение D.70) для i = п. Для ее решения используется метод
прогонки, поскольку ао = 0 и сп = 0.
4.7.4. Метод пристрелки численного решения крае-
краевых задач для ОДУ. Метод пристрелки сводит решение кра-
краевой задачи для ОДУ к решению итерационной последовательно-
последовательности задач Коши. Этот метод рассмотрим на примере следующей
первой краевой задачи для ОДУ 2-го порядка :
§4.7]
Численные методы решения краевых задач для ОДУ
181
D.71)
D.72)
D.73)
Вместо краевой задачи D.71)-D.73) рассматривается следу-
следующая задача Коши:
у" = /(ж,у,у')> а < х < Ь;
у (а) = уо, х = а;
yi, x = b.
у" = f(x,y,yf), a < х < 6;
у (а) = уо, х = а;
y/(a)=tga, a:
D.74)
D.75)
D.76)
в которой интегральная кривая у(х,а) зависит не только от
переменной ж, но и от параметра а, который называется углом
a b х
Рис. 4.5. Геометрическая интерпретация метода пристрелки
пристрелки. Он выбирается из условия равенства значения ин-
интегральной кривой на правой границе у(Ь, а) значению у\ с на-
наперед заданной точностью е (рис. 4.5):
\у(Ь,а)-У1\^е. D.77)
Угол пристрелки, удовлетворяющий неравенству D.77), обо-
обозначим через а*. Интегральная кривая, полученная из решения
182 Решение задач для обыкновенных дифференциальных уравнений [ Гл. IV
задачи Коши D.74)-D.76) с углом, близким к этому значению,
в соответствии с неравенством D.77) и будет решением краевой
задачи D.71)-D.73) с точностью е.
Таким образом, алгоритм метода пристрелки следующий.
1. Выбирается а^, например из условия
, 2/1-2/0
tga0 = -г •
о — а
2. С этим значением а$ одним из методов решается задача
Коши D.74)-D.76) с получением у(х^ао) и у(Ь,ао); если при
этом выполняется условие D.77), то краевая задача D.71)-D.73)
решена с точностью е.
3. В противном случае могут быть следующие два варианта:
а) ?/(Ь, ао) > 2/1; тогда угол пристрелки каким-либо способом
уменьшается и решается задача Коши D.74)-D.76) тем же мето-
методом до тех пор, пока не выполнится условие у(Ь, а\) < у\\
б) ?/(Ь, ао) < ух; тогда угол пристрелки каким-либо способом
увеличивается и решается задача Коши до тех пор, пока не
выполнится условие 2/(fe, ai) > у\.
4. Таким образом, угол пристрелки находится внутри интер-
интервала а ? (ao,o:i), после чего истинное значение а* угла при-
пристрелки определяется методом половинного деления с реализа-
реализацией следующей цепочки :
а) OLk+i = (ak-i + ak)/2]
б) у(х,ак+1);
в) у(Ь,ак+1);
г) анализируется неравенство \y(b,ak+i) — у\\ ^ е; если оно
выполнено, то а* « (ак + ак+{)/2 и у(ж, а*) — истинная инте-
интегральная кривая; если неравенство не выполнено, то итерацион-
итерационный процесс повторяется начиная с п. 4 а.
4.7.5. Метод пристрелки с использованием итераци-
итерационной процедуры Ньютона. Метод половинного деления
очень медленно сходится и приходится решать значительное
число задач Коши для различных значений углов пристрелки
ак. Для ускорения сходимости итерационного процесса будем
полагать, что у\ = уF, а$ + Аа), где Да подлежит определению.
Для определения Аа разложим у F, ао + Аа) в окрестности
ао в ряд Тейлора до второй производной включительно, получим
у(Ь, а0 + Да0) = у{Ь, а0) + 9у(?'ао)Аао + 0{Аа2) =
§4.7] Численные методы решения краевых задач для ОДУ 183
откуда
т/1 -у(Ь,а0) , ,
А^о = л (и ч—. D.78)
ду(Ь,а0)
да
ду(Ь,а0) х
Для определения —^- выбирается малое приращение о
да
угла пристрелки и со значением угла а о + S решается задача
Коши D.74)—D.76) с получением y(b,ao + S). Тогда для опре-
определения производной, входящей в выражение D.78), используем
отношение конечных разностей:
ду{Ь,а0) _ у(Ь, ар + д) -у(Ь,а0) . .
да ~ S ' l4-'9j
Подставляя D.79) в D.78), получаем
2/F, ао +5) -2/F,а0)
Итерационный процесс продолжается до выполнения условия
D.77) с помощью процедуры
1 ^
y[b,ak) -y(b,ak-i)
сходящейся значительно быстрее метода половинного деления.
Пример 4-3- Методом конечных разностей с использова-
использованием метода прогонки решить следующую краевую задачу для
ОДУ 2-го порядка, приняв h = 0,25 (а = xq = 1; b = X4 = 2):
у'A) + уA) = 1, (б)
уB) = 1. (в)
Решение. Эта задача допускает аналитическое решение,
имеющее вид у (х) = х4/8 х2 + 9/2, значения которого у (х{)
в узлах сетки xq = 1; х\ = 1,25; Х2 = 1,5; жз = 1,75; х^ = 2,0
занесем в таблицу (в эту же таблицу занесем и полученные ниже
результаты численного решения у^, г = 0,4).
184 Решение задач для обыкновенных дифференциальных уравнений [ Гл. IV
г
Xi
У(Хъ)
Уг
0
1
3,25
3,18
1
1,25
2,6568
2,60
2
1,5
2,039
2,00
3
1,75
1,462
1,44
4
2,0
1,0
1,0
Производные первого и второго порядков, входящие в диффе-
дифференциальное уравнение, в узлах Х{ аппроксимируются со вторым
порядком:
Подставляя эти выражения в дифференциальное уравнение для
узлов Х{, г = 1, 3, получим
yi+1 - 2ц + ц-! Jц+1 - ц-! = Ж2 + о /fe2) i=I73 (g)
k -^
2/г
Поскольку на правой границе (г = 4, ж 4 = 2) задано гранич-
граничное условие 1-го рода, т. е. значение искомой функции в этом
узле известно и равно у4 = 1, то уравнение для этого узла не
выписывается (но значение у^ будет использовано в конечно-
разностной аппроксимации (г) при г = 3). Будем аппроксими-
аппроксимировать со вторым порядком левое краевое условие {б) в узле г =
= 0, жо = 1. Разлагая на точном решении у\ в ряд Тейлора
в окрестности граничной точки xq = 1 до третьей производной
включительно, получим
У1 = у {х0 + h) = yo
Подставим сюда вместо у
y'oh
О (/г3) .
значение второй производной из
дифференциального уравнения (а) при xq = 1: у$ = —у$ + х$ .
Затем разделим все выражение на h и выразим из полученного
равенства значение у^ получим
Уо =
У\ ~Уо
Л 1 +
h
h
+ О (h2) .
Подставим это выражение в левое краевое условие (б) вместо
производной первого порядка, получим (у A) = у$)
§4.7]
Численные методы решения краевых задач для ОДУ
185
У\ -
hxi
^ 2 1 +
2х0
= 1 + О (h2) ,
откуда при жо=1 и h = 0,25 получаем алгебраическое уравнение
в узле xq = 1 со вторым порядком:
-2,556у0 + 3,556yi = 1,111 + О @,0625). (д)
Приписывая к этому уравнению алгебраические уравнения,
полученные из аппроксимации (г) для г = 1,3 (х\ = 1,25; х2 =
= 1,5; жз = 1,75; h = 0,25), получим следующую СЛАУ с трех-
диагональной матрицей:
-2,556?/о + 3,556yi = 1,111
(а0 = 0; Ьо = -2,556; с0 = 3,556; d0 = 1,111);
= 0,0977
(аг = 1,1; &i = -2; а = 0,9; d± = 0,0977);
l,0831yi - 2у2 + 0,9167у3 = 0,141
(а2 = 1,0831; Ъ2 = -2; с2 = 0,9167; d2 = 0,141);
1,071у2-2у3 =-0,737
(а3 = 1,071; Ь3 = -2; с3 = 0; d3 = -0,737),
которая решается методом прогонки:
В() = — =
Ьо -2,556
do 1,111
&о -2,556
-0,9
=
1
bi + сцАо -2 + 1,1-1,3912
-с2 -0,9167
= -0,4347;
= 1,9162;
= -1,226;
-2 + 1,1-1,3912
0,0977-1,1 (-0,4347)
-2 + 1,0831-1,9162
= -12,091;
186 Решение задач для обыкновенных дифференциальных уравнений [ Гл. IV
_ d2-a2B1 _ 0,141-1,0831 (-1,226) _
В2 - 62 + a2A, ~ -2 + 1,0831-1,9162 ~ 1
3
d3 ~ а
-0,737 - 1,071 ¦ 19,3765
-2+ 1,071-(-12,091)
' '
?3 = -Вз = 1,4375;
У2 = А2у3 + В2 = -12,091 • 1,4375 + 19,3765 = 2,00;
Уг = А1У2 + Вг = 1,9162 • 2,00 + (-1,226) = 2,60;
Уо = АоУ1 + В0 = 1,3912 • 2,60 + (-0,4347) = 3,18.
Эти значения занесем в 3-ю строку таблицы под значениями
аналитического решения, сравнение с которым показывает, что
действительно конечно-разностная аппроксимация (г) и (д) име-
имеет второй порядок относительно шага (h? = 0,0625):
Д (у). = {|3,25 - 3,18| = 0,07; |2,6568 - 2,60| = 0,0568;
|2,039 - 2,00| = 0,039; |1,462 - 1,44| = 0,022; 0}
Для более точного расчета необходимо уменьшить шаг h.
Пример 4-4- Методом пристрелки с использованием алго-
алгоритма Эйлера с шагом h = 0,25 и методом половинного деления
и Ньютона уточнения корней нелинейных уравнений решить
следующую первую краевую задачу для ОДУ 2-го порядка (точ-
(точность е = 0,05):
у" = -у' + х2
2/A) = 0,
, 2/B) = 1.
Эта задача допускает следующее аналитическое решение:
4 1-7 "I
п. ( rv*\ ю^> I
§4.7]
Численные методы решения краевых задач для ОДУ
187
Сведем данную краевую задачу к следующей задаче Коши
для того же ОДУ:
'(l) = tga, a = a*:y{2,a*) = l.
Уравнение D.76) для этой задачи, а именно уравнение / (а) =
= у B, а) — 1 = 0, как нелинейное уравнение относительно угла
пристрелки а можно решить одним из рассмотренных ранее
итерационных методов с параллельным решением задачи Коши
на каждой итерации. Здесь вначале будет использован метод
половинного деления, а затем метод Ньютона.
Метод половинного деления.
1-я итерация. Пусть угол пристрелки а^ определен из соот-
соот= —— — = 1; ао = 45°. Тогда задача Коши
ношения
для ОДУ 2-го порядка и соответствующая задача Коши для
нормальной системы ОДУ 2-го порядка будут иметь вид
у" = -у'
х2
= 0,
= -z + x2,
X
Метод Эйлера с шагом h = 0, 25 для этой системы имеет вид
Уг+1 = У1 + h- Z{,
у . . -, — у . A- h [ у . I v . A. rp^\ j — Г) 1 О Ч 4
^г+1 — ^г п^ '^ у^гI ^г \ г ) ? — ? ±,^,о,^±.
Решая эту систему, получаем
г
Xi
Уг
Zi
0
1,0
0
1
1
1,25
0,25
1,50
2
1,5
0,625
2,19
3
1,75
1,173
3,1
4
2,0
1,953
4,33
188 Решение задач для обыкновенных дифференциальных уравнений [ Гл. IV
у B; 45°) = 1,953.
Итак,
f1 D5°) = у B; 45°) - 1 = 1,953 - 1 = 0,953 > 0.
Следовательно, необходимо уменьшить угол пристрелки а,
причем так, чтобы / (а) на следующей итерации было меньше
нуля. Примем ol\ = 0, тогда задача Коши будет иметь вид:
2-я итерация (а\ = 0°).
У = 2,
, 1
z = —z +
X
у A) = О,
z(l) = 0.
У" = V
X
tf(l) = О,
у'A) =tgai = 0,
Методом Эйлера с шагом h = 0,25,
= Уг
= Zi
h
+ xfj , г = 0,1, 2, 3, 4,
получаем
г
Xi
Уг
Zi
0
1,0
0
0
1
1,25
0
0,25
2
1,50
0,0625
0,69
3
1,75
0,235
1,368
4
2,0
0,577
2,33
у B; 0°) = 0,577;
/2 @°) = у B; 0°) - 1 = 0,577 - 1 = -0,423 < 0.
Следовательно, угол а* находится внутри интервала ol\ —
= 0° < а* < а$ = 45°. После этого для уточнения угла пристрел-
пристрелки а используем метод половинного деления.
§4.7]
Численные методы решения краевых задач для ОДУ 189
итерация
= 0,414.
+
45° + 0°
о i o
= 22,5 ; tg22,5 =
X
уA) = 0,
z(l) = 0,414.
Решая эту задачу Коши методом Эйлера с шагом h = 0,25,
получим
г
Xi
Уг
Zi
0
1,0
0
0,414
1
0,
0,
1
,25
104
768
0
1
2
1,5
,296
,312
1
0,
2,
3
,75
624
093
1
3
4
2,0
,147
,153
у B; 22,5°) = 1,147;
/3 B2,5°) = у B; 22,5°) - 1 = 1,147 - 1 = 0,147 > 0;
|/3B2,5°)| = 0,147 > е = 0,05.
Сравнение значения функции / (а) на 2-й итерации
(/2 @°) < О) и на третьей итерации (/3 B2,5°) > 0) означает,
что 0° < а* < 22,5°.
4-я итерация (а3 = ° +О22'5 = 11,25°, tg 11,25° = 0,2 ).
Решение задачи Коши
X
г/ A) = о,
методом Эйлера с шагом h = 0,25 сведено в таблицу
190 Решение задач для обыкновенных дифференциальных уравнений [ Гл. IV
г
Уг
Zi
0
1
0
0,2
1
1,25
0,05
0,5
2
1,5
0,175
0,991
3
1,75
0,423
1,719
4
2,0
0,853
2,73
у B; 11,25°) = 0,853;
/4 A1,25°) = у B; 11,25°) - 1 = 0,853 - 1 = -0,147 < 0;
|/4A1,25°)| = 0,147 > е = 0,05.
Сравнение / (а) на третьей итерации (/3 B2,5°) > 0) и на
четвертой (/4 A1,25°) < 0) означает, что 11,25° < а* < 22,5°.
/ 11 2^° 4- 22 "i0
5-я итерация (а4 = ' ^—— = 16,875°; tg 16,875° =
= о,з).
Решение задачи Коши
z1 = -z + ж2,
X
2/A) = 0,
2A) = 0,3
методом Эйлера с шагом h = 0,25 сведено в таблицу
i
Xi
Уг
2 •
0
1,0
0
0,3
1
1,25
0,075
0,625
2
1,5
0,23
1,14
3
1,75
0,515
1,89
4
2,0
0,99
2,93
у B; 16,875°) = 0,99;
/5 A6,875°) = у B; 16,875°) - 1 = 0,99 - 1 = -0,01;
|/5A6,875°)| =0,01 < 0,05.
§4.7]
Численные методы решения краевых задач для ОДУ
191
Таким образом, угол пристрелки принимается равным а* =
= 16, 875°. На этом угле интегральная кривая имеет значения у{
из последней таблицы.
Метод Ньютона.
Как видно из проведенного расчета, метод половинного де-
деления при уточнении нуля а* функции / (а) очень медленно
сходится. Для ускорения итерационного процесса применим ме-
метод Ньютона, для чего на первой итерации примем а$ = 45°.
Результаты расчетов по методу Эйлера с использованием мето-
метода половинного деления приведены в таблице первой итерации,
из которой следует, что у B; 45°) = 1,953. Для проведения 2-й
итерации вычислим а± так:
у B) -у B; 45О) х
и у B; 45°+ 6)-у B; 45°) '
где 6 примем равным —10° (угол а нужно уменьшать, поскольку
f1 D5°)=0,953>0, а /(а*)=0).
С углом а = ао + S = 45° — 10° = 35° решается задача Коши
методом Эйлера с шагом h = 0,25. В результате получаем таб-
таблицу
i
Xi
Уг
Zi
0
1,0
0
0,7
1
1,25
0,175
1,125
2
1,50
0,456
1,74
3
1,75
0,89
2,59
4
2,0
1,538
3,73
у B; 35°) = 1,538.
На второй итерации
У B) -у B; 45°) (
tg22,5° = 0,404.
С этим ai на второй итерации решается задача Коши, результа-
результаты решения которой приведены в таблице на 3-й итерации метода
половинного деления, откуда уB; 22,5°) = 1,147, а |/2B2,5°)| =
= |1,147 - 1| = 0,147 > е = 0,05.
192 Решение задач для обыкновенных дифференциальных уравнений [Гл. IV
На 3-й итерации
у B) -у B; 22,5°)
OL2 = «1 +
у B; 45°) -у B; 22,5°)
D5° - 22,5°) =
tg17,8° = 0,32.
Решая задачу Коши с этим углом а2 = 17,8°, получаем
г
Уг
Zi
0
1,0
0
0,32
1
1,25
0,08
0,65
2
1,5
0,243
1,17
3
1,75
0,535
1,93
4
2,04
1,016
2,97
у B; 17,8°) = 1,016;
/3 A7,8°) = \у B; 17,8°) - 1| = |1,016 - 1| = 0,016 < е = 0,5.
Таким образом, точность выполнена, и итерационный про-
процесс останавливается. Кроме этого, видно, что метод Ньютона
сходится значительно быстрее метода половинного деления.
Ответом являются значения yi из этой таблицы.
УПРАЖНЕНИЯ.
4.6. Методом конечных разностей с использованием метода
прогонки решить следующие краевые задачи для ОДУ 2-го по-
порядка (аппроксимацию производных в краевых условиях выпол-
выполнить с О (/г2), h = 0,1):
а)
у'@) + у@) = 0, б)
у" = sin ж • у' — ж2,
3/' @) = 0,
2/ A) = 1;
§4.7]
Численные методы решения краевых задач для ОДУ
193
у" = ху' - ех,
у' @) + у @) = 1,
г <
У — е У * •ь У1
у'@) - у @) = 1,
у'A) + у A) = 0;
Д)
у" = еху'
х,
2/' @) = 1,
у' A) - у A) = 0;
е)
у" = ху + 1,
у'@) + У @) = 1,
ж)
" = 2V + 2,
3/A) = 0;
з)
у" = -ХУ' + 1,
j/' @) - 2j/ @) = 1,
2/A) = 0.
4.7. Методом пристрелки с использованием метода половин-
половинного деления или Ньютона с точностью е = 0, 01 решить следу-
следующие краевые задачи для ОДУ 2-го порядка (применить один
из методов: Эйлера, Эйлера-Коши или Рунге-Кутта):
а)
у" = cos ж • у' — ж2,
2/@) = 1,
у у±J — 1,0,
б)
у" = -ху'
У @) = 0,
в)
г <
у = sin ж • у — cos ж,
2/ @) = 0,
у' A) = 1;
д)
у" = х2у - ех,
1/@) = 1,
J/ A) = 0;
е)
У @) = 0,
2/' A) = 2;
7 В.Ф. Формалев, Д.Л. Ревизников
194 Решение задач для обыкновенных дифференциальных уравнений [ Гл. IV
Указание: В случае задания граничного условия 2-го рода
на правой границе итерационный процесс осуществлять до вы-
выполнения условия
2/A) — 2/A — Л) /,-
h * v
причем в качестве начального угла пристрелки можно принять
а$ = arctgy'(l).
ГЛАВА V
ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМИЗАЦИИ
Программа
Численные методы безусловной минимизации функции одной пере-
переменной, прямые методы: перебора, половинного деления, золотого се-
сечения. Методы минимизации, использующие производные. Численные
методы безусловной минимизации функций многих переменных: гра-
градиентного спуска, наискорейшего спуска, сопряженных направлений.
§ 5.1. Классификация численных методов
оптимизации
Задачи оптимизации, за редким исключением, решаются
с помощью вычислительных процедур, поэтому названия гла-
главы «Методы оптимизации» и «Численные методы оптимизации
(ЧМО)» практически равносильны. Среди важнейших методов
оптимизации широко распространены следующие методы.
1. Безусловной минимизации функций одной переменной:
— прямые методы (перебора, половинного деления, золотого се-
сечения);
— методы, использующие производные первого и второго поряд-
порядка (Ньютона, ломаных, касательных).
2. Безусловной минимизации функций многих переменных:
— градиентного спуска;
— наискорейшего спуска;
— сопряженных направлений.
3. Условной оптимизации:
— линейное и квадратичное программирование;
— нелинейное программирование;
— динамическое программирование.
Из перечисленных методов будем рассматривать только чис-
численные методы безусловной минимизации, поскольку широкий
класс методов математического программирования входит в от-
отдельный курс «Методы оптимизации».
196 Численные методы оптимизации [Гл. V
§ 5.2. Численные методы безусловной минимизации
функций одной переменной. Прямые методы
Под минимизацией функции /(ж) на множестве X С R будем
понимать следующую задачу: найти хотя бы одну точку мини-
минимума ж* и минимум /* = /(ж*) на множестве X.
Задача нахождения точки максимума ж* функции f(x)
и максимального значения функции /(ж*) сводится к задаче ми-
минимизации функции —/(ж), поэтому ниже будем рассматривать
только задачу минимизации.
Число ж* Е X называется точкой абсолютного (глобального)
минимума функции /(ж), а значение /(ж*) — глобальным мини-
минимумом, если /(ж*) ^ /(ж) для всех ж Е X.
Число ж Е X называется точкой локального минимума, ес-
если существует такое число S > О, что выполняется неравен-
неравенство /(ж) ^ /(ж) для всех точек ж, удовлетворяющих условию
|ж — ж| < 5] значение /(ж) называется локальным минимумом.
Будем рассматривать унимодальные функции /(ж) — функ-
функции, имеющие один минимум в области X.
Функция /(ж) называется унимодальной на отрезке [а, 6],
если она непрерывна на [а, Ь] и существуют числа а и /3,
а ^ а ^ /3 ^ 6, такие, что
1) на отрезке [а, а] /(ж) монотонно убывает;
2) на отрезке [/3, Ь] /(ж) монотонно возрастает;
3) на отрезке ж Е [а, /3] /(ж) имеет минимум /* = min /(ж).
же[а,/3]
Существует два критерия унимодальности, используемые на
практике:
1) если функция /(ж) дифференцируема на отрезке [а, Ь]
и производная /'(ж) не убывает на этом отрезке, то /(ж) унимо-
унимодальна.
2) Если функция /(ж) дважды дифференцируема на отрезке
[а, Ь] и /"(ж) ^ 0 на этом отрезке, то /(ж) унимодальна.
Пример 5.1. Показать, что функция /(ж) = ж4 — 10ж3 +
+ Збж2 + 5ж унимодальна на отрезке [3; 5].
Решение. Вторая производная функции /(ж) равна /"(ж) =
= 12ж2 — 60ж + 72. Корни полученного квадратного трехчлена:
х\ = 2 и Ж2 = 3. Следовательно f"(x) ^ 0 при ж Е (—ос, 2] U
U [3, ос). Пересечением этих промежутков с заданным отрезком
§5.2] Методы безусловной минимизации функций одной переменной 197
будет отрезок [3; 5] и по второму критерию унимодальности
заключаем, что f(x) унимодальна на х ? [3; 5].
Прямые методы минимизации основаны на вычислении толь-
только значений минимизируемой функции и не используют значе-
значений ее производных.
Из прямых методов минимизации рассмотрим методы пере-
перебора, половинного деления, золотого сечения.
5.2.1. Метод перебора. Метод перебора является про-
простейшим методом из прямых методов минимизации, но он яв-
является и самым надежным методом в смысле гарантированного
нахождения минимального значения.
Пусть f(x) унимодальна на х ? [а, Ь]. Требуется найти точку
минимума ж* и минимум /(ж*) с точностью е > 0.
Отрезок [а, Ь] разбивается точками xi = а + г • , г = 0, п,
на п равных частей, где п ^ (в простейшем случае п =
b — a b — а ч
= или = г).
xn =
Рис. 5.1. К методу перебора
Вычислив значения f(xi), i = 0, п, путем сравнения находим
(см. рис. 5.1)
'-> J
198
Численные методы оптимизации
[Гл. V
Ясно, что значения ж* и /(ж*) являются приближенными.
Поэтому для вычисления минимума с большей точностью е\
(е\ < е) рассматривается отрезок ж Е [жт-ъ %+i], где находит-
находится минимальное значение /(ж*), на нем вычисляются значения
f(xj), j = 0, к, к = (жш+1 - xm-i)/ei, и путем сравнения f(xj)
находим более точное значение минимума функции.
Достоинства метода — простота и надежность, недостаток —
большое число вычислений значений функции /(ж).
Пример 5.2. Методом перебора с точностью е = 0, 05 найти
точку минимума ж* и минимальное значение /* функции /(ж) =
= ж4 + 8ж3 - 6ж2 - 72ж на отрезке [1, 5; 2].
Решение. Функция f(x) на заданном отрезке уни-
унимодальна, так как по второму критерию унимодально-
унимодальности /"(ж) = 12ж2 + 48ж — 12 ^ 0 на промежутках ж Е
Е (-оо,-1 - >/2] U [-1 + л/2,оо), где -1 ± л/2 — кор-
корни квадратного трехчлена 12ж2 + 48ж — 12. Выбрав п =
= B — 1,5)/0,05 = 10, вычислим значение f(xi) в точ-
точках Х{ = 1,5 + г • 0,05, г = 0, 10, поместив их в таб-
таблицу:
Xi
f(Xi)
1,50
-89,4
1,55
-90,2
1,60
-91,2
1,65
-91,8
1,70
-92,08
1,75
-92,12
1,80
-91,9
1,85
-91,4
1,90
-90,5
1,95
-89,4
2,00
-88,0
Путем попарного сравнения значений /(ж^), г = 0,10, нахо-
находим ж* и 1,75, /* = -92,12.
5.2.2. Метод деления отрезка пополам. Метод деления
отрезка пополам сродни итерационному методу деления пополам
уточнения корней нелинейных уравнений. Он позволяет постро-
построить систему вложенных отрезков:
[а/Ь Ьк] С [ак-ъ bk-i] С ... С [а, Ь],
внутри которых содержится точка минимума ж*.
Пусть е — требуемая точность определения ж*. Выбрав
S E @;2s), построим последовательности {а&}, {6^}, < Жлев к
§5.2] Методы безусловной минимизации функций одной переменной 199
\ ЖпР к к = О,1, 2, . . . (из интервала (О, 2е) S выбирается как
можно меньше) по следующей схеме (см. рис. 5.2):
I
I
I
I
I
I
I
I
I
Рис. 5.2. Геометрическая интерпретация метода половинного деления
' ^.(°) _ aP + ^p ~ ^ (o) _ «p + 6p + S ш
i\ = ao, 6i = ЖпР, если / жлев ^ / ^пР (рис. 5.2 a);
= Ьо, если /
/ (жпр) (рис. 5.2 5);
^лев —
Qfe-1
L 1]) < / (x{nP 1}) ;
(/C — 1 ) | |
''/c — «^лев -> uk — uk — \t
Процесс останавливается, когда выполняется неравенство
?к = к 2ак < ?-
Окончательное значение точки минимума ж* вычисляется
следующим образом: ж* « — -, /* « / (ж*).
200 Численные методы оптимизации [Гл. V
Метод деления отрезка пополам использует значительно
меньшее количество вычислений функции /(ж), чем метод пе-
перебора, т. е. является существенно более экономичным.
Пример 5.3. Методом деления отрезка пополам решить
задачу из примера 5.2.
Решение. Положим S = 0,02 < 2е = 0,1 и построим после-
последовательность [a/,, bk] вложенных отрезков по выше приведен-
приведенному алгоритму:
а0 = 1,5, 60 = 2,0
@) _ ар + Ьр- 5 _ 3,5-0,02 _ (о) _ а0 + Ьо + 5 _
J-- Жлев — ~ — ~ — *-•)*% жпр — су —
= 1,76; / (хЩ = -92,135; / (ж^Л = -92,096. Поскольку
< / (жпр J, то ж* Е (а0, Жпр J; тогда ai = а0 = 1,5; 6i =
-„ biai 1,76-1,5 niQ^ nnt;
= 1,76; ei = —-— = = 0,13 > е = 0,05.
A) _ Ql + Ьг - 5 _ 1,5 + 1,76-0,02 _ m
Жлев — ^ — ^ — J-9^^? ЖПр —
h±± = 1,64; / (xiil) = -91,486; / (sg>) = -91,696.
ПОСКОЛЬКУ / (жлев) > / (жпр Ь ТО Ж* ^ (^лев?^); ТОГДа CL2 =
(!) 1 ^О А А 17^^ ^2 -Q2 1,76- 1,62
= Жлев = 1?Ь2; о2 = 6i = 1,76; ?2 = —-— = = 0,07 >
> е = 0,05.
B) _ а2 + Ь2 - д _ 1,62 + 1,76-0,02 _ B) _
«J- ^лев — су — су — ±)\JO) «^пр —
= а2 + Ь22 + 6 = 1,70; / (хЩ = -91,995; / (*g>) = -92,084.
ПОСКОЛЬКУ / ^Жлев! > / f ЖщЛ , ТО Ж* Е (жлев?^); ТОГДа п3 =
= х& = 1,68; Ь3 = Ь2 = 1,76; е3 = ^ = ^^-1^ = 0,04 <
<е = 0,05.
Заданная точность достигнута, и, следовательно х* =
= ^^ = 1,72; /* = / A,72) = -92,13.
5.2.3. Метод золотого сечения. Метод золотого сечения
так же является прямым методом, не использующим производ-
производные функции /(ж). Он позволяет сократить вычисления функ-
функции /(ж) по сравнению с методом деления пополам, вычисляя не
два значения на каждой итерации, а одно.
§5.2] Методы безусловной минимизации функций одной переменной 201
Деление отрезка на две неравные части так, что отношение
длины всего отрезка к длине большей части равно отношению
длины большей части к длине меньшей части, называется золо-
золотым сечением.
Золотое сечение отрезка [а, 6] осуществим двумя точками х\,
х2 (рис. 5.3):
xi = а -\ —F - а), х2 = а-\ —F - а),
причем х\ < х2 и х\ — вторая (большая) точка золотого сечения
отрезка [а, х2], a х2 — первая (меньшая) точка золотого сечения
отрезка [#i,6]. Эти значения х\ и х2 получены следующим об-
образом.
Пусть х\ — а = /i; 6 — х\ = fa, I = h + fa — b — а. Тогда по
определению золотого сечения
J_ _ fa
fa " h '
откуда
l2 = (h + fa)h; [ — ) + — -1 = 0; — = —-—;
-h,
2
h = L
Из этой системы находим
3-V5 л/5-1.
1 = 2 = 2
Отсюда получаем
о _ /к
Ж1 = а + -——(Ь - а) = а + 0,38F - а),
х2 = а Н —F - а) = а + 0,62F - а),
причем, зная одну из точек золотого сечения, можно найти дру-
другую из равенств
х\ = а + 6 — а?2) х2 = а + b — х\.
Таким образом, алгоритм метода золотого сечения следую-
следующий (см. рис. 5.3 а и б):
202
Численные методы оптимизации
[Гл. V
xf> =д
а б
Рис. 5.3. К методу золотого сечения
Строится система вложенных отрезков
внутри которых находится точка минимума ж , и последователь-
» @) @) A) A) (/с) (к)
ности золотых сечении х\\ ху2 ; ж^ , ж^ ; . . .; ж^ , ху2 ; . . .,
причем ж^ < Жз , fc = 0,1, 2, . . . , тогда
Рис. 5.3 а
Рис.
= а; Ьо = Ь\
ь (°)
= ао; oi = х2 ;
если
@)\
i?/ @)ч
т. е. вторая точка х\ золотого сечения на
следующем шаге имеется, вычисляем первую
\> = а\ + Ь\ —
\ \
ж* G
^ ) =
@К
а\ = х\ ]\ Ъ\ = Ьо;х\ = х\ , если f(x\
т. е. первая точка ж^ ^ золотого сечения на
следующем шаге имеется, вычисляем вторую
х* €
„A) .
м
§5.2] Методы безусловной минимизации функций одной переменной 203
Рис. 5.3 а <
Рис. 5.3
если
bk-x\
(k-i) i ,
ak = xx ; ok = bk-i',
если
>
(k) , i (/c) * / 0-1) /
^y = ak + bk - x\ \ x e (x\ \bk_
Значение ж* определяется следующим образом:
х
х
(к)
1 J
(к) л/ (к)\ ^
ху2 , если }[х\ ) >
Останов происходит тогда, когда выполняется неравенство
\Ьк - ак\ ^ е.
Погрешность метода золотого сечения оценивается по фор-
формуле
\х* — х
(Ь-а),
и если задана точность г, то, поскольку погрешность не превы-
превышает точности, из неравенства
к
(Ь-а)^е
-1
до начала процесса вычислений находим нижнюю оценку числа
шагов к:
b - a
In
Oil
-2,1 • In
b — а
Пример 5.4- Решить задачу примера 5.2 методом золотого
сечения.
Решение. В соответствии с алгоритмом clq = 1,5,
Ьо = 2; жр = ао -\ —(Ьо-ао) = 1,691; ху = а0 +
&о - «о) = 1,809.
204 Численные методы оптимизации [Гл. V
1-й шаг. / (х^Л = -92,049; / (х^А = -91,814. Поскольку
/ D ) < / D )> то х* G (ао> 4); а\ = ао = 1,5; &i = ж20) =
= 1,809; ei = 6i - oi = 1,809 - 1,5 = 0,309 > е = 0,05; х{2] =
= 4°' = 1,691.
2-й шаг. Значение х2 = 1,691 имеется, а также имеется
/ (XW\ = / (xf]) = -92,049. Вычисляем ж{Х) = a1 + b1- х{2] =
= 1,5 + 1,809 - 1,691= 1,618 и / (х\) = / A,618) = -91,464. По-
Поскольку / D1') > / D1}У то х* е («i^.bi) = С1'618! 1,809);
а2 = ж^ = 1,618; Ъ2 = Ьг = 1,809; е2 = 62 - а2 = 1,809 - 1,618 =
= 0,191 > ? = 0,05; ж[2) = 41} = i»691-
5-й шаг. Значения хг = 1,691 и f [х\ ) = /(ж2) =
B) B)
= —92,049 уже имеются. Вычисляем х2 = а,2 + Ь2 — х\ =
= 1,618 + 1,809 - 1,691 = 1,736 и / (хB2)) = /A,736) =
= -92,138. Поскольку / (х^Л > f (хB2)\ то х* € (х^; Ь2) =
= A,691; 1,809); а3 = х^ = 1,691; 63 = Ь2 = 1,809; е3 = 63 - а3 =
= 1,809 - 1,691 = 0,118 > ? = 0,05; ж^ = ж^2) = 1,736.
4-й шаг. Значения хг = 1,736 и / (ж^ ) = / (х2 I =
= —92,138 уже имеются. Вычисляем ж2 = о3 + 63 — ж^ =
= 1,691 + 1,809 - 1,736 = 1,764 и f (хBЛ = /A,764) =
= -92,083. Поскольку / (х^Л < / (х{23)\ то ж* € (а3,хBЛ =
= A,691; 1,764); а4 = а3 = 1,691; 64 = 43) = 1,764; е4 = &4 - «4 =
= 1,764 - 1,691 = 0,073 > ? = 0,05; ж^4) = ж^3) = 1,736.
5-й шаг. Значения ж2 = 1,736 и / (ж2 1 = / (ж-[ J =
= -92,138 уже имеются; х{4) = а4 + 64 - ж^4) = 1,691 + 1,764 -
- 1,736 = 1,719; / (ж54)) = /A,719) = -92,129. Поскольку
/ D4)) > / D4)), то ж* € (ж54), 64) = A,719; 1,764); а5 =
= 1,719; Ъ5 = 1,764; е5 = Ьь - а5 = 1,764 - 1,719 = 0,045 < е =
= 0,05.
§5.3] Методы минимизации. Метод Ньютона 205
Требуемая точность достигнута. Поскольку / (х\ ) =
= —92,138 < / (х\ М = —92,129, то в качестве точки минимума
принимается точка х* ж х^ — 1,736; /* = —92,138.
§ 5.3. Методы минимизации, использующие
производные. Метод Ньютона
Метод Ньютона, как метод с квадратичной скоростью схо-
сходимости, используется на завершающем этапе какого-либо более
грубого метода.
Он использует производные 1-го и 2-го порядков, что обеспе-
обеспечивает очень быструю сходимость.
Множество точек X С R называется выпуклым, если отре-
отрезок [жх, Ж2], соединяющий любые две точки х\, Х2 ? X, принад-
принадлежит множеству X, т. е. точки а х\ + A — а)х2 ? X, О < а < 1.
Функция f(x) называется выпуклой на множестве точек х ?
? X, если для двух точек х\, х<± ? X выполняется неравенство
f(ax! + A - а)х2) ^ af(xi) + A - а)/(ж2), 0 < а < 1.
Будем рассматривать выпуклые функции f(x) на отрезке ж ?
? [а, 6].
Для того чтобы дважды дифференцируемая функция была
выпуклой на отрезке х ? [а, 6], необходимо и достаточно, чтобы
выполнялось неравенство f"(x) ^ 0 для всех точек.
Для выпуклой дважды дифференцируемой функции f(x) на
х ? [а, Ь] метод Ньютона заключается в построении следующей
итерационной последовательности (сравнить с методом Ньютона
уточнения корней нелинейных уравнений B.46), B.47)):
k\ к = 0,1, 2 . . .
Отсюда видно, что производная второго порядка f"(x) на
отрезке х ? [а, Ь] не должна быть равна нулю. Для выпуклых
функций f(x) это действительно так, в противном случае точки,
в которых f"{x) = 0, являлись бы точками перегиба функции,
а в этих точках минимум (или максимум) функции f(x) отсут-
отсутствует.
206
Численные методы оптимизации
[Гл. V
Если задана точность ?, то останов осуществляется при вы-
выполнении условия
т.е. когда касательная к графику функции в точке
почти горизонтальна. Тогда
ж* « хк и /(ж*) « /(ж/,).
Можно показать, что верхняя оценка погрешности в методе
Ньютона представима в виде следующего неравенства:
|^|<2 |/'Ы|
/с = 0, 1, 2, . . . ; Mi = max |/' (ж)| ; ш2 = min \f" (ж)| ,
xe[a,b] xe[a,b]
причем для сходимости метода Ньютона достаточно, чтобы на-
начальное приближение х$ удовлетворяло условию q < 1.
Пример 5.5. Методом Ньютона найти точку минимума ж*
и минимальное значение /* функции / (ж) = (ж — 2) — In ж на
отрезке ж Е [2; 3] с точностью е = \ff (жд.)| < 10~7.
Решение. В окрестности этой точки функция / (ж) являет-
является выпуклой, поскольку f" (ж) = 12 (ж — 2) -\—о > 0. Вычисле-
х
ния по методу Ньютона сводятся в следующую таблицу (за жо
принимается любой конец отрезка [2;3]):
0
1
2
3
4
5
3
2,6972477
2,5322701
2,4736906
2,4663735
2,4662656
-9,86-Ю-2
-0,7558859
-0,8488508
-0,8553636
-0,8554408
-0,8554408
3,67
0,985
0,208
0,0201
0,0003
5 • Ю-8 < Ю-7
Окончательно получаем ж* « 2,4662656, /* « —0,8554408.
§5.4] Безусловная минимизация функций многих переменных 207
§ 5.4. Безусловная минимизация функций многих
переменных
5.4.1. Метод градиентного спуска. Будем рассматри-
рассматривать выпуклые функции многих переменных /(ж), х =
= (х\ Х2 . . . хп) , определенные на выпуклых множествах X
из n-мерного евклидова пространства х ? X С Еп. Для того
чтобы функция одной переменной была выпуклой, необходимо
и достаточно, чтобы 2-ая производная на всем отрезке [а, Ь] была
неотрицательна.
Для функций многих переменных используется следующий
критерий выпуклости.
Если f (х) — дважды дифференцируемая на выпуклом мно-
множестве X С Еп функция и матрица ее частных производных
~ 2
второго порядка (матрица Гессе) ——^—^- , г, j = 1, п, положи-
\_OXiOXj J
тельно определена для всех ж^Х, то функция f (х) является
выпуклой на множестве точек X.
С использованием критерия Сильвестра формулировка этого
критерия упрощается и принимает следующий вид.
Если все диагональные миноры матрицы \f'x'iX (ж) , i,j =
= 1,п, положительны на множестве точек х ? X, то функ-
функция f (x) выпукла на этом множестве точек X.
Понятие выпуклости функций является исключительно важ-
важным, поскольку в численных методах оптимизации выпуклых
на множестве х ? X функций задача о нахождении локального
минимума на всем множестве точек х ? X совпадает с задачей
нахождения глобального минимума на этом множестве.
Пример 5.6. Выяснить, является ли функция /(#i, Ж2) —
= 2х\ + х\ + sin (а?1 + Ж2) выпуклой в двумерном простран-
пространстве Е2.
Решение. Составим матрицу вторых производных:
/"(х) =
f" fll
f" f»
JX2X1 JX2X2
4 — sin (x\ + X2) — sin (xi + X2)
— sin (x\ + X2) 2 — sin (xi + X2)
из которой видно, что диагональный минор первого порядка
Ai = 4 — sin(#i + Х2) ^ 3 > 0 на всей плоскости x\Ox<i, по-
поскольку |sin(#i + #2)! ^ 1- Минор второго порядка А2 = 8 —
208 Численные методы оптимизации [Гл. V
— 6 sin (х\ + х%) ^ 2 > 0 по той же причине. На основании кри-
критерия Сильвестра заключаем, что матрица вторых производ-
производных f" (ж) положительно определена на всей плоскости х\Ох2,
а следовательно, заданная функция является выпуклой на этом
множестве.
Пусть /(ж), х = (х\ . . .хп)Т', — выпуклая дифференциру-
дифференцируемая функция на всем множестве точек х ? X в евклидовом
пространстве Еп. Требуется найти точку ее минимума ж* и мини-
минимум /(ж*). Выбрав произвольное начальное приближение ж'0' ?
GXc En, построим следующую итерационную последователь-
последовательность:
х(к+1) = х(к) _ ак gmd /(ж(*))? jfe = о, 1, 2 . . . , E.1)
где величины а^ (параметрические шаги) выбираются доста-
достаточно малыми из условия
< /(я(*>), fc = 0,1,2... E.2)
Остановимся подробнее на векторном соотношении E.1). По-
Поскольку градиент функции многих переменных в ортонормиро-
ванном базисе ei, в2, . . . , еп определяется как вектор grad f(x) =
df{x) df{x) df(x)
= _ e\ -\—_ в2 + . . . H— en, то координатами вектора
OX\ OX2 OXn
градиента функции многих переменных являются частные про-
изводные , % = 1,п, этой функции по переменным ж^, г =
ОХ
= 1, п.
Тогда алгоритм E.1) в скалярной форме принимает вид
(k+1) {к) 9f
X\ } = X\ } -OLk
dx\
df '
T(*+l) _ r(*) _ „ 9f
дхп
§5.4] Безусловная минимизация функций многих переменных
209
Окончание процесса устанавливается по близости к нулю
, т.е. при выполнении неравенств
df (*<*>)
г = 1, п,
E.3)
где е — заданная точность, или
grad/(x<*>)| =
\
Е
1=1
(*<*>)
E.4)
Если условие E.2) не выполняется, то а& уменьшается вдвое
и алгоритм E.1) повторяется и т.д. При выполнении усло-
условий E.3) или E.4) полагают
ж* &ХМ и f(x*)&f(
Алгоритм E.1) для функции f(x,y) двух переменных приоб-
приобретает вид
х
д х
= „(*) _
ду
Пример 5.7. Методом градиентного спуска с точностью е =
= 0,05 минимизировать функцию / (х) = / (жх, х2) = х\ + 2х\ +
+ ехр {х\ )
Решение. Вначале необходимо проверить выпуклость
функции на множестве х Е X С Е2, для чего составляется мат-
матрица частных производных второго порядка:
/"(х) =
т. е.
х2)
ехр {х\
4 + ехр (xi + X2)
= 8 + 6 ехр (х\ + х%) > 0,
А2 > 0; Ai = 2 + ехр (xi + х2) > 0.
Таким образом, по критерию Сильвестра заданная функция вы-
выпукла на всей плоскости х\Ох2.
210 Численные методы оптимизации [Гл. V
Для решения задачи выберем начальное приближение х^ =
1-й шаг: к = 0; х\' = 0; х\ = 0; ао = 1; f lx\ ', ху2 ' \ =1,
Н ^ = L По формуле <5Л
A) (О ^ И) , A) @)
1 1 д
дх2
т. е. условие E.2) не выполнено, вследствие чего необходимо
уменьшить параметрический шаг «о- Уменьшаем его вдвое, при-
приняв «о = 0,5, и повторяем по E.1) вычисления с х\ = 0 и Жг> =
= 0:
х\ = 0 - 0,5 • 1 = -0,5; х\ = 0 - 0,5 • 1 = -0,5;
условие E.2) не выполнено. Уменьшаем «о вдвое: «о = 0,25:
df (х{°Л
(-1) (Г)\ U J \Х )
х\1> = х j - а0—^ '- = 0 - 0,25 • 1 = -0,25;
иХл
A) @) df (ж@))
Х2 = Х2 ~ «о—^ = 0 - 0,25 • 1 = -0,25;
/ (Ж11}> 41]) = / (-0,25; -0,25) = 0,794 < / D°\ 4°') = 1;
= -0,5 + ехр (-0,25 - 0,25) = 0,106;
+ ехр [x\L) + хB
= 4 (-0,25) + ехр (x(i] + х^Л = -0,393;
§5.4] Безусловная минимизация функций многих переменных 211
grad / (жA)) I = у/0Д062 + (-0,393J = 0,407 > е = 0,05.
2-й шаг: к = 1; х^ = -0,25; х^] = -0,25; ах = 0,25;
df
42) =
df
- ах
= 0,774 < /
Сохраняем значение а\, приняв «2 = 0,25:
f ^ 2 > = 2х
8f
{2)
= -0,25 - 0,25 • 0,106 = -0,2765;
= -0,25 - 0,25 • (-0,393) = -0,1518;
= 0,794.
ехр (ЖР + 42)) = 0,0983;
ехр D2) + 42)) = 0,0451;
grad / (хBА I = ^0,09832 + 0,04512 = 0,108 > е = 0,05.
3-й шаг: к = 2; ж^ = -0,2765; ж22) = -0,1518; а2 = 0,25;
х\ = х\ - а2-
= -0,2765 - 0,25 • 0,0983 = -0,301;
df (х{
43) = 42) - «2—^ = -0,1518 - 0,25 • 0,0451 = -0,163;
ОХ
дх2
= 0,772 < 0,774;
\
|
= д/о,О2622 + (-0,023J = 0,03486
<
Точность достигнута, следовательно, ж* = (ж^; х\)
(-0,301; -0,163); /* « 0,772.
212 Численные методы оптимизации [Гл. V
5.4.2. Метод наискорейшего спуска. Метод наискорей-
наискорейшего спуска отличается от метода градиентного спуска E.1)
оптимальным способом определения параметрического шага а^,
который находится из условия
фк(<*к) = min^fc(a), E.5)
где
М") = f(x(k) " «grad f(x^)). E.6)
Здесь
{k)
После минимизации функции ф(а) одной переменной а най-
найденное значение а* принимается за скц., после чего реализуется
метод градиентного спуска:
= х(к) _ ак grad /(Ж(Л))? А; = 0,1, 2, . . .
Окончание итерационного процесса устанавливается при вы-
выполнении условия E.3) или E.4).
Таким образом, на каждом шаге метода наискорейшего спус-
спуска решается задача минимизации E.5), E.6) функции ф(а) одной
переменной а.
При таком выборе а& достигается максимально возможное
уменьшение функции f(x).
Можно показать, что в методе наискорейшего спуска
grad f(x^) и grad/(#(fe+1)) ортогональны, т.е. скалярные про-
произведения (grad/(#(*)), grad/(aj(fe+1))) = 0.
Пример 5.8. Методом наискорейшего спуска решить задачу
примера 5.7.
Решение.
1-й шаг: к = 0.
Выберем начальное приближение
§5.4] Безусловная минимизация функций многих переменных 213
Тогда
df
df
<ф0 (а) = f @ - а • 1, 0 - а • 1) = / (-а, -а) = За2 + ехр Bа) .
Для минимизации ф$ (а) используем метод перебора, для чего
составляется сеточная функция для функции ф$ (а):
а
^о(а)
0,18
0,7949
0,20
0,7903
0,22
0,7892
0,24
0,7916
0,26
0,7973
Отсюда ясно, что а = «о = 0,22 и
х
х
A)
1
A)
О
О
-а0
О
О
-0,22
-0,22
-0,22
grad /
\
|
= \/@,204J + (-0,236J = 0,312 > e.
2-й шаг: k = 1; a?W = (x^\ x?A = (-0,22; -0,22);
df
= 0,204;
Of
Ox-,
= -0,236;
<фх (a) = / (-0,22 - 0,204a; -0,22 + 0,236a) =
= (-0,22-0,204aJ +
+ 2 (-0,22 + 0,236aJ + exp (-0,44 + 0,032a) =
= 0,1452 - 0,1179a + 0,153a2 + exp (-0,44 + 0,032a)
Минимизируем ф\ (a):
214
Численные методы оптимизации
[Гл. V
а
0,28
0,774
0,30
0,77384
0,32
0,7738
0,34
0,77387
0,36
0,7741
т. е. а = а.\ = 0,32;
х
B)
1
Л2)
-0,22
-0,22
-0,32
0,204
-0,236
-0,2853
-0,1445
grad / (V2)) | =
\
дхл
дхо
3-й шаг: к = 2;
df
= 0,08;
= ^0,082 + 0,072642 = 0,1081 > е.
{^\ х^]\ = (-0,2853; -0,1445);
df (xW)
^^ = 0,07264;
С/Ж2
a) = (-0,2853 - 0,08aJ +
+ 2 (-0,1445 - 0,07264aJ + exp (-0,43 - 0,1526a)
Минимизируем fa («):
a
^2 (a)
0,20
0,77273
0,22
0,77241
0,24
0,77240
0,26
0,77241
0,28
0,77244
т.е. a = ot2 = 0,24. Тогда
x
x
C)
l
C)
X
X
B)
1
B)
df (*
V 8X2 /
-0,2853
-0,1445
-0,24
0,08
0,07264
-0,3045
-0,1619
§5.4] Безусловная минимизация функций многих переменных 215
grad /
\
+
дх<2
= д/(-0,0183J + (-0,0203J = 0,0273 < е = 0,05.
Заданная точность достигнута. Следовательно,
ж* « жC) = (-0,305; -0,162); /* и / (жC)) = 0,772.
Можно показать, что если f (х) — квадратичная функция,
/ (х) = -(Qx,x) + (г, ж), где Q — симметрическая матрица
коэффициентов при квадратичных слагаемых (Q = QT), x =
= (х\ Х2 . . . хп) , г = (ri, Г2, ... , гп) — коэффициенты при
линейных слагаемых, (х,у) — скалярное произведение, то вели-
величина параметрического шага а& может быть найдена в явном
виде:
(grad / (ж «), grad/(ж «))
= -± V-Л / L > E-7)
(Q grad /(^(/e)), grad / ((/е)))
причем grad / (ж^^) = фж^ + г.
5.4.3. Метод сопрялсенных направлений. Метод со-
пряженных направлений состоит в построении последовательно-
последовательности
= а;(*)-аЛр(*), к = 0,1,2,... , E.8)
где а/» выбирается так же, как и в методе наискорейшего спуска:
), фк(а) = /(ж(/г)
a>0
а направление спуска pW — с помощью выраж:ения
ft = 1,2,...; E.9)
@)); E.10)
216
Численные методы оптимизации
[Гл. V
grad/(;r
Е
г=1
df(x
д
ЕопхУ '
dxi
Критерием останова является выражение E.3) или E.4), т.е.
2 *
E.11)
Таким образом, метод сопряженных направлений отличает-
отличается от метода наискорейшего спуска только выбором направ-
направления уменьшения функции на каждом шаге (—р' ' вместо
-grad/(s(*))).
Отметим, что pW в E.9) определяется не только антигра-
антиградиентом — grad/(ж^)), но и направлением спуска —р(к~г) на
предыдущем шаге. Это позволяет более полно, чем в методах
градиентного и наискорейшего спуска, учитывать особенности
функции /(ж) при построении итерационного процесса E.8). Для
квадратичных функций в Еп требуется не больше п итераций
метода сопряженных направлений.
Пример 5.9. Методом сопряженных направлений найти
точки минимума ж* функции / (х) = х\ + 2х\ + х\ • Х2 — 7х\ —
— 7x2-
Решение. Поскольку f (х) — квадратичная функция, за-
заданная в i?2, то точка минимума ж* может быть найдена после
двух шагов метода сопряженных направлений.
Шаг 1: к = 0. Выбрав начальное приближение х^ = @; 0),
по формулам E.9)—E.11) находим
р(°) = grad f(x^) = BЯ1 + х2 - 7; 4ж2 + хх - 7)|ж@) =
= (-7; -7); ф0 {а) = 98 Bа2 - а) .
(ао) = 0 минимума фо (а) получим а$ = 0,25.
Из условия
Отсюда
-0,25
§5.4] Безусловная минимизация функций многих переменных 217
Шаг 2: к = 1;
g«d/(*<»)-(-!;?),
откуда с учетом E.11) имеем
-7/4 \ 1 / -7 \ / -35/16
J 16 1 -7 J
Поэтому ф\ (а) = — (-а2 - 4а - 392) и а\ = 4/7.
Окончательно:
A (р?Л = (У*\ 4/-35/1б
U'V ""' Uv " WV "'
Итак, ж* = (x$, x*2) = C; 1); /* = / (ж*) = -14.
УПРАЖНЕНИЯ.
5.1. Показать, что следующие функции на отрезке [а, Ь] яв-
являются унимодальными:
а) / (ж) = х2 - Зж + х • In ж, же [1; 2] ;
б) / (ж) = In A + ж2) - sin ж, ж G [0; тг/4] ;
в) / (ж) = -ж2 — sin ж, ж е [0; 1] .
5.2. Методом перебора с точностью г = 0,05 найти точку
минимума ж* функции / (ж) на отрезке [а, Ь] и минимум /*:
а) / (ж) = ж2 - 2ж + е"ж, ж е [1; 1,5];
б) / (ж) = tg ж — 2 sin ж, ж ? [0; тг/4] ;
218 Численные методы оптимизации [Гл. V
в) / (ж) = ж3 - 3 sin ж, ж е [0,5; 1,0];
г) / (ж) = -ж3 - 5ж + ж • In ж, ж Е [1,5; 2];
д) / (ж) = \/l + ^2 + е~2ж, ж Е [0; 1] .
5.3. Методом деления отрезка пополам с точностью е найти
точку минимума ж* функции / (ж) на отрезке ж Е [а, 6] и мини-
минимум /*:
а) / (ж) = ж • sin ж + 2 cos ж, ж Е [—5; —4] , е = 0,02;
б) / (ж) = Юж • In ж - —, ж Е [0,5; 1] , е = 0,05;
о
в) / (ж) = Зж4 - Юж3 + 21ж2 + 12ж, ж € [0; 0,5] , е = 0,01;
г) / (ж) = ех - ^ж3 + 2ж, же [-1,5; -1] , е = 0,01;
д) / (ж) = ж6 + Зж2 + 6ж - 1, же [-1; 0] , е = 0,1.
5.4. Методом золотого сечения с точностью е найти точку
минимума ж* функции / (ж) на отрезке ж е [а, Ь] и минимум /*:
а) / (ж) = ж2 + Зж (In ж - 1), же [0,5; 1] , е = 0,05;
б) / (ж) = Юж • In ж - —, ж Е [0,5; 1] , е = 0,05;
о
в) / (ж) = (ж + IL - 2ж2, ж е [-3; -2] , е = 0,025;
г) / (ж) = ж4 + 2ж2 + 4ж + 1, же [-1; 0] , е = 0,1;
§5.4] Безусловная минимизация функций многих переменных 219
д) / (х) = ж5 - 5ж3 + Юж2 - 5ж, ж е [-3; -2] , е = ОД.
5.5. Методом Ньютона на всей числовой оси минимизировать
функции / (ж) с точностью ? = 10~4:
а) / (ж) = 2х2 + х + cos2 ж;
б) f(x) = ex + e-2x + 2x;
в) / (ж) = ж2 + ж + sin ж;
г) /(ж) = ж2 -ж + е"ж;
д) /(ж) = ж2 + е~ж.
5.6. Убедиться в выпуклости следующих функций / (ж) на
всем пространстве Е2:
а) / (жь ж2) = у 1 + ж| + х\ ;
б) / (Ж1, Х2) = х\ + х\ — COS -
2 '
в) / (жь ж2, ж3) = ехр (ж2 + х\ + ж2) ;
г) / (жх, Ж2, жз) = 5ж2 + 5ж^ + 4ж2
5.7. Методом градиентного спуска с точностью е найти точку
минимума ж* и минимум /* на отрезке ж ? [а, 6]:
а) / (ж) = 2x1 + Х1 + xix2 + xi + ж2, ж@) = @; 0)
для ао = 0,265; ао = 0,5;
220 Численные методы оптимизации [Гл. V
б) / (ж) = х\ + х\ + х\ + Ж1Ж3 + ж2ж3, ж@) = @; 1; 0)
для ао = 0,1; ао = 0, 638; ао = 10.
в) / (х) = ехр (xj) + (ял + ж2 + ж3J , ж@) = A; 1; 1);
а0 = 0,1; а0 = 0,2127.
5.8. Методом наискорейшего спуска с точностью е = 0,05
найти точку минимума ж* и минимум /*:
а) / (х) = 2х\ + xl + Х1х2, ж@) = @; 0);
б) / (х) = х\ + х\ + х\ + хгх3 + х2х3, ж@) = @; 1; 0);
в) / (х) = exp (xj) + (ял + х2 + х3J , ж@) = @; 1; 0);
г) / (х) = х\ + 4ж1Ж2 + 17ж^ + 5ж2, ж@) = @; 1; 0) .
5.9. Методом сопряженных направлений с точностью е
0,001 найти точку минимума ж* и минимум /*:
а) / (х) = х\ + 5ж2 + ехр (х\ +
б) / (ж) = х\ + 3^2 + cos (#i +
в) / (х) = х\ + exp (#i + ж|) + 4ж1 +
г) / (ж) = ж^ + 2ж^ + ж^Ж2 + 2ж1 +
д) / (ж) = ехр {х\ + х\) + In D + х\ +
е) / (ж) = х\ + ж2 - 5жз + ехр {х\ + 2ж^
Часть II
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ
ЗАДАЧ ДЛЯ УРАВНЕНИЙ
МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Наиболее распространенными численными методами реше-
решения задач математической физики в настоящее время являются
следующие: метод конечных разностей (МКР), метод конечных
элементов (МКЭ), метод граничных элементов (МГЭ). Ниже
наиболее подробно рассматриваются методы конечных разностей
и конечных элементов.
ГЛАВА VI
МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ
Программа
Постановка задач математической физики для уравнений различ-
различных типов. Основные определения при замене дифференциальных
операторов конечно-разностными: сетка, сеточная функция, шаблон,
временной слой, явная и неявная конечно-разностные схемы. Конечно-
разностные схемы для уравнений математической физики различных
типов. Основные понятия, связанные с конечно-разностной аппрокси-
аппроксимацией дифференциальных задач: аппроксимация и порядок аппрок-
аппроксимации, устойчивость, сходимость и порядок сходимости, консерва-
консервативность и корректность. Теорема эквивалентности. Анализ порядка
аппроксимации. Исследование устойчивости. Метод гармонического
анализа, принцип максимума, спектральный метод, энергетический
метод для явных и неявных схем. Метод конечных разностей ре-
решения параболических задач, однородные и консервативные схемы.
Неявно-явные схемы, схема Кранка—Николсона. Методы прямых. Me-
222 Метод конечных разностей [ Гл. VI
тод конечных разностей решения эллиптических задач, явные, неяв-
неявные, неявно-явные схемы. Конечно-разностная аппроксимация крае-
краевых условий, содержащих производные. Метод установления и его
обоснование для эллиптических задач. Разностно-итерационный метод
Либмана.
§6.1. Постановка задач математической физики
Чтобы поставить задачу математической физики, необходимо
вывести дифференциальное уравнение в частных производных,
описывающее рассматриваемый физический процесс, а также на-
начальные и краевые условия. При этом начальные условия ставят-
ставятся для уравнений, содержащих частные производные по времени
(уравнения описывают нестационарные физические процессы).
Краевые (граничные) условия ставятся для уравнений, описыва-
описывающих физические процессы в ограниченных областях.
Задачи математической физики, содержащие начальные
и краевые условия, называются начально-краевымщ задачи, со-
содержащие только граничные условия — краевыми, а задачи,
содержащие только начальные условия (в бесконечных обла-
областях) — задачами Коши.
Известно, что количество условий и вид начальных и крае-
краевых условий зависят от типов уравнений математической физи-
физики, среди которых различают параболический, гиперболический
и эллиптический типы, количества границ, количества разрывов
в граничных условиях, порядка дифференциальных уравнений.
Вывод основных уравнений математической физики, началь-
начальных и краевых условий к ним дается в курсе «Уравнения ма-
математической физики». Здесь же ограничимся математической
формулировкой типовых задач математической физики.
6.1.1. Постановка задач для уравнений параболиче-
параболического типа. Классическим примером уравнения параболиче-
параболического типа является уравнение теплопроводности (диффузии). В
одномерном по пространству случае однородное (без источников
энергии) уравнение теплопроводности имеет вид
5 = а2Й' 0<х<1, t>0. F.1)
ut ox
§6.1] Постановка задач математической физики 223
Если на границах х =0 и х = / заданы значения искомой
функции и(х, t) в виде
u@, *) = <pi(t), х = 0, * > 0, F.2)
u(l,t) = (p2(t), x = l, О 0, F.3)
т. е. граничные условия первого рода, и, кроме того, заданы на-
начальные условия
и(х, 0) = ф(х), 0 ^ х ^ /, 4 = 0, F.4)
то задачу F.1)—F.4) называют первой начально-краевой задачей
для уравнения теплопроводности F.1).
В терминах теории теплообмена u(x,t) — распределение
температуры в пространственно-временной области ft x T =
= {0 ^ х ^ /; 0^?^ Т}, а2 — коэффициент температуропро-
температуропроводности, а F.2), F.3) с помощью функций (fi(t), (f2(t) задают
температуру на границах х = 0 и х = I.
Если на границах х = 0 и х = / заданы значения производных
искомой функции по пространственной переменной:
х = 0, О 0, F.5)
^ = (p2(t), x = I, t > 0, F.6)
т.е. граничные условия второго рода, то задачу F.1), F.5), F.6),
F.4) называют второй начально-краевой задачей для уравнения
теплопроводности F.1). В терминах теории теплообмена на гра-
границах в этом случае заданы тепловые потоки.
Если на границах заданы линейные комбинации искомой
функции и ее производной по пространственной переменной:
du@,t)
дх
du{l,t)
дх
т.е. граничные условия третьего рода, то задачу F.1), F.7), F.8),
F.4) называют третьей начально-краевой задачей для уравнения
теплопроводности F.1). В терминах теории теплообмена гранич-
ж = 0, * > 0, F.7)
/3u(l,t) = <p2(t), x = l, t > 0, F.8)
224 Метод конечных разностей [ Гл. VI
ные условия F.7), F.8) задают теплообмен между газообразной
или жидкой средой с известными температурами (pi(t)/a на
границе х = 0 и <^2 (?)//? на границе х = I и границами расчетной
области с неизвестными температурами г^@, ?), u(l, t). Коэффи-
Коэффициенты а, /3 — известные коэффициенты теплообмена между
газообразной или жидкой средой и соответствующей границей.
Для пространственных задач теплопроводности в области
ft = ft + Г первая начально-краевая задача имеет вид
Г ди
'у'г)^'*>0; ( }
= <p(M,t), M(x,y,z)eT, t>0; F.10)
П t>0. F.11)
Аналогично ставится вторая и третья начально-краевые за-
задачи для пространственного уравнения F.9).
На практике часто ставятся начально-краевые задачи теп-
теплопроводности со смешанными краевыми условиями, когда на
границах задаются граничные условия различных родов.
6.1.2. Постановка задач для уравнений гиперболиче-
гиперболического типа. Классическим примером уравнения гиперболиче-
гиперболического типа является волновое уравнение, которое в области 0 <
< х < /, t > О имеет вид
^ = а2^5 0<х<1, t = 0.
Здесь u(x,t) — малые продольные или поперечные переме-
перемещения (колебания) стержня, а — скорость звука в материале, из
которого изготовлен стержень.
Если концы стержня движутся по заданным законам, то есть
на концах заданы перемещения (или значения искомой функ-
функции), то первая начально-краевая задача для волнового уравнения
имеет вид (причем, если концы стержня жестко закреплены, то
§6.1]
Постановка задач математической физики
225
д2и
at
д
ax
= 0,
t>0;
0;
0;
t = 0;
i = 0.
F.12)
F.13)
F.14)
F.15)
F.16)
u(l, t) = ^2(^M x = I, 1
u(x,0) = ф\{х), 0 ^ x ^
Как видно, в задачах для волнового уравнения, кроме на-
начального распределения искомой функции, задается еще распре-
распределение начальной скорости перемещения.
Если на концах стержня заданы значения силы, которая по
закону Гука пропорциональна значениям производной переме-
перемещения по пространственной переменной (т. е. на концах заданы
значения первых производных по переменной ж), то ставится
вторая начально-краевая задача для волнового уравнения:
д2и _ 2д2и
du{0,t) _
дх ~
du{l,t) _
дх ~
у(Т Г)) —
и{х, и; —
д и(х, 0)
Yt =
0 < х < Z, t > 0;
ж = 0, t > 0;
х = Z, * > 0;
0 ^ х ^ Z, t = 0;
В условиях, когда концы стержня свободны, функции (fi(t) =
Наконец, в условиях, когда концы закреплены упруго, т. е. на
концевые заделки действуют силы, пропорциональные переме-
перемещениям, ставится третья начально-краевая задача для волнового
уравнения:
я2 я2
9 4' 0 < ж < /, t > 0;
dt2
du{0,t)
дх
= а
0яа
x = 0, * > 0;
8 В.Ф. Формалев, Д.Л. Ревизников
226 Метод конечных разностей [ Гл. VI
^M + /3«(Z,t) = y>2(t), ж = /, t>0;
(У X
и(х, 0) = ipi(x), 0 < х < /, < = 0;
Аналогично ставятся двумерные и трехмерные начально-
краевые задачи для двумерного и трехмерного волнового урав-
уравнения.
Необходимо отметить, что волновое уравнение легко транс-
трансформируется в систему уравнений акустики, являющихся про-
простейшей линейной моделью газодинамических течений.
Действительно, введем следующие обозначения:
?=Р, F.17)
(«.«)
Продифференцируем F.17) по переменной ?, а F.18) — по пе-
переменной ж, результат подставим в волновое уравнение, получим
Продифференцируем затем F.17) по ж, а F.18) — по t и,
полагая, что смешанные производные от u(x,t) по переменным
ж и t не зависят от порядка дифференцирования, получим
^7 = 1Г-
at ox
Здесь р, v — возмущения (слабые колебания) давления и ско-
скорости в акустической волне, а систему F.19), F.20) называют
уравнениями акустики. Поскольку F.19), F.20) — линейное при-
приближение уравнений газовой динамки, они используются для
исследования устойчивости численных методов решения урав-
уравнений газовой динамики.
6.1.3. Постановка задач для уравнений эллиптиче-
эллиптического типа. Классическим примером уравнения эллиптическо-
эллиптического типа является уравнение Пуассона
§6.1] Постановка задач математической физики 227
д х2 д у2
или уравнение Лапласа при /(ж, ?/) = 0.
Здесь функция и(х,у) может иметь различный физический
смысл, например: стационарное, независящее от времени, распре-
распределение температуры, скорость потенциального (безвихревого)
течения идеальной (без трения и теплопроводности) жидкости,
распределение напряженностей электрического и магнитного по-
полей, потенциала в силовом поле тяготения и т. п.
Если на границе Г расчетной области ft = ft + Г задана ис-
искомая функция, то соответствующая первая краевая задача для
уравнения Лапласа или Пуассона называется задачей Дирихле:
—о "^ 2 = /(ж> у)-> (ж' у) ^ ^> F.21)
Т* A11
.(ж, у)\г = ip(x, у), (ж, у) е Г. F.22)
Если на границе Г задается нормальная производная искомой
функции, то соответствующая вторая краевая задача называется
задачей Неймана для уравнения Лапласа или Пуассона:
тг4 + ^4 = /(ж> y)i (ж> у) ? п; F.23)
дх ду v y
ди(х,у)
дп
При этом п — направление внешней к границе Г нормали.
Более приемлемой является координатная форма краевого
условия F.24):
— cos(n,z) + — cos(n, j) = <р(х,у),
ох о у
где cos(n, г), cos(n, j) — направляющие косинусы внешнего век-
вектора единичной нормали к границе Г, i и j — орты базисных
векторов.
Наконец третья краевая задача для уравнения Пуассона (Ла-
(Лапласа) имеет вид
228 Метод конечных разностей [ Гл. VI
' д2и д2и
дх2 ду2
ди(х,у)
дп
+ аи\г = (р(х,у), (х,у) е Г.
г
Замечание: следует отметить, что в вышеперечисленных по-
постановках число начальных условий равно порядку дифференци-
дифференциального уравнения по времени, а старший порядок производной
по времени в начальных условиях на единицу меньше порядка
дифференциального уравнения по времени.
Старший порядок производной по пространственной пере-
переменной в краевых условиях равен порядку дифференциального
уравнения по пространственной переменной минус единица. Ко-
Количество краевых условий для многомерных задач не ограни-
ограничено, так как на разных участках границы могут быть заданы
граничные условия различных родов.
В одномерных задачах с одной пространственной переменной
количество граничных условий точно равно порядку дифферен-
дифференциального уравнения по пространственной переменной.
§ 6.2. Основные определения и конечно-разностные
схемы для различных задач математической
физики
6.2.1. Основные определения. Основные определения,
связанные с методом конечных разностей, рассмотрим на при-
примере конечно-разностного решения первой начально-краевой за-
задачи для уравнения теплопроводности F.1)-F.4). В этом же
параграфе будут рассмотрены простейшие конечно-разностные
схемы для задач математической физики, содержащих диффе-
дифференциальные уравнения различных типов.
Нанесем на пространственно-временную область 0 ^ х ^ /,
О ^ t ^ Т конечно-разностную сетку оон,т:
Uh,r = {xj = jh, j = 0,N; tk = кт, к = О, К}, F.25)
с пространственным шагом h = I /N и шагом по времени т =
= Т/К (рис. 6.1).
Введем два временных слоя: нижний t = кт, на котором рас-
распределение искомой функции u(xj,tk), j = 0, Л/", известно (при
§6.2] Определения и схемы для задач математической физики 229
к = О распределение определяется начальным условием F.4)
u(xj, t°) = tl>(xj)), и верхний временной слой tk+1 = (к + 1)т, на
котором распределение иско-
искомой функции u(xj,tk+1), j =
= О, Л/", подлежит определе-
определению.
Сеточной функцией зада-
ни F.1)-F.4) (обозначение ик-)
назовем однозначное отобра-
жение целых аргументов j,
к в значения функции ик- =
= u(xj, tk).
На введенной сетке F.25)
введем сеточные функции ик-^
T
y-i,
k+l
h
k+l
j+l
к
k+l
h
к
h
k+l
j+l
к
к
/ X
первая ИЗ которых ИЗ- Рис. 6.1. Конечно-разностная сетка
вестна, вторая — подлежит
определению. Для ее определения в задаче F.1)-F.4) заме-
заменим (аппроксимируем) дифференциальные операторы отноше-
отношением конечных разностей (см. §3.4 «Численное дифференциро-
дифференцирование»), получим
д и
~dt
02u
— U A
dx2
n
F.26)
F.27)
Подставляя F.26), F.27) в задачу F.1)-F.4), получим явную
конечно-разностную схему для этой задачи в форме
Ц*+1-Ц* _ ^2<1-2ц?+<1 о. ПЛ. -
F.28)
^п =
В каждом уравнении этой задачи все значения сеточной функции
известны, за исключением одного, и- , которое может быть
230
Метод конечных разностей
[Гл. VI
определено явно из соотношений F.28). В соотношения F.28)
краевые условия входят при значениях j = lnj = N — l,a на-
начальное условие — при к = 0.
Если в F.27) дифференциальный оператор по пространствен-
пространственной переменной аппроксимировать отношением конечных разно-
разностей на верхнем временном слое:
д2и
дх2
/с+1
J?
F.29)
то после подстановки F.26), F.29) в задачу F.1)-F.4) получим
неявную конечно-разностную схему для этой задачи:
j = 1, TV — 1, к = 0, К -1;
F.30)
= 0, K-l-
Теперь сеточную функцию и + на верхнем временном слое
можно получить из решения СЛАУ F.30) с трехдиагональной
матрицей. Эта СЛАУ в форме, пригодной для использования
метода прогонки, имеет вид
= 0;
cn-1 = 0;
,/e+l
л — о /V — 9
j — z, iv z,
j = N -
где uj = a, j = 2, TV - 1; 6j = -A + 2a), j = 1, TV - 1; Cj = a,
j = 1,7V-2; d,- = -uj, j = 2, TV-2; ^ = -(^ +
a2r
Шаблоном конечно-разностной схемы называют ее геометри-
геометрическую интерпретацию на конечно-разностной сетке.
На рис. 6.2 приведены шаблоны для явной F.28) и неявной
F.30) конечно-разностных схем при аппроксимации задачи F.1)-
F.4).
§6.2] Определения и схемы для задач математической физики 231
Рис. 6.2. Шаблоны явной (а) и неявной F") конечно-разностных схем для
уравнения теплопроводности
6.2.2. Конечно-разностная аппроксимация задач для
уравнений гиперболического типа. Рассмотрим первую
начально-краевую задачу для волнового уравнения F.12)—F.16).
На пространственно-временной сетке F.25) будем аппроксими-
аппроксимировать дифференциальное уравнение F.12) одной из следующих
конечно-разностных схем:
= l,N-l; Л = 1,2,... F.31)
с шаблоном на рис. 6.3 а и
к+\
k-i
'Jfc+i
k-i
j y-i j i+i
а б
Рис. 6.3. Шаблоны конечно-разностных схем для волнового уравнения
4-
= a2
//с+1
-1 + О (г + h2) ,
с шаблоном на рис. 6.3 б\
i = l,7V-l; Л = 1,2,... F.32)
232 Метод конечных разностей [Гл. VI
При этом схема F.31) является явной. С ее помощью решение
?iy+1, j = 1, N — I, fc = 1, 2, . . . , определяется сразу, поскольку
значения сеточных функций uk-~l, г^ на нижних временных
слоях должны быть известны. В соответствии с шаблоном для
этой схемы порядок аппроксимации равен двум как по про-
пространственной, так и по временной переменной (достаточно раз-
разложить на точном решении нецентральные значения сеточной
функции и-~1,и-^1, Uj-i, uIj+i B РЯД Тейлора в окрестности
центрального узла (xj,t) до производных четвертого порядка
включительно соответственно по переменным tux).
Схема F.32) является неявной схемой, ее можно свести
к СЛАУ с трехдиагональной матрицей, реализуемой методом
прогонки. В обеих схемах необходимо знать значения и-~ , и-^
j = 1, N — 1, fc = 1, 2, . . . , на нижних временных слоях. Для к =
= 1 это делается следующим образом:
u5 = V>i(^), j = O^V, F.33)
где ф\(х) — функция из начального условия F.15).
Для определения и1- можно воспользоваться простейшей ап-
аппроксимацией второго начального условия F.16):
т
Отсюда для искомых значений и1- получаем следующее вы-
выражение:
Недостатком такого подхода является первый порядок ап-
аппроксимации второго начального условия. Для повышения по-
порядка аппроксимации воспользуемся следующей процедурой.
Разложим и1- в ряд Тейлора на точном решении по времени
в окрестности t = 0:
1 / ^ . \ п . ди
Uj-u{Xj^ + T)-u3 , m
о и
Т+ —
3
dt
3
2
Для определения второй производной в полученном выраже-
выражении воспользуемся исходным дифференциальным уравнением
д2и
dt2
0
о О U
= а
дх
о
§6.2] Определения и схемы для задач математической физики 233
В результате получаем искомое значение сеточной функции
и1- со вторым порядком точности:
и) =
F.34)
Для определения и2- из схемы F.31) или F.32) достаточно
F.33), F.34) подставить в соответствующие схемы. При к = 2
значения vh, и2- сеточной функции известны, a v$ определяются
из схемы F.31) или F.32) и т. д.
Краевые условия F.13) и F.14) в схемах F.31), F.32) исполь-
используются автоматически соответственно при j = lnj = N — 1, так
же как в схемах F.28), F.30) для задачи теплопроводности.
6.2.3. Конечно-разностная аппроксимация задач для
уравнений эллиптического типа. Рассмотрим краевую
задачу для уравнений Лапласа или Пуас-
Пуассона F.21), F.22) в прямоугольнике х ?
? [0, /i], у ? [0, /2], на который наложим сет-
КУ о
Uj
F.35)
^ тт
Рис. 6.4. Центрально-
симметричный шаб-
Ha этой сетке аппроксимируем задачу лон для уравнения
F.21), F.22) с помощью отношения конеч- Лапласа
ных разностей по следующей схеме (вводит-
(вводится сеточная функция щ^ г = 0, Л/i, j = 0, N2)'
'
Х п /,2 , h2\
г U {ti! + ti2) —
-1, j =
F.36)
которая на шаблоне F.4) имеет второй порядок по переменным
х и ?/, поскольку шаблон центрально симметричен.
СЛАУ F.36) имеет пятидиагональный вид. Решать ее мож-
можно различными методами линейной алгебры, например методом
Гаусса, итерационными методами, методом матричной прогонки
и т. п.
234
Метод конечных разностей
[Гл. VI
Рассмотрим разностно-итерационный метод Либмана числен-
численного решения задачи Дирихле F.21), F.22). Для простоты изло-
изложения этого метода примем hi = h<i = h, тогда из схемы F.36)
получим (п — номер итерации)
(п+1) 1
(п)
(п)
(
fij = f(xi,yj), i = l,iVi-l, j = 1, iV2 - 1. F.37)
На каждой координатной линии (например, yj = const, j =
= 1, N2 — 1) с помощью линейной интерполяции (см. рис. 6.5)
u2j
lh
Рис. 6.5. К разностно-итерационному методу Либмана
граничных значений (р(х,у) определим щ ¦ на нулевой итера-
итерации, подставив которые в F.37), получим распределение u\j на
первой итерации:
@)
г =
- 1, j = 1,7V2 - 1.
Это распределение г^ • снова подставляется в F.37), полу-
B)
чаем распределение щ • и т. д. Процесс Либмана прекращается,
когда
гг"^х' - ик"П\ ^ ?, \\иу J\\ = max
где е — наперед заданная точность.
(n)
§6.3] Основные понятия конечно-разностной аппроксимации задач 235
Замечание. Метод простых итераций для решения СЛАУ,
возникающих при аппроксимации уравнения Пуассона (Лапла-
(Лапласа), отличается довольно медленной сходимостью. Этот недо-
недостаток может стать существенным при использовании мелких
сеток, когда число уравнений в системе становится большим.
С более эффективными методами решения таких СЛАУ можно
познакомиться, например, в [2].
§ 6.3. Основные понятия, связанные
с конечно-разностной аппроксимацией
дифференциальных задач
К основным понятиям, связанным с методом конечных раз-
разностей, относятся следующие: аппроксимация, порядок аппрок-
аппроксимации, устойчивость, сходимость, порядок сходимости (или
точность), консервативность и корректность. Определим каждое
из этих понятий.
6.3.1. Аппроксимация и порядок аппроксимации.
Запишем дифференциальную задачу в операторной форме
где L — один из дифференциальных операторов:
L =
— а2—о ~~ диффузионный;
ot ох
д2 2 д2
—2 — а —2 — волновощ
оъ ох
д2 д2
—2 H о ~~ лапласиан;
ох ду
U(x,y) — искомая функция, удовлетворяющая дифференциаль-
дифференциальной задаче; / — входные данные (т. е. начальные и краевые
условия, правые части и т.п.). Операторная форма (LU)h = fh
описывает дифференциальную задачу в узлах сетки, а оператор-
операторная форма LfrUh = fh описывает конечно-разностную схему на
точном решении [/(ж, t) , т. е. в конечно-разностной схеме вместо
значений сеточной функции подставлены точные (неизвестные)
значения искомой функции. Для перечисленных дифференци-
дифференциальных операторов L конечно-разностные операторы L^ имеют
вид
236 Метод конечных разностей [Гл. VI
д 9д2
L=
— — о2—2- — диффузионный;
2
А2 ,Д
—^ — а —~ — волновой;
т
h
А А
—^ -\ 2" — лапласиан.
Наконец, операторная форма конечно-разностной схемы (на-
(например, схемы F.28) или F.30)) имеет вид
Lhuh = fh. F.38)
Введем норму сеточной функции с помощью выражения
= max
j J
nfc
к = 0,1,2,... F.39)
Определение. Конечно-разностная схема F.38) аппрокси-
аппроксимирует дифференциальную задачу на точном решении, если
какая-либо норма разности (не обязательно в виде F.39))
\\(LU)h — LfrUhW стремится к нулю при г, h —> 0:
\\(LU)h-LhUh\\-j-^0. F.40)
Определение. Конечно-разностная схема F.38) аппрокси-
аппроксимирует дифференциальную задачу на точном решении с поряд-
порядком р по времени и порядком q no пространственной переменной,
если какая-либо норма разности \\(LU)h — L^f/^Ц удовлетворяет
равенству
\\(LU)LU\\ O{* h<) F.41)
Таким образом, если конечно-разностная схема аппроксими-
аппроксимирует дифференциальную задачу, то речь идет о близости диффе-
дифференциального и конечно-разностного операторов в узлах сетки.
6.3.2. Устойчивость. Пусть в конечно-разностной схеме
F.38) входные данные Д получили возмущения и приняли зна-
значения Д. Тогда сеточная функция и^ также получит возмуще-
возмущение и примет значение и^.
Определение. Конечно-разностная схема F.38) устойчива
по входным данным, если найдется такая ограниченная кон-
константа К > 0, не зависящая от сеточных характеристик г,
§6.3] Основные понятия конечно-разностной аппроксимации задач 237
h и входных данных Д, что выполняется неравенство
К-йлКА-Ц/л-лЦ. F.42)
Таким образом, понятие устойчивости интерпретируется сле-
следующим образом: конечно-разностная схема устойчива, если для
малых возмущений входных данных (начально-краевых условий
и правых частей) конечно-разносная схема F.38) обеспечивает
малые возмущения сеточной функции и^, т.е. решение с помо-
помощью конечно-разностной схемы находится под контролем вход-
входных данных.
Если во входные данные Д входят только начальные условия
или только краевые условия, или только правые части, то гово-
говорят об устойчивости соответственно по начальным условиям, по
краевым условиям или по правым частям.
Определение. Конечно-разностная схема F.38) абсолют-
абсолютно (безусловно) устойчива, если неравенство F.42) выполня-
выполняется при любых значениях сеточных характеристик т и h, т. е.
на шаги сетки не накладывается никаких ограничений.
Определение. Конечно-разностная схема F.38) условно
устойчива, если неравенство F.42) выполняется для сеточных
характеристик т и h, на которые накладываются определенные
ограничения.
6.3.3. Сходимость и порядок сходимости. Определе-
Определение. Решение и^, полученное с помощью конечно-разностной
схемы F.38), сходится к точному решению U, если какая-либо
норма разности \\U — и^\\ стремится к нулю при стремлении
к нулю сеточных характеристик т, h:
\\U-uh\\——+0. F.43)
т,/г-^0
Определение. Конечно-разностная схема F.38) имеет р-й
порядок сходимости (порядок точности) по времени и q-й поря-
порядок сходимости по пространственной переменной, если какая-
либо норма разности \\U — и^\\ удовлетворяет равенству
\\U-uh\\ = O{rP + hq). F.44)
Таким образом, порядок сходимости (порядок точности) ха-
характеризует близость конечно-разностного и точного (неизвест-
(неизвестного) решения.
238 Метод конечных разностей [Гл. VI
6.3.4. Теорема эквивалентности о связи аппроксима-
аппроксимации и устойчивости со сходимостью. При численном реше-
решении задач математической физики в общем случае необходимо
исследовать и аппроксимацию, и устойчивость, и сходимость.
Однако следующая теорема утверждает, что достаточно исследо-
исследовать аппроксимацию и устойчивость, и, в случае положительного
ответа, сходимость будет обеспечена.
Теорема эквивалентности. Если конечно-разностная
схема F.38) аппроксимирует на точном решении дифферен-
дифференциальную задачу с р-м порядком по времени и q-м порядком
по пространственной переменной и эта схема устойчива, то
решение с помощью этой конечно-разностной схемы сходится
к решению дифференциальной задачи с р-м порядком по времени
и q-м порядком по пространственной переменной.
Действительно, следующая цепочка доказывает теорему:
\\U - uh\\ < К ||/ - А|| = К \\{LU)h - LhUh\\ = O(rP
откуда
что и требовалась доказать.
В приведенной выше цепочке первое неравенство записано
по условию устойчивости, а последнее равенство — по условию
аппроксимации.
6.3.5. Консервативность и корректность. Все диффе-
дифференциальные, интегральные и прочие уравнения характеризу-
характеризуют некоторые законы сохранения какой-либо субстанции (массы,
энергии, импульса и т.п.). Заменяя дифференциальную задачу
конечно-разностной схемой, можно нарушить эти законы сохра-
сохранения.
Определение. Конечно-разностная схема консервативна,
если для нее выполняются законы сохранения, на основе которых
поставлена дифференциальная задача.
В противном случае конечно-разностная схема является
неконсервативной, т.е. решение с ее помощью не соответ-
соответствует решению дифференциальной задачи (решается другая
задача). Поэтому неконсервативными схемами пользоваться не
рекомендуется.
Свойство корректности конечно-разностных схем вытекает
из свойств аппроксимации и устойчивости.
§6.4] Анализ порядка аппроксимации разностных схем 239
Определение. Дифференциальная задача поставлена кор-
корректно, если выполнены следующие два условия:
1) задача однозначно разрешима при любых входных данных;
2) решение задачи непрерывно зависит от входных данных.
По аналогии определяется и корректность разностной задачи.
Определение. Конечно-разностная задача F.38) постав-
поставлена корректно, если при любых достаточно малых шагах г
и h сетки выполнены условия:
1) решение и^ существует и единственно при всех входных
данных из некоторого допустимого семейства]
2) решение и^ непрерывно зависит от входных данных Д,
причем эта зависимость равномерна относительно величины
шагов сетки (т.е. конечно-разностная схема устойчива).
Таким образом, основными характеристиками конечно-
разностной схемы, которые обязательно должны быть проана-
проанализированы, являются: аппроксимация, устойчивость и консер-
консервативность.
§ 6.4. Анализ порядка аппроксимации разностных
схем
Из определения порядка аппроксимации ясно, что чем выше
порядок аппроксимации, тем лучше конечно-разностная схема
приближается к дифференциальной задаче. Это не означает,
что решение по разностной схеме может быть так же близко
к решению дифференциальной задачи, так как разностная схема
может быть условно устойчивой или абсолютно неустойчивой
вовсе.
Для нахождения порядка аппроксимации используется аппа-
аппарат разложения в ряды Тейлора точных (неизвестных, но диф-
дифференцируемых) решений дифференциальной задачи в узлах
сетки (подчеркнем: значения сеточной функции и^ дискретны,
следовательно, не дифференцируемы и поэтому не разлагаются
в ряды Тейлора).
В соответствии с определением порядка аппроксимации про-
проанализируем порядок аппроксимации конечно-разностной схемы
F.28), для чего эту схему запишем на точном решении и!?:
ттк+1 _ ттк ттк _ уттк | ттк
Uj т Uj =a2Uj+1 2UJ+Ui~\ F.45)
240
Метод конечных разностей
[Гл. VI
Разложим в ряды Тейлора по переменной х значения ?/^+1,
f/f_i в окрестности узла (j,k) до четвертой производной вклю-
включительно, а значение U ¦; + — в ряд Тейлора по переменной t
в окрестности узла (j, к) до второй производной включительно,
получим
ди
дх
\, д2и
а -\ 2"
3 и X
д2и
2
. 6
+ О (/г4) , F.46)
дх1
д3и
. 6
= U
htk + т) = ?/*
И-
, F.47)
F.48)
Подставляя F.46)—F.48) в F.45), находим
LhUh = -1-
тк <)Т1к
j + l ~ ZUj
— а
Таким образом,
\\{LU)h-LhUh\\ = O{r + h2),
т. е. явная схема F.28) для уравнения теплопроводности име-
имеет первый порядок аппроксимации по времени и второй — по
пространственной переменной. Аналогично, тот же порядок ап-
аппроксимации можно получить и для неявной схемы F.30).
§ 6.5. Исследование устойчивости
конечно-разностных схем
Поскольку устойчивость является одной из основных ха-
характеристик конечно-разностных схем, то в данном параграфе
рассматриваются различные методы исследования устойчивости
§6.5] Исследование устойчивости конечно-разностных схем 241
конечно-разностных схем по начальным условиям. Наиболее рас-
распространенными методами исследования устойчивости являются
следующие [10-14]:
— метод гармонического анализа (Фурье);
— принцип максимума;
— спектральный метод;
— энергетический метод.
Каждый из этих методов имеет достоинства и недостатки.
6.5.1. Метод гармонического анализа. Из математи-
математической физики известно, что решение начально-краевых задач
представляется в виде следующего ряда:
u(x, t) =
п=1
где Лп — собственные значения, а ехр(гЛпж) = cos(An#) +
+ г sin(Anx) — собственные функции, получаемые из решения
соответствующей задачи Штурма-Лиувиля, т. е. решение может
быть представлено в виде суперпозиции отдельных гармоник
и(х, t) = un{t) ехр(гАпж), каждая из которых есть произведение
функции времени t и функции пространственной переменной ж,
причем последняя по модулю ограничена сверху единицей при
любых значениях переменной х.
В то же время функция времени un{t), называемая ампли-
амплитудной частью гармоники, никак не ограничена, и, по всей ве-
вероятности, именно амплитудная часть гармоник является источ-
источником неконтролируемого входными данными роста функции и,
следовательно, источником неустойчивости.
Таким образом, если конечно-разностная схема устойчива, то
отношение амплитудной части гармоники на верхнем временном
слое к амплитудной части на нижнем временном слое по модулю
должно быть меньше единицы.
Если разложить значение сеточной функции и- в ряд Фурье
по собственным функциям:
оо
ик. — V rii piX^xJ ((л АО)
71=1
где амплитудная часть 7]^п может быть представлена в виде
произведения
rikn = Un-qk, F.50)
242
Метод конечных разностей
[Гл. VI
Un — размерный и постоянный сомножитель амплитудной части,
а к — показатель степени (соответствующий номеру временного
слоя) сомножителя, зависящего от времени, то, подставив F.49)
в конечно-разностную схему, можно по модулю оценить отноше-
отношение амплитудных частей на соседних временных слоях.
Однако поскольку операция суммирования линейна и соб-
собственные функции ортогональны для различных индексов сум-
суммирования, то в конечно-разностную схему вместо сеточных зна-
значений достаточно подставить одну гармонику разложения F.49)
(при этом у амплитудной части убрать индекс п), т.е.
и) =
F.51)
Таким образом, если конечно-разностная схема устойчива по
начальным данным, то
F.52)
Vk
т. е. условие F.52) является необходимым условием устойчи-
устойчивости.
6.5.2. Исследование устойчивости методом гармони-
гармонического анализа явной и неявной схем для уравне-
уравнения теплопроводности. Подставим выражения F.51) в яв-
явную конечно-разносную схему F.28) для уравнения теплопро-
теплопроводности, получим
Vk+i
а2т
= 1 - 4сг • sin ——, а = -^-. F.53)
Vk I h
Здесь использована формула, вытекающая из формулы Эй-
Эйлера:
ехр(гЛп/г) — 2 + ехр(—i\nh) = —4 sin2
An h
2 '
и формула 1 — cos Xnh = 2 sin2 —^—, причем О < sin2
Z
поскольку An ф 0 и h ф 0.
В соответствии с F.53) получаем выражение
Vk
Xnh
l-4asin2^
= |1 — 4am\ , m = sin
^
Xnh
1,
2 лп
§6.5]
Исследование устойчивости конечно-разностных схем
243
или, с учетом F.52), неравенство
|l-4crm| ^ 1.
Отсюда получаем следующие два неравенства:
-1 ^ l-4crm ^ +1,
из которых правое выполнено всегда, а из левого следует зна-
знаменитое условие устойчивости Куранта: am ^ 1/2, или более
жесткое для а условие
а2т
F.54)
Из F.54) следует, что явная схема для уравнения теплопро-
теплопроводности условно устойчива с условием F.54), накладываемым
на сеточные характеристики т и h.
Подставим теперь гармоники F.51) в неявную конечно-
разностную схему F.30) для уравнения теплопроводности, по-
получим
откуда
А„А
всегда, так как а и квадрат синуса больше нуля.
Следовательно, неявная схема для уравнения теплопроводно-
теплопроводности абсолютно устойчива, так как для выполнения неравенства
С 1 на сеточные характеристики г и h не накладывалось
никаких ограничений.
Комплекс —2~ называют числом Куранта для уравнения теп-
h
лопроводности.
6.5.3. Исследование устойчивости методом гармони-
гармонического анализа явной и неявной схем для волнового
уравнения. Конечно-разностные схемы F.31) и F.32) для вол-
волнового уравнения являются трехслойными, а не двухслойными,
как для уравнения теплопроводности, поэтому подстановка в эти
схемы гармоник в форме F.51) не приведет к неравенству F.52).
244 Метод конечных разностей [Гл. VI
При исследовании устойчивости конечно-разностных схем
для волнового уравнения методом гармонического анализа
в конечно-разностные схемы подставляется отдельная гармоника
ряда F.49) с амплитудной частью в форме F.50), т. е. гармоники
вида
Д-э -ш- у [у? 'J А | /Т* • h I к? Т Т к? О А *Т* •
— ип Ч е ) aj — ип Ч е 1
F.55)
= Un • qk±l
Подставляем F.55) в явную схему F.31), получаем квадрат-
квадратное уравнение относительно параметра q:
q2 — q B — 4am) + 1 = 0, a = —^—, m = sin2 —?— > 0,
h 2
с корнями
q12 = A - 2am) ± у A - 2amJ - 1.
Комплекс a = —^- называют числом Куранта для волнового
уравнения.
Таким образом, если явная схема F.31) устойчива, то в соот-
соответствии с F.50) и F.52) величина q по модулю не превышает
единицы
A - 2ат) ± у A - 2сгшJ - 1
1, F.56)
или
-1 ^ A - 2ат) ± у A - 2сгшJ - 1 ^ +1. F.57)
Здесь правое неравенство выполняется всегда.
Из левого неравенства F.57) имеем
- 1) сгт ^ am- 1. F.58)
Для положительного знака в левой части F.58) получаем, что
am > 1. Действительно, в этом случае выполняется следующая
цепочка неравенств: (am — 1)ат ^ (am — IJ, (am — 1)(ат —
— сгт + 1)^0. Однако при этом не выполняется исходное нера-
неравенство F.56), в чем можно убедиться непосредственной подста-
подстановкой am ^1 в F.56).
§6.5] Исследование устойчивости конечно-разностных схем 245
Для отрицательного знака в левой части F.58) имеем:
1, поскольку выполняются неравенства: л^(ат — \)ат ^
^ 1 — dm, (am — 1)ат ^ A — шJ, A — ат)A — am +
+ am) ^ 0, am ^ 1. Это неравенство не противоречит неравен-
неравенству F.56), а поскольку 0 < т < 1, то вместо неравенства am ^ 1
принимается более жесткое неравенство а ^ 1 или
ет = ^ < 1. F.59)
Таким образом, явная конечно-разностная схема F.31) для
волнового уравнения условно устойчива с условием F.59), накла-
накладываемым на сеточные характеристики т и h.
Для неявной схемы F.32) результатом подстановки в нее гар-
гармоник F.55) с амплитудой в форме F.50) является квадратное
уравнение
2 2g + l = 0,
решением которого являются комплексные числа
1 .
' 1 + 4cr7n
1 + 4cr7n 1 + Аат
Модуль этих комплексных чисел всегда не больше единицы:
. , VI + 4<тга
91,2 = —г—Л ^ 1,
' 1 + 4сгт
что доказывает абсолютную устойчивость неявной схемы F.32)
для волнового уравнения.
6.5.4. Принцип максимума. В математической физике
известен принцип, в соответствии с которым решение начально-
краевой задачи внутри расчетной области не может превышать
значений искомой функции на пространственно-временной гра-
границе. Этот принцип положен в основу метода исследования
устойчивости конечно-разностных схем, называемого принципом
максимума.
Для его использования рассмотрим явную конечно-
разностную схему F.28) для уравнения теплопроводности
в форме
= aukj+1 + A - 2а) и) + аи)_х F.60)
246 Метод конечных разностей [Гл. VI
и введем норму сеточной функции и- в виде ||г/ || = max
Тогда из F.60) получим
A - 2а) ик + сгик_г ^
^ 111С1Л С'
Если
\uk+1 Umax
mj
о < ?, F-62)
то из F.61) имеем неравенство
L*+1II < LHI
откуда, продолжая цепочку неравенств вплоть до начального
условия, получим
где ф(х) — начальное условие F.4).
Неравенства F.63) в вычислительной математике называ-
называют принципом максимума. Он является достаточным условием
устойчивости явной схемы F.60) для уравнения теплопровод-
теплопроводности.
Таким образом, если выполнено условие Куранта F.62), то
из цепочки F.63) видно, что значение сеточной функции на лю-
любом временном слое по норме не превысит начального условия,
т. е. рассматриваемая схема устойчива по начальному условию,
причем условие F.62) является теперь не только необходимым
в соответствии с методом гармонического анализа, но и доста-
достаточным.
6.5.5. Спектральный метод исследования устойчи-
устойчивости. Рассмотрим сеточные функции ик- и uk+1, j = 0, Л/", на
двух временных слоях tk = кг и tk+1 = (к + 1)т и представим
конечно-разностную схему в следующей операторной форме:
S-uk, F.64)
где S — оператор перехода от слоя tk к слою tk+1. Такой опера-
оператор можно построить не для всякой конечно-разностной схемы
§6.5]
Исследование устойчивости конечно-разностных схем
247
(например, метод прогонки нельзя представить в форме F.64)).
Для явных конечно-разностных схем F.28) или F.31) оператор S
представляется следующей матрицей перехода:
S =
1-2<7
а
1-2G
О
1-2сг
\
\
1-2G
Составим от левой и правой частей равенства F.64) опера-
операцию нормы и используем свойство нормы: норма произведения
операторов не превышает произведения норм, получим
\и
k+i\
\и
Если выполнено неравенство вида
F.65)
F.66)
то из условий F.65) и F.66) следует принцип максимума
Таким образом, если схема устойчива, то норма оператора
перехода S не превышает единицы и, следовательно, условие
F.66) является необходимым условием устойчивости конечно-
разностных схем.
Почему этот метод называют спектральным?
Для ответа на этот вопрос рассмотрим векторы ик и ик+1
на соседних временных слоях в виде произведения сомножите-
сомножителя qk, зависящего от времени (здесь к — показатель степени), на
вектор v(ж), зависящий от пространственной переменной (для
линейных задач метод разделения переменных легко обосновы-
обосновывается), получим равенства
ик = qk ¦ v,
uk+1 = qk+1 ¦ v,
подставляя которые в F.64), будем иметь
Sv = qv.
F.67)
248 Метод конечных разностей [Гл. VI
Равенство F.67) является задачей на собственные векторы v
и собственные значения q оператора перехода S.
Составим от F.67) операцию нормы, получим
откуда
\q\^\\S\\, F.68)
Но для необходимого условия устойчивости выполняется нера-
неравенство F.66), т.е. из F.66) и F.68) следует неравенство
\q\ ^ 1. F.69)
Таким образом, если схема устойчива, то выполняется нера-
неравенство F.69), называемое условием устойчивости фон Нейма-
Неймана, из которого ясно, что в этом случае все собственные значе-
значения qj (или полный спектр оператора S) находятся внутри круга
радиуса единица с центром в начале координат на комплексной
плоскости.
6.5.6. Энергетический метод исследования устойчи-
устойчивости конечно-разностных схем. Как видно из предыдущих
разделов, метод гармонического анализа и спектральный ме-
метод являются необходимыми условиями устойчивости конечно-
разностных схем, а принцип максимума — достаточным усло-
условием устойчивости. В данном пункте рассматривается один из
самых мощных и распространенных методов — энергетический
метод, развитый в работах А. А. Самарского и базирующий-
базирующийся на понятиях энергетического пространства с энергетической
нормой, энергетического тождества (неравенства) и принципа
максимума. Ниже будет показано, что условия, используемые
в энергетическом методе, являются достаточными условиями
устойчивости конечно-разностных схем.
Для понимания энергетического метода рассмотрим примене-
применение его с целью исследования устойчивости конечно-разностных
схем при численном решении следующей первой начально-
краевой задачи для уравнения теплопроводности с однородными
краевыми условиями:
§6.5] Исследование устойчивости конечно-разностных схем 249
м@,*) = 0, ж = 0, t > 0; F.71)
tz(l,t) = 0, ж = 1, <>0; F.72)
гх(ж,0) = ^(ж), же[0;1], t = 0. F.73)
На сетке F.25) будем аппроксимировать эту задачу с по-
помощью явной F.28) и неявной F.30) конечно-разностных схем,
записанных в векторно-операторной форме следующим образом:
uk+1 - uk 1
= ЛгД F.74)
/c+l k
и ~и =Аик+\ F.75)
где конечно-разностный оператор Л аппроксимирует дифферен-
дифференциальный оператор по пространственной переменной ж, т.е.
Аик = а2(м}+1 - 2и) + u^2
Энергетическое пространство. Введем энергетическое про-
пространство На сеточных функций и^, являющееся гильбертовым
пространством, в котором определено скалярное произведение
для двух элементов и^ ? На и v^ Е На'
N
, vh)A = (Auh, vh) = ^2 AujVjh, F.76)
и, следовательно, с нормой
1/2
= (Auh,uhI/2 =
N
F.77)
Как известно, гильбертово пространство — это полное нор-
нормированное пространство, в котором определено скалярное про-
произведение. Здесь полнота определяется в том смысле, что если
последовательность сеточных функций {uhn} сходится к своему
пределу при hn —> О (в данном случае — к решению диффе-
дифференциальной задачи), то она является фундаментальной, т.е.
выполняется условие Коши
F.78)
71,771—)>ОО
250 Метод конечных разностей [ Гл. VI
Действительно, если конечно-разностная схема аппроксими-
аппроксимирует дифференциальную задачу и устойчива, то по теореме эк-
эквивалентности решение с помощью конечно-разностной схемы
сходится к решению дифференциальной задачи при измельчении
сетки.
Для двух сеточных функций и\1п и и\1ш (двух элементов
гильбертова пространства На) на различных сетках с шагами hn
и hm понятие полноты означает, что при измельчении сетки, т. е.
при hn —> 0 (или hm —> 0) последовательности {uhn} и {и^т}
сходятся к одному и тому же пределу, т.е. выполняется F.78).
В дальнейшем потребуются следующие понятия, характери-
характеризующие конечно-разностные операторы: сопряженность, самосо-
самосопряженность, положительная определенность.
Определение. Конечно-разностный оператор Л* называется
сопряженным оператору Л, если выполняется равенство
(Au,v) = (u,A*v). F.79)
Например, если оператор А — симметрическая матрица с дей-
действительными элементами (А = Лт), то А — сопряженный опе-
оператор (это можно проверить непосредственно).
Определение. Конечно-разностный оператор А называется
самосопряженным, если выполняется равенство
(Au,v) = (u,Av). F.80)
Определение. Конечно-разностный оператор А называется
положительно определенным (А > 0) или положительно полу-
полуопределенным (А ^ 0) на гильбертовом пространстве сеточных
функций Uh ? Яд, если
(Auh, uh) > 0 или (Auh, uh) ^ 0. F.81)
Можно показать, что разностный оператор —Л = А является
самосопряженным, т. е.
(—Аи, v) = (и, — Av).
С целью определения собственных функций и собственных
значений конечно-разностного оператора Л, рассмотрим вначале
задачу на собственные значения и собственные функции опера-
оператора Л:
А(р = \<р. F.82)
§6.5] Исследование устойчивости конечно-разностных схем 251
Собственные функции (fn(xj) должны удовлетворять следу-
следующим условиям:
1) быть ортогональными на отрезке х ? [0; 1] при п ф т, т. е.
(?>п? фт) = 0 на х G [0; 1] при п ф т\
2) удовлетворять однородным краевым уравнениям F.71),
F.72);
3) их число должно совпадать с числом собственных значе-
значений Ап.
Таким условиям удовлетворяют функции:
, ч . UTTXj 1
{) ^ h / 1 h
т. е.
т п \ 3) Л/" ' '' ' ' \ ' )
Для нахождения собственных значений Лп подставим F.83)
в F.82), получим
или
^2
U7TJ
откуда
4а2
2—, n = l,N-l. F.84)
Из F.84) видно, что все собственные значения оператора Л
отрицательны, а собственные значения оператора А = — Л поло-
положительны, т. е. оператор А = — Л положительно определен.
При исследовании устойчивости явной конечно-разностной
схемы F.74) энергетическим методом воспользуемся следующи-
следующими тождествами:
uk+1 - uk
щ = ;
и uk+1 + uk uk+1 - uk uk+1 + uk t
uk = = -ut.
252 Метод конечных разностей [ Гл. VI
Умножим скалярно явную схему F.74) на вектор 2тщ, полу-
получим
2т(иищ)+ (Аик,2ти^ = 0,
или, после подстановки сюда тождеств F.85),
2т(иищ)+ (Лик+\ик+Л
- т2 (Ащ, щ) - (Аик+\ик) + (Аик,ик+1\ = 0.
В силу самосопряженности оператора А и коммутативности
скалярного произведения, последние два слагаемых сокращают-
сокращаются, после чего получим следующее энергетическое тождество:
2т ((я - Т-А) иищ) + [Auk+\ uk+l) = [Аи\ик) . F.86)
Если оператор
Е-(т/2)А^0, F.87)
то из F.86) получаем следующее энергетическое неравенство:
(Auk+1, ufc+1) ^ [Аик, ufc) , F.88)
ИЛИ
\\ик+1\\ < \\ик\\
откуда сразу следует принцип максимума
\\ \\А \\ \\Л ^И На ~" И^ \Х)\\А '
являющийся достаточным условием устойчивости.
Если теперь от неравенства F.87) вычислить любую норму
(||Е|| = 1), например норму, которая равна максимальному по
модулю собственному значению оператора А, то с использовани-
использованием выражения F.84) получим
откуда
^ < I F-89)
§6.5] Конечно-разностный метод решения параболических задач 253
Таким образом, условие устойчивости Куранта F.54) явной
конечно-разностной схемы для уравнения теплопроводности, вы-
выведенное с помощью метода гармонического анализа, является
и достаточным условием.
Исследуем теперь устойчивость неявной конечно-разностной
схемы F.75) энергетическим методом, для чего к тождествам
F.85) добавим тождество
uk+l = ик + т-щ = М"+12+ "" +^щ. F.90)
Умножим скалярно схему F.75) на вектор 2т • щ, получим
2т {ии щ) + А(ик + т- ии 2т • u^j = 0,
2т ((е + ^а)щ,щ) + [Аик+\ик+1) - (Аик,ик) -
= 0.
Таким образом, для неявной схемы энергетическое тожде-
тождество имеет вид
2т ((# + 1д) щ, щ) + [Auk+\ ufc+1) = (Auk, uk^j . F.91)
Здесь первое слагаемое всегда положительно определено, по-
поэтому энергетическое неравенство имеет вид
Uuk+1,uk+1) ^ Uuk,uk),
F.92)
IH1Llb1L
откуда следует принцип максимума
Таким образом, неявная схема F.75) безусловно устойчива,
так как оператор Е -\—А всегда положительно определен.
254 Метод конечных разностей [ Гл. VI
§ 6.6. Конечно-разностный метод решения задач
для уравнений параболического типа
Конечно-разностные схемы и методы численного решения
одномерных и многомерных по пространству начально-краевых
задач для уравнений параболического типа, излагаемые в этом
параграфе, можно использовать и для соответствующих задач
для уравнений гиперболического типа, а некоторые — методы
расщепления — и в задачах для уравнений эллиптического типа.
6.6.1. Однородные и консервативные конечно-раз-
конечно-разностные схемы для задач теплопроводности с гранич-
граничными условиями, содержащими производные. В задачах
математической физики вообще, и в задачах теплопроводности
в частности, граничные условия 1-го рода аппроксимируются
точно в узлах на границе расчетной области и этот факт никак
не влияет на порядок аппроксимации во всей расчетной области.
Этого нельзя сказать об аппроксимации граничных условий 2-го
и 3-го родов, поскольку в них присутствует производная перво-
первого порядка искомой функции по пространственной переменной,
в результате чего порядок аппроксимации в граничных узлах
может быть ниже порядка аппроксимации во внутренних узлах
расчетной области.
В этой связи необходимо ввести понятия локального порядка
аппроксимации — порядка аппроксимации в отдельно взятом уз-
узле, и глобального порядка аппроксимации — порядка аппроксима-
аппроксимации во всей расчетной области. Анализ порядка аппроксимации,
рассмотренный в § 6.4 осуществлен для отдельного узла сетки, и,
следовательно, там речь идет о локальной аппроксимации. Для
задач с граничными условиями 1-го рода на равномерной сетке
локальный порядок аппроксимации совпадает с глобальным.
Для задач с граничными условиями, содержащими производ-
производные, порядок аппроксимации в граничных узлах может быть ни-
ниже порядка аппроксимации во внутренних узлах, если конечно-
разностная схема в граничных узлах не использует дифферен-
дифференциальное уравнение (ниже будет показано, что в этом случае
нарушается консервативность). Тогда глобальный порядок ап-
аппроксимации равен наименьшему относительно всех узлов сетки
порядку аппроксимации.
Рассмотрим методологию сохранения на границах с гранич-
граничными условиями 2-го и 3-го родов порядка аппроксимации, ко-
§6.6] Конечно-разностный метод решения параболических задач 255
торый дает аппроксимация дифференциального уравнения во
внутренних узлах, т. е. получение конечно-разностной схемы
с однородной аппроксимацией. Для этого рассмотрим третью
начально-краевую задачу для уравнения теплопроводности, со-
содержащего как конвективные члены (пропорциональные произ-
производной ди/'дх), так и источниковые члены, содержащие искомую
функцию и(х, t):
^L = a2^1 + b^i + cu о<ж</, t>0; F.93)
at ox их
a6"^ +Pu{0,t) = vo(t), x = 0, t>0; F.94)
7^-^ + <MM) = ?>i(*), x = l, t>0; F.95)
и(х,0) = ф(х), O^x^l, t = 0. F.96)
Во внутренних узлах конечно-разностной сетки F.25) неяв-
неявная конечно-разностная схема для уравнения F.93) имеет вид
л
l_ (y _ 2 л+1 , /с+л , A (yk+i _ /с
h2 W+1 i ^-V 2/г V ^+1 i
-O(r + hz), j = 1, TV — 1. F.97)
Если производные первого порядка в граничных условиях
F.94) и F.95) аппроксимировать по следующей схеме (с помо-
помощью отношения конечных разностей справа и слева):
ди
~дх
ди
~дх
lN UN-1
h
O(h),
j = N
то граничные условия аппроксимируются с первым порядком,
и глобальный порядок будет равен первому порядку, несмотря на
то что во всех остальных узлах порядок аппроксимации по про-
пространственной переменной равен двум. Для сохранения порядка
аппроксимации, равного двум, в граничных узлах разложим на
точном решении значение и^ в окрестности точки х = О в ряд
256
Метод конечных разностей
[Гл. VI
Тейлора по переменной х до третьей производной включительно,
а и^}г — в аналогичный ряд в окрестности точки х = /, получим
(в предположении что функция и(х, t) в граничных узлах имеет
первые производные по времени и вторые — по х):
**1 = и (
о
ди
k+i
д2и
дх1
+ О (hs) , F.98)
%-1 =
N
дх
k+1
h
d2u
N
дх1
+ О (/i3) . F.99)
N
Подставим сюда значения второй производной в граничных
узлах, полученные из дифференциального уравнения F.93):
д2и
дх2
j=0N
1 ди b ди с
a dt а дх а
k+l
j=0N
и найдем из полученных выражений F.98), F.99) значения
k
первой производной ——
дх
в граничных узлах с порядком
ди
~дх~
¦ + Л2):
к+1 2а2
j=0,N
h Bа2 - bh)
\и\+х - и%+1
h
ди
2а2 - bh dt
k+l
ch
2а2 - bh
+l + О (h*) ,
ди
~дх
fe+i
N
2az
h Bа2 + bh)
h
du
2а2 + bh dt
k+l
N
ch
2a2 + bh
и
+
§6.6] Конечно-разностный метод решения параболических задач 257
Подставляя ——
ох
k+i
в F.94), а ^
о
k+1
в F.95) и аппрокси-
N
мируя полученные соотношения в соответствующих граничных
к+1
( ди
узлах (при этом —-
~им)
0
- «*) /т + О (г), ^
/т + О (т) ), получим алгебраические уравнения
для граничных узлов, в каждом из которых два неизвестных:
- с0 •
= 0;
F.100)
п , 2а
= 0, 60 = ^—
h
2а2 h
— Н
h т
C ( 2 ч 2а2
[2а - bh) ; с0 = -^—;
a v y /г
do = *
2а2 - bh
а
О (
F.101)
2а
2а 2а h 5 , 2 , »/\ п
= -р-; »7v = -: 1 с/г Н— • Bа + о/г) ; сп = 0;
/г h т 7
ft
-
г
2а2 + bh
Таким образом, F.100) — конечно-разностная аппроксимация
граничного условия 3-го рода F.94) на левой границе х = 0,
а F.101) — конечно-разностная аппроксимация граничного усло-
условия 3-го рода F.95) на правой границе х = /, которые сохраняют
тот же порядок аппроксимации, что и в конечно-разностной
аппроксимации F.97) дифференциального уравнения F.93).
Приписывая к граничным конечно-разностным уравнениям
F.100), F.101), каждое из которых содержит два значения се-
сеточной функции, алгебраические уравнения F.97), записанные
в виде
dj + O(T + h2) , j = 1,УУ-1;
F.102)
_ a2 b _ 2a2
_ 1 k
9 В.Ф. Формалев, Д.Л. Ревизников
258
Метод конечных разностей
[Гл. VI
получим СЛАУ с трехдиагональной матрицей, решаемую мето-
методом прогонки (ао = 0; cjy = 0)
А ¦ -
F.103)
ukj+1 =
+
j = N, N - 1,... , 0.
F.104)
Покажем, что изложенный метод аппроксимации краевых
условий, содержащих производные по пространственным пе-
переменным, не только повышает порядок аппроксимации, но
и сохраняет консервативность конечно-разностной схемы, т. е.
в конечно-разностной аппроксимации соблюдаются законы со-
сохранения, на основе которых выведены дифференциальные со-
соотношения задачи F.93)—F.96). Для этого рассмотрим вначале
вывод дифференциального уравнения теплопроводности F.93)
в случае b = с = 0 (см. рис. 6.6 а).
q(xrAx/2)
п
Ax=h
Ax/2 Xj Ax/2
q{Xj+Ax/2)
о >
j+i ^
Ах/2 Ах/2 X! Ах/2 Ах/2 х2
Рис. 6.6. К аппроксимации краевых условий, содержащих производные, с со-
сохранением консервативности
Из физики известно, что тепловой поток, согласно закону
, л ди л . .
Фурье, в одномерном случае равен q = — Л • j—, где Л — коэффи-
С/ X
циент теплопроводности. Для элемента длиной Ах = /г, в центре
которого помещен узел х«, запишем сумму тепловых потоков:
§6.6] Конечно-разностный метод решения параболических задач 259
q(xj —Дж/2) — q(xj + Дж/2), подходящих к левой и правой
границам элемента. По закону сохранения энергии сумма этих
тепловых потоков равна изменению энергии в этом элементе Дж,
которая пропорциональна массе элемента рДж, теплоемкости
материала с и производной первого порядка от температуры
u(x^t) по времени
du(xj-Ах/2) ( du(xj+Ax/2)\ _ ди
— А • I —Л • I — с - р • Аж • -7—.
ох у их ) ot
Разделив это равенство на Дж и перейдя к пределу при Дж —> О,
получим одномерное уравнение теплопроводности
ди _ 2 92и 2 _ ^
C/L С/Т СО
Таким образом, конечно-разностная аппроксимация F.97)
дифференциального уравнения F.93) учитывает и тепловые по-
потоки, и энергию, поглощенную элементом Дж, т. е. все виды энер-
энергии, участвующие при выводе дифференциального уравнения.
Рассмотрим теперь вывод граничного условия F.94) на левой
границе (см. рис. 6.6 б) расчетной области (для правой границы
х = I вывод аналогичен).
К граничному узлу ж = 0 примыкает масса объемом Дж/2
со стороны расчетной области. При задании граничного условия
3-го рода на левой границе ж = 0 осуществляется теплообмен
с окружающей средой по закону Ньютона: qe = /3 (ие — и (О, ?)),
где ие — температура окружающей среды, а /3 — коэффициент
теплообмена на границе ж = 0, имеющей температуру n@, t),
с окружающей средой, имеющей температуру ие. Справа к эле-
элементу Дж/2 подводится тепловой поток, описываемый законом
Фурье. Тогда разность тепловых потоков, подводимых к поло-
половине элемента, равна энергии, пошедшей на повышение тем-
температуры элемента Дж/2, пропорциональной массе этого эле-
элемента рДж/2, теплоемкости с и производной температуры по
времени:
q( (п +\\ ( \ ди@ + Ах/2)\ Ах ди ( .
C(ие-и @, *)) - (-Л ^ М =ср- — -—. F.105)
Переходя здесь к пределу при Дж/2 —» 0, получим левое гра-
граничное условие 3-го рода F.94) (с точностью до коэффициентов)
260 Метод конечных разностей [Гл. VI
Л • ди^ ^ +/3(ие-и @, <)) = 0. F.106)
Таким образом, конечно-разностная аппроксимация гранич-
граничного условия F.106) или F.94) должна сопровождаться появле-
появлением консервативного слагаемого, стоящего в правой части ра-
равенства F.105). Физически это означает, что граничные условия
F.94), F.95) записаны для границ, не имеющих ни массы, ни объ-
объема. В конечно-разностной аппроксимации к границе примыкает
масса с одномерным объемом, равным Аж/2, в котором необ-
необходимо учитывать дифференциальное уравнение, действующее
во внутренних точках расчетной области, и не действующее на
границе.
В конечно-разностной аппроксимации краевого условия, со-
содержащего производную по переменной х, нестационарный член
в правой части выражения F.105) с помощью дифференциаль-
дифференциального уравнения можно заменить на дивергентный член, пропор-
пропорциональный д2и/дх2 \х=о •
Аналогичный подход можно осуществить в краевых задачах
для дифференциальных уравнений любых типов.
6.6.2. Неявно-явная конечно-разностная схема
с весами. Схема Кранка—Николсона. Явная конечно-
разностная схема F.28), записанная в форме
2
= <У ' Uj + i + A — 2сг) Uj + <J ' Uj_i, <J = —2~,
j = l,N-l, к = 0,1,2... , F.107)
обладает тем достоинством, что решение на верхнем временном
слое tkJrl получается сразу (без решения СЛАУ) по значениям
сеточной функции на нижнем временном слое t , где решение
известно (при к = 0 значения сеточной функции формируются из
начального условия F.4.)). Но эта же схема обладает существен-
существенным недостатком, поскольку она является условно устойчивой
с условием F.54), накладываемым на сеточные характеристики
т и h.
С другой стороны, неявная конечно-разностная схема F.30),
записанная форме
+ bju^1 - CjU^+l = dj, j = 1,7V- 1, к = 0,1, 2,. . . ,
F.108)
§6.6] Конечно-разностный метод решения параболических задач 261
приводит к необходимости решать СЛАУ, но зато эта схема
абсолютно устойчива.
Проанализируем схемы F.107), F.108). Пусть точное реше-
k-\-i
ние, которое неизвестно, возрастает по времени, т.е. и- >
> ик-. Тогда, в соответствии с явной схемой F.107), разностное
решение будет заниженным по сравнению с точным, так как
и-^~ определяется по меньшим значениям сеточной функции
на предыдущем временном слое, поскольку решение является
возрастающим по времени.
Для неявной схемы F.108) на возрастающем решении, на-
наоборот, решение завышено по сравнению с точным, поскольку
оно определяется по значениям сеточной функции на верхнем
временном слое.
На убывающем решении картина изменяется противополож-
противоположным образом: явная конечно-разностная схема завышает реше-
решения, а неявная — занижает (см. рис. 6.7).
Точное решение
Неявное решение
Явное решение !
ft % ft+^ ft X ft+^ t
Рис. 6.7. Двусторонний метод аппроксимации
На основе этого анализа возникла идея о построении более
точной неявно-явной конечно-разностной схемы с весами при
пространственных конечно-разностных операторах, причем при
измельчении шагов тик точное (неизвестное) решение может
быть взято в «вилку» сколь угодно узкую, так как если явная
и неявная схемы аппроксимируют дифференциальную задачу
и эти схемы устойчивы, то при стремлении сеточных характери-
262
Метод конечных разностей
[Гл. VI
стик т и h к нулю решения по явной и неявной схемам стремятся
к точному решению с разных сторон.
Проведенный анализ дал блестящий пример так называемых
двусторонних методов, исследованных В. К. Саульевым [15].
Рассмотрим неявно-явную схему с весами для простейшего
уравнения теплопроводности:
JU_|_1 jU к-\-Л ^ к-\-Л h I 1
/II1 fb I /II1 9 П Ш ' l/l#'
n
F.109)
где 0 — вес неявной части конечно-разностной схемы, 1 — 0 — вес
для явной части, причем 0 ^ 0 ^ 1. При 0 = 1 имеем полностью
неявную схему, при 0 = 0 — полностью явную схему, и при 0 =
= 1/2 — схему Кранка-Николсона.
В соответствии с гармоническим анализом для схемы F.109)
получаем неравенство
1-4GA-0)
откуда
1 < +1, F.110)
причем правое неравенство выполнено всегда.
Левое неравенство имеет место для любых значений сг, если
1/2 ^0^1. Если же вес 0 лежит в пределах 0 ^ 0 < 1/2, то
между а и 0 из левого неравенства устанавливается связь
о-
0^0 < 1/2,
F.111)
2-A-2(9)'
являющаяся условием устойчивости неявно-явной схемы с веса-
весами F.109), когда вес находится в пределах 0 ^ 0 < 1/2.
Таким образом, неявно-явная схема с весами F.109) абсолют-
абсолютно устойчива при 1/2^0^1 и условно устойчива с условием
F.111) при 0 ^ 0 < 1/2.
Рассмотрим порядок аппроксимации неявно-явной схемы
с весами F.109), для чего разложим в ряд Тейлора в окрестности
§ 6.6 ] Конечно-разностный метод решения параболических задач 263
узла (xj,tk) на точном решении значения сеточных функций
uk+1 по переменной t, и^±1, uk±l по переменной х и полученные
разложения подставим в F.109):
ди
~dt
к
3
д2и
" dt2
к
3
=
т
в
• а
д2
дх2
и
+
ди
dt
т + О (г2)
д2и
дх2
+ о (h2).
д2
В этом выражении дифференциальный оператор —^ от
дх
квадратной скобки в соответствии с дифференциальным урав-
уравнением F.1) равен дифференциальному оператору —^ —, в соот-
а оъ
ветствии с чем вышеприведенное равенство приобретает вид
ди
д2и
dt2
2 d2U
1 дх2
д2и
д2и
дх2
После упрощения получаем
-ва'
д2и
дх2
ди 2д2и\к ( 1 \ д2и
откуда видно, что для схемы Кранка-Николсона (в = 1/2) по-
порядок аппроксимации схемы F.109) составляет О (т2 + /г2), т.е.
на один порядок по времени выше, чем для обычных явных или
неявных схем. Таким образом, схема Кранка-Николсона F.109)
при 0 = 1/2 абсолютно устойчива и имеет второй порядок ап-
аппроксимации по времени и пространственной переменной х.
264
Метод конечных разностей
[Гл. VI
Аналогично схема Кранка-Николсона записывается и иссле-
исследуется для других нестационарных уравнений, например для
волнового уравнения.
6.6.3. Метод прямых. Метод прямых представляет собой
метод частичной дискретизации, когда часть дифференциаль-
дифференциальных операторов, входящих в дифференциальную задачу, аппрок-
аппроксимируется с помощью отношения конечных разностей, а осталь-
остальные дифференциальные операторы сохраняются в дифферен-
дифференциальной форме. Ниже рассматриваются два варианта метода
прямых: поперечный и продольный варианты применительно
к эволюционным задачам математической физики (теплопро-
(теплопроводности, малых колебаний и т. п.) с простейшими граничными
условиями первого рода.
В поперечном варианте метода прямых дифференциальные
операторы по времени аппроксимируются с помощью отноше-
отношения конечных разностей, дифференциальные операторы по про-
пространственным переменным сохраняются, а решение отыскива-
отыскивается вдоль прямых t = const (рис. 6.8).
tk+i
Рис. 6.8. Схема поперечного варианта метода прямых
В случае первой начально-краевой задачи для одномерно-
одномерного уравнения теплопроводности F.1)-F.4) этот вариант метода
прямых имеет вид (в уравнении F.1) коэффициент переноса
§6.6] Конечно-разностный метод решения параболических задач 265
примем равным а)
ат \ - uk+1 = -uk + О(т), к = 0,1, 2,. . . , К, F.112)
, Л = 0,1,2,... , X, F.113)
u(l, tk+1) = ик+1{1) = (p2{tk+1), к = 0,1, 2, . . . , К, F.114)
т. е. дифференциальная задача F.1)-F.4) сведена к системе неза-
независимых краевых задач F.112)—F.114) для обыкновенных диф-
дифференциальных уравнений (ОДУ) 2-го порядка в количестве,
равном числу К + 1, с граничными условиями первого рода.
Решением этой системы ОДУ, каждое из которых является
ОДУ второго порядка, будут следующие явные функции:
x,
+1 (х) = С\ ехр(ж/\/~ат )
— \/Bл/ат) ехр(х/л/ат ) • ик(х) ещ>{—х/л/ат)A
j
г
+ \/Bл/ат) ехр(—х/^/ат) • ик(х)
j
к = 0,1,2,... ,К; F.115)
и°(х) = и(х, 0) = ф(х), F.116)
где постоянные интегрирования С\, С2 определяются путем под-
подстановки F.115) в краевые условия F.113), F.114) соответствен-
соответственно при х = 0 и х = I.
Аналогично, в случае первой начально-краевой задачи для
волнового уравнения F.12)—F.16) схема поперечного варианта
метода прямых на неявном шаблоне имеет вид
a2r2 9^ _ uk+1 = _2uk + uk_, +
ОХ
к = 1,2,... ,К; F.117)
266
Метод конечных разностей
[Гл. VI
и(х, 0) = и0 = фг(х);
и(х, г) = и1 = ф\(х) + гф2{х) + О(т2);
u@,tk+1) = uk+1@) =
F.118)
F.119)
F.120)
F.121)
Аналитическое решение краевых задач для ОДУ 2-го порядка
F.117) также не вызывает затруднений.
В продольном варианте метода прямых с помощью отноше-
отношения конечных разностей аппроксимируются пространственные
дифференциальные операторы, а дифференциальные операторы
по времени сохраняются. Решения отыскиваются вдоль прямых
х = const (рис. 6.9).
О у у v v v V V
л | ... •^/—l •*•/ /+1 •*• JV—1 N
Рис. 6.9. Схема продольного варианта метода прямых
В результате получаем следующую задачу Коши для нор-
нормальной неоднородной системы ОДУ (N — 1)-го порядка (на гра-
границах х = 0 и х = I решения известны из левого F.2) и правого
F.3) краевых условий соответственно):
§6.6] Конечно-разностный метод решения параболических задач 267
Ul@) =
Ы*)) + ° W > F.122)
Здесь искомыми являются функции
), u2(t), . . . , UN-i(t). Задачу Коши F.122) можно
представить в следующей векторно-матричной форме:
u'(t) = Аи
и = {и\ и2 . . .
F.123)
х =
-2a2/h2 a2/h2
a2/h2 -2a2/h2 a2/h2
A =
a2/h2 -2a2/h2 a2/h2
a2/h2 -2a2/h2
Ее решение можно найти методом вариации произвольных
постоянных, для чего, интегрируя формально однородную си-
268 Метод конечных разностей [Гл. VI
стему, соответствующую F.123), получим общее решение одно-
однородной системы uoo(t) в виде матричной экспоненты
uoo(t) = [exp (At)] С, С = (Ci... CN-if ,
в котором, разлагая матричную экспоненту в матричный ряд,
получим
^oo(^) — [tii + Л г + -Л г + -Л г + . . . I • О = ?>т • О,
V z о /
где B(t) — функциональная матрица, полученная суммировани-
суммированием ограниченного числа членов ряда.
Поскольку матрица B{t) невырождена (матрица А невы-
невырождена), то определитель этой матрицы, являющийся опреде-
определителем Вронского Wsit) фундаментальной системы решений
однородной системы, соответствующей системе F.123), не равен
тождественно нулю, и, следовательно, в соответствии с методом
вариации произвольных постоянных общее решение uOH(t) неод-
неоднородной системы F.123) выписывается в виде
uOH(t) = B(t)C(t),
где C(t) — вектор-функция (C\{t) C2(t) . . . CN-i(t)) , опреде-
определяемая из решения СЛАУ
B(t) ¦ С'{t) =
откуда
C(t)= l
где D = (Z?i Z?2 • • • Djv-i) — вектор произвольных постоян-
постоянных.
Таким образом, общим решением системы F.123) будет век-
вектор _
I
§6.7] Метод конечных разностей для волнового уравнения 269
где WBj(t), j = 1, N — 1, — определители, получающиеся из
определителя Вронского Weit) заменой j-ro столбца на вектор
правых частей F(t).
Аналогично можно применить продольный вариант метода
прямых к решению первой начально-краевой задачи для волно-
волнового уравнения и к задаче Дирихле для уравнения Лапласа или
Пуассона.
§ 6.7. Метод конечных разностей решения задач
для волнового уравнения с граничными
условиями, содержащими производные
Рассмотрим 3-ю начально-краевую задачу для волнового
уравнения в общем виде:
д2и чд2и . ди _ . /~-,гч~\
—2" = а —ъ + Ь— + си, О < х < /, t > 0; F.125)
^ +aou(O,t) tpl(t), x = 0, <>0; F.126)
ОХ
+ aiu(l,t) <p2{t), x = l, t>0; F.127)
= 0; F.128)
), O^x^l, t = 0. F.129)
Конечно-разностная схема для уравнения F.125) на неявном
шаблоне (рис. 6.3 6):
и^+1 - 2и) + икгХ = с
+ /? («J+!1 - «*+}) + 7 «?+1 + О(т + /г2), i = 1, 7V-1,
А = 1,2,..., a = a2T2/h2, {3 = bT2/2h, j = ct2, F.130)
270
Метод конечных разностей
[ Гл. VI
имеет только первый порядок аппроксимации по времени, а на
явном шаблоне (рис. 6.3 а):
- 2u>j
+ /3 (ukj+l - «}_!) + 7 и) + O(r2 + /i2), j = 1, УУ-1,
А; = 1,2,..., a = a2r2/h2, /3 = Ьт2/21г, 7 = ст2,
— второй порядок. Второй порядок по времени имеет и неявно-
явная схема с весом в = 1/2 (схема Кранка-Николсона):
ц*+1 + 2ц,* + ukfl
=
nk+1 -
2»»J+1
2uj+1
In
+ О(И + Л2), j = 1, TV - 1, Л = 1, 2,...
с шаблоном, представленным на рис. 6.10.
При аппроксимации граничных усло-
условий F.126), F.127), содержащих произ-
производные по пространственным перемен-
переменным, аппроксимация их с помощью от-
ношения односторонних конечных разно-
разностей приводит не только к первому поряд-
порядку аппроксимации по пространственной
переменной (в этом случае аппроксима-
Рис. 6.10. Шаблон схе- Ция всеи начально-краевой задачи имеет
мы Кранка-Николсона порядок O(h\ несмотря на второй поря-
для волнового уравне- дОК аппроксимации во всех внутренних
ния узлах расчетной области), но и к некон-
неконсервативности конечно-разностной схемы, поскольку на про-
пространственных шагах, примыкающих к границам, не учитыва-
учитывается дифференциальное уравнение, т. е. на границах в конечно-
разностной схеме не соблюдаются законы сохранения, на основе
§6.7]
Метод конечных разностей для волнового уравнения
271
которых выведено дифференциальное уравнение. Для устране-
устранения этого явления в конечно-разностной аппроксимации крае-
краевых условий F.126), F.127) учтем дифференциальное уравнение
F.125), для чего сделаем предположение о существовании на
границах производной второго порядка искомой функции u(x,t)
по пространственной переменной, а затем разложим на точном
решении в ряд Тейлора до третьего слагаемого включительно
в окрестности граничных узлов значения сеточной функции и^
к-\-\ /
и и^_^ (т.е. в узлах, непосредственно примыкающих к гранич-
граничным), получим
ил =
_ М1 ди
0 + дх
к+1
к+1^
о Т
F.131)
uk+l -
aN-l ~
N
ди
~dx~
к+1
I
N
N
F.132)
причем производные второго порядка в F.131), F.132) опре-
определим из дифференциального уравнения F.125). В результате
ди к+1 ди ^+1
значения производных первого порядка —— и —— на гра-
дх о дх n
ницах определяются со вторым порядком следующим образом:
ди
~дх~
- Ur,
h - р
2аЛ • р дг
к+1
ch
2а2р
,к+1
ди
дх
к+1
N
.к+1
— U
к+1
N-1
h • q
h
2а
д2и к+1
^~qW
N
ch
2a2q
+ o(/i2), 4 = i + 5>;
Подставляя их в граничные условия F.126), F.127), а затем
аппроксимируя вторые производные по времени на верхнем (к +
+ 1)-м временном слое (т.е. с порядком О(т))\
д2и
dt2
272
Метод конечных разностей
[ Гл. VI
dt2
получим алгебраические уравнения для граничных узлов, каж-
каждое из которых содержит два неизвестных, в следующей форме:
do + О(т + /г2); F.133)
где
= dN + О(т + /г2),
а0 = 0;
F.134)
1
hp
/г
ch
2pr2 2a2p
1
«о;
do =
/г с/г
Для внутренних узлов расчетной сетки неявная конечно-
разностная схема F.130) представляется в виде
= 1,2,... , F.135)
где
= а — /3;
§6.8] Метод установления и его обоснование 273
bj = -2сг -1 + 7;
с j = а + /3;
СЛАУ F.133)-F.135) имеет трехдиагональную матрицу, что
позволяет решать ее на каждом временном слое методом прогон-
прогонки. При к = 1 vP- и и1-, j = О, N, вычисляются в соответствии
с начальными условиями F.128), F.129):
Ua =
^ ^) + O(r2), j = О, N.
Аналогично строятся конечно-разностные аппроксимации со
вторым порядком по пространственной переменной на явном
(рис. 6.3 а) и неявно-явном шаблонах, в частности на шаблоне
(рис. 6.10) для схемы Кранка-Николсона.
§ 6.8. Метод установления и его обоснование
Из теоретических основ механики сплошных сред, и, в част-
частности, из газовой динамики, известно, что в сверхзвуковых тече-
течениях, описываемых уравнениями гиперболического типа возму-
возмущения газодинамических функций, возникающие в какой-либо
точке (например, погрешности численного решения), локализу-
локализуются в так называемом сверхзвуковом конусе Маха, расположен-
расположенном вниз по течению от точки возмущения, с углом раствора,
обратно пропорциональным числу Маха (число Маха — отноше-
отношение скорости течения к скорости звука в среде). В околозвуковых
[трансзвуковых) течениях, описываемых уравнениями параболи-
параболического типа, возмущения локализуются в окрестности точки
возмущения. По этой причине большинство встречающихся на
практике параболических задач хорошо обусловлены по устой-
устойчивости и сходимости.
В дозвуковых газодинамических течениях, описываемых
уравнениями эллиптического типа, возмущения, возникающие
в точке, передаются во все стороны. В соответствии с этим
численные методы в задачах для уравнений эллиптического типа
274 Метод конечных разностей [Гл. VI
плохо обусловлены, поскольку погрешности счета с одинаковой
скоростью передаются как в область, где уже проведен расчет,
так и в область, где расчет еще не проводился. Это затрудняет
применение к эллиптическим задачам так называемых марше-
маршевых методов, когда численное решение осуществляется после-
последовательным переходом от одного пространственного сечения
к другому.
Этот факт стимулировал поиск путей перехода от эллиптиче-
эллиптических задач к эквивалентным (при определенных условиях) па-
параболическим задачам. Оказалось, что решение параболических
задач при t —> оо асимптотически стремится к решению соответ-
соответствующих эллиптических задач, т. е. к решению нестационарных
задач, в которых искомая функция уже не зависит от времени.
В соответствии с этой особенностью нестационарных задач
был разработан и обоснован метод установления. В его разра-
разработке и обосновании активное участие принимали отечественные
математики, и, в частности, С. К. Годунов.
Рассмотрим обоснование метода установления на примере
задачи Дирихле для уравнения Пуассона:
2 v в2 у
q-2 + ^ = ЯЖ' У)> (Ж> У) G fi> F.136)
ox oy
u(x, y)\v = cp(x, у), (ж, у) е Г. F.137)
В соответствии с методом установления вместо задачи
F.136), F.137) рассмотрим следующую начально-краевую зада-
задачу для уравнения параболического типа (двумерного уравнения
теплопроводности), добавив в правую часть уравнения F.136)
дифференциальный оператор —- и дополняя входные данные
однородным начальным условием, сохранив при этом независи-
независимость от времени краевого условия F.137):
dt дх2 ду2 ' ' F138)
(ж, у) G О,
§6.8] Метод установления и его обоснование 275
u(x,y,t)\ = <р(х,у),
F.139)
(х,у) еГ,
|о = О,
F.140)
где О — плоская двумерная область, ограниченная границей Г.
Покажем, что при t —> оо решение задачи F.138)-F.140) стре-
стремится к решению задачи F.136), F.137). С этой целью для задачи
F.136), F.137) введем пространственную сетку с^, на которой
дифференциальную задачу F.136), F.137) будем аппроксимиро-
аппроксимировать с помощью отношения конечных разностей, в результате
чего получим следующее векторно-матричное уравнение:
Аа = /, F.141)
т. е. СЛАУ для функции а(х{, yj).
В соответствии с продольным вариантом метода прямых для
задачи F.138)—F.140) можно записать следующую задачу Коши
для векторно-матричного ОДУ 1-го порядка:
+ A^ f, F.142)
^@) = 0, F.143)
ДЛЯ фуНКЦИИ 1p(Xi, yj,t).
Параллельно рассмотрим задачу на собственные значения
и собственные векторы матрицы А:
Аик = \кик, к = Т^г, F.144)
где и — собственные векторы, А& — собственные значения мат-
матрицы А.
Если матрица А — симметрическая (Л = Лт), положительно
определенная ((Аи, и) > 0), а именно к таким матрицам чаще
всего приводит конечно-разностная аппроксимация дифферен-
дифференциальных задач, то имеется полный вещественный положитель-
положительный спектр А& > 0, к = 1, п, а собственные векторы ик, к = 1, п,
ортогональны.
276 Метод конечных разностей [ Гл. VI
рам ик, получим
Разложим функции ip,a,f в ряд по собственным векто-
uk, F.145)
и\ F.146)
k=l
к=1
/*•"*, F-147)
к=1
где ак = (а,ик), фк = (ф,ик), fk = (f,uh) — коэффициенты
разложений F.145)-F.147).
Для определения коэффициентов ак разложения решения
конечно-разностной задачи F.141) подставим F.145) и F.147)
в F.141), получим
(п \ п
J2ak-uk\ =J2fk-uh,
k=i / к=1
а поскольку
п
fc) = 5>,.(A,^),
TO
k=l k=l
откуда следует, что
F.148)
поскольку ик, к = 1, п, ортогональны, и, следовательно, линейно
независимы.
§6.8] Метод установления и его обоснование 277
Таким образом, решение F.145) стационарной задачи F.136),
F.137) с учетом F.148) приобретает вид
Подставим теперь F.146), F.147) в задачу Коши F.142),
F.143), получим
к = 1 / \к = 1 / к = 1
к=1
Поскольку собственные векторы ик линейно независимы, то,
учитывая равенство Аик = \kUk, получим следующую задачу
Коши для функции
F.150)
dt
^,@) = 0, fc = l~rc, F.151)
решением которой является функция
фк(Ь) = у- A - exp (-Xkt)) . F.152)
Подставляя F.152) в разложение F.146), получим решение
задачи F.142), F.143), а следовательно, и задачи F.138)-F.140)
в виде
ик. F.153)
Для положительно определенных матриц А все собственные
значения положительны, и, следовательно, при t —» ос из F.153)
получаем решение
п
ф = Х^А.ик F.154)
278 Метод конечных разностей [ Гл. VI
совпадающее с решением F.149) стационарной задачи F.136),
F.137).
Таким образом, вместо решения задачи Дирихле F.136),
F.137) можно решать нестационарную задачу F.138)-F.140) для
двумерного уравнения теплопроводности при больших значе-
значениях времени. Решение останавливается тогда, когда оно уже
несущественно изменяется по времени.
При этом для нестационарной задачи F.138)-F.140) можно
использовать богатейший арсенал численных методов, включая
методы расщепления.
ГЛАВА VII
МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ РЕШЕНИЯ
МНОГОМЕРНЫХ ЗАДАЧ МАТЕМАТИЧЕСКОЙ
ФИЗИКИ. МЕТОДЫ РАСЩЕПЛЕНИЯ
Программа
Экономичность конечно-разностных схем для многомерных урав-
уравнений математической физики. Методы матричной прогонки, пере-
переменных направлений Писмена-Рэчфорда, дробных шагов Н. Н. Янен-
ко, центрально-симметричный А. А. Самарского, переменных направ-
направлений с экстраполяцией В. Ф. Формалева и полного расщепления
Формалева—Тюкина. Методы расщепления численного решения эллип-
эллиптических задач. Численные методы решения задач для многомерных
уравнений гиперболического типа: метод характеристик решения ква-
квазилинейных гиперболических систем, метод С. К. Годунова. Задача
о распаде произвольного разрыва.
При численном решении многомерных задач математической
физики исключительно важным является вопрос об экономично-
экономичности используемых методов.
Конечно-разностную схему будем называть экономичной,
если число длинных операций (операций типа умножения) про-
пропорционально числу узлов сетки.
За последние 50 лет разработано значительное количество
экономичных разностных схем численного решения многомер-
многомерных задач математической физики, основанных на расщепле-
расщеплении пространственных дифференциальных операторов по ко-
координатным направлениям и использовании метода скалярной
прогонки вдоль этих направлений. При этом большинство раз-
разработанных схем активно используют явную аппроксимацию
дифференциальных операторов, и поэтому при определенных
соотношениях сеточных характеристик в задачах с граничными
условиями, содержащими производные, или в задачах, содержа-
содержащих смешанные производные, такие схемы становятся условно
устойчивыми [10-16].
280 Метод конечных разностей. Методы расщепления [Гл. VII
Из экономичных конечно-разностных схем, получивших наи-
наибольшее распространение, в данной главе рассматриваются сле-
следующие:
— схема метода переменных направлений Писмена-
Рэчфорда A955г.);
— схема метода дробных шагов Н. Н. Яненко A956 г.);
— схема центрально-симметричного метода А. А. Самарско-
Самарского A958 г.).
Эти схемы аппроксимируют смешанные дифференциальные
операторы на нижних временных слоях (явным образом), что
при определенных условиях может приводить к неустойчивости
решения. От этих недостатков свободны следующие экономич-
экономичные, абсолютно устойчивые методы:
— метод переменных направлений с экстраполяцией
В.Ф. Формалева A987г.) [17-19];
— метод полного расщепления Формалева-Тюкина A996 г.)
[20-21].
Все эти методы будем называть общим термином — методы
расщепления.
Среди неэкономичных, полностью неявных, а потому абсо-
абсолютно устойчивых, методов можно отметить метод матричной
прогонки.
Рассмотрим эти методы на примере задачи для двумерного
уравнения параболического типа в прямоугольнике со сторона-
сторонами ^i, ?2 и граничными условиями 1-го рода.
Рассматриваемые методы можно использовать и для эллип-
эллиптических задач, если с помощью метода установления (§ 6.8) све-
свести их к параболическим задачам, а также для гиперболических
задач.
Для пространственно-временной области Gt = Gx [0,T],tG
G [0, T], G = G + Г, G = i\ x I2, рассмотрим следующую задачу:
?т = а(й + й)> xe(o,h), ye(o,?2), о 0; G.1)
ot \ox oy J
u(x,0,t) = <p1(x,t), x€[0, ?1], y = 0,t>0; G.2)
:,t), x€[0,?i], y = h, О 0; G.3)
;), x = 0,y€[0,?2], O0; G.4)
§7.1]
Метод матричной прогонки
281
,t), x = ?1,y€[0,e2], t>0; G.5)
и(х,у,О) = ф(х,у), хе [0,4], у€[0,?2], * = 0. G.6)
Введем следующую пространственно-временную сетку с ша-
шагами /ii, /12, т соответственно по переменным ж, у, t:
u)h1,h2 = \xi = ^Ь^ = 0,/; ж^- =
= fcT, Л = 0,1,2,...}, G.7)
и на этой сетке будем аппроксимировать дифференциальную
задачу G.1)—G.6) методом конечных разностей на верхнем вре-
временном слое tk+1 = (к + 1)т:
h\
Ь+1 - 2ик+1 + ик+1
lk+1)
i = 1, / - 1 ; j = 1, J - 1; Л = 0,1, 2,. . . ; G.8)
modi- ik+1)-
iJ
V>T А =
uyj), г = 0,/; j = 0, J.
7.1. Метод матричной прогонки
Выберем три произвольных сечения i — 1,г,г + 1,г = 1,/ — 1,
и запишем неявную схему G.8) в следующей векторно-матричной
форме:
где Л^, Bi, Сi — квадратные матрицы размера J — 1 вида
ах 0 ... О
О ах ... О
О 0 ... G1
282
Метод конечных разностей. Методы расщепления
[Гл. VII
Gi = —^ сг2 = —2" — сеточные числа Куранта; г^_х,
,k+l
г = 1,7 — 1, — векторы значений сеточной функции размера
/1 7|fc+i _ f7|fc+i7|fc+i 7|fc+i АТ. Е7. 7- _ 1 г _ 1 _ RPK
j 1, гб^ — i ^iX г^2 . . . uiJ_1\ , гг, г — 1, i 1, век-
векторы правых частей размера J - 1, Fj = (/^i /г2 ... fij-\)T.
Из векторно-матричной СЛАУ G.9) видно, что матрица
СЛАУ представляет собой трехдиагональную матрицу, на глав-
главной диагонали которой стоят матрицы В{, г = 1,7 — 1 , на
нижней диагонали — матрицы А{, г = 1, 7 — 1 , а на верхней
диагонали — матрицы С^,
в2 с2
Л3 В3 С3
i В,
F2
Fl-2
, G.10)
A\ = 6, Сi-\ = 6,6 — нулевая матрица.
Матрица А\ равна нулевой матрице, поскольку при г = 1
первое матричное уравнение системы G.9) имеет вид
§7.1] Метод матричной прогонки 283
4+1 = ^з (у,, tk+1) , з = 1^=1, G.П)
т. е. после вычисления вектора F\ с помощью матрицы А\ в урав-
уравнении G.11) матрицу А\ можно положить равной нулевой мат-
матрице в.
Аналогично, матрица С\ _ i равна нулевой матрице, посколь-
поскольку последнее уравнение системы G.9) имеет вид
j = l,J-l, G.12)
т.е. после вычисления вектора F/_i с помощью матрицы С\-\
последнюю можно принять равной нулевой матрице в.
Как видно теперь, система G.9) или G.10) по форме совпада-
совпадает с системой B.1) для одного координатного направления, и эту
систему формально можно решить с помощью метода прогонки.
Будем искать решение системы G.9) в виде
^ Qi, i = 1,7-1, G.13)
где Pi — прогоночные матрицы, Qi —прогоночные векторы.
Для определения Р^, Qi выразим из G.11) и^+1 через
получим
откуда, сравнивая с G.13) при г = 1, находим
Рл — В~1Пл Oi — R~LFi 7//c+1 — Рл ?//c+i 4- Пл G ЛА\
Выразим из 2-го уравнения системы G.9) ?i2+ через и^ :
откуда
г4+1 = (Б2 - Л2Р1Г1 C2uk+1 + (В2 - ^Pi) (F2 + A2Qi),
Р2 = (Б2 - ЛгР!)^; Q2 = (В2 - Л2Р1) (F2 + A2Qi).
G-15)
Продолжая этот процесс, получим
Р»# / г>. Л.р. А /^. • /^). ( T-Z ¦ А • Р- \ ( Т-Р- —\— Л • Г^) • \
г = 1, / — 1, G.16)
284 Метод конечных разностей. Методы расщепления [Гл. VII
причем при г = 1 эти выражения трансформируются в G.14),
поскольку А\ = в. При г = I — 1, P/_i = #, поскольку C/_i = #,
тогда
Q/-1 = (Б7_! - Л/_1Р/_2)-1(Р/_1 + A/.iQ/.a). G.17)
После вычисления выражений G.16), G.17) прямой ход мето-
метода матричной прогонки завершен. Обратный ход по определению
векторов Ui, i = I — 1, / — 2, ... , 1, осуществляется с помощью
равенств G.13):
G.18)
К достоинству метода матричной прогонки относится его
абсолютная устойчивость, поскольку аппроксимация осуществ-
осуществляется на верхнем временном слое (неявно) с порядком
О{т +|/i|2), \h\2 = hl + hl
а к недостатку — его неэкономичность, поскольку метод вклю-
включает в себя обращение матриц вида Pi = Bi — А{Р^-\.
§ 7.2. Метод переменных направлений
Писмена—Рэчфорда
В схеме метода переменных направлений (МПН), как и во
всех методах расщепления, шаг по времени т разбивается на
число, равное числу независимых пространственных переменных
(в двумерном случае — на два). На каждом дробном временном
слое один из пространственных дифференциальных операторов
аппроксимируется неявно (по соответствующему координатному
направлению осуществляются скалярные прогонки), а остальные
явно. На следующем дробном шаге следующий по порядку диф-
дифференциальный оператор аппроксимируется неявно, а осталь-
остальные — явно и т. д. В двумерном случае схема метода переменных
направлений для задачи G.1)-G.6) имеет вид
§7.2]
Метод переменных направлений Писмена-Рэчфорда
285
и
fc + 1/2
Li, G-19)
т/2
i+lj
a ( к
•A)- G-20)
В подсхеме G.19) на
первом дробном шаге
т/2 оператор
аппроксимируется
д2
а оператор а —^
а- о
неявно,
— явно
= 1,7-1, j = 1,J-1,
на временном полуслое
В подсхеме G.20) опера-
д2
(в результате весь конечно-
разностный оператор по
переменной у переходит
в правые части, поскольку
и\- известно). С помощью х
скалярных прогонок
в количестве, равном
числу J — 1, в направлении
переменной х получаем
распределение сеточной
функции г?- 2, г =
У
Рис. 7.1. Шаблон схемы метода пере-
переменных направлений
тор а-
ду
tk+1 = L
аппроксимируется неявно на верхнем временном слое
j а оператор а
дх1
— явно в момент времени
j.k+i/2 _ j.k _^_ T j2 (конечно-разностный аналог этого оператора
переходит в правые части). С помощью скалярных прогонок
в направлении переменной у в количестве, равном числу 7 — 1,
получаем распределение сеточной функции u-fl, i = 1,7 — 1,
х-.
286 Метод конечных разностей. Методы расщепления [Гл. VII
j = 1, J — 1, на полуслое tk+1 = tk+1/2 + r/2. Шаблон схемы
МПН представлен на рис. 7.1.
Исследуем схему МПН G.19) , G.20) на порядок аппроксима-
аппроксимации и устойчивость, для чего запишем ее в следующей оператор-
операторной форме:
Uk+1^uk G.21)
G.22)
uk+1 _ uk+1/2
T I
где Ai = a—?, A2 = a—5, и = (unui2 . . . uj-u-i
Исключим из равенств G.21), G.22) сеточную функцию
fl/2
в виде
uk+i/2 на промежуточном временном слое, для чего запишем их
=(Е+ Т-\2) ик, G.23)
- Т-А2) ик+1 =(Е + |Ai) uk+1/2, G.24)
где Е — тождественный оператор (например, единичная матри-
матрица). Умножим G.23) слева на оператор ( Е + —А\ J, а G.24) — на
оператор (Е Ai j и, складывая результаты, получим
(Е - lAj) (Е - Т-А2) ик^ =(Е+ т-А,) (е + Т-А2) ик,
G.25)
т. е. G.25) является уже двухслойной схемой. Раскроем в G.25)
скобки и разделим полученное выражение на т:
Агик) + I (\2ик^ + \2ик) -
fc+1 - ик) . G.26)
В векторно-операторном равенстве G.26) первые два сла-
слагаемых в правой части аппроксимируют дифференциальные
д2и д2и
операторы —^ и —^ по схеме Кранка-Николсона с поряд-
дх ду
ком 0{т2 + \h\ ), а последнее слагаемое мож:но представить
§7.2]
Метод переменных направлений Писмена-Рэчфорда
287
как —-А±А2щ = 0(т2), поскольку щ =
разностная производная по времени. Поэтому
.к
- ик
— конечно-
- ик
AlUk) + \
А2ик)
т. е. схема МПН имеет второй порядок по времени и поэтому
является высокоточной.
Исследуем устойчивость схемы G.19) , G.20) методом гармо-
гармонического анализа, для чего вместо значений сеточной функции
подставим гармонику
uij = Vk ехр [г
Xi + XmVj)], G.27)
получим для подсхемы G.19) равенство
Vk+1/2 ~ Vk = <JiVk+i/2 [exp(^n^i) "" 2 + ехр (—iXnhi)] +
+ сг2г]к [ехр (iXmh2) - 2 + ехр (-iXmh2)] ,
откуда (см. п. 6.5.2)
Vk + l/2
Vk
1 — G2
где bi = 4 sin2 -JL-L\ b2 = 4 sin
Г1л
ar
ar
Аналогично, подставляя гармонику G.27) в подсхему G.20),
получим
Vk+i
Vk + l/2
Тогда отношение амплитуд
Vk
гармоник будет равно
Vk+i
Vk
Vk+i
Vk + 1/2
Vk + 1/2
Vk
1 — 0 ftl 1 — <72&2
l + 0-lftl 1-
< 1. G.28)
Отсюда видно, что схема МПН абсолютна устойчива.
Проанализируем выражение G.28). Из него видно, что ослаб-
ослабление устойчивости по переменной у в подсхеме G.19) (уменьше-
(уменьшение числителя второго сомножителя) компенсируется большим
усилением устойчивости по направлению у в подсхеме G.20)
288 Метод конечных разностей. Методы расщепления [Гл. VII
(знаменатель второго сомножителя). Аналогично для перемен-
переменной х. Ослабление устойчивости по переменной х в подсхе-
подсхеме G.20) (уменьшение числителя первого сомножителя) компен-
компенсируется большим усилением устойчивости по направлению х
в подсхеме G.19) (знаменатель первого сомножителя).
Таким образом, в схеме метода переменных направлений
ослабление устойчивости по какому-либо направлению, вслед-
вследствие явной аппроксимации по этому направлению, компенси-
компенсируется увеличением устойчивости по другому направлению. Из-
за этого явления МПН не применяется к трехмерным задачам,
поскольку в этом случае он становится условно устойчивым.
К достоинствам метода переменных направлений можно от-
отнести высокую точность, поскольку метод имеет второй порядок
точности по времени. При малых числах Куранта а± <С 1, сг2 <С 1
с помощью МПН в двумерном случае можно тестировать другие
численные схемы.
К недостаткам можно отнести условную устойчивость при
числе пространственных переменных больше двух. Кроме этого,
МПН условно устойчив в задачах со смешанными производными
уже в двумерном случае. Таким образом, запас устойчивости
у метода довольно низок. Можно показать, что в задачах с крае-
краевыми условиями 2-го или 3-го рода схема МПН также условно
устойчива.
§ 7.3. Метод дробных шагов Н. Н. Яненко
В отличие от МПН, метод дробных шагов (МДШ) исполь-
использует только неявные конечно-разностные операторы, что делает
его абсолютно устойчивым в задачах, не содержащих смешан-
смешанных производных. Он обладает довольно значительным запасом
устойчивости (сохранение устойчивости при числах Куранта,
значительно превышающих единицу) и в задачах со смешанными
производными.
Для задачи G.1)-G.6) схема МДШ имеет вид
/с + 1/2 k
1а аа о,
L2
§7.3]
Метод дробных шагов Н. Н. Яненко
289
С помощью чисто неявной подсхемы G.29) осуществляются
скалярные прогонки в направлении оси х в количестве, равном
J — 1, в результате чего получаем сеточную функцию и{- ' .
На втором дробном шаге по времени с помощью подсхемы G.30)
осуществляются скалярные
прогонки в направлении оси у
в количестве, равном / — 1,
в результате чего получаем
сеточную функцию и^1.
Шаблон схемы МДШ
приведен на рис. 7.2.
Для определения порядка
аппроксимации схемы МДШ
запишем ее в следующей
операторной форме:
- ик+1'2
-=Л2« , Q
(Е - тЛ2) и = Ей + ' . Рис. 7.2. Шаблон схемы метода дроб-
ных шагов
Исключая здесь сеточную
функцию на промежуточном временном слое
получим двухслойную схему
(Е - тАг) (Е - тЛ2) ик+1 = Еик,
откуда получаем порядок аппроксимации по времени:
(Е-т (Лх + Л2) + т2Л!Л2) ик+1 = Еик,
= tk -\— ,
ик+1 - ик
= \lUk+1 + \2uk+1 -
G.31)
Из G.31) видно, что схема МДШ G.29), G.30) имеет порядок
O(r + |/i| ), т.е. первый порядок по времени и второй — по
переменным хну.
10 В.Ф. Формалев, Д.Л. Ревизников
290 Метод конечных разностей. Методы расщепления [Гл. VII
Для исследования устойчивости схемы МДШ G.29), G.30)
подставим в нее гармонику G.27), получим
Ьг = 4 sin2 ^i > 0;
Vk+1/2 — 0f?ife+l( —62)? ^2 = 4 Sin2 ^ > 0.
Тогда отношение амплитуд гармоник равно
1 1
Vk+i
Vk
Vk+i
Vk + l/2
Vk + 1/2
rjk
т. е. схема метода дробных шагов абсолютно устойчива.
Достоинства схемы МДШ: 1) проста в алгоритмизации
и программировании; 2) абсолютно устойчива с большим запасом
устойчивости даже для задач, содержащих смешанные производ-
производные.
Недостатки: 1) на каждом дробном шаге достигается ча-
частичная аппроксимация, полная аппроксимация достигается на
последнем дробном шаге; 2) имеет первый порядок точности по
времени; 3) в задачах со смешанными производными для устой-
устойчивости МДШ на коэффициенты накладываются жесткие огра-
ограничения, при невыполнении которых схема становится условно
устойчивой.
§ 7.4. Метод переменных направлений
с экстраполяцией В. Ф. Формалева
Как видно из изложенных выше конечно-разностных схем
для многомерных задач математической физики, конечно-
разностная схема может быть либо абсолютно устойчивой, но не
экономичной (метод матричной прогонки), либо экономичной, но
условно устойчивой, как схема МПН. Желание получить схемы
экономичные и одновременно абсолютно устойчивые с большим
запасом устойчивости приводит к необходимости использовать
апостериорную информацию о сеточной функции, которая полу-
получается в процессе счета. К таким схемам относится схема метода
переменных направлений с экстраполяцией (МПНЭ). Эта схема
использует распределение сеточной функции в левом (от рас-
расчетного) пространственном сечении, уже полученное на верхнем
временном слое, т. е. неявно. В правом пространственном сечении
§7.4] Метод переменных направлений с экстраполяцией 291
значения сеточной функции в первом приближении и с кон-
контролируемой точностью определяются линейной экстраполяцией
по времени с нижних временных слоев на верхний. Затем эти
значения уточняются с помощью скалярных прогонок.
Рассмотрим задачу, аналогичную задаче G.1)-G.6), в кото-
которой дифференциальное уравнение G.1) содержит смешанные
производные (наличие последних не обязательно):
ди д2и Л д2и д2и
--11вж2 ¦ —дхду ¦ —ду^
xe@;h), ye@;?2), t > 0. G.32)
На сетке G.7) аппроксимируем это дифференциальное урав-
уравнение с помощью следующей схемы:
п.к
4hih
CL22
%•-! J ' G-33)
G-34)
Здесь значения сеточной функции й^-, помеченные волнистой
чертой, определяются с помощью линейной экстраполяции:
о к к-1/2 . Л . . . -,
= 2umj+i ~ umj+i , rn = г - 1, г, г + 1,
ю*
292
Метод конечных разностей. Методы расщепления [Гл. VII
Шаблон схемы МПНЭ представлен на рис. 7.3
i+l j-
-- k+\
it+1/2
i+l j+\ <^>—Узлы с известными значениями
к о — Узлы с неизвестными значениями
X — Узлы с экстраполяционными
значениями
Рис. 7.3. Шаблон схемы метода переменных направлений с экстраполяцией:
а — подсхема G.33); б — подсхема G.34)
В подсхеме G.33) значения ui_1
к+1/2 к+1/2 к+1/2
l u
являются
искомыми, определяемыми из скалярных прогонок в направле-
к+1/2 к+1/2 к+1/2
нии переменной х , значения иг_г '._1? иг-[ , ui+1 /-1 уже извест-
известны на верхнем полуслое из прогонки вдоль координатной линии
/. -,ч7 ~к+1/2 ~к+1/2 ~к+1/2
Уj-1 = (j - 1)^2, а значения г^_^-+1, uij+{ , ui+1'j+1 с порядком
О(т2) определяются экстраполяцией по распределениям функ-
функции на двух предыдущих временных полуслоях. При этом все
конечно-разностные операторы по пространственным перемен-
переменным, за исключением оператора по переменной ж, переводятся
в правые части (хотя они и являются практически полностью
неявными).
В подсхеме G.34) значения ^Й, u\tX-> uit+i являются ис-
искомыми, определяемыми из скалярных прогонок вдоль перемен-
переменной у, значения ui^h_1, Ui-ij, ^^i?+i известны как значения
сеточной функции в левом пространственном сечении, а зна-
~к-\-Л ~к-\-\ ~к-\-Л /^л / 9\
чения ui^1j_1, u^j, иг+ц+1 с порядком О[тА) определяются
экстраполяцией по двум предыдущим временным полуслоям.
При этом все пространственные операторы, за исключением опе-
оператора по переменной у, переводятся в правые части, хотя они
практически являются полностью неявными.
§ 7.4 ] Метод переменных направлений с экстраполяцией 293
7.4.1. Аппроксимация. Для анализа аппроксимационных
свойств схемы G.33), G.34) прибавим и вычтем в подсхеме G.33)
«22 k+1/2 2а12 ( k+1/2 k+1/2 \
выражения —^-и--,\ , ——— \и-,Л'-,Л —и-л'-,л , а в подсхеме
G.34) — выражения —у^^Н, ~l~t~ \ui+ij+i ~ ui+ij-i)' полу-
получим эквивалентную схему
-(Г22 + 2Г{2)й*+1/2) G.35)
г/2
+ 1 _,,А+1/2
^-^ = Аик+1 + (Гц + 2Г{27) «fc+1, G.36)
где Л = Лц + 2Ai2 + Л22,
Ли и = ^
^ (
4ftift2
fc+l/2
rn ?7/c+i _ 2ai2 Г
12 ~ 4/z^^
Справедлива следующая теорема.
Теорема 7.1. Пусть решение задачи G.32), G.2)-G.6)
u(x,y,t) € С| (GT), где GT==Gx [0,T], t € [О, Г], С™ -
тсласс функций, т раз непрерывно дифференцируемых по t и п
раз — по ж, у. Тогда схема G.33), G.34) и, следовательно, эк-
эквивалентная ей схема G.35), G.36) аппроксимирует на точном
294 Метод конечных разностей. Методы расщепления [Гл. VII
решении дифференциальную задачу G.32), G.2)-G.6) с порядком
О(т + |/1|2 + т(/ц + /12)), где \h\2 = h\ + h\.
Доказательство. Действительно, рассматривая «оско-
«осколочные» операторы Г22, Г^2, Гц, Г^2, можно заметить, что
выполняются следующие тождества :
fc+1/2 и _
к-1/2 _
k к к-1/2 к-1/2
- (uk+i
fe+l/2 _ jfe _
Uilj
r/2 ~AM ' r/2
- Uij) _ _ {Ujj - Ujj-i)
. U fi —
h2
k-l/2\
fti rA/4
a12r
<та = -п-Г, г = 1,2,
Тогда справедлива следующая цепочка равенств:
7.4 ] Метод переменных направлений с экстраполяцией 295
_ *-l/2\ _
\Uij + l ZUIJ + 1 + U )
f [(
__О22 / fc+l/2_ fe
- h2 \Uij + l ZUIJ + 1
f
rI ~
1 12U
Таким образом,
T22uk+l'2 = -^AV+1/2 + О (rh2). G.37)
Аналогично,
Гцй*+1 = -^^A2mA;+1 + O(t/ii); G.38)
fc+1/2 „ fc fc-l/2
- 2u + u
296 Метод конечных разностей. Методы расщепления [Гл. VII
k к \ T2hi
к \ T2
= -2G12 (иких + и* г) rhx - ^f (ukttxy - икШу) г2 =
= О (г/ц + г2) ; G.39)
гЦйк+1 = О (rh2 + г2) . G.40)
Подставляя выражения G.37)-G.40) для «осколочных» опе-
операторов в схему G.35), G.36) , получим
т/2 2
+ \h\2 + r(h1 + h2) + г2) , G.41)
Gц
= AuAu +
r/2 2
+ О (т + \h\2 + r (fci + /г2) + r2). G.42)
Исключение сеточной функции г^+1/2 на промежуточном
временном полуслое приводит к следующей эквивалентной двух-
двухслойной схеме:
uk+1 - uk
/ , G.43)
где а = сгц + a22 > 0, b = аца22 > О.
Из G.43) следует аппроксимация с порядком Оут + \h\ +
+ т (h\ + h2) \. Теорема доказана.
7.4.2. Устойчивость. Будем исследовать устойчивость
схемы G.33), G.34) методом энергетических неравенств.
Имеет место следующая теорема.
Теорема 7.2. Пусть выполнены условия ац > 0, а22 > 0.
Тогда схема G.33), G.34) абсолютна устойчива по начальным
условиям.
§ 7.4 ] Метод переменных направлений с экстраполяцией 297
Для доказательства этой теоремы докажем следующую
лемму.
Лемма 7.1. Оператор
[2 3 1
- A + (ГЦ + СГ22) ^Л + ((ГЦ + СГ22) уЛ2 - С^3
в эквивалентной схеме G.43) является положительно опреде-
определенным и самосопряженным.
Действительно, этот оператор можно переписать в виде
C = {l + a)T-A + a1jA2 + bT^A\
в котором каждое слагаемое является положительно определен-
определенным и самосопряженным оператором, поскольку — Л = А — по-
положительный, самосопряженный оператор, действующий в гиль-
гильбертовом пространстве Н (см. гл. 6). Следовательно, оператор С
является положительно определенным, самосопряженным опе-
оператором, что доказывает лемму.
Таким образом, G.43) можно переписать в виде
k-\-l к
{ии)
Умножая это равенство скалярно на щ = и ис-
т
пользуя известные тождества
„*+!_ (uh+1+uh) , («»+1-f*) _ («fc+1+Q тщ
U - 2 + 2 - 2 + 2 '
получим следующее энергетическое тождество:
([я + т- (А + АС)] щ, щ) + ^ [((А + AC) uk+\ uk+1) -
=0, G.44)
при выводе которого использована положительность и самосо-
самосопряженность оператора D = А(Е + С).
Вводя энергетическое пространство Н^> элементов и, v, ...
. . . ? Hd со скалярным произведением (гх, г>)^ = (Du, v) и нор-
нормой ||ix||D = (Du,u), в силу положительности оператора Е +
-\— (А + АС) из G.44) получаем энергетическое неравенство
(Оик+\
298 Метод конечных разностей. Методы расщепления [Гл. VII
откуда следует принцип максимума
являющийся достаточным признаком устойчивости конечно-
разностной схемы G.33), G.34), что доказывает теорему.
Поскольку не накладывалось никаких ограничений на се-
сеточные характеристики т, /ii, /12, схема G.33), G.34) является
абсолютно устойчивой.
По запасу устойчивости метод МПНЭ превосходит все суще-
существующие экономичные методы расщепления для задач как со-
содержащих, так и не содержащих смешанные дифференциальные
операторы.
К достоинствам МПНЭ можно отнести следующие: 1) эко-
экономичность; 2) абсолютную устойчивость; 3) полную (не частич-
частичную, как в МДШ) аппроксимацию дифференциального урав-
уравнения; 4) применимость к задачам с любой размерностью по
пространственным переменным и к задачам, содержащим сме-
смешанные дифференциальные операторы; 5) отсутствие ограниче-
ограничений на величину коэффициентов ац, ai2, &22, кроме ограничений
ЙЦ > 0, 0-22 > 0, СЬцСЬ22 > tt12"
§ 7.5. Схема метода полного расщепления
Формалева—Тюкина
Аналогичной схемой, использующей апостериорную инфор-
информацию, является схема метода Формалева-Тюкина. Эта пол-
полностью неявная, но экономичная схема основана на более глу-
глубоком расщеплении смешанных дифференциальных операторов
по сравнению со схемами, разобранными выше.
Для задачи G.32), G.2)-G.6) на сетке G.7) эта схема имеет
следующий вид [20,21]:
fe + l/2 k
^^ a
fc+1/2 fc+1/2 fc+1/2
-u-u
G-45)
§7.5] Схема метода полного расщепления Формалева-Тюкина 299
h22
uk+1
1-сг
2 /iii
причем a = —1, если ayi < 0, cr = 1, если ai2 > 0. Значения
ац > 0, a22 > 0, ац * &22 — ^12 > 0- Коэффициент а введен для
того, чтобы анализ устойчивости не зависел от знака коэффи-
коэффициента ai2-
Шаблоны схемы G.45), G.46) приведены на рис. 7.4.
Я;
О—
У
i+l j
о=1
D
Q
ij-l i+l 7-1
а
У
i-l 7+1
a=l
О
i+l 7+1
a=-l
* У-16
? — Узлы с известными значениями
О— Узлы с искомыми значениями
Рис. 7.4. Шаблоны схемы полного расщепления: а, б — подсхема G.45); в,
г — подсхема G.46)
Подсхема G.45) реализуется с помощью скалярных прого-
прогонок в направлении координатной оси Ож, при этом значения
сеточной функции в нижнем (j — 1)-м сечении уже известны на
300 Метод конечных разностей. Методы расщепления [Гл. VII
верхнем временном полуслое. В подсхеме индекс г изменяется от
1 до / — 1, а индекс j — от 1 до J — 1.
Подсхема G.46) реализуется с помощью скалярных прогонок
в направлении координатной оси Оу, при этом значения сеточ-
сеточной функции в левом (г — 1)-м сечении (шаблон 7.4 в) или в пра-
правом (г + 1)-м сечении (шаблон 7.4 г) уже известны на верхнем
временном слое.
В подсхеме индекс j изменятся от 1 до J — 1, а индекс г — от
1 до / — 1 (шаблон 7.4 в) или от / — 1 до 1 (шаблон 7.4 г).
Таким образом, схема полного расщепления G.45), G.46) яв-
является экономичной, поскольку реализуется с помощью скаляр-
скалярных прогонок, несмотря на то что дифференциальное уравне-
уравнение содержит смешанные производные, и полностью неявной,
вследствие чего можно ожидать, что схема является абсолютно
устойчивой.
Как и схема метода дробных шагов Н. Н. Яненко, схема G.45),
G.46) обладает частичной аппроксимацией на каждом дробном
шаге и полной аппроксимацией — на целом шаге по времени.
Разлагая значения сеточной функции в окрестности узла
(ж^, yj, tk) на точном решении в ряд Тейлора до второй про-
производной по времени и до четвертой производной по простран-
пространственным переменным, можно показать, что порядок полной
аппроксимации в схеме G.45), G.46) составляет О (т + h\ + h^).
Аналогично схеме G.33), G.34) с помощью метода энерге-
энергетических неравенств можно показать абсолютную устойчивость
схемы G.45), G.46) полного расщепления.
Таким образом, за счет более глубокого расщепления смешан-
смешанного конечно-разностного оператора в рассматриваемой схеме
удалось смешанные производные аппроксимировать неявно, чего
не достигалось в классических схемах, рассмотренных выше.
В соответствии с этим достоинствами схемы полного расщеп-
расщепления являются следующие:
— экономичность;
— неявная аппроксимация всех дифференциальных операто-
операторов, включая смешанные и, как следствие, абсолютная устойчи-
устойчивость;
— применимость схемы к задачам любой размерности по
пространственным переменным;
§7.7] Методы решения задач для уравнений гиперболического типа 301
— отсутствие ограничений на величину коэффициентов ац,
&12 = &2Ъ а22, за исключением естественных ограничений вида
ац > 0, а22 > 0, \
§ 7.6. Методы расщепления численного решения
эллиптических задач
Для стационарных многомерных задач математической фи-
физики искомая функция не зависит от времени и, следователь-
следовательно, уравнение G.1) в задаче G.1)-G.6) становится уравнением
эллиптического типа (нет производной -^-), т.е. уравнением
Лапласа или Пуассона, а поскольку и начальное условие G.6) от-
отсутствует, то рассмотренные выше методы приходится несколько
видоизменить.
Однако если при решении задач для уравнений Лапласа или
Пуассона используется метод установления (см. § 6.8), то ста-
стационарное уравнение Лапласа или Пуассона трансформируется
в нестационарное уравнение G.1), являющееся уже уравнени-
уравнением параболического типа, с введением однородного начального
условия G.6), т.е. ф(х,у) = 0. В этом случае все вышерассмот-
ренные методы применяются без изменения.
Методы расщепления напрямую можно применять также
и к решению стационарных задач, заменив номер временного
слоя номером итерации. При этом в соответствующем конечно-
разностном методе конечно-разностная производная по времени
— будет отсутствовать.
В качестве начального приближения на нулевой итерации
можно использовать линейную интерполяцию краевых условий
G.2)-G.5) так, как это делалось в разностно-итерационном ме-
методе Либмана (п. 6.2.3).
§ 7.7. Методы решения задач для уравнений
гиперболического типа
Одним из наиболее мощных методов решения задач для урав-
уравнений гиперболического типа является метод характеристик,
применимый как к задачам с начальными условиями, так и
к краевым задачам и начально-краевым задачам [22], [23].
302 Метод конечных разностей. Методы расщепления [Гл. VII
В п. 6.1.2 задача для волнового уравнения сводилась к анало-
аналогичной задаче для гиперболической системы, которая могла быть
решена численно конечно-разностным методом. В более общей
постановке квазилинейные гиперболические системы описывают
газодинамические течения с вектором скорости, имеющим ком-
компоненты и(х,у) и v(x^y) в плоской системе координат хОу.
7.7.1. Метод характеристик решения квазилинейных
гиперболических систем. Рассмотрим следующую систему
дифференциальных уравнений в частных производных.
где и, v — искомые функции переменных ж, у ; а^, b^j, h 3 —
= 1,2 — коэффициенты, С{ — правые части, а их, vx, uy, vy —
частные производные первого порядка. В общем случае а^-, 6^-,
г, j = 1,2, с^, г = 1,2 являются функциями ж, у, и, v. Такие
системы называют квазилинейными (линейными относительно
первых производных их, г>ж, иу, vy).
Пусть в плоскости хОу задана кривая Г уравнением у =
= у(х) и пусть в точках этой кривой заданы значения функций
и(х,у{х)), v(x,y(x)) (рис. 7.5).
Поставим задачу: по значениям решения и(х,у), v(x,y) на
кривой Г найти на той же кривой значения частных производных
uXl uy, vXl vy, используя уравнения G.47). Если эту задачу
удастся решить, то с точностью до малых второго порядка можно
определить решения и(х,у), v(x,y) в точках М', близких к точ-
точкам кривой Г, используя разложения
=vM + A + A
Для этого к системе G.47) присоединим следующие диффе-
дифференциальные соотношения на кривой Г:
du
dx
dv
dx
G.49)
Поскольку на кривой Г функции и(х, у(х))\г и v(x,y(x))\r
являются функциями одной переменной, то полные производные
§7.7] Методы решения задач для уравнений гиперболического типа 303
и, v
Рис. 7.5. К методу характеристик
du
G.49) существуют. При этом —
(XX
dv
Г dx
известны, так как
известны u\y и v\r- Решаем СЛАУ G.47), G.49) относительно
их, vx, uy, vy, для чего из G.49) определим их, vx (индекс Г
опущен):
_ du , _ dv t
dx dx
подставляя которые в G.47), получим систему относительно иу,
vy на кривой Г:
d и dv
(Ьц - ацу')иу + F12 - a\2y')vy = c\ — an- ai2^-5
dx dx
(b - a f)u +(b -a f)v = с a du a dv
d т d т
G.50)
Для определения иу, vy составим определитель матрицы си-
системы G.50):
Д =
Ьц - any' 612 - a12yf
G.51)
304
Метод конечных разностей. Методы расщепления [Гл. VII
Тогда возможны следующие два случая:
1) если А ф 0 во всех точках кривой Г, то существует един-
единственное решение иу, vy в этих точках, а следовательно и един-
единственное решение их, vx\
2) если А = 0, то решение (если оно существует), неединствен-
неединственное.
Будем предполагать, что решение СЛАУ G.50) существует,
и, желая получить не только иу, vy, но и геометрические места
точек (ж, у), в которых ищется решение, будем рассматривать
второй случай:
Ьп-auA 512-а12Л
Д =
где Л = у'(х).
Раскрывая определитель в G.52), получаем квадратное урав-
уравнение, которое называется характеристическим:
а\2 - 2ЬХ + с = 0.
Его решением будут следующие два обыкновенных дифферен-
дифференциальных уравнения:
G.53)
1.2
Общие интегралы этих уравнений на плоскости хОу дадут
два семейства интегральных кривых, называемых характери-
характеристиками 1-го и 2-го семейства, а уравнения G.53) называются
дифференциальными уравнениями направления характеристик
{или просто дифференциальными уравнениями характеристик).
Эти уравнения нелинейные, поскольку коэффициенты зави-
зависят не только от ж и у, но и от искомых функций и(х, у), v(x,y).
Поэтому проинтегрировать их можно численно.
Из курса математической физики известна классификация
системы уравнений G.47) в зависимости от знака дискриминанта
Ь2 - ас.
Если Ь2 — ас > 0, то система G.47) является системой
гиперболического типа, характеристическое уравнение дает два
семейства вещественных характеристик с различными направ-
направлениями характеристик Ai ф A2.
§7.7] Методы решения задач для уравнений гиперболического типа 305
Если Ь2 — ас = 0, то система G.47) — система параболи-
параболического типа, и при Ъ2 — ас < 0 система G.47) — система
эллиптического типа.
Будем рассматривать гиперболическую систему G.47) с раз-
различными и действительными корнями характеристического
уравнения Х\ = у1 (ж), Л2 = у' (х).
Таким образом, дифференциальные уравнения направления
характеристик G.53) определят геометрические места точек на
плоскости хОу в окрестности кривой Г, в которых должно
быть определено решение и(х, у), v(x,y) исходной задачи G.47),
для чего необходимо составить еще два уравнения относительно
и(х,у), v(x,y).
Для их составления рассмотрим определители второго поряд-
порядка Ai, A2 системы G.50), первый из которых Ai образован из
определителя А G.51) заменой первого столбца на столбец пра-
правых частей, а второй А2 — из определителя А заменой второго
столбца на столбец правых частей.
Поскольку сделано предположение о существовании решения
СЛАУ G.50), то в соответствии с теоремой Кронекера-Капелли
ранг матрицы СЛАУ равен рангу расширенной матрицы (для
СЛАУ G.50) ранг матрицы СЛАУ равен единице, т. е. меньше
порядка матрицы, равного двум). Следовательно, поскольку А =
= 0, то в условиях предположения о наличии решения системы
G.50) и Ai = A2 = 0. Поэтому достаточно рассмотреть одно из
уравнений Ai = 0 или А2 = 0, например Ai = 0. Получим
Ai =
du dv ,
dx dx = 0, i = ТД G.54)
du dv ,
- O21- a22~r- 022 - Q>2
dx dx
Эти два уравнения называются дифференциальными соотно-
соотношениями на характеристиках. После умножения G.54) на dx
и раскрытия определителя можно записать
(v4Ai + B)du + Cdv + Mdx + Ndy = 0,
G.55)
(AX2 + B)du + Cdv + Mdx + Ndy = 0,
где
306
Метод конечных разностей. Методы расщепления
[Гл. VII
Л = det
а12
= det
bl2 «12
&22 «22
В = det
6i2 an
&22 «21
М = det
N = det
«12 Ci
a22 c2
Таким образом, решив систему ОДУ G.55) относительно и, г>,
ответим на поставленный в задаче вопрос.
Поскольку система G.47) квазилинейная, то уравнения G.53)
и система G.55) могут быть решены только численно. Рассмот-
Рассмотрим метод Массо численного решения системы G.53), G.55)
(рис. 7.6).
Характеристики
1-го семейства
Характеристики
2-го семейства
— А—
Рис. 7.6. К методу Массо
На заданной кривой Г наносится система точек с известными
координатами и известными значениями функций и |г, v |г • Для
точек а(ха,уа) и ЫуХъ^уъ) (рис.7.6 а) известны значения иа, va,
иь, Уь- Из системы двух линейных алгебраических уравнений
хс - Ха),
G.56)
§7.7] Методы решения задач для уравнений гиперболического типа 307
полученной из конечно-разностной аппроксимации двух урав-
уравнений характеристик G.53), определяются координаты точ-
точки с(жс, ус) как точки пересечения касательной к характеристике
первого семейства, выходящей из точки а, и касательной к ха-
характеристике второго семейства, выходящей из точки Ь. Таким
образом, точки пересечения характеристик различных семейств,
выходящих из двух соседних точек, определяются как точки пе-
пересечения отрезков касательных к этим характеристикам в этих
точках.
Зная координаты точки с, из конечно-разностной аппрокси-
аппроксимации системы дифференциальных соотношений на характери-
характеристиках G.55):
(АХ1а + В)(ис - иа) + C(vc - va)+
+ М(ХС - Ха) + N(Vc - Уа) = 0,
(А\2Ь + В)(ис - щ) + C(vc - vb)+
+М(хс - хъ) + N(yc - yb) = 0,
определяются значения uCl vc искомых функций в точке с.
Этот алгоритм реализуется для всех точек на кривой Г.
В результате получаем точки с, of, ... в окрестности кривой Г,
для которых известны координаты и значения функций и(х, у),
г;(ж, у). Если теперь из точки с провести отрезок касательной
к характеристике первого семейства, а из соседней точки d —
отрезок касательной к характеристике 2-го семейства до пересе-
пересечения в некоторой новой точке, то координаты последней можно
получить из решения системы G.56), а значения функций и и v
в этой точке — из решения системы G.57). И так далее.
Таким образом, в методе характеристик отыскиваются не
только значения искомых функций и и г?, но и координаты точек,
в которых эти решения находятся (рис.7.6 5).
7.7.2. Метод сквозного счета. Задача о распаде про-
произвольного разрыва. Метод С. К. Годунова. В задачах
механики сплошных сред приходится иметь дело с течениями,
в которых возникают сильные разрывы (например, ударные вол-
волны, местные скачки уплотнения и т. п.), хотя начальные условия
были гладкими. При расчете таких течений приходится либо
308
Метод конечных разностей. Методы расщепления [Гл. VII
явно выделять поверхности разрыва, используя законы сохране-
сохранения, либо использовать методы сквозного счета, позволяющие
получать сквозные решения, включая поверхности разрыва.
Одним из таких методов является метод С. К. Годунова [24,
25], использующий точные решения на кусочно-постоянных на-
начальных данных и гибкие пространственно-временные сетки,
связанные с поверхностями разрывов.
Рассмотрим метод С. К. Годунова на примере следующей
задачи Коши для уравнений акустики, являющихся следствием
волнового уравнения:
?Г + -^ = О> -оо<ж<+оо, t>0; G.58)
ot ро ox
+ ^^ = 0, -оо < х < +ос, * > 0; G.59)
и(х*-0,0) = иц р(х*- 0, 0) =рь х<х\ t = 0; G.60)
и(х* + 0, 0) = и2; р(ж* + 0, 0) = р2, х > ж*, 4 = 0, G.61)
где u(x,t), p(x,t) — возмущения скорости и давления в акусти-
акустической волне; ао, ро — скорость звука и плотность в невозмущен-
невозмущенном газе; и\, u<i, pi, Pi — постоянные, причем и\ ф и2 и р\ ф р2,
т. е. в точке ж* наблюдается разрыв первого рода функций и и р.
Будем решать задачу Коши G.58)-G.61) методом характери-
характеристик (система G.58), G.59) является гиперболической системой),
для чего запишем ее в форме G.47):
ацщ + CLuPt + Ьцих +
где ai2 = bn = c\ = a2\ = b22 = c2 = 0; an = a22 = 1; b\2 = —,
Po
b2i = po^o-
На начальной кривой Г в плоскости xOt выполняются диф-
дифференциальные соотношения G.49), из которых следуют равен-
равенства
ut = ^-ux-x'(t), G.62)
Pt = ^-px-x'(t). G.63)
§7.7] Методы решения задач для уравнений гиперболического типа 309
Подставляя G.62), G.63) в G.58), G.59), получим следующую
СЛАУ относительно их, рх:
, 1 du
-х'их -\ рх = - —
ро at
, dp
G.64)
G.65)
Д =
-x' —
Po
-х'
= х — а0 = 0, х12 =
х = =Ьао^ + с; при t = 0 х = х*.
Таким образом, характеристиками 1-го и 2-го семейства
в плоскости xOt являются прямые
х =
+ x\ G.66)
Приравнивая нулю один из определителей расширенной мат-
матрицы СЛАУ G.64), G.65), получим два дифференциальных со-
соотношения на характеристиках (х^ 2 =
— du
dt
—dp
dt
1
Po
= ±ao
du 1 dp
— + ——
at po dt
= 0,
или
dp du
— ±аоро— = 0.
dt dt
G.67)
Проинтегрируем G.67) по времени, получим комплексы p zb
± uqPqU = С ИЛИ
/± =р±аорои, G.68)
называемые инвариантами Римана. Они сохраняют свои зна-
значения вдоль соответствующих характеристик ж = =Ьао? + ж*,
выходящих из точки ж* начальной кривой при t = 0.
Пусть в точке (ж*,0) в начальный момент t = 0 функции и
и р претерпевают разрыв первого рода, а именно: слева от
310
Метод конечных разностей. Методы расщепления
[Гл. VII
точки (ж*,0) значения этих функций равны и(х* — 0,0) = г/i,
р(ж* -0,0)= pi, а справа и(х* + 0, 0) = г/2, р(ж* + 0, 0) = р2-
С течением времени слева от характеристики х + a$t (область I
на рис. 7.7) значения функций u(x,t) и p(x,t) будут равны
и\ и р\ соответственно, а справа от характеристики х — a^t —
значениям г/2 и р2- Таким образом,
р =
и =
х < ж* — a{)
(область I);
G.69)
р = Р2-, и = г/2, х > х* + dot (область II). G.70)
0 (х*,0) х
Рис. 7.7. Характеристики в точке (ж*,0)
На характеристиках х =Ь a$t (рис. 7.7) в окрестности точки ж*
выполняются соотношения (в соответствии с инвариантами Ри-
мана):
U*+o = / U*+o
Pi
= P +
G.71)
/_ \х*—о — I \х*— о : Р2 ~ &оРои2 — Р ~ &оРои- G.72)
Складывая G.71), G.72), а затем вычитая G.72) из G.71),
получим значения функций г/(ж,^), p(x^t) внутри области III
между характеристиками х + a^t и х —
Р2+Р1
Р = —^ аоро
U =
2
и2 + ¦
2
Р2 -Pi
< х < х* +
2aopo
t (область III).
G.73)
§7.7] Методы решения задач для уравнений гиперболического типа 311
Таким образом, начальный разрыв функций u(x,t), p(x,t)
в точке (ж*,0) трансформируется в пространстве (x,t) вдоль
характеристик ж* = х =Ь ао?, т.е. распадается. Поэтому решения
G.69), G.70), G.73) задачи G.58)-G.61) называются решениями
задачи о распаде произвольного разрыва. Эти решения являются
обобщенными решениями задачи G.58)-G.61).
На основе решения задачи о распаде произвольного разрыва
разработан метод С. К. Годунова численного решения газодина-
газодинамических задач. Изложим его существо. Пусть в момент време-
времени t = 0 заданы непрерывные функции щ(х), ро(х) (рис. 7.8).
Х0 Хт~-\ Хт~-У2 Хт Хт+1/2 Xm+l X
Рис. 7.8. Замена непрерывных начальных функций кусочно-постоянными
Заменим область непрерывного изменения переменной х дис-
дискретным множеством точек жт, га = 0,1,2,...,с шагами раз-
разностной сетки hm = хт — жт_1, т = 1, 2, . . . , и допустим, что
функции ад (ж), Ро{%) постоянны между узлами жт_1, хш рас-
расчетной сетки и равны pm_i/2, ит-1/2-
В узлах жт, т = 0,1,2,..., разрыва начальных данных воз-
возникают распады разрыва, т. е. в каждом узле сетки, где наблю-
наблюдается разрыв первого рода на начальных кривых, образуются
звуковые волны, распространяющиеся вправо и влево от точек
разрыва со скоростью звука clq. Тогда, согласно решениям G.69),
G.70), G.73) задачи о распаде произвольного разрыва, решение
312 Метод конечных разностей. Методы расщепления [Гл. VII
в окрестности точки хт будет (см. рис. 7.9.) иметь вид
и = um_i/2, Р = Pm-i/2, xm-i + aot < х < хт - aot; G.74)
- dot; G.75)
ит-1/2
= U = '
i Х
X
Ргп-1/2
хт — aot < х < хт + aot; G.76)
Prn-l/2 + Рт + 1/2
= Рт = —^ "
На рис. 7.9. изображена структура решения G.74)-G.77),
которая сохраняется до тех пор, пока характеристики различных
т+1/2 ~ ^т-1/2
хт — aot < х < хт + dot. G.77)
\
хч
X X
\ <>
ш
У
\\
\^-
X
У4
/
/
/
\_ _
/у
J/
У
\
\
\
/
/
л
0/
/
я'
ж
X
\ У
А/
Рис. 7.9. К методу Годунова С. К.
семейств, вышедшие из соседних узлов, не пересекутся между со-
собой (в точках пересечения получается неоднозначность решения,
чего нельзя допустить).
Для предотвращения этого явления шаг по времени г вы-
выбирается таким образом, чтобы упомянутые характеристики не
пересекались. Новые средние значения ит~1'2, рт~1/2 на слое т
§7.7] Методы решения задач для уравнений гиперболического типа 313
подлежат определению с помощью интегральных законов сохра-
сохранения.
Предположим, что искомые функции u(x,t), p(x,t), домно-
женные на некоторые коэффициенты, являются компонентами
векторной функции на плоскости xOt. Тогда к этой векторной
функции можно применить законы векторного анализа (фор-
(формулу Грина на плоскости или формулы Остроградского-Гаусса
и Стокса в пространстве). Применим к этому векторному полю
формулу Грина, в соответствии с которой циркуляция вектор-
векторного поля а(ж,у) = P(x,y)i + Q(x,y)j по некоторому замкну-
замкнутому контуру С, равна двойному интегралу по площади S от
8Q дР
функции
-. Коэффициенты у компонентов векторной
дх ду
функции и(х, ?), р(ж, t) подбираются такими, чтобы двойные ин-
интегралы от левых частей уравнений G.58), G.59), равные нулю,
были равны циркуляциям соответствующих векторных полей по
t=x
Рис. 7.10. К выбору шага т
замкнутому контуру С. Тогда для контура, представленного на
рис. 7.10, можно записать
ф (udx dt) =
1 Ро
С
дх
G.78)
314 Метод конечных разностей. Методы расщепления [Гл. VII
J) (pdx - poaludt) = ( я7 + Ро^о ^ ) dxdt = О, G.79)
J JJ V vt их J
S
откуда видно, что двойные интегралы равны нулю в соот-
соответствии с уравнениями G.58), G.59). Записывая соотношения
G.78), G.79) в плоскости xOt вдоль прямоугольной ячейки х =
= жт_ь х — хт, t = 0, t = г, получим для G.78)
Г Г
u(x,0)dx — u(x,r)dx+
Xm-1
или
Um l/2 = иш_1/2 \(Prn ~ Pm-l). G.80)
Для G.79) циркуляция векторного поля равна
Хт Хт Т
Г Г Г 2
p(x,0)dx — p(x,r)dx — (poaQu(xm,t))dt+
J J J
Xm-l Xm-1 0
T
Г 2
J Ш
0
откуда
ргп- I _ pm_1^2 — pQao-(um — um-i). G-81)
В соотношениях G.80), G.81) верхний индекс относится
к верхнему временному слою t = г, а нижний — к начальному мо-
моменту t = 0. Значения иш и рт в этих выражениях определяются
соотношениями G.76), G.77) в задаче о распаде произвольного
разрыва.
§7.7] Методы решения задач для уравнений гиперболического типа 315
Из соотношений G.80) и G.81) (а также в соответствии с ме-
методом гармонического анализа исследования устойчивости) сле-
следует, что
откуда получаем неравенство по ограничению шага численного
интегрирования задачи G.58)—G.61) по времени:
т ^ —. G.82)
ГЛАВА VIII
МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ
Программа
Основы метода конечных элементов (МКЭ). Система базисных
и весовых функций. Методы взвешенных невязок: коллокаций, Галер-
кина, наименьших квадратов. Конечно-элементный метод Галеркина
решения краевых задач для ОДУ. Слабая формулировка метода Га-
Галеркина. Формирование локальной и глобальной матриц жесткости.
Ансамблирование элементов. Случай граничных условий, содержащих
производные. МКЭ в многомерных стационарных задачах математиче-
математической физики. Принципы разбиения на конечные элементы. Ленточные
матрицы жесткости. Формирование многомерных базисных функций,
ансамблирование и построение глобальных СЛАУ. МКЭ в многомер-
многомерных нестационарных задачах математической физики. Оценка по-
погрешности МКЭ в задачах для ОДУ и уравнений в частных производ-
производных. Вариационный принцип в МКЭ. Вариационный принцип Релея-
Ритца. Решение задач с помощью конечно-элементного вариационного
принципа.
Метод конечных элементов (МКЭ) на основе вариационного
принципа возник из решения задач теории упругости, что и опре-
определило, в основном, терминологию, используемую в процессе его
применения в других разделах механики сплошных сред (теории
теплопроводности, газовой динамике и др.) [26].
Использование в МКЭ методов взвешенных невязок (та-
(таких, например, как методы коллокаций, Галеркина, наименьших
квадратов) позволило отказаться от вариационного принципа
в МКЭ, тем более что не для всякой задачи можно построить
функционал, минимум которого дает исследуемое дифференци-
дифференциальное уравнение. Тем самым круг решаемых задач механики
сплошных сред был существенно расширен [27-29].
§8.1] Основы МКЭ 317
§8.1. Основы МКЭ
Пусть в области ft = ft + Г необходимо решить некоторую
дифференциальную задачу. Тогда в МКЭ осуществляется сле-
следующая цепочка процедур.
1. Область ft разбивают на подобласти в количестве Е штук
(е = 1, Е), называемые конечными элементами, такие что
п= и fte, г= и ге.
е=1 е=1
2. В каждом конечном элементе ft = fte + Ге выбирает-
выбирается система нумерованных узлов, в которых значения искомой
функции являются неизвестными величинами.
3. Каждому нумерованному узлу приписывается базисная
функция, такая что в этом узле она равна единице, а в остальных
нумерованных узлах расчетной области — нулю. Число базисных
функций в расчетной области равно числу нумерованных узлов,
причем для различных узлов они обладают свойством линей-
линейной независимости (или ортогональности) по всей расчетной
области.
4. Решение искомой дифференциальной задачи приближенно
строится в виде линейной комбинации базисных функций по
всем нумерованным узлам расчетной области с коэффициентами
линейной комбинации, равными значениям искомой функции
в нумерованных узлах.
5. Это решение подставляется в дифференциальную задачу,
и, поскольку решение приближенное, результатом подстанов-
подстановки будет не тождественный нуль, а некоторая функциональная
невязка.
6. С помощью известных методов взвешенных невязок (кол-
локаций, Галеркина, наименьших квадратов) функциональная
невязка минимизируется по всей расчетной области путем при-
приравнивания нулю скалярного произведения функциональной
невязки и весовых функций (скалярное произведение от непре-
непрерывных функций равно определенному интегралу по расчетной
области от произведения этих функций), причем в методе взве-
взвешенных невязок Галеркина весовые функции в нумерованных
узлах совпадают с базисными функциями. В результате получа-
получается система линейных алгебраических уравнений (СЛАУ) от-
относительно значений искомой функции в нумерованных узлах,
318
Метод конечных элементов
[Гл. VIII
коэффициентами в которой являются интегралы по всей расчет-
расчетной области от базисных функций и их производных.
7. Определенные интегралы по всей расчетной области заме-
заменяются на сумму интегралов по конечным элементам, что, в си-
силу ортогональности базисных функций, делает матрицу СЛАУ
сильно разреженной, с ненулевыми элементами, расположенны-
расположенными в окрестности главной диагонали (так называемые ленточные
матрицы, частным видом которых является трехдиагональная
матрица).
8. Решается СЛАУ относительно узловых значений иско-
искомой функции каким-либо известным методом (Гаусса, простых
итераций, Зейделя и т.п.). Результаты решения подставляются
в приближенное решение по п. 4. При этом полученные значе-
значения искомой функции в нумерованных узлах каждого конечного
элемента могут быть использованы для получения решения во
всех точках конечного элемента ft = fte + Ге с помощью так
называемых функций элементов, простейшим случаем которых
является линейный интерполяционный многочлен в Rn.
Узлы
Рис. 8.1. Представление решения в МКР (а) и МКЭ (б)
Таким образом, существенным отличием МКЭ от метода ко-
конечных разностей (МКР) является то, что в МКЭ решение на
каждом элементе получается в виде непрерывных (или гладких)
функций, в то время как в МКР — в виде сеточной функции
(рис. 8.1).
§ 8.2. Система базисных функций
В качестве базисных функций будем рассматривать два
вида ортогональных базисных функций, а именно: кусочно-
постоянные базисные функции и линейные кусочно-непрерывные
базисные функции.
§8.2]
Система базисных функций
319
8.2.1. Кусочно-постоянные базисные функции.
Пусть в вещественном пространстве R1 рассматривается
класс функций <р(ж), непрерывно дифференцируемых
необходимое число раз на отрезке х Е [0; 1]. Разобьем этот
отрезок точками жт, га = 1, М, на М элементарных отрезков
[жт_1,жт], га = 1, М, и представим функцию ^(ж) в виДе
следующей линейной комбинации:
м
ф) « ?(ж) = ^ ^т ' #т(ж), (8.1)
где Nm(x) — кусочно-постоянные функции на каждом отрез-
отрезке [жт_1,жт], и, если эти функции линейно-независимы (или
ортогональны) при различных индексах га, будем называть их
кусочно-постоянными базисными функциями, определяемыми
равенствами
I 1, если xm-i < х < хт,
Nm{x) = t (8.2)
I 0, если х < xm-i или х > хт, га = 1, М,
а <Рт — значения функции (р(х) в нумерованных узлах, находя-
находящихся в середине каждого отрезка [хш-\, хт].
Ф(х)
У'
JC=1
0
1
М
Рис. 8.2. Аппроксимация функции с помощью кусочно-постоянных базисных
функций
Тогда аппроксимация (8.1) функции (р(х) на отрезке х Е [0; 1]
с помощью кусочно-постоянных базисных функций (8.2) геомет-
геометрически представляется ступенчатой функцией (рис. 8.2). При
320
Метод конечных элементов
[Гл. VIII
этом каждая базисная функция, приписанная нумерованному
узлу, принимает значение, равное единице только на отрезке,
внутри которого расположен этот нумерованный узел; во всех
остальных нумерованных узлах расчетной области эта базисная
Рис. 8.3. Глобальные (а) и локальные (б) кусочно-постоянные базисные
функции
функция равна нулю (рис. 8.3). Такие базисные функции назы-
называют глобальными (рис. 8.3а), т.е. заданными в форме (8.2) на
всей расчетной области.
В отличие от этого, базисную функцию, заданную на от-
отрезке [жт_1,жт] (рис. 8.3 5), называют локальной базисной
функцией.
Как видно из определения (8.2) глобальных кусочно-
постоянных базисных функций и из рис. 8.3 а, эти функции
ортогональны на отрезке ж G [0; 1] в смысле скалярного произ-
произведения, т. е. для двух кусочно-постоянных базисных функций
§8.2] Система базисных функций 321
с номерами г и j (г ф j, г, j = 1, М) имеет место равенство
1 Xi — 1
(Ni(x),Nj(x))={Ni(x)Nj(x)dx= I Ni(x)Nj(x)dx +
о о
+ f Ni(x)Nj(x)dx+ f Ni(x)Nj(x)dx+ \ Ni{x)Nj{x)dx +
8.2.2. Линейные кусочно-непрерывные базисные
функции. Если в качестве базисных функций принять
функции вида
Nm(x) =
-, ж
-,ж Е [xm,xm+i] ; (8.3)
U,
называемые линейными кусочно-непрерывными базисными функ-
функциями, то аппроксимация (8.1) функции <р(ж) на каждом отрез-
отрезке х ? [жт_1,жт] будет линейной и непрерывной в узлах хш.
В этом случае в качестве нумерованных узлов принимаются узлы
разбиения (рис. 8.4).
Для отдельного отрезка х Е [жт,жт+1.] с нумерованными
узлами т и т + 1 глобальные линейные кусочно-непрерывные
базисные функции представлены на рис. 8.5 а, а локальные — на
рис. 8.5 б. Из рис. 8.5 видно, что глобальные базисные функции,
построенные для различных узлов и действующие на различных
отрезках, ортогональны на всей области изменения перемен-
переменной х.
Можно построить и другие базисные функции, в том числе
и нелинейные.
11 В.Ф. Формалев, Д.Л. Ревизников
322
Метод конечных элементов
[Гл. VIII
Нумерованные
узлы
Хт+2
Рис. 8.4. Аппроксимация функции с использованием линейных кусочно-
непрерывных функций
Nm(x)
Nm+l(x)
Рис. 8.5. Глобальные (а) и локальные (б) линейные кусочно-непрерывные
базисные функции
8.3. Методы взвешенных невязок. Весовые
функции
Пусть в области (] =
задача
Lu
С Rn рассматривается краевая
• = 0 в П;
Ви + q = О на Г,
(8.4)
(8.5)
где L и В — линейные дифференциальные операторы, арид-
известные функции независимых переменных.
Для аппроксимации функции и в нумерованных узлах об-
области О выбирается система базисных функций 7Vm, т = 1, М,
с помощью которой строится приближенное решение
§8.3] Методы взвешенных невязок. Весовые функции 323
М
LL г*~> (Jj 7 UjTYI ^ * 1711 V /
m=l
где иш — значения искомой функции в нумерованных узлах.
Подставляя это приближенное решение в задачу (8.4), (8.5),
получим не тождественный нуль, поскольку (8.6) — прибли-
приближенное решение, а некоторую функциональную невязку Rn по
области ft и невязку 7?г по границе Г:
м м
R$i = 2_. UmL^Nm) + p; Ry = / j umB(Nm) + q.
m=l m=l
С целью нахождения искомых значений иш, т = 1, М, ор-
тогонализуем невязки Rq и 7?г с помощью специальным обра-
образом подобранных функций Ws, s = 1, М, называемых весовыми
функциями, т. е. приравниваем нулю скалярные произведения
невязок Rq и Rr и весовых функций Ws, s = 1, М, в результате
чего получается следующая система линейных алгебраических
уравнений относительно узловых значений иш искомой функ-
функции:
s- RndU + lWa ' RrdT =
г
lws (JTumL(Nm)+p\
dU
, (8.7)
где весовые функции Ws и W s для области ft и границы Г могут
быть разными.
Этот метод ортогонализации невязок 7?г и Rq с помощью
весовых функций называют методом взвешенных невязок, раз-
различные варианты которого отличаются способом задания весо-
весовых функций Ws, s = 1, М.
8.3.1. Метод поточечной ко л локации. В расчетной об-
области ft выбирается s = 1, М точек коллокации (совпадающих
с нумерованными узлами расчетной области), в которых невяз-
невязка Rq полагается равной нулю. В этом случае в качестве весовых
и*
324 Метод конечных элементов [Гл. VIII
функций принимаются дельта-функции Дирака, которые в п-
мерном вещественном пространстве имеют вид
где г s — длина радиуса-вектора точки кол локации, а дельта-
функция 6(г — rs) обладает следующими свойствами:
,0, если г ф rs;
о {г -г8) =
оо, если г = rs;
r>rs
I S(r-ra)dr = l, s=Tj\4; (8.8)
r<rs
r>rs
Rn(rM(r-ra)dr = Rli(r8), s = l,M. (8.9)
r<rs
В соответствии со свойством (8.9) и условием ортогонально-
ортогональности (8.7) получаем следующую систему из М линейных алгебра-
алгебраических уравнений относительно узловых значений ит искомой
функции:
Г . ч . ч - . ч
I А? ( гр \ А / /v» /v» |/7 \/ /-? \ Т* | (| Q 1 Л//
8.3.2. Метод Галеркина. В этом методе в качестве весо-
весовых функций выбираются базисные функции в нумерованных
узлах расчетной области Ws = Ns, s = 1, М.
В результате СЛАУ (8.7) относительно иш приобретает вид
dT = °> s = Т^Ж'
причем, в силу ортогональности базисных функций, матрица
этой СЛАУ будет иметь разреженный вид.
§8.4] Конечно-элементный метод Галеркина решения краевых задач 325
Среди методов взвешенных невязок метод Галеркина являет-
является одним из наиболее популярных.
8.3.3. Метод наименьших квадратов. Метод наимень-
наименьших квадратов заключается в минимизации функционала, явля-
являющегося интегралом по области ft от квадрата невязки R^:
и2, . . . , им) = - Rfidto-
Необходимым условием минимума этого функционала яв-
является равенство нулю частных производных 1-го порядка по
ди лт -—yt
параметрам и\, и2, . . . , им-» а учитывая, что —— — Ns, s = 1, М,
ous
приходим к следующей СЛАУ относительно иш, m = 1, М:
г г
\ Rn • L (Ns) du + \ Rr • В (Ns) dF = 0, 5 = 1, M.
j j
§ 8.4. Конечно-элементный метод Галеркина
решения краевых задач для обыкновенных
дифференциальных уравнений
Все содержание метода конечных элементов ниже излагается
на примере следующей первой краевой задачи для обыкновенно-
обыкновенного дифференциального уравнения (ОДУ):
^-<и = 0, 0 < ж < 1; (8.10)
dx
«@) = 0, х = 0, (8.11)
«A) = 1, х = 1, (8.12)
допускающей аналитическое решение, которое имеет вид
и(х) = [ехрA — ж) — ехрA + ж)]/A — е2).
Разобьем отрезок [0; 1] на три конечных элемента (е = 1, Е\
Е = 3), при этом нумерованные узлы т принимаются в точках
разбиения, т.е. т принимает значения 1, 2, 3, 4.
326 Метод конечных элементов [Гл. VIII
Каждому нумерованному узлу приписывается базисная
функция Nm(x), m = 1,4, определяемая с помощью выраже-
выражения (8.3). Решение задачи (8.10)—(8.12) записывается в виде
4
и(х) « и(х) = ^ Um ' Nm(x), (8.13)
т=1
где ит — значения искомой функции в нумерованных узлах,
подлежащие определению.
Если они определены, то на конечных элементах с номерами
е = 1,Ёи произвольными нумерованными узлами т и т + 1 ис-
искомая функция в точках этих элементов описывается следующи-
следующими линейными функциями (можно показать, что они совпадают
с интерполяционными многочленомами первой степени):
7/е/ \ _ е лте / \ , е дге / \ _ i о о
Такие функции называют функциями элемента.
Подставляя (8.13) в ОДУ (8.10) получаем следующую функ-
функциональную невязку:
d2u ^
Поскольку на границах заданы граничные условия первого
рода, выполняющиеся точно, то невязка Rr на границах рав-
равна нулю.
В соответствии с методом взвешенных невязок Галеркина ве-
весовые функции Ws(x), s = l,4, принимаются равными базисным
функциям Ns(x), s = l,4 (Ws(x) = Ns(x)). Тогда в соответствии
с методом Галеркина получаем следующую СЛАУ относительно
ит, т = 1,4:
[ Ns (^ -u)dx = 0,s = l, 2, 3, 4. (8.14)
о
8.4.1. Слабая формулировка метода Галеркина. Из-
Известно, что определенный интеграл существует в случаях, ког-
когда подынтегральная функция является кусочно-непрерывной на
заданном отрезке с конечным числом точек разрыва первого
рода и ограниченной (разрывы второго рода в подынтегральных
функциях не допустимы).
Однако во вторую производную подынтегральных функций
СЛАУ (8.14) входят линейные кусочно-непрерывные базисные
§8.4] Конечно-элементный метод Галеркина решения краевых задач 327
функции Nm(x), m = 1,4 (8.3), производные второго поряд-
порядка от которых претерпевают разрывы второго рода (стремятся
к zboc). Возникает вопрос, допустимо ли использование базисных
функций вида (8.3) в аппроксимации (8.13), т.е. достаточна ли
гладкость базисных функций в классе С0 (в классе непрерывных
функций)?
dNm/dx
dNm/dx
оо
d2Nm/dx2
А х
Рис. 8.6. Поведение функций и их производных: а — разрывных, б — непре-
непрерывных, в — непрерывно дифференцируемых
Для ответа на этот вопрос рассмотрим поведение трех ти-
типов функций Nm(x) и их производных до третьего порядка
включительно в окрестности точки А стыковки двух соседних
элементов (рис. 8.6), а именно разрывных, непрерывных (класса
С0) и непрерывно дифференцируемых (класса С1).
Из рис. 8.6 видно, что класс разрывных функций (рис. 8.6 а)
не годится для аппроксимации дифференциальной задачи
(8.10)—(8.12), поскольку уже первая производная претерпевает
328 Метод конечных элементов [Гл. VIII
разрыв второго рода. То же самое относится и к классу непре-
непрерывных функций (рис. 8.6 б) поскольку вторые производные
претерпевают разрыв второго рода. Класс непрерывно диф-
дифференцируемых функций (рис. 8.6 в) можно использовать для
конечно-элементной аппроксимации дифференциальной задачи
(8.10)—(8.12), поскольку производные второго порядка являются
кусочно-непрерывными с разрывами первого рода, т. е. опреде-
определенные интегралы от вторых производных таких функций суще-
существуют.
Таким образом, в МКЭ на гладкость базисных функций на-
накладываются жесткие ограничения. Покажем, как можно осла-
ослабить требования к гладкости базисных функций. Такие спосо-
способы ослабления гладкости базисных функций называют «слабой
формулировкой» в МКЭ. Эти способы в одномерных задачах
основаны на интегрировании по частям, а в многомерных — на
использовании формул Грина.
Проинтегрируем в (8.14) первое слагаемое по частям, полу-
получим
dNs du ЛГ ^\ . ГЛГ du\ Л
? + N)d+\Nte\ =0' S =
o
(815)
откуда видно, что теперь требуется непрерывность только при-
приближенного решения и (а следовательно, и базисных функ-
функций 7Vm, входящих во соответствии с (8.13)), и его первой
„ du
производной -—.
d х
В СЛАУ (8.15) в сумме для и при каждом s = 1, М + 1,
перебираются все т = 1, М + 1, где s — номер уравнения (и од-
одновременно номер весовой функции), а т — номер неизвестного
иш в (8.13) (и одновременно номер базисной функции).
8.4.2. Формирование локальной и глобальной мат-
матриц жесткости. Ансамблирование элементов. Предста-
Представим СЛАУ (8.15) в следующей векторно-матричной форме:
Ки = /, и = (иг и2 ... uM+i)J\ f = (/i /2 • • • /m+i)T, (8.16)
где К = [fcsm], s, m = 1, М + 1, причем элементы матрицы К
и компоненты вектора правых частей вычисляются следующим
образом (достаточно в (8.15) подставить (8.13)):
§8.4] Конечно-элементный метод Галеркина решения краевых задач 329
kSm=
fs= \N.
du
' dx
= N,
du
dx
-Nt
x=l
du
dx
= 1, M + l.
ж=0
Элементы ksrn и компоненты fs вычисляются таким образом,
что для s-Pl весовой функции 7V5, s = 1, М + 1, перебираются все
базисные функции 7Vm, m = 1, М + 1, и после интегрирования
образуется s-я строка матрицы К и s-й элемент в векторе /.
В каждый коэффициент ksrn и компонент fs в общем случае
делает вклад каждый конечный элемент расчетной области с ис-
использованием выражений
Е
e=l
где
he — he
-Т(
dNes dNem
dx dx
Е
e=l
, (8.17)
he =
s = m.
(8.18)
Для конечного элемента с нумерованными узлами т и т + 1
построим с помощью (8.17), (8.18) матрицу Ке:
Хт+1
-I
/ x 2
/ dNm \
\dx )
dNem+1
dx
-\-Ne
f (w™J
.(JVJ,
dx
С
dx
V/Ve
XiVm+l
^m + 1 ,
y +
(8.19)
причем для e =
330
Метод конечных элементов
[Гл. VIII
Матрицу (8.19) называют матрицей элемента или локальной
матрицей жесткости, в отличие от матрицы К в (8.16), назы-
называемой глобальной матрицей жесткости, построенной для всей
расчетной области.
Процесс суммирования локальных матриц жесткости, назы-
называемый ансамблированием конечных элементов, осуществляет-
осуществляется таким образом, чтобы каждая поэлементная составляющая
коэффициента ksm глобальной матрицы жесткости К была
на своем месте. Рассмотрим процесс ансамблирования в задаче
(8.10)-(8.12), для которой Е = М = 3 (рис. 8.7).
е=1
О
1
2
jc2=1/3
1И-1
/и+1
да+2 ... Af+1
Рис. 8.7. К вычислению локальных матриц жесткости
1) Пусть е = 1, тогда при s = lra = l, га + 1 = 2; при s = 2
га = 1, га + 1 = 2.
Локальная матрица жесткости (8.19) в узлах 1-го конечного
элемента вычисляется следующим образом. Элементы матрицы
(8.19), стоящие в s-и строке и га-м столбце (s, га = 1, 2) вычис-
вычисляются по правой ветви базисной функции (8.3), приписанной
левому нумерованному узлу, и по левой ветви базисной функции
(8.3), приписанной правому нумерованному узлу (на рис. 8.7 эти
ветви для га-го и (га + 1)-го узлов нанесены жирно).
Таким образом, элементы этой матрицы равны (жт+1 — хш =
= 1/3, га = 1,2,3)
1/3
(-
1 /
1 1
-ЗJ +
X — Х\
v 1/3
(Х2 — Х^
V V3 )
\ (х2-
)\ V3
2
1
\
X
)
1 (Х2~х\ (
1 v 1/з Д
Ч2 1 Iх ~
3 +1 1/
>+
' X — Ж1^
, 1/3 )
з )
dx =
§8.4] Конечно-элементный метод Галеркина решения краевых задач 331
28/9 -53/18
-53/18 28/9
Вектор правых частей глобальной СЛАУ содержит второе
слагаемое выражения (8.15), имеющего место только для гра-
граничных узлов:
11
du
dx
du
dx
x=l
du
dx
x=0
Первый элемент содержит только левую границу, и, следова-
следовательно,
du
dx
О
ж=0
Таким образом, локальная СЛАУ для первого конечного эле-
элемента имеет вид
28/9 -53/18
-53/18 28/9
U2
- (du/dx)\x=0
О
(8.20)
-53/18
28/9
0
0
0
0
0
0
0
0
0
0
Щ
u2
u3
U4
— (du/' d
0
0
0
Эта локальная СЛАУ, построенная для элемента е = 1, учи-
учитывается в глобальной СЛАУ (8.16) следующим образом:
га = 1 т = 2
28/9 —оо/ ±о и и а\ — уии/ (jlju) \x=q
= 2 -53/18
О
О
(8.21)
т.е. элементы матрицы К1 и вектора правых частей f1 рас-
расширяются до размеров глобальной матрицы К(м+1)х(м+1)
и глобального вектора /м+ъ гДе М = 3, причем при s =
= 1 (m = 1, m + 1 = 2) первая строка матрицы К1 ставится
в первую строку и в 1-й и 2-й столбцы расширенной матрицы.
При s = 2 (га = 1, га + 1 = 2) соответствующие элементы ста-
ставятся во вторую строку расширенной матрицы.
2) Пусть е = 2, тогда при s = 2 га = 2, га + 1 = 3; при s = 3
т = 2, т + 1 = 3.
332
Метод конечных элементов
[Гл. VIII
Аналогично элементу е = 1 из (8.19) имеем
28/9 -53/18
-53/18 28/9
т = 2 т = 3
О О
К2 =
/2 = (о o)J
s = 2
0 0 0 0
О 28/9 -53/18 О
О -53/18 28/9 О
0 0 0 0
ui
и2
и3
и4
0
0
0
0
(8.22)
3) Для e = 3 при s = 3m
m + 1 = 4, из (8.19) получаем
= 3, m + 1 = 4; при s = 4 m = 3,
0
0
0
0
28/9
-53/18
т = 3
0 0
0 0
0 28/9
0 -53/18
-53/18
28/9
т = 4
0
0
-53/18
28/9
f-
' щ'
и2
и3
U4
@ (du/dx)\x=1
0
0
0
(du/dx)x
s = 3
(8.23)
Завершается процесс ансамблирования обычным сложением
систем (8.21), (8.22), (8.23), в результате чего получается итого-
итоговая СЛАУ (8.16) с глобальной матрицей жесткости К и векто-
вектором /:
28/9 -53/18 О О
-53/18 56/9 -53/18 О
О -53/18 56/9 -53/18
О 0 -53/18 28/9
и2
U4
du
dx
x=0
О
О
du
dx
x=\ -
(8.24)
§8.4] Конечно-элементный метод Галеркина решения краевых задач 333
В силу того что на границах х = 0 и х = 1 значения искомой
функции известны из граничных условий первого рода (8.11),
(8.12), первое и последнее уравнение в системе (8.24) можно ис-
исключить, положив в остальных уравнениях и\ = и@) = 0 и и± =
= иA) = 1. Тогда из (8.24) имеем
56/9 -53/18
-53/18 56/9
U2
о
53/18
откуда U2 = 0,2885; г^з = 0,6098 (точные значения и<х = 0,2889;
г^3 = 0,6102).
Глобальная система (8.24) позволяет на границах, где заданы
граничные условия первого рода, определить производные пер-
первого порядка. Из (8.24) получаем
du
dx
28
ж=0
53
~18U2'
du
dx
53
28
x=l
откуда
(du/dx)x=0 = (-53/18) • 0,2885,
(du/dx)x=1 = (-53/18) • 0,6098 + B8/9) • 1.
8.4.3. Случай граничных условий, содержащих про-
производные. В случае, когда на границах расчетной области за-
заданы граничные условия второго или третьего рода (или сме-
смешанные краевые условия), вместо слабой формулировки мето-
метода Галеркина (8.15) необходимо воспользоваться общей схемой
взвешенных невязок (8.7) и на ее основе сформулировать слабую
формулировку метода Галеркина.
Рассмотрим такую формулировку на примере следующей
краевой задачи для ОДУ 2-го порядка:
d2u
0 < ж < 1;
(8.25)
и@) = 0, х = 0;
(8.26)
334
Метод конечных элементов
[Гл. VIII
du(l)
dx
— 1 т — 1
Тогда из (8.7) имеем
1
d2u ^Л ,
—т - и ) dx
dx2 ]
dx
= 0,
(8.27)
(8.28)
x=l
где невязка на левой границе равна нулю, поскольку на ней
задано значение искомой функции.
Для граничных условий, содержащих производные, базисные
функции Ws на соответствующей границе можно подобрать так,
чтобы эти производные и производные первого порядка, возник-
возникшие на той же границе от операции интегрирования по частям,
сократились, что существенно упрощает решение.
Интегрируя первое слагаемое в (8.28) по частям, получим
dWs du
dx dx
о
du
—
dx
= 0.
x=l
Положим здесь И^| х = — VK5|X=
тодом Галеркина Ws = Ns, s = 1, М +
l
dNs du ,r ^\ . |~,r du
-r^^ + Nsu) dx = - \N8 —
dx dx j dx
(а в соответствии с ме-
), будем иметь
x=0
+ [N,]X=V (8-29)
Проводя те же рассуждения, что и в задаче (8.10)—(8.12) с гра-
граничными условиями первого рода, из (8.29) получим следующую
глобальную СЛАУ, в которой граничное условие на границе х =
= 1 учтено естественным образом ([Ns]x=q = 1):
28/9 -53/18 О О
-53/18 56/9 -53/18 О
О -53/18 56/9 -53/18
О 0 -53/18 28/9
Ul
U2
и,
U4
du
dx
0
0
1
ж=0
(8.30)
§8.5] Метод конечных элементов в задачах математической физики 335
Краевое условие на левой границе и\ = и@) = О учитывается
вычеркиванием первого уравнения в (8.30) и равенством и\ = 0
в остальных уравнениях.
Решая глобальную систему (8.24) или (8.30) относительно
узловых значений искомой функции и подставляя их в линейную
комбинацию (8.13), получим решение задачи методом конечных
элементов не только в нумерованных узлах, но и в любой точке
любого конечного элемента с помощью функции элемента.
§ 8.5. Метод конечных элементов в стационарных
задачах математической физики
8.5.1. Основные этапы решения стационарных задач
математической физики методом конечных элементов.
Перечислим основные этапы решения двумерных стационарных
задач математической физики с помощью МКЭ на основе метода
Галеркина взвешенных невязок.
1. Расчетная область f] = П + Г G й2, которая может быть
и многосвязной, разбивается на элементы О = 0е + Ге того же
пространства. Для двумерной расчетной области в качестве ко-
конечных элементов принимаются треугольные или четырехуголь-
четырехугольные элементы, причем последние можно разделить диагональю
на два треугольных элемента. Достоинствами треугольных эле-
элементов являются возможность хорошей аппроксимации грани-
границы области и возможность аппроксимации искомой функции на
треугольном элементе с помощью простейшей поверхности —
плоскости, определяемой значениями искомой функции в ну-
нумерованных узлах элемента (обычно это вершины треугольного
элемента). Разбиение на элементы должно удовлетворять усло-
условию U ft = Л, причем смежные элементы должны иметь общие
стороны и общие нумерованные узлы (рис. 8.8).
2. В нумерованных узлах фиксируются узловые значения
искомой функции, являющиеся неизвестными величинами, под-
подлежащими определению.
3. С помощью узловых значений в нумерованных узлах эле-
элемента искомая функция аппроксимируется поверхностью (ча-
(чаще всего линейной функцией, описывающей плоскость), назы-
называемой функцией элемента, позволяющей определить искомую
функцию в любой точке конечного элемента. При этом если
336
Метод конечных элементов
[Гл. VIII
количество нумерованных узлов элемента на единицу больше
размерности пространства /?п, то элемент называется линейным.
Если в элементе число нумерованных узлов больше чем п + 1,
то этот элемент называется нелинейным, а искомая функция на
нем аппроксимируется с помощью нелинейной функции.
Рис. 8.8. Разбиение двумерной расчетной области: а — правильное разбиение;
б — неправильное разбиение
4. Каждому нумерованному узлу расчетной области ft + Г
приписывается базисная функция, равная единице в узле, кото-
которому она приписывается, и нулю во всех остальных узлах расчет-
расчетной области. Базисные функции для различных нумерованных
узлов являются линейно независимыми.
5. Приближенное решение задачи формируется в виде ли-
линейной комбинации базисных функций по всем нумерованным
узлам расчетной области с коэффициентами линейной комбина-
комбинации, равными узловым значениям искомой функции.
6. Это решение подставляется в дифференциальную задачу,
что приводит не к тождественному нулю, поскольку подставляет-
подставляется приближенное решение, а к невязкам по расчетной области Rn
и границе /?г-
§8.5] Метод конечных элементов в задачах математической физики 337
7. В соответствии с различными методами взвешенных невя-
невязок, наиболее эффективным из которых является метод Галер-
кина, невязки ортогонализируются с системой весовых функций
(в методе Галеркина в качестве весовых функций принимаются
базисные функции). Результатом такой ортогонализации явля-
является глобальная система линейных алгебраических уравнений
(СЛАУ) относительно узловых значений искомой функции. Чи-
Число уравнений в этой системе совпадает с количеством нуме-
нумерованных узлов расчетной области. Каждый элемент матрицы
и вектора правых частей этой СЛАУ содержит в той или иной
степени вклады элементов матриц и правых частей локальных
СЛАУ, сформированных для каждого конечного элемента. Про-
Процесс суммирования таких вкладов конечных элементов называют
ансамблированием конечных элементов, т. е. локальным номерам
узлов конечных элементов ставятся в соответствие глобальные
номера узлов расчетной области.
8. Решая полученную глобальную СЛАУ каким-либо из из-
известных методов, получаем узловые значения искомой функции,
с помощью которых из функций элементов определяются значе-
значения искомой функции в любых точках конечных элементов.
8.5.2. Принципы разбиения плоских областей на ко-
конечные элементы. Будем разбивать плоскую расчетную об-
область Q + Г G R2 на треугольные конечные элементы, при этом
номер элемента обозначается верхним индексом е, а локальные
номера узлов в элементе — нижними индексами г, j, fc, причем
если зафиксирован какой-либо узел под номером г, то остальные
узлы под номерами j и к нумеруются против часовой стрелки.
Перечислим основные принципы разбиения плоских расчет-
расчетных областей.
1. Сложные плоские области вначале разбивают на подобла-
подобласти, которые затем разбивают на конечные элементы.
2. При разбиении на конечные элементы тонкостенных об-
областей каждый конечный элемент должен содержать как мини-
минимум один нумерованный узел, находящийся внутри расчетной
области, так как если все нумерованные узлы расположены на
границе расчетной области, то при аппроксимации учитываются
только граничные условия и не учитывается дифференциальное
уравнение (рис. 8.9).
338
Метод конечных элементов
[Гл. VIII
Рис. 8.9. Конечные элементы в тонкостенных расчетных областях: а — непра-
неправильное, б — правильное разбиение
3. Глобальную нумерацию узлов в расчетной области необ-
необходимо осуществлять таким образом, чтобы в отдельном конеч-
конечном элементе разность между максимальным и минимальным
номерами была как можно меньше, поскольку от этой разницы
зависит полуширина b ленты матрицы (рис. 8.10) в глобальной
Г 1 2 3
м
Рис. 8.10. Вид ленточной матрицы глобальной системы линейных алгебраи-
алгебраических уравнений
§8.5] Метод конечных элементов в задачах математической физики 339
матрице результирующей системы алгебраических уравнений,
которая является ленточной, если все ее ненулевые элементы
на полуширине b расположены около главной диагонали.
Чем меньше полуширина b ленточной матрицы, тем устой-
устойчивее решение СЛАУ. Таким образом, нумерация узлов в тон-
тонкостенной расчетной области, представленной на рис. 8.9, осу-
осуществляется чередованием номеров на верхней и нижней грани-
границах (нумерация узлов сначала по верхней, а затем по нижней
границе приведет к значительной разности номеров в каждом
конечном элементе и такому же увеличению полуширины ленты
матрицы).
4. В многосвязных областях внутренние полости вписывают
в многоугольники, в вершины которых помещают нумерованные
узлы, соединяемые гранями с другими нумерованными узлами,
расположенными внутри расчетной области.
8.5.3. Аппроксимация линейными многочленами и
базисные функции. Применение метода конечных элементов
рассмотрим на примере следующей третьей краевой задачи для
уравнения Пуассона в области, представленной на рис. 8.11.
О 7
Рис. 8.11. Расчетная область
Тх А(Ж,у)-)+-
(х,у) ей;
(8.31)
340
Метод конечных элементов
[Гл. VIII
+ а и\г = <р (ж, у) , (ж, у) е Г.
(8.32)
Разобьем вначале область ft на три подобласти в виде трех
четырехугольников. Затем внутри каждого четырехугольника
введем по одному внутреннему узлу, которые соединим с узлами
в вершинах четырехугольников. Пронумеровав все узлы, полу-
получим разбиение всей области на двенадцать треугольных конеч-
конечных элементов с общим числом нумерованных узлов, равным
одиннадцати.
Каждому нумерованному узлу приписывается базисная
функция Nm (ж, у) в виде линейного многочлена, значение кото-
которого равно единице в узле, которому она приписана, и нулю — во
Ж
Рис. 8.12. Базисная функция Nf
всех остальных узлах расчетной области. На рис. 8.12 приведен
пример базисной функции Nf(x,y), приписанной узлу г в ло-
локальной нумерации узлов в конечном элементе е. Такая базисная
функция имеет вид
Nf (х, у) = а\ + Cfx
(8.33)
где коэффициенты а|, /3|, jf находятся из условий Nf (ж^, yi) =
= 1, Nf (xj, yj) = 0, Nf (ж/,, yk) = 0. При этом координаты ну-
нумерованных узлов определены положением узлов в расчетной
области относительно начала координат. Выполнение этих трех
§8.5] Метод конечных элементов в задачах математической физики 341
условий приводит к следующей системе из трех линейных алгеб-
алгебраических уравнений относительно коэффициентов а|, /3|, jf:
1 Xi Уг
Л if* • 11 •
i х3 y3
1 xk yk
решением которой являются выражения
- xkyj) ,
fit
It
=
1
0
0
(8.34)
2Ае
2Ае
- ук) ,
где Ае — площадь элемента,
Ae = ^det
хк ук
Для остальных узлов j и к конечного элемента е базисные
функции N? (ж, у) и ЛГ| (х,у) формируются аналогично. Тогда
равенство (8.33) для этих узлов будет иметь вид
7VJ (х, у) = а] + Щх + -у]у,
а система (8.34) сохраняется, за исключением двух групп неиз-
неизвестных а?, /3|, 7?5 а%-> &%•> !%-> и ДВУХ векторов правых частей
[О 1 О ]Т для 7VJ и [ 0 0 1 ]Т для Щ.
Приближенное решение задачи (8.31), (8.32) находится в ви-
виде линейной комбинации базисных функций, коэффициентами
которой являются значения искомой функции в нумерованных
узлах, т. е. в форме
м
и (ж, у) « и (ж, у) = ^2 итМш (ж, у), (8.35)
га=1
где М — число нумерованных узлов.
342 Метод конечных элементов [Гл. VIII
Для отдельного элемента е решение (8.35) представляется
в виде
ие (ж, у) = и\(х, у)Щ(х, у) +
+ и){х, у)Щ{х, у) + и%(х, у)Щ(х, у) (8.36)
и называется функцией элемента. С ее помощью значение ис-
искомой функции можно определить в любой точке конечного
элемента, как только станут известными узловые значения и\,
ие-, ие^. Система базисных функций ЛГт(ж, у), т = 1, М, обладает
свойством полноты, поскольку при М —» оо решение (8.35) может
сколь угодно точно аппроксимировать искомую функцию.
8.5.4. Слабая формулировка конечно-элементного
метода Галеркина. Если подставить приближенное решение
(8.35) в дифференциальную задачу (8.31), (8.32), то результатом
подстановки будет не тождественный нуль, поскольку (8.35) —
приближенное решение, а некоторая функциональная невяз-
невязка Rn(x,y) по расчетной области О и невязка Rr(x,y) — по
границе Г:
ди
—
Rr(x,y) = X
аи\ - ip(x,y).
г
В соответствии с методами взвешенных невязок требуем
ортогональности этих функциональных невязок и специаль-
специальным образом подобранных весовых функций Ws(x,y), s =
= 1, М, для невязки R^(x^y) и Ws(x,y), s = 1, М, для невяз-
невязки Rr(x,y). Для непрерывных функций Д^(ж,у), Rr(x,y) это
означает равенство нулю скалярных произведений (/?о? Ws) =
= 0 и (Яг? W's) — 0 или (/?о, Ws) + (Дг? И^^) = 0, s = 1, М, что
приводит к равенству нулю суммы двойного и криволинейного
интегралов соответственно по области ft и границе Г:
§8.5] Метод конечных элементов в задачах математической физики 343
= 0,8= ТЖ (8.37)
где Ws(x,y) — весовые функции для внутренних узлов расчет-
расчетной области, a Ws(x,y) — весовые функции для граничных
узлов расчетной области, s = 1, М. Весовые функции выбира-
выбираются таким образом, чтобы они были ортогональны невязкам по
области ft и по границе Г. В соответствии с методом Галеркина
взвешенных невязок весовые функции равны базисным: Ws =
= Ns,Ws=lVs.
Для базисных функций вида (8.33) интегралы от вторых
производных базисных функций (в соответствии с (8.35) при-
приближенное решение й(ж, у) содержит базисные функции) не су-
существуют, поскольку они стремятся к +ос или —ос. Для ослаб-
ослабления гладкости подынтегральных функций в (8.37) используем
первую формулу Грина, согласно которой для двух достаточ-
достаточное число раз непрерывно дифференцируемых функций и(х,у)
и v(x,y) имеет место равенство
\v — Л— + — A — dxdy =
J [дх \ дх) ду \ ду)\
п
dv .ди dv .6
П ~ "г
являющееся обобщением на двумерный случай формулы инте-
интегрирования по частям в определенном интеграле.
Тогда, подставляя в (8.37) решение (8.35) и применяя к по-
полученному выражению первую формулу Грина, в которой вме-
вместо функции v(x^y) подставлена функция Ns(x,y), а вмес-
вместо и(х,у) — функция и(х,у), получим слабую формулировку
конечно-элементного метода Галеркина:
Л / l\dNs xdNm^dNs ,dNm],, ^
V ит • < - —— • А^-— + —— • А^^ dxdy +
^ I J L дх дх ду ду \
NS- X^dr +\NS- X^dr +\NS- aNmdr ) =
344 Метод конечных элементов [Гл. VIII
= lf(x,y)Nadxdy+llV8<p(x,y)dr, s=TJI. (8.38)
п г
Весовые функции Ns на границе Г можно выбрать таким
образом, чтобы криволинейные интегралы по границе (второй и
третий интегралы в левой части выражения (8.38)) сократились,
т.е. принять Ns = — Ns. Тогда выражение (8.38) примет вид
dxdV
= - /(», y)Nsdxdy + Na(p(x, y)rfr, s = 1,M. (8.39)
n г
Выражения (8.39) — это неоднородная система линейных
алгебраических уравнений порядка М, которая в векторно-
матричной форме имеет вид
Аи = F, (8.40)
где элементы asm матрицы А и правых частей F образованы
суммированием вкладов отдельных конечных элементов (в со-
соответствии с аддитивным свойством кратных и криволинейных
интегралов):
Е Е
= /'
е=1 е=1
СЛАУ (8.39) или (8.40) называют глобальной СЛАУ, матри-
матрицу Л и вектор правых частей F — соответственно глобальной
матрицей (или матрицей жесткости) и глобальным вектором
правых частей.
Для отдельного конечного элемента 0е + Ге с локальными
номерами узлов г, j, k на основе глобальной СЛАУ (8.40), эле-
элементы матрицы и вектора правых частей которой определяются
выражением (8.39), можно построить локальную СЛАУ
Аеие = Fe (8.41)
§8.5] Метод конечных элементов в задачах математической физики 345
с локальной матрицей Ае = [afm], s = i,j,k; m = i,j,k и ло-
локальным вектором правых частей Fe = [/*], s = i,j,k, т.е.
Ае =
. 4i 4j Чк .
Fe =
F?
п
Элементы ае8т, s = г, j, к;т = г, j, fc, имеют вид выражений
в фигурных скобках СЛАУ (8.39), где интегралы вычисляются
по конечному элементу 0е + Ге, а компоненты F5e, s = i,j,k
имеют вид правых частей СЛАУ (8.39) на конечном элементе
Ое + Ге, т.е.
asm
дх дх ду ду
Ге
(8.42)
re
= i,j,k. (8.43)
В выражениях (8.42), (8.43) криволинейные интегралы равны
нулю, если конечный элемент не содержит граней, являющихся
граничными. Элемент aesrn локальной матрицы Ае вычисляется
таким образом, что для каждого номера s перебираются все
номера га. Например, для локального номера s = г перебираются
все номера га = г, j,fc; для s = j, га = г, j, fc; для s = fc, га =
При вычислении двойных интегралов в выражениях (8.42),
(8.43) используются базисные функции (8.33) и теорема о сред-
среднем
8NI
дх ду
ду
,m = i,j,k; (8.44)
346
Метод конечных элементов
[Гл. VIII
;, y)Nesdxdy = /cep • -Де, s = i,j, к, (8.45)
где в соответствии с теоремой о среднем
Ж* = -
Xj +Xk), у* = - (yi + yj + yk) ,
Ае — площадь треугольного элемента, /3|, 7| ~~ коэффициенты
в базисных функциях (8.33).
При вычислении криволинейных интегралов в выражениях
(8.42), (8.43) положим для определенности, что на границу Г
выходят узлы г и к элемента 0е + Ге (рис. 8.13).
К
Рис. 8.13. К вычислению криволинейных интегралов
Тогда произведения N%(ж, у) • Л^(ж, у), s, m = г, /с, геомет-
геометрически представляют собой поверхности второго порядка, а их
сечения плоскостью qik являются кривыми второго порядка,
а точнее — квадратными параболами. Таким образом, криво-
криволинейный интеграл в выражении (8.42) геометрически равен
заштрихованной площади на рис. 8.13, т.е.
- XiJ + (ук - Vi
(8.46)
§8.5] Метод конечных элементов в задачах математической физики 347
I
Ге
(yk - Vif ,
(8.47)
поскольку площадь криволинейного треугольника qik в соответ-
соответствии с теоремой о среднем равна 1/3ДГ, где АГ — расстояние
между узлами ink.
По той же причине имеет место равенство
J
Ге
где а
:* =
Vе (
1 (
2 ^
>, j/) rfr =^
i + xk); у*
о {х
1
~ 2
(ук -
(8.48)
+ ук), среср = <р(х*,у*).
Таким образом, в соответствии с выражениями (8.44)-(8.48)
локальная матрица Ае и вектор правых частей Fe СЛАУ для
конечного элемента ft = fte + Ге имеют вид (в случае, когда на
границу Г выходят узлы г и к конечного элемента)
Xecp-Ae-
+ ыJ рхщ + iti] mi +
1 0 1/2
0 0 0
1/2 0 1
, (8.49)
Fe =
'ср
-/,
е
ср
- /cep • Ae/3
- /cep • Ae/3
. (8.50)
В случае, если решается первая краевая задача для того
же уравнения (8.31), слабая формулировка (8.38) примет вид
(Ws = Ns)
348 Метод конечных элементов [Гл. VIII
dNadN
Л
ду ду
dxdy
п
где
' v)dxdV ~ \ N*<P (я, y)dT, s = ТЖ (8.51)
dNm dN
~^~~ cosA'n) +
ox
oy
n — вектор внешней нормали к границе Г.
Поэтому к вычислению интегралов (8.44)—(8.48) необходимо
добавить вычисление криволинейных интегралов от произведе-
произведения весовых функций на производные по нормали от базисных
функций. Тогда
^* ~ Xif + (Vk ~ У if >
(8.52)
если на границу Г выходят узлы ink.
Если конечные элементы ни одной гранью не выходят на гра-
границу области Г, то соответствующие криволинейные интегралы
равны нулю.
8.5.5. Ансамблирование элементов и построение гло-
глобальной СЛАУ. Для построения глобальной матрицы жест-
жесткости А и вектора правых частей F системы (8.40) необходимо
локальным номерам узлов г, j, k каждого элемента поставить
в соответствие глобальные номера узлов т, т = 1, М. При этом
§8.5] Метод конечных элементов в задачах математической физики 349
каждая локальная матрица Ае элемента расширяется до разме-
размера М х М, т.е. в глобальной матрице А ненулевые элементы
локальной матрицы Ае становятся на места, определяемые гло-
глобальными номерами узлов элемента 0е. Аналогично для вектора
правых частей F.
Затем расширенные таким образом матрицы и векторы пра-
правых частей всех конечных элементов складываются, в результате
чего получаем глобальную матрицу А и вектор правых частей
F, или глобальную СЛАУ (8.40).
Такой процесс объединения локальных СЛАУ для конечных
элементов в глобальную СЛАУ называется ансамблированием
конечных элементов.
Для рассматриваемого примера (рис. 8.11) М = 11. Тогда,
например, для элемента с номером 4 определено следующее со-
соответствие локальных и глобальных номеров узлов: г = 1, j = 4,
к = 5. Тогда локальная матрица элемента 4, имеющая вид
4 а4 а4
life
4
4 4 4
«?„• at- at.
преобразуется в расширенную матрицу Л4ас размера 11 х 11
следующим образом:
т 1 2 3 4 5 6 ... 11
S
1
2
3
4
5
б
11
?, О 0 а?
О
О
„4
О О
о о
о о
14
о
о
Х44
«15
о
о
а
\ь
о
о
о
«51 ° 0 «54
0 0 0 0
а45 О
О О
о
о
о
о
о
о
0 0 0 0 0 0 ... 0
350 Метод конечных элементов [Гл. VIII
Аналогично вектор правых частей F4 = \Ff, Fj, F^ ло-
локальной системы (8.41) преобразуется в расширенный вектор
с одиннадцатью компонентами:
<с = [Ft 0 0 Ff Ft 0 ... 0]Т . (8.53)
Операция суммирования осуществляется в соответствии с ад-
аддитивным свойством кратных и криволинейных интегралов. При
этом в памяти достаточно хранить матрицу-сумматор и вектор-
сумматор, а также буферные матрицу и вектор текущего эле-
элемента. Результирующую СЛАУ (8.40) можно решить одним из
известных методов, а значения искомой функции во внутренних
точках конечного элемента определяются по узловым значениям
с помощью функции элемента (8.36).
§ 8.6. Метод конечных элементов в многомерных
нестационарных задачах математической
физики
В нестационарных задачах математической физики искомая
функция зависит не только от пространственных переменных,
но и от времени, а дифференциальные уравнения и начальные
условия могут содержать производные по времени. Конечно-
элементную аппроксимацию в таких задачах можно осуществить
по пространственным переменным, сохранив дифференциаль-
дифференциальные операторы по времени, в результате чего получается си-
система обыкновенных дифференциальных уравнений порядка М
(М — число нумерованных узлов в пространственной расчетной
области О), т.е. один из вариантов метода прямых (см. раз-
раздел 6.6.3).
Однако существует более простой и эффективный метод,
согласно которому дифференциальный оператор по времени ап-
аппроксимируется конечно-разностным оператором, а простран-
пространственные операторы аппроксимируются конечно-элементным ме-
методом Галеркина. Рассмотрим этот метод на примере следующей
двумерной нестационарной задачи теплопроводности с гранич-
граничным условием 3-го рода для функции и(х, у, t):
}8.6] Метод конечных элементов в многомерных задачах 351
ди д (л , ч ди\ д (' , ч ди\ ,, ,
дх) ду\ Х'У ду) Х'У ' ^854)
(ж, у) GO, t > 0;
+ аи\Г = (р(х, у), (ж, у) е Г, t > 0; (8.55)
г
и(х, у, 0) = ф(х, у), (ж, у) G П, t = 0. (8.56)
Решение задачи (8.55)-(8.57) представляется в виде линейной
комбинации базисных функций УУт(ж,у), т = 1, М, с коэффи-
коэффициентами линейной комбинации, равными узловым значениям
искомой функции um(t), зависящими от времени:
м
и(х, у, *) и й(ж, у, t) = ^2 urn(t) • Nm(x, у), (8.57)
г?г=1
где базисные функции определяются соотношениями вида (8.33).
Тогда в соответствии со слабой формулировкой конечно-
элементного метода Галеркина (8.38) для задачи (8.54)-(8.56)
можно записать следующее нестационарное выражение:
м
I I I / И N ИМ ИМ И N \
\dxdy+
м
aN.NmdY %
, s = TJW, (8.58)
в котором функцию um(t) будем аппроксимировать на верх-
верхнем временном слое, обозначив um(tk+1) = г^1, а производную
dum(t)
^ — с помощью отношения конечных разностей по времени
dt
справа:
dum(t) = г4+1 ~ икт + q, ч
dt т
352 Метод конечных элементов [Гл. VIII
Тогда (8.58) будет иметь вид
М
aNsNmdr > =
m=1
s- f(x, y)dxdy + f Na(p(x, y)dr, s = Щ (8.59)
n г
Систему линейных алгебраических уравнений (8.59) отно-
относительно неизвестных узловых значений г^1, т = 1, М, на
верхнем временном слое в методе конечных элементов получа-
получаем с помощью аддитивного свойства кратных и криволинейных
интегралов путем суммирования локальных СЛАУ (8.41) для от-
отдельных конечных элементов с локальными номерами узлов г, j
и к. При этом элементы локальной матрицы и вектора правых
частей для конечного элемента ft выписываются на основе (8.59)
следующим образом:
Я/dNe 0Ne 0Ne
\dx A 8X + дУ Л дУ
+ f aNlN^dF, s,m = i, j, k. (8.60)
Ге
8=TJ4. (8.61)
Кратные и криволинейные интегралы в выражениях (8.60),
(8.61) вычисляются путем использования выражений согласно
(8.44)-(8.52). В (8.61) г^, как константа, выносится за знак
интеграла.
§8.7] Решение пространственных задач методом конечных элементов 353
В остальном алгоритм тот же, что и для стационарных задач.
Исключение составляет тот факт, что глобальную СЛАУ прихо-
приходится решать на каждом временном слое.
§ 8.7. Особенности решения пространственных
задач математической физики методом
конечных элементов
Рассмотрим эти особенности на примере следующей третьей
краевой задачи для трехмерного уравнения Пуассона в обла-
области П е Я3:
Ъх Vix) + ду IхJy) + Tz
= f(x,y,z), (x,y,z)eSl; (8.62)
А
ди
~дп
+ аи\г = (р(х, у, z), (ж, у, z) e Г. (8.63)
г
Приближенное решение ищется в виде следующей линейной
комбинации базисных функций Nm(x, у, z\ m = 1,М:
м
и(х, у, z) « u(x, y,z) = ^2um- Nm(x, у, z), (8.64)
т—\
где коэффициентами линейной комбинации являются значения
иш, т = 1, М, искомой функции в нумерованных узлах трехмер-
трехмерных конечных элементов fte.
В трехмерном случае в качестве конечных элементов прини-
принимаются тетраэдры с нумерованными узлами г, j, fc, / в вершинах
или параллелепипеды с узлами г, j, fc, /, m, n, о, р. Тетраэдр
является линейным конечным элементом, поскольку число ну-
нумерованных узлов на единицу больше размерности простран-
пространства Я3.
Если расчетная область ft разбита на тетраэдры, то базисные
функции, ассоциируемые с каждым нумерованным узлом конеч-
конечного элемента 0е, формируются в виде линейных функций пере-
переменных ж, у, z, удовлетворяющих условиям равенства единице
в узлах, для которых они определены, и нулю — в остальных
12 В.Ф. Формалев, Д.Л. Ревизников
354
Метод конечных элементов
[Гл. VIII
узлах. Для узла г, например, базисная функция имеет вид
Nf{x, у, z) = ai + Щх + 7геУ + Sfz, (8.65)
причем
Nf(x,y,z) =
1 в узле г;
О в узле j, /с, /.
Аналогично определяются базисные функции в узлах j, /с, /.
С учетом этих требований к базисным функциям формиру-
формируется следующая СЛАУ для определения коэффициентов af, /3|,
7|, Sf базисной функции Nf(x,y,z) (8.65):
yk zk
It
0
0
0
(8.66)
откуда
= det
= det
6Де
Jb -i
xk
_Xl
1
1
' г
Уз
Ук
Vl
Xj
Xk
6Де'
Z3
Zk
Z3
Zk
5
1
h
Д| =
6Де'
= -det
-det
"* 6Де
1 Уз
1 Ук
[l У1
1 Xj
1 xk
Z3
Zk
*l J
Уз'
Ук
6Ae = det
zk
у/
§8.7] Решение пространственных задач методом конечных элементов 355
Здесь Ае — объем элемента Пе (как известно, объем тетраэд-
тетраэдра равен шестой части объема параллелепипеда, который, в свою
очередь, равен модулю смешанного произведения трех векторов,
исходящих из одной точки, например из узла г в узлы j, /с, /).
Если узловые значения искомой функции иШ1т = i,j,k,l
станут известными, то значения искомой функции u(x,y,z) во
внутренних точках конечного элемента 0е определяются с помо-
помощью следующей функции:
7/^1 1* II У| 11^ /V^l Т II 7 1 —I- 11^ /V^l О" II У\ -\-
U \Х, у, Z) — U^ 1\i [Ж, у, Z) i" Uj 1\j [Ж, у, Z) -f
+ u%Nek(x, у, z) + ufNfix, y, z), (8.67)
называемой функцией элемента.
Слабая формулировка конечно-элементного метода Галерки-
на, изложенная выше для двумерных задач, полностью сохраня-
сохраняется для трехмерных задач за исключением того, что криволи-
криволинейные интегралы первого рода заменяются на поверхностные
интегралы первого рода, а двойные интегралы по области О —
на тройные интегралы.
При этом первая формула Грина, используемая в слабой
формулировке метода Галеркина, имеет вид
Г Г я / я \ я / я \ я / я \ 1
\ о ( ду\ д ( ду\ d/\dv\ii
\и Га~ А^~ + ^~ А^~ + ^~ А^~ dxdydz =
J [дх \ дх) ду \ ду) dz\ dz )\
Кди Лду диЛ ду ди л ду\ . . . Г Г л ду |тп
-—А-—h тг- А——Ь -^—л—- \axayaz + \\ и • А—— dY .
ох ох оу оу oz oz) JJ on
п г
В соответствии с количеством нумерованных узлов в конеч-
конечном элементе fte локальная матрица Ае в системе (8.41) имеет
размерность 4x4, причем интегралы в элементах матрицы Ае
и компонентах вектора правых частей Fe вычисляются с помо-
помощью тех же принципов (теорем о среднем), что и в двумерном
случае.
Процедура включения трехмерного элемента 0е в ансамбль
элементов, локальной матрицы жесткости Ае в глобальную А
и локального вектора правых частей Fe в глобальный вектор F
остается такой же, как и в двумерном случае.
12*
356 Метод конечных элементов [Гл. VIII
§ 8.8. Оценка погрешности метода конечных
элементов
8.8.1. Погрешность конечно-элементного метода ре-
решения задач для обыкновенных дифференциальных
уравнений. Границы погрешности конечно-элементного мето-
метода оценим вначале на примере первой краевой задачи для обык-
обыкновенного дифференциального уравнения второго порядка [29]:
Lu = -^ + а{х)и = /(ж); и@) = иA) = 0, (8.68)
dx
где а(х) — известная положительная функция, удовлетворяю-
удовлетворяющая условию
О < Рх ^ а(х) ^ р2 < оо, х е [0; 1]. (8.69)
Пусть конечно-элементное решение имеет вид (М — число
конечных элементов)
М+1
и(х) « и(х) = ^2 umNm(x). (8.70)
т—\
Для нахождения погрешности решения (8.70) введем функ-
функциональное пространство Соболева Wp[a, b] — пространство, для
любого элемента и(х) которого выполняется условие
—- G Lp[a, b] для всех а ^ п, (8-71)
где Lp — пространство функций, интегрируемых со степенью р
(интегрируемых по Лебегу). Для задачи (8.68) будем рассматри-
рассматривать пространство Соболева И/^[0;1] функций и(х) со скаляр-
скалярным произведением и нормой вида
1
/ / \ /w Г/ dudv
(u{x),v{x)) = «v + --
1
(и(х),и(х)) = ||«(a;)||^i = I
Здесь нижний индекс р = 2 указывает на то, что сама функ-
функция и(х) и ее первая производная (верхний индекс п = 1) дол-
должны быть интегрируемы с квадратом. Таким образом, верхний
§8.8]
Оценка погрешности метода конечных элементов
357
индекс 1 определяет наивысший порядок непрерывной производ-
производной в подынтегральном выражении.
Например, нормы функций и\ = х2 и u<i — sin x в простран-
пространстве Соболева W^[0; 1] будут соответственно
1
2
1
Г (ж4 + 4х2) dx
-О
(sin2 х + cos2 x) dx
1_0
Введем далее М-мерное подпространство S функций v(x) E
о
Е Sh С W\, где М = l//i, h — шаг разбиения области х Е [0; 1],
а кружок над символом пространства W означает, что функции
у(х) в граничных точках х = 0 и х = 1 обращаются в нуль.
Рассмотрим класс функций, принадлежащих этому подпрост-
подпространству.
Во-первых, это линейно-непрерывные глобальные базисные
функции Nm(x), т = 2, М, определяемые соотношениями (8.3),
поскольку эти функции кусочно-непрерывно дифференцируемы,
т.е. интеграл (8.72) существует, Nm(x) E W\[0; 1] и на границах
Ж*)
т=2
т=Ъ
М
Af+1
Рис. 8.14. Глобальные базисные функции Nm(x)
отрезка х Е [0; 1] они принимают нулевые значения (рис. 8.14).
При этом базисные функции для граничных узлов пока не уч-
учтены.
358 Метод конечных элементов [Гл. VIII
Во-вторых, это линейная комбинация и(х) базисных функ-
функций (8.70), поскольку в силу однородных краевых условий пер-
о
вого рода задачи (8.68) функция и(х) Е W\.
В-третъих, функция п(х), интерполирующая функцию и(х)
из задачи (8.68) и совпадающая с и(х) в нумерованных узлах,
то есть п(хт) = и(хт), т = 1, М + 1, поскольку п(х) на гра-
границах отрезка х ? [0; 1] также равна нулю и имеет кусочно-
непрерывные производные первого порядка.
На основе этого можно заключить, что и разность v(x) =
о
= п(х) — и(х) принадлежит подпространству Sh С W\. Таким
о
образом, к функциям \{х) ? W\ можно отнести множество
функций {Nm(x), и(х),п(х),п — и}.
о
Пространство W\ интересно тем, что если в качестве кон-
о
трольной функции взять элемент этого пространства v (х) ? W^
например базисную функцию Nm(x), то скалярные произведе-
произведения, записанные на основе (8.68) и (8.70), будут иметь вид
(L«,v) = (/,v), (8.73)
(Lu,v) = (f,v) + (R,v), (8.74)
где R(x) — невязка, являющаяся результатом подстановки (8.70)
в (8.68). Для v = Nm(x) скалярное произведение G?, v) = 0 в силу
метода Галеркина взвешенных невязок и ортогональности R(x)
и Nm(x).
Тогда, вычитая (8.74) из (8.73) (при (Д, v) = 0), получим
(Le,v) = 0, (8.75)
'е = и — и, причем можно показать, что (8.75) имеет место для
любой функции v(x) из перечисленного множества функций про-
о
странства W\.
В методе конечных элементов оценку погрешности будем
сравнивать с оценкой погрешности известных методов, например
метода интерполяции.
Тогда в соответствии с линейным свойством скалярного про-
произведения имеем следующее равенство:
(Le4, е) = (Le4, еГ+ п — п) = (Le4, и — п) + (Ь^е^п — и) . (8.76)
§8.8]
Оценка погрешности метода конечных элементов
359
Поскольку разность и — и принадлежит подпростран-
о
ству S С VK2 5 то в соответствии с (8.75) второе слагаемое в пра-
правой части выражения (8.76) равно нулю и оно принимает вид
(L'e, е) = (Le4, и — п) ,
или
1
,2^ \ Г / i2'
—| + а(х)е) edx = ( -^-| + а(ж)^) (и -u)dx. (8.77)
dx
dx
о
После интегрирования по частям первых слагаемых в подын-
подынтегральных выражениях равенство (8.77) приводится к виду
(с учетом однородных граничных условий задачи (8.68))
)[(§)'Нн[
о L J о
de d
-——
dxdx
— г^) + а(х)е (и — и)\ ах.
(8.78)
Обозначим левую часть в (8.78) через /, тогда на основе
неравенства Шварца
b /Ь \ 2 /Ь
/ Г 2 1 Г о
и - vdx ^ и dx - I \ v dx
Г /Г \ I Г
и - vdx ^ I u2dx I • I г;
j \ j / \ J
а
для любых и и v имеем
.0
-— 1 dx
— (и - и)\ dx\ +
\о / Lo
. (8.79)
Из определения соболевской нормы (8.72) следует, что
360
Метод конечных элементов
[Гл. VIII
т)dx
Lo
e'dx
Тогда из (8.79) находим
\\e\\w} х
dx
_о
(и — и) dx
Lo
max(l,/32)
— (и - и)\ dx > +
ах
\(и-пJ
.0
dx
2
тахA,
- u\\wi . (8.80)
Здесь /?2 — верхняя граница коэффициента а(х) в ограничениях
(8.69). Третье неравенство в цепочке (8.80) основано на известной
теореме о том, что среднее арифметическое двух неотрицатель-
неотрицательных выражений (а± ^ 0, а2 ^ 0) не ниже их среднего геометри-
геометрического:
(ai + а2)/2 ^ у/ах • а2 . (8.81)
На основе этого неравенства требуется доказать, что
\12
V2 (ai
(8.82)
Действительно, прибавим к левой и правой частям (8.81)
сумму (ai + a2), получим
a2)
a2 =
/ )
откуда сразу следует (8.82) и третье неравенство в (8.80). Таким
образом, из (8.80) получаем верхнюю оценку для выражения /:
§8.8]
Оценка погрешности метода конечных элементов
361
dx
О
max(l,
\e\\wi \\u - u\\wi
2 2
(8.83)
Для нижней оценки оператора / = (LeT, e) заметим, что
1
-Ш)
+ ае \\ dx
(8.84)
где /?i — нижняя грань коэффициента а{х) в (8.69).
Из сравнения оценок (8.83) и (8.84) следует, что
Х\Л 1 Т~1 I I 1°л -t I • I /Э I ^"^ гп о Л/" I П / Л И/ / I Z5 I -< 1^1 1 I II -*
111111^-L^ /-^ 1 / ||^|| ^ 111с1Л^ ±5^2/V^ П^П VK II II VK 5
откуда
||е^| = || j/ — й|| ^ с ||гх — гх|| , с = л/2 max A, /З2) / min (I, f3\) ,
(8.85)
т.е. норма погрешности конечно-элементного решения (8.70) не
превышает нормы погрешности интерполяционной функции.
Наконец, свяжем норму погрешности конечно-элементного
решения и с размером h конечного элемента. Используем по-
погрешность линейной интерполяции по Лагранжу п(х) в точке х
на отрезке [xj-±,Xj] (решение на каждом конечном элементе
с помощью базисных функций (8.3) является линейной функ-
функцией):
\и — и(х)\ =
2!
- Xj
max
г -I
2
= cljh2,tie(xj-1,xj), (8.86)
dx
(и — и(х))
362 Метод конечных элементов [Гл. VIII
^ max \u"(x)\2h/2 ^ c2jh. (8.87)
Интегрируя погрешности (8.86) и (8.87) по всему отрезку х Е
Е [0; 1] и выбирая максимальные на этом отрезке константы,
получаем
Г Г Г /7 12
(tj — гх) dx ^ ci/г4; -— (гх — гх) о!ж ^ С2/12.
J J |_^ж J
о о
Тогда соболевская норма погрешности интерполяционной
формулы оценивается выражением
сф. (8.88)
На основе (8.85) и (8.88) заключаем, что погрешность
конечно-элементного решения (8.70) оценивается сверху выра-
выражением
\\и - и\\ ^ c3V2 • [max A, /32) / min (I, /?i)] • /г, (8.89)
т. е. имеет место первый порядок по шагу, что согласуется с ли-
линейностью конечных элементов для задачи (8.68).
8.8.2. Погрешность конечно-элементного метода ре-
решения задач для уравнений в частных производ-
производных. Изложенный выше метод оценки погрешности конечно-
элементного метода решения задач для обыкновенных диффе-
дифференциальных уравнений легко распространяется на уравнения
в частных производных.
Погрешность конечно-элементного метода для задач мате-
математической физики рассмотрим на примере следующей задачи
Дирихле для уравнения Пуассона в плоской области ft + Г:
/\7/ I —L I —I— nil* II ill П\1* 7/1 \ 1* 7/i ^ О i& QOl
lull — [ о 2 ^ q 2 I ^ O^X, y)U — СДХ, У), ^Х, у) t ЛД, {O.VV)
и(г 11) — 0 (г и) G Г Г8 91"!
§8.8] Оценка погрешности метода конечных элементов 363
в которой а (ж, у) — положительная функция, удовлетворяющая
условиям
0<71^а(Ж,у)^72<ос, (8.92)
а оператор Lu положительно определен.
Для задачи (8.90), (8.91) введем пространство Соболева W\
функций и(х,у) со скалярным произведением
( дид\ ди д\
и нормой
п
ди\2
in: I + ( ^ ) \dxdy.
Повторяя выкладки, аналогичные выкладкам для обыкно-
обыкновенных дифференциальных уравнений, вплоть до соотношения
(8.77), находим
^4
dyz
d2e d2e\ 1
—~г + —-j + а(ж, y)e\ • (u-u) dxdy. (8.93)
Применим к первым двум слагаемым подынтегральных вы-
выражений левой и правой частей равенства (8.93) первую формулу
Грина, в которой криволинейный интеграл по границе Г равен
нулю, поскольку гх|г = 0; и\Г = 0] ^е = и — и = 0^ получим
Л^\ 2 / „\ 2
де\ , (де\
дед, _ч , де д
364
Метод конечных элементов
[Гл. VIII
Правую часть этого равенства оценим сверху с помощью
неравенства Шварца, обозначив выражение в левой части че-
через /:
L п
dxdy > +
де I,,
— dxdy
ду
L n
— (и-и)\ dxdy
Г Г
\\{и — 'иJ dxdy
+ 72 I e dxdy
) и
В соответствии с соболевской нормой имеем неравенства
. (8.94)
де
dxdy\
/\\e\\wi
$$e2dxdy) /\\e\\wi ^ 1.
Используя эти неравенства, из (8.94) получаем
д
max A,72)
дх
(и — и)\ dxdy > +
д
(и — и)\ dxdy > +
— uJdxdy
. (8.95)
Чтобы связать выражение в круглых скобках неравенства
(8.95) с соболевской нормой, воспользуемся неравенством
§8.9] Вариационный принцип в МКЭ 365
справедливым для любых неотрицательных а, 6, с.
Используя это неравенство, из (8.95) получаем оценку
max A, 72)
+ (и — пJ > dxdy ] = л/3 max A, 72) ||ё
или
я
^ л/3 max A, 72) ||е||Ж1 ||гх - u\\wi . (8.96)
Используя положительную определенность оператора Lu,
находим нижнюю границу интеграла в левой части выраже-
выражения (8.96):
. (8.97)
Сравнение неравенств (8.96) и (8.97) приводит к оценке для
нормы погрешности \\и — п\\ в пространстве Соболева:
ll^llv^1 ^ D \\u -u\\w± , D = л/3 max A,72) /min(l,7i) ,
(8.98)
из которой следует, что и для уравнений в частных производных
погрешность конечно-элементного метода не превышает погреш-
погрешности интерполяции с точностью до константы D.
§ 8.9. Вариационный принцип в МКЭ
При решении краевых задач для дифференциальных урав-
уравнений с помощью вариационного метода необходимо строить
такой функционал, минимум которого достигается на допусти-
допустимых функциях, удовлетворяющих уравнению Эйлера для этого
366 Метод конечных элементов [Гл. VIII
функционала, причем уравнение Эйлера совпадает с искомым
дифференциальным уравнением. То есть минимум упомянутого
функционала достигается на функциях, удовлетворяющих реше-
решению исходной дифференциальной задачи.
8.9.1. Введение в вариационное исчисление. Вариа-
Вариационное исчисление связано с отысканием стационарных зна-
значений функционалов [26,27], представляющих собой определен-
определенные интегралы от специальным образом построенных функций
и принимающих числовое значение при подстановке каждой кон-
конкретной функции в подынтегральное выражение.
Основная задача вариационного исчисления состоит в отыс-
отыскании такой функции F (ж), чтобы при произвольном бесконечно
малом изменении этой функции SF (х) величина функционала
(определенного интеграла от этой функции) оставалась неизмен-
неизменной, т. е. функционал принимал стационарное значение.
Рассмотрим функционал
ь
I=\F(x,(p, <px)dx, (8.99)
а
где х — независимая переменная; (р (х) — функция этой пере-
переменной, (рх = dip/'dx. Варьирование функционала / вызывается
бесконечно малым изменением (варьированием) функции F (х):
(8.100)
Чтобы вынести за скобку подынтегрального выражения в (8.100)
вариацию Scp, воспользуемся равенством
1'ь <8Л01>
после чего, проинтегрировав второе слагаемое в (8.100) по ча-
частям, получим
I I S(fdx + 5(р . (8.102)
а
§8.9] Вариационный принцип в МКЭ 367
Функционал (8.99) принимает стационарное значение, если
61 = 0, откуда, в силу произвольности Scp, имеем
^-^|^ = 0; (8.103)
й(р ах й(рх
или
6(р(а) = S(p{b) = 0, (8.105)
что соответствует постоянству функции (р на границах х = а,
х = 6, т. е. (р (а) = consti, ip (b) = const2-
Рассмотрим теперь функционал от функции трех независи-
независимых переменных в области V, ограниченной границей Г:
/ = F (ж, у, z, <р, <рх,<Ру, (Pz)dV. (8.106)
V
Произвольному бесконечно малому изменению функции
F (ж, у, z) соответствует вариация функционала
61 =
v
Используя соотношение (8.101), получаем выражение
хт - ,^Fr . OF д /е. ч . OF д ,Р ч . OF д
о! = \ \ ——
хдх v ^J dipydy v ^J dipzdz
v
(8.108)
Применяя ко второму слагаемому формулу дифференциро-
дифференцирования произведения, а затем формулу Остроградского-Гаусса,
находим
\w.~h(M dv = I h {wJ4) dv~[^ (Юs<pdv =
', (8.109)
\ )
V V V
г v
где пх — первый направляющий косинус нормали к границе Г.
368 Метод конечных элементов [Гл. VIII
Таким образом, из (8.108) и (8.109) имеем следующее выра-
выражение:
ХТ [\&f д (dF\ & (dF\ д fdF\]x „.^
61 = J [aj ~ Тх WJ ~ о~у Wv) ~ Tz WJ\ S<pdV+
V
Г Г dF OF 8F1
\\nx^— + ny^— + nz^—\8VdT. (8.110)
J [ д<рх у дуу d(pz\
г
Стационарное значение функционала (8.106) достигается при
равенстве нулю подынтегральных выражений в квадратных
скобках равенства (8.110), т.е. получаем уравнение Эйлера
OF \д (8F\ д FF\ д (8F
WX) ду \Wy) Tz \W.)\ - ( }
с ограничением
пх^- + пу^- + nz^- = 0. (8.112)
д(р o(f d(p
Соотношения (8.110)—(8.112) соответствуют вариационной
формулировке задач переноса тепла и массы.
Действительно, рассмотрим функционал
/ = F((p,<px,(py,(pz)dV =
V
Г Г / ?J \ ^ / ?) \ ^ /" ?1 \ ^
(8.113)
Тогда для уравнения Эйлера (8.111) и ограничений (8.112)
имеем
Кх-^пх + Хуу-^Пу + ^zz-^nz = 0, (8.115)
т. е. получаем стационарное уравнение теплопроводности с ис-
источниками Q в ортотропной среде с главными компонентами
тензора теплопроводности Лжж, \уу, Xzz и граничное условие
второго рода на границе Г, ограничивающей тело V.
§8.9] Вариационный принцип в МКЭ 369
Граничное условие (8.115) автоматически удовлетворяется
при задании функционала в форме (8.113) и поэтому называется
естественным.
8.9.2. Конечно-элементный вариационный принцип
на основе симметричного дифференциального операто-
оператора. Вариационный метод Релея—Ритца. Если задан функ-
функционал (вариационный принцип), то, как правило, можно найти
уравнение Эйлера. К сожалению, для дифференциальной задачи
не всегда можно построить функционал. Однако в одном важном
случае, а именно в случае симметричного дифференциального
оператора, это можно сделать.
Пусть дана дифференциальная задача
Ьср + р = О в ft; (8.116)
В(р + г = 0 на Г, (8.117)
где L и В — линейные дифференциальные операторы, ариг —
известные функции.
Пусть множество Ф функций в ? Ф непрерывно дифферен-
дифференцируемых в области ft + Г, удовлетворяет на границе Г однород-
однородному краевому условию (8.117), т.е.
Вв = О на Г. (8.118)
Тогда оператор L называется симметричным относительно
множества Ф, если для двух элементов в и $ этого множества
скалярное произведение удовлетворяет равенству
(в, Ы) = (#,L0)
или
1вЫс1П= \dL6dft, (8.119)
п п
т. е. оператор L — самосопряженный в ft с однородным гранич-
граничным условием на Г.
Симметричный оператор L называется положительно опре-
определенным относительно этого множества функций Ф, если для
370
Метод конечных элементов
[Гл. VIII
любого элемента в из данного множества
6L6 dtt
(8.120)
где равенство имеет место в том и только в том случае, когда
в = 0 в п.
Например, оператор L = —d2/dx2 на отрезке х Е [0; 1] и мно-
множестве функций, удовлетворяющих условиям в @) = в A) = 0,
является симметричным и положительно определенным. Дей-
Действительно, для двух элементов в и # после двойного интегри-
интегрирования по частям будем иметь
dx2
dx
——dx =
dx dx
Так как
d<d
dx
dO
dx
= 0,
), что и требовалось доказать.
Кроме того, заменяя в первом равенстве $ на ^, получаем
причем равенство нулю в (8.123) имеет место тогда и только тог-
тогда, когда d6/dx = 0, а это при однородных граничных условиях
0 @) = в A) = 0 выполняется при в = 0.
Таким образом, оператор L = —d2/dx2 ^ 0.
Пусть дана задача (8.116), (8.117) и L — симметричный опе-
оператор относительно множества ip ? Ф, удовлетворяющий одно-
однородному краевому условию (8.118), а ф — некоторая функция,
для которой на границе Г выполняется неоднородное краевое
§8.9] Вариационный принцип в МКЭ 371
условие
Вф + г = О на Г.
Тогда функционал
/ = I (^ - ф) JIl (ip - ф) + Lф + р] du (8.123)
принимает стационарное значение на решении (р краевой задачи
(8.116), (8.117).
Действительно, вариация функции ср (т. е. переход от ср к ср +
+ Sip) определяет вариацию функционала (8.123):
= | {S(p [\
51 = | {S(p [\L ^-
(8.124)
В силу симметричности оператора L на множестве функций,
удовлетворяющих (8.118), выполняется равенство
\ ((р - ф) L (S(p) du= \3(рЬ((р-ф) du. (8.125)
Тогда из (8.124) имеем
51 =
п
Г Г
= \S<p [L (ip - ф) + Ьф + р] du = S(p (Lip + р) dSl, (8.126)
п n
и так как Scp произвольно, то для стационарности функционала
(8.123) (т.е. при 61 = 0) выполняется равенство
L(p + p = 0 на О, (8.127)
т.е. получается исходное дифференциальное уравнение (8.116).
На основе понятия симметричного оператора L рассмотрим
вариационный метод Релея-Ритца приближенного решения за-
задачи (8.116), (8.117), в которой оператор L — симметричен отно-
относительно множества функций, удовлетворяющих краевому усло-
условию (8.118). Для этого выберем функцию ф, удовлетворяющую
372 Метод конечных элементов [Гл. VIII
неоднородным краевым условиям (8.117) задачи, т.е.
Вф + r = 0наГ, (8.128)
и определим систему базисных функций 7Vm, т = 1, М, такую
что
BNm = 0 на Г. (8.129)
Тогда аппроксимация для функции ср имеет вид
м
(рър = ф+^2ат-Мгп, (8.130)
771=1
а краевые условия (8.117) на Г выполняются автоматически для
всех значений постоянных ai, a2, . . . , &м- Метод Релея-Ритца
состоит в получении для функционала
1=1(<р-<Ф) [±l (<р - ф) + ьф + р] cm (8.131)
стационарного значения относительно параметров ai, a2, ...
Подставляя (8.130) в (8.131), находим
мм
I =
J
1=1 т=1
М р
. (8.132)
Выражение (8.132) принимает стационарное значение, если
91
Вычислив эти производные от (8.132), приходим к системе
линейных уравнений относительно ai, a<i, . . . , clm'-
м
(Ьф + р) dft,
m=l
§8.9] Вариационный принцип в МКЭ 373
Эта система в матричной форме записывается так:
Ка = /, (8.135)
где К — симметрическая матрица.
Компоненты матрицы К и вектора / вычисляются следую-
следующим образом:
klm=[NlLNmdU; ft = - J Nt (Ьф + p) dU. (8.136)
В системе (8.134) весовые функции TV/ совпали с базисными,
что тождественно методу Галеркина. Таким образом, методы
Релея-Ритца и Галеркина совпадают для симметричных опе-
операторов L. Разумеется, метод Галеркина справедлив для всех
операторов и в этом смысле является общим.
8.9.3. Решение задач с помощью конечно-элементно-
конечно-элементного вариационного принципа. Рассмотрим конечно-элемент-
конечно-элементный вариационный метод на примере решения задачи
|-§-р = 0, яе@;1); (8.137)
М°)д = 0, х = 0; (8.138)
dx
^р + a (ip A) - /3) = 0, х = 1. (8.139)
Составим следующий функционал, удовлетворяющий этой
задаче:
1
Действительно, вариация функционала (8.140) приводит к соот-
соотношению (с учетом интегрирования по частям)
1 , 1
51= -
dX у Ы*; q
- [q- a(<p- /3)]5(p,
374
Метод конечных элементов
[Гл. VIII
причем стационарное значение функционала достигается на
функциях (р, удовлетворяющих задаче A.137)—A.139). Предста-
Представим решение в виде линейной комбинации кусочно-линейных
базисных функций 7Vm, т = 1, М + 1 (8.3),
М+1
(р « ? = ^ VmNm (8.141)
т=1
и, подставив его в функционал (8.140), получим
d
dx
М+1
т=1
т=1
m - /3
dx—
. (8.142)
m=l
m=l
Необходимыми условиями минимума функции I(<pi,...
. . . , у м+i) многих переменных является равенство нулю ее част-
частных производных по переменным <?>/, / = 1, М + 1:
д!
= 0, 1 = 1, М + 1.
(8.143)
В результате получаем следующую систему М + 1 линейных
алгебраических уравнений относительно <?>/, Z = 1, М + 1:
М+1
dx
/М+1
+ TV/
- qNi +
m=l
=0, / = 1,
. (8.144)
m=l
В силу того что базисные функции 7Vm, m = 1, М + 1, в виде
равенств (8.3) кусочно-линейны, выражения (8.144) не равны
нулю на отрезках расчетной области х Е [0; 1], где не равна нулю
соответствующая базисная функция.
§8.9]
Вариационный принцип в МКЭ
375
Поэтому, разбив область [0; 1] на М одномерных элементов
и использовав аддитивное свойство определенного интеграла,
будем иметь
где ж|, ж| — соответственно координаты левого и правого ну-
нумерованных узлов элемента 0е, причем для внутренних нуме-
нумерованных узлов третье и четвертое слагаемые равны нулю, для
узла / = 1 третье слагаемое равно — д, а четвертое — нулю и, на-
наконец, для I = М + 1 третье слагаемое равно нулю, а четвертое —
выражению (<^V?m+i ~ ol0).
Для конечного элемента с локальными номерами г и j все
интегралы под знаком суммы в (8.145) будут равны нулю для
элементов, не ассоциируемых с узлами i и j, т.е. для системы
алгебраических уравнений
ktm = °> если 1,
(8.146)
м
e=l
M
Л = E ft,
e=l
если / = г, m = j или / = j, m = г;
he — he —
гг — Kjj —
376 Метод конечных элементов [Гл. VIII
если I = т = i или I = т = j.
Таким образом, в каждый элемент к\ш матрицы К и ком-
компонент // вектора / дают вклад только те конечные элементы,
которые ассоциируются с глобальными номерами узлов /ига.
УПРАЖНЕНИЯ
1. Используя подходящую систему базисных функций в виде
многочленов, аппроксимировать функцию ip = 1 + sin (тгж/2) на
отрезке [0; 1]. Применить методы коллокаций и Галеркина.
2. Для одномерной стационарной задачи теплопроводности
d2(p/dx2 + (p + l = 0;
d(f A)/dx = —(f
найти приближенное решение методом Галеркина, исследовать
скорость сходимости путем сравнения с аналитическим ре-
решением.
3. Рассмотреть функционал
- [а/2 • ср2 - qip] rfr,
г
где Л, Q, ср суть функции только ж, у. Найти уравнение Эйлера
и вид естественных краевых условий.
4. Доказать, что следующие операторы являются симметрич-
симметричными и положительно определенными:
a) L = —d?/dx2 относительно функций, удовлетворяющих
условиям
dip @)/dx + а<р @) = 0;
= 0;
а < 0; b > 0;
б) L(p = d2[a (x) d2cp/dx2]/dx2 + b (x) cp относительно мно-
множества функций, удовлетворяющих условиям (р = d(p/dx = 0 на
ж = 0 и на ж = 1;
§8.9] Вариационный принцип в МКЭ 377
в) оператор дА/дхА + 2дА /дх2ду2 + дА/дуА в области О,
ограниченной замкнутой границей Г относительно функций, удо-
удовлетворяющих условию (р = д(р/дп = О на Г.
5. Решить задачи конечно-элементным вариационным мето-
методом:
a) d2(p/dx2 + ехр (-х) = 0; <р @) = 0; dip (l)/dx = 1;
б) d*<p/dx* = sin тгх; <р(О) = <р A) = 0; *А = ^- = 0.
1 ах ах
6. Конечно-элементным методом Галеркина решить задачи
в квадрате х Е [0; 1], у ? [0; 1], разбив его на 18 треугольных
конечных элементов:
, д2и д2и
а) ^+v=0'
и(х, 0) = ж,
и(х, 1) = х2 + 1,
^ 92г. , д2и .
аж ду
и(х, 0) = ж,
и(х, 1) = х2 + 1,
ч 9?i 92г^ д2и
378 Метод конечных элементов [Гл. VIII
и(х, О, t) = X,
и(х, 1, t) = X2 + 1,
ГЛАВА IX
МЕТОД ГРАНИЧНЫХ ЭЛЕМЕНТОВ
РЕШЕНИЯ МНОГОМЕРНЫХ
СТАЦИОНАРНЫХ ЗАДАЧ
МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Программа
Метод граничных элементов (ГЭ) решения задач математической
физики. Использование фундаментальных решений, основной инте-
интегральной формулы Грина и граничного интегрального уравнения.
Формирование ГЭ, базисных функций и итоговой СЛАУ. Достоинства
и недостатки метода ГЭ.
Метод граничных элементов основан на представлении кра-
краевой задачи для уравнений Лапласа или Пуассона в виде гра-
граничного интегрального уравнения с использованием во второй
формуле Грина фундаментальных (без краевых условий) реше-
решений уравнения Лапласа [30].
Известно, что фундаментальными решениями уравнения Ла-
Лапласа Аи = 0 являются функции
и(М) = In = - In у/{хм ~ xwJ + (Ум ~ ywJ
К{М, М\у)
(9.1)
в двумерном случае и
и{М) = °"<]mw) =
. \ -1
\хм - xwJ + (ум - ywJ + (zm - zwJ J (9.2)
в трехмерном случае. В (9.1), (9.2) /?(М, Муу) — расстояние
между точкой расчетной области М Е ft и граничной точ-
точкой Mw е Г.
Применяя к фундаментальному решению (9.2) и к искомой
функции и вторую формулу Грина, получаем в трехмерном
случае тождество, называемое основной интегральной формулой
Грина:
380 Метод граничных элементов решения стационарных задач [Гл. IX
и(М) = -
1 ГГГ 1 du{Mw)
4тг JJ [R(M,MW) дп
Г
где п — направление внешней нормали к поверхности Г (для
внутренней нормали знак в тождестве меняется на противопо-
противоположный). Если и удовлетворяет уравнению Лапласа, то объем-
объемный интеграл в (9.3) равен нулю, а для уравнения Пуассона
этот интеграл известен и в дальнейшем это слагаемое рассмат-
рассматриваться не будет. Здесь М1 ? О (М ф М1) — переменная точка
в области О.
Для произвольной граничной точки Р\у ? Г в (9.3) необходи-
необходимо перейти к пределу при стремлении внутренней точки М ? ft
к точке Р\у ? Г. Получим следующее интегральное уравнение:
du{Mw)
R(PW,MW) дп
г
-u(Mw)-
дп \R(PW,MW)
называемое граничным интегральным уравнением.
Если задано граничное условие 1-го рода
(9.4)
u{Mw) = (р(х, у, z), Mw e Г, (9.5)
то значения и(Руу) и и(Муу) в (9.4) известны, поэтому из (9.4)
du(Mw) .
можно определить значения —т- -, которые, будучи подстав-
дп
ленными в (9.3), явно определяют значения и(М), М ? О, в нуж-
нужных точках расчетной области.
При задании граничного условия второго рода
или третьего рода
du(Mw)
Ъп
Mwer, (9.6)
+ au(Mw) = <р(х, у, z), Mw ? Г, (9.7)
Гл. IX] Метод граничных элементов решения стационарных задач 381
du(Mw)
нормальная производная —т- на границе 1 определяется
on
или явно из (9.6) или через u{Mw) из (9.7). Подставляя затем
в (9.4), решаем полученное интегральное уравнение
du(MW)
дп
относительно и(М\у), в результате чего на границе Г будут
известны и и(М\у), и —7- -. Подставляя затем их в (9.3),
дп
получаем явное выражение для определения и(М), М Е ft.
В двумерном случае основная интегральная формула Грина
и граничное интегральное уравнение имеют соответственно сле-
следующий вид:
1 du(Mw)
дп
,d \ 1 Г fi х du(Mw)
г
дп\ R(PW,MW)
). (9.9)
Таким образом, достоинством метода граничных интеграль-
интегральных уравнений является снижение на единицу порядка диф-
дифференциального уравнения. К недостаткам можно отнести
необходимость отыскания фундаментальных решений, которые
известны не для всех уравнений математической физики.
В соответствии с методом граничных элементов для числен-
численного решения граничного интегрального уравнения (9.9) в дву-
двумерном случае граница Г разбивается точками P\vK ^ Г, к =
= 1,п, на п частей (граничных элементов АГ^), причем уз-
узлы с номерами 1 и п + 1 совпадают. Искомая функция и(Руу)
аппроксимируется следующей линейной комбинацией базисных
функций Nk((p):
(9.10)
к=1
где коэффициенты ик линейной комбинации суть узловые зна-
значения искомой функции на границе Г, а (р — полярный угол
радиуса-вектора, соединяющего каждую точку Р\^г Е Г, г = 1, п,
382 Метод граничных элементов решения стационарных задач [Гл. IX
как центра локальной полярной системы координат, с точка-
точками М\ук, к = 1, п, к ф г.
В качестве базисных функций Nk, k = 1, п, рассматриваются
кусочно-линейные функции
((р - (pk-l)/(<Pk - 4>k-l)i 4>k-l ^ V ^ Фк\
Nk = < (
<р < (pk-i, ?
если за нумерованные узлы к принять точки разбиения, или
кусочно-постоянные функции
h **-^*<™ (9.12)
О, <р < ipk-i, V > <Pk,
если за нумерованные узлы принять точки Рк, леж:ащие в геомет-
геометрических центрах граничных элементов АГ^. Именно последний
вид базисных функций, как более простых, будет использован
в данной главе.
Представляя криволинейный интеграл в граничном инте-
интегральном уравнении (9.9) в виде суммы по граничным элемен-
элементам:
тг u{PWi)-
= l,n, (9.13)
и подставляя в (9.13) вместо и линейную комбинацию (9.10),
получаем систему линейных алгебраических уравнений относи-
относительно uw , к = 1, п.
Рассмотрим применение метода граничных элементов для
численного решения стационарной задачи теплопроводности
в многосвязных областях, которая формулируется в виде сле-
следующей краевой задачи для квазилинейного уравнения тепло-
теплопроводности (рис. 9.1):
д /л/ ,ди\ д
Гл. IX] Метод граничных элементов решения стационарных задач 383
aw(uel-uw)-X(u) -^
дп
= о,
(9.15)
-uw) + X(u)
fu
дп
= 0.
(9.16)
w2
Поскольку использование для решения интегральной форму-
формулы Грина (9.8) и граничного интегрального уравнения (9.9) пред-
Рис. 9.1. Разбиение границы многосвязной области
полагает линейность задачи, необходимо задачу (9.14)-(9.16) ли-
линеаризовать, для чего используется следующая замена искомой
переменной, называемая подстановкой Кирхгофа:
(9.17)
Тогда
д
—
ох
— = — А(«)—-—
ох I ох о А дх
dA
дА
д2А
ди
д2А
384 Метод граничных элементов решения стационарных задач [Гл. IX
и уравнение (9.14) трансформируется в следующее уравнение
Лапласа:
В краевых условиях (9.15), (9.16) подстановка (9.17) линеари-
линеаризует слагаемое с нормальной производной искомой функции, од-
однако линейные члены становятся нелинейными. Для сохранения
линейности этих слагаемых примем в начальном приближении
Х(и) постоянным и равным Лс. Тогда из (9.17) имеем
и краевые условия (9.15), (9.16) будут трансформированы следу-
следующим образом:
дА
- AwJXc)
дп
дА
дп W2
= 0, (9.20)
= 0. (9.21)
Если решение Л(ж, у) в точке (ж, у) линейной третьей краевой
задачи (9.18), (9.20), (9.21) для уравнения Лапласа подставить
в (9.17) и после интегрирования решить соответствующее алгеб-
алгебраическое уравнение, степень которого на единицу выше степени
функции А (г/), то получим значение искомой функции и(х,у)
в той же точке. При этом в радикалах решается уравнение
степени не выше четвертой:
ao^i4 + aiu3 + a2U2 + а%и + а^ = Л, (9.22)
что соответствует заданию Х(и) в виде многочлена степени не
выше третьей.
Итак, решается стационарная задача (9.18), (9.20), (9.21) ме-
методом граничных элементов с использованием базисных функ-
функций (9.12) в многосвязных областях, представленных на рис. 9.1.
Всякая функция Л(ж, ?/), непрерывная вместе с первыми про-
производными в замкнутой области ft + Гцг, где Г\у = ^Wi + ^W2 ~
достаточно гладкая граница, и имеющая вторые производные
внутри О, удовлетворяет основной интегральной формуле Грина
Гл. IX] Метод граничных элементов решения стационарных задач 385
(9.8) и граничному интегральному уравнению (9.9), которые для
задачи (9.18), (9.20), (9.21) имеют вид
Л(М) = ^
- In R(M,
on
dF(Mw), (9.23)
= -j \\(Mw)-^lnR(Pw,Mw)-
dT{Mw). (9.24)
Упростим подынтегральные выражения в (9.23), (9.24), для
чего введем локальную полярную систему координат с центром
У
Рис. 9.2. Локальная полярная система координат
в граничной точке Рц/-, полярным расстоянием г = R(Pw,
и углом (р (рис. 9.2). Тогда в (9.24) первое слагаемое подынте-
подынтегрального выражения преобразуется следующим образом (Гук =
= T(MW)):
ТЬ
§ С/ ТЬ
13 В.Ф. Формалев, Д.Л. Ревизников
386 Метод граничных элементов решения стационарных задач [Гл. IX
) - cos(r, п) д/г2 + (dr I dipJ dip =
г
dip = A(Mw)dip, (9.25)
так как из равенств
х = г • cos (/?, у = г - sin (p, dF\y = ydx2 + dy2
следует, что
д х д х
dx = -^—dr + -^—dip = cos (p dr — r • sin ip dip;
or dip
д у д у
ay = ^—dr + ——dip = sin w dr + r • cos w dip;
ОГ О if
dTw = ^dr2 + r2dip2 = ^/r2 + (dr/dipJdip. (9.26)
Кроме этого, если элемент касательной к дуге в точке Муу
определяется выражением (9.26), то отрезок нормали M\yN име-
имеет длину
\MWN\ = ^/r2 + (dr/dipJ
и, следовательно,
|^ = cos(r, п) = „/ ЛГ, = Г (9.27)
дп v J \MWN\ ^/r2 + {d/dJ V }
Таким образом, из (9.26), (9.27) следует (9.25). Используя
выражение (9.25) и краевые условия (9.20), (9.21) в граничном
интегральном уравнении (9.24), получаем это уравнение для гра-
граничных точек Руу в следующем виде:
A(PW) = - \ A(Mw)d(p-- [ 1пг^[Лс^е
(9.28)
где
aw = [aWi,aW2] , ue =
Разобьем границу Fvv — Tw\ + Ги/2 многосвязной расчетной
области на п граничных элементов АГ|^, i = 1,п, и будем вы-
вычислять с помощью формулы (9.28) функцию Л в нумерованных
Гл. IX] Метод граничных элементов решения стационарных задач 387
узлах P\Vii i — 1? п, находящихся в середине граничных элемен-
элементов АГ|^. Количество граничных элементов на наружной грани-
границе W\ принимаем равным нескольким десяткам, уменьшая шаг
разбиения в местах увеличения кривизны наружной границы.
На каждой из внутренних границ W<i принимается до десяти
граничных элементов, но не меньше четырех.
Используя аддитивное свойство криволинейного интеграла,
заменяем интегралы в (9.28) суммами интегралов по граничным
элементам АГ|^ и считаем величины olw-> ue-> A(Pvy) посто-
постоянными в пределах каждого граничного элемента. Получаем
следующую систему п алгебраических уравнений относительно
значений функции Л(Р^) = Л^л, г = 1, п:
(г-\,гф\ п \
Е + Е Ybk^ i=I^> (9-29)
где
ак
Vfc-1/2
/2 АГ^
Г
\nr-dTw.
В выражениях (9.29) для каждой зафиксированной точки
г-го участка (г = 1,п) пробегаются все к (к = 1,г — 1, г ф 1
и к = г + 1,п, г ф п) срединных точек Mwk, за исключением
точки Pwi- При этом угол (р изменяется от 0 до тг.
Вычисление интегралов в коэффициентах ак, Ьк можно
осуществить с помощью квадратурных формул трапеций или
Симпсона.
Система (9.29) является системой с наполненной матрицей
(т.е. очень мало нулевых элементов матрицы системы). Для ее
решения можно использовать как прямые, так и итерационные
методы.
13*
388 Метод граничных элементов решения стационарных задач [Гл. IX
Результатом решения системы (9.29) будет распределение
функции А\у^ i = 1, п, на границе Г^ расчетной области.
Гранично-элементная аппроксимация основной интегральной
формулы Грина (9.23) будет аналогична аппроксимации (9.29)
с той лишь разницей, что вместо коэффициента 1/тг при криво-
криволинейном интеграле будет стоять коэффициент 1/2тг, а значения
функций A(Mvv), дА(Мцг)/дп уже известны из решения систе-
системы алгебраических уравнений (9.29) и краевых условий (9.20),
(9.21). Таким образом, получаем явные выражения для опреде-
определения Л(М), MgH, в следующем виде:
к=1 к=1
Здесь в коэффициентах а&, 6& углы (р — это углы между
линиями М Муук, соединяющими точку М Е О с точками М\ук Е
Е Гvi/, ^ = 1, ^, и осью ж, которые изменяются от 0 до 2тг.
После определения функции Л в области О + Г\у из подста-
подстановки (9.17) определяется искомая функция и(х^у) в каждой
точке расчетной области. Например, если Х(и) задана в виде
многочлена третьей степени
Л() ^ + а\и2 + u2U + аз,
то в каждой точке расчетной области необходимо решить алгеб-
алгебраическое уравнение четвертой степени
^V + |V + |V + azu = Л(М), М € п + Г,
которое можно решить в радикалах [30].
В результате распределение функции и(х,у) в области О +
+ Г будет определяться в первом приближении, поскольку гра-
граничные условия (9.20), (9.21) учитывали постоянное значение
коэффициента Лс. В соответствии с этим будем обозначать это
решение верхним индексом A) г^1); (соответственно Л^1)).
Для определения второго приближения Л^2) (соответственно
и^) разложим функцию А^(и) в ряд Тейлора в окрестно-
окрестности г^1), оставив в нем только линейные члены:
О{Аи2). (9.31)
Гл. IX] Метод граничных элементов решения стационарных задач 389
Полагая здесь
получаем
(9-32)
Применим теперь к производным исходной задачи (9.14)—
(9.16) подстановку Кирхгофа (9.17), а вместо искомой функции
в краевых условиях (9.15), (9.16) — приближение (9.32), получим
следующую третью краевую задачу для уравнения Лапласа от-
относительно функции
(9.33)
el
кBЛ -
д п
B) ^ "
)
дп
(9.34)
(9.35)
w2
где
S2) -
Из сравнения задачи (9.33)-(9.35) с задачей (9.18), (9.20),
(9.21) следует, что для определения Л^2) формально можно ис-
использовать решение (9.29) для точек на границе Гцг и реше-
решение (9.30) для внутренних точек области О, заменяя коэффи-
коэффициенты а&, Ь^ следующим образом:
ак=
Г Г
= dip + о$к
ln r
390 Метод граничных элементов решения стационарных задач [Гл. IX
B) B) I
Ь/г = OLyy uek In Г • dT\y^
J
д г1 к
где
Искомая функция и^ в точках М G ft + Г определяется
путем решения уравнения (9.17).
СПИСОК ЛИТЕРАТУРЫ
1. Демидович Б. /7., Марон И. А. Основы вычислительной мате-
математики. — М.: ГИФМЛ. 1963.
2. Самарский А. А., Николаев Е.С Методы решения разност-
разностных уравнений. — М.: Наука. 1978.
3. Бахвалов П. С. Численные методы. — М.: Наука. 1975.
4. Форсайт Дж., Молер К. Численные методы решения систем
линейных алгебраических уравнений. — М.: Мир, 1969.
5. Крылов В. /f., Бобков В. В., Монастырный П. И. Вычисли-
Вычислительные методы. — М.: Наука. 1976. Т. 1,2.
6. Плис А. И., Сливина П. А. Лабораторный практикум по выс-
высшей математике. — М.: Высшая школа. 1983.
7. Турчак Л. И. Основы численных методов. — М.: Наука. 1980.
8. Корн Г., Корн Т. Справочник по математике для научных
работников и инженеров. — М.: Наука. 1968.
9. Сборник задач по математике для ВТУЗов. Методы опти-
оптимизации, уравнения в частных производных, интегральные
уравнения/ Под. ред. Ефимова А. В. — М.: Наука. 1990.
10. Самарский А. А., Гулин А. В. Устойчивость разностных
схем. — М.: Наука. 1973.
11. Самарский А. А. Теория разностных схем. — М.: Наука. 1983.
12. Самарский А. А., Попов Ю. П. Разностные методы решения
задач газовой динамики. — М.: Наука. 1980.
13. Самарский А. А., Гулин А. В. Численные методы. — М.: Нау-
Наука. 1989.
14. Яненко П. П. Метод дробных шагов решения многомерных
задач математической физики. — Новосибирск: Наука. 1967.
392 Список литературы
15. Саульев В. И. Интегрирование уравнений параболического
типа методом сеток. — М.: Физматгиз. 1960.
16. Марчук Г. И. Методы расщепления. — М.: Наука. 1988.
17. Формалев В. Ф. Экономичный абсолютно устойчивый алго-
алгоритм численного решения двумерных уравнений параболиче-
параболического типа. //Сборник научных трудов «Численные методы
решения задач аэродинамики». — М: Издательство МАИ.
1987. С. 56-59.
18. Формалев В. Ф., Тюкин О. А. Экономичный абсолютно устой-
устойчивый метод расщепления с экстраполяцией численного ре-
решения задач, содержащих смешанные дифференциальные
операторы. //Вычислительные технологии. 1995. Т. 4. № 10.
С.290-299.
19. Формалев В. Ф., Воробьева О. Р. Метод переменных направ-
направлений с экстраполяцией численного решения задач тепло-
теплопроводности с тензором теплопроводности и конвективными
членами. — М: Вестник МАИ. 1997. Т. 5. №1. С. 41-48.
20. Формалев В. Ф., Тюкин О. А. Неявный экономичный ме-
метод численного решения параболических задач, содержа-
содержащих смешанные производные //Математическое моделиро-
вание.1996. Т. 8. №6. С. 27-32.
21. Формалев В. Ф., Тюкин О. А. Неявный метод дробных шагов с
расщеплением смешанных дифференциальных операторов.//
Вычислительные технологии. 1998. Т. 3. №6. С. 82-91.
22. Березин И. С, Жидков Н. П. Методы вычислений. — М.: На-
Наука. 1960. Т. 2.
23. Когпляр Я. М. Методы математической физики в прикладных
задачах. — М.: Издательство МАИ. 1978.
24. Пирумов У. Г. Численные методы. — М.: Издательство МАИ.
25. Годунов С. К., Забродин А. В., Иванов Н. Е. и др. Численные
методы решения многомерных задач газовой динамики. — М.:
Наука. 1976.
26. Сегерлинд Л. Применение метода конечных элементов. — М.:
Мир. 1979.
Список литературы 393
27. Зенкевич О., Морган К. Конечные элементы и аппроксима-
аппроксимация. — М.: Мир. 1986.
28. Формалев В. Ф. Метод конечных элементов в задачах тепло-
теплообмена. — М.: Издательство МАИ. 1991.
29. Ши Д. Численные методы в задачах теплообмена. — М.: Мир.
1988.
30. Галицейский Б. М., Совершенный В. Д., Формалев В. Ф. и др.
Тепловая защита лопаток турбин. — М.: Издательство МАИ.
1996.
31. Тихонов А. //., Самарский А. А. Уравнения математической
физики. — М.: Наука. 1972.
ОГЛАВЛЕНИЕ
I. Численные методы алгебры и анализа
Глава 1. Элементы теории погрешностей 11
Глава 2. Численные методы алгебры 16
§2.1. Численные методы решения СЛАУ 17
2.1.1. Метод Гаусса A7). 2.1.2. Метод прогонки B6).
2.1.3. Обоснование метода прогонки C1). 2.1.4. Мат-
Матричная прогонка C3). 2.1.5. Нормы векторов и мат-
матриц C4). 2.1.6. Итерационные методы решения СЛАУ. Ме-
Метод простых итераций C8). 2.1.7. Метод Зейделя реше-
решения СЛАУ D5). 2.1.8. Метод Зейделя для нормальных
СЛАУ D7).
§ 2.2. Численные методы решения нелинейных и трансцендент-
трансцендентных уравнений 50
2.2.1. Способы отделения корней E1). 2.2.2. Методы уточ-
уточнения корней E2). 2.2.3. Скорость сходимости. Процедура
Эйткена ускорения сходимости F6). 2.2.4. Замечания к
методам отделения корней F8).
§ 2.3. Численные методы решения систем нелинейных уравнений 69
2.3.1. Метод простых итераций и метод Зейделя решения
систем нелинейных уравнений G0). 2.3.2. Метод Ньюто-
Ньютона G2).
§ 2.4. Численные методы решения задач на собственные значения
и собственные векторы матриц линейных преобразований . 76
2.4.1. Основные определения и спектральные свойства мат-
матриц G6). 2.4.2. Метод вращений Якоби численного реше-
решения задач на собственные значения и собственные векто-
векторы матриц (80). 2.4.3. Частичная проблема собственных
значений и собственных векторов матрицы. Степенной ме-
метод (91).
Глава 3. Теория приближений 97
§3.1. Исчисление конечных разностей 99
§ 3.2. Задача интерполяции 100
3.2.1. Интерполяционный многочлен Лагранжа A01).
3.2.2. Интерполяционный многочлен Ньютона A03).
3.2.3. Погрешность многочленной интерполяции A04).
3.2.4. Интерполяционный многочлен Ньютона, построенный
Оглавление 395
с помощью разделенных разностей A06). 3.2.5. Сплайн-
интерполяция A08).
§3.3. Метод наименьших квадратов 118
§ 3.4. Численное дифференцирование 127
3.4.1. Метод Рунге уточнения формул численного диффе-
дифференцирования A30).
§ 3.5. Численное интегрирование функций 134
3.5.1. Формула прямоугольников численного интегрирова-
интегрирования A35). 3.5.2. Численное интегрирование с помощью
формулы трапеций A36). 3.5.3. Формула Симпсона числен-
численного интегрирования A40). 3.5.4. Процедура Рунге оценки
погрешности и уточнения формул численного интегрирова-
интегрирования A44).
Глава 4. Численные методы решения задач для обык-
обыкновенных дифференциальных уравнений 150
§4.1. Основные определения и постановка задач Коши для обык-
обыкновенных дифференциальных уравнений 150
§ 4.2. Метод Эйлера численного решения задач Коши для ОДУ и
систем ОДУ 154
4.2.1. Метод Эйлера для нормальных систем ОДУ A55).
§ 4.3. Метод Эйлера-Коши (Эйлера с пересчетом) 156
4.3.1. Метод Эйлера-Коши для нормальных систем A57).
§ 4.4. Метод Рунге-Кутта 158
4.4.1. Метод Рунге—Кутта для нормальных систем
ОДУ A61).
§ 4.5. Выбор шага численного интегрирования задач Коши 162
§ 4.6. Процедура Рунге оценки погрешности и уточнения числен-
численного решения задач Коши 163
§ 4.7. Численные методы решения краевых задач для ОДУ 175
4.7.1. Постановка краевых задач для ОДУ A75).
4.7.2. Конечно-разностный метод с использованием
метода прогонки решения краевых задач для ОДУ A76).
4.7.3. Конечно-разностная схема со вторым порядком
аппроксимации краевых условий, содержащих производ-
производные A78). 4.7.4. Метод пристрелки численного решения
краевых задач для ОДУ A80). 4.7.5. Метод пристрелки с
использованием итерационной процедуры Ньютона A82).
Глава 5. Численные методы оптимизации 195
§5.1. Классификация численных методов оптимизации 195
§ 5.2. Численные методы безусловной минимизации функций од-
одной переменной. Прямые методы 196
396 Оглавление
5.2.1. Метод перебора A97). 5.2.2. Метод деления отрезка
пополам A98). 5.2.3. Метод золотого сечения B00).
§ 5.3. Методы минимизации, использующие производные. Метод
Ньютона 205
§ 5.4. Безусловная минимизация функций многих переменных . . 207
5.4.1. Метод градиентного спуска B07). 5.4.2. Метод наи-
наискорейшего спуска B12). 5.4.3. Метод сопряженных на-
направлений B15).
II. Численные методы решения задач для
уравнений математической физики
Глава 6. Метод конечных разностей 221
§6.1. Постановка задач математической физики 222
6.1.1. Постановка задач для уравнений параболического ти-
типа B22). 6.1.2. Постановка задач для уравнений гиперболи-
гиперболического типа B24). 6.1.3. Постановка задач для уравнений
эллиптического типа B26).
§ 6.2. Основные определения и конечно-разностные схемы для
различных задач математической физики 228
6.2.1. Основные определения B28). 6.2.2. Конечно-
разностная аппроксимация задач для уравнений
гиперболического типа B31). 6.2.3. Конечно-разностная
аппроксимация задач для уравнений эллиптического
типа B33).
§ 6.3. Основные понятия, связанные с конечно-разностной ап-
аппроксимацией дифференциальных задач 235
6.3.1. Аппроксимация и порядок аппроксимации B35).
6.3.2. Устойчивость B36). 6.3.3. Сходимость и порядок
сходимости B37). 6.3.4. Теорема эквивалентности о свя-
связи аппроксимации и устойчивости со сходимостью B38).
6.3.5. Консервативность и корректность B38).
§ 6.4. Анализ порядка аппроксимации разностных схем 239
§6.5. Исследование устойчивости конечно-разностных схем 240
6.5.1. Метод гармонического анализа B41). 6.5.2. Ис-
Исследование устойчивости методом гармонического ана-
анализа явной и неявной схем для уравнения теплопро-
теплопроводности B42). 6.5.3. Исследование устойчивости ме-
методом гармонического анализа явной и неявной схем
для волнового уравнения B43). 6.5.4. Принцип мак-
максимума B45). 6.5.5. Спектральный метод исследования
устойчивости B46). 6.5.6. Энергетический метод исследо-
исследования устойчивости конечно-разностных схем B48).
Оглавление 397
§ 6.6. Конечно-разностный метод решения задач для уравнений
параболического типа 254
6.6.1. Однородные и консервативные конечно-разностные
схемы для задач теплопроводности с граничными усло-
условиями, содержащими производные B54). 6.6.2. Неявно-
явная конечно-разностная схема с весами. Схема Кранка—
Николсона B60). 6.6.3. Метод прямых B64).
§ 6.7. Метод конечных разностей решения задач для волнового
уравнения с граничными условиями, содержащими произ-
производные 269
§ 6.8. Метод установления и его обоснование 273
Глава 7. Метод конечных разностей решения много-
многомерных задач математической физики. Методы расщеп-
расщепления 279
§ 7.1. Метод матричной прогонки 281
§ 7.2. Метод переменных направлений Писмена-Рэчфорда 284
§ 7.3. Метод дробных шагов Н. Н. Яненко 288
§ 7.4. Метод переменных направлений с экстраполяцией В. Ф.
Формалева 290
7.4.1. Аппроксимация B93). 7.4.2. Устойчивость B96).
§ 7.5. Схема метода полного расщепления Формалева-Тюкина . . 298
§ 7.6. Методы расщепления численного решения эллиптических
задач 301
§ 7.7. Методы решения задач для уравнений гиперболического
типа 301
7.7.1. Метод характеристик решения квазилинейных гипер-
гиперболических систем C02). 7.7.2. Метод сквозного счета. За-
Задача о распаде произвольного разрыва. Метод С. К. Году-
Годунова C07).
Глава 8. Метод конечных элементов 316
§ 8.1. Основы МКЭ 317
§ 8.2. Система базисных функций 318
8.2.1. Кусочно-постоянные базисные функции C19).
8.2.2. Линейные кусочно-непрерывные базисные
функции C21).
§ 8.3. Методы взвешенных невязок. Весовые функции 322
8.3.1. Метод поточечной коллокации C23). 8.3.2. Метод Га-
леркина C24). 8.3.3. Метод наименьших квадратов C25).
§ 8.4. Конечно-элементный метод Галеркина решения краевых за-
задач для обыкновенных дифференциальных уравнений .... 325
8.4.1. Слабая формулировка метода Галеркина C26).
8.4.2. Формирование локальной и глобальной матриц жест-
398 Оглавление
кости. Ансамблирование элементов C28). 8.4.3. Случай
граничных условий, содержащих производные C33).
§ 8.5. Метод конечных элементов в стационарных задачах мате-
математической физики 335
8.5.1. Основные этапы решения стационарных задач ма-
математической физики методом конечных элементов C35).
8.5.2. Принципы разбиения плоских областей на конечные
элементы C37). 8.5.3. Аппроксимация линейными много-
многочленами и базисные функции C39). 8.5.4. Слабая фор-
формулировка конечно-элементного метода Галеркина C42).
8.5.5. Ансамблирование элементов и построение глобальной
СЛАУ C48).
§ 8.6. Метод конечных элементов в многомерных нестационарных
задачах математической физики 350
§ 8.7. Особенности решения пространственных задач математиче-
математической физики методом конечных элементов 353
§ 8.8. Оценка погрешности метода конечных элементов 356
8.8.1. Погрешность конечно-элементного метода решения
задач для обыкновенных дифференциальных уравне-
уравнений C56). 8.8.2. Погрешность конечно-элементного ме-
метода решения задач для уравнений в частных производ-
производных C62).
§ 8.9. Вариационный принцип в МКЭ 365
8.9.1. Введение в вариационное исчисление C66).
8.9.2. Конечно-элементный вариационный принцип на
основе симметричного дифференциального оператора.
Вариационный метод Релея-Ритца C69). 8.9.3. Решение
задач с помощью конечно-элементного вариационного
принципа C73).
Глава 9. Метод граничных элементов решения много-
многомерных стационарных задач математической физики . . 379
Список литературы 391
Учебное издание
ФОРМАЛЕВ Владимир Федорович
РЕВИЗНИКОВ Дмитрий Леонидович
ЧИСЛЕННЫЕ МЕТОДЫ
Редактор Н.Б. Бартошевич-Жагелъ
Оригинал-макет: А.Л. Жигарев
Оформление переплета: А.Ю. Алехина
ЛР №071930 от 06.07.99. Подписано в печать 02.06.04.
Формат 60x90/16. Бумага офсетная. Печать офсетная.
Усл. печ. л. 25. Уч.-изд. л. 25. Тираж: 1000 экз. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997, Москва, ул. Профсоюзная, 90
E-mail: fizmat@maik.ru, fmlsale@maik.ru
http://www.fml.ru
Отпечатано с готовых диапозитивов
в ППП «Типография «Наука»
121099, Москва, Шубинский пер., 6
ISBN 5-9221-0479-9
9 785922 104791