К. К. ПОНОМАРЕВ
СОСТАВЛЕНИЕ
ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
ИЗДАТЕЛЬСТВО «ВЫШЭЙШАЯ ШКОЛА»
МИНСК 1973

w7.»
Π 5(1
.УДК 817.9 (07S.8)
Научный редактор
докт. физ.-мат. наук нр»
Пономарев К. К.
Пбб Составление дифференци.
ред. Ю. С. Богданова. Мн., <-
560 стр. с илл.
Учебное пособие для матера ι пче·
химических, биологических,
университетов, педагогическил илиит)
РУКОВОДСТВОМ ПО Составлению uUblKMUt-·
нений, а также простейших уравненш
адресована широкому кругу лиц, bciмеч
уравнениями в учебной, производствен:
работе.
0223—021
7—72
М304(05)—73
Пономарев К
СОСТАВЛЕНИЕ ДИФФЕРЕНЦИАЛ
Редактор Т. К- Майборода. Обложка В. И. Шёлка. Худо»
ноа. Техн. редактор М- Н. Кислякова. Корректоры Е. А. Нас.
ΛΤ 170211. Сдпио в набор 3/VIII 1972 г. Подписано к печати 26/11 19/;
Tititnrp, № 3. Печ. л. 35. Уч.-изд. л. 31,27. Изд. J* 70-92. Зак. lilt
Цена 1 руб. 01 коп.
ИЗДЙТ*.'! и ни ι «Нышчйшая школа» Государственного комитета Совета Мн.
долим iiiAimvihCTn, полиграфии и книжной торговли. Редакция литературы ..
и мятемвтиир. 1!ЙШ). Минск, ул. Кирова, 24. Ордена Трудового Красного Знам-
и 1Дптши,стиа ЦК КП Белоруссии. Минск, Ленинский пр., 79.

ПРЕДИСЛОВИЕ
В приложениях математики к различным отраслям науки
дифференциальные уравнения занимают важное место. Использование
НХ-™ наиболее эффективное и распространенное средство решения
прикладных задач естествознания и техники. Многие реальные
процессы с помощью дифференциальных уравнений описываются
просто н полно. Поэтому вполне понятно то внимание, которое уделяет-
СИ иопросу составления дифференциальных уравнений.
Однако многочисленные и разнообразные приложения теории
обыкновенных дифференциальных уравнений требуют в первую
очередь знания соответствующих теоретических положений и
законов естествознания, техники и других отраслей, которые изучаются
обычно после дифференциальных уравнений. По этой причине в
курсе дифференциальных уравнений решению практических задач на
составление уделяется все еще недостаточное внимание.
Прослушавшие этот курс не имеют достаточного навыка в решении задач,
выдвигаемых жизнью, производством. Кроме того, в учебниках и
учебных пособиях вопросы-составления дифференциальных
уравнений обычно ограничиваются элементарными задачами
геометрического или кинематического типа. Поэтому целесообразно
вернуться к составлению дифференциальных уравнений при изложении
специальных дисциплин, а также в процессе практической или
научно-исследовательской работы.
Цель автора — создание учебного пособия, которое широко
охватило бы различные задачи естествознания и техники и
способствовало овладению современной методикой составления
дифференциальных уравнений прикладных задач, возникающих в процессе
производства или научной деятельности.
Характерной особенностью освоения навыков составления
дифференциальных уравнений является изучение многочисленных
примеров. В связи с этим полнота изложения имеет здесь существенное
значение.
Книга содержит 325 задач на составление дифференциальных
уравнений, из которых 194 задачи анализируются подробно.

4
Предисловие
Рассматриваемые задачи классифицируются по их
математическому признаку: описываемые обыкновенными дифференциальными
ураииениями первого, второго, третьего и четвертого порядков,
системами этих уравнений первого и второго порядков, а также
дифференциальными уравнениями в частных производных,
приводящимися к обыкновенным дифференциальным уравнениям.
Д.;]я самостоятельного решения подобрана 131 задача,
большинство из которых аналогичны разобранным и снабжены
ответами, а более трудные — краткими пояснениями к решению.
Учебное пособие предназначено для студентов всех отделение
математических, физических, механических, химических,
биологических, геофизических, экономических факультетов университетов г.
педагогических институтов, а также высших технических учебных
заведений.
Книга рассчитана на широкий круг читателей, встречающихся
с дифференциальными уравнениями в учебно-методической,
производственной и научно-исследовательской практике.
Автор выражает глубокую и искреннюю благодарность
научному редактору книги профессору, доктору физико-математических
наук Ю. С. Богданову за ценные советы и замечания, во многом
способствовавшие улучшению книги.
Aerof.

Глава I
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
§ 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Уравнение для определения функции называют дифферен-
щаьным, если в нем участвуют дифференциалы или производные
номоп функции. Таким образом, дифференциальное уравнение
■ НТЫилет не только величину искомой функции, но и поведение ее
"ррждо всего скорость изменения в том или ином направлении)
"иЧ'Копечно малой окрестности рассматриваемого значения ар-
ΜΡΙΠ.Ί.
Решением дифференциального уравнения называют функцию,
ЧАНИую на связном множестве и обращающую дифференциальное
ι иппсиие в тождество. Характерной особенностью дифференциаль-
К) уравнения является то, что каждое уравнение определяет сразу
низ семейство решений, зависящее от некоторой совокупности
ι ,ΐ|οιιι»ιχ или функциональных параметров.
Дифференциальное уравнение обычно выражает некоторый
tiUlfi .чакон, которому подчиняется бесконечное множество кон-
••Tiiijx процессов. Для выделения конкретного процесса, которому
иТИстствует отдельное решение дифференциального уравнения,
иАынаются дополнительные условия — начальные и граничные,
< нанпомые в совокупности краевыми.
| 2. КЛАССИФИКАЦИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ
Существуют два основных типа дифференциальных уравнений:
щкнпвенные, определяющие функции одного переменного, и в ча-
ИЫХ производных, в которые входят производные от искомой
vIIKIUih по нескольким переменным.
Порядком дифференциального уравнения называют порядок
ιφΙΙΗ'ί'ι производной, участвующей в уравнении.
Дифференциальное уравнение имеет нормальную форму, если
m рп.'фешено относительно старшей производной. В противном
iVMtto форма дифференциального уравнения считается общей.
К отдельному виду относятся линейные дифференциальные
У|1И|НН'11ИЯ.
Аналогично классифицируются системы дифференциальных
уравнений.

б
Г л I. Основные понятия
§ 3. ОБЩЕЕ СЕМЕЙСТВО РЕШЕНИИ, ЧАСТНОЕ И ОСОБОЕ РЕШЕНИЯ
Семейство решений обыкновенного дифференциального
уравнения зависит от скалярных параметров, что проявляется в
присутствии произвольных постоянных в решении уравнения. Если число
произвольных постоянных совпадает с порядком уравнения, то
найденное семейство решений называется общим решением уравнения.
Общее решение может быть заданным как в явном, так и в
неявном виде. В частности, общее решение уравнения первого
порядка, разрешенное относительно произвольной постоянной,
называется общим интегралом.
Придавая произвольным постоянным фиксированные значения,
получим частные решения уравнения. Решения уравнения, которые
нельзя получить из общего, придавая произвольным постоянным
определенные числовые значения, называются особыми. В
некоторых случаях (см. задачи § 4 гл. VIII) именно особые решения и дают
ответ на поставленный вопрос.
Общим решением простейшего дифференциального уравнения
первого порядка
f(x,y,y')=o, (1)
где f — заданная функция, называется общее выражение
бесконечного множества функций, удовлетворяющих данному
дифференциальному уравнению, определяемое в явном виде
y = F(x, С) (2)
или в неявном
Ф(х,у,С)=0, (3)
где С — произвольная постоянная.
Если график особого решения дифференциального уравнени;
расположен внутри или на границе общего решения, то он обяза
тельно является огибающей интегральных кривых, составляющи.
указанное общее решение. С другой стороны, все невырожденны
огибающие интегральных кривых общего решения приводят к осе
бым решениям, если только они сами не оказываются в обще-
решении. Указанное обстоятельство позволяет строить особые реше
пня, отправляясь от известного общего решения. Основные факть
относящиеся к взаимоотношению общего, частного и особого peim
ниц дифференциальных уравнений, указаны Η. Μ. Матвеевы
[8; гл. I—IV]. Детальное исследование всей проблемы в целом прс
ведено Н. П. Еругиным [2, гл. 1—3, 8].

§ 4. Элементарные дифференциальные уравнения
§ 4. ЭЛЕМЕНТАРНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Все решения некоторых дифференциальных уравнений могут
быть найдены с помощью конечного числа простейших
аналитических операций и квадратур (интегрирований). Такие уравнения
называются элементарными.
Среди дифференциальных уравнений первого порядка
M(x,y)dx+N(x,y)dy=0
важнейшим элементарным уравнением является уравнение в
полных дифференциалах, т. е. уравнение с условием
дМ(х,у) _ dN(x,y)
ду дх
и односвязной области задания, все решения которого (общий
интеграл) дает формула
[х, У)
J Μ (χ, у) dx+N (χ, у) dy = С,
(Jfo, Vo)
где С — произвольная постоянная, а криволинейный интеграл
берется, по произвольному пути с фиксированным началом (Хо, Уо)
и переменным концом (х, у).
Основным элементарным дифференциальным уравнением
произвольного порядка является линейное дифференциальное
уравнение с постоянными коэффициентами а% (t=l, 2, ... , η):
г/(«)+а1г/(»-*)+.. ,+any = f(x).
Общее решение однородного уравнения [f(.\:)==0] можно
построить с помощью алгебраических операций. Общее решение
неоднородного уравнения дает сумма общего решения
соответствующего однородного уравнения и любого частного решения
неоднородного уравнения. Частное решение неоднородного уравнения
при специальных правых частях f(x), например при
m
f(x) = 2j Pk(x)elhx,
где pu(x) — многочлены, a kh — комплексные числа, получают
методом неопределенных коэффициентов. При произвольной правой
ч.чети f (x) частное решение неоднородного уравнения находят
метолом вариации произвольных постоянных. Линейные уравнения

8
Гл. I. Основные понятия
с постоянными коэффициентами и системы таких уравнений
подробно рассмотрены Н. М. Матвеевым [8, гл. VII, X].
В некоторых случаях дифференциальные уравнения приводятся
к основным элементарным формам с помощью преобразования
уравнения или замены переменных. Особую роль играют
равносильные и допустимые преобразования и замены. При равносильных
преобразованиях семейство решений транспонированного
уравнения совпадает с семейством решений исходного уравнения.
Примерами равносильных преобразований уравнения служат
умножение или деление обеих его частей на положительную
дифференцируемую функцию или перенос слагаемых из одной части
уравнения в другую.
Преобразование уравнения некоторой прикладной задачи
называется допустимым, если оно сохраняет решения, имеющие
смысл с точки зрения условия поставленной задачи (при
допустимых преобразованиях могут теряться или приобретаться только
решения, не имеющие физического смысла).
Примером допустимого преобразования служит деление обеих
частей уравнения на искомую функцию у=у{х), если по смыслу
задачи разыскиваемое решение не должно обращаться в нуль.
В настоящее время именно элементарные дифференциальные
уравнения служат главным поставщиком математических моделей
различных устройств и процессов. В частности, рассматриваемые
в данной книге прикладные задачи чаще всего приводят к
элементарным дифференциальным уравнениям, что позволяет довести
исследование до конца.
Известные типы элементарных дифференциальных уравнений
собраны в справочниках Э. Камке [4, 5].
§ 5. ВЫДЕЛЕНИЕ ИНДИВИДУАЛЬНЫХ РЕШЕНИИ
Большинство прикладных задач сводится к построению
функций, удовлетворяющих как некоторым обыкновенным
дифференциальным уравнениям, так и различным дополнительным условиям,
общее число которых обычно совпадает с порядком уравнения.
Особенно часто задаются начальные условия для решений и их
производных и тогда возникает начальная задача, называемая
задачей Коши. Для дифференциального уравнения я-го порядка
задача Коши состоит в построении того решения у = у(х) данного
уравнения
F(x,y, у',..., #<»>)= О,
которое вместе со своими η—1 первыми производными принимает
в заданной точке х=Ха заданные значения г/о, г/о', . .. , г/о<п_1):
У(Хо) =Уо, У'Ы =г/о', · · · , У(п-*Ы =ί/ο(η-1)-

§ 5. Выделение индивидуальных решений
9
Поскольку по определению у(°Цх) =у(х), то задача Коши для
уравнения первого порядка сводится к заданию значения искомой
ФУНКЦИИ у (х) При Х = Хй.
Геометрически это означает, что на плоскости задана точка
(л'о, г/о)· Решить задачу Коши в этом случае — значит построить
интегральную кривую, проходящую через точку.
Из общего решения можно получить любое частное решение.
Для этого достаточно в уравнение (2) или (3) из § 3 подставить
\ =лг0, у=Уо, тогда получится единственное соответствующее
нами льным условиям значение С=С0.
Подставив найденное значение С0 в уравнение (2) из § 3,
получим единственное частное решение
y=F(x, Co),
удовлетворяющее выбранным начальным условиям.
Если значения решения и его производных указаны при разных
шачениях аргумента х, то получается краевая (граничная) задача
|,чя обыкновенного дифференциального уравнения. Например,
периодическая краевая задача для уравнения
F{x,y,y' ζΛ>)=0
<■ ω-периодической функцией F,
F(x+«>, У, У',..., yW).^F(x, у, у', .. . , #<»>),
состоит в построении решения у = г/(х), удовлетворяющего условиям
!1(Хо+«>)=У(Хо), у'(Хо+«>)=Уо(Хо), ... , у(п-Ч(Хо+(й)=у(п-»(Хо).
Если располагать полным семейством решений, т. е. общим
решением и набором всех особых решений, то выделение
индивидуальных решений данного уравнения, удовлетворяющих
некоторым дополнительным условиям, сводится к составлению на основе
общего решения системы конечных уравнений для определения
произвольных постоянных, определяющих подходящие частные
решения, и к отбору тех особых решений, которые соответствуют
поставленным условиям.
Начальные и краевые задачи для неоднородных линейных
дифференциальных уравнений удобно решать с помощью функций
Коши и Грина, как это показано, например, А. М. Колобовым и
А. П. Черенковой [6, § 3.3—3.6].
Построение общего решения пеэлементарных
дифференциальных уравнений наталкивается на принципиальные трудности,
поэтому описанный способ решения задач с дополнительными условиями
для таких уравнений малоэффективен. В указанных случаях отроят
искомые индивидуальные решения с помощью разложения решения
в степенной или итерационный ряд и т. д.

10
Гл. I. Основные понятия
§ 6. ПОСТРОЕНИЕ РЕШЕНИЯ В ВИДЕ СТЕПЕННОГО РЯДА
Рассмотрим дифференциальное уравнение в нормальной форме:
y^=f(x, у,у',...,у{п~*).
Поставим для этого уравнения задачу Коши
ИЫ =Уо, У'(хо) =Уо', ■■■ , У{п~*{хо) =№("-«.
Если функция f {χ, у и г/2, ... , Уп) голоморфна, т. е. разлагается
в степенной ряд в окрестности точки (х0, г/о, г/о', ·. · , г/о(п_1)), то Ука_
заПная задача Коши имеет единственное решение у=у(х), которое
представляется рядом
оо
y(x)=yjBh(x-x0)k. (Ц
)i=0
Решение у=у(х) может быть найдено методом
неопределенных коэффициентов путем подстановки выражения (I) в исходное
уравнение и последовательного приравнивания друг к другу
коэффициентов при равных степенях разности х—х0.
Построение степенных рядов, решающих линейные
дифференциальные уравнения в окрестности тех значений аргумента х, при
которых коэффициенты голоморфны, описано в книге [8, гл. VIII].
Если точка (ха, у0', . . . , г/о(п_1)) оказывается особой для
функции f, то в ряде важных случаев решение задачи Коши находится
в виде обобщенных степенных рядов
у(х) = (х—Хо)Р/, Bk(x—x0)\
/i=0
причем для их построения снова применим метод неопределенных
коэффициентов.
Так, в частности, будет, если уравнение является линейным,
а коэффициенты его в точке х-— Хо удовлетворяют условию Фукса,
т. е. коэффициент при г/С1' имеет при х=х0 полюс порядка не выше
п-— k. Линейные уравнения с условием Фукса являются главными
поставщиками специальных функций.
Подробно об использовании обобщенных степенных рядов см.,
например, во второй части курса В. И. Смирнова [11, гл. V и VI].

§ 7. Метод последовательных приближений 11
§ 7. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
Задача Коши
УЫ —Уч, ■ ■ ■ , У{п-1)Ы =г/о<п-1)
для обыкновенного дифференциального уравнения
y№=f (χ, у, у' г/(»-»))
яниивалентна задаче о построении решения системы уравнений
X
2o(x)=i/o+J Zi(t)dt,
хо
χ
2i(x)==i/0'+ )z2(t)dt,
ХО
χ
ζη-2 (х) = у0(п-У+ J zn_! {t) dt,
Xt>
X
zn-i(x)=yJn-»+5f[t, z0(t),..., zn-i(t))dt,
xo
если считать у (χ) = z0(χ), y№(x) = zW (x). Решение этой системы
может быть найдено методом последовательных, приближений,
называемым методом итераций или методом Пикара.
Для краткости изложения ограничимся случаем п=1. Тогда
первые и—1 уравнений системы отпадают и она сводится к одному
\равнению
t(x)=yo+if[t,z{t)]dt.
Для решения последнего построим последовательность функций
iin(x), ui(x), ... , Uh(x) по правилу
и0(х)=у0,
X
Uk(x)=yo+]f[t, uh-i(t)]dt.
хо
Если функция f (x, у) непрерывна и имеет непрерывную частную
Производную —- в окрестности точки (х0, г/о), то решение
задачи Коши

12
1 л. ι. основные понятия
существует, единственно и представляется в виде равномерного
предела
у(х)= Hm Uh(x)
k->-o°
или в виде равномерно сходящегося ряда
у(х)=Уо+ 2-i [Uk(x)—uk-i(x)].
§ 8. ПРОДОЛЖЕНИЕ РЕШЕНИЙ
В случаях, когда решения дифференциальных уравнений
получаются в виде бесконечных разложений, возникает вопрос о
существовании решения вне интервала сходимости ряда, т. е. о
возможности продолжения решения уравнения за границы указанного
интервала. Этот вопрос имеет принципиальное значение, так как
оценка промежутка существования решения дифференциального
уравнения позволяет судить о тех значениях аргумента, при которых
данное дифференциальное уравнение способно моделировать
изучаемый процесс.
Решение линейного дифференциального уравнения продолжимо
на любой интервал, на котором коэффициенты уравнения
интегрируемы. Таким образом, если коэффициенты уравнения на любом
конечном отрезке изменения аргумента ограничены и имеют лишь
конечное число точек разрыва, то решение такого уравнения с
любыми начальными значениями существует для всех значений
аргумента.
Решение нелинейного дифференциального уравнения
-^=f(x,y,y',.-.,y^)
с правой частью f(x, у\, ... , уп), непрерывной вместе со всеми
—— для х^Хо, —оо<г/п<;+ОС1. заведомо беспредельно продол·
дун
жимо вправо от х=Хо, если для f(x*yu ... , уп) можно указать
линейную оценку
If (х, Уи ■ ■ ■ , Уп) | <А(х) [1+Ы+. · .+ \Уп\],
где положительная функция А(х) интегрируема на любом
промежутке [х0, xo+α], 0<а<+оо.
Проблема продолжимости решений дифференциальных
уравнений исследована Н. П. Еругиным [3].

Глава П
СОСТАВЛЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
ПО УСЛОВИЯМ ПРИКЛАДНЫХ ЗАДАЧ
§ 1. ОБЩИЕ ПРИНЦИПЫ
Дифференциальные уравнения объединяют и обобщают многие
идеи математического анализа, раскрывают сущность метода
бесконечно малых как важнейшего средства познания явлений
действительности.
Дифференциальные уравнения возникают при математической
формулировке прикладных задач в дифференциальных символах.
Составить дифференциальное уравнение — это значит найти
зависимость между аргументом, функцией и ее производной (или
дифференциалом).
Составление дифференциальных уравнений является важным
и вместе с тем трудным вопросом. Универсального метода,
пригодного во всех случаях, указать нельзя. Необходимо приобретение
опыта и определенных навыков в решении различных задач, что
достигается разбором большого количества решенных задач и
самостоятельным решением аналогичных примеров. Необходимо также
.шание данной прикладной дисциплины.
§ 2. МЕТОДИКА СОСТАВЛЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Составление дифференциального уравнения по условию задачи
(механической, физической, химической, технической или любой
другой) состоит обычно в определении математической зависимости
между переменными величинами и их приращениями, которые
сразу же заменяются соответствующими дифференциалами.
В ряде случаев дифференциальное уравнение получается без
рассмотрения приращений — за счет их предварительного учета.
~ ds
Так, представляя скорость выражением v = ~т—, мы не привлекаем
приращений As и At, хотя они фактически учтены в силу того, что
ds ,. As
Ускорение в любой момент времени t выражается зависимостью
d2s άυ dv
й= ~d¥~ = ~df =VΊϊΓ-

14 Гл. П. Составление дифференциальных уравнений по условиям задач
Изучение любого процесса сводится к определению его
отдельных моментов и установлению общего закона его течения.
Отдельный момент процесса (элементарный процесс)
выражается дифференциальным уравнением, связывающим переменные
величины процесса с их дифференциалами или производными; закон
общего течения процесса, получаемый после интегрирования,
выражается уравнением, связывающим переменные величины процесса.
Исчерпывающих правил для составления дифференциальных
уравнений нет.
В большинстве случаев методика решения прикладных
задач с применением обыкновенных дифференциальных уравнений
сводится к следующему:
1) подробный разбор условий задачи и составление чертежа,
поясняющего ее суть;
2) составление дифференциального уравнения
рассматриваемого процесса;
3) интегрирование этого уравнения и определение его общего
решения;
4) определение частного решения задачи на основании данных
начальных условий;
5) определение по мере необходимости вспомогательных
параметров (например, коэффициента пропорциональности и т. д.)
с использованием для этой цели дополнительных условий задачи;
G) вывод общего закона рассматриваемого процесса и
числовое определение искомых величин;
7) анализ ответа и проверка исходного положения задачи.
Некоторые из этих рекомендаций в зависимости от характера
задачи могут и не использоваться.
Как и при составлении алгебраических уравнений, при решении
прикладных задач с помощью дифференциальных уравнений многое
зависит от навыков, приобретаемых упражнением. Однако здесь
еще в большей степени требуется изобретательность и глубокое
понимание сути изучаемых процессов. Можно делать упрощающие
допущения, например, заменять существующий сложный
(криволинейный) элемент прикладной задачи более простым
(прямолинейным), неравномерное движение материальной точки за малый
промежуток времени равномерным, предполагать скорость
протекания любого процесса за малый промежуток времени постоянной.
Идея замены одних бесконечно малых другими требует
обязательного соблюдения эквивалентности заменяющего и заменяемого
бесконечно малых элементов.
В математической модели задачи надо учитывать только
основные параметры.

§ 3. Схема составления дифференциального уравнения 15
§ 3. СХЕМА СОСТАВЛЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
Подготовительный этап
1. Установление в результате анализа задачи аргумента (неза-
нисимой переменной) и искомой функции.
2. Исследование наличия конкретного смысла у производной
искомой функции.
3. Поиск соотношения между дифференциалами переменных,
если производная не имеет конкретного смысла.
4. Фиксирование произвольного значения аргумента и
соответствующего ему значения функции; придание аргументу приращения
и определения соответствующего приращения функции.
Основной этап
1. Попытка найти соотношение между приращением Ау
функции и приращением Ах ее аргумента, т. е. выражение Ау в виде
функции Ах и х. Искомую функцию у можно также выразить
элементарным суммированием ее последовательных приращений на
отрезке от а до х.
2. Введение (в случае невозможности определения
соотношения между Ах и Ау) условного элемента, заменяющего приращение
Ау искомой функции и характеризуемого условным приращением,
которое получила бы искомая функция при наличии допущений,
упрощающих характер ее изменения и не отражающихся на
точности результата. Этот элемент принимается в качестве
дифференциала искомой функции.
3. Проверка корректности допущений, которые по мере
приближения Ах и Ау к нулю с возрастающей степенью точности
приближались бы к полной истинности. Уравнение, связывающее
дифференциалы dy и dx, должно составляться на основе известных
законов математики, физики, химии, механики и т. д.
4. Установление зависимости между дифференциалами искомой
функции dy и ее аргумента dx в общем случае в виде простейшего
уравнения
f (x, y)dx+(f(x, y)dy=0
(или дифференциального уравнения более высокого порядка) на
основе сделанных допущений, которые дают возможность заменить
неравномерный процесс равномерным, используя
общетеоретические законы или соотношения данной прикладной области.
5. Интегрирование полученного дифференциального уравнения
задачи и определение искомой функции с учетом начальных (и
дополнительных) условий.
6. Исследование полученного закона задачи в предельных
случаях и изучение характера зависимости решений от параметров.

Глава ΠΙ
ЗАДАЧИ, ПРИВОДЯЩИЕ К ДИФФЕРЕН
УРАВНЕНИЯМ ПЕРВОГО ПОРЯД
РАЗРЕШЕННЫМ ОТНОСИТЕЛЬНО ПРОШ:
Наиболее общий вид дифференциального у,
порядка
М(х, y)dx+N(x, y)dy=0,
где Μ (χ, у) и Ν(χ, у) — функции χ и у.
Разрешив уравнение (1) относительно произ^-
dy Μ (χ, у)
~dT =~ Ν (χ, у) =^*' У)·
Общее решение уравнения (2) имеет вид
y=F(x, С),
где С — постоянная.
Неполное дифференциальное уравнение — npocTt
вид уравнения (2):
в котором правая часть не зависит от искомой функц
непосредственным интегрированием:
У= )f(x)dx>
или
откуда
„ Г 'аУ -
J В(У) '
§ 1. ПРИТЯЖЕНИЕ СТЕРЖНЯ И МАТЕРИАЛ*.
Задача 1. Материальная точка массой т находится ..
жении оси тонкого однородного стержня массой М, длиною
стоянии а от erto левого конца. Определить силу притяжения
ня и точки.
Решение. По закону Ньютона сила F притяжения межр
мя материальными точками с массами mj и т2, расположена

§ 1. Притяжение стержня и материальной точки
17
на расстоянии г друг от друга, выражается зависимостью
F=k m'm2 ,
(1)
где k — коэффициент притяжения.
Определим притяжение dF данной точки элементом стержня dx
(рис. 1).
m
iml
^^~ ^~ ^™ ^^
ι
^-
. * . $х.
Рис. 1
Так как масса однородного стержня М, то масса mi элемента dx
m.\ dx
находится из пропорции —г-г-
/
-, откуда
ту=
Mdx
~1
Расстояние.между т и dx будет г=а-\-х. По закону Ньютона
(1) запишем дифференциальное уравнение задачи
mMdx
dF=k-
l(a+x)2
Интегрируя его, получаем общее решение
w-i*LJ
dx
(а+х)
тМ
I
а-\-х
+С
Начальное условие: при х = 0 /г=0, откуда
. тМ 1
0=
или
C=k
I й+0
тМ 1
+С
I a
Притяжение массы т отрезком χ стержня будет
f=A_^M_(J 1 ).
/ \ а а-\-х ι
При х—1 получаем притяжение массы т всем стержнем:
F = k
тМ
(-V
ι
а-\-1
)-'
тМ
а(а-\-1)

18
Гл. III. Простейшие уравнения
§ 2. ДВИЖЕНИЕ ТЕЛ ПОСТОЯННОЙ МАССЫ
Прямолинейное движение с постоянным ускорением
Задача 2. Материальная точка движется по прямой с
постоянным ускорением а. Найти закон движения точки.
Решение. Ускорение а представляет производную от
скорому
сти ν по времени t, т. е. ~т— =а, поэтому
dv = adt. (1)
Интегрируя уравнение (1), находим
v^at+Ci. (2)
Для определения Ci положим, что начальная скорость равна v0,
т. е. при i=0 v = vo. Подстановка начальных условий в
уравнение (2) дает
uo=0+Ci или Ci = v0-
Таким образом, уравнение (2) примет вид
v=at+v0. (3)
Так как скорость представляет производную пути s по време-
ds
ни т, т. е. ϋ= —77-, то равенство (3) преобразуется к виду
ds
= αί+ν0
dt
или
ds=atdt-\-v0dt.
Интегрируя последнее равенство, получим общее решение
задачи
s=-^-aP+u0t+C2. (4)
Для определения С2 будем считать, что начальное положение,
равное расстоянию при t~0, будет s0, т. е. s=s0 при /=0.
Подставим эти значения в уравнение (4):
s0=0+0+C2 или Cz=s0.
Следовательно,
s = -77т~ atz+v0t+s0. (5)

§ 2. Движение тел постоянной массы
19
Положив в уравнениях (3) и (5) a=g, v0—О, s0=0, s=h,
Получим закон свободного падения тела в пустоте:
v=gt и h=—-gt2.
Прямолинейное движение с переменным ускорением
Задача 3. Скорость движущегося тела возрастает обратно
пропорционально пройденному пути. В начальный момент движения
тгло находилось на расстоянии 5 м от начала отсчета пути и имело
скорость 1>о=20 м/сек. Определить пройденный путь и скорость
Tivia через 10 сек после начала движения.
Решение. Пусть / — время, s — путь, пройденный телом.
Скорость движения тела есть производная пути по времени.
По условию дифференциальное уравнение задачи
ds * (1)
dt
где k — коэффициент пропорциональности.
Разделяя переменные и интегрируя уравнение (1), получим
sds=kdt; ~ =kt+C,
откуда
s2=2(kt+C)
или
s=12ikt+C. (2)
Дифференцируя функцию (2), найдем скорость движения
V=S'={2 .= k (3)
2ikt+C I2ikt+C
Начальное условие: при t=0 s = 5,
v=s'=20. (4)
Тогда
s(0) =-|/ 2 Υ k-0+C=i 2C=5.
Постоянная интегрирования
C-%-. (5)

20
Гл. III. Простейшие уравнения
Используя второе условие (4) и равенство (5), получаем
равенство для определения коэффициента пропорциональности:
v0=s'(Q) = k = _k__ = 20,
i2ik-0+C l/2-|/C
откуда
k=20 f2 fC=20 f2-^ =100. (6)
12
Подставим найденные значения (5) и (6) в уравнение (2):
!=1 2)/I00t+Ц-= 1 2^ ■
200^+25
или
s=i 200/+25. (7)
Так как
100 100
v=s =
V2]/l00i+-y- 12]/-
200ί+25
то
_ , J_00_
1200ί+25
Искомый путь найдем, подставляя в уравнение (7) значение
/=10:
s(10)=-|/ 200- 10+25=У 2025=45 ж.
Определим скорость
,.,_, 100 20
i>w=s (10) = ,_ = -7— н сек.
4t> 9
Задача 4. Ускорение локомотива, имеющего начальную
скорость vo, прямо пропорционально силе тяги F и обратно
пропорционально массе поезда т. Сила тяги локомотива
F=b—kv,
где υ — скорость, Ъ и k — постоянные величины. Найти силу тяги
локомотива по истечении времени t, если в начальный момент при
i=0 F=F0=b-kv0.
Решение. Пусть скорость ν движения локомотива является
функцией времени, т. е. v = v(t). Тогда ускорение локомотива

5 /. движение тел постоянной миссы
dv
а=
dt '
По условию
dv F
а=
dt m '
"де F=b—kv.
Поэтому дифференциальное уравнение задачи
dv b—kv
(О
dt m
После разделения переменных уравнение (1) принимает вид
= dt.
b—kv m
Интегрируя, имеем
1— 1и (b-ku) = — t+C,
k m
>ткуда общее решение уравнения
m
t=—-—\n{b—kv)+C. (2>
/ν
Начальное условие: при ί —0 u = uo. Отсюда
m
0= — ЩЬ—kvo) +C
171
C=-£-ln(b—kv0).
Найденную постоянную интегрирования подставляем в общее
Решение (2) и получаем
m b—kvo m F0
t== ~ΊΓ ln ~u—T~ = ~ΪΓ1η -W~- (3)
k b—kv k F ч '
Искомая сила тяги находится из равенства (3) путем его потен-
шрования
kt , F0
=ln——
m F
1ЛИ
ht
F=F0e~ m.

2
Гл. ill. Простейшие уравнения
Вращение вокруг оси
Задача 5. Материальная точка массой m расположена на кри-
юй АВ (рис. 2), вращающейся вокруг вертикальной оси с постоян-
юй угловой скоростью ω. Найти уравнение кривой АВ, если мате-
)иальная точка находится в равновесии в произвольном положении
ia кривой.
Решение. В положении равновесия равнодействующая R
:илы тяжести и центробежной силы направлена по нормали к кри-
зой АВ, так как реакция связи направлена по нормали. На точку Μ
действуют сила тяжести P=mg и центробежная сила F=m<u2x.
Здесь g — ускорение силы тяжести.
Пусть искомое уравнение кривой АВ имеет вид у—у(х). Угло-
зой коэффициент нормали'к кривой АВ равен —; угловой коэф-
У
tng g
рициент равнодействующей равен —= . Следовательно,
к J ιηω2χ ώιχ
1 = g
у' (ύ2Χ
dy ω2
dx g
du= xdx.
e
Интегрируя это уравнение, получим семейство парабол
у-~^+с,
где С — расстояние между кривыми семейства.
Свободная поверхность жидкости во вращающемся сосуде
Задача 6. Цилиндрический сосуд с радиусом основания г и
высотой h наполовину заполнен водой. Какую форму примет
поверхность воды, если сосуд вращать вокруг продольной оси с угловой
скоростью ω?
Решение. Начало координат поместим в центр основания
сосуда (рис. 3). Ось χ возьмем.в любом направлении на плоскости
его основания, ось ζ направим по продольной оси сосуда.
или
откуда
Рис. 2

§ 2. Движение тел постоянной массы
23
Определим сечение искомой поверхности плоскостью xOz.
На частицу воды Μ поверхности вращения с массой m
действуют силы: тяжести P—mg, центробежная F=m(o2;*: и реакции во
1ы R (рис. 4).
Рис. 3
Определим направляющие углы этих сил:
(pfx)=90°, (P?z) = 180°, (ffx)=0,
(F-fz)=90°, (tffx)=90°+a, (/?fz)=a.
Направляющие косинусы этих сил:
Л Л Л
cos(P,x)=0, cos(P; z) = — l, cos(r; лг) = 1,
л л dz
cos(F;z)=0, cos(i?; x)=—sin a= —
ds'
/пЛ \ dx
cos(R; z)=cos a—
ds '
Составляющие сил, действующих на частицу воды:
Рх=0, Pz=-P=-mg, Fx=F=m<i>4, Fz=0,
(i)
Система сил, действующих на частицу воды поверхности вра-

24
Гл. III. Простейшие уравнения
щения, находится в равновесии и поэтому суммы составляющих по
осям должны равняться нулю:
Px+Fx+Rx = 0,
PZ+FZ+RZ = Q.
Принимаем во внимание обозначения (1):
—R— ηΐω2χ--
ds
=о,
dx
-mg=0.
ds
Из системы (2) исключаем величину
циальное уравнение задачи
ωζχ
ds
(2)
и тогда дифферен-
откуда
dz
dz=
8
dx
xdx.
После интегрирования найдем общее решение
2g
(3)
Итак, искомое сечение принадлежит семейству парабол с
вершинами в точках (О, С) и параметром р-
"47
Так как ось χ взята
в произвольном направлении на плоскости дна цилиндрического
сосуда, то аналогичные параболы получим для всех сечений
поверхности плоскостями, проходящими через ось г. Таким образом,
искомая поверхность есть параболоид вращения с осью, направленной
по оси цилиндрического сосуда.
Для определения постоянной интегрирования в уравнении (3)
обозначим на рис. 5 отрезки ОА и ΒιΒ символами /ι2 и hi. При х=0
ζ=/ι2; при x=r z=hi. Подставляем эти значения в общее
решение (3),откуда
ωώ
•02+С, hi =
или
2g
C=hz; С=/ц—■
ω2Γ2
~2g~
+ C
(4)

§ 2. Движение тел постоянной массы
95
В двух равенствах (4) имеются три неизвестные постоянные с,
it и h2. Для составления дополнительного третьего уравнения
обратим внимание на объем жидкости, который ввиду слабой
сжимаемости воды не изменяется от вращения. До вращения высота воды
ι сосуде равнялась —, а соответствующий объем воды —— п. Такой
збъем воды остается и при вращении, но теперь его можно опре-
Рис. 4
Рис. 5
делить как разность объемов цилиндрического сосуда высотой /ΐι
ι сегмента параболоида вращения высотой h\—h2. Первый объем
)удет nrzhi, второй объем — nr2^—h2). Таким образом, объем воды
тавен ——- (/ΐι+/ι2).
Сравниваем этот объем с первоначальным
ш*
h=
пгл
(fti+M
1ЛИ
h=hi-\-h2.
(5)
Следовательно, имеем три условия (4) и (5) для определения
юстоянных. Исключаем /ΐι и h2 из трех уравнений и получаем
С=

ι л. ш. Простейшие уравнения
Итак, уравнение искомого сечения
ω2 „ . h ω2/-2
ИЛИ
2g 2 Ag
■h ,
2 + 2g \X 2 '
Уравнение параболоида вращения получится после замены х2
выражением х2-{-у2. Уравнение искомой поверхности воды будет
h , ω2 / „ , „ г2 \
§ 3. ДВИЖЕНИЕ ТЕЛ ПЕРЕМЕННОЙ МАССЫ (БЕЗ УЧЕТА ВНЕШНИХ СИЛ)
Скорость полета ракеты
Задача 7. Ракета с начальной массой т0 кг взлетает с земной
поверхности в вертикальном направлении. Газы выбрасываются
постоянными долями а кг/сек и с постоянной скоростью b м/сек
относительно ракеты, где й>0 и 6>0. Найти скорость ракеты и
расстояние, пройденное за время t, не учитывая действия внешних сил
на ракету.
Решение. Движение ракеты вызывается реакцией струи
раскаленных газов, образованных сгоранием топлива и вытекающих
с большой скоростью из отверстия, расположенного в нижней части
корпуса ракеты. Ракета несет с собой весь запас топлива, который
составляет главную часть переменной массы ракеты.
Извержение массы газа увеличивает скорость ракеты, что дает
ей возможность продолжать движение. Для исследования движения
ракеты необходимо сначала рассмотреть движение тела с
переменной массой.
Согласно второму закону динамики, изменение количества
движения пропорционально движущей силе и происходит по
направлению той прямой, по которой эта сила действует.
Если К — количество движения тела с массой т, F —
действующая сила, то в момент времени i
dK
dt
или
d{mv)
F=
dt
Применим второй закон Ньютона к движению ракеты.

§ 3. Движение тел переменной массы
27
Предположим, что общая масса ракеты в момент времени t
будет гп, а в последующий момент времени t-\-At — составит m-\-Am
(масса газа, выброшенного за время At, равна —Am, так как
является отрицательной (убывающей) величиной и поэтому
m— (—Am) =m-{-Am).
Предположим, что скорость ракеты относительно Земли в
момент времени t будет и, а в момент t-\-At будет υ-\-Αν, и примем
вертикальное направление ракеты в качестве положительного.
Выброшенная струя газа будет иметь скорость v-\-vt
относительно Земли, где υι — отрицательная величина, так что —vi
представляет действительную величину скорости газа относительно
ракеты, которую будем считать постоянной.
Общий момент движения ракеты перед выхлопом газа будет
mv, а после выхода газа (m-\-Am) (υ+Δυ). Количество движения
газа —Am(v-\-Vi), так что общее количество движения после выхода
струи будет (m+Am) (v-\-Av)—Am(v-\-Vi).
Изменение количества движения, т. е. общее количество
движения после выхода струи газа минус общее количество перед
выходом, составит
(m-\-Am) (v-\-Av)—Am(v-\-v1)—mv=mAv—viAm-\-AmAv.
Производная изменения количества движения есть предел
изменения количества движения, деленный на At, когда Δί-Ю, т. е.
/ Αυ Am , Am A \ dv dm
Δί-И)
At At ' At ι dt dt
Производная от количества движения тела равна по величине
действующей силе F и совпадает с ней по направлению. Поэтому
„ dv dm
Уравнение (1) является исходным уравнением движения
ракеты. При отсутствии внешних сил его левая часть F=0.
Так как ракета выбрасывает а кг/сек газа, то в течение t сек
она выбросит at кг/сек, и поэтому ее масса, спустя t сек, составит
т=т0—at. Скорость газа относительно ракеты дана: υι = —Ь.
Таким образом, на основании уравнения (1) получаем
,ч dv
0= (то—at) —— ab
или
dv = ab (2)
/ dt тй—at'

28
Гл. III. Простейшие уравнения
Интегрируя уравнение (2), находим
v = -bj
d(m0—at)
mo—at
откуда
u——b ln(m.0—at)-\-Ci.
Начальное условие: при ί=0 υ.=0. Отсюда постоянная
интегрирования
Ci=6 In tn0.
Общее решение уравнения
u = b In m0— b ln(m0—at) (3)
представляет искомую скорость ракеты.
Пусть χ — расстояние, измеряемое от поверхности Земли, кото-
, ~ ах
рое проходит ракета за время г. Тогда скорость υ= —— и, согласно
равенству (3), получаем
dx
= 6 In mQ—b ln(m0—at) =—b[\n(m0— at) — In m0] =
dt
= _6ln(^=^-).
Интегрируем это уравнение:
m0—at
m
Так как
»_-»Jin(^iL)*+c.
J In zdz=z In 2—z+C,
TO
mo—at I mo—at \ ( mo—at Y\ . r_
m0 \ mo ' \ m0 ' J
6m0 Г
r= —— -
a L
b(m0—аЛ (тй—at) b
■In (mo-af)+C (4)
a m0 a
Начальное условие: при ^=0 л:=0. Отсюда 0=0 т0-\-С
и постоянная интегрирования С= — т0. Подставляя ее в
уравнение (4), получаем искомое расстояние
x=bt+±(m^at) In (-^-). (5)

§ 3. Движение тел переменной массы
29
Уравнения (3) и (5) действительны только для t<C ■ , что
федставляет теоретический предел времени полета. Практический
федел значительно меньше теоретического.
Высота подъема ракеты
Задача 8. Ракета с начальной массой /п0 запускается верти-
;ально вверх с начальной скоростью υ0. Масса ракеты уменьшается
: постоянной скоростью и в момент t составляет m=m0—kt, где k —
юстоянный коэффициент. Предполагается, что убывающая масса
цзижется назад с постоянной скоростью b относительно ракеты.
1айти высоту подъема ракеты в любое время ί, учитывая лишь
?е силу тяжести tng.
Решение. Движение ракеты происходит путем выброса
:труи горящего газа назад с определенной скоростью относительно
)акеты. Это образует реактивную силу FR в направлении движения
закеты.
Если FH — внешняя сила, действующая на ракету, то
суммарен сила FH-\-FR и дифференциальное уравнение движения
~{mv)=FH+FR. (1)
Для определения силы FR принимаем, что она равна скорости
вменения количества движения убывающей массы.
Если Δ/η — убыль массы за время At и масса Δ/η имеет ско-
юсть ν—и, т. е. скорость —и относительно ракеты, то количество
шижения убывающей массы Δ/η (υ—и). Следовательно,
Подставляя соотношение (2) в уравнение (1), получаем
дифференциальное уравнение движения
d / dm ,
(mv) = Fa+—n-(O+u).
at κ ' " ' at
Раскрываем скобки в левой части равенства и сокращаем по-
,обные члены:
άυ dm
тчг+и-чг=Рн- (3)
По условию задачи положительное направление χ вверх, поэто-
:у уравнение (3) записывается в виде

30
Гл. III. Простейшие уравнения
dv
(tn0—kt) --T- + (—k)b = —(mD—kt)g
или
dv kb
= S-
dt пц—kt
Интегрируя, получаем общее решение
O =—b\n(rn0—kt)—gt+Ci. (4)
Начальное условие: при ^=0 ν = ϋο- Отсюда, согласно
равенству (4):
Ci=vQ-\-b In m0.
Тогда
v=v0—gt+b In I 1 I .
1Л dx
Интегрируя повторно, учитывая v = —ττ, получаем
x=0ei_^L_.-*_(me_«) [ln(l ^-) -l] +C2.
Начальное условие: при /=0 х=0. Отсюда
n bm0
Cz=—τ-
Искомый закон движения
x=(u0—b)t— — gt2 —I 1 ) In I 1 I .
§ 4. РАСТЯЖЕНИЕ УПРУГОЙ НИТИ
Работа растяжения переменной силы
Задача 9. Стальная проволока длиной / с поперечным
сечением F растягивается с силой, постепенно возрастающей до
величины Р. Найти работу растяжения.
Решение. Удлинение проволоки Δ/ под влиянием
растягивающей силы Ρ определяется по формуле
ρ
Al=k—=r-l0,
г
где k — коэффициент удлинения, /о — первоначальная длина
проволоки.

§ 4. Растяжение упругой нити
31
Рассмотрим элементарный процесс:
dl=-^-dP. (1)
Принимая на бесконечно малом участке удлинения dl силу Ρ
постоянной, получим работу, производимую этой силой на
рассматриваемом участке,
dW=Pdl
или, используя уравнение (1), дифференциальное уравнение
процесса:
άψ=-ψ~ΡάΡ. (2)
Интегрируя уравнение (2), получим общее решение
W^-^r-Pz+C.
2F
Для определения С используем начальные данные: при Р=0
W=Q, следовательно,
о—!£-.о+с.
откуда
с=о.
Итак, искомая работа растяжения
2F
Удлинение от собственного веса
Задача 10. Стальная проволока длиной L м защемлена в одном
из концов и под действием своего веса находится в положении
равновесия (рис. 6). Определить удлинение проволоки. Объемный вес
стали у Т/мя..
Решение. Величина натяжения Τ меняется в зависимости
от места сечения. Это натяжение равно весу ниже расположенной
части проволоки. Поэтому различные элементы проволоки
растягиваются по-разному. В точке на расстоянии χ от закрепления
элемент dx испытывает натяжение Т, определяемое из пропорции
PL' (Ч
где Ρ — вес всей проволоки.

32
Гл. III. Простейшие уравнения
Из уравнения (1)
(L-x).
Удлинение проволоки AL (м) под влиянием растягивающей
силы Τ (κΓ) будет
где k — коэффициент удлинения, F — площадь поперечного
сечения, см1.
Для растяжения элемента dx находим
dL = k-
■ dx
или
Рис. 6
dL =
kP
LF
(L~x)dx.
С другой стороны, Р=
yLF
1000
(2)
кГ, если L
в см. Подставляя последнее выражение в
уравнение (2), получим дифференциальное
уравнение процесса
dL=
ky
Γδοο"
(L-x)dx.
'Интегрируя, получим полное удлинение
1—1§О.Ь^)Л
ИЛИ
L=
о
ky
2000
D- м.
Форма каната цепного моста
Задача 11. Найти кривую, которую образует канат цепного
моста?
Решение. Часть каната АВ (рис. 7) находится в равновесия
под действием трех сил: горизонтального натяжения Η в точке А,
натяжения Г, направленного вдоль каната, в точке В и веса части
моста между точками А и В. Весом каната ввиду малости
пренебрегаем.

§ 4. Растяжение упругой нити
33
Вес части моста между А а В пропорционален длине χ и
рацеи kx. На основании уравнений статики сумма проекций всех
действующих сил на вертикальную и горизонтальную оси равна нулю,
Отсюда получаем условия равновесия сил — вертикальных:
горизонтальных:
Г sincp=&x,
Tcoscp=#.
(1)
(2)
Рис. 7
Разделив уравнение (1) на уравнение (2), получаем
tg«P=-jEp*.
Как известно,
Таким образом,
tgq>=
dy
dx
dy. k
Интегрируя последнее равенство, получим уравнение свешива-
пия каната
у=ж-хг+с-
(3)
Уравнение (3) представляет семейство парабол.

•у* Гл. 111. Простейшие уравнения
§ 5. РАБОТА ОПОРОЖНЕНИЯ СОСУДОВ
Задача 12. В вертикальном цилиндрическом резервуаре
диаметром 2г находится жидкое топливо с удельным весом γ. Высота
жидкости в резервуаре /г, а
общая высота резервуара Η
(рис. 8). Найти работу,
которую необходимо затратить для
опорожнения резервуара.
Решение. Работа
постоянной силы F па
прямолинейном пути s равна
Л —/\s cos α,
где α — угол между F и s.
Работу А при выкачивании
примем за искомую функцию
расстояния χ слоя жидкости до
рис g крапа, т. е. А = А(х).
Аргументу χ дадим приращение Δ*,
выделив из всей жидкости слой малой толщины. Производящая
работу сила F остается постоянной на высоте Ах и определяется весом
слоя: F=nr2yAx. Приращение работы, необходимой для
выкачивания слоя толщиной Ax=dx на высоту х, будет ее дифференциалом
dA, величина которого равна произведению силы па расстояние, или
5;
сг
/
-—^=^
. г
i
"\
-=— ~ ■
'
■
d А = nr^dx ■ χ=nrzyxdx.
(1)
Общее решение дифференциального уравнения (1)
Α=π/*γ —+С.
(2)
Начальное условие: при х=0 Л = 0. Отсюда, согласно
уравнению (2), постоянная интегрирования С=0. Тогда равенство (2)
принимает окончательный вид
-пг2у-
Работа Αι при х—Н будет
Я2
Αι=η/2γ--—,

§ 6. Изменение яркости света в стеклянной пластине
работа Аг при x=H—h будет
(Я-/г)2
Λ2=π/"2γ s
Работа, затраченная на выкачивание всего топлива,
Α=αΑι_Αζ=ηήΊ (__ _+ЯА-—) =лгуЦЯ- —) .
Величина
яг2у/г=Р,
где Ζ5 — вес всей жидкости. Тогда искомая работа
§ 6. ИЗМЕНЕНИЕ ЯРКОСТИ СВЕТА В СТЕКЛЯННОЙ ПЛАСТИНЕ
Задача 13. Найти закон изменения яркости света после
прохождения через стеклянную пластину, если при прохождении через
слой толщиной xj = 2,5 мм яркость света Βι составила 30 межд. ед.,
л на поверхности (х0=0) начальная яркость Во=ЮО межд. ед.
(рис. 9). Лучи падают на поверхность пластины под любым углом,
а его изменение отражается на величине коэффициента k.
Решение. Величина яркости света В, пропускаемого
стеклянной пластиной, изменяется в зависимости от толщины пластины.
Часть световой энергии поглощается стеклом, и сила света
уменьшается. Так как яркость света зависит от толщины пластины, то
силу света / будем рассматривать как функцию толщины х, т. е.
1—1(х). Если при толщине стеклянной пластины χ мм сила света
/ межд. ед., то при увеличении толщины пластины на величину Ах
получим уменьшение яркости света.
Пусть сила света на участке Ах уменьшается равномерно. Тогда
условное уменьшение яркости после прохождения через слой
толщиной Ах можно определить
dl=—kldx, (1)
где k — коэффициент пропорциональности, Ax—dx. Знак минус
указывает на уменьшение яркости с утолщением стеклянной
пластины.

36
Гл. III. Простейшие уравнения
Из дифференциального уравнения (1) после разделения
менных находим
—γ- =—kdX,
откуда после интегрирования получаем
In /=— kx-\-C.
\\
\ \ 1
—N
\
\ N. \
Рис. 9
Начальное условие: при л;0=0 /о= 100. Отсюда, согласно
уравнению (2),
In 100=—yfe-0+С
и
C=ln 100.
Подставляя найденное значение С в общее решение (2),
получаем
ln/=—fcc+ln 100,
тогда
1п-шг=-**· (3)
Дополнительное условие: при χι=2,5 /ι=30 дает равенство
, 30
100
=—2,5ft,
откуда коэффициент пропорциональности
ft=—-l-'ln 0,3=0,481.
(4)

§ 7. Нагрев тела
37
Найденное значение коэффициента пропорциональности (4)
подставляем в равенство (3), после чего искомый закон
принимает вид
lnw=-°'481*
ИЛИ
/=Ю0 е-0·481*.
§ 7. НАГРЕВ ТЕЛА
Теплота нагрева
Задача 14. Найти количество теплоты, необходимое для нагрева
I кг железа от 20 до 21° С. Удельная теплоемкость с железа
выражается зависимостью с=0,1053+0,000142/, где /— температура.
Решение. Количество теплоты Q, необходимое для нагрева,
будет функцией температуры, т. е. Q — Q(t). Теплоемкость тела
представляет изменение количества теплоты Q при изменении тем-
пературы / и. определяется как производная —тт- Удельная тепло*
dQ
емкость представляет производную —тг-
По условию
■~~ =0,1053+0,000142/
at
или
dQ= (0,1053+0,000142/)d/.
Интегрируем это уравнение:
Q = 0,1053/+0,000071/2+C. (1)
Начальное условие: при /=0 Q = 0. Отсюда, согласно
уравнению (1), находим, что С=0.
Тогда
Q = 0,1053/+0,000071/2.
Для определения количества теплоты, необходимого для
нагрева 1 кг железа от 20 до 21° С, находим
Q (21) =0,1053-21+0,000071-441 =2,2426 ккал,
Q (20) =0,1053-20+0,000071-400=2,1344 ккал,
откуда
Q (21) — Q (20) =0,1082 ккал&0,\\ ккал.

3β
ГЛ III. ПрОСТейШие: уриопспиЛ
Прохождение теплоты через пластину
Задача 15. Пластина из графита толщиной 10 мм на
поверхностях имеет постоянные температуры ίι= 1300° С и i2=100°C.
Найти удельный поток теплоты q, проходящий через графитную
<__
пластину с коэффициентом теплопроводности λ= 144 -10 200°.
Решение. По закону Фурье
»--*(')-£■. (о
где q — удельный поток теплоты, λ — коэффициент
теплопроводов
ности, -— скорость изменения температуры.
CLX/
Подставляя данные задачи в соотношение (1), получим
дифференциальное уравнение процесса
gdjf-» —144-10 ww-dt,
которое после интегрирования принимает вид
144 —
qx = — ..JO 2000 +С. (2)
2000
In 10
Начальное условие: при толщине пластины л:=0 ί=ίι=
= 1300° С. Отсюда
И
288000—g-
ln 10
Подставляем значение С в общий интеграл- (2):
In 10 v '
Дополнительное условие: при x=10 mm i=i2=100°C, откуда
288 000 / 10_i5"_io~"S") =8,32-106 ккал/мЧ.
In 10 х '

§ 7. Нагрев тела
39
Распределение температуры внутри ограждающих поверхностей
Задача 16. Кирпичная стена толщиной 30 см имеет температуру
ia внутренней поверхности 20° С, а на наружной 0°С (рис. 10).
1айти зависимость температуры внутри стены от расстояния до ее
шружного края и количество теплоты, которое отдает наружу 1 м2
тепы в течение суток.
Рис. 10
73 е ш е н и е. Количество теплоты, проходящее через единицу
и dt
юверхности в единицу времени, равно k—-j—, где t— температура,
: — расстояние до наружной стены, k — коэффициент теплопровод-
тети (для кирпича — 0,2 ккал/м-ч-град).
т . dt
хемпературныи градиент —г— характеризует интенсивность па-
|дч|ия температуры по направлению теплового потока перпендику-
υιριιο к поверхности стены'.
Пусть температура внутри стены есть функция расстояния до
оружной поверхности х, т. е. t=i(x) (рис. 10). Интенсивность
шдения температуры по нормали к поверхности стены определяется
dt
пюизводнои
dx
Возьмем на расстоянии χ от наружной стены слой
•'олщиной dx с постоянной (внутри этого элементарного слоя)
температурой t. Количество теплоты Qi, проходящее через этот слон,
будет постоянным и по условию
Q1 = -fe-^-S.
dx
(1)

40
Гл. III. Простейшие уравнения
Так как поверхность S = \ м2, то
at
Q^-*^· (2)
Общее решение дифференциального уравнения (2) имеет вид
t=--Q-x+C. (3)
Начальное условие: при х—0 t=Q, откуда, согласно
уравнению (3), С=0.
Тогда искомый закон температуры внутри стены
Qi
ί==~ΊΓ*· (4)
Дополнительное условие: при χ — 0,3 м t = 20°, k =
=0,2 ккал/м-ч-град дает возможность определить из уравнения (4)
величину
Ы 0,2-20 40_
Qi~ χ ~ 0,3 ~ 3 "
Подставляя найденное значение Qi в равенство (4), получим
искомую зависимость
40 200
t— ■■ п п х= —-—х.
3-0,2 3
Количество теплоты, которое отдает наружу 1 м2 стены за сутки
(24 часа), будет
Q=24Qi = — 320 ккал.
§ 8. ИЗМЕНЕНИЕ СОСТОЯНИЯ ГАЗОВ В СОСУДАХ
Работа сжатия
Задача 17. В цилиндрическом сосуде объемом V0=0,1 м3
заключен атмосферный воздух, который адиабатически (без обмена
тепла с окружающей средой) сжимается до объема Vi=0,01 м3.
Определить работу сжатия.
Решение. При адиабатических изменениях состояния газа
его давление и объем связаны уравнением Пуассона
ρ / Vo \k
пп ~ \ ν I'
ра ν V
где k — постоянная для данного газа величина. Для воздуха &« 1,4.
Атмосферное давление /?о= 1Ό 330 кГ/м2.

§ 8. Изменение состояния газов в сосудах
41
Пусть: S — площадь поршня; V —· объем газа и ρ — давление
газа, когда поршень находится на высоте χ; —άχ — бесконечно
малое перемещение (опускание) поршня при сжатии; dW—
бесконечно малая работа; ~dV — бесконечно малое изменение объема;
ро — первоначальное давление газа;
1/ц — первоначальный объем газа. [
Бесконечно малая работа прл
опускании поршня (рис. 11)
dW=~pSdx.
Но
Sdx=dV,
отсюда следует, что
dW=-pdV.
Из уравнения Пуассона
/ V0 \h poVoh
]/h
(1)
(2)
BE
minimi
s
ШШШ1ЧИ
■'.I
wmw.
iSi
Puc. 11
Подставляя выражение (2)
в уравнение (1), найдем дифференциальное уравнение процесса
dW=~poVoh
dV
у*. -
Интегрируя, получим общее решение:
W=-p0V0b jVrhdV= —
poVoh
PoV0h
l-k
Vi-b+C--
paVoh
_ i/-(ft-i)_LC= — +C.
Как видно из начальных условий, при V—V0 W=Q. Отсюда
_ PoVoh
PoVo
С=-
к—\

42
Гл. III. Простейшие уравнения
Таким образом, работа адиабатического сжатия
»-Ш(-г-Г-']·
Подставляя числовые данные, получим искомое значение
работы:
10 330 -^-0,1 м*
W— — [ 100·4-1]= 2582,5(IО0·4—1) кГи*«3904,4 кГм.
Работа расширения
Задача 18. Водород расширяется при постоянной температуре
от своего первоначального объема Vo, имея первоначальное
давление р0, при некотором внешнем давлении, которое бесконечно мало
отличается от давления газа. Найти произведенную водородом
работу.
Решение. Аналогично уравнению (1) задачи 17, учитывая
фактор расширения, запишем дифференциальное уравнение
процесса:
dW^pdV.
В данном случае газ расширяется изотермически и поэтому
подчиняется не закону Пуассона, а закону Бойля — Мариотта
pV=p0V0,
откуда
PoV0
Тогда дифференциальное уравнение процесса примет вид
dW=p0V0-y-. (1)
Интегрируя уравнение (1), получим общее решение
W=p0V0\n V+C.
Из начальных условий следует, что при V—Vo W=0, отсюда
0=p0Voln V'o+C
и
C=—p0Vo\n V0.
Таким образом, работа расширения
V
W—p0Vo\n
V0

Глапа IV
ЗАДАЧИ, ПРИВОДЯЩИЕ К ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЯМ С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ
Если в дифференциальном уравнении первого порядка
функции Μ и N представлены в виде
М(х, У) =/ι (*)φι(ί/), Ν (χ, у) =/2(x)q^(i/),
то уравнение
M(x,y)dx+N(x,y)dy=Q (1)
примет вид дифференциального уравнения с разделяющимися
переменными
h{x)fpt(y)dx+hix)(pi(y)dy=0. (2)
Делим уравнение (2) на Μ*)φι(ί/)> откуда
h(x) , , Чг(у) _, п
ах-\- ■ —-■ ш/=0
Н(х) φι(ί/)
или
R(x)dx+S(y)dy=0, (З)
где переменные χ и у разделены.
Общий интеграл уравнения (3)
JR(x)dx+$S{y)dy=C. (4)
Если φι(ί/) и fz(x) равны единице, то уравнение (2)
вырождается в простейшее дифференциальное уравнение с разделенными
переменными, общий интеграл которого получается
непосредственным интегрированием:
J fi(x)dx+ J q>z(y)dy=C.
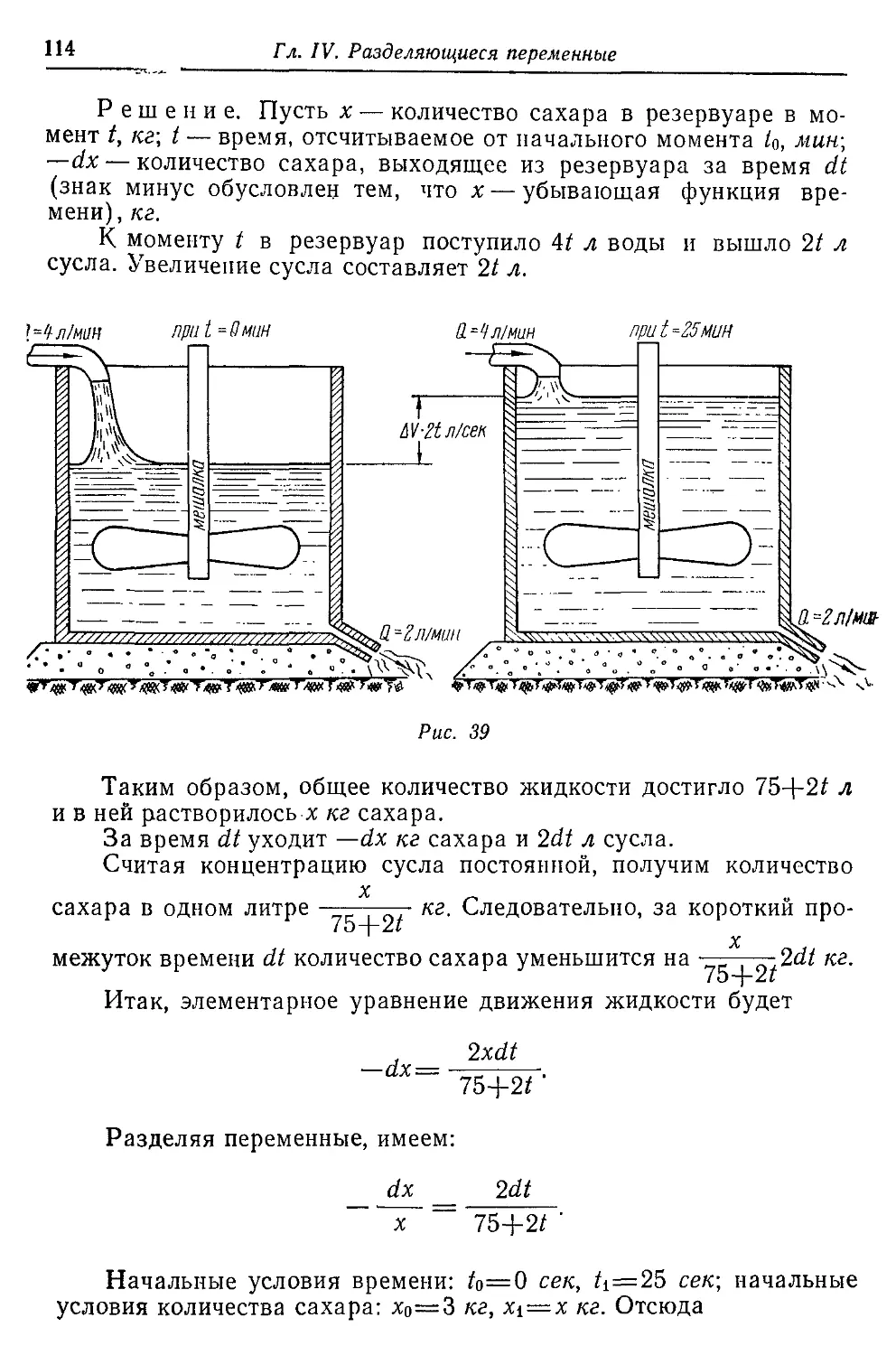
§ 1. ОХЛАЖДЕНИЕ ТЕЛ
Задача 19. Температура вынутого из печи хлеба в течение
20 мин падает от 100 до 60° С (рис. 12). Температура окружающего
воздуха 25° С. Через какое время от момента начала охлаждения
температура хлеба понизится до 30° С?
Решение. Скорость охлаждения тела представляет
понижение температуры Τ в единицу времени τ и выражается производ-

44
Гл. IV. Разделяющиеся переменные
ной ——. По закону Ньютона скорость охлаждения тела
пропорциональна разности температур тела и окружающей среды. Это процесс
неравномерный. С изменением разности температур меняется и
скорость охлаждения тела.
Дифференциальное уравнение охлаждения хлеба будет
dT
άτ
= k{T-t),
где Τ — температура хлеба, t — температура окружающего воздуха,
h ^ dT
k — коэффициент пропорциональности, — скорость охлажде-
,. ах
ния хлеба.
Пусть τ — искомое время охлаждения. Тогда, разделяя
переменные, получим
Для условий задачи
T—t
dT
-kdx.
Ввиду того что
Г-25
dT d(T—25)
Г-25
Τ—25 '

$ 1. Охлаждение тел
45
интегрируя, получаем
или
1п(Г-25)=/гт+1пС.
Потенцируем обе части последнего равенства:
gin (Т-25) _ ehx-\In С — ehx. gin C_
Так как
е^с=С,
то
Г—25=Се*. (1)
Произвольную постоянную С определяем из начального
условия: при τ = 0 мин Г=100°. Отсюда
100-25=Ceh0= С или С=75.
Величину eh определяем, исходя из данного дополнительного
условия: при τ=20 мин 7=60°. Получаем
60-25=75 (eh)
20
20
Уравнение охлаждения хлеба в условиях задачи примет вид
/ 7 \20
Г=75(-—) +25. (2)
15
Из уравнения (2) определяем искомое время τ при температуре
хлеба Τ =30°:
τ t
5=75 ( — ) или -^=(-у5-) ·
Окончательно,
-20 In 15 -20-2,7081
τ = —— —— « ^^7^— «71 мин.
In 7—In 15 —0,7622
Итак, после 1 ч 11 мин хлеб охлаждается до температуры 30° С.

46
Гл. IV. Разделяющиеся переменные
§ 2. НАГРЕВ ТЕЛ
Задача 20. Найти время нагрева 1 кг воды электроприбором
от комнатной температуры 20°С до температуры кипения 100° С,
если напряжение тока 120 в, сопротивление спирали 14,4 ом, и если
известно, что 1 кг воды остывает от 40 до 30° С за 10 мин.
Решение. Пусть Q — количество теплоты, доставленное
электроприбором к моменту времени t, Θ — температура воды.
По закону Джоуля — Ленда
Q = 0,24i2tf/,
где Q — количество теплоты в малых калориях; i — сила тока, а;
R — сопротивление, ом; t — время, сек.
Приращение количества теплоты AQ за промежуток времени Δ/
состоит из: 1) теплоты, идущей для повышения температуры
на ΔΘ0, т. е.
AQi=cmA6,
где с — теплоемкость и т — масса; 2) теплоты, идущей на
компенсацию охлаждения воды в результате теплообмена с окружающим
воздухом в комнате за время At, т. е.
AQZttcmk(<d—20) At,
где k(@—2Q)dt — по закону Ньютона дифференциал температуры
охлаждающего вещества.
Полное приращение количества теплоты за время At
AQ ж cmAQ+cmk (Θ—20) At
или
dQ = cmd<d+cmk (Θ—20) dt.
Скорость нагревания 1 г воды будет
1 dQ d<d
т dt dt
так как теплоемкость воды с=Ь
По закону Джоуля — Ленца
+*(θ-20), (1)
dQ E2
v =0,24i'2R=0,24'
dt ' v ' R '
Подставляя в последнее уравнение данные числовые значения
напряжения тока и сопротивления, получим
"О =0,24.-^=240. (2)
dt ' 14,4

§ 2. Нагрев тел
Прит = 1 кг=1000г
1 dQ
m dt
= 0,24.
По условию в течение 10 мин температура воды понижается
с 40 до 30° С и дифференциальное уравнение задачи
dQ =-£(Θ_20),
dt
откуда после разделения переменных
dQ
Θ—20
= -kdt (3)
Интегрируя уравнение (3), получаем
30 600
40 W Δν 0
ИЛИ
30
1η(θ—20)
In 10-ln20=-600£,
= -£•600;
40
откуда
k--^- (4)
к~ 600 ' W
Учитывая соотношения (1), (2) и (4), получим
дифференциальное уравнение
d<d In 2 In 2
0 24= ———-Ι ·θ
df + 600 30 '
откуда
dt = 600de
144+20 In 2-θ In 2 ' b)
Интегрируя, получим
100
/=60oJ - d@
20 144+20 In 2—θ In 2
100
600 1η(144+201π2-Θ1η2)
In 2
Итак, /ж422 сек =7 лшн 2 сек
«422
20

48
Гл. IV. Разделяющиеся переменные
§ 3. РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ ВНУТРИ ТЕЛ
Полая сферическая оболочка
Задача 21. Стальная шаровая оболочка, внутренний радиус
которой 6 см и внешний 10 см, находится в стационарном тепловом
состоянии. Температура ее внутренней поверхности 200° С, а
внешней 20° С (рис. 13). Найти температуру на расстоянии г от центра
и количество теплоты, которое в 1 сек шар отдает наружу
(коэффициент теплопроводности стали &=0,14).
т
Рис. 13
Рис. 14
Решение. Благодаря симметрии можно считать, что теплота
в шаре распространяется радиально. На расстоянии г от центра
площадь, через которую протекает теплота, равна площади
поверхности шара:
F=4w2.
Ввиду того что между отдельными сферическими
поверхностями количество теплоты остается неизменным, через две любые
поверхности протекает одно и то же количество теплоты по закону
теплопроводности Фурье. Скорость, с которой теплота
распространяется через площадку F, равна
Q = -kF
dT
dr
(1)
где Τ — температура тела, k — коэффициент теплопроводности
вещества.
Уравнение (1) принимает вид
dT
—4nkr2 , =Q=const.
dr

§ 3. Распределение температуры внутри тел
49
Разделяя переменные и интегрируя, получаем общее решение
4π£Γ= — +С. (2)
г
Для отыскания частного решения подставляем начальные
условия Т—20, г=10; Т=200, г=6 в уравнение (2) и определяем
величины С и Q:
80яЛ=-р-+С, |
800л/г= -§- +С.
о
Отсюда
С== — ΙΟΟΟπΛ
и
Q=10 800it&.
Таким образом, искомая температура
а количество теплоты, отдаваемое шаром· в течение 1 сек,
Q=10 80(k&=4750 кал.
Полая цилиндрическая оболочка
Задача 22. Трубопровод тепловой магистрали (диаметр 20 см)
защищен изоляцией толщиной 10 см; величина коэффициента
теплопроводности /г=0,00017. Температура трубы 160°, температура
пнсшнего покрова 30° (рис. 14). Найти распределение температуры
пиутри изоляции, а также количество теплоты, отдаваемой 1 и
трубы.
Решение. Если тело находится в стационарном тепловом
состоянии и температура Τ в каждой его точке есть функция только
одной координаты х, то, согласно закону теплопроводности Фурье,
количество теплоты, испускаемое в секунду,
Q =—kF(x) —— = const,
где F(x) —площадь сечения тела на расстоянии х, k —
коэффициент теплопроводности.

50
Гл. IV. Разделяющиеся переменные
В задаче
F(x)=2ial,
где I — длина трубы, см, χ — радиус трубопровода, см.
Таким образом, после разделения переменных
дифференциальное уравнение задачи примет вид
dT-.
Q
dx=-
Q
kF(x) k-2nl
Интегрируя обе части равенства (1), находим
30 20
Q f ах
7 ■ 9л1.
ю
ах
χ
0)
[ dT= Q f dx
2 0,00017·Ы"" J x '
\dT=-
Q
160
0,00017·2π/ J χ
ί
dx
(2)
(3)
или
30
20
ЧП 1 fid
зо 160- 000017.2π/
160
Τ 1 ΑΠ In r
Τ т~ 0,00017·2π/1Πλ
In x
χ
= - Q In 2
10 0,00017 ·2π/
® Infill·
0,00017 ·2π/ '"^ "
(4)
(5)
Разделив почленно уравнение (5) на уравнение (4), получим
Г—160 In 0,1* IgO.lje
-130
In 2
lg2
Отсюда закон распределения температуры внутри изоляции
Г=591,8—431,8 lgx.
Из уравнения (4) при /=100 см находим
130·0,00017·2π· 100 _ 200π· 130-0,00017
Q~ In 2" " ~~ 0,69315
Количество теплоты, отдаваемое в течение суток, равно
24.60-600 = 86 400 ^i|:?,00017_ = } m&jQ ^
0,69315

§ 4. Брус равного напряжения
51
} 4. БРУС РАВНОГО НАПРЯЖЕНИЯ
SM*dSlx)
Задача 23. Металлический брус равного напряжения
(напряжение во всех поперечных сечениях которого одинаково) длиной
/ — 100 м рассчитан на растягивающую нагрузку 2 Т. Допустимое
напряжение металла σ= 1000 кГ/см2,
и его удельный вес у = 7,6 Г /см3.
Определить площадь верхнего
сечения бруса.
Ρ е ш е и и е. Напряжением
напивается сила, рассчитанная на
I см2 поперечного сечения бруса.
'Гак как в каждом поперечном
сечении бруса растягивающая сила
равна нагрузке Ρ π весу ниже
расположенной части бруса, то эта сила
возрастает с повышением сечения,
а поэтому для равенства
напряжений необходимо, чтобы в той же
мере возрастала площадь сечения
с. удалением от нижнего конца
бруса. Наибольшую площадь должно
иметь верхнее сечение бруса.
Ось χ направим вертикально
(рис. 15) и введем обозначения:
Si·—искомая площадь верхнего
сечения; S2 — площадь нижнего сечения бруса; S — переменная
площадь сечения бруса на высоте х; Q — вес части бруса ниже
сечения S; Ρ — допустимая нагрузка бруса; σρ — допустимое и во всех
сечениях бруса одинаковое напряжение растяжения.
Напряжение в сечении S(x) будет
а в сечении S (x) -f-dS (x)
S+dS
= P+Q(x)
S(x) '
P+Q(x)+dQ(x)
S(x) +dS (x)
Так как в брусе эти напряжения одинаковы и равны
допустимому напряжению σρ,·το
P+Q(x) _
" S(x) ~°р'
P+Q(x)+dQ(x)
S(x)+dS(x)
jp )

52
Гл. IV. Разделяющиеся переменные
или
P+Q(x)=opS(x);
P+Q (x) +dQ (χ) =opS (χ) +opdS (x)
}
Вычитая из второго равенства первое, находим вес части бруса
между бесконечно близкими сечениями S(x) и S(x)-\-dS(x):
dQ(x)=opdS(x). (1)
Принимая эту часть бруса цилиндрической, получим
dQ(x)=yS(x)dx. (2)
Приравниваем правые части уравнений (1) и (2) и получаем
дифференциальное уравнение
yS (x) dx=opdS (x)
или
dS(x) γ
S (χ) σρ
Интегрируя, получим
dx.
lnS(x) = x+Ci
σρ
или после потенцирования
ν
S(x)=Ce°P
где С=ес>.
Начальное условие: при х=0 S = F0. Отсюда
JL.o
F0=Ceav =С. (Ъ
Тогда после подстановки значения постоянной интегрировь
ния (3) в общее решение находим
ν
S(x)=F0e°pX . (4)
По закону (4) можно определить площадь сечения бруса на
любой высоте х.
При х=1 площадь верхнего сечения
F=F0e>
y.i

§ 5. Давление зерна на стенки хранилища
53
Подставим числовые значения параметров.
« Р
Напряжение в нижнем сечении σρ= ——, откуда
„ Ρ 2000 0°
F0= = =2 еж2.
σρ 1000
Так как
то показатель
σΡ= 1000 кГ/см2= 1 000 000 Г/см2,
/=Ю0л=10 000 см.
γ ι= 7:6;Α0.°ϋΡ ^ο,ο76.
1 000 000
Таким образом, искомая площадь верхнего сечения
F=2e°'m ж 2 -1,08=2,16 см2.
§ 5. ДАВЛЕНИЕ ЗЕРНА НА СТЕНКИ ХРАНИЛИЩА
Задача 24. Давление ps зерна на стенки принимается
пропорциональным давлению ρ зерна на горизонтальную площадь ps=kp.
Найти закон изменения ρ и ps с возрастанием глубины h с учетом
трения зерна о стенки хранилища.
Решение. Рассмотрим условия
равновесия бесконечно тонкого слоя
между двумя горизонтальными плоскостями
на глубине h и h-\-dh (рис. 16). На
первую плоскость действует давление ρ
сверху вниз, на вторую — давление p-\-dp
снизу вверх.
Умножая силы ρ и p-\-dp на площадь
поперечного сечения S хранилища,
получим силу, действующую вверх:
S(p+dp)-Sp=Sdp.
1
«=1
t
dh
I
-: —
■Π . ρ ■
-<ττ~
• \γ:
·\·\ p+ijp
Μ-
Рис. 16
На слой действует также
собственный вес ySdh, где dh — высота слоя.
Кроме этих сил, если открыть нижнее отверстие хранилища,
в самом начале движения вследствие давления зерна на стенки
возникает направленное вверх сопротивление трения.
Пусть Ρ — периметр сечения хранилища. Тогда поверхность
части стенок, ограничивающей рассматриваемый слой, будет Pdh.
Тик как величина dh бесконечно малая, то боковое давление на
единицу площади в пределах этого слоя можно принять постоянным.
Полное боковое давление равно kPpdh, а вызванное им тре-
IIИС \ikPpdh.

54
Гл. IV. Разделяющиеся переменные
Условие равновесия всех действующих сил
Sdp+y,kPpdh—ySdh = О
или
dp+(-^p-y)dh=0. (1)
ukP
Вводим обозначение λ= —=—. Тогда дифференциальное урав-
нение (1) после преобразования примет вид
dp
λρ-y
или
dp
+dh = Q
= dh.
y-λρ
Общее решение этого уравнения
у—Хр = Се-ы. (2)
Начальное условие: при /г = 0 р = 0. Отсюда
γ—λ·0=Οβ-λ·°
или
С=у.
Найденное значение постоянной интегрирования подставляем
в общее решение
γ—Хр=уе ЛН,
откуда
е-^=1- — р. (3)
Υ
Из равенства (3) находим, что
γ yS 1 h\
, nc
ство (4), после сокращения получим
Ps
Так как ps=kp, то ρ— —τ- и, подставляя это значение в равен-
/с
УЛР h
Ps=-7nr{l-e S ')· (5)
μΡ
Из соотношений (4) и (5) видно, что давления ρ и ps
возрасти
тают непропорционально глубине h. При любом h величина ps<Z—^.

§ 6. Барометрическая формула и глубинное давление
55
§ 6. БАРОМЕТРИЧЕСКАЯ ФОРМУЛА И ГЛУБИННОЕ ДАВЛЕНИЕ
Задача 25. Найти зависимость высоты h места над уровнем
моря от давления воздуха ρ (кГ/м2). Вычислить при нормальных
атмосферных условиях давление воздуха на высоте /г = 1000 м,
предполагая, что нижележащие слои воздуха имеют постоянную
температуру 0° С. Нормальное
давление атмосферы на
поверхности Земли /)о=ЮЗЗО кГ/м2.
Плотность воздуха на
поверхности при нормальных
атмосферных условиях δο= 1,29 кГ/м3.
Решение. На высоте h
давление воздуха ρ
определяется весом той части столба
воздуха, которая опирается на
рассматриваемое
горизонтальное сечение АВ площадью 1 м1
(рис. 17). Плотность воздуха δ.
Увеличение высоты h па
бесконечно малую величину dh
приводит к уменьшению давления на величину dp, которая
измеряется весом слоя воздуха между сечением АВ на высоте h и
сечением CD на высоте h-\-dh, т. е. иначе изменение давления воздуха
равно весу столба воздуха с площадью основания 1 м2 и высотой dh.
Принимая на протяжении dh плотность δ неизменной, получим,
что вес такого столба равен 8dh, и поэтому имеем
дифференциальное уравнение
—dp=8dh. (1)
Заменим величину δ через р. Так как температура всех слоев
воздуха постоянна и равна 0°С, то, следуя закону Бойля — Ма-
риотта, получим
δ ρ
Уродень моря
Рис. 17
пли
δο
6 =
Ро
Ро
■р-
(2)
Выражение (2) подставляем в правую часть соотношения (1).
Получаем дифференциальное уравнение барометрического давления
—dp= pdh,
Ро
которое принимает вид
dp
^-^~dh.
Ро
(3)

56
Гл. IV. Разделяющиеся переменные
Интегрируем дифференциальное уравнение (3):
1п/> = - —й+С.
Ро
После потенцирования получим общее решение
h+Ct h
р = е Ро =Се Ро . (4)
Начальное условие: при h=0 р=ро. Тогда
С=р0.
Барометрическая формула (4) принимает окончательно вид
р = р0е р0 . (5)
Решим уравнение (5) относительно h:
ft=^LlnjPiL. (6)
δο ρ
Уравнение (6) позволяет судить о высоте подъема над уровнем
моря по давлению воздуха.
Для подстановки числовых данных в формулу (5) вычислим
показатель
60 -Н= 12?:1Г «0,125,
ро 10 330
откуда искомое давление
/7 = 10 330е-°'125=9116 кГ/м2.
Предположим, что температура воздуха переменна и газ
подчиняется закону
ι
pKn=const и а———рп.
Ρ
Тогда исходное уравнение процесса
dp ро
ι
= — Ρ
dh p
Разделяя переменные, имеем

§ 6. Барометрическая формула и глубинное давление
57
*Р --JULdh.
jl/n
Откуда после интегрирования
ι
+1
Ρ n =_-£L/l+c. (7)
ι—L. ρ
η
Начальное условие: при ft=0 р=ро- Отсюда постоянная
интегрирования
ι
1-±
П
Подставляя значение С в уравнение (7) и сокращая подобные
члены, получаем
ι ι
Ρο
■h:
Ρ
—Г(ро »-ρ - ) =
1 1
1 . ι .
= J5AlJL_[,_(JL) ·]. (8)
η—Ι ι ν ρ0 ι J 7
Так как при /ι=0 ρ = ρο и α=α0, το
Ρο — Ρο Οο
α0= · -ρ0" или = —π—.
ρ ρ Ρο1/η
Подставляя эти значения в уравнение (8), получаем
ι
η—1 α0 L χ Ρο ; J
Так как pV=RT (где Г=/°+273° и # = 8,32 дж на 1°), то
-&Г—ТГ (,0)

58
Гл. IV. Разделяющиеся переменные
Тогда
ι
V \п . / р0 \ "~ V
— 1~тг/ -1 или I 7 ~
Pa V Vo ' V Ρ ' W
откуда, подставляя эти значения в уравнение (10), получаем
г qjL)~~=(JL)'T („)
Го ро ^ Ра ' v ро '
Подставляя равенство (11) в уравнение (9), окончательно
имеем
,= _«'ϋΐ.(! 7 ).
η—1 α0 ν Γ ο '
Аналогично решается задача о глубинном давлении.
Если ρ — гидростатическое давление, h — глубина ниже уровня
моря, то тогда
dp=bdh,
откуда
dp
где δ — вес 1 м3 морской воды.
§ 7. ПРЯМОЛИНЕЙНОЕ ГОРИЗОНТАЛЬНОЕ ДВИЖЕНИЕ
Сила, действующая на тело, зависит от скорости: F=F(v)
при сопротивлении, пропорциональном скорости
Задача 26. Моторная лодка движется в спокойной воде со
скоростью и0=20 км/ч. На полном ходу ее мотор выключается и через
40 сек после этого скорость лодки уменьшается до Ui=8 км/ч
(рис. 18). Сопротивление воды пропорционально скорости движения
лодки. Определить скорость лодки через 2 мин после остановки
мотора.
Решение. На движущуюся лодку действует сила F=—kv,
где k — коэффициент пропорциональности. По закону Ньютона сила
dv
равна произведению массы на ускорение F=m——. Откуда
дифференциальное уравнение движения
dV и 1Л\
m~dT=~ О

§ 7. Прямолинейное горизонтальное движение
Очевидно,
ИЛИ
άυ
ν
In y= —
: at
m
m
t+d
Потенцируя, получим общее решение уравнения (1)
к к к
v = e m =ec>e m =Ce m .
i=0
I, -Wwk
Рис. 18
Начальное условие: при ^ = 0 у=20 км/ч. Откуда
h
20=Се
и С=20.
Тогда общий закон движения для условий задачи
k
.t
u — 2Qe m .
(2)
Дополнительное условие указывает, что при ί=40 сек= — ч
скорость лодки составляет 8 км/ч.
Отсюда
k ι
3=20е m 90 или е
— I 5
= (4)·
Подставляя числовые данные в найденный закон движения (2),
учитывая при этом, что t = 2 мин= -^~ ч, получим
30
у=20
1
ΊχΓ
У \ 2 ·/ J ^ 2 * 25
:20
Ш
32
1,28 км/ч.
Итак, скорость лодки, спустя 2 мин, снизится до 1,28 км/ч.

60
Гл. IV. Разделяющиеся переменные
Сила, действующая на тело, зависит от скорости
при сопротивлении движению, пропорциональном скорости
и силе тяжести тела
Задача 27. Судно водоизмещением в 12 000 τ (рис. 19)
движется прямолинейно со скоростью Уо=20 μ /сек. Сопротивление воды
пропорционально квадрату скорости судна и равно 36 Τ при
скорости 1 м/сек. Какое расстояние пройдет судно после остановки
двигателя, прежде чем скорость станет равной υ = 5 м/сек? За какое
время судно пройдет это расстояние?
А .П . f \
a. „ I...9 Aj=S
\Л-'ψ№"/Ό . -ПГ v^=
-—":
/IWWu^MBis^
f^^=Jr^^-^ -^=r^^^T^^=^
_
sJLr^ v
=^-
~ -"" ~ ~—:
— —
t = ?
Рис. 19
Решение. Количество движения системы
количеству движения центра масс системы, т. е.
(судна) равно
Q=mvc,
где vc — скорость центра масс, т — масса всей системы.
Производная вектора количества движения системы по времени
равна геометрической сумме всех внешних сил, действующих на
систему. Для движения.центра масс имеем
dQ
dt
mdvc
dt
-Ρ,
Центр масс системы движется, как материальная точка с
массой, равной массе всей системы, к которой приложены все
действующие на систему внешние силы. Движению судна препятствует
сопротивление воды, равное —kv2.
Таким образом, дифференциальное уравнение задачи
т
du
Ж
= -ku2
или
12 000 dv
g
dt
-36у2.

§ 7. Прямолинейное горизонтальное движение
Разделяя переменные и принимая g=9,81 м/сек2, получим
v-2dv=—0,03dt
ИЛИ, проинтегрировав,
- —^-СЦШ+Сь
ν
Определяем частное решение, исходя из начального условия:
t=Q, v = 16 м/сек. Отсюда
с- '
16
т-от+-1е· (1)
Прежде чем скорость судна станет равной 5 м/сек, пройдет
время
25(16—1») 25(16-5) 55
/_ — = = __ «;4,6 сек.
\2v 12-5 12
Определим расстояние, которое пройдет судно за время
ί=4,6 сек. Интегрируем еще раз уравнение (1) и, принимая пред-
ds
варительно υ— ——, получаем
dt 400di
ds=
откуда
s=Mln(12i+25) + C2.
О
Начальное условие: при t=0 s=0. Отсюда
0=-^-ln25+C2 и С2=-^°-1п25.
О О
Таким образом, закон движения судна
100 , / 12 , . , \ .

62 Гл. IV. Разделяющиеся переменные
. __ S
За время ί=4,6 сек судно пройдет расстояние
s= ~ In 3,20«38,8 м.
О
Итак, судно после остановки двигателя, прежде чем его
скорость станет 5 м/сек, пройдет расстояние 38,8 м.
Сила, действующая на тело, зависит от скорости при
сопротивлении движению, пропорциональном квадрату скорости
Задача 28. При небольших скоростях сопротивление движению
поезда определяется эмпирической формулой
tf=(2,5+0,05u)Q/cr,
где Q — вес поезда, Την — скорость, м/сек. Найти, через какое
время и на каком расстоянии поезд приобретет на горизонтальном
участке, пути скорость υ ==12 км/ч, если вес поезда с электровозом
Q=40 Τ, а сила тяги электровоза /г=200 кГ. Определить также
силу тяги iV электровоза при дальнейшем равномерном движении.
Решение. Масса поезда
Q-1000 Г кГ-сек2
т=- - '
Г κι ■ сек2 1
L м J'
Составляя уравнение равновесия действующих на состав сил
(рис. 20), после деления на т получим
dv , g-2,5 , g-0,05 Fg
или
dt ' 1000 ' 1000 Q-1000
dv
dt
dv
+24,5· 10-3+0,49-10-3i>—49-10"3=0;
24,5·10-3+0,49-ΙΟ-3 ν = 0.
dt
Разделяя переменные, приходим к дифференциальному
уравнению
\03-dv
24,5-0,490 · Ш
Интегрируя уравнение (1), находим общее решение
103
0,49
1пС(24,5—0,49ι»)-=/. (2)

ί /. Прямолинейное горизонтальное движение 63
Постоянную интегрирования С определяем из начального усло-
мпн; И])и /=0 ν = 0. Следовательно,
103
0,49
1пС(24,5-0)=0
НЛП
1п24,5С=0.
Потенцируя, находим
m-Ml
-^
и =
\J
24,5'
О
ЧУ
f
Рис. 20
Согласно условию, в искомое время t = T скорость поезда
составит о=12 км/чхЗ,33 м/сек. Таким образом, из уравнения (2),
проводя очевидные алгебраические преобразования, получаем:
0,49
0,49
22,9
сек.
Переходим к определению расстояния, при котором скорость
поезда достигнет 12 км/ч.
и άυ
Величина —— может быть выражена так:
at r
dv
~аТ
dv. ds
dv
ds dt ds
Тогда уравнение (1) примет вид
\03-vdv
24,5-0,49и
~ds.
(3)

64
Гл. IV. Разделяющиеся переменные
Интегрируя равенство (3), получим общее решение
103 г 94 ^ ι
~ W L ϋ+ W ln (24,5-0,49.)+С J =S. (<
Определяем постоянную величину С, используя начальное уел
вие: npks=0 u = 0.
Следовательно,
С_ 0,49 lni4'b·
Подставляя найденное значение С и скорость и = 3,33 лг/с<
в уравнение (4), находим
103 Г 24,5 , 24,5 1 ._
M^W 24,5-0,49, -V\=M»·
При дальнейшем равномерном движении (и=3,33 м/vei
сила тяги
АГ= Q(2,5+0,05-3,33) =40(2,5+0,05·3,33) = 106,6 кГ.
Сила, действующая на тело, зависит от положения точки:
F = F(x)
Задача 29. Проходя через лес и испытывая сопротивление д
ревьев, Befep теряет часть своей скорости. На бесконечно малс
пути эта потеря пропорциональна скорости в начале пути и дли:
его. Найти скорость ветра, прошедшего в лесу 150 м, зная, что ,
вступления в лес начальная скорость ветра ι>ο=12 м/сек. Пос.
прохождения в лесу пути s=l м скорость ветра уменьшилась
величины Vi= 11,8 м/сек.
Решение. Пусть на расстоянии s от начала леса скорое
ветра ν, потеря скорости на пути ds равна — dv (процесс убыва:
щий). Эта потеря пропорциональна υ, и поэтому дифференциальн
уравнение процесса представится в виде равенства
—dv=kvds.
Разделим переменные:
dv
=—kds.
υ
Интегрируя, получим общее решение
υ = Ce~hs.

§ 8. Вертикальное движение тел
65
Ищем частное решение, используя начальное условие: при s = 0
v--v0. Отсюда
v0=Ce-h-°
ИЛИ
C=v0.
Закон процесса
v — v0e-hs. (1)
Для определения коэффициента пропорциональности исполь-
|усм дополнительное условие: при s=l м u = Di=ll,8 м/сек.
Тогда
пли
„ fi 11,8
Уо 12
=0,983.
Числовые значения подставляем в уравнение процесса (1),
откуда искомая скорость
у=12(0,983)150=12-0,0776«0,93л</се/с.
Итак, скорость ветра, углубившегося на 150 м в лес, составит
0,93 м/сек.
§ 8. ВЕРТИКАЛЬНОЕ ДВИЖЕНИЕ ТЕЛ
Падение вниз под действием силы тяжести
Задача 30. Падающее под действием силы тяжести тело
(рис. 21) получает ускорение а= —-—, где k — коэффициент про-
порциональности, г — расстояние падающего тела от центра Земли.
Найти время падения тела, если оно находится от Земли на
расстоянии /? = 60,27гз, равном удалению Земли от Лупы. Радиус Земли
г3 = 6377/ш = 6,377-106л.
Решение. Пусть R — расстояние Луны от центра Земли;
g — ускорение силы тяжести на поверхности Земли.
Согласно общей формуле, это ускорение на поверхности Земли
k
равно -—-, поэтому
k
Знак минус взят потому, что расстояние считается от начала
(R = 0), а ускорение направлено к началу. Из уравнения (1) имеем

Гл. IV. Разделяющиеся переменные
Общее выражение для ускорения примет вид
gr32
а=—
Г*
С другой стороны, предполагая, что тело падает к центру
Земли О прямолинейно (рис. 21), имеем
dr
ϋ- dt>
a dv
dv
a~ df
vdv
a^— ■
откуда
ν dr ' dr
Таким образом, дифференциальное уравнение задачи
vdv _ gr32
dr r2
Разделяя переменные и интегрируя, получим
V2= JST^_ +c ,r
Г ч
Из начальных условий известно, что при r=7? v = 0. Подстав
ляя эти значения в уравнение (2), находим
C=-2g-
R
Одновременно
—зг-У^-У.
R
откуда
dt=-V ^ -dr.
Г 2gr3*(R~r) Τ·
Интегрируя, получим
t==-\ У 2grs4R-r) dr=
R , ,
= J Угй^яЬг*· (3>
2gr?(R~r)
'з

§ 8. Вертикальное движение тел
67
Интеграл (3) вычисляется подстановкой
г
R-r
= tg*q>, (4)
лгиуда
1+tg^cp
я
dr=2R sin φ cos φίίφ.
Из равенства (5) имеем
/"3
3ΐη2φι=——, sin2 ф2== 1,
φι
= arcsiny-|-; cp2= —. (6)
Значения (4) —(6) подставляем в выражение (3):
*= У^ТТ J 1§ Φ 2i? sin Φ cos Ф^Ф=
. ф2 . . ф2
R ι/ R I sin 2ψ2 , sin 2φι \
= — V-2g\^^——+-1—Η
R ι/ R ( η . -ι/ гз , sin 2φι \
= -^-KirlT-arcsmrir+~-2— )·
Подставляя числовые значения, найдем время в секундах, раз-
/цмин на 3600, искомое время в часах:
60,27 -ι/ 60,27·6,377·106 /я sin 2φι \
/8=-ЗбЖК 1^62 Ιτ-φι+-^—) *тч
(φι=7°24,33,,=0,1292 pad).
Итак, тело, находящееся от Земли на расстоянии, равном уда-
19МИЮ Земли от Луны, упадет на Землю через 116 ч (почти 5 суток).

68
Гл. IV. Разделяющиеся переменные
Задача 31. Метеор, находящийся под исключительным
влиянием земного притяжения, из состояния покоя начинает
прямолинейно падать на Землю с неограниченно большого расстояния h.
С какой скоростью он ударился бы о Землю при отсутствии земно?
атмосферы? Длина радиуса Земли #=6377 км=6,377-106 л.
Лина
Рис. 21
Рис. 22
Решение. В точке Μ (рис. 22), находящейся на неограничер
но большом расстоянии от Земли, на тело действует сила тяжестк
-.та.
(1)
где т — масса тела, а — ускорение.
На поверхности Земли в точке N на тело действует сила
тяжести
P=mg, (2)
где g — ускорение силы тяжести на поверхности Земли.
По закону Ньютона эти силы обратно пропорциональны
квадратам расстояний падающего тела от центра Земли:

§ 8. Вертикальное движение тел
69
R2
Ϊ- (3)
Ρ (h—x)
С другой стороны, учитывая соотношения (1) и (2),
F ma a
Ρ ~ mg ~ g "
(4)
Ввиду равенства левых частей уравнений (3) и (4) приравни-
1IIM их правые части, откуда
е
или
R2
{h-xy
R2g
(h-x)
Как известно, переменное ускорение
а= -ττ-zrr (5)
а= -β-. (6)
Подставляем выражение (6) в равенство (5) и получаем
dv _ gR2
~df~ (h-x)2'
(7)
В уравнении (7) три переменные величины v, t и χ. Одну из них
(■ремя ί) можно исключить, так как
dv dv dx dv
■υ. (8)
at dx dt dx
Подстановка полученного соотношения (8) в левую часть
уравнения (7) дает дифференциальное уравнение движения
dv gR2
ν —г- =
dx (h—x)2
Решаем это дифференциальное уравнение, выполняя предвари-
WH»iio очевидные преобразования,
gR2
^=7ft=^'

70 Гл. IV. Разделяющиеся переменные
откуда после интегрирования получаем общее решение
-γ- h^x +c·
Начальные условия: при /=0 х=0 и v=0. Отсюда
02 sR2 , г,
или
gR2
h '
Подставляем найденное значение постоянной интегрирования
и находим закон движения тела:
Φ gR4
h(h-x)
На Земле в точке N величина x=h—R. Отсюда искомая
скорость тела у поверхности Земли
у2 gR(h~R)
2 hR
Так как по условию задачи высота h считается неограниченно
большой, то в космосе
gRz(h-R) I gR* V
= im —йо = im U*—г-1 =
hR h-+oo h
Из полученного равенства
gR.
v=i2gR.
Подставляя значения радиуса Земли #=6337 кж=6 377 000 м
и ускорения силы тяжести g=9,81 м/сек2, получаем
v = i2-9,81 -6 377 000=11 180 м/секх 11 км/сек.
В действительности сопротивление земной атмосферы ослабит
этот удар и уменьшит скорость тела.

§ 8. Вертикальное движение тел
71
Выброс вверх
Злдача 32. Ракета запущена вертикально вверх с начальной
(Жиростыо 1>о=ЮО м/сек (рис. 23, а). Сопротивление воздуха замед-
Лйит ее движение, сообщая ракете отрицательное ускорение D, рав-
1,'Т О1/ = 0
h=max
t=OQV0=100M/ceK
Рис. 23
ШШ§ ·· 1<υ2 (где ν — мгновенная скорость ракеты, a k — аэродинами-
ЩСИИп коэффициент). Определить время достижения ракетой
ШИВыешего положения.

72
Гл. IV. Разделяющиеся переменные
Решение. Силы, действующие в вертикальном
прямолинейном полете на ракету, представлены на рис. 23, б, где F — сила тяги.
Движение ракеты принимаем условно за движение
материальной точки Λί.
Тогда общее ускорение ракеты а при движении вверх будет
a=—g—kv2. (1)
Но
du
а=чг
и тогда уравнение (1) примет вид
dv
= -(g+№). (2)
dt
Разделяя переменные, получим
dv ..
или
1+ ки
ё
Для интегрирования проводим преобразования уравнения (3):
*(V4»)
ё =-gdt
или
U Ц^-—**. (4)
8
Уравнение (4) интегрируется почленно
fh=—=-igk\dt.
•+(Ут°)

§ 8. Вертикальное движение
Общее решение уравнения (2)
arctg(]/-^u) = -fg~kt+C.
Для условий задачи, при t — 0 ν = ν0= 100 м/сек, величина
C=arctg(]/—vq) = arctg 100^-
g ' ' g'
Тогда частное решение
arctg]/—ν—arctg 100 ]/—= —fgkt. (5)
В момент достижения ракетой высшей точки t=T и мгновенная
скорость ν равна нулю. Подставляя в равенство (5) t — T, v=0
и принимая g=9,81 м/сек2, имеем:
arctg ( 100]/~)
g I arctg(31,32VA)
(6)
igk 3,132 У й
Итак, ракета достигнет своего наивысшего положения через
и|к»мя Т, определяемое зависимостью (6).
Падение вниз при сопротивлении среды,
пропорциональном скорости
Задача 33. С некоторой высоты брошено вертикально вниз тело
Мйгсой т. Найти закон изменения скорости ν падения этого тела,
§рли па него действуют сила тяжести и тормозящая сила
сопротивлении воздуха, пропорциональная скорости (коэффициент
пропорциональности k).
Решение. Задача заключается в определении закона
изменении скорости υ с течением времени t, т. е. u = f(t).
II;) второго закона Ньютона
dv
m4T=F'
ГА· —-г, ускорение движущегося тела, г — сила, действующая hi
ΐ#Λ» ι направлении движения.

74
Гл. IV. Разделяющиеся переменные
Сила F складывается из двух сил: силы тяжести Fi=mg и силы
сопротивления воздуха Fz=—kv (рис. 24).
Итак, уравнение движения
dv
т—~- = mg—kv.
at
Разделяя переменные, получим
mdv dv ,t.
dt= — = г—-. (1)
mg—kv k
Интегрируем обе части равенства (1):
t=-
1 d (g ν ) , и
m
k~ ~~ k *" V s m
m(g- — v)+c.
g ν
Решая последнее уравнение относительно ν, имеем
Ι„(
e~°) = 4rV-t)
m ι m
или
ft ft ft ft
k (C-i) С t t
g v = em =em e m =C\e m
m
откуда
ft
m _ ' , mg
k "
Обозначая постоянную величину -— d через С*, придем
к уравнению
h
1) = С*е~"Г< + -^-. (2)
Чтобы найти частное решение, используем дополнительное
условие: при сбрасывании тела ему придана начальная скорость fo.
Считаем ее неизвестной. Тогда искомая функция v=f(t) должна
быть такой, чтобы в начале движения при t=Q выполнялось
условие и = ϋο. Подставляя ί=0, ν = υ0 в уравнение (2), получаем

§ 8. Вертикальное движение тел
75
v0=C*+
откуда
C* = v0-
Итак, искомая функция
mg
k '
mg
k '
_(^JS.).~+.
mg
Падение вниз при сопротивлении среды, пропорциональном
квадрату скорости
Задача 34. Сила тяжести летчика с парашютом 80 кГ. Сопро-
Тннлсние воздуха при спуске парашюта пропорционально квадрату
§го скорости ν (коэффициент пропорциональности £=400).
Определить скорость спуска в зависимости от времени и установить
максимальную скорость спуска.
Решение. При спуске действует сила тяжести парашютиста
С парашютом P=mg (направлена книзу) и сопротивление воздуха,
окапываемое этому спуску F=—kv2 (направлено кверху). Таким
Образом, равнодействующая сила
R = mg—kv2. (1)
Согласно второму закону Ньютона,
«-»-£ (2)
Приравнивая равенства (1) и (2), получим дифференциальное
урвппение спуска парашютиста:
dV U 9
Найдем общее решение

76
Гл. IV. Разделяющиеся переменные
ИЛИ
_ Л1 ms Се2
о2 1
1т J
kJ-t
Се*' "» +1
Начальное условие: при ί—Ο и = 0, откуда
= Се°
и произвольная постоянная
С=1.
Закон спуска парашютиста примет при этом искомое выраже
ние (для вычисления скорости парашютиста)
у*
: г m
У_^ _е»У^-1 ш (3
У^£
! Г т
t
+ 1
Как видно из уравнения (3), правая часть равенства представ
ляет дробь, всегда меньшую единицы. Предел дроби при i-»-ou
равен 1. Таким образом, максимальное значение скорости
t
. - у^<
0шх= lim У-М- -fJ^Zi- = У-^. (4)
*- * у^г *
е2 Г m _J_1
Такой скорости парашютист никогда не достигнет, так как
v = vmax при ί->οο. Практически дробь формулы (3) уже при
£=2 сек очень мало отличается от единицы, поэтому можно считать,
что максимальная скорость достигается парашютистом через 2 сек

§ 8. Вертикальное движение тел
жк'лс начала спуска. Величину максимальной скорости спу^пл молу-
ЧййМ после подстановки числовых данных задачи в равенство (4):
-У
80 000-981
400
;443 см/сек»4,4 м/сек.
Задача 35. Определить скорость, которую будет иметь через
У ССК после начала падения находившаяся до того в покое горизон-
1=0
X
^Ψψψί
Р
m it
Рис. 24
тельная квадратная пластинка со стороной 1 м и силой тяжести
ϋ κΓ. Сопротивление воздуха пропорционально квадрату скорости.
Решение. По закону Ньютона
d2x
m—~-~mg—n^v'!· (l)

78
Гл. IV. Разделяющиеся переменные
или
-£-=«-*". (2)
где k2— . Ньютон дал также приближенную формулу для
определения к2 в виде
vyS
k2=
Q
где S — площадь проекции тела на плоскость, перпендикулярную
направлению движения, м2; Q — сила тяжести тела, кГ; у — сила
тяжести 1 м3 воздуха, кГ (сухой воздух при температуре 0°С и
давлении 760 мм рт. ст. имеет γ= 1,293); ν — коэффициент
сопротивления, зависящий от формы тела.
Для рассматриваемой задачи γ= 1,225, v=0,631, S = l и Q=2,
откуда k2—0,386.
Так как скорость падения
dx
v =
dt '
то уравнение (2) примет вид
dv
g—k2v2
= dt.
Интегрируя это выражение с учетом начального условия: при
t=Q v = 0, имеем
fg+ku »/ϊ*
—" >
i g—kv
откуда
u==i|-th(Ayi/).
При ί = 2 сек искомая скорость ν = 5,034 м/сек, что почти не
отличается от 1>тах=-!-~-=5,038 м/сек, так как при t-*-oo th(kifgt)-*~l.
/Ζ
Задача 36. Бомбардировщик начинает пикировать без
начальной скорости. Сила сопротивления воздуха пропорциональна
квадрату скорости. Найти зависимость между вертикальной скоростью
в данный момент, пройденным путем и максимальной скоростью
пикирования самолета.

§ 8. Вертикальное движение тел 79
Решение. Пусть ν — вертикальная составляющая скорости
dv
пикирования, а —-г вертикальная составляющая ускорения
пикирования.
Мели Ρ — сила тяжести самолета, то вертикальная
составляющий силы, действующей на самолет, будет P—kv2. Масса самолета
Ρ
m β —.
&
За время t самолет (рис. 25) проходит по вертикали путь у.
Пи основании второго закона Ньютона уравнение движения
запишется в виде
Так как
го
или
dv
m^rr =P—kv2.
at
dv dv dy
dt dy dt
dv dy n , ■>
m — 4- = P—kv2
dy dt
dv , „
tnv —j \-kv2—mg=0.
uy
Разделяя переменные, получим
mv dv
=dy. (1)
mg—kv2
Интегрируя дифференциальное уравнение (1), имеем:
tn
--Yk-\nC(mg-kv2)=y. (2)
Начальные условия: при t=0 y=0 и v=0, откуда
m
■ ]nC-mg=0
2k
или
\nC-mg=0
И потенцируя, имеем
Cmg— 1

80
Гл. IV. Разделяющиеся переменные
или, наконец,
mg
Подставляя найденное значение С в уравнение (2), получим
k
т 1 /, « о\
9k \ та ι *
Ik \ mg
Потенцируем это равенство:
2ft
& V
1 и2=е т . (3)
mg
Очевидно, что при у->оо самолет достигнет наибольшей
скорости i)max.
В этом случае
2ft
υ Ι
lim e m ' = lim =0
ет
и
& 2
1 vmax=0. (4)
Из уравнения (4) находим максимальную скорость:
v2 - mg ■
^max—
k '
flmax
=ίψ- <6>
Для нахождения искомой зависимости используем уравнение
(3), подставляя значение предельной скорости из уравнения (5).
Тогда
2ft
ν2 -·—-у
_е т
V2
max
и скорость
1-е m = иШах К 1-е r2ma*.

§ 9. Падение тел переменной массы
81
§ 9. ПАДЕНИЕ ТЕЛ ПЕРЕМЕННОЙ МАССЫ
Задача 37. Капля воды, имеющая начальную массу гп0 г и
равномерно испаряющаяся со скоростью mi г/сек, движется по инерции
с начальной скоростью Vo см/сек. Сопротивление среды
пропорционально скорости движения капли и ее радиусу. В начальный момент
(/ -()) оно равно f0 дин. Найти зависимость скорости движения
капли от времени.
Решение. По второму закону Ньютона
dv
F=m-df'
где F — сила, m — масса, ν — скорость, t — время.
Для решения этой задачи надо учесть, что масса m —-
переменная величина, зависящая от времени t\ v — искомая функция.
Так как капля воды испаряется со скоростью mi г/сек, то в
момент времени t масса капли будет равна
m=mu—mit. (1)
Сила, действующая на каплю, есть сопротивление среды,
которое по условию задачи пропорционально vR, т. е.
F=kvR,. (2)
где k — коэффициент пропорциональности.
Ввиду испарения капли воды ее радиус зависит от времени и от
Массы. Принимая удельный вес воды равным единице и каплю
шаровой формы, можем записать, что масса капли
4
m= ^r-nR3.
О
Отсюда
или, учитывая соотношение (1),
У3(т0—niit)
-Ч,—· (3)
4π
Значение (3) подставляем в равенство (2), откуда
-i/3(mo-mif)
Мо J/ „__ . (4)

82
Гл. IV. Разделяющиеся переменные
Начальные условия: при t=0 F=f0 и v=vQ. Отсюда
fo=kv<> ]/-
3m0
4π
и коэффициент пропорциональности
k,- fo ч/ 4π
■У-
υ0 r 3m0
Подставляя найденное значение k в уравнение (4), имеем
т/3(т0— mtQ f0 -ι/ 4π _ -ι/mo—mtf f0
' 4π oo ^ 3m0 ~ ' m0 y0 '
Так как сопротивление среды направлено в сторону,
противоположную движению капли, то дифференциальное уравнение
движения капли примет вид
. άυ -ι/ mo—tfiit /о
(m0—«if) -77- =—υ ν ί—
После разделения переменных
ν υ0 V
m0—mit
at
v0 V m0(m0—miu)3
или
dv f0 dt
v v0 ,/, m. ,i
m0
Интегрируя уравнение (5), получаем
(5)
lno= ■ -l/l—- /+In С (6)
Потенцируя уравнение (6), имеем общее решение

§ 10. Криволинейное движение
S3
Начальное условие: при t=Q v = Vo. Отсюда
З/а
vo = Се υ<>™'
З/о
Тогда искомая скорость
tii>o \ Г то ι
υ = Voe m^o
§ 10. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ (КРИВАЯ ПОГОНИ)
Задача 38. Судно выходит из точки О и с постоянной скоростью
плывет по направлению прямой Оу (рис. 26, а). Одновременно
(/=0) из точки А, расположенной па расстоянии ОА = а от судна,
ныходит вдогонку на пересечение катер, плывущий со скоростью,
дважды превышающей скорость судна. Найти уравнение описанной
катером кривой погони и минимальное время, необходимое для
достижения судна.
Ώ
О
\
С
Рис. 26
Решение. Пусть χ и у — координаты катера в момент t;
и ятот момент судно находится в точке В и прошло путь OB = vt
(рис. 26,6).
Пусть / — длина дуги АС. Вычислим угол наклона касатель-
dy
Мой —f- в точке С:
ах
dy
dx
= tga=
ё CD V χ
) =
y—vt

84
Гл. IV. Разделяющиеся переменные
С другой стороны, l=2vt. Таким образом,
/
у—и——
dy y 2v
dx
dx J 2
Как известно, длина дуги
^У t /IN
dl=1 \-\-у* dx.
Дифференцируя уравнение (1), получаем
dy dzy dy __ 1 dl
' 1 —{— X "
dx dx2 dx 2 dx
или, подставляя выражение длины дуги, находим
--£-—^·
Разделяем переменные:
dy' 1 dx
yi+i/'2 2 *
Интегрируем уравнение (2) почленно, откуда
(2)
Щу'+ 1 l+y'2) = Y In х+С
Определяем величину С, используя начальные условия: при
t=0 г/'=0 и х=а. Таким образом,
0=-у Ιηα+C
и
С=—-^-Ιηα.
Тогда
1п(г/'+ /ϊ+Ρθ = -i- In х- у In α=1η]/-^-.

§ 10. Криволинейное движение 85
После потенцирования
y'+ilW2=Y^; (3)
или
1
Продолжаем преобразования
-=У-.
75 II χ
У'-I 1+У'2
'-У1+Г2) г х
G/'+yi+rW-yi+r2)
у'-УТ+гГ2 =i/"g",
У'2— 1— У'2 » *
и тогда
у'~уТ+^=~]/-^. (4)
Сложив равенства (3) и (4) и разделив результат на 2, получим
Jy__j_( ιίΣιΓΚ \
dx 2 V V а V χ ι
или
2
Интегрируя, находим
*-ИУт-Ут)*
»-НУт<—ИУт*+с
ИЛИ
y=Jil£__yflJC+c (5)
зу«
Для нахождения частного решения используем начальное усло-
_ 2а
ИИС: при х=а у=0. Таким образом, С= ——, и уравнение
искомой кривой
х тГх :—- , 2й
у= - ^ -У Ω*+ ■ ·
зу«

86
Гл. IV. Разделяющиеся переменные
Катер догоняет судно при х=0. Отсюда, полагая в
равенстве (5) х=0, найдем путь, пройденный судном,
У--
2а
и искомое время
*=
JL
ν
2а_
Зо
§ 11. ВРАЩЕНИЕ ТЕЛ В ЖИДКОСТИ
Задача 39. Замедляющее действие трения на диск,
вращающийся в жидкости, пропорционально угловой скорости вращения
(рис. 27). Найти зависимость угловой скорости от времени, если
известно, что диск, начав вращаться со скоростью 200 об/мин, по
истечении 1 мин вращается со скоростью 120 об/мин.
Решение. Пусть ω — угловая скорость вращения диска,
об/мин; k — коэффициент пропорциональности; — изменение
угловой скорости вращения диска в жидкости.
Силовому воздействию вращения оказывает сопротивление
переменное трение, возникающее при вращении диска в жидкости
и зависящее от изменения скорости вращения.
Таким образом, из уравнения действующих сил
άω
или
ска
~аТ
-k<a=Q
= &ω.

§11. Вращение тел в жидкости
87
Разделяя переменные, получим
=kdf-,
ω
и, интегрируя,
1пв>=Ы+1пС.
После преобразований
In—=£*,
— pht
Общее решение уравнения
о=Сем.
Необходимо определить значения С и коэффициента
пропорциональности k.
Из начальных условий:
/0=0 мин, ωο=200 об/мин;
ti= 1 мин, ωι= 120 об/мин.
Тогда
o)(0)=Cefe·0=200 и С=200.
Далее, имеем
i»(l) = Cefei=120.
Из этого равенства определим величину k:
3
200efe=120 или efe= —,'
о
откуда
U 1 3
£ = 1п—.
о
Искомая зависимость угловой скорости от времени
Mni In- / 3 \*
о)=200е 5=200(е 5)* = 200(—).

88
Гл. IV. Разделяющиеся переменные
§ 12. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ
Выстрел снаряда на Луну
Задача 40. На основании закона всемирного тяготения иссле
довать возможность достижения Луны путем выстрела снаряда
космического корабля из гигантского орудия. Определить
начальную скорость, которую необходимо сообщить снаряду для
достижения Луны. Среднее расстояние от Земли до Луны «=384 395 км;
радиус Земли R3=^6377 км; ускорение силы тяжести Земли g=
=9,81 м/сек2; ускорение силы тяжести Луны £л=1,62 м/сек2
(около 1/6 g); масса Земли т3 = 81,53тл, где тЛ — масса Луны.
Решение. Хотя практически такой способ транспортировки
тел на Луну непригоден и для этой цели используются космические
ракеты, тем не менее задача представляет теоретический интерес,
в частности, для определения' той громадной скорости, которую
орудие должно сообщить снаряду для достижения Луны.
Сила взаимодействия F любых двух тел во Вселенной прямо
пропорциональна произведению их масс и обратно
пропорциональна квадрату расстояния между ними:
где mi, т2 — массы тел, d — расстояние между ними, k —
коэффициент пропорциональности (постоянная тяготения).
В основу исследования положим следующие предпосылки:
1) Земля и Луна являются шарообразными телами с
радиусами соответственно R3 и Ял и массами т3 и тл;
2) снаряд (или космический корабль) массы т выпускается
из вертикально расположенного ствола к центру Луны с начальной
скоросты» v0;
3) вращение Земли и Луны ие принимается во внимание;
4) влияние Солнца и других планет не учитывается;
5) сопротивление атмосферы не принимается во внимание.
Согласно рис. 28, принимая направление от центра Земли
к Луне за положительное, на основании закона всемирного
тяготения и соотношения (1), имеем
d2r _ km3m kmnm
F-mg:=m~dF~ ~~ ~~(r+R3)2 + (a+Rn-r)2
или
d2r km3 kmn
dt2 ~ (r-\rR3)2 + (a+Rn-r)2·
(2)
Равенство (2) показывает, что результат не зависит от массы
снаряда (космического корабля).

§ 12. Закон всемирного тяготения
89
Выразим произведение km3 общепринятыми величинами.
Очевидно, что сила притяжения массы m к Земле равно весу mg.
Отсюда, согласно соотношению (1),
km3m
■■mg
пли
km3=gR3*.
(3)
Аналогично, обозначая через gji ускорение, вызванное
притяжением Луны, получим
kmn=gnRj?. (4)
Рис. 28
Подставляем выражения (3) и (4) в уравнение (2):
dh gR? , gnRn2
dt2
+
(r+Rs)2 {a+Rn-r)2'
dr
(5)
Начальные условия: при t=0 r=0 и —т— = 0. Так как
уравнение (5) не включает в себя переменной t, то примем —— =v.
откуда
dt
dv
§R32
gnRn2
dr {r+R3)2 {a+Rn-ry*
Интегрируя, полуяаем
-SRz
d(r+R3)
(г+Яз)2
+gjiR
л2 J
d{a+Rn-r)
{a+Rn-ry
+Ci

90
Гл. IV. Разделяющиеся переменные
или, обозначая 2Ci=C,
r+R3 + a+Rn-r ^ ■
Начальные условия: при t=Q r=0, υ = υ0. Отсюда
2gnRn2
C=v<?-2gR3-
a+Rn
Подставляя найденное значение постоянной интегрирования,
получаем уравнение
ν2— -—τ-γτ- -\ .-= Ио2— 2gR3 -7-5—. (Ρ)
r+R3 a+Rn—r а+Кл
которое дает возможность определить мгновенную скорость v.
Определим начальную скорость (у дула) орудия, необходимую
для достижения нейтральной точки (расположенной между Землей
и Луной, в'которой притяжение равно нулю) с нулевой скоростью.
Положение этой точки, обозначаемое г=гя, определяется из
уравнения
т3 тл .^
(гн+#з)2 (я+Ял-гн)2'
полученного после приравнивания нулю (так как в нейтральной
точке скорость нулевая, следовательно, ускорение также равно нулю)
правой части уравнения (2). Так как при г=га и=0, то из
уравнения (6) получаем
Vo -2gR3~ TfRn^n+ a+Rn ra+R3- (8)
Так как по условию т3=81,53тл, το уравнение (7) запишется
81,53тл fjbi
(гн+#з)2 ~ (а+Ял-г*)2
или
81,53 1
(Гн+Яз)2 («+^Л-Гн)2'
Разрешаем последнее равенство относительно гн:
9,03(й+Ял)-#з
гн= .
10,03
(9)

§ 12. Закон всемирного тяготения
91
Подставляем выражение (9) в равенство (8):
._„ D 20,0б£л#л2 , 2^л#л2 20,06gfl32 ,,m
vo -2gR3- а+Ял+Йз + ~^^-л 9>03(а+^л+^з) " {Щ
На основании соотношений (3) и (4), а также того, что tn3=
= 81,53тл, получаем
£Я32=81,53Ы?л2 (И)
g
и так как gnfv —, то
b
*«*ш** (|2)
Подставляем соотношение (11) в уравнение (10):
"_2р/? 201,20g^32 , 2g/?32 _ n,
0 ё*3 81,53(а+/гл+/г3) 81,53(а+Дл) " l
Так как аж60Я3 и, согласно соотношению (12), Ял~ ~~r R$
ТО уравнение (13) записывается:
''U "&'\J _ Q. «О С, Г,» ^
81,53-61,25 ' 81,53-60,25
= 2£Дз (1-0,02+0,0002) = 2#Я3( 1-0,01 )2
ИЛИ
va=i 2gR3 (1-0,01).
Следовательно, скорость, необходимая для достижения
нейтральной точки, приближенно равна
v0=Q,99l2gR3.
Подставляя данные значения g и R3, находим, что начальная
скорость
ι>ο~11,1 км/сек.
Из уравнения (10) можно найти скорость, которую должен бы
иметь снаряд (космический корабль), чтобы покинуть Землю и
никогда больше не возвращаться, не принимая во внимание влияния
других планет, Солнца или еще каких-либо тел (т. е. при условиях,
принятых в начале задачи).
Для определения этой скорости необходимо в уравнении (10)
Принять £л = 0 и а->оо. Тогда

92
Гл. IV. Разделяющиеся переменные
2
^адз- 20'°6^-
9,03(а+Ял+Яз)
и
lim v02=2gR3,
α-χχ
откуда
u02=2gfl3
или
v0=i2gR3.
Таким образом, эта скорость только на 1 % больше скорости,
необходимой для достижения нейтральной точки.
Выброс вверх материальной точки
Задача 41. Определить скорость материальной точки,
запускаемой в направлении, радиальном к Земле, и находящейся под
воздействием лишь силы притяжения Земли.
Решение. Предполагаем, что движение материальной точки
начинается на прямой, проходящей через центр Земли.
Согласно закону всемирного тяготения, ускорение
Материальной точки должно быть обратно пропорциональным квадрату ее
расстояния до центра Земли. Пусть г — переменное расстояние
точки от центра Земли, R — радиус Земли. Если обозначим t — время,
ν — скорость материальной точки, а — ускорение и k —
коэффициент пропорциональности, то
dv k
dt ή "
Ускорение отрицательно, так как скорость убывает. Поэтому
постоянная k тоже отрицательна. При r=R ускорение
материальной точки а=—g, т. е. равно ускорению силы тяжести на
поверхности Земли. Таким образом,
откуда
R2
gR2
Выразим ускорение в виде функции скорости и расстояния.
Имеем зависимости а— ——- и и= —-гг. Следовательно,
at at
dv dr dv dv
a=~dT = ~di IF =V ~dT'

§ 12. Закон всемирного тяготения
93
ΊйК что дифференциальное уравнение для скорости имеет вид
dv gR*
dr r2
Разделим переменные:
vdv = —gR
2
dr
Г* '
откуда после интегрирования получим
2
или
где C=2d.
Предположим, что материальная точка отрывается от
поверхности Земли с начальной скоростью υ0. Тогда начальное условие:
при r—R v=va, откуда после подстановки этих значений в
уравнение (1) получаем
C = v<?~2gR.
Итак, закон движения материальной точки, запускаемой в
космос с начальной скоростью υ0, будет
у2= 28R2 +Vo2__2gR. (2)
На поверхности Земли (при r=R) скорость ν = υ0
положительна. Исследование правой части уравнения (2) показывает, что
скорость материальной точки υ остается положительной тогда
и только тогда, если
vo*-2gR^0. (3)
Так как скорость, заданная уравнением (2), должна быть
положительной (если удовлетворено неравенство (3)) и не может
исчезнуть, то она является непрерывной и положительной при r=R.
С другой стороны, если неравенство (3) не удовлетворяется, т. е.
Уо2—2gR<.0, то должно существовать критическое значение г, при
котором члены в правой части уравнения (2) равны нулю. Это
изменило бы скорость с положительной па отрицательную и
материальная точка могла бы вернуться на Землю.
Материальная точка запускается с Земли со скоростью ι>ο так,
что при va^i 2gR будет отрыв от Земли. Поэтому минимальное

94
Гл. IV. Разделяющиеся переменные
значение такой скорости отрыва
называется стартовой скоростью.
Так как радиус Земли # = 6377 км, ускорение силы тяжести
на поверхности Земли g = 9,81 м/сек2, то стартовая скорость для
Земли составляет
уз.ст = У2-9,81-6377» 11,2 км/ч.
Гравитационное влияние других небесных тел — Луны, Солнца.
Марса, Венеры и пр.— в этой идеализированной постановке задачи
не учитывается.
Если под материальной точкой, подразумевать идеализацию
баллистической ракеты, то надо учитывать дополнительные
элементы, в частности, сопротивление атмосферы.
§ 13. РАДИОАКТИВНЫЙ РАСПАД
Задача 42. Скорость распада радия прямо пропорциональна
наличной его массе. Определить, какой процент массы т0 радия
распадется через 200 лет, если известно, что период полураспада
радия (период времени, по истечении которого распадается поло·
вина наличной массы радия) равен 1590 лет.
Решение. Скорость распада радия измеряется его
количеством, распавшимся в единицу времени. За малый промежуток
времени Δ/, истекший с некоторого момента времени t, количество
распавшегося радия равно kmAt, где т — количество радия в
данный момент, k — коэффициент пропорциональности. Это же
количество, взятое с отрицательным знаком (масса убывает), равно
приращению массы за время Δ/:
Дт=—kmAt. (1)
Обе части равенства (1) делим на At и переходим к пределу
при Δί->0. Тогда
Am dm
hm -——- = —τ— =—km.
дг^о At at
Разделяем переменные:
dm
т
Интегрируя уравнение (2), находим
\nm=-kt+\nC
-.—kdt. (2)

§ }4. Электрические заряды 95
или после потенцирования
m = Ce-fti. (3)
Начальное условие: m = m0 при t=0, где то— масса в
начальный момент t=0.
Подставляя эти величины в уравнение (3), имеем
m0=Ce-k-°,
откуда
С=т0.
Уравнение (3) представляется теперь следующим образом:
т = тое~м.
График этой функции показан на рис. 29. Коэффициент k опре-
делится из дополнительного условия: при Г=1590 т— ——,
Таким образом,
то
= m0e-159№
2
или
— 1590ft = —In2, fe=0,00044.
Искомая функция
m(t)=m0e-°'oooiit.
Количество радия, не распавшегося через 200 лет,
m(200)=moe-0'00044-200=m0e-0'088=0,9l5mo.
Следовательно, через 200 лет распадется лишь 8,5% радия.
§ 14. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ
Потеря заряда проводником
Задача 43. Изолированному проводнику сообщен заряд Qo=
= 1000 к. Вследствие несовершенства изоляции проводник
постепенно теряет свой заряд. Скорость потери заряда в данный момент
пропорциональна наличному заряду проводника. Какой заряд
останется на проводнике по истечении времени ^=10 мин, если за пер-
иую минуту потеряно 100 /с?
Решение. К моменту t заряд проводника равен Q. Скорость
dQ „
потери заряда в этот момент равна —-. Так как эта скорость

96
Гл. IV. Разделяющиеся переменные
пропорциональна заряду Q, то дифференциальное уравнеш
процесса
dQ
где k — коэффициент пропорциональности.
т
Μ
^Υ*
А
®У/Г
у
УУ
X
К
ч\
β
§
Рис. 29
Рис. 30
откуда
Интегрируя это уравнение, получим общее решение
Q = Ce~kt.
Начальное условие: при' t=О Q = Q0. Отсюда
Qo=Ce-ft-°
C=Q0.
Следовательно, закон протекающего процесса
Q = Q0e-M.
Согласно дополнительному условию, при t= 1
Q = 900 к,
900=1000e-fel, е-'г = 0,9.
Подставляя найденное значение в общее решение, получим
<2 = 1000-0,9(.
Таким образом, через 10 мин на проводнике останется за[
Qs= 1000 ·0,910λ; 348,7 к.

§ 14. Электрические заряды
97
Эквипотенциальные линии электрического поля
Задача 44. На расстоянии а друг от друга в точках А я В
сосредоточены два равных разноименных заряда -\-q и —ц. Приняв точку
А за начало координат и направив ось χ по линии АВ, составить
уравнение семейства эквипотенциальных линий электрического
поля, создаваемого указанными зарядами.
Решение. Эквипотенциальные линии, или линии равного
потенциала, ортогональны силовым линиям поля. Силовая линия
и любой своей точке направлена по вектору электрической силы,
действующей на положительный заряд, помещенный в эту точку.
Пусть в точке М(х, у) ноля помещена положительная единица
заряда (+1).
По закону Кулона на эту единицу действуют силы (рис. 30):
P = k
Q = fe
Я
R2>
Где k — диэлектрическая постоянная среды.
Проекции этих сил па соответствующие оси будут:
q χ
Ρχ—k—- cos φ—kq
г' "г5
Py=k—-un<f=kq-
гг —τ ■-■» rs
Qx—k---cosQ = kq
Здесь
R2 f R3 '
X . Ц
cos rp= —, sin φ= —
r r
a—x . „ у
cos 0= —-—, sin 0= —.
R , R
Составляющие равнодействующей силы F равны
/ χ α—χ \ x(R3—r3)+ar3
Fx=Px+Qx=kq [ — + ——} =kq
Rs ι - r*Rs

vo
Γα. IV. Разделяющиеся переменные
(У У \
*y = Py+Qy=kq [ — — / =
kq
y{R3-r3)
г* R* ' v r*R*
Направление этой силы (угловой коэффициент)
tga=
y(R3-r3)
Fx x(R3-r3)+ar*'
Такое же направление имеет силовая линия в точке М(х, у).
Направление в этой точке эквипотенциальной линии, как
ортогональной к силовой линии, будет
tgai =
С другой стороны,
x(R3—r3)+ar3
dy
tgai=
dx
Таким образом, дифференциальное уравнение искомого
семейства эквипотенциальных линий
dy
x(R3—r3)+ar3
dx y(R3—r3)
Введем новые переменные R и г, полагая
r2 = JC2+£/2. ί
Дифференцируя последние равенства, имеем
RdR = — (a—x)dx-\-ydy, \
rdr=xdx-\-ydy. )
dy
(О
(2)
Из системы (2) определим dx, dy и
dx
dx=
dy=
dy
dx
rdr-RdR
(a—x)rdr-\-xRdR
ay
(a—x)rdr-srxRdR
= ~' у (rdr-RdR)
(3)

§ 15. Поверхность фрезы
99
Сравнивая уравнение (1) с уравнением (3), получим
(a—x)rdr+xRdR x{R*—r*)+ar*
y(rdr-RdR) = y(R3-r3)
мЛН После упрощения
R4r=r2dR,
>. i, дифференциальное уравнение с разделяющимися переменными,
• it нуда
*-=**-. (4)
Интегрируя уравнение (4), получим общее решение
которое указывает на основное геометрическое свойство эквипотен-
ин<ш>пых линий рассматриваемого поля.
Разность величин, обратных расстояниям текущей точки, от
•пряженных центров поля, есть величина постоянная. Переходя
И декартовым координатам, получим уравнение искомого семейства
t 1 =с.
1(а-х)*+у* у*2 + у2
§ 15. ПОВЕРХНОСТЬ ФРЕЗЫ
Задача 45. Острозаточеиная фреза имеет форму, показанную
Ни рис. 31. После использования шлифуется ее передняя грань АС.
Поверхность" сечением которой является кривая АВ, должна быть
тикой, чтобы угол α между радиус-вектором произвольной точки
Ириной и касательной к кривой АВ в этой точке оставался
постоянным. Найти уравнение кривой АВ.
Ρ е ш е и и е. Пусть уравнение искомой кривой в полярной
системе координат Γ=/(φ) и полюс совмещен с началом
прямоугольной системы.
Рассмотрим геометрический смысл производной
, ,. Аг dr
г = hm -r— = —г- =г (φ)
Λφ^ο Δφ αφ
урйнпения кривой r=f (φ) в полярной системе координат.
Пусть Pi и Ρ две точки кривой r=f(q>), которые в пределе при
Αφ-*Ο совпадают (рис. 32). Перед переходом к пределу радиус-

100
Гл. IV. Разделяющиеся переменные
Ь
вектор точки Ρ и секущая Р\Р образуют угол ψ. При переходе этот
угол переходит в угол ψ, образуемый радиус-вектором точки Р\ и
касательной, проведенной в этой точке, т. е. -ψ = ίim ψ. Следователь-
Δφ-Μ)
но (см. рис. 32):
, - BPt
τΔφ
Ar
Ar
Αφ
У
0
у
Ш/
J/\f
Μ(Ψ)\Ρ I
' /w
/^ 1
Рис. 31
Рис. 32
Таким образом, после предельного перехода
tgi|i = lim -т- =
Дф-Й) ΙΛΙ
Δφ
hm ——
д<р_»о Δφ
Г
В условиях задачи углу ψ соответствует угол α и,
следовательно,
, г
откуда после разделения переменных
t аГ А
tga =άψ.
г
Интегрируя равенство (1), имеем
tgalnr=q+Ci
(1)

§ 16. Трение ременной передачи
101
и III
lnr=(qH-d)ctga. (2)
Потенцируя равенство (2), получаем уравнение
г — gf<p+d)ctg а. — е® ctgot gC, ctgot_Cgij: clg a
Искомая кривая является логарифмической спиралью.
§ 16. ТРЕНИЕ РЕМЕННОЙ ПЕРЕДАЧИ
Задача 46. На барабан радиуса г натянута ременная передача,
нагруженная силами Р0 и Fit так, что /_АОВ = а (рис. 33, а). Благо-
чнри трению между цилиндром и передачей даже значительно
меньший сила F0 может уравновешиваться большей силой Fi. Найти
иннбольшую силу Fu которая может быть уравновешена силой F0,
ШУ1Н коэффициент трения равен μ.
Решение. Рассмотрим на барабане произвольную точку Λί,
Η Которой действует переменная сила F, а рядом в точке Μι пусть
деигтует сила F-\-dF (рис. 33, б).
Для определения силы трения на дуге ΜΜι необходимо найти
МКЖим dN, который равен
dN=F sin
αφ
2
■ + (F+dF),
χ углах
sin
sin-
d<f
Τ
dcp
2
- «
= 2F
dcp
2
sin
dq>
2
■ -\-dF sin
dtp
2 '
И тогда
dq> 1
dN = 2F-j- + — dFdy. (1)
Второй член в правой части уравнения (1) можно отбросить,
Кик величину бесконечно малую высшего порядка, чем dq>. Тогда
dN=Fdy.
Так как μ — коэффициент трения, то сила трения
В начале скольжения
F+dR = F+dF
II
\iFdy=dF.

102
Гл. IV. Разделяющиеся переменные
Таким образом, дифференциальное уравнение трения передачи
dF
d<f
= μ^
или после разделения переменных
dF
= μίίφ.
Рис. 33
Интегрируя это уравнение, имеем
In F=|itp-1-Ci
или общее решение
F=Cew.
Рис. 34
(2)
Начальное условие ср=0 F=F0 определяет произвольную
постоянную C~Fo, и тогда уравнение (2) принимает вид
F=Foew.

§ 17. Истечение жидкости
103
Для наибольшего значения силы F=Fi при φ=α получаем
1м мшую величину
Fi— Fuev-a.
Суммарная сила трения равна разности сил Fi и F0, т. е.
R==Fi—F0=F0(ev»—l).
§ 17. ИСТЕЧЕНИЕ ЖИДКОСТИ ИЗ СОСУДОВ
Цилиндрический сосуд
Задача 47. Заполненный водой цилиндрический сосуд высотой h
II площадью дна F имеет в дне отверстие, площадь которого f.
Найти время истечения воды через отверстие.
Решение. Пусть в момент t высота воды в сосуде над
площадью / составит χ (рис. 34). За время dt эта высота изменится на
ш'лнчину —dx. За это время вытечет вода объемом —Fax.
С другой стороны, этот объем воды равен объему столба воды
ι основанием f и высотой vdt, где ν — скорость истечения, т. е. объем
равен fvdt.
Скорость истечения определяется по формуле
v = i2gh,
ι /м· h — глубина погружения отверстия в данный момент, g —
ускорение силы тяжести.
В нашем случае /i=x и поэтому и=у 2gx. Следовательно,
искомый объем
fOdt=f ilgx dt.
С другой стороны, этот объем можно представить так:
—Fdx=f ^2gxdt
ИЛИ
F dx
-j—— =dt,
ι 12gx
•ifкуда после интегрирования получаем общее решение
Начальное условие: при t—0 x=h, откуда

J 04
Г.л. IV. Разделяющиеся переменные
-i-ϊ
2~+с
ИЛИ
/
•V-
Подставляем значение постоянной интегрирования в
равенство (1), и тогда закон процесса
ί=-Γ]/-^(ΐΗ^χ).
В момент опорожнения сосуда t=T и высота воды в сосуде
х=0, откуда искомое время
f
или
= -тУт(ул~уо)
Задача 48. В дне цилиндрического резервуара, наполненного
жидкостью, образовалась щель (рис. 35). Принимая скорость
истечения жидкости пропорциональной высоте уровня ее в резервуаре
и зная, что в течение первых суток вытекло 10% содержимого,
определить время истечения половины жидкости.
Решение. Пусть R— радиус резервуара; h — высота;
χ — высота уровня жидкости в резервуаре по истечении t дней.
Тогда объем жидкости в резервуаре в момент / равен nR2x,
а скорость изменения объема nR'2--^—. По условию эта величина
пропорциональна х, так что дифференциальное уравнение задачи
nR2 —— =kx,
at
где k — коэффициент пропорциональности.
Разделяя переменные, получим
nR4x UAi
или, проинтегрировав, находим
яЯ2 In x=kt+C.

§ 17. Истечение жидкости
105
Начальное условие: при t=0 резервуар полностью наполнен,
йк что x=h. Следовательно,
nR2\nh=C
ι уравнение (1) примет вид
nR2 In x=kt+nR2\nh
1ЛИ
nR2ln-r=kt.
h
—Щель —
II
-*=κ
Рис. 35
Время
IB/ушках)
и=?
Дополнительное условие: при t=\ x=-—h, и тогда коэффи-
шснт пропорциональности
k=nR4n
10'
Для рассматриваемого случая |прих=—-J искомое время
, 1
nR2 In -
= 6,57 суток.
10
Итак, для истечения из резервуара половины жидкости через
-11«ль потребуется 6 суток 14 часов.

106 Гл. IV. Разделяющиеся переменные
Сферический сосуд
Задача 49. В дне котла, имеющего форму полушара радиуса
R= 1 м и наполненного водой, образовалась щель площадью
σ=0,25 см2. Найти время истечения воды из котла.
Решение. Пусть в момент t глубина погружения щели χ
(рис. 36). За короткое время dt эта глубина изменится на величину
—dx, так как процесс убывающий.
I
Рис. 36
За время dt вытечет вода, объем которой равен
—πρ2 dx, (1)
где ρ — радиус сечения котла на уровне х.
С другой стороны, тот же расход воды равен объему столбика
воды с основанием σ и высотой vdt, где υ — скорость истечения.
Схематически это представляется: σ (площадь сечения) Хи
(скорость истечения) Xdi (время истечения) =σν (расход воды в
единицу времени)y^dt (время истечения) =avdt.
Скорость истечения υ = У 2gx, где χ — высота столба воды над
отверстием в данный момент, g — ускорение силы тяжести.
Следовательно, искомый объем
a-f2gxdt. (2)
Приравнивая выражения (1) и (2), получаем
—np4x=o.12gxdt. (3)
На основании теоремы Пифагора
р2= #2_ (#_χ)2_2RX—X*.
(4)

§ 17. Истечение жидкости
107
Подставляя соотношение (4) в равенство (3), получим
дифференциальное уравнение процесса
—n(2Rx—χ2) άχ=σ У 2gx at.
Разделяя переменные, имеем
dt= "—- (2R у x-xjx)dx.
ai2g
Проинтегрировав, найдем общее решение
£ η 5
■2 £
3 -' 5
«~-М4-**"-4-*т)+*
a12g
Начальное условие: при t = 0 x=R. Отсюда
5
3 5
0= *L-(±R-R2-\R2) +с
oi2g
с—=_.Jf«i
oj2g lb
Итак, закон процесса истечения
<=-М-И-М+-И·
В момент опорожнения t=T; лг=0 и искомое время истечения
14π#2 ι/ Я
У-
15σ Г 2g
Подставляя числовые значения, получаем
_ 14π·1002 -ι/ 100 · Qft
Г= — l·/ « 26 376 сек=7 ч 19 лшм 36 се/с.

108
Гл. IV. Разделяющиеся переменные
§ 18. НАПОЛНЕНИЕ СОСУДОВ
Задача 50. В резервуар глубиной 4 м, имеющий в поперечном
сечении форму квадрата со стороной 6 м, стекает вода со скоростью
10 м3 в минуту. Найти время наполнения резервуара, если
одновременно из него вытекает вода через имеющееся в дне квадратное
отверстие со стороной 1/12 м.
Решение. Пусть к моменту времени t в резервуаре уровень
воды будет h. За время dt он повысится на dh, а объем воды
увеличится на 36 dh. В резервуар по условию втекает 10 м3/мин воды.
Поэтому скорость повышения уровня воды в резервуаре будет
тгх м/мин или —— м/сек. Объем за время dt равен -ггтг -36dt=
-эо j 216 г v 216
= — dt. За это же время вытекает —'— у 2gh dt воды.
Итак, уравнение процесса
или после разделения переменных
mdh
~=dt. (1)
1 °>6 /о ι
>._ γ 2gh
6 144 ' s
Интегрируя уравнение (1), получаем
12 1 72
t= r^ „In
При ft = 4 ж искомое время
ί л; 14,7 ишм.
§ 19. УСТАНОВЛЕНИЕ УРОВНЯ В СООБЩАЮЩИХСЯ СОСУДАХ
Задача 51. Два сообщающихся сосуда имеют форму
параллелепипедов, у которых площади оснований S и Si (рис. 37). Найти
время установления одинаковых уровней жидкости в сосудах, если
S = Si=100 м2, начальная разность уровней h=2,5 м, площадь
отверстия между сосудами σ=0,5 м2, коэффициент гидравлического
сопротивления η=0,62.
Решение. Количество жидкости, теряемое первым сосудом,
равно количеству жидкости, полученному вторым сосудом.

§ 19, Установление уровня в сообщающихся сосудах 109
Поэтому
■тсюда
—Sdz=Sidzi,
S+S^dz.
dz—dzi=
Si
3 течение воемени dt через отверстие АВ площадью ω пройдет
Рис. 37
vn~)/2g(Z—zi)dt жидкости, и поэтому дифференциальное уравнение
;пдачи
-Sdz=r\o У 2^(2—2^ dt
1ЛИ
^i-^dt=.
Полагая z—Zi = u, получим
dz
iz—Zi
О)
du=dz—dzi= ■—-—— dz,
пкула
dz=
Sidu
S+Si "
Вследствие этого уравнение (I) примет вид
ησ
■ У 2g </*=-■
Si
S+Si
du
fa

110 Гл. IV. Разделяющиеся переменные
а отсюда
-^№■=--5^/-^--—/-^ <2)
5 s+s- „ у и S+S, „ /ϊ
Интегрируя дифференциальное уравнение (2) и подставляя
числовые значения, находим
Т= — = 114,5 сек.
vp(S+Si)ig
§ 20. КРИВАЯ ДЕПРЕССИИ
Задача 52. Определить уравнение кривой, но которой
располагается уровень грунтовых вод вблизи круглого колодца,
простирающегося до непроницаемого слоя (рис. 38).
Рис 38
Решение. Пусть АВ — поверхность земли; CD —
поверхность грунтовых вод до устройства колодца; EF —
водонепроницаемый слой, ограничивающий снизу поток грунтовых вод.
Если высота воды в колодце поддерживается вычерпыванием
на постоянном уровне GH, то поверхность грунтовых вод вблизи от
колодца понижается определенным образом.
Линия поверхности грунтовых вод CD переходит в две
искривленные ветки CG и D'H, которые замыкаются на уровне воды GH.
Поверхность уровня грунтовых вод представляет собой поверхность
вращения вокруг оси Оу меридиональной линии GC или HD'.
Кривая HD' определяется на основании эмпирического
правила, по которому скорость υ течения воды в точке Ρ пропускающего

§ 20. Кривая депрессии
111
(дренирующего) грунта пропорциональна наклону кривой в
точке Λί', лежащей на вертикали точки Р.
Обозначая коэффициент пропорциональности через k, получим
ЛЫрпжение скорости:
dy
v=k-
dx '
Через боковую поверхность цилиндра N'NMM' радиально
внутрь протекает количество воды
Ли
Q=2nxyv — 2nxyk--:—, (l)
которое для всего цилиндра радиуса χ равно расходу воды
и колодце.
Разделим переменные в дифференциальном уравнении (1):
dx 2nk ,
= —к— УаУ·
χ Q
Интегрируя, получим
In x=~y*+C. (2)
Постоянную интегрирования находим из условия, что кривая
Поверхности D'H переходит в поверхность колодца GH.
Если диаметр колодца 2г, а глубина воды в колодце h, то при
К*=г y = h, т. е.
1пг=-^-АЧ-С
или
С = 1пг--^-А2. (3)
Постоянную интегрирования (3) вводим в уравнение (2) и
получаем уравнение искомой кривой
In-f = -^(y*-h>)
ИЛИ
9 <2 , х , иг.
у2= —г- In \-№.

112
Гл. IV. Разделяющиеся переменные
§ 21. ОБЕДНЕНИЕ РАСТВОРА
Задача 53. Через сосуд емкостью а л, наполненный водным
раствором некоторой соли, непрерывно протекает жидкость, причем
в единицу времени втекает b л воды и вытекает такое же количество
раствора. Найти закон изменения содержания соли в сосуде в
зависимости от времени протекания жидкости через сосуд.
Решение. В данный момент времени t в сосуде содержится
χ кг соли, следовательно, в каждом литре раствора содержится
χ , Ьх
— кг соли, а в о литрах кг.
a v a
Если бы в течение единицы времени, начиная с момента t,
концентрация раствора оставалась неизменной, какой она была в
момент t, то количество соли в сосуде за эту единицу времени умень-
Ьх
шилось бы на кг; такова скорость уменьшения количества соли
в сосуде для момента t.
С другой стороны, производная
dx x(t+At)—x(l)
lim
dt Δί-ю At
равна скорости прироста количества соли в момент t, поэтому ско-
dx
рость уменьшения количества соли в момент t равна — —^-.
dt
Итак,
dx bx
dt
Разделяя переменные, получим
dx b i
■— at,
χ α
откуда
\nx= ί+ln С ι.
a
Потенцируя, найдем
_ j>
x=Cie at , (1)
где Cj — произвольная постоянная.
Предположим, что в некоторый начальный момент f=0
количество соли в сосуде равно с кг.

§ 22. Растворение твердых тел
113
Полагая в равенстве (1) /=0, найдем
Ci=c.
Искомый закон изменения содержания соли
ь
_ t
х=се а .
§ 22. РАСТВОРЕНИЕ ТВЕРДЫХ ТЕЛ
Пусть при постоянной температуре скорость растворения
твердого тела в жидкости пропорциональна количеству этого вещества,
•мце могущего раствориться до полного насыщения жидкости.
Пусть Ρ — количество вещества, дающее насыщенный раствор;
χ — количество растворившегося вещества.
Тогда дифференциальное уравнение процесса
-?г=*(Р-х).
где k — эмпирический коэффициент пропорциональности, t — время.
Разделяя переменные и интегрируя, находим
х = Р+Се-Ч (1)
Начальное условие: при t=0 x=0, откуда
0=P+Ce-fe0
и постоянная интегрирования
С=-Р. (2)
Подставляем выражение (2) в общее решение (1) и получаем
(икон зависимости количества растворившегося вещества от
времени:
*=Р(1—е-").
Растворение вещества при прохождении жидкости
Задача 54. Резервуар наполнен 75 л сусла, содержащего 3 кг
|>пстворенного сахара. Приток воды составляет 4 л в минуту, а
расход смеси из сосуда 2 л в минуту. Концентрация поддерживается
ршшомерной посредством перемешивания (рис. 39). Найти количе-
iino сахара, которое будет содержаться в резервуаре через 25 мин.

114 Гл. IV. Разделяющиеся переменные
Решение. Пусть χ — количество сахара в резервуаре в
момент /, кг; / — время, отсчитываемое от начального момента /о, мин;
—dx— количество сахара, выходящее из резервуара за время dt
(знак минус обусловлен тем, что χ — убывающая функция
времени), кг.
К моменту / в резервуар поступило 4/ л воды и вышло 2/ л
сусла. Увеличение сусла составляет 2/ л.
)М л/мин
при! =0мин
II'1л/ми н
nput=2SMUH
Q =Ζ'л/мин
1д =глш
Рис. 39
1^
Таким образом, общее количество жидкости достигло 75+2/ л
и в ней растворилось χ кг сахара.
За время dt уходит —dx кг сахара и 2dt л сусла.
Считая концентрацию сусла постоянной, получим количество
X
сахара в одном литре
75+2/
кг. Следовательно, за короткий
промежуток времени dt количество сахара уменьшится на
75+2/
Итак, элементарное уравнение движения жидкости будет
2dt кг.
—dx =
2xdt
75+2/
Разделяя переменные, имеем:
dx 2dt
75+2/
Начальные условия времени: /о=0 сек, /ι=25 сек; начальные
условия количества сахара: х0=3 кг, Χι—χ кг. Отсюда

§ 22. Растворение твердых тел
115
dx Г 2dt
J^-ί
или
χ ί 75+2/
Χα ίο
dx f "d (75+2/)
-J4=J
75+2/
Интегрируем:
25
— In a;
= ln(75+20
о
Откуда
, 3 ,125 ,5
In — = η —— = In
-τα: 75 3
Потенцируя последнее равенство, получаем
χ ~ 3
или искомое количество сахара в резервуаре
9
х= — =-1,8 кг.
5
Итак, через 25 мин в резервуаре останется 1,8 кг сахара.
Растворение вещества с течением времени
Скорость растворения пропорциональна наличному количеству
к нерастворенного вещества и разности концентрации насыщенного
раствора и концентрации раствора в данный момент Ct-
Пусть Μ — исходное количество вещества. Тогда растворенное
к данному моменту количество вещества будет М—х.
Концентрацией раствора в данный момент называется
отношение количества растворенного вещества к объему V растворителя:
г М-х
V
При достижении величиной Сг некоторого определенного для
данного растворителя и растворяемого вещества значения Со раст-
нор становится насыщенным и дальнейшее растворение
прекратится.
Задача 55. Подвергая 10 кг соли действию 90 л воды,
обнаружили, что в течение часа растворилась половина этого количества.

116
Гл. IV. Разделяющиеся переменные
Считая концентрацию насыщенного раствора соли равной 1/3,
найти количество растворенной соли в течение часа, если за это время
было влито 180 л воды.
Решение. Скорость уменьшения нерастворенного вещества
dx
~—~ должна быть пропорциональна χ и C0—Ct, что приводит к
дифференциальному уравнению
~=-kx(C0-Ct),
где k (предполагается, что &>0) —коэффициент
пропорциональности, подлежащий определению.
В правой части поставлен знак минус, так как каждый из мно-
. . ^ ^ dx
жителей k, x, Co—Ct, через произведение которых выражается —τ—,
dx
положителен, в то время как —т— <0, поскольку с течением
времени количество нерастворенного вещества должно убывать.
Преобразуя произведение этих множителей и выражая Ct
через М, V и х, получаем
Со — ) =-у-(С„У-М+х).
Пусть
k
= а\
ν ι о
CaV-M=b. j v '
Тогда
kx(C0—Ct) = ax (b-\-x)
и искомое дифференциальное уравнение задачи принимает вид
-~=-ах(Ь+х). (2)
Начальное условие:
при /=0 х=М. (3)
Условие для определения коэффициента а:
Μ
при t=\ ч х=——. (4)

§ 22. Растворение твердых тел
117
Разделяя переменные в уравнении (2) и интегрируя, имеем
^=-^taft (5)
Разложим подынтегральное выражение первого интеграла на
простейшие дроби:
Г их Г их (_}___]_]
J x(b+x) ~J ~ΊΓ \ χ b-\-x' '
Теперь, умножив обе части уравнения (5) на Ь, можем записать
где In C=6 In Ct, или, потенцируя,
_^-=Се-«Ч (6)
о-\-х
Полагая в уравнении (6) t=0 и принимая во внимание
начальное условие (3), находим
Тогда уравнение (6) примет вид
χ Μ
-abt
b+x b+M
Решая последнее равенство относительно х, имеем
x(b+M)=M(b+x)e-abt
или
χ (b+M—Me-abt) =Mbe~abtt
откуда общее решение
Mbe-abt
Х~ 6+М(1-е-°ь')' '
Выполним проверку; полагая в уравнении (8) t=0, получим
Mbe° Mb
Ь+М(1-е°) b ~ '
т. е, начальное условие соблюдается.

118
Гл. IV. Разделяющиеся переменные
Дифференцируя уравнение (8) по t, найдем
dx ., «., ,, b+M
= —Mab2e~abt
dt [6+M(l—е-«ь*)]2-
Составим с помощью уравнения (7) выражение
МЬе~аЫ bz+Mb{\—e-abt)+Mbe-°-bt
Ь-\-х = Ь-\-
Ь+М(\—е~аЫ) 6+М(1—е~аЫ)
Итак,
b(b+M)
+Х Ь+М(]-е-"ь*)'
По условию М=10 кг, К=90 л, С0=1/3, поэтому по второму
из соотношений (1)
6=4" ·90-10=20>0.
о
Равенство (8) примет вид
200е-20аг 20е~2°аг
20+10(1—e^at) 3—е-20аг '
Согласно условию (4),
20е-20а
= 5,
3-е-200
откуда
е-20а=0,6;
д ln0>6 'g°'6 1,7782 0,2218 ,
α~ 20 _ 20-0,4343 __ 20-0,4343 _ 8,685 ,UU
Согласно первому из соотношений (1),
&=0,0255- 90=2,295.
При У=Жл
О 02^5 1
а= ' =0,01275; 6=180- — -10=50; ай=0,6375.
Δ о
Искомое количество растворившейся сЪли
500е-°·6375 60(1—е-0·6375)
М—л;=10—
60— 10е-°·6375 6—е-°·6375
и, так как
е-о.6375^0,53,
то
Λί—л; «5,2 кг.

§ 23. Вентиляция производственного помещения
119
§ 23. ВЕНТИЛЯЦИЯ ПРОИЗВОДСТВЕННОГО ПОМЕЩЕНИЯ
Задача 56. Рассмотрим вентиляцию производственного
помещения объемом V м3, в котором технологический процесс
сопровождается равномерным накоплением вредных выделений в количестве
X единиц в час. Обмен воздуха в течение 1 ч составляет Μ м3/ч,
причем приточный воздух содержит вредные выделения в
концентрации μ на 1 м3. Найти концентрацию ζ (на 1 м3) выделений в
помещении через t ч после начала работы, если начальное значение этой
концентрации zo (остаток загрязнения от работы предыдущего дня).
Решение. За короткий промежуток времени at
концентрация ζ увеличится на άζ. Общее количество выделений составит Vdz.
Оно состоит из выделений, принесенных приточным воздухом μΜάί,
и выделений технологических процессов Zdt за вычетом количества
вредных выделений, которое содержалось в извлеченном из
помещения за промежуток at воздухе. Пренебрегая изменением
концентрации ζ за бесконечно малый промежуток времени, полагаем это
количество равным zMdt.
Итак, основное уравнение вентиляции
νάζ=Μμάί+Ζάί—Μζάί. (1)
Уравнение (1) можно представить в виде
Vdz
Μμ+Ζ—Μζ
Интегрируя это уравнение, имеем
— dt.
V ΐά{Μμ+Ζ-Μζ) Г
~ ~М~J ~Μ~μ+Ζ-Μζ = J dt+Ci
или
\η(Μμ+Ζ-Μζ)= ~ (i+Ci),
откуда общее решение
м
Μμ+Z-Mz—Ce v г. (2)
Начальное условие: при t=0 z=z0. Отсюда
0=Μμ+Ζ—Μζ0.
Найденную постоянную интегрирования подставляем в
уравнение (2), откуда получаем
(7 \ / _ *L· \ — -*L
*+-w)v-e vt)+z°e vt·

120
Гл. IV. Разделяющиеся переменные
§ 24. ГАЗОВЫЕ СМЕСИ
Задача 57. Сосуд емкостью в 1 л снабжен двумя трубками и
заполнен воздухом, содержащим 21 % кислорода по объему. Через
одну трубку в сосуд медленно поступает чистый кислород, через
другую вытекает смесь воздуха с кислородом. Какое количество
газа нужно пропустить, чтобы наполнить сосуд чистым кислородом?
Сколько процентов кислорода будет содержать сосуд после
пропуска 10 л газа?
Решение. В момент, когда через сосуд прошло χ л газа,
в нем содержится а%, т. е. а/100 л кислорода.
Пусть через сосуд пройдет еще dx л газа: в сосуд входит dx л
кислорода и выходит а/100-dx л кислорода. Тогда в сосуде будет
α / α \ α+(100—a)dx _
-—г- + ydx — dx ) = — л кислорода. Этот объем
кислорода составит а+(100—a)dx% всего объема газа.
Таким образом, процент кислорода увеличился на величину
da= (100—a)dx. (1)
Уравнение (1) является дифференциальным уравнением
процесса. Разделив переменные, получим
da
= ах.
100—α
Интегрируем это уравнение:
d(100-a)
-J-
=x+d
100—а
или
ln(100—a)= —(jc+Cj),
откуда
100—а=ес> е-х=Се~х
и, наконец, общее решение
а=Ю0—Се-х.
Начальное условие: при х=0 а=21. Отсюда
21 = 100—Се°
или
С=79.
Подставляем найденное значение С в общее решение:
а= 100-79 е-*. (2)

§ 25. Ионизация газов
121
При лг= 10
а= 100-79 е~10да 99,9964%.
Можно считать, что после пропуска 10 л газа сосуд наполнен
Чистым кислородом.
Исследуем закон процесса (2) с целью определения количества
Гпза, которое нужно пропустить для наполнения сосуда чистым
кислородом, т. е. при й=100%.
В этом случае уравнение (2) принимает вид
100=100—79 е-*
пли
е~х= =0,
ех
что возможно лишь, когда х = оо.
§ 25. ИОНИЗАЦИЯ ГАЗОВ
Задача 58. Под действием постоянного излучения в газовой
среде происходит процесс ионизации, при котором за 1 сек
образуется q положительных и q отрицательных ионов в данном объеме
газа. Так как положительные и отрицательные ионы снова
соединяются между собой, то количество их убывает. Из общего
количества η положительных ионов в каждую секунду соединяется часть,
пропорциональная квадрату их количества. Коэффициент
пропорциональности k зависит от природы и состояния газа. Найти
зависимость количества ионов η от времени t.
Решение. Непосредственно из условия можно записать
дифференциальное уравнение процесса ионизации
dn=qdt—kn2dt. (1)
После разделения переменных в уравнении (1) получаем
dn
q—kn2
или
dn
-.dt
kn^q ="««.
откуда

122
Гл. IV. Разделяющиеся переменные
Общий интеграл уравнения (2) будет
+/= ^- In С,
n-f
k
откуда после потенцирования имеем
-У1
η+γ-
-2 V hq t
= Ce
или общее решение
' « V fea t - V hat
— ykqt у hq t
у ft? t — у hq i
e —Ce
Начальное условие: при f=0 /ι=0. Тогда
да
C= — l.
Подставляя найденное значение постоянной интегрирования
в уравнение (3), получаем искомый закон
n(0 = |/-|-th(i^0·
§ 26. ХИМИЧЕСКИЕ РЕАКЦИИ
Реакции первого порядка
Задача 59. Определить константу скорости реакции первого
порядка.
Решение. Порядок химической реакции равен общему числу
молекул, входящих в левую часть химического уравнения. Так,
RaB->RaC есть реакция первого порядка. Скорость реакции есть
скорость ν, с которой система компонентов левой части
превращается в систему компонентов правой части уравнения реакции.

§ 26. Химические реакции
123
Действующая масса или концентрация реагирующего
вещества А есть количество молей * этого вещества в единице объема.
Согласно закону действующих масс, скорость реакции
пропорциональна действующим массам в данный момент.
Математическое выражение реакции первого порядка будет
нижеследующее:
Л->(конечные продукты реакции).
Если а— начальная концентрация вещества А, х — количество
молей на литр, прореагировавших за время t от начала реакции, то
dx
скорость реакции —тг, а действующая масса к этому моменту а—х.
Закон действующих масс выразится дифференциальным
уравнением реакции первого порядка
dX =k(a-x), (l)
dt
где k — коэффициент пропорциональности (константа скорости),
зависящий от рода и условий химического процесса.
Общим решением дифференциального уравнения (1)
= kdt
а—х
будет
ln-£—=JW. (2)
а—х ч '
Начальное условие: при t=0 x=0. Откуда
In—^—=k-0
а—О
или
С=а. (3)
Подставляем это значение в общее решение (2) уравнения:
а—х
пткуда
&= —-In
t а—х
•Моль (или грамм-молекула) вещества — число граммов этого вещества,
1 ■ и иное его молекулярному весу. Например, 1 моль кислорода равен 16 г, 1 моль
йоды — 18 г и т. д.

124
Гл. IV. Разделяющиеся переменные
Задача 60. Радиоактивный элемент RaB распадается
наполовину, образуя радиоактивный элемент RaC, в течение 26,7 мин
Найти время распада 0,2 первоначального количества RaB.
Решение. Здесь имеет место реакция первого порядка:
RaB->RaC.
Поэтому дифференциальное уравнение реакции
dx
dt
=k(a—x).
Разделяя переменные, имеем:
dx
а—х
--kdt. (1)
Интегрируем дифференциальное уравнение (1), и тогда общее
решение
, ' If- С
k а—х
Начальное условие: при ί=0 χ=0, откуда
0—!-1«. С
k α—0
или
С—а.
Подставляя в общее решение, получим
ί * !„_£_. (2)
k а—х ч '
Дополнительное условие: при ί==26,7 мин х=а/2, откуда
26'7=Tln-V = Tln2
или
£«0,026. (3)
Подставляя значение (3) в уравнение (2), имеем:
4 ! 1 а ! 1 5 ОС
t= . In — = —^пгг- In —- « 8,6 мин.
0,026 α—0,2 0,026 4

§ 26. Химические реакции
125
Задача 61. Вещество А превращается в вещество В. Спустя 1 ч
после начала реакции осталось 44,8 г вещества А, а после 3 ч —
11,2 г вещества. Определить первоначальное количество а
вещества А и время, когда останется 1/64 часть этого вещества.
Решение.. Рассматриваемая реакция — первого порядка
Л-*~В. Дифференциальное уравнение реакции первого порядка
dX U, S
— А (а—х)
dt
после разделения переменных принимает вид
dx
а—х
Интегрируем уравнение (1):
d(a—x)
= kdt. (1)
-J-
a—x
откуда
1η(α—χ) = — (*/+&), (2)
Потенцируем уравнение (2):
gIn(a-x)_-g-(«+Ci) —g-ki gCi
или
а-х=Се~м, (3)
где C = eCl.
Начальное условие: при t=0 x=Q. Откуда
a—0=Ce-ho
или
C=a.
Подставляем найденное значение С в общее решение
уравнения (3). Тогда
а—х—ае-м
или
х=а—ae-kt = a(l—e~ht). (4)
Дополнительные условия: при ί=1 х=а—44,8; при /=3
л:=а—11,2. Таким образом,
a—44,8=a(l—е-*·1), 1
а— 11,2=о(1— e-ft·3) J
или после сокращений

126
Гл. IV. Разделяющиеся переменные
=44,8, ^
а =11,2.'
(5)
(efe)3
Из системы (5) находим значения а и ek:
ek = 2; α = 89,6.
Найденные значения подставляем в уравнение (4):
х=89,6 (1-2-'),
откуда
89,6
2 = 89^=? (6)
По условию задачи в искомый момент t
Тогда, подставляя это значение в равенство (6), получим
2'.- 89>6
или
89,6 -
2*=64
t=6 ч.
89,6
64
откуда искомое время
Реакции второго порядка
Задача 62. Определить коэффициент пропорциональности
реакции второго порядка при различных концентрациях а и b веществ
А и В.
Решение. Рассмотрим математическое выражение закона
действующих масс (или концентраций) в реакции второго порядка:
Ai-\-Az-*-(конечные продукты реакции).
Пусть й! и α-ι — начальные концентрации веществ А\ и Л2;
χ — число прореагировавших к моменту / молей вещества А\, а
следовательно, и вещества Аг, так как каждый моль вещества Л ι
соединяется с молем вещества Л2, и поэтому число прореагировавших
молей обоих веществ одинаково.

§ 26. Химические реакции
127
τ, · dx _ „
В момент ι скорость реакции будет ——. Действующая масса
шщества Αι равна а\—х\ действующая масса вещества А2 будет
™ dx
<ι· -χ. Так как скорость реакции ——- пропорциональна величинам
κι χ и а2—х, то она пропорциональна также их произведению.
11оэтому закон действующих масс выразится дифференциальным
уравнением реакции второго порядка
dx
= k (αϊ—χ) (α2—χ). (1)
dt
Уравнение (1) представим в виде
dx
(αϊ—χ) {α2—χ)
= kdt. (2)
Рациональную дробь в левой части последнего равенства
интегрируем методом неопределенных коэффициентов:
Г ^ ,=!-?-dx+S-l-dx, (3)
J (α,ι—χ) (α2—χ) J CLy—x J a2—x '
ι ггкуда
m (a2—x) -\-n («i—x) = 1,
и, приравнивая соответствующие коэффициенты при неизвестных
и свободные члены в обеих частях равенства, получаем систему
уравнений
—т—n=0; \
α2ιη-{-α1η=1. )
Решая эту систему относительно неопределенных
коэффициентов тип, имеем
т= ; п= . (4)
а2—«ι oi—«2
Подставляем значения (4) в правую часть уравнения (3) и
получаем
т ( Г η 1 [ d (α,ι—χ)
dx-\- J dx-
αι—χ a2—x αι—α2 ai—x
1 f d(a2—x) 1
ai—a2 a2—x a.i—a2
[In («i—x) —In (a2—x) ] =
1 , α,ι—χ
In-
«i—a2 a2—χ

128
Гл. IV. Разделяющиеся переменные
Подставляем полученное значение в уравнение (2), и после
интегрирования его правой части общий интеграл
1 In Ui~X -=ki+C. (5)
а\—α2 α2—χ
Начальное условие: при t=0 х=0. Откуда
Лп- — =k-Q-\-C
αϊ—α2 α2—0
или
С= —*— In -*-. (6)
αϊ—α2 α2
Искомая константа скорости реакции получается путем
подстановки значения постоянной интегрирования (6) в общее
решение (5), откуда
1 с2 (αϊ—χ)
k— — г- In —-. -.
ί(αι—α2) αι(α2—χ)
Задача 63. Реакция омыления уксусноэтилового эфира едким
натром
CH3COOC2H5+NaOH->CII3COO.Na+C2H5OH.
уксусноэтилооый едкий уксуснокислый этиловый
эфир натр натр спнрт
Первоначальные концентрации уксусноэтилового эфира и
едкого натра соответственно а=0,01 и 6 — 0,002. Спустя 23 мин
концентрация уксусноэтилового эфира уменьшилась на 10%· В какое
время она уменьшится на 15%?
Решение. Это химическая реакция второго порядка; «ι и а2—■
начальные концентрации веществ А\ и А2; χ — число
прореагировавших к моменту / молей вещества А и а следовательно, и
вещества Л2 (каждый моль Αι соединяется с молем Л2, и поэтому число
прореагировавших молей обоих веществ одинаково).
Скорость химической реакции определяется изменением
количества вещества χ в единицу времени /, т. е. в момент t произ-
„ ах
ВОДНОЙ —г—·
at
Действующая масса (или концентрация реагирующего
вещества) Ai, указывающая количество молей вещества в единице
объема, равна αϊ—χ и α2—-χ и пропорциональна их произведению.
Поэтому закон действующих масс выразится дифференциальным
уравнением химической реакции второго порядка
—- =k(ai—x) (az—x).

§ 26. Химические реакции
129
Разделяя переменные, получим
dt= — % (1)
к (αϊ—л;) («2—х)
Для решения уравнения (1) применяем интегрирование
рациональных функций методом неопределенных коэффициентов:
J_ Г dx J_ С Adx 1 f Bdx _
~~ k ^ (ai—x) (a2—x) ~ k J Й!—χ k ■' α2—·": —
= T^W Πη(α1-χ)-1η(αΓ-χ)-1π C] =
k(ai—an) L(az—x)
Уравнение (2) является общим решением задачи. Для
определения величины С используем начальное условие: при t=0 x=0.
Тогда
η 1 . αϊ
0_ _^ |п.
k(ai—a2) Са%
или
αϊ
С=
«2
Подставляя значение С в общее решение (2), получим частное
решение
1 a-iiai—x)
ί=ΊΓ, Г1п~Ч Г- (3)
k(ai—a2) αι(α2—χ)
Коэффициент пропорциональности определим из
дополнительных условий: при ί=23 мин дг=0,1, αι=0,1 -0,01=0,001. Отсюда
1 0,002(0,01-0,001)
23= . , , In V '
£(0,01-0,002) 0,01(0,002-0,001)
н
й»3,19.
Подставляя полученные числовые значения в решение (3),
определим искомое время:
1 0,002(0,01-0,0015)
/= -—————-х-тг^г- In ■
3,19 (0,01 -0,002) 0,01 (0,002-0,0015)
1000 ,17
In ——- «47,9 мин.
8-3,19

130
Гл. IV. Разделяющиеся переменные
Здесь χ=0,15αι=0,0015.
Итак, примерно через 48 мин количество уксусноэтилового
эфира уменьшится на 15%.
Реакции третьего порядка
Задача 64. Определить константу скорости реакции третьего
порядка при разных концентрациях а\, а2 и а3 веществ Аи Αι и А3.
Решение. Математическое выражение закона действующих
масс в реакции /г-го порядка получается аналогично, как и для
реакций первого и второго порядков:
^ι+^2+· · .+Ли->(конечные продукты реакции).
Тогда па основании тех же соображений дифференциальное
уравнение реакции /г-го порядка
dx ч , ч
= k{ai—х){а2—х).. .{ап—х), (1)
at
где щ, а2, ... , ап — концентрации веществ Ль Αι, ... , Αη.
Уравнение (1) для реакции третьего порядка принимает вид
dx
—β- ^k(ai-x) (а2—х) (аз—*),
откуда после разделения переменных получим
dx
(αϊ—χ) (α2—χ) (α3—χ)
kdt. (2)
Интегрируем уравнение (2) методом неопределенных
коэффициентов, как в предшествующей задаче.
В итоге выполнения аналогичных алгебраических выкладок
найдем общее решение уравнения (2):
— г-т— г In (αϊ—χ) + ■-— — In (a2—x) -f-
(αϊ—аг) (α3—αϊ) (αϊ—α2) (αζ—α3)
+ -, \η ~\n{a3-x)=kt+C. (3)
(α2—α3) (α3—αϊ) '
Начальное условие: при / = 0 х=0. Откуда
1 1η(αι—0) + - г^ Γ1η(α2-0) +
(αι—α2) (α3—αϊ) (αϊ—α2) (α2—α3)
+ - ~~. . ln(a3-0)^6-0+C
(α2—α3) (α3—αϊ)

§ 26. Химические реакции
131
ИЛИ
1η αϊ 1ηα2 . In a3
J~ (а1—а2)(а3—а1) (а1—а2)(а2—а3) (α2—α3) (α3—αϊ)'
Подставляем найденное значение постоянной интегрирования
к уравнение (3) и, разрешая его относительно искомой константы
скорости реакции, получим
ш (-*=* )™ +1п (-*=!)α-α' +ш (-*=£)а'"аз
х αϊ ' \ а2 ; х а3 '
* (αϊ—а2) (а2—аз) (а3—а,)
Задача 65. В реакции третьего порядка
2FeCl3+SnCl2->2FeCl2+SnCl4
хлорное хлористое хлористое хлорное
железо олово железо олово
первоначальные концентрации SnCI2 и FeCl3 соответственно а=
-0,0625 и 2а=0,125. Через минуту концентрация SnCl2 стала
0,04816. Найти концентрацию SnCI2 спустя 11 мин после начала
реакции.
Решение. В задаче имеет место случай одинаковых молекул
рс-пкции п-то порядка.
В реакции п-го порядка некоторые вещества Аи А2, ... , Ап
могут оказаться одинаковыми. Химическое уравнение такой ре-
икции будет
тИ1+т2Л2+.. .+т„/4„-ν(конечные продукты реакции).
Его можно записать в виде
,Λΐ+Λΐ + · ■ .+Αι+Α2+Α2+. ■ .+^2 + . . .+Ап+Ап + . . .+ЛП-»
mi раз таг раз тп раз
-у(конечные продукты реакции),
по теперь всю концентрацию αϊ вещества Αι придется разбить на mi
чистей. Тогда концентрация отдельной компоненты Αι будет ——,
л β2
концентрация отдельной компоненты А2 и т. д., т. е. имеет
место случаи равных концентрации.
В реакции п-го порядка некоторые из веществ Αι, А2, ... , Ап
могут быть с одинаковыми концентрациями. В этом случае
дифференциальное уравнение реакции примет вид
dx
= k (d—χ)m' (α2—χ)m*.'.'. (αη—χ) ™»; (1)
dt

132
Гл. IV. Разделяющцеся переменные
где trii — число веществ с концентрацией аи тг — число веществ
с концентрацией а% и т. д.
При этом
/ni+m2+/n3+.. .+m„ = n.
Для случая равных концентраций из уравнения (1) получаем
^=кА^—хГ(^-х)т\..(^—х)тп
или
dx k\
—^ = . , 1а тхущ1а тх\т2 _ /а ЩпХ)тп =
12 и
=к(ах—ηΐιχ)^(αζ~т2х)т>... (ап—тпх)т*.
В условиях рассматриваемой задачи дифференциальное
уравнение реакции третьего порядка
dx
=k(2a-2x)2(a-x)
dt
или
dx
чг=Ща-ху. (2)
Разделяя переменные и проводя интегрирование, получим
общий интеграл уравнения (2)
1 =Ш+С.
2(a-x)z
Начальное условие: при t=^0 х=0. Откуда
1
2(а-0)2
или
с= 1
=4£-0+С
2а2
Подставляем значение С в общее решение:
1 =Ш+- 1
2(а~х)2 ' 2а2
или
а
а—х= —ιζζ^τ-·
y8a2fe/+i
(3)

§ 27. Рост населения
131
Дополнительное условие: при /=1 а—л:=0,04816. Откуд;)
0,0625
0,04816 =
У 8-ОТ06252Аг-1 + 1
k «21,89.
(4)
Подставляем значения константы скорости (4), а и t в
уравнение (3). Искомая концентрация
а—х=
0,0625
50,02141.
У 8-0,06252-21,89· 11 + 1
§ 27. РОСТ НАСЕЛЕНИЯ
Непрерывный рост или убывание
Пусть скорость прироста (или убывания) некоторой величины
чависит от ее наличного количества Ρ в данный момент t. В
начальный момент ί=0 эта величина равна Pq. Найти зависимость
игличины Ρ от времени /.
Для построения
математической модели простейшего
типа роста принимаем, что
скорость изменения количест-
ιι.Ί населения пропорциональна
лому количеству. Скорость
прироста выражается произ-
■ dP
«одной ——, если k — коэ
φαί
фициент пропорциональности,
то и случае роста
dP
Ρ >
Естественный
прирост
Л>0
dt
-.kP
(1)
И η случае убывания
= —kP.
dt
Рис. 40
Схематически-это представлено на рис. 40.
Разделяя в уравнении (1) переменные, имеем
dP
=kt,

134
Гл. IV. Разделяющиеся переменные
откуда после интегрирования находим
P(t)=CeM. (2)
Начальное условие: при ί=0 Ρ=Ρο, поэтому
Po=Cefto
или
С=Р0. (3)
Подставляем выражение (3) в уравнение (2) и имеем закон
прироста
Ρ (0 = Рое*'.
Для процесса убывания
P(t) = P0e-M.
Регулируемый прирост
Предположим, что количество населения Ρ увеличивается
с искусственно уменьшаемой скоростью.
Будем считать, что обстоятельства, препятствующие росту
количества Р, не превышают значения М. Кроме того, предположим,
что скорость роста количества Ρ пропорциональна произведению Ρ
и разности М—Р, Когда прирост М-Р мал, то скорость роста
замедляется. По предположению
dP
-5Γ-*Ρ(Αί-Ρ).
где k — постоянный положительный коэффициент.
Чтобы найти Ρ как явную функцию времени, проведем
разделение переменных:
Р(М~Р) '
откуда после разложения левой части равенства на простейшие
дроби получим
[-Х77Г + -1Г77,1 Пч ]dP = d(kt). (1)
L MP М(М—Р) J v ' w
Равенство (1) может быть представлено в виде
^d{^-r\n-J T \=i'\t).
\ Μ Μ—Ρ < · '

§ 27. Рост населения
135
Лнтегоируя последнее равенство, имеем
1 Ρ
In-,. „ =Ы+С,
Μ Μ—Ρ
Ρ
ιη-
Μ—Ρ
=Mkt+MC
Рис. 41
после потенцирования
Ρ
М-Р
Пусть
Тогда
— eMht+MC —
s __ емс емм
ггкуда
М-Р
=s,
Р =
sM
(2)
При ί->οο величина eMfti->oo, так как для процесса прироста
Л>0; следовательно, s->oo. Очевидно, что при t-*-oo дробь -—-—И
И иа основании зависимости (2) P-WW.

136
Гл. IV. Разделяющиеся переменные
С целью лучшего понимания процесса преобразуем далее
равенство (2). Пусть Р0 — количество населения в начальный момент
t=0. При t=0 s = eMC. Поэтому
Р°- ~Т+^· (3)
Разрешая равенство (3) относительно емс, находим, что
Выполнив алгебраические преобразования равенств (2) и (4),
получаем
ρ Mil f 5)
Уравнение (5) дает зависимость роста количества населения
при обстоятельствах, препятствующих ему. регулированное
размножение, возможные эпидемии и другие факторы. Оно называется
логистическим уравнением. На рис. 41 показан схематический
график этого закона.
Тип I — количество населения на определенную дату
Задача 66. Население Земли в 1970 г. составляло 3 600 млн. чел.,
а годовой прирост населения равнялся 60 млн. чел. Найти
предположительное количество населения в 2000 г.
Решение. В задачах типа I о росте населения известно
исходное количество населения и время прироста, а искомым
является конечное количество населения.
Определим коэффициент k естественного прироста:
60 · 106
= 0,017 (т. е. 1,7%).
3,6-109
Тогда через ^=30 лет имеем
Ρ(30) =P0ek ■ 30=3,6· 109 e°w ■ 30=3,6· ΙΟ9 e0·51,
откуда
Ряйб-109 чел. (т. е. 6 000 млн. чел.).
Задача 67. Пусть скорость прироста населения прямо
пропорциональна его количеству. Найти зависимость между количествол
населения А и временем t, если известно, что в некоторый момент
принимаемый за начальный, количество населения равнялось Ло
й 'U'pivi год оно увеличилось на а%.

§ 27. Рост населения
137
Вычислить предполагаемое на этой основе:
1) количество населения СССР на 15 января 1980 г. и 15
января 2000 г., если 15 января 1970 г. оно составляло 241,7 млн. чел.,
а годовой прирост за 1969 г. составил 1 %;
2) население г. Москвы (без пригородов) па 15 января 2000 г.,
если 15 января 1970 г. оно составляло 6,942 млн. чел. Годовой
прирост составил 1,25%;
3) население г. Минска (без пригородов) па 15 января 2000 г.,
если 15 января 1970 г. оно составляло 0,907 млн. чел. Годовой
прирост за 1969 г. составил 4,2%.
Решение. Скорость изменения количества населения есть
dA
производная от количества населения по времени, т. е. ——.
По условию задачи можно написать следующее
дифференциальное уравнение:
dA , л
-df=kA-
Разделяя переменные, получим
dA им
—-г— =kdt.
А
Интегрируя это выражение, находим
1пЛ = 1пе"'+с
или, потенцируя,
A=ehtec< = Ceht. (1)
Количество населения через год определяется следующим обра-
п/ л аА<>
зом: годовой прирост а % от Ао составит -.-тпг-, количество населения
через год
аАо (ЮО-г-а)Ло
^ 100 100
Подставляя в общее решение (1) соответствующие значения
количества населения и времени, а именно А=А0 и ^=0, определим
постоянную интегрирования С:
Ло=С-еь-°=С-е°,
С=Ао.
Таким образом, общее решение уравнения (1) принимает вид
А=А0еМ. (2)

138
Гл. IV. Разделяющиеся переменные
Для вычисления множителя ек используем дополнительные
данные, подставляя значение количества населения через год,
т. е. при t=l,
(100+а)Л0
А== 100-
в уравнение (2). Имеем
(100+а)Л0
100
=Аоек-1=А0ек
.»- т+а
100 ·
(3)
Подставляя найденное значение (3) в уравнение (2), получим
частное решение
„ „ / 100+а \(
выражающее зависимость количества населения от времени.
Пользуясь формулой (4), вычислим:
1) количество населения СССР, согласно принятой модели, на
15 января 1980 г. (через/=10 лет):
/ 101 \10
^1980=241,7 (~щ) »279,4 млн. чел.;
на 15 января 2000 г. (через /=30 лет):
/ 101 \30
Л2ооо=241,7 \—— ) л;325,3 млн. чел.;
2) количество населения г. Москвы на 15 января 2000 г.:
/ ιοί 25 \30
Д2ооо=6,942 (—-j— ) «9,52 млн. чел.;
3) количество населения г. Минска на 15 января 2000 г.:
/ 104 2 \30
Л20оо=0,907 (■ 1QQ ) «3,12 млн. чел.

§ 27. Рост населения
139
Тип II — динамика роста по времени
Задача 68. Население г. Минска 15 января 1970 г. насчитывало
0,907 млн. чел., а годовой прирост за 1969 г. составил 4,2%. Считая
темп прироста населения неизменным в ближайшем будущем,
определить, когда население города: удвоится; возрастет на 50%;
составит 2 млн. чел.?
Решение. В задачах второго типа о росте населения
искомым является время прироста, а начальное и конечное количество
населения (или их отношение) являются известными.
Так как дифференциальное уравнение прироста
dP
dt
= kP,
(1)
то, разделяя переменные, имеем
dP
= kdt.
(2)
1. Интегрируя и подставляя начальное и конечное условия
в качестве пределов интегрирования, получаем
S^-=kjdt=0,OA2 5dt,
(3)
откуда
In P
■■0,042t
или
и искомое время
t=
1π2=0,042ί
In 2 0,693
0,042 0,042
= 16,5 лет.
Итак, население города удвоится в 1987 г.
2. Рост населения на 50% означает, что количество его будет
и 1,5 раза больше исходного.
Поэтому уравнение (3) примет вид
1,5
J-=-=0,042 J Л,

140
Гл. IV. Разделяющиеся переменные
откуда
или
1,5
In P
=0,042/
и искомое время
In 1,5=0,042*
In 1,5 0,406
0,042 0,042
= 9,7 «10 лет.
Итак, население города возрастет на 50% в 1980 г.
3. Эту задачу можно решать двумя способами. Так как
количество 2 млн. чел. в 2,25 раза больше исходного, то можно это
отношение подставить в качестве верхнего предела интегрирования
в левую часть уравнения (3) и решать его.
Решим эту задачу иначе.
Интегрируя уравнение (2), имеем
\nP=kt+Cl
и, потенцируя, получаем общее решение уравнения (1) в виде
Р=Сем. (4)
Начальное условие: при *=0 Р = 907 000, откуда после
подстановки в уравнение (4)
С=907 000.
Тогда закон роста населения города
Р = 907 000е0.°42<.
Если Р = 2 000 000, то
е0,042( = 2,25,
откуда
U
In 2,25 0,811
= 19,3 «20 лет.
0,042 0,042
Итак, население города достигнет 2 млн. чел. в 1990 г.
Тип III — конкурентная динамика роста
Задача 69. Население г. Минска 15 января 1970 г. составляло
0,907 млн. чел., а годовой прирост населения за 1969 г. равнялся
4,2%. Население г. Новосибирска составляло в это же время
1,161 млн. чел. при годовом приросте за 1969 г. в 2,5%. Предполагая

$ 27. Рост населения
141
темпы прироста населения этих городов установившимися,
определить время, по истечении которого количество жителей г. Минска
станет равным количеству жителей г. Новосибирска.
Решение. В задачах третьего типа о росте населения
сравниваются темпы прироста населения в различных городах или в
других административных единицах.
В этой задаче известными являются исходные и конечные
количества жителей в двух городах, а искомым является время
достижения ими точки равпостояпия, т. с. момента, когда город с меньшим
количеством населения, по более высоким приростом, догоняет
город с большим количеством населения, но более низким приростом.
Так как дифференциальное уравнение прироста
dt
то общее решение этого уравнения
Р = Сеы.
Начальные условия: для г. Минска при ^=0 Р=907 000,
откуда С=907 000; для г.Новосибирска при i=0 Р=1161000,
откуда С=1 161 000.
Поэтому закон роста населения г. Минска
Р = 907 000е0·042',
а закон роста населения г. Новосибирска
Р=\ 161 000е°.°25г.
Так как количество населения этих городов через некоторое
время сравняется, то для этого момента
откуда
или
и
следовательно,
Отсюда
907 000е°.°ш=1 161 000е°>025<,
907e°.°42i=l 161e°'025t
ео,о42( __ j 28e°>025i
e(0,042-0,025)t I 28
eo,oi7(=1;28.
In 1,28 0,2469
0,017 ~ 0,017 ~14'5·
Итак, население обоих городов сравняется в 1985 г.

14U
Гл. IV. Разделяющиеся переменные
Истощение ресурсов
Задача 70. В настоящее время для обеспечений пищей одного
человека необходима площадь 0,1 га. На земном шаре 4 000 млн. га
пахотной земли. Поэтому население его должно быть, если не
учитывать появления в будущем новых источников пиши, ограничено
количеством 40 000 млн. чел. Когда будет достигнут этот предел
насыщения населения, если оно непрерывно растет со скоростью
1,7% в год?
Решение. Закон роста населения
Ρ(0=ΡοβΜ·
Так как в 1970 г. (ί=0) население Земли составляло 3,6· 109 чел.,
то Ρο=3,6·109, £=0,017, и получаем
Р(*)=3,6-109е°'0Ш.
Ищем такое t, чтобы
Ρ (/) =40-109.
Тогда
40-109=3,6-109-е°>017г,
откуда
40-109
eo,oi7i _ ч" =1111
3,6-ю9 ,п·
Логарифмируя последнее равенство, имеем
0,017/=1п 11,11 «2,408,
откуда
ί=142.
Итак, в 2112 г. мир достиг бы предела насыщения, если бы
сохранился темп роста населения и не появилось новых
источников пищи.
§ 28. ПРОЦЕССЫ РОСТА В ПРИРОДЕ И ПРОИЗВОДСТВЕ
Рост листьев растения
Задача 71. Скорость увеличения площади молодого листа
виктории-регии, имеющего форму круга, пропорциональна окружности
листа и количеству солнечного света, падающего на него. Последнее
пропорционально площади листа и косинусу угла между
направлением лучей и вертикалью к листу. Найти зависимость между
площадью S листа и временем t, если в б часов утра эта площадь
равнялась 1600 см2, а в 18 часов того же дня — 2500 см2·.

§ 28. Процессы роста в природе и производстве
143
Принять, что угол между направлением луча Солнца и
вертикалью в 6 часов утра и в 18 часов равен 90°, а в полдень — 0°.
Решение. Пусть t — время, отсчитываемое от полуночи, ч.
Если S — переменная площадь листа, то скорость роста листа
= ki 2nrQ,
at
где 2nr — длина окружности, Q — количество солнечного света,
&i — коэффициент пропорциональности.
Площадь листа S=nr2, откуда
-=У4
Тогда
По условию
^.=ki-^riSQ. (1)
at у π
Q=£2S cos α, (2)
где α — угол между направлением лучей и вертикалью, кг —
коэффициент пропорциональности.
Угол а является линейной возрастающей функцией аргумента t
(времени):
a=k3t+b.
Параметры k3 и b определяются из трех дополнительных
данных условий:
, „ π -
при t = 6 α= —,
при t=\2 α=0,
νιο Я
при /=18 α= —.
Из первых двух условий имеем
о=т3+ь.
Решая эту систему, получаем

144
Гл. IV. Разделяющиеся переменные
т. е.
«=-^('-12).
Проверка по третьему условию дает тождество
л л л
_ = „18_я=_
Значение α подставляем в равенство (2), откуда
Q = hS cos [~ (ί-12)] .
Полученное значение Q подставляем в уравнение (1):
dS
dt
in 1г
Вводим обозначение k=kikz. Тогда после разделения
переменных
dS U 2Л Г " и ,ο\Ί А*
——■ =k—^^-cos [~7}г (/—12) J dt.
sis in
Интегрируя, получим
2 24k
-^-.1а[-Ц-«-12)]+С.
is in
(3)
Начальные условия: при ί=6 S = 1600 и при t= 18 S = 2500.
Отсюда
20
1
iл
25 Υπ
Решая эту систему, находим

§ 28. Процессы роста в природе и производстве 145
Подставляя значения (4) в равенство (3), получим
-2 24 У^ . Γ π Ί 9
—— = -IT sin [ -Ίγ С"12) J ~ ОТИТ'
l/S 24-200Уя U 2UU
откуда
160 000
[9-sin-^-(f-12)]2
Рост дерева
Задача 72. Найти закон роста дерева любой породы, учитывая,
что зрелое растение в процессе роста сохраняет геометрическое
подобие. Свободную энергию (активное вещество) растение получает
путем фотосинтеза. Она расходуется на процесс фотосинтеза, на
рост дерева (т. е. на построение живой ткани) и на подъем раствора
пз почвы. За большие промежутки времени растение получает
постоянное количество света на единицу поверхности и может
поглотать необходимые вещества из неограниченного запаса.
Решение. Пусть x—x(t) —линейный размер дерева,
который изменяется со временем и может служить для выражения
высоты, площади поверхности зеленой части и объема растения.
Составим уравнение баланса энергии.
Свободная энергия Еа образуется путем фотосинтеза в зеленой
части растения, и ее величина возрастает пропорционально
поверхности зеленой части дерева:
Ea=kxX2,
где ki — коэффициент пропорциональности, зависящий от размеров
и формы листвы, а также от интенсивности фотосинтеза; величиной
ν- будет измеряться площадь поверхности зеленой части (например,
суммарная площадь поверхности листьев).
Расход энергии на:
а) процесс фотосинтеза пропорционален х2, т. е.
Ε синт == kiX ,
где кг — коэффициент пропорциональности (&2<&ι);
б) транспортировку питательного раствора во все части
растения пропорционален объему растения и высоте х, так как расход
связан с преодолением силы тяжести, т. е.
E^v.v~k3x3-x=kzxk;

146
Гл. IV. Разделяющиеся переменные
в) увеличение массы растения (на рост) пропорционален
скорости роста, т. е. производной по времени от массы,
т=ух3,
где у — средняя плотность растения, х3 — объем, т. е.
dm d
£р=**-5Г=**-5г(^)·
На основании закона сохранения энергии расход энергии равен
ее поступлению, откуда
■Сп^^синт-г^тр.рТ-Ср
ИЛИ
dx
krf^kzxZ+ksxb+hy-Sx2-^. (1)
h h
Уравнение (1) делим па Зк^х2 и, вводя обозначения ——— =а,
k У
-—г— =β, получаем дифференциальное уравнение задачи
dx
^Γ=α-βχ2· (2)
dx
Здесь α>0, β>0. Дерево растет, и производная ——- >0,
т. е. α—βχ2>0 и х2<С—. Разделим переменные в уравнении (2),
тогда
dx =dt. О)
α—β*2
Интегрируя уравнение (3), получаем
Интеграл в левой части равенства (4) находим методом
неопределенных коэффициентов:
dx 1 f* dx 1 f* dx
~z^1 , (5)
α—βχ:
(Η-Ήΐ/τ**)

§ 28. Процессы роста в природе и производстве
Ш
так как подынтегральная функция
1
_^_. + _^L
ТО
(V-i-*)(Vi+*) У|- Н+*
(A-B)x+(A+B)~]/j=\
(6)
и решение системы
Л—β = О,
1
дает значения неопределенных коэффициентов
1
А = В--
■У-·
» α
(7)
Подставляя значения (7) в новое выражение (6)
подынтегральной функции крайнего правого интеграла (5), имеем
1
ах
2Уоф
+
ах
2Υαβ
"(Vf+«) Г^У^—)
У?
In
2 У αβ
V--*
Тогда уравнение (4) примет вид
У^+*
ι г β
-In
2"|/оф
Ут-
= i+C.
(8)

ш
Гл. IV. Разделяющиеся переменные
Начальное условие: при t=t0 х = 0. Отсюда
. !—— 1п1 = /о+С
2|Όφ
или
C=-U. (9)
Постоянную интегрирования (9) подставляем в общий
интеграл (8):
Ц+* _
1П —JL =2 У αβ {t-U),
η
χ
β
откуда закон роста дерева
*(о=У
. 2 у αβ (ί—ίο)
α е —1
β 2 у αβ (ί—f0)
1+е
(10)
Так как для каждой породы величины α и β известны, то теперь
можно вычислить средний рост дерева данной породы в
зависимости от возраста, т. е. от времени t.
Исследуем этот закон при изменении t.
Дифференцируя уравнение (2), получим
dH
=—2βχ.
dP
d2x
Так как высота дерева всегда положительна, то х>0 и —гг<;0.
at2
Таким образом, функция (10) представляет возрастающую
вогнутую кривую (рис. 42).
Применяя к функции (10) правило Лопиталя, видим, что
предел функции x(t) при ί->οο равен
, , 2γ"αβ"(ί-ίο)
ι· /α η/ α ,. 2У сфе π/ α η/ α
t-*oa ' ρ ί-э-оо , 2 V αβ (ί—ίο) 'Ρ ' Ρ .
2 у сфе

§ 28. Процессы роста в природе и производстве
149
Величина
У а
—, при которой
» dx
ξ0, соответствует случаю,
когда поступающая энергия расходуется на процесс фотосинтеза
и транспортировку питательного раствора, а дерево при этом не
растет.
х,
Ц
Рис. 42
Зависимость (10) дает ответ на вопрос, почему деревья любой
породы сначала растут быстро, а потом их рост замедляется, пока
совсем не прекратится.
Увеличение количества фермента
Задача 73. В культуре пивных дрожжей быстрота прироста
действующего фермента пропорциональна наличному его количеству х.
Первоначальное количество фермента α в течение часа удвоилось.
Во сколько раз оно увеличится через 3 ч?
Решение. По условию задачи дифференциальное уравнение
процесса
dx
где k — коэффициент пропорциональности.
Разделяя переменные, получим
dx
=kdt.
Общее решение этого уравнения
х=Сем.
Определяем С из начального условия: при ί=0 χ=α. Отсюда
a—Ceh0 или С=а.

150
Гл. IV. Разделяющиеся переменные
Подставляя постоянную интегрирования С в общее решение,
получим частное решение
x—aeht. (1)
Коэффициент пропорциональности определяем из данных
дополнительного условия: при t=\ ч х=2а. Отсюда
2a=aekl или eh = 2.
Подставляя это выражение в частное решение (1), получим
закон рассматриваемого процесса:
х=а2г.
При г=3 ч х=8а. Следовательно, количество фермента спустя
3 ч увеличится в 8 раз.
§ 29. ЭКОЛОГИЯ* ПОПУЛЯЦИЙ
Изолированная колония организмов
Задача 74. Колония микроорганизмов обитает в идеальных
(или искусственно созданных) условиях, располагает
неограниченными ресурсами питания и не подавляется никаким другим видом.
В силу естественных процессов размножения (путем
самооплодотворения) и гибели число живых организмов колонии меняется
с течением времени: прирост пропорционален количеству взрослых
членов. Найти закон изменения общего количества живых
организмов в колонии.
Решение. Пусть x(t) — число живых организмов в момент t,
a x(t-\-At) — число живых организмов в момент t-\-At. Тогда за
промежуток времени Δ^ приращение функции x(t) будет
x{t+At)—x{t)=Ax.
За время At все взрослые члены колонии (или часть их)
произведут потомство, а часть членов колонии может погибнуть.
Тогда
Ax=N-M, (1)
где N — число родившихся за время Δ/, Μ — число погибших за
время Δ/.
Число родившихся N зависит от длины промежутка At (чем
больше At, тем больше N) и от количества родителей (чем больше
* Экология — раздел биологии, изучающий взаимоотношения организмов
и окружающей среды.

§ 29. Экология популяций
151
взрослых организмов, тем больше потомство), т. е.
N=F(x, At),
где функция F возрастает с ростом χ или At и равна нулю, если
равна нулю одна из этих переменных.
Можно полагать, что
N=hxAt, (2)
где ki — коэффициент пропорциональности.
По аналогии для процесса гибели
M=k2xAt. (3)
Подставляя равенства (2) и (3) в уравнение (1), имеем
Ax=kixAt—fexAt
или
Ax={ki—k2)xAt=kxAt, (4)
где k^ki—ki — специфическая скорость естественного увеличения
популяции.
В реальных колониях величины χ, Ν, Μ могут принимать только
целочисленные значения. Поэтому трудно говорить о непрерывности
пли о дифференцируемости функции x(t). Однако, когда колония
велика, а интервал времени At мал, функция x(t) по своим
свойствам напоминает непрерывную функцию и в равенстве (4) ее
можно считать непрерывной при условии, что она удовлетворительно
описывает реальную функцию x(t).
Разделив обе части равенства (4) на Αϊ и перейдя к пределу
при Δ/->0, имеем дифференциальное уравнение задачи
ι· Δχ dx и /сч
iZ^r = -dr=kx- (5)
После разделения переменных уравнение (5) примет вид
*L =kdt.
χ
Интегрируя последнее равенство, получим
\nx=kt+C,
откуда общее решение
x = Cekt. (6)
Начальное условие: при ί=ίο . x=x(to), где to — время начала
наблюдения за колонией, χ (to)—количество живых организмов
и колонии в начальный момент.

152
Гл. IV. Разделяющиеся переменные
Отсюда
C=x(t0)e-kt°.
Найденную постоянную интегрирования подставляем в
равенство (6) и получаем искомый закон изменения числа организмов
в колонии по времени (модель Мальтуса):
χ(ί)=χ(ίο)β*«-4
Заблуждение Мальтуса заключалось в том, что это уравнение
для нереальных условий он считал универсальным законом для всей
природы и человеческого общества.
Задача 75. Скорость размножения бактерий пропорциональна
их количеству. В начальный момент имелось 100 бактерий, а в
течение 3 ч их число удвоилось. Найти зависимость количества бактерий
от времени. Во сколько раз увеличится количество бактерий в
течение 9 ч?
Решение. Пусть χ — количество бактерий, имеющихся в
данный момент. Тогда скорость размножения будет —г—. Согласно
условию, дифференциальное уравнение задачи
dx
kx.
dt
где k — коэффициент пропорциональности между скоростью
размножения бактерий и их числом. Осуществляя разделение
переменных χ и t, получим
-^=kdt.
Проводя интегрирование и обозначая для удобства при
последующем потенцировании постоянную интегрирования через In С,
найдем
J ^L =k\ dt+\n с
или
lnx=kt+\nC. (1)
Потенцируем равенство (1):
х = ем+ы с — ein с ем __ £еы.
Итак, общее решение
х=Сем. (2)

§ 29. Экология популяций
153
Начальное условие: при ί=0 χ=100. Подставляя эти
значения в общее решение (2), получаем уравнение для определения
постоянной интегрирования
100=Се°,
откуда
С=100. (3)
В общем решении (2) осталась неизвестной постоянная k.
Дополнительное условие: при ^=3 х=200. Подставляя эти
значения в уравнение (3), получаем для определения k равенство
200=100e3t.
Сокращая на 100 и логарифмируя, находим
In 2 = 3/г,
откуда
1п2
*= —
Тогда
In 2 t_ t
eht = e~3~~ ' — (еШ2) 3 =2F.
Итак, искомая функция
i
х=100-2"з.
Ответ, на второй вопрос дает отношение
х(9) 100-29/3
. . — __03__0
х(0) 100 '
т. е. в течение 9 ч количество бактерий увеличится в 8 раз.
Учет самоотравления организмов
Задача 76. Колония организмов обитает в реальных природных
условиях — конкурентная борьба внутри популяции, недостаток
места и пищи, передача инфекции из-за тесноты и т. п. Найти закон
изменения общего количества живых организмов в колонии.
Решение. Фактор самоотравления учитывается при подсчете
прироста популяции Ах путем уменьшения его на величину h(x, At),
характеризующую действительные условия существования колонии.
Тогда уравнение (4) задачи 74 запишется
Ax—kxAt—h(x, At). (1)

154
Гл. IV. Разделяющиеся переменные
Без особой ошибки можно считать, что величина h(x, At) будет
линейно зависимой от At, т. е.
h(x, At)=f(x)At.
Функцию f(x) считают квадратичной, т. е.
f(x)=Kxz,
где λ —коэффициент самоотравления (или внутренней борьбы
в популяции).
Тогда
h(x,At)=lx2At. (2)
Величина (2) становится заметной по сравнению с kxAt только
при больших значениях х, при малых χ она становится бесконечно
малой более высокого порядка малости. Поэтому зависимость (2)
удовлетворительно отражает тот факт, что конкуренция внутри
популяции начинает заметно ощущаться только при большой
плотности, т. е. при больших значениях χ на ограниченной площади. Кроме
того, конкуренция увеличивается с ростом количества встреч между
членами колонии, а оно пропорционально произведению х-х, т. е. х2.
Таким образом, равенство (1) принимает вид
Ax=kxAt—%x2At. (3)
Равенство (3) делим почленно па At:
-—- =kx—Kx2
At
и после перехода к пределу при t-^Ο получим дифференциальное
уравнение
dx
—- =/bc—λχ2. (4)
at '
Уравнение (4) можно преобразовать следующим образом:
А
= kx{\-\x)=kA±-r—\. (5)
dt \ k ι \ k
k
Пусть μ= —. Тогда уравнение (5) запишется так:
λ
dx , / μ—χ \
~df-kxy-^rl·

§ 29. Экология популяций
155
Разделим переменные:
μάχ
χ(μ~χ)
=kdt.
(6)
Применив к уравнению (6) метод неопределенных
коэффициентов, получим
(J__j !_) dx=kdt.
\ χ μ—χ'
Х = ШоИ iff-
β-"ο+χοΕ
Рис. 43
Если μ>χ0, то для всех моментов времени μ>χ(/) и после
интегрирования имеем
In χ—In (μ—χ) = kt+\n С,
откуда, потенцируя, получаем
χ
μ—χ
:СеЧ
(7)
Упрощенные начальные условия: при ί0=0 х(0) —Χο<μ. Тогда
μ—Χο
Следовательно, уравнение (7) примет вид
X Хо
μ—χ
μ—Хо
ем

156
Гл. IV. Разделяющиеся переменные
и искомый закон (модель Ферхюльста — Перла)
x(t) =
УХо
μ—Хъ+х<>ем
График этого закона называют логистической кривой. Закон
роста колонии показан на рис. 43 сплошной линией, скорость
роста — пунктиром.
Учет скрещивания организмов
Задача 77. Колония организмов обитает в реальных природных
условиях. Найти закон изменения количества организмов в колонии,
учитывая в основе размножения только скрещивание.
Решение. Прирост будет тем выше, чем больше количество
встреч между членами колонии разных полов. Количество встреч
пропорционально как численности одного, так и численности
другого пола, т. е. произведению χ·χ=χζ.
Для идеальных (или искусственно созданных) условий — без
учета внешних факторов, при неограниченных резервах питания
и т. п., для популяции можно написать, что
dx
~df
—vxz,
где ν — коэффициент пропорциональности.
Пусть: t — среднее время между двумя последующими
оплодотворениями; τ — среднее время вынашивания плода,
фиксированное для данного вида.
Среднее время, в течение которого может состояться встреча,
ведущая к оплодотворению, tcv=t—τ. Вероятность такой встречи
будет тем большей, чем большую часть /ср занимает в интервале t,
т. е. чем больше отношение -γ-· Поэтому коэффициент ν
целесообразно принять
*ср *ср
ν=α—— =а-
где а — коэффициент пропорциональности.
Величина tcp зависит от плотности, т. е. рт х, и тем меньше, чем
больше χ на ограниченной площади, т. е.

§ 30. Плотность муравьев вне муравейника
157
Таким образом,
β
dx icp „ Χ „,
= α -—г— x2= α -^ 'χ
dt icp+τ _β_
χ
или
dx βΧ^
d/ β+τχ
В частном случае при малом τ по сравнению с β и малой общей
плотности (т. е. малых х) получим
dx
= ах2.
dt
В случае, если β мало по сравнению с τ (т. е. мало tcv), а общая
плотность большая (т. е. большие х), получим
dx β
= α — χ.
dt τ
Дальнейшее решение уравнения (1) дает искомый закон.
Исходя из уравнения (1), можно аналогично предыдущей
задаче найти также закон, учитывающий конкуренцию внутри
популяции, внешние факторы, периодичность размножения и т. п.
Во всех до сих пор рассмотренных задачах популяция считается
однородной по возрасту, т. е. не учитываются различные возрастные
группы в популяциях.
§ 30. ПЛОТНОСТЬ МУРАВЬЕВ ВНЕ МУРАВЕЙНИКА
Задача 78. Основанием муравейника служит круг радиуса г
(рис. 44), и пространство вне муравейника однородно по
распределению питательных веществ и по проходимости. Муравьи переходят
с одного места на другое, пока не найдут пищу или строительный
материал, и если они не погибают по дороге, то приносят свою
добычу в муравейник. В связи с этим вблизи муравейника больше
муравьев, чем вдали от него. Найти плотность муравьев вне
муравейника.
Решение. По условию задачи все точки, лежащие на
окружности радиуса R, будут равноправны в смысле своей значимости для
муравьев. В связи с этим плотность (количество насекомых в
окрестности, поделенное на ее площадь) муравьев во всех точках
окружности радиуса R (/?>?") будет одинаковой.
Таким образом, для анализа плотности как функции
расстояния R можно ограничиться рассмотрением точек одного луча.

158
Гл. IV. Разделяющиеся переменные
Пусть плотность в каждой точке не меняется со временем.
Поисковые перемещения муравьев считаем случайными, т. е. если
некоторое количество муравьев покинуло определенную окрестность
за единицу времени, то приблизительно столько же пришло в эту
окрестность из соседних участков, а также, если некоторые муравьи
скрылись в муравейнике со своей ношей, то приблизительно
столько же вышло из него в ее поисках.
Рис. 44
Рассмотрим две точки А и В, лежащие па одном луче (рис. 44),
и исследуем обмен муравьями между их окрестностями. Обозначим:
N(R) —количество муравьев в окрестности точки A, N(R-\-&R) —-
их количество в окрестности точки В.
В поисках муравьи разбегаются в разных направлениях,
которые в поисковом отношении равноценны, и поэтому доля выходящих
муравьев не зависит от направления выхода. Если из окрестности
точки А в направлении к точке В вышло kiN(R) муравьев, то из
окрестности точки В в направлении к точке А выйдет kiN(R-\-/S.R)
муравьев. Здесь &i«<l—коэффициент пропорциональности,
определяющий долю муравьев, выходящих в фиксированном
направлении.
Часть муравьев, вышедших из точки А к точке В, не дойдет до
окрестности этой точки, так как они найдут по дороге пищу или
строительный материал и вернутся в муравейник. Количество таких
насекомых будет тем больше, чем длиннее путь, т. е. чем больше
расстояние /\R между точками А и В.
Количество муравьев, вышедших из окрестности точки А и
дошедших до окрестности точки В, будет
NAn=kiN(R)-k2klN(R)AR,
где &2 — коэффициент пропорциональности, определяющий долю
вернувшихся в муравейник муравьев и зависящий от ценности
пространства — чем оно богаче, тем он больше.

§ 30. Плотность муравьев вне муравейника
159
К количеству муравьев ktN (R-\-AR) прибавятся муравьи,
которые вышли из окрестности точки В не к точке А, но по дороге нашли
пищу или строительный материал и, изменив направление, пошли
к муравейнику. Такие муравьи, если не успели выйти из сектора
OPS, также попадут в окрестность точки А, и их количество будет
том больше, чем больше расстояние AR.
Итак, количество муравьев, которые вышли из окрестности
точки В и попали в окрестность точки А, будет
NBA=kiN(R+AR)+k2kiN (R+AR)AR.
Так как количество муравьев в окрестности любой точки
должно быть постоянным, то
NAB = NBA
или
kiN(R)-k2klN(R)AR = kiN(R+AR)+k2kiN(R+AR)AR.
Сокращая полученное равенство на ki и учитывая, что
количество муравьев равно их плотности, умноженной на площадь,
Получим
f(R)FA-k2f(R)FAAR = f(R+AR)FB+k2f(R+AR)FBAR, (1)
где f(R), f(R-\-AR)—соответствующие плотности в окрестностях
точек А и В; FA, FB — площади окрестностей соответственно точек
А и В. Площади в полярных координатах выражаются:
FAttRAyh; Fbtz {R+AR)Ayh. (2)
Подставляем выражения площадей (2) в равенство (1) и
получаем
/ (/?) RAyh-k2f (R) RAq>hAR=f(R+AR) (R+AR) Δφ/ι+
+k2f(R+AR){R+AR)AyhAR. (3)
Сокращая равенство (3) на /ιΔφ и группируя слагаемые, имеем
(R+AR)f(R+AR)-Rf(R) =
= -h [f(R+AR) (R+AR)+f(R)R]AR.
Делим последнее уравнение на AR и переходим к пределу при
ΔΛ-Ч), в результате чего получим
-±-[Rf{R)] = -2kzRf(R). (4)

160
Гл. IV. Разделяющиеся переменные
Пусть k=2k2. Тогда уравнение (4) можно представить в виде
[Rf(R)Y
Rf(R)
откуда
= -Л.
d[Rf(R)]
Интегрируем полученное уравнение плотности:
\n[Rf(R)]=-kR+C. (5)
Начальные условия: при R = r f(R)—f(r), откуда
C=ln[rf(r)]+kr.
Найденное значение постоянной интегрирования подставляем
в уравнение (5) и тогда
In / =-k{R-r), (6)
г j {г)
откуда искомый закон плотности
f(R)=-j-f(r)<r**-o. (7)
Величину коэффициента k можно вычислить из равенства (6),
которое верно для всех R>r и, в частности, для R = rt. Подставляем
R=ri в уравнение (7) и имеем
f(ri)= —/(Ое-^-г
откуда
1 ή (г)
к-^=гыЖпу (8)
т. е. надо знать еще значение плотности / в точке R=rt. Подставляя
значение k по формуле (8) в уравнение (7), получим кривую
плотности f (R).

§ 31. Рост денежных вкладов 161
§ 31. РОСТ ДЕНЕЖНЫХ ВКЛАДОВ
Задача 79. Сумма А руб. положена в сберегательную кассу
на г% в год. Найти закон изменения суммы при условии, что
приращение начисляется непрерывно.
На основании полученного закона решить частные задачи.
а) Сумма 10 000 руб. положена в сберегательную кассу на 2%
и 1'од. Через сколько лет она составит 20 000 руб.?
б) Через сколько лет удвоится 1 руб., хранящийся на 3-про-
ιιιίιτηομ счету?
Решение. Общая сумма Ρ вклада в результате начисления
процентов-один раз в конце года составит
Р=А(\+г).
Если проценты будут начисляться по истечении полугодия, то
если поквартально,
и если ежемесячно, то
2
'-*('+-г)'·
Р=л(1 + -|-)к
12
В общем случае наращенная сумма в конце года составит
\ m I
m
при г% годовых, начисляемых m раз в год (например, 365 раз в год,
т. е. ежедневно).
По истечении η лет общая сумма будет
'-[('+^П*
Если число m начислений процентов в год будет беспредельно
увеличиваться, то
=ЛНт[(ц-^)Г]ПГ. (1)

162
Гл. IV. Разделяющиеся переменные
Так как
т
lim(l+-Mr =e,
т
то равенство (1) принимает вид
Р=Аепг.
Заменяя η через t, получим сумму, накопившуюся по истечении
времени t,
P=Aert.
В течение короткого промежутка времени dt приращение
суммы Ρ будет
dP=d(Aert)=rAertdt=rPdt.
Разделяя переменные, получим дифференциальное уравнение
задачи
dP
-p~=rdt. (2)
а) Интегрируя уравнение (2) и подставляя начальные и
конечные условия в качестве пределов интегрирования, имеем
20 000 (
С dP С
J -ρ-=0,02 J dt,
10 000 О
оТкуда
20 000 t
In Ρ Ι =0,02 J
10 000 0
или
In 2=0,02*
и искомое время
. In 2 0,693
ί== w=~w =34'66 года·
б) Интегрируя уравнение (2) с учетом условий задачи,
получаем
J-^-=0,03 j Л,
ι о
откуда
In 2=0,03*
и искомое время
. In 2
i==w~23,lro*a·

Глава V
ЗАДАЧИ, ПРИВОДЯЩИЕ К ОДНОРОДНЫМ
ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ПЕРВОГО ПОРЯДКА
Однородной функцией f(x, у) называется функция,
удовлетворяющая условию
f(lx,Xy)=hnf(x,y),
где λ — произвольное число; η — степень однородности.
Интегрирование однородного дифференциального
уравнения вида
M(x,y)dx+N(x,y)dy=Q (I)
производится методом подстановки.
Если М(х, у) и N(x, у) однородные функции своих аргументов
одинаковой степени, то уравнение (1) сводится к уравнению с
разделяющимися переменными подстановкой
у=их,
откуда
dy=udx-\-xdu.
Можно также пользоваться подстановкой
x=zy,
откуда
dx=zdy-\-ydz.
§ 1. ИЗОГОНАЛЬНЫЕ ТРАЕКТОРИИ
Задача 80. Найти изогональные траектории пучка прямых
с центром в начале координат.
Решение. Изогональными траекториями называются кривые,
образующие в каждой своей точке постоянный угол а с проходящей
через эту точку прямой пучка (рис. 45).
Пусть уравнение данного пучка у=ах. Положим tg α=β.
Обозначим текущие координаты точки траектории через (х, у);
угловой коэффициент касательной к траектории в этой точке
dy
будет —.
По условию
&=tga=
dx
1+-
—а
dy
1а

164
Гл. V. Однородные уравнения
В любой точке (х, у) всегда а=— (из уравнения лучка).
Поэтому
dy
У ψ»
k=
У_
dx x
1 +
или
dy_
dx
χ dx
У+kx
x—ky
(1)
Уравнение (1) является
однородным уравнением, и для его решения
применим подстановку
Рис. 45
у=их, dy=udx-\-xdu.
Подставляя выражения (2) в уравнение (1), получаем
xdu—kuzdx—kxudu—kdx=0
(2)
или после группировки членов
х(\—ku)du—k(l+u2)dx=0.
В уравнении (3) разделяем переменные
1 1— ku . dx
— · —r~.—г- du— ■
k l+«2 χ
= 0.
Интегрируем:
1 Г Г du
-[J-
k f d(}+uz) 1 С dx
Τ"1 1-fu2 '■" ~^ ΊΓ=(
или
(3)
— arctg и+ln C=ln x+ γ ln(l+«2) =ln χ У l+«2. (4)
Учитывая, что u= — и In e=l, придаем уравнению (4) вид
— arctg — =lnyx2-fi/2—In С
или
y*2_j-i/2=Ce*
,_arctg^_

§ 2. Геометрические приложения
165.
Переходя к полярным координатам, т. е. полагая x=r cos φ,
//=r sin φ, находим, что изогональными траекториями являются
логарифмические спирали
ф_
r=Cek~.
§ 2. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
Задача 81. В любой точке кривой длина поднормали равна
среднему арифметическому координат этой точки. Найти уравнение
кривой при условии, что она проходит через точку (—3, 2).
Решение. Длина поднормали кривой y=f(x) равна у
dx
(.реднее арифметическое координат текущей точки ——.
По условию задачи получаем дифференциальное уравнение
искомого семейства кривых
У dx 2 ' К }
которое является однородным уравнением. Преобразуем его к виду
_L (x+y)dx-ydy=0 (2)
и нводим подстановку
у=их, dy—udx-\-xdu.
Тогда уравнение (2) принимает вид
{х-\-их—2uzx)dx—2ux2du=0,
откуда после сокращения на χ получаем дифференциальное
уравнение с разделяющимися переменными
(1+«—2uPjdx—2uxdu=0. (3)
Уравнение (3) делим на произведение (1+«-2«2)ги получаем
2udu dx
1+u—2u2 = ~х~' ( '
Преобразуем левую часть этого уравнения. Представляя
знаменатель в виде произведения —2{х—\) (*+~τγ) и сокращая чис-
яитель и знаменатель на 2, получаем

166
Гл. V. Однородные уравнения
udu dx
_(„-1)(«+±) "~ Х '
Избавляемся от дроби в знаменателе левой части и
интегрируем полученное уравнение:
^Τ^ΪΤΙ^Ϊ)-='"+'" С,=1п С,*. (5)
Применяя метод неопределенных коэффициентов, находим
и А В
(и— 1)(2и+1) и—1 ' 2«+Г
откуда
Л(2и+1)+В(и—1)=ы
или
(2А+В)и+А—В=и,
и в итоге приравнивания коэффициентов получаем систему
2Л+Я=1, |
решая которую находим А — В=]/3.
Раскрывая интеграл в левой части уравнения (5), получим
= --| [ΐη(«-1) + -ίΐη(2«+1) ] =—~1η(α—1)/2Ϊ7+Τ =
== In ■—■__ = In Cix
[(ti.-l)y"2T+i]v.
или
Ci*(m—l)'/'(2u+I),/»=l,
У
откуда после подстановки и= — и сокращения на χ имеем
Ct(y-x)'H2y+xyh=l- (б)
Уравнение (6) преобразуем к виду
(у-х)Н2у+*Ук=*-^ *=С

§ 2. Геометрические приложения
167
И обе стороны полученного равенства возведем в куб
(у-х)*(2у+х)=С<.3=С.
Таким образом, общее решение уравнения (1)
(у-х)*(2у+х) = С.
Дополнительное условие: точка (—3, 2) является точкой
кривой, следовательно,
(2+3)2(2-2-3) = С
или
С=25.
Тогда уравнение искомой кривой
(у-хУ(2у+х)-25=0
или
2у3—Зху*+х3—25=0.
Задача 82. Радиус-вектор любой точки кривой меньше длины
подкасательной на величину абсциссы точки касания. Найти
уравнение кривой, если она проходит через точку (—3, 4).
Решение. Радиус-вектор любой точки кривой равен ix2-\-y"-.
dx
У
Длина подкасательной равна ~, .
dy
По условию задачи дифференциальное уравнение искомого
семейства
dx
1*+*=у-^ -χ
или
(рё+у*+х)ау-уах=0. (I)
Уравнение (1) является однородным дифференциальным
уравнением, которое можно привести к уравнению с разделяющимися
переменными. Целесообразнее -принять подстановку
x=zy, dx=zdy-\-ydz. (2)
Подставляем выражения (2) в уравнение (1) и получаем
уравнение
У 22+1 dy—ydz=0,
которое после разделения переменных принимает вид
dy dz
__2 ____— =о
у tz2+l

t68 Гл. V. Однородные уравнении
ИЛИ
dy dz
Интегрируем уравнение (3) и в итоге получаем
(3)
1ηy=\n(z+ /ζ2+Τ)+1η С,
откуда
y=C(z+1z*+l). (4)
Уравнение (4) преобразуем следующим образом:
y—Cz=C-]/z*+]
или
C2(z2+1) =y2—2Cyz+C2z2,
откуда общее решение дифференциального уравнения (1)
r/2=2Ci/z+C2=2Cx+C2.
Начальное условие: точка (—3, 4) лежит на кривой, т. е.
16=2(-3)С+С2,
откуда
Ci=8; С2=—2.
Итак, получаем две кривые: параболу
i/2=16x+64
и параболу
у2=— 4х+4.
Задача 83. Найти кривую, для которой площадь, заключенная
между осью абсцисс, кривой и двумя ординатами, одна из которых
постоянная, а другая переменная, равна отношению куба
переменной ординаты к переменной абсциссе (рис. 46).
Решение. Пусть N(x, у)—переменная точка на кривой.
Площадь криволинейной трапеции равна / ydx. По условию
Хо
X
$ydx=-£-. (1)
Берем производную от обеих частей равенства (1) и тогда
Зу*у'х-у3
У= -г .

§ 2. Геометрические приложения
169
)ткуда
dy_
dx
х2У+У3
ЪуЧ
(2)
Однородное дифференциальное уравнение (2) подстановкой
i = ux du=udx~{-xdu приводим к уравнению
dx
3udu
~l-2u2
(3)
Рис. 46
Общее решение уравнения (3) имеет вид
\пх+ ~ ln(2u2_i) = il£.
4 4
и после потенцирования запишется так:
х4(2«2-1)3=С.
Переходя к переменной у, имеем
2(/2—х2 \3
пли
., / 2(/2—х2 \3
(2(/2—х2)3=Сх*.

170
Гл. V. Однородные уравнения
§ 3. ЗЕРКАЛО, ФОКУСИРУЮЩЕЕ ПАРАЛЛЕЛЬНЫЕ ЛУЧИ
Задача 84. Какой формы зеркало собирает все лучи,
параллельные его оптической оси, в одной точке? Найти уравнение
зеркальной поверхности, если ее фокальная хорда равна 8.
Решение. Пусть отраженные лучи фокусируются в начале
координат. Ось абсцисс направим по оптической оси зеркала и со-
Рис. 47
ставим уравнение сечения искомой поверхности зеркала плоскостью
хОу (рис. 47). Любой луч QM параллельного пучка должен после
отражения пройти через начало координат. По закону отражения
Ζ.α=Ζ-β. Следовательно, треугольник ΜΟΝ равнобедренный и
ΟΜ=ΟΝ, τ. е. радиус-вектор точки М(х, у) равен отрезку,
отсекаемому на оси абсцисс нормалью:
ixz+y2=x+y~ (1)
Уравнение (1) представляет дифференциальное уравнение
семейства кривых, к которому принадлежит также искомое сечение.
Общее решение этого однородного уравнения
y2=2Cx+Cz
или
y*=2c(x+-j-)
представляет семейство парабол с общим фокусом в начале коор-
лнмит и параметрами р = С.

§ 4. Траектории полета самолетов
171
Так как фокальная хорда искомой параболы
о
р = С=4.
Уравнение искомого сечения представляет параболу
у2=8(х+2).
Так как плоскость хОу выбрана произвольно, то аналогичные
•очения получатся в любой плоскости, проходящей через ось Ох.
"аким образом, искомая зеркальная поверхность представляет па-
>нболоид вращения
у2+22=8(х+2).
§ 4. ТРАЕКТОРИИ ПОЛЕТА САМОЛЕТОВ
Задача 85. Летчик ведет самолет в направлении к городу В,
неположенному на одной параллели западнее взлетной площадки.
1айти уравнение траектории полета самолета, если его скорость
' км/ч и ветер дует с юга со скоростью w км/ч. Взлетная площадка
тходится на расстоянии а км от города В.
Рис. 48
^ешение. Пусть М(х, у)—положение самолета в момент
времени t (рис.*48). Вектор, представляющий его скорость, имеет вели-
•ину ν и направлен к точке В. Пусть φ — угол, образованный векто-
>ом с горизонталью, соединяющей взлетную площадку и город В.
)ектор скорости ветра направлен на север и имеет величину w.

172
Гл. V. Однородные уравнения
Тогда диагональ параллелограмма, образованного векторами ν и w,
представляет действительное направление вектора скорости
самолета в момент t. Диагональ должна касаться траектории самолета
в точке М. Следовательно, она образует наклон —— с искомой кри
ах
вой. Поэтому задача сводится к определению уравнения, которо<-
выражает производную —-— в виде функции хну.
Соответствующие составляющие скорости самолета в напраь
лениях χ и у будут
dx dy .
-усоБф, —r~=—vsm(f. (1)
dt ^ dt
Поэтому действительная скорость самолета в направлении у
с учетом скорости ветра
dy
= —fsincp-f-ay. (2)
dt
Из рис. 48 очевидно, что
У
sin φ— , соэф=
1х*+у* ix2+y*
Подставляя эти значения в первое уравнение (1) й в
уравнение (2), получим
dx —vx dy vy
- - +w. (3)
dt ix2+y2 dt ix*+y2
Деление второго уравнения (3) на первое уравнение (1) дает
w
dy — vy-\-w Ух2+у2 ν
у_ уХ2+у
г2
dx —vx
Пусть теперь
(4)
w
т. е. k — коэффициент отношения скоростей ветра и самолета.
Следовательно, равенство (4) примет вид
xdy=(y-kix*+!/*)dx. (5)

§ 4. Траектории полета самолетов
1?3
Уравнение (5) является однородным уравнением. Преобразуем
его к интегрируемому выражению
xdy
χ2 χ V \ χ ι
или
У'+ш!
= - — dx. (6)
X
Начальные условия: при ^=0 х=а, у==0, у'= — =0.
Интегрируя уравнение (6), имеем
У/х
d
Ш
X
У>+Ш'
откуда
Пусть
(8)
У
и= —
χ
Тогда равенство (7) принимает вид
или
1п(и+У 1+«2)=— /г In — -
а
или
,-ft
откуда
χ \~2h _ / χ \-h

174
f л. V. Однородные уравнения
Отсюда получаем, что
—Н(тГ-(тЛ·
Возвращаясь, согласно соотношению (8), к прежней перемен
ной, имеем:
*-τΝτ)"*-(τΠ--γ[(τΓ-(τΠ-
Подставляя k=
W
окончательно получаем уравнение
траектории
»~Н(тГ-(тГ]·
(9)
Исследуем зависимость решения от параметров.
Случай 1. Скорость ветра w равна скорости самолета v. В этом
случае решение (9) принимает вид
2 V 1 да / '
откуда
Х2=_2а («/*),

§ 4. Траектории полета самолетов
175
Г. е. уравнение траектории представляет параболу (рис. 49).
Самолет никогда не достигнет места назначения.
Случай 2. Скорость ветра w больше скорости самолета v.
ш W W
В этом случае—— >1, так что 1 <0. Поэтому при х->-0
юличина
1--
/ χ \ v __ / а \ v
' a J \ χ ι
*0О.
'ледователыю, согласно равенству (9), При Ло>0 у-+°о. Опять
имолет никогда не достигнет места назначения. Траектория пока-
niia на тшс. 49 пои w=2v.
NiOfi) wsinot (α,Ο)
Рис. 50
.лучай 3. Скорость ветра w меньше скорости самолета v.
W W
ь этом случае <1, так что 1 >0. Из уравнения (9) оче-
шдно, что при х=0 у = 0. Поэтому самолет достигнет города В.
w 1
1риблизительная траектория приводится на рис. 49 при = —.
Задача 86. Летчик ведет самолет, передняя часть которого на-
фавлена к городу N, расположенному на одной параллели запад-
ice взлетной площадки на расстоянии а км, Найти уравнение
траектории полета, если ветер дует со скоростью w в направлении,
>бразующем угол α с вертикалью (рис. 50).

176
Гл. V. Однородные уравнения
Решение. Как видно из рис. 51, равнодействующая
действительных скоростей ветра и самолета в направлениях χ и у
примет вид
dx , ■ dlJ · , /,\
=—ν cosqp+tiy sin α, —τ— = — υ sin φ+ο> cos α. (1)
dt
dt
Рис. 51
Разделим второе уравнение (1) на первое, в результате чего
получим
dy —υ sincp-fo; cos α
dt — υ cosqH-ш sin α '
В уравнении (2) выполняем замены:
У х
sin φ=
и cos φ=
У X2+t/2 "J/ Х2_|_у2
В итоге получаем однородное уравнение
-vy
f¥+y-
-fay cos
α ) dx= у
vx
ix*+y*
-fay sin α j dy, (3)
в котором величины υ, w cos α и w sin α постоянны. Уравнение (3)
преобразуем при помощи подстановки у=их, dy=udx-\-xdu, откуда
vu
У 1-fu2
■ -fay cos
α ) dx= (
vu
fT+tf
■ -fay sin α ) (udx-\-xdu).

Гл. VI. Уравнения в полных дифференциалах
177
Выполняя умножение, последующее сокращение и приведение
подобных членов, имеем
w (cos α—sin α) dx=x I w sin α ■ ) du,
откуда после деления равенства на χ получаем
w (cos α—sin α) = ( w sin α — ) du. (4)
v уТЙ? '
Интегрируя уравнение (4) и вместо и подставляя —, приходим
к равенству
w
(cos α—sin cc)lnx=aysin α Η In ( \-y 1 + -^-) +C1(
Χ λ Χ ' Χ1 ι
которое элементарными преобразованиями приводится к виду
XW(cos α—sin a)—I ц
In — =w sin a-^--\-Ci.
У+1х2+У2 X
После потенцирования общий интеграл уравнения примет вид
У
, , w sin ос .
xW(cosa-sina)-l_C(y.f ух2_|_у2)е *. (5)
Начальное условие: при х=а у=0. Отсюда
%w(cos α—sin α)—1== Qq
ИЛИ
Q— ^rofcos α—sin a)—I
a
Подставляя найденное значение С в уравнение (5), после
сокращения на xw(cos α-sin α)-ι получаем искомое уравнение траектории
полета
у
—w sin a
у+1х2+у2=ае

Глава VI
ЗАДАЧИ, ПРИВОДЯЩИЕ К ДИФФЕРЕ
УРАВНЕНИЯМ В ПОЛНЫХ ДИФФЕР
Дифференциальное уравнение
М(х, y)dx+N(x, y)dy=0,
где М(х, у) и N(x, у) —функции χ и у, будет ypt.
дифференциалах, если существует такая функция г
М(х, y)dx+N(x, y)dy=dF(x, у).
Условие
дМ _ dN
ду дх
является необходимым и достаточным, для того ч
было уравнением в полных дифференциалах.
Общий интеграл уравнения (2)
F(x, у)— С.
Функция F(х, у) может быть найдена
1) по формуле
X V
F(x,y)=\M{l,yC~' I "'"
где Хо и уо произвольны. Они выбираются так, "
вались конечными при х—а и у=Ь. Ооычни и и с
О или 1;
2) по формуле
}M(x,y)d,:-- -; , „; „.
Иначе, общее решение может оыть наи
\м(х,у)ах+\ [N(x,y)~J
"У
или
f dN(x, г/)
дх
5N(x,y)dy+5[M(x,y)-)-

§ 1. Параболическое зеркало 179
Если левая часть уравнения (1) не является полным
дифференциалом какой-то функции F(x, у), можно подобрать интегрирующий
множитель μ, который обратит уравнение (1) в уравнение в полных
дифференциалах
μΜ(χ, ι/)άχ+μΝ(χ, y)dy=Q
и тогда
δμΜ(χ, у) δμΝ(χ^)
ду дх
Интегрирующий множитель μ=μ (χ, у) удовлетворяет
уравнению:
м/ Ν <31ημ ... . din μ дМ dN
причем любое частное решение этого уравнения является
интегрирующим множителем.
Отыскание μ не всегда практически выполнимо.
Рассмотрим случаи простого определения интегрирующего
множителя.
Случай 1. Функции М(х, у) и Ν(χ, у) однородные одного
измерения:
μ=μ (χ, у) = M{xy)x+N(Xjy)y-
Случай 2. а) Отношение
дМ dN
д In μ ду дх
Ъ~х~ ~ N(x,y) ' =(Ρ(χ)'
где φ (χ) — функция только от х. Тогда
„S Ф(ж)йж.
μ—с ,
б) если
дМ dN
дх ду
—Mix^-f-=^'
где ψ (г/) — функция только одного у, то
., „J Ш№у

180
Гл. VI. Уравнения в полных дифференциалах
Случай 3. Если
дМ dN
=N(x, y)q,(x)-M(x, у)У(у),
ду дх
то интегрирующий множитель
μ = β
§ 1. ПАРАБОЛИЧЕСКОЕ ЗЕРКАЛО
Задача 87. Источник света помещен в точке О. Какова должна
быть форма зеркала, чтобы отраженные от него лучи были
параллельны оси Ох?
Рис. 52
Решение. Рассмотрим кривую сечения поверхности зеркала
плоскостью хОу и на этой кривой произвольную точку Р(х, у)
(рис. 52). Угол падения луча равен углу отражения и поэтому
AOQP=a.
Так как Z^OQP—a, то AOPQ — равнобедренный. Таким
образом, \OQ\ = \OP\=fx^+yi.
Считая у>0, получаем
dy
dx
= tga=
1^1
№\
УхЧ_у2 + х
Умножая числитель и знаменатель дроби на выражение
1 хг-\-уг—х, имеем

§ 1. Параболическое зеркало
181
,_ У х2+у2—χ
У~ У
откуда
х+УУ'
ix2+y2
или
d
Проинтегрировав последнее равенство, получаем
1х*+уг=х+С
у*=2Сх+С2=2с(х+~). (1)
или
С
2
По условию кривая должна быть симметричной относительно
оси Ох, т. е. уравнение (1) будет выполняться и при г/<0.
Равенство (1) показывает, что искомая кривая есть парабола с осью
симметрии Ох.
Пусть дано расстояние от источника света О до центра
зеркала S: \OS\ —а. Тем самым получаем начальное условие:
при х=—а у=0. (2)
Подставляя эти значения в уравнение (1), имеем
0=2с(-а+-^-),
откуда
С=2а.
Значение С=0 не подходит по физическому смыслу задачи.
Таким образом, искомая парабола:
у2=4а(х-\-а).
Для этой параболы ρ —2α и, следовательно, фокусное
расстояние — =а, т. е. источник света О находится в фокусе. Плоскость
хОу, в которой лежит парабола уг=4а(х-{-а), проходит через
ось Ох. Уравнение параболы не изменится, если эту плоскость
вращать вокруг оси Ох. Это значит, что поверхностью зеркала будет
служить параболоид вращения. Этот параболоид в сечении с любой
плоскостью, проходящей через ось Ох, будет давать параболу,
уравнение которой найдено выше. (Ср. с задачей 84.)

182
Гл. VI. Уравнения в полных дифференциалах
§ 2. КОНЦЕНТРАЦИЯ ВЕЩЕСТВА В ЖИДКОСТИ
Задача 88. Установить закон изменения концентрации глюкозы
в крови по времени при постоянном внутривенном введении в
количестве, колеблющемся от 155 до 630 мг/мин, если известно, что оно
продолжалось 60 мин, в течение которых брались пробы крови через
равные интервалы времени.
Решение. Если количество глюкозы в крови q, а ее
концентрация — =|, где V. — объем распространения в крови, то
вводимая глюкоза определяется в количестве, пропорциональном ее
наличному содержанию в крови. С другой стороны, концентрация
глюкозы повышается в результате постоянного ее введения.
В итоге этих двух взаимосвязанных процессов находим, что
изменение концентрации глюкозы в крови по времени
dl ~ Р -Αξ, (1)
dt V
где k — постоянная скорость вливания, ρ — количество вводимой
глюкозы, мг/мин.
Если глюкоза не прибавляется, р=0, уравнение (1) сводится
к равенству
1-*
тогда как при отсутствии вливания k = Q и уравнение (1) примет вид
dl ρ
dt V '
Представляя уравнение (1) в виде
г
замечаем, что оно имеет интегрирующий множитель е =ем, так
что, умножая на него обе стороны равенства (2), имеем
dt + е V '
и так как в левой части равенства полный дифференциал %ем, то
дифференциальное уравнение процесса
dt 4β ' V

§ 2. Концентрация вещества в жидкости
183
откуда
Интегрируя последнее равенство, находим
lektz=JLekt+C,
где С — постоянная интегрирования.
Начальное условие: при ί=0 |=0, поэтому
откуда
°=^+с·
С=-
Следовательно,
W
Ρ Ρ
^ekt=-Weht—kv
пли после деления на eht:
l=-jy(l-e-"). (3)
Концентрация глюкозы в крови при t=0 не равна нулю, но
формула (3) остается правильной, если С представляет
концентрацию глюкозы, превышающую в момент введения первоначальное
значение.
Экспериментальными наблюдениями установлено, что
ξ=53,8(1-6-°·0519ί). (4)
Сопоставляя уравнения (3) и (4), находим:
£ = 0,0519, -£7-=53,8.
Количество вводимой глюкозы ρ=297 мг/мин, так что объем
распространения глюкозы ]/=10,6 л.

Глава VII
ЗАДАЧИ, ПРИВОДЯЩИЕ К ЛИНЕЙНЫМ
ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ПЕРВОГО ПОРЯДКА
Дифференциальное уравнение
М(х, y)dx+N(x, y)dy=0,
разрешенное относительно производной у' и принявшее вид
y'+P(x)y=Q(x), (1)
называется линейным неоднородным дифференциальным
уравнением первого порядка. При отсутствии члена Q(x), т. е. при
Q(x) =0, уравнение (1) называется однородным.
Искомая функция у и ее производная входят в уравнение
линейно, т. е. в первой степени. В частном случае переменные
величины Р(х) и Q(x) или одна из них могут быть постоянными. Тогда
уравнение (1) в первом предположении примет вид
y'+Py=Q.
Общий интеграл уравнения (1) находится:
1) подстановкой Бернулли y—uz, и, следовательно,
dy = udz-\-zdu,
где «иг — неизвестные функции х, которые определяются из двух
условий
u'dV=Qix)'
2) при помощи интегрирующего множителя μ = £ —
путем приведения к полному дифференциалу
y=e-fpw* [ j Q {χ) J pwx dx+c ].
3) если известно какое-либо частное решение yi(x) линейного
уравнения, по формуле
y=yi(x)+Ce-S™dx;

§ 1. Геометрические приложения 185
4) если известны два линейно независимых частных решения
lli(x) и уг(х) (т. е. решения, линейная комбинация которых Cit/i-f·
-\-СгУ2 ни при каких значениях Ci и С2, кроме Ci = C2=Q, не
обращается тождественно для всех значений χ на данном интервале
н пуль), по формуле
y=yi+C(yz— t/i).
§ 1. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
Задача 89. Найти кривую, проходящую через точку (1, 1), у
которой отрезок, отсекаемый касательной на оси ординат, равен
абсциссе точки касания.
Решение. Наклон кривой в какой-либо точке определяется
угловым коэффициентом k касательной в этой точке и, следователь-
„ , dy „_,
по, производной « = tga=-i—. Поэтому уравнение касательной
У—Уо=-£г(х—Хо)· (1)
Точка пересечения касательной с осью ординат имеет
координаты, удовлетворяющие системе
dy , ч
У-Уо=-^-(х-Хо),
д;0=0.
Координаты точки касания #о=0, у0=у—х ——. Отрезок, отсе-
, ay
каемыи касательной на оси ординат, равный у0, будет y—x-j—.
Ι Ιο условию этот отрезок равен абсциссе χ точки касания. Отсюда
дифференциальное уравнение искомого семейства
у-х ■%■=*· (2)
Уравнение (2) является линейным уравнением, которое после
преобразования принимает вид
dy ±y=-i. О)
dx χ
Применяем» подстановку Бернулли
y=uz, dy=udz-\-zdu

186
Гл. VII. Линейные уравнения
Тогда уравнение (3) приводится к виду
dz , / du и \
и—— +z(— ) == —1.
dx \ dx χ ι
Неизвестные функции и и ζ определяются из условий:
. du. и
а) —— =0 или после интегрирования и=х;
лч dz ι С
б) х—г- = — 1 или после интегрирования г=1п ·.
ил %
Искомое общее решение уравнения (2) принимает теперь вид
, С
y=uz=x In .
а χ
Начальное условие: точка (1,1) лежит на кривой, отсюда
С
1 = 1 In
1
или
С=е.
Уравнение кривой будет
у=х In —■ =x(ln е—In χ) =д:(1—In χ) =χ—χ In x.
Задача 90. В точке с ординатой 2 кривая наклонена к оси Оу
под углом 45°. Касательная отсекает на оси абсцисс отрезок,
равный квадрату ординаты точки касания. Найти уравнение этой
кривой.
Решение. Отрезок, отсекаемый касательной на оси абсцисс,
dx π
равен χ—у ——. По условию задачи
dx „
х—у —г- =у2
dy
или дифференциальное уравнение искомого семейства
dx I ,,ч
— х=-у. (1)
dy У
Уравнение (1) является линейным относительно х, общий
интеграл его
х+у*-Су=0. (2)

§ 1. Геометрические приложения
187
Дополнительное условие: при г/=2
dx
dy
:tg45°=l.
Дифференцируя почленно уравнение (2) по у, имеем
^=С-2у
dy
и частное значение этой производной при у=2
dx
dy
:С-2-2=С-4,
У=2,
in куда
пли
С—4=1
С=5.
Уравнение искомой кривой
х+у2—5г/=0.
Задача 91. Площадь треугольника, образованного радиус-век-
Гором любой точки кривой, касательной в этой точке и осью
абсцисс, равна 2. Найти уравнение кривой, если она проходит через
,·ιιιιι/λγ /о 2).
Рис. 53
Решение. Основанием треугольника ОМА является отрезок
Μ (рис. 53), отсекаемый касательной на оси Ох. Аналогично за-
inче 89 для отрезка, отсекаемого на оси Ох касательной, найдем
dx
шражение х—у ——.

Ιββ
Гл. VII. Линейные уравнения
Высотой треугольника будет ордината у. Площадь
треугольника
По условию задачи
1 / dx \
Ty\x~y-dT> =%
откуда дифференциальное уравнение искомого семейства
dx 1 4
dy у у2
Уравнение (1) является линейным относительно х, а его общее
решение
2
ί/
Дополнительное условие: кривая проходит через точку (2, —2),
откуда
и
Уравнение искомой кривой
3ί/2+2χί/—4=0.
§ 2. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
Закон движения — алгебраический многочлен
Задача 92. В любой момент t скорость υ точки превышает
среднюю скорость за время t с начала движения на величину t2. Найти
закон движения, если при t=0 s=so, υ = 0.
ds
Решение. Скорость в момент t будет υ = ~тг- Средняя ско-
s—so „
рость за время t с начала движения иСр= —: ■ Но условию
задачи v—vcv=t2. Отсюда дифференциальное уравнение движения

§ 2. Движение материальной точки
189
as
dt
ds
dt
S — So
t
1 ,2
Ts=l-
= t2
So
t '
или
ds 1 ,<ϊη
(1)
τ, о. это линейное уравнение.
Общее решение уравнения (1)
s = s0+y-'3+C/. (2)
ds
Начальное условие: при ί=0 υ= —j-~ = 0. Дифференцируя
общее решение (2), получаем зависимость
dt ~ 2 ' +С'
откуда
0=^--02+С
или
С = 0. (3)
Подставляя значение (3) в общее решение (2), получим
искомый закон движения
s = s0-by*3.
Периодический закон движения
Задача 93. Скорость υ, путь s и время t связаны уравнением
V cos t-\-s sin f = 1. Найти закон движения, если при ^ = 0 s = 2.
ds
Решение. Так как ν——,—, то, подставляя это значение ν
at
В данное уравнение, получаем дифференциальное уравнение
движения
—— cos t-\-s sin г= 1.
dt
Решая это линейное уравнение, получаем
s = sin t-\-C cos t.
Начальное условие: при ί=0 s = 2, откуда
2 = sinO+CcosO

190
Гл. VII. Линейные уравнения
ИЛИ
С=2. (1)
Подставляя выражение (1) в общее решение, получаем
искомый закон движения
s=sin t-\-2 cos t.
Падение тела переменной массы
Задача 94. Капля с начальной массой Μ г, свободно падая
в воздухе, равномерно испаряется и ежесекундно теряет т г. Сила
сопротивления воздуха пропорциональна скорости движения капли.
Найти зависимость скорости движения капли от времени,
прошедшего с начала падения капли, если в начальный момент времени
скорость капли равна нулю. Принять, что коэффициент
пропорциональности k=£m.
Решение. Ввиду равномерного испарения капли ее масса
в момент t равна M—tnt, а сила тяжести капли — {M—mt)g, где g—
ускорение силы тяжести. Силу тяжести считаем положительной, т. е.
направленной вниз.
По условию сила сопротивления воздуха Fi=—kv (знак минус,
так как она направлена вверх). Равнодействующая всех сил,
приложенных к капле,
F=(M—mt)g—kv,
а так как по второму закону Ньютона
F=(M-mt) dV
dt '
то дифференциальное уравнение задачи
(M—mi) —- = (M—mt)g—kv
или
dv , k
Решая это линейное уравнение подстановкой v = uw, находим
k
w=(M—mt)m
и
k
а +1
и= jg(M-mt) « dt= — -k—■ УС.
т

Отсюда
§ 3. Температура охлаждающегося тела 191
v = uw=^~^+C(M-mOm. (1)
k—m iv'
Начальное условие: при t=0 t>=0. Следовательно,
0=-^-, +СЖ"^,
откуда
ft и
ι
С=
m—k m—k
Найденную постоянную интегрирования подставляем в
равенство (1), и тогда скорость движения капли
ft
§ 3. ТЕМПЕРАТУРА ОХЛАЖДАЮЩЕГОСЯ ТЕЛА
Задача 95. Найти закон изменения температуры Τ
охлаждающегося тела массы m и теплоемкости с. Температура окружающей
среды t, причем T>t. Когда температура окружающей среды t=0,
температура тела равна Τι.
Решение. По закону Ньютона бесконечно малое количество
теплоты dQ, отданное телом в течение бесконечно малого
промежутка времени dt, пропорционально разности температур тела и
окружающей среды:
dQ = -k(T—t)dt,
где k — коэффициент пропорциональности. Знак минус указывает,
что потеря теплоты dQ — величина отрицательная.
С другой стороны,
Q=mc(T-t), (1)
где m — масса тела, с — его теплоемкость.
Предполагая, что теплоемкость есть величина, не зависящая
от температуры, после дифференцирования уравнения (1) находим
dQ=mcdT.
Следовательно,
mcdT=—k(T—t)dt.

192
Гл. VII. Линейные уравнения
Разделяя переменные и интегрируя полученное уравнение,
имеем:
и
T=t+Ce~me. (2)
Начальное условие: при t=0 температура Г=7\. Отсюда
k
Ti=t+Ce »*'
или
C=Ti-t. (3)
Подставляя найденное значение постоянной интегрирования
(3) в общее решение (2), получаем искомый закон
T=t-\-(Ti—t)e "™с.
§ 4. НАГРЕВ ТЕЛА ПРИ СТАЦИОНАРНОМ ТЕПЛОПОТОКЕ
Задача 96. Найти закон нагрева теплообменника при
постоянном притоке теплоты.
Решение. ^Пусть: dT — изменение температуры
отопительного аппарата в течение времени dt; G — вес аппарата; с —
специфическая теплота материала аппарата; λ — коэффициент тепло-
переноса поверхностью аппарата (на единицу площади для
повышения температуры на 1°С); Q — количество поступающей теплоты
в единицу времени; 5 — поверхность теплопередачи аппарата;
Τι — наружная температура; Τ—Τι— превышение наружной
температуры теплообменника.
В течение времени dt происходят следующие процессы:
а) в теплообменник поступает количество теплоты, равное Qdt;
б) в аппарате накапливается количество теплоты, равное GcdT;
в) отдается в окружающую среду количество теплоты, равное
S(T-Ti)ldt.
Суммируя эти количества, получаем уравнение теплового
баланса
GcdT+S(T—Tl)Mt=:Qdt
или
(Г-Г,)=-^.
, дифференциальное уравнение про-
+a(T-Ti)=b.
Полагая а=
dT
dt
SX
г и
Gc
:а запишем в виде:
- + ■
Ъ =
dT
SI
Gc
Q
Gc
- 4-a

§ 4. Нагрев тела при стационарном теплопотоке
193
Разделяем переменные
dT
b-a(T-Ti)
=dt. (1)
Для облегчения интегрирования преобразуем левую часть
уравнения (1) так, чтобы в числителе получить дифференциал
знаменателя:
1 а[Ь—а(Т—Т$]
а Ь—а(Т—Т1
Умножаем это уравнение на (—а) и тогда
d[b-a(T-Ti)]
=dt.
b-a(T—Ti)
Интегрируя равенство (2), получаем
In [b-a(T-T1)]=-at+Cl
и после потенцирования
b—a(T—Ti) = ес* e-at = Ce~*t,
откуда
Т—Т1= — + — <?-«<= ^- +Cv-°i
а а а
Начальное условие: при/ = 0 Т=Т\. Отсюда
С—А
а
Тогда уравнение процесса принимает вид
= -adt. (2)
Τ- 7Ί= — (!-<?-«<) (3)
или, подставляя значения а и Ь, имеем:
βλ
Т-Т'=-Ъ-(1-е~ав*
При Γι=0 из уравнения (3) получим
Г= — (l-e-ai)· W
а

194
Гл. VII. Линейные уравнения
Исследуем этот закон. При t^-oo получаем
Ь
Т=
■Тк,
где Тк — конечная температура теплообменника.
Уравнение (4) может быть записано в виде
T=TK(l-ir*t).
(5)
1
Подставляя теперь в уравнение (5) значение /= — =τ,
получаем
Г=7к( 1-—) = 0,63ГК.
Время τ= — называется постоянной времени.
§ 5. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
Составление уравнений для токов в электрических цепях
основывается на законах Кирхгофа.
Первый закон Кирхгофа. Алгебраическая сумма всех токов,
притекающих к любой точке цепи, равна нулю (рис. 54).
\h
Ι, Ни* О
Рис. 54
h-'h^ti^O
Второй закон Кирхгофа. Для каждого замкнутого контура
цепи алгебраическая сумма падений напряжения в отдельных ветвях
контура равна нулю (рис. 55).
При составлении дифференциальных уравнений электрических
цепей следует учитывать, что падения напряжения на самоиндук-
. di
ции, сопротивлении и емкости выражаются соответственно L-
Ri,
Q
dt '
а заряд конденсатора

§ 5. Электрические цепи
195
Q(t)= $i(t)dt+Q(0).
Параметры R, С, L предполагаются постоянными, кроме особо
inпиоренных случаев. Здесь U — падение напряжения на каком-
■iiirto определенном участке контура.
и,+и3-о
и2
и,щ<иго
Рис. 55
и,*-иг+и9+ич~о
Цепь «сопротивление — самоиндукция»
а) Постоянная электродвижущая сила
Задача 97. При размыкании цепи (в момент появления искры)
сопротивление цепи R быстро возрастает от первоначальной
величины Ro до бесконечности. На основании опыта допускают, что за-
ипсимость R от t в этом процессе выражается
R=Ro-
-f
|де τ — время всего процесса размыкания. Найти силу тока i в
люпин момент в цепи при постоянной электродвижущей силе Ε и
самоиндукции L.
Решение. Так как в цепи действуют электродвижущая сила
, di
■L—гг-, ТО
источника Ε и электродвижущая сила самоиндукции
результирующая электродвижущая сила
dt '
V=E—L
di
~dt

196
Гл. VII. Линейные уравнения
По закону Ома
iR=V
или
iR=E L * .
at
В процессе размыкания цепи R = Ro .
дифференциальное уравнение процесса
di R0r . Ε
dt ' L(x—t) l~ L '
Отсюда получаем
(1)
которое является линейным.
Общее решение уравнения (1)
ЙОТ ЙОТ
t= -j- (τ-0 *· [ J (τ-0 ь dt+C ] .
Возможны два случая: —-—ф\ и—-—= 1.
В первом случае после раскрытия интеграла в квадратных
скобках общее решение будет
Во втором случае общее решение примет вид
/=_^-(т-0[С-1п(т-0]. (3)
Начальное условие: в момент начала размыкания при t=Q
Ε
сила тока i=i0= ——. Тогда в первом случае
до
Ε Ε (τ-0) СЕ , -^
-^ i + -7-(T-0) L ,
R0 R0x—L
откуда
СЕ EL -S£-
L Ro(RQx-L)
(4)

§ 5. Электрические цепи
197
Выражение (4) подставляем в общее решение (2) и получаем
Дот
_ . t
Ro(Rot-L)
Аналогично во втором случае
[Ru{T-t)-L(l---)L ]
R0 L
и ι куда
Е =4-(*-0)[С-1п(т__0)],
Ror
или, так как>—-— = 1, то
С=1 + 1пт. (5)
Подставляя выражение (5) в общее решение (3), имеем
(_-f (T-Ofl + In^].
Задача 98. В цепи поддерживается напряжение £=300 в.
Сопротивление цепи #=150 ом. Коэффициент самоиндукции
/. -30 гн. За какое время с момента замыкания цепи возникающий
и ней ток ι достигнет 99% своей предельной величины?
Решение. Электродвижущая сила самоиндукции
пропорциональна скорости нарастания силы тока. Коэффициентом
пропорциональности служит коэффициент L самоиндукции цепи.
В процессе замыкания цепи в ней действуют две прямо нроти-
имположпые электродвижущие силы: напряжение цепи Ε и электро-
пишущая сила самоиндукции £ι =—L——.
Алгебраическая сумма этих электродвижущих сил
V=E-L-di
dt '
По закону Ома сила тока в цепи
V
ι=ΊΓ
пли
Е- ■ di
i=. *L (i)
1 R W

198
Гл. VII. Линейные уравнения
Преобразуем последнее равенство
Ri=E-L-di
dt
или
Ridt=Edt—Ldi,
откуда
Ldi=(E—Ri)dt
и
Ldi
dt= Ί=*Γ <2>
Интегрируя равенство (2), имеем:
С di L С d(E—Ri)
E—Ri R " E—Ri
или
*=--!-In (£-#i)+C.
К
Начальное условие: при ί=0 ι—0, следовательно,
0=-~ In (£-/?· 0)+C,
откуда
С--±-ЫЕ.
Таким образом, закон процесса:
* L ι F
t= —7Г-1П-
R E-Ri'
Ε
Так как предельным значением i будет /= —--, то по условию
Ε R
ί=0,99 ——, и поэтому искомое время
А
'=-5-1пЁ=Ш=-й-|п,оа <3)
Подставляя в равенство (3) числовые значения L и R,
окончательно получим
30
t—~— In 100^0,92 сек.
150

§ 5. Электрические цепи
199
б) Периодическая электродвижущая сила
Задача 99. В цепи с сопротивлением R и самоиндукцией L дей-
t шует периодическая электродвижущая сила
Ei = a sin—=—г,
ι Μι· Τ — период, t — время, а — постоянное число, равное, очевидно,
Миксимальному значению величины Ει. Определить силу тока i
И lU'iiH в любой момент времени, если в начальный момент при t=0
сила тока равна нулю.
Решение. В цепи действуют две силы:
электродвижущий сила
Ει=α sin-^=— /
и противоположная ей электродвижущая сила самоиндукции
E2=-L.di
dt '
Общая электродвижущая сила
с- с- , с- . 2п , т di
Ε=Ει-\-Εζ=α sin —=- t—L -
Τ dt
По закону Ома сила тока в цепи
Ε
l=-R-'
Таким образом,
2π , , di
a sin—;=-£—L
Τ dt
t= ^ .
2π
Обозначая для краткости -=— = &, запишем дифференциальное
уравнение процесса
L—τ— -\-Ri=a sin kt. (1)
Уравнение (1) является неоднородным линейным
дифференциациям уравнением первого порядка.

200
Гл. VII. Линейные уравнения
Решаем соответствующее однородное уравнение
di , Я · π di R а<
-\ — 1 = 0 ИЛИ —-—= γ— at.
dt L i L
Интегрируя, найдем
ί-f—Μ*.
откуда
In ί= ^- ί+1η С
Потенцируя обе части равенства, получим
д
i=Ce~~r\
Частное решение неоднородного уравнения (1) ищем в виде
г'частн=Л sin kt-\-B cos kt. (2)
Коэффициенты А и В подлежат определению. Дифференцируем
равенство (2), считая А и В постоянными:
Лчастн =AkcQskt-Bks\nkt. (З:
dt
Подставляя значения (3) и (2) в уравнение (1), после очевид.
ных алгебраических преобразований имеем:
( А ~ Bk) sin kt+ ( Ak+B ~-) cos kt= —- sin kt.
Приравнивая коэффициенты обеих частей этого тождества
получаем систему
Л * ВА= а
L L '
Ak+B -т-=0.
(4*
Решая систему (4) относительно неизвестных А и В, получи:
aR akL
= k2L*+R* ' = k*L2+Rz "

§ 5. Электрические цепи 201
Итак, частное решение, согласно равенству (2),
aR . , ± akL
части-
^.+/ρ ^kt—mJ+prcoskL
Общее решение неоднородного дифференциального уравнения
(I) будет
Постоянную интегрирования С определим из начального
условия: при t = 0 i=0. Отсюда
JR
— —. о ag akL
0=Се " +^LH^Sink-°--MJ+R^COsk·0
И
с '-^L— (6)
Подставляя выражение (6) в общее решение (5), получим
t'= , р2 ( &Le ь +Я sin kt—kL cos &ί ) .
Для упрощения частного решения вводим сдвиг фаз φ при
помощи соотношений
R kR
cos φ= —— -, sin φ= —-— ■, 0^φ^2π.
У k2L2+R2 У k2L2+R2
Тогда частное решение
*частн= - ' ■ S'm(kt—φ),
У &L*+R2
η общее решение
akL —— ί . а
i= е l _j sin (fez1—φ).
k2L2+R* ik2L2+R2 K J
затухающая часть периодическая часть

202
Гл. VII. Линейные уравнения
Цепь «сопротивление — емкость» (постоянная
электродвижущая сила)
Задача 100. Конденсатор емкостью С включается в цепь с
напряжением U и сопротивлением R. Определить заряд q
конденсатора в момент t после включения.
Решение. Сила ι электрического тока представляет
производную от количества электричества q, протекшего через проводник,
, dq
по времени г: ——-.
т> . dq
В момент τ заряд конденсатора q и сила тока t= —тг\ в цепи
действует электродвижущая сила V, равная разности между напря-
л а
жением цепи и и напряжением конденсатора -^-, т. е.
V=U—· "
С
V
По закону Ома сила тока i= —^- или иначе,
dq
U—ir
dt R
Тогда дифференциальное уравнение процесса примет вид
«!="--£-■ ">
Интегрируя линейное уравнение (1), получим общее решение
ί_
q = CU—Cie~cR. (2)
По условию при t = 0 q = 0, откуда
о
0 = Ct/—Cte' с«
d=CU. (3)
Таким образом, закон рассматриваемого процесса
t
q=Cu(l-e с")

§ 6. Рационализаторские предложения
203
§ 6. РАЦИОНАЛИЗАТОРСКИЕ ПРЕДЛОЖЕНИЯ
Задача 101. Предприятие установило, что скорость изменения
((исходов по реализации взаимосвязана с рационализаторскими
Предложениями в производстве. В частности, если у — расходы по
реализации (в тыс. руб.), а х-—число новаторских предложении
Ы производстве, то изменение у в зависимости от изменения χ равно
1/8 у. Определить расходы по реализации в виде функции рацио-
пнлизаторских предложений производства, если известно, что когда
чпгло рационализаторских предложений 4, то расходы по
реализации составляют 3000 руб.
Решение. По условию зависимость переменных величин
dy 1
= -— у,
dx
откуда
du 1
Общее решение этого однородного линейного уравнения пер-
иого порядка
j.
у=Се~^х.
Начальное условие: при х=А у=3. Тогда
ι
3 = Се~ Т = 0,607С,
откуда постоянная интегрирования
С=4,9.
Искомый закон принимает вид
χ
y==4,9e~'i.
Это уравнение позволяет оценить расходы по реализации при
разных количествах рационализаторских предложений.
Так, при отсутствии рационализаторских предложений в
определенный период расходы по реализации составили бы
ι
у=4,9е~~* =4,9е°=4,9,
т, е. 4900 руб. С другой стороны, если за этот же период было еде-

204
Гл. VII. Линейные уравнения
лано 8 рационализаторских предложений, то расходы по
реализации сокращаются до размера.
ι
£/=4,9*?"«"' = 4,9<г1=4,9-0,368=1,8,
т. е. до 1800 руб.
§ 7. РАБОТА СЕРДЦА
Задача 102. Найти закон изменения давления крови в аорте во
время работы сердца человека.
Решение. Сердечно-сосудистая система представляет собой
замкнутую систему, состоящую из множества крупных и мелких
сосудов, по которым непрерывно движется кровь.
От сердца кровь по артериям идет ко всем органам и
возвращается обратно по венам к сердцу. Самая большая артерия (аорта)
постепенно разветвляется на все более мелкие артерии (артериолы),
которые заканчиваются тончайшими кровеносными сосудами
(капиллярами), снабжающими все органы человека кровью.
Для того чтобы кровь могла достигнуть самых отдаленных
участков тела, необходимо в сосудах поддерживать определенное
давление. Это достигается работой сердца, а также обусловлено
состоянием стенок сосудов, особенно артерий.
Сердце — полый мышечный орган, состоящий из четырех
полостей: двух предсердий и двух желудочков. Оно работает по
принципу нагнетательного насоса: при сокращении сердца кровь
с силой выталкивается из левого и правого желудочков в сосуды.
Артерии представляют собой полые трубы, в стенках которых
имеются мышцы и эластичные волокна, которые могут
растягиваться и сокращаться. Когда волна крови, нагнетаемой сердцем,
проходит по артериям и давит па их стенки, сосуды растягиваются,
а затем под действием эластичных волокон суживаются. При
сужении сосуды давят на кровь, находящуюся внутри них. Таким
образом в сосудах создается давление крови.
Давление крови в сосудах во время сокращения (систолы)
сердца называется систолическим (или максимальным), а во время
покоя (диастолы) сердца называется диастолическим (или
минимальным).
Рассмотрим математическую модель сердечно-сосудистой
системы, учитывая лишь основные ее свойства. В связи с этим
представим аорту (рис. 56) в виде упругого объемного сосуда, емкость
которого зависит от давления, развиваемого во время работы
сердца.
Этот упругий сосуд связан с трубкой, оказывающей потоку
крови определенное сопротивление, которое назовем артериальным.
Будем различать две последовательные фазы:

§ 7. Работа сердца
205
1) диастолическую фазу — количество притоков от сердца
аорте равно нулю;
2) систолическую фазу — кровь поступает в аорту из сердца.
Диастолическая фаза.
При рассмотрении работы сосуда учтем дополнительно:
а) линейную зависимость между объемом и давлением в нем;
б) подчинение системы закону Пуазейля.
Артериальное сопоотиожие.
Рис. 56
Линейная зависимость между давлением и объемом выражает
с я отношением
dp
dV
--k,
(О
где k — постоянная, ρ — давление во вмещающем сосуде, V —
объем крови. Чем больше сопротивление вмещающих сосудов, тем
больше давление в момент сокращения сердца и во время диастолы.
По закону Пуазейля объем жидкости, протекающей за секунду
через сечение трубки, прямо пропорционален разности давлений
у входа в трубку, и на выходе из нее, четвертой степени диаметра
трубки и обратно пропорционален длине трубки и коэффициенту
Нязкости.
Если принять давление на наружном конце трубки равным
пулю, то закон Пуазейля можно записать
dV
dt
ω
(2)
где
ω =
8/μ
Здесь ω — постоянное сопротивление; г — радиус трубки;
μ — вязкость крови; / — длина трубки.
Знак минус обозначает, что большему давлению ρ в сердце
соответствует большее уменьшение объема в единицу времени.
Исключая из равенств (1) и (2) величину dV, получаем
дифференциальное уравнение

206
Гл. VII. Линейные уравнения
dp kdt. (3)
ρ ω
Решение уравнения (3) находится непосредственным
интегрированием
k
р = С*е~ ω ',
где С* = ес.
При t=0 C* = p(0)=po, и тогда
ь_
р = р0е ω '.
Таким образом, в течение диастолического периода (клапаны
аорты закрыты) давление в аорте падает по показательному закону.
Систолическая фаза.
Особенностью этой фазы является то, что кровь накачивается
в аорту путем сокращения мышцы сердца. Скорость изменения
объема в аорте является результатом двух факторов: количества
притоков (от сердца) и оттоков (вытеканий) по артерии.
Количество вытеканий на основании закона Пуазейля
dV ρ
dt ω
„ dV
Знак минус отсутствует, так как теперь —т— является не
изменением объема в единицу времени в аорте, а объемом потока,
проходящего через поперечное сечение в единицу времени.
Обозначим объем потока, поступающего в единицу времени
в аорту, функцией i(t).
Очевидно, что изменение объема в аорте
Ρ dV
Если ι> , то отношение —— положительно, т. е. объем по-
ω dt
тока крови в аорте увеличивается, и наоборот. Учитывая равенство
(1), уравнение (4) перепишем в виде
dp
= *[i(0-—1
dt L ω
или
■££- + JLP=W(0. (5)

§ 8. Задача о сигарете
207
Функция i(t) является неизвестной. В качестве приближения
принимаем закон i=A sin Bt, т. е. число вытеканий потока крови
и аорту аппроксимируется функцией синуса. Тогда уравнение (5)
принимает вид
dp , k , . . _.
н + ■ p=kA sin Bt.
dt ω
Интегрирующий множитель μ=£ ω и искомое значение
ft ft - k
р=Се~~^~'+е~~<»~1 J kA sin Bt e ω 'Λ.
Применяя метод интегрирования по частям {и=е ω , i/y =
= sin.SW/) и решая полученное затем равенство относительно
искомых интегралов, получим
ft
( I sin Bt~B cos
Bt
p=Ce »*+Ак—^ . (6)
ω2
При t=0 p—Po, откуда
Окончательно, после подстановки в равенство (6) значения (7),
получаем
.„„ . ft Ak\ sm Bt—B cos Βίλ
kAB \ —— * L ω J
P= Ρ0+-Τ-, \e ω +
«r / ω2
§ 8. ЗАДАЧА О СИГАРЕТЕ
Задача 103. Исследовать вопрос фильтрации дыма (газового
потока) через горящую сигарету.
Решение. Это задача о фильтрации с подвижным краем.
Она может быть обобщена на другие аналогичные модели задач
о фильтрации и горении.

208
Гл. VII. Линейные уравнения
Предположим, что:
1) в продолжение непрерывного вдыхания (т. е. при
постоянной скорости воздуха и горящих газов, проходящих .через сигарету,
и установившемся коэффициенте горения) в табаке сохраняется
постоянная доля а любой его составляющей Z, а оставшаяся часть
1—α улетучивается в воздух;
2) относительно фильтрации составляющей Ζ коэффициент
абсорбции (поглощения) табака постоянен и равен Ь, аналогично
I >
I I »—
I '
I I ι |
t Χ Χ+ΔΧ
Рис. 57
при наличии фильтра у наконечника коэффициент абсорбции
наконечника также постоянный и равен β;
3) скорость изменения длины при сгорании является настолько
медленной, что можно пренебречь временем отставания, вызванным
конечной скоростью газового потока вдоль сигареты, т. е. отложение
доли а определенного количества составляющей Ζ по длине
сигареты от фильтрации проходит непрерывно при сгорании этого
количества до наконечника.
Рассмотрим абсорбцию составляющей Ζ при курении по длине
сигареты.
Пусть χ — расстояние вдоль сигареты, исчисляемое с любого
ее конца. Предположим для простоты, что дым движется вдоль
сигареты с постоянной скоростью, и рассмотрим очень тонкий слой
сигареты толщиною t, который будет передвигаться при курении
(рис. 57). Пусть общий вес составляющей Ζ в слое, когда он
проходит сечение х, будет w(x). Тогда общий вес в сечении х-\-Ах
составит w(x-\-Ax). Следовательно, из определения коэффициента
абсорбции Ь вес составляющей Z, перемещаемой со слоем, когда он
движется от сечения χ к сечению х-\-Ах, составит bwAx.
Поэтому
w (х) — w (χ+Δχ) = bwAx.
При Δχ->-0 получаем
или после интегрирования
w = w0e~bx,
где wo — значение w при х=0.

§ 8. Задача о сигарете
209
Так как вес, заключенный между сечениями χ и х-\-Ах, равен
bwAx, то вес, приходящийся на единицу длины в точке х, будет
bwAx , ,
— =bw0e-bx. (2)
ΖΛΛ-
Если в сечении х—Х прекращено курение сигареты, то, оче-
нндно, что это не влияет на результат анализа от сечения х=0 до
х=Х и дым идет через сечение л;=Х так же, как и раньше.
Вес части составляющей Ζ, которая проходит через сечение
χ ~Х, может быть найден путем вычисления количества, которое
могло бы находиться в интервале от х=Х до бесконечности, если
бы сигарета была бесконечно длинной. Таким образом, согласно
мыражепию (2), имеем:
J bw0e-bxdx=w0e-bx. (3)
χ
Аналогично, если сигарета имеет в интервале Ο^χ^ξ
коэффициент абсорбции бив интервале ξ^χ^Χ коэффициент
абсорбции β, то, подставляя их в уравнение (3), получим:
w = w0e-bx при Os^Ar^g,
w=We-t* при ξ^χ^Χ,
где постоянная W определяется из условия непрерывности w в
точке x=l·,, т. е.
w0e-b's=We-№
или
Вес, приходящийся на единицу длины в сечении х>|, будет
βΐϋοβ-^-Μ*-^ (4)
а вес, который проходит через сечение х—Х, составляет
а>0<гЫ-И*-а. (5)
Следовательно, отношение веса части составляющей Z, которая
проходит через сечение х=Х при наличии фильтра (5), к
аналогичному весу без фильтра (3) будет
е-(Э-ь) (χ-ΐ)_ (6)
Оно зависит только от длины фильтра, но не от длины сигареты.
В действительности задача более сложная, чем выше
рассмотренная.

210
Гл. VII. Линейные уравнения
Предположим, что сигарета имеет начальную длину / и конец
ее сгорает со скоростью ν, так что в момент времени / длина
сигареты l—vt (рис. 58).
Пусть W(x, t) —вес составляющей Ζ па единицу длины
сигареты в сечении χ в момент t, где χ измеряется от начального
положения с левого (горящего) конца сигареты при t — Ο. Вес Ζ на
единицу длины при горящем конце будет W(vt, t).
Горящий
коней
ι
л Vt , ■
1 "
!
X
Куриный
конец
Рис. 58
За время At сгорает кусок сигареты длиною vAt, содержащий
vAtW(vt, t) составляющей Ζ табака, часть которой avAt W(vt, t)
проходит в сигарету.
Согласно выражению (2), количество, заключенное между
сечениями χ и х-\-Ах, будет
abvAt W(vt, t)e~b^-^)Ax.
Поэтому общий вес, сохраненный дисперсией во время t между
сечениями χ и х-\-Ах, составляет
abv J Ψ(υτ, τ)β-^χ-Ώτ) dxAx=w(x, t)Ax,
(7)
причем он определяется функцией w(x, t). Общий вес в этом
сечении определяется добавлением W(x, 0)Δχ к количеству,
определяемому зависимостью (7), и в результате должен быть равным
W{x, t)Ax.
Следовательно,
t
W(x, t) = W(x, 0)+abve~bx§ W(vx, x)eb™dx.
(8)
Можно получить уравнение, из которого найдется функция
W(vt, t), подставляя в уравнение (8) x=vt.

$ 8. Задача о сигарете
m
Имеем:
W{vt, t)eb^ = W{vt, 0)eb*t+abv j" W(vx, x)eb™dx (9)
о
или, полагая
f(t) = W{vt,t)e™, (10)
уравнение (9) запишем в более компактном виде
f(t) = W(vt,0)el>*t+abvj f(x)dx. (11)
о
Уравнение (11) может быть решено дифференцированием.
Ограничимся случаем, когда начальная концентрация
постоянна— не зависит от х, т. е. W(x, 0)—Wo- Тогда дифференциальное
уравнение задачи после дифференцирования уравнения (11) будет
df(t)
—abvf(t)=bvW0ebvt.
dt
Решая это линейное неоднородное уравнение с учетом
соотношения (10), находим
W(vt, t) = -^- +Се-Ь('-<Ф",
где постоянная интегрирования С определяется из начального усло-
ния W{0,0) = WQ.
Отсюда
С= Wo- -^- = - -т^— Wo.
1—Ω Ι—Ω
Таким образом,
Wo
W(vt, 0= -гг~ [l-ae-bWt]. (12)
Подставляя это выражение в уравнение (8), окончательно
получаем
W(x, t) = W0[ l+-r?—е-Ъх{еш-еаШ) ].
Если ξ — длина сгоревшей части сигареты, так что ui=f|, то
W(x, t) = W0[ 1 + —^-e-b*(ebS-e<^) ].

512
Гл. VII. Линейные уравнения
Это выражение не зависит от скорости сгорания υ, что
принималось в третьей предпосылке.
Вес части составляющей Ζ, которая будет проходить через
конец сигареты при х=Х во время ее курения до сечения х=\, полу-
|
чается из уравнения (7), так как ί= —, с учетом соотношения (12):
со ν
J ш (*.-·) dx=ave~bx J W(vx, x)ehvxd% =
χ υ о
aWo е-ьх(е^-еаЪЪ). (13)
b(\-a)
При наличии фильтра наконечника в интервале ξ,^χ^,Χ при
х>|, учитывая соотношение (4), имеем:
w
(χ, ί)=α$υ\ Ψ(υτ, τ)е-ВД-чЬР<*-6)dx.
Таким образом, вес части составляющей, прошедшей через
сечение х = Х, равен
i
Ωϋβ-βΧ+(β-6)| J ψ(ΌΧι x)ebvx fa. (14)
о
Отношение веса части составляющей Z, которая проходит через
сечение х=Х при наличии фильтра (14), к аналогичному весу при
его отсутствии (13) составляет е-(Р-б) (-*-!). Это отношение совпадает
с отношением (6) и зависит только от длины фильтра, но не от
длины самой сигареты.

Глава VIII
ЗАДАЧИ, ПРИВОДЯЩИЕ К СПЕЦИАЛЬНЫМ
ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ПЕРВОГО ПОРЯДКА
(УРАВНЕНИЯМ БЕРНУЛЛИ, РИККАТИ, ЛАГРАНЖА
И КЛЕРО)
§ 1. УРАВНЕНИЕ БЕРНУЛЛИ
Дифференциальное уравнение Бернулли имеет вид
y'+P(x)y=Q(x)yn, (1)
где η — постоянная, не равная 0 или 1.
Это уравнение после деления на уп и введения переменной
Ζ= -ΙζΓ =у-"+* = У1-п (2)
У
решается, как обычное линейное уравнение первого порядка
относительно ζ. Обратной подстановкой получается общее решение:
ι
у=е ~/№ [ С+ (\-п) J Q(х)е ^«&* dx ] 1_я. (3)
Геометрические приложения
Задача 104. Нормаль отсекает на оси абсцисс отрезок, равный
квадрату радиус-вектора любой точки кривой. Найти уравнение
кривой, если она проходит через точку (0, 3).
Решение. Отрезок Хо, отсекаемый нормалью на оси Ох,
равен абсциссе точки пересечения нормали с осью Ох. Координаты
этой точки удовлетворяют системе:
dx
y-y°=-^y-(x-xJ'
ί/ο=0,
образованной уравнением нормали и уравнением оси Ох. Решая
систему, получим
, dy
Хо=Х+У1х--
Квадрат радиус-вектора любой точки равен xz-\-y2.

2k
Гл. VIII. Специальные уравнения
По условию задачи имеем дифференциальное уравнение
искомого семейства
которое преобразуется в уравнение Бернулли
Уравнение (2) приведем к виду
dy
* dx
и выполним замену
Л— ..«_< — ..-■> —у >
откуда
—yZ = XZ—X (3)
yn-i и-г
г- , dz
y=iz и dy= —. (4)
2iz
Подставляем значения (4) в уравнение (3) и тогда получаем
линейное уравнение
dz—2zdx=2 (χ2—χ) dx,
которое в результате подстановки z=uv, dz=vdu-{-udv приводится
К виду
и (dv—2vdx) -j-vdu=2 (xz—x) dx.
Будем искать такую функцию и, которая обращала бы в нуль
первое выражение в скобках. Для этого решаем уравнение
dv—2vdx=0,
откуда вспомогательная функция
и=е2х.
Тогда
eZxdu=2(xz—x)dx
и
f (χ2—χ) f хЧх f xdx
Интегралы в правой части последнего равенства находятся
интегрированием по частям:

§ 1. Уравнение Бернулли
215
2 J JLfL = _ J e-z^c? (_2χ) = —xe~2*+ J e-»*dx=
=-(х+т)е"2х'
2 f ^ =— \е-**хЧ(—2х)=—х2е-г*— \e~^xd{—2x) =
= -(X2+x+±)e-2x,
чЯорая вспомогательная функция
u=C—x2e~2x.
Тогда
z=uu = Ce25C—χ2,
а общее решение дифференциального уравнения (2) ввиду
соотношения z=y2 примет вид
х2+у2=Се2х.
Дополнительное условие: кривая проходит через точку (0, 3),
откуда
02+32=Се20
или
С=9.
Уравнение искомой кривой
х2-|-1/2=9е2ж.
Задача 105. Среднее геометрическое координат точки касания
равно отношению отрезка, отсекаемого касательной на оси ординат,
к удвоенной ординате точки касания. Найти уравнение кривой, если
она проходит через точку (1, 1).
Решение. Среднее геометрическое координат точки касания
У ху. Отрезок, отсекаемый каеательной на оси Оу, равен ординате
точки пересечения касательной с осью Оу. Координаты этой точки
удовлетворяют системе
dy ,
У-Уо=~£^(х-Хо),
хо=0,
образованной уравнением касательной и уравнением оси Оу. Решая
систему, получим

216
Гл. VIII. Специальные уравнения
dy
По условию задачи получаем уравнение
dy
— y~X~dT
У**=—^. (1)
которое является дифференциальным уравнением искомого
семейства. Уравнение (1) может быть представлено в виде
_ffc Ly=2x-lyl. (2)
dx χ
Это уравнение Бернулли.
Общее решение этого уравнения
х—у(х—С)2=0. (3)
Дополнительное условие: кривая проходит через точку (1, 1),
откуда
1-1(1-С)2=0
и
Ci=0; C2=2. (4)
Получаем две искомые кривые:
ху=\ и х—у(х—2)2=0.
§ 2. УРАВНЕНИЕ РИККАТИ
Дифференциальное уравнение Риккати имеет вид
y'=P(x)y*+Q(x)y+R(x). (1)
Уравнение (1) в общем случае не интегрируется в квадратурах,
т. е. нахождение его решения не может быть сведено к конечному
числу последовательных интегрирований.
Возможны следующие способы определения общего решения:
1) если известно одно частное решение уу уравнения (1), то
подстановка
, 1
У=У1+-£-,
где ζ — новая переменная, приводит уравнение Риккати к линей
ному уравнению;

§ 2. Уравнение Риккати
217
2) если известны два решения ух и у2, то zt= будет
ί/2—ί/ι
частным решением линейного уравнения относительно 2, что
позволит упростить его интегрирование;
3) если известны три частных решения yit y2 и у3, то общий
интеграл будет
У—Уг . Уг—Уг =Q
У—yi ' ί/з—ί/ι
Уравнение Риккати заменой переменных (/= ——— —|-β (-*■)
сводится к более простому виду
du ~, ■,
что облегчает нахождение общего интеграла исходного уравнения.
Падение тел
Задача 106. Тело массы m падает под действием силы тяжести
в среде, оказывающей сопротивление, пропорциональное квадрату
скорости падения. Найти закон движения тела.
Решение. Пусть s — расстояние, пройденное телом к
моменту t. Тогда движение определяется уравнением
d2s , 1 ds \2
m4t^-ms-k\~dTh
которое может быть представлено в виде
dz
dv
m-—=mg-kv2, (1)
ds
где скорость и=——-. Дифференциальное уравнение (1) является
уравнением Риккати.
Разделяя в нем переменные, имеем
mdv ,_,
■ ——- =dt
mg—kv2
или после сокращения левой части равенства на m

218
Гл. VIII. Специальные уравнения
Интегрируя это равенство, получаем
dv
g y2
m
= t+d. (2)
Для вычисления интеграла в левой части уравнения' (2)
применяем метод неопределенных коэффициентов, и тогда
dv (* Αάυ С* Bdv .„.
+ Ι ;ζζ—. \ά)
J*-»- )iH-l· J^+yi»
откуда
или
m ν ι m
A+B: l
A — B-.
Is
1
2fg
Подставляя найденные значения коэффициентов в интеграл
(3), имеем
'(*+Vjl·)
d(g-V^v)
Х V m =t+c,
8-
■V#-v
Г т
Для краткости обозначим у —— =г. Тогда после умножения
равенства на 2 I/ находим
t m
Г d(g+rv) f d(g-rv)
=2r(/+d)
g+rv g—rv
или
In (g+rv) —In (g—rv) =2rt+2rCu

§ 2. Уравнение Риккати
219
откуда
lnJ?±i5 2Г/+С·.
g—rv
где C*=2rd.
Потенцируя уравнение (2), получаем
g-\-ri) _e2rt+C* _£** e2rt
g—rv
ИЛИ
g+rv= (g—rv)C**e2rt,
откуда
rv (C**e2ri+1) —g (C**e2rt— 1)
и искомая функция
r**en \ en ί )
g (C**e2rt— 1) r2m V C**e»·' '
(4)
rm ert—Ce~rt
~~k ert+Ce~rt '
1 r2m
^ C= —, a * = —.
Из уравнения (4) очевидно, что при t, стремящемся к
бесконечности, скорость ν достигает предельного значения
Umax = V,
для которого
Следовательно, уравнение (4) записывается в виде
/ е*—Сег* \ ...
V = V\ en+Ce-n )· (5)
Начальное условие: при t=0 ν = υ0.
Пусть ради краткости записи ыо= ~тг· Тогда постоянная
интегрирования С в уравнении (5) принимает значение
η - 1—"о
1+«о

220
Гл. VIII Специальные уравнения
Подставляя это значение в уравнение (5), замечаем, что υ
может быть записана в виде
/ uo+thrt ν
' ^ 1 +ио th rt ι
Принимая, что при i=0 s—О, можем теперь определить s:
i
f V
s= J v(t)dt= · ln(ch rt-\-Uo sh ri).
о r
Подставляя r= —— и Ыо= —^- в это равенство, окончательно
получаем искомый закон движения
s= In
(ch__ + ___sh_j.
§ 3. УРАВНЕНИЕ ЛАГРАНЖА
Дифференциальное уравнение Лагранжа — это уравнение типа
χ=φ(ί/, (/') или ί/=ψ(χ, </)> ис разрешенное относительно
производной искомой функции.
Вид уравнения Лагранжа
а(у')х+Ь(у')у+с(у')=0, (I)
где а (у'), Ь(у'), с (у') —функции у'.
Уравнение (1) интегрируется подстановкой
/ dy
У'= ± =Р,
после выполнения которой, разрешая уравнение (1) относительно у,
получаем
ί/=*φ(Ρ)+ψ(ρ)·
Величина ρ рассматривается как вспомогательная переменная.
Продифференцировав это уравнение по р, получим уравнение
dx
[ρ-φ(ρ)1 -^--φ'(ρ)*-ψ'(ρ)=ο>
линейное относительно х.

§ 3. Уравнение Лагранжа
221
Общий интеграл уравнения
К
(Ρ)ιίρ
х=е р-ф(р)
J />-<р
(ρ)
~Μ
(p)dp
р-ф(р) flip
].
(2)
Исключая из уравнения (2) ρ, получаем общий интеграл
исходного уравнения.
Поверхность вращения, фокусирующая параллельные
световые лучи
Задача 107. Какую форму должен иметь меридиан поверхности
вращения, чтобы световые лучи, падающие на эту поверхность
параллельно оси вращения, после отражения сходились в одной точке
на оси вращения.
р
5/^
\
f
У
/ 1 \\
с 4 1 \
\V I а"
Рис. 59
Решение. Пусть фокус будет началом принятой нами
системы координат (рис. 59). Луч Ρ падает в точку Μ поверхности и,
отразившись, проходит через фокус F. В точке Μ проводим
касательную, пересекающую ось абсцисс в точке Q, и нормаль,
пересекающую ось абсцисс в точке S.
Пусть α — угол между касательной и положительным направ-
лепием оси абсцисс.
Тогда
Z.FSM = a-Z-SMQ = ее- -£-,

222
Гл. VIII. Специальные уравнения
так как внешний угол треугольника равен сумме внутренних непри-
легающих углов.
Далее
/LSMΡ = ZJSM = α- γ,
так как это накрест лежащие углы, образуемые пересечением
прямой параллельных линий;
Z.SMF=/LSMP = a- γ
на основании теоремы об углах падения и отражения лучей;
/_QFM = /_FSM+/_SMF,
так как внешний угол треугольника равен сумме внутренних непри-
легающих углов, или
/LQFM—a —+α— — =2α—π.
Обозначая координаты точки Μ через хну, имеем:
У
Как известно,
χ =tg(2a—Ji)=tg2a.
tg2a= St"
l-tg2a '
но, с другой стороны,
tg a=y'.
Поэтому
χ Ι—ι/'»
или
Это уравнение Лагранжа. Дифференцируя обе части
равенства (1), имеем:
у_21-г2+ (1-у2)2 у-
Пусть
dp
у'=р, у"--
ах

§ 3. Уравнение Лагранжа
223
Тогда
dx __ 2х
Ύ/Γ^ р{\—р2)
или после разделения переменных
f dx = f 2dP (о)
J x J p(\-p2) · K '
Преобразуем интеграл в правой части равенства (2):
f Ыр Г
2pdp
p№-\) j Рг(р2-\)
Применяем подстановку
p2=t, 2pdp=dt.
Тогда
f- 2dP = f dt =\ (J L) dt=
J р(рг-\) J t(t—\) J W-l / /
. /-ι p2-i
= 1П ; =1Π·
|2
t ρ
Подставляя полученное значение в равенство (2), после
интегрирования, полагая С=—In а, имеем
р2—1
In л:—In α=1η
Ρ2
откуда
л: ρ2— Ι
в
α ρ
ρ2—1
х=а-^-. (3)
Из уравнения (1) получаем
ρ ρ2—1 /7 2α
1—/72 /72 Ι—ρ2 ρ
или
2α .

224
Гл. VIII. Специальные уравнения
Это выражение подставляем в уравнение (3):
4а2
х—а-
У2
■—1
1а1 '
~УТ
отсюда
у2=—4ах-\-4а2.
Итак, меридиан описывается уравнением параболы, симметрич
ной относительно оси абсцисс. (Ср. с задачей 84.)
§ 4. УРАВНЕНИЕ КЛЕРО
Дифференциальное уравнение Клеро имеет вид
у=хр+$(р), (1)
где
dy
р= Ύχ-
Уравнение (1) является частным случаем уравнения Лагранжа.
Общий интеграл уравнения Клеро находится путем
подстановки вместо ρ произвольной постоянной С, т. е.
у=Сх+у(С).
Особое решение (см. гл. I) находится исключением ρ из
уравнений:
*+ψ'(ρ)=0, 1
ι/ = χρ+ψ(ρ). J
Геометрические места точек
Задача 108. Найти кривую, если произведение перпендикул>-
ров, опущенных из двух данных точек на касательную в любой
точке, имеет постоянную величину ±й2.
Решение. За ось абсцисс принимаем прямую, проходящую
через данные точки Μι и М2. Начало координат — в середине отрез
ка ΜιΜ2.
Пусть М1М2=2с. Тогда точки Мх(с, 0) и М2(—с, 0) лежат пг
одну сторону от касательной. В этом случае длины перпендикулг
ров имеют одинаковые знаки и получаем уравнение

§ 4. Уравнение Клеро
225
1+р
ИЛИ
(и—хр)2—с2р2
у=хр+1/а2р2+Ь^, (2)
где
#Ч-с2=а2.
Общее решение уравнения Клеро (2) имеет вид
у=Сх+1а2С2-\-Ь2. (3)
Ответ задачи дает его особое решение, которое находится
путем исключения С из уравнения (3) и уравнения, которое
получается из уравнения (3) дифференцированием по С, т. е.
а2С
0=х+
У а2С2-\-Ь2
откуда
х== ■ (4)
У а2С2+Ь2
Подставляем это значение χ в уравнение (3):
Ь2
У= —=^~. (5)
У а2С2+Ь2
Исключая С из уравнений (4) и (5), получаем уравнение
х2 у2 а2С2-\-Ь2
а2С2+Ь2
эллипса с фокусами в данных точках.
В случае, когда данные точки лежат по разные стороны от
касательной, надо в правой части уравнения (1) поставить минус.
Поступая аналогично и обозначая с2—Ь2=а2, получим
уравнение гиперболы
jc2 У1_=1
Задача 109. Найти кривую, если геометрическое место середин
отрезков касательных, заключенных между осями координат, есть
/
прямая y=kx-\- —.

zzo
Гл. VJJI. Специальные уравнения
Решение. Координаты середины отрезка будут
Xt
ρχ—y
2р '
Yt
η=-2- =
y—ρχ
Здесь Xt ■— отрезок, отсекаемый касательной на оси Ox; Yt —
отрезок, отсекаемый касательной па оси Оу; p = y'=tg a.
Так как точка (ξ, η) описывает заданную прямую, то
У—рх _иРх~У ι 1
~~2T~-k~^p~ + T
или
у=рх+
1р
k+p ■
(1)
Уравнение (1) представляет уравнение Клеро, особое решение
которого
Ы
у--
(k+p)2 ■
дает в параметрической форме решение задачи.

Глава IX
ЗАДАЧИ, ПРИВОДЯЩИЕ К ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЯМ ВТОРОГО ПОРЯДКА, РАЗРЕШЕННЫМ
ОТНОСИТЕЛЬНО ВТОРОЙ ПРОИЗВОДНОЙ (/' = С)
§ 1. СКОЛЬЖЕНИЕ ТЕЛА ПОД НАКЛОНОМ
Задача 110. По наклонной плоскости длиной /=10 м скользит
тело А (рис. 60). Угол наклона плоскости а = 45°. Коэффициент
трения тела по поверхности плоскости k = 0,5. Определить закон
движения тела и время, в течение которого тело пройдет вдоль всей
наклонной плоскости, если в начальный момент оно находилось
в покое на верхней грани этой плоскости.
Решение. В любой момент t на тело действуют три силы;
вес Р, сила трения F и реакция плоскости Νι. Нормальная и
тангенциальная составляющие Ν η Τ силы Ρ равны
N = Pcosa, T~P sin a.
Как известно, сила трения
F——kN——kP cos a.
Действующие силы Ρ, F, Nt заменяем эквивалентной системой
сил Τ и F (так как силы Ν η Νι взаимно уравновешиваются, а
система сил Τ, Ν эквивалентна силе Р). Равнодействующая
эквивалентной системы
R = T+F
или
R = P sin a—kP cos a
действует по направлению движения.
С другой стороны,
d d2s
P=mg, R = m
откуда дифференциальное уравнение движения
d2s
=g(sin a—k cos a).
dt2
Это уравнение типа у"=С.
Решая его непосредственным интегрированием, получаем
ds
g(sin a—k cos a)t-\-Cx
dt

228
Гл. IX. Уравнение у" = С
и общее решение
s= — (sin α—k cos α) i2-fCif-fC2.
Постоянные Ct и С2 определяем из начальных условий: при
ds
t=0 s=0 и ——- =0. Получаем систему
0=g(sin α—k cos α) -Ο+Ci,
0= -|- (sin a—ft cos a) -O+Ci-O+Ca,
ЩЩйЯГ
Рис 60
откуда
Ci=C2=0.
Подставляя эти значения в общее решение, получим искомый
закон движения
s= — (sin a—k cos α)ί2.
(1)
Для определения времени прохождения тела вдоль плоскости
подставляем в уравнение (1) числовые данные
s= -|- (sin 45°-0,5 cos 45°) t2= —- Ρ
2 о
(2)

§ 2. Движение в плоскости
229
И решаем уравнение (2) относительно t:
g
При s=/=10 м искомое время соскальзывания тела
§ 2. ДВИЖЕНИЕ В ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ
ПРИ СОПРОТИВЛЕНИИ, ПРОПОРЦИОНАЛЬНОМ СИЛЕ ТЯЖЕСТИ
Задача 111. Электровоз движется по горизонтальному
железнодорожному пути со скоростью 72 км/ч. Машинист включает тормоз
и сопротивление движению после начала торможения равно 0,2 веса
электровоза. Найти время от момента включения тормоза до полной
остановки электровоза и расстояние, пройденное за это время.
Решение. Пусть m — масса электровоза. Тогда сила тяже-
с'ш электровоза
P=mg, (1)
где g — ускорение силы тяжести. Расстояние, пройденное центром
тяжести электровоза после начала торможения, есть неизвестная
функция времени s=/(f).
Скорость движения электровоза
а ускорение
а=чг="ж- (2)
На основании второго закона Ньютона (произведение массы
на ускорение движущегося тела равно действующей на него силе)
та=-0,2Р, (3)
1де минус указывает, что сила торможения направлена против
движения электровоза.
Подставляем значения (1) и (2) в уравнение (3), откуда
dP-s
m~^-=—0,2mg
ΙΙ.ΊΙΙ
d2s
dt2
u =
dv
ds
dt
>
d2s
—0,2g. (4)

230
Г л IX. Уравнение у" = С
После первого интегрирования уравнения (4) получаем
ds
~dT
= u=-0,2gJrfi+Ci = -0,2gi+Ci. (5
Начальное условие: при t=0 начальная скорость электровозг
(в начале торможения) ио=72 км/ч = 20 м/сек. Отсюда'
20=-0,2^-0+С!
и
d = 20. (6
Подставляем значение постоянной интегрирования (6) в равеь
ство (5) и получаем уравнение скорости
-~=O=-0,2gt-\-20. (7
η t ds t
В момент t остановки электровоза его скорость ν= ~τ— = 1
Подставляя это значение в уравнение (7), находим искомое BpeMf
остановки электровоза
f--Jg-= 20 ^Ю2 се/с
l- 0,2g 0,2-9,81 ~™>гсек-
Интегрируем далее уравнение скорости (7) и получаем
s= J (-0,2^+20)^+C2=-0,lg/2+20i+C2.
Начальное условие: при t=0 s = 0. Следовательно,
0=-0,lg-02+20-0+C2
и
С2=0.
Тогда уравнение пройденного электровозом пути будет
s=-0,l^2+20i.
За время ί=10,2 сек электровоз пройдет расстояние
s« -0,1-9,81 ·10,22+20·10,2« 102 л.
Таким образом, электровоз остановится через 10,2 сек, пройдя
после начала торможения расстояние 102 м.

§ 3. Выброс вверх
23
§ 3. ВЫБРОС ВВЕРХ (БЕЗ УЧЕТА ТРЕНИЯ)
Задача 112. Тело брошено вертикально вверх с начальной
скоростью υ0. Определить закон движения, предполагая, что тело
движется только под влиянием силы тяжести.
Решение. Под влиянием силы тяжести тело движется с
постоянным ускорением, равным g. Ввиду того, что ускорение
выражается производной второго порядка от пути по времени,
дифференциальное уравнение (после сокращения на массу) в данном
случае
d'is /η
-w=-*· (1)
Интегрируя дважды, получим
dS =-gt+Cu (2)
dt
откуда
s= J" (-gH-Ci)d/=- -ψ- +Cii+C2. (3)
Постоянные d и С2 определяем из начальных условий.
Так как отсчет пути ведется от начального момента, то при
t — 0 s=0 и, следовательно, C2=0.
„, , ds
Так как при г=0 начальная скорость υο= —тг, то из
уравнения (2) получаем
C1=v0.
Итак, зависимость пройденного телом пути s от времени t:
gt2
§ 4. РАСПРЕДЕЛЕНИЕ ТЕПЛОТЫ В СТЕРЖНЕ
Задача. 113. Стержень длиною 2/ и площадью поперечного
сечения S на концах имеет одинаковую температуру ί0. По стержню
. /
проходит ток постоянной величины /, плотность которого ι= —.
Найти распределение теплоты по стержню, если максимальная
температура в центре стержня tmax. Пренебречь потерей теплоты
и окружающую среду.
Решение. Рассмотрим элемент стержня dx (рис. 61). Поток
dt(x)
Ί оплоты через сечение ΚΚι по закону Фурье — XS—-—, а через

232
Τ л IX. Уравнение у" = С
dt(x-\-dx)
сечение LLi составит — XS . Различие этих потоков обует
ловлено нагреванием элемента стержня током, выделяющим
теплоту в количестве
pi
0,24PR = 0,24i2S2-
S '
где ρ — удельное электрическое сопротивление.
К L
1
I
χ ι+dx
Рис. 61
При установившемся состоянии
dt{x+dx) dt{x) pi
-XS ■ -IS —.— = 0,24i2S2 -V
dx dx S
откуда дифференциальное уравнение задачи
d4(x) 0,24i2p/
dx2'
λ
(1)
(2)
Обозначая для краткости правую часть равенства (2) симво
лом А, имеем:
d4(x)
(3)
dx2
•=А.
Интегрируя это уравнение дважды, получим
t(x)=Ax2+CiX+C2.
(4)
Начальные условия: при х=0 t=t0 и при x=l i=imax
dt
и ■——- =0. Отсюда
dx
Ci=-2Al, C2=0. (5)

§ 5. Расстояние между фермами моста
233
Найденные значения постоянных интегрирования подставляем
N уравнение (4), откуда искомое распределение температур по
Стержню
t(x)=Ax2-2Alx+t0.
§ 5. РАССТОЯНИЕ МЕЖДУ ФЕРМАМИ
ЖЕЛЕЗНОДОРОЖНОГО МОСТА
Задача 114. Расстояние между рельсами железнодорожного
Пути с=1,6 м. Наибольшая нагрузка от паровоза на каждый рельс
Составляет Р=9 Т. Поперечный брус железнодорожного моста
лежит на двух фермах, расположенных на расстоянии / друг от друга.
Момент инерции площади сечения бруса 7=45 000 еж4, модуль
упругости £=105 кГ/см2. Найти расстояние I между фермами из
условия, чтобы допустимый прогиб поперечного бруса в середине
рпииялся 0,2 см.
Решение. Задача требует определения упругой линии балки
И нычисления прогиба в ее середине. Мерой изгиба балки может
служить кривизна ее упругой линии. В курсе сопротивления
материалов выводится формула радиуса кривизны Д упругой линии для
оллок любого сечения, которая имеет вид
*=-Щ*)~' (1)
где £ — модуль упругости балки, / — момент инерции поперечного
сечения относительно нейтральной оси,* М(х)—изгибающий
момент для данного сечения, равный алгебраической сумме моментов
относительно нейтральной оси всех внешних сил, приложенных
к брусу с одной стороны сечения (справа или слева).
Обычно изгибы балок чрезвычайно малы, и упругая линия мало
отклоняется от оси абсцисс. Поэтому в любой ее точке угловой коэф-
фпциент касательной —,— весьма мал, и в известном из диффе-
ренциалыюго исчисления выражении для радиуса кривизны
R— . можно пренебречь величиной у'2.
Отсюда на основании формулы (1) получаем
дифференциальное уравнение упругой линии в упрощенном виде
_J EJ
У" ~ М(х)
* Нейтральной осью данного сечения балки называется прямая пересечения
нейтрального слоя с плоскостью данного сечения. Нейтральный слой — слой, в
котором волокна балки не деформируются (не растягиваются и не сжимаются) под
действием сил.

234
Гл. IX. Уравнение у" = С
ИЛИ
«/"=
Μ (χ)
~εΊΓ~'
Очевидно, что
M(x)=EJy»=EJ-2r
Поперечный брус представляет собой балку на двух опорах /
и В, нагруженную двумя сосредоточенными силами Р, приложен
ными в точках D и Е.
Цшшмшт.'шипЙ
мго—м!
Рис. 62
Реакции опор N=P.
Для любого сечения F па участке DE (рис. 62) изгибающш
момент
М = Р(1—а—х)—Р(1—х)
или
М=— Ра.
Дифференциальное уравнение упругой линии принимает вид
dly Pa
dx2
EJ
(2)
Интегрируя уравнение (2), как уравнение типа у"=С, получим
общее решение
^-^r(4-+Ci*+C2)· (3)
Из начальных условий *=0, у=0 и х = 1, у—0 следует
(4)
С2=0.

§ 5. Расстояние между фермами моста
235
Подставляя выражения (4) в общее решение (3), получим
урпвнение упругой линии участка DE:
Pax ,
У=~2ЕГ{1-Х)-
I
При х= — прогиб середины поперечного бруса
Pal2
Так как 1=2а-\-с, то
/l=~s£ra(2a+c)2·
Преобразуя это кубическое уравнение, получим
8>EJh
4a3+4ca2+c2a =0. (5)
Подставляем числовые данные. Тогда уравнение (5) примет вид
a3+160a2+6400a-200 000=0.
тт а
Для упрощения вводим новую неизвестную z= - — или иначе
а = 10г. Тогда
1000г3+16 000г2+64 000г-200 000=0.
Сокращая на 1000, получим
23+16г2+64г—200 = 0.
Разлагаем левую часть последнего равеяства на множители:
(2-2)(22+18г+100)=0. (6)
Алгебраическое уравнение (6) имеет три корня: Ζι=2 и два
комплексных корня z-i и 23, которые не соответствуют физическому
смыслу рассматриваемой задачи.
Таким образом,
а= 102=20 см,
и искомое расстояние между фермами
Z=2a+c=2-20+160 = 200 см=2 м.

Глава X
ЗАДАЧИ, ПРИВОДЯЩИЕ К НЕПОЛНЫМ
ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ВТОРОГО ПОРЯДК
Общий вид дифференциального уравнения второго порядка
F(x,y,y',y")=o.
Разрешив его относительно второй производной (если это во'
можно), получим
y"=f(x,y,y')-
В приложениях часто встречаются следующие пять специаль
ных типов уравнений, называемые неполными дифференциальным
уравнениями второго порядка
U"=f(x),
y"=f(y),
y"=i{y'), \ (i
y"=f(*,y'),
y"=f(y,y').
Уравнения (1) решаются методом понижения порядка, т. е
введением новой искомой функции
dy r
Тогда
dp
У =~
dx
или (во втором и пятом случаях при наличии у)
dp dp dy dp
У
dx
dy dx
= ~dfP-
(2
(3
(3a
Подстановка значений (2) и (3) или (За) в уравнения (1) свс
дит их к уравнениям первого порядка
dp=f(x)dx,
pdp=f{y)dy,
dp =dx,
f(P)
dp=f(x, p)dx,
pdp=f(y,p)dy.
(4

§ I. Переходная кривая
237
Общее решение уравнении (4) имеет вид
р=ц>(х)+С
или
Используя зависимость (2), получаем уравнение
или
dy
dx
=Ш+С-
I. УРАВНЕНИЯ ТИПА у" =/(JC)
§ 1. ПЕРЕХОДНАЯ КРИВАЯ ЖЕЛЕЗНОДОРОЖНОГО ПУТИ
Задача 115. Найти уравнение кривой железнодорожного пути,
переходящей плавно от прямого направления к круговому, если
длина переходной кривой /, а радиус кругового пути г.
Решение. Кривизна переходной кривой — равномерно из-
1 R
меняется от пуля до — (рис. 63).
Следовательно, -=- =ks, где k — коэффициент пропорциональ-
ности, s — длина дуги от начала переходной кривой до текущей
точки М(х, у).
Коэффициент k определяется из условия: при s=l — = —■
А Г
откуда
1
г
h=
1
R ~
= М
1
rl
s
rl '
Итак, имеем:
Переходная кривая по всей длине I незначительно отклоняется
от оси абсцисс, и величину 5 можно заменить абсциссой χ точки М.

238
Гл. X. Неполные уравнения второго порядка
Следовательно, угловой коэффициент касательной —г— в точке
Μ будет очень мал, и поэтому в дифференциальной формуле
кривизны
1
У"
R (1+гг2)''*
величиной у2 можно пренебречь.
Прямолинейный
пщпь
Рис. 63
Таким образом, полагаем s=x и
Упрощенное дифференциальное уравнение переходной кривой
χ
У" =
rl
Общее решение этого уравнения
У=
6rl
+ Cix+C2.

§ 2. Прямолинейное движение точки в горизонтальной плоскости 239
Начальные условия: при х=0 у—0 и г/=0, откуда
С1=0, С2=0.
Подставляя эти значения в общее решение, находим искомое
уравнение переходной кривой
у—
Ы
§ 2. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
В ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ
Сила зависит от времени: F = F(t)
Задача 116. Вожатый трамвая, выключая постепенно реостат,
увеличивает мощность вагонного двигателя таким образом, что
сила тяги возрастает от нуля пропорционально времени,
увеличиваясь на 120 кГ в течение каждой секунды. Найти закон движения
вагона, если сила тяжести вагона Р= 10 Т; сопротивление трения
постоянно и равно 200 кГ; начальная скорость равна нулю.
-7(ШкГ Ж
Рис 64
Решение. Центр тяжести вагона движется по
горизонтальной прямой. Начало координат поместим в начальное положение
центра тяжести вагона (рис. 64). Проектируя внешние силы,
приложенные к вагону, на ось абсцисс, получим силу тяги, равную 120Z,
и силу сопротивления, равную 200 кГ, где t — время с момента
выключения реостата. На основании второго закона Ньютона запишем
дифференциальное уравнение движения вагона
Ρ άϊχ
—^-=120ί—200. (1)
g at2
Начало движения вагона не совпадает с моментом выключения
реостата. Время ίο соответствует началу движения и определяется
из условия равенства силы тяги и силы сопротивления
120/о=200,
откуда
5
ta= — сек.

240 Гл. X. Неполные уравнения второго порядка
Для удобства вычислений величину 120ί—200 обозначим через
120ii. Тогда
ίι_/—"Ϊ20 — ^ 3'
где ί — время начала выключения реостата.
Дифференциальное уравнение (1) примет вид
Ρ d2x
120fi=0. (2)
g dP
Интегрируя уравнение (2), получим
dx 120g U2
dU~ Ρ 2 +Cl- (3>
dx
Определим постоянную интегрирования С ι. При ίι=0 -^-=0.
Отсюда
С ι=0.
dti
Интегрируя уравнение (3), находим общее решение
уравнения (2):
,-»&-. «-+0 (4,
Определяем величину Сг. При ti=0 х=0. Следовательно,
С 2=0.
На основании равенства (4) находим решение уравнения
движения вагона
_ 120£ /, 5 \*_ 120-9,81 / К \3
или
6Р ^ 3 ' 6-10 000 \ 3 '
x=0,01962 ( ί 1~ )3ж·
Сила обратно пропорциональна кубу расстояния
Задача 117. Найти закон движения материальной точки массой
m по прямой ОА (рис. 65) под действием отталкивающей силы,
обратно пропорциональной третьей - степени расстояния точки
х=ОМ от неподвижного центра О.
Решение. Дифференциальное уравнение движения точки,
согласно второму закону динамики,

§ 2. Прямолинейное движение точки в горизонтальной плоскости 241
m
d4
χ3 '
где k — коэффициент пропорциональности.
Уравнение (1) можно представить в виде
пли
d4
dP
k 1
m x3
x"=a2Ar
χ3
(О
χ*
Μ
Hg>
Рис. 65
Умножим обе части уравнения на 2x'dt:
x'nt
2x'x"dl = 2a2-^^-.
χ3
Левая часть последнего равенства есть дифференциал от х'2:
*(д*)=:2*-£.=а*/(- -L-);
отсюда
а? х2—С,
х'=±
fc'i
или
dx a
'х2—С1
χ
l/x2-Ci
Разделяя переменные, получим
xdx a
fx^d
dt.
У С!
(2)

242
Гл. X. Неполные уравнения второго порядка
Решая уравнение (2), придем к равенству
Г xdx a
Окончательно
или
ix2—d
1С,
{t+Сг).
jX2-Cl=± (Ч-С2)
1С]
χ2—Cr-
~с~7
(t+C2)*.
§ 3. УПРУГАЯ ЛИНИЯ БАЛОК
Консоли
Задача 118. Консольная стальная балка длиной /=6 м
нагружена сосредоточенной силой Р=2Т в конце В (рис. 66). Найти
уравнение упругой линии (кривой изгиба) и определить величину
прогиба конца балки (модуль упругости £=2100 000 кГ/см"1,
/=30 000 см'').
Рис. 66
Решение. Определяем изгибающий момент Μ для Ъечения
с центром в точке Ν(χ, у) (рис. 66). В данном случае Μ равен
моменту силы Ρ относительно точки Ν, взятому со знаком плюс (сила
приложена к балке справа от сечения и вращает правую часть
балки по часовой стрелке), т. е.
М = Р(1-х).
(1)

§ 3. Упругая линия балок
243
Подставляя выражение (1) в уравнение (2) задачи 114, полу-
ί.ιομ дифференциальное уравнение упругой линии
Непосредственным интегрированием находим
dy Ρ С Ρ (1-х)
г ρ (1-Х)2
J {i-x)d{i_x)==_ ir^+Ci,
dx EJ ч ' ч ' EJ
откуда общее решение
ρ (1-х)3
у= -Ej- · —^- +Cix+c2. (3)
Константы С\ и С2 определяем из начального условия: на заде-
dy
ланном конце х=0, у=0 и --— =0. Отсюда
dx
Ρ I3 ^
и окончательно
Ρ I2
°—it·—+c-
Ρ I2 PI3
(4)
Ci= ——— ■ —г—, Сг= —
EJ 2 ' EJ 6 '
Подставляя значения Ct и С2 в общее решение (3), получим
искомое уравнение упругой линии
»=-ш-(^-г)· (5)
Прогибом балки называется ордината упругой линии в
рассматриваемом сечении. Величина прогиба h на конце балки В
получается из уравнения (5) при х=1:
h=-L.lp-JL)
Р13
2EJ V 3 / 3£/'
Подставляя числовые значения и приводя их к единой
размерности, находим величину прогиба
и — 2000-6003 _
Н~ 3-2 100 000-30 000 ~2'асМ-

244
Гл. X. Неполные уравнения второго порядка
Задача 119. Труба для стока воды выходит из стены на длину .
Внутренний диаметр трубы й?=16 см. Толщина стенки 2 см. Челг
должна равняться длина /, чтобы прогиб на конце трубы /г=0,5 см
Удельный вес стали γ=7,8; модуль упругости £=2· 10е кГ/см2.
Решение. Трубу можно рассматривать как консольную ба/·
ку, нагруженную равномерно распределенной нагрузкой q. На
элемент трубы d% (рис. 67) действует элементарная нагрузка qd%.
wL·/».
ξ
dS
k
</'
i"?
1 V\\\\\\\v\\
Рис. 67
Ее момент относительно точки N равен <?(£—x)dl·,, откуда
изгибающий момент
М=) q(l—x)d£=q .
X
Подставляя это значение в дифференциальное уравнение
упругой линии,получим
&У _ Я „ .ч2
dx* 2EJ (/ Х)К
Интегрируя уравнение (1), находим общее решение
(/-x)4+CiX+C2.
У=
24EJ
(О
(2)
Начальные условия: в заделанном конце балки х=0, у=0,
у'=0, откуда
ql3 ^ qlk
Ci=
6£/'
С2=-
24£/ '
(3)
Подставляя значения (3) в общее решение (2), запишем иско
мое уравнение упругой линии
У-
24£/
(б/2*2—Ш3+хк).

§ 3. Упругая линия балок
245
Прогиб на конце
"=-^ffir<6/,-4"+">=w· <4)
Решая уравнение (4) относительно искомого I, получим
., 8E~Jh
1-
Определяем нагрузку q и момент инерции /.
Пусть <7ι — вес 1 см трубы; <7г — вес воды на 1 см длины трубы.
Тогда общая нагрузка q = ql-\-q2. Так как
qi== ~ (202-162)7,8=882 Г/см,
<72=-^-162· 1=201 Г/см,
то
<7=1083 Г/см= 1,083 кГ/см.
Момент инерции круга относительно диаметра d равен -z-r-.
64
Таким образом, момент инерции относительно нейтральной оси
площади поперечного сечения трубы
/= ~ (204-164)=4710 см\
64
Подставляя найденные и данные величины в уравнение (5),
найдем искомую длину трубы
у±*
106·4710·0,5
— =431 см.
1,083
Балки на двух опорах
Задача 120. На двухопорную балку ОА длиной / действует
сосредоточенная сила Р, приложенная к точке В на расстояниях U и h
от концов. Найти уравнение упругой линии и определить прогиб h
в точке В.
Решение. Для определения неизвестных опорных реакций
Νι и N2 напишем в точках О и А уравнения моментов действующих
сил относительно этих опор:
Nil=Pl2 и Nzl=Plu

24b
Гл X. Неполные уравнения второго порядка
откуда
*~^ »*~Ц-
Составим уравнение для изгибающего момента.
I
Рис 68
В любом сечении С(х, у) части ОБ балки (рис. 68) получим
Μ=Ρ(Ιι-χ)—Ν2(1—χ)
или
M=P(h-x)-
Ph
I
(1-х).
В любом сечении D(|, η) части ΒΑ балки имеем:
Μ=-Ν2(1-1)=-
Ph
ι
(i-i).
(О
(2)
Моменты (1) и (2) подставим в дифференциальное уравнение
упругой линии и получим два разных дифференциальных уравнения
соответственно для частей ОВ и ВА балки:
d2y Р_
dx% ~~Ш
d2t]
(h-x)-
PL·
IEJ
(1-х),
Pk
IEJ
(l-D-

§ 3. Упругая линия балок
247
Решая оба эти уравнения типа y"=f(x), получим для левой
части балки: первый интеграл
^-=-w<''-*>!+w<'-*>!+c'·
Второй интеграл, т. е. общее решение,
Ρ PI
»-iw^3-iut{l-x)3+CiX+c>-
Для правой части балки: первый интеграл
dx] _ Ph
~сй[~ 21EJ
второй интеграл, т. е. общее решение,
{1-IY+C,
Начальные условия на опорах О и А:
1)л:=0иг/=0; 2) |=I и η=0;
в точке В приложения силы Р:
3) х=%=11, ί/=η (общая ордината);
d-У dx\ , „
4) ^=1=/!, —— = ——- (общая касательная).
Подставив начальные условия в первые и вторые интегралы,
найдем:
PU \
с>= Нет <-"-'»·
Ь4= — Сз1,
C2-\-CiU = Ci-{-C3li,
Ci=C3.
Решаем систему (5):
PI PI
(5)

248
Гл. X. Неполные уравнения второго порядка
Подставляем найденные значения С ι, С%, С3 и С4 в общее
решение и получаем уравнение упругой линии для левой части балки
У —
для правой части балки
Рк
Рк
ЪЕЛ
(-х3+Рх-кЧ),
η=
6ЕЛ
Стрела прогиба h при х=1=к
y—x\==h=
(Ε3+2/2Ε-3/ξ2+Ζι2χ-//ι2).
ЪЕЛ
Задача 121. Балка на двух опорах длиной I прогибается под
действием равномерно распределенной нагрузки, общий вес которой
равен Р. Определить уравнение упругой линии и прогиб в середине
пролета.
<
У,
0
mm
шшшИ
s .
ι
ί
i
k
в
X
Рис. 69
Решение. Опорные реакции равны + —; на единицу длины
Ρ 2
приходится нагрузка —.
Рассмотрим сечение С балки на расстоянии χ от начала коор
Ρ
динат (рис. 69). Вправо от сечения сила + -ζ- дает момент:
(4-*)(+т)·
Вычислим момент относительно сечения С, создаваемый
равномерно распределенной нагрузкой.

§ 3 Упругая линия балок
249
Нагрузка на элемент длины балки d\ с абсциссой ξ имеет величи-
Р Ρ
ну —dl·,, а ее момент относительно сечения С будет — (|—x)—rdl·,.
Полный момент всей нагрузки, соответствующей части балки СВ,
равен
-\{i-x)Z-di
Следовательно, суммарный момент
M{x)=-\{t-x)Tdt+
χ
+ (-Ь)(+т)=+4(т-т)·
Как известно, дифференциальное уравнение изогнутой балки:
Mix)
где Ε — модуль упругости, / — момент инерции.
Для условий задачи уравнение (1) принимает вид
У"
(^--4-)· «
2EJ \ 4 I
Начальные условия: при х=0 у—0 и г/'=0.
Решая полученное уравнение (2) при данных начальных
условиях, получаем
Ρ С Ι Ι χ2 \ , Ρ I lx xs \
y==w0J \T—r>dx=-wr\-r—зп·
и общее решение
Р_
У~ 2EJ
(т-ж)-т-^*г)

UOU
Гл. X. Неполные уравнения второго порядка
Стрела прогиба в середине пролета ( х= —) ρ
\61 4 / 16/ ~Т ■
h—
авна
Р13
48EJ
48EJ
Задача 122. Найти уравнение упругой линии и стоелу· πι
бруса длиной / и шириной Ь, опирающегося па яве пппш-
(рис. 70) и подверженного напору воды, уровень кишиии
ся против верхней опоры.
НроктШы
i
Νι
/ -—-~- ι
j
\ . —
/ —
—
R
Рис. 70
Решение. На глубине ξ выделим элементарную пли
бруса шириной Ъ и высотой d\. Поскольку площадь ее bdl·,, ι
бина погружения ξ, то гидростатическое давление воды на пл<
ку будет dQ = bldl. Это элементарное давление вызовет на о
элементарные реакции
l-l IdQ
dNi=——dQ и dN2=-
или
I
{l-l)bldl
dNi= —■— и dN2=
ι

§ 3. Упругая линия балок
251
откуда опорные реакции
ι
Nl=±$(i-tm=-^r~, Nt=j-I&i=
ы*
Момент элементарной нагрузки b\d\ относительно точки D
будет bldld—x). Отсюда изгибающий момент для сечения D от всех
действующих сил
ι ι
M=b J <Ц-хШ-Ыг{1-х)=Ъ J (l-x)ldl- ~ (1-х) =
= -^(x3-l2x).
о
Дифференциальное уравнение упругой линии
dx2 6EJ
Это уравнение типа y"=f(x). Его общее решение
Ь 1 X* IW Ч
Начальные условия: при х=0 </—Оиприл:=/ у=0. Отсюда
получаем систему уравнений для определения постоянных
интегрирования
6EJ '
откуда
Ci==~wli' Cz=°- (1)
Подставляем значения (1) в общее решение и получаем
искомое уравнение упругой линии:
у=-Шш{3х5-Шх3+71'х)-
Стрела прогиба ft = (/max-
Для удобства отыскания максимума у введем новую
переменную t подстановкой x=lt. Когда χ изменяется в интервале (0, /),

юг
Гл X. Неполные уравнения второго порядка
величина t изменяется в интервале (О, 1). После подстановки
получим
360£/
dy Ы5
dt 360£/
(Ш4-30*2+7). (2)
Для определения максимума приравниваем нулю переменную
часть уравнения (2):
15ί4-30/2+7 = 0. (3)
В интервале (0, 1) уравнение (3) имеет корень
U=\ 1-2 У-^-=0,519,
15
соответствующий максимуму для у, что легко проверяется второй
производной.
Итак, стрела прогиба
Ыь hi5 hi5
Многопролетная балка
Задача 123. Для любого сечения изогнутого под давлением Ρ
рельса железнодорожного пути изгибающий момент
где k — коэффициент жесткости упругого основания пути.
Составить уравнение упругой линии и вычислить прогиб h
рельса в точке приложения силы давления Ρ (рис. 71), учитывая, что
3 -i/ AEJ dy
у=0 при х= — it у —-— и -j—· =0 при х=0.
Решение. Вводим обозначения:
pVw="" Vw-»·

§ 3. Упругая линия балок
253
Тогда уравнение упругой линии
<й/ Μ (χ)
ли
dx2-
dx2
a
EJ
e-b*(cos bx—sin bx).
0)
Рис. 71
Интегрируя уравнение (1), получим
—- I J e~bx cos bxdx— J e~bx sin bxdx I.
dy
dx EJ
(2)
Для вычисления правой части первый из интегралов берем по
встям.
Пусть
и=е~Ьх, du =—be-bxdx, dv=^cos bxdx, v= —- sin bx,
b
Тогда
J e~bx cos bxdx= — e~hx sin bx-\- J e~bx sin bxdx.
Для вычисления второго интеграла из уравнения (2) полагаем
и~е-Ьх, g?u —sin bxdx.
Тогда
du——be-hxdx, v = — cos Ьх.
Следовательно,
J e~bx sin bxdx— j- e~bx cos bx— J e~bx cos bxdx.

254
Г л X. Неполные уравнения второго порядка
Подставляя полученные выражения для интегралов в равеь.
ство (2), получаем
Так как при л:=0 —;— =0, то
0=-|-е-ь «sinfc.O+d
bEJ
и
Ci=0.
Таким образом, первый интеграл равен
dy а и . ,
~- = -Т777- е-Ьж sin bx.
ах bEJ
Интегрируя вторично, получим второй интеграл
У=— 2b"EJ e-bx(sinbx+cosbx)-\-C2. (4"
т ■ 3 -ι/ AEJ 3π
Так как при х= ~—п V—т~ = -тт~ (/=0, то
4 г k 4ft
3π
α -ь _ / 3it , . 3it \ , _
и
C2=0.
Уравнение упругой линии
У= 2ЬЖГе ~bx(smbxJrcosbx)
или, возвращаясь к данным величинам,
р -X
У= ; е
4L (см*у * +elnJty * )
У 64£//г3
и пои х=0 находим абсолютную величину стрелы прогиба
ъ= р .
У 64£"/fe3

§ 4 Геометрические приложения
255
II. УРАВНЕНИЯ ТИПА /' = /СУ)
§ 4. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
Задача 124. Радиус кривизны в произвольной точке кривой
рацеи кубу длины нормали в этой точке. Найти уравнение кривой,
проходящей через точку (0, 1) и в этой точке параллельной оси абсцисс.
Решение. Длина нормали у У 1-\-у'2. По условию задачи
получаем дифференциальное уравнение искомого семейства
(1+У2)
У
или
t
Решая это дифференциальное уравнение, находим
1
x+Ci=-F-iC1y^-l. (1)
w
Дополнительные условия: кривая проходит через точку (0, 1)
и при χ=0 (/'=0. Отсюда
0+Ca=-i-VCflz-l
или
Ci2C22=C1-l. (2)
Так как, дифференцируя уравнение (1), находим
d(x+C2)
у = —^=_ ■
yCi(*+C2)4-l
то
Ci(0+C2)
0= г_ _.-· (3)
fCi(0+C2)2+l
Для определения постоянных интегрирования имеем систему
уравнений (2) и (3). Из равенства (3) находим CiC2=0, т. е. С4=0
или С2=0. Если Ci=0, то уравнение (2) дает —1=0,
следовательно, ϋιφΟ и Со=0. Тогда из уравнения (2) Ci= 1.
Подставляем значения Ci=l и Сг=0 в общее решение (1)
и получаем уравнение искомой кривой

256 Гл. X. Неполные уравнения второго порядка
§ 5. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ ПОД ДЕЙСТВИЕМ
СИЛЫ ПРИТЯЖЕНИЯ
Задача 125. Материальная точка массой m движется по прямо!
mk-
линии к центру О (рис. 72), притягивающему ее с силой ——
где г — расстояние точки от центра. Движение начинается с
состояния покоя при г=а. Найти время, по истечении которого точкг
достигнет центра.
Рис. 72
Решение. По условию задачи в любой момент t на точку
действует сила г = — ——.
Отсюда получаем дифференциальное уравнение движения
dzr km
m
или
dfi
d2r
dp
ή
Решая его как уравнение типа #"=/(#), находим общее
решение
/+С2
У di*+k
Ci
(1)
dr
Начальные условия: при ^=0 г=а и -—■ =0* Из первого
условия имеем:
Второе условие
о+с2=-
ds
i cia*+k
Ci '
У ClJ* + k
dt

§ 6 Определение кривой по радиусу кривизны
ίο ι
1ЛИ
fCitf+k
0 = —
Для определения постоянных интегрирования Ci и С% имеем
•истему
>ткуда
Подставляя значения (2) в общее решение (1), получим
afaF^T2
fk
Когда точка достигает центра О, расстояние г—0 и
исковое время
а?_
III. УРАВНЕНИЯ ТИПА /=/(У)
§ 6. ОПРЕДЕЛЕНИЕ КРИВОЙ ПО РАДИУСУ КРИВИЗНЫ
Задача 126. Кривая, проходящая через точки Л (5, 7) и β(6, 6),
имеет радиус кривизны R — b. Найти уравнение этой кривой.
Решение. Радиус кривизны
[1+{/'2Р
А= Г, ·
У
По условию задачи R = 5 и получаем дифференциальное
уравнение искомого семейства
[1+у2]3/2
= 5. (1)
У"
Общее решение дифференциального уравнения (1) типа
У"=){у') будет
(*-Ci)*+(y-C2)2=25.

258
Γα Χ. Неполные уравнения второго порядка
Дополнительное условие: кривая проходит через точки Л (5, 7)
и В(6, 6), откуда
(5-С1у+(7-С2у=25, \
(6-d)2+(6-C2)2=25. / К '
Из системы (2) определяем Ci=2, C2=3. Подставляя эти
значения в общее решение, получим
(*-2)2+ ((/-3)2=25.
Задача 127. Проекция радиуса кривизны R на ось абсцисс
равна постоянной величине а=]. Найти уравнение кривой, если она
проходит через начало координат и в этой точке ортогональна оси
абсцисс.
(1+J/'2)'/·
Решение. Радиус кривизны R— -. Направляющий
косинус радиуса кривизны как направляющий косинус нормали
У'
cos α= .
По условию задачи
R cos a = a,
откуда дифференциальное уравнение искомого семейства кривых
У'(\+У'2)=ау"·
Решаем это уравнение типа {/"=/({/') и получаем его общий
интеграл
х~ Ci . . у—С2
■ · =1п sin- ·
а а
или общее решение
x-Ci
у=а arcsin e a -\-С2.
Начальные условия: точка (0, 0) лежит на кривой и при х=0
у'=оо. Тогда
0-Ci
0—a arcsin е а +С2
и, так как
x-Ci
У

§ 7. Горизонтальное движение тела при наличии трения 259
ТО
O-Ci
е а
У 2(0- С,)
1-е «
Для определения постоянных интегрирования имеем систему
уравнений
Ci
a arcsin e α -f-C2=0,
Отсюда
2Ci
1-е « =0.
Cl=0; Ci=-m
2
Подставляем найденные значения в общее решение и получаем
— ал
у=а arcsin е а —.
При а= 1 имеем уравнение искомой кривой
it
у= arcsin ех —■
или
х=\п cos у.
§ 7. ГОРИЗОНТАЛЬНОЕ ДВИЖЕНИЕ ТЕЛА ПРИ НАЛИЧИИ ТРЕНИЯ
Сила зависит от скорости: F=F(v)
Задача 128. Вагон с силон тяжести Q=9216 кГ приходит в
движение под действием ветра, дующего но направлению полотна, и
движется по горизонтальному участку пути (рис. 73).
Сопротивление движению R вагона равно 1/200 его силы тяжести. Сила
давления ветра P = kStfi кГ, где S — площадь задней стенки вагона,
подверженная давлению ветра и равная 6 м2, и — скорость ветра
относительно вагона, а &=0,12 кГ-сек21м'\ Абсолютная скорость
нетра ω= 12 м/сек. Считая начальную скорость вагона равной нулю,
найти:
1) наибольшую скорость вагона;
2) время Т, необходимое для достижения этой скорости;
3) путь Χι, который должен пройти вагон, чтобы приобрести
скорость 3 м/сек.

260
Гл X Неполные уравнения второго порядка
Решение. Проектируя все действующие силы на
горизонтальную ось, получаем уравнение равновесия рассматриваемой
системы
Скорость ветра относительно вагона равна
dx
или после дифференцирования
du d2x
dt
dP
(2)
'#
γ////////////////?//////λ '/////У/////////////,
αϊ
Рис. 73
Подставив значения сил в уравнение (1) и разделив его на пг,
получаем
d2x Q kSuz
dt2 + m-200 m K '
Используя равенство (2), уравнение (3) приведем к виду
_ J*L· _L -JL _ kSu2
dt + 200 m
= 0.
Разделяя переменные и интегрируя, находим
du
200
1-
200AS_
mg
и2)
- = —f+C.
(4)
(5)

§ 7. Горизонтальное движение тела при наличии трения 26|
Для удобства вводим обозначение ■ =<х2. Тогда из урав-
mg
нения (5) получаем
200 Г 1 C-d(au) 1 Г d(au) 1
~a~g '-TJ (a«+l)+TJ (au-1) J =-/+C
или
100, сш-1
■ In —- =—H-C.
ag· ссы+1
Постоянную интегрирования в общем решении уравнения (4)
определяем, используя начальные условия: при t=0 ~гг =0, « = ω.
Тогда
_ 100, αω-1
С= -—In*
ag αω+1
Искомое частное решение
100 (au—1)(αω+1)
— t= In
ag (аы+1) (αω—1)
откуда при t = Q
'200kS 1
OL-
mg
,-У:
1. Максимальная скорость вагона i>max будет достигнута при
t-*-oo. Тогда
аи—1=0,
/ dx I \ , Л
Отсюда
-Т— 1/^s^-f
dx.\ 1 ι/ т# .„ ί 9216
rfHcc о ' 200kS Г 200-0,12-6'
Таким образом,
Ay
=4 м/сек.
dx
2. Время, которое потребовалось бы для достижения этой
скорости,
Т—>-оо.

262
Гл. X. Неполные уравнения второго порядка
3. Найдем путь χ ι, который должен пройти вагон, чтобы
приобрести скорость —тт =3 м/сек:
du du άζ, du
dt
du
du
dl
= U = (u—
d4
dl
dt
dx
dt '
dt dl dt d%
dl
dt dfi '
Интегрируем предпоследнее равенство:
1=ωί—χ.
Таким образом, уравнение (4) примет вид
du g kSuz
~~dTU+2№ m~ ~0'
Разделяя переменные, находим
udu
kSu*
= dl
200 m
или
200 udu
Τ' (,.*:*»,,) =* (6)
* mg ι
Вводя предыдущее обозначение α2= ■ и интегрируя,
приходим к равенству, представляющему общее решение
уравнения (6):
~i^,nC(1~a2"2)=l=Cui_x
Постоянную интегрирования С определяем из начальных
условий: при х=0 t=0, « = ω. Тогда
С= 1
1 — α2ω2
Искомое частное решение:
m l — a2«2
χ=ωί+ -^г^- In —-.
2kb l — α2ω2

§ 7. Горизонтальное движение тела при наличии трения 263
При Χ=Χι
dx
~dT
-3 м/сек, «=9 мIсек и
,= 1^-1^=99,8 сек
1 17-4.
имеем:
*ι=99,8·12-
9216 , 0,265
In . „ =187 м.
9,81 -0,12-6 1,25
Задача 129. Самолет на лыжах приземляется на
горизонтальное поле; летчик подводит самолет к посадочной площадке без
вертикальной скорости в момент приземления (рис. 74). Коэффициент
Рис. 74
трения лыж самолета о снег μ=0,08. Сила сопротивления воздуха
движению самолета пропорциональна квадрату скорости. При
скорости, равной 1 м/сек, горизонтальная составляющая силы
сопротивления #ж=0,09 кГ, а вертикальная составляющая, направленная
вверх, Ry=Q,7 кГ. Сила тяжести самолета 2000 кГ. Найти длину
и время пробега самолета до остановки.
Решение. Горизонтальная составляющая силы сопротив-
чения
где
/гж=0,09 кГ-сек2/м2.
Вертикальная составляющая силы сопротивления
где
kv=0,7 кГ-сек2/м2.

264
Гл X. Неполные уравнения второго порядка
„, ds
Так как v= —тт, то горизонтальная и вертикальная
составам
ляющие соответственно равны
Rx=kx( — ), Ry=ky(-^).
Составляя дифференциальное уравнение движения самолета,
получим
d2s
или
«-ж+М№-[-*-*.(■!?-Л-* о
Делим уравнение (1) на т. Тогда дифференциальное
уравнение задачи
d4
dtz m \ dt
Вводим обозначения:
. kx—\kkv I ds \2
т А' М=В-
Кроме того,
d2s _ dv
dP ~~dsV'
Уравнение (2) можно записать:
dv
v -|_^ϋ2+β=0.
ds
Разделив переменные, получаем дифференциальное уравнение
vdv
Интегрируя обе части равенства (3), получаем
f vdv I f ά{Β+Ανη 1

§ 7. Горизонтальное движение тела при наличии трения 265
Определяем постоянную интегрирования С, используя началь-
юе условие: при s=0 v = v0. Тогда
и искомое частное решение
Li ( Β+Αυ2 \ _
2А lnV В+Ащ* ι — *
При скорости у=0 находим длину пробега самолета до
остановки:
~=iir4i+4o«0 =
2А \ ' В
= ^8ί·10β1η(1+-ΤΓ·10-4·18'52)=216Λ·
Время пробега определяем, используя уравнение (2) и соотно-
cfis dv
шение —τ— = —77-· Уравнение (2) принимает вид
at1 at
dv
+Αό*+Β = 0. (4)
dt
В уравнении (4) разделяем переменные:
άυ
Αν*+Β
Таким образом,
1
= -dt.
arctg(]/^-.y) =-t+T.
iAB
При ί=0 ν = υ0 и искомое время пробега
Т=
ΙΑΒ
i_arctg(y-T-.0o) =

266
Гл. X. Неполные уравнения второго порядка
Движение тела в воде
Задача 130. Корабль водоизмещением Р=1500 τ преодолевает-
сопротивление воды, равное R = avzm, где сс=0,12, m — масса,
а υ — скорость корабля. Сила упора винтов направлена по скорости
в сторону движения и изменяется по закону:
Γ=Γο(ι—iL·),
Х us I
где 7O=120m — сила упора винтов, когда корабль находится без
движения, a i>s=const=33 м/сек. Начальная скорость равна щ.
/77 d X
Рис. 75
Найти зависимость:
1) скорости корабля от времени;
2) пройденного пути от скорости;
3) пути от времени при у0= 10 м/сек.
Решение. Проектируя действующие силы на горизонталь
(рис. 75) с учетом знаков и скорости движения корабля в виде
dx
v= —тг> получаем уравнение движения корабля
d4 I dx
или
dx
dzx d I dx \ 1 , dt ) I dx
Разделяя переменные, имеем
dx
= dt

§ 7. Горизонтальное движение тела при наличии трения 267
ИЛИ
\ dt I
-m
т ^L·
dx V . ° dt
= dt.
(1)
/ dx γ dt
Интегрируя уравнение (1), найдем общий интеграл
m
*VM«+&)
In
V Μ-+£)-£-.
dx
Ρ·(*&)
2vs
-a-
dx
Ж J
Вводим обозначение:
= t+C.
(2)
УМ
α+
ivs
■)-!·■
Частный интеграл находим из уравнения (2), используя началь-
4. О dX
ное условие: при г=0 скорость
dt
■■ϋ0.
Вычисляем постоянную интегрирования
Го
г m 1
С = г—In
2β
β-
2vs
-αί>ο
πι Γθ .
2vs
Искомый частный интеграл
Го dx
2β
(»--£+«-£)(»+&+■*)
(β+
2vs
ο , dx
+ a-
dt
)(p-St-«·)
(3)
Подставляя числовые значения, согласно условиям задачи,
получаем
Го
β=4,2;
2у0
= 1,8; -^-=0,055.
m

268
Гл. X. Неполные уравнения второго порядка
Тогда уравнение (3) принимает вид
(50+~йг) (20-ϋο)
(20-—) (50+о°)
— p0,055f
dx
Разрешая последнее равенство относительно ——, находим
dx
~dt
= υ·-
70uo+20(uo+50)(e°.055i-l)
70+(uo+50)(e°.°55i-l)
(4)
Здесь υ0 в м/сек.
Зависимость пройденного пути от скорости находится
следующим образом.
Уравнение (1) может быть записано в виде
mvdv
аи2-\- и—То
=—dx.
(5)
Интегрируя уравнение (5), находим
mvdv
х=
+Хо
Т0-
■ ν—αν2
или
~»=->{ΐ- (ψ-)'} +
9лу I V 1/ р. ' ■*
2α
ζαε
Здесь для упрощения принято
Г,
φ-f-y
Уе
1 φ-Η>
Ve
(6)
φ=
= 15 м/сек; ε =
ί ! + Т^Ч ) =1225 м*/сек\
2aos ---/ > - α \- 4aus2/
Подставляя числовые значения φ и ε в уравнение (6), получаем
,„-,= 637.5 1„{1-(^Г}+273,9,„{-|5}.

§ 7. Горизонтальное движение тела при наличии трения 269
Пользуясь начальными условиями, определим величину Xq.
При t=0 x=Q, ϋ=υ0. Следовательно,
Λ=β37,54_(^)>73,91η(|^).
Таким образом, искомая зависимость:
ϋο2+30ϋ0-1000 (ϋ—20)(ι>+50)
χ=637,5 In -^--- ——+273,9 In
у2+30у-1000 ' (wo—20) (уо+50) '
Найдем зависимость пути от времени при начальной скорости
Уо=10 м/сек.
Из уравнения (4) имеем:
20(wo+50) (e°.°55i-l)+70uo
И γ— , . . , /7/ —
(uo+50)(e°'055i-l)+70
70(20— O0)dt
=2(Ш (^qi50)>,055i+ (20-wo) ~ (7)
Интегрируя уравнение (7), получаем
C+,=20i-70^ f % . (8)
J ^ fo+50
20-uo
Вводим обозначение ζ = — и применяем подстановку
Уо+50
eo,055i^y. Тогда dt= - dy. Равенство (8) принимает вид
U,Uooi/
C+x=20f- '"* In
0,0552 nnrr, , 20—v0 '
^ уо+50
Находим постоянную интегрирования С, используя начальное
условие: при ί=0 дг=0. Следовательно,
+ уо+50
Подставляя значение Уо=Ю м/сек, находим искомую
зависимость пути от времени:
gp0,055i
ιη , =20ί—127Мп —-——-ρ-196,3.

270 ?л X Неполные уравнения второго порядка
Движение пули внутри вещества
Задача 131. Пуля входит в брус толщиной 12 см со скоростыг
200 м/сек, а вылетает, пробив его, со скоростью 60 м/сек. Брус С(·
противляется движению пули с силой, пропорциональной ква£
рату скорости движения (рис. 76). Найти время движения nv.m
через брус.
Ком
Рис. 76
Решение. Внутри бруса в любой момент t на пулю деис-
вует сила сопротивления бруса F. Она направлена против движе
пия, а по величине пропорциональна квадрату скорости движени>
пули в данный момент. Таким образом,
F=—kv*.
На основании второго закона динамики сила равна произведи
нию массы точки на ускорение а, которое сообщается точке, т. t
F=zma.
Сопоставляя уравнения, получим
та=—kv2.
Как известно, скорость точки
а ускорение
v =
du
ds
dt
»
d*s
dt dt2
(1)
(2)
(3)

§ 7. Горизонтальное движение тела при наличии трения 271
Здесь s — путь, / — время.
Подставляя значения υ и w в дифференциальной форме из ра
ионств (2) и (3) в уравнение (1), получим дифференциальное урав
пение движения
d2s__ k_ I ds γ
7ΐ~ _ m. V fit ι '
di2
(4)
Уравнение (4) представляет собой неполное линейное
уравнение второго порядка типа
у"=!(у')
и решается методом понижения порядка путем введения новой
искомой функции:
, dy
Р=У =
Р' = У" =
dx'
dp
dx
(5)
Применение этого метода для рассматриваемого уравнения (4)
приводит к следующему:
ds d2s dp
~~аТ=Р'' dt2 =~df
Уравнение (4) примет вид
dp k__ 2
dt m P '
Разделяя переменные ρ и t,
^-=-±-dt
ρ2 m
и почленно интегрируя, получаем
_ J-— _
Ρ ~
m
t+Ci
Подставляем значение ρ и интегрируем еще раз:
dt
ds
m
t+Cu

272
Гл. X. Неполные уравнения второго порядка
dt
m
di — t-d)
= -— In ■ t-CA+C* (6)
г—Cj
m
Для перехода от общего решения (6) к частному решению
определим значения произвольных постоянных Ci и С% по условию
задачи.
ds
Начальные условия: при i=0 s = 0 и —τ— =200 м/сек. Кроме
того, продифференцировав уравнение (6), получим
ds 1
dt k t-Ci
(7)
m
Из уравнения (7) определим Ci:
J
•0-Ci
200=— ; Ci=-
200'
°=-^ы(~-°+ш)+с>
m
а из уравнения (6) — C2:
m
- in ι -
m 200
или
Подставляя найденные значения С4 и С2 в общее решение (6),
получим частное решение, изображающее уравнение движения
в условиях задачи:
s= JL ln{^t+ J- )+^1п2оо=
b \ m 9ПП / b
β « m[(-*-*+ ^r)2oo] = ^-in(2oo-^-i+i);
& L\ m 200 ' ■« k x m ι
s=J!L\n(mA-t+\). (8)

§ 7. Горизонтальное движение тела при наличии трения 273
Разрешая уравнение (8) относительно t, получим
200 f-f-l=e"Sr
m
или
hs
m
200&
(em-l). (9)
Как видно из уравнений (8) и (9), для определения искомого
времени t необходимо найти величины кит.
Коэффициент пропорциональности k определим из
дополнись
тельного условия: при s=h= 12 сж = 0,12 м —τ— =60 м/сек.
Для применения этого дополнительного условия необходимо
продифференцировать уравнение (8):
ΤΓ — Ψ— <>о,
200 Н-1
т
Найденную величину / из уравнения (9) подставляем в
уравнение (10), которое примет вид
* 200
dt h*
ет
Подстановка дополнительных условий приводит к равенству
60—?ϋ°-. 02,
h
0,12 "
е т
откуда
1пт
k= -m^ 10,03m.
Анализируя полученную формулу, замечаем, что k является
линейной функцией т и нет надобности в определении т,
а достаточно найти величину е т . Это упрощает выкладки.

274
Гл. X. Неполные уравнения второго порядка
Из уравнения (12)
h
(4-)
3
k
Подставляя числовые значения величин k и ет в уравнение
(9), получим
25
"0,12
Итак, время прохождения пули через брус равно 0,00114 сек
(немногим более одной тысячной доли секунды).
§ 8. ДВИЖЕНИЕ В ВЕРТИКАЛЬНОЙ ПЛОСКОСТИ
Падение тела в воздухе
Задача 132. Тело массой т падает с некоторой высоты со
скоростью υ. При падении оно испытывает сопротивление,
пропорциональное квадрату скорости. Найти закон движения падающего тела.
Решение. В момент времени t тело находится под действием
двух сил: тяжести и сопротивления среды. Сила тяжести равна mg,
сила сопротивления среды направлена в сторону, противоположную
движению, и равна kv2. Следовательно, равнодействующая этих сил
равна mg—kvz. С другой стороны, величина силы, действующей на
тело, пропорциональна ускорению движения а и равна та.
Итак,
ma—tng—kv2. (1)
Если путь, считая от начала отсчета, равен s, то скорость
ds d2s
υ= —гг, и при прямолинейном движении а= . Равенство (1)
at at1
принимает вид
d2s . I ds \2
m-
=m-k m · (2)
dt2 ° v dt
Так как —гг =v, то, дифференцируя это равенство по t, имеем
d2s dv
dt2 ~~aT'
откуда правая часть представляется в виде

§ 8. Движение в вертикальной плоскости
275
и тогда
dv
dt
dv
ds
d2s
ds dv
dt ds
du
dt2 ds
Преобразуем уравнение (2):
dv
m
или
откуда
или
ds
mvdv
mg—kv2
v = mg~kv2
=ds,
J-
mvdv
mg—kv2
= jds
m
~2k
\n\mg— kv2\+C=s.
(3)
Пусть в начальный момент времени /=0 тело находилось
в начале отсчета пути, т. е. s=0, и начало падать с начальной
скоростью, равной нулю, т. е. и = 0.
Подставив в уравнение (3) s=0 и v = 0, находим
m , Л „ пг ,
\nmg-\-C=0 и C=-^- In mg.
2k
Таким образом,
2k
— -^ ln\mg—kv2\ + — In mg=s
или
m
mg
ds
Так как —т— = ν, то
dt
m ,
2*
mg—kv2
mg
mg-
-*(-£)
(4)
Уравнение (4) представляет дифференциальное уравнение пер-
вого порядка. Решаем его относительно -——:

276
Гл. X. Неполные уравнения второго порядка
In
mg
Так как тело падает, то, согласно уравнению (2), т-т^г>0;
2ks_
т
следовательно,
d2s
dt*
mg
-*(-*-) >о
mg
mg
-*(£)
■>o,
а поэтому имеем:
mg
2hs_ mg—k (—ίτ-)
2fes
tng-k(^r)
=e
mg
^=±/^(,-rv)
ds
Так как s — возрастающая функция t, то -— >0 и перед
корнем берется знак плюс:
ds
~dT
νψ(
2hs
1-е m J.
Разделив переменные, получим
ds
отсюда
У,
У,
—е
ds
—е
2Jts
т
2hs
т
-У^«
Пе-'+
-м-с.
(5)
Интеграл в левой части равенства (5) берется подстановкой
its , ks
— , k ·— .
z=em, dz= em ds,
m

§ 8. Движение в вертикальной плоскости
277
ι тогда
res ,
m ■ m dz
ds==—--e m dz= —-— ·
Таким образом,
ds m Г* dz m [* dz
Z|/i_JL * .W*-i
\ — e m .IV ■&
V.-.-ΐ \ЬУ'
m
^гТ)=^_1п(Д+УД11)=у^
= —— ln(2+-|/22-l)=—--In \em + Г em—lj = V -~ t+C.
Fi R, ■ R,
Подставляя в последнее равенство начальные условия f=0
л s —0, получим С—0.
Итак, уравнение (5) принимает вид
fts
.У.?-.)-У?
m \n\em+1 em — \) = ~]/^r~t,
откуда
±L ]/ J^L· ν4ι*
em + r e m — l==e , (6)
Λΐ JUL·
■ Г e m —l = i
r m
ks ~|/ 2hs
e~^-\- V e m — 1
(7)
Умножая числитель и знаменатель левой части равенства (7)
на выражение
юлучаем
и, учитывая
I
ks
em —
равенство (6)
fes
em -
t
J
-Ь
2ks
m _
Zhs
• m .
-1 =
-1,
У tn
-e

278
Гл. X. Неполные уравнения второго порядка
Закон движения падающего тела:
У щ У m
m ,
—— In-
+e
Погружение тел в воду
Задача 133. Подводная лодка, ие имевшая хода, получив
небольшую отрицательную плавучесть Р, погружается на глубину,
двигаясь поступательно (рис. 77). Сопротивление воды при
небольшой отрицательной плавучести можно принять пропорциональным
первой степени скорости погружения и равным kSv, где k — коэф-
"-$4
..
.
р_:
**#
__ -__- — "iim~ — ;
._.. .. _ _
Рис. 77
фициент пропорциональности, S — площадь горизонтальной
проекции лодки, υ — скорость погружения. Масса лодки равна т.
Найти:
1) скорость погружения ν, если при ί=0 начальная скорость
Уо=0;
2) путь, пройденный погружающейся лодкой за время Т.
Решение. Проектируя действующие при погружении лодки
силы на вертикальную ось, получаем дифференциальное уравнение
движения
mJ^+kS^-P=0. (1)
dfi
dt

§ 8. Движение в вертикальной плоскости
279
d2y
Здесь от — произведение массы на ускорение (сила тяже-
ati
ти погружающейся лодки), &S—тт сопротивление воды.
Вводя подстановку у=—тг и деля уравнение (1) на пг, получим
dV ' kSv P =0. (2)
di m m
В уравнении (2) отделяем переменные и приходим к равенству
mdv
T=ks-v=dt (3)
Интегрируя уравнение (3), получаем зависимость
ΪΪΙ
- — \nC(P-kSv) = t. (4)
Постоянную С определяем из начального условия: при ί=0
0 = 0:
с= 1
Ρ '
Таким образом, уравнение (4) принимает вид
-•S-h-jrC-**')—£"-('--ϊγ*')-<·
После простых алгебраических преобразований найдем
искомую скорость погружения:
'-(
1-
1-
=.
Ρ
k
Ρ
Ρ
kS
-Sv
■Sv =
('-
) =
= e
-e
= — ■
ftS
m
hS
m >
m
t
')·
■t,
(5)
Для определения пути, пройденного погружающейся лодкой за
Время Т, уравнение (5) переписываем в виде

280
Гл. X. Неполные уравнения второго порядка
as
( 1-е m ' )
dt kS
или
Ρ I - — t\
ds=—-(l-e m )dt.
Интегрируя это уравнение первого порядка с разделенными
переменными, находим путь в зависимости от времени:
Определим постоянную С, используя для этого начальное
условие задачи: при t=0 s = 0. Из уравнения (6) получим
<-£(£-+<0
kS V kS
или
„ m
kS
Тогда искомое частное решение
(7)
Ρ I m 1 tn \
kS \ ' kS kS
[^-^(l-.— . j. (8)
kS L kS
При t—T пройденный путь s=z выразится соотношением
Ρ Γ Ρ ' hS
U-irb--^)]-
kS L kS
§ 9. РАВНОВЕСИЕ ТЯЖЕЛОЙ НИТИ
Задача 134. Определить форму, которую принимает под
влиянием собственного веса гибкая тяжелая нить, подвешенная за
концы С и D.
Решение. Построим систему координат в плоскости нити
(рис. 78). Начало координат выберем на некотором, пока не
определенном, расстоянии ОА от самой низкой точки А кривой.

§ 9. Равновесие тяжелой нити
281
Рассмотрим часть кривой CD — дугу АВ. На эту часть
действуют силы: в точке А — горизонтальное натяжение Н, в точке В—
направленное по касательной натяжение Τ и вес части нити АВ,
пропорциональный длине нити. Собственный вес участка нити
АВ равен ps, где ρ — вес единицы длины нити, s — длина дуги АВ.
Рис. 78
Согласно условиям равновесия статики, сумма проекций
вертикальных и горизонтальных составляющих равна нулю. Проектируя
все силы на оси Ох и Оу, получаем соответственно
Tcosa=H, 1
Τ sin a—ps. '
Деля второе равенство на первое, находим
то
sin α
= tga=
ps
Так как
cos α Я
tg a=y',
, dy_ _ _ps_
У ~ dx - Η ■
(1)
Для устранения третьей неизвестной s дифференцируем
уравнение (1) по х. Тогда
ρ ds
«/"=■
Я dx "
Так как
ds
dx
=1 i+y2,

282
Гл X. Неполные уравнения второго порядка
то уравнение примет вид
y"=~ff-У1+У'2· (2
Уравнение (2) представляет уравнение типа y"=f{y'). Решаел
его подстановкой y'=z. Отсюда y"=z', и уравнение (2), полагая
Ρ 1
—-z-r = —> перепишем в виде
Я α
2'= -g- yl+z*= -i- fi+A (3)
Разделяем переменные:
У 1+22
откуда после интегрирования найдем
ln(z+yi+z*) = —-fCt.
Постоянную интегрирования определяем из начальных условий.
Касательная в точке А параллельна оси абсцисс, так что при х=0
y'=z=0. Таким образом,
In 1 = СЬ
т. е.
С 1 = 0.
Итак, для условий задачи
In (Z+У 1+г*)=— (4)
или, потенцируя обе части равенства (4), получим
г+У1+г2 = е«. (5)
Уравнение (5) можно преобразовать, умножив обе его части
на ζ— У 1 +z2. Тогда
— 1—(z-yi+z*)e«,
откуда
ζ— yi+22=— e а. (6)

§ 10. Гибкая нить равного сопротивления
283
Складывая уравнения (5) и (6) и деля обе части полученного
уравнения на 2, находим
г=у'= —(е^-е~« ). (7)
Интегрируем уравнение (7):
υ=γ( е^+е"^) +C2=ach^-+C2.
Если начало координат расположено на расстоянии а от
точки А, то при х=0 у = а, а поэтому С2=0. При этом уравнение
кривой приводится к уравнению цепной линии:
(X X
еа 4-е а ) =ach—.
' а
Форму цепной линии, в частности, принимает подвешенная за
концы цепь (поскольку цепь с некоторым приближением можно
считать гибкой нитью), отсюда и происхождение наименования линии.
§ 10. ГИБКАЯ НИТЬ РАВНОГО СОПРОТИВЛЕНИЯ
Задача 135. Найти уравнение подвешенной за оба конца гибкой
нити, площадь поперечного сечения которой всегда
пропорциональна натяжению.
Решение. При отыскании уравнения цепной линей
предполагалось, что поперечные размеры нити во всех сечениях
одинаковы. По условию данной задачи площадь поперечного сечения нити
изменяется пропорционально натяжению. Очевидно, что в этом
случае напряжения в любых сечениях нити по величине одинаковы.
Пусть ρ — плотность нити; F — переменная площадь ее
поперечного сечения.
Уравнения равновесия части AB = s нити принимают вид
—Н-\-Т cos α=0,
s
Τ sin α— J p Fds =
о
0)
где Я — натяжение нити в нижней ее точке А; Т — натяжение в лю-
Рой точке нити; α — угол между натяжением Τ и осью абсцисс.
Из первого уравнения системы (1)
г—ϋ-.
COS QS

284 Гл. X. Неполные уравнения второго порядка
а из второго уравнения
s
Т=—1—\pFds.
sin α 0
Приравнивая эти значения, умножая почленно на sin а и
учитывая, что tg a=y', имеем:
S
Η tga=Ну'= $pFds. (2)
о
Дифференцируем уравнение (2), откуда
Hy"dx=p Fds.
Пусть σ — одинаковое для всех сечений напряжение. Тогда
H=F0a, T^Fa,
где Fo — площадь поперечного сечения, центр тяжести которого по
сравнению с центрами тяжести других сечений имеет самое низкое
положение. В этой точке расположим начало координат. Граничные
условия: при х=0 у = 0 и tg a=y'=0. Тогда
τ ρ Η Hds
следовательно,
F=
cos a dx
Hds
adx
*-$№■
Так как
то
ds=i l-\-y'2dx,
у"=-у(1+у*У. (3)
Уравнение (3) есть дифференциальное уравнение типа
Ϊ {у'> У") =0. Преобразуем его к виду
dy' pdx

§ П. Кривая и радиус кривизны
285
ггкуда после интегрирования получим
ρ
arctgi/'= —х-\-С.
На основании второго граничного условия (при х=0 у'=0)
находим С=0.
Следовательно,
откуда
у = In cos — х,
Ρ ο
так как новая постоянная интегрирования на основании первого
граничного условия (при х=0 у=0) также равна нулю.
Уравнение цепной линии равного сопротивления имеет вид
е° vcos — x=\.
σ
IV. УРАВНЕНИЯ ТИПА у" =/(х, у')
§ 11. КРИВАЯ И РАДИУС КРИВИЗНЫ
Задача 136. В точке (1, —2) кривая параллельна оси абсцисс.
В любой точке радиус кривизны R равен квадрату абсциссы этой
точки. Найти уравнение кривой.
Решение. По условию задачи R = x2 и, приравнивая это
значение дифференциальной формуле радиуса кривизны, получаем
дифференциальное уравнение искомого семейства кривых
U+(y'nk 2
■ =х2.
У
Решение этого дифференциального уравнения типа y"=f(x, у')
приводит к первому интегралу
С 1 Р
х У1+Р2
dy
Постоянную интегрирования определяем из дополнительного
условия: в точке (1, —2) кривая параллельна оси абсцисс, т. е. при

286
Г л X. Неполные уравнения второго порядка
х=1 —г— =р=0, откуда
с, ' °
1 у ι—о2
или
С1==1.
Первый интеграл принимает вид
или
dy χ—1
"* У2х—1
Интегрируя далее, получим второй интеграл
у+С2= ~ (2х-1)\ (1)
Так как кривая проходит через точку (1, —2), то
-2+С8=-^(2-1-1)'/.
или
13
С2=
Подставляя значение (2) во второй интеграл (1), получим
уравнение искомой кривой
6у=(2х-1)3/*-13.
V. УРАВНЕНИЯ ТИПА у"=/(у,У)
§ 12. НАХОЖДЕНИЕ УРАВНЕНИЯ КРИВОЙ ПО НОРМАЛИ
И РАДИУСУ КРИВИЗНЫ
Задача 137. Длина нормали в любой точке кривой равна
радиусу кривизны R кривой в этой точке. Найти уравнение кривой,
параллельной оси абсцисс в точке (0, 1).
Решение. Длина нормали у У 1+У'2· По условию задачи она
равна радиусу кривизны. Поэтому дифференциальное уравнение
искомого семейства кривых
АЩА-=у11+у,г

§ 12. Кривая по нормали и радиусу кривизны
287
ИЛИ
У-
\+У'2
У"
(1)
Общий интеграл дифференциального уравнения (1) типа
У"=}{У>У') бУДет
х+Сг
У+1у2-С?=С& с, .
Дополнительное условие: кривая проходит через точку (0, 1)
и в этой точке у'=0. Тогда
О+Сг
и так как
«/'=-
ι+yi2-
х+Сг
—е Ct
1+ *
-Ci2=Cle ci
х+Сг
е Ci y«/2—С^
y+yy2_Cl2
(2)
Уу2_Сд2
то при х=0, у=1 получим
О+Сг
е с' У I2—G2
=0.
l+yi^-Ci2
(3)
Постоянные интегрирования найдем из системы уравнений
(2) и (3)
Сг
1+У1-С12=С1ес',
Сг
eci у 1-Ct2
= 0.
ι + yi-Ci2
Решая ее, находим
С|=1, С2=0.
Подставляем найденные значения постоянных интегрирования
в общий интеграл и получаем уравнение искомой кривой
У+1у2-\=е*
или
х=1п(у+Уу2-1).

Глава XI
ЗАДАЧИ, ПРИВОДЯЩИЕ К ЛИНЕЙНЫМ
ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ВТОРОГО ПОРЯДКА
С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Общий вид линейного неоднородного дифференциального
уравнения второго порядка с постоянными коэффициентами
Aiy"+A2y'+A-iy=f(x), (1)
где Αι, А2, Аз — постоянные действительные коэффициенты, f(x) —
некоторая данная функция χ или (в частном случае) постоянное
число.
При f (x) =0 уравнение принимает вид
Aiy"+A2y,+Aiy=Q (2)
и называется однородным линейным уравнением.
Если соответственно данному уравнению (2) составить
алгебраическое уравнение вида
А^2+А2г+Аг=0, (3)
то такое уравнение называется характеристическим по отношению
к уравнению (2). Вид общего решения уравнения (2) зависит от
рода кор'ней характеристического уравнения (3).
Случай 1. Корни характеристического уравнения г ι и г2—
действительные и разные числа.
Общее решение
y = der'x-\-C2er'x.
Случай 2. Корни уравнения (3) — кратные (равные)
действительные числа п=г%=г.
Тогда
y = Clerx+C2xerx= {Ci+C2x)erx.
Случай 3. Корни характеристического уравнения —
комплексные сопряженные числа: г\$=а±Ы.
Общее решение:
y = eax(CiCOsbx+C2sin bx). (4)
Общее решение (4) может быть также представлено в
эквивалентной тригонометрической форме
у=Меах sin(6x+<p),
где Μ и φ — постоянные величины.

Гл. XI. Уравнения второго порядка
289
Общее решение неоднородного дифференциального уравнения
У представляет собой сумму общего решения соответствующего од-
юродного дифференциального уравнения у и какого-либо одного
lacTHoro решения неоднородного дифференциального уравнения V:
Y=y+V.
Определение частного решения, зависящего от вида правой
части уравнения (1) f{x), в практически встречающихся случаях
сводится к следующему.
Случай 1. Правая часть представляет многочлен вида
f(x) =a0xm+a1xm-i+a2xm-z+.. .+am-ix+am.
Тогда
V=A0xm+Aixm-l+.. .+Am-iX+Am.
Если характеристическое уравнение имеет" корень, равный
нулю, кратности k (k=\, 2), то тогда
V=xk{A0xm+A1xm-l+.. .+Am-iX-\-Am).
Случай 2. Правая часть представляет собой показательную
функцию вида
f{x)=aePx,
где а — постоянная величина или многочлен от χ; ρ — постоянное
число. Тогда
V=Aevx,
где А —соответственно константа или многочлен.
Если характеристическое уравнение имеет корень ρ кратности k
(*=1,2),то
V=AxkePx.
Случай 3. Правая часть — тригонометрический многочлен
f(x) =αι sin bx-\-a2 cos bx.
Тогда
V=Ai sin bx-\-A2 cos bx.
Если характеристическое уравнение имеет корни ±6ί
кратности k, то
V=xk(Ai sin bx+A2cos bx).
Случай 4. Правая часть представляет собой комбинированный
случай вида
f(x).=eax(Cism bx-\-c2co^bx).

290
Гл. XI. Уравнения второго порядка
Тогда
V=eax(Cisin bx+C2 cos bx).
Здесь й, с2 и соответственно Ci и С2 могут быть многочленами
или постоянными величинами.
Если характеристическое уравнение имеет корни а-\-Ы и а—Ы
кратности k, то
V=xheax(Clsin Ьх+С2 cos bx).
Случай 5. Если правая часть f(x) представляет сумму функций
рассмотренных видов, то частное решение V равно сумме
соответствующих функций.
Коэффициенты А, А ь А%, ... , Ат, Си С% являются
коэффициентами или многочленами, подлежащими определению. Они должны
определяться так, чтобы V действительно являлось частным
решением уравнения (1): после подстановки V в уравнение (1) оно
обратится в тождество, из которого приравниванием коэффициентов
подобных членов обеих частей определяются искомые
коэффициенты или многочлены при условии, что их полная форма
предварительно задана.
Динамика точки
Если материальная точка находится под воздействием силы
t( dx λ
f\x, —тг, г) , то уравнение ее движения вдоль прямой имеет вид
d2x „ / dx
т-
rU4b<)· 0)
dt* ' \ · dt
Рассмотрим частные случаи дифференциального уравнениг
движения точки.
dx
Случай 1. Сила f зависит только от скорости v= —77-.
а) Сила сопротивления fc (сопротивление среды) пропорцио
нальпа скорости fc — kv.
б) Сила сопротивления fc пропорциональна квадрату скорост!
Уравнение движения точки (1) принимает вид
dv ... I dx
Это уравнение типа y"=F(y').
Случай 2. Сила f зависит только от пройденного расстояния л
Уравнение движения точки (1) принимает вид
т ■=—kx. (2
dt2

Гл. XI. Уравнения второго порядка
291
Это уравнение типа y"=F(x).
Уравнение (2) решаем не общим методом, а как линейное
уравнение с постоянными коэффициентами.
Случай 3. Сила / зависит от пройденного расстояния χ и ско-
dx
|)(>сти v — —тт-,1Ю не зависит явно от времени ι (или зависит от вре-
dx
мени t и скорости v= —тт, но не зависит явно от х).
а) Прямолинейное движение материальной точки подчинено
упругой связи с трением, причем сила трения пропорциональна
скорости. Уравнение движения. (1) принимает вид
d2x , „ dx
Это однородное линейное дифференциальное уравнение с
постоянными коэффициентами и ■.
mm
б) На материальную точку действует· периодическая сила
/=Л sin ωί. Сопротивление среды пропорционально скорости
движения V.
Уравнение движения (1) принимает вид
d2x . . J n dx
Это неоднородное линейное дифференциальное уравнение с
постоянными коэффициентами.
в) На материальную точку действует периодическая сила
f=A sin ωί. Сопротивление среды пропорционально квадрату
скорости.
Уравнение движения (1) принимает вид
=Λ5ίηωί-β (~).
dzx . . , „ / dx \2
τη-
dt2 K v dt
Понижаем порядок уравнения подстановкой —тт- =ν·
dv
m —- =А sin at—βυ2. (3)
Уравнение (3) интегрируется приближенными способами.
Случай 4 (общий). Сила f зависит от времени /, расстояния χ
dx
и скорости v= —тт-, τ· е· имеют место вынужденные колебания

292
Гл. XI. Уравнения второго порядка
материальной точки, подчиненной упругой связи под действием
внешней периодической силы.
Уравнение движения (1) примет вид
<Рх
m ———\-ах=A sin at
at2
или с учетом сопротивления среды
m
d2x
dt2
dx
~df
-\-ax=A sin ωί,
т. е. представляет неоднородное дифференциальное уравнение с по-
л.х. k a
стоянными коэффициентами и .
mm
Исследование колебаний
Свободные колебания
Пусть груз массой m подвешен на пружинной рессоре.
Отклонение груза от положения равновесия у, направленное
вниз, считается положительным, вверх — отрицательным.
Положение
та.
Π
Упригошь
пружины
Сила сопротивления
адижению
//////////////// /7777777777ТП7
Рис 79
В положении равновесия сила тяжести равна упругости
пружины. Силу, стремящуюся вернуть груз в положение равновесия,
будем считать пропорциональной отклонению, т. е. равной ky,
где k — постоянная для данной рессоры величина (рис. 79).
Предположим, что движению груза препятствует сила сопро-
dy
тивлеиия, пропорциональная скорости —— движения груза, т. е.
du
сила λ —77-, где λ — коэффициент пропорциональности.

Гл. XI. Уравнения второго порядка
293
Таким образом, на груз действует сила ky-\-%---. На
основании закона Ньютона
где знак минус означает, что, сила действует против движения.
Уравнение (1) может быть представлено в виде
«-£-+*!-+*=<>
ПЛИ
dt2 m dt m
λ k
откуда, обозначая =р, ■ =q, имеем:
J mm
y"+py'+qy=0- (2)
Характеристическое уравнение, соответствующее уравнению
(2), будет
rz+pr+q=0,
а его корни
Случай 1. Если сопротивление ρ настолько велико, что
подкоренное выражение положительно, то корни г ι, г2 будут
действительными отрицательными числами.
Общее решение будет
у=Суе-г*-\-С2е-т*. (3)
Из равенства (3) следует, что отклонение у стремится к нулю
(груз движется к положению равновесия) при возрастании
времени t. Колебаний в этом случае не будет.
Случай 2. Если сопротивление таково, что \-x-f =<7, то
Ρ
Г1=Г2=_Т
Общее решение будет

294
Гл XI. Уравнения второго порядка
Здесь отклонецис у стремится к нулю при возрастании t, но
более медленно благодаря наличию сомножителя t.
Случай 3. Если сопротивление отсутствует, т. е. р=0, то корни
/·ι,2= ±βί,
где β="|/<7-
Общее решение будет
yz^d cos βί+Ca sin β/. (4)
В уравнении (4) постоянные Ci и С2 заменим другими, для чего
разделим и умножим правую часть на у Ci2+C22, откуда
y = VCi2+C22( 'Cl cosPH-· sing^) . (5)
У Cf+Cz2 У Ci2+C22
Вводим обозначения
Л = У Ci2+C22, sincpo=— - , cos(po=— -.
Тогда уравнение (5) принимает вид
у=А (sin φο cos βί+cos φο sin βί)
или
у=А βίηίβί+φο).
Колебания в этом случае называются гармоническими. Пром1-
жуток времени Т, за который аргумент синуса изменяется на 2г.
2я
называется периодом колебаний, в данном случае Т= ——-. Части-
Ρ
той колебаний называется число колебаний за время ^=2π; в
данном случае частота будет β. Величина А наибольшего отклонения
равновесия называется амплитудой колебания; величина φο —
начальной фазой.
Случай 4. Если сопротивление настолько мало, что подкоренное
выражение отрицательно, то корни будут комплексными
Γι = --|-+βι, Γ2=--|--βί,
где

Гл XI. Уравнения второго порядка
295
Общее решение
ρ
у=е '2~ г (Q cos p/+C2 sin β*)
или после аналогичной замены постоянных интегрирования Ci и С2
имеем
г/= —— sin(pi+cpo).
е2
Здесь величина представляет амплитуду, зависящую от
ρ
е 2
премени ί и стремящуюся к нулю с его возрастанием. Колебания
будут затухающими.
Вынужденные колебания
Пусть сопротивление движению отсутствует (р=0), а нижняя
точка рессоры совершает колебания по закону z=l sin ω/, т. е. груз
колеблется при наличии внешней периодической силы. В этом
случае сила, стремящаяся вернуть груз в положение равновесия, будет
lt(y-\-l sin ω^), и по закону Ньютона получаем уравнение
йгц
ky-\-kl sin ωί= — m -
dt2 '
которое можно представить в виде
m-—j-—\-ky=—kl sin at
at1
или
d2y , k kl .
-j%- + - У = sin at. (6)
dt2 m m ч '
k kl
Обозначая =q и —а, уравнение (6) запишем
y"-\-qy=a sin wt. (7)
Так как gX), то общее решение соответствующего однородного
уравнения будет
Уоцп= Ci cos βί+Сг sin β/=Λ sin (βί-f-qO)·
Если частота внешней силы ω не равна частоте собственных
колебаний, то частное решение неоднородного уравнения будем
искать в виде
г/частп=^1 cos a>t-{-A2 sin ωύ.

296
Гл. XI. Уравнения второго порядка
Подставляя это выражение в уравнение (7), находим
Л,=0, А2= ?—.
q—ω2
Общее решение
г/=г/оДн+г/частн=^4 sin(β/+φο) + ■■ _ 2 sin ω/.
Колебания груза получаются в результате наложения
собственного колебания с частотой β и вынужденного колебания с
частотой ω.
Если частота внешней среды ω совпадает с частотой
собственных колебаний β, то частное решение будем искать в виде
y4&cTu=t(Ai cos ωί-\-Α2 sin ωί).
Подстановка этого выражения в уравнение (7) приводит
к определению значений:
Следовательно,
Общее решение
Λι=--5—, Α2=0.
2ω
«/частн= t COS ωί.
2ω
a
г/=#одн+г/частн=Л sin (βί+cpo) — у- / cos ωί. (8)
Второй член правой части равенства (8) показывает, что
амплитуда колебаний неограниченно возрастает с увеличением t. Это
явление (при совпадении частоты собственных колебаний системы
с частотой внешней силы) называется резонансом.
I. НЕПОЛНЫЕ ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
§ 1. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Колебательное движение от силы, пропорциональной
расстоянию, до центра притяжения
Задача 138. Определить закон движения материальной частицы
массой m под влиянием силы, направленной к центру О и прямо
пропорциональной удалению χ частицы от центра притяжения
(рис.80). "ί:
Решение. Если^на материальную частицу массы m действуе1)
центральная сила {, пропорциональная удалению χ частицы от цен

§ 1. Гармонические колебания
297
тра притяжения О, то такая сила называется восстанавливающей.
Восстанавливающая сила для рассматриваемой задачи равна
/= —ах.
По второму закону динамики она выражается уравнением
d2x
f=m
dt2
f=-nx/n
Рис. 80
Отсюда дифференциальное уравнение движения
d2x
т
или
dt2
d2x
--—αχ
dt2
+ω2*=0,
где ω2= —; здесь а — коэффициент упругости, ω — частота
колебаний.
Это неполное линейное однородное дифференциальное
уравнение второго порядка. Соответствующее характеристическое
уравнение
/·2+ω2=0
имеет корни
г\, 2=± V —ω2=±ωϊ.
Так как корни характеристического уравнения мнимые, то
общее решение имеет вид
или
χ—Ci sin ωί+Сг cos ωί
*= Ci (sin (ut-\- ·—- cos at J
Введем вспомогательный угол φ соотношением
С2
Ci
= tgcp.

298
Г л XI, Уравнения второго порядка
Тогда
х~ ■ (cos φ sin ωί+sin φ cos ωί)
cos φ 'τ /
или, обозначая
получим
cos φ
χ—A sin(o)i+cp). (1)
Выражение (1) представляет собой гармоническое колебание
с амплитудой А и начальной фазой φ. Период колебания Τ найдем
из формулы:
ω(ί+Τ)-\-ψ=ωί+ψ+2π,
где 2л —- период синуса, откуда
2л
Г=
ω
или
<■> = -ψ- (2)
Подставляя значение (2) в общее решение (1), получим
х=А sin (-~ί+φ) .
Притяжение материальной точки
двумя равномощными центрами
Задача 139. Материальная точка Μ массой m притягивается
двумя равномощными центрами А п В, расположенными один от
другого на расстоянии 2а. Сила притяжения пропорциональна
расстоянию от центра до точки М. В начальный момент точка
находится в повое на линии центров, на расстоянии Ь от ее середины
(рис. 81). Найти закон движения точки.
Решение. В любой момент на точку Μ действуют две силы
притяжения центрами А и В
fA=—K(a+x), 1
fB=tt(a—x), )
где κ — коэффициент пропорциональности.
Равнодействующая этих сил
R=fA+fB=-2xx.

§ 1. Гармонические колеЬания
На основании второго закона динамики получим дифференци-
ильное уравнение движения
т ... =— 2кх
пли
dt2
d4 , 2κ
dt2 m
(1)
i · Г
Щ
Рис 81
2κ .
Вводим обозначение k2= \ и тогда уравнение (1)
принимает вид
d2x
+k2x=0.
dt2
Общее решение этого уравнения
x=Ci sin kt-\-C2cos kt.
Начальные условия: при / = 0 х=Ь, —гг =0. Отсюда
и так как
то
b = Clsin{k-0) + C2cos(k-0),
dx
dt
= Cifecos kt—Czk sin kt,
0=C,kcos{k-0) — C2ksm(k-0).
(2)
(3)
(4)
Решая систему уравнений (3) и (4), получаем искомые
постоянные интегрирования
С1=0, С2=Ь. (5)
Подстановка значений (5) в общее решение (2) определяет
закон движения материальной точки
X=zb COS kt.

300
Τ л XI. Уравнения второго порядка
Притяжение камня, упавшего в глубь Земли,
ее центром
Задача 140. Допустим, что через земной шар проложен узкий
трубопровод, проходящий через центр Земли (рис. 82). Упавши!
в него камень притягивается центром Земли с силой, прямо прг
порциональной расстоянию между ними. Через какое время каменг
пролетит сквозь всю Землю?
Решение. В любой момент на точку Μ действует сила f
притяжения к центру Земли, пропорциональная расстоянию χ тел;
от этого центра и направленная к центру, т. е. при положительном ;.
в сторону его убывания F=—%х. На основании второго закот
динамики получим дифференциальное уравнение движения тела
или
—Г7„ Х=0. (1
dt2 т т v
Вводим обозначение fe2= · . Тогда неполное линейное диш
т
ференциальное уравнение (1) примет вид
d2v
-£-+**=* <2'
Общее решение уравнения (2):
χ—Ci sin kt-\-C2 cos kt. (3
dx
Начальные условия: при ί=0 χ=— R, ——- =0. Отсюда
и, так как
то
-^ = C1sin(/z-0)+C2cos(^-0) (4
dx
—— =Cik cos kt—C2k sin kt,
dt
0=Clkcos(k-0)—C2ksin(k-0). (5
Решая систему уравнений (4) й (5), находим
d = 0, Cz=-R. (6
Значения постоянных интегрирования (6) подставляем в обще·:
решение (3) и тогда
х=— R coskt,

§ 1. Гармонические колебания
301
откуда
/=Tarccos(--^),
На противоположном конце трубопровода x=R и
искомое время
'-т
Рис 82 Рис. 83
Дополнительное условие: при t=0 F=mg и х=— R. Исходя
из этого, имеем
mg=%R
или
к = _&_
т R
и коэффициент
Таким образом,
t= -г- =л Ц =п у — ^ ?»42,3 лш«.
к ' § ' У,о1

302
Гл. XI. Уравнения второго порядка
Математический маятник
Задача 141. Найти закон движения и определить период Г
математического маятника длиной / при малых отклонениях.
Решение. Силу тяжести Ρ в точке М, разложим на две
составляющие: N по направлению нити и f — по касательной к
траектории. Сила N уравновешивается сопротивлением нити, и, таким
образом, вся система сил эквивалентна силе /. Из рис. 83 видно:
|/| =Р sin a = mg sin a,
где m — масса, g — ускорение силы тяжести.
Так как для положительных углов а касательная
составляющая f направлена в отрицательную сторону, то
f=—mg sin аж—mg а,
так как при малых отклонениях нити sin α?»α.
о
Ввиду очевидного равенства а= -г- составляющая
Здесь s=AM — длина пройденного шариком криволинейного
пути. На основании второго закона динамики запишем
дифференциальное уравнение движения:
d2s ma
т~ж =—~s
или
d2s , g
dP ' /
s = 0.
Интегрируя это неполное линейное уравнение второго порядка,
получим общее решение
s = Ci sin ]/-^- t+C2 cos У-у t.
Используем начальные условия: при i=0 s=a и —τ—
Отсюда
Ci=0, C2=a.
Подставляя эти значения в общее решение, получим

§ 1 Гармонические колебания
303
s = acosy -η-t,
где а —· амплитуда колебания.
Движение математического маятника представляет
гармоническое колебание с периодом
>п-
= 2п]/ —
Физический маятник
Задача 142. Найти закон движения физического маятника
(ось Oz перпендикулярна к плоскости чертежа).
Решение. Физическим (или сложным) маятником назы-
мается твердое тело, вращающееся вокруг горизонтальной оси Oz
под действием силы тяжести (рис. 84). Обозначим расстояние ОС
центра тяжести маятника от оси вращения через а и силу тяжести
маятника через Р, причем P=Mg, где Μ — масса маятника.
Так как заданной силой является только сила Р, то главный
момент (сумма моментов всех сил системы) относительно оси Oz
равен
Mz = — Mga sin φ,
где φ — угол отклонения маятника от вертикали, отсчитываемый
и направлении, обратном движению часовой схрелки.
Как известно из динамики, дифференциальное уравнение
вращательного движения твердого тела вокруг неподвижной оси
d2®
'*-Ж=м» 0)
где J г —· момент инерции тела относительно оси вращения Oz.
Тогда уравнение (1) примет вид
d\
Jz-^r=-Mgasmy. (2)
Уравнение (2) представляет дифференциальное уравнение
движения физического маятника.
При малых отклонениях маятника приближенно можно принять
ΒΪηφΛίφ. Получим приближенное дифференциальное уравнение
малых колебаний маятника
d2®
= —Mga<p.
dP

304
Гл XI. Уравнения второго порядка
Пусть
Mga
= k*
откуда
dt*
+^2φ=0.
(3)
Уравнение (3) представляет дифференциальное уравнение
гармонических колебаний.
Рис. 84
Интегрируем уравнение (3), предполагая, что начальная
угловая скорость маятника равна нулю
/ άψ \
\ωο= —— =0/ . Так как
корнями соответствующего характеристического уравнения rz-\-k2=0
являются мнимые числа ±ik, то общее решение уравнения (3)
выразится
Ф==С± cos /г^+С2 sin /ei. (4)
Постоянные интегрирования Ci и С% вычисляем из равенства
(4), используя начальные условия:
1) при t=0 φ=φο:
cpo=Ci- l+C2-0,
(?ι=φο;

§ 1. Гармонические колебания
305
2) при ί=0 ωο= —тг =0:
άψ
= —kd sin kt+kCz cos &/,
—/eqxrO+/s-C2-l=0,
C2=0.
Подставляя найденные значения в уравнение (4), получим
уравнение движения физического маятника при малых колебаниях
φ=φο cos kt.
Полный период колебаний
k * Mga
Mgc
Колебание удлиненной упругой пружины с грузом
Задача 143. К вертикальной пружине, силой тяжести которой
пренебрегаем, подвешен груз Р, удлиняющий ее на величину /
(рис. 85). Оттянув груз на длину а вниз, его оставляют свободно
колебаться. Найти закон этого движения, пренебрегая побочными
сопротивлениями.
Решение. Ось Ох направим вертикально вниз и начало О
иозьмем в том месте, где находился груз в положении статического
равновесия. В любом положении А на груз действуют две силы:
сила тяжести P = mg и упругая восстанавливающая сила
пружины f.
По закону Гука при малых деформациях упругие силы
пропорциональны соответствующим деформациям.
В точке О упругая сила равна силе тяжести Р, а
соответствующая деформация /. Следовательно,
\P\=kl. (1)
В точке А упругая сила /, соответствующая деформация
равна 1-\-х:
\f\=k(l+x). (2)
Поделив почленно равенство (2) на равенство (I), получим
m _ ι+χ
\р\- ι '
откуда абсолютная величина силы /:
\П=р+~х.

306
Гл XI. Уравнения второго поряока
Так как при положительном χ сила f действует в отрицатель
ную сторону, ее надо считать силой отрицательной, а поэтому
f—P—^x.
Равнодействующая обеих сил
R=P+f
или
*=-—*=—rx-
На основании второго закона динамики дифференциальное
уравнение движения
d2x me
m^= ΊΓΧ
или
d2x g
~ж-+тх=°-
Это неполное линейное уравнение второго порядка. Интегрируя
его, получим общее решение
дс=Ci sin |/-^- i+C2 cos У-j ί. (3)
Используем начальные условия. В самом нижнем положении
оттянутого груза имеем:
^=0, х=а, -——=0.
at
На основании этих условий находим
Ci=0, Сч=а.
Подставляя эти значения в общее решение (3), получим закон
гармонического колебания
x = acos |/-у t
с периодом Т=2л у -
ё

§ 2. Движение тела без трения
307
§ 2. ДВИЖЕНИЕ ТЕЛА БЕЗ ТРЕНИЯ
Горизонтальное скольжение цепи
. ача 144. Цепь длиной /=4 м соскальзывает с гладкого
!зонтального стола. В начальный момент движения со стола
1Л конец цепи длиной а=0,Ъ м (рис. 86). Пренебрегая трением,
ч впемя соскальзывания всей цепи.
Рис. 86
j е и и е. В любой момент времени на цепь действует си-
, равная силе тяжести свесившейся со стола к этому моменту
■ή цепи длиной х.
~' >значая силу тяжести всей цепи Р, получим очевидную про-
шию
F _ х,
Ρ ~ Г
куда
Ρ mg
F=
х,
ι ι
ie m — масса.
На основании второго закона динамики
■т-
d2x
(1)
(2)
Приравнивая зависимости (1) и (2), получим дифференциаль-
ое уравнение движения цепи

308
Гл XI. Уравнения второго порядка
агх mg
или
агх е
-dtr-Tx=°-
Подставляя числовые значения и принимая приближенно
g"= 10 м/сек2, неполное линейное дифференциальное уравнение
второго порядка запишем в виде
Соответствующее характеристическое уравнение
г>-2,5=0
имеет корни
Г1=Ут- Г2=-Ут·
Общее решение
VI* -V%<
x=de +C2e . (3)
Определим произвольные постоянные Ci и С2 из начальных
dx
условий: при ί=0 х = а=0,Б м, и= ——- =0, откуда
at
и, так как
то
a=Cieo+C2e°=Ci+C2 (4)
.,/— Ут* ί/~ -Κϊ'
о^1/4с1ео-У-|с2ео.
(5)
2 Г 2
Из системы уравнений (4) и (5) находим
Ci=C2=-|-=0,25.
Подставляя эти значения в общее решение, получим частное
решение уравнения (3):
(VI· -УТЛ
x=0,25le +e /. (6)

§ 2 Движение тела без трения
309
Разрешаем уравнение (6) относительно /. Имеем
е +е = 4х
или _
е +1
е
•Ах.
t
Это выражение приводит к квадратному уравнению относи-
VI'
тельно е :
(VT'X VT<
\β ] —4xe +1 = 0.
Решая его, получим
Vf
2 \ 4х± У 16х2—4
е I = =-^ =2х±У4х2-1. (7)
В выражении (7) знак минус перед корнем отбрасывается, так
как при t~>0 e >е . Следовательно,
V-
'τ·
= 2х+ У4х2—1,
откуда
;=У-|-1п(2;с+У 4х2-1)
и при х=/=4 ж искомое время
f= ]/^- In (8+ /63) «1,75 сек.
Итак, в течение 1,75 сек вся цепь соскользнет со стола.

ош
Гл. XI. Уравнения второго порядка
Вертикальное скольжение цепи
Задача 145. Цепь длиною / м переброшена через блок. С однок
стороны свисает а=10 м цепи, с другой 6 = 8 м цепи (рис. 87)
Через какое время цепь сойдет с блока?
Решение. В любой момент на цепь действует сила F, равная
разности сил тяжести Pi и Р2 двух концов цепи с разных сторор
блока. Если в момент t больший конец цепи имеет длину х, то
меньший конец имеет длину α-f Ь—х.
Обозначим силу тяжести цепи Р. Тогда получим пропорцию
Pi х
Р2 а+Ь—х
или
Pi—Рг 2х—а—Ь
Р1+Р2 а+Ь
(1)
Так как общая сила тяжести цепи Ρι-\-Ρζ=Ρ, а длина a-\-b = l,
то соотношение (1) примет вид
F _ 2х—1 .
~Р~~~ I '
откуда
F=-£-(2*-/)=-^-(2x-/).
На основании второго закона динамики получим
дифференциальное уравнение движения цепи
или
или
Введем
гда
новую
d4
m dP =
d4
dP
переменную
d*y
dP
d4
dP
d2y
mg
I
f(2x-
2x—I
-=2-
1
2
2g
-(2x-
~l) =
-0
= 0.
=y. Тогда
dPx
dP
d2y
dP
г; —Г
t
)
& 1 —· <2)

§ 2. Движение тела без трения
311
Обозначим
2g
k2=
I
Тогда уравнение (2) запишется
d2y
dt2
—k2y=0.
Общее решение этого неполного линейного уравнения второго
порядка
t/=Ciefct+C2e-«. (3)
dx dy
Начальные условия: при /==0 х=10 м, г/=1, —ту = —тт- =0.
()тсюда
\ = С1ек-°+С2г* °, (4)
и так как
di
то
0=Cikeh0-C2ke-k °. (5)
Решая систему уравнений (4) и (5), находим постоянные
интегрирования
Ci=T' С*=Т- (6)
Значения (6) подставляем в общее решение (3)
У= γ (efti+e-fei)
или
1 е2М+\
2y=e*t+ -— = ^,
e2ht—2yeht+\=0,
откуда
Знак минус перед корнем надо отбросить, так как при ^>0
,./if-xj-fci с другой стороны, мы имели ем-\-е~м = 2у.
Следовательно, еы>у. Итак,
eM=y+iy2-\. (7)

312
Гл. XI. Уравнения второго порядка
Разрешая равенство (7) относительно /, имеем
1
/=т In (г/+У г/2-1)
или
t=]f~ln[(2x-l)+i(2x-iy-\]
и при х=1
г 2ё У 9,81
сек.
а* о-х
Рис. 87
Рис.
§ 3. ДИФФЕРЕНЦИАЛЬНЫЙ МАНОМЕТР
Задача 146. Манометр, применяемый для измерения давления
в гидромеханической лаборатории, работает под давлением воздуха
ρ кГ/см2 и принимает положение, показанное на рис. 88. Определить
уравнение движения столба жидкости, когда давление ρ внезапно
понижается до нуля, если общая длина жидкости в манометре /,
а удельный вес у кГ/см3.

§ 4. Распределение теплоты в стержнях
313
Решение. Для трубки диаметра d общий вес жидкости
G=——d2ly. Возмущающая сила обусловлена разностью уровня
в двух рукавах манометра. Если она взята как среднее
арифметическое общей разницы уровней, то ее величина
F=2(~dz)xy.
4
Поэтому дифференциальное уравнение
dt* '
причем знак минус обозначает, что длина координаты χ берется
от начала отсчета в направлении, положительном вниз.
Следовательно,
-2(τ*)*ν
Td4v л
или
4 '"' в dP
d4 +Ц-*=Ъ.
dtz
Общее решение
x = Ci sin ]/-^- t+C2 cos]/-у-1.
Частота колебаний
' 2π Г /
§ 4. РАСПРЕДЕЛЕНИЕ ТЕПЛОТЫ В СТЕРЖНЯХ
Распределение теплоты в стержне
от стационарного источника
Задача 147. На левом конце стержня (при х=0) постоянная
температура то. В точках стержня, лежащих па разных расстояниях
χ от левого конца, устанавливается температура т=т(л:). Найти
температуру в точке с абсциссой х.
Решение. Стержень отдает свою теплоту в воздух и поэтому
охлаждается. Теплота переходит от более теплых частей стержни
к менее теплым. Левый конец постоянно подогревается, чтобы урав-

314
Гл. XI. Уравнения второго порядка
повесить потерю теплоты. В каждой точке стержня будет своя
собственная температура, не зависящая от времени.
Пусть на расстоянии χ от произвольной точки стержня до его
нагретого конца температура х(х). Во всем элементе от χ до x-\-dx
будет приблизительно одна и та же температура х(х).
В единицу времени элемент dx потеряет kx(x)dA теплоты,
где dA — площадь соприкосновения с воздухом, k — коэффициент
пропорциональности.
Если Φ — поперечное сечение стержня, то количество теплоты,
dx
полученное холодным концом элемента, благодаря градиенту
равно
dx
—λΦάί
dx
dx
где λ — коэффициент теплопроводности, а количество теплоты,
потерянное теплым концом элемента, будет
—λΦ dt
dx
dx
x+dx
Так как температура стационарна, т. е. не меняется со
временем, то количество притекшей теплоты равно количеству потерянной
теплоты:
λΦάί
dx
dx
= —ΧΦάί
dx
dx
x+dx
-x-kx{x)dAdt.
o;
Так как dx бесконечно мало, то
dx
dx
dx
x+dx
dx
d2x
dx2
dx.
Величина dA равна длине окружности поперечного сечения
стержня С, умноженной на длину элемента dx.
Подставляя эти значения в уравнение (1), после
преобразований получим
d2x
kxCdxdi—'ΚΦ dt
или
d2x
dt2
kC
λΦ
dt2
τ=0.
dx
(2)
Обозначая
kC
~λΦ~
=p2, уравнение (2) запишем в виде
τ"-ρ2τ=0.

§ 4. Распределение теплоты в стержнях
3lu
Характеристическое уравнение
откуда
Г\,г=±Р-
Общее решение
Учитывая, что на больших расстояниях от начала координат
(х-э-оо) температура τ=0, получим 6^=0, что дает зависимость
T = C2e-J«.
Начальное условие: при х=0 τ=το, и тогда
С2=То·
Температура в точке с абсциссой χ будет
т=х0е-1>х.
Задача 148. Один конец стержня нагрет до 100° С. На
расстоянии единицы длины от этого конца температура равна 95° С. Найти
температуру в точке, удаленной от конца стержня на 10 единиц.
Решение. На расстоянии χ от начала стержня (нагретого
конца) выделим элемент длиною dx. Температуру Т(х) на данном
элементе можно считать постоянной.
По закону Ньютона элемент стержня за время dt теряет
теплоту в количестве
k(T—T0)Pdxdt,
где k — коэффициент пропорциональности, Ρ — периметр
поперечного сечения стержня, Pdx — площадь поверхности элемента,
соприкасающаяся с окружающей средой, Го — температура
окружающей среды.
Пусть Φ — площадь поперечного сечения стержня. По закону
Фурье количество теплоты, полученное холодным концом элемента
стержня за время dt, равно
dT(x)
и количество теплоты, потерянное теплым концом элемента
стержня, будет
dT(x+dx) / dT d2T \
"λφ —Ίχ— dt=-m <1F + -Жdx) dU
ι до λ — коэффициент теплопроводности.

316
Гл. XI. Уравнения второго порядка
На элементе dx температуру Т(х) можно считать постоянной,
и количество притекшей теплоты должно равняться количеству
потерянной.
Следовательно,
-λΦ ~ Μ=-λΦ —— dt-λΦ -— dt dx+k(T—To)Pdxdt,
CLX (XjC CIJC
откуда
d.4 kP .„ „ч „
&p
или, обозначая для краткости =п2, получим
с/2(Т-Го)
__ п2(Г-Го)=0. (1)
Общее решение неполного однородного дифференциального
уравнения второго порядка с постоянными коэффициентами (1)
T(x)=To+Cie^+C2e-nx. (2)
Начальные условия: а) при х=0 7=100; б) на очень
большом расстоянии стержень должен иметь температуру, как и
окружающая среда, т. е. при x-)-oo (Г—Го)-^0. Но тогда е~пж->-0,
а епх—>-оо.
Так как Т(х) не может обращаться в бесконечность, то
постоянная интегрирования Ci должна быть равна нулю, т. е. Ci=0,
а Сг=100, так как при х-+оо Г=Г0=0.
Тогда равенство (2) принимает вид
Т(х) = Же-пх. (3)
Для определения параметра η используем дополнительное
условие: при х=1 Т=95°, откуда
95=100е-пж.
Следовательно,
—п = 1п0,95.
Подставляем эту величину в уравнение (3) и получаем закон
изменения температуры по длине стержня
Т(х) = 100 (0,95)х.
При л:= 10 искомая температура
Τ(10) «59,9° С.

§ 4 Распределение теплоты в стержнях
317
Распределение теплоты в продольном ребре
прямоугольного сечения
Задача 149. Найти распределение температуры в продольном
ребре жесткости прямоугольного сечения металлической
конструкции (рис. 89) длиной /. Условия работы: 1) тепловой поток
постоянней, т. е. температура в любой точке ребра жесткости не изменяется
ι течением времени; 2) материал ребра однородный и теплопровод-
Рис 89
пость постоянная; 3) коэффициент передачи теплоты сплошной
ι ранью поверхности ребра постоянный; 4) температура
окружающей жидкости постоянная; 5) не имеется других источников
теплоты, кроме самого ребра; 6) отсутствуют температурные
градиенты (перепады) поперек ширины ребра.
Решение. Рассмотрим небольшой элемент ребра высотой Ах.
Элемент имеет площадь поперечного сечения А = Ы, а площадь
поверхности AS = 2(/+6)/\x, которая будет AS —2/Δχ, если принять,
что длина и высота ребра очень большие по отношению к его
ширине (/»δ, ό>δ).

318
Гл XI. Уравнения второго порядка
Пусть Г — температура ребра в элементе Ах. Поскольку
окружающая жидкость рассматривается при постоянной температуре Ts,
то избыток температуры или разница между температурой ребра
и окружающей жидкости О —Г—Ts, откуда, дифференцируя,
получаем dQ = dT.
Предполагаем, что ребро передает теплоту окружающей среде.
Тепловой баланс: поступающая теплота равна убывающей из
элемента высотой Ах теплоте. Поступающая теплота в сечении х,
согласно закону Фурье,
ил dT
:—kA
= —Ш~г-
ах
dx
где k — теплопроводность.
Аналогично выходящая из элемента в сечении х-\-Ах теплота
ил dT I и., dQ
dx I ж+дж dx
х+Ах
Следовательно, теплота выходит из элемента Ах через
поверхность AS путем конвекции.
Таким образом, эта теплота
qs=fiAS(T-Ts) = 2hlAxQ.
Тепловой баланс примет вид
qx—Qx+Ax-\-qs
или
dQ
-ш m
dx
= —Ш-
dx
-\-2hxAxQ,
χ+Αχ
который может быть представлен
dQ I dQ
dx Iж+дж dx
2h
Ax kb
В предельном случае, когда Ах стремится к нулю, уравнение (1)'
принимает вид неполного линейного уравнения второго порядка
ащ -m«e=o.
dx2
где
'2h
m=]/-

§ 4. Распределение теплоты в стержнях
319
Общее решение этого уравнения
Q = Clemx+C2e-mx.
В случае отсутствия теплового потока на конце ребра, где х=Ь,
q\x=b = ~k&l
с?е
dx
x=b
_dQ_
dx
=0,
x=b
(2)
так как ни k, ни б или / не равны нулю.
Кроме того, при постоянной температуре излишек у основания
0|ж=0=Эо.
(3)
Уравнения (2) и (3) образуют начальные условия. Чтобы
использовать первое из них, необходимо продифференцировать общее
решение дифференциального уравнения. Тогда
dx
— tnCiemx—mC2e-mx
и, подставляя условие (2), получаем
dx
или
Ciemb=C2e-mb.
= 0=mCiemb—m C2e-mb
x=b
(4)
У основания излишек температуры равен разности температуры
основания и окружающей среды и тогда
м>—Ts—θο= С\-\-С2.
(5)
Уравнения (4) и (5) используются для определения
постоянных интегрирования:
em&Ci—е-тЬС2=0, 1
Ci+C2=0, )
откуда
0 —е~тЬ
Q0e~mb
Cl=
θο 1
gmb Q—mb
1 1
етЪ-\-е
-mb
в0е-тЬ
2 ch mb
С2=
emb 0
2 ch mb
в0етЬ
2ch mb

320
Гл. XI. Уравнения второго порядка
Таким образом, искомое решение
о α
Q— (g—mb gmxigmb ρ—rnx\ —— ["gtn(b—x)_l_g—m(b—ж)1 -_.
2chmb K ^ ' 2chmb L ^ J
Ooch m(b—x)
ch /n£>
Оно представляет избыток температуры в л!обой точке ребра
как функцию расстояния χ от его основания.
§ 5. ПРОДОЛЬНЫЙ ИЗГИБ ПРЯМОГО СТЕРЖНЯ
Стержень постоянного поперечного сечения
со свободными концами
Задача 150. Определить критическую нагрузку стержня ОА
длиной /, если оба его конца подвижны, но не могут сходить с
первоначальной неискривлепной оси стержня (рис. 90).
Решение. Критическим называется то значение силы Р, при
котором начинается искривление оси стержня. Для любого сечения
D(x, у) изгибающий момент
М=-Ру.
В дифференциальном уравнении упругой линии
d2y M
dx2 ~~~ EJ
определяем изгибающий момент для сечения в точке D(x, у) и тогда
d2y Ρ
dx2 EJ
У, (О
где Ε — модуль упругости, / — момент инерции площади
поперечного сечения стержня.
Дифференциальное уравнение упругой линии (1) можно
преобразовать к виду
d2y P
+ ~ЕГГУ=а
dx2 ' EJ
Ρ
или, обозначая q2-
d2»
EJ'
&У
dx2

§ 5. Продольный изгиб прямого стержня
321
Общее решение полученного уравнения
у= Ci sin qx-\-C2 cos qx.
(2)
Граничные условия: так как концы стержня О к А должны
оставаться на оси х, то при χ—Ο у=0 и при х=1 у=0. Отсюда
0=Cisin((7-0)+C2cos(i7-0), \
0=Cismq[-\-C2cosqt /
ИЛИ
С2=0, 1
ι sin ql=0. У
(3)
z^^:
7
"V
k
1
щу>
Рис, 90
Одно из решений системы (3) будет Ci=0, C2=0. Подставляя
и общее решение (2), получим
г. е. упругая линия совпадает с осью χ и стержень не искривлен.
Этот случай, очевидно, соответствует такой нагрузке Р, которая
меньше критической нагрузки Ркр.

322
Гл. XI. Уравнения второго порядка
Для искривления стержня необходимо, следовательно, чтобь
Ci#0. Согласно системе (3), это возможно лишь при условии
откуда
или
где η — любое целое число.
sin ql=0,
ql=tm
ηπ
Я-
l '
Если η=0, 1, 2, 3,... , то соответственно <7=0,
π 2π 3π
Γ Ι ' Ι '·'
Подставляя эти значения q в общее решение и принимая в<
внимание, что С2=0, получим соответственно такие уравнения упру
гой линии
t/=Cisin(0-x)=0,
y—Cism — x,
y=C1sm—j-x,
y = C1sm-1—x,
Первое уравнение дает упругую линию еще не искривленное
стержня. Второе уравнение дает для упругой линии одну полуволн
синусоиды (у обращается в нуль на протяжении длины стержня
только 2 раза: при х=0 и при х=1), и стержень уже искривлен
Третье уравнение дает синусоиду, состоящую из двух полувол]
(у обращается в нуль на протяжении длины стержня / 3 раза: пр
я=0, — и /). Упругая линия, заданная четвертым уравнением
π
содержит три полуволны синусоиды и т. д.
Итак, стержень впервые искривляется при q= ■—-. Это и буде
π
критическим значением <7кр=—-.
С другой стороны,
Поэтому
<?кр
=У:
ЁТ'

§ 5. Продольный изгиб прямого стержня
323
откуда
У_Рк_ _£_
EJ I '
Разрешая последнее равенство относительно Рк, получим
значение критической нагрузки
EJ .
Ρ„=π2-
Р
Стержень постоянного сечения с защемленным концом
Задача 151. Найти критическую нагрузку упругого стержня
ι· одним защемленным и другим свободным концом, если стержень
нагружен центрально приложенной сжимающей силой Ρ (рис. 91).
Решение. Составим дифференциальное уравнение задачи,
исходя из условий равновесия. При определении момента внешних
сил необходимо учесть действующую поперек стержня опорную
реакцию А, которая связана с моментом защемления зависимостью
Мзащ=А1.
Изгибающий момент Μ в произвольном сечении χ выражается
через момент внешних сил:
М(х)=Ру—Ах. (1)
С другой стороны, изгибающий момент выражается
зависимостью
M(x) = -EJy", (2)
где Ε — модуль упругости материала, / — постоянный момент
инерции стержня.
Приравнивая уравнения (1) и (2), имеем:
EJy"=-(Py~Ax). (3)
Уравнение (3) приводится к виду
у"+тту=4тх- <4>
Общее решение соответствующего однородного уравнения
имеет вид
i/cwi=ClSin (y-gj-x)+CiCos \y-jyx)· (5)

324
Гл. XI. Уравнения второго порядки
Частное решение, исходя из вида правой части уравнения (4]
ищем в форме
Участн = «1Х+Й0. (6
Подстановка t/частн, согласно (6), и у"частн=0 в уравнение (4
приводит к уравнению
р , . ν А
откуда, приравнивая коэффициенты при соответствующих стеш
нях х, имеем
А
а0=0, αι= -ρ-.
Тогда частное решение (6) принимает вид
_ А η
ί/частп— ρ Χ· (ι
Суммируя решения (5) и (7), получаем общее решение неоднс
родного уравнения
y=J~-x+Clsm(~\/-£jx) +C2cos(Y^j-x) . (8
Начальные условия: на шарнирпо опертом конце стержн
(л:=0) прогиб у=0, отсюда С2=0; на защемленном неподвижно
конце (х=1) прогиб у и наклон у' должны быть равны нулю, т. ι
У=у' — 0, откуда, подставляя эти значения в функцию (8) и ее прс
изводную, получаем систему
0=^-l+C,sin(")/7^i),
„=4+С,уХс„з(У-^).|
Таким образом, имеем два значения для постоянной интегр!
рования:
с= А1__
Ci=-
EJ
А
1/-£тМШ

§ 5. Продольный изгиб прямого стержня 325
Эти два равенства только тогда взаимосвязаны, если
I 1
Решение трансцендентного уравнения (9) невозможно в замк-
ivtom виде.
Рис. 91 Рис 92
Если надо решить уравнение tg*=*, то берут функции
/ -=.χ и y = tgx и находят бесконечно много точек пересечения этих
шний. С точки зрения технических приложений интерес
представит только наименьшее положительное число х, которое
удовлетворяет уравнению.
Из графика (рис. 92) можно получить, что первая точка
пересечения этих двух линий приближенно имеет абсциссу л:=4,5.

326
Гл XI. Уравнения второго порядка
Применяя правило хорд, уравнение приводим к виду
i/=tgx-x=ctg (-—.—*) —x=ctg(4,7124—*)—■*
и находим корни этой функции, значения которых приведень
в нижеследующей таблице
X
4,500
4,450
4,492
4,493
4,494
3
— π — χ
2
0,2124
0,2624
0,2204
0,2194
0,2184
igx
4,637
3,723
4,463
4,485
4,506
У
0,137
— 0,727
— 0,029
— 0,008
0,012
Итак, х=4,4934.
Таким образом, решение уравнения (9) будет
V ΕΙ
/==4,493.
Следовательно, положение равновесия будет нарушено, когд.
сила Ρ достигнет критического значения
20,19£/
ρ Г '
■"КО
нр
Ρ
(ίο;
Так как 20,19«2π2, то выражение (10) можно записать такж
в виде
2π2£/
кр ·
/2
Ступенчатое поперечное сечение
Задача 152. Стержень ОА (рис. 93) со ступенчатым изменение!
сечения в средней части сжимается с обоих концов одинаковыми п
величине, но противоположными по направлению силами Р. Найт
величину критической силы Ркр.
Решение. Если изгиб малый, то, выбрав точку О за начал
координат и расположив оси так, как указано на рис. 93, получи!
для участка / уравнение
Е]1У"=-Ру
Р
или, обозначая ш^=
Eh'
y"-\-mi2y=0.
(1

§ 5. Продольный изгиб прямого стержня 327
Для участка // дифференциальное уравнение примет вид
EJ2y" = -Py
Ρ
или, обозначая т22= -^т-, получим
tJ2
y"+m£y=0. (2)
Общие решения уравнений (1) и (2) примут вид
y=Ci cos m,iX-\-С2 sin τπχΧ, у—С3 cos m2x-\-Ci sin m2x.
Граничные условия: 1) при х=0 у=0, откуда
0=CiCosmi-0+C2sinm1-0
или
Ci = 0;
2) при я=а ординаты обоих участков совпадают, т. е.
С2 sin rriia= С3 cos m2a-\-Ci sin /η2α; (3)
3) изогнутая ось в точке В имеет в частях I и II общую
касательную (производные от ординат равны), что дает
C2mi cos mia= — C3m2 sin m2a-\-Ckm2 cos m2a; (4)
4) в середине стержня при x=a-\-b касательная параллельна
«си абсцисс, откуда
—С3 sin т2(а-\-Ь)-\-С1 cos m2(a-\-b) =0. (5)
Пусть f — ордината изогнутой оси при х=а-\-Ь; тогда
С3 cos m2(a-\-b)-\-Ci sin m2(a-\-b)=f. (6)
Уравнения (3), (5) и (6) дают
C3=f cos m2(a-\-b), C4=f sin m2(a-\-b).
Подставляем эти значения в уравнение (4) и получаем
tgmla-tgm2b=~±-. (7)
m2
Так как
m
m2
И полагая
7-Н

328
Гл XI. Уравнения второго порядка
■1Ь
имеем
my = m2k.
Уравнение (7) примет тогда вид
tgm2a-tg m2b = k.
(8)'
//
я/
\
i
Τ"
\
,
I
Ρ
/ ар,
II В\[Зг
1
. {_
1
// s\e37
\
1
/ U γ J,
A _i_
Ρ
I
л
Рис, 93
Рис. 94
Из уравнения (8) находим наименьший положительный корень
т2 и определяем тогда критическую силу
PK9=EJ2m22=EJ1mi2.
§ 6. ДВИЖЕНИЕ ШАРИКА В ТРУБКЕ (ЗАДАЧА АМПЕРА)
Задача 153. Трубка наклонена к вертикальной оси под углом а
и вращается вокруг нее с постоянной угловой скоростью ω. В трубке
катится без трения шарик (рис. 94). Найти закон движения шарика
вдоль оси трубки, если в начальный момент он находился на оси
вращения и имел скорость ν0, направленную в положительном на'
правлении оси трубки.

§ 6. Движение шарика в трубке
329
Решение. В любой момент на шарик действуют сила тяжести
p=mg и центробежная сила /=тш2. Составляющая их
равнодействующей на оси χ
Х= -Р cos a+F cos (90°—ее)
или
Х=т(ш2 sin a—g cos α).
Так как
г~л: sin a,
то
X=m(xa>2s'm2a—g cos a).
На основании второго закона динамики получаем
дифференциальное уравнение движения шарика вдоль оси трубки
d2x
т ■ = m(xazs'm2a—g cos a)
или
d2x
-~— ((u2sin2a)x=— g cos a. (1)
Вводим обозначение &2=ω2 sin2a. Тогда уравнение (1)
примет вид
d2x
— k2x——g cos a. (2)
Общее решение неоднородного линейного уравнения второго
порядка (2) будет
x=Cie"+C2e-«+-^^.. (3)
dx
Начальные условия: при ί=0 х=0, — — =υ0. Отсюда
0=С1(* °+С2е-ь °+^^, (4)
и так как
dx
--r-=Cikekt-C2ke-M,
at
ΊΟ
v0=Cikeh-0-C2ke-h о. (5)
Уравнения (4) и (5) образуют систему
g cos a
Ci—Cz= —r~.

330
Гл. XI. Уравнения второго порядка
Решая ее, получаем значения постоянных интегрирования
vok—g cos a n v0k-\-g cos α
Cl= m ' C2= 2iP · (6)
Подставляем значения (6) в общее решение (3) и получаем
х= -гтг" [ (vok—g cos α) efti— (t>ofe+g cos a) e-kt-\-2g cos α],
где &=ω sin a.
II. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
§ 7. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
Движение материальной точки под действием
восстанавливающей силы с учетом сопротивления
Задача 154. Определить закон движения материальной частицы
массы m под действием силы, притягивающей точку к
неподвижному центру О и прямо пропорциональной удалению χ частицы от
центра притяжения О. Материальная частица колеблется в среде
с сопротивлением, пропорциональным скорости движения v.
Исследовать три случая:
1) коэффициент сопротивления h невелик по сравнению с
коэффициентом упругости № ( k2= — ) , так что /ι2—&2<0;
2) /г2-&2>0;
3) /г2-/г2=0.
Решение. Если материальная частица массы m движется
под действием восстанавливающей силы в среде с сопротивлением
fi, пропорциональным скорости ν, то fi называется силой
сопротивления. На частицу, кроме восстанавливающей силы fz=—ax,
действует также сила сопротивления среды fl =—bv.
Равнодействующая R этих сил будет R = f-\-f±, откуда на
основании второго закона динамики получим дифференциальное
уравнение движения
d2x , dx
т~ж-=-ах-ьчт
или
-£-+»*-+**-,». ^ (1)
где h= — коэффициент сопротивления, k2= коэффици-
циент упругости.

§ 7. Затухающие колебания
331
Уравнение (1) является линейным однородным уравнением
нторого порядка.
Характеристическое уравнение
г2+2/гг+/е2=0.
Корни характеристического уравнения
п, 2=—h±i~h2^k2.
Рассмотрим три случая значений дискриминанта h2—k2.
Случай 1: h2—/е2<0.
Введем обозначение h2—k2=—p2. Тогда
riiZ=—h±pi.
Общее решение имеет вид
x=e-ht(Ci sin pi+C2cos pt)
или
x=Cie-M (sin pt-\- —β- cos pt) .
Вводим вспомогательный угол φ посредством зависимости
С2 ,
Тогда
Q
х= — е~ы (cos φ sin pi+sin φ cos pt)
cos φ
или, обозначая для краткости
Ci
=л,
cos φ
получим
л:==Ле-'1г51п(р^+ф). (2)
Уравнение (2) представляет затухающее гармоническое
колебание с начальной амплитудой А и начальной фазой φ.
Множитель е~ы характеризует быстроту убывания амплитуды.
При t=0 амплитуда Ao=Ae-h-°=A,
при t=T амплитуда Ai=Ae-hT,
при ί=2Γ амплитуда A2=A(e-hT)z.
Таким образом, амплитуда колебаний убывает в
геометрической прогрессии со знаменателем e~hT. Период колебания Τ
находится из равенства
ρ(/+Γ)+φ=ρί+φ+2π,

332
Γα. XI. Уравнения второго порядка
откуда
т= 2л
Ρ
или
р= -γ-· (3)
Подставляем значение (3) в общее решение и имеем:
2л
Х—Ае и sin | _JL ;_|_φ j
Случай 2: h2~k2>0.
Введем обозначение h2—k2=q2. Тогда корни
характеристического уравнения примут вид
ri, 2= — h+q= — (h^Fq).
Общее решение будет
х=de-e^X+С2е-('!+<?>*.
Итак, получаем апериодическое движение.
При положительных С4 и С2 величина χ во все время движения
будет тоже положительной, но убывающей и скорость -— — все
время отрицательной, т. е. направленной к центру О.
При 1 = 0 x=Ci+C2, при /-коо лг-коо.
Случай 3: h2—k2—0.
Характеристическое уравнение имеет кратные корни
ri=r2= — /г.
Общее решение в этом случае
х=е-™(СН-С20,
т. е. получаем опять апериодическое движение.
Величина χ будет иметь некоторый максимум, после которого
она начнет убывать и частица будет приближаться к точке О.
Момент этого максимума, т. е. наибольшего удаления частицы
от центра притяжения, находится из уравнения
dx
— =-he-ht(Cl+C2t)+C2e-ht=0
или
Cz-dh-Czht^O,

§ 7. Затухающие колебания
333
111 куда
Cz-Cj
c2h ■
В случаях 2 и 3 вязкость среды, характеризуемая величиной h,
слишком велика и не допускает возникновения колебаний.
Колебания маятника в среде с сопротивлением,
пропорциональным скорости качания
Задача 155. Определить закон и период колебаний маятника
и среде с сопротивлением, пропорциональным скорости качания v.
ΐΐΐϋ
Решение. Кроме восстанавливающей силы f= —s
магматического маятника (задача 141), здесь действует еще сила
t опротивления flz=—bv. Равнодействующая этих сил
R=f+fl=-(l?jLs+bv).
На основании второго закона динамики получаем
дифференциальное уравнение движения
d2s
m
dt2
(ψε+bv)
ИЛИ
-|£_+2„^+й=„, (1)
b g
|де п= — коэффициент сопротивления, &2= —
коэффициент упругости.
Характеристическое уравнение
г2+2/гг+/г2=0
и его корни
n,2=—h±ih2—k2.
Так как h мало по сравнению с k2, то здесь имеем случай
/ι2— /е2<0.
Общее решение дифференциального уравнения (1) для этого
глучая
s=e-ht (СΊ sin pt+C2 cos pi), (2)
1де p=i k2—h2.

334 Гл. XI. Уравнения второго порядка
ds
Начальные условия: при ί=0 s = «, —77- =0. Имеем:
ds
=—fierh* (d sin pt+C2 cos pt) +e~ht (dp cos pt—C2p sin pt). (3)
dt
При ί=0 уравнения (2) и (3) приводят к системе, уравнений:
a = e~h ° [Cisin(p-0)+C2cos(p-0)],
0 = —fte-*-° [dsin(p-0) + dcos(p-0)] +
+έτ* ° [dp cos (ρ ·0)-dp sin (ρ ·0)].
Отсюда
С φ—С2/г=0
или
d=«, 1
ah
d= , С2=а. (4)
Ρ
Значения (4) подставляем в общее решение (2) и тогда
1.4 / ah \
s=:e~ht I sin pt-\-a cos pt I
или
s= e-]xl
Введем обозначение
( sm pt+-^-cos pt) . (5)
Тогда уравнение (5) примет вид
°h , 4 . / ,
s= ■ e~ht sin (ρί+φ).
ρ cos φ
Период колебания Г= , но величина
и тогда
4/n2g—/o2

§ 8. Затухающие колебания в электрической цепи 335
При Ь = 0, т. е. без учета сопротивления среды, этот результат
пишадает с результатом предыдущей задачи
7=2π
ff
§ 8. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
Колебательный замкнутый контур
Задача 156. Колебательный контур, представляющий собой
шмкнутую электрическую цепь, обладает емкостью С,
самоиндукцией L и активным сопротивлением R. При переходе энергии элек-
фического поля конденсатора в энергию магнитного поля катушки
а
~\ о
/ ?,
Рис. 95
(и обратно) часть энергии контура затрачивается на активных
сопротивлениях, в результате чего величина напряжения на
конденсаторе постепенно уменьшается. Найти законы изменения заряда
конденсатора q и тока в контуре i, а также напряжения на конден-
t'iiTope.i/ (рис. 95, а).
Решение. Ток в контуре определяется как частное от
деления падения напряжения на сопротивлении на величину этого
сопротивления:
UR Uc-UL ,
R
R
Здесь Uс — напряжение на конденсаторе, Ul ■
катушкеиндуктивности, т. е.
di
напряжение на
UL=L-
dt

336
Гл. XI. Уравнения второго порядка
Проводим алгебраические преобразования и получаем
исходное дифференциальное уравнение цепи
at
_ . dq
Ток в контуре ι = ——, где q — заряд конденсатора;
di _ d2q _q_
dt dt2 '
Тогда уравнение цепи примет вид
или
** +A_.^ + _i__=0 (i)
dt2 ' L dt ' LC
Подставляя в уравнение (1) величину q — CU, запишем
дифференциальное уравнение изменения напряжения на конденсаторе
d2U R dU U
dt1 ' L dt ' LC
Уравнение (1) дифференцируем по t.
Так как
d3q d2i d2q di dq
di3 di2 ' dt2 dt ' dt
то уравнение для определения тока будет
d2i R di i
+ —ι ТГ + ~T7^ =υ·
dt2 ' L dt ' LC
Решение уравнения (1) будем искать в виде q=Aemt. Тогда
^9 л . d2q л „ ,
—-у =Лте"", —~ =Am2emt.
dt dt2
Подставляя эти значения в уравнение (1), получаем
Aemt (m2+JLm+ L_) =
LC 1 -°·
Выражение Лет{ не равно нулю, так как отсутствие заряда на
конденсаторе обозначало бы отсутствие колебательного процесса.

§ 8. Затухающие колебания в электрической цепи 337
Следовательно,
т2+-т-т+тг=0'
(М'куда
Для краткости введем обозначения:
1 2 *
Тогда
"ii, 2=—α± У α2—ωυ2=—α±7 У ωί/2—α2.
Обозначая Усо^2— α2=ωΡ, получим
mi — — α+/ωρ,
m2= —α—/ωρ.
Заряд конденсатора
q=Aiem't-\-A2em2t = e~at(AieJ<0Pt+A2e-J<°Pt).
Используем формулу Эйлера:
eiwpi =cos ωρί+/sin ωρί,
e-iu>p< = cos (ύρί—j sin ωρ/.
Тогда
q=e-at [(Ai+Az^cos <uPt-\-j(Ai—Az)s'm aPt].
Обозначая Л1+Л2—М, j(Al—A2)=N, получим
q=e-at(M cos tupt+N sin ωpt). (2)
Значения М и N находятся из начальных условий:
При f = 0 q=QmsiX,
при ί=0 t=0.
Таким образом, при ί=0 па конденсаторе максимальный заряд
</=Qmax, но по уравнению (2) при t=0 q=M.
Следовательно,
q=e~at(Qmax cos ωpt-\-N sin ωpt), (3)

338
Гл. XI. Уравнения второго порядка
i= JL=—e-at [((ύΡΝ—aQm&x)cos apt—
— (topQmax+aN) sin ωΡί]. (4)
В начальный момент, при t=0, разряда конденсатора нет
(<7=0) и ток в цепи отсутствует (£=0).
Из второго начального условия и уравнения (4) следует, что
(ϋρΝ— aQmax = 0,
откуда
N=Qmax .
(ύρ
Подставляя значение N в уравнения (3) и (4), получим
<7=Qmaxe-°" I cos ωρί-\ sin apt j , (5)
X (Up '
i= Qmax ( ti>p-\ ) e~at Sin dipt. (6)
Член Qmax ( (ύΡ-\ ) =/max представляет максимальное зна-
V (Up '
чепие тока.
Итак,
i = /maxe-ai Sin (apt.
Используя зависимость {/= —^- и равенство (5), получим
напряжение на конденсаторе
U= t/max e~at ( cos ωρί+ -^- sin aPt ) . (7)
ν ωρ '
Уравнения затухающих колебаний (5), (6) и (7) изображены
графически на рис. 95, б.
Колебательный разряд конденсатора
Задача 157. Конденсатор емкостью С, заряженный до разности
потенциалов Vo, разряжается через проводник с сопротивлением R
и самоиндукцией L. Исследовать характер разряда при различных
значениях R, L и С.
Решение. В процессе разряда конденсатора разность
потенциалов на его обкладках переменна. Пусть в момент t эта
разность V. Тогда разряд конденсатора Q в этот момент будет
Q = CV. (1)

§ 8. Затухающие колебания в электрической цепи 339
При изменении V будет изменяться величина Q. Скорость — —
и ого изменения равна силе тока в цепи t. Поэтому
. dQ
l~ dt ·
Дифференцируя соотношение (1), получаем
dQ dV
dt dt '
Подставляем это значение в равенство (2) и имеем:
i=-c dv
(2)
dt '
В любой момент t в цепи действуют две противоположные элек-
|родвижущие силы: напряжение конденсатора V и
электродвижущая сила самоиндукции —L-—. Общая электродвижущая сила
будет
B-V-L-%, (3)
По закону Ома iR=E. Подставляя это соотношение в левую
часть уравнения (3), получим
или с учетом зависимости (2)
откуда
dP ^ L dt ^ CL к >
R 1
Вводим обозначения h= -—r- и &2=
2L CL '
Дифференциальное уравнение задачи (4) принимает вид
d2V dV
— +2^+^=0. (5)
Это уравнение затухающих колебаний.

340
Гл. XI. Уравнения второго порядка
Характеристическое уравнение
r2+2hr+№=0
имеет корни
ri,2=— /г±у/г2—№.
Исследуем три возможных случая.
Случай 1. Сопротивление R мало, т. е. h<k, или h2—&2<0
или R<2y—£-.
Общее решение уравнения (5) в этом случае
V■=е-м (СΊ sin pt+Cz cos pt), (6)
где
p=y/?2-/i2="|/-
1 R2
CL 4L2 *
dV
Начальные условия: при t=0 У=Уо, t=—C-—=0, откуда
V0=e-" °[Cisin(p-0)+C2cos(p.O)]
и так как
dV
-— =—he-ht {Сι sin p^+C2 cos p0 +е-Лг (dp cos pt—C2p sin pi),
то
0=—fte-*-o [Cisin(p-0)+C2cos(p-0)] +
+e~h °[Cipcos(p-0)-C2psin(p.O)],
откуда
n=c2,
0=-/iC2+Cip
Решаем систему (7):
} Μ
Ci= — У0> С2= У0. (8)
ρ
Подставляем значения (8) в общее решение (6) и получаем
h
или
у~е-ы (__yosin pt+Vo cos pt)
V=Voe-ht (— sinpi+cospi) .

§ 8. Затухающие колебания в электрической цепи 341
Вводим вспомогательный угол φ соотношением
h
Ctgq>=y.
Тогда разряд совершается по закону
V= —-е~н* sin(p/+m).
sin φ
В исследуемом случае цепь является вибратором, в котором
происходят электрические затухающие колебания с периодом
т= 2п = 2п
Ρ
l/-k-
CL 4L*
При достаточно малом R, которым можно пренебречь, получим
формулу Томсона для периода колебательного разряда
T=2nfCL.
Случай 2. Сопротивление R велико, т. е. h>k, или Л2—&2>0
или
иеус
V = de<«-ft>f+Сяв-tt+W, (9)
С
Общее решение уравнения (5) принимает вид
где
При тех же начальных условиях имеем
V0= Cie(9-'1) · о+С2е-(з+'1) ·«,
и так как
dV
= Ci (<7—h) eL9~*>)t—C2 (q+h) e-ftrt*)*,
dt
то
0=Ci(q—h)e(4-h)-o-C2(q+h)e-«i+h)·0,
откуда
CrfC2=l/o,
(<7-Л)Сх-(<7+Л)С2
=0.} <10>

342
Гл XI. Уравнения второго порядка
Решение системы (10) дает значения постоянных
интегрирования
Подставляем значения (11) в общее решение (9) и получаем
2q 2q
или
V= ~е~ы [(q+h)e4t+(q-h)e-<it].
J.q
В этом случае разряд происходит апериодически. Разность
потенциалов V асимптотически приближается к нулю.
Случай 3. При h=k или /ι2—№=0 сопротивление R=2 у —^—.
Общее решение уравнения (5) будет
V=e-«(Ci+Cai). (12)
При тех же начальных условиях имеем
Уо=ег+ »(Ci+C2.0),
и так как
то
откуда
= -Ле-«(СН-СаО+е-'"С2,
0=—Ле-ь -"(Ci+Ca-O) +С2е-Л0,
o°=-Cift+c2.} (13)
Решение системы (13) определяет значения постоянных
интегрирования
d=V0, C2=hV0. (И)
Подставляя значения (14) в общее решение (12), имеем
V=erht(V0+hVoi)
или
V=V0e-ht(\+ht).
Разряд происходит апериодически, а разность потенциалов V
стремится к нулю.
Изменяя постепенно сопротивление R цепи, можно переходить
от одного вида разряда к другому.

§ 9. Магнитная стрелка
343
§ 9. КОЛЕБАНИЯ МАГНИТНОЙ СТРЕЛКИ
БЕЗ И ПРИ НАЛИЧИИ УСПОКОИТЕЛЯ
Задача 158. Магнитная стрелка помещена в равномерное маг-
штное поле, отклонена на угол сро от положения равновесия и предо-
■тавлена самой себе. Исследовать характер движения магнитной
трелки, пренебрегая внешними сопротивлениями, а также при на-
тичии успокоителя.
Решение. На каждый полюс стрелки действует магнитная
•ила F поля. Таким образом, магнит находится под влиянием вра-
цающей его пары сил F.
Обозначим: Η — горизонтальную составляющую напряжения
>днородного магнитного поля, m — равные, разноименные
количества магнетизма на полюсах.
Тогда
F=Hm. (1)
Обе силы F разложим па составляющие Ρ и / (рис. 96). Силы Ρ
взаимно уравновешиваются и поэтому пара сил F эквивалентна
паре сил /.
Из рис. 96 очевидно, что
/=—F sin φ=-—m# sin φ.
Знак минус показывает, что сила f действует в сторону
убывания угла φ.
Элементарная работа dA пары / при повороте стрелки на бес-
Конечно малый угол —άψ будет
dA = 2}do=—2F sin ψάσ. (2)
Дуга do круга равна линейной мере угла, умноженной на
радиус, т. е. ίίσ= — άψ.
Отсюда
dA = — 2F sin φ — с?ф=— Fl sincpdcp. (3)
Учитывая соотношение (1), равенство (3) запишем в виде
dA = —tnlH sin φώρ. (4)
Величина ml=M называется магнитным моментом стрелки.
Тогда соотношение (4) принимает вид
dA = —MH sin ψάψ. (5)
С другой стороны, элементарная работа dA равна приращению
dH кинетической энергии U стрелки.

344
Гл XI. Уравнения второго порядка
Кинетическая энергия тела, вращающегося вокруг оси,
άφ
~~dt
"-±'№.
dt
где / — момент инерции тела относительно оси вращения, а
угловая скорость вращения.
Отсюда
2 dt dP
или
dt/=cM = /-^f-dq>. (6)
Сравнивая зависимости (5) и (6), получаем
/ —~- d<p= —ΜΗ sin φίίφ
dt2·
ИЛИ
iftp , ΜΗ .
Ή — sin φ=0.
dfl·
При малых колебаниях sin<p«<p. Обозначая постоянную вели-
МН «
чину —-— =д2, получаем дифференциальное уравнение магнита
d2(p +^2φ=0. (7)
dP
Общее решение неполного линейного дифференциального
уравнения (7) имеет вид
<p=Cisin kt-\-C2coskt. (8)
Начальные условия: при /=0 φ=φο, —η- =0. Отсюда
φο=Ci sin(/e-0)+C2 cos(&·()). (9)
Дифференцируя уравнение (8), находим
—-j- = Сф, cos kt—Czk sin kt
dt
и
0=CiAcos(A-0)-C2^sin(A-0). (10)

§ 9. Магнитная стрелка
345
Из системы уравнений (9) и (10) получаем:
Ci=0, C2=(po·
Подставляя значения постоянных интегрирования в общее
решение (8), находим закон колебаний
<p=(pocos kt
или
φ—φο cos у —-— t.
Стрелка совершает чисто гармонические колебания с периодом
т__ 2π
или

346
Гл. XI. Уравнения второго порядка
Итак, период Τ колебаний магнитной стрелки обратно
пропорционален У Н. Следовательно, число η колебаний стрелки в секунду
прямо пропорционально "|/77. Этим обстоятельством пользуются для
определения напряжения Η магнитного поля при помощи
наблюдения за колебаниями магнитной стрелки.
Исследуем движение магнитной стрелки при наличии
успокоителя, т. е. расположенной вблизи стрелки массы немагнитного
металла, например меди.
При вращении магнитной стрелки в успокоителе возникают
индукционные токи, которые, действуя обратно на стрелку,
препятствуют ее движению. Сила токов в успокоителе и их действие на
стрелку в каждый момент пропорциональны угловой скорости
вращения стрелки.
Кроме магнитного ноля, на стрелку действует еще пара сил /ι
(рис. 97), момент которой противоположен по знаку моменту пары
сил f, а по величине пропорционален угловой скорости —-
вращения стрелки.
Этот момент
άψ
μ=-η—.
Пусть стрелка поворачивается на бесконечно малый угол — άψ.
Определим приращение dU ее кинетической энергии U, работу dA
пары сил f и работу dAi пары сил fi.
Аналогично вышеизложенному находим
d2w
dU=I-~dy, (11)
dA = — ΜΗ sin ψάψ (12)
и
aA1=-2fl(-do) =2fi-^- άψ=!ι1άψ.
Так как момент пары μ = /ν, то
άψ
άΑι = μάψ=—η—-άψ. _ (13)
Приращение dU кинетической энергии стрелки должно
равняться совершенной над стрелкой работе и поэтому
dU=dA+dAl.
Подставляя соотношения (11), (12) и (13) в равенство (2),

§ 9. Магнитная стрелка
347
получаем
d\ άψ
I ——— άψ= — ΜΗ sin ψάψ—η —— άψ
at2· at
ИЛИ
ά*ψ η άψ ΜΗ
η , ΜΗ ,.
Для малых колебаний sincp^cp. Обозначая —- =h, —-— =к%
Получим дифференциальное уравнение движения
ά2ψ άψ
Коэффициент сопротивления h является мерой успокоения.
Коэффициент упругости k2 пропорционален напряжению Η поля и
является мерой силы поля.
Характеристическим уравнением для однородного линейного
уравнения (14) будет
г2+2/гг+&2=0.
Это уравнение имеет два корпя
η,2=—h±ihz—kz.
Исследуем три возможных случая значения подкоренного
выражения.
Случай 1. Успокоитель слабый: h<ck или /ι2—&2<0.
Общее решение уравнения (14) имеет вид
9=e-',i(C1sinpi+C2CospO. (!5)
где h2—k2=—p2.
Начальные условия: при ί=0 φ=φο' —τ— =0. Отсюда
tfo=e-h о [Cisin(/?-0)+C2cos(p-0)],
и так как
άψ
:=—he-ht(Ci sin pt-\-Cz cos pt) -\-e~ht (dp cos pt—C2p sin pt),
at
TO
0=-he~h ο [Cisin(p-0)+C2cos(p-0)] +
+e-'10 [Cipcos(p-O)— dp sin(p-0)],
откуда
фо=С2, 1 ,.„.
Q=-hC2+CiPJ K }

348
Гл XI. Уравнения второго порядка
Решая систему (16), находим
г h г
Ρ
Подставляем найденные значения в общее решение (15) и
получаем
φ_6-/ιί ^ — φο sin ρί+φο cos р^ )
или
φ=φοβ~Μ ( — sin pt-\-cos pt) .
r
Вводим вспомогательный угол α соотношением
ctga= —
Ρ
и получаем
φο
φ= — e~ht sin (ρί+φ).
sin a
Стрелка совершает затухающие гармонические колебания с
периодом
__ 2π 2π 2п
ν*'-"2 ., _№
У-^--(
Случай 2. Успокоител'ь сильный: h>k или h2—k2~>0.
Общее решение уравнения (14) в этом случае
^r=Cle(i-h)t^c2e-(i+h)t, (17
где q~}/h2—k2.
άφ
Начальные условия: при t=0 φ=φο, —rr =0· Отсюда
и так как
dm
—— = (q—h) de<e-*)'— (q+h) C&rtoW,
то
0= (q—h) de^-h) o_ (q+h) C2e^+h) · о_
откуда
С1+С2=фо, 1 . .
(q-h)Cl-(qi-h)C2=0.) (l0)

§ 9. Магнитная стрелка
349
Решая систему (18), находим
с'=^· с<=^»· (19)
Подставляем значения постоянных интегрирования (19) в
общее решение (17) и получаем
φ= !±A(poe(g-b)i+ 1ίΖ*ί e-(g+h)f
2q 2q
или
φο
φ=-——e-hi [(q-\-h)eit+(q—h)e~^].
zq
Приближение стрелки к положению равновесия
апериодическое.
Случай 3. h=k или h2—k2=0.
Общее решение уравнения (14)
q>=e-fc'(Ci+C80. (20)
Начальные условия прежние: при / = 0 φ=φο и —тт- =0.
φο=β-Λ 0(Ci+C2-0),
и так как
dw
_L =-he-ht(Cl+c2t)+C2e-M,
то
0=—he-b °(C1+C2-0)+C2e-'l0>
откуда
о=-лсн-сЛ (21)
Решая систему (21), находим постоянные интегрирования
Ci=«po, С2=/иро. (22)
Подставляем значения постоянных интегрирования (22) в
общее решение (20) и имеем
<p=e-ht(<po-\-hq>ot)
или
^—^е~ы(\-\-Ы).
Итак, имеем опять апериодическое приближение стрелки к
положению равновесия.

αου
Гл. XI. Уравнения второго порядка
§ 10. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
Колебания материальной точки под действием
восстанавливающей силы, сопротивления среды
и внешней периодической силы
Задача 159. Определить закон движения материальной частиць
массы m под влиянием восстанавливающей силы (силы, 'направлен
ной к центру О и прямо пропорциональной удалению χ частицы от
центра притяжения О), силы сопротивления и внешней силы
F=d sin(g/-fcpo) для случая /ι2—&2<0.
0
f, .
—_.
χ
f
ί
Λ
ч
Рис. 98
Решение. Кроме восстанавливающей силы f=— ax и силы
сопротивления fi=—bv, на частицу действует внешняя сила
F=ci sin(gi-fcpo). Как видно из рис. 98, равнодействующая всех сил
На основании второго закона динамики дифференциальное
.уравнение движения
сРх dx
m -jp- +6 — +ах=а sin (<//+φ>)
или
d2x dx
_+2fc_+#JC==ClSin(«/f+«pD)l (1)
b a
где 2h= , k2--
m m
Это неоднородное линейное дифференциальное уравнение
второго порядка. Решаем его для случая h2—k2<.0 (случай малого
сопротивления).
Пусть
h2—k2=—p2.
Тогда
ri=:—h+pi, 1
r2=—h—pi. )

§ 10. Вынужденные колебания механических систем 351
Характеристическое уравнение дифференциального
уравнения (1)
/·2+2/ι/-+&2=0
имеет комплексные корни
/ч,2=—Л± У/ι2—&2= —h± i—p2=—h±pi.
В этом случае общее решение соответствующего однородного
уравнения
x = e~hl (Ci sin pf+C2 cos pt)
или
л;=Cje-'1' (sin pt-\- —~ cos pi J ,
Вводя вспомогательный угол φ соотношением
имеем:
я= e~ht (cos φ sin ρί+sincpcos ρ/).
cos φ
Обозначая
cos φ
получим
x=i4e_ili sin(pi+(p).
Частное решение уравнения (1) будем искать в виде
вспомогательной функции V. Вспомогательная функция и ее производные
равны:
V=М sin (<?ί+φο) +Ν cos (<7Η-φο),
dV
Mq cos (qt-\-<fo)— Nq sin (<?ί+φο),
dt
d2V
■■ —Mq2 sin (<?ί+φο) —iV<?2 cos (^i+cpo).'
dt2
Подстановка этих выражений в уравнение (1) дает равенство:
—Mq2 sin (qt+ψο) —Nq2 cos (qt+ψο) +2hMq cos (qt+ψ)) —
—2hNq sin (qt+(fo) +&M sin (qt+ψο) +kzN cos (ίί+φο) =
= c εΐη(ί?ί+φο)

352 Гл. XI. Уравнения второго порядка
или
(k2M—Mq2-2hNq) sin (qt+φ,) +
+ (k2N—Nq'i+2hMq) cos (qt+щ) = с sin (qt+yo).
Приравнивая соответствующие коэффициенты, получим систему
уравнений
k2M—Mq2—2hNq=c,
k2N—Nq2+2hMq
Решая ее, находим значения N и М>.
2hqc
= 0. J
N--
М =
M^+^—q2)2'
c(k2—q2)
4h2q2+(№—q2Y '
Таким образом, общее решение
х=Ае~м sin(pf+q>) + 4h2q2+{k2_q2) sin(<7f-Hpo)-
2hqc
cos (qt+qx))
4h2q2+ (k2—q2)
или
c(k2 q2) Г
x=Aer*t sin(pH-q>) + 4h2q2+{k2_q2) Lsin(<74-q>„)-
~ ы-иг cos(qi+m) ].
&2—/l2
Вводя вспомогательный угол φι соотношением
2hq
k2—h2
и обозначая
c(k*—q2)
tg<Pl =
к it-
-02ϊ
5,
[4h2q2+(k2— q2)2] cos φι
окончательно получим
x=Ae~ht sin(pH~cp)+S sin(<7i+cpo—φι). (2)
Колебательное движение, описываемое уравнением (2),
состоит из двух частей: собственного (свободного) колебания Χι—
=Ae-htsm(pt-\-(p) и вынужденного колебания х2=В sin (^ί+φο—φι).

§ 10 Вынужденные колеоания механических шакм
Первая часть оказывает существенное влияние на общее
колебание только при малом t, т. е. в первое время движения. Это
объясняется тем, что множитель е~м с возрастанием t быстро стремится
к пулю. Таким образом, первая часть имеет значение только во
нремя установления процесса. В
дальнейшем величина χ почти исключительно
определяется вторым слагаемым, которое
дает закон установившегося
вынужденного колебания.
Упругая пружина с подвешенным
грузом, совершающим периодические
колебания с учетом сопротивления
Задача 160. Груз массы т подвешен
на пружине с жесткостью с. Конец
пружины К совершает вертикальные
гармонические колебания по закону KL =
=А sin(/?/). Найти закон движения
груза, если сила сопротивления движению
пропорциональна скорости груза.
Решение. Начало координат
поместим в точке L, ось χ направим по
вертикали вниз. Дифференциальное
уравнение движения груза в данном случае
будет
d2x
т ——- —mg—cK—k
где λ — удлинение пружины, сК — проекция на ось χ реакции
пружины, k — коэффициент сопротивления.
Если /о — естественная длина пружины, то, согласно рис. 99,
удлинение
K—x—~KL—lo=x—A s'm(pt)—lo. (2)
Подставляя выражение (2) в уравнение (1), находим
d'^x dx
т ■ =mg—cx+cA sin (pi) +cl0—k ——. (3)
Произведем замену переменного χ. Пусть
где ξ — новая переменная, Χι — постоянная величина.
Ч
dx
~ΊΓ'
ο/ί
о
о
Φ
о
-®-
Рис. 99
ч
(О

354
Гл XI Уравнения второго порядка
Тогда
ах _ _dg_ аЧ _ с№^
ЧГ ~ ~df' dP ~ ~d¥'
и вместо уравнения (3) получаем
d2l dl·
m~—-==mg—cl—cXi-{-cA sm(pt)+ck—k-~. (4)
Выберем χι так, чтобы в правой части уравнения (4) исчезли
постоянные члены, т. е. пусть
mg—cxi+c/o—О,
отсюда
х^Ь+ЛШ-, (5)
с
Согласно закону Гука, сила упругости (реакция) пружины F
пропорциональна ее удлинению, т. е. F=c%, где с — коэффициент
пропорциональности, называемый жесткостью пружины. Так как
в положении равновесия модуль силы F равен силе тяжести Р, то
Р = сХст,
где λοτ — статическое удлинение пружины.
Отсюда
Ρ
Обратно, зная жесткость с пружины, находим ее статическое
удлинение
Ρ _ mg
Лет—*— '_ —
С С
Тогда равенство (5) примет вид
Как видно из вышеизложенного, замена переменной
эквивалентна переносу начала координат из точки L в положение
равновесия груза О, если конец пружины закрепить в точке L. После
замены дифференциальное уравнение (4) будет
d2l· dt
m-ur+k-if+c^cAsmipt)

§ 10. Вынужденные колебания механических систем
ооо
ИЛИ
dt2 ' dt
где
d2£ dl
αδ +2n~}-+s2l=h sm (pt), (6)
cA n k
2n--
m m
и
1 m У λοτ
Уравнение (6) есть линейное неоднородное дифференциальное
уравнение второго порядка с постоянными коэффициентами. Общее
решение этого уравнения можно представить в виде
ξ=Χ1+Χ2) (7)
где Χι — общее решение соответствующего однородного уравнения
(без правой части), Х2 — какое-либо частное решение данного
линейного неоднородного дифференциального уравнения.
Находим общее решение ΛΊ соответствующего однородного
уравнения
-|L+2niL+s2^o. (8)
Для интегрирования этого уравнения применим способ замены
переменной.
Пусть
1=Ψ~η1, (9)
где η — новая переменная.
Дифференцируя равенство (9) по t, получим
dl _„_„, / d4
nf (_
ηη
dt \ dt
и вторая производная
"'(-3~*-2-+'*π)·
dP v dP dt
Подставляя значения функции ξ и ее производных в
дифференциальное уравнение (8), после сокращения на общий множитель
e~ni находим
ί/2η ац dr\
—2п —τ- +η2η+2η — 2n\+s\= О
dt2 dt ' * ' dt

356
Гл. XI. Уравнения второго поряока
ИЛИ
dtz
-f(s2—η2)η=0.
Допустим, что s>n; полагая тогда s2—n2=s12, последнее
уравнение приведем к виду
■+sih\=0. (10)
dtz
Это неполное линейное однородное дифференциальное
уравнение второго порядка с постоянными коэффициентами.
Проведем подробное интегрирование уравнения (10).
Соответствующее характеристическое уравнение r2-\-Si2—Q
имеет мнимые корни
/Ί,2= ± i—Siz=±isi.
Частные решения дифференциального уравнения (9) будут:
у\2=еГг1 = e_S|ii,
Так как корни мнимые, а частные решения независимые (отно-
шение _sit — переменное), то общее решение уравнения (10)
выразится функцией
η=βαί [Cicos(sii)+C2sin(sii)],
причем α=0. Окончательно:
t)=Clcos(sit)+C2sm(slt). (11)
В практических применениях это общее решение
дифференциального уравнения обычно преобразуется путем замены двучлена
в правой части выражения (11).
В равенстве (11) выносим за скобки величину yCi2-fC22. Тогда

§ 10. Вынужденные колебания механических систем 357
причем
С? 4- Сг1 = Cl2+C22 =
d2+C22 ' Ci*+C22 d2 + C22
На основании вышеизложенного величину — - можно
принять за sin φ, а — ■ за cos φ.
У Cl2+C22
Таким путем из равенства (12) находим
η= У Ci2-f-C22 [sin φ cos (sit) +cos φ sin (sit) ].
Обозначая
i~cffC22=c*
и применяя формулу синуса суммы
sin(i4+S) —sin Л cos β-fcos A sin В,
получим
T)=C*sin(siH-cp). (13)
Уравнение (13) представляет уравнение гармонических
колебаний.
Так как |=ηβ_,ιί, то, следуя обозначению, принятому в
соотношении (7), общее решение уравнения (8) запишем в виде
Xi=C*e-nt sin(sif+q>), (14)
где С* и φ — произвольные постоянные, a Si = y s2—ή1.
Уравнение (14) представляет уравнение затухающих колебаний.
Найдем частное решение Х2 данного неоднородного
уравнения (6).
Предположим, что
X2=C"sin(pf-H>),
где С** и ψ — некоторые постоянные величины, которые нужно
подобрать так, чтобы это значение Х2 тождественно удовлетворяло
данному дифференциальному уравнению (6).
Находим
—j- =C**p cos(pt+$)

358
Гл XI Уравнения второго порядка
Л2У
2 =_ С**р2 sin (ρί+ψ).
dt2
Подставляя эти значения производных, а также значение Хг
в дифференциальное уравнение (6), получим
— С**р2 sin (ρ/+ψ) +2nC**p cos (ρ/+ψ) -f
-fs2C** sin(p/+i|0 =h sin (pt)
или, полагая для краткости ρ/+ψ = θ,
С** (s2—p2) sin Q+2nC**p cos 0 = /i sin (0—ψ)
и
С** (s2—ρ2) sin 0+2rcC**pcos 0 = ft sin 0 cos ψ—/ι cos 0 sin ψ.
Так как это равенство должно выполняться тождественно (при
всяком Θ), то коэффициенты при sin 0 и cos 0 в левой и правой
частях должны быть равными, т. е.
/icos^=C**(s2—ρ2), \
/isin^=—2/гС**р. J " '
Из системы (15) находим
h
С**= ■ ·,
Y(s2—ρψ+Αηψ
. , 2ηρ
s2—p2
Тем самым частное решение Х2 линейного неоднородного
дифференциального уравнения определено полностью.
Таким образом, общее решение данного дифференциального
уравнения, представляющее закон движения точки при наличии
возмущающей силы, выражается зависимостью
l=Xi+X2=C*e «« sin(Si/+cp) + C** sin(pi+^).
Ввиду того что множитель e~nt быстро стремится к нулю,
то через достаточно большой промежуток времени можно
пренебречь членом, выражающим затухающие колебания. Тогда
|=С** sin(p/-pi|)). т. е. груз совершает только вынужденные
колебания около положения равновесия О.

§ 10 Вынужденные колебания механических систем
ла
Вынужденные колебания двигателя на балке
Задача 161. На балке, свободно лежащей на двух опорах,
установлен двигатель, маховик которого насажен на вал с небольшим
эксцентриситетом ε, и на вал действует центробежная сила,
расшатывающая систему. Найти закон вынужденных колебаний системы,
Рис 100 Рис. 101
а также исследовать влияние сопротивления среды,
пропорционального скорости движения.
Решение. Центробежная сила
ν2
где μ — масса маховика, — центробежное ускорение.
Так как ϋ=ωε, где ω — угловая скорость маховика (рис. 100),
ιό центробежная сила Ρ1ξ=μω2ε.
При колебаниях, вызываемых небалансированным ротором
машины при его равномерном вращении, можно считать, что
центробежная сила дает чисто гармоническую силу в заданном
направлении с частотою оборотов машины.
Допустим, что на массу m машины, стоящей на упругих опорах
(рис. 101), действует внешняя периодическая сила P(t),
изменяющаяся во времени.

360
Гл. XI. Уравнения второго порядка
Вертикальная составляющая центробежной силы, вызывающая
поперечные колебания балки, равна тогда Р^ътЫ.
Без учета сопротивления среды в любое мгновение груз
находится под действием трех взаимно уравновешивающихся сил
d2x
(рис. 101): силы инерции —от , силы упругости балки —kx
и вертикальной составляющей возмущающей силы Рц sin ωί. Здесь
k — коэффициент жесткости балки (в н/м, кГ/см и т. п.).
Проектируя действующие силы на вертикальную ось, получаем
уравнение движения
d2x
Рц sin (nt—kx—m <JO ■ =0,
at2
которое принимает вид
d2x , ,
in -irkx=Pn sin ωί
или
d2x , k I n
,,„ ■ + x= Рц sin at.
at2 in in
k
Обозначая n2= , дифференциальное уравнение задачи
записываем в виде
d2x
-\-п2х=Р sin at, (l)
dt
где Ρ— .
от
Характеристическое уравнение соответствующего однородного
уравнения
гЧ-п2=0
имеет корни
/Ί, 2=±т.
Общее решение однородного уравнения
*одн= Ci cos nt+Cz sin ηί.
Частное решение ищем в форме
*частн=Л cos ωί-\-Β sin ωί. (2'
Так как
#'частй=—Αω sin ωί+^ω cos ωί
и
x"4nc-ni=—Aa2 cos ωί—Βω2 sin ωί,

§ 10 Вынужденные колебания механических систем 361
ТО ПОСЛ6 ПОДСТаНОВКИ X части И Хчастн по формуле (2) в уравнение (1)
получим
Α (η2—ω2) cos ωί+Β(η2—ω2) sin ωί=Ρ sin ωί,
откуда, приравнивая коэффициенты при соответствующих членах,
находим систему
Л(п2-о2)=0, 1
В(п2—ω2)=Ρ.
В результате решения этой системы
Ρ
л=о, в=
Ρ
η2—ω2
и частное решение
-^частп—— ' ή Г~ Sin 0)ί.
Общее решение неоднородного дифференциального уравнения
(1) принимает вид
η t ι η ■ , . Ρ Sinwt
x=C\ cos nt4-C2 sin nt+ —.
η2—ω2
Рассмотрим влияние сопротивления среды. Так как
сопротивление среды пропорционально скорости, т. е. k——, где k — 2h —
Коэффициент пропорциональности, то дифференциальное уравнение
(1) примет вид
d2x άχ
-— \-2h ——- +"2л:=Р sin ωί.
at2 at
Характеристическое уравнение соответствующего однородного
уравнения
r2+2/ir+n2=0
имеет корни
г i,2=—h±i h2—n2.
Тогда при h<Cn
xom=e-ht(CiCos qt+C2 sin qt),
где —q2=h2—n2.
Частное решение ищем в виде
*частн=^ cos ωί-^Β sin ωί.

362
Г л XI. Уравнения второго порядка
В результате проведения аналогичных действий получаем
общее решение неоднородного уравнения, т. е. закон вынужденных
колебаний процесса
v,tlr> j. , ^ · ι\ 2ωΡ/ι
х= е~™ (С, cos qt+C2 sin qt) - (η2_ω2)2+4ω%2 cos ωί+
Ρ(η2-ω2)
+ (η2-ω2)2+4ω%28ΐηωί·

Глава XII
ЗАДАЧИ, ПРИВОДЯЩИЕ К ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЯМ ВТОРОГО ПОРЯДКА
С РАЦИОНАЛЬНЫМИ КОЭФФИЦИЕНТАМИ
I. УРАВНЕНИЕ ЭЙЛЕРА
1. Дифференциальным уравнением Эйлера второго порядка
называется уравнение вида
айхгу'''+aixy''+а2у=; { q 0)
где а0, «ι, «2 — постоянные, т. е. оно может быть однородным и
неоднородным.
Подстановкой х=е( уравнение (1) приводится к линейному
уравнению с постоянными коэффициентами. При этом
и"
У —
, dy dt dy
У ~ dt ' dx ~~ dt
,( 1 dy \
d(y') \ et dt ι
dx ~ d(e') ~
d*y
dt2
1
Xt'
1
dy
dt'
1 dy
~~ et ' dt '
d?y 1
' ~dt* ' et
el
dy
dt
2. Уравнение вида
Au(ax+b)Zy"+A1(ax+b)y'+A2y=f(x),
где Ao, Αι, Az, an b — постоянные коэффициенты, приводится к
уравнению с постоянными коэффициентами подстановкой
ах-}-Ь = е(.
§ 1. РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ В ПРОДОЛЬНОМ РЕБРЕ
ПАРАБОЛИЧЕСКОГО СЕЧЕНИЯ
Задача 162. Найти распределение температуры в продольном
ребре жесткости параболического профиля (рис. 102). Предпосылки
исследования такие же, как в задаче 149.
Решение. Здесь профиль определяется уравнением

364 Гл. XII. Уравнения второго порядка с рациональными коэффициентами
так что площадь поперечного сечения задана на единицу длины
в виде функции
А(х)=2у=6й(^-У. (1
Разница между входящим в элемент dx и выходящим из неге
количеством теплоты
'=-ж-[м«-£-]"*
1
X
So
^"^
X*
*^*"^//да/;
ih
χ
x*-dx
0
Высота В
в
χ=ο
Конец {Вершина
Рис 102
должна быть равной количеству выходящей из ребра теплоты путел
конвекции (также на единицу длины)
так что
qa~2h{T-Ta)dx,
k~[A(x) ^-]dx=2h(T-Ts)dx.
(2
Подставляя Q = T—Ts и dQ=dT, приводим уравнение (2) к вид·1
kA(x)
d20 dA (x) dO
dx2
+k
dx dx
--2Ш
и, используя равенство (1) для определения А(х) и ее производной
после преобразований получаем
dx2
+2х
dB
dx
-m2b2B = Q,
(3

§ 1. Температура ребра
365
где
2А
m
kdn
Уравнение (3) является уравнением Эйлера. Оно решается
подстановкой
х=е1 или / = ln*.
Тогда
dO _ dO dt _ 1 dO
dx dt dx χ dt
и
\ dO \ , I dQ
d20
d(T4r) ι do . ι d("3r)
+
dx2 dx x2 dt χ dx
1 dx . 1 ' d20
+
x2 dt ' x2 d/2 '
При этих условиях уравнение (3) принимает вид
* \ х2 di2 χ2 dt I+2X χ dt mb ϋ-υ
или, после сокращения подобных членов,
Это однородное дифференциальное уравнение имеет решение
0 = dev 2 2 ; +C2ev 2 2 ;
и, возвращаясь снова к независимой переменной х, имеем
Q=C1xp'+C2xp;
где
1 1
Ρι,2=- γ ± γ 1 1 +4m2i>2.
Общее решение
-4- + 4-V I+4m'6« Со
e=dx 2 2 + 2

366 Гл. XII. Уравнения второго порядка с рациональными коэффициентами
и можно заметить, что при л: = 0 избыток температуры будет
неограниченным, если не принять Сг=0.
Следовательно, общее решение окончательно принимает вид
Q=dxp>. (4)
Излишек температуры у основания при х=Ь составляет
Ъ0=Сфр\
поэтому постоянная интегрирования
ьр<
Подставляя найденное значение Ct в уравнение (4), получаем
искомый закон распределения температуры
Θ = Θ°(τΓ·
II. ЛИНЕЙНОЕ ОДНОРОДНОЕ УРАВНЕНИЕ
С РАЦИОНАЛЬНЫМИ КОЭФФИЦИЕНТАМИ
Линейное однородное дифференциальное уравнение второго
порядка с рациональными коэффициентами имеет вид
y"+p(x)y,+q(x)y = 0, (1)
где р(х) η q(x) — рациональные функции х.
Его общее решение
i/=Cii/l+C2i/2,
где г/ι и г/г — частные линейно независимые решения уравнения (1).
Если известно одно решение, то можно определить второе по
формуле
№
=Ayi\e-Sv(-x)dxdX
У?
где А — произвольное постоянное.
§ 2. ТОЛСТОСТЕННАЯ ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА
ПОД ДАВЛЕНИЕМ (ЗАДАЧА ЛЯМЭ)
Задача 163. Составить дифференциальное уравнение
деформации толстостенной трубы под действием внутреннего давления
(рис. 103). Длина трубы равна единице, и продольные деформации
во внимание не принимаются. Под влиянием внутреннего давления
труба расширяется.

§ 2 Толстостенная цилиндрическая оболочка под давлением 367
Решение. Рассмотрим неизвестное пока упругое
удлинение и, возникающее под действием внутреннего давления на стенку
трубы радиусом х. На рис. 103 показано сечение трубы, на котором
двумя радиусами с центральным углом da и двумя дугами радиусов
χ и x-\-dx выделена элементарная площадка.
Рис. 103
Тангенциальное растяжение трубы равно отношению удлинения
периметра окружности к первоначальному периметру окружности:
ε< =
2πα
2лх
и
χ
(1)
Радиальное удлинение получается при рассмотрении изменения
длины отрезка AB=dx, расположенного на радиусе. Точка А
радиуса х=МА передвигается на отрезок и, а точка В радиуса x-\-dx
соответственно на отрезок u-\-du, т. е. элемент ах удлиняется на
величину du. Относительное радиальное удлинение в
рассматриваемом месте
^ ~dx- <2>
Рассмотрим совместное действие напряжении на вырезанный
элемент стенки (рис. 104).
Силы напряжения σι, действующие в тангенциальном
направлении, па обеих сторонах элемента равны atdx, а их
равнодействующая CD равна daotdx.

368 Гл. XII. Уравнения второго порядка с рациональными коэффициентами
Напряжение, действующее в радиальном направлении внутрь,
обозначим Or- Приложенная к стороне элемента радиальная сила
xdaar. На противоположной стороне элемента напряжение ог-\-ааг,
а соответствующая сила
(ατ·\-άθγ) (x-}-dx)da= (aix-\-xdor-\-OrdxJrdardx)da.
Слагаемое dardx, как малое по сравнению с другими, можно
отбросить, а
xdor-}-Oi dx=d (xor).
Тогда равнодействующая радиальных сил d(xar)da.
Рис. 104
Между равнодействующими радиальных и тангенциальных сил
должно существовать равновесие
откуда
daotdx—d (xar) da,
d (xar)
Of-
dx
(3)
Для взаимосвязи формулы (3) с выражениями (1) и (2)
примем во внимание законы теории упругости.
Закон Гука в своей общей форме, учитывающий радиальные
и тангенциальные напряжения, дает следующие зависимости для
удлинений:

§ 2 Толстостенная цилиндрическая оболочка под давлением 369
где Ε — модуль упругости, коэффициент Пуассона.
μ
^ешим уравнение (4) относительно ot и а,:
Ot= 2_. (μβί + вг), аг= 2_ (μβτ+βί). (5)
IX J LI 1
Подставляем выражения (1) и (2) в соотношение (5):
μΕ I и , du \ μΕ I du , и \
а<=-^1^Т + Ж>> σ'=-]^ΓΓΐ^1Γ + τ)· (6)
Полученные равенства (6) подставляем в уравнение (3), в
результате чего
μΕ ( и du \ d Г μΕ I du и \Л
или
и , du d \ ( du и \л
Так как в правой части равенства (7)
d \ I du и \ ] I du d2u \ du ,
то после сокращения подобных членов
d2u du и
Делим последнее уравнение на μχ и окончательно, имеем
дифференциальное уравнение второго порядка с рациональными
коэффициентами:
dx* ^ χ ' άχ χ2 к }
Дифференциальное уравнение задачи (8) является
одноразмерным. Этим обстоятельством можно воспользоваться для упрощения
решения дифференциального уравнения.
Если χ и у считаются первого измерения и все члены
дифференциального уравнения оказались одного измерения, то удобно ввести

370 Гл. XII. Уравнения второго порядка с рациональными коэффициентами
новые переменные ν и 2 с помощью подстановок
x=ev, y=zev. (9)
Отсюда после дифференцирования
dy __ dy dv / dz cv \ dv
dx dv dx Wv ' dx
При этом
dx
dv
и, следовательно,
dv
=
βαχ
Поэтому
dy dz , . ЛЧ
•/7 = ^Г+2· (10)
Аналогичным образом
Производим при и=у подстановки (9) — (И) и этим приводим
уравнение (8) к более простому виду
d2z +2^=0.
dv2 dv
После подстановки
£-' <12»-
получаем уравнение первой степени
dp
+2р=0. (13)
dv
Разделяя переменные в уравнении (13.), находим
dv_ 1 dp
2 ' Ρ
или после интегрирования
v = Ci— — In ρ,

$ Ί. Толстостенная цилиндрическая оболочка под давлением 371
откуда
p — e*Ci-v)m (14)
Подставляем значение (14) в правую часть соотношения (12):
dz=e^c^)dv. (15)
Интегрируем почленно уравнение (15) и получаем общее
решение
z=Ca--|-e*c·-*). (16)
Из равенства (16) при помощи равенства (9) находим
u=xz=С2х — e2<c'-v).
Замечая, что x=ev, окончательно получаем
1 е2С|
и=С2х .
2 χ
Если обозначить
С2=С, -±-е™> = С*,
то общее решение дифференциального уравнения (8) примет вид
и=Сх+^-, (17)
где С и С* — постоянные интегрирования. Для определения
постоянных интегрирования подставим равенство (17) в уравнение (6).
Тогда
Для упрощения выкладок вводим обозначения:
-V*Lc=A, -i^-C* = B. (18)
μ—1 μ+1
В итоге получаем
στ=Α —
χ*

372 Гл. XII. Уравнения второго порядка с рациональными коэффициентами
Для определения новых постоянных А и В заметим, что на
внутренней стороне стенки (при х=г) радиальное напряжение ог
должно равняться давлению ρ внутри трубы со знаком минус.
При x=R (на внешней поверхности) радиальное напряжение ог
равно нулю.
Таким образом, начальные условия:
при х=г —р=А-
при x=R 0=A-
В
В
Разрешая эту систему относительно А и В, имеем:
А=-.
ргй
£2_r2 »
в=
р&г*
R2-r* '
(19)
Подставляем найденные значения постоянных (19) в правые
части уравнений (18) и находим значения постоянных
интегрирования С и С*:
prz
(μ-l); С* =
pR*r2
Подставляя значения (20) в уравнение (19), получаем
(μ+D. (20)
и=
рг
R2
μ£(/Ρ_^)-[^-1^+(«+ΐ) х
]■
Напряжения аг и σ/ получаются соответственно равными
ог=р-
-R2
Ot = p
x2+R2
R}—fl
(21)
Чем меньше χ, тем большие значения получают оба главных
напряжения. Материал будет наиболее напряжен внутри трубы.
Из уравнений (21) видно, что во всех точках абсолютное
значение ot больше абсолютного значения аг.
Наибольшее напряжение в трубе получится, если во втором
уравнении (21) принять χ равным его наименьшему возможному
значению х=г. Тогда
_ Rz+a2

§ 2. Толстостенная цилиндрическая оболочка под давлением 373
III. ЛИНЕЙНОЕ НЕОДНОРОДНОЕ УРАВНЕНИЕ
С РАЦИОНАЛЬНЫМИ КОЭФФИЦИЕНТАМИ
Вид линейного неоднородного дифференциального уравнения
второго порядка с рациональными коэффициентами
y"+p(x)y'+q(x)y=f(x),
где р(х), q(x), f(x) — непрерывные рациональные функции.
Общее решение
y = Ciyi+C2y2+V,
где г/ι и 1/2 — линейно независимые решения соответствующего
однородного уравнения; V — частное решение неоднородного уравнения.
Частное решение V находится способом Лагранжа (методом
вариаций произвольных постоянных), который дает возможность
проинтегрировать неоднородное линейное уравнение, если известно
общее решение соответствующего однородного уравнения y=Ciyi-\-
+C2I/2, считая при этом Ci и С2 уже не постоянными, а новыми
неизвестными функциями Ci(x) и Сг{х).
Частное решение неоднородного дифференциального уравнения
V(x) ищется в виде
V(x)=Cl(x)yl+C2(x)yz. (1)
Тогда
^ = (Cfa+Cfa) + {Сф'+Сгуг') (2)
и
dx2 = (С^+С^г) +2 (CiV+C2V) + (С^'Ч-W). (3)
Предполагаем, что С/ и С/ удовлетворяют системе
Ci'i/1+C/y2=0, 1
CiV+C2V=f(*)· J l
Дифференцируя первое уравнение системы (4), получаем
(Ci"0i+C2"ife) + {Сх'ух'+Сг'уг') = 0.
Тогда уравнения (1) — (3) примут вид
V=Ciyi+C2y2,
-^У-=С,у,'+СгУг',
ах
^L=Ciyi"+C2y2"+f{x).
(5)

374 Г л XII. Уравнения второго порядка с рациональными коэффициентами
Умножив первое уравнение (5) на q(x), второе на р(х), третье
на 1 и сложив почленно, получаем
d2V , / ч dv , / м, t, \
Ввиду того что t/i и t/2 — решения однородного уравнения, то
yi"+P(x)yi+q(x)yi = 0
Уг"+Р(х)Уг'+Ч&)Уг = 0.
Решая систему (4), находим
f(*)
с/=-
с2'--
'■('-£)
fM
Уг
У1
Интегрируя, получаем
Ci = d(x) и С2=С2(х).
§ 3. СКОРОСТЬ ТЕЧЕНИЯ ЖИДКОСТИ В ТРУБОПРОВОДЕ
Задача 164. Жидкость течет в трубопроводе, длина которого /
велика по сравнению с радиусом R поперечного сечения. Разность
давлений на концах трубопровода р. Нанти скорость движения
жидкости.
Решение. Рассмотрим установившееся движение жидкости
в трубопроводе. Скорость движения жидкости υ по мере удаления
от стенок и приближения к оси трубопровода увеличивается
(рис. 105).
Вообразим внутри потока жидкости плоскую площадку
площадью S, параллельную оси трубопровода.
Верхние слои жидкости над S действуют ускоряюще на нижние.
Нижние тормозят движение верхних.
По закону Ньютона действующая па площадку сила F равна
dv
kS ——, где k — коэффициент пропорциональности.
Рассмотрим далее поток жидкости, имеющий форму полого
цилиндра (рис. 106). Так как величина dr мала, то скорости частиц
жидкости в цилиндре можно считать одинаковыми.

§ 3. Скорость течения жидкости в трубопроводе
375
Пусть длина цилиндра равна 1. Тогда на внутреннюю поверх-
dv
пость площадью 2лг-1 действует сила 2nrk-——. На наружную по-
порхность действует сила — 2nrk — d I 2nkr —— ) .
dr x dr '
У
У/А/ //////////' Ч_^/ Ъ^^
Рис 105 Рис. 106
Сумма этих сил равна —2nkd ( г —;— ) .
Л dr *
При установившемся движении сила трения равна силе,
которая передвигает полый цилиндр вдоль оси. Эта сила равна разности
давлений ρ на концах полого цилиндра длиной 1. Тогда движущая
сила равна 2nprdr. Итак,
-2пЫ у—г— ) =2nprdr,
dr
откуда дифференциальное уравнение процесса
d2v 1 dv _ ρ
dr2 r dr k '
Это неполное линейное неоднородное уравнение с
рациональными коэффициентами. Для интегрирования его сделаем подста-
dv
новку z= ——.
В результате получим линейное уравнение первого порядка
dz ζ ρ
dr r k'

376 Гл XII. Уравнения второго порядка с рациональными коэффициентами
Общее решение его
dv
dr 2k
Интегрируя еще раз, имеем:
·/-+■
Ρ
2k
r*+Ci In r+Ci.
Постоянная интегрирования Ct должна быть равна нулю, так
как скорость течения жидкости по оси трубы не может быть
бесконечно большой (при r=0 v обращается в бесконечность).
Постоянная интегрирования С2 определяется из начального условия: при
r=R ι> = 0 (скорость течения около стенок трубы равна нулю),
г Р&
откуда С2= —ТТ-.
Искомая скорость движения жидкости
§ 4. ИЗГИБ КРУГЛОЙ ПЛАСТИНЫ
Задача 165. Найти упругую деформацию изгиба плоской
круглой пластины от действия равномерно распределенной
симметричной нагрузки.
Решение. Предположим, что:
1) закрепление по краям пластины всюду одинаковое;
2) ординаты у упругой поверхности *, отсчитываемые от
первоначального положения срединной поверхности, остаются
небольшими (малые деформации);
3) ввиду симметрии у зависит только от расстояния χ от оси
симметрии (от перпендикуляра к срединной плоскости в ее центре),
т. е. упругая поверхность должна быть поверхностью вращения;
4) преиебрегается по сравнению с ординатами у теми
составляющими упругих перемещений точек срединной поверхности,
которые параллельны начальному положению этой плоскости;
5) все точки, лежавшие прежде на одной прямой,
перпендикулярной к срединной плоскости, после деформации остаются опять
на одной прямой, которая вследствие симметрии должна
пересекаться с осью симметрии пластинки;
6) сохраняется закон Гука.
1. Выясним вопрос изменений длины, происходящих при изгибе.
* Упругой поверхностью называется поверхность, в которую переходит
срединная плоскость пластины при ее деформации.

§ 4. Изгиб круглой пластины
377
В точке А на расстоянии χ от оси симметрии и на расстоянии ζ
от срединной поверхности (рис. 107) возникают удлинения в
тангенциальном и радиальном направлениях et и ег. Так как нормаль
к упругой поверхности получает наклон φ по отношению к оси
симметрии, то радиус χ круга, проходящего через данную точку,
увеличивается на ζψ.
Рис. 107
Принимаем ввиду малости угла φ sincp^cp.
Длина окружности возрастает пропорционально радиусу.
Поэтому относительное удлинение в тангенциальном направлении
ε; =
ζψ
(1)
Проведем на расстоянии ах вторую нормаль к упругой
поверхности и обозначим через dy угол между двумя нормалями. Длина
волокна, проходящего через точку А и заключенного между двумя
нормалями, увеличится на ζάψ по сравнению с длиной волокна,
лежащего в срединной поверхности, которое остается без изменений.
Разделим величину ζάψ на первоначальную длину dx и получим
относительное удлинение
Удлинения (1), (2) и соответствующие им нормальные
напряжения σ, и θ( в перпендикулярных направлениях взаимосвязаны
основными соотношениями теории упругости
1
гг-
\ ot Or) , εΓ= —=— (σΓ— ■— ot) ,
v μ ' Ε \ μ '
где Ε — модуль Юнга, разрешив которые относительно at и аг,

378 Гл. XII. Уравнения второго порядка с рациональными коэффициентами
получим
ОГ-
μ2-1
(μεί+εΓ), σ.
μΕ
(μεΓ+ε;).
(3)
Подставляем в равенства (3) значения удлинений (1), (2)
и в итоге имеем:
μ2—1 ~ ν *~ Χ ' dx
μΕ 1 Λρ φ \
σ'=-μ^Τζ\μΊΐχ+Ύΐ'
(4)
т. е. напряжения пропорциональны расстояниям от срединной
плоскости.
2. Рассмотрим равновесие элемента пластины и составим
уравнение равновесия действующих сил.
т,
бг—
(V—\
dx
«°*
-^
X
,
U-6r
-^6г
'τ
fl
б.
Рис. 108
Проведем через ось симметрии две меридиональные плоскости,
образующие бесконечно малый угол da, и между обеими
плоскостями проведем два цилиндрических сечения с радиусами χ и x-\-dx.
Получим элемент пластины, представленный на рис. 108 (разрез
и план).
На четырех поверхностях сечений возникают напряжения аг
и at, которые на каждой поверхности приведем к паре. На
цилиндрических сечениях появляются также касательные напряжения τ, при
помощи которых нагрузка средней части пластины передается
на опору.
а) Напряжения at- Каждой элементарной площадке dF одного
меридионального сечения соответствует элементарная площадка
другого, на которой напряжение имеет такую же величину. Линии
действия обеих сил atdF пересекаются в плоскости симметрии
элемента пластины. Эти силы можно привести к равнодействующей
atdFda, приложенной в точке их пересечения и лежащей в
плоскости симметрии.

§ 4. Изгиб круглой пластины
379
Момент силы OtdFda относительно любой точки срединной по-
иерхности равен aizdFda. Для всей плоскости симметрии, учитывая
равенство (4), получаем
Μ {at) =da $etzdF=da -^ ( μ -\ + ■£-) jW.
Распространенный по всей площади сечения интеграл / z2dF
Рис. 109
твисит от вида сечения и представляет момент инерции меридио-
h3
пального сечения, равный ——-dx. Поэтому момент пары at
«с.)=1Й--й-(^ + -^)^ <5>
Ординаты ζ считаем положительными при направлении их вниз.
άφ
Г.сли величины φ и -;— также положительны, то в нижней части
dx
будут растягивающие напряжения ot и равнодействующая этих
напряжений в меридиональных плоскостях направлена в плоскости
ι имметрии элемента в сторону центра пластины, как показано в
разрезе (рис. 109).
Наверху при отрицательных ζ направления сил
противоположны и пара, образованная всеми напряжениями at, будет вращать
цемент пластины против часовой стрелки. Тогда момент (5) будет
иметь отрицательный знак,

380 Гл. XII. Уравнения второго порядка с рациональными коэффициентами
б) Напряжения аг. В поверхности сечения, соответствующей
радиусу х, напряжения σΓ образуют пару сил, момент которой с
учетом равенства (4) равен
i»"«=i§r (■"£+*)'*"·
Интеграл / z2dF представляет момент инерции прямоугольника
шириной xda и высотой h. Поэтому последнее равенство
принимает вид
/σ^=-^τ.-^-(μΧ-^-+φ)ί/α. (6)
К этому выражению присоединяется еще пара сил от
напряжений 0Г на противоположной поверхности сечения, имеющая обратное
направление вращения. Таким образом, остается лишь разница
между обоими моментами, которая представляет дифференциал
выражения (6), соответствующий приращению расстояния χ на dx:
4^--w( **£-*)**] =
μ£ h3 I d2® dm dm \ , .
μ2—1 12 * dx2 dx dx
Таким образом, момент всех напряжений σ,:
dm
Если величины φ и —τ— положительны, то напряжения аг в
нижней половине растягивающие и пара в сечении χ вращает против
часовой стрелки.
В сечении x-\-dx вращение направлено тогда по часовой
стрелке. Если предыдущий дифференциал положителен, то он дает
момент, вращающий в положительную сторону, т. е. момент всех
напряжений σΓ вводится в уравнение моментов без изменения знака.
в) Касательные напряжения т.
Для того чтобы привести касательные напряжения к паре сил,
момент которой мы должны найти, определим передающуюся
перерезывающую силу. Предположим, что в пластине проведено
кольцеобразное сечение радиуса х. Ограниченная этим сечением впутреь.
няя часть пластины находится под нагрузкой лх2р, которая
уравновешивается перерезывающими силами по кольцеобразному сечению.

§ 4 Изгиб круглой пластины
381
На часть кольца, заключенного между меридиональными сечениями
, da π
с центральным углом da, приходится —— сечения. Поэтому на эле-
2л
мент пластины в сечении χ передается перерезывающая сила
к2р
— da. В сечении x-\-dx перерезывающая сила больше только что
найденной на величину дифференциала. Следовательно, разница
между ними соответствует нагрузке, приходящейся на элемент.
Эта разница как бесконечно малая высшего порядка не имеет
существенного значения и поэтому
M(x)=^-dadx. (8)
Знак момента, как следует из рис. 109, положителен.
3. Элемент пластины относительно вращения будет в равпо-
иесии, если алгебраическая сумма всех моментов равна нулю:
Μ(σι)+Μ(σ,-)+Μ(τ)=0. (9)
Подставляем в уравнение (9) найденные значения моментов
(5), (7), (8) с учетом их знаков и получаем
μΕ h3 Ι φ dm
Ι φ αφ \ , ,
\μ Т + -Й71 dxda+
μ2-1 12 \r Χ ' dx
μΕ h3 Ι ά2φ , dm dm \ χ2ρ
^^T-^2^X4x^^Yx- + 4x-fdxda+-2-dadX-°
или'после сокращения на dadx и выполнения упрощений
μ2£ /г3 / d2m dm φ \ рх2
откуда
μ2—1 12 \ dx2 ' dx
d2m άφ φ 6(μ2—1)
* ~~dF+ ~dx χ,== μ2£/ζ3 ρΧ%
или, разделив обе части равенства па х, приводим задачу к
следующему неоднородному дифференциальному уравнению с
рациональными коэффициентами
сРср 1 dm φ 6(μ2-1)
dx2 x dx χ2 μ2ΕΙτ3
Здесь: φ — угол, образуемый нормалью к элементу пластины
после изгиба с первоначальным ее положением; χ — расстояние

а&г 1 л. XII Уравнения второго порядка с рациональными коэффициентами
элемента пластины от центра; коэффициент Пуассона
μ
h — толщина пластины; ρ — давление на пластину.
Соответствующее однородное уравнение для уравнения (10)
iftp 1 άψ φ
dx* +Τ ' Чх~~x^=0 (H)
совпадает с уравнением (8) предыдущей задачи и поэтому имеет
общее решение
ψ=αιΧ+-^. (12)
Для нахождения общего решения данного неоднородного
уравнения (10) предположим, что оно имеет такую же форму (12),
но Ci и С2 являются теперь функциями х, т. е.
С2(х)
φ= d (χ) χ-\ .
Функции Ci(x) и Сг(х) нужно определить, чтобы удовлетворить
дифференциальному уравнению (10).
Для этой цели· применим к дифференциальному уравнению (10)
метод вариации постоянных.
Краткости ради введем обозначение
6(μ2-0
ρ—Ν,
μζΕ№
Тогда уравнение (10) примет вид
ά2^ 1 άψ φ
ч* +т-4хг-ж=-"х- <I3>
Два частных решения соответствующего однородного
уравнения (11)
Φι=*. q*=—· (14)
С помощью линейно независимых частных решений (14) будем
искать общее решение уравнения (13) в виде
4>=Οι{χ)φι+ϋ2{χ)φ2. (15)

§ 4. Изгиб круглой пластины
383
Дифференцируя это равенство, получаем
άψ
dx
= С1'ф1 + С1ф1' + С2'ф2+С2ф2'- (16)
Так как С4 и С2 неизвестны, то для них поставим какие-то усло-
иия. В виде первого условия поставим
С1'ф1+С2/Ф2=0, (17)
после чего уравнение (16) упрощается и принимает вид
dw
—-=Cm'+Cm'. (18)
Дифференцируя еще раз уравнение (18), получим
ί/2φ
dx*
= Cm"+Cm"+Ci'<fl'+Ci'<v2'. (19)
Подставим выражения φ, —ι—, , % из уравнений (15), (18)
(19) в уравнение (13) и после группировки слагаемых получим
Мчн'Ч-уЧН' ^qH)+C1(q*''+^q*'--^q*) +
+ψ'0ι'+ψ20^'=-Νχ.
Так как ψ1 и <рг удовлетворяют уравнению (11), то уравнение
(13) превращается в нижеследующее
Ci · 0+С2· 04Vci'+<P2'C2' =-ЛГл:
или
Vi'Ct'+tfCi^-Nx. (20)
Решая теперь систему уравнений (17) и (20), находим GY и С/:
Nx Nx
Li = ; -, ϋ2 =
ф2фГ— <№' ψΐψ2—(Μ>1
Тогда величины Ct и С2 находятся простым интегрированием:

384 Гл. XII. Уравнения второго порядка с рациональными коэффициентами
ι l —~xdx
С ψλχαχ \ χ
Cl=_tfJ—-I r+C=-N \ ■ +С=
φ*Ρι — φιφ2 I J / 1_\
N С , _ Мс* _ } (21"
J φιφ2 —ψ2φι 2 ^ 8
Подставляем полученные значения (21) в уравнение (15) и ποι-
ле упрощения найдем общее решение уравнения (13):
где В и С — постоянные интегрирования.
Написанное выражение для φ является наиболее общим реше
нием, так как оно содержит две произвольные постоянные.
Для определения постоянных интегрирования из граничны:
условий заметим, что в середине пластины при х=0 и φ=0, τ. t
С*=0. Постоянная С зависит от условия, которому подчиняете?
пластина на краях.
Полагаем края пластины защемленными, т. е. считаем, чте
упругая поверхность касается по кругу радиуса х=г горизонталь
пой плоскости, с которой вначале совпадала срединная плоскосъ
пластины. Поэтому φ должно обращаться в пуль также при х=г
Тогда
N
0= -~г3+Сг
о
или
с—?-*
Итак, для защемленной по периметру пластины
Ν 3(μ2-1)
φ= __ (Λί_*)_ _____ р{гЧ-х*). (22
Подстановка значения φ из равенства (22) в соотношения (1
и (2) дает значения упругих удлинений и напряжений:
N N
ег= — (/*-**) ζ, 6Г= — (r*-3x*)z.

Глава XIII
ЗАДАЧИ, ПРИВОДЯЩИЕ К СПЕЦИАЛЬНЫМ ЛИНЕЙНЫМ
ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ВТОРОГО ПОРЯДКА
С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ
(УРАВНЕНИЯМ БЕССЕЛЯ, ЛЕЖАНДРА И МАТЬЕ)
Интегрирование дифференциальных уравнений второго
порядка с помощью рядов применяется, когда затруднительно
нахождение общего решения уравнения.
Рассмотрим интегрирование дифференциальных уравнений
второго порядка с переменными коэффициентами при помощи рядов.
Метод неопределенных коэффициентов
В уравнении
у"+р(х)у'+я(х)у=о
ρ (χ) и q{x) раскладываются в степенные ряды
00 ОО
ρ {χ)— 2*ίαίχ1 и я{х)=2ш1biXl-
г, 1=0 г, 1—0
Решение определяется в виде
У
=2 αχΐ-
г, 1=0
Коэффициенты Ci находятся способом неопределенных
коэффициентов; подставляя значения у, у' и у" в уравнение и приравнивая
нулю коэффициенты при одинаковых степенях х, получаем
уравнения для определения коэффициентов ее
х1
X2
2-\с2.+а0с1+Ь0Со=0,
3 · 2c3+2aoCZ+a1Ci-{-b0ci+bic0—0,
4-3c4+3aoC3+2aiC2+cz2Ci+froC2+6iCi+i>2Co=0,
Чтобы получить два частных решения ι/ι и ι/г, принимаем для
г/ι Со= 1 ci=0, для г/г Со=0 Ci=l.
После определения сг необходимо удостовериться в сходимости
полученного ряда.

386 Гл. XIII. Специальные линейные уравнения второго порядка
Метод разложения в ряд Тейлора или Маклорена
Решение уравнения
y"=f(x, У, У')
'можно искать в виде ряда Тейлора и Маклорена, если задать для
пего начальные условия и если ряд при этом получается
сходящимся.
Пусть начальные условия:
при χ=ω У=Ь;
» х=а y'z=bu
» χ=α y" — b2.
В таком случае общее решение уравнения
х—а (х—а)2 (х—а)3
y = b+bi-jr+bz±^r~+y"'{a)^rL +
(х—а)*·
+i/IV(a) -—-+■■ ■
Значения у"'(a), t/IV(а) находятся из заданного
дифференциального уравнения и из уравнений, полученных из него
дифференцированием, подстановкой в них заданных постоянных a, bi, b2
вместо χ, у, у', у".
Ряд Тейлора
х—а (х—а)2 (х—а)п
f(x)=f(a) + -^~f'(a) + ^~f"(ay+...+ y—^-i«(a)+...
Ряд Маклорена представляет собою частный случай ряда
Тейлора, когда разложение функции f(x) по степеням χ производится
при α=0, τ. е.
X У2 Хп
fW=f(0) + 1T-r(0) + -2pr(0)+...+ -^rf(il40)+..·
Решения нижеизложенных специальных дифференциальны."
уравнений второго порядка с переменными коэффициентами
основываются на принципе интегрирования уравнений с помощью рядов.
I. УРАВНЕНИЕ БЕССЕЛЯ
Линейное дифференциальное уравнение
у"+^у'+Ь-~)у=о
или
х*у"+ху'+(х2-п*)у=0, (1)
где η — любое число, называется уравнением Бесселя п-го порядка

Гл XIII. Специальные линейные уравнения второго порядка 387
Известно, что для уравнения типа x%y"-\-xp(x)y'-\-q(x)y=Oi
если функции р(х) и q(x) разлагаются в сходящиеся ряды по
степеням х, методом неопределенных коэффициентов могут быть
найдены решения вида y=xr(a0-\-aiX-{-a-2X2-{-. . .). Значения показателя
г находятся из характеристического уравнения
r(r~l)+p(0)r+<7(0)=0.
Для уравнения (1) характеристическое уравнение
г {г— 0 +г—п2=г2—и2=0,
Откуда
г=+п.
Подставляя
у=хп (a0-\-aix-\-a2X2-{-.. .)
В уравнение и приравнивая нулю коэффициент при xn+h, находим
k(2n+k)ah+ah-2=0.
При k=l получим:
(2η+1)αι=0,
£i2m+i=0 (m=l, 2, 3 . . .).
Придавая k значения 2, 3, 4, ... , имеем:
а0
а2= —
Й4-
2(2п+2) '
а0
2-4(2и+2)(2и+4) '
причем ао — произвольно.
Полученный сходящийся ряд при ао= - . .■ определяет
* Понятие факториала распространяется на любые числа χ (в том числе и
на комплексные) при помощи гамма-функции Т(х), определяемой двояким
образом: оо
( = Г е~( 1Х~1 dt (интеграл Эйлера) (только при х>0)
Г/ 1 ] ° П\ПХ~1
ι (X) -\ = lim ■ ■ (для любых значений х, отйич-
п-»„ х(х+\) (х+2).. .(х+п-1)
К ных от неотрицательных целых).
Основные свойства гамма-функции:
Т(х+1)=хТ(х),
Т(п) = (п— 1)! при целом положительном п.
Понятие факториала и', определенное сначала для целых положительных п,
обобщается для любого действительного η в виде функций П(д;) =Г(л:+1).
При целом положительном х; 11(х) =х! = 1 -2 · 3 · . . · х, при x — Q;
1Т(0)=Г(1) = 1.

388 Гл. XIII. Специальные линейные уравнения второго порядка
цилиндрическую функцию (функцию Бесселя) п-то порядка
1-го рода:
nW 2пГ{п+1) \ 2(2η+2) + 2·4(2η+2)(2η+4) "/~
со
Σ
ζ γ \n-i2k
. (2)
Л!Г(п+Л+1) ' V ;
ίι=0
которая является решением уравнения (1). Здесь |х|<;оо.
Решение уравнения Бесселя может быть представлено также
функцией Бесселя в виде
оо
j (х)-(±)яу (~1)ft ( х )2h
Jn(x)-\ 2 ; ,/j k[U(n+k) [ 2 ) >
ft—0
лоичем
n(n+k)=T(n+k+])=n(n) (л+l) (n+2) ... (n+ft). (2a)
Общее решение уравнения Бесселя, если η не целое число,
имеет вид
у=С,1п{х)+Сг1-п{х), (3)
где J-n{x) определяется рядом, получающимся из приведенного
выше ряда для Jn(x) заменой и на —п.
При η целом
/_п(*) = (-1 )"/„(*),
1
при п= —
J t (х) = 1/ -sinx,
при « = -γ
iw-l^
/ j (χ) = I/ cos x.
В этом случае функции /п и J-n ■>— линейно зависимые и и
линейная комбинация (3) уже не является общим решением урав
нения (1).
В общем решении в этом случае J-n{x) должна быть заменен
бесселевой функцией второго рода Yn{x), называемой функцие

Гл. XIII Специальные линейные уравнения второго порядка 389
Вебера (или Неймана) и определяемой равенством:
Jm (x) COS mn—J-m (х)
Уп(х)= lim
sin tnn
При помощи этих функций общее решение уравнения Бесселя
может быть записано в виде
y = ClJ„(x)+C2Yn{x)
(как при целом, так и не при целом п).
Уравнение
xhf+xy'— (χζ+ηη у=0
называется модифицированным уравнением Бесселя. Его отличие —
последний член всегда отрицательный.
Модифицированное уравнение Бесселя может быть приведено
к виду
χψ+χι/+ (/ах2_„2)у==о.
Обобщенное дифференциальное уравнение Бесселя
d I dii \
~dT \XP~dT' +(™}+bxk)y=0 (j>k)
сводится к уравнению Бесселя
У"+ — у'+(т2-^)у=0.
Общее решение (если η — целое число) будет
_ L 1
у=х « [d/n (ωχ α ) +CzYn (ωχ"«) ].
Здесь:
2 α(1—ρ) Ι—ρ
α= — Π-' β =
2-p+f M 2 2-ρ+Γ
У (1—/7)2—46 .—
k=p~2: /г= „ , .—■ и ω=αΥα.
2-ρ+/

390 Гл. XIII Специальные линейные уравнения второго порядка
§ 1. УСТОЙЧИВОСТЬ СТЕРЖНЯ ФОРМЫ УСЕЧЕННОГО КОНУСА,
СЖИМАЕМОГО ПРОДОЛЬНОЙ СИЛОЙ
Задача 166. Найти уравнение продольного изгиба стержня,
имеющего форму усеченного конуса, закрепленного в одном конце
и сжимаемого силой Р. Найти критическую силу, если радиус
нижнего основания конуса R = 2r (r — радиус верхнего основания).
Решение. Как известно, дифференциальное уравнение
упругой линии
dx2 J
Радиус ρ некоторого сечения S—S
определяется из соотношения (рис. ПО):
р—г χ
R—r = Т'
/1
R
т. е.
R-
■х.
т-т R—r
Полагая · =β и замечая, что
пп
Рис. ПО
= /о,
где /о — момент инерции верхнего сечения, имеем
/-/.(■+-£)'.
Начальные (граничные) условия: при х=0 ι/=0, при х=1
dy
dx
=0.
Уравнение упругой линии примет вид
«.-3-+(.+*-)-ч-ь
(1)
Пусть
1 +
βχ
Уравнение (1) принимает вид

§ 1. Устойчивость конуса, сжимаемого продольной силой 391
'>|+*»=i W
где
РР
£/οβ2
ζ
ζ
В уравнении (2) положим у— . Тогда получаем
дифференциальное уравнение Бесселя
?■"**
+/ *+(«*_' )а_ц
dt2 ' dt
которое представим в виде
Замечая, что п= —, получим общее решение
z=CiJL(at)+Czf_ ι (at)
2 2
ИЛИ
2
2= 1/ (Ci sin ai+^cos αί)»
f παί
где Ci и Сг— произвольные постоянные интегрирования, / ι и / ι
функции Бесселя первого рода и половинного порядка.
Возвращаясь к переменным хну, находим
где
ί πα » πα
Так как при х=0 ордината у—О, то
At sin a+Лг cos a=0,
A2=—Αι tg a.
Следовательно,
14-йх , . a&x
y= ——— -i4isin·
/ cos α ί+β*

392 Гл. XIII. Специальные линейные уравнения второго порядка
Находим производную
dy _ Лф / 1 . αβχ α αβχ \
^7__1ο^ν'Τδΐη1+βΤ+ /+βχ cos"7+fi7'· (3)
Производная (3) равна нулю при х=1. Это дает уравнение
ё ι+β ι+β' w
из которого при данном β определяем а.
Критическая сила
α2β2£/ο
FKP_ —
Если R — 2r, то β=1. Из уравнения (4) имеем
, α α
и
α = 4,06.
Тогда искомая критическая сила
4,062£Уа 17,08£/о
Лф_ - _ - - .
§ 2. УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКОГО СТЕРЖНЯ
ПОД ДЕЙСТВИЕМ СОБСТВЕННОГО ВЕСА
Задача 167. Найти критическую длину цилиндрического
стержня с закрепленным нижним концом и со свободным верхним концом
под влиянием силы собственного веса. (Критическая длина
стержня— длина, при которой может произойти прогиб стержня.)
Решение. Верхний конец стержня примем за начало
координат, ось Ох направим вертикально, а ось Оу — горизонтально
(рис. 111).
Рассмотрим элемент стержня длиной ds и с координатами
центра тяжести К (и, υ).
Момент силы тяжести элемента относительно точки S в
предположении, что изгиб достаточно мал, равен
q(y—v)ds&q(y—v)du,
где q — вес единицы длины стержня.

§ 2. Устойчивость цилиндрического стержня
393
Изгибающий момент в сечении S
X X
M=q J (y—v)du=qxy—qj vdu.
о о
Граничные условия:
/mm run п п
Рис. Ill
1) при х=0 г/=0, 2) при х=0 М=
л dy
вследствие защемления конца Л —— =0.
ах
d2y
ахг
Так как
EJ
d2y
dx2
:-М,
то, дифференцируя это равенство, получим
d?y dM
EJ-
dx3
dx
С другой стороны,
dM
-0, 3) при x=l
dy г п dy

394 Гл. ХШ. Специальные линейные уравнения второго порядка
и поэтому
£/-£-—*.■"»
ахг ах
или, обозначая αζ= -=-г и 2= —г-, имеем
EJ ах
^Г+*хг=0. (1)
/ 3 \3 —
Полагая ;с= I ——I t3, уравнение (1) запишем в виде
х λα. '
* d%Z ι l dz ι / η
Заменим функцию ζ через и с помощью подстановки z=v^t
и получим уравнение Бесселя
Ρ
d2v , , dv , / „, 1
+<^ + (<4-)»=°· и
1
Здесь параметр п= .
О
Общее решение уравнения (2)
f = C1/1(0+C2/_1(0
3 3
или
Подставляя функции Бесселя / ι ( —5— х2) и /_ ι ( —— χ2 J
з " ~"з
в уравнение (3), имеем:
dy
(3)
dx
= Ci(Ax+Bxi+Cx'1+.. .)+С2(К+Ьхз+Мх*+. ..).
d2y -
Находим вторую производную 2 и, учитывая второе
граничное условие, получим Ci = 0. Ввиду этого

§ 3. Устойчивость вращения гибкой нити
395
На основании третьего граничного условия
3
Приняв С2=0, получим прямолинейную форму равновесия
у=0. Другие формы равновесия получим, приняв
..(^М
3
2 -
т. е. считая, что —— /2 является корнем функции Бесселя / ι.
3 "J
Корни этой функции 1,87; 4,49; 8,13; ...
Наименьшему положительному корню соответствует критичес-
\ПЕГ
кая длина /Itp = 1,99 I/ .
Первое граничное условие будет удовлетворено, если,
проинтегрировав уравнение (3), выбрать новую постоянную интегрирования
так, чтобы изогнутая ось проходила через начало системы
координат.
§ 3. УСТОЙЧИВОСТЬ ВРАЩЕНИЯ ГИБКОЙ НИТИ
Задача 168. Найти критическое значение угловой скорости
вращения тяжелой гибкой нити вокруг вертикальной оси.
Решение. Тяжелая гибкая нить (рис. 112), прикрепленная
в точке О, вращается вокруг вертикальной оси Ох. Горизонтальную
ось обозначим Оу. Пусть m — масса единицы длины нити.
Рассмотрим элемент нити ΜΜι длиной As, обозначив через Τ
и 7\ натяжения нити соответственно в точках Μ и Μι. Натяжения
направлены по касательным к изогнутой оси нити и образуют с осью
абсцисс углы α и αι. Кроме того, к элементу ΜΜι приложены
центробежная сила maP-yAs и сила тяжести mgAs, где ω — угловая
скорость вращения, g— ускорение силы тяжести.
Проектируя действующие на элемент силы на координатные
оси, имеем:
Γι cos αϊ—Г cos a-\-mgAs = Q, 1
Tt sin at—Τ sin as4-mm2t/As = 0 -»
или
Τι sin αϊ—Τ sin a*f-ffi(u2yAs = 0
A^cos a)-{-mgAs = 0,
A (T sin a)-\rtn&2yAs=^Q
A(T cos a)+mgAs = 0, 1
=0. J ^ '

396 Гл. XIII. Специальные линейные уравнения второго порядка
Так как
cos ос =
dx
ds '
sin α=
dy
ds '
то после подстановки этих значений в систему (1) и деления
уравнений на As, переходя к пределу в предположении, что As -> О,
получим
ds
Рис. 112
Если отклонение нити от оси вращения мало, то, полагая
ds—dx, уравнения (2) запишем в виде
dT _ d*y , dy dT ,
Интегрируем первое из этих уравнений и в итоге получаем
T=-mgx+C. (4)
Граничное условие: при х—1 (в точке А) 7=0, отсюда
0=~mg/+C, C=mgl. (5)
Подставляя найденную постоянную интегрирования (5) в
общее решение (4), имеем:
T=mg(x—l).
(6)

§ 3. Устойчивость вращения гибкой нити
39?
Второе уравнение (3) можно представить в виде
<Ру , 1 dT dy , 1 „
dx2 ' Τ dx dx
или с учетом зависимости (6)
d2y ,1 dy , ω2Μ
dx2 x—/ сЬс g(x—l)
откуда
d2y 1 dy ω2ί/
dx2 Ζ—λ; dx g(l—x)
= 0.
, получим
d2w , 1 dy
dz2 ζ dz
Общее решение уравнения (7) примет вид
1/ = С1/о(2)+С2У0(2)
или
Граничные условия: при х=/ ордината у должна быть
конечной. Но Ко(0) = оо. Поэтому надо положить Сг=0.
При х=0 у=0, откуда
С!/о(2шУ—) =0.
Можем принять Ci = 0 и получим прямолинейную форму
равновесия.
Возможно также предположение, что
У4-
2со
" 8
где α — корень функции Jo{t), которая обращается в нуль при
ί = 2,40; ί=5,52; ί=8,65; . ..

398 Гл. XIII. Специальные линейные уравнения второго порядка
Для наименьшего из этих корней имеем
2ω|/— =2,40,
8
и тогда
ω=1,20
Vf («О
При угловой скорости со<1,20у— нить сохраняет
прямолинейную форму.
Если же ω равна значению (8), то нить может искривиться.
Итак, критическое значение угловой скорости
ωκρ=1,20
п
§ 4. РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ В КОЛЬЦЕВОМ РЕБРЕ
ПРЯМОУГОЛЬНОГО ПРОФИЛЯ
Задача 169. Кольцевое ребро прямоугольного профиля
приварено к теплообменнику (рис. 113). Начало радиус-вектора г
находится на его оси с положительным направлением от центра.
Сохраняются в силе расчетные теплотехнические предпосылки задачи 149.
Найти закон распределения температуры.
Решение. Площадь поперечного сечения отдельного
элемента высотой dr будет А = 2лг6. Площадь поверхности этого элемента
dS=2(2rtr)dr=4nrdr. Разностью между подводимой в направлении
г теплотой в отдельный элемент при г и выходящей из отдельного
элемента теплотой при r-\-dr является
dT
(2nr8k — )dr, (l)
dr \ dr
где Τ ■— температура в отдельном элементе.
Для температуры окружающей среды Тв имеем
Q = T-TS и dQ=dT.
Предполагаем, что ребро теплее окружающей среды.
В установившемся состоянии общий тепловой баланс требует,
чтобы теплота, протекающая через элемент dr, равнялась
отдаваемой путем конвекции двумя гранями ребра, т. е.
qKom=hQdS=4ithrQdr. (2)

§ 4. Температура в кольцевом ребре
399
Приравнивая уравнения (1) и (2), имеем
dT
I йЧ dT \
2пШ ——- +2пЫг —— dr—4nhrQdr=0
\ dr2 dr ι
или
dr2
■+/·■
dQ
-mzr2Q = 0.
dr2 ""■"' dr "*' "-"· (3)
Это модифицированное уравнение Бесселя пулевого порядка
2Л
с параметром m
-У-
/гб
ОсноВанщ
Ширина
Грань
Рис. 113
Общее решение уравнения (3) может быть непосредственно
записано в виде
0=Ci/o(mr)+C2/Co(ffir),
где постоянные интегрирования Ct и Сг определяются заданными
начальными условиями.
Здесь Кп(х)—модифицированная функция Бесселя второго
рода η-го порядка. Для целочисленных значений η имеет вид
Кп(х) =
dJ-n(x) din(x)
cos ηπ
дп
дп
]■

400 Гл. XIII. Специальные линейные уравнения второго порядка
И. ОБОБЩЕННОЕ УРАВНЕНИЕ БЕССЕЛЯ
§ 5. МАЯТНИК ПЕРЕМЕННОЙ ДЛИНЫ
Задача 170. Обыкновенный маятник состоит из невесомой нити
и веса W па нижнем конце. Найти уравнение движения маятника
при малых колебаниях, если его длина непрерывно увеличивается.
Решение. Если при колебании маятника его длила /
непрерывно увеличивается, то в момент / она будет A+Bt.
Угловой момент количества движения (кинематический момент)
W
есть произведение центробежного момента инерции /= г2 во-
о
круг основания и угловой скорости. Здесь г — радиус инерции.
Для сосредоточенного веса г=1 и поэтому момент количества
движения равен
W μΜ
g dt '
Скорость изменения углового момента количества движения,
согласно закону динамики, должна быть связана с
восстанавливающей силой. Как видно из рис. 114, эта сила равна Wsin G или ввиду
малых угловых перемещений приближенно равна 1F0.
Восстанавливающая сила образует вокруг опоры момент, плечо
которого /, и таким образом
d I W dQ
dt \ g dt
) =-WQl,
где знак минус указывает, что скорость изменения углового момента
количества движения уменьшается при положительном значении
угла 0.
Тогда дифференциальное уравнение движения маятника
(>-£-+»4"£)+™.
= 0
и при l=A-\-Bt принимает вид
™ ■ 2В * +^ге=о. („
dt* ' A+Bt dt ' A+Bt
Уравнение (1)—линейное дифференциальное уравнение
второго порядка с постоянными коэффициентами.
Пусть
A+Bt A
u=—r^ = ~+t,

§ 5. Маятник переменной длины
401
тогда
dQ dQ
au=at,
du dx '
и уравнение (1) принимает вид
s
где т2=
В '
Уравнение (2) может быть сопоставлено с обобщенным
уравнением Бесселя
d I dQ
(up-τ—) -\-(aui-\-buk)Q=0.
du \ du
Если сравнение покажет, что p~k-\-2 или 6=0, то уравнение
(2) приводится к уравнению Бесселя.
В этом случае 6 = 0 и решение
0=ц» [cjn (<nx*)+CtYn (сох« ) ],
если η — целое число.
Так как р=2, j= 1 и а=тг, то получаем значения постоянных:
«= 2=1+7=2; β=2=5τ/=--1; <* = «1~а=2т;
y(1_p)2_46
П= 2-р+/ -1·
Общее решение уравнения движения маятника при малых
колебаниях будет
θ= — [C1Ji(2mu)+C2Yi(2mu)].
* fu
Так как
и= 4- +*.
то

402 Гл. XIII. Специальные линейные уравнения второго порядка
§ 6. УСТОЙЧИВОСТЬ СТЕРЖНЯ ПЕРЕМЕННОГО СЕЧЕНИЯ
ПОД ДЕЙСТВИЕМ ПЕРЕМЕННОЙ РАСПРЕДЕЛЕННОЙ НАГРУЗКИ
Задача 171. Найти критическую нагрузку для защемленной
с одного конца стержня переменного момента инерции под дейст
вием переменной распределенной нагрузки (рис. 115). Момен-
инерции стержня изменяется по закону J(x)=J0 \ 1 г-) , а нг-
(х \п
1 J , где т, η принимают положительны-
целочисленные значения.
Рис. 114
Рис. 115
Решение. Изгибающий момент в сечении (х, у)
определяется так:
Ι χ χ
M(x)=-\p{l)dl{4-y) = \w(l)dl-y\p(S)dl=-EJ{x).y".
χ Ι Ι
Дифференцируя это уравнение с учетом условий задачи,
получим т
У х У + (п+1)£/о \1 I I У~^ [1)

§ 6. Сжатие стержня
403
При помощи подстановок
χ , 1 dy 1
/ I du I
У ~-п
I dv
-, Г" = --«
1 d2v
pol3
I2 du' * /з du2' (n+l)£/0
уравнение (1) приводим к виду
d2v m dv
= &2
du2 и du
(2)
сравнение (2) решается при помощи цилиндрических
функций Zp р-то порядка:
v = u2vZp( 2kvu2v ) ,
I m—1
— ^n—m+3 p= »__
ν · ra—m+3
Для псцелочислешюго параметра р имеем:
о = и ** [ С J р ( 2kvuJ» ) +С2/_р ( 2fevu*r ) ] ,
do
= — to 2v" [ Ci/P+1 (2fou2v ) — C2/_P-i ( 2&vu2v ) ] ·
Для целочисленного параметра p = Qi, если пг=^2+1»
,n= (^1+1)^2—2, а ^ и ?2 принимают целочисленные значения,
имеем:
v = u
dv
4>i2 г / 2k — <?Λ / 2& -92\1
[^/βι( —и» )+C2A/gi(—α2 )],
_i-5i((ij-i)-ir ι 2k —q2
-—~—ku 2 Ci/gi+i I u2
du L v <7г
Начальные условия:
а) прих=0 у'=0, т. е. u=l; и=0,

404 Гл XIII. Специальные линейные уравнения второго порядка
dv
б) при х=1 у"=0, т. е. и=0; -т— =0.
В силу
lim \и~ i»~ Jp+l (2Ьи*^") 1=0, п—/п+2>0,
и /_р_1(0) = оо или соответственно Ν51+ι (0) = оо из второго условия
следует, что С2=0.
Первое условие дает для всех значений ρ уравнение потери
устойчивости
/Р(2Ь)=0.
Первый корень Χι=2&ιν ввиду того, что
/W3
-*- Ш
(n+l)EJ0 "х * 2v
дает возможность определить критическую силу
\2 EJ0
j _ р0кр* _ / *1 Г
/2
Частный случай п—т+3 = 0, т. е. ν=οο, приводит, согласно
уравнению (3), к дифференциальному уравнению Эйлера
ά2υ , я+3 άυ , k2
άΦ
и
du
с критической нагрузкой (m=n+3):
F"»~ n+1 - 4 ("+2) /2 ·
Критические нагрузки для различных тип приводятся
в таблице:
т=0
т=1
т=2
т=4
0
1
2
3
4
7,87
16,1
27,3
41,3
5,78
13,0
23,1
36,1
52,1
3,67
9,87
18,9
30,9
45,8
1,0
6,59
14,7
25,7
39,5
—
2,25
10,2
20,2
33,0

§ 7. Колебания круглой мембраны
405
III. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
В ЧАСТНЫХ ПРОИЗВОДНЫХ
§ 7. КОЛЕБАНИЯ КРУГЛОЙ МЕМБРАНЫ
Задача 172. Исследовать колебания круглой тонкой мембраны
радиуса R и массой ρ педеформированного состояния на единицу
площади.
Решение. Для составления дифференциального уравнения,
описывающего движение мембраны, рассмотрим усилия,
действующие на ее элемент (рис. 116).
Χ Χ+ΔΧ
Рис 116
Так как деформации мембраны и углы наклона малы, то
стороны элемента приближенно равны Ах и Ау.
Натяжение Τ является силой на единицу длины. Поэтому силы,
действующие на края элемента, приближенно равны Τ Ах и ТАу.
Так как мембрана абсолютно гибкая, то эти силы являются
касательными к мембране.
Рассмотрим сначала горизонтальные составляющие сил. Эти
силы получаются умножением действующих сил на косинусы углов

406 Гл. XIII. Специальные линейные уравнения второго порядка
наклона. Поскольку углы малы, то их косинусы близки к
единице. Следовательно, горизонтальные составляющие сил на
противоположных краях приблизительно равны. В связи с этим движение
частицы мембраны в горизонтальном направлении будет ничтожно
малым. Отсюда заключаем, что движение мембраны можно
рассматривать как поперечное, т. е. каждая ее частица перемещается
вертикально.
Вертикальные составляющие сил вдоль краев, параллельных
плоскости уОи, будут ТАу sin β и —ТАу sin α, причем минус
указывает, что сила па левом конце направлена вниз. Так как углы малы,
то их синусы можно заменить тангенсами. Поэтому
равнодействующая этих двух вертикальных составляющих
ТАу (sin β—sin α) « ТАу (tg β—tg α) =
=my L ~L· (χ+Δχ>yi) ~ "J- (x> у*) ]' (l)
где г/ι и г/г — значения между у и у-\-Ау.
Аналогично равнодействующая вертикальных составляющих
сил, действующих на двух других краях вырезанного элемента
мембраны, будет равна
Τ Ах [ ~ (хи у+Ау) - -g- (xit у) ] , (2)
где Χι и хг — значения между χ и х-\-Ах.
На основании второго закона динамики сумма сил, заданных
зависимостями (1) и (2), равна массе рАхАу = рАА элемента иде-
алыю ровной мембраны, умноженной на ускорение —^—-.
Таким образом,
д2и Г ди ди 1
pAxAy~dW~ = У 1~дх (χ+Δχ> у^~~дх~(х' Уг) \ +
+ ТАХ [~^"-^1' У+АУ^~ ~д\ (Х2' У) ] '
где производная в левой части равенства вычислена в некоторой
определенной точке (х, у) элемента мембраны.
После деления последнего равенства на рАхАу имеем:
д*и
— {x+Ax,yi)~—(x,y2)
Ах +

§ 7. Колебания круглой мембраны
407
+
dU Ι ι А Ч dU , \
— (хиу+Ьу)-—{Хъу)
Ау
Переходя к пределу при Δχ-Μ) и Ау-^-0, получаем
д2и
Ρ
lim -
Дж->0
ди
дх
(χ+Δχ, г/ι)-
ди
дх
(X Уг)
Ах
+
+ lim -
Ау-+0
~-(хиУ+Ьу)-^-(хг,У)
Ау
_ Τ Г д I ди \ д 1 ди \1 Τ I д*и д2и \
~ о \- дх \ дх > + ди \ дй>* о \ дх2- + ди* '
И, полагая
случая
дх
Τ
дх ! ' ду ^ ду ! J ρ ν дхг дф
-а\ получаем волновое уравнение для двумерного
д*и
дР
= а2(
д2и
~дх?
+
д2и
)■
(3,
Так как выражение в скобках представляет оператор Лапласа
V2M для функции и=и(х, у), то выражение (3) записывается
д2и
дР
= a2V2ii.
(4)
Рассмотрим теперь колебания круглой мембраны радиуса R
(рис. 117). Применяя полярные координаты x=rcosq> и y=r sin φ,
волновое уравнение (4) запишем в виде
д2и
дР
= а2 (
д*и
~~дп
J_ ди_ J_ д2и
+ γ "дг +~г2 dlf'
)■
(5)
Будем рассматривать решения u(r, t) уравнения (5), которые
являются радиально симметричными, т. е. не зависят от φ. Тогда
волновое уравнение примет упрощенный вид
д2и
= α2(
д2и
дг2
+
1 ди
дг
)■
(в)
Так как мембрана защемлена по окружности r=R, то краевое
условие
u(R, t)=0 при Z^O. (7)

408 Гл. XIII. Специальные линейные уравнения второго порядка
Решения, независимые от φ, будут иметь место, если начальные
условия не зависят от φ, τ. е. если они вида
и(г,0)=/(г),
где f (г) — начальное отклонение, и
ди
dt
где g(r) — начальная скорость.
ί=0
=g(r),
(8)
(9)
Рас. 117
Применяя метод разделения переменных (метод Фурье),
определим решения уравнения (6), удовлетворяющие краевому
условию (7). Пусть
u(r,t) = W(r)G{t). (10)
Дифференцируя и подставляя равенство (10) в уравнение (6),
после деления полученного уравнения на azWG найдем
1
аЮ
dP
dW
1 / d*W 1 __
W \ dn + r ' dr
(И)
Для получения решений, удовлетворяющих краевому условию
без наличия тождественного нуля, выражения в обеих частях равен-

§ 7. Колебания круглой мембраны
409
ства (11) приравняем постоянной, которая должна быть
отрицательной, например, — k2. Таким образом,
1 d2G 1 / d2W .1 dW\
— W ' dr2 ^ г dr' ~ '
a2G dt2
откуда получаем обыкновенные дифференциальные уравнения
d2G
dt2
+λ2Ο = 0, K=ak, (12)
Введем в уравнение (3) новую независимую переменную s=kr,
откуда
_1_А dW — dW 1*1 dW
r s ' dr ds dr ds
и
d2W d2W
k\
dr2· ds2
Подставляя эти выражения в уравнение (13) и сокращая на
общий множитель k2, получаем уравнение
d2W ,1 dW , т п
Ч —~ + W=0,
ds2 s ds
которое представляет уравнение Бесселя нулевого порядка.
Общее решение
W=CJo(s)+C2Yo(s),
где /о и Уо — функции Бесселя первого и второго рода нулевого
порядка.
Так как отклонение мембраны всегда конечно, а функция Уо
становится бесконечной при s->-0, то нельзя ее применять и следует
положить С2=0. Определенно С^фО, так как иначе №=0.
Можем принять Ct= 1 и тогда
W(r)=J0(s)=Jo(kr).
На окружности r=R должно быть u(R, t) = W(R)G(t)=0.
Так как Gs=0 будет предполагать «=0, потребуем, чтобы

410 Гл. XIII. Специальные линейные уравнения второго порядка
Обозначая положительные корни функции Jo(s) символами
αϊ, α2, ■ · ·, получим
(Хгп
kR=am или k=km=
R '
где т=\, 2, 3,...
Поэтому решениями уравнения (13), которые исчезают при
r=R, будут функции
Wm(r)=Jo(kmr)=J0(-^-r).
R
Корни s = am функции Бесселя нулевого порядка Jo{s)
т
1
2
3
4
5
6
7
8
9
10
ат
2,4048256
5,5200781
8,6537279
11,7915344
14,9309177
18,0710640
21,2116366
24,3524715
27,4934791
30,6346065
т
11
12
13
14
15
16
17
18
19
20
(Хт
33,7758202
36,9170984
40,0584258
43,1997917
46,3411884
49,4826099
52,6240518
55,7655108
58,9069839
62,0484692
Соответствующие общие решения уравнения (12) при λ=λ,η=
= akm будут
Gm(t) =am cos Kmt-\-b τη Sin hmt.
Следовательно, решения волнового уравнения (6),
удовлетворяющие краевому условию (7), представляются
um(r, t) = Wm(r)Gm(t) = (amcoshmt+bms'mKmt)J0(kmr). (14
Функции (14) называются собственными функциями, а значе
ния Хт — характеристическими числами. Колебания мембраны,
соответствующие ит, называются главными колебаниями tn-το по
рядка. Виды главных колебаний показаны на рис. 118.
При т= 1 все точки мембраны перемещаются вверх (или вниз,
Когда т=2, то функция W2(r)=J0 \—р-г) равна нулю πρι
= αι или г
αι# „ αι#
. Окружность радиуса г= является,
R аг " аг
следовательно, линией узлов, и когда в некоторый момент централь

§ 7. Колебания круглой мембраны
411
1ая часть мембраны движется вверх, внешняя часть 1г> I
доижется вниз, и наоборот.
Решение um(r, t) имеет т—\ линий узлов, представляющих
концентрические окружности (рис. 118).
т^1
m=J
Для получения решения, удовлетворяющего также начальным
условиям (8) и (9), рассмотрим ряд
со со
и(г' 0 = / }Wm(r)Gm(t)--^/ ,(am cos Kmt+bm sin Kmt)Jo \-jp-r).
(15)
m=l
ro=l
Подставляя ί=0 и используя равенство (8), получаем
оо
u(r,0)=XamJo(-^r)=f(r).
m=l
Следовательно, чтобы ряд (15) удовлетворял условию (8), ве-'
.'шчины ат должны быть коэффициентами Фурье ряда Фурье —
Г)есселя, который представляет разложение f(r) по членам функции
., , I а,т \
Ьссселя /о \—w~r) > τ· е·
ат=
ЯЧ^(От)
R
irf(r)h(-^-r) , m=l, 2, 3, ...
Дифференцируемость функции f(r) в интервале Os=:rs=:#
является достаточным условием существования разложения,

412 Гл. XIII. Специальные линейные уравнения второго порядка
Коэффициенты bm определяются с учетом условия (9)
подобным образом:
н
Для получения числовых значений коэффициентов ат и Ьт
можно использовать любой метод приближенного интегрирования,
применяя таблицы функций Бесселя /0 и /ι.
IV. УРАВНЕНИЕ ЛЕЖАНДРА
Дифференциальное уравнение Лежандра имеет вид
(1-я?)у"-2ху'+п(п+1)у=0, (1)
где η — целое положительное число (п=0, 1, 2, ... , k).
Одним из решений уравнения (1) является сходящийся ряд,
называемый полиномом Лежандра или шаровой функцией,
1·3...(2η—1) / n(n-l)
ρ· w= n< (*·- 2(k=i7 *"!+
n(n—l)(n—2)(n—3) \
■χη~1—...+... / =
2·4(2η—1)(2η—3)
1 dB[(*a—1)»]
2n n\ dxn
Фундаментальная система решений (1):
yi=Pn(x),
η
Уг= Qn (Χ) = γ Ρ η (Χ) In -iij- - 2 \ рь-1 (*) pn-h (Χ) ■
ίι—1
Qn(x) называется функцией Лежандра второго рода.
Тогда общее решение уравнения Лежандра
y—CiPn(x)+CzQn(x).
Основные свойства полиномов Лежандра следующие:
2) Ро(х) = 1, Λ (*)*=*, Р2(х) = ~(3х2-\У,

§ 8. Электрический потенциал двух равносильных зарядов 413
Ps(x) = i- (5л:3-3л:), P4(jc) = -J- (35x4-30x2+3),
2 о
Р5(*) = — (бЗх5—70*3+15х),
о
Р„(*)= -L (231л:6—315л;4+-105л;2—5);
lb
3) nP„(x) = (2n—1 )*?„-!(*) —(η—1)Р„_2(х);
4) Рп(х) имеет η нулевых точек, расположенных между
+ 1 и-1;
+Г ί °
5) }Pm(x)Pn(x)dx = _J_
_, 1 2пА
+i f 0 при пфт,
при п=т;
2л+1
§ 8. ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ ДВУХ РАВНОСИЛЬНЫХ ЗАРЯДОВ
Задача 173. Найти в произвольной точке пространства
электрический потенциал, создаваемый двумя равными и находящимися на
расстоянии 2d зарядами.
Решение. Задача представляет вращение вокруг прямой,
соединяющей эти массы на плоскости (рис. 119).
Пусть ±<7 — заряды точек А и В, расположенных на
расстоянии 2d, а Р(х, у) — точка, потенциал которой надо определить.
Потенциал
V--
Обозначим ОР=г и /LPOx=0. Тогда
/2d d2 \
Г12=га_|_</2_2с/г cos0 = r2 (l Cos0+—p)
ί 2d d2 \
r22=r2+d2+2dr cosQ = r2 (l-\ cos ОН -)
и в результате потенциал
V--
_i —-i
Я I , 2d n d2 \ 2 q I . 2d а , d2 \ 2

414 Гл. XIII Специальные линейные уравнения второго порядка
Предположим, что величина г значительно больше ά.
Используя полиномы Лежандра, можно написать новое выражение
потенциала
оо со
7!=0 ?1=0
а/
-7
У
0
Ь
У /
/ V -J
Ав /в
d *t{
Р(х,у)
X
Рис. НО
Так как полипом Рп(х) является функцией своего показателя,
то потенциал
со
п=0
2п+1
(О
Замечая, что величина- г является очень большой по сравнению
с d, можно ограничиться первым членом ряда (1), играющим
важную роль в разложении. Поэтому потенциал
V--
2q
2qd cos θ Μ cos θ
— Pi(cos θ) Ι — Ι = —ί— = ;
г \ г ' г2 г
где M=2qd— электрический момент диполя (—q, -\-q).

§ 9. Уравнение потенциала
415
Очевидно, что если г меньше d, то тогда
I 2г ή \
пг=а, (!____ cos θ+-^).
r2W2(l+ —cose+^r)
и, проводя аналогичные выкладки,
oo
n=0
§ 9. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
В ЧАСТНЫХ ПРОИЗВОДНЫХ ПОТЕНЦИАЛА
Закон всемирного тяготения гласит, что между двумя
материальными точками с массами Mum, которые находятся на
расстоянии г, действует сила
F=-kJf< (I)
где k — постоянная притяжения, а знак минус обозначает, что сила
стремится уменьшить расстояние между точками (рис. 120).
Если точка Μ находится в начале прямоугольной системы
координат, то в формулу (1) можно подставить r2=xz-\-y2-\-z2 и тогда
F=-k- Mm
x2+y2+z2 ·
Составляющие силы F по трем координатным осям
соответственно равны:
kMm χ kMmx
Γχ^= —
х2+У2+г2 V χ2+ί/2+ζ2 (χ2+ί/2+ζ2)3/*
_ kMmy _ kMmz
V~~~ (x2+i/2+22)3/* ' Z~~ (A;2+y2+z2)3/2·
Существует такая функция Ф(х, у, ζ), что
ρ _дф. ρ — a®L. f _дф
дх ' у ду ' z dz '

416 Гл. XIII. Специальные линейные уравнения второго порядка
которая называется силовой функцией и имеет вид
kMm
Φ:
(*2+У2+22)'/2
Отрицательное значение Φ обозначается V=—Φ и называется
потенциалом точки Μ на точку т.
Функция
Рис. 120
V=-
kMm
удовлетворяет дифференциальному уравнению в частных
производных
giy giy dW
■ + -ξ-γ=0,
дх2 \ ду2
dz2
(2)
что легко проверяется подстановкой в это уравнение
соответствующих частных производных.
В сферических координатах г, ν, φ уравнение (2)
представляется
дг2 ^ δμ L ^ μ^μ J ^ 1—μ2 &?
где ради сокращения записи обозначили cos v через μ.
(3)

§ 10. Потенциал притягивающих масс
417
§ 10. ПОТЕНЦИАЛ ПРИТЯГИВАЮЩИХ МАСС
Задача 174. Найти потенциал северного полюса N шара
единичного радиуса на точку Ρ (рис. 121).
Решение. Предположим, что количество сосредоточенных
в обеих точках притягивающих масс равно единице.
Если квадрат расстояния между двумя точками (северным
полюсом N и точкой Р) (Л/Р)2=./?, то потенциал V= —.
Рис. 121
Полярные координаты полюса N (1, 0, 0) и на основании
равенства -{-У/? = +у 12-{-г2—2r cos ω получаем
fR = у 1— 2rcosv+r2,
так как
cos cu=cos v cos vi+sin ν sin vi cos(cp—φι) =cos v.
Тогда потенциал
У 1— 2r cos v-f-r2
Следовательно, потенциал V северного полюса N (1, 0, 0) на
точку Ρ (г, ν, φ) зависит лишь от радиус-вектора г и широты v.
При г<1 выражение (1) разложимо по степеням г в ряд Мак-
лорена
ПО) Г(0)
v=f(r)=№+f'(o)r+--T:±r*+-j-^r*+..:

418 Г л XIII. Специальные линейные уравнения второго порядка
Здесь:
f(0) = l;
f/(r)=/?-J,/»(cosv-r), f'(0)=cosv;
r(r)=-^-3A+3^-%(cosv~r)2, f"(0)=3cos2v-l;
f" (r) = —9/?-'/» (cos v—r) +15/?-'/» (cos v—r)3,
f'"(0) = 15cos3v-9cosv.
Тогда
ι/ ι , ,, 3cos2v—1 , , 5cos3v—3cosv . ,n
V= 1 +'' cos v+r2 [-r3 (-... (2
Если коэффициенты при rn обозначить через Pn(cosv), то раз
ложепие (2) примет вид
оо
V= Р0 (cos ν) -\-rPi (cos v) -\-r2P2 (cos v) +. .·=2ΐι '"JMcosv)
η=0
или
оо
ν=^Γ»Ρη(μ), (3
где μ=α)8ν.
Здесь функции
(2п)! Г η (η—Ι) η(η—\) (η—2) (п—Ъ)
ρ Ι.Λ . i_ „n_ _J ί ,."-21 - — . — - цП-4_
η(μ1"2ηηΙηΙΐμ 2(2η-1)μ ^ 2·4{2η-]){2η-3) μ
η(η—1)(η—2)(η—3)(η—4)(η—5) η_β 1
2 · 4 · 6(2η-1) (2η^3) (2η-5) μ" 6+''" ^ '
Простые шаровые функции Лежандра (4) являются целыми
рациональными. Так:
•Ро(и)—cos0 —Ь
Ρι(μ)=α>8 ν —μ,
^(μ)=γ(3ε052ν-1)=|-(3μ2-1),
^(μ) = -у (5 cos3v—3 cos ν) = — (5μ3—3μ),
ρ4(μ)= JL (35cos4v-30cos2v+3) = ~ (35μ4-30μ2+3).

§ 10. Потенциал притягивающих масс
419
Потенциал V должен удовлетворять уравнению (3, стр. 416).
Так как он не зависит от φ,'το это уравнение принимает
упрощенный вид
dHrV) . д Г dV Ι
Подставляем сюда выражение потенциала по формуле (3):
оо
2> {(η+1)^(μ) + ^[(1-μ2)~^]}=0. (5)
-п=0
Уравнение (5) может иметь место лишь в случае равенства
нулю коэффициентов при отдельных степенях г:
(»+1)«Ρ»(μ) + -^-[(1-μ")^^]=0. (6)
После выполнения дифференцирования в квадратных скобках
уравнение (6) принимает вид
άΨη(μ) dP» (μ)
Это дифференциальное уравнение Лсжандра.
Общее решение любого линейного дифференциального
уравнения второго порядка представляет линейную комбинацию двух
частных решений этого уравнения, т. е.
у=С1у1-\-С2у2-
Одно частное решение может быть представлено в виде
степенного ряда с неопределенными коэффициентами и показателями
степеней:
оо
у1= 2 Αημ™Η. (7)
Тогда производная этого частного решения
оо
-?-= y\Akm^mk~\
а второй член уравнения (6)

120 Гл. XIII. Специальные линейные уравнения второго порядка
= 2л*т*(т*+1Ьт*— ^Аь.тк{тк—\)^т^-г. (8)
Подставляя выражения (7) и (8) в уравнение (6), имеем
оо оо
η(1+1) ^W"*=2j Льт*(тк+1)ц"Ч—
ft=l ft=l
оо
— ^,^ftmfc(mft—Ομ1»1*-2
Ь=1
или
2^b{[n(n+l)-mft(mft+l)] μ™ί.+ίηβ^-1)μ™Λ-2}=0. (9)
fc=l
Ряд (9) будет тождественным с рядом
оо
^{Л/,тЛ(тЛ—Ομ^-^+Λ^-ι [/ι(η+1)—mWi(mft+1+l)] μ™*+ι}
fc=0
при Л0=0.
Выполнение равенства (9) возможно, если nth—2 — mh+l, т. е.,
если показатели степени членов ряда представляют убывающую
арифметическую прогрессию, разность которой равна 2, т. е.
зависимость между показателями степени двух рядом стоящих членов
будет
mt—2=m2,
m2—2=m3=mi—4,
m3—2 = ml=mi—6,
mfe—2 = m,i+i—mi—2/г,
mft=mi—2^+2.
Тогда ряд приводится к виду
оо
2 {Ak(ml-2k+2) (ml-2k+l)+Ah+l [n(n+l)-
fc=0
— (mi—2ft)(mi—2Л+1)]} μ™·"2'', Αο=0.

§ 10. Потенциал притягивающих масс
421
Первый член степенного ряда
i4i[n(n+l)—mi(mi+l)] μ"·· (10)
)бращается в нуль, если т4 равно η или —(п-\-1).
Остальные члены обращаются в нуль при
(ml~2k+2) (mi~2k+l)
Ak+i = —Ah —
n(n+l) — (mi—2k) (mi~2k+l)
— h (n—mi+2fe)(n+mi-2fe+l) ' ( '
Соотношение (11) представляет рекуррентную формулу для
определения коэффициентов Ah при условии, что выбрано одно из
позможных значений mi:=n или mi=— (n-\-\).
Пусть в уравнении (10) nii = n. Тогда получаем значения
искомых коэффициентов
п(п— 1)
(я—2)(гс—3) (п—3)(п—2)(п—1)п
А3=-А2 -^Щ^1^)~ ==AiT.i(2'n^3)j2V~l) '
(n—2k+2) (n—2k+l)
Ah+i = -Ah -^^-^-^ .
или
δ -ι пы ("-2fe+l)(^-2fe+2)...(M-l)n
ЛА+1_(-1)Л1 2*А!(2п-2"Щ)...(2п-1) '
Таким образом, искомое частное решение
оо
„ А ( пл.У г n> (^-2fe+D(n-2fe+2)...(n-l)M \
(12)
Ряд (12) прекращается при k=—, если η — целое положи-
тельное четное число и при k= ——, если η — нечетное число.
В уравнении (12), несмотря на неопределенный коэффициент
{2п)\
Ai, yi после умножения на ——-— представляет собой шаровые
функции Ρη(μ) первого рода.

422 Гл. XIII. Специальные линейные уравнения второго порядка
Пусть теперь в уравнении (10) т\= — (п+1).
Тогда вместо рекуррентной формулы (11) получим для
определения коэффициентов А рекуррентную формулу
(n+2fe-l) (n+2k)
Ak+i~Ak~~~2k(^+2k+lT~-
Так как mh= — (n+1) — 2&+2, то получим ряд,
представляющий второе искомое частное решение
Уг=А1 [μ-("+ΐ)+
, У Мт^2! и -(^+2^-l)(n+2fe) Ι
^ ~ 2*£!(2/г+3)(2/г+5)...(2/г+2£+1) μ J ' U;
2ηη'η|
Умножим ряд (13) на ———-rrr и тогда
(2/г+1)!
2"/г!п! _ и!
Уи {μ) - Тг^+ТУГ У2~ Т1Г5ГД2Я+1Т №
представляет шаровые функции ζ?η(μ) второго рода.
При /г=0:
л / ϊ ]л.! 1-ь1 ]л-! ] ■
μ ' 3 μ3 ' 5 μ5 ' 7 μ7 '
Между шаровыми функциями Qn(\i) и Ρ?ι(μ) существует завн
симость
«3„w=±PnWInu±L_{i!t±p„_lW+|tEiyP„_,w+
+ 5(Н)Р"-5<"»+···}' -'«•Х1·
которая дает возможность получения функции £?η(μ) из шарово{
функции Ρη(μ) первого рода и логарифмической функции.

§ 10. Потенциал притягивающих масс
423
V. УРАВНЕНИЕ МАТЬЕ
Дифференциальное уравнение Матье имеет вид
у"+(К—2h cos 2х) у=0. (1)
Если μ — характеристический показатель уравнения (1), то
существует решение у(х) такое, что
у(х+п)=е^у(х).
Если г/i (х) —решение уравнения Матье, удовлетворяющее
начальным условиям
ί/ι(0) = 1, ί/ι(π)=0,
то параметр μ вычисляется по формуле
ώ(μπ)=ί/ι(π).
При малых значениях коэффициента h применяется
приближенная формула
,-г , , „ η i λ sin n i λ
г/! (π) « cos π У λ+/ι2 --'__{у— +
(15λ2—35λ+8)πνλ sin π /λ—2λ(λ— 1) (λ—4)π2 cos nfk
В случае г/ι(π)#± 1, т. е. μ^ΐη (η=0, ±1; ±2...), общее
решение уравнения Матье
y = de^ р(х)+С2е-^ р(-х),
Где р(х) —периодическая функция периода π.
Ее коэффициенты Фурье могут быть определены из
дифференциального уравнения. Если г/ι (π) = ± 1, общее решение уравнения
Матье
у=dpi (x)+С2 [χρι (χ) +Р2 (х) ],
где ρι(χ) и pi (χ) —периодические функции периода π [если
г/j (я) = +1 ] или 2π [если г/ι (π) = — 1 ].
Решение у(х) называется устойчивым, если у(х) при %->-оо
остается ограниченным; в противном случае решение неустойчивое.
При |ί/ι(π)|<1 общее решение устойчиво, при |«/ι(π)|^1
существуют неустойчивые частные решения.

vzi Гл ΧΙΙί. Специальные линейные уравнения второго порядка
§ 11. ДИНАМИЧЕСКАЯ УСТОЙЧИВОСТЬ СТЕРЖНЯ
ПОД ДЕЙСТВИЕМ ПЕРЕМЕННОЙ ПРОДОЛЬНОЙ СИЛЫ
Задача 175. Исследовать устойчивость шарнирно закрепленногс
на концах стержня длиной / под действием переменной продоль
ной силы
Р(/)=Р0 cos at,
где Ро — наибольшее значение продольной силы, ω — круговая ча<
тота изменения продольных сил, t — время. При рассмотренш
поперечных колебаний стержня под действием указанных сил выя<
нить, когда это движение неустойчиво. Площадь попеоечного сече
ния стержня F, жесткость стержня EJ и плотность γ.
У
Рис. 122
Решение. Когда идеально прямой стержень -находили а ш
кое, то под действием периодических сил P=Pocoscoi в не
возникают переменные напряжения сжатия и растяжения. Есл
какой-либо импульс искривит ось стержня, то начнутся поперечик
колебания.
Составим дифференциальное уравнение движения стержн
Выделим элемент АВ (рис. 122) изогнутого стержня длиною а

§ 11. Динамическое сжатие
425
Так как деформации малы, то dsttdx. Тогда дифференциальное
уравнение изогнутой оси
откуда после двукратного дифференцирования
Ei~dW^
где q — сплошная нагрузка на единицу длины, которая состоит из
yF d2y
силы инерции · ■ и разности поперечных сил по концам
элемента, отнесенной к единице длины стержня.
Здесь g— ускорение силы тяжести.
В сечении А поперечная сила (—Qi) будет равной Qi = P——t
а в сечении В равна Qz=P ( —; —,— dx ) .
\ dx dx1 ι
Разность поперечных сил на элемент будет —Ρ , „ dx и па
Л2 UX
г, и У
единицу длины стержня — Ρ % .
Поэтому дифференциальное уравнение движения стержня будет
EJ Фу = уЕ d2y P d2y
dxi g dx2 dx2
И после деления на EJ принимает вид
dky yF d2y Pocosat d2y
dx^ gEJ dt2 EJ dx2
(1)
yF Po
Пусть —— =a2 и -=— = £2. Тогда уравнение (1) запишется
dhj d2y d2y
^+°2^Г+*2с°-^=0. (2)
Для интегрирования уравнения (2) полагаем
y=X(x)T(t). (3)
Подставляем это значение у в уравнение (2)
d^X d2T d2X

426
Гл. ΧΙΠ. Специальные линейные уравнения второго порядка
и делим равенство на произведение XT:
1 / &Х , d2X \ 1 d2T
_(_+*,„*__)+ -г<й__--α (4)
Полученное уравнение распадается на два уравнения:
1 / №Х . ,„ , d2X
(-^-+k2cosat-^r) =α+β*2οοδωί, (5)
= — α—p&2cos ωί, (6)
Χ \άχ" ^ wou" dx2
α2 ά4
Τ di2
где α и β — неизвестные постоянные расщепления уравнения (4).
Интегрируя уравнение (5), будем рассматривать ί как
постоянную величину и искать частное решение в виде
Х=&*. (7)
После подстановки выражения (7) в уравнение (5) имеем
qteqx+& cos ωί ■ q2eix=e<ix(a+pk2 cos ωί)
или, сокращая обе части последнего равенства на eix, получим
qk-\-k2 cos ωί- q2= α+β£2 cos ωί.
Отсюда
ft2cos ωί
q2 = -
_y jW(oJ_ + (a+pfe2 cQs ωί) = _^1±^2
2
Вводим обозначения:
-•Ri+fl2=zi2,
Тогда общее решение уравнения (5) будет
X=Ciez'x+C2e г'х+С3 cos z2x+C,t sin zzx.
d2X
Начальные (граничные) условия: при л:=0 Х=0 и 2 =0
d2X
при %=/ Jf=0 и =0.
На основании этих четырех условий получаем систему для опре
деления постоянных интегрирования:

§ 11. Динамическое сжатие
427
откуда
а
Ciez''+C2e-^+C3 cos z2/+C4 sin z2l=0,
(Cl+C2)Zl2-C3Z22 = 0,
(С^'Ч-Сге-1'')^!2—(C3 cos z2/+C4 sin z2/)z22=0,
Ci = C2= C3= 0,
C4 sin z2/—0.
Так как sin z2/=0, то
z2l=nn, n=l, 2, 3, ...
Таким образом,
&4cos2coi , . „,„ ,ч / n%r2 &2coscoi \2
+ (a+P&2coscof)=(
или
ft4 cos2coi
+a+p£2cos ωί;
4ττ4
η4π'
/2
nbi2
4 ' ~ ' r /4 /2
Откуда после сокращения подобных членов
α-(-ββ2 cos ωί=
η4π4
ηΔηΔ
k2 cos ωί+
&2cos cat.
kk COS2Cui
(8)
Равенство (8) будет справедливым при любом t, если соблю
даются условия
η4π4 „ η2π2
а-
/4
и β = -
I2 "
О)
Каждому решению уравнения (5)
Хп = Сп sin
плх
будет соответствовать определенное решение Тп уравнения (6),
и общее решение уравнения (3) выразится суммой
У== 7 ιΧηΤη.
n=i
Значения (9) подставим в уравнение (6) и тогда
а2 сРТ
П'1Я
2тг2
WW
at2
/4 + I2
■ k2 COS Cut

428 Гл. XIII. Специальные линейные уравнения второго порядка
Т
или, умножая обе стороны этого равенства на —— и перенося все
члены в левую часть уравнения, получаем
d2T , η4π4 Γ №
[ггъг τ
dt2 ' /4α2 L nW
m2jx2
Пусть рп= — частота собственных (свободных) попереч-
* .. . 2 № m Po
ных колебании порядка η стержня; &»а=-^т = ^~^j = уж^~
η
отношение наибольшего значения продольной силы к Эйлеровой
нагрузке порядка η стержня.
Тогда уравнение (10) принимает окончательный вид
d2T
+P«2(l-&™2coscu0r=0. (Π)
dt2
Уравнение (11) является уравнением Матье.
Для решения этого уравнения введем новую независимую
переменную ti подстановкой
Тогда
2/Ί=ω/ или ti=——t.
dT dT 2 dT.
dti , Ι ω , \ ω dt '
"(tO
a
m
d I dT \ d2T _ d /2 dT \ _ d /2 dT \ _
dti ' dU I ~~ dU2 ~ dti \ ω dt ' — J / ^ ^\ \ ω dt '
~2
___2_ 2 d2T 4 с/2Г
~ ω ' ω Λ2 ~' ω2 dt2 '
откуда
d2T ω2ά2Τ
dt2 AdU
Уравнение (11) принимает вид
ω2 d2T
4 dh2
или
+Pn2(l-&n2cos2ii)r=0
^ +^(1-&п2со52^)Г=0. (12)
dti2

§ 11. Динамическое сжатие
•u-j
Пусть
4р„2 _ 4р„2
Тогда уравнение Матье (12) приводим к виду
аЧ
Здесь
d/ ^ + (φο+2φι cos 2ii) Г=0.
2pn2 , „ &η2
φι= j-bnz=— φο-
ω* ■ 2
Уравнение (13) может быть представлено в виде
dtf
+ [<Po+q>i(e2<t'+e-2<t')] T=0.
(13)
(14)
Будем искать общее решение этого уравнения методом Хилла
в форме
--Σ
bmeict+2imt,
(15)
где bm—постоянные коэффициенты; ί=]/— 1; с — функция φ0 и φι.
Подставляя выражение (15) в уравнение (14), получаем
т=+оо т=+оо
- Σ &т(с+2т)2е'-сг+2™'+[фо+ф1(е2"+е-2")] [ Σ bmeict+2imt]=0.
т=—с» т=~оо
Отсюда получаем бесконечную систему уравнений, общий вид
которых
Ьт [(с+2т)2-С^]-ф1 [&m_l+&m+l]=0. (16)
Обозначая для краткости
.[m'] = [(c+2m)2-cpo],
запишем систему уравнений (16) в развернутом виде:
-(fib-з+Ь-2[—2]— φι&_ι =0,
—φι&-2+ [ — 1 ] —φι&ο = 0,
—φι6_ι+6ο[0]—φι6ι =0,
—φι&ο+&ι[ΐ]—φι&2 =0,
—φι6ι+62[2]— φι&3=0,
(17)

430 Гл λ ΙII Специальные линейные уравнения второго порядка
Исключая из системы (17) величины bi, получаем определитель
£>(с)=0.
Уравнения (16) не меняются при замене с на c-f-2s или на —с,
где s — целое число, т. е. все корни уравнения заключаются в
интервале ±Со+2г, где г — положительное или отрицательное целое
число. Отсюда можно сделать вывод, что определитель D(c)
имеет вид
D (с) =А [cos (от) —cos (con) ], 4 (18)
где А — постоянная величина.
Подставляя в равенство (18) г==0 и заменяя с0 на с, благодаря
общему виду выражения для с имеем:
D(0)=A [I-cos(ot)]. (19)
Для определения величины А рассмотрим частный случа!
—φι = 0, тогда с—^φο и определитель D(0) переходит в новый опр<-
делитель со значимыми диагональными элементами
где
Тогда
1—cos (от)
1 —cos У срол
D'(0)=A [l-cos(Vqjon)],
0'(0)=[0(0)]Ф1=о.
si"2 {-ψ-)
η2( —}/φοπ)
SI
Д(0)
Л'(0)
= Д(0),
Здесь
Д(0) =
1—cos(OT)=sin2 (ίφο-^-) -Д(0)=А(0).
1
φι
Φι
22-φο
0
42-ψο
1
φι
0
0
02-φο
0
О
О
φι
22-φ0
1
φι
22-φο
О
О
О
φι
02-φ0
1
φι
42—φο
0
0
0
φι
22:=φ7
1

§ 11 Динамическое сжатие
Отсюда
cos(cjt) = 1—Δ(0).
Вопрос об устойчивости движения сводится в каждом отдель-
ipM случае к вычислению определителя Δ(0).
Если
-1<1-А(0)<1,
зеличина с вещественная и движение устойчиво; в другом случае
1—Δ(0) | = |cos(cjt) I > 1, величина с становится мнимой и дви-
кение неустойчиво. Величиной с, разграничивающей
действительнее значения с от мнимых, является с—1.
Очень существенно установить зависимость между
коэффициентами φο и φι, соответствующую переходу от мнимых к вещественным
качениям с.
Проанализируем вопрос о переходе с от мнимых значений
л действительным.
Пусть величина с будет комплексной, т. е.
с = а-\-Ы,
_"де а и 6 — действительные числа.
Тогда
cos(cit) =cos an cos ibn—sin an sin ibn.
Так как величина cos(cjt) по существу всегда действительная,
о или 6=0 или a — s, где s — целое число.
Если 6 = 0, то с — действительная величина; если же a=s, то
cos (ел) = ±cos ι'6π= 1 —Δ (0),
ричем это уравнение в каждом частном случае дает лишь одно
ействительное значение 6.
В случае, когда 1— Δ(0)>0, величина
c=±ib+2s\ (20)
во втором случае, когда 1—Δ(0)<0, то
cos(cit) =—cos ibn
и величина
c=±ib+2s+\, (21)
а общее выражение для Τ будет
ОО ОО
7=ebf 2 bseil^+2^+e-bt ^ Ь/еи№*). (22)

432 ί α λ Ш Специальные линейные уравнении οτυρυ^'ο поряОка
Переходу величины с от действительных значений к мнимым
соответствует обращение в нуль величины в формулах (20) и (21).
Таким образом, основными величинами с, разграничивающими
действительные значения от мнимых, будут
с=1 и с=0.
В случае с=1 общее выражение Т=Тп при 6 = 0, согласно
соотношению (22), принимает вид
оо оо
s=0 s=0
и общее решение уравнения (2) при переходе от действительного
значения с к мнимому запишется
«,= 2*.Г„= Σ c sin UH [ Zb,e->+ Σ Ь.'<> ) ■
η=1 η=1 s=0 s=0
Общее решение для действительного с, равного —с=а, будет
оо оо
У= /.,ХпТп= / , cnsin—^Х
п=1 п=1
.· . оо . . оо
Χ[δ2 2j^ 2 +e 2 2j **'e 2 J ·
/i=i ;ι=·ι
Общее решение для мнимого c=±ib-\-2s-{-\ примет вид
оо оо
Σ,, _, X1 пях
ХпТп— £i С„ Sin —— X
«=1 п=1
Г *ί?νΐ ί^1(1+28) _Ьги~ ^ί(Η26-)Ί
Χ [ е 2 2j 6se 2 +e * 2j 6*'e 2 J ·
S=l 8 = 1
В случае с=0 из равенства (18) получаем
Д(0) = 0,
откуда в развернутом виде

§ II Динамическое сжашс
433
D(0).
Ι3—φο
—φι
0
0
0
—φι
22-φο
—φι
0
0
0 0
-φι 0
φο —φι
φι 22—φο
0 -φι
0
0
0
—φι
42—φο
Учитывая, что φι = — φο
2 '
φο=
получаем
4Ρη2 η
ω"
тгеюда следует рп=0 или ω->-οο, что практического значения
ла имеет.
Следовательно, можно ограничиться исследованием
случая с=1.
Из равенства (18) аналогично получаем
1+cos(ct) . D(\)
l+cosd/φπ) D'^
(23)
Как уже известно, величина с, разграничивающая мнимые и ве-
дественные значения, равна 1. Подставив с=1 в уравнение (23),
юлучаем искомое условие
Д(1)=0.
(24)
В развернутом виде бесконечный определитель (24) записы-
зается
D(l) =
1 β2 1 0 0 0
0 1 «ι 1 0 0
0 0 1 «ι 1 0
0 0 0 1 β2 0
= 0,
(25)
φο—Ι φο—9 φο—25
где αι= , «2= , as= и т. д.
φι φι φι
Раскрывая определитель (25) и приравнивая его нулю,
получаем уравнение для нахождения критического соотношения
коэффициентов φο и φι.

434 Гл. XIII. Специальные линейные уравнения второго порядка
Решение находится методом последовательных приближений.
Первое приближение, включающее только четыре центральных
элемента определителя, будет
1 αϊ Ι
или
αϊ*—1 = 0,
откуда
Qi = ±l. (26)
аё
[(«-^)"-1
Второе приближение дает уравнение
j_\2
«2
или
1
flt ·=±1.
«2
Третье приближение дает уравнение
1
«1 : = + 1 И Т. Д.
а2 ■
Критическое уравнение (25), устанавливающее связь между bnz
An 2 -
и φο= £-, принимает вид
«ι =±1. (27ч
а2-
1
а3— ■—
Необходимые величины:
Фо—1 2(φο—Ι) 2(φο-9)
αι= = . α2=_.
φι Ьг?Щ ' Ьп^щ
-2(φο—25)
α3= —
Ьп^Щ
Придавая величине 6„2 определенные значения, можно длг
каждого из них вычислить приближенно отношение φο= —^-.

φ 11 Динамические сжатие
4оо
Правая часть уравнения (27) имеет два знака и поэтому для
каждого значения 6„2 распадается на два уравнения", дающих по два
корня для каждого значения Ьп2.
При Ьп2—0 оба уравнения совпадают и первое приближение
Рп2
дает точное значение критического соотношения .
ω2
Итак, первое приближение по формуле (26)
βι = ±1
или
2(«ро-1)
_ L· =-1-1,
откуда
2(φο— \)=+Ьп2ф>.
Когда величина Ьп2->-0, то
φο=—:т=1,
Ро
т. е. при очень малых значениях отношения будет резонанс,
11
когда
ω=2ρ„,
т. е. когда частота изменения силы Ρ вдвое превышает одну из
частот собственных (свободных) поперечных колебаний стержня.

Глава XIV
ЗАДАЧИ, ПРИВОДЯЩИЕ К СИСТЕМАМ ЛИНЕЙНЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА
Непосредственный метод интегрирования систем
дифференциальных уравнений сводится к образованию путем сложения,
вычитания, деления данных уравнений интегрируемых комбинаций, т. е.
дифференциальных уравнений вида
где U — некоторая функция от искомых функций, не содержащая t.
В случае линейной однородной системы с постоянными
коэффициентами интегрируемая комбинация есть уравнение с разделенными
переменными, в случае неоднородной линейной системы — линейное
уравнение первого порядка. Каждая интегрируемая комбинация
дает один первый интеграл; если число их равно числу уравнений
системы, интегрирование закончено; в противном случае получается
система с меньшим числом неизвестных функций.
Рассмотрим системы линейных уравнений с постоянными
коэффициентами. Существуют различные способы интегрирования таких
систем. Проще всего пользоваться методом Даламбера, который
вытекает из непосредственного интегрирования.
Пусть дана система двух уравнений
dx
— =alx+biy+F1(t),
-~=a&+b2y+F2(t).
(1)
Обозначим через λ множитель, на который надо умножить
второе уравнение, чтобы получить интегрируемую комбинацию
d(x+Xu)
= (α1+α2λ)χ+(61+62λ)ί/+^1+λ^2.
dt
Цель достигнута, если
61+62λ=λ(«ι+β2λ)
или
β2λ2+(βι-62)λ-6ι=0. (2)
Тогда имеем интегрируемую комбинацию (U=x-\-%y):

Гл. ΧIV. Системы уравнений первого поряока
■Ιό ι
dU_
(αι+Ω2λ) U+Fi+KF2 ~ w
(линейное уравнение).
Пусть общий интеграл уравнения (3) есть
и=х+Ху=Ф({, λ, С).
Различают три случая:
1) корни квадратного уравнения (2) действительные и
различные. Тогда имеем два интеграла системы (1):
x+Xly=Q>(t,K,Cl),
*+Яву = Ф(/, λ, С2);
2) корни комплексные, λ=α±βι. Приравнивая действительные,
а также мнимые компоненты обеих частей уравнения
*+(α+βί)ί/=Φ(ί, «+β*. Α+ΒΙ)>
получим также два интеграла (А, В — произвольные постоянные);
3) корни действительные и кратные, λι=λ2-
В этом случае получаем только один интеграл, который
позволяет свести вопрос к интегрированию одного линейного уравнения
с одной неизвестной функцией.
Рассмотрим систему трех уравнений
ах
= OiX+biy+CiZ+F ι (t),
dt
dy_
dt
dz
It
=a2x+b2y+c2z+F2(t),
= a3x+bsy+csz+F3(t).
Умножаем второе уравнение на λ, третье на μ и затем
складываем. Получаем
d(x-\-Ky-\-\iz)
— = (α1_|-α2λ+α3μ)χ+(6ι+62λ-τ-63μ)ί/-τ-
dt
+ (ει+ε2λ+ί3μ)ζ+^ι+λ^2-τ-μ^3·
Подберем теперь λ и μ так, чтобы имели место равенства:
6ι+62λ+63μ= (βι+β2λ+α3μ)λ, Ί ·4·
ίι+ε2λ+ε3μ==(βι+α2λ+α3μ)μ· >

438
Г л XIV Системы уравнений первого порядка
Вводим подстановку U=x-\-Xy-\-\xz. Находим линейное ■
уравнение
ни
-Ж
Пусть его общее решение
ί/=Φ(/,λ;μ, с).
Определяем λ и μ. Запишем систему (4) в виде
«ι+Ω2λ+β3μ &ι+£ϋλ+&.*μ ει+ε2λ+ε3μ
(5)
1
■=s.
Отсюда
«2λ+«3μ=5—«!,
(62—5)λ+63μ=—6ι,
С2Я+(с3—«)μ=—Ct.
Условие совместности системы (6):
(б;
«2
62—s
с2
а3
Ьг
Cz—S
fli—S
&1
Й
= 0.
(7)
Это кубическое уравнение относительно s.
Различают три случая:
1) среди корней уравнения (7) нет равных, s^s^s^.
Определив для каждого корня из системы (6) соответственные значения
для λ и μ (т. е. λι, μι; λ2, μ2; λ3, μ3), из уравнения (5) получаем вс^
три интеграла;
2) среди корней есть двукратный; тогда найдем лишь два иь
теграла системы. Для окончания потребуется еще интеграция одш
го уравнения;
3) корень трехкратный; тогда найдем лишь один интеграл
а поэтому интегрирование будет сведено к системе двух уравнение
В случае комплексного корня поступают аналогично излс
женному.
§ 1. РАЗЛОЖЕНИЕ ВЕЩЕСТВА
Задача 176. Некоторое вещество А разлагается на два веществе
Ρ и Q. Скорость образования каждого из них пропорциональна кг
личеству неразложенпого вещества. Пусть χ и у — количества
веществ Ρ и Q, образовавшихся к моменту t. Определить закон и;
изменсний, зная, что в начальный момент лг=0, г/=0, а через 1 '
3 1
х=—с, у= — с, где с — первоначальное количество вещества л

§ L Разложение вещества 439
Решение. В момент t скорости образования веществ Ρ и Q
будут:
--ki(c-x-y),
dt
dy
dt
--k2(c—x—y),
(О
так как к этому моменту количество неразложившегося еще
вещества А равно с—х—у. Уравнения (1) представляют систему двух
линейных дифференциальных уравнений первого порядка.
Дифференцируя первое уравнение, получим
d2x , / dx dti \
Подставляя в уравнение (2) значение —~ из второго уравнения
системы (1), имеем:
d2x Г dx 1
-W-=-kihu+k*{c^X-y)\. (3)
Исключая у из уравнения (3) и первого уравнения системы (1),
находим
d2x ,, , , ч dx
__ + (fel+fe2)_==0. (4)
Уравнение (4) является однородным линейным уравнением
второго порядка. Его характеристическое уравнение:
^+(*ι+*ζ)γ==0.
Это неполное квадратное уравнение имеет два корня:
П=0 и r2—~(ki-\-k2).
Таким образом,- общее решение уравнения (4)
x=Cl+C2e-^+W.
Для нахождения второго решения дифференцируем найденное
dx
рыражение для х, подставляем χ и —j— в первое уравнение системы
и решаем его относительно у.

440
Гл. ΧΓν. Системы уравнений первого порядка
Получим
dx
~dJ
= -С2(Л1+*2)е-(*«+*«)',
—C2(ki+ka) e-№i+fci' = jfe| (с—d— C2e-(fe>+^i—у)
и второе решение
у=с— ~ C2e-(fe>+M«_Ci.
Таким образом, решения системы
г/=с+ -^- С2е-№.+*#—Сь
«ι
(5)
Определим d и С2, используя начальные условия: при ί=0
х=0 и t/ = 0. Таким образом,
С,+Са=0,
Ci-
k2
С2=С,
откуда
Ci=
k\C
С2=-
ki-\-k2'
kiC
h+kz
(6)
Подставляя значения (6) в решения (5), получим законы
изменения величин χ и у в виде
х=
KiC
У=
«1+Й2
k2c
kl + k2
[1—e-(b.+ft2)i],
[l_g-(fc,+ft2)f].
(7)
Неизвестные коэффициенты «ι и &2 найдем из дополнительных
3 1
условий задачи: при ί= 1 х= — с, г/= — с. Имеем:
he
J3c =
8 К1+К2
с k2c
8 &1+/г2
[1—е-Оч+Ы],
[l_e-(ft,+ft>)].
(8)

§ 1. Разложение вещества
Из системы (8) определяем ki и k2:
и тогда
или
Отсюда
или
к
с
~8
2
-т<
e-4h2==
4£2=
*4
*-i
«i==
1-е-
1
2"
In 2
In 2.
In 2.
ύκ2,
-4ftA
Тогда
Суммируя уравнения (9) и (10), имеем
fn+k2=ln2
или, потенцируя,
Далее
eki+k2—2.
h+k2 4 '
1
h+ki 4 '
Подставляя эти значения в систему (7), находим:

442
Гл. XIV. Системы уравнений первого порядка
§ 2. ОТНОСИТЕЛЬНАЯ КРИВАЯ ПОГОНИ
Задача 177. Бомбардировщик, летящий со скоростью νβ,
преследуется истребителем, скорость полета которого vK. Hoc
истребителя постоянно направлен к бомбардировщику, который летит в
направлении, образующем с горизонталью угол β. Найти траекторию
полета истребителя, наносимую на карту наблюдателем внутри
бомбардировщика. Задачу рассмотреть в полярной системе
координат.
Mir, Ψ)
У*ШШ
V6C05(4>-fi)
Решение. Наблюдателю в бомбардировщике, который
движется вправо, кажется, будто он стоит неподвижно, а истребитель
движется влево, й если бо'мбардировщик движется со скоростью ν$,
то наблюдателю кажется, что истребитель движется со скоростью »g
(рис 123).
Радиальные и поперечные составляющие верхнего вектора »е
бразуют систему дифференциальных уравнений
dr
dt
άφ
~dT
= —D6COS(<jp—β),
= u6sin(q>—β).
Поэтому, как видно наблюдателю из бомбардировщика, дей-
вительная скорость истребителя в радиальном направлении (это
умма двух скоростей в том же отрицательном направлении г) будет
dr
dt
■ — Va—Vs COS (φ—β),
О)

§ 2. Относительная кривМ-ЩМОШ
443
поперечном направлении
Γ-^-=ι»β8ίπ(φ-β). (2)
Делим равенство (1) на равенство (2) и в итоге получаем урав-
ие с разделяющимися переменными:
dr cos (φ—β) ν„
-г- ^ г—, ττ cosec (φ—β).
Γάφ sin (φ—β) уб
Решение этого уравнения
Ό
In r+ln C= —In sin (φ—β) — In [cosec (φ—β) — ctg (φ—β) ],
орое после потенцирования упрощается к виду
°«
ygfU&fs. '
Г l-CQS<f·^ Ι
sin (φ—β) L sin{?~$
1
[sin (φ—β) 3 ""Ml—COS (φ—β)] «Γ
(3)
Начальные условия: при ί=0 /·'=/<>, φ=φο.
Изучим характер зависимости решения (3) от параметров.
Случай /..Если скорость бомбардировщика »б равна скорости
требителя ии, то уравнение (3) упрощается к виду
СГ== 1 —С08(ф—β)' (4)
Уравнение (4) представляет параболу.
Траектория полета истребителя, наблюдаемого из бомбарди-
вщика, приводится на рис. 124, а.
Очевидно, что в этом случае истребитель никогда не достигнет
мбардировщика.

444
Гл. XIV. Системы уравнений первого порядка
Случай 2. Если скорость истребителя уи превышает скорость
уи
бомбардировщика не, тогда 1 <0 и уравнение (3)
записывается
1»б
Сг=-
[sin(<p—β)] »б
[1—cos (φ—β)] "β
График траектории полета истребителя, наблюдаемого с борта
бомбардировщика (при ии=2иб) приводится на рис. 124,6.
а
Рис. 124

§ 3 Давление в двух цилиндрах
445
§ 3. ДАВЛЕНИЕ В СИСТЕМЕ ДВУХ СОЕДИНЕННЫХ
ЦИЛИНДРОВ С ГАЗОМ
Задача 178. В двух цилиндрах, соединенных трубкой с краном,
аключеи газ под разными давлениями pi и р2. Объемы цилиндров
оответственно Vi и 1/2. Нсли открыть кран, то газ пойдет из ци-
индра с большим давлением, например ри в цилиндр с меньшим
авлением р2. Скорость течения газа в каждый момент t пропорцио-
альна разности квадратов давлении газа в обоих сосудах в мо-
[ент t. Найти закон изменения давлений в цилиндрах.
Решение. Пусть pi и /72 — давления газа в цилиндрах в мо-
[ент /.
За время dt из первого цилиндра во второй перейдет масса
аза dM. Скорость течения будет —-. По условию задачи эта
скорость пропорциональна р42— /722. Следовательно,
dM
_=α(Ρι2_^), (1)
де а — коэффициент пропорциональности.
Соотношение (1) можно представить
dM = a(pl2—p#)dt. (2)
С другой стороны, масса dM равна убыли массы Μι в цилиндре
■ давлением ри а также прибыли массы М2 в цилиндре с давлением
>2за время at. Но:
Μι=δι1/ι, Μ2=δ2ν2)
'де δ — плотность газа, которая изменяется пропорционально дав-
1ению ρ при постоянной температуре.
Следовательно,
bi = bp{, |
δ2=6ρ2, f
[•де b — коэффициент пропорциональности.
Отсюда
Mi = bpiVu \ (о.
M2=bp2V2. I W
Дифференцируя систему (3), получим
dM = —bVidpi (убыль массы Μι) (4)
и
dM = bVidpi (прибыль массы Λί2). (5)

446
Г л XIV. Системы уравнений первого порядка
Сравнивая уравнения (4) и (5) с равенством (2), получим си
стему двух дифференциальных уравнений процесса
-δνιάρι=α(ρ^-ρ2ηάί, 1
bV2dp2=a(pi2—p22)dt ί
или
dPl а I 2 2\
-df=--bv7(Pi -rt*
dp% α
dt bV2
(/Ί2-Ρ22).
(6
Проведем преобразования системы.
. Первое уравнение системы (6) умножим на Vi, второе на V
складываем и умножаем на dt.
Получим
Vidpi+Vzdpz^O. (7
Далее первое уравнение системы (6) умножаем на pzViV
а второе на ριί^Ι/ο и вычитаем. Отсюда
V^(p^-P^) =-~(Р12-Р22)(р-гУг+р^). (8
Система (7), (8) легко интегрируется, так как левая част
уравнения (7) есть полный дифференциал
d(VlPl+V2p2)=0,
откуда первое решение системы
ViPi-\-V2Pi=Ci. (9
На основании решения (9) уравнение (8) примет вид
dt ri dt
Pi
или, полагая ■ =х, имеем
рг
dpi dp2
(10
_ d I Pi \
dt. \ п., I
Pz4f-pidt
dt dt ' p2 ' p22
откуда
dpi dp2 , dx
чт-р1чг=р*-ш
Р2-ТГ - Pi -ГТ =P22 -TJ-. (11

φ 4, Напряженное состояние пиши
Подставляем соотношение (11) в уравнение (7) и получаем
Vi Vzpf —=,- — ClP2* (ж*-1)
ИЛИ
dx
■Ci(tf--l).
(12)
Уравнение (12) является уравнением с разделяющимися
переменными, общий интеграл которого
ViVz . х+1
Г— 1П 7
-jdi+Ca.
(13)
Итак, уравнения (9) и (13) представляют общие интегралы
системы (7), (8).
Начальные условия: при /=0 pi==Pi, р2=Р2. Отсюда
V1Pi-T-y2P2-=C1>
Vly2 Pi+p2 а
-2~ln~P^p;-TCl-0+C2
или
C1=V1Pl+V2P2,
С2
ViVz ln P1+P2
Pi-Ρ г
Подставляем постоянные интегрирования в общие решения (9)
и (13) и получаем систему уравнений, определяющую pi и р% как
функции t:
Pi-Pi V2
Р2-Р2 Vi '
(Ρι+Ρ*) (Ρ1-Ρ2) 2a
(Pt+Pz) (Pi-Pi) ~ bViVi
(PiVl+P2V2)t.
§ 4. НАПРЯЖЕННОЕ СОСТОЯНИЕ ДИСКА
ПОД ДЕЙСТВИЕМ ЦЕНТРОБЕЖНЫХ СИЛ
Задача 179. Диск радиуса R и постоянной толщины s с
концентрическим отверстием радиуса г вращается с угловой скоростью ω
вокруг вертикальной оси. Найти кольцевые и касательные
напряжения, возникающие в диске под действием центробежных сил.
Решение. Условия равновесия вырезанного элемента диска
(рис. 125) показывают, что между тангенциальными силами Τ
в кольцевых сечениях ввиду симметрии сохраняется равновесие,

448
Γα XIV. Системы уравнений первого порядка
а в кольцевом направлении действуют наружу две силы:
центробежная
dZ= ( х-\——· ] &Чт= ί χ-\ —- ) (o2psxd(fdx,
где ρ — плотность, т — масса, и в сечении x-\-dx сила
" Fx+dx=(ax+dax)(x-\-dx)sd(p,
где ах— кольцевое напряжение.
Внутрь направлены сила
Fx=oxxsd(Q и вертикальные
составляющие
равнодействующих сил касательных
напряжений
Tsin
,η ίί-
t^T^t
Tsin
df
Рис 125
2σφ sin ——- sdxfaotfSdydx,
где σφ — касательное
напряжение.
Проектируя эти силы на
вертикаль, получаем
( *+ ~К~ ) (u2psxdxd<p-\- (ox-\-dox) (x+dx) sdq=
=σκΛ;5ί/φ-}-σφ5ί/Λ:ί/φ. (1)
Равенство (1) делим на общий множитель si/φ, откуда
I dx \
\ х-\ — J &2pxdx-\- (ax+dax) (x-\-dx) =σχχ-\-σφάχ.
Выполняя умножение, сокращая подобные члены и пренебрегая
выражениями (dx)2 и dxdax как бесконечно малыми высшего
порядка, получаем
χ2ω2ράχ-\-σχάχ-\-χάσχ=σφάχ. (2)
Равенство (2) делим на dx, вводим ради краткости подстанов-
dox
ку —j—=ах' и получаем в итоге первое дифференциальное
уравнение для искомых функций
хох'-\-ах—σφ=— ρω2χ2. (3)

§ I Напряженное loctoiiiiuc опека
44U
Второе дифференциальное уравнение получится из зависимости,
связывающей кольцевые и тангенциальные удлинения.
Если и — направленное наружу кольцевое перемещение, то du
представляет его изменение между внутренним и наружным краем
du
вырезанного элемента, а величина —-—= εχ— кольцевое удлинение.
При равномерном, перемещении от внутреннего до наружного
края i/u=0. При перемещении и удлиняется периметр узкого кольца
на расстоянии χ от срединной оси от 2пх до 2л,(х-{-и).
Разделив приращение на первоначальный периметр, получаем
тангенциальное удлинение
_ 2л,(х+и)—2лх _ и
ф 2юс χ '
Разрешая это уравнение относительно и, имеем и=хеч>, откуда
после дифференцирования
аи=а(хг<р) =εφ+χεφ.
Тогда искомая зависимость между удлинениями
du ά(χΕφ) άεψ
гх= ~dx~= dx = Ч+Х ~d~T· (4)
В это уравнение подставляем вместо удлинений &х и εφ их
выражения через напряжения, полученные по закону Гука,
гх= —ψ- (σχ—νσφ) и εφ= -=- (σφ—νσ«),
где ν = 0,3 — коэффициент Пуассона (для металлов), Ε — модуль
упругости.
Тогда, подставляя эти выражения в уравнение (4) и умножая
затем его на Е, имеем
σχ—\σφ=σφ—ναχ-\-χ —— (σφ—νσχ) =σφ—νσχ+ΛΓ(σφ'—νσ/),'
откуда после приведения подобных членов получаем второе
дифференциальное уравнение, связывающее напряжения ах и σφ:
x(a9'—vax) + (1 +ν) (σφ—σ*) =0. (5)
Итак, задача описывается системой дифференциальных
уравнений (3) и (5).

4M
ι .ι Λ/Ι LiiLWMhi ijpuuiniiiiu ία pi, иго пориика
В уравнении (5) имеются неизвестные функции ох и σφ, а так»
их производные, в то время как в уравнении (3) отсутствует прои.
водная функции σφ. Поэтому целесообразно уравнение (3) разр|
шить относительно σφ, продифференцировать по χ и функцию с
и ее производную σ</ подставить в уравнение (5). Тогда
σφ=χσχ+σχ+ρω2χ2,
σ4,,=θχ,-\-χσχ"+σχ,-\-2()(ύζχ, (6
откуда
χ(χσχ"+2σχ+2ρ&4—νσ«') + (1+ν) (χσ/+σ*+ρω2Λ:2—σχ) =0. (7
Группируя члены уравнения (7) по порядку производных, пол?
чаем линейное дифференциальное уравнение второго порядка дл
одной лишь функции ах:
χ?σχ"+3χσχ'=—ρ&(3+ν)χ?. (δ
Так как в это уравнение искомая функция ах не входит в явно
виде, то ее производную ох'=у введем в качестве новой переменно1
Таким образом, соответствующее однородное дифференциал!
ное уравнение сводится к линейному дифференциальному уравш
нию первого порядка
х2у'+3ху=0.
Разделяя переменные, получим уравнение
dy Ых .
У ~ х '
которое почленно интегрируется, и общий интеграл этого уравнени
С=х3у.
Начальное условие: при х=х0 у=Уо, откуда
С—Хо3уо-
Тогда
x3y=x03yQ
»-(-f-)V <f
Так как, согласно принятой подстановке,
' d°x /if
у=ах==ЧГ' (1С

^S / iiull/) I >K(-ltH()c till ttillHllL Ullliiil
то, приравнивая правые стороны равенств (9) и (10), имеем:
άΰχ I Хо \3 С
=т»=± с")
dx
Повторное интегрирование приводит уравнение (11) к виду
одн I t>
иди ■ — . п
ах =_-_.__+С,.
С
Пусть —- — Сг; тогда общее решение соответствующего
однородного уравнения
*Г = С1+^-. (12)
Частное решение дифференциального уравнения (8) будем
искать в виде
ος=β*2, (13)
откуда
σ';=2βχ и a"j=2B.
Постоянную В определяем путем приравнивания
соответствующих коэффициентов при х1 в обеих частях уравнения, т. е.
2Вх*+Ъх ■ 2Вх = -ρω2 (з+v) χ2,
8Вх?= —ρω2(3+ν)Λ;2
и
В 3+V 2
8~р
•Частное решение (13) принимает теперь вид
3+ν
σ;=-^-ρω2*2. (14)
Общее решение дифференциального уравнения (8) получается
путем суммирования уравнений (12) и (14):
ai==Ci+-§—-^-ρω^. (15)
Тангенциальное напряжение σφ получается подстановкой
кольцевого напряжения ах, согласно уравнению (15), и его производной
в уравнение (6),откуда

452
Гл. XIV. Системы уравнений первого порядка
ο,^—^—^ψ-ρω**. (16)
Постоянные интегрирования определяются начальными
условиями.
Незагруженные края диска имеют кольцевые напряжения
(на внутреннем и внешнем краях), равные нулю: при х=г ох=0
и x=R σχ=0. Тогда для определения постоянных Ci и С% получаем
систему уравнений
откуда
Ci=^±^pM2(^2+r2); С2=--^р<й^2Л (17)
о о
Окончательно искомые напряжения ох и σφ получаются
подстановкой значений постоянных интегрирования (17) в уравнения
(15) и (16):
3-fv ,1 п,, , R2r
ох— —j-— ρω2
/ D2r2 \
l^2+'-2--^ *2)> (Ι8)
„.^(^^-Jg.,). (19)
Кольцевые удлинения получаются непосредственной
подстановкой полученных соотношении (18) и (19) в равенство
х , \
α=χεφ= —— (σφ—νσχ),
откуда окончательно
Удлинения на внутреннем крае (х=г) и соответственно на
наружном крае (x=R) получаются из уравнения (20) в виде частных
случаев:
г3 Г R2 1
«Γ=ρω2-4^-[ (l-v) + (3+v)-^rJ;
R3 Г г2 1
u* = pco2—- [ (i_v) + (3+v) -rY J ·

§ 5 Превращение одного вещества в другое
453
§ 5. ПРЕВРАЩЕНИЕ ОДНОГО ВЕЩЕСТВА В ДРУГОЕ
Задача 180. Одна грамм-молекула вещества А превращается
постепенно в промежуточное вещество М, которое далее
превращается в вещество В. Найти количество вещества В в любой момент
времени t.
Примечание. Скорость превращения вещества А в любой момент
пропорциональна наличному его количеству Скорость образования вещества В в
любой момент пропорциональна наличному к этому времени количеству вещества М.
Скорость накопления промежуточного вещества Μ равна разности скоростей
превращения вещества А н образования вещества В.
Решение. Пусть χ — количество вещества А в момент t,
у — количество вещества Μ в момент t, z — количество вещества В
в момент /, &ι и k2 — коэффициенты пропорциональности.
Так как первоначально была взята одна грамм-молекула
вещества А, а веществ Μ и β не было, то
x+y+z=l.
Скорость превращения вещества А:
dx
Скорость образования вещества В:
dz
dt
fay-
Скорость накопления вещества М:
dy dx dz
~dT= dt dT
-kiX—k2y.
Таким образом, система дифференциальных уравнений
процесса
dx ,
= —kiX,
dt
= kix—k2y, ■
= k2y.
dt
dz
dt
(0
Из системы (1) необходимо определить величину ζ как
функцию t.

454
Гл. XIV. Системы уравнений первого порядка
Дифференцируя последнее уравнение системы (1), находим
d2z , dy
=k2-
dt2 dt
или с учетом второго уравнения системы (1)
d2z
kik2x—k22y. (2)
dt2
Правую часть уравнения (2) преобразуем следующим образом:
d2z
■—— ^kikzx—kz^y+kifhy—kikzy
или
d2z
-— = klk2(x+y) — (ki-^-k2)k2y.
dz
Так как &2г/= —тт, a x-\-y=\—z, то
d4 -_klk2(]-z)-(ki+k2) dz
dt2 ^ ' νί ' v dt
или
~ + (kt+k2) — +^2(z-l) =0.
Введем новую переменную
« = 2—1.
Тогда получим
йЧ +{h^k2)~+hk2u=Q. (3)
dt2 ' v ' *' dt
Общее решение линейного однородного дифференциального
уравнения (3)
a=Cie-*''+C2irw,
откуда
ζ— \ = Cie-W-\-C2e-™
или
Начальные условия: а) при /=0 2=0; б) так как при /=0
у=0, то из третьего уравнения системы (1) получим, что при ί=0
и^г=0·

§ 5. Превращение одного вещества в другое
455
Дифференцируя последнее равенство, находим, что
dz
—- =— Jnde-ы—!г2Сге-ы,
at
Начальные условия дают тогда систему
0=— kyde-ь ■ о—к2С2е-ь ■ °, /
откуда
Решаем систему (4) и получаем постоянные интегрирования
ki—k2' ki—k2
Значения (5) подставляем в общее решение и в результате
получаем закон изменения количества вещества В от времени:
kie-w—kzer-w
2=1
ki—k2

Глава XV
ЗАДАЧИ, ПРИВОДЯЩИЕ К НЕПОЛНЫМ
ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ
ВЫСШИХ ПОРЯДКОВ
Дифференциальные уравнения вида
Общий интеграл уравнения находится η последовательными
интегрированиями:
-^^- = Jf (x)dx+Clf
Дифференциальные уравнения вида
J d«-iy dny \
'\ dv.n-i ' dv.n I
Вводя новую функцию
dn~^y
dxn~l
■-ζ,
получаем уравнение·первого порядка
Если, интегрируя это уравнение, получим общее решение в виде
ζ=ψ(χ, Ci),
то, заменяя ζ через
dn~ly
άχη-ι '■
приведем уравнение к виду, рассмотренному выше.

Гл. XV. Неполные уравнения высших порядков
457
Дифференциальные уравнения вида
/_ф^_ d"~2y \
' Wvn ' dY.n-2 I
dny
Решая это уравнение относительно ■ , находим
dxn ~~Ύ \ dxr>
dny
ι dn~2y \
π dn~2y
Применяя подстановку z= A„„_,*■> получаем
d2z
dx2
dxn~2
=φ(ζ).
Полагая
юлучим
)ткуда
Тогда
ι, следовательно,
ггкуда
dz
dp
dx
=4>(z).
dp=(p(z)dx-
φ(ζ)άζ
2pdp=2y(z)dz,
ρ2=2 J<v(z)dz+Cu
dz
dx
= l2f<p(z)dz+Clt
x=
dz
— +Cz
J I2f<p(z)dz+Cl
Дифференциальные уравнения вида
dky d^y . dny
f(*.
dxk ' dx^ ' -'" ' dx
η I
0
Эти уравнения допускают понижение порядка па k единиц, если
двести новую функцию ζ, положив
dky
dxh
= z.

458
Τ л XV. Неполные уравнения высших порядков
В частном случае уравнение f [х, —~, 2 ) = 0 при помощи
dy
подстановки —;— =р приводится к уравнению первого порядка
'(**-&)=*
dx
Дифференциальные уравнения вида
' \у· dx' dx* '···' dtr ι
Порядок таких уравнений может быть понижен на единицу,
если принять за новую независимую переменную у, а за новую функ-
dy ~
цию р= —т—. Тогда
Фу
dx2
d3y
dxs
=p-
= p2
dp
dy'
d2p
dy2
+P
[dp y
\dy I
Преобразованное уравнение будет иметь вид
/ dp dn-ip \
^y'p'4i'---'^ly^r)=°-
В частном случае уравнение
/ dy d*y \
f\y'-dx"-dxr)=0
приводится к уравнению первого порядка
^{у'Р'^)=°-
§ 1. ЛИНИЯ ПРОГИБА НЕРАЗРЕЗНОЙ БАЛКИ
ОТ РАСПРЕДЕЛЕННОЙ НАГРУЗКИ
Задача 181. Найти линию прогиба неразрезной балки
постоянного сечения на жестких шарнирных опорах, в каждом из пролетов
нагруженной распределенной нагрузкой w(x).
Решение. Рассмотрим участок балки между сечениями χ
и х-\-Ах (рис. 126).
Пусть Μ и Λί+ΔΛί — соответственно изгибающие моменты
в этих сечениях. Распределенная нагрузка w{x) представляет на-

§ 1 Прогиб неразрезной балки
459
грузку на единицу длины в точке х, поэтому w(x)Ax представляет
«грузку участка между сечениями χ и χ-{-Ах без учета бесконечно
лалых высшего порядка, чем Δ*.
Пусть Q — поперечная сила в точке х, т. е. алгебраическая
•умма вертикальных сил по одну сторону от сечения х, например
зпоаво. a 0-\-AQ — соответствующая поперечная сила в сечении
Из условий равновесия рассматриваемого участка балки
заключаем, что
AQ+w(x)Ax+a(Ax)2=0
чпроекция сил на вертикальную ось равна нулю) и
ΔΛΓ + (Q+Δ<2)Δλ:+w (χ) ΔχΘΔχ=0,
де0^9^1 (сумма моментов относительно любой точки равна
гулю). Здесь α — коэффициент при бесконечно малой высшего
второго) порядка.
Полученные равенства делим на Δ*, и тогда
AQ
Ах
AM
Ах
-{-w(x)-{-aAx=0,
+Q+AQ+W (χ) ΘΔχ=0.
Пусть теперь длина элементарного участка Δχ-Я), тогда
AQ , , ч , А..\ ,.._ ^Q , _..,„, dQ
дх-*о . Δλ;
Um(~+w(x) + aAx) = lim ~ +w(x) = -^- +α>(х)=0

460 Г л XV. Неполные уравнения высших порядков
lim ( -Т7 +<2+Δ0+α>(χ)ΘΔχ ) = Hm 4^· +Q= 4^ +Q = 0
\x-*o /лл ' \x->0 ΔU αχ
Δχ->0" Δ·^
Отсюда
dQ
dx
dM
dx
Дя-М)
-w(x),
-Q.
Используя уравнение EJy"=M(x), после двукратного диффе
ренцирования получаем
EJyiy^w(x),
(1)
где EJ — постоянная жесткость балки.
Рис 127
Промежуточный пролет /& неразрезной многопролетной балю
показан на рис. 127. Балка разрезается в непосредственной близоеп
вправо от опоры i и соответственно влево от опоры k. Положитель
ные направления действующих усилий и деформаций показань
стрелками.
В дальнейшем будем рассматривать усилия и деформацш
только на правом крае сечения.

§ 1. Прогиб неразрезной балки 4Ы
Общее решение дифференциального уравнения (1) и его
последующие производные с учетом правила знаков, указанного на
"рис. 127, получаются последовательным интегрированием:
EJhy™(xh) =wk(Xh) —Wh(Xh),
xh
■\EJhyh'" (xh) =Qk(xk) = jwh(l)dl+Ci =
0
= Qho(Xk)+Cu
BJkyh"(xh) =Mh(xh) = §Qho(l)dl+Clxh+C2 =
о
=MM(Xh)-\-CiXh+C2,
xk
Ehyh'(xh) = -Ejhyk{xk) =EJh j ^^-dl+C^+C^+C^
о
t2
Xh
= — EJbSfuo (Xh) +Ct ——- +C2Xfc+C3;
"■h
,3 v,2
EJhyh{xh) =-EJk iq)fto(i)di+Ci-^- +C2-'- +Ca*ft+C4 =
о b z
= EJhwh0(Xk) +Ci -~ +C2-~- +C3Xft+C4.
Здесь: поперечная сила
xh
Qho(xh) = ] wk(%)dl,
0
изгибающий момент
h
Mh0(xh) = $Qko(l)d£,
0
угол наклона
xh
. С ΛίΜ(|)
-фмЫ= J ν, dl>
0 C,,ft
(2)

462
Г л XV. Неполные уравнения высших порядков
прогиб
хн
-\-wM(xk) = — J φΜ(%)άΙ
о
при 0<g<xfe и 0<хй</й.
Начальные условия: па левом конце &-го пролета хи=0, откуда
Qk(0) = Qu Cl= Qi^QuiQ), так как QM(0) =0,
ΛίΛ(0)=Λί,, C2=Mi = Mh(Q),
фй(0) —ψϊ, C3=—EJkq>i = —EJhyh(0)J
Уи(0)=Уи Ck=EJhyi=EJhyh(0).
Таким образом, четыре произвольные постоянные
интегрирования представляют усилия и деформации на левом краю балки.
Подставляя значения Cj (ί=1, 2, 3, 4) в уравнения (2),
упорядочив члены и разделив щ(хи) и уь.(хп) на EJh, получаем общее
решение совместно с первыми четырьмя производными
yh(Xk) =
fft(Xh) —
Mh(Xh) =
Qh(xu) =
Wh (Xh) =
Uk(0)-
-*ифй(0) + -
φ*(0)--
Xh1
2EJk
Xh
EJh
-M,
-Mh
Mi
.(<>) + ■
t(0)--
.(0)
Xh3
6EJk
Xh2
2EJk
-Qn(P)+yu.
-Qfc(0)+q>M
)(Xk),
•(Xh),
+XhQh(0)+Mho(Xh),
Qft(0)+Qfto(xft).
Wh (Xh) ·
Таким образом, уже известна линейная зависимость усилий
и деформаций между левым краем и любым сечением xh &-го
пролета. Первое уравнение представляет искомую линию прогиба
в пределах &-го пролета.

Глава XVI
ЗАДАЧИ, ПРИВОДЯЩИЕ К ЛИНЕЙНЫМ
ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ
ТРЕТЬЕГО ПОРЯДКА С ПОСТОЯННЫМИ
КОЭФФИЦИЕНТАМИ
§ 1. ПАРОВАЯ МАШИНА С РЕГУЛЯТОРОМ
Задача 182. Найти дифференциальное уравнение движения
паровой машины с регулятором, если радиус кривошипа г=0,3 м,
а длина шатуна /= 1,5 м.
Решение. Известно, что вращательное движение паровой
машины неравномерно. Угловая скорость вала переменна и период
равен продолжительности одного оборота машины.
Поэтому при изучении движения машины вопрос сводится:
1) к исследованию изменения угловой скорости вала в течение
одного оборота в зависимости от угла кривошипа;
2) к определению зависимости угла кривошипа от времени.
Определим кинетическую энергию L системы тел, состоящей
из паровой машины и регулятора.
I. Кинетическая энергия паровой машины 1пм определяется
следующим образом. На рис. 128 изображена передача
одноцилиндровой паровой машины. Прямая АВ представляет шатун машины.
В шарнире А можно сосредоточить общую массу Μ всех частей
машины, двигающихся только по горизонтали (поршень, поршневой
шток и ползун), между тем как вращающиеся части (маховик, вал,
кривошип) можно объединить вместе и приписать им момент
инерции 0.
Шатун совершает как горизонтальное, так и вращательное
движение и поэтому должен рассматриваться отдельно.
Как известно, кинетическая энергия материальной точки
массы т, вращающейся со скоростью υ, равна
Кинетическая энергия системы тел равна сумме кинетических
энергий отдельных масс. В связи с этим определим величину L для
отдельных частей паровой машины.
Кинетическая энергия ползуна и связанных с ним масс
1 >л I dx V
dx
где —— мгновенная скорость ползуна.

464
1л XVI. Уравнения третьего порядка
Кинетическая энергия частей, совершающих только одно
вращение:
£вращ= -г- 0ω2 =
-l· (-£)'·
dt
где ω =
άϋ
dt
угловая скорость паровой машины.
Определим кинетическую энергию шатуна. Все его точки имеют
различные скорости и.
Рис. 128
Представим стержень разделенным на элементы массы dm
бесконечно близкими сечениями, перпендикулярными длине.
Кинетическая энергия одного такого элемента
dL·
1
dm · и2.
(2)
Пусть λ — расстояние рассматриваемого элемента от конца
шатуна. Тогда его координаты по отношению к левой мертвой
точке Κι будут
xi=x-\-Kcos$, 1
ί/1=λ sin β. ί
Отсюда вытекает:
2 ΙάχΛ\ (аУЛ* ( dx Ϋμ
v2= \-иТ)+ \ЧГ)=\-аГ) +
dt
dt
I d& \2 dx du
+λ2 (-fi- ) -2λ sin β μ
dt
d
dt dt
(3)

§ 1. Паровая машина с регулятором
465
После подстановки уравнения (3) в равенство (2) и интегриро-
!ания находим кинетическую энергию шатуна:
А-= γί «>dm= ±- (i£-)'Jdm-sin β-^- -Й-J Wm+
+i (!)>-·
Введем обозначения и названия соответствующих величин:
f Jm=Aim — масса шатуна, / kdm=Sm — статический момент
шатуна относительно ползуна, f Kzdm = Qm — момент инерции шатуна
относительно ползуна.
Таким образом, кинетическая энергия всего механизма паровой
машины
1 / dx \2
-SmSir^
dx
At . _L
dt 2
dt dt ' 2 ш \ di
Если воспользоваться соотношениями:
М£)Чо(£)
(4)
x=r(l —cos O)-f-/(l — cos β),
dx . „ d# , , . „ dR
— ^rsinO-^+Zsmp^p
r
/ sin β=/-sin # (или sin β= — sin #),
/ cos β
dp
df
:Г COS #
dft
di'
то уравнение (4) после подстановки этих соотношений
принимает вид
1 Г I r cos ft\2
1п.м= т[ъ+(М+Мш)1**тЧ ( 1 + т . _) _
г3 „ I , , г cos # \ cos θ ,
-2Sm -— sin2# ( 1 -f- -y- · τ-) —z- +
Z2 V / COS β ' COS β
2 cos2# 1/ dft \2 1 „,л. ( d# \2,
+ΘΠ
cos2p
(5)
В последнем выражении угол β можно выразить еще через ϋ
с помощью равенства
sin β= —sin Ό.

466
Гл XVI. Уравнения третьего порядка
Величина £(#) зависит только от аргумента (переменного
угла) ■& и содержит в качестве коэффициентов массы и моменты
инерции частей системы.
II. Энергия регулятора Lp (обыкновенный регулятор изображен
на рис. 129) равна общей кинетической энергии вращающихся
шаров и муфты. Влияние масс соединительных стержней можно учесть
js", lis",
I
Рис 129
путем соответствующей прибавки к массе шаров или муфты. Кроме
того, часть энергии муфты, происходящую от величины —тт, отнесем
к энергии паровой машины.
Центр системы вращающихся шаров находится в точке с
координатами
x = l(\—cos τ),
у= (a-|-/sin t)cos #,
2= (а-{-1 sin τ) sin #.
Середина муфты имеет координату
г=2/(1—cos τ),
причем χ отсчитывается от положения середины при τ=0.
Дифференцируя уравнения системы по времени, возводя в
квадрат и складывая, находим

§ 1 Паровая машина с регулятором
467
Для муфты
2 I dx γ . Ι dx γ
уМуфт= \-[f) =4/2sin2T^—) .
Следовательно,
Энергия системы паровой машины и регулятора L определяется
III. Для составления дифференциального уравнения движения
лашины применим формулу (1), согласно которой величина L свя-
;ывается с силами, действующими на отдельные части машины.
Зти силы представляет равнодействующая r(T—W)
тангенциального момента гТ силы поршня и тангенциального момента rW сопро-
"ивления, преодолеваемого машиной. При этом последнее считается
тостоянным, а Т является известной функцией Ό.
Величина r(T— W) легко находится, если дана индикаторная
диаграмма машины (кривая режима работы). Тогда эту величину
ложно считать известной функцией Ό:
r(T—W)=F{Q).
Для дальнейшего необходимо знать зависимость силы F(#) от
зеличины отклонения регулятора τ. Регулятор действует на момент
тарового давления гТ, среднюю величину которого rTm он меняет.
" подъемом' регулятора уменьшается величина г'Гт и наоборот. Эта
зависимость выражается уравнением
гТт=г(Т0—kx).
Величина момента давления пара колеблется около величины
Тт согласно зависимости
rT=r(To—kx)+rT(Q).

468 Гл. XVI. Уравнения третьего порядка
— . ■ ■ — ■ . ii'ihiii
Для простоты дальнейших вычислений отбросим влияние
колебаний и тогда
r(T-W)=r{T0-kx-W).
Для τ необходимо вычислить силы, действующие на
вращающуюся шаровую систему вместе с муфтой.
При расчете сил учитываем влияние:
а) моментов масс Λίι и М2 — {M2-\-Mi)gl sin τ;
б) пружины— //(1—cos τ) sin τ;
в) масляного тормоза, пропорциональное скорости движения
муфты умуфТ=2/ sin τ — —.
άτ
Так как тормозящая сила муфты K™Vm=R fMy<j>T=2/i<! sin τ-тг,
где R — коэффициент пропорциональности, то приведенный к
вращающимся шарам момент равен
ах
ΚίοτιμΙ Sin T = 2/2i? Sin2T —г:-.
at
Силы, действующие на систему регулятора, считаются
отрицательными на правой стороне, потому что они противодействуют
возрастанию величины τ. Они образуют функцию ΰ(τ), которая,
учитывая вышеизложенную систему влияющих усилий, равна
άτ
G(t) = — (Mi+M2)g/ sin τ—//(1—cos τ) sin τ—2l2R sin2t
dt '
Связь между кинетической энергией L системы тел и силами,
под действием которых происходит движение системы,
устанавливается дифференциальным уравнением Лаграпжа.
Последнее является выражением следующей теоремы.
Если L — кинетическая энергия системы масс, которая зависит
только от величины #, и если при этом движение системы
происходит под действием силы r(T— W), которая также является функцией
F(-&) той же переменной, то существует дифференциальное
уравнение
= F(G) (6)
dt Λ άϋ· dO
d~dT
В данном случае имеем равенство (5). Поэтому

§ 1. Паровая машина с регулятором
469
dL г/пч <5θ dL 1 _„„. ( άϋ γ Ί
. do
d dL
dt
dt' δϋ 2
Λ2 '
dt
(7)
Если соотношения (7) подставить в уравнение (6), находим
/равнения движения машины
Ε{ϋ)
d2®
dt2
+т£,(#) (4г)а==/7(д)==г^°-*т-^
(8)
dh- I dr \2
/2(M2+4Mi sin2t) -^- -4/2Mi sin τ cos τ (-^-) -
/ dft \2
—/M2 (α-f / sin τ)cos τ ^-—- J = — (M2-f Mi)g/ sin τ—
—//(1—cos τ) sin τ—2/2# sin2T
df
(9)
Это система дифференциальных уравнений с двумя зависимыми
и одной независимой переменными.
IV. Допускаем некоторые упрощения, вытекающие из смысла
задачи.
Прежде всего в функции £(#) можно исключить все слагаемые,
которые не учитывают в своих множителях влияния вращающегося
колеса машины, после чего уравнение (8) принимает вид
QjL2-=r{T0-kx-W).
dt2
(10)
Пусть
τ=το+η,
— ωο+<ο
dt
и, ограничиваясь изучением малых колебаний, отбросим все
слагаемые, содержащие произведения η и ω или их производных. Таким
образом, будем изучать только малые отклонения регулятора τ от
начального положения το и малые колебания угловой скорости
машины ω относительно их начальных значений ωο· Кроме того, в
уравнении (9) примем для установившегося режима

470
Гл XVI Уравнения третьего порядка
. άτ η dH
T0=const, — =0, — =0
соотношение
Ш2(а-\-1 sin t0)cos τοωο2= (M2+Mi)g/ sin τ0+//(1—cos το)sin το.
После изложенных замечаний и введения сокращенных
обозначений
m=/2(M2+4Misin2T0),
6 = 2#/2sin2T0,
c=fl [(1 —cos το) cos To+sin2T0] + (M2 + Mt)gl cos τ0+
-f-/M2 [{a+l sin τ0)sin τ0—/ cos2t0] ωο2,
κ=21Μ2(α+1 sin το)ωο
вместо уравнений (9) и (10) получаем
— . -^- =-ki\+T0-kx0-W. (12)
г at ·
Исключим ω из этих уравнений, для чего дифференцируем
равенство (11)
άω 1 / dh\ , dh\ dr\
~df = -^\m^F+b-ir+c^r
и, подставляя полученное выражение в уравнение (12), имеем
dh\ , , d\ , ώι , km. (T0-kx0-W)
Λ3 ' Λ2 ' dt ' θ ' 0
Таким образом, вместо системы уравнений получено искомое
уравнение движения, которое является линейным
дифференциальным уравнением третьего порядка с постоянными коэффициентами,
числовые значения которых находим, подставляя данные задачи.

Глава XVII
ЗАДАЧИ, ПРИВОДЯЩИЕ К ЛИНЕЙНЫМ ОДНОРОДНЫМ
ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ВЫСШЕГО ПОРЯДКА
С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Однородными линейными дифференциальными уравнениями
η-го порядка с постоянными коэффициентами называются
уравнения вида
у(п) + а1у(™-1) + а2у(П-2) + . . . + Оп-1у' + апу = 0,
где αϊ, а2, ... , ап — постоянные величины.
Для нахождения общего решения этого уравнения следует
предварительно решить характеристическое уравнение
1. Если все корни этого уравнения п, г2, ... , гп различны и
действительны, то общее решение
у—С^х-{~С2<?ГгЖ+.. .+CneV,
где С\, С2, . .. , С„ — произвольные постоянные.
2. Если среди корней характеристического уравнения
содержится k равных действительных корней /ί=γ2— ... =ru=r,
а остальные корни rh+i, m+i, ... , rn — действительные, различные
и г не равные, то общее решение
«/== (d+CzX+Cs^-b . .+Chxh-i)e™+Ch+ierb+i*+.. .+C„<?V.
3. Если среди корней характеристического уравнения
содержатся комплексные попарно сопряженные /Ί=αι+βιϊ и r2=ai—βι1,
а остальные корни r3, а, ... , гп — действительные и разные, то
общее решение
y=ealX [(d+C2)cos βιΧ+ί(6Ί—C2)sin $lx]+C3er>x+С4ег«ж+
+. .-f CneV=ea*x [C* cos βιχ+C* sin βιχ] +C3er^-f
+C4<?r<*-b..+Cnernx.
Здесь C* = Ci+C2, C* = i(d-C2).
4. Если среди корней характеристического уравнения
содержатся комплексные, попарно сопряженные и k раз кратные, то часть
"бщего решения, соответствующая этим корням, будет
у* = <?«.* [(d+C2x+.. .+Chxh-l)cos$iX+
+ (Ch+1+Cft+2x+.. .+C2ftxfc-i) sin β!χ].

472
Г л XV П. Уравнения высшего порядка
§ 1. КОЛЕБАНИЯ ВАЛА ОТ ДЕЙСТВИЯ ЦЕНТРОБЕЖНЫХ СИЛ
Задача 183. Найти критические скорости тонкого
вращающегося вала длиной /. Радиус поперечного сечения вала а, сила тяжести
Ρ и модуль упругости материала Е.
Решение. При увеличении угловой скорости вращающегося
вала от значения ω = 0 до некоторого предельного значения ω=ωι,
называемого критической угловой скоростью, вал сохраняет свою
L
К
ξ..
'
iff
Жу)
Рис. 130
прямолинейную ось. В момент достижения критической скорости ωι
вал искривляется и начинает колебаться. При дальнейшем
увеличении ω колебание прекращается, а затем вновь возникает при
второй критической скорости со2, и так периодически.
При вращении изогнутого вала на каждый его элемент
действует центробежная сила, которую можно считать непрерывно
распределенной нагрузкой.
На элемент dl·, вала (рис. 130) действует центробежная сила
/7=/ηω2η,
где т — масса элемента ά\, ω — угловая скорость вращения,
η — прогиб, равный радиусу вращения элемента dl·,.
Ρ Ρ
Сила тяжести элемента dl·, равна ——d%, а масса т= ——j-dl·,.
I
gl
Элементарная центробежная сила dF——-ah\dl·,. Прогиб η
является функцией ξ, определяемой уравнением упругой линии.
Таким образом, выражение
бежная сила
dF=f{t)dt
ш%)=/(|) и элементарная центро
Ρ
gl
ω^ηί/ξ.
(1)
Момент этой силы относительно произвольного сечения В будет
dF(x-t) = (x-t)f(t)dt.

§ 1 Колебания вала от действия центробежных сил
473
Аналогично предыдущим рассуждениям изгибающий момент
χ
о
Дифференцируя под знаком интеграла дважды это выражение
ло параметру х, получим
х χ
= $ϊ(1)άξ+(χ-χ)ί(χ) -^--(*-0)/(0) ~- (0)= Jf(|)rfS;
о
χ
dxl -Jo.«+/W-§-«0)-^(0)=f(x). (2)
Так как на основании равенства (1)
х> выражение (2) примет вид
dM
dx
= J/(E)
0
d2M
d2M d2 ( d*y \ Ρω2
2 \^ пу2 I
dx2 dx2 \ dx2 I gl
Дифференциальное уравнение упругой линии
d^y Ρω2·
У-
dxk EJgl
У=0. (3)
Ρω2
Вводим обозначение - - = qi. Тогда уравнение (3) представ-
(EJ gl
яется так;
<1кУ , η
Для того чтобы решить это неполное линейное уравнение чет-
зертого порядка, записываем характеристическое уравнение
1ЛИ
(r-q) (r+q) (r2+q2) = 0.

J л λ VI J. Уравнения высшего порядка
Корни характеристического уравнения:
n=q,
r3=qi,
ri= — qi.
Таким образом, общее решение дифференциального уравнения
упругой линии вала
у —Cie^-f С2е-чх-\~С3 sin qx-\~С4 cos qx.
(4)
Для определения постоянных интегрирования С ι, С2, С3 и С4
используем граничные условия задачи. На опорах вала прогиб и
кривизна оси вала равны нулю. Математически это выражается
четырьмя граничными условиями:
при х=0
при х=0
при х=1
при х=1
d2y
dx2
У=0,
=о,
У=0,
d2y
dx*
= 0.
Дифференцируя дважды общее решение (4), получим
dy
dx
d2y
dx2
= Ciqevx—C2qe-4x-\~C3q cos qx—Сщ sin qx,
— Ciq2eix+C2.q2e-4X—C3qz sin qx—Ctf cos qx.
Граничные условия дают систему четырех уравнений для
определения постоянных интегрирования:
Ciei 0+С2е-9 °-f C3 sin(^-O) +С4 cos(<7-0) =0,
Ciq2ei °+C2q2e-i °—C3q2sm(q-0)—Ciq2cos(q-0)=0,
Cle4lJrC2e-(il+C3 sin ql+Ci cos ^/=0,
Ciq2e4l-\~C2q2e-4l— C3q2 sin ql—Сщ2 cos ql=0
или
Ci+C2+C4=0,
Ci+C2-C4=0,
Ci^+C2e-«l-f C3 sin ql+Ck cos g/==0,
Cie<il+Cze-4l— C3 sin g/— C4 cos ql=0.

§ 1. Колебания вала от действия центробежных сил 475
Складывая и вычитая два первых уравнения системы, получаем
d+cUo' ί (5)
или
-Си 1
0. J
Поступая аналогично с двумя последующими уравнениями
той же системы, имеем:
C3sin<7/-fC4cosi7/=:0, 1 ,fis
Подставляя выражение (5) в систему (6), получим
С3 sin ql=Q, 1
Ci(e«l—е-в»)=0· J
Так как при /=^0 и с?=И=0 последнее выражение в скобках не
может равняться нулю, то
Ci=0,
С2=0,
С4=0,
С3 sin ί?/=0.
Если С3=0, уравнение упругой линии вала у=0, т. е. упругая
линия совпадает с осью χ и вал не искривлен. При искривлении вала
необходимо, чтобы С$ф0. Но тогда необходимо, чтобы
sin<?/=0.
Отсюда
ql=kn
и
4 I '
где £=0, 1,2,...
При k=0 получим q—Ο, и уравнение упругой линии вала
i/ = CH-C2+C4=0,
т. е. вал прямой.
При остальных значениях q вал искривляется. В таких случаях
уравнение упругой линии
у = С3 sin ql

476
Гл. XVII. Уравнения высшего порядка
при
π 2я Зя
7ι=—. Я=Чг=—, 4=<1г-у-
Упругая линия будет синусоидой:
у=С3 sin —-— χ,
п . 2π
y=C3sm-y-x,
у=С3 sin ——χ,
содержащей по длине вала одну, две, три и больше полуволн.
Таким образом, при критическом значении
/кр-
упругая линия — синусоида с k полуволнами по длине.
Вернемся к введенному обозначению
Ф=
EJgl
Подставляя в последнее равенство критические значения qKp
и (о1ф, получим
</кр =
- kW
Ρω
кр
EJgl'
Ρ
Ρωιφ
EJgl
или
kbi2
ωκρ=
У
PI
Вычислим момент инерции площади сечения вала.
Момент инерции / материальной точки относительно оси
представляет собой, как известно, произведение ее массы на квадрат
расстояния точки от оси. Момент инерции площади поперечного
сечения вала

§ 2. Балка на упругом основании
477
/= lim Σ R2&>n= j" R2dm,
Лт-s-O
\e Am — масса элементарной частицы, R — расстояние любой точ-
и элементарной частицы от оси, dm — дифференциал однородной
ассы, имеющей форму круга (для вала) при плотности р=1.
В общем случае dm=^pdv и / —ρ / R2dv.
Момент инерции / площади поперечного сечения вала относи-
ельно диаметра:
ρπα4
Эту величину можно получить из справочных таблиц или вы-
ислить при помощи определенного интеграла, решив задачу опре-
.еления момента и-нерции круга относительно его диаметра.
Масса вала
Ρ
т — ряаЧ= .
8
Таким образом, момент инерции сечения вала
Ра2
4g/
ι для определения критической скорости получим выражение
k2n2a ·—·
Минимальная критическая скорость
я2а -=
\ 2. БАЛКА (ЖЕЛЕЗНОДОРОЖНЫЙ РЕЛЬС) НА УПРУГОМ ОСНОВАНИИ
Задача 184. Рельс бесстыкового пути лежит на упругом
основании и прогибается сосредоточенной силой Р. Составить уравнение
упругой линии рельса и определить стрелу прогиба в точке О
(рис. 131).
Решение. Реакция ρ упругого основания, рассчитанная на
единицу длины рельса, пропорциональна прогибу — у, так что
р — —пу,
где η — коэффициент пропорциональности (коэффициент упругости
основания).

478
Гл. XVlf Уравнения высшего порядка
Исходя из симметрии упругой линии относительно оси ординат,
„ Ρ
можно рассматривать правую часть рельса, нагруженную силой —.
Определим изгибающий момент Μ для любого сечения А(х, у)
правой части рельса. Прогиб рельса —у представляет собой
некоторую функцию х, определяемую уравнением упругой линии. Таким
образом, реакция упругого основания
p = —ny=f(x),
т. е. является функцией х.
На элемент dl·, рельса (рис. 131) действует реакция основания
pc/|=f(|)c/|. Момент силы реакции относительно сечения А, равен
/(|)с/|(х—ξ). Сумма моментов всех элементарных реакций,
действующих слева от сечения А на правую часть рельса, равна
J(x-i)f(|)rf(|).
Момент сосредоточенной силы —- равен
■х.
Изгибающий момент в сечении равен алгебраической сумме
моментов относительно нейтральней оси всех внешних сил,
приложенных к балке с одной стороны (справа или слева) от данного
сечения. Отсюда изгибающий момент
•ν
M=\{x~l)f{l)d{l)-^-x.
(О
К равенству (1) применим формулу дифференцирования по
параметру под знаком интеграла:
^«.x)«-J£«.w.*>£-^*)£.

§ 2 Балка на упругом основании
479
В данном случае ц=0, υ = χ.
Кроме того,
f(|,x) = (x-|)/(|), ~=/(|).
Дифференцируя равенство (1), получаем
dM d f/ еч*/ечл d (Р \
= J f(|)rf|+(x-x)/(x) -^_(χ_0)[(0) -^- (0)-γ· =
dx v dx 2
ж
i/(6)d(6)--|- (2)
Дифференцируя- повторно уравнение (2) и учитывая, что
дР
■ (|, х) =/(|) и -^— =0, имеем:
£*2М dr.... d
J ,«>«-£(£) =
dx2 dx J 'vw b dx \ 2
dx IK ' dx
= J 0-#+/(*) -^--f(O) — (0)-0=f(x)=p=-ny. (3)
Дифференциальное уравнение упругой линии
d2y M
dx2 "~ EJ
Уравнение (4) преобразуем к виду
(4)
И-Ц—М. (5)
Дифференцируя дважды уравнение (5), получим
d4t/ _ _d2M_
dx4 dx2
чли на основании равенства (3)

480
Гл. XVII, Уравнения высшего порядка
откуда
Вводя обозначение —=-- =4£4, получим неполное линейное диф-
tJ
ференциальное уравнение четвертого порядка
Соответствующее характеристическое уравнение
г4+4/г4=0.
Это уравнение решаем разложением левой части на квадратные
множители:
г4+4/г4+4г2/г2—4г2£2=о,
(г2+2/г2)2—4г2£2=0,
(г2+2/г2—2rk) (r2+2fe2+2r/s) =0.
Последнее уравнение равносильно
г2-2/гг+2/г2 = 0,
г2+2/гг+2/г2=
Определяем корни
ч
0. J
Г3 = —-fe-j-t*,
Г4=—£—ί'β.
Таким образом, общее решение дифференциального уравнения
упругой линии
y—ehx(d sin kx-{~Сг cos kx) -\-е-кх(С3 sin &x+C4 cos kx):
Для определения неизвестных постоянных используем
начальные условия.
1. В бесконечно удаленных от силы Ρ точках практически
прогиб и кривизна рельса равны пулю. Так как множитель eliX
возрастает при возрастании х, то в уравнении не должно быть первого
слагаемого ehx(d sin kx-\-Cz cos kx), что возможно при условии
d=c2=o.

§ 2. Балка на упругом основании
Ίβΐ
Уравнение упругой линии примет вид
y=e~hx(C3 sin^+C4cos kx).
2. В начальной точке (х = 0) касательная к упругой линии
dy
тараллельна оси х, а поэтому —.— =0. Так как
= — ke-hx(C3 sin kx+Ci cos kx)-\-e-hx(C3k cos kx—CJi sin kx),
dx
—for*·0 [Cssin(Jfe-0)+C4cos(ife-0)]+e-k·0 [C3k cos(fc-O)-
— C4Jfesin(Jfe.0)]=0
C3-C4=0,
>ткуда
Сз=С4.
Уравнение упругой линии принимает вид
y = C3e-hx(sinkx-\-coskx). (6)
3. Для определения постоянной С3 используем уравнение (2)
in х=0:
dM
dx
С Ρ Ρ
=J/(IK—*-=--5-. (7)
2 2
Дифференцируя уравнение упругой линии (5), получим
cfx cfx3 ч '
Величину третьей производной для равенства (8) определяем
I уравнения (6). Трижды дифференцируя уравнение (6), имеем:
d3y =AC3k3e-hxcoskx. (9)
dx3
Зависимость (9) подставляем в уравнение (8). Отсюда
dM
dx
При х = 0
dM
■-AC3EJk3e~hx cos kx.
=4C3EJk*. (10)
αχ χ=ο

482
Гл. XVII. Уравнения высшего порядка
Приравниваем выражения (7) и (10):
Ρ
2 '
откуда
С3=-
AC3EJk3=-
Р
8EJk3 '
Таким образом, уравнение упругой линии
Ρ
У = 8ЕЛгз е-** (sin fcx+cos kx).
Стрела прогиба в середине рельсовой плети (при х=0)
h = L_
8EJk3 '
где коэффициент
*=Vw-
ΑΕΙ
§ 3. КОЛЕБАНИЯ ОДНОРОДНОЙ БАЛКИ (ПРИВЕДЕНИЕ
ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ В ЧАСТНЫХ
ПРОИЗВОДНЫХ К ОБЫКНОВЕННОМУ)
Задача 185. Однородная балка длиною I, жесткостью EJ и
массой т на единицу длины свободно опирается на колонны (рис. 132).
Найти основную гармонику колебаний.
Решение. Пусть один конец однородной горизонтальной
балки расположен в начале системы координат хОу. Предположим,
что малые колебания балки происходят в плоскости координатных
осей. Если элемент max на расстоянии χ от начала О системы
координат в момент t имел отклонение у, то действующая на элемент
сила равна
mdx д2у
т. е. следствием колебаний является такое нагружение до, где
т д2у
до= —
dt*
Уравнение прогиба

§ 3. Колебания однородной балки 483
Приравнивая эти два уравнения, запишем дифференциальное
'равнение в частных производных, описывающее колебания:
ρ τ d4t/ m д2у
Гармонические колебания периода задаются зависимостью
(о
у=Х cos ωί,
,е Х—Х(х). Подставляя это значение у в уравнение (1), получаем
///
k
L 1 .—.J
Рис. 132
обыкновенное дифференциальное уравнение относительно X
ФХ
άχί
И«-=?-*-0. (2,
Пусть
«=у.
gEJ ■
Тогда уравнение (2) принимает вид
<" ·α'Χ=0.
(3)
cfx4
Общее решение этого уравнения
Х=Ci ch αχ+Сг sh ax+C3 cos ал:+С4 sin ax, (4)
где С ι, C2, C3 и С4 — постоянные интегрирования.
Периоды колебаний зависят от способа закрепления концов
балки.
По условию задачи балка свободно опирается, т. е. прогибы
и изгибающий момент на каждой опоре равны нулю.

484 Гл. XVII Уравнения высшего порядка
Итак,
сРХ'
при х = 0 Х=0 и при х = 1 —-—- =0. (5)
Подставляя условия Х=0, Х"=0 при х=0 в уравнение (4),
имеем
С1+С3=0==а2(С1-Сз),
так что
С1=Сз=0,
и уравнение (4) принимает вид
X— С2 sh ax-\-Oi sin ах.
Оставшиеся два условия в уравнении (5) Х=0, Х" = 0 при х=1
после подстановки в уравнение (4) дают систему
C2sh a/+C4 sin a/=0, 1
a2C2 sh al—a2Ci sin al=0.>
Следовательно, C2=0 и если С4=£0, то
sin a/=0.
Тогда
где λ — целое число.
Из соотношения (3) получаем
-f
./g£/ λ2π2
т /2
Основная гармоника соответствует низшей частоте при λ=1.
Гармоники высших частот получаются при λ=2, 3, 4, ...

Глава XVIII
*^Цачи, приводящие к линейным неоднородным
дифференциальным уравнениям
четвертого порядка с постоянными
коэффициентами
Неоднородными линейными дифференциальными уравнениями
г-го порядка с постоянными коэффициентами называются уравне-
шя вида
y(n)+aiy(n-i)+a2y(n-2)+-. .+αη-&'+αη=ί(χ), (Ι)
~де cti, а,2, ... , αη — постоянные, а {(х) — непрерывная функция х.
Для получения общего решения уравнения (1) применяют два
летода.
1. Метод Лагранжа (вариации произвольных постоянных)
Общее решение уравнения будет иметь вид
У=С1у1+С2у2+.. .+Спуп,
лде уи уг, ... , уп — частные решения соответствующего однород-
ioro уравнения, а Си С2, ... , С„ — функции х, определяемые
системой уравнений:
dd dC2 . . dCn
У1+ -IT №+· · ·+ -ΊΠΓ У« = 0'
(2)
dx dx ' dx
dx dx dx dx dx dx '
iCi d"-'t/i dC2 ап-*уг dCn dn~lyn
dx ' dxn~l + dx ' dxn-i ~t_'' '~t_ dx ' dxn~^ П >'
Решая систему (2) относительно ('=1, 2, ... , η),
толучим
dCi
dx
dC2
dx
dCn
=h(x).
=h(x),
= fn{x),

486 Γα XVШ Неоднородные уравнения четвертого порядка
откуда
Cl = ^fl(x)dx+Al,
C2=$f2(x)dx+A2, ,
Сп = ) fn(x)dx+An.
2. Метод неопределенных коэффициентов
Для получения общего решения неоднородного уравнения
достаточно к его частному решению прибавить общее решение
соответствующего однородного уравнения. Нахождение частного решения
может быть упрощено методом неопределенных коэффициентов
в следующих случаях:
а) когда правая часть
М*)=е«ф(*),
где α — постоянное число, φ(χ) — целая функция m-й степени.
Частное решение у0 ищется в виде
y0=e<*xxh{A0xm-{-AiX™-t+.. ,+Am-iX+Am),
где Ао, Αι, ... , Am-i, Am — неопределенные коэффициенты, k —
порядок кратности корня α для характеристического уравнения.
Если α не является корнем характеристического уравнения,
то & = 0;
б) когда правая часть
f(x)=eaxcos$X(f>(x)
или
f{x)=eaxsm$x<p{x),
где α и β — постоянные числа, φ(χ) — целая функция m-й степени.
Частное решение t/o такого уравнения имеет вид
y0=eaxxh [(A0xm+AiXm-l+. · .+Am)cos βχ+
+ {B0xm+Blxm~1+.. .+£m)sin βχ],
где Л о, Αι, ... , Am и В0, Бь ... , Вт — неопределенные
коэффициенты, a k — порядок кратности корня α±βί для характеристического
уравнения.
Если α±βί не является корнем характеристического уравнения,
то k=0.

§ J. Деформация стенок цилиндрического резервуара 487
§ 1. ДЕФОРМАЦИЯ СТЕНОК ЦИЛИНДРИЧЕСКОГО РЕЗЕРВУАРА
Задача 186. Цилиндрический резервуар для хранения жидкости,
толщина D стенок которого мала по сравнению со средним
радиусом R (рис. 133), а меридиональное сечение стенки —
прямоугольник, подвергается силовому воздействию давления жидкости. Найти
дифференциальное уравнение деформации стенок резервуара.
Ρ е щ е н и е. На элемент стенки
с основанием abed и высотой ах,
взятый на глубине х, действуют:
сила давления жидкости, равная
yxRdqdx и приложенная к грани ab
(V — вес единицы массы жидкости);
силы упругости Γι и Г2,
приложенные к граням be и ad и вследствие
симметрии равные между собой.
Обозначая прогибы точек
элемента через у, получим, что
относительное удлинение их
первоначального расстояния от оси
цилиндра равно ——. Ввиду малости тол-
Н
щины стенок величины у для всех
точек элемента можно считать
равными и положить, что эти точки
равноудалены от оси цилиндра.
Относительное увеличение
длины окружности цилиндра на уровне
У
R
вызванные
взятого элемента будет также
Поэтому напряжения,
в стенках силами упругости, равны Ε ■
сти материала стенки.
Силы упругости
Рис 133
где Ε — модуль
упругого Т2=
Еу
Ddx.
Равнодействующая сил, приложенных к элементу, будет
_ , , _ dw dq>
dQ=yxRd((idx—Ti sin —^ Г2 sin -~-
или,считая
sin-
άφ d(f

488 Г л XVIII. Неоднородные уравнения четвертого порядка
получаем
цЕ
dQ=yxRd(fdx fi—Dd<pdx.
R
Эта сила dQ представляет приращение поперечной силы,
соответствующее приращению dx глубины элемента.
Известно, что изгибающий момент Μ и поперечная сила Q
связаны соотношениями
dx Ц'
d*y
M = EJ
dx* '
где / — момент инерции площади abed относительно нейтра
ной оси.
Учитывая вышеизложенное, получим
Так как
D3Rd<p
/=
12
то после подстановки этого выражения в уравнение (1) и сокраще
ния на Rd(f найдем
ED3 d^y yED
или
где
12
d'y
dxi
η
dx4
-+4
4
ηί —
— ул
a4y=
3
#2D2
12γ
mkx
R}
t
(2;
ED3'
Общее решение полученного уравнения
y = z+y0,
где ζ — общее решение соответствующего однородного уравнения
t/o — частное решение уравнения (2).

§ 1. Деформация стенок цилиндрического резервуара 489
Соответствующее однородное дифференциальное уравнение
имеет вид
~^+^У=0. (3)
Характеристическое уравнение
/·4+4α4 = 0,
корни которого
ri—(l+i)a, гг=(\—1)а, r3={ — \+i)a и г4=( — 1— ι)α.
Составляем общее решение однородного уравнения (3):
z=deax cos ах+С2еах sin ах+С3е-ах cos аХ+Ске~ах sin ax.
Частное решение уравнения (2) находим методом
неопределенных коэффициентов. Так как правая часть уравнения представляет
двучлен первой степени относительно х, то частное решение ищем
в виде
Уо=Ах+В.
Здесь А и В — постоянные, подлежащие определению. Находим
их в предположении, что частное решение у0 есть решение
уравнения (2). Дифференцируем уй по х:
У'0=А, у"о=у'-=у^=,0.
Подставляем эти значения в уравнение (2)
4а4(Лх+Б)=т4л;
или
4aiAx+4aiB = mix.
Приравнивая коэффициенты соответствующих степеней х,
получим систему уравнений
4aiA = mi,
= 0. J
откуда
4й4Б = 0,
т4 „
А=-—1- В = 0.
4 а4
Тогда частное решение неоднородного уравнения (2)
mkx
Уо=-4^·

490 Гл. XVIII. Неоднородные уравнения четвертого порядка
Таким образом, общее решение неоднородного линейного
уравнения (2) имеет вид
ΐϊϊ^Χ
y=Cieax cos ax+C2eax sin ах+С3е~ах cos ах+С^~ах sin αχ Η .
4 α4
Произвольные постоянные Си С2, С3 и С4 определяются из уело
вий на концах вертикальной полоски MN, имеющей фигуру abcu
поперечным сечением.
В случае, например, когда резервуар имеет недеформирующее-
ся днище, эти условия будут таковы: при х=0 у=0 и у'=Ь и при
х=Н у = 0 и у'=0, где Η — высота цилиндрического резервуара.
§ 2. ЖЕЛЕЗНОДОРОЖНАЯ ШПАЛА
Задача 187. Определить изгиб железнодорожной шпалы
постоянного сечения под действием нагрузки и распределение давления
под нею. Зависимость прогиба шпалы от возникающего при этом
давления балласта на нее принимается прямо пропорциональной.
Решение. Нижний край шпалы АВ под влиянием нагрузки
РР деформируется, принимая форму кривой ΑιΒι, и погружается
в балласт. Пусть величина прогиба шпалы на расстоянии χ от
левого конца равна у (рис. 134).
в
-ilk
Рис. 1S4
Предположение относительно зависимости между прогибом
(упругой осадкой) у и давлением р, передаваемым на балласт
единицей длины шпалы, может быть выражено уравнением
P=ky,
где k — коэффициент упругости балласта (коэффициент постел
шпалы).

§ 2. Железнодорожная шпала
491
Рассмотрим более общий случай, к которому может быть всегда
•ведена силовая схема, изображенная на рис. 134,— шпалу, нагру-
кенную непрерывно распределенной нагрузкой q=f(x) (рис. 135).
Под влиянием этой нагрузки различные точки шпалы погрузят-
:я в балласт на глубину у, зависимость которой от χ подлежит
опрела Й|[ГЯ
Ί^-φ ■'
Рис. 135
делению. При этом давление нагрузки уравновешивается реакцией
упругих сил балласта, т. е. должно соблюдаться равенство
J f(x)dx=— k) ydx.
о о
Пользуясь дифференциальным уравнением упругой балки
сРу
EJ-
dx2
-Μ
знак минус ставится в силу того, что положительный момент вызы-
зает отрицательную кривизну), после двукратного
дифференцирования получаем
Ε J
dly
dx^
1ЛИ
EJ
d2M
dx*
d'y
dx^
-.q—ky=f(x)—ky
+ky=f{x).
(1)
Для решения этого уравнения рассмотрим соответствующее
>днородное уравнение
EJ-?pL+ky=0
dx^ ^

492 Тл. XVIII. Неоднородные уравнения четвертого порядка
ИЛИ
άχί ' EJ
Характеристическое уравнение
а1ц k
+ —~у=0. (2)
ri+4r=°
имеет четыре корня:
/ π , . . π \ τ/ k , I 3n , . . 3π \ τ/ k
Π= |cosT+lSinT) γ—, r2=^cos — +ism —) |/-g-,
/ π . . π \ η/ k Ι 3π . . 3π \ τ/ k
Гз= lC0ST~iSinT/ V Ж' n=[cosT-ismT) уж
После упрощений эти корни принимают вид
ι=(1+ί) rw· г*—^-1ч
4EJ ' Λ Λ ' Г 4£/'
Полагая
У-
= ос,
4£/
получаем общее решение однородного уравнения (2)
у= (Ci cos ax+C2 sin ах) eax+ (C3 cos ах+С4 sin ах) е~ах. (3)
Для получения общего решения неоднородного
дифференциального уравнения (2) применяем метод вариации постоянных
интегрирования.
k 1
Уравнение (2) типа y(^)-\-ay=bf (χ), где α= -=rr, b — -=—.
hj hJ
Изложим схему решения этой громоздкой своими выкладками
задачи.
Постоянные d (ί=1, 2, 3, 4) в уравнении (3) будем полагать
переменными. Попробуем выбрать эти переменные так, чтобы
функция у удовлетворяла уравнению (2).

§ 2. Железнодорожная шпала
493
Продифференцируем уравнение (3) три (т. е. п— 1) раза. Тогда
i=l г—1
Вторую сумму, содержащую производные С,·, при каждом
дифференцировании полагаем равной нулю, что возможно, так как
имеем право наложить на неизвестные С, такое требование. Таким
образом,
У'= 2 СгУ/
г=1
2 С/Уг = 0. (4)
г'=1
Продолжая дифференцирование, имеем
ί/"=2θ//'
г=1
2?Сг-'г//=0; (5)
г=1
y'"=%ZCiyi'"
г=1
2<W = 0. (6)
г=1
Наконец, представим в виде ряда производную четвертого
порядка
yPV)= g Ctyfi*)+ *Σ Сг'Уг'", (7)
г—Ι ί=1
не налагая на вторую сумму требования равенства ее нулю.
Подставляя соотношения (7) и (3) в дифференциальное
уравнение (1), получаем новое уравнение
1?С; 3W*-ft)+ao If Ci'yi"' = \{x) , (8)
г=1 fe=0 г'=1
^де a.k — символическое обозначение постоянных коэффициентов.
Так как каждая функция у, удовлетворяет уравнению
2a^ft)=0,

494 Гл. XV111. Неоднородные уравнения четвертого ηορι
то из уравнения (8) остается только
г=1
которое совместно с уравнениями (4) — (6) дает возможность
определить величины С/ (i=l, 2, 3, 4), т. е. первые производные
неизвестных функций С,·.
Итак, имеем систему уравнений относительно С/:
2?а«/№>=0, k=0, 1,2;
г'=1
Пусть
Ci'=^i{x), i=l,2,3,4.
Интегрируя эти равенства, получаем
X
Сг=Аг-\- ^i(x)dx.
хо
Подставляя эти значения в уравнение (3), находим общее
решение неоднородного линейного дифференциального уравнения (2):
ί=4 ΐ=4 с
У = Σ АгУг+ Σ Уг J ψί (*) d*·
О
Первая сумма в правой части полученного равенства
представляет общее решение однородного уравнения, а вторая сумма —
частное решение соответствующего неоднородного уравнения.
Для определения четырех постоянных Л, используем начальные
условия. На концах шпалы изгибающие моменты и поперечные силы
равны нулю, т. е.
Ma=mb=-ej-^L=o
и
dMA dMB d3y
QA = QB=-dx- = -dr=~EJ-d^-Q-
Таким образом, получаем четыре уравнения для определения
постоянных интегрирования:
у"(0)=0, у'"(0)=0, у" (') = 0 и у'"(')=0.

Глава XIX
ЗАДАЧИ, ПРИВОДЯЩИЕ К СИСТЕМАМ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА
Решение системы дифференциальных уравнений, содержащей
производные второго порядка, можно свести к решению системы
дифференциальных уравнений первого порядка, введя новые
неизвестные функции.
Пусть
d2x , / dx dy dz \
—fi \ t, x, y, z, ——, ——, —- ) ,
dt2 (1 \ ·'"""-' dt ' dt ' dt
d*y
, / dx dy dz \
—h \ t, x, y, z, —, —, — J,
dt2 ~h \ ' X' У' Z' dt' dt' dt ι '
dt2
d*z
Вводя новые неизвестные функции
, dx , dy
dz .
систему (1)
заменяем с
dx
dt
dy
dt
dz
dt
dx'
dt
dy'
dt
dz'
dt
dt'y-~
ледующей:
= £',
=h(t, x, y,
=fz(t, x, y,
=f3(A x, y,
dt
г,
ζ,
*,
> *
χ'
χ'
χ',
У',
У',
У',
' dt '
ΐ
ζ'),
ζ'),
ζ'),
(1)
(2)
где / — аргумент, χ, у, ζ, χ', у', ζ' — искомые функции.

496 Гл XIX Системы второго порядка
Система (2) состоит из шести уравнений первого порядка
с шестью неизвестными функциями: х, у, ζ, χ', у', ζ'.
Система (2), разрешенная относительно всех входящих в нее
производных, называется нормальной. Решить систему (2) — значит
найти систему уравнений вида
Fi(t, χ, у, ζ, х', у', ζ', Си С2, С3, ... , С6) =0,
F2(t, х, у, ζ, х', у', ζ', Си С2, Сз, . .. , С6) = 0,
Fe(t, χ, у, ζ, х', у', ζ', С и С2, С3,..., С6) = 0,
обладающую следующими двумя свойствами:
1) функции х, у, ζ, х', у', ζ', определяемые системой (3), долж
ны удовлетворять системе (2);
2) систему (3) можно разрешить относительно произвольны,
постоянных Си С2, ... , Се, т. е. все эти постоянные не могут быть
исключены из системы.
Разрешая систему (3) относительно произвольных постоянных
получим
Ci=q,1{i,x,y,z,x',y',z'),
C2=yi{t,x,y,z,x',y',z'), ·4.
Cs=(pe(t, x, у, ζ, χ', у', ζ'). .
Функции
(pi=(pi{t, χ, у, ζ, χ', y',z'),
ф2=ф2(/, X, У, Ζ, Χ', у', Ζ'), (5-
φβ= φβ(/, χ, У, ζ, χ', у', ζ')
называются интегралами системы.
Если φι, ψ2, ·.. , φβ — интегралы системы (2), то и произвольна*
функция F(<pi, ф2, ... , φβ) от этих интегралов будет интегралом си
стемы, так как
^(φι, φ:, ■ ■ . , φβ) —F(CU С2, ... , Се)=С.
Таким образом, система имеет бесчисленное множество
интегралов. Среди них можно выбрать не более шести независимых
интегралов, где /г=6 — число уравнений первого порядка,
составляющих систему.
Независимыми интегралами называются такие интегралы
φι, φ2, ... , φβ, между которыми не может существовать никакого
тождественного соотношения вида Φ (φι, ψ, .. ■ , φβ) =0, т. е. ни один
из них не является функцией остальных.

§ 1. Движение точки под действием отталкивающей силы 497
Разрешая систему общих интегральных уравнений (3) или
систему независимых интегралов (4) относительно искомых функций,
получим общее решение системы:
χ =$i(t, Си С2, . .
У =ψ2(/, С ι, С2, . .
ζ =ψ3(/, Си С2, ..
*'=гМ*> Си С2, ■ ■
У'=$ьЦ, Си С2, . .
ζ'=-ψ6(/, Си С2, ..
■ , Св),
• , Се),
• , Се),
.,С„),
• ,Св),
. ,С«). J
Таким образом, решение системы уравнений (2) сводится
к определению одной из систем уравнений (3), (4) или (5).
В прикладных вопросах особое значение приобретают системы
дифференциальных уравнений второго порядка, к которым, в
частности, сводятся задачи, связанные с движением системы
материальных точек и твердых тел в пространстве.
§ 1. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ ПОД ДЕЙСТВИЕМ
ОТТАЛКИВАЮЩЕЙ СИЛЫ, ПРОПОРЦИОНАЛЬНОЙ РАССТОЯНИЮ
Задача 188. Материальная точка массы гп, в начальный момент
(ί=0) находящаяся на расстоянии а от центра О, имеет скорость
vq, перпендикулярную к прямой, соединяющей начальное положение
— " \Μο(0ι[Ι}
Рис. 136
материальной точки с центром О, от которого точка отталкивается
силой, прямо пропорциональной расстоянию от центра (рис. 136).
Найти траекторию движения материальной точки.

498
Гл. XIX. Системы второго порядка
Решение. В любом положении М(х, у) на точку действует
сила Р, направленная по радиус-вектору точки и пропорциональная
ему по величине Р=кг.
Составляющие этой силы на оси абсцисс и ординат
Х—кг cos сс=хл:, "I
Y=xr sin α=κι/. J
На основании второго закона динамики получим
дифференциальное уравнение движения
т-щГ=кХ'
или
т
d2x
dt2
d2y
dt2
jPx_
dt2
dzy
dt2
m
κ
m
=xy
■x=0,
■y=0.
(1)
Вводим обозначение k2-
нения (1) принимают вид
т
-. Тогда неполные линейные урав-
d2x
dt2
d*y
dt2
—k2x=0,
—k2y=0.
(2)
Общие решения уравнений (2)
x=CieM+Cze-kt, J
y=C3ekt-T-Cie-kt. J
(3)
dy
dt
dx η
Начальные условия: при /=0 х—а, у=0, —j- =v0 cos — =0,
= u0cos 0°=ио.Подставляя эти значения в систему (З), имеем:
a=C1eft-0+C2e-ft0,
Так как
0=
dx
dt
dy
dt
-.Сгек-°+Сф-к0. J
= Cikekt—Ctke~kt,
= C3kekt—Cike-M,

§ 1. Движение точки под действием отталкивающей силы 499
ТО
0=Cikek-°— C2ke-h0, l
uo=C3keh·0— СЖе-ь °. I
Для определения четырех постоянных интегрирования имеем
систему алгебраических уравнений
Ci+C2=a,
Ci—С2=0,
С3+С4=0,
Сз—Са=
Vo
Решая систему (4), находим:
Vo
(4)
с ~а с - а г —
с4=-
2k
Подставляя найденные значения постоянных интегрирования
з общие решения (3), имеем уравнения движения:
х— у (eft4-e-fti), y-
Ур
2k
(ем—е~м).
(5)
Для получения уравнения траектории движения исключим t из
уравнений (5), которые преобразуем следующим образом:
ekt+e
,-ht.
okt.
-е~м =
2х
2ky
Vo '
(6)
Суммируя левые и правые части системы (6), получим
2(voX-\-aky)
откуды
ekt=
2ем=
VoX+aky
avo
e~kt=
αυ0
(7)
αυο ' eht VoX+aky
Подставляя выражения (7) во второе уравнение (5), получим
Vo / VoX+aky avo \ (v0x-\-aky)2—a2v02
2k
avo
VoX+aky
■)-
2ak(voX-\-aky)
(8)

500
Гл. XIX. Системы второго порядка
Уравнение (8) преобразуем к виду
2aky(v0x+aky) = (v0x+aky)2—a2vet.
(9)
После умножения, возведения в степень и сокращения подобных
членов уравнение (9) примет вид
α4ψ=ϋοζχ2—α2υ02
или
Щ2
= 1,
откуда окончательно получаем траекторию движения данной точки
в виде гиперболы
х2
У
ш
■л.
§ 2. ВЫБРОС ТЕЛА ПОД УГЛОМ
Задача 189. Камень брошен под углом α к горизонту и
движется в среде, сопротивление которой пропорционально скорости υ.
Найти траекторию движения камня.
Решение. В любой точке траектории Ν(χ, у) на камень
действуют две силы: тяжести P=mg и сопротивления среды F=kv.
Составляющие их равнодействующей по осям координат
(рис. 137) будут
Но
X=Pcos{P,X)+Fcos(F,X), 1
Y=Pcos(P, Y)+Fcos(F, Υ). J
cos(P, X)=0, cos(P, Y) — l,

§ 2. Выброс тела под углом
501
cos(F, *)=--£-, cos(F,Y)=-4L
Следовательно,
X = -kv
dx
ds
Y=—mg—kv
ds
dy
ids '
Как известно, υ= -——. Тогда система (2) примет вид
X=-k
Y=-k
dx
~dT'
dy
dt
-mg.
(1)
На основании второго закона динамики дифференциальные
уравнения движения

turn
d2x
dP
d*y
dtz
рЛН
d2x
IF
d*y
dP
+
+
= -k
k
m
k
m
dx
~df'
dy
dt
dx
ЧГ
dy
dt
-mg
=0,
= —&·
(2)
Решая первое уравнение системы (2) как неполное линейное
однородное дифференциальное уравнение второго порядка, а второе
как линейное однородное дифференциальное уравнение второго
порядка, получим общие решения
__Li
х= Ci+C2e m ,
Для частного решения используем начальные условия: при t=0
~ dx dy
!#=(), у = 0, —τ— =ϋο cos α, —r- =v0 sin α.
at at

Гл. XIX. Системы второго порядка
Получаем:
Так как
Q=Ci+C2e m ,
0=С3+С4е
-JL.o
gm
■0.
(3)
dx
IT
k _ -»-t
m
Cze
dy
dt
= C4e
m
gm
k '
k „ -— °
y0 cos a= C2e m ,
m
k ±o gm
yosina= Сф m r—■
m ft
(4)
Из уравнений (3) и (4) определяем произвольные постоянные:
Ci=
m
Уо cos a,
С2=-
m
■ vq cos a,
Ca=
m
(gm+kvos\n a),
Сл=-
m
(gm+feuosin a).
Подставляя найденные значения в общие решения, получим
астные решения:
m -J-t -it .
х= —г— Uo cos a (1-е m )=a(l—e c ),
/2
1
_£г
l=-zr (gm+kv0sina){\—e c ) — ^-t=b(\— e с )_с/.
(5)

§ 3 Сброс груза с самолета в заданную точку 503
gm k g
Здесь с= —τ—, следовательно, — —
k m с
Значения α и Ъ очевидны из уравнений (5). Для получения
траектории движения камня исключаем время t.
Из первого уравнения (5) находим,что
l_e-{t=x_
а '
Подставляя полученное выражение во второе уравнение (5),
получим
и Х
у = о ct,
откуда
Ьх—ау
ас
Полученную величину времени подставляем в первое
уравнение (5), и тогда
М_ (Ьх-ау)
х=а [1-е а& ]
или траектория движения камня
ас2 , а—х
ау—ох= In —.
g a
§ 3. СБРОС ГРУЗА С САМОЛЕТА В ЗАДАННУЮ ТОЧКУ
Задача 190. Самолет летит на высоте h м над землей со
скоростью ν км/ч. На каком расстоянии χ от данной точки А
необходимо сбросить груз с самолета без начальной относительной
скорости и пренебрегая сопротивлением воздуха, чтобы он попал
в точку Л?
Решение. Начало координат помещаем в начальном
положении груза (рис. 138).
Дифференциальные уравнения движения по координатным
осям принимают вид
d4
d2y
тчг=тё-

4
Гл. XIX. Системы второго порядка
Интегрируя каждое из них дважды, получаем
x = Cit+C2,
У= γ gP+U+Cb
Начальные условия — при t=0: х=0,
dx
гкуда, так как —г—
at
= Ci и
dy_
dt
dx
~dT
= gt-\-C3, имеем
(1)
= ό; y=0, t/'=0,
\
\
0=d-0+C2,
v = Cu
0=0+С3-0+С4,
0=0+Сз
или
\
\
Л-
Ci=v, С2=С3=С4=0.
Тогда система (1)
принимает вид
x=vt,
У
Рис. 138
гкуда общее решение
При y=h находим
gt\
У=
gx2
2υ2
' g
§ 4. ДВИЖЕНИЕ ПЛАНЕТ
Задача 191. Найти закон движения планет Солнечной системы,
частности, движения Земли вокруг Солнца, основываясь на законе
семирного тяготения, не учитывая при этом влияния других планет.
Решение. Пусть Солнце находится в начале системы коор-
инат хОу, а Земля в момент t движения по солнечной орбите имеет
екущие координаты (х, у).
В качестве положительных направлений векторов примем на-
равления -\-х и -\-у.
Из рис. 139 очевидно, что действующая на Землю сила F рас-
ладывается на горизонтальную и вертикальную составляющие
оответственно F cos θ и F sin θ.

§ 4. Движение планет
505
Пусть Μ — масса Солнца, m — масса Земли.
Тогда на основании закона всемирного тяготения
F=
kMiM2
d~
(1)
и второго закона динамики F=ma получаем
d2x „ kMm
m—r^r- =—r cos θ = —cos θ,
m
d2y
dt2
kMm .
= —F sin θ = r—■ sin Θ.
(2)
(3>
Так как sin θ= — и cos θ= ■—, то уравнения (2) и (З)
примут вид
где v=kM.
d2x
~dW
vx dzy
vy
dt2
(4)
Принимая во внимание, что r—~]/x2-{-y2, систему уравнений (4)
запишем в виде
d2x
dt2
vx
J?y_
(x2+y2)^' dt2
vy
(x2+y2Y
<5>

6
Гл. XIX. Системы второго порядка
При ί=0 Земля находится на оси абсцисс на расстоянии а от
элнца и движется в положительном направлении оси ординат со
юростью и0.
Начальные условия: ί=0, х=а, у=0, —г— =0, ——- =υ0.
at at
Остается решить систему дифференциальных уравнений (5),
ювлетворяющую этим начальным условиям.
Предварительно запишем систему уравнений (5) в полярных
юрдинатах (г, Θ).
Так как x=r cos θ и y=r sin θ, то дифференцируя эти выраже-
1я по t и обозначая соответствующие производные сверху точкой,
неем:
x=r cos θ—(г sin θ)θ,
x=r cos θ—2 {r sin θ) θ— (r sin θ) θ— (r cos θ) θ2,
y=r sin B+i/'cos θ)θ,
y=r sin 0+2(r'cos B^+ircos θ)θ— (r sin θ)θ2.
Таким образом,
x= {r—rfc)cos θ—(2r θ+r θ) sin θ,
y'= (r—rQ2)sin Θ+ (2r θ+г 6)cos Θ.
(6)
С учетом соотношений (6) система дифференциальных уравне-
m (5) принимает вид
■· .... ν COS θ
(r-r92)cos θ- (2r θ+r θ) sin θ= ~2—
(r—rQ2) sin Θ+'(2γ Q+r θ)cos θ = — V S'"
(7)
Умножая первое уравнение системы на cos θ, второе на sin θ
складывая, получаем
г-г¥=-~ (8)
Аналогично, умножая первое уравнение на sin θ, второе на cos θ
вычитая, получаем
2гЬ+гЪ=0. (9)
Соответственно необходимо представить начальные условия
полярных координатах:

§ 4 Движение планет
507
Vn
при f=0 г=а, θ=0, г=0, θ=——. (10)
Теперь необходимо решить систему дифференциальных
уравнений (8) и (9), удовлетворяющую начальным условиям (10).
Замечая, что левая часть уравнения (9) представляет
выражение — · —г- (гЩ), можем его заменить уравнением
d (γ2Θ)=0 (11)
dt
или
r*Q=Ci. (12)
вательно, из уравнения (12)
Из условий (10) видим, что при ^=0 г=а и θ= ——. Следо-
С!=ащ. (13)
Таким образом, уравнение (12) принимает вид
r2Q=av0, (14)
откуда
и уравнение (8) будет
«--=4 О»)
·· а2Уоа ν
'= ——7Г· (16)
Уравнение (16) не содержит θ и непосредственно не включает t.
поэтому, полагая г=р, это уравнение запишем в виде
dp dp dr dp Фщг ν
dt dr dt dr
|ли
dp α2ι>02 ν
p-dF = — —?-- (17)
Разделяя переменные и интегрируя уравнение (17), получаем
ρ2 ν с'ро8 , r MRv
Τ" "Τ—2^-+С2· (18)

18
Гл. XIX Системы второго порядка
Из уравнения (18), так как р=г = 0, где г=а, имеем:
V02 V
c-^-f. ow
Таким образом, уравнение (18) принимает вид
г2 ν α2ν0ζ Щ2 _ ν
2 г 2г2 ' 2 α
ли, рассматривая только положительный квадратный корень,
dr
dt
г-П^^)+~^- <2°>
Отсюда можно получить г в виде функции времени t и найти
естоположение Земли (или другой планеты) относительно Солнца
любое время. Однако значительно больший интерес представляет
писание траектории Земли при ее движении. Для этого необходимо
равнение, содержащее гиб.
Задача описывается теперь системой уравнений (20) и (15).
[ифференциальное уравнение, содержащее г и Θ, но не включаю-
lee ί, может быть получено делением уравнения (20) на уравнение
15), откуда
dr
dQ
:/-уЛ/-2+2Вг-1, (21)
це
м ' --» в-
α3υο2' oPW
Разделяя переменные и интегрируя, получаем
dr
ί"
njAr2+2Br— 1
= JdO=6+C3. (22)
гт l a du
Применяя подстановку r= —, dr= —, имеем:
и и2
-ί
1А+2Ви—и2
d(u-B)
= Q+C3,
iA+B2—(u—B)z
е.
_ arccos U~B — =Q+C3. (23)
iA+B2

§ 5. Система двух связанных электрических контуров 509
--де
Общее решение
и=В+ 1А+В2cos(6+C3) =β [l+ecos(e+C3j], (24)
е=Щ*=а»*_^ (25)
β
1
Так как и= —, то
г
α2ν02
Г~ 1+есоз(е+Сз) - (26)
Начальное условие: при 6=0 г=а. Отсюда
й2Уо2
α (1 +е cos С3) = .
ν
Сокращаем на α и переносим единицу в правую часть урав-
1ения:
е cos C3= ■ —\=е.
ν
Сокращая опять обе части равенства на е, получаем cos C3=l,
-. е. С3=0.
Таким образом, искомая зависимость r=f(Q) будет
а2у02
v(l+ecos6)'
§ 5. СИСТЕМА ДВУХ СВЯЗАННЫХ ЭЛЕКТРИЧЕСКИХ КОНТУРОВ
Задача 192. Две цепи А и В (рис. 140) находятся в магнитной
".вязи при заданном коэффициенте Μ взаимной индукции. Дано: Li,
?ι и G — коэффициент самоиндукции, сопротивление и емкость
депи Л; L2, R2 и С2 — аналогичные величины для цепи В. Найти
,акон изменения силы тока ί в цепи А, предполагая, что:
а) сопротивления цепей /?ι и /?2 весьма малы;
б) цепи настроены в унисон, т. е. CiLi=C2L2.
Решение. В цепи А возникают силы: электродвижущая сила
,. di2 т dh
гадукции —Μ —тг, электродвижущая сила самоиндукции — L —тг,
1апряжение конденсатора

510
Гл. XIX. Системы второго порядка
Отсюда по закону равновесия электродвижущих сил
... ir$iidL
Аналогично для цепи В
RlXl^-M — -.Ll —
Rziz=—M
dii
IT
diz
~dt
1
ί
izdt.
(1)
(2)
vww-
i
L>i
-yrNkl·
ft
Рис. 140
Из уравнений (1) и (2) получаем систему дифференциальных
уравнений процесса
Μ
diz
~dt
+L
dk
1 dt
-Rih+
1
-] iidt=0,
U2
dt ' ~s dt
или, дифференцируя,
M^+U^i+R^+'i^O,
dt2
dH
м^+и
dP
dP
dHz
dt*.
+R
diz
dt
+
1
c2
t'2 = 0.
(3)
Это система двух дифференциальных уравнений второго
порядка. Исключим из системы (3) величину —|. Тогда

§ 5. Система двух связанных электрических контуров 511
Дифференцируя уравнение (4), находим
В уравнении (5) заменяем величину Μ ■■■■■ - выражением из
di
первого уравнения системы (3)
и получаем
+ (-£+**)£+ £'-5-£-* О
Дифференцируя уравнение (6), находим
(LlL2_M2) -gL + (L^i+L^2) -~- +
Вторично заменяя величину Μ ■ выражением из первого
/равнения системы (3), получим
(14, dsi,
(ULt-M*) -^f + {URl+UR2) -|£- +
+ 7τ^-ίι=0. (7)
Сокращаем уравнение (7) на LVL2:
( М2 ) dHl \ ( Ri R* ) d4i
' UL2 ι Л4 + \ U ^ L2 I dt* +

12
Гл. XIX Системы второго порядка
, ( 1 , 1 . Ri Rz \ dHi
>2i>2 CiLi Li Lz ' di2
+ (-Bl _J , _?i. _1_\^_,_J 1_/=η (Μ
**" V U C2L2 ^ U dU I dt **" dU C2L2 i ' K '
Уравнение (8) представляет неполное линейное однородное
ифференциальное уравнение четвертого порядка, решение которого
пределит силу тока ιΊ в цепи А.
Так как цепи настроены в унисон, т. е. CiLi=C2Lz, и сопротив-
ениями Ri и R2 можно пренебречь, то уравнение (8) примет вид
/ М2 \ dHi 2 d4i 1 .
\l-T^i^tr+-cz;-^tr+-c^jh=0- (9)
Соответствующее характеристическое уравнение
/ Μ2 \ 2 1
(1-гж-)'ч-«7'ч-здг-*п- (10)
Обозначим для краткости:
LiL2 CiLi
Тогда уравнение (10) примет вид
(1— £2)/-Ч-2п2/-2+п4=0. (И)
Корни уравнения (11):
ni ni
/V
ni ni
11—k f\^k
Искомое общее решение
η η
i=Ci sin -t+Cz cos ί+
Vl+ft Y1+*
_ η · η
+Сз sin i+C4 cos -^^zzr '·
У1—ft yi-ft

§ 6. Потенциал электролинии
513
§ 6. ИЗМЕНЕНИЕ ПОТЕНЦИАЛА ЭЛЕКТРИЧЕСКОЙ ЛИНИИ
ПО ВРЕМЕНИ (ПРИВЕДЕНИЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ К СИСТЕМЕ
ОБЫКНОВЕННЫХ УРАВНЕНИЙ)
Задача 193. Линия длиной / с сопротивлением R и утечкой G
* G
а единицу длины свободна от искажении (т. е. --— = -τς—, где L —
амоиндукция и С — емкость на единицу длины) и заряжена до
ютенциала Uq. Конец линии (х—1) изолирован. В момент времени
= 0 начало линии (х=0) заземляется. Найти закон изменения
ютенциала в любой точке линии в зависимости от времени t.
Решение. Прохождение электрического тока по проводу
: равномерно распределенными на единицу длины сопротивле-
шем R, самоиндукцией L, емкостью С и утечкой G характеризуется
:илой тока i(x, t) и напряжением U(x, t), которые являются
функциями положения точки χ и времени t.
Величина потерь пропорциональна напряжению в
рассматриваемой точке провода.
Величины i(x, t) и U{x, t) связаны следующей системой
уравнений:
61 +c^L+gu=o,
дх ' di
dUx , , di
дх dt
+Ri=0,
(A)
называемой системой телеграфных уравнений.
Из системы (А) легко получается уравнение силы тока
дЧ <52ί di
~eXT=CL-a^- + {CR+GL)-dT+Gm ™
и уравнение напряжения
Каждое из них называется телеграфным уравнением..
Если можно пренебречь потерями через изоляцию и
сопротивление очень мало, т. е. G«0, i?»0, то приходим к уравнению
-дё-=а2-дхТ (°0

514
Гл. XIX Системы второго порядка
и к уравнению
1
d2U , d2U
= az-
(D2)
где αΔ
CL
dt2 дх* '
Каждое из этих уравнений называется волновым
уравнением.
Потенциал U{x, t) и сила тока i(x, t) в кабеле удовлетворяют
системе телеграфных уравнений (А) при 0<х<1 и 0<^<+°°.
Из данных задачи вытекают начальные условия
i/(x,0) = i/0, i(x, 0)=0
и граничные условия
{/(0,0=0 при />0, i{l,t)=0.
(1>
(2)
Кроме того, из первого уравнения системы (А), которое должно·
оставаться справедливым из физических соображений при /=0,
следует еще одно начальное условие для потенциала
дх
+ GU(x, 0)=0
или с учетом соотношения (1) имеем:
dU
dt
ί=0 L
(3)
Из второго уравнения системы (А), которое должно быть
справедливым и при х=1, следует еще одно граничное условие для
потенциала
дх
*=«+ dt
χ=ί
+Ri(l,t)=0
или с учетом соотношения (2) имеем:
dU
дх
= 0.
(4)
Итак, задача сводится к интегрированию телеграфного уравне
ния для потенциала U(x, t):
G
а*
d2U
dW
дх2 dt2
при начальных условиях
+ (■
L
+
ди +ϊίυ
dt
U(x,0) = U0,
dU
G
dt (==o С
LC
(0<х<1)
(5

§ 6. Потенциал электролинии
515
и граничных условиях
С/(0, 0=0 при t>0, —— =0.
Пусть
-l/^L + JL.),
2 \ J, С /
tf(*,f)=<? V (*,*). (6)
где V(x, t) —новая искомая функция.
Так как кабель —линия без искажений, то —— = -—— и
получим для функции V{x, t) волновое уравнение
d*V dW
= «2-^· (7)
дР дх*
Из начальных и граничных условий для функции U(x, t)
вытекают соответствующие условия для функции V(x, t), а именно:
dV
V(x,0) = Uo,
дх
V{0, ί)=0,
дУ
дх
= 0 (0<*</); (8)
*=i
=0. (9)
Решение дифференциального уравнения в частных
производных (7) сведем к решению системы обыкновенных
дифференциальных уравнений.
Для этой цели воспользуемся методом разделения переменных,
т. е. решение будем искать в виде
V(x,t)=X(x)T(t). (10)
Требуем, чтобы функция Х(х) удовлетворяла граничным
условиям (9), а также, чтобы X(x)T(t)^0,
Подставляем равенство (10) в уравнение (7), откуда
ХТ"=а2ТХ"
и после разделения переменных получаем уравнение
Равенство (11) возможно лишь в случае, если каждое из этих
отношений равно постоянной. Очевидно, что если эта постоянная
не отрицательна, то граничным условиям (9) удовлетворяла бы
только функция, тождественно равная нулю.

516
Гл. XIX. Системы второго порядка
Пусть λ2 — общая постоянная. Тогда
λ2
α2
Γ"+λ2Γ=0.
(12)
Таким образом, уравнение задачи в частных производных (3)
приведено к системе двух обыкновенных дифференциальных
уравнений второго порядка (12).
Общие решения этих уравнений
Х=A cos — х4-В sin — χ,
а а
Т=A* cos λί+Β* sin It.
Из условий (9) следует:
А = 0, λ=—тг,— ал.
03)
Из начального условия
Итак,
dV
dt
ί=0
2/
= 0 вытекает, что В*=0.
,,, ,ч г,Л · (2m+1)ju; (2η+1)παί
1/(jc, t)=BA* sin- ^—cos- ^'
21
21
_ . 2n+l 2n+l
= Csin ——-roc cos·———παί, (14)
где C=BA0*.
Функция (14) удовлетворяет всем условиям задачи, кроме
V(x, 0) = Csin (2η]"/)π хфиа. (15)
Чтобы удовлетворить и это условие, будем искать решение
задачи в виде ряда
п=0
(2я+1)л (2η+1)πα ,
sin ——irr1— x cos ——j^r1 1,
21 21
в котором коэффициенты Сп выбраны так, что
Σ (2л+1)я
Сп Sin
(16)
n=0
21
x — Uo.
(17)

§ 6 Потенциал электролинии
Для нахождения этих коэффициентов рассмотрим нечетную
функцию
/ Ι/,, при 0<х<21,
Пх)=\-ивщ>н-21<х<0, (18)
а вне интервала {—21, 21) продолженную периодически с
периодом 4/.
Коэффициенты Фурье этой функции
ZI
OIL
2U0 f . ηπ l-(-l)"
Поэтому
f(x) = ~Z~Zu
2i/„ X1 i_(_i)n nn
π ~ η 21
τι=1
oo
4t/„ V 1 . (2η+1)π
ΣΙ . (2η+1)π
8ΙΠ_^Χ. (19)
n=0 '
Отсюда следует, что коэффициенты Сп должны быть
коэффициентами Фурье функции f(x).
Если функцию f(x) найти трудно, то можно было бы тогда
функцию V(x, 0) разложить в интервале (0, /) в ряд по функциям
. (2п+1)я
sin —L-x.
Если функция V(x, 0) удовлетворяет некоторым ограничениям,
то такое разложение возможно и Сп будут его коэффициентами.
Пусть теперь далее
С—Лш- <20)
Тогда
4ί/0 У1 1 . (2η+1)π
sin —————x=Uo, 0<л:<2/.
я S2n+1 2/
Следовательно,
τ// ^ 4t7° V L_ · (2«+1)я (2м+1)ал ,
τι=0 '
Остается проверить, удовлетворяет ли полученное решение
уравнения (21) всем условиям задачи.

18
Гл. XIX. Системы второго порядка
Представим функцию V(x, t) в виде
V(x, t) =ψ(χ-\-αί)-\-φ(χ—at),
'Де
(22)
. 2Ι/ο γ 1 . (2n+l)n(x+at)
φ(χ+αί) =—~Ζ^~—г-r sin-
π <-*. 2η+1
τι=0 '
2/
. 2ί/ο γ 1
η=0 '
. (2η+1)π(χ—at)
2η+\ Sm 2/
-Bl
-Ы
-η
ι Ύ(ζ)
-21
?\
ΊΙ
1)1
81
—n
Рис 141
Из соотношений (18) и' (19) следует, что φ(ζ)--
__Uo
f(2) =
2
С/о
при —2/<2<0,
при 0<z<2/,
■f{z), т. е.
(23)
а вне интервала (—2/, 2/) продолжается периодически с периодом 4/
(рис. 141).
Значения функции V(x, t) представлены на рис. 142.
Во всех точках плоскости (х, t), кроме лежащих на прямых
x±_at=2nl, где п=0, ±1, ±2, ... , называемых характеристиками
данного уравнения, функция V(x, t) (21) удовлетворяет уравнению
(7), начальным условиям (8) и граничным условиям (9).

§ 7. Стационарные системы
oJ9
Учитывая соотношение (6), искомая функция
U{x,t)=e L V{x,t) =
Wo
= e
oo
'* V l
■H 2n+l
(2η+1)π (2η+1)απ ±
Рис. 142
§ 7. СТАЦИОНАРНЫЕ ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
В ТЕОРИИ СИСТЕМ СОВРЕМЕННОЙ
ТЕХНИКИ И ЕСТЕСТВОЗНАНИЯ
Системы автоматического регулирования
Под термином система подразумевается взаимосвязь самых
различных элементов.
Физическая система, характеристики которой не изменяются
по времени, называется стационарной. Если же они изменяются
очень медленно, то система называется квазистационарной, и
соотношения между различными свойствами системы приблизительно
такие, как в стационарном состоянии.
Линейными стационарными системами называются такие
системы, свойства которых (упругость, масса и коэффициент трения

520
Гл. XIX. Системы второго порядка
в механической системе, емкость, индуктивность и активное
сопротивление в электрической системе) не зависят от величин,
характеризующих состояние системы (от смещений и скоростей в случае
механической системы, напряжений и токов в случае электрической
системы).
Нелинейной системой называется система, которая содержит
хотя бы одно звено, описываемое нелинейными уравнениями.
Процессы в линейных системах описываются линейными
дифференциальными уравнениями (откуда и произошло их название,
так как параметры системы, которые входят в коэффициенты
уравнений, не зависят от переменных и их производных, определяющих
состояние системы).
В теории систем современной техники и естествознания
стационарные линейные дифференциальные уравнения находят широкое
применение. Особо велико их значение в автоматическом
регулировании. В частности, эти уравнения описывают действие
электромеханических следящих систем, служащих для управления
положением тела в пространстве, так, чтобы оно с требуемой точностью
копировало (отслеживало) положение другого тела и имело
возможность изменить положение некоторого элемента в зависимости
от характера сигнала управления (задающего сигнала).
Примерами следящих систем являются: автоматический
потенциометр для измерения температуры электропечи, системы
управления антеннами радиолокационных станций, автопилоты (на
самолетах), гирорулевые системы (на кораблях) и т. д. Во всех этих
системах регулируемой величиной является положение
механического объекта.
В более широком смысле следящими системами называют
любую систему автоматического регулирования, предназначенную для
того, чтобы какая-либо выходная величина с заданной точностью
повторяла изменения входной величины часто другой физической
природы.
Поэтому следящие системы находят самое широкое
применение: в копировальных станках, у которых фреза или резец станка
«следит» за перемещением щупа по копиру; в артиллерии, где
орудие или о'рудийная башня «следит» за рукояткой управления,
перемещаемой наводчиком, и т. д.
Составление дифференциальных уравнений систем
автоматического регулирования
Системы автоматического регулирования в большинстве
случаев являются сложными устройствами, динамика которых
описывается совокупностью дифференциальных уравнений.
Для получения такой совокупности необходимо составить
дифференциальное уравнение для каждого элемента
автоматической системы так, чтобы общее число уравнений было не меньше

§ 7 Стационарные системы
521
числа независимых обобщенных координ.ат,* определяющих
состояние системы.
При составлении дифференциального уравнения каждого
элемента необходимо выявить физический закон, определяющий его
поведение. Например, закон сохранения вещества (для объектов
регулирования уровня давления), закон сохранения энергии (для
объектов регулирования температуры), закон равновесия моментов
(для объектов регулирования скорости или угла поворота), закон
равновесия электродвижущих сил (для электрических цепей) и т. д.
Математическая формулировка соответствующего физического
закона является исходным дифференциальным уравнением данного
элемента автоматической системы.
Так, для электродвигателя закон равновесия моментов,
приведенных к исполнительной оси, т. е. на его валу, представляется
уравнением
άω
J ,, =-Мвращ—МТОрМ, ( 1)
где / — приведенный момент инерции двигателя, ω — угловая
скорость двигателя, МВращ — вращающий момент двигателя, Мторм —
тормозной момент внешних сил (момент нагрузки).
Далее необходимо определить факторы, от которых зависят
переменные, входящие в это дифференциальное уравнение. В
условиях уравнения (1) надо выяснить, от каких величин зависят" и
какими соотношениями определяются вращающий момент двигателя
•Мвращ и тормозной момент Мторм на его валу.
Следующим этапом является линеаризация полученных
уравнений, допустимая при отсутствии разрывных, многозначных или
резко изгибающихся характеристик, и если уравнения являются
стационарными, т. е. справедливы в течение всего времени
регулирования.
В итоге линеаризации получается совокупность
дифференциальных уравнений, описывающих движение рассматриваемой системы:
an(p)xl~\-ai2l(p)x2-Jr.. .+aik(p)xh=fl(t),
a2l{p)Xi-\-a22{p)X2+---+a2k(p)Xk=f2(i), . (2)
aki(p)Xi+ah2(p)X2+.. .+akk(p)xh=fk{t),
где Χι, Χ2, ... , Xh — обобщенные координаты системы, в том числе
регулируемая величина y(t) и ошибка x(t); p= —т- алгебраизи-
* Обобщенными координатами называются величины, характеризующие
изменение положения системы Обобщенными координатами могут быть прогибы
отдельных· точек, углы поворота узлов, взаимные углы поворота стержня и т. п.

22
Гл. XIX Системы второго порядка
ованный оператор дифференцирования; fi(t), f2(^), ·.. , fk{t) —
>ункции времени, представляющие управляющие и возмущающие
оздействия (будем считать, что к системе приложены только два
оздействия — управляющее h(t) и возмущающее f(t)); а^(р)—
екоторые многочлены оператора р.
Совокупность дифференциальных уравнений (2) может быть
(азрешена относительно любой обобщенной координаты.
Обычно это производится относительно отклонения регулируе-
юй величины от заданного значения, т. е. ошибки (рассогласова-
шя) x(i), или относительно регулируемой величины y(t).
В первом случае получается дифференциальное уравнение
D(p)x(t)=Q(p)h(t)+R(p)f(t). (3)
Здесь характеристический многочлен п-п степени
D(p) =Ω0ριι+αιΡη-1+α2Ρη-2+.. .+αη-φ+αη, (4)
~де Ωο, αϊ, аг, ... , ап — постоянные коэффициенты линеаризованной
:истемы, характеризует свободное движение регулируемого объекта
г регулятором; многочлен n-ή степени
Q (р) =С0рп + С1Рп-1+Сгрп-2+. . ,+Сп-ф + Сп, (5)
где со, Си с2, ... , сп — постоянные коэффициенты, определяет
влияние управляющего воздействия h{t) (т. е. требуемого закона изме-
1ения регулируемой величины y(t)) на характер изменения ошибки
x(t); R(p)—многочлен, определяющий влияние . возмущающего
воздействия f(t) на характер изменения ошибки x(t).
Во втором случае при решении системы дифференциальных
уравнений (2) относительно регулируемой величины y(t)
подстановка выражения для ошибки x(t) =h(i)— y(t) в равенство (3)
дает уравнение движения регулируемого объекта:
D(p)y(t)=S(p)h(t)-R(t)f(t), (6)
где S(p)=D(p)—Q(p) —многочлен степени т^.п:
S(p) =f>0pm+f>ipm-1+i>2Pm-2+. ■ .+Ьт-ф+Ьт.
Если функции времени, стоящие в правой части
дифференциальных уравнений (3) и (6), заданы, то эти уравнения
интегрируются относительно искомых функций времени, т. е. можно определить
изменение ошибки регулирования во времени χ(ί) из уравнения (3)
и движение регулируемого объекта с регулятором y{t) из
уравнения (6).

§ 7. Стационарные системы
523
Следящая система
Следящая система работает на принципе обратной связи —
путем сравнения заданного положения объекта с действительным
его положением и использования фиксированных отклонений для
автоматического регулирования объекта. Желательное положение
•объекта задается значением напряжения или силы тока, плотности
излучения, перемещения и других физических величин.
Рис. 143
Обозначим элементы схемы электрической следящей системы
■следующим образом: / — маховичок датчика; 2 — ведомый вал;
3 — регулируемый объект; 4 — усилитель; 5 — электродвигатель
постоянного тока; 6 — шестеренная передача; Ri— движковый
реостат датчика; R2— движковый реостат ведомого вала; U
■—напряжение задания (т. е. напряжение неуравновешения моста
сопротивления, регулирующего усилитель); Uz — напряжение питания моста.
Пусть имеется некоторая ось АА' (рис. 143), которую назовем
задающей. Угол поворота α этой оси задается извне и является
установленной величиной.
Задача следящей системы состоит в том, чтобы угол поворота β
другой оси ВВ', которую назовем приемной, равнялся а. Величина
угла α может быть представлена в общем случае любой функцией
времени. Ось ВВ' должна автоматически следовать за осью АА'.
В качестве измерительного органа системы автоматического
регулирования применена цепь, состоящая из двух потенциометров
(или реостатов) Ri и R2, движки которых укреплены на осях АА'
и ВВ'.
Если аф$, то потенциалы движков U и Uz равны и их
разность At/ (т. е. напряжение между движками Ρ и Q) равна нулю.
Если α=β, то напряжение AU=U—Uz=/=0 приложено к входным
зажимам усилителя с коэффициентом усиления &о· На выходе
усилителя образуется напряжение £/Β=&0Δί7, вызывающее ток iB в
обмотке возбудителя генератора Г.
Появление электродвижущей силы генератора Ет вызывает
ток г'я в цепи якоря двигателя Μ независимого возбуждения.
Последний через шестеренную передачу с передаточным числом q вращает

524
Гл. XIX. Системы второго порядка
приемную ось до" тех пор, пока AU не обратится в нуль. Тогда
напряжение U-b станет равным нулю и система придет к состоянию
равновесия.
В структурной схеме системы регулирования (рис. 143) датчик 1
в виде круглого движкового реостата Ri предназначен для
установки желательного углового положения а, которое должен принять
ведомый вал 2, передвигающий регулируемый объект 3. Каждому
углу α соответствует определенное положение движка реостата Ri.
На ведомом валу 2, имеющем действительное угловое положение β,
находится второй движковый реостат Rz, который совместно с
реостатом Ri образует мостовую схему. Если положения α и β движков
двух реостатов Ri, R2 не совпадают, то мост не находится в
равновесии и на его диагонали появляется напряжение U, управляющее
усилителем 4.
Усилитель за счет питающей энергии производит ток i„,
необходимый для приведения в движение двигателя 5.
Двигатель постоянного тока приводит в движение при помощи
передачи 6 .ведомый вал и работает до тех пор, пока движки двух
реостатов Ru R2 не займут тождественного положения α=β.
Напряжение U и ток г'я становятся равными нулю, и двигатель
останавливается.
Такого рода структурная схема позволяет точно регулировать
положение больших и инертных масс часто на большие расстояния
при небольшой затрате энергии (перевод движка реостата Ri).
В следящей системе замеряются физические величины,
подлежащие контролю (выход информации), и этот замер сопоставляется
с другими физическими величинами (входная информация).
Разница между выводом и вводом информации называется погрешностью
по регулирующему воздействию и используется, чтобы вызвать
изменение физической системы с целью минимизации этой
погрешности или сведения ее к нулю.
В частности, рассогласование (ошибка) системы
AU=U— υ г
представляет разность между напряжением задания U и
напряжением питания моста Uz.
Задача 194. Для следящей системы (рис. 144) определить угол
поворота командной оси как функцию времени при следующих
параметрах: напряжение аккумуляторной батареи £п.т=4 в,
коэффициент усиления линейного усилителя &о=Ю в/в (вольтов/вольт),
коэффициент пропорциональности вращения &Вр=1 кГ- м/а,
самоиндукция якоря 1Я=0,02 гн, сопротивление якоря #я=0,74 ом,
осевой момент инерции вала 7=0,5 кГ-м-сек2, коэффициент отношения
угловой скорости к напряжению якоря /Ся=6,43 в/рад/сек,
коэффициент вязкого затухания С=0,5 кГ-м/рад.

§ 7. Стационарные системы
525
Решение. В структурной схеме следящей системы (рис. 144)
показаны усилитель, двигатель постоянного тока и два
потенциометра. При такой схеме соединения потенциометр выхода можно
расположить перед входным потенциометром.
Усилитель
}_<оэ-Л^--<£
Т=к 1Я -ш<^\ ρ Χ
*4L
с
Рис 144
Угол поворота β командной оси, замеренный вторым
потенциометром,
νΒΗΧ = β·£π.τ» (1)
а угол поворота α исполнительной оси можно вручную установить
равным заданному углу при помощи вращающего вала входного
потенциометра
νΒχ=α£π.τ· (2)
Рассогласование представляет разность между выражениями
(1) и (2), т. е.
β = νΒχ—Vsbix· (3)
Напряжение якоря мотора получается путем усиления
рассогласования
£я=/гое (4)
и связано с угловой скоростью мотора зависимостью
£я=#я1'я+-£-я —— +Кя
dt
dt'
где RH — сопротивление якоря; La — самоиндукция якоря; гя — ток
якоря двигателя; Кя — коэффициент соотношения угловой скорости
и напряжения якоря.

526
Гл. XIX. Системы второго порядка
Пусковой (вращающий) момент, приложенный к валу двига
теля, является функцией силы тока якоря
У =йцр'я
и, когда этот момент действует на вал двигателя, вращение вал^
описывается дифференциальным уравнением
У =kBVl„ = J —775- +C
dt2
dt '
где / — момент инерции всех вращающихся частей, приведенных
к валу двигателя; С — коэффициент вязкого затухания.
Очевидно, что уравнения, описывающие работу следящей
системы, будут
/4t+cdp
dt2
dt
din
LR —-r.—г"^я^я+УХя
«вр'я—0;
dp
dt
Ея.
Кроме того, согласно уравнениям (1) — (4), напряжение якоря
Ея может быть представлено в виде
£h=&o(vBx—Vbi,ix) =EnTko(a—β)
и поэтому система дифференциальных уравнений, описывающая
работу следящей системы, будет представлена явными функциями
углов поворота осей и силы тока якоря
Ln —-77—\-Rnin-\-Kn —тг +-Επ.τ^οβ=£π.τ^οα.
Дифференциальные уравнения движения с учетом условий
задачи примут вид
0,5 *L +о,5*
dt2
dt
-*я=0,
0,02 -~- +ο,74ίβ+6,43-^- +40β = 40α.
d
(5)
Пусть оператор —г— =D. Тогда в операторной форме система
(5) запишется

§ 7. Стационарные системы
527
(ΰ2+ΰ)β-2ί„=0;
(321,5Ζ)+2000)β+φ+37)ίΗ=2000α.
Характеристический определитель системы
D2+D —2
(6)
f{D) =
321.5D+2000 D+37
= D3+38D2+680D+4000=0
представляет уравнение третьей степени с постоянными
коэффициентами.
Характеристическое уравнение
имеет корни
r3+38r2+680r+4000=0
■ Ю; r2l3= —14± 14,28г.
Общие решения соответствующих однородных
дифференциальных уравнений (6) будут
$от=Сне-т+е-ш{С125\п 14,28/+С13 cos 14,28/), }
ioflH=c21e-ioi+e-14'(C22sin 14,28/+C23cos 14,28/). '
(7>
Число произвольных постоянных можно уменьшить, если
использовать первое уравнение системы (6). С помощью решений (7)
и их соответствующих производных получаем
0=(90С11-2С21)е-1°(+(385,72С13-22С12-2С22)е-14г sin 14,28/—
-(385,72C12+22Ci3+2C23)e-14i cos 14,28/,
откуда, приравнивая соответствующие коэффициенты и сокращая;
полученные равенства на 2, имеем
45Сц-С21 = 0;
192,86С13—IICu—Csb=0;
-192,86С12-11С а— С23= 0
или
C2i=45Cllf
С22=192,86С13—ПС12,
С23=-192,86С12-11С13.
Тогда общие решения соответствующих однородных уравнений!
(6) принимают вид
βοηΗ=Cue-10i+e-14i(Ci2sin 14,28/+Ci3cos 14,28/),
годн=45С11е-1°'+(192,8бС12—11С13)е-1« sin 14,28/—
- (192,86С12+ UCts) е~ш cos 14,28/.
(8>

528
Гл. XIX. Системы второго порядка
Пусть частные решения системы неоднородных
дифференциальных уравнений (7)
§частн=-Д> 'ячастп:=о·
Подставляя их в исходную систему дифференциальных
уравнений (6). получаем
-2Б = 0; 1
2000Л+37Б = 2000а, J
откуда
Л = о, В = 0. (9)
Таким образом, общее решение для угла поворота командной
оси получается путем суммирования соответствующих уравнений
(8) и (9):
P^die-^+e-^Cizsin 14,28/+С13 cos 14,28*)+α.
d& d2R
Начальные условия: при *=0 β = 0, —τ— =0, —τ— =0.
at ar
Отсюда получаем систему алгебраических уравнений для
определения постоянных интегрирования
Cn+Ci3=— α;
— 10СИ+14.28С12—14Cis=0;
ЮОСц—400Ci2—8C1S=0.
Решение этой системы
Сц=-1,82а; С12=-0,471а; С13=0,82а.
Частное решение для угла поворота β командной оси
принимает вид
β = α [1-1,82е-10г+(0,82 cos 14,28^-0,471 sin I4,28i)e-«*].

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
I. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ПЕРВОГО ПОРЯДКА
1. Определить работу, которую нужно затратить, чтобы насы-
тать из песка конус, радиус основания которого /?= 1,2 м, а высота
Ί=1 м. Удельный вес песка γ=2 Γ/см3. Песок поднимают с поверх-
-юсти Земли.
Ответ: А « 754 кГм.
2. Концы каната цепного моста находятся на высоте #=5 м,
а середина на высоте /ι=4 м от проезжей части моста. Длина моста
2/=20 м. Найти кривую свешивания каната.
х2
Ответ: парабола у—4= ——-.
3. Пластинка, имеющая форму половины эллипса, погружена
вертикально в жидкость так, что малая ось 26 лежит на поверхности
жидкости. Найти давление на стороны этой фигуры, если длина
погруженной полуоси эллипса равна а, а удельный вес жидкости γ.
Ответ: дифференциальное уравнение задачи
с?р= —- χ i a2—x2 dx\
а
2 , ,
при χ=a p=—-byaz
О
4. Ракета с начальной массой Ма г взлетает с Земли в
вертикальном направлении. Газ выбрасывается постоянными долями
а Г'/сек и с постоянной скоростью b см/сек относительно ракеты
(а>0; &>0). На ракету действует постоянное гравитационное поле.
1) Показать, что уравнение движения
dV
{М0—at) —Tr—ab = —g{M0—at);
2) найти скорость ракеты в любое время ί< после старта
с Земли, принимая начальную скорость ракеты равной нулю;
3) определить высоту подъема ракеты в момент t.
М0 \ , „ _ Mo
Ответы: 2) V=b In ( „. ° ) —gt, 0<*<
v Mo—at ι
3) x=w_|(M„_ai)ln(_^_)_|gi!, 0<i<^

530
Задачи для самостоятельного решения
5. Легкое тело массы m падает с высоты 250 м под действием
силы тяжести, встречая противодействие силы трения воздуха.
Предполагая, что сила трения пропорциональна скорости
(коэффициент пропорциональности k), установить:
1) через сколько секунд после начала падения тело достигнет
Земли;
2) закон движения h=f(t).
171 **
Ответ: 1) /= — In
k k
g ·υ
m
„, , mg , m2g I - — l\
2) h=-ft rf (1-е - )
k2
6. Шар массы m падает свободно без начальной скорости под
действием силы тяжести из точки О, которую примем за начало
координат. Сопротивление воздуха F пропорционально скорости
падения, т.е. F=—ku (k — коэффициент пропорциональности).
Найти закон движения шара.
ё g
Ответ: у= — t — (1— e~nt).
7. Материальная точка массы m брошена вертикально вверх
с начальной скоростью v0. Сопротивление воздуха пропорционально
квадрату скорости движения.
Найти: 1) время tt подъема точки до наибольшей высоты;
2) наибольшую высоту h подъема точки;
3) скорость U2 точки в момент ее падения на Землю;
4) время t2 падения материальной точки на Землю.
dv
Ответы: 1) m -— = — mg—kv2;
t=~=(arctgu0y^-aTctgv']/-j), а=-^Г;
у ag ё s
1 , ΐ/~α"'
при υ = 0 h= arctg υ0 |/ —;
lag g
1 , g+av02 n , 1 g+avo2
2)5=Ύα1η7+^;πρΗϋ=° h=Ta^—j->
dv 1 , ёГ
3) при падении -^- =g—av2, s= γ α In g_ai)2 ;
при s=h vz=v0 у
g
g+ava2

/. Дифференциальные уравнения первого порядка
531
ι , ie+via
4) t=—~ln — _;
2iag У g—υ У α
1 , fo fa+yg+afo2
При V = V2 h= 1П — «J t»2<fo, t2>«l.
fag 1ё
8. Период распада радия 1600 лет. В настоящее время имеется
500 мг. Какое количество останется через 250 лет?
Ответ: 449 мг.
9. За 30 дней распалось 50% первоначального количества
радиоактивного вещества. Через сколько времени останется 1 %
первоначального количества вещества?
Ответ: 2=200 дней.
10. В куске горной породы содержится 100 мг урана и 14 мг
уранового свинца. Определить возраст горной породы, если
известно, что уран распадается наполовину за 4,5· 109 лет и при полном
распаде 238 г урана образуется 206 г уранового свинца. Принять,
что в начальный момент образования горная порода не содержала
свинца, и пренебречь наличием промежуточных р'адиоактивных
продуктов между ураном и свинцом ввиду их значительно более
быстрого распада, чем урана.
Ответ: 975· 106 лет.
11. Футбольный мяч, сила тяжести которого 0,4 кГ, брошен
вверх со скоростью 20 м/сек. Сопротивление воздуха
пропорционально квадрату скорости и составляет 0,48 Г при скорости 1 м/сек.
Найти время и наибольшую высоту подъема мяча. Исследовать
изменение результатов, пренебрегая сопротивлением воздуха.
Ответ: 2=1,75 сек, /imax=16,3 м. Без учета сопротивления
воздуха 2=2 сек и /imax=20 м.
12. Масса ракеты с полным запасом топлива равна М, без
топлива — т, скорость истечения продуктов горения из ракеты — с,
начальная скорость ракеты равна нулю. Найти скорость ракеты
после сгорания топлива, пренебрегая силой тяжести и
сопротивлением воздуха.
Μ
Ответ: v = c In (формула Циолковского).
13. Замедляющее действие трения па диск, вращающийся
в жидкости, пропорционально угловой скорости движения.
1. Диск, начавший вращаться с угловой скоростью 3 об/сек,
через 1 мин вращается с угловой скоростью 2 об/сек. Какова будет
угловая скорость диска через 3 мин после начала вращения?
2. Диск, начавший вращаться с угловой скоростью 5 об/сек,
через 2 мин вращается с угловой скоростью 3 об/сек. Через сколько

632
Задачи для самостоятельного решения
времени после начала вращения диск будет обладать угловой
скоростью, равной 1 об/сек?
о
Ответ: 1. — об/сек. 2. Через 6 мин 18 сек.
14. Найти расстояние, которое пройдет за t сек тело, брошенное
вертикально вниз с начальной скоростью 30 см/сек.
Ответ: s= —-gtz-\-30t.
15. Из точки, находящейся на высоте 18 м над уровнем Земли,
брошено вертикально вверх тело со скоростью 30 м/сек. Найти
высоту, на которой тело находится в момент t, как функцию времени.
Найти также наибольшую высоту подъема тела.
Ответ: s=h=— -— ^2+30^+18; hmaK^63,9 м.
16. Пуля проходит через доску в 7,5 см толщины, которая
задерживает ее движение, сообщая ей постоянное отрицательное
ускорение. Скорость пули в момент, когда она достигает доски,
составляет 300 м/сек, а в момент, Когда она вылетает из доски,—150 м/сек.
Сколько времени заняло движение пули сквозь доску?
0твет: *=-шсек·
Примечание. По условию ускорение a=—w ■ (где w — постоянное
положительное число).
17. Катер, сила тяжести которого 300 кГ, движется
прямолинейно. Его начальная скорость 16 м/сек. Сопротивление воды
пропорционально скорости катера и равно 10 кГ при скорости 1 м/сек.
Какое расстояние пройдет катер, прежде чем его скорость станет
8 м/сек, и за какое время он пройдет это расстояние?
Ответ: s=25 м; t—2,1 сек.
18. При движении катера в спокойной воде сопротивление среды
вызывает замедление, пропорциональное скорости движения.
В момент остановки мотора катер двигался со скоростью 200 м/мин,
а через 1/2 мин — со скоростью 100 м/мин. Найти скорость катера
через 2 мин после остановки мотора.
Ответ: и=12,5 м/мин.
19. Самолет А летит со скоростью 200 км/ч в направлении,
наклон которого к горизонтальной линии равен 3/4. Самолет В из
точки 50 км севернее вылетает на перехват его со скоростью
300 км/ч. Нос самолета В непрерывно направлен к А. Найти
уравнение траектории полета самолета В, наблюдаемой с борта
самолета А. Задачу решить:

/. Дифференциальные уравнения первого порядка oSd
1) в прямоугольной системе координат;
2) в полярной системе координат.
Ответы: 1) дифференциальное уравнение в прямоугольной
системе
dy _ ЗОбу + 120 Ух2 + у* _
ах 300* + 160 Ухг + ~уг'
при t—0 x=0, у=50. Здесь координаты (х, у) определяют
положение самолета В в любой момент t относительно подвижной
системы координат (положения самолета А в момент t);
2) решение в полярных координатах
_ 50 f¥ (4 sin φ—3 cos φ)1/г
(5—4 cos φ—3 sin φ)3/*
20. Кислород поступает через трубку в бутылку емкостью в 1 л,
а смесь кислорода с воздухом вытекает через другую трубку.
Процесс проходит настолько медленно, что в каждый момент можно
считать газ в бутылке однородным. Вычислить, сколько процентов
кислорода будет содержать бутылка, после того как через нее
пройдет 10 л газа (принимается, что воздух содержит 21% кислорода).
Ответ: ρ=99,9964%.
21. Если тело медленно погружается в воду, то его скорость ν
и ускорение а приближенно связаны уравнением a=—g—kv, где g
и А — постоянные. Выразить пройденное телом расстояние как
функцию времени, если в момент ^=0 тело находилось в покое.
Ответ: s=-f"^ r~ (1—е~м).
22. Паропровод диаметром 20 см защищен изоляцией толщиной
10 см (k—0,00017). Допуская, что труба имеет температуру 160° С,
а внешняя поверхность изоляции 30° С, найти распределение
температуры внутри слоя, а также количество теплоты, отдаваемое
паропроводом наружу в течение суток на протяжении 1 м.
Ответ: 7=592-187,6 In г; около 1 731 000 кал.
23. Влага, содержащаяся в свежеиспеченном хлебе, испаряется
в окружающую среду со скоростью, пропорциональной количеству
влаги в хлебе, а также разности влажности окружающего и
насыщенного воздуха. Некоторое количество свежеиспеченного хлеба,
содержащее 3 кг влаги, положено в помещение объемом 100 м3,
воздух которого первоначально имел влажность 25%. Насыщенный
воздух при той же температуре содержит 0,12 кг влаги на 1 м3.

534 Задачи для самостоятельного решения
Если в течение первых суток хлеб потерял половину своей влаги,
то сколько влаги в нем останется по истечении вторых суток?
Ответ: дифференциальное уравнение задачи
ds
—— =fes(s+6); 0,82 кг.
at
24. В течение какого времени хлеб (в предыдущей задаче)
потеряет 90% своей влаги, если начальную влажность 25%
поддерживать постоянной при помощи вентиляции?
Ответ: 3 суток.
25. Дно резервуара вместимостью 300 л покрыто смесью соли
и нерастворимого вещества. Допуская, что скорость растворения
соли пропорциональна разности между концентрацией раствора
в данный момент и концентрацией насыщенного раствора (1 кг соли
на 3 кг воды) и что данное количество чистой воды растворяет
1/3 кг соли в 1 мин, найти, сколько соли будет содержать раствор
по истечении 1 ч.
Ответ: 18,1 кг.
26. Человек в среднем дышит 18 раз в 1 мин, выдыхая каждый
раз 2000 см3 воздуха, содержащего 4% С02. Какой процент
углекислоты будет содержать по истечении 30 мин воздух аудитории
вместимостью 400 м3, если в ней находятся 50 человек и если
вентиляторы доставляют в 1 мин 40 м3 свежего воздуха? (Свежий воздух
содержит 0,04% С02.)
Ответ: 0,17%.
27. В торговое помещение вместимостью 10 000 м3 втекает через
вентиляторы в 1 мин 1000 м3 свежего воздуха, содержащего 0,04%
С02. В 9 ч утра в помещение входят служащие и через 30 мин
содержание С02 в воздухе повышается до 0,12%. Какой процент С02
можно ожидать в воздухе к 2 ч дня?
Ответ: 0,124%.
28. После лекции воздух в аудитории объемом 10 800 м3
содержит 0,12% С02. Сколько кубических метров воздуха, содержащего
0,04% С02, надо ежеминутно доставлять в зал, чтобы через 10 мин
после перерыва содержание углекислоты в аудитории
составило 0,0650?
Ответ: «1500 м3. Если с — искомая величина, а у —
количество углекислоты в данный момент, то дифференциальное
уравнение задачи
4,^(0,0004--^)'*.

Л Дифференциальные уравнения первого порядка
535
29. Определить коэффициент скорости реакции второго порядка
при равных концентрациях вещества А п В: а=Ь.
1 χ
Ответ: k=— ; дифференциальное уравнение реакции
tit С* Д-
dX = k{a-x)\
at
30. Определить константу скорости реакции третьего Порядка
при двух равных концентрациях: а — сфЬ.
гл и ! Г (ь—а)х , , Ь(а—х) Л
° Т В 6 Т: k= t{b-ay I Я^Т) +1П 7{Ь=х) J ' ««Hep™-
альное уравнение реакции
dx = k(a-x)2(b-x).
dt
31. Определить константу скорости реакции третьего порядка
при равных концентрациях веществ Л ι, Α ζ, Α3: а1=а2=аз=я.
Ответ: k= —-— [ ·. _ — I ; дифференциальное урав-
пение реакции
-§- =На-х)*.
32. Реакция омыления уксусно-этилового эфира едким натром
CHaCOOCaHa+NaOH-^CHgCOONa+CzHsOH
происходит при равных концентрациях а = 0,01 уксусно-этилового
эфира и едкого натра. Найти концентрацию реагентов спустя 2 ч
после начала реакции. При измерении времени в минутах константа
скорости реакции k=3,\9.
а
Ответ: концентрация а—х= ——— «0,002, что составляет
20% первоначальной концентрации.
33. В воде растворяется бензойная кислота (СвРЬСООН).
Спустя 10 мин после начала растворения крепость раствора
составляет 6%. Найти крепость раствора спустя 30 мин, считая скорость
растворения пропорциональной разности крепостей насыщенного
и существующего в данный момент растворов.
Крепость насыщенного раствора бензойной кислоты равна 28%.
Ответ: х=28(1 — e~ht) « 14,4%.
34. Вертикальный цилиндрический резервуар имеет высоту
й=11,5 м, а его диаметр D = 23 м. Найти время, в течение которого

536
Задачи для самостоятельного решения
нефть, заполняющая резервуар, вытечет из него через круглое
отверстие радиуса 15 см, сделанное в дне?
35. Два вертикальных резервуара, каждый из которых имеет
4 м высоты и 4 м в диаметре, поставлены рядом и соединены у дна
коротким круглым шлангом диаметра 1/6 м. Если вначале один
резервуар наполнен водой, а другой пуст, то по истечении какого
времени вода будет находиться в них на одном уровне?
Принимается, что скорость протекания воды через шланг определяется как
скорость воды, вытекающей из отверстия под тем же давлением.
Ответ: t=7,27 мин.
36. В резервуар глубиной 4 м, имеющий в поперечном сечении
квадрат со стороной 6 м, втекает нефть со скоростью 10 ж3 в 1 мин.
В какое время резервуар будет наполнен, если в то же время нефть
вытекает из него через квадратное отверстие со стороной в 1/12 м,
имеющееся в дне?
Ответ: t=li,7 мин.
Дифференциальное уравнение задачи
{-g-—o,6 f2gil (-1- )2} dt=36dh.
37. На дне котла, имеющего форму полушара радиуса R=l м,
образовалась щель площадью σ=0,25 см2. Найти время истечения
всей воды из котла.
Ответ: Т= ———· I/ —— = 7 ч 19 мин 36 сек.
15σ 1 2g
38. За какое время вытечет вода через отверстие 0,5 см2 на дне
конической воронки высотой /ι=10 см с углом при вершине сс=60°?
Ответ: t=9,9 сек.
39. Найти зависимость давления воздуха ρ от высоты h, если
известно, что это давление на уровне моря (h=0) равно 1 кГ'/см2
и на высоте 500 м равно 0,92 кГ/см2.
Ответ: p=e-o,oooi7ft.
40. Некоторое количество нерастворимого вещества содержит
в своих порах 10 кг соли. Подвергая вещество действию 90 л воды,
нашли, что в течение 1 ч растворилась половина содержавшейся
в нем соли. Сколько соли растворилось бы в течение того же
времени, если количество воды удвоить? Скорость растворения
пропорциональна количеству нерастворенной соли и разности между
концентрацией раствора в данный момент и концентрацией
насыщенного раствора (1 кг на 3 л).
Ответ: дифференциальное уравнение задачи

/. Дифференциальные уравнения первого порядка
41. Металлический шар, температура которого 12° С, погружен
в воду с температурой 0° С. В течение 8 мин шар охлаждается до
9° С. Найти время охлаждения шара до 6° С.
Ответ: tzal9 мин.
42. По закону Ньютона скорость охлаждения тела в воздухе
пропорциональна разности температур тела и воздуха. Известно,
что температура тела в течение 20 мин падает от 100 до 60° С.
Температура воздуха равна 20° С. Через сколько времени (от момента
начала охлаждения) температура тела понизится до 25°?
Ответ: t= 1 ч 20 мин.
43. Стена (коэффициент теплопроводности £=0,0015) .имеет
30 см толщины. Найти зависимость температуры от расстояния
точки до наружного края стены, если температура равна 20° С на
внутренней и 0° С на внешней поверхности стены. Найти также
количество тепла, которое стена (на 1 м2) отдает наружу в течение суток.
2
Ответ: 7= — х; 864 000 кал.
О
44. Цилиндрический сосуд высотой Я=20 см и с площадью дна
S= 120 см2 имеет на дне отверстие площадью σ=0,4 см2. Найти
время истечения через отверстие воды, заполняющей сосуд.
Указание. Скорость истечения u=y2g/i, где h — глубина
погружения отверстия в данный момент.
,_^Т/2Я.
σ V σ
η τ ~ 1/2Я ,
Ответ: 7 = ·— |/ —- « 1 мин.
8
45. Коническая воронка с радиусом верхнего отверстия
jR==20 см, радиусом нижнего отверстия г=0,3 см и высотой h=
= 20 см наполнена водой. За какое время вода вытечет из воронки?
_ _ 2R2 -ι/ h
Ответ: Τ = —-— Ι/ ——ж65 сек.
46. Допустим, что в вертикальном воздушном столбе давление
на каждом уровне обусловлено давлением вышележащих слоев.
Найти зависимость давления от высоты, если на уровне моря это
давление равно 1 кГ/см2, а на высоте 500 м — 0,92 кГ/см2.
Указание. Использовать закон Бойля — Мариотта, в силу
которого плотность газа пропорциональна давлению.
Ответ: дифференциальное уравнение задачи
dp=—kpdh,
откуда
ρ _ g-0,00016h_

538
Задачи для самостоятельного решения
47. Если движение воздуха от одного уровня к другому
совершается адиабатически (т. е. теплота не приобретается и не теряется),
то давление p=kpn, где ρ — плотность и k — постоянная. Допуская
адиабатический характер распространения воздуха, найти высоту
атмосферы, если на уровне моря плотность воздуха составляет
0,0013 Г/см3, а давление 1 кГ/см2.
Ответ: дифференциальное уравнение задачи
ι
„Τι
dp= — -Z—dh.
1
Высота атмосферы 26,923 км.
48. Найти форму зеркала, отражающего пучок лучей,
стремящихся сойтись в одной точке так, что после отражения все лучи
пересекаются в некоторой другой точке.
Ответ: гиперболоид вращения. Дифференциальное уравнение
задачи dr—dr'=0.
49. Металлическое ядро (удельный вес γ=7,25 Г/см3) радиусом
2 см падает с высоты 1200 м. Через какое время и с какой скоростью
ядро достигнет Земли? Задачу решить, предполагая отсутствие
сопротивления воздуха и при сопротивлении воздуха,
пропорциональном квадрату скорости падения.
Указание. На тело, падающее в пустоте, действует сила
притяжения Земли, которая сообщает ему ускорение g=9,81 м/сек2.
При сопротивлении воздуха возникает усилие,
пропорциональное квадрату скорости падения.
При расчете принять коэффициент пропорциональности
2G
где G — сила тяжести тела, кГ; б — 1,293 — сила тяжести 1 м3
воздуха, кГ; F — перпендикулярное к направлению движения
наибольшее поперечное сечение тела, м2; ψ — постоянное число, зависящее
от формы тела; для шара ψ = 0,5.
Ответы: 1) t= 15,64 сек, v=gt= 153,4 м/сек;
2) ί=21,04 сек, и=75,92 м/сек.
50. Деревянный ч шар (удельный вес у = 0,9 Г/см3) радиусом
г=3 см падает с высоты: 1) Л= 100 м, 2) h=20 м. Найти время
падения и конечную скорость.
Ответы: 1) < = 5,21 сек; υ = 30,19 м/сек;
2) t=2,08 сек; и = 18,16 м/сек.

/ Дифференциальные уравнения первого поряака
51. Найти суточную потерю теплоты (в кал) паропроводом,
транспортирующим пар температурой 100° С. Длина паропровода 20 м,
диаметр 30 см. Паропровод защищен слоем бетона толщиной 10 см.
Температура внешней поверхности бетона 35° С. Найти также
температуру в середине бетонного слоя (принять коэффициент
пропорциональности й=225-10-5 кал/см-град■ сек).
Указание. Количество (кал/сек) выделяемой источником
площадью А см2 теплоты
где χ — радиус цилиндрического источника теплоты, и —
температура источника по Цельсию, k — коэффициент пропорциональности.
du
Величина —-— представляет собой температурный градиент.
&л
Ответ: 3,1 МО8 кал/сутки; 63,4°С.
52. Сферический резервуар диаметром D=2,75 м наполнен
водой. Найти время, необходимое для истечения всей воды через
круглое отверстие в днище диаметром d = 3,7 см. Коэффициент
пропорциональности й=4,8.
Ответ: 57,6 мин ?» 58 мин.
53. Горизонтальный цилиндрический резервуар имеет длину
6 м и диаметр 4 м. Найти время истечения воды из резервуара через
круглое отверстие радиуса 1/12 м, сделанное в дне.
Ответ: 18,5 мин.
54. Количество света, поглощающегося при прохождении через
тонкий слой воды, пропорционально толщине слоя и количеству
света, падающего на его поверхность. Если при прохождении через
слой толщиной 3 м поглощается половина первоначального
количества света, то какая часть света дойдет до глубины 30 м7
0твет:ж·
55. По шероховатой наклонной плоскости, составляющей с
горизонтом угол сс=30°, спускается тяжелое тело без начальной
скорости. Определить, в течение какого времени Τ тело пройдет путь
длиной L=39,2 м, если коэффициент трения μ=0,2.
Ответ: уравнение движения
dx . . . . Л
m——· — mg(sm α—μ cos α) =0;
■-ν-
2L
= 4,94 «5 сек.
g(s'ma—μ cos α)

.40
Задачи для самостоятельного решения
56. Определить предполагаемое количество населения
Украинкой ССР и Белорусской ССР на 15 января 2000 г., если известно,
ιτο 15 января 1970 г. в Украинской ССР проживало 47 136 000 чело-
зек и прирост за 1969 г. составил 0,82%, а в Белорусской ССР
троживало 9 003 000 человек и прирост за 1969 г. составил 0,97%.
Ответ: «60,45 млн. чел.; «12 млн. чел.
57. Вычислить предполагаемое на 15 января 2003 г. количество
«селения городов, если известно число их жителей на 15 января
1970 г. и темпы прироста за последние 11 лет (см. таблицу), которые
ю условию будут сохраняться в дальнейшем.
Город
Население
иа 15/1
1970 г.
(в тыс чел.)
Прирост
за 11 лет
(в %)
Ленинград
Киев
Ташкент
Баку (с пригородами)
Харьков
Горький
Новосибирск
Куйбышев
Свердловск
Одесса
Тбилиси
Донецк
Челябинск
Казань
Днепропетровск
Пермь
Омск
Волгоград
Ростов-на-Дону
Уфа
Ереван
Саратов
Рига
Алма-Ата
Фрунзе
Душанбе
Вильнюс
Таллин
Кишинев
Ашхабад
3513
1632
1385
1261
1223
1170
1161
1047
1026
892
889
879
874
869
863
850
821
818
789
773
767
758
733
730
431
374
372
363
357
253
18
47
49
30
28
24
31
30
32
34
27
24
27
30
31
35
41
38
32
41
55
31
26
60
96
65
57
29
65
49
Примечание. 11-летний период принять
за расчетную единицу времени Г, т. е. период
в 33 года составит 3 Т.
58. Естественный прирост населения большого города
пропорционален наличному количеству жителей и промежутку времени.
Кроме того, население города увеличивается благодаря мигра-

/. Дифференциальные уравнения первого поряока тч-ыщща
ции: скорость прироста населения этим путем пропорциональна
времени, отсчитываемому от момента, когда население города
равнялось Ло. Найти зависимость числа жителей города от времени
(считая процесс непрерывным).
59. Население колонии животных удваивается в течение 50 дней.
Через сколько дней ее население утроится?
Ответ: 79 дней.
60. Население страны удвоилось в течение 50 лет и составляет
теперь 20 млн. чел. Когда население достигнет 30 млн. чел. и каким
оно будет через 10 лет?
Ответ: через 29 лет; 22 970 000 чел.
61. Население города в течение 50 лет удвоилось за счет
естественного прироста и составляет 40 000 чел. Определить население
города через 10 лет. Решить также задачу в условиях механического
уменьшения населения на 400 чел. в год.
Примечание. Сначала найти коэффициент пропорциональности
естественного прироста.
Ответ: 50 240 чел.; 41 660 чел.
62. Служащий 30-летнего возраста планирует в течение 20 лет
откладывать по 50 руб. в месяц, с тем чтобы иметь к моменту
выхода на пенсию (через 30 лет) 12 000 руб. Какую сумму необходимо
ему ежемесячно откладывать в сберегательную кассу на
3-процентный счет, чтобы выполнить намеченное?
63. Как долго необходимо держать 1 руб. на 3-процентном счету
в сберегательной кассе, чтобы эта сумма удвоилась?
Ответ: ί«23 года.
64. Отец новорожденного ребенка планирует накопить до
момента достижения ребенком 20-летнего возраста 3000 руб. путем
ежемесячных взносов в сберегательную кассу на 3-процентный
вклад. Какую ежемесячную сумму он должен вносить, чтобы по
истечении срока накопить желаемые деньги?
65. Некто для поступления в жилищно-строительный
кооператив одалживает 3500 руб. с условием, что погашение долга будет
производиться постепенно путем открытия на имя
одалживающего 3-процентного вклада в сберегательной кассе и ежемесячного
вклада должником определенной суммы до накопления полного
размера долга. Каков ежемесячный размер вклада, когда будет
погашен долг и сколько в действительности денег отдаст должник из
собственных средств?
66. Какой формы должен быть хирургический нож, чтобы боль,
причиненная во время операции, была минимальной, т. е. чтобы

542
Задачи для самостоятельного решения
было повреждено минимальное количество тканей и кровеносных
сосудов?
Ответ: p=Ceft<f.
67. Радиус Луны #л=1740 км. Ускорение силы тяжести на ее
поверхности около 0,165g, где g — ускорение силы тяжести на
поверхности Земли. Определить начальную скорость запуска ракеты
с Луны.
Ответ: 2,41 км/сек.
68. Определить с точностью до двух значащих цифр скорости
запусков ракет для каждого небесного тела (исходные данные
указываются ниже).
Небесное
тело
Ускорение силы
тяжести на
поверхности
Радиус, км
Венера 0,85g 6 100
Марс 0,38g 3 400
Юпитер 2fig 69 200
Солнце 28g 625 000
Ответы: 10,1 км/сек; 5 км/сек; 60 км/сек, 612 км/сек.
69. Найти кривую, проходящую через точку (4, 6), для которой
длина подкасательной равна среднему арифметическому координат
точки касания.
Ответ: длина подкасательной равна у ——.
Кривая 3 (х—у)2—2у=0.
70. Кривая имеет в точке с абсциссой 2 наклон 45°. Отрезок,
отсекаемый касательной на оси ординат, равен квадрату абсциссы
точки касания. Найти уравнение этой кривой.
Ответ: х2—Бх-\-у=0.
71. Касательная к кривой на оси ординат отсекает отрезок,
равный радиус-вектору точки касания. Найти уравнение кривой, если
она проходит через точку (—УТД 3/2).
Ответ: 1) х2= — 10t/+25; 2) х2=4у+4.
72. На оси χ касательная отсекает отрезок, равный длине
касательной. Найти уравнение кривой, если она проходит через точку
(-2,4).
Ответ: х2-\-у2—5у=0.

/ Дифференциальные уравнения первого порядка
543
73. Поднормаль равна отрезку, отсекаемому касательной на
оси у. Найти уравнение кривой, если она проходит через точку (1, 1).
Ответ: х=у(\-\-\п у).
74. Отрезок касательной от точки касания до оси ординат равен·
отрезку, отсекаемому этой касательной на оси ординат. Найти
уравнение кривой, если она проходит через точку (2, 4).
Ответ: х2+у2— 10х=0.
75. Радиус-вектор любой точки кривой равен отрезку,
отсекаемому на оси ординат нормалью, проведенной через эту точку. Найти
уравнение кривой, если она проходит через точку (4, 3).
Ответ: I) х2—\у—4 = 0; 2) х2+\6у—64 = 0.
76. Отношение квадрата радиус-вектора любой точки кривой
к отрезку, отсекаемому на оси χ нормалью, проходящей через эту
точку, равно половине абсциссы точки. Найти уравнение кривой,
если она проходит через точку (3, 4).
Ответ: 25х4—81(х2+у2) =0.
77. Квадрат радиус-вектора любой точки кривой равен отрезку,
отсекаемому па оси ординат нормалью, проведенной через эту точку.
Найти уравнение кривой, если она проходит через точку (3, 0).
Ответ: х2+4у2—9е2У.
78. Кривая в точке с абсциссой /2 наклонена к оси абсцисс под
углом 45°. Отрезок, отсекаемый касательной на оси абсцисс, равен
длине касательной. Найти уравнение кривой.
Ответ: х2-\-у2-\-4у—0; х2-\-у2—Ау=0.
79. Найти ортогональные траектории семейства кругов:
х2+у2+2пу=0,
где η — произвольный параметр.
Ответ: х2+у2—Сх=0.
80. Найти ортогональные траектории семейства кривых у=ахп,
где а — произвольный параметр.
Ответ: х2-\-пу2=С.
81. Найти ортогональные траектории семейства кривых х3—
—Зху2-\-Ь = 0, где Ъ — произвольный параметр.
Ответ: у3—Ъхгу—С = 0.
82. Аквалангист переплывает реку шириной 100 м, все время
направляясь на дерево, которое стоит на другом берегу напротив
места старта. Он плывет со скоростью 3 м/сек. Найти уравнение
траектории аквалангиста, если течение будет сносить его вниз по
реке со скоростью 1 м/сек; 3 м/сек; 4 м/сек.

544
Задачи для самостоятельного решения
Ответ: j,=5o[( JL)"1- (JL·)'1· ] ; *.=-200<»-50);
-»[(шГ-(ж)'"1.
83. Летчик ведет самолет в направлении к городу,
находящемуся в 400 км западнее взлетной площадки. Ветер дует с юга со
со скоростью 20 км/ч, скорость самолета 300 км/ч. Найти уравнение
траектории полета.
14 _16_
Ответ: у=200 [(^) " - (^) " ] .
84. В любой момент t скорость υ точки превышает среднюю
скорость за время t с начала движения на постоянную величину k.
Найти закон движения, если при i=0 s = So=0, а при t=\ s = k.
Ответ: s = kt(\nt+l).
85. В любой момент t скорость υ точки превышает среднюю
скорость за время t с начала движения на величину квадрата
пройденного за это время пути. Найти закон движения, если при ί=0
s = so=0 и у=уо=1.
Ответ: s=
2—t2'
86. Скорость υ, путь s и время t связаны уравнением
v-\-s cos i=sin t cos t.
Найти закон движения, если при t=0 v = 0.
87. Капля сферической формы с начальной массой Λί г,
свободно падая в воздухе, равномерно испаряется и теряет ежесекундно
m г. Сила сопротивления воздуха пропорциональна произведению
скорости капли на площадь ее поверхности. Плотность жидкости у.
Найти зависимость скорости движения капли от времени,
прошедшего с начала падения, если в начальный момент времени ее
скорость равна нулю. Принять, что коэффициент пропорциональности
k Φ m.
t
s . ρ s
Ji l/ — <M-mi>2 \ - — 1/ — ι**-***
Ответ: v=ge2m V У J e 2m Г ν2 at.
о
88. Разность потенциалов на зажимах катушки равномерно
падает от величины внешней электродвижущей силы £Ό=2 в до вели-

л. Дифференциальные уравнения второго поряока 545
чины £Ί=1 в в течение 10 сек. Сопротивление катушки 0,12 ом,
коэффициент самоиндукции 0,1 гн. Найти силу тока в конце десятой
секунды, если в начале опыта она составляла 16 — а.
о
Ответ: дифференциальное уравнение задачи
*-£"+«'=*■
ί(10) = 9,03α.
89. Найти кривую, касательная в любой точке которой образует
а.
с осями координат треугольник постоянной площади —-.
а
Ответ: xw= -—.
4
90. Найти кривую, если отрезок касательной, заключенный
между осями координат, равен а.
Ответ: астроида χ2/3+ί/2/ι=α2''3·
91. Найти кривую, если перпендикуляры, опущенные из двух
данных точек на касательную, имеют постоянную сумму 2s.
Ответ: x2-\-y2=s2.
92. Найти кривую, если геометрическое место оснований
перпендикуляров, опущенных из данной точки Ρ на касательные к
кривой, есть окружность радиуса г, а расстояние точки Ρ от центра
круга равно с.
Примечание Начало координат надо поместить в центре О данной
окружности, за ось абсцисс принять ОР. Координаты основания перпендикуляра
будут
р(рх~у)+с _ рх-у-ср
1+Р2 ; η~ 1+Р2
Подставляя эти значения в уравнение окружности я2+(/2 = а2, получим
уравнение Клеро.
X2 У2
Ответ: —— -\— = 1; дифференциальное уравнение
у=рх-1г2(1+р2)-с2, р=у'.
II. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ВТОРОГО ПОРЯДКА
93. Материальная точка массой m движется по прямой линии
tnk2
к центру, притягивающему ее с силой ——, где г — расстояние
точки от центра. Движение начинается с состояния покоя при г=а.
Найти время достижения точкой центра.
а2
Ответ: г= —т=-

546
Задачи для самостоятельного решения
94. Тяжелое тело скользит по шероховатой наклонной
плоскости, причем угол наклона равен а, а коэффициент трения μ. Найти
закон движения, если начальная скорость равна нулю.
Ответ: s= — g(s'm α—μ cos α)/2.
95. Найти время достижения Земли метеором, падающим с
высоты 400 000 км.
Ответ: дифференциальное уравнение задачи
d2r k
—τϊγ-= τ-, причем £=£(6400)2; t&\22 4.
96. Цепь переброшена через гладкий гвоздь. С одной стороны
свисает часть цепи длиной 8 ж, а с другой стороны — длиной 10 м.
При скольжении ускорение пропорционально разности длин частей
цепи, свисающих с обеих сторон. Через какое время сосколь-"
знет цепь?
Ответ: /= —= In(9+ /80) «2,76 сек.
ig
97. Материальная точка движется по прямой линии к точке А
таким образом, что ускорение ее равно kr~4\ В начальный момент
t=0 движущаяся точка находилась в покое на расстоянии / от
точки А. Когда она достигнет точки Л?
98. Сопротивление, оказываемое воздухом падающему телу,
вызывает отрицательное ускорение —kv2, где υ — скорость тела,
a k — постоянная. Показать, что снаряд, выпущенный вертикально
вверх со скоростью υ ι, возвратится к исходной точке со скоростью
-у.
gvf
g+kv.
где g — ускорение силы тяжести.
Указ а н и е. Дифференциальное уравнение движения тела
вверх
d2s dv
m^T-"lv—=-mg-kv2.
Падение происходит по закону
mv —— = —mg-\-kv2.
99. Катер движется в спокойной воде со скоростью у = 10 км/ч.
На полном ходу его мотор выключается и через 20 сек скорость
катера уменьшается до ι>ι=6 км/ч. Сопротивление воды движению

//. Дифференциальные уравнения второго порядка
nfc
катера пропорционально его скорости. Найти скорость катера черв!
2 мин после остановки мотора.
Ответ: к2=0,467 км/ч.
100. Цепь длиной / лежит на гладком столе так, что ее конец
длиной Ъ свисает над краем стола. Из этого положения цепь им·
чинает скользить вниз. Через какое время цепь соскользнет
со стола?
Ответ: /== Ι/ — In — ·.
V g b
101. Bee 1000 м телеграфной проволоки 40 кГ. Укрепленные
концы проволоки находятся на расстоянии 120 м, а середина
провисла на 3 м. Определить горизонтальное натяжение в нижней точке
проволоки.
Ответ: Я==24 кГ.
102. Найти закон движения тела, свободно падающего без
начальной скорости, допуская, что сопротивление воздуха
пропорционально квадрату скорости и предельная скорость равна 75 м/сек.
gt_ gt
_ (75)2 с еп+е~пл
Ответ: s= -——\п\ -; У .
g I 2 )
103. Тело медленно погружается в жидкость. Сопротивление
пропорционально скорости. Найти закон движения тела,
погружающегося в жидкость без начальной скорости.
tn2s — — tns
Ответ: s=—-(e mi—\)-\ $-t.
№ к
104. Частица массой в 1 г движется по прямой к точке А под
действием некоторой силы притяжения, пропорциональной
расстоянию ее от точки А. На расстоянии 1 см действует сила 0,1 дн.
Сопротивление среды пропорционально скорости движения и равно 0,4 дн
при скорости 1 м/сек. В момент / = 0 частица расположена на 10 см
правее точки А и скорость ее равна нулю. Найти зависимость
расстояния от времени и вычислить это расстояние для t=3 сек
(с точностью до 0,01 см).
Ответ: s = e-°·2' [ 10 cos (0,245ί) +8,16 sin (0,245ί) ];
s|i=3«7,07 см.
105. Вагон на прямолинейном горизонтальном участке
железнодорожного пути приходит в движение вследствие силы давления
ветра, пропорциональной квадрату скорости ветра относительно
вагона. Найти уравнения движения вагона при постоянной скорости

548
Задачи для самостоятельного решения
ветра и силе трения, пропорциональной его весу. Исследовать
изменение скорости движения вагона с увеличением времени.
d2s ., / ds \2
В A—B+(A+B)e2Dt
d2s I ds \2
Ответы: 1) m —k2 \ a -—-J—K2mg;
υ = α-
k B—A+(A+B)e2Dt'
m , (A+B)em-(A—B)e-Dt
s=at rr-ln-
k2 2B
где A=ak, B=Kimg, D=kly
2) lim t) = a
m
В
106. Материальная частица массой m движется по прямой
линии к центру О, которым она отталкивается с силой,
пропорциональной расстоянию ее от центра. В начальный момент (t=0) частица
находится от центра на расстоянии Ь и имеет скорость v0,
направленную к центру О. Найти закон движения частицы.
Ответ: х= ±[( Ь+ -£-) е*+ ( Ь-^-) е-ы] .
107. Найти закон падения тела в воздухе, считая сопротивление
воздуха пропорциональным квадрату скорости движения, если в
начальный момент тело находилось в состоянии покоя.
m
,·1
/ m _|_e ' I
2
1 gft
I m
Ответ: s=
108. На двухопорную балку О А длиной / действует
сосредоточенная сила Р, приложенная в середине балки. Найти стрелу
прогиба балки.
Р13
0твет: н=-шг-
109. На консольную балку длиной / м с закрепленным концом О
действуют равномерно распределенная нагрузка q кГ/м и
сосредоточенная сила Ρ κΓ, приложенная к концу балки А. Составить
уравнение упругой линии и определить прогиб балки в точке А (рис. 145).
Жесткость балки EJ.
г. η р ί ι 2 χ3 \ , Я1 I № х3 , I3 \
Ответ: 1) ы=—— ( 1х2 —- ) + -^— I — ττ + —ζ) '.
; у 9.FJ \ 3 / ' 9.EJ \ 2 3 т 2/'
2EJ \ 3 ' ' 2EJ \ 2 3 ' 12
I3
3EJ
Is I 3ql \
2) прогиб конца балки Ла = орт \ ^Ч о—).

//. Дифференциальные уравнения второго порядка
ПО. Консольная балка длиной / (рис. 146) нагружена ранни·
мерно распределенной нагрузкой интенсивности q на погонную
единицу длины*. Составить уравнение упругой линии и определить
величину прогиба h конца балки В. Жесткость балки EI.
Ответ: 1) у= Я (6/2х2—4/хЗ+х*);
24£У
2) прогиб конца балки hB=
JUL
8EJ
•tojJDIttl
А
,A,)iAi\plf\J^i>]±\^i ■&>&>»/)> Л >*>>\>>\j\i)/A/b/y.
А
y-ffX)'?
A <*.'
Рис 145
111. Плотина высотой Н=2 м состоит из ряда вертикальных
деревянных столбов (рис. 147) с дощатой обшивкой, закрепленных
в нижних концах. Расстояние между осями двух смежных столбов
с=1 м. Момент инерции площади поперечного сечения столба от-
ПопоНино Высоты
Бшти
Рис. 146
носительно нейтральной оси /=9000 си4. Составить уравнение
упругой линии деформированного под напором воды столба и определить
прогиб h верхнего конца столба, если вода доходит до верхнего края
плотины. Модуль упругости дерева Е=\0Ъ кГ/см2.

550
Задачи для самостоятельного решения
Указание. Давление, передаваемое элементарной полоской
высотой d\ на каждый столб, будет q=c(H—Qd%.
Ответ:
г/= -гтт^т [{н-х)*+ьнь-н*},
60£/Я2
h =
QtP_
1беГ
1 ,2 см,
где Q — общая нагрузка столба.
112. Материальная точка массы m притягивается каждым из
двух центров с силой, пропорциональной расстоянию х. Крэффи-
ilpaBeHb воды
±
If
'ЛГ
■r-t
— _ и/.;
Τ
Рис 147
>'W<№
У
циент пропорциональности равен k, расстояние между двумя
центрами 2Ь. В начальный момент (/ = 0) точка находится на линии
соединения центров на расстоянии х=с от ее середины. Начальная
dx TI „
скорость—-— равна нулю. Наити закон движения.
Ответ: дифференциальное уравнение движения (начало
координат в середине расстояния между центрами)
ач
*_=*(*-
-x)—k(b+x)=—2kx.
Закон движения
: С COS ■
№4
113. Тело совершает 90 колебаний в минуту. В течение 15 сек
амплитуда колебаний уменьшается вдвое. Найти дифференциальное
уравнение движения.

П. Дифференциальные уравнения второго поряОп,,
Указание. Движение характеризуется законом
x=Ae-atcos($t+Q).
Согласно условию, Т= -—— или β = 3π; далее
Ρ
15α ! 1П 2
g-15a_ —- И CC =
2 15 '
d^x dx
Ответ: ——- +0,092—— +88,8x=0.
at'· at
114. На тело, сила тяжести которого 10 кГ, действует упругая
сила, стремящаяся вернуть его к положению устойчивого
равновесия. Сила пропорциональна смещению и равна 2 кГ при смещении
в 1 м. Сопротивление среды пропорционально скорости. Амплитуда
после трех колебаний уменьшается в 10 раз. Найти период
колебаний.
Указание. Предполагаем закон движения в форме, как.
в предыдущей задаче. Дифференцируя, находим
d2x dx
■ 2α~- + (α2+β2)χ=0.
df2- ' dt
С другой стороны, по условию
10
е
Сравнивая, получаем
кроме того,
е-а
откуда
d2x , dx , „
άμ +k dt +2*=0.
α2+β2= JL
-a *L ,
3T — e β —
_ 10 '
Ответ: период колебаний
2π
1 -. / С
= -3-УуУ(6я)2+1пМ0.
115. Круглый диск радиуса а, погруженный в жидкость, вращя-
1гтся вокруг оси, проходящей через центр диска перпендикулярно
к его плоскости. Сопротивление трения равно kv на единицу
площади в каждой точке диска, где ν— скорость точки, Л— постоянная.

S52
Задачи для самостоятельного решения
Найти закон движения при начальной угловой скорости ωο,
допуская, что момент силы трения, обусловленный осью, равен постоянной
величине К.
пгп
Указание. Момент инерции диска равен —-—, где m — его
масса.
dQ
Элементарный момент силы трения есть —kr-——r-rdrd(p,
где rdrdy ■— элемент площади диска в полярной системе координат.
Полный момент равен
—k ——■ \ dw I r3dr= — α4 ——.
dt l ψ1 2 dt
Ответ: дифференциальное уравнение движения с учетом
трения
ma2 d2Q kn , dQ
2 dt2 2 dt
πΑα2
ml , 2Κ \ ,, * 2К ±
116. Если ось вала турбины расположена горизонтально,
а центр тяжести диска, насаженного на вал, не лежит на оси, то
прогиб у (рис. 148) оси вала при вращении удовлетворяет
уравнению
d*y
+ ( ω2) y=g cos ωί4-ω2β,
dt2 \ ma
где m — масса диска, a — постоянное число, зависящее от рода за
крепления концов А и В, ω — угловая скорость вращения, е — экс
центриситет центра тяжести диска. Найти общий интеграл этоп
уравнения.
Ответ: если >ω2, то
та
а
у— С^ cos Ы+Сг sin kt-\- -—2—— cos ωί-\-
eco2
ft2—ω2 r k2 '
где
k2= ©2',
та
если <ω2, то
та
У=С^+С2е^~ -^ cos ω/- -^

//. Дифференциальные уравнения второго порядки
где
№--
■■ω'
ma
117. Колонна длиной / неподвижно закреплена в нижнем конце.
Под действием силы Ρ верхний конец отклонился на расстояние α
от своего первоначального положения. Найти изгибающий момент
и форму изогнутой колонны.
Центр о <>
тяжести диет
Рис. 148
Проверить, что критическая нагрузка
крит-
№■
Указание. Нижний конец колонны принимаем за начала
координат, колонну — за ось х.
dy
Полагая р-
изгиба
dx'
получаем дифференциальное уравнение
EJ-Й- =Е1р. ^~ =М=Р(а-у).
dx*
dy
Ответы: 1) у=а ( 1—cosl/ —=у- χ J ;
2) так как колонна выдерживает груз при х=1, у=а, то
Ρ -Ε/(-±-Υ
118. Горизонтальная трубка вращается около вертикальной оси
с постоянной угловой скоростью ω. Шар, помещенный внутри
трубки, скользит по ней без трения. Найти закон движения шара, если
в начальный момент он находится на оси вращения и имеет скорость
ν0 (вдоль трубки).
Указание. Дифференциальное уравнение движения
d4
~dF
— (й"Г.

554
Задачи для самостоятельного решения
Начальные условия: г=0, -—— —υ0 при t=0.
Ответ: г= ~- [βωί+β-ωί].
Ζ (О
119. Материальная точка массы m притягивается каждым из
двух центров, лежащих на прямой, с силой, пропорциональной
расстоянию. Множитель пропорциональности равен k. Расстояние
между центрами равно 2Ь. В начальный момент точка находится на
линии соединения центров на расстоянии с от ее середины.
Начальная скорость равна нулю. Найти закон движения.
Ответ: дифференциальное уравнение движения (начало
координат в середине между центрами)
d2x
m ■ = k(b—x)—k(b-\-x)=—2kx.
dx τ/ 2k
Начальные условия х=с, ——=0 при ί=0; x=acos\/ 1.
120. Тело, сила тяжести которого 2 кГ, брошенное вертикально
вверх со скоростью 20 м/сек, испытывает сопротивление воздуха,
которое при скорости υ м/сек равно 0,04и кГ; g=9,81 м/сек2. Найти,
через сколько секунд тело достигнет наивысшего положения.
Ответ: дифференциальное уравнение задачи
d2s ds
m~dr+k~dT+m8=Q'' >=^сек- ■
121. Тело, брошенное с начальной скоростью vo под углом а
к горизонту, движется под влиянием силы тяжести Ρ и
сопротивления воздуха R. Определить наибольшую высоту h тела над
уровнем начального положения, считая сопротивление
пропорциональным первой степени скорости: R=kPv.
Ответ: дифференциальное уравнение задачи
п= ; г- 1η(1+βϋο sin α).
gk gk2
122. Тело, сила тяжести которого 1,96 кГ, подвешено на
пружине, которая силой 1 кГ растягивается на 20 см, при движении
встречает сопротивление, пропорциональное первой степени скорости и
при скорости ] см/сек равное 0,02 кГ. В начальный момент пружина

///. Системы дифференциальных уравнений первого порядк
растянута из положения равновесия на 5 см, и тело приходит и ι ни
жение без начальной скорости. Найти закон движения тела.
Ответ: дифференциальное уравнение задачи
m-dtr+k4T+cx=0>
x=5e~5t(5t+\) см.
123. Температура па поверхности сферы радиуса α задана
функцией /(φ). Ввиду симметрии результирующее распределение
температуры и (г, φ) является функцией лишь г и φ, т. е. не зависит от
сферической координаты Θ. Используя метод разделения
переменных, определить распределение температуры по всей этой сфере.
Ответ:
ОО
и (г, φ) = Σ CnrnPn (cos φ),
η=0
где
я
2η-\-\ С
Cn=~~2tfT~J f(cp)sin<pP„(coscp)dcp.
124. Найти числовые значения радиусов линий узлов Иг и Из
колеблющейся круговой мембраны при /?=1.
Ответ:
и*. г= — =0,43565,
аг
и3: г= — =0,27789,
аз
г= — =0,63788.
а3
Ш. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ
ПЕРВОГО ПОРЯДКА
125. В химической реакции вещество с разлагается на два
вещества: χ и ί/.'Скорость образования каждого из продуктов
разложения пропорциональна наличному количеству вещества с. Найти
зависимость χ и у от времени, если в начале процесса с=1, х=0,
1 1 3
г/=0, а по истечении 1 ч с= —, х= -^-, у= -г-.
zoo
Ответ: х= —■ (l-2'')i //-= \ (1-2-<).

556
Задачи для самостоятельного решения
126. В химической реакции вещество χ преобразуется в
вещество у со скоростью, пропорциональной наличному количеству х.
В то же время образовавшееся вещество у обратной реакцией
переходит в вещество χ со скоростью, пропорциональной наличному
количеству у. Химический анализ дал такие результаты:
Ί
X
У
0
10
0
3
6
4
■°°
5,5
4,5
Найти зависимость х и у от времени ί.
Ответ: г/=4,5(1—е-0·7324'); χ=10—у.
127. Преобразование радиоактивных: веществ происходит со
скоростью, пропорциональной их наличному количеству. RaB
преобразуется^ RaC с такой скоростью, что половина количества RaB
оказывается преобразованной по истечении 27 мин. В свою очередь
половина данного количества RaC преобразуется в другое вещество
в течение 19,5 мин. Принимая первоначальное количество RaB за
единицу, найти количество RaB и RaC по истечении 1 ч.
Ответ: RaB = 0,124; RaC = 0,249.
128. Скорость роста культуры микроорганизмов
пропорциональна их количеству и количеству питательных веществ (коэффициент
пропорциональности равен k). Скорость убывания питательных
веществ пропорциональна наличному количеству микроорганизмов и
времени (коэффициент пропорциональности равен kx). В начале
опыта в сосуде имелось А0 г микроорганизмов и В0 г питательных
веществ. Найти зависимость количества А микроорганизмов и
количества В питательных веществ от времени.
Ответ:
1—$eakt
а' l+$eakt '
где
α=ρ,+ψΑι, р=л±

IV. Системы дифференциальных уравнений второго порччп,
IV. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНКНИН
ВТОРОГО ПОРЯДКА
129. Снаряд вылетает из орудия со скоростью υ о, направленной
под углом а, к горизонту. Пренебрегая сопротивлением воздухе,
найти закон движения снаряда.
Ответ: x=t;o^cosa; y=v0t sin а, — gt2.
130. Снаряд вылетает из орудия со скоростью 800 м/сек под
углом 45° к горизонту. Найти, пренебрегая сопротивлением воздуха,
наибольшую высоту, на которую поднимается снаряд, и место его
падения.
Ответ: /imax=16,3 км; s«65 км.
131. Материальная точка Μ массы m в начальный момепг
(^=0) имеет скорость υ0, перпендикулярную к прямой,
соединяющей начальное положение Μ с центром О, который притягивает
точку Μ с силой, прямо пропорциональной расстоянию от центра.
Найти траекторию движения точки М.
х2 и2
Ответ: эллипс—— + · г~ = 1·
а Ш
ЛИТЕРАТУРА
1. Г орт В Дифференциальные уравнения Л.—Μ , 1933.
2. Ε ρ у г и н Н. П. Книга для чтения по общему курсу дифференциальных
уравнении Минск, 1972
3 Ε ρ у г и н Н. П. О продолжимости решений дифференциальных уравнений
«Прикладная математика и механика», 1951, т. 15, № 1, сгр 55—58.
4. Камкэ Э. Справочник по обыкновенным дифференциальным уравнениям.
М, 1965.
5. К а м к э Э. Справочник по дифференциальным уравнениям в частных
производных первого порядка. Μ , 1966.
6. Колобов А. М, Черенкова Л. П. Избранные главы высшей
математики. Минск, 1967.
7 Креер Л. И. Сборник упражнений но дифференциальным уравнениям.
Μ , 1940.
8. Матвеев Η. Μ Методы интегрирования обыкновенных
дифференциальных уравнений. Μ , 1963.
9. Μ а т в е е в Η. Μ. Сборник задач и упражнений по обыкновенным
дифференциальным'уравнениям. Минск, 1970
10. Пономарев К. К· Составление и решение дифференциальных
уравнений инженерно-технических задач. М., 1962.
11. С м и ρ н о в В И. Курс высшей математики Т. III. Л.—М., 1958.
12. С τ е π а н о в В. В. Курс дифференциальных уравнений. М., 1959.

ОГЛАВЛЕНИЕ
Предисловие
ГЛАВА I ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
1 Дифференциальные уравнения . ,
2 Классификация дифференциальных уравнений
3 Общее семейство решений, частное и особое решения
4 Элементарные дифференциальные уравнения
5 Выделение индивидуальных решений .
6 Построение решения в виде степенного ряда
S 7 Метод последовательных приближений . ,
§ 8 Продолжение решений ... , ,
ГЛАВА 11 СОСТАВЛЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ПО УСЛОВИЯМ
ПРИКЛАДНЫХ ЗАДАЧ ..,,,.,
§ 1 Общие принципы , , . . , , ,
§ 2 Методика составления дифференциальных уравнений . ,
§ 3 Схема составления дифференциального уравнения
ГЛАВА Ш ЗАДАЧИ, ПРИВОДЯЩИЕ К ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ
ПЕРВОГО ПОРЯДКА, РАЗРЕШЕННЫМ ОТНОСИТЕЛЬНО ПРОИЗВОДНОЙ
§ 1 Притяжение стержня и материальной точки
§ 2 Движение тел постоянной массы
§ 3 Движение тел переменной массы (без учета внешних сил)
§ 4 Растяжение упругой нитн ... ...
§ 5. Работа опорожнения сосудов
6. Изменение яркости света в стеклянной пластине
7. Нагрев тела . , ...
8 Изменение состояния газов в сосудах
ГЛАВА IV ЗАДАЧИ, ПРИВОДЯЩИЕ К ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ
С РАЗДЕЛЯЮЩИМИСЯ ПЕРЕМЕННЫМИ . ,
I
§ 1 Охлаждение тел .,,..,,,,
§ 2 Нагрев тел . , ,
| 3 Распределение температуры внутри тел
§ 4 Брус равного напряжения
§ 5 Давление зерна на стенки хранилища
§ 6 Барометрическая формула и глубинное давление
§ 7 Прямолинейное горизонтальное движение .
§ 8 Вертикальное движение тел
§ 9 Падение тел переменной массы
§ 10 Криволинейное движение (кривая погони)
§ II Вращение тел в жидкости .
§ 12 Закон всемирного тяготения
§ 13 Радиоактивный распад . ....
§ 14 Электрические заряды . ....
§ 15 Поверхность фрезы
§ 16 Трение ременной передачи
§ 17. Истечение жидкости из сосудов
§ 18 Наполнение сосудов
§ 19 Установление уровня в сообщающихся сосудах
§ 20 Кривая депрессии , . ....
Обеднение раствора . . «
Растворение твердых тел . -
Вентиляция производственного помещения
§ 24 Газовые смеси , ...
§ 25 Ионизация газов . , . .
§ 26 Химические реакции
§ 27. Рост населения
§ 28 Процессы роста в природе н производстве
§ 29 Экология популяций
I 30 Плотность муравьев вне муравейника . «
§ 31 Рост денежных вкладов
§ 21
§ 22
§ 23
ГЛАВА V ЗАДАЧИ, ПРИВОДЯЩИЕ К ОДНОРОДНЫМ ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЯМ ПЕРВОГО ПОРЯДКА
§ 1 Изогональные траектории . . ...,.,
§ 2 Геометрические приложения
§ 3 Зеркало, фокусирующее параллельные лучи .....
§ 4 Траектории полета самолетов .... ......
ГЛАВА VI ЗАДАЧИ, ПРИВОДЯЩИЕ К ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ
В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ . .
§ 1 Параболическое зеркало . . ,.»...,
§ 2 Концентрация вещества в жидкости . . . ....
ГЛАВА VII ЗАДАЧИ, ПРИВОДЯЩИЕ К ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЯМ ПЕРВОГО ПОРЯДКА . .... . .
§ 1. Геометрические приложения
§ 2 Движение материальной точки ...
3
5
s
5
6
7
8
10
II
12
13
»
13
16
&
18
26
30
34
35
37
40
43
43
46
48
51
53
55
58
65
81
83
86
88
94
95
99
101
103
108
108
ПО
112
ИЗ
119
120
121
122
133
142
150
157
161
163
гез
165
170
171
17а
ISO
182
184
Ш5
188

Оглавление
т
ill
as№
т
227
337
W
§ 3 Температура охлаждающего тела . I'll
§ 4 Нагрев тела при стационарном теплопотоке . . . Ш
§ 5 Электрические цепи . ■ ... . . - · . (И
§ 6 Рационализаторские предложения . ...
§ 7. Работа сердца ... . .
§ 8 Задача о сигарете .
ГЛАВА VIII ЗАДАЧИ, ПРИВОДЯЩИЕ К СПЕЦИАЛЬНЫМ
ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ПЕРВОГО ПОРЯДКА (УРАВНЕНИЯМ БЕРНУЛЛИ, РИК"
КАТИ, ЛАГРАНЖА И КЛЕРО)
§ 1 Уравнение Бериулли .... . ...
$ 2 Уравнение Риккати . ......
| 3 Уравнение Лагранжа . . . ....
§ 4 Уравнение Клеро .... ....
ГЛАВА IX ЗАДАЧИ, ПРИВОДЯЩИЕ К ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ
ВТОРОГО ПОРЯДКА, РАЗРЕШЕННЫМ ОТНОСИТЕЛЬНО ВТОРОЙ
ПРОИЗВОДНОЙ (у"=С) . . . .
§ I Скольжение тела под наклоном
§ 2 Движение в горизонтальной плоскости при сопротивлении, пропорциональном
силе тяжести .... ·
§ 3 Выброс вверх (без учета трения) ... . 231
§ 4 Распределение теплоты в стержне ... . 231
§ 5 Расстояние между фермами железнодорожного моста . 2.111
ГЛАВА X ЗАДАЧИ. ПРИВОДЯЩИЕ К НЕПОЛНЫМ ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЯМ ВТОРОГО ПОРЯДКА . . . 236
I Уравнения типа y"—f(x)
§ 1 Переходная кривая железнодорожного пути . 237
§ 2 Прямолинейное движение материальной точки в горизонтальной плоскости 230
§ 3 Упругая линия балок . . . 242
II Уравнения типа y"=f((y)
§ 4 Геометрические приложения . . . . . ... 255
§ 5 Движение материальной точки под действием силы притяжения . . 256
III. Уравнения типа y"=f(y')
§ 6 Определение кривой по радиусу кривизны . ...... 257
§ 7. Горизонтальное движение тела при наличии трения 259
§ 8 Движение в вертикальной плоскости 274
§ 9 Равновесие тяжелой нити . .... . . 280
§ 10 Гибкая нить равного сопротивления .... . . 283
IV. Уравнения типа y"=f(x, у')
§ II Кривая и раднус кривизны . . . ... 285
V. Уравнения типа у"—\{у, у')
§ 12 Нахождение уравнения кривой по нормали и радиусу кривизны . . 286
ГЛАВА XI ЗАДАЧИ, ПРИВОДЯЩИЕ К ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЯМ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 288
I. Неполные линейные дифференциальные уравнения
§ I Гармонические колебания . . .... 296
§ 2 Движение тела без трения .... . . ... 307
§ 3 Дифференциальный манометр . . . 312
§ 4 Распределение теплоты в стержнях 313
§ 5 Продольный изгнб прямого стержня , . ЗЛ)
§ 6 Движение шарика в трубке (задача Ампера) . . . 328
II. Линейные дифференциальные уравнения
§ 7 Затухающие колебания . . . . . . . . 330
§ 8 Затухающие колебания в электрической цепи . . . 335
§ 9 Колебания магнитной стрелки без и при наличии успокоителя . . 343
§ 10 Вынужденные колебания механических систем . ... 350
ГЛАВА XII ЗАДАЧИ, ПРИВОДЯЩИЕ К ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ
ВТОРОГО ПОРЯДКА С РАЦИОНАЛЬНЫМИ КОЭФФИЦИЕНТАМИ . . 363
I. Уравнение Эйлера
§ 1. Распределение температуры в продольном ребре параболического сечения 363
ΪΙ. Линейное однородное уравнение с
рациональными коэффициентами
§ 2 Толстостенная цилиндрическая оболочка под давлением (задача Лямэ) , . 366
III. Линейное неоднородное уравнение с рацио и
ильным и коэффициентами
§ 3 Скорость течения жидкости в трубопроводе Я74
§ 4 Изгиб круглой пластины « 976

Оглавление
§
§
II
§
§ 6
III
S 7
IV.
ГЛАВА XIII ЗАДАЧИ. ПРИВОДЯЩИЕ К СПЕЦИАЛЬНЫМ ЛИНЕЙНЫМ
ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ВТОРОГО ПОРЯДКА С ПЕРЕМЕННЫМИ
КОЭФФИЦИЕНТАМИ (УРАВНЕНИЯМ БЕССЕЛЯ. ЛЕЖАНДРА И МАТЬЕ)
I Уравнение Бесселя
§ 1 Устойчивость стержня формы усеченного конуса, сжимаемого продольной
силой . . . .
2 Устойчивость цилиндрического стержня под действием собственного веса
3 Устойчивость вращения гибкой нити . . .
4 Распределение температуры в кольцевом ребре прямоугольного профиля
Обобщенное уравнение Бесселя
5 Маятник переменной длины ... ....
6 Устойчивость стержня переменного сечения под действием переменной
распределенной нагрузки . ....
Дифференциальные уравнения в частных
производных
Колебания круглой мембраны . . . . , ,
Уравнение Лежандра
§ 8 Электрический потенциал двух равносильных зарядов
§ 9. Дифференциальное уравнение в частных производных потенциала
§ 10 Потенциал притягивающих масс . . .... . .
V Уравнение Матье
§ П Динамическая устойчивость стержня под действием переменной_продолыюй
силы ... ...."*
ГЛАВА XIV ЗАДАЧИ, ПРИВОДЯЩИЕ К СИСТЕМАМ ЛИНЕЙНЫХ ДИФФЕРЕП
ЦИАЛЫ1ЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА .
§ 1 Разложение вещества . . . .
§ 2 Относительная кривая погони . ...
§ 3 Давление в системе двух соединенных цилиндров с газом
§ 4 Напряженное состояние диска под действием центробежных сил
§ 5. Превращение одного вещества в другое . . .
ГЛАВА XV. ЗАДАЧИ, ПРИВОДЯЩИЕ К НЕПОЛНЫМ ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЯМ. ВЫСШИХ ПОРЯДКОВ
§ 1 Линия прогиба неразрезиой балки от распределенной нагрузки
ГЛАВА XVI ЗАДАЧИ. ПРИВОДЯЩИЕ К ЛИНЕЙНЫМ ДИФФЕРЕНЦИАЛЬНЫМ
УРАВНЕНИЯМ ТРЕТЬЕГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
§ 1 Паровая машина с регулятором ... .
ГЛАВА XVII ЗАДАЧИ, ПРИВОДЯЩИЕ К ЛИНЕЙНЫМ ОДНОРОДНЫМ ДИФФЕ-
РЕЦИАЛЬНЫМ УРАВНЕНИЯМ ВЫСШЕГО ПОРЯДКА С ПОСТОЯННЫМИ
КОЭФФИЦИЕНТАМИ ,.,.,,
§ I Колебания вала от действия центробежных сил
§ 2 Балка (железнодорожный рельс) на упругом основании
§ 3 Колебания однородной балки (приведение дифференциального уравнения
в частных производных к обыкновенному) . . -. . .
ГЛАВА XVIII ЗАДАЧИ, ПРИВОДЯЩИЕ К ЛИНЕЙНЫМ НЕОДНОРОДНЫМ
ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ ЧЕТВЕРТОГО ПОРЯДКА С
ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ ... . .
§ I Деформация стенок цилиндрического резервуара
| 2. Железнодорожная шпала ...
ГЛАВА XIX ЗАДАЧИ. ПРИВОДЯЩИЕ К СИСТЕМАМ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ ВТОРОГО ПОРЯДКА . . . ...
1.
пропор-
Движение материальной точки под действием отталкивающей силы,
циональиой расстоянию . . . . ...
Выброс тела под углом . . . *
Сброс груза с самолета в заданную точку ... ,
Движение планет . . . .... . .
Система двух связанных электрических контуров
Изменение потенциала электрической линии по времени (приведение системы
дифференциальных уравнений в частных производных к системе
обыкновенных уравнений) . . ... ...
Стационарные линейные дифференциальные уравнения с постоянными
коэффициентами в теории систем современной техники и естествознания
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
I Дифференциальные уравнения первого порядка »
II Дифференциальные уравнения второго порядка
III Системы дифференциальных уравнений первого порядка
IV Системы дифференциальных уравнений второго порядка
§ 7
385
390
392
395
398
400
402
405
413
41т
417
424
43ϋ
Ш
442
411
447
453
456
«8
463
♦6S
477
482
485
487
490
495
497
500
503
504
509
513
519
529
529
545
555
557