С. А ЧАПЛЫГИН
(с портрета художника О. Делла-Вос-Кардовской)

Классики
ЕСТЕСТВОЗНАНИЯ

КЛАССИКИ
ЕСТЕСТВОЗНАНИЯ
Математика
Механика
Фнз ижа
Астрономия
Государственное Издательство
ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
Москва 1950 Ленинград

С.А.ЧАПЛЫГИН
Новый МЕТОД
ПРИБЛИЖЕННОГО
ИНТЕГРИРОВАНИЯ
ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
Государственное Издательство
ТЕХНИКО ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ
Москва 1950 Ленинград

О РАБОТАХ С. А. ЧАПЛЫГИНА ПО ПРИБЛИЖЁННОМУ
ИНТЕГРИРОВАНИЮ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
Замечательный русский учёный — Сергей Алексеевич
Чаплыгин создал вместе со своим учителем, «отцом
русской авиации» Николаем Егоровичем Жуковским новую
науку — аэродинамику и заложил основы для создания
газовой динамики — теоретической базы для развития всей
современной авиации. Его работы в этой области
представляют собой одно из замечательнейших достижений русской
науки.
Кроме работ в области аэродинамики, С. А. Чаплыгин
занимался и многими другими вопросами механики и
прикладной математики. В этой книге собраны его работы,
в которых он дал свой, ставший ныне классическим, метод
приближённого решения дифференциальных уравнений.
С. А. Чаплыгин начал заниматься вопросом о
приближённом интегрировании дифференциальных уравнений
в 1905 г. К этому времени относится его переписка с проф.
В. П. Ермаковым об использовании для изыскания
интегралов дифференциальных уравнений с остаточным членом
теоремы, названной С. А. Чаплыгиным «обобщённой
теоремой Ролля». 26 апреля 1905 г. С. А. Чаплыгин прочёл

6
Μ. В. КЕЛДЫШ И Д. Ю. ПАНОВ
в Московском математическом обществе доклад
«Приближённое интегрирование дифференциальных уравнений
первого порядка», без сомнения развивавший эти идеи.
С. А. Чаплыгин сам не публиковал эти свои работы,
видимо считая их незавершёнными, пока они не
распространены на уравнения п-го порядка. В его рукописях
имеются наброски доказательства теоремы, обобщающей
нужным образом теорему Ролля, однако полного
доказательства этой теоремы в бумагах С. А. Чаплыгина найти
не удалосы
Видимо, трудности, связанные с доказательством этой
теоремы, заставили С. А. Чаплыгина искать других путей,
в результате чего и был создан уже в советское время
«Метод Чаплыгина», представляющий одно из наиболее
выдающихся достижений советской науки в области
прикладной математики.
Метод приближённого решения дифференциальных
уравнений, созданный С. А. Чаплыгиным, был задуман им как
метод, позволяющий удобно оценивать погрешность
приближённого решения. Он заключается в том, что искомое
решение дифференциального уравнения у всё более точно
аппроксимируется двумя последовательностями функций
уп и Yni такими, что
Vn<y<Yn-
Построение таких последовательностей, очевидно, позволяет
приближённо решать дифференциальное уравнение с
заранее известной степенью точности, определяемой разностью
Уп—уп. Этого не даёт ни один из известных
методов. Однако значение метода С. А. Чаплыгина не
исчерпывается этим. Дело в том, что при построении после-

О РАБОТАХ С. А. ЧАПЛЫГИНА
7
довательностей уп и Уп С. А. Чаплыгин использовал прием,
представляющий собой обобщение на случай
дифференциальных уравнений знаменитого «метода касательных»,
предложенного Ньютоном для решения алгебраических
уравнений. Лишь сейчас становится ясным всё значение
этой замечательной идеи — построения для решения
функциональных уравнений метода, аналогичного самому
сильному методу решения алгебраических уравнений — методу
Ньютона.
Метод С. А. Чаплыгина, опубликованный им в 1919—
1920 гг., некоторое время оставался мало известным, так
как соответствующие статьи были помещены в изданиях,
не имевших большого распространения. В 1932 году эти
статьи были переизданы в Трудах Центрального
аэрогидродинамического института им. Η. Е. Жуковского°и сразу же
привлекли к себе внимание. Академик Η. Н. Лузин
обратил внимание на аналогию между методом А. С. Чаплыгина
и методом Ньютона и показал, что для метода С. А.
Чаплыгина имеет место такая же быстрая сходимость, как и для
метода Ньютона (сходимость погрешности к нулю,
начиная с некоторого я, имеет порядок 2~2^). Вскоре метод
С. А. Чаплыгина был распространён на интегральные
уравнения и тем самым показано, что основные идеи С. А.
Чаплыгина имеют универсальное значение для решения
функциональных уравнений вообще. В последнее время эти идеи
полечили широкое развитие в работах Л. В. Канторовича,
который показал, как можно построить метод решения
весьма общего класса функциональных уравнений,
аналогичный методу Ньютона. Но ещё и сейчас далеко не
полностью использовано всё богатство оригинальных и глубоких
идей, заложенных в этих замечательных работах С· А.
Чаплыгина. Как и большинство его работ, работы по приближён-

$ Μ. В. КЕЛДЫШ И Д. Ю. ПАНОВ
ному интегрированию дифференциальных уравнений,
несомненно, ещё долго будут привлекать внимание исследователей
и послужат источником новых изысканий в этом
направлении.
М. В. Келдыш и Д. Ю. Панов

С.А.ЧАПЛЫГИН
[OS
Новый МЕТОД
ПРИБЛИЖЕННОГО
ИНТЕГРИРОВАНИЯ
ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ

ПРЕДИСЛОВИЕ
Приближённое интегрирование дифференциальных
уравнений есть один из основных вопросов технической
математики, а потому всякий шаг в этой области, если он даёт
сколько-нибудь новое освещение процесса, представляет
интерес. Вот почему я считал правильным собрать воедино
свои работы по этому вопросу, частью помещённые в виде
журнальных статей в периодической лечати, частью
изданные в виде отдельных брошюр. Все эти издания стали
библиографической редкостью, а между тем, по моему
мнению, в намеченном мною направлении работу следовало
бы продолжить.

^\^^^^^^y^^^\^^y^\^y^^^^^^^^^^^\^^^\^^^\^y^\^^\^^\^\^^i
I. ОСНОВАНИЯ НОВОГО СПОСОБА ПРИБЛИЖЁННОГО
ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
§ 1. Основная идея метода. При отыскании
приближённого интеграла данного дифференциального уравнения
обычно ставится один из двух вопросов: либо требуется
с возможной точностью построить аналитическое
выражение искомой функции, либо вычислить её числовую
величину при заданном значении независимого переменного·
Для решения первого вопроса единственным, дающим
практически удобный приём вычисления способом является
разложение интеграла в ряд. Приём этот, однако, даже
в простейших случаях, приводит обычно к чрезвычайно
сложным, а при значительном числе подлежащих подсчёту
членов — практически едва преодолимым трудностям
вычисления,— обстоятельство тем более тягостное, что при
пользовании лишь этим приёмом большею частью не
оказывается возможным установить величину остающейся
погрешности и узнать, насколько удовлетворительно разрешена
поставленная задача.
Для отыскания числовых значений интеграла уравнения
с числовыми коэффициентами известен ряд способов,
наилучшим из которых нам представляется метод Адамса

14 С. А. ЧАПЛЫГИН
(Adams)-IUTepMepa (Stormer), позволяющий быстро подойти
к решению достаточной точности. Пределы остающейся
ошибки, однако, и при этого рода приёмах не
устанавливаются с достаточной строгостью и точностью. Что же
касается характера интегральной кривой, то её при этом
приходится вычерчивать по точкам и, следовательно, лишь
графически определять её ход, опять-таки без ясного
представления о тех уклонениях от истинных значений ординат,
которые при этом имеют место.
Υ
τ
I
I
I
1
1
λ_ ъ—-
в
"Т^^-ч
1 f
ь »».
Фиг. 1.
Предлагаемый нами приём по идее существенно
отличается от известных до сих пор. Мы ставим себе
следующую задачу: по данному дифференциальному уравнению,
разрешённому относительно высшей производной,
v(»)—/(*, у, у', у", ...,/»-!>) = 0, (1)
отыскать две функции, z = z{x) и и = и (х), равные
искомому интегралу в начальной точке χ = xQ, так, чтобы на
прилегающем к этой точке участке соблюдалось двойное
неравенство
* > У > и-

I. ОСНОВАНИЯ НОВОГО СПОСОБА
15
Переводя это требование на геометрический язык, мы
можем сказать, что на плоскости OXY надлежит выделить
ленту ABC, по возможности узкую, внутри которой
необходимо должна лежать интегральная кривая Ау (фиг. 1).
Само собой ясно, что уравнения y = z(x) иу = и(х)
определяют в таком случае граничные кривые АВ и АС.
Решить поставленную задачу позволяет нижеследующая
основная теорема.
§ 2. Основная теорема о дифференциальных
неравенствах. Допустим, что мы нашли функцию ζ = ζ {χ) с такими
свойствами:
1) при х = х0
г=У=Уо> *'=У'=Уо>
ζ" =у" == у" , ^(n-i) =у^п-1) =уп—1 ;
2) всюду на участке (л:0, х), прилегающем к л*0, где,
значения χ более х0, результат подстановки ζ на место у
в уравнение (1) более нуля, т. е.
zin) —/(χ9 Zt z\ z\ ..., ^-1}) > 0. (2)
Предположим, далее, что на этом участке искомый интеграл
' и его производные до порядка η конечны и непрерывны
что такими же свойствами обладает функция ζ и что функция
/ и её частные производные по аргументам у, у\ ..., yfo-i)
в области интересующих нас значений перечисленных
аргументов и независимого переменного также всюду конечны;
тогда для всех х, больших л*0 и не превосходящих
некоторого определённого предела, будет существовать
неравенство
г>у-
Знак этого неравенства был бы обратный в случае
противоположного знака в неравенстве (2); неравенство будет

16
С. А. ЧАПЛЫГИН
также обратного знака в области прилегающих к точке х0
значений независимого переменного, меньших х0 для η
нечётного.
Будем называть определённую таким образом функцию
верхней или нижней границей интеграла, смотря по знаку
неравенствами условимся в последующем через ζ
обозначать именно верхнюю, а через и — нижнюю границу, так
что интеграл у будет заключён между ζ и и:.
г>у> и.
Обратимся к доказательству теоремы и проведём его,
последовательно переходя от более простых к более
сложным случаям.
§ 3. Доказательство основной теоремы для
уравнения первого порядка. Дано уравнение первого порядка
и неравенство
z'—f(x, z)>0 (3)
при условии χ > лг0, причём z—y=yQ для х = х0.
Данные соотношения приводят к неравенству
*'—·/—ρ (*—j0>o.
где
f(x, z)—f(x, у)
Ρ ζ—у
представляет собою на основании наложенных на г и у
условий вполне определённую, хотя и неизвестную нам
функцию л:, всюду конечную в области интересующих нас
значений переменных: для χ = х0 функция эта, очевидно,
имеет значение

I. ОСНОВАНИЯ НОВОГО СПОСОБА
17
Умножим построенное нами неравенство на положительный
в наших условиях множитель
χ
— J ρ dec
s dx = ex<> dx;
интегрируя результат в пределах х0 и х, получаем
X
XQ
так как ζ—у при д: = х0, то по упрощении это
неравенство приводит к искомому результату
*>у.
Если бы χ было менее лг0, то на пути интеграции dx было
бы отрицательно, и, следовательно, при умножении на 5 dx
неравенства (3) в нём пришлось бы изменить знак, а это
повело бы к изменению знака результата. Само собою
ясно, что функция и, удовлетворяющая неравенству
u'—f(x, «)<0,
будет нижнею границею интеграла.
Приведённое нами доказательство, как мы увидим ниже,
с соответственным изменением распространяется и на
уравнения ^высших порядков; что же касается, в частности,
уравнений первого порядка, то для них можно дать
другое, почти очевидное, геометрическое доказательство, на
возможность которого обратил моё внимание Η. Е.
Жуковский. Для ясности и полноты приведём такое
доказательство. Уравнением
/—/(*. .У) = о
на плоскости ΟΧ Υ определяется семейство кривых,,
идущих, вообще говоря, раздельно, так что через каждую
2 Зак. 1799. С. А. Чаплыгиг.

18
С. А. ЧАПЛЫГИН
точку проходит определённая кривая. Ряд таких линий
изображён на фигуре 2. Пусть АС есть та из
интегральных кривых y=zy(x), которая соответствует начальным
данным лг = л:0, у=у0, т. е. проходит через точку А
Фиг. 2.
с координатами х0, у0. Кривая у = ζ (л:), изображённая на
чертеже линиею ADB, удовлетворяющая неравенству
и проходящая через ту же точку А, вправо от А
необходимо должна подниматься вверх над интегральной
кривой, пересекая последовательные кривые интегрального
семейства, и, как легко усмотреть, не может пересечь
линию АС прежде, чем прикоснётся к одной из последующих
линий семейства в точке В; после этого, если знак
неравенства меняется, она начинает вновь встречать те
интегральные линии, которые пересекла ранее. Ясное дело, что
неравенство
z>y
будет справедливо на некотором участке за точкою В.
В нашем распоряжении, однако, нет средств ответить на
вопрос, как далеко будет ещё простираться этот участок.

I. ОСНОВАНИЯ НОВОГО СПОСОБА 19
§ 4. Доказательство основной теоремы для
линейного уравнения второго порядка. Обратимся теперь
к линейным уравнениям высших порядков и начнём
с уравнения второго порядка
У—РУ—Р1У = <1> W
в котором /?, рг и q суть конечные и непрерывные
функции χ на прилегающем к точке χ = х0 участке. Пусть
найдена функция
г = ζ О),
имеющая при х = х0 значение z=y=y0, причём
zf —у' =Ур Функция ζ на некотором участке,
прилегающем к х0, будет верхнею границею интеграла, если
ζ" —рг' — pxz — q>0. (5)
Чтобы в этом убедиться, составляем при помощи
уравнения (4) неравенство
/'_/'+<Ф'-У)-(°+р)(*,—/)—р, (*-.?)> о,
где σ — подлежащая определению функция х.
Определим σ так, чтобы удовлетворялось условие
-±{o-{-p)s=p1s, (6)
где
χ
J adx
s = ex*
Умножив неравенство (5) на sdxt мы можем переписать
его в виде
-£$(г'-У)-175(°+Р)(г-У)>0·

20
С. А. ЧАПЛЫГИН
Проинтегрировав это неравенство в пределах х0 и х, мы
по упрощении результата приходим к неравенству
*'—у' — (°+р)(*—у)>о,
откуда, так же как в § 3, заключаем о справедливости
неравенства
ζ— у>0
для значений переменного χ > х0.
Приведённое рассуждение справедливо до тех пор, пока
множитель s остаётся положительным, что будет иметь
место, пока определённая выше функция σ сохраняет
конечные значения. Уравнение (б), определяющее эту
функцию, в раскрытой форме напишется в виде
σ' + σ* +рз -)- Р' — Pi = °.
Таким образом, пределом применимости неравенства явится
то значение х, для которого σ приобретает бесконечно
большую величину, короче говоря, полюс функции о.
В этой точке функция s обращается в нуль и может
переменить знак. Сама функция s, как нетрудно убедиться,
удовлетворяет линейному уравнению
s" + (psy-Pls = 0,
сопряжённому с (4), если из этого последнего удалить
вторую часть.
Итак, пределом применимости теоремы будет
значение х) являющееся полюсом σ и в то же время
представляющее собою корень функции s\ при этом необходимо
иметь в виду, что присутствие в функциях а и s
произвольных постоянных позволяет до известной степени
отодвинуть отмеченный предел. Однако предел этот может
и в некоторых случаях будет существовать, хотя бы нера-

1. ОСНОВАНИЯ НОВОГО СПОСОБА
21
венство (5) было справедливо при всяком х, большем
начального х0.
Для значений χ < х0 в результате приведённого выше
рассуждения мы пришли бы по интеграции неравенства (5)
к неравенству
*'—у'—(°+р)(*—у)<о.
откуда следовало бы по § 3, что и здесь опять
ζ— у>0.
Таким образом, для уравнения второго порядка ζ будет
верхнею границею интеграла по обе стороны начальной
точки х0.
§ б. Доказательство основной теоремы для
линейного уравнения любого порядка. Доказательство
теоремы для линейного уравнения порядка η может быть
проведено способом перехода от /ι — 1 к п. Пусть,
в самом деле, известна функция ζ, которая по вставке на
место у в уравнение
у№ — /fy(»-i)_ Plj/("-2)— ... —Vn^y=q (7)
даёт в результате неравенство
*ώ—ρ*(»-υ_Α*0»-2)— . . . —pn-xz — q> О, (8)
удовлетворяя в то же время условиям
z=y=y0, z'—yf—y'^ ..., <г(п--1)=Уп-1)==У0я-1)
при
X · ΛΛι
Само собою разумеется, что общие условия
непрерывности, приведённые в тексте основной теоремы, соблюдаются
и в рассматриваемом частном случае, как это предполага-

22
С. А. ЧАПЛЫГИН
лось в ранее рассмотренных и будет предполагаться
в дальнейшем.
Составляем вытекающее из соотношений (7) и (8)
неравенство
• · · —К-2+Аг-2) [*'—/! — Λ,-ι \*—у\ > 0 (9)
и определяем функции σ, σχ, σ2, ..., σΜ_2 так, чтобы при
χ
было
dx
(° + P)s = — <V>
■7Γ(σι + Λ)ί== — V»
ί/л:
(10)
откуда
"57 (вя-а+Рп-в) s = —Pn-\S,
о' -\-а*-\-рз-\-р' = —ση
<г-2 + ση-2σ +Ρ»-ϊσ +Ρή-2= — Рн-г j
(И)
Пока определённые этими уравнениями функции α, σχ, ..., ση-2
остаются конечными и непрерывными, а, следовательно,
величина s положительной, мы можем, умножив
неравенство (9) на интегрирующий множитель sdx,
проинтегрировать результат в пределах х0 и χ > х0 и по сокраще-

I. ОСНОВАНИЯ НОВОГО СПОСОБА
23
нии прийти к дифференциальному неравенству (п — 1)-го
порядка
^(!Ι-1)_^(η-1)_(σ_|_ρ)[^(»-2)_^(η-2)]
— (σι+Ρι)[^-3)— У<?-Щ — . ..
··· — (°η-* + Α·-9)[*— У1>0- (12)
Если я = 3, то неравенство (12) будет второго порядка?
и потому, на основании рассуждения, приведённого в § 4,
мы должны заключить, что ζ будет верхнею границей
интеграла. Таким образом теорема оказывается
справедливою для линейного уравнения третьего порядка. Положив
η = 4, убеждаемся, что она верна для уравнения
четвёртого порядка, и т. д.
Определение предела приложимости неравенства z>y
приводится к обследованию полюсов интегралов данной
выше системы уравнений (10). Нетрудно убедиться, что
изучение этих уравнений с указанной точки зрения
приводится к рассмотрению линейного уравнения, которому, как
оказывается, удовлетворяет множитель s. В самом деле,
система (11) при помощи очевидных соотношений
■s ' s
приводится к следующему виду:
s" + (psy = -s^,
— W + (ps)' = + so2,
(s°2)4-(Pas)'== — s°3>
(- l)n"21(w,-8)' + Ow)'] = (-1)"-1^,

24
С. А. ЧАПЛЫГИН
Продифференцировав первое из этих уравнений η— 2 раза,
второе η — 3, третье η — 4 раза и т. д. и сложив
результаты, получим
sW+(ps)(»-i)_(piS)(«-2) + (/,2s)(»-3)_ т, ^
...+(-1)и->п_, = 0, (13)
уравнение, сопряжённое заданному уравнению (7) без его
второй части. Предельным значением независимого
переменного, до которого ζ остаётся верхней границей
интеграла уравнения (7), будет корень функции s, являющийся
в то же время полюсом для σ, σ1? σ2, ..., ση-2.
Отмеченный предел может быть отодвинут в известной мере путём
подбора частного интеграла уравнения (13) в качестве
интегрирующего множителя неравенства (9), как это было
замечено выше при доказательстве теоремы для линейного
уравнения второго порядка.
В заключение этого, пункта отметим, что
неравенство (12) изменит знак в точках х<х0\ нетрудно будет
убедиться, что при η чётном ζ будет верхнею границею
по обе стороны от χ = х0, а при η нечётном та же самая
функция при χ < х0 окажется уже нижнею границею.
интеграла. В самом деле, будем считать теорему
доказанной для уравнений порядка η—1; тогда при η — 1
нечётном (стало быть, при чётном п) неравенство (12)
приводит к соотношению ζ > у при χ > х0\ это же самое
соотношение должно иметь место и для χ < х0 ввиду
того, что здесь неравенство (12) будет иметь
противоположный знак. Если же η — 1 чётное, an — нечётное
число, то из неравенства (12) будет следовать ζ—^>0
при χ > х0; но при χ < х0 тогда окажется уже ζ < у,
так как в этих точках опять-таки знак неравенства (12)

1. ОСНОВАНИЯ НОВОГО СПОСОБА
25
изменится, а с ним ввиду чётности числа /г— 1 должен
измениться и знак неравенства, связывающий функцию ζ
с .интегралом.
§ 6. Доказательство основной теоремы для
нелинейного уравнения второго порядка. Перейдём теперь
к рассмотрению нелинейных уравнений высших порядков
и начнём опять с уравнения второго порядка
/'—/(*. */) = <>. (I4)
предполагая, что у и / удовлетворяют всем условиям,
указанным в тексте основной теоремы. Пусть конечная и
непрерывная вместе с двумя своими первыми производными
функция ζ удовлетворяет в начальной точке х = х0
требованию z = y — yQ, zf—y'==yr0 и оправдывает на
участке (х0, х) неравенство
*"—/(*, г, г')>0.
Это соотношение при помощи уравнения (14) мы можем
привести к виду
z"-f-p (*'-У') -Pi (г—у) > 0, (15)
положив
f{x.z,z')—fjx,z%y) _п
'г'—у* ~Pi
f{x,z, y')—f(x, У, У)
Так как по условиям, наложенным на у, ζ, /, функции ρ
и рг всюду в интересующей нас области конечны и
непрерывны, то из линейного неравенства (15) на основании
§ 4 приходим к выводу, что ζ будет верхнею границею
интеграла уравнения (14) при χ > χθ9 пока значение χ
не превзойдёт некоторого предела.

26
С. А. ЧАПЛЫГИН
§ 7. Доказательство основной теоремы для
нелинейного уравнения любого порядка. Последний шаг,
доказательство теоремы для общего случая, приводится
к рассуждению, совершенно аналогичному с только что
изложенным для нелинейного дифференциального
уравнения второго порядка. Уравнение порядка η
y(n)_f{Xj у9 yt уг>у βββ> ^г-1)) = 0
будет иметь верхнею границею величину г,
удовлетворяющую сверх начальных условий неравенству
*(»)—/(*, г? г>% z*9 _# г(*-П)>0
на участке (х0, х); а это неравенство приводится к
линейному неравенству
г(п)—у(п)—p[z(n~i)—j/(«-i)j —
_Pl [г(^2) —у»-*)] _ ... -.рн_г [z—y] > о,
если мы введём обозначения
__ f(x,z,z/iz">...,z(n-2),z(n-i))-f(x,z,zr,...,z(>i-2),y(»>-i))
_/(х,г,г',...,г(*-2),у(»-У)—/(х,г,г',...,у(п-*),у{п-1))
Pl~ Z(n-2)—y(?l-2)
я _f(xizif„,.y{n^),y{n^)-f{xyyfyr,...)y^^)iy{n-l))
Pn-i — JZT-y ·
Из этого неравенства на основании § 5 вытекает
соотношение
ζ— у>0,
так как по условиям непрерывности р, рх, . .., рп_х суть
функции, всюду в интересующей нас области конечные
и непрерывные.
К изложенному добавим, что ζ будет верхнею
границею интеграла по обе стороны от точки χ = а*0, если

I. ОСНОВАНИЯ НОВОГО СПОСОБА
27
данное дифференциальное уравнение чётного порядка;
в противном случае неравенство, связывающее гну,
меняет знак при переходе через χ = х0. Доказательство
этого положения в общем случае ничем не отличается
от того, которое мы привели в случае уравнений
линейных.
§ 8. Пределы применимости основной теоремы.
Развитое нами доказательство основной теоремы намечает
одновременно и путь, которым следует итти для того,
чтобы отыскать предел применимости доказываемого
положения; предел этот, как было выяснено, определяется
полюсами системы функций, которые сами определяются
дифференциальными уравнениями. Разыскание таких
полюсов само по себе представляет сложную и трудную
задачу, которая нами лишь ставится.
Если бы мы задались лишь целью показать
справедливость основной теоремы, не вдаваясь в определение
путей к отысканию пределов её приложимости, то самое
доказательство можно было бы до чрезвычайности
упростить и при этом пользоваться либо аналитическим, либо
геометрическим методом.
Аналитическое доказательство можно свести к
следующему рассуждению. Допустим, что на участке значений
независимого переменного, прилегающем к начальной
точке χ = О (для простоты принимаем х0 = 0), интеграл
дифференциального уравнения
у(п) _/ (Х) у9 уf у} ... ,y*-D) = 0 (16)
имеет значение
^Л+^+Хп+^+Г1' 1.2.3^,-1) +
+^,)1.2:Г...Я+^

28
С. А. ЧАПЛЫГИН
допустим, далее, что для функции г, которая при χ = О
удовлетворяет соотношениям ζ =yQJ ζ' —y'Q, - . · , z^1—^^
=y(Jl~1\ оправдывается неравенство
*(Ό—/(*,*,*',*", ... ,z<fi~1))>0 (17)
при λγ, достаточно близком к нулю. В таком случае мы
будем иметь:
*=Уо+У'ох + У'оТЪ+ · · · +-Уо>~1) 1-2-3^7(/»-1) +
+ Ζ° 1.2.3...η+ύη'
а тогда по условию (16)
^-^ = [4'°-^П)] 1.2Х3...п +S«-K»·
Так как £η и Rn заключают в себе множитель а;п+1, то
при достаточно малом χ знак г—jj зависит от первого
члена; но по условию (17)
4'0-.ώη)>ο,
а следовательно, для х, отличного от нуля, мы получим
z—y>0
при η чётном; если же η есть число нечётное, то при
х>0 и ζ будет более у, т. е.
ζ— у>о,
а при χ < 0 окажется
г— у<0.
Обратимся к геометрической интерпретации теоремы.
Пусть интегральная кривая данного дифференциального
уравнения
yw — f(x,y,y',... ,/Λ-1>) = ο

I. ОСНОВАНИЯ НОВОГО СПОСОБА 29
изображается линиею ADC и пусть ABC представляет
собою верхнюю границу интеграла (фиг. 3). Неравенство
zW—f(x,z,z', ... ,0(^~1))>О,
(18)
существование которого мы предполагаем на участке
оси ОХ вправо от х0, показывает, что интегральные
кривые, проведённые во всех точках границы так, чтобы
они имели с нею наитеснейшее возможное прикосновение
порядка η — 1, будут справа от точки касания уходить
под граничную кривую, оказываясь слева выше или ниже
этой кривой в зависимости от того, будет ли порядок
прикосновения чётный или нет. Это вытекает из
приведённого выше аналитического рассуждения. При
пересечении граничной кривой с интегральной могут
представиться два различных случая, которые мы и
рассмотрим последовательно.
Первый случай изображён на фигуре 3 и имеет место,
если последовательно прикасающиеся к граничной кривой
интегральные кривые не пересекаются и не пересекают

30
С. А. ЧАПЛЫГИН
линии ADC; тогда по мере отступления от начальной
интегральной линии ADC последующие интегральные
линии будут встречать границу в точках, всё более
близких между собою, пока для некоторой определённой
линии они не сольются в одну точку В; в этом месте
соответственная интегральная кривая будет иметь с
граничною кривою прикосновение порядка высшего, чем
η—1, и вправо от В выйдет наружу из-под границы.
Очевидно, в этой самой точке В нарушится и основное
неравенство (18), и, следовательно, теорема наша
оказывается справедливою на всём участке, находящемся влево
от точки χν где неравенство соблюдается, ибо здесь
граничная кривая всюду выше интегральной линии ADC.
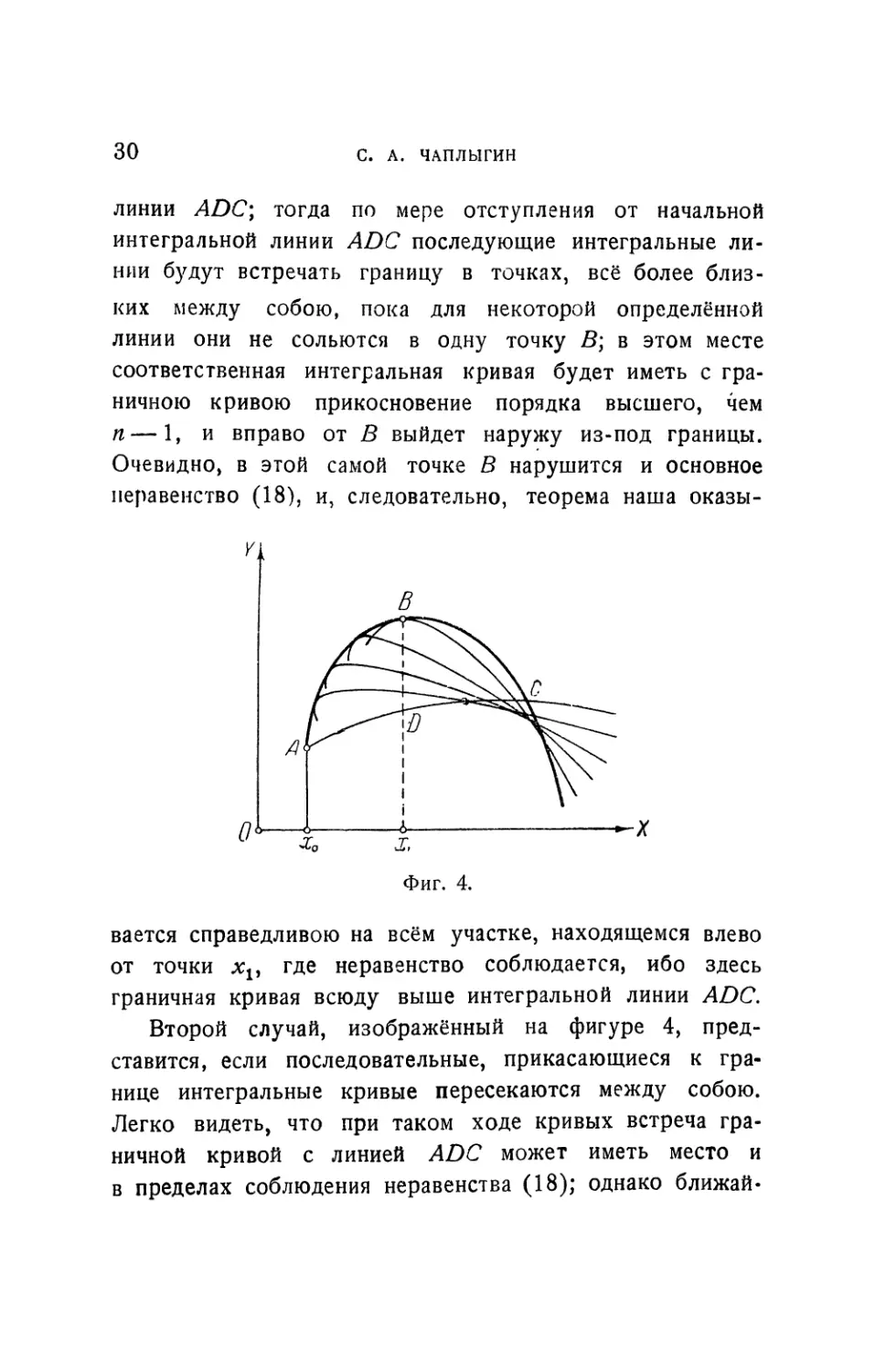
Второй случай, изображённый на фигуре 4,
представится, если последовательные, прикасающиеся к
границе интегральные кривые пересекаются между собою.
Легко видеть, что при таком ходе кривых встреча
граничной кривой с линией ADC может иметь место и
в пределах соблюдения неравенства (18); однако ближай-

I. ОСНОВАНИЯ НОВОГО СПОСОБА
31
шая к началььой точка пересечения С не может лежать
ближе, чем та точка Д где первая из интегральных
кривых пересекается с бесконечно близкой к ней
последующей. Точка Д очевидно, мэжет быть также
определена как предельная точка пересечения начальной
интегральной кривой ADC с другой, также интегральной
линией, проходящей через ту же начальную точку А и
имеющей здесь с кривою ADC прикосновение (я — 2)-го
порядка, причём производные порядка η — 1 дли обеих
указанных кривых отличаются на бесконечно малую
величину. Заметим, что, предположив иное расположение
последовательных пересечений интегральных кривых, или,
говоря иначе, дри ином ходе их огибающей мы
неминуемо пришли бы к прерывности высшей производной
интеграла в пределах изменения х.
§ 9. Порядок действий при приближённом
интегрировании уравнения. Способ, при помощи которого,
опираясь на доказанную теорему, можно приближённо
проинтегрировать данное дифференциальное уравнение,
очевиден: всё сводится к отысканию верхней и нижней
границ интеграла. Для уравнений высших порядков вопрос
весьма осложняется отысканием предела приложимости
теоремы; для уравнений же первого порядка этого
затруднения не существует. Что касается условий
непрерывности интеграла, то исследовать их в приложениях,
которые мы главным образом имеем в виду, обычно
никакой необходимости не встречается, так как физическое
значение определяемой функции бывает известно, а этим
значением вполне характеризуются пределы
непрерывности.
Итак, предположив, что мы имеем дело с уравнением
У-/(*,Х> = 0, (19)

32
С. А. ЧАПЛЫГИН
поступаем так: меняя по возможности мало вид
уравнения, стремимся привести его к интегрируемой форме;
интеграл изменённого уравнения, имеющий то же
начальное значение, как искомое решение уравнения (19),
подставляем в это последнее и определяем знак результата;
если он положителен, то мы нашли верхнюю границу
интеграла уравнения (19) для л;, превышающих начальную
величину; противоположный знак результата показал бы,
чго мы имеем дело с нижнею границею. Установив обе
границы и воспользовавшись ими как первым
приближением, можно в том или другом частном случае ближе
подойти к интегралу, подставив в некоторые члены
функции / (х, у) на место у его верхнюю или нижнюю
границу. Знак результата подстановки найденного таким
образом второго приближения позволит судить, имеем ли
мы дело с нижнею или верхнею границею искомого
интеграла.
Указанный приём оставляет значительное место
интуиции во всякой реальной задаче и с этой точки зрения
представляется как бы не вполне выработанным. Мы, со
своей стороны, однако, усматриваем в этом лишь
большое удобство и гибкость метода, позволяющего
направить анализ по наиболее простому пути во всяком
определённом частном случае. С другой стороны, возможно
использовать основную теорему и таким образом, чтобы
дать способ, если не всегда удобный, то во всяком
случае приложимый: стоит только для определения границ
интеграла пользоваться его разложением в тот или иной
ряд. Подстановка известной группы первых членов ряда
в левую часть уравнения (19) своим знаком определит
нам, будем ли мы иметь верхнюю или нижнюю границу
интеграла, если остановимся на этой группе, как прибли-

I. ОСНОВАНИЯ НОВОГО СПОСОБА
33
жённом выражении искомой функции. Практически, однако,
такой путь весьма часто может оказаться чрезвычайно
громоздким ввиду крайней сложности вычислений.
Примеры реального применения к отдельным задачам
всего лучше иллюстрируют метод. В дальнейшем мы даём
такое применение к интеграции уравнения движения
поезда, почему считаем себя в праве в предлагаемом
изложении общих оснований способа примеров не касаться.
§ 10. Распространение основной теоремы на
уравнения с частными производными. В заключение этой
части считаем полезным изложить ещё одну теорему,
которая показывает, как могут расшириться перспективы
в приложениях аналогичного метода, применимого, как
оказывается, и κ некоторым уравнениям с частными
производными.
Теорема. Пусть мы имеем уравнение с частными
производными
где ρ — существенно положительная в данной области
функция координат или нуль. Пусть, далее, мы нашли
некоторую функцию координат ψ, внутри области
конечную и непрерывную вместе со своими первыми частными
производными и имеющую конечные вторые производные,
на границах области всюду равную искомому интегралу φ
уравнения (20), который должен обладать в той же степени
свойствами непрерывности. Функция ψ будет нижнею
границею интеграла для внутренних точек области, если
результат её подстановки в уравнение (20) всюду
положителен; верхней границе соответствует обратный знак
указанного результата.
3 Зак. 1799. С. А. Чаплыгиг.

34 С. А. ЧАПЛЫГИН
Будем для краткости письма в дальнейшем обозначать
операцию
д* . д2 д2
дх2 τ ду2 ' dz2
знаком Δ, так что уравнение (20) перепишется в виде
Δφ —/?φ = 0,
а ψ внутри области удовлетворяет неравенству
Δψ_ρψ>0; (21)
условимся также в обозначениях
3Ϊ = Й cos <*' ^ + "%■ cos0v«) + -fj cos (^),
где (λ;, λ) есть угол между осью ОХ и внутреннею нор-
малью к данной замкнутой_поверхности, (у, п) и (г, /г) —
подобные же углы осей OF и OZ с внутренней нормалью;
-^- есть так называемая производная функция φ по нормали.
Из формул (20) и (21) вытекает неравенство
Δ (Ψ — ?) — Ρ (Ψ — φ) > 0. (22)
Составим выражение
(Ψ — ?) {^ (Ψ — ?) —Ζ7 (Ψ — ?)} ^ ^У ^г
и проинтегрируем его по всему объёму области. Теорема
Грина позволяет изобразить результат в форме тождества
/ J /(ψ_?ΜΔ(ψ —?)— Ρ(Ψ—9)}dxdydz =
— J Jw-»)^*-
— J J j* {£>(ψ — <?)+/> (ψ — <p)«}dxrfy<fe<0. (23)

I. ОСНОВАНИЯ НОВОГО СПОСОБА 35
Выражение, стоящее в последней строке, непременно
отрицательно, так как двойной интеграл, распространённый по
поверхности области, есть нуль по условию равенства
ψ — φ = 0 на границах, а в тройном интеграле подинте-
гральная функция существенно положительна. Таким
образом, преобразуемый тройной интеграл первой строки
уравнения (23) есть величина отрицательная, а так как
выражение, стоящее в витых скобках, по условию (22) более
нуля, то ψ — φ не может быть всюду положительно.
Таким образом, относительно этой функции может быть
сделано два предположения: или 1) она всюду внутри
области отрицательна, или 2) объём разбивается на части,
из которых в некоторых ^частях соблюдается неравенство]
ψ—φ<0, а в других имеет место обратное неравенство.
Легко показать, что второе предположение не может
иметь места в действительности; в самом деле, на
поверхности, отграничивающей ту часть объёма, где ψ — φ менее
нуля, от части, где имеет место обратное неравенство,
должно иметь место равенство ψ — ? = 0; а отсюда ясно,
что, применив к последней части объёма соотношение (23)
мы придём к противоречию, так как на основании
сделанного предположения и неравенства (22) выражение,
стоящее в верхней строчке рассматриваемого соотношения,
оказалось бы положительным, тогда как нижняя строчка
содержала бы попрежнему отрицательное количество ввиду
обращения в нуль двойного интеграла. Итак, единственное,
не приводящее к противоречию предположение, которое
можно сделать о знаке функции ψ — φ, приводит к
неравенству
ψ_φ<0.
Заметим ещё, что изложенная теорема допускает
некоторое обобщение. В самом деле, легко усмотреть, что
3*

36
С. Л. ЧАПЛЫГИН
она применима и в том случае, если дифференциальное
уравнение, определяющее функцию φ, имеет вид
где А, В, С, ρ— какие угодно знакоположительные
функции. Доказательство в этом случае ничем не отличается от
предыдущего, с тою разницею, что в преобразованном
неравенстве вместо производной по нормали от разности
ψ — φ будет стоять количество
+ С^1>С08(Г»),
а это обстоятельство не поведёт ни к йаким изменениям
в заключении, вытекающем из неравенства.
Как частный пример уравнения гипа (24) укажем
уравнение установившегося течения газа при обычном
предположении, что давление есть функция плотности. В таком
случае мы имеем
д ду , д_ дер , _д_ д<р ^
дх9дх~\ дур ду* dzP dz~~ '
если ρ = k[jn, то
/ι ^V
и мы приходим к уравнению
т·.
п — \
дх\ vl) дх^ ду[ vl) ду^~
где
дг \ vl ) dz

1. ОСНОВАНИЯ НОВОГО СПОСОБА
37
Отметим ещё одно интересное обстоятельство.
Предположим, что мы нашли две функции ψχ и ψ2,
удовлетворяющие условиям нашей теоремы и имеющие равные
с основной функцией значения на границах области. Таким
образом, пусть
/ι = ΔΨι—ΡΨι > 0, /2 = Δψ2 — ρψ2 > 0, Δφ — ρφ = 0.
По теореме
Ψΐ >% ^2 > ?·
Тогда из приведённого доказательства теоремы можно
непосредственно усмотреть, что при fx > /2 мы имеем
/ι—Λ = Δ(Φι —W—Ρ(Ψι —Ψ»)>0, Ψι<ψ2
и, следовательно, функции по величине во всех точках
области располагаются в таком порядке:
Ψι < ψ2 < ?·
Изложенная теорема в частном случае, когда φ не
зависит ни от у, ни от ζ, позволяет установить верхнюю и
нижнюю границы решения обыкновенного линейного
уравнения второго порядка
для 'того случая, когда интегральная кривая должна
проходить через две заданные точки. Любопытно отметить,
что никакого ограничения, вроде предела приложимости,
который проявляется при применении основной теоремы,
на этот раз мы не встречаем.

II. НОВЫЙ МЕТОД ИНТЕГРИРОВАНИЯ ОБЩЕГО
ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ДВИЖЕНИЯ
ПОЕЗДА
§ 1. Общая постановка задачи. При исследовании
влияния профиля на работу железнодорожных поездов
приходится искать зависимость основных переменных
движения поезда: времени t, пути s и скорости ν от того
независимого переменного, через которое мы условимся
выражать влияние профиля. В самом общем виде, когда
профиль представляет собою произвольную кривую,
влияние его на движение поезда состоит в том, что в каждый
данный момент, если все остальные условия движения
остаются прежними, благодаря изменению профиля,
появляется слагающая силы тяжести отдельных элементов
поезда, т. е. паровоза, тендера и вагонов, направление
которой либо совпадает с направлением движения при
уклонах, либо противоположно последнему при подъёмах. Так
как профиль мы берём криволинейный, то направление
движения поезда, а также обратное направление в каждый
момент для отдельных элементов поезда совпадают с
положительным или отрицательным направлением касательных
к кривой профиля в различных точках. Если считать, что
силы тяжести каждого отдельного элемента поезда при-

II. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ ПОЕЗДА 39
ложены в центре тяжести соответствующего элемента, то
означенные точки будут точками пересечения кривой
профиля с отвесными линиями, проходящими через отдельные
центры тяжести.
Если взять начало координат в какой-либо точке
кривой профиля и ось абсцисс ОХ направить по горизонтали
[в сторону движения], а ось ординат OY — по вертикали
вниз, то кривая профиля изобразится каким-либо
уравнением
f(x, у) = о.
Касательная к этой кривой в произвольной точке (х, у)
будет составлять с осью ОХ угол, который обозначим
через φ, причём
Так как сила тяжести направлена по вертикали, т. е. по
оси OF, то её слагающая по направлению касательной
будет равна самой силе тяжести, помноженной на sin φ,
причём
dy
sin со = --— .
ds
При обозначении веса отдельного элемента поезда через Qn
слагающая этого веса по касательной к кривой профиля
в точке (хП1 уп) будет равна
F =0 Ш-
г« —Чп ds'
Так как углы φ для различных точек кривой будут
различны, то для нахождения равнодействующей
[касательных] слагающих [сил тяжести] от всех элементов поезда
следовало бы спроектировать все [касательные
составляющие] силы на оси координат. Однако ввиду того, что

40
С. Л. ЧАПЛЫГИН
означенные проекции получаются весьма сложного вида
Σ~ dy dx \У^. /dy\*
Q"-di^F И 2dQ»Vdi)'
приходится прибегать к упрощениям, вытекающим из
характера кривой профиля. Самой существенной чертой этой
кривой является то, что её абсциссы χ значительно
превосходят её ординаты у, конечно, если только железная
дорога не представляет собой типа фюникюлерного пути.
Ввиду сказанного с большой степенью точности для
железных дорог, проходящих по равнинам, всегда можно
принять, что на расстоянии от 1 до 2 км от точки,
выбранной за начало координат, абсцисса χ по горизонтали
весьма мало отличается по величине от дуги кривой s.
А так как длина поезда не превосходит 1 км, то для
всех элементов его можно допустить, что
dx -
т. е. что сумма проекций касательных слагающих сил
тяжести отдельных элементов на ось ОХ равна
r* ZA4n ds '
а сумма проекций тех же сил на ось OY равна
Но раз мы сделали допущение, что dx = ds, то это
значит, что на протяжении, равном длине поезда, профиль
представляет собой прямую линию, наклонённую к
горизонту под углом φ, для которого
dy

II. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ ПОЕЗДА 41
Отсюда следует, что
dy γι dy
s ds ы^сп ^ ds
■.-(Ш«.-«(#У·
где Q — вес всего поезда; относя слагающие силы
тяжести по касательной к одной тонне веса поезда, получим,
разделив предыдущие выражения на Q:
Таким образом, мы представляем кривую профиля
в виде наклонённых к горизонту под различными углами
отрезков прямой линии, длина которых не превосходит
длины поезда. Но это представление можно откинуть и
рассматривать любой криволинейный профиль, если только
допустить предположение, что и по криволинейному
профилю поезд движется так же, как и по прямолинейному,
т. е. как одна материальная точка с массой, равной массе
всего поезда, сосредоточенной в центре тяжести всего
поезда. В этом случае касательные слагающие силы
тяжести, появляющиеся благодаря наклону профиля, выразятся
теми же формулами (1) и (2).
При прямолинейном профиле, если принять во
внимание, что ds = dx, формула (1) даёт
, где величина / есть уклон (+) или подъём (—) в промил-
лях (%0), иначе, число килограммов добавочной силы на
1 т веса поезда.

42
С. А. ЧАПЛЫГИН
§ 2. Различные формы приведённого уравнения
движения поезда. Зная выражение величины /в, можно теперь
при исследовании влияния профиля применить основное
дифференциальное уравнение движения поезда, представив
его в следующем виде:
1 d2s 1 dv 1 dv , , ο d у ,_ч
ς fitf2 ξ dt ξ ds ' rfs ' ч '
здесь по принятому в инженерной практике обозначению
ε=-ί!οβ127 */**'·
где g·—ускорение силы тяжести, выраженное в км/час2.
Разрешить это уравнение в таком общем виде невозможно,
но если задаться кривой профиля и выразить ординату
её у как функцию пути 5 или времени /, то решение
для многих случаев вполне возможно, т. е. возможно,
например, определить скорость ν в зависимости от t или 5
или вообще одно из трёх переменных определить в
зависимости от двух других и от некоторых параметров. Мало
того, если нам даже неизвестна кривая профиля, но
известна лишь производная -jr- = -^" как функция от t или
от 5, то и в этом случае мы можем определить одну
переменную через две другие и через параметры, а также
определить неизвестную кривую профиля.
Итак, положим, что мы задались соотношением
■£-'<·>.
где F(s) есть произвольная заданная функция от s; тогда,
очевидно,
у == j F(s)ds

II. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ ПОЕЗДА 43
представляет кривую профиля, и дифференциальное
уравнение (3) изобразится следующим образом:
Lv^ = a — bv + cv*-F(s), (4)
т. е. нелинейным уравнением первого порядка,
разрешённым относительно -т-. Если бы-—- было задано в
функции времени, то мы должны были бы интегрировать
уравнение
|| = й-^ + «Ч/(0. (5)
Из изложенного видно, что исследование влияния
профиля на движение поезда сводится к вопросу о том,
какой функцией мы можем выразить переменную
величину i подъёма или уклона профиля. В дальнейшем мы
рассмотрим частные виды уравнений (4) и (5),
соответствующие частным предположениям о виде функций,
которыми характеризуется профиль пути.
§ 3. Приближённое интегрирование уравнения
движения поезда на криволинейном подъёме: пример
первый. В виде примера рассмотрим уравнение
—- = ξ (α — bv — cv2 — k sin nt). (6)
Полагаем г> = α -|- #, где постоянной α можно придать
значение начальной скорости ν0 или какой-либо из
последующих скоростей; и будем считать количеством
настолько малым, что си2 можно отбросить по сравнению
с остальными членами при первом приближении. Числовой
пример покажет, что такое предположение весьма
возможно, если подъём не слишком длинен и изменение
скорости не выходит из некоторых довольно, впрочем,

44
С. А. ЧАПЛЫГИН
широких границ. Предположим, например, что начальная
скорость перед подъёмом ν0 = 40 км/час, скорость в конце
подъёма ^ = 20 км/час. Положив α = 30 км\час, для и
будем иметь максимальный предел 10 км/час. При а= 16,
£ = 0,47, с = 0,003 имеем
а — bv + cv* = а — Ьа -{- со? — (ft — 2са) и-}-си2 —
= 16 — 14,1 + 2,7 — (0,47 — 0,18) и + 0,003 и*,
и последний член при # = 10 значительно меньше
предыдущих. Преобразовав уравнение (6) указанной
подстановкой в следующее:
^ = ξ{Α_6α + £α8 —(ft —2са)« +
-\-си2—k sin ηέ}9 (7)
и рассматривая взамен его уравнение
^ = ξ{α — $а+яха— (ft — 2ca)Ul— k sin nt},
находим его интеграл в виде
(Ь — 2с<*)ах = а — fta + ™2 + Ce~^ +
-\- h cos /г/ + / sin ηέ> (8)
где β— ξ (ft — 2£<α), С—произвольное постоянное
интеграции, a h и / имеют такие значения:
Эти значения показывают, что чем короче промежуток
неровности пути, тем меньше h и /, тем меньше меняется
скорость, что и должно быть. Подставив теперь
выражение ах из равенства (3) на место и в член си2 в
уравнение (7), мы найдём по интеграции полученного таким

II. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ ПОЕЗДА 45
образом уравнения второе приближение, а затем можем
снова повторить процесс, если это понадобится.
Что касается связи между полученными таким образом
приближённым и истинным интегралами уравнения (6), то
о ней можно судить на основании моей теоремы о
дифференциальных неравенствах, а именно: если в результате
подстановки в левую часть уравнения
i21_6(fl —fo + «>a-^Asin«0 = 0.
вместо ν, такой функции t, которая при t = О имеет
должную начальную величину ν = ν0 и всюду непрерывна,
получится результат, больший нуля, то указанная функция
больше истинного ν; если же результат подстановки
окажется отрицательным, то это значит, что подставленная
функция меньше v.
В нашем случае результат подстановки первого
приближённого значения будет
— fc«f<0;
следовательно, это приближение даст нижний предел
интеграла.
При помощи той же теоремы убеждаемся, что и
второе приближение — результат интеграции уравнения
EL^\(a — bv + cul — k sin nt), (9)
получающегося из уравнения (7) заменой в нём члена си*
через си\, также окажется менее истинного значения и
(всегда предполагается, что при £ = 0 приближённое и
истинное значения и совпадают). Третье приближение будет,
в свою очередь, нижним пределом интеграла и т. д.

46
С. А. ЧАПЛЫГИН
Если бы в уравнении (9) их имело иное значение,
именно, если бы оно представляло собой численно
наибольшую предельную величину истинного значения и, то
интеграция уравнения (9) дала бы верхнюю границу
искомого интеграла. Легко видеть, что вместо истинного
максимального значения можно вставить и вообще какую-либо
постоянную, заведомо превышающую численно это
количество; такая постоянная найдётся, например, из
рассмотрения выражения (8) для и{. В самом деле, так как α-f ^
есть величина, меньшая истинной скорости a-f-#> то при
убывании ν от начального значения v0 функция их будет
всё время величиной отрицательной, численно большей и,
после того как перейдёт через нуль (если a = v0> то это
будет иметь место с самого начала); поэтому крайнее
значение uv даваемое формулой (8), может
послужить для определения верхней границы #, а стало
быть и V.
Верхнюю границу ν можно было бы определить и иначе:
в самом деле, достаточно в основном уравнении (6)
заменить cv2 через cv0v, чтобы получить интегрируемое
уравнение для определения интересующей нас функции, т. е.
верхнего предела v.
Любопытно отметить несколько иную форму основного
уравнения, которая поддаётся точной интеграции; в
некоторых случаях она могла бы оказаться полезной. Дело
в следующем: при переходе поезда с горизонтального пути
на подъём он лишь короткое время будет находиться на
участке криволинейного профиля. Это обстоятельство
позволяет всякую функцию f{t) на этом участке представить
в виде α + β^ где α=/(0), β=/' (0). Имея это в виду,
мы можем приближённо при любом профиле на
криволинейном участке уравнение движения поезда изобразить

II. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ ПОЕЗДА
в виде
с
где
а' — а -\~ α, ξλ = β<\
Положив затем
а'с-т
мы преобразуем вышеприведённое уравнение так:
d4
Ζ :
^2г
■ = — λοζ.
Введя обозначения
*1 * 9 . Я 1" 9 . Я . Λ . ft 9.ft.K.fi.ft.9 ~t"
-.(ι
*Q = σ 1
2-3 ] 2.3.5-6 2.3.5.6.8-9
λσ3 , λ2σ6 λ3σ9
„2 —*^ι — 374 "Γ 3.4.6-7 — 3.4.6.7.9.ΙΟ
мы изобразим интеграл ζ в виде
ζ = Αζχ -j- Яг2,
после чего найдём:
cv-
zt+Cz2 '
с А '
если через s обозначить пройденный путь.

48
С. А. ЧАПЛЫГИН
Вышеприведённый ряд можем вычислить и
табулировать, руководясь аргументом λο3 = τ, и тогда вычисления
всякий раз весьма просто доводятся до конца при любых
частных значениях входящих в задачу постоянных.
Если бы в уравнении (10) коэффициент при ζ был λσ^,
то в ζχ и ζ2 пришлось бы заменить σ3 через σ2+^ и в
знаменателях 2 · 3; 5-6; 8 · 9; .. . через
(1+μ)(2 + μ); (4+ ,i)(6-i-μ); ' (7 + μ)(8 + |ΐ),...,
т. е. всякое η через η—1 + μ.
§ 4. Приближённое интегрирование уравнения
движения поезда на криволинейном подъёме: пример
второй. Рассмотрим теперь уравнение
Здесь
« = T& = 127 */«*",
где g — ускорение силы тяжести в единицах км/час2.
Требуется получить закон изменения бкюрости на
криволинейном подъёме, где
y==h+ XAfiCOs-j-;
в этом случае
dy _ \\ 2%hn . 2ks ,
ΊΓ~ Ζι~ζΓ8ΐη ln '
в написанном выше уравнении
Α.-1000-^.
Для нахождения приближённого интеграла пользуемся
нашей теоремой; если в уравнение

II. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ ПОЕЗДА 49
подставим функцию £($), имеющую при s = s0 значение
z=yQ, и получим результат, больший нуля, то на участке
s> s0 и ζ 'будет больше у:
в противном случае знак последнего неравенства будет
обратный. Вместо уравнения (11) рассмотрим уравнение
•S-«{—*+(-£)"-Σ*.*τ}. <12>
получаемое из уравнения (11) путём умножения члена —bv
во второй части на -^ ( 1- -~); v0 может не совпадать
с начальной скоростью; множитель этот близок к единице,
если поле изменения ν не очень широко; так, если
большее из крайних значений превосходит меньшее даже в два
раза и если за vQ мы примем среднюю скорость, то при
*т« = 4mn> 2*Ό = *max + ^mm>
4 2
13
наш множитель колеблется в пределах 1 и т^ ; при более
близких <ршах и vmin его отличие от единицы будет ещё
менее значительно. Например, при
<П — _ σj <п — ^max + pmin
^max 2 min» u0 2
получится
6 4
^max = J v0> *\nin = J V0>
и, следовательно,
1 << JL^-L^^ll
^ 2UrW440'
4 Зак. 1799. С. А. Чаплыгин.

50
С. А. ЧАПЛЫГИН
Ещё более тесные пределы изменения множителя
получатся, если за ν0 мы будем принимать среднее
геометрическое между i;raax и vmin: если
^0 = *W.nin>
то
•<Ki+^)<T(/s+/a>
тогда при ©ти = 2от1п
1<4·(ϋ. + 3ΐ)<^1»1,06;
^ 2 \щ ι ν/^ 4 > '
3
ПРИ ^гаах = "2 ^niiu
к i(iL+a)<5J^«i,02.
^ 2 V^o ϋ/ 12
Итак, при правильном выборе vQi даже и при широких
пределах изменения ν, уравнение (12) оказывается весьма
близким к уравнению (11). Интеграл его, как ясно из его
вида, весьма просто получается в форме
я=Чс-£)(·
где С—произвольное интеграции, а σ — частный интеграл
уравнения (12), который будет иметь вид
Подстановка его в уравнение (12) даст для определения
Η и К уравнения
2^L = mHn, -2-^^mKn-2ikn;
*«. * п.

П. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ ПОЕЗДА 51
отсюда
5Я,=^, SKn = 2mten9 S = m*-y^.
ln ln
Произвольное постоянное С определяется так, чтобы при
s = sQ скорость ν имела должную величину.
Полученное таким образом выражение v = v' будет
менее истинного на основании теоремы о
дифференциальных неравенствах, так как в результате подстановки его
в уравнение (11) мы получаем в левой части выражение
-si (*-*)-.
меньшее нуля.
Составим теперь новое дифференциальное уравнение;
заменив в уравнении (11) член bv через bv\ будем иметь
•o% = ^(a-bv' + c^-^kn^). (13)
Проинтегрировав это уравнение, найдём значение ν = ν"
интеграла, который имеет должную величину при s = s0.
Нетрудно убедиться, что истинное ν будет меньше и",
ибо результат подстановки истинного значения ν в
уравнение (13) даст —1Ъ (ν — ν'), что по предшествующему
менее нуля; поэтому истинное значение ν менее интеграла
уравнение (13), т. е. менее ιΛ Итак
ν"> ν>ν'-
Вставляя ν' вместо ν0 в уравнение (12), мы по интеграции
получили бы более точное значение нижнего предела;
проинтегрировав уравнение (13), в котором ν' заменено более
точным значением, мы нашли бы более близкий к
истинному значению интеграла верхний предел и т. д.
Однако указанное интегрирование на деле привело бы
к чрезвычайно сложным квадратурам, и потому для практи-
4*

52
С. А. ЧАПЛЫГИН
ческого применения нужно найти иной путь. Можно
поступить так: можно подставить в то же самое уравнение (13)
на место ν' более грубый нижний предел функции ν,
меняющийся с s. Для этого надо найти такую функцию
от s, которая давала бы по подстановке в левую часть
основного уравнения отрицательную величину, по
возможности малую. Для приискания такой функции можно
поступать различно. Один из путей таков: полагаем ι/ = β-|-#,
где β — некоторое значение скорости, которое, в частности,
можно положить равным начальной скорости. Получаем:
= ξ \а-Ь$+сР-{Ь-2ф) «-J К sin ^} - a(g - Uu).
Отбросим последний член в правой части и интегрируем
остающееся уравнение; его интеграл имеет вид
(b — 2c$)u = a — Ь?-\- с$2-\-Се~^-\-
+ Σ (^cos~7^ + К'пsin"r9>
Λ=|(*-2*β).
Коэффициенты определяются путём подстановки.
Подставив затем результат в отброшенный член и определив его
значение на участке, прилегающем к точке s = s0, мы
на основании теоремы о дифференциальных неравенствах
узнаем, по какую сторону истинного значения интеграла
лежит найденное приближение.
§ 5. Приближённое интегрирование уравнения
движения поезда при переходе с горизонтального пути на
наклон. Среди различных частных случаев,
представляющихся вниманию исследователя при изучении уравнения

II, ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ ПОЕЗДА 53
движения поезда, естественно обращает на себя внимание
тот, когда поезд, схематизируемый как определённой длины
материальная цепь, входит с горизонтального пути на
наклон. Нетрудно составить уравнение, соответствующее
промежутку времени, когда совершается этот переход.
Обозначив через L длину поезда и полагая γΖ, = 1, назвав,
кроме того, через 5 длину той части поезда, которая уже
поднялась на подъём / (или спустилась под уклон —ί)
мы, очевидно, будем иметь
ν ^ = £ (a — bv-\- cv2— γβ). (14)
Этим уравнением определится движение в промежутке от
5 = 0 ДО
s = i = I.
Τ
Полагаем в уравнении (14) для определённости а = 15;
6 = 0,5; с = 0,004; ξ = 125; γ==2,5; i = 5; smax = 0,4;
vQ = 50;
a — bvQ -\- cvl — 0.
Нижний предел ν = и находим из уравнения
«£-«{«-*-(£-0·'-4 <15>
приняв во внимание, что "о"("ь"4"7г) близко к единице,
если h принадлежит к числу имевших место в
действительности скоростей. В данном случае ввиду обращения
в нуль — в уравнении (14) при 5 = 0 правильнее всего
принять h—v0, так как тогда и -^ в уравнении (15) удо-
du А „ Л
влетворяет тому же условию -=- = 0 при $ = Ό.

54
С. А. ЧАПЛЫГИН
Обозначим для краткости и2 через г; введя все
принятые числовые значения, найдём из уравнения (15)
^-=625—4 — 3125$.
ds 4
Это уравнение имеет общий интеграл
8
φ = ζ = Ае~ -f 52 500 — 12 5005.
Произвольное постоянное А в нашем случае ввиду
соотношений
г0 = ^ = 2500, s0 = 0
имеет величину — 50 000. Итак,
ζ = 52 500 — 12 5005 — 50 000е~~ * . (16)
При максимуме 5 = 0,4 достаточно взять разложение
показательной функции, сохранив степени s до четвёртой
включительно:
—"j 1 5 , 52 53 , 54
4 '32 3-128 π 3.8.256'
поэтому формулу (16) можно переписать в виде
52 , 3125 53 3125 5*
я2=г = 2500—3125
3 8 3 128'
При вычислении нижнего предела интеграла нужно
в разложении показательной функции остановиться на
положительном члене, уменьшая, таким образом, этот
предел, как явствует из формулы (16). Минимальное
значение zmiu = zl найдётся из уравнения (16) при подстановке
5 = 0,4:
z{ = 2500 _ 250 Η- 8 ^ — |f = 2258,125;
ux = Y7[tt 47,52 км/час.

II. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ ПОЕЗДА 55
При нахождении нижнего предела, в сущности, мы из
ξ
правой части уравнения (14) вычли выражение ^—b(v—τ>0)2,
которое при ν = ν0 обращается в нуль, а при близких
к этому значению величинах скорости имеет очень малое
значение по сравнению с остающимся ускорением, особенно
с последним членом -—γ/^. Уравнение (14) может быть
переписано в форме
которая и показывает, что в результате подстановки
в уравнение (14) значения и, определённого из
уравнения (15), получается отрицательная величина
•9^("-%>2<0.
Для нахождения верхнего предела можно поступить
аналогичным образом, именно прибавить к правой части
tfo + fi
выражение, обращающееся в нуль при v = v0 и ν = νχ
(где Oj — нижний предел скорости) и положительное при
промежуточных значениях скорости. Уравнение (14) может
быть переписано в виде
ds I VC+O, Wo+σι / ' J^
Легч'о сидеть, что интеграл уравнения
Ί=ο,
dw * Г , vnVi
dS I V0+V±
b
-C )W* — 41S

56
С. А. "ЧАПЛЫГИН
имеющий начальное значение w = v0> и будет давать
верхний предел истинной скорости, определяемой из
уравнения (14), ибо результат подстановки w в уравнение (17),
тождественно совпадающее с уравнением (14), даёт
i (*Y>—w) (w— vi)> 0.
^o + ^i
За vt мы можем принять определённое выше v1 = 47,52
или, проще, 47,5; после чего, по замене букв числами,
уравнение (18) дает
§ = 2500 · Э-Я*-312&.
где
Ζ = иР.
Отсюда
/39\2
tw4==Z=3125.(j?)',+
-j-2500 — 3125-у? 5— 3125-(~)%
или, по разложении в ряд показательной функции,
£=2500— ^-s2 +
, 3125 s3 11 3125 s4 /Ц\« . 3125 s* /11\з
3 2 39 3 8
/Ιΐγ . 3125 so /11\з
439/ "τ" 3 40 V39/ '
Здесь при разложении показательной функции необходимо
было остановиться на отрицательном члене, опять-таки
ввиду формулы (16). При 5 = 0,4
Ζ1-2260 + 84-(ΐ + |·)-έ(1 + » + έ) +
Н-13-Ш)3^2259'145·
Но

II. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ ПОЕЗДА 57
где ε есть единица с небольшой дробью; это меняет лишь
сотые доли километра в скорости, и мы получаем
верхний предел часовой скорости
г = ΫΖ1 = 47,53 км/час.
w
§ 6. Нахождение .вторых, более близких пределов
для скорости в задаче о переходе поезда с
горизонтального пути на наклон. Итак, положим, что мы нашли
две функции и и w, между которыми заключается искомая
функция ν и которые суть первые пределы. Как найти
более тесные пределы для ν, т. е. такие функции иг и wv
которые с большим приближением подходят к ν снизу и
сверху на заданном участке от s — 0 до smax ?
Напомним, что нижний предел и определяется из
уравнения
du
и —
ds
■«[«-^-(^-'У-Н-0· <19>
причём основное уравнение (14) преобразуется для этого
случая в следующее:
.0-ί[«-^^(έ-«)--Η-
-is; с—»»>'=■<>; (2°)
а верхний предел w определяется из уравнения
da ■ L v0 + u-
dw ft [л u v^u'
v0 + u'
Ч^-'К-^Н· (21)

58
С. А, ЧАПЛЫГИН
где и! есть наименьшее значение и, соответствующее
наибольшему s. Основное уравнение (14) преобразуется при
этом так:
·£-«1-»^-(5Ϊτ-«)"-Η+
+ '<-^ТГ (»о-»>(»-«') = Λ (22)
Если теперь в последний член уравнения (20) вместо ν
внесём верхний предел w, то это равенство нарушится.
Для восстановления его мы должны уже взять не ν,
а другую функцию, назовём её через их; для её
определения имеем следующее уравнение:
'.£-«[—!?-(&-0'!-Н-
-l±-(w-v^-0. (23)
Подставим в последнее уравнение вместо ut искомую
функцию V] тогда, принимая во внимание уравнение (20),
найдём, что уравнение (23) преобразуется в следующее
неравенство:
= l±(v + w — 2v0)(v — да)>0,
так как множители ν — w и v-\-w — 2v0 оба
отрицательны на всём участке. Поэтому по теореме о
дифференциальных неравенствах мы заключаем, что
их <v.
Подставляя в уравнение (23) вместо их функцию и,
на основании уравнения (19) получим в результата
подстановки
_Е^.(«,_„0)«<0,

П. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ ПОЕЗДА 59
т. е. и < их\ иначе говоря, ых будет более близким
нижним пределом к vy чем и.
Подставляя в тот же последний член уравнения (20)
вместо ν функцию и, получим следующее уравнение для
определения новой функции w{.
dw
ι t Г bvo f b \ 9 .1
-£2F0 ("-%)2 = 0; (24)
внося же сюда, вместо wlt искомое ν, на основании
уравнения (20) получим
ζ2^~ и)(? + и — 2г>0)<0,
так как ν — и положительно, а ν -\- и — 2ν0 отрицательно
на всём участке. Поэтому по теореме о дифференциальных
неравенствах заключаем, что
это показывает, что w1 есть верхний предел интеграла v.
Но будет ли wx < w, т. е. будет ли w1 более близким
пределом к ν, чем ранее определённый w, об этом нельзя
судить на основании анализа в алгебраическом виде.
В самом деле, подставляя в уравнение (24) вместо wl
функцию w, на основании уравнения (21) получим в
результате подстановки, что на всём участке
(Ро-«)(«--«0 _ ( 2 _ ц2) ^^_ > о, (25)
так как при u = v0 неравенство (25) имеет такой вид:

60
С. А. ЧАПЛЫГИН
а при и = а' оно имеет вид
Следовательно, теорему о дифференциальных неравенствах
в данном случае применить нельзя; тем не менее, в
результате подстановки числовых величин получается w >wu
что не противоречит соображениям, на основании
которых выведена теорема о дифференциальных неравенствах.
Что касается уравнений (21) и (22), то, проделав
с последним из них аналогичную операцию подстановки,
как вышеизложенная, найдём в результате неравенство,
знак которого будет изменяться с изменением 5 на
рассматриваемом участке, и потому к нему не может быть
приложена теорема о дифференциальных неравенствах.
Подсчёт пределов и здесь не представляет труда, но
я не нахожу нужным выписывать всех этих вычислений.
Замечу только, что в результате второго приближения
оказывается возможным в точке наибольшего расхождения
обычно определить .часовую скорость до долей метра.
§ 7. Приближённое интегрирование уравнения
движения поезда в случае, когда начальная скорость
равна нулю. Данный нами путь приближённого
интегрирования уравнения
v*!L — t(a — bv + cv* — 4is) = 0 (26)
неприложим в одном частном случае, именно если v0 = 0.
Тогда все приведённые выше рассуждения падают. Но
в этом случае легко усмотреть совершенно иной, столь
же естественный подход. Заметим, что [интервал
изменения расстояния] s, на котором имеет место уравнение (26),

II. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ ПОЕЗДА 61
не превышает длины поезда, почему и время, в течение
которого происходит исследуемый процесс, также в общем
невелико. Пока скорость не превосходит 10—15 км/час,
член cv2 мал по сравнению с bv\ в самом деле, при
b = 0,5 и с = 0,004, как было принято выше, имеем
для «σ=1,0: £-0 = 5,0; ст2 = 0,4;
» ν =15: £г> = 7,5; с<оа = 0,9;
поэтому для первого приближения мы отбрасываем
квадратичный член. Остающееся уравнение
иЖ~^а — ** —Tffe)-° (27)
преобразуем к виду
и интегрируем его точно, как линейное уравнение с
постоянными коэффициентами, потребовав, чтобы при /=0
было
ds Л
5=*Г = 'г==0·
Отысканную таким образом функцию
ds
4t=u
мы можем принять за нижнюю границу скорости ν, ибо
подстановка в уравнение (26) функции и вместо ν даёт
в левой части — %cv*\ стало быть,
и <τ>.
Более близкий нижний предел найдётся из уравнения
(26) по замене в нём ν в квадратичном члене %cv* через

62
С. А. ЧАПЛЫГИН
найденное и. В самом деле, обозначив функцию,
удовлетворяющую преобразованному таким образом уравнению,
через αν легко находим, что
"ι > я,
так как по замене в уравнении
Ul ^ — ξ (а — Ьих + си* — lis) = 0 (28)
и1 через и мы получаем в левой части, как это вытекает
из уравнения (27), величину
— Есиа<о.
С другой стороны, подстановка в уравнение (28) вместо
ах скорости ν даёт
lc(v*—u*)>0.
Таким образом,
г; > ttj > й.
Чтобы найти верхнюю границу интеграла, рассуждаем
так. Обозначим эту функцию через w; по условию te>0 = 0;
что же касается конечного значения w, то оно вообще
неизвестно. Назовём его через а. Легко усмотреть, что
интегрирование уравнения
w2jj — l[a — (b — ca)w — vs] = 0 (29)
определит искомую верхнюю границу; в самой деле,
подстановка w — v в уравнение (29) даёт
U {ν—α)ν < О,
ибо а во всяком случае более v.
Для отыскания α будем иметь выражение скорости w,
в конце процесса равной а, через известные величины

П. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ДВИЖЕНИЯ ПОЕЗДА 63
и через то же а. Таким образом, получим некоторое
определённое уравнение, из которого и найдём а. Через
замену в квадратичном члене уравнения (27) функции и
через найденную функцию w найдём новое
дифференциальное уравнение
Wl *?L _ ξ (д _ ьщ 4- cw* — γ/5) = 0, (30)
которое определит нам следующую, более близкую к
искомой скорости верхнюю границу её wv Это вытекает из
того соображения, что в результате замены wx через w
в левой части уравнения (30) мы получаем
\cw (а — w) > 0;
следовательно,
w > ад1#
С другой стороны, подстановка ν на место w1 даёт
а стало быть,
W{ > V.
Таким образом, мы получаем первое и второе
приближения, а*именно
w > wx > ν > их > и.

UO<n>V^*W^T*»4*'^4Xl^Vn(*'^T^^
III. ИНТЕГРИРОВАНИЕ ОСНОВНЫХ УРАВНЕНИЙ
БАЛЛИСТИКИ ПРИ ЗАКОНЕ СОПРОТИВЛЕНИЯ,
ДАННОМ ЛОРЕНЦОМ
§ 1. Постановка задачи. В предлагаемой статье мы
даём приём для приближённого интегрирования уравнения
баллистики в случае выражения силы сопротивления
формулой
R = kmg*[l -f- (v2_^+c?v,],
тле а — скорость звука, с—особая скорость затухания
колебаний, ν — скорость снаряда, m — масса снаряда. Для
простоты я рассматриваю лишь случай отлогой стрельбы.
При навесной придётся пользоваться разбивкой
траектории на участки обычными приёмами баллистики. Всё дело
в интеграции основного уравнения между скоростью и
углом наклона (уравнения годографа). Если этот угол
будем обозначать через 0 и скорость через vy то
(1)
m
mg
di
сЦ
rv cos θ)
dt
2 d§
ds
g"cos6
υ cos Θ)
"5θ :
= —
_ г/2
_ Ρ
= —
=*vR
Rcos
= —
db
0,
g
cos6, j
J

III. ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ БАЛЛИСТИКИ 65
Последнее уравнение и надо интегрировать прежде всего.
Разумеется, можно говорить лишь о приближённом
интегрировании этого уравнения.
Я опираюсь на следующую доказанную мною теорему:
пусть задано дифференциальное уравнение первого
порядка
£—f(x. У) = 0, (2)
разрешённое относительно производной искомой функции;
пусть далее ζ— некоторая функция х, имеющая при
начальном значении переменной χ = х0 то же значение j/0,
которое должен иметь искомый интеграл; пусть, далее,
в результате подстановки ζ на место у в наше
дифференциальное уравнение получается величина, большая нуля
при всех значениях переменной χ на интересующем нас
участке, примыкающем к точке х — х0; тогда, если этот
участок лежит в области обыкновенных точек функции
/(#, у) и если как г, так и у по смыслу задачи не
обладают здесь особенными точками, то мы будем иметь ζ^> у
для χ > х0 и ζ < у при χ < х0.
§ 2. Преобразование уравнения годографа.
Приведём уравнение (1) годографа к общему виду (2)
уравнения первого порядка. Его можно преобразовать двумя
способами.
а) Избрав новые переменные
будем иметь
At-— dv-—2a*—·
ах ~ cos θ ' ау — Ш ν* '
Sin0 = ^qn = th*
5 Зак. 1799. С. А. Чаплыгин.

66
С. А. ЧАПЛЫГИН
R
mgv*
где
41+ (^-уУ+ьуУ
Подставляя в уравнение (1) годографа в раскрытом виде'
mgYcos 0 —^- — ν sin Ь)—vR= О,
и преобразовывая его к новым переменным, получим:
£ + 2^h* + «[l + (T=3^] = 0, (3)
где
η = 2&я2.
б) Подставляя
я cos 0 = <?σ
или
V2 COS2 θ '
то же уравнение представим в виде
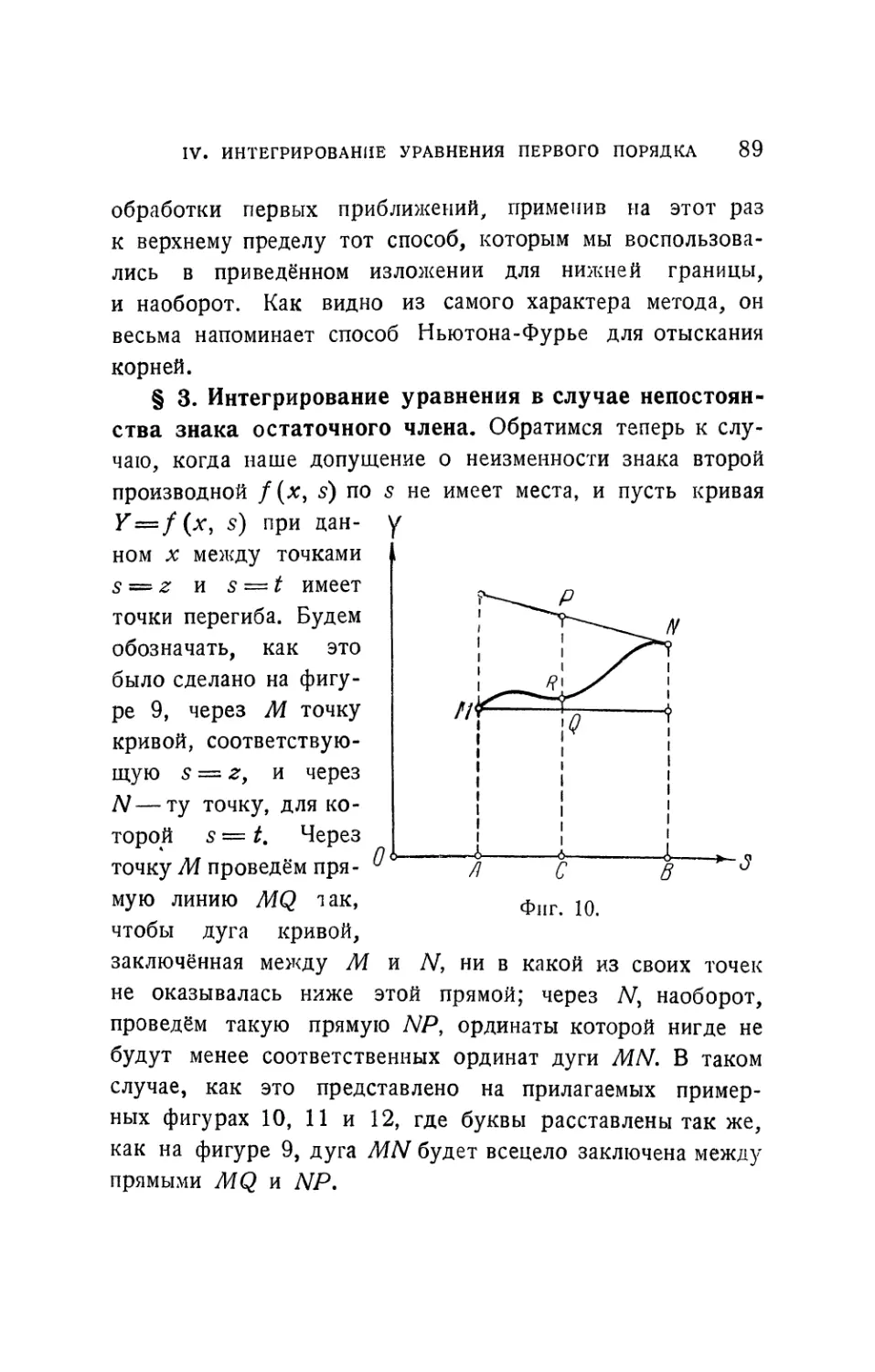
§ 3. Интегрирование уравнения годографа,
записанного в первой форме. С точки зрения теории, пожалуй,
прямее путь приближённого интегрирования уравнения (3),
особенно если иметь в виду только это уравнение, не
обращая пока внимания на прочие уравнения баллистики.
При отлогой стрельбе величина ху начиная с начального
значения х0, всё время убывает. Заметим, что и
гиперболическая функция th χ будет убывать. Проинтегрируем
уравнение
•£ + 2«th*0-*[l+ ж^ ]-0. (5)

111. ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ БАЛЛИСТИКИ 67
Возьмём интеграл, который при х = х0 равен у0, и
подставим его в уравнение (3). Получим в левой части,
приняв во внимание равенство (5):
H=2z(thx — thx0);
так как х0>х, то #<0, и, следовательно, по
приведённой теореме z>y. При
χ = χ^ z0 —Уо
по дифференциальному уравнению следует
/ dz\ (£У_\ .
\ dx/o V dx /о'
поэтому искомая интегральная кривая, прикоснувшись
в точке х = х0 к кривой z = z(x)1 должна далее итти
ниже её.
у
I
ί/ό —6 ό 1—*~-χ
Фиг. 5.
Так как в нашем случае, по условию вопроса, у должно
ς течением времени, т. е. с убыванием перехменного д:,
возрастать, то х, вычисленное из уравнения г = г(х), будет
более х, которое получилось бы из интегрального
соотношения у=у(х) при y = z; это видно непосредственно
5*

68
С. А. ЧАПЛЫГИН
из фиг. 5, на которой ОЛ соответствует интегральной
функции у, а ОВ— функции г.
На этом основании, назвав через х1 = χ (ζ) выраженное
в зависимости от ζ решение уравнения
ζ = ζ (χ),
будем иметь
th ATj>th х\
но, с другой стороны, ясно, что
thA,0>thjf1,
так как х0> хх; на чертеже Ох0 > ОВ; лишь в начальный
момент хг = д*0.
Представим теперь себе, что мы проинтегрировали
уравнение
•g-+gglth^1 + "[i+(1,Jt|y + tol]-o, (6)
где переменные опять разделяются, так как хг = хх (zt).
Подставив интеграл уравнения (6), имеющий начальное
значение z0=y0, в уравнение (3), мы получим в
результате подстановки
H1 = 2(thx — ihx1)z1<0,
так как
x<xv *ι>0,
а следовательно, у<г; но подстановка zx в уравнение (5),
определяющее ζ, даёт
Ha = 2(thAT0 —th^)^ >0,
так как л:0 > х. Поэтому ζγ < ζ. Окончательно

III. ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ БАЛЛИСТИКИ 69
Итак, мы приблизились к искомому интегралу. Повторив
операцию, мы найдём г2 такое, что
y<z2<zu
и так далее.
С другой стороны, если за исходное уравнение вместо
(5) мы возьмём уравнение
^ + ^th^ + «[i + u=5>)4+s>]-o,
в котором хг есть постоянное, определяемое углом
падения bv заранее неизвестное, подлежащее определению по
прочим уравнениям баллистики и удовлетворяющее
неравенству χ > х', то интеграл этого уравнения, имеющий
значение у0 при χ = х0, даст нам нижний предел
интегральной кривой; мы будем иметь у > ζ'\ переходя от zr
к z'x и z'2 аналогично тому, как мы выше переходили
от ζ к гг и ζ2, будем иметь
У>г'2>*\>*'·
ЯснХ), что таким образом мы можем постепенно подходить
к искомому интегралу.
§ 4. Интегрирование уравнения годографа,
записанного во второй форме. Изложенный приём, совершенно
ясный с математической стороны, неудобен по причине
значительных вычислительных трудностей. С точки зрения
возможного упрощения вычислений удобнее исходить из
другой формы основного баллистического уравнения, именно
уравнения (4):
W" cos^O L +(1—ocos»e)*-|-frjcos2e J^0· (7)

70
С. А. ЧАПЛЫГИН
Назовём через σ0 значение σ при θ = θ0 = <*. Отыскав
интеграл уравнения
~Ж~" ТоРТГ l1^ 7^2—Ί>) τ COS2 α + τ2"] ~ °' (8)
который имеет значение τ = σ0 при θ = α, и подставив
его в уравнение (7), получим в результате
г _ пА [τ (2 — 5) (cos2 θ — cos2 a + τ2 (1 —· cos* θ)]
— cos» θ 11-(2— b) τ cos2 θ -f τ2 cos* θ] [1 — (2 — δ) τ cos* α+τ2]'
Ясно, что G>0 пока cos2 0 > cos2 α, 0<α, и
следовательно, по основной теореме здесь τ менее σ. На участке
пути, где cos2 θ < cos2 α, т. е. в точках, близких к месту
падения снаряда, числитель G будет также более нуля,
потому что в этих точках, вообще говоря, τ, отношение
квадрата скорости звука к квадрату [проекции] скорости
снаряда [на горизонталь], уже значительно более единицы,
и мы будем иметь в числителе в самой неблагоприятной
точке, точке падения (Θ = а'),
(2 — Ь) (sin2 а — sin2 α') -f τ sin2 а' (1 + cos2 а') > 0,
по причине указанного значения количества τ > 2 — b.
Если бы τ не было более единицы вблизи точки падения,
то можно было бы в формуле (8) ввести вместо
начального угла а угол падения а', и тогда никаким сомнениям
о знаке выражения О не осталось бы места.
Вместо τ можно взять мало отличающуюся от него
функцию s, меньшую τ, которая найдётся в результате
интеграции уравнения
~t~cos2e [ 1 «"1—.(2—&)scos2a + s2J^
x(i+!f'_Jp] = o. (9)

Ш. ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ БАЛЛИСТИКИ 71
Интеграл этого уравнения, равный σ0 при 0 = а, наверное
меньше τ. В самом деле, результат его подстановки
в уравнение (8) даёт
G' = tf2f_J i_ig!i+J£IW0
так как
_1 Λ , tg2Q lg*6\2_ tg66 tg8Q
cos26 V1*"» 2 8 j " 8 64 ^
Начать можно с интеграла уравнения, которое
получится из уравнения (9) заменою последней скобки просто
единицей, стало быть, уравнения
ds , η Г ^ · А 1 п
)s20[1^ 1 — (2 — fc)scos2a-|-s2 J —'
if θ ' cos
Проинтегрировав его и найдя tg θ = F (s), в интеграле
уравнения (9) член
tg3 6 tg5Q
6 40
можем заменить выражением
Таким образом, мы придём к более точному значению tg θ
и найдем s, т. е. нижний предел σ:
σ >5.
Далее можно поступать способом, аналогичным тому,
который мы употребляли при интегрировании уравнения (3).
А именно, так как 6Х и θ2, определённые для равных
значений s и σ из уравнений
*=/(<·), * = ф(0),

72
С. А. ЧАПЛЫГИН
будут, как видно из фигуры 6, удовлетворять неравенству
где
01== 0 = /-!(*), 09 = 0 = φ-ΐ(σ),
то, проинтегрировав уравнение
tg26t tgiOA
dSj ■ « Λ ι tg^t tg*6A
de ι" cosseA1 '2 8 /Λ
Xi
[■
= 0,
мы опять найдём ^<ои подойдём несколько ближе к
искомому интегралу, так как^ будет более s. Но легко видеть,
что мы не в состоянии будем повторением этого приёма
подойти как угодно близко
к искомому интегралу, так
как коэффициент при s2
в знаменателе дроби
А
1 _ (2 _ b) s cos2 θ + s2
приходится оставлять рав-
дь j **-ff ным единице, что суще-
. п ственно меняет вид урав-
Фиг. 6. J*
нения.
Другая, а именно, верхняя граница σ найдётся
интегрированием уравнения
rfe+^Fe(1+i-_(2-6)x/ + T'2cos4aV °' (10)
причём τ0 = α0, где а'— угол падения; вместо этого
уравнения можно взять
d^^cos^V^r 2 Д1 Τ" 1_(2 — b)s'+s'2
=0.
cos4 a/

III. ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ БАЛЛИСТИКИ 73
Будем иметь s' > τ' > а, если s'Q = τ^ = σ0. От s' можно
перейти к ^ < s' путём интеграции уравнения
d^
η ( tg2 8\/
= 0,
db ι cos26\ ~ 2 /\ n i^-(2_^)^ + s/2cos4^
где 0 нужно определить через sr± из уравнения s^ — Fx (θ),
полученного путём замены s' через s't в интеграле
предшествующего уравнения.
Таким образом, окончательно найдём
s' > s[ > σ > s± > s.
Пределы s^ и s± будут ближе друг к другу, чем
начальные приближённые интегралы sf и 5.
§ 5. Другой способ интегрирования уравнения
годографа, записанного во второй форме. Практически
окажется, может быть, более удобным следующий приём
приближённой интеграции уравнения (7), т. е.
da . η л т Λ
db ' cos3 θ
1 + 1 — (2 - b) σ cos2 θ 4- σ2 cos* θ J = °" (10)
Что касается количества —-г, то его попрежнему будем
заменять через
р, = 1+itg^e или P(r = l + |tg«e-Itg*0,
смотря по тому, определяем ли мы верхний или нижний
предел интеграла. Знаменатель же дроби, стоящий в
скобках, заменим через 1 — (2 — Ь) Ασ -|- Α'σ2, где количества А
и А' суть правильные дроби, чрезвычайно мало
отступающие от единицы, так как они должны лежать в
пределах 1 > А > cos2 а и 1 > А' > cos4 α',

74
С. А. ЧАПЛЫГИН
Проинтегрировав уравнения
d?/ пр, Λ , А
Ж + ЩЦ [ "^ 1 — (2 — 6) Λ,σ, + h'rf
de \ cos2 e ^ ' ι _ (2— b) h„a„ + h**i J v '
интегралы этих уравнений, имеющие значения σ, = σ„ = σ0
при θ = α, подставим затем в левую часть
уравнения (10); в результате получим соответственно G, и Grr
Затем подыскиваем коэффициенты h, и К (лежащие в
указанных пределах) под условием, чтобы было О, < 0;
коэффициенты же hn и h'„ должны приводить к
неравенству G„ >0. Тогда σ, >σ>σ„. Разумеется, чем ближе
к равенству количества К и Н1П с одной стороны, h и
А„ — с другой, тем пределы будут теснее, и тем точнее
будет искомый интеграл.
Однако это уравнение (10) само по себе не даст
возможности с достаточной точностью определить
коэффициент h. Для этого придётся обратиться к другим
уравнениям баллистики и определить по ним сначала пределы,
в которых лежат а' и — ν/, значения величин σ и θ в точке
падения. Лишь тогда мы будем иметь перед собою всю
область изменения величин σ и 0, а стало быть, лишь
тогда вполне строго можно судить о знаках выражений О,
и Оп в пределах изменения переменных при изучаемом
движении.
§ 6. Общий ход решения задачи. Подводя
окончательное резюме сказанному, намечаем нижеследующий
путь решения задачи. Интегрируем уравнение (11).
Найденное значение функции σ1 будет более σ при должном
= 0, (11)

HI. ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ БАЛЛИСТИКИ 75
подборе подлежащих определению величин h{ и h'v Далее}
обращаемся к уравнениям
dft g , /— 0,. dx a dy , n
-· = — Α γ0 cos2 0, — = -=, f = tg Θ,
fi^ я dt у a dx
которые дают
£ У σ £ σ g α
где для краткости письма введено обозначение
p = tg0.
Эти уравнения можно переписать в виде
dt , α
Τ
rf/? £У σ
Допустим, что мы вместо σ подставим в эти
уравнения количество а1У которое для ясности рассуждений будем
себе представлять выраженным через /?, и таким образом
определим приближённое время tx и координаты снаряда хг
и yv Чтобы охарактеризовать соотношение между этими
приближёнными и истинными значениями функций t, χ, у,
подставим отысканные их выражения в уравнения (13),
(14), (15), в которых будем под σ понимать его истинную
величину. Соответственные значения левых частей
а_/_\ \_\ i*VJ__J_\ ff/_l 1\
все будут положительны, если <Jj>c; следовательно, мы
нашли нижние пределы значений искомых функций.

76
С. А. ЧАПЛЫГИН
Исходя из интегралов σ„ уравнения (12), найдём таким же
способом t2, х2, у2, которые при надлежащем выборе й„
и h'„ явятся верхними границами количеств t, χ и у.
В обоих случаях σ определяется при одном и том же
угле 0, или, что всё равно, неизменном значении
количества ρ = tgO.
Положив ух = О, найдём рг = — tg α', т. е. тангенс
угла падения, который будет, как нетрудно сообразить,
численно менее истинного р'. Из уравнения у2 = 0 найдём
/?2 > Р' (не надо забывать, чт0 Рг отрицательно). Эти
соотношения пояснены
на фигуре 7, где А
будет истинная точка
падения {О А — истинная
траектория); здесь
р = р',х = х',у=/,
Af и ATf будут
неизвестные нам
положения снаряда,
характеризуемые значением
ρ = рг = — tg α'
переменного ρ на
приближённых траекториях ΟΒ,Α, и ОВ„А„. Значение ρ =р[
соответствует точке В, траектории/,/?^ — точке Вп
траектории //; соответственно о, и σ„ в этих точках будут
равны о, и σ',.
Теперь обращаемся, наконец, к выражениям G, и G„
на стр. 74. Так как G, должно быть менее нуля, то,
отыскав в найденных пределах σ0 и <з' изменения σ
максимальное значение G,, приравняем его нулю; тогда условие,
наложенное на G„ будет удовлетворено, и мы найдём
одно соотношение между й и й,'.
Фиг. 7.

Ш. ИНТЕГРИРОВАНИЕ УРАВНЕНИЙ БАЛЛИСТИКИ 77
Таким же образом, требуя, чтобы наименьшая величина
G„ была нулём, найдём соответствующее соотношение
между hn и h'/r Два остальных соотношения между h
могут быть определены из различных соображений, если
иметь в виду возможное сближение найденных пределов
изменения величин, фигурирующих в задаче. Кажется,
всего естественнее было бы требовать, чтобы границы,
найденные для дальности полёта снаряда {х1 —Хх и
х2 = Х2 при соответственных ординатах, равных нулю) и
для времени его нахождения в воздухе Т, были возможно
ближе между собою, т. е. Х2 — Хх и Т2 — Тг должны
иметь наименьшую возможную для них величину. Может
быть, вместо 7'2 — Тг практичнее рассматривать разность
ординаты Yu которую кривая / имеет в точке Х2, и
У2 — ординаты кривой //, определённой для точки Х=ХХ,
и требовать наименьшего числового значения разности
γ*—Υχ σι<ο, r2>o).
Что задача, которая нами поставлена, имеет решение
искомого типа, явствует из следующих соображений: при
интегрировании уравнения (10) ранее рассмотренным нами
приемрм были найдены значения функций s' и s, из
которых первая представляет верхний предел σ и соответствует оп
вторая, как и σ„, является нижним пределом для σ:
s'>a>s.
Легко увидеть, что 5 есть частное значение о/9 получаемое
при A, ss=l, ti, = cos4α',, а σ„ — частное значение s,
соответствующее hlf = cos2 α, h'„ = 1.
Кстати сделаем здесь ещё замечание об определении а'.
После того как по найденному s' будет найдено у, из

78
С. А. ЧАПЛЫГИН
равенства у = 0 мы найдём соответственное значение
угла 0 = — а' путём совместного решения уравнения у = О
с уравнением tg θ = — tg α7 = / (У).
Если пределы σ/ и σ„, между которыми находится
искомый интеграл, недостаточно близки, то, подставив в
уравнение (10) вместо ocos6 по очереди значения этого
количества и определив их в функции σ при помощи
уравнений tg61 = /7(o1), tg β/7 = F(of/)$ мы получим путём его
интегрирования более близкое значение о; при этом для
решения вопроса о том, в каком соотношении стоят новые
значения с истинной величиной σ, должно опять
воспользоваться нашей основной теоремой о дифференциальных
неравенствах.

1^1<и?уп*у»т*'У»У'г^г*Утх^Ут^У'УУ^
IV. ПРИБЛИЖЁННОЕ ИНТЕГРИРОВАНИЕ
ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
ПЕРВОГО ПОРЯДКА
§ 1. Основная теорема о дифференциальных
неравенствах. В брошюре автора «Основания нового способа
приближённого интегрирования дифференциальных
уравнений» *) изложена основная теорема, на которую
опирается способ, и в общих чертах охарактеризован порядок
интегрирования. Здесь я приведу доказательство этой
теоремы, называемой мною также теоремою о
дифференциальных неравенствах, ограничиваясь уравнением первого
порядка
g-/(*, j0 = o. О)
Теорема. Допустим, что мы нашли функцию t — t(x) *)
с такими свойствами:
!) 'о=.Уо ПРИ х = *о'>
2) всюду на участке (х0, X), прилегающем к х0, где
значения χ более х0, результат подстановки t на место у
в уравнение (1) более нуля, т. е.
£-/(*, У)>°- (2)
1) Журнальная статья в повременном издании НКПС, Москва,
1919 [стр. 13 настоящей книги].
*) [На стр. 15 эта функция обозначена через z(x),]

80
С. А. ЧАПЛЫГИН
Предположим, далее, что на этом участке искомый инте*
грал у и функция t не обладают особенными точками.
Тогда для всех х, больших х0 и не превосходящих
определённого выше предела X, будет существовать
неравенство
t>y.
Знак этого неравенства был бы обратный в случае
противоположного знака в неравенстве (2); неравенство будет
также обратного знака в области прилегающих к точке х0
значений независимого переменного, меньших х0.
Для доказательства теоремы из выражений (1) и (2)
составим неравенство
где
f(x, t)-f(x,y)
Р = - t-y
представляет собою на основании наложенных на t и у
условий вполне определённую, хотя и неизвестную нам
функцию х, всюду конечную в области интересующих
нас значений переменных; для х = х0 функция эта,
очевидно, имеет значение
Умножим построенное нами неравенство на положительный
в наших условиях множитель
χ
— Ι" ρ dx
s dx = e χο dx.
Интегрируя в пределах х0 и х, получаем
χ
I (t—y)s>0.

IV. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 81
Так как tQ=y0, то по упрощении это неравенство
приводит к искомому результату
t>y.
Если бы χ было менее х09 то на пути интеграции dx
было бы отрицательно, и, следовательно, при умножении
на sdx неравенства в нём пришлось бы изменить знак,
а это повело бы к изменению знака результата.
Само собою ясно, что функция ζ1), удовлетворяющая
неравенству
§-/(*, г)<0
и условию
^>"Л.
даст
z<y-
Будем называть определённую таким образом функцию
верхней или нижней границей интеграла, смотря по знаку
неравенства, так как интеграл у будет заключён между t
и ζ:
t>y>z.
Ясно, что для приближённого интегрирования уравнения (1)
достаточно тем или иным путём определить верхнюю и
нижнюю границы интеграла так, чтобы разность между
значениями t и ζ при всех значениях независимого
переменного была возможно меньше. Переводя это на
геометрический язык, мы можем сказать, что на плоскости ΟΧΥ
надлежит выделить ленту ABC, по возможности узкую,
внутри которой необходимо должна лежать интегральная
кривая Лу (фиг. 8). Понятно, что уравнения t=t(x) и
gvm%(x) определяют в таком случае граничные
кривые АВ и АСь
г) [На, стр. 16 эта функция обоначема через и (х)>]
6 Зак. 17W. <2. А» Чаплыгин*

82
С. А. ЧАПЛЫГИН
Способ, при помощи которого, опираясь на доказанную
теорему, можно приближённо проинтегрировать данное
дифференциальное уравнение, очевиден: всё сводится
к отысканию верхней и нижней границ интеграла.
*~Х
Фиг. 8.
Имея дело с уравнением (1), можно поступить так.
Меняя по возможности мало вид уравнения, стремимся
привести его к интегрируемой форме; интеграл
изменённого уравнения, имеющий то же начальное значение, как
искомое решение уравнения (1), подставляем в это
последнее и определяем знак результата; если он
положителен, то мы нашли верхнюю границу интеграла
уравнения (1) для х, превышающих начальную величину;
противоположный знак результата показал бы, что мы имеем
дело с нижнею границею.
Установив обе границы и воспользовавшись ими как
первым приближением, можно в том или другом частном
случае ближе подойти к интегралу, подставив в
некоторые члены / (Ху у) на место у его верхнюю или нижнюю
границы. Знак результата подстановки найденного таким

IV. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 83
образом второго приближения позволит судить, имеем ли
мы дело с нижнею или верхнею границею искомого
интеграла.
Указанный приём оставляет значительное место
интуиции во всякой реальной задаче, и с этой точки зрения
представляется как бы не вполне выработанным. В
настоящей заметке я даю'совершенно определённый метод,
применимый ко всякому уравнению первого порядка,
удовлетворяющему условиям основной теоремы, и позволяющий
как угодно близко подойти к интегралу данного
уравнения.
§ 2. Интегрирование уравнения в случае
неизменности знака остаточного члена. Итак, пусть требуется
проинтегрировать дифференциальное уравнение
&-/<*.*)-°·
Допустим, что, опираясь на основную теорему о
дифференциальных неравенствах, мы нашли функции л:,
представляющие собой верхний и нижний пределы интеграла.
Тогда мы будем иметь на участке значений х,
заключённых 4 между х0 и X, большем х0, следующие
соотношения:
Ό = *о =Уо ПРИ х = *о» (3)
t>y>z, (4)
£—/(*. ') = ?(*)<<>> (5)
dt
dx
-/(*> 0=Ψ(*)>0, (6)
причём три последние справедливы для всякого х>
лежащего на участке (л:0, Х)9 т. е. при х0<х<Х.
6*

84
С. А. ЧАПЛЫГИН
Допустим сначала, что пределы ζ η t сближены между
* d*f(x, s)
собою настолько, что \ ъ по замене 5 каким угодно
числом, лежащим между соответствующими значению χ
величинами t и г, при любом возможном а сохраняет
неизменный знак. Будем для определённости предполагать,
что знак этот — плюс. Впоследствии мы увидим, как
изменяется решение задачи в противоположном случае.
Введём обозначения:
у— * = ζ, /—yz=τ.
В силу соотношения (5) имеем
3J-—/ (*, y)+f (*. *) + φ (*) - 0;
^i)C + ?W«-cc, (7)
с9>о,
а отсюда
rfC
Ах
где
,_ 1 д»/(х,8)
2 ds*
так как по теореме Тейлора
где 5 — величина, промежуточная между у и z\ на
рассматриваемом же участке значений независимого
переменного χ вторая производная, входящая в остаточный член,
по условию положительна. Отметим, что при х = х0 мы
должны иметь ζ0 = 0 в силу соотношения (3), а при
прочих значениях χ получим ζ > 0 на основании условия (4).
Отыскиваем обращающийся в нуль при χ = х0 интеграл
Линейного уравнения

IV. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 85
ои будет таков:
X ,
X
ξ = — е х» φ (х) е х* dx,
х0
где через fg обозначена для краткости частная производ-
df(x ζ)
ная -^-—^—-. Подстановка нуля на место ξ в уравнение (8)
даёт результат, меньший нуля, так как φ (л:) < 0; поэтому
по теореме о дифференциальных неравенствах
0<ξ;
та же теорема ввиду того, что замена ξ через С в
уравнении (8) по равенству (7) даёт в результате α > 0,
приводит к неравенству
о?,
или
y — z>t
Резюмируя отмеченные неравенства, мы приходим к
следующему окончательному результату:
y>z + t>z, (9)
и, стало быть, мы нашли новый, также нижний предел
zx — z-\-l,
более близкий к интегралу. По теореме о
дифференциальных неравенствах мы должны иметь
g—/(*,*!) =9х(*)< 0, (10)
так как, кроме неравенства (9), zx удовлетворяет также
и требованию
*ю —*ο=υΌ ПРИ * = *<>·

86
С. А. ЧАПЛЫГИН
Повторяя по отношению к уравнению (10) тот же
процесс, мы получим новый, ещё более близкий нижний
предел интеграла ζ2 = ζ1-\-^ и т. д.
Обратимся к изысканию более близкого верхнего
предела. На основании уравнения (6), имея в виду, что
t=y-\-%, получаем
—fix, о+я*, JO - Ψ (*)=о.
Преобразуем это уравнение, приняв во внимание, что по
условию сохранения знака второй производной функции /
кривая
где Υ и 5 — текущие координаты, при всяком данном χ
обращена своею вогнутостью в сторону положительных у,
как это изображено на фигуре 9: здесь
ΟΑ=ζ, ΟΒ = έ, ОС=у.
RC=f(x,y), MA=>f(x, ζ), NB=f(x, t),

IV. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 87
MQ — касательная в точке М. Легко усматриваем, что
RQ = f(x, у)—f{x, ζ)— JKdz 4 = —др-^2"=«э
PR=f(x, *)—/(*, ,ν)-/(^^(χ'^τ = ρ>0.
Последняя строка даёт
если для краткости письма в дальнейшем воспользоваться
обозначением
/(.г, t)—f(x, ζ) = ^ , ν
Преобразуя при помощи приведённого соображения
вышеуказанное дифференциальное уравнение для ty найдём
£-/?(χ)τ-ψ(*) = Ρ>0. (11)
Отмечаем также, что τ0, т. е. значение τ при х — х0, есть
нуль и что во всей области значений х, кроме начальной
точки, τ положительно. Отыскиваем обращающееся в нуль
при χ = х0 частное решение линейного уравнения
αΛ^Ρ{χ)Ύί-ύ(χ) = 0. (12)
Такое решение выражается формулою
X X
iFclx® -JFdx
η = ехо Г ψ (χ) e χ» dx.
χ0
Легко усмотреть, что η > 0, как это и должно быть, так
как результат подстановки нуля в уравнение (12)
отрицателен вследствие неравенства ψ (χ) > 0. Наоборот, замена η

88
С. А. ЧАПЛЫГИН
через τ в силу уравнения (11) приводит к положительному
результату, а потому
τ = /—^>η>0;
отсюда
t>t—-q>y.
Таким образом, функция
*! = /—η
даёт верхний предел интеграла, более близкий, чем ранее·
найденная функция L
По основной теореме будем иметь
§-/(х, О = Ψι (*)><>·
Применив только что описанный процесс к этому новому
уравнению, найдём в результате следующее, ещё более
тесное приближение ^2» которое также будет верхнею
границею интеграла, и т. д. В конце концов у нас будет
налицо два ряда функций
Ь *1» *2» ' ' ' > w» · · ·>
Ζ, Ζ±, Ζ^ . . . , Ζη^ . . .,
из которых первые для одного и того же значения
независимого переменного убывают с возрастанием индекса,
а последние возрастают при том же условии. Способом,
указанным Η. Н. Лузиным, можно обнаружить, что
разность tn — zn при этом быстро стремится к нулю.
В заключение отметим, что если бы мы приняли
противоположное предположение о знаке второй
производной функции fix, s) в пределах изменения s, то нам
пришлось бы переместить данные нами два процесса

IV. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 89
обработки первых приближений, применив на этот раз
к верхнему пределу тот способ, которым мы
воспользовались в приведённом изложении для нижней границы,
и наоборот. Как видно из самого характера метода, он
весьма напоминает способ Ньютона-Фурье для отыскания
корней.
§ 3. Интегрирование уравнения в случае
непостоянства знака остаточного члена. Обратимся теперь к
случаю, когда наше допущение о неизменности знака второй
производной /(#, s) по s не имеет места, и пусть кривая
К = /(х, s) при
данном χ между точками
5 = ζ и s = t имеет
точки перегиба. Будем
обозначать, как это
было сделано на
фигуре 9, через Μ точку
кривой,
соответствующую s = ζ, и через
N — ту точку, для
которой 5 = t. Через
точку Μ проведём
прямую линию MQ так,
чтобы дуга кривой,
заключённая между Ми W, ни в какой из своих точек
не оказывалась ниже этой прямой; через Ν, наоборот,
проведём такую прямую ΝΡ, ординаты которой нигде не
будут менее соответственных ординат дуги ΜΝ. В таком
случае, как это представлено на прилагаемых
примерных фигурах 10, 11 и 12, где буквы расставлены так же,
как на фигуре 9, дуга ΜΝ будет всецело заключена между
прямыми MQ и ΝΡ.

90
С. А. ЧАПЛЫГИН
Иногда одна из граничных прямых может оказаться
касательной в одной из конечных точек, как это имеет
место для прямой ΝΡ на
фигурах 10 и 11; на
фигуре 11, кроме того,
вторая граничная прямая
совпадает с хордой ΜΝ,
так что здесь мы имеем
случай, совершенно
аналогичный изображённому
на фигуре 9. Наконец,
фигура 12
предусматривает такое более общее
предположение,когда
граничные прямые не столь
просто связаны с ходом
кривой в её конечных точках Μ и N. Следует иметь в виду,
что приведёнными чертежами отнюдь не исчерпываются
все возможные, весьма
разнообразные, вообще говоря,
случаи и особенности хода
кривой между точками Μ и N.
На чертежи эти нужно
смотреть лишь как на
иллюстрации разных типов течения
кривой.
Угловые коэффициенты
прямых ΝΡ и MQ будут иметь
совершенно определённые
величины при данном значе-
/I
в
С
Фиг. 12.
нии χ и изменяются вместе с изменением этого
переменного. Обозначим поэтому через А (х) угловой коэффи-

IV. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА ' 91
циент прямой MQ и через В {х) — то же количество для NP;
при этом, как обыкновенно, будем угол каждой из
граничных прямых отсчитывать от оси OS в сторону,
противоположную часовой стрелке, иными словами, от OS
к OY. Непосредственно из чертежа мы легко выводим:
СР = /(лг, ί)—Β{χ)τ,
CQ=f(x, *) + Л(*К,
RP=f(x,t) — B(x)z—f(x,y) = p>0, J (1 }
где попрежнему
x = t—у, i=y — z.
Затем преобразуем уравнения (5) и (б). По формуле (5)
имеем
§■—/(*> у)+/(*> *)+?(■*) = о,
а по формуле (6)
dx
—fix, ')+/(*, jO—Ψ(*) = ο.
Функции φ и ψ определяются теми же соотношениями, что
и в предшествующем § 2. Отсюда на основании формул (13)
|1_Л(л-)С + с?(х) = «, (14)
£_β(*)τ_φ(*)==β. (15)
Проинтегрировав уравнения
|--^W5+?W = o, (16)
^_β(χ)η_ψ(χ)==0( (17)

92
С. А. ЧАПЛЫГИН
и отыскав их частные решения, обращающиеся в пуль
для χ = х0, убеждаемся, прилагая теорему о
дифференциальных неравенствах, из сопоставления уравнений (14)
и (16), что
а из сопоставления уравнений (15) и (17), что
z = t— у>%
Так как, заменив нулями ξ и η в определяющих их
уравнениях, мы в обоих случаях получаем результаты
отрицательные, то ξ и η должны быть более нуля. Приняв во
внимание сказанное, мы приходим к окончательному
неравенству
t>t — r\>y>z+t>z. (18)
Неравенство (18) показывает, что tx — t — η и z1 = z-\-i
суть новые, притом более тесные пределы интеграла у.
Исходя из tx и zt и повторив процесс, мы получим
функции t2 и z2, ещё более тесно охватывающие
интегральную функцию, и т. д., так же как в случае, описанном
в § 2. Разница будет лишь в том, что дифференциальные
уравнения для второго и последующих приближений нельзя
указать в раскрытой форме, так как функции Л(х) и
β (χ) могут иметь весьма разнообразный характер в
конкретных случаях, и выразить их в общей форме и
зависимости от / (л:, ζ) и / (лг, t) не представляется возможным.
Лишь в одном случае можно это сделать, несмотря на
то, что требование § 2 не будет соблюдено: именно, если
дуга MN в направлении от Μ к N переходит из
вогнутой в выпуклую (в сторону положительных у), и если на
ней имеется не более одной точки перегиба. Тогда дуга
будет лежать или между касательными в концах её, или

IV. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 93
между касательною в одном из концов и хордою, и вид
функции А (х) и В (х) определяется так же, как и в § 2.
В заключение заметим, что прямые ЛЩ и NP можно
было бы заменить иными прямыми, не проходящими через
концы дуги Μ и /V, лишь бы дуга ΜΝ целиком лежала
между этими линиями. Если мы условимся для угловых
коэффициентов этих прямых сохранить прежние
обозначения Л(х) и В(х), то, как нетрудно усмотреть, всё
изменение, которое будет в таком случае внесено в уравнения
(16) и (17), определяющие поправки первого приближения,
сведётся к добавлению в левых частях определённых
функций от х.
§ 4. Примеры. Для пояснения описанного метода на
конкретных случаях рассмотрим два простых примера.
а) Пример первый. В качестве первого примера
возьмём уравнение Рикатти
£+У-1-* = 0 (19)
и будем отыскивать интеграл- этого уравнения,
удовлетворяющий условию
у = 1 при χ = 0.
В первом грубом приближении примем
Подстановка этих значений в уравнение (19) даёт
функции, определяемые формулами (5) и (б); в данном случае
?(*) = — *> Ψ (■*) = **+ т·
Функция / уравнения (19) есть
f(x,y) = i + x—A

94
С. А. ЧАПЛЫГИН
так что
= - 2 < О,
и мы находимся в условиях, предусматриваемых § 2.
А так как отмеченная производная отрицательна, то для
верхнего предела придётся применить приём, описанный
подробно в § 2 для изыскания нижней границы интеграла,
и наоборот, [для нижнего предела использовать указание
для нахождения верхней границы,] как это было указано
в § 2. Составив поэтому выражения
df(x, t)_ 9 2
(20)
мы будем иметь для определения поправок по
формулам (8) и (12) (в обращенном порядке) следующие
линейные уравнения:
ё+(2+т>-*=°>
Отсюда ввиду обращения в нуль искомых поправок в
начальной точке л: = 0 получим:
если
S = 2x + ^, Г = 2дг + ^.
dx,

IV· ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 95
По совершении в формуле для ξ одной интеграции по
частям, составим затем:
χ
г, = Ж = Н?-
-*/(*" + !?) *srf*.
ί1 = ί-η = 1+^-β-2'/(*4-^)βτ^.
(21)
Если мы предположим χ заключённым в пределах 0 и 1,
то функции
а?3 я*
еТ и еТ (22)
не будут далеко уклоняться от единицы. Приняв во
внимание это замечание и несколько раздвигая пределы,
определяемые формулами (21), мы можем за новые границы
интеграла считать функции
χ
/x = 1 + у· — е"*»./ + β"8*/;
здесь введены обозначения:
(23)
У:
"/(*+?)
e2aJ г/л: =
7 (*2*_ι)_!^(7*_7*»Η-2*8 — ^),
16
и;
7'=JxVdx = ^(^-l)-l^ +
о
_|-^.(Нбл:2—145х—92x8-l-39х4—ЮхБ _|_ 2х6).
(24)

96
С. А. ЧАПЛЫГИН
Так же просто составится и формула для
as
Г (х) = J χ*/ dX.
о
Я не выписываю её в развёрнутом виде ввиду её
громоздкости.
Формулы (23) получаются из равенств (21) путём
интегрирования по частям, причём показательные функции (22)
стоящие перед знаками интегралов, принимаются за
дифференцируемые множители, а остающиеся выражения — за
интегрируемые. Такое интегрирование совершается в
первой из формул (21) два раза, а во второй — один раз;
затем в последних членах полученных формул
показательные функции (22) выносятся из-под знаков интегралов,
что ведёт к увеличению числовых значений указанных
членов; а следствием этого явится уменьшение г1 и
увеличение ^; таким (бразом, новые пределы, выраженные
формулами (23), далее отстоят от искомого интеграла уравнения,
чем приведённые в формулах (21).
Формулы (24) получаются из общего соотношения
/*-*_с-(£_*;+£-5+...).
правая часть которого будет содержать конечное число
членов, если буквою Μ без штрихов обозначим какой-либо
многочлен, а тою же буквою со штрихами — его
производные соответственных порядков.
Для характеристики приближений в смысле числового
определения интеграла уравнения рассмотрим крайнюю
точку участка изменения независимого переменного дг==1,

IX. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 97
в которой пределы наиболее расходятся. Здесь будем иметь
,,-2/—.1 — е-2 -
6 J"~"16 16* '
|~7^ = S + a = 1.2467f
^2/Ч1) = ^_|7Ш. = о,0015,
г1== 1,2617, ^ = 1,2797.
Приняв
у = .£цЬ£.= 1,2707,
мы будем иметь максимальную ошибку менее трёх
четвертей процента от определяемой величины, тогда как первое
приближение приводило к ошибке, которая могла возрасти
при том же способе определения числовой величины
интеграла до 20%·
В точках, более близких к началу, ошибка весьма резко
уменьшается. Само собою разумеется, что она была бы во
втором приближении гораздо менее значительна, если бы
мы исходили из первого приближения, более близкого
к интегралу уравнения; например, мы могли бы, оставив
тот же верхний предел, принять за нижнюю границу
функцию
1 , х2 х3
ζ— 1п""2 3 '
что привело бы к гораздо лучшему результату во втором
приближении.
б) Пример второй. Насколько быстро падает
величина возможной ошибки в процентном отношении к опре-
7 Зак. 1799. С. А. Чаплыгин.

98
С. А. ЧАПЛЫГИН
деляемой функции в отдельных случаях, показывает
пример следующего дифференциального уравнения:
dy
dx
+ У-*2 = °>
для которого мы постараемся изыскать предел интеграла,
обращающегося в нуль при х = 0. Приняв в первом
приближении
Z = 0, t = -3- ,
так что ошибка в
_ г + t _ χ*
может достигнуть 100% определяемого количества,
перейдём к определению второго приближения. По правилам § 2
составляем:
cp(x) = _x2,
а:9
Ψ(*)="27>
df(x, t) χϊ_
dt ~ 3 '
Затем для определения поправок получим уравнения
dx^ 9 ς х υ'
£+4ч-£-°.
откуда
X7 Х X7
о
-х-!х* -

IX. ИНТЕГРИРОВАНИЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 99
После совершения в этих формулах потребного количества
интеграции по частям, несколько уменьшая поправки ξ, η
и раздвигая соответственно пределы, найДём:
__ X* X™ , Х*1 хЫ
Zl~~~ 3 270 "+"270.153 270-153 216'
__ χ* хю хп
1 — 3 270 "т~ 270 · 51 '
и можем принять для у:
_ Xs χ™ , χ**
У~3 270 "г 135.153'
При χ = 1 ошибка в процентном отношении будет менее
0,073% искомой величины.

ОГЛАВЛЕНИЕ
Стр.
О работах С. А. Чаплыгина по приближённому
интегрированию дифференциальных уравнений (М. В. Келдыш
и Д. Ю. Панов) 5
С. А. ЧАПЛЫГИН
НОВЫЙ МЕТОД ПРИБЛИЖЁННОГО ИНТЕГРИРОВАНИЯ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ.
Предисловие 11
I. Основания нового способа приближённого
интегрирования дифференциальных уравнений 13
§ 1. Основная идея метода 13
§ 2. Основная теорема о дифференциальных
неравенствах 15
§ 3. Доказательство основной теоремы для
уравнения первого порядка 16
§ 4. Доказательство основной теоремы для линейного
уравнения второго порядка 19
§ 5. Доказательство основной теоремы для
линейного уравнения любого порядка 21
§ б. Доказательство основной теоремы для
нелинейного уравнения второго порядка 25
§ 7. Доказательство основной теоремы для
нелинейного уравнения любого порядка 26
§ 8. Пределы применимости основной теоремы ... 27
§ 9. Порядок действий при приближённом
интегрировании уравнения 31
§ 10. Распространение основной теоремы на
уравнения с частными производными 33

ОГЛАВЛЕНИЕ
101
Стр.
И. Новый метод интегрирования общего
дифференциального уравнения движения поезда 38
§ 1. Сбщая постановка задачи 38
§ 2. Различные формы приведённого уравнения
движения поезда 42
§ 3, Приближённое интегрирование уравнения
движения поезда на криволинейном подъёме:
пример первый 43
§ 4. Приближённое интегрирование уравнения
движения поезда на криволинейном подъёме:
пример второй 48
§ 5. Приближённое интегрирование уравнения
движения поезда при переходе с горизонтального
пути на наклон 52
§ 6. Нахождение вторых, более близких пределов
для скорости в задаче о переходе поезда с
горизонтального пути на наклон 57
§ 7. Приближённое интегрирование уравнения
движения поезда в случае, когда начальная скорость
равна нулю 60
III. Интегрирование основных уравнений баллистики
при законе сопротивления, данном Лоренцом ... 64
§ 1. Постановка задачи 64
§ 2. Преобразование уравнения годографа 65
§ 3. Интегрирование уравнения годографа,
записанного в первой форме 66
§ 4. Интегрирование уравнения годографа,
записанного во второй форме 69
§ 5. Другой способ интегрирования уравнения
годографа, записанного во второй форме 73
§ §. Общий ход решения задачи 74

102
ОГЛАВЛЕНИЕ
Стр.
IV. Приближённое интегрирование обыкновенного
дифференциального уравнения первого порядка . 79
§ 1. Основная теорема о дифференциальных
неравенствах 79
§ 2. Интегрирование уравнения в случае
неизменности знака остаточного члена 83
§ 3. Интегрирование уравнения в случае
непостоянства знака остаточного члена 89
§ 4. Примеры 93

Редактор В. R. Гольцман.
Техн. редактор С. Ы. Ахламов.
Переплёт и графическая орнаментация
книги художника А. П. Радищева.
-*
Подписано к печ. 6/IX 1950 г. Бум. 84x108/16
1,656 бум. л. 5,33 печ. л. 4- 1 вклейка.
4,17 уч.-изд. л. 30 816 тип. зн. в печ. л.
Т-05978. Тир. 4 000 экз. Заказ № 1799
Цена книги 4 руб. 50 коп.
4-я тип. им. Евг. Соколовой Главполиграф-
издата при Совете Министров СССР
Ленинград, Измайловский пр., 29