ОГЛАВЛЕНИЕ
ИЗ ПРЕДИСЛОВИЯ АВТОРА К ТРЕТЬЕМУ ИЗДАНИЮ................	8
От редакции .................................................. 8
Глава 1. Аналитическая геометрия на плоскости ................ 9
§ 1.	Координаты точки на прямой и на плоскости. Расстояние
между двумя точками..................................... 9
§2.	Деление отрезка в данном отношении. Площадь треуголь-
ника и многоугольника.................................. 11
§3.	Уравнение линии как геометрического места точек ....	12
§ 4.	Уравнение прямой: 1) с угловым коэффициентом, 2) об-
щее, 3) в отрезках на осях............................. 14
§5.	Угол между прямыми. Уравнение пучка прямых, прохо-
дящих через данную точку. Уравнение прямой, прохо-
дящей через две данные точки. Точка пересечения двух
прямых ................................................ 16
§6.	Нормальное уравнение прямой. Расстояние от точки до
прямой. Уравнения биссектрис. Уравнение пучка пря-
мых, проходящих через точку пересечения двух данных
прямых ................................................ 19
§7.	Смешанные задачи на прямую........................... 21
§8.	Окружность........................................... 22
§9.	Эллипс............................................... 24
§ 10.	Гипербола........................................... 26
§ 11.	Парабола............................................ 29
§ 12.	Директрисы, диаметры и касательные к кривым второго
порядка ............................................... 32
§ 13.	Преобразование декартовых координат. Параболы у =
= ах2 + Ьх + с и х = ay2 + Ьу + с. Гипербола ху = к . . .	35
§ 14.	Смешанные задачи на кривые второго порядка.......... 38
§ 15.	Общее уравнение линии второго порядка............... 40
§ 16.	Полярные координаты ................................ 44
§ 17.	Алгебраические кривые третьего и высших порядков . .	48
§ 18.	Трансцендентные кривые ............................. 49
Глава 2. Векторная алгебра................................... 51
§ 1.	Сложение векторов. Умножение вектора на скаляр ....	51
§ 2.	Прямоугольные координаты точки и вектора
в пространстве ........................................ 53
§3.	Скалярное произведение двух векторов................. 55
§ 4.	Векторное произведение двух векторов ................ 58
§5.	Смешанное произведение трех векторов................. 60
Оглавление
Глава 3. Аналитическая геометрия в пространстве ............ 62
§	1. Уравнение плоскости ................................ 62
§2	. Основные задачи на плоскость ...................... 63
§3	. Уравнения прямой................................... 65
§	4. Прямая и плоскость.................................. 68
§5	. Сферические и цилиндрические поверхности........... 70
§6	. Конические поверхности и поверхности вращения ....	72
§	7.	Эллипсоид, гиперболоиды и параболоиды............... 74
Глава 4. Высшая алгебра .................................... 78
§ 1.	Определители........................................ 78
§2.	Системы линейных уравнений.......................... 80
§3.	Комплексные числа................................... 83
§ 4.	Уравнения высших степеней и приближенное решение
уравнений................................................ 86
Глава	5. Введение в анализ................................ 90
§ 1.	Переменные величины и функции....................... 90
§2.	Пределы последовательности и функции. Бесконечно ма-
лые и бесконечно большие................................. 93
§3.	Свойства пределов. Раскрытие неопределенностей
§ 4.	Предел отношения --- при a —> 0 ................... 98
a
§ 5.	Неопределенности вида оо — оои0-оо................. 99
§ 6.	Смешанные примеры на вычисление пределов.......... 100
§7.	Сравнение бесконечно малых........................ 101
§8.	Непрерывность функции............................. 102
§9.	Асимптоты ........................................ 105
§ 10.	Число е ......................................... 106
Глава 6. Производная и дифференциал .................. 108
§ 1.	Производные алгебраических и тригонометрических
функций........................................... 108
§2.	Производная сложной функции.................. ПО
§ 3.	Касательная и нормаль к плоской кривой...... 111
§4.	Случаи недифференцируемости непрерывной функции .	.	113
§5.	Производные логарифмических и показательных функций	114
§6.	Производные обратных тригонометрических функций .	.	116
§7.	Производные гиперболических функций ............... 117
§ 8.	Смешанные примеры и задачи на дифференцирование	.	118
§9.	Производные высших порядков................. 119
§ 10.	Производная неявной функции................ 121
Оглавление	5
§ 11.	Дифференциал функции.............................. 123
§ 12.	Параметрические уравнения кривой.................. 124
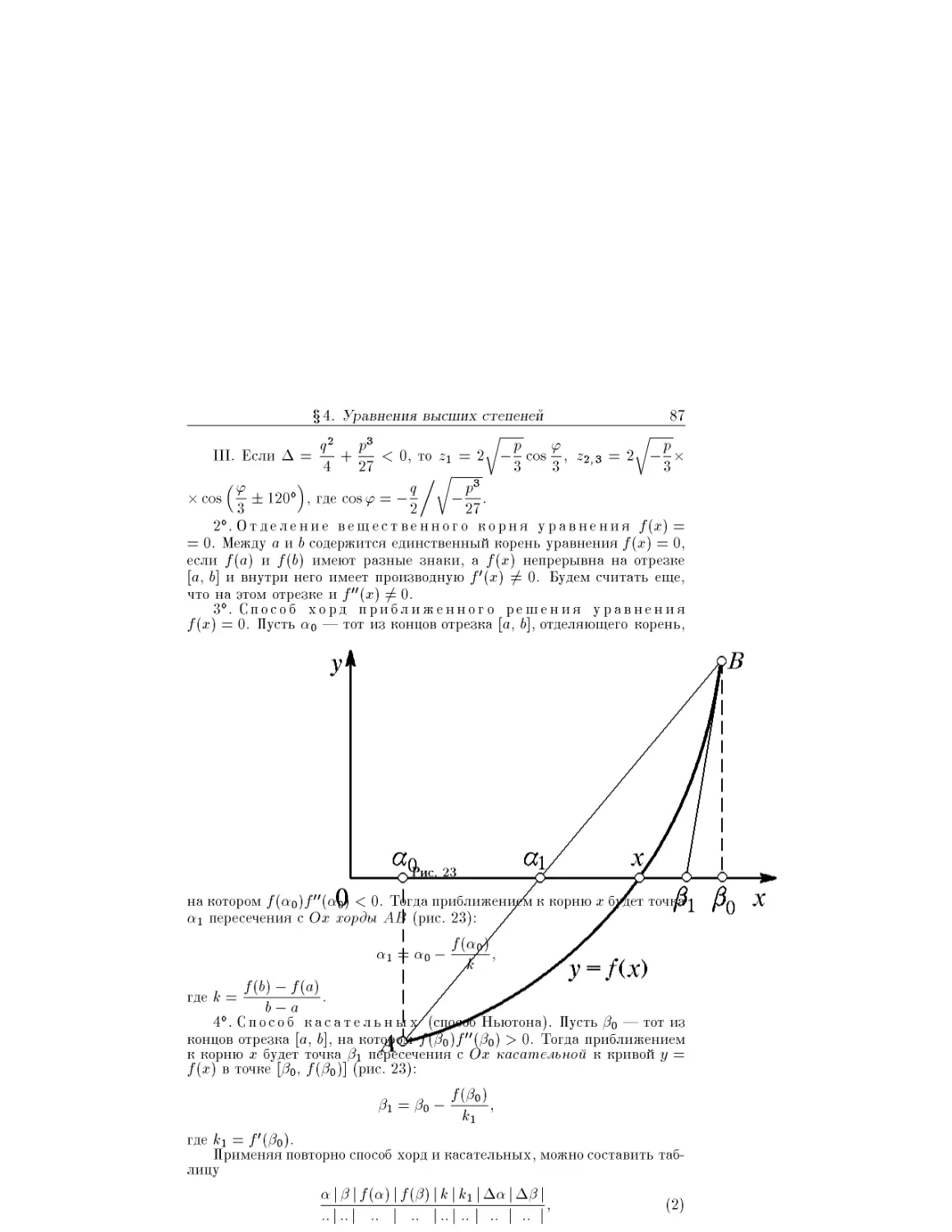
Глава 7. Приложения производной ........................... 127
§ 1.	Скорость и ускорение............................... 127
§2.	Теоремы о среднем ................................. 128
§3.	Раскрытие неопределенностей. Правило Лопиталя ....	131
§ 4.	Возрастание и убывание функции. Максимум и минимум 133
§ 5.	Задачи о наибольших и наименьших значениях величин 136
§ 6.	Направление выпуклости и точки перегиба кривой.
Построение кривых................................... 138
Глава 8. Неопределенный интеграл........................... 140
§ 1.	Неопределенный интеграл. Интегрирование разложением 140
§2.	Интегрирование подстановкой и непосредственное ....	142
[	dx f	dx f	dx
§3.	Интегралы вида /	/	/
J x2±a2 J y/a^ — x2 J \/x2 + k
и к ним приводящиеся................................ 145
§ 4.	Интегрирование по частям........................... 147
§5.	Интегрирование тригонометрических функций.......... 148
§6.	Интегрирование рациональных алгебраических функций 150
§ 7.	Интегрирование некоторых иррациональных алгебраиче-
ских функций........................................... 152
§8.	Интегрирование некоторых трансцендентных функций 155
§9.	Интегрирование гиперболических функций. Гиперболи-
ческие подстановки..................................... 156
§ 10.	Смешанные примеры на интегрирование............... 157
Глава	9. Определенный интеграл .......................... 160
§ 1.	Вычисление определенного интеграла................. 160
§2.	Вычисление площадей ............................... 163
§3.	Объем тела вращения................................ 165
§ 4.	Длина дуги плоской кривой.......................... 167
§5.	Площадь поверхности вращения....................... 169
§6.	Задачи из физики................................... 170
§ 7.	Несобственные интегралы............................ 172
§8.	Среднее значение функции........................... 175
§9.	Формула трапеций и формула Симпсона................ 176
Глава 10. Кривизна плоской и пространственной кривой ....	178
§ 1.	Кривизна плоской кривой. Центр и радиус кривизны.
Эволюта................................................ 178
§ 2.	Длина дуги кривой в пространстве................... 180
§3.	Производная вектор-функции по скаляру и ее механиче-
ское и геометрическое значение. Естественный трех-
гранник кривой ...................................... 180
§ 4.	Кривизна и кручение пространственной кривой .... 183
Глава 11. Частные производные, полные дифференциалы
и их приложения ........................................ 185
§ 1.	Функции двух переменных и их геометрическое изобра-
жение ............................................... 185
§2.	Частные производные первого порядка ............ 187
§3.	Полный дифференциал первого порядка............. 189
§4.	Производные сложных функций .................... 191
§5.	Производные неявных функций..................... 192
§ 6.	Частные производные и полные дифференциалы высших
порядков............................................. 194
§ 7.	Интегрирование полных дифференциалов............ 198
§8.	Особые точки плоской кривой..................... 199
§9.	Огибающая семейства плоских кривых.............. 200
§ 10.	Касательная плоскость и нормаль к поверхности.	201
§ 11.	Скалярное поле. Линии и поверхности уровней.
Производная в данном направлении. Градиент........... 203
§ 12.	Экстремум функции двух переменных.............. 205
Глава 12. Дифференциальные уравнения ................... 207
§ 1.	Понятие о дифференциальном уравнении............ 207
§ 2.	Дифференциальное уравнение первого порядка с разделя-
ющимися переменными. Ортогональные траектории . . .	208
§ 3.	Дифференциальные уравнения первого порядка:
1)	однородное, 2) линейное, 3) Бернулли.......... 211
§ 4.	Дифференциальные уравнения, содержащие дифферен-
циалы произведения и частного........................ 213
§ 5.	Дифференциальные уравнения первого порядка в полных
дифференциалах. Интегрирующий множитель ............. 213
§6.	Дифференциальные уравнения первого порядка, не раз-
решенные относительно производной. Уравнения
Лагранжа и Клеро................................. 215
§ 7.	Дифференциальные уравнения высших порядков, допус-
кающие понижение порядка............................. 217
§8.	Линейные однородные дифференциальные уравнения с
постоянными коэффициентами........................... 218
§9.	Линейные неоднородные дифференциальные уравнения
с постоянными коэффициентами......................... 219
§ 10.	Примеры дифференциальных уравнений разных типов 221
§ 11.	Линейное дифференциальное уравнение Эйлера хпу^ +
+ а1хп-1у(-п~1'> + ... + ап_}ху' + апу = f(x) ... 222
Оглавление	7
§ 12.	Системы линейных дифференциальных уравнений с по-
стоянными коэффициентами ........................... 223
§ 13.	Линейные дифференциальные уравнения в частных про-
изводных второго порядка (метод характеристик)......	224
Глава 13. Двойные, тройные и криволинейные интегралы . .	226
§ 1.	Вычисление площади с помощью двойного интеграла . .	226
§ 2.	Центр масс и момент инерции площади с равномерно рас-
пределенной массой (при плотности jj, = 1).......... 228
§3.	Вычисление объема с помощью двойного интеграла . . .	230
§4.	Площади кривых поверхностей......................... 231
§5.	Тройной интеграл и его приложения .................. 232
§6.	Криволинейный интеграл. Формула Грина............... 234
§ 7.	Поверхностные интегралы.
Формулы Остроградского-Гаусса и Стокса .............. 238
Глава	14. Ряды............................................ 242
§ 1.	Числовые ряды....................................... 242
§2.	Равномерная сходимость функционального ряда......... 245
§3.	Степенные ряды...................................... 247
§ 4.	Ряды Тейлора и Маклорена............................ 249
§5.	Приложения рядов к приближенным вычислениям ....	251
§ 6.	Ряд Тейлора для функции двух переменных............. 254
§ 7.	Ряд Фурье. Интеграл Фурье........................... 255
Ответы ..................................................... 260
Приложение. Некоторые кривые (для справок) ................. 332
ИЗ ПРЕДИСЛОВИЯ АВТОРА
К ТРЕТЬЕМУ ИЗДАНИЮ
В настоящем «Сборнике» подобраны и методически распреде-
лены задачи и примеры по аналитической геометрии и математи-
ческому анализу.
В начале каждого параграфа приведены формулы, определения
и другие краткие пояснения теории, необходимые для решения
последующих задач.
В конце каждого параграфа «Сборника» приведены (после чер-
ты) задачи для повторения, составляющие около одной трети всего
материала «Сборника». Эта особенность поможет преподавателю в
подборе задач для работы в классе и для домашних заданий или
для повторений перед контрольными работами. Кроме того, при
таком распределении задач легко определить минимум, необходи-
мый для усвоения курса, который можно рекомендовать заочни-
кам или для работы на вечерних факультетах.
«Сборник» может быть использован как для работы под ру-
ководством преподавателя, так и для самостоятельного изучения
курса высшей математики во втузах, так как почти все задачи
имеют ответы, а некоторые и решения и, кроме того, ко многим
задачам в тексте или в ответах даны указания к их решению.
Этому же способствуют краткие пояснения теории.
ОТ РЕДАКЦИИ
Издание настоящего «Сборника» осуществлено в связи с много-
численными заявками, поступившими в наш адрес от математи-
ческих кафедр, библиотек, студентов и преподавателей различных
втузов России.
В связи с тем, что автора, Василия Павловича Минорского,
увы, давно уже нет с нами, редакция предельно бережно отнеслась
к тексту, осуществив лишь новый набор, верстку и оформление, не
внося при этом никаких существенных изменений в текст, кроме
исправлений замеченных опечаток.
Мы считаем своим приятным долгом подарить новому поколе-
нию учащихся этот широко известный в математическом образо-
вании «Сборник», тем более, что его предыдущее издание было в
1987г.
Глава 1
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
§ 1. Координаты точки на прямой и на плоскости.
Расстояние между двумя точками
1°. Расстояние d между точками A(«i) и В(х2) на оси:
d = |Ж2 - Ж1| = у/(х2- Ж1)2.	(1)
2°. Величина АВ (алгебраическая) направленного отрезка на
оси:
АВ = х2 — Xi.	(2)
3°. Расстояние d между точками A(xi; t/j) и В(х2; у2) на плос-
кости:
d = V(®2 - »i)2 + (t/г - t/1)2•	(3)
4°. Проекции на оси координат направленного отрезка, или век-
тора I Д на плоскости с началом А(хр, г/Д и концом В(х2; у2):
прхлЗ = X = х2 - хъ пру~А& = У = у2 - t/i.	(4)
1.	Построить на числовой оси точки А( —5), В(+4) и С( —2) и
найти величины АВ, ВС и АС отрезков на оси. Проверить, что
АВ + ВС = АС.
2.	Выполнить предыдущее упражнение для точек А(+1), В(—4)
и С(+5).
3.	Построить треугольник с вершинами А(—4; 2), В(0; —1) и
С(3; 3) и определить его периметр и углы.
4.	Доказать, что треугольник с вершинами А( — 3; —2),В(0; —1)
и С( — 2; 5) прямоугольный.
5.	Построить точки А(—4; 0), В(— 1; 4) и точки Aj, В^, сим-
метричные данным относительно оси Оу. Вычислить периметр
трапеции АВВ^А^.
6.	Точка В симметрична А(4; —1) относительно биссектрисы
первого координатного угла. Найти длину АВ.
10	Гл.1. Аналитическая геометрия на плоскости
7.	Найти точку, удаленную на 5 единиц как от точки А(2; 1),
так и от оси Оу.
8.	На оси ординат найти точку, удаленную от точки А(4; —1) на
5 единиц. Пояснить построением, почему получается два решения.
9.	На оси абсцисс найти точку, удаленную от точки А(а; Ь) на
с единиц. Исследовать решение при с > |&|, с = |&| и с < |6|.
10.	На оси Ох найти точку, одинаково удаленную от начала
координат и от точки Л(8; 4).
11.	Найти центр и радиус круга, описанного около треуголь-
ника с вершинами А(4; 3), В(—3; 2) и 0(1; —6).
12.	Даны точки А(2; 6) и В(0; 2); построить вектор 4/1. его
компоненты на осях и вычислить и р.,.1 /к пруА^ и длину АВ.
13.	В точке А(2; 5) приложена сила, проекции которой на оси
координат равны: X = 3 и Y = 3. Определить конец вектора 1 /к
изображающего силу, и величину силы.
14. В точке А( —3; —2) приложена сила, проекция которой Y =
= — 1, а проекция X положительна. Определить конец вектора
JTi , изображающего силу, если ее величина равна 5д/2.
151)	. На числовой оси построить точки А(1), В( —3) и О(—2)
и найти величины АВ, ВС и С А отрезков на оси. Проверить, что
АВ + ВС + СА = С
16.	На плоскости построить точки А( —7; 0) и В(0; 1) и точки
Д1 и В], симметричные точкам А и В относительно биссектрисы
первого и третьего координатных углов. Вычислить периметр тра-
пеции АВВ^Ар
17.	На оси ординат найти точку, одинаково удаленную от на-
чала координат и от точки А( — 2; 5).
18.	На оси абсцисс найти точку, удаленную от точки А( — 2; 3)
на ЗД5 единиц.
19.	Определить центр и радиус круга, описанного около тре-
угольника с вершинами А(—3; — 1), В(5; 3) и 0(6; —4).
20.	Даны точки A(xj; yi) и В(х2', уг)- В начале координат при-
ложены силы, изображаемые векторами О1 и О/к Построить их
равнодействующую 0(3 и доказать, что проекция равнодействую-
щей на координатную ось равна сумме проекций составляющих
на ту же ось.
21.	Даны точки А(1; 2), В(3; 5), 0(5; 2) и 0(2; —2). В точке
А приложены силы АВ, аЗ и аЗ. Найти проекции на оси коор-
динат равнодействующей силы и ее величину.
])	В каждом параграфе после черты приведены задачи, которые рекоменду-
ются для задания на дом или для повторений.
§ 2. Деление отрезка в данном отношении
11
§ 2. Деление отрезка в данном отношении.
Площадь треугольника и многоугольника
1°. Деление отрезка в данном отношении. Даны точки
А(хр, уД и В(х2; у2). Координаты точки М(ж; у), делящей отрезок АВ
в отношении AM : МВ = А, определяются по формулам:
Ж1 + Хх2 t/i + Лг/2
В частности, при делении пополам, т. е. в отношении А = 1 : 1 = 1,
«1 + х2 t/i + J/2	/ОА
1 =	V =	(2)
2°. Площадь многоугольника с вершинами А(хр, уД, В(х2;
Уъ), С{х3-, у3), . . В(хп; уп) равна
е-+Ч|г1	S/1I , |«2	X/21 ,	, Нп	уп\]
±2 I.K	У2\ + К	г/з| +	'"+|ж1	yi IJ	•	>
Выражение вида Г1 "(И равно хру2 — х2у^ и называется определи-
I2 У2|
uii.ii.vi второго порядка1).
22.	Построить точки Д( —2; 1) и В(3; 6) и найти точку М(х; у),
делящую АВ в отношении AM : МВ = 3:2.
23.	Даны точки Д( — 2; 1) и В(3; 6). Разделить отрезок АВ в
отношении AM : МВ = —3 : 2.
24.	В точках A(®i) и В(х2) оси Ох помещены массы тд и т2.
Найти центр масс этой системы.
25.	В точках Д(ж1), В(х2) и С(хД оси Ох помещены соот-
ветственно массы mi, т2 и т3. Показать, что центр масс этой
m-ix-i + т2х2 + ГП3Х3
системы будет в точке х = -------------------.
т1 + т2 + тз
26.	На концы однородного стержня длиной 40 см и массой 500 г
насажены шары массой 100 г и 400 г. Определить центр масс этой
системы.
27.	В точках Д( —2; 4), В(3; —1) и 0(2; 3) помещены соответ-
ственно массы 60 г, 40 г и 100 г. Определить центр масс этой си-
стемы.
28.	Определить середины сторон треугольника с вершинами
4(2; -1), В(4; 3) и С(-2; 1).
29.	В треугольнике с вершинами 0(0; 0), 4(8; 0) и В(0; 6)
определить длину медианы ОС и биссектрисы OD.
]) Об определителях подробно изложено в гл. 4, § 1.
12	Гл.1. Аналитическая геометрия на плоскости
30.	Найти центр масс треугольника с вершинами Д(1; — 1),
В(6; 4) и С(2; 6).
Указание. Центр масс треугольника находится в точке пересече-
ния его медиан.
31.	Вычислить площадь треугольника с вершинами А(2; 0),
В(5; 3) и С(2; 6).
32.	Показать, что точки Д(1; 1), В(—1; 7) и С(0; 4) лежат на
одной прямой.
33.	Вычислить площадь четырехугольника с вершинами Д(3; 1),
В(4; 6), С(6; 3) и В(5; -2).
34.	В точках Д(—3; —1) и В(4; 6) приложены параллельные
силы, соответственно равные ЗОН и 40 Н. На отрезке АВ найти
точку приложения равнодействующей.
35.	В точках 0(0; 0), А(2; —5) и В(4; 2) помещены соответст-
венно массы 500 г, 200г и 100 г. Определить центр масс этой си-
стемы.
36.	В треугольнике с вершинами А( — 2; 0), В(6; 6) и 0(1; -4)
определить длину биссектрисы АЕ.
37.	Найти центр масс треугольника с вершинами A(xj; t/i),
В(х2; у2) и С(ж3; у3).
38.	Найти центр масс четырехугольной однородной доски с вер-
шинами А(—2; 1), В(3; 6), 0(5; 2) и 0(0; —6).
Указание. По формулам, полученным в задаче 37, найти центры
масс треугольников АВС и ADC и разделить расстояние между ними
в отношении, обратном отношению площадей треугольников.
39.	Даны точки Д(1; 2) и В(4; 4). На оси Ох определить точку
О так, чтобы площадь АДВС была равна 5, и построить АДВС.
40.	В треугольнике с вершинами Д( — 2; 2), В(1; —4) и С(4; 5)
каждая сторона продолжена в направлении обхода периметра про-
тив часовой стрелки на одну треть своей длины. Определить
концы М, N и Р продолжений сторон и найти отношение к пло-
щади £\MNP к площади АДВС.
§ 3. Уравнение линии как геометрического места точек
Уравнением линии называется уравнение с переменными х и
у, которому удовлетворяют координаты любой точки этой линии и
только они.
Входящие в уравнение линии переменные х и у называются теку-
щими координатами, а буквенные постоянные — параметрами. На-
пример, в уравнении окружности (задача 41) х2 + у2 = R2 переменные
х и у — текущие координаты, а постоянная R — параметр.
Чтобы составить уравнение линии как геометрического места точек,
обладающих одинаковым свойством, нужно:
§ 3. Уравнение линии как геометрического места точек 13
1)	взять произвольную (текущую) точку М(х; у) линии;
2)	записать равенством общее свойство всех точек М линии;
3)	входящие в это равенство отрезки (и углы) выразить через теку-
щие координаты точки М(ж; у) и через данные в задаче.
41.	Показать, что уравнением окружности с радиусом R и с
центром в начале координат будет х2 + у2 = R2.
42.	Написать уравнение окружности с центром <7(3; 4) и радиу-
сом R = 5. Лежат ли на этой окружности точки А( —1; 1), В(2; 3),
<9(0; 0) и В(4; 1)?
43.	Написать уравнение линии, по которой движется точка
М(ж; у), равноудаленная от точек А(0; 2) и В(4; —2). Лежат ли
на этой линии точки С( — 1; 1), В(1; —1), В(0; —2) и В(2; 2)?
44.	Написать уравнение траектории точки М(ж; у), которая
при своем движении остается втрое дальше от точки А(0; 9), чем
от точки В(0; 1).
45.	Написать уравнение траектории точки М(ж; у), которая
при своем движении остается вдвое ближе к точке А( —1; 1), чем
к точке В(—4; 4).
46.	Написать уравнения биссектрис координатных углов.
47.	Написать уравнение геометрического места точек, сумма
расстояний от каждой из которых до точек В(2; 0) и Fi(-2; 0)
равна 2-\/5. Построить линию по ее уравнению.
48.	Написать уравнение геометрического места точек, равно-
удаленных от точки F(2; 2) и от оси Ох. Построить линию по ее
уравнению.
49.	Написать уравнение линии, по которой движется точка
М(ж; у), оставаясь вдвое дальше от оси Од, чем от оси Оу.
50.	Построить линии: 1) у = 2ж + 5; 2) у = 7 — 2ж; 3) у = 2ж;
4) у = 4; 5) у = 4 — х2.
51.	Определить точки пересечения линии у = х2 — 4ж + 3 с
осями координат и построить ее.
52.	Определить точки пересечения с осями координат линий:
1) Зх — 2у = 12; 2) у = х2 + 4ж; 3) у2 = 2ж + 4. Построить эти
линии.
53.	Написать уравнение геометрического места точек, равно-
удаленных от оси Оу и от точки F(4; 0), и построить линию по
ее уравнению.
54.	Написать уравнение линии, по которой движется точка
М(х; у), равноудаленная от начала координат и от точки А(—4; 2).
Лежат ли на этой линии точки В( — 2; 1), (7(2; 3), D(l; 7)?
14	Гл.1. Аналитическая геометрия на плоскости
55.	Написать уравнение траектории точки М(х; у), которая
при своем движении остается вдвое ближе к точке А(0; —1), чем
к точке В(0; 4). Построить траекторию движения.
56.	Определить точки пересечения с осями координат линий:
1) 2ж + 5у + 10 = 0; 2) у = 3 — 2ж — ж2; 3) у2 = 4 — х. Построить
линии.
57.	Написать уравнение геометрического места точек, равно-
удаленных от оси Ох и от точки F(0; 2), и построить линию по
ее уравнению.
58.	Написать уравнение геометрического места точек, разность
расстояний от каждой из которых до точек Fj(—2; —2) и F(2; 2)
равна 4. Построить линию по ее уравнению.
§4. Уравнение прямой: 1) с угловым коэффициентом,
2) общее, 3) в отрезках на осях
1°. Уравнение прямой с угловым коэффициентом
у = kx + b.	(1)
Параметр к равен тангенсу угла а наклона прямой к оси Ох (к =
= tga) и называется угловым коэффициентом, или иногда наклоном
прямой. Параметр Ь — величина отрезка на оси Оу, или начальная
ордината.
2°. Общее уравнение прямой
Ах + Ву + С = 0.	(2)
Особые случаи:
а)	при С = 0 у =---х — прямая проходит через начало координат;
В
С
б)	при В = 0 х = —- = а — прямая параллельна оси Оу;
_?Т
с
в)	при А = 0 у =---= Ь — прямая параллельна оси Ох;
В
г)	при В = С = 0 Ах = 0, х = 0 — ось Оу;
д)	при А = С* = 0 By = 0, у = 0 — ось Ох.
3°. Уравнение прямой в отрезках на осях
где а и Ь — величины отрезков, отсекаемых прямой на осях координат.
59.	Построить прямую, отсекающую на оси Оу отрезок b =
= 3 и составляющую с осью Ох угол: 1) 45°; 2) 135°. Написать
уравнения этих прямых.
60.	Построить прямую, отсекающую на оси Оу отрезок b =
= — 3 и составляющую с осью Ох угол: 1) 60°; 2) 120°. Написать
уравнения этих прямых.
§4. Уравнение прямой	15
61.	Написать уравнение прямой, проходящей через начало ко-
ординат и составляющей с осью Ох угол: 1) 45°; 2) 60°; 3) 90°;
4) 120°; 5) 135°.
62.	Построить прямую, проходящую через начало координат и
через точку ( — 2; 3), и написать ее уравнение.
63.	Определить параметры к и Ь для каждой из прямых:
1)	2х - Зу = 6; 2) 2х + Зу = 0; 3) у = -3; 4) ^ + | = 1.
64.	Построить прямые:
1)	Зх + I // = 12; 2) Зх - I // = 0; 3) 2х - 5 = 0; 4) 2у + 5 = 0.
65.	Определить параметры к и Ь прямой, проходящей через
точку А(2; 3) и составляющей с Ох угол 45°. Написать уравнение
этой прямой.
66.	Уравнения прямых: 1) 2х — Зу = 6; 2) Зх — 2у + 4 = 0
привести к виду в отрезках на осях.
67.	Даны точки 0(0; 0) и Д(—3; 0). На отрезке ОА построен
параллелограмм, диагонали которого пересекаются в точке В(0; 2).
Написать уравнения сторон и диагоналей параллелограмма.
68.	Написать уравнение прямой, проходящей через точку Д(4; 3)
и отсекающей от координатного угла треугольник площадью, рав-
ной 3.
69.	Прямые у = —2 и у = 4 пересекают прямую Зх — I // — 5 = 0
соответственно в точках А и В. Построить вектор .1 /Л определить
его длину и его проекции на оси координат.
70.	Лежат ли точки Д(3; 5), В(2; 7), С( —1; —3) и D(— 2; —6) на
прямой у = 2х — 1 или же они «выше» или «ниже» этой прямой?
71.	Каков геометрический смысл неравенств:
1)	у > Зх + 1; 2) у < Зх + 1; 3) 2х-\-у — 4 + 0; 4) 2х-\-у — 4 < 0?
72.	Построить области1), координаты точек которых удовле-
творяют неравенствам:
1)	у < 2 — х,	х	>	—2,	у	> —2;
2)	у > 2 — х,	х	<	4,	у	< 0;
3)	^ + | + 1,	у	+	д + 2,	х	+ —4.
73.	Точка М(х; у) движется так, что разность квадратов рас-
стояний от нее до точек А( — а; а) и В(а; —а) остается равной 4а2.
Написать уравнение ее траектории.
]) Слово «область» здесь означает часть плоскости хОу, координаты каждой
точки которой удовлетворяют некоторым условиям (например, неравенствам).
Область называется замкнутой, если в нее включены точки, лежащие на гра-
нице области. В противном случае область называется открытой.
16
Гл. 1. Аналитическая геометрия на плоскости
74.	Написать уравнение траектории точки М(х; у), проекция
которой на ось Ох движется со скоростью тед/с, а на ось Оу —
со скоростью п ед/с. Начальное положение точки М0(а; Ь).
75.	Построить прямые, заданные параметрами: 1) Ь = —2, (р =
= 60° и 2) Ь = —2, р = 120°, и написать их уравнения.
76.	Определить параметры к и Ь прямой, проходящей через
точку ( — 2; 3) и составляющей с Ох угол 45°. Построить прямую
и написать ее уравнение.
77.	Равнобедренная трапеция с основаниями 8 см и 2 см имеет
острый угол 45°. Написать уравнения сторон трапеции, приняв за
ось Ох большее основание и за ось Оу — ось симметрии трапеции.
78.	Написать уравнения сторон ромба с диагоналями 10 см
и 6 см, приняв большую диагональ за ось Ох и меньшую — за
ось Оу.
79.	Написать уравнение прямой, проходящей через точку (—4; 6)
и отсекающей от осей координат треугольник площадью 6.
80.	Написать уравнение линии, по которой движется точка
М(х; у), оставаясь вдвое дальше от оси Ох, чем от прямой х = —3.
81.	Прямые х = — 1 иг = 3 пересекают прямую у = 2s + 1 в
точках А и В. Определить длину вектора АВ и его проекции на
оси координат.
§ 5.	Угол между прямыми. Уравнение пучка прямых,
проходящих через данную точку. Уравнение прямой,
проходящей через две данные точки.
Точка пересечения двух прямых
1°. Угол р, отсчитанный против часовой стрелки от прямой у =
= kix + до прямой у = к%х + определяется формулой
/'2 ~ ^1
1 +
W =
(1)
Для прямых, заданных уравнениями
А^х + В^у + С\ = 0 и А2Х + В2У + С*2 = 0,
формула (1) примет вид
_ Д1В2 — И2В1
А-уА2 + В-уВ2
Условие параллельности: р = К2 или — = —-.
А2 В2
Условие перпендикулярности: к2 =-----или ЛдДг + В1В2 = 0.
k-i
§5. Угол между прямыми. Уравнение пучка прямых 17
2°. Уравнение пучка пр я м ы х, проходящих через данную точ-
ку -4(^1; t/i):
У - У1 = k(x - «J.	(2)
3°. Уравнение прямой, проходящей через две данные
точки A(«!; yj и В(х2; У2)-
У ~У1 _ х - Xj
У2 ~У1 х2 - «1'
4°. Чтобы найти точку пересечения непараллельных прямых
А-ух + Bly + С\ = 0 и А2х + В2у + С2 = 0, нужно решить совместно их
уравнения. Получим:
—C*i BA	IAj —Ci
IAi BA ’ y |Aj BA '
Ц2 -B2|	\a2 b2\
82.	Определить угол между прямыми:
1)	у = 2ж - 3, у = |ж + 1;
2)	5ж — у + 7 =	0,	2ж —	Зу + 1	= 0;
3)	2ж + у = 0,	у =	Зж —	4;
4)	Зж + 2у = 0,	6ж	+ 4у	+ 9 =	0;
5)	Зж — 4у = 6,	8ж	+ бу	= 11;
83.	Среди прямых Зж —2у+7 = 0, 6ж—4у—9 = 0, 6ж+4у—5 = 0,
2ж + Зу — 6 = 0 указать параллельные и перпендикулярные.
84.	Написать уравнение пучка прямых, проходящих через точ-
ку А(2; 3). Выбрать из этого пучка прямые, составляющие с осью
Ох углы: 1) 45°; 2) 60°; 3) 135°; 4) 0°, и построить их.
85.	Построить точку А( — 2; 5) и прямую 2ж — у = 0. Напи-
сать уравнение пучка прямых, проходящих через А, и выбрать из
пучка: 1) прямую, параллельную данной; 2) прямую, перпендику-
лярную к данной.
86.	В точках пересечения прямой 2ж — 5у — 10 = 0 с осями
координат восставлены перпендикуляры к этой прямой. Написать
их уравнения.
87.	Написать уравнение прямой, проходящей через точки
А(-1; 3) и В(4; -2).
18	Гл.1. Аналитическая геометрия на плоскости
88.	В треугольнике с вершинами А( — 2; 0), В(2; 6) и С(4; 2)
проведены высота BD и медиана BE. Написать уравнения сто-
роны АС, медианы BE и высоты BD.
89.	Найти внутренние углы треугольника, стороны которого
заданы уравнениями х + 2// = 0, х + I // — 6 = 0, х — I // — 6 = 0.
Указание. Чтобы найти внутренние углы треугольника, нужно
угловые коэффициенты сторон выписать в порядке убывания: > &2 >
> Кз, затем вычислять тангенсы углов по формулам ---——, ---——,
1 +	1 “И ^2^3
/'3 - h
-----——. Убедиться в этом из чертежа, поместив одну из вершин в
1 + ЛД&3
начале координат.
90.	Написать уравнения прямых, проходящих через начало ко-
ординат под углом 45° к прямой у = 4 — 2х.
91.	Написать уравнения прямых, проходящих через точку
Д( —1; 1) под углом 45° к прямой 2ж + Зу = 6.
92.	Из точки Д(5; 4) выходит луч света под углом = arctg2
к оси Ох и от нее отражается. Написать уравнения падающего и
отраженного лучей.
93.	Определить вершины и углы треугольника, стороны кото-
рого заданы уравнениями х + Зу = 0, х = 3, х — 2у + 3 = 0.
94.	Отрезок прямой Зх + 2у = 6, отсеченный осями коор-
динат, служит гипотенузой равнобедренного прямоугольного тре-
угольника. Найти вершину прямого угла, если известно, что она
лежит «выше» данной прямой.
95.	Дан треугольник с вершинами А(—2; 0), В(2; 4) и С(4; 0).
Написать уравнения сторон треугольника, медианы АЕ, высоты
AD и найти длину медианы АЕ.
96.	Написать уравнения сторон и найти углы треугольника с
вершинами Д(0; 7), В(6; —1) и С(2; 1).
97.	Прямая 2х — у + 8 = 0 пересекает оси Ох и Оу в точках
А и В. Точка М делит АВ в отношении AM : МВ = 3:1. На-
писать уравнение перпендикуляра, восставленного в точке М к
прямой АВ.
98.	Построить треугольник, стороны которого заданы уравне-
ниями х-\-у = 4, Зх — у = 0, х — Зу — 8 = 0; найти углы и площадь
треугольника.
99.	Найти точку пересечения медиан и точку пересечения вы-
сот треугольника, вершины которого А(—4; 2), В(2; —5) и С(5; 0).
100.	Из точки Д( —5; 6) выходит луч света под углом <р> =
= arctg ( —2) к оси Ох и отражается от оси Ох, а затем от оси
Оу. Написать уравнения всех трех лучей.
§6. Нормальное уравнение прямой	19
§ 6. Нормальное уравнение прямой. Расстояние
от точки до прямой. Уравнения биссектрис.
Уравнение пучка прямых, проходящих через точку
пересечения двух данных прямых
1°. Нормальное уравнение прямой
х cos/3 + t/sin/3 — р = 0,	(1)
где р — длина перпендикуляра (нормали), опущенного из начала коор-
динат на прямую, а (3 — угол наклона этого перпендикуляра к оси Ох.
Чтобы привести общее уравнение прямой Ах + By + С = 0 к нормаль-
ному виду, нужно все члены его умножить на нормирующий множитель
М = ± yjppi д2 ’ взятый со знаком, противоположным знаку свобод-
ного члена С.
2°. Расстояние d от точки («q; j/q) до прямой найдем,
если е левую часть нормального уравнения прямой на место теку-
щих координат подставим координаты (ху, уо) и полученное число
возьмем по абсолютной величине:
d = |«qcos (3 + t/o sin [3 — p|,	(2)
или
_ |Ажр + Byo + C|
У. I2 + В2 '	1 ’
3°. Уравнения биссектрис углов между прямыми Аж + Вг/+
+ С = 0 и А^х + В^у + С\ = 0:
Ах + By + С _ А^х + В^у + С\
У. I2 + В2 “	/12 + в?
4°. Уравнение пучка прямых, проходящих через точку пере-
сечения двух данных прямых:
а(Ах + By + С) + /3(А1Х + В^у + C*i) = 0.	(4)
Можно положить а = 1, исключив этим из пучка (4) вторую из дан-
ных прямых.
101.	Привести к нормальному виду уравнения прямых:
1)	Зж — 4у — 20 = 0; 2) х + у + 3 = 0; 3) у = кх + Ь.
102.	Построить прямую, если длина нормали р = 2, а угол
(3 наклона ее к оси Ох равен: 1) 45°; 2) 135°; 3) 225°; 4) 315°.
Написать уравнения этих прямых.
103.	Найти расстояния от точек А(4; 3), В(2; 1) и С(1; 0) до
прямой Зх + I // — 10 = 0. Построить точки и прямую.
20	Гл.1. Аналитическая геометрия на плоскости
104.	Найти расстояние от начала координат до прямой 12® —
- 5у + 39 = 0.
105.	Показать, что прямые 2® — Зу = 6 и 4® — бу = 25 парал-
лельны, и найти расстояние между ними.
Указание. На одной из прямых взять произвольную точку и найти
расстояние от нее до другой прямой.
106.	Найти к из условия, что прямая у = кх + 5 удалена от
начала координат на расстояние d = у/5.
107.	Написать уравнение геометрического места точек, удален-
ных от прямой 4® — Зу = 0 на расстояние d = 4.
108.	Составить уравнение прямой, удаленной от точки А(4; —2)
на расстояние d = 4 и параллельной прямой 8® — 15у = 0.
109.	Написать уравнения биссектрис углов между прямыми
2ж + Зу = 10 и Зж + 2у = 10.
110.	Написать уравнения биссектрис углов между прямыми
3® + 4у = 12 и у = 0.
111.	Написать уравнение траектории точки М(х; у), которая
при своем движении остается втрое дальше от прямой у = 2® — 4,
чем от прямой у = 4 — 2®.
112.	Написать уравнение прямой, проходящей через точку М
пересечения прямых 2ж-Гу-|-6 = 0иЗж-Г5у — 15 = 0и через
точку 2V(1, —2) (не находя точки М).
113.	Написать уравнение прямой, проходящей через точку М
пересечения прямых 5ж — у-Г10 = 0и8ж-Г4у-Г9 = 0и парал-
лельной прямой ж + Зу = 0 (не находя точки М).
114.	Найти длину высоты BD в треугольнике с вершинами
А(-3; 0), В(2; 5)и С(3; 2).
115.	Написать уравнение прямой, проходящей через точку
А(2; 4) и удаленной от начала координат на расстояние d = 2.
116.	Проверить, что точки А(—4; —3), В( — 5; 0), С(5; 6) и
D(l; 0) служат вершинами трапеции, и найти ее высоту.
117.	Через начало координат проведена прямая на одинаковом
расстоянии от точек А(2; 2) и В(4; 0). Найти это расстояние.
118.	Написать уравнения геометрического места точек, удален-
ных от прямой ж + 2у — 5 = 0 на расстояние, равное л/5.
119.	Написать уравнение траектории точки М(х; у), которая
при своем движении остается вдвое дальше от прямой у = ж, чем
от прямой у = —ж.
120.	Написать уравнение прямой, проходящей через точку М
пересечения прямых 2ж — Зу-|-5 = 0иЗж-Гу — 7 = 0 и перпенди-
кулярной к прямой у = 2® (не находя точки М).
§ 7. Смешанные задачи на прямую
21
§ 7. Смешанные задачи на прямую
121.	Через начало координат провести прямую, образующую с
прямыми ж + у = аиж = 0 треугольник площадью а2.
122.	Даны точки А( —4; 0) и В(0; 6). Через середину отрезка
АВ провести прямую, отсекающую на оси Ох отрезок, вдвое боль-
ший, чем на оси Оу.
123.	Даны точки А( —2; 0) и В(2; —2). На отрезке О А построен
параллелограмм OACD, диагонали которого пересекаются в точке
В. Написать уравнения сторон, диагоналей параллелограмма и
найти угол CAD.
124.	Найти углы и площадь треугольника, образованного пря-
мыми у = 2®, у = —2ж и у = х + Ь.
125.	Из начала координат проведены две взаимно перпендику-
лярные прямые, образующие с прямой 2ж + у = а равнобедренный
треугольник. Найти площадь этого треугольника.
126.	Найти внутренние углы треугольника, если даны уравне-
ния его сторон: (АВ) х — Зу + 3 = 0 и (АС) х + Зу + 3 = 0 и
основание D(— 1; 3) высоты AD.
127.	Даны уравнения боковых сторон равнобедренного тре-
угольника Зж + у = 0иж — Зу = 0и точка (5; 0) на его основании.
Найти периметр и площадь треугольника.
128.	В треугольнике АВС даны: 1) уравнение стороны (АВ)
Зх + 2у = 12; 2) уравнение высоты (ВМ) х + 2у = 4; 3) уравнение
высоты (AM) 4s + у = 6, где М — точка пересечения высот.
Написать уравнения сторон АС, ВС и высоты СМ.
129.	Две стороны параллелограмма заданы уравнениями у =
= х — 2 и 5у = ж + 6. Диагонали его пересекаются в начале коор-
динат. Написать уравнения двух других сторон параллелограмма
и его диагоналей.
130.	Дан треугольник с вершинами А(0; —4), В(3; 0) и С(0; 6).
Найти расстояние вершины С от биссектрисы угла А.
131.	Написать уравнение траектории точки М(х; у), движу-
щейся так, что сумма расстояний от нее до прямых у = 2ж и
у = —ж/2 остается постоянной и равной у/5.
132.	Построить области, координаты точек которых удовлетво-
ряют неравенствам:
1) ж — 2<у<0иж>0; 2) —2 у х 2;
3)	2 < 2ж + у < 8, ж > 0 и у > 0.
133.	Стороны АВ и ВС параллелограмма заданы уравнениями
2ж — у+ 5 = 0 и х — 2у + 4 = 0, диагонали его пересекаются в точке
М(1; 4). Найти длины его высот.
134.	Найти вершины прямоугольного равнобедренного тре-
угольника, если дана вершина прямого угла С(3; —1) и уравне-
ние гипотенузы Зх — у + 2 = 0.
Cl
Гл. 1. Аналитическая геометрия на плоскости
135.	Даны две вершины треугольника А(—4; 3) и В(4; -1) И
точка пересечения высот М(3; 3). Найти третью вершину С.
136.	Вычислить координаты вершины ромба, если известны
уравнения двух его сторон: ж-Г2у = 4иж-|-2у = 10, и уравнение
одной из его диагоналей: у = х + 2.
137.	Составить уравнения сторон треугольника, зная одну его
вершину Д(0; 2) и уравнения высот: (ВМ) х + у = 4 и (СМ)
у = 2ж, где М — точка пересечения высот.
138.	Даны прямая х + 2у — 4 = 0 и точка Д(5; 7). Найти:
1) проекцию В точки А на данную прямую; 2) отражение С точки
А в данной прямой.
Указание. Написав уравнение перпендикуляра АВ и решив его
совместно с уравнением данной прямой, найдем точку В, которая есть
середина АС.
139.	Дана прямая 2ж + у — 6 = 0 и на ней две точки А и В с
ординатами уд = 6 и ув = —2. Написать уравнение высоты AD
треугольника АОВ, найти ее длину и MDAB.
§ 8. Окружность
Уравнение окружности с центром в точке С(а; Ь) и радиусом,
равным R:
(х - а)2 + (у - b)2 = R2.	(1)
Если в уравнении (1) раскрыть скобки, то оно примет вид
ж2 + у2 + тх + пу + р = 0.
(2)
Чтобы от уравнения (2) опять перейти к уравнению вида (1), нужно
в левой части уравнения (2) выделить полные квадраты:
(3)
140.	Написать уравнение окружности с центром С(—4; 3), ра-
диусом R = 5 и построить ее. Лежат ли на этой окружности точки
Д(-1; -1), В(3; 2), <9(0; 0)?
141.	Дана точка (—4; 6). Написать уравнение окружности, диа-
метром которой служит отрезок О А.
142.	Построить окружности: 1) ж2 + у2 — 4ж + бу — 3 = 0;
2) ж2 + у2 — 8ж = 0; 3) ж2 + у2 + 4у = 0.
143.	Построить окружность ж2 + у2 + 5ж = 0, прямую ж + у = 0
и найти точки их пересечения.
144.	Написать уравнение окружности, касающейся осей коор-
динат и проходящей через точку Д(1; 2).
§ 8. Окружность
23
145.	Найти угол между радиусами окружности х2 + у2 + 4ж —
— бу = О, проведенными в точки пересечения ее с осью Оу.
146.	Написать уравнение окружности, проходящей через точки
А(-1; 3), В(0; 2) и С(1; -1).
Указание. Написать уравнение искомой окружности в виде х2 +
+ у2 + тх + пу + р = 0, подставить в него координаты каждой точки и
затем найти т, п и р.
147.	Написать уравнение окружности, проходящей через точки
пересечения окружности ж2 + у2 + 4ж — 4у = 0 с прямой у = —х и
через точку А(4; 4).
148.	Определить область расположения кривой у = — \j—x2 — 4s.
Построить кривую.
149.	Написать уравнение касательных к окружности х2 + у2 —
— 8х — 4у + 16 = 0, проведенных из начала координат.
150.	Дана точка А(а; 0). Точка М движется так, что в ЛОМА
угол ОМА остается прямым. Определить траекторию движения
точки М.
151.	Даны точки Д( — 6; 0) и В(2; 0). Найти геометрическое
место точек, из которых отрезки ОА и ОВ видны под равными
углами.
152.	Определить траекторию точки М(х; у), движущейся так,
что сумма квадратов расстояний от нее до точек А( — а; 0), В(0; а)
и С (а; 0) остается равной За2.
153.	Определить траекторию точки М(х; у), движущейся так,
что сумма квадратов расстояний от нее до биссектрис координат-
„	2
ных углов остается равной а .
154.	Дана окружность х2 + у2 = а2. Из ее точки Д(а; 0) про-
ведены всевозможные хорды. Определить геометрическое место
середин этих хорд.
155.	Даны точки Д( — 3; 0) и В(3; 6). Написать уравнение ок-
ружности, диаметром которой служит отрезок АВ.
156.	Найти центры и радиусы окружностей: 1) х2-\-у2 — 6х-\-
+ 4у — 23 = 0; 2) х2 + у2 + 5х — 7у + 2, 5 = 0; 3) х2 + у2 + 7у = 0.
Построить окружности.
157.	Окружность касается оси Ох в начале координат и про-
ходит через точку Д(0; —4). Написать уравнение окружности и
найти точки пересечения ее с биссектрисами координатных углов.
158.	Написать уравнение окружности, проходящей через на-
чало координат и через точки пересечения прямой s+y+a=0c
окружностью х2 + у2 = а2.
Гл. 1. Аналитическая геометрия на плоскости
159.	Написать уравнения касательных, проведенных из на-
чала координат к окружности, проходящей через точки Л(1; —2),
В(0; -1) и С(-3; 0).
160.	Найти угол между радиусами окружности ж2-|-у2 — 4ж-Г
+ бу — 5 = 0, проведенными в точки пересечения ее с осью Ох.
161.	Показать, что точка Л(3; 0) лежит внутри окружности х2 +
+ у2 — 4s + 2у + 1 = 0, и написать уравнение хорды, делящейся в
точке А пополам.
Указание. Искомая хорда перпендикулярна к С А, где С — центр
окружности.
162.	Точка М(ж; у) движется так, что сумма квадратов рассто-
яний от нее до начала координат и до точки А( — а; 0) остается
равной а2. Определить траекторию движения точки М.
163.	Дана окружность х2 + у2 = 4. Из точки ее Л( — 2; 0) про-
ведена хорда АВ и продолжена на расстояние ВМ = АВ. Опре-
делить геометрическое место точек М.
164.	Отрезок AM = а перемещается по плоскости хОу, оста-
ваясь параллельным Ох, так, что левый конец его А скользит
по окружности х2 + у2 = а2. Определить траекторию движения
точки М.
§ 9. Эллипс
Эллипсом называется геометрическое место точек, сумма рас-
стояний от каждой из которых до двух данных точек F и Fi (фоку-
сов) есть постоянная величина 2а, большая F^F.
Каноническое (простейшее) уравнение эллипса
4 + $ = 1-	m
Эллипс, заданный уравнением (1), симметричен относительно осей
координат (рис. 1). Параметры а и Ь называются полуосями эллипса.
У“
Рис. 1
Пусть а > Ь, тогда фокусы F и Fi находятся на оси Ох на расстоянии
с = \/а2 — Ь2 от центра. Отношение — = е < 1 называется эксцентри-
§9. Эллипс	25
ситетом эллипса. Расстояния от точки М(ж; у) эллипса до его фокусов
(фокальные радиус-векторы) определяются формулами
г = а — ех, r-у = а + ех.	(2)
Если же а < Ь, то фокусы находятся на оси Оу, с = \/Ъ2 — а2, е = -,
b
г = b ± еу.
165.	Построить эллипс х2 + 4у2 = 16, найти его фокусы и экс-
центриситет.
166.	Написать каноническое уравнение эллипса, зная, что:
1) расстояние между фокусами равно 8, а малая полуось 6=3;
2) большая полуось а = 6, а эксцентриситет е = 0, 5.
167.	Найти малую полуось b и эксцентриситет е эллипса, име-
ющего большую полуось а = 5 и параметр с, равный: 1) 4,8; 2) 4;
3) 3; 4) 1,4; 5) 0. Построить каждый из эллипсов.
168.	Земля движется по эллипсу, в одном из фокусов которого
находится Солнце. Наименьшее расстояние от Земли до Солнца
равно приблизительно 147,5 млн км, а наибольшее 152,5 млн км.
Найти большую полуось и эксцентриситет орбиты Земли.
169.	Эллипс, симметричный относительно осей координат, про-
ходит через точки М(2; ^/3) и В(0; 2). Написать его уравнение и
найти расстояния от точки М до фокусов.
170.	Эллипс, симметричный относительно осей координат,
фокусы которого находятся на оси Ох, проходит через точку
3
М(—4; а/21) и имеет эксцентриситет е = -. Написать уравнение
эллипса и найти фокальные радиус-векторы точки М.
171.	Найти длину хорды эллипса х2 + 2у2 = 18, делящей угол
между осями пополам.
172.	Найти эксцентриситет эллипса, если расстояние между
фокусами равно расстоянию между концами большой и малой по-
луосей.
173.	В эллипс х2 + 4у2 = 4 вписан правильный треугольник,
одна из вершин которого совпадает с концом большой полуоси.
Определить координаты двух других вершин треугольника.
Указание. Написать уравнение одной из сторон, имеющей наклон
k = tg30°, и найти точки ее пересечения с эллипсом.
174.	На эллипсе 9ж2 + 25у2 = 225 найти точку, расстояние от
которой до правого фокуса в четыре раза больше расстояния от нее
до левого фокуса.
175.	Ординаты всех точек окружности х2 + у2 = 36 сокращены
втрое. Написать уравнение полученной новой кривой.
176.	Определить траекторию точки М, которая при своем дви-
жении остается вдвое ближе к точке F( — 1; 0), чем к прямой
х = —4.
26
Гл. 1. Аналитическая геометрия на плоскости
177.	Отрезок АВ постоянной длины a + b движется так, что
его конец А скользит по оси Ох, а конец В — по оси Оу. Опре-
делить траекторию движения точки М отрезка, делящей его на
части ВМ = а и МА = b (эллиптический циркуль Леонардо да
Винчи).
178.	Даны окружности х2 + у2 = Ь2 и х2 + у2 = а2 (6 < а).
Произвольный луч ОБА пересекает их соответственно в точках В
и А, из которых проведены прямые, параллельные осям коорди-
нат, до пересечения их в точке М. Определить геометрическое
место точек М.
179.	Написать простейшее уравнение эллипса, у которого рас-
стояния от одного из фокусов до концов большой оси равны 5 и 1.
180.	Эллипс, симметричный относительно осей координат, про-
ходит через точки М(2-\/3; ^/б) и А(6; 0). Написать его уравнение,
найти эксцентриситет и расстояния от точки М до фокусов.
ж2 у2
181.	Найти длину хорды эллипса — + — = 1, направленной
а2 о2
по диагонали прямоугольника, построенного на осях эллипса.
182.	Найти общие точки эллипса х2 + 4у2 = 4 и окружности,
проходящей через фокусы эллипса и имеющей центр в его «верх-
ней» вершине.
183.	На прямой х = —5 найти точку, одинаково удаленную от
«левого» фокуса и от «верхней» вершины эллипса х2 + 5//2 = 20.
184.	На эллипсе х2 + 5//2 = 20 найти точку, радиус-векторы
которой перпендикулярны.
Указание. Искомые точки суть точки пересечения с эллипсом
окружности, проходящей через фокусы эллипса и имеющей центр в на-
чале координат.
185.	Абсциссы точек окружности х2 + у2 = 4 увеличены вдвое.
Определить полученную кривую.
186.	Определить траекторию точки М, которая при своем дви-
жении остается втрое ближе к точке А(1; 0), чем к прямой х = 9.
§ 10. Гипербола
Гиперболой называется геометрическое место точек, разность
расстояний от каждой из которых до двух данных точек F и Fi (фо-
кусов) есть постоянная величина 2а (0 < 2а < FiF).
Каноническое (простейшее) уравнение гиперболы
ж2
а2
Mi.
b2
(1)
§10. Гипербола
27
Гипербола, заданная уравнением (1), симметрична относительно осей
координат (рис. 2). Она пересекает ось Ох в точках А(а; 0) и Ai(—a; 0) —
вершинах гиперболы и не пересекает ось Оу. Параметр а называется ве-
щественной полуосью, b — мнимой полуосью. Параметр с = л/а2 + &2
есть расстояние от фокуса до центра. Отношение — = е > 1 называется
а
b
эксцентриситетом гиперболы. Прямые у = ± — х называются асимп-
а
тотами гиперболы. Расстояния от точки М(х; у) гиперболы до ее фо-
кусов (фокальные радиус-векторы) определяются формулами
г = \ех — а |, п = \ех + а|.	(2)
Гипербола, у которой а = Ь, называется равносторонней, ее уравне-
х2 у2
ние х2 — у2 = а2, а уравнения асимптот у = ±ж. Гиперболы — — — = 1
а2 Ь2
у2 X2
и —------ = 1 называются сопряженными.
Ь2 а2
187.	Построить гиперболу ж2 — 4у2 = 16 и ее асимптоты. Найти
фокусы, эксцентриситет и угол между асимптотами.
188.	На гиперболе х2 — 4у2 = 16 взята точка М с ординатой,
равной 1. Найти расстояние от нее до фокусов.
189.	Написать каноническое уравнение гиперболы, зная, что:
1) расстояние между фокусами 2с = 10, а между вершинами 2а =
= 8; 2) вещественная полуось а = 2-\/5, а эксцентриситет е =
=
190.	Гипербола симметрична относительно осей координат, про-
ходит через точку М(6; — 2^/2) и имеет мнимую полуось 6 = 2.
Написать ее уравнение и найти расстояния от точки М до фоку-
сов.
28
Гл. 1. Аналитическая геометрия на плоскости
191.	Написать уравнение гиперболы, имеющей вершины в фо-
х^ у2
кусах, а фокусы — в вершинах эллипса — + — = 1.
192.	Написать уравнение гиперболы, имеющей эксцентриситет
е = -\/2, проходящей через точку (2а; а-\/3) и симметричной отно-
сительно осей координат.
193.	Построить гиперболу у2 = а2 + х2, найти координаты ее
фокусов и угол между асимптотами.
194.	Написать уравнения касательных к гиперболе х2 — I//2 =
= 16, проведенных из точки Д(0; —2).
ж2 у2
195.	Найти расстояние от фокуса гиперболы — — — = 1 до ее
а2 о2
асимптот и угол между асимптотами.
х2
196.	Найти сторону квадрата, вписанного в гиперболу — —
а2
у2
— — = 1, и исследовать, в какие гиперболы можно вписать квадрат.
о2
197.	Найти эксцентриситет гиперболы, асимптота
ставляет с вещественной
осью угол: 1) 60°; 2) а.
198. Определить область
которой со-
расположе-
ния кривой у = —-\/9 + х2. Построить
кривую.
199.	Определить траекторию точки
М(х; у), которая при своем движении
остается вдвое ближе к прямой х = 1,
чем к точке F(4; 0).
200.	Даны точки Д( — 1; 0) и В(2; 0).
Точка М движется так, что в ЛАМ В
угол В остается вдвое больше угла А.
Определить траекторию движения.
201.	Дана точка А(а; 0). По оси Оу
движется точка В. На прямой BE, па-
раллельной Ох, откладываются отрезки
ВМ и BMi, равные АВ. Определить
геометрическое место точек М и М-р
= ±6 и х = ±а (Ь < а). Произвольный
202. Даны прямые х
луч ОА (рис. 3) пересекает прямую х = b (или х = —6) в точке В
и прямую х = а (или х = —а) в точке А. Радиусом ОА описана
дуга, пересекающая Ох в точке С. Из точек В и С проведены
прямые, параллельные соответственно Ох и Оу, до пересечения в
точке М. Определить геометрическое место точек М.
203.	Написать каноническое уравнение гиперболы, зная, что
расстояния от одной из ее вершин до фокусов равны 9 и 1.
§11. Парабола	29
204.	Найти точки пересечения асимптот гиперболы х2 — Зу2 =
= 12 с окружностью, имеющей центр в правом фокусе гиперболы
и проходящей через начало координат.
205.	Гипербола проходит через точку М(6; 3-\/5/2), симметрич-
на относительно осей координат и имеет вещественную полуось
a = 4. Написать уравнения перпендикуляров, опущенных из ле-
вого фокуса гиперболы на ее асимптоты.
206.	На гиперболе 9ж2 — 16у2 = 144 найти точку, расстояние
от которой до левого фокуса вдвое меньше, чем до правого.
207.	На гиперболе х2 — у2 = 4 найти точку, фокальные радиус-
векторы которой перпендикулярны (см. указание к задаче 184).
208.	Точка М делит расстояние между фокусами гиперболы
9ж2 — 16у2 = 144 в отношении F^M : MF = 2:3, где Fi — левый
фокус гиперболы. Через точку М проведена прямая под углом 135°
к оси Ох. Найти точки пересечения этой прямой с асимптотами
гиперболы.
209.	Определить траекторию точки М, которая движется так,
что остается вдвое дальше от точки F( — 8; 0), чем от прямой
х = —2.
210.	Даны точки А( — а; 0) и В (За; 0). Точка М движется так,
что угол МАВ остается втрое меньше внешнего угла АМС тре-
угольника АМВ. Определить траекторию движения точки М.
§ 11.	Парабола
Параболой называется геометрическое место точек, одинаково
удаленных от данной точки (фокуса) и данной прямой (директрисы).
Каноническое уравнение параболы имеет два вида:
1)	у2 = Зрх — парабола симметрична относительно оси Ох (рис. 4);
2)	х2 = 2ру — парабола симметрична относительно оси Оу (рис. 5).
Рис. 4
Директриса
Рис. 5
В обоих случаях вершина параболы, т. е. точка, лежащая на оси
симметрии, находится в начале координат.
30
Гл. 1. Аналитическая геометрия на плоскости
Парабола
у2 = 2рт
Парабола
имеет фокус F
и директрису х =
точки М(ж; у) на ней
х2 = 2ру
фокальный радиус-вектор
имеет фокус F
точки М(х; у) на ней
и директрису
. Р
г = У F —
р
у = —фокальный радиус-вектор
211.	Со ставить уравнение геометрического места точек, одина-
ково удаленных от точки F(0; 2) и от прямой у = 4. Найти точки
пересечения этой кривой с осями координат и построить ее.
212.	Со ставить уравнение геометрического места точек, одина-
ково удаленных от начала координат и от прямой х = —4. Найти
точки пересечения этой кривой с осями координат и построить ее.
213.	Построить параболы, заданные уравнениями: 1) у2 = 4ж;
2) у2 = — 4ж; 3) х2 = 4у; 4) х2 = — 4у, а также их фокусы и
директрисы и написать уравнения директрис.
214.	Написать уравнение параболы: 1) проходящей через точки
(0; 0) и (1; —3) и симметричной относительно оси Ох; 2) прохо-
дящей через точки (0; 0) и (2; —4) и симметричной относительно
оси Оу.
215.	Канат подвесного моста имеет форму параболы (рис. 6).
Написать ее уравнение относительно указанных на чертеже осей,
если прогиб каната О А = а, а длина пролета ВС = 26.
216.	Написать уравнение окружности, имеющей центр в фокусе
параболы у2 = 2рх и касающейся ее директрисы. Найти точки
пересечения параболы и окружности.
217.	Написать уравнение параболы и ее директрисы, если па-
рабола проходит через точки пересечения прямой х + у = 0 и
Рис. 6
окружности х2 + у2 + 4у = 0 и симметрична относительно оси Оу.
Построить окружность, прямую и параболу.
§11. Парабола
31
218.	На параболе у2 = 6х найти точку, фокальный радиус-
вектор которой равен 4,5.
219.	Зеркальная поверхность прожектора образована враще-
нием параболы вокруг ее оси симметрии. Диаметр зеркала 80 см,
а глубина его 10 см. На каком расстоянии от вершины параболы
нужно поместить источник света, если для отражения лучей па-
раллельным пучком он должен быть
в фокусе параболы?
220.	Определить область располо-
жения кривой у = —у/—х. Постро-
ить кривую.
221.	Из вершины параболы у2 =
= 1рх проведены всевозможные хор-
ды. Написать уравнение геометриче-
ского места середин этих хорд.
222.	Определить геометрическое
место центров окружностей, касаю-
щихся окружности ж2 + у2 = ‘lax и
оси Оу.
223.	Даны точки Д(0; а)иВ(а; а).
Отрезки ОА и АВ разделены на п
равных частей точками Ai, А%, Аз, ...нВ], В2, В3, ... (рис. 7).
Пусть Mk — точка пересечения луча ОВ^ с прямой АкМк\\Ох. По-
казать, что такие точки Мь лежат на параболе у2 = ах. Построить
этим приемом параболы у2 = 4ж, у2 = 5ж, у2 = Зж.
224.	Со ставить уравнение геометрического места точек, одина-
ково удаленных от начала координат и от прямой х = 4. Найти
точки пересечения этой кривой с осями координат и построить ее.
225.	Со ставить уравнение геометрического места точек, оди-
наково удаленных от точки F(2; 0) и от прямой у = 2. Найти
вершину параболы, точки пересечения ее с Ох и построить ее.
226.	Написать уравнение параболы: 1) проходящей через точки
(0; 0) и ( — 1; 2) и симметричной относительно оси Ох; 2) прохо-
дящей через точки (0; 0) и (2; 4) и симметричной относительно
оси Оу.
227.	Написать уравнение параболы и ее директрисы, если па-
рабола проходит через точки пересечения прямой у = х и окруж-
ности ж2 + у2 + 6ж = 0 и симметрична относительно оси Ох. По-
строить прямую, окружность и параболу.
228.	В параболу у2 = 2ж вписан правильный треугольник.
Определить его вершины (см. указание к задаче 173).
229.	Написать уравнения касательных к параболе у2 = 8ж,
проведенных из точки А(0; —2).
32
Гл. 1. Аналитическая геометрия на плоскости
230.	Через фокус параболы у2 = — 4ж проведена прямая под
углом 120° к оси Ох. Написать уравнение прямой и найти длину
образовавшейся хорды.
§ 12.	Директрисы, диаметры и касательные
к кривым второго порядка
х2 у2
1°. Директрисами эллипса — + — = 1 (при а > Ь) и гиперболы
а2 о2
х2 у2
—------ = 1 называются прямые, параллельные оси Оу и отстоящие от
а2 Ь2
а
нее на расстояние —, где е — эксцентриситет кривой.
е
Уравнения директрис:
а
<‘>
Свойство директрис: отношение расстояний от точки кри-
вой до фокуса и до соответствующей директрисы равно эксцентри-
ситету кривой
(2)
d ‘
2°. Диаметром кривой второго порядка называется гео-
метрическое место середин параллельных хорд. Диаметрами эллипса
и гиперболы оказываются отрезки и лучи прямых, проходящих через
центр, а диаметрами параболы — лучи, параллельные ее оси.
Уравнение диаметра, делящего пополам хорды с наклоном
tgа = к, будет
х2 у2
кривых — ± f- = 1:
а2 о2
ДЛЯ
для
параболы г/2 = 2рт:
Ь2
a2k
(3)
(4)
Два диаметра эллипса и гиперболы, из которых каждый делит по-
полам хорды, параллельные другому, называются взаимно сопряжен-
ными. Их угловые коэффициенты к и к\ связаны зависимостью кк\ —
—------- (у эллипса) и кк\ = — (у гиперболы).
к
к
3°. Уравнения касательной:
к X2 у2	\ хх0	уу0
эллипсу — + — = 1	+ —— = 1;
bz	) az	bz
X	Ц	\ ХХс\	UUo
гиперболе — - — = 1 —---------— = 1;
\ а2	о2	/ а2	о2
к параболе (г/2 = 2рт) ////о = р(х + «о), где («q; j/q) — точка касания.
§ 12.	Директрисы, диаметры и касательные к кривым 2-го порядка 33
231.	Построить эллипс — + — = 1, его директрисы и найти
расстояния от точки эллипса с абсциссой х = —3 до правого фокуса
и правой директрисы.
тт	ж2 У2
232.	Построить гиперболу — —— = 1, ее директрисы и найти
расстояния от точки гиперболы с абсциссой х = 5 до левого фокуса
и левой директрисы.
233.	Написать каноническое уравнение эллипса, директрисами
, 4
которого служат прямые х = ±—и большая полуось которого
равна 2.
234.	Написать уравнение гиперболы, асимптоты которой у =
= ± х, а директрисы х = ±-\/б.
тт	7	7	Х
235.	Построить эллипс х£ + 4у2 = 16, диаметр у = — и сопря-
женный ему диаметр и найти длины (д и 1д построенных полу-
диаметров.
236.	Построить гиперболу х2 — I//2 = 4, диаметр у = —х и
сопряженный ему диаметр и найти угол между диаметрами.
х2 у2
237.	Найти длину того диаметра эллипса +	= 1, который
а2 о2
равен своему сопряженному диаметру.
х2 у2
238.	Асимптота гиперболы — — — = 1 составляет с осью Ох
а2 о2
угол 60°. Написать уравнение диаметра, сопряженного с диамет-
ром у = 2ж. Выбрав произвольно отрезок а, построить кривую,
диаметры и хорды, параллельные данному диаметру.
239.	Определить геометрическое место середин хорд параболы
у2 = 4ж, составляющих с Ох угол 45°.
х2 у2
240.	Дан эллипс — + — = 1. Через точку ( — 2; 1) провести
хорду, делящуюся в этой точке пополам.
241.	Дана парабола у2 = —4ж. Через точку ( — 2; —1) провести
хорду, делящуюся в этой точке пополам.
242.	На примере задачи 235 проверить теорему Аполлония:
а2 + Ь2 = а2 + Ь2 и аДд sin р = ab, где (д и Ь-у — длины со-
пряженных полудиаметров, а и b — полуоси эллипса, а р — угол
между сопряженными диаметрами.
243.	Написать уравнения касательных к кривым:
1)	ж2 + 4у2 = 16; 2) Зж2 — у2 = 3; 3) у2 = 2ж в точке с абсциссой
х0 = 2.
34	Гл.1. Аналитическая геометрия на плоскости
244.	Показать, что если прямая Ах + By + С = 0 есть каса-
тельная к эллипсу — + — = 1, то Д2а2 + В262 = С2.
а2 о2
Указание. Из пропорциональности коэффициентов уравнений
хх0 уу0
—-—|----— = 1 и Ах + By + С = 0 определить х0 и t/о и подставить
а2 Ь2
X2 у2
их в уравнение — + — = 1.
а2 Ь2
245.	Написать уравнения касательных к эллипсу ж2+4у2 = 20,
параллельных биссектрисе первого координатного угла.
246.	Написать уравнения касательных к эллипсу ж2 + 2у2 = 8,
проведенных из точки (0; 6).
ж2 у2
247.	Написать уравнение касательной к эллипсу — + — = 1,
а2 о2
отсекающей на осях координат равные положительные отрезки.
248.	Показать, что если прямая Ах + Ву + С = 0 есть касатель-
ж2 у2
ная к гиперболе — — — = 1, то Д2а2 — В262 = С2 (см. указание
а2 о2
к задаче 244).
249.	Написать уравнения касательных к гиперболе 4ж2 —9у2 =
= 36, перпендикулярных к прямой ж + 2у = 0.
250.	Доказать, что нормаль к эллипсу есть биссектриса угла
между радиус-векторами соответствующей точки эллипса.
251.	Доказать, что касательная к гиперболе есть биссектриса
угла между радиус-векторами точки касания.
252.	Доказать, что лучи, выходящие из фокуса параболы, от-
ражаются от параболы по прямым, параллельным ее оси.
Указание. Нужно написать уравнение нормали MN, найти точку
N пересечения ее с осью параболы и доказать, что FM = FN, где F —
фокус параболы.
253.	Найти точки пересечения асимптот гиперболы--= 1
с ее директрисами.
254.	Построить эллипс ж2 + 4у2 = 16, его диаметр у = ж и
сопряженный ему диаметр и найти угол между этими диаметрами.
255.	Определить геометрическое место середин хорд гиперболы
ж2 — 4у2 = 16, составляющих угол 45° с осью Ох.
256.	Дана гипербола 4ж2 — у2 = 4. Через точку (2; 2) провести
хорду, делящуюся в этой точке пополам.
257.	На эллипсе ж2 + 2у2 = 6 взята точка М с ординатой 1
и отрицательной абсциссой. Найти угол касательной к эллипсу в
точке М с прямой ОМ.
§ 13. Преобразование декартовых координат
35
258.	Показать, что если прямая Ах + By + С = 0 есть каса-
тельная к параболе у2 = 2рх, то В2р = 2АС (см. указание к
задаче 244).
259.	Написать уравнение касательной к параболе у2 = 8х, па-
раллельной прямой х + у = 0.
§ 13.	Преобразование декартовых координат.
Параболы =	2 +	+ и =	2 +	+ .
Гипербола =
1°. Координаты (х; у) в данной системе преобразуются к координа-
там (X; У) в новой системе по формулам:
1)	при параллельном сдвиге осей и перенесении начала координат
в точку 01 (а; /3)
х = X + а, у = У + /3;	(1)
2)	при повороте осей на угол р
х = X cos р — У sin р, у = X sin р + У cos р.	(2)
2°. Уравнение у = а(х — а)2 + /3 переносом начала координат в
точку 01 (а; /3) приводится к виду У = аХ2 и, следовательно, опреде-
ляет параболу с вершиной Oi(a; /3) и осью симметрии, параллельной
Оу (рис. 8). Уравнение у = ах2 + Ьх + с выделением в правой части
полного квадрата приводится к предыдущему и поэтому тоже определяет
параболу. При а > 0 парабола от вершины направлена «вверх», при
а < 0 — «вниз».
3°. Уравнение ху = к при повороте осей координат на угол
р = 45° приводится к виду X2 — У2 = 2к и, следовательно, определяет
равностороннюю гиперболу, асимптотами которой служат оси коорди-
нат (рис. 9). Уравнение (х — а) (у — (3) = к переносом начала координат
в точку 01 (а; /3) приводится к виду XY = к и поэтому тоже определяет
равностороннюю гиперболу.
36	Гл.1. Аналитическая геометрия на плоскости
260.	1) Точка А(3; 1) при параллельном сдвиге осей координат
получила новые координаты (2; —1). Построить данные и смещен-
ные оси координат и точку А.
2) Найти острый угол поворота осей координат, при котором
точка А(2; 4) получит новую абсциссу 4. Построить обе системы
координат и точку А.
261.	Перенесением начала координат упростить уравнения:
(х — 2)2	,	(х + З)2 (у — I)2
1)	k^	+	(y+i)2 = i;	2)	=
3) (у + 2)2	= 4(ж — 3);	4)	2у	=	—(ж + 2)2;
5) х2 + 4у2	—	6х + 8у = 3;	6)	у2	—	8у = 4ж;
7) х2 — 4у2	+	8ж — 24у = 24;	8)	х2	+	6ж + 5 = 2у.
Построить старые и новые оси координат и кривые.
262.	Поворотом осей координат на 45° упростить уравнения:
1)	5ж2 — бху + 5у2 = 32;	2) Зж2 — Юху + Зу2 + 32 = 0.
Построить старые и новые оси координат и кривые.
263.	Построить по точкам кривую ху = —4 и поворотом осей
на угол /р = —45° преобразовать уравнение.
264.	Переносом начала координат привести к виду ху = к урав-
нения кривых:
1)	ху — 2х = 6;	2) ху — 2х — у + 8 = 0;
3)	ху — х + 2у = 6; 4) ху + 2х = Зу.
Указание. Уравнение ху + Ах + By + С = 0 можно написать в
виде (ж + В) (у + А) = АВ — С.
265.	Построить параболы:
1)	у — (ж -2)2; 2) у — (ж-2)2 + 3;
3)	у = (ж + 2)2; 4) у = (ж + 2)2 - 3.
266.	Построить параболы:
1)	у = ж2 — 4ж + 5;	2) у = ж2 + 2ж + 3;
3)	у = —ж2 + 2ж — 2,
выделив в правых частях уравнений полные квадраты.
267.	Построить параболы:
1)	у = 4ж — ж2 и 2) 2у = 3 + 2ж — ж2,
найдя их точки пересечения с осью Ох.
268.	Струя воды фонтана достигает наибольшей высоты 4 м на
расстоянии 0,5 м от вертикали, проходящей через точку О выхода
струи. Найти высоту струи над горизонталью Ох на расстоянии
0,75м от точки О.
§ 13. Преобразование декартовых координат
37
269.	Составить уравнение параболы, симметричной относитель-
но оси Оу и отсекающей на ней отрезок Ь, а на оси Ох — отрезки
а и —а.
Указание. В уравнении параболы вида у = Ах2 + Вх + С под-
ставить координаты данных на параболе точек (—а; 0), (а; 0) и (0; Ь) и
затем найти А, В и С.
270.	Парабола у = ах2 + Ьх + с проходит через точки 0(0; 0),
А(—1; — 3)иВ(-2; —4). Написать уравнение окружности, диамет-
ром которой служит отрезок оси Од, отсеченный параболой.
271.	На какой угол нужно повернуть оси координат, чтобы ис-
чез член, содержащий жу, в уравнениях:
1) х2 — ху + у2 — 3 = 0;	2) 5s2 — 4ху + 2у2 — 24 = 0?
Построить старые и новые оси координат и кривые.
272.	Определить траекторию движения пули, брошенной под
углом /р к горизонту с начальной скоростью v0. Определить также
дальность полета пули и наивысшую точку траектории (сопроти-
влением воздуха пренебречь).
273.	Написать уравнение геометрического места точек М(х; у),
отношение расстояний от которых до точки F(4; 0) к расстояниям
до прямой х = —2 равно 2.
274. Показать, что переносом начала координат в левую Bep-
s'2 у2
шину эллипса — + — = 1 или в правую вершину гиперболы
а2 о2
х2 У2	2
— — — = 1 оба уравнения приводятся к одинаковому виду: у =
а2 о2
, &2 ,
= 2рх + qx , где р = —,ag = e—1.
а
275.	По результатам задачи 274 определить эксцентриситет и
тип кривой: 1) у2 = х — -х2; 2) у2 = s-|--s2; 3) у2 = х. Построить
кривые, найдя для первых двух точки пересечения их с осью Ох
и параметры а и Ь.
276.	Выделением полных квадратов и переносом начала коор-
динат упростить уравнения линий:
1)	2s2 + 5//2 - 12s + 10у + 13 = 0;
2)	s2 — у2 + 6s + I // — 4 = 0;
3)	у2 + 4у = 2s;
4)	s2 — 10s = 4у — 13.
Построить старые и новые оси и кривые.
38	Гл.1. Аналитическая геометрия на плоскости
277.	Поворотом осей координат на 45° упростить уравнение
Зж2 — 2жу + 3у2 — 8 = 0. Определить координаты фокусов в старой
системе координат.
278.	Написать уравнение окружности, диаметром которой слу-
жит отрезок, отсекаемый на оси Ох параболой у = 3 — 2ж — ж2.
Построить обе кривые.
279.	Написать уравнение окружности, диаметром которой слу-
жит отрезок примой ж + у = 6, отсеченный гиперболой ху = 8.
Построить все три линии.
280.	Точка А — вершина параболы у = ж2 + 6ж + 5, В — точка
пересечения параболы с осью Оу. Написать уравнение перпенди-
куляра, восставленного из середины отрезка АВ.
281.	Составить уравнение параболы, симметричной относитель-
но оси Ох и отсекающей на ней отрезок —4, а на оси Оу — отрезки
4 и —4.
Указание. Уравнение параболы должно иметь вид ж = ay2 + с
(почему?).
282.	Построить по точкам пересечения с осями координат па-
раболы:
1) Зу = 9 — ж2; 2) у2 = 9 — Зж;
3) у2 = 4 + ж; 4) ж2 = 4 + 2у.
283. Написать уравнение геометрического места точек М(х; у),
отношение расстояний от которых до точки F(4; 0) к расстояниям
до прямой ж = 10 равно 1/2.
§ 14.	Смешанные задачи на кривые второго порядка
284.	Написать уравнение окружности, диаметром которой слу-
ж У
жит отрезок прямой —h — = 1, отсеченный осями координат.
a о
285.	Найти расстояние от центра окружности ж2 + у2 + ay = 0
до прямой у = 2(а — ж).
286.	Через центр окружности ж2 + у2 = 2аж проведена прямая,
параллельная прямой ж + 2у = 0 и пересекающая окружность в
точках А и В. Найти площадь АЛОВ.
287.	Показать, что геометрическое место точек М, которые уда-
лены в m раз дальше от данной точки А, чем от другой данной
точки В, есть прямая при m = 1 и окружность при m ф 1.
288.	Отрезок АВ разделен на части АО = а и ОВ = Ь. Пока-
зать, что геометрическое место точек, из которых отрезки АО и
ОВ видны под равными углами, есть прямая при a = b и окруж-
ность при a b (аполлониева окружность).
§ 14. Смешанные задачи на кривые второго порядка 39
289.	Определить траекторию точки М(х; у), движущейся так,
что сумма квадратов расстояний от нее до прямых у = кх и у =
= — кх остается постоянной и равной а2.
290.	Эллипс, симметричный относительно оси Ох и прямой
х = —5, проходит через точки ( — 1; 1,8) и ( — 5; 3). Написать урав-
нение эллипса и построить его.
291.	Найти площадь равностороннего треугольника, вписан-
ного в гиперболу х2 — у2 = а2.
292.	Найти угол между диагоналями прямоугольника, вершины
которого находятся в точках пересечения эллипса х2 + Зу2 = 12Z2
и гиперболы х2 — Зу2 = 6Z2.
293.	Окружность с центром в начале координат проходит че-
рез фокусы гиперболы х2 — у2 = а2. Найти точки пересечения
окружности с асимптотами гиперболы.
294.	Построить гиперболы ху = —4 и х2 — у2 = 6 и найти
площадь ДАВС, где А и В — вершины двух пересекающихся
ветвей гипербол, a С — точка пересечения двух других ветвей
гипербол.
295.	Доказать, что произведение расстояний любой точки ги-
а2Ь2
перболы от ее асимптот есть величина постоянная, равная ——.
с2
296.	Найти длину и уравнение перпендикуляра, опущенного
х2
из фокуса параболы у =-----на прямую, отсекающую на осях
8
координат отрезки а = Ь = 2.
297.	Построить эллипс х2 + 4у2 = 4 и параболу х2 = бу и
найти площадь трапеции, основаниями которой служат большая
ось эллипса и общая хорда эллипса и параболы.
298.	Из фокуса параболы у2 = '2р.г. как из центра, описана
окружность так, что общая хорда кривых одинаково удалена от
вершины и от фокуса параболы. Написать уравнение окружности.
299.	Найти длину и уравнение перпендикуляра, опущенного из
вершины параболы by = х2А2ахАа2АЬ2 на прямую, отсекающую
на осях координат отрезки а и Ь.
300.	Построить по точкам пересечения с осями координат па-
раболы 4у = 12 — ж2 и 4ж = 12 — у2 и найти длину их общей
хорды.
301.	Найти площадь четырехугольника с вершинами в точках
пересечения параболы у = 4 — х2 с осью Ох и с прямой у = Зх.
302.	Написать уравнение окружности, проходящей через на-
х2
чало координат и через точки пересечения параболы у = — —
а
— 2. г + а с осями координат.
40
Гл. 1. Аналитическая геометрия на плоскости
303.	Дан эллипс х2 + 4у2 = 16. Из его вершины А(4; 0) про-
ведены всевозможные хорды. Определить геометрическое место
середин этих хорд и построить кривые.
304.	Определить траекторию точки М(х; у), движущейся так,
что разность квадратов расстояний от нее до биссектрис коорди-
натных углов остается равной 8.
305.	Со ставить уравнение геометрического места центров ок-
ружностей, проходящих через точку А(3; 4) и касающихся оси Ох.
306.	Выделением полных квадратов и переносом начала упро-
стить уравнение линии х2 — у2 — 4ж — бу — 9 = 0. Построить старые
и новые оси координат и кривую.
307.	Найти геометрическое место середин фокальных радиус-
векторов, проведенных из правого фокуса ко всем точкам гипер-
х2 у2
болы	= 1.
9	16
308.	Написать уравнение эллипса, проходящего через точку
А(а; —а), если фокусы его находятся в точках F(a; а) и Fi(— а; —а).
Упростить уравнение поворотом осей координат на 45°.
309.	Поворотом осей координат на угол р = arctg - упростить
уравнение линии Зж2 + 8жу — Зу2 = 20. Построить старые и новые
оси координат и кривую.
310.	Написать уравнение геометрического места точек, раз-
ность квадратов расстояний от которых до прямой Зж + 4у = 0
и до оси Ох остается постоянной и равной 2,4.
311.	Написать уравнение геометрического места точек М(ж; у),
( р \
отношение расстояний от которых до точки F -------; 0 к рас-
\е + 1 /
Р
стояниям до прямой ж =----------- равно е.
е(е + 1)
312.	Построить области, координаты точек которых удовлетво-
ряют неравенствам:
1)	R2 < ж2 + у2 < 4F2 и ж2 > F2/4;
2)	ж2 - у2 > а2 и ж2 < 4а2;
3)	жу > а2 и |ж + у| < 4а;
4)	2ж < у2 + 4у и ж2 + у2 + 4ж + 4у < 0.
§ 15.	Общее уравнение линии второго порядка
1°.Линией второго п о р я д к а называется линия, определяемая
уравнением 2-й степени, которое в общем виде можно написать так:
Ах2 + ‘2Вху + Су2 + ‘2Dx + ‘2Ey+ F = 0.	(1)
§15. Общее уравнение линии второго порядка
41
Составим из коэффициентов уравнения (1) два определителя:
А
В
А В
D
Е
F
Определитель А называется дискриминантом уравнения (1), a S —
дискриминантом старших его членов. В зависимости от значений S и
А уравнение (1) определяет следующий геометрический образ:
	А ± 0	А = 0
S > 0	Эллипс (действительный или мнимый)	Точка
S < 0	Гипербола	Пара пересекающихся пря- мых
<5 = 0	Парабола	Пара параллельных прямых (действительных или мни- мых)
2°. Преобразование уравнения (1) к центру. Если S =
И В\ -L О
= Ig (J г2 то линия имеет центр, координаты которого находятся
из уравнений
<Н(^ у) = О, Ф>, у) = 0,	(2)
где Ф(ж, у) — левая часть уравнения (1). Перенеся начало в центр
О1(жо! Уо) (рис. 10), приведем уравнение (1) к виду
Ах2 +	+ Су2 + Fi = 0,	(3)
где
Fi = Dx0 + Еу0 + F =	(4)
о
3°. Преобразование уравнения (3) к осям симметрии.
Поворотом осей О-ух-у и Oij/i на некоторый угол р (рис. 10) уравнение
(3) приводится к каноническому виду:
h-V2 + (\У2 + F1 = 0.	(5)
Коэффициенты Ai и С\ являются корнями уравнения
A2-(A + G)A + J = 0.	(6)
Угол поворота р находится по формуле
42
Гл. 1. Аналитическая геометрия на плоскости
4°. Преобразование уравнения линии второго поряд-
ка, не имеющей центра. Если S = 0, то линия не имеет центра
или не имеет определенного центра. Ее уравнение можно тогда записать
в виде
(ах + /Зу)2 + 2Dx + 2Еу + F = 0.	(8)
Случай 1. D и Е пропорциональны а и /3: D = ma, Е = т/3.
Уравнение (2) примет вид (ах + (Зу)2 + 2т(ах + (Зу) + F = 0, откуда
ах + (Зу = — т ± \/т2 — F — пара прямых.
Случай 2. ОиЕне пропорциональны а и /3. Уравнение (8) можно
переписать в виде
(ах + (Зу + n)2 + 2т((3х — ay + q) = 0.	(9)
Параметры т, п и q найдутся сравнением коэффициентов в уравне-
ниях (8) и (9). Далее, приняв за ось О\Х прямую ах + (Зу + п = 0, за
ах + (Зу + п
ось СДУ прямую рх — ay + q = 0 (рис. 11), найдем: У = - г,
±vq2 + /З2
(Зх — ay + q	„
X = --- г. После этого уравнение (9) примет вид У = 2рХ, где
±vq2 + /З2
Рис. 10
Рис. 11
р = —	:. Ось О-уХ направляется в ту полуплоскость, в которой
\/ а2 + /З2
(Зх — ay + q имеет знак, противоположный знаку т, как это следует из
уравнения (9).
313.	Выяснить геометрический смысл уравнений:
1)	4ж2 — у2 = 0; 2) 4ж2 + у2 = 0;
3)	ж2 + у2 + 2ж + 2 = 0;
4)	ж2 + у2 — 6ж — 8у + 25 = 0; 5) ж2 + жу = 0;
6)	у2 — 16 = 0; 7) ж2 — Зжу + 2у2 = 0.
§ 15. Общее уравнение линии второго порядка	43
314.	Найти центры и преобразовать к центру уравнения линий:
1) 2ж2 + Зу2 — 4ж + бу — 7 = 0;
2)	ж2 — у2 — 4ж + 2у — 4 = 0;
3)	2ж2 + 5жу + 2у2 — 6ж — Зу — 8 = 0.
315.	Поворотом осей координат преобразовать уравнения к ка-
ноническому виду и построить кривые:
1)	5ж2 — 4жу + 2у2 = 24; 2) 2ж2 + 4жу — у2 = 12.
316.	Преобразовать к каноническому виду уравнения и постро-
ить кривые:
1)	Зж2 — 2жу + Зу2 — 4ж — 4у — 12 = 0;
2)	ж2 — бжу + у2 — 4ж — 4у + 12 = 0.
317.	Преобразовать к каноническому виду уравнения линий:
1)	ж2 + 4жу + 4у2 — 20ж + 10у — 50 = 0;
2)	ж2 — 4жу + 4у2 — 6ж + 12у + 8 = 0
и построить их.
318.	По дискриминантам 6 и А определить геометрический
смысл уравнений:
1)	ж2 — 4жу + Зу2 — 8ж + 14у + 15 = 0;
2)	ж2 + 2жу + 4у2 — 2ж + 4у + 4 = 0;
3)	ж2 + 4жу + 4у2 + Зж + бу + 2 = 0.
Решив первое и третье уравнения относительно у, построить ли-
нии, определяемые этими уравнениями.
319.	Привести к каноническому виду уравнение кривой у =
Зж2 — 12ж + 4
= ------------- и построить ее.
4ж - 8
320.	Написать уравнение кривой второго порядка, имеющей
центром точку Oi(l; 2) и проходящей через начало координат и
через точки (0; 4) и (1; —1).
321.	Показать, что уравнение у/х + ^/у = ^/а определяет дугу
параболы, построить параболу и найти ее вершину.
Указание. Повернуть оси координат на угол = —45°.
322.	Написать уравнение геометрического места точек М(х; у),
отношение расстояния от каждой из которых до точки F(m; п)
к расстоянию от нее до прямой ж cos а + у sin а — q = 0 равно
е. Обозначив коэффициенты полученного уравнения через А, В,
С, ..., определить инварианты А + С и 6 \р ^\.
44
Гл. 1. Аналитическая геометрия на плоскости
323.	Выяснить геометрический смысл уравнений:
1)	х2 — 4у2 = 0;
2)	х2 + 2у2 + 4® — 8у + 12 = 0;
3)	х2 + 5ху — бу2 = 0.
324.	Преобразовать к каноническому виду уравнения и постро-
ить кривые:
1)	х2 — ху + у2 — 2® — 2у — 2 = 0;
2)	Зж2 + Юху + Зу2 — 12® — 12у + 4 = 0.
325.	Преобразовать к каноническому виду уравнения:
1)	х2 — 2ху + у2 — 10® — бу + 25 = 0;
2)	х2 + 2жу + у2 — 4ж — 4у + 3 = 0
и построить линии, изображаемые ими.
326.	По дискриминантам 6 и А определить геометрический
смысл уравнений:
1) ж2 — 2жу + у2 — 4ж + 4у + 3 = 0;
2) ж2 — 2жу — Зу2 + 6® + 10у — 7 = 0.
Решив каждое уравнение относительно у, построить линию, опре-
деляемую им.
327.	Написать уравнение геометрического места точек М(х; у),
отношение расстояний от которых до точки F(3; 3) к расстояниям
до прямой ж + у = 0 равно: 1) е =	2) е = 2.
328.	Написать уравнение геометрического места точек М(ж; у),
одинаково удаленных от точки F(a/2; a/2) и от прямой ® + у = 0,
и привести его к каноническому виду.
329.	Написать уравнение геометрического места точек, раз-
ность квадратов расстояний от которых до прямой х — 2у = 2
и до оси Ох остается постоянной и равной 3,2. Преобразовать его
к каноническому виду и построить кривую.
§ 16. Полярные координаты
Пусть на плоскости дана точка О — полюс и луч ОР — полярная
ось (рис. 12). Тогда положение точки М на плоскости определится:
1)	полярным углом р = Z.MOP',
2)	длиной г радиус-вектора О л/: г = |Ол/|.
При изучении уравнений, связывающих г и р, бывает полезно рас-
сматривать полярные координаты р и г принимающими какие угодно
положительные и отрицательные значения. При этом отрицательные
углы р отсчитываются по часовой стрелке, а отрицательные г отклады-
ваются не по лучу, а по его продолжению за полюс.
§16. Полярные координаты
Если принять полюс за начало декартовых прямоугольных коорди-
нат, а полярную ось ОР — за ось Ох, то декартовы координаты (х; у)
точки М и ее полярные координаты (9?; г) бу- .
дут связаны зависимостью	м( . -
х = г cos р, у = г sin 9?;
(1)
Г = \/х2 + у2, tgcp = -
(2)
Если принять фокус эллипса, гиперболы и О'	' х
параболы за полюс, а фокальную ось симме-
трии за полярную ось, направленную в сто-
рону, противоположную ближайшей вершине, то уравнение всех трех
кривых в полярных координатах будет одинаковым:
1 — е cos tp ’
(3)
где е — эксцентриситет, ар — параметр. Для эллипса и гиперболы
330. В полярной системе координат (<р; г) построить точки
UUU.	нимлрпип LliLlClViC ПиирДППаТ	' ) llULipuniD 1U11U1
А(0; 3), В(тг/4; 2), С(д/2; 3), В(д; 2), £^(37г/2; 3).
331. Построить точки А(тг/2; —2), В( — тг/2; 3), С( —д/4; —4),
В(2д/3; -3).
332. Построить линию г = 2 + 2 cos </?.
Указание. Составить таблицу значений г для = 0; ±тг/3; ±тг/2;
±2тг/3; тг.
333. Построить линии (см. с. 334 и 335, рис. 80, 81 и 86):
(архимедова спираль);
(кардиоида);
(лемниската);
(гиперболическая спираль);
(улитка Паскаля).
1)	г = a/р	(архимедова спираль);
2)	г = а(1 — cos 93) (кардиоида);
3)	г2 = a2cos2<p	(лемниската);
4)	г = a/ip	(гиперболическая спираль);
5)	г = а(1 + 2 cos <р) (улитка Паскаля).
7Г
334.	Построить линии: 1) г = а; 2)	= —; 3) г =
4	sin д
335.	Написать в полярных координатах уравнения: 1) прямой,
отсекающей от полярной оси отрезок а и перпендикулярной к ней;
2) прямой, проходящей через точку А(сн; а) и параллельной по-
лярной оси.
336.	Написать в полярных координатах уравнение прямой, про-
ходящей через точку А(а; а) и составляющей с полярной осью
угол (3.
337.	Написать в полярных координатах уравнение окружности
с центром в точке С(0; а) и радиусом, равным а.
46	Гл.1. Аналитическая геометрия на плоскости
338.	Построить кривые:
1)	г = 3 — 2 sin 2^?;	2) г = 2 + cos З92;
3)	г = 1 — sin Зр.
Указание. Определить углы, при которых имеем rmax и rmjn.
339.	Построить линии (см. с. 334, рис. 82 и 83):
1)	г = asin3<^ (трехлепестковая роза);
2)	г = asin2<^ (четырехлепестковая роза).
340.	Преобразовать к полярным координатам уравнения ли-
ний:
1) х2 — у2 = а2;	2) х2 + у2 = а2;
3) х cos а + у sin а — р = 0; 4) у = х;
5) х2 + у2 = ах;
6) (ж2 + у2)2 = а2(х2 — у2).
341. Преобразовать к декартовым координатам уравнения ли-
ний и построить линии:
1) г cos р = а; 2) г = 2а sin р;
3)	г2 sin 2у: = 2а2;
4)	г sin (р + —) = ал/2;
5)	г = а(1 + cos </?).
342. Написать канонические уравнения кривых второго по-
рядка:
х	9	х	9
1) г = ---------;	2) г = ------;
5 — 4 cos р	4 — 5 cos р
3)r=-^----------.
1 — COS ф
343.	К онхоида. Через точку Л(тг/2; а) проведена прямая,
параллельная полярной оси. Произвольный луч ОВ пересекает
эту прямую в точке В. На луче от точки В по обе ее стороны
отложены отрезки ВМ = BMj = b. Определить геометрическое
место точек М и М^ в полярных координатах и построить кривую.
344.	Строфоида. Прямая х = а пересекает ось Ох в точке А
и произвольный луч ОВ в точке В. На луче от точки В по обе ее
стороны отложены отрезки BMj и В М2, равные АВ. Написать
уравнение геометрического места точек М^ и М2 в полярных и
декартовых координатах (рис. 84, с. 335).
§16. Полярные координаты
47
345.	Овал Кассини. Точка M(ip; г) движется так, что про-
изведение расстояний от нее до точек F(Q; а) и Fi(tt; а) остается
равным Ь2. Написать уравнение траектории движения точки М в
полярных координатах.
346.	Кардиоида. На произвольном луче О А от точки А пе-
ресечения его с окружностью г = a cos р откладывается по обе
стороны отрезок AM = АМ\ = а. Составить уравнение геометри-
ческого места точек М и М\ в полярных и декартовых координа-
тах.
347.	Кар диоида (эпициклоида). Круг диаметра а ка-
тится без скольжения по кругу такого же диаметра снаружи его.
Написать уравнение кривой, описанной точкой М катящейся ок-
ружности, если за полюс и начальное положение точки М принять
точку касания кругов, а полярную ось провести через центры кру-
гов (в начальном положении).
348.	Построить кривые: 1) г = 3 + 2cos2y; 2) г = 3 — sin З92;
3)	г = acos2y (см. указание к задаче 338).
349.	Построить:
1)	г = 4(1 + cos </?); 2) г = 2 — sin
350.	Написать в полярных координатах уравнение прямой, про-
ходящей через данные точки А(а; а) и В((3; 6).
Указание. Рассмотреть зависимость между площадями треуголь-
ников АОМ, ВОМ и АОВ, где 1/(у: г) — произвольная точка прямой.
351.	Написать канонические уравнения кривых второго по-
рядка:
ч 1
1) г = ------—-----;
2 — уЗ cos у
ч 1
2) г = ------=-----;
2 — у5 cos у
2 — 2 cos у
352.	Л емниската Бернулли. Точка М(рр; г) движется
так, что произведение ее расстояний от точек F(0; с) и Fi(tf; с)
остается равным с2. Написать уравнение траектории движения в
полярных и декартовых координатах.
Указание. По теореме косинусов FМ2 = г2 + с2 — 2rccos<^> и
F-yM2 = г2 + с2 + 2rccos<£>, причем по условию FМ2  F^M2 = с4.
48	Гл.1. Аналитическая геометрия на плоскости
353.	Улитка Паскаля. На произвольном луче О А от точки
А пересечения его с окружностью г = a cos (/2 по обе стороны отло-
жены отрезки AM = AMi = Ь. Составить уравнение геометриче-
ского места точек М в полярных координатах.
354.	Че тырехлепестковая роза. Концы отрезка АВ =
= 2а скользят по осям декартовых координат. Из начала коор-
динат опущен на АВ перпендикуляр ОМ. Написать уравнение
геометрического места точек М(х; у) при всевозможных положе-
ниях отрезка АВ.
§ 17.	Алгебраические кривые третьего и высших порядков
355.	Построить кривые (см. с. 332, рис. 66-69):
1)	у = ж3/3 (кубическая парабола);
2)	у2 = х3 )
> (полукубическая парабола);
3)	у* = х2 J
4)	у2 = х(х — 4)2 (петлевая парабола).
356.	Построить кривые:
1)	ж2/3 + у2/3 = а2/3 (астроида равносторонняя);
/#\2/3	/ту\2/3
2)	(^—J	+ (^—j	= 1, b у? а (астроида неравносторонняя).
Указание. Найти точки пересечения кривых с осями Ох и Оу и
b
первой кривой с прямыми у = ±ж, а второй — с прямыми у = ±—х
(рис. 78 на с. 334).
357.	Построить на отрезке [—1; 1] кривые: 1) у = ж2п+1; 2) у =
= х2п; 3) x2n + y2n = 1 при n = 1, 2, 4. К каким ломаным
приближаются эти кривые, когда п —> сю?
Указание. Найти точки пересечения первой кривой с прямой у =
х	1
= —, второй кривой с прямой у = — и третьей кривой с прямой у = х.
2п	2п
За единицу масштаба принять 10 клеток клетчатой бумаги.
358.	Астроида. Концы отрезка АВ = а скользят по осям
декартовых координат. Прямые АС и ВС, параллельные осям
координат, пересекаются в точке С. Из С опущен на АВ перпен-
дикуляр СМ. Написать уравнение геометрического места точек
М(х; у) при всевозможных положениях отрезка АВ.
§18. Трансцендентные кривые
49
359.	Построить кривые:
2)
1) У2 =
8а3
х2 + 4а2
(циссоида, рис. 85, с. 335);
(локон, рис. 76, с. 333).
360.	Каждая точка Р(х0; у0) параболы у2 = 2 у.г смещена па-
раллельно оси Ох на расстояние PM = POP. Найти геометри-
ческое место точек М.
361.	Стержень ОА = а вращается вокруг начала координат О.
В точке А к нему прикреплен шарниром стержень АВ = 2а, конец
которого скользит по Ох. Написать уравнение линии, которую
будет описывать при этом середина М отрезка АВ.
362.	Ц и с со и да. Произвольный луч О А (рис. 85, с. 335) пе-
ресекает окружность х2 + у2 = ах в точке А и прямую х = а в
точке В. На луче откладывается отрезок ОМ = АВ. Составить
уравнение геометрического места точек М.
363.	Произвольный луч ОВ (рис. 85) пересекает прямую х = а
в точке В. С — проекция точки В на ось Оу и М — проекция
точки С на прямую ОВ. Показать, что геометрическое место точек
М есть циссоида.
364.	Если из вершины параболы у2 = — 4аж опускать перпенди-
куляры на касательные к этой кривой, то геометрическим местом
оснований перпендикуляров будет циссоида. Доказать.
365.	Локон. Произвольный луч О А пересекает окружность
х2 + у2 = 2ау и прямую у = 2а в точках А и В, из которых
проведены прямые, параллельные соответственно оси Ох и оси
Оу до пересечения в точке М. Определить геометрическое место
точек М.
366.	Декартов лист ж3 + у3 — Заху = 0. Показать, что это
уравнение поворотом осей координат на 45° приводится к виду
Х3(ЗЬ — Х)	а
}	= -----------—, где о = —=. Построить кривую, определив в
3(о + X)	у/2
новой системе координат область расположения кривой и ее сим-
метрию, точки пересечения с прямой у = х (т. е. с новой осью
ОХ) и асимптоту. Показать, что уравнение асимптоты в новой
системе координат будет X = —Ь, а в старой х + у + а = 0 (см.
рис. 79, с. 334).
§ 18. Трансцендентные кривые
367.	Циклоида. Круг радиуса а катится по прямой ОХ без
скольжения. Составить параметрические уравнения кривой, опи-
санной точкой М окружности, приняв за параметр t угол поворота
50	Гл.1. Аналитическая геометрия на плоскости
катящегося круга и положив, что при t = 0 точка М находится в
начале координат.
368.	Развертка круга. Нить, намотанная на окружность
х2 + у2 = а2, разматывается, оставаясь натянутой. Составить па-
раметрические уравнения кривой, описанной концом нити, если
вначале конец нити находится в точке (а; 0). За параметр t при-
нять длину смотанной дуги (в радиусах).
368.	Квадратриса. Произвольный луч ОМ, составляющий
с осью Оу угол t (в радианах), пересекает прямую х = at в точке
М. Написать уравнение геометрического места точек М.
370.	Эпициклоида. Круг радиуса г катится без скольжения
по кругу радиуса R снаружи его. Составить параметрические урав-
нения кривой, описанной точкой М катящейся окружности. (При
г = R эпициклоида обращается в кардиоиду. См. задачу 347.)
371.	Гипоциклоида. Круг радиуса г катится без скольже-
ния по кругу радиуса R > г внутри него. Составить параметриче-
ские уравнения кривой, описанной точкой М катящейся окружно-
сти. (При г = Л/4 гипоциклоида обращается в астроиду ж2/3+
+ у2/3 = а2/3.)
Глава 2
ВЕКТОРНАЯ АЛГЕБРА
§	1. Сложение векторов. Умножение вектора на скаляр
1°. Определения. Вектором называется направленный отрезок
М> (рис. 13), в котором точка А рассматривается как начало, а точка
В — как конец. Вектор обозначается или указанием его начала и конца
М> со стрелкой наверху, или одной какой-нибудь буквой, выделенной по-
лужирным шрифтом, например а. Модуль (длина) вектора обозначается
Л или |а|, или АВ, или а. Векторы, параллельные одной прямой,
называются коллинеарными. Векторы, параллельные одной плоскости,
называются компланарными. Два вектора а и b (рис. 13) называются
равными, если они: 1) имеют равные модули; 2) коллинеарны; 3) на-
правлены в одну сторону.
2°. Умножение вектора на скаляр. Произведением век-
тора а на число (скаляр) т называется новый вектор, имеющий длину
а|т| и направленный одинаково с а (при т > 0) или противоположно а
(при т < 0).
3°. Сложение векторов. Суммой векторов a+b + с называется
вектор R = 0(3 (рис. 14), замыкающий ломаную ОАВС, построенную
Рис. 13	Рис. 14
из данных векторов. В частности, в параллелограмме, построенном на
данных векторах О А = а и 0/5 = Ь, одна вектор-диагональ 0(3 есть
сумма а + Ь, а другая есть разность а — b данных векторов.
4°. Проекция вектора на ось. Пусть вектор а составляет угол
р с осью Ох. Тогда проекция вектора на эту ось определяется форму-
лой
прга = |а| cos р = a cos (а, Ох).
52
Гл. 2. Векторная алгебра
Проекция суммы векторов на ось равна сумме проекций составля-
ющих векторов на ту же ось:
прг(а + Ь) = прга + пргЬ.
372. По сторонам ОА и ОБ прямоугольника ОАСВ отложены
единичные векторы
Рис. 15
i и j (рис. 15). Выразить через i и j векторы
Ж', С^,вЗ,О^ и ВА, если О А = 3 и
ОБ = 4.
373.	Пусть на рис. 15 М — середина ВС
и N — середина АС. Определить векторы
ОЙ, Ы\Г И Ш при О А = 3 И ОБ = 4.
374.	На плоскости даны точки Д(0; —2),
В(4; 2) и С(4; —2). В начале координат при-
ложены силы ol, Oil И 0(5. Построить их
равнодействующую найти ее проекции
на оси координат и величину. Выразить си-
лы , ов, 0(1 и OIvl через единичные век-
торы i и j координатных осей.
375.	Даны три компланарных единичных вектора m, п и р,
причем (т, п) = 30° и (пДр) = 60°. Построить вектор u = m +
+ 2п — Зр и вычислить его модуль.
Указание. В ломаной, построенной из векторов т, 2п и —Зр,
продолжить первое звено до пересечения с третьим.
376.	Проверить аналитически и геометрически векторные тож-
дества:
. b — а а-|-Ь	.	а-|-Ь а — b
1)	а Д------= ------:	2) а-------= ------.
’	2	2 ’	’	2	2
377.	На трех некомпланарных векторах О А = a, Oil = b и
0(1 = с построен параллелепипед. Указать те его вектор-диагонали,
которые соответственно равны а + b — с, а — b + с, а — Ь — с и
b — а — с.
378.	С помощью чертежа задачи 377 проверить переместитель-
ное свойство векторной суммы
а-|-Ь — с = а — с-|-Ь = Ь-Га — с = Ь — с-Га.
379.	Даны векторы О1 = а и Oil = Ь. Вектор 0(1 = с — меди-
ана СО АВ. Разложить аналитически и геометрически: 1) вектор
с по векторам а и Ь; 2) вектор а по векторам b и с.
380.	В прямоугольнике ОАСВ (рис. 15) М и N — середины
сторон ВС = 3 и АС = 4. Разложить геометрически и аналити-
чески вектор 0(3 = с по векторам ОМ = а и 01^ = Ь.
Указание. В условие с = ma + nb подставить выражения а, b и
с через i и j и сравнить коэффициенты слева и справа при i и j.
§ 2. Прямоугольные координаты точки и вектора в пространстве 53
381.	Дан правильный шестиугольник OABCDE со стороной
ОА = 3. Обозначив единичные векторы направлений оХ, Л/).
В(1 через m, п и р, установить зависимость между ними (напри-
мер, рассмотрением трапеции О АВС). Выразить затем через m
и п векторы 011, В(1, Ёб, O~t) и вХ.
382.	В равнобедренной трапеции О АС В (рис. 16) угол ВО А =
„ .	-	у — середины сторон ВС
= 60°, ОВ = ВС = С А = 2, М и
Рис. 16
ON и MN через тип — единич-
ные векторы направлений о!иО1
383.	Даны векторы а и Ь, угол
между которыми 120°. Построить век-
тор с = 2а — 1,5b и определить его
модуль, если a = 3 и Ь = 4.
384.	На плоскости даны точки
А(3; 3), В( —3; 3) и С( —3; 0). В начале координат приложены
силы ol, oil и 0(5. Построить равнодействующую ОМ, найти
ее проекции на оси координат и величину. Выразить силы ОА,
Oil, 0(5 и ОА! через единичные векторы i и j координатных осей.
385.	1) В трапеции ОАСВ имеем ВС = ОД/3 и ВС\\ОА. Раз-
ложить геометрически и аналитически вектор О А = а по векторам
Указание. Из ЛОВС можно с выразить через b и а и затем
решить полученное уравнение относительно а.
2) Точка В делит дугу окружности АС= 90° в отношении 1 : 2.
О — центр окружности. Разложить вектор оЗ = с по векторам
О А = а и 0/1 = Ь.
§ 2.	Прямоугольные координаты точки и вектора
в пространстве
1°. Определение. Пусть даны три взаимно перпендикулярные ко-
ординатные оси с общим началом О и дана точка М (рис. 17). Проекции
ее радиус-вектора О1\1 = г на оси координат ОМ^ = х, ОМ? = у и
ОМ3 = z называются прямоугольными координатами точки М или
вектора г = О1\1.
2°. Радиус-вектор точки в пространстве. Модуль или
длина радиус-вектора О1\1 = г:
(1)
54
Гл. 2. Векторная алгебра
Единичные векторы координатных осей i, J и к называются ортами.
Радиус-вектор выражается через орты:
г = «i + t/j + zk.	(2)
3°. Вектор, заданный коор-
динатами начала и конца. Пусть
даны точки A(«!; ур, z-y ) и В(х2; У2', ^г)-
Проекции вектора и = на оси коор-
динат будут:
П|),.1 /( = X = Х2 — Хр
= У = г/2 - У1,	(3)
пр,! /( = Z = z2 — zp
Можно написать формулы, аналогичные формулам (1), (2):
и = \/Х2 + Y2 + Z2 = у/(х2 - Ж1)2 + (г/2 - У1)2 + (z2 - z-i)2,	(4)
u =	= Xi + yj + Zk.	(5)
Если a, /3 и 7 — углы вектора u = Л /1 с осями координат, то
X	У	У
cos а = —, cos (3 = —, cos 7 = —,	(6)
и	и	и
причем
cos2 а + cos2 (3 + cos2 7=1,	(7)
т. е. сумма квадратов направляющих косинусов вектора равна 1.
Из формул (4)-(6) следует, что вектор и вполне определяется тремя
числами: X, У и У — его проекциями или его координатами. Поэтому
иногда пишут или говорят: дан вектор u{Jf; У; У}.
386.	Построить точку М(5; —3; 4) и определить длину и на-
правление ее радиус-вектора.
387.	Построить вектор г =	= 2i + 3j + 6k и определить
его длину и направление (проверить по формуле cos2 а + cos2 (3 +
+ cos2 7=1).
388.	Вектор составляет с осями Ох и Oz углы 40° и 80°. Найти
его угол с осью Оу.
389.	Радиус-вектор точки М составляет с осью Ох угол 45° и
с осью Оу угол 60°. Длина его г = 6. Определить координаты
точки М, если ее координата z отрицательна, и выразить вектор
ОМ = г через орты i, j, k.
390.	Даны точки А(1; 2; 3) и В(3; —4; 6). Построить вектор
А1~3 = и, его проекции на оси координат и определить длину и на-
правление вектора. Построить углы вектора и с осями координат.
§ 3. Скалярное произведение двух векторов
55
391.	Построить параллелограмм на векторах О А = i+j и
= к — 3j и определить его диагонали.
392.	В точке А(2; 1; —1) приложена сила R = 7. Зная две
координаты этой силы X = 2 и Y = —3, определить направление
и конец вектора, изображающего силу.
393.	На плоскости хОу даны точки А(4; 2). В(2; 3) и С(0; 5)
и построены векторы о! = а, = b и ОС = с. Разложить
геометрически и аналитически вектор а по векторам b и с.
394.	Даны точки А(2; 2; 0) и В(0; —2; 5). Построить вектор
ЛI) = и и определить его длину и направление.
395.	Вектор ОМ = г составляет с осями координат равные
острые углы. Определить эти углы и построить вектор г, если его
длина равна 2д/3.
396.	Вектор составляет с осями Оу и Oz углы 60° и 120°. Какой
угол он составляет с осью Ох?
397.	Даны три последовательные вершины параллелограмма
Д(1; —2; 3), В(3; 2; 1) и С(6; 4; 4). Найти его четвертую вер-
шину D.
Указание. Из равенства Л!) = следует, что равны и их коор-
динаты: х — 1 = 6 — Зит. д.
398.	На плоскости хОу построить векторы О А = а = 2i, Of) =
= b = 3i + 3j и 0(5 = c = 2i + 6j. Разложить геометрически и
аналитически вектор с по векторам а и Ь.
§ 3. Скалярное произведение двух векторов
1°. Определение. Скалярным произведением двух векторов на-
зывается произведение их модулей, умножен-
ное на косинус угла между ними.
Скалярное произведение вектора а на век-
тор b обозначается а • Ь. Итак,
а • b = ab cos р.	(1)
Из рис. 18 видно, что bcosp = праЬ. Поэтому
а • b = ab cos р = а npab = Ь прьа. (2)
2°. Свойства скалярного произве-
дения:	Рис. 18
I. а • b = b • а — переместительный закон.
И. а • (Ь + с) = а • b + а • с — распределительный закон.
III.	Если а||Ь, то a-b = ±ab. В частности, а2 = аа = аа cos 0° = а2;
остюда
а
(3)
56
Гл. 2. Векторная алгебра
IV.	Если а ± Ь, то а • b = ab cos 90° = 0.
V. Скалярное произведение ортов:
i • j = 0, j • k = 0, i • k = 0, ii=l, j j = 1, kk=l.
VI.	Если векторы а и b заданы координатами a{c.r. ay, az} и
Ь{6Ж, by, bz}, TO
a • b = axbx + ayby + azbz.	(4)
3°.Угол между векторами:
a b	axbx + ayby + azbz
cos = —- =	= .	(5)
ab y/aX + ay + aly/bX + by + bl
Условие параллельности: b = ma или
Условие перпендикулярности: a • b = 0 или axbx + ауЬу + azbz = 0.
399.	Определить угол между векторами а = -i-|-j и b = i -
— 2j + 2k.
400.	Определить углы ДАВС с вершинами А(2; —1; 3), В(1; 1; 1)
и С(0;0;5).
401.	Даны точки А(а; 0; 0), В(0; 0; 2а) и С(а; 0; а). Построить
векторы 0(5 И ТГ и найти угол между ними.
402.	На плоскости дан треугольник с вершинами 0(0; 0),
А(2а; 0) и В(а; —а). Найти угол, образованный стороной ОВ и
медианой ОМ этого треугольника.
403.	Найти угол между биссектрисами углов хОу и yOz.
404.	Из вершины квадрата проведены прямые, делящие проти-
воположные стороны пополам. Найти угол между этими прямыми.
405.	Найти угол между диагоналями параллелограмма, постро-
енного на векторах a = 2i-|-jHb = —2j + к.
406.	Даны векторы a = i-Tj-T2kHb = i— j + 4k. Определить
пр6а и npab.
407.	Раскрыть скобки в выражении
(2i - j) • j + (j - 2k) • k + (i - 2k)2.
408.	Вычислить: 1) (m+n)2, если m и n — единичные векторы
с углом между ними 30°; 2) (а — Ь)2, если а = 2у/2, Ь = 4 и
(а, Ь) = 135°.
409.	Раскрыть скобки в выражениях:
1)	(а + Ь)2;	2) (а + Ь)2 + (а - Ь)2
и выяснить геометрический смысл полученных формул.
410.	Даны компланарные векторы а, b и с, причем а = 3, b = 2,
с = 5, (а, Ь) = 60° и (Ь, с) = 60°. Построить вектор и = а-Гb — с
§ 3. Скалярное произведение двух векторов
57
и вычислить его модуль по формуле
u = -\/(а + b — с)2.
411.	Найти величину равнодействующей четырех компланар-
ных сил, приложенных к точке О, если величина каждой силы
равна ЮН, а угол между двумя последовательными силами ра-
вен 45°.
412.	Определить длины диагоналей параллелограмма, постро-
енного на векторах а = 2m + п и b = m — 2п, где тип —
единичные векторы, угол между которыми 60°.
413.	Дан вектор а = 2m — п, где тип — единичные векторы
с углом 120° между ними. Найти cos (а, т) и cos (аДп).
414.	Определить угол между биссектрисами двух плоских углов
правильного тетраэдра, проведенными из одной его вершины.
Указание. Если m, п и р — единичные векторы ребер, то m + п
и m + р — векторы, направленные по биссектрисам.
415.	На осях Ох, Оу и Oz отложить равные отрезки а = 4 и
на них построить куб. Пусть М — центр верхней грани, a N —
центр правой боковой грани куба. Определить векторы ОМ и О1\Г
и угол между ними.
416.	Даны векторы О.'\ = а и Oil = Ь, причем a = 2, Ь = 4, а
(а, Ь) = 60°. Определить угол между медианой OJ\i треугольника
АОВ и стороной оХ.
417.	Из вершины прямоугольника со сторонами 6 см и 4 см
проведены прямые, делящие противоположные стороны пополам.
Найти угол р между ними.
418.	Даны три последовательные вершины параллелограмма:
Д( —3; —2; 0), В(3; —3; 1) и С(5; 0; 2). Найти его четвертую вер-
шину D и угол между векторами лё и В15.
419.	Даны точки Д(3; 3; -2), В(0; -3; 4), С(0; -3; 0) и
В(0; 2; —4). Построить векторы All = а и СВ = b и найти
праЬ.
420.	В равнобедренной трапеции ОАСВ (см. рис. 16) М и
N — середины сторон ВС = 2 и АС = 2. Острый угол трапеции
60°. Определить угол между векторами ОА% и О1\Г.
421.	Найти угол между векторами а = 2m + 4п и b = m — п,
где тип — единичные векторы, образующие угол 120°.
422.	Показать, что угол между диагоналями прямоугольника,
построенного на векторах а и b (а ± Ь), определяется формулой
а2 - Ь2
cos<p = ±
а2 + о2
58
Гл. 2. Векторная алгебра
423.	Проекции перемещения s движущейся точки на оси коор-
динат sx = 2 м, sy = 1м, sz = —2 м. Проекции действующей
силы F на оси координат равны Fx = 5 Н, Fy = 4 Н и Fz = 3 Н.
Вычислить работу А силы F (Л = F • s) и угол между силой F и
перемещением s.
424.	К вершине правильного тетраэдра с ребром а приложены
три силы, изображаемые его вектор-ребрами. Определить вели-
чину равнодействующей.
Указание. Искомая величина равна ay/(m + п + р)2, где т, п и
р — единичные векторы данных сил.
425.	Квадрат разделен на три полосы одинаковой ширины и за-
тем свернут в правильную треугольную призму. Найти угол между
двумя смежными звеньями ломаной, образованной при этом диа-
гональю квадрата.
§4. Векторное произведение двух векторов
1°. Определение. Векторным произведением вектора а на век-
тор b называется такой третий вектор с (рис. 19), который:
1)	имеет модуль, численно равный площади параллелограмма, по-
строенного на векторах а и Ь;
2)	перпендикулярен к плоскости параллелограмма;
3)	направлен в такую сторону, с которой кратчайшее вращение от
а к b рассматривается совершающимся против часовой стрелки. Такое
расположение векторов а, b и с называется
с = ахЬ	правой связкой.
Векторное произведение обозначается
hу	—у а х Ь. Итак,
/	77	а х Ь = с,
q	а	е ели.
1) с = |а х b| = ab sin р,
Рис- 19	2) с 1аи с 1b,
3)	а, Ь, с составляют правую связку.
2°. Свойства векторного произведения:
I.	а х b = —b х а.
II.	а х (Ь + с) = а х b + a х с — распределительный закон.
III.	Если а||Ь , то а х b = 0; в частности, а х а = 0.
3°. Векторные произведения ортов:
i х j = k, jxk = i, kxi=j.	(1)
Вообще произведение любых двух смежных векторов в последова-
тельности
—- +
ijkij
дает следующий вектор со знаком +, а в обратной последовательности —
со знаком —.
§4. Векторное произведение двух векторов
59
4°. Выражение векторного произведения через коор-
динаты сомножителей а{аг, ау, аг} и b{6r, by, bz}:
а х b =
i	j	k
«у «г
bx by	bz
(2)
5°. Площадь параллелограмма, построенного на векторах
а и Ь:
S^j = |а х b|,
(3)
а площадь треугольника, построенного на векторах а и Ь:
5д = ||ахЬ|.	(4)
426.	Определить и построить вектор с = а X Ь, если: 1) а = 3i,
b = 2k; 2) а = i + j, b = i — j; 3) а = 2i + 3j, b = 3j + 2k.
Найти в каждом случае площадь параллелограмма, построенного
на векторах а и Ь.
427.	Вычислить площадь треугольника с вершинами А(7; 3; 4),
В(1;0;6)иС(4;5;-2).
428.	Построить параллелограмм на векторах a = 2j + knb =
= i + 2k и вычислить его площадь и высоту.
429.	Раскрыть скобки и упростить выражения:
1)	i х (j + k) - j х (i + k) + к х (i+j + k);
2)	(a + b + с) X с + (a + b + с) X b + (b — с) X a;
3)	(2a + b) X (c — a) + (b + с) X (a + b);
4)	2i • (j x k) + 3j • (i x k) + 4k • (i x j).
430.	Доказать, что (a — b) X (a + b) = 2a X b, и выяснить
геометрическое значение этого тождества.
431.	Векторы а и b составляют угол 45°. Найти площадь
треугольника, построенного на векторах а — 2Ь и За + 2Ь, если
|а| = |Ь| = 5.
432.	Найти площадь параллелограмма, диагоналями которого
служат векторы 2m — пи 4m — 5п, где тип — единичные
векторы, образующие угол 45°.
Указание. Имеем а + b = 2m — п и а — b = 4m — 5п, где а и b —
векторы-стороны параллелограмма. Перемножив, найдем вектор 2b х а,
модуль которого и равен удвоенной искомой площади.
433.	Построить векторы а = 3k — 2j, b = 3i —2j и c = axb. Вы-
числить модуль вектора с и площадь треугольника, построенного
на векторах а и Ь.
434.	Построить треугольник с вершинами Д(1; —2; 8), В(0; 0; 4)
и С(6; 2; 0). Вычислить его площадь и высоту BD.
60
Гл. 2. Векторная алгебра
435.	Вычислить диагонали и площадь параллелограмма, по-
строенного на векторах а = k — j и b = i + j + к.
436.	Доказать, что (2а + b) X (а + 2Ь) = За X Ь.
437.	Найти площадь параллелограмма, построенного на векто-
рах а = m + 2n и b = 2m + п, где тип — единичные векторы,
образующие угол 30°.
§ 5.	Смешанное произведение трех векторов
1°. Определение. Смешанным произведением векторов а, b и с
называется выражение вида (а х Ь) • с.
Если векторы а, b и с заданы своими координатами, то
(а х Ь) • с =
Ьу
СХ Су
az
С
Cz
(1)
2°. Свойства смешанного произведения.
I.	От перестановки двух любых сомножителей смешанное произве-
дение меняет знак:
(а х Ь) • с = —(а х с) • b = —(с х Ь) • а.
(2)
II.	Если два из трех данных векторов равны или параллельны, то
их смешанное произведение равно 0.
III.	Знаки операций «точка» и «крест» можно поменять местами,
(а х Ь) • с = а • (b X с); поэтому смешанное произведение принято
записывать в виде abc, т. е. без знаков действий и без скобок.
3°	. Объем параллелепипеда, построенного на векторах а, b и с.
V = ±abc (+ при правой связке, — при левой связке).
Объем пирамиды, построенной на векторах а, Ь, с:
клир = ixabc.
6
4°	. Условие компланарности. Если а, b и с компланарны,
то abc = 0, и обратно. При этом между а, b и с существует линейная
зависимость вида с = ma + nb.
438.	Построить параллелепипед на векторах а = 3i + 4j, b =
= — 3j + k, с = 2j + 5k и вычислить его объем. Правой или левой
будет связка векторов (а, Ь, с)?
439.	Построить пирамиду с вершинами 0(0; 0; 0), Д(5; 2; 0),
В(2; 5; 0) и 0(1; 2; 4) и вычислить ее объем, площадь грани АВС
и высоту пирамиды, опущенную на эту грань.
440.	Показать, что точки Л(2; —1; —2), В(1; 2; 1), 0(2; 3; 0) и
В(5; 0; —6) лежат в одной плоскости.
441.	Показать, что векторы а = — i + 3j + 2k, b = 2i — 3j — 4k,
c = — 3i-T12j-|-6k компланарны, и разложить вектор с по векторам
а и Ь.
§ 5. Смешанное произведение трех векторов
61
442.	Показать, что:
1)	(а + Ь) • [(а + с) X b] = —abc;
2)	(а + 2Ь — с) • [(а — b) X (а — b — с)] = ЗаЬс.
443.	Найти объем тетраэдра, построенного на векторах оА,
И 0(5, если эти векторы направлены по биссектрисам коорди-
натных углов и длина каждого вектора равна 2.
444.	Построить пирамиду с вершинами А(2; 0; 0), В(0; 3; 0),
0(0; 0; 6) и -0(2; 3; 8), вычислить ее объем и высоту, опущенную
на грань АВС.
445.	Построить векторы а = i+j+4k, b = i—2j и с = 3i—3j+4k,
показать, что они компланарны, и найти линейную зависимость
между ними.
446.	Показать, что объем параллелепипеда, построенного на
диагоналях граней данного параллелепипеда, равен удвоенному
объему данного параллелепипеда.
447.	Даны единичные векторы m, п и р. Угол (т, п) =
= [р, (т X п)] = а. Доказать, что тогда (m X n) X р = - sin 2а.
448.	При любых векторах а, b и с векторы а — Ь, Ь — с и с — а
компланарны. Доказать это аналитически и геометрически (рас-
смотрением параллелепипеда, построенного на векторах а, Ьис).
449.	Вычислить объем параллелепипеда ОАВСО^А^В^С^, в
котором даны три вершины нижнего основания 0(0; 0; 0),
Л(2; —3; 0) и 0(3; 2; 0) и вершина верхнего основания Bj(3; 0; 4),
лежащая на боковом ребре BBj, противоположном ребру ООр
Глава 3
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
§ 1. Уравнение плоскости
1°. Уравнение плоскости, проходящей через точку М-у («i; t/j; zi)
и перпендикулярной к вектору N{A; В; С}.
I. D = 0, Ax + By + Cz
Пусть М(ж; у, z) — произвольная
точка плоскости (рис. 20). Тогда ±
i N и по условию перпендикулярности
векторов
А(х - Xi) + В(у - yi) + C(z - zt) = 0.
(1)
2°. Общее уравнение плос-
кости:
Ax + By + Cz + D = 0.	(2)
Вектор N{A; В; С} называется нор-
мальным вектором к плоскости (2)
или (1).
3°.Особые случаи уравнения
Ах + By + Cz + D = 0:
= 0 — плоскость проходит через начало
координат.
II.	С* = 0, Ах + By + D = 0 — плоскость параллельна оси Oz.
III.	С = D = 0, Ах + By = 0 — плоскость проходит через ось Oz.
IV.	В = С = 0, Ах + D = 0 — плоскость параллельна плоскости
yOz.
V.	Уравнения координатных плоскостей: х = 0, у = 0, z = 0.
4°.	Уравнение плоскости в отрезках на осях:
450.	Построить плоскости: 1) 5ж — 2у + Зг — 10 = 0; 2) Зх +
+ 2у — z = 0; 3) Зх + 2г = 6; 4) 2г — 7 = 0.
451.	Построить плоскость 2ж + Зу + 6г — 12 = 0 и найти углы
нормали к плоскости с осями координат.
452.	Даны точки Mi(0; —1; 3) и A^l; 3; 5). Написать уравне-
ние плоскости, проходящей через точку и перпендикулярной к
вектору N = М1М2.
§2. Основные задачи на плоскость	63
453.	Написать уравнение плоскости, проходящей через точку
М(а; а; 0) и перпендикулярной к вектору ОМ. Построить плос-
кость.
454.	Написать уравнение геометрического места точек, равно-
удаленных от точек А(а; а) и В(0; а/2; 0).
455.	Написать уравнение плоскости, параллельной оси Ох и
проходящей через точки Mi(0; 1; 3) и Мг(2; 4; 5) и построить ее.
456.	Написать уравнение плоскости, проходящей через ось Ох
и точку Mi(0; —2; 3). Построить плоскость.
457.	Написать уравнение плоскости, проходящей через ось Oz
и точку Mi (2; —4; 3). Построить плоскость.
458.	Написать уравнение плоскости, параллельной оси Оу и
отсекающей на осях Ох и Oz отрезки а и с. Построить ее.
459.	Написать уравнение плоскости, проходящей через точку
М(2; —1; 3) и отсекающей на осях координат равные отрезки.
460.	Написать уравнение плоскости, проходящей через точку
Mi(—4; 0; 4) и отсекающей на осях Ох и Оу отрезки а = 4 и
6 = 3.
461.	Построить плоскости: 1) 2ж + у — z-j-6 = 0; 2) x — y — z = 0;
3) у — 2г + 8 = 0; 4) 2ж — 5 = 0; 5) х + z = 1; 6) у + z = 0.
462.	Построить плоскость 2ж — 2у + г — 6 = 0 и найти углы ее
нормали с осями координат.
463.	Через точку М(—1; 2; 3) проведена плоскость, перпенди-
кулярная к ОМ. Написать ее уравнение.
464.	Написать уравнение плоскости, проходящей через ось Оу
и через точку (4; 0; 3). Построить плоскость.
465.	Написать уравнение плоскости, параллельной оси Oz и
проходящей через точки Mi (2; 2; 0)иМг(4; 0; 0). Построить плос-
кость.
466.	Написать уравнение плоскости, проходящей через точку
Mi(l; —3; 5) и отсекающей на осях Оу и Oz вдвое большие от-
резки, чем на оси Ох.
§ 2. Основные задачи на плоскость
1°.Угол, образованный двумя плоскостями:
N-Nj
COS ip = ±-
ЯМ
M4i + ВВг + СС\
ЯМ
(1)
где N и Ni — нормальные векторы к плоскостям Ах + By + Cz + D = 0
и А^х -|- В^у -|- O\z -|- 2?1 = 0.
Условие параллельности:
А _ В _ С
Ai В, С\
(2)
64	Гл.З. Аналитическая геометрия в пространстве
Условие перпендикулярности:
AAi + BBi + СС\ = 0.	(3)
2°. Р ас с т о я ни е от точки Mq(xq; у^; zq) до плоскости Ах +
+ By + Cz + D = 0:
, _ |Нжр + Ву$ + Czq + D\	, ч
Я	U
3°. Уравнение пучка всех п л о с к о с т е й, проходящих через
линию пересечения двух данных плоскостей:
a(Ax + By + Cz + D) + (3(Aix + В^у + C^z + Di) = 0.	(5)
Можно положить a = 1, исключив этим из пучка (5) вторую из данных
плоскостей.
467.	Найти угол между плоскостями:
1)	ж — 2у + 2г — 8 = 0 и х z — 6 = 0;
2)	ж + 2г — 6 = 0 и ж + 2у — 4 = 0.
468.	Найти плоскость, проходящую через точку (2; 2; —2) и
параллельную плоскости ж — 2у — Зг = 0.
469.	Написать уравнение плоскости, проходящей через точку
(—1; —1; 2) и перпендикулярной к плоскостям ж — 2у + г — 4 = 0
и ж + 2у — 2г + 4 = 0.
470.	Написать уравнение плоскости, проходящей через точку
(0; 0; а) и перпендикулярной к плоскостям ж — у — г = 0и2у = ж.
471.	Написать уравнение плоскости, проходящей через точки
Mi(—1; —2; 0) и 1И2(1; 1; 2) и перпендикулярной к плоскости ж +
+ 2у + 2г - 4 = 0.
472.	Написать уравнение плоскости, проходящей через точки
-1; 2), М2(2; 1; 2) и М3(1; 1; 4).
473.	Через ось Oz провести плоскость, составляющую с плос-
костью 2ж + у — y/5z = 0 угол 60°.
474.	Найти расстояние от точки (5; 1; —1) до плоскости ж —
— 2у — 2г + 4 = 0.
475.	Найти расстояние от точки (4; 3; 0) до плоскости, прохо-
дящей через точки Mi(l; 3; 0), М2(4; —1; 2) и М3(3; 0; 1).
476.	Найти расстояние между параллельными плоскостями
4ж + Зу — 5г — 8 = 0 и 4ж + Зу — 5г + 12 = 0.
Указание. Взять на первой плоскости любую точку, например
(2; 0; 0), и найти ее расстояние от другой плоскости.
477.	1) Написать уравнения плоскостей, параллельных плос-
кости ж — 2у + 2г — 5 = 0 и удаленных от нее на расстояние,
равное 2.
§ 3. Уравнения прямой
65
2) Написать уравнения плоскостей, делящих пополам двугран-
ный угол, образованный плоскостями 2ж + 2у = z и z = 0, и
построить данные и искомые плоскости.
478.	1) Написать уравнение плоскости, проходящей через ли-
нию пересечения плоскостей 2ж — у + Зг — 6 = 0, ж + 2у — г + 3 = О
и через точку (1; 2; 4).
2)	Найти две взаимно перпендикулярные плоскости, проходя-
щие через прямую пересечения плоскостей х = у и z = 0, если
одна из искомых плоскостей проходит через точку (0; 4; 2). По-
строить прямую и искомые плоскости.
479.	Найти точку пересечения плоскостей 2ж — у + Зг — 9 = 0,
ж + 2у + 2г—3 = 0иЗж + у — 4г + 6 = 0.
480.	Написать уравнение плоскости, проходящей через точку
(2; —1; 1) и перпендикулярной к плоскостям Зж + 2у—г + 4 = 0и
ж + у + г — 3 = 0. Построить ее.
481.	Написать уравнение плоскости, проходящей через точки
(0; —5; 0) и (0; 0; 2) и перпендикулярной к плоскости ж + 5у +
+ 2г — 10 = 0. Построить ее.
482.	Найти угол плоскости, проходящей через точки 0(0; 0; 0),
Mi(a; —а; 0) и М2(а; а; а), с плоскостью хОу.
483.	Найти расстояние от начала координат до плоскости, про-
ходящей через точки Mi(a; 0; 0), 4^(0; а; 0) и М^(а; а; а).
484.	Написать уравнение плоскости, проходящей через ось Ож
и составляющей угол 60° с плоскостью у = ж.
485.	Найти расстояние от точки (а; Ь; с) до плоскости, отсека-
ющей на осях координат отрезки а, b и с.
486.	Написать уравнения плоскостей, параллельных плоскости
2ж + 2у + г — 8 = 0 и удаленных от нее на расстояние d = 4.
487.	Написать уравнение плоскости, проходящей через линию
пересечения плоскостей 4ж — у + Зг — 6 = 0иж + 5у — г + 10 = 0
и перпендикулярной к плоскости 2ж — у + 5г — 5 = 0.
§ 3. Уравнения прямой
1°. Уравнения прямой, проходящей через точку А(а; Ь; с) и па-
раллельной вектору Р{т; п; р}. Пусть М(ж; у; г) —произвольная точка
прямой (рис. 21), тогда ,\.\i || Р и по условию параллельности векторов
х — а у — b z — с
---- = ~--- = ----• 1
т п р
Уравнения (1) называются каноническими уравнениями прямой. Век-
тор Р{т; п; р} называется направляющим вектором прямой.
66	Гл.З. Аналитическая геометрия в пространстве
2°. Параметрические уравнения прямой получим, прирав-
няв каждое из отношений (1) параметру t:
х = mt + а, у = nt + b, z = pt + с.
(2)
3°. Уравнения прямой, прохо-
дящей через две точки:
x-Xj _ у-У! _ Z- Zj
Х2 - X! у2- У1 z2 - Z! '
4°. Общие уравнения прямой:
Ах -|- By -|- Cz -|- D — 0,	. .
А^х + Вху + C^z + Di = 0.	'
5°. Уравнения прямой в проекциях получим, исключив из
общих уравнений (4) один раз у, другой раз х:
х = mz + а, у = nz + b.
(5)
Уравнения (5) можно записать в канонической форме:
х — а у — b z — 0
т n 1
488.	Найти следы прямых:
1) х = z + 5, у = 4 — 2г и 2) —-— = —-—
на плоскостях хОу и xOz и построить прямые.
Указание. Положить в уравнениях прямой: 1) z = 0; 2) у = 0.
489.	Уравнения прямой х + 2у + 3z — 13 = 0, Зх + у + 4г — 14 =
= 0 написать: 1) в проекциях; 2) в канонической форме. Найти
следы прямой на координатных плоскостях, построить прямую и
ее проекции.
490.	Написать уравнения прямой, проходящей через точку
А(4; 3; 0) и параллельной вектору Р{ —1; 1; 1}. Найти след пря-
мой на плоскости yOz и построить прямую.
491.	Построить прямую х = 4, у = 3 и найти ее направляющий
вектор.
492.	Построить прямые: 1) у = 3, г = 2; 2) у = 2, г = х + 1;
3) х = 4, г = у и определить их направляющие векторы.
493.	Написать уравнения прямой, проходящей через точки
А(—1; 2; 3) и В(2; 6; —2), и найти ее направляющие косинусы.
494.	Построить прямую, проходящую через точки А(2; —1; 3)
и В(2; 3; 3), и написать ее уравнения.
§ 3. Уравнения прямой
67
495.	Написать уравнения траектории точки М(х; у; г), кото-
рая, выйдя из точки А(4; —3; 1), движется со скоростью v{2; 3; 1}.
496.	Написать параметрические уравнения прямой:
1) проходящей через точку ( — 2; 1; —1) и параллельной вектору
Р{1; —2; 3};
2) проходящей через точки А(3; —1; 4) и В(1; 1; 2).
497.	Написать уравнения прямой, проходящей через точку
(a, b, с): 1) параллельно оси Oz; 2) перпендикулярно к оси Oz.
498.	Найти угол прямой х = 2z — 1, у = — 2г + 1 с прямой,
проходящей через начало координат и через точку (1; —1; —1).
499.	Найти угол между прямыми: х — у z — 4 = 0, 2s + у —
— 2г + 5 = 0и® + у-|-г — 4 = 0, 2s + Зу — z — 6 = 0.
Указание. Направляющий вектор каждой из прямых можно опре-
нормальных векторов плоскостей
делить как векторное произведение
(Р = N х NJ.
500. Показать, что прямая —
прямой ж = г + 1, у = 1 — z.
У z
= — = — перпендикулярна к
501.	Написать уравнения прямой, проходящей через точку
(—4; 3; 0) и параллельной прямой х — 2у + z = 4, 2s + у — z = 0.
502.	Написать уравнения перпендикуляра, опущенного из точки
(2; —3; 4) на ось Oz.
Указание. Искомая прямая проходит еще через точку (0; 0; 4).
503.	Найти расстояние от точки М(2; —1; 3) до прямой
у + 2	г-1
х + 1
3
4	5
Указание. Точка А(—1; —2; 1) лежит на прямой; Р{3; 4; 5} —
направляющий вектор прямой. Тогда
АМ\РхАА%\ |Р х АА%\
d = AM sin a = -!-----= J-------
P  AM	P
504.	Найти расстояние между параллельными прямыми
s — 2 у + 1 г + 3 х — 1 у — 1 г + 1
1 “ 2 “ 2 И 1 “ 2 “ 2
505.	Найти следы прямой —-— = —-— = —- на координат-
ных плоскостях и построить прямую.
506.	Уравнения прямой 2s + у + 8г — 16 = 0, х — 2у — г + 2 =
= 0 написать: 1) в проекциях; 2) в канонической форме. Найти
следы прямой на координатных плоскостях, построить прямую и
ее проекции.
68	Гл.З. Аналитическая геометрия в пространстве
507.	Написать уравнения прямой, проходящей через точку
А(0; —4; 0) и параллельной вектору Р{1; 2; 3}, найти след пря-
мой на плоскости xOz и построить прямую.
508.	Построить прямую х = 3, z = 5 и найти ее направляющий
вектор.
509.	Найти направляющий вектор прямой х + у — z = 0, у = х
и углы прямой с осями координат (см. указание к задаче 499).
510.	Написать уравнения перпендикуляра, опущенного из точки
(2; —3; 4) на ось Оу.
511.	Найти угол между прямыми 2ж — у — 7 = 0, 2ж — г + 5 = 0
и Зж — 2у + 8 = 0, z = Зж.
512.	Написать уравнения прямой, проходящей через точку
( —1; 2; —2) и параллельной прямой ж — у = 2, у = 2 г + 1.
513.	Найти расстояние от точки М(3; 0; 4) до прямой у = 2ж +
+ 1, z = 2ж (см. задачу 503).
§4. Прямая и плоскость
х — ay — b z — с
1. Угол между прямой 	 = 	 = 	 и п л ос-
те----------------------------п-р
костью Ах + By + Cz + D = 0:
• ft lN'Pl
sin 0 = ---
NP
|Ате + Bn + Cp\
Wp
(1)
Условие их параллельности (N||P):
Ате + Bn + Ср = 0.	(2)
Условие их перпендикулярности (N 1 Р):
А _ В _ С
те п р
(3)
2°. Точка пересечения прямой и плоскости. Написав
параметрические уравнения прямой х = mt + а, у = nt + b, z = pt + с,
подставим в уравнение плоскости Аж + By + Cz + D = 0 вместо ж, у,
z их выражения через t. Найдем to, а затем жо, Уо, zq — координаты
точки пересечения.
3°. Условие расположения двух прямых в одной плос-
кости:
а — di Ь — &1 с — ci
те	п	р
mi	«1	pi
(4)
514. Найти угол прямой у = Зж — 1, 2г = —Зж + 2 с плоскостью
2ж + у + г — 4 = 0.
§ 4.	Прямая и плоскость
515. Показать, что прямая ——
-1
параллельна
3
--- лежит
3
2
-1
плоскости 2ж + у — z = 0, а прямая
в этой плоскости.
516.	Написать уравнение плоскости, проходящей через точку
(—1; 2; —3) и перпендикулярной к прямой х = 2, у — z = 1.
517.	Написать уравнение плоскости, проходящей через прямую
х — 2 у — 3 z
—— =	= —j— и точку (3; 4; 0).
518.	Написать уравнение плоскости, проходящей через прямую
+ 2
-— и перпендикулярной к плоскости 2ж + 3у —
2	2
z = 4.
519. Написать уравнение плоскости, проходящей через парал-
х — 3 у z — 1 х + 1 у — 1 z
и ----- = ------ = —.
лельные прямые
1	2	12	2	12
520.	Написать уравнения прямой, проходящей через начало
координат и составляющей равные углы с плоскостями 4у = Зж,
у = 0 и z = 0. Найти эти углы.
521.	Найти точку пересечения прямой х = 21 — 1, у = t + 2,
z = 1 — t с плоскостью Зх — 2// + z = 3.
х у — 1 г + 1
522.	Найти точку пересечения прямой — = —-	—
с плоскостью х + 2// + 3z — 29 = 0.
523.	Найти проекцию точки (3; 1; —1) на плоскость х + 2// +
+ 3z - 30 = 0.
524.	Найти проекцию точки (2; 3; 4) на прямую х = у = z.
525.	Найти
2
кратчайшее расстояние между непараллельными
прямыми:
х — a у — Ь z — c х — a-i у — bi z — q
1)		= ----- = ----- и -------= ------= ------;
m n р	mi П} pi
ж + 1 у	z— 1 х у+1	г — 2
2)	----= — = ----- и — = ------= ------.
’	1	1	2	13	4
Указание. Предполагая прямые в общем случае скрещивающи-
мися, нарисуем параллельные плоскости, в которых они расположены.
Из точек А(а; Ь; с) и 4i(ai; bp cj) проведем векторы АВ = AiBi =
= P{m; п; р} и 4(3 = AiC'i =	пр /д}. Высота призмы
ABCAiBiC'i и равна искомому расстоянию.
526.	Показать, что прямые
х — 2 У ~ 4 z — 2
х = z — 2, у = 2г + 1 и --------= ------= -------
’ У	3	1	1
пересекаются, и написать уравнение плоскости, в которой они рас-
положены.
70	Гл.З. Аналитическая геометрия в пространстве
527.	Написать уравнения перпендикуляра, опущенного из точки
(2; 1; 0) на прямую х = 3z — 1, у = 2г.
528.	Построить плоскость х у — z = Ои прямую, проходя-
щую через точки А(0; 0; 4) и В(2; 2; 0). Найти точку пересечения
прямой с плоскостью и угол между ними.
529.	Построить плоскость у = z, прямую х = —z +1, у = 2 и
найти: 1) точку их пересечения; 2) угол между ними.
530.	Найти проекцию точки (3; 1; —1) на плоскость Зж + у +
+ г - 20 = 0.
х — 1 у
531.	Найти проекцию точки (1; 2; 8) на прямую —-— = —- = z.
532.	Написать уравнение плоскости, проходящей через парал-
х — 1 у + 1 z — 2 х у + 1 z — 1
лельные прямые -= ----= ---- и — = --= ----.
1	1-231-23
х+3 у+lz+l
533.	Показать, что прямые —-— = —-— = —-— и х = 3z — 4,
у = z + 2 пересекаются, найти точку их пересечения.
534.	Написать уравнения перпендикуляра, опущенного из точки
х + 1 у — 1 Z
(1; 0; —1) на прямую -= -= —.
1	2	3
535.	Найти кратчайшее расстояние между прямыми х = —2у =
= гиж = у = 2.
§ 5. Сферические и цилиндрические поверхности
1°. Уравнение сферической поверхности с центром
С (а, Ь, с) и радиусом R:
(х - а)2 + (у - Ь)2 + (г - с)2 = R2.	(1)
2°. Уравнение F(ж, у) = 0, не содержащее z, определяет цилин-
дрическую поверхность с образующей, параллельной оси Oz. Анало-
гично каждое из уравнений: 1) F(y, z) = 0 и 2) F(x, z) = 0 опреде-
ляет цилиндрическую поверхность с образующей, параллельной: 1) Ох;
2) Оу.
3°. Уравнение цилиндрической поверхности с напра-
вляющей F(x, у) = 0, z = 0 и с образующей, параллельной вектору
х — Xq
P{m; я; р}. Уравнение произвольной образующей будет -- =
m
у — Уо z
= -----= —, где (Уо; Ж 0) — точка на направляющей.
п р
Определив отсюда и Уо и подставив их в уравнение направляющей,
получим уравнение цилиндрической поверхности:
F
m	п \
х----F У---z
р	р J
= 0.
(2)
§ 5. Сферические и цилиндрические поверхности	71
536.	Найти центр и радиус сферы:
1)	ж2 + у2 + г2 — Зж + 5у — 4г = 0;
2)	ж2 + у2 + г2 = 2аг
и построить изображение второй сферы.
537.	Написать уравнение сферической поверхности, вписанной
в тетраэдр, образованный плоскостями
Зж — 2у + 6г — 18 = 0, ж = 0, У = 0, г = 0.
538.	Написать уравнение геометрического места точек, распо-
ложенных вдвое ближе к точке А(2; 0; 0), чем к точке В(—4; 0; 0).
539.	Написать уравнение сферической поверхности, проходя-
щей через окружность ж2 + у2 + г2 = а2, ж + у + г = а и через
точку (а; а; а).
Указание. Искомое уравнение должно иметь вид
ж2 + у2 + г2 — а2 + А(ж + у + г — а) =0.
540.	Построить в левой системе координат поверхности:
1)	у2 + г2 = 4; 2) у2 = ах; 3) жг = 4; 4) ж2 + у2 = ах.
541.	Написать уравнение геометрического места точек, одина-
ково удаленных от прямой ж = а, у = 0 и плоскости yOz. Постро-
ить поверхность.
542.	Написать уравнения трех цилиндрических поверхностей,
описанных около сферы ж2 + у2 + г2 — 2аж = 0 с образующими,
параллельными соответственно: 1) оси Ох; 2) оси Оу; 3) оси Oz.
543.	Нарисовать в первом октанте левой системы координат
кривую Вивиани:
ж2 + у2 + г2 = 16, ж2 + у2 = 4ж,
построив ее точки при ж = 0; 2 и 4. Показать, что проекция кривой
на плоскость xOz есть парабола.
544.	Найти центр и радиус окружности
ж2 + у2 + г2 = 10у, ж + 2у + 2г — 19 = 0.
Указание. Центр окружности есть проекция центра шара на плос-
кость (см. задачу 530).
545.	Написать уравнение цилиндрической поверхности с на-
правляющей у2 = 4ж, г = 0 и с образующей, параллельной вектору
Р{1; 2; 3}.
546.	Построить в первом октанте поверхность (ж + у)2 + аг = а2
по сечениям плоскостями ж = 0, у = 0, г = 0, г = А^аи
показать, что эта поверхность цилиндрическая с образующими,
параллельными прямой ж + у = a, z = 0.
Гл. 3. Аналитическая геометрия в пространстве
547.	Шар х2 + у2 + z2 = 4г освещен лучами, параллельными
прямой х = 0, у = z. Найти форму тени шара на плоскости хОу.
Указание. Нужно написать уравнение цилиндрической поверхно-
сти, образованной лучами, касательными к шару. За ее направляющую
принять линию сечения шара плоскостью, проходящей через центр шара
и перпендикулярной к лучам.
548.	Написать уравнение плоскости, проходящей через центр
С поверхности х2 + у2 + z2 — 2s + у — Зг = 0 и перпендикулярной
к прямой ОС.
549.	Написать уравнение геометрического места точек, удален-
ных вдвое дальше от начала координат, чем от точки (0; —3; 0).
550.	Найти проекцию на плоскость z = 0 сечения шаровой
поверхности х2 + у2 + z2 = 4(ж — 2у — 2г) плоскостью, проходящей
через центр шара и перпендикулярной к прямой х = 0, у + г = 0.
551.	В левой системе координат построить поверхности:
1) г = 4 — х2; 2) у2 + г2 = 4г; 3) у2 = х3.
552.	Построить в первом октанте левой системы координат кри-
вую пересечения цилиндров х2 + г2 = а2 и х2 + у2 = а2.
Указание. Построив в плоскостях xOz и хОу четверти направля-
ющих окружностей, разделить их приближенно на равные части (напри-
мер, на 4) и через точки деления провести образующие цилиндров до их
пересечения (см. рис. 60, с. 320).
553.	Написать уравнение цилиндрической поверхности с обра-
зующей, параллельной вектору Р{1; 1; 1}, и с направляющей х2 +
+ у2 = 4ж, г = 0.
554.	Построить тело, ограниченное поверхностями у2 = х,
z = 0, г = 4, х = 4, и написать уравнения диагоналей грани,
лежащей в плоскости х = 4.
§ 6.	Конические поверхности и поверхности вращения
1°. Конические поверхности. Пусть коническая поверхность
имеет вершину в начале координат, а направляющую F(x, у) = 0 на
х у Z
плоскости z = h. Уравнение образующей будет: — = — = —, где
''о Уо
(xq; уо', h) — точка направляющей. Определив отсюда хо и уо и подста-
вив их в уравнение F(x, у) = 0, получим уравнение конической поверх-
ности с вершиной в начале координат:
(1)
§ 6. Конические поверхности и поверхности вращения 73
Если вершина конуса будет в точке (а; Ь; с), то уравнение примет
вид
(у - b)(h - с)
(2)
Уравнение (1) однородно относительно х, у, z, а уравнение (2) од-
нородно относительно х — а, у — b и z — с. По однородности уравнения
можно узнать уравнение конической поверхности.
2°. Поверхности вращения:
Уравнения кривой	Ось вращения	Уравнение поверхности вращения
J-5. 5? II II	Ох Оу	F(x, \/ у2 + z2) = 0 F(\/х2 + z2, у) =0
J-5. 5? II II	Ох Oz	II II -1- “Г <м |Чз > К К
J-5. II II	Оу Oz	F(y, \/х2 + z2) = 0 F(\/x2 + у2, z) = 0
555.	Написать уравнение конической поверхности с вершиной
в начале координат и направляющей х2 + у2 = a2, z = с. Постро-
ить изображение поверхности.
556.	Написать уравнение конической поверхности с вершиной
в точке А(0; —а; 0) и направляющей х2 = 2ру, z = h. Построить
изображение поверхности.
557.	Определить вершину конуса х2 + (у — а)2 — z2 = 0, его
направляющую в плоскости z = а и построить конус.
558.	Определить вершину конуса х2 = 2уг, его направляющую
в плоскости z = h и построить конус.
559.	Исследовать поверхность коноида1) или клина (а2 — х2)х
Ху2 = h2z2 по сечениям плоскостями z = 0, у = h, х = ±с (с а)
и построить коноид в области z 7> Q.
560.	Написать уравнение поверхности, образованной враще-
нием кривой z = х2, у = 0: 1) вокруг оси Oz; 2) вокруг оси
Ох. Построить обе поверхности.
]) Коноидом называется поверхность, образованная движением прямой, па-
раллельной данной плоскости и пересекающей данную кривую и данную прямую.
74	Гл.З. Аналитическая геометрия в пространстве
561.	Написать уравнение поверхности, образованной враще-
_ 2	4
нием вокруг оси Oz: 1) кривой z = е х , у = 0; 2) кривой z = —,
х1
у = 0. Построить обе поверхности (в левой системе координат).
562.	Написать уравнение конической поверхности с вершиной
0(0; 0; 0), направляющей ж2+(у—6)2+г2 = 25, у = 3 и нарисовать
поверхность.
563.	Написать уравнение конической поверхности с вершиной
0(0; —а; 0), направляющей х2 + у2 + z2 = 25, у = 3 и нарисовать
поверхность.
564.	Написать уравнение поверхности, образованной враще-
нием прямой z = у, х = 0: 1) вокруг оси Оу; 2) вокруг Oz, и
нарисовать обе поверхности.
565.	Показать, что сечение конуса z2 = ху плоскостью х + у =
= 2а есть эллипс, и найти его полуоси.
§ 7. Эллипсоид, гиперболоиды и параболоиды
1°. Канонические уравнения. Кроме цилиндрических, су-
ществуют шесть основных видов поверхностей второго порядка, опре-
деляемых следующими каноническими (простейшими) уравнениями:
х2 у2 Z2
I. Эллипсоид: —- + — 4—- = 1.
а2 о2 с2
II. Гиперболоиды:
(2	2	2
X	и	Z
—7+77-----9=1 ---- однополостный,
a	Ь	с
2	2	2
X	U	z
—7+77-----7 = — 1 — двуполостный.
a	Ь	с
х^	у%	z%
III. Конус второго порядка: —7 + —--------- = 0.
а2	о2	с2
IV. Параболоиды (при pq > 0):
х и
----Н — = 2г — эллиптический,
р q
х2 у2
----— = 2г — гиперболический.
р q
2°. Прямолинейные образующие. Через каждую точку од-
нополостного гиперболоида проходят две его прямолинейные образу-
ющие:
§ 7. Эллипсоид, гиперболоиды и параболоиды
75
Через каждую точку гиперболического параболоида тоже проходят
две его прямолинейные образующие (при р > 0 и q > 0):
и
3°. Круговые сечения. На всех поверхностях, имеющих эллип-
тические сечения, имеются также и круговые сечения. Наибольшие
х2	у2	z2
круговые сечения эллипсоида —- Ч---	 Ч	- = 1 (при а > Ь > с) на-
ст	Ь2-с2
ходится на сфере х2 Ч- у2 Ч- z2 = b2. Круговые сечения эллиптического
ж2 у2
параболоида-----1---= 2г, проходящие через вершину, находятся на
Р 7
сфере ж2 Ч- у2 Ч- z2 = 2/г. (при р > </).
566.	Написать уравнение поверхности, образованной враще-
X2 Z2
нием эллипса —Ч—у = 1, у = 0 вокруг оси Oz.
а2 с2
х2 у2 z2
567.	Построить поверхность —— = 1и найти площади
ее сечений плоскостями: 1) z = 3; 2) у = 1.
568.	Написать уравнение поверхности,
X2 Z2
нием кривой —------- = 1, у = 0: 1) вокруг
а2 с2
оси Oz; 2) вокруг оси Ох. Построить обе
поверхности (в левой системе координат).
569.	Построить поверхности:
1)	х2 Ч- у2 - z2 = 4;
2)	х2 - у2 Ч- z2 Ч- 4 = 0.
тт	ж2 У2
570.	Построить гиперболоид -—h —---
z2
-----= 1 и найти его образующие, прохо-
36
дящие через точку (4; 1; —3).
571.	Нитяная модель цилиндра «закру-
чена» поворотом верхнего круга на а°
(рис. 22). Определить уравнение получен-
ной «линейчатой» поверхности, если ок-
образованной враще-
Рис. 22
76
Гл. 3. Аналитическая геометрия в пространстве
ружности ее оснований лежат в плоскостях z = ±с, их центры —
на оси Ог, а их радиусы равны 2а. Рассмотреть частные случаи
при a = 90°, 120°, 180°.
Указание. Точка М(х; у; z) делит расстояние между точками
A(2acos/; 2а sin/; —с), В(2а cos (t + а); 2а sin (/+ а); с)
в отношении AM : МВ = (с + z) : (с — z).
572.	Написать уравнение поверхности, образованной враще-
нием параболы az = ж2, у = 0 вокруг оси Oz. Построить по-
верхность по сечениям плоскостями: z = a, х = 0, у = 0.
573.	Построить поверхности:
574.	Построить (в левой системе координат) поверхность х2 —
— у2 = 4г и найти ее образующие, проходящие через точку (3; 1; 2).
575.	Написать уравнение геометрического места точек, отно-
шение расстояний от каждой из которых до плоскости х = 2a
к расстояниям до точки F(a; 0; 0) равно ^/2. Построить поверх-
ность.
576.	Написать уравнение геометрического места точек, отно-
шение расстояний от каждой из которых до точки F(0; 0; 2a) и до
плоскости z = а равно ^/2. Построить поверхность.
577.	Написать уравнение геометрического места точек, одина-
ково удаленных от точки F( — a; 0; 0) и от плоскости х = а. По-
строить поверхность.
х2
578.	Найти наибольшие круговые сечения эллипсоида ----- +
579.	Определить круговые сечения эллиптического параболоида
х2 у2
---1---= z, проходящие через начало координат.
580.	Назвать и построить каждую из поверхностей:
1)	ж2	+	у2	+	z2 = 2аг; 6)	х2 = 2аг;
2)	ж2	+	у2	=	2аг;	7)	х2 = 2уг;
3)	ж2	+	г2	=	2аг;	8)	z = 2 + х2	+	у2;
4)	х2	—	у2	=	2аг;	9)	(г — а)2 =	ху;
5)	ж2 — у2 = z2;	10) (г — 2ж)2 + 4(г — 2х) = у2.
§ 7. Эллипсоид, гиперболоиды и параболоиды
77
581.	Написать уравнения прямолинейных образующих гипер-
болоида х2 — у2 + z2 = 4, проходящих через точку (2; 4; 4).
582.	Написать уравнение геометрического места точек, одина-
ково удаленных от точки F(Q; 0; а/2) и от плоскости z = — а/2.
Построить поверхность.
583.	Написать уравнение геометрического места точек, одина-
ково удаленных от точки F(Q; 0; а/2) и от плоскости z = За/2.
Построить поверхность.
584.	Найти наименьшие круговые сечения гиперболоида
™2	,,2
F = 1.
25
585. Написать уравнения прямолинейных образующих гипер-
х2 у2
болического параболоида---------= 2г, проходящих через точку
16	9
(4; 3; 0).
25	9
Глава 4
ВЫСШАЯ АЛГЕБРА
§ 1.	Определители
1°. Определители. Определителем второго порядка называ-
ется число, обозначаемое символом Г1
’	К
&11
и определяемое равенством
01 &1 I	,
т, = 0102
02 Ъ2\	12
— a2&i-
(1)
Определителем третьего порядка
символом
01
02
аз
Ь1
Ъз
С1
С2
Сз
называется число, обозначаемое
и определяемое равенством
01
02
аз
bi
Ъз
С1
С2
Сз
- п 1&2 с2
“Ч&з с3
02 С2
Оз с3
а2 Ь21
аз &зГ
(2)
Определители второго порядка, входящие в правую часть равенства
(2), получаются из данного определителя третьего порядка вычеркива-
нием одной строки и одного столбца и называются его минорами. Фор-
мула (2) называется формулой разложения определителя третьего по-
рядка по элементам первой строки.
2°. Свойства определителей:
I.	Величина определителя не изменится от замены строк столбцами.
II.	Величина определителя от перестановки двух любых параллель-
ных его рядов меняет знак на обратный.
Из свойств I и II следует, что определитель можно разложить по
элементам любого ряда, так как этот ряд можно сделать первой строкой.
III.	Определитель с двумя одинаковыми параллельными рядами ра-
вен нулю.
IV.	Общий множитель элементов одного ряда можно вынести за знак
определителя.
V.	Величина определителя не изменится, если к элементам одного
ряда прибавить элементы параллельного ряда, умноженные на произ-
вольное одинаковое число. Например:
01	&1	С1
а2 Ь2 с2
аз Ьз сз
01 + mci
о2 + тс2
аз + тс3
&1 + ПС1 С1
Ь2 + пс2 с2
Ъз + пс3 с3
§ 1. Определители
79
С помощью этого свойства можно в любом ряду определителя третьего
порядка сделать два нуля, чем упростится разложение определителя по
элементам этого ряда.
3°. Площадь треугольника с вершинами А(хр, yi), В(х2', Уз),
С(х3; у3):
(3)
Вычислить определители:
see. |3 1\.
587-|б -io|-
S8S.|J I
589.
591.
у/а —1
а у/а
sm ct cos^ ct
sin2 /3 cos2 /3
590. I Sm °
| — cos a
cos al
sin a | ’
Вычислить определители, разложив их по элементам первого
столбца:
592.
а
593. -1
1 а
а 1
— 1 а
Вычислить определители, разложив их по элементам того ряда,
который содержит наибольшее число нулей:
594.
595. О
Упростить и вычислить определители:
596.
597.
1
3
-3
2	5
—4	7
12 -15
598.
599. у2 у
600.
1 + cos а
1 — sin a
1
1 + sin a 1
1 + cos a 1
1 1
o 9	i
2 cos^ sm a 1
2 cos2 2 sin /3 1
1	0	1
1
1
1
80
Гл. 4. Высшая алгебра
602.	Найти площадь треугольника с вершинами
А{2- 3), В(4; -1) и С(6; 5).
603.	Лежат ли на одной прямой точки
4(1; 3), В(2; 4) и С(3; 5)?
604.	Написать с помощью определителя третьего порядка урав-
нение прямой, проходящей через точки:
1) (жн У1) и (ж2; Уг); 2) (2; 3) и (-1; 5).
остить и вычислить определители:
Упр
	2 -3 1		
605.	6-6 2	606.	
	2-12		
	ах а2 +	а?2 1	
607.	ау а2 + у2 1		
	az а2 +	Z2 1	
т + a т — a a
п + a 2n — a a
a — a a
	sin За	cos За	1
608.	sin 2а	cos 2а	1
	sin а	cos а	1
Указание. В задаче 607 вынести а за знак определителя, затем
из первой и второй строк вычесть третью и вынести (х — z) и (г/ — z) за
знак определителя.
609. Доказать, что
Xi + х2 У1 + у2
2	2
~ х2 У1 ~ У2
2	2
Х1	У1
1
= 1|®1 У11
1	2 1Ж2 У2\'
1
610. Найти х из уравнений:
и проверить подстановкой корней в определитель.
§ 2. Системы линейных уравнений
1°.Система двух линейных уравнений с двумя неиз-
вестными
«1® + &1У = ci,
«2® + Ь2у = с2
(1)
§ 2. Системы линейных уравнений
81
имеет решение
lei	&i|	lai	cd
|с2	&г|	_	К	с2|
lai	&i| ’ У ~	lai	611
la2	&2I	la2	&2I
(2)
при условии, что определитель системы А =
2°. Система двух однородных линейных
0.
уравнений с
тремя неизвестными
a-yx + biy + c-yz = 0,
«2® + Ь2у + c2z = 0
(3)
имеет решения, определяемые формулами
-‘12 22 ’=-‘12 Sb -‘12 21’ w
где к — произвольное число.
3°. Система трех однородных линейных уравнений с
тремя неизвестными
а-ух + biy + c-yz = 0,
«2® + b2y + c2z = 0,
азх + Ь3у + c3z = 0
(5)
имеет отличные от 0 решения, если определитель системы
ai 61
а2 Ь2
ад Ь3
С1
С2
сз
= о,
и обратно.
4°.Система трех линейных уравнений с двумя неиз-
вестными
ai« + &ij/ = ci,
а2х + Ь2у = с2,	(6)
а$х + Ь3у = с3
совместна, когда А =
Ь1
Ъ2
Ъз
С1
С2
сз
= 0 и система не
содержит попарно
противоречивых уравнений.
5°. Система трех линейных уравнений
с тремя неиз-
вестными
а-ух + biy + c-yz = c?i,
а2х + b2y + c2z = d2,
азх + Ь3у + c3z = d3
(7)
82
Гл. 4. Высшая алгебра
при условии, что определитель системы
01
02
аз
61 С1
&2 с2
Ъз сз
имеет следующее единственное решение:
где
di	61	ci
С?2	&2	с2
d3	Ьз	сз
^0,
(8)
di di ci
02 d2 с2
оз d3 с3
01	61	di
о2 62 d2
03 63 d3
6°. Несовместные и неопределенные системы. Обозна-
чим левые части уравнений (7) через Xi, _\'2 и Х3. Пусть определитель
системы (7) А = 0. При этом возможны два предположения.
I. Элементы двух строк определителя А пропорциональны, например
02	62	с2	_
— = — = — = т. Тогда _\2 = тХ-у и:
01	61	С1
1) если d2 ф mdi, то система несовместна (первые два уравнения
противоречивы);
2) если d2 = mdi, то система неопределенна (если первое и третье
уравнения не противоречивы).
II. В определителе А нет строк с пропорциональными элементами.
Тогда существуют отличные от 0 числа тип такие, при которых mXi +
+ пХ2 = Х3, и:
1) если mdi + nd2 ф ds, то система несовместна;
2) если mdi + nd2 = d3. то система неопределенна.
Числа тип можно подобрать или же найти их из уравнений ар и +
+ о2п = 03, 61m + 62п = 63, cim + с2п = с3.
Решить с помощью определителей системы уравнений:
611.
Зж + 2у = 7,
4ж — 5у = 40.
- 3У = 1
[ ах — 2у = 2
613.
5ж + 2у = 4,
7ж + 4у = 8.
тх — пу = (т — п)2,
2ж — у = п (при т 2п).
Решить системы уравнений:
( 2ж — Зу + z — 2 = О,
615. < ж + 5у - 4г + 5 = О,
[ 4ж + у — 3z + 4 = 0.
_ Г 2ж - 5у + 2г = О,
t ж + 4у - Зг = 0.
( 2ж — I // + Зг = 1,
616. < ж - 2у + 4г = 3,
[ Зж — у + 5г = 2.
( Зж + 2у — г = О,
618. 2ж - у + Зг = О,
[ ж + Зу — 4г = О,
§ 3. Комплексные числа
83
Г Зх + 2 у — z = О,
619. 1 2х - у + 3z = О,
[ х + у — z = О.
( х + 2у + 3z = 4,
621. < 2х+ у - z = 3,
[ Зх + Зу + 2z = 7.
Г х + 2у + 3z = 4,
620. 2s + I// + 6г = 3,
[ Зх + у — z = 1.
( х + 2у + 3z = 4,
622. < 2s + у - z = 3,
[ Зх + Зу + 2z = 10.
623. Пересекаются ли в одной точке прямые:
1) 2х — Зу = 6, Зх + у = 9, х + I // = 3;
2) 2х — Зу = 6, х + 2у = 4, х — 5у = 5?
Выполнить в обоих случаях построение.
Решить системы линейных уравнений:
Г 2х — у + z = 2,
624. < Зх + 2у + 2z = —2,
[ х — 2у + z = 1.
J + 2г = О,
t 5s + 2у + 3z = 0.
Г 2s — у + 3z = О,
628. < s + 2у - 5г = О,
[ 3s + у — 2г = 0.
Г х + 2у — Зг = 5,
625. < 2s — у — г = 1,
[ х + Зу + 4г = 6.
Г 3s — у + 2г = О,
627. < 2s + Зу - 5г = О,
[ х + у+ г = 0.
!х — 2у + г = 4,
2x + 3y-z= 3,
4s— у + г = 11.
§ 3.	Комплексные числа
1°. Определения. Комплексным числом называется выражение
вида х + г/г, в котором жиг/ — вещественные числа, аг — некоторый
символ, если при этом приняты условия:
1)	х + Ог = х, 0 + г/г = г/г и 1г = г, (—1)г = —г;
2)	х + г/г = «1 + у-yi тогда и только тогда, когда х = .щ и у = у^,
3)	(s + г/г) + («1 + г/р) = (ж + Ж1) + (г/ + г/1)г;
4)	(s + г/г)(ж1 + г/р) = (жЖ1 - г/г/i) + (жг/i + xxy)i.
Из условий 1) и 4) получаются степени числа г:
г2 = —1, г3 = —г, г4 = 1, г5 = г нт. д.	(1)
Комплексное число ж + г/г, в котором у ф 0, называется мнимым
числом. Число г называется мнимой единицей.
2°. Действия над комплексными числами. Сложение,
вычитание, умножение и возведение в степень комплексных чисел можно
выполнять по правилам этих действий над многочленами с заменой сте-
пеней числа г по формулам (1).
Деление комплексных чисел и извлечение корня из комплексного чи-
сла определяются как действия обратные.
84
Гл. 4. Высшая алгебра
3°. Тригонометрическая форма комплексного числа.
Комплексное число x + yi определяется парой вещественных чисел (х, у)
и поэтому изображается точкой М(х; у) плоскости или ее радиус-векто-
ром г = 04 ( (см. рис. 12). Длина этого вектора г = ^/ж2 + г/2 называ-
ется модулем комплексного числа, а угол его р с осью Ох называется
аргументом комплексного числа. Так как х = rcosp, у = г sin р, то
х + yi = г (cos р + i sin р).	(2)
4°. Действия над комплексными числами в тригоно-
метрической форме:
r(cos р + i sin <£>)ri(cos pi + i sin pi) =
= (ny) [cos (pp + 9?!) + i sin (p + <^i)],	(3)
r(cosp + «sin<£>) г г ,	.	. . ,	...
—---------------- = — cos (p - ^>1 + ism (p - ^>1 ,	4
7*1 (cos pi + г sin pi) Vi
[r(cos p + i sin <£>)]" = rn (cos np + i sin np),	(5)
/—-------------г i- ( p + Q/k'K . . p + 2&тг\
л/r(cos p + г sin p) = 1/r cos---H г sin------- ,	(6)
\ n	nJ
где к = 0, 1, 2, . . ., n — 1.
Формулы (5) и (6) называются формулами Муавра.
5°. Формула Эйлера:
elifi = cos р + i sin р.	(7)
6°. Логарифм комплексного числа:
In z = In г + ipo + 2&тгг,	(8)
где ро — значение аргумента р, удовлетворяющее неравенствам —тг <
< р iZ 7Г. Выражение lnr + г^о называется главным значением лога-
рифма.
630.	Выполнить действия: 1) (2 + Зг) (3 — 2г); 2) (а + Ы) (а — Ы);
3) (3 — 2г)2; 4) (1 + г)3; 5)	6)
631.	Решить уравнения: 1) ж2 + 25 = 0; 2) ж2 — 2ж + 5 = 0;
3) ж2 + 4ж + 13 = 0 и проверить подстановкой корней в уравнение.
Следующие комплексные числа изобразить векторами, опреде-
лить их модули и аргументы и записать в тригонометрической
форме:
632.	1) г = 3; 2) z = -2; 3) г = Зг; 4) г = -2г.
633.	1) г = 2 - 2г; 2) г = 1 + /3) г = -л/3 - i.
§ 3. Комплексные числа
85
634.	1) ->/2 + гл/2; 2) sin a + г(1 — cos a).
635.	Числа, данные в задачах 632-634, записать в форме revt
(при —7Г < X тт).
636.	Построить области точек z по условиям:
1)	|г| < 3; 2) |г| < 2 и д/2 <	< д;
3)	2 < |г| < 4 и —тт < i/> < —7г/2.
637.	Показать, что |^i — г2| есть расстояние между точками
z\ и г2.
638.	Дана точка z0 = —2 + Зг. Построить область точек г, для
которых |г — г0| < 1.
639.	Число, сопряженное с г, обозначается через ~z. Доказать,
что z • z = | z|2.
640.	Вычислить по формуле Муавра:
1) (1 + г)10; 2) (1-г^З)6; 3) (-1фг)5;
4)	(1 + cos + г sin ; 5) (л/З + г)3.
641.	Выразить sin За и cos За через функции утла а, используя
тождество (cos а + г sin а)3 = cos За + г sin За.
642.	Найти все значения z = и изобразить их радиус-
векторами, построив крут радиуса, равного 1.
643.	Найти: 1) </1; 2)	3) ^1; 4) </-2 + 2г.
644.	Найти: 1) \/i; 2) \/—1 + г; 3)	8 + 8г-\/3.
645.	Решить двучленные уравнения: 1) s3+8 = 0; 2) s4+4 = 0.
646.	Найти главное значение логарифма: 1) In ( — 2); 2) In (1 + г);
3) In г; 4) In (х + уг); 5) In (2 — 2г).
647.	Найти сумму sin х + sin 2s + sin Зх + ... + sin nx.
exi — e~xi
Указание. По формуле Эйлера заменить sins = ----—---- и т. д.
2г
648.	Найти сумму cos х + cos 2s + cos3s + ... + cos nx.
649.	Доказать тождество
s5 — 1 = (s — 1) (s2 — 2s cos 72° + 1) (s2 — 2s cos 144° + 1).
650.	Вычислить:
4 - 3?
1)	2) (° + M3-(a-M3.
Следующие комплексные числа изобразить векторами, опреде-
лить их модули и аргументы и записать в тригонометрической
форме и в форме revt (при — тг < (f> + тг):
86
Гл. 4. Высшая алгебра
651.	1) г = 4 + 4г; 2) г = -1 + г^З; 3) г = 1 - г.
652.	1) г = 5; 2) z = -i; 3) z = -у/2 - ^2.
653.	Построить область точек z по условиям
1 < |^| < 3 и 7Г/4 < ip < Зд/4.
654.	Дана точка z0 = 3 — 4г. Построить область точек z, для
которых \z — г0| < 5.
655.	Вычислить по формуле Муавра:
(7Г	7Г \
l + cos- + zsin- .
О	О '
656.	Выразить sin 4a и cos 4a через функции утла а, используя
тождество (cos а + г sin а)4 = cos 4а + г sin 4а.
657.	Найти все значения корней: 1) \/—1; 2) д/1 и изобразить
их радиус-векторами.
658.	Решить уравнения:
1)	х3 - 8 = 0; 2) х6 + 64 = 0; 3) х4 - 81 = 0.
659.	Найти сумму (см. задачу 647)
cos х + cos Зх + cos 5s + ... + cos (2гг — l)s.
§ 4.	Уравнения высших степеней и приближенное
решение уравнений
1°. Кубическое уравнение:
х3 + ах2 + Ьх + с = 0.
(1)
Если si, Х2, хз — корни уравнения (1), то уравнение можно записать
в виде (х — Ж1)(ж — хз)(х — хз) = 0. Отсюда а = —(»i + ж2 + хз),
b = Х]Х2 + Ж1Ж3 + ж2жз, с = — Х1Х2Х3.
Уравнение х3 + ах2 + Ьх + с = 0 приводится к виду z3 + pz + q = 0
а	-
подстановкой х = z — —. Уравнение z pz + q = 0 решается по формуле
Кардано:
qz <>	«1 + гь
I.	Если А = — + — > 0, то гд = U1 + г)1; г2)3 =--------------- ±
± -------гл/З, где ui и гд — вещественные значения корней и и v.
тт р Л q2 _1_ Р3	n	3q	3t	Z1
4	27	p	2p	2
§4. Уравнения высших степеней
87
2°.Отделение вещественного корня уравнения f(x) =
= 0. Между а и Ь содержится единственный корень уравнения f(x) = 0,
если f(a) и f(b) имеют разные знаки, a f(x) непрерывна на отрезке
[а, Ь] и внутри него имеет производную f'(x) ф 0. Будем считать еще,
что на этом отрезке и f"(x) ф 0.
3°. Способ хорд приближенного решения уравнения
f(x) = 0. Пусть «о — тот из концов отрезка [а, Ь], отделяющего корень,
ctn
дТис. 23
ет точ
y=f(x)
Ньютона). Пусть /3q — тот из
> 0. Тогда приближением
[ с Ох касательной к кривой у =
некотором f(ap)f"(oQ) < 0. тАгда приближени
«1 пересечения с Ох хорды АЙ (рис. 23):
! /(«
«1 Ф «о-----
№ - №)
где к =	.	,
о — а	.
4°. Способ касательны
концов отрезка [а, Ь], на кот^
к корню х будет точка Д пересечения
f(x) в точке [Х?о, f(M] (рис. 23):
«1
где h = f'(fdo)-
Применяя повторно способ хорд и касательных, можно составить таб-
лицу
a\/3\f(a) |/(Я | fe | fei | Аа I А/3|
(2)
88
Гл. 4. Высшая алгебра
где к и к-у — наклоны хорд и касательных, а
к	к\
Последовательности получаемых в таблице (2) значений а и > схо-
дятся к искомому корню.
5°. Способ итераций. Если уравнение f(x) = 0 можно привести
к виду х = <р(х), причем в некоторой окрестности корня |^>,(а?) | < О <С 1 и
xq — любое число в этой окрестности, то сходящаяся последовательность
приближенных решений будет
Ж1 = <£>(ж0), х2 = ‘р(х1), х3 = ip(x2), . . .
В уравнениях задач 660, 661 среди целых множителей свобод-
ного члена подобрать один корень, разделить левую часть на x — xi
и затем найти остальные корни:
660.	1) х3 — 4х2 + х + 6 = 0; 2) х3 — 4s2 — 4s — 5 = 0. Решение
проверить составлением выражений
+ х3, Х}Х2 + 2?2жЗ + х 1 х3 , ®1®2Ж3-
661.	1) X3 - 5s2 - 2ж + 24 = 0;
2) х4 + х3 + 2s — 4 = 0;
3) 9s3 + 18s2 — х — 2 = 0; 4) 4s3 — 4s2 + х — 1 = 0.
Решить по формуле Кардано следующие уравнения:
662. 1) z3 - 6z - 9 = 0; 2) z3 - 12г - 16 = 0.
663. 1) z3 - 12г - 8 = 0; 2) г3 + 6г - 7 = 0.
664.	х3 + 9s2 + 18ж + 9 = 0.
665.	Дано уравнение /(ж) = х4 — х — 10 = 0. Составив таблицу
знаков /(s) при х = 0, 1, 2, ..., определить границы положитель-
ного корня и вычислить его с точностью до 0,01 по способу хорд и
касательных.
666.	Построить график функций у =
3
У’
определить графиче-
ски границы корней уравнения ж3 —6ж + 3 = 0 и вычислить корни
с точностью до единицы третьего знака.
667.	По способу итераций (последовательных приближений)
найти вещественные корни уравнений: 1) х3 + 60s — 80 = 0;
2) 27; = 4s; 3) s3 + l2x + I3 = 0; 4) х4 - 2s - 2 = 0.
668.	Подбором одного корня среди целых множителей свобод-
ного члена решить уравнения:
1) s3 + 8s2 + 15s + 18 = 0; 2) s3 — 3s2 + 4 = 0.
Для проверки составить выражения J^Sj, J^SjSj и Х]Х2х3.
§4. Уравнения высших степеней
89
669. По формуле Кардано решить уравнения:
1) г3 + 18г-19 = 0; 2) г3 - 6г - 4 = 0;
3) г3 — Зг + 2 = 0;	4) х3 + 6ж2 + 9х + 4 = 0.
670. Построив график функции у =
^4
Т’
определить границы
корней уравнения ж4 + 3ж — 15 = 0 и вычислить корни с точностью
до 0,01.
671. Найти с точностью до 0,01 положительные корни уравне-
ний: 1) х3 + 50ж — 60 = 0; 2) х3 + х — 32 = 0.
672. По способу итераций найти вещественный корень уравне-
ния ж3 + 2ж — 8 = 0, вычисляя последовательные приближения по
формуле х = \/8 — 2ж.
Глава 5
ВВЕДЕНИЕ В АНАЛИЗ
§ 1. Переменные величины и функции
1°. Отрезки и интервалы. Множество чисел х, удовлетворяю-
щих неравенствам а < х < Ь, называется интервалом и обозначается
(а, Ь). Множество чисел х, удовлетворяющих неравенствам а <( х <( Ь,
называется отрезком и обозначается [а, Ь].
Эквивалентные неравенства (при а > 0)
х2 < а2, или |ж| < а, или — а < х < а
определяют интервал, симметричный относительно нуля.
2°. Переменные величины и функции. Если каждому зна-
чению переменной х поставлено в соответствие одно число, то перемен-
ная у, определяемая совокупностью этих чисел, называется однозначной
функцией х. Переменная х называется при этом аргументом, а данная
совокупность значений аргумента — областью определения функции.
То, что у есть функция х, символически записывают в виде у =
= f(x), или у = F(x), или у = р(х) и т. п. Символ f(x) или F(x) и
т. п. обозначает закон соответствия переменных х и у, в частности, он
может означать совокупность действий или операций, которые нужно
выполнить над х, чтобы получить соответствующее значение у.
673. Построить области изменения переменной х, удовлетворя-
ющей неравенствам:
1) |ж| < 4; 2) ж2 9; 3) |ж — 4| < 1;
4) -1 < х - 3	2; 5) ж2 > 9; 6) (ж - 2)2 4.
674.	Записать неравенствами и построить интервалы измене-
ния переменных: [—1, 3]; (0, 4); [—2, 1].
675.	Определить область изменения переменной х = 1 — где
t принимает любое значение 1.
В задачах 676-678 построить по точкам на отрезке |ж|	3
графики указанных функций:
676.	1) у	= 2ж;	2) у = 2ж + 2;	3)	у =	2ж - 2.
677.	1) у	= ж2;	2) у = ж2 + 1;	3)	у =	ж2 — 1.
678.	1) у	= ^;	2)у=^ + 1;	3)	у =	-	1.
§ 1. Переменные величины и функции
91
679.	Построить графики функций: 1) у = —; 2) у = 2Ж; 3) у =
= log2s. Какую особенность в расположении этих кривых отно-
сительно осей координат можно заметить?
680.	Построить на одном чертеже графики функций: 1) у =
= sin ж; 2) у = coss по точкам, в которых у имеет наибольшее,
наименьшее и нулевое значения. Сложением ординат этих кривых
построить на том же чертеже график функции у = sin х + cos ж.
681.	Найти корни sj и х% функции у = 4ж — ж2 и построить ее
график на отрезке [sj — 1, х^ + 1].
682.	Построить графики функций:
1)	У = Ы; 2) у = -|ж - 2|; 3) у = |ж| - х.
В задачах 683-686 найти области определения вещественных
Значений функций и построить их графики.
683.	1) у = у/х + 2; 2) у = д/9 — ж2; 3) у = а/4ж — ж2.
--	/ж — 1
684.	1) у = у—ж + у4 + ж; 2) у = arcsin —-—.
685.	1) у = ж(2 ±	;	2) у =
686.	1) у = -V2sins; 2) у = _ж^16 ~ ж2_.
687. 1) /(ж) = ж2 -	- ж + 1; вычислить /(0), /(1), /(-1), /(2),
/(а + 1); 2) ф(х) = 1	2х — 3	/3\ 2	।  вычислить	</>(—1), ф 1
V - , ~7
\х/
688. F(s) = ж2; вычислить:
F(b) — F(a)	.	bаh\	b а — h\
—Ч-----2 F I - F I ------------
b — a ’ 1	[ 2 J	\ 2 J
689.	f(x) = ж2, со(ж) = ж3; вычислить	.
690.	F(s, у) = ж3 — Зху — у2; вычислить F(4, 3) и F(3, 4).
691.	Функция /(ж) называется четной, если /( — ж) = /(ж);
нечетной, если /( — ж) = —/(ж). Указать, какие из следующих
функций четные и какие нечетные:
. „. . sin ж .	, . ах — 1	.	.	1
1) /(ж) = ---! 2) ф(х) =	; 3) F(s) = ах + —;
х	ах + 1	ах
4) Ф(ж) = ах----5) Ф(ж) = ж sin2 ж — ж3; 6) Д (ж) = ж + ж2.
92
Гл. 5. Введение в анализ
692.	Середина любой хорды графика некоторой функции /(s)
лежит выше графика этой функции. Записать это свойство функ-
ции неравенством. Проверить, что этим свойством обладает функ-
ция /(s) = ж2.
693.	Какая из элементарных функций обладает свойствами
/(1) = 0, /(а) = 1, f(xy) = f(x) + /(у)?
694.	Какая из элементарных функций обладает свойствами
/(0) = 1, /(1) = a, f[x + у) = /(®)/(у)?
695.	Построить области изменения переменной х, удовлетворя-
ющей неравенствам:
1) |s| < 3; 2) х2 4; 3) |ж — 2| < 2; 4) (х - I)2	4.
696.	Определить область изменения переменной х = 2+ -, где
t принимает любое значение 1.
697.	Построить графики функций:
х3
1)	у = 4---— на отрезке |s|	2;
х2
2)	у = 3, 5-ГЗд —— между точками пересечения с осью абсцисс.
698.	Построить графики функций:
1)	у = х — 4 + |® — 2| на отрезке [—2, 5];
2)	у = 1 — coss на отрезке |s| 2тг.
699.	Построить графики функций:
\	4 ч
1)	у= 2) у = 2—.
700.	Найти области определения вещественных значений функ-
ций:
1)	у = у/ 4 — х2;	2) у = V® + 1 — л/3 — х;
3) у = 1 — ^/2 cos 2s; 4) у = --------
1 + V х2 — 4
и построить их графики.
2ж “I- 1
701. 1) Для функции /(ж) =	----
/(-1/2), /(s - 1), /(1/2); Х +
2)	для функции tp(x) = х3 вычислить
вычислить /(0), /( — 2),
tp(x + h) — tp(x — h)
h	’
3)	для функции /(ж) = 4s — х2 вычислить /(а + 1) — /(а — 1).
§ 2. Пределы последовательности и функции
§ 2.	Пределы последовательности и функции.
Бесконечно малые и бесконечно большие
1°. Числовая последовательность. Пусть каждому нату-
ральному числу n = 1, 2, 3,... по некоторому закону поставлено в со-
ответствие число хп. Тогда говорят, что этим определена последова-
тельность чисел «1, Х2, хз, . . . или, короче, последовательность {жп} =
= {«1, Х2, хз, . . Отдельные числа последовательности {жп} называ-
ются ее элементами. Говорят еще, что переменная хп пробегает значе-
ние последовательности {жп}.
2°. Предел последовательности (предел переменной).
Число а называется пределом последовательности {жп}, или пределом
переменной хп (обозначается хп —> а), если для всякого е > 0 найдется
зависящее от е число «о такое, что \хп — а| < е для всех натуральных
п > HQ. Интервал (а — е, а + е) называется е-окрестностью числа а
(или точки а). Таким образом, хп —> а обозначает, что для всякого е > О
найдется такое число по, что для всех п > hq числа хп будут находиться
в е-окрестности числа а.
3°. Предел функции. Пусть функция f(x) определена в некото-
рой е-окрестности точки а, за исключением быть может самой точки а.
Говорят, что число Ь является пределом функции f(x) при х —> а (пишут
f(x) —> Ь при х —> а или lim f(x) = Ь), если для любого е > 0 существует
х—¥а
зависящее от е число S > 0 такое, что |/(ж) — Ь\ < е при 0 < |ж — а| < S.
Аналогично, lim f(x) = Ь, если для всякого е > 0 существует завися-
х—¥а
щее от е число N такое, что |/(ж) — Ь\ < е при |ж| > N. Употребляется
также запись lim f(x) = сю, которая обозначает, что для всякого числа
х—¥а
А > 0 существует зависящее от А число S такое, что |/(ж)| > А при
О < |ж — а| < S.
Если х —> а и при этом х < а, то пишут х —> а — 0; аналогично,
если х —> а и при этом х > а, то пишут х —> а + 0. Числа f(a — 0) =
= lim f(x) и f(a + 0) = lim f(x) называются соответственно пре-
х—ta — 0	х—>а+0
делом слева функции f(x) в точке а и пределом справа функции f(x)
в точке а. Для существования предела функции f(x) при х —> а необхо-
димо и достаточно, чтобы было f(a — 0) = f(a + 0). Вместо х —> 0 — 0 и
х —> 0 + 0 пишут х —> —0 и х —> -j-О соответственно.
4°. Бесконечно малые. Если lim а(ж) = 0, т. е. если |а(ж)| < е
х—¥а
при 0 < |ж — а| < <5(е), то функция а(ж) называется бесконечно малой
при х —> а. Аналогично определяется бесконечно малая а (ж) при х —> сю.
5°. Бесконечно большие. Если для любого сколь угодно боль-
шого числа N существует такое S(N), что при 0 < |ж — а| < S(N) вы-
полнено равенство |/(ж)| > N, то функция f(x) называется бесконечно
большой при х —> а. Аналогично определяется бесконечно большая f(x)
при х —> сю.
94
Гл. 5. Введение в анализ
702.	Полагая п = 0, 1, 2, 3, ..написать последовательности
значений переменных:
1
1
2” ’
1\"
2 )
Начиная с какого п модуль каждой из переменной сделается и бу-
дет оставаться меньше 0,001, меньше данного положительного е?
703.	Написать последовательность значений переменной х =
(-1)”
= 1-|------. Начиная с какого п модуль разности х — 1 сделается и
2п + 1
будет оставаться меньше 0,01, меньше данного положительного е?
704.	Прибавляя к 3 (или вычитая из 3) сначала 1, затем 0,1,
потом 0,01 и т. д., записать «десятичными» последовательностями
приближения переменной к пределу: хп —> 3 + 0, хп —> 3 — 0.
705.	Записать «десятичными» последовательностями прибли-
жения переменных к пределам: хп —> 5 + 0, хп —> 5 — 0, хп —>
—> — 2 + 0, хп —> — 2 — 0, хп —> 1 + 0, хп —> 1 — 0, хп —> 1, 2 + 0,
хп —> 1, 2 — 0.
706.	Доказать, что lim х2 = 4. Пояснить таблицами значений
х—>2
9
X И X .
707.	Доказать, что lim (2s — 1) = 5. По данному числу е > 0
х—>3
найти наибольшее число 6 > 0 такое, чтобы при любом х из
5-окрестности числа 3 значение функции у = 2. г — 1 оказалось в
е-окрестности числа 5. Пояснить графически.
708.	Доказать, что lim (3 — 2s — s2) = 4. Из какой наиболь-
X—> — 1
шей 5-окрестности числа —1 нужно взять значение s, чтобы зна-
чение функции у = 3 — 2s — s2 отличалось от ее предела меньше
чем на е = 0, 0001?
709.	Доказать, что sin а есть бесконечно малая при a —> 0.
Указание. Сделать чертеж и показать, что | sin a | < |а|.
710.	Доказать, что lim sin s = sin a.
x—^a
Указание. Положив x = a + a, составить разность sins — sin а и
затем положить a —> 0.
3s + 4
711.	Доказать, что lim --- = 3. Пояснить таблицами зна-
Зж Ч- 4
чений s и ------ при s = 1, 10, 100, 1000, ...
4s — 3
712.	Доказать, что lim --- = 2. При каких s значения
s—2s -Г 1
функции будут отличаться от своего предела меньше чем на 0,001?
§ 2. Пределы последовательности и функции
95
713.	Доказать, что lim % д 2 = —^,5. При каких х значения
функции будут отличаться от своего предела меньше чем на 0,01?
714.	Доказать, что lim 0, 333.. .3 = -, составив разности-
п-Юо ' -v—' 3	3
п знаков
- 0,3; - - 0,33; - - 0,333; ...; - - 0, 333.. .3.
’ ’ 3	’ ’ 3	’	’	’3	'
пзнаков
715.	Написать последовательности:
Существует ли
lim хп в каждом примере и чему он равен?
и->+со
716.	Найти lim ----- и lim ------- и пояснить таблицами.
х—>2ДО X 2 х—>2—О X 2
717.	Найти lim 21/ж и lim 21/ж и пояснить таблицами.
х—>04-0	х—>0—0
718.	Выяснить точный смысл «условных» записей:
1) — = 0; 2) | = ±оо; 3) Зто = ос; 4) 3"°° = 0;
сю	О
5)	1g 0 = —сю; 6) tg90° = ±сю.
719.	Показать, что lim sin х не существует, составив последо-
вательности значений sins:
1)	при х = пд; 2) при х = — + 2дп; 3) при х = — — + 2лп
(п = 0, 1, 2, 3, 4, ...).
720.	Показать, что lim sin — не существует.
ж->0 х
721.	Показать, что lim ж sin — = 0 при любом способе прибли-
ж->0 х
жения х к 0.
722.	В круг радиуса R вписан правильный многоугольник с
числом сторон п и стороной an. Описав около круга квадрат, по-
казать, что an < е, как только n > SR/e^ т. е. an —> 0, когда
п —> сю.
723.	Пусть гп — апофема правильного, вписанного в круг п-
угольника. Доказать, что lim rn = R, где R — радиус круга.
Гл. 5. Введение в анализ
724.	Вершина В треугольника АВС перемещается по прямой
ВЕ\\АС, неограниченно удаляясь вправо. Как будут при этом
изменяться стороны треугольника, его площадь, внутренние углы
и внешний угол BCD?
725.	Написать «десятичные» последовательности приближений
переменных к пределам: хп —> 4 + 0; хп —> 4 — 0; хп —> —1,5 + 0;
хп —> —1,5 — 0.
726.	Доказать, что:
1) lim х3 = 27: 2) lim (х2 + 2s) = 3.
ar-j-З	ж-Ы
тт	V 5ж + 2
727.	Доказать, что lim ---- = 2,5, показав, что разность
хЧ-со 2./'
5х + 2
—-------2,5 есть бесконечно малая при х бесконечно большом.
Пояснить таблицей, полагая х = 1, 10, 100, 1000, ...
728.	Доказать, что lim cos ж = cos а (см. задачу 709).
х—Ya
729.	Написать последовательности значений переменных:
1)	Жп = 1+(-|) ;	2) Хп= (-1)«+^;
«Пт — (-В\п(9г, д_ П- Кт — 2^sin (шг/2)
Какая из последовательностей имеет предел при п —> +оа?
730.	Найти: 1) lim 21^х~1^ ; 2) lim 2|/(';_|5
ж-Ы-0	хч- 1+О
2
3) lim 3tg2a;; 4) lim 3tg2a;; 5) lim ------------------—;
x—>тг/4—О	x—>тг/4+0	х—>тг/2+0 1 “Г 2tSa'
ч ,	2	.	,	a
6) hm -----------—; 7) hm ------------.
x—>тг/2—О 1 “Г 2 &х	X—> + СО 1 -|- (Iх
2	2
731. Доказать, что lim 0, 666.. .6 = -, составив разности-----
п-1-со 4—'	3	3
пзнаков
2	2
— 0,6;----0, 66; ...;---- 0, 666.. .6.
’ ’ 3	’	’	’3	—v—'
пзнаков
732. Пусть ып — внутренний угол правильного п-угольника.
Доказать, что lim an = тг.
733. На продолжении отрезка АВ = а справа взята точка М
на расстоянии ВМ = х. Найти lim
§ 3. Свойства пределов
97
§ 3. Свойства пределов.
О	оо
Раскрытие неопределенностей вида — и —
О	оо
1°. Предел постоянной равен самой постоянной.
2°. lim (u + v) = limu + limu, 1
о0	\ к к	> если limu и limt) существуют.
3 . lim (uv) = lim u • lim v, I	j j
u limu
4 . lim — = ----, если limu и limu существуют и limu ф 0.
u limu
5°. Если для всех значений х в некоторой окрестности точки а,
кроме, быть может, х = а, функции f(x) и <р(х) равны и одна из них
имеет предел при х —1 а, то и вторая имеет тот же предел.
Это свойство применяется при раскрытии неопределенностей вида
0	оо	х2 — а2
- и —. Например, ------ = х + а при любых х, кроме х = а. По свой-
0	оо	х — а
х2 — а2
ству 5° lim------ = lim (х + а) = 2а.
х—1а X — а	х—1а
Найти пределы:
. , s2 — 4s + 1	. ,	1 + sin 2s
734. 1 lim -----------—:	2 lim —------------.
x—>2	2s 4“ 1	x—1тг/4 1 — cos 4s
д2 — 4
735. lim -----— (пояснить таблицей).
x 12 X 2
736. lim
x—12
x — 2
s2 — Зх + 2
737. lim —-----------
x2 — 2s — 3
Указание. Решить задачу 736 двумя способами: 1) полагая х =
= 2 + а; 2) разлагая знаменатель на множители.
, tff s
738. lim .
хч-тг sin 2s
740. lim ,	----.
^/1 + 3s — 1
— 1
742. lim А=-------.
739.
sin s — cos s
lim -----------------
жН-тг/4 cos 2s
741. lim
, Vl + mx — 1
743. lim -2—----------
x-10	S
Указание. В задаче 742 положить х = te, а в задаче 743 1 +
+ mx = t3.
... Г VI + ^ - VI -
744. lim ---------------------.
а;-10	S
745. li,n
ж-nr	sin 2s
98
Гл. 5. Введение в анализ
746. 1) lim
2s2 — 1 _
Зж2 — 4ж’
. ,	5ж3 — 7х
2) lim ---------
Указание. Можно решить двумя способами: 1) разделив числи-
тель и знаменатель на ж в высшей степени; 2) положив х = 1/а.
747. lim	Зх — 1	x3 — 1 .	748. hm X2 + 1	s4oo X2 + 1
749. lim	x/x — 6s	3n 		.	750. hm 	. 3x + 1	n-J-co 1 — 2n
751. lim n—>oc	V2n2 + 1	r l + 2 + 3 + ... + n 	. 752. hm 	,		. 2n — 1	n-J-co	C9n4 + 1
Найти пределы:
5ж2 — Зх + 2
. lim —--------------.
3:400 2ж2 + 4ж + 1
9 - х2
754. hm ,
у/Зх — 3
,	л/1 + cos х
756. lim -3—:-----------
ж-J-ir+O Sill X
Зп + 1
758. lim
л/Зп2 + 1
,	/ 5ж2	. /
759. lim -- + г1/27
2400 \ 1 — X2
760. lim
п—>ос
1 + 3 + 5 + ... + (2п — 1)
1 + 2 + 3+ ...-Гп
761. lim
м"
2 — \/х — 3
х2 - 49
762. lim
х—>тг/4
sin 2ж — cos 2х — 1
cos х — sin х
sin
§ 4. Предел отношения ---- при	—> О
Если угол а выражен в радианах, то
sin о	a
lim ----= 1; lim —----- = 1.
а->о a	twOsina
§ 5. Неопределенности вида сю — сю и 0 • сю
Найти пределы:
, sin 4®	, sin(s/3)
763. lim ------.	764. lim ---
И) X	И) X
Указание. В задаче 763 умножить числитель и знаменатель на 4
(или положить 4s = а).
, tgs	, sin2 (s/2)	,	1 —cos 2s
765. lim —.	766. lim ---767. lim ------------;.
x—Ю X	>0	X2,	>0 X SID X
, sin 3s	, sin (s + li) — sin (s — li)
768. lim ,	------=.	769. lim --v 7 ,---------
s-ю V® + 2 - V 2	M)	h
. arctgs . arcsin (1 — 2s)
770. 1 lim ----2 lim ---------------4-------
x—Ю	S	ж-Ы/2	4s2 — 1
Указание. Положить в примере 1) arctg s = а, а в примере 2)
arcsin (1 — 2s) = a.
,	1 — cos s	, tff s — sin s
771. lim --------.	772. lim —---------.
s—>0	S2	s—>0
Найти пределы:
773. lim ——.
>0 Sin 3s
,	a/1 — cos 2s
775.	lim ------------
x^-0	S
774. lim
x—>0
sin 4s
, 2s sin s
776.	lim ---------
s—>o sec s — 1
777. lim
x—>0
1 — cos mx
s2
,	1 — cos 2s + tg2s
778. lim ---------.	8
>0 s sin s
779. lim
x—>2
Sin (Ж - 2) , 9-1/(s-2)2
S2 -4	+
(положить s = 2 + a).
780. 1) lim -------——
h—>0	h
. 9
sin X
;	2) lim
arcsin (s + 2)
s2 + 2s
781. lim
§ 5. Неопределенности вида oo - oo и 0 • oo
Найти пределы:
___________________	/ 1	2
782. lim (V®2 + 3s — s).	783. lim--------------
s->+co	ж-ы \ s — 1 s2 — 1
100
Гл. 5. Введение в анализ
785. lim
х—>2
786. lim [ у
\ sin
12
х3 — 8/
1
4 sin2 (ж/2)
787. lim
п-Юо
,	.	. 7Г
788. hm (1 — ®)tg — х
(положить х = 1 — а).
789. lim (V®2 + 1 — а/ж2 — 4ж).
790. lim
х—> — 2
Найти пределы:
791. lim (ж — л/х2 — х -f- 1).
792. hm (ж — x2 — a2
,	( sin х
793. hm --------------—
.г.^тД'2. \COS2 X
1 + 3 + ... + (2п — 1)
п + 3
794. hm
n-Kx>
795.	hm (1----I tg x (положить x = —h a
x^/2 \	2) & [	2
§ 6.	Смешанные примеры на вычисление пределов
Найти пределы:
ч , л/ж + 4 — 2	. ,	1 + х sin х — cos 2х
796.	1) lim	; 2 lim —---------~.
ж-ю sm 5х	ж-ю sin х
797.	1) lim ;	2) lim Л/ --------.
ж-н ^/х - 1	ано ^/1 + 2х - 1
798.	lim (-\/ж2 + ах — \/х2 — ах).
§ 7. Сравнение бесконечно малых
101
799.	1)
800.	1)
801.	1)
802.	1)
803.	1)
804.	1)
lim
1 - 2s
J/l + 8s3
. , s2 + s — 2
2) hm —--------------.
x—^ — 2 x2 + 2s
, , cos(s/2)
2 lim -------
х—^-тг S — 7Г
1 — COS X
x(y/l + X — 1)
lim
_ 21/-
1 - 2s4
^/1 + cos 2s
lim --------------=-
v:—>тг/2+О л/тг — V2s
§ 7.	Сравнение бесконечно малых
1°. Определения. Пусть при х —> а функции a(s) и /3(х) являются
бесконечно малыми. Тогда:
I.	Если lim — = 0, то /3 называется бесконечно малой высшего
х—^а а
порядка относительно а.
II.	Если lim — = А (конечен и отличен от 0), то /? называется
г-la сип
бесконечно малой n-го порядка относительно а.
Р
III.	Если lim — = 1, то /3 и а называются эквивалентными беско-
х—>а а
нечно малыми. Эквивалентность записывается так: (3 Rs а.
2°. Свойства эквивалентных бесконечно малых:
1) Разность двух эквивалентных бесконечно малых есть бесконечно
малая высшего порядка относительно каждой из них.
2) Если из суммы нескольких бесконечно малых разных порядков
отбросить бесконечно малые высших порядков, то оставшаяся часть, на-
зываемая главной, эквивалентна всей сумме.
Из первого свойства следует, что эквивалентные бесконечно малые
могут сделаться приближенно равными со сколь угодно малой относи-
тельной погрешностью. Поэтому знак Rs мы применяем как для обозна-
чения эквивалентности бесконечно малых, так и для записи приближен-
ного равенства их достаточно малых значений.
805.	Определить порядки бесконечно малых: 1) 1 — coss;
2) tgs — sin s относительно бесконечно малой s. Показать на чер-
теже, что при уменьшении угла s вдвое величина 1 — coss умень-
шается приблизительно в четыре раза, а величина tgs — sins —
приблизительно в восемь раз.
102	Гл. 5. Введение в анализ
806.	Определить порядки бесконечно малых:
1)	2 sin4 ж — х5; 2) \/sin2 х + х4; 3) д/1 + ж3 — 1
относительно бесконечно малой х.
807.	Определить порядок малости «стрелы» кругового сегмента
относительно бесконечно малой дуги сегмента.
808.	Доказать, что при х —> 0:
1)	sin тх рй тх; 2) tgms рй тх; 3) у/1 х — 1 рй -х.
809.	Коэффициент объемного расширения тела принимается
приближенно равным утроенному коэффициенту линейного рас-
ширения. На эквивалентности каких бесконечно малых это осно-
вано?
/3
810.	По теореме lim — = lim —, если а рй од, [3 ~ Д и один из
a «1
пределов существует, найти пределы:
sin 5ж	sin ax + ж2	Зж + sin2 ж
1) hm —----; 2) hm -----------; 3) hm —---------
ж-ю sin 2ж ж-ю tg ох	ж-ю sin 2ж — ж3
811.	Капля воды испаряется так, что ее радиус стремится к
нулю. Определить порядки бесконечно малых поверхности и объ-
ема капли относительно ее радиуса.
812.	Определить порядки бесконечно малых:
1)	д/1 + ж2 — 1; 2) sin 2ж — 2 sin ж; 3) 1 — 2 cos (ж +
относительно бесконечно малой ж.
813.	Доказать, что при ж —> 0: 1) arctgтх рй тх;
2)	^/1 + ж — 1 рй -ж; 3) 1 — cos3 ж рй 1, 5 sin2 ж.
§ 8.	Непрерывность функции
1°. Определение. Функция f(x) называется непрерывной при
х = а, если она определена в некоторой окрестности а и
lim /(ж) = /(а).
х—
Это определение содержит такие четыре условия непрерывности:
1)	f(x) должна быть определена в некоторой окрестности а;
2)	должны существовать конечные пределы lim f(x) и lim /(ж);
х—У а — 0	х—>а+0
3)	эти пределы (слева и справа) должны быть одинаковыми;
4)	эти пределы должны быть равны /(а).
§ 8. Непрерывность функции
103
Функция называется непрерывной на отрезке [a?i, х2], если она не-
прерывна в каждой точке внутри отрезка, а на его границах lim f(x) =
х—> ar 14-0
=/(«1) и lim f(x) = f(x2).
х—— 0
Элементарные функции: степенная хп, показательная ах, логариф-
мическая, тригонометрические и им обратные, а также их сумма, про-
изведение, частное непрерывны при всяком х, при котором они имеют
определенное значение.
2°. Разрывы функции. Функция имеет разрыв при х = а, если
она определена слева и справа от а, но в точке а не соблюдено хотя бы
одно из условий непрерывности. Различают два основных вида разрыва.
1)	Разрыв I рода — когда существуют конечные пределы lim f(x)
х—0
и lim f(x), т. е. когда выполнено второе условие непрерывности и не
х—>а+0
выполнены остальные (или хотя бы одно из них).
х — а
Например, функция у = --------, равная —1 при х < а и +1 при
|ж — а|
х > а, имеет при х = а разрыв I рода (рис. 24), так как существуют
пределы lim у = —1 и lim у = +1, но эти пределы не равны.
х—¥а— 0	х—>а+0
2)	Разрыв II рода — когда lim f(x) слева или справа равен ±оо.
х—¥а
Например, функция у = f(x) = ------ (рис. 25) имеет при х = а
х — а
разрыв II рода. Все дробные функции, знаменатель которых при х = а
Т ic. 24	|	---- I ис. 25 I _
О \а	\а
равен 0, а чис; итель не равен 0, имеют при х = а рЬ&рыв II рода.
Функция /(a;)j=: 21/® (задача 819, рис. 38 на с. 27И:) такж^ им^ет при
X = П рячрт.~Т-1 рлтгя та» ия! |И|| )'(./') = 0, НО lim f (ж) =¥хЭ. I
х—> — 0	х—О	I I
4	\ 1
814.	Указать точку разрыва функции у =---------, найтщ Aim у,
X Ч 2	Vp+2-О
lim у, lim у и построить кривую по точкам
х—>2+0	ж+±со
х = —2, 0, 1, 3, 4 и 6.
104
Гл. 5. Введение в анализ
815.	Найти точки разрыва и построить графики функций:
6	4
1)у=--; 2) у = tgs; 3) у = -------г
х	4 — ж2
816.	Построить график функции
!ж/2 при х у? 2,
0 при х = 2
и указать точку ее разрыва. Какие из четырех условий непрерыв-
ности в этой точке выполнены и какие не выполнены?
817.	Построить графики функций: 1) у = 1-----г и 2) у =
|ж + 1|
х + 1
= х + -j----. Какие из условий непрерывности в точках разрыва
\х + 1|
этих функций выполнены и какие не выполнены?
818.	Построить график функции
2 при х = 0
и указать точку ее разрыва. Какие из условий непрерывности в
ней выполнены и какие нет?
819.	Указать точку разрыва функции у = 2|/';. найти lim у,
х—> —О
lim у, lim у и построить график функции. Какие условия не-
ж-Ц-0	ж-)-±со
прерывности в точке разрыва не выполнены?
820.	Построить график функции
	' 0, 5ж2	При 2	’ < 2,
У = /(ж) = *	2,5	при |я	1 = 2,
	k 3	при |я	’ >2
и указать точки ее разрыва.
821.	Найти точки разрыва и построить графики функций
1	а	х3 — х2
^ У = ТД2^' 2)9 = arctgTXT! 3> « = ф-ц-
822.	Сколько однозначных функций задано уравнением х2 —
— у2 = 0? Определить из них: 1) четную функцию; 2) нечетную
функцию так, чтобы они имели конечные разрывы (I рода) при
х = ±1, ±2, ±3, ..., и построить их графики.
§9. Асимптоты
105
823.	Указать точку разрыва функции у =--, найти lim у,
X + 2	14-2-0
lim у, lim у и построить график по точкам х = —6, —4, —3,
ж->-2+0 ж->±со
- 1, 0, 2.
824.	Построить график функции
' 2 при х =
О и х = ±2,
|ж| < 2,
У = /(ж) =
при 0 <
при |ж| > 2
и указать точки разрыва. Какие условия непрерывности выпол-
нены в точках разрыва и какие нет?
825.	Найти точки разрыва и построить графики функций:
1)у = 2-^; 2) г/= 21/<ж-2>;	3) г/= 1 — 21/27;
х х г\ 4 — х
4>»=-ЭД-; 5),= 14Г7|-
826.	Сколько однозначных функций задано уравнением ж2 +
-|- у2 = 4? Определить из них: 1) две непрерывные на отрезке
|ж|	2; 2) ту из них, которая отрицательна на отрезке |ж|
0 и положительна для всех остальных допустимых значений х.
Построить график и указать разрывы последней функции.
§ 9.	Асимптоты
Асимптотой кривой называется прямая, к которой неограни-
ченно приближается точка кривой при ее удалении по кривой в беско-
нечность.
I.	Если lim f(x) = ±оо, то прямая х = а есть асимптота кривой
х—¥а
у = f(x). Например, кривая у = ---- имеет асимптоту х = а (рис. 25).
х — а
II.	Если в правой части уравнения кривой у = f(x) можно выделить
линейную часть у = f(x) = кх + Ь + а(ж) так, что оставшаяся часть
а(ж) —> 0, когда х —> ±оо, то прямая у = кх + Ь есть асимптота кривой,
тт	ж3 + х2 + 1	1
Примеры: 1) кривая у = ------------ = х + 1 -|---- имеет асимптоту
(Z?	X
а	а
у = х + 1 (и асимптоту х = 0); 2) кривая у = --- = О Н----имеет
х — а х — а
асимптоту у = 0 (рис. 25).
fix)
III.	Если существуют конечные пределы lim ------------- = к и
г->+оо или-оо х
lim [/(ж) ~ кх] = к, то прямая у = кх + Ь есть асимптота.
X —>4-00 ИЛИ —00
4
827.	Определить асимптоты кривой у = 1 — — и построить
х2
кривую по точкам х = ±1, ±2, ±4.
106
Гл. 5. Введение в анализ
В задачах 828-830 найти асимптоты кривых, выделив из дроби
линейную целую часть; построить асимптоты и кривые:
2,т	2	2
ООО 11	х + 1	Х	Q\	х
828.	1 у=——; 2)у= —у;	3 у = Г-
х	X Т	X + 1
ооо п _ 2 i	_ х2 - х - 1 х _ ax + b
829.	1) у — । ।	1, 2) у —	, 3) у —	.
tZ/	tZ/	lib |	/ v
ooa n 1 - 4®	... x3	ч 4ж - ж3
830.	1) у = . , n ; 2) у =	;	3) у = —5.
,У 1 + 2®’ ,y х2 + Г ,У x2 + 4
Найти асимптоты кривых и построить кривые:
831.	1) х2 — у2 = а2;	2) х3 + у3 = Заху;
3)	у = х — 2 arctg х; 4) у = arctg Ж .
832.	1) у = Vx2 + 1 - Vx2 - 1;
2)	у = V®2 + 1 + V®2 — 1; 3) у = х — —j=.
+ + 1	х3 + х2 — 2
833.	Построить кривые: 1) у = -----; 2) у = --------- и
Зх	х + 1
параболы, к которым эти кривые асимптотически приближаются.
2
834.	Найти асимптоты кривых: 1) у =
4---- и построить кривые по точкам х = +-, ±1, ±2.
ж2	2
835.	Найти асимптоты кривых и построить кривые:
_ Л	Л	™3
tZ/	.	tZ/
2^4’ )//=Т^74'
1)у=-—- 2}у= —---; 3) у =
,У 2®+ 4’ ,У 2-2®’ ,У
§10. Число
Числом е называется предел
lim | 1 4---)
п->оо у nJ
lim (1 + n)1/" = е.
а—>0
Это число иррациональное и приближенно равно е = 2,71828. . . Ло-
гарифмы с основанием е называются натуральными и обозначаются
loge х = In х.
Десятичный логарифм: 1g ж = Mln®, где М = 0,43429. . .
§ 10. Число е
107
Найти пределы:
836.	lim I 1-----) (положить------= а).
п^гсо \ П J	п
\ П	/	\ «+3
1------) ; 2) lim I 1 + - I
Зп/	п->-со у nJ
838.1) lim (1 + 2хУ^х;
х—>0
2) lim (1 — 4ж)(х х)/х.
х—>0
839. 1) lim --------
n-Юо \ п + 1
2х - 1\
2. г + 1 j
2х
84	0.1) lim n[ln (п + 3) — In n]; 2) lim (1 + 3 tg2s)ctg2a;.
841.	lim (coss)ctg2a; (положить sin2 x = a),
x—>O
. , In (1 + a) . , e — 1
842.	1) hm -----------; 2) hm ------------; 3) hm
а—Ю	CH	x—ю	X	x—>0
Указание. В примере 2) положить е х — 1 = а.
843.	Найти последовательные целые числа, между которыми
содержится выражение 6(1 — 1, 01“ 10°).
Найти
пределы:
/ o \ 3n
п/2
844. 1)
lim
lim
2х
p-3x _ i
lim ------.
x-m	x
846. hm (sin 2s)tg 2x (положить cos2 2s = a).
x—>тг/4
. , t
847. 1) hm —---------:
7 wo In (1 + xt)
845. 1)
lim
n п — In (n + 2)].
Глава 6
ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ
§ 1. Производные алгебраических
и тригонометрических функций
1°. Определения. Производной функции у = f(x) в точке х на-
зывается предел
f(x + Аж) - f(x)
пт —----------
Длт->0	Дж
г Аг/
lim ——.
Длт->0 Дж
(1)
Если этот предел конечный, то функция f(x) называется дифферен-
цируемой в точке х; при этом она оказывается обязательно и непрерыв-
ной в этой точке.
Если же предел (1) равен +оо (или —сю), то будем говорить, что
функция f(x) имеет в точке х бесконечную производную, однако при
дополнительном условии, что функция в этой точке непрерывна.
и	к	/ еы \ dV
Производная обозначается у или j (ж), или —, или —-—.
ах	ах
ждение производной называется дифференцированием функции.
2°. Основные формулы дифференцирования:
Нахо-
1) (с)' = 0;	2) (ж")'
4) (и + v)' = и' + и1-,
8) (sin ж)' = cos ж;
Ю) (tg«)' =
1
cos2 ж ’
= пхп \	3) (си)' = си';
5) (ии)' = и'v + uv';
7) (^У =
2уж
9) (cos ж)' = — sin ж;
И) (ctgz)' = —•
sin ж
Ay
848. Вычислением hm —— найти производные функций:
Дж-Ю Дж
1) у = х3;	2) у = х4;	3) у = уТ;	4) у = sin х;
.1.1 .1 .
5)у=-;	6) у =	Г)у=—-	8)y = tgs;
9)у=^; 10) у = 71 + 2ж; И)у=^Г_;
12) у = V1 + ®2.
§ 1. Производные алгебраических и тригонометрических функций 109
Найти по формулам производные функций:
ж3 849. 1) у =	- 2ж2 + 4ж - 5 О	
850. 1) у=^--^- + х- О	о	/	2\ 2 2) У = (1 - y) •
851. 1) у = ж + 2-Уж;	2) У = (л/a - /7 )2 .
.	10	. 1 1 1
852. 1)у=-- ,г‘	2) У — —1	у 4	у ж ж2 ж3
853. 1) у = ж +	- -*т; гр	гр О	2) у = Зж — 6-\/ж.
854. 1) у = 6\/ж-4^/ж;	/ 1 \ 2 2)У= 1-1Й • \	Vх /
. 1 1	.	8	6
855. 1) у = —		- 2ж2 Зж3	2 У = ~п= - ~^=- ч/ X	/ X
856. 1) у = ж — sin ж;	2) у = ж — tgж.
857. 1) у = ж2 cos ж;	2) у = ж2 ctgж.
ч	COS X	ж2
858. 1 у= —г- X1	У~ ж2 + Г
859. 1) у =	\ ; ’ у 1 - 4ж ’	2)9=W-
860 11 fix']	cosx .	21 сИж!
7V/	1 — sm х	И } “ ^+Г
861. 1) 8 =	2) ж = a(t — sin t).
862.	/(ж) =----ж2 + х; вычислить /'(0), У’/(1), /'( —1).
3
863.	/(ж) = ж2 — вычислить /'(2) — /'( — 2).
Г /ж — I)2
864.	/(ж) = -------; вычислить 0, 01 • f'(0, 01).
Найти производные функций:
865.	1) у = (а — 6ж2)3;	2) у = (1 + \/ж)2.
а 11.32
866.	1 у= —; 2 у=
10ж&	4ж4	ух Jx
по
Гл. 6. Производная и дифференциал
867.	1)	у	=	х + sin х;	2)	у	=	х + ctg х.
86	8.1)	у	=	ж2 sin х-	2)	у =	х2 tg х.
/2
869.	1)	у	=	у/х cos ж;	2)	s =	— j-
870.	1)	у	=	ж — |	2)	у	=4^-
х Зх'5	xz + 1
/ I \ з
1 \	/ -1 ,	1	\	cos X
871.	1) у — ( 1 -р .— ] : 2) у — т; j п ;	.
J \	^/х J J	1 + 2 sm х
872.	/(ж) = найти /'(— 8).
873.	/(ж) =	найти /'(0), /'(2) и /'(-2).
§ 2. Производная сложной функции
Если у = f(u), а и = <р(х), то у называется функцией от функции
или сложной функцией от х. Тогда
dy dy du
dx du dx
или у' = f'(u)  и'.
(1)
Формулы предыдущего параграфа примут теперь общий вид:
1) («")' = nu"-1u/;	2) (sin и)' = cos и • и';
и'
3) (cos и)' = — sin и • и'; 4) (д/й)' =	;
2л/ «
11?
5)(tg«)'= -----;	6) (ctg и)'= —.
cos2 и	sm и
Найти производные функций:
874.	1) у = sin 6ж;
875.	1) у = sin + cos
876.	1) у = (1 - 5ж)4;
877.	1) у =	1	;
(1 — ж2)&
878.	у = ч/2® — sin 2ж.
2) у = cos (а — &ж).
2) у = 6 cos —.
3
2) у = W + Зж)2.
2) у = VI —ж2;	3) у = ч/СО84ж
879. у = sin4 ж = (sin ж)4.
880. 1) у = sin2 ж; 2) у = cos2 ж; 3) у = sec2 ж.
881. у = sin3 ж + cos3 ж. 882. у = tg3® — 3 tg ж + Зж.
883. у = \/Т + cos2 ж.
884. у — sin
§ 3. Касательная и нормаль к плоской кривой
111
885. у = Vl + sin 2® — у/1 — sin 2s.
886‘ = П । 1 л 15- 887- У = ctg3|-
(14-cos4s)&	3
ООО sin2 х	ооп	гт> -
888. у = ------.	889. у = хм х1 — 1.
cos х
\/2х — 1	9 t
890. у = --------.	891. s = a cos2 —.
х	a
892.	1) г = ay/cos 2^?;	2) г = ^2^ + cos2 + —
893.	f(t) = л/а2 + fr2 — 2а6cost; вычислить
X Чтг \
/ЪМ /'И, f’//-/
894.	/(ж) = у/ х + 2л/х; найти /'(1).
Найти производные функций:
895.	у = а/4ж + sin 4s.	896. у = х2у/1 — s2.
897. у = sin4 s + cos4 s. 898. у =	4- cos 6s.
2	1
899. 1) у = tg s 4— tg3s 4— tg5s; 2) у = sin2 s3.
3	5
900. у =
1 4- sin 2s
1 — sin 2s ’
a/4s 4- 1
s2
904. f(t) = a/1 4- cos2/2: найти f
§ 3. Касательная и нормаль к плоской кривой
Угловой коэффициент касательной к кривой у = f(x)
в точке кривой (sq; Уо) равен значению производной функции f(x) в
точке xq:
k = tgp = f'(x0) = у'\х=Хо.	(1)
Число к называют иногда наклоном кривой в точке (sq; Уо)-
Уравнение касательной в точке M(xq; уф) на кривой (рис. 26):
у - уо = к(х - х0).	(2)
112
Гл. 6. Производная и дифференциал
Уравнение нормали:
У - Уо = ~т(х - ж0),
к
(3)
где к определяется формулой (1).
Отрезки ТА = уо ctg р, AN = уо tg р (рис. 26) называются соот-
ветственно подкасательной и поднормалью, а длины отрезков МТ и
MN — длинами касательной и нор-
905. Найти наклоны параболы
: х2 в точках х = ±2.
906. Написать уравнение каса-
тельной и нормали к параболе у =
= 4 — ж? в точке пересечения ее с
(при х > 0) и построить
параболу, касательную и нормаль.
Рис. 26
ньк:
в
-1.
х3
— в точке х =
)07. К крр1ВОЙ
ных г кривым и
задачах 907-910 написать
строить кривые и касатель-
g
909.	К локону у = ------ в точке х = 2.
910.	К синусоиде у = sin х в точке ж = 7Г.
911.	Под каким углом кривая у = sin х пересекает ось Ох?
912.	Под каким углом пересекаются кривые
2// = х2 и Ту = 8 — ж2?
913.	Найти длину подкасательной, поднормали, касательной и
нормали кривой: 1) у = ж2; 2) у2 = ж3 в точке ж = 1.
914.	Доказать, что подкасательная параболы у2 = 2рж равна
удвоенной абсциссе точки касания, а поднормаль равна р.
915.	В уравнении параболы у = ж2 + Ьх + с определить бис,
если парабола касается прямой у = ж в точке ж = 2.
916.	Написать уравнения касательных к гиперболе ху = 4 в
точках Ж1 = 1 и Ж2 = —4 и найти угол между касательными.
Построить кривую и касательные.
§4. Случаи недифференцируемости непрерывной функции 113
В задачах 917-919 написать уравнения касательных к кривым
и построить кривые и касательные к ним:
917.	у = 4ж — ж2 в точках пересечения с осью Ох.
918.	у2 = 4 - х в точках пересечения с осью Оу.
919.	у2 = (4 + х)3 в точках пересечения с осями Ох и Оу.
920.	Найти расстояние вершины параболы у = х2 — 4ж + 5 от
касательной к ней в точке пересечения параболы с осью Оу.
921.	Под каким углом прямая у = 0,5 пересекает кривую
у = cos ж?
922.	В какой точке касательная к параболе у = х2 + 4ж парал-
лельна оси Ох?
923.	В какой точке параболы у = ж2 — 2ж + 5 нужно прове-
сти касательную, чтобы она была перпендикулярна к биссектрисе
первого координатного угла?
924.	Найти длину подкасательной, поднормали, касательной и
2
нормали кривой у = ------- в точке ж = 1.
1 _|_
ж2
925.	Какие углы образует парабола у = — с ее хордой, аб-
сциссы концов которой равны 2 и 4?
§ 4.	Случаи недифференцируемости
непрерывной функции
1°. Угловая точка. Точка А(ху г/i) кривой у = f(x) (рис. 27)
называется угловой, если в этой точке производная у' не существует,
но существуют левая и правая различ-
г	I.
ные производные: пт -— = ki и
Дж->-о Дж	у/ :
Дг/	J
lim —— = k’2- Из угловой точки вы-
ходят два касательных луча с наклонами
ki и /.Д,
2°. Точка возврата с верти-
кальной касательной. Точка
В(х2', г/г) (рис. 27) называется точкой
возврата с вертикальной касательной,
если в этой точке производная у' не су-
ществует, но существуют левая и пра-
вая бесконечные производные разного
Рис. 27
знака (+оо и —сю). Такая точка является частным случаем ^гловой. Из
нее выходит один вертикальный касательный л гч или, мо
что из нее выходят два слившихся касательных
3°. Точка перегиба с вертикально!
ка С(ху, уз) (рис. 27) называется точкой nept
касательной, если в ней существует б0конечная
|но считать,
луча. 1
касательной. Точ-
114
Гл. 6. Производная и дифференциал
/ г ~^У г ~^У	।	(	\ |>
у' = lim —— = lim —— = +оо (или —сю). В такой точке сущест-
Дж->-о Дж Дж-ц-о Дж
вует вертикальная касательная.
В точках А и В функция у = f(x) не имеет производной; в точке
С она имеет бесконечную производную. Во всех трех точках функция
непрерывна, но недифференцируема.
926.	Построить график функции у = a/ж2 (или у = |ж|) и найти
левую у'_ и правую у'+ производные в угловой точке графика.
927.	На отрезке [0, 4] построить график функции у = 0,5х
X у/ (х — 2)2 и найти левую у'_ и правую у'+ производные в угловой
точке графика функции.
928.	На отрезке [—7Г, 7г] построить график функции у = Vsin2 х
и написать уравнения касательных в угловой точке кривой.
929.	На отрезке [0, 2тг] построить график функции у = а/Г+созж,
написать уравнения касательных в угловой точке кривой и найти
угол между ними.
930.	На отрезке [—2, 2] построить график функции у = \/ИА и
написать уравнение касательной в точке х = 0.
931.	На отрезке [0, 4] построить график функции у = 1 —
— у/ (х — 2)2 и написать уравнение касательной к ней в точке
х = 2.
932.	На отрезке [—2, 2] построить кривую у3 = 4ж и написать
уравнение касательной к ней в точке х = 0.
933.	На отрезке [0, 4] построить кривую у3 = 4(2 — ж) и напи-
сать уравнение касательной к ней в точке х = 2.
934.	На отрезке [0, 7г] построить график функции у = 1 —
— Vcos2 х и написать уравнения касательных к кривой в угловой
точке.
935.	На отрезке [—2, 0] построить график функции у =
= -у/(ж + I)2 — 1 и написать уравнение касательной к кривой в
точке ж = — 1.
936.	На отрезке [—1, 5] построить график функции у = |4ж — ж2|
и написать уравнения касательных в угловой точке ж = 0 и найти
угол между ними.
§ 5. Производные логарифмических
и показательных функций
Основные формулы:
и?
(фиу = —- (еиу = еи-и1-, (аиу = аи1па-и'.
§ 5. Производные логарифмических и показательных функций 115
1 + 2s
1 - 2s’
Найти производные функций:
937.	1) у = х In х; 2) у = —•—---;	3) у = 1g (5s).
2	1
938.	1) у = In х-------2) у = In (х2 + 2s).
s 2s2
839. 1) у = In (1 + cos s);	2) у = In sin s — - sin2 s.
940. у = In (^/s + y/x + 1).
a2 + s2	s2
941. у = In —----942. у = In -------------
(!/ — S2	1 — S2
943. у = In tg ) . 944 у = In
945.	у = In (s + л/a2 + s2) •
946.	у = 2^/s — 4 In (2 + y/x).
.	COSS , S	X“
947.	1) у = +lntg-; 2)y = ln —
sin's 2	v 1 - as4
948.	Написать уравнение касательной к кривой у = In х в точке
пересечения ее с осью Ох. Построить кривую и касательную.
s2
949.	Показать, что парабола у = — касается кривой у = 1ns,
2е
и найти точку касания. Построить кривые.
Найти производные функций:
950.	1) у = s2 + 3х- 2) у = s2 • 2Ж; 3) у = х2ех.
951.	1) у = а81ПЖ; 2) у = е х2-	3) у = х2е 2х.
952.	у = 2(еж/2 — е-ж/2). 953. у = у/хе^.
1 + ех	, х
954. у = -------.	955. у = ex'a cos —.
1 — ех	а
956. 1) у = е~х(sins + coss); 2) у = In (е х + хе х').
957. у = In ------.	958. у = (еах - е~ах}2.
У s2 + l	1	’
959.	/(£) = In (1 + a~2t); найти /'(О).
960.	Под каким углом кривая у = е2х пересекает ось Оу?
961.	Доказать, что длина подкасательной в любой точке кривой
у = ех/а равна а.
116	Гл. 6. Производная и дифференциал
962.	Предварительным логарифмированием найти производ-
ные функций: 1) у = Xх; 2) у = ж81ПЖ.
Найти производные функций:
,	1	7
963.	у = m cos х — - cos
|	у/g.2 _i_
964.	у = In (Дх - y/x - 1).	965. у = In ——-------—
966.	у = In (sin x + \/l + sin2 XY
x	1
967.	у = In	:.	968. у = - In tg x + In cos x.
yl — s2	2
969. у = In
sin 2s
1 — sin 2s
970. у = In (1 + sec s).
971.	у = a In (-^/s + a + ^/s) — V®2 + ax.
972.	у = ae~x/a + xe~x!a. 973. у = |(еж/“ + е~хД.
974. у =e +e—.	975. у = In (е2ж + у/e4x + 1).
еж _ e-x
976. у = In
977. у = xx!x.
978. /(£) = In	найти /'(тг/З).
979. Написать уравнение касательной к кривой у = 1 — <J'/2 в
точке пересечения ее с осью Оу. Построить кривую, касательную
и асимптоту кривой.
§ 6. Производные обратных тригонометрических функций
/	• V	«'	/	V	«'
arcsin и = —,	; arccos u =-- ;
v 7	Vi^2	v	7
.	, u'	. u'
arctg u =——arcctgu =
1 + uz	1 + uz
Найти производные функций:
980. у = \/Т — s2 + arcsin s.
§ 7. Производные гиперболических функций
117
981. у = х — arctg ж.
982. у = arcsin -\/1 — 4ж.
983. у = arcsin —.
а
985. у = arccos (1 — 2s).
984. у = arctg —.
а
1 +
986. у = arcctg -—
987. 1) у = х\/1 — х2 + arcsin ж; 2) у = arcsin (е3j ).
988. у = arctg х + In \	.	989. у = arccos —=.
V 1 — X	у/Х
X а / 9	9\
990.	у = х arctg------- m (ж + а ).
Найти производные функций:
991.	у = arcsin у/х. 992. у = arctg Сбж — 1.
993.	1) у = arccos (1 — ж2);	2) у = arcctgж-----.
994.	у = < ' \/1 — <2х + arcsin ех.
995.	у = ж arccos ж — V1 — х2.
996.	у = arctg е2х + In
997.	s = л/47 — t2 + 4 arcsin .
998.	у = arccos у/1 — 2. г + л/2ж — 4ж2.
999.	f(z) = (г + l)arctge-2^; найти /'(О).
е2х + 1
е2ж - Г
§ 7.	Производные гиперболических функций
ех —е~х ех + е~х
1.	Определения. Выражения --------, ----- и их отноше-
ния называются соответственно гиперболическими синусом, косинусом,
тангенсом и котангенсом и обозначаются
ех — е х	ех + е х	sh х	ch ж
sh х = --------, ch х = ----------, th х = ——, cth x = ——
2	2	ch ж	sh ж
2°. Свойства гиперболических функций:
1)	ch2 ж — sh2s = l; 4) sh 0 = 0, ch 0 = 1;
2)	ch2 ж + sh2 ж = ch 2ж; 5) (sh х)' = ch ж, (сЬж)/ = 811ж;
3)	sh 2ж = 2 sh ж ch ж; 6) (th ж)' = —_—, (cth ж)' =-_—•
7	! V ! ch2 ж V ! sh2 ж
118
Гл. 6. Производная и дифференциал
Найти производные функций:
1000.	1) у = sh2 ж; 2) у = х — th ж; 3) у = 2Veh ж — 1.
1001.	/(ж) =	sh — + ch —;	найти	/'(0) + /(0).
1002.	1) у =	In [ch ж];	2)	у =	th ж + cth ж.
1003.	1) у =	ж — cth ж;	2)	у =	In [th ж].
1004.	1) у =	arcsin [th ж];	2)	у =	\/1 + sh2 4ж.
a /	/	ж
1005.	Линия у = — (ех'а + е~х'а) = асп — называется цепной.
Написать уравнение нормали к этой линии в точке ж = а. Постро-
ить кривую и нормаль.
1006.	Написать уравнение касательной к кривой у = sh ж в
точке ж = —2. Построить кривую и касательную к ней.
1007.	Доказать, что проекция ординаты любой точки цепной
, х
линии у = a ch — на ее нормаль есть величина постоянная, рав-
а
ная а.
§ 8. Смешанные примеры и задачи
на дифференцирование
Найти производные функций:
ч V®2 — 1	1 ч 1г2ж
1008.	1) у = --------h arcsin —; 2) у =--------h In cos ж.
ж	ж	2
1009.	у = ф\х - 1 + arcctg ^4ж — 1.
1010.	ж = In (e2t + 1) — 2 arctg (е*).
1011.	у = 4 In (V® — 4) + V®2 — 4ж.
1012.	s = tg4t — | tg2t — In (cos t).
1013.	/(ж) = (ж2 + a2) arctg-аж; найти
Г «21
1014.	1) у = In ж----;	2) у = ж (cos In ж + sin In ж).
1015.	/(ж) = arcsin-------; найти /'(5).
1016.	у?(м) = e~“/“ cos —; показать, что </?(0) + а<//(0) = 0.
§9. Производные высших порядков	119
1017.	/(у) = arctg - — In у/у4 — а4; найти f'(2a).
1018.	F(z) = -------5—; показать, что F (—— 3F1 (—= 3.
V 7	1 + sin2 г	\4/	\4/
1019.	Показать, что функция s = —--- удовлетворяет диффе-
t m ct
ds	9
ренциальному уравнению t-----h s = —ts .
dt
t - e~t2
1020.	Показать, что функция x = ——— удовлетворяет диф-
dx	,2
ференциальному уравнению t——\-2х = е .
dt
§ 9. Производные высших порядков
Пусть мы нашли для функции у = f(x) ее производную у1 = f(x).
Производная от этой производной называется производной второго по-
d2y
рядка функции fix) и обозначается у" или f"(x) или —Аналогично
dx2
определяются и обозначаются
производная третьего порядка у1" = f"'(x) =
d3y
dx3 ’
производная четвертого порядка t/IV = /IV (ж) =
и вообще
уп у
производная п-го порядка t/") = /^(х) =
d4y
dx4 ’
1021.	Найти производную второго порядка функции:
1) у = sin2 ж; 2) у = tg ж; 3) у = 71 + ж2.
1022.	Найти производную третьего порядка функции:
1)	у = cos2 ж; 2) у = —;	3) у = ж sin ж.
1023.	Найти производную третьего порядка функции:
1)	у = ж In ж; 2) s = te-t; 3) у = arctg —.
t ,—у	t	d3s
1024.	s = -V2 — t2 + arcsin —=\ найти .
2	72	dt3
Найти производную n-го порядка функции:
1025.	1) е~х/а- 2) In ж; 3) у/х.
1026.	1) ж":	2) sin ж; 3) cos2 ж.
120	Гл. 6. Производная и дифференциал
1027.	Последовательным дифференцированием вывести фор-
мулы Лейбница:
(uv)" = u"v + 2u'v' + uv";
(uv)"' = u"'v + 3u"v' + 3wV' + uv"’;
(w)IV = mivv + 4u"'v' + 6u"v" + 4u'v"' + wIV и т. д.
1028.	По формуле Лейбница найти производную второго по-
рядка функции:
1) у = ех cos ж; 2) у = ахх3; 3) у = ж2 sin х.
1029.	По формуле Лейбница найти производную третьего по-
рядка функции:
1) у = е~х sin х; 2) у = ж2 In х; 3) у = х cos ж.
1030.	/(ж) = хех?а; найти /"'(ж), /И(ж), /И(0).
1031.	/(ж) = (1 + ж)т; найти /(0), /'(0), /"(0), /"'(0), ...
•••, /(п)(°)-
1032.	/(ж) =	; показать, что при п 2
у 1 -J- ж
1033.	f( ж) = ---показать, что
J V ’	1-х2'
= fn! при " = 2"'-
2	' '	[0 при п = 2т—1.
Указание. Применить тождество
1 - 1 ( 1	1 А
1 — ж2 2\1 + ж”'~1 — х J
1034.	Продифференцировав тождество (ж — 1)(ж2 + ж3 + ...
... + ж" ) = жп+1 — ж2 три раза по ж и положив затем ж = 1, найти
А , х (п + 1)п(п - 1)
сумму цк - 1) = -	---- и затем сумму квадратов
k=i	з
чисел натурального ряда
Е 9	9	9	9	TL (п -|“ 1) (2TL -|“ 1)
к2 = 12 + 22 + ... + п2 = v л
6
к=1
1035.	Найти производную второго порядка функции:
\	_ 2	х	х	. X
1)	у — е ; у — ctgж; 3) у = arcsm —.
§ 10. Производная неявной функции	121
1036.	Найти производную n-го порядка функции:
1)у = аж; 2) у =	3)y = sin2x.
1037.	/(ж) = arcsin —; найти /(2), f'(2) и f"(2).
1038.	По формуле Лейбница найти производную третьего по-
рядка функции:
1) у = х3ех; 2) у = ж2sin—;	3) у = xf'(a — ж) + 3/(а — ж).
1039.	Показать, что функция у = е^созж удовлетворяет диф-
ференциальному уравнению yIV + 4у = 0.
1040.	Показать, что функция у = же-1/ж удовлетворяет уравне-
нию х3у" — ху1 + у = 0.
уу f уу _ 1 1 f_
1041.	/(ж) = ж2е-Ж//“; показать, что /W(0) = -3—п_2	’ •
1042.	/(ж) = е~х ; показать, что
/Ь)(о) = —2(п - 1)/(п-2>(0), /(2т-!)(0) = 0,
/2т(0) = (—2)"'(2ш - 1)(2т - 3) •... • 5 • 3 • 1.
1043.	/(ж) = ж": показать, что
/(1) + £Ш + ф + ... + 44ф)=2Л.
§ 10.	Производная неявной функции
Если уравнение F(x, у) = 0, неразрешенное относительно у, опреде-
ляет у как однозначную функцию х, то у называется неявной функцией
х. Чтобы найти производную у1 этой неявной функции, нужно обе части
уравнения F(x, у) = 0 продифференцировать по ж, рассматривая у как
функцию от х. Из полученного уравнения найдем искомую производную
у1. Чтобы найти у", нужно уравнение F(x, у) = 0 дважды продиффе-
ренцировать по ж и т. д.
Найти у' из уравнений:
ж2 и2
1044.	1) ж2 + у2 = а2;	2) у2 = 2рх; 3)	— — = 1.
а2 о2
1045.	1) ж2 + жу + у2 = 6;	2) ж2 + у2 — ху = 0.
1046.	1) ж2/3 + у2/3 = а2/3; 2) еу — е~х + жу = 0.
1047.	ех sin у — е у cos ж = 0.
122	Гл. 6. Производная и дифференциал
1048.	х = у + arcctg у.
1049.	еху — х2 + у3 = 0; найти —— при х = 0.
dx
1050.	Найти у” из уравнений:
1)	х2 + у2 = а2;	2) ax + by — ху = с; 3) хтуп = 1.
х2 ц2
1051.	— + — = 1; найти у” в точке (0; 6).
а2 Ь2
1052.	Написать уравнения касательных к кривой ж2 + у2 + 4ж —
— 2у — 3 = 0 в точках пересечения ее с осью Оу.
1053.	Найти точки пересечения нормали гиперболы х2 — у2 = 9,
проведенной из точки (5; 4), с асимптотами.
1054.	Написать уравнение касательной в точке (ж0; у0) к кри-
вой:
х2 и2
1)	+ ?2 =!; 2) у2 = 2рж-
а2 Ь2
1055.	Написать уравнения касательных к астроиде ж2/3+у2/3 =
= а2/3 в точках пересечения ее с прямой у = х.
1056.	Под каким углом пересекаются кривые
х2 + у2 = 5 и у2 = 4ж?
1057.	Найти у' из уравнений:
х2 и2
1)	“Т + 77 = 1;	2) х3 + у3 - Заху = 0.
а2 Ь2
1058.	Найти у" из уравнений:
1)	х2 — у2 = а2;	2) (ж — а)2 + (у — /З)2 = R2;
3)	arctgу = х + у; 4) х2 + ху + у2 = а2.
1059.	Написать уравнения касательных к окружности х2-\-у2 +
+ 4ж — 4у + 3 = 0в точках пересечения ее с осью Ох. Построить
окружность и касательные.
1060.	Написать уравнение касательной к эллипсу ж2 + 4у2 = 16
в точке, в которой делится пополам отрезок касательной, отсечен-
ный осями координат, и которая лежит в первой четверти.
ds
1061.	te~s!2 + se-^2 = 2; найти — при t = 0.
dt
dx
1062.	i In ж — ж In i = 1; найти — при t = 1.
’ dt F
1063.	ж2 sin у — cos у + cos 2// = 0; найти у' при у = 7г/2.
§11. Дифференциал функции
123
§ 11. Дифференциал функции
Если функция у = f(x) дифференцируема в точке х, т. е. имеет в
/	Л£/	/ ,	v о
этой точке конечную производную у , то —— = у + а, где а —> О при
Аж
Аж —> 0; отсюда
Аг/ = у' Аж + а Аж.	(1)
Главная часть у'Ах приращения Аг/ функции, линейная относи-
тельно Аж, называется дифференциалом функции и обозначается dy:
dy = у1 Ах.	(2)
Положив в формуле (2) у = ж, получим dx = ж'Аж = 1 • Аж = Аж, и
поэтому
dy = у' dx.	(3)
Формула (3) верна и в том случае, если ж есть функция новой пере-
менной t.
Из (1) следует, что Аг/ Ай dy, т. е. при достаточно малом dx = Аж
приращение функции приближенно равно ее дифференциалу.
В частности, для линейной функции у = ах + Ь имеем: Аг/ = dy.
Найти дифференциалы функций:
1064.	1) у = хп-	2) у = х3 — Зж2 + Зх.
______	„^2
1065.	1) у = л/1 + х2;	2) s =
1066.	1) г = Др — sin 2^?;	2) х = —.
1067.	1) d(sin21);	2) t/(l — cosm).
1068.	1) d (- + arctg —2) d(a + In a);
3)	d (cos ;	4) d ^arcsin —.
1069.	Нахождением дифференциала каждого члена уравнения
dy
найти — из уравнений:
dx
1) х2 + у2 = а2;	2) ху = а2;	3) х2 — ху — у2 = 0.
1070.	1) у = ж2; найти приближенно изменение у (фАу ай dy),
когда х изменяется от 2 до 2,01; 2) у = у/х; найти приближенно
изменение у, когда х изменяется от 100 до 101.
1071.	1) Сторона куба х = 5м±0,01м. Определить абсолют-
ную и относительную погрешность при вычислении объема куба.
124
Гл. 6. Производная и дифференциал
/	2/2\
2) Длина телеграфного провода s = 2i> ( 1 Д-— ), где 26 —
\ Зо2 /
расстояние между точками подвеса, a f — наибольший прогиб.
На сколько увеличится прогиб /, когда провод от нагревания удли-
нится на ds?
1072.	1) С какой точностью нужно измерить абсциссу кривой
у = х2у/х при х 1, чтобы при вычислении ее ординаты допу-
стить погрешность не более 0,1?
2) С какой относительной точностью нужно измерить радиус
шара, чтобы при вычислении объема шара допустить погрешность
не более 1 %?
1073.	Определить приближенно: 1) площадь кругового кольца;
2) объем сферической оболочки. Сравнить с их точными значени-
ями.
Найти дифференциалы функций:
1074.	1)	у =-----2)	г = cos (а — Ьф);	3)	s = а/1 — 72-
1075.	1)	у = In cos х;	2)	г = arctg— 1;	3)	s = e~2t.
1076.	1)	d(y/x + 1);	2)	d(tga — а);	3)	d(bt — e-W).
1077.	1) у = ж3; определить Ay и dy и вычислить их при
изменении ж от 2 до 1,98.
2)	Период колебания маятника Т = 2д-y/Z/980 с, где I — длина
маятника в сантиметрах. Как нужно изменить длину маятника
I = 20 см, чтобы период колебания уменьшился на 0,1с?
3)	С какой точностью нужно измерить абсциссу кривой ху =
= 4 при х 0,5, чтобы при вычислении ее ординаты допустить
погрешность не более 0,1?
§ 12.	Параметрические уравнения кривой
Пусть кривая задана параметрическими уравнениями х = f(t) и
у = Обозначая точками производные по параметру, найдем:
dy _ У	d2y _ d(j)/x) _ ух - ху
dx х’ dx2 dx	х3
1078.	Построить кривые по параметрическим уравнениям:
1	t3
1)	х = t2, у = -t3;	2) х = t2, у = —— t.
Исключив из уравнений t, написать уравнение каждой кривой в
обычном виде: F(x, у) = 0.
§12. Параметрические уравнения кривой
125
Привести к виду F(x, у) = О (или у = /(ж)) уравнения кри-
вых, заданных параметрически:
1079.	1) х = a cost, y = bsint;
2)	х = acos3t, у = asin3t.
x e* + e~f F - e~f
1080.	1) x = -------, у = --------:
’	2 y 2
2) x = tgt, у = cos2 t.
1081.	Построить «развертку», или «эвольвенту», круга (см. за-
дачу 368)
х = a(cos t + t sin t), у = a(sin t — t cos t),
давая t значения: 0, д/2, 7Г, Зтг/2, 2тг.
1082.	Положив у = xt, получить параметрические уравнения
«декартова листа» х3-\-у3 — Заху = 0 (см. задачу 366) и исследовать
движение точки по кривой при монотонном изменении t: 1) от 0
до +сю; 2) от 0 до —1; 3) от —сю до —1.
1083.	Написать уравнение касательной к циклоиде (см. задачу
367) х = a(t—sin t), у = а(1 —cost) в точке, где t = тг/2. Построить
кривую и касательную.
1084.	Написать уравнение касательной к гипоциклоиде (астро-
иде) х = acos3t, у = asin3t в точке t = тг/4. Построить кривую и
касательную.
Указание. Для построения кривой составить таблицу значений х
и у при t = 0; тг/4; тг/2; Зтг/4 и т. д.
</2у
1085.	Найти из уравнений:
ах2
1)	х = a cost, у = asint;
t3
2)	х = t2, у = —— t;
3)	х = a(t — sin t), у = a(l — cos t).
1086.	Построить кривые, заданные параметрическими уравне-
ниями:
1) х = 2t — 1, у = 1 — 4t2;	2) х = t3, у = t2 — 2,
найдя точки пересечения их с осями координат и заметив, что для
<7у
второй кривой — = сю при t = 0. Написать уравнения кривых в
ах
виде F(x, у) = 0.
126
Гл. 6. Производная и дифференциал
1087.	Написать уравнение касательной к циклоиде
х = a(t — sin i), у = а(1 — cos i)
в точке t = Зтг/2. Построить кривую и касательную.
1088.	Написать уравнение касательной к развертке круга
х = a(cos t + t sin i), у = a(sin t — t cos i)
в точке t = 7t/4.
<72//
1089.	Найти из уравнений:
dx2
l)® = 2cos£, y = sint; 2) x = t2, y = t + t3;
3) x = e2t, у = e3t.
Глава 7
ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
Пусть точка движется по
х = f(t). Тогда в момент t
§ 1. Скорость и ускорение
Ох и в момент t имеет координату
оси
dx
dt ’
dv
dt
скорость v = lim —— = 
At->o Ш
Ar
ускорение w = lim —— =
At->o AZ
1090.	Зенитный снаряд выброшен вертикально вверх с началь-
ной скоростью а м/с. На какой высоте х он будет через t се-
кунд? Определить скорость и ускорение движения снаряда. Через
сколько секунд снаряд достигнет наивысшей точки и на каком рас-
стоянии от земли?
t3
1091.	Тело движется по прямой Ох по закону х = —— 2Z2 + 3Z.
Определить скорость и ускорение движения. В какие
тело меняет направление движения?
1092.	Колебательное движение материальной точки
ется по закону х = a cos cot. Определить скорость и ускорение
движения в точках х = ±а и х = 0. Показать, что ускорение
d2x
Ht2 и
d2x
dt2
1093.	Вращающееся маховое колесо, задерживаемое тормозом,
за t секунд поворачивается на угол р = а + bt — ct2, где а, b и
с — положительные постоянные. Определить угловую скорость и
ускорение вращения. Когда колесо остановится?
1094.	Колесо радиуса а катится по прямой. Угол поворота
t2
колеса за t секунд определяется уравнением х = t-\—. Определить
скорость и ускорение движения центра колеса.
1095.	Пусть v — скорость и w — ускорение точки, движущейся
по оси Ох. Показать, что w dx = vdv.
dPx
dt2
моменты
соверша-
отклонение х связаны «дифференциальным» уравнением
,2
128
Гл. 7. Приложения производной
1096.	Точка движется прямолинейно так, что v2 = 2ах, где v —
скорость, х — пройденный путь и а — постоянная. Определить
ускорение движения.
1097.	Тело с высоты 10 м брошено вертикально вверх с началь-
ной скоростью 20 м/с. На какой высоте х оно будет через t секунд?
Определить скорость и ускорение движения. Через сколько секунд
тело достигнет наивысшей точки и на какой высоте?
1098.	Сосуд в форме полушара радиуса Лем наполняется водой
с постоянной скоростью а л/с. Определить скорость повышения
уровня на высоте уровня /гем и показать, что она обратно пропор-
циональна площади свободной поверхности жидкости.
Указание. Объем шарового сегмента V = тг/г2 \R — — )• Обе
\ d J
dV
части этого равенства нужно продифференцировать по t, причем - = а
dt
(по условию).
1099.	Зависимость между количеством х вещества, получае-
мого в некоторой химической реакции, и временем t выражается
уравнением х = А(1 — e-/rf). Определить скорость реакции.
dp	dtjj
1100.	Пусть угловая скорость —— =	угловое ускорение —— =
dt	dt
d(uj2)
= е. Показать, что —-— = 2е.
dp
§ 2.	Теоремы о среднем
1°. Теорема Ролля. Если f(x): 1) непрерывна на отрезке [а, Ь],
2) имеет производную внутри него, 3) /(а) = f (b), то между а и Ь най-
дется такое х = с, при котором
Г(с) = 0.	(1)
2°. Теорема Лагранжа. Если f(x): 1) непрерывна на отрезке
[а, Ь], 2) имеет производную внутри него, то между а и Ь найдется такое
х = с, при котором
=	(2)
3°. Теорема Коши. Если f(x) и р(х): 1) непрерывны на отрезке
[а, Ь], 2) имеют производные внутри него, причем р1 (х) ф 0, то между а
и b найдется такое х = с, при котором
7(0 ~ 7(«) = Ш
р(Ь) — р(а) р'(с)'
§ 2. Теоремы о среднем
129
Эти теоремы носят название теорем о среднем потому, что в них
говорится о некотором значении х = с, среднем между а и Ь.
Геометрически теоремы Ролля и Лагранжа утверждают, что на дуге
АВ непрерывной кривой у = f(x), имеющей в каждой точке определен-
ную касательную и не имеющей точек возврата, найдется внутренняя
точка, касательная в которой параллельна хорде АВ.
На дугах, содержащих угловые точки или точки возврата, условия
теорем о среднем, очевидно, не выполнены.
Теорему Ролля в частном случае при f(b) = f(a) = 0 формулируют
так: между двумя корнями а и Ь функции f(x) найдется по крайней мере
один корень ее производной f (х), если f(x) непрерывна на отрезке [а, Ь]
и имеет производную внутри него.
1101.	Проверить, что между корнями функции /(ж) = ж2 —4ж +
+ 3 находится корень ее производной. Пояснить графически.
1102.	Применима ли теорема Ролля к функции /(ж) = 1 — \[хА
на отрезке [—1, 1]? Пояснить графически.
1103.	Построить дугу АВ кривой у = | sin ж | на отрезке
[—7г/2, 7г/2]. Почему на дуге нет касательной, параллельной хорде
АВ? Какое из условий теоремы Ролля здесь не выполнено?
1104.	В какой точке касательная к параболе у = х2 парал-
лельна хорде, стягивающей точки А(—1; 1) и В(3; 9)? Пояснить
графически.
1105.	Написать формулу Лагранжа для функции /(ж) = х2 на
отрезке [а, Ь] и найти с. Пояснить графически.
1106.	Написать формулу Лагранжа для функции /(ж) = у/х на
отрезке [1, 4] и найти с.
1107.	Показать, что на отрезке [—1, 2] теорема Лагранжа не-
4	з/—
применима к функциям — и 1 — \/х2. Пояснить графически.
1108.	Построить АВ кривой у = | cos х| на отрезке [0, 2тг/3].
Почему на дуге нет касательной, параллельной хорде АВ? Какое
из условий теоремы Лагранжа здесь не выполнено?
1109.	Пусть /(ж) = при |ж| > 2? Построить график этой
функции и, взяв на нем точки 0(0; 0) и В(2; 1), показать, что
между О и В на этом графике нет точки, касательная в которой
была бы параллельна ОВ. Какие условия теоремы Лагранжа для
этой функции на отрезке [0, 2] выполнены и какие нет?
1110.	Поезд прошел расстояние между станциями со средней
скоростью v0 = 40 км/ч. Теорема Лагранжа утверждает, что был
момент движения, в который истинная (а не средняя) скорость
<7s
движения — была равна 40 км/ч. Показать это.
130
Гл. 7. Приложения производной
1111. Дано, что /(ж) непрерывна на
взводную в каждой точке внутри него,
к функции
X /(ж)
отрезке [а, Ь] и имеет про-
Применив теорему Ролля
ДЬ)
1
1
1
получить теорему Лагранжа. Выяснить геометрическое значение
функции Ф(ж).
1119 и ж к Ж-/И Лс)
1112.	Написать формулу Ноши —— ---— = —— для функ-
‘Л») - уДс)
ций /(ж) = х3 и <Дж) = ж2 и найти с.
1113.	Геометрически теорема Коши утверждает, что на дуге
кривой х = у = f(t) для значений t на отрезке а t b
найдется внутренняя точка, в которой касательная параллельна
хорде, если функции ip(t) и f(t) на отрезке [а, Ь] удовлетворяют
условиям теоремы Коши. Доказать это.
1114.	Написать формулу Лагранжа в виде f(x + Аж) — /(ж) =
= Дж/'(ж + 0Дж), где 0 < 0 < 1, для функций: 1) /(ж) = ж2;
2) /(ж) = ж3, и показать, что для первой функции 0 не зависит от
ж, а для второй зависит от ж и Аж.
1115.	Показать, что д/101 = 10 Д-.	~ 10, 05.
2 V100 + 0
1116.	С помощью формулы Коши доказать, что если
/(0) = /'(0) = /"(0) = ... = /^(о) = о,
то
где 0 < 0 < 1.
1117.	Написать формулу Лагранжа
Ж - /(а) = (Ь - а)/'(с)
для функции /(ж) = ж3 и найти с.
1118.	Написать формулу Лагранжа и найти с для функций:
1)	/(ж) = arctg ж на отрезке [0, 1];
2)	/(ж) = arcsin ж на отрезке [0, 1];
3)	/(ж) = In ж на отрезке [1, 2].
§3. Раскрытие неопределенностей. Правило Лопиталя
131
1119.	Написать формулу Коши и найти с для функций:
1)	sins и coss на отрезке [0; тг/2];
2)	s2 и у/х на отрезке [1, 4].
1120.	Построить график функции у = |s — 1| на отрезке [0, 3].
Почему здесь нельзя провести касательную, параллельную хорде?
Какое из условий теоремы Лагранжа здесь не выполнено?
1121.	В какой точке касательная к кривой у = 4 — s2 парал-
лельна хорде, стягивающей точки А( —2; 0) и В(1; 3)? Пояснить
графически.
§ 3. Раскрытие неопределенностей.
Правило Лопиталя
1°. Неопределенность Первое правило Лопиталя.
У* (л?)
Если lim f(x) = lim р(х) = 0, то lim ——— = lim ———, когда послед-
x^a	x^a	x^a ip( X) x^a tp'( X)
ний существует.
2°. Неопреде ленность —. Второе правило Лопиталя.
F г /( г	(	г	г
Если lim j(x) = lim = сю, то lim ———- = lim , когда послед-
x-¥a	х-¥а	х-¥а <f>(X)	х-ьа \Х)
ний существует.
3°. Неопределенности 0- сю, сю — сю, 1°° и 0° сводятся к не-
0 оо
определенностям - и — 0 сю Найти пределы: , sin 3s 1122. lim 	. s ,	s — a 1124. lim 	. x-S-a xn — an ,	1	—	cos ax 1126.	lim		— Ж-Ю	1	—	cos OS ,	s	—	sin s 1128.	lim		г	. s3 1130. 1) lim x^+oo S3 In s 1132. lim 	. Ж-Ю ctg s	путем алгебраических преобразований. ex — 1 1123. lim 		. ж-ю sm 2s 1125. lim Ж-Ы In s ,	1 — cos s 1127. lim 			. Ж-m	S2 , tg s — sin s 1129. lim —	;	 ж-ю s — sm s .	,	ex	,	In s 2) hm —. 1131. hm 	. ж->-со s3	ж-j-co s tg S 1133. hm жН-тг/2 tg3s
132
Гл. 7. Приложения производной
1134.
1136.
lim (тг — s)tg —
lim xn  е~х.
1135. lim х In x.
1137. lim Xх.
ж-Ю
/	3
1138. lim (sins)tg;E. 1139. lim ( 1 H—
ж-Ю	жн-со у X
1140.	Определить порядок бесконечно малой хех — sin х отно-
сительно х —> 0.
1141.	Доказать, что при х —> 0:
х3
arctg ж рй —;
а
2) а — о рй х In —;
о
3) е2х — 1 — 2s рй 2s2; 4) 2s — In (1 + 2s) рй 2s2.
s3
1142.	Доказать, что (при х —> 0) х — sin х рй — и отсюда sin s рй
Рй х с погрешностью, приближенно равной х3/6. Вычислить sin 1°
и sin 6° и оценить погрешность.
1143.	Доказать, что (при а —> 0)	+ а — 1 — -а
-----	1	о?
и отсюда у/1 + а Рй 1 4—а с погрешностью рй —. Вычислить
3	9
.2
9
^/1, 006, ^/0, 991,	д/210 и оценить погрешность.
Найти пределы:			
1144.	~ах 	 pbx lim 	;	. ж-ю Sin S	1145.	s — arctg s lim
			®-10	S'5
1146.	1 — sin ах lim	1147.	ax — Iх lim 	.
1148.	ж->тг/2а (2as — 7Г)2 1 — 2 sin s lim 	.	1149.	ж-Ю tg S 1-tgs lim 	.
1150.	хЧ-тт/6 COS 3s (2х _ Х lim -—			1151.	x^-v/4 COS2S In s lim 	
1152.	ж-ю In (1 + 2s) lim (1 — e2;E)ctg s.	1153.	Ж-Ы 1 — XJ lim x1^1-^.
1154. 1156.	r ( 1 1 \ lim	.	„ . ®-10 \s sin s	s2/ Доказать, что при s	1155. lim (e2x + x)1^ ж-Ю x3 —> 0 arcsin s — s рй — 6	
§ 4. Возрастание и убывание функции
133
_____ <1	О!
1157. Доказать, что (при a —> 0) у/1 + a — 1 — — рй--------и
2	8
2
.---- a	a
отсюда у1 + а рй 1 4— с погрешностью, приближенно равной —.
2	8
Вычислить ^/1, 006, ^/1, 004, ^/0, 998, ^/0, 994, -\/б5, д/85 и оценить
погрешность.
§ 4.	Возрастание и убывание функции.
Максимум и минимум
1°. Определения:
I.	Функция f(x) называется возрастающей в точке xq, если в не-
которой е-окрестности этой точки
f(x0 - h) < f(x0) < f(x0 + h)
при любом положительном h < е.
II.	Функция f(x) называется возрастающей на отрезке [а, Ь], если
для любых «1 и «2 на этом отрезке f(xi) < /(жг), когда ./ц < «2-
Аналогично определяется убывание функции в точке и на отрезке.
III.	Функция f(x) называется имеющей экстремум (максимум или
минимум) в точке xq, если f(xg) является наибольшим или наименьшим
значением функции в некоторой двусторонней окрестности этой точки.
2°. Достаточные признаки возрастания и убывания
функции у = f(x) (в точке и на отрезке):
если у' > 0, то функция возрастает;
если у' < 0, то функция убывает.
3°. Необходимое условие экстремума. Функция у = f(x)
может иметь экстремум только в точках, где у' = 0 или не существует.
Такие точки называются критическими. В них касательная или гори-
зонтальна (у' = 0), или вертикальна (в точке возврата), или нет опре-
деленной касательной (например, в угловой точке). В двух последних
случаях у' не существует.
4°. Достаточные условия экстремума. Если функция/(ж)
непрерывна в точке xq и имеет в некоторой окрестности xq, кроме, быть
может, точки xq, конечную производную и если при переходе х через ху
у' меняет знак с + на —, то /(жо) = .'/max-
у' меняет знак с — на +, то /(жо) = J/min,
у' не меняет знака, то экстремума нет.
Третий случай имеет место в обыкновенной точке (при у' > 0 или
у' < 0), а также в точке перегиба и в угловой точке.
Итак, чтобы найти экстремум функции, нужно:
1) Найти у' и критические точки, в которых у' = 0 или не суще-
ствует.
2) Определить знак у' слева и справа от каждой критической точки,
составив таблицу, например, вида
134
Гл. 7. Приложения производной
Xi
О
Далэе можно найт i
: гостпое ла итнщая. торт
Х2
не суще-
ствует
ХЗ
О
кривую На pi c. 28
озтастаетВз1ше т ице-
J3 . дос т ат о	л )
экстремума (второй о^соб иссле-
дования).
Если
1) У'
max 1
2/min и ПОСТРОИТЬ
а
у" > 0, то f(x0) =
.ИсследоваЬ^
возрастание и|убывание функций:
1
у" = 0, то вопрос
ным и нужно обра-
способу исследова-
остается iHepeni
Житься к перво
ния. I
в некоторой точно х
= О,
___	^0 •
у” < 0, то f(x0) =
0 1158. 1) $4= ж2;
1159. 1) у = tg®; 2) у = еж; 3) у = 4ж — ж2.
Найти экстремум функции и построить ее график1):
ж3
1161. у = 4ж-----.
У 3
4
1 + 2ж2 - —.
4
1160.
1162.
1164.
1166.
1168.
1170.
,з
з
И
4
,з
ж2 — 6ж + 13

1163.
1165.
1167.
1169.
1171.
,У,бывает
перегиб
убывав']
х 2
2 + х'
1
1 _|_ э-2
.2
]) В задачах 1165, 1168, 1173 и некоторых других для построения кривой
нужно найти ее асимптоты (см. гл. 5, §9).
§ 4. Возрастание и убывание функции
135
1172. у = х + cos 2s в интервале (0, 7г).
/ 7Г 7
1173. х = 4s — tgs в интервале I----, -
1174. у = —	.		1175. у = a		: — arctg 2x.
1176. 1) у	= хе ж/2;	2) У =	= x In	X.
И77. 1) у	= Vsin х2;	2) У =	= y/e3	2 -1.
1178. у =	sin4 х + cos4 х	. 1179.	У = з	;д/1 — x.
1180. у =	4^/х	1181.		X
	х + 2		У~ (	'x — 1) (x — 4)
1182. у =	х2 1 Т + х'	1183.	У = a	:2/3+(ж_ 2)2/3
1184. у =	™5 111	4,4 	X + X . 5	1185.	У = a	"3(s + 2)2.
1186. у =	2 f- - -V) •	1187.		x3
			У ~ ’	c2 — 3
1188. у =	2 tg х — tg2s.	1189.	У = a	7 + In (COS s).
1190.1) у	= In -\/l + x2	— arctg a	”	2) у = s (a? + 2).	
1191.у = х2е х.
1192. у = 3{/(s + I)2 - 2s.
Найти экстремум функции			и построить ее график
1193.	у = 4s — s2.	1194.	у = s2 + 2s — 3.
	s3		
1195.	У = у + x2.	1196.	у = s3 + 6s2 + 9s.
	X2		ж4
1197.		1198.	У = X3 +
	У	' х — 2		
	ж4		
1199.	у =	2s2. У 4	1200.	у = 2х — 3\/ х2.
1201.	„= (ж~ i)2 У х2 + 1 ’	1202.	-т2 Iе! у — хе
1203.	у = х — 2 In х.	1204.	у = s2/3(s — 5).
136
Гл. 7. Приложения производной
1205.	у = sin 2s — х в интервале (—тг/2, тг/2).
1206.	у = 2s + ctgs в интервале (0, 7г).
1207.	у = х + arcctg2s.
1208.	у = 1 + {/(ж - I)2.
1209.	у = 2 sin х + cos 2s в интервале (0, 7г).
1210.	у = 3s4 - 8s3 + 6s2. 1211. у =—.
1214. 1) у = ае х cos s (при х > 0); 2) у = 3s5 — 5s3.
1215. у =
1217. у =
(4 — s)3
9(2 —s)’
2s2 - 1
1219. у =
ч s + З3
1221. 1) у = ;	( •
S + 22’
12л/(ж + 2)2
1216. у = —
s2 + 8
1218. у = (1 - s2)(l - s3).
1220. у = х + 2-\/—
2) у = л/1 — cos s.
§ 5.	Задачи о наибольших и наименьших
значениях величин
1222.	Решеткой длиной 120 м нужно огородить прилегающую к
дому прямоугольную площадку наибольшей площади. Определить
размеры прямоугольной площадки.
1223.	Разложить число 10 на два слагаемых так, чтобы произ-
ведение их было наибольшим.
1224.	В треугольник с основанием а и высотой h вписан прямо-
угольник наибольшей площади. Определить площадь прямоуголь-
ника.
1225.	Из квадратного листа картона со стороной а вырезаются
по углам одинаковые квадраты и из оставшейся части склеивается
прямоугольная коробка. Какова должна быть сторона вырезаемого
квадрата, чтобы объем коробки был наибольшим?
1226.	Определить размеры открытого бассейна с квадратным
дном объемом 32 м3 так, чтобы на облицовку его стен и дна пошло
наименьшее количество материала.
1227.	Боковые стороны и меньшее основание трапеции равны
10 см. Определить ее большее основание так, чтобы площадь тра-
пеции была наибольшей.
§5. Задачи о наибольших и наименьших значениях величин 137
1228.	В полукруг вписана трапеция, основание которой есть
диаметр полукруга. Определить угол трапеции при основании так,
чтобы площадь трапеции была наибольшей.
1229.	Сечение тоннеля имеет форму прямоугольника, завер-
шенного полукругом. Периметр сечения 18 м. При каком радиусе
полукруга площадь сечения будет наибольшей?
1230.	Вблизи завода А проводится по намеченной прямой к
городу В железная дорога. Под каким углом а к проектируемой
железной дороге нужно провести шоссе с завода А, чтобы доставка
грузов из А в В была наиболее дешевой, если стоимость 1 тонно-
километра при перевозке по шоссе в т раз дороже, чем по желез-
ной дороге?
1231.	Два источника света расположены в 30 м друг от друга.
На прямой, соединяющей их, найти наименее освещенную точку,
если силы света источников относятся, как 27 : 8.
1232.	Два самолета летят в одной плоскости и прямолинейно
под углом 120° с одинаковой скоростью v км/ч. В некоторый мо-
мент один самолет прилетел в точку пересечения линий движения,
а второй не долетел до нее на а км. Через какое время расстояние
между самолетами будет наименьшим и чему равно это расстоя-
ние?
1233.	Балка прямоугольного сечения со свободно опертыми кон-
цами равномерно нагружена по всей длине. Стрела ее прогиба
обратно пропорциональна моменту инерции сечения балки I =
ху3
~12~’
где х и у — размеры балки.
Определить размеры балки
при наименьшей стреле прогиба, если балка вырезана из круглого
бревна с диаметром D.
1234.	Во сколько раз объем шара больше объема наибольшего
цилиндра, вписанного в этот шар?
1235.	Два коридора шириной 2,4м и 1,6 м пересекаются под
прямым углом. Определить наибольшую длину лестницы, кото-
рую можно перенести (горизонтально) из одного коридора в дру-
гой.
1236.	В конус с радиусом 4 дм и высотой 6 дм вписан цилиндр
наибольшего объема. Найти этот объем.
1237.	В полукруг радиуса R вписан прямоугольник наибольшей
площади. Определить его размеры.
1238.	На параболе у = х2 найти точку, наименее удаленную от
прямой у = 2ж — 4.
1239.	Картина повешена на стене. Нижний ее конец на 6см, а
верхний на а см выше глаза наблюдателя. На каком расстоянии
от стены должен встать наблюдатель, чтобы рассмотреть картину
под наибольшим углом?
138
Гл. 7. Приложения производной
1240.	Общая длина стен изображенного на плане дома (рис. 29)
должна быть равна 90 м. При какой ширине х коридора площадь
трех остальных комнат будет наибольшей?
1241.	В прямоугольный треугольник с гипотенузой 8 см и углом
60° вписан прямоугольник, основание которого расположено на ги-
потенузе. Каковы должны быть размеры прямоугольника, чтобы
его площадь была наибольшей?
1242.	Даны точки Л(0; 3) и В(4; 5). На оси Ох найти точку
М так, чтобы расстояние S = AM + МВ было наименьшим.
1243.	Сопротивление балки продольному сжатию пропорцио-
нально площади поперечного сечения. Определить размеры балки,
вырезанной из круглого бревна диаметром D, так, чтобы сопроти-
вление ее сжатию было наибольшим.
1244.	Из круга вырезается сектор, содержащий угол а, а затем
сектор свертывается в конус. При каком значении угла а объем
конуса будет наибольшим?
1245.	Груз весом Р, лежащий на горизонтальной плоскости,
нужно сдвинуть приложенной к нему силой F (рис. 30). Под каким
1°. Выпуклость. Кривая называется выпуклой «вверх» («вниз») в
точке х = xq, если в некоторой окрестности этой точки (слева и справа)
кривая расположена «ниже» («выше») касательной в этой точке. Если в
точке х = xq:
1) у" > 0, то кривая выпукла «вниз»;
2) у" < 0, то кривая выпукла «вверх».
2°. Точкой перегиба называется точка, в которой кривая пере-
ходит с одной стороны касательной на другую (и, следовательно, меняет
направление выпуклости). Необходимым условием точки перегиба явля-
ется то, что в ней у" = 0 или не существует, а достаточным — то, что
у" при этом меняет знак.
§ 6. Направление выпуклости и точки перегиба кривой
139
3°.Для построения кривой рекомендуется определить: ^сим-
метрию; 2) область расположения; 3) точки пересечения с осями Ох и
Оу; 4) точки разрыва функции у = <р(х) или х = f(y) и асимптоты;
5) возрастание или убывание у или х и экстремальные точки; 6) напра-
вление выпуклости и точки перегиба.
1246. Исследовать направление выпуклости и построить кри-
вые:
1) у = ж2;	2) у = ж3;	3) у = ех;
4) у = In ж; 5) у = ж5/3.
1247. Определить экстремальные точки и точки перегиба кри-
вых и построить кривые:
1)*/=у-ж2;	2) у = е-^2;	3) у = 1	;	4) у = 21/*.
Применяя некоторые из правил п. 3°, построить кривые, за-
данные в задачах 1248-1262 уравнениями:
1248. у2 = 2ж + 9.	1249. у = -ж2 - 4ж.
Указание. В задаче 1248 определить симметрию, область располо-
жения и точки пересечения с осями, а в задаче 1249 — точку экстремума
и точки пересечения с Ох.
1250. у = sin ж, у = cos ж. 1251. у = з11ж, у = сЬж.
Указание. В задачах 1250, 1251 определить точки экстремума и
перегиба.
1252. у = In (х + 2).	1253. у = е~х.
Указание. В задачах 1252, 1253 определить область расположения
точки пересечения с осями, асимптоту и направление выпуклости.
1254.	1) у2 = ж3;	2) у2 = (ж + З)3.
12	3	1
1255.	1) у = 2+^—: 2) у =-----------
Ж4 __ /|	гр	гр О
ХГ	*С	*С
. е In ж
1256.	1) у = ---;	2) у = еже х.
4	12
1257. 1) у = ж +-----;	2) у = —-----
)У ж+ 2’ )У ж4 ж2
1258. 1) у = ж — In ж; 2) у = ~(ех/а + е~х^а).
т4	4	1
1259. I ) у =^—:	2) у = — + —.
1260. 1) у2 = 2ж2 — ж4;	2) ж(у — ж)2 = 4.
1261. у = (ж + 2)2/3 - (ж - 2)2/3.
1262. у2 = хе~х.
Глава 8
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. Неопределенный интеграл. Интегрирование
разложением
1°.Неопределенным интегралом f f(x) dx называется функ-
ция F(x) + С, содержащая произвольное постоянное С, дифференциал
которой равен подынтегральному выражению f(x) dx, т. е.
/(ж) dx = F(x) + С,
если
d[F(x) + С] = f(x) dx.
2°. Таблица основных интегралов:
1.
6.
2.
3.
4.
5.

а
In а
dx
cos2
dx
sin2
dx
,.2
dx
a/1 - x2
—ctg х + С.
arctg х + С
или
—arcctg х + С\.
' arcsin х + С
< или
— arccos х + С.
3°. Свойства неопределенного интеграла:
§1. Неопределенный интеграл. Интегрирование разложением 141
Интегрирование разложением есть приведение данного интеграла
(по свойству IV) к сумме более простых интегралов.
1263. В следующих равенствах заполнить пропущенные места:
1) d( ) = 2s dx;	2) d( ) = x' 3) d( ) = cos x dx; 4) d( ) = — x ,/ x	dx	.	. 5 d =	;	6) d = COS2 X	1 Найти затем интегралы J 2s dx, Найти интегралы: 1264.1) У (s2 + 2s + -) dx; 1265.1) [	dx; J ' 1266.1) У (д/х + f/x) dx; x f	I)3 , 1267.1) / —	— dx; 1268. 1) [ ex ( 1 - e— ) dx; J \ x2 J . f cos 2s 1269.1) / 			—dx; J cos2 x sin2 x x f	dx 1270. 1) / . 2	; J sin X COS2 X 1271.1) У sin2^ds; , ft 2	3 1272. 1 /				, f J \i + ®2 Vi-жС	3 dx; X dx + s2 1 s3 dx и т. д. x f 10s8+ 3 , 21J dx- f (x2 + I)2 2) J	x3	dx- , r / 1	1 \ 2) / I —=	—= I dx. . 7 s — 1 , 2 J dx' .	7 „ / a~x \ 2) / a 1 1 4—-= j dx. J \ vs3/ 2) /etg’.S.. 2) [3-2XX^ J	COS2 X 2)	У cos2 — dx. \	7 s4 I	dx;	2)	/  -dx. J	’	4 1 + s2
142
Гл. 8. Неопределенный интеграл
Найти интегралы:
1273.1)	f ~ dx;
. [ х - 2 ,
1274.1) J —j=dx;
Г (1	1	1 \
1275. 1) /	- + — + — ] dx;
/ \ *Z/	*Z/ “	& /
1276.1)	[ ех (1+ '	] dx;
J \ COS2 X J
/1 — sin3 х ,
——.-------dx. 1278.
sin2 х
tg2s dx.
§ 2.	Интегрирование подстановкой и непосредственное
Положив х = р(и), dx = <р'(м) du, получим
У f(x)dx = У f[p(u)]p'(u)du.	(1)
Такое преобразование интеграла называется интегрированием под-
становкой.
В простых случаях введение новой переменной и рекомендуется вы-
полнять в уме, применяя следующие преобразования дифференциала dx:
dx = — d(ax + 6); 2ж dx = с/(ж2);
cos x dx = d(sin x);	— = d(ln x) и т. п.,
и обозначая мысленно выражение в скобках через и. Такой прием инте-
грирования называют непосредственным.
Найти интегралы:
1279.У cos Зж t/ж.	1280. У sin — dx.
Указание. Задачу 1279 можно решить двумя способами: 1) по-
ложив Зж = и, х = и/3, dx = du/3; 2) приведя интеграл к виду
- / cos Зж с/(3ж).
О
§2. Интегрирование подстановкой и непосредственное 143
1281.	1е~3хdx.	1282.	f dx ' cos2 5x
1283.	[ (ех/2 + е~х!2^ dx.	1284.	f л/4ж — Idx.
1285.	(3 — 2ж)4 dx.	1286.	f \/5 — 6x dx.
1287.	Г dx	1288.	f sin (a — bx) dx
	1 V3 - 2ж		
1289.	Г 2х-5	1290.	7 x dx
	J	Q	(X «Л/ • 1 х2 — 5х + 7		1 x2 + 1
Указание. Задачи 1289-1298 решаются по формуле
т. е. если числитель подынтегральной дроби есть производная от
знаменателя, то интеграл равен логарифму знаменателя.
1291.	7 dx	1292.		7 e2x dx
	1 1-10®’			1 1 — 3e2x'
1293.	f ctgxdx.		1294.	ftg ® dx.
1295.	7 cos 2®	- dx.	1296.	7 sin x dx
	1 sin x cos x			' 1 + 3 cos x
1297.	f COS X	- dx.	1298.	7	dx
	1 1 + 2 sin a			' ®(1 + In x)
1299.	/ sin2 x cos:	r dx.	1300.	/ cos3 x sin x dx
Указание. Задачу 1299 можно решить подстановкой sin ж = и или
непосредственно, заменив cos х dx через d(sin®).
	7 cos x dx	7 sin x dx
1301.	/ ——.	1302. / 	—. ’ sm x	J cos'5 x
1303.	7 1 - 2 cos x ,	7 . / 		dx. 1304. / sin x cos x dx. ' sin2 x	J
144
Гл. 8. Неопределенный интеграл
1305. / ecosx sin х dx.
1306.
Указание. Задачу 1306 можно решить подстановкой х3
непосредственно, заменив х2 dx через -d(s3).
и
или
1309. / \42 + Ixdx. 1310. / \/х3 - 8x2dx.
Указание. Задачу 1309 можно решить подстановкой х2 + 1
или непосредственно, записав интеграл в виде - f (х2 + I)1/2 d(x2 -
= и
-!)•
f х2 dx		
1311. J		1312.
	у/1 + X3	
1313. J	Г sin х dx	1314.
	\/1 + 2 cos х	
1315. У л/1 + 4 sin х cos х dx. 1316.
д/1 + In ж dx
Найти интегралы:
1317. J	1 (еж + е х )2 dx.	1318.	1 sin3 x cos x dx.
1319. J	Г dx	1320.	f cos (a — bx) dx.
	' у/1 — 4ж		
1321. J	+ Зх dx.	1322.	1 \/l — 2s3s2 dx
1323.	Г х dx	1324.	f 1 — 2 sin x
	' а/1 + х2		f	COS2 X
1325.	Г 1 + sin 2s / 		dx. ' sin2 х	1326.	esin x cos x dx.
1327. J	Г x2 dx	1328.	f dx
	’ 1 — X3		1 (a — bx)3
§ 3. Интегралы специального вида
145
§ 3. Интегралы вида
2 -£	2’
и к ним приводящиеся
1329. Показать , что:
/dx	1	х
—---- = — arctg —h С, положив х = atgt;
а2 + х2	a	a
/dx	х
,	= = arcsin —h С, положив x = asint;
Va2 -	a
+ С, разложив
1	1 a + x + a — x	1 / 1	1
x2 — a2	2a x2 — a2	2a \x — a	x + a
I	QX	I--- --------------------------
4)	/	: = In |ж + v x2 + k\ + С, положив у/x2	k = t — x.
J у/ x к
/dx	,	f dx
—----;	2)	/ —-.
x2 -25’	’	J x2 + 9
/dx	.	f dx
,	;	2 / ;
л/4 - ж2	J л/®2 + 5
/dx	, f dx
,	;	2) / —---.
’ J x2 + 3
/dx	.	[	x2 dx
;	2)	/	 -.
y/5^2	’ J 4 + s6
/x dx	.	f	dx
,-----Л 2 / —------.
V3 - s4	J b2x2 - a2
/dx	. [ x3 dx
V3 - 4s2 J Vx8 - 1
x Г 5x - 2 , x Г 3x - 4 ,
1336.1)	—-----dx;	2)	—----dx.
’ J s2 + 4	’	7 J s2 — 4
. Г x + 1 ,	.Г x + 1
1337.1)	/	' dx; 2) /	' dx.
’ J	J ^l^T2
146
Гл. 8. Неопределенный интеграл
1338.
1339.
2-3
Указание. В задачах 1338, 1339 нужно из подынтегральной
неправильной дроби исключить целое выражение.
1340.	f	dx	1341. J	Г	dx
	J х2 + 4s + 5		1 х2 + 6х + 13
Указ выделить	ание. В задачах 1340-1347 нужно из квадратного трехчлена полный квадрат.		
1342.	Г	dx	П43. }	Г	dx
	J у/х2 + 2ж + 3		-\/1 — 2ж — х2
1344.	Г dx	П45. }	Г	dx
	J \/йх — X2		х2 + Зх + 3
1346.	Г	dx	4347. }	Г	dx
	J V2 + Зж - 2ж2		1 V3x2 - 2ж - 1
Найти интегралы:
3
6
1348.
2-3
1349.
1350.
1352.
1354.
1356.
1358.
/ 1 W2 - ж2 +	1 >	| dx.
	72 + ж2;	
4ж — 5 —	ах. х1 + 5	1351. J	С ж2 dx
		x2 - 2
х4 dx	1353. j	f ex dx
ж2+ 2’		y/1 — e2x
х dx	1355. j	f	dx
ж4+ 0,25’		x2 + 4ж + 29
dx	1357. J	f	dx
ж2 — 2ж + 5		y/5 — 4x — x2
ж dx	1359. j	f	dx
ж2 + ж + 1		\/4x2 + 4ж + 3
§4. Интегрирование по частям
147
§ 4. Интегрирование по частям
Из формулы дифференциала произведения d(uv) = u dv + v du полу-
чается формула интегрирования по частям
и dv = uv
J v du.
Эта формула чаще всего применяется тогда, когда под интегралом
имеется произведение алгебраической и трансцендентной функций, на-
пример f х2ех dx или / ж2 In х dx. При этом за и принимается функция,
которая дифференцированием упрощается, а за dv — та часть подын-
тегрального выражения, содержащая dx, интеграл от которой известен
или может быть найден.
Из трансцендентных функций за и обычно принимаются In х, arctg х
и arcsin х.
Например, в интеграле f х2 In ж dx за и нужно принять In х (а не ж2),
а в интеграле f х2ех dx за и нужно принять ж2 (а не ех).
Найти интегралы:
1360. У In х dx.	1361. У х In (ж — 1) dx.
1362. У хе2х dx.	1363. ж arctg ж t/ж.
1364. У ж2 cos ж t/ж. 1365. У t '; si о ж t/ж.
1366. Показать, что г 	 1		
1 у/ж2 + к dx = - [ж\/х2 + к + /г In (ж + -у/(ж2 + к))] + С.
Найти интегралы:
/	.->	к х dx
1367. /(In ж)2 t/ж.	1368. / —5—.
J	J sin2 ж
к In ж dx	к arcsin ж dx
1360	/	137ft /
J X2	J 71 + Ж
1371. У arcsin ж t/ж.	1372. J х3е~х dx.
1373. / In (ж2 + 1) dx. 1374. / cos (In ж) t/ж.
148
Гл. 8. Неопределенный интеграл
Найти интегралы:
1375.	1 у/х In 5	c dx.	1376.
1377.	arctgж	1 dx.	1378.
1379.	ех cos:	c dx.	1380.
1381.	Г X COS X	dx	1382.
	' sin3	X	
arctg у/2.
COS2 X
arcsin (ж/2)
----,	— dx.
2е X!2dx.
§ 5. Интегрирование тригонометрических функций
1°. Интегралы от квадратов и других четных степеней си-
нуса и косинуса находят, применяя следующие формулы пониже-
ния степени:
. 2	1 — cos 2ж 2	1 + cos 2ж .	sin 2ж
sin х = -----; cos х = --------; sm х cos х = -.
2	2	2
2°. Интегралы от кубов и других нечетных степеней синуса
и косинуса находят, отделяя от нечетной степени один множитель и
полагая кофункцию равной новой переменной и.
Интеграл J cos™ х sin" х dx находится по правилу 1°, если тип оба
четные, и по правилу 2°, если m или п нечетно.
Найти интегралы:							
1383.	1 sin2	Зж dx.		1384.	/(1 + 2	COS X	)2 dx
1385.	/и-	sin 2ж)	2 dx.	1386.	f 4	dx.	
1387.	sin2	ж cos2 a	' dx.	1388.	f • 4 / sin X	4 COS e	v dx.
1389.	sin2	4 x cos a	' dx.	1390.	/" sin5 ж	dx.	
1391.	sin2	x cos a	' dx.	1392.	/" sin3 ж	Q COS e	v dx.
1393.	f 7 / cos	ж dx.		1394.	/U + 2	COS X	)3 dx
1395.	Г cos3	x dx		1396.	Г sin3 ж	dx	
	/ sin	l2 ж			1 cos2	X	
§5. Интегрирование тригонометрических функций 149
sin2 х + cos2 х
2 sin х cos x
1397.
dx =7
1398. 1) 1399. У	f dx J sin x ’ COS X + sin 2 sin 2s	.	[ dx 2 / 	. J COS X -dx. 1400.	-— J sin X	dx
			 — COS X
1401. /	tg3s dx.	1402. / ctg3:	v dx.
Указание. В задаче 1401 положить tgs = t, х = arctg/.
1403.У sin Зх cos х dx. 1404. J cos mx cos nx dx.
Указание. В задачах 1403-1406 применить формулы
sin a cos /3=7; [sin (« + /?)+ sin (a — /?)],
cos a cos /3 = i [cos (a + /3) + cos (a — /?)],
sin a sin /3 = i [cos (a — /3) — cos (a + /?)].
1405.
sin 3x sin 5x dx;
sin mx sin nx dx.
1406.
dx.
1407. Интегрируя по частям, вывести формулы «понижения
степени»:
. п , 1
sin х dx =----------cos х sin
п - 1 Г . п_2
----- / sin” 2
cos” x dx = — sin x cos'
п - 1 Г п_2
----- / cos” 2
и по этим формулам найти:
cos6 x dx.
1408. Найти интегралы:
dx
cos3 x
Указание. Применить формулы задачи 1407 к интегралам
f dx
и / ----.
COS X
150	Гл. 8. Неопределенный интеграл
Найти интегралы:
1409.	/(1 + 3	cos 2ж)2 dx.	1410.	1 sin4 ж t/ж.
1411.	[ • 4 / sm х	cos2 x dx.	1412.	1 cos5 ж t/ж.
1413.	1 sin3 х	cos2 x dx.	1414.	^"(1 + 2 sin ж)3 dx.
1415.	Г (sm x — cos ж)2 / 	;	 dx. 1	sm 2ж		1416.	1 sin Зж sin ж t/ж.
1417.	Г sin3 x 1 cos2	+ 1 , ;	dx. ' X	1418.	1 sin (ж + —) cos ж dx
§ 6. Интегрирование рациональных
алгебраических функций
1°. Если подынтегральная дробь неправильная, то нужно исключить
из нее целое выражение.
2°. Знаменатель правильной дроби разлагается на множители вида
(ж — а)а и (ж2 + рх + а правильная дробь разлагается на сумму
элементарных дробей следующим образом:
Р(ж)	А1 Аг	Аа
-----------—----------= —  1---------—н... н----------н
(ж — а)"(ж2 + рх + q)!3 . . . х — а (ж — а)2	(ж — а)"
Л71ж + #1 М%х + #2	Mpx + Np
ж2 + рх + q (ж2 + рх + </)2	(ж2 + рх + q)/3	’
где Р(х) — полином степени ниже степени знаменателя.
Найти интегралы: 1419.1) /	2) J ['	ж — 4 1420. / 		—	-dx. J (ж_2)(ж-3) f Зж2 + 2ж — 3 , 1422. / 	+	dx. J	X3 — X f ж + 2	, 1424. / —— -dx. J x3 — 2ж2	Г ™4	г	..5 '		.dx- 3) /		— dx. ж2 + a2	J x ~ a f 2ж + 7	, 1421. / —		dx. J x2 + ж — 2 Г (x + I)3 , 1423. / v	’ dx. J X2 — X f Зж — 2a 1425. / —	dx. J x4 — ax6
§ 6. Интегрирование рациональных алгебраических функций 151
[' 2ж2 - 5ж + 1 , 1426. / —	—dx. J ж3 — 2ж2 + ж	Г 5ж - 1 1427. / —	dx. J ж3 - Зж - 2
[' 5ж + 2 1428. / —		dx. J ж2 + 2ж + 10	Г 4ж —2,4 1429. / —	-	dx. J ж2 — 0, 2ж + 0,17
Указание. В задаче 1428 выделить в знаменателе полный квадрат
и затем положить х + 1 = t.
['	2ж2 + ж + 4 1430. / —			dx. J ж3 + ж2 + 4ж + 4	[' 7ж - 15 1431. / —			dx. J ж3 — 2ж2 + 5ж
f dx 1432. / —	. j ж3 + 8	[ Зж2 + 2ж + 1	, 1433. / 		„ —-dx. J (ж + 1)2(ж2 + 1)
.	[ dx 1434‘ J (ж2 + 62)2’	Г dx 2) J (ж2 + 62)3’
Указание. Положить х = btgt и затем (во втором примере) ис-
пользовать формулу 2) задачи 1407.
. Г (2ж + 1) dx 1435. 1) / —\: ’ J (ж2 + 2ж + 5)2’ Г	4ж dx J (1 + ж)(1 + ж2)2’	Г	dx J (ж2 — 6ж + 10)3 1437. [ Ж + 1	dx. J ж4 + 4ж2 + 4
Найти интегралы, не применяя общего метода неопределенных
коэффициентов:
/dx	[ dx
—------Г-	1439. / 7--77---ТУ-
х ( х + a)	J ( х + а) ( х + о)
Указание к задачам 1438-1442. В числителе подынтегральной
дроби написать разность множителей знаменателя, разделив интеграл
на соответствующее число.
/dx	[ dx
-----•	1441. /
ж2 — 2х	J (ж2 — 3) (ж2 + 2)
/dx	f dx
---у.	1443. / —---.
ж4 — ж2	J ж3 + 4ж
152
Гл. 8. Неопределенный интеграл
Найти интегралы:			
1444.	{'	2х “ 1	Л / 7		Г аХ. / (ж — 1)(ж — 2)	U45. j	/ Зх + 2 л / —		ах. 2ж2 + х — 3
1446.	Г	5ж - 14 / / д'3 — х2 — 4ж + 4	1447' J	Г Пж + 16 ' (ж —1)(ж + 2)2 Х
1448.	[ 5х -8 / —о	5	dx. / х6 — 4ж2 + 4ж	U49. }	(' ж + 2 / —			ах. х6 — 2ж2 + 2ж
1450.	Г х — а	1451' J	f	dx
	1 х3 + а2х Х'		х3 + х2 + 2s + 2
1452.	Г dx	U53. }	7	х dx
	1 х3 — 8		' (х2 + 2х + 2)2'
В задачах 1454-1457 выполнить интегрирование, не прибегая
к методу неопределенных коэффициентов:
/dx	[ dx
—-----•	1455. / —---
х2 + 5х	J х4 Зх2
/dx	[ dx
—-----•	1457. / —----------------.
х4 — 1	J х4 — х2 — 2
§ 7. Интегрирование некоторых иррациональных
алгебраических функций
1°. Интеграл / R\x, \/ax + b] dx, где R(x, у) —рациональная
функция, находится подстановкой ax + b = tn, а интеграл более общего
вида [ R (xm V^+b} х™~' dx подстановкой ах™ + Ь -
1эг1ДС1 / J L I tL i v Wet-	U I	UjiL	НиДС 1 drlUrirtUrl CltL	U — L
.. TT	f Mx + N
2 . Интеграл / -------------- dx находится подстановкой
J (x — a)\/ax2 + bx + c
1
3°. Тригонометрические подстановки. К рациональному
тригонометрическому виду приводятся интегралы
а2
— подстановкой х = a sin/,
dx — подстановкой х = a tgf.
§ 7. Интегрирование иррациональных алгебраических функций 153
f aoxm +	1 + . . . + am
4 . Из интеграла / -----------------------dx можно выде-
J /ах1 + Ьх + с
лить алгебраическую часть по формуле
/dx
ж ’
где W = /ах1 + Ьх + с. Коэффициенты А находятся после дифферен-
цирования равенства и освобождения его от знаменателя сравнением ко-
эффициентов слева и справа при одинаковых степенях х.
5°. Интеграл от дифференциального бинома
У xm(a + bxn)p dx берется в конечном виде в трех случаях: 1) когда
"' + 1
р — целое число, разложением; 2) когда----целое число, подста-
п
тп И- 1
новкой а + bxn = ts; 3) когда--Н р — целое число, подстановкой
п
ах~п + Ь = ts, где s — знаменатель дроби р.
Используя подстановки п. 1°, найти интегралы:
	[ х + 1	,			х dx
		1459. J		
	' </3s + l		* /2х	+ 1 + 1
				
		1461.	f х/а	— х dx.
1460. J	-у/ж + /х			
1462- J	Г х3 dx	1463. J	[' X3	dx
	1 + y/s4 + 1		/ х2	+ 2
Используя подстановку п. 2°, найти интегралы:
1466.
/dx
х/2х2 + 2s + 1
/dx
----,
(x + 1)-\/ж2 + 2s + 2
Найти интегралы, используя подстановки п. 3°:
140S.	[	dx 1469. /	, 7 y/(4 + s2)3
1470. /а/4-^.	(' s2 dx 1471. /	; J y/(a2 + x2/
1472. У у/з + 2s - x2dx.	[ x2 dx 1473. /	, J y/(2 - s2)3
154	Гл. 8. Неопределенный интеграл
Найти	интегралы, применяя правило п. 4°: Г х2 + 4s	Г	х dx
1474.	/	,	=dx. 1475. /	,	=. / Vs2 + 2s + 2	J a/3 — 2s — s2
1476.	+	1477./^-^.
Найти	интегралы от дифференциальных биномов: f dx	f dx
1478.	/ x-y/l-f-x3	J s3\/2 — s3 f'	dx	f' x3 dx
1480.	1 s2v/(l + s2)3	J (a — 6s2)3/2
Найти интегралы:		f	dx	
	Г х - 1	,		
1482.		1483.	
	/ V2s - 1		/ //Зх +1 — 1
1484.	f у/х dx	1485.	/ ^^dx-
	/ рг + Г		
1486.	[ ж + 1 А	1487.	Г x3 dx
	1 ху/х — 2		1 у/x2 +1-1
1488.	Г	х dx	1489.	Г x3 dx
	1 s2 + 2 + 2^/1 + х2		1 2 + y/4 — x2
1490.	Г	dx	1491.	Г	dx
	/ ху/х2 + 2s		/ (s — 1)-\/ж2 — 2s
1492.	Г s2 dx	1493.	f 1 X dx
	1 д/4 — s2		/ V 2 - S
Указание. В задаче 1493 положить х			= 2 sin21. Г	T2
1494.	1 у/ 4х + s2 dx.	1495.	'	—dx J y/5 + 4s — s2
1496.	Г dx	1497.	f	dx
	1 х3у/1 + S2		J X2y/1 + s2
1498.	Г dx	1499.	f	dx
	/ Ху/1 — X3		J ху/Зх2 — 2s — 1
§8. Интегрирование некоторых трансцендентных функций 155
§ 8. Интегрирование некоторых трансцендентных функций
К рациональному алгебраическому виду приводятся интегралы:
/ R(e ) dx — подстановкой е = t, х = mt, dx = —;
— подстановкой tg ж = t, х = arctg/, dx
sin х, cos х) dx — подстановкой tg — = t, sin x =
dt
~ 1 +t2’
2/
------, COS X =
1 + t2’
1 — t2 2dt
------ dx = ---
1+t2	1+t2
Найти интегралы:
2х
!500. j	/ —		dx. ' e2x + 1	1501.
1502' J	f e3x dx	1503.
	' ex + 2'	
1504' J	Г dx	1505.
	5 + 3 cos x	
1506.	Г dx	1507.
	1 • 4	
SHI X
dx
1 + 3 cos2 x
dx
3 sin x + 4 cos x
dx
Указание. В задачах 1506, 1507, 1512, 1513, где под интегралом
sin ж и cos ж содержатся только в четной степени, лучше применять под-
становки
t2 2	1	dt
= ------о, cos ж = -----dx = ---------
1 + t2’	1 +t2 ’	1+t2
Найти интегралы:
1509.
1511. [-----
J 3 +
dx
1 + 3 sin2 ж
156
Гл. 8. Неопределенный интеграл
dx
2 sin x + sin 2ж
„----dx.
sind х
1516.
——-— dx.
Sin Z.X
§ 9. Интегрирование гиперболических функций.
Гиперболические подстановки
1. У ch х dx = sh х + С. 2. J sh x dx = ch x + C.
3. [ —j— = th« + G.	4. [ —j— = — cth x + C.
J chr x	J str x
Интегралы от квадратов и других четных степеней ch ж и sh ж находятся
применением формул:
2 ch 2ж + 1	2 ch 2ж — 1	sh 2ж
ch ж = ---------, sh ж = ----------, sh ж ch ж = ------.
2	2	2
Интегралы от нечетных степеней sh ж и ch ж находятся тем же спо-
собом, что и интегралы от нечетных степеней sin ж и cos ж.
Гиперболические подстановки иногда применяются при нахождении
интегралов вида
[ R (х	dx	подстановкой	ж - a chf
I 11 I Ф ,	у	•!	(J	I	UjiL	11иДС1С1г1и1эХ\иг1еЪ — (J Cll t,
[ R (x	dx	подстановкой	ж - a sht
/ 11 I Ф ,	у	•!	(J	I	UjiL	11иДС1С1г1и1эХ\иг1	-L — (J oil t.
При этом: если ж = a cht,
то t = In
a
если ж = a shl,
to t = In
2
a
Найти интегралы:
sh2 Зж dx',
1519.
з
dx
ch ж + 1
1520.
dx
th ж — 1
§10. Смешанные примеры на интегрирование
157
1523.
a2 dx.
1524.
ж2 — a2 dx.
dx
\/(x2 + 4)3
dx
V(^2-5)3
Найти интегралы:
1527. У 8Ь3Зжс/ж.
1529. У 8114жс11жс/ж.
1531. У л/ch ж + 1 dx.
/ж2 dx
— з
1528.
1530.
2 х ch2 x dx.
2
1 + 2 sh x
-----=----dx.
ch2 x
----dx.
§ 10. Смешанные примеры на интегрирование
Найти интегралы:
1535.		f arete ж dx	
	f л/1 + ж dx	15И-	J	
			'	1 + ж2
1537.	Г dx	15М-	J	Г dx
	1 ж3 + ах2		1 + sin ж
1539.	Г	dx	1МО- J	Г	dx
	' \/х(1 — ж)		sin2 ж/a2 + cos2 x/b2
1541.	жсов2жс/ж.	1М2- J	Г dx
			’ e2x + ex
/cos2 ж dx
sin4 ж
1545. / жtg2 ж dx.
1546.
/sin ж dx
7Т~--2—
+ cosz ж
/ах — b
----TTTdx.
(ax + b)4
1548.
1550.
cos2 ж dx
sin ж
dx
\[x? + 2л/ж
dx
ж4 + ж2
158
Гл. 8. Неопределенный интеграл
Г dx
1551‘ / г-—т--------V2- 1552-
J (sin X + COS X)2
/ж2 dx
7------•	1554.
(a — bx3)n
f dx
1555. / -------—.	1556.
J (1 + V^)3
f e* - 2 ,
1557. / —------dx. 1558.
J e2- + 4
1559. У ctg4«d«.	1560.
/COS X ,	4 f
21 /
1562-x) [ г 2) I
J \/x + a + у/x	J
f x4 + 1
1563. / ,	, с/ж. 1564.
J X3 — X2
f dx
1565. / —	.	1566.
J x\/x3 — 1
/arcsin x/~x ,
-----dx. 1568.
/cos 2ж ,
dx.	1570.
sin4 x
f dx
1571. / —------.	1572.
J e3x - ex
f In (x + 1) dx
1573. / v ;.	1574.
J x2
f dx
1575.	/ ----------------1576.
J 1 + sin x
1577.	j e~^dx.	1578.
1575.	[	1580.
J sin 2ж
/ax dx
—------.	1582.
a2x + 1
b dx
J x\/a + 6 In ж
/arctg ж dx

f	dx
J (2ж+ 1)(1 +V2TTT)
J
sin ж
—----dx.
sin Зж
dx
+ 1 — ж
[	+ 2ж
J -др—'ь-
b dx
J 1 Н^ж'
/sin 2ж
——dx.
cos4 ж
/In (cos ж) dx
sin2 ж
/sin3 ж dx
cos5 ж
/ж dx
ж4 — ж2 — 2
у arctg y/x dx
f In (ж2 + 1) dx
J '
f 1 — sin л/ж
/ ----=---dx.
§10. Смешанные примеры на интегрирование
159
1583.
--------dx.
V2ax + х2
cos3 х + 1
---2-----dx.
sinJ x
x arcsin x dx
1584. j	' VI - X2
,588. j	Г x2 dx
	' (x+lV
,588. j	r 4x+l
	' 2x3 + x2 — x
,58». j	f dx
	' x4 + 4
dx.
Глава 9
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. Вычисление определенного интеграла
Пусть на отрезке [а, Ь] определена функция f(x). Разобьем отрезок
[а, Ь] на п частей точками а = xq < х^ < х% < . . . < хп = Ь. Из каждого
интервала (жг_1, жг) возьмем произвольную точку £г- и составим сумму
п	п
/(в)Ажг-, где Аг; = Xi — жг_1. Сумма вида	называется
г = 1	г = 1
интегральной суммой, а ее предел при iiiaxA.r, —> 0, если он существует
и конечен, называется определенным интегралом от функции f(x) в
пределах от а до Ь и обозначается
f(x)dx = lim ) f^i)Axi.
max >0
г=1
(1)
Функция f(x) в этом случае называется интегрируемой на отрезке
[а, Ь].
Для интегрируемости достаточно, чтобы на отрезке [а, Ь] функ-
ция была непрерывна или же имела конечное число конечных разры-
вов.
Пусть f(x) непрерывна на [а, Ь]. Тогда на этом отрезке существует
неопределенный интеграл
(2)
и имеет место формула
ь
У /(ж) dx = F(b) - F(a) = f f(x)dx\ba,	(3)
т. e. определенный интеграл от непрерывной функции равен разности
значений первообразной функции (или неопределенного интеграла) при
верхнем и нижнем пределах. Формула (3) называется формулой Нью-
тон а-Л е й б и и ц а.
§ 1. Вычисление определенного интеграла
161
1591. Составлением интегральных сумм и переходом к пределу
найти интегралы:
a
sin х dx.
о
Указание. При решении второго и четвертого примеров восполь-
зоваться результатами задач 1034 и 647.
1592. Вычислить «нижнюю» и «верхнюю» интегральные суммы
2
г dx
S5 и 6*5 для интеграла / —, разбив отрезок [1, 2] на пять равных
1
частей. Сравнить с точным значением интеграла.
5	5
Указание. S5 = гпг-Аж, S5 = М^Лх, где тг- — наименьшее,
г = 1	г = 1
a Mi — наибольшее значение подынтегральной функции в г-м частичном
промежутке.
Вычислить:
3
1597. f ,dX .. 1598. f ex/3dx.
J a2 + '	J
a	0
1	тг/4
г	dx	f
1599. /	.	1600. / sin4sds.
J	J
0	0
9	vr/3
f dx	f 1 + tg2s
1601. / —--------.	1602. / -— & dx.
J ^-1	J (l + tgs)2
4	тг/4
Указание. В задаче 1601 нужно применить подстановку х = /2;
при этом пределы интеграла изменятся, что записывается в виде таб-
х I 4 I 9
лицы —	. Аналогично в задаче 1602 при интегрировании подстанов-
/23
кой tg« = t нужно соответственно изменить пределы.
162
Гл. 9. Определенный интеграл
dx
1 -Г ^/2s -J- 1
1604.
1603.
1606.
1613. Из формулы задачи 1407 получить, что
Вычислить:
1614.
1615.
1616.
/dx
cos2 2s
тг/8
1618.
1619.
§ 2. Вычисление площадей
163
/х dx
у/ 4s + 5
i
тг/2
1622. / х cos х dx.
1624. Из формулы задачи 1407 получить, что
§ 2. Вычисление площадей
1°. Площадь криволинейной трапеции А^АВВ^, приле-
жащей к оси Ох (рис. 31):
х2
S = йт ^^уДх = у dx.	(1)
Дифференциал переменной площади АуАММ^ равен dS = у dx.
164	Гл. 9. Определенный интеграл
2°. Площадь криволинейной трапеции, прилежащей к
оси Оу:
У2
S = ^Нш жАу = У х dy.	(2)
У1
Дифференциал переменной площади dS = х dy.
3°. Площадь сектора О АВ (рис. 32) кривой, заданной в
полярных координатах:
S = Alimn 12	/ |г2	(3)
' 2	J 2
Дифференциал переменной площади dS = -г2 dp.
Вычислить площадь, ограниченную линиями:
1625. у = 4 - ж2, у = 0.	1626. 3-+У- = 1.
а21 Ь2
1627. у2 = 2рх, x = h.	1628. у = 3 - 2ж - ж2, у = 0.
1629. ху = 4, ж = 1,	1630. у = In ж, ж = е, у = 0.
ж = 4, у = 0.
1631. у2 = 2ж + 4, ж = 0.	1632. у2 = ж3, у = 8, ж = 0.
1633. у2 = (4 — ж)3, ж = 0. 1634. Петлей кривой
4(у2 — ж2) + ж3 = 0.
1635. у = ж2, у = 2 — ж2.	1636. у = ж2 + 4ж,
у = ж + 4.
1637. а2у2 = ж3(2а — ж).	1638. (у — ж)2 = ж3, ж = 1.
1639. Петлей строфоиды у2(2а — ж) = ж(ж — а)2.
1640. Цепной линией у =
, ж = ±а и у = 0.
1641.	Одной аркой циклоиды ж = a(t — sin i), у = а(1 — cos i) и
осью Ох.
1642.	Астроидой ж = acos3t, у = asin3t.
1643.	Лемнискатой г2 = a2cos2<^.
1644.	Кардиоидой г = а(1 — cos 92).
1645.	г = 3 + sin 2</з между смежными наибольшим и наимень-
шим радиус-векторами.
1646.	г = 2 — cos 3^ между смежными наибольшим и наимень-
шим радиус-векторами.
§ 3. Объем тела вращения
165
1647. г = a cos 2р.
1648. г = a sin Зр.
1649.
1651.
a(sin p + cos<^). 1650. r = —, — p 2тг.
p 4
• ? V
asm —, лежащей ниже полярной оси.
1652.	Петлей декартова листа х3 + у3 — Заху = 0 (см. рис. 79
на с. 334) (перейти к полярным координатам).
/sin2 р cos2 р dp
„--------—— положить tg р = U,
(sim р + cos3 р}1
разделив сначала числитель и знаменатель на cos® р.
Вычислить площадь, ограниченную линиями:
1653.	у = 6ж — ж2, у = 0.
1654.	у = ж3, у = 8, х = 0.
1655.	у2 = 1 — х и х = —3.
1656.	у2 + х' = ж2.
1657.	у = ж2 + 4ж + 5, х = 0, у = 0 и минимальной ординатой.
1658.	Одной полуволной синусоиды у = sin х и у = 0.
1659.	I// = ж2 и у2 = 4ж.
1660.	жу = 6иж + у — 7 = 0.
1661.	Петлей кривой х3 + х2 — у2 = 0.
1662.	г = 3 — cos 2р между смежными наибольшим и наимень-
шим радиус-векторами.
1663.	г = 2 + sin Зр между смежными наибольшим и наимень-
шим радиус-векторами.
1664.	г = a sin 2р.	1665. г = a cos Зр.
1666.	г = аг2 от р = —7Г до р = тг.
х2 у2	х2 у2
1667.	Общей части эллипсов +	= 1 и —+	= 1 (перейти
а2 о2	о2 а2
к полярным координатам).
1668.	г = a(l + sin2 2р) и г = а.
§ 3. Объем тела вращения
1°. Объем тела, образованного вращением вокруг оси Ох криволи-
нейной трапеции А^АВВ^ (рис. 33), где АВ — дуга кривой у = f(x),
определяется формулой
lim лу2 Ах =
V =
(1)
Дифференциал переменного объема dV = ту2 dx.
166
Гл. 9. Определенный интеграл
2°.
нием во
ции, п
формтйог
ла, обра юванно!
окрчг
(И
и
И
пр 33
гж? ау.
ем тела, образованного враще-
г оси Оу криволинейной трапе-
ащей к оси Оу, определяется
У2
/ тгж2 dy. (2)
ДиНэференц ил переменного объема dV =
о вращением фигуры, огра-
круг/оси Оу.
0/вокруг оси Ох.


Определить
ниченной линиями:
1669. у2 = 2р./- и х
х2 у2
1670. — -	= 1
a- о-
1671. ху = 4, х = 4, у
1672. у2 = (ж + 4)3 и х = 0 вокруг оси Оу.
1673.	ж2 + у2 = а2 вокруг прямой х = Ь > а.
Указание. dV = тг(& + ж)2 dy — тг(6 — ж)2 dy = 4тг6ж dy.
1674.	у = a ch —, х = ±а, у = 0 вокруг оси Ох.
а
1675.	у2 = 4 — х, х = 0 вокруг оси Оу.
1676.	(у - а)2 = ах, х = 0, у = 2а вокруг оси Ох.
1677.	у = cos X и у = —1 вокруг прямой у = — 1 при —7Г	X 7Г.
1678.	у = ху/—х, х = —4 и у = 0 вокруг оси Оу.
1679. у = COS
, х = 0, у = 0 (при х > 0) вокруг оси Ох.
х2
1680.	у = а----и х + у = а вокруг оси Оу.
а
Определить объем тела, образованного вращением фигуры, огра-
ниченной линиями:
1681.	у = sins (одной полуволной), у = 0 вокруг оси Ох.
1682.	х2 — у2 = 4, у = ±2 вокруг оси Оу.
1683.	у = ----х = ±1, у = 0 вокруг оси Ох.
§4. Длина дуги плоской кривой	167
ж2 у2
1684.	— + — = 1 вокруг оси Оу.
а2 о2
1685.	ж2/3 + у2/3 = а2/3 вокруг оси Ох.
1686.	у = ж3, ж = 0, у = 8 вокруг оси Оу.
1687.	ж2 — у2 = а2, ж = ±2а вокруг оси Ох.
1688.	у = ж2, у = 4 вокруг прямой ж = 2.
Указание. dV = тг(2 + ж)2 dy — тг(2 — ж)2 dy.
1689.	Одной арки циклоиды ж = a(t — sin t), у = а(1 — cost)
вокруг оси Ох.
1690.	(у — З)2 + Зж = 0, ж = —3 вокруг оси Ох.
§ 4.	Длина дуги плоской кривой
1°. Длина дуги АВ кривой у = /(ж):
S = У + у'2 dx.	(1)
Я? д
Дифференциал дуги ds = у/1 + у'2 dx = у/dx2 + dy2.
2°. Длина дуги АВ кривой ж = f(t), у = tp(t):
tB
s = У у/x2 + у2 dt.	(2)
t А
3°. Длина дуги АВ кривой г =/(<£>):
4>в
s = / V7"2 + г'2 dtp.	(3)
tPA
Определить длину дуги кривой:
1691.	у2 = ж3, отсеченной прямой ж = 4/3.
1692.	Всей кривой ж2 + у2 = а2.
1693.	Всей кривой ж2/3 + у2/3 = о2/3.
1694.	у2 = (ж + I)3, отсеченной прямой ж = 4.
1695.	Одной арки циклоиды
х = a(t — sin t), у = а(1 — cos t).
t&	/'
1696.	x = —, у = 2------между точками пересечения осями
6	4
координат.
168
Гл. 9. Определенный интеграл
х2
1697.	w =----1, отсеченной осью Ох.
у 2
между прямыми х = ±а.
Указание. J у 1 + х2 dx можно или найти по частям, или напи-
сать по формуле задачи 1366.
1698.	у = |(еж/“ + е~
1699.	у = In х от х = 3/4 до х = 12/5.
л/1 + х2 dx
--------- находится подстановкой
Указание.
х2 = t2.
1700.	у = In (2 cos ж) между смежными точками пересечения с
осями координат Оу и Ох.
1701.	1) 9у2 = х(х — З)2 между точками пересечения с осью Ох.
2)	е2у th х = 1 от х = 1 до х = 2.
1702.	1) Кардиоиды г = а(1 — cos </?).
2)	Первого завитка спирали г = сир.
з У3
1703.	Всей кривой г = a sin —.
1704.	Гибкая нить подвешена в точках А и В, находящихся
на одной высоте на расстоянии АВ = 26, и имеет стрелу прогиба
f. Считая форму нити параболой, показать, что длина нити s рй
/	2 f2\	f
~ 26 1 ------- при достаточно малом —.
\	3 о2 J	о
Указание. Применить приближенную формулу л/1 + а ~ I + — а
задачи 1157.
Определить длину дуги кривой:
4
у2 = -(2 — ж)3, отсеченной прямой ж = —1.
у = In (sin ж) от ж = 7г/3 до ж = 2тг/3.
у = In (1 — ж2) от ж = —1/2 до ж = 1/2.
у2 = 2рх, отсеченной прямой ж = р/2.
х = t2, у = —{I2 — 3) между точками пересечения с
3
1705.
1706.
1707.
1708.
1709.
осью Ох.
§5. Площадь поверхности вращения	169
§ 5.	Площадь поверхности вращения
1°. Площадь поверхности, образованной вращением вокруг оси
Ох дуги АВ кривой у = f(x):
Рх = 2тг У yds, где ds = \/dx2 + dy2.
АВ
2°. Площадь поверхности, образованной вращением вокруг оси
Оу дуги АВ кривой х = <р(у):
=	где
АВ
Определить площадь поверхности, образованной вращением кри-
вой:
1710.	х2 + у2 = R2 вокруг оси Ох.
1711.	у = ж2/2, отсеченной прямой у = 1, 5, вокруг оси Оу.
1712.	у = a ch — между х = ±а вокруг оси Ох.
а
1713.	4ж2 + у2 = 4 вокруг оси Оу.
Указание. Приняв у за независимую переменную, получим, что
2
искомая площадь Р = тг j Д16 — Зу2 dy. Далее применяем подстановку
о
4 .
у = smt.
7з
1714.	Одной полуволны кривой у = sin х вокруг оси Ох.
1715.	Одной арки циклоиды х = a(t — sin t), у = а(1 — cost)
вокруг оси Ох.
1716.	Петли кривой х = t2, у = -(t2 — 3) вокруг оси Ох.
3
1717.	х2 + у2 = а2 вокруг прямой х = Ь > а.
Указание. dP = 2тг(6 + х) ds + 2тг(6 — х) ds.
Определить площадь поверхности, образованной вращением во-
круг Ох:
1718.	Дуги кривой у — — от х = —2 до х = 2.
3
170
Гл. 9. Определенный интеграл
1719.	Дуги кривой у2 = 4+ х, отсеченной прямой х = 2.
1720.	Всей кривой х = a cos3 i, у = a sin3 7.
/3	t2
1721.	Дуги кривой х = —, у = 4 — — между точками пересе-
чения с осями координат.
§ 6. Задачи из физики
1722.	Определить силу давления воды на вертикальный пря-
моугольный шлюз с основанием 8м и высотой 6м. Определить
также силу давления на нижнюю половину шлюза.
1723.	Определить силу давления воды на вертикальную тре-
угольную площадку, основание которой а расположено на поверх-
ности воды, а высота равна h.
1724.	Определить силу давления воды на вертикальный полу-
круг, диаметр которого 2/? расположен на поверхности воды.
1725.	Плотина имеет форму трапеции с верхним основанием
20 м, нижним 10 м и высотой 6 м. Определить силу давления воды
на плотину.
1726.	Найти моменты инерции относительно осей Ох и Оу
площади прямоугольника, ограниченного линиями х = 0, х = а,
у = 0 и у = Ь.
Указание. Разбив прямоугольник на горизонтальные площадки,
умножим каждую площадку на квадрат ее расстояния от оси Ох, т. е.
на у2. Суммируя и перейдя к пределу, получим
ь
Jx = lim > aAt/t/2 = / ay2 dy.
Д.7^0^	J
о
Аналогично Jy = j" bx2 dx.
о
1727.	Найти момент инерции относительно осей Ох и Оу пло-
щади треугольника, ограниченного линиями х = 0, у = 0 и
х У
—1“ Т ~
а о
1728.	Найти момент инерции относительно оси Оу площади,
ограниченной линиями х = 2, у = х2 и у = 0.
1729.	Найти статические моменты относительно Ох и Оу и
координаты центра масс треугольника, образованного линиями
х = 0, у = 0их4~у = а.
Указание. Статические моменты: М3
о	о
К	МУ М- Q	Ж
Координаты центра масс: хс = —д~, Ус = —гг, где 5 — площадь фигуры.
О	о
§6. Задачи из физики
171
1730.	Найти центр масс площади, ограниченной линиями а2у =
= Ьх2, х = а и у = 0.
1731.	Найти центр масс полукруга х2 + у2 = а2, отсеченного
осью Ох.
1732.	1) Вычислить работу, которую нужно затратить на выка-
чивание воды из цилиндрического бассейна с радиусом основания
0,5 м, если в начальный момент уровень воды в бассейне равен
2,8 м и на 0,2 м ниже выпускающего воду отверстия в цилиндре.
2) Вычислить работу, которую нужно затратить на выкачива-
ние воды из полушара радиусом Rm.
1733.	Определить работу, которую нужно затратить, чтобы под-
нять массу т с поверхности земли на высоту h.
Указание. Сила F земного притяжения на расстоянии х от центра
земли определяется из пропорции F : mg = R2 : х2, где R — радиус
земного шара.
1734.	Котел имеет форму параболоида вращения глубиной Н =
= 0,5 м и радиусом основания R = 0,4м. Определить работу,
которую нужно затратить на выкачивание воды из такого напол-
ненного котла.
1735.	В цилиндре под поршнем находится воздух объемом Уо =
= 0,1м3 с давлением ро = 1, 033 • 105 Па. Определить работу изо-
термического сжатия воздуха до объема Vi = 0,03м3. (По закону
Бойля-Мариотта pV = PqVo-)
1736.	Вычислить работу растяжения на 0,001м медной прово-
локи длиной 1м с радиусом сечения 2 мм.
Указание. Сила F Н натяжения проволоки длиной I м и площадью
сечения s мм2 при удлинении ее на х м определяется формулой F =
SX
= Е — , гДе Е — модуль упругости. Для меди можно принять Е к,
1,2 • 105Н/мм2.
1737.	За какое время вода, наполняющая цилиндрический со-
суд с площадью основания S = 420 см2 и высотой Н = 40 см,
вытечет через отверстие на дне площадью s = 2 см2?
Указание. Скорость истечения жидкости при уровне ее на высоте
ж см определяется по формуле v = y^/Hgx, где у — коэффициент, зави-
сящий от вязкости жидкости, формы сосуда и отверстия. Мы примем
здесь, как и в задаче 1738, у = 0, 6.
1738.	За какое время вода вытечет из конической воронки вы-
сотой Н = 40 см, радиусом нижнего основания г = 0,3см и верх-
него R = 6см (см. указание к задаче 1737)?
1739.	Определить силу давления воды на вертикальную тре-
угольную площадку высотой h, основание которой а параллельно
172
Гл. 9. Определенный интеграл
поверхности воды, а противоположная вершина находится на по-
верхности воды.
1740.	Определить силу давления воды на вертикальный пара-
болический сегмент, основание которого равно 4м и расположено
на поверхности воды, а вершина находится на глубине 4 м.
1741.	Найти глубину х, на которой прямоугольный шлюз вы-
сотой h разделится горизонтально на такие две части, величина
силы давления на которые одинакова.
1742.	Цилиндрическая цистерна с горизонтальной осью напо-
ловину наполнена маслом (плотность 0,9). Определить силу давле-
ния масла на каждую из плоских стенок цилиндра, если радиус ее
равен 2 м.
1743.	Определить момент инерции относительно Ох площади
четверти круга х = a cos t, у = a sin 7.
1744.	Найти координаты центра масс площади, ограниченной
линиями у = 4 — ж2иу = 0.
1745.	Вычислить работу, необходимую для выкачивания воды
из ямы, имеющей форму конуса (с вершиной на дне), высота ко-
торого Н = 2 м, а радиус основания Л = 0,3 м.
1746.	Определить работу адиабатического сжатия воздуха объ-
емом Vo = 0,1м3 нс давлением ро = 1,033 • 105 Па до объема
Vi = 0, 03 м3. (Адиабатическое сжатие происходит по закону Пуас-
сона: р\' = PqVq, где 7 рй 1,4.)
1747.	За какое время вода, наполняющая чашу формы по-
лушара радиусом 40 см, вытечет из отверстия на дне площадью
2 см2? (См. указание к задаче 1737; положим коэффициент вязко-
сти р = 0, 8.)
§ 7. Несобственные интегралы
1°. Определения:
+сю	b
I. Интегралом j f(x) dx называется lim J f(x) dx, если этот
предел существует и конечен. Аналогично определяются интегралы
Ь	+сю
У /(ж) dx и У /(ж) dx.
II. Если f(x) непрерывна для всех значений х отрезка [а, Ь], кроме
точки с, в которой f(x) имеет разрыв II рода, то интегралом от f(x) в
пределах от а до Ь называется сумма
с —в	b
lim У /(ж) dx + lim J f(x)dx,
a	c+$
если эти пределы существуют и конечны.
§ 7. Несобственные интегралы	173
Интегралы с бесконечными пределами и интегралы от разрывных
(неограниченных) функций называются несобственными.
Если приведенные выше пределы конечны, то говорят, что несобст-
венные интегралы сходятся, если нет, — то расходятся.
2°. Сходимость несобственного интеграла часто устана-
+сю
вливается методом сравнения: если при х > a\f(x) | р(х) и j ip(x) dx
+сю
сходится, то сходится и У f(x) dx. Аналогичный признак сходимости
можно указать и для интеграла от разрывной функции.
Вычислить интегралы:
1752. Исследовать сходимость интегралов:
/sin х dx . f х dx . f	^2 ,
—;	5) J 6) J e dl-
12	0
174
Гл. 9. Определенный интеграл
1	Ь
/dx . f dx
2)	J ("Р"4 > »)
О	a
Указание. Рассмотреть три случая: n = 1 — а < 1, n = 1 и
n = 1 + a > 1.
1754.	Вычислить площадь, заключенную между локоном у =
1
= ------- и асимптотой этой кривой.
1 + X2
1755.	Вычислить площадь, заключенную между кривой у =
= хе~х /2 и ее асимптотой (при х > 0).
1756.	Вычислить площадь, заключенную между циссоидой у2 =
= ------ и ее асимптотой.
2а — х
Указание. Положив х = 2а sin2/, перейти к параметрическим
уравнениям.
1757.	Найти объем тела, образованного вращением циссоиды
жз
у2 = ------ вокруг ее асимптоты (см. задачу 1756).
2 а х
1758.	Определить площадь поверхности, образованной враще-
нием вокруг оси Ох бесконечной дуги кривой у = е~х при поло-
жительных х.
1759.	Найти объем тела, образованного вращением вокруг оси
Ох бесконечной ветви кривой у = 2 (------- ) при ж 1.
\ Ж Ж /
1760.	Показать, что при m целом и положительном }):
1)	У e~xxmdx = ml- 2) j е~х2x2m+1 dx =	.
о	о
1761.	Вычислить интегралы:
оо	оо	оо	е
/dx . [ 9	,.з ,	. [ In х dx , f dx
— 	2 / x2e~ dx- 3 /	4 / ——.
x* J	J	xz	J x mx
2	0	i	i
oo
]) Функция У e~xxt-1 dx = Г(/) называется гамма-функцией от t. При целом
о
t > 1, как это следует из задачи 1760, 1), Г(() = (t — 1)! Полагая здесь t = 1,
ОО
получим условно 0! = Г(1) = / е~хх° dx = 1. Поэтому принято считать 0! = 1.
§ 8. Среднее значение функции
175
Указание. В примере 3) при нахождении
правило Лопиталя.
In ж
lim --- применить
/dx	. [ dx	. [ dx
--	;	2 /	,	;	3 /	----т.
жл/1 + х2 J а/(1 + ж)3 J х2 + х
1	О	1
1763.	Вычислить площадь, заключенную между кривой у =
= е~2х и осями координат (при х > 0).
1764.	Найти объем тела, образованного вращением вокруг оси
Оу площади бесконечной длины, заключенной между линиями:
ху = 4, у = I, х = 0.
1765.	Определить объем тела, образованного вращением кри-
вой у = хе~х/2 (при х > 0) вокруг ее асимптоты.
§ 8.	Среднее значение функции
Теорема о среднем. Если на отрезке [а, 6] функция/(ж) непре-
ъ
рывна, то между пределами интеграла j f(x) dx найдется такое ж = с,
при котором
ь
У f(x)dx = (6- a)f(c).	(1)
Значение функции
ъ
f f(x) dx
Ут = f(c) = а b_a	(2)
называется средним значением функции /(ж) на отрезке [а, Ь].
1766. Определить среднее значение функции:
I)	у = sin х на отрезке [0, 7г];
2)	у = tgs на отрезке [0, тг/З];
3)	у = In х на отрезке [I, е];
4)	у = х2 на отрезке [а, Ь];
5) У =
I + х2
на отрезке [—1, I].
Указать на чертеже среднее значение функции в каждом примере.
176
Гл. 9. Определенный интеграл
§ 9. Формула трапеций и формула Симпсона
1°. Формула трапеций:
(I)
где h = (b—a)/n, a j/q, t/j, у2, . . yn — равноотстоящие ординаты кривой
у = /(ж) на отрезке [а, Ь]. Погрешность формулы (I):
ФХ (&~12a)fc\/zUx.	(1)
2°. Параболическая формула Симпсона для двух полос:
ь
/h
f(x) dx Pd -(г/о + 4г/1 + y2),
(П)
где h = (b — a)f‘1.
3°. Формула Симпсона для 2n полос:
(HI)
где h = (b — a)/2n. Погрешность формул (II) и (III):
(2)
т. е. формула (II) является точной для парабол второй и третьей степе-
ней: у = a + Ьх + сх1 2 + dx3.
2
/dx
— и оценить
1
погрешность по формуле (1).
5
1768. По формуле Симпсона (III) вычислить интегралы х3 dx
1
2
" /	<1:С. оценить погрешность „о формуле (2) и результаты орав-
О
нить с точными значениями интегралов.
§ 9. Формула трапеций и формула Симпсона
177
1769.	По формуле Симпсона (III) вычислить интегралы:
2	тг/2
х3dx (2п =
— cosZxdx (2п = 6);
о
о
4
f dx
/ ------- (2n = 4) и оценить погрешность, полагая в фор-
I 1-1- т-4 v	'
о
муле (2) приближенно h4|yIV|max рй |A4y|max.
1770.	Найти по формуле Симпсона (II) объем бочки высотой
50 см с диаметром каждого дна 20 см и с диаметром среднего сече-
ния 30 см.
1771.	Вывести формулы объема пирамиды и шара из формулы
Симпсона (II).
2
/* dx
1772.	Вычислить In 2 = / — по общей формуле Симпсона (III)
1
(при 2п = 10) и оценить погрешность по формуле (2).
1773.	Найти длину дуги эллипса х = 5cost, у = 3sint, при-
менив к интегралу, определяющему первую четверть всей дуги,
формулу Симпсона (II).
1774. Вычислить приближенно 7Г =
интегралу формулу Симпсона (II).
1
/dx
—.	, применив к
74^2
о
1
[ dx
I I ..2
по общей формуле Симпсона
1775.	Вычислить — = I
4 J
о
(III)	(при 2п = 10) и оценить погрешность, полагая в формуле (2)
приближенно h4|yIV|max |A4y|max.
1776.	Рассматривая площадь части круга, ограниченного кри-
4
вой х2 + у2 = 32, показать, что j
о
вычисляя интеграл по формуле Симпсона (при 2п = 4).
1777.	Вычислить по формуле Симпсона (III) длину дуги полу-
волны синусоиды у = sin х, разбив отрезок [0, 7г] на шесть равных
частей.
х2 dx = 4д + 8; найти 7Г,
Глава 10
КРИВИЗНА ПЛОСКОЙ
И ПРОСТРАНСТВЕННОЙ КРИВОЙ
§ 1. Кривизна плоской кривой.
Центр и радиус кривизны. Эволюта
1°. Кривизна:
2°. Радиус кривизны:
(1 + г/'2)3/2	(ж2 + у2)3/2
\у"\	\ух — ху\
(О
(2)
3°. Координаты центра кривизны:
(3)
, _	_ У"
~ ds ~ (1 + j/'2)3/2 '
R =
Геометрическое место центров кривизны С(Х; У) называется эво-
лютой. Уравнения (3) и будут параметрическими уравнениями эво-
люты.
4°. Радиус кривизны кривой г = f(p), где г и р— полярные
координаты:
=	(г2 + ,,/2)3/2
1	|г2 _|_ 2г'2 — гг"|'	'
Определить радиус кривизны и построить кривую и круг кри-
визны кривой в ее вершине:
1778. у = 4ж — х2.	1779. у = е~х2.
1780. х2 + 4у2 = 4. 1781. х = a(t — sin t),
1782.	у = хе х.	у = а(1 — cost).
Определить координаты центра кривизны и построить кривую
и круг кривизны кривой:
1783.	ху = 4 в точке х = 2.
§ 1. Кривизна плоской кривой	179
1784.	у = In х в точке пересечения с Ох.
хз -j- 1
1785.	у =------- — в точке пересечения с Ох.
3
Написать уравнение эволюты кривой и построить кривую и ее
эволюту:
х2
1786.	у = 1-у. 1787. х = 2cost, у = sint.
1788.	ж2 - у2 = a2 ( или х = a ch t и у = a sh i).
1789.	x = a(cos t + t sin i), у = a(sin t — t cos i).
1790.	Найти максимальную кривизну кривой у = ех.
1791.	Доказать, что радиус кривизны цепной линии у = a ch —
a
у2
в любой точке равен — и равен отрезку нормали между кривой и
a
осью Ох.
1792.	Определить радиус кривизны в произвольной точке кри-
о2
вой: 1) г = а(1 — cos 92); 2) г2 = a2cos2<^; 3) г2 = -—.
Определить радиус кривизны и построить кривую и круг кри-
визны кривой в ее вершине:
1793.	у = ——-. 1794. ж2 - у2 = 4.
1 + х1
1795. у = sin х. 1796. 2у = х2 + 4ж.
Определить координаты центра кривизны и построить кривую
и круг кривизны кривой:
1797.	у = ех в точке пересечения ее с Оу.
,.3
1798.	у = — в точке (—1; —1/3).
3
1799.	у2 = ж3 в точке (1; 1).
7Г
1800.	у = cos ж в точке ж = —.
Написать уравнение эволюты кривой и построить кривую и ее
эволюту:
73
1801.	у2 = 2(ж + 1). 1802. ж = t2, у = —.
3
1803. ху = 4.	1804. ж = a cos31, у = a sin3 7.
180 Гл. 10. Кривизна плоской и пространственной кривой
1805. Показать, что в любой точке астроиды ж2/3 + у2/3 = а2/3
радиус кривизны равен 3 у/а\ху\.
§ 2.	Длина дуги кривой в пространстве
Дифференциал дуги: ds = dx2 + dy2 + dz2, или
ds = ^i2 + у2 + i2 dt.
^2
Длина дуги: s = j у/ x2 + y2 + z2 dt.
Найти длину дуги кривой:
2/3
1806.	х = t, у = t2, z = — от t = 0 до t = 3.
3
1807.	x = 3 cost, у = 3 sin t, z = 4/ от t = 0 до произвольного t.
1808.	у = —, z = — от x = 0 до x = 3.
У 2 ’	6
Найти длину дуги кривой:
t
1809.	х = t — sin t, у = 1 — cos t, z = 4 sin - от t = 0 до t = it.
1810.	x = ег, у = e-*, z = ty/2 от t = 0 до t = 1.
1	x2
1811.	у = - In x, z = — от x = 1 до x = 2.
y 2	’	2
§ 3.	Производная вектор-функции по скаляру
и ее механическое и геометрическое значение.
Естественный трехгранник кривой
Радиус-вектор г =	+ yj + zk точки кривой х = x(t), у = y(t), z =
= z(t) есть вектор-функция скаляра/. Производная г = ii + yj + zk есть
_____________________________________________________ ys
тангенциальный вектор и имеет модуль |г| = ^/ж2 + у2 + i2 = s = —.
Поэтому, если t — время, а кривая — траектория движения, то г = v
есть вектор скорости, г = w — вектор ускорения.
Через точку М(ж; у; z) кривой (рис. 34) проведем три плоскости:
1)	перпендикулярную к г; она называется нормальной;
2)	содержащую гиг; она называется соприкасающейся;
3)	перпендикулярную к первым двум.
Они образуют естественный трехгранник (триэдр) кривой.
§ 3. Производная вектор-функции по скаляру
181
В пересечении плоскостей имеем три прямые: касательную, бинор-
маль и главную нормаль, определяемые векторами:
1)	г — тангенциальный,
2)	В = г х г — бинормальный,
3)	N = В х г — главный нормальный.
Единичные векторы этих направлений обозначим т, (3, ы: они свя-
(1т
ds
бт
заны зависимостью —
as
I/ и /3 = т х и.
Пусть ЛГДХ; У; Z) — точка касательной (рис. 34). Тогда MMi||r и
из условия параллельности векторов получим уравнения касательной
X — х У — у Z — z
— =	= — • И
X	у	Z
Пусть М2(Х] Y] Z) — точка
на нормальной плоскости.
Тогда ММ2 1 г и из усло-
вия перпендикулярности векторов
получим уравнение нормальной
плоскости:
х(Х - х) + y(Y - у) +
+ z(Z — z) = 0. (II)
Уравнения бинормали и глав-
ной нормали получим, заменив в
уравнениях (I) х, у, z соответст-
венно на Вх, Ву, Bz или на Nx, Ny, Nz.
плоскости получим, заменив в уравнении (II) х, у, z на В
Рис. 34
Уравнение соприкасающейся
х Д/, Bz .
1812.	Радиус-вектор движущейся точки в момент t задан урав-
нением г = 4ti — 3tj. Определить траекторию, скорость и ускоре-
ние движения.
1813.	Уравнение движения г = Зй + (4£ — £2) j. Определить тра-
екторию и скорость движения. Построить траекторию и векторы
скорости в моменты t = 0, 1, 2 и Зс.
1814.	В задаче 1813 определить ускорение w движения и его
dv	ГХ.-----2
тангенциальную wT = — и нормальную wn = Jwz — wz. соста-
dt
вляющие в любой момент t и при t = 0.
1815.	Уравнение движения г = a cost • i + b sin t • j. Определить
траекторию, скорость и ускорение движения и построить векторы
скорости и ускорения в точках t = 0, тг/4, тг/2.
В задачах 1816-1818 написать уравнения касательной прямой
и нормальной плоскости кривой:
1816.	х = t, у = t2, z = t3 в любой точке и при t = 1.
182 Гл. 10. Кривизна плоской и пространственной кривой
1817.	у = ж2, z2 = х в любой точке (ж 0) и при ж = 4.
1818.	ж2 + у2 = 10, у2 + z2 = 25 в точке (1; 3; 4).
Указание. Взяв дифференциал от левой и правой частей каждого
уравнения, найти затем отношения dx : dy : dz.
1819.	Найти тангенциальный г, бинормальный В и главный
нормальный N векторы кривой ж = 1 — sint, у = cost, z = t в
точке t = 0. Найти также т, (3 и и в той же точке.
1820.	Написать уравнения главной нормали, бинормали и со-
прикасающейся плоскости к кривой ж = t, у = t2, z = /3 в точке
t = 1.
1821.	Написать уравнения главной нормали и бинормали кри-
вой ж = ег, у = е-*, z = t в точке t = 0.
1822.	Показать, что уравнения ж = tcost, у = t sin t, z = t
определяют коническую винтовую линию, и написать уравнения
главной нормали, бинормали и касательной к ней в начале коор-
динат.
1823.	Написать уравнения касательной к винтовой линии ж =
= a cost, у = a sin t, z = bt в любой точке и при t = тг/2. Показать,
что винтовая линия пересекает образующие цилиндра ж2 + у2 = а2
Ь
под одинаковым углом 7 = arccos	=.
уа2 + 62
1824.	Найти углы с осями координат тангенциального вектора
кривой ж2 = 2аг и у2 = '2bz в точке z = y/ab.
1825.	Плоскость у = 0, на которой дана кривая 2г = ж2, у = 0,
накручивается на цилиндр ж2 + у2 = 2у. Написать параметриче-
ские уравнения образованного кривой винта и определить бинор-
мальный вектор кривой в любой точке и в точке t = тг/2, где t —
угол поворота плоскости.
1826.	Радиус-вектор движущейся точки в момент t задан урав-
нением г = a(t — sin t)i + а(1 — cost)j. Определить и построить
векторы скорости и ускорения при t = д/2 и t = д.
В задачах 1827-1829 написать уравнения касательной к кри-
вой:
1827.	у = ж, z = 2ж2 в точке ж = 2.
1828.	ж2 + у2 + z2 = 14, ж + 2// — z = 2 в точке (1; 2; 3) (см.
задачу 1818).
1829.	ж = 2t, у = In t, z = t2 в точке t = 1.
§4. Кривизна и кручение пространственной кривой
183
1830.	г = е4 + e“*j + t-\/2k. Найти углы с осями координат
бинормального вектора b в точке t = 0.
1831.	Написать уравнения главной нормали и бинормали кри-
вой у = х2, z = у2 в точке х = 1.
1832.	Написать уравнения главной нормали и бинормали кри-
. t
вой х = t — sin t, у = 1 — cos t, z = 4 sin - в точке t = 7Г.
§4. Кривизна и кручение пространственной кривой
Кривизна 1/R есть предел отношения угла р поворота касательной
к длине дуги As, когда As —> 0. Кручение 1/р есть предел отношения
угла в поворота бинормали к As, когда As —> 0. Так как р к, |Дт| и
0 ss ±|АД|, то 1/R и 1/р численно оказываются модулями векторов:
dr	1	d/3	1
— = —v, — =-----------V.
ds	R	ds	p
Если кривая задана уравнением г = r(t),	то
1 |г X г| 1 г г г
R	|г|3 ’ р	|г	х г|2
(1)
(2)
1833.	Продифференцировав равенство v = vt по t, с помощью
первой формулы (1) получить разложение ускорения w на танген-
циальное и нормальное:
v
2
W = VT + —V.
1834.	Точка движется по параболе х = t, у = t — t2, где t —
время движения. Определить кривизну 1/R траектории и танген-
циальное и нормальное ускорения в момент t и при t = 0.
1835.	Точка движется по эллипсу х = 4cost, у = 3sint, где
t — время движения. Определить кривизну 1/R траектории и
7Г
тангенциальное и нормальное ускорения при t = —.
2
1836.	Для движения с уравнением г = ti + /2j + опре-
делить кривизну 1/R траектории и тангенциальное и нормальное
ускорения в любой момент t и при t = 1.
Определить кривизну 1/R и кручение 1/р кривой:
1837.
1838.
1839.
х = t, у = t2, z = /3 в любой точке и при t = 0.
х = е/ у = е *, z = t-\/2 в любой точке и при t = 0.
3
z = — в любой точке и при х = 1.
184 Гл. 10. Кривизна плоской и пространственной кривой
1840.	Показать, что на правом винте (х = a cost, у = a sin 2,
z = bt) кручение положительно, а на левом (х = a cost, у =
= — a sin 2, z = bt) — отрицательно.
Определить кривизну 1/2? и кручение 1/р кривой:
1841.	х = 22, у = In 2, z = 22 в любой точке и при 2=1.
у2 9
1842.	х = —, z = х в любой точке и при у = 1.
1843.	х = е1 sin 2, у = <L cos 2, z = е* в точке 2 = 0.
Глава 11
ЧАСТНЫЕ ПРОИЗВОДНЫЕ, ПОЛНЫЕ
ДИФФЕРЕНЦИАЛЫ И ИХ ПРИЛОЖЕНИЯ
§ 1. Функции двух переменных
и их геометрическое изображение
1°. Определение. Переменная z называется однозначной функ-
цией переменных жиг/, если каждой паре значений х и у в некоторой
области их изменения поставлено в соответствие одно значение z. Функ-
циональную зависимость z от х и у записывают в виде
z = F(x,y).	(1)
2°. Геометрическое изображение. Уравнение (1) геометри-
чески определяет некоторую поверхность. Пара значений жиг/ опреде-
ляет на плоскости хОу точку Р(х; у), a z = F(x, у) — аппликату соот-
ветствующей точки М(ж; у; z) на поверхности. Поэтому говорят, что z
есть функция точки Р(х; у), и пишут z = F(P).
3°. Предел функции lim F(P) = А, если разность F(P) — А
Р —>Р0
есть бесконечно малая, когда р = PqP —> 0 при любом способе прибли-
жения Р к Pq (например, по любой линии).
4°. Непрерывность функции. Функция F(ж, у) называется
непрерывной в точке Pq, если lim F(P) = F(Pq). Иначе говоря, функ-
P—^Pq
ция Р(ж, у) непрерывна в некоторой точке (ж; у), если
lim F(x + Аж, у + Аг/) = Р(ж, у).
Дг—>о
Ду—>о
1844. Указать области изменений х и у, для которых следую-
щие функции имеют вещественные значения:
Г
4)
6)
х2 + у2;	2) az = а2 — -2 — "2
у/ а2 — х2 — у2; 5)
1	7)
д/1 — х2 — у2
ху
4
-Кг/2;
и построить геометрические изображения функций по сечениям
поверхностей плоскостями х = 0, у = 0, z = Q и z = h.
186 Гл. 11. Частные производные, полные дифференциалы
1845.	Дан периметр 2у треугольника. Определить площадь S
треугольника как функцию двух его сторон х и у. Определить и
построить область возможных значений х и у.
1846.	Для функции F(s, у) = --- вычислить F(3,1), F(l, 3),
F(l, 2), F(2, 1), F(a, a), F(a, —a).
1847.	Доказать, что если F(s, у) = у/x4 у4 — 2ху, то F(tx, ty) =
= t2F(x, у).
1848.	Для z = x2 — ху = у2 определить Л.,;г. A.yz и Аг.
Вычислить А,;г. А^г, Аг, если х изменяется от 2 до 2,1, а у
изменяется от 2 до 1,9.
1849.	Показать, что уравнение х2 — у2 — г2 = 0 определяет
г как бесчисленное множество однозначных функций х и у, из
которых две непрерывны. Указать область определения всех этих
функций и построить геометрическое изображение положительной
непрерывной функции. Привести пример однозначной, но раз-
рывной функции г = F(x, у), определяемой тем же уравнением
х2 — у2 = г2.
1850.	Построить линии уровней (при г = 0, 1, 2 и т. д.) функ-
ций:
/	^2
1) г = у 1 —-— у2; 2) г = х2 — у;
3) г = х2 — у2;	4) г = ху.
У
1851. Показать, что при х —> 0 и у —> 0 выражение и = --
ж - у
может стремиться к любому пределу. Привести примеры такого
приближения точки (х; у) к точке (0; 0), при котором lim и = 3,
lim и = 2, lim и = 1, lim и = 0, lim и = — 2.
Указание. Рассмотреть изменение х и у вдоль прямых у = кх.
1852. Показать, что:
1) Um 2-ДГГ+4 = _1; 2| Um sin (Zy) = 1;
ar-Ю Ху	4	а;—Ю	®У
У->О	у->О
х d sin (ху}
3 lim ------= О
х—И)
У->О
при любом способе приближения точки (х; у) к точке (0; 0).
Указание. Положить ху = а.
§ 2. Частные производные первого порядка
187
1853. Изобразить геометрически функцию
1 при
z = Р(ж, у) = <
О при
— 1 при
ху > О,
ху = о,
ху < О
и указать линии ее разрыва.
1854. Указать области определения функций:
/I	z I т2 ?/2
1)г = ж + у; 2)г=—; 3) - = J1 -	- У~-
х + у с V од
2	2
4) - = 1 -	5) z = х + \/х2 - у2;
с a- о-
6) yfz = yfx + yfy
и построить геометрические изображения этих функций.
1855.	Доказать, что если F(x, у) =-, то F(a, F)+F(b, а) = 1.
х — у
4
1856.	Показать, что уравнение z2 = ---------- определяет z
4 — х2 — у2
как бесчисленное множество однозначных функций х и у, из ко-
торых две непрерывны. Указать область определения всех этих
функций и построить геометрическое изображение функции, по-
ложительной в области ж2 + у2 0 и отрицательной вне ее.
1857.	Построить геометрическое изображение однозначной
функции z = F(x, у), определяемой уравнением x2-\-y2-\-z2 = а2,
,	, а2
положительной в области ж + у — и отрицательной вне ее.
Указать линию ее разрыва.
§ 2. Частные производные первого порядка
Производная функции z = F(x, у) по ж, найденная в предполо-
жении, что у остается постоянным, называется частной производной z
Qz
по ж и обозначается — или 0(ж, у). Аналогично определяется и обо-
д z
значается частная производная z по у: — = F'(x, у).
Оу у
Найти частные производные функций:
1858. z = ж3 + Зж2у — у3.	1859.г	= In (ж2 + у2).
у 1860. z =	1861.г	У = arctg —.
XII 1862. г = —— .	1863.и	= !п (- ~^=
X - у		\ \/х y/t
188 Гл. 11. Частные производные, полные дифференциалы
1864. с = л/а2 + fr2 — 2а6 cos a.
1865. u = - + - -	1866. u = xe~yx.
У z
2s — t
1867. u = ------.
x + 2t
1869. Доказать , что
1868. ci = arcsin (ty/x).
если z = In + y/y), to
dz	dz	1
X —--H V~— =
dx	dy	2
г-  У
1870. Доказать, что если z = ф./'sin —, то
dz dz z
X ——|- у— = —.
dx dy 2
1871. Доказать, что если и = ех^2, то
du du
2ж —	t-^— = О-
dx dt
1872. Доказать, что если и = ху, то
х du 1 du
у dx In ж dy
= 2и.
1873. Ниже, в задаче 1898, будет доказана следующая теорема
Эйлера:
Если z = F(x, у) — однородная функция степени п, то
dz	dz
х — +	= nz-
dx	dy
Проверить эту теорему Эйлера для функций:
1) z = ж3 + ху2 — 2у3; 2) z = -\/ж2 + жу + у2;
3) z =
1
ж3 — У3’
4) г = ех!у.
Найти частные производные функций:
Ту
1874. z = cos (аж — by). 1875. z = arcsin —.
1876. z = -------.	1877. и = In sin (ж —
Зу — 2ж
1878. и = sin2 (ж + у) — sin2 ж — sin2 у.
§ 3. Полный дифференциал первого порядка
189
1879. Доказать, что если и = -\/х2 ф у2 ф z2, то
1880. Доказать, что если z = e^lny, то
dz dz z
dx + V dy	In у
1881. Доказать, что
IT	dT	dT
если Т = 7га/-, то /—-+у—— = 0.
V в	dl	dg
1882. Доказать, что
если z = е
, то
dz dz\2 1 T . 2
~di + Ihi J - 2е sm
1883. Проверить теорему Эйлера об однородных функциях (см.
задачу 1873) для функций:
1) z = ——;	2) z =	3) z = arctg -.
х — у	х‘у‘	х
§ 3. Полный дифференциал первого порядка
Если функция z = F(x, у) имеет в точке (х; у) непрерывные частные
производные, то ее полное приращение может быть представлено в виде
Л dz dz
Аг = —Аж + -д—Аг/ + ер,
Ох оу
(1)
где е —> 0 при р = л/| Аж 12 + I Аг/|2 —> 0. Тогда выражение —Аж + —Аг/
dx dy
есть главная часть полного приращения Аг; она называется полным
дифференциалом функции и обозначается dz:
dz	dz
dz = —Дж + —A;/.
Ox	Oy
(2)
Полагая в формуле (2) г равным: 1) ж; 2) у, найдем: dx = Аж, dy = Аг/.
Поэтому
, dz dz
dz = -—dx + -—dy.
dx dy
(3)
2
190 Гл. 11. Частные производные, полные дифференциалы
Из (1) следует, что
Аг Рй dz,
(4)
т. е. при достаточно малых Аж и Ду полное приращение функции при-
ближенно равно ее полному дифференциалу (тл. 5, §7).
Функция F(x, у) называется дифференцируемой в точке (х; у), если
она имеет в этой точке полный дифференциал.
1884.	Найти полные дифференциалы функций:
1)	z = х2у; 2) z = ——;	3) и = es^; 4) z = у/ж2 + у2.
х — у
1885.	Найти значение полного дифференциала функции:
1)	z = — при х = 2, у = 1, dx = 0,1, dy = 0, 2;
2)	и = еху при х = 1, у = 2, dx = —0,1, dy = 0,1.
1886.	Вычислить dz и Аг для функции z = ху при х = 5,
у = 4, Аж = 0,1, Ау = —0, 2.
у
1887.	Подсчитать приближенно изменение функции ф = arctg —,
когда х изменяется от 2 до 2,1, а у — от 3 до 2,5.
1888.	При деформации цилиндра его радиус R увеличился с
20 см до 20,5см, а высота Н уменьшилась со 100 см до 98 см.
Найти приближенно изменение объема V по формуле АН рй dV.
1889.	Катеты прямоугольного треугольника, измеренные с точ-
ностью до 0,1см, оказались равными 7,5 см и 18 см. Определить
абсолютную погрешность при вычислении гипотенузы.
1890.	Найти полные дифференциалы функций:
1) z = — — —;	2) s = х In t- 3) и = у/ж2 + у2 + г2,
ж у
1891.	Найти значение dz и Аг для функции г = In (ж2 + у2),
когда ж изменяется от 2 до 2,1, а у — от 1 до 0,9.
тт	• У
1892.	Подсчитать приближенно изменение функции г = arcsin —,
когда ж изменяется от 5 до 4,5, а у — от 3 до 3,3.
1893.	При деформации конуса его радиус R увеличился с 30 см
до 30,1см, а высота Н уменьшилась с 60 см до 59,5см. Найти
приближенно изменение объема по формуле АН рй dV.
§4. Производные сложных функций
191
(1)
(2)
2t
§4. Производные сложных функций
1°. Если z = F(x, у), х = fit), у = pit), то z называется сложной
функцией от t. При этом
dz dz dx dz dy
dt dx dt dy dt ’
если функции F, f и ip дифференцируемы.
2°. Если z = F(x, у), где x = f[u, v), у = p(u, v), и если функции
F, f и ip дифференцируемы, то
dz	dz dx	dz dy	dz	dz dx	dz dy
du	dx du	dy du ’	dv	dx dv	dy dv
dz
1894.	Найти по формуле (1) — из уравнений:
1)	z = x2 + ху + у2, х = t2, у = t;
2)	z = у/х2 + у2, х = sint, у = cost.
Проверить предварительной подстановкой значений ж и у в выра-
жение для функции z.
dz
1895.	Найти —, если
dt
dz
1896.	Найти ——, если
ах
dz
1897.	Найти —, если
ах
1898.	Функция z =
F(xt, yt) = tn  F(x, у).
ства по t и полагая в результате t = 1, доказать теорему Эйлера об
dz	dz
однородных функциях: х——h у— = nz.
dx	dy
dz	dz	x2
1899.	Найти —— и ——, если z = —, где х = и — 2г>, у = v + 2м.
du	dv	у
dz	dz	dz	dz
1900.	Пусть z = Fix, у). Выразить —— и —— через —— и ——,
dx	dy	du	dv
если:
1)	и = mx + ny, v = px + qy; 2) и = xy, v = y/x.
1901.	Пусть и = F(x, у), где x = r cos ip, у = r sin ip.
du	du	du	du
Выразить —— и —— через —— и —— и показать, что
dr	dp	dx	dy
( ди\2	/1du\2_ /du\2	/du\2
\dr J	\r dip J \dx J	\dy J
uv, где и и v — функции от х.
z = хеу, где у — функция от х.
F(x, у) называется однородной, если
Дифференцируя обе части этого равен-
192 Гл. 11. Частные производные, полные дифференциалы
1902.	Пусть z = у + F(w), где и = х2 — у2. Доказать, что
d z	d z
у——|- х— = х для любой дифференцируемой функции F(u).
dx	оу
1903.	Найти — из уравнений:
dt
1)	z = Ах2 + 2Вху + Су2, х = sin t, у = cost;
2)	z = arctg —, x = e2t + 1, у = e2t — 1.
1904.	Доказать, что если z = ху + xF(u), где и = у/х, то
dz	dz
z — + УРГ = z + xy.
dx	dy
1905.	Доказать, что если z = уф(и), где и = х2 — у2, то
1 dz	1 dz	z
х dx	у dy	у2
dz	dz	dz	dz
1906.	Пусть z = F(x, у). Выразить —— и —— через —— и ——,
dx	dy	du	dv
если: 1) и = x + 2y, v = x — y; 2) и = y/ху, v = x + y.
§ 5.	Производные неявных функций
1°. Уравнение F(x, у) = 0, имеющее решение («q; j/q), опреде-
ляет в окрестности xq переменную у как непрерывную функцию х при
ЭР
условии, что производная —— i 0 и непрерывна в некоторой окрестно-
dt/
сти точки («о; уф).
Если сверх того, в окрестности точки («о; уф) существует и непре-
dF	г	dy
рывная производная ——, то неявная функция имеет производную —,
dx	dx
определяемую формулой
dt/ _ dF/dx
dx ~ dF/dy'	1 ’
2°. Уравнение F(x, у, z) = 0 при аналогичных условиях опре-
деляет z как неявную функцию х и у, имеющую частные производные
dz	dF/dx dz	dF/dy
dx	dF/dz’ dy	dF/dz'
tt dy
Найти — из уравнений:
dx
1907.	x2 + у2 — 4s + бу = 0.
§ 5. Производные неявных функций
193
1908.	1) s2/3 + y2/3 = a2/3;	2) xe2y — ye2x = 0.
1909.	Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0.
Найти угловой коэффициент касательной к кривой:
1910.	х2 + у2 = 10у в точке пересечения ее с прямой х = 3.
1911.	х3 + у3 — 2аху = 0 в точке х = у = а.
1912.	Найти точки, в которых касательная к кривой х2 + у2 +
+ 2ж — 2у = 2 параллельна: 1) Ох; 2) Оу.
тт dz dz
Найти —— и —— из уравнений:
1913.	х2 + у2 + z2 — 6s = 0.	1914. z2 = ху.
1915.	cos (ах A by — cz) = k(ax A by — cz).
1916.	Доказать, что если xyz = а3, то
dz dz
1917.	Показать, что дифференциальному уравнению
dz dz
удовлетворяет неявная функция г, определяемая уравнением (ко-
нических поверхностей) zjx = ф(у/х).
тт dy
Найти — из уравнений:
ах
1918.	х2 — 4у2 = 4. 1919. ху + In у + In х = 0.
1920. х + у = еу!х. 1921. 2 cos (х — 2у) = 2у — х.
1922. Найти угловой коэффициент касательной к кривой у2 —
— ху = 4 в точках пересечения ее с прямой х = 3.
dz dz
1923. Пусть х2 + у2 + z2 — 2z.r = а2. Найти — и —.
dx dy
1924.2 sin (х + 2// — 3z) = х + 2// — 3z. Показать, что
dz dz
я—I- ~я~ =
dx dy
1925. Показать, что дифференциальному уравнению
dz dz
удовлетворяет неявная функция z, определяемая уравнением (ци-
линдрических поверхностей): х — mz = ф(у — nz).
194 Гл. 11. Частные производные, полные дифференциалы
§ 6. Частные производные и полные дифференциалы
высших порядков
Пусть дана функция z = F(x, у), имеющая частные производные
dF dF тт
—— и ——. Частные производные от этих производных называются част-
от dy
ными производными второго порядка. Они обозначаются:
d(dF/dx) _ d2F d(dF/dx) _ d2F
dx dx2 ’ dy dx dy ’
d(dF/dy) _ d2F	d(dF/dx) _ d2F
dx	dydx’ dy dy2
Аналогично определяются и обозначаются частные производные
третьего порядка и других высших порядков.
Смешанные производные, отличающиеся только порядком диффе-
ренцирования, равны, если они непрерывны:
d2F	d2F	d3F d3F	d3F
----- = -----,	----- = ------- = ------ и т. д.
dx dy	dydx	dx2dy	dxdydx	dydx2
Получим следующую таблицу производных высших порядков:
d2F d2F d2F
второго порядка —— ,	, —— ;
dx£ dx dy dyz
d3F d3F d3F d3F
третьего порядка ——,	,	—— и т. д.
dxs dx^dy dx dyz dya
Полные дифференциалы высших порядков определяются так:
,2 d2z 2 d2z	d2z 2
d z = — dx2 + 2 dx dy + — dy2.
dx£	dx dy	dyz
Символически это равенство можно записать так:
d2z =	dx + —- dy z.
\dx	dy	J
Аналогично	, п	п	\ 3
,з / о , d , \
d z = dx + —- dy z
\dx	dy	J
и т. д.
1926.	Найти частные производные третьего порядка функции
Z = X3 -Г х2у -Г у3.
d2z d2z
1927.	Проверить, что ——— = ——— для функций:
Ох оу Оу Ох
1) z = sin (ax — by); 2) z = x2/у2;	3) z = In (x — 2y).
§ 6. Частные производные высших порядков
195
1928.	Найти частные производные четвертого порядка функции
и = х4 + Зж2у2 — 2у4.
1929.	Найти частные производные третьего порядка функции
и = у/х.
„	, /1	1\	d2s d2s 1
1930.	Пусть s = In--; проверить, что ———+ —=
\х	t J	dx dt dx2 х2
1931.	Найти частные производные второго порядка функции
У
z = arctg —.
тт	. (X у\
1932.	Доказать, что если z = sin-— , то
\a о)
1933.	Доказать, что если u = arctg (2s — £), то
d2u d2u
я 9 + 2——— = 0.
d.r- ox dt
1934.	Доказать, что если s = \/ax bt, to
f d	d\2	2s
\ dx	dt J	9
1935.	Показать, что функция и = хе~у/х удовлетворяет диффе-
ренциальному уравнению
d2u	/ du du\	d2u
dx dy + \dx + dy)	dy2
1936.	Доказать, что если z = F(s, у) — однородная функция
n-го измерения, то
2d2z d2z 2d2z
х + 2хУ я л + У = п<п ~ 1)z’
dr- dx dy dy-
или символически
2
Указание. Равенство х——Н г/—— = nz (см. задачу 1898) продиф-
аг оу
ференцировать: 1) по х\ 2) по у, и результаты, умноженные соответ-
ственно на х и на у, сложить почленно.
196
Гл. 11. Частные производные, полные дифференциалы
1937.	Проверить равенство I х ——h у — I z = n(n — l)z для
\ dx dy J
однородных функций: 1) z = х2 + ху + у2; 2) z = —; 3) z =
= _2_; 4) s = in(2- i).
— у*	\х /
2
1938.	Найти d2u, если: 1) и =	2) и = х In —.
1939.	Доказать, что если z = cos (mx + ny), то d2z =
= — z(mdx + ndy)2.
1940.	Доказать, что если z = In (ax + by), to:
1)	d3z = 2dz3;	2) dnz = (-l)n"1(n - 1)1 dzn.
1941.	Доказать, что если z = F(u, v), где и = mx + ny и v =
d2z / d d\2 d2z ( d d\
= px+qy, to —— = m— + p— z, = m— + p— X
OX£ \ OU ov J ox oy \ OU OV J
( d d\ d2z ( d d\2
x nF~	+ Чтг	F 7ГХ = n4~ +	z-
\ OU dv J dy2	\ OU	ov J
d2z d2z d2z
1942. Преобразовать выражение —— — 4 ——-—|-3-z—z- к новым
dx2 ох dy dy2
переменным и = 'фг + у \\ с = г + у (см. задачу 1941).
d2z d2z d2z
1943.	Преобразовать выражение —— — 4 ——-—|-4 —— к новым
Ох2 ох оу оу2
переменным и = 2х-\-унх = у (см. задачу 1941).
1944.	Доказать, что если z = F(u, v), где и и v — функции от
х и у, то
d2z ( , д , д \2 п dz п dz
dx2 \ du dv J	du dv
d2z	d2z
Определить аналогично ——— и ——
dx dy dy2
d2z	d2z
1945.	Преобразовать выражение x2—— — у2тгд к новым пере-
dx2	dy2
менным и = ху и v = у/х (см. задачу 1944).
d2z 1 d2z
1946.	Преобразовать выражение —— 4—дтглу
от2 г2 d<p2
1 dz
4——— к новым
г dr
переменным х = гсояф и у = г sin 92 (см. задачу 1944).
§ 6. Частные производные высших порядков
197
1947. Найти частные производные второго порядка
™2
функции
1-2у
1948. Найти частные производные третьего порядка
функции
тт	ХУ
1949. Доказать, что если z = --------, то
d2z d2z d2z 2
dx2 + dx dy + dy2 x —
1950. Доказать, что если
s = In (ах — bt), то
d\3
+	) s — 2.
dt)
1951. Доказать, что если
z = 2 cos2
i \
- , то
2/
d2z d2z
dt2 + dx dt
тт	т/«	^Z
1952.	Доказать, что если z = е то у ——— = ——
dz
1953.	Пусть и = In х. Найти d2u и d3u.
d2 z	d2z
1954.	Преобразовать выражение —— — а2—— к новым пере-
dx2	dy2
менным и — ах у и v — ах — у (см. задачу 1941).
d2z	d2z
1955.	Преобразовать выражение х—~— + у——д— к новым пере-
dx2 ох оу
У
менным и = у и v = — (см. задачу 1944).
1956. Показать, что функция и =
при любых
дважды дифференцируемых функциях f и р удовлетворяет диф-
ференциальному уравнению
198 Гл. 11. Частные производные, полные дифференциалы
§ 7. Интегрирование полных дифференциалов
1°. Чтобы выражение Р dx + Qdy, где Р и Q — дифференцируе-
мые функции х и у, было полным дифференциалом du, необходимо и
ЗР 3Q
достаточно выполнение условия —— = ——.
ду дх
।	~	ди о ди о
Для нахождения	и из условии	——	= Р	и ——	= Q	получим и =
дх	Оу
= f Р dx + рд(у), и = f Q dy + (pz(x). Выписав из первого выражения
все известные члены, а из второго — члены с у, недостающие в первом,
получим функцию и.
2°. Чтобы выражение Р dx + Q dy + Rdz, где Р, Q и R — диффе-
ренцируемые функции от х, у и z, было полным дифференциалом du,
необходимо и достаточно выполнение условий:
ao__dR
ду дх ’ dz дх ’ dz ду
Для нахождения и имеем:
и = У Pdx + p^y, z), и = У Qdy + cp2(x, z), и = j Rdz + p3(x, у).
Выписав из первого выражения все известные члены, а из второго и
третьего — недостающие члены с у и z, получим функцию и.
Нахождение функции по ее полному дифференциалу называется ин-
тегрированием полного дифференциала.
Проверить, что следующее выражение является полным диф-
ференциалом du, и найти и:
1957.(2ж + у) dx + (ж — 2у — 3) dy.
1958.	х sin 2у dx + х2 cos 2у dy.
1961.(yz -
1962. - -
1959.	(x + In y) dx + I —h sin у I dy.
\У J
x dy — у dx
1960.	---.
- У2
2x) dx + (xz + y) dy + (xy — z) dz.
1 \ dy ( x 1	\
—- I dx -|--------I — -|- -------— I dz
ZY* !	Q f	\ A	I _l yL /
Проверить, что следующее выражение является полным диф-
ференциалом du, и найти и:
1963. (у2 — 1) dx + (2жу + Зу) dy.
1964. (sin 2у — у tg ж) dx + (2ж cos 2у + In cos ж + 2у) dy.
§8. Особые точки плоской кривой	199
( sin2y\ ,	/ sin 2у \ ,
1965.	I у-------— I dx + I x H-------h 1 I dy.
\	£ j	\	Cy*	j
I x 1 + aA2 + 1 ,
1966.	t. / --dt H-------—=-----dx.
V i2 + 1	2^
1967.	(In у — cos 2г) dx + —Pzj dy + (y + 2s sin 2г) dz.
dx — 3 dy 3y — z ,
1968.		---- + J „ dz.
z	z2
§ 8.	Особые точки плоской кривой
Точка кривой У (ж, у) = 0 называется особой, если в этой точке
дх и ду
Угловой коэффициент к = у' касательной в такой точке находится из
уравнения А + 2Вк + Ск2 = 0, где А, В и С — значения производных
d2F d2F d2F
, ——— и	в этой особой точке. При этом возможны три случая:
дх2 дх ду ду2
1)	В2 — АС >0 — две касательные; точка называется узлом',
2)	В2 — АС <0 — нет касательной; точка изолированная',
3)	В2 — АС = 0 — или изолированная точка, или точка возврата,
или точка самосоприкосновения', в точках возврата и самосоприкосно-
вения существует одна общая касательная к двум ветвям кривой.
Чтобы в третьем, сомнительном, случае решить вопрос окончательно,
нужно узнать, имеются ли точки кривой в сколь угодно малой окрестно-
сти исследуемой точки.
Определить области расположения, точки пересечения с осями
координат, особые точки кривых и построить кривые:
1969. х3 + х2 - у2 = 0. 1970. у2 = (х + 2)3.
1971. х3 - х2 - у2 = 0. 1972. у2 + ж4 - х2 = 0.
1973. (у - х)2 = х3.	1974.	у2 = х(х - 2)2.
Определить области расположения, особые точки и асимптоты
кривых и построить кривые:
1975. (х + 2а)3 + ху2 = 0. 1976. х3 - у3 - Зу2 = 0.
1977. х3 + у3 — Заху = 0.	1978. у2(ж2 — а2) = х4.
200 Гл. 11. Частные производные, полные дифференциалы
Определить области расположения, точки пересечения с осями
координат, особые точки кривых и построить кривые:
1979. у2 + ж3 - 2ж2 = 0.
1981. у2 = х(х + 2)2.
1983. 4у2 = ж5 + 5ж4.
1980. а2у2 = х2(‘2ах — ж2).
1982. ху2 = (ж + а)3.
1984. у2 — ж4 + ж2 = 0.
1985. Найти точки пересечения с осями координат, утах, осо-
бую точку и асимптоту кривой 4ж2 — у2 + ж3 — у3 = 0 и построить
кривую.
Определить области расположения, особые точки и асимптоты
кривых:
1986. 1) у2(2а — ж) = ж(ж — а)2 (строфоида);
2) а2(ж2 + у2) = х2у2.
1987.	1) ж(ж2 + у2) = а(ж2 — у2); 2) а(ж2 + у2) = ж(ж2 — у2).
§ 9.	Огибающая семейства плоских кривых
Кривая называется огибающей семейства кривых F(x, у, а) = 0,
если: 1) она касается каждой кривой семейства; 2) каждая ее точка явля-
ется точкой ее касания с кривой семейства, отличной от нее самой.
Огибающая семейства кривых F(x, у, а) = 0, если она существует,
находится исключением параметра а из уравнений
F(x, у, а) = 0 и F&(x, у, а) = 0.
Может, однако, случиться, что полученная этим способом кривая бу-
дет не огибающей, а геометрическим местом особых точек кривых се-
мейства (см. ответ к задаче 1990, 2)).
Найти огибающую семейства кривых и построить огибающую
и кривые семейства:
1988.	1) у = аж + а2;	2) у = аж2 -|—.
а
1989.	1) (ж — а)2 + у2 = Л2; 2) 4ау = (ж — а)2.
1990.	1) у — 1 = (ж — а)2;	2) (у — I)3 = (ж — а)2;
3)	(у — I)2 = (ж — а)3; 4) 9(у — а)2 = (ж — а)3.
1991.	Отрезок постоянной длины а скользит своими концами
по координатным осям. Найти огибающую семейства таких от-
резков.
1992.	Найти огибающую семейства окружностей, проходящих
через начало координат и имеющих центр на параболе у2 = 4ж.
1993.	Найти огибающую семейства окружностей, имеющих диа-
метрами радиус-векторы точек гиперболы жу = а2.
§ 10. Касательная плоскость и нормаль к поверхности 201
1994.	Из начала координат выпускается снаряд с начальной
скоростью b под углом а к оси Ох. Найти огибающую семейства
траекторий при различных а.
1995.	Найти огибающую: 1) семейства прямых х cos а-\-у sin а —
— р = 0 при постоянном р; 2) семейства прямых у = ах ---;
а
3) семейства кубических парабол у — 1 = (ж — а)3.
1996.	Найти огибающую семейства окружностей с центрами на
оси Ох, радиусами которых служат соответствующие ординаты
параболы у2 = 4ж.
X2 у2
1997.	Найти огибающую семейства эллипсов — + — = 1 при
а2 о2
условии, что сумма полуосей имеет постоянную длину I.
1998.	Найти огибающую семейства парабол, имеющих ось сим-
метрии, параллельную оси Оу, и проходящих через точки ( — а; 0);
(За; 0) и (0; За2) при различных а.
§	10. Касательная плоскость и нормаль к поверхности
Пусть поверхность задана уравнением F(x, у, z) = 0; возьмем на ней
точку М(ж; у, z).
Уравнения нормали к поверхности в этой точке будут
X — х Y — у Z — z
dF/дх = dF/dy = dF/dz'
Уравнение касательной плоскости:
dF	дР	дР
^-(X-x) + ^-(Y-y) + ^-(Z-z) = 0.	(2)
dx	оу	OZ
В уравнениях (1) и (2) X, Y, Z — текущие координаты нормали или
касательной плоскости.
т. _ f dF дР дР 1
Вектор N < -т—; -т—; -т— > назовем нормальным вектором поверхно-
ох оу dz J
сти.
тл	dF м dF
Если на поверхности есть точка, в которой = 0, -т— = 0,
ох	оу
dF
= 0, то она называется особой. В такой точке нет ни касательной
dz
плоскости, ни нормали к поверхности.
Написать уравнения касательной плоскости к поверхности:
1999.	z = х2 + 2?/2 в точке (1; 1; 3).
202 Гл. 11. Частные производные, полные дифференциалы
2000.	ху = z2 в точке (ж0; Уо', Zq).
2001.	xyz = а3 в точке (ж0; Уо', zo).
х2	у2	z2
2002.	— + —------- = 1 в точке (ж0; Уо! z0) и в точке (а; Ь; с).
а2	о2	с2
2003.	Определить плоскость, касательную к поверхности х2 +
+ 4у2 + z2 = 36 и параллельную плоскости х + у — z = 0.
2004.	Написать уравнения нормали в точке (3; 4; 5) к поверх-
ности конуса х2 + у2 = z2. В какой точке конуса нормаль неопре-
деленна?
2005.	Найти углы с осями координат нормали к поверхности
ж2 + У2 ~ xz — yz = 0 в точке (0; 2; 2).
2006.	Написать уравнения нормали к поверхности ж2г-|-у2г = 4
в точке ( — 2; 0; 1). Построить нормаль и поверхность.
2007.	Показать, что касательные плоскости к поверхности xyz =
= а2 образуют с плоскостями координат пирамиды постоянного
объема.
2008.	Показать, что сумма квадратов отрезков, отсекаемых на
осях координат плоскостью, касательной к поверхности ж2/3 +
+ У2/3 + г2/3 = а2/3, равна постоянной величине а2.
2009.	Найти расстояние начала координат от касательной плос-
Z	тт
кости к геликоиду у = х tg — в точке (а; а; 7га/4). Построить по-
верхность по сечениям: z = 0; да/4; да/2; ла.
2010. Написать уравнение касательной плоскости к поверхно-
9.9
сти az = х + у в точках пересечения ее с прямой х = у = z.
х2
2011.	Показать, что касательная плоскость к поверхности — +
а2
= 1 в точке на ней (ж0; Уо', z0) определяется уравнением
ХХр ууо ZZp
а2	Ь2	с2
2012.	Написать уравнения нормали к поверхности х2 + у2 —
— (z — 5)2 = 0 в точке (4; 3; 0). Построить в первом октанте по-
верхность и нормаль.
2013.	Найти углы с осями координат нормали к поверхности
2г = ж2 — у2 в точке (2; 2; 0).
2014.	Найти расстояние начала координат от касательной плос-
кости к коноиду (2а2 — г2)ж2 — а2у2 = 0 в точке (а; а; а).
§11. Скалярное поле. Линии и поверхности уровней 203
2015.	Показать, что сумма отрезков, отсекаемых на осях коор-
динат плоскостью, касательной к поверхности ж1/2 + у1/2 + г1/2 =
= а1/2, равна постоянной величине а.
2016.	В какой точке касательная плоскость к поверхности z —
= 4 — ж2 — у2 параллельна: 1) плоскости хОу; 2) плоскости 2ж +
+ 2у + г = 0? Написать уравнения этих касательных плоскостей.
§ 11. Скалярное поле. Линии и поверхности уровней.
Производная в данном направлении. Градиент
Уравнение u = F(x, у) определяет и в каждой точке (х; у) некоторой
области, которая называется полем скаляра и. Вдоль каждой из линий
F(x, у) = «1, F(x, у) = «2, • • ., где «1, «2, • • • — постоянные, скаляр и
остается постоянным и меняется только при переходе точки (х; у) с од-
ной линии на другую. Эти линии называются изолиниями (изотермами,
изобарами и т. п.) или линиями уровней.
Уравнение и = F(x, у, z) определяет поле скаляра и в некоторой
части трехмерного пространства. Изоповерхностями, или поверхно-
стями уровней будут
F(x, у, z) = «1, F(x, у, z) = «2,
Пусть точка (х; у; z) перемещается по прямой х = xq + I cos а, у =
= t/о + I cos/3, z = zq + /cosy со скоростью — = 1. Тогда скаляр
dt
и = F(x, у,	z)	будет	изменяться со	скоростью
du	du	dF	dF	dF
t: =	—	=	—	=	— cos a +	— cos Д +	— cos 7 = N • l0,
dt	di	dx	dy	dz
f dF dF dF }
где N < ——; ——; —— > — нормальный вектор изоповерхности, a
( dx dy dz J
lo{cosa; cos/3; cosy} — единичный вектор направления 1.
Производная
du	dF	dF	dF
— = — cos a + — cos /3 + — cos у = N • l0
dl	dx	dy	dz
называется производной от функции и = F(x, у, z) в данном напра-
влении lo{cosa; cos /3; cosy}.
Градиентом скаляра и = F(x, у, z) называется вектор grad и =
du.	du. ди
= —— 1 + —j + —к. Градиент есть вектор скорости наибыстрейшего
dx	dy	dz
изменения скаляра и.
2017.	Пусть z = 4 — ж2 — у2. Построить линии уровней и grad z
в точке А(1; 2).
204 Гл. 11. Частные производные, полные дифференциалы
У
2018.	Пусть z = arctg—. Построить линии уровней и grad г:
1)	в любой точке прямой у = х; 2) в любой точке прямой
у = —х, в частности в точках (1/2; ±1/2), (1; ±1), ...
2019.	Горизонтали возвышенности определяются уравнением
ж2
h = 20-------у2. Построить горизонтали, соответствующие от-
меткам h = 20 м, 19 м, 18 м, 16 м и 11м. Направление grad h
определяет здесь направление линии наиболее крутого ската, а ве-
личина — крутизну этого ската возвышенности. Построить grad h
в точке х = 2 и у = 1.
2020.	Найти наибольшую крутизну поверхности z2 = ху в
точке (4; 2).
2021.	Найти производную функции u = In (ех ± еу) в напра-
влении, параллельном биссектрисе координатного угла.
2022.	Найти производную функции и = х2 ± у2 ± z2 в точке
(1; 1; 1) в направлении l{cos45°; cos60°; cos60°} и найти gradrr
в той же точке и его длину. Построить поверхности уровней.
2023.	Построить поверхности уровней скаляра и = х2 ± у2 —
— 2г и найти и построить gradrr в точках пересечения оси Ох с
поверхностью и = 4.
X2	у2	Z2
2024.	Найти производную функции и = —- ± — -|—-в точке
а2	о2	с2
(а; Ь; с) в направлении радиус-вектора этой точки.
2025. Пусть
точке (—1; 2) и
Построить линии уровней и grad г в
найти |grad^|.
2026. Пусть и = xyz. Найти производную — в направлении,
dl
составляющем с осями координат равные углы, в любой точке и
в точке (1; 2; 1).
2027.	Построить поверхности уровней скаляра и = х2 фу2 — г2,
определить gradrr на поверхности, проходящей через начало коор-
динат, и построить его в тех точках этой поверхности, в которых
у = 0 и z = 2.
2028.	Пусть и = -\/ж2 ± у2 ± г2. Найти gradrr и его длину.
9	9
z х у
2029.	Построить изоповерхности поля функции и =----- — —
с а2 о2
и найти производную от и в точке (а; Ь; с) в направлении радиус-
вектора этой точки.
§12. Экстремум функции двух переменных
205
§ 12. Экстремум функции двух переменных
1°. Необходимые условия. Функция z = F(x, у) может иметь
dF	dF
экстремум только в точках, в которых —— = 0 и —— = 0. Эти точки
дх	Оу
называются критическими.
2°. Достаточные условия. Обозначим через А, В и С значения
d2F d2F d2F
производных , ——— и в критической точке («о; уф).
дх2 Ох Оу Оу2
Тогда, если:
1)|д с| > °’ то F(XOj у°) = Zmax при Л < °’ F(XOj у°) = Zmin
при А > 0;
9ДД В\ / о
2) Ig (j\ < 0, то экстремума нет;
., ч IА ВI „	_	к/
3) Ig q = 0, то экстремум может быть, а может и не быть (сомни-
тельный случай).
3°. Условный экстремум. Чтобы найти экстремум функции
z = F(x, у) при условии, что х и у связаны уравнением р(х, у) = 0,
составим вспомогательную функцию и = F(x, у) + Хр(х, у).
Координаты экстремальной точки (х; у) должны удовлетворить трем
ди	ди
уравнениям: <р(ж, у) = 0, —— = 0, —— = 0, из которых и находятся А,
дх	ду
хну.
Найти экстремум функции:
2030.	z = х2 — ху + у2 + 9ж — бу + 20.
2031.	z = уфФ — у2 — х + бу.
2032.	z = х3 + 8у3 — бху + 1.
2033.	z = 2ху — 4х — 2у.	2034. z = ех/2(х + у2).
2035.	z = sin х + sin у + sin (х + у) при 0 х ф. тг/2 и ОД
С // С 7Г/2.
1 1
2036.	z = —|— при х + у = 2.
х У
1	1	1
2037.	z = х + у при — + — =
х2	у2	2
2038.	Определить размеры прямоугольного открытого бассейна,
имеющего наименьшую поверхность при условии, что его объем
равен V.
2039.	Построить эллипс х2 + 4у2 = 4 и прямую 2ж + Зу — 6 =
= 0 и на эллипсе найти точки, наиболее и наименее удаленные от
прямой.
2040.	На гиперболе х2 — у2 = 4 найти точку, наименее удален-
ную от точки (0; 2).
206 Гл. 11. Частные производные, полные дифференциалы
2041.	Определить размеры цилиндра наибольшего объема при
условии, что его полная поверхность равна 5 = 6дм2.
2042.	1) В эллипс х2 + Зу2 = 12 вписать равнобедренный тре-
угольник с основанием, параллельным большой оси, так, чтобы
площадь треугольника была наибольшей.
2)	Ось Ох расположена на границе двух сред. По какому пути
должен пройти луч света из точки А(0; а) в точку В (с; —Ь), чтобы
затратить на прохождение этого расстояния наименьшее время
(а > 0, Ь > 0, с > 0)?
а	b
Указание. Нужно найти минимум функции Т =-------1------
Vi cos a V2 cos р
при условии a tg а+Ь tg/З = с, где гд и гд — скорости света в двух средах,
а а и (3 — углы падения и преломления.
Найти экстремумы функций:
2043.	z = Зх + бу — х2 — ху — у2.
2044.	z = х2 + у2 — 2ж — 4^/жу — 2у + 8.
2045.	z = 2ж3 — ху2 + 5ж2 + у2.
2046.	z = Зж2 — Эх^/у + у — 8х + 8.
2047.	z = ху при условии, что х2 + у2 = 2.
2048.	Найти наибольший объем прямоугольного параллелепи-
педа при условии, что длина его диагонали равна 2д/3.
2049.1) На параболе у2 = 4ж найти точку, наименее удаленную
от прямой х — у + 4 = 0.
х2 у2
2) В эллипс — + — = 1 вписан прямоугольник наибольшей
а2 о2
площади. Найти эту площадь.
2050. Определить размеры конуса наибольшего объема при усло-
вии, что его боковая поверхность равна S.
Глава 12
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§ 1. Понятие о дифференциальном уравнении
1°. Обыкновенным дифференциальным уравнением
п - г о порядка называется уравнение вида
F(x,y,y',y", ...,у^)=0,	(1)
где у = у(х) — искомая функция. Любая функция у = р(х), обращаю-
щая уравнение (1) в тождество, называется решением этого уравнения,
а график этой функции — интегральной кривой. Если решение за-
дано в неявном виде Ф(ж, у) = 0, то оно обычно называется интегралом
уравнения (1).
Функция у = р(х, С\, . . ., Сп), содержащая п независимых произ-
вольных постоянных, называется общим решением уравнения (1), если
она является его решением при любых значениях постоянных С\, ...
. . ., Сп- Если эта функция задается в неявном виде выражением
Ф(ж, у, С\, . . ., Сп) = 0, то это выражение называется общим инте-
гралом уравнения (1). Придавая в выражении у = р(х, С\, . . ., Сп)
или в выражении Ф(ж, у, С\, . . ., Сп) = 0 определенные значения по-
стоянным С\, . . ., Сп, получаем частное решение или соответственно
частный интеграл уравнения (1).
Обратно, имея семейство кривых, задаваемых уравнением
Ф(ж, у, С\, . . ., Сп) = 0, и исключая параметры С\, . . ., Сп из системы
уравнений
с/Ф	(ГФ
Ф = 0, — = 0, ... , -— = О,
ах	ахп
получим, вообще говоря, дифференциальное уравнение вида (1), для ко-
торого Ф(ж, у, С\, . . ., Сп) = 0 является общим интегралом.
2°. Дифференциальное уравнение первого порядка
имеет вид
(2)
тэ	/ОА
Решив уравнение (2) относительно —, если это возможно, получим
ах
S = ^х’
(3)
208	Гл. 12. Дифференциальные уравнения
Уравнение (3) определяет наклон k = tga = — = f(x, у) инте-
гральной кривой в точке (х; у), т. е. определяет поле направлений ин-
тегральных кривых.
Если в некоторой области функция f(x, у) непрерывна и имеет огра-
ниченную частную производную fy(x, у), то оказывается, что через каж-
дую внутреннюю точку (ж0; Уо) этой области пройдет единственная ин-
тегральная кривая.
В такой области уравнение (3) имеет общее решение у = р(х, С),
или общий интеграл Ф(ж, у, С) = 0, из которого можно найти единст-
венное частное решение, или единственный частный интеграл, удовле-
творяющие начальным условиям: у = у0 при х = х0.
2051.	Проверить подстановкой, что функция у = Сх3 является
решением дифференциального уравнения Зу — ху1 = 0. Построить
интегральные кривые, проходящие через точки:
1) (1; 1/3);	2) (1; 1);	3) (1; -1/3).
2052.	Проверить подстановкой, что дифференциальные уравне-
ния 1) у" + I // = 0 и 2) у'" — 9у' = 0 имеют соответственно общие
решения: 1) у = cos ‘ix + C^ sin 2s и 2) у = + С2е3х + Сзе~3х.
2053.	Построить параболы у = Сх2 при С = 0, ±1, ±2 и со-
ставить дифференциальное уравнение семейства таких парабол.
2054.	Построить изображения семейства: 1) окружностей х2 +
+ у2 = 2Сж, 2) парабол у = х2 + 2Сх и составить их дифферен-
циальные уравнения.
2055.	Построить изображения полей направлений, определяе-
мых каждым из уравнений:
dy	У	dy	dy	2
— =	2)— = у — х; 3) — = у + хР
ах	х	ах	ах
2056.	Построить изображение поля направлений, определяе-
dy	гдд—2
мого уравнением — = Дх£ + у2, с помощью окружностей, вдоль
dx
dy 1
которых — =	1; 2; 3; ... Нарисовать приближенно интеграль-
dx 2
ную кривую, проходящую через начало координат.
§ 2.	Дифференциальное уравнение первого порядка
с разделяющимися переменными.
Ортогональные траектории
1°. Дифференциальное уравнение первого порядка
Pdx + Qdy = Q,	(1)
где Р и Q — функции жиг/, называется уравнением с разделяющимися
переменными, если коэффициенты Р и Q при дифференциалах разлага-
ются на множители, зависящие только от х или только от у, т. е. если
§ 2. Дифференциальное уравнение первого порядка 209
оно имеет вид
/(ж)у(г/) dx + /1 (ж)у1 (у) dy = 0.	(2)
Разделив оба члена уравнения (2) на ip(y)fi (х), получим
f(x)dx уд (у) dy
№) + Л»)	"
Общим интегралом уравнения (3), а следовательно, и (2) будет
Г f(x)dx Г уч (г/) dy _
J Кх) Д Лу)	u
2°. Ортогональными траекториями семейства линий
F(x, у, а) = 0 называются линии, пересекающие линии данного семей-
ства под прямым углом. Продифференцировав уравнение F(x, у, а) = 0
по I и исключив а из полученного и данного уравнений, получим диф-
ференциальное уравнение линий данного семейства у' = f(x, у). То-
гда дифференциальным уравнением ортогональных траекторий будет
у' =-------—•
f(x, у)
В следующих дифференциальных уравнениях: 1) найти об-
щий интеграл; 2) построить несколько интегральных кривых;
3) найти частный интеграл по начальным условиям у = 4 при
х = —2:
2057.	ху1 — у = 0. 2058. ху1 + у = 0.
2059. уу' + х = 0. 2060. у' = у.
Найти общие интегралы уравнений:
2061. х2у' + у = 0.	2062. х + ху + у'{у + ху) = 0.
2063.	Д dr + (г — a) dip = 0.
2064.	2st2 ds = (1 + t2) dt.
В следующих уравнениях найти общий и частный интегралы
по начальным условиям:
2065.	2у\/ж = у, у = 1 при х = 4.
2066.	у' = (2у + 1) ctg ж, у = 1/2 при х = тг/4.
2067.	х2у' + у2 = 0, у = 1 при х = — 1.
2068.	Построить интегральные кривые каждого из уравнений:
1) у'(х2 — 4) = 2жщ 2) у' + wtgs = 0, проходящие через точки:
1) (0; 1); 2) (0; 1/2); 3) (0; -1/2); 4) (0; -1).
2069.	Найти кривую, проходящую через точку (1; 1/3), если
угловой коэффициент касательной к ней в любой точке кривой
втрое больше углового коэффициента радиус-вектора точки каса-
ния.
210	Гл. 12. Дифференциальные уравнения
2070.	Кривая проходит через точку А(0; a), MN — произволь-
ная ордината кривой. Определить кривую из условия, что площадь
OAMN = as, где s — длина дуги AM.
2071.	Найти кривую, проходящую через точку (а; а), если под-
касательная в любой точке ее равна удвоенной абсциссе точки ка-
сания.
2072.	Найти кривую, проходящую через точку ( — 1; —2), если
поднормаль ее в каждой точке равна 2.
2073.	За какое время тело, нагретое до 100 °C, охладится до
25 °C в комнате с температурой 20 °C, если до 60 °C оно охлажда-
ется за 10 мин? (По закону Ньютона скорость охлаждения пропор-
циональна разности температур.)
2074.	Нагрузка на канат висячего моста (см. рис. 6) от каждой
единицы длины горизонтальной балки равна р. Пренебрегая весом
каната, найти его форму, если натяжение каната в низшей точке
принять за Н.
Указание. Возьмем на дуге ОС (рис. 6) произвольную точку М.
На часть каната ОМ будут действовать три силы: горизонтальная Н
(влево от точки М), вертикальная — вес рх и тангенциальная сила на-
тяжения Т (вправо от точки М\ Для равновесия сумма проекций сил
на Ох и Оу должна равняться 0.
2075.	Определить и построить кривую, проходящую через точку
Р( — а; а), если отрезок АВ любой касательной к ней, заключен-
ный между осями координат, делится точкой касания М пополам.
2076.	Найти ортогональные траектории семейства парабол ау =
= ж2. Построить их.
2077.	Найти ортогональные траектории семейства гипербол
ху = с.
2078.	Найти ортогональные траектории семейства полукубиче-
ских парабол ay2 = ж3.
2079.	Найти ортогональные траектории семейства эллипсов
ж2 + 4у2 = а2.
Решить уравнения:
2080. у'ж3 = 2у.	2081. (ж2 + х)у' = 2у + 1.
2082. у'у/а2 + ж2 = у. 2083. (1 + ж2)у' + 1 + у2 = 0.
2084.	dr + г tg ф dip = 0; г = 2 при ф = 7Г.
2085.	у1 = 2^/у In ж; у = 1 при ж = е.
2086.	(1 + ж2)у' + уу/1 + ж2 = ху; у = 1 при ж = 0.
2087.	Определить кривую, проходящую через точку А(—1; 1),
если угловой коэффициент касательной в любой точке кривой ра-
вен квадрату ординаты точки касания.
§ 3. Дифференциальные уравнения первого порядка
211
2088.	Кривая проходит через точку А(0; a), MN — произволь-
ная ордината кривой. Определить кривую из условия, что площадь
OAMN = a(MN - a).
2089.	Определить и построить кривую, проходящую через точку
(—1; —1), для которой отрезок ОТ, отсекаемый на оси Ох каса-
тельной к кривой в любой ее точке, равен квадрату абсциссы точки
касания.
2090.	Найти ортогональные траектории семейства гипербол х2 -
— 2у2 = а2.
2091.	Определить кривую, радиус-вектор любой точки которой
равен отрезку нормали между кривой и осью Ох.
2092.	Определить линию, если площадь, ограниченная осями
координат, этой линией и произвольной ее ординатой, равна 1/3
площади прямоугольника, построенного на координатах конечной
точки кривой.
§ 3. Дифференциальные уравнения первого порядка:
1) однородное, 2) линейное, 3) Бернулли
1°. Однородное уравнение. Уравнение Р dx + Q dy = 0 назы-
вается однородным, если Р и Q — однородные функции от х и у оди-
n	dy (У\
накового измерения. Оно приводится к виду — = ip 1 — 1 и решается
dx \х/
„ У
подстановкой — = и или у = их.
2°. Линейное уравнение. Дифференциальное уравнение назы-
вается линейным, если оно первой степени относительно искомой функ-
ции у и всех ее производных. Линейное уравнение первого порядка
имеет вид у' + Ру = Q. Оно сводится к двум уравнениям с разделя-
ющимися переменными подстановкой у = uv. Другой способ решения
(вариация произвольной постоянной) состоит в том, что сначала ре-
шаем уравнение у' + Ру = 0; получаем у = —Ae~fpdx. Подставляем
это решение в данное уравнение, считая А функцией х, и затем находим
А' и А.
3°. Уравнение Бернулли у' + Ру = Qyn решается так же,
как и линейное, подстановкой у = uv или вариацией произвольной по-
стоянной. Уравнение Бернулли приводится к линейному подстановкой
г = г/1-".
Решить дифференциальные уравнения:
2093. уу' = ‘2у — х.
2094. х2 + у2 — 2хуу' = 0.
ds	s	t
2095. — =---------.	2096. г/-
dt	t	s
.	2у	е~х2
2097.	у' + — = -----.
2098.	у' cos х — у sin х = sin 2s.
212
Гл. 12. Дифференциальные уравнения
2099.	у'х + у = —ху2.	2100. у' — ху = — у3е х2.
. у	у
2101. ху cos — = у cos--х.
2102. х2у' = у2 + ху.	2103. ху' + у = In х + 1.
2104.	х2у2у' + ух3 = 1.
В задачах 2105-2107 найти частные интегралы по данным на-
чальным условиям:
2105.	у + -у/ж2 + у2 — ху' = 0; у = 0 при х = 1.
о ds
2106.	t2— = 2ts — 3; s = 1 при t = —1.
dt	’ F
2107.	xy' = у (1 + In — Y у = —j= при x = 1.
\ x) Де
2108.	Найти семейство кривых, подкасательная в любой точке
которых есть среднее арифметическое координат точки касания.
2109.	Найти ортогональные траектории семейства окружностей
х2 + у2 = ‘lax.
2110.	Сила тока i в цепи с сопротивлением Л, самоиндукцией
L и электродвижущей силой Е удовлетворяет дифференциальному
уравнению
L— + Ri = Е.
dt
Решить это уравнение, считая R и L постоянными, а электро-
движущую силу Е линейно нарастающей: Е = kt. Начальные
условия: i = 0 при t = 0.
2111.	Найти форму зеркала, отражающего все лучи, выходя-
щие из данной точки, параллельно данному направлению.
Указание. Рассматривая плоское сечение зеркала, примем в нем
данную точку за начало координат, а данное направление — за ось Оу.
Касательная к искомой кривой в точке М образует равные углы с ОМ и
осью Оу, т. е. отсекает на оси Оу отрезок ON = ОМ.
Решить дифференциальные уравнения:
2112. ху + у2 = (2ж2 +	ху)у'. 2113.	(а2 + х2)у' + ху = 1.
2114. ху' + ly/ху = у.	2115.	(1х + 1)у' + у = х.
2116. у' — у tg х = ctg х.	2117.	t ds — Is dt = t3 In t dt.
2118. y' + xy = xy3.	2119.	у' + у cos x = sin lx.
2120.	у' =	; у = 1 при x = —1.
£ A £
2121.	Зу2у' + у3 = ж-Г1; у = — 1 при x = 1.
§4. Уравнения с дифференциалами произведения и частного 213
2122.	(1 — х2)у' — ху = жу2; у = 0, 5 при х = О.
2123.	Определить кривую, проходящую через точку А(а; а),
если расстояние от начала координат до касательной в любой точке
кривой равно абсциссе этой точки.
§ 4.	Дифференциальные уравнения, содержащие
дифференциалы произведения и частного
,/у\ х dy — у dx , (х\	у dx — х dy
d(xy) = х dy + у dx; d ( — ) = ---; d — = -----------.
\xJ x1	\y J y2
Такие уравнения иногда легко решаются, если соответственно поло-
« У
жить ху = и, у = — или — = и, у = их.
Решить дифференциальные уравнения:
2124.	х2 dy + ху dx = dx. 2125. у2х dy — у3 dx = х2 dy.
Указание. В примере 2125 уравнение приводится к виду
у2 d ) = dy или у2 du = dy.
2126.	у dx + (х — у3) dy = 0.
2127.	у dx — (ж — у3) dy = 0.
2128.	у cos ж dx + sin ж dy = cos 2ж dx.
ds
2129.	t—--s = s2 In t. 2130. x2y2 + 1 + ж3уу' = 0.
dt
2131. t2s dt + t3 ds = dt. 2132. ж dy — у dx = x2 dx.
2133. жу' + tg у = 2ж sec у. 2134. у (уе-ж/2 + 1) = жу'.
§ 5. Дифференциальные уравнения первого порядка
в полных дифференциалах. Интегрирующий множитель
1°. Если в дифференциальном уравнении
Р dx + Q dy = 0
dP 9Q	„
—— = ——, то оно приобретает вид du = (J и его общин интеграл будет
ду дх
и = С.
дР dQ
2°. Если —— ф ——, то при некоторых условиях существует функция
ду дх
у,(х, у) такая, что рР dx + pQ dy = du. Эта функция у(ж, у) называется
интегрирующим множителем.
214
Гл. 12. Дифференциальные уравнения
Интегрирующий множитель легко найти в случаях:
dP/dy — dQ/dx	г
1) когда -----—------ = Ф(ж), тогда In у = J Ф(ж) ах;
Д
dQ/dx — dP/dy .	г. .	,
2) когда -----—------ = Фг(у), тогда In у = J ФДу) dy.
Дифференциальные уравнения § 4 являются частными случаями урав-
нений, рассматриваемых в настоящем параграфе.
Решить следующие дифференциальные уравнения «в полных
дифференциалах»:
2135.	4 - dx + — dy = 0.
\	£ А /
2136.	Зж2еу dx + (х3еу - 1) dy = 0.
2137.	е~у dx + (1 - хе~у) dy = 0.
2138.	2s cos2 у dx + (2у — х2 sin 2у) dy = 0.
Найти интегрирующие множители и решить дифференциаль-
ные уравнения:
2139.	(ж2 — у) dx + х dy = 0.
2140.	2х tg у dx + (ж2 — 2 sin у) dy = 0.
2141.	(е2х — у2) dx + у dy = 0.
2142.(1 + Зж2 sin у) dx — ж ctg у dy = 0.
Показать, что левые части следующих дифференциальных урав-
нений суть полные дифференциалы, и решить уравнения:
2143. (Зж2 + 2у) dx + (2ж — 3) dy = 0.
2144. (Зж2у — 4жу2) dx + (ж3 — 4ж2у + 12у3) dy = 0.
2145.	(ж cos 2у + 1) dx — ж2 sin 2у dy = 0.
Найти интегрирующие множители и решить уравнения:
2146.	у2 dx + (уж — 1) dy = 0.
2147.	(ж2 — Зу2) dx + 2жу dy = 0.
2148.	(sin ж + еУ) dx + cos ж dy = 0.
2149.	(ж sin у + у) dx + (ж2 cos у + ж In ж) dy = 0.
§ 6. Уравнения Лагранжа и Клеро
215
§ 6. Дифференциальные уравнения первого порядка,
не разрешенные относительно производной.
Уравнения Лагранжа и Клеро
1°. Если уравнение F(x, у, у1) = 0 второй степени относительно у1,
то оно имеет два решения относительно у': у1 = fi(x, у) и у' = f%(x, у),
непрерывных относительно х и у в некоторой области, а геометрически
определяет в любой точке («о! Уо) этой области два направления инте-
гральных кривых.
Такие дифференциальные уравнения F(x, у, у') = 0, кроме общего
интеграла Ф(ж, у, С) = 0 и частных интегралов, иногда имеют еще осо-
бый интеграл, не содержащий произвольной постоянной и в то же время
не получающийся из общего ни при каком значении постоянной.
Особый интеграл, если он существует, можно получить, исключив
р = у' из уравнений F(x, у, р) = 0 и Fp(x, у, р) = 0 или же исключив
С из общего интеграла Ф(ж, у, С) = 0 и Ф) = 0. Геометрически особый
интеграл определяет огибающую семейства интегральных кривых1).
2°. Уравнение Лагранжа
У = xf(j>) + Hr),	(!)
где р = у', интегрируется следующим образом.
Продифференцировав (1) по х, найдем:
Р = f(p) + [xf'(p) + P'ip)]^--
ах
dx
Это уравнение линейное относительно х и —. Решив его, получим:
ар
х = СА(р) + В(р).
(2)
Уравнения (1) и (2) будут параметрически определять общий инте-
грал. Исключив из них параметр р (если это возможно), получим общий
интеграл в форме Ф(ж, у, С) = 0.
3°. Уравнение Клеро
у = рх + р(р)	(3)
является частным случаем уравнения Лагранжа. Оно имеет общий ин-
теграл у = Сх + р(С) и особый, получающийся исключением параметра
р из уравнений у = рх + р(р) и х = —р'(р).
2150.	Построить несколько интегральных кривых уравнения
у'2 = 4у. Какие две интегральные кривые проходят через точку
М(1; 4)?
]) См. определение огибающей на с. 200
216
Гл. 12. Дифференциальные уравнения
2151. Построить интегральные кривые уравнения у'2 + у2 —
— 1 = 0. Какие две интегральные кривые проходят через точку
М(д/2; 1/^2)?
2152.	Показать, что интегральные кривые уравнения ху'2 —
— 2уу' + 4ж = 0 содержатся внутри острого угла между прямыми
у = ±2х. Построить интегральные кривые, полагая в общем ин-
теграле постоянную С = ±-, ±1, ±2 и т. д.
2153.	Решить уравнения:
1) УУ12 + у'(,х — у) — х = 0;	2) ху12 + 2ху' — у = 0
и построить интегральные кривые.
2154.	Решить уравнения, не содержащие явно одной из пере-
менных:
1) У = 1 + У12',	2) х = 2у' -
Указание. Обозначив у' через р, продифференцировать первое
уравнение по ж, а второе — по у.
2155.	Найти общие и особые интегралы уравнений Лагранжа:
1) У = ху'2 + у'2-	2)у = 2ху'+-^-	3) 2у =	.
2156.	Найти общий и особый интегралы уравнения Клеро и
построить интегральные кривые:
1) у = ху'- у12;	2) у = ху' -ад'! + у'2;	3) у = ху' + —L—.
2157.	Построить интегральные кривые уравнения у'2 + у = 1.
Какие две интегральные кривые проходят через точку М(1; 3/4)?
2158.	Решить уравнения, не содержащие явно одной из пере-
/7 /з \	аУ/
менных: 1) у = у £ + у °; 2) х = —	.
Д1 + У12
х2
2159. Решить уравнение у = 2у'х + — + у'2.
2160.	Найти общий и особый интегралы уравнения Клеро и
построить интегральные кривые:
!')у = у'х+—;	2) у = ху' + у' + у'2.
У'
2161.	Найти кривую, касательные к которой образуют с осями
координат треугольник постоянной площади, равной 2а2.
2162.	Найти кривую, касательная к которой отсекает на осях
координат отрезки, сумма которых равна а.
§ 7. Дифференциальные уравнения высших порядков
217
§ 7. Дифференциальные уравнения высших порядков,
допускающие понижение порядка
1°	. Уравнение вида = f(x) решается последовательным
n-кратным интегрированием правой части. При каждом интегрирова-
нии получается одна произвольная постоянная, а в окончательном ре-
зультате — п произвольных постоянных.
2°	. Уравнение F(x, у', у") = 0, не содержащее у в явной форме,
„ ,	„ dp
подстановкой у = р, у = — приводится к виду
dx
к (	dP\	о
\	dx J
3°	. Уравнение F(y, у', у") = 0, не содержащее х в явной форме,
dp	dp
подстановкой у' = р, у" = — = р— приводится к виду
dx	dy
к (	dP\	n
г р, р, р—	= U.
\	dyj
Решить уравнения:
6
2163. 1) у'" = —; начальные условия: у = 2, у' = 1, у" = 1
при х = 1; 2) у" = 4соз2ж; у
1
1 + х2
2164. х3у" + х2у' = 1.
2166. у" + у' tg х = sin 2s.
2168. у"х In х = у'.
2170. 1) ху" — у' = ехх2\
: 0, у' = 0 при х = 0; 3) у" =
2165. уу" + у'2 = 0.
2167. у"+ 2у(у')3 = Ъ.
2169. y"tgy = 2(y')2.
2) у" + 2жу/2 = 0.
2171.	Определить кривую изгиба горизонтальной балки, один
конец которой наглухо заделан, а на другой действует сосредото-
ченная сила Р (весом балки пренебречь и считать изгиб настолько
малым, что 1 + у'2	1).
2172.	Определить кривые, у которых радиус кривизны вдвое
больше длины нормали.
2173.	Определить кривые, у которых радиус кривизны равен
длине нормали.
2174.	На отрезке [0, 1] определить кривую, касающуюся оси
Ох в начале координат, если кривизна ее к = х, т. е. равномерно
нарастает вдоль оси Ох (переходная кривая). Принять прибли-
женно, что 1 + у'2 к, 1.
218
Гл. 12. Дифференциальные уравнения
Решить уравнения:
1	In 2	7Г
2175. у" = ---— у = —, у' = 1 при х =
cos^ х 2	4
2176. (1 + х2)у" + 2ху' = х3. 2177. у”у3 = 1.
d2s ds
2178. 2уу" = (у')2.
2179. t— + — + t = 0.
dlz dt
2180. 2yy" = 1 + y'2.	2181. y"tgs = y' + 1.
2182. Определить кривые, у которых радиус кривизны равен
кубу длины нормали.
2183. В интервале (—тг/2, тг/2) определить кривую, касающу-
юся оси Ох в начале координат, если кривизна ее в любой точке
к = cos ж.
§ 8. Линейные однородные дифференциальные уравнения
с постоянными коэффициентами
Однородное линейное дифференциальное уравнение
У(п) +Pit/(n-1) + • • • рпу = 0,	(1)
где pi — функции х, имеет общее решение вида
У = 0*11/1 + C2J/2 + • • • + Спуп,	(2)
где г/i, г/2, • • • , Уп — линейно независимые частные решения уравнения
(1), а С\, С'2, • • Сп — произвольные постоянные.
Если коэффициенты pi, р^, . . рп уравнения (1) постоянны, то част-
ные решения г/i, г/2, • • •, Уп находятся с помощью характеристического
уравнения
Гп + Р1ГП-1 + ... + Рп = 0.	(3)
1) Каждому вещественному корню г = а уравнения (3) кратности т
соответствуют т частных решений еах, хеах, . . ., хт~геах.
2) Каждой паре мнимых корней г = а ± (3i кратности т соответ-
ствуют т пар частных решений:
e"rcos/3s, cos/Зж, ..., хт~1еах cos/Зх,
eaxsin/3x, xeaxsin/3x,	хт~1еах sin/Зх.
Решить уравнения:
2184.	у” - 4у' + Зу = 0.	2185.	у" - 4y' + 4y = 0
2186.	у" - 4у'+ 13у = 0.	2187.	у" — 4y = 0.
2188.	у" + 4у = 0.	2189.	У" + 4y' = 0.
2190.	d2x	dx -—у + 3 —	4s = 0. dt2	dt	2191.	d2p 4t4+-° = 0- t/<p2
§9. Линейные неоднородные дифференциальные уравнения 219
d^s ds
2192.	— + 2 — + 2s = 0; при t = 0 s = 1, s' = 1.
dt2 dt
2193.	y"' - 5y" + Sy' - 4 у = 0.
2194.	yIV - 16y = 0.	2195. y'" - 8y = 0.
2196. y'" + 3ay" + 3a2y' + a3y = 0.
2197. yIV + 4y = 0.	2198. 4yIV - Зу" - у = 0.
2199.	Определить уравнение колебаний маятника, состоящего
из массы т, подвешенной на нити длиной I (сопротивлением пре-
небречь и положить, что при малом угле а отклонения sin а рй а).
Определить период колебания.
2200.	Два одинаковых груза подвешены к концу пружины. Под
действием одного груза пружина удлиняется на а см. Определить
движение первого груза, если второй оборвется (сопротивлением
пренебречь). Определить период колебания.
2201.	Решить задачу 2200 с учетом сопротивления, пропорци-
онального скорости движения.
Решить уравнения: 2202. у"+ Зу'+ 2у = 0.	2203.	у" + 2ау' + а2у = 0.
2204. у"+ 2у'+ 5у = 0.	2205.	d2x	dx —гтр — 2 —	Зх = 0 dt2	dt
d2x	„ 2206. — + (Лх = 0. dt2	2207.	d2s	ds —I-	= О’ dt2	dt
2208. б Т 2ту Т Зх — 0.	2209.	у'" — Зу" + 4y = 0.
2210. yIV - Зу" - 4у = 0.	2211.	yIV + 8y" + 16y = 0.
2212. Найти интегральную кривую уравнения у" — у = 0, ка-
сающуюся в точке (0; 0) прямой у = х.
§ 9. Линейные неоднородные дифференциальные
уравнения с постоянными коэффициентами
1°. Основное свойство. Пусть даны уравнения:
У{п) + Р1У{п~1} + • • • + РпУ =	— неоднородное,	(1)
У(п) + Р1У(п~1} + • • • + РпУ = 0 — однородное	(2)
и пусть и — общее решение уравнения (2), а ух — частное решение
уравнения (1). Тогда общее решение у уравнения (1) будет
у=« + ух.	(3)
220
Гл. 12. Дифференциальные уравнения
2°. Метод неопределенных коэффициентов. При посто-
янных pi, Р2,   , Рп частное решение t/i находится методом неопреде-
ленных коэффициентов в следующих случаях:
1)	f(x) — многочлен;
2)	f(x) = етх (a cos nx + b sin пх);
3)	f(x) есть сумма или произведение предыдущих функций.
В этих случаях частное решение t/i имеет тот же вид, что и f(x),
отличаясь от нее только коэффициентами.
Исключения составляют особые случаи, когда:
1) f(x) — многочлен, но г = 0 — корень характеристического урав-
нения кратности к;
2) f(x) = етх (a cos nx + b sin пх), но г = т ± ni есть корень харак-
теристического уравнения кратности к.
В этих особых случаях t/i отличается от f(x) не только коэффициен-
тами, но еще и множителем хк.
3°. Метод вариации произвольных постоянных. Более
общим приемом решения неоднородного линейного уравнения является
метод Лагранжа, или метод вариации произвольных постоянных.
Если t/i и г/2 — независимые частные решения уравнения у" + ру' +
+ qy = 0, то решение уравнения у"+ру' +qy = f(x) по методу Лагранжа
находится в виде у = At/i + В у2, где А и В — функции х, удовлетворя-
ющие системе уравнений
A'yi + В'у^ = 0,
A't/i + В'у2 = f(x).
Отсюда
yzf(x)
W
в, = yif(x)
W ’
У1 У2
У1 У2
a w =
Решить уравнения:
2213. у" -2у' +	у = е2х.	2214. у"	-	4у = 8ж3.
2215. у" + Зу' +	2у = sin 2ж	+ 2 cos 2s.
2216. у" + у = х	+ 2ех.	2217. у"	+	Зу' =	9ж.
2218. у" + 4у' +	5у = 5ж2	—	32ж + 5.
2219.	у" - Зу'+	2у = ех.
(1^Х
2220.	—— + k2x = 2k sin kt.
dtz
2221.	у" -2y= xe~x.	2222. y" - 2y' = x2 - x.
2223. y" + 5y' + 6y = e~x + e~2x.
2224. x + 2kx + 2k2x = bk2 sin kt.
§10. Примеры дифференциальных уравнений разных типов 221
2225. у'" + у" = бх + е~х.	2226. yIV - 81y = 27e-3E
2227. х + х = 3t2.	2228. y'" + 8y = e~2x.
2229. 1) х + 4s + 4s = e~2t;	2) a3x + as = 1.
„ 1	е2ж
2230. у" + 4 у =  	.	2231. у" - йу' + 5y = 	
sm 2s	COS X
2232. y" — 2y' +y = x~2ex.	2233. y" + y = tgs.
	<•-2j'
2234. 1) / + //= T^-?:	2 у" + йу + 4y - S'5
2235. Единица массы движется по оси Ох под действием по-
стоянной силы а, направленной по оси, при сопротивлении дви-
жению, численно равном скорости движения. Найти закон дви-
жения, если при t = 0 имеем х = 0 и скорость v = 0.
Решить уравнения:
2236. у" + у' -2у= 6s2.	2237.	у" - 5у' + бу = 13 sin Зх.
2238. у" +2у' +у = ех.	2239.	у" + у' + 2, 5у = 25 cos 2s.
2240. I//" — у = х3 — 24s.	2241.	у" — у = е~х.
d2s	ds	о
2242. —- + 2-----1- 2s = 2t3 - 2.
dt2	dt
2243.1) у" — 2my' + m2y = sin mx; 2) n3y" — 4ny = 8.
2244. yIV + 5y" + I// = 3 sin x.
2245. у'" — Зу" + Зу' — у = ex.
Следующие уравнения решить методом вариации произволь-
ных постоянных:
2246. у" + 4у' + I // = е~2х In х.
2247. 1) у" + у =	2]у"+\у=^^.
cos0 х	sm х
2248. у"-2у'+у= J
V4 - s2
§ 10. Примеры дифференциальных уравнений
разных типов
Определить тип дифференциального уравнения и решить его:
2249. у' 4--— = е~х.	2250. у' + у tg х = tg х.
1 + х
2251. (ж — х3)у' + (2s2 — 1)у = х3.
Ш
Гл. 12. Дифференциальные уравнения
2252. (1 + х2)у' + у(х - V1 + х2) = 0.
2253. t2 ds + 2ts dt = e* dt. 2254. xy' = 4(y + ^/y).
2255. 2xyy' = 2y2 + y/y4 + x4.
2256. xy" + y' = In x.
2258. y" - m2y = e~mx.
2260. xy' + у In — = 0.
2262. y'" - 2y" +y' = x2.
2257. yy" - 2y'2 = 0.
2259. y'x In x + у = 2 In x.
2261. 2y' + у = у3(ж - 1).
2263. у" = у'+ у'2.
2264. —— — 3 --- 2s = sin t + 2 cos t.
dt3 dt
2265.1) sin t ds = |4tsin2—h s ) dt;
\	2 J
2266. 1) xy' + y(x tgs + 1) = sec x;
e3x
2267. 1) y"-3y' + 2y=—^;
1 + ezx
2268. Цилиндр радиуса адм и массой
при вертикальном положении оси. Найти период колебания, ко-
2) уу'х - у2 = 1.
2) у"'+ у = е~х.
2) у'"у = у"у'.
т = а° кг плавает в воде
торое получится, если цилиндр немного погрузить в воду и затем
отпустить. Сопротивление движению принять приближенно рав-
ным нулю.
2269. Полый железный шар с радиусами поверхностей а и 2а
имеет постоянную температуру внутренней поверхности 100 °C и
наружной 20 °C. Определить температуру внутри стенки на любом
расстоянии г от центра (а г 2а) и при г = 1, 6а.
V	г	dT
Указание. Скорость падения температуры —— в проводнике со
dr
стационарным распределением температуры обратно пропорциональна
площади поперечного сечения.
§ 11. Линейное дифференциальное уравнение Эйлера
П (п) + г П-1 (п-1) +	+ п_г > + п =	( )
Частное решение однородного уравнения (при f(x) = 0) можно найти
в виде у = хг, где г — постоянное число. Для нахождения г нужно под-
ставить у = хг в однородное дифференциальное уравнение и решить
полученное характеристическое уравнение относительно г. При этом:
1)	каждому вещественному корню г = а кратности т соответствует
т частных решений ха, ха In х, ж“(1пж)2, . . .;
2)	каждой паре мнимых корней г = a±/3i кратности т соответствует
т пар частных решений:
ха cos (/? In х), ха cos (/? In х) In х, ...;
ха sin (/31ns), ха sin (/? In x) In x, ...
§12. Системы линейных дифференциальных уравнений 223
Неоднородное дифференциальное уравнение Эйлера решается мето-
дом вариации постоянных.
Решить уравнения:
2270. 1) х3у'" - Зху' + Зу = 0;	2) х2у" - 2у = 0;
3)	х2у" + 2жу' — п(п + 1)у = 0.
2271. 1) ж2у" + 5ху' + 4у = 0;	2) х2у" + ху' + у = 0.
2272. 1) ху" + 2у' = Юж; 2) х2у" — бу = 12 In х.
2273. 1) х2у" - 2ху' + 2у = 4ж;
2) х3у" + Зх2у' + ху = 6 In х.
2274. 1) х2у" — йху' + бу = ж5;
2) х2у" + ху' + у = х.
dy
dt
dy
§ 12. Системы линейных дифференциальных уравнений
с постоянными коэффициентами
Решить уравнения:
dx	dx
2275.	— + у = 0, —
dt	dt
d х	i * и	i
2276.	——h x — у = e', — x + у = e'.
dt y ’ dt У
dt
Указание к задаче 2275. Продифференцировав первое из уравне-
dy
ний по t, исключаем из трех уравнений у и —.
at
dx	dy	,
2277.	5— - 2—+ 4ж - у = е~'
dt	dt
dx	.
— + 8ж - Зу = 5е '.
dt	У
2278.	х — 4ж + 4ж — у = 0,
у + 4у + 4у — 24ж = 16е*.
Решить уравнения:
2279.	x + Зж + у = 0,
у — ж + у = 0, ж = 1, у = 1 при 7 = 0.
2280.	ж = у, у = ж + 2 sh t.
224
Гл. 12. Дифференциальные уравнения
§ 13.	Линейные дифференциальные уравнения
в частных производных второго порядка
(метод характеристик)
2281.	Найти общее решение (содержащее две произвольные
функции) уравнений:
, д2и	, д2и	, д2и 1ди
17Г^Г	= 0; 2 7Г^ = 0; 3 )	-----7Г = 0;
дх ду	ду2	дхду х ду
д2и	х
4) я—я- = 2а—
дх ду	у
V	тт	ди
Указание. Положить —— = z.
ОУ
2282. Найти частное решение уравнения
д Z
Q L7-‘	9	1
ным условиям: z = у , — = у при х = 1.
дх
2283. Преобразовать уравнение
d2z
—— = 0 по началь-
дх2
д2и д2и д2и
-----4--------к 3--
дх2 дх ду ду2
к канонической форме и найти его общее решение.
2284. Преобразовать уравнение
7д2и д2и ~д2и
д~д + ^УД-ДГ + У ДДД = 0
дх2 дх ду ду2
к канонической форме и найти его общее решение.
В следующих дифференциальных уравнениях найти общие ре-
шения, а если даны начальные условия, то и частные решения:
д2и д2и д2и
2285.	4-— +4— = 0.
дх£ дх ду ду£
д2и
2286. —-
дх2
д2и	ди
—— = 0; и = sm у, — = у при х = 0.
ду2	дх
„ „ д2и	ди
2287. х—— + у	=0; и = 2у + 1, — = у при х = 1.
дх2 дх ду	дх
д2и
дх2
§13. Метод характеристик
225
7d2u 7d2u	7 du 7
2288. t2—— — х2—— = 0: u = 2s2, — = x2 при t = 1.
dtz dxz	dt
Найти частные решения дифференциальных уравнений:
d2u	d2u	du	du
2289. — + —— + — = 0; u = 0, —
dtz	dx dt	dt	dt
d2u	7du
- д— + 2а2 —
dlz	dx
d2u
вД' tl =
dx dt
d2u
2290. 4a2s—
dxz
7d2u
2291. a2—- =
dxz
— x — 1 при t = 0.
= 0; u = 0,
du
—- = ax при t = 0.
dt
du
~dt
при t = 0.
Глава 13
ДВОЙНЫЕ, ТРОЙНЫЕ И КРИВОЛИНЕЙНЫЕ
ИНТЕГРАЛЫ
§ 1. Вычисление площади с помощью
двойного интеграла
1°. Двойным интегралом от непрерывной функции F(x, у), распро-
страненным на ограниченную область (S) плоскости хОу, называется
предел соответствующей двумерной интегральной суммы:
у"У F(x, у) dx dy =
Д')
lim „ ЕЕ F(xi, yk)XxiXyk,
max Д1Г,—>0	•	,
л . г» г	к
max /лук —>0
где Джг- = жг+1 — Xi, Д.ук = yk±i — ук и сумма распространена на те
значения г и к, для которых точки (жг-; ук) принадлежат области (S).
Площадь S области (S) определяется формулой
S = уУ dx dy.
Д)
2°. Если область (S) определяется неравенствами а ж 6, уДх) SZ
<	< У2(.х), причем каждая из непрерывных кривых у = уДх) и у =
= yz(x) пересекается с вертикалью х = X (ад < X < жг) только в одной
точке, то
Ь У2Д)
F(x,y)dxdy = j" dx j" F(x,y)dy,
(s)	a
УзД)
где при вычислении интеграла j F(х, у) dy величину х полагают по-
У1(.Д
стоянной.
3°. Если область (S) определяется неравенствами h <Z у <Д, ад(г/)
< ж < Х2(у), причем каждая из непрерывных кривых ж = жДг/) и ж =
= Х2(у) пересекается с горизонталью у = У (гд < У < а/г) только в
одной точке, то
I х2(у)
F(x,y)dxdy = j" dy j" F(x,y)dx,
(S)	h X1(y)
§ 1. Вычисление площади с помощью двойного интеграла 227
х2(у)
где при вычислении интеграла j F(х, у) dx величину у полагают no-
tify)
стоянной.
4°. Если область (S) определена в полярных координатах неравен-
ствами tp\ tp рд, ri(v) С r С г2(^); то площадь этой области
V2 ’’2(¥’)
S = JУ г dr dtp = У dtp J г dr.
(S)	Vi гДД)
Записать с помощью двойных интегралов и вычислить пло-
щади, ограниченные линиями:
2292.	ху = 4, у = х, х = 4.
2293.	1) у = ж2, I// = ж2, у = 4; 2) у = ж2, I// = ж2, ж = ±2.
2294.	у2 = 4 + ж, ж + Зу = 0.
2295.	ay = ж2 — 2аж, у = ж.
2296.	у = In ж, ж — у = 1 и у = — 1.
2297.	Построить области, площади которых выражаются инте-
гралами:
ах	а	\/а2 — у2	а	у/ 2а2 —ж2
1) У dx	dy; 2) J dy J dx; 3) J dx J dy.
ОО	О	а —у	0	x
Изменить порядок интегрирования.
Указание. Чтобы получить уравнения линий, ограничивающих
область, нужно пределы интеграла по dx приравнять х, а пределы инте-
грала по dy приравнять у.
2298.	Построить области, площади которых выражаются ин-
1	2-х2	о о
тегралами: 1) dx dy; 2) dy dx. Изменить порядок
о х	-2 у2_4
интегрирования и вычислить площади.
2299.	Вычислить площадь, ограниченную линиями г =
= а(1 — cos 92) и г = а и расположенную вне круга.
2300.	Вычислить площадь, ограниченную прямой г cos р> = а
и окружностью г = 2а.
Вычислить площади, ограниченные линиями:
9
а	9 х
2301.	ху = —, ху = 2а , у = —, у = 2ж.
Указание. В задаче 2301 выгодно перейти к новым координа-
там ху = и и у = vx, после чего площадь определяется по формуле
228 Гл. 13. Двойные, тройные и криволинейные интегралы
jj | J\ du dv, где J =	дх ди дх dv	ду ди ду dv	и называется якобианом. В задаче 2302
9	9 положить у = их, vy =		х3,	а в задаче 2303 перейти к обобщенным
полярным координатам х = г cos3 и у = г sin3 р>.
2302.	у2 = ах, у2 = 16ах, ау2 = х3, 16ау2 = х3.
2303. х2/3 + у2/3 = а2/3.
Вычислить площади, ограниченные линиями:
2304.	у = х2, у = х + 2.
2305.	ах = у2 — ‘lay и у + х = 0.
2306.	у = sin ж, у = cos х и х = 0.
2307.	у2 = а2 — ах, у = а + х.
2308. г = 4(1 + cos </?), г cos р = 3 (справа от прямой).
2309.	г = а(1 — cos 92), г = а и расположенную вне кардиоиды.
2310.	ху =1, ху = 8, у2 = х, у2 = 8®.
2311.	Построить области, площади которых выражаются инте-
гралами:
Изменить порядок интегрирования и вычислить площади.
§ 2.	Центр масс и момент инерции площади
с равномерно распределенной массой
(при плотности = 1)
Координаты центра масс площади S с равномерно распределенной
на ней массой:
_ Д х dx dy _ ff у dx dy
s	s
Моменты инерции площади S'.
,,г = ЦуЧЫу.	,,0 = ЦгЧЫу (2)
(S)	(S)	(S)
§ 2. Центр масс и момент инерции площади	229
Определить центр масс площади, ограниченной линиями:
2312.	у = 0 и одной полуволной синусоиды у = sin X.
2313.	у = х2, х = 4, у = 0.	2314. у2 = ах и у = х.
2315.	ж2 + у2 = а2 и у = 0.
2316.	Определить центр масс площади, ограниченной астрои-
дой ж2/3 + у2/3 = а2/3 и осью Ох.
Указание. Перейти к обобщенным полярным координатам
х = г cos (р и t/ = rsm ip.
2317.	Определить моменты инерции Jx, Jy и Jo площади пря-
моугольника, ограниченного линиями х = 0, х = а, у = 0 и
У = ь.
2318.	Определить момент инерции относительно оси Ох пло-
щади, ограниченной линиями у = ж/2, х = а, у = а.
2319.	Определить момент инерции относительно оси Оу пло-
щади треугольника с вершинами А(0; 2а), В(а; 0) и С(а; а).
В задачах 2320-2323 определить полярный момент инерции
площади, ограниченной линиями:
2320.	х + у = а, х = 0, у = 0.	2321. г2 = a2 cos 2</>.
2322.	Окружностью г = а.
2323.	у2 = ах, х = а.
Определить центр масс:
2324.	Полусегмента параболы у2 = ах, х = а, у = 0 (при
у > 0).
х2 у2
2325.	Полуэллипса — + — = 1, отсеченного осью Ох.
а2 о2
2326.	Определить момент инерции относительно оси Оу пло-
х2
щади, ограниченной линиями у = а -----, у = 2ж и ж = 0.
а
2327.	Определить момент инерции относительно оси Ох пло-
щади треугольника с вершинами А(1; 1), В(2; 1), С(3; 3).
Определить полярный момент инерции площади, ограничен-
ной линиями:
2328.	- + у = 1, х = 0, у = 0.
а о
2329.	у = 4 - ж2 и у = 0.	2330. г = а(1 — cos </?).
230
Гл. 13. Двойные, тройные и криволинейные интегралы
§ 3. Вычисление объема с помощью двойного интеграла
Объем тела, ограниченного сверху поверхностью z = F(x, у), сни-
зу — плоскостью z = 0 и с боков — цилиндрической поверхностью,
вырезающей на плоскости хОу область (S), равен
V =
Д')	Д')
Вычислить объемы тел, ограниченных поверхностями:
2331.	z = ж2 + у2, х + у = 4, х = 0, у = 0, z = 0.
2332.	г = ж + у + а, у2 = ax, х = a, z = 0, у = 0 (при у > 0).
2333.	(ж + у)2 + az = а2, ж = 0, у = 0, г = 0 (поверхность
построить по сечениям: ж = 0, у = 0, z = 0, z = h Д. а; см.
задачу 546).
2334.	ж2 + у2 = а2, ж2 + z2 = а2 (см. задачу 552).
2335.	z2 = жу, ж = а, ж = 0, у = а, у = 0.
2336.	az = ж2 — у2, z = 0, ж = а.
2337.	z2 = жу, ж + у = а.
2338.	ж + у + z = За, ж2 + у2 = а2, z = 0.
Указание. В задачах 2338—2344 перейти к полярным координа-
там.
2339.	z = тх, ж2 + у2 = a2, z = 0.
2340.	az = а2 - ж2 - у2, z = 0.
2341.	ж2 + у2 + z2 = 4а2, ж2 + у2 = а2 (вне цилиндра).
2342.	ж2 + у2 + z2 = а2, ж2 + у2 ± ах = 0 (внутри цилиндров).
£
2343.	Первым завитком геликоида у = ж tg — внутри цилиндра
а
ж2 + у2 = а2 и плоскостью z = 0.
2344.	z2 = 2аж, ж2 + у2 = ах.
Z	X	V
2345.	- = 1 - — z = 0.
с	<Д	ir
Указание. В задачах 2345 и 2346 перейти к обобщенным (элли-
птическим) полярным координатам: х = ar cos р, у = br sirup.
2	2
2346. г = cef-^2/»2)-^2/62) и	= 1.
а2	о2
2347. ж2/3 + у2/3 + г2/3 = а2/3 (положить ж = г cos3 92, у =
= г sin3 </?).
§ 4. Площади кривых поверхностей
231
Вычислить объемы тел, ограниченных поверхностями:
2348. z = a — х, у2 = ах и z = 0.
2349. z = ж2 + у2, у = х2, у = 1, z = 0.
2350. у2 + z2 = йах, у2 = ах, х = За (вне цилиндра).
2352.	Коноида х2у2 + h2z2 = а2у2 при 0 у h (см. задачу
559).
2353.	ж2/3 + z2/3 = а2/3, ж2/3 + у2/3 = а2/3.
2354.	4г = 16 — х2 — у2, г = 0, х2 + у2 = 4 (вне цилиндра).
Указание. В задачах 2354—2358 перейти к полярным координа-
там.
2355.	z2 = (ж + а)2, ж2 + у2 = а2.
4
2356.	z = —--z = 0, ж2 + у2 = 1, ж2 + у2 = 4.
ж2 + у2
2357.	az = ж2 + у2, z = 0, ж2 + у2 ± ах = 0.
2358.	az = а2 — ж2 — у2, z = 0, ж2 + у2 ± ах = 0 (внутри
цилиндров).
Указание. Положить х = ar cos <р, y = brsin(p.
§ 4. Площади кривых поверхностей
Площадь а части поверхности F(x, у, z) = 0, проекция которой на
плоскость z = 0 определяет область (<тг), равна
Г Г JidF/dxF + (dF/dyF + (dF/dz)’2 , ,
” = .1.1-----------|W4----------------*=
FY
= 11 TFWHT\dxdy-
JJ \dF/dz\
FY
Аналогично при проектировании на две другие координатные плос-
кости получим
[[ N . . [[ N . .
J J \dF/dy\	J J \dF/dx\ У
232 Гл. 13. Двойные, тройные и криволинейные интегралы
Вычислить площадь:
2360.	Поверхности цилиндра 2г = ж2, отсеченной плоскостями
у = х/2, у = 2ж, х = 2-\/2.
2361.	Поверхности конуса г2 = 2жу, отсеченной плоскостями
х = а и у = а, при х 0 и у 0.
2362.	Поверхности конуса у2 + z2 = х2, расположенной внутри
цилиндра х2 + у2 = а2.
2363.	Поверхности az = ху, расположенной внутри цилиндра
х2 + у2 = а2.
2364.	Поверхности конуса х2 + у2 = г2, расположенной внутри
цилиндра z2 = 2р.г.
Вычислить площадь:
2365.	Поверхности цилиндра х2 + z2 = а2, расположенной вну-
три цилиндра х2 + у2 = а2.
2366.	Поверхности шара х2 + у2 + z2 = а2, расположенной вну-
три цилиндров х2 + у2 ± ах = 0.
2367.	Поверхности параболоида х2 + у2 = 2аг, расположенной
внутри цилиндра х2 + у2 = За2.
2368.	С помощью двойного интеграла определить площадь ча-
сти земной поверхности, ограниченной меридианами 0° и /3°, эква-
тором и параллелью а°. Рассмотреть частный случай при а = 30°,
(3 = 60°.
§ 5. Тройной интеграл и его приложения
Тройным интегралом от функции /(ж, у, z), распространенным на
область (V), называется предел соответствующей трехмерной интеграль-
ной суммы:
/ / / Р(ж, у, z) dx dydz= lim EEE F(xp yj, zk)AxiAyjAzk,
J J J	maxA^t->0	,
(V)	тахДщ-Ю ’	3 *
max Дг* —>0
где A.Xi = xi+1 - Xi, A.yj = yj+1 - yj, Szk = zk+1 - zk и сумма распро-
странена на те значения у и к, для которых точки (жг-; г/у; zk) принадле-
жат области (V).
Если область (V) определена неравенствами
а < х Ь, г/1(ж) у уДх), гДх, у) z z2(x, у),
то
Ь у2(.Д	Z2(x,y)
JУУ F(x, у, z) dx dy dz = J dx J dy J F(x, y, z) dz.
(V)	а У1(Х)	Z1(x,y)
§ 5. Тройной интеграл и его приложения
233
При F(x, у, z) = 1 получаем объем V. Координаты центра масс одно-
родного тела объемом V вычисляются по формулам:
хс = — УУУ х dx dydz, ус = — J У dx dydz,
(V)	(V)
(V)
2369.	Определить объем тела, ограниченного поверхностями
az = ж2 + у2, 2az = a2 - х2 - у2.
2370.	Определить объем тела, ограниченного поверхностями
ж2 + у2 — z2 = 0, ж2 + у2 + z2 = а2, внутри конуса.
2371.	Показать, что поверхность конуса ж2 + у2 — z2 = 0 делит
объем шара х2 + у2 + z2 = 2az в отношении 3 : 1.
2372.	Определить массу пирамиды, образованной плоскостями
х F у F z = а, х = 0, у = 0, z = О, если плотность в каждой ее
точке равна аппликате z этой точки.
Определить центр масс однородного тела, ограниченного по-
верхностями:
2373.	х + у + z = а, х = 0, у = 0, z = 0.
2374.	az = а2 - х2 - у2, z = 0.
Определить момент инерции относительно оси Oz тела, огра-
ниченного поверхностями (плотность р = 1):
2375.	х = 0, у = 0, у = a, z = 0, х + z = а.
2376.	х + у + z = а-\/2, х2 + у2 = a2, z = 0.
2377.	Определить объем тела, ограниченного замкнутой по-
верхностью:
1) (ж2 + у2 + z2)2 = а3х; 2) (ж2 + у2 + z2)2 = az(x2 + у2).
Указание. Перейти к сферическим координатам по формулам х =
= г sin 0 cos <£>, у = г sin 0 sin <£>, z = г cos ip; элемент объема dV =
= г2 sin 0 dr dip d0.
Определить объемы тел, ограниченных поверхностями:
2378.	az = ж2 + у2, х2 + у2 + z2 = 2а2.
2379.	ж2 + у2 — z2 = 0, z = 6 — ж2 — у2.
2380.	az = ж2 + у2, z2 = х2 + у2.
2381.	Определить массу тела, ограниченного поверхностями
ж2 + у2 — z2 = 0 и z = h, если плотность в каждой точке его
равна аппликате этой точки.
234 Гл. 13. Двойные, тройные и криволинейные интегралы
2382.	Определить массу тела, ограниченного поверхностями
2ж + z = 2а, х + z = а, у2 = ах, у = О
(при у > 0), если плотность в каждой его точке равна ординате у
этой точки.
2383.	Определить центр масс однородного полушара ж2 + у2 +
+ z2 = a2, z = 0.
2384.	Определить момент инерции относительно оси Oz тела,
ограниченного поверхностями z2 = 2аж, z = 0, х2 + у2 = ах.
2385.	Определить объем тела, ограниченного поверхностью
(ж2 + у2 + z2)2 = axyz (перейти к сферическим координатам) (см.
задачу 2377).
2386.	Определить массу сферического слоя между поверхно-
стями ж2 + у2 + z2 = а2 и ж2 + у2 + z2 = 4а2, если плотность
в каждой его точке обратно пропорциональна расстоянию от точки
до начала координат (перейти к сферическим координатам).
§ 6. Криволинейный интеграл. Формула Грина
1°. Определение криволинейного интеграла. Пусть на
дуге АВ, спрямляемой кривой, определена непрерывная функция Р(х,у,z).
Разобьем дугу на части точками А(жо; Уо', Zo), М-Дхр ур, гД, ...
..Мп_Дхп_р, уп_р, гп_Д и В(хп\ уп- zn) и пусть жг--жг_1 = Джг-. То-
п
гда lim P(xi, Vi, Zi)Ax; называется криволинейным интегралом,
Дж>->ог=1
взятым по дуге АВ, и обозначается J Р(х, у, z) dx. Аналогично опреде-
АВ
ляются интегралы / Q(x,y,z)dy, f B(x,y,z)dzn f P dx + Q dy +
AB	AB	AB
+ Rdz как сумма предыдущих интегралов. Наконец, встречается еще
криволинейный интеграл вида
/п	____.
P(x,y,z)ds = lim У'',Р(хр ур гДАвр где Ast = М^Мр
As,—>0
_	2 = 1
АВ
2°. Вычисление криволинейного интеграла. Пусть кри-
вая АВ задана уравнениями х = f(t), у = рДД, z = ДД), а параметр t
при перемещении точки М(2) по дуге АВ в одном направлении изменя-
ется монотонно; тогда
[ Р(Х,У, z)dx= i P[f(t), p(t), ip(t)]f(t)dt,
§ 6. Криволинейный интеграл. Формула Грина
235
т. е. все переменные и дифференциалы под знаком криволинейного ин-
теграла нужно выразить через одну переменную (t) и ее дифференциал
(dt) из уравнений кривой.
3°. Механическое значение криволинейного интегра-
ла. Интеграл вида f Р dx + Q dy+ R dz определяет работу при переме-
АВ
щении единицы массы по дуге АВ в поле, образованном силой F{Р; Q', R}.
4°.Случай полного дифференциала. Если в некоторой обла-
сти (V) Р dx + Q dy + Rdz = du, то / P dx + Q dy + Rdz = ив — ид,
AB
т. e. равен разности значений функции и(х, у, z) в точках В и А и не
зависит от пути интегрирования АВ, взятого в области (V).
5°. Формула Грина
J	JJ \ох ду J
(С)	(S)
dx dy
преобразует криволинейный интеграл от Р dx + Q dy, взятый (против
часовой стрелки) по замкнутому контуру (С), в двойной интеграл по
области (S), ограниченной этим контуром.
6°. Площадь, ограниченная контуром (С):
S =
(с)
у dx.
2387. Даны точки Л(2; 2) и В(2; 0). Вычислить J (х + у) dx :
(С)
х1 2
1) по прямой О А; 2) по дуге О А параболы у = —; 3) по ломаной
ОБА.	2
2388. Даны точки Л(4; 2) и В(2; 0). Вычислить
У (х + у)
(С)
dx — х dy :
1) по прямой О А; 2) по ломаной ОБА.
2389. Решить задачу 2388 для интеграла
у dx + х dy.
(С)
Почему здесь величина интеграла не зависит от пути интегриро-
вания?
236 Гл. 13. Двойные, тройные и криволинейные интегралы
2390.	Даны точки Д(а; 0; 0), В(а; а; 0) и С(а; а; а). Вычи-
слить интеграл
У у dx + z dy + х dz
по прямой ОС и по ломаной О АВС.
2391.	Поле образовано силой F{F; Q}, где Р = х — у, Q =
= х. Построить силу F в каждой вершине квадрата со сторонами
х = ±а и у = ±а и вычислить работу при перемещении единицы
массы по контуру квадрата.
2392.	Поле образовано силой F{F; Q}, где Р = х + у, Q =
= 2. г. Построить силу F в начале каждой четверти окружности
х = a cost, у = asint и вычислить работу при перемещении еди-
ницы массы по окружности.
Решить эту же задачу при условии Р = х + у, Q = х. Почему
здесь работа равна 0?
2393.	Поле образовано силой F{y; а}. Определить работу при
перемещении массы m по контуру, образованному полуосями ко-
ординат и первой четвертью эллипса х = a cost, у = bsini.
2394.	Поле образовано силой F{s; у; z}. Вычислить работу при
перемещении единицы массы по ломаной ОАВСО, соединяющей
точки 0(0; 0; 0), Д(0; а; 0), В(а; а- 0), С(а; а; а).
2395.	Написать и проверить формулу Грина для
У (х + у) dx — 2s dy
(С)
по контуру треугольника со сторонами х = 0, у = 0, х + у = а.
2396.	Вычислить интегралы:
1)	У 2ху dx + х2 dy; 2) J cos 2y dx — 2s sin 2y dy;
AB	AB
^^yliz + l^yliy
AB
по любой линии от точки Д(1; 7г/6) до В(2; тг/4).
2397.	Применив формулу Грина, вычислить интеграл
У у2 dx + (s + у)2 dy
(С)
по контуру ДАВС с вершинами А(а; 0), В(а; а) и 0(0; а).
§ 6. Криволинейный интеграл. Формула Грина
237
2398.	Определить криволинейным интегралом площадь элли-
пса х = a cos t, у = b sin t.
2399.	Определить криволинейным интегралом площадь петли
кривой х3 + х2 — у2 = 0 (см. рис. 48 на с. 304).
Указание. Перейти к параметрическим уравнениям, положив у =
= xt.
2400.	Определить криволинейным интегралом площадь петли
декартова листа х3 + у3 — Заху = 0 (см. указание к задаче 2399 и
рис. 79 на с. 334).
2401.	С какой силой притягивает масса М, равномерно рас-
пределенная по верхней полуокружности х2 + у2 = а2, массу т,
сосредоточенную в начале координат?
Указание. Пусть у — линейная плотность, ds — элемент длины
полуокружности, 0 — угол радиус-вектора с осью Ox, а X и У — про-
екции силы притяжения. Тогда
Г кту cos 6 ds	f кту sin 0 ds
(С)	(с)
где к — гравитационная постоянная.
2402.	Даны точки А( — а; а) и В (а; а). С какой силой масса М,
равномерно распределенная по отрезку АВ, притягивает массу т,
сосредоточенную в точке (0; 0).
2403.	Даны точки А(а; 0), В(0; а) и С( — а; 0). С какой силой
масса М, равномерно распределенная по ломаной АВС, притяги-
вает массу т, сосредоточенную в начале координат.
2404.	Даны точки Л(0; 1), В(2; 5) и С(0; 5). Вычислить
У (ж + у) dx - 2ydy :
(С)
1) по прямой АВ; 2) по дуге АВ параболы у = х2 + 1; 3) по
ломаной АСВ.
2405.	Даны точки Л( — а; 0) и В(0; а). Вычислить работу силы
F{P; Q}, где P = ynQ=y - х, при перемещении единицы
массы: 1) по прямой АВ; 2) по ломаной АОВ; 3) по дуге АВ
х2
параболы у = а-----.
а
2406.	Показать, что
У у dx + (х + у) dy
(С)
238 Гл. 13. Двойные, тройные и криволинейные интегралы
по любому замкнутому контуру равен нулю. Проверить, вычислив
интеграл по контуру фигуры, ограниченной линиями у = х2 и
У = 4.
2407.	Написать и проверить формулу Грина для интеграла
J У х
(С)
взятого по контуру ЛАВС с вершинами А(1; 1), В(2; 1) и С(2; 2).
2408.	С помощью криволинейного интеграла определить пло-
щадь фигуры, ограниченной астроидой х = acos3t, у = a sin3 Г
2409.	С помощью криволинейного интеграла определить пло-
щадь, ограниченную кривой у2 + х4 — х2 = 0. (Перейти к параме-
трическим уравнениям, положив у = xt.)
§ 7. Поверхностные интегралы.
Формулы Остроградского-Гаусса и Стокса
1°. Поверхностные интегралы. Пусть F(x, у, z) — непре-
рывная функция и z = <£>(ж, у) — уравнение поверхности S, причем
у) др(х, у)
существуют ------ и ------.
дх	ду
Поверхностный интеграл первого типа представляет собой предел
интегральной суммы:
п
F(x, у, z)dS = lim У^Р(хр yi; Zi)SSi,
i = l
где A.Si — площадь г-го элемента поверхности S, точка (ау; г/г-; гг) при-
надлежит этому элементу, причем максимальный диаметр элементов
разбиения стремится к нулю. Если проекция а поверхности S на плос-
кость хОу однозначна, т. е. всякая прямая, параллельная оси Oz, пере-
секает поверхность S лишь в одной точке, то соответствующий поверх-
ностный интеграл первого типа может быть вычислен по формуле
F(x, у, z) dS =
(А
Если Р = Р(х, у, z), Q = Q(x, у, z), R = R(x, у, z) — непре-
рывные функции и S+ — сторона поверхности S, характеризуемая на-
правлением внешней нормали n{cos а; cos/3; cosy}, то соответствующий
§ 7. Поверхностные интегралы
239
поверхностный интеграл второго рода выражается следующим образом:
УУ Р dy dz + Q dz dx + Rdx dy =
(5 + )
JУ (P cos a + Q cos /3 + R cos 7) dS.
2°. Формула Остроградског о—Г а у с с а:
УУ (Р cos a + Q cos P + R cos 7) dS =
(S')
J J J \dx dy dz J
(V)
dx dy dz,
где a, P и 7 — углы внешней нормали замкнутой поверхности S и осями
координат, а V — объем тела, ограниченного этой поверхностью. Пер-
вый интеграл можно записать в виде
± [[ (PdJ_ + Q9J- + RdJ\
J J \ dx 4 dy dz J dF/dz ’
(sp
где F(x, y, z) = 0 — уравнение поверхности, a Sz — проекция S на
плоскость xUy.
3°. Формула Стокса:
Р dx + Q dy + Rdz =
(С)
dR
dy
dP\
-7— cos 7
dS,
где a, P, 7 — углы, образованные осями координат с нормалью к по-
верхности S, направленной в ту ее сторону, с которой обход контура С
рассматривается происходящим против часовой стрелки.
2410. Вычислить
УУ (ж cos a + у cos Р + z cos 7) dS
(S)
по верхней поверхности плоскости х + у + z = а, расположенной в
первом октанте.
2411. Вычислить
[ж2 cos (n, i) + у2 cos (n, j) + z2 cos (n, k)] dS
(S)
по верхней поверхности параболоида ж2 + у2 + 2аг = а2, располо-
женной во втором октанте (где ж < 0, у > 0, z > 0).
240 Гл. 13. Двойные, тройные и криволинейные интегралы
Указание. Приведя интеграл к виду
Ц^ + ^ + az2)^
пе-
(8Й)
рейти к полярным координатам. Угол будет изменяться от тг/2 до 7Г.
2412.	Написать и проверить формулу Остроградского для ин-
теграла
[ж cos (n, i) + у cos (n, j) + z cos (n, k)] dS,
взятого по поверхности шара x2 + у2 + z2 = a2.
2413.	Написать и проверить формулу Остроградского-Гаусса
для интеграла
[х2 cos (n, i) + у2 cos (n, j) + z2 cos (n, k)] dS,
(S)
взятого по наружной поверхности тела, ограниченного поверхно-
стями х2 + у2 + 2a z = a2, х = 0, у = 0, z = 0, внутри первого
октанта.
Указание. Двойной интеграл по плоским граням тела равен 0,
ибо, например, на плоскости z = 0 и cos (n, i) = 0 и cos (n, j) = 0.
2414.	Полагая в формуле Остроградского-Гаусса Р = х, Q = у,
R = z, получить формулу для объема:
V = - J J [х cos a + у cos (3 + z cos 7] dS.
(S)
Вычислить по этой формуле объем эллипсоида
„,2	./2
2 Ь2 с2
ди
2415.	Полагая в формуле Остроградского-Гаусса Р = —, Q =
ди	ди
= и = ~dz
доказать, что
(т. е. полагая вектор {Р; Q; R} равным gradrr),
(S)
Л д2и
где Дм = —- +
дх2
(V)
д2и д2и
—— + —— — оператор Лапласа.
ду2 dz2
§ 7. Поверхностные интегралы
241
2416.	Проверить полученную в предыдущей задаче формулу для
функции и = х2 + у2 + z2 на поверхности х2 + у2 + z2 = a2.
2417.	Показать с помощью формулы Стокса, что
У yz dx + xzdy + xydz
(С)
по любому замкнутому контуру равен нулю. Проверить это вы-
числением интеграла по контуру ЛОЛВ с вершинами 0(0; 0; 0),
А(1; 1; 0) и В(1; 1; 1).
2418.	Написать и проверить формулу Стокса для интеграла
У (z — у) dx + (х — г) dy + (у — ж) dz,
(С)
взятого по контуру ДАВС с вершинами А(а; 0; 0), В(0; а; 0) и
0(0; 0; а).
Указание. Двойной интеграл можно взять по любой поверхности,
проходящей через периметр треугольника АВС, например по плоскости
х + у + z = а.
2419.	Написать и проверить формулу Остроградского-Гаусса
для интеграла
У[ж3 cos (п’ + У3 cos (n’ j) + z3 cos (n’ k)] dS,
(S)
взятого по поверхности шара x2 + у2 + z2 = a2.
Указание. Тройной интеграл преобразовать к сферическим коор-
динатам.
2420.	Написать и проверить формулу Стокса для интеграла
У x(z — у) dx + у(ж — г) dy + z(y — ж) dz
(С)
по контуру треугольника с вершинами А(а; 0; 0), В(0; а; 0) и
С(0; 0; а) (см. указание к задаче 2418).
2421.	С помощью формулы Остроградского-Гаусса вычислить
I/ dy X + ^dZlb + ?М.
(5)
взятый по наружной поверхности пирамиды, образованной плос-
костями х + у + z = а, х = 0, у = 0, z = 0.
Глава 14
РЯДЫ
§ 1.	Числовые ряды
1°. Ряд Mi + «2 + "з + • • • + пп + . . . называется сходящимся, если
сумма Sn его п первых членов при п —> сю стремится к конечному пре-
делу S: lim Sn = S. Число S называется суммой сходящегося ряда.
П—>00
Несходящийся ряд называется расходящимся.
Для сходимости ряда необходимо (но не достаточно), чтобы ип —> О
при п —> сю.
2°. Интегральный признак сходимости ряда с положитель-
ными убывающими членами:
Если ип = f(n), где f(x) — убывающая функция, и
/(А, то ряд сходится,
f (х) dx — \
J v 7	1 схэ, то ряд расходится.
1
3°. Признак Даламбера сходимости ряда с положительными
членами: если
то ряд сходится,
то ряд расходится,
то вопрос остается нерешенным.
4°. Сравнение рядов с положительными членами:
и1 + и2 + из + • • • + ип + . . . ;	(1)
^1 + v2 + v3 + • • • + vn + • • •	(2)
1) Если ип vn и ряд (2) сходится, то сходится и ряд (1).
2) Если ип ип и ряд (2) расходится, то расходится и ряд (1).
5°. Ряд с чередующимися знаками ui — и-2 + из — щ + . . .
сходится, если и± > и2 > из > . . . и lim ип = 0.
П—>00
6°. Абсолютная сходимость. Ряд
и1 Н- и 2 Н- из + . . . + Un + • • •	(3)
сходится, если сходится ряд
|^1| + |^2 | + К| + • • • + \ип | + . . .	(4)
§ 1. Числовые ряды
243
В этом случае ряд (3) называется абсолютно сходящимся. Если же
ряд (3) сходится, а ряд (4) расходится, то ряд (3) называется условно
(неабсолютно) сходящимся.
Выполняется ли необходимое условие сходимости ряда:
1	3	5	7.
2 + 4 + 6 + 8
1111
I + 3 + 5 + 7 4
2	4	6	8
3 + 9 + 27 + 81+’”
Исследовать по интегральному признаку сходимость ряда:
111.
3 + 5 + 7
2422.
2423.
2424.
2425.
2426.
2427.
2428.
2429.
2430.
1	1	1
1 + ^4	 +	,— + •
	а/7	д/10
1	2	3	
23 + З3 ’	4 “щ- 4- 43	
1	1	1
1 + 12 1	1 + 22	1 1 + 32
1	2	3
1 + 12	1 + 22	1 + 32
1	1	1
З2 - 1 1	52 - 1	1 72- 1
1	1	1
. . о . 1		1 .о
2431.
2 In2 2
31п23	4 In2 4
Исследовать по признаку Даламбера сходимость ряда:
2	4
3 + 9 +
1 + 4 +
1 • 2
1 + гд
1+2-
2-3
1	_3!_
2	+ 2^4
1
V3 + V2 • З2 1 л/З • З3 1 д/4-34
2432.
2433.
2434.
2435.
2436.
2437.
6	8
27 + 81 4
4_	_8
3!+ 4! +
1-2-3
+ 1-3-5
З2
+ 22 • 5 +
5!
+ 2-4-6
5
З3
23 • 7 + ’ ’ ’
7!
+ 2-4-6-8
9	13
244
Гл. 14. Ряды
Сравнением с гармоническим рядом или с убывающей прогрес-
сией исследовать сходимость ряда:
1 1 1
2438.
2439.
2440.
л/2
1 + Г5 +
1 1
In 2 + In 3
4
1
' 4-53
1
In 5
/3
1
3 • 52
1
+ In 4
2441. Методом сравнения рядов показать, что ряд ------------ +
1 + х1
------- -|------- + ... при |ж|	1 расходится, а при |ж| > 1
сходится.
Указание. Для сравнения в первом случае заменить х2, х4, х6, .
единицами, во втором случае отбросить в знаменателях единицы.
Найти сумму ряда:
1 1 1
2442. ----Г---Г------Г ...
1-22-3	3-4
Указание. Разложить ип на элементарные дроби.
1 1 1
2443.----|-----|------h ...
1-44-77-10
Исследовать сходимость ряда:
1 1 1
2444.1 -
2445.1 -
2446.
2447.
л/2 V3 у4
1 1 1
32 + 52 “ 72 +
1	1	+	1
2 In 2	31п3		4 In 4
sin ct 1 +	sin 2а 22	+	sin За З2
2448. Показать, что сумма S условно сходящегося ряда 1-1-
1 1
+ - — - + уменьшится вдвое, если после каждого положитель-
ного члена ряда поместить два последующих отрицательных, и
увеличится в полтора раза, если после каждых двух положитель-
ных членов поместить один отрицательный.
§2. Равномерная сходимость функционального ряда 245
Исследовать сходимость ряда:
2449.	1 + -^-= + -^-= + ...
3/1	5^5
1	1	1
2450.	Ц-------1----1-------1- ...
101	201	301
1	2	3
2451.	------ +------ +------- + ...
1 + I4 1 + 24	1 + З4
2452.	1 + - + -+ — + ...
4	9	16
2453-	1 + ^2 + 72 +	+ • • •
13	5	7
2454-7 + ^ + ^ + ^ + ---
2455.
21	41	61
2456.
2457.
3	9	27
2	4	6
Т + 3! + 5! +
1 1
2458.1 -
2459.1 -
1 1 1
23 + З3 ~43 + -
1 1 1
2а2 + За4	4а6
Найти сумму ряда:
1 1 1
2460.--|----|---h ...
1-33-55-7
2461.
1 , 1 । 1 ।
1-2-3 + 2-3-4 + 3-4-5 + ’ ’ ’
§ 2. Равномерная сходимость функционального ряда
1°. Совокупность значений х, при которых функциональный ряд
Ы1(ж) 4- и2(х) 4- • • • 4- ип(х) 4" • • •
(1)
сходится, называется областью сходимости этого ряда.
Функция S(x) = lim Sn(x) называется его суммой, а разность
П—>00
Rn(x) = S(x) — Sn(x) — остатком ряда.
1 -
3
5
246
Гл. 14. Ряды
2°. Ряд (1) называется равномерно сходящимся на отрезке [а, Ь],
если для всякого е > 0 можно найти такой номер N, что при п > N и
любом х на отрезке [а, Ь] будет выполнено неравенство |/?„(ж)| < е.
3°. Признак равномерной сходимости. Ряд (1) сходится
абсолютно и равномерно на отрезке [а, Ь], если существует числовой
сходящийся ряд с положительными членами
Cl + С2 + Сз + . . . + Сп + . . .
такой, что |ып(ж)| сп при а ж 6.
2462.	Определить при |ж| < 1 сумму и остаток ряда 1 + ж +
+ ж2 + ж3 + ... и показать, что он сходится равномерно на отрезке
[О, 1/2]. При каком п остаток |2?га(ж)| < 0,001 для любого ж на
этом отрезке?
2463.	Показать, что ряд
ж + ж(1 — ж) + ж(1 — ж)2 + ж(1 — ж)3 + . . .
сходится неравномерно на отрезке [0, 1] и равномерно на отрезке
[1/2, 1]. При каком п остаток |2?га(ж)| < 0,01 для любого ж на
отрезке [1/2, 1]?
2464.	Показать, что ряд — —
на отрезке [0, 1]. При каких п и
< 0,1?
9	*4
eZ/ ~ X
----1------... сходится равномерно
2	3
любом ж на этом отрезке |2?га(ж)| <
ж3	ж3
2465. Показать, что ряд ж3 4------ + -----— + ... сходится
1 + ж3 (1 + ж3)2
неравномерно при ж > 0 и равномерно при ж 1. При каком п
остаток |2?га(ж)| < 0,001 для любого ж 1?
тт	111
2466. Показать, что ряд ,	-,	----,	+
у/ТТХ 3V1 + Зж 3271 + 5ж
1
+	= + ... сходится равномерно в интервале 0 ж < сю.
33л/1 + 7ж
При каком п (и любом неотрицательном ж) остаток ряда |2?га(ж)| <
< 0,01?
Указание. Сравнить данный ряд с числовым сходящимся рядом.
2467. Показать, что ряд
1
ж2 + 1
1 1 1
ж2 + 4~1~ж2 + 9 ж2 + 16 +
сходится равномерно на всей числовой оси. При каком п (и любом
ж) остаток ряда |2?га(ж)| < 0,0001?
§3. Степенные ряды	247
2468.	Показать, что ряд
1 1 1
х(х + 1) + (х + 1)(ж + 2) + (х + 2)(х + 3) +
сходится равномерно к — в интервале 0 < х < сю. При каком п (и
любом х > 0) остаток ряда |Лга(ж)| < 0,1?
2469.	Показать, что ряд
1111
VI + ж + V22 + 2х + а/24 + Зх + ^2^+4® + ’
сходится равномерно в интервале 0 х < сю. При каком п остаток
ряда \Rn(x) I < 0, 01?
§ 3. Степенные ряды
Пусть дан степенной ряд
2	г?
<зо + <31 х И- а^х И- ... И- “I- . . .
(1)
Число R называется радиусом сходимости ряда (1), если при |ж| < R
ряд сходится, а при |ж| > R — расходится. R можно найти или иссле-
дованием абсолютной сходимости ряда (1) по признаку Даламбера, или,
когда все ai отличны от нуля, по формуле R = lim
В частности,
если этот предел равен сю, то ряд (1) абсолютно сходится на всей оси Ох.
Степенной ряд сходится не только абсолютно, но и равномерно на
любом отрезке [а, Ь], лежащем внутри интервала сходимости (-R, R).
Определить интервал сходимости ряда и исследовать его схо-
димость на границах интервала:
9	*4
X	X ~	X
2470.	1 4------1- —---1- —--1- ...
3-2	32-3	33-4
Q	С
X	X	X
2471.	1 ----- +-------------- + ...
5^2	52V3	53л/1
2х	4ж2	8ж3
2472.	1 +------ +--— +------— + ...
32V3	52W 72V3^
~ хп	™ (-др"1
2473.	£ —.	2474. £	---.
П=1	П=1
3ПХП
2475. £	,
п=1 7(3п- 2)2П
248
Гл. 14. Ряды
2476. 1) £ т"-1 • п\-
п=1
2)
(х + I)2
2477. (х + 1) +	+
(х + I)3 ' (х + I)4
3 -42 + 4 • 43 +
2ж — 3 2х - З2 2х - З 3
2478.----------- ...
1	3	5
Определить интервал сходимости ряда и найти его сумму:
2479. 1 + 2х + Зх2 + 4ж3 + ...
Указание. Для нахождения суммы S найти сначала j S dx.
о
Q	Е	7
ьСьС ьС *
2480. х------|-------h...
3	5	7
v	и -	dS
Указание. Наити сначала —.
dx
2481. 1 + Зх + 5ж2 + 7х3 + ...
Указание. Обозначив сумму ряда через S, составить выражение
S — Sx в виде суммируемого ряда.
2482. 1 + —х +
т(т — 1) (т — 2) 3
1-2-3 Х
S'	S'х
Указание. Показать, что----1----= S,
т т
циальное уравнение.
и решить это дифферен-
Определить интервал сходимости ряда и исследовать его схо-
димость на границах интервала:
2х
2483. 1 + ,____+
4ж2	8ж3
а/9 -52	д/13 • 53
9	4
2484. 1 --------- 4----------
3 • 2^2 З2 • Зу/З
З3 • I /Т + ’ ’ ’
2485. £
п=1
2486. УJ-I)"-1-----
’ 2п - 1
х — 1 (х — I)2 (х — I)3
2487.--------1- ----4- + ------4- + ...
1-2	3 • 22	5 • 23
§ 4. Ряды Тейлора и Маклорена
249
2488.
2s + 1
1
(2s+ 1)2 ' (2s + I)3
4	+	7	+
Определить интервал сходимости ряда и найти сумму:
2489. 1 - Зх2 + 5s4 - 7х6 + ...
Указание. Для нахождения суммы S найти сначала j S dx.
о
9	3
е?/ ~	Ху
2490. х + — + у + ...
v	и -	dS
Указание. Наити сначала
dx
2491. 1 — 4s + 7s2 — 10s3 + ...
Указание. Составить выражение S + Sx.
§4. Ряды Тейлора и Маклорена
1°. Формула Маклорена:
/И = /(о) + фиф? + ... + ед, (1)
где Rn(x) = —rfl'n'>(0x), 0	0 < 1.
п\
2°. Формула Тейлора:
/(ж) = /(а) + yp(s - а) + у^(« - °)2 + • • • +	(2)
где Rn(x) =	ft”1') [а + в(х - а)].
3°.Ряды Маклорена и Тейлора. Если в формулах (1) и (2)
Rn(x) —> 0 при п —> сю, то из этих формул получаются бесконечные
ряды:
fW = /(0) +
/'(о) , /"(о)
_ж + _ж +...
(з)
f(x) = f(a) +	- ») + y^(s - а)2 + • • • ,	(4)
сходящиеся к f(x) при тех значениях х, при которых lim Rn(x) = 0.
250
Гл. 14. Ряды
4°. Разложение в ряды элементарных функций:
2	„3
1!	2!	3!
„3	„5
3!	5!
2	4
сходятся к соответствующей
функции при всех значениях х;
2!	4!
m m(m — 1) „
(1 + x) = 1 + — x 4----—  x + . . . — биномиальный ряд; он
сходится к биному (1 + х)т при |ж| < 1;
„2 „з
v 7	2	3	v 7 '
х3 х5
arctg x = x-------1----... сходится к arctg x при I x I < 1.
3	5
2492.	Разложить в ряд по степеням х функции: 1) cos (х — а);
2) sin1 2 ж; 3) хех; 4) sin (in.г 4-) и написать и исследовать фор-
мулу остаточного члена.
2493.	Написать первые три члена разложения в ряд функции
/(ж) = In (1 4- екх).
2494.	По формуле Маклорена написать разложение в ряд по сте-
пеням х бинома (14—и показать, что полученный ряд схо-
дится при |ж| < а.
2495.	С помощью биномиального ряда показать, что при |ж| < 1
—. = i _ Зж + 6ж2 _ 10жз +	= у
(1 + ж)3	2-^2
v	7	П=1
2496.	С помощью биномиального ряда получить разложение в
ряд функции
1	1 2 Ь 3 4	1-3-5 6	. .	1
,	: = 1---х 4---з--;Х---------х 4- . . . при ж < 1.
2	22-2!	23-3!	1	1 1
2497. Разложить в ряд по степеням х функции:
1) In ; 2) In (2 — Зх 4- ж2); 3) In (1 — ж 4- ж2).
2498. Интегрированием полученного в задаче 2496 ряда напи-
сать ряд для In (ж 4- д/1 + ®2)-
§ 5. Приложения рядов к приближенным вычислениям 251
2499.	Разложить ех'а в ряд по степеням х — а; написать и ис-
следовать формулу остаточного члена ряда.
2500.	Разложить функцию /(ж) = ж3 — Зх по степеням х — 1.
2501.	Разложить х4 по степеням х + 1.
2502.	Разложить в ряд по степеням х + 2 функцию /(ж) = — и
исследовать сходимость ряда по признаку Даламбера.
2503.	Разложить в ряды функции: 1) /(ж) = cos — по степеням
х — —; 2) /(ж) = sin Зх по степеням х + —.
2504. Разложить в ряд по степеням ж 4-1 функцию /(ж) = \/х и
исследовать по признаку Даламбера сходимость полученного ряда.
2505. Разложить в ряд по степеням х функции: 1) 2х;
2) cos (in.г 4-) и написать и исследовать формулы остаточных
членов разложения.
2506.	Разложить функцию /(ж) = х4 — 4ж2 по степеням х + 2.
7Г
2507.	Разложить в ряд по степеням х — — функцию /(ж) = cos2 х
и написать и исследовать формулу остаточного члена ряда.
2508.	Разложить в ряд по степеням х — 1 функцию /(ж) =
. 7ГЖ
= sm —.
3
2509.	Разложить в ряд по степеням х — 4 функцию /(ж) = у/х и
исследовать по признаку Даламбера сходимость полученного ряда.
2510.	С помощью биномиального ряда показать, что
1	1 2	I’3 4	I’3’5 К	II,
.	: = 14—х 4—а----;х 4--------ж 4- • • • при ж < 1.
V1 - ж2 2	22 • 2!	23 • 3!	1 1
2511. Почленным интегрированием ряда, полученного в задаче
2510, написать ряд для arcsin ж.
§ 5. Приложения рядов к приближенным вычислениям
2512. Написать биномиальный ряд для д/1 4- ж и вычислить
у/1, 004, ^/0, 992, а/ЭО, ограничившись двумя членами ряда. Оце-
нить погрешность.
2513. Написать биномиальный ряд для \/1 4- ж и вычислить
^/1, 006, ^/0, 991, а/130, ограничившись двумя членами ряда. Оце-
нить погрешность.
252
Гл. 14. Ряды
2514. Вычислить sin 12°, ограничившись двумя членами ряда
для sins, и оценить погрешность.
Указание, х = 12°, в радианах х = тг/15 = 0,2094. Верхнюю
границу погрешности определить из условия х < 0,3.
2515. Делением числителя дроби
лучить разложение ------ = V ( — 1)
1 + х2 п=1
1
----- на ее знаменатель по-
Г х2
1х2п~2 и, проинтегрировав
почленно полученный ряд, написать разложение в ряд arctg ж.
2516. Полагая х = —= в разложении arctg х = V --------
V 3	П=1 2п - 1
получить ряд для вычисления тг:
.=2лу, (~1)711-
(2п - 1)3П-1
2517. Вычислить 7Г, взяв пять членов ряда задачи 2516.
2518. С помощью полученного в задаче 2497 ряда
вычислить In 2, In 3, In 4, In 6.
тт	1 + x
Указание. Положив ----- = 2, найти х и т. д.
1 — х
2519.	Определить в виде рядов интегралы —--dx и — dx.
2520.	Определить в виде ряда функцию Ф(ж) = е~х dx и
о
вычислить Ф(1/3), взяв столько членов, сколько нужно для того,
чтобы погрешность была меньше 0,001.
2521.	Определить в виде ряда функцию Ф(ж) =	х2 dx
о
и вычислить Ф(1/5), взяв столько членов, сколько нужно для того,
чтобы погрешность была меньше 0,00001.
2522.	Найти в виде ряда решение уравнения у" = х2у с на-
чальными условиями: при х = 0, у = 1, у' = 1.
2523.	Найти первые четыре члена ряда, определяющего реше-
ние уравнения (Риккати) у' = 1 + s — у2 с начальными условиями:
у = 1 при х = 0.
§ 5. Приложения рядов к приближенным вычислениям
253
2524.	Написать в виде ряда решение уравнения Бесселя ху" +
+ у' + ху = 0 с начальными условиями: у = 1, у' = 0 при х = 0.
2525. Вычислить /1/005, /1,0012, ^/0/993, </0/997, /ПО,
/70, /40, ограничившись двумя членами биномиального ряда
т(т — 1)ж2
(1 + х)т = 1 + тх 4-----j-----1- ..., и оценить погрешность.
2526. Вычислить cos 12°, ограничившись двумя членами раз-
ложения в ряд coss. Оценить погрешность.
2527.	Полагая в разложении в ряд arcsin ж (задача 2511) х =
= 1/2, вычислить 7Г, ограничиваясь тремя членами ряда.
Указание. Сначала вычислить первый из отброшенных членов,
затем выразить десятичной дробью каждый из первых трех членов с
погрешностью не больше первого отброшенного члена.
тт	7Г	1	1
2528.	Пользуясь тождеством — = arctg - + arctg-, написать
выражение для 7Г через сумму двух бесконечных рядов.
2529.	Полагая х = 1/N в разложении In (1 + ж) в ряд, получить
формулы:

2)lg(JV + l) = lgW + 0,4343 /-/I + s/-
2530.	Зная In 2 = 0,6931, вычислить In 5 и In 10 и показать,
что модуль М = 1 1 рй 0,4343.
2531.	Вычислить 1g 101 и 1g 102.
2532.	Определить в виде ряда длину дуги эллипса.
0,5
2533.	Вычислить f /1 + ж3 t/ж, взяв столько членов ряда, сколько
о
нужно для того, чтобы погрешность была меньше 0,001.
г х%
2534.	Определить в виде ряда функцию Ф(ж) = / cos — dx и
о
вычислить Ф I - I с точностью до 0,000001.
\2 )
254
Гл. 14. Ряды
2535.	Написать первые три члена ряда, определяющие решение
уравнения у' = ж2 + у2, удовлетворяющее условию: у = 0 при
х = 0.
2536.	Написать в виде ряда решение уравнения у" + ху = 0 с
начальными условиями: при х = 0, у = 1, у' = 0.
2537.	Написать в виде рядов уравнения переходной кривой,
вдоль которой кривизна к нарастает пропорционально длине дуги s.
dp 8
Указание. Из условия — = —, где С — постоянная, найти р и
as С
затем решить уравнения dx = ds cos р и dy = ds sirup.
§ 6. Ряд Тейлора для функции двух переменных
Формулу Тейлора для функции двух переменных можно написать в
трех следующих видах:
F(x + h, у + Г) = F(x, у) +
+ П h7T + l7F F(x’ + ?! hF~ + lF~ Р(Х’У) + ---, (I)
1! [ ох оу]	2! [ ох	оу_
Т(Ж; у) = F(a, Ь) +
F(a, b) +
dz	d2z	dnz
1!	2!	п!	г=10+8Дх
У=Уо+0Ау
(HI)
2538.	Написать разложение функции F(s + ?, y-f-Z) по формуле
Тейлора (I), если Р(ж, у) = х2 + ху + у2.
2539.	Разложить функцию F(x, у) = ж3 + 2жу2 по степеням
ж — 1 и у — 2 (формула (II)).
2540.	Разложить функцию F(x, у) = In (ж — у) по степеням ж
и у + 1, написав члены 1-го и 2-го порядков и остаточный член
(формула (Н)).
2541.	Разложить функцию F(x, у) = sin (тх + пу) по степеням
жну, написав члены 1-го, 2-го и 3-го порядков и остаточный член
(формула (II) при а = Ь = 0).
2542.	Разложить по степеням жну функцию е~х ~у (формула
(II) при а = Ъ = 0).
2543.	Определить приращение Аг функции z = ж2 — ху + у2
(формула (III)) и вычислить его при условии, что ж изменяется с
2 до 2,1, а у изменяется с 3 до 2,8.
§ 7. Ряд Фурье. Интеграл Фурье	255
2544.	Определить приращение Az функции z = cos(ax — by),
написав два члена формулы (III) и остаточный член.
2545.	Функцию F(x, у) = х2у разложить по степеням х — 1 и
у + 1 (формула (П)).
У
2546.	Функцию F(x, у) = arctg — разложить по степеням х — 1
и у, ограничившись членами 1-го и 2-го порядков.
2547.	Разложить функцию z = ух по степеням х — 2 и у — 1,
написав члены 1-го и 2-го порядков, и вычислить 1,12,1.
2548.	Определить приращение Az для функции z = х2у — у2 и
вычислить его с точностью до 0,0001 при условии, что х изменя-
ется от 2 до 1,99, а у — от 5 до 5,02.
§ 7.	Ряд Фурье. Интеграл Фурье
1°. Определение. Функция f(x) называется удовлетворяющей
условиям Дирихле на отрезке [а, Ь], если она на этом отрезке:
1)	имеет конечное число разрывов, причем все они первого рода;
2)	имеет конечное число экстремумов;
оа \	- 0) + f(x + 0)
3)	f(x) = --------------- во всех точках (о, о).
2°. Функция f(x), удовлетворяющая условиям Дирихле на отрезке
[—/, /], может быть определена во всех точках этого отрезка рядом Фурье:
«о Г n7VX .
ап cos
J v 7	2	1 n = l где i 1 f ,, . плх an = j j(x) cos —— -I Если f(x) = f(—x), t. e. f(x) - ft A /(-) = Д Если f(x) = —f(—x), t. e. f(x) f(O =	I	I J ’	v 7 I 1 f	П7ГХ dx; bn = -	/(^)sin--—dx.	(2) -i — функция четная, то bn = 0 и j	—л	117ГХ	. . - + > , «n cos ——.	(3) n = l — функция нечетная, то ап = 0 и у—\	. П7ГХ X&nsm—.	(4) П = 1
256
Гл. 14. Ряды
Если функцию f(x), определенную рядом (1) на отрезке [—I, I], про-
должить по периодическому закону с периодом 2/, потребовав, чтобы
/(/-о) + д/ + о)
f(l) = ------------------, то она будет определяться рядом (1) и на
всем своем продолжении.
3°. Если функция f(x) абсолютно интегрируема в промежутке
+сю
(—сю, сю) ^т. е. У |/(ж)|с/ж сходится^ и удовлетворяет условиям Ди-
рихле на всяком конечном отрезке, то она может быть представлена ин-
тегралом Фурье:
+сю +сю
f(x) = — J da f(t) cos cv(^ — t) dt =
0	-00
+ c*0
=	+	(-5)
0
(6)
Разложить в ряды Фурье следующие периодические функции с
периодом 2д:
2549. /(ж) = 1 при 0 < х < 7Г и /( — ж) = — /(ж). С помощью
полученного ряда показать, что
1 - - + - - -
3	5	7
2550. f(x) = x при 0 х :
полученного ряда показать, что
1+1+1-
32	52
2551. /(ж) = х2 при —7Г х
показать, что
4
/( — ж) = f(x). С помощью
2
1
h 72 ' "	8 '
7Г. С помощью полученного ряда
1	1	1	7Г2
2^	+ З2	— + • • • — 42	12’
ч 1	1	1	7Г2
2)1 + ^	+ р	+ + • • • — 42	Т’
2552. /(ж	) = 1	7Г	при 7Г — X при	— 7Г 0
§ 7. Ряд Фурье. Интеграл Фурье
257
Разложить в ряд Фурье периодические функции с периодом 27:
2553. /(ж) = 1 при 0 < х < I и /( — ж) = — /(ж).
2554. /(ж) = 1 — х при 0 х 1, /( — ж) = /(ж), I = 1.
2555. /(ж) =
при
при
— I < ж О,
О ж < I.
2556. /(ж) в области (0, 2] задана графиком (рис. 35) и про-
должена: 1) по четному; 2) по нечетному периодическому закону с
периодом 27 = 4. Разложить каждую из этих функций в ряд Фурье.
2557. Распространение тепла
уравнением
1 ди
в стержне длиной I определяется
д2и
a2 dt дх2’
где и(х, t) — температура, и условиями
1) граничными: и = 0 при ж = 0 и при ж = I;
( х при ж < Z/2,
2) начальными: и = <	. при 7 = 0.
[I — х при ж > 7/2
Определить методом Фурье функцию и(х, 7).
2558. Продольные колебания стержня длиной I, у которого один
конец (при ж = 0) закреплен, а другой (при ж = 7) свободен, опре-
деляются уравнением
1 д2и _ (Ри
a2 dt2 дх2'
где и(х, 7) — продольное смещение, и условиями
ди
1) граничными: и = 0 при ж = 0; —— = 0 при ж
дх
ди
2) начальными: и = /(ж), — = 0 при 7 = 0.
Определить методом Фурье функцию м(ж, 7).
258
Гл. 14. Ряды
2559. Поперечные колебания стержня длиною I с закреплен-
ными концами определяются уравнением
1 д2и д4и
a2 dt2 + дх4
и условиями
1)	граничными: и = 0 и 7—7 = 0 при х = 0 и х = /:
дх2
г/ \ ди
2)	начальными: и = f(x) и — = 0 при t = 0.
Определить методом Фурье функцию и(х, £).
В задачах 2560-2562 написать интеграл Фурье для функции:
, fl при 0 < х < 1,	.
2560.	/(ж) = < Р	’ и f (-х = -f (х .
J v ’	[0 при х > 1 J v	J v ’
2561.	/(ж) = e~^x при ж 0 и /( — ж) = /(ж).
2562.	/(ж), заданной на отрезке [—2; 2] графиком на рис. 36 и
равной нулю вне этого отрезка.
Разложить в ряды Фурье функции:
2563.	/(ж) = —-— при 0 < ж 7Г,
/( —ж) =/(ж), /(ж + 2д) =/(ж).
2564.	/(ж) = | sin ж|; с помощью полученного ряда показать, что
1 1 1 _ 1
ЬЗ + 3J5 + 5^7 + "'~ 2'
f ж при 0 < ж < 7Г/2,	.
2565./(ж) = <	Р	/ и f -ж = -/ ж .
7	[7Г-Ж при д/2 Ж 7Г	7	7
2566. /(ж) = ж при 0 ж Z,
f(-x)=f(x), f(x+ 21) = f(x).
r. fl при —1 < ж < 0,	„/ х „/х
2567./ж	Р	/ и/ж + 2=/ж.
J 7 7 [ж при	0 < ж 1 J 7	7	777
2568. /(ж) = ех при — I < ж < I и /(ж + 21) = /(ж).
§ 7. Ряд Фурье. Интеграл Фурье
259
2569. Методом Фурье решить уравнение
д2и д2и
dt2 дх2
при условиях:
ди
1) и = 0 при х = 0, —— = 0 при х = 7г:
дх
ди
2) и = /(ж) и — = 0 при 7 = 0.
2570. Написать интеграл Фурье для функции
fl при -1 < х < 1,
/(ж) — I о при |ж| > 1.
ОТВЕТЫ
1. АВ = 9, ВС = -6, АС = 3,9 — 6 = 3. 3. 5(2 + ^), 90°, 45°. 5. 20.
6. 5у7. 7. (5; 5), (5; -3). 8. В(0; 2) и В(0; -4). 9. х = а ± С С - Ь2;
при с > |6| две точки, при с = |6| одна, при с < |6| ни одной. 10. М(5; 0).
11. Центр (1; -1), R = 5. 12. пРа,Л^ = -2, пруЛ^ = -4, \А^\ = 2^5.
13. В(5; 8), \А^\ = Зу^. 14. В(4; -3). 15. -4, 1, 3. 16. 18у^.
17.(0; 2,9). 18.В(4; 0), Bi(-8; 0). 19. Центр (2; -1), R = 5. 21.Х = 7,
У = -1; 5у7. 22. М(1; 4). 23. АГ(13; 16). 24. х =	* ^2
26. В 26см от центра шара массой 100г. 27. (1; 2,5). 29. ОС = 5,
24л/2
OD = —— . 30. (3; 3). 31. 9. 33. 13. 34. (1; 3), если силы напра-
влены в одну сторону, и (25; 27), если — в разные стороны. 35. (1; — 1).
Ж1 + Ж2 + Ж3 t/i + у2 + Уз ,о <37 13\
36. -----. 37. х = ----------------, у = -------------. 38.	—; — .
3	3	3	\27 27 J
39. (71(3; 0), (72(—7; 0). 40. М(2; -6), Я(5; 8), Р(-4; 1), к = 7/3.
42. х2 + у2 — 6 т — 8г/ = 0, А и О лежат на окружности.
I) и Г лежат на линии. 45. х2 ± у2 = 8. 46. у = Ех.
х2
48. у = —~х+2. 49. у = ±2х. 51. (1; 0), (3; 0), (0; 3).
54. 2х — у + 5 = 0. Точки В и D лежат на линии.
43. х- у- 2 = 0,
х2 2
47. — + у2 = 1.
5
53. у2 = 8(ж —2).
55. х2 + у2 = 4.
ж2	_________________ _____________________
57. у = — + 1. 58. ^/(т ± 2)2 ± (г/± 2)2 - ^(т - 2)2 ± (г/- 2)2 = 4
или ху = 2; при х = ±1/2, ±1, ±2, ±4, у = ±4, ±2, ±1, ±1/2; по этим
точкам можно построить кривую. 59. 1) у = х ± 3; 2) у = —х ± 3.
60. 1) у	= х,/3	- 3;	2)	у	=	-х^/З - 3. 62.	у = -1, Ьх.	63. 1) к = 2/3,
Ь = -2;	2) к = -2/3,	Ь	=	0;	3) к = 0, Ь	= -3;	4) к	= -3/4, Ь	=	3.
65. к =	1, b =	1, у	=	х	±	1.	66. 1) - ±	— =	1; 2)	—± -	=	1.
’	’ У	7 3	-2	’ 7	-4/3 2
67. у = 0; 4ж — Зу = 0; у = 4; 1т — Зу ± 12 = 0. 68.-------- = 1 или
2	3
С — на прямой, В — «выше», a D — «ниже» прямой. 71. Неравенства
определяют: 1) все точки, лежащие «выше» прямой у = Зх ± 1 (по-
луплоскость); 2) все точки, лежащие «ниже» прямой у = Зх ± 1; 3) все
точки, лежащие «выше» прямой у = 4 — 2х и на самой прямой; 4) точки,
Ответы	261
лежащие «ниже» прямой у = 4 — 2ж. 73. х — у = ±а. 74. Через t
секунд координаты точки М будут х = а + mt, у = b + nt. Исключив
х — а у — Ь	/-
t, получим уравнение траектории: --- = -----. 75. 1) у = жуЗ — 2;
тп п
2) у = -ж73-2. 76. к = 1, b = 5. 77. х + у-4 = 0, х-у + 4 = 0; у = 3,
X	у	X	у	X	у	,	,
y = Q. 78.-±|=±1. 79.- + | = 1и— + -^ = 1. 80. г/= ±2(ж + 3).
5	3	4	3	—2	—6
81. АВ = 4^5, прОхАЁ = 4, прОг,А^ = 8. 82. 1) arctg |; 2) 45°; 3) 45°;
s	4
а? — 62
4) 0°; 5) 90°; 6) arctg ——-—. 86. 5х + 2г/ + 4 = 0, 5х + 2г/ = 25.
88. х - Зу + 2	= 0, 5х - у = 4, Зж	+ у = 12. 89.	28°, 12°30' и
139°30'. 90. у	= Зх и	у = — -х. 91.	х — 5г/ + 6 = 0,	5ж + у = —4.
92. у = 2ж —6, у = -2ж + 6. 93. (3; -1), (3; 3), (-9/5; 3/5); 45°, 71°34',
63°26'. 94. (5/2; 5/2).	95. АЕ: 2ж -	5г/ = -4, AD:	х - 2г/ = -2;
V29- 96. А =	18°26',	В = 26°34', С	= 135'. 97. х + 2г/ - 11 = 0.
98. tgA = 4/3, tgB = tgC = 2; S = 16. 99. (1; -1), (8/3; -2).
100. 2ж + у = —4, 2х - у = —4, 2х + у = 4. 103. 2, 8; 0; 1,4. 105. У13/2.
106. к = ±2. 107. Две прямые, параллельные данной: 4ж — Зг/ ± 20 = 0.
108. 8ж — 15г/ + 6 = 0, 8ж — 15г/ = 130. 109. х — у=0их+у— 4 = 0.
110. Зх — у = 12 и х + Зу = 4. 111. х + у = 2 или 4ж + у — 8 = 0.
112. 31ж + 26г/= —21. ИЗ.ж + Зг/ = 2. 114. л/10- 115. Зж - 4г/+ 10 = 0;
ж = 2. 116. h = 18/-\/34. 117. Прямые: ж + г/ = 0иж — Зг/ = 0;
расстояния: «/, = 2»/2, с?г = 0,4л/Т0. 118. Пара прямых: ж + 2г/ = О
и ж + 2г/ = 10. 119. ж + Зу = 0 и Зж + у = 0. 120. 11ж + 22г/ = 74.
121. у = —ж/2 и у = —Зж/2. 122. ж + 2г/ = 4. 123. у = 0, 2ж + Зу = -4;
у = —4, 2ж + 3г/ = 0; ж + 2г/ = —2; у = —х, tgа = -. 124. 18°26', 108°27';
,3Л = 2Ь2/3. 125. а2/5. 126. А = 36°52', В = 127°52'. 127. 4(^10 +V5);
20. 128. 2ж—г/+6 = 0, ж—4г/ = 4, 2ж—Зг/+2 = 0. 129. у = ж+2, ж—5г/ = 6,
у = —х, 2у = х. 130. л/ТО. 131. Точка движется по сторонам квадрата,
ограниченного прямыми ж — Зу = ±5, Зж + г/ = ±5. 133. hi = h% =
134. (3/5; 19/5), (-9/5; 17/5). 135. (4; 5). 136. (0; 2), (4; 0), (2; 4),
(-2; 6). 137. у - ж = 2, ж + 2г/ = 4, 2ж + у = 8. 138. 1) В(2; 1);
2)С(-1;-5). 139. у — 2ж + 6; 12/^5; ADAB 53°. 140. ж2 + г/2+8ж -
— 6г/ = 0; А и О — на окружности, В — вне ее. 141. ж2 + г/2+4ж —6г/ = 0.
143. (0; 0), (—2, 5; 2, 5). 144. (ж —1)2 + (г/—I)2 = 1 или (ж —5)2 + (г/—5)2 =
= 25. 145. tga = -2,4, а = 112°37'. 146. (ж + 4)2 + (г/+ I)2 = 25.
147. ж2 + г/2 — 8г/ = 0. 149. у = 4ж/3 и у = 0. 150. г/2 = ж(а — ж).
262
Ответы
/	(1 \ 2
151. (х - З)2 + г/2 = 9. 152. т2 ± [у --J = у. 153. т2 ± г/2 = а2.
154. т2 + у'2 = ах. 155. т2 ± у2 - 6г/ - 9 = 0. 156. 1) (3; -2), R = 6;
2) (-5/2; 7/2), R = 4; 3) (0; -7/2), R = 7/2. 157. т2±г/2±4г/ = 0; (0; 0),
(2; —2), (—2; —2). 158. т2 ± у2 ± ах ± ау = 0. 159. у = 0, 15т ± 8г/ = 0.
160.90°. 161. т±г/ = 3. 162. т2 ± у2 ± ах = 0. 163. (т - 2)2 ± г/2 =
= 16. 164. х2 + у2 = 2ат. 165. а = 4, b = 2, с = 2л/3, е = л/З/2.
2	2	2	2
166. 1) —	+ —	= 1; 2) — +	—	= 1. 167. 6=1,4; 3; 4; 4, 8; 5;	е = 0, 96;
7 25	9	’ 7 36	27	,,,,,,,
х2 г/2
0,8; 0,6; 0,28; 0. 168. а = 150млн км, е = 1/60. 169.----1----= 1,
/	16	4
а/3	т2 г/2
е = —, г = 4 — у/З, т*1 = 4 + \/3. 170.--1----= 1 г = 11, ri = 5.
2 ’	’	V 64	28
171.	4^3. 172.	173. (2/7; ±4^3/7). 174. (-15/4; ±^63/4).
х2	у2	х2	у2	х2	у2	х2	у2
175.	^ + ^г = 1- 176- 7Г + L 178‘ —> + 77 = 1 или 77 +	= !•
36	4	4	3	а2	62	62	а2
2	2	2	2	2	2
X V	X V	X 4J	г- ,
179.	Н — = 1 или-------1-- = 1. 180.----н — = 1; е = %/3/2, г = 3,
9	5	5	9	36	9	’	7 ’
П = 9. 181. 72(а2 + 62). 182. (±4^2/3; 1/3) и (0; -1). 183. (-5; 7).
184.	(±715; ±1). 185. х2 ± 4г/2 = 16. 186. — ± — = 1. 187. е = 75/2,
9	8
2	2	2	2
53°08'. 188. г = 1, п = 9. 189. 1) у - У— = 1; 2) |- - У— = 1.
10 У	2U 4
2	2	2	2
190.	-----— = 1; 2^3 и бТЗ. 191. -----------— = 1. 192. х2 - у2 =
12	4	’	16	9	У
= а2. 193. (0; ±а72); 90°. 194. у ± 2 =	195. 6, 2 arctg-.
196.	=, 6 > а. 197. 1) е = 2; 2) е = sec а. 198. у < -3, у < — |т|.
X2 tP	4/2
199.	— - у = 1. 200. т2 - у = 1 (при х > 0). 201. х2 - у2 =
22	2	2	/	2	2	\
о	XZ U	XZ U	( ХЛ 4Г	\
= а2. 202. — - /- = 1. 203.------------ — = 1 ( или---------— = — 1 | .
а2 Ь2	16	9	\	9	16	/
4	'__
204.	(0; 0) и (6; ±2л/3). 205. у = ±-(х + 5). 206. (-9, 6; ±3^119/5).
о
207.	(±7б; ±72). 208. (-4; 3) и (-4/7; -3/7). 209. |- - ^- = 1.
16	48
2	2	2
210.	= 1 (при х > 0). 211. у = 3 - 1-. 212. у2 = 8(т ± 2).
а2 За2	4
214.	1) у2 = 9т; 2) у = -т2. 215. у = ут2. 216. (т -	± у2 = р2;
2
(у ±ру 217. у = -у. 218. (3; ±3^2). 219.40см. 221. у2 = рх.
Ответы
263
х2
222.	у2 = 4ах и у = 0. 224. у2 = 8(2 - х). 225. у = х - —, Oi(2; 1).
226.	1) у2 = -4х; 2) у = х2. 227. у2 = -Зж. 228. (0; 0), (6; ±2^3).
229.	ж = 0, ж ± г/ ± 2 = 0. 230. у = -^3(ж ± 1); 16/3. 231. г = 7,4,
d = 9,25.
ж2
233. — +
4
232. Директриса ж = ±3,2, е = 1,25, г = 10,25, d = 8,2.
у2 = 1. 234. ж2 — у2 = 12. 235. Сопряженный диаметр
У = ai = 61 = л/10.
236. Сопряженный диаметр 4г/ ± ж = 0; 81°.
237.	Уравнение диаметра у = — ж,
а
его длина ^/2(а2 ± 62).
238.	у = 1, 5ж.
239.	г/= 2. 240. 8ж — 9г/± 25 = 0.
241.	у = 2ж ±3. 243. 1) ж ± 2^3г/ = 8;
2)	2ж ± у = 1; 3) ж ± 2г/ = -2. 245. ж - у = ±5. 246. у = ±2ж ± 6.
247. ж ± у = \/а2 ± 62.	249. у = 2г/ ± 4^2.	250. Уравнение нор-
мали MN: а2уох — Ь2хоу = с2жог/о- Положим у = 0, найдем абсциссу
точки N пересечения нормали MN с осью Ох: Ж1 = е2жо- Тогда
FN = с — е2жо = er, FyN = с±е2жо = е/д, т. е. нормаль MN делит FFi
в отношении г : п и поэтому есть биссектриса. 252. Нормаль к параболе
у2 = 2рж имеет уравнение у$х ±ру = Уо(р + Жо). Положив у = 0, найдем
Ж1 = р ± жо, FM = Ж1 — ^ = ^±жо = FM, т. е. FFMN = FF N М.
253. (±3,2; ±2,4). 254. Диаметры у = ж и у = —ж/4, угол 59°02'.
255.	г/= ж/4. 256. 4ж - у = 6. 257. arctg 3 » 71°31'. 259. ж ± у ± 2 = 0.
260.	1) 01(1; 2); 2) tgy> = |. 261. 5) X2 ± 4У2 = 16; 6) У2 = 4Х;
7)	X2-4Y2 = 4; 8) У = Х2/2. 262. 1) X2 + 4Y2 = 16; 2) X2-4Y2 = 16.
263. X2 - У2 = 8.
264. 1) XY = 6; 2) XY = -6; 3) XY = 4; 4) XY =
= — 6. 268. Уравнение струи: у = 16(ж — ж2); у = 3 м при ж = 0, 75м.
/ ж2 \
269.	у = 6 г/------ . 270. ж2 ± г/2 ± 4ж = 0. 271. 1) 45°; 2) arctg 2.
\ /
2
272.	у = ж tgр---£-------. 273. г/2 = 24ж ± Зж2 (гипербола). 275. 1) Эл-
2vqcos р
X2 У2
липе; 2) гипербола. 276. 1) ——|—— = 1, Oi(3; —1); 2) X2 — У2 = 9;
3)	У2 = 2Х; 4) X2 = 4Y. 277. X2 ± 2У2 = 4. Фокусы в старой системе
(1; 1) и (-1; -1). 278. (ж ± I)2 ± у2 = 4. 279. (ж - З)2 ± (г/ - З)2 =
(ж - 212	г/2
= 2. 280. ж ± Зг/ = 0. 281. г/2 = 4(ж ± 4). 283. v	= 1.
„	,	ал/5
284. ж2 ± у2 — ах — by = 0. 285.	.
286. Основание АВ = 2а, высота
9
а	а
OD = площадь 287. За начало примем точку О, делящую АВ
у5	у5
264
Ответы
в отношении АО : ОВ = т, а за ось Ох — прямую ОВ; пусть ОВ = а,
тогда координаты точек Ан В будут: А(—та; 0), В(а; 0). Уравнение ис-
комой линии: (т— 1)т2 + (т — 1)г/2 = 2тах; при т 1 окружность: т2 +
•> 2та
у = ------х; при т = 1 прямая: х = 0. 288. Точку О примем за начало,
т — 1
а О В — за ось Ох. Уравнение искомой линии: (а — Ь) (ж2 + у2) = 2abx;
2а6
при а ф b окружность: х + у = -------х; при а = b прямая: х = 0.
а — Ь
289. 2(k2x2 + y2) = a2(k2 + l); эллипс при k 1, окружность х2 + у2 = а2
х2 —I- Ют	г/2	3
при k = 1. 290. —-------н — = 0. 291. 3а2?3. 292. arctg -	36°52'.
25	9	4
293. (±а; ±а). 294. А(?6; 0), В(2; -2), О(-2^2; ?2); S&ABC =
2 4- \/3	(	2
= V2 + V3 + V6. 296.2^2; у = т-2. 297. У . 298. (т - ^) +у2 =
9р2	I dl) I
= ---. 299. ах — by + а2 + b2 = 0; d =	300. Вычитая урав-
16	Va2 + b2
нения почленно, получим 4(г/ — т) = (у + х)(у — т), отсюда: 1) у = т;
2) х + у = 4; следовательно, точки пересечения парабол лежат на прямой
у = т или на прямой т + у = 4; найдем tj = 2, Т2 = —6; длина хорды
(х - 2)2
8?2. 301. 30. 302. т2 + у2 = а(т + г/). 303. 1—Н у2 = 1 (эллипс с
/^>2____________________________________I 25
центром (2; 0)). 304. ху = 4. 305. у = --------. 306. X2 — У2 = 4;
(т — 2 5)2 V2
01(2; —3). 307. 1—2~25------~4~ = (гипербола с центром (2,5; 0)).
308. Пусть М(т; у) — точка эллипса. Тогда FМ + FiM = AF + AFi или
\/(х — а)2 + (у — а)2 + У(т + а)2 + (г/ + а)2 = 4а; Зт2 — 2тг/ + Зг/2 = 8а2;
после поворота осей на 45°: X2 + 2У2 = 4a2. 309. cos р = —,	= =
ушу?
2	1
= —=, sin р = —=; новое уравнение X2 — Y2 = 4. 310. Зт2 + 8тг/ —
V	V
— Зг/2 = 20; поворотом осей на угол р = arctg (1/2) приводится к виду
X2 — Y2 = 4 (см. 309). 311. у2 = 2рх + (е2 — 1)т2. 313. 1) Пара пря-
мых у = ±2т; 2) точка (0; 0); 3) мнимая окружность; 4) точка (3; 4);
5) пара прямых т = 0, у = —т; 6) пара прямых у = ±4; 7) пара
т	X2 У2
прямых у = т и у = —. 314. 1) (1; —1),------Н — = 1; 2) (2; 1),
X2 Y2
X2 - Y2 = 9; 3) 2Х2 + 5XY + 2У2 = 8. 315. 1) -------- + — = 1;
г	7 24	4
ул2	у2 у*2	у2 у*2
2)--------= 1. 316. 1) — + — = 1; 2)-----------= 1. 317. 1) У2 =
7 4	6	! 8	4	7 8	4	7
= 2?5Х; 2) пара прямых т — 2г/ = 3 ± 1. 318. 1) Зг/ = 2т — 7 ± (т — 2);
Ответы
265
2) точка (2; —1); 3) 4г/ = —2ж — 3 ± 1. 319. 4J72 — У2 = 8; центр
(2; 0); tg <^> = —1/2. 320. 5(ж — I)2 + (г/ — 2)2 = 9. 321. Повернув оси
X2 а
на —45°, получим У = —— 4---------=. Уравнение л/ж + ^Jy = yja опре-
ау2 2у2
деляет дугу АВ этой параболы (рис. 87), на которой х а и у а.
322. (ж — т)2 +	(г/ — п)2 — е2(ж cos а + у sin а + д)2	=	0;	А +	С = 2	— е2;
S = 1 — е2. 323. 1) Пара прямых х ± 2г/	= 0; 2) точка	(—2;	2); 3)	пара
X2 У2	X2	У2
прямых у = х,	х + Qy = 0. 324. 1)	4—— =	1;	2)	—------—	= 1.
325. 1) У2 = I \/'2. V; 2) прямые х 4- у = 2 ± 1. 326. 1) у = х — 2 ± 1;
2) Зу = х - 5 ± 2(ж + 1). 327. 1) Тх2 - 2ху + 7г/2 - 48ж - 48г/ + 144 = 0;
2) х2 4- 4жг/ 4- г/2 4- 6ж 4- 6г/ — 18 = 0. 328. (ж — г/)2 — 2а(ж 4- у) 4- а2 = 0;
У2 = ал/2Х. 329. ж2 - 4жг/ - у2 - 4ж + 8г/ - 12 = 0; X2 - У2 = 3, 2^/5.
.	а . а sin а	asin(/3 —а)
335. 1 г = ----; 2) г = —--------. 336. г =	.	337. г =
cos р	sin р	sin (j3 — р)
= 2acos<£>. 338. 1) rmax = 5 при р = 135°, 315°; rmjn = 1 при р = 45°,
225°; г = 3 при р = 0°, 90°, 180°, 270°; 2) rmax = 3 при р = 0°, 120°,
240°; rmjn = 1 при р = 60°, 180°, 360°; 3) rmax = 2 при р = 90°, 210°,
330°; гт;п = 0 при р = 30°, 150°, 270°. 339. 1) rmax = а при р = 30°,
150°, 270°; г = 0 при р = 0°, 60°, 120°, 180°, 240°, 300°; 2) г = а при
р = 45°, 225°; г = -а при р = 135°, 315°; г = 0 при р = 0°, 90°,
а2
180°, 270° (см. с. 334, рис. 83). 340. 1) г2 = -—; 2) г = а; 3) г =
р
= ----------4) tg р = 1; 5) г = а cos р-, 6) г2 = а2 cos 2р. 341.1) ж = а;
cos \рр — а)
2) ж24-г/2 = 2ау; 3) ху = а2; 4) ж 4-г/ = 2а; 5) (ж24-г/2 — аж)2 = а2(х2 + у2).
9	9	9	9
х х	гг	ч х	v	ч	о	а
342. 1 -----1- — = 1; 2)-----— = 1; 3 г/2 = 6ж. 343. г = -------± Ь.
7 25	9	7 16	9	7	sin^
а(1 ± sin р)	..
344.	г = ОВ ± АВ = ------------- или в декартовых координатах у =
cos р
= —------—. 345. FМ2 = г2 4-а2 — 2га cos р, F\M2 = г2 4-а2 4-2га cos р,
2а — х
FМ2  FiM2 = (г2 4- а2)2 — 4г2а2 cos2 р = Ь4, отсюда г4 — 2a’2r2 cos 2р =
= Ь4 — а4.	346. г = а(1 4- cos р); (ж2 4- у2 — аж)2 = а2(ж2 4- г/2).
347.	Пусть С — центр неподвижного круга, С\ — центр смещенного
круга и М(р; г) — текущая точка,
и СО = С\М = |а, то ОМ || СС\.
Так как АОСС\ = АМС\С = р
Спроектировав ломаную ('()М('\
на CCi, получим
ct	Ct	/ -I	\
— cos р 4- г 4- — cos р = а. Отсюда г = а (1 — cos р).
348.1) rmax = 5 при р = 0°, 180°; rmin = 1 при р = 90°, 270°; 2) rmax = 4
266
Ответы
при ip = 90°, 210°, 330°; rm;n = 2 при ip = 30°, 150°, 270°; 3) г = а при
ip = 0°, 180°; г = -а при ip = 90°, 270°; г = 0 при ip = 45°, 135°,
ab sin (в — а)	. х2 „
225°, 315°. 350. г = ——-----------Д , . ’ -------. 351. 1 — ± у2 = 1;
a sin (ip — а) + b sin (р — ip)	4
х2
2)	—— у2 = 1; 3) у2 = х. 352. г2 = 2с2 cos 2<^>; (х2 ± у2)2 = 2с2(т2 — у2).
На рис. 80 положено сл/2 = а. 353. г = b ± a cosip. 354. Из АО AM:
г = ОМ = OAcosip, но из ДОЛЯ: О А = 2а sin ip, откуда г = a sin 2ip.
358.	Пусть точка А на оси Ох, точка В на оси Оу и АО АВ = t. То-
гда х = В М cost = ВС cos21 = a cos3/, у = AM sin t = AC sin2/ =
= asin3/; итак, x = acos3/, у = asin3/, откуда ж2/3 ± г/2/3 = a2/3.
2
360.	у2 = —---. 361. (Зг/2 + х2)2 = 4х2(а2 — у2). 362. В полярных
р + х
координатах г = ОМ = АВ = BDsinip = a tg ip sin ip\ в декартовых
х3
у2 = ----- (рис. 85). 365. Обозначив через / угол луча О А с Ох, най-
а — х
 2	8a3
дем х = 2actg/, у = 2a sin /. Исключив /, получим у = —----------—г.
х1 + 4a2
367.	х = а(/ — sin/), у = а(1 — cos/). 368. х = a(cos/ ± / sin/), у =
ж	(R + г)/
= a(sm/—/cos/). 369. у = х ctg —. 370. х = (R+r) cos/ — г cos------,
а	г
(R _|_
у = (R + r) sin / — г sin 2-где / — угол поворота линии центров.
г
R — г	R — г
371.	х = (R -	г) cos / + г cos---/,	у =	(R — г)	sin / — г sin /.
374.	X =	= 8; У =	=	-2;	ОМ	=	^64 ± 4 = 2^17.
375.	^8 + 2^3.	379. 1) с =	2)	а =	2с - Ь.	380. с = |(а - Ь).
381.	m ± р = п; О t) = 3(т ± п), +('’ = 3(п — т), Е(5 = 3(т — п),
ot) = 3(2n — т), dX = 6(т — п). 382. . IД = 2(n — т), О\( = 2п ± т,
О + = Зт + n, мА = 2т — п. 383. 6л/3- 384. X =	± Х% ± Хл =
= - 3, У =	= 6, ОМ = Д9±“36 = 3^5. 385. 1) а = 3(с - Ь);
2)	с = 2Ь — ал/З- 386. ОМ = г = 5л/2; cos а = 0, 5у/2, cos (3 = —0, Зл/2,
cos7 = 0,4^2. 387. г = 7; cos a = 2/7. 388. /3 к 52° или 128°.
389. М/Зл/2; 3; —3), г = 3(V2i±j — к). 390. u = 2i — 6j ± Зк, и = 7.
391. ОС = i - 2j + к, ОС = V6; А^ = к - 4j - i, АВ = 3^2.
392.	Конец В(4; —2; 5) или Д (4; —2; —7), cos a = 2/7; cos /3 = —3/7;
г-	2
cos 7 = ±6/7. 393. а = 2b — 0,8c. 394. и = Зл/5, cos a =---------=.
3y5
395.	cos a = cos /3 = cos 7 = 1/л/3. 396. 45° или 135°. 397. D(4; 0; 6).
398.	c = 2b - 2а. 399. 135°. 400. В = С = 45°. 401. cos^> =
Ответы
267
= 1/VTO = 0,316; <р = 71°35'. 402. cos^ = 2/^5 = 0,894; p 26°37'.
403. 60°. 404. arccos 0, 8. 405. 90°. 406. npba = 4^2/3. 407. 2.
408. 1) 2 + У+ 2) 40. 409. (a + b)2 = a2 + 62 + 2a6 cos p (теорема коси-
нусов); (а + b)2 + (а — b)2 = 2a2 + 262 (свойство диагоналей параллело-
грамма). 410. 7. 411. R = 7(a + b + c + d)2 = 10^4+ 2^2 к 25, 3H.
r- r—	______ (2m —11)111	5	,	,
412. V7 и V13. 413. cos (a, m) = —.	---— = —cos (apn) =
V ’	7(2m-n)2 • 1	2^7
= - 2/V7. 414.5/6. 415. ОЛ? = 2(i + j + 2k),	= 2(i + 2j + k);
cos в = 5/6. 416. cos p = 2/л/7. 417. cos<^> = 0, 26л/10; p & 34°42'.
418.	D(-l; 1; 1); p = 120°. 419. npab =	= -6- 420. OM =
= ^(2n + m)2 = V7, ON = ^(3m + n)2 = /Тб: cos p =	=
17	17	4a/2
=	0, 891, p = 27°. 421.120°. 423. 80 Дж, cos 0 =	.
2^91	19,08	15
424.	ал/б. 425. cos p = —1/4. 426. a x b равно: 1) —6j; 2) —2k;
3) 6i — 4j + 6k. Площадь равна: 1) 6; 2) 2; 3) 2^22- 427. 24, 5. 428. y/21,
h = д/4Д 429. 1) 2(k - i); 2) 2a x c; 3) a x c; 4) 3. 430. Пло-
щадь параллелограмма, построенного на диагоналях данного паралле-
лограмма, вдвое больше площади данного параллелограмма. 431. 50л/2.
432. 1,5^2. 433. ЗУГ7, SA = ЗУГ7/2. 434.	= 7^5, BD = 2у/21/3.
435. |а + Ь| = |а — Ь| = \/Ъ, S = л/б- 437. 1, 5. 438. V = 51, левая.
439. V = 14, Н = 7v^/3. 441. с = 5а + b. 443. 2^2/3. 444. V = 14,
Н = V14. 445. с = а + 2Ь. 446. V = |(а + Ь) • [(b + c) х (а + с)]| = 2|abc|.
447. (т х п) • р = |т х п| • 1 • cos а = sin a cos а = 0, 5 sin 2а. 449. 52.
2	3	6
451. cos а = cos(3 = COS7 =	452. х+4у—2г = 2.
454. х — y + z = а. 455. 2у — Зг + 7 = 0. 456. Зг/ + 2г = 0.
458. - + - = 1. 459. х + у + г = 4. 460. - + - + - = 1.
ас	4	3	2
2	1
cos/3 = --, cos7 = -; а = 48°11', /3 = 131°49', 7 = 70°32'.
О	о
453. х+у = 2а.
457. 2ж + у = 0.
2
462. cos а = -,
3’
463. х -
— 2у — Зг + 14 = 0. 464. Зж —4г = 0. 465. х + у = 4. 466.- + - + - = 1.
2	4 4
467.	1) 45°; 2) 78°30'. 468. х - 2у - Зг = 4. 469. 2х + Зу + 4г = 3.
470.	2ж+г/+г = а. 471. 2x-2y+z = 2. 472. 2x-y+z = 5. 473. 3x-y = 0
и ж + Зг/ = 0. 474.3. 475. V0. 476. 2^2. 477. 1) ж - 2г/+ 2г = 11,
ж —2г/ + 2г = —1; 2) х + у — 2г = 0 и x + y + z = 0. 478. 1) ж —8г/ + 9г = 21;
2) ж — г/ + 2г = 0иж — у — г = 0. 479. (1; —1; 2). 480. Зж — 4г/ + г = 11.
481. 2г/ — 5г + 10 = 0. 482. Уравнение плоскости ж + у — 2г = 0; угол
268
Ответы
ее с плоскостью z = 0: cos р = \/б/3 Ай 0,8165, р = 35°15'. 483.
\ 3
4S4.y = ±z. 485.	” С	486.2т + 2г/+ г = 20 и 2т + 2г/ +
\/а2Ь2 + а2с2 + Ь2с2
+ г+4 = 0. 487. 7т+14г/+24 = 0. 488.1) (5; 4; 0) и (7; 0; 2); 2) (0; -4; 0)
и (2; 0; 2). 489. т = — z + 3, у = — z + 5; ——- =
490. —р =	491. Р{0; 0; 1}. 492. 1) Р = i; 2) Р = i + к;
I 1 у____ Q 2, _ 3
3)	Р = j + k. 493. —-— = —-— = ——; cos а = 0, 3^2, cos /3 = 0, I \/2.
3	4—5
cos 7 = —0, 5^2. 494. т = 2, г = 3. 495. Через t секунд координаты
точки М будут т = 4 + 2/, у = —3 + 3/, z = 1+/; -=	.
496. 1)
497. 1)
т = —2+/, у = 1 — 2/, z = —1 + 3/; 2) т = 1 +/, у = 1—/, z = 2 + /.
у-ь
0
т — а
0
z — с
1
что значит т = а, у = Ь; 2) z
с и
-----= -----. 498. cost? = ~~/=- 499. cos р = —. 501. Направляющий
т п---------л/3	26
|	у __ 2	%
вектор Р = NxN] = i + 3j + 5k. Уравнения прямой: —-— = —-— = —.
502. Зт + 2г/ = 0, г = 4. 503. 0,3^38. 504. 4^2/3. 505. (4; 2; 0),
-г — К у — Л 7
(3; 0; 2), (0; —6; 8). 506. т = 6 — Зг, у = —2г + 4; - = ---- = —;
следы: (6; 4; 0), (0; 0; 2). 507. |	= |. 508. Р{0; 1; 0}.
509. Р{1; 1; 2}; а = /3 = arccos^^. 510. у = —3, 2т — г = 0.
V6
511. Приведем
т у — 4
3“
уравнения к канонической форме:
г	20
= -; cos^> = — ай 0,952,
6	21
сав уравнения
данной прямой в виде
2
3/-2
2
т у + 7 г — 5
1 “	2	“	2
17°48'. 512. Напи-
г - 1/3
—	, получим
1
513. Л(0; 1; 0),
уравнение искомой прямой: ——
ЛЛ?{3; -1; 4}, Р{1; 2; 2}, d = л/Г7. 514. sin в = 1/л/б- 515. Для обеих
И 2

У
2
1
прямых Ат + Вп + Ср = 2 • 2 + 1(—1)
вой (—1; —1; 3) не лежит на плоскости,
лежит на плоскости. 516. у + г + 1 =
т — 2 у — 1 г\
записать в виде —-— = —-— = —
+ (—1) • 3 = 0, но точка пер-
а точка второй (—1; —1; — 3)
0 уравнения прямой можно
517. т — 2г/ + г + 5 = 0.
Ответы
269
518.	8ж — 5г/ + г — 11 = 0. 519. х + Чу - 4z = 1. 520. | = = |;
17°33'. 521. (5; 5; -2). 522. (6; 4; 5). 523. (5; 5; 5). 524. (3; 3; 3).
, ЛТ|рР| 1	х — Ч г/-1	7
525.	d = -— -7 =	526. х + Чу-5г = 0. 527.--=  -----= —.
|Р х Pi| V3	-9	8	11
528.	(1; 1; 2); 70°. 529. (-1; 2; 2); 30°. 530. (6; 2; 0). 531. (3; -1; 1).
532. x-y-z = 0. 533. (-1; 3; 1). 534.	535. Точки
на прямых: 0(0; 0; 0) и А(Ч; 2; 0); направляющие векторы прямых:
Р{0; 0; 1} и Pi{2; -1; 2}, d = ^P^>1 = -^=. 536. 1) 0(1, 5; -2, 5; 2),
|Р х Pi I у5
R = 2, 5^2; 2) 0(0; 0; a), R = а. 537. (ж - I)2 + (г/ + I)2 + (г - I)2 = 1.
538. ж2 + г/2 + г2 = 8х. 539. ж2 + г/2 + г2 — а(ж + у + г) = 0. 541. г/2 =
= Чах — ж2. 542. ж2 + г/2 = Чах, ж2 + г2 = Чах, y2 + z2 = а2. 544. (1; 7; 2),
R = 4. 545. (ЗУ — 4Z)'2 = 12(ЗХ — Z). 546. 1) у = 0, ж2 = а'2 — az (пара-
бола); 2) ж = 0, у2 = а'2 — az (парабола); 3) z = h, х + у = ±^/а(а — /г) —
прямая, параллельная х + у = а (см. рис. 59 на с. 320). Цилиндрическая
„	„	ж2 (г/ + 2)2
поверхность 2ж + (г/ — г + 2) = 8, форма тени ——|------------ = 1 —
4	8
эллипс. 548. 2ж — у + Зг — 7 = 0. 549. ж2 + (г/ + 4)2 + г2 = 4.
(ж — 2)2	(г/ + 4)2	.	.
550 1______L__l ’____О = 1	5?;ч	_ -X _i_ (>, _ -X — л(
36	18
ж2 + г/2
554. ж = 4, г ± у = 2. 555. —А^-
а2
(0; а; 0), направляющая — окружность г = а, ж2 + (г/ — а)
557.
z2
— . 556. h'2x'2 = 2рг[/г(г/ + а) — аг].
2 -
558.	Вершина (0; 0; 0), направляющая — парабола г = h, ж2 = 4hy.
559.	При г = 0 ж = ±а; при у = h ж2 + у2 = а2; при ж = ±с пря-
Оа2 - с2
мые г = ±-----------у, т. е. поверхность образована движением пря-
h
мой, параллельной плоскости уОг и пересекающей окружность АВС
(см. рис. 65 на с. 321) и ось Ох. 560. а) г = ж2 + г/2; б) ^/г/2 + г2 =
= ж2. 561. 1) г = е~е2+у2); 2) г = —------ 562. 9(ж2 + г2) = 16г/2.
(Г 4“ у
563. ж2 + г2 = г(г/ + а).	564. а) ж2 + г2 = г/2; б) г2 = ж2 + у2.
565. Повернув оси Ох и Оу вокруг оси О г на 45°, получим уравнения
поверхности и плоскости в виде 4Z2 = X2 — У2, X = ал/Ч. Отсюда
Г У2 Z2	г
сечение: X = ау2, —г + —- = 1 — эллипс с полуосями ау2 и а.
Ча2 а2
ж2 + г/2	г2	.	,45	, ж2 + г/2	г2
566. —ААХ +	= 1- 567. a 3, 84тт; б —тг. 568. a —------------ = 1
а2	с2	’	’ 4	’а2	с2
_|_ ^2
(однополостный гиперболоид); б) —----------— = 1 (двуполостный ги-
270
Ответы
перболоид). 570.------1— = - ( 1 + -
1	7	4	6	3 V ‘
= 1 + |. 571. х =
’4	6	3
4	6
= 1 - -,----
2’4	6
= 1 + cosa; при а = 90°
Зг2
—	= 1, при а = 180°
с2
574. х + у = 4, х — у = z;
2 I ,,2
2а2
2 I
4а2
1	т2 + у2 z2
а)], откуда	- —(
г2
------ = 1, при а = 120°
с2
г2
------ = 0 (конус).
с2
2 I ,,2
2
572. ж2 + у
2
х + у = 2г, х — у = 2. 575.
9
' = az.
+ г2 _
а2 “ '
+ , ,,2
2а2
577. х
576. т2+г/2—г2 = —2а2 (двуполостный гиперболоид).
578. 9т = ± 13г.
радиусом R = а; 2) параболоид вращения вокруг Oz; 3) цилиндр; 4) ги-
перболический параболоид; 5) конус; 6) параболический цилиндр; 7) ко-
нус; 8) параболоид вращения; 9) конус; 10) цилиндр. 581. х + у = 2 + г,
х — у = 2 — z; х + у = 3(г — 2), 3(г/ — х) = г + 2. 582. т2 + г/2 =
4а
579. 4г/ = ±3г. 580. 1) Сфера с центром (0; 0; а) и
о w	х2 + у2
= 2аг. 583. г = а — —-----------.
2а
Зх — 4г/ = 12г; г = 0, Зх = 4г/.
590. 1. 591. sin (а + /3) sin (а —
595. -2т. 596. —4а3.
584. 2г/ = ±3г.
586. 26.
/3). 592. -10.
585. Зх + 4г/ = 24,
587. -38. 588. 7. 589. 2а.
593. 4а. 594. -262.
597. 144. 598. 72. 599. (т - г/)(г/ - z)(x - z).
600. 1.	601.	sin	(Р	— а). 602.	10.	603. Лежат			на прямой у = т + 2
	X	У	1		т	У	1		
604. 1)	Х\	У1	1	= 0; 2)	2	3	1	= 0.	605. 10. 606. атп
	Х2	У2	1		-1	5	1		
607. а(х — z)(y — z)(y — х). 608. 4 sin a sin2 —.
610. 1) Ti = 2, т2 = 3;
4
2) ti = 0, х-2 = —2. 611. т = 5, у = —4. 612. т = —, у = 1. 613. т = 0,
у = 2. 614. т = т, у = 2т - п. 615. 5; 6; 10. 616. -1; 0; 1. 617. 7к,
8к, 13к. 618. 5к, —life, — 7к. 619. т = у = г = 0. 620. Несовместна.
тт	2 + 5г 5 - 7г
621. Неопределенна: т = —-—, у = —-—. 622. Несовместна. 624. 2;
-1; -3. 625. 1; -1; 2. 626. 2к, к, -4к. 627. т = у = г = 0. 628. -к,
13А?, 7>к. 629. Неопределенна: у = 7 — Зт, г = 18 — 7т. 630. 1) 12 + 5г;
/*	3 7Г	3 7Г
2) а2 + 62; 3) 5 — 12г; 4) —2 +2г; 5) г; 6) 1 + г. 634. 1) 2 ( cos — + г sin — J ;
2) 2 sin — (cos — + г sin —) . 640. 1) 32г; 2) 64; 3) 4(1 — г); 4) 2(3 + 2л/2)г;
5) 8г'. 641. sin За = 3 sin а cos2 а — cos3 а, cos За = cos3 а — 3 sin2 а cos а.
Ответы
271
ктг . кк ,	.	—1±гуЗ	г ± л/3
642. cos----Нг sin —; к = 0, 1, ..5. 643.1) 1, ------------; 2) —г, ----;
3	3’	’ ’	’	7 ’	2	7	2
3) ±г, ±V^±?; 4) 1 + i, -1, 36 + 0, 365г', 0, 365 - 1, 36г'. 644. 1) ±^-±Д;
2) </2(cos <р + i sin ^), 9? = 45°, 165°, 285°; 3) ±2(Тз + г'), ±2(-1 + г'^4).
645. 1) —2, 1 ± г'73; 2) ±1 ± г'. 646. 1) 1п2 + ттг'; 2) |1п2 + у; 3)
, ,	---s-	V . 3 , тт sin (пх/2) sin Г(п + 1)/21ж
4 In V®* 2 + г/2 + г' arctg -; 5 - In 2 - -г'. 647. -V 7 7	1 о J 7/ J .
х 2	4	sm(^/2)
sin (пх/2) cos i(n + 1)/21ж	ч 7 — 24г ч о
648. -------' { , , О 	650. 1 ----------; 2 26 За2 - 62 г.
sm(^/2)	25
651. 1) 4л/2е7Гг/4; 2) 2e2"/3; 3) V2e-"/4.	652. 1) 5(cos 0 + г sin 0);
2) е-7"/2; 3) 2е-37Гг/4. 654. Точки внутри круга с центром C(zq) и г = 5.
±1 ± г
655. 1) 8г; 2) 512(1 — г'л/З); 3) —27. 657. 1) ——^=—; 2) cos р> + г sin р>, где
р = 0°, 72°, 144°, 216°, 288°. 658. 1) 2, -1±г'л/3; 2) ±2г', ±7з±г'; 3) ±3,
sin2n«	.	.	— 1±гу5
±3г. 659. —;------. 660. 1 -1, 2, 3; 2 5, -----------—. 661. 1 хх = 3,
2 sin х	2
ж2 = 4, «з = —2; 2) «j = 1, ж2 = —2, 13 4 = ±г'л/2; 3) Xi = —2,
ж2)з = ±1/3; 4) Xi = 1, ж2)3 = ±г'/2. 662. 1) А = 49/4 > 0, щ = 2,
—3 ± i\/3
«1 = 1, гх = 3, г2)3 = ---------------; 2) А = 0, zi = 4, г2 = z3 =
= — 2. 663. 1) А < 0, р = 60°, гу = 4cos20°, г2)з = 4cos (20° ± 120°).
/3	/(а) /(/3) к Да
Д/3
665.
1,85 < х < 1,86.
666. 2,15; 0, 524; -2, 66. 667. 1) 1, 305; 2) 4 и 0, 310; 3) -0, 682/; 4) Х1 =
= 1,494, ж2 = —0,798 ^жх найдено по формуле х = \/2х + 2, а ж2 —
__________________________2 \
по формуле х = ------------- I. 668. 1) —6, —1 ± г'х/2; 2) —1; 2; 2.
О J
669. 1) А =	> 0, ггх = 3, щ = -2, zx = 1, г2>3 =
2) А = —4 < 0, <р = 45°, zi = 2^2	cos 15° = 1 + г/З,	г2	=	-2,	z3	=
= 1 — х/З; 3)	А = 0, z\ = —2, г2)з	=	1; 4) положив х =	z	— 2, получим
г3 — Зг + 2 = 0; А = 0; гу = —2, г2 = z3 = 1; жх = — 4, ж2 = х3 = —1.
670. 1,76 и -2,15. 671. 1) 1,17; 2) 3,07. 672. 1,67. 675. О < х < 1.
681. жх = 0,	ж2 = 4. 683. 1) х -2; 2) -3 < х <	3;	3)	0 <	х	<
< 4. 684. 1)	—4 < х < 0; 2) -1	<	х < 3. 685. 1) х	0;	2) х	<	4.
272
Ответы
686. 1) 2h < г < (2к +1)тг; 2) -4 < х < +4. 687. 1) /(0) = 1, f (1) = 1,
/(-1) = 3, /(2) = 3, f(a + 1) = а2 + а + 1. 688. 1) Ь + а; 2) 2а/г.
689. о Ь + а—690. Г(4; 3) = 19, F(3; 4) = -25. 691. 1) Четная:
b2 + ab + a2	v '	v '	'
2) нечетная; 3) четная; 4) нечетная; 5) нечетная; 6) и не четная, и не
Лж1) + Лж2)	+	х
нечетная. 692. ——----------—- > г -------- . 693. log„ х. 694. а .
2	\	2	)	а
696. 2 < х 3. 700. 1) |ж| <7 2; 2) —1 <7 х 3; 3) — — + &тг <7 х — + ктг;
4) |ж| 7> 2. 701. 2) 6т2 + 2h2; 3) 4(2 — а). 702. |а| < 0, 001, как только
3	3	1 f 1 / &\
п > -- или п > -- = 10; I а I < е, как только п > -. 703. х = 2;
1g 2	0,3	’ 1 1	’	1g 2
2161 , ,
1-;	1-; . . . —> 1; х — 1 < 0, 01, как только п > 50; х — 1 < е,
3	5 7	9	'	1	/	> ।	।
как только п > --. 704. х = 4; 3,1; 3, 01;...	3 + 0; х = 2; 2, 9;
2е	’ ’ ’ ’	’	’	’ ’ ’
2, 99; ...-) 3 - 0. 705. х = 6; 5,1; 5, 01; ...	5 + 0; х = 4; 4, 9;
4,99; ...	5 - 0; х = -1; -1,9; -1,99; -1,999; ...	-2 + 0; х = -3;
—2,1; —2, 01; -2, 001; ...-) -2 - 0. 707. 8 = е/2. 708. <7 = 0, 01.
712. При |ж| > 2500,5. 713. При |ж| > 7,036. 715. lim х в первом
примере равен 1, во втором —1, в четвертом 0, в пятом 2, в шестом 0, в
третьем не существует.
716.
X	3;	2,1;	2,01;	...	-> 2 + 0
eo 1	3;	30;	300;	—> +oo
lim -----
r->2+0 X -
2
X	1;	1,9;	1,99;	-4-2-0
1	-3;	-30;	-300;	. . .	—> —00
lim
а^2-0 X -
2
х	1;	0,1;	0,01;	...	->+0
717.------------------------------------------------; lim 21/х = +оо;
21/!	2	210;	2100;	...	-> +оо	а^+о
X	-1;	-о, 1;	-0,01;	...	-4 -0	lim 2^/^ — 0
2l/x	1/2;	1/210;	1/2100;	...	-4 0	97^-0
2	2	2
718. 1) lim — = 0; 2) lim — = +оо; lim — = —сю; 3) lim 3r = сю;
r->oo X	r-Ц-О X	г—>0 X	r-Ц-оо
4) lim 3r = 0; 5) lim lg« = —сю; 6) lim tga: = +oo;
r->-oo	r-H-0	r-»90c,-0°
lim tg x = — сю. 724. AB —> сю, СВ —> сю, ABCD —> 0,
г-^ЭО’+О»
AACB 180°.
Ответы
273
725. х = 5; 4,1; 4, 01; 4, 001; ...-) 4 + 0;
х = 3; 3,9; 3,99; 3,999; ...-) 4 - 0;
х = -0,5; -1,4; -1,49; -1,499; ...—>—1,5 + 0;
х = -2,5; -1,6; -1,51; -1,501; ...—>—1,5—0.
729. Только первая последовательность имеет предел: lim х = 1.
п—>оо
В остальных примерах lim х не существует. 730. 1) 0; 2) сю; 3) сю;
4) 0; 5) 2; 6) 0; 7) 0 при а > 1, 1/2 при а = 1, а при 0 < а < 1. 733. 1.
734. 1) -0,6; 2) 1. 735. 4. 736. 1. 737. 3/2. 738. 1/2. 739. -1/^2.
740. 2/3. 741. —1/2 при а > 0 и сю при а < 0. 742. 2/3. 743. т/3.
744. 1. 745. -1/2. 746. 1) 2/3; 2) -2,5. 747. 0. 748. сю. 749. -2.
750. -3/2. 751. 1/л/2- 752. 1/6. 753. 1/4. 754. -12. 755. -1.
756. lim -------lSma;l = — 1/л/2- 757. 2,5. 758. у/З. 759. -4.
Г->7Г+О sin Ху/1 — COS X
760. 2. 761. — 1/56. 762. -V2. 763. 4. 764. 1/3. 765. 1. 766. 1/4.
767. 2. 768. 6^2. 769. 2 cos ж. 770. 1) 1; 2) -1/2. 771. 1/2. 772. 1/2.
773.1/3. 774.8. 775. lim ^18ШЖ1 =	776.4. 777. га2/2 778.3.
779.1/4. 780.1) —2 sin ж; 2) -1/2. 781.1. 782.1,5. 783.1/2. 784.1.
785. 1/2. 786. 1/4. 787. -3. 788. 2/тг. 789. -2. 790. -1/4. 791. |.
792. 0. 793. 1/2. 794. -1/2. 795. -1. 796. 1) 1/20; 2) 3. 797. 1) 3/4;
2) 2 [положить в примере 1) х =	Z12, а в примере 2) 1 + 2ж	= t4]. 798.	—а.
799. 1)	-1; 2) -0,2. 800. 1) 3;	2) 3/2. 801. 1) 1; 2) -1/2. 802.	1)	-2;
2) -0,1. 803. 1) -2,5; 2) 1,5. 804. 1)	2) -1. 805. 1) 2; 2) 3.
806. 1)	4; 2) 1; 3) 3. 807. 2.	809. При а -> 0 (1 +	а)3 - 1	рй	За.
810. 1)	2,5; 2) а/6; 3) 1,5. 811.	2 и 3. 812. 1) 2; 2) 3; 3)	1. 815.	1)	При
л	2п - 1
х = 0; 2) при х = —-—тг; 3) при х = ±2. 816. При х = 2 выполнены
первые три условия и не выполнено четвертое.
{—1	при	ж <	— 1,	[ х — 1	при	х < — 1,
2) г/=
1	при	ж >	— 1;	( ж + 1	при	ж > — 1.
При ж = — 1 функции имеют разрыв I рода (выполнено только второе
условие непрерывности). 818. При ж = 0 не выполнено только четвертое
условие (рис. 37). 819. Разрыв при ж = 0, lim у = сю, lim у = 0,
lim у = 1 (рис. 38). 820. Разрывы при ж = ±2. 821. 1) Разрыв I рода
при ж = 0, при этом lim у = 0, lim у = 1, lim у = -, lim у =
274
Ответы
= - (рис. 39); 2) разрыв I рода при х = а, при этом
lim
У
lim у =
г->а+0
при X = 1
2’ ЛУУ = °’ у = У при х > 1 и “У при
Рис. 37
Рис. 38
Рис. 39
822. Уравнение х2 — у2 = 0 определяет у как бесчисленное множество
однозначных функций х. Из них две: у = х и у = —х непрерывные.
Остальные (разрывные) на одних участках оси Ох определяются урав-
нением у = х, а на других — уравнением у = —х. Четную с разрывами
при х = ±1, ±2, ±3, . . . можно определить так:
при
при
2п — 1 < х < 2п,
2п < х < 2n + 1,
нечетную так:
{—х при
+х при
2п — 1 < х < 2п,
2п < х < 2n + 1,
где п = 0, ±1, ±2, ±3, ...
823. Разрыв II рода при х = —2; lim ^у = +00, lim ^у = —сю,
lim у = 1. 824. При х = 0 не выполнено только четвертое условие
Ответы
275
непрерывности; при х = ±2 — еще и третье. 825. Точки разрыва: 1) х =
= 0; 2) х = 2; 3) х = 0; 4) х = 0; 5) х = ±2 и х = 0. 826. Бесчисленное
множество. Из них: 1) непрерывные у = л/4 — ж2 и у = — \/1 — х2;
2) искомая разрывная:
{—V4 — ж2 при |ж|	1,
_____
+V4 — ж2 при 1 < |ж|	2.
827. х = 0 и у = 1. 828. 1) х = 0 и у = х; 2) х = — 1 и г/ = х — 1; 3) у = 1.
829. 1) х = 0, у = —1; 2)ж = 0иг/ = ж — 1;3)ж = —п/m и у = а/тп.
830. 1) х = —1/2 и у = —2; 2) у = х; 3) у = —х. 831. 1) у = ±ж;
2) х + у = —а; 3) у = х ± тг; 4) у = —тг/4. 832. 1) у = 0; 2) у = ±2ж;
3) х = 0 и у = х. 833. Параболы: 1) у = ж3/3; 2) у = х2. 834. 1) х = 0 и
г/=1;2)ж = 0иг/ = —х. 835. 1) х =
= -2, у = 1/2; 2) х = 1 и у =
3) х = 2, х = —2, у = 1 (рис. 40);
4) х = 1, х = — 1 и у = —х. 836. 1/е5.
837. 1) в”1/3; 2) е4. 838. 1) е2; 2) е~4.
839. 1) е-1; 2) е~2. 840. 1) 3; 2) е3.
841. 1/VF. 842. 1) 1; 2) -1; 3) 21па.
843. 3 и 4.	844. 1) е6; 2) —
845. 1) 1/е2; 2) -3.	846. l/^F.
847. 1) 1/х; 2) —2. 848. 1) Зж2; 2) 4ж3;
3) —т=', 4) cos ж; 5)-6)-----
7 2^F 7	’ !	ж2’ !	2х^’
9	13	1
7)---8)----9) -4; 10) ;	;
7 ж3 7 cos2 ж 7 ж4	7 у/1 + 2ж
11)  ---——; 12)	. Х 849. 1) (.
’ (Зж + 2)2	> VTT^2
Рис. 40
- 2)2; 2) -. 850. 1) (ж2 - I)2;
.	1	. Га .	30 . ж2 + 2ж + 3
2 ж3 - 2ж. 851. 1 1 + —=, 2 1 - 1/-. 852. 1 ---------2---------л .
yjx	уж	ж4	ж4
/	1 \2	/	1 \	о 1	2
853. 1)	1 -	—	; 2)	3 1-^.	854. 1) —=	- -=,	2) — х
\	ж3/	7 V V* J	tfx2 х/ж3 Зж
4= ). 856. 1)
2 sin2
.	„	.	... ж(зт2ж — ж)	. ж sin ж
2)— 1^2ж. 857.1) ж(2 cos ж — ж sin ж); 2) —--=-858.1)-------------Н
sin ж	ж3
2 cos ж
7з ’ %)
2х
.	1	. 4ж — sin 2ж
859. 1	--------; 2	---------—.
(1 — 4ж)2 4жл/жсо82ж
276
Ответы
860. 1) -------; 2)
1 — sm т
1
0; 4. 863. 8,25.
ч 2т - 1
864. -90. 865. 1) -6bx(a -
,1/1	1 A
861. 1) gt- 2) 2a sin2 |. 862. 1;
2/1	\
6т2)2; 2)	— + 1 .
867.
1) 2 cos2
868. 1) т(2з!пт
2)
2)
ds 1	2
Л = 2 + ё 8™'1>
И2.-1/3
.4
COS2 T
;2)
869. 1)
-; 2) -ctg2T.
cos x — 2x sin x
2
873. -1, — 1/9, -1/25.
874. 1) 6 cos 6т;
2)
6sin(a — Ьх).
2
cos----sm — ;
2	2/’
__ ..	10т
877. 1) ------;
2) — 2 sin—.
О
- 2>
. 879.4 sin3 т cos t. 880. 1) sin 2т;
882. 3tg4T.
876. 1) -20(1 - 5т)3; 2)
t/4 + Зт
______	9 si n 2 т
3) — 2 tg 4tVcos4t. 878.	,
л/2т — sin 2т
3
2)	—sin2т; 3) 2tgTsec2T. 881. —sin 2т sin
— sin 2т	cos л/т	, г-------	,-------.
-. 885. ±(-\/l — sin2т + Vl + sin2т);
при cos 2т < 0, а при cos 2т = 0 у' не
20 sin 4т
hm у = —л/2). 886. —-----------—
’	(1 +cos 4т)6
2т2 — 1	1 — т
,	890. ---,
т2л/2т — 1
2 sin2 2р
COS л/
883. --,	884. —-/=
4^(1 + cos2 t)3	2^t
знак «+» при cos 2т > 0, знак «—»
существует ( lim у' = л/2, а
х —>тг/4— О	X-
ctg2(T/3)	.	„ .
887.—Л v z,./. 888. sm т(1 + sec2 т). 889.
891.
893.
sin2 (т/3)
. 2t	.	dr
— sm —. 892. 1)	—
a	dp
(^\	ab
894.
1
2 sin 6x
895.
898.-----,
y/(l + cos 6т)
ds
901- -г - -----,	=
dt 2y/t/2- sin (t/2)
904.
a sin 2р dr
Vcos 2<^ ’ 7 dp \/2p + cos2 (2p + tt/4) '
f'W = 0,
4 cos2 2т	t(2 — 3т2'
= .	896.	\
л/4т + зш4т	л/1 — т2
= . 899. 1) зес6т; 2) Зт28ш2т3.
sin2 (t/4)
dr
902. —
dip
1
- cos^>.
ab
897. — sin 4т.
4 cos 2т
(1 — sin 2т)3
2(3t + 1)
903.----} ,	’ .
т3у4т + 1
905. к = tga = ±4. 906.
у = 8 — 4т, т — 4г/ = 2.
Ответы
277
2
907. у = х +	908. у = 0, у
3
910. у = тг - х. 911. 45° и 135°.
= ±|(3ж - 1). 909. у = -| + 2.
4	1	д/5 г-
912. arctg-. 913. 1) -, 2, А
2)	-—, -—. 915. у = ж2
! 3 2’ 3	2	У
условия у' = 2х +6=4+6= 1, ас — из условия, что (2; 2) — точка ка-
1	15
сания. 916. у = —4ж + 8, у = — -х — 2;	= arctg — к, 62°. 917. у = 4ж,
у = —4ж+16. 918. х ± 4г/ = 8. 919. у = ±(3ж + 8) и у = 0. 920. 4/V17.
921. 40°54' или 139°6'. 922. (-2; -4). 923. (1/2; 17/4). 924. 1; 1; У+
— Зх + 4. Параметр Ь находится из
V2. 925. 11°20' и 7°7'. 926. у'_ = -1, у'+ = 1. 927. у'_ = - 1/2;
у'+ = 1/2. 928. у = ж и у = -ж. 929. у =	Ю9°30'. 930. ж = 0.
931. ж = 2. 932. ж = 0. 933. ж = 2. 934. г/-1 = ±
936. у = ±4ж; 28°. 937. 1) 1пж + 1; 2) -^; 3)
X2
939.1) — tg —; 2) ctg ж cos2 ж. 940.
2
. 935. х = -1.
2)
2
942. ——
.	2 ctg2 х
947. 1 -----; 2 -
Sin X X
точке (л/ё; 1/2). 950. 1)
951. 1) +1"'' cos ж In a; 2)
1 /- ( 1 \
953. -еУх 1 + —= .
2	\ Jx)
0,4343 _
-------. 938. 1)
1
2\/ х2 + ж
1
945. ,
941.
Ж3 ’
4а2ж
.4 _ ж4 •
1
~ 2’ ' '
1
943. ----. 944.
cos ж
2
— аж5
2ж + Зг1пЗ; 2) (2ж + ж2In2)2Г; 3) ж(2 + х)ех.
—2хе~х2-, 3) 2ж(1 — ж)е_2г. 952. <х/‘2 + е~х!2.
2ех
954. ------
1 — 4ж2'
946.
948. у = ж — 1.	949. Касаются в
955.
— 2д?
1
— e^1 “ ( cos--------sin —
2
956. 1) —2е х sin ж; 2) —
957.
958. 2a(e2ax - e~2ax
959.-Ina. 960. 26°35'.
963. — tg х sin2 х.
967.
1
964.-----
2^^
1 1
. 965.-------==
968. ctg2«.
971.—
972.----е
sin X
cos x m x H-------.
2е2х
975.	,
2
ctg 2ж
969. ----------
1 — sin 2ж
973.-(ех1а-е~х1а
2V
. , 1 — In ж
977. xrlx-----—.
cos ж
966.	,
V 1 + sin2 ж
tg ж
970. ----------.
4
974.----------
(ех — е
978. 16. 979. у =
976.
-. 980.
ж2	1
. 981. -----982.-------,	983.
1 + ж2	^ж - 4ж2
2 _ ,.2
278
Ответы
984	а	985	1 986
а2 + х2 ч Зе3х	2 2) ,	988.		— т2 1 989.	^=.
' VI - е6х	1 - Т4	2тл/т — 1
992. 	/	993. 1) 2т7бт - 1	’	—Э—; 2) |т|л/2 — т2
-----987. 1) 2^1 - т2;
1 + x2
X	1
990. arctg —. 991. —,
a 2\/x — x2
_ 1 .. 994. 2r'Vl - e2x.
x2 + X4
4e2r	/4
995. arccos x. 996. -----—. 997. л/- — 1.
1 - e8x V t
1000. 1) sh 2т; 2) th2T; 3) л/ch т + 1.
/2
998. 1/-- 4. 999. (7г-4)/4.
1001. 1,5.	1002. 1) th x;
2) — l/sli2 2т. 1003. 1) cth2 x; 2) 2/sh2T. 1004. 1) 1/сЬт; 2) I sli l.r.
1 — X
1005. x + 1,175г/ = 2,815a. 1006. г/= 3, 76т + 3, 89. 1008.1) - ;
т2ут2 — 1
2) tg3T. ds 1012. — dt	л/4т — 1	dx	2е‘(е‘ - 1)	X
	1009.	. 2х = tg5t. 1013. — —.	1021. 1) За	7	1010. — dt . 1014.1) -	= V 1 • 1011- e2t + 1 t2 + a2 . ; 2) 2 cos (1пт) (x2 — a2)	л/т2 — 4т 1 . 1015.— 15 1 (1 + т)3/2'
1017. -		2 cos 2т;	2) 2tgTsec2T; 3)	
1022. 1)	—4sin2T; 2) —	—3) —(tcost + 3sinT). 1023. 1)		 X	'	X2		
e
2)
2)
2)
2)
. . x x 2a(3x2 — a2)	2	. / l\n ,
I-1'""'"-1/ 3) (-D’-l	„
Xn	2ny/x2n~1
(7Г \	/
x + n— J; 3) 2п-1со8^2т +
xax(x2ln2a + 6x In a + 6);	3)
7Г
2
1028. 1)
2 sin x + 4т cos x
—2ex sin x;
— x sinx.
1029. 1) 2e x(sinx + cost); 2) 2/t; 3) TsinT — 3cost. 1030. f"'(x) =

1031. 1, m,
(4— ж2)3/2-
1036. 1) ar(lna)n;
1оет. 1, _2I,
6’	6 ’ 36
m(m — 1), m(m — l)(m — 2), . . .,
1035. 1) 2<~''2(2t2 - 1); 2)	3)
sin т
2n . «I	/
2) (-l)n7------——; 3) -2"-' cos (2a
7 V 7 (1+ 2т)п+1	7	V
1038. 1) И? + 9т2 + 18т + 6); 2) — (ба2 cos----бах sin----т2 cos — );
a3 \ a	а	а/
( l\n
3) —T/IV(a—т). 1041. По формуле Лейбница/(п)(т) = х2е~х!а (----j 4-
п — 2
. Отсюда /^п\0) =
2те x!a (—
1 • 2
Ответы
279
a2
1049. 1/3. 1050. 1)----;
Г
=	1042‘ f'H = -^2 = -2xf(x).
Далее по формуле Лейбница	(ж) = Г—2ж/(ж)1	^ит.д. 1044.1) ;
У
, V . Ь2х	, 2ж + у , 2ж — у	, /V е~х + у
2	3 -Т-. 1045. 1 ------— 2) --------1046. 1)	2) ------—.
г/ а2у	:
ех sin у + е~у sin ж
1047.---------—------------
ех cos у + е у cos ж
2(г/— а)
! (Ж -6)2’
1053. (40/9; 40/9) и
; 2)
ж + 2г/ ж — 2г/
. 1048. -4 + 1.
У2
b
. 1051.------.
а2
1054. 1)
1052. у = 3 — x n у = x -
xxo , УУо 1
—5- +	= 1; 2) yy0
a2 b2
1056. arctg 3. 1057. 1)
. ; 4) -
2T2
(40; 40).
b2x
a2y ’
6a2
= p(x + жо). 1055.
9
4 x — ail
2 --------1. 1058. 1 -
ax — y2
V2
Л2
;2)
1071. 1) dV =
1072. 1) dx <
а2
г/3’2)	(г/ - Д)3 ’ 'J) у5 ' (ж + 2г/)3'
1059. 2г/ = - ж - 3 и 2г/ = ж + 1. 1060. ж + 2г/ = 4^2. 1061. 1 - -.
е
1062. е(е — 1). 1063. ±2. 1064. 1) dy = пхп~1 dx', 2) dy = 3(ж — I)2 dx.
1065. 1) dy =	-; 2) ds = gt dt. 1066. 1) dr = 4 sin2 p dtp', 2) dx =
VI + ж2
2 dt	.	.	.	.	,	. a3 dx	. (a + 1) da
=-----—. 1067.1 )sm2tdt-2 )sinudu. 1068.1 — ----------— • 91 ———----•
t3	'	'	'	ж2(а2 + ж2
3) -|sin^d^; 4)--------dx 1070. 1) 0,04; 2) 0,05.
2	2	xyjx2 — 1
= Зж2 dx = 0,75;	= 0,006 или 0,6%; 2) d = 44.
ж3	8 f
0 1-2
</ ——-= < 0,005; 2) радиус нужно измерить с погрешностью не более
5жл/ж
1	4
-%. 1073. 1) S = тгЛ2, AS « dS = 2rRdR- 2) V = -тгЛ3, AV к
О	о
рз dV = 4ttR2 dR. 1074. 1) ----2-----• 2) b sin (a — bp) dp; 3) —	=.
1075. 1) — tgxdx; 2) --dU ; 3) -2e~2t dt. 1076. 1)	2) tg2ada;
2ггу4гг — 1	‘2\/x
3) 6(1 + e~bt)dt. 1077. 1) Ay = Зж2Аж + ЗжАж2 + Аж3 = -0,2376,
14	ж2•0 1
dy — Зх2 dx = —0, 24; 2) dl =--4, 46 см; 3) \dx\ --------——— <С 0, 006.
7Г	4
1078. 1) 4г/2 = ж3; 2) у2 = ж (- - 1V. 1079. 1) ^- + ^- = 1; 2) ж2/3 +
\3	/	а2 Ь2
+ г/2/3 = а2/3. 1080. 1) ж2 - у2 = 1; 2) у =	1	1082. ж =
280
Ответы
За/2	(4 — тг)а	а	.	1
Ю83. г/ = t+V ’ . 1084. ж + г/= —=. 1085.1 ------------— ;
1 + /3	2	V2	а sin3t
t2 + 1	1
2)	3)-------. 1086. 1) у = -х2 - 2х; 2) (у + 2)3 = х3.
7	I/3 ’ 7	4asin4(//2)	7 У	’ ’	’
/Зтг \	атг	.	1
1087. х + у = а------Н 2 . 1088. у = х-----------1089. 1)----------
\ 2 J	У 2^2	4sin3/
. З/2 — 1	. 3	gt2 dx	d2x
2) ----т—: 3) —1090. х = at------------: — = a — gt; —- = —а: через
7	4/3 ’ 7 4e‘	2 ’ dt У ’ dt2 У’ P
u	a	u.t
t = —, x = — (высшая точка . 1091. — = О
д' 2g У	’	dt
At + 3; fi = 1, t2 = 3.
1095. v = —; — = w; перемножим почленно. 1096. 2v— = 2a— =
dt dt	dt dt
= 2av, откуда w = — = a. 1097. x = 10 + 20/------; — = 20 — gt;
dt	2 dt
d2x	dx	20	dh
—- =	— a. В наивысшей точке	—	= 0; / =	—	Pi 2,04c. 1098.	—	=
dt2	di	g	dt
a	a	dx , . ,
= —-------— = —-. 1099. — = k A - x . 1100. d U) = 2wdw,
nh(2R-h) яг2	dt v 7	7
—-— = 2w— = 2w ——— = 2we— = 2e. 1101. Корни функции 1; 3.
dip	dp dt dp ш
Корень производной f'(x) = 2x — 4 равен 2; 1 < 2 < 3. 1102. He при-
менима, ибо при x = 0 нет производной. 1103. Потому, что точка х = О
угловая (две касательные). 1104. Наклон хорды (АВ): к = ---- = 2;
3+1
f(x) = 2х = 2, х = 1; в точке х = 1 касательная параллельна хорде.
1105. f(b) = b2, f(a) = a2, f'(c) = 2с; подставим это в формулу Ла-
гранжа Ь2 — а2 = (Ь — а) • 2с; откуда
дуге есть угловая точка при х =
7Г
2’
b + а	9
с = ——. 1106. с = -. 1108. На
2	4
в которой функция не имеет про-
изводной. 1109. Функция непрерывна и имеет производную внутри от-
резка [0; 2], но разрывна на его правом конце. 1110. Пусть s = f(t) —
уравнение движения, а /j и t2 — начальный и конечный моменты дви-
жения. По теореме Лагранжа между /j и t2 найдется /3, при котором
f(A)~f(A)	,,	,, ds
= f (t3), т. e. 40 = f(t3) = — в момент /3.
+ — А
1111. Ф'(ж) = b f(b)
1
/(«) 1
. Так как Ф(6) = Ф(а) = 0 и в интервале
(а, Ь) имеется производная Ф'(ж), по теореме Ролля между а и b найдется
Ответы
281
= с, при котором Ф'
= 0, откуда f(b) —
b f(b) 1
a f(a) 1
— /(а) = (6 — a)f (с). Функция Ф(ж) есть удвоенная площадь ДАМБ,
Ь3 — а3 Зе2
где М — любая точка на дуге АВ. 1112. —-------- = ——, откуда с =
_ а2 2с
2(а2±а6±62)	dy	f(t)
=	----Л—- ИИ. Угловой коэффициент касательной — =	,
1	dx	f (t)
Угловой коэффициент секущей к\ = ------ =
«2 — «1
а в точке t = с к =
fW-f(a)	„
= ——------—; по теореме Ноши между а и о найдется t = с, при котором
+W - ^>(а)
к\ = к, т. е. касательная параллельна хорде. При этом так как (t) ф О,
то <р(а) < <р(с) < <р(Ь) (или наоборот), и точка касания находится внутри
/а2 + аб + 62	. /4	. Г 4~ . 1
дуги. 1117. с = J -----------. 1118. 1 J- - 1; 2 J1 - —; 3 —.
V 3	у тг	V Д' In 2
тт //15\2
1119. 1) -; 2) О I — \ я 2,4. 1120. Функция у = |ж — 1| не имеет
производной при х = 1. 1121. В точке х = —1/2. 1122. 3. 1123. 1/2.
1124. —3—-. 1125. 1. 1126. а2/62. 1127. 1/2. 1128. 1/6. 1129. 3.
пап 1
ИЗО. 1) оо; 2) 0. 1131. 0. 1132. 0. 1133. 3. 1134. 2. 1135. 0. 1136. 0.
1137.1. 1138.1. 1139. е3. 1140. 2-го порядка. 1144. а - Ь. 1145.1/3.
1146. 1/8. 1147. 1п^. 1148. 1/л/3. 1149. 1. 1150. 1. 1151. -1/3.
1152.-2. 1153. 1/е. 1154.1/6. 1155. е3. 1160. При х = -2 t/min = 1.
1161. При х = —2 г/min = —16/3; при х = 2 t/max = +16/3; точки
пересечения с Ox: Xi = 0, Ж2,з = ±2л/3 Ай ±3,4. 1162. При х = —1
t/max = 5/3, при х = 3 t/min = —9; точки пересечения с Ox: xi = 0,
^2, з ай 1, 5 ± 3, 3. 1163. При х = ±2 t/max = 5, при х = 0 г/min = 1, при
у = 0 ж Ай ±2, 9. 1164. При х = 0 у = 0 — перегиб; при х = 3 t/min =
= —27/4. 1165. При х = —2 t/max = —2, при х = 2 t/min = 2; асимптоты
х = 0 и у = ж/2. 1166. При х = 0 t/min = —1 (точка возврата) точки
пересечения с осью Ох: х = ±1. 1167. При х = 0 t/maX = 1, при х —> оо
у —> 0, т. е. у = 0 — асимптота. Кривая симметрична относительно
оси Оу (почему?). 1168. При х = 1 t/maX = —4, при х = 5 t/min = 4;
асимптоты х = 3иу = х — 3. 1169. При х = 0 t/min = 0, при х = 2/3
t/max = 4/27. 1170. При х = 4 t/maX = 1, при у = 0 х = 3 или х = 5, при
282
Ответы
у = —3 х = —4 или х = 12. 1171. При х = 0 t/max = 1; асимптота у = 0.
ТГ	ТГ	л/3
= Утах =	+ V ~
ТГ	4тГ
— Утах — “ГД — V 3
ТГ
—2,45. Асимптоты х = ± —.
Симметрична относительно Оу. 1172. При
» 1,1, при х = || ymm ай 0,4. 1173. При
тг	г 4тг
Ай 2,45, при X = -- ymin = V3-------—
О	о
1174. При х = 1 ymax = 1
Асимптоты х = 0 и у = 0.
1пж = —1, х = е-1 Ай 0,4.
при X = г/тах » 0, 28.
Утах = 2/е. Асимптота у = 0. 2) При х = 1/е утт = -1/е;
= 0 — концевая точка; при х = 1 у = 0. 1177. 1) При х = 0
Точка пересечения с осью Ох: 1 + In ж = О,
1175. При х = -
1 ТГ
Утт = 2 “ 4	~0’28’
7Г
Асимптоты у = х ± —. 1176. 1) При х = 2
= 2/е. Асимптота у = 0. 2) При х = 1/е t/mjn
lim у =
г—>4-0
t/min = О
/4п + 1
(угловая точка), при х = ±О —-—тг ymax = 1; 2) при х = 0
(угловая точка). 1178. t/mjn = 1/2 при х = тг/3; Зтг/4; 5тг/4; . . .; ymax = 1
при х = 0; тг/2; тг; Зтг/2; . . . 1179. Область расположения кривой х 1;
t/max = —— при х = -; у = 0 при Xi = 0 и х% = 1. 1180. При х = 2
2л/2	2
t/max = л/2; область расположения кривой х > 0. 1181. Асимптоты х = 1
г/min = О
и х = 4 (разрывы) г/min = —1/9 при х = —2, ymax = —1 при х = 2.
1182. При х = 1 г/min = 1,5. Кривая асимптотически приближается к
параболе у = ж2/2 и к оси Оу. 1183. При х = 0 и х = 2 t/mjn = -^4 Ай 1, 6,
при х = 1 утах = 2 (в точках минимума точки возврата). 1184. При
X = 0 Уперег = о, при х = 1 утах = 0, 2, при х = 3 ymin = -5, 4.
1185. При xi = —2 утах = 0, при Х2 = —1,2 г/тт	—1,1, при х = 0
Уперег = 0. 1186. При X = 2 утах = |, При у = 0
х = 1; асимптоты —
оси координат. 1187. При х = —3 утах = —4, 5, при х = 0 уперег = 0,
при х = 3 ут\п = +4,5; асимптоты у = х, х = ±л/3- 1188. При
7Г	7Г	7Г
х —	Утах = 1, при х — —	— разрывы. 1189. При X — —-\-2kK
утах = ^ + 2йтг-|1п2. 1190.1) При X = 1 ymin = | In 2-2) при х =
= — 1 Утах = 1, при х = 0 утт = 0 (угловая точка с наклонами к = ±2).
1191. При х = 0 t/min = 0; при х = 2 Утах = 4/е2 ай 1/2; асимптота
у = 0. 1192. При х = — 1 точка возврата t/mjn = 2, при х = 0 утах = 3,
при у = 0 ж ай 4. 1193. При ж = 2 утах = 4; при у = 0 Ж1 = 0, х-2 = 4.
Ответы
283
1194. При х = —1 t/mjn = —4; при у = 0 Xi = 1, х2 = —3. 1195. При
X = О t/min = О, при X = -2 г/тах = 4/3; при у = О «1 = О, х2 = -3.
1196. При х — —1 t/min = — 4, при х — —3 г/тах = 0. 1197. При х = О
Утах —
X = 4 г,
У = « + !
Рис. 41
t/min = -6, 75, при X = О г/перег = 0; при у = О = О, х2 = —4 (рис. 42).
1199. При х = ±2 г/тт = —4, при х = О г/тах = 0; при у = О Xi = О,
«2,з = ±V8 Pi ±2, 8. 1200. При х = 0 точка
возврата г/тах = 0, при 1201. При х = 1 г/тт =
= —1; при у = 0 «1 = 0, «2 = 27/8 (рис. 43).
х = -1 г/тах = 2, при X = 1 ymin = 0, При
х = 0 у = 1. Асимптота у = 1. 1202. При
х = — 1 г/mm = — 1/V®	—0,6, при х = 1
г/max Р^ 0, 6; ось Ох — асимптота. 1203. При
х = 2 г/min = 2(1 — In 2) рй 0,6; ось Оу —
асимптота при х = 1 у = 1; при х = е2 Pi 7, 4
г/ Pi 3,4. 1204. При х = 0 точка возврата
Утах — 0, При X = 2 г/min — 3 \/4 Pi 4, 8,
при х = 5 у = 0. График подобен графику на рис. 43. 1205. При х = 4—
6
7Г	7Г	7Г
Утах Р^ о, 34, при X = -- j/min рр -О, 34, при х = ±- у = =F- = 4=1, 57.
о	2	2
284
Ответы
1206. При х
асимптоты х
1, 85, при
7Г
“ 4
= О
Зтг
Утах — +3,71;
1 Зтг
“2 + Т
Асимптота
= 0 у = 2,
= 1,5, при
Уперег — 1•
Утах
7Г
УтЫ = - + 1 АЙ 2, 57, при X
и х = тг. 1207. При х = — -
| УтЫ АЙ 1,28, при X = 0 у = тг/2.
у = X. 1208. При х = 1 точка возврата t/min = 1, при х
при х = 2 у = 2. 1209. При х = тг/6 и х = 5тг/6 утах
х = тг/2 t/min = 1. 1210. При х = 0 ymjn = 0, при х = 1
1211. При X = е Утах = 1/е Ай 0,4, при у = О х = 1. Асимптоты X = О
и у = 0. 1212. При х = —3 t/min = 6, при х = —2 у = сю (разрыв), при
х = —1 утах = 2. Точки пересечения с осями: х = 0, у = 1, 5; у = О,
х = ±л/3 ай ±1, 7. Асимптоты х = —2 и у = 2 — х. 1213. При х = 1
Ут1п = 2, при х = —1 Утах = ~2, при х = 0 — разрыв. Асимптоты
у = х и х = 0. 1214. 1) При х = 0 у = а. Точки пересечения с осью
Ох: х = — + &тг. Экстремум: при Xi = ——Н 2/.-тг — минимум, при
7тг
Х2 = ——Н 2ктг — максимум. Кривая — график затухающих колеба-
ний; она вписана в кривые у = ±ае~х, на которых и находятся точки
экстремума. Построение нужно начать с кривых у = ±ае~х. Ось Ох —
асимптота. 2) При х = —1 утах = 2, при х = 0 — точка перегиба, при
х = 1 t/min = ~2; при у = 0 «1 = 0, «2,з ай ±1,3. 1215. При х = 1
t/min = 3, при X = 2 у = СЮ (разрыв), при X = 4 t/neper = 0, при X = О
у АЙ 3,6. 1216. При X = —2 t/min = 0, при X = —4 Утах = 0,8, При
х = 1 Утах Ай 2,8; ось Ох — асимптота. 1217. При х = ±1 ymax = 1;
при у = 0 х = ±1 /л/2 ай ±0, 7. Асимптоты — оси Ох и Оу. 1218. При
х = 0 Утах = 1, при х = 1 t/min = 0; при у = О X = ±1. 1219. При
х = — 1 t/min = 1/3, при х = 1 Утах = 3, при х = 0 у = 1; асимптота
у = 1. 1220. При х = —1 Утах = 1; при у = 0 «1 = 0, «2 = — 4; область
расположения кривой х 0. 1221. 1) При х = —2 у = сю (разрыв),
при х = —3 Уперег = 0, при х = 0 t/min ай 27/4; асимптоты х = —2
и у = х ± 5; 2) t/min = 0 при х = 2птг, ymax = л/2 при х = (2п ± 1)тг.
В точках минимума у' не существует (угловые точки). 1222. ЗОмхбОм.
1223. 5 и 5. 1224. ah/b. 1225. а/6. 1226. 4мх4мх2м. 1227.20см.
1228. 60°. 1229. —ай 2,5. 1230. cos а = — (однако при усло-
1	а
вин, что — < ----, где а — проекция АВ на направление железной
т	АВ
Ответы
285
дороги). 1231. В 18м от более сильного источника света,
а
— часов наименьшее расстояние будет равно а/2км.
2е
У = ОДД 1234. В Уз » 1,7 раза.
,	2,4
как максимум функции I = —-----Н
sin а
высоте х = 2 дм. 1237. Smax = 7?2
1232. Через
1233. х = D/2,
1235. I Pi 5,6м; определяется
1,6	128тг	о
----. 1236. етах = —— дм15 при
cos а	9
R
при высоте х = —1238. (1; 1).
1239. Vab. 1240. При х = 2 м. 1241. 4см и Уз » 1, 7см. 1242. х= 1,5.
1243. Сечение — квадрат со стороной D/Д. 1244. При а = ЧкДД
иР
радианов Pi 294°. 1245. F = ---------;; tg а = у = 0,25, a Pi 14°.
cos а + у sin а
1246. 1) у = х2, у" = 2 > 0, кривая всюду выпукла «вниз»; 2) у = ж3,
у" = 6ж, кривая выпукла «вниз» при х > 0 и «вверх» при х < 0,
х = 0 — точка перегиба; 3) у = ех, у” = ех > 0, кривая всюду вы-
пукла «вниз», (0; 1) — точка пересечения с Оу; 4) у = In х (х > 0),
у” =------- < 0, кривая всюду выпукла «вверх», (1; 0) — точка пере-
х2
сечения с Ох; 5) (0; 0) — точка перегиба. 1247. Точки перегиба кри-
вых: 1) (2; -8/3); 2) (±1/^2; е~^2); 3) (±Д; ±Уз/2) и (0; 0); 4) при
In 2
х =-----— Pi —0,35. 1252. Область расположения х > —2. Точки пе-
ресечения с осями (—1; 0) и (0; 1п2). у всюду взрастает, кривая вы-
пукла «вверх». Асимптота х = —2. 1253. у > 0, у = 0 — асимптота.
1254. 1) Симметрична относительно Ох. Область расположения х /> 0.
Верхняя ветвь выпукла «вниз», нижняя — «вверх». Обе ветви касаются
Ох в точке (0; 0). Кривая называется «полукубической параболой» (вме-
сте с осью Оу образует букву К); 2) такая же, как предыдущая кривая,
но сдвинута влево на 3 единицы. 1255. 1) При х = 0 утах = — 1, асимп-
тоты х = —2, х = 2 и у = 0 (три ветви); 2) при х = 1 t/max = 2,
при х = —1 г/min = ~2, пересекается с Ох при х = ±Д>, перегиб при
х = ±«/2, асимптоты — оси Ох и Оу. 1256. 1) Область расположе-
ния х > 0, при у = 0 х = 1, асимптоты — оси Ох и Оу, при х = е
Утах — 1? 2) При X = 1 Утах = 1, При X = 2 Уперег — 2/е Pi 2/3, ОСЬ
Ох — асимптота, при х = 0 у = 0. 1257. 1) При х = 0 ym;n = 2,
асимптоты х = —2 и х — у = 0; 2) симметрична относительно Оу, при
у = 0 х = ±«/2/2 Ай ±0,7, при х = ±1 ymin = —1, асимптота —ось
Оу. 1258. 1) Область расположения х > 0, при х = 1 ym;n = /вы-
пукла «вниз»; асимптота — ось Оу; 2) Оу — ось симметрии, при х = 0
286
Ответы
г/min = а, всюду выпукла «вниз»; кривая называется цепной линией.
1259. 1) При х = 0 t/max = 0, при х = -^4 ай 1,6 t/min 2,1, при
х = — -^2 ай —1,3 t/перег —0,8, асимптоты X = 1 и у = х\ 2) при
х = —1 t/min = —3, при у = 0 х = —-у^О, 25 ай —0,6, асимптоты —
оси Ох и Оу. 1260. 1) Симметрична относительно Ох и Оу, область
расположения |т| < у/2, при х = ±1 уэ = ±1, при у = 0 х = О
2
или х = ±»/2; 2) на ветви у = х ± —^= t/min = 3 при х = 1, ветвь
2
у = х — —j= пересекает Ох при х = \/4 Ай 1,6, обе ветви имеют асимп-
тоты у = х и х = 0. 1261. При X = -2 t/mm = -W -2,52,
при х = 2 t/max 2,52 (обе точки возврата), ось Ох — асимптота,
8т
ибо у = -------—тт-— ----------т-г----—т- —> 0, когда х —> ±оо.
У (т ± 2)4/3 ± (т2 — 4)2/3 ± (т — 2)4/3
1262. Симметрична относительно От, область расположения т	0, асимп-
тота — ось От ( lim у = 0), при т = 1 экстремум уэ = ±1/е Ай ±0,3.
1264. О — ± т2 ± In |тI ± О; 2) 2т5 - Д- ± С. 1265. 1)	± О;
3'	/р о	'	/р Л
х1	1	/2	3	\
2)	—	+	2 In	|ж|	—	— -	+ С.	1266.	1)	х	I ~у/х +	— х/^г I	Н-	С;	2)	’2\/х	—
Z	ZX	\ О	х	!
— 4^/т ± С.	1267. 1)	——	Зт ±	б^т	— In |т| ±	С;	2) -(т	—	4) е/х ±	С.
О	х
1268.1)	ех-\--\-С; 2) --у=+С. 1269.1) — ctg т—tg т±О; 2) — ctg т—
т	Ina у/х
dx	С sin2 т ± cos2 т
—5----~5----------------5-----ат = tg т — ctg т±
sin т cos2 т J sin т cos2 т
„ „. „	„	„	... т sin т „ „. т sin т „
±О; 2) 3 tg т ± 2 ctg т ± С. 1271. 1) — — —--Н О; 2) — ± —--Н С.
т3	т4 - 1
1272.1)	2 arctg т — 3 arcsin т±О; 2)--T±arctgT±G. 1273.1) ----
3	2т2
-	2 In |т|±О; 2) 3^±-|=±О. 1274. 1) ^±^±О; 2) 41п |т| -	-
-	- ± С. 1275. 1) In |тI -  -± О; 2) т ± cos т ± С. 1276. 1) ех ±
X	х	X 2х2
± tgT±G; 2)	—±О. 1277. cos х — ctg х + С. 1278. tg х —
In а 4ж4
1	х	1
-х + С. 1279. - sin Зт ± О. 1280. -2 cos - ± С. 1281. —е-3г ± О.
3	2	3
1282.	| tg 5т ± С. 1283. 2(ег/2 - е"27/2) ± С. 1284. |(4т - I)3/2 ± С.
О	о
-т ± С. 1270. 1)
Ответы
287
1285. ~^3	+С. 1286.-|(5 - 6ж)4/3 + С. 1287. -^3 - 2ж + G.
1288. | cos (а - Ьх) + С. 1289.1п (ж2 - 5ж + 7) + G. 1290. | In (ж2 + 1) + С.
1291.-0, llnll - 10ж| + С. 1292.--In 11 - 3e2r| + G. 1293.1n I sinж| + С.
6
1294. — In | cos ж| + C. 1295. In | вт2ж| + С*. 1296. — In |1 + 3 cos ж| + C.
3
1297. - In |1 + 2зтж| + G. 1298. In |1 + In ж| + C. 1299.	+ C.
2
1300.	+ c 130i.------------L—h c. 1302. ——н c.
4	3 sin ж	2 cos2 ж
2 — cos ж „	sin2	„	1 s „
1303.----:-----|-G. 1304.—-------HG. 1305.—e +G. 1306.-G +G.
sm ж	2	3
1307. -je-^2 + G. 1308. 2г/7 + G. 1309. |^(ж2 + I)3 + G.
z	о
1310. -^(ж3- 8)4 + G. 1311. 0, 5^(1 +ж3)2 + G. 1312. -y/1 - x2 +
2	1
+ G. 1313. -Vl + 2 cos ж + G. 1314. -^(1 + 1пж)3 + G. 1315. -(1 +
о	0
+ 4япж)3/2 + С. 1316.—-(1-6ж5)4/3+С. lZ17.‘2x+-(e2x-e-2x')+C.
1318.	+ С. 1319. --V1 - 4ж + G. 1320. sin (а - 6ж) + G.
4	2	b v 7
1321. |(1 + Зж)4/3 + С. 1322.-|(1 - 2ж3)7/6 + G. 1323. V1 + ж2 + G.
1324. Sm Ж ~ 2 + G. 1325. 21п|8тж| - ctg ж + С. 1326. esinr + G.
COS X
1	1	х — 5
1327.--1п|1-ж3| + С. 1328.—--------—+ G. 1330. 1) 0,1 In ----- +
3	2b(a — bxy	ж + 5
+ G; 2) - arctg —H G. 1331. 1) arcsin —-G: 2) In (ж + л/®2 + 5) + G.
3	3	2
1332.1) In |ж + V'ж2 — 4| + G; 2) —j= arctg —^ + C. 1333.1) arcsin —^= + C;
V3 v3	V5
1 ж3
2) - arctg — + G. 1334. 1)
1	2ж
1335. 1) - arcsin —j= + G; 2)
2	V3
1	•	z ....	1
- arc-sill — + G: 2) —— In ------------- + G.
2 V3	lab bx + a
| In (ж4 +	- 1) + G. 1336. 1) 2,5x
x 3
x In (ж2+4) — arctg —+G; 2) - In |ж2 —41—In
ж — 2
ж + 2
+G. 1337.1) V^2 + l +
+ In (ж + л/®2 + 1) + G; 2) —л/1 — ®2 + arcsin ж + С. 1338. ж — arctg ж +
+ G.
1340. arctg (ж + 2) + G.
288
Ответы
1 х _ з
1341. - arctg —-— + С.	1342. In (х + 1 + л/®2 + 2т + 3) + С.
. т + 1	. т — 2	2	2т + 3
1343. arcsin ———Н С. 1344. arcsin	Н С. 1345. —= arctg V2	2	V3			+ 7з
+ 0.1346. —= arcsin	 V2	5 + О. 1348. V3 ^arctg	- + О. 1347.— х/з 1	. т — л/3 —= + In 	— \/3	х +	п |Зт — 1 + л/9т2 — 6т + 3| + | + О. 1349. arcsin ~^+ )	V?	
+ In (т + л/2 + т2) + О.	1350. 21п(т	+ 5) — V5 arctg-	+ о. /5
1 т - V2 1351. т + —= In 	— т + V2	т3 + О. 1352. — - 2т + 2^2 arctg О		+ О. V2
ж + 2
1353. arcsin (ех) + С. 1354. arctg (2т2) + С. 1355. О, 2 arctg —--Н С.
1 ж — 1	х -1~ 2	1
1356. - arctg-НО. 1357. arcsin-НО. 1358. - In (т2 + т + 1) —
1 2т + 1	1
— —2= arctg —+ С. 1359. - In (2т + 1 + V4t2 + 4т — 3) + С.
1 (\
1360. х In |ж| — х + С. 1361. — In — 1| — - ( — + ^ + 1п|ж — 1М + С.
1362. |е2;г (т - 0 + С.
+ 2т cos т — 2 sin х + С.
1363. —-— arctg т — — + С. 1364. т2 sin т +
1 , .
1365. -е (sin т — cos т)
2 V	’
+ С.
1367. т[(1п|т| -
In IX I I 1
— I)2 + 1] + С. 1368. —т ctg т + In | sin т| + С. 1369.--------------+ С.
1370. 2л/1 + т arcsin т + 4л/1 — т + С. 1371. т arcsin т + \/1 — х2 + С.
1372.
—е
+ 6т + 6) + С. 1373. т In (т2 + 1) — 2т + 2 arctg т +
2 ___________________________/	2\
+ С. 1374. —(coslnT + sinlnT) + С. 1375. -\/х^ I In |т| — - ) + С.
Z	0	\	о /
1376. —2е г/2(т2 + 4т + 8) + С. 1377. т arctg т — - In (1 + т2) + С.
1378. т tg т+ln | cos т|+С. 1379. О, 5er(sin т + cos х) + С. 1380. 4л/2 + т —
- 2^2^ т arcsin — + С.	1381. — - (	----HctgT) + С.
2	2 \sin2 т J
1382. т arctg У 2 т - 1 -	+ q 1384. Зт + 4 sin т + sin 2т + С.
Зт	sin 4т „ Зт sin 2т sin 4т „ т
1385.-----Н cos 2т---------НО. 1386.------Н---------Н------НО. 1387.------
2	8	8	4	32	8
sin 4т „	Зт sin 4т sin 8т „	т sin 4т sin3 2т
----------НО. 1388.----------------Н------НО. 1389.-------------Н---------Н
32	128	128	1024	16	64	48
Ответы
289
„	2	„ cos5 х „	sin3 х sin5 x „
+ С. 1390. — cos x 4— cos3 x------H С. 1391.---------------Н С.
3	5	3	5
11	3	1
1392. - sin4 х-sin6 ж + С*. 1393. sin х — sin3 х 4— sin5 х-sin7 х + С.
4	6.	57
8 sin3 х	1
1394. 7ж + 14 sin ж + Ззт2ж —------Н С. 1395. —;-----sin ж + С.
3	sin ж
1396.------Н cos ж + С. 1397. - In I tg ж| 4-С. 1398. 1) Inltg—I +
cos ж	2	12 1
+ С- 2) In |tg (| +	| + C. 1399. | [in |tg || + In |tg (| + J) |] + C.
dx
sin ж — cos ж
= “Fln
a/2
7	dx	1	7 dx
J sin ж — sin (тг/2 — ж) л/2 J sin (ж — тг/4)
tg2 X , .	,	ctg2 ж
+ C. 1401.-^—4-In | cos ж14-C. 1402.- 6
2
— In | 8тж| + С*.
1403. —-(cos 4ж + 2 cos 2ж) + C. 1404.-
8	2
sin (m —
+ С при m ф n и
ж 1
--H --зт2тж + С при m = n.
2 4m
sin (m — n)x 8т(т + п)ж
1405. 1) - sin 2ж-sin 8ж + C: 2) -
’ 4	16	’ ’ 2
X 1
при m Ф n и — — ----sin 2тж + C
2	4m
1	5
— - зт4ж + C. 1407. 1) —ж — cos ;
8	16
cos ж 1 I ж I
+ 5in|tg5| + e; 2
9	„
1409.----H 3 sin 2ж 4— sin 4ж + C. 1410. -ж-sin 2ж 4-sin 4ж
2	8	84	32
ж sin 4ж sin3 2ж	.2 sin3 ж sin5 ж
""	--------------H C. 1412. sin ж--------1-------H
64	48	3	5
cos3	.8 cos3 ж
--------H C. 1414. 7x — 14 cos ж — 3 sin 2ж 4	h
3-------3
1415. - In I tgж| — ж 4- С. 1416. -(2вт2ж — 8т4ж) 4- С. 1417. -
2	8	cos ж
1	/	7Г \	1	Ж3
4- cos ж 4- tg ж 4- С*. 1418. — cos Оы- _i— I j—141а П--_
ж3
4- 4ж4-81п|ж — 21+С; 2) —
+ С 1420.
1408. 1) -----5—
2 sin2 ж
11ж	„ .
2
1411.------
16
К
cos
1413. -----
5
1 .
2
ж2
1423. — + 4ж + In
при m = n. 1406. — — созбж —
5 sin3 ж 5 sin ж \	„
—+—)+c‘
1 . I (x 7Г\ I
 2 1П l‘g (2 + I + C
1 . „ 1 .
/ • 5
I sin ж
6
sin ж
2 cos2 ж
3
4	32
o-3	• I
2 sin ж	sin
1412. sin x — --
3
8
3
х	а3
— arctg —+С; 3) 1п |^3
о о
Ст3
+ С. 1422. In-----
1421. In
I)8
з
1424. - + In
290
Ответы
£ _ q	2
---— + С. 1426. 1пС*т(т — 1) + ------------
ах2	х —
+ С. 1428. - In (ж2 4- 2т — 10) — arctg —±-F
2	о
Ют - 1
1429. 2 In (т2 — 0, 2т + 0,17) — 5 arctg----Н С.
1425. Д-In
1427. In
2
1430. 1п|т+ 1|Vt2 + 4 + C. 1431. 3 In
2
л/т2 ~ 2т + 5	т —
----Ы------+2“C‘S —
+ C. 1432. — In.,	,
24 t2 - 2т + 4 4^3
1
2) 864
1 т — 1	, v t2 + 1
4----arctg ———H C. 1433. In —---------—
J	V3	|t + 1|
.	1 ( x bx \
1434. 1) — arctg - 4-	4- (
' 263 \ b x2 + b2 J
т 4- 9	1
+ 2t + 5) “ 16
+ arctg т + C.
1 Гт(562 + Зт2)
— --------------- + - arctg — + C. 1435. 1) —
' b J
3)(3т2 - 18t +32) o
2 g ^,„,2--------- + 3 arctg Ж - 3
x2 — от + 10)J
3
(t2 + 62)2 ' b
x arctg —— + C- 2) -
2	о
1436. In
1438. - In
1
1441. Ii
10^3
x — V3
т + V3
1
1439.----
1437. —---------
4(t2 + 2)
т + b
In
л/2 т
+ — arctg —
1 , a
2
2
+ С. 1440. - In 1-----
1442.
-- 2
1 1 ,
--1— In
T 2
, С*(т — 2)3
1444. In —
1 x
dl = 11„ w =
t2)	4 V4 + T2
1445. In C(x - 1V2t + 3. 1446. In z ~ ------г. 1447. 3 In ~
v ;v	(t + 2)2(t -2)	t + 2
2	, С(т-2)	1
-------.	1448. 2 In —------------
1449. In
1450. — In
+2 arctg (t — 1) + C.
1,	|т + 1|	1
- In ,	: 4----= arctg
/т2 + 2	3^2 V2
(т — 2)2	1 x +
t2 + 2т + 4 “ 4Vf MCtg V3
1451.
1452.
— In
24
2
V®2 — 2т + 2
1 x
+ - arctg — + G .
1453.
1
2
^ + 2» +2 +	11 + 1) +C-
1454.
lln
т + 5
1455.
1 [ t2 4- 3 — t2	1
- / —.., „---т dx =----
3 J t2(t2 4- 3) 3т
1	т
—— arctg — 4- G.
3^3	V3
Ответы
291
1456.
1 fx2 + l-(x2-O	1
- /	z--— dx = - In
2 J (ж2 + 1)(ж2 - 1)	4
- arctg x + C.
1 f	x2+ 1 - (ж2 - 2) ,	1	,	ж-^2	1
1457.	- /	——--—----2- dx =	—-= In	 =-arctg x + C.
3J	(ж2 + 1)(ж2-2)	6^2	x + V2	3 S
1458. ^-^(Зж+ I)2 + C. 1459. 2ж 1 (2^2ж + 1 - 3) + C.
Э	1Л
1460. 6
2
1461. — (Зж2 — ax — 2а2)л/а — x + C.
10
3
1462. -
4
(ж2 _ 4к/ж2	2	1
1463.	---------H C. 1464. arcsin — + С (— при x > 0 и
3	x
.	,	Сх	1 /2а — x
+ при x < 0). 1465. In-----------,	1466. —\ ------- +
x + 1 + 72ж2 + 2ж + 1	а V x
+ С. 1467. In-----*-(( + )	1468. - Гж^а2 — ж2 + а2 arcsin —1 +С.
1 + 7ж2 + 2ж + 2	2 L	aJ
1469. —,	+ С. 1470. 2 arcsin------(2 — ж2) V4 — ж2 + С.
4^4 + ж2	2	4
1471. о „ 7/ „	„ +С. 1472. / У4 - (ж - I)2 dx решаем подстанов-
За2 V (а2 + ®2)3 J
кой ж — 1 = 2 sin/,
[ /--------—. 9	,	. ж — 1 (ж — 1)л/3 + 2ж — ж2
/ V 4 — 4 sin2 t 2 cos t dt = 2 arcsin —---------------------------H C.
1473. —L--------— arcsin + C.
yj2 - x2	V2
1474. | (ж + 5)7ж2 + 2ж + 2 - 3, 5 In (ж + 1 + \/x2 + 2ж + 2) + С.
1475. —л/3 — 2ж — ж2 — arcsin —±-----Н С.
ж — а ,--а . ж — а
1477. —-—у2аж — ж2 + — arcsin-Н С.
1	л4/1 гз _ 1	9	_______
1478. - In	—- + - arctg + ж3 + С*.
о	у 1 + ж3 + 1	о
^/(2 - ж3)2
1479.	---z-^-
4ж2
292
Ответы
//4 “Г -L	—" “Г -L О	_о
1480.-------\-р = ------Н- равняется целому числу; положив х +1 =
= Z2, получим
С х~2х~3 dx у t2 — 1	1 + 2т2
J (ж-2+ 1)3/2 = - J	+ С-
//4 Т ±	| ±	о	о
1481. ------ = ------ равняется целому числу; положив а — ох = t ,
п	2
получим
1 ft2 -а
b2 J t2
dt =
2а — bx2
Ь2\/а — Ьх2
+ С. 1482.
(х - 2)72т - 1
------а--------Г
1483. (Зж+2Х) Z + (Зж +1)1/3 + 1п |(3ж + I)1/3- 1| + С. 1484. х-2уД +
+ 2 In (у/х + 1) + С. 1485. -О, 3(2т + За) ^/(а - х)2 + С.
1486. 2у/х — 2 + \/2 arctg
3(т2 + 1) / ^(т2 + I)2	7т2 + 1	1\
2 у 5	+	4	+ Зу +
1488. In (1 + VI + т2) +---/	+ С.
1 + V1 + х2
+ |У(4^
О
1489. т2
ж2)3 + С; в этом примере выгодно сначала освобо-
диться от иррациональности в знаменателе.
1490.
+ С.
1494.
1х + 2	1
=Рд /------\~ С (— при х > 0 и + при х < —2). 1491. arccos--------- +
\ х	х — 1
1492. 2 arcsin — — |74-т2 + С. 1493.2 arcsin
2 -к х ______ _____________________
—-—V4;r +	— 2 In + 2 + ^4х + х2\ + С.
Гх
— 72т — х2 + С.
1495.
_|_ (j
——75 + 4т — ж2 +
17	. х - 2
— arcsm-------
2	3
+ G.
1496.
71 + х2
2х2
11,.^^+Ос
1497.
1498. Положив 1 — х3 = t2, найдем
х2 dx	2 Г dt	1	л/1 — я?3 — 1
т371 — х3	3 J t2 — 1	3	71 — ®3 + 1
1499. Положив х = 1/t, найдем
Г dt	Г dt	х + 1
— / —,	,	---- = arccos------
J 73 - 2/ - t2 J 74 - (t + I)2	2т
Ответы
293
1500. - In (е2х + 1) — 2 arctg (ех) + С. 1501. - tg3 х — tg х + х + С.
2	3
е2х	I х I
1502. — - 27 + 4 In [ех + 2) + С. 1503. In tg -1 + С.
1	(\ х\	„	1
1504. - arctg ( - tg — I + С. 1505. - In
2	S\2 S 2/	5
2tg (ж/2) + 1
tg(«/2) - 2
ctg3 x
1506.------—
3
1	/ X \
ctg x + C. 1507. - arctg f —— J + C.
,4	1-2
1508. X' + ln 17 - lUC. 1509.	- In I cos 7 + C. 1510. ex +
11	4	2
1 , ex — 1	1	/tg(x/2)\	lg3-'’
+ -In ------ + C. 1511. — arctg 6 V 7 + C. 1512. —----------1-
2	о1' + I	л/2	X л/2 7	3
+ Ig./ + t'. 1513. | arctg (2tgx) + C. 1514. |ln|tg|| + |tg2| +
Z	4 I z I о	z
+ C. 1515. -In Itg || - - ctg2 | + C. 1516. 2In 7 - 1| - x + C.
Z I Z I ± z
1517. |(tg х + In | tgx|)+G.
„	. , sh3 x
+ C. 1519. 1) sli ./ +
x	sh 2 т
2 +
1522. -
1525.
4^4 + x2
sh It
X	X , sill.с
-о+^;2) -+сЬ2т+ —
1 — ch х
sll 6.C X „ X
1518.1--------
7 12	2	’ ' 2
o , C. 1520. Inlchxl + G. 1521.-	,
3	sh x
sh2 x
2~
1523.
1526.-----,	+
5V^2 - 5
e	sh5 x
и 1524. См. задачу 1366.
„	ch3 ->x ch ->x
C. 1527.-------------------H
9	3
1528.	- - + C. 1529.	+ C. 1530. x - cl I it + C.
______32	8	5
2 Veh x — 1 + С (под интегралом умножить сначала числитель и
sh х — 2 „	3 , .	.
—-------\-С. 1533. - In ж + V»2 — 3 +
ch х	2
1531.
знаменатель на У<-|, ,r - 1). 1532.
x	\/x^ I 3'
+ ^Vx2 - 3 + C. 1534. 111 I./- + \/-'-2 + "-I — —-+ C. 1535.2V^n +
Z	X
+ In	+ c
- — + C. 1538. tg -
ax	\2
X = sin2t). 1540. ab arctg
(arctg x)2	1 x + a
1536. -----2-7- + C. 1537. — In -
2	a2 x
7Г \	_
— + C. 1539. 2 arcsin y/x + С (положить
4/	v \
- tg x ] + C.
1541.
+ x sin 2x 4— cos 2x
2
+ C. 1542. Int'C '' + 1) - x - e
1
4
f /1 — X f 1 — X	. i---------
1543. / 1/---dx = /	,	: dx = arcsin x + \/1 — x2 + C .
J V 1 + X J y/T^
294
Ответы
ctg3 X „	, .	Т2 _	, I х I
1544.-------------Н С. 1545. х tg х + In | cos т|------— + С. 1546. In |tg — | +
+ cost + С. 1547. —arctg------------------------Н С. 1548. Зт1/3 — 12./-|//6+
Ь Ь
А _ Ч о Т'
+24 In (т1/6 + 2) + С. 1549. —---------— + С
оа(ах + о)15
1550.----+ arctg х + С. 1551.-----------------
х	tg х + 1
знаменатель на cos2 ж и положить tg ж = t).
(положить ах + b = t).
(разделить числитель и
2 ,________
1552. -у/а + bln х + С.
Ь
15И- 36(„ - 1)(а - М— + С "РИ " * 1 "	1,11“ - М + С
при п = 1. 1554. Выделив под корнем полный квадрат, положить х +
+ 1 = V2sint (или же решить методом неопределенных коэффици-
х + 1 ,----------------. х + 1	2л/т +1
ентов); -----у1 — 2т — х2 + arcsin ———Н С. 1555. — -——-— + С.
%	(V^+i)
1 , т2 arctg х „	1 ех 1	1 , ,	„
1556. - In-----------------\-С. 1557. - arctg-------т+ - In (4 + е2 ) + С.
2	1 + т2 т	2	& 2	2	4 V 7
1558. In
О^2т + 1
1 + ^/2т + 1
1559. т + ctg т - ‘XLjL + с.
3
1560.
V4 — т2
т	1
arcsin —Н С. 1561. 1) —— In
2	’ 2^3
у/З + ctg т
л/3 — ctg т
= —-—= In
2^3
sin (т + тг/6)
sin (т — тг/6)
+ G; 2) -^1п
2^3
\/3 + tg т
л/З - tgT
+ С. 1562. 1) Осво-
2 г/
бодиться от иррациональности в знаменателе; — (
За
1 ________ _______________ х 2	1
2) - Гт^ж2 + 1 + In (т + л/х2 + 1) + т2( + С. 1563. — + т 4--+
2	2	т
, С(х - I)2	1 /т + 2\3/2	/	1\
+ 1п^--------1564. -- —:—	+ С положить т = - .
т	3 \ т /	\	t)
2
1565. - arctg У./-3 — I + С
3
(положить т3
1566. О, 5[т + In | sin т + cos т|] + С. 1567. 2 [у/х arcsin у/х + л/1 — т] + С.
1568. tg2 т + С или ---------Н G1.
cos2 т
/cos2 т — sin2 т , f о	, f ,,
-------------dx = — ctg т d(ctg т) + / d(ct£
sin т--------J	J
---------H C. 1570. — ctg т In | cos t| — x+C. 1571. e~x + - In
3	2
1	X “I- 1
1572. - tg4 т + С (положить tg x = t). 1573. In |t|-----In
= ctg х—
е'
+С.
Ответы
295
У l------:--- ,	/ сои х ах	,----;-- „	,
VI — sin х dx = ± /	, = = ±2V1 + sin х + С (+ при
J VI + sin X
cos х > 0 и — при cos х < 0). 1575. —arctg (л/2 tg х) + С.
1 Г с/(ж2)	1 [' х2 + 1 — (ж2 — 2)	9
1576. - / —--------------- = - / —:----А-----2 d ж2 =
2 У (ж2 + 1)(ж2- 2)	6 J (ж2 + 1)(ж2- 2) V ’
1	|а;2 — 21
= «ln 2----Г + С- 1577- -2е-2^(7^+ 1) + С. 1578. 2л/ж arctg л/ж —
6 ж2 + 1
— In |1 + ж| + С. 1579. д/tg х + С (положить tg ж = I). 1580. In |ж| —
ж2 + 1	1
— -----— 1п(ж2 + 1) + С. 1581. -----arctg (аг) + С. 1582. 2(л/ж +
Z х	in d
+ cos y/x) + C. 1583. —-—У-—-	+ 1 + 2^2 In	—ДД + C (no-
3	y/x + 1 + V2
дожить ж + 1 = t2). 1584. ж — л/l — ®2 arcsin ж + C. 1585. -----------
/	1\	Зж2 + Зж + 1
положить ж = - .	1586.----------—— + G (положить ж + 1 =
\	V	3(ж +
= t). 1587. л/2аж + ж2 — 2а In |ж + а + л/2аж + ж2| + С (с. 153, п. 4°).
, (2ж — I)2	„	1 + cos ж + sin2 ж „
1588. In 2—---+ С. 1589.----------------—-------+ С.
\х2 + ж|	sin ж
1 , С*(ж2 + 2ж + 2)	1 2ж z
1590. — In---------------Н - arctg ------- (знаменатель разлагается на
16 ж — 2ж + 2	8	2 — ж2
множители так: ж4 + 4 = ж4 + 4ж2 + 4 — 4ж2 = (ж2 + 2)2 — 4ж2 и т. д.).
2
1592. s5 = 0,646, S5
14	7Г
1595. —. 1596.
3	6
f dx	21
= 0,746, / — = 0,693. 1593. 20. 1594. —.
J х	8
1
1597.	1598. 3(е - 1). 1599. In (1 + ^2).
1600. |
1601. Положив ж = t2 и изменив соответственно пределы, полу-
3
ЧИМ [ —— = (2t + 21n(t- 1))||= 2(1 +In 2). 1602.-—1603.2 —
J I 1	2
2
,	тт V3	, 2е	а(тг — 2) .
— In2. 1604.-------. 1605. In-----. 1606. —------- (положить ж =
3	2	е + 1	4 v
. 9 .	1 тга2 ,	V2 + ln(l + V2)
= asm2t . 1607.-. 1608.--. 1609. 2 In 2-1. 1610.^—^----v +
7	3	16	2
V3-V2	,3	ч 1	тт	4 1 - 3	7Г	4 1-3-5	7Г
1611. -----1612. In-. 1613. 1---------: 2-------: 3-----------.
2	2	; 2	2’	; 2-4	2’	; 2-4-6	2
296
Ответы
	а3	1	\/3-1	1
1614. 1619.	6 ' arctg е 1 - In 2	1615. -. 1616. 1. 1617. 		. 1618. 21п1,5	 6	2	’	3 ~ 0 433	1620	1621	1622	1
		4	6 '	4	2 , 1 тг , 1 • 3 тг , 1-3-5 тг	32
1623.	2	. 1624. 1 - •	2 	 •	3 	 • -. 1625. — 7 2 2’ 7 2-4 2’ 7 2-4-6 2	3
1626.	тгаб.	1627. - произведения основания (2л/2р/г) на высоту h 0
1628.	—. 1629. 81п2. 1630. 1. 1631. —. 1632. 19,2. 1633. 25,6 0	0	
1634.	1635.	1636. ——. 1637. тга2 (см. рис. 56 на с. 309).
1638. 0, 8 (см. рис. 53 на с. 307). 1639.- ^4—; положить х = 2а sin21
(рис. 84, с. 335). 1640. 2a2shl = а2(е — е-1) ай 2,35а2. 1641. Зтга2.
Зтга2	„	Зтга2
1642. ——. 1643. а2. 1644. —. 1645. rmax = 4 при 2Г~ = 90° +
+ 360°п, т. е. при р = 45° + 180°п = 45°, 225°; гт;п = 2 при 2<^> =
= — 90° + 360°п, т. е. при р = —45° + 180°п = 135°, 315°. Смеж-
ные экстремальные радиус-векторы при 45° и 135°. Искомая площадь
Зтг/4
If, .	,9 ,	19тг	Зтг	тга2	тга2
равна	- / (3 +	sm 2<£>)2 dtp	=	——.	1646.	—.	1647.	——.	1648.	——.
2 J	8	4	2	4
тг/4
тг	тг
= 0, р = - rmin = 0 при р - -
Зтг/4
S = - [ (ал/2)'2 cos2 (р--------------dp =
j ч ' max — u V - при.	—
тг	тг Зтг
-, р = -- И —. Площадь
7ГС1^
——. Ответ получается проще, если
— тг/4
перейти к декартовым координатам: х'2 + у2 = а(х + у) — окружность.
7а2	Ютг + 27^3 а2	За2
1650. ----. 1651.	1652. ----. 1653. 36. 1654. 12.
4тг	64	2
32	4	14	16
1655. —. 1656. - (см. рис. 52 на с. 307). 1657. —. 1658. 2. 1659. —.
0	0	0	0
о
1660. 17, 5 — 61п6. 1661. 2 У —x\Jx + Idx = 7^7 (см. рис. 49 на с. 307).
-1
1662. rmax = 4, когда 2р = 180°+360°n, р = 90о + 180°п = 90° или 270°;
f’min = 2, когда 2р = 0° + 360°п, р = 180°п = 0° или 180°. Площадь
Ответы
297
тг/2
If., „	, 19тг	Зтг	тга2	тга2
S=- / (3 + cos 2<z>)2 dtp =------. 1663. —. 1664. --------. 1665. -----.
2 ./	'	8	4	2	4
о
Ь	11
1666. —(e2?r — e-2,r) = —sH2tt. 1667. \ab arctg-. 1668. —тга2.
4 V	7	2	а	8
О д 2
1669. тгр/г2. 1670. ——.	1671. 12тг.	1672. 58, 5тг. 1673. 2тг2а26.
„/sh2	\	512тг	7 о	„	512тг
1674. тга3 ------1- 1. 1675. ----. 1676. -тга3. 1677. Зтг2. 1678. -----.
\ 2 J	15	6	7
тг /бтг а/з\	тга3	тг2	64тг	(тг + 2)тг
4 у 3	2 у 6	6	3	4
4	„	З2тга3	8тга3
1684. -тга26. 1685. ——. 1686. 19, 2тг. 1687. ——.	1688. V =
3	105	3
128тг	„ „	112	670
= -------. 1689. 5тг2а3. 1690. 72тг. 1691. ----. 1693. 6а. 1694. ------.
3	27	27
1695. 8а. 1696. Точки пересечения с осями при tj = 0 и t2 = ^^8,
^8
у/О+ l-t3dt =	1697. V6 + ln(V2 +V3). 1698. 2авЬ1Ай
О
12/5
2,35a. 1699. s =
3/4
-| 2,6
д/1 + х'2	..	..
--------ах; полагаем 1+ж = t ; s
13/5
Г t'2 dt
J ё^Т
5/4
1 , t - 1
= t + - In-------
2 t + 1 j i 25
7Г
ОСЯМИ при X\ = 0 И X2 = —;
О
1, 35 + In 2 Ай 2, 043. 1700. Точки пересечения с
dx f cos x dx
J COS X J COS2 X
о	0
1701. 1) 4^3; 2) 0,5 In (2 ch 2)
a ,	,-----Зтга 28
+ — In (2тг + л/1 + 4тг2). 1703.—. 1705.—. 1706.1n3. 1707.21n3-l.
14тг
1708. p[V2 + In (1 + V2)] « 2,29р. 1709. 4^3. 1711.—. 1712. тга2х
/ 4тг "\	64
x(sh2+2). 1713. 2тг 1 + —= . 1714. 2тг[Т2+1п (1 + %/2)]. 1715.-х
\ ЗуЗ/	3
Зтг.	1717. 4тг2а6.	1718.	34ёё-	2^.	62тг
9	3
1721. 29, бтг. 1722. 1,44 • 106Н; на нижнюю половину
г,	ah’2
1,08 • 106Н. 1723. --
6
S
хтга2. 1716.
1720. 2,4тга2.
сила давления
У a sin х ,	,	/—х
V . 7 = In (2 + ёз) ай 1, 31.
1 — sin х
о
1,009. 1702. 1) 8а; 2) тга^! + 4тг2 +
2
1724. -Л3. 1725. 2,4 • 106Н.
О
298
Ответы
ab3	a3b
1726. Jx = ----, Л = -------• 1727.
3 ’ y 3
a3
1729. Mx = Mv = —; xc = yc =
Л	У	g , С	УС
My = У xy dx = -^ba2; S = У у dx =
о	ъ
2j\y/2)ydx	4
= °, Ус =	° ----2--- = R" ™
(J,O7raz	Зтг
R+h
2) 2,5 • 103тгЛ4Дж. 1733. [ rR)R
ab3
= ~12’ Jy
a3b
---. 1728. 6,4.
12
1730. Mx = / |t/ dx = 0, lab2,
ab	3
— • xc = -a, yc = 0, 36. 1731. xc =
3	4 ’ y
4
-a.	1732. 1) 1,12 • 104тгДж;
9
mgRh	1000тгЛ2Я2
„	, . 1734. -----------
H
210 Дж. 1735. 12410 Дж. 1736. 0, 24тг Дж. 1737.6=/—S dx_
j 0,6sy/2gx
о
= 100c.
1738. t =
R2
0,6r'2H'2y/2g
H+h
J xy/xdx, где h Ki 2 — высота довод-
h
нительного конуса. Вычислив, получим t Ki 42 с.
1741.-^=. 1742. 2,4 • 104Н на каждую стенку.
ah2	1
1739. ----. 1740. 17-.
3 а	5
1743. 1Х = У y2xdy =
о
тг/2
/д-9	9 тга4
a sin t cos t dt = -.
16
1744. xc = 0, yc
fy2dx
о _ °
2	— 5'
2 f у dx
1745. *R ’1°°° f(H - x)2x dx Ki ЗООтг Дж. 1746.
H2 J	7-1
о
U A
УМ
Ki 15 980 Дж. 1747. t =	419 c. 1748. 1) 1;
15 • s • 0,8 у 2g 3
/dx 1
— = ------- при n > 1; pacxo-
xn n — 1
1
дится при n 1. 1749. 1) 1; 2) 1/2; 3) тг/4; 4) 1; 5) In 2; 6) 16.
1750. 1) —; 2)---1----; 3) -----. 1751. 1) 6-^2; 2) расходится; 3) 6.
6	4	2	8
Ответы
299
f dx	1	1 C dx
1752. 1) / —== сходится, ибо	: <	. , а /	. сходится
J Vl + ж3	Vl + X3 Ж3/2’ J Ж3/2
О	1
/dx	11
z расходится, ибо	- > —, а
\ЛЕ3 — 1	л/Т3 — 1 X
/dx	[' е х dx	е х _r
— расходится; 3) / ------ сходится, ибо -- <ie при х 1, а
2	О
1
сходится (см. задачу 1749); 4) j
1
sin х dx
абсолютно сходится,
2
ибо
|sin«| 1 Г dx
------— <С —, а / — сходится (см. задачу
1
2
расходится, ибо
.4
расходится;
сходится.
е х dx сходится,
ибо
_ 2	_
е е при
при
п < 1, расходится
_ 2
е
1
о
о
1
1
1
1 — п
а
2
1
о
ь
Г dx (6 — а)1-п
при п > 1; 2) / —------— = -----------при п < 1, расходится при п > 1.
J (6 — х)п 1 — п
1754.7г. 1755.2. 1756. Зтга2. 1757. 2тг2а3. 1758. тг[^2 + In (1 + \/2)] •
4тг	1	1
1759. —. 1761. 1)	2)	3) 1; 4) расходится. 1762. 1) In (1 + ^2);
3	2	3
2) 2; 3) 1 - -. 1763. -. 1764. 16тг. 1765. 2тг. 1766. 1) -; 2)
4	2	7Г 7Г
1 a2 -I- ah -I- 62 тг	4
3) —р 4)	+	+ ; 5) - 1768. 1) ф) = 0; 2) \e(h)\ < - < 0,3.
с J.	О	Я	J. О
55	2•10-4
1770. — тг 28,8 дм3. 1772. In 2 = 0,6932; |е(/г)| < ——— < 0,001.
О	10
1773. 8,167Г. 1777. Приближенно 1, 22тг. 1778. R = -. 1779. R = -.
1780. В вершине (2; 0) Ri = -; в вершине (0; 1) /О = 4. 1781. R =
= 4а. 1782. t/max = - при х = 1; R = е. 1783. (4; 4). 1784. (3; -2).
е
300
Ответы
1785. (0; 1). 1786. 27Х2 ± 8У3 = 0. 1787. (2Х)2/3 ± У2/3 = З2/3.
1788. X2/3 —У2/3 = (2а)2/3. 1789. X = асов/, У = asin/ илиХ2 + ¥2 =
= а2. 1790. к = ех(1 ± е2^)-3/2; £тах =	2 —= в точке х = зТз	in 2 Г й
2 ,а2 ъ - 0,347. 1792. 1) R = -V^ar; 2) —; 3	Зг	^3	। 3) -. 1793. -.	1794. 2
1795. 1. 1796. 1. 1797. (-2; 3).
ТГ 3
1800. X =-----0,7:	У =	-
4	2
/	t2\
1802. X = -t2 1 + — , У = 4/
\	2 /’
/	4
1798. 0: —
к 3
л/2	—1,4. 1801. 8Х3 - 27У2 = 0.
л л
14---; для построения кривой и
\	3 /
1799.
11 16
Т’ У
эволюты составить таблицу значений х, у, X, У для t = 0; ±1; ±3/2.
1803. (Х±У)2/3-(Х-У)2/3 = 4. 1804. (X±У)2/3±(Х-У)2/3 = 2a2/3;
при повороте осей на 45° это уравнение примет вид х^3 + у^3 = (2a)2/3,
т. е. эволюта астроиды есть тоже астроида с увеличенными вдвое раз-
мерами и повернутая на 45°. 1806. 21. 1807. 5/. 1808. 7,5. 1809. 2тг.
3 I 1п 2	t/i*
1810. 2 sh 1	2, 35. 1811. —--------. 1812. Зх ± 4г/ = 0; — = 4i - 3i.
’	2	У ’ dt	J
4 х2 dv	d2v
1813. у = -x----------; — = 3i ± 2(2 - /)j. 1814. w = — = -2j,
y 3	9 ’ dt	v '	dt2 J’
41/ — 21	6	...
wT =	,	, wn =	,	; при t = 0 wT = 1,6;
/I/2 - 16/ ± 25	V4/2 - 16/ ± 25
wn — 1,2.
1816.
1818‘ 12
X	У	л	.. J	.
1815. — + — = 1; v = —asmZi + ocos/j, w = —r.
a2	b2
у — t2 z — t3	X — x Y — x2 Z — Xx
----- = 	—. 1817. 	 = 	 = ,, C-
2/---3/2	1---2т 1/(2^/^)
у _ Q g
: —— = ——. 1819. r = —i ± к, В = i ± k, N = -2j;
г
главной нормали:
г - 1
—-— и соприкаса-
т = ----——; /3 = —v = — j. 1820. В = r x
У2 .. V2
N = (r x r) x r = —22i — 16j ± 18k, уравнения
x — 1 У ~ 1 z — 1	x — 1 У ~ 1
-----= ------ = -----; бинормали: ---- = ----- =
11	8	-9	3	-3 .
ющейся плоскости: Зх — Зг/±г=1. 1821. N = 3(i ± j), В = —i ± j ± 2k.
х — 1 у — 1
Уравнения главной нормали: х = у, z = 0; бинормали: ---— = —-— =
= —. 1822. Исключив /, получим х2 ± у2 = z2 — уравнение кониче-
ской поверхности, г = (cos/ — / sin/)i ± (sin / ± /cos/)j ± k = i ± k;
г = (—2 sin / — /cos/)i ± (2 cos / — / sin/)j = 2j;B = rxr = 2i± 2k,
N = 4j. Касательная: x = z и у = 0; главная нормаль: ось Оу; би-
Ответы
301
нормаль: х + г = 0иу = 0.	1823. При t =------= ---------;
2 —а b_________
\/~а	. Vb	tf4ab
у = а. 1824. cos а = ±-----, cos р = ±--------, cos 7 = ±---------у=;
л/а + v b	у/а + v &	\/~а + v b
выбор знака зависит от выбора направления на каждой ветви кривой.
1825. Уравнения винтовой линии: х = sin 2/, у = 1 — cos 2/, z = 2/2,
где t — угол поворота (рис. 44). Единичный бинормальный вектор /3
в точке С (при t = тг/2): /3 = —~*~ ** ~*~ . 1826. При t = — v =
V2 + тг2	2
Рис. 44
..	.	х — 2 У — 2 z — 8	х — 1
= a(i+j), w = ai. 1827. —— =	= ——. 1828.	=
1	1	О	z
= и z = 3. 1829. —- = - = Z~—-. 1830. 120°, 60°, 45°.
-1	212	’	’
1831. N = —26i - 31j + 22k, В = 16i - 12j + 2k; —- =	- = Z~—
26	31	—22
---- = ------ = ---. 1832. N = — 4j — 4k, В = 2i — 2k. Уравнения
8-61---------------j , j и
главной нормали: x = тг, z = у + 2; бинормали: x = тг, у + z = 6.
.1 |р х w| 2
1834. v = r = i + (1 - 2/)j, w = r = —2j, — = --------— = —;
R vA vA
I/ _ 2	p2	2
p = л/2 — 4/ + 4/2; wT = p = ,	= — л/2, wn = — = — = л/2-
V2 - 4/ + I/2	R	v
—4i + 3i .. 4i + 3i
1835. v = r = —4sinh + 3cosh = -----——, w = r =--------——;
V2	V2
12	/---д-s------------— . ISIIIZI	7Г
—, p = у 16sin t + 9cos2t, v = --------------; при t = — p _
p3	2p	4	^2
302	Ответы
7	„ „ г-	г? 12	12^2	„ . г-
wT = v = —— = 0, 7л/2, wn = — = — = -------- = 2, 4л/2- 1836. v =
5^2	R v 5
= г = i + 2fj + 2f2k, w = 2j + 4/к; v = 2t2 + 1, — = J------—- =
= (2/2 + I)2 = l’ = V = = 4’ = 7? = m2 + IP = 2 (B ЛЮб°Й
точке). 1837. Сначала составим матрицу координат векторов
t
1
0
0
6/2
I2 I3
2/	З/2
2	6/
0	6
-6/ 2
Затем найдем:
1) |r| = V1 + 4/2 + 90; 2) |г х г| = 2^90+ 90 + 1;
3) гг г = 12; 4) —
R
2V9O + 90 + 1 _ 2	1 _	12
V(1+4O + 9O)3 “ ’	“ 4(90 + 90 + 1)
1838. - = ———— = — _ =
R (х + у)2	4 р
1
«правой» винтовой линии: —
Р
1 _	2/	_ 2 1 _
1841‘ R ~ (2f2+ 1)2 - 9’ ~р ~
A X = 9^4 + 4г/6 +1 =
4 ’ R2 (у2 + 1 + г/6)3
V2	1	V2 1	1
- —. 1839. - = —, - =	1840. На
4	R	3 ’ р	3
b	1 b
= -5---на «левой»: - =----------------—.
az + b2	р a2 + b2
2t	2	у2 .
“(2O + 1)2 “ “9 1842-r - y1 + ^J +
14 1	3	1	72 1	1
—, - =	1843. — = —, - =
27’ p	7	R 3 ’ p	3
1844. 3) Вся плоскость, кроме точки (0; 0); 4) х2 + у2 <1 а2", 5) тг/ > О
(первый и третий квадранты); 6) х2 + у2 < 1; 7) вся плоскость, кроме
прямой у = х. Уравнения 1) и 2) определяют параболоиды вращения;
4
3) — поверхность вращения вокруг оси Oz кривой z = — и у = О
X2
(рис. 45); 4) полусферу; 5) конус, для изображения которого возьмем
сечения: х = a, z2 = ay и у = b, z2 = Ьх — параболы (рис. 46); 6) по-
верхность вращения кривой z =	у = 0 вокруг Oz; 7) конус
71 — х2
кх
с образующими у = кх, z = --- и направляющими — равносторон-
к — 1
ними гиперболами у = h, (х — h)(z + h) = —h2, имеющими вершины
на оси Оу и одну из асимптот на плоскости у = х (х = h, у = /г); та-
кие же гиперболы получаются в сечениях х = h или z = h (рис. 47).
Ответы
303
1845. s = у/р(р — х)(р ~ у)(х + У ~ р)- Область существования функ-
ции: 0 < ж < р, 0<у<рих + у>р, т. е. множество точек внутри
треугольника, ограниченного линиями х = р, у = р и х + у = р.
Рис. 46
1848. Arz = (2ж — у + Аж)Аж = 0, 21, Ауг = (2г/ — х + Аг/)Аг/ = —0,19,
Аг = А^г + Ауг — АжАг/ = 0, 03. 1849. Непрерывные и однозначные
Рис. 47
в области |г/| <С |ж| функции z = +^/х'2 — у'2 и г = —^/х'2 — у'2 изо-
бражаются верхней и нижней поверхностями кругового конуса (с осью
Ох). Примером разрывной функции, определяемой уравнением z =
304
Ответы
= ± ^/т2 — г/2, может служить функция
	+У«2 -	У2	при	0 х <	1,
Z = <	-\/х2 -	У2	при	1 <С х <	2,
	. +V«2 -	У2	при	2 <С х <	3
и т. д. Прямые х =	1, х = 2	И т	д. —	- линии	разрыва. Изображе-
нием будут чередующиеся полосы верхней и нижней поверхностей ко-
нуса. Область определения этой функции |г/| <С |ж|, т. е. множество
точек внутри острого угла между прямыми у = ±ж и на этих прямых.
1854. 2) Вся плоскость, кроме прямой у = —х; 3) точки внутри эллип-
- + ^
2	62
= 1 и на эллипсе; 4) вся плоскость; 5) точки внутри угла
|t/| <С |ж| и на его сторонах; 6) квадрант плоскости х 0 и у 0.
Поверхность 2) цилиндрическая с образующими z = h, х + у = 4/h и
направляющей z = 4/ж, у = 0 (рис. 48). Поверхности 5)-6) конические;
Рис. 48
поверхность 4) — параболоид. 1858. Зж(т+2г/), 3(т2 — у2).
У 1
1860.-
1861.
1863.

^/х	дс a —b cos а дс
3t(\/t - ^х)' 'да с ’ дЬ
(/II	(/II
1866. — = е~ху(1 — ху), — = — х2е~ху.
дх	v yh ду
Ь —a cos а дс ab sin а
с ’ да с
du 5t ди
1	___ — __________ ___
дх (т + 2/)2’ dt
Ответы
305
5ж	да	t да I х
______ 1868 _____ = ___________ ____ = /________
дх 2у/х - x2t2 ’ dt }/ 1-xt2'
dz ,  /	<9г
—— = Ь sin (ах — by). 1875. —— = —
ду	дх
_ dz	Зу dz
1876. ТГ = (ъ \ w тг = -
дх (Зу — 2х)2 ду
ди	О ui
2t), — = — 2 ctg (ж — 2t). 1878. — = 2sinj/x
dt	дх
2 sin ж cos (ж + 2г/). 1885. 1) 0,075; 2) —0,1е2 ай
dz
1874. —
дх
x2y/x2 — y2 ’
Зж
— (Зг/ —2ж)2'
<Эгг „ .
дх	У
= —a sin (аж — by),
dz	| я? |
д У	ху/ ж2 — у'2
1877.	= ctg (ж -
дх
х cos (2ж + у), — =
Ай - 0,739. 1887.-0,1. 1888. 1,2тг дм3. 1889.0,13см. 1890. 1) dz =
= — (dx + (—|—dy; 2) ds = Int dx 4--------------. 1891. Аг =
\ж2	г// \x у2 J	t
= 0,0431, dz = 0,04. 1892.0,15. 1893.-ЗОттсм3. 1895. — = -(е‘ +
,	dz	dy	dz 2x ( x\
+	= -2cht 1897. — = ey + xey-/~. 1899. — = — 1 -----------,
dx	dx	ди у \ у J
dz	x (.	x\	dz	dz du	dz dv	dz	dz
Г~ =-------( 4— )' 1900. 1)	д---'"fl-fl- = mTi---1" PTT
dv	У \	У J	Ox	du dx	dv dx	du	dv
dz	dz	dz	. dz	dz	у dz	dz	dz	1 dz	du
тг = nTr + qTT’^ тг = yT----------ТТГ ТГ = XTT + ~TT 1901‘ ТГ =
oy	OU	OV OX	OU	xz ov	oy	OU	X ov	or
du	du	. du	f	du	. du	\	dz
= — cos + — sin —- = - 7— Sin + T— COS r. 1903. 1) —- =
dx	dy dp	\	dx dy	J	dt
dz
= 2 [(Аж + Вг/) cos t — (Bx + Cy) sin t] = (A — C) sin 2t + 2B cos 2t; 2) — =
2e2t	1906. 1) dz dz + дГ dy e2y —. 1910. e2r (-3; 1). 1 dz 1915. — dx xy + y'2 жг/ 0; 6. 192£	dz	dz dz du ”1” dv ’ dz =+ —. 190' / dv 1911. -1. 3 — ж z ’ dz	b ду c 4 1 1922. -, - 5’ 5 2 0; 0. Ж*5	dz	pz	dz	dz dy	du	dv ’	dx =	„(,8.1) _ .Д дх у + 3	у ж 1912. 1) (-1; 3) и (-1; -1); dz	у	dz	у — = -У~. 1914. — = р, ду	z	дх	2z dy	х	у 1918.	1919. --. аж	4г/	ж dz	dz	у . 1923. — = 1, — = ох	оу	X — Z 2хи	и2, — х2 1931
~ e4t + 1' _ dz y/y du 2y/x 21 2ye^ ~ 2же2У — 2) (1; 1) и dz	x dy	2z x2 + 1920. —— 1926. 6; 2;		dx dz y/x du 2^/1 4 dz 913. — dx a c ’ 1 )21. -. 2 6 г/ ж4		
				‘ (ж2 + г/2)2’ (ж2 + г/2)2’
—2xy	2	„ , „	,	, ,	„ , „. „. y(dx — ж dy)
----—-. 1938. 1) —~(3y2 dx2 — 4жг/dx dy + x2dy2); 2)-----------
(x2 + у2)2	ж4	xy2
306
Ответы
1942.
<Э2х _ / Э _Э_\2	-о,— 6 д2%	д2%
дх2 \ ди ”1” dv)	ди2 ди dv dv2 ’
д2 z ( д д\ ( д д\	д2 z	д2 z	д2 z
dx dy \ du dv) \du dv J du2	dudv	dv2'
<Э2х _ / d_ д_\2	_ Э2х 2 d2z d2z
dy2 \3u + dv J	du2 + du dv dv2 ’
d2z d2z d2z	d2z
______4_______l з___	= _4______
dx2 dx dy dy2	du dv
d2 z
1943. Записывая так же, как и в задаче 1942, получим 4 —
dv2
1945.
d2z _	2d2z	^у2 д2 z	у2 d2z	2у dz	2
дх2	ди2 х2 ди dv	х4 dv2	х3 dv ’
Э2г _	д2 z 2 д2 z	1 д2 z	2
ду2	ди2 + ди dv	х2 dv2 ’
2d2z	2д2z	2 д2z 2у dz
дх2 ду2	ди dv х dv
d2z 1946. — + ох2 8х2		32г 1947‘ оу2 1ОЛ0 п. п.	d2z	2	d2z	4x	d2z
			dx2	1 4	— 2y’ dx dy	(1 —2г/)2’ dy2 28т	у , „
+ +	(1 —2г/)3' — 2 , ,	„	2г/ , „ — ах ау, а и = — ах — v2 dz	х2 — ——. 1959. и =	Н и dv	2		gt2//t’	m3//t'	“ “	т2 3	„	„ d2z	.. d2z — dx2dy. 1954.4a2-——. 1955.—г:2-—— X2	OU OV	OU ov X	1 x In у — cos у + C. 1962. и = —|	Hint/ Z	X	
Зг/2
arctg г + С. 1963. и = ху2 — х 4------------Н С. 1964. и = х sin 2г/
+ у In cos х + г/2 + С. 1965. и = ху 4—'—- + у + С. 1966. и = у/х х
х(1 4- лА2 4- 1) 4- С. 1967. и = х In у — х cos 2г 4- yz 4- С. 1968. и =
------- 4- С. 1969. у = 4=тл/1 4" х: область расположения: 1 4- х / 0;
z
х / — 1. Точки пересечения с Ох: у = 0, х = 0 или х = — 1. Особая точка
2	2	2
0(0; 0) — узел. Экстремум у при х =---, г/э = —т= Ай (рис. 49).
3	3v 3	5
1970. у = 4=(т 4- 2)л/® 4- 2; х / —2 — область расположения. Особая
точка: (—2; 0) — точка возврата. Точки пересечения с осями: при х = 0
у = 4=2л/2; при у = 0 х = —2 (рис. 50). 1971. у = ±х-/х — 1. Область
Ответы
307
расположения ж 1, ж = 0, у = 0 — особая изолированная точка. При
х = 1 у = 0, при х = 2 у = ±2. Точка перегиба:
4	4
“ 3’ У ~
— 1 <С х	1. Точки пересечения с осями: при у = 0 Xi = 0, Х2 = 1, хз =
= — 1. Особая точка 0(0; 0) — узел. Экстремумы при х = ±—±0,
Уэ = ±| (рис. 52). 1973. у = х ±
4
тремум имеет функция у = х — Ху/х', при х = -
9
4
г/max = (рис. 53).
1974. у = ±(ж — 2)л/ж; область расположения х 0; при у = 0 х = 0 или
308
Ответы
х = 2; особая точка (2; 0) — узел. Кривая имеет такой же вид, как и
/ х + 2а
на рис. 52, но сдвинута вправо. 1975. у = ±(ж + 2а)О-------; кривая
расположена в той области, где х и х + 2а имеют разные знаки, т. е. при
—2а <С х < 0. Особая точка (—2а; 0) — точка возврата; х = 0 — асимп-
тота. Кривая — циссоида, такая же, как на рис. 85, но смещенная на 2а
I х3 — у3
влево. 1976. у = ±а/-------; область расположения у <С х. Точки пере-
V о
сечения с осями: при х = 0 у = 0 или у = —3. Особая точка (0; 0) —
точка возврата. Найдем асимптоту вида у = кх + Ь. Разделим члены
уравнения наг3: 1= ( —) — 3	) — = 0. Отсюда к = lim — = 1,
—Зг/2
b = lim (у — х) = lim —------------ = — 1. Итак, асимптота у = х — 1.
r->oo	1-ЮТ X2 + ху + у2
Экстремум функции х = <р(у) = \/у3 + Зу"2: при у = —2 хэ = -^4 Ай 1, 6;
при х = 0 у = —3 — перегиб (рис. 54). 1977. х3 + у3 — Заху =0 —
декартов лист (см. задачу 366). Особая точка 0(0; 0) — узел с каса-
тельными у = 0 и х = 0. Найдем асимптоту у = кх + Ь. Приведем
/ г/ \ 3	/ у\ 1	. f У\
уравнение к виду 1 + — J — За — J— = 0; откуда к = lim Q—J = — 1,
Рис. 54
Рис. 55
b = lim (г/ + х) = lim —------------ = —а. Итак, у = —х — а — асимп-
r->oo	r->oo X2 — ху + у2
.О
тота (рис. 79). 1978. у = ±	--. Симметрична относительно Ох
уж2 — а2
Ответы
309
и Оу. Область расположения |ж| > а и |г/| > |ж|. 0(0; 0) — особая
изолированная точка. При х = ±ал/2 экстремум у = ±2а. Асимптоты
х = ±а и у = ±х (рис. 55). 1979. у = ±жл/2 — х; область расположе-
ния х 2. Точки пересечения с осью Ох: при у = 0 Xi = О, Х2 = 2.
4	1^2
Особая точка (0; 0) — узел. Экстремумы у: при х = - уэ = ±—-= =
3	3v 3
= ± 1,08. (Кривая имеет такую же форму, как на рис. 49.) 1980. у =
= ± — ^/а2 — (ж — а)2; область расположения |ж — а| </ а, или —а
</ х — a а, или 0 </ х 2а. При у = 0 х± = 0, х-2 = 2а. Точка (0; 0)
/------- х(а — х)
особая (точка возврата). При у = 0, т. е. л/2аж — ж2 4-	— =
л/2аж — ж2
= 0, ж = —, уэ = ±—а ай ±4а (рис- 56). 1981. у = ±(ж + 2)л/ж.
Область расположения ж^ Он еще изолированная точка (—2; 0). Точка
перегиба при ж = 2/3. Кривая такая же, как на рис. 51, но смещена влево.
> 0; 2) ж < —а. Асимптоты:
— и ж = 0. Точка возврата (—а; 0). Экстремумы
Зл/За	ж2 .----
—-— ай ±2, 6а. 1983. у = ±—у/х + 5; область
1982. Две области расположения:
За
г/ = ^ + у
1)
У при ж = -
расположения ж /> —5. Особая точка (0; 0) — точка самоприкосновения.
Экстремумы у: при ж = -4 |t/|max = 8, при ж = 0 |г/|ты = 0 (рис. 57).
310
Ответы
1984. у = ±тл/ж2 — 1- Области расположения |ж| /> 1 с изолированной
точкой 0(0; 0). График такой же, как и на рис. 51, с добавлением еще до
симметрии кривой слева. 1985. При у = 0 ij = 0 и = —4; при х = О
г/1 = 0, г/2 = ~ 1. Особая точка (0; 0) — узел с наклоном касательных
к = ±2. При х = —8/3 г/max = 1, 8 и при х = 0 г/т;п = —1. Асимптота
у = ж + 1. Кривая пересекает асимптоту при х = —0, 4 и затем описывает
петлю, пройдя через (0; 0) и (0; — 1).
1986. 1) у = ±(ж — а)
д-----; кри-
2а — х
вая расположена там, где х и 2а — х имеют одинаковые знаки, т. е. при
0 </ х 2а. Точка (а; 0) особая — узел с наклоном касательных к = ±1.
ах
Асимптота х = 2а (рис. 84). 2) у = +	----; область расположения
»/ж2 — а2
|ж| > а и |г/| > а с изолированной точкой (0; 0). Асимптоты х = ±а и
у = ±а. Между каждой парой этих асимптот точек кривой, кроме особой,
нет, ибо |ж| > а и |г/| > а. Кривая состоит из четырех симметричных
ветвей, приближающихся к асимптотам х = ±а и у = ±а. 1987. 1) у =
1а — х
= ± хО-----; область расположения —а < х < а. Точки пересечения с
V х + а
осью Ох: у = 0, Xi = 0, Х2 = а. Особая точка (0; 0) — узел. Асимптота
х = —а. Кривая — строфоида и получается перегибанием рис. 84 по оси
Оу и смещением затем оси Оу влево на а. 2) Области расположения:
х а; х < —а и х = 0. Точка (0; 0) изолированная. Асимптоты х = —а,
а(^5 + 1)	1 R	„
у = а — хиу = х — а. При х =----------------- Ай —1,оа уэ ~ ±3,3а.
1988. 1) у = —ж2/4; 2) у = ±2х. 1989. 1) у = ±Л; 2) у = 0 и у = —х.
1990. 1) г/ = 1; 2) г/ = 1 — геометрическое место точек возврата, но не
огибающая; 3) у = 1 — и геометрическое место точек возврата и огибаю-
щая; 4) у = х — 4/3 — огибающая, у = х — геометрическое место точек
г3
возврата. 1991. ж2/3+г/2/3 = а2/3. 1992. у2 =---1993. (х2+у2)2 =
дх^
= 4а2жг/.	1994. Семейство траекторий у = х tg а — —--------—. Их
2о2 cos2 а
62	9Х^	2	2
огибающая (парабола «безопасности») у = -----26^ 1995. 1) х + у =
= р2- 2) у2 = 4х; 3) у = 1. 1996. у2 = 4(х + 1). 1997. х2/3 + у2/3 =
= I2/3. 1998. у = —4ж2/3. 1999. 2х + 4у - г = 3. 2000. ху0 + ух0 =
о	ХХо min ZZo
= 2гг0. 2001. xyozo + yxozo + zxoyo = За3. 2002. -г- +	----— = 1.
а2 о2 с2
У~4 z ~5	/поп»
— -----; в точке (I); (J; U).
—5
2003. х + у - z = ±9. 2004. -------
3
4
Ответы
311
2005. cos а = — cos /3 = cos 7 =	2006. г/ = О, х + z + 1
V 3
поверхность изображена на рис. 45, с. 303. 2009. Касательная
тга	тга
кость х — у + 2z = —. Ее расстояние от начала равно
коид — поверхность «линейчатая». Прямые линии получаются в сече-
ниях z = h. При z
Зтга
= 0;
плос-
Гели-
тга
= 0 у = 0, при z = —
х = 0, при z
2
тга
у = x, при г = —
у = —х, при z = тга у = 0 (рис. 58). 2010. z =
г	2
-. 2013. cos а =
5	3
2012. ----
4
1
г/-з
3
п 2	1	а
cosр = —-; cos7 = —-. 2014. Плоскость z + у — х = а, р = —
2016. 1) z = 4; 2) 2х + 2у + z = 6. 2017. gradz = — 2«i — 2t/j = — 2(i + 2j).
3
2018. 1) grad г = -------; 2) grad г =
2 т
= ^7- 2019. grad/г = -|i - 2j.
/х^ -р и^
2020. tg<£> = |gradz| = i /--------- =
V 4жг/
/Л)	du	\/2
= ъ 0,79. 2021. — =
4	dl 2
2022. — = 2 + V2; grad и = 2i + 2j +
dl
+ 2k, |gradtt| = 2^3. 2023. grad а =
6
± 4i.
2024.
Рис. 58
2025. grad z = 0, 32i—О, 64J, |grad z| =
г- du yz + xz + xy
= 0, 32л/5. 2026. — = У	y =
5
=	2027. grad а = 2(«i + t/j — zk), |grada| = 2z\[2. 2028. grad а =
а/ 3
ж! + t/j + zk	3
= ---------------, |gradtt| = 1 в любой точке. 2029.------------/	.
2030. zmin = -1
= у = 4. 2032.
мума. 2034. zmjn
тг
3
при х = —4, у = 1.
‘-|п||| = 0 при X = 1,
2
=-----при х = —2, у
е
2036. zmjn = 2 при х = у = 1.
У
2031. ,:maz
2033.
1
2
= 0.
2035. ‘.та/
2037. zmax
= 12 при х =
Нет экстр е-
зТз
= — при
= —4 при
х = у = — 2 и zmjn = 4 при х = у = 2. 2038. х = у = \/'2\', z = 0, 5 \/21'.
2039. (8/5; 3/5), (-8/5; -3/5). 2040. Нужно найти минимум функции
312
Ответы
z = d2 = х2 + (у — 2)2 при условии х2 — у2 — 4 = 0. Искомая точка
(±л/5; 1). 2041. R = 1, Н = 2. 2042. 1) Вершины (±3; —1) и (0; 2);
2) луч должен пройти так, чтобы sin а : sin (3 = гд : V2, как это и проис-
ходит в природе. 2043. zmjn = 9 при х = 0 и у = 3. 2044. zmjn = 0 при
х = у = 2. 2045. zmjn = 0 при х = 0 и у = 0. 2046. zmjn = 0 при х = 2,
У = 4. 2047. zmax = 1 при х = у = ±1,	= -1 при х = -у = ±1.
ж — у Я- 4
2048. V = 8. 2049. 1) Нужно найти минимум d = --—---- или мини-
мум z = х — у + 4 при условии \.г — у2 = О', искомая точка (1; 2); 2) 2а6.
/ 5	жз
2050. R = < /—2051. Уравнения интегральных кривых: 1) у = —;
V 7TV 3	3
х3
2) у = х3- 3) у = —-. 2053. ху' = 2у. 2054. 1) у2 - х2 = 2хуу';
2) х2 + у = ху'. 2057. у = Сх, у = —2х. 2058. ху = С, ху = —8.
2059. х2 + у2 = С2, х2 + у2 = 20. 2060. у = Сех, у = 4ег+2. 2061. у =
= Се1/х. 2062. х + у = lnG(« + l)(t/+l). 2063. г = Се1У + а. 2064. s2 =
t2 — 1 + Ct	г г •>	С* sin2 ж — 1
= ---------. 2065. у = СеУ, у = гУ-2. 2066. у = ---------------;
о	1	11
у = 2 sin х---. 2067. 1— = С; у = —х. 2068. Общие интегралы:
2	х у
1) у = С(х2 — 4); 2) у = Ceos х. Все интегральные кривые первого урав-
7Г
нения пересекают ось Ох при х = ±2, а второго — при х = (2п — 1) —
х3
(особые точки). 2069. у = —. 2070. I
о
у'"2 dx, откуда
о
О
у = ал/1 + у'2, у' = ±-\/—- — 1; положим у = a ch и, тогда a sh и х
V а2
х и' = ±shiz. Отсюда: 1) sh и = 0, ch и = 1, у = а; 2) a du = ±dx,
х + С
аи = ±(ж + С), у = a ch и = a ch---; при ж = О у = <аиС = 0. Итак,
ж	а	„
или у = a ch-----цепная линия, или у = а — прямая. 2071. у = ах.
а
2072. у2 = 4(ж + 2). 2073. За 40мин. Решение. Пусть через t секунд
dT
температура тела будет Т; = —к(Т — 20°С), где к — пока неизвест-
ный коэффициент пропорциональности; In (Т — 20°С) = —kt + С; при
800 С
t = О Т = 100°C, поэтому С = In80°C, kt = In——	; подставив
1 — ZD \_z
сюда Tj = 25 °C и = 60 °C и разделив почленно, исключим неизвест-
kij	In 16
ное к: ----- = -----, t = 40 мин. 2074. V Xi — —Н + Тcos а = 0,
к • 10	m 2
Ответы
313
v-v	, -г • n	+	dy px	p .
2^ У = -px + 1 sin a = 0, откуда tga = — = —, у =	+ О
(парабола). 2075. Уравнение касательной У — у = у'(X — х). Поло-
жив У = 0, найдем абсциссу точки А пересечения касательной с осью
г/	у
Ох: Ха = х — —. По условию Ха = 2ж, х =------------; решив это диффе-
У	У
ренциальное уравнение, найдем искомую кривую ху = —а2 (гипербола).
2076. ж2 + 2г/2 = С2. 2077. у2 - х2 = С. 2078. Чх2 + Зг/2 = За2.
Сх2
2079. у = Сх4. 2080. у = Се~4!х . 2081. 2г/ = ------------— - 1. 2082. у =
(1 -I-
2084. г = С cos р, г = —2 cos р.
2085. y/у = х In х — х + С, y/у = ж In ж — ж + 1.
cVTTlc
х + л/1 + X2
2086. у =
1	2	2
у =	2087. ху = -1. 2088. у = аех/а. 2089. у = --.
ж + VI + ж2	1 — ж
2090. х2у = С. 2091. Радиус-вектор ОМ = ^/ж2 + г/2, отрезок нор-
мали MN = ------ = уу/1 + tg2 а = у у/1 + у'2. Искомая кривая или
cos а
х2 + у2 = С2 (окружность), или ж2 — у2 = С (гипербола). 2092. у = Сх2.
С
2093. у - ж = СехКУ~хХ 2094. ж2 - у2 = Сх. 2095. s2 = 2/21пу.
„ „	„	С — е~х	С — соз2ж
2096. у = Сх3 - ж2. 2097. у = ———. 2098. у = —--------------.
2ж2	2 cos ж
1	ех2
2099. г/= ,	. 2100. у2 = ——-. 2101. sin - +1п ж = С. 2102. у =
У ж!пСж У 2ж + G	ж	У
= —4-----. 2103. у = In ж + -. 2104. у3 =	+ Д. 2105. у =
С — In х	х	2х хл
2   1	11
= -----. 2106. 8 = Ct2 +	8 = 4t2 + -. 2107. у = хеСх, у = хе~х12.
Ч	t	t	У ’ У
2108. (ж —г/)2 = Су. 2109. ж2 + г/2 = ЧСу. 2110. i =	+ ^Me~Rt/L - 1).
R R
2111. Положив X = 0 в уравнении касательной У — у = у (X — ж),
найдем Уо = —ON = у — ху', ON = ху' — у = ОМ = ^/ж2 + г/2.
ж2 - С2
Отсюда у = ———. Зеркало должно быть параболоидом вращения.
9	~	/	1пС*(ж + л/a2 + х2\
2112. у2 = Схе~у/ . 2113. у = -----\	2114. При ж > О
у/ а2 + ж2
</^ = In—, при ж < 0 <	= 1пС*ж. 2115. у =----------Н
V х х	V ж	3 у/Чх + 1
InCtg (ж/2)	о
2116. у = 1 + -----1	2117. s = f3 Inf - 1 + Ct2. 2118. у2 =
cos ж
314
Ответы
=	,	,2- 2119. г/= 2(sin т — 1) 4-Ge-sinr. 2120. у = ---—, у =
1 + Сех	1 — Cxz
2х	1
= -------. 2121.г/3 = х+Се~х, у3 = х-2е1~х. 2122. у = —,
1 - Зт2 ''	''	У 3V1 - т2 - 1
2123. (х - а)2 + у2 = а2. 2124. у =	. 2125. у2 = х(Су - 1).
и4	х v2	С
2126. ху =	+ С. 2127. - +	= С. 2128. у = cos х + ------.
4	г/2	sin х
t	Ct — 1
2129. s = -----------—. 2130. х2у2 + 21пт = С. 2131. s = -------—.
С + t-tlnt	У	t2
С	х
2132. у = т2 + Сх. 2133. sin у = х + —. 2134. у = ------------л-.
У	У	х	У С + 2е~хС
2135. 4т2 + у2 = Сх. 2136. х3еу - у = С. 2137. у + хе~у = С.
1 V
2138. х2 cos2 у + у2 = С. 2139. у = —; х 4— = С. 2140. In у = In cos у,
х2 sin у + 0, 5 cos 2г/ = С. 2141. у = е 2х; у2 = (О — 2х)е2х. 2142. у =
1 X
= —----------\-х^ — С. 2143. ж3+2жу—Зу = С. 2144. х^у—2ж2у2+3у4 =
sin у sin у
= С. 2145. Х СО82г/ + т = С. 2146. у = тг/-1пг/ = 0. 2147. у = Д-;
2	г/	х4
у2 = Сх3 + х2. 2148. у = е~У; е ycosx = C + x. 2149. In у = — In х, у =
= —; х sin г/ + у In х = С. 2150. у = (С ± х)2. Через точку М (1; 4) прохо-
дят кривые у = (14-т)2 и у = (3 —ж)2. 2151. у = sin (С ± х). Через точку
. /	7Г\	. /Зтг
проходят кривые у = sin ( х----I и у = sin —
2152. у = Сх2 + —; особые интегралы у = ±2т. 2153. 1) у = х
/ /------ \ 2
и х2 + у2 = О2; 2) х (. /1 + — ± 1 ) = С или (г/ — С)2 = 4Сх.
бые интегралы х = 0 и у = —х. Область расположения парабол:
Осо-
при
х > 0 у —х, при х < 0 у < —х. Параболы касаются оси Оу и
(х — С)2
прямой у = —х. 2154. 1) у = 14------------; особый интеграл у = 1;
1	2	,____
2) х = 2р-----у = р2----------Н С. 2155. 1) у = (С 4- Vх + I)2; осо-
р2	р
бый интеграл у = 0; 2) х = Ct2 — 2t3, у = 2Ct — 3t2, где t =
р
3) Су = (т — С)2; особые интегралы у = 0 и у = —4т. 2156. 1) у =
/2 _____________________________________________________
= Сх — С2’, особый интеграл у = —; 2) у = Сх — ау/1 4- С*2; особый
интеграл х2 4- у2 = а2’, 3) у = Сх 4-	2 5 особый интеграл у = 1, 5т2/3.
Ответы
315
(ж + С)2	7 3\	ж2
2157. у = 1-------; через М II; - I пройдут две кривые: у = 1 ——
ж2	3
и у = ж—2158. 1) ж = 2р+ -р2 + С, у = р2+р3; 2) х2 + (у+С)2 = а2.
2159. у = — — + Сх + С2', у = —2160. 1) у = Сх + —; особый ните-
трал у2 = 4ж; 2) у = С(х + 1) + С2', у = — -—7 . 2161. Отрезки каса-
У
тельной У — у = у'(X — ж) на осях координат: Ха = х-, Yg = у — ху'.
У'
Ув
По условию ------- = 2а2; (у — ху')2 = — 4а2у', у = ху' ± ^/—4а2г/' —
уравнение Клеро. Любая прямая семейства у = — Сх ± 2ал/С, а также
кривая, определяемая особым интегралом ху = а2, дает решение задачи.
2162. Парабола (у — ж — а)2 = 4ах. 2163. 1) у = 31пж + 2ж2 — 6ж + 6;
2) у = 1 — cos 2ж; 3) у = С\х + ж arctg ж — In у/1 + ж2 + С2. 2164. у =
= —Н Ci In ж + С2. 2165. у2 = — С1Ж + С2. 2166. у = С\ sin ж — ж —
— -8т2ж + С*2. 2167. у3 + Сру + С2 = Зж. 2168. у = С*1ж(1пж —
2169. ctg у = С2- С\х. 2170. 1) у = ех(х - 1
1	Ж	1
= arctg + ^2 (при Ci > 0), In
yCi	V^l	^V—^1
C*i < 0), С*2-(при Ci = 0). 2171. у" = —(/ — ж). При ж = 0 у = 0 и
™	EI
х3\
2---— — уравнение кривой изгиба. 2172. Сру =
О /
+ С2 (при
у' = 0, у =
4
ж3
2174. у = —
о
= —In cos ж.
2173. у = a ch
2175. у =
2176. у =
2178.
2 к	г
С1Ж + С2 — In cos ж; частный интеграл у =
— — — + С\ arctg ж + С*2-	2177. t'i//2 =
/2
у = (С1Ж + С^)2. 2179. s = —— + C*i Int +
+ С2. 2180. 4(С\у - 1) = (С1Ж + С2)2. 2181. у = С2 - С\ cos ж -
- ж. 2182. См. 2177. 2183. у = -йгсовж. 2184. у = Схех + С2е3г.
2185. у = (Ci + С2х)е2х. 2186. у = е2х(А cos Зж + В sin Зж). 2187. у =
= C*ie2j; + С2е~2х = A ch 2ж + В sh 2ж. 2188. у = A cos 2х + В sin 2ж =
= a sin (2ж + ip). 2189. у = С\ + С2е~4х. 2190. ж = С^е* + C2e~4t.
2191. р = Acos^ + Bsin^. 2192. s = e-t(Acost + Bsint); s =
316
Ответы
= e-t(cos/+2sint). 2193. у = С\ех+ (С’2+Сзх)е2х. 2194. у = С\ ch 2т +
+ С2 sh 2т + Сз cos 2т + С4 sin 2т. 2195. у = Cie2j; + е~х(С2 cos тл/3 +
+ Сзвттл/З). 2196. у = (Ci + С2х + Сзх2)е~ах. 2197. у = A sin т sh т +
В sin т ch т + С cos т sh т + D cos т ch т. 2198. у = A ch т + В sh т +
Ceos — + Osin—. 2199. Отклонение т = a sin
, период
2201. т
2тг
2200. х — a cos </-t, период Т = 2тг
ае kt sin (ait + ср), где ш = л/у-
к2
—. 2202. у = С\е~2х + С2е~х.
22ОЗ.у=(С1х + С2)еах
2204. у = е Х(С1 cos 2т + С2 sin 2т). 2205. т =
= Cie3t + С2е *. 2206. т = С\ cos act + С2 sin act. 2207. s = C\ +
+ C2e~at. 2208. т = е-‘(Асо8/С2 + BsintC2). 2209. у = C\e-X +
+ (С2х + Сз)е2х. 2210. у = С\е2х + С2е~2х + Сз cos т + С4 sin т. 2211. у =
= (Ci + С2х) cos 2т + (Сз + С4т) sin 2т. 2212. у = -----   =	sh т.
2214. у = Cie2j; + С2е~2х - 2т3 - Зт. 2215. у = С1е~х + С2е~2х +
+ 0, 25л/2 cos — 2т) . 2216. у = С\ cos т + С2 sin т + т + ех. 2217. у =
3
= Ci + С2е~3х + -т2 — т. 2218. у = e~2x(Ci cos т + С2 sin т) + т2 —
— 8т + 7. 2219. у = С\е2х + (С2 — х)ех. 2220. т = Asinfc(t — to) —t cos kt.
Г-	t3
2221. у = CC'^ +	_ (x _ 2)e“C 2222. у = Ci + C2e2x--------.
6
2223. у = -e~x + t<’;' + Cxe~2x + C2e~3x. 2224. т = О/СуоС/ +
+ C2 sin kt) +sin kt — 2 cos kt. 2225. у = Ci +C2x + (Сз + х)е~х +т3 — Зт2.
2226. у = Cre3x + (с2 - |) е~3х + С3cos Зт + С4 sin Зт. 2227. т = Ci +
+ С2 cost + Сз sin / + t3 — 6/. 2228. у = (Ci 4-) е~2х + (С2 cos т^З +
/	I2 \	t
+ Сз sin тСЗ)еС 2229. 1) т = I Ci + C2t + — I e-2t; 2) т = A cos - +
/	1	x
+ В sin —I—. 2230. Здесь y\ = cos 2ж,	= sin 2ж, w = 2;A=—— + C*i;
a	a	2
1	/ x \	f 1	\
В = - In sin 2т + C2 и у = I Ci-I cos 2т + C2 4— In sin 2т sin 2т.
4	\2/	\	4	/
2231. у = [(Ci +ln cos x) cos x + [C2 + x) sin t] e2x. 2232. у = (Ci — In x +
+ C2x)ex. 2233. у = C\ cos x+C2 sin x—cos x In tg + —) . 2234.1) у =
= Ci + C2e x — (1 + e ' ) In (I + ex) + t; 2) у = e 2x ^Ci + C2x +	.
2235. т = a(e-‘ + t - 1). 2236. у = C\ex + C2e~2x - 3(t2 + t + 1, 5).
Ответы
317
2237. у = Cie2x + C2e3x + -(5 cos Зх — sin Зж). 2238. г/= (Сгж 4-G2)e х +
6
1	Z* 3 х	3 х
+ —ех. 2239. у = е~х!’2 ( С\ cos----------Н G2 sin — | — 6 cos 2ж + 8 sin 2ж.
4	\	2	2 /
2240. у = С\ех!2 + С2е~х!2 - ж3. 2241. у =	+ (с2 - |) е~х.
2242. s = e-t(G1cosZ4-G2sinZ)4-(/-l)3. 2243. 1) у = етг(С1 + С2ж) +
4------—; 2) у = С\е2х!п + G2e-2r/n------. 2244. у = A cos х + В sin х +
2m2	п
1	(	х*\
+ С cos 2х + D sin 2х---х cos х. 2245. у = C*i + С^х + С&с2, Н------
2	\	6 у
/*	1 -j-. j,	о ^,2	\
2246. у = (—------------— + Ci + С2х ] е~2х. 2247. 1) у = Gisinz +
+ G2 cos х 4------; 2) у = (Gi — In I sin ж I) cos 2ж 4- ( G2 — ж-ctg ж ) x
2 cos ж	\	2	/
x sin 2ж.
2248. у =
x2 + x arcsin —
2
e'
2249. у =
= ------1 у-------. 2250. у = 1 + Geos ж. 2251. г/ = ж(1 + С^1 - ж2),
7 х \	е* 4- С
линейное. 2252. у = С 1 + —^=  2253. s = -----------—. 2254. Jy =
\ V1 + х2 /
= Сх2 — 1. 2255. 2С*г/2 = ж(С*2ж2 —1). 2256. у = ж!пж — 2ж4-С*11пж4-С*2.
2257. t/(G2 - (Лж) = 1. 2258. у = Схетх + (с2 - е~тх. 2259. у =
С	1
= In ж + ----. 2260. у = хес1х~х. 2261. у2 = --------——. 2262. у =
In ж	ж 4- Оех
ж3
= (С,1 + С2ж)е;Г + С,з+ — + 2ж2 + 6ж. 2263. Сгу = 1 + С2ес'х. 2264. s =
О
= С1е2Че-((С2 + С;Х)-^. 2265.1) s = (t2 + C) tg 2) у2 = Сж2-1.
. sin ж 4-Geos ж .	ж\	„ /о	жуЗ
2266. 1) у = --------------; 2) у = е~ Gi + - + G2G/2cos +
х	\	3 /	2
4- С'зех/2 sin —• 2267. 1) у = (Gi — In у/1 4- е2х)ех 4- (G2 4- arctg ех)е2х;
—	—	a2 d2x
2) у = С1е^сх + С2е~^сх му = Сгж + G2. 2268.---------— + ЮООж = О,
<7 аО
„ iovw4 , n . ioVW4	™ т dT
х = Л cos---------1 4- В sin-----1, период 1 = —-------. 2269. —— =
а	а	5л/1О<7	dr
k k	k
=-------T =----------|-G; к и G находим из условий: 20°С =--------Н G
4тгг2 8тгг	8тг • 2а
и 100°C = —— +С; Т = 160 °’а - 60°C = 40°C. 2270. 1) у =
8тг • а	г
= С1Х + С2ж-Х + С3ж3; 2) у =	+ С2ж2; 3) у = С1ЖП + С2ж-<п+1).
318
Ответы
2271.1) у = х 2(C*i +С’2 In х); 2) у = С\ cos In хАС? sin In х. 2272.1) у =
=	+ С\х 1 + С'2', 2) у = C*it3 + —z- — 2Inх + —. 2273. 1) у =
3	х2	3
= С\х + С-2х2 - 4т Inх- 2) у = С1 + С21°Ж + 1П Х  2274. Х) У =
/3	\
= (— + Cix + СУ т2; 2) у = ^+Ci cos In т+С*2 sin In т. 2275. ж = С±е* +
+ iy~3'. J/ = —-7- = Сдв* —3C*2e-3t. 2276. т = ?+С1 +G2e-2t, у = е‘ +
at
+ C1-C-2e-2t. 2277. х = 2е~* АСте* AC2e~2t, у = Зе“‘+3C'iet+2G2e-2t.
2278. х = е‘ + C\e3t + O2e-3t + G3cos (t + <?). 2279. x = e~2t(l - 2t).
2280. x = Cie* + C*2e-t At chC 2281. 1) и = <p(x) Атр^у)', 2) и = y<p(x) +
+ ^(x)', 3) и = х(р(у) + -ф(х); 4) и = ax2 In у+Ьху+(р(х) + -ф(у). 2282.7 =
д2и д2и д2и
= у2(х+у— 1). 2283. Чтобы уравнение А—-+2В-—-—= F при-
Ох2 Ох Оу оу2
вести к каноническому виду, нужно решить характеристическое уравне-
ние A dy2 — 2В dx dy + С dx2 = 0; в двух его интегралах <р(х, у) = £
и "ф(х, у) = г) произвольные постоянные £ и г) принять за новые пере-
менные и преобразовать к этим новым переменным данное уравнение
(см. задачи 1941 и 1942). В нашем примере нужно решить уравнение
dx2 + \dx dy + 3dy2 = 0, откуда dy A dx = 0, dy + 3dx = 0, у + x =
<92ы
у А Зх = у. В новых переменных уравнение примет вид ——— = 0.
ОТ]
Отсюда и =	+ V’(7?) = v(y + х) + "Ф(у + Зт). 2284. Характеристиче-
ское уравнение т2 dy2 — 2ху dx dy + у2 dx2 = 0, или (т dy — у dx)2 = 0,
или d J =0; — = Решения равные; за у принимаем у. Итак,
задачу 1944.)
У е	v	/
характеристики: — = £ и у = у. Уравнение примет вид (см. задачи
О2 и
1944 и 1945) 7^—^- = 0; и = Ар((,) + ip(£.), или и = yip(y/x) + -ф(у/х).
2285. и = у<р(у + 2т) + -ф[у + 2т). 2286. и = ху + sin у cos т. 2287. (См.
и = г/In т + 2у + 1. 2288. и = y/xtip ( — ) + Tp(xt); част-
ное решение
ное решение
1
3
и
у----2289. и = е Х(р(х — t) + ^(т); част-
/)е“‘ - т. 2290. Частное решение и = xat +
x+at
ooqi „ _ f(x - at) + f(x + at) 1
ll —	“Г
2a
2292. 6 -
2
32	125	9a2	1	1
- 41n2	3,28. 2293. 1) —; 2) 4. 2294. ---------. 2295. -----. 2296.--------
’	7 3 ’ 7	6	2	2	e
Ответы
319
2297.
2
1
1
2
9
тга

dx = 1-;
6’
О
о о
1
О
о
о
о
о
dy
16
У
2299.
2. 2300. Пло-
-2
у2-4
— 4
щадь
меньшего
сегмента
4тг
3
3
2302.
3
2308.
ь
8
4
2315.
2321.
2326.
868 9	3 9
---а2. 2303. -тга2.
15
8
2304.4,5.
За2
2,457а2.	2301. ----In2.
’	2
2	9
2305.—. 2306. ^2-1. 2307.-а2.
6	2
2
ь
8тг + 9^3. 2309.
’Ч 2
4/ а
2310. 7In2.
ь
2
dx =
2
о
о
У
о
а2(3тг
-2).
12
а-У
4
о
о
4
У2/4
dx+
о
о
о
2312.
2313. (3; 4,8).
2314.
2а
У’
2
О
( 4а
Ьу
тга4	„„„
—. 2322. —. 2323.	2324.
8
„4
( Ж&а\
2316. 0; — .
\	315тг)
88а4
4
тга
2
105
17а4
2318. ----.
96
За
У’
а4
2319. —
4
За
У
30'
2
2331. 42-.
3
2327. 3.
2328.
79 о
2332. —а3.
60
12
2329. 47,5.
а4
2320. —
6
(У)
\ Зтг/
35тга4
2330. ----.
16
2325.
2333. Сечение плоскостью z
= ± Уа(а — h) — параллельные прямые, т. е. поверхность цилиндри-
320
Ответы
ческая (рис. 59). Искомый объем V = 2 J dx j
о о
(рис. 60). 2335. (См. рис. 46, с. 303.) -а3.
9
, а3 16
z dy = —. 2334. — а3
тга3
2337. ----------------.
12
а ‘1
а3
2336. —
3
Рис. 59
Рис. 60
тг/2	а
/('	4m3
т cos dtp / г2 dr = (рис. 61).
о	о
2340.— .2341.4тг^3а3. 2342. —— (Зтг — 4) (рис. 62). 2343.тг2а3 (рис. 58).
2	9
Рис. 61
Рис. 62
Ответы
321
Рис. 64
Рис. 63
128
ноида, умноженной на половину высоты (рис. 65). 2353.-а3. 2354.18тг.
105
3	5тга3
2355. 2тга3. 2356. 8тгIn2 (см. рис. 45, с. 303). 2357.—тга3. 2358.-.
16	16
322
Ответы
2359.2360.13. 2361. ^L2. 2362. 2тга2. 2363.^7(272-1).
3	3	3 V V 7
14
2364. 2тгр272.	2365. 8а2.	2366. 4а2(тг - 2).	2367. —тга2.
__________ о
f [ Vх2 + У2 + J .	р2 •	я ЙПО ОНО
2368. <т = / / —---------ах dy = sin а; при р = 60 и а = 30
тг//2
77
(S)
2369.
радиус сечения г =
а \	2тга3 ,
. 2370. -(2 -72).
V о /	О
2372.
2375.
2379.
2384.
dx dy / z dz = —. 2373.	- -Y 2374. (б; 0; -Y
J J ' J 24	\4’ 4 4/ V ’	3/
0	0	0
а5	тга5	. тга3	. тга3	тга3 ,
— . 2376. —. 2377. 1 ----------; 2 ----. 2378. ----- 872 - 7.
4	72	7 3 ’	7 60	6 V	V 7
32	тга3	тг/z4	a4	( За\
—тг.	2380. —. 2381. ——.	2382. —. 2383. 0; 0; — .
3	6	4	12	у 8 J
32777	a3	„
	. 2385. -. 2386. бктга , где к — коэффициент пропор-
135---------------360
циональности.
4 по прямой ОА,
Ю
< — по дуге О А,
О
2 по ломаной ОБА.
2388. 1) 8; 2) 4. 2389. J (х dy + у dx) = 8 в обоих случаях.
дО	дР
что здесь —— = ——. 2390. 1) 1,5a2; 2) a2. 2391. 8a2.
дх	ду
тгтаЬ	. 5тг	.	1	1
2393. -----. 2394. 0. 2396. 1 —; 2 —: 3 2 -----------= .
4	' 6	'	2	' 7з
8	3 „	2kmM
2398. тгаб. 2399. —. 2400. -а2. 2401. X = 0, У = ----—
15	2	’ тга2
Это потому,
2392. тга2.
2а3
2397. —.
О
2402. У =
ктМ
а2л/2
2403. У =
ктМ
59	За2
2404. 1) -16; 2)—3) -12. 2405. 1) —;
О	7
а2	11а2	3	.,	4	а3	тга4
2 —: 3 -------. 2408. -тга2. 2409. -. 2410. —. 2411. ----. 2412. Каж-
7 2 ’	7 6	8	3	2	48
дая из частей формулы равна 4тга3. 2413. Каждая из частей формулы
а4 /4	тг \	12 к
равна — —|-------. 2419. Каждая из частей формулы равна —тга .
3 \5	16/	5
2421. 0, 15а5. 2422. Нет. 2423. Да. 2424. Да. 2425. Расходится.
/х dx 3
--------— = -. 2428. Сходится,
7 + 1)3	8
1
Ответы
323
дится,
dx
_1_ ,.'2
7Г	С
— . 2429. Расходится, ибо /
4	J
1
— dx = сю. 2430. Схо-
dx
J (2х + I)2 - 1
1
— In
4
= - In 2. 2431. Сходится.
Ji 4
2432. Сходится. 2433. Сходится. 2434. Сходится, ибо lim n+1 = - <
n->oo ип 2
< 1. 2435. Расходится. 2436. Расходится. 2437. Сходится. 2438. Расхо-
дится. 2439. Сходится. 2440. Расходится. 2442. 1. 2443. -. 2444. Схо-
3
Сходится абсолютно. 2446. Сходится не
абсолютно. 2448. После первой переста-
Л 1	<1	Л	1
в виде 1------— - +------------— - +
\	2/	4	\ 3	6/	8
дится не абсолютно. 2445.
абсолютно. 2447. Сходится
новки членов напишем ряд
/1 1 \ 1
+ I - — — I — ^ + - • • Выполнив действия в скобках, получим ряд, члены
которого вдвое меньше членов данного ряда,
новки членов преобразуем n-ю тройку членов:
1 1
4п — 3 4п — 2 +
первые четыре члена
два — ряд с суммой
1	1 1
4п — 1 4п ”1” 4п — 2
образуют данный ряд
g
—.	2449. Сходится.
2451. Сходится, ибо j
1
После второй переста-
1 1	1
4п — 3 + 4п — 1	2п
—; при п = 1, 2, 3, . . .
4п
суммой S, а последние
2450. Расходится, ибо
f dx
J 100ж — 99
i
дится,
2х - 1
,.2
2453. Сходится. 2454. Сходится, ибо
i
ТГ	„
— = —. 2452. Расхо-
4	8
1
м„+1	1	20п + 21
hm ------ = - < 1. 2455. Сходится, ибо hm ------ = hm ----------— =
n->oo Un 2	n->oo Un П->ОО 3(20n + 1)
= - < 1. 2456. Сходится. 2457. Сходится не абсолютно. 2458. Сходится
абсолютно. 2459. При а > 1 сходится абсолютно, при а = 1 сходится
Сумма
л 1 1
не абсолютно, при а < 1 расходится. 2460. -. 2461. -. 2462.
1	хп
ряда S(x) = ------- при х < 1, остаток Rn = S — Sn = ----------•
На от-
резке [0; 1/2] |Rn | < ^п-1 < 0,001, как только п — 1 >	;
324
Ответы
2463. Ряд имеет
х I 1 при 0 < х 1,
сумму S = ---------- = <
1 — (1 — х) I 0 при х = О
) (1 — х)п при О < х 1,
и остаток Rn = <
I 0 при х = 0.
При любом п остаток Rn будет больше, например, 0,9, как только х < 1 —
— -/0,9, т. е. на отрезке [0; 1] ряд сходится неравномерно. Но на отрезке
[1/2; 1] он сходится равномерно, ибо тогда при любом ж|7?п| < — < е,
2П
— 1g £
как только п > ——— ; в частности, |7?п| < 0, 01 при п / 7. 2464. Оста-
ток знакочередующегося ряда меньше по модулю первого отброшенного
жп+! 1
члена. Поэтому на отрезке [0; 1] |7?п(ж)| < ----- < ----- < 0,1, как
п + 1 п + 1
только п + 1 / 10 или п / 9. 2465. Ряд имеет
и остаток Rn
{1 + ж3 при
0 при
х > 0,
х = 0
1
<	(1 + Т3)П-1
о
при х > 0,
при х = 0.
При любом п остаток Rn будет больше, например, 0,1, как только х3 <
< п~/Тб — 1, т. е. при ж / 0 ряд сходится неравномерно. Но при
ж / 1 он сходится уже равномерно, ибо тогда при любом ж / 1 |7?п| /
1	— 1g е
< ------ < е, как только п — 1 > —-; в частности, \R„ \ < 0,001 при п >
\ 2„-i	’	jg2 ’	’ 1	1	’	F
/11. 2466. При любом неотрицательном ж члены данного ряда меньше
.	\	л 1	1	1
(или равны) членов числового сходящегося ряда 1+- + — + — + ...
0	0 о
Следовательно, ряд сходится равномерно для всех х 0, Rn(x) меньше
остатка числового ряда, т. е.
< /^7 =	< 0,01, как
только Зп 1 > 50, или п > 5, при любом ж / 0. 2467. |7?п(ж)| < —- <
п2
/ 0,0001, как только п 100, при любом ж. 2468. ип = -------------------- —
ж + п — 1
— -----. Поэтому Sn =---------------; S = lim Sn = — при любом ж / 0.
Ответы
325
В частности, при х > 0 Rn(x) = ---- < — 5$ 0, 1, как только п 10.
х + п п
2469. При любом неотрицательном х члены данного ряда меньше (или
а	.111
равны) членов числового сходящегося ряда 1 + 77 + 7+ 0+ - • • Поэтому ряд
(1/2)п	1
сходится равномерно для всех х 0, Rn(x) < -------< 0,01,
как только 2п~1 > 100, или п	8. 2470. — 3 х < 3. 2471. —V5
х л/5- 2472. — <х <	2473. Абсолютно сходится на всей
л/2	л/2
числовой оси. 2474. — 1 < х 1. 2475. —— < х < —-. 2476.1) R = 0;
О	о
2) R = е. 2477. -5 < х < 3. 2478.1 < х < 2. 2479. ----— при |ж| < 1.
(1 —
2480. arctgх при |ж| <С 1. 2481.
2
V 5	\/5
2483.	< х < —. 2484. -
2	2
2
Г?2
1 _ 2х
при |ж| < 1. 2490. — In (1 — ж) при —1 <С х < 1.2491. ---—
.3	„5
1!	3!	5!
2!	4!
2	„4
2493. ln(l + efej;)
Ь/р	Х>2/р2	е4 /р4
f\j d>	t\i d-у	f\; d-y
= In 2 + — + 2!22 - 4!23 + • • •
. , 1 + X Г ж3 ж5
2497. 1 In ------= 2 ж + — + — + ...
1 — ж	3	5
326
Ответы
2) In (2 — Зт + ж2) = In (1 — х) (2 — х) = In 2 — У~^(1 + 2 ")—;
П = 1
1 4- г3
3) In (1 — х + ж2) = In----------- =
2498. In (ж + \/1 + ж2) = х + У~^(—1)
П = 1
ед = (£^Ге1+«о/а-1).
п!ап
2500. х3 - Зх = -2 + 3(т - I)2 + (х - I)3.
2501. х4 = 1 - 4(т + 1) + 6(т + I)2 - 4(т + I)3 + (х + I)4.
1
2502. -
2(1- (т + 2)/2)
при — 4 < х < 0.
х	\ Г1
2503. 1) cos - = —
’ ‘1 ‘1
' _ (ж - 7г/2)
1!2
(ж — тг/2)2
2!22	+'"
(х — л/‘2)п~1	(2п — 1)тг
(п- 1)!2П“1	4
принимая 0! условно равным 1 (см.
сноску на с. 174 к задаче 1760);
2504.
(х + 1) = -1 + ж + 1 + 2(ж + Х)2
1 + ’	+ 3-1! + З2 • 2!
2 • 5(т + I)3
З3 3!
2  5  8 ...  (Зп - 1)
3
.	ж In 2
2505. 1) 2r = 1 + ——
ж2 In2 2	,	, тп1пп2
Ответы
327
mx
mx
7Г
cos (2n — 1)— (полагая 0! = 1).
2506. ж4 - 4ж2 = (х + 2)4 - 8(ж + 2)3 + 20(ж + 2)2 - 16(ж + 2).
2507. COS2 X —
1 л/з х — тг/З 22(ж — тг/З)3 24(ж — тг/З)5
4 “ Т [ 1!	3!	+	5!	''
1 Г2(ж — тг/З)2 23(ж - тг/З)4 25(ж - тг/З)6
+ 2	2!	4!	+	6!
2509. y/i = 2
(х - 4)2	1 • 3(ж — 4)3
26 • 2! +	29  3!
1 • 3 • 5(ж — 4)4
212  4!
1 ж3 1-3 ж5 1•3 • 5 ж7	,______
2511. arcsin х — х-\—------1— ---------1------------Н . . . 2512. 7092 =
2 3	22 - 2! 5	23  3! 7	v ’
VI - 0,008
» 1 _ 0, 004 = 0, 996; 790 = 7810 = 9 л/1 + | к,
V 9
= 9,5. 2513. 707991 = 71 - 0,009 » 0,997; 7130 =
= 7125 + 5 = 5/71 + ^ » 5(1+7-
76
15'
2515. arctg ж =
1
ж3 ж5	/11	1	1 \
----Н--... 2517. тг = 273 1-Н---г +-т =
3	5	\	3-35- З2 7 • З3 9 • З4/
/•	а	г>
— dx = c + x-T- + T--..-
х	3’3 5’5
[ ех ,	ж	ж2	ж3
7 J х	1!	2!2	3!3
ж3 ж5 ж7	/ 1 \	1
= Х ~ ТТз + 2!5 “ 3!7 + ' Ф \ 3) ^3
... 2520. Ф(ж) = J е~х2 dx =
О
- —	0,419 с погрешностью
328
Ответы
1	ч [ Зл-------о ,	1 ж3 2 ж5
< -----.	2521. Ф(т) = / л/1 + х2 dx = х 4—•------— •----Н
2430	J	3 3	322! 5
о
2•5 ж7	/1\	1	1
+ ^з“Ч7 ' V - • • •; ф F	- + О О СЗ	°’ 2008 с погрешностью
Зл • 3! 7	\5)	5	3 • 3 • 5Л
< —------ < 0,0001. 2522. Продифференцировав уравнение п раз и под-
32 • 5Ь
ставив х = 0, получим г/дП+2^ = п(п — 1)уд" 2\ Отсюда j/q = t/g" = 0,
t/gV = 2 • 1, t/У = 3-2, t/У1 = 0 и т. д. Подставив эти значения в формулу
л/г	, Уо , Уо 2 ,	।	"	"4
Маклорена у = г/0 + —ж + ~^х + • • находим у = 1 +
^5	^8	^2	^.3	^4
4-------1-----------Н ... 2523. у = 1 4----------1-----...
4-5	3-4-7-8	2	36
нием является «функция Бесселя нулевого порядка»: 1о(х)
X4	X6
+ +Г+4 - 02	х-> + • • • 2525‘ У1Ж 1,0025; л/ТДЙ2 1,0004;
• I2 22 • 42 • б2
7Щ993 » 0,9965; (/ОПТ » 0,999; /ГН) = V100 + 10 ~ 10 U + /О =
13-4
2524. Реше-
2
22
= 2, 1.
2527. тг = 6 | - + - •
\2	2
1	1-3
3 • 23 + 22 - 2!  5  25 + '''
3(1 + 0,0417+ 0,0047) » 3,14.
2528. тг = 2 1-----3— + -1—
3 •22	5 • 24
1
7 • 26
, 4 L 1 , 1	1
+ 3 1 “ 3 • З2 + 5 • З4 “ 7 • З6 + '''
= 1£ + 2ЕЫГ
3	2п - 1
П = 1
2
9П • 3) '
тг/2	тг/2
2532. s = 4 У \/a2 sin21 + b'2 cos21 dt = 4a j у/1 — e'2 cos2 t dt =
о	о
e2 p-3V g4 /1-3-5Л2 e6
г2 ~ \F4J ' У ~ \2-4-6J ' У
где e — эксцентриситет эллипса, a a — его большая полуось (см. № 1624
Ответы
329
0,5
и его ответ). 2533. J у/1 + х3 dx =
о
Н— • — • — —	0, 508 с погрешностью
2 4 2	128
1 ж5 1 ж9	ж /1\	1
= х —-------4----------—	 ф —	= — —
2! 42  5	4! 44 - 9	’	\2 J 2
с погрешностью <
-----—. 2535. у = — +
27 • 220 У 3
< -----г;;- 2534. Ф(ж) =
7 • 210	v !
^То + ... ^ 0,499805
,.7	о .	11
•С
З2 • 7 + З2  7  11 + '''
2536. Продифференцировав уравнение п раз и подставив х = 0, получим
(п+2)	(п-1)	i / п II п III	1 IV
Уо = -пу'о , отсюда у0 = 1, у0 = 0, у0 = 0, у0 = -1, у1^ =
v п Vi , .	, х3 1 • 4 • х6 1 • 4 • 7 • х'1
— УО — 0, УО —	' ,   ; У —	~ -gj- 4 gj	gj
s4
2!(2C*)2 • 5 + '' J ’
s4
I - 91/о42 7 + • • • ’ где постоянная С = R-L,
.3	3’(2С)2 • 7
!' s2 Г
2537. x = / cos —— ds = s 11 —
J
0
/ . s2 2
О
R — радиус круговой кривой и L — длина переходной кривой. Кривая
называется клотоидой (рис. 88, с. 336). 2538. F(x + h, у + I) = х2 +
+ ху + у2 + /г(2ж + у) + l(2y + х) + h2 + hl + I2. 2539. х3 + 2жг/2 =
= 9 +11(ж — 1)+ 8(г/ —2)+ 3(ж—1)2+8(ж — 1)(г/ —2)+ 2(г/ —2)2 +(ж — I)3 +
х2	(и О- I)2
+ 2(ж —1)(г/—2)2. 2540. In (ж - у) = ж-(г/+1)- —+ж(г/+1)-------------Н
(х — у — I)3
+ R3, где R3 = оГ ' ,	' 1А1Ч. 2541. sin (тх + пу) = тх + пу —
3[f)x + 1 - 0(у + 1)]л
(тх + пу)3 (тх + пу)4 .
—   — -—Н   — — sin в(тх + пу). 2543. dx = 0,1, dy = —0, 2,
Аг = (2ж — у) dx + (2г/ — х) dy + dx2 — dx dy + dy2 = —0, 63. 2544. Аг =
= — (a dx — b dy) sin (ax — by) — —(adx — b dy)2 cos (ax — by) + R3, где
R3 = — (a dx — b dy)3 sin [а(ж + в dx) — b(y + в dy)]. 2545. x2y = — 1 —
- 2(x- 1) + (г/+1)-(x — 1)2+(ж- 1)(г/+1). 2546. arctg | = г/-(ж-1)г/+. . .
(u — 1)
2547. yx = 1 + 2(y - 1) + (x - 2)(y - 1) + [У > + ...; 1Д2-1 as
0,12
as 1 + 2 • 0,1 + 0,1 • 0,1 +	= 1, 215. 2548. dx = -0, 01, dy = 0, 02;
Аг = 2yx dx + (x2 — 2y) dy + у dx2 + x dx dy — dy2 + -dx2 dy к —0, 1407.
330
Ответы
2549.
4 sin (2n — 1)ж
тг 2n — 1
n=l
+<E(-i)
n=l
2552.
2550.
Зтг
T “
cos (2n —
(2n — I)2
sin x sin 2т sin 3x
~1	2~ +	3
ТГ
2551.--------H
3
1	2
... + -x
ТГ
cos x cos 3x cos 5x
“I2”+ 32 + 52
2553.
4 Г . тгх	1 . Зтгт
- sm — + - sm ——H
ТГ I	3 I
1 . 5тгт
+ - sm —----H
5 I
1	4
2554. - + —
2 ТГ2
cos Зтгт
ТГ./'	1
cos — + — cos
/	3Z
l Г ТГ./'	1	2тгт
+ - sm —----------------- sm —--------H . . .
7Г 12	1
3	4 Г тг./'	2 2тгт 1 Зтгт
2556‘ X) 4 + [cos -y “ г2 C°S + ip C°S
1 5тгт 2 бтгт
+ycos^-ycos^ + --- ;
2)
2
ТГ
. ТГ./'	1	.	2тгт 1 .	Зтгт
sm---------1— sm------------1— sm---------H • • •
2	2	2	3	2
4 Г . тгх 1 . Зтгт 1 . 5тгт
s,nT-3Ss,n^ + ps,n^-' '
2557. к =
1 . птг
~^sm —
п/ 2
. птгх
 sm —-—е
(п2тг2а24)//2
2558.
Е2п + 1	. 2п + 1
а„ cos-;—airt sm-;—тгх,
21	21
п=0
где ап
2 [ • 2n + 1
о
Е°°	. птгх	атг’2п’Ч
bn sm —-— cos ———, где bn
I	I2
2 I • П7Г^
J / Ж)8Ш— у.
о
е. .	2 fl — cos Л . .
2560. f(x) = —	--------sin Ах dA.
о
л/ ч 20 f cos Аж „
2И1-Л’' = тУ
о
Ответы
331
.	4 f (1 —cos A) sin А . ,
2562. f(x) = —	-------—~4-----зтАжс/А.
тг J	А2
о
2564. | sin ж |
2	4 соз2ж соз4ж cos 6ж
1-3 + 3-5 + 5-7
I
2566. -
41 cos(ttx/1) сов(3тгж//)
^2 р +	32
з
2567. -
4
2 cos тгж cos Зтгж	1 sin тгж cos 2тгж
^2 I2 + ~З2	+ ' ' ' ~ к 1	+	2
, , 1	, (cos (тгж/I)
2568. sh I - - 2/ —
I у + 1
, о_ f1 -sin (тгж//)
+ 27Г -------------— 
\ ТГ2 + /2
2 sin (2тгж/7)
22тг2 + /2
2569. и =
ап cos
п=0
2n + 1 . 2n + 1
—-—t sin —-—х
где ап
11 Ж)sm
о
2п + 1<^
.	2 f sin A cos Аж
2570. /(ж) = - / ----------------
7Г J А
о
dX.
Приложение
Некоторые кривые (для справок)
Приложение	333
Рис. 73. Цепная линия
Рис. 74. График гиперболического синуса
334
Приложение
Рис. 78. Астроида	Рис. 79. Декартов лист
Рис. 80. Лемниската Бернулли
Рис. 81. Кардиоида
Рис. 82. Трехлепестковая роза
Рис. 83. Четырехлепестковая роза
Приложение
335
Рис. 84. Строфоида
Рис. 85. Циссоида
Рис. 86. Гиперболическая спираль
Рис. 87. Дуга параболы,
вписанной в угол хОу
336
Приложение
Рис. 88. Клотоида