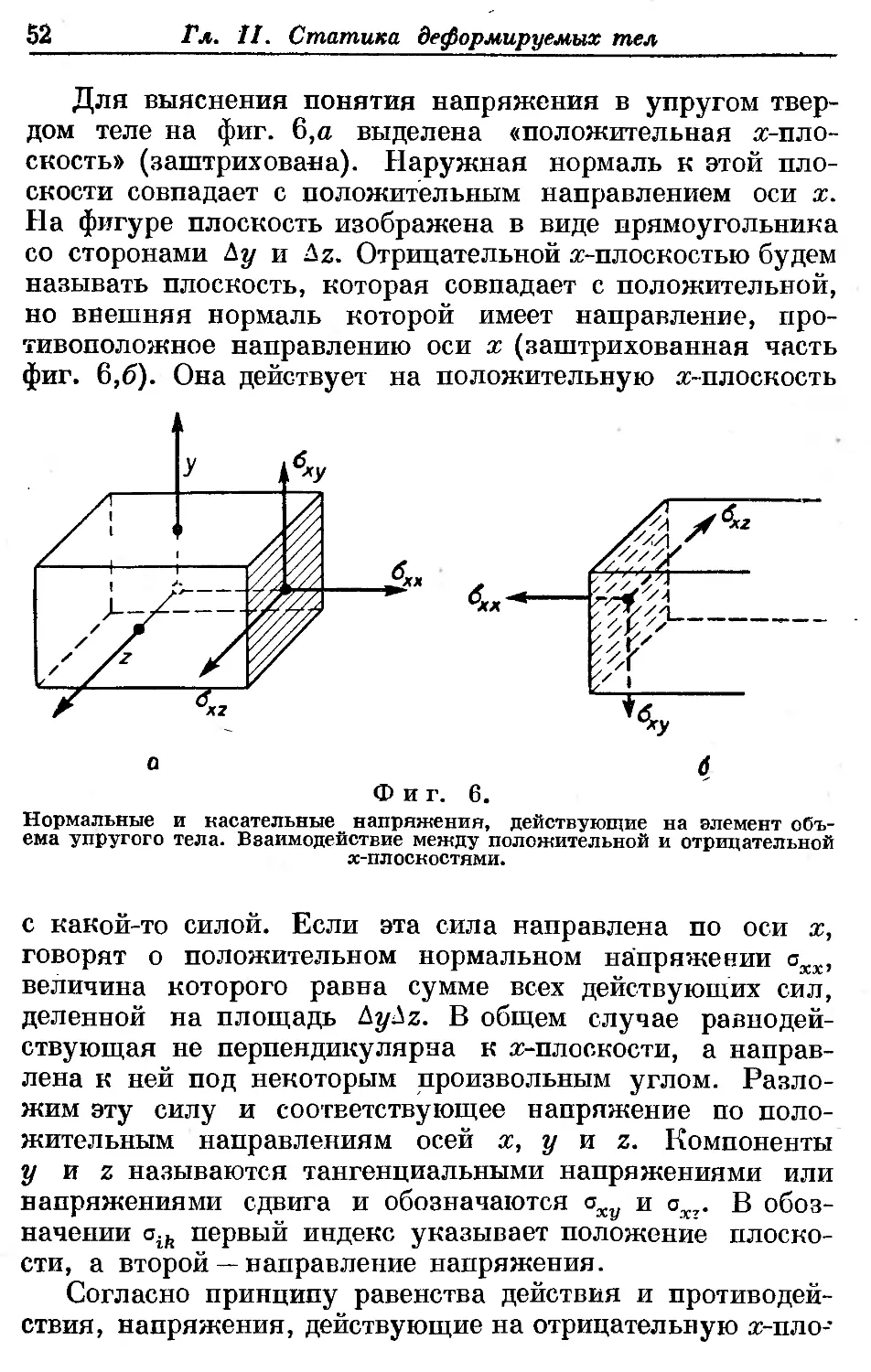
Текст
А. ЗОММЕРФЕЛЬД
МЕХАНИКА
ДЕФОРМИРУЕМЫХ СРЕД
Перевод с немецкого
Е. М. Л ИФШИЦА
и * л
ИЗДАТ ЕЛЬСТВ О
ИНОСТРАННОЙ ЛИТЕРАТУРЫ
Москва, 1954
VORLESUNGEN
OBER THEORETISCHE PHYSIK
BAND II
MECHANIK DER
DEFORMIERBAREN MEDIEN
von
ARNOLD SOMMERFELD
Zweite, neubearbeitete Auflage
LEIPZIG, 1949
ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКА
С изданием настоящей книги советский читатель по-
получает в русском переводе еще один том «Лекций по
теоретической физике» известного немецкого физика *
А. Зоммерфельда г).
Общий характер этой книги не отличается от других
томов, написанных им же, где автор не стремится к ис-
исчерпывающей полноте и систематическому изложению
предмета. Это, пожалуй, в особенно сильной степени
относится именно к данному тому, посвященному меха-
механике сплошных сред—гидродинамике и теории упругости.
В первых трех главах дается изложение общих основ
кинематики, статики и динамики сплошных сред, причем
основные уравнения механики жидкости и твердых упру-
упругих тел излагаются параллельно, что позволяет подчерк-
подчеркнуть общие черты, свойственные как тем, так и другим.
Остальные пять глав посвящены рассмотрению ряда
конкретных вопросов гидродинамики и теории упругости,
выбранных автором более или менее произвольно из
огромного материала, содержащегося в современной ме-
механике сплошных сред.
Характерным для этого выбора является его физиче-
физическая направленность. Так, в гл. VIII («Дополнения
к теории упругости») наряду с вопросами изгиба и кру-
х) До настоящего времени были изданы: том I—«Механика»,
ИЛ, 1947; том IV—«Оптика», ИЛ, 1953; том VI—«Дифференциаль-
VI—«Дифференциальные уравнения в частных производных физики», ИЛ, 1949. Соот-
Соответствующие ссылки в тексте даются по русским изданиям.
Предисловие переводчика
чения стержней излагается теория упругих колебаний
в конечных телах с точки зрения применения ее к кванто-
квантовой теории теплоемкости твердых тел.
В области гидродинамики рассматриваемые вопросы
относятся в основном к тем разделам этой науки, которые
в настоящее время принято называть «классическими»:
потенциальные течения идеальной жидкости, теория вих-
вихрей, ряд вопросов теории вязкой жидкости, теория волн
-на поверхности жидкости. Заметим, кстати, что последний
вопрос, которому посвящена гл. V, излагается автором
сравнительно подробно и с присущим ему математическим
изяществом.
В то же время необходимо предупредить читателя,
что многие важнейшие вопросы современной гидродина-
гидродинамики освещены здесь весьма поверхностно. Это относится
Ь первую очередь к газодинамике. Например, ударным
-волнам посвящен всего один параграф (§ 37), а теории
¦пограничного слоя—всего три страницы (§ 33). Кроме
того, изложение некоторых вопросов, в которых автор,
повидимому, не являлся специалистом, не находится на
современном уровне; мы имеем прежде всего в виду
изложение теории турбулентности (§ 38). Для более
глубокого ознакомления со всеми этими вопросами чита-
читатель может обратиться к ряду других курсов и специаль-
специальным монографиям, имеющимся в советской литературе
по гидродинамике.
Следует заметить, что книга отличается оригинально-
оригинальностью, свежестью изложения и широтой физического
кругозора. В ряде случаев автор делает интересные
отступления в другие области физики, не обычные для
курсов механики. Именно эти особенности придают цен-
ценность «Лекциям по теоретической физике».
Необходимо сделать несколько замечаний о харак-
характере, исторических справок, даваемых автором. Больший-
Предисловие переводчика
ство их посвящено немецким механикам и физикам, роль же
ученых других стран освещается весьма не полно. Это в
первую очередь относится к нашим отечественным ученым.
Совершенно не отмечена роль великих создателей теории
полета аэроплана—Н. Е. Жуковского и С. А. Чаплыгина
(фамилия первого упомянута лишь один раз вместе с фа-
фамилией второстепенного механика Кутта, а фамилия вто-
второго не упоминается вовсе). Нет никаких указаний на
работы ученых советского периода, в том числе на работы
А. Н. Колмогорова, А. Н. Обухова и др., в значительной
степени выяснивших физическую картину турбулентно-
турбулентности. Читателю, специально интересующемуся вопросами
истории механики, можно порекомендовать сборник
«Механика в СССР за 30 лет», М.—Л., 1950.
В целом книга Зоммерфельда представляет интерес
для широкого круга физиков, математиков и механиков,
а также научных работников, аспирантов и студентов.
Е. М. Лифшиц.
ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
Увеличение объема второго тома по сравнению с пер-
первым г) произошло за ' счет довольно полного изложения
в нем необходимых математических методов, которые
часто выделяются в отдельный курс «Введение к теорети-
теоретической физике». Как уже говорилось в предварительных
замечаниях к первому тому, более точным названием
второго тома было бы: «Механика системы с бесконечным
числом степеней свободы». В этом случае вместо обыкно-
обыкновенных' дифференциальных уравнений, которые описы-
описывают законы механики систем с конечным числом степе-
степеней свободы, здесь используются уравнения в частных
производных, а вместо векторлой алгебры—векторный
анализ, краткое изложение которого дается в гл. I.
Кроме того, излагаются основы тензорного анализа,
являющегося необходимым инструментом в теории упру-
упругого тела и вязкой жидкости. Это изложение проделано
не только для декартовых координат, но и, в известной
степени, для ортогональных криволинейных координат.
Здесь уместно перечислить некоторые вопросы, кото-
которые, как я полагаю, изложены мною полнее, чем в элемен-
элементарных учебниках.
В гл. I, § 2, доказывается, что операция rot предста-
представляет собой аксиальный вектор (антисимметризный тен-
тензор) и поэтому его компоненты правильнее обозначать
двумя индексами.
В гл. III, § 16, следуя Осборну Рейнольдсу, вводится
два закона подобия и два соответствующих инварианта,
а именно, обычное число Рейнольдса ^ дополняется
!) Sommerfeld A., Mechanik, 1944. (См. перевод: 3 о ад-
мер фельд А,, Механика, ИЛ, 1947.—Прим. перее.)
Из предисловия к первому изданию
безразмерной величиной S, характеризующей зависимость
давления.
В § 15 этой же главы рассматривается квазиупругое
тело (гироскопический эфир); оно также является
сплошной средой и поэтому подчиняется основной тео-
теореме кинематики (см. § 1). Мы стремились здесь, разу-
разумеется, не к модельному объяснению уравнений Макс-
Максвелла, а к тому, чтобы показать фундаментальное отличие
электродинамики от механики. •
В гл. V, § 27 и 28, дается полный расчет довольно
сложных задач о кольцевых и корабельных волнах, для
чего используется метод стационарной фазы (который
представляет собой упрощение метода перевала).
В гл. VI более доступно излагаются задачи Гельм-
гольца—Кирхгофа об отображениях, но при этом не
используются (в отличие от обычного метода) безраз-
безразмерные величины, а с самого начала вводятся размеры
пластинок, сопел и т. д. В § 32, следуя. Мауэ, обобщаются
рассмотрения вихревых цепочек Кармана на асимметрич-
асимметричный случай (направление распространения не совпадает
с направлением цепочки).
В гл. VII, §36, коротко рассмотрена гидродинамическая
теория смазки. В § 37 рассмотрена теория ударных волн
Римана, а также приводятся результаты для некоторых
случаев, которые поддаются элементарному расчету. Су-
Существенные вопросы, связанные с проблемой турбулент-
турбулентности, кратко изложены в § 38. Там же излагается мате-
математическая модель турбулентности Бургерса.
В гл. VIII, § 43, в задаче о деформации винтовой пру-
пружины рассматриваются одновременно изгиб с кручением.
В § 44 на примере упругого параллелепипеда показана
роль граничных условий и сделаны краткие замечания
по поводу квантовой термодинамики твердого тела.
Октябрь 1944 е.
А. Зоммерфельд.
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Во втором издании в отличие от первого, согласно
первоначальному плану, к гл. VII и VIII добавлены
задачи. Общее тензорное исчисление дано в книге в каче-
качестве приложений, причем мы ограничились случаем трех
измерений и ортогональных элементов длины. Еще в пре-
предисловии к первому изданию этого же, второго, тома было
указано, что здесь будут довольно полно излагаться
математические методы теоретической физики. Поэтому
методы тензорного исчисления целиком здесь не опу-
опускаются, так как они оказались весьма плодотворными
в общей теории относительности, несмотря на то, что
(как будет показано в последнем приложении) они не
д%ют упрощения при решении стоящих здесь перед нами
частных задач по сравнению с простыми методами вектор-
векторного анализа.
• Рассмотрение вопроса о турбулентности, которое еще
в первом издании причинило мне много забот, пришлось
пересмотреть на основе новых, еще не опубликованных
работ Вейцзекера и Гейзенберга. Мое давно составившееся
мнение о том, что можно достичь цели путем интегрирова-
интегрирования уравнений Навье—Стокса в их полной нелинейной
форме, в особом случае «изотропной турбулентности»,
исследованном этими двумя авторами, не подтвердилось:
здесь, как и в кинетической теории газов, оказались
плодотворными статистические методы. Конечно, было
невозможно полностью отразить эти новые результаты,
но прежние представления были во многих местах испра-
исправлены в соответствии с новой точкой зрения. Все осталь-
остальные изменения носят более формальный характер.
Мюнхен, август 1948 ?,
А, воммерфелъд.
Глава I
КИНЕМАТИКА ДЕФОРМИРУЕМЫХ ТЕЛ
§ 1. ОСНОВНАЯ ТЕОРЕМА КИНЕМАТИКИ
В начале своей статьи «Об интегралах гидродинами-
гидродинамических уравнений, отвечающих вихревым движениям»1),
Гельмгольц устанавливает следующую теорему: наиболее
общее движение достаточно малого элемента деформируе-
деформируемого (т. е. не твердого) тела может быть представлено
в виде суммы:
1) параллельного переноса,
2) вращения,
3) растяжения в трех взаимно перпендикулярных на-
направлениях. *
Доказательство основано на разложении в ряд Тейлора
относительного смещения двух соседних точек по перво-
первоначальным разностям их координат.
Пусть Р — точка рассматриваемого элемента объема;
х, у, z — ее координаты в прямоугольной системе, начало
которой О лежит внутри элемента объема (в общем случае
движения тела обе точки Р и О изменят свое положение);
?, т], С и ?0, т]0, Со — соответственно координаты точек Р и О
после смещения. Согласно формуле Тейлора, имеем
Для краткости введем обозначения
д\ __ д^__ дч\ _ df] _
HelmbolU Ц., Crelles Journ.., 55, 25A858).
10
Гл. I. Кинематика деформируемых тел
и запишем каждую из величин aik как сумму симмет
ричного и антисимметричного по индексам членов
-in 2 ' 2
Теперь A.1) можно переписать в следующей форме:
I «Я1
+0 +
+
+
2
«21 ~ «12
— у+-
«23— «32
~«13 „. i «32~~ «23
"о ХТ О '
, «1
1х '
У+0
A.3)
где члены выше первого порядка по х, у, z опущены.
Для полного изменения положения Р введем символ s;
вертикальные линии в A.3) показывают, что смещение s
состоит из трех частных смещений sy, sx, s2, или
s = so+s1 + s2. * A.4)
Смещение s0 с компонентами Ео, т]0, Со одинаково для всех
точек Р элемента объема и поэтому представляет собой
параллельный перенос.
Средняя часть A.3)—Sj представляет собой вращение.
Вводя вектор 9 c компонентами
ftgo — O-23 «13 «31 ^21 ^12 /Л С\
CD = • CD = • СР„ = — I 1.0 I
и радиус-вектор ОР, равный г, получаем
вх = [*»]. A.6)
Это смещение хорошо известно из кинематики твердого
тела1) и соответствует бесконечно малому повороту 9, ось
и величина которого заданы компонентами срх, <pv, <pz.
Следует заметить, что 9 является аксиальным векто-
вектором2), который отличается от обычного (полярного) ве-
вектора, характеризующего параллельный перенос.
х) См. «Механика» (т. I), равенство B2.3).
2)
2) Более подробно об аксиальных векторах см. § 2.—Прим,
перев.
§ 1. Основная теорема кинематики 11
Из рассмотрения смещения sx с точки зрения кинема-
кинематики твердого тела следует, что оно не вызывает изме-
изменения длины вектора ОР. Это можно показать независи-
независимо. Напишем выражение для квадрата длины ОР:
Но, согласно A.6),
Пренебрегая, как и в A.3), членами второго порядка,
находим
|r + Sl|2 = |r|2 = r2.
Отметим, что здесь, как и во всех последующих рас-
рассуждениях такого характера, выражение «без изменениям
следует понимать как «без изменения в первом прибли-
приближении» .
Для того чтобы перейти от бесконечно малых вели-
величин к конечным, надо рассмотреть зависимость смещений
от времени, что приводит к введению скоростей вместо
смещений, а именно:
s = vAz, ср = <*>А*? A-7)
или в компонентах
Здесь v—скорость рассматриваемой частицы, a to—вектор
ее угловой скорости. Важный смысл последней величины,
как вихря скорости, был впервые указан Гельмгольцем.
Вектор угловой скорости, согласно A.8), A.5) и A.2),
в системе х, у, z имеет следующие компоненты:
l/dw
dzj ' у 2\oz dxj z 2\дх dyj v '
Более полное рассмотрение этого основного определения
будет дано в следующем параграфе.
Перейдем теперь к третьей группе членов правой части
выражения A.3) — sa, которая характеризует деформи*
12 Гл. I. Кинематика деформируемых тел
руемость, в то время как два первых члена соответствуют
движению тела как целого. Смещение s2 есть линейная
векторная функция радиус-вектора г. Обозначим компо-
компоненты s2 через ?2, f\2,X2 и напишем их выражения в виде
= %хх + вууУ + V, A -10)
Согласно A.2) и A.3), коэффициенты eife выражаются сле-
следующим образом:
_^i _ -Lfdl.M
ехх —дх » еху — вух 2 V ду ~т~ дх
df\ 1 /' дч\ ¦
Величины eik являются компонентами тензора деформа-
деформации. Сам тензор может быть представлен в виде квадрат-
квадратной матрицы
/ ? Р ? \
/ &хх &ху wxz \
A.12)
"zz/
В настоящем случае тензор симметричен (т. е. компоненты
симметричны по отношению к главной диагонали, соеди-
соединяющей верхний левый угол с нижним правым). Это
непосредственно следует из определения третьего частного
смещения s2 в A.3). С другой стороны, система коэффи-
коэффициентов частного смещения sx представляет собой анти-
антисимметричный тензор. Согласно определению, данному
в A.6) или в A.3), группа членов между вертикальными
линиями представляет собой матрицу
A.12a)
Введенные обозначения <pz = — чху = <рух и т. д. устанав-
устанавливают соответствие с обозначениями посредством двойных
§ 1. Основная теорема кинематики 13
индексов в A.5). Заметим, что антисимметричный тензор
всегда может быть представлен в виде вектора, что, ко-
конечно, не является справедливым для симметричного
тензора (см. § 2).
Так же как и для момента инерции1), при анализе тен-
тензора деформации воспользуемся понятием тензорной по-
поверхности. Рассмотрим с этой целью скалярное произве-
произведение
(szr) = sxxx2+2exyxy + eyyyz+ т .. ^ffa уъ z). A.13)
Полагая f{x, у, z) = const, получим поверхность второго
порядка, называемую также эллипсоидом деформации;
этот термин не означает, что поверхность представляет
собой обязательно эллипсоид, как, например, в случае
тензора инерции. Она может являться любой поверхно-
поверхностью второго порядка: одно- или двуполостный гипербо-
гиперболоид или поверхность, вырождающаяся в пару пло-
плоскостей. Чтобы выяснить это, приведем тензор деформа-
деформаций к главным осям. При введении соответствующих пря-
прямоугольных координат Хг, Х2, Х3 уравнение A.13) при-
принимает вид
F(Xlt X2, ХаНвД + е^ + в,*;** const. A.14)
Коэффициенты ег, е2, е3 называются главными растяже-
растяжениями (или сжатиями, если они отрицательны).
Согласно A.13), линейную вектор-функцию A.10)
можно переписать в виде
Введение главных осей координат соответственно упро-
упрощает линейную вектор-функцию:
E-i^-eX S=I^-SJ S-i^-sI
!~ 2 дХх~ х х' 2 2 dXz~~ 2 2' 3~~ 2 дХъ~~ 3 3'
A.16)
Главные компоненты смещения S. являются проекциями
вектора s2 на главные оси Xt.
1) См. «Механика» (т. I), § 22.
14 Гл. 1. Кинематика деформируемых тел
Теорема Гельмгольца окончательно доказывается уста-
установлением соотношений A.16), которые указывают на то,
что третье частное движение состоит из трех растяжений
(сжатий) во взаимно перпендикулярных направлениях
по главным осям эллипсоида деформации. Действительно,
любая точка Р нашего элемента объема с координатами Х{
в главной системе переходит, согласно A.16), в точку Р'
с координатами
Х4 + Е4 = Х<A+е.). A.17)
Понятие тензорной поверхности, введенное здесь фор-
формальным образом, в § 4 будет углублено, причем вместо
координат х, у, z будут введены дифференциалы коор-
координат или соответствующие им направляющие косинусы
[см. выражение D.21)].
Перейдем теперь от линейных растяжений ei к объем-
объемному расширению В, которое определяется как удельное
изменение объема (т. е. его изменение на единицу перво-
первоначального объема):
где AV — первоначальный, a AV — растянутый (или сжа-
сжатый) объем элемента. Легко вычислить объем элемента,
имеющего форму прямоугольного параллелепипеда с реб-
ребрами, параллельными главным осям. Пусть одна из вершин
совпадает с точкой О. Обозначим ребра до и после рас-
расширения соответственно через ai и в|. Тогда
AV = axa2a3, AV=a'1a'2ars.
Согласно A.17), а| = а4A+е4), поэтому
AF' = AF A + ^A+^A+4)
и, согласно A.18),
<^(l+e1)(l + s2)(l+e3)-l=e1+e2 + e3 A.19)
(члены второго порядка опять опущены).
Представление В в виде A.19) справедливо для любой
декартовой системы координат. Возьмем, например, перво-
первоначальную систему х, у, z; в этом случае всегда будет
справедливо соотношение
е^+вуу-к~г, A-20)
§ 1. Основная теорема кинематики
15
Для доказательства используем определенные свойства
преобразования, переводящего поверхность / = const [урав-
[уравнение A.13)] в поверхность F = const [уравнение A.14)].
Написав преобразование в виде определителя
причем
A.21)
*x
x2
X3
X
ax
a2
a3
У
Px
P2
Рз
z
Ti
T2
Тз
читая определитель A.21) слева направо (т. е. разрешив
относительно X,-), получим при подстановке в A.14)
Это выражение должно совпадать с A.13), поэтому
axPisx + a2P2e2 + азРз8з»
PiTxsi + P2T2S2 + РзТз8з»
TiaiSl + T2a282 + T3a3S3 •
A.22)
A.22a)
Используя равенство A.22) и принимая во внимание со-
соотношения ортогональности A.21а), окончательно по-
получаем
?х* + %у + szz = sl + Ч + Ч- A -23)
Следовательно, сумма элементов главной диагонали
тензора деформаций не зависит от выбора системы коор-
координат; она является инвариантом тензора. В § 4 этот
результат будет дополнен исследованием всех инвариан-
16 Гл. I. Кинематика деформируемых тел
тов тензора. Соотношения A.22а) будут там рассмотрены
полнее.
Используя A.11), можно выражение A.20) записать
в простой форме:
* =1 + 1 + 1- A-24)
Установив геометрическое значение главных растяже-
растяжений S|, перейдем к геометрической интерпретации ком-
компонент еи и eife тензора деформации в общем виде. Что
касается диагональных компонент ехх, ..., то в этом слу-
случае не будет отличия от величин ех, ..., так как ехх
представляет собой относительное приращение длины
отрезка в направлении оси ж. Если в теле выбрать такой
отрезок между точками х — 0 и х — Al, то его длина
после деформаций будет равна
а относительное изменение длины
ДГ —AZ_?-?q
д/ ~" дг '
Но это выражение, как легко видеть, равно
дх~ ехх>
если подставить в A.1) частные значения х = Д/, у = 0, z — 0.
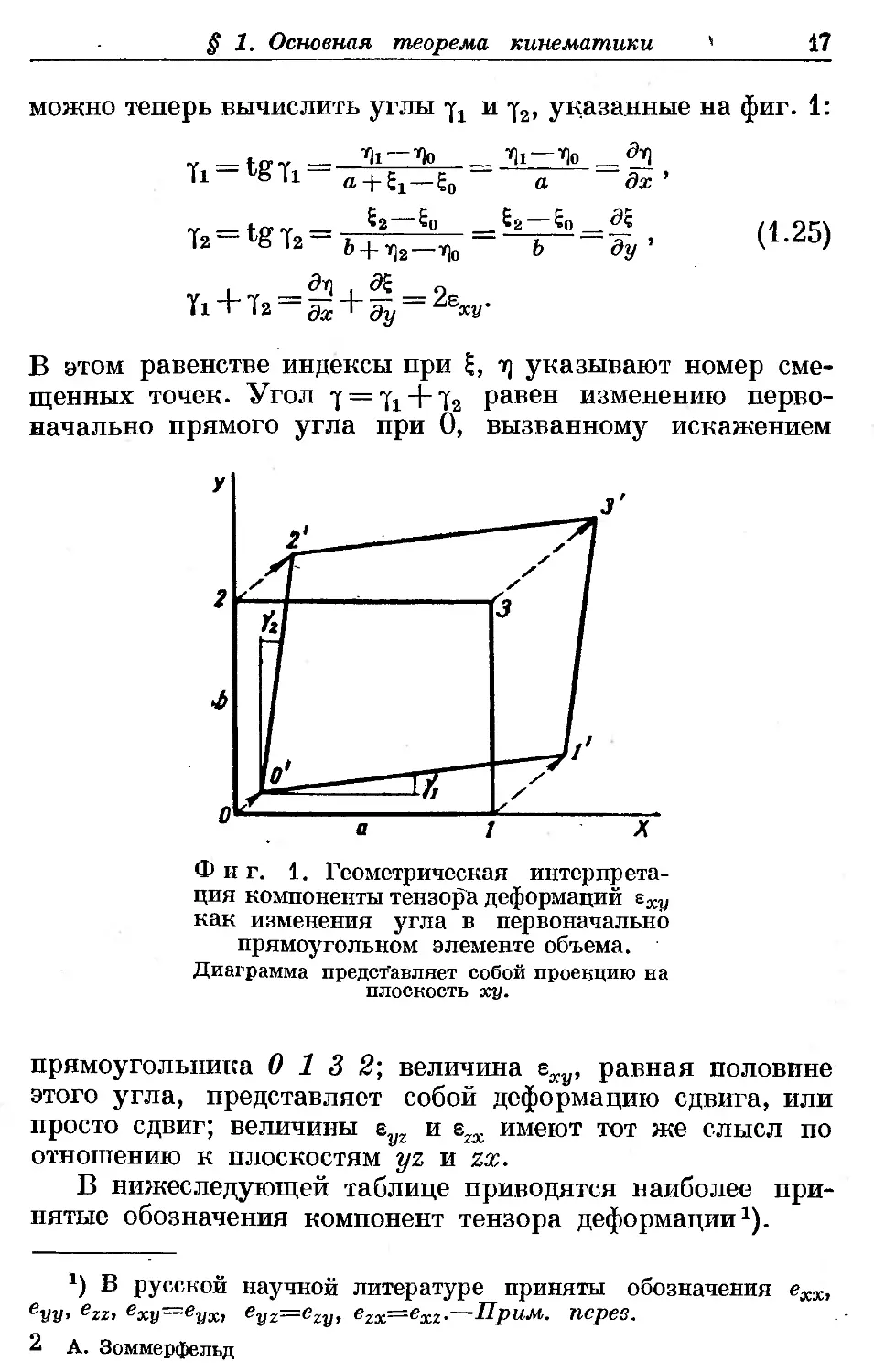
Для интерпретации компоненты еху вместо направле-
направления оси х рассмотрим плоскость ху. Обозначим через
0 13 2 бесконечно малую прямоугольную площадку со
сторонами а ж Ьу лежащую в плоскости ху (фиг. 1).
В процессе деформирования точки 0, 1, 2 переходят
в 0', 1', 2', и прямоугольник превращается в парал-
параллелограмм. (Заметим, что мы отвлекаемся от смещения
в направлении оси z, т. е. представляем себе, что дефор-
деформированная фигура спроектирована на плоскость ху,
тогда проекция точки 3', в которую перешла точка 3,
совпадает с четвертой вершиной параллелограмма, по-
построенного на 0' 1' и 0' 2', если пренебречь членами
высшего порядка.) Опуская опять члены высшего порядка,
§ 1. Основная теорема кинематики * 17
можно теперь вычислить углы ^ и-[2, указанные на фиг. 1:
A.25)
__df\ &z
В этом равенстве индексы при ?, -rj указывают номер сме-
смещенных точек. Угол T = Ti + T2 равен изменению перво-
первоначально прямого угла при 0, вызванному искажением
3'
Фиг. 1. Геометрическая интерпрета-
интерпретация компоненты тензора деформаций гху
как изменения угла в первоначально
прямоугольном элементе объема.
Диаграмма представляет собой проекцию на
плоскость ху.
прямоугольника 0 13 2; величина еху, равная половине
этого угла, представляет собой деформацию сдвига, или
просто сдвиг; величины eyz и ezx имеют тот же слысл по
отношению к плоскостям yz и zx.
В нижеследующей таблице приводятся наиболее при-
принятые обозначения компонент тензора деформации1).
г) В русской научной литературе приняты обозначения ехх,
еуу, ezz, exy—eyXj eyz=ezy, ezx—exz.—Прим. перев.
2 А. Зоммерфельд
18
Гл. t. Кинематика деформируемых теЛ
Данная книга
Кирхгоф, Планк
Английская ли-
литература
Немецкая техни-
техническая литера-
литература
ехх
«,
е
ех
гУУ
Уу
i
ezz
г,
8
еху —
1
Yxy —
1
1 __
еух
1
2
а
1
2" Тузе
•
1
1
~2~1
уг = ^у
1
1
уг—гЛгу
?zx =
1 _
1
2
1
-gYzx-
вхг
1
С
1
Включение множителя х/2 в данное здесь определение
е ... соответствует системе обозначений, принятой в тен-
тензорном анализе. Ниже будет показано, что выбор Кирх-
Кирхгофом обозначений ху . . . имеет определенные преиму-
преимущества при получении простого выражения для величины
энергии (см. § 40).
§ 2. ОБЗОР ВЕКТОРНОГО АНАЛИЗА !)
Поскольку в данной книге будет широко использован
векторный анализ (исчисление, связанное с векторными
величинами), представляется целесообразным выяснить
некоторые основные положения этого раздела математики.
Предполагается, что читатель знаком с векторной алгеб-
алгеброй и первоначальными понятиями векторного анализа.
Прежде всего повторим определение вектора и скаляра,
данное в т. I, § 22. Величина называется вектором, если
при ортогональном преобразовании системы координат
она подчиняется тем же законам преобразования, что
и радиус-вектор г = х, у, z; величина называется скаляром,
если при подобном преобразовании она остается неиз-
неизменной.
Используем это определение для доказательства того,
что величина G [см. A.24)], полученная из вектора s=E, tj, С,
является скаляром. Заменим s произвольным вектором
!) В качестве подробного руководства по векторному и тензор-
тензорному анализу можно рекомендовать книгу: К о чин Н. В.?
Векторное исчисление и начала тензорного исчисления, ОНТИ,
1934.—Прим. перев.
§ 2. Обзор векторного анализа
19
А = Ах, Ау, Az и рассмотрим вместо G более общее выра-
выражение
дАх , dAv , dAz /о ..
+ ^^ B.1)
dlV А =
дх
ду
dz
которое называется дивергенцией векторного поля А.
Инвариантность divA, которая будет сейчас доказана,
выражается следующим равенством:
дАх, dAv, dAz,
5ж' ' ду' ' 5z'
Вместо того чтобы обозначать координаты (со штрихом
или без него) различными буквами, обозначим их одной
и той же буквой с различными численными индексами.
В этом случае преобразование A.21) запишется более
просто:
B.2)
х'2
<
хг
а11
а21
а31
х%
а12
а22
a32
Х3
а1з
а23
B'2а)
Символ 8|у понимается в обычном смысле: •
_И Для г = /,
ij=\0 для г^=/.
Для произвольной функции U (хг, х2, х3), которая
в силу B.2) будет в то же время функцией от х[, х'2, х'3,
имеем:
Если определитель коэффициентов B.2) читать сверху
вниз, то B.3) можно переписать в виде
—-= уа-ь^г—. B.3а)
h
2*
20 Гл. 1. Кинематика деформируемых тел
Согласно определению вектора, можно правило преобра-
преобразования радиус-вектора г [см. B.2)] применить к векто-
вектору А. Таким образом, читая B.2) слева направо, получим
^ = 2«гА- B-4)
Примем теперь в качестве произвольной функции U
в B.3а) компоненту вектора А{. Проделав это для
? — 1, 2, 3 и суммируя, получим
v ^!i _ w v r, г, dAi — v -v к dAi
2л дх:~2j2j2jаЛ^~2л2л°ыщ •
г г i k I k I
Здесь первый член представляет собой div'A, а послед-
последний—div А, при условии использования свойств 8-символа.
Таким образом, инвариантность дивергенции доказана.
Объемное расширение A.24) может быть теперь записано,
как 0 = divs. Операция дивергенции превращает вектор
в скаляр. С другой стороны, простейшим дифферен-
дифференциальным оператором, превращающим скаляр в вектор,
является оператор градиента. Обозначив через U скаляр-
скалярную функцию точки, построим вектор
ди dU dU /о сч
-^, -^, -^. B.5)
Векторный характер этой функции сразу следует из со-
соотношения B.3а), которое может быть записано с помощью
символа grad:
grad? U = 2 aifegradh U. B.5a)
Следовательно, градиент преобразуется таким же образом,
как и радиус-вектор.
Рассмотрим дифференциальную операцию, введенную
в A.9), для которой применяется символ rot. Написав A.9)
с помощью этого символа, получаем
B = rotA, rotxA = ^f-^ и т. д. B.6)
Здесь 2Ю1) заменено на В, а \ = и, v, w — на А. Равен-
х) Позже будет опять выделен множитель г/2 [см. A.9)], который
теперь включен в определение В.
§ 2. Обзор векторного анализа ' .21
ство A.6) содержит уже определение вектора со. Согласно
A.7),
тогда A.6) перейдет в
v1 = [»r]. B.7)
Из § 1 следует, что определение ю из равенства B.6)
или A.9) совпадает с определением из равенства B.7) или
A.6); это будет непосредственно проверено в задаче 1 гл. I.
Перепишем B.7) в тех же обозначениях, что и B.6);
вместо 2со будем писать В, a vx заменим на А, поскольку
в'дальнейшем нас будет интересовать только векторный
характер этой величины, а в этом смысле rot vx иденти-
идентичен rotv. Тогда B.7) примет вид
2А=[Вг]. B.7а)
Покажем, что величина В в определенном смысле имеет
векторный характер. Это доказательство, позволяющее
лучше уяснить понятие ротора, безусловно не является
лишним, хотя оно не приводится в большинстве учебников.
Формальное доказательство может быть основано на
определении B.6), но в этом случае оно сопровождается
громоздкими вычислениями (задача 2 гл. I); тот же
результат может быть получен, если исходить из равен-
равенства B.7а), где компоненты В являются коэффициентами
линейной векторной функции, подобно величинам eife
в A.10). Вводя двойные индексы и нумеруя компоненты
вектора (вместо того чтобы обозначать их буквенными
индексами), запишем:
Ву = В2 = Вгг = - Вп, Ау = А2, B.8)
BZ = B3 = В21 = — В12, Az = А3.
Такое обозначение, компонент В соответствует значению ф,
представленному равенством A.12а); в обоих случаях
диагональные компоненты (Вн, <ри) исчезают и «вектор»
В действительно является антисимметричным тензором,
подобным ф.
22 Гл. I. Кинематика деформируемых тел
Равенство B.7а) примет теперь простую форму
2А = 2я«**; B-9)
k
это можно проверить для i, равного, например, единице.
Из B.8) и B.9) получаем
2Аг = 2 Ах = Вхххх + В12х2 + В13х3 = -Bzy + Byz = [Br]x,
что находится в согласии с B.7а).
Для определения величин В в повернутой системе
координат х' запишем равенство B.9) в этой системе
2А1 = %В'шх'к B.10)
h
и введем новые х и А, согласно B.2):
I
Тогда B.10) переходит в
2!1!Я1- B.11)
2*Л 2!1
Если подставить в первый член этого равенства выражение
2Ah='^iBklxl [которое является соотношением B.9),
только с другими индексами], то равенство B.11) при-
примет вид
2 2 вы aih xi = 2 2 B'ih Ща xt;
hi hi
оно должно тождественно выполняться для любых зна-
значений независимых переменных хг, х2, х3. Приравнивая
коэффициенты, получаем следующие три уравнения,
связывающие В и В':
2#ыагл = 2#«ам> /==1' 2, 3, B.12)
откуда должны быть определены В[к. Это производится
путем умножения уравнений B.12) на ajt и суммирова-
суммирования по /. После суммирования правых частей уравне-
уравнений B.12) получаем
2 2 Blh akl an = 2 B'ik 2 4i «я = 2 B'ik *kj = Blj. B.12a)
I ft ft I h
§ 2. Обзор векторного анализа 23
Поступая таким же образом с левой частью B.12), получаем
VI У\ Вы aik an ; сравнивая с B.12а), найдем:
i h
7 \ 7\ "^ ^ik ^ji r~= *-*%]• \ )
I h
Следовательно, каждая В' есть линейная функция всех
девяти компонент В. Учет условия Bkl= —Bik и Вш — 0
приводит к тому, что число членов сокращается до трех.
Написанные развернуто выражения для В' имеют вид
-f B21 (ai2 aд - an ay2). B.14)
Выпишем одно из них, например, для ? = 3, / = 2:
^32 = ^32 (a33 a22 ~ а32 а2з) + ^13 (a3l a23 ~ a33 a2l) +
Коэффициенты при В в A.15) суть не что иное, как
миноры элементов первой строки определителя преобра-
преобразования B.2). В зависимости от того, равен ли этот
определитель + 1 или — 1, миноры равны соответствую-
соответствующим элементам или отличаются от них на множитель— 1х).
Поэтому равенство B.15) может быть переписано как
± В'г = а11В1 + a12Z?2 -f a13B
3,
где для В вновь введены ординарные индексы. Подобным
образом получаются выражения для В'2 и В'3.
Результат может быть записан в форме
±B'i=4%ailBl. B.16)
Равенство B.16) совпадает с точностью до двойного знака
с B.4).
Отсюда могут быть сделаны два вывода:
1. Величина В = rot А ведет себя подобно обычному
(полярному) вектору при поворотах, т. е. при орто-
ортогональных преобразованиях координат с определителем -}-1;
при этом обычно пользуются простой терминологией
«вектор rot», которой мы также будем придерживаться,
х) См. «Механика», (т. I), задача 10 к гд, I,,
24 Гл. I. Кинематика деформируемых тел
2. Говоря точнее, ротор представляет собой не поляр-
полярный, а аксиальный вектор, так как при переходе от пра-
правой системы координат к левой или, в более общем случае,
при вращениях с последующей инверсией {определитель—1)
новые компоненты ротора принимают обратный знак
по сравнению с компонентами полярного вектора.
Теперь легко видеть, чго использование в предыдущем
доказательстве двойных индексов дает определенное пре-
преимущество: не совсем верно изображать аксиальный
вектор стрелкой в направлении оси; более правильным
символом была бы круглая стрелка, расположенная
вокруг оси; в этом случае плоскость круглой стрелки,
скажем плоскость yz, принимает на себя роль оси х,
и лучше было бы писать левый член равенства B.6) в виде
гс*даА = ^-^. B.17)
vz оу dz v '
Обозначение rotxA дает отображение аксиального вектора
на полярный. Это возможно в случае чистого вращения;
согласно выводу 1 такое обозначение помогает нагляд-
наглядному представлению.
В этой связи следует упомянуть известное и часто
применяемое правило, которое помогает запомнить струк-
структуру выражения B.6) или B.17) и в особенности после-
последовательность знаков в этих формулах. Оно гласит:
д д д
rotA= ~fa ду~ dz
B.18)
здесь i, j, k—единичные векторы1) в направлений осей
х, у, z.- С помощью этих единичных векторов любой
вектор В можно представить в виде
B=tiBx + jBy + kBt. B.18а)
Умножение на djdx, djdy, d/dz означает дифференцпро-
г) В оригинале автор не обозначает i, /, к как векторы, руко-
руководствуясь историческими соображениями (аналогией с кватернио-
кватернионами Гамильтона и т. п.). Мы изменяем здесь эти обозначения на
векторные, как принято в нашей литературе.—Прим. перее.
§ 2. Обзор векторного анализа 25
вание по соответствующей переменной. Раскрытие опре-
определителя B.18)
B.186)
показывает, что он действительно дает правильную струк-
структуру компонент ротора.
Следует заметить, однако, что отображение аксиаль-
аксиального вектора на полярный возможно только в трехмерном
пространстве. Это может быть выведено из сравнения
числа компонент полярного вектора, которое равно,
конечно, числу измерений пространства п, и числа ком-
компонент аксиального вектора, для которого в общем случае
оно равно
v=n(w--l)> или дляп=1} 2, 3, 4, ... v = 0, 1, 3, 6, ...
Число v связано с обозначением компонент аксиального
вектора двойными индексами: оно представляет собой
число сочетаний из п направлений в пространстве по два.
То, что v совпадает с п, для п==3 является случайностью.
Число компонент v = 6 в четырехмерном пространстве
играет решающую роль в электродинамике, где оно сов-
совпадает с числом компонент электромагнитного поля (три
электрические и три магнитные компоненты).
Вернемся к нашему исходному уравнению A.9)
и запишем его в векторной форме
(o = -irotv. B.19)
Нельзя отрицать, что наличие множителя х/2 вредит
изяществу этой формулы. Однако именно (о есть «вра-
«вращение», связанное с распределением скоростей v. Фор-
Формальное введение символа rot в B.6) означает, что «фи-
«физическое вращение» составляет только половину «матема-
«математического вращения». Этот парадокс нельзя устранить
включением множителя х/2 в определение операции rot,
так как это имело бы очень неприятные последствия
для общего векторного анализа, а в особенности для
электродинамики. Поэтому остается только констатировать
наличие этого недостатка.
26
Гл. I. Кинематика деформируемых тел
Три оператора grad, div и rot были пока определены
с помощью дифференциальных операций. Однако суще-
существует очень удобный способ введения div и rot посред-
посредством интегральных операций. Начнем с дивергенции.
Представим себе векторное поле А как поле течения,
т. е. пусть величина скорости и направление потока
задаются везде -величиной и направлением А. Окружим
точку Р поля замкнутой поверхностью, и пусть Ат — объем,
Фиг. 2.
Вычисление divA путем интегрирования по поверх-
поверхности бесконечно малого параллелепипеда.
заключенный внутри этой поверхности. Если п — внешняя
нормаль по отношению к элементу поверхности До, то
Ап — количество вытекшей за единицу времени жидкости
через единицу площади, нормальной к поверхности.
Составляя выражение
-т— V А„ do
и находя предел его при стремлении Ат (или с) к нулю,
получаем
1 Г
iv А — lim -г- \
Дт-э-О АХ J
div A
Ап do.
B.20)
Соответствие этого определения и B.1) сразу видно
в особом случае, когда в качестве Ат выбран прямо-
прямоугольный параллелепипед с центром в Р и сторонами Аж,
A?/, Az (фиг. 2). Если Ах в точке х-{-&х разложить в ряд
Тейлора и пренебречь высшими степенями Аж, как это
делалось раньше, получаем для ^-поверхностей (т. е. для
§ 2. Обзор векторного анализа 27
поверхностей, нормальных к оси х)
\.nda=\ [Ах(х + Ах)- Ах{х)] dy dz =
=л
Ox
Аналогично получаются два других члена для двух пар
плоскостей у и z; складывая, можно получить выраже-
выражение B.1) для divA. Математики писали бы B.20) с оговор-
оговоркой, что указанный предел существует. Мы эту оговорку
опускаем, так как ограничения, накладываемые этой
оговоркой на векторное поле и его непрерывность, не.
сильнее, чем ограничения, содержащиеся в определе-
определении B.1). Таким образом, оба определения B.1) и B.20)
эквивалентны, но следует предпочесть определение B.20)
как менее формальное.
Ротор может быть определен соответственно путем
следующего построения. Пусть через точку Р проходит
произвольно выбранная ось а; в плоскости, содержащей
Р и нормальной к а, начертим замкнутую кривую s,
окружающую Р, и обозначим поверхность, заключенную
внутри s, через До. Пусть As — компонента А в направ-
направлении элемента дуги ds, выбранного так, что направление
обхода кривой образует с а правовинтовую систему.
Рассмотрим теперь криволинейный интеграл ф As ds, для
которого Томсон (Кельвин) ввел удачное обозначение —
циркуляция. Предел отношения циркуляции к площади
До дает
rotaA = lim-?-<6 A%ds. B.21)
Соответствие этого определения предыдущему B.17) может
быть опять легко показано в случае специального выбора
кривой s. Проверим B.21) для ^z-компоненты ротора.
В этом случае а совпадет с положительным направле-
направлением оси х, и s может быть выбрано в виде прямоуголь-
прямоугольника с центром в Р и сторонами Ау, Дг (фиг. 3). Как
и прежде,, разлагая в ряд вклад от каждой пары сторон,
получаем для первой пары (которая параллельна оси у)
28
Гл. I. Кинематика деформируемых тел
и для второй пары
4 ds — ~ Ay As.
s ду и
Складывая, получим, согласно B.21),
. д . д dAz dAv
roL, A = rotwz A = -~ — -=-? .
Другие компоненты можно получить путем простой цикли-
циклической перестановки координат.
Таким образом, введенные ранее формально, аналити-
аналитическим путем, понятия div и rot получают геометри-
геометрический смысл. Выясним далее существо операции gradC/.
йу
Фиг. 3.
Вычисление rotA путем криволинейного интегрирова-
интегрирования вдоль прямоугольного контура.
Для этой цели рассмотрим «поверхности-уровня» U = const
и траектории в пространстве, ортогональные этим поверх-
поверхностям. Направление градиента будет везде касательно
к траектории; его величина dU/dn определяется густотой
поверхностей уровня, следующих друг за другом; если
Ы1 постоянно, то dU/dn тем больше, чем меньше Ьп.
По сравнению с первоначальными определениями B.1),
B.5) и B.17) преимущество геометрических определений
заключается не только в меньшей формальности. Они
справедливы для произвольной системы координат, что,
в частности, позволяет легко перейти к любой системе
криволинейных ортогональных координат.
§ 2, Обзор векторного анализа 20
Покажем это для общего случая системы трех взаимно
перпендикулярных семейств поверхностей. Случай более
элементарных систем координат, например полярных,
будет рассмотрен в задаче 3 гл. I. Пусть р1г р2, р3 —
параметры трех семейств поверхностей. Вследствие их вза-
взаимной ортогональности в аналитическое выражение ква-
квадрата расстояния между двумя соседними точками не
будут входить смешанные члены типа dpi dpk. Обозначим
коэффициенты при квадратичных членах посредством g\\
тогда квадрат элемента длины запишется как
ds*=g\ dpi + d dpi + gl dpi B.22)
Отсюда, в частности, вытекают следующие выражения
для дифференциалов в трех координатных направлениях:
Эти выражения заменяют dx, dy, dz, если вместо декар-
декартовых координат пользуются ортогональными криво-
криволинейными координатами. Прежние компоненты градиента
г dU dU dU
запишутся в виде
л атт л лтт л лтт
B.24)
gs
Выражение для дивергенции в новых координатах может
быть получено из B.20), если в качестве объема Ат выб-
выбрана бесконечно малая ячейка с криволинейными сторо-
сторонами As1} As2, As3:
div A =
B.25)
Выражение для первой компоненты ротора может быть
получено, если выбрать поверхность, содержащую прямо-
прямоугольный контур, ортогональный координатному напра-
направлению рг:
rotlА = -А- Гэ_ЩА^_ЩА? 1 ^ B 26)
1 gzgs L dVi ^Рз J х '
Вторая и третья компоненты получаются путем цикли-
циклической перестановки индексов 1, 2, 3.
30 Гл. I. Кинематика деформируемых тел
§ 3. ТЕОРЕМЫ ОСТРОГРАДСКОГО—ГАУССА,
СТОКСА И ГРИНА
От интегральных определений дивергенции и ротора
в B.20) и B.21) всего один шаг к интегральным теоре-
теоремам Остроградского—Гаусса1) и Стокса.
Пусть векторное поле А дифференцируемо внутри
замкнутой поверхности с; тогда в любой точке внутрен-
внутреннего объема существует div А. Интегральное соотношение,
составляющее теорему Остроградского—Гаусса, имеет вид
\ =\ Anda. C.1)
Здесь п—внешняя 2) нормаль к элементу поверхности do.
Для доказательства этого соотношения разделим объем х
на ряд маленьких ячеек &tm; в соответствии с матема-
математическим понятием определенного интеграла при неогра-
неограниченном увеличении числа ячеек и их одновременном
уменьшении левую часть C.1) можно записать, как обычно,
в виде предела
т=М
lim 2 divAAxm, C.1a)
М->со
где значение div А может быть взято в любой точке ячей-
ячейки Атт. Если для div А принять интегральное определе-
определение B.20), то вместо C.1а) получим
Так как объем Дт^ сохраняет сначала конечную вели-
величину, то его можно внести под знак предела; кроме
того, поскольку суммирование производится по конеч-
конечному числу членов, можно поменять местами знак сум-
суммирования со знаком предела. Тогда выражение C.16)
х) В немецком оригинале йаписано «теорема Гаусса».—Прим. ред.
2) Это условие может вызвать некоторое неудобство, например,
в случае A=grad U, где dU/dn, вообще говоря, снаружи о может быть
не определено; однако в таком случае можно заменить dU/dn на—
OUJdn', где п'—внутренняя нормаль.
§ 3. Теоремы Остроградского—Гаусса, Стокса и Грина 31
примет вид
Предположим, что объем Дт, служащий для определения
дивергенции, тождественен с Дтт, относящемуся к опреде-
определенному интегралу1). В то же время da заменим на dam.
Это указывает на то, что теперь dam является элементом
поверхности Дтт. После этих изменений C.1в) перейдет в
При суммировании по т части поверхностей ат, лежащие
внутри о, уничтожатся попарно, так как знаки норма-
нормалей п противоположвы. Остается только вклад, даваемый
элементами поверхностей, прилегающих к поверхности da;
отсюда сумму в (-3.1г) можно написать в виде
где интегрирование производится по поверхности задан-
заданного первоначально в интеграле C.1) объема. Так как
интеграл не зависит от способа разбиения на ячейки Дтт,
предельные переходы как в C.1г), так и в C.1а) ничего
не изменят. Поэтому выражение C.1д) совпадает с C.1а),
которое, в свою очередь, представляет собой лишь иной
способ записи объемного интеграла, стоящего в левой
части C.1). Таким образом, C.1д) идентично правой
части C.1), что и требовалось доказать.
Приводимое обычно в учебниках формальное доказа-
доказательство теоремы Остроградского—Гаусса основывается
на интегрировании по частям в прямоугольных коорди-
координатах; было показано, что его можно заменить рассужде-
рассуждением, использующим только общие принципы интеграль-
интегрального исчисления и векторного анализа. То же можно
сказать и о теореме Стокса, для которой наметим только
общий путь доказательства.
х) Это означает, что процессы стремления Дт—>0 и Ахт—>0
(или т—>оо) происходят одновременно, хотя, согласно C.16),
они могут происходить независимо.
32 Гл. 1. Кинематика деформируемых тел
Если говорить о потоке жидкости, то правая часть C.1)
представляет собой количество жидкости, проходящей
за единицу времени через граничную поверхность (отри-
(отрицательный знак соответствует случаю, когда жидкость
поступает в объем). Левая часть C.1) представляет собой
алгебраическую сумму интенсивностей всех источников,
или стоков, распределенных непрерывно внутри поверх-
поверхности. Так что интуитивно равенство этих двух членов
очевидно.
В теореме Стокса рассмотрим произвольную (криво-
(криволинейную) поверхность о, ограниченную замкнутой кри-
кривой (контуром) s, которой приписываем определенное направ-
направление обхода. Для каждого элемента поверхности da по-
построим нормаль п, направленную так, что она образует
с направлением обхода s правовинтовую систему. Тогда
теорема Стокса читается следующим образом: для любого
векторного поля А, непрерывного в окрестности о,
rotn A da = & As ds. C.2)
Для доказательства разделим о на малые элементы,
которые можно рассматривать как части соответствующих
касательных плоскостей; их границам sm приписываем
то же направление обхода, что и у s. Напишем равен-
равенство B.21) для каждого элемента Дот, умножим его на Дст
и просуммируем по т. В результате получаем
lim ^ '< АДст= lim 2 Ф lim ^T А* dsm- C-3)
J Д0
2 Ф
т-мэо *J Дс->0
т
Приравнивая &а = &ат и поступая в дальнейшем, как
в равенствах C.1а)—C,1г), учтем, что в правой части
C.3) вклад от всех внутренних границ исчезнет, так как
каждый отрезок принадлежит двум соседним элементам
и поэтому будет проходиться дважды в противоположных
направлениях. Останегся только вклад от элементов,
прилегающих к границе, который в результате суммиро-
суммирования дает криволинейный интеграл, стоящий в правой
части C.2).
Если говорить о потоке жидкости, то из соотноше-
соотношения C.2) следует: циркуляция, взятая по замкнутой
§ 3. Теоремы Остроградского—Гаусса, Стокса и Грина 33
кривой s, равняется потоку вихревого вектора (ротора)
через произвольную поверхность с, натянутую на s.
Если поверхность замкнутая, то интеграл, взятый
по граничной кривой, исчезает, т. е.
= 0; C.4)
при этом, конечно, предполагается непрерывность rot A
(что подчеркивалось и прежде).
Если, в частности, в качестве вектора А выбран гра-
градиент, А = gradf/, то дифференциальное выражение
As ds = Ах dx + Ау dy -J- Az dz C.5)
будет полным дифференциалом dU. В этом случае
0 C.6)
для любой замкнутой кривой. Тогда левая часть в C.2)
исчезнет для любой поверхности о^и любого направления
нормали п. Отсюда следуег, что
rot gradtf = 0. C.7)
Эту формулу можно также вывести из дифференциаль-
дифференциального определения ротора B.6).
Равенство rotA = 0, написанное в прямоугольных
координатах, равносильно условию, что дифферен-
дифференциальное выражение Ах dx -\- Ay dy -\- Az dz является пол-
полным дифференциалом [см. равенство C.5)]. Было показа-
показано1), чю те же самые условия требуются для существо-
существования потенциала в силовом поле; теперь они могут
быть записаны в легко запоминаемом виде rotA = 0.
Заметим, кстати, что операция rot grad имеет совер-
совершенно определенное значение, в то время как grad rot
не имеег никакого смысла, так как по своему определе-
определению операция grad не может быть применена к вектору.
Если применить теорему Остроградского—Гаусса к век-
векторному полю ротора, т. е. если в C.1) вместо А под-
подставить rot В, то правая часть C.1) превратится в интег-
интеграл вида C.4) и поэтому обратится в нуль. Следовательно,
х) См. «Механика» (т. I), равенства A8.17).
3 А. Зоммерфельд
34 Гл. I. Кинематика деформируемых тел
левая часть C.1) будет равна нулю для любой замкну-
замкнутой поверхности о в объеме т. Это означает, что всегда
div rot В — 0; C.8)
тождество C.8) можно также вывести непосредственно
из дифференциальных определений B.1) и B.6). Опять-
таки обратный символ rot div не имеет смысла, так как
операция ротора не может быть применена к скаляру.
Рассмотрим также символы div grad и grad div. Пер-
Первый можно применять к скаляру, например U. Напишем
divgrad?/ = A*7; C.9)
в декартовых координатах оператор Д есть
В криволинейных ортогональных координатах рг, р2, р3
соотношения B.24) и B.25) дают
\
ёх
Символ Д называется оператором Лапласа или лапласи-
лапласианом, а также вторым дифференциальным параметром.
Первый дифференциальный параметр определяется как
Оба символа действуют на скалярные функции точки.
Другим принятым обозначением для лапласиана яв-
является V2 х).
*) Знак V символически определяется, как
Vя означает скалярное произведение
§ 3. Теоремы Остроградского—Таусса, Стокса и Ppuha S5
Обратный символ grad div применим к векторам.
Можно, кстати, упомянуть, что он содержится в полез-
полезной формуле
rot rot A = grad div A — div grad A = grad div A — ДА, C.10)
которую, однако, надо применять с осторожностью, так
как здесь оператор Д - div grad применен к вектору,
что, строго говоря, запрещено. В действительности же фор-
формула относится к декартовым компонентам вектора А,
и Д действует на каждую из компонент А, взятую в от-
отдельности и рассматриваемую как скаляр. Доказатель-
Доказательство C.10) соответственно можно провести в декартовых
координатах. Оно будет заключаться в доказательстве
равенства обеих частей путем простой подстановки; при
этом можно также пользоваться символическим методом,
изложенным в примечании на стр. 34.
Наоборот, формула C.10) может служить для опреде-
определения величины ДА в произвольных координатах (до сих
пор ДА была определена только в декартовых коорди-
координатах). Перепишем C.10) в виде
ДА = grad div A — rot rot А. (ЗЛОа)
Согласно B.24) —B.26), правая часть C.10а) определена
для произвольных ортогональных координат, поэтому
левая часть приобретает определенный смысл. Это выра-
выражение будет применено в § 9 после равенства (9.18).
В задаче 4 гл. I будет объяснена разница между пра-
правильно и неправильно вычисленными компонентами ДА
в цилиндрических координатах.
Произведение V на скаляр <р есть grad<p- Скалярное произве-
произведение (VA), если действовать формально по правилам векторной
алгебры, дает дивергенцию А:
дх ду dz
Векторное произведение [VA] обозначает соответственно rot А;
учитывая, что [ij] = k, [jk]=i, [ki]^j, [ji] = —k, [kj] = —i,
[ik] = —j, [ii]= [jj] = [kk] = O, можно получить, как в B.186),
з*
36 Гл. 1. Кинематика деформируемых МеЛ
Перейдем к теореме Грина1), наиболее существенной
среди интегральных теорем векторного анализа. Она очень
часто применяется в математической физике, имеет фунда-
фундаментальное значение в теории потенциала (для которой
Грин доказал ее впервые), необходима для гидродинамики,
электродинамики и оптики, а также чрезвычайно полезна
для чистой математики. Риман основывал свою теорию
функций комплексного, переменного на теореме Грина
для двухмерного пространства; она используется также
в вариационном исчислении, теории собственных функ-
функций и интегральных уравнений. Грин доказывал свою
теорему путем интегрирования по частям, что часто де-
делается и в настоящее время. Докажем ее гораздо проще
с помощью теоремы Остроградского—Гаусса, которая,
кстати, не была известна Грину. Ilycib U и V—две ска-
скалярные функции точки, удовлетворяющие необходимым
требованиям непрерывности (существование вторых и не-
непрерывность первых частных производных). Примем в ка-
качестве А в C.1) выражение
A=*7gradF —Fgradtf; C.11)
следовательно,
Вычисляем?):
div (*7 grad F) = (grad Г/, grad V) + U div grad V, C.13a)
div (F grad ?7) = (grad F, grad U) -f V div grad U. C.136)
Находим из C.11) и C.9) выражение для div A:
divA = CMivgradF-Fdivgrad?7==GAF-FA[7. C.14)
Подставляя C.14) и C.12) в соотношение C.1) теоремы
г) Green G., Трактат о применениях математического анализа
к теориям электричества и магнетизма, Nottingham, 1828 (Ostwalds
Klassiker der exakten Wissenschaften, Nr. 61). Теорема сформули-
сформулирована и полностью доказана в § 3; вычисления, конечно, проводи-
проводились не.в векторной форме, а в декартовых координатах. Обозна-
Обозначения, использованные в C.11), введены Грином.
2) Для произвольного скаляра ф и произвольного вектора А
легко вывести формулу div i^A=^ div A+(Agrad (];).
§ 3. Теоремы Остроградского—Гаусса, Стокса и Грина 37
Остроградского—Гаусса, получаем
\^-V^)da. C.15)
Полученное выражение является первой формой теоремы
Грина. Оно справедливо для любых двух функций U tlV
и любой границы о объема т. Напомним, что за поло-
положительное направление нормали п принято внешнее на-
направление. До сих пор считалось, что объем т имеет
только внешнюю граничную поверхность. Если в теле
имеются одна или несколько полостей, то интегрирование
в правой части C.15) должно производиться также по
внутренним граничным поверхностям. Это, в частности,
имеет место, если объем содержит точки, где функция U
или V обращается в бесконечность или имеет какую-ни-
какую-нибудь другую особенность, так что эти точки должвы
быть исключены путем введения ограничивающих их по-
поверхностей oi. Тогда в правой части C.15) дополнительно
появляются соответствующие интегралы.
Если в качестве А в теореме Остроградского—Гаусса
принять выражение -А = Ugrad V, т. е. An=U (дУ/дп), то
подставляя C.13а) в C.1), получаем
(gradf/, gradV)dx+[ UAVdx=^U^da. C.16)
Выражение C.16) является второй формой теоремы Грина.
Приняв V = U и введя обозначение из C.9в), получим
формулу
^ {VUfdT+ ^ UbUdx= ^U~dc C.16a)
Последнее равенство приводит к выводам, чрезвычайно
важным для теории потенциала, которая, говоря матема-
математически, есть не что иное, как теория дифференциаль-
дифференциального уравнения
0, C.17)
решения которого известны под названием гармонических
или потенциальных функций. Из формулы C.16а) можно,
например, сразу получить следующую теорему: потенци-
потенциальная функция, которая обращается в нуль на замкну-
замкнутой поверхности а и регулярна внутри этой поверхности,
38 Г л I. Кинематика деформируемых тел
тождественно равна нулю внутри поверхности о. Дейст-
Действительно, в силу C.17) и граничного условия U — 0 из
C.16а) вытекает
[ (VUJd-z = 0 внутри о, C.17а)
Но из C.17а) следует, что VE/" = 0, так как подинтеграль-
ное выражение не отрицательно. Это означает, что U — const,
а так как U исчезает на границе, то ?7 = 0.
Однозначность решения граничной задачи в теории
потенциала может быть также доказана с помощью C.16а).
Сформулируем эту задачу следующим образом: требуется
найти решение уравнения C.17), принимающее задан-
заданные значения на граничной поверхности и регулярное
внутри. Если бы имелись два решения Ux и U2, удовле-
удовлетворяющих условиям задачи, их разность U = U1 — U2
удовлетворяла бы условиям предыдущей теоремы; таким
образом, U= 0 внутри о и, следовательно, Ux—if2.
Путем слегка измененных рассуждений тот же резуль-
результат может быть получен в случае, если на границе вместо
функции U задана dU/dn (см. задачу 5 гл. I).
Эти немногочисленные замечания дают обшее пред-
представление о значении теоремы Грина. В § 20 будет рас-
рассмотрен характерный случай ее применения.
§ 4. НЕКОТОРЫЕ ЗАМЕЧАНИЯ О ТЕНЗОРНОМ АНАЛИЗЕ
Различают симметричные, антисимметричные и про-
произвольные, или асимметричные, тензоры.
В настоящем параграфе мы будем иметь дело только
с симметричными тензорами, так как произвольный теезор
можно представить в виде суммы симметричного и анти-
антисимметричного тензоров точно так же, как в случае
коэффициентов ой в § 1, а антисимметричный тензор—в
виде вектора (аксиального), как в A.12а). Так как рас-
рассмотрение ограничивается тензорами второго ранга (т. е.
тензорами, компоненты которых имеют не более двух
индексов), то в качестве отправного пункта может быть
взято представление тензора деформации A.12). Наши
замечания будут сделаны по отношению к тензору дефор-
деформации, но они, конечно, сохраняют смысл для любого
§ 4. Некоторые замечания о тензорном аналиае 39
симметричного тензора второго ранга, в частности, для
тензоров напряжения и трения (см. гл. II).
Поведение тензора при преобразованиях координат
может быть изучено или с помощью его представления
в виде схемы коэффициентов линейной векторной функ-
функции, как в A.10), или с помощью его связи с квадра-
квадратичной формой A.13). Переписывая эти два соотношения,
заменим х, у, z на хг, х%, х3, ехзс, exii ... на eih, вектор &2,
т]2, С2 на произвольный вектор А с компонентами Av A2,
Л3; в результате получим
2 2 Bik xi xk = const. D.2)
i h
Для того чтобы найти связь между компонентами тензо-
тензоров е и е', сравним D.1) и D.2) с аналогичными соотно-
соотношениями в преобразованных уравнениях:
D.1а)
h
2 2 &im z'i я'т = const. D.2а)
I
2
I m
Воспользуемся следующими соотношениями между ком-
компонентами векторов х, А и х'', А';
Чл^к, D.3)
xi = 2j ati %l» Xh== 2j amfe ^w D-4)
1 m
Сравнивать D.1) и D.1а) здесь не требуется, так как эта
процедура формально идентична с преобразованием анти-
антисимметричного тензора, проведенным в B.9)—B.13); надо
только везде заменять Bih на eih. В этом случае B.13)
запишется в следующем виде:
D.5)
i k
Тот же самый результат может быть получен при срав-
сравнении D.2) с D.2а). Подставив, в D.2) из D.4), xi и xh,
40 Гл. I. Кинематика деформируемых тел
переменим порядок суммирования. Выражение
2 2 2 2 е1йа,|айАж[жт = const
I m i k
должно совпадать с D.2). Поэтому
eim = 2 2 SikWmh D-6)
i ft
совпадает с D.5), если отвлечься от наименования индексов.
Второй метод вывода правил преобразования, конечно,
проще, но он не может быть применен в случае анти-
антисимметричного тензора вращения. Попытка связать квад-
квадратичную форму с подобным тензором приводит к обра-
обращению этой формы тождественно в нуль: коэффициенты
при квадратах равны нулю (<р^ = 0), произведения разно-
разноименных компонент уничтожаются попарно, так как
Результат D.6) может быть выражен в форме следую-
следующего предложения: компоненты симметричного тензора
преобразуются как произведения и квадраты координат',
наоборот, это утверждение может быть принято в качестве
определения тензора.. Соответствующим утверждением для
полярного вектора было бы: компоненты преобразуются,
как сами координаты.
Равенства D.6) являются обобщениями предыдущих
равенств A.22) и A.22а); однако в D.6) имеются суммы
шести членов, в то время как в A.22) и A.22а)— суммы
только трех членов. Причина этого очевидна: в § 1 тен-
тензор деформации рассматривался в «диагональной форме»,
т. е. он был приведен к главным осям; но прямоуголь-
прямоугольный параллелепипед с ребрами, параллельными главным
осям, останется прямоугольным и после растяжения, а так
как угловых изменений нет, то, следовательно, и не будет
сдвигов. Таким образом, когда е относится к главным
осям, то из шести компонент тензора в D.6) три обра-
обращаются в нуль
Рассмотрим инварианты, тензора, дополнив то, что
было сказано ранее [см. A.23)] по поводу инвариантности
суммы диагональных членов, и докажем, прежде всего,
что определитель коэффициентов квадратичной формы
D.2) является инвариантом при ортогональных преобра-
преобразованиях координат:
§ 4. Некоторые замечания о тензорном анализе
41
-11
'21
'12 cl3
'22 fc23
D.7)
31 Е32 Е33
где D' — определитель для е' в равенстве D.6). Доказа-
Доказательство основано на теореме умножения определителей:
если определитель е умножается на определитель коэффи-
коэффициентов преобразования а, результат является тоже опре-
определителем со следующими элементами:
hi = 2 eihau-
i
Умножая определитель р еще раз на определитель а,
получим в результате элементы определителя
2 hiamk=^ 2 2 ei/Ai°w
k k i
Согласно D.6), это выражение совпадает с выражением
для преобразованных компонент тензора г[ъ, определитель
которого обозначен через D'. Таким образом,
Д' = Д.К|К,|. D.7а)
Это соотношение совпадает с D.7), так как определитель
а равен единице.
Если поверхность / = 2 2 4nxixn='coris\> при ортого-
ортогональном преобразовании переходит в /' = 2 2 г'гкх\хк=const,
то квадратичная форма ср = 2 %\ переходит в ср' = 2 #i2
(определение ортогонального преобразования). Следова-
Следовательно, любая поверхность семейства / -f- Хер = const при
ортогональных преобразованиях перейдет в /' + Хер' = const,
причем для одной и той же поверхности второго поряд-
порядка параметр X в этих двух уравнениях будет иметь одно
и то же значение. Но так как определитель коэффициен-
коэффициентов этой поверхности тоже будет инвариантен, отсюда
следует
D.8)
-и
'12
'21
S31
'22'
S32
'23
S33
Это должно выполняться для произвольных значений па-
параметра X; этим самым обобщается соотношение D.7).
42 Гл. I. Кинематика деформируемых тел
Определитель Бл может быть представлен в виде раз-
разложения по степеням X:
DA « D + ХД -Ь Х28 + X3, D.8а)
где в — сумма диагональных членов из A.23), а А —
квадратичное выражение
А = ?Пе22 + e22S33 + S33eil — Sl2e21 ~ E23S32 ~ S31S13- О4-9)
Выполняя то же разложение для Б'л и обозначая анало-
аналогично D.8а) коэффициенты через D', Д', в', получим
в силу D.8)
D + ХД + Х2в 4- X3 = D' 4- ХД' 4 Х28' + X3.
Это равенство должно выполняться для любого значе-
значения X, поэтому
D = D\ Д = Д', 8 = 8'. D.10)
У симметричного тензора имеются три инварианта,
т. е. три характеристических скаляра, которые не за-
зависят от системы координат, в которой заданы компо-
компоненты тензора. Геометрическая связь между инвариан-
инвариантами и тензором рассматривается в задаче 6 гл. I.
В случае механической интерпретации инвариант В пред-
представляет собой объемное расширение, как было показано
раньше. В общем случае 8 называется следом тензора.
Предыдущее рассуждение относится к произвольным
квадратичным формам и поэтому должно оставаться
справедливым для антисимметричного тензора в такой
же степени, как и для симметричного. Отсюда следует,
что антисимметричный тензор должен иметь три инва-
инварианта, но инвариант 8 тождественно равен нулю (диа-
(диагональные члены отсутствуют) и определитель D также
исчезает (что справедливо для любого антисимметричного
определителя нечетного порядка). Остается только инва-
инвариант Д, для которого D.9) принимает особую форму:
т. е. он равен сумме квадратов компонент соответствую-
соответствующего аксиального вектора. Таким образом, в случае
аксиального вектора точно так же, к,ак и для полярного,
существует только одна величина, не зависящая от вы-
выбора системы координат.
§ 4. Некоторые замечания о тензорном анализе 43
Разберем некоторые частные случаи тензорных по-
поверхностей и, прежде всего, простейший случай сфери-
сферической поверхности. Она соответствует однородному рас-
растяжению или сжатию во всех направлениях: сдвигов при
этом совсем не возникает, так как любая ось может быть
выбрана в качестве главной; все прямые углы сохра-
сохраняются.
Одноосное расширение, например в направлении оси
х, при условии, что во всех направлениях, нормальных
к оси х, растяжение отсутствует, соответствует квадра-
квадратичной поверхности х2 — const, что представляет собой
пару плоскостей. Это состояние, однако, не является дефор-
деформацией, которое фактически реализуется при односторон-
одностороннем растяжении в направлении оси х, так как в этом случае
(см. § 9) дополнительно возникает сжатие в направлении,
нормальном к х. Соответствующей поверхностью второго
порядка будет однополостный гиперболоид, для которого
ось х служит осью симметрии.
Представляет некоторый интерес состояние деформа-
деформации, при котором точки тела смещаются вдоль концен-
концентрических окружностей, расположенных вокруг неизмен-
неизменной оси г = О таким образом, что смещения обратно про-
пропорциональны расстоянию г от оси. Этот пример будет
полезен при рассмотрении кручения стержня круглого
сечения. Для того чтобы определить компоненты вектора
смещения, естественно ввести цилиндрические координаты,
в которых
Компоненты тензора деформации могут быть сразу
найдены для тех же координат с помощью выведенных
ниже формул D.26) и D.28). Эти формулы годятся для
произвольЕшх ортогональных криволинейных координат
и в настоящем случае дают
er'i = — ~^г » егг = е?? = Чг — V = ?zr = О, D.13)
Напишем уравнение тензорной поверхности, приняв, что
?, f\, С — обычные прямоугольные координаты в направле-
направлении приращений dr, c?cp, dz
2еГуЬ\ = const. D,14)
44
Гл. I. Кинематика деформируемых тел
Коэффициент егр меняется с расстоянием г, но в равен-
равенстве D.14), которое соответствует определенной точке
в теле, он сохраняет постоянное значение. Поэтому мно-
множитель 2егр можно включить в постоянную правую часть
равенства и вместо D.14) получить уравнение равносто-
равносторонней гиперболы
b] = const. D.15)
Тензорная поверхность в этом случае представляет собой
равносторонний гиперболический цилиндр. Оси гиперболы
D.15) образуют угол 45° с асимптотами ? = 0, tj = O.
Элемент объема, вырезанный параллельно dr, dy, dz,
после деформации находится в состоянии чистого сдвига.
г=0
Фиг. 4а.
В состоянии чистого сдвига первоначально пря-
прямоугольный элемент объема переходит в ромбо-
ромбоидальный.
Фиг. 46.
Главные деформации
образуют с направле-
направлениями сдвигов угол
45е; они равны друг
другу по величине и
противоположны по
знаку.
Первоначально прямоугольный элемент объема при де-
деформации принимает ромбоидальную форму (на фиг. 4а
обозначен пунктиром). Полагая
s9 (г) = s0 -Ь 8s, s, (г + dr) = s0 — 8s,
можно увидеть, что только 8s соответствует искажению,
в то время как s0 представляет собой простой перенос
(на фигуре не указан). С Другой стороны, элемент объема,
изображенный на фиг. 46, ориентированный параллельно
главным осям тензорной поверхности, не только не испы-
испытывает деформации сдвига (что требуется по определению
главных осей), но и не меняет объема.
Это является следствием равносторонней формы тен-
тензорной поверхности; из D.13) видно, что 'след © обра-
§ 4. Йекоторые замечания о тензорном анализе 45
щается в нуль, следовательно, он должен исчезать также
для элемента объема, вырезанного параллельно главным
осям (инвариантность следа). Так как в = e1-f-e2+e3 = О
и ед=ея=О, то е2= — ег
Состояние чистого сдвига характеризуется главными
деформациями, равными по величине и противоположны-
противоположными по знаку.
В заключение выведем формулы, выражающие пре-
преобразование тензора деформации в криволинейных коор-
координатах [они уже использовались для
получения D.13)]. Эти формулы не
могут быть выписаны сразу, как это
было сделано для grad, div, rot в / ds+Sda
равенствах B.24) —B.26), так как у ds I /
нас нет определения тензора, кото- / ^<~*^Q
рое имело бы наглядный, геометри- pl~~~^T
чески инвариантный смысл, подобно
определениям grad, div, rot в § 2. Ф и г. 5.К преобразо-
Для углубления представления о тен- ванию тензора дефор-
« г мадии в произволь-
зорнои поверхности необходимо ни- нь? ортогональных
жеследующее рассмотрение1). Хотя это координатах: смеще-
рассмотрение довольно трудоемко, оно ние qb элемента дли-
будет весьма полезно впоследствии, ны ds-
например в задаче о кручении в § 42.
Пусть ds — расстояние между двумя соседними точ-
точками Р и Р' рассматриваемой среды, dx, dy, dz — раз-
разности их декартовых, a dplt dp2, dp3 — разности ортого-
ортогональных криволинейных координат. Согласно B.22),
ds* = <h* + dy* + dz* = g\ dp\ + g\ dp\ + g\ dpi D.16)
/ d
s I /
/ ^
При деформировании среды все точки претерпевают сме-
смещения, задаваемые A.10), которые обозначим теперь через
Sq. Символ dbq обозначает разность их смещений, и
можно доказать, что
dbq = bdq. D.17)
Это поясняется на фиг. 5; переход от Р к Q и соот-
соответственно от Р' к Q' обозначается буквой Ь, переход от
Р к Р' и соответственно от Q к Q' — буквой d; стороны
х) См. Beltrami E., Ann. di Math, 10, 183 A881), Ges. Werke,
Bd. Ill S. 183.
46 Гл. I. Кинематика деформируемых тел
четырехугольника понимаются как векторы. Тогда имеем
а также
Здесь левая часть представляет собой dbq, а правая —
bdq', следовательно, соотношение D.17) доказано и его
геометрический смысл пояснен.
Вернемся теперь к A.10). В декартовых координатах
мы имели
( d Ьх = е^ dx + exy dy + exz dz,
dbq = \ dby — eyxdx + eyy dy -\-eyzdz, D.18)
' d bz = ez;x. dx + ezy c?2/ ~b ezz ^2-
Подставим вместо с?ж, dy, dz элементы длины в криволи-
криволинейных координатах из равенства B.23)
ds1 = g1dp1, ds2 = g2dp2, dss = gsdps. D.19)
Изменение смещения B.18) примет вид
d bs1=en dsx + e12 ds2 + e13 c?s3,
d bs2 = eal c?5x + e22 ds2 -f e23 dss, D.20)
dbq =
= e31 ffSjL + e32 ds2 + e33
Необходимо, зная компоненты смещения 8gx, og2, bq3
в направлениях jDlf /?2,* р3, вычислить криволинейные
компоненты тензора zik, как это делалось в A.11).
Сначала определим в декартовых координатах изме-
изменение квадрата длины ds2, вызванное смещением. Из
D.16) — D.18) получаем
^-bds2 = dx Ь dx + dy Ь dy + dz b dz = e^ dx2-\- eyy dy2 -+-
4- ezz dz2 + 2exy dx dy + 2eyz dy dz + 2ezx rfz da;. D.21)
Правая часть представляет собой тензорную поверхность
A.13), где х, у, z заменены на dx, dy, dz. Левая часть
D.21) может быть записана в форме dsbds. Разделив на
ds2, получим величину bdsjds, которая представляет
собой относительное растяжение отрезка ds. Тот же
§ 4. Некоторые замечания о тензорном анализе 47
смысл имеет выражение тензорной поверхности, если
в него вместо прежних переменных х, у, z подставить
направляющие косинусы (dxjds), (dyjds), (dzjds). В этом
заключается более наглядный смысл тензорной поверх-
поверхности (ср. стр. 14).
Этот метод может быть непосредственно перенесен на
обобщенные криволинейные координаты рх, р2, р3. Исполь-
Используя D.19), напишем квадрат элемента длины, как
ds2 — dsl~\-dsl-\-dsl. На основании D.17) и D.20) получим
— Ь ds2 = dsx Ь dsx -f- ds% b ds2 -f- ds3 о ds3 =
= en ds\ + e22 ds\ + e33 ds23 +
+ 2e12 dsx ds2 -J- 2e23 ds2 dss -\- 2e3l ds3 dsv D.22)
Разделив на ds2, получим, как прежде, растяжение от-
отрезка ds.
Чтобы определить eik, надо выразить у § ds2 с по-
помощью первоначального соотношения D.16). Записывая
D.16) в сокращенном виде
получаем
-i Ь ds2 = 2 Si tet dpi + 2 Si dPi Ь dPi.
i i
Введем теперь
h
после этого получим
4
.^«adp' + 22«<жd"'dft- <4-23>
i ft i ft
Теперь, согласно D.19), можно вместо dpt ввести dsit
а для bpk, согласно смыслу bqk из фиг. 5, можно вос-
воспользоваться формулой, аналогичной D.19):
48 Гл. I. Кинематика деформируемых тел
После этих подстановок первая из двух сумм" правой
части D.23) преобразуется следующим образом:
—-p-dz!, D.23а)
Sigh dPk V '
ft
а вторая —
(
gh dpk V gi
i k
или, производя дифференцирование, получаем
ds J)J\^LlfLds ds D.236)
г k ^ Д gigk dph » Л v '
gk fyk г k ^ Д gigk
i ft i ft
Из выражений D.23а) и D.236) определим коэффициенты
при некотором определенном dsf. Выражение D.23а)
дает вклад
^1 D.24а)
^" gigk
ft
В D.236) вместо к надо подставить данное г, в резуль-
результате чего обе двойные суммы сведутся к одному члену
ji|L^L. D.246)
gi dpi g\ dpi v '
При сложении D.24а) и D.246) два члена взаимно уни-
уничтожаются и получаем
±(^,+ у\^р.Л, D.25)
gi \dPi ' <*- gk dPkJ V '
ki=i
Сравнение D.23) с D.22) показывает, что это выражение
и есть еи. Следовательно,
dgl Ьд3 dg
_
e22
22
D.26)
33
g3 \ dps "*" ft ^l "^ g2 ^2 / '
При определении компонент сдвига eik мы прежде
всего отметим, что D.23а) не дает вклада, так как туда
§ .4. Некоторые аамечания о тенаорном анализе 49
входят только квадраты ds\, а не произведения dsi dsk.
Если заданы определенные i и к, то в D.236) надо брать
два члена, а именно один член с dsi dsk и другой с dskdsi.
Тогда вместо D.25) получаем четырехчленное выражение
gk dPh gi dPi gigh V Vl dPk *ft dpi J V '
которое равно 2eik [это видно из сравнения D.22) с D.23)].
В развернутом виде
gx dPl
Формулам D.26) и D.28) может быть придан более
удобный вид, если пользоваться обозначениями общего
тензорного анализа, как это сделано в приложении I.
Применим эти формулы для подтверждения равенств
D.13). В случае цилиндрических координат рх — г, /?2=~ср,
~p3 — z, причем g1 = g3 = l, g2 = r и, согласно D.12),
Ч ^0 Ьд
В результате, вклад дадут только те члены в D.26) и
D.28), которые содержат bq2 или dbq2jdpx и не содержат
исчезающих коэффициентов [например, dgjdy в первом
из равенств D.26)]. Этим условиям удовлетворяет только
е12, а именно:
1 А
2gi dPl 2 г»
И
2
Таким образом, в нашем случае из D.28) получим
ei2 — ~ (-4/г2)- Этим доказана справедливость утверждения
А. Зоммерфельд
$0- Гл. I. Кинематика деформируемые тел
Дадим, наконец, интерпретацию поля смещений D.12)
как поля скоростей, полагая
г;г = 0, г;, = А} ^ = 0. D.29)
Это движение имеет фундаментальное значение в теории
вихрей. В дальнейшем покажем, что во всех точках, где
г > О (т. е. везде, кроме оси), это движение безвихревое.
Такое утверждение верно, несмотря на то, что происхо-
происходит вращение вокруг оси г = 0. Обозначим это движение
как «простой вихрь», чтобы указать, что на оси имеется
особенность: концентрированная «вихревая нить».
Этот вопрос будет рассмотрен подробнее в § 19, где
будет также показан безвихревой характер такого дви-
движения; последнее, однако, можно ноказать также с по-
помощью формул к задаче 3 гл. I. Надо только
принять в качестве вектора А в формулах, дающих ком-
компоненты ротора в цилиндрических координатах, вектор,
приведенный в D.29).
В этой главе было развито понятие тензора и изучено
его поведение в декартовой системе координат. При ис-
исследовании более общих преобразований должны быть
применены методы общего тензорного анализа, о которых
кратко сказано в приложениях I — IV.
Глава II
СТАТИКА ДЕФОРМИРУЕМЫХ ТЕЛ
§ 5. РАЗДЕЛЕНИЕ ТЕЛ НА ТВЕРДЫЕ И ЖИДКИЕ,
СЖИМАЕМЫЕ И НЕСЖИМАЕМЫЕ, ИДЕАЛЬНЫЕ И ВЯЗКИЕ
Как и в случае механики систем с конечным числом
степеней свободы, статика — это наука о силах, действую-
действующих на вещество1). Можно различать силы внешние
и внутренние, определяя последние как силы, которые, дей-
действуя внутри рассматриваемой системы, подчиняются прин-
принципу равенства действия и противодействия. Из внешних
сил в механике деформируемых тел обычно рассматривают
силу тяжести и центробежную силу2), а также капил-
капиллярные силы, которые действуют со стороны внутренних
молекул на молекулы пограничного слоя или между
стенкой и пограничными молекулами жидкости. К внут-
внутренним силам относятся также реакции (напряжения,
давления, поверхностные напряжения), которые возни-
возникают вследствие заполнения пространства веществом. В ме-
механике деформируемых тел эти силы играют главную роль 3).
В случае твердого тела реакции, отнесенные на еди-
единицу поверхности, называются напряжениями, в случае
жидкости разумно говорить о давлениях (отрицательных
напряжениях). Напряжения4) и давления имеют размер-
размерность не силы, а сала\площадь (в системе CGS — дина]см2).
х) Определение статики см. «Механика» (т. I), § 5, особенно при^
мечание на стр. 48.
2) Центробежная сила как сила инерции относится, собственно
говоря, к динамике (см. гл. III). Ее можно, однако, рассматривать
в статике, так как для наблюдателя, движущегося в телом, она
эквивалентна внешней силе.
3) Разделение на внешние и внутренние силы, вообще говоря,
не совпадает с разделением на силы физического и геометрического
происхождения, из которых последние возникают вследствие на-
наложения на систему пространственных ограничений.
4) Термин несколько неудачен, так как в обычной механике, го-
говоря о напряжении каната, имеют в виду силу, передаваемую кана-
канатом.
4*
52
Гл. //. Статика деформируемых тел
Для выяснения понятия напряжения в упругом твер-
твердом теле на фиг. 6,а выделена «положительная ж-пло-
скость» (заштрихована). Наружная нормаль к этой пло-
плоскости совпадает с положительным направлением оси х.
На фигуре плоскость изображена в виде прямоугольника
со сторонами Ау и &z. Отрицательной sc-плоскостью будем
называть плоскость, которая совпадает с положительной,
но внешняя нормаль которой имеет направление, про-
противоположное направлению оси х (заштрихованная часть
фиг. 6,6). Она действует на положительную ^-плоскость
Шк
/С/, ¦
Фиг. 6.
Нормальные и касательные напряжения, действующие на элемент объ-
объема упругого тела. Взаимодействие между положительной и отрицательной
эс-плоскостями.
с какой-то силой. Если эта сила направлена по оси х,
говорят о положительном нормальном напряжении ахх,
величина которого равна сумме всех действующих сил,
деленной на площадь Ay^z. В общем случае равнодей-
равнодействующая не перпендикулярна к se-плоскости, а направ-
направлена к ней под некоторым произвольным углом. Разло-
Разложим эту силу и соответствующее напряжение по поло-
положительным направлениям осей х, у и z. Компоненты
у и z называются тангенциальными напряжениями или
напряжениями сдвига и обозначаются аху и ахг. В обоз-
обозначении aik первый индекс указывает положение плоско-
плоскости, а второй — направление напряжения.
Согласно принципу равенства действия и противодей-
противодействия, напряжения, действующие на отрицательную se-пло-
§ б. Разделение тел на твердые и жидкие 53
с кость (фиг. 6, б), должны быть противоположно направ-
направленными. Здесь положительное напряжение о^ направ-
направлено в отрицательную сторону оси к. То же самое спра-
справедливо для отрицательной ге-плоскости элемента объема
(фиг. 6, а), которая получается путем простого смещения
рассмотренной ранее отрицательной ^-плоскости на длину
ребра Да>.
Совокупность величин aik, характеризующих элемент
объема, обозначим как тензор напряжений, хотя доказа-
доказательство его тензорного характера будет дано только
в § 8 (будет доказана симметрия aik и выведены правила
их преобразования при переходе в другую систему коор-
координат). Кстати, выражение «тензор напряжений» является
тавтологией, так как латинское слово tensio означает на-
напряжение.
Силы, с которыми окружающие элементы объема дей-
действуют на рассматриваемый элемент, могут быть направ-
направлены как внутрь, так и наружу. В первом случае пред-
предпочитают говорить не о напряжениях, а о давлении. Мы,
однако, сохраним для упругого твердого тела название
«напряжение», говоря о давлении как об «отрицатель-
«отрицательном напряжении».
Иначе в случае жидкости, где силы сцепления малы
и ее предел прочности по сравнению с твердым телом чрез-
чрезвычайно мал. Другими словами, жидкость почти не ока-
оказывает сопротивления положительному нормальному на-
напряжению. Поэтому в случае жидкости разумно говорить
не о напряжении о, а о давлении р; на фигуре, подобной
фиг. 6, положительное давление рхх изобразилось бы стрел-
стрелкой, направленной внутрь1). Что касается напряжений, то
в жидкости они почти никогда не бывают значительными.
Совокупность давлений pik, действующих на элемент
жрздкости, также назовем тензором. Однако между нор-
нормальными давлениями рн и тангенциальными давления-
давлениями pih, по крайней мере в случае покоящейся или мед-
медленно движущейся жидкости, есть существенная разница.
х) Следовательно, рху, />х2и т. д. должны изображаться стрелками,
направление которых противоположно направлению стрелок, изо-
изображенных на фиг. 6, т. е. р^ положительно, если оно направлено
в отрицательном направлении оси у. Это будет учтено в даль-
дальнейшем.
54 Гл. Л. Статика деформируемых тел
Слой жидкости может двигаться над лежащим под ним
слоем без существенной затраты энергии, если скорость
достаточно мала. В случае медленного перемещения отно-
относительно друг друга двух прилегающих слоев танген-
тангенциальные давления p{k будут также незначительны. По-
Поэтому следует принять, что в состоянии покоя танген-
тангенциальные давления pik равны нулю. В § 6 будет пока-
показано, как существенно упростится при этом тензор дав-
давлений.
В случае больших относительных скоростей частиц
жидкости тензор давлений должен рассматриваться в об-
общем виде и должна, кроме того, исследоваться его зави-
зависимость от градиентов скорости. Это будет проделано
в § Ю.
Понятие жидкости можно также распространить на
газы и пары, но они отличаются большой сжимаемостью.
Обычные жидкости, в отличие от газов, не могут быть
существенно сжаты. Конечно, они могут быть несколько
сжаты, если на них действуют очень большие внешние
силы. Но в сравнении с газами эта сжимаемость незна-
незначительна, и ею в большинстве случаев можно прене-
пренебречь. Так, например, воду чаще всего считают несжи-
несжимаемой. Согласно A.24), условие несжимаемости выра-
выражается как в = 0; переходя от вектора смещения s к
вектору скорости v [как в A.7)], получим для этого
условия выражение
divv=0. E.1)
«Из каждого элемента объема Дх вытекает столько же
жидкости, сколько втекает».
Обозначив через Am содержащуюся в Дх массу, полу-
получим
Дт = рДх, E.2)
где р — плотность. Это значит, что для однородной не-
несжимаемой жидкости плотность постоянна во времени
и пространстве.
Что соответствует равенству E.1) для сжимаемой
жидкости? В этом случае сохраняется не объем, а масса.
Масса Дт не может уменьшиться, если только часть ее
не выйдет из объема Дх через его границу. Поток мае-
§ б. Разделение тел на твердые и жидкие 55
сы в любой точке границы задается нормальной состав-
составляющей вектора pv. Полное изменение массы за время AZ
равно [ср., например, B.20)]
\ pvndc A?=div(pv) Дт At. E.3)
С другой стороны, потеря массы за то же время может
быть найдена из E.2), т. е.
Сравнение с E.3) приводит к условию сохранения массы
|+div(pv) = 0, E.4)
известному под названием уравнения неразрывности.
Его можно также писать в форме
E.4а)
Здесь (ср. стр. 121) полная производная означает, что
| | E.46)
В случае постоянства р в пространстве и времени из
E.4) опять вытекает условие несжимаемости E.1). Для
несжимаемой неоднородной жидкости, где р непостоянно
в пространстве, из E.46) получаем
| = 0, т. е. |?=_(v,gradP). E.4в)
Полученное выражение дает зависимость р от времени
для определенного места наблюдения. В прямоугольных'
координатах равенства E.1), E.4) и E.4а) запишутся
как
Й + pffi + ^ + ^W E.4а')
dt ' г \дх ду ' dz J \ i
Если вместо всего объема жидкости будем рассматри-
рассматривать только ее поверхностные слои (капиллярность), то.
56 Гл. II. Статика деформируемых тел'
введенная прежде поверхность раздела заменится теперь
линией раздела, проведенной через поверхностную плен-
пленку. При эгом должны изучаться силы реакции, с кото-
которыми один берег разреза будет действовать через линию
раздела на другой. Сила, отнесенная к единице длины
разреза, называется поверхностным натяжением. Ее раз-
размерность—дина/см, в отличие от размерности давления
в жидкости и напряжения в твердом теле, которая рав-
равна дина/см2.
§ 6. ГИДРОСТАТИКА
В этом параграфе рассматривается не только вода
(hydor), но и любая жидкость в состоянии равновесия,
поскольку в состоянии покоя различия в вязких харак-
характеристиках у разных жидкостей не играют роли (см. стр. 54).
Там же было показано, что в состоянии равновесия тан-
тангенциальные компоненты тензора давлений обращаются
в нуль:
Pik = O,i*k. F.1)
Это равенство может служить определением состояния
покоя жидкости — в противоположность состоянию затвер-
затвердевания; стекло, которое не имеет кристаллической струк-
структуры, может быть физически охэрактеризовано как
затвердевшая жидкость, для которой равенство F.1),
конечно, не выполняется.
Из F.1) вытекает фундаментальное следствие: тензор-
тензорной поверхностью гидростатического давления является
сфера. Согласно F.1), в качестве главных осей могут
быть выбраны любые оси; давление действует перпенди-
перпендикулярно к любой поверхности раздела i в жидкости и
одинаково во всех направлениях'. рп = ргг = рВ8. Впервые
атот вакон открыл Паскаль1).
Таким обравом, гидростатическое давление есть ска-
скалярная величина. Как это обычно делается, обозначим
ее через р (опуская ненужные индексы у рн). Напри-
Например, под действием силы тяжести будут находиться не
*) Влав Паскаль A624—1662 гг.) был не только великим гевметрем
(теорема Паскаля), математиком (треугольник Паскаля, основание
теории вероятностей), писателем, он изучил также законы атмосферно-»
Го давления и первый произвел барометрическое определение высоты.
§ 6. Гидростатика * 57
только горизонтальные сечения в воде, но это же давле-
давление р будет действовать на любую поверхность раздела,
в том числе и на вертикальную. Направленный харак-
характер действующей силы не сказывается на всесторонности
давления.
Как же зависит величина давления от величины и
направления внешней силы? Обозначив последнюю через F,
будем считать, что это — сила, действующая на единицу
объема жидкости (а не приложенная к точке, как в т. I).
Размерность F в физической системе единиц будет
дина .п о\
Выберем, для простоты, в качестве элемента объема прямо-
прямоугольный параллелепипед (Дт = Ьх &у &z) и пусть отрица-
отрицательная ж-плоскость находится в точке х, а положитель-
положительная—в точке (x-\-kx) (ср. стр. 52), так что в положи-
положительном направлении оси х будут действовать следую-
следующие силы:
На отрицательную На положительную На элемент
ж-плоскость зс-плоскость объема
FxAx F.3)
Первый и второй члены при сложении дадут
-§f Да;ДуД2=-|?Дт, F.3а)
и после деления на Дх получаем в сумме
a? F.36)
или для произвольного направления и любой точки в
жидкости
F. F.4)
Очевидно, чте соотношения F.36) или F.4) для компо-
компонент силы являются необходимыми условиями равнове-
равновесия. Являются ли эти условия достаточными? В статике
твердого тела имелось еще условие равенства нулю сум-
суммы моментов сил. Ясно, что условие, необходимое для
твердого тела, будет необходимо и для нетвердого тела
С ослабленными внутренними связями. Но в случае
58 Гл. II. Статика деформируемых тел
жидкости это условие выполняется само собой. Нормальное
давление р не может давать момента относительно ка-
какой-нибудь оси. Относительно оси х момент могут давать
только тангенциальные давления руг и ргУ, но, согласно
равенству F.1), они обращаются в нуль. То, что и внеш-
внешняя сила F не дает момента, непосредственно оче-
очевидно при непрерывном распределении силовых линий
в бесконечно малом объеме, как в поле тяжести.
Если же силовые линии имеют внутри рассматриваемого
элемента объема особую точку, в которой пересекаются
две или более линии, то в этой точке сила F, а тем бо-
более ее момент обращаются в нуль. Таким образом, F.4)
представляет собой не только необходимое, но и доста-
достаточное условие равновесия.
Равенство F.4) содержит в себе замечательную тео-
теорему: равновесие возможно только тогда, когда внешняя
сила имеет потенциал, т. е. если F может быть пред-
представлена в виде градиента скалярной функции. В этом
случае можно написать [знак минус объясняется связью
с потенциальной энергией1)]
F= -gradC/. F.5)
Недостаточно одного существования потенциальной функ-
функции U; она также должна быть однозначной в объеме,
занятом жидкостью. Только при этих предположениях
можно найти р из F.4) как однозначную скалярную
функцию точки в виде
/?+{/ = const. F.6)
Постоянная интегрирования в F.6) определяется специаль-
специальным соглашением о нормировках давления и потенциала.
Пояснение этой теоремы мы перенесем в конец пара-
параграфа, а сейчас займемся обычным случаем, когда сила F
имеет однозначный потенциал, выбрав, прежде всего, силу
тяжести.
Пусть z = О на поверхности жидкости (назовем ее
просто водой); ось z направим вертикально вниз. Тогда
F = Fz = 9g = i, U=-pgz=-iz. F.7)
-1) См. «Механика» (т. Л), стр. 139.
§ 6. Гидростатика 59
Здесь 7~~ удельный вес воды в собственном значении
этого слова; в отличие от удельной массы или плотности
р в значение f в виде множителя входит ускорение силы
тяжести. При написании формулы F.7) функция U выбрана
таким образом, что на поверхности воды она равна нулю.
Тогда из F.6) следует
jo = fz + const. F.8)
Здесь const означает давление на поверхности (при2 = 0),
равное атмосферному давлению. Если же под р понимать
давление, превышающее атмосферное (что удобнее для
дальнейшего), то можно просто написать
p — ^z. F.8а)
Эта формула содержит все, что нужно для описания
явлений, которые мы наблюдаем в сообщающихся сосу-
сосудах. Независимо от ширины обоих колен и от того, как
они изогнуты, уровень воды во втором колене будет тот
же, что и в первом, а именно: z = 0; на одинаковой глу-
глубине z под поверхностью в обоих коленах будет одно
и то же давление.
Тот же результат можно получить не только из инте-
интегральной формулы F.8а), но и из дифференциальной
формулы F.4). Внутри сосуда проведем ломаную линию,
огибающую его границу и состоящую частью из верти-
вертикальных, а частью из горизонтальных отрезков и нахо-
находящуюся целиком в воде. На горизонтальных отрезках
dp = 0, на вертикальных dp = ^dz. Суммирование послед-
последних дает, что p = -^z на глубине z.
Приведем здесь некоторые численные постоянные: нор-
нормальное атмосферное давление на уровне моря измеряется
весом ртутного столба высотой 76 см\ плотность ртути
равна 13,596 г/смь. Поэтому из F.8а) следует
ратм. = 76 • 13,596 • g г/см2 = 1033 • g г/см2 = 1,033 кГ/см2.
Следовательно, на каждый квадратный сантиметр поверх-
поверхности воды действует сила, равная 1 кГ, а на 1м2— 10 т.
Если атмосферное давление измерять весом водяного
столба, а не ртутного, то высота столба равна 10,33 м.
Здесь для воды принято, что р=1 и
Ратм. — ЮЗЗ • 1 • g ejcM2 — 1,033 кГ/см2. . >. .-
60 Гл. II. Статика деформируемых тел
Отсюда следует, что в море на каждые 10 м глубины
давление возрастает примерно на 1 атм. Поэтому р мож-
можно измерять не только в атмосферах, но и в десятимет-
десятиметровых столбах воды.
Рассмотрим пример, когда одновременно действуют
сила тяжести и центробежная сила: жидкость в барабане
(центрифуге) врашается с постоянной угловой скоро-
скоростью со вокруг вертикальной оси. Центробежная сила,
действующая на единицу объема, равна
/• = /?г = рГиJ. F.9)
Эта сила обладает потенциалом
Суммарный потенциал силы тяжести и центробежной силы
без учета произвольной постоянной равен
ТТ 1 О 9 f i r2W2 \
и = — ogz —гг р/^со = — y ( z + -п— ) .
^ ч *ё у
На основании F.6) можно вычислить давление во вра-
вращающейся жидкости:
const. F,10)
Чтобы определить постоянную, обозначим высоту жидко-
жидкости на оси барабана, т. е. для г — 0, через z0. Если через р
опять обозначить превышение давления над атмосферным,
то из F.10) для случая z — z0 и г—0 имеем
0 — 7Z0 -f const, const = — fzo
и для любой точки
F.11)
Уравнение свободной поверхности, согласно вашему
условию, задается уравнением /? = 0, т. е.
«o-* = i5~. (б-12)
Эта поверхность представляет собой параболоид враще-
вращения (фиг. 7), как в «опыте с ведром» Ньютона1). Так
х) См. «Механика» (т. I), стр. 16,
§ 6. Гидростатика
61
как ось z направлена вниз, ординаты параболического
профиля z0 — z отсчитываются вверх. Пусть h — разность
уровней воды на периферии и в центре, a v — скорость
на периферии, тогда из F.12) получаем
* = -?, F-13)
т. е. h равна величине «скоростного напора» *). Поверх-
Поверхности постоянного давления представляют собой кон-
груентные параболоиды, по-
полученные путем смещения
поверхностного параболоида
вертикально вниз.
Вернемся опять к случаю
чистого поля тяжести, а имен-
именно, рассмотрим равновесие ко-
корабля. На фиг. 8 представ-
представлено сечение, перпендикуляр-
перпендикулярное к продольной оси судна
(ось у направлена вперед, ось
х — вправо, ось z — вниз). Кор-
Корпус судна будем рассматри-
рассматривать как цилиндрическую обо-
оболочку, параллельную оси у.
О—центр тяжести судна,
С — центр тяжести вытеснен-
вытесненного объема жидкости; этот
объем называется также водо-
водоизмещением.
Определим выталкивающую силу, действующую на
судно, как равнодействующую всех сил давления, дей-
действующих на корпус. Можно доказать, что эта равно-
равнодействующая проходит через С. Точку С можно назвать
центром пловучести.
Рассмотрим элемент поверхности стенки судна do =
= dsdy. На фиг. 8 виден только элемент длины нашего
сечения ds; элемент длины dy расположен параллельно
оси судна. Давление ^z действует перпендикулярно к da,
z
Фиг. 7.
Параболоидальная поверхность
вращающейся жидкости. Подъем
у стенок может рассматриваться
как скоростной напор.
См. «Механика» (т. 1)г стр. 30, формула C.13а).
62
Гл. II. Статика деформируемых тел
сила, действующая на da, равна ^zda, а ее вертикаль-
вертикальная составляющая —
fs da cos (п, z),
где п — внутренняя нормаль к da. Но da cos (п, z) пред-
представляет собой, с другой стороны, проекцию da на гори-
горизонтальную плоскость (плоскость ху), в качестве которой
выбрана поверхность воды. Отсюда можно найти равно-
равнодействующую R всех сил давления:
iV1 F.14)
где V — объем вытесненного количества жидкости, равный
сумме объемов столбов воды zdxdy, находящихся под
Равновесие цилиндрического корпуса корабля. Подъемная си-
сила представляет собой равнодействующую всех сил давле-
давления, действующих на оболочку.
элементами dx dy. По абсолютной величине сила R равна
весу iV вытесненной жидкости, но направлена вверх —
это выталкивающая сила. Точка приложения R совпадает,
естественно, с центром тяжести С объема V, так как
выталкивающая сила определяется как равнодействующая
сил тяжести всех рассматриваемых столбов воды.
При равновесии С ml О должны лежать на одной
вертикали и выталкивающая сила R должна быть равна
весу G, как это показано на фиг. 8:
§ 6. Гидростатика 63
Это условие определяет глубину погружения судна,
которая, естественно, зависит от нагрузки судна. Гори-
Горизонтальные составляющие сил давления, действующие
на два противоположных элемента da1 и dc2, расположен-
расположенные на одной и той же глубине, уравновешивают друг
друга (даже в случае несимметричного нагружения судна!).
Это следует немедленно из равенства обеих проекций
на вертикальную плоскость
cos (wx, х) dcx = cos (n2, х) е?о2.
Сделаем несколько замечаний по поводу колебаний
судна при нарушении состояния равновесия. Чтобы не
выходить из области гидростатики, рассмотрим только
статику колеблющегося судна. Распределение давлений
в жидкости в каждый момент можно считать (с хорошим
приближением) установившимся и поэтому вычисления
производить на основе соотношений статики.
Рассмотрим боковую качку судна, т. е. вращение его
вокруг горизонтальной продольной оси (ось у). Меридио-
Меридиональная плоскость судна при этом выйдет из вертикаль-
вертикальной плоскости; обозначим угол, который в некоторый
момент образуют эти плоскости, через ft. Во время качки
форма вытесненного объема жидкости и положение точ-
точки С будут меняться. Точка С перейдет в С или,
при другом направлении качки, в С". Построим для
точки С центр кривизны М кривой С'СС", найдя для
этого точку пересечения нормали из С с соседней нор-
нормалью, например из точек С' или С", как это показано
на фиг. 9. В судостроении точку М называют метацен-
метацентром. В положении, изображенном на фиг. 9, равнодей-
равнодействующая выталкивающих сил R приложена в точке С".
Она расположена справа от центра тяжести судна О.
Момент М пары сил R и G (его направление на фигуре
указано стрелкой) стремится уменьшить угол отклоне-
отклонения Ь. Это является необходимым и достаточным условием
для устойчивости судна. Оно выполняется, если точка М
расположена над О. Если метацентр М был бы располо-
расположен ниже центра тяжести О, то момент М способствовал
бы увеличению отклонения Ь, что привело бы к опроки-
опрокидыванию судна.
Гл. II. Статика деформируемых тел
Расстояние между О и М называется высотой мета-
метацентра и обозначается через h. Для малого Ь (см. фиг. 9)
|М| = hG sin b^hGb.
Дифференциальное уравнение качания будет таким же,
как и для физического маятниках) (в — момент инерции
судна относительно продольной оси):
F.15)
и круговая частота колебаний равна
- F.16)
В практикэ судостроения величина h выбирается равной
нескольким значениям (от трех до пяти) расстояния СО.
z=0
^Ф и г. 9. Корпус судна в наклоненном состоянии.
Метацентр и возвращающий момент.
"Мы рассмотрели здесь бесконечно малые колебания
и, следовательно, положение метацентра М при 9-—>0.
В практике судостроения надо, конечно, исследовать усло-
условия равновесия и при конечных Ь и соответственно учи-
учитывать изменение положения М для соответствующего Ь.
Перейдем к рассмотрению интересных явлений, кото-
которые возникнут в силовом поле, не имеющем однознач-
х) См. «Механика» (т. I), § 16.
§ 6. Гидростатика 65
ного потенциала. Вместо общих рассуждений приведем
простой пример, который легко может быть осуществлен
экспериментально.
Нальем слабо проводящую жидкость (например рас-
раствор CuSO4) в плоский цилиндрический сосуд с изоли-
изолирующим дном и проводяшей боковой стенкой. Вдоль оси
сосуда расположим медную проволоку. Между проволокой
и боковой стенкой приложим разность потенциалов в не-
несколько вольт. В сосуде возникнет электрический ток,
идущий через жидкость от оси к боковой стенке. Пусть
/ -полный ток, идущий через жидкость, a J —удельный
ток на расстоянии г от оси (равный полному току, делен-
деленному на площадь цилиндрической поверхности радиуса г),
т. е.
4 <6Л7>
где h — высота слоя жидкости. Наложим однородное маг-
магнитное поле Н, силовые линии которого будут перпен-
перпендикулярны к слою жидкости. На каждый элемент тока
будет действовать электромагнитная сила
F = [JH], F.18)
перпендикулярная к J и Н и поэтому направленная каса-
касательно к окружностям, концентричным с боковой стен-
стенкой. Принимая во внимание F.17) и F.18), напишем
Эта сила имеет потенциал
tf=-4cp. F.20)
Действительно, если вычислить отрицательный градиент
U в цилиндрических координатах, то составляющие в на-
направлениях г и 2 обратятся в нуль, а составляющая
в направлении ср будет
, ТТ 1 dU A „
— grada U = 5— = — = F9.
Но этот потенциал в (двусвязной!) области нашей жидко-
жидкости неоднозначен. А именно, при каждом обороте вокруг
оси г = 0 он меняется на величину 2пА.
5 А. Зоммерфельд
бб Гл. II. Статика деформируемых тел
Так как гидростатическое давление должно быть одно-
однозначной функцией точки, то не будет существовать рас-
распределения давлений, удовлетворяющего этому потенциалу
в смысле равенства F.6). Следовательно, жидкость будет
находиться в движении под действием силы Fy. При этом
возникнет описанный в D:29) простой вихрь; его круговая
скорость будет в данном случае равна
А г
V=Vr,— ,
где t— время, прошедшее после включения магнитного
поля, р — плотность. Скорость возрастала бы непрерывно,
если бы не возникало трения.
Что делает математик, если он изучает многозначную
функцию и хочет выделить ее различные однозначные «вет-
«ветви»? Он проводит в области значений функции «разрез».
Проделаем то же самое здесь, поставив твердую разделитель-
разделительную перегородку между осью и боковой стенкой. С одной
стороны этой перегородки жидкость поднимется, а с дру-
другой — опустится. Теперь потенциал в области, занимаемой
жидкостью, будет однозначен; возникнет гидростатиче-
гидростатическое давление р = Ау, уравновешивающее потенциал U\
движение прекратится. Распределение давления можно
определить по форме поверхности жидкости. С одной
стороны разделительной перегородки жидкость будет
стоять выше, чем с другой; разность высот ЪкА будет
равна прежнему «периоду» потенциала.
§ 7. СТАТИКА СЖИМАЕМОЙ ЖИДКОСТИ
В сжимаемых газах и парах плотность пе постоянна,
а зависит от давления. Между ними имеется зависимость
вида
или с учетом нормального состояния р0, р0
G.1)
Ро \ Ро
В технике и астрофизике это уравнение называется урав-
уравнением политропы, а п — показателем политропы.
§ 7. Статика сжимаемой жидкости 67
Для изотермического случая п= 1. Это следует из урав-
уравнения состояния газа
R — универсальная газовая постоянная, ji — молярный
вес1) газа (например, fi = 32 г для О2), Т — абсолютная
температура.
В адиабатическом случае п для двухатомных газов
равно 1,4. Значение показателя п в адиабатическом слу-
случае совпадает, как известно из термодинамики, с отноше-
отношением теплоемкости ср при постоянном давлении к тепло-
теплоемкости cv при постоянном объеме.
Условимся в случае сжимаемой жидкости измерять
внешнюю силу иначе, чем мы это делали для несжимае-
несжимаемой жидкости. В последнем случае внешняя сила F отно-
относилась к единице объема. Теперь оказывается более удоб-
удобным относить ее к единице массы. Вместо буквы F обо-
обозначим ее буквой Р (от латинского pondus — тяжесть).
Тогда получаем
FAx = PAm, или F = pP. G.3а)
В случае поля тяжести вместо F — pg будет просто
p = pz==±g G.36)
в зависимости от того, как направлена ось z (вверх или
вниз); для центробежной силы, где, согласно F.9),
F — prio2, будет
jP = ra>2. G.4)
Целесообразность такого обозначения становится ясной,
если рассмотреть условие равновесия F.4), пригодное как
для сжимаемой, так и для несжимаемой жидкости.
г) Под «молем» понимают, как известно, массу газа в граммах,
равную сумме атомных весов его составляющих. Вместо молярного
веса часто говорят «молекулярный вес», но мы сохраним это выра-
выражение для веса (или, более правильно, для массы) отдельной моле-
молекулы (см. ниже). Определение моля зависит от величины единицы
массы. Если вместо грамма взять килограмм, моль перейдет
в киломоль. То же относится к молярному объему и числу Лошмидта
(см. стр. 71). В системе CGS газовая постоянная имеет значение
Я=8,31 • 10' эрг/град.
68 Гл. II. Стат ика деформируемых тел
В нашем случае оно может быть записано как
iP; G.5)
здесь справа стоит известная величина, а слева — вели-
величина, которая может быть вычислена, если известна связь
между р и р.
Если эта связь задается равенством G.1), то G.5) мож-
можно записать в форме
grad<^ = P, G.6)
где
Легко видеть, что такая форма равенства G.6а) годится
и для неполитропического случая, если под е^ понимать
величину
в
\, G.66)
где Л — фиксированная точка, Л —текущая точка с коор-
координатами х, у, z.
Точно так же, как в случае F.4), из G.6) сразу сле-
следует, что в случае сжимаемой жидкости равновесие воз-
возможно только тогда, когда внешняя сила имеет потен-
потенциал (в данном случае—сила Р, отнесенная к единице мас-
массы). Обозначим этот потенциал через V; тогда из G.6)
следует
grad (^ + V) = 0, <^ + F = const. G.7)
В случае поля тяжести
V = gz G.7а)
(z положительно при отсчете вверх). Принимая во вни-
внимание G.6а), получаем
„1/п ,
i°-ni-(i/n> = —(const —gz). G.8)
Ро п
§ 7, Статика сжимаемой жидкости
Подставив значения z = 0 и р = р0 для поверхности земли,
определим постоянную из равенства
р0 п—1
— = const.
р0 п
Путем простых преобразований из G.8) получаем
'=*0-"Hr»"№l~'>- <7-9>
Используя G.1), имеем
Формулы G.9) и G.9а) дают выражение для давления
и плотности в произвольной политропической атмосфере.
Отсюда можно определить высоту атмосферы, подставив
р = 0 или р = 0, а именно:
/г= " JP». G.96)
После подстановки этого значения в G.9) и G.9а) эти
равенства приобретают более простой вид:
nl(n~l) С Z\ll(n-1) „ п
A GЛ0)
Если воспользоваться уравнением состояния газа G.2),
то из отношения pfp можно сразу определить распределе-
распределение температур в политропической атмосфере:
Таким образом, мы получили линейное распределение
между z = 0 и z = h от Го = (j./?o/poi? до Т = 0.
Из G.96) можно найти численное значение для высоты
атмосферы (см. задачу 1 гл. II). Для адиабатического
случая, когда п—1,4, получаем, что высота h равна
только 28 км, для политропы с показателем п — 1,2 высота
h = 48 км, а для изотермического случая п = 1 высота
атмосферы бесконечна.
- Из измерений с помощью шаров-зондов известно, что
равенство Т = const для всей атмосферы совершенно
несправедливо. В низшей части, тропосфере, температура
резко падает с увеличением высоты; в стратосфере на про-
70 Гл. II. Статика деформируемых тел
тяжении нескольких километров температура сохраняется
постоянной, а затем возрастает. Граница между тропо-
тропосферой и стратосферой находится на высоте, равной
~ 12 км (на полюсе ниже, чем на экваторе). Но для
небольших разностей высот, например при восхождении
на гору, подсчеты ведут, считая температуру постоянной.
При этом распределение давления и плотности выражается
известной барометрической формулой. Так как эта фор-
формула часто употребляется, мы выведем ее, воспользовав-
воспользовавшись основным равенством G.5).
Положим, что Р — —g [z отсчитывается положитель-
положительным вверх; см. G.36)], и из G.2) имеем
Р = Ср; С = -^. G.12)
Из G.5) можно получить
р dz °б-
Интегрирование дает
In p=-Cgz + \np0, G.13)
где р0 — атмосферное давление на поверхности земли
B = 0); или в другой форме1):
р = pQe-^z = poe-wlRT. G.14)
Для распределения плотности та же формула дает [со-
[согласно G.12), имеем р/р0 = /]
Равенство G.13) показывает, что высота над поверх-
поверхностью земли может быть определена по барометру
с логарифмической шкалой давлений. Распределе-
Распределение G.15) можно представлять себе как «седиментацию»
воздушных масс над землей. Жан Перрен использовал
такое представление для создания лабораторной модели
атмосферы (атмосферой ему служила эмульсия мастики)
с целью определения фундаментальной постоянной атом-
1) Равенство G.14) может быть получено непосредственно из
общего соотношения G.9) путем предельного перехода при п -*¦ 1
с использованием известного определения показательной функции
§ 7. Статика сжимаемой жидкости 71
ной теории. Это станет понятным, если в равенство G.15)
подставить
p — Lm,
где L — число Лошмидта (или число АвогадроI),
т. е. число молекул в моле, а т — масса одной молекулы,
которая, будучи умноженной на g, дает «вес молекулы»
в собственном смысле этого слова. Из G.15) можно
получить тогда
р = poe-L(™0z№T>. G.15а)
В то времй как массу молекулы т невозможно опре-
определить прямым измерением, величина т частиц модели
Перрена измеряется непосредственно (путем взвешивания
достаточно большого числа капелек мастики). В этом
случае равенство G.15а) может служить для определе-
определения L, если известны плотности р и р0. Таким путем
Перрен получил значение L = 6,8-1023, которое нахо-
находится в удовлетворительном согласии с известным
теперь значением L — 6,02-1023.
Если в G.15а) вместо газовой постоянной на моль R
ввести газовую постоянную по отношению к одной моле-
молекуле 2)
к = 4» G-156)
то показательная функция в G.15а) примет вид
e-mgzlkT = e-VlkT > G.15в)
х) Иногда число молекул в 1 см? называют числом Лошмидта
в отличие от числа Авогадро, характеризующего число молекул
в 1 моле. Первый из этих терминов был предложен Больцманом
в речи, посвященной памяти Лошмидта. (См. Boltzmann,
Populare Schriften, Leipzig, 1905, S. 243.) Лошмидт, действительно,
рассматривал только первое из этих чисел, которое он оценивал
с помощью различных газокинетических методов; второе же число
он мог бы легко получить затем на основании закона Авогадро. С дру-
другой стороны, Авогадро в то время вообще не мог оценить, даже по
порядку величины, какое-либо из этих чисел. Поскольку число
молекул в 1 моле вещества является очень существенной величиной
для всей атомной физики, представляется справедливым дать спе-
специальное наименование только этому числу, связав его с именем
человека, который впервые придумал методы его определения.
2) Она обычно называется постоянной Больцмана, хотя впервые
она была введена Планком, который развивал идеи Больцмана,
72 Гл. II. Статика деформируемых, тел
где V — потенциальная энергия частицы массы т, подня-
поднятой в поле тяжести на высоту z. Выражение G.15в) назы-
называется множителем Больцмана. Оно может быть пере-
перенесено с рассмотренного специального случая поля тяже-
тяжести на энергетическое состояние любой физической системы;
в этом случае G.15в) будет представлять собой, вообще
говоря, относительную вероятность такого состояния по
отношению к нулевому состоянию при данной темпера-
температуре Т.
Множитель Больцмана играет большую роль во всех
статистических исследованиях. В этом небольшом отсту-
отступлении в область атомной теории мы указали на его связь
с элементарной барометрической формулой.
Так как в выражение G.15) входит молярный вес (л,
то это указывает на возможность разделения смеси тяже-
тяжелого и легкого газов путем осаждения. Практически
в поле тяжести это проделать вряд ли возможно. Использо-
Использовать для этой цели поле центробежных сил является более
эффективным. Займемся сейчас соответствующими вычи-
вычислениями.
Потенциал центробежной силы, отнесенной к единице
массы G.36), равен
F=-i-r2aA G.16)
Согласно G.7),
& = const +~ г2ы2; G.16а)
здесь, как и в F.9а), ш считается постоянной для всех
г во вращающемся барабане. Для изотермического со-
состояния газа или газовой смеси из G.66) и G.12) имеем
, ()
V- 3 Р V- Ро V
где pQ — давлениз на оси барабана, т. е. для г = 0.
Тогда постоянная в G.16а) обращается в нуль, и из
G.16) и G.17) получаем
In -? = -|_1г2ш2, р^ро&Ю^ЧИП. G.18)
Таким образом, в барабане давление также меняется
по экспоненциальному закону. В случае смеси двух газов
§ 7. Статика сжимаемой жидкости 73
с молярными весами [ах и (л2 из G.18) получаем два пар-
парциальных давления рх и р2 с двумя постоянными pQl и
/?02, зависящими от состава смеси. Суммарное давление
равно p — Pi-tP2- Равенство G.18) указывает, что пар-
парциальное давление, соответствующее большему молярно-
молярному весу {J., растет к периферии быстрее, чем для меньшего.
Так как при данной температуре плотности пропорциональ-
пропорциональны давлению, смесь на периферии будет обогащаться
более тяжелой компонентой. В задаче 2 гл. II будет
определено численное значение величины (вернее показа-
показана незначительность) этого эффекта для воздуха B1 объем-
объемный процент О2 и 79 объемных процентов N2).
Если здесь, как и в случае несжимаемой жидкости,
примем во внимание, кроме центробежной силы, силу
тяжести, то необходимо в выражение V в равенстве
G.16) добавить потенциал силы тяжести —gz. Тогда из
G.18) получаем
МНТ) (-0Z+- Г2со2)
p = pQe 2 \ G.19)
Поверхностями равного давления (а следовательно, и
равной плотности) будут опять параболоиды вращения.
р0 — это давление на параболоиде
Отсюда можно получить остальные поверхности уровня
путем параллельного смещения вверх или вниз. В этом
случае не возникает свободной поверхности, отвечающей
вакууму (р — 0), так как экспоненциальная функция не
принимает нулевого значения ни для какого конечного
значения аргумента. ,
Центрифуги, вращающиеся с чрезвычайно большой
скоростью, созданы Сведбергом. Число оборотов в них
достигает 100 000 в минуту. Центробежная сила в них
превосходит силу тяжести в 750000 раз. Одна из обла-
областей их применения — разделение тяжелых белковых
молекул (молярный вес которых достигает 30000). Основ-
Основной областью применения этих ультрацентрифуг являются
коллоидная химия и биология, где объекты исследования
можно рассматривать скорее как несжимаемые жидкости,
чем как сжимаемые газы.
74
Гл. II. Статика деформируемых тел
§ 8. НАПРЯЖЕННОЕ СОСТОЯНИЕ УПРУГОГО ТВЕРДОГО ТЕЛА
Математическая характеристика напряженного со-
состояния в твердом теле будет полной только тогда, когда
мы покажем, что напряжения образуют симметричный
тензор второго ранга. Иначе говоря, необходимо показать
не только то, что в опре-
определителе
ух
ху
zyy
"гу
компоненты, симметричные
относительно главной ди-
диагонали (соединяющей ле-
левый верхний и правый ниж-
нижний углы), равны друг
ДРУГУ
(8.1)
ух
т. д.
Фиг. 10. К симметрии тензора
напряжений.
Равновесие элемента объема упругого
тела относительно вращения.
-у
J но и что ее компоненты при
переходе к другой прямо-
прямоугольной системе коорди-
координат преобразуются как
квадраты и произведения
координат (см. стр. 40).
Симметрия тензора может быть легко доказана из
условия равновесия моментов. Вычислим, например,
момент сил относительно оси z, действующих на элемент
объема со сторонами их, by, Az (фиг. 10). Нормальные
напряжения не дадут вклада в этот момент, так как их
направления пересекают ось z\ из тангенциальных на-
напряжений следует принять во внимание только аху и аух.
Соответствующие им силы реакции, действующие на
элемент объема и их плечи, равны
oxybybz, уДя, а также oyxAzbx, -^ Ay.
Сумма их моментов будет равна (если принять во вни-
внимание обозначения на фиг. 10 и введенное на стр. 53
условие, по которому направление напряжения указы-
§ 8. Напряженное состояние упругого твердого тела 75
вается вторым индексом у о при условии, что оно дей-
действует на «положительную» поверхность)
Ах
'ух
(8.2)
В случае действия внешней силы F (отнесенной к едини-
единице объема) ее момент равен
где плечо I имеет тот же порядок малости, что и сторона
элемента объема (ср. стр. 58). Следовательно, выражение
(8.2) должно равняться
нулю; это дает условие
симметрии (8.1). Остальные
два условия симметрии вы-
вытекают из равенства нулю
моментов относительно
осей х и у.
Более сложно доказа-
доказательство тензорного харак-
характера по отношению к из-
изменению системы коорди-
координат. Оно основывается на
векторном характере сил
реакции, действующих на
некоторую плоскость раз- ф ..
реза, ТОЧНО так Же, Как СО- равновесие С1ШИДующих на эле-
ответствующее доказатель- ментарный тетраэдр.
ство для тензора дефор-
деформаций основывается на векторном характере соответству-
соответствующих смещений.
С этой целью рассмотрим условия равновесия тетраэд-
тетраэдра, отрезанного от нашего прямоугольника элементом
объема и секущей плоскостью с произвольно направлен-
направленной нормалью п (фиг. 11). Пусть площадь этой стороны
равна Fn, а площади сторон, перпендикулярных к осям
х, у, z, равны Fx, Fy, Fz. Последние равны проекциям Fn
на плоскости х = 0, у = 0, 2 = 0, а именно:
Fx = Fncos{n, х); Fy = Fncos(n, у); Fz = Fncos(n, z). (8.3)
Действующие на тетраэдр реакции находятся в равно-
76 Гл. II. Статика деформируемых тел
весии, и поэтому для проекции на ось х имеем1)
Откуда, согласно (8.3),
°nx = ai°xx + Pi V + Ti°2x> (8- 5)
если направляющие косинусы обозначить сокращенно
согласно следующей таблицы:
п t t'
а3
Р«
Г1 , ГЗ
Ti Ъ Is
Равенство (8.5) дает напряжение, действующее на п-
плоскость в направлении х. Напряжения, действующие
соответственно в направлении у и z, равны
Из (8.5) —(8.7) в результате векторного сложения полу-
получаем, что нормальное напряжение, действующее на
n-плоскость, равно
>пп = а\Спх + Plcny + Tl°r7Z =
iVa- (8.8)
Выберем теперь в «-плоскости два взаимно перпенди-
перпендикулярных направления t и V и спроектируем векторные
суммы (8.5) —(8.7) вместо нормали тг на эти направления;
в результате получим тангенциальные напряжения, или
напряжения сдвига:
°nt = Ч°пх + hany +¦ T2°nz =
= а1а2Сас=с + PlPa°wi/ + TlT2C2z + (Pla2 + aA) °xy +
a ^ PiTa) °yz + («iTa + a2Ti") <W (8-9)
x) Заметим, что, согласно фиг. 11, Fx, Fy, Fz представляют собой
отрицательные плоскости х, у, z нашего элемента объема (который
не изоРражен целиком на фиг. И). Поэтому члены с ахх, аух, azx
вначале присутствуют со знаком минус, но так как в равенстве (8.4)
они находятся в правой части, то они берутся со знаком плюс.
§ 8. Напряженное состояние упругого твердого тела 77
аналогичное выражение получим для оп1>. Упростим
запись, обозначив первоначальные напряжения ахх, аху,...
через aik{i, к — 1, 2, 3), а преобразованные спп, cnt,...—
через Oik, и соответственно этому введем направляющие
косинусы с двойными индексами aik. Тогда можно будет
написать формулу, являющуюся обобщением выражений
(8.8) и (8.9), а также условий для остальных плоскостей
элемента объема, вырезанного параллельно /г, t at':
SSwiffl
1 m
Это то же самое правило преобразования компонент
тензора, которое было получено ранее в D.5) для тен-
тензора деформаций. Мы имеем теперь основание говорить
о тензоре напряжений и характеризовать напряженное
состояние в окрестности некоторой точки поверхностью
тензора напряжений (эллипсоид, гиперболоид и т. д.).
Главные оси поверхности тензора напряжений определяют
по величине и направлению главные напряжения. Точно
так же, как и в теореме Гельмгольца (§1) для деформа-
деформаций, всякое напряжение в окрестности некоторой точки
состоит из трех взаимно перпендикулярных тензоров
более простого характера; в данном случае они представ-
представляют собой чистые односторонние растягивающие или же
(в случае обратного знака) сжимающие натяжения.
В наших условиях равновесия (8.4) учитывались
только силы реакции, действующие на грани тетраэдра,
и не учитывались внешние силы, действующие на весь
объем тетраэдра. Это было отчасти оправдано тем, что
их вклад в равенство пропорционален объему тетраэдра,
в то время как вклад напряжений был порядка величины
граней тетраэдра.
Однако положение меняется, когда речь идет о равно-
равновесии невырезанного элемента объема, имеющего форму
параллелепипеда, под действием внешних и внутренних
сил. В этом случае получается соотношение, аналогич-
аналогичное F.4) в гидростатике. Точно так же, как и в равен-
равенстве F.3), для обеспечения равновесия в направлении
оси х мы приравняем вклад внешних сил вкладу поло-
положительной и отрицательной ж-плоскостей, но в отличие
от жидкостей, где напряжения сдвига равны нулю, здесь
78 Гл. II. Статика деформируемых тел
придется добавить вклад тангенциальных напряжений,
действующих на плоскости у и z. Внешнюю силу, отне-
отнесенную к единице объема, обозначим, как прежде, через
вектор F. Сократив на множитель А% = Ax&yAz, получаем
условие равновесия в виде
*-» *-» <\
= 0. (8.11)
дх ду д.
Циклической перестановкой индексов можно получить
условия для направлений осей х и у. То, что сила F
здесь стоит слева, а в гидростатическом условии равно-
равновесия F.4) она стояла справа, объясняется тем, что здесь
идет речь о напряжениях, а там —о давлениях (отрица-
(отрицательных напряжениях).
Равенство (8.11) и остальные два уравнения сокра-
сокращенно запишутся в виде
Divo + F = 0. (8.12)
Здесь Div означает «векторную дивергенцию», которая
ставкт в соответствие тензору некоторый вектор, в то
время как наша прежняя, с формальной стороны так же
введенная операция div ставила в соответствие вектору
скаляр. В общем тензорном исчислении (см. приложения
I — IV в конце книги), которое занимается изучением
тензоров любого ранга и применяется в общей теории
относительности, подобная операция называется «диф-
«дифференцирование с последующим свертыванием»; в резуль-
результате ее применения ранг тензора снижается на единицу.
Определение Div, содержащееся в (8.12), относится,
очевидно, к декартовым координатам. Введем определе-
определение, пригодное для любой ортогональной системы коор-
координат, рассмотрев, как и в B.20), предел поверхностно-
поверхностного интеграла. Окружим точку Р, для которой будет
определяться операция Div, замкнутой поверхностью /
и обозначим через п внешнюю нормаль к элементу df
поверхности / и через Дх — заключенный в ней объем.
Тогда
' " npdf. (8.13)
Здесь апр — компонента напряжения, действующего на
§ 8. Напряженное состояние упругого твердого тела 79
элемент поверхности df в направлении р, в котором
определяется компонента векторной дивергенции.
Можно показать, что в частном случае прямоуголь-
прямоугольных координат х, у, z вновь появятся три первых члена
левой части (8.11) [как и при переходе от B.20) к B.20а)],
если в качестве поверхности / выбрать гранипу элемента
объема ДгеД^Дг. В более общем случае криволинейных
ортогональных координат, введенных в B.22), в качестве /
выбирается поверхность, ограничивающая элемент объема,
образованный координатными линиями и имеющий стороны
Si^Pi» #2ДР2> 8з*Рз- Из (8.13) можно получить гогда
компоненту векторной дивергенции в направлении dph:
Divfeo = —— \ir-
(8.14)
Здесь aik означает напряжение, действующее в направ-
направлении dpk на плоскость, перпендикулярную к dp{.
Можно выражение (8.14) подставить в (8.12) и вы-
выразить F в компонентах Fk по направлениям /?,., чтобы
получить к-ю компоненту условия равновесия в обобщен-
обобщенных координатах. Однако для того, чтобы по заданному
вектору F определить тензор напряжений о, недостаточ-
недостаточно условий равновесия. Симметричный тензор имеет
шесть независимых компонент, в то время как (8.12)
представляет собой три независимых соотношения.
В качестве недостающих трех соотношений условия
равновесия для моментов служить не могут, так как они
(см. стр. 74) выражают собой только симметрию тензора.
Для определения напряженного состояния необходимо
установить связь между напряжением и деформацией,
что будет сделано в следующем параграфе.
В этой связи можно задать вопрос, какие условия
надо добавить к равенствам (8.12), чтобы шесть величин
о характеризовали собой некоторое физически возможное
состояние напряжения. Эти соотношения называют усло-
условиями совместности.
Такой же вопрос можно было бы задать в случае
состояния деформации, где шесть компонент е зависят
только от трех компонент Е, yj, С и, конечно, не могут
быть произвольно заданы.
80
Гл. П. Статика деформируемых тел
Закончим этот параграф таблицей, в которой сопо-
сопоставляются, различные обозначения.
Данная книга
ахх
°уу
*zz
аху — аух
°yz — °zy
czx = Gxz
Обозначения
Кирхгофа—
Планка
-хх
— Yy
—zz
~Xy= — Yx
У 7
1 z ?jy
-zx=-xz
Немецкая техни-
техническая литера-
литература
Ox
ау
°z
*хи = *ух
Xyz — Xzy
tzx — xxz
авторы
P
Q
R
S
T
и
§ 9. СООТНОШЕНИЯ МЕЖДУ ДЕФОРМАЦИЕЙ И НАПРЯЖЕ-
НАПРЯЖЕНИЯМИ. УПРУГИЕ ПОСТОЯННЫЕ. УПРУГАЯ ЭНЕРГИЯ
Будем считать, что нагрузки невелики, поэтому мож-
можно пренебречь второй и более высокими степенями ком-
компонент напряжений и деформации. В этом случае между
напряжением и деформацией будет существовать, вообще
говоря, линейная связь. В примитивной форме эта связь
была впервые установлена Гуком, современником Ньютона
(закон Гука). В § 39 гл. VIII будут сделаны некоторые
замечания о тех пределах пропорциональности и упру-
упругости, где кончается действие линейного закона.
Так как твердые тела имеют обычно поликристал-
поликристаллическую структуру, то предположим далее, что упругое
тело изотропно, т. е. его свойства не зависят от направ-
направления. Будем также рассматривать такие элементы
объема, которые велики по сравнению с микроструктурой,
т. е. содержат большое число микрокристалликов, ориенти-
ориентированных произвольным образом. По поводу упругих
свойств макроскопического монокристалла будут сделаны
некоторые замечания в гл. VIII.
Элемент объема удобно вырезать таким образом, чтобы
его стороны были параллельны главным осям эллипсоида
напряжений. Тогда на три пары плоскостей, ограни-
ограничивающих элемент объема, будут действовать только
§ 9. Соотношения между деформацией и напряжениями 81
главные напряжения о1? с2, с3; согласно определению,
напряжений сдвига aih в этом случае возникать не будет.
Следовательно, если в напряженном состоянии элемент
объема имеет прямоугольную форму, он будет оставаться
прямоугольным и под действием с1? o2, с3. Угловые изме-
изменения, соответствующие сдвигам e]fe, будут поэтому равны
нулю, так что возникающая деформация будет также
состоять из чистых растяжений в направлениях главных
осей эллипсоида напряжений. Но это означает, что глав-
главные оси поверхности тензора напряжений совпадают
с главными осями поверхности тензора деформаций. Обоз-
Обозначим возникающие при этом главные деформации, как
и в A.14), через ех, е2, е3.
Между главными напряжениями и главными деформа-
деформациями существуют связи следующего типа: в силу линей-
линейности напряжений
ох = аех 4- Ьг% -\- се3 (9.1)
и в силу предположенной изотропии тела
c2 = ae2-f- Ье3-\-св±, о3 = ае3 4- Ъгг -+- се2. (9.1а)
Согласно последнему предположению, Ъ = с в (9.1), так
как обе главные оси 2 и 3 равноправны по отношению
к главному напряжению сг Добавив и отняв Ыг в (9.1),
перепишем его в виде
ai — (a — b) е-! + b («! + е2 -f- e3),
или, изменив обозначения1), получаем
+ е2-Ь е3). (9.2)
Если то же самое проделать с равенствами (9.1а), то
возникнут еще два соотношения, которые могут быть
получены из (9.2) путем циклической подстановки индек-
индексов, которые вместе с (9.2) запишутся в виде
+ ea + e.). (9.3)
г) То, что в равенстве (9.2) перед \>. введен множитель 2, в даль-
дальнейшем окажется более удобным [см. ниже (9.16) и (9. 18)].
6 А. Зоммерфельд
82 Гл. ТТ. Статика деформируемых тел
ото выражение можно легко обобщить для произволь-
произвольно ориентированного прямоугольного элемента объема.
Воспользуемся уравнениями преобразования A.22) и
(\.22s), которые справедливы как для тензора напряже-
напряжений, так и для тензора деформаций:
?хх = ai?i + а2?2 4- <ф8, еху = a^ej -f а2Р2е2 -f а3р3е3,
ху ^j f 2Р22 f 3р33,
Умножая (9.3) на а* и на a^it складывая и применяя
(9.4), получаем
°хх = 2V*xx -+ ^ («J + «2 + «5) (ei 4- Ч + es)» / 9 5)
+ е2 + е3).
В силу условия ортогональности во вторых членах пра-
правой части сумма квадратов а равна единице и сумма
произведений ай равна нулю. Использовав инвариантность
следа тензора, заменим e1-f-s2-f- е3 на е^ -\- еуу + ezz, так
что (9.5) перейдет в
Ovv = 2{А6„„ -f" A. (Svv -}- ?,... -f- Етт),
ЛЛ( " «А-Л» \ ^.^r yj/ Л.1,1
(9.6)
ху * осу*
или, в сокращенной записи,
е, (9.7)
где символ 8ift понимается в том же смысле, что и на стр. 19.
Эти равенства (96) представляют собой обшую форму
соотнон ений между напряжениями и деформацией для
произвольного элемента объема.
Равенства (9.6) могут быть легко обращены. При
сложении первых трех раяенст,в получается
?-"« + %у 4оя = B{х + За) (гхх + еуу-f ej;
§ 9. Соотношения между деформацией и напряжениями 83
отсюда каждое из равенств (9.6) немедленно дает
(9.6а)
— —9 '
или, в сокращенной записи,
eife = 2K-4ftH-x'8iuE- (9.7а)
Последнее равенство представляет собой общую форму
соо. ношений между деформацией и напряжениями; вместо
постоянных 2ц, X в них входят 2р/ и X', определяемые
как
1 IX
2' Х' (976)
Равенства (9.6) или (9.6а) показывают, что у изотроп-
изотропного тела имеются две упругие константы; они зависят
как от материала тела, так п от его температуры. У кри-
кристалла в зависимости от его симметрии имеется до 21 упругой
константы (как мы увидим в гл. VIII). Константы [х и X
были введены Ляме и называются модулями упругости
Ляме1). Эти модули удобны для общих исследований,
но не имеют наглядного физического смысла. Мы, однако,
выразим их через две другие постоянные, которые
имеют совершенно наглядный смысл.
Пусть на нижний конец вертикального призмати-
призматического бруса действует нагрузка Р, а верхний конец
бруса закреплен (заделан). Поперечное сечение F бруса
имеет произвольную форму. Будем считать, что нагруз-
нагрузка Р приложена не в определенной точке, а равномерно
распределена по сечению F на конце бруса. Напряжение
в этом сечении и в любом другом, ему параллельном,
будет равно a = PjF. Так как боковых сил нет, то
1) Принято называть коэффициенты в соотношениях между
напряжешшми и деформациями модулями упругости, а в соотно-
соотношениях между деформациями и напряжениями [как, например,
наши р/ и \' в равенствах (9.7а)]—упругими коэффициентами.
84 Гл. II. Статика деформируемых тел
напряжения сдвига будут отсутствовать, и поэтому а
является главным напряжением. Ему соответствует глав-
главная деформация е = Д///, где / — длина, а Д/—удлинение
бруса. Отношение напряжения к деформации представ-
представляет собой материальную константу, т. е-, величину,
которая при не очень больших нагрузках не зависит
от Р, F и /. Ее обозначают через Е и называют модулем
упругости или модулем Юнга (введен в 1807 г. Томасом
Юнгом, с именем которого также связано открытие
интерференции света). Итак, для растянутого бруса имеем
Е = ±. (9.8)
Так как е — безразмерная величина, то Е имеет раз-
размерность напряжения, т. е. сила (площадь. Для стали и
ковкого железа ;
Е = 2-10е кГ1см*.
Из опыта следует, что при растяжении не только
увеличивается длина бруса, но и уменьшается его по-
поперечное сечение. В увеличенном масштабе мы наблю-
наблюдаем это явление при растяжении резинового шнура и
воспринимаем его как вполне естественное с точки зрения
приспосабливания материала к растяжению. Обозначим
это сжатие, одинаковое для всех поперечных сечений,
через — е' и введем
. ?i=*v, (9.9)
или, согласно (9.8),
v также является материальной константой; ее называют
коэффициентом Пуассона. Пауссон не только ввел это
число, но и вычислил его из соображений молекуляр-
молекулярной теории, сделав, правда, при этом далеко идущие
допущения. Найденное им численное значение равно 1/4.
Современная теория кристаллического состояния уточ-
уточнила вычисления Пуассона и показала, что v = ХД ~~ не
единственно возможное значение..
§ 9. Соотношения между деформацией и напряжениями 85
Если брус подвергается не растяжению, а сжатию, то
поперечное сжатие переходит в поперечное расширение,
а продольное расширение — в продольное сжатие. Но
величины Е и v как материальные константы сохраняют
свое значение и при изменении знака деформации, если,
конечно, нагрузка попрежнему не достигает предела
упругости (см. § 39).
Перенесем теперь наше рассмотрение на случай общего
напряженного состояния, которое обсуждалось в связи
с (9.3). Это состояние представлялось как наложение трех
односторонних напряжений в направлениях трех главных
осей. При этом будет происходить то же, что и при
растяжении бруса. В силу линейности всех наших соотно-
соотношений можно использовать принцип суперпозиции как
для напряжений, так и для соответствующих деформаций.
А именно, деформация в направлении главной оси 1
зависит не только от напряжения ах, но и (как попереч-
поперечное сжатие) от напряжений, действующих вдоль главных
осей 2 и 3. Из равенств (9.8) и (9.9) можно, таким
образом, получить ,
и, в общем виде, для г = 1, 2, 3
?i~-E~Ci~E
(9.10)
Отсюда для величины гх -f- е2 + е3 = в получаем путем
сложения
e = A=^S, 2 = ^8. (9.10а)
Подставив Е в (9.10), имеем
•+таг «О-
Сравним коэффициенты такого представления с коэффи-
коэффициентами в равенстве (9.3):
86 ^ Гл. //. Статика деформируемых тел
Последние равенства выражают связь р. и X с более на-
наглядными константами Е и v.
Теперь вместо одностороннего растяжения или сжатия
рассмотрим случай всестороннего сжатия, как, напри-
например, в цилиндре гидравлического пресса. Эллипсоид на-
напряжений, как и эллипсоид деформаций, представляет
собой сферу (ср. стр. 43); откуда имеем
о1 = с2 = с3= — р, Е=— Зр, ei = 62 = 63= — -3-I О |,
так что (9.106) дает
Определяя для этого случая, аналогичпо (9.8), модуль
сжатия К с помощью равенства
Я-ffj (9.13)
и сравнивая с (9.12), получаем
(9Л4)
В случае несжимаемости в = 0 и, следовательно,
К=оо, так что v = 1/2. Эта величина представляет собой
верхнюю границу возможных значений коэффициента
Пуассона. Для v > х/2 состояние тела было бы неустойчи-
неустойчивым: при внешнем давлении оно не уменьшало бы своего
объзма, а увеличивало его, в > 0.
Рассмотрим последний пример, а именно случай, на-
называемый чистым сдвигом. Будем считать, что z-плоскосгь
нашего прямоугольного параллелепипеда свободна от
напряжений, в то время как в х- и ^-плоскостях дей-
действуют касательные напряжения аху — аух = т. Это —
«плоский» случай, так как от z ничего не зависит, и
он может быть представлен сечением, параллельным пло-
плоскости ху (см. фиг. 12а). Касательное напряжение х пре-
преобразует первоначальный прямоугольник (фиг. 12а) в па-
параллелограмм; при этом два прямых угла увеличатся на
величину ^» а Два других — уменьшатся на ту же вели-
величину. Поверхность тензора напряжений, как и поверх-
поверхность тензора деформаций, в случае «чистого сдвига»
§ 9, Соотношения меокду деформацией и напряжениями 87
(см. на стр. 44 фиг. 4а и 46) представляет собой цилиндр,
параллельный оси х, основанием которого является рав-
равносторонняя гипербола. Главные оси расположены под
углом 45° к осям х и у. Оба главных напряжения
равны друг другу и противоположны по згтаку: о2 = — сг
(третье главное напряжение о3, естественно, равно, нулю).
Это следует из инвариантности следа S и из того, что
для элемента объема, из которого мы исходили, а<х =
= ауу = azz = 0. Элемент объема, вырезанный в направле-
Фиг. 12а.
Изменение формы в слу-
случае чистого сдвига.
Фиг. 126.
В случае чистого сдви-
сдвига главные напряжения
равны и противополож-
противоположны по знаку.
нии главных осей (фиг. 126), будет растянут в напра-
направлении 1 и сжат в направлении 2. Если аг =с, то ог= — о.
Такое состояние чистого сдвига служит для опреде-
определения модуля сдвига, который мы, как это принято в тех-
технике, обозначим через G. По некоторой аналогии с (9.8)
и (9.13) запишем
G=±. (9.15)
Эта аналогия не полна, так как в (9.8) и (9.13) в зна-
знаменателе стоит удлинение или, соответственно, сжатие,
вызванные напряжением, стоящим в числителе; здесь же
в знаменателе стоит вызванное напряжением угловое из-
изменение, которое, согласно нашему определению A.25),
представляет собой удвоенную компоненту тензора де-
деформации. Для определения G в общем случае восполь-
воспользуемся соотношением (9.6)
¦•эсу
2е
ху
88' Гл. II. Статика ' деформируемых тел
которое в обозначениях нашего примера запишется как
т
— — V-
Из сравнения этого соотношения с~(9.15) и(9.11) следует
Оказывается, что модуль сдвига совпадает с модулем
упругости Ляме р, так что обозначение G нам больше
не понадобится. Эту константу называют также модулем
кручения; он появляется в задачах о крутильных* коле-
колебаниях (стр. 135) и о кручении (см. § 42).
Теперь мы можем решить задачу, поставленную в кон-
конце предыдущего параграфа, а именно задачу о полном
определении напряжений из условий равновесия (8.12).
Они представляют собой только три условия для шести
напряжений aik, вследствие чего часть напряжений
остается неопределенной. Однако если теперь cik выра-
выразить через eik, которые, согласно их первоначальному
определению в A.11), можно выразить через вектор сме-
смещения, то получим три уравнения, определяющих ком-
компоненты этого вектора смещения. . *
Поставленная задача очень просто решается в прямо-
прямоугольных координатах. Исходя из смысла векторной
дивергенции и из равенства (9.6), можно написать
xx divx , dez
или, используя A.11),
TV - /S g2? , W , дЦ дЪ дК \ у д@
UIVX О - f» ^ g-Г, + ^2 + ду ЭХ "Г- 0Z2 -Г QZ дх) "Г" ^ -Q^ •
Это выражение легко преобразуется к виду
(9.17)
Подставляя (9.17) в равенство (8.12) и произведя цикли-
циклическую подстановку индексов в (9.17) для получения
§ 9. Соотношения между деформацией и напряжениями 89
остальных двух компонент векторной дивергенции, имеем
(9.18)
Эти три фундаментальных уравнения определяют век-
вектор смещения ?, у\, С, во всем объеме упругого тела, если
его поведение на границе задается соответствующими
граничными условиями. Зная ?, т], С, можно с помощью
соотношений между напряжениями и деформациями опре-
определить 6, а также напряжения о. Условия (9.18) яв-
являются дифференциальными уравнениями, полностью
определяющими равновесие. То, что в (9.18) входит р.,
а не 2р, определило наш выбор обозначений на стр. 81.
Уравнения (9.18) относятся к декартовым координа-
координатам. Чтобы они годились для произвольных ортогональ-
ортогональных координат, надо," согласно C.10а), символ Д пред-
представить как операцию grad div—rot rot. Обозначая дальше
вектор смещения ?, ц, С через Sq, как это делалось в со-
соотношениях D.17)—D.28), напишем (9.18) в законной
векторной форме:
[д. grad div Sq — ц rot rot &q + (p 4- X) grad 9 -^ F = 0;
используя 9 = div §q, можно упростить это выражение:
Bfi + X) grad 9 - ц rot rot bq + F = 0. (9.19)
Переход к обобщенным координатам plt /?2, pz может
быть теперь осуществлен, если использовать соотношение
B.22) и B.24) — B.26). Используя сокращенное обозна-
обозначение Р — rot Sq, получаем сразу
(9>20)
8s gi
Гл. II. Статика деформируемых тел
Согласно B.25) и B.26), величины в и Р имеют вид
(9.20а)
JP == I ОД "л __ од V.
1 gigs \ др2 др3 J
Дополнительные граничные условия, задаваемые к
уравнениям (9.18) или (9.20), могут относиться или к сме-
смещениям, или к напряжениям, или (см. § 44) частично
к тем и другим (смешанные граничные условия). Если
на всей поверхности упругого тела заданы смещения
в виде
&==$о> -Ч = Чо. С = С0 (9.21)
(?0, щ, Со — заданные функции точки), то эта задача ана-
аналогична граничной задаче теории потенциала на стр. 38,
но значительно сложнее ее. Если должны быть заданы
напряжения, то надо представлять себе систему внешних
сил, распределенных на поверхности тела в виде
F = Ыо,
где поверхностная плотность i задается на поверхности
в виде конечной векторной величины. Она должна нахо-
находиться в равновесии с действующими на тело напряже-
напряжениями. Поэтому для каждого элемента поверхности (на-
(направление нормали п) должно выполняться условие
°n* + U = 0, °пу + U - 0' в« + /х = °" (9'21а)
Если поверхность не находится под действием сил, то
граничные условия имеют вид
«n. = e»y = «nz = 0. (9.216).
Этот случай имеется, например, на поверхности изогну-
изогнутой балки (см. § 41) или закрученного стержня (см. § 42).
Если в (9.21а) и (9.216) о выразить через ?, ч\, С, то по-
получим граничные условия для первых производных \, ~г\, С.
При этом возникает проблема интегрирования, подобная
приведенной в задаче 5 гл. I, в так называемой второй
граничной задаче теории потенциала, но опять-таки зна-
значительно более сложная.
§ 9. Соотношения между деформацией и напряжениями 91
Однозначность перечисленных здесь граничных задач,
в частности в случае односвязного тела, доказывается
аналогично тому, как ато делается в теории потенциала
(см. стр. 38) путем применения формулы Грина. При
этом предполагается, что материал однороден, темпера-
температура постоянна всюду и предел упругости не достигается.
Так как в технике мы всегда имеем остаточные напря-
напряжения (температурные напряжения, напряжения после
литья), то эти условия в сопротивлении материалов не
выполняются, и в этом случае доказательство однознач-
однозначности не имеет смысла.
Рассмотрим, наконец, энергетическую сторону соотно-
соотношений между напряжением и деформацией и определим
работу деформации. Вычисления будут опять проведены
для декартовых координат х, г/, z и компонент смеще-
смещения i, 7], С-
Рассмотрим обе я-плоскости нашего элемента объема
Дт = Д#Дг/Дг при изменении смещений
6, 7), с-
Работа напряжений на отрицательной я-плоскости равна
dAx = - (ахх & + аху d-ц + axz dl) ^y Az
и соответственно на положительной
axy d-ц 4- о„ dC) by Az +
4 z dl) Дя by Дг.
Складывая оба выражения алгебраически, получаем вто-
второй член последнего равенства. В сумме с работой внеш-
внешней силы F в направлении х получаем
| (*« К + аху d-n + охг dr.) +Fxdt) Их by Az. (9.22)
Сложим это выражение с соответствующими вкладами от
у- и z-плоскостей и преобразуем сумму согласно урав-
уравнениям равновесия (8.12), в результате чего исчезнут те
члены, в которые войдут в качестве множителей dZ, d*q
92' Гл. II. Статика деформируемых тел
или (К. Если обозначить работу, отнесенную к единице
объема, через dW, то для нее получается
Здесь использовалась симметрия тензора напряжений
(aife— °fei) и учитывалось, что изменение во времени d,
очевидно, коммутативно с пространственным изменением
д/дх, д/ду, djdz (их порядок может быть переставлен).
Вводя тензор деформации, вместо (9.23) можно написать
dW = ахх dexx + oyy deyy + ozz tfezz + 2axy dexy +
+ 4* deyz + 2o« rfez:K = S 2 aift de^. (9.24)
i fe
В последней двойной сумме индексы ink пробегают
все значения х, у, z.
Если, наконец, использовать соотношения между на-
напряжениями и деформацией из равенств (9.7), то из
(9.24) получаем
dW = 2р. 2 S eiftdeift-f Ш rf8. (9.25)
i fe
Это выражение представляет собой полный дифферен-
дифференциал при условии, что константы [х и X действительно
постоянны в случае рассматриваемой деформации. По-
Поэтому можно говорить о работе деформации W незави-
независимо от пути, по которому тело приводится из началь-
начального состояния, свободного от напряжений, в конечное
напряженное состояние. Иными словами, работа дефор-
деформации представляет собой функцию состояния. Если ее
выразить в функции от деформации, она принимает, со-
согласно (9.25), следующий вид:
^+Te\ (9-26)
Будучи функцией состояния, работа деформации, конечно,
не должна зависеть от случайно выбранной системы'
§ 9. Соотношения между деформацией и напряжениями 93
координат х, y,.z. To, что это действительно так, пока-
показывает следующая элементарная выкладка:
21 24 = (ец + ем -ИззJ +
+ 2 (?j2 4- els + eji - eue22 - e22e33 - e33en) = в2 - 2Д,
где, согласно равенству D.9), А является инвариантом
тензора. Поэтому вместо (9.26) получаем инвариантное
представление
W = О±± е2 - 2р.Л. (9.26а)
Возможна симметричная запись, которая также выявляет
.инвариантность
Стоящая справа величина представляет собой простей-
простейший совместный инвариант обоих тензоров о и е. Выра-
Выражая о через е или е через о, получаем две квадратич-
квадратичные формы
W(e) или W(a). (9.27)
Первая получается из (9.266) при использовании соотно-
соотношения между напряжением и деформацией (9.7) и совпа-
совпадает с (9.26), вторая — если использовать соотношения
между деформацией и напряжением (9.7а), а также если
в (9.26) подставить о, S вместо е, в и, кроме того, р.', X'
вместо р., X из (9.76).
Множитель 1/2, входящий, например, в (9.266), соот-
соответствует, очевидно, закону Гука, т. е. линейной зави-
зависимости между напряжениями и деформациями.
Из обеих форм (9.27) компоненты напряжения или
же деформации могут быть получены как частные произ-
производные работы деформации по соответствующим дефор-
деформациям или же напряжениям:
_ 6W (е) _ 8W (а)
дг
ш
W, взятое со знаком минус, называют также упругим
потенциалом единицы объема.
94 Гл. //. Статика деформируемых тел
На стр. 83 было отмечено, что р, и X зависят от тем-
температуры. Если в течение рассматриваемого процесса
температура сохраняется постоянной (изотермический про-
процесс), то р. и X действительно постоянны и наше пред-
предшествующее определение W справедливо. Если этот про-
процесс в каждом элементе объема происходит без притока
или отвода тепла (адиабатический процесс), то можно
показать, что энергия деформации опять является функ-
функцией состояния. Но адиабатические значения fi и X отли-
отличаются от их изотермических значений. Это различие,
как и следовало ожидать, особенно заметно при рассмо-
рассмотрении газообразного состояния; мы вернемся к этому
опять в § 13 при подсчете скорости звука. В общем слу-
случае для тела с неравномерным распределением темпера-
температур работа деформации не является функцией состояния,
так как она зависит от пути, по которому тело пришло
в данное состояние; в этом случае тело не имеет упру-
упругого потенциала.
§ 10. ВЯЗКИЕ СИЛЫ И ИХ РАБОТА, В ЧАСТНОСТИ
В НЕСЖИМАЕМЫХ ЖИДКОСТЯХ
Начнем с некоторого весьма частного случая, рассмо-
рассмотренного еще Ньютоном. Пусть направление скорости
жидкости и (у) всюду параллельно оси х и как-то возра-
возрастает в направлении оси у. Силы реакции, вызванные
вязким трением и передаваемые через плоскости, нор-
нормальные к оси у, согласно Ньютону, пропорциональны
градиенту скорости с некоторым множителем пропорцио-
пропорциональности [а, зависящим от природы жидкости. Рассмо-
Рассмотрим силы реакции, отнесенные к единице плошади,
и назовем их вязкими давлениями; можно для них написать:
р«--р?- <10Л>
Чтобы объяснить обозначение рУх и знак минус в правой
части A0.1), рассмотрим фиг. 13 и вспомним общие обо-
обозначения из § 5. На фиг. 13 изображена воображаемая
плоскость раздела sS. Для нижней части жидкости она
играет роль положительной ^-плоскости (внешняя нор-
нормаль совпадает с положительным направлением оси у),
§ 10. Вязкие силы и их работа
а для верхней части жидкости — отрицательной ^-пло-
^-плоскости (см. § 5, стр. 52). Жидкость в верхней части,
текущая более быстро, стремится увлечь за собой жидкость
нижней части и двигать ее в положительном направле-
направлении оси х, как это изображено на фиг. 13 стрелкой внизу.
и (У)
Фиг. 13.
Вязкое трение, переносимое при ламинар-
ламинарном течении. Простейшее предположение
Ньютона.
Жидкость нижней части стремится удержать жидкость
верхней части, т. е. двигать ее в отрицательном напра-
направлении оси х (стрелка вверху фиг. 13). В случае напря-
напряжений необходимо было бы обозначить обе стрелки через
Сух (положительное направление оси х на положительной
^-плоскости, отрицательное направление на отрицатель-
отрицательной г/-плоскости). Но поскольку мы имеем дело с давле-
давлениями, в обозначение вошел знак минус, т. е. равенство
A0.1) гласит: так как и растет с увеличением у, для
положительной ^/-плоскости давление рух отрицательно,
а для отрицательной — положительно г).
Обобщим это специальное соотношение на случай
произвольного течения жидкости. Будем исходить из
основной теоремы кинематики (см. § 1) о разложении
х) См. примечание на стр. 53. По приведенному там правилу на
положительной у-плоскости условие рух > 0 означает, что давление
направлено против оси х, а на отрицательной ^-плоскости—в обрат-
обратном направлении.
Гл. II. Статика деформируемых тел
бесконечно малого смещения на трансляцию, вращение
и деформацию. Первые две части соответствуют движе-
движению твердого тела, при котором, конечно, не имеется
никакого трения. Поэтому трению соответствует только
третья часть, которая выражается тензором деформации е.
Но в случае жидкостей, как указывалось в § 5, оно за-
зависит не от смещений, а от их изменения во времени,
поэтому будем считать, что вязкое трение зависит не от'е,
а от е. Сделаем предположение, которое дальше будет
доказано, что
А*=-2мЛ, l]=x,y,z. A0.2)
Множитель пропорциональности р, стоящий в A0.1)t
является постоянной внутреннего трения. Назовем эту
постоянную коэффициентом вязкости. Он зависит не
только от природы жидкости, но очень сильно и от ее
температуры (с ростом температуры вязкость падает).
Покажем, что соотношение A0.2) в простейшем слу-
случае течения (см. фиг. 13) совпадает с соотношением A0.1).
Из фиг. 13 следует
и = и{у), г; = 0, ш = 0.
Если от ?, т], С перейти к и, v, w, то, согласно A.1.1)
и A.12),
0 1? ' °'
2 ду
0
Поэтому равенства A0.2) сведутся к равенству, идентич-
идентичному с A0.1),
ди
Рху ~ Pyx = ~ Iх ~Щ »
а все остальные pik исчезнут.
Равенства A0.2) находятся также в соответствии с
результатами предыдущего параграфа, по крайней мере
для несжимаемой жидкости; ограничимся использованием
равенств A0.2) только для этого случая. Согласно E.1),
6 = 0 и соотношения между напряжениями и деформа^
§ 10. Вязкие силы и их работа 97
циями (9.7) перейдут непосредственно в A0.2), если заменим
напряжения на давления (с изменением знаков) и дефор-
деформации на скорости деформаций. Поэтому, кроме A0.2),
не будет существовать другой тензбрно-инвариантной
связи. При этом надо заметить, что введенный здесь коэф-
коэффициент вязкости fA и модуль упругости fA из предыдущего
параграфа отличаются по физическому смыслу. ¦
Выясним прежде всего следующее: в теории упруго-
упругости путем рассмотрения равновесия тетраэдра было пока-
показано, что о является симметричным тензором. Что касается
тензора вязкого трения р, то переход к достаточно малому
элементу объема не будет законным, как это было в случае
твердого тела (ср. стр. 98). Поэтому можно было бы
сначала предположить, что
Pih Ф Рм-
Однако подобный асимметричный тензор давления может
быть представлен в виде симметричной части р~ и анти-
антисимметричной тс, для которых
Антисимметричный тензор может быть представлен в виде
вектора (см. стр. 12), который инвариантным образом свя-
связывается только с величиной того же характера. В ка-
качестве такой величины в рассмотрение может быть взята
угловая скорость <о; статически-кинематическая связь
между it И(о могла бы иметь вид
A0.3)
= —ХО),
Таким образом, вопрос о возможной асимметрии тен-
тензора вязкого трения р находится в связи с вопросом о
существовании вихревого трения в том виде, как оно
представлено равенством A0.3). Последнее, однако, дол-
должно быть немедленно отвергнуто, иначе уже при рас-
рассмотрении простейшего примера мы придем к бессмыслен-
бессмысленному результату.
Представим себе барабан, наполненный вязкой жидко-
жидкостью и приведенный во вращение вокруг своей оси.
Жидкость постепенно будет увлекаться стенками. Есте-
Естественно, что в первый период дополнительно к враща-
7 А. Зоммерфельд
98 Гл. II. Статика деформируемых тел
тельному моменту, необходимому для ускорения бара-
барабана и жидкости, потребуется момент сил, уравновеши-
уравновешивающий силы вязкого трения в жидкости. В конечной
стадии, несомненно, вся жидкость будет вращаться
с одной и той же угловой скоростью ш. Жидкость будет
тогда вращаться как твердое тело, и для поддержания
этого состояния не потребуется никакого вращательного
момента, если будет отсутствовать трение в подшипниках
и т. п. В противоположность вышесказанному равенство
A0.3) привело бы к наличию сил трения внутри барабана
и для конечного состояния, которые передавались бы на
стенки барабана и должны были бы уравновешиваться
внешним вращающим моментом.
Это рассуждение, как и предыдущие, носит фено-
феноменологический характер, в соответствии с общей точ-
точкой зрения, принятой в этой книге. Деформируемые
среды рассматриваются как континуум, но ничего
не говорится о молекулярном происхождении возникаю-
возникающих напряжений или давлений. В случае сжимаемых
жидкостей этими вопросами занимается кинетическая тео-
теория газов. Она выявляет настоящую причину возникно-
возникновения вязких давлений, которая заключается в пере-
переносе количества движения вследствие теплового" движе-
движения, или, как иногда говорят, диффузии количества дви-
движения. Эта более глубокая и далеко идущая теория х)
приводит неизбежно к соотношению A0.22) между давле-
давлением и скоростью деформации для сжимаемых жидкостей,
которое будет приведено позже и которое в случае несжи-
несжимаемой жидкости дает равенство A0.2). Перенос этих
рассуждений на' собственно несжимаемые жидкости не
может быть сделан без довольно произвольных допуще-
допущений. Несомненно, что и здесь отдельные элементы объема
участвуют в обмене количеством движения с удаленными
элементами объема; в этом и заключается физическая
причина возникновения вязкого трения. С другой сто-
стороны, именно -это обстоятельство не дает возможности
переходить к рассмотрению изолированного достаточно
малого элемента объема жидкости.
х) Критическое рассмотрение этого вопроса см., в частности:
Fues E., Zs. f. Phys., 118, 409 A941); 121, 58 A943).
§ Ю. Вязкие силы и их. работа 99
Если на поток будет действовать внешняя сила F,
то одновременно с вязкими давлениями, поведение кото-
которых нами рассмотрено, будет присутствовать и всесто-
всестороннее нормальное давление. Как и раньше, обозначим
его скалярной (без индексов) величиной р, несмотря на
то (см. ниже), что оно будет отличаться от гидростати-
гидростатического давления р. Тогда суммарный тензор давления
Р примет вид
/ + Рхх> Рху> Pxz
x> P + Pw> Pyz
x> Pzy> P + Pz
Теперь можно написать уравнения, аналогичные урав-
уравнениям равновесия (8.12). Правда, мы имеем здесь не
находящееся в покое упругое тело, а текущую жидкость,
но", рассматривая движение без изменения величины или
направления скорости, можно сказать, что каждый эле-
элемент объема действительно находится в механическом
равновесии; поэтому будем говорить об «условиях равно-
равновесия», которые можно написать в виде, аналогичном
(8.12) (заменив напряжения давлениями и переменив
в связи с этим знаки):
DivP = F. A0.5)
Здесь Div обозначает введенную инвариантным обра-
образом в (8.13) векторную дивергенцию. В декартовых коор-
координатах A0.5) напишется в виде
др ¦ дрхх друх ¦ dpzx _ „
дх^ Эх "г" ду "г" dz ~Гх>
д в э*
ду ' дх ' ду
*J>p> = F Aа6)
' dz У1 v 7
др ¦ дрхг , дРУг ¦ dpzz _ р
dz "i" дх "г ду "^ dz z'
Эти равенства, однако, будут определять стационарное
течение, если, согласно A0.2), выразить шесть величин
Pik через три компоненты скорости и, v, w. Из первого
равенства A0.6) получаем
дЬ?\_
дх "'
7*
100 Гл. II. Статика деформируемых тел
¦С помощью условия несжимаемости выражение
«? + *? + - = 0 A0.8)
дх ' ду ' dz v '
может быть приведено к виду
%-?bu = Fx. A0.8a)
Соответствующими уравнениями для у- и z-направлений
будут
A0.86)
Соотношения A0.8)—A0.86) представляют собой четыре
уравнения для определения четырех неизвестных и, v, w, p.
Поэтому давление р характеризуется не своим гидроста-
гидростатическим значением, а этими четырьмя уравнениями,
одновременно с и, v, w.
Уравнения A0.8)—A0.86) можно рассматривать также
как приближенные для течений, в которых ускорения не
исчезают совершенно, но настолько малы, что ими можно
пренебречь. Подобные движения мы будем называть
«ползущими». Их подробное рассмотрение будет дано
в § 35 и 36.
В обоих случаях, стационарных и приблизительно
стационарных движений, необходимо к дифференциальным
уравнениям добавить граничные условия. Лишь после
зтого задача будет иметь однозначное решение точно
так же, как и для дифференциальных уравнений упру-
упругости в § 9. Однако граничные условия в этом случае
и в случае идеальной жидкости существенно различны.
В то время как для идеальной жидкости выполнялось
только одно граничное условие vn — 0, а касательная
скорость vs вдоль жестких стенок принимала любые
значения, в данном случае необходимо потребовать, чтобы
жидкость прилипала к поверхности жесткой границы.
Скачок величины гя на границе означал бы, что ее
градиент имел бы бесконечно большое значение, а это
приводило бы к бесконечно большим значениям вязкого
трения pns, чего в действительности быть не может.
Соответствующая экспериментальная проверка проводи-
§ 10. Вязкие силы и их работа 101
лась в опытах с капиллярами (см. ниже). Итак, гранич-
граничные условия гласят
vn=0, vs = 0. A0.9)
Это существенное различие между идеальной и вязкой
жидкостями приводит к тому, что предельный переход
аналитическим путем от малого к исчезающе малому
трению затруднен. Мы вернемся к этому опять в § 33
(пограничный слой Прандтля).
В качестве простейшего приложения наших условий
равновесия A0.8) и граничных условий A0.9) рассмотрим
классический пример течения Гагена — Пуазейля в капил-
капиллярах1). Капилляр расположен горизонтально, имеет
круглое сечение радиуса а, который настолько мал, что
течение будет прямолинейно и параллельно оси капилляра
(«ламинарное течение»; дополнительно о нем, а также об
условиях его устойчивости см. § 16). Примем ось капилляра
за ось х\ расстояние от нее равно г=у y2-\-z%. Тогда
имеем
v=w = 0, ю = и(г); A0.10)
равенство A0.8) указывает в этом случае, что и не зави-
зависит от ж, а в силу цилиндрической симметрии может
зависеть только от г. Внешняя сила F не действует, так
как вследствие горизонтального положения капилляра
силой тяжести можно пренебречь. Из A0.86) следует
8? = *-°. ¦* = *<*>• A0Л1>
Поскольку в A0.8а) первый член зависит только от ху
а второй — только от г, а их разность должна тождест-
тождественно равняться нулю, то оба члена должны рав-
равняться некоторой постоянной, скажем, —А. Поэтому имеем
%=-А, Д»=-?, A0.11.)
где А — градиент давления вдоль трубы, т. е. деленный
на длину трубы I перепад давления П между началом
х) Н ag en G., PoggendorffsAnn., 46A839). P о i s eu i 11 e J.,
Compt. Rend., 11 A840); 12 A841). Гаген был производителем работ
в Берлине, Пуазейль—врачом в Париже. Независимо друг от друга
они установили соотношение A0.15) экспериментальным путем.
102 Гл. IT, Статика деформируемых тел
и концом трубы. Значение Ам в цилиндрических коор-
координатах г, ср, z вычисляется в задаче 3 гл. I; если и не
зависит от ср и z, то
А Id/' du\
&U= -г ( Г-т- ) .
г dr\ dr J
Поэтому из A0.11а) можно вывести следующее заключение:
d f du\ A du A г2 , „
dr\ dry [x ' dr (a 2 ¦ i
Здесь Сх должно равняться нулю, чтобы du/dr имело
конечное значение при г = 0. Еще одно интегрирование дает
A0.12)
Для определения С2 служит граничное условие A0.9)
и = 0 для г = а. A0.13)
Жидкость прилипает к стенкам трубы. То, что A0.13)
справедливо, следует однозначно из опытов, проведенных
не только для воды, но и для несмачивающих жидкостей
(ртуть в стекле). Итак, из A0.12) следует
так что A0.12) переходит в
и=-?(а2-г2). A0.14)
Профиль скорости представляет собой параболу (фиг. 14).
Все частицы жидкости, которые в момент t—0 заполняли
поперечное сечение трубы, в момент времени t > 0 будут
располагаться на параболоиде вращения, который с уве-
увеличением t вытягивается, так как точки соприкосновения
его со стенкой остаются на месте.
Объем жидкости Q, вытекающей в единицу времени,
равен
а
— а4. A0.15)
§ 10. Вязкие силы и их работа 103
В течение 100 лет с помощью этой формулы определя-
определялось большинство коэффициентов вязкости. Усредненная
по сечению скорость истечения
равна половине максимальной скорости имакс. [равен-
[равенство A0.14) при г = 0]. Из A0.15) и A0.16) для перепада
давления следует
П = 8р./^. A0.17)
Перепад давления, вызванный вязким трением, пропор-
пропорционален первой степени средней скорости протекания
и обратно пропорционален квадрату радиуса. Это утвер-
утверждение, пригодное в соответствующей форме для других
Фиг. 14.
Ламинарное течение в капилляре. Прилипание
к стенкам; параболический профиль скоростей.
ламинарных течений (см. задачи 3 и 4 гл. II и фиг. 19а
и 196 на стр. 153), находится в характерном противо-
противопоставлении с утверждением, относящимся к турбулент-
турбулентным течениям (см. гл. III, § 16): перепад давления здесь
примерно пропорционален квадрату средней скорости про-
протекания и обратно пропорционален первой степени ради-
радиуса трубы.
Перейдем теперь к энергетической стороне процессов,
связанных с вязкостью. Чтобы вычислить работу сил
вязкого трения, начнем с равенств (9.22). При этом
заменим напряжения а на давления р (с изменением знака),
а также виртуальные изменения смещений d\, dt\, dC, на
действительные смещения в жидкости udt, vdt, wdt,
которые происходят за время dt. Тогда вместо (9.22)
получаем
- q-x {{Р + Рхх) U + PxyV )
104 Гл. II. Статика деформируемых тел
Это выражение представляет собой работу, произведенную
всесторонним давлением р и давлениями вязкого трения
pik, действующими на я-плоскость, сложенную с работой
^-компоненты внешней силы. Выполняя дефференцирова-
ние по х и добавляя соответствующие выражения по у
и z, получим после преобразования с помощью уравне-
уравнений равновесия A0.6) и деления на
дм dv dw /" ди dv Л
— Рхх дх—Руу-Щ J}zz-Q^ — P+J
f dv ,idw\ / dw , du\ ,лг\ ло\
— РиЛ 7Г+1Г ) — Pzxi ir-\-ir ) ; A0.18)
rVz \dz ' ду J ^zx\dx ' dzj ' ч 7
члены, куда входит р, исчезнут вследствие, условия
несжимаемости A0.8). Выражение A0.18) представляет
собой величину, так сказать, избыточной энергии, по-
поскольку для поддержания стационарного движения энергии
не требуется. Поэтому она будет переходить в тепло.
Следовательно, A0.18) дает величину тепла, выделенного
за счет вязкого трения, отнесенную к единице объема
и единице времени.
Обозначая, как это делается в термодинамике, коли-
количество тепла, подведенного за время dt к единице объема,
через dq и вспоминая определение eih из A.11), можно
вместо A0.18) написать
С учетом связей A0.2) между pik и eik получаем (оба
отрицательных знака взаимно уничтожаются!)
Естественно, определенное из A0.20) количество тепла dq
не является полным дифференциалам, как, например,
упругая энергия dW из аналогичного равенства (9.25);
не имеется также термодинамической функции состояния
С dq, которая соответствовала бы упругой энергии дефор-
деформации из равенств (9.26) и последующих.
§ 10. Вязкие силы и их работа 105
В заключение рассмотрим совсем кратко те измененияг
которые потребуется внести в наши рассуждения в слу-
случае сжимаемой жидкости. В первую очередь сравнение-
с соотношениями между напряжениями и деформациями
в виде (9.7), так как теперь © Ф 0, показывает, что вме-
вместо A0.2) должно быть
ftfe=-2H.h-X8ifee. A0.21)
Кроме [а сюда входит еще вторая вязкая константа X1),.
которая определяет скорость объемного расширения ©.
Условия равновесия A0.5) и A0.6) сохраняются,,
только в них надо, как в G.3), заменить F на рР^
Уравнение A0.8а) при этих условиях примет вид:
^_^ди_(р1 + Х)^в = рРя« A0.22)
Оно вместе с такими же уравнениями для у и z ,a также-
уравнением неразрывности E.4) определяет четыре неиз-
неизвестных u, v, w и р, если задана связь между р и р. То, что
при этом решения значительно усложняются, видно уже-
при применении их к задаче Гагена — Пуазейля для газа:
в этом случае нельзя получить уравнения только для и,
как это было сделано выше, а получаются два уравнения,
в которые одновременно входят мир. Что касается выра-
выражения A0.20) для теплоты вязкого трения, то оно из-
изменяется вполне понятным образом, а имение:
|^ A0-23>
г) Мы намеренно оставляем ее величину Неопределенной. В лите-
литературе она обычно принимается равной Х=-—B{л./3) на основании
кинетической теории газов, примененной к одноатомным газам.
(Enskog, Diss. Uppsala, 1917). Нетрудно показать из A0.21), что
в случае всестороннего давления возникает изотропное вязкое
трение, равное величине Г ^[х + Х )в. Можно поэтому обозначить
«з H-+^ как объемную вязкость в отличие от [л, которую назы-
называют ламинарной вязкостью. Объемная вязкость одноатомных
газов тождественно равна нулю. Для других газов она отлична
от нуля.
Глава III
ДИНАМИКА ДЕФОРМИРУЕМЫХ ТЕЛ
§11. УРАВНЕНИЯ ЭЙЛЕРА ДЛЯ ИДЕАЛЬНОЙ
НЕСЖИМАЕМОЙ ЖИДКОСТИ
Переход от статики к динамике заключается в доба-
добавлении сил инерции к внешним силам1). Сила инерции,
действующая на частицу массы Атг равна
А dv A dv
— Am -у- = — р Дт __ .
dt r dt
Если мы отнесем ее к единице объема, т. е. разделим
на Дт, то получим
Чтобы получить уравнения движения, необходимо в усло-
условие равновесия F.4) для несжимаемой и идеальной
{т. е. невязкой) жидкости добавить к внешней силе
величину A1.1), также отнесенную к единице объема.
Перенесем A1.1) с положительным знаком в левую часть
равенства, в результате получаем
P^ + gradp = F. A1.2)
Здесь надо четко различать полное, или материальное
ускорение dxjdt, и локальное ускорение ду/dt. Рас-
Рассмотрим, например, ^-компоненту скорости
и(х, у, z, t).
Ее полное изменение при движении материальной частицы
равно
«и = я~ d t + д- dx + -к- ay -\- -д- dz.
х) См. «Механика» (т. I), § 10.
§ 11. Уравнения Эйлера для несжимаемой жидкости 107
Подставив в предыдущее равенство dx = udt, dy = vdt,
dz = w dt, получим для полного ускорения в направлении х
du ди , ди , ди , ди ... о.
dt dt ' дх ' ду l dz ч '
разность между полным и локальным ускорением в
направлении х равна
du ди ди , ди , ди ... о ч
+ v + w AO)
Наличие этой разности можно, например, наглядно вы-
выяснить в случае стационарного течения жидкости через
трубу переменного сечения. Ось трубы примем за ось х,
так чтобы она соответствовала компоненте скорости и.
В случае предположенной стационарности du/dt=±O, что,
конечно, не относится к dujdt. Напротив, в местах, где
труба сужается, скорость будет возрастать, убывая
в местах расширения трубы. Таким образом, будет суще-
существовать разность ускорений (полного и локального),
задаваемая правой частью равенства A1.3а), в частно-
частности ее первым членом, соответствующим компоненте и.
Члены, стоящие в правой части A1.3а), называют иногда
конвекционной частью ускорения.
Если A1.2) записать в развернутой форме и ввести
выражение A1.3), а также соответствующие равенства
для dv/dt, dwjdt, образующиеся путем циклической под-
подстановки координат, то получим
(ди ди , ди . ди\ , dp n
(dv , dv , dv , d
'dt + U^ + Vdy + Wd
четвертым дифференциальным уравнением является усло
вие неразрывности
108 Гл. III. Динамика деформируемых тел
Это и есть уравнения Эйлера1) для идеальной жидкости.
Давление р входит сюда совместно с компонентами иу
v, w в качестве четвертой неизвестной и не совпадает со
своим гидростатическим значением.
Уравнения Эйлера можно записать в сокращенном
виде, используя для этого символическую форму
= F; A1.5)
вместо (vgrad) можно также писать (vV) (см. стр. 35),
Но такая форма непригодна для перехода к криволиней-
криволинейным координатам (см. задачу 1 гл. III), так как операция
градиента может быть применена только к скалярной
величине. Однако псевдовекторный символ (v grad) v можно
преобразовать к законной векторной форме, которую
можно затем рассматривать как общее определение этой
операции для любых координат. Это преобразование
гласит
V2
(vgrad) v = grad у — [v rot v]. A1.6)
Действительно, ^-компонента левой части A1.6) может
быть преобразована к виду
ди , ди , ди
дх oy oz
ди dv\ . / ди
Здесь правая часть совпадает с ^-компонентой правой
части A1.6). Путем циклической подстановки можно
получить соответствующие соотношения для у- и z-kom-
поненты.
г) Жизнь и научная деятельность Леонарда Эйлера A707—1783)
была тесно связана с Российской Академией Наук, членом
которой он состоял. Приехав в Россию в двадцатилетнем
возрасте, он прожил в Петербурге почти всю свою жизнь, временно
покинув Россию лишь в эпоху «бироновщины». Уравнения движения
идеальной жидкости были впервые опубликованы Эйлером в 1755 г,
в трактате «Общие принципы движения жидкости».—Прим перев*
§ 11. Уравнения Эйлрра для несжимаемой жидкости 109
Теперь, используя A1.6), можно преобразовать урав-
уравнение A1.5) к виду
^ )F. A1.7)
Добавляя условие несжимаемости
divv = 0, A1.7а)
получаем уравнение Эйлера в виде, позволяющем без
труда выписать их в любых криволинейных координатах,
например в полярных. При этом надо использовать выра-
выражения для grad, div и rot в общем виде из B.24) — B.26)
или уже вычисленные для полярных координат, которые
приведены в ответах к задаче 3 гл. I.
Рассматривая математический характер уравнений
Эйлера, можно сразу заметить, что в противоположность
большинству уравнений математической физики (теории
потенциала, теплопроводности, электродинамики и т. д.)
они являются нелинейными. Эта нелинейность вызвана
наличием конвекционных членов
ди , ди , ди г . 1 . 1 "V2
+ v + w~te и т< д' или [v rot v]+grad ~2-.
Нелинейность чрезвычайно затрудняет интегрирование
уравнений, так как в этом случае не выполняется принцип
суперпозиции, согласно которому сумма двух частных
решений дает более общее решение. Поэтому интегриро-
интегрирование уравнений гидродинамики Эйлера представляет
гораздо более сложную математическую задачу, чем,
например, интегрирование уравнений электродинамики
Максвелла, которые па первый взгляд кажутся более
сложными.
Только для безвихревого движения представляется
возможным написать сразу первый интеграл уравнений
Эйлера. В этом случае
Достаточно, чтобы это соотношение выполнялось в неко-
некоторый момент времени. Тогда, как будет показано в гл. IV,
оно будет выполняться постоянно, если можно пренебречь
вязким трением.
110 Гл. III. Динамика деформируемых тел
Кроме того, ограничимся случаем стационарного тече-
течения, так что
?-0, A1.8а)
и примем, что внешняя сила F, как в равенстве F.5),
имеет потенциал
F=— grad?7. A1.86)
Тогда из A1.7) следует
или, интегрируя, получаем
р -77-+ p-\-U = const. A1.9)
Выражение A1.9) представляет собой известное уравне-
уравнение Бернуллих). Оно было получено, еще до вывода
Эйлером его уравнений, с помощью рассуждения, кото-
которое можно назвать прообразом закона сохранения энергии.
Бернулли рассматривал потенциальную энергию только
в случае силы тяжести, где U = pgz (z положительно при
отсчете вверх). Уравнение A1.9) в этом частном случае
имеет вид
-^- + —+ gz = const. A1.9a)
z р
Уравнение Бернулли является одной из важнейших
теорем в учении о течении жидкости и используется
в многочисленных технических приложениях (расчет
турбин, аэродинамика и т. д.). Первый член в равен-
равенстве A1.9) представляет собой кинетическую энергию
единицы объема, третий.член — потенциальную энергию
внешней силы, также отнесенную к единице объема.
Давление жидкости р входит в A1.9), в известном смысле,
в качестве потенциальной энергии внутренних сил, кото-
х) Даниил Бернулли A700—1783 гг.), как и Эйлер, был членом
Российской Академии Наук. На титульном листе трактата Бернул-
Бернулли «Гидродинамика» A738 г.) указано, что это—«академический
труд, выполненный автором во время работы в Петербурге».—
Прим. перев.
§ 11. Уравнения Эйлера для несжимаемой жидкости 111
рые действуют в единице объема и которые в силу
несжимаемости возникают при действии элементов объема
друг на друга. Более глубокое математическое рассмо-
рассмотрение р будет сделано в следующем параграфе.
Используем сейчас равенство A1.9а) для получения
формулы Торичелли для скорости истечения. Торичелли*
был учеником Галилея, жил до Бернулли и, конечно,
не мог использовать уравнение Бернулли для получения
этого результата.
Представим себе сосуд, наполненный жидкостью*
и имеющий на уровне дна (сбоку или снизу) кран. Пусть
на поверхности жидкости 2 = 0, а у дна z=—h. Если
кран закрыт, то во всем объеме v = 0 и р — 0 на поверх-
поверхности (мы понимаем под р превышение давления над
атмосферным), поэтому в A1.9а) надо принять const = 0.
У дна сосуда, согласно A1.9а), p~pgh^=^h (p — гидро-
гидростатический избыток над атмосферным давлением, как
в § 6). Если кран открыт, то можно предположить, чта
v на поверхности практически все еще равно нулю;
а так как р = 0, то снова const = 0. Но теперь р —- 6
и возле крана, так что A1.9а) для z= —h даст
v = ]/2gh, A1.10)
как в случае свободного падения. Полученное выражение
представляет собой содержание теоремы Торичелли.
Другим примером является стационарное течение
через горизонтальную трубу переменного сечения. В силу
несжимаемости, количества жидкости, протекающие в еди-
единицу времени через различные сечения, будут равны;
следовательно, скорость v при возрастании сечения будет
падать, а при убывании возрастать, как было уже отме-
отмечено на стр. 107 (в данном случае v фактически совпа-
совпадает с рассмотренной ранее аксиальной компонентой и).
Согласно A1.9а), давление ведет себя обратным образом.-
Если у трубы имеется ряд открытых сверху вертикаль-
вертикальных отростков, в которые может подниматься жидкость,
то высота ее в этих отростках покажет распределение-
давления вдоль трубы.
Жидкость ведет себя гораздо разумнее толпы людей,,
которой надо пройти через узкий проход. Их скорость
при этом убывает, а давление друг на друга растетг
112
Гл. III. Динамика деформируемых тел
в противоположность тому, что происходит при движении
жидкости.
Иллюстрацией уравнения Бернулли служит опыт,
который можно очень легко воспроизвести. Положим на
левую руку листочек бумаги (например, величиной 5 X о еж),
приложим сверху второй и третий пальцы правой руки
и будем дуть сильно в середину листка через узкую
щель между пальцами. Бумага при этом не будет при-
прижиматься к левой руке, а наоборот, поднимется к паль-
дам правой руки, где и будет висеть в течение неко-
некоторого времени. Объяснить
это можно так: воздух, про-
проходящий между пальцами
и бумагой, протекает через
канал возрастающего сече-
сечения (фиг. 15); его скорость
падает, а давление возра-
возрастает. Но в конце канала
давление равно атмосфер-
атмосферному давлению р0, следо-
следовательно, в канале будет
давление р < р0; так как
снизу на бумагу действует
атмосферное давление р0,
то возникает разность дав-
давлений р0 — р, действующая снизу вверх, или, как иногда
говорят, всасывающее действие, направленное сверху вниз.
Если этот опыт провести в большом масштабе с по-
помощью сжатого воздуха, струя которого направлена на
перпендикулярно расположенную пластину, то эту пла-
пластину можно еще нагрузить довольно значительным
весом.
В этом и предыдущем опытах мы применяли к сжи-
сжимаемому воздуху уравнение Бернулли, выведенное для
несжимаемых жидкостей. Это допустимо, так как скорость
течения не очень велика. В общем случае можно показать
{см. приложение к § 13), что различие между сжимаемой
и несжимаемой жидкостью становится существенным при
скоростях, близких к скорости звука.
Рассмотрим, как изменится уравнение Бернулли
в случае нестационарного течения. Иначе говоря, отбросим
Всасывающее действие
потока, продуваемого
воздушного
через щель
между двумя пальцами и листом бу-
бумаги. Листок при этом не сдувается,
а прижимается к пальцам.
§ 11. Уравнения Эйлера для несжимаемой жидкости 113
предположение A1.8а), но сохраним A1.8) и A1.86).
Равенство A1.8) представляет собой необходимое и доста-
достаточное условие того, что udx-\-vdy-\-wdz есть полный
дифференциал. Поэтому положим
udx + vdy + wdz = — йФ A1.11)
и назовем Ф потенциалом скорости. В этом случае
дФ дФ дФ
дх ' дг/ ' dz '
или
v= — gradO, а следовательно, -^- = — grad -^— . A.1.12)
Заметим, что отрицательный знак в A1.11) и A1.12)
выбран только по аналогии с силовым потенциалом
[см., например, A1,86)].
Так как divv = 0, то в данном случае Ф удовлетво-
удовлетворяет уравнению потенциала C.17), т. е.
АФ = 0. A1.13)
С учетом A1.8), A1.86) и A1.12)"уравнение Эйлера A1.7)
принимает вид
grad(-p^ + p^- + ^ + C/) = O, A1.14)
или, если использовать введенное в C.9а) обозначение
для первого дифференциального параметра, имеем
—^+у?Ф +} (/> + #) = const. A1.15)
Полученное выражение является обобщенным уравне-
уравнением Бернулли для нестационарных движений и предста-
представляет собой так же, как и равенство A1.9), первый инте-
интеграл уравнений Эйлера. Как показывает переход от A1.14)
к A1.15), постоянная, входящая в A1.15), не зависит
от пространственных координат, но в общем случае может
зависеть от t. Она представляет собой функцию (единую
во всем объеме жидкости), которая может быть определена
из граничных условий течения (заданным образом меня-
меняющихся со временем). Заметим, что эта зависимость от t
может быть включена в определение потенциала скоро-
8 А. Зоммерфельд
114 Гл. 777. Динамика деформируемых тел
сти Ф, так как уравнение потенциала A1.13) задает про-
пространственную, а не временную зависимость Ф.
До сих пор мы рассматривали только безвихревое дви-
движение. Посмотрим, что может быть сказано по поводу
общего случая вихревого движения.
Рассмотрение A1.7) показывает, что и в этом случае
может быть проведено однократное интегрирование, если
производить его в направлении линии тока, т. е. в пере-
переменном направлении v. Тогда интеграл от второго члена
левой части A1.7) обратится в нуль, так как
[х rot vj
направлен перпендикулярно к v и при интегрировании
не дает никакого вклада. Если сохранить условия A1.8а)
и A1.86) (стационарное течение в силовом поле, имеющем
потенциал, но не имеющем потенциала скорости), то
равенство A1.9) все еще будет справедливым, но с той
разницей, что входящая сюда постоянная не будет теперь
одинаковой во всем объеме жидкости, а будет меняться
от одной линии тока к другой.
Понимаемое в этом смысле выражение A1.9) назовем
модифицированным уравнением Бернулли. Его обобщение
на случай нестационарных движений здесь рассматри-
рассматриваться не будет.
§ 12. ВЫВОД УРАВНЕНИЙ ЭЙЛЕРА ИЗ ПРИНЦИПА
ГАМИЛЬТОНА. ДАВЛЕНИЕ КАК МНОЖИТЕЛЬ ЛАГРАНЖА
Несомненно, понятие давления в несжимаемой жидкости
представляет некоторое затруднение для физического
истолкования. Давление представляет собой функцию
состояния, но, однако, не сказывается на поведении
жидкости но отношению к занимаемому ею объему. Для
сжимаемой жидкости эта трудность отпадает, так как
в этом случае давление определяет плотность. Поэтому
рассмотрим понятие давления для несжимаемой жидкости
с точки зрения аналитической механики.
Подвергнем частицу массы жидкости виртуальному
смещению
8s = «, Ч К,
§ 12. Вывод уравнений Эйлера из принципа Гамильтона 115
которое, однако, не нарушает условия несжимаемости
6 = 0 [ср. A.24)J. Тогда выражение
80 =^i + ^- + -? = div8s A2.1)
дх ' ду dz v '
должно обращаться в нуль. Это условие будет выпол-
выполнено, если в подинтегральное выражение в принципе
Гамильтона добавить величину Ъ®, умноженную на множи-
тель Лагранжа X. Если это записать в форме уравнения
C3.10) из т. I, то получим
dt \dx {ЬТ + ЬА + Х8О) = 0. A2.2)
Интегрирование по dr распространяется на весь объем
жидкости. Величины ЬТ и ЬА относятся к единице объема,
так же как и S© в A2.1). Поэтому
T = |-v2, ЬТ==9(х,Ьу), A2.3)
а для виртуальной работы внешней силы
84 = (F, 8s). A2.4)
Подставим в A2.3) действительную скорость
v = |- A2.4а)
и для ее виртуальной вариации соответственно получим
Sv = 8-5T = 48s- A2-4б>
Преобразуем член с ЬТ путем интегрирования по частям
по t и заметим, что, согласно положениям принципа
Гамильтона, время t не варьируется и 8s на краях интер-
интервала tQ и /j должно обращаться в нуль1). Тогда получаем
'о to to
х) См. «Механика» (т. I), равенства C3.1) и C3.2).
116 Рл. III. Динамика деформируемых тел
Кроме того, в A2.2) преобразуем интеграл с подинте-
гральным выражением Х8© = X div (8s) согласно соотно-
соотношению
X div (8s) = div (X8s) - (grad X, 8s).
Используя теорему Остроградского — Гаусса, получим
в результате интегрирования
Xdiv (8s) dx = ^ \bsndc - ^P(grad X, 8s) dx. ' A2.6)
К поверхностному интегралу, стоящему на первом месте
в правой части, мы еще вернемся, а пока обозначим его
точками. Таким образом,
div(8s) rft=...-^(gradX, 8s)^т. A2.7)
Вводя A2.1), A2.4), A2.5) и A2.7) в A2.2), получаем
^ ( ^ ) . .. =0. A2.8)
'о
Благодаря введению множителя X смещение 8s может
быть выбрано произвольным образом внутри объема жидко-
жидкости т и интервала времени от t0 до 1г. Но так как при
этом должно выполняться равенство A2.8), то множитель,
стоящий при 8s, в скалярном произведении должен обра-
обращаться в нуль во всей области интегрирования. Поэтому
можно записать, что
P^ + gradX = F. A2.9)
Это выражение является уравнением Эйлера, написанным
в форме A1.2), если X отождествляется с давлением р.
Таким образом, с точки зрения аналитической механики,
гидродинамическое давление представляет собой реакцию
против условия несжимаемости, которому должен удо-
удовлетворять выбор X. В соответствующем случае сфериче-
сферического маятника1) мы считали, что X представляет собой
1) См. «Механика» (т. I), равенство A8.7).
§ 12. Вывод уравнений Эйлера из принципа Гамильтона 117
силу реакции, удерживающую точечную массу на сфе-
сферической поверхности. Здесь условие несжимаемости можно
рассматривать как жесткую связь, не совершающую
работы; это толкование помогает устранению трудности,
связанной с понятием давления в несжимаемой жидкости.
Следует заметить, что можно было бы эти рассужде-
рассуждения основывать не на условии A2.1), а на обычной форме
условия несжимаемости и его вариации:
divv = 0, 8divv = div8v = O. A2.10)
Оставляя выражения A2.3) и A2.4) для ЬТ и ЬА, напишем
вариационный принцип A2.2) как
h
\dt\ dx{p{v, 8v) + (F, 8s) + X'div8v}=0. A2.11)
to
В этом выражении мы обозначили множитель через X',
потому что он, уже по соображениям размерности, не
совпадает с прежним X. Чтобы воспользоваться 8v в каче-
качестве независимой вариации, необходимо преобразовать
средний член в A2.11). Положив
F^=\Fdt, A2.12)
получим
tl tl t\
to to to
В последнем преобразовании было использовано равен-
равенство A2.46), а также учтено, что при интегрировании
по частям члены, соответствующие пределам t0 и tx, обра-
обращаются в нуль, как в равенстве A2.5). Преобразовав,
как в A2.7), член, содержащий X', получим из A2.11)
h _
to
Те же рассуждения, что и для равенства A2.7), приводят
к выражению
pv-F-gradX' = 0. A2.13)
118 Гл. III. Динамика деформируемых тел
Теперь необходимо продифференцировать это выражение
по времени [с учетом A2.12) для F] для того, чтобы
опять получить уравнения Эйлера (р в силу предполо-
предположенной несжимаемости ведет себя как величина, не зави-
зависящая от времени):
p-^ + grad^F, где Р=-^-. A2.14)
С этой точки зрения давление опять определяется мно-
множителем Лагранжа X', правда, иначе, чем в предыдущем
случае, что, однако, нас не должно удивлять после заме-
замечания, сделанного к A2.11).
Рассмотрим теперь поверхностный интеграл из равен-
равенства A2.6), обозначенный в равенстве A2.7) точками,
который дает нам граничные^ условия, требующиеся для
полного определения давления. Заменив в этом поверхно-
поверхностном интеграле X на р и bsn на Bv, запишем его в виде
V pbvda.
A2.15)
Прежде всего вместо полученного выражения рас-
рассмотрим аналогичный интеграл, отвечающий силам сцепле-
сцепления в жидкости. Чтобы сделать это, надо воспользоваться
некоторыми представлениями молекулярной теории. Дей-
Действие частиц жидкости друг на друга определяется
не только давлением р (в силу постоянства их объема),
но и силами связи, действующими между соседними
частицами на коротком расстоянии, возникающими благо-
благодаря электрическому строению молекул. Для внутрен-
внутренних элементов объема эти силы взаимно уничтожаются
вследствие того, что в среднем они равномерно распреде-
распределены по направлениям. Для элементов объема, располо-
расположенных вблизи поверхности, эти силы дадут равнодей-
равнодействующую N, направленную по внутренней нормали
п к поверхности (обозначение N принято для силы,
отнесенной к единице площади). Ее виртуальная работа
при смещении Sv будет равна
ЬА= -
Поэтому в* принципе Гамильтона, кроме написанного
в A2.2) объемного интеграла от ЬА, куда силы сцепления
§ 12. Вывод уравнений Эйлера из принципа Гамильтона 119
не вошли, должен войти поверхностный интеграл
\ bAda = - \ Nbvda. A2.16)
Это выражение совместно с поверхностным интегралом
A2.15), соответствующим условию несжимаемости, при-
приведет к
^(p-N)lvda. A2.17)
Согласно принципу Гамильтона, теперь должен обра-
обратиться в нуль не только пространственно-временной инте-
интеграл A2.7), но и образованный из A2.17) поверхностно-
временной интеграл:
h
[ dt \ {р - N) 8v do = 0. A2.18)
to
Для вывода отсюда некоторых следствий рассмотрим три
возможных вида границ: а) жидкость граничит с твердой
стенкой; б) жидкость имеет свободную поверхность, т. е.
она граничит с пустотой или с воздухом; в) две жидкости
граничат друг с другом, например масло и вода, причем
поверхность раздела может иметь произвольную форму.
Рассмотрим каждый из этих случаев:
а) При наличии твердой стенки невозможно движение
жидкости нормально к стенке. Это справедливо как для
реального, так и для виртуального смещения жидкости.
Отсюда следует, что Sv = O, так что условие A2.18) выпол-
выполняется само собой. В случае твердой стенки на давление
не накладывается никаких граничных условий на поверх-
поверхности жидкости.
б) Если жидкость имеет свободную поверхность, то Sv
произвольно. Равенство A2.18) требует тогда равенства
p = N A2.19)
для любого элемента свободной поверхности и любого
момента времени t.
в) В случае поверхности раздела между двумя жидко-
жидкостями 1 и 2, в которых могут иметься гидродинамиче-
гидродинамические давления рх и р2 и давления сцепления Nx и iV2,
120 Гл. III. Динамика деформируемых тел
для каждого элемента поверхности do и любого t, соглас-
согласно A2.18), должно выполняться условие
N2) Bv2 = 0. A2.20)
Соприкосновение жидкостей 1 и 2 в результате вирту-
виртуальных смещений не должно нарушаться. Поэтому
где знак минус соответствует нашему соглашению отно-
относительно направления нормали п. Таким образом,
из A2.20) следует
Рг-Рг = Пг2, Nn = Nx-Nr A2.21)
Вдоль поверхности раздела двух жидкостей имеется раз-
разность давлений, обусловленная силами сцепления. Она
зависит от природы жидкостей и формы поверхности раз-
раздела, но не зависит от движения жидкостей.
Принцип Гамильтона1) приводит не только к диффе-
дифференциальным уравнениям задачи (в данном случае
к уравнениям Эйлера), но и к граничным условиям для
давления на поверхности, если они вообще имеются.
К их рассмотрению мы еще обратимся в § 17.
§ 13. УРАВНЕНИЯ ЭЙЛЕРА ДЛЯ ИДЕАЛЬНОЙ СЖИМАЕМОЙ
ЖИДКОСТИ. ИХ ПРИЛОЖЕНИЕ К АКУСТИКЕ
Переход от статики к динамике происходит здесь, как
и в случае несжимаемых жидкостей, путем добавления
к внешним силам сил инерции.
Так как у нас имелись основания в случае сжима-
сжимаемой жидкости относить внешние силы не к единице объема,
а к единице массы (обозначение Р), то аналогичным
образом следует поступить и с силами инерции. В этом
случае в уравнения равновесия вместо Р необходимо
будет подставить величину
r dt '
в результате чего G.5) преобразуется к виду
См. «Механика» (т. I), § 33,
§ 13. Уравнения Эйлера для идеальной сжимаемой жидкости 121
Совместно с уравнением неразрывности E.4)
^ 0 A3.2)
получаем уравнения Эйлера для сжимаемой жидкости.
Связь между р и р в достаточно общем виде задается
уравнением политропы G.1). Теперь от х, у, z и t зави-
зависит не только р, но и р.
В акустике нас интересуют, как правило, только
малые колебания воздуха. Для этого случая отпадают
трудности, связанные с наличием в уравнениях Эйлера
квадратичных членов A1.3а). А именно, мы можем здесь
прямо заменить
dv д\
ЧГ чеРез ~эТ'
Однако квадратичные члены необходимо сохранить
в случае § 37, где будет проведено исследование ударных
процессов с большими скоростями, как, например, явле-
явления, сопровождающие выстрел из орудия. В акустике вели-
величину р можно также рассматривать как отклонение от
нормального атмосферного давления р0, которое как вели-
величина постоянная в пространстве в равенство A3.1) не
войдет, так как там давление стоит под знаком градиента.
Далее, пренебрегая членами второго порядка малости,
можно величину р в знаменателе A3.1) и под знаком
дивергенции в A3.2) заменить на нормальное значение
плотности р0 в невозмущенной атмосфере. В этом случае р
и производные р, а также v являются малыми величи-
величинами. И, наконец, для целей акустики можно считать,
что Р = 0.
Тогда получаем очень простую систему уравнений:
O, A3.3)
| O. A3.4)
Учтем связь между р и р:
(^) с*=(^-)о, A3.5)
122 Гл. III. Динамика деформируемых тел
где с —постоянная, относящаяся к нормальному состо-
состоянию атмосферы. Таким образом, вместо A3.3) получаем
Po!f + c2gradp = O. A3.6)
Из A3.4) и A3.6) можно исключить v, для чего возьмем
частную производную по t от A3.4) и подставим туда
выражение для pv(d\jdt) из A3.6). В результате получим
= с2 div grad p = с2Др. A3.7)
dt2
Такое же уравнение справедливо и для р. Согласно A3.5),
grad/?, а поэтому Д/? и d2p/dt2 равны соответственным
выражениям, образованным из р, если их умножить
на коэффициент пропорциональности с2. Поэтому
% A3.8)
Наконец, то же самое дифференциальное уравнение
описывает и поле скоростей. В этом случае оно относится
собственно не к v, а к потенциалу скоростей Ф, поскольку
он существует. Подставляя [см. A1.12)] v= — grad<E>,
преобразуем A3.4) и A3.6) к виду х)
дФ
Дифференцируя второе уравнение по t и сравнивая с пер-
первым, сразу же получаем
^ = с2ДФ A3.9)
Уравнения типа A3.7) — A3.9) называются волно-
волновыми уравнениями. Они играют большую роль в при-
приложениях математической физики, например в колеба-
колебаниях струны (одномерное, Д = д2/дх2) или в уравнениях
колебаний мембраны (двухмерное, Д = д2/дх2 -+- d2jdy2).
х) Во второе из нижеследующих уравнений надо было бы дописать
постоянную, не зависящую от ж, у, z, но зависящую от t. Однако ее
можно включить в Ф при определении потенциала скоростей (ср.
стр. 113).
§ 13. Уравнения Эйлера для идеальной сжимаемой жидкости 123
Наша задача сводится к уравнению колебаний струны,
если рассматривается состояние, в котором все зависит
только от координаты х. В этом случае уравнение A3.8)
принимает вид
%¦-*&. A3.10)
Это уравнение может быть сразу проинтегрировано. Инте-
Интеграл может быть задан в виде решения Даламбера
р = Fx (х -f ct) +- F2 {x - ct), A3.11)
где Fx и F2— действительные функции, совершенно про-
произвольные вплоть до необходимых условий непрерывности
(существование первой и второй производных). Действи-
Действительно, любая функция от х ± ct удовлетворяет диффе-
дифференциальному уравнению A3.10), что справедливо (бла-
(благодаря тому что мы пренебрегли в уравнениях Эйлера
квадратичными членами!) и для их суммы.
Выражение A3.11) представляет собой общее решение
волнового уравнения в одномерном случае, так как оно
справедливо при любых начальных условиях. Пусть
в момент t = 0 задано
тогда достаточно положить
откуда сразу следует
х0
Проиллюстрируем это на фиг. 16, где принято /2 = 0.
Начальное возмущение давления fx (x) смещается наполо-
наполовину направо и наполовину налево, причем обе части
движутся без изменения формы, как говорят «неиска-
«неискаженными», со скоростью с. Таким образом, становится
очевидной роль коэффициента с как скорости звука.
124 Гл. III. Динамика деформируемых тел
На фиг. 16 графически изображено первоначальное воз-
возмущение в виде горба давления в центре и состояние
в некоторый последующий момент времени: два горба
половинной высоты слева и справа. На языке акустики
график изображает распространение некоторого шума
(имеющего произвольную форму, но с амплитудой,
постоянной вдоль плоскостей, перпендикулярных к оси х).
Фиг. 16. Иллюстрация решения Даламбера.
Вначале области повышенного давления, смещающиеся впра-
вправо и влево, перекрывают друг друга. С течением времени
между ними возникает невозмущенное пространство.
Указанный график характеризует также колебания струны,
оттянутой в момент t = 0 и затем отпущенной, причем
в случае конечных размеров струны следует мысленно
добавить отражение возмущений, идущих вправо и влево
от ее концов.
В акустике речи и музыки интересуются не столько
однократными, сколько периодическими возбуждениями
воздуха. Пусть <о=.2тс/т — круговая частота, откуда
v = и>/2% = 1/т —высота тона, т. е. число колебаний в 1 сек.
Будем считать, что Fx и F2 являются тригонометриче-
тригонометрическими функциями, например, следующего вида:
, A3 13)
Fx (x+ct) = b cos [kx + Ы + P),
где а и Ъ — амплитуды, а и [3 —постоянные фазы;
о 2п
К — —ч
С А.
есть волновое число, равное числу длин волн X в отрезке
длины 2тс. Функция F2 представляет собой плоскую
волну, распространяющуюся в положительном направле-
направлении оси х, Fx — b отрицательном направлении оси х.
§ 13. Уравнения Эйлера для идеальной Сжимаемой жидкости 125
В случае равных амплитуд а и Ъ наложение обеих волн
дает стоячую волну. Отметим также,'что
Прежде всего рассмотрим вопрос о направлении
колебаний. Согласно A3.5), направление градиента р
совпадает с направлением градиента р; согласно A3.6),
направление d\jdt, а потому и направление v совпадает с на-
направлением градиента р. Таким образом, для наших волн
(как бегущих, так и стоячих) направление колебаний
или совпадает с направлением распространения, или же
имеет противоположное направление в случае противо-
противоположной фазы, т. е. волны являются продольными;
поперечных волн в идеальной жидкости не бывает. Про-
Процесс, представленный на фиг. 16, изображает, конечно,
распространение продольного возмущения.
В настоящее время обычно применяется удобная для
волновой теории замена тригонометрических функ-
функций A3.13) комплексными показательными функциями
A pi {kx—4>t) А — пРш
ле >, л-ае , A3.15)
При этом, естественно, имеется в виду действительная
часть этих комплексных выражений, совпадающая с пра-
правыми частями A3.13). Знак перед i выбран таким обра-
образом, что временная зависимость в обоих случаях имеет вид
е~ш.
Если этот временной множитель считать раз навсегда
заданным, то вместо A3.15) можно написать еще более
простое выражение:
х—плоская волна, распространяющаяся в положительном
направлении оси х, , . _, . _ .
г, ь A3.15а)
Jt>e~inx—плоская волна, распространяющаяся в отрицательном ,
направлении оси х.
Такое представление пригодно в равной степени (при
соответствующем изменении значений А и В) для давле-
давления, плотности и потенциала скорости. Как будет пока-
126 Гл. III. Динамика деформируемых тел
зано в гл. V, этот способ записи с помощью показа-
показательных функций приведет к значительному сокращению
формул.
Сделаем еще замечания по поводу численного значе-
значения скорости звука. Положим в основу рассмотрения
изотермическое изменение состояния. Показатель п поли-
политропы можно тогда считать равным единице; в этом слу-
случае из G.1) получаем
dp _ Ро
d? Ро '
и, согласно A3.5),
' A3.16)
В случае нормального состояния атмосферы (на поверх-
поверхности земли), согласно стр. 59,
р0 = 1,033 кГ/см2 = 1033-981 г/см-сек2,
ро= 1,293-10 г/см3.
Откуда
с = 1/ , 293 • 103 см/сек = 280 м/сек.
Эта величина скорости звука, которая гораздо меньше дей-
действительной, была вычислена еще Ньютоном. Рассмотрим
теоретическую формулу, которой пользовался Ньютон,
а именно:
= у Упругость 6а)
г Плотность ч '
В нашем случае термин «упругость» аналогичен модулю
сжатия; он задается в случае упругого твердого тела
равенством (9.13) и для газов соответственно выражается
через
Tf /^ л (~\ ар
Таким образом,
К = Р^- A3.166)
§ 13. Уравнения Эйлера для идеальной сжимаемой жидкости 127
и, согласно A3.16а),
что совпадает с ранее полученным выражением A3.5).
Возникает вопрос, допустимо ли считать изменение
состояния изотермическим. Как впервые заметил Лаплас,
при быстрых колебаниях воздуха почти не происходит
обмена теплом и изменение состояния можно практи-
практически считать адиабатическим. В таком случае показа-
показатель политропы равен не 1, а 1,4 (см. стр. 69); в этом
случае, согласно G.1), имеем
<13Л7>
т. е. в 1,4 раза больше, чем в A3.16). Скорость звука
при этом увеличивается в |/ 1,4 раза и составляет
с = |/ТД. 280 = 332 м/сек,
что находится в достаточно хорошем согласии с опытомг).
В заключение перенесем метод интегрирования Далам-
бера с плоских волн на сферические. Пусть источник
сферических волн расположен в начале сферической
системы координат г, Ь, <р. Распределение давления будем
считать сферически симметричным, т. е. не зависящим
от & и ср. Тогда выражение для Д/? (см. задачу 3 гл. I)
может быть написано как
Р ~ г дг* '
и равенство A3.8) примет вид
дг*
Оно может быть проинтегрировано в виде A3.11)
rp = Fx(r + ct) + F2 (г — ct).
х) Разница в значениях с, связанная, согласно A3.166). с раз-
различием в К, иллюстрирует упомянутую в конце § 9 зависимость
упругих констант от характера изменения состояния.
128 Гл. III. Динамика деформируемых тел
Отсюда любое распределение р и dp\dt при ? = 0 и г > 0
может быть продолжено для t > 0, причем только зна-
значение F2 для отрицательных аргументов должно быть
таким, чтобы обеспечить конечность р в точке г = 0.
Здесь мы также интересуемся главным образом перио-
периодическим случаем и можем записать решение в ком-
комплексном виде; опуская, как в A3.15), временной мно-
множитель е~ш, имеем
р = Ле*г, A3.18)
или
р е-1^
A3.18а)
В таком же виде могут быть представлены величины р
и Ф. Так как gradCD имеет составляющую только в на-
направлении г, колебания скорости v здесь будут также
продольными.
Выражение A3.18) описывает расходящуюся сфери-
сферическую волну, у которой сферические поверхности рав-
равной фазы кг,— о)^ = const с увеличением t движутся из
начала координат с фазовой скоростью
dr to
c
Можно представить себе, что такой колебательный про-
процесс вызван колебаниями сферы, помещенной в начале
координат.
Наоборот, выражение A3.18а) характеризует сходя-
сходящуюся сферическую волну; поверхности равной фазы
— кг— оJ = const движутся здесь к началу координат
со скоростью
dr w
__= —-?-= —С.
Физически такой колебательный процесс не может быть
реализован; он требовал бы искусственного создания
системы сил давления, действующих на очень большом
удалении.
§ 13. Уравнения Эйлера для идеальной сжимаемой жидкости 129
ПРИЛОЖЕНИЕ
Сравнение течения сжимаемых и несжимаемых
жидкостейг)
Рассмотрение течений в сжимаемых средах гораздо
сложнее, чем в несжимаемых. Возникает вопрос: когда
сжимаемую среду можно с достаточной точностью считать
несжимаемой? Термин «с достаточной точностью» здесь
означает, что для интересующих нас величин (р, р, г;)
не превосходится известная, заранее заданная ошибка.
Будем исходить из уравнения неразрывности. Из него
следует, что в случае сжимаемой среды поперечное сече-
сечение трубок линий тока отличается от сечения для не-
несжимаемой среды. Чтобы показать это, рассмотрим ста-
стационарный случай, которым мы и ограничимся в даль-
дальнейшем. Тогда, согласно E.4), выполняется равенство
div (pv) = 0.
G помощью теоремы Остроградского — Гаусса, применен-
примененной к трубке тока, ограниченной малыми сечениями F
и Fo, перпендикулярными к линиям тока, это равенство
приводит к соотношению
. . pFv = ро/>о = const = М, A3.19)
v, v0 и соответственно р и р0 — абсолютные значения ско-
скоростей и плотности в F и Fo. (Поверхность трубки тока,
образованная линиями тока, не дает вклада в интеграл.)
Для несжимаемых сред A3.19) принимает вид
Fv = Fovo = const = V. A3.19a)
В A3.19) и A3.19а) М означает массу, а V — объем, про-
протекающий через поперечное сечение F в единицу времени.
Вычислим теперь давление в случае стационарного
течения сжимаемой жидкости и сравним его с давлением
в случае несжимаемой жидкости. Уравнение Бернулли
х) См. также Prandt 1—Т i e t j e n s. Hydro- und Aero-
mechanik, Bd. I, S 208. (См. перевод: Прандтль и Титьенс,
Гидро- и аэромеханика, т. I, М.—Л., 1933.—Прим. перев.)
9 А. Зоммерфельд
130 Гл. III. Динамика деформируемых тел
для сжимаемой жидкости, если сила тяжести — единствен-
единственная внешняя сила, согласно A1.9а) и G.66), дает
№ vl)±g{hh)+\lf O A3.20)
а для несжимаемой жидкости
Y (*2 -»;) + *(*- ho) + ~- = 0. A3.20а)
Величины без индекса относятся к произвольному, а с ин-
индексом 0 —к заданному «конпевому сечению». В основу
вычисления интеграла в A3.20) полошим уравнение по-
политропы р—Срп
v
Г dp __ п Г р^_ _ро_\ _ п р0 Г f ±_\п~1 _ 1 1 _
J P n-lVp Ро У п — 1 Ро LVpo / J
п—1
~1 Ро
Последнее выражение впин:ем в A3.20) и разрешим
относительно р. Поело этого получим
" . A3.21a)
, Если предположить, что
-^ (г^2 — vi) -f g (/г — h0) < ^—^ — , A3.216)
то, разлагая бином A3.21а) в ряд, получим
что совпадает с значением р, взятым из A3.20а), если
пренебречь квадратичным членом и членами более высо-
высокого порядка.
Произведем оценку ошибки для одного важного ча-
частного случая. В потоке находится твердое тело. Пусть
§ 13. Уравнения Эйлера для идеальной сжимаемой жидкости 131
концевое сечение с р0, v0 расположено вдали от тела;
разностью высот пренебрежем, т. е. положим h -=/г0. Вычи-
Вычислим давление в точке остановки (см. ниже фиг. 46 и 48),
или, проще говоря, скоростной напор р—р0- Согласно
определению [см. ниже B9.7)], в точке остановки v = 0
и во втором приближении из A3.21в) получаем
Введем здесь скорость звука, соответствующую нашей
политропе. Согласно A3.17), для нормального состояния,
в качестве которого примем состояние на конце р0, р0,
• A3-21г>
Тогда предыдущее равенство перейдет в
О A3-22)
в то время как A3.20а) можно написать в виде
P-A)=4po<- A3.22а)
Ошибка, которую мы совершим, вычисляя скоростной
напор в сжимаемой среде с помощью равенства A3.22а)
для несжимаемой жидкости вместо правильного равен-
равенства A3.22), оцененная по величине квадратичного члена,
не превышает 1%, ^если г;0<0,2с0. Для адиабаты, т. е.
политропы с 7г = 1,#4, это означает, что г;0< 66,4 м\сек,
так как с0 = 332 м/сек. Если ошибка может составить 10%,
то можно допустить, что г;0%0,63с0, т. е. в адиаба-
адиабатическом случае v0 < 209 м/сек.
Изменение плотности, соответствующее изменению да-
давления в силу уравнения политропы, можно получить
из A3.21а), если заменить р, р0 на р, р0, показатель
п/(п — 1) на 1/(/г — 1), оставляя при этом квадратные
скобки без изменения. При h—hQ соответствующее выра-
выражение имеет вид
(^) A3-23)
132 Гл. III. Динамика деформируемый тел
Вычислим теперь изменение скорости вдоль трубки
тока. В случае несжимаемой жидкости, если h = k(j, из
A3.20а) получаем
где Др=ро-ри р = Ро; A3.24)
с другой стороны, для сжимаемой жидкости, при-
применяя A3.20) и подставляя последнее из значений инте-
интеграла, вычисленного в A3.21), имеем
подставляя р = р0 - -Ар и разлагая по степеням Ар, по-
получаем
С1+?¦?+•••)• A3-24б)
Это выражение совпадает с A3.24) с точностью до члена
второго порядка по Ар.
Вернемся еще раз к равенствам A3.19) и A3.19а),
характеризующим изменение сечения трубок тока в случае
сжимаемой и несжимаемой сред. Беря логарифмическую
производную уравнения неразрывности A3.19), получаем
^ ^L ^^o. A3.25)
+ ^ +
р ' F v
Дифференцирование уравнения Бернулли A3.20) при
h=-h0 дает
vdv + ^- = 0, A3.26)
а из уравнения политропы получаем
^=п^-. A3.27)
Р Р v
Первый и последний члены в A3.25) могут быть выра-
выражены с помощью A3.27) и A3.26). Тогда
dF dp г. ?v2\__dP
§ 13. Уравнения Эйлера для идеальной сжимаемой жидкости 133
Здесь с означает политропическую скорость звука в сече-
сечении F, не совпадающую с с0 — скоростью звука в сече-
сечении Fo. Для течения несжимаемой жидкости надо заме-
заменить A3.27) на dp = O и вместо A3.28) получим
Щ
F
A3.28а)
Из сравнения A3.28) и A3.28а) сразу следует, что раз-
различием в изменении сечений для сжимаемой и несжи-
несжимаемой жидкостей можно пренебречь, если v <C с, точно
так же, как было в случае различия в изменениях давле-
давлений при сравнении A3.22) и A3.22а). Из A3.28) и A3.28а)
можно вывести еще одно важное заключение. Для не-
несжимаемой среды dF и dp имеют один и тот же знак, т. е.
поперечное сечение увеличивается с возрастанием давления
и падает с убыванием давления. Для сжимаемой среды
это так только в случае v < с, т. е. при дозвуковых
скоростях. При сверхзвуковых скоростях сечение растет
при уменьшении и падает при увеличении давления. Это
обстоятельство приводит, в случае сжимаемой жидкости
к существенному различию между течениями со сверх-
сверхзвуковой скоростью и с дозвуковой скоростью, а также
с поведением несжимаемой среды, для которой, по опре-
определению, скорость звука бесконечна. Далее, из A3.28)
следует, что сечение трубки тока при достижении ско-
скорости звука (?; = с) имеет экстремум, а именно минимум.
Заметим еще, что формулы A3.19) и A3.19а) играют
большую роль в машиностроении. С их помощью опре-
определяют поперечное сечение потока в трубопроводах, вен-
вентилях, сечение турбинных лопаток и т. д.
Равенства A3.24), A3.24а) определяют скорость исте-
истечения через сопла замкнутого сосуда, где ,р0—давление
внутри (поддерживаемое постоянным) и р — также постоян-
постоянное давление снаружи сосуда; значением v0 можно в хо-
хорошем приближении пренебречь; A3.24а) называют форму-
формулой Сен-Венана и Вантцеля A839 г.).
Особый интерес представляет сопло Лаваля1), которое,
как и все сопла, служит для того, чтобы энергию высо-
х) Впервые создано шведским инженером Лавалем, который
является создателем хорошего сепаратора для молока и первой
паровой турбины, использованной на практике.
134 Гл. III. Динамика деформируемых тел
кого давления и низкой скорости преобразовать в энергию
низкого давления и высокой скорости, но при этом, что
и характеризует сопло Лаваля, могут быть достигнуты
сверхзвуковые скорости. Из предыдущего мы знаем, что
поперечное сечение потока до достижения скорости звука
должно сужаться, а затем опять возрастать.
§ 14. ДИНАМИКА УПРУГОГО ТЕЛА
Переход к динамике упругого тела осуществляется
путем добавления к внешней силе F сопротивления инер-
инерции в основном уравнении статики. Так как в твердом
теле наблюдаются небольшие смещения [только при до-
достижении предела текучести, т. е. вне области чисто
упругого поведения (см. § 39), имеют место сравнительно
большие смещения], здесь можно полное ускорение ото-
отождествить с локальным. Сила инерции, как и F, отне-
отнесенная к единице объема, будет тогда равна
где s = E, т], С.
Используя основное уравнение статики в форме (8.12),
получаем дифференциальное уравнение упругости
** A4.1)
или, согласно (8.11), в декартовых компонентах имеем
дЧ дохх доух дагх
Ч _
Р dt* ~~ дх ~т~ ду ^ dz
Ж _ daxz davz догг „
Р ЭР ~~ дх "•" ду "*" dz ' г'
Используя более подходящую форму основного уравнения
статики (9.18), мы получим дифференциальное уравнение
упругости в форме
Р ijjjr = (Iх + х) ?rad в + H-As 4- F, в = divs. A4.16)
§ 14. Динамика упругого тела 135
Это уравнение следует читать в декартовых координатах;
в других случаях необходимо исходить не из (9.18), а из
более общего соотношения (9.19).
Мы главным образом интересуемся случаем свободных
колебаний, поэтому положим F = 0. Из A4.16) можно
сразу вывести, что в общем случае имеют место как
колебания сжатия, так и колебания кручения, первые —
продольного, а вторые — поперечного характера.
Волны сжатия. Взяв дивергенцию от каждого члена
в A4.16), получаем
Р ^J- = (р- Ч- X) АО -h tx div As.
Можно, однако, заменить
div As на A div s -— А0,
в результате получаем простое скалярное уравнение
Сравнение A4.2), например, с A3.8) показывает, что ско-
скорость распространения волн сжатия, обозначим ее через а,
дается формулой
a* = 2-t±±. A4.3)
В линейном или сферически симметричном случае
метод Даламбера A3.11) дает для бесконечного упругого
тела чисто периодическое решение с круговой частотой ш,
которое имеет вид
егкх и соответственно —шегкг, к — — , A4.4)
что соответствует плоским или сферическим волнам, ко-
которые распространяются с постоянной скоростью а.
Волны кручения. Подобным жр образом возьмем ротор
от равенства A4.16) и, вводя в соответствии с B.19) обо-
обозначение
rots= 2ср,
136 Гл. III. Динамика деформируемых тел
получим из A4.16) в силу того, что rotgrad = 0 [см. C.7)],
fg A4.5)
Здесь ^р по величине и направлению представляет угол
закручивания рассматриваемого элемента объема. Сравне-
Сравнение с A3.8) показывает, что скорость распространения
волн кручения, назовем ее Ь, задается в виде
Ь2=^. A4.6)
Поэтому константу Ляме ц, как уже отмечалось на стр. 88,
можно называть модулем кручения. Метод интегрирова-
интегрирования Даламбера опять дает плоские и сферические волны,
которые, как и волны сжатия, могут быть представлены
в виде A4.4), если только там определить волновое число
как k = wjb.
Сравнение A4.3) с A4.6) сразу показывает, что а > Ъ,
так как
^L — 9 ¦ Х — 2~2v •
Ь2 ~ ~ГУ~ 1 —2v '
последнее следует из (9.11). Так, для железа v = 0,3 и
| =/1=1,87.
Это соотношение, очевидно, означает, что упругое сопро-
сопротивление материалов, вызванное изменением объема, зна-
значительно больше их сопротивления к изменению относи-
относительного положения, что вполне естественно.
Конечно, абсолютное значение b для твердых тел
гораздо больше скорости звука с в воздухе. Так, для
железа (Е — 2Л06кГ/см2) р = 7,8 г /см3, откуда
Ъ = 3100 м\сек.
Обе формулы A4.3) и A4.6) соответствуют правилу Ньютона
A3.16а), если только термину «упругость» в каждом слу-
случае придать соответствующее значение.
Рассмотренные здесь колебания сжатия и кручения
представляют собой трехмерные волны, распространи-
§ 15. Квазиупругое тело как модель эфира 137
ющиеся в упругой среде, которую мы считаем неограни-
неограниченной. Кроме того, существуют и поверхностные волны,
распространяющиеся на свободной поверхности среды,
которые играют особую роль в сейсмических явлениях.
Они будут рассмотрены в § 45. Поверхностные волны
распространяются с меньшей скоростью, чем объемные
волны (земля оказывает вторым большее упругое сопро-
сопротивление, чем первым). Они обусловливают главный удар
в случае наблюдаемого землетрясения; объемные волны,
которые приходят раньше, ощущаются как более слабый
предварительный толчок.
Фундаментальная теорема векторного анализа, кото-
которую мы рассмотрим в § 20, позволит выяснить существо
различия между волнами сжатия и кручения.
§ 15. КВАЗИУПРУГОЕ ТЕЛО КАК МОДЕЛЬ ЭФИРА
Как известно, в XIX в. считалось, чтс световые волны
есть колебания эфира, которому приписывали свойства
обычной упругой среды. Но при этом уже в простейших
проблемах отражения и преломления возникали трудности,
которые будут рассмотрены подробнее в § 45. Еще в 1839 г.
Маккуллаг попытался отбросить связь с обычной теорией
упругости и развить представления оптики, свободные
от этих трудностей; как выяснилось позднее, его фор-
формулы формально совпадают с формулами электромагнит-
электромагнитной оптики Максвелла, в частности в случае прозрач-
прозрачных сред. То, что будет рассмотрено ниже, представляет
собой истолкование уравнений Маккуллага.
Вернемся к § 1. Там мы раскладывали в общем слу-
случае смещение непрерывной среды на три части: трансля-
трансляцию, вращение и деформацию. Реакцией упругого тела
на деформацию является возникновение напряжений;
тензор напряжений может быть определен из тензора
деформаций, оставаясь, конечно, нечувствительным к вра-
вращению и к трансляции- Представим квазиупругое тело,
которое не реагирует на деформации, но реагирует на
повороты относительно абсолютного пространства! Так
как вращение имеет характер антисимметричного тензора
[см. равенство A.12а)], то предположим, что напряжения,
вызванные вращением и действующие на элемент объема,
138
Гл. III. Динамика деформируемых тел
имеют также вид антисимметричного тензора. Наплшем
их в виде определителя:
О °ху О„\
сух 0 ol oift=-oM. A5.1)
'гу
Предполагаемые здесь соотношения между напряжениями
и поворотами проиллюстрированы на фиг. 17. Повернем
Фиг. 17.
Связь между напряжением и поворотом для
квазиупругого тела.
наш элемент объема Ат на угол <рг (стрелка вокруг поло-
положительной оси z в направлении правого винта). Чтобы
произвести этот поворот, приложим, согласно нашей
гипотезе, момент сил вокруг оси z:
Мг:=%?.т, A5.2)
где к — «модуль поворота» квазиупругого тела. Этому мо-
моменту сил соответствуют на фиг. 17 два касательных
й
напряжения
и — а
ух,
действующие на положительные
х- и ^/-плоскости, и два касательных, антипараллельных
§ 15. Квазиупругое тело как модель эфира 139
первым, напряжения, действующие на отрицательные х-
и ^-плоскости. Для того чтобы имелось соответствие
с A5.2) и A5.1), надо положить
Действительно, тогда момент сил, действующих на обе
я-плоскости, равен (см. также соответствующее рассужде-
рассуждение, относящееся к фиг. 10)
а момент сил, действующих на обе «/-плоскости, равен
-2oyxAxAz ^- = -|сргДх,
что дает в сумме такой же момент, как в равенстве A5.2).
Из A5.3) путем циклической подстановки можно сразу
получить
Суг = — azy = Y ?*' °« = "" °« ^ Т ЧУ A5'3а)
Уравнения движения этого квазиупругого тела могут
быть получены из A4.1а). Для этого припишем телу
инерцию (р — масса единицы объема) и будем считать его
движение медленным (пренебрежем квадратичными кон-
конвекционными членами, т. е. dujdt = dufdt). Кроме того,
не будем принимать во внимание внешние силы (F=0).
Тогда с учетом A5.3) и A5.3а) получаем из A4.1а)
ди _ доух да2Х __ _ к_ Г д^_ _ d?y N .
Р dt ду ^ dz ~ 2\^ду dz J1
после циклической подстановки в векторной форме оно
записывается следующим образом:
dV к
Это уравнение движения может быть дополнено связью v
с угловой скоростью to. Она выражается следующим
образом, если здесь также заменим d^>jdt на d^jdt:
| l A5.5)
140 Гл. III. Динамика деформируемых тел
Предположим еще несжимаемость и добавим условие,
следующее из того, что ^ представляет собой ротор век-
вектора смещения:
divv = 0, div? = 0. A5.6)
Система уравнений A5.4) — A5.6) поразительно проста
и симметрична. Она имеет такую же форму, как и урав-
тзения Максвелла в пустоте.
Чтобы уточнить это утверждение, положим, что
а) v= ± аЕ, 9= ^ РН
или
б) v=±aH, ?==FPE,
где Е — напряженность электрического поля, Н —напря-
—напряженность магнитного поля, а и (S — множители пропорцио-
пропорциональности, которые зависят от выбора единиц, в кото-
которых измеряются Е и Н, а также от выбора знака элек-
электрического заряда и магнитной полярности.
В любом случае равенства A5.4) — A5.6) примут форму
0^ , ,
Ж ' <15-7>
jx0 -qj-= — rotE, divH = 0.
Коэффициенты s0, ц0 называются соответственно диэлек-
диэлектрической постоянной и магнитной проницаемостью ваку-
вакуума; в наших обозначениях они выражаются как
• р 2а 2?
€\\ G — .* .. ft —— L
а; ?о - k р » f*o - а
или
-v p 2а 2^
Их произведение не зависит от выбора единиц измерения
(а и Р). А именно, в обоих случаях имеем
^0 = ^=4- A5.8)
Определенная таким образом величина с представляет
собой скорость света в пустоте. Заметим при этом, что
§ 15. Квазиупругое тело как моВелъ эфира 141
она, как и скорость звука в § 13 и 14, подходит под
формулировку Ньютона A3.16а), если под термином
«упругость» понимать х/4 нашего модуля поворота к.
Мы далеки от того, чтобы приписывать этой модели
эфира какой-нибудь реальный физический смысл. Еще
в конце прошлого столетия стало ясно, что все попытки
дать механическое объяснение уравнениям Максвелла
обречены на неудачу. Мы приводим здесь не механиче-
механическое объяснение, а скорее механическую аналогию. Урав-
Уравнения Максвелла лежат в основе теории электрического
строения материи, так что не следует ожидать, чтобы
они объяснились с помощью механических свойств тел.
Более того, согласно одной из последних работ Шредин-
гера1) представляется возможным связать их с той же
общей основой, что и уравнения гравитации, именно
с пространственно-временной метрикой. Наше рассмотре-
рассмотрение, возможно, оправдывается тем, что оно показывает, что
если лостроить «эфир», для которого выполнялись бы урав-
уравнения Максвелла, то он обладал бы свойствами, диаме-
диаметрально противоположными свойствам обычных упругих
тел, а именно, для него играла бы роль абсолютная
ориентация относительно пространства, а не относитель-
относительная ориентация элементов объема относительно друг
друга, что имеет место в случае упругого тела.
Можно' сделать следующие исторические замечания.
Вслед за Маккуллагом в 80-х годах В. Томсон раз-
развил идею квазиупругого, или, как он его называл, «квази-
«квазитвердого» , эфира2). Он не удовлетворился простым посту-
постулированием действия сил A5.2), как это сделали мы,
а попытался смоделировать его с помощью волчков. Мы
знаем, что быстро вращающийся волчок стремится
сохранять направление своего вращения и под действием
довольно сильного момента сил только немного изме-
изменяет направление вращения3). Но модель эфира, основан-
г) Schrodinger E., Proc. Roy. Irish Academy, 49, 43 A943).
(Выдвинутые Шредингером в этой работе идеи не получили в совре-
современной физике никакого признания.—Прим. перев.)
2) Thomson W. (Kelvin), Mathematical and Physical Papers,
vol. 3, Art. 49, 50, 52.
3) См. «Механика» (т. I), § 27.
142 Гл. III. Динамика деформируемых тел
ная на гироскопических явлениях, чрезвычайно сложна.
В каждом элементе объема должно находиться множе-
множество волчков, ориентированных относительно друг друга
так, чтобы желаемое сопротивление вращению наблюда-
наблюдалось по отношению ко всем трем направлениям коор-
координатных осей, а не к одной оси. Только путем такого
построения мог бы осуществляться «гиростатический»,
т. е. основанный на свойствах волчка, эфир.
Томсон считал, что е0 и ji0 определяются выражениями
«а», т. е. он связывал поворот своего гиростатического эфира
с вектором магнитного поля Н. Значения вектора элек-
электрического поля Е он не устанавливал и, таким образом,
отказывался от исчерпывающего моделирования уравне-
уравнений Максвелла. Несомненно, что эта точка зрения физи-
физически наглядна, так как Н обладает свойствами аксиаль-
аксиального вектора, аналогично 9» a E, напротив, свойствами
полярного вектора, как и v. С другой стороны, соотно-
соотношения «б» представлялись более предпочтительными, так
как они дают квазиупругуго модель не только для чистого
эфира и диэлектриков, но и для проводников1). В связи
с этим Больцман2), однако, отметил, что возникают
трудности, связанные с существованием «свободных элек-
электрических зарядов». Позтому, отвлекаясь от толкования
электродинамики проводников, мы сделаем еще некото-
некоторые замечания по поводу соотношений «а».
К соотношениям «б» мы вернемся еще в § 20, в свя-
связи с теорией вихрей Гельмгольца.
В случае диэлектриков могут быть использованы те
же два основных уравнения A5.7), что и в случае ваку-
вакуума, но с другими значениями е, [х вместо е0, [х0. Оба урав-
уравнения для дивергенции при этом существенно изменяют-
изменяются. Вместо div H = 0 должно быть
divВ = 0, В = (аН = Магнитная индукция. A5.9)
Поэтому необходимо связывать с поворотом ^ не Н,
а В, что не приводит к трудностям. С другой стороны,
^Sommerfeld A., Ann. d. Phys., 46, 139 A892).
2) В о 1 t z m a n n L., Ann. d. Phys., 47, 743 A892); См. также
Vorlesungen uber Maxwells Theorie, Bd. II, Leipzig, 1893, § 1, S. 6.
§ 16. Динамика вязкой жидкости 143
условие div E = 0 переходит в
divD = pe, D = еЕ = Электрическое смещение, A5.10)
где ре —объемная плотность свободных электрических
зарядов. Если теперь вместо Е свяжем D со скоростью
течения v и постоянные е, р надлежащим образом с /с,
р, а, р, то в этом случае формально также получатся
уравнения Максвелла для диэлектриков. Но с точек зре-
зрения предположения «а» и уравнения неразрывности
сушествование свободных зарядов представляет трудности.
.Чтобы обойти эту трудность, можно сделать математи-
математическое допущение, однако совершенно неудовлетвори-
неудовлетворительное с точки зрения физики. Можно просто заставить
нашу жидкость вытекать из поля или втекать в него
в местах расположения свободных зарядов, в зависимости
от их знаков. Правда, куда она вытекает или откуда
втекает — остается неясным. В качестве извинения за
такое предположение можно сослаться на великого
Римаиа1), который в статье «Новые математические прин-
принципы физики» использовал его для объяснения явлений
тяготения и электростатики. Но гораздо правильнее будет
считать, что не существует никакой механической или
квазимеханической модели фундаментального факта суще-
существования электрических зарядов.
Во всяком1 случае, у нас не будет оснований возвра-
возвращаться к обсужденной здесь модели эфира в т. III, посвя-
посвященном теории электромагнетизма. Напротив, электри-
электрический заряд и электромагнитное поле будут там рас-
рассмотрены как явления, выходящие за рамки механики.
§ 16. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ. ГИДРОДИНАМИКА
И ГИДРАВЛИКА. КРИТЕРИЙ ТУРБУЛЕНТНОСТИ
РЕЙНОЛЬДСА
Для того чтобы рассмотреть нестационарное движе-
движение вязкой жидкости, добавим в уравнения A0.8а) и
A0.86) для стационарного движения силы инерции, т. е.
г) R i e m a n n В., Ges. Werke, 2 Aufl., S. 528. Цитированная
статья была написана им вскоре после присз'ждения ему степени
доктора A851 г.) и опубликована после его смерти.
144 Гл. 111. Динамика деформируемых тел
заменим F на
Таким путем мы получим уравнение Навье—Стокса г)
дх
р ~dt + р (v grad)v ~ ^Ау + grad P ='F» ^16- ^
которое написано здесь в псевдовекторной форме. Чтобы
привести его к собственно векторной форме, пригодной
для любой системы координат, надо использовать равен-
равенства A1.6) и C.10а):
(vgrad)v = grad -»—[vrotv],
Ду = grad div v — rot rot v.
Для несжимаемой жидкости к уравнению A6.1) необ-
необходимо добавить соотношение
divv = 0. A6.1а)
В случае сжимаемой жидкости вместо A6.1а) будет вы-
выполняться уравнение неразрывности E.4); в то же время
в A6.1), согласно A0.22), войдет еще дополнительный
член, содержащий множитель (ц + ^>)-
В настоящее время уравнение Навье—Стокса является
основным при расчете всех явлений, связанных с жидко-
жидкостями. В XIX в. считали, наоборот, что между физико-
математической гидродинамикой и технической гидрав-
гидравликой лежит глубокая пропасть. ' Английский инженер
и физик Рейнольде своими экспериментальными2) и тео-
теоретическими3) работами перебросил мост через эту про-
пропасть.
Он производил эксперименты со стеклянными труб-
трубками различного сечения, при различных перепадах
!) Навье A822 г.); Стоке A845 г.).
2) Reynolds О., Экспериментальное исследование условий,
определяющих, будет ли движение воды ровным или завихренным,
и закон сопротивления в параллельных каналах, Phil. Trans. Roy.
Soc<, 174 A883).
3) Reynolds О., По поводу динамической теории несжимае-
несжимаемого вязкого течения и определение критерия, Phil. Trans. Roy.
Soc, 186 A895). В связи с этим см.: Lorentz H.A., Ges. Werke,
Bd. I, S. 43.
§ 16. Динамика вязкой жидкости 145
давления или, что одно и то же, с различными средними
(по сечению) скоростями жидкости. Впуская окрашенную
струйку жидкости во входное сечение, он наблюдал пове-
поведение этой окрашенной струйки в трубе. В случае ма-
малого поперечного сечения трубы и не очень большой
средней скорости струйка двигалась ровно и параллельно
оси трубы. При большем сечении или большей скорости
появлялось направленное в стороны нерегулярное движе-
движение, которое постепенно захватывало всю трубу, струйка,
ровная у входа, разбивалась затем на множество изви-
извилистых струек. В первом случае движение называют
ламинарным (в виде правильных слоев, как при течении
Гагена — Пуазейля), в последнем случае, следуя Рей-
нольдсу, его называют турбулентным.
Рейнольде, однако, не был бы в состоянии упорядо-
упорядочить свои экспериментальные исследования, если бы он
не рассматривал их с точки зрения «правила подобия».
Рассмотрения подобного рода имелись уже на заре раз-
развития физики в работе Галилея1). Вообще говоря, они
состоят в сравнении двух явлений, отличающихся только
в масштабах.
В нашем случае речь идет о двух трубах соответ-
соответственно радиуса а1 и а2. Пусть соотношение
. ай = аа1 A6.2а)
выражает изменение единицы длины при переходе от
явления 1 к явлению 2. Это не обязательно относится
к радиусам и может относиться ко всему, что имеет
размерность длины, например к координатам двух соот-
соответственных точек в обеих трубах. Для всех таких точек
будет
Пусть vx и v2 средние скорости в соответственных сече-
сечениях труб. Положим
v2 = $vx. A6.26)
х) См. его последнюю работу: Galilei G., Беседы и мате-
математические доказательства о двух новых науках, 1638 г. (Ostwalds
Klassiker der exakten Wissenschaften, Nr. 11 A und 2 Tag.); Nr. 24
C und 4 Tag.); Nr. 25 E und 6 Tag.).
Ю А. Зоммерфельд
{46 Рл. III. Динамика деформируемых Мел
Так как размерность скорости есть длина, деленная на
время, то р определяет также и изменение единицы времени
при переходе от явления 1 к 2; согласно A6.2а) и A6.26),
это изменение равно а/В. Допустим также, что обе трубы
наполнены различными жидкостями, которые имеют раз-
различные плотности и вязкости. Пусть
P» = 7Pi- A6.2b)
Так как размерность плотности есть масса/объем, то
множитель ^ определяет также и изменение единицы
массы при переходе от 1 к 2; это изменение, согласно
A6.2а) и A6.2в), равно ?а8.
Вместо коэффициентов вязкости ц введем более удоб-
удобные кинематические вязкости v, определив их как v = р/р.
Положим
v2 = ?V A6.2г)
Наконец, для сравнения давления в соответственных
сечениях обеих труб положим
p2 = ePl. A6.2д)
Очевидно, исходя из размерности р, можно выразить е
через а, В и f.
Напишем теперь равенство A6.1) еще раз в схема-
схематическом виде, причем все члены разделим на р и опу-
опустим внешнюю силу F, так как в случае течения по
трубе она роли не играет.
Ускорение — vAv-1—grad/? = O. A6.3)
Размерность ускорения — скорость/время или ско-
скорость2/длина. Поэтому этот член при переходе от явле-
явления 1 к явлению 2, согласно A6.2а) и A6.26), изме-
изменится на множитель
?• A6.4а)
С другой стороны, второй член в A6.3), согласно
A6.26) и A6.2), меняется в
4 (i6-46)
раз, так как входящее в Av двухкратное дифференци-
дифференцирование по координатам в смысле размерностей означает
§ 16. Динамика вязкой жидкости 147
то же, что двухкратное деление на длину. Наконец,
в последнем члене A6.3), согласно A6.2а), A6.2в) и
A6.2д), изменение масштаба равно
Примем, что равенство A6.3) выполняется для явле-
явления 1. Если оно справедливо для явления 2, то отно-
отношения приведенных трех множителей A6.4а) —A6.4в)
должны равняться единице:
?-:8l:-! = l:l:l. A6.5)
Деля первый член слева на второй и третий на пер-
первый, получаем, что
^ = 1 A6.5а)
jpr=l- A6-56)
Согласно A6.2а), A6.26) и A6.2д), выражение A6.5а)
означает, что
vial v%u2 /лек р.\
vl V2
Подобным • образом, согласно A6.26) — A6.2д), выраже-
выражение A5.56) означает
-?i- = -^i-. A6.7)
Равенства A6.6) и A6.7) представляют собой резуль-
результат теории подобия Рейнольдса. В литературе обычно
равенство A6.6) называют критерием Рейнольдса, хотя,
как мы здесь видели, равенство A6.7) тоже составляет
его часть. Взятые вместе, они дают необходимые и доста-
достаточные условия гидродинамического подобия. В дальней-
дальнейшем мы используем и равенство A6.7).
Если предположить, что выполняются оба критерия,
то можно заключить, что оба течения 1 и 2 или одно-
одновременно ламинарны, или турбулентны. В обоих случаях
течение в трубе 2 представляет собой копию течения
в трубе 1 только с измененным масштабом.
10*
148 Гл. III. Динамика деформируемых тел
Определяемое равенством A6.6) выражение предста-
представляет собой безразмерную величину. Назовем A6.6) чис-
числом Рейнольдса и обозначим его следующим образомг):
&,=™, A6.8)
причем а может обозначать любой линейный характери-
характеристический размер эксперимента (например, расстояние
между двумя пластинками, глубина канала, радиус падаю-
падающего шара). Безразмерную величину, введенную в A6.7),
обозначим через S:
S = -^- A6.9)
В частности, переход от ламинарного к турбулентному
течению для наших труб 1 и 2 представляет собой по-
подобное явление, которое поэтому характеризуется одним
и тем же численным значением Si. Это так называемое
критическое число Рейнольдса:
= (—') • A6.10)
<^крит.
Его значение, однако, сильно зависит от формы входной
части трубы. В случае закругленного входа, напоминаю-
напоминающего формой рожок, течение с самого начала устанавли-
устанавливается ламинарным и продолжает им оставаться до боль-
больших Si. Если сосуд на входе трубы имеет с ней незакруг-
незакругленное соединение с острыми углами, то течение у входа
будет возмущено в боковом направлении, причем силы
трения не смогут сразу ликвидировать это возмущение;
переход к явно выраженной турбулентности произойдет
при меньших значениях Si. Область критических чисел
Рейнольдса лежит примерно между значениями 1200
(случай весьма нерегулярного входа) и 20000 (хорошо
закругленный вход). Таким образом, наше заключение
о равенстве критических чисел Рейнольдса должно отно-
относиться к течениям с одинаковыми условиями на входе.
Возникает вопрос, почему происходит переход от ла-
ламинарного течения к турбулентному. Наше рассмотрение
х) Это обозначение введено впервые автором (см. Intern. Math.
Kongress, Vol. 3, S. 116,1908, Rom). В технической литературе часто
пользуются обозначением Re.
§ 16. Динамика вязкой жидкости 149
ламинарного течения в капиллярах на стр. 101 не накла-
накладывает ограничений на ламинарный характер при малых
диаметрах и малых скоростях. Более того, из него сле-
следует, что течение Гагена—Пуазейля является возможной
формой течения при любых обстоятельствах. Но для
М > 5?Крит. течение становится неустойчивым. Критерий
Рейнольдса для границы между обеими формами движения
выступает поэтому в опытах как критерий устойчивости.
Рассмотрим, в чем заключается его физический смысл.
Силы вязкости сглаживают боковые движения, возникаю-
возникающие в то или иное время вследствие различных неровно-
неровностей стенок, обеспечивая тем самым ламинарность течения.
Напротив, инерция жидкости, стремящаяся сохранить эти
боковые составляющие, если они уже возникли, действует
в пользу турбулентности. При статическом рассмотрении
капилляров в § 10 подобные боковые составляющие не
учитывались, так как инерция отсутствовала; поэтому
нам казалось, что полученные результаты могут быть
распространены на сколь угодно быстрые течения и сколь
угодно широкие трубы. Связь между вязкостью и инер-
инерцией видна из рассмотрения структуры величины v = fi/p,
стоящей в знаменателе A6.8): при увеличении р. можно,
не нарушая устойчивости, увеличивать значения va; уве-
увеличение же р ограничивает возможные значения va, об-
облегчая возникновение турбулентности.
То, что здесь было сказано по поводу устойчивости,
находится в согласии с уже упомянутой кажущейся не-
неопределенностью момента перехода; этот факт можно
сравнить с известным в термодинамике явлением пере-
переохлаждения воды: ее можно охладить до температуры
ниже 0° С, и она не превратится в лед до тех пор, пока
на нее не будет оказано возмущающего воздействия. По-
Подобным же образом ламинарное течение может казаться
устойчивым, если тщательно избегать возникновения бо-
боковых движений у входа или вследствие шероховатости
стенок.
Чтобы установить, существует ли точно определенное
идеальное критическое число Рейнольдса, надо было бы
изучать течение в достаточно длинных трубах с достаточ-
достаточно гладкими стенками и на достаточном удалении от
входа. В устойчивом случае возмущения, вызванные на
150 Гл. III. Динамика деформируемых тел
входе,, будут иметь время улечься, причем новые боковые
возмущения от стенок не будут возникать. Если бы при
этом для определенных значений Э{ наблюдалась лами-
нарность, а для больших значений Э1 — турбулентность,
и если бы верхняя граница первых совпадала с нижней
границей последних, то соответствующий предел и был бы
идеальным значением 5$КрИт.х). Практически не могут
быть осуществлены подобные идеальные опыты, и поэтому
в литературе приводятся весьма различные значения
ал 2\
^крит- )•
Начало турбулентности проявляется, однако, не только
в форме движения жидкости, но и в изменении закона
давления. Переходя к рассмотрению этого явления, вместо
равенства A6.8) рассмотрим второй закон подобия —ра-
—равенство A6.9). Заменим в нем величину р на перепад
давления П между началом и концом трубы, введенный
еще на стр. 74. Конечно, величина П должна иметь ту же
самую размерность, что и р. При такой замене необхо-
необходимо также ввести в рассмотрение длину трубы /, кото-
которая в равенстве A6.9) могла иметь произвольное значение.
Так как в равенстве A6.9) стояла безразмерная величина,
то введем в рассмотрение не /, а также безразмерную
величину l/а и напишем вместо A6.9) выражение
H = pv2~S, A6.11)
которое справедливо для обоих подобных движений 1 и 2
при одном и том же S, но при различных П, р, v, I, a.
Сравним A6.11) с принятой в гидравлике формулой
для потери напора в трубах^и каналах
Л=х|/?. A6.11а)
х) Возможно, что при дальнейшем сглаживании условий экспери-
эксперимента (улучшении регулировки на входе и изготовлении более глад-
гладких стенок) величина 5?крит может принять сколь угодно большие
значения. В таком случае подобного идеального значения не имеется
совсем и граница устойчивости Реинольдса имеет только практиче-
практический смысл, зависящий от условий эксперимента.
2) Зависимость значения 5?крит от характера входа системати-
систематически исследовал Шиллер.
§ 16. Динамика вязкой жидкости 151
Здесь X — безразмерная величина (гидравлический коэф-
коэффициент трения), F — поперечное сечение жидкости, U —
омываемый периметр сечения. Для круглого сечения, це-
целиком заполненного жидкостью, U = 2%a, F = ku2, так
что A6.11а) переходит в
/г=Х — -, A6.116)
что совпадает с A6.11), если положить S— \ и П выра-
выразить через гидростатический напор
Если, с другой стороны, в A6.11) подставить вместо
S также безразмерную величину 8/31, т. е.
S — — — 8^
va pva '
то получим формулу Гагена — Пуазейля
П = 8^?, A6.12)
которая отличается от прежней формулы A0.17) только
тем, что вместо величины v мы имели там более точно
определенную величину средней по сечению скорости ггср..
Сравнение A6.11а) и A6.12) показывает, что закон
давления, о котором упоминалось на стр. 103, ламинар-
ламинарного и турбулентного течений различен: в A6.11а) зави-
зависимость от скорости и радиуса определяется множителем
v2ja, а в A6.12) —vja2. Формально можно перебросить
мост между этими двумя случаями путем надлежащего
выбора безразмерной величины S, которая не устанавли-
устанавливается соображениями подобия.
Заметим, что используемая в технике формула A6.11а)
имеет такую же структуру, как и принятый Ньютоном
закон сопротивления воздуха, согласно которому тело,
движущееся в воздухе со скоростью v, испытывает сопро-
сопротивление, пропорциональное г;2, или, что одно и то же,
движущийся воздух давит на покоящуюся плоскость
с силой, пропорциональной гА В баллистике при дозву-
дозвуковых скоростях также используется закон, по которому
сопротивление приблизительно пропорционально vz%
152 Гл. III. Динамика деформируемых тел
Более точное представление о перепаде давления при
турбулентном течении в гладких трубах может быть по-
получено в рамках нашего общего уравнения A6.11), если
предположить, что S слабо зависит от Э1 [а не вовсе не
зависит, как в равенстве A6.116), и не пропорцио-
пропорционально ¦ 9ГЛ, как в равенстве A6.12)]. Для больших Э1
применялись формулы
S = 19TX и S = \ + \19TX1 A6.13)
где % принимает значения от х/4 до */5 в первой формуле
и несколько большее во второй.
Вместо прежней квадратичной зависимости от скоро-
скорости, принятой в технике A6.11а), первая из формул A6.13)
дает г?2~х (у Блаэиуса х — х/4), что
почти в точности совпадает с преж-
прежними наблюдениями Гагена и Рей-
нольдса (см. также задачу 2 гл? III),
Более подробное изложение изме-
изменения давления при переходе^от
ламинарного течения к турбулент-
у ному, а также влияния неровно-
и=1\Рит стей стенок трубы дано в книге
Фиг. 18. Зависимость Прандтля1).
перепада давлений от Изменение закона давления в
средней скорости v. переходной области схематически
^™Гч^ТкЦехоа: представлено на фиг. 18: при ма-
дит в турбулентное. ЛЫХ СКОрОСТЯХ, V < г?крит., ВЫПОЛ-
няется прямолинейный закон Га-
гена —Пуазейля, при скоростях v > укрит. перепад дав-
давления растет как v2~~x. Пунктирное продолжение прямо-
прямолинейной части за точку А означает, что при соответству-
соответствующих условиях граница устойчивости ламинарного тече-
течения может быть повышена, как уже было указано на
стр. 150.
ИзменениЪ закона давления в критической точке Л
сопровождается или, правильнее, вызывается существен-
х) Р г a n d 11 L., Fuhrer durch die Stromungslehre. (См. пере-
перевод: Прандтль Л., Гидроаэромеханика, ИЛ, 1951. Подробное
изложение этих вопросов можно найти в книгах: Л ойцянс к-и й
Л. Г., Аэродинамика пограничного слоя, М.—Л., 1941, и Механика
жидкостей и газов, М.—Л., 1950.—Прим, перев.)
§ 16. Динамика вязкой жидкости
153
ным изменением распределения скоростей по сечению.
В то время как при ламинарном течении мы имели пара-
параболическое распределение (см. фиг. 14), в случае турбу-
турбулентного течения скорость внутри трубы, усредненная
по времени, почти постоянна, за исключением погранич-
пограничной зоны, где, согласно условию торможения, она быстро
падает до нуля (см. фиг. 65, § 38).
Зависимость границы турбулентности от степени вяз-
вязкости жидкости поучительным образом иллюстрируется
У///ЛО
'/////////////////А
2h
Фиг. 19а.
Характер ламинарного течения между
двумя покоящимися пластинами.
Фиг. 196.
Ламинарное течение в реке под
влиянием силы тяжести. Сво-
Свободная поверхность при у=0.
случаем, имевшим место у Фёппля, известного исследова-
исследователя во всех областях прикладной механики. Один из
его учеников прокладывал в России дальний нефтепровод.
Он спроектировал его, воспользовавшись формулой A6.11),
и получил выход, значительно больший ожидаемого. Он
попросил совета у Фёппля, и тот сразу заметил, что в слу-
случае такой тяжело текущей жидкости, как нефть, несмотря
на большую величину сечения используемых труб, дол-
должно иметь место не турбулентное, а ламинарное течение,
и поэтому расчеты, положенные в основу проекта, были
ошибочны.
Противоположность между ламинарным и турбулент-
турбулентным течениями имеет место не только для труб круглого
или еще какого-либо сечения, но также и для течения
между двумя покоящимися пластинами. Этот случай
представляет собой двухмерную аналогию трехмерного
течения Гагена — Пуазейля (задача За гл. II). На фиг. 19а
показано распределение скоростей, имеющее также пара-
параболическую форму; однако здесь мы имеем параболиче-
параболический цилиндр, а не параболоид вращения, как на фиг. 14.
154
Гл. III. Динамика деформируемых тел
Если фиг. 19а разрезать посредине, т. е. на высоте
y — h над основанием, и наклонить основание под углом
а к горизонтали, то получим картину ламинарного тече-
течения воды в реке (фиг. 196). Ширина реки для наших
целей может считаться бесконечно большой. Вместо пере-
перепада давлений мы имеем здесь компоненту силы тяжести
pg sin а. Гопфх) предпринял тщательное исследование
такого ламинарного течения, осуществив его экспери-
экспериментально. Он определил также пре-
У делы его устойчивости. Полученное
.. им число Рейнольдса равно примерно
7
Фиг. 19в.
Характер ламинарного
течения между покоя-
покоящейся и движущейся
пластинами. Прямоли-
Прямолинейное вырождение в
случае так называемого
куэттовского течения.
Рассмотрим наиболее простой слу-
случай, когда из двух пластин, изобра-
изображенных на фиг. 19а, одна покоится,
а другая движется с постоянной ско-
скоростью U. Тогда при ламинарном те-
течении профиль скоростей прямолинеен
(фиг. 19в). Обозначив скорость через
и, при выбранном расположении на-
направления оси х имеем
u=^-U, v = w = 0. A6.14)
Вероятно, не лишним будет заметить, что, хотя здесь
нет никакого вращения, в гидродинамическом смысле это
движение вихревое.
Действительно, мы имеем здесь
9| | _ 9 _ дх> ди __ U
В силу своей большой аналитической простоты A6.14)
часто используются при теоретических исследованиях
устойчивости (см. § 38).
Экспериментально этот случай течения был красиво
реализован Куэттом2) с помощью двух коаксиальных
цилиндров. Если внутренний цилиндр покоится, а на-
наружный вращается с линейной скоростью U, то, согласно
х) Н о р f L., Диссертация, частично опубликованная в Ann,
d. Phy^ 32, 777 A910).
2) Couette M., Ann. de chim. et phys., 21 A890),
§ 17. Некоторые замечания о капиллярности 155
Куэтту, турбулентность возникает при числе Рейнольдса
Обратный случай, когда внутренний цилиндр двигался,
а наружный покоился, был исследован Тейлором1).
Мы интересовались здесь только внешней стороной про-
проблемы турбулентности и не затрагивали основных вопро-
вопросов, которые заключаются в следующем. С чем связана
неустойчивость при критическом числе Рейнольдса? Воз-
Возможно ли дать математическое описание колебаний ско-
скорости, возникающих при турбулентности? Достаточны ли
для описания явлений турбулентности уравнения Навье—
Стокса? К этим вопросам мы вернемся в § 38. Достаточно
полного ответа на них не дано до сих пор.
§ 17. НЕКОТОРЫЕ ЗАМЕЧАНИЯ О КАПИЛЛЯРНОСТИ 2)
Молекулярные силы сцепления, вызывающие явления
капиллярности, были нами учтены уже в конце § 12
в форме нормального давления N, действующего на по-
поверхность жидкости. Однако во время нашего короткого
экскурса в' эту область нам будет удобнее исходить не
из молекулярных сил, как это делал Лаплас3), а, следуя
Гауссу4), исходить из принципа минимальности поверх-
поверхностной энергии [см. A2.16)] и на этом основании вычис-
вычислить упомянутое ранее нормальное давление N.
1) Т а у 1 о г G., Phil. Trans., 223, 289 A923). (Подробное изло-
изложение исследования устойчивости движения жидкости между вра-
вращающимися цилиндрами можно найти в книге: Кибель И. А.,
Кочин Н. Е., Розе М. В., Теоретическая гидромеханика,
часть 2, М.—Л., 1948.—Прим. перев.)
2) Так как явление капиллярности будет рассмотрено здесь
только в такой степени, в какой это необходимо в общем курсе гид-
гидродинамики, то желающих подробно ознакомиться с этим вопросом
мы отошлем к статье Минковского Г., напечатанной в Enzykl.
d. Math. Wiss., Bd. V, I, S. 55. Там приводится также молекулярно-
теоретическое объяснение капиллярности, значительно более глу-
глубокое, чем наше, чисто феноменологическое рассмотрение.
3) Laplace P., Mecanique celeste, Supplement de l'action
capillaire, Bd. 10, 1806.
4) Gauss К., Общие принципы теории жидкости в состоянии
равновесия, см. Ges. Werke, Bd. 5, 1830.
156
Гл. III. Динамика деформируемых тел
С этой точки зрения надо представлять себе, что на
поверхности F жидкости действует всюду одинаковое тан-
тангенциальное поверхностное натяжение Т, так что поверх-
поверхность F как бы покрыта плотно прилегающей мембраной,
которая, как тоненькая резиновая пленка, сама по себе
не обладает упругостью по отношению к изменению
формы; ее сопротивление при изменении формы жидкости
обязано только постоянному натяжению Т, действующему
Фиг. 20а.
Натяжение Т колеблющейся струны и со-
соответствующая ему возвращающая сила N;
такая же картина будет в случае цилиндри-
цилиндрической поверхности жидкости данного про-
профиля.
на край пленки в касательных к ней плоскостях нор-
нормально к границе.
Мы сделаем еще один шаг в сторону упрощения, рас-
рассматривая цилиндрическую поверхность жидкости или,
что одно и то же, мембрану такой же цилиндрической
формы. В этом случае равновесие напряжений будет та-
таким же, как в случае колеблющейся струны, форма ко-
которой в данный момент времени совпадает с профилем
цилиндрической мембраны.
Пусть и — смещение струны между двумя соседними
точками Р и Р', a ks — расстояние между ними. Отделим
этот кусок струны от остальной части разрезами в точ-
точках Р и Р' (фиг. 20а) и заменим действие отрезанных
§ 17. Некоторые замечания о капиллярности 157
частей напряжениями Т и Т', перпендикулярными к обоим
разрезам, т. е. направленными по касательным к струне.
Напряжения Т и Т' равны по величине и составляют
друг с другом угол Ае. Замыкающую силового треуголь-
треугольника, образованного Т и Т', назовем Д71. Из треуголь-
треугольника сил (фиг. 20а, справа внизу) следует
замыкающая ЬТ направлена перпендикулярно к As.
В то же время Д71, взятое с обратным знаком, предста-
представляет собой равнодействующую Т и Т'. Обозначим ее
через iVAs, так что N будет представлять собой совмест-
совместное действие Г и Г, отнесенное к единице длины, и при-
приложим N на фиг. 20а к As в направлении, следующем
из построения силового треугольника. Таким образом,
получаем, что
NAs^TAe. A7.1)
По определению, кривизна
1 ,. Де дх2 ., „ г>\
R Л с Г /" Ян \2 1 З/о ' \ ' /
ЬКЮТ'
где и — отклонение, а х — абсцисса, взятая вдоль неоткло-
ненной струны. Следовательно,
^~7\ A7.3)
или для достаточно малого отклонения и
N=-^T, A7.4)
где знак минус показывает, что N действует в сторону
уменьшения кривизны (на фиг. 20а д^и/дх2 отрицательно;
указанное там направление соответствует положитель-
положительному N; знак его меняется, если д2и/дх2 положи-
положительно).
Соотношение A7.4) превращается в дифференциальное
уравнение колебаний струны [о котором уже говорилось
вслед за равенством A3.9)], если величину N заменить
158
Гл. III. Динамика деформируемых шел
на силу инерции, отнесенную на единицу длины струны:
(р —линейная плотность); именно
д2и т д2и
дх2 '
A7.5)
Если мы от цилиндрической перейдем к произвольной
поверхности, обладающей двойной кривизной, то вместо
A7.3) будем иметь
206.
Колеблющаяся мем-
мембрана с радиусами
кривизны главных се-
сечений Ri иЕг. Такая
же картина будет для
поверхности жидкости
данной формы.
давление Дт
где i?j и R2 — главные радиусы кри-
кривизны в рассматриваемой точке поверх-
поверхности. Главные радиусы кривизны
определяются как величины, обратные
кривизнам двух главных сечений, т. е.
сечений, в которых соседние норма-
нормали к поверхности пересекаются в оп-
определенных точках — центрах кривизны
Сг и С2 (фиг. 206). Рассматривая рав-
равновесие поверхностных натяжений Т,
действующих на бесконечно малый пря-
прямоугольник ^sxus2 на фиг. 206, ориен-
ориентированный в направлении обоих глав-
главных сечений 1 и 2, и построив для обоих
главных сечений силовые треуголь-
треугольники, как на фиг. 20а, получим две
замыкающие стороны Д7\ и АТ2, а из
них, согласно равенству A7.1), два нор-
нормальных давления Л^ и N
в A7.6) получается
р
2. Нормаль-
сложением Nx
ное
и N2.
Из A7.6) сразу следует дифференциальное уравнение
колебаний мембраны в форме, упомянутой вслед за A3.9).
Оно получится, если, 'согласно A7,2), подставить
ду*
A7.7)
§ I't. Некоторые замечания о капиллЛрности 159
и если вместо N ввести силу инерции
пг д2и i \
N— — р-^72 (р — поверхностная плотность).
Получающееся таким образом из A7.6) уравнение
с
годится для координат, взятых не только в главных на-
направлениях, но в силу инвариантности оператора Д и для
произвольных взаимно перпендикулярных координат х и у.
Входящая в A7.6) величина
М = ~Л-~ ' A7.9)
называется средней кривизной поверхности, в то время
как введенная Гауссом мера кривизны1)
к=вк A7-9а)
называется гауссовой или просто кривизной.
В наших рассуждениях о колебаниях струны и мем-
мембраны мы, казалось, отвлеклись от капиллярности. В дей-
действительности же равенства A7.3) или соответственно A7.6)
без всяких изменений описывают капиллярные явления
для цилиндрической или произвольной формы поверх-
поверхности и позволяют, если их ввести в равенства A2.19)
или A2.21), следующие из принципа Гамильтона, опре-
определить поверхностные граничные условия для гидродина-
гидродинамического давления р.
Например, для свободной поверхности (вода, грани-
граничащая с воздухом), согласно A2.19), p = N. Если по-
поверхность имеет цилиндрическую форму, как в случае
плоской капиллярной волны, распространяющейся в на-
направлении оси х, то N задается равенствами A7.3) или
х) В цитированной статье (см. примечание на стр. 155) Минков-
1/1 1 \
ский определяет среднюю кривизну как М = к I -jr + -б~ ) » чт0
более соответствует названию «средняя кривизна». Мы сохраним
здесь обычное определение A7.9); для последующих результатов
это, конечно, не имеет значения.
160 Гл. III. Динамика деформируемых тел
A7.4) и мы получаем
р = ^ или р=-Т^; A7.10)
последнее равенство получается в том случае, когда сме-
смещение и от положения равновесия может считаться до-
достаточно малым. Мы вернемся еще к этому равенству
в § 25. Точно так же в случае произвольной формы по-
поверхности, согласно A7.6),
ъ+ъ)- A7И)
Здесь, как и в A7.10), р означает гидродинамическое
давление в жидкости, на которую, как мы воображаем,
натянут капиллярный слой1).
Мыльная пленка, натянутая на жесткую граничную
кривую (каким-то образом изогнутую проволоку), может
рассматриваться как изолированный капиллярный слой
(без соответствующей жидкой основы). Здесь р = 0 (давле-
(давление воздуха с обеих сторон взаимно уравновешивается).
Согласно A7.11), средняя кривизна М также будет равна
нулю. Это условие выполняется и для соответствующим об-
образом ограниченной мембраны, находящейся в равновесии;
в случае почти плоской мембраны условие равновесия
Ам = 0, следующее из A7.8), совпадает с A7.11), где надо
положить р = 0.
Условие М = 0 означает, что главные радиусы кри-
кривизны равны друг другу и противоположны по знаку.
Поверхности, обладающие этим свойством, называются
минимальными, так как они имеют наименьшую площадь
по сравнению с другими поверхностями, натянутыми на
ту же границу. С точки зрения капиллярных явлений
это легко объясняется путем следующего рассуждения.
Поверхностная энергия U, заключенная в капиллярном
х) В дополнение к равенствам A7.10) и A7.11) отметим, что нэ
плоскую, невозмущенную поверхность также действует давление,
названное Ван дер Ваальсом внутренним давлением, возникающим,
как отмечалось на стр. 118, в результате молекулярного взаимодей-
взаимодействия. На плоской поверхности имеется также поверхностное натя-
натяжение Т, но оно вступает в силу только при распространении волн
на поверхности, когда^его направление меняется от точки к точке.
§ 17. Некоторые замечания о капиллярности 161
слое, равна
A7.12)
.Виртуальное смещение при постоянной границе и по-
постоянном Т изменит эту величину на
W = TbF. A7.13)
Это и есть виртуальная работа, которая в случае равнове-
равновесия должна обращаться в нуль. Отсюда вытекает усло-
условие равновесия bF = O, т. е. поверхность F, входящая
в выражение для энергии A7.12), должна иметь наимень-
наименьшую площадь.
Хорошо известный опыт, подтверждает этог): если на
плоскую, произвольным образом ограниченную мыльную
пленку положить петлю из нитки и проткнуть пленку
внутри петли, то последняя примет форму окружности.
Окружность является кривой, охватывающей наибольшую
площадь при данном периметре, поэтому остающаяся
часть мембраны будет иметь наименьшую площадь при
данной длине границы и нити.
Внутри замкнутого мыльного пузыря имеется превы-
превышение давления р над давлением воздуха снаружи. Если
пренебречь силой тяжести, то мыльный пузырь имеет
сферическую форму. Радиус сферы может быть определен
из A7.11) в виде
R = -p->
так как /f^-ffg по соображениям симметрии. При нали-
наличии пены в отдельных пузырьках мы будем иметь слегка
отличающиеся давления. Разность давлений по обеим
сторонам стенки, разделяющей два пузырька, постоянна,
и поэтому стенка, согласно A7.11), принимает форму
поверхности постоянной средней кривизны.
Чтобы применить условие минимума A7.13) к вычис-
вычислению краевого угла, рассмотрим фиг. 21. Пусть в точке
Р встречаются три среды: 1 — жидкость, 2 — воздух, 3 —
твердая вертикальная стенка. Р представляет собой точку
граничной линии, перпендикулярной к плоскости рисунка.
х) Этот и многие другие опыты с подробным описанием техники
получения мыльных пузырей см. Boys С, Soap Bubbles,
London, 1931. (См. перевод: Бойс Ч., Мыльные пузыри, М.—Л.,
1938.— Прим. ред.)
На. Зоммерфевьд
162
Гл. III. Динамика деформируемых тел
Рассмотрим единицу длины этой линии. При виртуаль-
виртуальном смещении точки Р на величину bw поверхность раз-
раздела F12 увеличится на
bF12 = cos $ • bw ¦ 1,
где Ь — краевой угол. Поверхность соприкосновения F1B
увеличится на
Согласно A7.13), полошим
^i2 + T13bF13 = (T12 cos
откуда, так как bw произвольно,
A7,14)
cos ft = —;
Фиг. 21. К уело- Для того чтобы угол был острым
вию равновесия. (вода на стекле), Т13 должно быть
и^ердаЬя стенкаГ/- Отрицательным И | Т13 | < Г„. Для БВ-
краевой угол. смачивающих жидкостей (ртуть на
стекле) угол Ь — тупой.
Совместное действие силы тяжести и поверхностного
натяжения приводит к капиллярному подъему и опуска-
опусканию (см. задачу 5 гл. III). Задача о капле жидкости под
влиянием силы тяжести приводит к сложному дифферен-
дифференциальному уравнению, решаемому лишь приближенно.
Проще выглядит теория красивого явления, которое
носит название «водяного колокола»J). Полная теория
капиллярности нуждается в использовании термодинами-
термодинамического рассмотрения (Гиббс).
Следует заметить, что в первоначальной теории Ла-
Лапласа к поверхностной энергии [см. равенство A7.12)] был
добавлен член, пропорциональный объему жидкости. Он
оказался существенным для Ван дер Ваальса при
построении им теории жидкого состояния и нашел свое
выражение в постоянной а в законе Ван дер Ваальса.
х) Buchwald E. und Konig H., Ann. d. Phys., 23, 557
A935); 26, 659 A936).
Глава IV
ТЕОРИЯ ВИХРЕЙ
§ 18. ТЕОРЕМЫ ГЕЛЬМГОЛЬЦА О ВИХРЯХ
В опубликованной в 1858 г. работе Гельмгольц не
только определил кинематически вихревое движение (ср.
примечание на стр. 9), но в основном довел до конца
и свою динамическую теорию. В дальнейшем не было
получено существенно новых результатов, хотя метод ис-
исследования был упрощен.
Основное содержание динамической теории заключается
в законе сохраненияJ): вихри не могут возникнуть и
вихри не могут исчезнуть. Или в более общей форме:
интенсивность вихря постоянна во времени. Эта теорема
основана на следующих предположениях: жидкость не<-
вязкая и несжимаемая; внешние силы имеют внутри жидко-
жидкости однозначный потенциал. Как будет показано ниже,
к сохранению вихря во времени добавляется сохранение
в пространстве: интенсивность вихря постоянна вдоль
каждой «вихревой линии» или «вихревой трубки»; эти
линии и трубки или замкнуты, или выходят на поверх-
поверхность жидкости.
1. Дифференциальная форма теоремы сохранения вихря
во времени
Следуя Гельмгольцу, будем исходить из уравнений
Эйлера в форме A1.2). Так. как внешняя сила F обладает
потенциалом U, мы можем написать
dt
A8.1)
г) Соответствующие теоремы были найдены в посмертных статьях
Дирихле, умершего в 1859 г., и опубликованы в его собрании со-
сочинений, изданном Дедекиндом.
11*
164 Гл. tV. Теория вихрей
Левая часть A8.1) есть «субстанциальная» производ-
производная, т. е. изменение скорости рассматриваемой мате-
материальной частицы при ее движении. Выразим ее через
«локальную» производную. Это было проделано в равен-
равенстве A1.7), которое мы при сделанных предположениях
относительно F можем написать в виде
^). A8.2)
Применим к этому равенству операцию ротора. При этом
правая часть исчезнет, так как rot grad = 0. Подставляя
1
со = -гг rot v, получаем
4?--rot[ve»]=0. A8.3)
Произведем преобразование, справедливое для любых
векторов v, со:
rot [wv] = (v grad) to — (w grad) v -f со div v — v div to. A8.4)
Эта формула, как и соответствующее ей выражение A1.6),
может быть проверена прямым вычислением в декартовых
координатах.
В данном случае A8.4) упрощается, так как divv = 0
и div со = div rot v = 0, и, подставив в A8.3)*, получаем
~- + (v grad) со = (со grad) v. A8.5)
Теперь в левой части у нас стоит субстанциальная ско-
скорость изменения со, так что вместо A8.5) мы можем на-
написать
¦^¦ = (»grad)v. A8.6)
Субстанциальная скорость изменения ы равна нулю всюду,
где равна нулю со. Отсюда Гельмгольц, не приводя более
подробного доказательства, сразу делает вывод: частицы
жидкости, находившиеся когда-либо в безвихревом движе-
движении, будут находиться в нем все время. При этом он,
очевидно, рассуждал следующим образом: пусть со = О
для t — t0; тогда, согласно A8.6), и dm / dt — O. Вместо
этого можно сказать, что у рассматриваемого материаль-
материального элемента объема со = 0 и в момент t — tQ-\-ht. Тогда
§ 18. Теоремы Гелъмголъца о вихрях 165
из A8.6) и для этого момента времени следует did/dt = O,
что означает со = 0 для t = t0 + 2Ai и т. д.
Для того чтобы дать более строгое математическое
доказательство, начнем издалека. Пусть А —вектор, опре-
определенный в текущей жидкости, da — элемент поверхности,
движущийся с жидкостью и вследствие
этого меняющий свое положение и фор-
форму , Ап — компонента А, перпендикуляр-
перпендикулярная к da. Рассмотрим поток А через da
в два близких момента времени tx и t2.
Соответствующие элементы длины c?sx и
ds2 границ dax и da2 переводятся друг в
„руга смещением w = у А. При „виже- ^ ?„?&
нии они образуют боковую поверхность ра через элемент по-
бесконечно малой области, для которой верхности а, кото-
поверхности dax и с?а2 служат основа- рый движется с
ниями (фиг. 22). Ее объем равен "™%%???
dx — Wnda
(при этом безразлично, принято ли здесь da — dax и wn_]_da1
или da = da2 и wn_]_da2).
Согласно теореме Остроградского — Гаусса, или, что
одно и то же, согласно определению дивергенции, имеем
\Ап da = div A dx = div Awn da. A8.7)
Интеграл в левой части распространяется на основания
и боковую поверхность нашего цилиндра.
На нашей фигуре элемент боковой поверхности за-
штрихова^. Его вклад в интеграл составит
(A, [tfsw]) = (cfe[wA]) = «fe[wA]8.
Индекс s в последнем члене этого равенства означает,
что берется компонента вектора в положительном на-
направлении ds, которое образует с внешней нормалью
верхнего основания правовинтовую систему (см. фиг. 22).
Поэтому интеграл по всей боковой поверхности будет
равен криволинейному интегралу, взятому по границе
верхнего основания:
ds [wA]s = da rotn fwA]; A8.7a)
166 Гл. IV. Теория вихрей
полученное выражение преобразовано по теореме
Стокса.
С другой стороны, вклад в левую часть A8.7) от верх-
верхнего и нижнего оснований может быть записан в виде
суммы (для нижнего основания внешняя нормаль направ-
направлена в сторону, противоположную к внешней нормали
верхнего основания)
Здесь 8 (Лп da) означает изменение потока А вследствие
движения и искажения элемента поверхности da.
Согласно A8.7) и A8.7а), можно написать
8 (Ап da) = (w div A - rot [wA])n da. A8.76)
Мы должны принять здесь во внимание изменение потока
А вследствие изменения самого А за время dt, т. е. при
смещении w. Оно равно
Если мы обозначим возникающее таким образом полное
изменение потока как
и вместо смещения w подставим его значение v dt, то,
деля на dt, получим, согласно A8.76),
^-Hn^)=(-^-bvdivA-rot[vA])nrfo. A8.7b)
Эта формула получена также Гельмгольцемг) в его по-
посмертной работе о принципе наименьшего действия в
электродинамике.
Теперь отождествим наш, до сих пор произвольно
выбранный вектор А с угловой скоростью to. Так как
х) Helmholz H., Ges. Werke, Bd. Ill, S. 476. См. в особенности
равенства (8а), (86), относящиеся к вектору виртуального смещения
А=§?, Ьч], К. Употребляемая Гельмгольцем система записи
в компонентах весьма громоздка; наша система записи и взятия
производных соответствует изложению: Lorentz H. A., Enzykl.
d. Math. Wiss., Bd. V, 2, S. 75. См. равенство E), где он показывает
фундаментальное значение этого соотношения в электродинамике
движущихся тел.
§ 18. Теоремы Гелъмголъца о вихрях 167
div@ = O, получаем из A8.7в) для произвольного на-
направления нормали п из da:
)e. A8.8)
Согласно A8.3), правая часть этого равенства обращается
в нуль. Таким образом, мы получаем
^(cotfc) = 0. A8.9)
Из этого равенства сразу следует теорема сохранения
вихря. Поток угловой скорости через каждый элемент
поверхности, движущийся с жидкостью, сохраняет постоян-
постоянное значение. Вихрь не может исчезнуть или возникнуть.
Вихревое движение есть свойство, присущее частицам
жидкости, которое переносится вместе с ними.
о
2. Интегральная форма теоремы сохранения вихря
во времени
Чтобы упростить теорию вихрей Гельмгольца, мы
воспользуемся введенным на стр. 29 понятием циркуляции,
которое с этой целью использовал еще Томсон1). Вместо
произвольного вектора А подставим наш вектор v и обра-
образуем
Z.— Ф vs ds = & (v, ds) = <T> (и dx -f- v dy -f w dz). A8.10)
Интегрирование производится по замкнутой кривой внутри
жидкости, которая передвигается вместе с частицами
жидкости (фиг. 23). С —кривая, по которой производится
интегрирование в момент времени t, С — искаженный
течением контур для времени ?-|-Д?- Под ds понимается
элемент дуги кривой С, a ds' — соответствующий элемент
дуги кривой С. Прямые стрелки на фигуре представляют
собой пути движения частиц жидкости за время At и для
точек i или i -\-1 соответственно равны
\i At или \i+i At.
Эти стрелки соответствуют вектору w на фиг. 22. Отличие
фиг. 23 от фиг. 22 заключается в том, что вместо беско-
г) Thomson W. (Kelvin), О вихревом движении, Trans.
Roy. Soc, Edinburgh, 25 A869).
168
Гл. IV. Теория вихрей
нечно малых контуров мы имеем здесь конечные кривые
С ж С. Нижеследующий расчет аналогичен тому, который
приводился ранее.
Из четырехугольника, образованного стрелками на
фиг. 23, следует
' = d& -f Vi+i At,
или
ds' — ds
' At
-vt. A8.11)
Фиг. 23. К понятию
циркуляции.
Понимая под2' циркуляцию вдоль
С, вычислим
dZ т Z' — Z d
*
Стоящий в последнем интеграле символ
<18-12)
есть не что иное, как предел величины, вычисленной
в A8.11); этот интеграл может быть приближенно записан
в виде, суммы по ?:
Совершая предельный переход от многоугольника ... i,
i + 1 ... к криволинейному интегралу вдоль С, получаем
Л 2 В
'' 2 V a'
где ^4 — произвольная точка начала интегрирования (соот-
(соответствующая i = 0) и 5 — совпадающая с ней точка конца
интегрирования. Таким образом, этот второй интеграл
обращается в'нуль.
Но и первый интеграл в правой части A8.12) ташке
обращается в нуль. Согласно уравнению Эйлера A8.1),
он равен криволинейному интегралу от отрицательного
градиента величины {p-\-U) / р, т. е.
Р+и
¦=о.
§ 18. Теоремы Гелъмголъца о вихрях 169
Таким образом, из A8.12) следует
^¦=0, Z = const. A8.13)
Циркуляция, взятая вдоль произвольного замкнутого кон-
контура, состоящего из частиц жидкости, сохраняет неизмен-
неизменным начальное значение в продолжение всего времени.
Циркуляция непосредственно связана с наличием
в жидкости вихревого движения. Согласно C.2) имеем
Z = <? (v, ds) = & vs dss — <? rotn v do = 2 \ wn do. A8.14)
Если через кривую С провести произвольную поверхность
и в каждом элементе do взять компоненту угловой скорости
о в направлении нормали, то Z равна удвоенному потоку
угловой скорости через эт.у поверхность. Согласно равен-
равенству A8.13), этот поток угловой скорости сохраняется
постоянным во время течения жидкости. Теорема Гельм-
гольца о вихрях выступает здесь в форме теоремы Том-
сона о сохранении циркуляции, полностью совпадая с ней
по содержанию.
Нет никакой необходимости рассматривать во время
движения в равенстве A8.14) одну и ту же поверхность а,
проходящую через кривую С. Через любую поверхность а,
натянутую на контур С, проходит один и тот же поток
угловой скорости u>ndo. Это доказывается опять-таки с по-
помощью теоремы Стокса, согласно которой можно восполь-
воспользоваться, произвольной поверхностью о, как об этом упо-
упоминалось вслед за равенством C.5). При этом, однако,
требуется, чтобы ее граница С состояла все время из одних
и тех же материальных частиц.
Выражения A8.13) и A8.14) переходят очевидным
образом в прежнее равенство A8.9), если поверхность
бесконечно мала, и наоборот, наш результат можно было
бы получить из A8.9) путем интегрирования по do. Однако
примененное здесь рассуждение проще и менее абстрактно,
чем предыдущее, и мы считаем, что как дополнение к
вышеизложенному оно не является лишним.
В то время как равенства A8.1) или A8.2) представляют
собой дифференциальную форму уравнений Эйлера, мы
170
Гл. IV. Теория вихрей
можем рассматривать закон сохранения циркуляции A8.13)
как интегральную форму уравнений Эйлера. Такое наи-
наименование принято по аналогии с электродинамикой.
Выписанные в § 15 равенства A5.7) представляют собой
дифференциальную форму уравнений Максвелла. В то же
время имеются аналогичные уравнения в интегральной
форме, выражающие связь между криволинейными и по-
поверхностными интегралами. Такая за-
запись во многих случаях более удобна.
3. Пространственный закон сохранения
в теории вихрей
Согласно Гельмгольцу, построим в
жидкости вихревые линии и вихревые
трубки. Пусть вектор со определяет в
каждом месте в данный момент времени
определенную положительную ось вих-
вихревого движения. По этим направлениям
можно построить вихревые линии точно
так же, как мы строим в произволь-
произвольном силовом поле силовые линии. За-
Затем построим перпендикулярно к вихре-
вихревой линии элемент поверхности Ад так, чтобы наша вих-
вихревая линия проходила через какую-нибудь точку грани-
границы Ад, а также построим вихревые линии, проходящие
через другие точки границы. Ад. В результате образуется
вихревая трубка. Циркуляция вдоль границы Ад, согласно
A8.14), равна
Z = 2[x, где [А = о)Дд; A8.15)
jj. — поток угловой скорости через вихревую трубку, или;
как говорят, ее интенсивность. Согласно A8.13), р- постоян-
постоянно во времени, в то время как вихревая трубка и огра-
ограничивающие ее вихревые линии могут во время движения
менять свою форму.
Интенсивность вихря постоянна не только во времени,
но и в пространстве (если мы будем двигаться вдоль
вихревой трубки, см. фиг. 24). Так как, согласно равен-
равенству B.8), divrot = 0, мы имеем
div ш = 0.
Фиг. 24.
Вихревая трубка.
Поток вихря через
ее ортогональное и
наклонное сечение.
§ 18. Теоремы Гелъмголъца о вихрях 171
Тогда из теоремы Остроградского — Гаусса следует для
части вихревой трубки между сечениями Aq и Aq'
0-= ^ div ш dx = ^ шп da. A8.16)
Поверхностный интеграл в правой части распространяется
на Aq, Aq' и на боковую поверхность нашего отрезка
трубки. Но' на боковой поверхности <on обращается в нуль,
так как вихревые линии всюду имеют направление <о.
Далее, компонента и>п, взятая в направлении внешней
нормали наших сечений, на Aq равна —<«, а на Aq'
равна +«)', где w и о/— модули (о в соответствующих
местах. Равенство A8.16) дает тогда
0 = ш'Д?'-шДд, т. е. {а' = (х. A8.17)
Итак, интенсивность вихря постоянна вдоль трубки
в пространстве. То же самое значение jjl получится, если
мы возьмем не перпендикулярное, а наклонное сечение.
Пусть Aq" — площадь такого косого сечения и <«„ — компо-
компонента со в направлении нормали к Aq". Тогда, согласно
теореме Остроградского — Гаусса, опять будем иметь
Таким образом, для любого произвольно направленного
сечения вихревой трубки произведение площади сечения
на нормальную компоненту угловой скорости вращения
жидких частиц постоянно. В § 20 мы увидим аналогию
между вихревыми трубками и проводниками электриче-
электрического тока.
Из постоянства интенсивности вихря сразу следует,
что вихревая трубка не может заканчиваться в жидкости.
Она либо достигает ее границы, либо замыкается.
До сих пор мы молчаливо подразумевали, что <« рас-
распределено в пространстве непрерывным образом. Тогда \i
имеет тот же порядок малости, что и сечение вихревой
трубки Aq. Можно, однако, представить себе предельный
случай, когда <о сконцентрировано в отдельных бесконечно
узких линейных областях (аналогично так называемым
линейным, т. е. бесконечно тонким, проводникам электри-
электрического тока). Тогда на этих особых линиях <о бесконечно
велико, в то время как всюду вне этих линий ш можно
172 Гл. IV. Теория вихрей
считать равным нулю. В таком случае мы говорим о вихре-
вихревой нити. Ее интенсивность имеет конечное значение,
не исчезающее с убыванием Ад, которое может быть пред-
представлено в виде
Дд. A8.18)
§ 19. ПОТЕНЦИАЛЬНОЕ ТЕЧЕНИЕ В ПЛОСКОСТИ
И В ПРОСТРАНСТВЕ
Термин «потенциальное течение» аналогичен названию
«в общем, безвихревое течение». Слово «в общем» означает
здесь «за исключением, быть может, особых точек или
линий». В § 11 было показано, что из условия безвихре-
безвихревого движения
2<о = rot v = О
следует существование потенциала скоростей Ф, и в § 18 —
что если течение в начальный момент было безвихревым,
то оно будет оставаться таким все время. Впрочем, в насто-
настоящем параграфе будем рассматривать только стационарные
течения, так что зависимость Ф от,времени фигурировать
не будет. Так как во всей этой главе мы считаем жидкость
несжимаемой, выполняется, вообще говоря, уравнение
потенциала A1.13)
ДФ = 0; A9.1)
термин «вообще говоря» опять означает «за исключением
особых точек или линий».
Исследуем свойства течения, описанного уравнением
A9.1). Рассмотрим наиболее простой случай плоского
течения. Тогда A9.1) запишется в виде
д2Ф д2Ф _0 Г1Я2^
Сравним A9.2) с уравнением колебаний A3.9)
4^г-^^г = 0- A9.2а)
Если положить t— у и с2= — 1, т. е.
с = ± i,
§ 19. Потенциальное течение в плоскости U в пространстве 173
то A9.2а) перейдет в A9.2). Так как нам известно общее
решение A9.2а), а именно решение Даламбера A3.11)
х — с1), A9.26)
то, следовательно, известно и общее решение уравнения
A9.2). Оно гласит:
if (ж + 1) + /* (ж ~ 1
Здесь необходимо было заменить функции Fx и F2 на взаимно
сопряженные функции / и /*, так как Ф, конечно, должно
быть действительным; так как мы ввели множитель г/2,
то Ф будет равно действительной части j{x-\-iy).
Таким образом, общее решение уравнения A9.2) за-
задается действительной частью произвольной аналитической
функции / комплексного переменного
z = x-\- iy.
Соответственно этому положим
f{z) = <S>(x, y) + iW{x, у). A9.4)
Соответствующая мнимая часть W представляет собой со-
сопряженный с Ф потенциал. В гидродинамике W называется
функцией тока.
Чтобы установить связь между Ф и W, продифферен-
продифференцируем A9.4) по х, а затем по у; производную функции
f(z) по z мы обозначим, как это принято, через /' (z):
/() /4) /'() +
A9.4а)
Исключая /' (z), получим
дх ду \ дх ду
Так как Ф и W действительны, то выполняются условия
Коши —Римана теории функций комплексного пере-
переменного:
дФ__№_ дФ__ __dW_ .q _
дх ду ' ду дх \ • /
1?4 Тл. IV. Теория вихрей
Объединим эти условия в одно уравнение
дФ dW
A9.5а)
ds дп '
где ds и dn представляют собой два любых взаимно пер-
перпендикулярных элемента длины плоскости ху, следующих
друг за другом в том же направлении, что и положитель-
положительны^ действительная и мнимая оси на числовой плоскости
Гаусса (фиг. 25). Если ds совместить с осью х, a dn,
следовательно, с осью у, то A9.5а) перейдет в первое из
уравнений A9.5); если, с другой стороны, ds совместить
с осью у, a dn — c, отрицатель-
отрицательнее/^ ной осью х, то из A9.5а) будет
~ следовать второе уравнение
A9.5). Но равенство A9.5а) го-
годится и для любого другого на-
направления ds и связанного с ним,
H=const согласно фиг. 25, направления
dn. Оно представляет собой удоб-
удобную векторную (т. е. не завися-
Ф и г. 25. Эквипотенциаль- щую от системы координат) фор-
ные линии: Ф=сопв1 и ли- условий Коши-Римана.
нии тока W=const в случае J ^
двухмерного безвихревого Положим, например, что на-
течения. правление ds (см. фиг. 25) сов-
совпадает с линией уровня потен-
потенциала скоростей, так что дФ /ds — О; тогда линия уровня
функции тока будет проходить в направлении dn, так
как, согласно A9.5а),
?=<>• <19-6>
Линии Ф = const и W = const образуют ортогональные
семейства кривых. Это положение обычно доказывается
с. помощью перекрестного перемножения равенств A9.5),
в результате чего получается, что
(grad<J>, gradW)-0. A9.6a)
Однако с помощью равенства A9.5а) эта ортогональность
может быть установлена еще более непосредственным
образом.
Фиг. 25 оправдывает также название функции тока.
Если мы направим ds по эквипотенциальной линии,
§ 19. Потенциальное течение в плоскости и в пространстве 175
то v= — grad Ф будет направлено по dn. Однако в этом
направлении, согласно A9.6), W = const. Отсюда следует,
что линии 4f = const являются линиями тока.
Семейство кривых Ф = const, W = const не только
ортогональны друг другу, но и изометричны, т. е.
масштаб изменения Ф в направлении dn и W в направ-
направлении ds один и тот же; согласно A9.5а), ds = dn при
заданном" бесконечно малом возрастании 8 = dФ = dW.
Кривые Ф, W, Ф + 8, W + 8 образуют бесконечно
малый квадрат. Вследствие этого отображение на плос-
плоскость Ф + iW какой-либо бесконечно малой фигуры,
нарисованной на плоскости х -J- iy, будет представлять
собой подобную фигуру. Отображение плоскости х + iy
на плоскость Ф + гЧР* будет конформным. Это справедливо
для любой аналитической функции f{x-\-iy). Масштаб
отображения задается величиной \f'(x-\-iy)\. Он изме-
изменяется от точки к точке, однако в каждой точке мас-
масштаб не зависит от направления.
Можно без преувеличения сказать, что теория ана-
аналитических функций комплексного переменного есть
не что иное, как двухмерная теория потенциала, или,
говоря на языке гидродинамики, плоского потенциаль-
потенциального течения, поскольку потенциал скоростей и функция
тока объединены в одну комплексную величину. В своей
диссертации в 1851 г. Риман, используя методы матема-
математической физики, создал теорию, в которой функции выра-
выражались не посредством формул, например в виде степенных
рядов, а отвлеченно, по их свойствам, как, например, по осо-
особым точкам, связности, точкам ветвления. Чтобы охаракте-
охарактеризовать прием, который сначала был оказан диссертации
Римана, уместно привести следующий случай, сообщенный
Вюльнером. В 70-х годах Вюльнер встретился на Риги
с Вейерштрассом и Гельмгольцем. Во время своего
отпуска Вейерштрасс занимался изучением диссертации
Римана и жаловался Гельмгольцу, что ему, специалисту
по теории функций, с трудом понятны методы Римана.
Гельмгольц попросил у него статью и во время следующей
встречи сказал, что ему соображения Римана кажутся
вполне естественными и очевидными.
В качестве простейшего примера приложения методов
теории функций комплексного переменного к гидроди-
176 Гл. IV. Теория вихрей
намике мы рассмотрим описанный еще на стр. 50 про-
простой вихрь. Положим
f(z) = iAlnz. A9.7)
Полагая z — re^, получим
/ (Z) = Ф + iW = — Ay + iA In г,
откуда
Ф=-Лср, W = A\nr. A9.7a)
Линии тока задаются равенством W = const, т. е. г = const.
Скорость течения может быть получена из условия
v= —дгас!Ф. -Так как в нашем случае Ф зависит только
от <р, скорость течения будет равна
^^=-grad^=-|^ = |, vr = 0, A9.76)
что находится в полном соответствии с равенством D.29).
В начале координат течение имеет особенность: v=oo.
Эта особенность видна уже в выражении A9.7) для/(;г),
так как f(z) при z = 0 обращается в бесконечность.
Течение всюду (кроме точки г = 0) безвихревое, соответ-
соответственно тому, что оно задается комплексной функцией /.
То же самое можно показать с помощью формул, вычи-
вычислив составляющую угловой скорости со" перпендикулярную
к плоскости ху, воспользовавшись при этом результатами
задачи 3 гл. I:
2ш = =о.
г дг г ду
Можно было бы не приводить соответствующего вычисле-
вычисления в декартовых координатах, но мы выполним его,
так как оно занимает немного места:
откуда в каждой точке, за исключением начала коор-
координат,
9 _dvv dvx_A 2Ax* , А 2Ауъ_(Л
дх ду г2 74 ' г2 гх
§ 19. Потенциальное течение в плоскости и в пространстве 177
Согласно инвариантному определению B.21), о> может
быть вычислена в любой точке с помощью циркуляции
вдоль бесконечно малого контура, заключающего внутри
себя рассматриваемую точку. Циркуляция вокруг любой
точки, кроме г -- 0, будет также равна нулю. Если,
с другой стороны, мы вычислим циркуляцию вдоль произ-
произвольной, - сколь угодно малой окружности с центром
в начале координат, то, согласно A8.10), получим
Z = & (v, ds) = ^vr d<? = 2ъА. A9.8)
Этот результат не зависит от г, т. е. он будет один и тот
же для двух окружностей с радиусами гг и г2; так и
должно быть, потому что внутри кругового кольца тече-
течение безвихревое. Все вихревое движение сконцентрировано
в одной особой точке — в начале координат. Интенсивность
вихря в этой точке, согласно нашему определению (а
в A8.15), равна
[x = iu4. A9.8а)
Если рассматривать наше движение как пространствен-
пространственное, то особая точка представляет собой вихревую нить,
перпендикулярную к плоскости ху. Вихревая нить той
же интенсивности, но другого знака \i = — к А находится
в этом случае на бесконечности, которую, как это обычно
делают в теории функций комплексного переменного,
представляют как точку. Приведем еще формулу, явля-
являющуюся следствием A9.76) и A9.8а):
* »» = ?¦ A9-9)
С помощью дробно-линейного преобразования пере-
перенесем обе вихревые нити в конечную часть плоскости,
например в точки z=±c. Именно, рассмотрим вместо
A9.7) функцию
/ G\ — / Л I n z с (\ Q 10^
12 а. Зоммер ?ольд
178
Гл. IV. Теория вихрей
Если положим здесь
z-f c =
A9.10a)
A9-106)
то р и ср будут представлять собой «биполярные коор-
координаты», и тогда, согласно A9.4), получаем
Ф = —
= 4р = т4 In ^ .
A9.11)
Так как геометрическим местом вершин равных углов,
опирающихся на отрезок, является дуга окружности,
Наложение двух равных противоположно направ-
направленных простых вихрей. Система биполярных ко-
координат.
то эквипотенциальными линиями Ф = const будут окруж-
окружности, проходящие через обе особые точки z — ± с; линии
тока ЧГ = const также будут представлять собой окруж-
окружности, поскольку окружность я'вляется геометрическим
местом точек, 'расстояния от которых до двух данных
точек находятся в определенном отношении. На фиг. 26
наглядно показана ортогональность обоих семейств
окружностей, а также разбиение плоскости на бесконечно
§ 19. Потенциальное течение в плоскости и в пространстве 179
малые квадраты, если параметры двух соседних окруж-
окружностей каждого семейства изменяются на равные вели-
величины Ь.
Методика вычисления в биполярной системе коорди-
координат показана в задаче 1 гл. IV. В математической
физике ими пользуются довольно редко, так как в этих
координатах не разделяются переменные уравнения коле-
колебаний (см. также задачу 1 гл. IV).
В рассматриваемом случае функция / (z) представляет
собой суперпозицию двух простых вихрей типа A9.7),
из которых один имеет центр в z = + с и постоянную
-\-А, а другой — центр в z — —с и постоянную —А:
f (z) = iA In (z - с) - iA In (z + c). A9.12)
Произвольный контур, проведенный вокруг z= -\-c, но не
включающий в себя точку z== — с, дает, согласно A9.8),
A9.12а)
контур вокруг z= — с, не включающий z= -\-c, дает
Z2=-2i:A, A9.126)
а контур, не включающий в себя этих точек или вклю-
включающий обе точки, дает
Так же как и в случае A9.8а), из A9.12а) и A9.126)
следует, что интенсивность вихревых нитей в z= -\-c
и соответственно z = — с равна
[х1 = '1гЛ и соответственно [х2= — к А. A9.13)
Так же как и функция f(z), соответствующее ей поле
течения возникает в результате суперпозиции двух полей
скоростей A9.9) простых вихрей, если в них подставить
вместо г величину | z — с | или соответственно | z -\- с |.
При этом получается
v _ Wi Р-Ф2 __ Wi W2 A9 14)
71 | ZС | TZ | Z | С I КГ КГ ' '
Здесь ip1 и ^р2 представляют собой единичные векторы
в направлении возрастающих углов <рх и <р2. В задаче 2
12*
180 Гл. IV. Теория вихрей
гл. IV этот результат сравнивается с представлением
в биполярных координатах, вытекающим из A9.11):
v = -4grad ср = — gradcp. A9.14а)
Другая ортогональная система координат, а именно
софокусные эллиптические координаты, играет большую
роль для течений, рассматриваемых в гл. VI. К ним
можно подойти более просто, если, рассмотреть отобра-
отображение комплексной плоскости z = x-\-iy на комплексную
плоскость C = ?-f-nq, задаваемое соотношением
или, если написать в развернутом виде,
вводя
e±iir) = с08 -q _j_ i sjn ^
сразу получаем из A9.15а)
x-\-iy = c (ch 5 cos ^ -f i sh k sin n)
или отдельно для действительной и мнимой частей
sc = cch?cos7], y = cshEsirnr]. A9.16)
Так как cos21\ + sin2 -q = 1, то исключение -ц приводит
к выражению
IT It
' A9.17a)
а так как ch2 \ — sh2 5=1, то после исключения 5 полу-
получаем
2 2
1- A9.176)
с2 sin2
Выражение A9.17а) при заданном 5 является уравнением
эллипса с полуосями
Его эксцентриситет равен
л/ пг — IJ — г 1Q 1Яя\
§ 19. Потенциальное течение в плоскости и в пространстве 181
т. е. не зависит от ?. Меняя параметр \, получаем си-
систему софокусных эллипсов с фокусами в точках
х=±с, у=0.
С другой стороны, A9.176) при заданном т] является
уравнением гиперболы с полуосями
а = с cost], 6 = с sin т].
Эксцентриситет этой гиперболы
У ф + Ъг = с A9.186)
также не зависит от tj и равен эксцентриситету эллипсов
в A9.18а). Меняя параметр tj, получаем из A9.176)
Фиг. 27а. Система софокусных эллипсов и ги-
гипербол ?=const и Tj=const.
систему гипербол, софокусных между собой и с системой
эллипсов (фиг. 27а).
Рассмотрим предельные значения параметра семей-
семейства эллипсов
\ = 0 и \ = оо.
182
Гл. IV. Теория вихрей
Согласно A9.17а), условие ? = 0 соответствует прямой,
соединяющей фокусы
у = 0, —с<х<-\-с.
Условие ? = оо соответствует бесконечно удаленному
эллипсу.
Что касается параметра i\ семейства гипербол, то зада-
зададимся значениями
-ц = 0, 7] = ± ~ ; 7] = ± ТТ.
Согласно A9.176), т] = 0 соответствует продолжению
прямой, соединяющей фокусы, в направлении оси х
у = 0, х>с.
Условие т] = ± (tz/2), согласно A9.176), соответствует х = 0,
т. е. оси у. -к; = ± тс соответствует части оси х, примы-
примыкающей слева к отрезку, соединяющему фокусы
у = 0, х<—с.
Для того чтобы соблюдалось однозначное соответствие
координат ?, ~г\ и точек плоскости ху, лучше всего дого-
договориться, что значения 0 < г\ < -к относятся к ветвям
А?
I
I
v-
Ф и г. 276. Отображение плоскости
(х-т-iy) на плоскость (;-f nrj).
гипербол в полуплоскости у > 0, а значения — тс < т] < О—
к ветвям гипербол в полуплоскости у < 0. В целом пло-
плоскость ху будет тогда отображаться на полосу на пло-
плоскости ?, у], изображенную на фиг. 276:
0<а<+оэ, -тс<7]<+тс. A9.19)
§ 19. Потенциальное течение в плоскости и в пространстве 183
Верхнюю и нижнюю границы полосы надо представлять
себе в однозначном точечном соответствии друг с другом,
так как они соответствуют одной и той же части оси х
плоскости ху.
В задаче 3 гл. IV на примере уравнения колебаний
будет показано преимущество эллиптических координат
перед биполярными (в смысле разделимости переменных).
В гл. VI с помощью эллиптических координат будет
решена задача об обтекании плоской пластинки. Там мы
воспользуемся выражением вида
.Ф-fiW = f(Q, например /(С) = const• shС A9.20)
Если в этом выражении заменить, согласно A9.15),
С на z, то /(С) станет комплексной функцией z, в согласии
с общей формой выражения A9.4).
Рассмотрим еще раз наше простое выражение (-19.7),
но отбросим в нем стоящий справа множитель i. Тогда
получим
W = Ay. A9.21)
Линии тока будут теперь являться прямыми ср = const,
исходящими из начала координат. Эквипотенциальные
линии будут представлять собой окружности г = const
с центром в начале координат. Центр, в зависимости
от знака А, будет представлять собой источник или
сток. В заключение заметим: общее центрально-симмет-
центрально-симметричное решение уравнения потенциала на плоскости
является логарифмическим потенциалом Ф = 1пг, с точ-
точностью до постоянного множителя и постоянного слагае-
слагаемого.
t В конце этого параграфа приведем некоторые заме-
замечания по поводу потенциального течения в пространстве.
Центрально-симметричное решение уравнения потен-
потенциала в пространстве представляет собой так называемый
потенциал Ньютона
Ф =у . A9.22)
Такое название не имеет исторического основания, так
как Ньютон никогда не упоминал о подобном потен-
184 Гл. IV. Теория вихрей
циале; оно связано только с тем, что этот потенциал
относится также к силовому гравитационному полю:
F= — grad<?= -^4grady . A9.22а)
В гидродинамике величина Ф, в зависимости от знака А,
является потенциалом скоростей источника или стока,
расположенного в начале координат.
Вообще говоря, в трехмерном случае потенциалу ско-
скоростей не соответствует никакая функция тока W.
Только в случае аксиально-симметричного течения можно
построить функцию тока1). Введем цилиндрическую
систему координат р, у, z, причем в качестве оси z
выберем ось симметрии. В этом случае аксиальная сим-
симметрия будет означать, что потенциал скоростей не
зависит от <р> т- е- Ф будет являться функцией только
от р и z:
Ф = Ф(р, z).
Уравнение потенциала A9.1), т. е. условие несжи-
несжимаемости, имеет вид (см. задачу 3 гл. I)
Его можно переписать в виде
Отсюда можно сделать вывод, что существует функция
для которой выполняется условие
_д_( дФ\ д_
dp dz dp \ dp у dz
Поэтому можно положить, что
dw_ dФ dw _ dФ ,Q 9/.
dz op dp ' dz v '
х) StokesF., Trans. Cambr. Phil. Soc, 7, 439 A842); Ges.
Werke, Bd. I, S. 1, в частности стр. 14 и далее.
§ W. Фундаментальная теорема векторного анализа 185
Перемножая крест-накрест уравнения A9.24), получаем
Р V^P ~др ~д* ~д* ) ~
Отсюда следует, что в каждой меридиональной плоскости
ср = const линии Ф = const и W = const взаимно ортого-
ортогональны. Линии W — const, следовательно, проходят
в направлении градиента Ф и представляют собой линии
тока, поэтому о функции W можно говорить как о функ-
функции тока. Из A9.24) и равенства v=—?гас1Ф можно
также, получить
vp= -=- , vz=— -д- , A9.25)
р р dz z p dp ' ч '
однако Ф и W нельзя объединить в одну комплексную
функцию Ф + iW переменного р + iz, как это мы делали
в двухмерном случае. Если бы это можно было сделать,
то равенства A9.24) совпадали бы с условиями Коши —
Римана A9.5), чего на самом деле нет, так как в A9.24)
имеется еще множитель р. Кроме того, Ф и W должны
были бы в этом случае удовлетворять уравнению
Лапласа, в то время как Ф удовлетворяет уравнению
A9.23), a W — уравнению
вытекающему из условия rotv = 0. Вследствие этого
методы теории функций комплексного переменного
не могут быть применены к теории потенциала в трех-
трехмерном пространстве.
Гильберт как-то высказался по поводу бесплодности
всех попыток в этом направлении: время одномерно,
пространство трехмерно, а число, т. е. совершенное комп-
комплексное число, двухмерно.
§ 20. ФУНДАМЕНТАЛЬНАЯ ТЕОРЕМА ВЕКТОРНОГО АНАЛИЗА.
ЭЛЕКТРОМАГНИТНАЯ АНАЛОГИЯ ВИХРЕВЫХ ПОЛЕЙ
Эта теорема может быть сформулирована следующим
образом. Любое непрерывное векторное поле V, заданное
во всем бесконечном пространстве и обращающееся на бес-
бесконечности вместе со своими первыми производными в нуль,
186 Гл. IV. Теория вихрей
может быть представлено в виде суммы безвихревой
части \г и части, не обладающей источниками, V2 (или
как говорят, соленоидалъной):
B0.1)
где
rotV1 = 0, divV2^0. B0.1a)
В этом случае все имеющиеся в заданном поле V источ-
источники (стоки) будут включены в первую часть — У1г а все
вихри—во вторую часть—V2; таким образом, усло-
условие B0.1а) также означает
divV1 = divV, rotV2 = rotV. B0.16)
Разложение B0.1) однозначно с точностью до векторной
постояннойг В основном эта фундаментальная теорема
была доказана еще Стоксом1) в 1849 г. В более полной
форме указанная теорема легла в основу работы Гельм-
гольца о вихревых движениях, опубликованной в 1858 г.,
где он (конечно, не в векторной, а в координатной
форме записи) также доказал ее. Эта теорема позволяет
глубже вникнуть в интегральные методы математической
физики. Она играет важнейшую роль в гидродинамике
и особенно в теории электромагнетизма. Мы докажем
ее в три приема.
x) Stokes F., О динамической теории диффракции, Trans.
Cambr. Phil. Soc, vol. 9, p. 1; Ges. Werke, Bd. II, S. 243, в особен-
особенности стр. 254 и дальше. Стоке, однако, не дал точного определения
векторного потенциала А. Вместо этого он вычислял V2 с помощью
формулы, представляющей собой комбинацию наших формул B0.5)
и B0.9):
4tcV2 = V — rot rot V dx.
Более строгое математическое доказательство дал в своей работе
Blumenthal О.,О разложении бесконечных векторных полей,
Math. Ann., 61, 235 A905). Он предположил только, что на беско-
бесконечности V с первыми производными стремится к нулю, не оговари-
оговаривая того, как быстро они убывают. При этом он получил интересный
результат, показывающий, что составляющие поля V (поля \\ и V2)
не только не должны исчезать, но даже могут определенным образом
обращаться в бесконечность. В дальнейшем мы сделаем несколько
неопределенное предположение, что V «достаточно быстро» исче-
исчезает на бесконечности.
§ 20. Фундаментальная теорема векторного анализа 187
1. Вычисление Vr Так как \г — безвихревой вектор,
то он может быть получен из скалярного потенциала Ф
в виде
Vj = — grad Ф + const. B0.2)
Тогда Ф удовлетворяет дифференциальному уравнению
div grad Ф = ДФ = — div \1г
откуда в силу B0.16) можно записать
AO=—divV. B0.3)
Постоянная, которая для общности была введена в B0.2),
при определении Ф не играет никакой роли. Из неодно-
неоднородного уравнения потенциала B0.3), у которого известна
правая част», мы можем, пользуясь теоремой Грина,
вычислить Ф в форме (см. ниже п. 1а)
г. B0.4)
Здесь г = rPQ — расстояние между точкой Р, в которой
вычисляется потенциал Ф, и местом расположения
источника Q, по координатам которого производится
интегрирование (т. е. элемент объема с?т располагается
в точке Q). Зртая Ф, можно определить с помощью
соотношения B0.2) \г с точностью до постоянной.
2. Вычисление V2. Можно ввести векторный потен-
потенциал А, положив
V2 = rot A + const B0.5)
и введя дополнительное условие
divA = 0. B0.6)
Такое введение возможно, так как вектор А определен
с точностью до градиента произвольной скалярной
функции. Из B0.5) следует
rot rot A = rot V2
или, согласно B0.16),
rot rot A-rot V. B0.7)
188 Гл. IV. Теория вихрей
Здесь опять постоянная, входящая в B0.5) при опреде-
определении А, не играет роли. Вспомним соотношение C.10а),
справедливое для декартовых координат:
АА = grad div A — rot rot A.
В силу B0.6) оно может быть упрощено
АА= —rot rot А,
так что B0.7) перейдет в
AA=-rotV. B0.8)
Таким образом, А, как и Ф, удовлетворяет неоднород-
неоднородному уравнению потенциала и поэтому может быть опре-
определено с помощью формулы, аналогичной B0.4):
г. * B0.9)
В п. 2а будет показано, что А, определенное с по-
помощью этого выражения, само по себе удовлетворяет
условию B0.6). Зная А, мы можем из -B0.5) определить
и V2 с точностью до постоянной.
3. Однозначность разложения V = V1 + V2. Допу-
Допустим, что, кроме разложения \г, V2, существует другое—
\[, Vg. Тогда безвихревой вектор V{ — \х был бы также
соленоидальным, так как, согласно B0.16),
div(Vi-V1) = 0.
Точно так же соленоидальный вектор V^—V2 был бы
безвихревым, так как опять, согласно B0.16), было бы
Вычисление потенциалов Ф и А для векторов \[ — Vt
и Vg— V2 с помощью B0.4) и B0.9) привело бы тогда
к следующему результату: Ф = 0, А=0; поэтому, со-
согласно B0.2) и B0.5), мы получили бы, что
V; —V1== const, Vj - V2 = const*.
Следовательно, наше разложение действительно является
однозначным с точностью до векторной постоянной.
§ 20. Фундаментальная теорема векторного анализа 189
1а. Вычисление Ф и А с помощью теоремы Грина.
В C.15) подставим и=Ф, V = \jr. Согласно A9.22),
V удовлетворяет уравнению потенциала, т. е. AF = 0
всюду, кроме особой точки г = 0, которую мы окружим
малой сферой (радиуса р), чтобы исключить ее при инте-
интегрировании. Прежде всего вычислим поверхностный ин-
интеграл по этой сфере, который будет входить в правую
часть C.15).
Обозначив соответственно телесный угол и элемент
поверхности единичной сферы через Я и dQ, получим,
что da = p2dQ. Далее, пусть dn—внешняя (по отношению
к области интегрирования) нормаль, так что
ап— ар, дп— 5р> дп~ dpp — +p2-
Тогда получаем те члены правой части C.15), которые
соответствуют сфере радиуса р в- виде
Ф ^cffi+^pdQ. B0.10)
Второй интеграл обратится в нуль при р —> 0, а первый
равен 4тс.
Рассмотрим теперь поверхностный интеграл по сфере
очень большого радиуса R. Если ввести da — R2dQ, то
получаем
-li&dQ-l^RdQ. B0.11)
Здесь оба интеграла обратятся в нуль, так как Ф на
бесконечности каким-то образом стремится к нулю,
а дФ/dR стремится к нулю быстрее, чем ijR, в силу
того" что V на бесконечности «достаточно быстро» стре-
стремится к нулю. При этих предположениях сумма поверх-
поверхностных интегралов по обеим сферам будет равна 4тсФ.
С другой стороны, в силу B0.3) и того, что AF = 0,
левая часть C.15) принимает вид
С divV ,
\ dx.
J r
Таким образом, равенство B0.4) справедливо. Доказа-
Доказательство справедливости B0.9) может быть проведено точно
так же.
190 Гл. IV. Теория вихрей
2а. Доказательство выполнения дополнительного
условия div А = 0. Если мы возьмем дивергенцию от диф-
дифференциального уравнения B0.8), то получаем
div ДА = — divrotV = 0.
Так как divA = Adiv, то div А удовлетворяет однород-
однородному уравнению Д = 0. Если провести такое же интегри-
интегрирование, как в п. 1а, то можно увидеть, что в выраже-
выражении Грина для div А обратится в нуль не только объем-
объемный интеграл, но и поверхностный интеграл, взятый по
сфере бесконечно большого радиуса.
Таким образом, на самом деле выполняется дополни-
дополнительное условие B0.6).
За. Замечания по поводу однозначности. Если век-
векторное поле V задано не во всем бесконечном простран-
пространстве, а внутри некоторой граничной поверхности Е, то
вместо равных нулю интегралов по поверхности беско-
бесконечно удаленной сферы в наши выражения войдут инте-
интегралы по этой граничной поверхности, которые, конеч-
конечно, не обращаются в нуль. Для Ф, например, вместо
B0.11) будет
Таким образом, равенство B0.4), а следовательно, и до-
доказательство однозначности перестают быть справедли-
справедливыми. То же можно сказать относительно B0.9). Оче-
Очевидно, что для ограниченной области пространства вместо
условия обращения в нуль на бесконечности надо задать
соответствующие граничные условия на поверхности И,
чтобы разложение векторного поля на безвихревую и соле-
ноидальную части приобрело в этом случае определенный
смысл.
Заметим также, что в случае неограниченного вектор-
векторного поля V постоянные, входящие в B0.2) и B0.5),
должны быть равны по величине и иметь разные знаки,
так как, согласно предположению, сделанному в этом
параграфе, их сумма V^^Vj + Vg должна обращаться
в нуль на бесконечности.
Доказанная нами однозначность в двухмерном случае
представляет собой известную теорему теории аналити-
§ 20. Фундаментальная теорема векторного анализа 191
ческих функций: функция f(x-\-iy), не имеющая особен-
особенностей во всей комплексной плоскости, включая и беско-
бесконечно удаленную точку, равна постоянной величине (Лиу-
виллъ).
Следовательно, такая функция должна иметь безвих-
безвихревую и соленоидальную действительную часть. То же
можно сказать и о ее мнимой части; следовательно, обе
части постоянны, так что / представляет собой комплекс-
комплексную постоянную.
4. Приложение фундаментальной теоремы к полю
скоростей, соответствующему заданному распределению
вихрей. Для простоты предположим
сначала, что все бесконечное про-
пространство заполнено движущейся
жидкостью, и отождествим вектор V
со скоростью течения жидкости v.
В силу условия несжимаемости
(divv = 0) имеем, согласно B0.4),
Ух = 0, т. е. V = v = V2 ^
с точностью до аддитивной постоян-
постоянной, которую опустим. Введем угло- фиг 28 Схемараз-
вуго скорость вращения жидких ча- реза элемента вихре-
стиц, которую будем пока представ- вой трубки по длине.
лять непрерывно распределенной в
пространстве. Так как rotv=2w, то, согласно B0.9)
и B0.5), получаем
-dx, v = rotA. B0.13)
Следовательно, \ выражается аддитивным образом через
вклады отдельных вихревых элементов шс?т. Рассмотрим
любой из таких элементов и построим проходящую через
него вихревую трубку (см. стр. 170). На фиг. 28 пред-
представлен разрез такой трубки по длине, равной |As|; ее
поперечное сечение равно Ад. Если, согласно A8.15),
обозначить (х = соДд, то вклад нашего вихревого элемента
в» векторный потенциал А (назовем его А') равен
2* А'= -?-Да. B0.14)
192 Гл. TV. Теория вихрей
Вклад в скорость течения (назовем его v') будет соста-
составлять
^() B0.15)
Величина, стоящая в скобках, как и вектор wrfx, из ко-
которого она получена, имеет направление As. Операция
rot, действующая на эту величину, относится к коорди-
координатам точки Р, в которой мы хотим определить v'. Чтобы
было удобнее производить дифференцирование, выберем
временно направление As за ось z прямоугольной системы
координат с началом в точке О элемента объема1"). В этом
случае
Согласно B0.15),
о / дЛг М- л V
2^x = -^-=-^As-f,
B0.16)
х
Три равенства B0.16) можно объединить и представить
в виде векторного произведения
f3[Asr]. B0.17)
Таким образом, скорость v' направлена перпендикулярно
к As и радиус-вектору г = ОР. По абсолютной величине
она равна
2'KV' = ti^Js[n^) B0.18)
где Ь—угол между As и г (см. фиг. 28). Векторы As,
г и v' образуют правовинтовую систему, так как v' сов-
совпадает по направлению с векторным произведением As и г.
Движение в точке Р, вызванное каждым вихревым
элементом (xAs, определяется выражением B0.17). Сум-
*) Вместо этого мы могли бы использовать общую формулу век-
векторного анализа rot(/a)=/rot a+[grad /, а], которая в случае
^t и f—V-jr переходит сразу в B0.17).
§ 20. Фундаментальная теорема векторного анализа 193
марная скорость v является векторной суммой частных
скоростей v'
v = 2v'. - B0.19)
5. Электромагнитная аналогия вихревых полей. Срав-
Сравним B0.18) с хорошо известным классическим выраже-
выражением закона Био—Савара
|tfF|=^ shift, B0.20)
где /—сила тока в элементе проводника ds и d?—сила,
с которой он действует на единичный магнитный полюс,
находящийся в точке Р; Ь и г имеют тот же смысл,
что и на фиг. 28. Наравление и знак d? совпадают с на-
направлением и знаком скорости v'.
Таким образом, между гидродинамикой и электродина-
электродинамикой существует полная аналогия, которая, как заме-
заметил Гельмгольц, весьма плодотворна как для той, так
и для другой области.
Сила тока / соответствует интенсивности вихря (х,
плотность тока J (ток, отнесенный к единице поверх-
поверхности)—угловой скорости to. Сила dF в законе Био—Сава-
Био—Савара, с которой отдельный элемент тока действует на еди-
единичный магнитный полюс, аналогична нашей частной
скорости 2irv', напряженность магнитного поля (сила,
с которой вся система токов действует на единичный
магнитный полюс) с точностью до множителя 2чг соот-
соответствует суммарной скорости течения v = 2v'. Точно
так же, как система электрических проводников окру-
окружена магнитными силовыми линиями, система вихревых
трубок окружена соответствующими гидродинамическими
линиями тока.
Заметим здесь, что эта аналогия соответствует той
связи, которая выражается соотношением, приведенным
на стр. 140, так как скорость течения v связывается
с напряженностью магнитного поля, а вращение (там у,
здесь w)—с напряженностью электрического поля.
Электромагнитные соотношения выглядят особенно
просто, если мы перейдем к линейным проводникам, т.е.
к проводникам достаточно малого поперечного сечения.
Им соответствуют в гидродинамике введенные на стр. 171
13 а. Зоммерфельд
194 Гл. IV. Теория вихрей
вихревые нити, которыми мы займемся в двух следую-
следующих параграфах.
6. Граничные задачи в случае жидкостей, занимаю-
занимающих ограниченный объем. В случае жидкости, распре-
распределенной по всему пространству, определение поля тече-
течения представляло собой задачу суммирования, а именно
вычисление векторного потенциала А путем простого ин-
интегрирования по всем вихрям, распределение которых
предполагалось заданным. При этом скалярный потен-
потенциал Ф не играл никакой роли, так как течение пред-
предполагалось свободным от источников. Другое дело в
случае жидкости, занимающей конечный объем. Здесь
надо принимать во внимание граничные условия на
поверхности для давления (например, /? —О на свобод-
свободной поверхности) и скорости (например, vn = 0 у твердой
стенки). Если в течении имеются источники, то их надо
исключить из области, где выполняются уравнения Эйлера,
и ограничивающие их поверхности рассматривать как
граничные поверхности жидкости. Простое представле-
представление А в виде интеграла становится недействительным,
и в дополнение к А появляется скалярный потенциал Ф
(см. выше п. За). Если имеются граничные условия, то
приходится решать граничную задачу, что не может быть
сделано путем простого суммирования вихрей и источ-
источников, а нуждается в таких вспомогательных методах
теории функций, которые соответствуют заданным гра-
граничным условиям (например, в двухмерном случае—кон-
случае—конформные отображения).
§ 21. ПРЯМОЛИНЕЙНЫЕ ПАРАЛЛЕЛЬНЫЕ ВИХРЕВЫЕ НИТИ
Рассмотрим двухмерную задачу. Задано некоторое
количество прямолинейных вихревых нитей, направлен-
направленных перпендикулярно к плоскости ху. Как они будут
взаимодействовать друг с другом в течение некоторого
промежутка времени? Для этого нам придется заняться
динамикой вихрей, в- то время как при нахождении поля
скоростей мы рассматривали только кинематическую сторо-
сторону теории вихрей. Основу динамики вихрей составляет тео-
теорема Гельмгольца из § 18, согласно которой вихревое
движение, связанное с жидкими частицами, перемещается
§ 21. Прямолинейные параллельные вихревые нити 195
вместе с ними, не меняя своей интенсивности. Если из-
известна скорость, с которой частицы нашей вихревой нити
движутся под влиянием других вихревых нитей, то из-
известна также скорость^ движения вихревой нити и харак-
характер изменения ее формы; однако в нашем двухмерном
случае вихревые линии остаются прямолинейными, т. е.
не меняют своей формы. Таким образом, динамика и ки-
кинематика вихревых нитей непосредственно связаны.
1. Единичная вихревая нить
Ее поле скоростей ничем не отличается от поля ско-
скоростей простого вихря [см. равенства A9.7), A9.7а)
и A9.76)]:
Ф-f ;? = Шп(ж+ iy), B1.1)
v = vv = -gradS^y^. B1.1a)
Линии тока представляют собой окружности с центром
в начале координат; источник вихря не принимает уча-
участия в течении.
Посмотрим, как связано поле этого течения с законом
Био—Савара, о котором говорилось в предыдущем пара-
параграфе. Для этого оставим пока нашу комплексную пло-
плоскость х -\- iy и рассмотрим координату z вдоль вихревой
нити — со < z < + °°- Пусть х, у, 0 и 0, 0, z соответ-
соответственно координаты точки поля и точки, пробегающей
вихревую нить, по которой мы будем интегрировать.
Элемент длины, который мы раньше обозначали через | As |,
будет теперь равен dz. Расстояние от элемента длины до
некоторой точки поля, которое раньше называлось г,
назовем теперь
так что обозначение г сохраняется для двухмерного рас-
расстояния в плоскости ху соответственно равенству B1.1а).
Вычисляя векторное произведение, получим из равенств
B0.17) и B0.19)
\ —^, B1.2)
13*
196 Гл. IV. Теория вихрей
в то время как vz, очевидно, равно нулю. Согласно из-
известной формуле, неопределенный интеграл
С dz —
Отсюда для определенного интеграла имеем
а
\ у '-= In (а + ]/ > + а ) - In г
о ' r ~^~z
и, дифференцируя по г, получаем
а
С dz r
— у \ — —.
О
если а —> оо, то первый член справа исчезнет, и мы
получим
+ ОО СО
dz г,
—со * Tz ) 0
Равенство B1.2) даст тогда
z^^. ч- tc/«. = ^ , Z/::=z z^tn :=г — , (Zii.^ai
Л • у гтг р& ' т ТС/*
что совпадает по величине и направлению с векторным
равенством B1.1а).
Если мы обозначим вектор длины (х в направлении
оси z, т. е. вихревой нити, через р, а радиус-вектор
точки х, у в плоскости ху—через г, то вместо B1.2а)
можно написать
v = ^j[jir]. B1.26)
Действительно, вычисленные отсюда компоненты vz и vy
совпадают со значениями vx и vy из B1.2а). Формула
B1.2а) отличается от B0.17) для v' в трехмерном слу-
случае отсутствием множителя 2, который имеется в левой
части B0.17), а также тем, что вместо г3 в правой части
стоит г2. Указанные отличия обусловлены тем, что мы
проделали интегрирование по z.
§ 21. Прямолинейные параллельные вихревые нити
197
2. Две вихревые нити равной интенсивности
с цротивоположными или одинаковыми знаками
Случай двух вихревых нитей с противоположным
направлением вращения уже рассматривался в равен-
равенствах A9.12) и далее. Из равенства A9.14), а также
непосредственно из фиг. 29а следует, что скорость vx,
*'/?-
f
^м с :>^
V.
Фиг. 29а.
Две параллельные вихревые нити
равны по интенсивности и противо-
противоположны по знаку. Их плоскость сим-
симметрии может быть заменена твердой
стенкой.
Ф и г. 296.
Две вихревые нити, равные по
интенсивности и по знаку, дви-
двигаясь по окружности, располага-
располагаются на противоположных концах
ее диаметра.
которую пить Fx сообщает F2, равна по величине и на-
направлению скорости v2, которую нить F2 сообщает Fv
т. е.
Z71=Z79=^ = Z7. B1.3)
1 2 2пс ч
С другой стороны, скорость v0 в точке М (середина пря-
прямой, соединяющей Fx с F2), вызванная действием Fx
и F2, равна
B1.3а)
Следовательно, обе вихревые нити движутся с одной
и той же скоростью v. Жидкость протекает между ними
с большей скоростью, но в том же направлении, в кото-
котором движутся Fx и F2. В точках, лежащих на продол-
продолжении линии их соединения, справа или слева от нее,
198 Гл. IV. Теория вихрей
жидкость течет в противоположном направлении (вблизи
F1 и F2 с весьма большой скоростью).
Не только в точке М, но и во всех точках перпен-
перпендикуляра М'М" к середине отрезка F1 F% равнодействую-
равнодействующая скоростей частиц, сообщенных им со стороны F1 и F2,
направлена вдоль этого перпендикуляра. Поэтому мы
можем заменить его твердой стенкой, ибо в этом случае
удовлетворяется соответствующее граничное условие (об-
(обращение в нуль нормальной составляющей скорости).
Изолированная, первоначально покоящаяся вихревая
нить, если к ней приблизить стенку, начинает двдгаться
параллельно этой стенке, причем с тем большей скоро-
скоростью, чем ближе к ней будет помещена стенка. Можно
говорить, что в этом случае на нее действует вообража-
воображаемое зеркальное изображение в этой стенке. Подробнее
это показано в несколько более сложном случае, изобра-
изображенном на фиг. 31.
Случай двух вихревых нитей одного знака описывается
равенством A9.12), при этом изменяется знак у второго
члена правой части. На фиг. 296 видно, как нити будут
в этом случае влиять друг на друга. Нить F1 сообщит
нити F2 скорость, равную по величине и противополож-
противоположную по знаку той, которую F2 сообщает F1. Величина
ее равна v из равенства B1.3). В то время как F1 на на-
нашем рисунке сместится вниз по окружности радиуса с,
F2 сместится на такое же расстояние вверх. Диаметр
Fx F2 будет при этом вращаться вокруг неподвижного
центра М. Поэтому обе вихревые нити будут двигаться
по одной окружности, располагаясь в диаметрально про-
противоположных точках.
3. Теорема о центре тяжести двух и более
вихревых нитей
Если две вихревые нити имеют две различные интен-
интенсивности \i1 и fi2, то точки F1 и F2 будут, вообще гово-
говоря,, двигаться по окружностям, которые теперь имеют
различные радиусы. Их общий центр будет являться цент-
центром тяжести [Xj и [х2, если \хг и [х2 представлять себе как
массы, расположенные в Fx и F2. Этот центр тяжести
располагается4 внутри линии, соединяющей Fx и Fs, если
§ 21. Прялюлинейные параллельные вихревые нити
199
\ьх и |х2 имеют одинаковый знак (фиг. 30, а), или снару-
снаружи ее, если \ix и [х2 имеют разные знаки (фиг. 30, б).
В последнем случае при определении центра тяжести
одна из масс считается отрицательной. Оба рисунка сде-
сделаны в предположении, что \i2 > р.х, т. е. |[л-21 >fii-
Можно построить изображенный на фиг. 30,а (\1г и \ь2
имеют одинаковое направление вращения) общий центр
окружностей, описываемых точками Fx и F2, если конец
вектора vx, приложенного в Fx, соединить с концом v2,
Фиг. 30.
Две прямолинейные вихревые нити произвольной интенсивности описы-
описывают окружности вокруг общего центра тяжести, который располагается
между ними или снаружи, в зависимости от того, одинаковы пли раз-
различны знаки у вихревых нитей.
приложенного в F2, и найти ючку пересечения S с линией,
соединяющей Fx с F2. Так как скорость v1 вызвана вих-
вихревой нитью F2, a v2 ~ нитью Fx, то очевидно, что
B1.4)
Из подобия обоих треугольников с катетами vx и
можно найти положение точки S:
SFj SF2
откуда, согласно B1.4),
таким образом, точка S действительно является центром
тяжести p-j и fi2,
200 Гл. IV. Теория вихрей
На фиг. 30,6 произведено подобное построение для
случая противоположных направлений вращения, так
что fi2 рассматривается как отрицательная масса. В пре-
предельном случае, когда IfJ^^fh» точка S уходит в беско-
бесконечность: обе окружности переходят в параллельные пря-
прямые, т. е. мы приходим к первому случаю, рассмотрен-
рассмотренному в разделе 2 данного параграфа. Точно так же рас-
рассмотренный там второй пример является предельным
случаем движения, изображенного на фиг. 30, а (если
окружности равны).
При этом следует заметить, что построенная нами
точка представляет собой только воображаемый центр
тяжести интенсивностей \ix и [х2 вихрей, и, конечно, если
его рассматривать как материальную точку жидкости,
то он не остается в покое. Действительно, в случае, изо-
изображенном на фиг. 30, а, его скорость будет
K-i У-% __ Ул f a V-jSF\
Согласно определению центра тяжести B1.5), выраже-
выражение в скобках равно
Таким образом, центр тяжести, понимаемый как частица
жидкости, ни в коем случае не имеет скорости, равной
нулю. Точно так же при обобщении теоремы о центре
тяжести, к которой мы сейчас перейдем, покоящийся
центр тяжести не означает того, что связанная с ним
жидкая частица находится в покое.
Рассмотрим произвольное количество вихревых нитей
Fx F2 . .. Fi ... Fk. Используя представление B1.26),
напишем выражение скорости v, вызванной нитью Fi
в некоторой точке Р:
где г — г{ — радиус-вектор из F{ в точку Р\ его роль
здесь аналогична роли радиус-вектора г в B1.26). Пусть
Р совпадает с Fk; просуммируем теперь по всем i, кроме
i — k, так как F^ не сообщает сама себе никакой ско-
§ 21. Прямолинейные параллельные вихревые нити 201
рости. (В нижеследующих уравнениях такое суммирова-
суммирование будем обозначать штрихом у знака 2-) В результа-
результате получим:
Упростим способ записи, для чего введем следующие
обозначения:
eife = ^i-=-efei, B1.7a)
где eih — единичный вектор в плоскости ху. Введем далее
единичный вектор е, перпендикулярный к плоскости ху,
который, совпадая по направлению с р,, позволяет выра-
выразить jii следующим образом:
Тогда равенство B1.7) запишется следующим образом:
Ч^Е'^1^- B1-76)
г
Теперь образуем выражение
"Ч^1^- B1-8)
k i
В двойной сумме справа вектор eih, а следовательно, и
[eeik] антисимметричны по г и Л, в то время как ^{^k
и rik, конечно, симметричны. Поэтому члены в двойной
сумме попарно уничтожаются и мы имеем
S № = <>• B1-9)
По этой же причине исчезнет также скорость центра
тяжести нашей системы вихрей vs (конечно, воображае-
воображаемая, а не материальная)
Il =0 B1.10)
202 Гл. IV. Теория вихрей
4. Закон площадей для системы вихревых линий
В определенном смысле здесь существует аналогия
с законом площадей в аналитической механике, посколь-
поскольку момент импульса системы вихрей также сохраняется
постоянным (в отсутствие внешних сил).
Определим импульс отдельной вихревой нити как
произведение (xfevfe и момент импульса всей системы вих-
вихрей, взятый относительно произвольно расположенного
начала координат О как
Подставив значение vh из- B1.76), получим
/I i
Переставляя индексы суммирования i и к и учитывая
антисимметричный характер eih, получим также, что
4'eeife]]. B1.11а)
Пк
Взяв полусумму B1.11) и B1.11а) и учитывая определе-
определение eik в B1.7а), имеем
S. B1.116)
k i
Теперь, согласно известной векторной формуле1),
[eife [eejh]] = e (eikeik) - eik (eeifc). B1.12)
Здесь первое скалярное произведение равно единице (elk —
единичный вектор!), второе равно нулю (е перпендику-
перпендикулярно к eih!). Правая часть B1.12), таким образом, не
зависит от ? и А:, а именно она равна е. При этом B1.116)
преобразуется к следующему виду:
B1ЛЗ)
l) См. «Механика» (т. I), равенство B4.7).
§ 21. Прямолинейные параллельные вихревые нити 203
5. Общие замечания о динамике вихрей
Как было показано ранее, динамика вихрей довольно
своеобразна и во многом отличается от динамики точеч-
точечных масс.
Уже первый закон Ньютона здесь изменяется. Изоли-
Изолированный вихрь (т. е. такой вихрь, на который не дей-
действуют силы) пребывает в состоянии покоя; равномерное
прямолинейное движение имеет место только при нали-
наличии второго вихря такой же интенсивности с противопо-
противоположным направлением вращения или при взаимодействии
с твердой стенкой.
Принцип относительности классической механики,
согласно которому покой и равномерное движение экви-
эквивалентны друг другу, здесь теряет сил. Это, конечно,
вызвано тем, что жидкость, в которой имеется вихрь,
по отношению к нему является избранной системой от-
отсчета.
Еще более разительно отличие во втором законе.
Внешнее воздействие, исходящее в данном случае от
другого вихря, является здесь причиной не ускорения,
а скорости. Соответственно этому меняется также закон
о движении центра тяжести: равно нулю не ускорение
центра тяжести, а его скорость. Что касается закона
площадей, то здесь, как и в случае системы масс, кото-
которая не подвергается воздействию внешних сил, момент
импульса системы вихрей остается постоянным, однако
постоянная однозначным образом определяется из равен-
равенства B1.13) через интенсивности вихрей, в то время как
для системы масс она представляет собой постоянную
интегрирования, которая может принимать произвольные
значения.
6. Атмосферные вихри
На первый взгляд кажется невозможным экспери-
экспериментально осуществить бесконечно длинные вихревые
нити. Однако еще Гельмгольц заметил, что в слое жидко-
жидкости, ограниченном двумя параллельными плоскостями,
расположенными перпендикулярно к вихревой нити,
может быть получено точно такое вихревое движение,
204 Гл. IV. Теория вихрей
как в случае жидкости, занимающей -все бесконечное
пространство.
Подобным слоем жидкости является наша атмосфера,
если пренебречь несущественной для этого случая кривиз-
кривизной поверхности Земли. Действительно, смерчи (воздуш-
(воздушные и водяные столбы) и торнадо можно представлять
себе как увеличенные изображения рассмотренных здесь
вихревых нитей (их диаметр равен 5 — 500 м), в то вре-
время как атмосферные циклоны и антициклоны, горизон-
горизонтальные размеры которых (диаметр больше 1000 км)
во много раз больше их вертикальной протяженности
A0—15 км), соединяют в себе свойства как вихрей,
так и волн.
В приложении к метеорологии классическая теория
вихрей развивается в двух направлениях. Нормальное
состояние атмосферы представляет собой не состояние
покоя, а равномерного вращения. С точки зрения наблю-
наблюдателя, находящегося на Земле, мы не можем теперь,
как мы делали раньше в этой главе, рассматривать
жидкость как не подвергающуюся воздействию внешних
сил, а должны учесть силу Кориолиса1), или же рас-
рассматривать не относительное, а абсолютное вихревое
движение.
К этой динамической поправке добавляется еще термо-
термодинамическая, связанная со сжимаемостью воздуха: плот-
плотность воздуха связана с его давлением уравнением со-
состояния p = F(р, Т, ...), куда входит не только давле-
давление, но и температура Т, а возможно, и другие пере-
переменные (например, влажность). Поэтому rot [(l/p)grad р],^
вообще говоря, не исчезнет и, следовательно, будет пред-
представлять собой силу, вызывающую исчезновение или воз-
возникновение вихрей.
Оба эти направления развития классической теории
вихрей мы встречаем в метеорологической литературе,
где рассматриваются и формулируются более общие за-
законы вихревого движения (Бьеркнес, Эртель2)).
х) См. «Механика» (т. I), гл. V.
2)Bjerknes V., Meteorol. Zs., 7 и 145 A900), а также 96
A902); Ertel H., Phys. Zs., 526 A942), а также Meteorol. Zs.,
277 и 385 A942).
§ 22. Кольцевые вихри
205
§ 22. КОЛЬЦЕВЫЕ ВИХРИ
В противоположность прямолинейным вихрям замкну-
замкнутые вихри, в частности имеющие форму круглого коль-
кольца, очень легко воспроизвести в малом масштабе. Не толь-
только курильщик знает о них и любит их пускать, но их
можно видеть также над дымовыми трубами. Кольцевые
вихри легко воспроизвести: проделаем в .передней стенке
картонного ящика круглое отверстие, а вместо задней стен-
стенки натянем кусок полотна. Внутри
поместим две чашечки, одну с соля- 7
ной кислотой, другую с нашатырным
спиртом. При этом ящик наполнится
м>
и.
а ' и
Фиг. 31. Кольцевые вихри.
а—схематическое изображение воз-
возникновения вихря при прохождении
струи дыма через отверстие; б-схема
движения вихря при приближении
к плоской стенке.
Фиг. 32.
При приближении
кольцевого вихря к
параллельной ему
плоской стенке он
расширяется; ско-
скорость его движения
падает.
густым дымом хлористого аммония. Щелкая по задней
стенке, мы будем выталкивать дым из отверстия, причем,
проходя мимо краев отверстия, он будет завиваться в виде
кольцевого вихря (фиг. 31, а). Возникший таким образом
вихрь может пройти по прямой линии расстояние, равное
многим метрам, с довольно значительной скоростью.
Согласно основной теореме (см. стр. 167), вихри свя-
связаны с материальными частицами и поэтому увлекают
с собой частицы воздуха; это можно заметить, если на
пути вихря поставить свечу. Она будет с тихим свистом
задута «вихревым ветром». Если уменьшить круглое
отверстие, а вместе с ним и радиус возникающего вихря,
206
Гл. IV. Теория вихрей
то его скорость увеличится. Если круглое отверстие
заменить прямоугольным, то в первоначально прямо-
прямоугольном вихре возникнут правильные колебания, кото-
которые будут стремиться придать вихрю форму окружности;
именно эта форма будет устойчивой, в то время как
прямоугольная форма является неустойчивой. Если коль-
кольцевой вихрь приближается к стенке, параллельной пло-
плоскости окружности, то его радиус будет увеличиваться
(см. фиг. 32).
Можно проделать следующий опыт, который плохо
удастся воспроизвести с помощью нашего прибора, но
Фиг. 33.
Схематическое изображение двух вихрей, движущихся друг за
другом; изменяя свои размеры, они проходят друг сквозь друга.
который удастся опытному курильщику: маленький вихрь
выпускается - вслед за большим. Благодаря большей ско-
скорости он догонит первый вихрь и пройдет сквозь него.
После этого маленький вихрь увеличится, а большой
уменьшится. Теперь второй будет двигаться быстрее,
так что он сможет пройти через первый. Теоретически
эта игра может повторяться много раз. Этот опыт нагляд-
нагляднее можно произвести с каплями окрашенной жидкости,
которые падают из пипетки на поверхность воды. Когда
капля упадет на поверхность, она превратится в вихре-
вихревое кольцо и, погружаясь в воду, будет одновременно
расширяться. Следующая капля и возникающее из нее
вихревое кольцо, которое сначала будет маленьким, до-
догонит большее и т. д. Такой эксперимент позволяет на-
наблюдать многократное прохождение вихрей друг через
друга (фиг. 33).
§ 22. Кольцевые вихри 207
Для объяснения приведенных выше опытов обсудим
некоторые вопросы, на которые можно ответить путем
элементарных рассуждений. Сюда не входит обратное
действие вихревого кольца самого на себя, вследствие
чего мы в дальнейшем можем рассматривать вихрь как
бесконечно тонкую нить.
В основу рассмотрения положим формулу B0.17),
аналогичную закону Био —Савара. Эта формула опреде-
определяет вклад скорости v', который сообщает какой-либо
точке отдельный вихревой элемент (хДя. Если в качестве
этой точки выбрать центр М вихревого кольца, то все
эти вклады будут равны по величине и направлению.
Если а —радиус кольца, то, согласно B0.17), получаем
, iiAs
v =
Отсюда, суммируя по всем As, получим скорость центра vM
Таким образом, скорость точки М возрастает с убыва-
убыванием а. Как было упомянуто раньше и как будет дока-
доказано ниже, скорость движения вихревого кольца как
целого также увеличивается с уменьшением а.
Если в качестве рассматриваемой точки выбрать произ-
произвольную точку А оси, проходящей через центр круга
и отстоящей от него на расстоянии z (расстояние ее от
точек кольца будет при этом равно г = \/ a2-\-z2), то v'
можно разложить на аксиальную и боковую компонен-
компоненты, причем последняя взаимно уничтожится со вкладом
диаметрально противоположного вихревого элемента.
Аксиальная компонента v' равна
v —.
г
Из B0.17) при суммировании по всем As следует
/S^W^- B2.2)
*~i г3 r (a2-\-z2) l2
Таким образом, скорость на оси падает по обе стороны
от точки М и при неограниченном возрастании z стре-
стремится к нулю.
208 Гл. IV, Теория вихрей
В случае произвольного положения рассматриваемой
точки скорость v не может быть получена из v' путем
элементарного суммирования; при этом задача сводится
к интегралам эллиптического типа. То же самое, как
известно, получается при вычислении магнитного поля,
создаваемого круговым током.
С другой стороны, некоторые из вышеописанных явле-
явлений могут быть объяснены качественным образом.
На фиг. 31, а схематически изображено возникнове-
возникновение вихря при истечении из отверстия в стенке ящика,
а на фиг. 31, б —его приближение к стенке, параллельной
плоскости кольцевого вихря. На этой плоскости выпол-
выполняется граничное условие vn = 0. Оно может быть удов-
удовлетворено, если воспользоваться методом зеркальных
изображений, согласно которому представим себе, что
помимо реально существующего вихря, находящегося
слева от стенки, имеется справа от стенки воображае-
воображаемый вихрь, так что наше гидродинамическое поле, огра-
ограниченное стенкой, можно теперь считать простирающимся
по всему пространству. При этом частице воздуха,
находящейся по соседству со стенкой, будет сообщаться
скорость vi от реального вихря [Xj и скорость v? от
воображаемого вихря (а2; причем, согласно формуле
B0.17), обе скорости будут перпендикулярны к соответ-
соответствующим радиус-векторам г{ и осям вихрей {xi# Обе
составляющие скоростей \[ и \'2 при сложении, очевид-
очевидно, приведут к движению, параллельному стенке, т. е.
наше граничное условие vn — 0 будет выполнено. Это
относится не только к изображенным на фиг. 31 (вверху
или внизу) вихревым элементам, но и к любым двум
элементам, расположенным зеркально друг к другу.
Выясним теперь, какое действие на наш реальный
вихрь оказывает его зеркальное изображение1), напри-
меряна верхнюю точку вихря ^ (см. фиг. 31,6). Силь-
Сильнее' всего на нее будет действовать ближайший к ней
элемент вихря (х2 (также расположенный вверху).
х) С физической точки зрения тут, конечно, может идти речь
только о действии стенки. Однако мы убедились, что это действие
может быть также правильно описано заданием воображаемого зер-
зеркального изображения нашего вихря.
§ 22. Кольцевые вихри 209
Согласно B0Л7), он сообщит верхней точке |хх скорость,
направленную вертикально вверх, которая графически
изображена на фиг. 31 вертикальной стрелкой слева
вверху. Все другие точки вихря (х2 будут частично усилить
это действие, а частично, как, например, нижняя точка
вихря {х2 (см. фиг, 31,6), ослаблять его, но в значительно
меньшей степени. То же самое рассуждение, применен-
примененное к нижней точке вихря {х17 позволяет определить на-
направление скорости, которая изображена на фиг. 31,6
внизу слева вертикальной стрелкой, направленной вниз.
Соответствующими вертикальными стрелками показано
на фиг. 31, б также действие реального вихря на его
зеркальное изображение.
Таким образом, наш,реальный вихрь при приближе-
приближении к стенке будет увеличиваться в силу гидродинами-
гидродинамического воздействия его зеркального изображения. То
же самое можно сказать о зеркальном изображении.
С увеличением радиуса кольца соответственно будет за-
замедляться скорость движения вихря по направлению
к стенке, так как, согласно вышесказанному, поступа-
поступательное движение вихря в основном происходит со ско-
скоростью, обратно пропорциональной его радиусу (это
утверждение уже было нами высказано, но не было еще
доказано). Таким образом, вихрь, не успев дойти до
стенки, будет становиться все больше и все слабее, пока
не исчезнет на бесконечности (см. по этому поводу
фиг. 32, где горизонтальные стрелки характеризуют
поступательное движение).
Попытаемся объяснить с помощью тех же качествен-
качественных методов прохождение двух вихрей друг сквозь
друга (см. фиг. 33). На фиг. 33, а радиусы и поступатель-
поступательные скорости обоих вихрей равны; так как они были
получены один за другим с помощью одного и того
же устройства; их направления вращения совпадают
(наоборот, на фиг. 31,6 направления вращения обоих
вихрей различны в силу того, что один является зер-
зеркальным изображением другого). Действие обоих вихрей
друг на друга будет состоять в этом случае в расшире-
расширении переднего и одновременном сужении заднего вихря;
это показано на фиг. 33, а вертикальными стрелками.
На фиг. 33, б и 33, в изображены вихри до и после про-
14 А. Зоммерфельд
210 Гл. IV. Теория вихрей
хождения друг сквозь друга; это прохождение оказывается
возможным в результате того, что у вихря, движущегося
позади, скорость больше (см.. горизонтальные стрелки
на фиг. 33, б). Вертикальные стрелки на фиг. 33, в пока-
показывают, как вихри будут действовать друг на друга
после прохождения: передний будет расширяться, а зад-
задний—сужаться, в то же время передний будет замед-
замедляться, а задний — ускоряться. Результат, изображен-
изображенный на фиг. 33, г, представляет собой повторение фиг. 33, а,
так что описанный процесс может начаться снова.
Однако эти качественные методы рассмотрения не смо-
смогут ничего объяснить, если мы попытаемся рассмотреть
обратное действие вихря самого на себя. Сюда относится
прежде всего вопрос о поступательном движении кольце-
кольцевого вихря. Чтобы его определить, необходимо предполо-
предположить, что поперечное сечение вихревого кольца имеет
конечные размеры, например представляет собой круг ра-
радиуса с, много меньшего чем а. Можно считать, что внутри
этого круга распределен конечный (например, постоян-
постоянный) вихрь скорости о>; интенсивность вихря (а, которую
мы раньше относили к вихревой нити, выразится теперь
через со следующим образом:
Лучше всего воспользоваться функцией тока W из A9.24),
причем так как с <С «, то можно кольцевой вихрь при-
приближенно рассматривать как прямолинейный вихрь.
Тогда внутри поперечного сечения вихря функция W
будет удовлетворять неоднородному дифференциальному
уравнению, левая часть которого совпадает с A9.26):
Уже у Гельмгольца имеется выражение функции W в ви-
виде полных эллиптических интегралов первого и второго
рода, которое справедливо для точек, расположенных
вне поперечного сечения вихря. Основанное на нем вы-
вычисление поступательной скорости вихря vE не только
связано с математическими трудностями, но и не совсем
правильно с физической точки зрения, поэтому мы его
§ 22. Кольцевые вихри 211
опускаем. В результате этого вычисления получается1)
причем слагаемое х/4 в скобках не вполне определено w
том смысле, что оно зависит от предполагаемого распре-
распределения интенсивности вихря по сечению. Равенство B2.3)
устанавливает зависимость, неоднократно использован-
использованную в наших рассуждениях, а именно, что ve растет
с убыванием а и падает с ростом а. Правда, в B2.3)
входит физически неопределенная величина а/с, которая
делает результат несколько иллюзорным. Сравнение B2.3)
с B2.1) показывает, что ve может быть больше или мень-
меньше .Vm, в зависимости от выбора этой величины.
Совершенно аналогичные трудности и формально точ-
точно такая же формула, как B2.3), появятся при вычисле-
вычислении самоиндукции провода, но с той существенной раз-
разницей, что в электрической задаче радиус провода с
имеет, конечно, вполне определенный физический смысл.
Как устранить эту неопределенность в случае кольце-
кольцевого вихря? Это можно было бы сделать только пу-
путем более подробного изучения образования вихря на
краях круглого отверстия. При этом мы если и не полу-
получим определенного радиуса с, то по крайней мере опре-
определим убывающее из середины наружу распределение со
по поперечному сечению. Но подобное исследование было
бы весьма трудоемким и явно не стоило бы затраченного
труда. Поэтому нам придется оставить интересную и пло-
плодотворную теорию кольцевых вихрей незавершенной
в весьма существенном отношении.
Чтобы сделать более понятным поступательное движе-
движение кольцевого вихря, мы сравним его еще с поступа-
поступательным движением пары прямолинейных вихрей (см.
§ 21, фиг. 29а). Эта пара вихрей получается геометри-
геометрически из кольцевого вихря, если рассматривать только
два диаметрально расположенных вихревых элемента, а
в качестве их продолжения вместо остальных вихревых
*) Критический обзор литературы см. в статье: Love А. Е.
Encykl. d. Math. Wiss., Bd. IV, 3, S. 118.
14
212 Гл. IV, Теория вихрей
элементов вообразить бесконечные пераллельные прямые
нити. Несмотря на это довольно внешнее сходство, посту-
поступательное движение пары прямолинейных вихрей весьма
сходно с движением кольцевого вихря. Если в равенст-
равенстве B1.3) половину расстояния между вихрями, обозна-
обозначенную через с, заменить на а (радиус кольцевого вихря),
то получим для поступательного движения
Это выражение представляет собой первый множитель
в правой части нашего равенства B2.3), определяюще-
определяющего ve- Скорость v направлена перпендикулярно к пло-
плоскости, проходящей через пару вихрей. Соответственно
и скорость Ve также направлена перпендикулярно к пло-
плоскости кольцевого вихря.
Во время гребли можно заметить, что в том месте,
где весло выходит из воды, образуются маленькие углуб-
углубления на поверхности — мы назовем их «вихревыми впа-
впадинами»,—которые пробегают по поверхности воды. Они
представляют собой концы вихревых дуг, которые обра-
образуются вслед за веслом при его прохождении через воду.
Чашеобразная форма этих углублений обусловлена тем, что
поверхность вращающейся жидкости должна располагать-
располагаться перпендикулярно к равнодействующей центробежной
силы и силы тяжести, подобно тому, как в случае отсут-
отсутствия вращения, поверхность жидкости перпендикулярна
к направлению силы тяжести. В то время как при вра-
щении жидкой массы с постоянной угловой скоростью о>
поверхность, как известно, принимает форму параболои-
параболоида, в данном случае ввиду быстрого падения угловой
скорости со при удалении от центра вихря и ее полного
исчезновения на некотором конечном расстоянии в жид-
жидкости образуются углубления только возле конца вихре-
вихревой нити. Они могут быть описаны как водовороты или
«вихревые впадины». Эта пара вихревых воронок пробе-
пробегает по воде с такой же скоростью, с которой происхо-
происходит поступательное движение соединяющей их вихревой
дуги.
Так как путем оптических исследований (по эффекту
Зеемана) установлено, что на солнечных пятнах имеются
§ 22. Кольцевые вихри 213
интенсивные вихревые движения солнечной материи, то
можно заключить, что здесь расположены концы вихре-
вихревых нитей, проходящих внутри Солнца; можно также
предположить, что для каждого солнечного пятна имеется
противоположное пятно с обратным направлением вра-
вращения, которое связано с первым вихревой нитью, про-
проходящей внутри Солнца и имеющей приблизительно
полукруглую форму. Конечно, при этом следует при-
принять во внимание, что солнечное вещество не является
идеальной невязкой жидкостью, так что такое перенесе-
перенесение представлений о вихревых движениях на Солнце
.является довольно рискованным.
• Глава V
ТЕОРИЯ ВОЛН
С давних пор в качестве модели физических пред-
представлений, связанных с теорией волн, использовались
волны на воде, несмотря на то, что они представляют
собой значительно более сложное явление, чем акусти-
акустические или оптические волны. Волны на воде —это по-
поверхностные волны, т. е. они связаны с поверхностью
раздела двух сред, в то время как обычные акустические
и оптические волны являются пространственными вол-
волнами.
Между вихрями и волнами имеется существенное раз-
различие: вихри увлекают с собой вещество, а при волно-
волновом движении частицы жидкости в среднем остаются на
месте.
По своей симметрии волны на воде разделяются на
плоские, кольцевые, имеющие круговую симметрию,
корабельные и волны Маха. Прежде всего рассмотрим
простейший тип плоских бегущих волн.
В зависимости от природы вызывающих их сил эти
волны разделяются на гравитационные и капиллярные.
Гравитационные волны являются волнами большого
масштаба; их обычно и имеют в виду, когда говорят
о волнах на воде.
§ 23. ПЛОСКИЕ ГРАВИТАЦИОННЫЕ ВОЛНЫ
В ГЛУБОКОЙ ВОДЕ
Рассмотрим чисто периодические волны; при этом
точно так же, как и на стр. 125, зависимость от времени
будем представлять в виде
§ 23. Плоские гравитационные волны в глубокой воде 215
причем волны, зависящие от времени каким-либо иным
образом, могут быть получены путем наложения волн
с различной круговой частотой со (см. § 26).
Далее, будем предполагать, что ветер, сотрясения
и др. сообщают воде волновые движения, выводя ее из
состояния покоя. В задаче 3 гл. VI мы рассмотрим,
при каких условиях ветер, дующий вдоль горизонталь-
горизонтальной поверхности воды, может привести ее в волновое
движение. Так как жидкость предполагается невязкой,
а в качестве единственной действующей силы в этом
и следующем параграфах будем рассматривать потен-
потенциальное поле тяжести, то, согласно § 18, движение
будет обладать потенциалом скоростей Ф, который
в случае плоской волны зависит только от двух про-
пространственных координат х ж у (х— направление распро-
распространения, у— направление вглубь от поверхности) и не
зависит от третьей пространственной координаты z, на-
направленной горизонтально и перпендикулярно к направ-
направлению распространения. Таким образом, по отношению
к пространственным координатам функция Ф является
двухмерным потенциалом и, согласно § 19, для несжи-
несжимаемой жидкости имеет форму
f(x±iy).
Пусть для оси у направление вниз является положи-
положительным. Поскольку мы хотим получить цуг волн, рас-
распространяющийся в положительном направлении оси х,
то необходимо предположить наличие тригонометрической
зависимости / от х, или, что одно и то же, зависимости
в виде комплексной показательной функции. При этом воз-
возможны следующие случаи:
Ф = / (ж -f iy) е~ш = AeWx-^V e~hv B3.1)
или
здесь к — волновое число, причем
где X —длина волны, а т — период колебаний.
B3.2)
216 Гл. V. Теория волн
Предположим, что вода имеет бесконечно большую
глубяну. Это означает, что координата дна г/ — h по
сравнению с X очень велика.
Для дна будем иметь
/h/ = ^_>oo. B3.2а)
Отсюда следует, что предположение B3.1а) несправед-
несправедливо, так как в результате мы получим на дне беско-
бесконечно большие амплитуды скорости. Напротив, предпо-
предположение B3.1) удовлетворяет всем требованиям, которые
мы до сих пор накладывали на наши волны, распро-
распространяющиеся в глубокой воде. Естественно, как только
это потребуется, мы можем от нашего комплексного
представления перейти к действительному представлению
(взяв действительную часть комплексной величины).
Выражение B3.1) содержит три параметра: А, со и к.
А — амплитуда волны при у = 0 и, подобно круговой
частоте со, зависит от способа возбуждения; поэтому обе
эти величины могут задаваться произвольно. Напротив,
величина к при этом должна быть определена, а именно
по отношению к ш. Согласно B3.2),
т. е. представляет собой скорость распространения волны.
Волновое число к можно определить из условия
р = 0 B3.4)
на свободной поверхности, где за нулевое значение
давления принято атмосферное давление. Равенство B3.4)
следует из A2.19), если пренебречь капиллярными сила-
силами (N = 0). В то время как все предыдущее рассмотре-
рассмотрение носило кинематический характер, выражение B3.4)
вносит в теорию волн элемент динамики.
Давление р связано с потенциалом Ф уравнениями
Эйлера. Воспользуемся ими здесь в наиболее удобной
интегральной форме закона Бернулли. Так как в дан-
данном случае мы имеем потенциал скоростей, зависящий
от времени, то необходимо для этого закона взять вы-
выражение A1.15). При этом квадратичный член ЛФ
§ 23. Плоские гравитационные волны в глубокой воде 217
в A1.15) можно опустить, предполагая, что амплитуд-
амплитудный множитель А есть малая величина (как это обычно
делается в механике колебаний). Тогда искомое уравне-
уравнение примет вид
~™ + jiP + U) = const; " B3.5)
как было сказано на стр. 113, здесь const есть величина,
не.зависящая от пространственных координат, но кото-
которая может зависеть от времени. В нашем случае един-
единственной функцией, зависящей только от времени pi не
нарушающей периодичности бегущей волны, является
const = F (t) = 0.
Учитывая это, а также воспользовавшись равенством
B3.4), можно упростить B3.5):
~w=T' ( 5a)
где U — потенциал силы тяжести единицы объема на
поверхности колеблющейся жидкости. Так как направ-
направление оси у вниз является положительным, то в общем
случае
U=-Pgy. _ B3.56)
Пусть у = т\ является уравнением поверхности; согласно
вышесказанному, положительные значения ч\ соответ-
соответствуют опусканию поверхности, отрицательные — подня-
поднятию поверхности. Из B3.5а) следует
ЭФ - /оо сч
Зависимость -ц от х и t имеет ту же форму, что и для
потенциала скоростей Ф, а именно:
•»l = ae*('lx-urf>. B3.7)
Введенная здесь постоянная величина а, вообще говоря,
комплексна, так как она включает в себя амплитуду
и фазу колебаний поверхности; мы считаем, что постоян-
постоянная а точно так же, как и А, мала. Подставляя B3.7)
218 , Гл. V. Теория волн
и B3.1) в B3.6) и сокращая на общий экспоненциаль-
экспоненциальный множитель, получаем
шАе-ъъ = ga. B3.8)
Разложим е—ьу по степеням к-ц и пренебрежем произве-
произведениями А-ц, Atf, .. . как членами более высокого по-
порядка. Тогда B3.8) упростится:
wA = ga. B3.9)
Это соотношение выражает связь между величинами А
и а, а не связь между к и ш, которую мы ищем. Ее
можно получить, если ввести дополнительное кинемати-
кинематическое условие. Оно весьма тривиально и состоит в том,
что движение поверхности должно совпадать с движе-
движением частиц жидкости, находящихся на поверхности,
причем здесь принимаются во внимание только состав-
составляющие этих движений в направлении нормали п к по-
поверхности (движение частиц жидкости по поверхности не
изменит формы последней и поэтому может не рассма-
рассматриваться). Если обозначить скорость поверхности через V,
а скорость частиц жидкости через v, то необходимо по-
потребовать, чтобы
Vn = vn. B3.10)
Скорость vn может быть выражена с помощью потенциала
Ф как
_ дФ
vn— — ~&г •
Однако в случае достаточно малого А (достаточно малой
амплитуды) с точностью до «ошибки в косинусе», т. е.
до величины второго порядка, можно заменить
дФ дФ ,по лг\ \
-т— на -д— . B3.10а)
On ду ч '
Соответственно для V также можно произвести замену
Vn на ^, B3.106)
т. е. выразить через скорость опускания поверхности.
Тогда из B3.10) получим
дг\ дФ
dt ду
B3.11)
§ 23. Плоские гравитационные волны в глубокой воде 219
Если сюда подставить выражения -ц и Ф из B3.7) и B3.1)
и сократить на общий экспоненциальный множитель, то
получим
— ша = кА. B3.12)
Сравнив выражения B3.9) с B3.12), сразу получим
^ = 4-=--^-. B3.13)
a ш к ч '
Отсюда можно сделать следующие выводы:
1. Величина а сдвинута относительно амплитуды А
по фазе на тс/2. Если считать А действительной, что мы
вполне можем сделать, то величина а будет чисто мни-
мнимой. Иначе говоря, прибегая к способу записи с помощью
действительных чисел и подставляя Ф, согласно B3.1),
имеем
Ф = A cos (кх — at) е-ьу, B3.14)
так что, согласно B3.7) и B3.13),
-ц = — — A sin (кх - со*) B3.14а)
о
или, опять-таки согласно B3.13),
-ц = --^А&т(кх — ы). B3.146)
2. Величины к и со связаны между собой следующим
образом:
co2 = g7L B3.15)
Поэтому, согласно B3.3), мы можем написать
/с2 к 2п
V=V-%-. B3.16)
Скорость распространения зависит от длины волны X;
волны с большей длиной волны распространяются бы-
быстрее, чем с меньшей.
Перед тем как обсудить этот результат, сделаем за-
замечание методического характера^ те, кого страшат вы-
вычисления с помощью комплексных величин, могут проде-
проделать предыдущий расчет с чисто действительными вели-
220
Гл. V. Теория волн
чинами и убедиться, что он также приведет к равенству
B3.16), хотя и несколько более сложным путем. При
этом надо выражение B3.1) заменить на B3.14), а
вместо B3.7) взять
т] = | а j cos (кх — coi -f- a),
где а — разность фаз между Ф и г\, которую надо опре-
определить.
Заключающаяся в равенстве B3.16) зависимость ско-
скорости распространения от длины волны называется
Фиг. 34. Зависимость фазовой скорости V от
длины волны X.
а—кривая дисперсии для гравитационных волн в слу-
случае A <gft; b—д^> h; с—xZh; h—глубина воды.
дисперсией (термин, заимствованный из оптики). Говорят
о нормальной" дисперсии в некоторой среде, если более
длинным волнам (красный свет) соответствует большая
скорость распространения (меньший показатель прелом-
преломления), чем более коротким волнам (фиолетовое излуче-
излучение). Таким образом, гравитационные волны в глубокой
'воде соответствуют оптическому случаю нормальной
дисперсии.
На фиг. 34 изображен график этой зависимости. Он
представляет собой обычную параболу, которая в точке
X = 0 касается оси V. Однако мы выделили только сред-
среднюю часть этой параболы (отрезок а), так как только
для нее справедливы сделанные нами предположения.
При дальнейшем возрастании, длина волны X станет
сравнимой с глубиной воды h. Но тогда наше предполо-
§ 24. Плоские гравитационные волны в мелкой воде 221
жение B3.2а) не будет справедливым. Этот случай мы
рассмотрим в следующем параграфе. С другой стороны,
для достаточно малых X причиной распространения волн
будет уже не сила тяжести, а поверхностное натяжение.
В этом случае закон дисперсии в корне изменится
(см. § 25).
§ 24. ПЛОСКИЕ ГРАВИТАЦИОННЫЕ ВОЛНЫ В МЕЛКОЙ
И В НЕ ОЧЕНЬ ГЛУБОКОЙ ВОДЕ
Будем теперь считать, что глубина воды h не беско-
бесконечно велика, а имеет конечное значение. Тогда мы уже
не сможем отбросить выражение B3.1а) как невозмож-
невозможное, а должны будем принять его во внимание наравне
с B3.1). В качестве выражения для потенциала скоро-
скоростей Ф надо взять
ф __ ci(fex-u>o {Ае-ъу + Ве+ъу}. B4.1)
Добавим к нему граничное условие на дне
vy = О или -у- = 0 для у = hi
Согласно B4.1), это условие эквивалентно равенству
__ Ae~hh + Be+kh = 0.
Чтобы удовлетворить ему, введем новую постоянную С
с помощью соотношений
откуда следует
А=уСе+№, ? = уСе-№, B4.1а)
а также
ф _ ei(fo>c-w0 ?_ /gft(h-y) _|_ e-k{h-y)} _
= ?*№*-«»>о С ch к {h - у). B4.2)
Выражение B3.7) для величины опускания поверхности
остается неизменным. Напишем его теперь в виде
ij = сеНь*-^).. B4.3)
222 Гл. V. Теория волн
Точно так же неизменными остаются динамическое усло-
условие для поверхности B3.6) и кинематическое условие B3.11).
В силу B4.2) и B4.3), если их сократить на общий
экспоненциальный множитель, они дадут для у = О
gc, B4.4)
— mc = Ckshkh. B4.5)
Для случая мелкой воды, а именно для
kh С 1, сЬЛЛ = 1, shkh = kh,
из B4.4) и B4.5) следует
или
С М-=—?-. B4.6)
с
Отсюда можно получить выражение для скорости
распространения
(О2 /
V2 = -—- = eh V = Veh B4 7V
Оно напоминает определение для скоростного напора1)
h — ¦—- .
Сходство это чисто формальное и связано только с со-
соображениями размерности.
В случае мелкой воды скорость распространения не
зависит от длины волны; в этом случае нет никакой
дисперсии.
На основании равенства B4.7) мы можем теперь
кривую, изображающую зависимость скорости v от дли-
длины волны \ (см. фиг. 34), продолжить в область боль-
больших значений \. Для X > h кривая должна приближать-
приближаться к горизонтальной асимптоте, отстоящей от оси X на
расстоянии }/gh (см. отрезок Ъ кривой на фиг. 34).
Равенства B4.4) и B4.5) отвечают на вопрос о пове-
поведении волн в не очень глубокой воде, где h имеет вели-
х) «См. «Механика» (т. I), равенство C.13а).
§ 24. Плоские гравитационные волны в мелкой воде 223
чину того же порядка, что и X. В этом случае из B4.4)
и B4.5) сразу получим
С - ё - Ы B4.8)
ш ch kh
kshkh
Отсюда следует
со2
gk
B4.9)
Введя обозначения x=kh и d = ^zhjg, напишем B4.9)
в виде
B4.9а)
th х = —
х
Воспользовавшись графическим приемом, который
применил еще Фурье при изучении теплопровод-
теплопроводности, построим (фиг. 35) гипер-
болу d\x и кривую гиперболиче-
гиперболического тангенса (монотонную кри-
кривую, приближающуюся к асимпто-
асимптоте, отстоящей от оси х на расстоя-
расстоянии, равном единице). Как легко
убедиться, обе кривые пересекутся
только в одной точке. Ее абсцисса
х = х0 даст нам корень уравнения
B4.9а), а также искомое значение
л = л
о
Ф и г. 35. Вспомога-
Вспомогательное -построение для
решения трансцендент-
трансцендентного уравнения B4.9а)
распространения волн
B4.10)
на основании которого можно по-
получить выражение для скорости
в не очень глубокой воде
V = ¦?-=—.
к х0
Таким образом, с помощью построения, изображенного
на фиг. 35, мы получили в неявном виде общее пред-
представление закона дисперсии. Теперь кривая на фиг. 34
построена полностью: разрыв между отрезками a (h > X)
и b(h <С X) заполняется отрезком c(h я» X), соответствую-
соответствующим равенству B4.10). Монотонный подъем этого отрезка
свидетельствует о том, что в этой области также будет
нормальная дисперсия.
224 Гл. V. Теория волн
Выражение для области перехода от а к с может
быть получено из формулы, являющейся непосредствен-
непосредственным следствием выражения B4.9):
F* = ^ = 4th^. B4.10а)
Из B4.10а) можно получить
для hyl: F2 -> ф- [равенство B3.16)],
для h < X: V2 —> gh [равенство B4.7)].
Сделаем несколько замечаний по поводу прибоя гра-
гравитационных волн у берега. Они будут носить качествен-
качественный характер и будут довольно нестрогими. Поскольку
в данном случае значения h очень малы и, следователь-
следовательно, величина x = kh также будет мала, то можно заменить
ihx на х. Тогда трансцендентное уравнение B4.9а) пе-
перейдет в алгебраическое уравнение
d
X '
корнем которого будет
xo = y2=wy A,
откуда, согласно B4.10), скорость распространения
B4.11)
т. е., как и следовало ожидать, мы опять получили
формулу B4.9) для мелкой воды.
Конечно, все предыдущее рассмотрение относится
к воде, имеющей постоянную глубину. Рассмотрим теперь
случай, когда глубина воды убывает по направлению
к берегу (фиг. 36). Так как мы пренебрегали квадратом
амплитуды, то наши прежние выводы относились только
к волнам с очень малой амплитудой. Несмотря на это,
применим их здесь к волне с конечной амплитудой
и будем считать, что определяющая гребень волны глу-
§ 24. Плоские гравитационные волны в мелкой воде 225
бина hT больше, чем глубина hB, определяющая впади-
впадину волны. Тогда из B4.11) получим
B4.11а)
Следовательно, гребень волны распространяется быстрее,
чем впадина, поэтому волна изменит свою форму (см.
правый горб на фиг. 36). Это весьма нестрогое рассуж-
рассуждение дает указание к объяснению образования прибоя.
Фиг. 36. Схема образования прибоя око-
около берега.
После этого отступления перейдем к интересному во-
вопросу о траекториях частиц при волновом движении;
в основу рассмотрения положим сначала соотношения
для достаточно глубокой воды.
Пусть в покоящейся воде рассматриваемая частица
имеет координаты х, у, а в воде, возмущенной волновым
движением, — координаты х', у'. Смещение по отношению
к состоянию покоя будет равно
Ь = х'-х, У1 = у'-у, B4.12)
где i\ обозначает смещение частицы не на поверхности,
как это было ранее, а на любой глубине у (то же самое
относится к &). Согласно B4.2), скорость частицы равна
vx = k = - 4r- = ~
*-**) Cchk (h - y),
>0 С sh k (h — y).
B4-13)
Нам, конечно, следовало бы дифференцировать не по
х и у, а по измененным координатам и подставить
15 д. Зоммерфельд
226 Гл. V. Теория волН
в B4.13) х', у' вместо х, у или, что, согласно B4.12),
одно и то же, ж + ?, y-\-f\- Однако получающееся при
этом различие было бы второго порядка малости по
сравнению с величинами С, ? и kj, которые здесь рас-
рассматриваются малыми, поэтому им можно пренебречь.
Интегрируя по t, из B4.13) получаем
k = — е***-**) С ch к (k - у),
ш. B4.14)
т] = i JL eHkx-wt) Cshk(h — у).
(Ввиду периодичности движения постоянную интегриро-
интегрирования надо положить равной нулю.) Введем сокращен-
сокращенные обозначения (причина введения этих обозначений
станет сразу понятна)
. a = ^-chk(h-y), b^^Bhk(h-y) B4.15)
и перейдем от комплексного представления к действи-
действительному:
^—асов{кх — ы), т]= — bsin(kx— ы). B4.16)
Чтобы получить уравнение траектории нашей частицы,
исключим t из B4.16). Для этого возведем ? и -ц в квад-
квадрат. (В этом и заключается причина перехода к действи-
действительным величинам, так как способ записи с помощью
комплексных величин годится только при линейных
операциях!) Тогда
Полученное выражение есть уравнение эллипса. Соглас-
Согласно B4.15), отношение малой оси к большой равно
ч B4.17а)
для у = 0 (поверхность).
Эксцентриситет, опять-таки согласно B4.15), будет
равен
6 = 1/^3^=-^, B4.176)
т. е. не зависит от глубины.
§ 24. Плоские гравитационные волны в мелкой воде 227
На фиг. 37, а изображены положение и величина этих
эллипсов в общем случае, на фиг. 37,6 — в предельном
случае глубокой воды и на фиг. 37, в — в случае мелкой
'///////////////////////,
о
о
77777777777777777/
в
Фиг. 37. Траектории частиц воды.
а—в не очень глубокой воде, б—в луОокой воде,
в—в мелкой воде.
воды. На фиг.37, а эллипсы, если их расположить коак-
сиально, будут, согласно B4.176), софокусными. В пре-
предельном случае kh~->oo, согласно B4.17а),
A = th(cx>)=l;
таким образом, эллипс перейдет в окружность (см.
фиг. 37, б). Чтобы определить радиус окружности, вычис-
вычислим из B4.15) величины а и Ь, воспользовавшись пер-
первым из равенств B4.1а):
а = ~ ch k {h — у) = -|- Ae~
hh
= А А (е-ъу + e-fcBh-y)) __> A Ae~hv,
M
Ъ = ML sh к (h - у) = -?- Ae-hh(eh(h~y) -
= А А
Таким образом, радиус окружности быстро уменьшается,,
с увеличением глубины. С другой стороны, в предельном
228
Гл. V. Теория воли
случае kh—->0 (тем более, k{h — у)—>0), согласно
B4.17а),
Эллипсы перейдут в горизонтальные прямые (см. фиг. 37,в);
можно сказать, что в случае мелкой воды не будет
вертикальных смещений. Горизонтальное смещение будет
иметь амплитуду е, не зависящую, согласно равенству
B4.176), от у.
Линии тока поля скоростей являются не менее инте-
интересными, чем траектории частиц воды. Так как для
наших плоских волн поле будет двухмерным, то, со-
согласно A9.5), функцию тока
W получим из равенств
rdW дФ dW дФ
дх
ду
Подставив сюда общее выра-
выражение для Ф из равенства
B4.2) (в частном случае мел-
мелкой воды все линии тока,
конечно, будут горизонталь-
горизонтальными), получаем
Фиг. 38. Картина линий то-
тока гравитационных волн на
воде, имеющей конечную глу-
глубину.
dW
ду
ot)Cshk{h — y),
w'> Cchk{h — y)
и, интегрируя одно из выражении по х или соответст-
соответственно по у (постоянная интегрирования опять будет рав-
равна нулю), имеем
W = - iei(b*-»t) Cshk(h-y).
Рассмотрим некоторый фиксированный момент времени,
например ? = 0, и перейдем к действительной части
W — С sin кх sh к (k — у).
B4.18)
Для сравнения выпишем, согласно B4.3), выражение для
опускания .поверхности ^, выразим из B4.6) с через С
§ 24. Плоские гравитационные волны в мелкой воде 229
¦и перейдем к действительной части и к моменту времени
т]=_ —Csin/b:. B4.19)
Из B4.18) сразу следует, что ? = 0 для y = h; дно
жидкости представляет собой линию тока, что само собой
разумеется. Далее мы получим ЧГ=О для kx = 0, ± ic,
± 2тс, где, согласно B4.19), т\ также равно нулю. Таким
образом, картина течения распадается на прямоугольные
поля, содержащие линии тока. Далее, из B4.18) следует,
что в точках, где cosA:a; = Or т. е., согласно B4.19), при
всех абсциссах, где у\ будет иметь максимум или мини-
минимум, для произвольного у обратится в нуль выражение
TjT- = кС cos kx shk(h — y).
Иначе говоря, в этих местах линии тока будут прохо-
проходить в горизонтальном направлении. После всего ска-
сказанного картина линиц тока, изображенная на фиг. 38,
становится достаточно понятной.
Красивые фотографии, изображенные на фиг. 39а и
396, находятся в прекрасном совпадении с теоретически
построенными картинами на фиг. 38 и 37, а. Жидкость
находится в стеклянном сосуде с плоскими стенками,
параллельными направлению освещения. В ней нахо-
находятся мелкие металлические частицы, поглощающие свет.
Чтобы получить линии тока, изображенные на фиг. 39а,
требуется кратковременное освещение. Наблюдатель легко
соединит элементы длины, образованные металлическими
частицами, в непрерывные кривые и представит их поло-
положение относительно достаточно резко выраженной по-
поверхности жидкости. В случае более длительного осве-
освещения, равного примерно половине периода колеба-
колебаний^ и при менее плотно расположенных металличе-
металлических частицах получим траектории в виде частей дуг
эллипсов, как это изображено на фиг. 396/В этом слу-
случае поверхность не резко выражена. Последняя фотогра-
фотография позволяет также заметить распространение , фазы,
с которой пробегаются эллипсы. Частицы при волновом
движении, по существу, остаются на месте (в случае
230 Гл. V. Теория волн
достаточно малой амплитуды, что и предполагалось при
пашем рассмотрении; при конечной амплитуде это уже
не совсем справедливо); распространяться будет только
фаза, скорость которой V мы вычисляли. Поэтому вели-
величину V правильнее всего будет назвать фазовой ско-
скоростью.
§ 25. ПЛОСКИЕ КАПИЛЛЯРНЫЕ И КАПИЛЛЯРНО-
ГРАВИТАЦИОННЫЕ ВОЛНЫ
Не будем вначале совсем принимать во внимание силу
тяжести, а учтем лишь поверхностное натяжение Т. Те-
Теперь поверхность не будет свободна от действия сил, а на
нее будет действовать нормальное давление N, вызван-
вызванное наличием поверхностного натяжения Т. Давление
на поверхности будет подчиняться не условию р = 0, как
в B3.4), а в случае плоской волны, согласно A7.10),
условию
(Величина и из A7.10) заменена на величину, характе-
характеризующую опускание поверхности yj, взятую со знаком
минус, т. е. она характеризует поднятие поверхности.)
Это значение р подставим в уравнение Бернулли с уче-
учетом того, что С/ = 0, так как силу тяжести мы временно
не принимаем во внимание. Таким образом,
дФ _Т Л,
{ }
В кинематическом рассмотрении, проведенном в начале
§ 23, использовались только общие свойства плоских
волн, следовательно, оно вполне пригодно и в настоящем
случае. Поэтому мы можем сразу воспользоваться выра-
выражением B3.1) для Ф, а также выражением B3.7) для tj.
Тогда из B5.2) получаем, сокращая на экспоненциаль-
экспоненциальный множитель и пренебрегая величинами второго по-
порядка,
шА = — №, B5.3)
§ 25. Плоские капиллярные волны
231
Точно так же останется в силе кинематическое условие
B3.11); оно, как и в B3.12), приведет ко второму усло-
условию
— iaa = kA. B5.4)
Из B5.3) и B5.4) следует
А__Т /с2 ш
а р ito к '
B5.5)
откуда можно найти связь между ш
и к:
B5.6)
Скорость распространения капиллярных волн будет равна
к2 р '
Она растет с убыванием X, в то время как для гравита-
гравитационных волн в глубокой воде с уменьшением X ско-
скорость V убывала. Таким образом,
в этом случае имеем аномальную
дисперсию. (Для гравитационных
волн при любых конечных значе-
значениях длин волн имеется нормальная
дисперсия.)
На фиг. 40 пунктирная кривая 1
изображает изменение V в зависи-
зависимости от X. Для сравнения изобра-
изображена пунктирная кривая 2, взятая
из фиг. 34, которая характеризует
зависимось V от X для гравитацион- Фиг. 40. Сопостав-
ных волн. Эти кривые пересекаются ление зависимости от
в точке, абсцисса которой X = Хп. Для х фазовой скорости V
•v ^ 1 -ш " капиллярных и гра-
Х<Х0 кривая 1 располагается над витаци0Нных волн.
кривой 2, что вполне понятно, так Минимум при А=
как сила, вызывающая распростра- = ^мин.
нение капиллярных волн, зависит
от кривизны профиля поверхности, которая в случае за-
заданной амплитуды растет с убыванием длины волны.
Этот факт является причиной того, что на фиг. 34 мы не
продолжали отрезка а до начала координат. Соответст-
Соответственно для X > XQ кривая 2 располагается над кривой 1.
232 Гл. V. Теория волн
Так как для длинных волн капиллярные силы не
сказываются, то становится ясным, почему в этом па-
параграфе использовалось выражение для потенциала ско-
скорости в глубокой воде. Даше при сравнительно неглубо-
неглубокой воде величины hfk и тем более hk будут очень боль-
большими в случае капиллярных волн.
Теперь не представит затруднений рассмотрение об-
общего случая совместного действия капиллярных сил
и силы тяжести. Для этого, кроме значения р из B5.1),
необходимо в уравнение Бернулли B3.5) добавить зна-
значение потенциала силы тяжести из B3.56):
Тогда вместо B5.3) получаем
mA = f—k2 + g^)a, B5.8)
а вместо B5.5) сразу получаем, воспользовавшись B5.4)
и B5.8),
+ g^^ B5.9)
р '.у к ч '
Вместо B5.6) и B5.7) будет
T B5.10)
<25-и)
Здесь Fj — скорость капиллярных волн из равенства
B5.7), a V2 — скорость гравитационных волн из B3.16).
Следовательно, квадрат скорости V равен сумме квадра-
квадратов скоростей V1 и F2.
Удовлетворяющая этому правилу кривая изображена
на фиг. 40 (сплошная линия). Вычислим из B5.11) ми-
минимум скорости V как функцию от X. Тогда
и далее
пп ~ о_ Г пп
B5.12)
§> 25. Плоские капиллярные волны 233
Это значение Хмин. равно абсциссе точки пересечения
кривых 1 ж 2, обозначенной на фиг. 4Q как Хо. Действи-
Действительно, в точке пересечения, согласно B5.7) и B3.16),
будет
/Т 2п | / gk0
р Ло Г /тс
принимая во внимание при этом B5.12),
В силу равенства Vx и V2 в этой точке соответствующее
значение FMHH. будет иметь значение
Пин. = 2V\ = 2V\ = 2 УЦ . B5.13)
Как легко показать, значение V2 в общем случае [ра-
[равенство B5.11)] может быть записано в изящной форме
У8 = 1 ( Хмин- X
V2 2
г мин.
Перейдем, наконец, к интересным численным соотно-
соотношениям. Для воды на границе с воздухом имеем1)
Т — 72 dimjCM = 72 г/сек2.
Приняв р = 1 и g = 9Si, из B5.12) и B5.13) получим
Хмин. = 2тт ]/ щ = 1,73 СЖ,
• 981 = 23,2 см /сек.
На воде не может существовать волн, распространяю-
распространяющихся со скоростью, меньшей 23 см/сек; не только волны,
имеющие длину больше Хмин.=7,73 см, но и волны с мень-
меньшей 'длиной распространяются со скоростью, большей
23 см/сек.
J) Заметим, что наиболее точное определение величины Т про-
производится именно с помощью метода капиллярных волн, возбуждае-
возбуждаемых колебаниями камертона; методы, связанные с измерением высоты
капиллярного подъема, не дают большой точности, так как на стен-
стенках трубок всегда имеются загрязнения.
234 Гл. V. Теория волн
Кельвин предложил называть волны с X < Хмин.
«рябью». Иногда можно наблюдать гравитационные вол-
волны, поверхность которых покрыта рябыо.
§ 26. ВВЕДЕНИЕ ГРУППОВОЙ СКОРОСТИ
В конце § 24 мы назвали скорость распространения
V фазовой скоростью. Действительно, со скоростью
V распространяется фаза волны. Переменная часть фазы
в наших выражениях B3.1), B3.7), B4.1). и т. д. за-
задается показателем i(kx — ш/). Если положить его рав-
равным постоянной величине и, таким образом, отыскать
положение поверхности равной фазы, занимаемое ею
в различные моменты времени, то получим условие
kdx-adt = 0, т. е. ~ = ~ = V. B6.1)
Для монохроматических волн (если опять употребить
выражение, заимствованное из оптики), т. е. для волн
с фиксированной частотой, единственной скоростью, кото-
которая может войти в рассмотрение, является фазовая ско-
скорость V.
При наложении волн различной частоты говорят
о группе волн, особенно если частоты волн мало отли-
отличаются друг от друга. (Вместо этого термина в настоя-
настоящее время, в особенности в квантовой механике, упо-
употребляют иногда менее удачный термин «волновой пакет».)
Группа волн распространяется с групповой скоростью U,
которая, вообще говоря, отличается от V. Лучше всего
писать выражение U в виде
и р62)
Законность этой формулы скоро будет нами доказана.
Если волны распространяются без дисперсии, т. е. если
V не зависит от длины волны X (или от волнового чис-
числа к), то, согласно B6.1),
и, согласно B6.2),
U=V, B6.2а)
§ 26. Введение групповой скорости 235
Только в случае отсутствия дисперсии групповая и фазо-
фазовая скорости совпадают.
В общем случае
c?w = V dk + k -jt- dk
или, используя B6.2),
U=V + k^ = V-k~. B6.26)
В случае нормальной дисперсии [(dV/dk) > 0] групповая
скорость меньше, а в случае аномальной дисперсии
\{dVIdk) < 0] — больше фазовой скорости.
Например, для гравитационных волн в глубокой воде,
согласно B3.16), имеем
. 2п ' dl 21 '
подставляя в B6.26), получаем
U=:V-\V <V. B6.2в)
Напротив, в случае чисто капиллярных волн, согласно
B5.7),
р I ' dl ~ 21
и
U = V-\-~V>V. B6.2г)
Из фиг. 40 следует, что для капиллярно-гравитацион-
капиллярно-гравитационных вол при X < Хмин, дисперсия аномальна и U > F;
для X > Хмин. она нормальна и U<V. Для Х = ХМИН,
групповая скорость U—V; этому условию соответ-
соответствует горизонтальная касательная к кривой фиг. 40
в месте ее минимума, кроме того, в этом случае исчезает
множитель dV/dk в равенстве B6.26).
В литературе рассмотрен также вопрос о том, могут ли
U и V, иметь различные знаки г).
х) См. Schuster A., Optik (deutsh bei Teubner, 1907,
S. 377). Здесь рассмотрено распространение света в сильно погло-
поглощающей среде.
236 Гл. V. Теория волн
Понятие «групповая скорость» имеет гидродинами-
гидродинамическое происхождение (работы Стокса, 1876 г.), но оно
приобрело также большое значение в оптике (Рэлей).
В квантовой механике фазовая скорость играет совершен-
совершенно формальную роль, в то время как групповая скорость
является важнейшей физической величиной, а именно,
она представляет собой скорость, которой обладает ча-
частица, представленная группой волн (Де-Бройль, 1924 г.).
Приведем сейчас, следуя Стоксу, обычный элементар-
элементарный вывод формулы B6.2). Рассмотрим наложение двух
волн с равной амплитудей, но несколько отличающимися
частотами и, следовательно, различными волновыми чис-
числами. Пусть эти волны распространяются в направлении
оси х:
-q = a {sin {кхх — ш^) + sin (k2x — ш2г)}. B6.3)
Возникающая при этом группа волн носит характер
биений1): во всех точках, где разность обеих фаз кх — Ы
равна 2тс (п — целое число), имеет место взаимное уси-
усиление, а в точках, где она равна Bп + 1) тс, — взаимное
уничтожение. Это следует из B6.3) после простого три-
тригонометрического преобразования
о /" кЛ—ко со,—со9 Л . /ki-A-kv coj-f-too N
t] = 2аcosf -—-?x l 2 2 t jsinf ^ -x ^ 2 t\.
B6.3a)
В точках, где разность фаз равна целому нечетному или
четному кратному тс, косинус соответственно становится
равным нулю или ± 1- Введя обозначения
перепишем B6.3а) в виде
= C sin(kQx— шог), С = 2а cos-к-(Ак х — Дшг). B6.36)
Легко видеть, что С представляет собой медленно меня-
меняющуюся величину. Назовем С «амплитудой группы».
Фазовую скорость этого сложного колебания можно
См. «Механика» (т. I), фиг. 34.
§ 2&, Введение групповой скорости 237:
получить из рассмотрения синусоидального множителя
в B6.36)
Эта скорость не отличается существенным образом от
фазовых скоростей составляющих колебаний
1=="Т~ и 2 = Tt'
Кроме этого, существует скорость, с которой распро-
распространяется «амплитуда» С. Для ее определения положим
Акх — Au>t = const,
откуда в результате дифференцирования следует
в пределе (при ДА:—>0) получаем формулу B6.2).
Мы можем освободиться от ограничений, наклады-
накладываемых специальным видом выражения B6.3), для чего
рассмотрим произвольную группу волн с частотами,
расположенными в узком интервале значений. Более
удобно опять вернуться к способу записи с помощью
комплексных величин. Положим
¦л— \ п lk\ pi (hx—u>t) ffh /9fi Л^
J
ко—*
где a (/b) c?/c — амплитуда единичной составляющей волны.
По волновым числам группа имеет весьма малую ширину
2s и сконцентрирована около среднего значения к0.
Соответственно этому перепишем показатель выражения
B6.4) в виде
кх — Ы = кох — u>0Z + (к — к0) х — (ш — оH) ?.
После этого B6.4) перейдет в
С=
B6.4а)
238 Рл. V. Теория волн
Так как х и t входят только в показатель степени в вы-
выражении для С, то надо последний положить равным
постоянной величине, для того чтобы определить ско-
скорость распространения амплитуды С. Мы получим для
всей группы волн практически постоянную скорость
dx со — соо Дсо
~dt= к — к0 =~Ш '
а при переходе к достаточно малым ДА: опять появится
групповая скорость из равенства B6.2).
Следует заметить, что формула B6.4), как и частный
случай B6.3), описывает бесконечно протяженный цуг
волн и, следовательно, никак не может быть использо-
использована для представления изолированного волнового воз-
возбуждения. Для описаний изолированной группы или
«волнового пакета» надо воспользоваться теорией инте-
интегралов Фурье и интегрировать не в узком интервале
волновых чисел 2s, как это делалось в B6.4), а по
всем значениям волновых чисел, от — оо до -f-oo. Этот
случай здесь рассматриваться не будет.
Только в среде, где отсутствует дисперсия, изолиро-
изолированная группа волн может распространяться без изме-
изменения формы. В общем случае в силу наличия диспер-
дисперсии она будет расплываться, так как составляющие
волны будут двигаться с различными скоростями. Пос-
Последний факт имеет очень большое значение при рассмот-
рассмотрении понятия частицы в квантовой механике. Первое
можно легко доказать (по крайней мере в случае доста-
достаточно малой амплитуды), воспользовавшись решением
Даламбера A3.11), которое справедливо как в акустике,
так и в гидродинамике для сред без дисперсии. А имен-
именно, если V не зависит от к, то в случае любого началь-
начального состояния f] — F(x) и соответствующей начальной
скорости для последующих моментов времени будет
т. е. движение действительно будет происходить без
изменения формы, независимо от вида функции F (х) вол-
волнового профиля.
Оба нижеследующих построения для нормальной
и для аномальной дисперсии (фиг. 41) становятся
§ 26. Введение групповой скорости
239
понятными, если воспользоваться равенством B6.26) и за-
зависимостью tg а = ± (dV/d\).
Рейнольде1) и одновременно Рэлей2) выяснили более
глубокий смысл групповой скорости, связав ее с перено-
переносом энергии. По их определению, отношение групповой
Фиг. 41. Построение групповой скорости по задан-
заданной фазовой скорости с помощью кривой дисперсии.
а—нормальная и б—аномальная дисперсии.
скорости U к фазовой скорости V аналогично отноше-
отношению потока энергии S, прошедшего через некоторое се-
сечение волны за время т, к энергии Е, содержащейся
в области пространства между нашим сечением и сече-
сечением, отстоящим от него на расстоянии Ft:
V
Е
B6.5)
Если под т понимать период колебаний (что удобно для
дальнейшего), то Ft попросту равно длине волны X.
Тогда Е представляет собой превышение энергии коле-
колеблющейся жидкости над энергией покоящейся жидкости.
Докажем это для волн достаточно малой амплитуды
в глубокой воде. Так как нам придется иметь дело
с энергиями, т. е с квадратичными величинами, то вос-
воспользуемся вместо комплексных выражений действитель-
х) Reynolds О., Ges. Werke, Bd. I, S. 198; Nature, 46,
343 A877).
2) Rayleigh, Ges. Werke, Bd. I, S. 322. (См. также: Рэлей,
Теория звука, т. I, М.—Л., 1940.—Прим. перев.)
240 . Гл. V. Теория волн
ными [см. B3.14) и B3.146)]:
Ф = A cos (кх — Ы
Для длины волны X в направлении х и ширины, рав-
равной 1, в направлении оси z величина потенциальной
энергии в поле тяжести, заключенной в области жидко-
жидкости между возмущенной (y = -t]) и невозмущенной (?/ = 0)
поверхностями, в некоторый момент t = const будет равна
] = gP^X. B6.7)
о
Воспользовавшись формулой дисперсии B3.15), получим
^пот. = -j кАЧ = -| тгЛ3. B6.7а)
Эта величина равна в то же время разности потен-
потенциальных энергий всей жидкости, которая в случае по-
покоя распространяется от у = 0 до у = оо, а в случае
колебаний — от у = т\ до у= со.
Кинетическая энергия жидкости в случае малых ко-
колебаний равна той же величине; мы докажем это в за-
задаче 1 гл. V. Суммарная энергия (или, точнее говоря,
ее отличие от энергии покоящейся жидкости) будет равна
Е = Етъ. + ЯПот. = ркА2. B6.8)
Определим, с другой стороны, поток энергии S через
сечение х = \ или, что одно и то же, через сечение х — 0.
Для этого нам надо знать давление р в этом сечении. Его
можно вычислить из уравнения Бернулли B3.5) и ра-
равенства B3.56):
+ + const. B6.9)
Так как давление действует перпендикулярно к плос-
плоскости х = 0, то для определения работы над элементом
§ 26. Введение групповой скорости 241
этой плоскости (высотой dy и шириной 1) за время dt
надо умножить давление на скорость и на dt:
dA = pvx dydt= — p -^— dy dt. B6.9a)
Из этого выражения можно получить полную работу
в сечении* х = 0 за время т, т. е. полный поток энергии
через эту плоскость за это же время. Согласно B6.9)
и B6.9а), получаем
Не зависящие от времени не выписанные здесь члены
Р 8У + const уничтожатся в результате умножения на
дФ/дх и интегрирования по t. Подстановка из B6.6)
дает
S = ршЫ2 ^ dt sin2 Ы К e~2hy dy
и после интегрирования
6' = |-^2е-2^=|-хЛ2. B6.11)
Последнее равенство справедливо с точностью до членов
более высокого порядка по А (в этом приближении мож-
можно считать e~2hr> — l).
Сравнение равенств B6.11) и B6.8) дает
4 = |, B6.12)
что действительно представляет собой, согласно B6.2в),
отношение U/V в случае волн на глубокой воде. Таким
образом, наш простой пример подтверждает общее энер-
энергетическое определение групповой скорости B6.5), кото-
которое подтверждается также в более сложном случае не
очень большой глубины, где, согласно B6.26) и B4.10а),
16 А. Зоммерфельд
242 Гл. V. Теория волн
имеем
U - i (' \ 1 2kh Л
Для того чтобы наш результат сделать более на-
наглядным, рассмотрим еще раз цуг волн длины X, огра-
ограниченный сечением х — 0. Если бы дисперсия отсутство-
отсутствовала, то за время т вся энергия этого цуга протекла бы
через сечение. Тогда
В действительности в случае нормальной дисперсии толь-
только часть (для глубокой воды — половина) энергии Е будет
перенесена дальше, в то время как остальная часть
останется в колеблющейся жидкости, находящейся перед
сечением. Особенно интересным с этой точки зрения пред-
представляется случай аномальной дисперсии; здесь через сече-
сечение проходит больше энергии, чем ее содержится в цуге
волн длины X; энергия, которая оставалась бы в этом цуге,
была бы отрицательной. В этом случае для поддержания
волнового движения надо затрачивать больше энергии
в сравнении с тем количеством, которое несет с собой
волна; в других случаях для такого же переноса энергии
требуется меньшая энергия возбуждения. Нормально
диспергирующая среда облегчает, а аномально дисперги-
диспергирующая среда затрудняет перенос энергии.
§ 27. КОЛЬЦЕВЫЕ ВОЛНЫ
Если в воду бросить. камень, то возникающие волны
являются, конечно, не прямолинейными, а представляют
собой систему кольцевых подъемов и впадин, которые
не будут иметь постоянной амплитуды и не будут нахо-
находиться на постоянном расстоянии друг от друга. Напротив,
с удалением от места падения камня амплитуда будет резко
уменьшаться, а расстояние двух максимумов друг от друга
увеличиваться по весьма своеобразному закону. Хотя
на первый взгляд эта задача может показаться простой,
при ее решении возникают значительные математические
трудности: нам потребуется не только теория функций
Бесселя и интегралов Фурье, но и так называемый «метод
§ 27. Кольцевые волны 243
перевала». Здесь мы ограничимся только теми поясне-
пояснениями метода, которые потребуются в ходе вычислений.
Для того чтобы схематически описать действие камня,
брошенного на поверхность воды, представим себе, что
в начале координат в воду погружен на глубину а
цилиндрический поршень радиуса г0, который внезапно
извлекается из воды в момент ? = 0. Обозначим опуска-
опускание поверхности снова через т\, так что начальное состоя-
состояние задается соотношениями
4 = 0, r>r0. B7Л)
Прежде чем рассматривать случай однократного воз-
возмущения, решим более простую задачу периодически
повторяющегося возбуждения.
1. Периодический случай. Некоторые замечания
о функциях Бесселя
Представим себе приспособление, которое применяется
для получения волн в купальном бассейне: пусть прямой
брус движется в точке ж = 0 с частотой ш; в результате
возникнут плоские гравитационные волны, которые будут
распространяться в направлении оси х, перпендикулярно
к брусу. Подобные волны мы рассматривали в § 23;
здесь также рассмотрим случай глубокой воды.
Чтобы воспользоваться результатами § 23 для нашей
задачи, решение которой, конечно, обладает осевой сим-
симметрией, введем цилиндрические координаты г, у, у
(у положительно при отсчете вниз). Если воспользоваться
решением задачи 3 гл. I, то условие несжимаемости для
потенциала скорости в этих координатах запишется, как
дЩ 1 дФ 1
Положим (с учетом осевой симметрии, т. е. независимости
от ср)
Ф = Af (r) е-ьуе-ш. B7.3)
Тогда, согласно B7.2), /(г) будет удовлетворять диф-
дифференциальному уравнению
10*
244 Гл. V. Теория волн
Сделав подстановку kr = p, напишем вместо B7.4)
<Р/4? 0. B7.4а)
Решение этого уравнения, регулярное в нуле и обра-
обращающееся там в единицу, обозначим через /0(р)# Срав-
Сравнивая коэффициенты, легко получить из B7.4а) разложе-
разложение /0(р) по степеням р:
Если, с другой стороны, Ф зависит от ср, то мы заменим
в B7.3) /(г) на fn{r)einf и получим вместо B7.4) и B7.4а)
следующие уравнения:
Решение B7.6а), регулярное в нуле, назовем /п(р)
и путем сравнения коэффициентов получим обобщение
разложения B7.5):
Функции Jn (целые трансцендевтные) называются функ-
функциями Бесселя и-ro порядка.
Между Jx и /0 существует связь
Л(Р)=-|[Л>(Р)]> B7-8)
что может быть легко установлено с помощью B7.5)
и B7.7).
Напишем для / = /0(р) уравнение B7.4а) в виде
что, согласно B7.8), эквивалентно
Л()[Л(
§ 27. Кольцевые волны 245
Интегрируя, получим для произвольного р0
6
Нам понадобится интегральное представление
Действительно, легко убедиться, что это выражение удо-
удовлетворяет уравнению B7.4а) и при р = 0 обращается в 1;
оно должно также совпадать с B7.5). То же самое можно
получить, правда, более сложным путем, если разложить
в ряд экспоненциальную функцию в B7.9). Вместо B7.9)
часто употребляют также'выражение
Ы. B7.9а)
Подставим теперь f = JQ(kr) в выражение B7.3)
и получим
Ф = AJ0 (кг) е-куе-шш ^27.10)
Это выражение удовлетворяет условию для глубокой воды:
Ф—>0 при у—>оо. Но оно также должно удовлетворять
условиям B3.6) и B3.11) на поверхности у=0. Пред-
Предположим, что опускание поверхности т] выражается фор-
формулой, соответствующей B7.10),
-г] = aJQ (кг) е~ш. B7.10а)
Тогда из вышеуказанных условий после сокращения
на 10(кг)е~ш, как и в равенствах B3.9), B3.12) и B3.13),
будет следовать
— = ¦?=-?, B7.11)
а но к ч '
а также прежний закон дисперсии
<u = \/"gk . B7.11а)
В силу B741) выражение для Ф будет иметь следующий
вид:
ф = аЛ J (кг) <r*v-b#, B7.12)
246 Гл. V. Теория волн
2. Однократное возмущение. Интегральное
представление Фурье—Бесселя
Теорема об интеграле Фурье гласит: произвольная
(не слишком иррегулярная) функция F(х) может быть
представлена для любых значений х в виде суперпозиции
sm
V .. Bill I
тригонометрических функции кх или, что то же самое,
показательных функций eihx следующим образом:
-foo -}-со
B7.13)
Существует аналогичная теорема для представления F
через функции Бесселя *
tdtF$)J0{kZ), 0<r<+oo.
о о
B7.13а)
Применим B7.13а) к начальному состоянию, задан-
заданному соотношениями B7.1), полагая
_( а для 0<г <г0,
(Г) = 7]==|О для г0<г<оо.
Тогда, согласно B7.13а),
^0 (кг) ^Zd$J0 (Щ. B7.14)
о о
Чтобы вычислить второй интеграл, воспользуемся равен-
равенством B7.8а) и получим при /с? = р, кго = ро
6
Вследствие этого B7.14) перейдет в
¦Ч«-о = aro ^ Jo №) Ji (Лго) dk. B7.14а)
§ 27. Кольцевые волны 247.
Докажем теперь, что выражения для т\ и Ф в любой
последующий момент времени t > 0 можно написать
в виде , ,
т] = аг0 ^ /0 {кг) /х (kr0) e~iV^' dk, B7.15)
а
со
Ф = - iagr0 \ Jo (kr) Jx (кг0) е-ьуе-1^' ^L . B7.16)
5 У ёк
Дли доказательства заметим, что при ? = 0 выраже-
выражение B7.15) переходит в B7.14а) и что оба выражения
B7.15) и B7.16) получаются из периодических решений
B7.10а) и B7.12) в результате действия одного и того же
«оператора»
с одновременным учетом закона дисперсии B7.11а). Так
как B7.10а) и B7.12) удовлетворяют решению нашей
задачи и граничным условиям для г/ = 0 и г/ — со, то
это же можно сказать и о выражениях B7.15) и B7.16).
А так как эти выражения; кроме того, удовлетворяют
начальному условию для / = 0, то они действительно
являются искомыми решениями.
3. Интегрирование по к. Метод стационарной фазы
В рассматриваемых кольцевых волнах мы наблюдаем
форму поверхности. Поэтому в дальнейшем будем зани-
заниматься только равенством B7.15). Если в нем вместо /0
подставить его значение из B7.9а) (с Jx мы вскоре
поступим иным образом) и переменить порядок интегри-
интегрирования, то получим двойной интеграл
dk Jx{kr0)e*'«»-*V^'. B7.17)
о о
5 интеграле по к, который мы обозначим буквой К,
введем новую переменную интегрирования й соответственно
248 Гл. V. Теория волн
сокращенное обозначение
Р = У*Ъ, 2т = 1/^|. ^ B7.17а)
Тогда
оо
B7.18)
о
r/r0 представляет собой очень большую величину, следо-
следовательно, с изменением р показательная функция будет
быстро меняться. Обозначим множитель при i (r/r0) через
/(/?) = /?2 cos а — 2рх. B7.19)
Вообще говоря, положительные и отрицательные значе-
значения подинтегральной величины уничтожатся вследствие
интерференции. Исключение будет представлять точка,
где
i' (г>\ — О г> — п т /97 IQa}
j \r/ if r-o coga \ /
На этом обстоятельстве основан метод стационарной
фазы; р = р0 является тем местом, где фаза быстро меня-
меняющейся экспоненциальной функции будет стационарна.
Интегрирование проводится только в окрестности этой
точки и поэтому может быть выполнено элементарным
путем. Этот метод был с большим искусством применен
Кельвином к решению многих гидродинамических и опти-
оптических задач. Оформленный более строго математически,
он и представляет собой тот самый метод перевала1),
о котором упоминалось выше, однако здесь мы на нем
подробнее останавливаться не будем.
Вместо B7.19) можно написать
*) W i d en b a u er H., Zs. angew. Math, u, Mech., 14, 321
A939). Здесь ваша задача о кощщевых водцах решена с
этого метода.
§ 27. Кольцевые волны 249
при этом, если ограничиться интегрированием в окрест-
окрестности р = р0, равенство B7.18) перейдет в
e-i
, B7.20)
где е <С 1. Здесь множители /х(/?2) и р изменяются мед-
медленно по сравнению с быстро изменяющейся экспонен-
экспоненциальной функцией и поэтому могут считаться постоян-
постоянными и равными своим значениям при р — р0. Подста-
Подстановка
= f cos a B7.20a)
'о
переводит B7.20) в
^.«^ B7.21)
Что касается положения критической точки р = р0) то
необходимо заметить: так как, согласно B7.17а), т поло-
положительно, то на основании B7.19а) имеем
р0 > 0 для 0 < а < у ,
р0 < 0 для -| < а < тт.
В первом случае p = pQ и, следовательно, 5 = 0 находятся
в области интегрирования 0 < к < оо, а во втором слу-
случае они находятся вне области интегрирования. Выраже-
Выражение B7.21) справедливо только в первом случае; в дру-
другом случае
К = 0, -|<а<тг, B7.21а)
что означает полное погашение вследствие интерференции.
Окончательный результат следует из B7.21) при исполь-
использовании хорошо известного интеграла
! ' dt—yK. {17.Zl)
250 _ -Гл. V. Теория волн
Если мы заменим здесь t на
t = е^<*/*>$, t2 = — is2, d? = e-WV ds,
то получим1) из B7.22)
^2(/5 = е^/4)/^. B7.22а)
Левая сторона идентична с интегралом, входящим в B7.21),
пределы которого также становятся бесконечными, если
при заданных в и cos а Ф 0 стремить г/г0 к бесконечно-
бесконечности. Подставив B7.22а) в B7.21), получим
В предположении, что
^-2«1, B7.24)
следующее из B7.17а) и B7.19а) значение
4т-2 cos a
будет всюду очень мало, за исключением а = тг/2. Тогда,
согласно B7.7), мы будем иметь с достаточной точностью
2\ Fp nil r&\ tl x ' *'nb~ X^2
J0/— о » /V'l\/yO/ о
2 V 4ra у cos3 a "
Наконец, подставив из B7.20а) выражение для q,
получим вместо B7.23)
COS7 а г2
К = |/-Vt- Г^-2 Y2 e-i(^2/4rcos«)+i(W4). B7.25)
V COS7 а г2 V4r у v 7
х) Интегрирование в B7.22а) проводится в комплексной «-пло-
«-плоскости не вдоль действительной оси s, а вдоль прямой, наклонённой
к ней под углом 45°, которая как раз представляет собой границу
сходимости B7.22а). Этот путь интегрирования может быть, однако,
заменен действительной осью и двумя дугами окружностей на бес-
бесконечности, которые при этом не дадут никакого вкладам интеграл.
§ 27. Кольцевые волны 251
4. Интегрирование по а. Рассмотрение предельного
случая
Вернемся опять к B7.17). Интегрирование по а в силу
B7.21а) должно проводиться в области 0 < а < тс/2. Если
ввести обозначение
Fo = izr^a
для вытесняемого в начальный момент объема, то полу-
получаем
71/2
Tjr=:-^- Л^!Л8/2 ( _^L_e-i(ff*2/4rCOS«)-MGl/4) /27 26}
1 г2 V 4nr J } cos7/2 a V '
Произведем предельный переход г0—>0. Для того чтобы
возмущение произвело конечный эффект, нужно сохранить
постоянным объем Fo; для этого необходимо определен-
определенным образом устремить к бесконечности глубину погруже-
погружения а, что следует в дальнейшем иметь в виду.
Выражение B7.26) зависит существенным образом
только от переменной
» = §:• B7.27)
Найдем асимптотическое значение для -ц при и —»оо. При
этом предельном переходе, экспонента в B7.26) опять
будет представлять собой быстро меняющуюся величину,
так что здесь мы еще раз применим метод стационарной
фазы. Обозначим теперь множитель при и в экспоненте,
в B7.26), через /(а):
j. / \ j/ i \ sin а
/ (а) == , /' (а) = —г-
1 х ' COS а ' * \ I cos2 а
и получим критическое значение а, для которого
„ „ Г\ X I \ Л у / \ Л I ^i \
2 COS7^2 а0
откуда
da. B7.28)
о
252 Гл. V. Теория волн
Подобно тому как мы имели в B7.22а), теперь для
и~»оо будет
е со
С ^-(i/2)u«2 da = у 1 ^ e-is* ds = у JL е-г(*/4).
о о
и, подставив в B7.28), получим для -ц
Ь B7.29)
Для проверки можно заметить, что, согласно B7.27),
величина и представляет собой безразмерную величину,
a V0/r2, как и tj, имеет размерность длины.
На первый взгляд кажется, что для границы области
интегрирования a = ir/2 наш метод непригоден, так как
обращается в нуль знаменатель cos a в B7.26). Однако,
согласно B7.21а), эта граница в то же время является
границей области исчезновения К, так что можно заклю-
заключить, что при интегрировании по а эта точка не требует
никакого особого исследования.
Согласно B7.29), действительная часть -ц равна
-п = ——?— и cos и;
¦ц обращается в бесконечность в точке г = 0; причина
этого заключается в том, что при нашем предельном пере-
переходе г0—>0, если величина Fo остается постоянной, глу-
глубина погружения а должна быть бесконечной. С ростом г
высота максимумов убывает, как и/г2, т. е. как 1/г3,
причем эти максимумы следуют друг за другом на рас-
расстоянии
что легко может быть получено, если сравнить выраже-
выражение для фазы и при и = 2тт и и = 2тс(п-\-1) для задан-
заданного t.
Таким образом, длина волны не будет постоянной,
как в случае типов волн, рассмотренных ранее, а будет
при постоянном t возрастать, как г2, и убывать при
постоянном г, как 1/р, На фиг. 42 изображен профиль
§ 28. Корабельные волны и угол Маха
253
поверхности при заданном t. Он хорошо совпадает с кар-
картиной поверхности воды, на которую брошен камень или
упала капля дождя.
За решение этой задачи Парижская Академия назна-
назначила в 1816 г. премию. Задача была решена Коши.
(По поводу этого решения, а
также о более поздней работе
Пуассона см. подробное изло-
изложение Буркхардта1).)
§ 28. КОРАБЕЛЬНЫЕ ВОЛНЫ И
УГОЛ МАХА
Каждый видел красивую кар-
картину, образованную волнами,
которые бегут вслед за движу-
движущимся судном. Она состоит из
системы продольных волн, при-
прилегающих к корме судна, кото-
которые пересекаются поперечными
волнами2). Вся картина пере-
перемещается вместе с судном, так
что с него она кажется непод- фиг. 42. Форма поверх-
вижной. Эту картину хорошо ности воды после возбуж-
наблюдать с крутого берега. Та- Дения кольцевых волн в
кую же картину, правда, сильно Г^ющиТ^о^о^Г
уменьшенную, можно наблю-
наблюдать за плывущей уткой.
В математической теории мы, конечно, не будем рас-
рассматривать ни корабля, ни утки, а будем представлять
источник распространения волн в виде точки (фиг. 43).
В этом случае можно схематически представить задачу
о корабельных волнах следующим образом: положение
судна в любой момент времени является источником
системы кольцевых волн; центр этой системы движется
равномерно и прямолинейно со скоростью судна v. Что
х) Burkhardt H., Jaresber. d. deutsch. Math. Ver., X, 429
A908).
2) Во избежание недоразумений следует отметить, что термины
«продольные» и «поперечные» волны здесь не имеют обычного (напри-
(например, как в акустике) смысла.— Прим. перев.
254
Гл. V. Теория волн
получится в результате наложения следующих друг
за другом кольцевых волн? Очевидно, что при этом воз-
возникнет картина, которая с судна будет казаться стационар-
стационарной, но детали этой картины весьма неожиданны и могут
быть выяснены только в результате точного анализа.
На фиг. 43 точка О представляет собой положение
судна в момент наблюдения t = 0, Q — его положение
Фиг. 43. Схема возникновения корабельных волн.
О—положение корабля в данный момент времени, Q, Q', ...—
его положения в предшествующие моменты времени, Р, Р', ...—
различные положения точек поля.
в предшествующий момент времени t, так что расстоя-
расстояние QO = vt. Р— точка, в которой будет вычисляться под-
поднятие поверхности воды tj. Оно складывается из подня-
поднятий t\t, вызванных во все предыдущие моменты времени,
согласно формуле
о
ritdt; B8.1)
Р —множитель, который должен иметь размерность' обрат-
обратную времени; положим, что он равен v/l, где в каче-
качестве I естественно взять кубический корень из Vo — вели-
величины вытесненного объема, входящей в равенство B7.29).,
Тогда из B8.1) и B7.29) получим
B8.2)
§ 28. Корабельные волны и угол Маха 255
где rt — расстояние QP, т. е. расстояние от рассматри-
рассматриваемой точки Р до точки Q, которая являлась источ-
источником возмущения в предшествовавший момент времени t.
Далее, пусть г и 8- будут полярными координатами
точки Р относительно полюса О, т. е. величинами,
не зависящими от времени.
Согласно фиг. 43 (t отсчитывается в отрицательную
сторону),
rf = г2 -f vH2 -f 2rvt cos 8. B8.3)
Учитывая B7.27), положим
Использованное в B8.2) представление B7.29) было
получено в предположении и > 1. В этом предположении
f(t) опять будет являться быстро изменяющейся функ-
функцией. Воспользуемся поэтому методом стационарной
фазы и будем искать корни уравнения
Из B8.4) и B8.3) получаем
А /' (г) = г± - ll (vH + rv cos Ь) = j-3 (vH2 + 3rvt cos Ь + 2r2).
B8.5)
Если последнюю скобку приравнять нулю, то для t полу-
получим два корня (если 8 — острый угол)
Обозначим их
«1=-тт(™*-УС0В'*-т)'
B8.6)
'2=-1П7 (cosft + j/сое»»--§-) .
Для того чтобы корни находились в нашей области
интегрирования — оо < t < 0, они должны быть не только
отрицательными, но и действительными. Отсюда следует,
что
4, \Ь\<
'о-
256
Гл. V. Теория волн
Здесь 9-0 является предельным углом, который впервые
был вычислен Кельвином,
= 4 или
B8.7)
Для 18-1 > 8-0 не существует области постоянной фазы;
вся картина волнового движения будет ограничена двумя
прямыми, расположенными под углами Ь= ±ЬЬ к напра-
направлению движения (фиг. 44). Ее можно пояснить следу-
следующим образом: интеграл B8.2) распадается на две части,
Фиг. 44.
Продольные и поперечные волны за корпусом движу-
движущегося судна.
возникающие в результате интегрирования в окрестности
t = tx и t = t2. Они содержат фазовые множители e~lf (*i)
и е~~*^*2). Полагая, что УAг) и f(t2) являются постоян-
постоянными, мы получим две системы волн, а именно, упомя-
упомянутые уже продольные и поперечные волны. Кривые,
изображенные на фиг. 44, представляют собой их макси-
максимумы, следующие друг за другом.
Для & = fr0, согласно B8.6), оба значения tx и t2 сов-
совпадают. Соответствующий источник возмущения распо-
расположен в точке Q' на фиг. 43. Согласно B8.6), он от-
отстоит от О на расстоянии
vt[ =
vt'2 =
r' cos
где r' — расстояние точек Р', лежащих на прямых 8- = ±9-0,
от точки О. Направление линии постоянной фазы / Aг) =
§ 28. Корабельные волны и уеол Мака 257
= /(^2) = const в точке Р' можно найти, если из точки Q'
провести небольшой отрезок дуги окружности радиуса
Q'P'. Обе кривые постоянной фазы, таким образом,
выходят из точки Р' в одном и том же направлении.
Если их рассматривать как единую алгебраическую
кривую, то в точке Р' эта кривая будет иметь точку
возврата.
С убыванием & < 9-0, согласно B8.6), — vt2 будет воз-
возрастать, а точка Q' будет смещаться на фиг. 43 влево
до положения Q, соответствующего fr = 0:
где г —теперь расстояние от О до точки Р'%, в которой
поперечная волна пересекает направление движения.
Дуга окружности, проведенная радиусом QIPI и совпада-
совпадающая в точке Р\ с направлением поперечной волны, рас-
расположена, естественно, перпендикулярно к направлению
движения. Таким образом, общая форма гребня попе-
поперечной волны более или менее очевидна.
С другой стороны [снова согласно B8.6)] с убыва-
убыванием 8- < Ьо расстояние — vtx будет убывать и точка Q'
перейдет вправо в положение Qx (см. фиг. 43), смеща-
смещаясь до положения Q'[. Касательная к исходящей из Рг
продольной волне будет постепенно становиться более
пологой; это видно, если из точки Qx провести окруж-
окружность радиусом QXPX. Для очень малых 8 расстояние 0Q{
будет равно
так что соответствующая точка Qx будет почти совпадать
с точкой кривой Р'х' и с точкой О. Поэтому продольные
волны касались бы в точке О направления движения
при условии справедливости нашего метода в окрестно-
окрестности О, что, однако, не выполняется (поэтому на фиг. 44
кривые до конца не доведены). Действительно, наш ме-
метод стационарной фазы не годится для малых интерва-
интервалов /. Тем не .менее мы выяснили в общих чертах форму
продольных волн.
17 А. Зоммерфельд
258 Гл. V. Теория волн
Полное аналитическое представление обоих семейств
кривых имеется как в книге Л амба1), так и в мюнхен-
мюнхенской диссертации Гопфа, о которой упоминалось на
стр. 154; в последней использован метод интегрирования
в плоскости комплексного переменного.
Рассмотрим кажущееся на первый взгляд парадок-
парадоксальным положение о том, что существует предельный
угол Ьо, не зависящий от скорости. Как согласовать
этот результат с хорошо известными моментальными
фотографиями снаряда, летящего со сверхзвуковой ско-
скоростью, полученными с помощью метода Теплера. В тео-
теории этого явления снаряд, как и наше судно, рассматри-
рассматривается в виде точки и принимается, что из места, где
находилась эта точка в любой предыдущий момент вре-
времени, исходит волна сжатия. В момент наблюдения эта
волна заполняет сферу радиуса r = ct, где с —скорость
звука; путь, который за это время прошел снаряд, равен
х = vt. Огибающая совокупности всех образованных сфер
будет являться круговым конусом, который называется
конусом Маха. Половина угла раствора этого конуса
называется углом Маха, который задается соотношением
sini8-n = —=—.
0 х v
Мы видим, что с ростом v этот угол стремится к нулю,
что противоречит существованию не зависящего от ско-
скорости предельного угла &0 = 19°28'.
Причина этого противоречия обусловлена законом
дисперсии. Звуковые волны распространяются с посто-
постоянной скоростью с без дисперсии. Наоборот, волны в глу-
глубокой воде распространяются, согласно закону диспер-
дисперсии, со скоростью V = |/g/k; их скорость зависит от
длины волны. Для любой скорости, с которой движется
судно, образуются волны, распространяющиеся вместе
с судном, в то время как при полете снаряда все волны
будут отставать от него. Из этого становится понятным
существование для корабельных волн угла 9-0, не зави-
зависящего от v.
То же самое можно получить, если рассмотреть кора-
х) L a m b H., Hydrodynamics. (См. перевод: Ламб Г.,
Гидродинамика, М.,1947.—Прим. перев.)
§ 28. Корабельные волны и угол Маха 259
бельные волны в мелкой воде (в смысле § 24). Так как
в этом случае, согласно B4.7), V = ygh, то не будет
никакой дисперсии, и мы можем применить изложенное
чисто геометрическое рассмотрение. Возникающий при
скорости v > V предельный угол должен при увеличении v
также стремиться к нулю. Однако при такой постановке
задачи наше судно должно рассматриваться плоскодон-
плоскодонным, что является слишком искусственным. Заметим
только, что в прежних работах1) о корабельных волнах
образующие их кольцевые волны рассматривались с по-
помощью соотношений для мелкой воды (работы Эйлера,
1759 г.; Лапласа, 1776 г.; Лагранжа, 1787 г.).
В заключение приведем несколько малоизвестных
фотографий, полученных Кранцем в его баллистической
лаборатории, которые иллюстрируют явление Маха.
На фиг. 45а изображен снаряд, летящий между двумя
параллельными стенками. Конус Маха правильным
образом отражается от этих стенок; кроме того, здесь
(так же как и на других фотографиях) виден «вихревой
хвост», который тянется вслед за снарядом. На фиг. 456
изображен снаряд, пробивший тонкую деревянную стенку,
которая находится за левым краем фотографии. Видны
конусы Маха как за снарядом, который, выйдя из стенки,
несколько отклонился, так и за многочисленными оскол-
осколками дерева, выбитыми из стенки. Последние вследствие
более малых, но все еще сверхзвуковых скоростей имеют
углы раствора большие, чем у конуса, образованного
снарядом. Наиболее поучительной является фиг. 45в:
снаряд пролетает сквозь цилиндр с кольцевыми отвер-
отверстиями (видна выходящая из цилиндра головка снаряда).
Из отверстий цилиндра выходят сферические волны, оги-
огибающей которых является конус Маха. Здесь мы видим
прямое экспериментальное доказательство представлений
о возникновении конуса Маха как огибающей отдельных
сферических волн, а также красивую иллюстрацию прин-
принципа Гюйгенса, оперирующего с поверхностями огибаю-
огибающие сферические волны; этот принцип имеет важнейшее
значение во всей геометрической оптике.
х) Ср. цитированный на стр. 253 обзор Буркхардта. стр. 352,
429 и 430.
17*
Глава VI
ТЕЧЕНИЯ С ЗАДАННЫМИ ГРАНИЧНЫМИ
УСЛОВИЯМИ
§ 29. ОБТЕКАНИЕ ПЛОСКОЙ ПЛАСТИНКИ
Так как в этом и следующих параграфах будут рас-
рассматриваться двухмерные течения, то можно воспользо-
воспользоваться мощными методами теории функций комплексного
переменного.
Рассмотрим опять эллиптические координаты ?, tj,
(см. фиг. 27а), которые связаны с прямоугольными коорди-
координатами х, у с помощью ра-венства A9.15)
cch(Z-j~iri), B9.1)
где с —половина фокального расстояния на фиг. 27а
и одновременно половина длины проекции нашей пла-
пластинки на плоскость ху; будем считать, что в направлении
оси z пластинка имеет бесконечную протяженность.
В эллиптических координатах передняя и одновре-
одновременно задняя стороны проекции нашей пластинки задаются
значениями
соответствующими бесконечно узкому эллипсу (см.
фиг. 27а). Для этих значений правая часть равенства
B9.1) действительна, так что г/ = 0 и —с < х < -{-с.
С другой стороны, для
i\=±-Y> 0< ?< со
правая часть B9.1) соответственно положительно или
отрицательно мнимая, так что х = 0 и у > 0 или у < 0;
это также следует из фиг. 27а.
Рассмотрим теперь аналитическую функцию
Ф + iW = const sh (& + щ), B9.2)
§ 29. Обтекание плоской пластинки
261
введенную еще в A9.20), и положим
.const = iqc;
B9.2а)
здесь q — действительная величина, имеющая размерность
скорости. В силу B9.1) Ф-f iW будет являться аналити-
аналитической функцией не только от ? + пг], но и от x-\-iy.
Поэтому, согласно § 19 , Ф можно рассматривать как
потенциал скоростей, a \F — как функцию тока при усло-
условии, что Ф и W удовлетворяют граничным условиям
нашей задачи в плоскости ху. Чтобы выяснить это,
рассмотрим следующую таблицу:
Плоскость
Е = 0
? —> оо
Плоскость
X = С COS Tfj, ^
ж = 0, у= —с s
ж = 0, y=+cs
2 2_с2 ^2=
ху
h|<0
—> оо
Поведение функций Ф, W
W = 0, Ф = — gc sin г]
""=0, * = ,""?> 0
ф= +?•«, ф = —ду
Смысл первых трех строк вытекает из наших преды-
предыдущих замечаний, если принять во внимание, что пра-
правая часть B9.2), с учетом B9.2а), действительна как
для Е = 0, так и для tj= ± (^/2). Что касается четвертой
строки таблицы, то, согласно B9.1) и B9.2), для ?—> оо
будет
B9.3)
« ас 1- . „. ас е
Ф = — ^- е- sin 7j, W = \ е* cos 73,
что совпадает со значениями, приведенными в таблице.
Отсюда можно вывести, что в плоскости ху на бесконеч-
бесконечности имеется поле однородного течения в направлении у:
vv=—-jr- = q, i?r=—-a- = 0, (z9.oa)
262 Гл. VI. Течения с заданными граничными условиями
С другой стороны, из первых трех строк таблицы
вытекает следующее: отрицательная ось у представляет
собой линию тока W = 0. В точке х — у = 0, т. е. в сред-
средней точке О передней стороны пластинки линия тока
разделяется на две ветви, обтекающие переднюю и зад-
заднюю стороны пластинки, которые соединяются опять
в средней точке задней стороны пластинки; оттуда линия
Фиг. 46. .
Течение, перпендикулярное к пластинке. Теоретиче-
Теоретическая картина течения за пластинкой представляет
собой зеркальное отображение течения перед пла-
пластинкой.
W == 0 идет дальше в направлении положительной оси у.
Эта линия тока представляет собой границу семейства
линий тока (фиг. 46)
W — const.
Особый интерес представляет точка О или, лучше
сказать, обе точки О на передней и задней сторонах
пластинки. Назовем их точками раздвоения течения или
(согласно терминологии теории функций) точками вет-
ветвления отображения. Они называются точками останов-
остановки, так как в этих точках скорость обращается в нуль
(vx = vy = 0). Согласно закону Бернулли, это соответствует
максрмуму гидродинамического давления.
§ 29. Обтекание плоской пластинки 263
Согласно A1.9), в случае стационарного течения и
отсутствия внешних сил (U = const)
р = const — р у • B9.4)
Если на бесконечности давление положить равным нулю,
т. е. считать, что давление р обусловлено только гидро-
гидродинамическим давлением, которое появляется при течении,
то const = p/2 • q2 и
P = i(q2~v2)- B9.4а)
Так как в точках остановки г; = 0, то давление там будет
действительно больше, чем в любых других точках.
Исследуем также изменение давления на передней
и задней сторонах пластинки. Как было показано,
передней стороне соответствуют координаты ? = О,
— тс < т] < 0, а задней стороне ? = 0, 0 < -ц < -J- тг; при этом
Ф=—дс sin ц, х = с cos tj,
ЭФ dt] cos ч]
V = ^— -;— = О —: ,
dir] dx * sin if]
и, согласно B9.4а),
р 2 q
Отсюда следует
p = — со , для т] =
f 0, х= +с 1
-- '» \ (ребра пластинки)
( ± те, ж= — с J ^ F 7
f « с Т
I ±f» ж==~^т7^1 (расстояние, равное
р = 0, для ^ = ^ Зтс с * 0»29с от ребер
| ±-?, ж=~^ пластинки),
и, как. было показано выше,
jo = /?макс. = -^- g2 для 7] = ± ~, ж = 0 (середина пластинки).*
Однако в силу наличия отрицательного (а на ребрах
даже бесконечно большого отрицательного) - давления
такое распределение давления е чдштнт жидкости осу^
264 Гл. VI. Течения с заданными граничными условиями
ществиться не может; под влиянием таких давлений
в течении должен произойти разрыв.
Имеется еще одно, не менее парадоксальное след-
следствие: суммарное давление текущей жидкости на пла-
пластинку, а также суммарный вращательный момент равны
нулю, так как давление на переднюю сторону пластинки
уравновешивается давлением на заднюю сторону пла-
пластинки.
Иначе говоря, если считать, что на бесконечности
жидкость покоится, а пластинка движется в жидкости
с постоянной скоростью q, то при этом работа не затра-
затрачивается. Пластинка и окружающая ее жидкость, однажды
приведенные в движение, будут перемещаться далее с по-
постоянной скоростью.
Рассмотрение этого парадокса, обобщенного на слу-
случай твердого тела произвольной формы, было произве-
произведено Даламбером и Эйлером1). Кирхгоф, Томсон и позднее
Минковский2) исследовали, с точки зрения абстрактной
гидродинамики, при каких условиях возможно стацио-
стационарное движение (как, например, в случае нашей пла-
пластинки); выяснилось, для того чтобы такое движение
было возможным, направление импульса пластинки
должно совпадать с направлением момента импульса.
На примере нашей пластинки мы видим, как разрешается
этот парадокс: появление отрицательного давления делает
такое стационарное движение иллюзорным.
Сравним с этой точки зрения фиг. 46 с фиг. 47а,
изображающей действительную картину течения. Изо-
Изображенные на этих фигурах картины течений на перед-
передней части пластинки в основном совпадают. В частности,
около середины пластинки, изображенной на фиг. 47а,
также имеется точка остановки. Но за пластинкой оба
рисунка коренным образом отличаются друг от друга.
г) Во введении к книге О seen С. W., Hydrodynamik,
AKademische Verlagsgesellschaft A927) упоминается Спиноза, как
более ранний исследователь этого вопроса. Отметим, кстати, что
В этой книге также излагается этот парадокс. Поучительное рассмо-
рассмотрение для двухмерного случая проведено в работе: Н a jjl e I G.,
Zs. angew. Math. u. Mech., 40, 52 A935).
2) Minkowski H., Ges. Werke, Щ, II, S. 283; Preuss, Akad.
$. Wiss., 15, 1095 A688).
§ 29. Обтекание плоской пластинки
265
На фиг. 47а за пластинкой имеются завихрения, кото-
которые возникают при обтекании ребер пластинки и дви-
движутся дальше вместе с жидкостью. Это явление будет
рассмотрено в § 30 и 32.
Продолжим теперь наше еще весьма несовершенное
теоретическое рассмотрение и перейдем к исследованию
обтекания косо расположенной пластинки. Для этого
воспользуемся системой координат х, у, повернутой
по отношению к системе %, у\ на угол f < (тс/2). При
этом равенства B9.1) и B9.2) перейдут в
х -f iy — cel"i ch (? + щ),
Ф + iW = iqc sh (E + if\ + щ
B9.5)
B9.6)
Таблица на стр. 261 изменится следующим образом:
Плоскость
Плоскость ху
Поведение функций Ф, W
5 = 0
5 —¦> оо
х — с cos if] cos -у
у = с cos ifj sin T
ж = -f- с sh 5 sin 7
у = + с sh 5 cos -у
C2 2 =
j2/2 e '
= O, Ф=—
^=4: gcshi sin-y
Ф = -J- qc ch 5 cos -у
Отсюда следует, что передняя и задняя стороны пла-
пластинки задаются значениями ? = 0, —тг < ч\ < 0 и соот-
соответственно 0 < т] < + и: и опять представляют собой
линию тока ^ = 0. На бесконечности, как и прежде,
для ? = сю имеем в плоскости ху поле однородного тече-
течения с постоянной скоростью д; линиями тока здесь
являются прямые х = const. Но линии у\— Т (^/2) больше
не являются линиями тока; геометрически они пред-
представляют собой две полупрямые, а именно нормали
к пластинке в ее средней точке, задаваемые уравнением
у= —xctg^ .(см. среднюю колонку таблицы). В конеч-
конечной области теперь совсем нет прямолинейных линий тока.
266 Гл. VI. Течения с заданными граничными условиями
Чтобы исследовать картину течения, опять найдем
точки остановки. Они совпадают с точками ветвления
отображения нашей плоскости Ф -\- г'Ч?* на плоскость
x~\-iy. Вообще говоря, они задаются условием
=0- B9.7)
Производная, стоящая в левой части, может быть вычи-
вычислена с помощью B9.5) и B9.6):
d(Ф + W) id{x-\-iy) iqch(S + щ + if) /9Q 7Я\
1 ^*IA>
Согласно B9.7),
ch(|+i7j + JT) = 0 B9.76)
или, отделяя действительную и мнимую части, получаем
ch&cos(-rj + T) = 0, sh?sinG] + 7) = °- B9.7в)
Так как сЪ^Ф 0, a shE = O только при ? = 0, решением
уравнения B9.7в) будет
т,= ±~т. 5 = 0. B9.8)
Мы опять получили две точки остановки, одну на перед-
передней и другую на задней стороне пластинки:
6 = 0, 72=_^-т и 1 = 0, tj=+|— т- B9.8а)
Однако теперь они расположены не в середине пла-
пластинки, а смещены в разные стороны на одно и то же
расстояние, которое, согласно B9.5), равно
На фиг. 48 они обозначены через Ох и О2. Здесь vx = vy = 0
и, согласно уравнению Бернулли B9.4а), давление имеет
максимальное значение:
Эти точки остановки теперь являются также «точками
раздвоения». Линия тока, раздваивающаяся в точке Olt
подходит перпендикулярно к пластинке точно так же,
как и линия тока, выходящая из 0%.
§ 29. Обтекание плоской пластинки
267
Рассмотренная в B9.7) производная дает в произ-
произвольной точке выражение для скорости течения в ком-
плексной форме
—р-.—. . . = —Vv-\-lV... (zy.y)
Это непосредственно следует из выражения A9.4а) для
/'(z) и из условий Коши —Римана A9.5). Если возьмем
модуль величины, стоящей в B9.9), и учтем B9.7а), то
получим
B9.10)
v =
В частности, для Е = 0, т. е. для контура пластинки
(как для передней, так и для задней стороны), „
cos (-ц + т)
B9.10а)
Течение, наклонное к пластинке. Теоретическая кар-
картина течения за пластинкой представляет собой кар-
картину течения перед пластинкой, повернутую отно-
относительно середины пластинки на 180?.
Отсюда следует, согласно уравнению Бернулли B9.4а),
что приводит к условию
p=z-*rca для 1} = | т. е. на ребрах пдастинки.4
268 Гл. VI. Течения с заданными граничными условиями
Далее,
р = 0 для cos2(Tj + T) = sin2Tj. B9.12)
Если вместо sin tj написать cos [(тс/2) — if]], то это усло-
условие запишется в виде
COS G] + 7) = ± COS
Отсюда следует, что либо
либо
.11 ТС У
Координата % положительна (так как f < тс/2), и точка
расположена на задней стороне, т]2 отрицательна, и точка
расположена на передней стороне пластинки. На задней
стороне между значениями т\ = 0 и 1C = % и на передней
стороне между f]= — тс и tj = tj2 Давление отрицательно.
Так как в жидкости не может быть отрицательного дав-
давления, то наше решение для наклонно расположенной
пластинки точно так же, как и для частного случая
перпендикулярной пластинки, не имеет физического
смысла.
Это подтверждается сравнением фиг. 48 с действи-
действительной картиной течения, изображенной на фиг. 476.
С передней стороны картина линий тока совпадает на
обоих рисунках, в частности точка остановки на фиг. 476
находится там, где ее и следовало ожидать. Но картина
с задней стороны пластинки коренным образом разли-
различается. Вместо антисимметричного повторения картины,
наблюдающейся на передней стороне, на фиг. 476 имеются
характерные завихрения.
Мы рассматривали здесь только стационарные течения.
В акустике, где рассматриваются нестационарные волно-
волновые поля, большое значение имеет задача о свободно
подвешенном легком диске, так называемом «диске Рэлея»,
помещенном в звуковой поток. Как показал Рэлей1), для
l) Rayleigh, Phil. Mag., Dezember A876); Lamb EL, Hydro-
Hydrodynamics, Ch. IV, Art. 78. (См. перевод: Лам б Г., Гидро-
Гидродинамика, М,, 1947.— Прим. перев.)
§ 30. Мертвая зона и поверхности разрыва 269
решения этой задачи можно использовать изложенные
выше методы. Поэтому наши выводы об отсутствии физи-
физического смысла у полученных решений мы будем относить
только к стационарному случаю.
§ 30. МЕРТВАЯ ЗОНА И ПОВЕРХНОСТИ РАЗРЫВА
«В природе жидкости, если ее рассматривать как
идеально текучую, т. е. лишенную всякого трения, нет
ничего, что мешало бы двум соседним слоям жидкости
двигаться относительно друг друга с конечной скоростью.
По крайней мере те свойства жидкости, которые вхо-
входят в гидродинамические уравнения, а именно, постоян-
постоянство массы в каждом элементе объема и равенство давле-
давления во всех направлениях, не препятствуют тому, чтобы
тангенциальная скорость движения жидкости по обе сто-
стороны от поверхности, проходящей внутри жидкости, от-
отличалась на конечную величину. Напротив, компоненты
скорости в направлении, перпендикулярном к плоскости,
а также давление по обе стороны такой поверхности
должны, конечно, быть равными» х).
Далее Гельмгольц указывает, что, для того чтобы
в жидкости не было отрицательных давлений, на острых
краях препятствия всегда должны возникать поверхности
разрыва. Он отмечает далее, что под влиянием трения
поверхность, которую мы первоначально представляли
геометрической, разобьется на ряд завихрений (Гельмгольц
говорит: «вихревых нитей»). Мы рассмотрим это явление
в § 32. Пока будем считать жидкость идеальной и невязкой.
С этой точки зрения рассмотрим опять нашу двух-
двухмерную задачу об обтекании пластинки, причем, как
и в начале § 29? будем для простоты считать, что пла-
пластинка расположена перпендикулярно к потоку. От острых
краев пластинки в двухмерном случае будут отходить
две линии разрыва, расположенные зеркальным образом
по отношению к оси у, форма которых, однако, нам еще
не известна (см. фиг. 49, где ребра пластинки обозначены
буквами А и В). Пространство между линиями разрыва
*) Helmholz H.,, О разрывных движениях жидкости, Sitzungsb.
d: Preuss. Akad. d. Wiss., 1868.
270 Гл. VI. Течения с заданными граничными условиями
и пластинкой мы представляем себе как неподвижную,
«мертвую зону». В ней скорость равна нулю и давление
постоянно, скажем, равно р0. Согласно приведенной выше
цитате, для жидкости, текущей снаружи линий разрыва,
имеют место следующие граничные условия для давле-
давления и нормальной составляющей течения:
Р = Ро, ^ = 0. C0.1)
С другой стороны, тангенциальную компоненту vs
можно определить из уравнения Бернулли B9.4а), кото-
которое с учетом C0.1) дает
C0.2)
Фиг. 49.
Течение, перпендикулярное к пла-
пластинке АВ. От А и В начинаются
линии разрыва AU и BU, ограни-
ограничивающие мертвую зону.
z = х + iy и / =
рассматривал также третью переменную
1
Итак, тангенциальная
компонента скорости вдоль
1/ обеих линий разрыва посто-
постоянна. О бесконечно больших
скоростях и отрицательных
давлениях теперь больше нет
речи.
Кирхгоф1), разработав-
разработавший идею Гельмгольца и при-
применивший ее к рассмотрению
нашей задачи об обтекании
пластинки, наряду с комп-
комплексными переменными
C0.3)
*) Kirchhoff G., Crelles Journ. 70 A869), а также Vorle-
sungen iiber Mechanik. Кар. XXII. (После работ Гельмгольца и Кирх-
Кирхгофа следующий крупный шаг в теории струй (разрывных течений)
был сделан в 1890 г. Н. Е. Жуковским, развившим совершен-
совершенные методы, позволяющие решать сложные задачи с большим числом
струй (см. Собрание сочинений, т. II, 1949). Изложение этих мето-
методов и их применения можно найти в книге Л. И. Седова «Плоские за-
задачи гидродинамики и аэродинамики», М.—Л., 1950.—Прим.перев.)
§ 30. Мертвая зона и поверхности разрыва
271
которая связана с двумя переменными, согласно B9.9),
следующим образом:
«, dz
-—5/" •
C0.4)
Кирхгоф исходил из предположения, которое лежит также
в основе картины, изображенной на фиг. 49, что мертвая
зона простирается вплоть до бесконечности. В этом слу-
случае давление р0 равно давлению на бесконечности, кото-
которое, согласно определению в равенстве B9.4а), равно
нулю. Из C0.2) следует тогда, что для любого места
на линиях разрыва
— //«—г~ IV,. = с/„ = и. , I OVJ.O)
Отсюда, согласно C0.3), получаем граничное условие
для С:
|С|= —. C0.5а)
я
Необходимо отметить, что предположение о том, что
линии разрыва уходят на бесконечность, носит слишком
частный характер. Замеча-
Замечания по этому поводу будут
сделаны в конце этого па-
параграфа.
Найдем в плоскости
комплексного переменного
С отображение границы
между областью течения
и мертвой зоной (фиг. 50).
Начнем с бесконечно удаленной точки z-плоскости.
В этой точке
vy — q, vx = Q и, согласно C0.3), С= •
Таким образом, отображение точки U в С-плоскости
лежит на отрицательной мнимой оси. Через эту точку,
согласно C0.5а), проходят также отображения обеих
линий разрыва. На фиг. 50 проведена полуокружность
радиуса \\q с центром в С = 0. Ее концы С=±A/<7)
соответствуют ребрам пластинки АВ (см. фиг. 49). На всей
и г. 50. Отображение z-пло-
скости на С-плоскость.
272 Гл. VI. Течения с заданными граничными условиями
пластинке, а также на ребрах vy — 0 и, согласно C0.3),
С действительно.
Рассмотрим, наконец, точку остановки О фиг. 49.
В этой точке vx — vy = 0 и, согласно C0.3), С=оо. Изо-
Изображение точки О в С-плоскости лежит в бесконечности.
Тем самым задается отображение обеих половин пластинки.
Ввиду того что вдоль пластинки С действительно, отре-
отрезок О А действительной оси фиг. 50 соответствует одной
половине пластинки, а отрезок ОВ — другой половине.
При обходе контура UAOBU на фиг. 49 область тече-
течения находится слева, а мертвая зона —справа. Поэтому
заштрихованная на фиг. 50 область, находящаяся слева
от пробегаемого в том же направлении контура, соответ-
соответствует области течения1), а незаштрихованная область —
мертвой зоне. Однако мы еще не получили аналитиче-
аналитического представления конформного отображения обеих
плоскостей друг на друга, так как еще неизвестна форма
линий разрыва на фиг. 49.
Иначе обстоит дело в случае отображения z-плоскости
на /-плоскость. Рассмотрим приведенную ниже таблицу.
Как и прежде, будем считать, что на линии тока, которая
раздваивается в точке остановки, 47 = 0. Тогда на всей
границе области мертвой зоны / будет действитель-
действительно. Далее будем считать, что в точке, остановки О
потенциал скоростей Ф равен нулю и, следовательно,
Ф отрицательно вдоль ОА, а также вдоль ОВ. Неиз-
Неизвестное еще нам значение, которое Ф принимает в точках
А и В, обозначим через /0:
+с —с
/о = - \ Vxdx = - \ vxdx' C0-6)
0 0
так как 47 = 0 в точках А и В, то /0 является также
значением / в этих точках. Так как отрицательная дей-
действительная ось / соответствует и верхней и нижней
границам области мертвой воды, то необходимо считать,
что в /-плоскости вдоль отрицательной действительной
х) Если вместо переменной С воспользоваться обратной величи-
величиной С = 1/С, то в плоскости этой переменной область течения ото-
отобразится на внутренность изображенного на фиг. 50 полукруга,
ограниченную сверху его горизонтальным диаметром.
§ SO. Мертвая зона и поверхности разрыва
273
оси имеется разрез (фиг. 51). С другой стороны, имеется
взаимнооднозначное соответствие между положительной
действительной осью и линией тока W = 0, т. е. между
г/ = — со и 2/ = 0 на фиг. 49.
Заштрихованная часть на
фиг. 51 означает, что вся
/-плоскость, ограниченная
только нашим разрезом, со-
соответствует области течения
на фиг. 49; область мертвой
зоны на фиг. 49 отображает-ся на второй лист . /-пло-
/-плоскости, соединенный с первым вдоль нашего разреза.
шшш,
Ф и г. 51. Отображение z-пло-
скости на /-плоскость.
А
В
О
и
z
+ с
— с
0
оо
С
1
Я
+-
i
Я
\ f
/о<О
/о<О
0
сю
Изменение
угла
1
2
1
т
1
"
Сравнивая фиг. 50 и 51, попытаемся найти прямое
отображение Г-плоскости на /-плоскость. Если бы это
отображение было всюду конформным, оно задавалось бы
линейной зависимостью Си/. Однако имеются места,
где конформность отображения нарушается, правда, не
внутри заштрихованных на фиг. 50 и 51 областей,
а на их границе. Они отмечены в последней колонке
приведенной выше таблицы. Величина х/2 в строках, соот-
соответствующая точкам А и В, означаем что угол тс, обра-
образованный границей /-плоскости возле Аи В (см. фиг. 51),
переходит в угол тс/2 в ^-плоскости (см. фиг. 50); точно
так же величина 1/2, соответствующая точке О, означает,
что угол 2тс, образованный границей /-плоскости возле
точки О (см. фиг. 51), переходит в угол тс в С-плоскости
(см. фиг. 50). Отсюда следует, что в искомую связь
18 а. Зоммерфельд
274 Гл. VI. Теченил 6 заданными граничными условиями
между Си/ эти величины должны входить соответственно
в следующем виде:
Рассмотрим соответственно этому отображение
0-f)"
Yh+Yf
или, в более удобной форме,
i лГ~ГГГ
C0.7)
Эта функция удовлетворяет требованиям нашей таблицы»
что может быть доказано разложением в ряд в окрестно-
окрестностях точек А, В, О; в следующем параграфе мы покажем
это несколько более систематически.
Вычислим теперь явным образом величину С. Приведя
C0.7) к общему знаменателю, получим квадратное урав-
уравнение
= 0, C0.7а)
решение которого имеет вид
Исключим нашу вспомогательную переменную ? с по-
помощью C0.4). При этом получим дифференциальное ура-
уравнение, связывающее обе первоначальные переменные
z и /, а именно:
Для того чтобы его проинтегрировать, введем параметр а
с помощью соотношения
1/ -jr- = sina, d/ = 2/0sinacosacfa,
у if-
Sin a
§30. Мертвая зона и поверхности разрыва 275
Если выражение C0.9) взять со знаком плюс, то получим
2/
dz = — (cos a + cos2 a) da.
В результате интегрирования находим
z= —
a)J . C0.11)
Правильность интегрирования легко может быть про-
проверена дифференцированием. Постоянную интегрирования
надо положить равной нулю, так как, согласно C0.10),
при а = 0 должно быть / = 0; согласно нашей таблице,
при / = 0 необходимо, чтобы z —0.
При a = тс/2, согласно C0.10), / = /0; из нашей таблицы
следует, что это соответствует ребру пластинки А, т. е.
2 = с. Иначе говоря, необходимо, чтобы
с=_?[оЛ + М -="-^Й. C0,12)
Этим соотношением определяется ранее неизвестная вели-
величина /0. Подставим ее выражение C0.12) в C0.11) и,
разделяя действительную и мнимую части, получим
уравнение поверхности пластинки в виде
4с Г 1 1
ж = —-г-, I sin a-f--о" (sin a cos a-j-a) V , C0.13)
где a пробегает значения
_-!<a<+?. C0.13а)
Если теперь а приписать комплексные значения,
начиная от значения тс/2:
а = |—ф, 0<р<оо,
то получаем
Так как /, согласно C0.10) и C0.12), продолжает оста-
оставаться действительным, то мы, очевидно, имеем дело
с продолжением линии тока 47 = 0 за точку А, т. е.
18*
278 Гл. VI. Течения с виданными граничными условиями
с нижней ветвью линии разрыва, изображенной на
фиг. 49. Если опять разделить действительную и мнимую
части и подставить /0 из C0.12), то, согласно C0.11),
C0.14)
Кривая эта трансцендентна, но легко может быть рассчи-
рассчитана численно; для больших р она может быть апроксими-"
рована обычной параболой.
В равенствах C0.10) — C0.12) содержится также общее
решение нашей задачи об обтекании пластинки. Если а
приписать произвольные комплексные значения, то получим
/ = Ф + *^= _-^L sin2aj C0.15)
z = х + iy = , -I sin a + -o" (sin a cos a + a) r • C0.16)
Явное представление Ф и 4f через х, у путем исключе-
исключения а невозможно, да в нем и нет необходимости.
Для проверки сравним значение C0.12) с первоначаль-
первоначальным определением /0 в C0.6). Согласно C0.6), должно быть
с
\ vxdx= $ Ц^ = ФС-ФО. C0.17)
о о
Здесь, согласно C0.15), надо положить
фс=-^Г4» так как а «у,
Ф0 = 0, так как а = 0.
Таким образом, C0.17) совпадает с C0.12).
В противоположность § 29, который приводит к па-
парадоксу Даламбера — Эйлера, наша настоящая теория
дает разумное значение для суммарного давления Р,
действующего на единицу длины пластинки.
Согласно B9.4а), имеем
\ \ ( f) C0.18)
§ 30. Мертвая зона и поверхности разрыва 277
Здесь вдоль передней стороны пластинки v=*vx, а так
как vy = 0, то, согласно C0.3),
и C0.18) перейдет в
+с
()x- C0Л9)
Этот интеграл может быть взят следующим изящным
и строгим способом. Воспользовавшись равенством C0.4),
в котором вдоль пластинки можно заменить dz на dx,
получаем
Теперь, согласно выражению C0.8), которое ошгаь
возьмем со знаком плюс, получаем
Отсюда после несложных вычислений следует
и
Это можно было бы показать непосредственно с по-
помощью квадратного уравнения C0.7а). Вместо C0.19а)
получаем
/о
y! C0.20)
Что касается пределов интегрирования, то, согласно
нашей таблице, / = /0 для обоих краев пластинки, т. е
для х— ± с, в то время как / = 0 для середины
пластинки. Поэтому последний интеграл распространен
278 Гл. VI. Течения с заданными граничными условиями
только на половину пластинки и при этом введен перед
интегралом множитель 2.
С помощью подстановки C0.10) получаем из C0.20)
те/2
Р = 4р/0? \ cos2ada=- p/og* . C0.21)
о
Используя значение /0 из C0.12), имеем
Таким образом, давление, действующее на единицу длины
пластинки, пропорционально квадрату скорости течения,
что находится в соответствии с общим эксперименталь-
экспериментальным гидравлическим законом (см., например, стр. ЮЗ);
вместо этого определения можно сказать: пропорциональ-
пропорционально кинетической энергии единицы объема невозмущенного
течения или, что одно и то же, пропорционально скоро-
скоростному напору в точке О. Численный коэффициент,
вообще говоря, совпадает с экспериментальными данными
только по порядку величины. Для нашего случая бес-
бесконечно длинной пластинки Прандтль приводит экспери-
экспериментальное значение, равное примерно 2,0, вместо нашего
коэффициента 0,88. Согласно Прандтлю1), причина рас-
расхождения заключается в том, что в действительности
область мертвой зоны не простирается до бесконечности,
а течение вдали за пластинкой сходится опять; завих-
завихрения, образующиеся с задней стороны пластинки, сни-
снижают давление за пластинкой по сравнению с невозму-
невозмущенной жидкостью, что приводит к «всасывающему
действию».
Последние замечания противоречат представлениям,
введенным Кирхгофом и встречающимся в литературе.
Введенное для упрощения предположение, что р0 = 0,
как было показано на стр. 271, совпадает с предполо-
предположением о том, что область мертвой зоны простирается
неограниченно. Более общее рассмотрение (см. приме-
примечание на этой стр.), свободное от этих предположений,
х) См. также SchmiedenC, Zs. furLuftfahrtforschung, 17,
37 A940) и KolscherM., там же, стр. 154.
§ 30. Мертвая зона и поверхности разрыва 279
слишком сложно, чтобы его здесь можно было воспро-
воспроизвести.
Сделаем, наконец, короткое замечание по очень
интересному вопросу об устойчивости. Будем считать, что
наша пластинка не закреплена жестко, а что в центре
у нее имеется ось, вокруг которой она может вращаться.
Будет ли тогда пластинка устанавливаться в направлении
течения? (В этом положении наше давление Р было бы
равно нулю.) Или же она будет оставаться в перпенди-
перпендикулярном положении? Опыт решает вопрос в пользу
последнего.
Полное исследование этого вопроса потребует знания
течения и соответствующих ему поверхностей разрыва
в случае косо расположенной пластинки. Они не потре-
потребуются нам, если мы будем считать, что наша картина
течения, изображенная на фиг. 48, качественно верна
в том смысле, что она правильно описывает положение
точки остановки с передней стороны пластинки. Это
предположение подтверждается экспериментальной кар-
картиной, изображенной на фиг. 476. Будем поэтому исходить
из того, что при вращении пластинки точка остановки
будет смещаться вперед на половину пластинки, обращен-
обращенную к течению. В эту же сторону сместится тогда и
максимум давления.
Если пластинка, как показано на фиг. 48, из пер-
перпендикулярного направления будет повернута против
часовой стрелки, то возникнет вращательный момент,
направленный по часовой стрелке, что препятствует вра-
вращению пластинки.
Таким образом, перпендикулярное к потоку положе-
положение пластинки является устойчивым. То же самое рас-
рассмотрение, примененное к пластинке, параллельной пото-
потоку, показывает, что параллельное положение является
неустойчивым.
Точно так же флюгер, если бы он вращался вокруг
оси, проходящей через его середину (в действительности
его заднее крыло всегда значительно больше переднего),
устанавливался бы не в направлении ветра, а перпенди-
перпендикулярно к нему. Диск Рэлея (см. стр. 268), подвешенный
за середину, также устанавливается перпендикулярно
к звуковому потоку.
280 Гл. VI. Течения с заданными граничными условиями
§ 31. РЕШЕНИЕ ЗАДАЧИ О СВОБОДНОЙ СТРУЕ С ПОМОЩЬЮ
МЕТОДА КОНФОРМНЫХ ОТОБРАЖЕНИЙ
Может показаться, что функция, введенная в выраже-
выражение C0.7) и задающая отображение, является результа-
результатом счастливой догадки, а не строгого вывода. Ниже-
Нижеследующее изложение покажет, что это не так.
Пусть требуется отобразить положительный квадрант1)
^-плоскости на верхнюю половину s-плоскости. Проще
всего это сделать с помощью соотношения
t^s1!*. C1.1)
Отображение конформно всюду в конечной области, кроме
начала координат обеих плоскостей, где угол тс (образо-
(образованный действительной осью) вблизи s = 0 переходит
в угол тс/2 (между положительной действительной и по-
положительной мнимой осями) вблизи ? = 0. Если теперь
произвести дробно-линейное преобразование (а —действи-
—действительно и положительно)
то положительная мнимая ось t перейдет в полуокруж-
полуокружность |С| = й, выходящую из точки [=-ои проходя-
проходящую через С= —ia в точку С= -{-а, в соответствии с тем,
что при дробно-линейном преобразовании прямые, вообще
говоря,- переходят в окружности. С другой стороны, по-
положительная действительная ось Z-плоскости перейдет
в обе части действительной оси С: а < С < + оо и
— оо<С<— а.
Отображение, возникающее в результате подстановки
C1.2) в C1.1) и возведения в квадрат
х) Наш квадрант представляет собой «прямолинейный двууголь-
двуугольник» с двумя прямыми углами, один из которых расположен при
¦?=(), другой—при t~cc>. Можно отобразить на полуплоскость про-
произвольный многоугольник с любыми углами и вершинами, располо-
расположёнными произвольным образом. Это может быть сделано с помощью
общей интегральной формулы Шварца—Кристоффеля. Надо здесь,
рднако, эта формула не потребуется,
§ 31. Решение задачи о свободной струе 281
переводит положительную мнимую s-полуплоскость на
область С-плоскости, заштрихованную на фиг. 50.
Теперь отобразим s-полуплоскость на /-плоскость
(изображенную на фиг. 51), которая разрезана вдоль
отрицательной действительной оси. Чтобы осуществлялся
переход угла тс при s—О в угол 2тс при / = 0, согласно
C1.1), проще всего воспользоваться подстановкой s=|//.
Но так как мы хотим при этом привести в соответствие
значения / и С (согласно таблице на стр. 273), то сна-
сначала подвергнем }/ / дробно-линейному преобразованию,
т. е. напишем
C1.3а)
Если величину а заменить на 1/д, то полученное выра-
выражение совместно с C1.3) дает
C1.4)
Для определения коэффициентов а, C, у, 8 даны следую-
следующие условия1):
=-i, /=/o. «
=+l, / = /o, -
=00, / = 0, р =
Если положить а=1, что мы вполне можем сделать,
то получим
х) Знак минус перед -у во второй строке приведенных условий
следует из фиг. 51: при переходе с верхнего берега разреза на ниж-
нижний значение V1 меняет знак, если этот переход осуществляется
в заштрихованной части фиг. 51, т. е. без пересечения разреза.
Поэтому значение |//0 в первой строке, соответствующей точке А,
во второй строке заменено на— V^/o, которое соответствует точке 2?i
282 Гл. VI. Течения с заданными граничными условиями
При этом C1.4) примет вид
_
(gc+iJ_ Vf-Vh _
i+
т/Т"
г /о
C1.4а)
Таким образом, мы вывели равенство C0.7) доста-
достаточно строгим путем.
Применим теперь тот же метод к классической задаче
об истечении из большого сосуда, связанной с именем
О'
U-
i
тх
Фиг. 52. Двухмерная схе-
схема границы и поперечного
сжатия струи и иллюстра-
иллюстрация характера сужения вы-
вытекающей струи.
Торичелли [см. равенство
A1.10), где было сказано без
доказательства, что жидкость
вытекает из отверстия в виде
U связной струи]. Гельмгольц пер-
первый указал, что образование
струи нуждается в гидродина-
гидродинамическом объяснении. В рабо-
работе, цитированной на стр. 269, он
в качестве примера, иллюстри-
иллюстрирующего свои предположения
о поверхностях разрыва, при-
приводит задачу, которую мы сей-
сейчас рассмотрим.
Будем исходить из карти-
картины, схематически изображен-
изображенной на фиг. 52, и для простоты, как и Гельмгольц, рас-
рассмотрим двухмерную задачу. Поэтому вместо цилиндри-
цилиндрического сосуда у нас будет плоская стенка, а вместо
отверстия, имеющего, например, круглую форму, —бес-
—бесконечно длинная щель шириной 2с. Не будем учитывать
влияние силы тяжести на вытекающую струю. Среднюю
линию струи примем за ось у, твердую стенку—за ось х.
На острых краях щели будут начинаться линии разрыва,
которые сблизятся вследствие притока воды в боковом
направлении. Поэтому сечение струи после выхода из
отверстия будет убывать; говорят о поперечном сжатии
струи (vena contracta). Наша основная цель заключается
в том, чтобы вычислить меру этого сжатия, т. е. отно-
отношение сечения струи вдали от выхода к сечению вблизи
рт него. Детали расчета мы рассмотрим весьма кратко,
§ 31. Решение задачи о свободной струе 283
так как они в основном совпадают с рассуждениями,
приведенными в § 30. Фиг. 52 изображена в плоскости
z — x-{-iy. Кроме этой плоскости рассмотрим (см.
стр. 270 и 271) плоскости
С- ^- и / = Ф + 1Ж C1.5)
— Vx+lVy ' V '
Снаружи вдоль обеих линий разрыва имеется постоянное
атмосферное давление, которое примем за начало отсчета
гидродинамического давления. Тогда из уравнения Бер-
нулли B9.4) следует, что v2 = const, а также
v — const = q.
Из C0.3) имеем
14=7'
где q обозначает, например, величину скорости v на краях
А, В или, иначе говоря, задаваемую формулой Тори-
Торичелли A1.10) скорость истечения в достаточном удале-
удалении от отверстия. ф
В бесконечно далеко отстоящей точке струи U, где,
очевидно, боковая компонента vx исчезнет, согласно
C1.5), будет
С=-|. C1.5а)
Вдоль внутренней границы сосуда, где vy обращается
в нуль, значение С будет действительным. Согласно
фиг. 52 и равенству C1.5), имеем
-J- оо > С > — на стенке О А,
9 C1.56)
— оо < С < ¦ на стенке О'В.
я
Область течения в С-плоскости, таким образом, имеет ту
же форму, что и на фиг. 50, но с несколько иным
обозначением характерных точек границы (фиг. 53); на
фиг. 51 также показано отображение бесконечно уда-
удаленной точки U', соответствующей неограниченному
продолжению средней линии струи в направлении, обрат-
обратном истечению.
284 Гл. VI. Течения с заданными граничными условиями
На фиг. 54 изображена соответствующая область
/-плоскости. В качестве линии тока W — О (действитель-
(действительная ось /-плоскости) мы выберем ось симметрии UU'
течения, вдоль которой Ф возрастает от U к U' (скорость
v~vy имеет здесь все время направление U'—>U).
Обозначим линии тока, проходящие вдоль стенок сосуда
и линий разрыва 1), через
Полоса /-плоскости, ограниченная этими двумя прямыми,
представляет собой отображение всей области' течения.
__?=*
Ф и г. 53. Отображение, z-пло- Фиг. 54. Отображение z-пло-
скости на С-плоскость. скости на /-плоскость.
Если мы припишем значения Ф = 0 эквипотенциальной
линии, проходящей через края щели, то отображения
точек А и В будут находиться на мнимой оси /-плос-
/-плоскости. Стенки сосуда соответствуют отрезкам АО и ВО'
границы полосы, границы струи соответствуют отрезкам
UА и UB.
Установим аналитическую связь между С-плоскостью
и /-плоскостью. Для этого воспользуемся таблицей
(см. стр. 285), построенной на основании фиг. 52—54 и
аналогичной таблице, приведенной на стр. 273.
Если прежде при отображении С на плоскость /, име-
имеющей разрез по действительной отрицательной оси, у нас
появлялась величина у /, то теперь вместо нее будет
показательная функция ew, так как мы имеем дело не
со всей /-плоскостью, а с полосой. Здесь w—введенная
х) Множитель гс/2 перед Wo, введенный для некоторого упроще-
упрощения формул, конечно, никак не скажется на результате.
§ 31. РеШеШё задачи о свободноц струе
285
A
В
0
0'
и
V
'z
+ с
— с
+ ОО
— оо
— ioo
С
1
Я
1
я
—со
i
Я
— ioo
f
i — W
2
— оо
-}-оо
Кирхгофом безразмерная величина, которая при наших
обозначениях равна1)
C1.6)
Воспользовавшись зависимостью вида C1.4) и опре-
определив при этом коэффициенты а, C, ^, Ь из приведенной
выше таблицы (для этого надо, например, использовать
условия для точек В, А и U, при этом остальные усло-
условия будут выполняться автоматически), получаем
х) Сравнение с изложением Кирхгофа, приведенным в его книге
Vorlesungen iiber Mechanik, Кар. XXII, § 3, показывает, что Кирхгоф
определяет потенциал скоростей с обратным знаком, систему коор-
координат выбирает несимметричным образом и проводит все вычисле-
вычисления в безразмерных величинах. Например, он полагает д=1, а соот-
соответствующие единицы измерения вводит значительно позже. Такой
прием используется в литературе весьма широко. Мы, однако, пола-
полагаем, что остроумный метод Кирхгофа будет легче понять, если
с самого начала проводить вычисления в определенных единицах
измерения.
286 Гл. VI. Течещя с заданными граничными условиями
Отсюда вытекает квадратное уравнение для дС, аналогич-
аналогичное (ЗО.7а):
решение которого имеет вид
Если воспользоваться зависимостью вида C0.4), в кото-
которой теперь заменим df на Wodw, то получим диффе-
дифференциальное уравнение
°
dz= -—°(^+У e*w+l)dw. C1.7)
Рассмотрим три прямые линии, изображенные на
фиг. 54,
Для ? = 0 значения / и, следовательно, w действительны,
поэтому правая часть C1.7) будет чисто мнимой. Вели-
Величина z описывает тогда, как это и должно быть, ось у
(см. фиг. 52) от у — — оо до у— +оо.
Для ^=±^-^0 значение ew будет чисто мнимым;
напишем, что
ew= ± is, dw — — ,
S
и, согласно C1.7), получим
Л-Ь-(±, + )/?П)^. C1.8)
Эта величина действительна при оо > s > 1; при этом z
является текущей координатой стенки сосуда
у=0, х>с и соответственно х<—с.
Так как мы интересуемся главным образом грани-
границами свободной струи, то поэтому рассмотрим условие
$< 1. В этом случае величина, выражаемая C1.8), будет
комплексной, что и должно быть в случае искривленных
границ струи.
§ 31. Решение задачи о свободной струе 287
Выражение C1.8) возьмем со знаком плюс, что соот-
соответствует нижней границе струи, изображенной на фиг. 52,
и положим
s = sina, -^-> a > 0.
Тогда C1.8) примет вид
Т ^0 / • I • \ C0S a J • ^0 гя C0S a J
e?z = — (sm a 4-1 cos a) -— c?a = i — e~ia -— da.
q ч ' Sin a q sin a
Интегрирование дает
Это может быть непосредственно проверено дифференци-
дифференцированием. В точке Л имеем z = c и a = тс/2. Отсюда сле-
следует, что
Wn т
const =• с ,
z = c-^Tl-,-e-i« + 4-lni±^-a>) . C1.9а)
у v 2 1 — cos a у ч '
Разложение на действительную и мнимую части дает
W
гр /» W / Л С "I Т"| rt\
Ji/ —— С 1 X ^^ olll СЛ I у
? C1.10)
у = —-I cos а—^m-p-! ).
у V л 1 — cos а J
Таким образом, мы получили в параметрическом виде
уравнение одной из границ струи; уравнение другой
границы получается из C1.10), если изменить знак у х.
Для а—0 равенство C1.10) дает
это есть координаты точки, которая обозначена на
фиг. 52 через U. Полуширина струи в точке U будет
поэтому равна
& = с-—°. C1.11)
288 Гл. VI. Течения с заданными граничными условиями
Здесь мы должны еще выразить WQ через q. Для этого
воспользуемся общими условиями Коши—Римана A9.5)
В сечении в точке U скорость всюду равна q и напра-
направлена по оси у. Поэтому правая часть C1.12) будет по-
постоянной; интегрирование C1.12) в пределах от х = 0
до х = Ь, соответствующих ? = 0 и ЧГ = (тг/2) Wo, дает,
следовательно,
C1.12а)
Из C1.12а) и C1.11) получаем
Ъ-с--Ь 2 + л Ь-с
L/ " О СУ ¦ ' СУ ' С- •
те п
Отсюда сжатие струи равно
Ъ л
с
= 0,611.
С подобными коэффициентами сжатия оперируют в тех-
технике, когда по размеру отверстия вычисляется величина
расхода жидкости.
§ 32. ВИХРЕВАЯ ЦЕПОЧКА КАРМАНА
Искусство физика-теоретика состоит в том, что он дол-
должен уметь так идеализировать стоящую перед ним физи-
физическую задачу, чтобы она стала доступной математиче-
математическому рассмотрению. Аналогично надо подойти к задаче,
поставленной еще Гельмгольцем (см. стр. 269), которая
формулируется так: каким образом рассмотренные в § 30
поверхности разрыва разбиваются на последовательность
отдельных вихрей? В случае, рассмотренном в § 30, они
возникают на острых краях пластинки, а в общем слу-
случае—на любых препятствиях, противодействующих тече-
течению. Фиг. 47а и 476 изображают картину таких
вихрей. Грубо говоря, вихри действуют как шарико-
шарикоподшипники, помещенные вдоль поверхностей разрыва
между мертвой зоной и текущей жидкостью. Это пред-
представление, во всяком случае, дает правильный ответ
§ 32. Вихревая цепочка Кармана 289
на вопрос о направлении их вращения с обеих сторон.
Но вихри не передвигаются со скоростью течения, как
это было бы в случае шариков в подшипнике. Такое
передвижение происходило бы, если бы вихри не дейст-
действовали друг на друга. В действительности в результате
этого взаимодействия возникает дополнительная скорость
вихря, которая накладывается на основную скорость тече-
течения и которая, как мы увидим, в простейших случаях,
направлена в обратную сторону.
Карман1) идеализированно представляет последова-
последовательность вихрей, исходящую от препятствия, в виде
прямолинейной вихревой цепочки, бесконечно протяжен-
протяженной в обе стороны; причем он не рассматривает возник-
возникновения вихрей, перенося их источник на беконечность.
С обеих сторон Цепочки вихри отстоят друг от друга на
равном расстоянии, что соответствует стационарному состо-
состоянию через бесконечно долгий промежуток времени после
их возникновения; но направление вращения вихрей с обеих
сторон цепочки различно, аналогично направлению вра-
вращения шариков с обеих сторон нашего шарикоподшип-
шарикоподшипника. Карман ограничился случаем, когда дополнитель-
дополнительная скорость направлена параллельно цепочке. Мы нач-
начнем также с этого случая.
Легко видеть, что в этом случае вихри должны либо
располагаться друг против друга, как показано на фиг. 55,
либо перемежаться друг с другом (фиг. 56). При этом вихри
мы представляем в виде концентрированных вихревых
нитей, так что на фигурах они изображены в виде точек.
Рассмотрим сначала фиг. 55,. где вихри перенумеро-
перенумерованы в интервале от —со до + со. Как будут воздей-
воздействовать на вихрь О остальные вихри? Вихри ± 1, рас-
расположенные на той же стороне цепочки, не будут сообщать
ему никакой скорости, что следует из общего закона
кинематики вихрей B1.26), согласно которому индуци-
индуцированная скорость направлена перпендикулярно к исхо-
исходящему из индуцирующего вихря радиус-вектору, в сто-
сторону, соответствующую вращению вихря. Поэтому ско-
х) К а г m а и ТЪ., О механизме сопротивления жидкости и воз-
воздуха, Gottinger Nachr., 1911 и 1912. См. также К arm an Th.,
Rubach H., Phys. Zs., 13, 49 A912).
19 А. Зоммерфельд
290 Гл. VI. Течения с заданными граничными условиями
рости, индуцированные вихрями ± 1, взаимно уничто-
уничтожаются. Такое же явление произойдет со вкладом от
вихрей ± к. В то же время другой вихрь О, находящийся
против нашего вихря, сообщит ему дополнительную ско-
скорость в направлении, противоположном направлению
Дополнительная Основная
скорость -• жорость
-/
К0
•>
+/
+/
a
+2
•>
+2
Фиг. 55.
Цепочка вихрей Кармана с расположенными друг против друга
вращающимися в разные стороны вихрями.
цепочки. Вихри ± 1 со стороны, противоположной преж-
прежней, радиус-векторы из которых расположены косо по
отношению к цепочке (см. фиг. 55), дадут равнодей-
равнодействующую в том же направлении. То же самое можно
сказать о вихрях ± к.
4)
•)
^——^
^ " ^^
•)
•>
'Фиг. 56.
Цепочка Кармана с вихрями, расположенными перемежаю-
перемежающимся образом.
Если, однако, вихри располагаются не точно друг
против друга, то соответствующее построение покажет,
что дополнительная скорость нашего вихря направлена
наклонно к цепочке. Исключение составляет случай пере-
перемежающихся вихрей (фиг. 56). Здесь действие вихрей О
и 1 противоположной стороны (показанное на фигуре
пунктирными линиями) опять даст составляющую, напра-
§ 32. Вихревая цепочка Кармана 291
вленную противоположно цепочке. В этом же направле-
направлении дадут вклад вихри — к и -\-k-\-l. На фиг. 56,
кроме этого, показано, как будет извиваться жидкость
в середине цепочки между^ перемежающимися вихрями.
Мы видим, что это течение по форме совпадает со сред-
средней частью течения, показанного на фотографиях 47а
и 476. Кроме того, фотографии показывают, что именно
перемежающееся расположение вихрей (см. фиг. 56), а не
расположение, изображенное на фиг. 55, соответствует
действительности. Для обоснования рассмотренной кар-
картины Карман исследовал устойчивость обоих располо-
расположений.
Что при этом надо" понимать под устойчивостью?
На фиг. 55 и 56 положение вихря
точно задается целыми положительными или отрица-
отрицательными числами к. При этом, как будет показано,
дополнительная скорость может быть легко вычислена
с помощью известных комплексных методов. Для иссле-
исследования устойчивости необходимо сообщить вихрю малые
смещения г)
Дополнительная скорость при этом также изменится.
Так, например, уже не будет справедливо утверждение,
что вихри, располагающиеся на той же стороне цепочки,
х) Эта вариация не имеет достаточно общего вида, так как она
берется только в плоскости ху, в то время как в перпендикулярном
к ней направлении z вихревая нить после вариации точно так же,
как и первоначальная, рассматривается прямолинейной. Более общая
форма вихревых нитей, меняющаяся в направлении z, рассмотрена
в мюнхенской диссертации Шлейера [Schl ayer К., Z s. angew.
Math, und Mech., 8, 352 A928)], где проведено исследование устой-
устойчивости в этом случае. В защиту рассмотренной Карманом вариации
можно заметить, что, как уже указывалось на стр. 203, «бесконечно
длинные» вихревые нити соответствуют реальному случаю течения
жидкости между двумя близко расположенными параллельными
пластинами. В случае достаточно малого расстояния между пласти-
пластинами устойчивость может быть исследована с помощью рассмотрения
вариации, приведенной в тексте. Шлейер нашел, что для общей вариа-
вариации здесь будет иметься небольшая неустойчивость, растущая с уве-
увеличением расстояния между пластинами.
19*
292 Гл. VI. Течения с заданными граничными условиями
что и рассматриваемый вихрь О, не сообщают ему допол-
дополнительной скорости. Напротив, дополнительная скорость
будет зависеть от всех bzh как для вихрей противополож-
противоположной стороны цепочки, так и для той же. Эту зависимость
можно рассматривать как линейную, если пренебречь
всеми высшими степенями bzh. Варьируемая скорость bz
определяет изменение положения нашего вихря со вре-
временем как линейную функцию всех остальных bz. Таким
образом, получаем бесконечную систему линейных диф-
дифференциальных уравнений первого порядка по bz, кото-
которая, однако, сводится только к двум дифференциальным
уравнениям того же характера (см. ниже). В теории ма-
малых колебаний1) отыскивают нормальные колебания
системы, т. е. решения, которые зависят от времени,
как е}Л. Если X чисто мнимая величина, то в нашем слу-
случае вихревая цепочка была бы устойчивой, так как
колебания будут затухать вследствие трения, которым
мы до сих пор пренебрегали. Если же X является ком-
комплексной величиной с положительной действительной
частью, то вихревая цепочка будет неустойчивой. Система
будет устойчивой только в том случае, когда все нор-
нормальные колебания устойчивы. Карман показал2), что
в этом случае расположение вихрей, изображенное на
фиг. 55, является неустойчивым для любого h, отлич-
отличного от нуля, а перемежающееся расположение (фиг. 56)
устойчиво только тогда, когда имеет место соотношение
shA« = lf т. е. - = 0,281. C2.1)
Фиг. 55 и 56 соответствуют примерно такому отноше-
отношению hja.
Ясно, что полное, математически строгое рассмотре-
рассмотрение вопроса устойчивости весьма сложно и потребовало бы
больше места, чем ему отведено в данной книге. Поэтому
наметим только путь этого рассмотрения и будем исхо-
исходить из более общих предположений.
х) Простейший случай см.: «Механика», (т. I), вслед за равен-
равенством C.24), и там же задачу 2 гл. IV.
2) Исследования Кармана были дополнены Долапчиевым [D о-
laptschiew В. L., Zs. angew. Math. u. Mech., 17, 313 A937);
18, 263 A938)], который принял во внимание члены второго порядка.
§ 32. Вихревая цепочка Кармана 293
Так же' как и Мауэ1), будем считать, что одна сто-
сторона цепочки сдвинута относительно другой на произ-
произвольный отрезок d < а (на фиг. 55 d = О, на фиг. 56
d = a/2). Это обобщение формально не вызовет трудно-
трудностей, если начало координат z-плоскости поместить
в середине отрезка, соединяющего обе точки О ж О. При
этом точки ± | & I одной стороны цепочки будут распо-
располагаться диаметрально противоположно точкам Т | & |
другой стороны:
4= -4, zb = zo + ka, zQ^\{d + ih), C2.2)
где верхние индексы 1 и 2 соответствуют верхней и нижней
сторонам цепочки, z0—координата вихря О верхней сто-
стороны цепочки в комплексной плоскости.
Прежде всего дадим весьма простое выражение для
комплексного гидродинамического потенциала / = Ф -f №,
пригодное для произвольного значения d, так как эта
величина не будет входить в него явным образом. Будем
исходить из равенства A9.10), которое описывает взаимо-
взаимодействие положительного и отрицательного вихрей. В этом
равенстве числитель и соответственно знаменатель выра-
выражения, стоящего под знаком логарифма, обращаются
в нуль в местах расположения положительного и соот-
соответственно отрицательного вихрей. Обобщением этого
равенства для нашей вихревой цепочки явится выражение
C2.3)
Действительно, числитель логарифма исчезает во всех
точках
Z
а знаменатель—в точках
z= —
!)Maue A. W., Zs. angew. Math. u. Mech., 20, 130 A940).
Равенства C2.6) и C2.8) в данной книге, выходящие за пределы рас-
рассмотрения, выполненного Карманом, заимствованы из указанной
работы. Приложение к этому параграфу было дано самим Мауэ,
294 Гл. VI. Течения с заданными граничными условиями
как и должно быть согласно C2.2). То, что координаты
любого вихря входят в это выражение совершенно равно-
равноправным образом, гарантируется периодичностью синуса.
Стоящий перед выражением A9.10) множитель А, опре- ч
деляющий интенсивность вихря, мы взяли из A9.8а),
выбрав знак таким образом, чтобы направление враще-
вращения вихрей соответствовало фиг. 56.
Дифференцируя / по z, получим. знакомые нам (соот-
(соотношения C0.3) и C0.4)
[ v = v* + ivv ¦ C2.4)
* = vx-ivy. к '
Здесь V—скорость частицы жидкости, характеризуемой
координатой z. Если мы захотим применить это правило
к координатам какого-либо вихря, например вихря О,
у которого z — z0, то мы должны принять во внимание,
что сам на себя он не оказывает никакого воздействия,
и поэтому из выражения для / его надо исключить.
Это будет выполнено, если к правой части C2.3) при-
прибавить
Если в отличие от v обозначить скорость рассматрива-
рассматриваемого вихря через \x=ux-\-iuy, то из C2.4) получим
sinч—¦—^~
Здесь после дифференцирования надо положить
Если ввести сокращенное обозначение
то, устремляя е к нулю, можно легко получить
и* = _ ilictg ?^o . C2.5)
а ° a v '
Эта формула пригодна не только для вихря z = z0, но
в силу периодичности цепочки и для любого другого
§ 32. Вихревая цепочка Кармана 295
вихря. Для того чтобы выражение C2.5) было действи-
действительным, т. е. чтобы и имело направление вихревой це-
цепочки ', выражение
ctg-^Гили в силу C2.2) ctg-{d + i
должно быть чисто мнимым. Это будет, если d — О и К = а/2.
В обоих случаях равенство C2.5) даст
d = 0, и* = ия=—?cth—тс,
C2.5а)
а — -^-, и* = и„= —— tn—it.
2 * а а
Используя критерий устойчивости C2.1) и соотношение
ch2 — sha=l,
можно вторую строку C2.5а) переписать в виде
?? = -, и* = их= i=^. C2.56)
2' х Yla V ;
Итак, мы весьма простым путем вычислили дополнитель-
дополнительные скорости, построенные на фиг. 55 и 56. Указанную
там же основную скорость (обозначим ее, как и прежде,
через q) мы нормировали к нулю путем выбора системы
отсчета: если z устремить к бесконечности по какому-
нибудь пути, не включающему в себя вихревой цепочки,
то выражение под логарифмом в C2.3) будет стремиться
к постоянному пределу, поэтому / будет постоянным
и q = 0.
Во всех случаях, кроме указанных в C2.5а), скорость и
направлена наклонно по отношению к вихревой цепочке.
Угол наклона f может быть элементарным путем вычис-
вычислен из C2.5):
sin 2тс —
fc?f C2-6)
sh 2тс—
a
296 Гл. VI. Течения с заданными граничными условиями
Абсолютное значение скорости и может быть также полу-
получено из C2.5):
/
X
ch2 тс sin2 тс —
C2.6а)
Эта формула представляет собой обобщение выражения
C2.5а), соответствующего случаю Кармана.
Если, как и в начале параграфа, считать, что вихре-
вихревая цепочка возникает при обтекании пластинки, то ра-
равенство C2.6) соответствует случаю, когда пластинка
расположена косо по отношению к течению. При этом
следует заметить, что, вообще говоря, угол f> опреде-
определяемый равенством C2.6), не совпадает с углом f на
фиг. 48 (первый гораздо меньше последнего). Из фиг. 476
не следует, что возникающая вихревая цепочка располо-
расположена косо, но она не говорит и о противном.
Рассмотрим теперь центральную часть нашей проблемы—
вопрос об устойчивости. Так же как и Мауэ, примем
несколько измененный подход к решению задачи: вместо
произвольно заданных смещений координат вихрей bzk
введем изменения синусоидальных функций, входящих
в C2.3),
sin (z — z0) — — Cj (z) и соответственно sin(z-\-z0) ——C2(z)
C2.7)
и определим предполагаемые достаточно малыми воз-
возмущения Сх, С2 так, чтобы нули функций C2.7) лежали
в точках Zft-j-Bzh и соответственно z\-\-bz\. Этого можно
достичь, положив
При этом величины С, определяются с точностью до пери-
периодической функции с периодом а. Скорость вихря после
возмущения может быть найдена, согласно равенству C2.4),
из функции /, изменившейся в результате появления
величин С. Если эту скорость выразить через производ-
производные по времени С и пренебречь высшими степенями С,
§ 32. Вихревая цепочка Кармана
297
то получим два линейных дифференциальных уравнения,
в которые одновременно войдут Ср С2> их первые и вто-
рые производные по z и Сх, С2« Рассмотрение этих уравне-
уравнений мы здесь опустим. Оно приводит к следующему
критерию устойчивости:
-, h . d
sn— ти = sm —
a a
C2.8)
Фиг. 57. К обобщенному
критерию устойчивости.
h—ширина вихревой цепочки в за-
зависимости от взаимного смещения
право- и левовинтовых вихревых
нитей.
что представляет собой прямое обобщение критерия
Кармана C2.1). Таким образом, для косо распростра-
распространяющейся вихревой цепочки
каждому значению d соответ-
соответствует однозначно определен-
определенное отношение h/a, при ко-
котором расположение вихрей
в возмущенной вихревой це-
цепочке остается неизменным
е точностью до остающихся
малыми колебаний.
Фиг. 57 качественно по-
поясняет это, включая частный
случай C2.1), рассмотренный
Карманом. На ней изображе-
изображена связь между величинами
d и h для всевозможных устойчивых вихревых цепочек.
Если в равенстве C2.8) кривую гиперболического синуса
в начале координат заменить ее касательной, то получим
между d и h синусоидальную зависимость. Так как, с дру-
другой стороны, гиперболический синус меняется монотонно,
истинная зависимость между величинами d и h будет
представлять собой лишь слегка искаженную кривую
обычного синуса, стоящего в правой части равенства
C2.8). Максимальная ордината соответствует случаю
Кармана d — a/2. Для й = 0 соответственно /г = 0 точно
так ше, как и в пе отличающемся от него геометрически
случае d = a\ при этом стоящие друг против друга вихри
соединятся и взаимно уничтожатся; конечные точки
нашей кривой устойчивости не имеют физического смысла.
Следует ожидать, что экспериментальное исследование
«косых» вихревых цепочек приведет к условию C2.8),
298 Гл. VI. Течения с заданными граничными условиями
подобно тому как исследование «прямых» вихревых це-
цепочек, предпринятое Карманом и Рубахом (см. приме-
примечание на стр. 289), привело к условию C2.1).
ПРИЛОЖЕНИЕ
Проблема лобового сопротивления
Получение правильного закона сопротивления было
той целью, которую преследовал Карман при изучении
вихревых цепочек. Для этого он рассматривал движу-
движущееся в жидкости тело, за которым образовывалась вих-
вихревая цепочка, уходящая на бесконечность. Вычисления
проводились в плоскости цепочки х -f- iy, где х отсчиты-
валось в направлении движения тела. Само тело предпола-
предполагалось бесконечно длинным в направлении, перпендику-
перпендикулярном к плоскости х -f- iy. В этой плоскости можно
выбрать достаточно большой «контрольный прямоуголь-
прямоугольник», в котором будут находиться тело и достаточно
длинный отрезок вихревой цепочки, и исследовать баланс
количества движения в этой области между силой, дей-
действующей со стороны тела на жидкость, увеличением
импульса в контрольной области в результате .образова-
.образования новых вихрей и потерей импульса через границы
этой области. Первая из ятих трех составных частей, взя-
взятая с отрицательным знаком, представляет собой ком-
комплексное число P-\-iQ, где действительная часть Р соот-
соответствует сопротивлению течения, а мнимая часть Q —
подъемной силе.
Карман здесь также ограничился случаем, когда напра-
направление вихревой цепочки совпадает с направлением дви-
движения тела, но и в этом частном случае вычисления
сопровождаются большими трудностями.
То же самое можно сказать о рассмотрении Мауэ,
который предполагал, что направление вихревой цепоч-
цепочки составляет с направлением движения тела некото-
некоторый угол и что это наблюдается тогда, когда тело не
обладает симметрией относительно направления дви-
движения.
Соответствующая формула сопротивления, в цитиро-
цитированной на стр. 293 работе, не приведена и публикуется
§ 32. Вихревая цепочка Кармана 299
нами впервые. Из этой формулы в качестве частного
случая может быть получена формула Кармана.
Здесь будут приняты обозначения, аналогичные тем,
которые мы имели в § 30 при рассмотрении обтекания
пластинки. Наше теперешнее сопротивление течения Р
соответствует давлению, проинтегрированному по всей
ширине покоящейся пластинки [см. равенство C0.22)].
Величина 2с является эффективной шириной тела в напра-
направлении, перпендикулярном к направлению движения
в плоскости х + iy (ранее 2с представляло собой просто
ширину пластинки); q — скорость тела относительно покоя-
покоящейся на бесконечности жидкости (в прежнем рассмотре-
рассмотрении q—скорость жидкости на бесконечности по отношению
к покоящейся пластинке); X—безразмерный коэффициент
сопротивления (ранее X имело у нас частное значение,
равное 0,88).
Величины h ж а, как и прежде, представляют собой
измерения вихревой цепочки; и—скорость ее распростра-
распространения, вычисленная в C2.5).
Тогда, согласно Мауэ, по аналогии с C0.22) имеем
?-4 в* <32-9)
C2.10)
здесь приняты следующие сокращенные обозначения
C2.11)
Входящие сюда безразмерные величины р и if] опреде-
определяются следующим образом:
Р = 7иТ' 4=7 • C2Л2)
Таким образом, коэффициент сопротивления, опреде-
определяемый равенством C2.10), зависит от трех отношений,-
а именно, от обеих величин, определяемых равенствами
C2.12), и от а/с.
300 Гл. VI. Течения с заданными граничными условиями
В случае Кармана d — aJ2 и, согласно C2.8), shC = l;
при этом из C2.11) следует, что
Л = 0,794, Б = 0,31, С = 0. C2.13)
Тогда из C2.10) получим, что коэффициент сопротивле-
сопротивления для случая Кармана равен
\ = ± [ 0,794^-0,314 (it"J] ; C2.14) ;
теперь коэффициент X содержит только два ^отношения:
а/с и u/q. Значения последних взяты Карманом из
экспериментов, где в качестве исследуемого тела исполь-
использовалась плоская пластинка; они приведены в цити-
цитированной на стр. 289 работе. Его результаты:
fc = 5,5, | = 0,20. C2.15)
Откуда, согласно C2.14), следует, что
Х=1,6, C2.16)
т. е. Карман получил величину, значительно большую,
чем коэффициент Кирхгофа, который равен 0,88 [см. C0.22)];
то, что последний имеет слишком малое значение, мы
уже заметили ранее, ссылаясь на исследования школы
Прандтля.
Гейзенберг1) попытался теоретически определить те
же величины, которые входят в C2.15)^ исходя из зако-.
нов сохранения, имеющих место при возникновении вихрей.
Он нашел, что
23 = 5,5, - = 0,23
(эти значения находятся в хорошем согласии с данными
Кармана) и, согласно C2.14),
х) HeisenbergW., Phys. Zs., 23, 363 A922), с дополнитель-
дополнительным примечанием Прандтля.
§ 33. Пограничный слой Прандтля 301
§ 33. ПОГРАНИЧНЫЙ СЛОЙ ПРАНДТЛЯ
Представляется неудовлетворительным, что во всех
рассмотренных в этой главе потенциальных течениях1)
жидкость считалась невязкой. Однако можно легко
показать, что это предположение скажется только на
граничных условиях, но не на дифференциальных уравне-
уравнениях. Это справедливо как для двухмерных, так и для
произвольных трехмерных потенциальных течений.
Будем исходить из уравнений Навье — Стокса A6.1).
Для потенциального течения (rot v = 0) и несжимаемой
жидкости (divv = 0) в силу соотношения
Av = grad div v — rot rot v
член ^Av, характеризующий вязкость, выпадает из
уравнений A6.1).
Найденные нами решения идеального уравнения Эй-
Эйлера будут также решениями уравнений Навье — Стокса:
силы вязкого трения не оказывают динамического воздей-
воздействия внутри жидкости.
Иначе обстоит дело на границе между жидкостью
и твердой стенкой. В то время как для[идеальной жидко-
жидкости граничное условие гласит, что
г>п=0, ^ — произвольно, C3.1а)
для вязкой жидкости имеется условие прилипания A0.9)
г?п = 0, г;8 = 0. C3.16)
Силы вязкого трения проявляются только вблизи стенок
вследстеие изменения граничного условия C3.16). Мы можем,
однако, предположить, что в случае больших чисел
Рейнольдса вызываемое вязкостью изменение картины
течения идеальной жидкости не распространяется далеко
вглубь жидкости.
Математическое противоречие между условиями C3.1а)
и C3.16) можно понимать следующим образом: то, что
в уравнения Навье —Стокса входят производные второго
г) Вихревая цепочка Кармана также является чисто потен-
потенциальным течением, за исключением особых точек (координат вих-
вихревых нитей). К таким же течениям принадлежат волновые движения,
рассмотренные в гл. V.
302 Гл. VI. Течения с заданными граничными условиями
порядка по координатам, влечет за собой наличие двух
векторных граничных условий на твердой стенке, в то
время как уравнение Эйлера, в которое входят только
первые производные, влечет за собой только одно такое
граничное условие, необходимое для получения решения.
Однако с физической точки зрения противоречие между
равенствами C3.1а) и C3.16) основывается на том, что
между областью потенциального течения и твердой стен-
стенкой должен находиться слой, который с уменьшением
величины {х может сделаться как угодно тонким. В этом
слое vs должно быстро убывать до нуля. Для конечного,
но малого {х (воздух, вода) и достаточно больших ско-
скоростей и размеров тела этот слой будет иметь весьма
малую толщину и, кроме того, основная часть течения
при этом будет иметь ту же картину, что й потенциаль-
потенциальное течение идеальной жидкости. В этом состоит, основная
идея теории пограничного слоя Прандтля, которую он
впервые предложил в 1904 г. х)
Эта теория носит приближенный характер2). В ней-
в основном рассматривают двухмерные задачи и прене-
пренебрегают в пограничном слое влиянием на вязкие члены
изменения скорости в направлении слоя, которое мало
по сравнению с сильным изменением в перпендикулярном
направлении. Толщина пограничного слоя для достаточно
малых {х пропорциональна \/ \i или, что то же самое,
1/j/ &l EU — число Рейнольдса потенциального течения).
Изменением давления в направлении, перпендикулярном
к пограничному слою, пренебрегают в силу тонкости
этого слоя и считают, что внутри слоя оно равно давле-
г) Verhandlungen des Internationalen Mathematiker-Kongres-
ses in Heidelberg. Подробности можно найти в учебнике: Р rand 11
und Tietjens, Hydro- und Aerodynamyk, Springer, 1931.
[См. русский перевод: Прандтль и Титьенс, Гидро-
Гидроаэромеханика, М.—Л., 1949 (т. I), 1951 (т. II). Следует заметить, что
теория пограничного слоя и ее многочисленные практические при-
применения глубоко развиты в работах советских ученых. Обзор этих
работ и подробная библиография имеются в статье Лойцянского
Л. Г. «Пограничный слой» в сборнике: Механика в СССР за
30 лет., М.—Л., 1950.—Прим. перев.]
2) Дальнейшие рассуждения этого параграфа мы приведем,
следуя докладу Кармана: К а г m a n Th., Vortrage aus dem Gebiet
der Hydro- und Aerodynamik, Innsbruck, 1922.
§ 33. Пограничный слой Прандтлп 303
нию в примыкающих областях потенциального течения.
Из уравнений Бернулли имеем для изменения давления
на внешней границе пограничного слоя в направлении
элемента длины слоя ds:-~= — pvs -—¦ . Отсюда следует,
что если в каком-нибудь месте dvs/ds меняется от поло-
положительных к отрицательным значениям, то жидкость
течет в направлении, противоположном перепаду давлений.
Дальнейшие вычисления показывают, что (d2vs/dn2) < 0
для тг = О вниз по течению за этим местом. Для доста-
достаточно больших перепадов давления возможно, что
(dvsldri)n=o < 0, т. е. может возникать обратное течение.
Это в дальнейшем ведет к образованию вихрей; так что
вниз по течению за этим местом ламинарное течение
заменится процессами другого характера.
Эта теория, несмотря на свой приближенный характер,
дает весьма точные результаты (так как на практике
числа Рейнольдса весьма велики) и позволяет в каждом
отдельном случае установить, будет ли течение всюду
прилегать к поверхности тела и поэтому оставаться
потенциальным всюду (за исключением тонкого погранич-
пограничного слоя) или же произойдет отрыв течения и вслед-
вследствие этого образование вихрей.
Для очень больших скоростей vs (т. е. для очень
больших чисел Рейнольдса) предположение о ламинарном
характере течения внутри пограничного слоя не спра-
справедливо. В этом случае течение будет турбулентным,
в результате чего точка отрыва может значительно сдви-
сдвинуться вниз по течению. На основании экспериментального
материала стало возможным приближенно вычислять
поведение такого турбулентного слоя.
Одной из важнейших прикладных задач, решаемых
на основании этой теории, является задача об обтекании
крыла. Двумерная теория крыла, основы которой раз-
разработаны Кутта и Жуковским1), рассматривает обтекание
г) Приоритет в создании теории подъемной силы крыла в дейст-
действительности неоспоримо принадлежит Н. Е. Жуковскому, который
совместно с С. А. Чаплыгиным создал основы' всей современной
теории полета. Теорема Жуковского о подъемной силе была опуб-
опубликована им в работе «О присоединенных вихрях» в 1906 г. (см.
Избр. соч., т. II, стр. 97).—Прим. перее.
304 Гл. VI. Течения с виданными граничными условиями
крыла как плоское потенциальное течение с циркуляцией,
не равной нулю; здесь в большой степени используются
методы конформных отображений. Трехмерная теория
крыла была развита Прандтлем. Здесь течение пред-
предполагается потенциальным, с наличием поверхности раз-
разрыва, которая идеализированно представляется в виде
системы вихрей. С помощью этой теории не только
выясняют распределение подъемной силы по поверхности
крыла, но -и определяют сопротивление, эквивалентное
остающейся в поле течения кинетической энергии. Эта тео-
теория развита настолько, что теперь возможно вычислить
распределение давления по крылу произвольной формы
(с отогнутыми элеронами и т. д.).
Глава VII
ДОПОЛНЕНИЯ К ГИДРОДИНАМИКЕ
§ 34. ГИДРОДИНАМИЧЕСКИЕ УРАВНЕНИЯ ЛАГРАНЖА
Рассмотрение этих уравнений в дополнениях обусло-
обусловлено тем, что они имеют неизмеримо меньшее практи-
практическое значение, чем уравнения Эйлера. Заметим, кстати,
что название «уравнения Лагранжа» исторически не точно:
впервые они появились в работе Эйлера, о которой мы
упоминали на стр. 108.
Прежде всего необходимо подчеркнуть, что уравнения
Эйлера не являются уравнениями того типа, которые
встречаются в обычной механике при описании движения
некоторой системы. Там мы рассматриваем материальную
точку с массой т (или какой-либо иной элемент системы),
приписываем ей определенные метки (координаты) q и опре-
определяем зависимость от времени импульса р, соответствую-
соответствующего координате q в соответствии с заданными силами
и связями. В случае уравнений Эйлера рассматривается
элемент объема dx и приписывается ему, а не элементу мас-
массы ре?т определенное значение координат (например, декар-
декартовых); при этом мы определяем вызванное силами и связями
(последние описываются здесь с помощью гидродинами-
гидродинамического давления р) изменение импульса по отношению
к месту, где находится dx, в то время как элемент массы,
содержащийся в dt, в дальнейшем в рассмотрение не входит.
Иначе обстоит дело в случае уравнений Лагранжа.
Здесь мы приписываем элементу массы dm определенные
метки а, Ь, с, роль которых, например, могут играть
его координаты х0, у0, z0 в момент t = 0, и отыскиваем
положение х, у, z элемента dm в момент t. Эти коорди-
координаты х, у, z совместно с давлением р представляют
собой зависимые переменные в уравнениях Лагранжа, в то
время как а, Ь, с совместно с временем t представляют
собой независимые переменные.
20 А. Зоммерфельд
306 Гл. VII. Дополнения к гидродинамике
В данном случае не надо различать локального
и полного ускорений
дх dx
тт
dt dt
Полное (или субстанциальное) ускорение, которое играет
решающую роль в балансе импульса, теперь может быть
непосредственно выражено1) через
д2х д2у d2z ,
~di?' д&' ~dt* при заДанных а> ь> с-
Уравнения, которые определяют значения а, Ь, с точно
так же, как и уравнения Эйлера, нелинейны; "если бы
они были линейны, они имели бы огромные преимущества
перед уравнениями Эйлера. Эти уравнения имеют вид
д2хдх . д2уду , d2z dz д U+p m .~r л\
сюда надо добавить два аналогичных уравнения, в кото-
которые вместо а входят Ъ и с. Равенство C4.1) вытекает из
равенства A1.2), если его компоненты умножить на
дх ду dz
да' да' да
и сложить. При этом надо учесть несжимаемость жидкости
(р = const) и существование потенциала у внешней силы
F= — gradtf.
Частное дифференцирование д/да означает, что, кроме Ъ
и с, остается постоянной и четвертая переменная t\
поэтому
dU_ = dUdx dUdy d_?dz
да дх да ду да dz да
Заметим, что в C4.1) производится дифференцирование
только по четырем независимым, переменным — а, Ь, с, t—
и что при этом дифференцируются только четыре зави-
зависимые переменные — х, у, z, p. К трем уравнениям, пред-
г) Это обозначение кажется нам более последовательным, чем
обозначение dPx/dt2 в уравнениях Лагранжа, которым пользовался
Кирхгоф и которое часто встречается в учебниках.
§ 34. Гидродинамические уравнения Лагранжа
307
ставленным в C4.1), в качестве четвертого добавляется
условие несжимаемости, выражающее собой постоянство
объема. Отношение объема dx к начальному объему е?т0
задается «функциональным определителем»
d%
дх дх дх
дх0 ' ду0 ' dz0
ду ду ду
дх0 ' ду0 ' dz0
dz dz dz
dxn дуп dzt\
C4.2)
C4.2a)
который, как это принято, можно записать сокращенно
в виде
dx_ _ d(x, у, z)
din d(x0, y0, z0) '
a-
Если представить себе, что координаты х0, у0, z0 выра-
выражены через а, Ъ, с, то правая часть C4.2), согласно
закону умножения определителей, разобьется на произ-
произведение двух функциональных определителей
d (x, у, z) d(a, Ъ, с)
d(a, Ъ, с) d(xQ, yQ, zQ) '
Последний, очевидно, не зависит от t. Независимость
выражения C4.2) от времени, т. е. условие несжимае-
несжимаемости, может быть поэтому записано в следующей форме:
^_О Л-
dt '
д(а, Ъ, с)
C4.3)
Это выражение также включает в себя только диф-
дифференцирование трех зависимых переменных х, у} z по
четырем независимым переменным а, Ъ, с и t.
Соотношения C4.1) и C4.3) являются уравнениями
Лагранжа для несжимаемой жидкости.
Соответствующие уравнения для сжимаемой жидкости
могут быть получены из C4.1), если заменить
через Р = \
dp
и
— через V,
C4.3а)
308 Гл. VII. Дополнения к гидродинамике
где V — потенциал внешней силы Р, отнесенной к еди-
единице массы. Кроме того, уравнение C4.3) надо заменить на
|(РД) = О. C4.36)
Кирхгоф1) воспользовался уравнениями Лагранжа
для строгого доказательства теоремы Гельмгольца о сохра-
сохранении вихрей; при этом ему не пришлось пользоваться
формулой A8.8), которая была нам необходима, так как
мы исходили из уравнений Эйлера.
§ 35. СТОКСОВО ТЕЧЕНИЕ И ФОРМУЛА СОПРОТИВЛЕНИЯ
Ползущим движением весьма метко называют такое
состояние, когда трение настолько препятствует инерции,
что последней можно пренебречь (см. стр. 100). Уста-
Установление такого состояния характеризуется числом
Рейнольдса A6.8)
<й т
которое при этом должно удовлетворять условию
¦51 «1. C5.1)
Под стоксовым движением понимают стационарное дви-
движение сферического тела в жидкости. В этом случае а
означает радиус сферы, v—зависящую от внешней силы
(разность между весом тела и выталкивающей силой,
электрическое поле- и т. п.) скорость, которая после
короткого начального периода устанавливается постоян-
постоянной. Для выполнения условия C5.1) не обязательно,
чтобы кинематическая вязкость v была велика. Условие
это выполняется также в случае достаточно малых зна-
значений а или v. Вместо движения шара можно рассма-
рассматривать обтекание жидкостью жестко закрепленного шара,
причем суммарное давление на шар будет равно сопро-
сопротивлению, которое он испытывал бы при движении
с той же скоростью в покоящейся жидкости.
Вычисление этого сопротивления сыграло большую
роль в решении основных физических вопросов. С его
1 Kirchhoff, Vorlesungen iiber Mechanik, Кар. XIV, § 1.
§ 35. Стоксово течение и формула сопротивления 309
помощью в 1905 г. Эйнштейн рассмотрел броуновское
движение и определил число Авогадро (см. стр. 71).
Знание этого сопротивления существенно также при
определении элементарного электрического заряда по
способу Милликена.
В качестве исходного пункта воспользуемся условиями
равновесия A0.8а) и A0.86) для вязкой жидкости, в кото-
которые перейдут уравнения движения Навье —Стокса, если
пренебречь инерционными членами. Внешнюю силу F
мы в этих условиях не будем принимать во внимание,
так как она уравновесится сопротивлением трения. Тогда
получаем (в прямоугольных координатах)
| = ,ДК,| = 11А,,^ = ,ДШ. C5.2)
Будем считать, что начало координат расположено
в центре сферы, а положительная ось z направлена против
движения. Таким образом, в этой системе рассматривается
не падающая сфера, а жидкость, обтекающая неподвиж-
неподвижный шар в положительном направлении оси z. Вместо
прямоугольных координат нам вскоре потребуются сфе-
сферические координаты г, Ь, ср, которые также отсчитыва-
ются от центра сферы. При этом, например, будет
cosO=y. C5.2а)
Рассмотрим несжимаемую жидкость; в этом случае
к уравнениям C5.2) добавим условие
du.dv.dw г. /ОК оч
-я-+-о-+-г-= 0. C5.3)
дх ' ду ' dz v '
Из C5.2) и C5.3) сразу следует, что
Др = 0. C5.4)
Сферически симметричное решение уравнения C5.4),
согласно A9.22), имеет вид
Р = $- C5.5)
Ввиду того что в нашей задаче имеется избранное
направление z, которое является направлением движения
жидкости относительно сферы, течение не будет обладать
310 Гл. VII. Дополнения к гидродинамике
сферической симметрией; поэтому вместо C5.5) рассмот-
рассмотрим выражение
P = Ai~FzT> ' C5-5а)
которое, очевидно, также является решением уравне-
уравнения C5.4). Если выражение C5.5а) продифференцировать
и воспользоваться равенством C5.2а), то, положив Аг = А,
получаем
^ C5.56)
Значительно более общее решение C5.4) дается рядом
со
71=0
начальные члены которого совпадают с выражениями C5.5)
и C5.5а). Ряд C5.5в) представляет собой разложение по
сферическим функциям Pn(cosb) и убывающим (отрица-
(отрицательным) степеням г. Мы не будем здесь приводить
общего определения сферических функций, а заметим
только, что множители 1 и cos Ь, входящие в C5.5)
и C5.5а), совпадают с нормированными обычным образом,
сферическими функциями Ро (cos Ь) = 1 и Рг (cos Ь) = cos 9v
Заметим также, что сферические функции более высокого
порядка представляют собой полиномы более высоких
степеней от cos 9-. Так как (см. ниже) в граничные
условия C5.12а) и C5.126) входит только первая степень
cos Ь, то в разложение C5.5в) для нашей задачи войдет
только член с п = 1, так что Ао = А2 — А3 = ... = 0.
Поэтому равенство C5.5в) перейдет в C5.56).
Чтобы определить поле скоростей, необходимо пере-
переписать уравнения C5.2) в законной векторной форме.
Для этого воспользуемся равенством C.10а). Так как
divv = 0, то вместо C5.2) получим
{a rot rot v= — gradjo. C5.6)
Теперь можно сразу перейти к нашим сферическим
полярным координатам. Взятые в этих координатах ком-
компоненты вектора v назовем
vr, г;*, v
§ 35. Стоксово течение и формула сопротивления 311
Последняя из них обращается в нуль вследствие сим-
симметрии нашей задачи. То же самое можно сказать
о любом дифференцировании по ср, которое может появиться
в дальнейшем:
v,^0, 1=0. C5.7)
Выпишем, в частности, r-компоненту равенства C5.6).
Используя пояснение к решению задачи 3 гл. I или
приложения III и IV, получаем
р. г д2{r2vr) , 1 д /* . ^dvr\ 1 dp ,пК ON
-^ —j~+^-ih sind-^ i =я • (o5.8)
г2 |_ дг2 ' sin ft 5i> V ew J \ . dr v '
Если здесь обозначить функцию, зависящую только от г,
через R,
rvr = Rcos§, C5.8а)
и ввести значение р из C5.56), то cos ft выпадет и мы
получим для R обыкновенное дифференциальное уравнение
^*™ г П )~~ г* >
которое можно также написать в виде
r*R" + 2rR' - 1R = — . C5.9)
Частным решением неоднородного уравнения является
выражение
а общим решением соответствующего однородного уравнения
Отсюда, согласно известной теореме1), следует, что общее
решение уравнения C5.9) имеет вид
J?= — — + Вг4- —
Л {JL ^ ПГ ^ г2 »
а выражение для vr, согласно C5.8а),
C5.10)
См. «Механика» (т. I), стр. 141.
312 Гл. VII. Дополнения к гидродинамике
Отсюда с помощью условия несжимаемости может,
быть получено выражение для г;», которое имеет вид
VQ. — Rx^'m^, где Иг опять означает функцию, зависящую
только от г. Легко можно получить
R — — — Я4- —
1 2ur 2r3
И
Xr~B + e0sinb- C5-И)
Постоянные интегрирования А, В, С должны быть опре-
определены так, чтобы удовлетворялись граничные условия
задачи. Если невозмущенную скорость на бесконечности
обозначить через q, то эти условия гласят:
г = п . vr = vq — и, ^оо. 1^а)
r= oo : vr = qcos &, v§=—# sin ft. C5.126)
Мы видим, что C5.126) удовлетворится сразу, если под-
подставить B = q. Решая уравнения C5.12а), получим
А — ^ г —я. з
[х~2а> 2й '
Таким образом,
( ^S'j.»-^ • s C5ЛЗ)
и, согласно C5.56),
F=-^ga^. C5.13а)
Результат показывает, что выбор частного решения C5.56)
вместо общего C5.5в) был вполне законным. Но мы не
доказали, что полученные нами равенства C5.13) и C5.13а)
представляют собой единственно возможное решение нашей
задачи. Однако будем считать, что правильно поставленная
задача математической физики может иметь только одно
решение.
Перейдем теперь к формуле для сопротивления дви-
движению шара, или, что одно и то же, для давления на
покоящийся шар. Оно будет складываться из двух частей:
§ 35. Стоксово течение и формула сопротивления 313
компоненты гидродинамического давления в направлении
положительной оси z и действия вязких сил в том же
направлении.
Гидродинамическое давление р действует в радиаль-
радиальном направлении. Его компонента в положительном
направлении z, согласно C5.13), для г = а равна
— р cos Ь = -^ [I — cos2 Q-.
Интегрирование по сфере (элемент поверхности 2тга2 sin Ь db)
дает
Т. +1
С С
3iz\Laq \ cos2 9- sin Ь d$ = 3it{xag \ x2 dx = liz^aq. C5.14)
Для определения вязких давлений ргг и рг& на поверх-
поверхности шара г —а начнем с соотношений A0.2), которые
выражают связь между тензорами pih и eik не только
в декартовых, но и в произвольных ортогональных и,
в частности, в наших сферических полярных координатах.
Предполагая, как и в A0.2), что жидкость несжимаема,
напишем, что
Prr= -2^err, РгЬ= -2^г&. C5.15)
Величины е в ортогональных криволинейных координатах
задаются равенствами D.26) и D.28). Из этих равенств
можно определить к, если в них заменить векторы сме-
смещения 8^1, bq2, Ьд3 на векторы скорости
и Ри Pv Рз на г> $> 9- Соответственно выражению
ds2 = dr2-[-г2 d$2-\-г2 sin2 Ь dy2 имеем g±= I, g2 = r, g3=r sin 9.
В результате из D.26) получаем
к„ = % C5.16)
и из D.28)
о« 1 dvr . дЩ 1 /ос лп\
2ег*=тж+-дР-т^- C5-17)
314 Гл. VII. Дополнения к гидродинамике
Если сюда подставить выражение C5.13), то для г = а
получим [из трех членов в C5.17) останется только
средний, так как при r = a vr и г>а исчезают]
и, согласно C5.15),
Компонента рг& в положительном направлении z равна
ргь sin ft = -к- — sin2 9-;
после интегрирования по поверхности шара получаем
те +i
Зтср,ад \ sin3ЬйЪ = Зтг{хад \ A —ж2)с?ж = 4тг{хад, C5.19)
о -1
что дает вместе с C5.14) известную формулу сопроти-
сопротивления Стокса
W^e^aq. C5.20)
Если мы имеем дело не с равномерным поступатель-
поступательным движением (скорость q), а с равномерным враще-
вращением (угловая скорость со), то ему будет противодей-
противодействовать вращательный момент (см. задачу 4 гл. VII),
равный х)
й. C5.21)
Наше рассмотрение относится к жидкостям и к до-
достаточно плотным газам. В случае сильно разреженных
газов в формулу C5.20) надо ввести поправку, вычис-
вычисленную Кеннингхемом. В этом случае в выражении C5.2)
появляется знаменатель вида
1 + сД, C5.22)
где I — длина свободного пробега молекул в газе, кото-
которая обратно пропорциональна плотности; физический
г) См. К i г с h h о f f, Vorlesungen fiber Mechanik, Кар. XXVII, § 3.
§ 35. Стоксово течение и формула сопротивления 315
смысл численного коэффициента а не вполне ясен1).
Поправка Кеннингхема имела большое значение при
определении элементарного электрического заряда по ме-
методу Милликена.
Вводя длину свободного пробега, мы, естественно,
выходим из рамок используемых нами представлений
о непрерывности и входим в область статистической меха-
механики. Теория непрерывных сред, на которой основана
формула Стокса, справедлива для явлений больших
масштабов (здесь —для радиуса сферы а) по сравнению
с величиной I. На этом же предположении основана по-
поправка Кеннингхема (если только ее рассматривать как
поправку). Это следует из самой структуры выражения
C5.22). Если 1^а, то соотношения становятся неясными.
Кроме того, наше рассмотрение предусматривает, что
числа Рейнольдса малы [см. неравенство C5.1)]. При
росте 91 начинает сказываться наличие инерционных
членов, которыми мы прежде пренебрегали, причем сна-
сначала ламинарный характер течения сохраняется, за
исключением отдельных вихрей за шаром. Сопротивле-
Сопротивление, которое, согласно Стоксу, растет линейно со ско-
скоростью q, все более приближается к квадратичной зави-
зависимости. Настоящая турбулентность наступает при
более высоком 91 =¦ .%крит., когда вихри возникают не
только за шаром, но и в поле течения, окружающем
шар, и тогда закон сопротивления внезапно меняет
свой характер.
Рассмотрим, наконец, насколько справедливо прене-
пренебрежение инерционными членами.
Из равенства C5.56) следует, что при г—> оо давле-
давление р изменяется как 1/r2, a gradp — как 1/г3. Тот же
порядок величины, что и grad/>, имеют содержащиеся
в равенствах C5.2) величины Аи, Av, Aw. Часть инер-
инерционных членов, которыми мы пренебрегли при г—> со,
убывают как 1/г3, а некоторые более медленно. Послед-
Последнее относится к инерционным членам
ди дх> dw /ос оо\
* г) S е х 1 Th., К газокинетическому обоснованию формулы
Стокса—Кеннингхема, Ann. Phys., 81, 855 A926).
316 Гл. VII. Дополнения к гидродинамике
которые, как показывает вычисление с помощью ра-
равенств C5.13), убывают только как 1/г2 (компоненты
и, v, w относятся к прямоугольным координатам).
Правда, если подходящим образом выбрать единицы
измерения (как было сделано в § 16), эти члены будут
иметь в уравнении в качестве множителя число Рейнольдса
которое, по нашему предположению, достаточно мало.
Наше предположение ничего не изменит, поскольку при
г —>оо отношение отброшенных нами членов C5.23) к остав-
оставшимся будет сколь угодно велико.
Это обстоятельство побудило Осеена1) сохранить
в принципе члены C5.23), заменив их в первом прибли-
приближении на
ди dv dw
Интегрирование уравнений Стокса, измененных таким
образом, отнюдь не просто и составляет основную часть
его книги, цитированной на стр. 264. В свете полученных
там результатов наши предыдущие формулы можно рас-
рассматривать как первые члены разложения по степеням М.
В частности, вместо равенства C5.20) получаем с точ-
точностью до следующего члена по Э1
> C5.24)
К счастью, мы видим, что эта поправка не меняет суще-
существенным образом результата Стокса, который так широко
применяется в экспериментальной и теоретической физике:
дело в том, что в силу условия C5.1) для того, чтобы
наше движение оставалось «ползущим», 91 должно быть
мало по сравнению с единицей. Из равенства C5.24)
можно понять, почему в нашем случае, как было указано
выше, с ростом Э1 переход от линейного закона сопро-
г) При этом, конечно, ошибка для больших г уменьшается,
но одновременно вводится ошибка для г=а, где в действительности
w Ф q, а обращается в нуль. • Надо заметить, что, несмотря на
этот факт, решение Осееном этот"! проблемы в смысле математи-
математической строгости не оставляет желать лучшего.
§ 36. Гидродинамическая теория смазки
317
тивления к квадратичному осуществляется непрерывным
образом. Появление настоящей турбулентности при
«5& = ^крит. таким путем, конечно, объяснено быть
не может.
§ 36. ГИДРОДИНАМИЧЕСКАЯ ТЕОРИЯ СМАЗКИ
Эта проблема занимает одно из важнейших мест
в области, связанной с «ползущими движениями».
В старых учебниках по технической механике
трение цапфы в подшипнике относилось к вопросам
сухого трения. Такое рас-
рассмотрение ничего общего с во-
вопросами гидродинамики не
имеет и будет здесь приведено
только для того, чтобы под-
подчеркнуть его отличие от даль-
дальнейшего изложения.
Чтобы можно было приме-
применить обычные представления
о трении1), представим себе,
что цапфа находится в не-
непосредственном соприкосно-
соприкосновении с внутренней поверх-
поверхностью подшипника (фиг. 58). _ _„ „ х
TTV чх v 'п Ф и г. 58. Положение цапфы
На фигуре давление цапфы Р в подшипнике. к теории сухо-
изображено в виде стрелки, го трения,
направленной вертикально
вниз. Так как это давление складывается из веса, ком-
компонент силы тяги, а также из действия сил инерции,
то в общем случае оно будет направлено наклонно
к вертикали. Это, однако, ничего не меняет в нижесле-
нижеследующем рассмотрении: надо только представлять наш
рисунок повернутым соответствующим образом. Заметим,
кстати, что Р отнесено к единице длины цапфы.
В точке соприкосновения В на цапфу действует тре-
нпе R, направленное противоположно вращению, и нор-
нормальное давление N. Их равнодействующая, обозначенная
на фигуре через Q, составляет с N угол трения а (а
х) См. «Механика» (т. I), § 14.
318 Гл. VII. Дополнения к гидродинамике
означает здесь угол трения скольжения, определяемый
из коэффициента трения скольжения / соотношением
/ = tga). Для равновесия сил, действующих на цапфу,
Q должно быть равно по величине и направлено противо-
противоположно Р. В этом случае пара сил QP образует момент
сил трения относительно оси цапфы, приходящийся на
единицу длины подшипника и уравновешивающийся
противоположно направленным вращательным моментом.
Если г—радиус цапфы, то г sin a — плечо пары сил:
M = Pr sin a. C6.1)
Момент сил трения в рассмотренном выше случае не за-
зависел бы от линейной скорости U на окружности и был
бы прямо пропорционален давлению цапфы Р. Точка
соприкосновения лежала бы тогда позади давления цапфы
(если вести отсчет в направлении вращения).
Русский военный инженер Н. П. Петров был первым,
который. рассмотрел эту проблему с точки зрения вязких
свойств смазки1). Он представлял, что цапфа в подшип-
подшипнике точно сцентрирована, так что слой смазки кругом
всей цапфы имеет постоянную толщину d (фиг. 59).
В этом слое скорость уменьшается примерно по линей-
линейному закону от значения U у цапфы к значению нуль
у подшипника. Тангенциальное давление трения у цапфы
тогда будет равняться
U
Суммируя по всей окружности, получим полный момент
этого давления на единицу длины подшипника:
^г2. C6.2)
х). См. статьи Петрова Н., 1883 г., РейнольдсаО.,
1886 г., Зоммерфельда А., 1904 г. и 1921 г.,иМитчелла А.,
1905 .г., о гидродинамической теории смазки в сборнике:
Ostwalds Klassiker, Nr. 218. Более поздняя лите-
литература указана в книге: Р г a n d 11, Stromungslehre, Braun-
Braunschweig, 1942, S. 144 und 145. [(См. перевод: ПрандтльЛ.,
Гидроаэромеханика, ИЛ, 1951.) См. также сборник: Гидродина-
Гидродинамическая теория смазки, М., 1934. Существенный вклад в гидроди-
гидродинамическую теорию смазки принадлежит также Н. Е. Жуковскому
и С. А. Чаплыгину; см. их статью «О трении смазочного слоя
между шипом и подшипником», 1906, переизданную в указанном
сборнике —Прим. перев. ]
§ 36. Гидродинамическая теорил смааки
319
Мы получили зависимость, обратную C6.1): пропор-
пропорциональность U и независимость от Р. Множитель (а в от-
отличие от а в C6.1) зависит от материала смазки, а не от
материала подшипника.
Однако общие статические условия равновесия не удов-
удовлетворяются равенством C6.2), так как давление цапфы
Р не уравновешивается силами трения. Отсюда Рейнольде
Фиг. 59. К гидродинамиче- Фиг. 60. Иллюстрация смеще-
скому трению в случае центри- ния цапфы в направлении, пер-
рованной цапфы. пендикулярном к ее давлению.
сделал заключение, что цапфа располагается не в центре
подшипника; такое положение может возникнуть только
в случае бесконечно большой скорости U. Далее Рей-
Рейнольде показал, что место наименьшей толщины слоя h
располагается относительно Р не позади, а впереди. Но фор-
формулы Рейнольдса не позволяют дать наглядного толкова-
толкования, так как он проводил подсчеты для незамкнутого под-
подшипника (как в случае осей железнодорожных вагонов).
Наглядные соотношения получаются для случая зам-
замкнутых вкладышей подшипников и всесторонней смазки,
как, например, в электрических машинах, работающих
на больших оборотах (см. третью работу из цитированных
на стр. 318). В этом случае цапфа смещается в направлении,
перпендикулярном к давлению цапфы (фиг. 60). К этой
работе непосредственно примыкает (по времени и по со-
содержанию) разработка Митчеллом конструкции подшип-
подшипников для тяжелых вертикальных турбин.
320
Гл. VII. Дополнения к гидродинамике
Основой теории служит приближенное вычисление
картины течения изображенной на фиг. 61. Пренебрежем
компонентой скорости v в направлении у по сравнению
с ее компонентой и в направлении ж (значение w в этой пло-
плоской задаче, конечно, тождественно равно нулю): Согласно
основным уравнениям пол-
ползущих движений C5.2) и
C5.3), имеем:
р = р(х), и = и(у),
У!
dp
dx
d2u
Фиг. 61. Упрощенная схема
слоя смазки переменной толщины.
откуда
и
в силу граничных
условии u = U при у = О
(цапфа) и и = О при у = h (внутренняя поверхность под-
подшипника):
C6.3)
Поток через сечение h равен
h
h тт Л3 dp
12р. dx
О
С л _ h тт __ h3 '
j 2 12р. i
Несмотря на изменяющееся /г (фиг., 61), поток должен
оставаться постоянным для всех сечений (условие несжи-
несжимаемости !). Если h0 означает некое воображаемое се-
сечение, где dp/dx обращается в нуль, то
тт- -f- = (h — ho)U.* (oo.4)
Из C6.3) и C6.4) следует выражение для вязкого дав-
давления на единицу поверхности границы у = О
du
Ah—3/?0
C6.4а)
Перенесем эти результаты с фиг. 61 на фиг. 60. При
этом введем следующие обозначения: О, г и О', г' —
§ 36. Гидродинамическая теория смазки 321
центры и радиусы цапфы и подшипника, е — эксцентри-
ситет, равный расстоянию 00', d — r'~r— зазор при сов-
совмещении точек О и О', А — произвольная точка, соот-
соответствующая углу ср. Из треугольника 00'А получаем
OA-=r-\-h, O'A = r', r+u
Последнее из этих равенств получается при проектиро-
проектировании ломаной 00'А на сторону треугольника OA = r-\- h,
откуда следует
/г = d -}-е cos ср. C6.5)
Введем это значение в равенства C6.4) и C6.4а), для
того чтобы они соответствовали случаю, представленному
на фиг. 60х):
C6.6а)
Отсюда следует после интегрирования по ср от 0 до 2it
р Bтс) - р@) = 6|ir«7 (/2 - Va). C6-7)
C6.7а)
Здесь М, как и прежде, обозначает передаваемый на цапфу
момент сил трения, отнесенный к единице длины под-
подшипника; через / обозначены выражения следующего
вида:
an
\
= 2тсй (d* - e2)-3/s C6.8)
2тс
С rfcP = 2к Гd2 + 4 e2 ) (d2 - e2)-5^.
г) Не представляет труда вывести эти уравнения непосред-
непосредственно в полярных координатах г, у, но в этом нет необходимости.
21 А. Зоммерфельд
322 Гл. VII. Дополнения к гидродинамике
Очевидно, что значения Jlf J2 и /3 связаны сле-
следующим образом:
J*~ dd ' Js~~ 2 del '
Так как величина р должна иметь периодом 2тг, то из
C6.7) и C6.8) следует
ho = ^ = d d2-.e2 . C6.9)
Подставляя значение Ло в C6.7а), получаем
C6.10)
Если аналогично C6.5) положить
/i0 = rf-j-ecoscp0, C6.11)
то из C6.9) имеем
coscp0=— -s- q— . C6.11а)
Для центрированного положения цапфы е = 0:
. coscp0.= o, фо=у или -2"тс;
с другой стороны, для е = d (наибольшего из возможных
значений эксцентриситета)
coscp0=—1, cpo = ir.
Согласно C6.6),
^ = 0 для h = h0.
Оба значения ср0, соответствующие h0, задают положение,
соответствующее максимальному и минимальному давле-
давлению. В случае центрированного положения они распо-
располагаются диаметрально противоположно друг к другу
относительно центра цапфы; в случае максимального
эксцентриситета, когда цапфа касается вкладыша под-
подшипника, оба эти положения совпадают (в точке сопри-
соприкосновения).
§ 36. Гидродинамическая теория смазки
323
'Ра
Пока что мы определили положение этих мест отно-
относительно линии 00', соединяющей центры (прямая ср = 0).
Выясним теперь, как они располагаются относительно дав-
давления цапфы. Для этого заметим: перепад давления dp/dy,
согласно C6.6), зависит только от h и является чет-
четной функцией от ср, если отсчитывать ср от нулевой линии
00'\ это следует из C6.5). Следовательно, с точностью до
постоянной интегрирования р0 давление р является не-
нечетной функцией от ср; обозна-
обозначим ее через рг. Постоянное
слагаемое р0, естественно, при
суммировании уравновешивает
само себя.- Обозначим через рл
и р-? значения рг в двух точках
Аи А, расположенных сим-
симметрично относительно ср = 0.
Если ра и р-? перенести в центр
цапфы О, то они дадут равно-
равнодействующую, перпендикуляр-
перпендикулярную к 00' (фиг. 62). Это же от-
относится и к вязким давлениям
(мы их обозначили на фигуре
как qA и q-~), которые, согласно
C6.6а), являются четными функ-
функциями от ср, причем надо принять во внимание их тан-
тангенциальное направление (в сторону, обратную возраста-
возрастанию ср).
Соответствующий параллелограмм сил показывает,
что и их равнодействующая будет перпендикулярна к 00'.
Таким образом, равнодействующая всех действующих
на цапфу сил будет также перпендикулярна к 00'. Так
как она должна уравновешиваться с давлением цап-
цапфы Р, последнее должно быть равно ей по величине и
противоположно по направлению. Иначе говоря: центр
цапфы О смещается в направлении, перпендикулярном
к давлению Р (как было заранее изображено на
фиг. 60).
Кроме направления, нам надо также определить вели-
величину смещения е. Для этого надо только приравнять
сумму упомянутых выше равнодействующих /? ид задан-
21*
\Р
Фиг. 62. Иллюстрация
условия равновесия между
гидродинамическими давле-
давлениями р, q и давлением
цапфы Р.
324 Гл. VII. ДоЛолнениА к Гидродинамике ^
ному значению Р. Это дает:
, — = \ р sin cp dy—Vgcoscpdcp. C6.12)
Первый интеграл можно преобразовать с помощью интег-
интегрирования по частям, причем подстановка пределов
в член, вышедший из-под знака интеграла, в силу
периодичности дает нуль. Тогда вместо C6.12) получаем
K^0cos^ C6Л2а)
Здесь можно пренебречь q по сравнению с dp/dy, так
как, согласно C6.6) и C6.6а), отношение dpjdy к q
имеет порядок г/Л. Поэтому можно написать более про-
простое выражение
6U(Jh0J6), C6.126)
где приняты сокращенные обозначения
Y С cos <p d<$ j С cos у d<p
4~~ J (d + ecos?J' 5~ J (d + ecos<?
Из C6.8) можно легко показать, что
Если подставить эти выражения в C6.126) и восполь-
воспользоваться значением h0 из равенства C6.9), то после
элементарных преобразований получаем
Р d* Зе d2 /ое 4оч
Отсюда можно определить е (вернее, отношение ejd)
как функцию левой части равенства C6.13). Если зна-
значение ё подставить в C6.10), то можно определить М
(причем далее будем интересоваться только величиной,
но не знаком у М). Особенно простое выражение для М
можно получить, если разделить C6.10) на C6.13):
. C6.13а)
§ 36. Гидродинамическая теория смешки 325
Рассмотрим теперь два предельных случая.
а) U—>co. Из равенства C6.13) получим тогда, что
е = 0; это соответствует центральному положению цапфы,
а из C6.10) следует
М = 2^г2^, C6.14)
т. е. приходим к формуле Петрова C6.2).
б) U—>0; Равенство C6.13) дает e — d, т. е. имеем
соприкосновение цапфы и подшипника. Равенство C6.13а)
показывает, что M = Pd, вместо чего лучше написать
M = r'P-j. C6.15)
Это выражение представляет собой формулу C6.1) для
сухого трения с частным значением входящего туда
угла трения, а именно
d
sinct=— .
г
в) Представляет интерес еще и третий случай, когда
при заданном давлении цапфы Р и заданном зазоре d вели-
величина М принимает минимальное значение. Если правую
часть C6.13а) продифференцировать по е и производную
приравнять нулю, то получаем
С этим значением е равенство C6.13а) дает
M = '^Pd = 0№Pd. C6.16)
Это значение только на 6% меньше предельного значе-
значения C6.15) для U~>0. Все эти результаты графически
представлены на фиг. 63. В качестве ординаты там вы-
выбрана безразмерная величина y = M/Pd, а в качестве
абсциссы — также безразмерная величина z, которая
является обратной величиной левой части равенства C6.13):
326
Гл. VII. Дополнения к гидродинамике
Приведенная на фигуре кривая представляет собой зави-
зависимость, задаваемую равенствами C6.10) и C6.13), из
которых исключена величина е. Параметрическое пред-
представление этой кривой лучше всего может быть задано
Фиг. 63. График теоретической за-
зависимости безразмерных переменных
y=M/Pd и z=2UBdz)
с помощью равенств C6.13) и C6.13а), если обозначить
e/d через {3:
z =
!=?. C6-18)
Кроме этой кривой, - на фиг. 63 пунктиром изображены
прямые, выражающие собой зависимости C6.1) и C6.2),.
которые в наших новых переменных представляют просто
у=1 и y = z;
они касаются кривой при z — 0 и z — со. Зависимость
нашей кривой только от безразмерной комбинации z
выражает собой закон подобия гидродинамической теории
смазки: при одном и том же z, согласно C6.18), C — e/d
и ?/ = M/Pd будут всегда иметь определенные значения
независимо от того, каким значениям U, P, r, d и \х,
соответствует z.
§ 36. Гидродинамическая теория смазки 327
Как согласуются экспериментальные факты с нашими
теоретическими результатами? Можно сказать: в окрест-
окрестности минимума, а также на некотором расстоянии
вправо от него наблюдается (в случае всесторонней
смазки) не только качественное, но и количественное
совпадение с нашей кривой. Из этого можно заключить,
что здесь смазка определяется только коэффициентом
вязкости \i и что наше, предположение о ползущем
характере движения справедливо. Но для больших
и очень малых значений z наблюдаются отклонения
от теоретической зависимости, которые указаны на фи-
фигуре штрихпунктирной линией. Так как здесь не будет
соблюдаться закон подобия для трения при вязкой
смазке, эти отрезки надо было бы рисовать не в виде
отдельных кривых, а в виде семейств кривых, зависящих
от Р, U и т. д.
Для больших z экспериментальная кривая идет ниже
теоретической. Это объясняют тем, что движение там
носит не ламинарный, а турбулентный характер.
Для очень малых значений z кривая идет значитель-
значительно выше теоретической. .Здесь кроме вязкости играют
роль совсем другие свойства смазочной среды, а именно
свойства, относящиеся к прилипанию этой среды к огра-
ограничивающим ее металлическим стенкам. Эти свойства
тесно связаны с изученными Ленгмюром мономолекуляр-
мономолекулярными слоями, которые возникают в результате того, что
длинные цепные молекулы масла на поверхности сма-
смазочного слоя вытягиваются в одном направлении. Однако
мы не будем углубляться в этот вопрос, так как это
выведет нас из рамок классической гидродинамики.
Мы рассматривали плоскую задачу, т. е. считали
подшипник бесконечно длинным. Учет конечной длины
подшипника влечет за собой появление новых граничных
условий для давления и скорости. Кроме того, перед
конструктором возникает задача, как подобрать приток
и утечку смазки, чтобы пространство между цапфой
и вкладышем было заполнено вдоль всего подшипника.
Одна из трудностей заключается в возможности воз-
возникновения отрицательных давлений. Переменная часть
величины р (мы назвали ее рг), как мы видели, пред-
представляет собой нечетную функцию угла ср. В то время
328 Гл. VII. Дополнения к гидродинамике
как в месте наиболее узкого зазора значение рг воз-
возрастает, при возрастании зазора оно должно убывать,
достигая затем отрицательного значения, равного по аб-
абсолютной величине максимальному положительному
значению. В результате возникает опасность разрыва слоя,
если постоянная часть давления (мы назвали ее р0) не
будет иметь такую величину, при которой /? = ро + рг будет
всюду положительным. Величина р0, зависящая от при-
притока и утечки на концах подшипника, в нашей теории
является свободным параметром, и получение необхо-
необходимых значений р0 определяется умением конструктора.
Ясно, что для такой практической проблемы, как
вышеизложенная, идеализированная теория может дать
только общие руководящие указания. То, что эти ука-
указания могут оказаться весьма полезными на практике,
показывает упомянутый на стр. 319—320 пример с под-
подшипниками Митчелла.
§ 37. УДАРНЫЕ ВОЛНЫ РИМАНА. ИНТЕГРИРОВАНИЕ
В ОБЩЕМ ВИДЕ УРАВНЕНИЙ ЭЙЛЕРА ДЛЯ СЖИМАЕМОЙ
ЖИДКОСТИ В ОДНОМЕРНОМ СЛУЧАЕ
В главе о волновых движениях мы всюду опускали
квадратичные члены в уравнениях Эйлера (ввиду того
что мы считали амплитуды бесконечно малыми; в случае
«ползущих движений» они, как инерционные, члены
выпадали сами). В этом параграфе мы непосредственно
перейдем к рассмотрению этих членов. Первым, кто осме-
осмелился это сделать, был не кто иной, как Бернгард
Риман1); вслед за ним этим вопросом занимались
Гюгонио, Адамар и многие другие.'
Метод Римана заключается в том, что в результате
замены зависимых и независимых переменных нелиней-
нелинейные гидродинамические уравнения становятся линейными.
Это удается сделать в одномерном случае. Метод,
с помощью которого Риман проинтегрировал полученное
линейное дифференциальное уравнение, стал прообразом
для общей задачи об интегрировании линейных уравне-
1)Riemann.B.J О распространении плоских воздущных
волн с конечной амплитудой, Abhandl. d. Gottinger Ges. d. Wiss.,
1860; Ges. Werke, S. 156. (См. перевод: Риман Б., Собр. соч.,
М., 1948.) '
§ 37. Ударные волны Римана 329
ний второго порядка в частных производных соответ-
соответствующего (гиперболического) типа.
Чтобы подойти к результатам исследований Римана,
вспомним решение Даламбера для соответствующей
задачи в случае бесконечно малых амплитуд колебаний
(см. § 13). Теперь, как и в том случае, из каждого воз-
возмущенного в начальном состоянии места будут распро-
распространяться две волны в противоположных направлениях.
Давление можно при этом представлять себе как функцию
плотности /? = <р(р), заданную, например, в форме урав-
уравнения политропы G.1). Приведем цитату из статьи
Римана х): «Скорость распре странения обеих волн в газе
равна |/<р'(р), однако относительно пространства она
будет увеличена на величину скорости газа в направле-
направлении распространения волны. Если, как это и бывает,
предположить, что <р' (р) при увеличении р не убывает,
то большие платности будут распространяться с большей
скоростью, откуда следует, что волны сжатия будут
убывать по ширине, переходя в конце, концов в скачок
уплотнения».
После этого вступления начнем с перехода от нели-
нелинейных уравнений к линейным. Пренебрежем действием
силы тяжести и других внешних сил и будем считать,
что ось х расположена в направлении движения. Как
это часто делается в математике, обозначим дифферен-
дифференцирование некоторой величины по какой-либо незави-
независимой переменной соответствующим индексом внизу
справа. Исходные уравнения запишутся тогда в виде
-=О, C7.1)
+±рх = 0. C7.2)
Величину рх в C7.2) можно заменить на р^, полагая
/? = ср(р):
Рх = с%, с2_-=^ = ср'(р); C7.3)
Коэффициент с, как и в A3.5), есть скорость звука,
но там он был постоянным в силу бесконечно малой
амплитуды, а здесь'является функцией р.
R i e m a n n В., Gottinger Nachr., Nr. 19, A859).
330 Гл. VII. Дополнения к гидродинамике
Учитывая выражение C7.3), можно записать C7.2)
в виде
и, + иия+-Ря = 0. C7.4)
Уравнения C7.1) и C7.4) линейны и однородны относи-
относительно дифференциалов х и Р, сами х и t туда не входят.
Наоборот, р и и и их дифференциалы dp и du входят
в уравнения в нелинейной форме. Поэтому, следуя
Риману, введем х и t как зависимые, арии как неза-
независимые переменные
х = х{р, и), t = t{p,u),
dx = x9dp-\-xudu, dt = t9dp-\- tudu.
Если выражения для dx и dt подставить в
du = uxdx-\- ut dt
и соответственно в
dp = pxdx.-\-pt dt,
то получим уравнения
du = {ихх9 -[- *МР) dp -f-(uxxu-\- uttu) du C7.5)
и
Сравнивая множители при dp и du, получим из C7.5)
ихх9 + uttp = 0
хи tu
и кя=-^, »f=--f' C7.7)
где А — функциональный определитель
C7.7а)
t
который предполагается не обращающимся в 0.
Точно так же из C7.6) следует
C7.8)
§ 37. Ударные волны Римана 331
Если в C7.1) и C7.4) подставить значения их, ut, px, pt
из C7.7) и C7.8), то получим
0, x9-ut9+jtu = O. C7.9)
Второе из этих равенств можно переписать в виде
(Х-Ш)= t==
dp ^ ' p ди dp ди '
где V = V(p, и) — новая зависимая переменная, через ко-
которую х и t могут быть выражены. следующим образом:
x-ut=Vu, t=-±V9. C7.10)
Если справедливы равенства C7.10), то удовлетворяется
и второе равенство C7.-9). Заменив теперь в первом ра-
равенстве C7.9) хи — utu и tp- через производные V, получим
одно линейное дифференциальное уравнение второго по-
порядка в частных производных для определения един-
единственной неизвестной V; оно имеет вид
Это уравнение можно упростить, если вместо р ввести
новую переменную
5*: 1=7- C7Л2)
Кроме того, вместо и будем далее писать г\. Тогда
получим
P &i V с p
Если теперь ввести в качестве зависимости между р и р
уравнение политропы G.1)
332 Гл. VII. Дополнения к гидродинамике
то, согласно C7.12),
Е- ЪУ^ 0(n-l)/2 d ^._3-П ^
Вместо C7.11) имеем
Vn-Vn+^V^O, C7.13)
где введено обозначение
A-jb?- C7.14)
В случае & = 0 равенство C7.13) переходит в уравнение
колебаний струны, решением которого, согласно A3.11),
является решение Даламбера
7i)f C7.15)
где F и G — произвольные (до необходимых условий не-
непрерывности) функции. Докажем, следуя Бехерту х), сле-
следующую теорему: если W есть решение уравнения
L = 0, C7.16)
' C7.16а)
Wrm + -L
то величина
является решением уравнения
Vx-V^ + i^V^O. C7.166)
Для доказательства надо только продифференцировать
C7.16) по ? и заменить, согласно C7.16а), Wg на %V.
Тогда
После выполнения дифференцирования в первом члене и
деления па ? мы сразу получаем уравнение C7.166).
Зная общее решение C7.15) уравнения C7.13) для
к —0, мы тем самым знаем также и общее решение для
1)Bechert К., К теории плоских возмущений в невязких
газах, Ann. d. Phys., 37, 89 A940); 38, 1 A940).
§ 37. Ударные волны Римана 333
к = 2] 4, 6 ... Согласно C7.16а), оно имеет следующий
вид:
Все эти элементарно интегрируемые случаи можно охва-
охватить, если в выражение C7.14) подставить к, равное
произвольному четному числу 2/г. Соответствующий «по-
«показатель политропы п» (это выражение употреблено здесь
в том же смысле, что и на стр. 86)' равен тогда, согласно
C7.14),
Эта рациональная форма л 'составляет главный предмет
исследования Бехерта, так как она, оказывается, имеет
поразительное термодинамическое значение.
Как известно, в адиабатическом случае
u=l+j, C7.18а)
где / — число степеней свободы молекулы газа. Для двух-
двухатомных газов, например для воздуха, / = 5, для одно-
одноатомных газов / = 3. В последнем случае играют роль
только три трансляционные степени свободы, так как
вращение отсутствует. В современной физике это сразу
следует из квантово-механических соображений, в то
время как Больцману для обоснования того, что / = 3
и соответственно / = 5 у одно- и двухатомных газов, при-
приходилось исходить из весьма искусственного предполо-
предположения о том, что одноатомная молекула имеет сфериче-
сферическую форму, а двухатомная молекула — форму эллип-
эллипсоида вращения. Таким образом, для указанных двух
случаев
Ih = 1 (для одноатомных газов),
n = Z (для двухатомных газов).
334 Гл. VII. Дополнения к гидродинамике
Вследствие этого как раз в этих двух наиболее инте-
интересных случаях мы можем интегрировать уравнения C7.17)
с помощью элементарных выражений F2 и F4 х).
В этом примере может броситься в глаза «заранее
предопределенная гармония» между физикой и матема-
математикой. Математические возможности кажутся приспособ-
приспособленными к потребностям физики. Чтобы не переоценить
этого «чуда», мы сразу же заметим, что для молекул,
состоящих из трех и более атомов (Н2О, NH4, ...), для
которых / = 6, необходимо к трем трансляционным сте-
степеням свободы добавить три вращательные. Таким обра-
образом, эти газы не соответствуют интегрируемому в нашем
смысле случаю. С другой стороны, наиболее просто инте-
интегрируемый случай /=1, & = 0 в природе не реализуется:
для его реализации надо было представить «одномерный
газ», в котором атомы не могли бы вращаться, а двига-
двигались бы только в одном направлении.
Для той же цели служит следующее замечание: не
следует думать, что если п не принимает одного из ра-
рациональных значений, даваемых формулой C7.18), то
интегрирование невозможно. Мы запишем2) последова-
последовательность равенств C7.17) в общем виде
V0, где С = |, ? = }/2С. C7.19)
Согласно известному обобщению теоремы Коши, в тео-
теории функций комплексного переменного мы можем сна-
сначала для целого h выразить стоящую в C7.19) h-ю про-
производную через комплексный интеграл
ГЛ = * Ь?<? 1*1Щ* dm. C7.20)
Интегрирование производится в комплексной плоскости
w по замкнутому контуру вокруг точки о> —С; в аргу-
аргументе Fo мы, согласно C7.19), вместо ? подставили У 2w,
х) Бехерт сообщил автору, что особое положение для случая
C7.18) было замечено раньше: Love А. Е. Г. and P i d d u с к
F. В., Trans. Roy. Soc, 222, 167 A922).
2) Согласно второй из статей, цитированных на стр. 332.
§ 37. Ударные волны Римана 335,
оставив irj без изменения.- Но в выражении C7.20) не
требуется, чтобы h было целым; здесь можно заменить
2/г на произвольную величину к, частным значением
которой и является 2/г. Заменим соответственно
на -к- -\-1, J-, на
щ на
\2
В результате вместо C7.20) получаем1)
У, ТО) , /or, О/1\
~-dw. C7.21)
(да— СJ
Может быть сразу показано что выражение C7.19), как
и C7.20), удовлетворяет уравнению *C7.13). Более того,
мы имеем теперь общее решение этого дифференциаль-
дифференциального уравнения, так как C7.21) содержит под знаком
интеграла две произвольные функции F и G. Наше
высказывание о том, что физически интересные случаи
одно- и двухатомных газов являются интегрируемыми,
теперь может быть уточнено: эти случаи отличаются от
других лишь тем, что общий интеграл для них имеет
элементарную форму.
Следуя Риману, мы рассмотрели здесь случай одной
пространственной координаты. Обобщение на случай двух
или трех переменных2) вызывает большие трудности.
Появляющиеся при этом уравнения в частных производ-
производных, аналогичные C7.13), до сих пор не были решены
в общем виде.
х) Здесь знак ф не обозначает простой обход вокруг точки ш=С,
как это было в C7.20); поскольку она является точкой ветвления
-+1
функции (w—СJ , то контур не замкнут. Этот знак означает
«двойную петлю» вокруг точек а>=? и ау=оо, часто используемую
в-теории функций комплексного переменного.
2) В ее her t К., Ann. Phys., 39, 169, 357 A941); 40, 207
A941). В первой из этих работ рассмотрен класс цилиндрических
и сферических волн, а в последней приняты во внимание трение и
теплопроводность.
336 Гл. VII. Дополнения к гидродинамике
Все вышеизложенное касалось весьма интересной, но
формальной стороны проблемы. Теперь следует перейти
к рассмотрению физической природы движения, как это
сделано в цитированной выше работе Римана. Для этого
мы не будем рассматривать готовое выражение для инте-
интеграла V, а обратимся к определению переменных J-, tj
в равенстве C7.12). А именно, следуя Риману, положим
C7.22)
причем предположение о выполнении уравнения поли-
политропы для дальнейшего не требуется. Эти величины в на-
нашем частном случае являются «характеристиками» диф-
дифференциального уравнения C7.13). В общей теории диф-
дифференциальных уравнений этого типа характеристики
играют важнейшую роль.
Обозначив, как и ранее, производные по первоначаль-
первоначальным координатам х и t через индексы справа внизу, вы-
вычислим, воспользовавшись C7.22),
и образуем выражение
C7.24)
В силу уравнений движения C7.1) и C7.4) скобка в пра-
правой части C7.24) обратится в нуль. Вычислив точно
так же из C7.22) st ш sx и построив выражение st +
-}- (и — с) sx, опять получим в правой части нуль. Можно,
таким образом, записать оба результата:
0- C7.25)
§ 37. Ударные волны Римана 337
Если теперь образовать полные дифференциалы
dr = rx dx.-\- rtdt .и ds = sxdx + st dt
и подставить значения rt, st из C7.25), то получим
dr f dx ~\ ds f dx \ /on Oe\
выражение C7.26) показывает, что определенное значе-
значение г или 5 распространяется со скоростью
? = и-\-с, или ~ = и~-с. C7.27)
Если |и|<с, то г распространяется в сторону возра-
возрастания х, a s — в сторону убывания, причем оба движе-
движения происходят с переменными скоростями. -
v,t>0
Фиг. 64. Распространение и одновременно искажение двух волн,
двигающихся вправо и влево.
Обозначения У, W означают то же самое, что и наши характеристические
параметры г и s, считаемые функциями х я t.
Сравнивая фиг. 64 и 16, заметим, что средняя кривая на фиг. 64 пред-
представляет собой каждое из возмущений V и IV, в то время как на фиг. 16
она представляет собой сумму возмущений, распространяющихся вправо
и влево.
Рассмотрим, в частности (подобно тому как это было
сделано на фиг. 16), пример, в котором в начальном
состоянии имеется возмущение давления в узком интер-
интервале оси х. Из него будут исходить две волны уплот-
уплотнения (при условии, что вначале мы имели увеличение
давления). Однако форма волны теперь не будет сохра-
сохраняться, как это было на фиг. 16. Напротив, фронт волны
будет делаться более крутым, так как в силу C7.27)
большие плотности будут распространяться с большими
22 А. Зоммерфельд
338 Гл. VII. Дополнения к гидродинамике
скоростями. Так будет происходить постепенный пере-
переход волны уплотнения в скачок уплотнения. Далее наше
рассмотрение перестает быть справедливым, так как в нем
не учитывались вязкость и теплопроводность. Развитие
этой теории имеется в работах Гюгонио и Адамара х).
На этом мы можем закончить изложение цитирован-
цитированной выше статьи Римана.
Фиг. 64 взята из работы Бехерта (первая из цитиро-
цитированных на стр. 332 статей). Она относится к простей-
простейшему случаю «одномерного газа» (см. стр. 334); этот слу-
случай, как показал Бехерт, несмотря на крайнюю идеали-
идеализацию, иллюстрирует характерные особенности [распро-
[распространения волн.
§ 38. О ТУРБУЛЕНТНОСТИ
Перейдем теперь к труднейшей проблеме гидродина-
гидродинамики, изложение которой разобьем на ряд разделов.
В разделе 1 рассмотрим ряд полу эмпирических, полу-
теоретических положений о свойствах турбулентного те-,
чения. Поскольку эти положения носят лишь теорети-
теоретический характер, они основываются на уравнениях
Навье — Стокса и на представлениях о «диффузии» ко-
количества движения, которые эти уравнения выражают
(см. стр. 98). В разделе 2 обсудим фундаментальный
вопрос: можно ли вообще, опираясь на эти уравнения,
дать объяснение экспериментальным явлениям. В частно-
частности, можно ли с помощью этих уравнений " предсказать
наступление неустойчивости при определенном критиче-
критическом числе Рейнольдса? Прежние исследования этого
вопроса с помощью метода малых колебаний дали отри-
отрицательный результат: согласно этим исследованиям не
должно быть никакого критического предела для числа
Рейнольдса, а течение должно оставаться стабильным
при любых di. С помощью метода малых колебаний
г) См. обзор Zemplen G., Enzykl. d. Matb. Wiss., Bd. IV,
3, Art. 19, дополненный более поздней работой: Becker R.,
Zs. Phys., 8, 321 A922). [Подробное изложение теории одномерных
движений сжимаемого газа и ударных волн можно найти в книгах:
Зельдович Я. В., Теория ударных волн и введение в газо-
газодинамику, М., 1946; Ландау Л. Д. и Лифшиц Е. М.,
Механика сплошных сред, М., 1953.—Прим. перев.]
§ 38. О турбулентности 339
исследовались установившиеся ламинарные течения: тече-
течение в трубах по закону Гагена — Пуазейля и куэттовское
течение между пластинами. Ввиду этих отрицательных
результатов такие знатоки этого вопроса, как Карман и
Тейлор, в своих работах в ряде мест склонялись к мне-
мнению, что турбулентность, подобно- теории газов, может
быть истолкована только с помощью статистических мето-
методов. В основе этой точки зрения лежит тот факт, что
жидкость представляет собой систему со многими (.в прин-
принципе—с бесконечно многими) степенями свободы, которые
начинают играть роль при больших числах Рейнольдса.
Движение тогда так усложняется,^ что можно ждать
простого ответа только на вопрос о его поведении в сред-
среднем. В особенности это относится к предельному случаю
так называемой «изотропной турбулентности», о которой
мы приведем некоторые сведения в разделе 4, ссылаясь
на еще не опубликованные работы Вейцзекера и Гейзен-
берга. Перед тем как обсуждать эти вопросы, относя-
относящиеся к так называемому «состоянию развитого турбу-
турбулентного равновесия», мы совсем коротко обсудим в раз-
разделе 3 исследования, связанные с процессом установле-
установления ламинарного течения: процессы у входа при тече-
течении в трубах и образование пограничного слоя Прандтля
возле движущейся пластины в случае течения между
пластинами. Прандтль сам начал изучать эту проблему,
которая затем была разработана его учениками Толми-
ном, Титьенсом, Гёртлером, Шлихтингом. Метод малых
колебаний применялся при этом не к профилю скоростей
установившегося ламинарного течения, а к промежуточ-
промежуточному профилю, который имеет место при возникновении
ламинарного течения. Еще в более ранних работах Рэлея,
который, однако, рассматривал только невязкую жидкость,
было замечено, что форма профиля скоростей играет роль
в вопросе об устойчивости. В упомянутых выше более позд-
поздних исследованиях в основу были положены уравнения
Навье —- Стокса для вязкой жидкости в полной форме
(вернее, в несколько сокращенной форме ввиду малости
колебаний). Эти исследования привели к установлению
предела устойчивости, правда, не для установившегося
ламинарного течения, а для процессов его возникно-
возникновения. Наконец, в разделе 5 мы рассмотрим пример,
22*
340 Гл. VII. Дополнения к Гидродинамике
в котором для соответствующе выбранных, нелинейных
дифференциальных уравнений (похожих на уравнения
Навье —Стокса, но более простых) имеют место такие же
явления, как и в турбулентной жидкости. Этот пример,
которым мы обязаны Бургерсу, укрепит нашу точку
зрения, согласно которой турбулентность также можно
отнести к классической гидродинамике, хотя математи-
математическое описание ее сильно затруднено.
1. Некоторые свойства турбулентного течения
В течение многих лет инженеры-гидравлики накопили
обширный экспериментальный материал, относящийся
к турбулентному движению в трубах и каналах. Для
того чтобы его упорядо-
упорядочить, надо исходить из
двух принципов: следует
рассматривать течения с
равными числами Рей-
нольдса и учитывать не-
Ф и г. 65. График распределе- ровности стенок. Что ка-
ния средней скорости турбулент- саетСя второго требования,
ного течения в трубе круглого ? ?
сечения (сплошная линия) ила- * о для того, чтоиы не yi
минарного течения (пунктирная лубляться слишком в тех-
линия). нику и чтобы можно было
провести вычисления, мы
рассмотрим случай гладких стенок, т. е. случай, когда
в пределе неровности стремятся к нулю.
Тогда в смысле первого требования мы имеем общий
результат: в развившемся турбулентном состоянии в
случае геометрически подобных сечений труб распреде-
распределение скоростей также будет подобным, т. е. отноше-
отношение скорости в некотором месте к значению скорости,
усредненному по всему сечению, не зависит от числа
Рейнольдса.
На фиг. 65 показано это распределение скоростей
в случае круглого сечения, а также распределение при
течении Гагена —Пуазейля. В последнем случае профиль
скорости представляет собой параболу; скорость в сере-
середине равна удвоенной средней скорости. В турбулентном
случае скорость на оси трубы лишь слегка превосходит
§ 38. О турбулентности 341
среднюю скорость, которая на фигуре выбрана равной
для обоих случаев. Только вблизи стенок скорость бы-
быстро падает до нуля; здесь образуется узкая краевая
зона, где играет роль вязкость и где течение более или
менее ламинарно.
Следует заметить, что когда мы говорим о скорости
в турбулентном состоянии, то это выражение не совсем
строго и при этом подразумевается скорость, усреднен-
усредненная по времени. Индивидуальная скорость какой-либо
частицы жидкости может при этом сильно меняться со
временем. Спектр ее значений во времени и пространстве
весьма широк. Мы приведем о нем более подробные све-
сведения для одного характерного предельного случая (см.
раздел 4). Обозначим усредненную по времени скорость,
которая направлена по оси трубы (ось х) через U, а до-
дополнительные компоненты индивидуальных скоростей ча-
частиц— через и, v, ... Пусть Р— усредненное по времени
давление; индивидуальное мгновенное отклонение давле-
давления от значения Р обозначим через р.
Закону распределения скорости поставим в соответ-
соответствие закон падения давления. Известно, что давление
не будет, как в случае ламинарного течения, пропор-
пропорционально скорости, а будет пропорционально ее квад-
квадрату (точнее — в степени 7/4, закон Блазиуса, см. стр. 152).
Выраженный рациональным образом, т. е. с помощью
инвариантов подобия R и S, этот закон, согласно ра-
равенствам A6.10) и A6.13), гласит:
где а—радиус трубы, X — численный коэффициент. В на-
наших теперешних обозначениях этот закон перепишется
в виде
^ W^wy/V/4>
Равенство C8.1) показывает, что в противоположность
случаю ламинарного течения коэффициент вязкости 'здесь
почти не играет никакой роли: он входит только в виде
множителя v1/4. Превалирует теперь другой вид потери
энергии, связанный с действием сил инерции и проявля-
342 Гл. VII. Дополнения к гидродинамике
ющийся в наличии множителя р (или р8^, если учесть
зависимость кинематической вязкости v от р).
С помощью некоторых дополнительных предположе-
предположений Прандтль и Карман вычислили из уравнения C8.1)
распределение скоростей в краевой зоне. Если предста-
представить, что' из трубы вырезан элемент длиной dx, то усред-
усредненное давление, действующее на оба поперечных сече-
сечения элемента, будет находиться в равновесии со взятым
у стенок трубы касательным напряжением т0, действу-
действующим на границе этого элемента:
—г- dx таг2 = хп dx 2таг,
т. е., согласно C8.1),
dP а Хр / vy/4r/7/ ~я 9.
т°- ~ш t=tw и • <38-2'
Пусть у— а — г — расстояние некоторой точки краевой
зоны от стенки. Тогда, согласно Прандтлю и Карману,
имеется единственное разумное, с точки зрения размерно-
размерностей, приближенное выражение для касательного напря-
напряжения1) в точке у:
х = const p Г-V4 С/7'4, C8.2а)
или, разрешая относительно U, получаем
U = const (^
Таким образом, скорость в краевой зоне растет от нуля
пропорционально степени 1/1 расстояния от границы. Эта
зависимость хорошо согласуется с опытом. Далее Кар-
Карман получил из этой зависимости формулу для тепло-
теплопередачи в краевой зоне, которая также хорошо согла-
согласуется с опытом.
х) То, что равенство C8.2а) для t/=0 не переходит в C8.2), а обра-
обращается в бесконечность, объясняется, согласно Карману [Zs. angew.
Math, und Mech., 1, 233 A921)], тем, что равенство C8.2а) претен-
претендует только на асимптотическое представление для бесконечно боль-
больших чисел Рейнольдса.
' § 38. О турбулентности 343
Теперь проанализируем путь, по которому пришел
к пониманию вопроса о турбулентности сам Рейнольдег)
и, следуя его идеям, Лорентц2). Рассмотрим основное
стационарное движение в направлении оси х с перепадом
давления —dP/dx, на которое налагается добавочное
нестационарное квазипериодическое движение. Будем рас-
рассматривать двухмерное состояние, зависящее -только от
х и. у. Скорость U основного движения будет тогда за-
зависеть только от у, а добавочное турбулентное движе-
движение будет иметь компоненты и и v, зависящие от t, x
и у. Рассмотрим усредненное по времени значение сум-
суммарной скорости v и суммарного давления &>:
vx = U + u,' vy = v, &> = P + p C8.4)
и потребуем
vx = U, vy = Q, ? = Р, т. е. п^О, v = 0, J=0. C8.5)
Отсюда следует
vxvx = U2 + 2Uu + ии = U2 + аи,
uv C8.5а)
и
В силу квазипериодичности движения, кроме этого, на-
например, будет
?? = 0 C8.5в)
и, далее, в силу C8.4) и C8.5),
Запишем уравнения движения в сокращенной векторной
форме A6.1), считая F = 0:
р ~ -f p (v grad)-v = - grad ^ + jiAv. C8.6)
г) См. работу Рейнольдса, цитированную на стр. 144.
2)Lorentz H. A., Amsterdamer Akademie, Zittingsveriag,
6,28A897); Ges. Abhandlungen, Teubner, 1907, S.43.
344 Гл. VII. Дополнения к гидродинамике
Произведем небольшое преобразование, используя усло-
условие divv = 0, а именно:
dvx . dvx д .д
Теперь ^-компоненту уравнения C8.6) можно написать
как
дЬх , д д доР А /оо е \
+ Р/А+Р? = + №х. C8.6а)
Образуем от этого уравнения среднее по времени и
с учетом C8.4) —C8.5г) получим
* ^? C8.7)
9Ш +
Здесь в левой части равенства стоят градиенты вязких
давлений, которые появляются наряду со стоящим справа
градиентом нормального давления Р. Обозначим эти ве-
величины, согласно системе обозначений, принятой в A0.4),
через
^.Рхх + ^Рху, где рхх = рии, pxy = puv. C8.7а)
Стоящий в правой части уравнения C8.7) член p&U, как
показано в уравнениях A0.6) — A0.86), тоже возник из
вязких давлений. Однако, в то время как прежние pih
отвечали молекулярному беспорядку микроскопических
частиц жидкости, теперешние компоненты рхх и рху
в C8.7а) возникают из-за молярного беспорядка макро-
макроскопических областей жидкости, принимающих участие
в турбулентном течении. В обоих случаях физическая
причина возникновения вязких давлений лежит в пере-
переносе импульса. Например, в случае молярного вязкого
давления рху речь идет о переносе импульса из движе-
движения в направлении х в боковое движение v, что, конечно,
не может не повлиять на баланс импульса основного
движения U. В этом и заключается причина того, что
в левой части уравнения C8.7) для основного движения
появляются члены C8.7а). Появление усредненных дав-
давлений C8.7а), к которым дальше нельзя применять
обычные методы дифференциального исчисления, и обу-
§ 38. О турбулентности 345
словливает то, что в этом подходе к проблеме тур-
турбулентности приходится использовать статистические
методы v
Из двух вязких давлений рху и рхх основную роль
играет первое. Поэтому мы обозначим вклад второго
в уравнение C8.7) только точками. Кроме того, удобно
в этой связи говорить не о вязком давлении, а о вязком
напряжении
Х = °ху = - Рху = - Р «*• C8-8)'
Тогда уравнение C8.7) перейдет в
? %+.-.. C8-9)
где вместо ДЕТ" можно писать dHJ / dy2, так как U дол-
должно зависеть только от у. Выражение C8.9) есть урав-
уравнение, определяющее основное течение.
Уравнение для ^-компоненты добавочного турбулент-
турбулентного движения мы получим из C8.6), если воспользо-
воспользоваться равенствами C8.4) и упростить результат с по-
помощью C8.5г) и C8.9):
где мы опять обозначили точками все члены второго
порядка по и и v. Имеется также соответствующее урав-
уравнение для ^-компоненты скорости v турбулентного дви-
движения и аналогичное C8.9) уравнение для дР/ду.
Конечно, нельзя дать количественного анализа харак-
характера турбулентности с помощью этих весьма сложных
уравнений. Мы привели их здесь главным образом для
того, чтобы сравнить с примером, рассматриваемым в раз-
разделе 5, и чтобы подчеркнуть значение молярного вязкого
напряжения т. Последнее приводит к представлению
о характеристической для турбулентности длине Z, так
называемой «длине перемешивания Прандтля» A926 г.),
соответствующей понятию длины свободного пробега
в газах.
346 Гл. VII. Дополнения к гидродинамике
Прандтль обосновал это понятие следующим образом1):
если «шарик жидкости» со средней скоростью U (у) пере-
переносится из точки у в точку у-\-1, то для дополнительного
движения это означает флуктуацию, равную примерно
Естественно предположить, что флуктуация бокового
движения v в процессах перемешивания имеет этот же
порядок величины. Тогда, согласно C8.8), для т полу-
получается выражение вида
f % ¦ C8-")
Если его подставить в C8.9), то получим дифференциаль-
дифференциальное уравнение, которое зависит только от величин, хара-
характеризующих основное движение, и которое теперь может
быть изучено. При этом, однако, требуется эксперимен-
экспериментальное подтверждение соотношения C8.11), которое носит
гипотетический характер.
2. Прежние попытки математического обоснования
критерия турбулентности Рейнольдса
Еще до теоретических исследований Рейнольдса вопрос
об устойчивости был исследован с помощью метода малых
колебаний Кельвином2), однако он не получил рконча-
тельных результатов. Двадцать лет спустя этот вопрос был
снова исследован3) для вырожденного случая куэт-
товского течения, отличающегося особой простотой мате-
математического выражения [формула A6.14)]. Если на пря-
прямолинейный профиль основного течения U, изображённый,
на фиг. 196, накладывается малое возмущение и, v, кото-
которое может быть представлено функцией тока ф, то возни-
возникающее в общем случае дифференциальное уравнение
x)Prandtl L., Stromungslehre, Vieweg, 1942, S.105. (См.
перевод: Прандтль Л., Гидроаэромеханика, ИЛ, 1951,
гл. III, § 4.—Прим. перев.)
а) Kelvin, Phil. Mag., 24, 188, 272 A887).
8) OrrW.M.F. Proc. Irish Acad.,27 A907); Sommerf eld A.,
Intern. Math. Kongress Rom, V. Ill, 1908, S. 116.
$38. О турбулентности 347
в частных производных четвертого порядка
в силу прямолинейности профиля {d2iUjdy2i = Qi) распа-
распадается на два уравнения второго порядка
I+и -к ~vA) *=°' АФ=*• C8- 12а>
Возьмем вместо ф и х их компоненты ряда Фурье
ф==/(у)еИвх-РО, х = ^1(у)в*(«с-РО C8.126)
и получим для / и F два обыкновенных дифференциаль-
дифференциальных уравнения второго порядка, решение которых может
быть получено во всем. интервале 0 < у < h в виде из-
известных функций (функций Бесселя порядка 1/3 и 2/3).
Граничные условия для г/ = 0 и y = h после исключения
постоянных интегрирования дадут трансцендентное урав-
уравнение для р в виде определителя второго порядка. Если
для заданного действительного а оно будет иметь решение р
с положительной мнимой частью, то это означает неу-
неустойчивость в том смысле, что для волнового числа а
возмущение будет возрастать со временем. Критическое
значение числа Рейнольдса, согласно этим представле-
представлениям, есть значение, при котором впервые появляется р
с исчезающей мнимой частью для какого-либо значе-
значения а.
Мизес1), однако, показал, что, согласно природе этого
трансцендентного уравнения, такого {3 вообще не может
существовать и что, таким образом, прямолинейное куэт-
товское течение при всех возмущениях а должно было бы
оставаться устойчивым. Этот вывод был подтвержден
Гопфом2), который показал это более прямым путем,
рассмотрев подробно типы возникающих колебаний.
Более того, согласно общему методу Нётер8), кажется
даже, что любое течение между двумя плоскими
x)Mises R., Heinrich-Weber-Festschrift, 1912, S.I 12
(Teubner); Jahresber. d. deutsch. Math. Ver., 6, 232 A926).
2) H о pf L., Ann. d. Phys., 43, 1 A914).
3) No ether F., Zs. angew. Math. u. Mecb., 6, 232 A926).
348 Гл. VII. Дополнения к гидродинамике
параллельными пластинами должно быть устойчивым
(если при этом нет особых нерегулярностей на входном
профиле).
Сексль1) рассмотрел уравнения, подобные C8.12) и
C8.126), не только для течений между плоскими пласти-
пластинами, но и для собственно куэттовского течения2) между
коаксиальными вращающимися цилиндрами и для течения
Гагена—Пуазейля в трубах. Во всех случаях соответствую-
соответствующее задаче трансцендентное уравнение привело к заклю-
заключению об устойчивости.
Таким образом, мы имеем очевидное противоречие
между теорией и экспериментом. Какое можно сделать
заключение? Должны ли мы усомниться в методе малых
колебаний, который оправдал себя во всех других обла-
областях механики, включая и астрономию, или же мы долж-
должны для доказательства неустойчивости рассмотреть не
малые, а конечные колебания и сравнить их с ламинар-
ламинарным движением? Может быть, необходимо считать, что
в нашем случае уравнения Навье—Стокса перестают быть
справедливыми? Это кажется недостаточно обоснованным,
так как из этих уравнений следуют не только все преды-
предыдущие теоретические выводы, но и сам закон подобия
Рейнольдса.
3. Новая формулировка проблемы возникновения
турбулентности
Выход из указанного выше затруднения можно найти,
если (следуя Прандтлю) обратить внимание на то, как
при эксперименте возникает турбулентное состояние
(см. также описание явлений в трубах, стр. 149). С этой
точки зрения, более простым, чем течение в трубах,
представляется куэттовское «течение между пластинами»,
при котором поле течения с одной стороны ограничено
плоской пластиной, движущейся в направлении х. На ней
в начале движения образуется пограничный слой Прандтля.
!) Sexl Th., Ann. d. Phys., 83, 835 A927); 84, 807 A927); 87,
570 A928).
2) В более тщательных исследованиях куэттовского течении, про-
проведенных Тейлором (см. стр. 155), было показано, что после перехода
предела устойчивости отклонения от ламинарного течения не имеют
аксиальной симметрии, а спиралеобразны, т. е. трехмерны.
§ 38. О турбулентности 349
Другую ограничивающую поле течения покоящуюся
пластину будем считать пока расположенной на беско-
бесконечности. Примем, что между ней и пограничным слоем
жидкость покоится или характер ее течения является
ламинарным, оно описывается условием U (у). Как впервые
показал Толмин1), для характера устойчивости основную
роль играет профиль скорости в пограничном слое. Из
критерия устойчивости Толмина2) следует, что профиль
скорости с точкой перегиба, возникающий в пограничных
слоях в случае возрастания давления, в высшей степени
неустойчив. Для того чтобы охарактеризовать относя-
относящиеся к этому вопросу исследования (определение соб-
собственных значений и приближенное вычисление соб-
собственных функций в полосе жидкости), приведем цитату
из работы Шлихтинга3): «В качестве основного течения
не следует брать линейное распределение скоростей,
а надо исследовать всевозможные профили скоростей,
возникающие между двумя параллельными плоскими
стенками, если одна из стенок приводится из состояния
покоя в движение с постоянной скоростью. На движущейся
стенке тогда образуется пограничный слой, толщина
которого растет со временем, и если течение остается
ламинарным, то происходит асимптотическое приближе-
приближение к линейному распределению скоростей. В противо-
противоположность этому окончательному линейному распре-
распределению скоростей «начальный профиль» обладает ко-
конечным критическим числом Рейнольдса, значение кото-
которого зависит от формы профиля скорости. Истинным
критическим числом Рейнольдса для куэттовского течения
является тогда самый низкий предел устойчивости для
различных профилей в начальный период».
Конечно, решение поставленной таким образом про-
проблемы значительно труднее, чем решение проблемы, со-
содержащейся в наших уравнениях C8.12). Для ее реше-
х) Tollmien W., О возникновении турбулентности, Got-
tinger Nachr.,. 1929.
2) Т о 1 1 m i e n W., Gottinger Nachr., 1935.
3)Schlichting H., Ann. Phys., 14, 905 A932). Он ссы-
ссылается на более ранние работы других учеников Прандтля, а именно:
Т i e t j e n s О., Zs. angew. Math. u. Mech., 5, 200 A925); Tol-
Tollmien W. (см. примечание 1 на данной стр.). См. также более
поздние работы Шлихтинга в Gottinger Nachr., 1932", 1933, 1935.
350 Гл. VII. Дополнения к гидродинамике
ния потребуется прибегнуть к методу последовательных
приближений, к численным,| и графическим методам,
а этим мы сейчас заняться не; можем. Но такое решение
приводит к определенному, имеющему практическое
значение пределу устойчивости, который, вообще
говоря, зависит от того, как возникает турбулентное
состояние.
Чтобы подчеркнуть измененный характер постановки
вопроса, мы можем сказать: с этой точки зрения не самр
ламинарное течение неустойчиво, что подразумевалось
в разделе 2, а тот путь, по которому происходит возникно-
возникновение этого течения, содержит промежуточные неустойчи-
неустойчивые состояния. В свете этого неустойчивость является
свойством не конечного состояния, а его предистории1).
4. О предельном случае изотропной турбулентности
Ввиду такой сложности проблемы имеет смысл поста-
поставить вопрос о том, не имеется ли идеального предельного
состояния, к которому стремится турбулентная жидкость,
т. е. своего рода турбулентного равновесия, не зависящего
от начального состояния и от предистории. Предположим,
что при этом в пространстве не имеется избранного на-
направления, и будем говорить об изотропной турбулент-
турбулентности. Пространство при этом разобьется на «турбулент-
«турбулентные элементы» («турбулентные ячейки») с непрерывно из-
изменяющимися размерами, распределенные каким-то ста-
статистическим образом; вихревое движение в них подчи-
подчиняется уравнениям Навье—Стокса, но слишком сложно
для полного математического рассмотрения. Равновесие
между различными турбулентными элементами может
быть поэтому описано только статистически. Можна
х) Данное Зоммерфельдом в разделах 2 и 3 изложение-вопроса об
устойчивости ламинарного движения не находится на современном
уровне, и результаты, к которым приходит автор, не могут в настоя-
настоящее время быть признаны правильными. Подробное изложение совре-
современного состояния этого сложного вопроса можно найти в книгах:
Кибель И. А., К о чин Н. Е., Розе Н. В., Теоретиче-
Теоретическая гидромеханика, часть II, М.—Л., 1948; Ландау Л. Д.
и Лифшиц Е. М., Механика сплошных сред, М.—Л., 1953.—
Прим. перев.
§ 38. О турбулентности 351
говорить о вероятности, с которой осуществляется некая
заданная величина турбулентного элемента. Этим самым
мы возвращаемся к затронутому еще на стр. 341 вопросу
о спектре турбулентных элементов.
В качестве примерной модели может служить кинети-
кинетическая теория газов. Здесь математически точное состоя-
состояние (координаты и скорости всех молекул газа) также
определяется предисторией. Однако в кинетической тео-
теории газов интересуются только статистически-вероятност-
статистически-вероятностным распределением (а также вероятностью отклонения
от него), задаваемым законом Максвелла—Больцмана.
Аналогичным Ьбразом, в данном случае мы интересуемся
не частностями, а только статистически-вероятностным
распределением вихрей, которое может быть описано
сведениями о частоте появления вихрей определенной
величины с определенной угловой скоростью.
Применяя метод подобия, Вейцзекеру удалось полу-
получить спектр скоростей (сравнивая турбулентные элементы
различной величины). При этом он исходил из предполо-
предположений о том, что состояние квазистационарно (его изме-
изменение за время, необходимое для возникногения статисти-
статистического равновесия, должно быть малым) и неупорядо-
чено. Закон распределения тогда гласит: средняя относи-
относительная скорость турбулентного элемента (по отношению
к окружающим его элементам) меняется как корень
третьей степени из его диаметра. Отсюда следует, что
в энергетическом спектре плотность энергии пропорцио-
пропорциональна степени—5/3 волнового числа. Этот закон спра-
справедлив лишь в средней части спектра, которая, однако,
при больших числах Рейнольдса весьма широка. Что
касается очень малых волновых чисел (больших турбу-
турбулентных элементов, размеры которых сравнимы с ха-
характерными размерами течения), то вместо статистиче-
статистического рассмотрения надо решать гидродинамическую гра-
граничную задачу для каждого элемента в отдельности.
В области очень больших волновых чисел (малых турбу-
турбулентных элементов) трение вызывает очень быстрый спад
спектральной интенсивности к нулю.
Гейзенберг получил тот же результат с помощью раз-
разложения в ряд Фурье, причем ему удалось вычислить мно-
множители пропорциональности, воспользовавшись исследо-
352 Гл. VII. Дополнения к гидродинамике
ванием предельных случаев малых и больших волновых
чисел и определяя флуктуации давлениях).
5. Математическая модель, иллюстрирующая проблему
турбулентности
После тщетных попыток объяснить статистическими
методами явления турбулентности Бургерс создал мате-
математическую модель2), свойства которой аналогичны свойст-
свойствам турбулентного течения и могут быть выведены совер-
совершенно строго. Упрощенная система уравнений, которую
Бургерс взял вместо предыдущих уравнений C8.9) и
C8.10), выглядит следующим образом:
— — Р — /у2 —
dt ~~
—- = Uu — vw.
dt
C8-13>
Эти уравнения, как и уравнения турбулентности,
нелинейны [см. член с и2 в первом и с Uu во втором
из уравнений C8.13)]; они также содержат диссипа-
тивные вязкие члены [vt/ в первом и vw во втором из
уравнений C8.13), соответствующие членам fiAE/" в C8.9)
и fi/рДи в C8.10)]; постоянная Р в C8.13) стоит вместо
перепада давлений dP/dx в C8.9) и, как последнее,
представляет собой движущую силу. Величины U и и,
как и прежде, —.зависимые переменные; U — основное
движение, и — добавочное турбулентное движение. Однако,
в то время как уравнения C8.9) и C8.10) имеют неза-
*) Развитие теории так называемых «локальных свойств турбу-
турбулентности» почти целиком является заслугой советских механиков.
В частности, Колмогорову А. Н. и Обухову А. М. принадлежит закон
пропорциональности частоты турбулентных пульсаций кубическому
корню из их пространственных масштабов; этот закон был открыт
ими в 1940—1941 гг. (между тем работы Вейцзекера и Гейзенберга,
которые упоминаются в тексте, относятся к 1948—1950 гг.). Подроб-
Подробное изложение этих вопросов можно найти в книгах: Ландау
Л. Д. и Л и ф ш и ц Е. М., Механика сплошных сред, М., 1953;
Седов Л. И., Методы подобия и размерностей в механике,
М., 1951.—Прим. перев.
2) Burgers J. М., Математические примеры, иллюстрирую-
иллюстрирующие соотношения, возникающие в теории турбулентного течения
жидкости, Amsterdamer Akademie XVII, S. 1, 1939.
§ 38. О*турбулентности
353
висимыми переменными три величины х, у, t, в C8.13)
имеется единственная независимая переменная t.
Нелинейные члены в уравнениях C8.13) выбраны
таким образом, что они выпадают из «выражения энергии»,
которое образуется, согласно общему правилу, путем
умножения первого уравнения C8.13) на U, а второго
на к и последующего сложения. В результате получим
C8.13а)
Здесь в правой части первый член представляет собой
работу, производимую в единицу времени давлением и
относящуюся к основному движению, а второй член озна-
означает диссипацию энергии при трении.
Существует ламинарное решение уравнения C8.13),
а именно:
C8.14)
Оно будет устойчивым, если
P<v2. C8.14а)
Это можно установить сразу, воспользовавшись методом
малых колебаний. Положим
и пренебрежем высшими степенями ?, v\. Тогда, соглас-
согласно. C8.13),
1 C8-146)
Так как v > 0, то первое из этих уравнений имеет экспо-
экспоненциально убьшающее решение, а решение второго будет
убывать, только если Uo < v, что в силу равенства C8.14)
совпадает с C8.14а). Если Uo > v, то Р > v2, и хотя
равенство C8.14) будет оставаться решением уравне-
уравнения C8.13), оно будет в силу второго из уравнений C8.146)
вести себя неустойчиво.
23 А. Зоммерфельд
354 Гл. VII. Дополнения к гидродинамике ¦
Однако для Р > v2 существуют два решения, которые
назовем турбулентными, поскольку в них присутствует
добавочное движение. Этими решениями являются
v*. C8.15)
Они оба устойчивы для Р > v2. Если положить
и, следуя методу малых колебаний, пренебречь опять
более высокими степенями ? и т\, то из C8.13) получим
C8.15а)
dt ~ U°K-
Чтобы их решить, удобно сделать обычную подстановку
Ь = Ае", ti = BeM. C8.156)
Тогда мы получим условия для определения X и В/А:
Ы= —чА — 2и0В,
\В = и0А,
из которых после исключения В/А сразу следует
C8.15в)
Оба корня \ будут действительными и отрицательными
при
V2 < Р < | V2
и комплексными с отрицательной действительной частью
ыри
§ 38. О турбулентности
355
Таким образом, наше возмущение, задаваемое C8.156),
убывает для всех Р > v2 по экспоненциальному за-
закону; решение C8.15) будет поэтому устойчивым для
всех Р > v2. Граница устойчивости лежит при P = v2,
где один из корней решения C8.15в) исчезает. Она совпа-
совпадает с границей устойчивости ламинарного решения C8.14)
и дает нам аналогию с критерием устойчивости Рей-
нольдса. Правда, в противоположность гидродинамике,
Фиг. 66. Диаграмма
модели Бургерса в «ла-
«ламинарном» случае, Р<\2.
Ф и г. 67.. Диаграмма
модели Бургерса в
«турбулентном» случае,
Р^
нб только ламинарное, но и турбулентное решение ста-
стационарно, т. е. не зависит от t. Наш пример, конечно,
дает только «модель» турбулентности, не давая ей ника-
никакого объяснения (об этом свидетельствует также и то,
что в отличие от гидродинамики в нашей модели воз-
возможны две формы турбулентного движения, в то время
как закон действительного турбулентного движения одно-
однозначным образом определяется числом Рейнольдса).
Следуя Бургерсу, мы приводим на фиг. 66 и 67 гра-
графическую интерпретацию результатов. На этих фигурах
изображены в координатах U и и обе кривые
§ = 0 и *-
Согласно C8.13), они задаются равенствами
C8.16)
C8.16а)
C8.166)
23*
356 Гл. VII. Дополнения к гидродинамике
Выражение C8.16а) представляет собой параболу, а
C8.166) — пару прямых, состоящих из оси абсцисс и линии,
параллельной оси ординат. Так как оба наших решения
C8.14) и C8.15) стационарны (не зависят от t), то точки,
которые их представляют, должны лежать на пересечении
кривых, описываемых уравнениями C8.16а) и C8.166).
На фиг. 66, где парабола проходит слева от прямой
Z7 = v, имеется только одна точка пересечения, которая
соответствует устойчивому решению C8.14); на фиг. 67
имеются три точки пересечения, из которых точка, лежа-
лежащая на оси абсцисс, соответствует теперь уже неустойчи-
неустойчивому решению C8.14), а две другие соответствуют устой-
устойчивому решению C8.15).
Бургерс во многом развил свой метод «математических
моделей», чтобы еще больше приблизить его к действи-
действительным соотношениям турбулентности. Например, он
рассмотрел систему трех дифференциальных уравнений,
в которые вошли как основное движение U, так и доба-
добавочные движения и и v, причем эти движения зависели
не только от времени, но и от пространственных коорди-
координат. Мы не будем ими здесь заниматься, так как ясно,
что уже примитивная модель, задаваемая уравнениями
C8.13), достаточно разъясняет математическую ситуацию:
нелинейный характер уравнений, как и в случае турбу-
турбулентности, создает здесь возможность двух совершенно
различных форм движения, которые мы в этом случае
назвали ламинарной и турбулентной. Соотношения, опи-
описывающие их устойчивость, некоторым образом анало-
аналогичны соотношениям гидродинамической турбулентности.
Переход одной формы в другую при достижении предела"
устойчивости можно сравнить с критерием устойчивости
Рейнольдса.
Глава VIII
ДОПОЛНЕНИЯ К ТЕОРИИ УПРУГОСТИ
§ 39. ПРЕДЕЛЫ УПРУГОСТИ, ПРОПОРЦИОНАЛЬНОСТИ И
ТЕКУЧЕСТИ. ПЛАСТИЧНОСТЬ И ПРОЧНОСТЬ
До сих пор мы предполагали, что твердое тело одно-
однородно и изотропно, и допускали только малые деформа-
деформации. Ниже мы совсем коротко обсудим важнейшие откло-
отклонения, возникающие при более общих условиях.
Рассмотрим цилиндрический стальной стержень, один
конец которого жестко закреплен, а на другой действует
растягивающая сила Р. Возникающее в поперечном сече-
сечении напряжение с будем относить, как принято в технике,
к нерастянутому сечению Fo, так что
¦=?. C9.1)
т. е. напряжение пропорционально нагрузке.
Если в качестве оси абсцисс принять измеренную де-
деформацию ?, а. в качестве ординаты—вычисленное из
выражения C9.1) напряжение, то при нагрузках, соответ-
соответствующих очень малым деформациям е, мы получим ли-
линию, практически не отличающуюся от прямой (см. сплош-
сплошную кривую на фиг. 68). Это справедливо до некоторой
точки Р, так называемого «предела пропорциональ-
пропорциональности».
Пределом упругости называют точку диаграммы, до
которой при возрастании или убывании нагрузки соответ-
соответственно возрастает или убывает деформация. Для стали
предел упругости расположен несколько ниже предела
пропорциональности.
Если нагрузка превосходит предел пропорционально-
пропорциональности, то линия се искривляется, достигает максимума, так
называемого верхнего предела растяжения So (его также
называют пределом текучести или пластичности), а затем
несколько падает до нижнего предела растяжения Su,
358
Гл. VIII. Дополнения к теории упругости
после чего на протяжении небольшого отрезка она слегка
колеблется, но в среднем остается параллельной оси е.
Иногда пределы растяжения вообще неясно выражены.
Различный характер поведения зависит от состава стали и,
возможно, от ее предыдущей обработки.
К этой переходной области примыкает область пластич-
пластичности, или текучести, где возникают остаточные дефор-
деформации. При малом изменении нагрузки деформации быстро
Фиг. 68. Диаграмма зависимости
напряжения от деформации при рас-
растяжении пластического материала
(стали).
возрастают, так что в этой области кривая сначала под-
поднимается медленно, затем постепенно искривляется и де-
делается вогнутой по отношению к оси е. Максимум В соот-
соответствует разрушающему усилию и соответственно раз-
разрушающему напряжению; разрушение, однако, наступает
в точке z, где кривая ае внезапно обрывается. Необ-
Необходимо добавить, что при этом стержень 1) испытывает
поперечное сжатие и 2), начиная с точки В, его сечение
весьма сильно уменьшается в окрестности того места,
в котором позже произойдет разрыв (образуется шейка).
Если вычислять напряжение в (переменном) наименьшем
сечении F, т. е. положить
а=-?, • C9.2)
§ 39. Пределы упругости, пропорциональности и текучести 359
и вычисленное таким образом напряжение поставить
в соответствие с измеренным е, то получим в пластической
области кривую, которая на фиг. 68 изображена пунк-
пунктиром. В области упругости эта кривая, естественно,
совпадает со сплошной кривой.
Сталь является важнейшим представителем пластиче-
пластических материалов, чугун же относится к хрупким матери-
материалам. У последнего отсутствует пластическая область и,
конечно, при разрыве не образуется шейка. Разрыв насту-
наступает почти сразу после резко ограниченной упругой
области. Согласно прежним опытам, для чугуна, вообще
говоря, закон Гука несправедлив, однако Грюнайзен1)
показал, что для достаточно малых е напряжение с также
меняется пропорционально е.
Материалы, которым может быть придана любая
форма (например, глина и свинец), естественно, совсем
не имеют упругой зоны и всюду ведут себя пластично.
В случае сжатия, изгиба и кручения материалы будут
вести себя так-же, как и при растяжении, причем следует
заметить, что разрушение при чистом сжатии наступает
только в случае хрупких, а не пластических тел. При всех
упомянутых опытах мы предполагаем, что нагрузка
растёт достаточно медленно, так как, кроме нагрузки,
деформация зависит еще.. и от времени.
Возникающие при этом явления получили название
упругого последействия: деформация в случае прило-
приложения определенной нагрузки (даже в упругой области)
принимает свое конечное значение только спустя значи-
значительное время. При этом говорят также о «ползучести»
рассматриваемых материалов.
Упругий гистерезис представляет собой явление, ана-
аналогичное поведению ферромагнитных тел при намагни-
намагничивании. Так же как и в случае магнитного гистерезиса,
площадь петли гистерезиса в плоскости се представляет
собой потерю энергии деформации за цикл.
В предыдущем рассмотрении нагрузка предполагалась
постоянной или медленно меняющейся. Большое значение,
особенно в машиностроении, имеет случай периодической
нагрузки, при котором напряжение колеблется в обе
Gruneisen E,, Ber. Deutsch. Phys. Ges.,
360 Гл. VIII. Дополнения к теории упругости
стороны от некоторого среднего значения на одну и ту же
величину. При этом разрушение наступает при значитель-
значительно более низкой нагрузке, чем в стационарном случае;
в таком случае говорят об «усталости» материалов. Если
откладывать среднее напряжение ат в зависимости от
числа циклов нагрузки z, необходимых для разрушения,
то мы получим монотонно убывающую кривую, которая
с ростом z приближается к горизонтальной асимптоте cas.
Это указывает на то, что если мы хотим с уверенностью
избежать разрушения вследствие усталости, то нельзя
допускать превышения среднего напряжения <зт над о^.
В случае разрушения при медленно возрастающей
нагрузке излом имеет крупнозернистую структуру, в то
время как при усталостном разрушении часть излома
имеет мелкозернистую структуру и обнаруживает распро-
распространение дефектных участков (см. ниже). Остальная
часть излома имеет обычную крупнозернистую структуру.
Отсюда можно заключить, что в результате действия мед-
медленно возрастающей нагрузки сечение уменьшилось на-
настолько, что стал возможен обычный излом. Укажем так-
также, что число циклов до излома z сильно зависит от со-
состояния поверхности. Мельчайшие, невидимые глазом
трещины могут сильно снизить значение z. В этой связи
следует заметить, что при измерении прочности каменной
соли Фойгт получил значение, равное только х/400 теорети-
теоретического значения, вычисленного с помощью представлений
о прочности кристаллической решетки. Причиной этого
также являются маленькие трещины и поверхностные не-
неровности. Если производить этот опыт под водой, когда
происходит сглаживание поверхности в результате рас-
растворения, то могут быть достигнуты значения прочности,
достигающие величины, равной 3/4 теоретического зна-
значения.
Твердые тела, используемые в технике, обычно являют-
являются металлами или металлическими сплавами, состоящими
из маленьких кристаллических зерен, между которыми
имеется более дисперсный промежуточный слой, состоя-
состоящий из других веществ. Между этим слоем и зернами
возникают весьма значительные силы сцепления; этот
слой также сообщает твердому телу известную однород-
однородность. Но в нем также располагаются менее прочные места,
§ 40. Упругость кристаллов 36J
так называемые «дефекты», в которых начинается раз-
разрушение.
Органические вещества, например дерево и кожа,
построены из кристаллоподобных частиц, между кото-
которыми вкраплены другие вещества. Напротив, стекло,
например, является аморфным веществом.
Что касается кристаллической структуры металлов,
то мы теперь знаем, что всякий кристалл представляет
собой пространственную решетку. Основу этой решетки
составляют атомы металла, располагающиеся по «кристал-
«кристаллическим плоскостям», а на плоскостях—по «кристалличе-
«кристаллическим прямым». Кристаллические плоскости могут быть
разбиты на три, вообще- говоря, неортогональных семей-
семейства параллельных плоскостей.
При малых нагрузках (в области пропорциональности)
пространственная решетка деформируется однородно, без
существенных изменений формы, причем со снятием на-
нагрузки эта деформация- исчезает. В пластической области
кристаллы деформируются с изменением их формы. Кри-
Кристаллические плоскости некоторого семейства (плоскости
скольжения), содержащие наиболее густо усеянные атома-
атомами кристаллические прямые, скользят относительно друг
друга в направлении этих прямых.
§ 40. УПРУГОСТЬ КРИСТАЛЛОВ
Обширная область физических явлений в анизотроп-
анизотропных телах весьма полно изложена в «Учебнике кристалло-
кристаллофизики» Фойгта х). В этой книге выведены весьма общие
соотношения, связанные со свойствами симметрии кри-
кристалла и с геометрическими понятиями, характеризу-
характеризующими рассматриваемые физические явления, как, напри-
например, скалярными или векторными полями, тензорными
полями второго и более высокого ранга. При рас-
рассмотрении упругих свойств кристаллов мы имеем дело
со связью между тензорами напряжения и деформации.
х) V о i g t W., Lehrbuch der Kristallphysik, Teubner, 1910
(второе издание, 1928 г.). Кроме свойств диэлектриков и провод-
проводников, здесь изложены, например, пироэлектрические и, ставшие
в последнее время весьма важными, пьезоэлектрические свойства;
в этой книге, однако, не излагаются вопросы кристаллооптики.
362 Гл. VIII. Дополнения к теории упругости
Так как они оба является симметричными тензорами
второго ранга, т. е. имеют по шесть компонент, то наи-
наиболее общий вид линейной связи между напряжениями
и деформацией будет зависеть от 6-6 = 36 коэффициентов.
Это количество, однако, сокращается до
6 + ^ = 21, D0.1)
при условии, что работа деформации W является функ-
функцией состояния, что впервые было постулировано Грином.
Было указано (см. стр. 94), что это предположение
выполняется в случае изотермических процессов (вопросы
равновесия), а также при адиабатических изменениях
(быстрые колебания). В этих случаях, которые нас только
и будут интересовать в дальнейшем, dW явится полным
дифференциалом. Наши общие обозначения aih и eih
с двойными индексами заменим обозначениями с простыми
индексами, для чего положим
°11=а1' <?22==О2» °33 = аЗ> а23=а4> °3l = °5> °12 = °в> D0 2)
?11 = S1> e22==S2» 833== 83' ^S23 == 84> ^Sgj = ?5» ^812 == S6#
Тогда двойная сумма (9.24) перейдет в
dW= S «Л D0.3)
и общая связь между напряжениями и деформацией буде!
иметь вид
°h= S **Л , D0.4)
где 5ih — модули упругости1) кристалла. Из условия, что
dW — полный дифференциал, имеем, согласно D0.3),
х) Об этой общепринятой терминологии, введенной Фойгтом,
говорилось еще в примечании на стр. 83. Коэффициенты . в соот-
соотношениях между деформацией и напряжениями, которые получают-
получаются, если D0.4) разрешить относительно е, Фойгт обозначил через
cik («упруги6 коэффициенты»).
§ 40. Упругость кристаллов 363
Полученное выражение совпадет с D0.4), если
. ¦ ** = *«• D0.5)
Расположив все s в виде квадрата, симметричного
относительно диагонали sn ... s66, сразу получим число
компонент, вычисленное в D0.1). То же самое, конечно,
можно сказать и об упругих коэффициентах с.
Следует заметить, что прежние молекулярные теории
Навье, Коши, Пуассона (центральные силы между моле-
молекулами) приводили к дальнейшему сокращению этого
числа до 15. Мы знаем, однако, что по отношению
к изотропным телам эта. теория недостаточна. Она дает
для коэффициента Пуассона v в равенстве (9.9) значе-
значение, равное 1/i, и таким путем позволяет сократить
число упругих констант изотропного тела с двух до
одной.
Современная теория кристаллического состояния по-
показала, что причина возникающих здесь трудностей
заключается не в молекулярной теории как таковой,
а в ее слишком узкой формулировке: кристалл, вообще
говоря, состоит- из нескольких налагающихся друг на
друга решеток, которые при упругих, деформациях могут
сдвигаться относительно друг друга, и в результате пред-
предположение о центральном характере сил перестает быть
справедливым.
Упомянутое ранее число 21 относится к кристаллу
с наиболее низкой симметрией, т. е. к триклинному
кристаллу. В дальнейшем мы воспользуемся следующим
принципом: симметрия физического процесса налагается
на симметрию кристалла. Упругая деформация имеет
по своей природе центр симметрии, или, иначе говоря,
растяжение в каждом направлении равно растяжению
в противоположном направлении. С другой стороны,
в отношении симметрии у триклинного кристалла есть
две возможности: в нем или имеется центр симметрии,
или его нет. В последнем случае мы, однако, можем
сказать, что деформация в известном смысле добавляет
недостающий центр симметрии. Поэтому обе подгруппы
триклинной системы по отношению к деформации ведут
себя одинаковым образом.
364 Гл. VIII. Дополнения к теории упругости
Всего имеется 32 группы (класса) симметрии1), кото-
которые относятся к 7 кристаллографическим системам:
триклинной,' моноклинной, ромбической, тетрагональной
или квадратной, ромбоэдрической или тригональной,
гексагональной и кубической. В каждой из трех первых
и двух последних систем все кристаллы ведут себя-
в отношении своих упругих свойств одинаковым образом,
только в тетрагональной и ромбоэдрической системах
можно выделить по две подгруппы, различающиеся по
упругим свойствам2). Мы рассмотрим ниже в качестве
примера некоторые из этих 5 -f- 2 • 2 = 9 различных воз-
возможных схем упругих констант.
Кристаллические оси обозначаются обычно через а,
Ь, с. В триклинной системе они имеют различные длины
и произвольные направления. В моноклинной системе
одна из них расположена перпендикулярно к двум
остальным и представляет собой ось симметрии второго
порядка. Если ее выбрать в качестве оси z некоторой
прямоугольной системы координат xyz и обозначить
упругие смещения через Е, tj, С, то при повороте на 180°
вокруг оси z произойдет следующий переход:
х, У, z -> —х, —у, z, I, т], С —> — I, — tj, С; (а)
согласно D0.2), с одной стороны,
si> е2> Ч, Ч перейдут в elt s2, е3, е6 (б)
а, с другой стороны,
е4, е5 перейдут в — е4> — е5; " (в)
действительно,
х) Как хорошо известно, они отличаются дрз^г от друга симмет-
симметрией относительно некоторой точки. Более глз^бокое разделение
на 230 пространственных групп, отличающихся друг от друга сим-
симметрией пространственной структуры, мы здесь рассматривать не
будем.
2) Эти подгруппы не отличаются друг от друга по числу неза-
независимых упругих констант; разница состоит лишь в большей или
меньшей свободе выбора главных осей деформации.—Прим. перее.
§ 40. Упругость кристаллов 365
при преобразовании (а), меняют свой знак, а, например,
компонента
6~ду ^ Эх
знака не меняет. Точно так же, как и е, ведут себя а,
для которых также справедливы правила преобразова-
преобразования (б) и (в). Если выписать приведенные выше соотно-
соотношения между напряжениями и деформацией D0.4) и,
кроме того, перед членами, меняющими знак, поставить
±, а остальные члены в правой части обозначить точ-
точками, то для к—1, 2, 3, 6 получим
Gh= ... ^ЫЕ4±^5 •••» (Г)
и для к = 4, 5
±ок= ... ±sMei±skte5 ... (д)
При фиксированном к выражение (г) представляет собой
систему из двух уравнений. Вычитая одно из другого,
получим
sm4 + sh-34 = 0 для к = \, 2, 3, 6. (е)
Соответственно из (д), прибавляя одно уравнение к дру-
другому, получим
из (е) следует, что
и = s14 = s2i — s3i = s64 = s15 = s25 = s35~ 565, DU.b)
а из (ж), напротив, не следует ничего нового, так как
На основании результата D0.6) становится ясным, как
меняется поведение модулей упругости при переходе от
триклинной системы к моноклинной:
Триклинная система
Осей симметрии нет, s1± s12 sl3 s14 s15 s16
21 константа s22 s23 s24 s25 s26
366
Гл. VIII. Дополнения к теории упругости
Моноклинная система
Ось симметрии второго
порядка А\\ 13 констант
'12
'13
'33
OOs
0 0 s,
0 0 s.
В ромбической системе (оси'а, Ь, с взаимно перпен-
перпендикулярны) к оси А\ добавляется еще одна ось симметрии
второго порядка А%\ кроме того, появится также ось А%,
но ее можно рассматривать как следствие первых двух,
и поэтому она никакого влияния на вычисления не
окажет.
Повторяя рассуждение, аналогичное тому, которое
приводит к D0.6), получим:
Ромбическая система
Две оси симметрии вто- s
рого порядка, 9 констант
'22
'23
S33
0
0
0
1 Л Л
0
0
0
0
0
0
0
0
о
'66
Точно так же можно получить в случае
Кубической системы
Три эквивалентные друг sn s12 s12
другу оси симметрии чет- su sJ2
вертого порядка, 3 кон- sn
станты
0
0
0
0
0
0
0
0
0
0
0
о
'44
Из последней схемы следует, что кубический моно-
монокристалл ведет себя не как изотропное тело. У послед-
последнего имеются только два модуля упругости, например
наши прежние (л и X. Чтобы предыдущая схема перешла
в схему, содержащуюся в (9.6), мы должны приписать
входящим в нее константам следующие значения:
§ 41. Изгиб балки 367
т. е. необходимо принять условие
которое для кубического кристалла, вообще говоря,
не выполняется.
Физически это означает следующее: так называемые
изотропные твердые тела не имеют однородной структуры,
а являются поликристаллами. Их поведение при упругих
деформациях выглядит проще, чем у монокристалла, так
как каждое наблюдение дает результат, усредненный по
большому числу отдельных кристалликов, расположен-
расположенных произвольным образом относительно друг друга.
Совсем иначе обстоит дело в оптике. В оптических
приборах, используемых в определенной части спектра,
вместо обычных изотропных (аморфных) стеклянных линз
применяются кристаллы флюорита или каменной соли.
Такая замена допустима только потому, что кубический
монокристалл оптически изотропен. Причина этого заклю-
заключается в том, что в оптике мы имеем дело не с тензор-
тензорной связью (как это имеет место в теории упругости
(связь напряжений с деформацией), а с вектор-векторной
связью (электрическое поле — диэлектрическое смещение),
и потому число коэффициентов связи уменьшается.
Мы не имеем здесь возможности останавливаться более
подробно на весьма интересных вопросах упругости
кристаллов. Что касается этого параграфа, то здесь мы
хотели подчеркнуть различие в упругом поведении изо-
изотропных тел по сравнению с однородными анизотропными
телами.
§ 41. ИЗГИБ БАЛКИ
Растянутые и изогнутые балки составляют основной
элемент конструкций в строительном деле; при проекти-
проектировании новой постройки все балки рассчитываются и рас-
расчет этот обязательно проверяется. Теория, которая при
этом используется в течение последних 200 лет, весьма
примитивна; основы ее были заложены Даниилом Бернул-
ли. Ниже мы обсудим, как с помощью более строгих
методов (Сен-Венан) можно обосновать эту теорию, но
вначале будем следовать ее историческому развитию.
368 Гл. VIII. Дополнения к теории упругости
Ограничимся наиболее простым случаем прямолиней-
прямолинейной балки, находящейся в состоянии чистого изгиба.
Сечение балки может иметь произвольную форму (напри-
(например, Т- или I-образную), но вдоль балки оно должно
быть постоянным. Весом самой балки будем пренебрегать.
Пусть на одном ее конце в вертикальном направлении
действует сила Р; другой конец будем считать жестко
закрепленным. При этом верхние волокна балки будут
растянуты, а нижние — сжаты.
, dx
-м
x+dx
х
а
Фиг. 69.
Элемент длины изогнутойТбалки: а —в первоначальном состоянии,
б — в изогнутом состоянии.
Берну л ли предполагал, что любое плоское сечение
балки после изгиба также останется плоским. Отсюда
Навье вывел, что нормальные напряжения, которые
действуют на сечение, будут распределяться в нем по
линейному закону. Рассмотрим два соседних сечения;
первоначально отстоящих друг от друга на расстоянии dx
{х, например, возрастает справа налево, см. фиг. 69, а).
Расположенные между ними волокна после изгиба будут
иметь длину dx-\-bdx, причем, так как сечения останутся
плоскими, удлинение bdx будет убывать сверху вниз
линейно, обращаясь в некотором определенном• слое NN
в нуль и переходя в силу той же линейности на нижнем
конце в сокращение (bdx < 0). Из этого «линейного
закона» можно получить деформации
bdx
§ 41. Изгиб балки 369
а также напряжения'[см. (9.8)J
o^Fe. D1.1)
Если <змакс. — напряжение в (верхнем или нижнем) по-
поверхностном волокне, а Л —его расстояние от слоя NN
(см. фиг. 69, б), то, согласно линейному закону,
где у равно расстоянию а-волокна от NN.
Чтобы определить максимальное напряжение амакс>,
рассмотрим равновесие сил, действующих на отрезок
Фиг. 70.
Равновесие между изгибающим моментом М
и нормальными напряжениями а.
балки длиной х (фиг. 70), причем можно рассматривать
балку неизогнутой. Во-первых, рассмотрим уравнение
моментов, вычисленных относительно оси, перпендику-
перпендикулярной к плоскости фигуры и проходящей через точку 7V
в сечении х, а во-вторых, уравнение компонент сил
в горизонтальном направлении х\ равновесие сил в верти-
вертикальном направлении у будет рассмотрено позже.
Момент внешних сил в нашем частном случае изгиба,
равен
М=--Рх, D1.3)
где М — общепринятое обозначение изгибающего момента.
Согласно уравнению D1.2), растягивающие усилия adf
дадут момент
^ \ D1.4)
24 А. Зоммерфельд
370 Гл. VIII. Дополнения к теории упругости
Величина / называется моментом инерции1} сечения.
В т. I, в задаче 1 гл. IV, мы ввели момент инерции
масс, распределенных в плоскости, причем различали
«полярный» и «экваториальный» моменты инерции. Здесь,
однако, речь идет не о массах, распределенных в пло-
плоскости, а о плоской площади. Поэтому наш момент
инерции / будет иметь размерность не г-си*2, а см*.
Так как ось в точке N, относительно которой вычис-
вычисляется величина /, лежит в плоскости сечения, то /
представляет собой экваториальный момент инерции. *
Если учесть противоположное направление вращения
моментов ва фиг. 70, то, согласно D1.3) и D1.4), урав-
уравнение моментов даст
hM ,,м г\
амакс. ~~J~ • {il.D)
Одновременно с определением оМакс.» согласно D1.2), мы
получим значение напряжения о в любом другом месте
сечения.
Инженера особенно интересует величина амакс., так
как он должен следить, чтобы возникающее наибольшее
напряжение не превышало допустимого • предела адоп-.
Он должен найти наиболее опасное сечение, т. е. такое,
в котором будет наибольший изгибающий момент М,
, и выбрать размеры сечения таким образом, чтобы напря-
напряжение на его границе амакс. было не больше адоп.. Для
сечений, употребляемых в технике, величины / и 1 jh
раз навсегда протабулированы в таблицах нормальных
профилей. Для круглого сечения радиуса а имеем
I = ±Fa* = ?-a*, D1-6)
а для прямоугольного сечения шириной Ъ и высотой 2/г
I = ^-bh3. D1.6а)
В обоих случаях мы предполагаем, что ось у — О, отно-
относительно которой должен вычисляться момент инер-
х) Мы не воспользуемся принятым в т. I обозначением в, со-
сохранив его для объемного расширения, а примем обычное для тео-
теории изгиба обозначение /.
§ 41. Изгиб балки 371
ции /, проходит через центр тяжести сечения, т. е. через
центр круга и соответственно прямоугольника.
Для доказательства этого в общем случае восполь-
воспользуемся уравнением компонент сил в направлении х.
Внешние силы не дадут никакого вклада в уравнение
не только в нашем случае, где единственная внешняя
сила Р действует вертикально, но и в более общем слу-
случае. Если бы это было не так, то нельзя было бы гово-
говорить о состоянии чистого изгиба, а мы имели бы дело
с комбинированным напряженным состоянием, куда вхо-
входили бы изгиб и растяжение (или сжатие). В результате
искомое условие запишется просто как
т. е. в силу D1.2)
Этот распространенный по поверхности сечения «момент
первого порядка»г) при обращении в нуль как раз
определяет центр тяжести сечения. Волокно, проходящее
через центры тяжести следующих друг за другом сечений
балки, называют нейтральным волокном, а горизон-
горизонтальный слой, образованный следующими друг за другом
осями г/ = 0, называется нейтральным слоем. Именно это
мы и имели в виду, приняв на фигурах обозначение NN.
Определим теперь форму нейтрального волокна в изо-
изогнутом состоянии. Она станет очевидной из рассмотрения
дифференциального уравнения упругой линии, которое
сразу может быть получено на основании фиг. 69,6;
здесь через с обозначен центр кривизны упругой ли-
линии NN, лежащий на пересечении продолженных следов
сечений х и x-\-dx. Сторонами треугольника CNN будут
р, р и dx (р—радиус кривизны). Подобный треуголь-
треугольник возникнет у верхнего края балки, если через
одну из точек N провести линии, параллельные
*) Вместо этого часто употребляют менее удачный термин «ста-'
тический момент». В то же время и вместо момента инерции гораздо
лучше говорить «момент второго порядка».
24*
372 Гл. VIII. Дополнения, к теории упругости
следам сечений х и х -\-dx. Соответствующими сторонами
треугольника будут h, h, bdx=zMgLKC.dx. Таким образом,
имеется пропорция
dx _ емакс. dx
р- h
которую в силу D1.1) и D1.5) можно переписать в виде
-= — D1 7\
Что касается выбранного здесь знака, то для краткости
сошлемся на фиг. 69, б. Правая часть представляет собой
известную функцию от х, или, вообще говоря (в случае
конечного искривления, когда вместо х надо вычислять
длину дуги s упругой линии), известную функцию точки
вдоль этой линии. Левая часть выражения D1.7) пред-
представляет собой дифференциальный инвариант — «кри-
«кривизну». Таким образом, уравнение D1.7) является иско-
искомым дифференциальным уравнением.
Как известно, в случае достаточно слабого искривле-
искривления с достаточной точностью будет выполняться соотно-
соотношение
и, следовательно,
^У MMt D1.8)
в частности, в силу уравнения D1.Зу
Интегрирование даст
т. е. получаем параболу третьего порядка. Постоянные
интегрирования А и В определяются из условий в месте
закрепления:
Су = О
для s = z|dy 0 ... А=--^-, В = ~. D1.9б>
§ 41. Изгиб балки 373
Так называемая «стрела прогиба», т. е. прогиб для х = О,
будет равна
Рассмотрим балку на двух опорах (отстоящих друг
от друга на расстоянии I), нагруженную только собствен-
собственным весом, величина которого на единицу длины равна
р — const. Силы реакции на обеих опорах будут в таком
случае равны —^ р, где знак минус указывает, что они
направлены вверх. Изгибающий момент слагается из- мо-
момента собственного веса и момента сил реакции
^ D1.10)
В этом случае интегрирование D1.8) даст
- D1Л0а>
т. е. получим параболу четвертого порядка.
Вместо D1.96) имеем теперь условия:
для ж = 0 | is
для х=1 ) у ~ ''' ~~ ' ~~ 12
Наибольший прогиб будет^ конечно, в середине. Он равен
D1Л0б>
^
Для дальнейшего представляет интерес случай, когда
на конце балки действует не одна сила, как на фиг. 70,
а пара сил, т. е. две действующие вблизи друг от друга
силы, направленные противоположно. Силы эти должны
быть равны по величине, а их момент должен быть конеч-
конечным. Тогда М = const и, согласно D1.8),
374 Гл. VIII. Дополнения к теории упругости
Если на другом конце х = 1, как и в D1.96), балка
жестко закреплена, то А—— I, В = — 12. Тогда прогиб
в точке х = 0 будет равен
р{^2. D1.11а)
В этом случае можно описывать упругую линию дугой
окружности, так как ее кривизна постоянна.
Только в этом последнем случае мы с помощью наших
условий равновесия приходим к чистому конечному резуль-
результату. А именно здесь, и только здесь, тождественно вы-
выполняется третье условие равновесия, которое мы должны
поставить:
Сумма всех вертикальных сил = 0. D1.12)
Во всех других случаях в результате этого условия
в каждом сечении х возникает вертикальная перерезыва-
перерезывающая сила, противодействующая внешней нагрузке. Сила
эта является суммой всех касательных напряжений, дей-
действующих в рассматриваемом сечении. Например, в случае
фиг. 70, кроме нормальных напряжений ахх, должны воз-
возникать и касательные напряжения аху, чтобы в каждом
сечении выполнялось соотношение
xvdf = P. D1ЛЗ)
При этом, однако, должны появиться угловые изменения
Y^, в результате которых первоначально плоское сечение
искривится.
Иными словами: гипотеза Бернулли о том, что сече-
сечения остаются плоскими, противоречит общим основам
статики. Отсюда следует, что закон Навъе о прямолиней-
прямолинейном распределении напряжений, который опирается на
гипотезу Бернулли, также теряет силу.
Прежде чем показать, как преодолевается эта трудность,
определим величину требуемых касательных напряжений.
Интегральное условие D1.13) для этой цели не годится.
Мы, однако, можем воспользоваться дифференциальным
условием (8.12). В отсутствии внешних объемных сил F,
и, например, для прямоугольного сечения, при котором о?х,
41. Иаеиб балки 37i
очевидно, исчезает, можно записать
Используя в качестве первого приближения выражения
D1.2), D1.3) и D1.5), получаем
В последнем выражении постоянную интегрирования А
надо положить равной /г2, чтобы аху при y=±h обраща-
обращалось в нуль.
Все это является следствием того, что значения аху
на верхнем и нижнем краях балки определяют на ее
наружной поверхности касательные напряжения, а также,
что эта поверхность должна быть свободна от напряже-
напряжений. Не представляет труда, зная аух и соответствующие
углы сдвига ^ху, определить, как исказится прямоуголь-
прямоугольное сечение.
И, наконец, кратко укажем, как можно освободить
теорию изгиба от упомянутого выше внутреннего про-
противоречия. Это было проделано Сен-Венаном в 1855 г.г)
Прежде всего надо подчеркнуть, что использованные до
сих пор соотношения между напряжениями и внешними
силами не являются достаточными для полного описания
упругого состояния. Для этого надо еще использовать
упругие смещения ?, т], С в том виде, в каком они входят
в основные уравнения теории упругости (9.18). Затем
необходимо указать, что в предыдущем изложении мы
не.говорили о напряжениях ауу, azz, ayz; действительно,
при рассмотрении равновесия изогнутой балки эти на-
напряжения не появляются и могут поэтому считаться рав-
равными нулю. Если же их выразить через ?, ?], С, то можно
получить простые дифференциальные уравнения между tj,
С и ?, в результате которых упомянутые основные уравне-
г) Полное изложение см. в сделанном Сен-Венаном переводе
прочитанных в Карлсруэ лекций Клебша о «Теории упругости твер-
твердых тел», где Клебш, в свою очередь, уточнил работы Сен-Венана.
376 Гл. VIII. Дополнения к теории упругости
ния (9.18) сильно упростятся и в конце концов могут
быть приведены к видуг)
i д2 дг д2 &* 1 д?
\ ^ = ~dy~2==~d#=zdy~d~z) д^" = 0' D1.15)
Отсюда немедленно следует, что растяжение д^/дх для
анволокон, а также соответствующее напряжение а = ахх
Представляют собой в сечении линейную функцию коорди-
координат у и z. Таким образом, линейный закон представляет
собой необходимое следствие основных законов теории упру-
упругости. Гипотеза Бернулли, которая, как мы видим, в дей-
действительности не выполняется, для вывода этого закона
не нужна.
Далее, уравнение D1.15) показывает, что деформация
я-волокна должна быть линейной функцией и от х, откуда,
согласно D1.5), следует, что изгибающий момент М также
должен зависеть от х по линейному закону. Это относится
к случаю одной или нескольких сосредоточенных сил или
. моментов (и несправедливо при непрерывно распределенной
нагрузке от собственного веса). Однако необходимо ука-
указать на следующее ограничение: сосредоточенная нагрузка
должна прикладываться так, чтобы она могла быть урав-
уравновешена касательными напряжениями аху; поэтому эта
нагрузка не должна быть приложена в точке, а распре-
распределяться по сечению точно так, как по нему распределяет-
распределяется наше напряжение аху. В действительности это, конечно,
никогда не выполняется. Однако можно сказать: различие
между силами, приложенной в точке и как-то распреден-
ной по сечению, если обе они одинаковы, скажется замет-
заметно только вблизи от этого сечения. Это можно показать
на выбранных соответствующим образом примерах, как
практических, так и теоретических. Результат такой про-
проверки, принятый в качестве аксиомы, называют принципом
Сен-Венана: отклонения от идеального состояния при
различных реальных способах приложения нагрузки сво-
сводятся лишь к местным возмущениям.
Таким образом, мы теоретически обосновали описан-
описанный в начале этого параграфа простой расчет, который
оправдал себя практически в огромном числе случаев.
х) Соответствующие несложные вычисления можно найти,
например, в учебнике: F oppl A., Techn. Mech.., Bd. Ill, § 73.
§ 42. Кручение
377
§ 42. КРУЧЕНИЕ *
Вначале рассмотрим простейший и наиболее важный
случай закручивания стержня круглого сечения. Действи-
Действительно, любой вал в машине подвергается кручению: на
одном его конце обычно прикладывается вращательный мо-
момент вокруг оси вала, а на другом конце находится та часть
машины, которая приводится в движение и действует на
вал в противоположном направлении
с моментом, равным по величине вра-
вращательному. Никаких сосредоточен-
сосредоточенных сил при этом не возникает. Все
это относится к более общему слу-
случаю кручения. При кручении пря-
прямолинейного стержня произвольного
сечения на одном конце всегда дей-
действует момент вокруг его оси; другой
конец стержня или закреплен, или
подвергается действию равного и про-
противоположно направленного момента;
если, кроме того, стержень подвер-
подвергается растяжению в направлении
своей оси, то мы уже не будем иметь
чистого кручения.
В случае стержня круглого сече-
сечения с закрепленным, например, ниж-
нижним концом можно легко установить
картину возникающих деформаций;
правда, при этом придется еще до-
доказать ее законность. Предположим
(фиг. 71), что каждое сечение стер-
стержня повернется на некоторый опре-
определенный угол ср, пропорциональный
Иначе говоря., положим
ср = ах., % — ..cons't.. D2.1)
При этом первоначально прямолинейные образующие
стержня перейдут в обычные винтовые линии. В цилиндри-
цилиндрических полярных координатах г, ср, х—компоненты вектора
смещения s, — согласно D2.1), равны
х=0
Фиг.
Кручение стержня круг-
круглого сечения. Стержень
закреплен только вни-
внизу, а вверху на него дей-
действует крутящий мо-
момент М.
координате х.
0.
D2.2)
378 Гл. VIII. Дополнения к теории упругости
Выражение для деформации можно получить отсюда про-
простым, но достаточно строгим способом, если вместо bqx,
bq2, bq3 подставим величины выражения D2.2) в уравне-
уравнения D.26) и D.28), и в силу того, что ds2 = dr2 -f- r2 dy2 +
-\-dx2, положим
а — 1 а — г Р — 1
61— А> 62 — '» 63— 1'
В результате из этих уравнений получаем
з7^0?~2^1 = аг е =0. D2>3)
Отсюда получаем соответствующие о, воспользовавшись
тензорной связью (9.7), которая- справедлива для про-
произвольных ортогональных координат:
О = Gmm = О = О =.Огф = 0,
rr W хх ^г гф 4
ах.р = х = [tar.
Для единственного действующего в сечении х = const
касательного напряжения принято обозначение х, упо-
употребительное в технике.
Для нашего напряженного состояния D2,4), как и для
изгиба, справедлив линейный закон; вместо выражения
D2.4) можно также написать
х = —хмакс, где хмакс. = (хеш. D2.4а)
Из предположения D2.2) видно, что поперечные сечения
в этом простейшем частном случае остаются плоскими:
5^ = 0 (как было показано, в случае изгиба такое пред-
предположение несправедливо). Сразу же необходимо подчерк-
подчеркнуть, что в случае кручения это предположение справед-
справедливо только"для круглого сечения.
Теперь надо доказать, что наша система напряжений
находится в соответствии с граничными условиями задачи.
Для боковой поверхности стержня (г = а) это очевидно.
Она должна быть свободной от напряжений, т. е.
агг = °г<Р = агх = 0,
что и выполняется в действительности согласно D2.4).
На нижнем сечении вместо условия отсутствия напряжений
§ 42. Кручение - ,379
имеется условие отсутствия смещений, которое сразу
выполняется в силу D2.2), поскольку здесь х = 0. На-
Наконец, на верхнем конце стержня необходимым усло-
условием будет
M=\rxdf, D2.5)
где М — момент закручивающей силы Р (см. фиг. 71).
Согласно D2.4а), можно также написать
М = \r?df~ Jp = [iaJp, /p=— a4, D2.5a)
где /р — полярный момент инерции сечения, который
в случае круга равен удвоенному значению экваториаль-
экваториального момента инерции, приведенному в D1.6).
Однако это условие не является достаточным. Внешний
вращательный момент М не только должен быть равен
суммарному моменту сдвигающих усилий относительно
оси стержня, но и должен распределяться по сечению
от точки к точке точно так же, как распределяется
момент г df, что для пары сил М = Pd, изображенной
в качестве примера на нашей фигуре, конечно, не вы-
выполняется. Эту трудность можно преодолеть, восполь-
воспользовавшись принципом Сен-Венана (см. стр. 376). Согласно
этому принципу, такое местное возмущение равновесия
распространяется только на ближайшую окрестность верх-
верхнего основания и не сказывается на упругом равновесии
в каком-либо другом месте стержня.
Для большей строгости необходимо показать, что
наше частное решение D2.2) удовлетворяет дифференциаль-
дифференциальным уравнениям теории упругости, написанным в смеще-
смещениях. Для компонент смещения ?, -ц, С в декартовых коорди-
координатах это были уравнения (9.18); в случае произвольных
ортогональных координат их место займут уравнения (9.20).
Мы, однако, не будем сразу выписывать их, а заметим
прежде, что входящие в них величины 0 и Р, как это
можно показать с помощью (9.20а), в нашем случае при-
принимают значения
380 Гл. VIII. Дополнения к теории упругости
После этого сразу станет ясно, что уравнения (9.20)
в действительности тождественно выполняются (величина
F в них положена равной нулю).
Теперь мы должны подробнее остановиться на уравне-
уравнении D2.5а). Оно определяет величину угла закручивания
нашего стержня (приходящегося на единицу его длины),
которая до сих пор в нашей задаче оставалась неопре-
неопределенной. Вместо этого найдем- полный угол закручива-
закручивания стержня, который, согласно D2.1), можно опреде-
определить как
где I равно длине стержня. Из D2.5а) получим
Ml
//о с\
Это равенство имеет вполне ясный смысл: угол закручи-
закручивания пропорционален вращательному моменту М и длине
стержня /, а также обратно пропорционален модулю
кручения [л. Из равенства D2.6) нельзя непосредственно
определить зависимость угла закручивания от размеров
сечения; она содержится в знаменателе /р. Надо, однако,
подчеркнуть, что входящая сюда зависимость от Jv не
сохраняется для стержня произвольного сечения, как
это было в случае величины / при изгибе. Напротив,
в случае сечения, не имеющего круглой формы, например
в случае рассмотренного ниже эллиптического сечения,
зависимость от размеров сечения отнюдь не определяется
величиной Jp рассматриваемого сечения.
Для сечения произвольной формы- не будет иметься
избранной системы координат, подобно цилиндрическим
полярным координатам в предыдущем, случае. Поэтому
мы поневоле вернемся к прямоугольным координатам х,
у, z и смещениям ?, rit ?, а также к уравнениям равно-
равновесия (9.18) (с F = 0).
Ось х, как и прежде, направлена вдоль оси стержня.
Теперь мы не можем положить ? = 0 [соответственно тому,
как прежде мы имели sx—0 в выражениях D2.2)], а должны
допустить коробление сечения. Однако вследствие цилин-
цилиндрической формы стержня мы должны будем предполо-
предположить, что это тчоробление не зависит от положения
§ 42. Кручение 381
сматриваемого сечения, т. е. от его координаты х. По-
Поэтому положим
. z), -||=0. ¦ < D2.7)
Предположим далее, что (как и в случае круглого сече-
сечения) 0 = 0, т. е. что при кручении отсутствует объемное
расширение. Мы еще более специализируем это предпо-
предположение и будем считать, что
4?=§ = 0. D2.8)
И, наконец, предположим, что аналогично прежнему
выражению D2.3) (ег? = 0) здесь также можно положить
Ч.«& + ?-0. D2.9)
То, что эти различные предположения допустимы, будет
выяснено в ходе дальнейших рассуждений.
Дифференциальные уравнения теории упругости (9.18)
в силу D2.7) и D2.8) упростятся и примут вид
ду2 "•" dz2 ~ '
ж
дх2
D2.10)
Первое из этих уравнений гласит, что введенная в D2.7)
функция должна удовлетворять двухмерному уравнению
'потенциала
ДФ = 0, А = ^ + -^. D2.11)
Остальные два уравнения D2.10) в силу условия D2.8)
удовлетворятся, если считать ч\ и С билинейными функ-
диями следующего вида:
tj = Ьо + Ъхх + Ьгг + Ьъхъ,
С = с0 + схх + с2у -f c3xy.
382 Гл. VI11. Дополнения к теории упругости
В силу D2.9) между постоянными бис должна сущест-
существовать связь: для каждого х
и поэтому
62=-с2, &3=-с3. D2.13)
Далее (как и на фиг. 71), будем считать нижнее основа-
основание стержня закрепленным, т. е. смещения в стороны
должны отсутствовать. Таким образом, для ж = 0и любых
у и z должно
откуда
Ьо = со = Ь2 = с2 = 0. D2.13а)
Кроме того, направление оси х относительно основания
должно быть фиксировано. Отсюда для х = 0 следует
11 = ^ = 0, § = Cl = 0. D2.136)
В силу D2.13), D2.13а) и D2.136) уравнения D2.12)
перейдут в
tq=— axz, I,—-\-axy, D2.14)
если вместо с3 написать а.
При наших предположениях относительно ?, ч\ и С,
заключающихся в D2.7), D2.11) и D2.Д4), естественно,
будут удовлетворены дифференциальные уравнения теории
упругости, а также граничные условия на нижнем осно-
основании. Возникает, однако, вопрос: удовлетворятся ли при
этом граничные условия на боковой поверхности цилиндра.
Если обозначить через п нормаль боковой поверхности
в некоторой точке Р, а через s—касательную к контуру
сечения в этой точке, то граничные условия запишутся
в виде
°nS = 0 и спЛ = 0. D2.15)
Совершенно ясно, что первое из этих уравнений будет
выполняться, а именно, мы можем ничем не фиксирован-
фиксированную в сечении ось у направить параллельно нормали п,
так что ось z будет направлена параллельно s. Тогда
§ 42. Кручение ' 383
°ns будет совпадать с ayz в точке Р. Но так как, согласно
D2.9), eyz = 0, то и ayz будет равно нулю в точке Р. Это
рассуждение может быть применено к любой точке Р
боковой поверхности. Остается только доказать, что
второе из условий D2.15) будет выполняться. Для этого
воспользуемся общим тензорным соотношением (8.5),
согласно которому в нашем случае
апх = havx + Tl°2x = 2P- (PiSx + Ъегх) =
Через рх и ^ в (8.5) обозначены направляющие косинусы
нормали п относительно осей у и z. Если направление 5
выбрать так, что s по отношению к п будет расположено
точно так же, как + у по отношению к + z, то получим
Рх = COS (Л, у) = — COS (S, 2) = — -^- ,
% D2.17)
Yj = cos (w, z) = -f cos (s, y) = + -gj- .
Тогда из второго соотношения D2.15), с учетом D2.16)
D2.17), D2.7) и D2.14), следует
(-^+aOdy- D2-18)
Это условие должно выполняться в любой точке контура
сечения. Оно может быть упрощено, если ввести потен-
потенциал, сопряженный потенциалу Ф, или, с гидродинами-
гидродинамической точки зрения, функцию тока, задаваемую условия-
условиями Коши —Римана A9.5). Из этих условий следует для
наших теперешних координат (г/, z вместо ос, у)
f -?¦ ?--¦?¦ ^
Тогда уравнение D2.18) перейдет в
или
= ~(y2-\-z2) + C ... (граничное условие). D2.19)
384 Гл. Vllt. Дополнения к теории упругости
Разумеется, функция W, так же как и Ф, должна удовле-
удовлетворять дифференциальному уравнению D2.11):
Д? = 0. D2.19а)
Из уравнений D2.19) и D2.19а) функция W может быть
однозначно определена как решение простой задачи
теории потенциала. Таким образом, доказана возможность
выполнения нашего граничного условия D2.18). Одно-
Одновременно с этим становятся оправданными предположе-
предположения, сделанные нами в уравнениях D2.8), D2.9) иD2.12).
Вернемся теперь еще раз к сечению круглой формы.
Если начало координат лежит в центре круга, то имеем
y2-\-z2 = a2', таким образом, согласно D2.19) и D2.19а),
на границе и внутри должно быть
W = const.
Тогда, согласно D2.18а),
Ф =const
и в силу D2.7)
? = const.
Таким образом, при этих условиях сечения остаются
плоскими. Обратно, если при некоторой форме сечения
вдоль стержня ? = 0, то, согласно D2.7), Ф = 0 и, соглас-.
но D2.18а), W = const. Тогда из D2.19) следует, что на
границе y2-\-z2~ const. Следовательно, сечение в этом
случае представляет собой круг.
В качестве менее тривиального примера рассмотрим
случай эллиптического сечения с границей
? + !- = 1- D2.20)
Так как общее решение D2.19а) гласит
(Re — действительная часть), то мы можем, в частности,
положить, считая / просто второй степенью аргумента
У + iz,
W = A(i/-z2). D2.21)'
§ 42. Кручение 385
Тогда, согласно D2.19), на эллипсе должно быть
Если подставить z2 из D2.20) и сравнить коэффициенты
при у2, то отсюда следует, что
. а а2 — Ъ2 //
А D
Теперь мы мошем вычислить из D2.18а) и D2.21)
дФ а2 — Ь2 дФ а2— Ь2
Отсюда с учетом D2.7) и D2.14) определятся касатель-
касательные напряжения
, D2.22)
Касательное напряжение т, состоящее из оху и оХ2, в каж-
каждой точке сечения направлено параллельно касательной
к контуру в конце радиус-вектора, проходящего через
эту точку, а вдоль этого радиус-вектора подчиняется ли-
линейному закону.
Согласно D2.22), момент касательных напряжений
относительно оси х будет определяться формулой, являю-
являющейся обобщением нашего прежнего соотношения D2.5):
м =
z. D2.23)
Проведение интегрирования, как это сделано в задаче 4
гл. VIII, показывает, что вместо множителя /р перед |ш
в D2.5а) получим выражение
D2-24>
не совпадающее с полярным моментом инерции эллипса.
25 А. Зоммерфельд
386 Гл. VIII. Дополнения к теории упругости
Одновременное рассмотрение потенциала Ф и функции
тока W наводит на мысль о гидродинамической анало-
аналогии, которая вполне оправдала себя для приближенного
решения более сложных задач, как, например, задачи
о кручении стержня I-образного профиля.
§ 43. КРУЧЕНИЕ И ИЗГИБ ВИНТОВОЙ ПРУЖИНЫ
Рассмотрим пружину, изображенную на фиг. 37 в т. I,
стр. 155. Речь идет о тонкой проволоке, навитой плотно
на круговой цилиндр. Если ее после этого снять с ци-
цилиндра и закрепить как-то верхний конец, а к нижнему,
прикрепить диск, как это изображено на фиг. 37 в т. I,
то под действием веса диска пружина несколько растя-
растянется, но так, что ее шаг будет- мал по сравнению с ра-
радиусом цилиндра. Если мы нагрузим пружину в направ-
направлении оси цилиндра добавочным весом, то шаг ее не-
несколько увеличится и пружина удлинится. При этом
проволока будет закручиваться. Если же на нижний
конец будет действовать пара сил (для этого, например,
можно закручивать диск двумя пальцами), то шаг пру-
пружины практически не изменится, а изменится ее радиус.
При этом проволока будет изгибаться.
Оба факта на первый взгляд кажутся парадоксаль-
парадоксальными, однако этот парадокс легко разъясняется. Действи-
Действительно, кручение означает, что на рассматриваемое се-
сечение действует момент сил относительно полярной
оси, а изгиб означает, что момент сил действует относи-
относительно так называемой экваториальной оси, лежащей в
сечении.
Рассмотрим плоскость (фиг. 72, а и б), проходящую
через ось цилиндра и через исследуемое сечение (на фи-
фигуре эти сечения заштрихованы). Действующая по оси
цилиндра нагрузка Р (фиг. 72, а) имеет относительно
центра сечения момент PR; назовем его крутящим мо-
моментом Мк. Если представить этот момент в виде векто-
вектора, то он будет направлен перпендикулярно к сечению.
На фиг. 72, б показан диск, на который действует пара
сил е моментом QR (на фиг. 72, б диаметр диска выбран
равным 2R, поэтому обе силы, составляющие пару, рав-
равны Q/2). Назовем этот момент изгибающим моментом М1г.'
43* Кручение и изгиб винтовой пружины
387
Он направлен по оси цилиндра, так что, если его сме-
сместить параллельно самому себе, он будет располагаться
в заштрихованном сечении. Его положение в сечении мы
обозначим через NN, чтобы подчеркнуть, что NN представ-
представляет собой .след нейтрального слоя в изогнутом, сечении.
В случае кручения (см. фиг. 72, а) в плоскости сече-
сечения возникнут касательные напряжения, пропорциональ-
пропорциональные расстоянию г от оси проволоки, которые мы, как
в предыдущем параграфе,
назовем т. При этом должно
выполняться соотношение
= MK. D3.1)
В случае изгиба (фиг.
72, б) на сечение будут дей-
действовать нормальные на-
напряжения о, пропорци-
пропорциональные расстоянию у от
экваториальной оси NN.
В этом случае
D3.2)
Ф и г. 72.
Спиральная пружина, подвергнутая:
а—кручению (сила Р, удлинение у)
и б—изгибу (момент QR, угол вакру-
чивания xIR).
Если провести вычисления
в выражениях D3.1) и D3.2), воспользовавшись D2.4а),
D2.5а) и соответственно D1.5), то получим
Jp = Мк и соответственно
D3.3)
Нас, однако, интересуют не столько максимальные
напряжения т^акс. и оМакс.» сколько смещения пружины
в вертикальном направлении у и соответственно в горизон-
горизонтальном направлении х. Для этого нам надо было бы знать
уравнение упругой линии при кручении и изгибе перво-
первоначально искривленного стержня, которое нами не полу-
получено. Однако мы можем применить болез простой энерге-
энергетический метод, согласно которому мы вычислим работу
деформации при кручении и изгибе нашей спиральной
пружины и приравняем ее работе вкешней силы Р или Q.
Мы сделаем это тем более охотно, что до сих пор мы
25*
388 Гл. VIII. Дополнения к теории упругости
еше не коснулись в нашем изложении вопроса об энер-
энергии деформации1), который играет в технике важнейшую
роль.
До сих пор мы вывели только общее выражение (9.266)
для энергии деформации. В случае чистого сдвига
•с
= °21 ~ Т» ?12 = ?21 = 2JI
и соответственно для чистого растяжения и сжатия (из-
(изгиба)
это соотношение принимает вид
W = у (°12?12 + °21?2l) = YJ
и соответственно
Эти выражения относятся к единице объема. Для напря-
напряженного состояния, меняющегося от точки к точке, они
должны быть умножены на элемент объема df ds {df—
элемент поверхности сечения, ds— элемент длины оси
стержня). В результате, согласно D3.4), для кручения
имеем
= -^ — dfds, х=~ %акс. ••• [согласно D2.4а)]. D3.6)
После интегрирования по сечению получаем
V 7ТТ7 *• МйКС» V О 7 J 7 МйКС» Т 7 / / О ?? \
\ dW =т> 5— \ r*df ds=—^—w-Jmds Do.oa)
и с учетом D3.3)
\ dW = ¦ г ¦ as. Dо.6б)
г) При решении всех «статически неопределимых» систем, в осо-
особенности стержневых систем, важную роль играют теоремы
Кастильяно о минимуме энергии деформации, а также теорема
Максвелла о взаимности перемещений.
§ 43. Кручение и изгиб бинтовой пружины 389
Отсюда следует выражение для полной работы при кру-
кручении WK, которое получается путем интегрирования
по всей длине I стержня (здесь — пружины):
Соответственно при изгибе, согласно D3.5), имеем
= ~dfds, о = |-омакс. ... [согласно D1.2)] D3.8)
и после интегрирования по сечению
Отсюда с учетом D3.3) следует выражение для полной
работы изгиба спиральной пружины
Выражения D3.7) и D3.9) представляют собой упругую
энергию деформации. Она равна механической работе
силы (или пары сил), постепенно возрастающей от нуля
до конечного значения Р (или QR), производимой ею
на рассматриваемом пути у (или х). Эта работа равна
-=т- D3Л°)
Если сравнить эти выражения с D3.7) и D3.9), то полу-
получим
HI т\ И I s-\ 1 ш о л Л \
Таким образом, с помощью энергетического метода мы
весьма просто получили искомые смещения пружины х
и у. Заметим также, что мы, согласно Кастильяно,
590 Гл. VIII. Дополнения к теории упругости
смогли бы получить соотношения D3.11), если бы обра-,
зовали г)
W(P,Q) = WK + Wat y = ~, х = д^. D3.11а)
С помощью уравнений D3.11) можно получить урав-
уравнения для свободных колебаний пружины, если мы
заменим Р и Q на силы инерции:
Что означают здесь массы М и Мприв.? Масса М
в основном составляется из массы колеблющегося дис-
диска Мо. Но так как масса т проволоки также участ-
участвует в колебаниях (в убывающей степени снизу вверх),
то к Мо в качестве поправки добавляется часть массы т.
Как показал Рэлей, эта часть равна 1/3. Итак, под М
мы будем понимать М = М04- (т/3). С другой стороны,
сопротивление инерции при крутильных колебаниях
вокруг оси цилиндра равно
где <p = x/R — угол закручивания диска (см. смысл х
на фиг. 72, б); в здесь также в основном состоит из мо-
момента инерции диска 60, к которому добавлена 1/3 мо-
момента инерции проволоки, mR2. Согласно этим замеча-
замечаниям, а также равенству A1.8) из т. I, МпрИв. опреде-
определяется из соотношения
, Уравнения свободных колебаний при кручении и из-
изгибе, согласно D3.12) и D3.11), гласят
с\ d^x EI л i/n ло\
*) Правило D3.11а) предполагает, что между у, жиР, Q имеется
линейная связь, так что W (P, Q) является квадратичной функцией
от Р и Q, как в D3.7) и D3.9). Иначе нам пришлось бы заменить W
на «модифицированное выражение энергии» в виде
W(P, Q)^yP + wQ-W(x, у),
согласно правилу преобразования Лежандра. [См. «Механика»
(т, I), стр. 315].
§ 43. Кручение и изгиб винтовой пружины 391
Соответствующие круговые частоты равны
Эти величины, вообще говоря, отличаются друг от дру-
друга1). Если бы они были равны, то оба колебания нахо-
находились бы в резонансе и очень сильно зависели бы
друг от друга. В этом случае вышеизложенная теория
больше не годится: мы должны учесть конечную вели-
величину шага пружины и изучить возникающую в резуль-
результате этого связь между обоими типами колебаний.
В случае конечной величины шага h угол подъема
винтовой линии задается следующим образом:
h
sina —
где а —угол наклона сечения проволоки относительно
вертикали. При этом моменты PR и QR разлагаются на
компоненты следующим образом:
Перпендикулярно
к сечению
Параллельно
к сечению
PR
QR
cos a PR
sin a QR
— sin a PR
cos a QR
В этой таблице слева стоят составляющие части кру-
крутящегося момента, а справа — изгибающего момента. По-
Поэтому
Мк = cos a PR -\- sin a QR, Ma = cos a QR — sin a PR.
x) Это можно показать опытным путем, если, как это изображено
на фиг. 37 в т. I, подвесить к пружине добавочный груз (на фиг. 37
он обозначен буквой Z). При этом масса М, сказывающаяся на коле-
колебаниях кручения, увеличится и, следовательно, частота шк упадет.
Напротив, поскольку груз расположен на оси, то Л/прив., а с нею и
частота «и заметным образом не изменятся.
392 Гл. VIII. Дополнения к теории упругости
Отсюда следует, согласно правилам, содержащимся
в D3.11а), что
dW R2l
у = -Qp — —j- (cos2 a P -fr sin a cos a
. (COS a 'J— smaPJ
+ ^7 ^J '
in2aP), D3.15)
5W7 i?2Z
ж = дтг = --jr- (sin a cos a P + sin2 a (?) -f-
+ ду (cos2 a^ — sin a cos cuP).
Эти уравнения заменяют уравнения D3.11). Если теперь
вместо Р и Q ввести сопротивления инерции D3.12),
то получим уравнения связанных колебаний
$ + <(y-kx) = 0, ~ + <{x-hy)^O, D3.16)
где приняты следующие обозначения (v— коэффициент
Пуассона):
D3.16а)
"v sin a cos a , -v sin a cos a ..
^ D
Коэффициенты связи k ш h при a = 0, естественно, обра-
обращаются в нуль; одновременно с этим выражения для <%
и ши принимают прежний вид D3.14), а уравнения
D3.16) переходят в D3.13)х).
Дальнейшее рассмотрение уравнений D3.16) принад-
принадлежит не теории упругости, а, скорее, механике. Его
х) При сравнении значений <ои в D3.16а) и D3.14) следует при-
принять во внимание связь JP=2I, которая имеет место для круго-
кругового сечения, а также формулу /Г=2(х A + \), которая уже была
использована при переходе от D3.15) к D3.16).
§ 44. Упругая энергия в прямоугольном параллелепипеде 393
результат в случае резонанса шк = ши уже упоминался
в т. I на стр. 155: энергия будет переходить от того
типа колебаний, который был первоначально возбужден,
к другому, так что колебания одного типа будут посте-
постепенно переходить в другой, после чего процесс повто-
повторится в обратном направлении, и т. д. Период биений N,
выраженный в периодах отдельных колебаний, может
быть весьма точно определен путем подсчета отдельных
колебаний в биении. В случае резонанса величина N
принимает максимальное значение. Большое значение
-^макс. й малость угла а позволяют весьма точно опре-
определять значения коэффициента Пуассона v1).
Указанный здесь эффект резонанса был впервые опи-
описан и объяснен Вильберфортом2). Однако для определе-
определения числа Пуассона он использовал не метод резонан-
резонанса, а менее изящные соотношения D3.14).
§ 44. УПРУГАЯ ЭНЕРГИЯ, СОДЕРЖАЩАЯСЯ
В ПРЯМОУГОЛЬНОМ ПАРАЛЛЕЛЕПИПЕДЕ
После того как в § 14 рассматривались упругие вол-
волны в неограниченном изотропном твердом теле, в послед-
последних двух параграфах мы будем говорить об упругих
колебаниях в ограниченных телах. Прежде всего рассмот-
рассмотрим прямоугольный параллелепипед со сторонами а, Ь, с.
Если его грани х= \ , у= \ , , z= \ свободны от
сил, то нормальные и касательные напряжения на них
должны исчезать. Колебания, возможные в этом случае,
называются собственными колебаниями; при таких коле-
колебаниях нет никакого обмена энергией с окружающей
средой.
Указанная проблема заключает в себе весьма боль-
большие математические трудности3). Это видно уже из того,
1) Подробности см.: «Механика» (т. I), стр. 155.
2) Wilberforth, РЫ1. Mag., 38, 386 A894).
3) Частный случай куба, который лежит в основе рассмотрения
аналогичных вопросов, связанных с теорией электромагнитного излу-
излучения (см. ниже), не представляет собой более простой задачи, чем
указанный более общий случай. Это следует уже из того, что в окон-
окончательном результате, содержащемся в уравнении D4.23), содержит-
содержится только объем тела V, а не его форма.
394 Гл. VIII. Дополнения к теории упругости
что ее частный случай, а именно случай прямоугольной
пластинки, до сих пор не имеет точного решения, хотя
в течение 150 лет уже известны красивые фигуры Хлад-
ни, побудившие многих математиков не раз приниматься
за эту задачу. Плодотворные исследования в этой обла-
области принадлежат Ритцу1). Они, однако, заключаются
не в прямом решении дифференциальных уравнений с
заданными граничными условиями, а в применении не-
некоторого минимального принципа, с помощью которого
решения получаются методом последовательных напря-
напряжений.
Условие отсутствия обмена энергией с внешним про-
пространством выполнимо не только при предположении,
что грани свободны от напряжений. Работа, производи-
производимая напряжениями на единице поверхности «ж-плоско-
сти» на пути ?т]С, равна
Она обращается в нуль не только когда
ахх — сху
ахх — сху = axz=0 (свободная поверхность) D4.2)"
или
? = т] = С = О (жестко закрепленная поверхность), D4.2а)
но и, например, когда
6 = 0, Ох» = «« = 0 D4.3)
или
о« = 0, ij = C = O. D4.3а)
Эти «смешанные» граничные условия, куда входят
как напряжения, так и смещения, как в 1902 г. пока-
показал Зомильяна2) для случая статической нагрузки,
позволяют решить нашу проблему весьма элементарным
путем. С другой стороны, что касается тех физических
приложений, которые мы имеем в виду, то «смешанные»
х) R i t z W., Теория поперечных колебаний квадратной пла-
пластинки со свободными краями, Ann. Phys., 28, 737 A909). Случай,
круглой пластинки, как показал Кирхгоф, допускает прямое
интегрирование.
2) См. Т е d о п е О., Enzykl. d. Math. Wiss., Bd. IV, 4, Art:
25, Nr. 2, где подробно изложен этот вопрос.
§ 44. Упругая энергия в прямоугольном параллелепипеде 395
условия для них эквивалентны «несмешанным» усло-
условиям D4.2) или D4.2а).
В основу нашего рассмотрения положим, например,
равенства D4.3) и следующие из них путем циклической
подстановки граничные условия для граней у и z. В си-
силу первого из равенств D4.3), следствием которого яв-
являются соотношения
дЧ _ д\ ^ п дч\ ^ дС
ду dz ХУ дх xz дх
эти граничные условия гласят:
fc_O 5y1-^-0 ппя х-1°
?-U' Эх—дх-" ДЛЯ Ж-\а'
ОС/С, C/Q r\ I U / / / / \
, =- = -тг =0 ДЛЯ V= 1 , , D4.4)
ду ду и \ Ъ v 7
„_п ?i_^_n f0
- — а — ¦-, ДЛЯ Z — 1
dz dz \ с
Так как сила F = 0, то наши дифференциальные уравне-
уравнения A4.16) запишутся в виде
ае
Й > D4-5)
Условия D4.4) будут выполнены, если положить
. . пЛпх Папу Иотсг ,-
= A sin -i— cos -— cos —— er-
а Ъ с
г> — В cos -J— sin -v^ cos -s— е~гш<, D4.6)
' a b с ' ч '
С Si ПаПХ ПаЖу . ПоЛ2 . N,
= с; cos —— cos -4-^ sin —— e—шг,
a b с '
где п{, п2, п3 — произвольные целые числа, 4, В, С —
постоянные, отношения которых определятся вместе
с круговой частотой to.
Если выражения D4.6) подставить в D4.5), то во все
три члена D4.5) войдут, те же тригонометрические мно-
396
Гл. VIII. Дополнения к теории упругости
жители, которые имеются соответственно у величин ?,
к), С Например, будем иметь
5?
р ^ = —
sin . .. cos .. . cos ...,
56 / . П?
¦5-= —( ^ -|
5ж V. a2
= — Л ^_|+g|+-ijTC2Sin ... COS ... COS ...,
iI2Sin . . . COS . . . COS . . .
Эти множители можно сократить, после чего уравне-
уравнения D4.5) перейдут в следующие уравнения, линейные
относительно А, В, С:
( й + ^
V а2
^
= 0,
где величина Q, введенная в качестве сокращенного обо-
обозначения, определяется из соотношения
п„,2 „2 2 „2
/¦V , \ f-w ри> »*1 . /fro , /fro iff < \
(Л -\- (i) U = (i5 — —¦, 5==~2 "гт| i "T • D4./aJ
Для того чтобы уравнения D4.7) были разрешимы отно-
относительно А, В, С, должен обратиться в нуль определи-
определитель
= 0. D4.8)
Ъа
аЪ '
ас
Если его разложить по степеням Q, то легко видеть,
что множители при Q0 и Q1 обратятся в нуль и оста-
останутся только множители при Q2 и Q3, равные соответ-
соответственно s и 1. Поэтому уравнение D4.8) примет форму
= 0. D4.9)
§ 44. Упругая энергия в прямоугольном параллелепипеде 397
Таким образом, мы получили двойной корень Й1 = Й2 = О
и простой Q3= — s. Согласно D4.7а), этим корням со-
соответствуют следующие значения ш2:
2 2 2 ^ о 2 2 'Ч" "F*1 „ /ЛА 4 Г^
1- 2 — % у I 3— ^— • \ ' )
Для этих значений ш можно, согласно D4.7), вычислить
отношения Л : В :С, после чего наша система решений
D4.6) будет определена с точностью до произвольно
выбранных общего множителя и чисел пх, п2, п3 для каж-
каждого из wi.
Что означает этот произвольный выбор? В соответ-
соответствии с числами и1? и2, п3 ребра а, Ь, с разобьются
на отрезки
к=^, 4=4' хс=?, D4Л1^
которые можно рассматривать как длины волн. В таком
случае в параллелепипеде уложится целое число волн.
Соответствующими волновыми числами будут
у 2it 2toti 7 2% 2т^Пс, 7 2it 2тъп<> •.
Если, в частности, рассмотреть структуру выражений
D4.6) вдоль оси x(y = z=0), то с учетом D4.11) можно
написать
? = ilsinrcf е-***, tj = C = O. D4.12)
Это выражение представляет собой стоячую волну, узла-
узлами которой являются границы нашего параллелепипе-
параллелепипеда ж = 0и х = а = п1Ка. Таким образом, уравнения D4.6)
задают систему стоячих волн, заполняющих параллеле-
параллелепипед, которые в общем случае не являются плоскими,
а представляют собой суперпозицию волн в направлениях
трех ребер.
С другой стороны, уравнения D4.10) указывают на
то, что эти волны являются частью поперечными, а ча-
частью продольными. А именно, если, согласно выраже-
выражениям A4.6) и A4.3), скорости звука (обозначенные
398 Гл. VI П. Дополнения к теории упруёости
в этих выражениях через b и а) теперь обозначить как
ct и Cj, то
Если, кроме этого, ввести волновое число kr —
= \r ka-\-kl-\-k%, являющееся результирующим трех вол-
волновых чисел ка, къ, кс, то, согласно D4.11а) и D4.7а),
В этом случае уравнения D4.10) примут простой вид
«Ч—о^усА, ш. = |сЛ. D4.14)
Вдвое большее число поперечных волн по сравнению
с продольными, связано с поляризацией в двух перпен-
перпендикулярных друг к другу направлениях.
Таким образом, мы получили бесконечную систему
упругих волн, которые могут быть возбуждены в адиа-
адиабатически изолированном от среды параллелепипеде. То,
что это система является полной, т. е. что при тех же
граничных условиях не может существовать никаких
других стоячих волн, следует хотя бы из возможности
разложения произвольного начального состояния по ре-
решениям D4.6) в момент 1 = 0г).
Определим число Z волн, частота которых не превос-
превосходит заданной величины v = u)/2'tc. Проведем вычисление
с помощью геометрических методов сначала для продоль-
продольных волн.
В прямоугольной системе осей ка, къ, кс отметим все
точки, соответствующие целочисленным значениям п1}
п2, п3. При этом мы получим ромбическую простран-
х) См. Orfvay R., Ann. Phys., 42, 745 A913); здесь проведено
также обобщение на анизотропные тела. Более глубокое рассмотре-
рассмотрение с точки зрения теории групп имеется в диссертации W i e г-
zejewski H., Упругие собственные колебания кристаллов при
«смешанных» граничных условиях, Zs. f. Kristallographie, Bd. 101,
1939.
§ 44. Упрубая энербия 6 прямоугольном параллелепипеде 399
¦€твенную решетку. Ребрами ее элементарной ячейки бу-
будут [см. D4.11а)]
2тг 2те 2и
о"' Т ' ~с '
Ограничим ее снаружи сферой kr = const, соответствую-
соответствующей частоте v. Согласно D4.14), ее радиус будет равен
к = —
ci
Далее заметим, что нам придется рассматривать только
положительный октант решетки, так как все пх, п2, п3
не должны быть меньше нуля. Ограниченный сферой
объем этого октанта равен
4 к* 4тг /2ttv\3
Разделим его на объем элементарной ячейки
При этом получим число элементарных ячеек в ограни-
ограниченном сферой октанте и тем самым число продольных
волн с частотой, не превышающей v:
Точно так же для обоих состояний поляризации по-
поперечных волн получается
Z' = "~' D4.16а)
Следовательно, полное число всех колебаний с часто-
частотами, не превышающими v, равно
Z = Zt + 2Zt = % аЫ* (~ + -i-) . A4.166)
Это число Z определено с точностью до ошибки, вызы-
вызываемой разностью* объемов сферы и примыкающей к ней
области, состоящей из целых ячеек. Эта ошибка имеет
порядок 1/abc [см. D4.15)], и в случае достаточно боль-
большого параллелепипеда ею можно пренебречь. Из D4.166),
400 Гл. VIII Дополнения к теории упругости
производя дифференцирование по v, получаем число ко-
колебательных состояний между v и v-f-dv:
dv> D4.i7)
где V = abc — объем нашего параллелепипеда.
Теперь мы можем приступить к рассмотрению про-
проблемы, упомянутой в названии этого параграфа. Энергия,
заключенная в нашем адиабатически замкнутом твердом
теле, как говорили раньше, состоит из энергии тепловых
колебаний его молекул. Вместо этого будет правильнее
говорить, следуя Дебаю1): из энергии упругих колебаний
тела, так как- молекулы тесно связаны друг с другом
и не могут быть приведены в колебание поодиночке. На-
Напротив, рассмотренные в выражении D4.6) волны не за-
зависят друг от друга,- и каждая самостоятельно удовле-
удовлетворяет дифференциальным уравнениям упругости.
Каждая из них может быть проквантована согласно за-
закону, установленному Планком для теплового излучения:
п = целому числу,
* „ Jf D4.18)
h = кванту действия . ч
х) D e b у е P., Ann. Phys., 39, 789 A912). В этой фундамен-
фундаментальной работе Дебай определил собственные колебания достаточ-
достаточно большой сферы, поверхность которой предполагалась свободной
от напряжений. Он положил в основу граничные условия, соответ-
соответствующие нашим уравнениям D4.2). Поскольку только пластинка
круглой формы допускает непосредственное интегрирование (см.
примечание 1 на стр. 394), то сфера является единственной формой
упругого тела, допускающей при «несмешанных» граничных условиях
интегрирование в известных (бесселевых) функциях. Но даже в этом
случае решение весьма громоздко и становится возможным только
с помощью полученных Дебаем асимптотических формул для бес-
бесселевых функций в случае больших значений аргумента и индекса.
Упрощение, которое приносят «смешанные» граничные условия, было
отмечено автором в его лекции по квантовой теории, прочитанной
в 1912 г., а затем развитой опубликовано Ортвеем(см. примечание
на стр. 398). Следует заметить, что, для того чтобы показать незави-
независимость распределения собственных функций от формы тела, Дебай
должен был предполагать, что радиус сферы «достаточно велик».
Та же причина заставила нас предположить, что размеры нашего
параллелепипеда достаточно велики. [Нам это потребовалось перед
уравнением D4.17) для того, чтобы мы могли пренебречь ошибкой,
связанной с поверхностными эффектами.]
§ 44. Упругая энергия в прямоугольном параллелепипеде 401
Здесь мы должны этот закон принять без всякого обо-
обоснования; он будет рассмотрен в т. V, посвященном
электродинамике. Опустим также уточнение этого закона,
полученное в квантовой механике, согласно которому п
в D4.18) надо заменить на и-}-1/2. Для дальнейшего это
значения не имеет.
Кроме этого квантового закона, мы используем в даль-
дальнейшем множитель Больцмана, который тоже без дока-
доказательства был введен в G.15в). В нашем случае, если
имеется N колебательных систем, находящихся в термо-
термодинамическом равновесии при температуре Т, то число Nn
систем, колеблющихся с энергией еп, задается выражением
Nn = Ae-*nlbT = A*n, 0L = e-h^lhT, D4.19)
где А — постоянная, определяемая из условия, что полное
число N всех колеблющихся систем должно быть равным
п=0
В нашем случае N означает (большое!) число dZ из
D4.17). Таким образом, имеем
A = (l-a)dZ. D4.20а)
Ту часть всей энергии колебаний U, которая отно-
относится к этим dZ колебаниям, назовем dU. Согласно D4.19)
и D4.20а), она равна
dU = 2 Nnen = Ahv 2 пап = A - а) Ь dZ 2 шп. D4.21)
п=0 • п=0
Входящая сюда сумма по п может быть сразу вычислена,
если продифференцировать по а ряд 1 + а -f- а2, . . .; она
равна а/A— аJ. Поэтому, согласно D4.21) и с учетом
определения а в D4.19), имеем
Выражение, стоящее в знаменателе D4.22), встречается
в законе излучения Планка и вообще в статистике Бозе.
Еели мы подставим dZ из D4.17) и проинтегрируем
по всем v от v = 0 до верхней границы vgi то получим
26 д. Зоммерфельд
402 Гл. VIII. Дополнения к теории упругости
<44-23>
Прежде всего надо определить верхнюю границу v0. Со-
Согласно Дебаю, она может быть найдена, если полное
число Zg всех колебаний с частотой, не превышающей vff,
мы приравняем числу степеней свободы нашего тела. Так
как отдельная точечная масса обладает тремя степенями
свободы1), то число, о котором идет речь, равно утроен-
утроенному числу молекул. Если, в частности, наше тело со-
состоит из моля рассматриваемого вещества, то, согласно
определению на стр. 71, число его молекул равно числу
Авогадро L. Поэтому мы потребуем, чтобы Zg — 2>L. Если
объем параллелепипеда abc заменить на объем моля, то,
согласно равенству D4.166), это дает
D4.24)
Этим равенством, с одной стороны, можно воспользоваться
для определения vff, ас другой стороны — для упроще-
упрощения D4.23), которое мы теперь можем написать в виде
тт 9Lh Г* v3dv ... окч
tfмгш. = -^г \ hyikT „' D4.25)
д J в —1
или с помощью сокращенных обозначений
y=w> x=ii = T> e = iv D4-26)
в еще более простой форме
X
о '
где @ — величина, известная под названием характери-
характеристической температуры Дебая. Она принимает значения
примерно от 100°К (алмаз, кварц и т. д.) до нескольких
х) См. «Механика» (т. I), стр. 67.
§ 44. Упругая энергия в прямоугольном параллелепипеде 403
градусов (мягкие металлы) ?•). Уравнение D4.27) в общей
находится в прекрасном соответствии с богатым опытным
материалом, собранным Нернстом и его учениками.
Не следует, конечно, ожидать, что в наших общих резуль-
результатах будут отражены детали, связанные с конкретной
кристаллической структурой, или строением молекул твер-
твердых тел.
Исследуем уравнение D4.27), в котором мы сначала
будем считать Т > в. Тогда х < 1, и поэтому во всей
области интегрирования ?/< 1. Для малых у мы можем
разложить
и с достаточной точностью получить выражение для инте-
интеграла в D4.27)
о
откуда
UMon. = 3RT, B = kL [согласно G.156)]. D4.28)
Соотношение D4.28) содержит в себе закон Дюлонга —
Пти:
сМол. = -^—^ = ЗЛ ~ 6 кал. D4.29)
Молярная теплоемкость смол. представляет собой коли-
количество тепла, необходимое для нагревания моля вещества
на 1° (той же буквой с, как известно, обозначают обычно
.удельную теплоемкость, т. е. количество тепла, необхо-
необходимое для нагревания единицы массы). Согласно нашим
представлениям, уравнение D4.29) должно годиться для
всех твердых тел в качестве предельного закона для вы-
высоких температур, при условии что можно не учитывать
собственных колебаний молекул. Последняя оговорка
необходима, так как в приведенном выше подсчете степе-
степеней свободы молекулы мы считали ее твердой и не при-
принимали во внимание ее внутренних степеней свободы.
В случае одноатомных металлов, где это ограничение
х) Здесь автором допущена ошибка в численных значениях:
следует читать от —1000° К до десятков градусов.—Прим. перее.
26*
404 Гл. VIII. Дополнения к Меории упрубосшй ,
отпадает, закон Дюлонга—Пти выполняется особенно
хорошо; в этом случае обычно вместо моля и молярной
теплоемкости говорят о грамматоме и грамматомной
теплоемкости.
Гораздо интереснее, чем предельный случай Т > ©,
обратный предельный случай. Для Т < ©, согласно D4.26),
х > 1. Интеграл в D4.27) можно записать в виде
D4.30)
Подстановкой z = ny все интегралы этой суммы могут
быть сведены к первому. При этом получаем
f ^ = 3!g. D4.30а)
n=i 0 n=i
Необходимое в конце этой выкладки суммирование свя-
связано с так называемыми числами Бернулли; оно обосно-
обосновано в т. VI в разделе, где рассматриваются ряды Фурье.
В силу D4.30) и D4.30а) уравнение D4.27) примет
вид
EW=-g--0r • D4.31)
Отсюда следует после дифференцирования по Т
) • D4.32)
Это есть так называемый «закон Г3» Дебая для моляр-
молярной теплоемкости твердых тел при низких температурах.
На фиг. 73 изображен общий ход молярной тепло-
теплоемкости, полученной путем дифференцирования по Т
уравнения Дебая D4.27). Здесь изображено поведение
теплоемкости как в предельном случае для больших 21
(прямая Дюлонга—Пти), так и для малых Т (парабола*-
Т3 Дебая). При этом видно, что последний предельный
случай является справедливым только для весьма низких
температур. Мы не коснемся здесь общего для всех ме-
металлов отклонения, которое наступает вблизи абсолют-
абсолютного нуля и зависит от степеней свободы электронов
в металле.
§ 44. Упругая энергия в прямоугольном параллелепипеде 405
В конце этого параграфа сделаем краткие замечания
по поводу энергии, содержащейся в пространстве, запол-
заполненном электромагнитным излучением. Свободные колеба-
колебания такого пространства могут быть описаны аналогично
(и даже значительно проще) колебаниям нашего упругого
параллелепипеда. Развитые Рэлеем и Джинсом методы
[включая и геометрический метод подсчета узлов решетки,
использованный в уравнении D4.16)] как раз и послужили
3R
I
I Закон Дю/юнга~Пти
I
IЗакон Т
Фиг. 73. График молярной теплоемко-
теплоемкости твердых тел согласно Дебаю.
Значение © разъясняется в D4.26).
прообразом развитой в этом параграфе теории для упру-
упругих тел. Результатом этих электромагнитных методов
явилось наше уравнение D4.23) со следующими упроще-
упрощениями:
1) Продольных волн в электромагнитном поле не
имеется, поэтому член \\с\ отсутствует.
2) Поперечные волны распространяются со скоростью
света с, поэтому член 2/с? заменяется на 2/с3.
3) Число степеней свободы электромагнитного поля
не зависит от какой-либо молекулярной структуры и,
насколько мы знаем, неограниченно, поэтому надо по-
положить vff = оо.
4) Если мы хотим определить удельную энергию, со-
содержащуюся в единице объема, так называемую «плот-
«плотность энергии», то мы должны положить в равенстве
D4,23) F — 1; при этом, как принято, будем писать и
406 Гл. VIII. Дополнения к теории упругости
вместо U. В результате D4.23) перейдет в
со
8izh
D4.33)
Если мы здесь используем подстановку D4.26) и ре-
результат, полученный в D4.30) и D4.30а), то получим
8яЛя*^йту 8«6 ft* ™ ///о/ч
м = ~ч~те -г- =те~^т^^ • D4.34)
с3 15 v h J 15с3 Л3 v '
Этот результат выражает так называемый закон Стефана
для черного излучения или равновесного излучения в уста-
установленной Планком окончательной форме. Закон 714 Сте-
Стефана— Больцмана для излучения имеет то же происхо-
происхождение, что и закон 714 Дебая для энергии, содержащейся
в твердом теле, и его же закон Ts для удельной тепло-
теплоемкости.
§ 45. УПРУГОЕ ПОЛУПРОСТРАНСТВО И ПОВЕРХНОСТНЫЕ
ВОЛНЫ В НЕМ
Рассмотрим бесконечное упругое тело, ограниченное
плоскостью у = 0, и изучим простейшие типы волн, ко-
которые могут распространяться в полупространстве у > 0.
Поверхность у — О граничит с воздухом (вакуумом) и сво-
свободна от сил. На ней имеют место условия, выражающие
отсутствие напряжений:
1. Отражение плоской поперечной пространственной
волны
Пространственные волны, рассмотренные в § 14, раз-
разделяются на поперечные и продольные. Первые из них
соленоида льны, а последние—потенциальны (см. § 20);
в § 14 они названы соответственно волнами кручения
и сжатия. Мы рассмотрим здесь плоские волны как наи-
наиболее простые в каждом из этих типов.
Пусть, например, плоская поперечная волна, поляри-
поляризованная в. плоскости падения ху, падает на поверхность
§ 45. Упругое полупространство и поверхностные волны в нем 407
у = 0 под углом а к положительной оси у (см. фиг. 74).
Последнее означает, что из трех компонент смещения I, т\, С
только U т] отличны от нуля. Воспользовавшись обозначе-
обозначениями теории функций комплексного переменного, напишем
Отренк. продолен.
Над. поперечн
ртраш. поперечн.
74.
Отражение поперечной волны, поляризованной
в плоскости падения; на свободной поверхности
возникает продольная компонента.
выражение для такой волны [всюду мысленно следует до-
добавить зависимость от времени в виде е~ш, см, замеча-
замечание к выражениям A3.15) и A3.15а)]:
т]е = sin a
ft—ycos
D5.2)
где к — волновое число; индексом е мы обозначили падаю-
падающую волну. Прежде всего в результате D5.2) будет авто-
автоматически выполнено условие соленоидальности
дх
ду
= 0.
Кроме того, плоскости постоянной фазы
х sin а — у cos а = const,
D5.3)
как и следовало ожидать, будут расположены перпенди-
перпендикулярно к направлению распространения (Н. Р.), кото-
которое определяется углом а. Вектор смещения (B.C.) ле-
лежит в фазовой плоскости. Знаки тригонометрических
функций могут быть получены из сравнения нашей фи-
фигуры с первой колонкой следующей ниже таблицы, в ко-
которой задаются направляющие косинусы Н.'Р. и В, С?
относительно положительных осей х и у.
408
Гл. VIII. Дополнения к теории упругости
Н. Р.
B.C.
sin a
COS а
-COS а
sin а
падающая попе-
поперечная
sin a cos а
COS а — sin а
отраженная по-
поперечная
sin сц
sin ац
cos
cos
отраженная про-
продольная
Уравнения теории упругости, которые для нашей попе-
поперечной волны (в = 0) сильно упрощаются, гласят
Р ~яж = \1^> Р~ш==\1^г1- - D5.4)
Эти уравнения удовлетворяются при подстановке соотно-
соотношений D5.2), если к будет связано с ш известным урав-
уравнением распространения
i?=J!: = c! = &a; D5.5)
/с2 р 1 ^ •
обозначение Ь в § 14 использовано для ct.
. ¦ Однако наше выражение D5.2) само по себе, конечно,
не удовлетворяет поверхностным условиям D5.1). Затруд-
Затруднение нельзя также избежать, если предположить суще-
существование одной отраженной поперечной волны
cos a \
_ I fieih (хsino+y cos «)# D5.6)
— sin а J
Выбранные здесь знаки у тригонометрических функций
можно проконтролировать по второй колонке приведенной
таблицы.
Величины А; и а должны совпадать с их значениями
в D5.2). Первое следует из дифференциального уравне-
уравнения D5.4), последнее—из граничных условий, точно
так же, как это имеет место в элементарной оптике. При
суперпозиции падающей и отраженной волн эти усло-
условия гласят:
§ 45. Упругое полупространство и поверхностные волны в нем 409
и с учетом © = 0
= — 2\xik (A + В) sin a cos a?ihx sin «,
D5.8)
55 , «
— 5) (cos2 а - sin2 a) eihx sina .
Третье условие, ayz = 0, выполняется само собой. Но два
предыдущих условия противоречат друг другу: согласно
одному, А=—В, согласно другому, А=-\-В. Заметим,
кстати, что это затруднение не будет устранено, если мы
предположим, что угол отражения не равен углу падения.
Тогда мы получим не два, а бесконечно много противо-
противоречащих друг другу условий, а именно для каждого
х — свое условие.
Нам остается единственный выход: предположить, что
при отражении, кроме поперечной, возникает также и про-
продольная волна, так что появится еще одна амплитуда С.
С учетом третьей колонки таблицы положим
k sin a( ^
I Ceiki(xsin«i+v cos eo. D5.9)
COSOCj J
Волновое число кг будет отличаться от прежнего к. Урав-
Уравнения теории упругости A4.16) требуют теперь
tf___Je}«... D5.10)
так как теперь к D5.4) добавятся члены с grad ©;
a = ct — сокращенное обозначение, которое мы исполь-
использовали еще в § 14; ш имеет такое же, заранее заданное,
значение, как и в D5.5). Из D5.5) и D5.10) следует
у- = и, D5.11)
где принято сокращенное обозначение
410 Гл. VIII. Дополнения к теории упругости
Угол af также будет отличаться от прежнего угла паде-
падения а. А именно, для отраженной продольной волны бу-
будет иметь место такой же закон, который имеется в эле-
элементарной оптике для преломленной поперечной волны:
sin a =/г sin a?. D5.12)
Назовем его поэтому «законом преломления», хотя он
относится не к преломлению, а к отражению. Коэффи-
Коэффициент п будем называть в переносном смысле «показа-
«показателем преломления».
Для доказательства соотношения D5.12) образуем
из D5.9)
e = ^4^=fc^i"ta"« для у-0;
тогда к первому из уравнений D5.8) добавятся в правой
части члены
2^ ^ + Хв = ikL Bц cos2 a, + X) Ceihix sin ai D5.12а)
и соответственно ко второму уравнению D5.8)
* (f + ^) = ikl2[Lsm*lcosalCeihi*^°i . D5.126)
Так как правая часть выражения D5.8) вместе с доба-
добавочными членами, согласно условию, должна обращаться
в нуль независимо от х, то экспоненциальные функции,
зависящие от х, должны совпадать у всех членов. Сле-
Следовательно, должен выполняться закон преломления
D5.12).
Учтя это, мы можем сократить оба уравнения D5.8),
дополненные членами D5.12а) и D5.126), на экспонен-
экспоненциальную функцию, а также на общий фазовый мно-
множитель i:
— 2fxfc sin a cos a {A + B) + kt Bjx cos2 at + X) С = 0,
D5.13).
cos2 a — sin2 a) (A — B) -f- k^ sin at cos at С = 0.
Таким образом, мы получили два линейных уравнения
с постоянными коэффициентами, откуда могут быть одно-
§ 45. Упругое полупространство и поверхностные волны в нем 411
значно определены неизвестные величины
А р Л '
которые определяют, какую часть от произвольно задан-
заданной падающей волны составляют отраженные волны.
Путем элементарного подсчета можно найти
• С п sin 4a
~А~~ cos2 2а 4-n2 sin 2a sin 2a( '
D5.14)
В cos2 2а — п2 sin 2a sin 2at
A cos2 2a -f- n2 sin 2a sin 2aj
Таким образом, задача об отражении поперечной волны,
поляризованной в плоскости падения, решена.
Если, напротив, падающая поперечная волна поляри-
поляризована перпендикулярно к плоскости падения, то к обыч-
обычной отраженной волне не добавляется никакой продоль-
продольной компоненты. С другой стороны, в случае падающей
продольной волны, кроме обычной отраженной продоль-
продольной волны, добавляется поперечная волна, поляризован-
поляризованная в плоскости падения. Оба случая будут рассмотрены
в задаче 5 гл. VIII.
В приведенных выше рассуждениях мы имеем в виду их
интерес не столько для теории упругости, сколько для
оптики. Как известно, в оптике XIX в. (начиная от
Френеля и Фраунгофера и кончая Нейманом и Герцем)
господствовали представления об упругом эфире,
В качестве .подготовки к т. V покажем, почему эти
представления должны были привести к неразрешимым
противоречиям.
После того как была точно установлена поляризация
света, в оптике можно было допустить существование
только поперечных волн. Правда, Рентген под влиянием
одной из последних работ Гельмгольца считал, что от-
открытые им рентгеновские лучи могут иметь природу про-
продольных колебаний. Однако своими опытами Баркла
установил наличие поляризации у этих лучей, в резуль-
результате чего отпала возможность приписать им продольный
характер.
Мы видим, однако, что уже простое явление отраже-
отражения упругих волн невозможно без возникновения про-
412 Гл. VIII. Дополнения к теории упругости
дольных волн. Даже если представить себе чисто попе-
поперечную волну, то видно, что при отражении к ней доба-
добавится продольная волна, существование которой в оптике
не допускается. Причина этого, в конечном счете, арифмети-
арифметическая.
Если мы вместо рассмотренного ранее чистого отраже-
отражения представим себе общий случай отражения с преломле-
преломлением, т. е. переход из среды 1 в среду 2, то в теории
упругости будем иметь шесть граничных условий: три
уравнения для напряжений и три уравнения, определяю-
определяющие непрерывность смещений ?, ij, С- В то же время для
поперечных световых волн нам надо будет определить
только четыре неизвестных, а именно по два отношения
амплитуд для каждой из двух возможных поляризаций.
Очевидно, что это противоречие разрешено быть не
может.
Положение изменится, если мы от упругого эфира
перейдем к квазиупругому эфиру, рассмотренному в § 15.
Напряжение будет тогда представлять собой не симме-
симметричный, а антисимметричный тензор, который может быть
представлен некоторым вектором. Для него ои = 0 и вместо
трех уравнений для напряжений останется только два;
то же произойдет с уравнениями для смещения. Возни-
Возникающие в этом случае граничные условия будут иметь
тот же вид, что и в электромагнитной теории света, в ко-
которой внутренние противоречия упругой теории света
прекрасно разрешаются.
2. Упругие поверхностные волны
Мы будем здесь возможно ближе придерживаться
изложения гл. V, где рассматривались гидродинами-
гидродинамические поверхностные волны. Так же как и там, рас-
рассмотрим плоские волны, распространяющиеся в положи-
положительном направлении х с заданной круговой частотой со,
но с еще не определенным волновым числом к. Посколь-
Поскольку волна плоская, состояние не зависит от третьей
координаты z. Волна будет складываться из продольной
и поперечной компонент.
Продольная компонента, как и в гидродинамике,
является безвихревой и поэтому может быть вычислена
§ 45. Упругое полупросшранстбо и поверхностные волны в нем 413
из некоторого потенциала Ф. Пусть
f- 9Ф ЭФ у ~
Здесь Ф будет удовлетворять не условию несжимаемости
ДФ = 0, как это было' в гидродинамике, а уравнению,
следующему из дифференциальных уравнений теории упру-
упругости для I и 7j:
^ D5.16)
Если предположить, что
ф^е* <**-«>*) ю (у), D5.17)
то из D5.16) для неизвестной функции и получаем
или
dy*
Предположим, что р действительно, и выберем знак плюс
для квадратного корня в.D5.18). Из двух частных интег-
интегралов уравнения D5.18)
и = е~РУ и и =
второй надо отбросить в силу его поведения при у = со.
В этом случае наше выражение D5.17) (если мы опять
опустим зависимость от времени) представится в виде
Ф = Aeihx~pv.
Отсюда, согласно D5.15), следует
*»~ ША ' D5.19)
ч = + pAeihx~py.
С другой стороны, поперечная составная часть нашего
волнового движения соленоидальна. Поэтому можно ввести
4l4 Гл. УТИ. Дополнения tt теории ynpyiocmu
функцию W, аналогичную гидродинамической функции
тока, и положить
Функция W удовлетворяет тому же дифференциальному
уравнению, что и ?t, y\t, а именно:
D5.21)
Положим
\jr _ fiei (hx-wo v (yj D5.22)
и получим из D5.21) дифференциальное уравнение для v
*—и^ D5-23)
р
с единственным допустимым решением
(q должно быть действительным и положительным).
Из D5.20) и D5.22) следует (зависимость от времени
опять опущена)
?, = qBeihx-w,
1 Ч //г-).24)
При суперпозиции решений D5.19) и D5.24) получим
для полного смещения ?, у\ выражение с двумя произ-
произвольными постоянными: волновым числом к и отноше-
отношением амплитуд А/В. Они должны быть определены из
двух граничных условий D5.1) ауу = аух—0 [третье усло-
условие D5.1), так же как и в разделе 1, будет выполнено
само собой, так как волна плоская]. Как легко показать,
эти два условия гласят, что если из полного смещения
\, т] вычислить вуу, еху, 0, а из них — напряжения ауу, аухУ
то
- 2{х (рЫ + ikqB) + X (к2 - р2) А = 0,
§ 45. Упру&ое полупрострамтбо и поберхНостНие болНы в Нем 415
Если здесь подставить для р и q их значения из D5.18)
и D5.23) и одновременно выразить X и jx через а и Ъ, то
получим
D5.25)
Приравнивая нулю определитель этой системы однород-
однородных уравнений, имеем
-F- <45-26>
Мы получили уравнение третьей степени относительно
неизвестной к2, так как член с к8 уничтожится при
возведении D5.26) в квадрат. После его решения отно-
отношение А/В может быть получено из D5.25).
Приведем только приближенное рассмотрение D5.26)
в предельном случае а—>оо (почти несжимаемая среда).
Тогда, деля на А;4, получаем
D5.27)
Нас интересует тот корень, который лежит в окрест-
окрестности а; = 1/2. Положив х = г12 — 8, получаем из D5.27)
2S, ij + A8+...=2S18~i. D5.28)
Отсюда, согласно D5.27), следует
со2
X = ¦
где со/Л — скорость распространения нашей поверхностной
волны. Она несколько меньше (правда, довольно незна-
незначительно) скорости Ъ поперечной пространственной волны.
Скорость а продольной волны, по предположению, зна-
значительно больше.
Выясним, .на какой глубине от поверхности г/ = 0
будут еще заметны поверхностные волны. Это можно
получить из рассмотрения экспоненциальных множителей
416 Гл. VIII. Дополнения к теории упругости
e-Qv в выражении D5.24) и ervv в D5.19). Если, как это
обычно принято, под глубиной проникновения мы будем
понимать расстояние, на котором амплитуда падает в
1/е раз, то она равняется у = — или соответственно
1
* Р
Воспользовавшись сокращенным обозначением х из
D5.29), получаем, согласно D5.23),
где /—длина волны и, согласно D5.18), при а—>оо
11 '
1
D5.30а)
В обоих случаях глубина проникновения составляет
только часть длины волны I, с которой волновое движе-
движение распространяется вдоль оси ж; эта последняя, конеч-
конечно, для обеих составных частей движения будет одина-
одинаковой; в противном случае, граничные условия не смогли
бы удовлетвориться тождественно на всей поверхности.
Однако глубина проникновения обеих составных частей,
как мы видели, различна.
Результаты, выраженные соотношением D6.30) и
D6.30а), указывают на то, что мы действительно имеем
здесь дело с упругим процессом, который распростра-
распространяется в непосредственной близости от поверхности и
возможен только при условии различия упругих констант
по обе стороны поверхности. Последним объясняется также
различие скоростей распространения. На поверхности
упругая сила меньше, а смещение осуществляется легче,
чем внутри материала. Поэтому скорость распространения
поверхностных волн меньше, чем пространственных волн.
Точно так же можно объяснить малую скорость попереч-
поперечных волн по сравнению с продольными пространствен-
пространственными волнами; в случае распространения последних
материал подвергается сжатию, при котором возникают
силы, большие, чем в случае сдвига, который имеет
место в поперечной волне.
§ 45. Упругое полупространство и поверхностные волны в нем 417
Еще в 1886 г. Рэлей, впервые изучая упругие поверх-
поверхностные волны, высказал предположение, что они могут
играть существенную роль при землетрясениях. Это пред-
предположение полностью подтвердилось дальнейшим раз-
развитием сейсмологии, которая во многом обязана теоре-
теоретическим работам и" экспериментальному искусству
Вихерта. Роль двухмерных поверхностных волн, рас-
распространяющихся вдоль земной поверхности, возрастает
при удалении от центра землетрясения по сравнению
с ролью распространяющихся внутри земли простран-
пространственных волн, рассеивающихся во всем объеме. Поверх-
Поверхностные волны составляют, таким образом, основную
часть наблюдаемых смещений земли. Они отличаются от
пространственных волн и по времени их появления.
Поверхностные волны достигают места наблюдения
несколько позднее поперечных пространственных волн",
частью в силу их несколько меньшей скорости, а частью
в силу того, что они проходят более длинный путь (дуга
окружности по сравнению с хордой). Продольные про-
пространственные волны в качестве первых предвестников
отмечаются сейсмографами раньше поперечных волн.
Сейсмические сигналы дают нам сведения не только
о среднем упругом поведении земной массы, но и о
возможных неоднородностях в ней. Анализируя эти сиг-
сигналы в связи с другими геофизическими и астрономи-
астрономическими данными, Вихерт пришел к представлению о
«твердом» земном ядре, состоящем в основном из железа,
которое окружено слоями более легких веществ: сульфи-
сульфидов и силикатов. Для этого вывода наряду с процессом
распространения сыграли роль также и процессы отра-
отражения от следующих друг за другом неоднородных земных
слоев, простейшая схема которых была рассмотрена
нами в разделе 1.
27 А. Зоммерфельд
ЗАДАЧИ
К ГЛАВЕ I
1.1. Сравнение определения rot А как линейной вектор-
векторной функции с дифференциальным определением. Показать,
что оба определения ротора [см. B.6) и B.7а)]
B = rotA
и
2(А-А0) = [Вг]
идентичны, если (как в § 1) г считать сколь угодно малой
величиной. "Следует заметить, что в тексте векторное
поле А в равенстве B.7а) при г = 0 исчезает, так как
оно соответствует вращательной части \х нашего движе-
движения. Поэтому мы вместо прежнего А написали А —Ао,
причем Ад соответствует трансляционной части v0
в соотношении so=voA?, аналогичном A.7); таким
образом, Ао равно значению теперешнего А при г = 0.
1.2. Векторный характер rot А. Исследовать вектор-
векторный характер ротора, воспользовавшись дифференциаль-
дифференциальным определением
В = rot A
и применяя формулы преобразования B.2) не только к
координатам, но и к вектору А.
1.3. Таблицы векторных операций в полярных коорди-
координатах. Дать выражения grad, div, rot, А и D в цилин-
цилиндрических и сферических полярных координатах.
1.4. К вычислению ДА. Вычислить выражение
grad div A — rot rot A
m Задачи 419
в цилиндрических координатах и сравнить его с выраже-
выражениями, которые получились бы при формальном при-
применении оператора А, вычисленного в задаче 1.3, к ком-
компонентам Ат, Av, Az. В соответствии с замечаниями к
C.10) оба выражения совпадают только для «декарто-
«декартовой» компоненты Ах.
1.5. К так называемой второй граничной задаче
теории потенциала. Показать, что задача теории потен-
потенциала, в которой на границе области задано не U, а
dU/dn, имеет однозначное решение с точностью до адди-
аддитивной постоянной.
1.6. Геометрический смысл инвариантов тензора.
Действительными геометрическими свойствами фигуры
являются такие свойства, которые остаются неизменными
при ортогональных преобразованиях. В свою очередь
каждый ортогональный инвариант допускает определен-
определенное геометрическое истолкование. Геометрическим образом,
лежащим в основе понятия тензора, является тензорная
поверхность, которую удобно предполагать эллипсоидаль-
эллипсоидальной. Истолковать три тензорных инварианта D.10) как
свойства эллипсоида.
1.7. Условия, при которых заданная картина силовых
линий принадлежит потенциальному полю. В случае
полностью заданного силового поля F условие суще-
существования потенциала U, согласно формуле C.7),
имеет вид rotF = 0. Если, однако, задана только карти-
, на силовых линий поля, то в каждой точке пространства
известны только отношения Fx:Fy:Fz, так что F задано
\ с точностью до некоторого скалярного множителя X.
Может ли X быть выбрано таким образом, чтобы F имело
потенциал? Показать, что необходимым условием для
: этого является
F0_LrotF0.
: Здесь Fo означает какой-либо вектор с заданными отно-
отношениями Fx:Fy:Fz, например единичный вектор, имеющий
всюду направление силовых линий.
; 27*
420 Задачи
К ГЛАВЕ II
II.1. Высота политропической атмосферы, а) Опреде-
Определить полную высоту политропической атмосферы для
и = 1,4 (адиабатический случай), п = 1,2 и п = 1 (изо-
(изотермический случай).
б) Как будет меняться давление с подъемом над по-
поверхностью земли, если последнюю считать не плоской,
как в § 7, а сферической? Показать, что при таком пред-
предположении давление в изотермической атмосфере не будет
обращаться в нуль не только на конечной высоте, но,
вопреки ожиданиям, и на бесконечности.
П.2. Разделение смеси газов путем центрифугирования.
Какое число оборотов в 1 мин. должен делать бара-
барабан диаметром 60 см, наполненный воздухом при 0°С,
чтобы между осью и периферией возникла разность дав-
давлений, равная 40 см водяного столба? Каков будет
состав воздуха на периферии барабана? Известно, что
воздух состоит из 21 объемных процентов О2 и 79
объемных процентов N2.
П.З. а) Двухмерная аналогия течения в капиллярах.
Жидкость течет вдоль оси х между двумя параллельны-
параллельными пластинами, расположёнными друг от друга на рас-
расстоянии 2h (см. фиг. 19а). Определить профиль скоростей
в плоскости ху и перепад давления П между двумя
сечениями, отстоящими друг от друга на расстоянии I.
Какая сила потребуется, чтобы удержать пластинки,
между которыми протекает жидкость?
б) Идеальный случай ламинарно текущей реки (см.
фиг. 196). Показать, что профиль скоростей задается
нижней половиной профиля случая П.3,а. Следует
принять во внимание граничное условие на свободной
поверхности у = 0; глубина реки h постоянна, угол накло-
наклона дна реки равен а. Роль внешней силы вместо пере-
перепада давления в случае П.З,а играет компонента силы
тяжести.
II.4. Прямолинейное и цилиндрическое куэттовское
течение. Прямолинейное течение, известное под назва-
Задачи 421
нием куэттовского (ср. фиг. 196), согласно A6.14),
задается выражением
u=%-U, v = w = 0. A)
Условия равновесия A0.8а) и A0.86) тогда удовлетво-
удовлетворяются при р = const; движущее усилие возникает здесь
за счет принудительного движения верхней пластины.
Требуемая для этого сила равна \iU/h.
При аналогичном куэттовском течении между двумя
коаксиальными цилиндрами радиусов га и г,- для жидкости
также не требуется перепада давления, а требуются
только моменты Ма и Mi для вращения наружного
и удержания внутреннего цилиндров. Вывести дифферен-
дифференциальное уравнение этого течения, проинтегрировать
его и сравнить результат в предельном случае,^—> оо
с уравнением A) настоящей задачи. Вычислить, далее,
моменты Ма и Mi и обратить внимание* на то, что они
отличаются друг от друга.
П.5. Задача Буссинеска. На упругое тело, ограничен-
ограниченное горизонтальной плоскостью, действует вертикальная
сила Р, которая приложена в некоторой точке поверх-
поверхности. Остальная поверхность свободна от напряжений;
тело заполняет все полупространство. Вычислить напря-
напряженное состояние тела, в частности возникающие в нем
«кольцевые напряжения», т. е. главные напряжения
вдоль окружностей вокруг направления Р.
К ГЛАВЕ III
III.1. Конвекционные члены течения в полярных
координатах. Показать на примере цилиндрических по-
полярных координат различие между правильным вычис-
вычислением конвекционных членов с помощью A1.6) и не-
неправильным применением символа (vgrad), при котором
grad просто заменяется на
д_ ^д_ д_
дг ' г ду ' dz '
Убедиться в том, что это различие не имеет места для
декартовой z-компоненты, но сказывается для г- и ср-ком-
422 Задачи
понент. Сравнить это различие с центростремительным
и кориолисовым ускорениями.
III.2. Соотношения подобия при течении в трубах.
Связь между перепадом давления на единицу длины П//
и: средней скоростью v для заданной трубы и определен-
определенной жидкости представляется соотношением
у = С*;п. A)
Здесь надо подставить для ламинарного течения п = 1,
а для турбулентного п = 1,722 по Рейнольдсу или
и = 1,75 по Гагену (схематическое представление см. на
фиг. 18).
Величина С может зависеть еще от плотности, кине-
кинематической вязкости и радиуса трубы а.
а) Предположить, следуя Карманух), что С пропор-
пропорционально произведению некоторых степеней этих вели-
величин, и определить показатели этих степеней по теории
размерностей.
б) Соотношение A) может быть представлено через
безразмерные величины R и S ж через безразмерное
отношение Ца. Наиболее общим представлением такого
типа является
Придавая этому соотношению снова вид произведения
степеней и выбирая по смыслу степень у отношения 1/а
равной 1, получим вместо B)
S = \±B*, C)
где X — безразмерная постоянная; 8 легко выразить через
п из A).
в) Показать, что соотношение S = XR~ 1l* в A6.13)
находится в соответствии со значением Гагена п =1,75.
Ш.З. Форма свободной поверхности жидкости, на
которую действуют внешние силы. С помощью принципа
х) К а г m a n Th., Phys. Zs., 12, 283 A911).
Задачи 423
виртуальной работы найти дифференциальное уравнение,
определяющее форму свободной поверхности жидкости.
Кроме капиллярных сил, на жидкость действуют внеш-
внешние силы, обладающие потенциалом. Следует заметить,
что объем рассматриваемой жидкой массы при виртуаль-
виртуальном перемещении остается постоянным.
III.4. Высота подъема в капиллярах. Использовать
результат предыдущей задачи, для того чтобы опреде-
определить высоту подъема или опускания смачивающей (или
несмачивающей) жидкости в узком капилляре. Заменить
для этого поверхность в капилляре сферой; поверхность
жидкости снаружи капилляра можно с достаточной точ-
точностью считать плоской.
К, ГЛАВЕ IV
IV. 1. Вычисления в биполярных координатах. Биполяр-
Биполярные координаты р, ср определяются уравнениями A9.10а)
и A9.106). Показать, что элемент длины имеет форму
Вычислить, далее, выражение для А и построить урав-
уравнение колеблющейся мембраны A7.8) в переменных р и <р;
оно не допускает «разделения переменных», т. е. интег-
интегрирования в форме
Ы- B)
IV.2. Поле течения двух равных простых вихрей
с противоположным направлением вращения. Соотношение
A9.10), совпадающее с A9.11), определяет поле скоростей
v=
где значение g берется из выражения A) предыдущей
задачи. Это представление v должно совпадать с равен-
равенством A9.14). Доказательство может быть весьма эле-
элементарно проведено геометрическим путем.
424 Задачи
IV.3. Вычисления вг эллиптических координатах.
Требуется вычислить элемент длины ds и оператор Д
в эллиптических координатах ?, ч\. Уравнение колебаний
мембраны может быть разделено в переменных ?, -ц,
т. е. [ср. IV. 1, уравнение B)] может быть проинтегри-
проинтегрировано в форме
IV.4. Переход от биполярных координат к кольцевым
и веретенообразным координатам. Из плоских биполяр-
биполярных координат в результате вращения вокруг оси р = 0
(фиг. 26) возникают так называемые кольцевые (или
тороидальные) координаты, а в результате вращения
вокруг оси <р = 0 — веретенообразные координаты. Найти
в этих координатах элемент длины и оператор Д. Далее,
рассмотреть вопрос о возможности разделения переменных.
К Г Л А В Е V
V.I. Кинетическая энергия волн в воде. В дополнение
к рассмотренному на стр. 240 примеру вычислить кинети-
кинетическую энергию глубинных гравитационных волн, содер-
содержащуюся в столбе жидкости сечением ДхДг = Х-1 между
свободной поверхностью и дном; сравнить ее с потен-
потенциальной энергией, содержащейся в том же столбе
жидкости.
Далее, перенести вычисления, проделанные на стр. 240
и далее, на случай не очень глубокой воды и показать
совпадение получающегося в этом случае значения SjF
со значением U/V в уравнении B6.13).
К Г Л А В Е VI
VI.1. Дрейфовое течение. Ветер, дующий вдоль поверх-
поверхности воды, вызывает в океане так называемое «дрейфо-
«дрейфовое течение». Приведенный ветром в движение поверхно-
поверхностный слой вследствие наличия сил трения передает дви-
движение нижележащим слоям. Океан предполагается бес-
бесконечным, его плотность и вязкость всюду постоянными.
Следует воспользоваться введенной в т. I на фиг. 49
системой координат ?, -»), С, ориентированной относительно
Задачи 425
вращающейся земли. При этом в уравнения Навье — Стокса
следует добавить силу Кориолиса1). В силу сделанных
предположений о неограниченности и однородности океана
Vg и г^, а также р не будет зависеть от ? и ч\\ компо-
компонентой Vx, можно пренебречь.
Исследовать стационарное состояние, возникающее
при давлении ветра, имеющего в координатах I, ч\ постоян-
постоянные направление и величину.
VI.2. Неустойчивость плоской поверхности раздела
между полями течений с различными скоростями. В на-
начале § 30 и 32 было указано, что поверхности разрыва
неустойчивы, а именно, что они под влиянием трения
разбиваются на последовательность вихрей. Эта неустой-
неустойчивость, однако, имеет место и при отсутствии трения.
Показать это в простейшем случае плоской поверхности
разрыва у = 0, разделяющей два течения одной и той же
жидкости.
При у > 0 жидкость течет с постоянной скоростью Ult
при у < 0 — с отличающейся от Ux постоянной скоро-
скоростью U2 (в обоих случаях в направлении х). Задача эта
двухмерна и остается таковой и в том случае, когда воз-
возмущение поверхности имеет форму синусоидального
цилиндра с образующими, параллельными оси z. Внеш-
Внешними силами здесь можно пренебречь.
Провести вычисления, воспользовавшись потенциалами
скоростей:
Основное движение Фх= —Uxx
Возмущение срх
Ф, = — U«x
У>0
У<0,
и теоремой Бернулли в виде A1.15), которая справедлива
для возмущения, зависящего от времени. Обсуждение
возникающих таким образом уравнений движения пока-
показывает, что основное движение^ для возмущения любой
длиной волны будет неустойчивым. Так как любое воз-
возмущение, согласно интегральной теореме Фурье, может
См. «Механика» (т. I), уравнения C0.2) или C0.5).
426 Задачи ,
быть разложено на синусоидальные компоненты, течение
будет в любом случае неустойчивым.
Согласно Гельмгольцу!), часто наблюдаемые в высо-
высоких слоях атмосферы перистые облака связаны с неустой-
неустойчивостью границы между двумя течениями воздуха в одном
и том же направлении с различными скоростями. Облака
возникают в результате конденсации водяного пара
в капельки тумана или кристаллики льда в местах пони-
пониженного давления. Перенос рассмотренной здесь неустой-
неустойчивости со случая несжимаемой на случай сжимаемой
жидкости допустим, так как все скорости здесь малы
по сравнению со скоростью звука (см. дополнение к § 13).
VI,3. Устойчивость горизонтальной поверхности воды
при различной силе ветра. С помощью вычислений, подоб-
подобных рассмотренным в предыдущей задаче, исследовать
устойчивость покоящейся поверхности жидкости под влия-
влиянием дующего вдоль нее ветра. При этом не следует
пренебрегать плотностью воздуха, как это делалось в гл. V,
несмотря на то, что отношение плотности воздуха к плот-
плотности воды равно 0,00129:1. Следует также принять
во внимание действие на поверхность воды силы тяжести,
К Г Л А В Е VII
VII. 1. Вычисление с помощью уравнений Лагранжа
формы поверхности жидкости во вращающемся барабане.
Решить с помощью уравнений Лагранжа задачу об опре-
определении формы свободной поверхности несжимаемой жидко-
жидкости в барабане, вращающемся с постоянной угловой ско-
скоростью. Как и прежде, ось барабана расположена вер-
вертикально.
VII.2. Переход от уравнений Эйлера к уравнениям
Лагранжа в одномерном сжимаемом случае. Получить
непосредственно из уравнений Эйлера и закона сохране-
сохранения массы уравнения гидродинамики в форме Лагранжа
в частном случае одномерного течения сжимаемой жидко-
жидкости, свободной от сил.
х) Гельмгольц, Об атмосферных движениях (лекции,
читанные в Берлинской академии в 1898 и 1899 гг.).
. Задачи 427
VII.3. Упрощенный вывод линейных дифференциальных
уравнений, по Адамару, для задачи об ударных волнах
Римана. Полученное в предыдущей задаче одномерное
уравнение Лагранжа позволяет, согласно Адамару1),
несколько упростить переход, к линейным дифференциаль-
дифференциальным уравнениям второго порядка, приведенным в § 37.
При этом следует предположить, что сжимаемая жидкость
в начальном состоянии имеет постоянную плотность,
а также воспользоваться преобразованием Лежандра2).
VII.4. Формула Стокса для вращающейся сферы. Иссле-
Исследовать вместо равномерного поступательного движения
сферы радиуса а (см. § 35) ее равномерное вращение.
Следует и в этом случае предполагать, что жидкость
несжимаема, а течение ползущее. Показать, что для поддер-
поддержания равномерного вращения с угловой скоростью ш тре-
требуется, внешний момент, указанный в C5.21): М 8
К Г Л А В Е VIII
VIII. 1. Изгиб балки на двух опорах под действием
сосредоточенной нагрузки. Балка длины 1 — а-\-Ъ концами А
и В свободно лежит на двух опорах равной высоты; на
расстоянии а от А она изгибается вертикальной силой Р.
Вычислить и изобразить ход срезывающего усилия и изги-
изгибающего момента вдоль балки и определить ее упругую
линию.
VIII.2. Колебания стержня, а) Вертикально подве-
подвешенный призматический стержень с жестко закреплен-
закрепленным верхним концом несет на нижнем конце массу М,
которая велика по сравнению с массой стержня т.
Система может совершать колебания в направлении оси
стержня (колебания растяжения — сжатия). Определить
круговую частоту колебаний. Для простоты можно пре-
пренебречь массой т по сравнению сМи упругостью тела М
по сравнению с упругостью стержня.
б) Описанная в «а» система может совершать, коле-
колебания вокруг оси стержня (крутильные колебания). При
'JHadamard J., Legons sur la propagation des endes,
Paris, 1903.
2) См. «Механика» (т. I) уравнение D2.8).
428 Задачи
определении круговой частоты можно не принимать
во внимание действующего в направлении оси стержня
веса М, так как он вызовет постояные во времени напря-
напряжения растяжения. Теперь разумно предположить, что
момент инерции в, соответствующий массе М, велик
по сравнению с моментом инерции стержня.
в) Наконец, рассмотреть горизонтальный стержень,
который либо на одном конце жестко закреплен, а на
другом конце нагружен массой М (как на фиг. 69), либо
(как в задаче VIII.1) поддерживается на обоих концах А
ж В ж нагружен массой М на расстоянии а от А (и соот-
соответственно Ъ от В); равновесие стержня нарушается
вертикальным возмущением. Определить и здесь круго-
круговую частоту колебаний, перпендикулярных к оси стержня
(колебаний изгиба), считая снова М > т.
VIII.3. Стержень, подвергнутый ударной нагрузке.
Масса М, приложенная к стержню, как в задаче VIII. 2, а,
действует не стационарно, а прикладывается к нему
в определенный момент времени t = 0. Скорость в момент
приложения равна г;0. Определить в общем случае макси-
максимальное смещение ?макс. массы М и максимальное напря-
напряжение Смаке, в концевом сечении стержня и показать,
в частности, что
а) для Vq = О значение амакс> вдвое больше, чем в ста-
статистическом случае, и
б) омакс. для больших v0 возрастает в соответствии с ки-
кинетической энергией М в момент приложения и зависит
только от объема стержня, а не от его отдельных размеров.
VIII.4. Добавление к задаче о кручении стержня эллип-
эллиптического сечения. Определить крутящий момент М
и угол закручивания ср? в случае эллиптического сечения
стержня путем проведения интегрирования в D2.43)
и сравнить возникающий при этом геометрический мно-
множитель с полярным моментом инерции эллипса.
VIII.5. Отражение плоской поперечной и плоской про-
продольной волн внутри упругого тела, ограниченного пло-
плоскостью. В качестве дополнения к § 45 показать, что
поперечная волна с колебаниями, перпендикулярными к пло-
¦ Указания к решению задач 429
скости падения, правильно отражается от плоской
поверхности, свободной от сил, без одновременного возник-
возникновения продольной волны; показать, что в случае пло-
плоской продольной волны, наоборот, кроме правильно отра-
отраженной продольной волны возникает поперечная волна
€ колебаниями в плоскости падения.
УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ
1.1. а) Следует взять частные производные z-компо-
ненты равенства
2(А-А0) = [Вг]
по у и ^-компоненты этого равенства по z и образовать
разность возникающих уравнений. Если пренебречь всеми
членами, исчезающими с г, то получится обычное диф-
дифференциальное представление х-компоненты от
В = rot А.
б) Убедиться, что опущенные при этом члены имеют вид
(г grad) Bx — х div В.
Это указывает на связь с общей формулой
rot [ab] = (b grad) a — (a grad) b + a div b — b div a,
которая выполняется для произвольных векторов а, Ь,
но только в декартовых координатах.
1.2. Согласно B.2),
-' У„ ~ ~ У„ ~'. л' "V « л
k i i
откуда можно вычислить
о -^ oxk о -^ о дА\ дАщ
dxi ^ dxi dxh ^ lk ^xh дхт dxi
Каждая из двух последних производных состоит из девяти
членов. При вычитании первой производной из второй
шесть членов попарно уничтожатся, а остающиеся две-
двенадцать членов могут быть попарно соединены. Каждая
компонента преобразованного ротора выразится при этом
430 Указания к решению задач
через три компоненты первоначального ротора с коэф-
коэффициентами, равными минорам схемы преобразования,
как в B.15). Это соответствует тому, что ротор имеет
характер аксиального вектора.
1.3. Искомые выражения можно получить из их опре-
определения в декартовых координатах при помощи соответ-
соответствующих ортогональных (но не аффинных) преобразо-
преобразований. Однако этот путь слишком длинен по сравнению
с непосредственным путем подстановки соответствующих
координатных систем в общие формулы B.24), B.25),
B.26), C.9а), C.96). Выпишем окончательные формулы,
которые сразу получаются при такой подстановке, так
как они нам понадобятся в дальнейшем. Выражения для
цилиндрических координат содержат также результаты
задач 1.4 и III.1; то же самое относится и к таблице для
сферических координат. Что касается действительного
значения используемых здесь символов ДА и (Agrad)A,
то мы еще раз сошлемся на выражения C.10а) и
A1.6).
Относительно знака ротора следует заметить, что три
полярные координаты, взятые в порядке г, ср, z и соот-
соответственно г, 9-, ср, должны образовать правовинтовую
систему. Только при этом условии будет законным при-
применение формул B.26). В случае сферических координат
это означает, что если, как обычно, отсчитывать 9- от
северного полюса на юг, то ср надо отсчитывать не с востока
на запад, как географическую долготу, а в обратном
направлении. Если мы будем отсчитывать ср в том же
' направлении, что и географическую долготу, то мы,
согласно уравнению B.16), должны будем изменить знак
у ротора, так как он является аксиальным вектором.
То же самое произойдет, если мы изменим порядок г, 9-, ср
на г, ср, 9-.
Цилиндрические полярные координаты
г, <р, z\ e?s2 = e?r2-J-r2 d
Указания к решению задач 4?Л
dz
, А \ дАг
rot,. А = ~ —
г д<р dz '
д дАг
dz дг
д
г a? J ^ dz \J dz J J ~
— 1-JL( dU\ 1 дЦ дЦ _
~ г дг \ дг ) ¦" Тз" 5«р2 ' dz2 ~
дЧТ 1 дЦ 1 аС/
5/-2 + "г 5г "г" га ду2 *
Г (A, grad^)--^-,
(A, grad^z),
Ar 2
ДА.
Сферические полярные координаты
г, Ъ, ср, ds2 = dr2 + r2 e$2-f r2 sin2
4S2 Указания к решению задач
rote. A = —7
rsin& dy r дг '
А.ГЛ
5ф V. sin
sin & р ) J V /
/. .gt/V 1 / g2t7 \ _ дЮ 2 д?7 1
X ^sm it ^& j -\- r2 gin2 & ^ d^ j — dr2 -t- r ar -f- r2
\d J ^ r2
\dr J ^ r2 ^ 5& у ^ г2 sin2 &
(Agrad)A =
AAr—
ЛА - 2 г ал Л ctg& дл9 i
л* "Г Г2 |_ 5& 2 sin2 & sin & <9<р J '
1.4. Согласно предыдущим формулам, г-компонента
rotrrotA равна
* А 13 * А 5 . А
rotrrotA = —-r— rot, A—^-rotn A =
далее, согласно той же таблице,
grad divA-^+^-A , Л
Указания к региению задач 433
Отсюда следует, если после вычитания собрать члены,
дающие ААГ, и обозначить их точками, что
griadrdivA-rotrrot A= ... _А._ JL_jl.
Точно так же можно найти
1.5. Из двух решений U1 и U2 этой задачи образуем
разность U = U2 — Ux, для которой LU внутри области,
а также dU/дп на ее границе обратятся в нуль. Из тео-
теоремы Грина C.16а), как и в случае первой граничной
задачи, следует U = const, откуда U2 — Ux -f const.
1.6. Пусть уравнение эллипсоида в прямоугольной
системе координат хх, хг, х3, повернутой произвольным
образом относительно главных осей эллипсоида а, Ь, с,
имеет вид:
2'?гЛ%=1- A)
а) 8 = 6'. Для х2 = аг3 = О мы получим eu = l/^i, где
^ — полуось эллипсоида в направлении хх. Приписывая
соответствующий смысл величинам х2 и х3, получим
Сумма обратных квадратов трех взаимно перпенди-
перпендикулярных полуосей не зависит от положения образуемого
ими триэдра] в частности, она равна
~ а* ~т~ б2 "г с2 *
б) А = А'. Для х3 =:0 мы получим уравнение эллипти-
эллиптического сечения
?11а'1 ~Т ^?12а'1'':;2 ~Т" S22*J:;2 == *
Его главные оси определяются корнями Хх, Х2 уравнения
?~К Iй х1-о. C)
е21» е22 •
28 А. Зоммерфельд
434 Указания к решению задач
а именно, они равны 1/|/Хх и 1/[/Х2, что можно дока-
доказать обычными методами аналитической геометрии. Пло-
Площадь этого эллипса равна
В силу C) и D) настоящей задачи, имеем
— _ 2 —
— е11?22 ?12 —
При соответственном определении Fx и F2 из опреде-
определения Д следует
(^^ i) E)
Сумма обратных квадратов площадей эллипсов, которые
образованы тремя взаимно перпендикулярными плоско-
плоскостями, пересекающимися в центре, не зависит от их
положения и, в частности, равна
в) D = D'. Эллипсоид возникает из сферы единичного
радиуса в результате трех взаимно перпендикулярных
растяжений в а, бис раз. При этом получается извест-
известная формула для объема эллипсоида
I —-^-abc. F)
В главных осях определитель D.7) сводится к произве-
произведению диагональных членов I/a2, 1/62, 1/с2, так что
G)
9/2 '
При ортогональном преобразовании D', согласно D.7),
переходит в D (закон умножения определителей). Поэтому
имеем также
Инвариантность D, таким образом, означает не что
иное, как независимость объема I от системы координат.
Указания к решению задач , 435
1.7. Из F = XF0 следует
rot F = X rot Fc + [grad X, Fo].
Умножая это равенство скалярно на Fa и применяя фор-
формулу
(А[ВС]) = (В[СА]),
получим уравнение, которое непосредственно удовлетво-
удовлетворится, если предположить, что Fo _L rot Fo.
Далее можно показать, что если U — потенциал,
соответствующий картине, силовых линий Fo и множи-
множителю X, так что XF0 = grad?7, и если V — произвольная
функция от U, то V также будет являться потенциалом;
при этом соответствующий множитель X' будет равен
" dU '
Таким образом, задача об определении потенциала и соот-
соответствующего скалярного множителя для картины сило-
силовых линий имеет бесконечное множество решений,
II. 1. а) Воспользовавшись значениями (см. стр. 126)
р0 = 1033 х 981 г/см • сек2, Ро == 0,00129 г/см3,
получим из формулы G.96) значения h для /г =1,4;
1,2 и 1, приведенные уже на стр. 69. Последнее значение
согласуется с тем, что показательная функция в G.14)
обращается в нуль для z=oo.
В адиабатическом случае (п = 1,4) для высоты h = 28 км
и линейного убывания .температуры с высотой [равен-
[равенство G.11)] получается, что если на поверхности земли
температура 0° С = 273° К, то на каждые 100 м темпера-
температура падает примерно на 1°. Такой «адиабатический
закон падения температуры в сухом воздухе» наблюдается
также в восходящих частях фенов между двумя точками
одной и той же линии тока, отстоящими друг от друга
по высоте на 100 м\ в вертикальном направлении, т. е.
при переходе к другим линиям тока, получается при-
примерно вдвое меньшее значение (соответственно среднему
температурному градиенту атмосферы).
28*
436 Указания к решению задач
б) Подставим теперь во второе уравнение G.7)
где G — гравитационная постоянная, М — масса земли»
г — расстояние от центра земли. Постоянная в G.7) опре-
определяется из условия, что на поверхности земли (r = i?)
опять должно быть р = р0. При этом мы получим из G.6а)
и G.7) для любого п
На поверхности земли будет
Ж"* B)
Для границы атмосферы r = R-\-h и /? = 0, так что,
согласно A) настоящей задачи,
п
что совпадает с G.96) для h < R.
Это совпадение, однако, не имеет места в пределе
п—»1, т. е. в изотермическом случае. В этом случае
из соотношений A) и B) в результате предельного пере-
перехода следует
р = рое роМ г) (г>Д). D)
Теперь уже не существует границы атмосферы, опреде-
определяемой из условия р — 0, так как при г—> со давление
стремится к конечному (хотя и очень малому) значению
Ро. р
р = Рое ро . E)
Этот парадоксальный результат указывает на то, что
предположение об изотермичности атмосферы недопустимо.
Укаёания к решению задач 437
II.2. Парциальные давления 02 и N2 в покоящемся
воздухе (w — 0), а также на оси (г = 0) равны
_ 21 _ 79 ...
Poi~ Ро|об> Рог~~ А) |об9 { '
ро = 1033x981 г/см-сек2 (как в И. 1).
Парциальные давления на периферии г, согласно G.18),
равны
Pi = Poie2 RT ...,^ = 32,
— B)
«r ..., 14 = 28.
Разность давлений задана равной 40 см вод. ст., т. е.
Pi + Рг — Ро = 40 X 981 г/см-сек2. Поэтому, согласно A)
и B) настоящей задачи,
Ввиду малой величины эффекта (на что указывалось еще
в § 7) мы можем в первом (и достаточно хорошем) при-
приближении ограничиться рассмотрением одних только
линейных членов обеих экспоненциальных функций. При
значениях i? = 8,31-107 эрг/град и, например, jT = 273°K
мы получим, сократив на g = 981 см/сек2:'
40=10,33B1.32 + 79-28) 2.8™?.т ¦
Отсюда
ш = 260 сек, и число оборотов п = 30 ш/тс = 2480 об/мин.
Отношение давлений и соответственно плотностей на
периферии будет равно
2
Pi Pi _ft>i 2 RT __21 1,043
/>a ~ P2 ~ fo2 . - t*2 ^2to2 ~ 79 • 1,038 '
¦*" 2 i?T
т. е. только на 0,5% больше, чем на оси. Таким обра-
образом, даже при увеличении числа оборотов центрифуги-
центрифугирование не может служить эффективным средством для
разделения смеси газов или изотопов. Даже ультра-
438 Указания к решению задач
центрифуга (см. стр. 73) разделяет только коллоидальные
частицы или гигантские молекулы белковых смесей.
II.3. а) Воспользовавшись уравнениями A0.11) и
A0.17), можно получить
и=?&*-У*)> ит = Ш = Л^^ П = Л/ = 3^, A)
т. е. параболический профиль скоростей, как на фиг. 14;
перепад давления оказывается пропорциональным первой
степени средней скорости течения и обратно пропорцио-
пропорциональным квадрату полуширины сечения потока [что
соответствует радиусу в формуле A0.17)]. На единицу
площади верхней и нижней пластинок жидкость будет
действовать в направлении течения с силой, равной
б) Компонента силы тяжести в направлении оси х
(фиг. 196) равна
(компонента, перпендикулярная к дну*2/= —h, нас здесь
не интересует). На свободной поверхности всюду имеется
атмосферное давление р = 0; перепада давления в напра-
направлении х, таким образом, не существует, но он и не
требуется, так как вместо него действует сила, опреде-
определяемая соотношением B). Поэтому дифференциальное урав-
уравнение A0.8а) переходит в
Условие на поверхности требует, однако, не только
р = 0, но и
ди г,
Это условие совпадает с условием в II. 3,а, где в силу
симметричности течения относительно оси х оно выпол-
выполняется само собой. Поэтому профиль скоростей будет
представлять собой нижнюю половину профиля случая
II. 3, а с соответственно измененным значением А.
Указания к решению задач 439
II.4. Будем исходить из формул, приведенных в ука-
указании к задаче 1.3 для цилиндрических полярных коорди-
координат, и положим v = vv, vr = vz = 0.
Условие несжимаемости
1 dv 4- — О
Г Of
требует, чтобы v не зависело от <р, так что v = v(r).
То же самое относится и к давлению р.
Формально вычисленное выражение для Аг; было бы
равно
d*v I dv .
dr* ~i~ r dr'
однако, согласно тем же формулам на стр. 431, надо ввести
поправку, в результате чего получится дифференциаль-
дифференциальное уравнение
d2v , 1 dv v г.
(давление, как и при прямолинейном куэттовском тече-
течении, постоянно). Общее решение составляется из част-
частных интегралов v = r и v = l/r. Постоянные интегриро-
интегрирования определяются из граничных условий
v = 0 при r = ri} v = U при r — ra.
Полученное, таким образом решение
при предельном переходе ra = ri-\-h, r^ri-\-y, ri —> со
совпадает с решением A6.14) для прямолинейного течения.
Моменты, действующие на наружную и внутреннюю
цилиндрическую поверхности, равны
Га—ri Га — ri
Их разность, отнесенная к единице поверхности внеш-
внешнего цилиндра, дает пару сил pU, которая равна паре,
действующей в случае прямолинейного куэттовского
440 Указания к решению задач
течения на наружную и внутреннюю пластинки (сила
ll/h, плечо /гI).
П.5. Ход решения этой задачи довольно утомителен.
Мы точно наметим его отдельные этапы, предоставляя
читателю самому связать их друг с другом. Задача пред-
представляет собой типичный пример применения основных
уравнений упругого равновесия.
Пусть направление силы Р совпадает с осью z, а точка
ее приложения — с началом цилиндрической системы
координат г, ср, z. Компоненты вектора смещения в на-
направлении этих координат равны
Объемное расширение в в этих координатах (см. формулы
к задаче 1.3) в силу симметрии задачи относительно
оси z запишется в виде
е=4!<п>>+|. A)
а) В качестве дифференциального уравнения для в
из (9.18) можно найти, как это было сделано в A4.2),
ДВ = О. B)
Решениями, обладающими соответствующей симметрией,
являются
1 Я 1 Я2 4
?) х _ L • R2 r2i72 / Ц\
® ~ ~R > dz~R ' dz* R ' ' ¦ • ' П ~ Г Т * {*)
(ср. стр. 310). Как и ранее, мы выберем из них второе
и положим
б) Дифференциальное уравнение для декартовой ком-
компоненты С, согласно (9.18) и формулам к задаче 1.3, имеет
вид
г) Здесь, повидимому, имеет место недоразумение, так как
моменты Ма и Mi должны быть одинаковыми по величине.—
Прим. перев.
Указания к решению задач 441
Его частным решением будет
2*
Общее решение получается в результате суперпозиции
решений вида C). Выбирая первое из них, напишем
^ ~~ R [I 2 R3 ' К }
в) Дифференциальное уравнение для р проще всего
получить из выражения A):
Отсюда мы можем получить
в 1+М±4«'*« (9)
dr-R l [l 2 dr R3 v '
Интегрирование дает
где /B) — постоянная интегрирования. Для ее определе-
определения служит условие гр = 0 при г = 0 и всех значениях
2> 0; так как в этом случае R = z, мы получим
В результате из A0) следует
г) Граничными условиями для z = Q и г > 0 являются
azr = 0, aztf = 0, ozz = 0. A2)
Согласно первому условию,
Второе условие удовлетворяется само собой из сообра-
соображений симметрии, причем не только на граничной пло-
442 Указания к решению задач
скости z = 0, но и во всем упругом теле (см. ниже пункт «е»).
Так как 0 = 0, третье условие для z = 0 и г > О можно
записать в упрощенном виде
и в силу G) полученное условие также всюду удовле-
удовлетворяется. Согласно G) и A1), мы можем в A3) для
z = 0 подставить величины
дг ~~ г2 ' dz~ V "^ и- у г2 '
после чего получим
д) Наше состояние деформации, таким образом, опи-
описывается выражениями
aAL г А
В?) '
к которым следует добавить
! ^. A6)
Теперь остается только связать постоянную интегрирова-
интегрирования А с внешней силой Р. Если мы рассечем тело на
некоторой глубине z плоскостью z = z0, то мы, очевидно,
должны потребовать
P
г=0
Так как
оо
=—2tz \ azzrdr для z = z0. A7)
1
3z3'
С rdr_ 1_
r=0 r=0
мы из A7) и A6) получим
A8)
Указания к решению задач 443
е) Из трех касательных напряжений огф, a9z, azr оба
первых, очевидно, обращаются в нуль во всем объеме
упругого тела. Отсюда следует, что нормальное напря-
напряжение а<р<р в любой точке сечения <р = const является
главным напряжением. Его называют кольцевым напря-
напряжением. Соответствующие «траектории напряжения»
являются окружностями, описанными вокруг направле-
направления Р. В каждом бесконечно тонком кольце постоянного
сечения, расположенном вокруг такой окружности, дей-
действует определенное напряжение оф<р, меняющееся от
кольца к кольцу. Подобные кольцевые напряжения воз-
возникают в трубах и паровых котлах, подверженных дей-
действию внутреннего давления; величина этих кольцевых
напряжений определяет, в конечном счете, прочность
этих конструкций. В нашем случае внешняя сила Р
действует на каждое кольцо подобно такому внутрен-
внутреннему давлению. Так как при этом радиус каждого
кольца меняется на р, изменение его длины равно 2ир,
а деформация — 2irp/2it/' = p/r. Поэтому имеют место соот-
нощения '
Т ^^ A9)
и в- силу A5)
Если числитель и знаменатель в последнем члене правой
части умножить на r2-=R2—z2, то, складывая с первым
членом, получим
^^) B0)
На первый взгляд кажется, что это выражение при г —О
обращается в бесконечность, однако это не так, по-
поскольку при этом обращается в нуль и множитель
Справедливость частных решений, выбранных в D)
и G), подтверждается тем, что они удовлетворяют всем
444 Уки*&»шя к решению задач
граничным условием и всем условиям непрерывности
нашей задачи. К граничным условиям относится также
исчезновение напряжений и смещений на бесконечности,
которое непосредственно видно из выражений A5), A6)
и B0).
Физически неприемлемое предположение "о сосредото-
сосредоточении нагрузки в одной точке значительно облегчает
математическое решение задачи. Общий случай нагрузки,
каким-то образом распределенной по заданной поверх-
поверхности, может быть легко решен с помощью интегриро-
интегрирования наших предыдущих формул.
Буссинеск опубликовал свое решение в 1879 г. и дал
его полное рассмотрение в своей книге «Приложения
теории прямого, обратного и логарифмического потен-
потенциала» г).
III. \. Неправильное применение оператора (vgrad)
привело бы к следующему выражению:
d)i;r = rr-^ + -f-^ + t;z-^. A)
Вместо этого A1.6) приводит к
dvr , dvv , dvz . , .
Если использовать выражения для rot? А и rotz А из
формул к задаче 1.3 и вычеркнуть при этом две пары
взаимно уничтожающихся членов, то это даст
ft JV^. + Л*_.1. B)
г ду z dz r v '
дг г ду z dz
Последний член, отсутствующий в A), представляет собой
центростремительное ускорение или, будучи умножен
на плотность р,—центробежную силу в единице объема,
взятую с обратным знаком.
*) Boussinesq, Applications des Potentials directs, inver-
inverses, logarithmiques, Paris, 1885.
Указания к решению задач 445
Соответствующее вычисление для ср-компоненты
(vgrad)v приводит к следующему выражению для до-
дополнительного члена:
где со означает угловую скорость, вектор которой на-
направлен вдоль оси z, соответствующую скорости vv.
В таком случае vru> = [covjq, представляет собой половину
кориолисова ускорения1). Наконец, можно убедить-
убедиться, что при вычислении z-компоненты (vgrad)v с по-
помощью A1.6) не возникает никакого дополнительного
члена. Все эти результаты приведены в формулах к задаче
1.3 для цилиндрических полярных координат; на сле-
следующей странице приведены также соответствующие
результаты для сферических полярных координат.
III. 2. а) Положим
где А—безразмерная величина, а а, р, f подлежат опре-
определению. Если сюда подставить размерности р, v и Н/1,
то получится следующее уравнение для размерностей:
г • см~2 • сек~2 = г« • См
Сравнивая показатели, получим а—1, [3 = 2 — п и
1 = п — 3. Таким образом,
б) Если в предыдущее равенство подставить значения
S и R из A6.9). и A6.8), то получим
П . I Г va \§
Для того чтобы это соотношение было эквивалентно
исходному уравнению нашей задачи, v должно входить
в него в степени п; поэтому надо положить 8 = п — 2,
и, следовательно,
H = lp-v2Rn~2.
r a
См. «Механика» (т. I), уравнение B9.4а).
446 Указания к решению задач
в) Для п — 1,75 (Гаген) предыдущее уравнение дает
что совпадает с первой формой уравнения Блазиуса
A6.13).
III. 3. Пусть виртуальное смещение жидкой массы
состоит в том, что элемент dF ее поверхности смещается
в направлении нормали на Ьп. Так как весь объем
сохраняется постоянным, то должны наблюдаться как
положительные, так и отрицательные смещения Ьп.
Виртуальная работа будет складываться из работы ка-
капиллярных и внешних сил. Первая получится из
A7.10а) в результате умножения на Ьп и интегрирования
по dF, последняя равна \ UbndF, если U—потенциаль-
U—потенциальная энергия единицы объема.
В силу постоянства всего объема возникает допол-
дополнительное условие
у»
A).
Его можно учесть, вводя множитель Лагранжа X.
Так как Ьп может быть произвольным, то можно
получить уравнение
= 0. B)
Если здесь заменить среднюю кривизну на ее выраже-
выражение через первые и вторые частные производные от ко-
координат поверхности жидкости, то B) будет представлять
собой дифференциальное уравнение в частных производ-
производных для определения формы этой поверхности. При этом
следует потребовать, чтобы поверхность проходила через
заданную точку, где множитель X определен (ср. следую-
следующую задачу).
III. 4. Высота подъема в капиллярах. Выберем в ка-
качестве оси z ось капилляра, расположенную вертикально,
Указания к решению задач 44?
причем будем отсчитывать z вверх от плоской поверх-
поверхности жидкости снаружи капилляра. Тогда
U = pgz. A)
Для смачивающей жидкости, которую мы рассмотрим
сначала, радиус сферы надо считать отрицательным, так
как поверхность вогнутая. Уравнение B) предыдущей
задачи перейдет тогда в
-T-|-+pgz + X = O. B)
Для свободной поверхности снаружи капилляра z —О,
R = co, так что Х = 0. С помощью краевого угла 9- ра-
радиус сферы можно выразить через радиус г капилляра
Если под h понимать среднее значение z для мениска
в капилляре, то из B) и C) следует выражение для
высоты подъема
Л = —-cosfl. D)
Для смачивающей жидкости можно считать, что
cosft = l. Для несмачивающей жидкости R следует счи-
считать положительным, в результате чего в правой части
D) появится знак минус и вместо подъема будем иметь
опускание.
IV.1. Из A9.10а) и A9.106) можно вычислить
z = x-\- iy как функцию р + гср и посредством дифферен-
дифференцирования выразить dx-\-idy через dp-\-idy. Если мы
напишем выражение для модулей обеих частей этого
выражения, то получим уравнение A) задачи.
То, что здесь множители при dp2 и ricp2, которые мы
•в B.22) обозначили через g\ и g\, равны друг другу,
означает, что плоскость x-\-iy делится соседними кри-
кривыми р = const и ср = const на бесконечно малые квадраты;
биполярные координаты «изометричны» в том смысле,
как и на стр. 175. (Заметим, что то же самое получает-
получается в случае обычных полярных координат, если вместо
i подставить z = e^+*?> т. е. р = 1пг!)
448 Указания к решению задач
При образовании оператора Д следует, конечно,
специализировать трехмерную схему C.96 )для случая двух
координат рг = р, р2 = ?» для чего надо положить в C.96).
В то время как в уравнении потенциала ДG —0 множи-
множитель ljg2 несущественен, в уравнении колебаний он
играет сущетвенную роль. Это уравнение получается из
A7.8) в случае периодической зависимости от времени
U i?t и имеет вид
CM* . С I* . у t\ о f\ у ш
dp2 5ф2 i о » ^
Если допустить слраведливость уравнения B) настоящей
задачи, то, деля на /х/2 и дифференцируя еще раз по р
или ср, мы получим противоречие.
IV.2. Как было указано в этой задаче, соотношение
A9.11) дает
Для произвольной функции /(р, <р) от биполярных коор-
координат р и ср имеем
g ар S аф
При / = ср отсюда, в частности, следует: г^ = 0, vlf=\lg,
что и упоминалось в задаче. Если . ^4 = (х/тг, равенство
A9.8а) даст
Это выражение следует сравнить со значением, по-
получаемым из A9.14):
B)
Вектор 9i/ri имеет длину 1/г1 и направлен перпендику-
перпендикулярно к радиус-вектору, проведенному из точки z= -\-c
в рассматриваемую точку; то же можно сказать и о
Указания к решению задач 449 ¦
векторе у2!г2- Поэтому оба вектора расположены под
углом <p = (Pi — ?'г ДРУГ к ДРУГУ- Их векторное сложение
дает
1 _1_ i 2 _
й I 5 COS ф —
= 1/ J/^ch p — cos ср.
Таким образом, выражения A) и B) совпадут, если
будет показано, что
A j/chp-cos? =
В справедливости этого можно убедиться, применив
теорему Пифагора к треугольнику, вершины которого
лежат в точках z — ± с и в рассматриваемой точке.
IV.3. Из определения эллиптических координат
в A9.15) следует (аналогично задаче IV. 1)
ds2 = g2 {d? + dtf), g = ~
у 2
Уравнение колебаний мембраны поэтому будет иметь вид
(соответственно IV. 1, но с измененным значением g)
?%* = 0. A)
Положив
после деления, дифференциального уравнения A) на
получим
L + ^ch26=f + ^coS21) = X. B)
Величина X представляет собой «параметр разделения»;
независимость его от % и ч\ следует из B) в результате
дифференцирования по -ц или ?. Дифференциальное урав-
уравнение в частных производных B) может быть поэтому
29 А. Зоммерфельд
450 Указания к решению задач
разделено на два обыкновенных дифференциальных урав-
уравнения:
^) ( ). C)
Их решения называются «функциями эллиптического
цилиндра» или функциями Матье.
IV.4a. Кольцевые координаты были впервые введены
Риманом в его посмертной работе «О потенциале коль-
кольца» *). Назовем их р, ср, ф и положим
0<Р<оо, 0<ср<2ти, 0<ф<2ти. A)
Значение р и ср следует из фиг. 26, причем вслед-
вследствие ограничения 0 <; р < со надо рассматривать только
правую половину этой фигуры. При этом ф означает
угол поворота в пространстве вокруг оси р = 0, а поверх-
поверхности ф = const представляют собой полуплоскости, про-
проходящие через эту ось. Из окружностей р = const при
вращении вокруг р = 0 возникают кольцевые (тороидаль-
(тороидальные) поверхности с круговым сечением, а из дуг окруж-
окружностей ср = const возникают шаровые сегменты.
Если комплексную переменную z, введенную в A9.10а),
обозначить теперь через z = x + iy, то из A9.10а) и
A9.106) получим
=___p_ csiny Bч
chp—coscp ' и chp—cos 9
Если ввести пространственные декартовы координаты ж,
у, z так, чтобы ось z совпадала с р==0, а начало —
с центром фиг. 26, то при уже описанном ф-повороте
переменные х, у перейдут в
ж = жсо8ф, у = xsinty, z = y. C)
Отсюда в результате дифференцирования следует (ср.
задачу IV. 1)
ds2 = dx2 + dy2 + dz2 = g2 (dp2 + dy2) + g\ йф2, D)
. с — cshp ,«
8 = 8i = §2= chp —cos <f * g3~ ~x== ^J
R i e m a n n В., Ges. Werke, XXIV, S. 431.
Указания к решению аадач 451
Согласно C.96), будем иметь
ЛГ7-_ 1 \ д
Если положить
U— Ychp — cos<pF(p, <p)eitn*f G)
то после довольно долгих преобразований мы получим
= (ch р - cos ту/. {-^- + cth p -^ +
Если мы имеем дело с уравнением потенциала Ш = О,
то решение соответствующего дифференциального урав-
уравнения для V может быть разделено в виде
V = f{9)e*«*, (9)
где / определяется из дифференциального уравнения
/==0. A0)
Решениями этого дифференциального уравнения являют-
являются обобщенные сферические функции.
В случае волнового уравнения AC/ -f- k4J = 0 мы для
V, определяемого из G), получим уравнение
dW , ., dV. dW
+ Cth +
др2
^^ *2'2 > = 0, (H)
(chp—СО8ф)б/
которое не может быть, решено с помощью выражения
вида Л(р)/2(ср.).
IV.46. Если фиг. 26 вращать не вокруг оси р = 0,
а вокруг оси ср = 0, то из окружностей р = const возник-
возникнут сферы, а из дуг <р = const —«веретена», причем это
название, собственно говоря, подходит лишь для поверхно-
поверхностей с <р < тг/2. Третьей координатой теперь служит угол
29*
452 Указания к решению задач
поворота ф вокруг теперешней оси вращения, так что
поверхности ф = const опять будут полуплоскостями.
Однако в противоположность кольцевым координатам
теперь будут справедливы неравенства
-со<р<4-оо, 0<<p<ir, 0<ф<2т:. Aа)
В пространственной системе координат х, у, z, ось z
которой совпадает с теперешней осью вращения <р = 0,
а начало — с центром фиг. 26, будем иметь вместо C)
[с тем же самым смыслом х, у, что и в B)]
x = ycosty, y = ys\nty, z.— x. (За)
Отсюда в результате дифференцирования получается то
же самое выражение для элемента длины с тем же
самым значением g, что и в D), однако значение ^3
изменится:
о -Z . _ сsin V i^~\
Выражение F) для АС/ остается справедливым. Если
воспользоваться выражением G) и теперешним значе-
значением g3, то отсюда будет следовать
= (ch р - cos vfl* { 4^- + ctg f -?¦ +
Если мы имеем дело с уравнением потенциала ДЕ/ = О,
то решение соответствующего дифференциального урав-
уравнения для V разделится, если положить
P, (9a)
где / удовлетворяет уравнению
^) = O. A0а)
Это уравнение, как и A0), интегрируется в обобщенных
сферических функциях.
Указания к решению задач 453
В случае волнового уравнения AC/-\-№U — Q здесь
также невозможно разделение.
V.I. Кинетическая энергия, подлежащая вычисле-
вычислению, определяется выражением
Л со
г- р L, f jf /дФ\2 , f дФ V i / ЭФ VI ,,ч
Вт.=\ \dx\dy\ ^) + (^) +Ы)\- (!)
О т>)
Если сюда подставить Ф из B6.6), то почти сразу получим
со "¦**
Янин. = рккА* \ е~2кУ dy=.t; *A2e~2h\ B)
что совпадает с выражением B6.7а) для Епот.г так как
амплитуда А, входящая в -ц [ср. B6.6)], считается бес-
бесконечно малой, и поэтому e~2hi> можно заменить на 1.
Так как в покоящейся жидкости ЕИИВ. = 0, выражение
B) одновременно означает разность кинетических энер-
энергий при волновом движении и состоянии покоя в рас-
рассматриваемом объеме.
Во второй части задачи следует положить
Ф — С cos (кх — utf) ch к (h — у)
и с учетом B4.3) и B4.S) .
7) = —— sin (кх — Ы) ch kh,
о
откуда получим-
S = ¦?- т:С2 (sh 2Л/г f 2ЛЛ), ^кин. = ^пот. = ± ^С2 sh 2^.
VI.1. Уравнения Навье — Стокса A0.8а) и A0.86), если
к ним добавить кориолисову силу, примут вид
= p. A)
Для"" компонент % и -q в северно^ полушарии следует
с принятыми в задаче упрощениями (i>e, v^ и р не зависят
454 Указания к решению задач
от ? и т), F — сила тяжести, направленная перпендику-
перпендикулярно к ? и т))
2ш sin <рг;ч + v -^- = О,
"\ „ B)
— 2о) sin <рг;5 + v -^ = О,
где <р — географическая широта; С-компонента A) ввиду
г;с = 0 дает просто закон возрастания гидростатического
давления с глубиной
dp
условие несжимаемости при наших предположениях удо-
удовлетворяется само собой. .Оба уравнения B) можно для
удобства объединить в одном комплексном выражении,
подобно тому как это делается в теории маятника Фуко1).
С помощью обозначения
V = v^ + iv^
получим
™L-2i\W = 0, X^sincp. C)
Интегрирование дает, если С считать положительным
вверх (т. е. в океане С отрицательно),
F = ile* (*_+*) с. D)
Постоянная Л определяется из возмущения, вызываемого
давлением ветра. Его компоненты должны быть равны
по величине вязким давлениям р^г р^ на поверхности
С = 0 и направлены противоположно им. Их комплексное
представление (v^ опять пренебрегаем!) имеет вид
vs ¦ d%\ dV
Из D) для С = 0 следует
-Р0 = ^ХA-М). E)
Это выражение одновременно дает комплексную форму
давления ветра на поверхности, величину и направление
х) См. «Механика» (т. I), уравнения C1.5) и далее.
, Указания к решению задач 455
которого можно считать заданными. Если положить
о I ol > о ylif*' '
то, подставив в D) значение Л из E), получим
cos (\z + -J-
Из F) можно вывести следующее заключение: поверх-
поверхностное дрейфовое течение повернуто относительно напра-
направления ветра на —45°. Далее, скорость v с возраста-
возрастанием глубины убывает по величине и направление- ее из-
изменяется так, что на «глубине трения Экмана», равной
7
I/
Г
— Sin
V
течение будет направлено противоположно течению на
поверхности. На этой глубине v в е~те раз меньше v0.
В работе Экмана «Динамические законы морских те-
течений» х) дается обоснование введенных упрощающих пред-
предположений и содержится более детальное рассмотрение
вопроса. Наличие турбулентности может быть учтено
введением повышенной вязкости, т. е. выбором для коэф-
коэффициента вязкости р. более высокого, чем обычно,
значения.
VI.2. Из уравнения A1.15) могут быть получены сле-
следующие уравнения для возмущенных потенциалов ФЛ -{- <рх
и Ф2 -+- ср2, если пренебречь высшими степенями <рг и ср2
и объединить постоянные члены 11Ц2 и Щ/2 уравнения
Бернулли с постоянными интегрирования Сг и С2:
at +Ul dx
дх
x) Cm. Verhandlungen des Internationalen Mathematiker-Kong-
ressen in Heidelberg.
/
456 Указания к решению задач !
отсюда следует, ввиду равенства обоих давлений при
0
A)
(где с = С1 — С2); в силу предположения о периодичности
срх и <р2 следует положить с = 0.
Синусоидальное возмущение поверхности удобнее
всего записать в форме
т] = Aelhx, к = y , А — функция от t. B)
Скорость частицы на поверхности, с одной стороны, равна
It = ~дГ + "i ~дх '
а с другой стороны,
ду •
Оба эти выражения справедливы с точностью до членов
более высокого порядка. Отсюда получим
А]
й ' vi ^ ду
и соответственно
C)
dt 2 дх ду ^ '
В силу того что задача двухмерна,
y2 = A2eih(x~iy\ * ! функции от t. E)
При такой зависимости будет удовлетворено условие не-
несжимаемости, а также условие конечности значений
срх при у = + со и ср2 при г/ = — со. Чтобы задача имела
решение, необходимо, чтобы к в E) имело то же значе-
значение, что и в B),
Указания к решению задач
457
Если подставить B) и E) в уравнения A), C) и D),
мы получим дифферентмальные уравнения для ^4, Аг, А2:
dt
dA
dt
+ ikU
^ = ^r + iW2A2,
= -kA2.
Так как эти уравнени линейны, выражения вида
F)
(8)
будут являться их pei «ниями. Можно вычислить аг и а2
из G) и (8) и подст! ить их значения в F). При этом
мы получим квадрать а уравнение для а. Его корнями
будут
Во всех случаях, когда 1/1ф U2, один из двух корней
будет иметь положительную действительную часть, что
соответствует монотонному возрастанию амплитуд А, А1У
А2. Таким образом, для любого волнового числа к будут
иметься такие синусоидальные возмущения, которые воз-
возрастают со временем, т. е. являются неустойчивыми.
VI.3. В уравнении A) предыдущей задачи мы заменим
для первой среды (воздух) Ux на U (скорость ветра),
а для второй среды (вода) U2 на 0 (покоящаяся вода).
Действие силы тяжести будет равно — g-ц {-ц возрастает
при отсчете вверх). Введем также две плотности рх и р2
и их отношение s = pjp2. Постоянную с, как и в 'преды-
'предыдущей задаче, мы будем считать равной нулю. Тогда
вместо уравнения A) получим
Выражения B) и E) сохраняют свой вид. То же отно-
относится и к уравнениям C) и D), причем следует принять
во внимание теперешние значения Ux и U2. Дифферен-
Дифференциальные уравнения для А, Ах, А2, соответствующие
458 Указания к решению задач ',
уравнениям F) —(8), позволяют опять выразить аг, а2
через а с помощью выражений (9), оставшихся неизмен-
неизменными. При этом для а получится квадратное уравнение
s (a + iWf + а2 = - gk (I - s). A0a)
Один из его двух корней имеет положительную действи-
действительную часть, если
Но \fg\k, согласно B3.16), означает фазовую скорость V
волн в глубокой воде, если пренебречь инерцией воздуха
(в противном случае величина V лишь незначительно
уменьшится, что может быть показано соответствующим
развитием вычислений в § 23). Условие неустойчивости
A1а) поэтому можно записать в виде
1 —S2
Чтобы вызвать возмущение с длиной волны X, скорость
ветра U должна быть значительно больше фазовой ско-
скорости V, соответствующей этой длине волны. Плоская
поверхность воды будет для длины волны X устойчива,
если скорость ветра
V
и
Если, кроме силы тяжести, принять во внимание капил-
капиллярность (которая будет усилипать стабилизирующее
влияние силы тяжести!), то поверхность волны будет
абсолютно устойчивой, т. е. устойчивой для всех длин
волн при скорости ветра
U < 28PW; FMHH. = 23,2 см/сек.
Здесь FMHH, — вычисленное на стр." 233 значение V, соот-
соответствующее Хмин. = 1,73 см. Следовательно, ветер со ско-
скоростью, меньшей 28 х 23,2 см/сек ъ 6,5 м/сек (ветер силой
в 2 — 3 балла), не может возмутить первоначально глад-
гладкую поверхность. При этом предполагается полная одно-
однородность ветра (в действительности он, конечно, турбу-
турбулентен).
Указания к решению задач 459
VII. 1. Пусть а, Ь, с — координаты произвольной ча-
частицы жидкости в момент ? = 0; если ввести цилиндри-
цилиндрические координаты г, <р, z, то
A)
Так как вращение равномерно (угловая скорость to),
можно получить отсюда координаты в любой момент
времени t, заменяя <р на tp-^wt. Воспользовавшись A),
получим
х — a cos u)t — b sin Ы,
у = b cos iat + a s'm iat, B)
z — c.
Отсюда легко убедиться в том, что условие несжимае-
несжимаемости C4.3) выполнено и что уравнения Лагранжа C4.1),
куда в качестве единственной внешней силы входит сила
тяжести, перейдут в
д2х . , д2у , 1 др л /ОЧ
dt* g +P dc ~u*
Здесь, как и на фиг. 7, ось z считается направленной
вниз. Если в C) подставить выражения для ускорений,
следующие из B), то получим для р следующую систему
дифференциальных уравнений:
1 др о 1 др „I 1 др //ч
р да ' р дЬ ' р дс ° v '
Можно убедиться, что в результате интегрирования от-
отсюда получится выражение для р, которое в силу B)
совпадает с выражением F.10).
Поучительно также провести рассмотрение для сжи-
сжимаемого газа. Уравнение неразрывности будет тогда иметь
вид dpjdt = O, а уравнение движения P = g\
460 Указания к решению задач
откуда в силу G.18) следует уравнение G.19) (с точностью
до выбранного здесь обратным знака z).
VII.2. Будем исходить из одномерного уравнения
Эйлера A3.1) без внешних сил:
du 1 dp ,i,
dt р дх' ^ '
Введем в качестве независимых переменных t та. а. Пусть
а = х0 — начальная координата: рассматриваемого элемента
объема, а х— его координата в более поздний момент
времени. Масса, содержащаяся в этом элементе объема,
равна
дх
для t — 0: poda, для t > 0: pdx = 9~^ ^а-
Сохранение массы требует, чтобы
— = ' B)
Отсюда следует
~dt
что совпадает с уравнением C4.36).
Учитывая замечание, сделанное в § 34 о способе запи-
записи частных производных, положим в A)
дх du д2х ...
далее запишем:
др др да др / дх „.
дх да дх да I да ' * '
Подстановка D) и E) в A) дает
dt^ да р да *
что совпадает с C4.1) тогда и только тогда, когда принято
во внимание указанное в C4.3а) изменение для сжимаемой
жидкости.
Указания к решению задач 461
VII. 3. Если в начальный момент времени плотность р0
в сжимаемой жидкости постоянна, то дифференцируя
уравнение B) предыдущей задачи по независимой пере-
переменной а, получим
откуда следует
р да ~~ а) да2 ' ^'
где, согласно Адамару, принято сокращенное обозначение
Если, далее, следуя Риману, подставить уравнение со-
состояния в форме /> = <р(Р) и принять во внимание B),
то получим
р да р да ш да2 ' ^ '
Уравнение F) предыдущей задачи перейдет при этом в
где Q представляет собой функцию только от ш, так
как, согласно уравнению B) предыдущей задачи, р об-
обратно пропорционально ш. Это наводит на мысль ввести
в качестве независимой переменной величину ш. В каче-
качестве второй независимой переменной подходит
дх /Лч
и = 1н- F)
Таким образом, в силу C) и F) мы будем иметь
dx = (ada-\-udt. G)
Если одновременно в соответствии с преобразованием
Лежандра1) ввести зависимую переменную
z(и, u>) = ut — u>a — x(t, а) (8)
и образовать ее полный дифференциал, то получим
dz = tdu-\-adu. (9)
х) См. «Механика» (т. I), стр. 315.
462 Указания к решению задач
Из (8) и (9) следует
u
дЧ
Согласно E) и A0), таким образом, получим
в,«9юв. A2)
Отсюда, применяя известное правило преобразования,
мы получим
o»=»Q*u. A3)
Это уравнение в силу A1) представляет собой линейное
дифференциальное уравнение второго порядка относитель-
относительно z, коэффициент которого Q зависит только от неза-
независимой переменной ш. Выражая C) через переменную z,
получим
Q
Это уравнение было положено Адамаром в основу при
рассмотрении ударных волн Римана. Отличие этого урав-
уравнения от аналогичного уравнения C7.11) объясняется тем,
что значения зависимых и независимых переменных не
совпадают с принятыми в § 37.
VII.4. Введем сферические полярные координаты
г, 9-, ср. Будем считать, что г = 0 в центре сферы, & = 0
на оси равномерного вращения ф = ш. Предположим, что
окружающая сферу жидкость движется по окружностям
вокруг оси, в направлении возрастания ср, и покажем,
что такое простейшее предположение вполне допустимо.
Из компонент скорости vr, v$, v9 = v в этом случае обе
первые обратятся в нуль, и в силу предположенной не-
несжимаемости будет иметь место соотношение
в то время как dvjdb и dv/dr отличны от нуля. Будем
исходить из уравнений C5.6) и воспользуемся выраже-
Указания к решению задач 463
ниями, приведенными в указаниях к задаче 1.3:
rotr rot v = rot» rot v = 0, A)
i д * 0 (sin ft?) m
т-ш-^ж B)
Из C5.6) и A) мы прежде всего получим
Так как в силу симметрии задачи gradj? также равен
нулю, то
р — const, C)
и. мы получаем дифференциальное уравнение для v
дЧ 2 dv 1 /дЧ ¦ ~dv v
Если принять для v выражение v = Cf(r)g(b), то полу-
получим (X — параметр разделения)
Решением1) этого уравнения, которое обращается в нуль
на бесконечности и остается конечным для всех значе-
значений 0 < Ь < тс, будет
Для v при соответствующем выборе множителя С, кото*
рый до сих пор играл роль свободного параметра, мы
получим
а3 . G /GЧ
г; = ш — sin ft. G)
Так как на поверхности сферы г = а величина v должна
принимать заданное граничное значение v — u>a sin 9s, то
наше частное значение Х = 2 в F) выбрано правильно,
Более общим решением было бы
где Р^—присоединенный полином Лежандра первого рода (см.
Дифференциальные уравнения в частных производных (т. VI),
гл. IV).
464 Указания к решению задач
и более общие решения, приведенные в примечании на
стр. 463, для нашей задачи излишни.
Чтобы перейти от G) к вязким давлениям, будем
проводить вычисления подобно тому, как это делалось
на стр. 48, для iero мы подставим в D.26), D.28)
значения 8gx = bq% = 0, bq3 = v = ш -§¦ sin Ь и получим
1 dv I dg3 ш . ft Г п а3 а3\
с 97 ein ft I У I
'-'ГФ о о о " о о Bill U Lj —г „ 1
r<? 2gx dr 2g3gx dr 2 V. г3 г3 у
3 . ft с3
При этом исчезнут все вязкие давления, кроме
prtf = — 2ргГ9 = Зрш -j sin 0. (8)
Отсюда мы получим выражение для момента М,
положив г = а:
— М = 2па3 \ pry sin2a d Ь = бтсрша3[ sin3 & d Ь = 8тгРша3, (9)
о
что совпадает с C5.21). Момент, требующийся для под-
поддержания равномерного вращения, равен по величине
моменту вязких давлений и направлен в противополож-
противоположную сторону, т. е. в сторону возрастания ср, чего и сле-
следовало ожидать.
Кирхгоф решил эту задачу (см. примечание на
стр. 314) изящным, но несколько более длинным спосо-
способом, проводя вычисления в декартовых координатах.
VIII.1. Реакции А и В в точках А и В, согласно
правилу рычага (ср., например, (9.2) в т. I), равны
Поэтому введенное вслед за уравнением D1.12) сре-
срезывающее усилие в области I (между А и Р) и соответ-
соответственно в области II (между Р и В) будет равно
Si = A, Su=-B. . A)
Указания к региению задач 465
Следует принять во внимание знаки и отсчитывать х
по направлению от А к J5, а также относить Si и Su
к положительной я-плоскости в смысле фиг. 6 на стр. 52.
Перерезывающая сила, согласно A), в обеих обла-
областях I и II постоянна, но в точке приложения Р она
претерпевает скачок на величину Р. Эта разрывность,
конечно, обусловливается фиктивным предположением
о сосредоточенности нагрузки Р.
Изгибающий момент в области I в сечении, находя-
находящемся на расстоянии х от А, равен
MI = Ax = P~xt • B)
а в области II в сечении, отстоящем от В на ?,
Mn = Bl*=P±t. C)
Здесь Мц относится к «положительной ^-плоскости»,
которая, очевидно, соответствует «отрицательной я-пло-
скости».
Графическое представление М состоит, таким обра-
образом, из двух прямых, которые пересекаются в точке х = а,
или, что то же, ? = ?. В этой точке М = ММ&КС. — Р ~г
согласно B) или C).
Прогиб г/i получается в области I из
dx* EJ I
ffls
и в области II из
, di2 EJ I k' v '
Постоянные, входящие в D) и E), определяются из гра-
граничных условий и условий непрерывности:
а) в А и В должны обращаться в нуль уг и г/п;
б) в точке приложения нагрузки (х == а или ? = Ь)
обе кривые должны переходить друг в друга непрерывно
30 А. Зоммерфельд
466 Указания к решению заЬач
и без излома. В результате получим
У1~ EJ Ы \аЧ а ~Ь у ,~
Уи = XT "fiT v ^лг" ~ъ ~п ) '
Х>«/ UI» \^ 1*1/ С/ 1л У
Из обоих уравнений можно получить выражение для
прогиба в месте приложения нагрузки:
_ _ Р аЧ* /7Ч
У — 2/макс. — EJ-зГ- \Ч
Между изгибающими моментами B) и C) и срезывающими
усилиями A) существует общая связь:
Если балка нагружена несколькими силами в произ-
произвольных местах, то легко получить выражения для пере-
перерезывающей силы, изгибающего момента и прогиба в ре-
результате суперпозиции выражений, полученных для одной
силы.
VIII.2. а) Пусть F — сечение стержня, а смещение ?
массы М (а также нижнего конца стержня) отсчиты-
вается положительным вниз. На массу М сила тяжести
действует вниз, а упругая сила стержня aF = FE (%jl) —
вверх. Уравнение для смещения ? в этом случае гласит
'i hl, k = ~, A)
или, в результате интегрирования, да
^ , B)
A = l/^ C)
М У ML ' \ '
Две постоянные А ж В определяются из начальных
условий. Таким образом, \ колеблется около постоян-
постоянного значения ?о = ё7<«о> которое представляет собой не
что иное, как чисто статическое значение ?, которое
получается из A) для ? = 0.
Указания к решению задач 467
б) Здесь, согласно D2.6), имеет место уравнение
так что
(/p — полярный момент инерции сечения стержня, кото-
которое мы считаем круглым, р —модуль кручения, ср — угол
закручивания М вокруг оси стержня.)
в) Движение М при малых прогибах с хорошим при-
приближением можно рассматривать как вертикальное сме-
смещение (в случае стержня на двух опорах, если а = Ь = 1/2,
это будет в точности так), поэтому в основу опять можно
положить уравнение A); ? теперь будет означать смеще-
смещение М перпендикулярно к оси стержня.
В случае стержня, закрепленного с одной стороны,
к_ЗЕ1
а в случае стержня на двух опорах
, ЪЕП
/ЗЁТ
где /— экваториальный момент инерции сечения стержня.
Отсюда следует в первом случае
и во втором случае
Точная теория колебаний растяжения — сжатия, крутиль-
крутильных колебаний и колебаний изгиба учитывает массу
самого стержня и вместо A) и E) приводит к дифферен-
дифференциальным уравнениям в частных производных второго
порядка. В результате кроме определенных выше основ-
основных колебаний с частотой ш0 получается бесконечный
ряд обертонов, соответственно тому5 что в действитель-
действительности стержень имеет бесконечное число степеней сво-
свободы.
30*
468 Указания к решению задач
VIII.3. Так как для ? = 0 должно быть ? = 0, \ = v0,
согласно уравнению B) предыдущей задачи, получается
смещение в виде
A)
так что
Максимальное напряжение может быть получено отсюда
с помощью закона Гука
амакс. == ~г ^ (}
Пусть a) vo = O. Тогда
t _9 g _2gMl _
'«макс. — & ^г" — ~~EF~ ' макс- —
9
EF ' макс- — F
в соответствии с утверждением «а» в тексте задачи,
б) v0 велико. Тогда
t _ v0 _1/Mv%l _
?макс. — Ш — у -j^p- , °макс. —
в соответствии с утверждением «б» в тексте задачи.
VIII.4. Параметрическое представление эллиптической
границы сечения гласит
у = а cos и, z — bsinu, 0 < и < 2чг.
Семейство подобных эллипсов задается выражениями
у = аК cos и, z=Uk sin и, 0 < X < 1;
входящие сюда параметры X и и являются подходящими
координатами для вычисления интеграла D2.23). Функци-
Функциональный определитель преобразования у, z—->X, и равен
ду
Ж
dz
д\
ду_
ди
dz
ди
Указания к решению задач 469
В результате получается
, Ml Я2 + 62
Полярный момент инерции /р эллипса удобнее всего
получить с помощью выражения для экваториальных
моментов инерции 1у и Iz, которые, в свою очередь,
получаются из экваториального момента инерции / — ~т «4
для круга радиуса а посредством равномерного сжатия
(множитель Ъъ\аг для 1у и b/а для /z). При этом имеем
что отличается от входящего в выражения для М и ср,
множителя
7Ш3Ь3
и совпадает с ним только в частном случае а = Ъ (круг).
VIII.5. Пусть плоскостью падения, как в § 45, будет
плоскость ху. Перпендикулярная поляризация означает,
что из трех смещений ?, т\, С только С = 0. Соответственно
таблице на стр. 408 для поперечной волны, падающей
под углом ах и отражающейся под углом <х2, имеют место
соотношения
Г —_ A(Ah (x sin «1—у cos оц)
С, = Beih (.X Sin «2+V COS «2)#
Волновое число к, согласно D5.5), одинаково у обеих
волн в силу равенства частоты ш. Три условия отсут-
отсутствия сил на граничной поверхности D5.1) переходят
в одно условие
Оно может быть выполнено без возникновения продоль-
продольной волны, если положить
а2 = аа и В=А. A)
470 « Указания к решению задач
Таким образом, мы имеем правильное отражение с по-
постоянной амплитудой.
Если, напротив, под углом аг падает продольная
волна, отражающаяся под углом <х2, то придется иметь
дело с обеими компонентами ?, ч\:
le \ sin <xx \
тг]е J — cos ax J
&г \ ,.
\ _ I ^gih (х sin О2+У cos 0-2) /3)
\] cosaj
Волновое число к в обоих случаях будет одинаковым,
так как здесь ш также равны друг другу. Оно будет
задаваться соотношением D5.10).
Из трех условий D5.1) для поверхности, свободной
от сил, теперь только ayz = 0 будет выполняться тожде-
тождественно. Оба других условия
) Ae (ж sin «l-y cos он)
j
sin a21
прежде всего потребуют, чтобы имело место правильное
отражение (a2 = a1 = a), однако они не смогут быть удо-
удовлетворены каким-либо выбором постоянной В/А. Поэтому
придется предположить существование отраженной попе-
поперечной волпы, поляризованной в плоскости падения
(ср. среднюю колонку таблицы на стр. 408):
It ) cos a,)
\= \ Ceiht &
•4,J — sinaj
at связано с a «законом преломления» D5.12):
sin a — n sin a,, n=f-= 2-^ I .
Из B), C) и E) можно вычислить полные смещения:
и получить из обоих уравнений D) два условия для двух
отношений А: В\ С [ср. аналогичные уравнения D5.13)
и D5.14)].
Приложение I
ПРЕОБРАЗОВАНИЕ ТРЕХМЕРНОГО ТЕНЗОРА
ДЕФОРМАЦИИ В ОРТОГОНАЛЬНЫХ
КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
Формулы D.26) и D.28) для деформаций еи и eik
значительно упростятся, если вместо смещения Ьд (име-
(имеющего размерность длины) ввести изменения координат Ьр,
которые, например, в случае полярных координат могут
также означать угловые изменения и поэтому не должны
всегда обязательно иметь размерность длины. Соответ-
Соответственно выражениям D.19) ^qk = gkbpk после простых вык-
выкладок (проведение дифференцирования dbqjdpt) мы полу-
получим
ih gk dpk gi дрг \ *
В A) мы употребили сокращенную запись, введенную
Эйнштейном и часто применяемую в тензорном исчисле-
исчислении: если греческая1) буква повторяется дважды, то по
ней производится суммирование. Поэтому в нашем слу-
случае трехмерных тензоров второй член в правой части A),
написанный в развернутом виде, выглядит так:
ХП ЪРа dgi
х) Суммирование только по греческим буквам предусмотрено для
того, чтобы мы не спутали ец или, далее, ili со следом рассматри-
рассматриваемого тензора. Вообще следует заметить, что без этого и подобных
ему ограничений обозначения в тензорном исчислении весьма удоб-
удобны и коротки, однако они могут иногда запутать начинающего.
472 Приложение I
Далее, чтобы упростить запись и воспользоваться сокра-
сокращенными обозначениями тензорного исчисления (верхний
индекс — контравариантный, нижний индекс — ковариант-
ный вектор), положим bpi = %t и перепишем уравнение A)
в виде
е..= —+ — -^- = 5*. Aа)
11 dpv gi др^ г'
Введенное здесь обозначение ?\ называется в тензорном
исчислении «ковариантной производной контравариант-
ного вектора Ег по координате р{», на что указывает
индекс i справа внизу; контравариантным при этом назы-
называется каждый вектор, который преобразуется как изме-
изменения координат dpit а ковариантной —каждая величина,
матрица преобразования которой транспонирована1),
т. е. строки которой совпадают со столбцами матрицы
преобразования dpif и наоборот. К последним величинам
относится производная скаляра по координатам (его
градиент), но не производная вектора, подобно д^г/др{.
В последнем случае для того, чтобы получить ковариант-
ную производную, к д?/дрг следует добавить содержа-
содержащуюся в Aа) сумму по а.
Прежде всего мы покажем, что входящий в Aа)
множитель при ?" является частным случаем так назы-
называемого «символа Кристоффеля».
х) Эти несколько странные обозначения были введены Эйнштейном.
Прежде вместо «контравариантный» говорили «когредиентный»,
а вместо «ковариантный»—«контр агредиентный». Следует заметить
еще, что было бы логичней писать вместо pi и dpi pl и dp1, однако
это не принято. То, что введенный в Aа) процесс дифференцирова-
дифференцирования ?\ действительно ковариантен в смысле Эйнштейна, мы здесь,
конечно, доказывать не будем; точно так же мы не будем обосновы-
обосновывать приведенную ниже формулу D) или правило «поднимания
и опускания индексов». Эти вопросы тщательно, хотя и сжато, изло-
изложены в книге Eddington A. S., Relativitatstheorie in mathe-
matischer Behandlung (см. перевод: Эддингтон А., Математиче-
Математическая теория относительности, Харьков—Киев, 1933.^—Прим. перев.),
где, например, в § 29, выводятся наши уравнения C5) и D). Далее
см. Levi-Civita Т., Der absolute Differentialkalkiil» Springer,
1928. (См. также указанную в примечании на стр. 18 книгу Н. Е.
Кочина.—Прим. перев.).
Преобразование трехмерного тензора деформации 473
Общее определение этого символа для произвольных
координат хг, х2, х3 гласит1):
В случае ортогональных координат, которыми мы огра-
ограничимся, входящие сюда выражения имеют следующий
вид:
? и — 8 8 Q 8ih — —
sih-bik8igk> 8 ~gigh-
Легко убедиться в том, что
{ai,i} = ±**L . (За)
* l Si дРа v '
Поэтому мы можем вместо Aа) писать также
Как обобщение этого выражения укажем без доказа-
доказательства выражение для ковариантной производной
5\ = |1 + «г}Г. D)
Если взять значение {ак, i) из C), то можно переписать D)
в виде •
<h~~dpk+gi dPh * g? dPi* * ^
Мы, однако, не сможем таким путем получить, как можно
было бы ожидать, величину sik из B), хотя бы потому,
что это выражение не удовлетворяет условию симметрии
sife = efti. Чтобы удовлетворить этому условию, мы должны
рассмотреть ковариантный вектор ?t и его контравариант-
ную производную ?*V Ее можно получить из Гь опуска-
опусканием верхнего индекса i и подниманием нижнего индекса к.
В случае ортогонального элемента длины первое произво-
х) Вместо {fxv,a} пишут также i У, или символ Эйнштейна Г
474 Приложение I
дится путем умножения на gf, а последнее — делением
на gl. В результате получим из E)
Если совершенно формально поменять местами индексы
г и /с, то получим
#^--!^4. F)
gi dPk v ;
Здесь оба последних члена в правой части равны друг
другу по величине и противоположны по знаку двум
последним членам в правой части E). Складывая E)
и F), получим
- dph-rg2 др.
или, если обе стороны умножить на gjgk,
— (^+U)-—^+—-^—. G)
Правая часть этого выражения совпадает с правой
частью B), если снова написать Ьр{~1ъ, bpk — ^h. Таким
образом, мы имеем следующее определение деформаций
в обозначениях тензорного исчисления:
2^ = -f(^ + ^), (8)
в котором также содержится представление Aа) для еи:
*« = «4г (8а)
Подчеркнем при этом, что оба эти уравнения полностью
аналогичны первоначальному определению в прямоуголь-
прямоугольных координатах A.11), если мы в последнем пронуме-
пронумеруем координаты и будем обозначать дифференцирование
с помощью верхнего (или нижнего) индекса.
Все это соответствует общей цели тензорного исчисле-
исчисления: ввести такие символы и такой формализм, чтобы
уравнения в криволинейных координатах возможно точнее
соответствовали бы элементарным, написанным в декарто-
декартовых координатах.
Конвекционные члены вектора ускорения в тензорной форме 475
При л ожение II
КОНВЕКЦИОННЫЕ ЧЛЕНЫ ВЕКТОРА
УСКОРЕНИЯ В ОБЩЕЙ ТЕНЗОРНОЙ ФОРМЕ
Переходя от рассмотренного в приложении I контра-
контравариантного вектора смещения bpt = ?г к контравариант-
ному вектору скорости bpt = vl, мы утверждаем, что
общая форма контравариантного вектора полного ускоре-
ускорения имеет вид
где индекс, обозначенный греческой буквой, опять озна-
означает, что по а производится суммирование. Эта форма
соответствует элементарному векторному уравнению
Однако, в то время как последнее выражение справедливо
только в декартовых координатах, первое годится для
произвольного элемента длины и автоматически дает воз-
возникающие при этом инерционные члены, которые мы
в случае цилиндрических полярных координат вычислили
более длинным путем в задаче III. 1.
На этом примере мы выясним структуру конвекцион-
конвекционных членов vav\ для i = l, 2, 3. Если рг = г, р2 = у,
pz = z и gx = 1, g2 = r, g3 = 1, то мы имеем
1 dr о d<p % о dz /ОЧ
v =di-vr> v2==-W = T-> v =dt-v*' C>
Составим, пользуясь уравнениями (За), C6) и E) прило-
приложения I, следующую таблицу:
v 1 - дг > v 2 ~ д(р ,. -г -у » v з - dz »
\ 2
476 Приложение II
Отсюда, умножая на v* из C), соответствующее каж-
каждому а, и суммируя по а, получим
в 2
г 5/* ^ гдср z dz т 9
dvz , dvz
±+v
Здесь мы в средней строке вынесли из всех членов
за скобку 1/г для того, чтобы было удобнее получить
окончательное уравнение движения (ср. приложение IV).
Интерес представляют стоящие друг под другом в чет-
четвертом столбце «инерционные члены»:
V
которые совпадают с членами, вычисленными в зада-
задаче III. 1.
В то время как с помощью псевдовекторного форма-
формализма (vgrad)v могут быть получены только первые три
члена [ср. также выражения на стр. 431, где эти члены
прямо обозначены как (A, grad-4r), (A, grad^l^),
(A, grad,4z)], наше тензорное вычисление дает все четыре
члена, причем первый из четвертых членов соответствует
обычному центростремительному ускорению, второй —
половине кориолисова ускорения; в случае третьей —
декартовой — координаты z, как и следовало ожидать,
четвертого члена не имеется.
Если шаг за шагом провести те же вычисления для
сферических полярных координат г, Ь, ср с ^ = 1, g2 = r,
g3 = rsin&, мы получим вместо C), D) и E):
1 dr о db % о d<? *><р ,п ч
7; 1_
dt — Г ' V - dt ""/-Sin»
1
1 dr ' 2~ rdb
Конвекционные члены вектора ускорения в тензорной форме 477
jil zL. ?;o »;2 — jK
i dvr . с 'о ^ cosu о ^
i dvr
6 d
(vgradz;r) f- ,
Ea)
На первом месте во всех трех строках стоят члены,
соответствующие элементарной векторной формуле
(vgrad)v, причем во второй строке за скобку вынесен
множитель 1/г, а в третьей — множитель 1/rsinft. Нас,
однако, здесь также интересуют преимущественно допол-
дополнительные инерционные члены: в первой строке —это
обычные центростремительные ускорения — #©2/г и — v$2/r.
Полный вклад последнего при движении по параллели
с радиусом г sin $ был бы равен —v92/rsinb, однако для
/•-направления входит лишь его умноженная на sin О
составляющая; при этом sin$ в Числителе и знаменателе
сократится.
По той же причине во вторую строку Eа) входит вы-
выражение vv2/r sin Q-, умноженное на cos&. Преимуществом
нашего тензорного представления является то, что при
нем не требуется специального геометрического рассмот-
рассмотрения. Кроме того, в среднем члене второй строки, точно
так же как и в двух последних членах третьей стро-
строки, мы легко можем узнать половину кориолисова ускоре-
ускорения. Доверяя нашему тензорному рассмотрению, мы
не будем пытаться выяснять наглядный смысл этих чле-
членов. Сошлемся на формулы на стр. 432, где эти члены
выведены путем вычислений с помощью векторного
анализа.
478 Приложение III
Приложение III
ТЕНЗОР ВЯЗКИХ ДАВЛЕНИЙ И ЕГО
ДИВЕРГЕНЦИЯ
(ДИФФЕРЕНЦИРОВАНИЕ С ПОСЛЕДУЮЩИМ
СВЕРТЫВАНИЕМ)
В случае несжимаемой жидкости, которым мы здесь
ограничимся, тензор вязких давлений связан с тензором
скоростей деформации eik с помощью соотношения A0.2):
Pik— —2[ieik. Дифференцируя по t уравнение (8) прило-
приложения I, мы получим
Согласно приложению II, этим определяются вязкие
давления в любой системе координат, в частности
в полярных координатах. Однако в уравнения движения
вязкие давления входят не сами по себе, а в виде «век-
«векторной дивергенции» [ср. уравнение A0.5)]. В декарто-
декартовых координатах она выражается через псевдовектор
— {j,Av [уравнение A0.8)], правильное векторное выраже-
выражение которого (для случая цилиндрических полярных
координат) было получено чисто векторным путем в за-
задаче 1.4. Чтобы провести это несколько трудоемкое вычи-
вычисление с помощью тензорного исчисления, заменим Av
дифференцированием с последующим свертыванием тен-
тензора vik-\-vki, входящего в A). Иначе говоря, мы про-
проделаем операцию
v\« + v™, B)
где двойной индекс а обозначает как суммирование, так
и ковариантное дифференцирование. Второй член в B)
в силу предположения о несжимаемости при суммирова-
суммировании по а даст нуль. В результате ?-я компонента нашего
дифференцирования с последующим свертыванием обра-
обратится в
=-l^4 C)
(мы будем обозначать эту компоненту как /)
Для фактического вычисления Div*/? нам потребуется
провести ковариантное дифференцирование тензора^ а не
Тензор вязких давлений и его дивергенция 479
вектора, но так как эта' операция несколько сложнее,
мы опять сошлемся на § 30 цитированной книги Эддинг-
тона. Б случае цилиндрических полярных координат
мы на основании уравнений D) приложения II получим
г дг
(A\
Первые три члена правой части представляют собой обыч-
обычный оператор Лапласа, действующий на vr, выражение
которого дано в задаче 1.3 на стр. 431 и который мы
можем обозначить как Д#г. Вторые два члена появляются
в результате того, что vr — не скаляр, а компонента век-
вектора. Как и должно быть, эти два члена, а также допол-
дополнительные члены в v%a совпадают с вычисленными
в задаче 1.4. Как мы знаем, в декартовой компоненте
v3aa такие дополнительные члены не появляются. Если,
подобно Lvr, ввести обозначения Ау9 и Avz, to мы получим
% \2dV
f /.2 1
v\« = Avz. E)
Во втором из этих уравнений, подобно уравнению E)
приложения II, вынесен множитель 1/г.
.В случае сферических полярных координат мы, про-
произведя аналогичные вычисления, получим вместо D)
«1«_ 1 д f 2дуг\ Г 3 / ^гл
Первые три члена, согласно стр. 432, опять совпадают
с выражением оператора Лапласа, действующего на Аг;г;
дополнительные члены могут быть преобразованы, если
воспользоваться условием несжимаемости. Если мы, кроме
того, введем в v2aa и v?aa сокращенные обозначения Дг;в
и LVj и вынесем в них за скобку множите ли 1/г и 1/r sin Q-,
480 Приложение IV
как это было сделано в уравнениях Eа) приложения II,
то получим
»v=1U»+i B iS - Jl - ^3l? ^
Приложение IV
УРАВНЕНИЯ ДВИЖЕНИЯ ВЯЗКОЙ
НЕСЖИМАЕМОЙ ЖИДКОСТИ
В ЦИЛИНДРИЧЕСКИХ И СФЕРИЧЕСКИХ
ПОЛЯРНЫХ КООРДИНАТАХ
Уравнения Навье — Стокса в форме, пригодной для
произвольной системы координат, гласят
= в- A)
Отдельные их члены в точности соответствуют векторному
уравнению A6.1), если в последнем рассматривать внеш-
внешнюю силу F как градиент потенциальной энергии V,
перенести ее из левой части в правую и объединить
в один член с гидродинамическим давлением. Обозначе-
Обозначение (р-\-У){ в A) означает контравариантное дифферен-
дифференцирование по i-й координате.
Уравнение A) дает возможность указать на закон
однородности тензорного исчисления по отношению к сте-
степени, в которой входят в уравнение отдельные индексы.
Мы видим, что во всех членах уравнения A) индекс i
входит в степени + 1, а индекс а в степени — 1, если
считать нижние индексы отрицательными, а верхние —
положительными. Уже благодаря этому обстоятельству
последний член A) следует писать в виде контравариант-
ной производной, в результате чего при переходе к гра-
градиенту мы получим существенный множитель l/gt.
Следует заметить еще, что vl есть скорость изменения
1-й. координаты, а не соответствующее изменение длины
Уравнения движения вязкой несжимаемой жидкости 481
пути; аналогично dvl/dt означает локальное ускорение
координаты, а не соответствующее ускорение вдоль траек-
траектории, которое отличается от dvl/dt на множитель i/gim
Обычное условие несжимаемости divv = 0 гласит теперь
vaa—-0; оно уже было использовано при преобразовании
вязких членов в уравнении A), что приводит [как и в B),
приложение III] к их упрощению.
Уравнение A) имеет самую общую форму и не пред-
предполагает даже ортогональности системы координат; про-
простота этого уравнения, однако, теряется, если его кон-
конкретизировать для какой-либо недекартовой системы
координат. Даже в случае ортогонального элемента длины
при введении конкретных gi через них должны быть
выражены неявно содержащиеся в A) символы Кристоф-
феля, что в значительной степени усложняет выражения.
Поэтому в дальнейшем мы опять ограничимся нашими
двумя частными случаями.
Цилиндрические полярные координаты
Мы воспользуемся выражениями E) из приложения II
для конвекционных членов и выражениями D) из при-
приложения III для вязких членов, причем среднюю строку
мы сократим на общий множитель 1/г. В результате
члены этой строки
д*__д*9 yJ_ I d(p+V)
перейдут в обычное ускорение и соответственно обычную
ср-компоненту градиента
OS. и EI .
dt гду
Если при этом опять использовать обычный скалярный
оператор Лапласа Д и сокращенное обозначение (v grad v),
то мы получим
~Ш ~^~ (V ^Г Vr' —*
31 А. Зоммерфельд
482 Приложение IV
-0. B)
dz
= 0.
К этому следует добавить условие несжимаемости v^ = 0,
а именно:
±«(„гН?Ь + *._0. C)
Точно так же в случае сферических полярных коорди-
координат мы из Eа) в приложении II и Dа) в приложе-
приложении III, если снова произведем сокращение на общие
множители, вынесенные за скобки, а также восполь-
воспользуемся оператором Лапласа Д и сокращенным обозна-
обозначением (vgradp), получим /
^9
Bа)
дуг , cos6^ t>y n
а также условие несжимаемости
10 1 d 1 0^a> л /о \
= 0. Ca)
Уравнения эти несимметричны, хотя мы старались,
чтобы добавляющиеся к выражениям Д инерционные
Уравнения движения вязкой несжимаемой жидкости 483
члены были по возможности похожи друг на друга.
Единственной полностью симметричной формой этих
уравнений, которая совпадает с формой уравнений
Навье —Стокса в декартовых координатах, является A).
Нельзя, правда, отрицать, что тензорные вычисления,
приводящие к предыдущим уравнениям, довольно гро-
громоздки, а для цилиндрических полярных координат даже
сложнее элементарного вывода с помощью векторного
анализа, как это сделано в задачах 1.4 и III. 1.
С другой стороны, в косоугольных четырехмерных ко-
координатах, с которыми неизбежно приходится иметь
дело в общей теории относительности, тензорное рас-
рассмотрение является единственно пригодным.
ОГЛАВЛЕНИЕ
Предисловие переводчика 3
Из предисловия к первому изданию 5
Предисловие ко второму изданию 7
Глава I. Кинематика деформируемых тел ........ 9
§ 1. Основная теорема кинематики 9
§ 2. Обзор векторного анализа 18
§ 3. Теоремы Остроградского—Гаусса, Стокса и Грина 30
§ 4. Некоторые замечания о тензорном анализе ... 38
Глава II. Статика деформируемых тел 51
§ 5. Разделение тел на твердые и жидкие, сжимаемые
и несжимаемые, идеальные и вязкие 51
§ 6. Гидростатика 56
§ 7. Статика сжимаемой жидкости 66
§ 8. Напряженное состояние упругого твердого тела 74
§ 9. Соотношения между деформацией и напряже-
напряжениями. Упругие постоянные. Упругая энергия . 80
§ 10. Вязкие силы и их работа, в частности в несжи-
несжимаемых жидкостях 94
Глава III. Динамика деформируемых тел 106
§ 11. Уравнения Эйлера для идеальной несжимаемой
жидкости 106
§ 12. Вывод уравнений Эйлера из принципа Гамиль-
Гамильтона. Давление как множитель Лагранжа ... 114
§ 13. Уравнения Эйлера для идеальной сжимаемой
жидкости. Их приложение к акустике 120
Приложение. Сравнение течения сжимаемых и
несжимаемых жидкостей 129
§ 14. Динамика упругого тела 134
§ 15. Квазиупругое тело как модель эфира 137
§ 16. Динамика вязкой жидкости. Гидродинамика и
гидравлика. Критерий турбулентности Рей-
нольдса 143
§ 17. Некоторые замечания о капиллярности 155
Глава IV. Теория вихрей 163
§ 18. Теоремы Гельмгольца о вихрях 163
§ 19. Потенциальное течение в плоскости и в про-
пространстве 172
Оглавление 485
§ 20. Фундаментальная теорема векторного анализа .
Электромагнитная аналогия вихревых полей . . 185
§ 21. Прямолинейные параллельные вихревые нити . . 194
§ 22. Кольцевые вихри 205
Глава V. Теория волн 214
§ 23. Плоские гравитационные волны в глубокой воде 214Ч
§ 24. Плоские гравитационные волны в мелкой и
в не очень глубокой воде 221
§ 25. Плоские капиллярные и капиллярно-гравитаци-
капиллярно-гравитационные волны 230
§ 26. Введение групповой скорости 234
§ 27. Кольцевые волны 242
§ 28. Корабельные волны и угол Маха 253
Глава VI. Течения с заданными граничными условиями . 260
§ 29. Обтекание плоской пластинки 260
§ 30. Мертвая зона и поверхности разрыва 269
§ 31. Решение задачи о свободной струе с помощью
метода конформных отображений 280
§ 32. Вихревая цепочка Кармана 288
Приложение. Проблема лобового сопротивления . 298
§ 33. Пограничный слой Прандтля 301
Глава VII. Дополнения к гидродинамике . 305
§ 34. Гидродинамические уравнения Лагранжа .... 305
§ 35. Стоке ово течение и формула сопротивления . . 308
§ 36. Гидродинамическая теория смазки 317
§ 37. Ударные волны Римана. Интегрирование в
общем виде уравнений Эйлера для сжимаемой
жидкости в одномерном случае 328
§ 38. О турбулентности 338
Глава VIII. Дополнения к теории упругости 357
§ 39. Пределы упругости, пропорциональности и
текучести. Пластичность и прочность 357
§ 40. Упругость кристаллов 361
§ 41. Изгиб балки 367
§ 42. Кручение 377
§ 43. Кручение и изгиб винтовой пружины 386
§ 44. Упругая энергия, содержащаяся в прямоуголь-
прямоугольном параллелепипеде 393
§ 45. Упругое полупространство и поверхностные
волны в нем 406
486 Оглавление
Задачи . . . 418
Указания к решению задач 429
Приложение I. Преобразование трехмерного тензора де-
деформации в ортогональных криволинейных координатах 471
Приложение II. Конвекционные члены вектора ускорения
в общей тензорной форме 475
Приложение III. Тензор вязких давлений и его дивер-
дивергенция (дифференцирование с последующим свертыва-
свертыванием) 478
Приложение IV. Уравнения движения вязкой несжима-
несжимаемой жидкости в цилиндрических и сферических поляр-
полярных координатах 480
А. Зоммерфельд
МЕХАНИКА ДЕФОРМИРУЕМЫХ СРЕД
Редактор У. Я. МАРГУЛИС
Технический редактор Б. И. Корнилов
Корректоры Т. Бопачева и А. Семенова
Сдано в производство 3/П 1954 г.
Подписано к печати 24/IV 1954 г.
Т02856. Бумага 84ХЮ81/32 = 7,7 бум. л.—
25,2 печ. л., в т/ч. 3 вкл.
Уч.-издат. л. 22,7. Изд. № 2/1918.
Цена 17 р. 40 к. Заказ 106.
Издательство иностранной литературы.
Москва, Ново-Алексеевская, 52.
16-я тип. Союзполиграфпрома Главиздата
Министерства культуры СССР.
Москва, Трехпрудный пер., д. 9.
ОПЕЧАТКИ
Стр.
18
23
45
75
79
133
150
*55
Строка
3 сн.
(сноска)
13 св.
Подпись
к фиг. 5
8 и 7 сн.
5 св.
10 сн.
17 св.
2 сн.
(сноска)
Напечатано
Кочин Н. В.
в.A.15)
от нашего прямо-
прямоугольника элементом
объема и секущей
плоскостью
от B.20) к B.20а)],
через сопла замкну-
замкнутого сосуда
на стр. 74
г) См. Verhandlun-
gen des Internationalen
Mathematiker-Kongres-
sen in Heidelberg.
Следует читать
Кочин Н. Е.
в B.15)
8q
от нашего прямо-
прямоугольного элемента
объема секущей
плоскостью
от B.20) к B.1)],
через сопло из зам-
замкнутого сосуда
на стр. 103
х) См. Vortrage aus
dem Gebiet der Hydro-
imd Aorodynamik, Inns-
Innsbruck, 1922.
Фиг. 39а. Фотография линий тока (короткая экспозиция).
Фиг. 396. Фотография траекторий (длинная экспозиция).
Зап. 106
Ф п г.. 45а. Фотография снаряда, летя-
летящего со сверхзвуковой скоростью между
двумя параллельными стенками.
Отражение конуса Маха от стенок.
¦Ф и г. 456. Фотография снаряда, про-
пробившего тонкую деревянную стенку.
¦Осколки дерева, летя со сверхзвуковой
скоростью, оставляют за собой след в виде
конуса Маха.
Ф п г. 45в. Фотография снаряда,
пролетевшего через цилиндр с
кольцевыми отверстиями.
Выходящие из отверстий сферические
волны огибаются конусом Маха этого
снаряда.
За,к. 106
Ф и г. 47а. Фотография действительной картины течения вокруг
пластинки, расположенной перпендикулярно к направлению течения.
Точка остановки в середине передней стороны пластинки.
Фиг. 476. Фотография действительной картины течения вокруг
пластинки, наклонно расположенной к направлению течения.
Точка остановки смещена к ребру, наклоненному против течения.