К 175-летию
МГТУим. Н.Э. Баумана

ПРИКЛАДНАЯ МЕХАНИКА
СПЛОШНЫХ СРЕД
В трех томах
Научный редактор доктор технических наук,
профессор В.В. Селиванов
ТОМ1
Москва
Издательство МГТУ имени Н.Э. Баумана
2004

А.В. Бабкин, В.В. Селиванов
ОСНОВЫ МЕХАНИКИ
СПЛОШНЫХ СРЕД
Рекомендовано Министерством
общего и профессионального образования
Российской Федерации
в качестве учебника для студентов
высших технических учебных заведений
Издание второе, исправленное
Москва
Издательство МГТУ имени Н.Э. Баумана
2004

УДК 531@75.8)
ББК 22.22
Б12
Рецензенты: зав. кафедрой газовой и волновой динамики
механико-математического факультета МГУ им. М.В.
Ломоносова академик РАН Е.И. Шемякин; зав. лабораторией
волновых процессов д-р физ.-мат. наук, проф. Н.Н. Смирнов;
зав. кафедрой теоретической и экспериментальной механики
Саровского государственного физико-технического
института д-р техн. наук} проф. С.А. Новиков; зав. кафедрой
прикладной математики МГТУ им. Н.Э. Баумана д-р техн. наук,
проф. B.C. Зарубин.
Бабкин А.В., Селиванов В.В.
Б12 Основы механики сплошных сред: Учебник для втузов. — 2-е
изд., испр. — М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. — 376 с:
ил. (Прикладная механика сплошных сред: В 3 т. / Науч. ред.
В.В. Селиванов; Т. 1).
ISBN 5-7038-2344-7 (Т. 1)
ISBN 5-7038-2343-9
В первом томе комплекса учебников серии "Прикладная механика
сплошных сред" приведены основные элементы векторного и
тензорного анализа, необходимые и достаточные для изучения краткого курса
"Основы механики сплошных сред", излагаемого с помощью
математического аппарата тензорного исчисления. Рассмотрены понятия и
соответствующие физические величины, используемые для описания
движения и состояния материального континуума. Выводятся уравнения и
соотношения, справедливые для описания поведения любых сплошных
сред независимо от их агрегатного состояния и физико-механических
характеристик.
Описаны основные реологические модели сплошных сред и
приведены соответствующие физические соотношения. Даны общие
принципы постановки задач механики сплошных сред и примеры постановки
ряда практических задач.
В приложении приведены примеры решения типовых задач.
В основу учебника положен материал лекций, читаемых авторами
студентам МГТУ им. Н.Э. Баумана.
Для студентов технических университетов и машиностроительных
вузов.
УДК 531@75.8)
ББК 22.22
© А.В. Бабкин, В.В. Селиванов,
1998; 2004, с изменениями
tqrn t; 7пчя оълл 7ГГ л\ © Издательство МГТУ
ISBN 5-7038-2344-7(Т. 1) им н э Баумана> 1998; 2004>
ISBN 5-7038-2343-9 с изменениями

ПРЕДИСЛОВИЕ
Механика сплошных сред — это раздел теоретической
физики, в котором изучается движение деформируемых сред: твердых,
жидких и газообразных. В отличие от теоретической механики,
изучающей движение материальных точек, дискретных систем
материальных точек и абсолютно твердых тел, механика сплошных
сред изучает движение таких тел, которые заполняют пространство
непрерывно, сплошным образом и расстояния между точками
которых во время движения изменяются. Целью механики сплошных
сред является установление наиболее общих свойств и законов
движения деформируемых сред с учетом физико-механических свойств
материалов этих сред. Значение механики сплошных сред
состоит в том, что эта дисциплина является основой для более узких,
прикладных дисциплин, изучающих движение газов, жидкостей или
твердых тел. К их числу относятся, например, газовая динамика
(в частности, прикладная газовая динамика — это физика взрыва),
аэродинамика, гидродинамика, теории упругости и пластичности,
теории прочности и разрушения твердых тел и т.д.
Развитие механики сплошных сред, служащей научной базой
многих прикладных технических наук, связано с широким
применением математических методов исследования различных процессов и
явлений, происходящих в сплошной среде при нагружении ее
внешними силами. Однако классический университетский курс механики
сплошных сред для механико-математических факультетов по
своему содержанию, смысловому построению, методике изложения
существенно расходится с содержанием учебных планов технических
университетов и не всегда доступен для усвоения студентами
технических университетов и машиностроительных вузов. Наш
многолетний опыт преподавания основ механики сплошных сред и
смежных дисциплин в Московском государственном техническом
университете им. Н.Э. Баумана убедил нас в необходимости введения в
учебные планы технических университетов и машиностроительных
вузов адаптированного курса механики сплошных сред —
прикладной механики сплошных сред, ориентированной на студентов
технических вузов и включающей в себя такие взаимосвязанные разделы,

как основы механики сплошных сред, механика разрушения
деформируемого твердого тела, а также вопросы численного
моделирования неустановившихся движений сплошных сред.
В плане фундаментального образования в технических
университетах нельзя обсуждать основные понятия и закономерности
механики независимо от тех приложений, физических моделей и научно-
технических проблем, которые уже существуют в практике
исследовательских и опытно-конструкторских работ, а также могут
появиться (и появляются!) в ближайшей перспективе в связи с
развитием новых высоких технологий и проектов. Очевидно, что
глубокое изучение студентами прикладной механики сплошных сред
будет полезным как для понимания уже известных решений и
приложений, так и для постановки и решения прикладных задач
механики, которые непрерывно возникают в процессе решения
сложнейших технических и технологических проблем современного и
перспективного машиностроения и приборостроения.
Курс прикладной механики сплошных сред состоит из трех
взаимосвязанных частей, содержание которых раскрывается в
соответствующих томах комплекса учебников серии "Прикладная механика
сплошных сред".
Первый учебник (том 1. Основы механики сплошных
сред) содержит изложение основных понятий и операций
тензорного исчисления, а также трактовку основных понятий, уравнений
и соотношений механики сплошных сред, достаточных для
усвоения ключевых элементов кинематики, динамики и термодинамики
материального континуума. Здесь же приведены базовые модели
сплошных сред и даны соответствующие физические соотношения.
Изложенный материал является самодостаточным для
выполненного в заключительной главе книги описания общих принципов
постановки практических прикладных задач механики сплошных сред.
Второй учебник (том 2. Механика разрушения
деформируемого тела) посвящен вопросам деформирования и разрушения
твердых тел в условиях статического, динамического и ударновол-
нового нагружения. В нем дано физическое представление о
строении твердого тела, описаны процессы деформирования и
разрушения тела при нагружении с позиций микро- и макроструктуры
материала, наличия различных дефектов и характера нагружения.
Приведена характеристика известных критериев прочности,
соотношений механики рассеянных повреждений и линейной механики
разрушения, рассмотрены модели механики хрупкого и вязкого
разрушения. В книге подробно описаны волновые процессы, сопрово-
6

ж дающие ударноволновое нагружение деформируемых сред,
выполнен анализ природы и структуры волн напряжений, отмечены
особенности их распространения с учетом фазовых переходов.
В третьем учебнике (том 3. Численные методы в
задачах физики быстропротекающих процессов) анализируются
проблемы численного решения задач механики деформируемого
тела и использования разностных методов вычислительной
математики применительно к задачам физики быстропротекающих
процессов (в том числе физики взрыва и удара). На примере
простейшей одномерной плоской газодинамической задачи рассмотрены
фундаментальные понятия теории разностных схем, представлены
основные сеточные методы, численный метод характеристик,
методы семейства "частиц в ячейках". Приведены постановки,
алгоритмы численного решения и результаты решения ряда одномерных и
двумерных нестационарных задач при использовании лагранжевых,
эйлерово-лагранжевых и эйлеровых методов. Обсуждены вопросы
технологии проведения вычислительного эксперимента и приведены
примеры, демонстрирующие возможности численного
моделирования как инструмента исследования быстропротекающих процессов.
Опираясь на методическую основу, заложенную в лучших
отечественных учебниках и монографиях по механике сплошных сред,
авторы избрали стиль изложения, который предполагает
достижение главной цели — научить читателя при минимальном объеме
информации ставить и решать конкретные задачи физики быстро-
протекающих процессов на базе фундаментальных основ механики
сплошных сред, механики разрушения деформируемого твердого
тела и численных методов анализа процессов и явлений, происходящих
в сплошных средах в условиях интенсивных динамических нагрузок.
Содержание учебников соответствует фундаментальному
курсу лекций, который авторы читают на протяжении многих лет в
Московском государственном техническом университете им. Н.Э.
Баумана как студентам, так и специалистам ряда
машиностроительных научно-исследовательских институтов,
научно-производственных объединений и конструкторских бюро. Основные разделы
лекционного материала в той или иной мере нашли отражение в
различных учебных пособиях, монографиях, статьях и обзорах,
опубликованных за последние 15 лет.
В.В. Селиванов

ВВЕДЕНИЕ
Подход к изучению движения деформируемых сред
заключается в переходе от реальных деформируемых сред к их
идеализированному представлению и соответствующему математическому
описанию. Будем в дальнейшем понимать под материальным телом,
независимо от его агрегатного состояния, систему материальных
частиц, которая заключена в некоторой области пространства Д
имеющей объем V и ограниченной поверхностью S.
Реальными материальными частицами, составляющими
материальное тело, являются атомы и молекулы. Они находятся в
непрерывном хаотическом движении и взаимодействуют между собой
за счет сил электромагнитного происхождения. Характер
хаотического движения и взаимодействия молекул различен для тел,
находящихся в различных агрегатных состояниях. Число
материальных частиц (молекул) N в практически малых объемах тела
огромно (в 1 см3 твердого тела содержится порядка 1024 молекул),
а электромагнитные силы взаимодействия между ними не всегда
известны. Поэтому изучение движения деформируемых сред
невозможно, если рассматривать тело как совокупность реальных
материальных частиц. При описании движения каждой молекулы как
абсолютно твердого тела для 1 см3 вещества потребовалось бы не
менее 6 х N = 6 х 1024 дифференциальных уравнений первого
порядка и такое же число начальных условий. Однако
необязательно знать движение каждой материальной частицы — на практике
нужно знать некоторые средние, суммарные характеристики. Это
положение определяет два основных подхода к изучению движения
деформируемых сред: статистический и феноменологический.
Статистический подход (развиваемый в физике) базируется
на методах статистической механики. Это — вероятностные
методы, применение средних характеристик по большому ансамблю
частиц, введение дополнительных гипотез о свойствах молекул и об
их взаимодействии с целью упрощения модели. Однако при сложном
строении молекул использование статистических методов
затруднено, так как недостаток информации не позволяет сформулировать
8

гипотезу о взаимодействии молекул, а получаемые уравнения
чрезмерно сложны.
Феноменологический подход (от греческого слова phainomenon
— явление) базируется на общих, полученных из опыта
закономерностях и гипотезах, которые принимаются за истинные и
используются для построения последующих уравнений и выводов. В
основу феноменологического подхода положены понятие материального
континуума и соответствующая этому понятию гипотеза
сплошности.
Материальный континуум (сплошная среда) есть состоящая из
большого числа малых частиц фиктивная субстанция, которая
непрерывно, сплошным образом заполняет область пространства D,
отведенную данному телу, независимо от его агрегатного состояния.
Следует отметить, что под частицей, составляющей материальный
континуум, понимается часть тела, малая по отношению к
геометрическим размерам тела, но большая по сравнению с размерами
молекул. Таким образом, в рамках феноменологического подхода
абстрагируются от реального атомно-молекулярного строения тел
и переходят к идеализированному представлению вещества в виде
материального континуума. Такая идеализация реального
дискретного вещества позволяет использовать при исследовании движения
деформируемых тел математический аппарат дифференциального
и интегрального исчисления непрерывных функций.
В соответствии с феноменологическим подходом к изучению
процессов движения деформируемых сред вводятся ряд понятий,
качественно определяющих эти процессы, система физических
величин, характеризующих их количественно, и между ними на
основании опыта устанавливаются взаимосвязи.
Во-первых, вводятся система характеристических функций,
определяющих движение частиц сплошной среды (вектор
перемещения и у вектор скорости и, тензоры деформаций (е) и скоростей
деформаций (ё)у поворота (и) и скоростей поворота (w)), и система
параметров, определяющих внутреннее состояние среды (плотность
р, удельная внутренняя энергия Е) энтропия 5, абсолютная
температура Т, давление р, тензор напряжений (а) и т.д.).
Во-вторых, между введенными физическими величинами
устанавливаются взаимосвязи, выражаемые определенными
уравнениями и соотношениями, которые основаны на полученных из опыта
данных и используются для математического описания поведения
деформируемых сред. К их числу относятся уравнения, выражаю-
9

щие такие фундаментальные законы природы, как закон
сохранения массы (уравнение неразрывности), закон сохранения импульса
(уравнения движения), закон сохранения энергии, или первое
начало термодинамики (уравнение энергии), и второе начало
термодинамики, а также конечные соотношения, отражающие физико-
механические свойства изучаемых сплошных сред.
В-третьих, устанавливаются начальные и граничные условия,
при которых все характеристические функции могут быть найдены
математическими методами.
Механика сплошных сред строится в рамках
феноменологического подхода при ограничениях и упрощениях, определяемых
гипотезами механики сплошных сред.
Первая гипотеза механики сплошных сред — гипотеза
сплошности — связана с понятием материального континуума.
Вторая гипотеза механики сплошных сред связана с
понятием пространства. Под пространством понимается бесконечно
большая совокупность точек, однозначно задаваемых с помощью чисел,
называемых координатами, которые определяют положение
произвольной точки относительно некоторой точки, принятой за начало
координат.
Мерность пространства обусловлена числом координат,
которыми определяется положение точек в пространстве. Например,
бесконечно большая совокупность точек в обычном физическом
пространстве составляет трехмерное пространство, так как положение
произвольной точки в декартовой прямоугольной системе
координат задается тремя координатами х\} г/i, z\. Совокупность точек
на плоскости составляет двумерное пространство, положение
произвольной точки задается двумя координатами х\, у\. Двумерным
является и пространство, составляемое совокупностью точек,
образующих сферическую поверхность, здесь положение точки может
быть однозначно определено двумя координатами: углами 0
(долгота) и (р (широта).
Предполагается, что пространство, в котором рассматривается
движение деформируемых сред, является евклидовым. Евклидовы
пространства — это такие пространства, в которых можно ввести
единую для всех точек декартову прямоугольную систему
координат (х, у, z), а расстояние между двумя произвольными точками 1
и 2 определить по формуле г = \/{х2 — х\J + (уг — УхJ + (*2 — ^iJ-
Следовательно, обычное физическое трехмерное пространство и
двумерное пространство на плоскости являются евклидовыми. Это
10

не относится к двумерному пространству на поверхности сферы,
так как нельзя определить расстояние между двумя произвольными
точками по приведенной выше формуле, не выходя за пределы этого
пространства.
Третья гипотеза механики сплошных сред — гипотеза
абсолютного времени. Согласно этой гипотезе, время течет одинаково
независимо от выбора системы отсчета, в которой рассматривается
движение деформируемой среды. Данная гипотеза является
хорошей идеализацией при решении большинства практических задач, в
условиях которых скорости движения тел не достигают таких
значений, чтобы возникала необходимость учета релятивистских
эффектов.

Глава 1
МАТЕМАТИЧЕСКИЙ АППАРАТ
МЕХАНИКИ СПЛОШНЫХ СРЕД
1.1. Характер математических объектов
математического аппарата
механики сплошных сред
Механическое движение, в том числе и движение
деформируемых сред, всегда определяется по отношению к
некоторой системе отсчета — к телу или точке отсчета и к связанной
с ними системе координат. Система координат — это
совокупность произвольной точки пространства, принятой за
начало отсчета, и правил, с помощью которых устанавливается
взаимно однозначное соответствие между точками
пространства и числами — координатами точек.
Для трехмерного пространства каждой точке М можно
поставить в соответствие три числа ж][^, ж^, ж^,
называемые координатами точки (рис. 1.1). Координаты однозначно
определяют положение точки
пространства относительно
принятой за начало координат
точки 0, имеющей координаты ж1 =
= ж2 = ж3 = 0. В
дальнейшем для краткости будем
обозначать совокупность координат
ж1, ж2, ж3 точки как ж1, где
индекс г = 1, 2, 3 принимает
значения в пределах, определяемых
мерностью пространства.
Рис. 1.1
12

Через любую точку пространства могут быть проведены
координатные линии и координатные поверхности (рис. 1.2).
Координатная линия— это геометрическое место точек в
пространстве, характеризуемое изменением только одной из
координат, тогда как две другие остаются неизменными
(линии М(х1)у М(я2), М(ж3) на рис. 1.2). Координатная
поверхность — это геометрическое место точек в пространстве,
характеризуемое изменением двух координат и постоянством
третьей (поверхности (x1)M(x^)J (x1)M(x2), (х2)М(я3) на
рис. 1.2). Через каждую точку трехмерного пространства
могут быть проведены три координатные линии и три
координатные поверхности.
В зависимости от вида координатных линий различают
прямолинейные и криволинейные системы координат.
Прямолинейные системы координат — это системы координат,
координатные линии которых являются прямыми линиями.
Криволинейные системы координат — это системы
координат, координатные линии которых являются кривыми
линиями.
М
Рис. 1.2
Рассмотрим три частных случая, которые чаще всего
используются в механике сплошных сред: прямолинейную де-
картову прямоугольную систему координат, криволинейные
цилиндрическую и сферическую системы координат.
В декартовой прямоугольной системе координат
положение произвольной точки М в пространстве характеризуется
координатами х1 = я, х2 = у, ж3 = z (рис. 1.3). Координатны-
13

ми линиями, проходящими через точку М, являются прямые,
параллельные координатным осям. Координатные
поверхности, проходящие через данную точку, представляют собой
плоскости, параллельные координатным плоскостям.
В цилиндрической системе координат положение
произвольной точки М в пространстве характеризуется
координатами х1 = г (расстояние данной точки от некоторой оси),
угловой координатой х2 = в и координатой х3 = z (рис. 1.4).
Из трех координатных линий, проходящих через
произвольную точку М, только две являются прямыми линиями. Так,
координатная линия ММ2, проходящая через точку М
параллельно оси z, соответствует изменению только координаты z.
Прямая MMi, проходящая через точку М и ось z
перпендикулярно последней, соответствует изменению только
координаты г. Третья координатная линия — окружность, лежащая в
плоскости, проходящей через точку М перпендикулярно оси z,
— соответствует изменению только одной угловой
координаты в. Координатными
поверхностями в случае
цилиндрической системы координат
являются плоскость,
проходящая через данную точку
перпендикулярно оси z
(неизменна только координата z),
плоскость, проходящая через
данную точку и ось z
(неизменна только угловая
координата 0), и проходящая через
данную точку цилиндрическая
поверхность, осью которой
Рис. 1.4 является ось z (неизменна
координата г).
В сферической системе координат (рис. 1.5)
положение произвольной точки М в пространстве
характеризуется координатой х1 = г (расстояние данной точки от
точки 0, принятой за начало координат) и двумя угловыми
координатами х2 = # и х3 = </?. Из трех координатных
14

Рис. 1.5
линий, проходящих через
произвольную точку М, только
одна является прямой — это
прямая ОМ, которая
соответствует изменению только
одной координаты г. Две
другие координатные линии —
окружности. Одна из них (с
центром в точке 0, принятой
за начало координат)
определяется пересечением
плоскости, проходящей через
точку М и ось z, и сферической
поверхности с центром в
начале координат, проходящей
через данную точку (изменяется только одна координата ф).
Третья координатная линия (окружность С с центром в точке
Oi) определяется пересечением этой же сферической
поверхности с плоскостью, проходящей через данную точку
перпендикулярно оси z. Этой координатной линии соответствует
изменение только угловой координаты в. Координатными
поверхностями для сферической системы координат являются:
сферическая поверхность с центром в начале координат
(неизменна только координата г); плоскость, проходящая через
точку М и ось z (неизменна только координата в); коническая
поверхность с осью, совпадающей с осью z, вершина которой
находится в начале координат. Координатная линия ОМ
является образующей, а окружность С — направляющей (здесь
неизменной остается только одна координата ц>).
Эти три системы координат наиболее часто будем
использовать при дальнейшем рассмотрении движений
сплошных сред.
Фундаментальное свойство математических объектов,
применяемых в математическом аппарате механики
сплошных сред, — их инвариантность (или независимость)
относительно выбора системы координат. Это утверждение может
быть обосновано следующим образом:
15

— явления и процессы, происходящие в природе и
технике, объективны (например, течение воды в реке или
воздушных масс в атмосфере, взрыв заряда взрывчатого вещества в
воздухе, высокоскоростное соударение метеорита с земной
поверхностью объективны, т.е. не зависят от человека,
наблюдающего или изучающего эти явления и процессы);
— очевидно, что так же объективны и законы, по
которым развиваются те или иные явления.
Система координат вводится исследователем для того,
чтобы можно было количественно описать механическое
движение деформируемых сплошных сред, сопровождающее
природные и технические процессы. Однако выбор системы
координат произволен. Например, при исследовании
высокоскоростного метеоритного удара допустимо использование как
декартовой прямоугольной, так и цилиндрической или
сферической системы координат. Конкретная система координат
выбирается исследователем главным образом из соображений
удобства при математическом описании движения.
Очевидно, что математические выражения объективных
законов, которым подчиняются явления и процессы, могут
содержать координаты, но не должны зависеть от субъективно
выбираемой исследователем системы координат. Иными
словами, математические выражения законов должны быть
инвариантными относительно выбора системы координат.
Следовательно, и математические объекты математического
аппарата механики сплошных сред, участвующие в записи этих
законов, должны быть инвариантными относительно выбора
системы координат. Как принято говорить, математические
объекты в механике сплошных сред должны быть
инвариантными относительно преобразования системы координат.
Математические объекты, инвариантные
относительно преобразования системы координат, называются
тензорами. Примерами наиболее простых тензоров являются
скалярные величины, определяемые одним своим числовым
значением: плотность р, температура Т, давление р, объем V
и др. Совершенно очевидно, что значения давления,
плотности, температуры в данной точке земной поверхности не
зависят от того, в какой системе координат (декартовой
прямоугольной, цилиндрической или сферической) рассматривается
16

движение воздушных масс. Скалярные величины
инвариантны относительно преобразования системы координат. Более
сложными математическими объектами являются векторные
величины, определяемые своим числовым значением и
направлением в пространстве. Прежде чем обосновать
инвариантность векторов относительно преобразования системы
координат, рассмотрим необходимые в дальнейшем изложении
основные элементы векторного исчисления.
1.2. Основные элементы векторного исчисления
1.2.1. Элементы векторной алгебры
Рассмотрим основные элементы векторной алгебры,
определяющей правила проведения операций с векторами,
применительно к декартовой прямоугольной системе координат.
Условие равенства векторов: два вектора, обладающие
одинаковой размерностью, считаются равными, если они
имеют одинаковые модули и одинаковые направления.
Сложение векторов осуществляется по правилу
параллелограмма или треугольника (рис. 1.6). Суммой двух векторов
является вектор, начало которого совпадает с началом
первого вектора, а конец — с концом второго вектора, причем конец
первого вектора и начало второго вектора совпадают.
Ь
c=o+b c=a—b;
Рис. 1.6 Рис. 1.7
Вычитание векторов определяется как действие,
обратное сложению. Разность двух векторов есть вектор, сумма
которого с вычитаемым вектором равна уменьшаемому вектору
(рис. 1.7).
17

Умножение вектора на скаляр определено следующим
правилом: при умножении вектора на скаляр получается
вектор, коллинеарный (параллельный) данному и направленный
в ту же сторону, когда скаляр положителен, и в
противоположную, когда скаляр отрицателен (рис. 1.8). Модуль
полученного вектора равен произведению модуля данного вектора
и модуля множителя.
т >0
b — т о
Рис. 1.8
т < О
Всякий вектор может быть разложен по трем
некомпланарным векторам (векторам, не лежащим в одной плоскости
при условии совмещения точек начала этих векторов) или
направлениям. Так, в декартовой прямоугольной системе
координат вектор а может быть представлен в виде суммы
трех составляющих векторов а^, ау, а^, каждый из которых
коллинеарен соответствующей координатной оси (рис. 1.9).
В свою очередь, каждый из
трех составляющих
векторов может быть
представлен в виде произведения
некоторой скалярной
величины и единичного
вектора, параллельного соот-
i
_y__i-
Рис. 1.9
/
ветствующей координатной
оси: ах = a>xh ау = ау3<>
az = azk. Скалярные
величины ах, а«, а2 называются
18

проекциями вектора на координатные оси или компонентами
вектора. Совокупность трех единичных взаимно
ортогональных векторов г, j, fc, направленных по осям координат,
образует ортонормированный базис декартовой прямоугольной
системы координат. Таким образом, всякий вектор может быть
представлен в виде суммы трех произведений его компонент и
базисных векторов: а = axi + ayj + azk.
Сумма квадратов компонент всякого вектора а в
декартовой прямоугольной системе координат равна квадрату модуля
этого вектора: ах + а** + а\ = а2 (см. рис. 1.9). Отношение
компоненты к модулю вектора определяет косинус угла,
составляемого данным вектором с соответствующей осью
координат, т.е. cos(a, х) = ах/а> cos(a, у) = ау/а, cos(a, z) = az/a.
Тогда тождество, связывающее направляющие косинусы
вектора, имеет вид
cos (а, х) + cos (а, у) + cos (a, z) = 1. A-1)
Скалярное произведение двух векторов определяется как
произведение модулей обоих векторов, умноженное на
косинус угла между этими векторами: а Ъ = а Ь cos а (рис. 1.10).
Если скалярно перемножаемые
векторы заданы своими
компонентами, т.е. а = axi + ayj + azk
и Ь = Ьхг + byj + 6zfc, то с
учетом равенства нулю скалярных ~" /> ""^
произведений разноименных ба- a»b= abcosa
зисных векторов (г-j' = 0, г-fc = 0
и т.д.) и равенства единице ска- Рис. 1.10
лярных произведений
одноименных базисных векторов (i-i = l,j'jf=l,fc*fc = l) скалярное
произведение двух векторов определяется выражением
a b = axbx + ayby + azbz. A.2)
Векторное произведение двух векторов определяется как
вектор, по модулю равный площади параллелограмма,
построенного на двух данных векторах, и направленный
перпендикулярно плоскости двух данных векторов, так, что с
19

его конца вращение первого вектора по кратчайшему пути
ко второму вектору должно происходить против хода
часовой стрелки (рис. 1.11). Векторное произведение может быть
выражено через компоненты перемножаемых векторов: а =
= axi + dyj + azk и b = bxi + byj + bzk. Так как единичные
векторы ортогонального базиса г, jf, к связаны между собой
соотношениями г х j = fc, j х г = — fc, jf x fe = г и т.д. (см.
рис. 1.9), векторное произведение двух векторов определяется
следующим образом:
a xb = (aybz - azby) г + (azbx - axbz) j
+ (o>xby — dybx) к =
ax
az
bz
¦ A-3)
Векторно-скалярное (смешанное) произведение трех
векторов не является самостоятельной операцией векторной
алгебры. Однако ввиду его частого использования в
тензорном исчислении отметим, что результатом смешанного
произведения трех векторов а • (Ь х с) = ±F является
скалярная величина, численно равная объему V параллелепипеда,
построенного на перемножаемых векторах (рис. 1.12).
Действительно, результатом векторного перемножения векторов
Ь и с является вектор d, направленный перпендикулярно
основанию этого параллелепипеда (параллелограмм, построенный
на векторах 6 и с на рис. 1.12) и равный площади этого
основания: d = S = 6с sin а. При дальнейшем скалярном умножении
20

вектора а на вектор d = 6 X с получается скаляр, равный
произведению площади основания параллелепипеда d = S и
проекции вектора а на направление вектора d, равной высоте
Д = a cos /3 параллелепипеда, построенного на перемножаемых
векторах: \а • (Ь х с)| = S/i = У. Знак смешанного
произведения определяется взаимной ориентацией векторов а, Ь, с.
Если векторы а, Ь, с составляют правую тройку, т.е. с конца
вектора а поворот вектора 6 по кратчайшему пути к вектору
с происходит против хода часовой стрелки (векторы а и Ь х с
составляют между собой острый угол), то знак смешанного
произведения положителен, в противном случае —
отрицателен.
Смешанное произведение трех векторов выражается
через их компоненты на основании аналогичных формул для
скалярного и векторного произведений следующим образом:
а (Ь х с) = (bycz - bzcy) ах + (bxcz - bzcx) ay +
(bxcy - bycx)az =
ах
bx
сх
ау
by
Су
bz
Cz
A.4)
Из приведенной формулы следует вывод о том, что если
два любых вектора, участвующих в смешанном векторно-
скалярном произведении, одинаковы или коллинеарны, то
результат смешанного произведения равен нулю (две строки
определителя третьего порядка одинаковы или
пропорциональны).
1.2.2. Элементы векторного анализа
В векторном анализе рассматриваются вопросы,
связанные с переменными векторами, дифференцированием и
интегрированием скалярных и векторных функций скалярного и
векторного аргументов. Скалярная функция скалярного
аргумента является обычной функцией у = f(x) одного аргумента
ж и с точки зрения векторного анализа интереса не
представляет.
Векторная функция скалярного аргумента считается
заданной, если задан вектор а, изменяющийся в
зависимости от некоторого скалярного аргумента *, т.е. а = a{t).
21

Рис. 1.13
В механике под скалярным аргументом чаще всего
понимается время. Рассмотрим некоторые необходимые в дальнейшем
понятия и положения на примере радиус-вектора г,
характеризующего положение материальной точки, движущейся
относительно декартовой прямоугольной системы координат. В
этом случае радиус-вектор является функцией времени t, т.е.
г = r(t) (рис. 1.13).
Годограф вектора есть геометрическое место точек
концов вектора, зависящего от скалярного аргумента. На
рис. 1.13 годографом радиус-вектора г, характеризующего
положение в пространстве движущейся материальной точки М,
является кривая L — траектория движения материальной
точки.
Производная векторной функции скалярного
аргумента определяется как предел отношения изменения векторной
функции Да к соответствующему изменению скалярного
аргумента при стремлении последнего к нулю. Для
приведенного на рис. 1,13 примера производная радиус-вектора dr/dt в
момент времени, соответствующий положению материальной
точки М,
dr 1# Дг
— = lim -— = v
dt д*->о Д*
представляет собой вектор скорости движения материальной
точки в момент времени t. Очевидно, что направление
производной вектора по скалярному аргументу совпадает с
направлением касательной к годографу вектора, т.е. вектор скорости
22

Mf(t+At)
Рис. 1.14
направлен по касательной к траектории движения
материальной точки.
Зависимость радиус-вектора г движущейся
материальной точки М от времени t может быть задана и более сложным
образом. Пусть радиус-вектор г является функцией другого
скалярного аргумента s — длины дуги кривой годографа,
отсчитываемой от некоторой начальной точки Л/о (рис. 1.14), а
сам путь 5, проходимый материальной точкой М по
траектории, — это функция времени: s = s(t). Тогда радиус-вектор
есть сложная функция времени: г = v[s(t)]. В соответствии с
правилами дифференцирования сложной функции
dr dr ds
V = —- = =: SV.
dt ds dt
т.е. производная радиус-вектора по скалярному аргументу
может быть представлена в виде произведения двух
сомножителей. Один из них — скалярный — представляет собой
модуль скорости движения материальной точки М по
траектории v = ds/dt. Второй сомножитель
dr 1в Дг
s = — = hm —
ds Д5->О As
является производной радиус-вектора по длине дуги
годографа и представляет собой единичный вектор s, направленный
23

по касательной к кривой годографа в сторону возрастания
длины дуги s. Это утверждение следует из того, что при
стремлении к нулю приращения длины дуги (As —> 0) секущая
кривой годографа Ат стремится занять положение
касательной к кривой, а значения длины дуги кривой (As) и секущей
(Аг) сближаются, т.е. (см. рис. 1.14)
п. &*¦ -1-
As-+o As
При изучении движения сплошных сред в рамках
феноменологического подхода для описания движения и
внутреннего состояния среды вводятся скалярные и векторные
величины: давление р, температура Т, скорость v и др.
Поскольку сплошная среда (материальный континуум) есть некоторая
субстанция, непрерывным, сплошным образом заполняющая
часть пространства, описание ее движения и состояния
связано с заданием характеризующих движение величин в каждой
точке какой-либо области пространства. Иными словами, при
описании движения сплошных сред приходится иметь дело с
полями скалярных и векторных величин.
Поле — скалярное или векторное — это совокупность
значений той или иной величины, заданных в каждой точке
рассматриваемой области пространства. В качестве примера
можно назвать скалярное поле давлений или температуры в
атмосфере, векторное поле скорости течения воды в реке и т.д.
Математическое описание поля связано с
установлением зависимостей величин от координат, однозначно
определяющих положение точек в пространстве: р = р(х, у, z),
Т = Г(х, 2/, z), v = v(x, у, z). Поскольку координаты точки
в пространстве я, у, z задают радиус-вектор г,
характеризующий положение этой точки относительно начала координат,
задать скалярное или векторное поле означает задать
скалярную или векторную функцию векторного аргумента г, т.е.
поставить в соответствие каждому радиус-вектору г значение
соответствующей физической величины: р = р(т), Т = Т(г),
v = v(r).
24

Тш Т2- const
T—T> — const
Рис. 1.15
Графически изображать поля удобно с помощью
поверхностей уровня и векторных линий. Поверхности уровня (изо-
поверхности) используются для графического изображения
скалярных полей. Это геометрическое место точек в
пространстве, соответствующее одному и тому же значению
скалярной величины (р(х, у, z) = const, Т(ж, j/, z) = const и т.д.).
В качестве примера на рис. 1.15 показаны изоповерхности
температуры (изотермы). По виду изотерм можно судить о
характере распределения температуры в пространстве. В
частности, более близкое расположение изотерм друг к другу
свидетельствует о более резком изменении температуры в данной
области пространства.
Векторные линии используются для графического
изображения векторных полей. Это такие линии в
пространстве, касательные к которым в каждой точке совпадают по
направлению с направлением вектора в данной точке.
Векторные линии, используемые для графического изображения
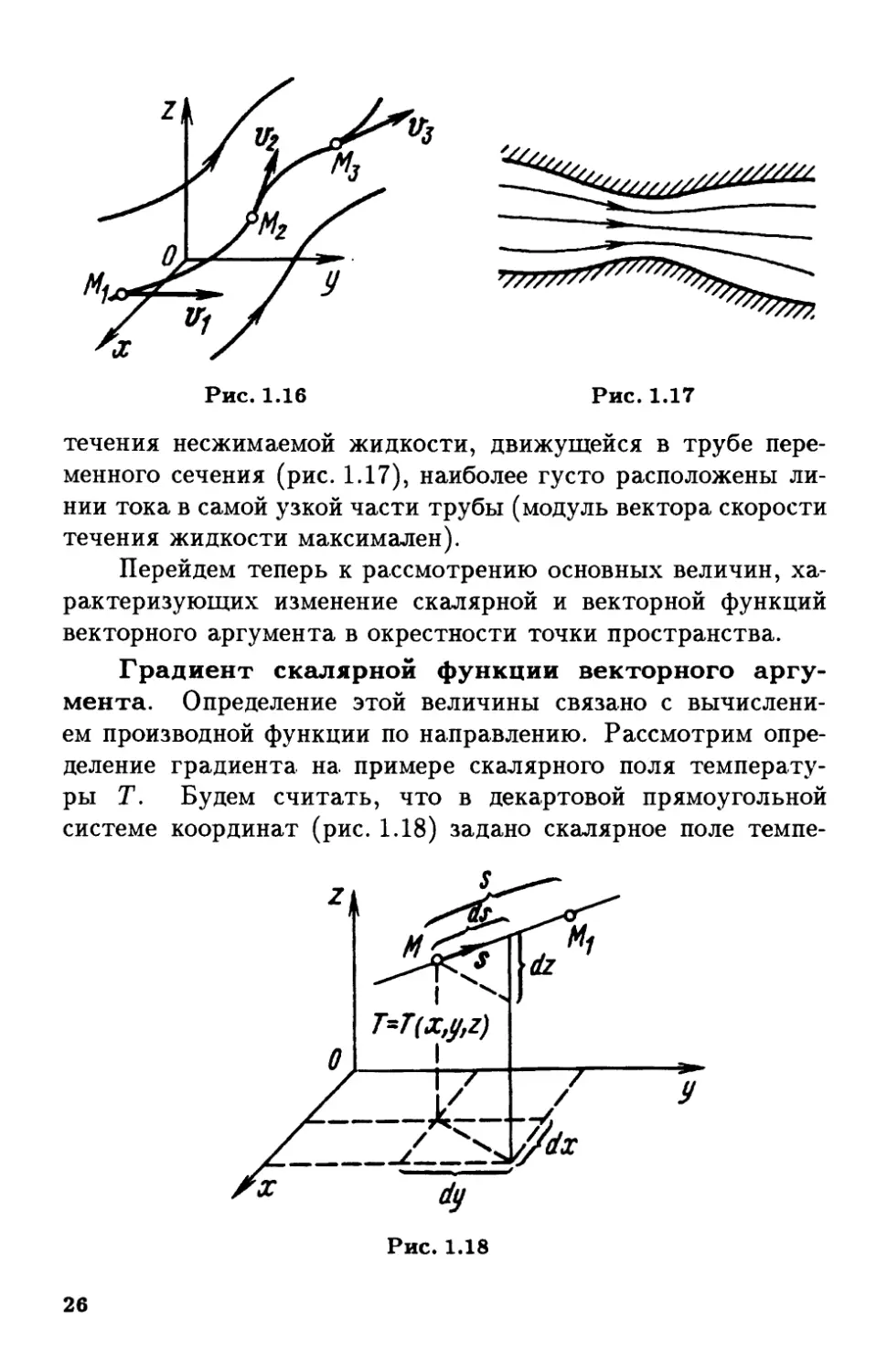
поля вектора скорости v, называются также линиями тока.
На рис. 1.16 с помощью линий тока показан поток жидкости,
Движущейся относительно декартовой прямоугольной
системы координат. В каждой точке (Mi, M2, М3) любой линии
тока вектор скорости v (t>i, i>2, V3 и т.д.) направлен по
касательной к ней. Модуль вектора в данной области векторного
поля графически связан со степенью сближения векторных
линий. Например, при графическом изображении поля скорости
25

*ъ*ъъ.
Рис. 1.16
Рис. 1.17
течения несжимаемой жидкости, движущейся в трубе
переменного сечения (рис. 1.17), наиболее густо расположены
линии тока в самой узкой части трубы (модуль вектора скорости
течения жидкости максимален).
Перейдем теперь к рассмотрению основных величин,
характеризующих изменение скалярной и векторной функций
векторного аргумента в окрестности точки пространства.
Градиент скалярной функции векторного
аргумента. Определение этой величины связано с
вычислением производной функции по направлению. Рассмотрим
определение градиента на примере скалярного поля
температуры Т. Будем считать, что в декартовой прямоугольной
системе координат (рис. 1.18) задано скалярное поле темпе-
Рис. 1.18
26

ратуры Т = Т(ж, у у z). Выберем произвольную точку М
пространства с координатами a; j, z и произвольное
направление М М\у которое будем характеризовать единичным
вектором s (|s| = 1). Вдоль прямой ММ\ координаты я, у, z
точек пространства изменяются в зависимости от
координаты 5, отсчитываемой от точки М по направлению вектора 5:
х = x(s), у = 2/E), z = z(s). Следовательно,
изменяющаяся вдоль произвольной прямой ММ\ температура Т
является сложной функцией только одного скалярного аргумента:
Т — Т(х, у, z) = T[x(s), 2/E), z(s)]. В соответствии с
правилами дифференцирования сложной функции производная по
направлению вектора s в точке М равна
ds дх ds ду ds dz ds
Дифференциалы координат dx,dyy dz отвечают изменениям
координат ж, 2/, z в соответствии с изменением координаты
5, отсчитываемой вдоль заданного направления вектора 5, на
величину ds. Из геометрических соображений (см. рис. 1.18)
следует, что
или
На основании известного тождества A.1),
связывающего направляющие косинусы вектора, величины dx/ds, dy/ds,
dz/ds могут рассматриваться как направляющие косинусы
вектора, характеризующего выбранное произвольное
направление. Так как для вектора единичной длины направляющие
косинусы тождественно равны его компонентам, приведенные
выше величины являются компонентами единичного вектора
s = sxi + Syj + 5zfc, характеризующего выбранное
произвольное направление, т.е.
dx _ dy _ dz _
27

Из последних соотношений и из A.2), A.5) следует, что
взятая в точке М пространства производная температуры по
направлению единичного вектора s определяется как скалярное
произведение двух векторов:
дт
дт. дт . ат
Один из сомножителей полученного скалярного произведения
— вектор, компонентами которого являются частные
производные скалярной функции по соответствующим
координатам, — называется вектором градиента скалярной
функции в данной точке пространства. Тогда
ОТ . дТ
дТ
С\гг\
A.6)
A.7)
Физический смысл градиента скалярной функции
векторного аргумента устанавливается с помощью
соотношения A.7) и рис. 1.19. Проведем через произвольную точку М
пространства, в котором задано скалярное поле
температуры Г = Т(ж, у, z), поверхность уровня Т = const. Пусть
направление вдоль поверхности уровня определено
единичным вектором sy направленным по касательной к поверхности
уровня в данной точке М (рис. 1.19, а). Значение
температуры вдоль поверхности уровня остается неизменным, поэтому
gradT
qradT
28

производная скалярной функции по выбранному направлению
dT/ds = 0. Но из соотношения A.7) следует, что скалярное
произведение вектора градиента температуры и единичного
вектора s, направленного по касательной к поверхности
уровня, также должно равняться нулю: gradT -5 = 0. Таким
образом, вектор градиента направлен по нормали к
поверхности уровня в данной точке пространства. Для уточнения
направления градиента рассмотрим семейство поверхностей
уровня в окрестности данной точки М (рис. 1.19, б). Выберем
направление единичного вектора s в сторону возрастания
значения скалярной величины. Тогда взятая в точке М
производная по выбранному направлению положительна (dT/ds > 0),
следовательно, положительно и скалярное произведение
вектора градиента и единичного вектора s: grad Т • s > 0. Тогда
угол между векторами grad Г и 5 а < тг/2, а вектор
градиента направлен в ту же сторону, что и единичный вектор s,
в данном случае в сторону увеличения скалярной функции.
Отметим также, что производная по направлению связана с
модулем вектора градиента соотношением
— = gradT-5 = |gradT| • \s\ cos a = |gradT|cosa. A.8)
OS
Очевидно, что максимальное значение производная по
направлению dT/ds = |gradT| получает в том случае, когда она
определяется по направлению нормали п к поверхности
уровня. В этом случае а = 0 (рис. 1.19, в). Поэтому относительно
модуля вектора градиента можно сказать, что он равен
производной скалярной функции, взятой по направлению нормали
п к поверхности уровня, т.е.
|gradT| = — = —,
а вектор градиента может быть определен и через единичный
вектор нормали п к поверхности уровня как
gradT= —n.
on
29

Таким образом, градиент скалярной функции векторного
аргумента — это вектор, направленный по нормали к
поверхности уровня в сторону быстрейшего увеличения скалярной
функции и равный производной по этому направлению.
Геометрический смысл градиента скалярной функции
векторного аргумента легко устанавливается из формулы
A.8). Согласно A.8), производная по какому-либо
направлению есть проекция вектора градиента на это направление.
Если на векторе градиента, построенном в данной точке М
пространства, построить, как на диаметре, сферическую
поверхность (рис. 1.20), то производная по направлению dT/ds
будет определяться длиной отрезка прямой ММ\,
заключенного внутри сферической поверхности. Максимальное по
модулю значение производная по направлению в данной точке
скалярного поля имеет в случае совпадения этого
направления с направлением вектора градиента, а минимальное
(равное нулю) значение достигается по касательной к поверхности
уровня.
Рис. 1.21
Аналитический смысл градиента скалярной функции
векторного аргумента устанавливается с использованием
соотношения A.7). Пусть в точке М скалярного поля
температуры Т = Т(я, t/, z) определен вектор градиента
температуры (рис. 1.21). Рассмотрим в бесконечно малой
окрестности точки М некоторую близко расположенную точку М\,
30

положение которой относительно исходной точки М
характеризуется вектором dr. Очевидно, что вектор dr может быть
представлен через единичный вектор s, характеризующий
направление dr как dr = sdsy где ds — модуль вектора dr или
расстояние между двумя близко расположенными точками М
и М\. Умножим теперь обе части соотношения A.7) на ds.
В результате
— ds = gradT • sds = gradT • dr.
as
Учитывая, что левая часть приведенного соотношения
определяет изменение значения скалярной функции dT при переходе
от точки М пространства к точке, расположенной в
окрестности данной точки М вдоль направления вектора s на
расстоянии ds, получаем
dT = gradTdr. A.9)
Нетрудно видеть, что градиент скалярной функции
характеризует изменение этой функции в окрестности
рассматриваемой точки. Зная градиент скалярной функции в данной
точке, мы можем определить изменение функции при переходе от
рассматриваемой точки к любой другой в ее окрестности. Для
этого достаточно знать положение точки относительно
заданной, характеризуемое вектором dr. Соотношение A.9)
является аналогом известного из математического анализа
соотношения, связывающего дифференциалы аргумента dx и
функции dy со значением производной у\х) функции скалярного
аргумента, т.е.
dy = y\x)dx. A.10)
Из сравнения формул A.9) и A.10) следует очевидный вывод
о том, что градиент скалярной функции координат Т(ж, у, z)
или векторного аргумента Т(г) играет по отношению к
функции векторного аргумента такую же роль, что и обычная
производная скалярной функции скалярного аргумента по
отношению к этой функции.
31

a(x,y,z)
Дивергенция (расхождение) вектора. Это одна из
величин, характеризующих изменение векторной функции
векторного аргумента а(г) или векторной функции координат
а(я> 2/> z) B окрестности точки векторного поля. Определение
дивергенции вектора
связано с понятием потока
вектора через поверхность. Если
в области пространства, в
котором задано векторное
поле а(я, у, z),
существует некоторая поверхность 5,
ориентация которой в
каждой ее точке
характеризуется единичным вектором
нормали n = nxi+nyj+nzky то
потоком вектора через поверхность S называется
поверхностный интеграл от скалярного произведения данного вектора а
и единичного вектора нормали п (рис. 1.22):
Рис. 1.22
andS= / (ахпх
аупу + aznz) dS.
Дивергенция вектора в данной точке векторного поля
есть отнесенный к единице объема поток вектора через
замкнутую поверхность, ограничивающую бесконечно малый
объем, окружающий рассматриваемую точку. На рис. 1.23
показана произвольная точка М векторного поля,
находящаяся в области пространства объемом V, ограниченной
поверхностью S. Согласно определению, дивергенция вектора а в
данной точке М пространства представляет собой следующий
предел:
) а • п dS
div(o) = lim
VО
A.11)
,0 V
Физический смысл дивергенции вектора
проанализируем на примере дивергенции вектора скорости течения потока
32

Рис. 1.23
Рис. 1.24
жидкости, в котором отсутствуют внутренние источники или
стоки (рис. 1.24). Будем считать заданным векторное поле
скорости v ~ v(x, у, г). Рассмотрим произвольную точку М
пространства. Выберем некоторый малый объем Vq
пространства, ограниченный поверхностью 5, охватывающей точку М.
В момент времени t этот объем включает вполне
определенные частицы жидкости. Очевидно, что с течением времени
при движении сжимаемой жидкости ее объем, включающий
те же самые (одни и те же) частицы, может изменяться.
Объем среды, включающий вполне определенные, фиксированные
(одни и те же) частицы среды, здесь и в дальнейшем будем
называть индивидуальным объемом.
Установим, каким образом индивидуальный объем
жидкости, имевший в момент времени t значение Vj)> будет
изменяться с течением времени. Для этого рассмотрим малый
участок dS поверхности 5, ограничивающей выбранный
индивидуальный объем в момент времени t. К моменту времени
t + At частицы жидкости, находившиеся на участке
поверхности dS (кривая АВ на рис. 1.24), совершат перемещение на
vAt, где v — вектор скорости течения жидкости на участке
dS поверхности 5, и будут находиться в положении,
соответствующем участку поверхности А'В'. Изменение
индивидуального объема, связанное с движением жидкости на
рассматриваемом малом участке, равно объему цилиндра ABB1 А1 и
определяется как dV — dSn(vAt), где dSn = dS cos а
представляет собой площадь поперечного сечения цилиндра ABB1 А!
2-9712
33

плоскостью, перпендикулярной вектору скорости v. Угол а
между этой плоскостью и площадкой dS равен углу между
единичным вектором нормали п к площадке dS и вектором
скорости движения частиц жидкости v. Поэтому
элементарное изменение рассматриваемого индивидуального объема за
интервал времени At
dV = dS cos a vAt = dSv nAt.
Полное изменение рассматриваемого индивидуального объема
за время At определяется интегралом по поверхности 5,
ограничивающей индивидуальный объем в момент времени t:
AV = Iv-ndSAt.
= Ф v
Следовательно, поток вектора скорости через замкнутую
поверхность 5 задает скорость изменения V индивидуального
объема жидкости, ограниченного в данный момент времени
этой поверхностью, т.е.
V= lim — = <bvndS.
At->0 At
Последнее выражение и формула A.11) приводят к
соотношению
)v • ndS
s V
div(v) = lim 77 = lim --.
Дивергенция вектора скорости течения жидкости в
данной точке векторного поля представляет собой
относительную скорость изменения бесконечно малого
индивидуального объема жидкости.
Бесконечно малый индивидуальный объем будем
называть в дальнейшем индивидуальной частицей. Под
индивидуальной частицей сплошной среды будем понимать часть
34

этой среды, малую по отношению к геометрическим размерам
тела и состоящую из вполне определенных, фиксированных
(одних и тех же) частиц вещества (с точки зрения
реального атомно-молекулярного строения вещества индивидуальная
частица при всех ее возможных движениях состоит из одних
и тех же атомов и молекул).
Физический смысл дивергенции вектора скорости связан
с изменением плотности жидкости в данной точке векторного
поля. Действительно, малый индивидуальный объем V,
имеющий неизменную массу тп, связан с плотностью р очевидным
соотношением V = т/р. Поэтому дивергенция вектора
скорости течения жидкости выражается через плотность как
= = . A,2)
Таким образом, дивергенция вектора скорости может быть
интерпретирована и как величина, характеризующая
относительную скорость изменения плотности индивидуальной
частицы сплошной среды, находящейся в данной точке
пространства.
Выражение для дивергенции вектора через его
компоненты в декартовой прямоугольной системе координат выводится
с помощью математического аппарата векторного анализа на
основании определения A.11):
Таким образом, дивергенция вектора равна сумме частных
производных компонент вектора по соответствующим
координатам.
С дивергенцией векторной функции тесно связана
одна из интегральных теорем векторного анализа — теорема
Остроградского — Гаусса, которая формулируется
следующим образом: поток вектора через замкнутую поверхность
> 35

равен интегралу, по объему ограниченному этой
поверхностью, от дивергенции вектора, т.е.
J>andS= fdiv(a)dV. A.14)
S V
Простое эвристическое (основанное на здравом смысле)
доказательство справедливости этой теоремы следует
непосредственно из определения дивергенции векторной функции.
На рис. 1.25 показана
область пространства /?, в
которой задано векторное
поле а(я, у, z). При этом
объем V ограничен
поверхностью 5. Разобьем
область пространства D на
большое число малых
областей, имеющих объем dV и
ограниченных каждая
своей поверхностью S*.
Очевидно, что для каждой из
введенных малых областей пространства на основании
определения A-П) дивергенции вектора в данной точке
пространства будет справедливо равенство
Рис. 1.25
div(a) dV = <f> a
п
A.15)
где правая часть представляет собой поток вектора через
замкнутую поверхность 5*, ограничивающую малую область
пространства объемом dV. При суммировании выражений
типа A.15) по всем малым областям, на которые была
подразделена область Z), приходим к выражению A.14)
теоремы Остроградского — Гаусса. Действительно, в результате
суммирования поверхностных интегралов, взятых по
поверхностям 5*, ограничивающим малые области, получится
только поверхностный интеграл (pan dS, взятый по поверхности
S
36

5, ограничивающей всю область D в целом. Поверхностные
интегралы, взятые по поверхностям, ограничивающим
внутренние области, при этом взаимно уничтожаются, так как
определенные для соседних малых областей потоки вектора
через одну и ту же граничную поверхность (S^B на рис. 1.25)
различаются только знаком в связи с противоположным
направлением единичного вектора внешней нормали п к
граничной поверхности. Так, на рис. 1.25 вектор п\
представляет собой единичный вектор внешней нормали для части
поверхности (SaB), ограничивающей малую область 1> а вектор
П2 является единичным вектором внешней нормали для части
поверхности (S^B), ограничивающей малую область 2.
Очевидно, что П2 — —Tii, поэтому
Ф а • п\ dS = — / а
dS
ИЛИ
/ а • п\ dS + / а • n*i dS = 0,
т.е. сумма поверхностных интегралов, взятых по внутренним
поверхностям, равна нулю.
Ротор (вихрь) вектора. Это вторая основная
величина, характеризующая изменение векторной функции
векторного аргумента а(т) или векторной функции координат
а (ж, у, z) в окрестности точки векторного поля. Определение
ротора вектора связано с понятием линейного интеграла или
циркуляции вектора по какому-либо контуру. Если в
области пространства, в которой задано векторное поле а(ж, у, z),
задана некоторая кривая Z, ориентация которой в каждой ее
точке характеризуется единичным вектором касательной /, то
линейным интегралом {или циркуляцией вектора по контуру
L) называется интеграл от скалярного произведения
вектора а и единичного вектора касательной I, взятый по длине
37

контура L, т.е.
I aldl,
L
где dl — длина бесконечно малого участка контура (рис. 1.26).
Рис. 1.26
Ротор вектора в данной точке векторного поля
вводится как вектор, проекция которого на направление,
характеризуемое единичным вектором нормали п, равна пределу
отношения циркуляции вектора по замкнутому контуру,
ограничивающему площадку, перпендикулярную единичному
вектору нормали, к ограниченной замкнутым контуром
площади при стремлении последней к нулю. На рис. 1.27 показана
произвольная точка М(ж, у, z) векторного поля, через
которую проходит плоскость, ориентация которой в пространстве
характеризуется единичным вектором нормали п. Точку М
на плоскости охватывает замкнутый контур С,
ограничивающий плоскую фигуру площадью S. Ориентация кривой С в
произвольной ее точке характеризуется единичным вектором
касательной /. В соответствии с определением ротор вектора
rot (а) есть вектор, проекция которого на направление
единичного вектора нормали п представляет собой следующий
предел:
\a-ldl
rot (а) • п = lim
A.16)
38

Выражение для ротора вектора через его компоненты в
декартовой прямоугольной системе координат выводится с
помощью соотношений векторного анализа на основании
определения A.16) и имеет форму
дах да
или более удобный для запоминания вид
rot(a)=
г з z
д_ д_ д_
дх ду dz
ах пу az
A.18)
Физический смысл ротора вектора проанализируем на
примерах определения ротора вектора скорости v при
вращении недеформируемого тела относительно неподвижной оси
и ротора вектора скорости течения жидкости. Рассмотрим
недеформируемое (абсолютно твердое) тело, вращающееся с
постоянной угловой скоростью а? вокруг неподвижной оси z
(рис. 1.28, а). Линейная скорость движения произвольной
Рис. 1.28
39

точки тела определяется угловой скоростью вращения и и
расстоянием г до точки от оси вращения как v — lot. Вектор
скорости направлен перпендикулярно оси вращения в сторону
вращения тела. Определим вектор ротора скорости rot (г?) в
некоторой точке 0, находящейся на оси вращения. Выделим
площадку, проходящую через точку 0 и ортогональную оси
вращения z. Ориентация этой площадки в пространстве
характеризуется единичным вектором нормали, совпадающим с
базисным вектором к. В качестве замкнутого контура,
охватывающего выбранную точку 0, примем окружность с
центром в точке 0 радиусом R и длиной 2тгД, ограничивающую
круг площадью 7гЛ2. В соответствии с определением ротора
вектора A.16) проекция ротора скорости на ось z находится
по формуле
rot {у) • к = [ rot (v)}z = lim
vldl
С
5-To S ¦
С учетом того, что в любой точке выбранного замкнутого
контура вектор скорости v направлен по касательной к этому
контуру, циркуляция вектора скорости по окружности
определяется как
/,„/„/„ / „ о
ф v - Idl = ф vdl = ф uR dl = ljR ф dl = uR - 2irR = 2тгД и.
J I J I
С С С С
Отсюда следует, что проекция вектора ротора скорости на
ось z
Выделим теперь прямоугольную площадку, проходящую
через точку 0 перпендикулярно оси х так, что нормалью к
этой площадке является базисный вектор г (рис. 1.28,6). В
каждой точке выбранного замкнутого контура вектор
скорости v ортогонален контуру ABCD, поэтому циркуляция
вектора скорости по замкнутому контуру ABCD равна нулю.
40

Да основании определения A.16) проекция вектора ротора на
ось х также будет равна нулю:
vldl
[ rot («)] ¦ г = [ rot (v)]x — Hm
ABCD
= 0.
Аналогично проекция ротора скорости на ось у [rot (v))y = 0.
Следовательно, вектор ротора направлен по оси вращения и с
точностью до постоянного сомножителя равен угловой
скорости вращения тела и. Ротор вектора скорости при вращении
абсолютно твердого тела относительно неподвижной оси
представляет собой удвоенный вектор угловой скорости вращения
тела: rot (у) = 2о>.
nkv(z,t/,z)
V
Аналогичным образом может быть интерпретирован
физический смысл ротора вектора скорости течения жидкости
(рис. 1.29). Рассуждения, подобные приведенным выше, могут
быть отнесены к бесконечно малой индивидуальной частице
жидкости, находящейся в данный момент времени в некоторой
точке М пространства (и включающей эту точку). Ротор
скорости течения жидкости в данной точке М пространства,
в котором задано векторное поле скорости v(x, у, г), будет
отличен от нуля, если найдется хотя бы одна площадка, на
которой циркуляция вектора скорости по охватывающему
данную точку замкнутому плоскому контуру будет отлична от
41

нуля:
• Idl ф 0. Но это означает, что индивидуальная
частица жидкости, находящаяся в точке М, участвует во
вращательном, вихревом движении (рис. 1.29, а). Равенство нулю
циркуляции вектора по любому из замкнутых контуров,
охватывающих точку М, означает, что индивидуальная частица
лишь расширяется (рис. 1.29, б) или сжимается (рис. 1.29, в),
но не вращается. Таким образом, ротор вектора скорости v
течения жидкости в данной точке поля характеризует модуль
и направление угловой скорости вращения бесконечно малого
объема жидкости: rot (г?) = 2о>.
С понятием ротора векторной функции связана еще одна
теорема векторного анализа — теорема Стокса, которая
формулируется следующим образом (рис. 1.30): циркуляция
вектора по замкнутому контуру равна потоку ротора вектора
через поверхность, ограниченную этим контуром, т.е.
Ф а • Idl = / rot (a) • пds.
Простое эвристическое
доказательство этого
утверждения следует
непосредственно из определения
ротора вектора A.16) и
проводится аналогично
доказательству теоремы
Остроградского — Гаусса.
Использование векторного дифференциального
оператора Гамильтона в дифференциальных
операциях первого порядка. Операции определения градиента
скалярной функции, дивергенции и ротора векторной функции
являются дифференциальными операциями первого порядка,
так как они связаны с вычислением частных производных
первого порядка скалярных величин или компонент векторов
по координатам. Градиент, дивергенция и ротор вводятся в
соответствии с их определениями A.6), A.7), A.11) и A.16), на
42

основании которых в декартовой прямоугольной системе
координат выводятся соответствующие выражения для этих
величин: A.6), A.13), A.17), A.18). В практическом обращении с
дифференциальными операциями первого порядка удобно
использовать символический подход, который основан на
применении векторного символического дифференциального
оператора Гамильтона.
Оператор Гамильтона представляет собой
символический вектор, компонентами которого являются частные
производные некоторых математических объектов по
соответствующим координатам:
V=^dxAi + 4yAj+^dTk- (Ы9)
С использованием векторного символического
дифференциального оператора Гамильтона градиент скалярной функции
<р — ip(x, у, z) определяется как результат воздействия этого
оператора на скалярную функцию, т.е.
Дивергенция векторной функции г?(ж, у, z) = vx(x, у, z)i +
+vy(x, у, z)j + vz(x, у, z)k может быть найдена как результат
скалярного умножения векторного символического оператора
Гамильтона на данный вектор, т.е.
т / \ •-> dvx dvv dvz
dlv(t,) = v. = — + ^ + ^.
Ротор векторной функции v(x, t/, z) определяется как
результат векторного умножения оператора Гамильтона на
заданную векторную функцию:
rot (г?) = V х v =
г j к
д^_ д_ д_
дх ду dz
vx vy vz
ду
к.
43

1.3. Основные элементы тензорного исчисления
1.3.1. Характеристика системы координат
В соответствии с общим определением тензора (как
математического объекта) основным его свойством в
физическом отношении является инвариантность относительно
выбора или преобразования системы координат. Опираясь на
это ключевое положение, рассмотрим основные понятия,
определения и положения тензорного исчисления, правила
проведения операций с тензорами в общем случае задания
криволинейной системы координат.
К числу характеристик произвольной криволинейной
системы координат в точке пространства относятся
совокупность трех векторов, образующих основной базис,
совокупность трех векторов, образующих взаимный базис, а также
метрические матрицы основного и взаимного базисов.
Основной базис системы координат. Произвольная
криволинейная система координат (ж1, ж2, ж3) представляет
собой совокупность точки 0, принятой за начало координат,
и координатных линий, проведенных через начало координат
(рис. 1.31). Рассмотрим произвольную точку М, имеющую
координаты ж1, ж2, ж3. Через нее могут быть проведены три
координатные линии (ж1), (ж2), (ж3) — геометрические места
точек, соответствующие изменению только одной из трех
координат. Положение произвольной точки М относительно точки
О начала координат определяется радиус-вектором г, который
обусловлен значением трех координат, т.е. г = г(ж1, ж2, ж3).
Найдем теперь для точки М пространства частные
производные радиус-вектора по соответствующим координатам:
дг дг дг / Л\
гз- (L20)
Согласно правилам дифференцирования векторной
функции по скалярному аргументу, векторы гь Г2, т*з
образуют тройку векторов, направленных по касательной к
соответствующим координатным линиям, проведенным в данной
44

Рис. 1.31
Рис. 1.32
точке пространства в направлении возрастания координат.
Совокупность этих трех векторов — основной базис системы
координат в данной точке.
Основной базис системы координат в данной точке
пространства есть совокупность трех векторов, определенных
как частные производные радиус-вектора, проведенного в
данную точку пространства, по соответствующим
координатам.
Соотношения A.20), согласно которым находятся
векторы основного базиса, могут быть записаны в виде дг/дхг = г;,
где г = 1, 2, 3 — свободный индекс, встречающийся лишь один
раз в каком-либо выражении (или, как в данном случае, по
одному разу слева и справа от знака равенства) и принимающий
значения в пределах, определяемых мерностью пространства.
Например, система координат (ж1, х2, х3) для краткости
записи может быть обозначена х\ а некоторая другая система
координат (у1, у2, у3) — yJ.
Необходимо отметить, что тройка векторов гг,
составляющих основной базис системы координат, в общем случае
задания криволинейной системы координат являе-тся
нестабильной характеристикой: векторы основного базиса могут
изменяться при переходе от одной точки пространства к другой.
Например, в декартовой прямоугольной системе координат в
45

любой точке пространства (точки О, М, М\ на рис. 1.32)
координатные линии — прямые, параллельные координатным
осям. При переходе от точки к точке пространства каждый из
векторов, составляющих основной базис, не изменяется ни по
модулю, ни по направлению, т.е. в декартовой
прямоугольной системе координат основной базис — стабильная
характеристика. В декартовой прямоугольной системе координат
основной базис является ортонормированным, его составляют
взаимно перпендикулярные единичные векторы т\ — г, т^ = j,
r3 = fe.
Несколько иначе обстоит дело в случае криволинейной
системы координат. Например, через произвольную точку
пространства в цилиндрической системе координат могут быть
проведены три координатные линии, две из которых
прямые, а третья является окружностью (штриховые линии на
рис. 1.33). Векторы основного базиса в точке М должны
быть направлены следующим образом: первый базисный
вектор 7*i =rr, соответствующий изменению только координаты
х1 = г (t»i = дг/дх1 = дг/дг), — вдоль соответствующей
координатной линии,
являющейся прямой, проходящей
через данную точку и ось z
перпендикулярно последней;
второй базисный вектор 7*2 =
= TQ, отвечающий изменению
только угловой координаты
х2 = 0, — по касательной к
соответствующей
координатной линии (окружности с
центром на оси z на рис. 1.33)
в сторону увеличения угловой
координаты 0; третий
базисный вектор т*з = rz — параллельно оси z. Аналогично
определяется направление векторов основного базиса при переходе
к другой точке пространства — М\. Очевидно, что при
переходе от одной точки пространства к другой в цилиндрической
системе координат изменяются два базисных вектора т\ = гг
Рис. 1.33
46

й Г2 = г^ при неизменном базисном векторе Г3 = rz, т.е. в
криволинейных системах координат основной базис является
нестабильной характеристикой (изменяется при переходе от
одной точки пространства к другой).
Понятие метрики пространства. Метрические
коэффициенты основного базиса. Пусть положение
некоторой точки М пространства относительно точки 0,
принятой за начало координат, характеризуется радиус-вектором
г = г(ж1, х2, х3). Рассмотрим еще одну точку
пространства — Mi, расположенную сколь угодно близко от точки М
(рис. 1.34). Положение
точки Mi относительно точки М
характеризуется вектором
dr — дифференциалом
радиус-вектора г. Расстояние
dl между двумя сколь угодно
близкими точками
пространства М и Mi определяется
модулем вектора dr: рис# 1#34
(dlJ = dr-dr. A.21)
Так как радиус-вектор г является функцией трех координат
х1, х2, ж3, то дифференциал радиус-вектора г имеет вид
дт
дт
дг
= Ti dx1 + r2 dx2 + r3 dz3. A.22)
Следовательно, вектор dr представляется в виде разложения
по векторам основного базиса г\, 7*2, гз через егр компоненты
— дифференциалы координат dx1, dx2, dx3.
Сформулируем широко применяемое в тензорном
исчислении соглашение о суммировании (правило суммирования
47

по двойному индексу, или правило суммирования
Эйнштейна). Так, выражение A.22) формально может быть
представлено в виде
3
dr = ridx1 + r2dx2 + r3dx3 = ^ r, dx% = r, dxl. A.23)
Использованное в соотношении A.23) правило
суммирования Эйнштейна формулируется следующим образом: если в
каком-либо выражении один и тот же индекс встречается
дважды (один раз внизу и один раз вверху), то
предполагается, что по этому индексу производится суммирование в
пределах, определяемых мерностью пространства; при этом
знак суммирования опускается.
Встречающийся дважды в одном и том же выражении
индекс носит название индекса суммирования. Индекс
суммирования может обозначаться любой буквой. Но какой бы
буквой ни был обозначен индекс суммирования, выражения
типа dr = Г{ dx* = tj dxJ = rj. dx* — .. . означают только
то, что дифференциал радиус-вектора г представляет собой
сумму трех слагаемых, каждое из которых определяется
произведением вектора основного базиса и дифференциала
соответствующей координаты.
С использованием соглашения о суммировании
выражение A.21) может быть представлено в виде
(dlJ = (гг dx{) • (tj dxj) = (г,- • Tj) dx{dxj. A.24)
Соотношение A.24) в краткой записи содержит сумму девяти
слагаемых (индекс г изменяется в пределах от 1 до 3, и
каждому из значений индекса г соответствует изменение индекса j
в этих же пределах).
Обозначим скалярное произведение базисных векторов
Ti-Tj = gij. A.25)
В выражении A.25) индексы г и j являются свободными
индексами, каждый из которых принимает значения от 1 до 3.
48

Следовательно, равенство A.25) в краткой форме содержит
девять соотношений типа
С учетом обозначений A.25) соотношение A.24) может быть
представлено в виде метрики пространства
(dlJ =д^AхЧхГ A.26)
Таким образом, метрика пространства с системой
координат х% есть квадратичная относительно дифференциалов
координат форма A.26), выражающая квадрат расстояния
между двумя сколь угодно близкими точками.
Метрические коэффициенты g±j основного базиса
системы координат (см. A.25)) — это постоянные
коэффициенты метрики пространства, определяемые как скалярное
произведение векторов основного базиса. Совокупность девяти
метрических коэффициентов g{j образует метрическую матрицу
11 9ij 11 основного базиса системы координат. Метрическая
матрица 11 g+j 11 является симметричной матрицей gij = gji,
что связано с коммутативностью скалярного умножения
векторов ri'Tj = rj Т{. Поэтому метрическая матрица основного
базиса системы координат в общем случае характеризуется
шестью различными величинами:
V V
Q-\ -г Q-\ п Q -| п 11
012 022 023 (L27)
013 023 033 JJ
Важным частным случаем криволинейных систем
координат являются ортогональные системы координат,
координатные линии которых в любой точке пространства
взаимно перпендикулярны, а следовательно, взаимно
перпендикулярны и векторы основного базиса. Ввиду взаимной
ортогональности базисных векторов из совокупности девяти
метрических коэффициентов g±j отличными от нуля являются лишь
49

три метрических коэффициента, имеющих одинаковые
индексы (гг • гj = 0 при г ф j, г, • гj• ф О при г = j). Поэтому
метрическая матрица основного базиса ортогональной
системы координат характеризуется только тремя отличными от
нуля величинами и является диагональной матрицей:
A28)
Отметим, что в дальнейшем будут использоваться главным
образом ортогональные системы координат. В частности,
ортогональными являются рассмотренные ранее декартова
прямоугольная, цилиндрическая и сферическая системы
координат.
Для ортогональных систем координат выражение A.26)
метрики пространства будет представлять сумму трех
слагаемых:
(dlJ = gu{dx1) +g22(dxz) + дгзЫх6) . A.29)
Отсюда вытекает способ нахождения значений метрических
коэффициентов основного базиса в ортогональных системах
координат. Для этого необходимо выразить квадрат
расстояния между двумя сколь угодно близкими точками через
дифференциалы координат. Коэффициенты при квадратах
дифференциалов будут определять значения метрических
коэффициентов. В качестве примера найдем значения
метрических коэффициентов g+j основного базиса для декартовой
прямоугольной и цилиндрической систем координат (рис. 1.35 и
1.36).
В декартовой прямоугольной системе координат (х1 = х,
х2 = у5 х3 = z) квадрат расстояния между двумя близкими
точками выражается через дифференциалы координат как
(dlJ = (dxJ + (dyJ + (dzJ = (dx1) + (dx2) + (dx*) .
50

Рис. 1.36
Из сравнения этого выражения с формулой A.29) следует, что
в декартовой прямоугольной системе координат метрические
коэффициенты основного базиса являются безразмерными
величинами, т.е.
#11 = #22 - #зз =
A.30)
В цилиндрической системе координат (а; = г, х — 0,
а;3 = z) выражение для метрики пространства принимает вид
= (drf + r2(dey +
Отсюда с учетом выражения A.29) получаем, что в
цилиндрической системе координат два метрических коэффициента #11
и 9зз являются постоянными безразмерными величинами,
тогда как третий коэффициент #22 зависит от координат точки
пространства и является размерной величиной, т.е.
#22 =
#33 =
С1-31)
Теперь на основании двух рассмотренных выше
примеров может быть установлен геометрический смысл
метрических коэффициентов основного базиса системы координат:
51

метрические коэффициенты есть коэффициенты
пропорциональности в выражении метрики пространства с данной
системой координат, приводящие в соответствие
размерности координат (размерности квадратов координат к
размерности квадрата длины). Действительно, в декартовой
прямоугольной системе координат все три координаты х1 = я,
х2 = у, ж3 = z имеют размерность длины, поэтому
метрические коэффициенты A.30) являются безразмерными
величинами. В цилиндрической системе координат только две
координаты х1 = г и х3 = z имеют размерность длины, тогда как
угловая координата х2 — в измеряется в радианах. Согласно
этому метрический коэффициент #22 = г2 является размерной
величиной с размерностью квадрата длины, в то время как
два других коэффициента являются безразмерными
величинами (см. A.31)).
Взаимный базис системы координат.
Метрические коэффициенты взаимного базиса. Взаимный (по
отношению к основному) базис системы координат в данной
точке пространства есть совокупность трех векторов г3
(или г1, г2, г3), которые взаимосвязаны с векторами
основного базиса соотношением
1 при г = j,
0 при i ф j.
Согласно определению A.32), скалярное произведение
векторов основного (г{) и взаимного (W) базисов обусловлено
значением символа Кронекера 6?: скалярное произведение базисных
векторов с одинаковыми индексами равно единице;
результатом перемножения базисных векторов с разными индексами
является нуль. Определение A.32) позволяет по известным
векторам основного базиса построить совокупность трех
векторов взаимного базиса. Например, для первого из векторов
взаимного базиса
г1-ri^l, r1-r2 = 0, г1 ^3 = 0. A.33)
52

Как следует из этих соотношений, первый вектор взаимного
базиса г1 должен быть ортогонален обоим векторам основного
базиса Г2 и г^. Следовательно, вектор г1 = т(г2 X гз)
должен быть коллинеарен векторному произведению г 2 X гз, где
значение скалярного множителя т определяется из первого
соотношения A.33): т»1 • т (?»2 X гз) = 1. Значение т обратно по
отношению к смешанному произведению векторов основного
базиса 7*1 • [г2 X гз), которое равно объему параллелепипеда,
построенного на векторах основного базиса. Для
ортогональных систем координат смешанное произведение определяется
произведением модулей базисных векторов гг. С учетом
определения метрических коэффициентов основного базиса A.25)
получим
г\ <(г2 X г3) = |н| • \т2\ -\Ы =
г3) =
где д = det I I g+j I I — детерминант метрической матрицы
A.28) для ортогональной системы координат. Таким образом,
скалярный множитель m — 1/у/д, что позволяет найти первый
вектор взаимного базиса: г1 = (г2 X т$\ Iу/д. Аналогично
2
определяются второй и третий векторы взаимного базиса г2
и г3.
Уточним геометрическое
представление взаимного
базиса. В общем случае
неортогональной криволинейной
системы координат (рис. 1.37)
векторы основного базиса
ГЬ Г2, гг не являются
ортогональными, а векторы
взаимного базиса г1, г2, г3 не
совпадают с одноименными
Рис. 1.37
53

(имеющими одинаковые индексы, например, rj и г1)
векторами основного базиса ни по направлению, ни по модулю.
В случае ортогональной криволинейной системы координат
векторы основного базиса взаимно перпендикулярны,
одноименные векторы основного и взаимного базисов совпадают
по направлению, но могут не совпадать по модулю (рис. 1.38).
Наконец, в декартовой
прямоугольной системе
координат векторы
взаимного базиса, построенные в
соответствии с
определением A.32), совпадают по
модулю и направлению с
единичными векторами
основного базиса: г1 =
Рис. 1.38
= г, г2 =
= J,
г3 = г3 = fc.
Метрические коэффициенты взаимного базиса системы
координат вводятся с использованием векторов взаимного
базиса как величины, определяемые скалярным произведением
соответствующих базисных векторов, т.е.
gtj = rl.rj. A.34)
Совокупность девяти метрических коэффициентов gl*
образует метрическую матрицу взаимного базиса I I g%J 1 1 , которая
так же, как и метрическая матрица основного базиса, является
симметричной:
[{ди д12 9й))
(И)" #И »22 »» •
IU13 9™ 9*4)
Для ортогональной системы координат метрическая матрица
является диагональной:
711 О О
(И) -
о
о
,22
54

Между метрическими коэффициентами основного и
взаимного базисов существует взаимосвязь, которую приведем
без вывода: дц — 1/дгг. Таким образом, в декартовой
прямоугольной системе координат (дц = дуг — #зз = 1)
метрические коэффициенты взаимного базиса системы координат
имеют следующие значения:
В цилиндрической системе координат (ди = #зз = 1, #22 = г2)
метрические коэффициенты взаимного базиса отличаются от
коэффициентов основного базиса:
," = 1, 922 = 1/г\ 533 = 1, ^ = 0, хф]. A.36)
В заключение отметим, что существует еще один тип
метрических коэффициентов — метрические коэффициенты
смешанного типа^ которые определяются как скалярные
произведения двух базисных векторов, один из которых
принадлежит к основному базису, а второй — к взаимному:
A-37)
О при г/j. v '
Согласно определению взаимного базиса A.32), значения
метрических коэффициентов д\ обусловливаются значениями
символов Кронекера Ь\. Совокупность девяти метрических
коэффициентов смешанного типа образует метрическую
матрицу 11 g\ I j , которая является диагональной единичной
матрицей:
Таким образом, система координат в данной точке
пространства характеризуется тройкой векторов т\, г%, т*з,
составляющих основной базис, тройкой векторов г1, г2, г3,
составляющих взаимный базис, а также тремя метрическими
матрицами 11 д%j\ 1 , I I g*J I I , 11 5^ I I > компонентами которых
55

являются метрические коэффициенты основного и взаимного
базисов, а также метрические коэффициенты смешанного
типа.
1.3.2. Преобразования координат
и базисных векторов
При анализе характера математических объектов
математического аппарата механики сплошных сред было
отмечено, что основное требование, предъявляемое к указанным
объектам, — их инвариантность относительно
преобразования системы координат. Такие математические объекты
называются тензорами. Простейшими тензорами являются
скалярные величины, так как их значения не зависят от того,
в какой системе координат (декартовой прямоугольной,
цилиндрической, сферической или какой-то другой)
рассматривается движение сплошной среды. Покажем, что векторные
величины также инвариантны относительно преобразования
системы координат, т.е. не изменяются при переходе от одной
системы координат к другой (при неизменности точки отсче-
та).
Для описания движения сплошной среды введем
некоторую систему координат хг (ж1, ж2, ж3), например декартову
прямоугольную систему координат (ж1 = ж, ж2 = у, ж3 = z).
Выберем произвольную точку М пространства, положение
которой относительно точки 0 начала координат
характеризуется радиус-вектором г, и сколь угодно близкую к точке М точку
Mi, положение которой относительно исходной точки
характеризуется вектором dr (рис. 1.39). Для описания движения
сплошной среды может быть выбрана и любая другая система
координат у3 (у1, у2, у3), например цилиндрическая система
координат (у1 — г, у2 — 0, у3 = z). Будем в дальнейшем для
краткости систему координат хг называть старой, а систему
координат у3 — новой. Предположим, что между
координатами точек пространства в старой и новой системах
координат существует взаимосвязь: хг = жг(у-?), у3 — у-7 (ж1), т.е.
каждая из трех координат ж1, ж2, ж3 зависит от трех координат
56

Рис. 1.39
У1? У2-> 2/3 и наоборот. Например, координаты точек
пространства в декартовой прямоугольной и цилиндрической системах
координат связаны известными соотношениями: х = г cos в,
у = rsin#, z = z.
В системе координат хг вектор dr может быть
представлен в виде разложения по векторам основного базиса Г{ в
точке М как сумма произведений векторов основного базиса
и дифференциалов координат:
дг
dr = •—г dx% — т{ dx\
дхг
где дифференциалы координат dxl являются компонентами
вектора dr в разложении по векторам основного базиса (см.
A.22) и A.23)). При переходе от старой системы координат
хх к новой системе координат у3 будут изменяться зналения
компонент вектора dr от dx% к dy3, а также будет
изменяться и совокупность трех векторов, образующих.основной базис
системы координат в данной точке пространства. В
соответствии с определением A.20) векторы основного базиса будут
изменяться от гг = дг/дхг (векторы основного базиса в
системе координат хх) к (гу)' = дг/ду3 (векторы основного базиса в
системе координат у3). Несмотря на изменение компонент
вектора dr и базисных векторов при переходе от одной системы
координат к другой, сумма произведений компонент вектора
57

и соответствующих векторов основного базиса остается
неизменной, т.е. вектор dr (как математический объект) является
инвариантным относительно преобразования системы
координат:
dr = v{ dx{ = (tjI dyj. A.38)
Преобразование координат проводится по закону,
носящему название контрвариантного закона преобразования.
Согласно предположению относительно взаимосвязи между
координатами старой и новой систем координат, каждая из
трех координат у1, у2, у3 зависит от трех координат ж1, ж2,
х3:
у1 = уV. х\ х% у2 = у2(х\ х\ х% у3 = yV, х\ х3).
Компоненты вектора dr в новой системе координат yi или
дифференциалы ее координат определяются в соответствии с
правилами дифференцирования функции нескольких
переменных и соглашением о суммировании:
Эти выражения могут быть записаны в общем виде
Следовательно, чтобы перейти от компонент dxk вектора dr
в системе координат хг к компонентам dy* этого же вектора
в системе.координат у-7, необходимо знать частные
производные dyi/dxk новых координат по старым. Величины,
преобразующиеся при переходе от одной системы координат к
другой подобно компонентам вектора dr в разложении по
векторам основного базиса, называются
контрвариантными (формальный признак — индекс вверху).
58

Преобразование векторов основного базиса при
переходе от одной системы координат к другой проводится по
закону, носящему название ковариантного закона
преобразования. Радиус-вектор г = г(ж1, ж2, ж3) является функцией
координат жг, каждая из которых, в свою очередь, связана с
координатами у3: хг = xl(y3). В соответствии с
правилами дифференцирования сложной функции векторы основного
базиса (rjI в новой системе координат связаны с векторами
основного базиса гг в старой системе координат
соотношениями
, _ j>r_ _ дг^дх^ дт^дх^ дг дхъ
3 ~W~+ +
дх1 Эх2 дх3
ду) дуЭ дуз
или
дх1
' <ы0>
при использовании соглашения о суммировании. Таким
образом, для перехода от векторов основного базиса т\ в данной
точке пространства в системе координат хг к векторам
основного базиса (rjI в той же точке пространства в системе
координат yi необходимо знать частные производные дх^/ду3
старых координат по новым. Величины, преобразующиеся при
переходе от одной системы координат к другой подобно
векторам основного базиса, называются ковариантными
(формальный признак — индекс внизу).
Ковариантный и контрвариантный законы
преобразования являются взаимно обратными, что и приводит к
инвариантности вектора dr относительно преобразования системы
координат. Действительно, в соответствии с соотношениями
A.39) и A.40)
59

Выражение, заключенное в скобки, представляет собой сумму
трех членов:
у* дх1 дуг
Согласно предположению о существовании взаимосвязи
между координатами точек в старой и новой системах координат:
х1 = ж^у1, у2, у3), уг = Уг(^у я2, х3), последнее выражение
представляет собой частную производную координаты х* по
координате х*, значения которой определяются значениями
символа Кронекера:
дх1 dyi дх1 . Г 1 при I = к,
дхк дхк к \ 0 при I ф к.
Действительно, в силу независимости координат ж1, х2, х3
друг от друга значение производной дх*/дхк будет отлично от
нуля только в одном случае I = к, когда какая-либо
координата дифференцируется по самой себе. С учетом проведенного
упрощения выражение A.41) принимает вид
Выражение, заключенное в скобки, представляет собой сумму
трех слагаемых (здесь суммирование выполняется по
индексу суммирования к). Однако отличным от нуля будет только
одно из слагаемых, для которого значение индекса
суммирования к = I. В результате упрощения dxk6^ = dx* и
окончательно (tjI dyi = ri dx^ — Г{ dx% — dr, т.е. вектор dr инвариантен
относительно преобразования системы координат. Несмотря
на то что при переходе от одной системы координат к другой
преобразуются компоненты вектора dr и базисные векторы,
законы этих преобразований (контрвариантный и ковариант-
ный) взаимно обратны и обеспечивают инвариантность
вектора dr в целом относительно преобразования системы
координат.
60

По аналогии с вектором dr любой вектор а является
математическим объектом, инвариантным относительно
преобразования системы координат. Инвариантность вектора
обеспечивается тем, что законы преобразований компонент
вектора и базисных векторов при переходе от одной
системы координат к другой являются взаимно обратными.
Любой вектор может быть представлен в виде разложения
по векторам основного базиса: а = агг{ = (aJ)l(rj)f. Векторы
основного базиса при переходе от одной системы координат к
другой преобразуются по ковариантному закону A.40), и
поэтому основной базис называют также ковариантным
базисом. Компоненты же вектора аг в разложении по векторам
основного базиса преобразуются по обратному
(контрвариантному) закону и носят название контрвариантных компонент
вектора:
В то же время любой вектор может быть представлен
в виде разложения по векторам взаимного базиса: а = а{Гг.
Можно показать (мы приведем без доказательства), что и в
случае такого представления вектора сохраняется его
инвариантность относительно преобразования системы координат.
При этом векторы взаимного базиса при переходе от одной
системы координат к другой преобразуются по
контрвариантному закону
| /рЗ \ — /р
и поэтому взаимный базис называют также
контрвариантным базисом. Компоненты at вектора в разложении по
векторам взаимного базиса преобразуются по обратному (ковари-
антному) закону и носят название ковариантных компонент
вектора:
Ы' =
A.44)
61

Итак, вектор может быть представлен через свои ковари-
антные компоненты а, при использовании в качестве
базисных математических объектов векторов г1 взаимного
(контрвариантного) базиса, а может быть представлен и через свои
контрвариантные компоненты аг при использовании в
качестве базисных математических объектов векторов г,
основного (ковариантного) базиса:
а = аУ = (а,-)' (г*")' = oV,- = (а*)' (г,-)'. A.45)
Следовательно, вектор представляет собой математический
объект, инвариантный относительно преобразования системы
координат, т.е. векторные величины, так же как и
скалярные, относятся к математическим объектам, называемым
тензорами,
1.3.3. Понятие тензора второго ранга
Тензоры второго и более высокого рангов могут быть
введены на основе аналогии с векторами. Идея введения тензора
второго ранга в самом общем виде может быть
представлена следующим образом. При введении вектора
использовались базисные математические объекты — векторы
основного (г,-) или взаимного (г4) базиса, которые в совокупности с
числами — компонентами аг или а,- вектора — приводили к
образованию математических объектов, инвариантных
относительно преобразования системы координат. По аналогии с
этим можно ввести более сложные базисные математические
объекты, которые, управляя числами, позволяют образовать
более сложные математические объекты, инвариантные
относительно преобразования системы координат.
При введении тензора второго ранга такими более
сложными базисными математическими объектами являются
диадные произведения базисных векторов. Диадные
произведения базисных векторов r^j, rlr3, Т{Т3 представляют
собой результат неопределенного умножения векторов или
62

основного базиса {rtrj), или взаимного базиса (rlrJ), или обо-
их базисов (r,-W). Отметим, что в каждом из записанных
вь1ражений индексы г и j являются свободными индексами,
каждый из которых принимает значение от 1 до 3. Поэтому,
например, выражение r^j в краткой форме обозначает девять
диадных произведений: г\г\, г\Т2, П**3> Г2Г\, • ••> ^3^3-
Неопределенное умножение векторов а и Ь есть некоторая
операция над этими векторами, приводящая к образованию не
скаляров (как при скалярном умножении векторов) и не
векторов (как при векторном умножении векторов), а некоторых
новых математических объектов аЬ — тензоров второго
ранга. Любая операция, выполняемая в матемяти^е над
математическим объектом, полностью определяется ее свойствами.
Это относится и к операции неопределенного умножения
векторов, приводящей к образованию их диадных произведений.
Отметим некоторые основные свойства неопределенного
умножения векторов:
— невыполнение переместительного закона
(некоммутативность неопределенного умножения векторов), например
аЬ ф Ьа; выполнение распределительного закона и
переместительного закона относительно скалярного множителя,
например
с(Аа + ВЬ) = сАа + сВЬ = Аса + ВсЬ;
— выполнение скалярного умножения диады аЬ на
вектор с, например
аЬ с = а(Ъ с), с • аЬ = (с • а)Ьу
результатом которого будет вектор, коллинеарный одному из
векторов (а или Ь — в зависимости от порядка перемножения),
составлявших исходное диадное произведение аЬ\
— выполнение векторного умножения диады аЬ на
вектор с, например
аЪх с = а(Ь х с), с х аЬ = (с х а)Ь,
результатом которого будут новые диадные произведения
(а(Ь х с) или (с х а)Ъ — в зависимости от порядка
перемножения).
63

С использованием в качестве базисных математических
объектов диадных произведений векторов основного или
взаимного базиса вводятся такие инвариантные относительно
преобразования системы координат математические объекты,
как тензоры второго ранга. По аналогии с выражением
вектора а через компоненты и базисные математические объекты
(см. A.45)) тензор второго ранга представляется как сумма
девяти слагаемых, каждое из которых является произведением
некоторого числа (компоненты тензора) и соответствующего
диадного произведения:
(а) = аХ)Т{т> = a^TiTj = а\т{Гу A.46)
В соответствии с соотношением A.46) можно дать полное
определение тензора произвольного ранга: тензор есть
математический объект, инвариантный относительно
преобразования системы координат, представляющий собой
сумму произведений некоторых чисел — компонент тензора
— и базисных математических объектов] инвариантность
тензора обеспечивается взаимно обратным характером
преобразования компонент и базисных математических
объектов при переходе от одной системы координат к другой.
Рассмотрим возможные формы представления тензора
второго ранга A.46). Тензор второго ранга может задаваться
своими компонентами а,-у с использованием в качестве
базисных математических объектов диадных произведений
векторов взаимного базиса rlrJ. Чтобы при переходе от одной
системы координат к другой тензор (как математический объект)
оставался неизменным, а именно
при условии, что векторы взаимного базиса преобразуются по
контрвариантному закону A.43), т.е.
64

компоненты a^j тензора должны преобразовываться по кова-
риантному закону
/ у дхк дх1
Ы =akiw^j (L48)
(сравним с формулой A.44) преобразования ковариантных
компонент вектора). Действительно, из формул A.47) и A.48)
следует, что
а)'(А'(гЛ' - aJ-^^r"^
a'V V ) V ) - Ч1 dyi dyi дх<*
Так как символ Кронекера принимает значения
1 при к = а,
О при к ф а,
окончательно получаем
«у)'(г1')'
что говорит об инвариантности тензора относительно
преобразования системы координат. Компоненты aij тензора,
преобразуемые при переходе от одной системы координат
к другой по ковариантному закону {1.48), носят название
ковариантных компонент тензора второго ранга
{формальный признак — индексы внизу). Ковариантный закон A.48)
преобразования ковариантных компонент а,-у тензора второго
ранга является обратным по отношению к
контрвариантному закону преобразования базисных математических
объектов A.47), что и обеспечивает инвариантность тензора
относительно преобразования системы координат.
3-9712 65

Тензор второго ранга может задаваться и своими
контрвариантными компонентами а1-7 при использовании в
качестве базисных математических объектов диадных
произведений векторов основного базиса r^rj. Компоненты atJ тензора
носят название контрвариантных компонент тензора
(формальный признак — индексы вверху) в связи с тем, что для
обеспечения инвариантности математического объекта
(a) = a^rtrJ = (a^)\ri)\rj)'
при условии преобразования векторов основного базиса по
ковариантному закону
' дха / \' дхР
они должны преобразовываться по обратному —
контрвариантному — закону
л =
дхк дх1
Наконец, третья возможная форма представления тензора
второго ранга определяется заданием смешанных компонент
а;- тензора при использовании в качестве базисных
математических объектов диадных произведений векторов основного и
взаимного базисов тхгу.
В этом случае при переходе от одной системы координат к
другой базисный вектор гг преобразуется по
контрвариантному закону, а базисный вектор rj — по ковариантному закону:
Для обеспечения инвариантности математического объекта
(а) относительно преобразования системы координат
необходимо преобразование компонент а\ по смешанному закону:

1.3.4. Ряд тензоров
Сформулируем понятие ранга тензора и построим ряд
тензоров (от простого тензора к сложному).
Ранг тензора — это число, определяющее количество
компонент тензора и равное количеству индексов у компонент.
Число компонент тензора N связано с рангом тензора г как
# = 3Г.
Тензор нулевого ранга (г = 0) является простейшим
тензором с числом компонент N = 1. Это скалярная величина,
характеризуемая только одним числовым значением.
Тензор первого ранга (г = 1) — более сложный тензор с
числом компонент N = 3. Это вектор а = а+гг (или а = а'г,-),
характеризуемый тремя числами — компонентами а\, a<i, «з
(или а1, а2, а3). Число индексов у компонент а, соответствует
рангу тензора и равно единице.
Тензор второго ранга (г = 2) имеет девять компонент
(JV = 9). Он может быть представлен либо через свои ко-
вариантные компоненты а,^, либо через свои
контрвариантные компоненты а%3, либо через свои смешанные компоненты
а? (см. A.46)). Каждому тензору второго ранга можно
поставить в соответствие матрицы размером 3.x 3.
Совокупность ковариантных, контрвариантных и смешанных
компонент образует соответствующие матрицы:
(М)
(И)
¦К
а21 а22 а23
«31 <*32 «33
((ап а12 а13))
а21 а22 а23 ;
На31 а32 а33 J J
(И)) -
а\ а{ а\
а\ а2 а\
19 4
\,а\ а2 а\
67

Тензор третьего ранга (г = 3) имеет число компонент
N — 27. Число индексов у компонент агд соответствует
рангу тензора. Тензор третьего ранга может быть выражен через
свои ковариантные компоненты а^ь контрвариантные
компоненты а%3\ смешанные компоненты различного вида а*-, а\
и т.д. В качестве базисных математических объектов в
данном случае выступают триадные произведения базисных
векторов Т{Т)Тъ, ггг3гк и т.д., представляющие собой результат
неопределенного умножения трех векторов основного и
взаимного базисов. Тензор третьего ранга имеет следующую
структурную запись:
(а) = dijkrlr3v = atj
В механике сплошных сред наиболее часто
употребляются тензоры нулевого ранга (скаляры), тензоры первого
ранга (векторы) и тензоры второго ранга. Примером тензора
второго ранга является фундаментальный метрический
тензор, компоненты которого — метрические коэффициенты
системы координат:
{я) = ttjrV = glJriVj = g\vlTy
При этом метрические коэффициенты g^j основного базиса
системы координат являются ковариантными компонентами
метрического тензора, метрические коэффициенты glJ взаимного
базиса представляют его контрвариантные компоненты,
метрические коэффициенты смешанного типа д\
соответствуют смешанным компонентам тензора (д). Покажем,
например, что совокупность девяти метрических коэффициентов gij
основного базиса дает ковариантные компоненты тензора
второго ранга. Ранее было доказано, что векторы основного
базиса при переходе от одной системы координат к другой
преобразуются по ковариантному закону A.40):
dxk ( у дх1
68

Соответственно метрические коэффициенты основного базиса,
определяемые как скалярные произведения векторов основного
базиса, преобразуются по закону
дхк дх1 дхк дх1
Сопоставление полученной формулы с формулой A.48)
показывает, что метрические коэффициенты g{j основного базиса
при переходе от одной системы координат к другой
преобразуются по закону преобразования ковариантных компонент
тензора второго ранга. Следовательно, совокупность девяти
метрических коэффициентов g{j действительно определяет кова-
риантные компоненты некоторого тензора второго ранга —
фундаментального метрического тензора.
В общем случае тензор второго ранга (а) = а^ггг^
характеризуется девятью различными компонентами a,j- (или а1*',
или а\). В двух важных частных случаях количество
различных компонент, которыми определяется тензор второго ранга,
менее девяти, так как некоторые компоненты взаимосвязаны
между собой. Это случаи симметричных и
антисимметричных тензоров.
Симметричным называется тензор, значения
компонент которого не изменяются при перестановке
одноименных индексов: а^- = а^. Под одноименными следует понимать
либо только нижние индексы, либо только верхние. В
последнем случае условие симметричности тензора записывается в
виде а%3 = aJ%. Очевидно, что симметричному тензору
второго ранга соответствует симметричная относительно главной
диагонали матрица 11 aij 11 , среди элементов которой не
более шести различных компонент:
ai3
J J
I I «13 «23 азз
Примером симметричного тензора второго ранга является
фундаментальный метрический тензор, для которого
выполняется условие симметричности g±j = gj{.
69

Антисимметричным называется тензор, значения
компонент которого изменяются на противоположные при
перестановке одноименных индексов: a^j = — ay, или alJ = —а3\
Компоненты антисимметричного тензора с одинаковыми
индексами равны нулю, а элементы соответствующей
тензору матрицы, симметричные относительно главной диагонали,
различаются знаками:
= -«12 0 а2г
I v -^13 -а23 0 ) )
Антисимметричный тензор второго ранга в общем случае
характеризуется только тремя отличными от нуля числами: ai2,
a13> a23- Поэтому он иногда называется псевдовектором,
поскольку вектор также характеризуется только тремя
компонентами.
1.3.5. Элементы тензорной алгебры
Тензорная алгебра является разделом тензорного
исчисления, в котором определяются правила проведения
алгебраических операций с тензорами: сложение и вычитание тензоров;
умножение тензора на скаляр; операции жонглирования
индексами; свертывание тензора; скалярное и векторное
умножение тензоров.
Сложение и вычитание тензоров. Операция
сложения тензоров выполняется при следующих ограничениях:
ранги суммируемых тензоров должны быть равными;
структура суммируемых тензоров должна быть одинаковой. Суммой
двух тензоров
(д ) ~ Дв'чТ* 7* — а щ в 7"-» — а • 7* 7*V
/ *J * J t J
и
(b) = bijrlr^ =
70

является тензор того же ранга и той же структуры
(с) = (а) + (b) = cxjrlri = ctjrtrj = с\г{т^
компоненты которого равны сумме соответствующих
компонент исходных тензоров (или только ковариантных, или
только контрвариантных, или только смешанных):
Суммирование компонент разных типов, например а^ +Ь%*, не
допускается.
Вычитание тензоров определяется как действие,
обратное сложению, и выполняется при аналогичных
ограничениях. Разностью двух тензоров (а) и F) является тензор
(с) = (а) - (Ь) того же ранга и той же структуры,
компоненты которого равны разности соответствующих компонент
тензора уменьшаемого и тензора вычитаемого:
сц = ац-Ъц, с« = а* - Ь«, с* = «?-*«.
Умножение тензора на скаляр. Эта операция
выполняется без каких-либо ограничений. Результатом умножения
произвольного тензора
(а) = <Lijr%r3 = a%3riTj = o\txtj
на скалярную величину а является тензор (с) = а(а) того
же ранга и той же структуры, что и исходный тензор (а),
компоненты которого равны произведению данной скалярной
величины и компонент исходного тензора:
с
г> = aalJ, с] = аа\.
Операции жонглирования индексами. Эти
операции позволяют осуществить переход от одного типа
компонент тензора (например, от контрвариантных) к компонентам
другого типа (например, к ковариантным). Необходимость
71

этих операций покажем на следующем примере. Уравнения
движения идеальной жидкости связывают вектор ускорения
индивидуальной частицы жидкости, имеющей плотность /э, с
градиентом давления gradp и вектором объемных сил F:
р— = F-gradp.
Это векторное уравнение эквивалентно трем скалярным
уравнениям, записанным через компоненты участвующих в
уравнении векторов — тензоров первого ранга:
В трех уравнениях A.51) в соответствии с правилами
суммирования тензоров участвуют только ковариантные
компоненты векторов ускорения dv/dt, градиента давления gradp,
вектора объемных сил F. Однако в общем случае для
любого из этих векторов, например для вектора объемных сил F,
могут быть известны только контрвариантные компоненты:
F — FJvj. Непосредственно использовать в уравнении A.51)
контрвариантные компоненты F3 вектора объемных сил
недопустимо в силу ограничений, накладываемых на операцию
суммирования тензоров. Необходим предварительный переход
от контрвариантных компонент FJ вектора к его ковариант-
ным компонентам F{. Для этой и других целей используется
одна из трех операций жонглирования индексами: опускание
индекса, поднятие индекса, замена одного индекса другим.
Операция опускания индекса. Эта операция
заключается в переходе от контрвариантных компонент тензора
(индекс вверху) к его ковариантным компонентам (индекс
внизу). Рассмотрим правила проведения этой операции на
примере тензора первого ранга (вектора)
(а) = а = atV = а? Ту A-52)
72

Будем считать заданными контрвариантные компоненты а-?
вектора. Определим неизвестные ковариантные компонен-
Tbi а{. Для этого выполним скалярное умножение обеих
частей равенства A.52) на вектор основного базиса гд., т.е.
аггг -тк = ajrj -rk.
С учетом определений метрических коэффициентов A.25),
A.34), A-37) получим
k =
*9jk-
%9k = a
В левой части полученного выражения выполняется
суммирование по индексу г. Единственным отличным от нуля
слагаемым в этой сумме будет член акд^ = ак (см. определение
A.37) метрических коэффициентов смешанного типа).
Окончательное выражение ковариантных компонент вектора через
его контрвариантные компоненты принимает вид
я* = aJgjk, A.53)
т.е. ковариантные компоненты тензора первого ранга
определяются суммой произведений его контрвариантных
компонент и соответствующих метрических коэффициентов
основного базиса.
В частном случае декартовой прямоугольной системы
координат из формулы A.53) следует, что в этой системе
координат отсутствует различие между ковариантными и
контрвариантными компонентами. Действительно, в декартовой
прямоугольной системе координат д^ — 0 при j ф А;, д^к — 1
при j = к (см. A.30)) и ак = ак. Этот же вывод следует из
структурной записи A.52) тензора первого ранга, так как в
декартовой прямоугольной системе координат тройка
векторов основного базиса совпадает с тройкой векторов взаимного
базиса — в обоих случаях это совокупность трех единичных
взаимно ортогональных векторов г, jy к.
Аналогичным образом выполняется операция опускания
индекса применительно к компонентам тензора второго ранга.
73

Если заданы контрвариантные компоненты а%3 тензора
второго ранга, то смешанные (акА и ковариантные (а^) компоненты
получаются также с использованием метрических
коэффициентов основного базиса — ковариантных компонент
фундаментального метрического тензора, т.е.
<*>[ = a%39ik> ак1 = aJk9jl = a%J9ik9jl- A-54)
Операция поднятия индекса. Эта операция
заключается в переходе от ковариантных компонент тензора
(индекс внизу) к контрвариантным компонентам (индекс
вверху). Правила проведения этой операции рассмотрим на
примере тензора первого ранга A.52). Будем считать заданными
ковариантные компоненты аг вектора. Для определения
неизвестных контрвариантных компонент выполним скалярное
умножение обеих частей равенства A.52) на вектор взаимного
базиса rk. По аналогии с изложенным выше получим
выражение для операции поднятия индекса применительно к тензору
первого ранга:
агг{ • rk = ajrj • г*, aiglk = a?g), ak = aigik. A.55)
Контрвариантные компоненты тензора первого ранга
определяются суммой произведений его ковариантных компонент и
соответствующих метрических коэффициентов взаимного
базиса — контрвариантных компонент фундаментального
метрического тензора A.55).
Аналогичным образом осуществляется операция
поднятия индекса применительно к компонентам тензора второго
ранга, т.е. переход от ковариантных компонент а^ к
смешанным ак- и контрвариантным akl компонентам тензора второго
ранга:
а) = aij9ik, akl = a)g*1 = ацд*?1. A.56)
Операция замены одного индекса другим. Бе
можно проиллюстрировать с помощью следующего примера. В
уравнении движения A.51) идеальной жидкости индекс г
является свободным индексом. В отличие от индекса
суммирования, который может обозначаться любой буквой (а = а,г* =
74

_ a-rJ — a^r^) и используется лишь для обозначения
суммы, свободный индекс в одном из членов выражения не может
произвольно заменяться каким-либо другим. Если же такая
необходимость возникает и в выражении A.51) вместо
компонент Ft вектора объемных сил с индексом г нужно применить
компоненты Fj с индексом j, то можно цспользовать свойство
метрических коэффициентов gj смешанного типа, которые
отличны от нуля и равны единице только в случае совпадения
индексов: г = j (см. A.37)). С учетом этого свойства
метрических коэффициентов получаем соотношение
ai = ajgl A.57)
которое отображает операцию замены одного индекса другим
применительно к тензору первого ранга. На основании
соотношения A.57) уравнения движения A.51) могут быть
выражены через компоненты Fj вектора объемных сил:
Аналогичным образом проводится операция замены одного
индекса другим применительно к компонентам тензора второго
ранга:
a>il = <*>ij9Jl> 4l = aij9k9Jr (L58)
Свертывание тензора. Это операция суммирования
компонент тензора по двум каким-либо индексам, один из
которых верхний, а другой — нижний. Так, например, сверткой
тензора второго ранга (а) = а\т%т^ заданного своими
смешанными компонентами а^, является сумма
а\ =
представляющая собой скалярную величину Ь. Сверткой
тензора третьего ранга (а) = а%;Т*г*гь по двум индексам,
например г и &, является вектор — тензор первого ранга с
компонентами
75

Как следует из приведенных правил свертывания тензора,
свертка представляет собой тензор, ранг которого на две
единицы меньше ранга исходного тензора. Отсюда вытекает
ограничение на эту операцию: ранг свертываемого тензора
должен быть не менее двух (г > 2).
Скалярное умножение тензоров. Рассмотрим
правила скалярного умножения тензоров на примере умножения
тензоров первого ранга (ri = т2 — 1): (а) = аггг и F) = 6jW,
имея в виду определения A.25), A.34), A.37) метрических
коэффициентов, а также правила выполнения операций
жонглирования индексами:
= аг (Ъ3д1)) = агЬ{ = ахЪ1 + a2b
Итак, скалярным произведением тензоров первого ранга
является скалярная величина, равная сумме попарных
произведений одноименных компонент. В частности, в
декартовой прямоугольной системе координат, где отсутствует
различие между ковариантными и контрвариантными
компонентами тензоров, полученная формула для скалярного
произведения тензоров первого ранга совпадает с аналогичной
формулой A.2) векторной алгебры.
При скалярном умножении тензора второго ранга (а) —
— dijT^vi (т\ = 2) на тензор первого ранга F) = Ькг^ (г2 — 1)
получается тензор первого ранга
(с) = (а) • (Ь) = (o0-rV) • (bkrk) = а^Ькт{ (г> ¦ тк) =
= atjbkrlgJk = ац(ькд>к) г1 = a^W = сУ
с ковариантными компонентами сг- = а^ЬК При получении
результата использовалось одно из свойств диадных
произведений векторов, проявляющееся при скалярном умножении
диады на вектор: аЬс — а{Ь • с). Следовательно, при
скалярном умножении тензоров результирующий тензор имеет ранг,
равный разности рангов перемножаемых тензоров: г = г\ — г2-
76

Векторное умножение тензоров. Определим
правила векторного умножения тензоров на примере двух тензоров
первого ранга (г\ — Т2 — 1): (а) = а%т{ и F) = Wtj. При
векторном умножении тензоров
(а) X F) = (alrt) X (Vrj) = aWfr, X г,-)
возникает необходимость в векторном перемножении
базисных векторов. В общем случае записи тензоров (или через ко-
вариантные, или через контрвариантные, или через
смешанные компоненты) необходимо определить векторные
произведения векторов основного базиса гг X гу, векторов взаимного
базиса rlxW, векторов основного и взаимного базисов гг х т3.
Любое из названных произведений является вектором, а
следовательно, может быть представлено в виде разложения по
векторам основного или взаимного базиса. Примем без
доказательства, что компонентами в разложении указанных
векторных произведений по векторам основного или взаимного
базиса являются компоненты тензора третьего ранга (Л) —
дискриминантного тензора (тензора Риччи):
тг х Vj = Aljkrk = Л* г*;
гг х
гг х
= Aljkrk = Л?г*; A.59)
Дискриминантпный тензор есть тензор третьего ранга,
компоненты которого являются компонентами в
разложении векторных произведений базисных векторов по
векторам основного или взаимного базиса. Дискриминантный
тензор может быть представлен через свои ковариантные,
контрвариантные и смешанные компоненты:
(Л) = AyfcrVr* = Л"*г<г,-г* = AfyrVrjfc = ...
Компоненты разных типов связаны между собой в
соответствии с правилами жонглирования индексами, например:
77

Л|-- = Aijkgkl. Поэтому, чтобы определить всевозможные
векторные произведения базисных векторов A.59), достаточно
установить значения ковариантных компонент Л^ дискрими-
нантного тензора. С этой целью выполним скалярное
умножение левой и правой частей равенства A.59) на вектор
основного базиса г/. В результате (с учетом операции замены одного
индекса другим) получим
(г,- х г Л • VI = Aijkrk - г/ = Aijkg{ = Лг;/;
V / ч A.60)
Kjl= \Ti XVjj Vh
т.е. ковариантные компоненты дискриминантного тензора
определяются смешанным (векторно-скалярным)
произведением трех векторов основного базиса.
Из формул A.60) следует заключение о численных
значениях компонент Aiji дискриминантного тензора. Компоненты
Aiji с любыми двумя одинаковыми индексами (или t = j, или
г = /, или j = /) равны нулю (см. формулу A.4) смешанного
произведения трех векторов). В противном случае при
разных значениях индексов г, j, l компоненты Л^/ определяются
значением смешанного произведения трех различных
векторов основного базиса, которое равно объему построенного на
базисных векторах параллелепипеда, взятого со знаком плюс
или минус в зависимости от взаимной ориентации векторов
ri-> rj> rl- Для ортогональных систем координат при i ф j,
j ф l,i ф1 A^i = i|rll' lr2l * 1гз|- С учетом определения A.25)
метрических коэффициентов основного базиса и
диагонального вида метрической матрицы 11 д^ ] I для ортогональных
систем координат получим
где д = det 11 g{j J j — детерминант метрической матрицы
основного базиса ортогональной системы координат. Таким
образом, ковариантные компоненты дискриминантного
тензора принимают в ортогональной системе координат следующие
значения:
0 при i=j, i = /, j = /,
при гф^ гф1, j*l. (
78

Знак (плюс или минус) компонент Л,^/ наиболее удобно
определять непосредственно из соотношения A.60) с учетом того,
чхо совокупность векторов основного базиса тч, Г2, т*з
образует правую тройку векторов (с конца вектора гз поворот
вектора г\ по кратчайшему пути к вектору v<i происходит против
хода часовой стрелки). Например, Лш = \т\ X т<Л гз = +д,
так как вектор г\ ХГ2 направлен в ту же сторону, что и вектор
гз (см- Рис- 1-31), а следовательно, (т\ хг2)-гз > 0. Напротив,
д213 =fr2 X ri J • гз = —у/ду так как вектор Г2 X г\ направлен
противоположно вектору гз, а следовательно, (гз X т\) гз < 0
и т.д. Нетрудно установить, что правило для определения
знака компонент Л^-/ сводится к правилу циклической
перестановки.
С установлением значений компонент дискриминантного
тензора представляется возможным определение правил
векторного умножения тензоров. Результатом векторного
умножения тензоров первого ранга
(а) X F) = а^(тг X rj) = alVAljkrk = ckrk
является также тензор первого ранга с компонентами с*. =
= а26^Л,д, в образовании которых участвуют
компоненты дискриминантного тензора и компоненты
перемножаемых тензоров. В частности, в декартовой прямоугольной
системе координат отсутствует различие между ковариант-
ными и контрвариантными компонентами тензоров, а
детерминант метрической матрицы есть постоянная величина
д = det 11 g{j 11 = 1. В связи с этим компоненты
дискриминантного тензора принимают значения 0, +1, — 1, а
полученная формула совпадает с формулой A.3) векторного
произведения векторов.
При векторном умножении тензора второго ранга (а) =
= aijrlrJ на тензор первого ранга (b) = bkrk получится тензор
второго ранга
(а) х F) = (atirV) X (&Ч) = a.A'V X rk) =
= ао-6*г''(л?,г') = (ацЬкА{,)
= сцт{т1
79

с компонентами сц = aijb^A^. При получении результата
использовалось одно из свойств диадных произведений векторов,
проявляющееся при векторном умножении диады на вектор:
аЬ х с = а(Ь х с). Итак, при векторном умножении тензоров
ранг результирующего тензора равен наивысшему из рангов
перемножаемых тензоров: г = max(ri, Г2).
1.3.6. Элементы тензорного анализа
В механике сплошных сред тензорные математические
объекты, как правило, зависят от координат и времени.
Раздел тензорного исчисления, в котором рассматриваются
операции дифференцирования и интегрирования переменных
тензоров, называется тензорным анализом.
Дифференцирование тензоров по координатам.
Специфика этой операции в общем случае криволинейной
системы координат связана с переменностью не только
компонент, но и базисных векторов. Действительно, только в случае
декартовой прямоугольной системы координат совокупность
векторов основного базиса не изменяется при переходе от
одной точки пространства к другой (см. рис. 1.32). Напротив, в
любой криволинейной системе координат, например в
цилиндрической, совокупность базисных векторов в разных точках
пространства различна (см. рис. 1.33), т.е. базисные векторы
являются функциями координат: гг — г^ж1, #2, ж3).
Именно этот факт и определяет особенности дифференцирования
тензоров по координатам.
Рассмотрим правила дифференцирования тензоров на
примере тензора первого ранга (вектора), заданного
контрвариантными компонентами, (а) = аггг. Будем считать,
что компоненты тензора зависят от координат и времени:
аг = аЧя1, я2, я3, ?), а также (в общем случае
криволинейной системы координат) что базисные векторы зависят от
координат: Г{ = Г{(х1ух2уХ^). Определим частную производную
тензора (а) по любой координате хК С учетом правил
дифференцирования произведения получим
80

Производная векторной функции Т{ = г^ж1, ж2, ж3) по
скалярному аргументу ж-7 представляет собой некоторый вектор,
который обозначим как
dri
гц = ^у. A.63)
Как и всякий вектор, вектор A.63) может быть представлен в
виде разложения по векторам основного или взаимного базиса:
Компоненты Гг^ производной вектора основного базиса Г{ по
координате х3 в разложении по векторам взаимного базиса
называются символами Кристпоффеля первого рода, а
компоненты Г*- производной вектора основного базиса Г{ по координате
х3 в разложении по векторам основного базиса носят
название символов Крисгпоффеля второго рода. С использованием
символов Кристоффеля второго рода (см. A.64)) выражение
A.62) для производной тензора (а) по координате xJ
принимает вид
д{а) да* ik
= г" + вГг*
Поменяем в выражении а* Г* г д. обозначения индексов
суммирования: г на А; и А; на г. Это допустимо, так как индекс
суммирования может обозначаться любой буквой,
существенно лишь его двукратное повторение в выражении: один раз
вверху, другой — внизу. Поэтому с точки зрения
соглашения о суммировании выражения агГ^г^ и a*Tji-г; полностью
эквивалентны. С учетом изменения обозначения индексов
суммирования получим
т.е. производной тензора первого ранга, заданного
контрвариантными компонентами, является вектор, компоненты
которого имеют специальное обозначение
fS a*r*' (L66)
81

и название абсолютной (ковариантной) производной
контрвариантных компонент тензора первого ранга. Очевидно,
что абсолютная производная компонент вектора отличается
от обычной частной производной дополнительными членами
а Г!-, связанными с переменностью базисных векторов по
координатам.
Остановимся более подробно на таких объектах
тензорного анализа, как символы Кристоффеля. По определению
A.64), символы Кристоффеля первого и второго рода
являются компонентами производной вектора основного базиса
по координате.
Геометрический смысл символов Кристоффеля
заключается в следующем. В декартовой прямоугольной системе
координат векторы основного базиса не зависят от координат,
поэтому производная любого базисного вектора г,- по любой
координате х-7 равна нулю: дг^/дх^ = 0.
Соответственно (см. A.64)) равны нулю и компоненты вектора дг{/дх^:
Гг^ = Г* = 0. В любой криволинейной системе координат в
общем случае векторы основного базиса зависят от координат:
Т{ — гДх1, ?2, х3), поэтому производная дг^/дх3 отлична от
нуля, а следовательно, отличны от нуля и компоненты этой
производной: Г^д. ф 0, Г*- / 0. Очевиден вывод: символы
Кристоффеля характеризуют искривленность координатных
линий системы координат ("криволинейность" системы
координат), т.е. символы Кристоффеля являются
характеристикой системы координат наряду с фундаментальным
метрическим тензором.
Символы Кристоффеля не являются компонентами
некоторого тензора третьего ранга. Действительно, кова-
риантные компоненты тензора третьего ранга при переходе
от одной системы координат к другой должны изменяться в
соответствии с ковариантным законом преобразования:
\*ijk) -а«/
дх
Очевидно, что если компоненты тензора третьего ранга
равны нулю в какой-то одной системе координат, то они будут
82

равны нулю и в любой другой системе координат. Символы
Кристоффеля не удовлетворяют этому условию: в декартовой
прямоугольной системе координат они равны нулю, а,
например, в цилиндрической — отличны от нуля.
Связь символов Кристоффеля первого и второго рода
устанавливается на основе определения A.64). Для этого
выполним скалярное умножение обеих частей равенства A.64)
на вектор взаимного базиса г*. С учетом выражений A.34),
A.37) для метрических коэффициентов взаимного базиса и
метрических коэффициентов смешанного типа, а также правил
выполнения операции замены одного индекса другим получим
rtjk rk-vl = Г*- П • г1, Tijkgkl = Г^1, Г|,. = Ttjkgkl.
Несмотря на то что символы Кристоффеля не являются
компонентами тензора третьего ранга, символы Кристоффеля
первого и второго рода взаимосвязаны подобно ковариантным
и смешанным компонентам тензора через метрические
коэффициенты взаимного базиса.
Вычисление символов Кристоффеля выполняется с
помощью метрических коэффициентов g±j основного базиса
системы координат. Составим частные производные метрических
коэффициентов по координатам с учетом выражения A.25) и
обозначений A.63), а также правил дифференцирования
произведения:
dJii--L(r..r.\-
(r.
дд* д (, ,}
_ dri _ ¦ - дгк
дх* ~ дх
drj drk
83

В правых частях выражений A.67) находятся одинаковые
члены, например r{j • г д. = гу,- • гд.. Это следует из выражения
A.63) и определения векторов основного базиса A.20), так как
/дт\ _
\дх*) ~
д2
dxi
а результат двукратного дифференцирования не зависит от
порядка дифференцирования. С учетом отмеченного факта и
определения символов Кристоффеля A.64) получим
^^__2 2Г. 1. _2Г.
дх* + дх> дхк~ %3 Гк-П^1Т Тк~Пчк-
Окончательное выражение для символов Кристоффеля
первого рода через метрические коэффициенты принимает вид
dgik ддц
Формула A.68) позволяет вычислить значения символов
Кристоффеля в любой системе координат, если известны
метрические коэффициенты gij основного базиса. Например, в
декартовой прямоугольной системе координат все 27 значений
символов Кристоффеля 1\уд. = 0, так как метрические
коэффициенты являются постоянными величинами (см. A.30)), а
в цилиндрической системе координат (ж1 = г, ж2 = 0, х3 = z)
в совокупности 27 значений символов Кристоффеля
присутствуют члены, отличные от нуля:
Абсолютная (ковариантная) производная ковариантных
компонент тензора первого ранга вводится в рассмотрение
84

при дифференцировании по координатам вектора (а) — а —
= аггг, заданного ковариантными компонентами п{. В этом
случае
хз дхЛ1 ) dxJ %дх3
дхз дхЛ1 ) dxJ %дх3
и возникает необходимость в определении производной
векторов взаимного базиса гг по координате хК Эта величина
находится из соотношения гг гд. = <$?, связывающего векторы
основного и взаимного базисов. Дифференцируя это
соотношение по координате х3 с учетом того, что при данной паре
векторов гг и Г}, символы Кронекера Ь\ есть постоянные
величины, получаем
или в соответствии с определением символов Кристоффеля
A.64)
Очевидно, что при скалярном умножении вектора дгг/дх3
на базисный вектор г*, получается скалярная величина —FJL-,
если компонентами первого вектора являются взятые со
знаком минус символы Кристоффеля второго рода, т.е.
-Д = -Рт;Гш, A.69)
так как
Теперь можно найти выражение для производной вектора,
заданного ковариантными компонентами, по координатам.
С учетом изменения обозначений индекса суммирования
получаем
-e*r«)ri=(v^)rl- (L70)
85

Производной тензора первого ранга, заданного ковариантны-
ми компонентами, является вектор, компоненты которого
1ё в*г& (L71)
являются абсолютными производными ковариантных
компонент исходного вектора. Так же как и в предыдущем случае,
абсолютная производная отличается от частной производной
дополнительными членами, учитывающими переменность
базисных векторов.
Абсолютная (ковариантная) производная
контрвариантных компонент тензора второго ранга вводится в
рассмотрение по аналогии с вектором, заданным
контрвариантными компонентами. При дифференцировании по координате
хк тензора второго ранга (а) = a^i^ry, заданного
контрвариантными компонентами а'-7, с учетом формулы A.64) и
изменения обозначений индексов суммирования получаем
д(а) _ d(ai^rlrj) _ даЦ
„-Яг,
•J дхк }
дхк ~ дхк •J дхк
Производной тензора второго ранга, заданного
контрвариантными компонентами, является также тензор второго ранга,
компоненты которого — абсолютные производные
контрвариантных компонент исходного тензора:
e°n* + el"lrk- (L72)
В заключение приведем вывод абсолютной (ковариант-
ной) производной ковариантных компонент тензора
второго ранга. С учетом выражения A.69) производную тензора.
86

второго ранга (а) = a^VW, заданного ковариантными
компонентами аг;, по координате xk запишем в виде
дац дгг •
= ^rV + a"—rJ+
+ aijT дх~Ь-~дхЪГГ ~ Ut}X *'r ' " Uy ' «
* - ^И JJ п П г1г> - a Tj r'V -
а1г r a*jLklr T ~
где абсолютная производная ковариантных компонент тензора
второго ранга определяется формулой
Vita,, = -^L - ayrl,- - а,7Г^, A.73)
Подчеркнем еще раз, что все абсолютные производные
отличаются от обычных частных производных
дополнительными членами, учитывающими искривленность
координатных линий системы координат. Полученные формулы A.66),
A.71)—A.73) для абсолютных производных компонент
тензоров первого и второго рангов являются фундаментальными
соотношениями тензорного анализа и широко используются
при постановке и решении задач механики сплошных сред.
Дифференциальные операции первого порядка с
тензорами. К числу дифференциальных операций первого
порядка относятся операции определения градиента,
дивергенции и ротора тензора. В тензорном анализе
дифференциальные операции первого порядка с тензорами вводятся с
использованием символического подхода. В принципе каждая из
перечисленных операций с тензорами первоначально
вводится с помощью соответствующего определения (см., например,
определения градиента скалярной величины, дивергенции и
ротора вектора). Однако в практическом использовании
более прост и удобен именно символический, абстрагированный
87

от изначального определения рассматриваемых операций
подход. В соответствии с этим подходом в тензорном анализе
вводится векторный символический дифференциальный
оператор Гамильтона
V = V,(...)r\ A.74)
компонентами которого являются абсолютные (ковариант-
ные) производные некоторых математических объектов.
Частным случаем этого символического оператора является
оператор Гамильтона A.19), используемый в векторном
исчислении в декартовой прямоугольной системе координат. С
помощью векторного символического дифференциального
оператора Гамильтона A.74) выполняются дифференциальные
операции первого порядка с тензорами. При этом следует иметь
в виду, что абсолютные производные Vt(...) берутся только
от компонент математических объектов, на которые
действует дифференциальный оператор A-74).
Градиент тензора — это результат действия оператора
Гамильтона на заданный тензор (или же результат
неопределенного умножения оператора Гамильтона на заданный
тензор — см. раздел 1.3.3), т.е.
grad(a) = V(a). A.75)
Градиентом тензора нулевого ранга (а) = а является вектор
grad(a) = Уг(а)гг, компоненты которого равны абсолютным
производным заданной скалярной величины а по
соответствующим координатам. Абсолютные производные скалярных
величин совпадают с обычными частными производными,
поэтому градиент тензора первого ранга представляется
выражением
да : да л да о да о
Очевидно, что в частном случае декартовой прямоугольной
системы координат полученные формулы для градиента
скалярной величины совпадают с формулой A.6) векторного
анализа.
88

Градиентом тензора первого ранга (вектора) (а) = ajrJ
является тензор второго ранга
grad (a) = V(a) = V^a,) rV,
компоненты которого — абсолютные производные компонент
исходного тензора. Очевиден вывод о том, что в
результате нахождения градиента тензора получается математический
объект, ранг которого на единицу выше ранга исходного
объекта.
Дивергенция тензора определяется как результат
скалярного умножения оператора Гамильтона на заданный
тензор, т.е.
div(a) = V • (a). A.76)
Дивергенция тензора первого ранга (a) = ujv* в соответствии
с A.76) определяется как
div(a) = [V,(...) г*] • (ajri) = V, (ay) г* • г> = V; (ay) д{>.
Отметим без доказательства, что компоненты </,-у, дг^ gj
метрического тензора ведут себя по отношению к абсолютному
дифференцированию как постоянные величины и их можно
вносить под знак и выносить из под знака абсолютной
производной. В соответствии с этой особенностью метрических
коэффициентов выражение для дивергенции тензора первого
ранга приобретает вид
div(a) = Vi(ajgiiy) = V.-a1' = Via1 + V2a2 + V3a3. A.77)
Очевидно, что в частном случае декартовой прямоугольной
системы координат, в которой отсутствует различие между
абсолютной и частной производными компонент вектора,
полученное соотношение приводит к известной формуле A.13)
векторного анализа. В случае же криволинейной системы
координат выражение A.77) дивергенции вектора отличается от
формулы A.13) дополнительными членами, учитывающими
искривленность координатных линий системы координат.
89

Дивергенцией тензора второго ранга (а) = а^т3гк
является тензор первого ранга, т.е. вектор
div(a)= [V,(...)r'] ¦(a]kr>rk) = V,
= Vt(a>fc)(r' • г>)г* =
компоненты которого — суммы абсолютных производных
соответствующих смешанных компонент исходного тензора.
Таким образом, операция нахождения дивергенции тензора
уменьшает ранг математического объекта на единицу.
Ротор тензора определяется как векторное произведение
оператора Гамильтона на заданный тензор, т.е.
rot(a) = Vx (a). A.78)
Операцию нахождения ротора тензора рассмотрим на примере
тензора первого ранга (a) = q?tj, В соответствии с A.78)
ротором тензора первого ранга является также тензор первого
ранга:
pot(a)= []
() r1 X rj = Vt-(a>) \)krk = ckrk. A.79)
В образовании компонент ск = Vj(a^) Л*^ полученного тензора
участвуют абсолютные производные компонент а-7 исходного
тензора и компоненты Агк дискриминантного тензора. Таким
образом, при определении ротора тензора ранг
математического объекта не изменяется.
Интегральные теоремы тензорного анализа. В
связи с опердциями интегрирования тензоров, переменных по
координатам, в механике сплошных сред наиболее часто
употребляются две интегральные теоремы: Остроградского —
Гаусса и Стокса. Эти теоремы являются обобщением известных
90

теорем векторного анализа на случай тензоров
произвольного ранга. Доказательство теорем Остроградского — Гаусса и
Стокса применительно к векторам (тензорам первого ранга)
следует непосредственно из определений дивергенции A.11) и
ротора A.16) вектора. Исходя из аналогии, ограничимся
формулировкой и записью этих теорем для случая тензоров
произвольного ранга.
Теорема Остроградского — Гаусса формулируется
следующим образом (см. рис. 1.23): поток тензора через
замкнутую поверхность равен интегралу по объему,
ограниченному этой поверхностью, от дивергенции тензора, т.е.
i(a) ndS = I div(a) dV. A.80)
В выражении A.80) под п = п^гк понимается единичный
вектор внешней нормали к замкнутой поверхности 5,
ограничивающей объем V. Если в качестве тензора (а) рассматривается
тензор второго ранга (a) = aijr%rJ, то выражение теоремы
Остроградского — Гаусса через компоненты тензоров будет
иметь вид
I пцп'т* dS= [ V, (afj r{ dV. A.81)
S V
Теорема Стокса имеет следующую формулировку
(см. рис. 1.30): циркуляция тензора по замкнутому контуру
равна потоку ротора тензора через поверхность,
ограниченную этим контуром, т.е.
i(a)-ldl= I rot (a) ndS, A.82)
где под I = /j.r* понимается единичный вектор,
направленный по касательной к замкнутому контуру С, а п = пага —
единичный вектор внешней нормали к поверхности 5,
ограниченной этим контуром.
91

Вопросы и задачи
1. В чем состоит предмет механики сплошных сред?
2. В чем заключается основное отличие механики сплошных
сред от теоретической механики?
3. Какова сущность статистического подхода к изучению
движения деформируемых сред?
4. В чем заключается сущность феноменологического
подхода к изучению движения деформируемых сред?
5. Сформулируйте понятие материального континуума.
6. С чем связана необходимость введения такой идеализации
реальной деформируемой среды, как материальный
континуум?
7. С чем связана возможность введения такой идеализации
реальной деформируемой среды, как материальный
континуум или сплошная среда?
8. Сформулируйте основные гипотезы механики сплошных
сред.
9. Что понимается под геометрическим пространством?
10. Чем определяется мерность пространства?
11. Какие геометрические пространства называют
евклидовыми?
12. Чем принципиально отличаются двумерные
геометрические пространства совокупностей точек, образующих
плоскость и сферическую поверхность?
13. Почему при решении прикладных задач механики
сплошных сред время можно считать абсолютным и не
зависящим от выбора системы отсчета?
14. В чем преимущество феноменологического подхода к
изучению движения деформируемых сред по сравнению со
статистическим при решении технических задач?
15. Сформулируйте понятия системы координат,
координатных линий и координатных поверхностей.
92

16. Постройте три координатные линии через произвольную
точку пространства в декартовой, цилиндрической и
сферической системах координат.
17. Постройте три координатные поверхности через
произвольную точку пространства в декартовой,
цилиндрической и сферической системах координат.
18. Как показать, что цилиндрическая и сферическая системы
координат являются криволинейными?
19. Почему математические объекты математического
аппарата механики сплошных сред должны быть
инвариантными относительно преобразования системы координат? Как
следует понимать это требование?
20. Каково основное свойство тензоров в физическом
отношении?
21. Сформулируйте основную идею, используемую при
введении в рассмотрение тензоров.
22. Определите понятия вектора, его составляющих,
компонент, направляющих косинусов.
23. Сформулируйте основные правила проведения
алгебраических операций с векторами: сложения, вычитания,
умножения вектора на скаляр, скалярного и векторного умножения
векторов.
24. В чем заключается геометрический смысл векторного
произведения векторов?
25. В чем заключается геометрический смысл смешанного
векторно-скалярного произведения трех векторов?
26. Приведите выражения скалярного и векторного
произведений двух векторов, а также скалярно-векторного
произведения трех векторов через их компоненты в декартовой
прямоугольной системе координат.
27. Докажите взаимную перпендикулярность векторов а —
= 2г - 4jf + 5fc и Ь = 4г - 3j - 4fc.
28. Определите площадь параллелограмма, построенного на
отложенных от одной точки векторах а = 2г - 4jf + 5fc и
Ь = 4г - 3jf - 4fe.
93

29. Определите объем параллелепипеда, построенного на
отложенных от одной точки векторах а = \г + 2jf + 3fc,
Ь = -2г + 3j + к, с = 2г - 5jf + 2fc.
30. Сформулируйте понятия векторной функции скалярного
аргумента, скалярной и векторной функций векторного
аргумента.
31. Определите понятие поля, приведите примеры скалярных
и векторных полей.
32. В связи с чем в механике сплошных сред приходится иметь
дело с полями физических величин?
33. Каким образом графически представляются скалярные и
векторные поля?
34. Как будут выглядеть векторные линии скорости движения
частиц абсолютно твердого тела при вращении его вокруг
закрепленной оси?
35. Как будут выглядеть в пространстве поверхности уровня
для поля температуры с равномерным распределением Г =
= Т(х, у, z) — const?
36. Задано поле температуры Т = Т(я, j/, z) — 2х + Зу — Ъг.
Что будут представлять собой поверхности уровня?
Каково значение температуры на изотермической поверхности,
проходящей через начало координат?
37. Каков физический, геометрический и аналитический
смысл градиента скалярной функции векторного
аргумента?
38. Задано поле скалярной величины р = р(х, у, z) = 2ху + z.
Для точки пространства с координатами х = 1, у = 2,
z = 3 определите значение производной по направлению
единичного вектора s = г/%/2 + j/\/2.
39. Задано скалярное поле температуры Г = Г(х, у, z) =
= ху - bz. В точке пространства (х = 2, у = 3, z = 0)
определите максимально и минимально возможные
значения производной по направлению.
94

40. В точке пространства с координатами х = у = z = 0
заданы значение давления р = 1 и градиент давления
gradp = 1г + 3j + 4fc. Определите приближенно
значение давления в точке, расположенной в малой окрестности
данной точки и имеющей координаты х = 0,01, у = 0,02,
z = -0,0L
41. Определите понятия потока вектора через поверхность,
циркуляции вектора по какому-либо контуру.
42. Дайте определения дивергенции и ротора вектора.
Приведите выражения для дивергенции и ротора через
компоненты вектора в декартовой прямоугольной системе
координат.
43. Каков физический смысл дивергенции вектора скорости
течения жидкости (в случае отсутствия источников
массы в потоке)?
44. Каков физический смысл ротора вектора скорости
движения частиц среды (на примерах вращения абсолютно
твердого тела вокруг закрепленной оси и движения
деформируемой среды)?
45. Чему равны дивергенция и ротор вектора скорости
движения частиц абсолютно твердого тела при вращении его
вокруг закрепленной оси с угловой скоростью и;?
46. Определите поток вектора напряженности
электрического поля точечного заряда. Е = q/D7re?or2), находящегося
в центре сферической поверхности радиусом Л, через эту
поверхность. Чему будет равна циркуляция вектора
напряженности электрического поля по замкнутому контуру,
лежащему на этой сферической поверхности?
47. Для некоторого момента времени задано векторное
поле скорости течения жидкости v = vxi + vyj + v2k =
= 3xyi - 5yj + xzk. Что можно сказать о характере
движения частицы среды, находящейся в точке пространства
с координатами ж = 1,у = 2,г = 3?
95

48. С использованием векторного символического
дифференциального оператора Гамильтона определите в декартовой
прямоугольной системе координат rot (grad ф) и
div(grad^), где (р — скалярная функция координат.
49. Сформулируйте теоремы Остроградского — Гаусса и
Стокса с использованием понятий векторного анализа и
дайте их эвристическое обоснование.
50. Дайте определения основного и взаимного базисов в точке
пространства в случае произвольной системы координат.
51. Получите выражения для векторов взаимного базиса через
векторы основного базиса.
52. Дайте определения метрики пространства и метрических
коэффициентов основного базиса, истолковав их
геометрический смысл.
53. Сформулируйте правило суммирования Эйнштейна.
Поясните различие между индексами суммирования и
свободным индексом на примере выражения а^Ы.
54. Сколько различных соотношений содержит выражение
9ij = г.--г,?
55. Приведите развернутую запись выражения А = а^хгхК
56. Как определяются метрические коэффициенты основного и
взаимного базисов, а также смешанного типа? Каковы
особенности соответствующих метрических матриц в общем
случае и для ортогональных систем координат?
57. Покажите, что в декартовой прямоугольной системе
координат основной и взаимный базисы совпадают, не
зависят от координат и образуют ортонормированный базис.
58. Определите для цилиндрической системы координат в
произвольной точке пространства векторы основного и
взаимного базисов и соответствующие метрические
коэффициенты?
59. Различаются ли матрицы, составленные из метрических
коэффициентов смешанного типа, в декартовой,
цилиндрической и сферической системах координат?
96

60. Докажите инвариантность вектора dr — dxlrx, который
можно рассматривать как дифференциал радиус-вектора
г, относительно преобразования системы координат,
получив контрвариантный закон преобразования координат хг
и ковариантный закон преобразования векторов основного
базиса гг.
61. Какие формы представления произвольного вектора Вам
известны? Каким образом обеспечивается инвариантность
вектора относительно преобразования системы координат,
несмотря на изменения при этом преобразовании и его
компонент, и базисных векторов?
62. Что является базисным математическим объектом при
образовании тензора второго ранга?
63. Что понимается под диадным произведением двух
векторов? Каковы основные свойства, проявляемые диадными
произведениями?
64. В каком из следующих случаев результат алгебраических
операций может отличаться от нуля: ax(ab-c)] ax(c-ab)]
{аЬ х Ь); а х (ab x с)?
65. Сформулируйте общее определение тензора как
математического объекта, инвариантного относительно
преобразования системы координат.
66. Какие формы представления тензора второго ранга Вам
известны? Каким образом обеспечивается инвариантность
тензора второго ранга относительно преобразования
системы координат, несмотря на изменение при этом
преобразовании и его компонент, и базисных векторов?
67. Что такое ранг тензора? Сколько компонент имеет тензор
четвертого ранга и какова его структурная запись?
68. Каким образом доказывается, что метрические
коэффициенты основного и взаимного базисов, а также смешанного
типа являются соответственно ковариантными,
контрвариантными и смешанными компонентами тензора второго
ранга — фундаментального метрического тензора данной
системы координат?
4-9712 97

69. Составьте матрицу из компонент следующего тензора
второго ранга: (а) = Згг + bij + 4ji - кк.
70. Обоснуйте утверждение: фундаментальный метрический
тензор в декартовой прямоугольной системе координат
имеет вид (д) = гг + jj + kk.
71. Каковы особенности матриц, составленных из компонент
симметричного и антисимметричного тензоров второго
ранга? Почему антисимметричный тензор второго ранга
называется псевдовектором?
72. Является ли фундаментальный метрический тензор
симметричным? Если является, то почему?
73. Каковы правила сложения и вычитания тензоров,
умножения тензора на скаляр?
74. Допустимо ли проводить сложение тензоров (а) = a^rV-?
и (Ь) = btjkrlr^rk?
75. Почему недопустимо проводить сложение двух тензоров
второго ранга, заданных в виде (а) = а^ггг^ и F) =
76. В чем состоит сущность операций жонглирования
индексами?
?
77. Докажите правомерность операции опускания индексов
применительно к компонентам тензора второго ранга
j
78. Докажите, что операция скалярного умножения тензора
второго ранга на тензор первого ранга обладает свойством
коммутативности лишь в случае симметричности тензора
второго ранга.
79. Определите результат скалярного умножения (а) • F) =
= (aijrWJ) • F*т*д.), где (Ь) = 1г\ + 2г2 + Згз, а
тензору второго ранга соответствует матрица [ I а,у 11 =
98

gO. Определите результат скалярного умножения тензоров
[(а) • F)] • (Ь) = [(а0т'г>) ()] ()
gl. Заданы тензор второго ранга (а) = 2ii + Sjk + кк и тензор
первого ранга (Ь) = Зг. Определите простейшим образом
результаты скалярного умножения (а) • F) и [(а) • F)] • F).
82. Каким образом и в связи с чем вводится в рассмотрение
тензор третьего ранга — дискриминантный тензор (тензор
Риччи)?
83. Как определяются значения ковариантных компонент
дискриминантного тензора? Чем обусловлен тот факт, что
компоненты тензора Риччи с любыми двумя одинаковыми
индексами равны нулю?
84. Какие значения имеют компоненты дискриминантного
тензора в декартовой прямоугольной системе координат?
85. Покажите, что векторное умножение тензоров первого
ранга с использованием дискриминантного тензора дает
результат, совпадающий в частном случае декартовой
прямоугольной системы координат с результатом,
получаемым с помощью известных правил векторной алгебры.
86. В чем заключается специфика дифференцирования
тензоров по координатам в общем случае произвольной системы
координат?
87. Чем отличается от обычной частной производной по
координатам абсолютная (ковариантная) производная
контрвариантных компонент тензора первого ранга?
88. Что такое символы Кристоффеля? В связи с чем они
вводятся? Чем различаются и как взаимосвязаны символы
Кристоффеля первого и второго рода?
89. Каков геометрический смысл символов Кристоффеля?
90. Является ли совокупность 27 значений символов
Кристоффеля компонентами тензора третьего ранга?
4* 99

91. Выведите формулу, выражающую символы Кристоффеля
первого рода через компоненты фундаментального
метрического тензора, и определите их значения для декартовой
прямоугольной (д^ = <722 — #33 = 1) и цилиндрической
(<7n = g33 = 1} <722 — г2) систем координат.
92. Выведите формулу для абсолютной производной
контрвариантных компонент тензора второго ранга.
93. В чем состоит сущность символического подхода к
определению дифференциальных операций с тензорами
произвольного ранга?
94. Чем отличается векторный символический
дифференциальный оператор Гамильтона в тензорном анализе от
аналогичного оператора, используемого в векторном анализе?
95. Каким образом определяется градиент тензора
произвольного ранга, как при этом изменяется ранг
получающегося математического объекта относительно ранга исходного
объекта?
96. Каким образом определяется дивергенция тензора
произвольного ранга, как при этом изменяется ранг
получающегося математического объекта относительно ранга
исходного объекта?
97. Каким образом определяется ротор тензоров первого и
второго рангов, как при этом изменяется ранг
получающегося математического объекта относительно ранга
исходного объекта?
98. Сформулируйте интегральные теоремы тензорного
анализа: теорему Остроградского — Гаусса и теорему Стокса.
99. Определите с использованием символического подхода
дивергенцию и ротср радиус-вектора в произвольной точке
пространства.

Глава 2
ОСНОВНЫЕ ПОНЯТИЯ,
УРАВНЕНИЯ И СООТНОШЕНИЯ
МЕХАНИКИ СПЛОШНЫХ СРЕД
2.1. Представление движения
материального континуума
2.1.1. Система отсчета наблюдателя
и сопутствующая система отсчета.
Индивидуализация точек
материального континуума
Всякое механическое движение представляет собой
происходящее в пространстве и во времени изменение положения
тел или составляющих их частиц относительно других тел.
На рис. 2.1 для некоторого начального момента времени t = to
t>t0
Рис. 2.1
101

(чаще всего полагают *о = 0) показана занятая сплошной
средой область пространства Dq объемом V'o, ограниченная
поверхностью Sq. Это может быть, например, твердое тело,
движущееся в воздухе, или же индивидуальный объем — часть
газообразной, твердой или жидкой среды.
Индивидуальный объем — часть сплошной среды,
состоящая (в процессе движения) из одного и того же материала,
включающая одни и те же частицы, а с точки зрения
реального молекулярного строения деформируемых сред — состоящая
из одних и тех же молекул. Значение индивидуального объема
V может изменяться в процессе движения под действием
внешних сил (например, твердое тело при всестороннем сжатии
будет сжиматься и его
объем будет уменьшаться).
При движении может
изменяться и форма
индивидуального объема (рис. 2.2).
Неизменным у
индивидуального объема остается
лишь его состав.
Бесконечно малый индивидуальный
объем (V -> 0) в механике
Индивидуальный -./—\ —
объем —
Индивиду альная~\ 1/.Z
частица ^
ИндивидуальнаяА
точка
Движущаяся
среда
сплошных сред называется
индивидуальной частицей.
Наконец, предельным
случаем индивидуального объ-
Рис. 2.2 ема является
индивидуальная точка —
математический объект, не имеющий размеров, объем которого V — 0
(см. рис. 2.2). С определенной долей условности можно
сказать, что при изучении макроскопических движений в рамках
феноменологического подхода индивидуальная точка
соответствует вполне определенной молекуле сплошной среды.
Следует отметить, что употребление термина "бесконечно малый
объем" корректно только в рамках феноменологического
подхода, при котором абстрагируются от реального молекулярно-
102

го строения сред и оперируют фиктивной субстанцией —
материальным континуумом, заполняющим пространство
непрерывно, сплошным образом. С точки зрения реального
строения тел понятие индивидуальной частицы можно определить
как индивидуальный объем, малый по сравнению с
размерами тела, но достаточно большой по сравнению с размерами
молекул среды.
Пусть к произвольному моменту времени t > to
выделенный в начальный момент времени индивидуальный
объем сплошной среды переместился и занимает область
пространства D\ объемом Vi, ограниченную поверхностью S\
(см. рис. 2.1). Для количественного описания механического
движения сплошной среды необходимо ввести систему
отсчета, представляющую собой совокупность тела или точки
отсчета, связанной с ними системы координат и указаний
о моменте начала отсчета времени. В механике сплошных
сред вводятся два типа системы отсчета: система отсчета
наблюдателя и сопутствующая система отсчета.
Система отсчета наблюдателя {эйлерова) — это
система отсчета, по отношению к которой определяется
движение материального континуума. На рис. 2.1 система
отсчета наблюдателя изображена в виде точки отсчета 0 и
проведенных через нее координатных осей. Положение
точек трехмерного пространства относительно этой системы
отсчета однозначно определяется тремя значениями координат
ж1, ж2, ж3. Выбор тела или точки отсчета и конкретного
вида системы координат (например, декартовой прямоугольной,
или цилиндрической, или какой-либо иной) произволен и
определяется соображениями удобства при исследовании движения
деформируемого тела. Существует, однако, ограничение на
выбор системы отсчета наблюдателя. Как правило, эта
система отсчета должна быть инерциальной. Напомним, что
система отсчета является инерциальной, если в ней
выполняется первый закон Ньютона [закон инерции): тело
движется равномерно и прямолинейно, если воздействия на
него со стороны других тел скомпенсированы или
отсутствуют. Как известно из физики, выполнение в какой-либо
системе отсчета закона инерции дает основание использовать при
103

рассмотрении движения и второй и третий законы Ньютона,
на базе которых получены основные дифференциальные
уравнения движения сплошных сред. При решении прикладных
задач в качестве тела или точки отсчета чаще всего
принимается Земля (или точка, неподвижная относительно Земли),
чем и обеспечивается выполнение требования инерциальности
системы отсчета наблюдателя.
Задача определения движения материального
континуума требует дополнительного пояснения. Движение одной
материальной точки М тела, размерами которого можно
пренебречь, перемещающейся
по какой-то траектории L
относительно системы отсчета
наблюдателя (рис. 2.3),
однозначно определяется
векторной функцией скалярного
аргумента — зависимостью
радиус-вектора г, который
характеризует положение
материальной точки в
пространстве, от времени t: r =
= v(t). Аналогично
определяется движение одной
выделенной индивидуальной
точки М сплошной среды
(см. рис. 2.1). Приведенному векторному уравнению
соответствуют три скалярных уравнения вида
Рис. 2.3
хг = *•'(*), * - 1, 2, 3,
B.1)
определяющих зависимость от времени текущих координат
материальной точки относительно системы отсчета
наблюдателя. Уравнения B.1) называются законом движения
материальной точки. Получение этого закона — основная задача
механики при изучении движения материальной точки.
Определить движение материальной точки — значит установить ее
текущие координаты в любой момент времени (см. B.1)).
104

Существенно сложнее описать движение материального
континуума. Определить движение материального
континуума — значит установить параметры движения всех его
индивидуальных точек. Но, с одной стороны, любой
индивидуальный объем сплошной среды в силу гипотезы непрерывности
(сплошности) состоит из бесконечно большого числа
индивидуальных точек. С другой стороны, индивидуальные точки
материального континуума на первый взгляд совершенно
равноправны и неотличимы друг от друга. Поэтому, для того
чтобы описать движение сплошной среды и знать движение
всех ее индивидуальных точек, необходимо ввести правило
индивидуализации точек материального континуума,
позволяющее различать индивидуальные точки континуума друг
от друга и получать закон движения для всех этих точек.
Индивидуализация точек материального континуума
осуществляется, как правило, путем задания значений их координат
в начальный момент времени.
Рассмотрим два близких по своей сущности способа
индивидуализации .
Первый способ индивидуализации точек сплошной
среды заключается в задании значений их начальных
координат относительно системы отсчета наблюдателя. На рис. 2.1
положение произвольной индивидуальной точки М
относительно системы отсчета наблюдателя в начальный момент
времени t = to характеризуется радиус-вектором R или же
тремя значениями начальных координат arj, х2, zjj, которые
указывают на вполне определенную, единственную
индивидуальную точку сплошной среды. При таком способе
индивидуализации точек материального континуума определить
его движение — значит найти зависимости текущих
координат индивидуальных точек хг от их начальных координат
хг0 и времени t: х1 = x1(xq, Xq, zjj, t), x2 = x2{x\, Zq, Zq, i),
re3 = #3(:Tq, ?q, Xq, t) или в сокращенной записи с
использованием свободного индекса
xlxlt). B.2)
105

Зависимости B.2) носят название закона движения
материального континуума. Этот закон в принципе действительно
определяет движение сплошной среды, так как дает
возможность знать движение каждой из бесконечно большого числа
ее индивидуальных точек, различаемых с помощью их
начальных координат относительно системы отсчета наблюдателя.
Второй возможный способ индивидуализации
заключается в задании координат индивидуальных точек в системе
отсчета, связанной с частицами среды, т.е. в сопутствующей
системе отсчета. Действительно, так как выбор тела или
точки отсчета достаточно произволен, в качестве последней
может быть взята вполне конкретная индивидуальная точка
материального континуума, например точка Oi (см. рис. 2.1).
Являясь индивидуальной точкой сплошной среды, она
движется вместе со средой, занимая в произвольный момент времени
положение 0^, чем и объясняется название системы отсчета.
В начальный момент времени через точку Oi могут быть
проведены координатные оси. Положение любой индивидуальной
точки материального континуума относительно точки Oi,
принятой за начало координат, определяется тремя значениями
координат ?1, ?2, f3. При таком способе индивидуализации
точек сплошной среды закон движения принимает вид
*' = хЧ*\ ?,?,*), B-3)
который также содержит информацию о движении всех ее
индивидуальных точек. При этом, задавая конкретные
значения ?*, ?2, ?3, указывают на одну (и только одну!)
индивидуальную точку сплошной среды, для которой закон движения
позволяет определить ее текущие координаты относительно
системы отсчета наблюдателя в зависимости от времени t.
Специфика сопутствующей системы отсчета не
исчерпывается тем, что в качестве точки отсчета принимается одна
из индивидуальных точек материального континуума.
Сопутствующей системе отсчета присуще также то, что
координатные линии (в частности, координатные оси, проходящие через
106

точку отсчета) всегда проходят через одни и те же
индивидуальные точки среды. Таким образом, вводимая при описании
движения сопутствующая система отсчета — это подвижная,
деформируемая, криволинейная в общем случае система
координат, координатные линии которой всегда проходят через
одни и те же индивидуальные точки сплошной среды.
Введенная указанным образом сопутствующая система
отсчета имеет следующие особенности.
Первая особенность сопутствующей системы координат
заключается в следующем. В начальный момент времени
t = Ц выбор системы координат зависит от желания
исследователя. Например, на рис. 2.1 при t = t$ в качестве
сопутствующей системы координат принята декартова прямоугольная
система координат: координатные оси f1, f2, ?3, проходящие
через точку отсчета Оь и координатные линии (?*), (f2), (f3),
проведенные через произвольную индивидуальную точку М
материального континуума, представляют собой взаимно
перпендикулярные прямые. Однако в дальнейшем, при движении
сплошной среды, сопутствующая система координат выходит
из под власти исследователя. По определению, ее
координатные линии, проходя всегда через одни и те же индивидуальные
точки, являются как бы "вмороженными" в среду, движутся и
деформируются вместе с ней (t > to на рис. 2.1).
Сопутствующая система координат рассматривается в основном для того,
чтобы по деформациям ее координатных линий ввести
величины, количественно характеризующие деформирование
материального континуума, — компоненты тензора деформаций
и тензор деформаций в целом.
Вторая особенность сопутствующей системы координат
состоит в том, что все индивидуальные точки сплошной
среды имеют не изменяющиеся во времени координаты f1, f2, f3
относительно данной системы отсчета. Это следует из самого
способа определения значений координат ^1,^2,^3,
индивидуализирующих точки материального континуума.
Действительно, три значения координат ?*, ?2, ?3 точек относительно
сопутствующей системы отсчета определяются для
фиксированного начального момента времени t = ?q, раз и навсегда
107

закрепляются за каждой индивидуальной точкой и в связи с
этим уже не могут изменяться в зависимости от времени.
Подтверждением может служить следующий пример частного
характера. В начальный момент времени t — Ц индивидуальная
точка Оь принятая за точку отсчета сопутствующей системы
координат, имеет в этой системе координаты (} — f2 = f3 = 0.
К произвольному моменту времени t > to (см. рис. 2.1)
индивидуальная точка перемещается в положение 0'1? продолжая
оставаться точкой отсчета, имеющей относительно самой
себя те же самые координаты f1 = ?2 = ?3 = 0. Таким образом,
все индивидуальные точки материального континуума как бы
покоятся относительно сопутствующей системы отсчета.
2.1.2. Сущность точек зрения Лагранжа и Эйлера
на изучение движения сплошной среды
Точка зрения Лагранжа на изучение движения
сплошной среды (лагранжев подход) заключается в исследовании
изменения величин (например, скорости t>, температуры Г),
описывающих движение и состояние сплошной среды для
каждой из ее индивидуальных точек. В качестве
независимых переменных при математическом описании движения с
позиций Лагранжа используются координаты ?*, ?2, ?3 (или
a?Q, Xq, zjj), индивидуализирующие точки сплошной среды и
называющиеся лагранжевыми координатами, и время t. Ла-
гранжевы координаты f1, f2, ?3 и время t носят название ла-
гранжевых переменных. Формально при использовании ла-
гранжева подхода находят зависимости величин,
описывающих поведение сплошной среды, от лагранжевых переменных
?Х> ?2> ?3> ^ например:
хг = х\е, i2, ез, о. ^=v(e, е, е3, о. т=г^1, е, е3, о-
Точка зрения Эйлера на изучение движения сплошной
среды (эйлеров подход) заключается в исследовании
изменения величин, описывающих движение и состояние среды для
каждой из точек пространства, в которые с течением времени
108

могут приходить различные индивидуальные точки. В
качестве независимых переменных при описании движения среды с
позиций Эйлера используются координаты ж1, ж2, ж3,
определяющие положение точек пространства относительно системы
отсчета наблюдателя и называющиеся эйлеровыми
координатами, и время t. Эйлеровы координаты ж1, ж2, ж3 и время t
называются эйлеровыми переменными. Эйлеров подход
предполагает поиск зависимостей всех величин, описывающих
поведение деформируемой сплошной среды, от эйлеровых
переменных ж1, ж2, ж3, ?, например:
v = г?(ж\ ж2, ж3, t), T = Т(ж\ ж2, ж3, t) и т.д.
Итак, различие подходов Лагранжа и Эйлера
заключается в том, что в первом случае следят за каждой
индивидуальной точкой (или индивидуальной частицей) движущейся
сплошной среды, а во втором — за каждой точкой
пространства, в котором движется сплошная среда.
Сущность лагранжева и эйлерова подходов и их
принципиальное различие можно уяснить на следующем простом
примере. Изучение движения земной атмосферы с
практической целью формирования метеопрогноза проводится с
позиций феноменологического подхода. Воздушная среда
рассматривается как сплошная, при этом необходимо знать такие ее
характеристики, как температура Т, давление р (величины,
описывающие состояние воздушной среды), скорость v
движения воздушных масс, т.е. скорость ветра. Основой
формирования достоверного метеорологического прогноза
являются данные наблюдений за текущим состоянием
атмосферы. Соответствующие данные могут быть получены
двояким путем: со стационарных метеостанций и с подвижных
метеозондов (рис. 2.4). Каждая стационарная метеостанция
размещена в определенной точке пространства с
неизменными координатами ж1, ж2, ж3 относительно системы отсчета
наблюдателя. При определении изменения во времени
значений интересующих исследователей величин на каждой
стационарной метеостанции и дальнейшем обобщении информации
109

Q 6- Q О
6 Й 6 6
Рис. 2.4
получают описание движения атмосферы с позиций Эйлера:
v = ^(ж1, ж2, ж3, *), Т = Т(ж2, ж2, ж3, «) и т.д. Подвижные
метеозонды, движущиеся в воздушном потоке, имеют
нулевую скорость относительно потока, а относительно системы
отсчета наблюдателя — скорость, равную скорости движения
воздушной массы. Они позволяют получить информацию об
изменении во времени значений интересующих
исследователей величин для каждой из индивидуальных точек воздушной
среды, в окрестности которых были запущены эти зонды в
начальный момент времени. Путем обобщения получаемой с
метеозондов информации получают описание поведения
атмосферы с позиций Лагранжа.
Подходы к описанию движения сплошной среды с
позиций Эйлера и Лагранжа с точки зрения механики
эквивалентны. Имея описание движения сплошной среды с позиций
Лагранжа, можно перейти к его описанию с позиций
Эйлера, и наоборот. Пусть, например, получено описание
движения сплошной среды с позиций Лагранжа для поля скоростей
v = «(f1* ?2> ?3> t) и определен закон движения B.3). Три
уравнения вида ж* = ж'^1, f2, f3, i), представляющие собой
закон движения материального континуума, могут
рассматриваться как три уравнения относительно трех неизвестных
величин f1, f2, f3. Можно определить эти величины из
уравнения закона движения и получить обратный закон движения в
виде ?1 = ^(ж1, ж2, ж3, *), который показывает, какая именно
индивидуальная точка сплошной среды (однозначно
определяемая — индивидуализируемая — тремя значениями f1, f2, f3)
но

находится в данный момент времени / в данной точке
пространства с координатами я1, ж2, ж3 относительно системы
отсчета наблюдателя. Подставляя эти выражения в
уравнение для поля скоростей, получаем v = «(f1, f2, ?3, t) =
= t,(fV, *\ *3> 0. fV>*2,*3,0, e{x\x\x\t),t) ипере-
ходим к зависимостям, характеризующим поведение сплошной
среды, от координат точек пространства и времени, т.е. к
описанию движения среды с позиций Эйлера: v = v(x1, я2, я3, t).
Следовательно, лагранжев и эйлеров подходы
действительно эквивалентны. Использование того или другого подхода
определяется спецификой решаемой задачи механики
сплошных сред.
2,2. Основы кинематики
материального континуума.
Теория деформаций
2.2.1. Тензор деформаций —
характеристика деформированного состояния
материального континуума
В соответствии с феноменологическим подходом к
изучению поведения деформируемых сред в механике сплошных
сред вводятся в рассмотрение различные физические
величины, количественно описывающие движение и состояние
исследуемой среды. К числу величин, описывающих движение
материального континуума, относятся такие известные из
курсов общей физики и теоретической механики векторные
величины, как радиус-вектор г, перемещение и, скорость v и
ускорение а.
Напомним, что радиус-вектор г определяет положение
индивидуальных точек материального континуума
относительно системы отсчета наблюдателя (см. рис. 2.1). Найти
зависимость г = г(^1, ?2, ?3, t) радиус-вектора г от лагран-
жевых координат f1, f2, ?3 (или xj, я2, zjj),
индивидуализирующих точки материального континуума, и времени t
означает найти закон движения сплошной среды и знать движение
111

любой ее индивидуальной точки из бесконечно большого их
числа.
По определению, перемещение и — векторная величина,
характеризующая изменение положения индивидуальных
точек относительно системы отсчета наблюдателя (см. рис. 2.1).
Перемещение вводится как разность радиус-векторов,
характеризующих текущее и начальное положения индивидуальной
точки: и = r — R. Как и всякий вектор (тензор первого ранга),
вектор перемещения может быть представлен в разложении по
векторам основного или взаимного базиса через свои ковари-
антные или контрвариантные компоненты: и — щгг = и%т{.
Компоненты перемещения связаны с компонентами радиус-
вектора (или координатами индивидуальных точек
относительно системы отсчета наблюдателя) согласно очевидным
соотношениям иг = х1 - хг0.
Скорость v — векторная величина, характеризующая
быстроту изменения перемещения индивидуальных точек (или
индивидуальных частиц) материального континуума
относительно системы отсчета наблюдателя. Значение скорости
определяется значением частной производной перемещения и
по времени t, вычисляемой при фиксированных значениях ла-
гранжевых координат f1, ?2, ?3:
v =
~dt
~dt
с
С учетом того, что в общем случае перемещения
индивидуальных точек различны, т.е. и = i^f1, f2, f3, *), а значения
лагранжевых координат f1, ?2, ?3 раз и навсегда
закрепляются за каждой индивидуальной точкой и от времени не зависят,
скорость, по существу, определяется как полная производная
перемещения и (или радиус-вектора индивидуальной
частицы) по времени, т.е.
du dr
V=~dt=~dt'
Вектор скорости может быть представлен в разложении по
векторам основного или взаимного базиса через свои ковари-
антные или контрвариантные компоненты: v = v,r* = vlr{.
112

При этом компоненты вектора скорости определяются
полными производными компонент вектора перемещения (или
текущих координат индивидуальных точек) по времени:
v% = du*/dt = dx*/dt.
Ускорение а — векторная величина, которая может быть
записана через свои компоненты как а = а,{Гг = ахт{ и
характеризует быстроту изменения скорости движения
индивидуальных точек относительно системы отсчета наблюдателя:
а —
Tt
dv
dt'
Компоненты вектора ускорения связаны с компонентами
векторов скорости и перемещения, а также с текущими
координатами индивидуальных точек следующими соотношениями:
аг = dvl/dt = d2u*/dt2 = d?x%/dt2. Необходимо отметить, что
в общем случае для криволинейных систем координат
взаимосвязь между компонентами аг вектора ускорения и скоростями
изменения компонент вектора скорости dv1/dt выглядит более
сложным образом в связи с зависимостью базисных векторов
Г{ от координат х3 точек пространства, изменяющихся при
движении индивидуальных точек (см. B.3)). Эта взаимосвязь
выявляется из преобразований
i dv d(vlvi)
а — а г; = — = -1——- =
1 dt dt
dv% t- dv{ dx3 dv1
и выглядит как
dt
Однако для большинства представляющих практический
интерес случаев (многомерные течения, рассматриваемые в
декартовой прямоугольной системе координат, двумерные и
одномерные осесимметричные течения, рассматриваемые в
цилиндрической системе координат, одномерные течения с
центральной симметрией, рассматриваемые в сферической
системе координат) vkv3Tlk • = 0. Поэтому в дальнейшем будем
полагать а1 = dvl/dt (см., например, разделы 2.4.3 и 4.1.3).
113

Для описания движения сплошной среды используются не
только приведенные выше кинематические величины. В связи
с тем, что объектом изучения в механике сплошных сред
являются деформируемые среды, расстояния между
индивидуальными точками которых могут изменяться в процессе
движения под действием внешних сил, в рассмотрение вводятся
дополнительные величины, количественно характеризующие
движение материального континуума. К их числу
относятся тензоры второго ранга: тензор деформаций (е) = ?,;r*W,
тензор скоростей деформаций (ё) = e^-r'W, тензор поворота
(и) = UijTlr3, тензор скоростей поворота (и) = U{jr%r3.
Тензор деформаций является характеристикой
деформированного состояния материального континуума и
определяется для его произвольной точки. Поле тензора деформаций,
найденного для любой индивидуальной точки материального
континуума, характеризует деформированное состояние тела
в целом. Тензор деформаций вводится в рассмотрение при
сравнении расстояний между данной индивидуальной точкой
и точками, находящимися в бесконечно малой ее окрестности,
до и после деформирования.
На рис. 2.5 показан индивидуальный объем
материального континуума, занимающий в начальный момент времени
t = to (соответствующий исходному недеформированному
состоянию) область пространства Do- Будем считать, что под
действием внешних сил индивидуальные точки
материального континуума совершили перемещения и к моменту
времени t > to этот индивидуальный объем занимает область
пространства D\. Выделим в начальный момент времени
произвольную точку М, для которой и определим тензор
деформаций. В исходном недеформированном состоянии
положение выделенной индивидуальной точки М относительно
системы отсчета наблюдателя характеризуется радиус-вектором
R. Выберем теперь в начальный момент времени t = Jo
произвольную индивидуальную точку М\, находящуюся в
бесконечно малой окрестности данной точки М. Положение точки М\
относительно точки М определяется вектором dRy который
114

Рис. 2.5
можно рассматривать как бесконечно малое приращение или
дифференциал радиус-вектора R. Очевидно, что расстояние
между двумя выбранными индивидуальными точками
определяется модулем вектора dR: (dlJ = dR • dR.
Введем в начальный момент времени сопутствующую
систему отсчета, выбрав в качестве точки отсчета
индивидуальную точку Oi и приняв декартову прямоугольную систему
координат. На рис. 2.5 для момента времени t = to показаны
три взаимно перпендикулярные координатные оси f1, ?2, f3,
проходящие через точку отсчета Oi, а также три взаимно
перпендикулярные координатные линии (?*), (f2), (f3),
проходящие через индивидуальную точку М. В общем случае такой
выбор сопутствующей системы координат не обязателен, но
удобен для дальнейшего выяснения геометрического смысла
компонент тензора деформаций. К текущему моменту
времени индивидуальная точка М совершает перемещение и и
занимает положение М\ определяемое радиус-вектором г.
Индивидуальная точка М\ также совершает перемещение, ее
новое положение М[ относительно нового положения М1 данной
точки М будет характеризоваться вектором dr, который
можно рассматривать как дифференциал радиус-вектора г.
Расстояние между выбранными индивидуальными точками
после деформирования будет определяться модулем вектора dr:
115

Радиус-векторы Лиг, характеризующие начальное и
текущее положения индивидуальной точки М относительно
системы отсчета наблюдателя, зависят от того, положение
какой именно точки материального континуума они
определяют, а следовательно, являются функциями лагранжевых
координат: R = Щ1, ?2,f3), r = г^1,^2, ?3). Это делает
возможным представление dR и dr в виде разложения по
векторам основного базиса сопутствующей системы координат с
помощью их компонент, в качестве которых выступают
бесконечно малые приращения (дифференциалы) лагранжевых
координат ?г, соответствующие переходу от данной точки М к
бесконечно близкой точке М\. Действительно, в соответствии
с правилами дифференцирования функций нескольких
переменных и определением векторов основного базиса имеем
dR = dR({\ e,e)
где R{ и Г{ — соответственно векторы основного базиса
сопутствующей системы координат в исходном
(недеформированном) и текущем (деформированном) состояниях, определенные
в индивидуальной точке М (М1) на рис. 2.5. При этом квадрат
расстояния между индивидуальными точками М и М\ до
деформирования
(dlJ = dR dR=
где gij = R{ • Rj — определенные в данной точке М
метрические коэффициенты основного базиса сопутствующей системы
координат в исходном состоянии. По аналогии квадрат
расстояния между теми же самыми индивидуальными точками
(М1 и М[) после деформирования
) fa ) = rt >rj de d? = 4- dc de,
116

где gjj = гг • rj — определенные в той же самой
индивидуальной точке метрические коэффициенты деформированной
сопутствующей системы координат. Изменение расстояния
между данной точкой и точкой, находящейся в бесконечно
малой ее окрестности, описывается выражением
- (dlJ = (д*3 - gtj) d?
из которого следует, что в качестве меры изменения
расстояний между данной индивидуальной точкой и точками,
взятыми в ее окрестности, может быть принята разность (#*• - g{j)
метрических коэффициентов, определенных в данной
индивидуальной точке после деформирования и до деформирования
сопутствующей системы координат.
На основе изложенного выше ковариантные компоненты
тензора второго ранга (тензора деформаций)
B-4)
Они образуют во взаимодействии с базисными
математическими объектами тензор деформаций
(е) = etjR%Rj. B.5)
В качестве базисных математических объектов при
образовании тензора деформаций наиболее удобно принять диадные
произведения базисных векторов R% W недеформированной
сопутствующей системы координат.
Получим явное выражение введенных формальным
образом компонент тензора деформаций B.4) через модули
базисных векторов и углы между ними (углы между
координатными линиями сопутствующей системы координат в данной
индивидуальной точке) в соответствии с рис. 2.6. Метрические
коэффициенты основного базиса сопутствующей системы
координат выражаются через указанные величины с помощью
соотношений
Я,=Я|--Я> = |Я.-| \Rj\ cos ф^
9ij = rt-rj = \ri\\rj\ cosф^,
где ф®- — углы между базисными векторами сопутствующей
системы координат в исходном состоянии; ф^ — углы между
117

<={
базисными векторами деформированной сопутствующей
системы координат. Так как ранее в качестве сопутствующей
системы координат принята декартова прямоугольная
система координат, то в начальный момент времени t = to
начальные углы между векторами основного базиса будут равны
тг/2 при г ф j,
О при г = j.
Относительно значений углов между базисными векторами
после деформирования можно определенно утверждать лишь
то, что t\){j — 0 при i = j (угол, который составляет любой
базисный вектор с самим собой, равен нулю). Значения углов
ifrij при г ф j могут быть произвольными вследствие
искривления координатных линий сопутствующей системы координат,
которые, как отмечалось в разделе 2.1, являются как бы
"вмороженными" в среду и деформируются вместе с ней.
Сопоставим модули одноименных базисных векторов в
данной индивидуальной точке М после деформирования и до
деформирования, определив их отношение
№1
dSOl
. B.7)
118

В процессе преобразования выражений B.7) числитель и
знаменатель исходного соотношения были домножены на
дифференциал df? соответствующей г-й лагранжевой
координаты ?* (суммирование по i в выражениях B.7) не
производится). Произведение частной производной dR/d?l (или дг/д?г)
радиус-вектора R (или г) по координате ?г и
дифференциала d?l этой же координаты определяет приращение вектора
dR\dci (или dr\^t%)y соответствующее приращению только г-й
координаты на величину df\ Задать приращение d?% какой-
либо координаты в исходном или в деформированном
состоянии физически означает перейти от данной индивидуальной
точки М (или М') к бесконечно близкой индивидуальной
точке, находящейся на г-й координатной линии сопутствующей
системы координат (на рис. 2.6 для определенности
изображен случай, когда i — 1). Поэтому модуль сШ|^,- определяет
длину dS${ элемента дуги г-й координатной линии,
проходящего через определенные индивидуальные точки
материального континуума до деформирования, а модуль
равен
длине dS{ элемента дуги координатной линии, проходящего
через те же самые индивидуальные точки, но после
деформирования. По существу, величины dS$i и dS{ представляют
собой длины материальных отрезков (материальных волокон),
направленных вдоль координатных линий сопутствующей
системы координат, до деформирования и после него.
Отношение изменения длины материального отрезка к его начальной
длине l{ = (dS{ - dSoi)/dSoi определяет коэффициент
относительного удлинения в данной индивидуальной точке вдоль
г-й координатной линии сопутствующей системы координат.
Таким образом, модули векторов основного базиса
сопутствующей системы координат до и после деформирования
взаимосвязаны с помощью коэффициентов относительных удлинений
вдоль соответствующих координатных линий:
К| = |Я,-|(/,- + 1). B.8)
Из соотношений B.4), B.6)—B.8) следует явное
выражение компонент тензора деформаций через коэффициенты
119

относительных удлинений, модули базисных векторов и углы
между ними:
Щ = [A + U) A + /,•) cos xptj - cos ^-] |Я,-| \Rj\.
Эти соотношения позволяют установить геометрический
смысл компонент тензора деформаций с одинаковыми
индексами ец. Действительно, в случае г = j получаем 2ец =
= [A + /гJ - 1] </,-,•, где дц — 1 — метрические коэффициенты
основного базиса недеформированной сопутствующей системы
координат. Компоненты тензора деформаций с одинаковыми
индексами в таком случае оказываются связанными с
коэффициентами относительных удлинений: /г- = A + 2ецI12 - 1.
При малых деформациях (ец мало) взаимосвязь /г и ец
имеет следующий вид: /г- = 1 + 0,5 • 2ец + о(ец) - 1 = ец, где
°(еп) — величины более высокого порядка малости, чем ец.
Следовательно, компоненты тензора деформаций с
одинаковыми индексами для случая малых деформаций совпадают
с коэффициентами относительных удлинений материальных
отрезков, ориентированных вдоль координатных линий
сопутствующей системы координат.
Геометрический смысл компонент тензора деформаций
с различными индексами (i ф j) следует из выражений B.4) и
B.6). При i ф j ipij = тг/2 и gij = 0. В этом случае
2eij = g*j = т{ • tj = |rt-| |ry| cos^-y,
где углы tfrij между координатными линиями
деформированной сопутствующей системы координат отличаются от
начальных углов ф^- = тг/2 на некоторую величину Xij: ipij =
~ ^tj ~ Xij = к/2 - X{j- Здесь Xij — изменение углов
между первоначально ортогональными координатными линиями
сопутствующей системы координат вследствие
деформирования. В рассматриваемом случае при г ф j
120

откуда следует, что компоненты тензора деформаций с
различными индексами связаны с изменением углов Xij
между первоначально ортогональными координатными линиями
сопутствующей системы координат. При малых
деформациях изменения углов малы и
,'о
а метрические
коэффициенты с одинаковыми индексами д*± сопутствующей
системы координат после деформирования мало
отличаются от одноименных коэффициентов дц в исходном состоянии:
g*i ~ дц = 1, 5?,- ~ 9jj — 1- Поэтому в случае малых
деформаций 2eij « х,о т.е. компоненты тензора деформаций с
различными индексами для случая малых деформаций
определяют изменения углов между первоначально
ортогональными координатными линиями сопутствующей системы
координат.
Компоненты тензора деформаций с различными
индексами €{j называются также сдвиговыми деформациями, так как
они, по существу, характеризуют относительный сдвиг
слоев среды в окрестности данной индивидуальной точки. Это
видно, например, на рис. 2.7,
где показана
индивидуальная частица
материального континуума, имевшая до
деформирования форму
элементарного прямоугольного
параллелепипеда и
приобретшая в результате
деформирования форму
непрямоугольного параллелепипеда.
Изменение угла между ко-
ординатными линиями
и (?3) на величину
ствительно
Рис. 2.7
соответствует
сдвигу слоя индивидуальных точек на верхней грани
элементарного параллелепипеда относительно нижнего слоя.
Выражения B.4), определяющие компоненты тензора
деформаций как полуразности метрических коэффициентов #*•
121

и g{j сопутствующей системы координат, не удобны в
практическом использовании. Чтобы вычислить компоненты
тензора деформаций в произвольной индивидуальной точке
сплошной среды, необходимо знать закон движения материального
континуума г = r(^, ?2, f3, t). Однако при решении задач
механики сплошных сред часто определяется не закон
движения, а поле перемещений сплошной среды и = ^(f1, ?2, f3, t).
В связи с этим более удобным является выражение
компонент тензора деформаций через компоненты вектора
перемещения и. Соотношения, выражающие компоненты тензора
деформаций через компоненты вектора перемещения,
называются геометрическими соотношениями. Их получают из
выражений B.4) с учетом определения метрических
коэффициентов основного базиса сопутствующей системы координат
(<7?. = г{ • rj, g{j = R{ • Rj) и очевидной взаимосвязи радиус-
векторов, характеризующих начальное и текущее положения
индивидуальных точек материального континуума, и вектора
перемещения (г = R -f и):
2eij = 9*j - 9ij = ?i • г, - Ri • Rj =
_ dr_ dr__ _d(R + u) d(R + u)
Полагая вектор перемещения заданным своими ковариантны-
ми компонентами в разложении по векторам взаимного базиса
сопутствующей системы координат в исходном недеформиро-
ванном состоянии (it = щИк — u\R}) и учитывая правила
дифференцирования тензоров первого ранга по координатам
(ди/дС = д(икИк}/д? = (ViUk)Rky получаем
2etJ = [^ + (ViUk) Rk] • [Rj + (Vyu,) Rl] - Ri ¦ Rj -
= (V.-ujt) Rk • Rj + (VjUl) Rt Rl + (Vtuk) (VjUl) Rk • R\
где V{uk — абсолютная (ковариантная) производная ковари-
антных компонент вектора перемещения по г-й лагранжевой
122

координате ?*. Учитывая далее, что скалярные произведения
базисных векторов определяют соответствующие метрические
коэффициенты (llk-Rj = g*j, Я, Rl = д\, Rk Rl = gkl),
являющиеся по отношению к ковариантному дифференцированию
постоянными величинами, и используя такую операцию
тензорной алгебры, как жонглирование индексами, получаем
Окончательно геометрические соотношения,
определяющие компоненты тензора деформаций через перемещения,
приобретают вид
etj -0,5 (ytuj + VjUi + Viti*Vjt**). B.9)
etj (y )
Здесь индексы г и j являются свободными, каждый из них
может принимать любое значение (г = 1,2,3; j = 1,2,3),
поэтому одной формулой B.9) с использованием индексных
обозначений записано девять различных соотношений.
Геометрические соотношения включают два члена, линейных
относительно абсолютных производных, и квадратичный член
ViUkVjUk, представляющий собой сумму трех попарных
произведений соответствующих абсолютных производных. Для
важного частного случая малых деформаций, когда
перемещения щ индивидуальных точек материального континуума
мало отличаются друг от друга, а следовательно, малы и
абсолютные производные V^uj компонент по координатам,
квадратичный член имеет более высокий порядок малости по
сравнению с линейным и им можно пренебречь.
Геометрические соотношения для случая малых деформаций
приобретают вид
eij^O^iViUj + VjUi). B.10)
В дальнейшем при изложении вопросов теории деформаций
будем считать, что деформации малы, а геометрические
соотношения имеют вид B.10).
123

(М) =
Приведем краткую характеристику введенного в
рассмотрение тензора деформаций — тензора второго ранга.
Значения его компонент, различающихся порядком чередования
индексов, одинаковы. Это следует, например, из
геометрических соотношений B.10):
Eij = 0,5(Чщ + VjUi) = 0,5 (Ч,щ + V.-Uj) = eji,
т.е. тензор деформаций является симметричным.
Совокупность девяти его компонент образует симметричную матрицу
второго ранга
?11 ?12 ?13 
^12 ?22 ?23
?13 ?23 ?33
задаваемую не более чем шестью различными членами. В
соответствии с установленным выше геометрическим смыслом
компонент тензора деформаций на главной диагонали
приведенной матрицы находятся коэффициенты относительных
удлинений материальных отрезков, взятых вдоль
координатных линий сопутствующей системы координат. Остальные
элементы этой матрицы {е\2, ?13, ?2з) характеризуют
изменения углов между координатными линиями сопутствующей
системы координат вследствие деформирования материального
континуума в окрестности данной индивидуальной точки.
Помимо введенных компонент 6{j тензора деформаций
(см. B.4)) в теории деформаций рассматривают также
физические компоненты е^л тензора деформаций, или
истинные деформации, что целесообразно по следующим причинам.
Тензор деформаций (е) = eijRlRJ введен в декартовой
прямоугольной системе координат, где базисные векторы не имеют
размерности. Не имеют размерности в этом случае и
компоненты тензора деформаций. Поэтому в исходной системе
координат тензор деформаций в целом является математическим
объектом, не имеющим размерности. Однако, как и всякий
тензор, он может быть представлен в любой другой системе
124

координат, оставаясь инвариантным по отношению к
такому преобразованию, а следовательно, оставаясь безразмерным
объектом:
В новой системе координат базисные векторы могут
приобретать размерность. Например, в цилиндрической системе
координат (ж1 = г, я2 = 0, я3 = z) два базисных вектора
П — дг/дх1 = дг/дг и гз = дг/дх^ = dr/dz не имеют
размерности, а третий Г2 = VQ = дг/дх2 = дт/дв обладает
размерностью длины, что является следствием выбора в качестве
второй координаты х2 угла в. Таким образом, в случае
задания тензора деформаций (е) = е^ггг3 в произвольной
системе координат базисные математические объекты могут
обладать размерностью. Но тогда обратной размерностью
должны обладать компоненты тензора деформаций в этой же
системе координат, так как только в этом случае тензор останется
безразмерным математическим объектом.
Итак, физические компоненты тензора деформаций
вводятся в случае его задания в произвольной системе
координат. Это компоненты, образующиеся при использовании в
качестве базисных математических объектов единичных
безразмерных векторов, коллинеарных векторам основного или
взаимного базиса. Выражение для физических компонент
получается при преобразовании тензора деформаций к виду, при
котором базисные математические объекты нормируются
относительно собственного модуля, что сопровождается
дополнительными преобразованиями для сохранения неизменности
тензора в целом:
где еге* — диадные произведения единичных безразмерных
базисных векторов; ?л-.\ = Eijyg"у/д^ — физические
компоненты тензора деформаций (суммирование по i и j отсут-
125

ствует!). Очевидно, что физические компоненты имеют
размерность деформации, т.е. являются безразмерными
величинами. Отметим также, что в общем случае введенные в
соответствии с B.4) компоненты Sijy которые в противовес
физическим компонентам могут быть названы геометрическими,
отличаются от физических компонент ?(,,)• В частном случае
декартовой прямоугольной системы координат (дгг = д^ = 1)
различие между ними отсутствует и S{j = ?(ij)-
Из курса теоретической механики известно, что движение
абсолютно твердого (недеформируемого) тела складывается
из поступательного движения центра масс и вращательного
движения вокруг оси вращения, проходящей через центр масс.
Движение деформируемой среды является более сложным, так
как возможно изменение расстояний между индивидуальными
точками материального континуума. При этом появляется
дополнительная деформационная составляющая движения.
Движение деформируемой среды усложняется еще и потому, что
вращательная и деформационная составляющие могут быть
совершенно неодинаковыми в различных индивидуальных
частицах среды.
На рис. 2.8 показано положение индивидуального объема
сплошной среды для момента времени t = to, принятого
за начало отсчета времени. Положение произвольной
индивидуальной точки М относительно системы отсчета
наблюдателя характеризуется радиус-вектором R = Л(^, f2, ?3).
t=t
Рис. 2.8
126

Выберем в бесконечно малой окрестности данной
индивидуальной точки М другую индивидуальную точку Mi,
положение которой относительно точки М характеризуется вектором
dR = (дИ/д?г) d?l = R{ <f?l, где Лг — базисные векторы неде-
формированной сопутствующей системы координат в данной
индивидуальной точке М; dt? — бесконечно малые
приращения переменных, индивидуализирующих точки сплошной
среды (лагранжевы координаты), соответствующие переходу от
точки М к точке М\. Будем считать, что к произвольному
моменту времени t > to индивидуальный объем переместился
в новое положение. При этом индивидуальная точка М
совершает перемещение и и занимает положение М\ а находящаяся
в ее окрестности точка М\ совершает перемещение и\ ф и и
занимает положение М[. Перемещение и\ отличается от
перемещения данной индивидуальной точки М на бесконечно
малую величину относительного перемещения du: и\ = и + du.
В общем случае перемещения, совершаемые разными
индивидуальными точками, различны: и — t^f1, f2, ?3).
Поэтому величина относительного перемещения определяется как
du = dt^f1, ?2, f3) = (du/d?%)d?%. С использованием
представления вектора перемещения через ковариантные
компоненты (и = u^Rk) и на основе правил дифференцирования
тензоров получим
d(ukRk)
= v J dC - (Viiijb) Rk
du = v J dC - (Viiijb) R i
В соответствии с правилами скалярного умножения
тензоров представим величину относительного перемещения du как
скалярное произведение вектора dR = R\d?',
характеризующего начальное положение точки М\ относительно данной
точки М, и некоторого тензора второго ранга (Vjtijb) RlRk,
компонентами которого являются абсолютные производные
компонент вектора перемещения:
du = (V,-«fc) Л*^ = (Л,#') • (у,-«кЛ>РЛ*).
127

Очевидно, что тензор второго ранга V {U^R1 R может быть
представлен как результат действия оператора Гамильтона
V = Уг(...)Л1 на вектор перемещения и = щК и в
соответствии с символическим подходом является градиентом
перемещения grad(tt) = ViUfclVR . Представим теперь
градиент перемещения в виде суммы двух тензоров второго ранга,
в связи с чем относительное перемещение разделится на две
составляющие:
du = (л, #') • [о, 5 (У,-!** + Чкщ) RlRk]
Первая составляющая в соответствии с B.5) и B.10)
равна скалярному произведению вектора dR и определенного в
данной индивидуальной точке М тензора деформаций (е) =
— SikRlRk. Очевидно, что эта составляющая относительного
перемещения индивидуальных точек за счет деформирования
равна
dUjx = (Л/ d^ . (eik&R^ = dR • (е) = (е) • с/Л. B.11)
Вторая составляющая равна скалярному произведению того
же самого вектора dR и некоторого определенного в данной
точке тензора второго ранга (а;) = u^R%Rг, компоненты
которого представляются как полуразности абсолютных
производных компонент вектора перемещения:
4-ib = 0,5(Vt-uib-Vjfctt1-). B.12)
Отметим, что вторая составляющая относительного
перемещения точки, находящейся в бесконечно малой окрестности
данной точки, связана с поворотом всей окрестности данной
точки как единого жесткого целого:
dun = (Ri d?l) • (uikR'R^ = dR • (и). B.13)
128

Тензор второго ранга (и) = и^КгК характеризует
относительное перемещение индивидуальных точек сплошной
среды за счет вращательной составляющей движения. Из B.12)
следует, что значения компонент, различающихся порядком
чередования индексов, противоположны:
utj = 0,5 (Vt-t?j - VjUi) = -0,5 (VjUi - Vtuj) = -uji.
Следовательно, тензор поворота является
антисимметричным. Совокупность компонент тензора поворота образует
матрицу второго ранга с равными нулю диагональными
членами:
0
(М) -
0
B.14)
, -CJ13 -CJ23 0
Тензор поворота характеризуется не более чем тремя
различными по модулю компонентами и представляет собой
псевдовектор.
Покажем, что составляющая dun относительного
перемещения действительно связана с поворотом окрестности данной
точки М. Из выражения B.13) следует dun = и^A^гКк, что
с учетом антисимметричности тензора поворота B.14)
приводит к развернутой записи: duu = Rl(—ui$d?* - ь>12^?2) -
-Я2(и;2з df3 ~ W12 dt1) + R3(u>m di1 + о?2з d?2). Правая часть
последнего выражения представляет собой результат
векторного умножения вектора П = П,-Д1 на вектор dR = d&Rj, так
что
ип = (П) х (dR) = (П.-Д1') х (d?jRj). B.15)
При этом компоненты вектора П определяются компонентами
тензора поворота п\ — и^ъ, ^2 = ~^133 ^3 = ^12-
Формула B.15) соответствует известным соотношениям
кинематики вращательного движения абсолютно твердого тела.
Действительно, при вращении абсолютно твердого тела вокруг
закрепленной оси линейная скорость v любой точки этого
тела равна векторному произведению вектора угловой скорости
5 - 9712
129

Со и радиус-вектора г, характеризующего положение
выбранной точки относительно оси вращения: v = uj х r (рис. 2.9).
В то же время перемещение, совершаемое рассматриваемой
точкой за бесконечно малый интервал времени <Й,
определится как duu = (a; di) х г = ft x т», где ft = a; dt — вектор
малого поворота, коллинеарный
вектору угловой скорости. Последнее
соотношение практически
эквивалентно выражению B.15).
Различие заключается лишь в том, что
для абсолютно твердого тела
рассматривается движение тела в
целом, а приведенное соотношение для
линейной скорости справедливо для
любой его индивидуальной точки.
В случае деформируемой среды
рассматривается вращательное
движение лишь бесконечно малой
окрестности точки М, а выражение B.15)
справедливо лишь для
индивидуальных точек, находящихся в этой
окрестности.
Таким образом, полное перемещение индивидуальной
точки Mi, находящейся в малой окрестности данной точки
М, складывается из ее поступательного перемещения
вместе с точкой М и относительных перемещений вследствие
деформирования, а также за счет поворота всей окрестности
данной точки как единого жесткого целого:
Рис. 2.9
щ =
duu.
B.16)
Установим теперь геометрический смысл тензора
деформаций в целом. Рассмотрим частный случай движения
индивидуальной частицы материального континуума и сопоставим
его с простейшим примером деформирования стержня при его
одноосном растяжении. Будем считать, что после
перемещения индивидуального объема материального континуума его
130

м
'////////////////////////
i i Vij
,()
(S)*O
Рис. 2.10
индивидуальная точка М не перемещается (it = 0) и остается
в исходном положении (рис. 2.10). Будем также считать, что
отсутствует и поворот бесконечно малой окрестности точки
М как единого жесткого целого, т.е. {и) = 0.
Предположим, что, несмотря на отсутствие перемещения точки М и
поворота ее окрестности, деформированное состояние в
данной точке определено и задается тензором деформаций (е). В
этом случае любая индивидуальная точка М\, находящаяся в
бесконечно малой окрестности данной точки Мив начальном
недеформированном состоянии занимающая положение,
задаваемое вектором dR, вследствие деформирования получает
перемещение, определяемое в соответствии с B.16) и B.11) как
и\ = <1иц = (е) • dR,
B.17)
и занимает новое положение М{. Это случай так называемой
чистой деформации.
Рассмотрим теперь стержень с начальной длиной /о,
один из торцов которого М—М неподвижно закреплен (см.
рис. 2.10). Будем считать, что стержень подвергается
одноосному растяжению, в результате чего он удлиняется, а его
торец М\—М\ получает перемещение А/ и занимает новое
положение Mj—М[. Полученное перемещение Д/ связано с
деформацией е в направлении растяжения очевидным
соотношением
Д/ =
B.18)
131

В обоих случаях существуют точка среды, остающаяся
при деформировании неподвижной (в первом случае это
индивидуальная точка М, а во втором — торец М—М стержня),
и точка с заданным (до деформирования) положением
относительно неподвижной точки (в первом случае это
находящаяся в бесконечно малой окрестности точки М индивидуальная
точка М\, положение которой характеризуется вектором dД, а
во втором случае это торец М\—Mi, начальное положение
которого задается скалярной величиной /о)- Точки с заданным
начальным положением совершают перемещения вследствие
деформирования, но в первом случае индивидуальная точка
может совершать пространственное перемещение,
характеризуемое вектором duR, а во втором случае торец Mi—Mi
совершает лишь осевое перемещение, характеризуемое скалярной
величиной Д/. В обоих случаях деформированное состояние
характеризуется с помощью специальной величины, но в
первом случае, когда возможно пространственное движение точек
в окрестности данной точки, используется тензор второго
ранга (г), а во втором, когда возможны лишь осевые перемещения
плоских сечений, достаточно скалярной величины осевой
деформации е. Наконец, в обоих случаях зависимость
перемещения вследствие деформирования от характеристик
деформированного состояния и начального положения точек описывается
совершенно одинаковыми по своей структуре соотношениями
B.17) и B.18): в левых частях соотношений содержатся
величины, определяющие перемещения за счет деформирования, а
в правых — скалярные произведения величины,
характеризующей деформированное состояние, и величины, определяющей
начальное положение индивидуальных точек.
На основании приведенного сопоставления можно сделать
вывод о том, что тензор второго ранга (тензор деформаций)
вводится в связи с переходом от простейшего случая
деформированного состояния, соответствующего одноосному
растяжению стержня при возможных перемещениях его плоских
сечений только в одном направлении, к более сложному случаю
деформированного состояния, когда имеют место
пространственные перемещения индивидуальных точек. Тензор
деформаций, по существу, является обобщением известной из курса
132

сопротивления материалов осевой деформации на этот более
сложный случай деформированного состояния.
Итак, тензор деформаций является характеристикой
деформированного состояния в индивидуальной точке
сплошной среды и позволяет определить перемещение любой
точки, находящейся в окрестности данной точки,
возникшее в результате деформирования.
Определив тензор деформаций в точке материального
континуума, можно установить коэффициент
относительного удлинения произвольно направленного бесконечно малого
материального отрезка, взятого в окрестности данной точки.
Действительно, полученное в результате деформирования
перемещение du^ индивидуальной точки М\ (см. рис. 2.10)
фактически означает, что бесконечно малый материальный
отрезок MMi, имевший до деформирования длину dR = \dR\
и ориентацию, задаваемую единичным вектором п так, что
dR = n dRy в результате деформирования изменяет свою
длину и подвергается сдвигу, занимая новое положение ММ[,
Изменение длины этого материального отрезка определится
величиной dun проекции вектора относительного перемещения
du^ на первоначальное направление этого отрезка, поэтому с
учетом B.17) получим
dun = du% • то =
Отношение изменения длины бесконечно малого
материального отрезка к его начальной длине dun/dR определяет
коэффициент относительного удлинения 1п материального отрезка
в данной индивидуальной точке в выбранном направлении тг,
поэтому получим
/„= ((е)-п).п B.19)
или с учетом правил скалярного умножения тензоров
ln = ((eijlVR?) • (nkRk)) • (nlRi) = Sijnlnj,
где eij, n — соответственно компоненты тензора деформаций
в данной точке и единичного вектора п, характеризующего
выбранное направление.
133

Очевидно, что в любой точке материального континуума
может быть выбрано бесконечно большое число различных
направлений (в телесном угле 4тг) и каждому из этих
направлений будет соответствовать свое значение коэффициента
относительного удлинения. Деформированное состояние в
индивидуальной точке сплошной среды можно считать полностью
охарактеризованным, если известна вся бесконечно большая
совокупность направлений и соответствующих им
коэффициентов относительных удлинений. Тензор деформаций как бы
содержит в себе всю эту информацию и позволяет определить
относительное удлинение для конкретного направления в
соответствии с приведенной выше формулой. Значит, тензор
деформаций является характеристикой деформированного
состояния в индивидуальной точке сплошной среды, т.е.
позволяет определить коэффициент относительного удлинения
материального отрезка в произвольном направлении в
окрестности данной точки.
2.2.2. Главные оси деформации
и главные деформации.
Геометрическое представление
тензора деформаций
Будем считать, что задано деформированное состояние в
индивидуальной точке сплошной среды, т.е. определен
тензор деформаций (г) = E{jR%W. В общем случае
элементарный материальный отрезок вдоль произвольного направления
п в результате деформирования испытывает изменение длины
и вследствие сдвига меняет ориентацию в пространстве (см.
рис. 2.10). Из множества направлений, которые могут быть
выбраны в данной точке, главными направлениями
{главными осями деформации) называются направления, в которых
материальные отрезки в результате деформирования
испытывают только изменение длины. Сдвиги в главных осях
деформации отсутствуют (рис. 2.11), т.е. индивидуальная
точка Mi, находящаяся в окрестности точки М на главной оси
134

Глабнаяось
деформации
Рис. 2.11
деформации, в результате деформирования получает
перемещение вдоль этого направления:
= A dR,
B.20)
где dR = ndR — вектор, определяющий главное
направление; п — единичный вектор главного направления; А —
некоторая скалярная величина. Величина А есть отношение
изменения длины \dup\ элементарного материального отрезка,
направленного вдоль главной оси деформации, к его
начальной длине \dR\ = dR, т.е. она является коэффициентом
относительного удлинения материального отрезка вдоль
рассматриваемого главного направления и соответствующей этому
главному направлению главной деформацией.
При известном деформированном состоянии главные оси
деформации и соответствующие им главные деформации
определяются из условий B.17) и B.20) как du^ = (e) dR = XdR,
что приводит к тензорному уравнению (е) • п — Хп = 0.
Результатом скалярного умножения тензора деформаций (е) =
= ?ijR%RJ на вектор п = n^R искомого главного
направления является вектор (е) • п = Sijn^R1. При скалярном
умножении А на тот же вектор п — riiR1 = n3gijR1 получается
вектор Xn3gijR%. В результате исходное тензорное уравнение
приводится к условию равенства нулю вектора:
135

что возможно только при условии равенства нулю всех трех
его компонент:
(eij-bgij)n* = 0,
где gij — метрические коэффициенты сопутствующей
системы координат в исходном (недеформированном) состоянии.
Так как ранее в качестве сопутствующей системы координат
принята декартова прямоугольная система координат (д^ = 1
при г = j и д^ = 0 при i\ф j), то в развернутой записи
система уравнений для определения главных направлений п (или
компонент п1, п2, п3, определяющих вектор п) и
соответствующих главных деформаций А принимает вид
(бц - Л) п1 + епп2 + ?13п3 = 0;
1 + F22 - А) п2 + ?23п3 - 0; B.21)
+ (гзз ~ А) п3 = 0.
Система трех уравнений B.21) включает четыре неизвестные
величины: п1, п2, п3 и А, поэтому необходимо ввести еще одно
уравнение — условие единичности направляющего вектора п:
= L B.22)
Из B.22) следует, что величины п1, п2, гг3 не могут
одновременно принимать нулевые значения, поэтому система B.21)
трех линейных относительно п1, п2, п3 однородных
уравнений имеет ненулевое решение. Из теории систем линейных
уравнений известно, что это может быть лишь в случае
равенства нулю определителя этой системы, т.е. когда
11 - А ?12 ?13
?12 ?22 - A ?23
= 0. B.23)
?13 ?23 ?33 ~ А
Раскрытие определителя приводит к кубическому
относительно А уравнению, носящему название характеристического
(или векового) уравнения. Решение уравнения B.23) дает три
действительных корня А = Ai = ?ь А = А2 = ?2 и А = Аз = ?з>
соответствующих трем главным деформациям для трех пока
не определенных главных направлений ni,ri2 И713.
136

Главные направления для каждой из трех главных
деформаций определяются на основе системы уравнений
B.21), B.22). Действительно, система B.21) справедлива при
использовании в качестве А любой из уже известных главных
деформаций. В то же время любая из главных деформаций
обращает в нуль определитель, составленный из
коэффициентов этой системы уравнений, что говорит о
пропорциональности строк определителя B.23), т.е. одно из трех
уравнений B.21) является следствием двух других. Это уравнение
может быть исключено из рассмотрения, а оставшиеся два
в сочетании с уравнением B.22) могут рассматриваться как
система трех уравнений относительно трех неизвестных
величин п1, п2, п3, определяющих искомое главное направление
для данной главной деформации (или ?i, или ?2, или ?з).
Итак, при заданном деформированном состоянии (?) =
= 6ijRlRJ в индивидуальной точке сплошной среды могут
быть установлены три главных направления гц, П2, пз и
соответствующие им главные деформации ?j, ?2, ?3- Можно
показать, что все три главных направления взаимно
перпендикулярны (щ • га д. = 1 при г — к и га, - гад. = 0 при г ф к).
Следовательно, с главными осями деформации можно связать
декартову прямоугольную систему координат (г/1, ?у2, г/3), у
которой единичные взаимно ортогональные базисные векторы
Я*, Я2, J?3 совпадают с единичными векторами rai, П2, П3,
определяющими соответствующие главные направления. На
рис. 2.12 в точке М
материального континуума показаны
координатные линии (f1), (?2),
(?3) недеформированной
сопутствующей системы координат
(взятой как декартова), в
которой задающий
деформированное состояние тензор
деформаций (е) — SijRlRJ имеет в
общем случае девять отличных
от нуля компонент E{j (отрезки
указанных координатных ли- Рис. 2.12
137

ний в процессе деформирования изменяют свою длину, углы
между ними также изменяют свои значения). На этом же
рисунке показаны оси 771,7/2, т;3, совпадающие с главными осями
деформации. Элементарные материальные отрезки,
направленные по главным осям до деформирования, не изменяют
направления и после деформирования, но изменяют свою
длину, что характеризуется соответствующими коэффициентами
относительных удлинений — главными деформациями ?ь ?2>
?3- Учитывая геометрический смысл компонент тензора
деформаций, можно утверждать, что в декартовой
прямоугольной системе координат G71, rj2, 773), связанной с главными
осями деформации, тензор деформаций имеет лишь три отличные
от нуля компоненты с одинаковыми индексами, равные
главным деформациям (ец = Е\, ?22 = ?2> ?зз = ?з)> и приобретает
простой вид:
(г) = EiRlRl + e2RlRl + ?3Я?< B.24)
Эти главные деформации называются также главными
значениями тензора деформаций.
Геометрическим образом тензора деформаций (?)
является поверхность второго порядка — поверхность деформации
Коши, которая вводится следующим образом. Для
индивидуальной точки М сплошной среды будем считать заданным
тензор деформаций (?) = е^ггг^ в произвольной системе
координат (рис. 2.13). Выберем в области пространства,
окружающей данную точку, произвольную точку М\. Ее положение
t з относительно точки М
характеризуется радиус-вектором
г = хкгь> где хк —
компоненты радиус-вектора г (для
декартовой прямоугольной
системы координат они
совпадают с координатами точки М\
относительно точки М).
138

Определим двойное скалярное произведение тензора
деформаций и радиус-вектора г, используя правила тензорной
алгебры:
((е) • г) ¦ г = (foyrV) • (хкгк)) ¦ (xlrt) = е^хК
В результате получена, скалярная величина, значение которой
зависит, во-первых, от деформированного состояния в данной
точке (компоненты ?,у), во-вторых, от выбранной точки М\
(компоненты хг радиус-вектора г). Тогда уравнение
S{jXlxJ — const B.25)
определит некоторое геометрическое место точек,
окружающих данную точку, и для них выполняется условие
(е) rr = const. B.26)
Это геометрическое место точек и определяет поверхность
деформации Коши.
Геометрический смысл поверхности деформации Коши
следует из условия B.26). Радиус-вектор, направленный из
данной точки М к точке М\ поверхности деформации, может
быть представлен как г = пг, где п — единичный вектор,
характеризующий направление от данной точки к точке
поверхности деформации. В этом случае уравнение B.26),
описывающее поверхность деформации, представляется в форме
(е)'П-пг2 = const и в соответствии с B.19) приводится к виду
1п - const/г2, где 1п — коэффициент относительного
удлинения бесконечно малого элементарного материального отрезка,
взятого в данной точке, по направлению к точке поверхности
деформации. Следовательно, поверхность деформации — это
геометрическое место точек, окружающих данную точку,
таких, что значение коэффициента относительного
удлинения по направлению от данной точки к любой точке
поверхности деформации обратно пропорционально квадрату
139

расстояния между этими точками. По виду поверхности
деформации Коши можно судить о характере
деформированного состояния в данной точке сплошной среды. Например, по
направлению к наиболее удаленным точкам поверхности
деформации относительное удлинение материальных отрезков
минимально и т.д.
Как следует из уравнения B.25), поверхность
деформации является поверхностью второго порядка. Ввиду
инвариантности скалярной величины относительно преобразования
системы координат это уравнение сохраняет свой вид в любой
системе координат (при этом, разумеется, изменяются и
компоненты тензора деформаций, и компоненты радиус-вектора,
однако эти изменения взаимно обратны и компенсируют друг
друга). В частности, в декартовой прямоугольной системе
координат (т/1, г/2, г/3), связанной с главными осями
деформации, уравнение поверхности деформации в соответствии с
B.24) приводится к наиболее простому (каноническому) виду:
+е2 (г?2) +?з(??3) = const,
где г/1, т/2, г/3 — координаты точек поверхности деформации в
указанной системе координат. Конкретный вид поверхности
деформации зависит от характера деформированного
состояния. Например, для деформированного состояния
всестороннего растяжения (?i > 0, е2 > 0, ?з > 0) поверхность
деформации представляется эллипсоидом, т.е.
а2 + Ь2 + с2 -1'
где а2 = const/бi; b2 = const je2\ с2 = const /е$. Для
равноосного растяжения (ei = е2 = ?з = е) поверхность деформации
является сферической поверхностью, а для более сложного
деформированного состояния (е\ > 0, е2 > 0, ?з < 0) —
сочетанием однополостного и двухполостного гиперболоидов и т.д.
140

2.2.3. Инварианты тензора деформаций
Тензор деформаций является математическим объектом,
характеризующим деформированное состояние в данной точке
материального континуума. Деформированное состояние
объективно определяется изменением расстояний между
индивидуальными точками сплошной среды и не зависит от
субъективно выбираемой для его описания системы координат.
Поэтому тензор деформаций инвариантен относительно
преобразования системы координат:
(е) = eijITRi = (?i;)'rV = ?l r\
Он остается неизменным математическим объектом в любой
произвольной системе координат. Как известно из тензорного
исчисления, именно поэтому компоненты тензора деформаций
зависят от выбранной системы координат и преобразуются
при переходе от одной системы к другой по определенному (в
данном случае ковариантному) закону:
Такая зависимость компонент тензора деформаций от
произвольно выбираемой системы координат затрудняет анализ
деформированного состояния и приводит к необходимости
введения так называемых инвариантов тензора деформаций.
Инварианты тензора деформаций — это скалярные
величины, составленные из компонент тензора деформаций, не
зависящие от выбора системы координат и не изменяющиеся
при переходе от одной системы координат к другой. Тензор
деформаций имеет три основных инварианта: первый Т\(е)
— линейный; второй ТгСО — квадратичный; третий Т${е) —
кубический.
Первый основной инвариант в произвольной системе
координат образуется с участием ковариантных компонент E{j
тензора деформаций и контрвариантных компонент g%J
фундаментального метрического тензора в этой же системе
координат и определяется как сумма их произведений: Т\(е) = ?ijglJ-
141

Образуемая указанным образом скалярная величина
действительно является инвариантом ввиду взаимно обратного
характера преобразования ковариантных компонент тензора
деформаций и контрвариантных компонент метрического тензора
при переходе от одной системы координат к другой. В
частном случае ортогональной системы координат (декартова,
цилиндрическая и т.д.) первый основной инвариант выражается
через физические компоненты тензора деформаций с
одинаковыми индексами:
Г1(?) = ?Ш11+?22<722 +
+ ^22уд22 уд22 + ?ззуд33 уд33 = ?(п) + ?B2) + ?(зз)-
Первый основной инвариант может быть также выражен и
через компоненты тензора деформаций в декартовой
прямоугольной системе координат, связанной с главными осями
деформации, как Т\(е) = в\ + е2 + ?з-
Второй основной инвариант в общем случае
образуется как сумма произведений ковариантных и контрвариантных
компонент тензора деформаций: Т2(е) = г^е1* = ?ij?a0gatg^*
Он может быть выражен через физические компоненты
тензора деформаций в какой-либо ортогональной системе координат
или же через главные значения тензора деформаций:
е22 (д22)' + е2ъ
V2 + 2eW V3
= е(П) + ?B2) + еC3) + 2бA2) + 2?A3) + 2?B3) =е1+€2 + еЗ-
Очевидно, что при записи второго основного инварианта в
ортогональной системе координат он представляет собой сумму
квадратов всех девяти физических компонент тензора
деформаций.
Третий основной инвариант образуется с
использованием смешанных компонент тензора деформаций и при
выражении через главные значения тензора деформаций определяется
суммой их кубов:
Г3(е) = фН = eiaej0ebrgaWkgTi = е} + е\ + е\.
142

Более удобными для анализа деформированного
состояния являются не основные инварианты Ti(e), T2(e), Гз(^)> а
производные инварианты — средняя деформация е и
интенсивность деформаций в{.
Средняя деформация является производным инвариантом
первого основного инварианта:
e=Ti(e)/3. B.27)
Физический смысл е наглядно выявляется в частном
случае деформированного состояния, когда деформации малы,
при сравнении объемов индивидуальной частицы
материального континуума до и после деформирования. Выделим в
окрестности индивидуальной точки М материального
континуума индивидуальную частицу, имеющую до
деформирования форму элементарного параллелепипеда с ребрами
длиной d^1, d7/2, dr/3, направленными по главным осям
тензора деформаций. Объем выделенной индивидуальной частицы
до деформирования определяется произведением длин ребер
dV = dr^drp'djf. В результате деформирования изменяются
длины ребер элементарного параллелепипеда (элементарных
материальных отрезков вдоль главных направлений). В
соответствии с геометрическим смыслом компонент тензора
деформаций с одинаковыми индексами длины ребер станут
равными rf?71(H-ei), drJ(l + S2), ^773A+?з)> а объем
индивидуальной частицы после деформирования dV* = dr^drf drpA + е\) X
хA + ?2)A + ?з)- Относительное изменение объема
индивидуальной частицы может быть охарактеризовано величиной
объемной деформации {коэффициента кубического
расширения) в = (dV* - dV)/dV. При малых деформациях, когда
произведениями главных деформаций можно пренебречь по
сравнению с самими главными деформациями, коэффициент
кубического расширения определяется суммой главных
деформаций, а следовательно, первым основным инвариантом тензора
деформаций или средней деформацией:
лу* - dV
в = — « ?i + е2 + е3 = Тг(е) = Зе.
143

Таким образом, средняя деформация и первый основной
инвариант тензора деформаций характеризуют изменение
объема индивидуальных частиц материального континуума.
Интенсивность деформаций в{ является производным
инвариантом первого и второго основных инвариантов тензора
деформаций и определяется как
et = ±.у/т(е)-Т?{е). B.28)
Учитывая возможность представления второго и первого
основных инвариантов через физические компоненты е^:\
тензора деформаций или же через его главные значения ?ь ?2> ?з>
получаем соответствующие выражения и для интенсивности
деформаций:
(^B2) "
е223)); B.29)
~ ?2J + (?2 - ?зJ + (?3 - ?lJ- B.30)
Значение коэффициента \/2/3 выбрано из условия равенства
интенсивности деформаций ?г главной деформации Е\ в
направлении растяжения для случая одноосного растяжения
несжимаемого стержня. При одноосном растяжении стержня
направление растяжения и два любых перпендикулярных ему
направления (радиальное и тангенциальное) являются
главными осями деформации. Главные деформации в радиальном
и тангенциальном направлениях связаны с главной
деформацией в направлении растяжения (?2 = ?з = —0,5?i), что
вытекает из принятого предположения о несжимаемости
материала стержня и физического смысла первого основного
инварианта тензора деформаций. Тогда из B.30) следует, что
действительно е% — ?\.
Физический смысл интенсивности деформаций
заключается в том, что эта величина является обобщенной
144

интегральной характеристикой сдвиговых деформаций в
окрестности данной индивидуальной точки материального
континуума. Так как сдвиговые деформации
определяются изменениями углов между координатными линиями
сопутствующей системы координат и связаны только с изменением
формы индивидуальных частиц (см. рис. 2.7), то
интенсивность деформаций характеризует формоизменение
индивидуальных частиц материального континуума.
Однако из выражений B.29) и B.30) не очевидно, что
интенсивность деформаций е{ действительно обобщенно
характеризует сдвиговые деформации в окрестности
индивидуальной точки материального континуума. Например,
интенсивность деформаций может быть выражена через
главные деформации — коэффициенты относительных удлинений
элементарных материальных отрезков, направленных вдоль
главных осей, испытывающих при деформировании лишь
изменение длины. Сдвиги же в главных осях отсутствуют.
Тем не менее отсутствие сдвиговых деформаций в главных
осях не означает их отсутствие вообще в окрестности
данной точки. В общем случае сдвиговые деформации
отличны от нуля и их экстремальные значения определяются
разностями главных деформаций. Это можно показать,
опираясь на геометрический смысл тензора деформаций в целом.
Будем считать тензор деформаций в индивидуальной
точке заданным в главных осях г/1, ту2, т/3: (е) = eiR^R^ +
+ 62ЩЩ + езЩЩ- Выберем в исходном недеформирован-
ном состоянии материальный отрезок единичной длины и
произвольного направления п = nlRi (рис. 2.14). Перемещение,
которое в результате деформирования получает конец М\
выбранного материального отрезка, в соответствии с B.17)
определится выражением
йиЛ = (е) • п = eijnJR1 = e\nlR\ + е2п2R2V +
Материальный отрезок изменяет свою длину на величину
dun — Aиц - п — е\п\ + ?2^2 + ?Зпз> а М°ДУЛЬ
тангенциальной составляющей перемещения duT определяет сдвиговую
145

деформацию в окрестности данной точки, соответствующую
выбранному направлению вектора п. Очевидно, что
9
99
п
9i»i9j9 9 9
du; = {du^y-dui = ef n\
или с учетом единичности длины вектора п получим
du\ = е\{\ -п\- п\) + е\п\ + е\п\ -
Значение тангенциальной составляющей перемещения du*
зависит от направления материального отрезка и
является функцией компонент п2 и щ направляющего вектора
п\ = i/l — ^2 "" пз )* Направления, которым
соответствуют максимальные значения тангенциальной составляющей
относительного перемещения, а следовательно, и
максимальные сдвиги, определяются из условии d(du^.j/dn2 = 0 и
didu\J дщ = 0. Например, из первого условия следует, что
[9 91
[?2 + Si) — 2в1 — (?2 — Si) 7l2 — (?3 " ?l) n3 = 0*
Это позволяет определить одно из направлений
экстремальных сдвиговых деформаций пз = 0, п\ = п2 = 1/\/2 и
соответствующую этому направлению максимальную
тангенциальную составляющую перемещения (dv%)
\ / max
146

или (duT) = (е\ —?2)/2. Аналогичным образом определя-
\ / max
ются и два других направления в окрестности данной точки,
которым соответствуют экстремальные значения сдвиговых
деформаций, и устанавливается тот факт; что они
характеризуются разностями главных деформаций.
Таким образом, интенсивность деформаций ?t
действительно является обобщенной характеристикой сдвиговых
деформаций в окрестности индивидуальной точки
материального континуума.
2.2.4. Шаровой тензор деформаций
и девиатор тензора деформаций
В общем случае при деформировании может происходить
изменение как объема индивидуальных частиц материального
континуума, так и их формы. В полных деформациях,
характеризуемых тензором деформаций (б), может быть выделена
часть, которая определяет изменение объема, и часть, которая
связана с изменением формы. Соответственно и тензор
деформаций в целом (е) может быть представлен в виде суммы двух
тензоров второго ранга — шарового тензора деформаций (Se)
и девиатора тензора деформаций (D?): (e) = (Se) + (D?).
Компоненты шарового тензора деформаций E?)
образуются на основе производного инварианта тензора деформаций
в целом — средней деформации — с использованием
компонент gij (или g*i, или gj) фундаментального метрического
тензора системы координат: Seij — egij. Совокупность
девяти компонент шарового тензора деформаций образует
диагональную матрицу, содержащую на главной диагонали
величину средней деформации. Поверхность деформации Коши
для определенного таким образом тензора будет являться
сферической, чем и объясняется его название "шаровой тензор".
Убедимся в том, что шаровой тензор деформаций
действительно характеризует часть полных деформаций,
определяющих изменение объема индивидуальных частиц
материального континуума и не связанных с изменением их формы.
147

Для этого необходимо определить производные инварианты
шарового тензора — среднее значение 5 и интенсивность St
— и сравнить их с соответствующими инвариантами тензора
деформаций в целом (е и ?,•). Действительно, первый и второй
основные инварианты шарового тензора деформаций в
соответствии с определением инвариантов и компонент шарового
тензора равны:
При определении выражений для основных инвариантов
имелось в виду, что сумма произведений ковариантных и
контрвариантных компонент метрического тензора gijg%* вследствие
взаимно обратного характера преобразования указанных
компонент является величиной, инвариантной относительно
преобразования системы координат. Значит, эта величина может
быть вычислена в любой ортогональной системе координат,
где отличны от нуля лишь метрические коэффициенты с
одинаковыми индексами, а метрические коэффициенты основного
и взаимного базисов взаимно обратны. Из соотношений B.27)
и B.28) следует, что среднее значение шарового тензора S
совпадает со значением средней деформации е, а интенсивность
шарового тензора St; = 0. Таким образом, производный
инвариант шарового тензора, характеризующий изменение объема
индивидуальных частиц сплошной среды, совпадает с
соответствующим производным инвариантом тензора деформаций
в целом, а производный инвариант шарового тензора,
характеризующий формоизменение, равен нулю. Это дает основание
утверждать, что шаровой тензор деформаций характеризует
ту часть полных деформаций, которая определяет
изменение объема индивидуальных частиц материального
континуума и не связана с изменением их формы.
Девиатор тензора деформаций (D?) (в дальнейшем — де-
виатор деформаций) представляет собой тензор второго ранга,
дополняющий шаровой тензор до тензора деформаций в целом.
148

Девиатор деформаций как бы показывает, насколько тензор
деформаций в целом отклоняется от шарового (от латинского
слова deviatio — отклонение). Компоненты девиатора
деформаций — это разности компонент тензора деформаций в целом
и компонент шарового тензора: D€{j = 6{j - egij. Первый и
второй основные инварианты девиатора деформаций
определяются выражениями
= eijgij - едцд%3 = Т^е) - 3? = 0;
T2(D?) = DeijDlJ = (?ij - egij) (е%> - eg") =
Но тогда среднее значение девиатора деформаций равно нулю,
а его интенсивность с учетом B.28) можно определить как
т.е. она равна интенсивности деформаций ?,-. Таким образом,
производный инвариант девиатора деформаций,
характеризующий изменение объема индивидуальных частиц, равен нулю,
а производный инвариант, характеризующий формоизменение
индивидуальных частиц, совпадает с соответствующим
производным инвариантом тензора деформаций в целом. Это
дает основание утверждать, что девиатор тензора деформаций
характеризует ту часть полных деформаций, которая
определяет изменение формы индивидуальных частиц
материального континуума и не связана с изменением их объема.
2.2.5. Понятие об уравнениях
совместности деформаций
Уравнения совместности деформаций устанавливают
взаимосвязи между компонентами тензора деформаций,
являющимися в общем случае функциями координат. В этом
разделе ограничимся обоснованием необходимости существования
149

уравнений совместности деформаций, описанием принципа их
получения и физического смысла.
Будем считать заданным поле перемещений сплошной
среды и = г^х1, х2,х3). В соответствии с этим для каждой
точки пространства с координатами х1, х2, х3 относительно
системы отсчета наблюдателя определяется вектор
перемещения, которое получила индивидуальная точка, находящаяся
в данной точке пространства. Векторное поле перемещения
можно считать заданным, если известны три скалярные
функции вида щ = щ(х^, х2, х3). В соответствии с
геометрическими соотношениями B.9), выражающими компоненты тензора
деформаций через компоненты щ вектора перемещения,
можно по заданному полю перемещений определить поле
компонент тензора деформаций. Тензор деформаций имеет девять
компонент, поэтому на основе трех функций, компонент
вектора перемещения от координат щ = щ(х1, х2, х3) получаются
девять функций компонент тензора деформаций от координат:
ij = ?ij{x\ х2, х3) =0,5 (V^-
Очевидно, что девять функций координат e+j = ^(х1, х2, х3),
определенные всего лишь по трем исходным функциям
координат щ = щ(х*у х2, х3), не могут быть совершенно
произвольными и должны быть определенным образом
взаимосвязаны, причем число устанавливающих взаимосвязи
соотношений должно равняться шести. Уравнения, устанавливающие
взаимосвязи между компонентами тензора деформаций как
функциями координат, называются уравнениями
совместности деформаций.
Уравнения совместности деформаций вытекают из
геометрических соотношений, в чем можно убедиться на
следующем частном примере. Будем считать поле
перемещений заданным в декартовой прямоугольной системе координат
(х1 = х, х2 = у, х3 = z). Предположим также, что
деформации малы. В таком случае геометрические соотношения B.10)
принимают вид
дщ duj
Ш + d
150

Из девяти приведенных здесь геометрических соотношений
выделим лишь три, необходимые для получения одного из
уравнений совместности деформаций:
дих
дх
диу
?22 = ?уу =V
?12 =
Продифференцируем теперь первое из выделенных
соотношений дважды по координате у, второе — дважды по координате
#, а результаты сложим:
д2ехх д2еуу _ д3их д\у _ д2 (дих дч
ду2 дх2 " ду2дх + дх2ду ~ дхду\ду дх
Полученная смешанная производная второго порядка
удвоенной сдвиговой деформации 2еху = дих/ду + диу/дх позволяет
записать одно из уравнений совместности деформаций:
д2ехх д2еуу д2еху
дУ2 + дх2 дхду'
Аналогичным образом могут быть получены остальные пять
уравнений совместности деформаций.
Физический смысл уравнений совместности
деформаций заключается в том, что их выполнение
соответствует сохранению сплошности материального континуума при
его деформировании. Напротив, если какое-либо тело
разбить на множество элементарных параллелепипедов и
задаться совершенно произвольными функциями координат Sij =
= Sij(x1y х2, х3), не связанными уравнениями совместности
деформаций, то из отдельных элементарных
параллелепипедов, деформированных в соответствии с заданными
произвольными деформациями, нельзя будет составить сплошное
деформированное тело.
151

2.2.6. Тензор скоростей деформаций
Тензор скоростей деформаций (ё) = ёцГгг* — еще одна
физическая величина, вводимая для описания движения
материального континуума. Он характеризует скорость
изменения деформированного состояния в индивидуальных точках
сплошной среды.
Тензор деформаций вводился в рассмотрение на
основе сравнения расстояний между индивидуальными точками
материального континуума до деформирования и после
него. Компоненты тензора деформаций определялись как
полуразности метрических коэффициентов деформированной и
исходной сопутствующих систем координат. По существу,
при введении тензора деформаций сравнивались два
состояния сплошной среды: исходное при t = t$ и текущее для
произвольного момента времени t. Тензор скоростей деформаций
также вводится на основе сравнения двух состояний:
текущего для произвольного момента времени t и отстоящего от него
на малую величину Д*. В общем случае происходит движение
сплошной среды, а быстрота изменения положения
индивидуальных точек относительно системы отсчета наблюдателя
характеризуется вектором скорости v =¦ dr/dt = du/dt = V{r%.
Индивидуальные точки сплошной среды за малый интервал
времени At получают малые перемещения Ащ = V{At. При
сравнении двух близких состояний t и t + At в соответствии
с геометрическими соотношениями B.9) можно найти
компоненты тензора малых деформаций
Аегз = 0,5
характеризующие приращения компонент тензора
деформаций, получаемые за малый интервал времени At.
Тензор скоростей деформаций вводится как тензор,
компоненты которого определяются пределом отношения
приращений деформаций к интервалу времени, в течение которого
эти приращения были получены, при стремлении последнего
к нулю:
До ^ = 0,5 (v.-t;,- + Vyt;,-). B.32)
152

Соотношения B.32), выражающее компоненты тензора
скоростей деформаций через компоненты вектора скорости,
называются кинематическими соотношениями. В целом же
тензор скоростей деформаций, как и всякий тензор второго
ранга, образуется при участии базисных математических
объектов — диадных произведений векторов взаимного базиса
системы координат:
(е) = eo-rV. B.33)
Из кинематических соотношений следует, что значения
компонент тензора скоростей деформаций, различающихся
порядком чередования индексов, одинаковы (eij = ?ji)<> т.е. тензор
скоростей деформаций является симметричным.
При движении материального континуума можно
выделить три его составляющие: поступательную,
деформационную и вращательную. Подтвердим это положение путем
сопоставления скоростей движения некоторой произвольной
индивидуальной точки М и точки Mi, находящейся в
бесконечно малой окрестности точки М (рис. 2.15). Будем
считать, что некоторая произвольная индивидуальная точка М,
положение которой относительно системы отсчета
наблюдателя для произвольного момента времени t характеризуется
радиус-вектором г, имеет скорость движения v. Выберем в
бесконечно малой ее окрестности индивидуальную точку М\.
Положение этой точки относительно точки М может быть
задано вектором dr, являющимся бесконечно малым
приращением радиус-вектора г (его дифференциалом). Ввиду
зависимости радиус-вектора г от координат индивидуальных точек
Рис. 2.15
153

вектор dr может быть представлен в разложении по базисным
векторам произвольной системы координат через свои
компоненты, в качестве которых выступают бесконечно малые
приращения соответствующих координат, отвечающие
переходу от точки М к точке М\\ dr — (dr/dxl)dx% = rtdx*.
В общем случае скорость движения v\ точки М\
отличается от скорости v точки М на бесконечно малую величину
dv = (dv/dxl)dxl. Учитывая зависимость скорости от
координат индивидуальных точек (v = v(xl, х2, х3)) и
опираясь на правила дифференцирования векторов по координатам,
правила скалярного умножения тензоров и правила
определения дифференциальных операций первого порядка с
тензорами, получаем, что различие в скорости движения
рассматриваемых индивидуальных точек определяется выражением
dv = —v/ . J dx% = (V.u,- ] r3 dxx =
= dr ¦ grad v.
= (ri dxl\
Здесь тензор второго ранга Vji;yrlW, т.е. результат
действия символического дифференциального оператора
Гамильтона V = V(...)r2 на вектор скорости v = Vjr^ является
градиентом вектора скорости (в этом случае действие
сводится к неопределенному умножению: Vv = [V,-(.. .)rl](vjrJ) =
= V{Vjr%ri — grad v). Указанный тензор второго ранга может
быть представлен в виде суммы двух тензоров: V{Vjrlr3 =
= 0,5(Vt-Vj + Vyv^rV + 0,5(Vt-t;j - VjV^rWK При этом
первый является тензором скоростей деформаций, а второй
— (и) = d>ijrlrJ — характеризует мгновенное вращение всей
окрестности данной точки М как единого жесткого целого и
называется тензором скоростей поворота. С учетом
разложения grad v = (ё) + (^) получаем v\ = v + dv = v + dvR + dvn,
где dvji = dr • (ё) определяется тензором скоростей
деформаций в данной точке, зависит от относительного положения
точки, взятой в окрестности данной точки, и представляет
собой деформационную составляющую относительной скорости
154

движения точек, adun = dr-(u) характеризует вращательную
составляющую относительной скорости движения.
Последнее утверждение можно обосновать по аналогии с
обоснованием геометрического смысла тензора поворота.
Действительно, компоненты тензора (и;), предположительно
ассоциированного с вращением окрестности данной точки,
определяются как полуразности абсолютных производных
компонент вектора скорости: lj{j = 0,5(Vt-Vj — Vj-v,-), что
приводит к выполнению условия антисимметричности этого
тензора: Cj{j = —Mji- Совокупность его компонент образует матри-
цу
О
(М) -
-и>\2
О
^23
О
B.34)
характеризуемую не более чем тремя различными и
отличными от нуля величинами: u>i2, ?13, ^>23- Тогда выражение для
соответствующей составляющей относительной скорости
движения точек может быть представлено в виде векторного
произведения некоторого вектора П = и^т1 и вектора dr = г, da;1,
характеризующего относительное положение точек, т.е.
dvu = dr . (и) =
=ftx dr,
где компоненты вектора П определяются компонентами
тензора (и): п\ — CJ23? ^2 — ~^13j ^3 = ^12- В справедливости
подобного преобразования можно убедиться, приведя его
развернутую запись применительно к некоторой декартовой
прямоугольной системе координат, в которой векторное
произведение векторов tl X dr находится наиболее простым образом
с помощью соответствующего определителя. Это не
отрицает справедливости подобного преобразования применительно
к произвольной криволинейной системе координат ввиду
инвариантности тензоров по отношению к преобразованию
системы координат, а следовательно, и результатов алгебраических
155

операций с ними. Выражение для составляющей
относительной скорости движения dvn = tlxdr соответствует
известному из теоретической механики выражению v = (Ъ х г для
линейной скорости движения точек абсолютно твердого тела при
его вращении вокруг закрепленной оси с угловой скоростью о;
(см. рис. 2.9). Поэтому тензор второго ранга (а;) = и^тгг3
действительно характеризует мгновенное вращение
окрестности данной точки как единого жесткого целого, а угловая
скорость вращательного движения Q определяется компонентами
этого тензора.
На основе проведенного кинематического анализа
представляется возможным уяснить кинематический смысл
тензора скоростей деформаций
в целом (рис. 2.16). Зная
тензор скоростей
деформаций в произвольной
индивидуальной точке М
сплошной среды, можно для любой
точки Mi, находящейся в ее
окрестности, определить
относительную скорость дви-
Рис. 2.16 жения, возникающую
вследствие деформирования:
*>д = (?).*•, B.35)
где dr = ndr\ dr — расстояние между этими точками или
текущая длина материального отрезка; п — единичный вектор,
характеризующий направление элементарного материального
отрезка, состоящего из индивидуальных точек между
точками М и М\. Проекция dvn вектора относительной скорости
движения точки М\ на направление элементарного
материального отрезка определит скорость изменения длины этого
отрезка: dvn = dvR -n = (e)-n-ndr. Но тогда скорость
относительного удлинения выбранного элементарного
материального отрезка ln = dvn/dr = (ё) • п • п = kijn%n3, т.е.
тензор скоростей деформаций позволяет найти и скорость
относительного удлинения материального отрезка в произвольном
направлении в окрестности данной точки.
156

2.3. Теория напряжений
2.3.1. Напряжение — мера интенсивности
внутренних сил
Основной особенностью движения деформируемых сред
является изменение расстояний между их индивидуальными
точками, происходящее под действием внешних сил. Это
приводит к появлению внутренних сил в деформируемых средах,
и деформированному состоянию всегда сопутствует
определенное напряженное состояние.
Процессу изменения расстояний между
индивидуальными точками материального континуума в реальных
дискретных средах соответствует изменение расстояний между
атомами или молекулами. Известно, что взаимодействие атомов
и молекул имеет электромагнитную природу: между ними
действуют силы притяжения и отталкивания, в исходном (не-
деформированном) состоянии уравновешивающие друг друга.
При изменении средних расстояний между молекулами
нарушается равновесие между этими силами, в результате чего
силы одного направления преобладают над силами
противоположного направления. Этому процессу появления сил
взаимодействия частиц реальной среды в рамках
феноменологического подхода соответствует возникновение внутренних сил
в материальном континууме. Чтобы количественно
характеризовать внутренние силы, вводится специальная физическая
величина — вектор полного напряжения.
Пусть на тело действуют внешние силы Fi, -F25 • • • >
приводящие к относительному перемещению его индивидуальных
точек и появлению внутренних сил (рис. 2.17). Мысленно
разобьем это тело плоскостью S на две части объемами V\ и V<i.
Выделим в сечении тела, заданном плоскостью 5,
индивидуальную точку М и включающую эту точку площадку dS>
ориентацию которой зададим единичным вектором нормали п. В
рассматриваемом теле (в частности, в сечении S)
существуют внутренние силы, поэтому на площадке dS на часть тела
157

Рис. 2.17
объемом V\ со стороны части тела объемом V2 действует
внутренняя сила dF. Интенсивность внутренних сил,
действующих в данной точке материального континуума на площадке,
ориентация которой задана единичным вектором нормали п,
определяется вектором полного напряжения
ап = dF/dS. B.36)
Полное напряжение характеризует поверхностную плотность
внутренней силы взаимодействия между частями тела на
данной площадке. Вектору полного напряжения на площадке,
ориентация которой задана единичным вектором нормали п,
соответствуют две скалярные величины — нормальное
напряжение а/п\ = ап п, представляющее собой проекцию полного
напряжения на направление нормали к площадке, и полное ка-
сателъное напряжение т = ./|сгта|2 — а? ч = Jcrn • ап — aj ч,
действующее на данной площадке.
2.3.2. Тензор напряжений —
характеристика напряженного состояния
материального континуума
Подобно тому как для описания деформированного
состояния материального континуума вводилась специальная
кинематическая величина — тензор деформаций, для описания
напряженного состояния также вводится специальная
физическая величина — тензор напряжений, являющийся
специфичной динамической характеристикой сплошной среды.
158

Тензор напряжений вводится на основе анализа
условий равновесия элементарного тетраэдра, ребра которого
совпадают с координатными линиями некоторой
декартовой прямоугольной системы координат, и определения
вектора полного напряжения на площадке произвольной
ориентации. Аналогичную операцию можно провести на
основе анализа уравнений движения для элементарного
тетраэдра. Рассмотрим произвольную индивидуальную точку М
индивидуального объема материального континуума,
занимающего область пространства D объемом V',
ограниченным поверхностью S и подверженным действию внешних
сил F (рис. 2.18). Введем в рассмотрение декартову
прямоугольную систему координат (ж1, х2, х3). Она может или
быть связанной с системой отсчета наблюдателя, или
вообще являться произвольной и быть связанной с какой-либо
точкой пространства.
Через данную точку М
можно провести три
координатные линии (х1), (ж2),
(ж3). Выберем теперь на
этих координатных
линиях точки Л, Б, С,
бесконечно близкие к данной
точке М. Тело,
ограниченное четырьмя
плоскостями, проходящими через
точки М, А у Б, С,
является бесконечно малым
элементарным тетраэдром
(на рис. 2.18 он показан в
увеличенном виде).
Гранями выделенного
тетраэдра являются площадки
МВС, MAC, MAB,
совпадающие с координатными поверхностями (основные
площадки), и площадка ABC произвольной ориентации,
задаваемой единичным вектором нормали п.
159

Площади dS\, dS2, dS$ основных площадок связаны с
площадью dS площадки произвольной ориентации через
компоненты пг (направляющие косинусы) единичного вектора
нормали п. Например, площадь dS% третьей основной площадки,
перпендикулярной координатной линии (х3), связана с углом
а наклона площадки произвольной ориентации и ее
площадью dS как dS$ = d5cosa (см. рис. 2.18). Но угол а наклона
площадки произвольной ориентации к третьей основной
площадке равен углу, который составляет единичный вектор
нормали п с третьей координатной линией (ж3). Следовательно,
dS^ = d5-n3, где n3 = cos a — направляющий косинус
единичного вектора нормали п по отношению к координатной линии
(ж3). Аналогичным образом выражаются площади двух
других основных площадок, поэтому
dSi = dS-n\ dS2 = dS-n2y dS3 = dS • n3. B.37)
По граням элементарного тетраэдра действуют
внутренние силы, количественно характеризуемые векторами полных
напряжений. На первой основной площадке действует вектор
полного напряжения о\, на второй — вектор полного
напряжения 0-2, на третьей — вектор полного напряжения <тз, а
на наклонной площадке произвольной ориентации, задаваемой
единичным вектором нормали п, — вектор полного
напряжения ап. Каждый из трех векторов полных напряжений,
действующих на основных площадках, может быть представлен
в разложении по базисным векторам системы координат:
0*1 = <гцг\ 02 = сг{2г\ <т3 = <7t-3r\ B.38)
Очевидно, что компонентами векторов полных напряжений
являются нормадьные и касательные напряжения,
действующие на площадках, совпадающих с координатными
поверхностями. Например, <7ц — нормальное напряжение на первой
основной площадке, а2\ и СГ31 — касательные напряжения на
этой же площадке и т.д.
Условие равновесия элементарного тетраэдра под
действием внутренних сил может быть выражено как стп dS =
160

= a\ dS\ + о dS2 + сгз dS$y что с учетом соотношений B.37)
приводит к выражению вектора полного напряжения на
площадке произвольной ориентации через векторы полных
напряжений на основных площадках и направляющие косинусы п%:
<тп = <т\п1 + <72П2 + азп3. Это позволяет ввести в
рассмотрение такую характеристику напряженного состояния, как
тензор напряжений. Действительно, выражая векторы o*i, 0*2, ^3
через их компоненты и базисные векторы, получаем
ап = <7tlnV + <7i2n2r% + а&пггх = <7t;nV,
что в соответствии с правилами тензорной алгебры дает
основание представить вектор полного напряжения ап на
площадке произвольной ориентации как результат скалярного
умножения некоторого тензора второго ранга на единичный вектор
нормали п к рассматриваемой площадке, т.е.
ап = <7tJnV = (*уrV') • (пкгк^ = {а) • п. B.39)
Полученный подобным образом тензор второго ранга
(а) = <ТцТгт*) компонентами которого являются
компоненты векторов полных напряжений на основных площадках или
нормальные и касательные напряжения на этих площадках,
является тензором напряжений.
Тензор напряжений — это тензор второго ранга. Он
вводится в рассмотрение в декартовой прямоугольной системе
координат, однако может быть представлен и в произвольной
системе координат своими ковариантными,
контрвариантными или смешанными компонентами:
(а) = <7yfV = a^TiTj = <т{г{Ту B.40)
Как уже указывалось, компоненты тензора напряжений
представляют собой нормальные и касательные
напряжения, действующие на площадках, совпадающих с
координатными поверхностями (рис. 2.19). Совокупность девяти
компонент тензора напряжений образует квадратную матрицу, на
6-9712

Рис. 2.19
Рис. 2.20
главной диагонали которой находятся нормальные
напряжения, а остальные ее элементы представляют собой
соответствующие касательные напряжения.
Тензор напряжений — это симметричный тензор.
Опуская общее доказательство этого положения, приведем
частное его подтверждение на примере условий равновесия
элементарного параллелепипеда при напряженном состоянии,
соответствующем чистому сдвигу (рис. 2.20). При чистом
сдвиге на гранях элементарного параллелепипеда
размерами dz, dy, dz действуют внутренние силы, значения
которых определяются касательными напряжениями тху и тух, а
также площадью граней. При равновесии результирующий
момент внутренних сил относительно оси z (тху dz dy) dx —
-(ryxdxdz)dy = 0. Это приводит к закону парности
касательных напряжений тху = тух или к условию
симметричности тензора напряжений a+j = <7yt.
Так же как и для тензора деформаций, для тензора
напряжений вводятся физические компоненты. Это связано с
тем, что в общем случае представления тензора напряжений
B.40) в произвольной системе координат базисные векторы
могут обладать размерностью, а поэтому и компоненты
тензора напряжений в этой системе координат будут иметь
размерность, отличную от размерности напряжений. По аналогии с
162

физическими компонентами тензора деформаций физические
компоненты тензора напряжений — это компоненты,
имеющие размерность напряжений и образующиеся при
использовании в качестве базисных математических объектов
единичных безразмерных базисных векторов. Физические
компоненты выражаются через метрические коэффициенты
системы координат как а/^\ = (Tijy/g^ y/g**, где
суммирование по г и j не предполагается.
Напряженное состояние в точке считается полностью
охарактеризованным, если для любой из бесконечно большого
числа площадок, которые могут быть проведены через данную
точку, известны полное, нормальное и касательное
напряжения. Тензор напряжений охватывает всю эту бесконечно
большую совокупность, позволяя определить конкретные значения
этих величин на любой площадке, ориентация которой
задается единичным вектором нормали п к ней. Действительно,
из определения тензора напряжений B.39) следует
соотношение, выражающее вектор полного напряжения на площадке
произвольной ориентации, ап = (а) • п = сгП|г*, где
компоненты вектора полного напряжения на выбранной площадке
определяются компонентами тензора напряжений и зависят от
ориентации этой площадки, т.е. от компонент п3 единичного
вектора нормали п к этой площадке:
ani = aijn*. B.41)
Нормальное напряжение определяется как проекция
вектора полного напряжения на направление нормали к площадке
*(п) = <*п • п = (а) • п • п = (<7t7Vr') • (jtkrk^ = crijnj(nkglkj
и также зависит от компонент тензора напряжений и
ориентации площадки:
cr(n) = (a)-n;n = a0-nV B.42)
(сравните с формулой B.19) для вычисления
коэффициента относительного удлинения бесконечно малого
произвольно ориентированного материального отрезка в окрестности
данной точки материального континуума). Наконец,
касательное напряжение г, действующее на выбранной площадке
6* 163

(см. рис. 2.17), в соответствии с очевидными
геометрическими соображениями определяется из выражения г2 = ап ап -
т =
>)
Таким образом, зная тензор напряжений в
индивидуальной точке сплошной среды, можно рассчитать полное,
нормальное и касательное напряжения на любой площадке,
проходящей через данную точку, что и позволяет рассматривать
тензор напряжений как характеристику напряженного
состояния среды в данной точке.
2.3.3. Главные оси, главные площадки
и главные значения тензора напряжений.
Геометрическое представление
тензора напряжений
Из бесконечно большого числа площадок, которые можно
провести через точку материального континуума, где
существует напряженное состояние, целесообразно выделить
главные площадки — площадки, на которых отсутствуют
касательные напряжения. Направления по нормали к этим
площадкам определяют главные направления, или главные оси,
тензора напряжений, а нормальные напряжения,
действующие на этих площадках, называются главными
напряжениями или главными значениями тензора напряжений. Из
приведенного определения следует, что на главной площадке
вектор полного напряжения <тп коллинеарен единичному вектору
п данного главного направления, т.е. ап = An, где
скалярная величина А характеризует главное напряжение на данной
164

главной площадке Главное у
(рис. 2.21). При по- направление^?
ложительном значении
А на данной главной
площадке действует
растягивающее напря- \" \ Главная
жение, а при отрица- >ч—./ площадка
тельном — сжимаю- рис 2
щее.
Главные оси и главные значения тензора напряжений
определяются по аналогии с принципом нахождения главных
осей и главных значений тензора деформаций. Единичный
вектор п будет определять главное направление, если
выполняется условие <7П = (<т)-п = An, где А — главное напряжение
на главной площадке, ортогональной искомому главному
направлению. Указанное уравнение с использованием
соотношения B.39) и правил тензорной алгебры может быть приведено
к условию (aij - Xgij) n^r1 = 0, что формирует систему
уравнений типа B.21), содержащую компоненты тензора
напряжений и включающую в качестве неизвестных величин три
компоненты (п1, п2, п3) единичного вектора искомого
главного направления и величину А соответствующего главного
напряжения. Полученная система уравнений замыкается
условием B.22) единичности вектора п.
Дальнейшее решение этой системы уравнений,
определение главных напряжений А = Ai = ffi, А = Аг = <Т2>
А = Аз = 0"з и соответствующих каждому из трех главных
направлений единичных векторов nj, пз, пз проводится
аналогично тому, как это выполнялось в теории деформаций.
Можно показать, что все три главных направления тензора
напряжений взаимно перпендикулярны, т.е. с ними можно связать
декартову прямоугольную систему координат G71, f/2, f/3),
единичные базисные векторы которой совпадают с единичными
векторами главных направлений Д* = ni, Д^ = П2, R^ = П3.
В этой системе координат площадки, совпадающие с
координатными поверхностями, являются главными площадками и
165

на них действуют только нормальные (главные) напряжения,
а касательные напряжения отсутствуют. В соответствии с
физическим смыслом компонент тензора напряжений в
декартовой прямоугольной системе координат, связанной с его
главными осями, отличны от нуля лишь три компоненты с
одинаковыми индексами <7ц = 01, ^22 = ^2> ^33 = ^З* поэтому
тензор напряжений в этой системе координат можно представить
через его главные значения:
B.43)
Так же как и при геометрическом представлении
тензора деформаций, геометрическим образом тензора
напряжений (<т), характеризующего напряженное состояние в
индивидуальной точке материального континуума, является
поверхность второго порядка — поверхность напряжений. Она
вводится в рассмотрение так же, как и поверхность деформации
Коши, и обладает аналогичными свойствами, поэтому в этом
разделе ограничимся лишь установлением геометрического
смысла поверхности напряжений.
Поверхность напряжений — это геометрическое место
точек, окружающих данную точку и подчиняющихся условию
(а) • г - г = const или (ТцХгх* = const, где г — радиус-вектор,
направленный из данной точки к точке поверхности; хх —
координаты точек поверхности относительно данной точки.
Поскольку радиус-вектор г может быть представлен как г = пг,
где п характеризует направление от данной точки к точке
поверхности, а г — расстояние от данной точки до точки
поверхности, уравнение, описывающее поверхность напряжений,
может быть записано в виде (а) • п • nr2 = const или с учетом
B.42) в виде <т/п\ = const /г2, где а/п\ = (а)-п-п — нормальное
напряжение на площадке, ориентация которой задается
нормалью п. Следовательно, поверхность напряжений — это
геометрическое место точек, окружающих данную точку,
таких, что величина нормального напряжения на площадках,
перпендикулярных направлению от данной точки к точке
поверхности, обратно пропорциональна квадрату расстояния
от данной точки до точки поверхности.
166

2.3.4. Инварианты тензора напряжений
Тензор напряжений ранее вводился в рассмотрение в
декартовой прямоугольной системе координат. Однако, как и
всякий тензор, он может быть представлен и в любой другой
системе, например в декартовой прямоугольной системе
координат, связанной с главными направлениями. Являясь
объективной характеристикой напряженного состояния
материального континуума, не зависящей от субъективно выбираемой
системы координат, тензор напряжений остается
инвариантным по отношению к преобразованию системы координат:
Из тензорного исчисления известно, что именно это
обстоятельство приводит к изменению компонент тензора при
переходе от одной системы координат к другой, что неудобно для
анализа напряженного состояния.
Проводить анализ напряженного состояния более удобно
с помощью инвариантов тензора напряжений — скалярных
величин, составленных из компонент тензора напряжений и
не изменяющихся при переходе от одной системы координат к
другой.
Основные инварианты тензора напряжений —
линейный Ti(a), квадратичный ?2@") и кубический Т^(а) —
вводятся аналогично основным инвариантам тензора
деформаций. Каждый из трех основных инвариантов может быть
выражен через компоненты а, у тензора напряжений в
произвольной системе координат и метрические коэффициенты д%3 этой
же системы координат, через физические компоненты 0ип в
какой-либо ортогональной системе координат или через
главные напряжения — компоненты тензора напряжений в
главных осях:
167

<J22g22 + <т3з<733 =
T2(a) = <тц*ч =
= *(
B.44)
= ^1 + ^2 + a3i
li = ^1
Однако наиболее удобно проводить анализ
напряженного состояния с помощью производных инвариантов тензора
напряжений — среднего напряжения а и интенсивности
напряжений О{.
Среднее напряжение является производным инвариантом
первого основного инварианта: а = Т\(а)/3 = (ai + о2 +
+<тз)/3. Физический смысл среднего напряжения установим
на частном примере напряженного состояния всестороннего
равноосного сжатия, реализуемого, например, при сжатии
поршнем жидкости в цилиндре (рис. 2.22). В этом случае
на гранях любой индивидуальной частицы жидкости
действуют одинаковые сжимающие напряжения о\ = —р, а2 = -р,
аз = —р. Среднее напряжение с точностью до знака равно
давлению, действующему в данной индивидуальной частице:
а = -р, т.е. среднее напряжение и первый основной
инвариант тензора напряжений определяют давление в
индивидуальной частице сплошной среды, появление которого связано
с изменением объема индивидуальных частиц.
Рис. 2.22
168

Интенсивность напряжений является производным
инвариантом первого и второго основных инвариантов тензора
напряжений, т.е.
<П = ^у/эТ2(*)-1?{*), B-45)
и с учетом B.44) может быть выражена через физические
компоненты аил в любой ортогональной системе координат или
же через главные напряжения fi, <?2, <т3:
л/2 Г/ ^2 ~, 72 *
°\ = "у у ^A1) ~ CTB2)J + (^B2) ~ <rC3)J +
f); B.46)
^Я + ^^ + ^^ОЗ B.47)
Форма B.47) представления интенсивности напряжений
позволяет обосновать выбор постоянного коэффициента \/2/2.
Он выбран исходя из того, что для простейшего случая
напряженного состояния одноосного растяжения (о\ ф О,
(j2 = аз = 0) интенсивность напряжений должна
равняться единственному отличному от нуля главному напряжению:
(Ji = О\.
Физический смысл интенсивности напряжений
заключается в том, что эта величина является интегральной
обобщенной характеристикой касательных напряжений,
действующих в окрестности данной точки
материального континуума. Так как появление касательных
напряжений связано с изменением формы индивидуальных частиц
материального континуума, то интенсивность напряжений —
это обобщенная характеристика напряжений, возникающих
в связи с формоизменением частиц сплошной среды.
Последнее утверждение нуждается в обосновании, так
как в выражение B.47) касательные напряжения вообще не
169

включены ввиду их отсутствия на главных площадках.
Однако это отсутствие вовсе не означает, что касательных
напряжений нет на любых других площадках, проведенных
через данную индивидуальную точку материального
континуума. Из курса сопротивления материалов известно, что
экстремальные значения касательных напряжений действуют на
площадках, равнонаклоненных к главным площадкам, и
определяются полуразностями главных напряжений. Поэтому
интенсивность напряжений действительно характеризует
экстремальные значения касательных напряжений, действующих
в окрестности данной точки.
2.3.5. Шаровой тензор напряжений
и девиатор тензора напряжений
Так же как и тензор деформаций, тензор напряжений (а)
может быть представлен в виде суммы двух тензоров —
шарового тензора напряжений (Sa) и девиатора тензора
напряжений (Dp), который в дальнейшем будем называть просто
девиатором напряжений.
Компоненты шарового тензора напряжений образуются
на основе его производного инварианта (среднего напряжения)
при использовании метрических коэффициентов системы
координат: Saij = og{j. Первый и второй основные инварианты
шарового тензора напряжений, согласно B.44), определяются
выражениями
Ti(Sff) = Srirfi = <гдцд{> = За;
T2(S<T) = SvijSH = agij(TgxJ = За2.
Но тогда среднее значение шарового тензора напряжений
5 = T\(S(r)/3 = о совпадает со средним значением
тензора напряжений в целом, а интенсивность шарового тензора,
определяемая в соответствии с B.45), St = 0. Это
позволяет утверждать, что шаровой тензор напряжений
характеризует лишь ту часть полных напряжений, появление
которой связано с изменением объема индивидуальных частиц
материального континуума и не связано с их
формоизменением.
170

Девиатор напряжений имеет компоненты, дополняющие
компоненты шарового тензора до полных напряжений:
Dpij = G{j - agij. При таком определении компонент деви-
атора его первый (T\(Do)) и второй (T2(Da)) основные
инварианты, а также среднее значение D и интенсивность /?,-,
согласно B.44) и B.45), имеют следующий вид:
rf j ) - Za = 0;
T2(Dff) = D* ( ) (
= сц** - 3a2 = T2{a) - *№.,
Таким образом, производный инвариант D девиатора
напряжений, связанный с реакцией сплошной среды на
изменение объема индивидуальных частиц, равен нулю, а
производный инвариант /?,-, характеризующий возникающие в связи
с формоизменением напряжения, совпадает с
соответствующим производным инвариантом тензора напряжений в целом.
Это дает основание утверждать, что девиатор напряжений
характеризует ту часть полных напряжений, появление
которой связано лишь с изменением формы индивидуальных
частиц материального континуума и не связано с изменением
их объема.
Следовательно, разделение тензора напряжений на
шаровой тензор и девиатор напряжений осуществляется с
целью выделения составляющих полных напряжений,
связанных с изменением объема или формы индивидуальных
частиц сплошной среды. Тензор напряжений в целом (а) =
= EV) + {Da) характеризует полные напряжения,
возникающие в индивидуальных частицах вследствие изменения как
их объема, так и формы.
171

Рп"
2.3.6. Условия равновесия
материального континуума
В общем случае на тело или индивидуальный объем
материального континуума действуют внешние
распределенные силы jP, р (рис. 2.23). Действие внешних сил
приводит к изменению расстояний между индивидуальными
точками сплошной среды, вследствие чего появляются внутренние
силы и возникает
соответствующее напряженное со-
Ьп стояние. Важным частным
случаем движения
материального континуума под
действием внешних сил
является случай равновесия,
когда в результате
совместного действия внешних и
внутренних сил каждая
индивидуальная частица тела и
Рис 2 23
" ' тело в целом не
испытывают ускорений. Для
обеспечения равновесия материального континуума внешние и
внутренние силы должны быть определенным образом
взаимосвязаны условиями равновесия.
Различают два вида внешних сил — поверхностные и
объемные (массовые) силы. Поверхностные силы — это
внешние силы, действие которых распространяется на
частицы материального континуума, находящиеся на
поверхности, ограничивающей область пространства, занятую
сплошной средой. Такими силами, например, являются
силы давления и трения. Для количественного описания
поверхностных сил вводится векторная физическая величина —
вектор удельной поверхностной силы р, по модулю равный
поверхностной силе, приходящейся на единицу площади
поверхности. Тогда можно определить поверхностную силу,
действующую на площадку dS, как pdS. В общем случае
интенсивность поверхностных сил может изменяться вдоль
поверхности тела, а величина р может быть переменной, так что
172

полная поверхностная сила, действующая на тело,
ограниченное поверхностью 5, определяется интегралом Ф pdS, взятым
S
по этой поверхности от вектора удельной поверхностной силы
р (в дальнейшем для краткости будем его называть вектором
поверхностной силы).
Объемные (массовые) силы — это внешние силы,
действие которых распространяется на все частицы
материального континуума, заключенные в объеме тела.
Такими силами, например, являются силы тяжести, инерции (в
неинерциальных системах отсчета), электромагнитные силы.
Для количественного описания объемных (массовых) сил
вводится специальная физическая величина — вектор удельных
объемных (массовых) сил F, по модулю равный объемной
(массовой) силе, отнесенной к единице объема (массы)
материального континуума. При этом объемная сила,
действующая на индивидуальную частицу материального континуума
объемом dV, определится как FdV. В общем случае
величина F может быть переменной. Тогда полная объемная
сила, действующая на тело объемом F, определится интегралом
FdV', взятым по этому объему от вектора удельных объем-
V
ных сил F (в дальнейшем для краткости будем его называть
вектором объемных сил). Например, на любую
индивидуальную частицу тела, находящегося в поле тяготения Земли,
действует сила тяжести dFT = drug = —dmgk = — р$ dVgk, где
/9o — плотность среды; dV — объем индивидуальной частицы;
д = -дк — ускорение свободного падения (рис. 2.24). Вектор
объемных сил F = dFT/dV = -родк, а вектор массовых сил
F= dFT/dm = -gk = д.
На рис. 2.23 показана индивидуальная точка М тела,
находящаяся сколь угодно близко к поверхности S тела.
Проведем через выбранную точку координатные линии (ж1), (ж2),
(я3) до пересечения с поверхностью S в точках А, В и С.
Образовавшаяся площадка А В С представляет собой
бесконечно малый участок поверхности тела, ориентация которого в
173

X
J
Рис.
dFT
2.24
пространстве может быть задана единичным вектором
нормали п = щт% = п^'гу. Поверхностные силы действуют на
поверхности S тела. В частности, они действуют и на
бесконечно малой площадке ABC, ориентация которой задается
единичным вектором нормали п. Очевидно, что вектор
поверхностной силы рп на рассматриваемой площадке заданной
ориентации однозначно определяет вектор полного
напряжения сгп = рп, действующего на данной площадке. Учитывая,
что вектор полного напряжения на площадке заданной
ориентации определяется тензором напряжений в данной точке
материального континуума и ориентацией площадки согласно
B.39), получаем взаимосвязь между напряжениями и
поверхностными силами на границе тела или граничные условия в
напряжениях:
(сг)-п = рп. B.48)
Тензорное соотношение B.48) иногда также называется
условиями равновесия на границе области, занятой сплошной
средой. Полагая тензор напряжений, единичный вектор нормали
п и вектор поверхностной силы заданными своими
компонентами, т.е. (а) = <JijT%T3) п = n3vj, pn = РщГ1, получаем из
B.48) запись граничных условий в напряжениях через
компоненты тензоров
°ijnj =Pni- B.49)
Согласно полученным условиям, компоненты тензора
напряжений на границе тела, где действуют поверхностные силы,
174

не могут быть совершенно произвольными и должны быть
определенным образом взаимосвязаны с компонентами
вектора поверхностных сил и с компонентами единичного вектора
нормали, задающего ориентацию поверхности в данной точке.
Условия равновесия в объеме тела выводятся из
рассмотрения равновесия тела в целом под действием объемных и
поверхностных сил (см. рис. 2.23). В общем случае на
каждый участок поверхности тела площадью dS, ориентация
которого задана единичным вектором нормали п, действует
поверхностная сила pndS, а в целом на тело действует
полная поверхностная сила Ф рп dS. На каждую индивидуальную
5
частицу тела объемом dV действует объемная сила FdV, а в
целом на тело действует полная объемная сила / FdV. Необ-
V
ходимым условием равновесия тела в целом является условие
равенства нулю главного вектора внешних сил (объемной и
поверхностной): R = FdV + Ф pndS = 0. При
V S
тор поверхностных сил рп для любой точки поверхности в
соответствии с граничными условиями в напряжениях B.48)
выражается через тензор напряжений на поверхности тела и
единичный вектор нормали к поверхности в данной точке, так
что полная поверхностная сила определяется потоком тензора
напряжений через замкнутую поверхность, ограничивающую
тело. Используя далее теорему Остроградского — Гаусса,
получаем
j>pndS = Ф(а) -ndS = / div(cr) d\\
S S V
что позволяет привести условие равенства нулю главного
вектора внешних сил R к виду
этом век-
()F = 0. B.50)
V
175

В полученном условии равновесия тела в целом
интегрирование ведется по объему V тела. Однако это условие должно
выполняться и для любого индивидуального объема
сплошной среды при ее равновесии, где в качестве поверхностных
сил (внешних по отношению к произвольному
индивидуальному объему) выступают напряжения, действующие на
границе этого объема со стороны окружающих его частиц среды.
Ввиду произвольности объема V, для которого должно
выполняться условие B.50), равновесие тела в целом будет иметь
место только в том случае, если тождественно равно нулю
подынтегральное выражение, т.е. если для каждой
индивидуальной точки будет выполняться условие
F+ div(<j) = 0. B.51)
Соотношение B.51) представляет собой условие равновесия в
объеме тела, согласно которому распределение напряжений в
находящемся в равновесии материальном континууме не
может быть произвольным, а должно быть определенным
образом взаимосвязанным с объемными силами.
Из тензорной формы записи условий равновесия B.51)
можно получить запись этих условий через компоненты
тензоров. Для этого необходимо представить каждый
участвующий в уравнении B.51) тензор через соответствующие
компоненты, например через контрвариантные: F = FlVi,
(а) = (Т^т^гу, а затем на основе символического подхода к
проведению дифференциальных операций первого порядка с
тензорами определить дивергенцию тензора напряжений:
rj =
) (r* • r.) rj =
= V*
В процессе преобразования приведенных выражений
использовались правила скалярного умножения тензоров,
учитывалось постоянство метрических коэффициентов по отношению
176

к абсолютному дифференцированию, принимались во
внимание возможность замены одного индекса другим и
возможность обозначения индекса суммирования любой буквой, а
также симметричность тензора напряжений. Из тензорного
условия B.51) следуют три условия равновесия в объеме тела,
выраженные через компоненты тензоров:
F{ + Vj<jij = 0. B.52)
2.4. Законы сохранения
в механике сплошных сред.
Элементы термодинамики сплошных сред
2.4.1. Полная, локальная и конвективная
производные
Поведение сплошных сред при их нагружении, движении
и деформировании подчинено основным фундаментальным
законам природы — законам сохранения массы, импульса,
энергии (первый закон термодинамики) и второму закону
термодинамики. Применительно к материальному континууму законы
сохранения выражаются через дифференциальные уравнения
в частных производных. К их числу относятся уравнения
неразрывности, движения и энергии.
Прежде чем перейти к выводу соответствующих
уравнений, рассмотрим частный вопрос, связанный с особенностями
вычисления производной какой-либо величины по времени при
описании движения с позиций Лагранжа и Эйлера, что
приводит к определению понятий полной, локальной и конвективной
производных.
Пусть движение сплошной среды описывается с
позиций Лагранжа, т.е. для любой величины, характеризующей
движение и состояние сплошной среды, определена ее
зависимость от лагранжевых координат f1, ?2, f3,
индивидуализирующих точки материального континуума, и времени t.
177

Для определенности будем считать заданным
изменяющееся во времени распределение температуры в сплошной среде:
Т = ТЧ^1, ?2, ?3, t). Найдем частную производную dT/dt ,
V
полагая фиксированными переменные ?*, ?2, ?3. Так как ла-
гранжевы координаты f1, f2, ?3 навсегда закрепляются за
каждой индивидуальной точкой (или индивидуальной частицей)
сплошной среды и не зависят от времени, рассматриваемая
частная производная является полной производной по
времени, т.е.
ЯГ _ d_
dt p " dt
и характеризует скорость изменения значения
рассматриваемой величины для выделенной, фиксированной лагранжевыми
координатами f1, f2, ?3 индивидуальной точки (или
индивидуальной частицы) среды. Определенная подобным образом
производная по времени называется полной, или
индивидуальной, или субстанциональной производной.
Нахождение полной производной по времени при
описании движения с позиций Эйлера существенно усложнено. В
этом случае изменяющееся во времени распределение какой-
либо величины в сплошной среде задается в виде
зависимости этой величины от времени t и от текущих
координат х1, х2, х3 индивидуальных точек среды относительно
системы отсчета наблюдателя (эйлеровых координат): Г =
= Т(х1у х2, х3, t). При движении сплошной среды текущие
координаты я1, а:2, ж3 ее индивидуальных точек зависят от
лагранжевых координат ?2, f2, f3, а также от времени t: х* =
= «4f1,f2>f3, *). Тогда
dt
dt ci
1 О Q v 1
dt
дт дх1
дх1 dt
дт дх2
дх2 dt
dr
dt
178

где дх%/dt\ = dxl/dt = v% — компоненты вектора скорости
движения индивидуальных точек материального континуума;
дТ/дх* — компоненты вектора gradT = (дТ/дх{)г\ В
целом полная производная по времени представляется в виде
суммы двух составляющих:
1ГТ"т •^Т^ .ЛТ^ .ЛТ"'
ч
первая из которых называется локальной, или местной,
производной, а вторая — конвективной производной.
Локальная производная определяется при фиксированных значениях
эйлеровых координат я1, я2, ж3 и характеризует скорость
изменения значения какой-либо величины в данной точке
пространства. Очевидно, что локальная и полная
производные по времени не совпадают и различие между ними,
характеризуемое конвективной производной v • grad T, связано
с движением сплошной среды (в конвективной производной
фигурирует вектор скорости движения индивидуальных
точек) и с неравномерностью пространственного распределения
рассматриваемой величины (неравномерность
характеризуется градиентом этой величины, фигурирующим в выражении
для конвективной производной).
Физический смысл полной, локальной и конвективной
производных и их взаимосвязи B.53) могут быть уяснены с
помощью следующего примера (рис. 2.25). Будем считать, что в
момент времени t в точке 1 пространства находится
индивидуальная частица сплошной среды температурой Т\. В течение
малого интервала времени At рассматриваемая
индивидуальная частица совершает малое перемещение Дг = vAt, при
этом в общем случае ее температура изменяется и к
моменту времени t + At становится равной Т[. Однако к моменту
времени t + At в точку 1 пространства приходит некоторая
другая индивидуальная частица температурой Т^,
находившаяся в момент времени t в точке 2 пространства и
имевшая температуру Тз, причем положение точки 2
относительно точки 1 задано вектором — Дг = -vAt. За время Д*
изменение температуры в точке 1 пространства с
фиксированными эйлеровыми координатами ж* определяется величиной
179

,-J/
т;
Рис. 2.25
(ATj = Т*2 - Гь а изменение температуры
индивидуальной частицы с фиксированными лагранжевыми координатами
^ = Г^ - Гг. Следовательно,
локаль— величиной
ное изменение температуры отличается от изменения
температуры индивидуальной частицы потому, что в данной
точке пространства начальное и конечное значения температуры
определяются температурой совершенно различных
индивидуальных частиц сплошной среды. Изменение температуры в
данной точке пространства может быть представлено в виде
суммы двух составляющих:
-Т1), B.54)
одна из которых выражает изменение температуры
индивидуальной частицы, а вторая (Т2 ~~ ^i) связана с
пространственной неравномерностью распределения температуры в
исходный момент времени t. Но для этого момента времени при
переходе от точки 1 пространства к точке 2 в соответствии с
аналитическим смыслом градиента скалярной функции
изменение температуры Т2~Т\ = -Дг-gradT, где gradT отнесен
180

к точке i, а вектор -Дг = -vAt характеризует
относительное положение точки #, взятой в малой окрестности точки 1.
Тогда изменение температуры в данной точке пространства
. = (дг) . - vAt- gradr,
что при At —> 0 эквивалентно взаимосвязи B.53) между
полной, локальной и конвективной производными.
Таким образом, конвективная производная определяет
ту часть изменения во времени какой-либо величины в
данной точке пространства, которая связана с движением
индивидуальных частиц сплошной среды и с неравномерным
распределением этой величины по частицам среды. Если же
среда не движется (v = 0) или пространственное
распределение величины равномерно (gradr = 0), значения полной и
локальной производных совпадают.
2.4.2. Закон сохранения массы —
уравнение неразрывности
Сущность закона сохранения массы состоит в том,
что при нагружении, движении и деформировании
материального континуума масса т любого его индивидуального
объема (или масса dm любой индивидуальной частицы)
остается неизменной:
т
- I pdV = const; B.55)
V
dm = pdV = ро dV0 = const, B.56)
где /9q, dVo — начальные плотность и объем индивидуальной
частицы; />, dV — текущие (после деформирования) плотность
и объем индивидуальной частицы; V — значение
индивидуального объема.
181

Более удобно выразить закон сохранения массы в
дифференциальной форме, установив взаимосвязь между скоростью
изменения плотности индивидуальных частиц и полем
скорости движения индивидуальных точек. С этой целью
рассмотрим движение материального континуума относительно
системы отсчета наблюдателя (ж1, ж2, ж3) (рис. 2.26).
п
V
Рис. 2.26
Выделим некоторую область пространства D* с
неизменным объемом V*, ограниченную неподвижной относительно
системы отсчета наблюдателя поверхностью 5*. При
движении материального континуума через поверхность 5*
происходит перенос массы через эту поверхность, что вызывает
изменение массы, содержащейся в объеме выделенной области
пространства. При этом для любого бесконечно малого
интервала времени dt ф О изменение массы, содержащейся в объеме
V*, равно массе, перенесенной через поверхность 5+ в течение
этого интервала времени.
Определим изменение массы материального континуума
в объеме V* за время dt ф 0. Выделим бесконечно малую
область пространства dV* вокруг точки пространства с
фиксированными эйлеровыми координатами ж1, ж2, ж3. При
плотности р среды в данной точке пространства можно представить
массу, содержащуюся в выделенном бесконечно малом объеме,
182

как pdV*. Скорость изменения массы в объеме dV*
характеризуется локальной производной по времени d(pdV*)/dt\xi =
:= d(pdV*)/dt. В связи с неизменностью во времени величины
dV* скорость изменения массы, содержащейся в объеме dV+,
равна (др/dt) dV*. За время dt ф О масса в объеме dV*
изменяется на (др/dt) dV* dt, В целом за время dt масса
материального континуума, содержащаяся в объеме выделенной области
пространства, изменяется на величину, равную сумме
элементарных изменений или же соответствующему объемному
интегралу
/ , а. \
B.57)
Теперь найдем значение массы, переносимой через
поверхность 5* за бесконечно малый интервал времени dt ф 0.
Рассмотрим бесконечно малый участок поверхности dS*
вокруг некоторой точки, причем ориентацию поверхности в этой
точке будем считать заданной единичным вектором нормали
п (см. рис. 2.26). При движении сплошной среды со
скоростью v через элементарную площадку dS* за время dt
переносится масса, заключенная в объеме косого цилиндра с
основанием d5*, образующей vdt и площадью поперечного сечения
dSn = dS* cos а, равной проекции площадки d5+ на
направление, перпендикулярное вектору скорости движения среды v
(рис. 2.27). Переносимая масса
р (dS* cos a vdt) = р dS* cos a v dt = p v - n dS* dt,
\
vdt
Рис. 2.27
183

где а — угол между площадкой dS* и плоскостью поперечного
сечения цилиндра, равный углу между вектором скорости v
и нормалью п к рассматриваемой площадке. Но тогда масса
материального континуума, переносимая за время dt через всю
поверхность 5*, определится поверхностным интегралом
pv-ndsAdt B.58)
или же потоком вектора pv через замкнутую поверхность,
ограничивающую выделенный объем V*. Вектор pv
называется вектором потока массы. Он совпадает по направлению с
вектором скорости и, а по модулю равен массе, переносимой
в единицу времени через единичную площадку,
перпендикулярную вектору скорости. Последнее вытекает, например, из
анализа размерности вектора pv.
Итак, масса, переносимая через неподвижную
поверхность 5*, определяется потоком вектора pv через эту
поверхность: при положительном потоке вектора pv масса среды в
выделенном объеме уменьшается (среда "вытекает" из
области), а при отрицательном — увеличивается (среда "втекает"
в область). Следовательно, соотношение, выражающее закон
сохранения массы (уравнение баланса массы), имеет вид
/^-dV*dt = - ApvndS+dt
V* 5*
или
v; s*
Используя далее теорему Остроградского — Гаусса A.14) и
преобразуя поток вектора pv через замкнутую поверхность 5*
в интеграл от дивергенции этого вектора по объему V*,
ограниченному этой поверхностью, получаем
/с
^ + div(/w)J dV* = 0.
V*
184

В силу произвольности выделенного объема V* приведенный
объемный интеграл равняется нулю в случае тождественного
равенства нулю подынтегрального выражения
B.59)
которое через компоненты вектора скорости можно записать
в виде
^ + V;(^') = 0. B.60)
Уравнения B.59) и B.60) эквивалентны, они являются
дифференциальным выражением закона сохранения массы и
называются уравнениями неразрывности. Согласно этим
уравнениям, скорость изменения плотности в данной точке
пространства, характеризуемая локальной производной плотности по
времени, определяется дивергенцией вектора потока массы,
взятой в этой же точке пространства.
Уравнение неразрывности может быть представлено в
иной форме и записано не только для точки пространства, но
и для индивидуальной частицы сплошной среды. В
соответствии с правилами дифференцирования произведения из B.60)
следует
при этом второй член представляет собой скалярное
произведение вектора скорости на градиент плотности, а именно
v%Vip = (v^Vj) • (Vipr%) = v • grad/9, и является
конвективной производной плотности. В соответствии с B.53) сумма
локальной и конвективной производных плотности есть
полная производная dp/dt, характеризующая скорость изменения
плотности индивидуальной частицы сплошной среды.
Поэтому уравнение неразрывности можно представить в виде
B.61)
185

или в виде эквивалентного тензорного уравнения
^ + pdivv = 0. B.62)
at
Согласно B.62), скорость изменения плотности
индивидуальных частиц материального континуума определяется
дивергенцией вектора скорости движения индивидуальных точек
сплошной среды.
Дифференциальное уравнение B.62), выражающее закон
сохранения массы, может быть получено более простым путем
на основе условия B.56) неизменности массы индивидуальной
частицы dm = pdV. Из этого условия следует, что скорости
изменения плотности и объема любой индивидуальной
частицы взаимосвязаны:
dm dp d(dV)
-dr = Ttdv+p^r = 0>
dp p d(dV)
dt dV dt
Учитывая, что относительная скорость изменения
бесконечно малого индивидуального объема определяется
дивергенцией вектора скорости, приходим к дифференциальному
уравнению неразрывности B.62).
Вывод уравнения неразрывности проводился без каких бы
то ни было ограничений относительно физико-механических
свойств рассматриваемой среды. Это позволяет говорить об
универсальности уравнения неразрывности: любая сплошная
среда, какими бы конкретными физико-механическими
свойствами она ни обладала (идеальная, упругая, вязкая, упруго-
пластическая и т.п.) и в каком бы агрегатном состоянии она
ни находилась (твердое, жидкое, газообразное), должна
подчиняться этому уравнению.
Отметим также, что при выводе закона сохранения
массы применительно к сплошным средам была введена в
рассмотрение скалярная физическая величина — плотность />,
характеризующая состояние материального континуума при
186

изменении объема его индивидуальных частиц. Из теории
деформаций следует, что текущий объем индивидуальной
частицы dV взаимосвязан с начальным ее объемом dVo и
объемной деформацией в (коэффициент кубического расширения):
dV = dVo(l + в). Но тогда из закона сохранения массы в
форме B.56) следует взаимосвязь начальной и текущей
плотностей и объемной деформации р = ро/A + в), показывающая,
что значение плотности частицы материального континуума
действительно характеризует объемную деформацию частиц
сплошной среды.
В заключение приведем вид уравнения неразрывности
для двух частных случаев: несжимаемого и однородного
материальных континуумов.
Сплошная среда называется несжимаемой, если не
изменяется объем ее индивидуальных частиц. Это условие
однозначно определяет объемную деформацию и плотность частиц
среды: в = 0; р = ро- Тогда с учетом B.61) и B.62)
уравнение неразрывности для несжимаемой среды можно записать в
виде
divt> = 0, Vtvf = 0.
Сплошная среда является однородной в том случае, если
плотность ее не изменяется по координатам, но при этом
не исключено ее изменение во времени. Условие однородности
материального континуума V±p = др/дх% = 0, в результате
этого с учетом B.60) получаем соответствующее выражение
для закона сохранения массы:
2.4.3. Закон сохранения импульса —
уравнения движения
Одним из фундаментальных законов механики
материальной точки является второй закон Ньютона, согласно
которому изменение импульса (количества движения)
материальной точки равно импульсу равнодействующей внешних
187

Рис. 2.28
сил, действующих на материальную точку: та = F, или
т dv/dt = F, или d{mv) = Fdt. Второй закон Ньютона для
материального континуума формулируется аналогично:
изменение импульса любого индивидуального объема материального
континуума равно импульсу внешних сил [объемных и
поверхностных), действующих на этот индивидуальный объем.
На рис. 2.28 показан ограниченный поверхностью 5
индивидуальный объем V сплошной среды, на который действуют
объемные силы F и поверхностные силы р, вследствие чего
частицы материального континуума движутся с определенной
скоростью v. Выделим индивидуальную частицу объемом dV
и плотностью /?, движущуюся со скоростью v. Тогда импульс
этой частицы равен vpdV, а полный импульс всего
индивидуального объема определяется интегралом / vp dV, взятым
V
по всему индивидуальному объему. Объемная сила,
действующая на малую индивидуальную частицу объемом dV, равна
FdV', а полная объемная сила, действующая на
индивидуальный объем в целом, определяется соответствующим
интегра/ FdV. На любой элементарной площадке dS (бесконеч-
V
но малом участке поверхности 5, ориентация которой задана
единичным вектором нормали п) действуют поверхностные
силы рп. Поверхностная сила, действующая на всю
площадку dS, равна pndS, а полная поверхностная сила определится
лом
188

взятым по замкнутой поверхности S интегралом Ф рп dS. То-
5
гда закон сохранения импульса для индивидуального объема
материального континуума может быть представлен в виде
интегродифференциального уравнения
vpdv) =
или эквивалентного уравнения
= J FdV + iPn dS. B.63)
V V S
Выражение B.63) закона сохранения импульса (а точнее,
закона изменения импульса) не удобно в силу привязки его
к определенному индивидуальному объему V и
ограничивающей его поверхности 5, которые в общем случае
изменяются при движении среды и заранее не известны. Более
удобным является дифференциальное выражение закона,
справедливое для любой индивидуальной частицы материального
континуума. Для получения дифференциального уравнения,
выражающего второй закон Ньютона для сплошной среды,
преобразуем выражение B.63). Прежде всего отметим, что
вследствие неизменности во времени массы индивидуальных
частиц dm = pdV скорость изменения полного импульса
индивидуального объема определяется только ускорениями
индивидуальных частиц:
V V
В то же время вектор поверхностных сил рп в любой
точке поверхности 5, ориентация которой задана единичным
вектором нормали п, однозначно определяет вектор полного
напряжения <тп = рп, действующий в данной точке на
соответствующей площадке. Но последний можно
представить как произведение тензора напряжений в сплошной
среде в точке на поверхности и единичного вектора
нормали п: <тп = (а) • п, так что полная поверхностная сила
189

равна потоку тензора напряжений через замкнутую
поверхность, ограничивающую выбранный индивидуальный объем:
<р pndS = Ф(сг) • ndS. Используя далее теорему Остроград-
S S
ского — Гаусса A.14), преобразуем B.63) в соотношение
которое в силу произвольности индивидуального объема V
может выполняться лишь при условии равенства нулю
подынтегрального выражения для любой индивидуальной частицы
материального континуума. Это и приводит к
дифференциальному уравнению, выражающему закон сохранения импульса
для сплошной среды:
dv
p— = F+diw(a). B.64)
at
Согласно B.64), получаемые индивидуальными частицами
ускорения определяются объемными силами F, плотностью р
данной частицы и зависят от пространственного
распределения напряжений.
Подчеркнем, что дифференциальное уравнение B.64)
математически описывает один из законов природы, который
является объективным и не зависит от субъективно
выбираемой исследователем той или иной системы координат. В
соответствии с этим в полученном математическом выражении
закона сохранения импульса участвуют тензоры,
инвариантные относительно выбора системы координат. Это тензор
нулевого ранга — плотность р, тензоры первого ранга — вектор
объемных сил F и вектор скорости i>, тензор второго ранга
— тензор напряжений (<т). Уравнение движения было
получено без каких-либо предположений и ограничений на
агрегатное состояние и физико-механические свойства среды, т.е. оно
справедливо для описания движения любых сплошных сред.
190

Частным случаем движения сплошной среды является ее
равновесие, когда индивидуальные точки или
индивидуальные частицы среды не получают ускорений и dv/dt = 0.
Уравнение движения в этом случае сводится к ранее полученному
условию равновесия материального континуума B.51).
В заключение приведем запись закона сохранения
импульса через компоненты соответствующих тензоров. Имея в виду,
что тензорному уравнению B.64) соответствуют три
скалярных дифференциальных уравнения, и определяя дивергенцию
тензора напряжений по аналогии с тем, как это делалось при
получении условий равновесия B.52) в объеме тела, получаем
искомые дифференциальные уравнения движения
P^ = r + V,4F« B.65)
2.4.4. Баланс механической энергии —
теорема "живых сил"
Из механики материальной точки известна теорема об
изменении кинетической энергии, являющаяся прямым
следствием второго закона Ньютона d(mv) = Fdt, При скалярном
умножении этого уравнения на вектор скорости движения
материальной точки v получаем d(mv) • v = Fdt • v, где левая
часть d(mv)-v = d(mv-v/2) = d(mv2/2) определяет изменение
кинетической энергии материальной точки за малый интервал
времени <Й, а правая часть Fdt • v = F- dr — работу
равнодействующей внешних сил, совершаемую над материальной
точкой при ее перемещении на dr = v dt. В конечном счете из
закона сохранения импульса следует, что изменение
кинетической энергии материальной точки равно работе внешних
сил:
2 2 *?
vi mvi [
2 2 ?
mvi mvi [ _
191

Для материального континуума полным аналогом
теоремы об изменении кинетической энергии является теорема
"живых сил", приводящая к уравнению баланса механической
энергии для сплошной среды. Теорема "живых сил" также
является прямым следствием закона сохранения импульса для
материального континуума и выводится из уравнений
движения B.65). Для доказательства теоремы "живых сил" и
вывода уравнений баланса механической энергии умножим каждое
из уравнений движения на соответствующую компоненту V{
вектора скорости, а результаты сложим. В итоге получим
соотношение, записываемое с использованием соглашения о
суммировании (см. раздел 1.3):
Проинтегрируем полученное выражение по индивидуальному
объему V материального континуума (см. рис. 2.28):
[p^VidV= [F{vidV + I(V,VJ) у{dV. B.66)
V V V
Рассмотрим физический смысл каждого интеграла в
выражении B.66). Объемный интеграл, стоящий в левой части
B.66), с учетом неизменности во времени массы
индивидуальных частиц dm = p dV и на основании правил
дифференцирования произведения и правил скалярного умножения векторов
может быть представлен в виде
v
d (vv\ d f v2 dEK
W)dV}dV
dt
192

Он определяет скорость изменения кинетической энергии
[ v2 f v2
Ек — \ dm — = I p dV — всего индивидуального объема ма-
V V
териального континуума (или тела в целом).
Первый интеграл, стоящий в правой части B.66),
определяет полную (для всего тела) мощность объемных сил:
/ В*у{ dV = I FvdV= f(FdV) -v = Nv.
V V V
Второй объемный интеграл в правой части B.66) с
использованием правил дифференцирования произведения может быть
представлен как разность двух интегралов:
/ (v^) vi dV = f V, (V-Ч) dV- [ a^VjVt dV. B.67)
V V V
В свою очередь, первый из вновь образовавшихся
интегралов B.67) представляет собой взятый по объему тела
интеграл от дивергенции вектора
(а) • v = [crljrirjj • [vkrkj = aljrivkgj = a%jvjri,
являющегося результатом скалярного умножения тензора
напряжений на вектор скорости. Тогда
div[(a)-v}=
На основании теоремы Остроградского — Гаусса A.14) этот
интеграл преобразуется в интеграл, взятый по
ограничивающей индивидуальный объем замкнутой поверхности 5 от
потока вектора (а) • v:
I Vj(<7гЧ) dV = I div[(<j) • v] dV = In- (o) • vdS.
V V S
7-9712 193

Но скалярное произведение тензора напряжений ((т) и
единичного вектора нормали п, задающего ориентацию площадки,
определяет вектор полного напряжения сгп на этой площадке,
совпадающий в рассматриваемом случае с вектором
поверхностных сил рп. Поэтому первый из интегралов правой части
выражения B.67) приводится к виду
J V, (а'Ч) dV = fpn.vdS = j>{pndS) -v = Ns B.68)
V S S
и определяет полную (для всего тела) мощность
поверхностных сил.
Второй из интегралов правой части B.67) с учетом
кинематических соотношений может быть преобразован к виду
/ <TijVjVi dV = I (Tijeij dV. B.69)
Действительно, абсолютная производная Vjt/,- может быть
выражена через компоненты тензоров скоростей деформаций и
скоростей поворота: Vjv± = eij — afy, что и приводит к B.69)
ввиду равенства нулю суммы произведений компонент
симметричного тензора напряжений и антисимметричного тензора
скоростей поворота.
Таким образом, на основе проведенных преобразований
B.66)—B.69) приходим к интегральному соотношению,
являющемуся прямым следствием закона сохранения импульса
B.65):
/ JikijdV = f FvdV+ lPnvdS
dt
V V S
или
V
194

Установим теперь физический смысл комплекса ^Sij для
каждой индивидуальной частицы материального континуума
и объемного интеграла / аг*ёц dV в целом. Отметим прежде
V
всего, что для каждой индивидуальной точки сплошной среды
величина сггН^ образуется как сумма произведений
контрвариантных компонент а%3 тензора напряжений и ковариантных
компонент e{j тензора скоростей деформаций. В силу этого
обстоятельства величина <jX3kij является инвариантной
относительно преобразования системы координат, а ее значение
не зависит от того, в какой конкретно системе координат оно
будет определяться. В частности, это значение можно
определить в декартовой прямоугольной системе координат,
связанной с главными осями г;1, 772, г/3 тензора напряжений, в
которой собственно тензор напряжений имеет наиболее простое
представление через свои главные значения B.43). В этом
случае девятичленная сумма crlHij сводится к трехчленной:
cj^Sij = агёп + <т2ё22 + <73?зз, B.70)
где ?ц, ?22? ?33 — компоненты тензора скоростей деформаций
в указанной системе координат.
На рис. 2.29 показаны индивидуальная точка М сплошной
среды и проведенные через нее главные оси г/1, 7/2, 7/3 тензора
напряжений (<т), характеризующего напряженное состояние в
данной точке, причем единичные взаимно ортогональные
векторы Л*, Л2 А3 — базисные векторы, связанные с главными
осями тензора напряжений. Выделим в окрестности точки М
индивидуальную частицу в форме элементарного
прямоугольного параллелепипеда с ребрами длиной dr/1, d7/2, tfy3,
направленными по главным осям тензора напряжений. По граням
этого параллелепипеда действуют внутренние силы,
представляемые главными нормальными напряжениями а\у оч, &ъ-
195

' f
Рис. 2.29
Преобразуем выражение B.70), умножив и разделив его
правую часть на объем выделенной индивидуальной частицы:
>
+
Очевидно, что произведение значений любого главного
напряжения и площади грани, на которую оно действует, в
сочетании с единичным вектором данного главного
направления определяет вектор полной внутренней силы, действующей
на данную грань элементарного параллелепипеда, а именно
dpx = <7id772d7/3JR*, dp2 = a2drildr^R2v, dp3 = u^dr]1dri1B?r}
(см. рис. 2.29). В то же время в соответствии с
кинематическим смыслом тензора скоростей деформаций (к) вторые
сомножители в числителе последнего соотношения
определяют относительную скорость движения граней элементарно-
196

го параллелепипеда B.35). Например, скорость движения
dvgi фронтальной грани относительно тыльной,
обусловленная развивающимся во времени процессом деформирования,
определяется как dvg\ = (ё) • (d^R*) = кцйгрВ^. По
аналогии задаются скорость движения правой грани относительно
левой (dvg2 = S22d7]2R^) и верхней грани относительно
нижней (dvgz = essdrj^Ry). В итоге интерпретируемая величина
clH{j представляет собой удельную (отнесенную к единице
объема среды) мощность внутренних сил, или, иначе говоря,
удельную мощность деформирования:
ij _ dPl dvgl + dp2 dvg2 + dp3 dvgZ _ diNs
° €i> - dv " ~W {2m71)
Отметим, что в ряде случаев удельная мощность
деформирования рассматривается относительно единицы массы среды:
/2 72ч
р рdV dm
Теперь несложно установить, что объемный интеграл
&lJeij dV от удельной мощности деформирования предста-
V
вляет собой полную (для всего тела) мощность внутренних
сил, или полную мощность деформирования:
J <т%- dV= I dNs = Ifs. B.73)
V V
Из физики известно, что всякая мощность определяется
скоростью выполнения какой-либо работы. В данном случае полная
мощность внутренних сил определяется скоростью
выполнения работы внутренних сил, или скоростью выполнения
полной работы деформации:
197

Под полной работой деформации следует понимать работу,
которую совершают внутренние силы (напряжения) над
всеми индивидуальными частицами тела в связи с
перемещениями индивидуальных точек (а следовательно, и граней частиц)
вследствие деформирования.
Уравнение баланса механической энергии можно записать
в виде
/ aijeij dV= f FvdV+ lpn-vdS B.75)
dE*
dt
V
или с учетом физического смысла входящих в это соотношение
объемных и поверхностных интегралов в виде
Последнее соотношение означает, что при нагружении,
движении и деформировании материального континуума
мощность внешних сил (объемных и поверхностных)
воспроизводится в виде мощности деформирования и определяет
скорость изменения кинетической энергии тела.
В заключение подчеркнем, что выражающее содержание
теоремы "живых сил" уравнение баланса механической
энергии B.75), как и закон сохранения импульса B.65), следствием
которого оно является, справедливо по отношению к любым
сплошным средам независимо от их агрегатного состояния и
конкретных физико-механических свойств.
2.4.5. Закон сохранения энергии
при отсутствии тепловых явлений
Рассмотрим частный случай движения материального
континуума, когда отсутствуют переход механической
энергии в тепловую и передача тепловой энергии телу со
стороны окружающей среды. В этом случае работа, совершаемая
внутренними силами над каждой индивидуальной частицей,
198

является мерой изменения внутренней энергии
индивидуальных частиц — внутренней потенциальной энергией
деформации. Вычисленная для всего тела работа внутренних сил As
определит потенциальную энергию деформации U тела в
целом: As = U. Таким образом, при отсутствии тепловых
явлений полная мощность деформирования определяет скорость
изменения потенциальной энергии деформации тела:
f. (,76)
Дальнейшее использование теоремы "живых сил" B.75)
позволяет получить соотношение, выражающее закон
сохранения энергии при отсутствии тепловых явлений:
(EK+U) = JFvdV + fpnvdS, B.77)
V S
согласно которому изменение полной механической энергии
тела (сумма кинетической энергии Е& и потенциальной
энергии деформации U) равно совершаемой над телом работе
внешних сил (объемных и поверхностных).
2.4.6. Закон сохранения энергии
при наличии тепловых явлений.
Первый закон термодинамики,
уравнение энергии
Рассмотрим общий случай описания движения
материального континуума, когда учитывается возможный переход
механической энергии в тепловую, а также принимается во
внимание обмен тепловой энергией между различными
частицами сплошной среды. Для описания происходящих в
сплошных средах тепловых процессов вводятся специальные
физические величины, характеризующие состояние материального
континуума. К их числу относятся абсолютная температура
Г, удельная внутренняя энергия 2?, вектор теплового потока
<7, энтропия S и т.д.
199

Удельную внутреннюю энергию Е удобно ввести на
основе определения внутренней энергии тела U при чисто
механических процессах, когда внутренняя энергия равна
потенциальной энергии деформации тела. В этом случае скорость
изменения потенциальной энергии деформации тела
определяется полной (для всего тела) мощностью внутренних сил, или
полной мощностью деформирования B.76). Но тогда
внутренняя энергия
dv }dt= / / —i-ipdv)dt.
Полученный интеграл с учетом неизменности во времени
массы индивидуальных частиц и независимости от времени t
переменной интегрирования во внутреннем интеграле можно
представить в виде
= [
EpdV= [ Edm.
В приведенном выражении Е определяется взятым по
времени интегралом от удельной (отнесенной к единице массы
среды) мощности деформирования B.72) и представляет собой
удельную работу деформации. При чисто механических
процессах работа деформации "переходит" во внутреннюю
потенциальную энергию деформации, так что удельная
внутренняя энергия материального континуума Е представляет собой
удельную (отнесенную к единице массы среды)
потенциальную энергию деформации. Отметим, что употребляемому в
рамках феноменологического подхода понятию
"потенциальная энергия деформации" в реальных деформируемых средах,
имеющих дискретное, молекулярное строение,
соответствует понятие "потенциальная энергия взаимодействия молекул
между собой".
200

В более общем случае, при наличии тепловых явлений и
процессов в сплошной среде, под удельной внутренней
энергией понимается внутренняя энергия единицы массы
среды, включающая как потенциальную энергию деформации
материального континуума (потенциальную энергию
взаимодействия молекул в единице массы среды), так и тепловую
энергию (в реальных средах — кинетическую энергию
хаотического движения молекул, взятых в единице массы среды).
Как и все величины, описывающие движение и состояние
сплошной среды, в общем случае удельная внутренняя энергия
различна для разных индивидуальных частиц материального
континуума, поэтому внутренняя энергия тела (или
индивидуального объема материального континуума) определяется
соответствующим интегралом, взятым по массе или объему
тела:
U= f Edm= [ EpdV. B.78)
т V
При наличии тепловых явлений внутренняя энергия тела в
целом представляет собой сумму потенциальной энергии
деформации тела и тепловой энергии.
Введем физическую величину, с помощью которой
характеризуется интенсивность обмена тепловой энергией между
различными частицами сплошной среды, — вектор
теплового потока q, который характеризует направление
наиболее интенсивной передачи тепловой энергии в окрестности
данной точки сплошной среды и по модулю равен
количеству теплоты, переносимой в единицу времени через
единичную площадку, перпендикулярную этому направлению. На
рис. 2.30 показана индивидуальная точка материального
континуума, в котором, по предположению, существуют условия
для теплообмена между индивидуальными частицами.
Выделим площадку d5, проходящую через эту точку, зафиксируем
малый интервал времени dt ф 0 и предположим, что известно
количество теплоты dQ, переносимой за малый интервал
времени через данную площадку. При фиксированных значениях
201

dS,
Рис. 2.30
Рис. 2.31
dS и dt количество переносимой теплоты dQ зависит от
ориентации площадки и при некоторой ее ориентации достигает
максимального для данной индивидуальной точки значения.
Направление нормали к такой площадке определяет
направление вектора теплового потока q в данной точке континуума,
модуль которого
В свою очередь, определенный в точке сплошной среды вектор
теплового потока q позволяет оценить количество теплоты
dQ, переносимой за малый интервал времени dt через
проходящую через данную точку площадку dS произвольной
ориентации, задаваемой единичным вектором нормали п (рис. 2.31).
Действительно, количество теплоты, переносимой за время
dt через площадку dS, равно количеству теплоты,
переносимой через площадку dSn — проекцию данной площадки на
направление, ортогональное вектору теплового потока q. В
соответствии с определением вектора теплового потока B.79)
dQ = qdSndt = qdS cos a dt, откуда следует выражение для
количества теплоты, передаваемой за малое время через
малую площадку произвольной ориентации:
= q-ndS dt.
B.80)
Известны три вида теплообмена (теплопередачи):
излучение, конвекция, теплопроводность. Из них лишь
теплопроводность реализуется в любых сплошных средах независимо
202

от их агрегатного состояния и физико-механических свойств,
в то время как теплообмен посредством излучения возможен
лишь в прозрачных средах, а теплообмен посредством
конвекции — в газообразных или жидких средах. Поэтому в
дальнейшем ограничимся анализом только одного вида
теплообмена между частицами сплошной среды — теплопроводности.
Теплообмен посредством теплопроводности происходит
лишь при условии существования неравномерного
распределения температуры Т в объеме сплошной среды. Поэтому
должна существовать взаимосвязь между вектором теплового
потока, характеризующим интенсивность теплообмена между
частицами сплошной среды, и величиной, характеризующей
неравномерность пространственного распределения
температуры в теле. В качестве последней может выступать вектор
градиента температуры gradT = Vi(T)r% — (дТ/дхг)г%,
модуль которого тем больше, чем неравномернее распределена
температура, т.е. чем больше значения производных по
координатам дТ/дхг. Такая взаимосвязь действительно
существует и выражается законом теплопроводности Фурье,
обобщающим опытные факты. Согласно закону
теплопроводности Фурье, вектор теплового потока в данной
индивидуальной точке сплошной среды прямо пропорционален градиенту
температуры в этой же точке:
q= -A gradT, B.81)
где А — коэффициент теплопроводности или просто
теплопроводность данной среды.
Физическое истолкование закона теплопроводности
Фурье может быть дано на основе определения
физического смысла градиента скалярной функции координат,
проиллюстрированного на рис. 2.32. В соответствии с векторным
анализом градиент температуры в какой-либо точке
сплошной среды направлен по нормали к проходящей через данную
точку изотермической поверхности, ориентирован в сторону
наиболее быстрого возрастания температуры, а по модулю
равен производной по этому направлению дТ/дп. Закон же
203

Рис. 2.32
Рис. 2.33
теплопроводности Фурье показывает, что тепловая энергия в
окрестности данной точки распространяется по направлению
наиболее быстрого убывания температуры, и тем
интенсивней, чем более резко изменяется температура в окрестности
этой точки, т.е. чем большее значение имеет производная
дТ/дп.
Для получения интегрального выражения первого
начала термодинамики рассмотрим индивидуальный объем V
материального континуума, ограниченный поверхностью S
(рис. 2.33). Будем считать, что материальный континуум
подвержен действию объемных F и поверхностных р сил.
Кроме того, примем во внимание теплообмен между частицами
сплошной среды и будем считать определенным поле вектора
теплового потока д, заданного для каждой индивидуальной
точки среды, включая точки, находящиеся на поверхности.
Закон сохранения энергии утверждает, что изменение
полной энергии выделенного индивидуального объема
материального континуума, которая равна сумме кинетической Ек
и внутренней U энергий, определяется работой внешних сил
(объемных и поверхностных) и количеством теплоты,
переданной телу через ограничивающую его поверхность.
Количество теплоты, передаваемой за малый интервал времени
dt через малый участок поверхности dS, ориентация которой
задается единичным вектором внешней нормали п,
определяется в соответствии с выражением B.80). Полное же
количество теплоты, передаваемой за время dt ограниченной
поверхностью S сплошной среде, определяется поверхностным
204

интегралом — (р q n dS dt или взятым со знаком минус пото-
S
ком вектора теплового потока q через указанную замкнутую
поверхность. При этом знак минус учитывает то
обстоятельство, что положительный поток вектора q (в каждой точке
поверхности вектор q направлен в одну сторону с единичным
вектором внешней нормали — индивидуальный объем отдает
теплоту) соответствует уменьшению полной энергии
индивидуального объема, а отрицательный поток того же вектора
соответствует увеличению полной энергии индивидуального
объема.
Работа, совершаемая за время dt объемными силами,
выражается объемным интегралом / (FdV) • vdt. За тот же от-
V
резок времени поверхностные силы совершают работу
(b(pdS)-vdt.
S
Закон сохранения (а точнее, изменения) полной энергии для
индивидуального объема материального континуума теперь
может быть выражен интегродифференциальным
соотношением
+ U)= I FvdVdt+ <bpnvdSdt- (bqndSdt
V S S
или эквивалентным уравнением
- j
J f jq-ndS. B.82)
V S S
Ранее было получено уравнение B.75) баланса
механической энергии, вытекающее из закона сохранения импульса
и справедливое поэтому для описания любого движения
материального континуума независимо от того, сопровождается ли
205

это движение тепловыми явлениями или же они отсутствуют.
Сопоставляя выражения B.75) и B.82), нетрудно убедиться,
что баланс механической энергии B.75) составляет часть
баланса полной энергии B.82). На основании этого закон
изменения полной энергии B.82) может быть сведен к закону
изменения внутренней энергии
^-= [ (Tijeij dV - iqndS, B.83)
V S
согласно которому изменение внутренней энергии тела dll
или индивидуального объема материального континуума
равно сумме работы внутренних сил (работы деформации)
a^eijdVdt и количества теплоты - Ф q ndS dt, nepe-
V S
данной материальному континууму через ограничивающую
его поверхность. Уравнение B.83) представляет собой
интегральное выражение закона изменения внутренней энергии
— первого закона, или первого начала, термодинамики.
Подчеркнем здесь еще раз следующее важное обстоятельство: из
закона изменения внутренней энергии B.83) в сочетании с
уравнением баланса механической энергии B.75) следует
закон изменения полной энергии B.82). В связи с этим
интегральное выражение первого закона термодинамики B.83)
также называют законом сохранения энергии.
Полученное интегральное выражение B.83) для первого
закона термодинамики не удобно ввиду его привязки к
изменяющимся во времени величинам: индивидуальному объему V и
ограничивающей его поверхности 5. Более удобным является
выражение первого закона термодинамики в виде
дифференциального уравнения, справедливого для каждой
индивидуальной частицы материального континуума. Такое
дифференциальное уравнение называют уравнением энергии. Для его
получения воспользуемся теоремой Остроградского — Гаусса
и преобразуем поток вектора теплового потока q через
поверхность тела 5 к интегралу по объему тела V от
дивергенции вектора теплового потока. Эта дивергенция
выражается через сумму абсолютных производных компонент q% этого
206

вектора. Тогда Ф q ndS = / div qdV = lViqxdV. Отме-
S V V
тим далее, что скорость изменения внутренней энергии
тела U — \ EpdV определяется скоростями изменения удель-
V
ной внутренней энергии Е индивидуальных частиц сплошной
не изменяю-
ур р у
среды: dU/dt = j(dE/dt)pdV, где dm = pdV —
V
щаяся во времени масса индивидуальных частиц. С помощью
указанных преобразований интегральное выражение первого
закона термодинамики B.83) приводится к условию равенства
нулю объемного интеграла:
Это условие должно выполняться для произвольного
индивидуального объема материального континуума, что приводит
к необходимости выполнения для каждой индивидуальной
частицы сплошной среды дифференциального уравнения
которое является уравнением энергии и выражает в
дифференциальной форме первый закон термодинамики для каждой
индивидуальной частицы сплошной среды.
Физический смысл уравнения энергии наиболее ясно
выявляется при представлении его в следующей эквивалентной
форме, полученной с учетом определения дивергенции вектора
теплового потока:
— Ф q • п dS dt
• dt + lim —* . B.85)
V-+0 pV
207

В полученном выражении член ox^k{jjp характеризует
удельную (отнесенную к единице массы среды) мощность
деформирования в данной индивидуальной частице сплошной
среды B.72). Соответственно (a^eij/pjdt представляет собой
отнесенную к единице массы работу деформации за малое
время eft, совершенную внутренними силами над индивидуальной
частицей. В то же время второй член в B.85) определяет
отнесенное к единице массы количество теплоты, отданной за
время dt индивидуальной частице окружающими ее
частицами. В целом же дифференциальное уравнение в форме B.84)
или B.85) эквивалентно хорошо известному из физики
выражению первого закона термодинамики dU = dA + dQ, согласно
которому изменение внутренней энергии dU системы может
быть осуществлено посредством передачи теплоты dQ этой
системе и путем совершения над ней работы dA. Различие
заключается лишь в том, что уравнение энергии B.84)
записано в удельных величинах, отнесенных к единице массы тела.
Таким образом, дифференциальное уравнение энергии
устанавливает, что изменение удельной внутренней энергии
индивидуальной частицы материального континуума равно работе
деформации, отнесенной к единице массы сплошной среды, и
количеству теплоты, переданной единице массы данной
индивидуальной частицы.
2.4.7. Второй закон термодинамики,
обратимые и необратимые процессы,
энтропия
Так же как законы сохранения массы, импульса и
энергии, второй закон, или второе начало, термодинамики
является фундаментальным законом природы. Второй закон
термодинамики тесно связан с понятиями необратимых
процессов, необратимых потерь энергии и с такой физической
величиной, как энтропия. Применительно к материальному
континууму второй закон термодинамики выражается
дифференциальным уравнением, определяющим закон изменения
энтропии индивидуальных частиц материального континуума.
208

Прежде чем получить это дифференциальное уравнение,
рассмотрим пример, с помощью которого определим качественно
понятия обратимых и необратимых процессов, необратимых
потерь энергии, выясним физический смысл энтропии и
обоснуем необходимость ее введения.
Пусть имеется изолированная система тел, не
обменивающаяся с окружающей средой ни массой, ни энергией,
причем входящие в эту систему тела взаимодействуют лишь
между собой и не взаимодействуют ни с какими другими телами
(рис. 2.34).
г
t = 0
о*-
„Полный порядок"
209

Закон сохранения энергии (или первый закон
термодинамики) по отношению к изолированной системе тел
устанавливает неизменность во времени ее полной энергии Wq = const.
Приведем здесь же как основу для дальнейшего анализа
наиболее простую формулировку второго закона термодинамики:
самопроизвольный, без затрат энергии извне, переход
теплоты возможен только от более нагретого тела к менее
нагретому.
Проанализируем развитие во времени данной
изолированной системы тел, т.е. рассмотрим ее эволюцию. Для
простоты и облегчения понимания физического смысла энтропии, а
также второго закона термодинамики в целом подобный
анализ целесообразно проводить при параллельном
использовании двух подходов к изучению поведения деформируемых сред:
феноменологического (на макроуровне) и подхода,
учитывающего реальное молекулярное строение тел (на
микроуровне). При рассмотрении эволюции указанной системы в
рамках феноменологического подхода будем использовать такие
понятия, как кинетическая энергия тела, тепловая энергия,
необратимые потери энергии. С позиций анализа,
выполняемого на микроуровне, кинетической энергии тела будет
отвечать кинетическая энергия направленного движения молекул,
из которых состоят тела, тепловой энергии — кинетическая
энергия хаотического (беспорядочного) движения молекул, а
накоплению необратимых потерь энергии — увеличение
степени хаотического движения молекул, т.е. увеличение
"степени беспорядка" в системе на микроуровне.
Рассмотрим начальное состояние системы при t = 0.
Пусть входящие в систему тела находятся в движении с
различными скоростями t?i, ^2,1?з, .. •, vn (рис. 2.34, а). Будем
также считать, что в начальный момент времени абсолютная
температура всех тел равна нулю (Т = 0). Это соответствует
отсутствию хаотического движения составляющих тело
молекул и равенству нулю тепловой энергии системы: UT = 0.
Итак, считаем, что в начальный момент времени полная
энергия рассматриваемой системы \Vq есть кинетическая энергия
210

движения тел Ек. Следовательно, вначале полная энергия
системы — это кинетическая энергия направленного,
упорядоченного движения молекул, из которых состоят тела. При
этом отсутствует кинетическая энергия хаотического
движения этих молекул. В целом же начальное состояние системы
на микроуровне можно охарактеризовать как состояние
"полного порядка", т.е. отсутствия молекулярного теплового
хаоса. Следует отметить, что подобная система тел способна к
дальнейшему развитию: составляющие ее тела будут
взаимодействовать между собой, совершать друг над другом работу,
обмениваться энергией и т.п. Образно говоря,
рассматриваемая система в начальный момент времени полна "жизненных
сил".
Характер процессов, которые происходят при
взаимодействии тел, может быть различным: бывают обратимые и
необратимые процессы. Обратимые процессы — это процессы,
допускающие обратное самопроизвольное протекание с
возвратом к исходному состоянию. Примером обратимого
процесса является взаимодействие двух абсолютно упругих шаров
при их соударении (рис. 2.35). В этом случае процесс
деформирования каждого шара вначале сопровождается
увеличением внутренней энергии U (потенциальной энергии
деформации), компонент тензоров напряжений a{j и деформаций Sij в
каждой индивидуальной частице взаимодействующих тел, а
затем самопроизвольно протекает в обратном направлении с
уменьшением этих величин и возвратом в итоге к исходному
состоянию.
Рис. 2.35
211

Необратимые процессы — это процессы, не
допускающие самопроизвольного обратного протекания с возвратом
к исходному состоянию. В механике особенно часто
встречаются две группы необратимых процессов: процессы, связан-
ные с переходом механической энергии в тепловую, и
процессы теплообмена между телами, нагретыми до
различной температуры. На рис. 2.36 показаны начальная и
конечная стадии процесса проникания тела вращения в преграду.
В процессе взаимодействия двух тел происходит интенсивное
пластическое деформирование каждого из них, приводящее к
образованию кратера в преграде, срабатыванию ударника и
сопровождающееся переходом кинетической энергии тела
вращения в тепловую энергию нагрева обоих тел. С позиций
анализа, выполняемого на микроуровне, следует сказать, что в
этом процессе кинетическая энергия упорядоченного,
направленного движения молекул переходит в кинетическую
энергию их хаотического движения. Подобный процесс необратим
в силу того, что самопроизвольный обратный ход событий
невозможен (охлаждение преграды и ударника, обратное их
деформирование, движение ударника в обратном направлении),
хотя это вовсе не противоречит закону сохранения энергии.
Еще одним примером необратимых процессов первой группы
является показанное на рис. 2.37 движение тела вращения с
высокой скоростью в атмосфере. В этом случае происходит
Рис. 2.36
Рис. 2.37
212

торможение тела, уменьшение его кинетической энергии,
переходящей в тепловую энергию нагрева самого тела и
воздуха. Необратимый процесс, относящийся ко второй группе,
показан на рис. 2.38. При
отсутствии внешних воздействий
теплообмен между двумя телами
может происходить только
посредством передачи теплоты от более
нагретого тела к менее нагрето- Рис. 2.38
му. Передача теплоты от менее
нагретого тела к более нагретому (обратный процесс)
самопроизвольно происходить не может, хотя это также не
противоречит закону сохранения энергии. Невозможность
обратного протекания необратимых процессов как раз и
утверждает рассматриваемый фундаментальный закон природы
— второй закон термодинамики.
В процессе эволюции изолированной системы тел (см.
рис. 2.34), когда тела взаимодействуют между собой, реально
все процессы взаимодействия в большей или меньшей степени
являются необратимыми. В конечном счете необратимые
процессы первой группы переведут всю механическую энергию
системы в тепловую, а необратимые процессы второй
группы обеспечат выравнивание температуры между
различными телами. В итоге своей эволюции к некоторому моменту
времени t = tK система придет в такое состояние, когда
полная ее энергия будет определяться только тепловой энергией
UT при обеспечении теплового равновесия между различными
частями системы (см. рис. 2.34, в). В такой изолированной
системе уже невозможно дальнейшее протекание процессов и
совершение какой-либо работы или взаимодействие тел — это
состояние "тепловой смерти".
Несмотря на то что полная энергия системы по
сравнению с начальным состоянием осталась неизменной (Wo = UT),
она не может быть использована в рамках этой изолированной
системы для совершения какого-либо активного процесса
(например, разгона тела) и является совершенно бесполезным
запасом. Такой процесс утраты полезности энергии, ее
"деградации", перехода из активной формы (кинетическая энергия,
213

потенциальная энергия положения или деформации) в
пассивную (тепловая энергия при состоянии теплового равновесия)
называется в рамках феноменологического подхода
накоплением необратимых потерь энергии. Подчеркнем, что этот
термин носит условный характер, так как в
действительности никаких потерь полной энергии не происходит, энергия
лишь переходит в форму, затрудняющую (или исключающую,
как в нашем примере) ее полезное использование для передачи
другим телам. Отметим также, что с позиций анализа,
выполняемого на микроуровне, к моменту времени t = tK полная
энергия Wo системы представляет собой кинетическую
энергию хаотического движения молекул, так что на микроуровне
конечное состояние системы по сравнению с начальным
можно охарактеризовать как состояние "полного беспорядка", т.е.
отсутствия какого-либо организованного, упорядоченного
движения молекул.
Таким образом, необратимые процессы приводят к
необратимым потерям энергии, а на микроуровне — к
увеличению "степени беспорядка" в системе (см. рис. 2.34). Для
количественного описания необратимых процессов, накопления
необратимых потерь энергии (а на микроуровне — для
определения "степени беспорядка" в системе) в термодинамике
вводится специальная физическая величина — энтропия S,
являющаяся мерой необратимости процессов. Необходимость ее
введения объясняется тем, что имеющимися величинами
(полная (Wo) и тепловая (UT) энергии системы) не представляется
возможным количественно охарактеризовать необратимые
потери энергии. Так, полная энергия Wq остается неизменной
в течение всей ее эволюции, следовательно, не может
характеризовать накопление необратимых потерь энергии.
Тепловая энергия UT предпочтительнее для характеристики
необратимых потерь энергии, тем более что их накопление связано
с переходом механической энергии в тепловую и с
теплообменом между телами. Однако и она не может служить
мерой накопления необратимых потерь энергии. Например, на
рис. 2.34, б показано некоторое промежуточное состояние
системы, когда необратимые процессы первой группы перевели
214

механическую энергию в тепловую (Wo = UT)> в результате
чего образовались две группы тел, нагретых до разных
температур (Т2 > Т\). В такой системе еще возможно развитие и
при определенных условиях (например, при прямом контакте
тел) будет происходить передача теплоты от более нагретого
тела к менее нагретому. При наличии в системе рабочего
тела (например, газа) можно "превращать" тепловую энергию в
механическую, отбирая от более нагретого тела теплоту dQ2
и отдавая менее нагретому телу теплоту dQ\. При этом
совершается работа dA = dQ2-dQi (например, по разгону какого-
либо тела). Очевидно, что тепловая энергия UT не позволяет
различать два качественно различных состояния системы (см.
рис. 2.34, б и в) и поэтому не может быть количественной
характеристикой необратимых потерь энергии.
Особенности определения энтропии S удобно рассмотреть
на примере элементарного процесса прямого теплообмена
между двумя телами, показанными на рис. 2.34, б. В этом
случае самопроизвольно может происходить лишь передача
теплоты dQ от более нагретого тела (температура Т2) к
менее нагретому (температура J\). Подобный процесс является
необратимым и представляет собой малый шаг на пути
эволюции системы от начального состояния (полностью
упорядоченного) к конечному состоянию (полностью беспорядочному).
Очевидно, что рассматриваемый процесс теплопередачи
приводит к увеличению необратимых потерь энергии в системе
(увеличение "степени беспорядка" в системе). Поэтому для
данного процесса вводимая величина — энтропия 5 системы
— должна изменяться в сторону увеличения. В то же время
у отдающего теплоту тела уменьшается внутренняя тепловая
энергия (кинетическая энергия хаотического движения
составляющих тело молекул), что соответствует уменьшению
"степени беспорядка" в данном теле. Напротив, у тела,
принимающего теплоту, увеличивается внутренняя тепловая энергия,
что соответствует увеличению "степени беспорядка" в этом
теле. Поэтому энтропия должна быть определена так,
чтобы в рассматриваемом процессе она уменьшалась для тела,
215

отдающего теплоту, и увеличивалась для тела, получающего
теплоту.
Сформулированным критериям удовлетворяет
физическая величина, изменение которой для тела при его
теплообмене с окружающей средой определяется как
dS = f, B.86)
где dQ — количество теплоты, получаемой (или отдаваемой)
телом; Т — температура, при которой тело получает (или
отдает) теплоту. Соотношение B.86) может быть
интерпретировано следующим образом. Величина dQ полученной (или
отданной) телом теплоты характеризует изменение тепловой
составляющей внутренней энергии dUT или изменение
кинетической энергии хаотического движения молекул тела.
Абсолютная же температура Г, как известно, определяет
среднюю кинетическую энергию J^o хаотического движения
молекул тела (для одноатомного газа Eq = 1,5&Т, где к —
постоянная Больцмана), а следовательно, с точностью до
постоянного множителя и кинетическую энергию хаотического
движения молекул тела в целом. Поэтому изменение энтропии
dS определяется отношением изменения кинетической энергии
хаотического движения молекул тела к полной кинетической
энергии их хаотического движения. Иначе говоря, изменение
энтропии определяет как бы изменение "степени беспорядка"
в данном теле.
Убедимся теперь, что вводимая на примере теплообмена в
соответствии с B.86) физическая величина (энтропия S)
удовлетворяет приведенным выше критериям и является мерой
необратимости процесса. В этом случае для тела,
получающего теплоту, dQi — -\-dQ и энтропия изменяется на величину
dS\ — +dQ/T\ > 0, т.е. "степень беспорядка" в данном теле
увеличивается. Для тела, отдающего теплоту, dQi = — dQ,
и энтропия уменьшается, т.е. dS2 = -dQ/Ti < О, что
соответствует уменьшению "степени беспорядка" в этом теле.
Изменение же энтропии системы в целом определится суммой
216

= dS1+dS2 = dQ {T2-T\)f (T2Ti) > О, что соответствует
увеличению "степени беспорядка" в системе в целом,
увеличению необратимых потерь энергии в системе и отражает факт
необратимости данного процесса. Следовательно, вводимая в
соответствии с B.86) энтропия действительно является мерой
необратимости процесса.
Теперь второй закон термодинамики может быть
сформулирован в несколько иной, более универсальной форме,
отличной от приведенной выше простейшей формулировки,
устанавливающей допустимость самопроизвольного перехода
теплоты только от более нагретого тела к менее нагретому. По
существу, второй закон термодинамики отражает
фундаментальный опытный факт: в изолированной системе
реальные процессы могут протекать лишь в сторону перехода
от более упорядоченного состояния системы к менее
упорядоченному, сопровождаясь увеличением необратимых потерь
энергии, увеличением энтропии системы. Второй закон
термодинамики определяет, таким образом, направленность
протекания реальных процессов.
В более общем случае возможно изменение тепловой
составляющей внутренней энергии тела dQ не только за счет
теплопередачи, но и за счет совершения над телом
механической работы cL4T, приводящей к выделению эквивалентного
количества теплоты (например, работы сил трения), так что
изменение энтропии тела выражается более общим
соотношением
dQ + dAT, B.87)
которое является количественным выражением второго
закона термодинамики применительно к равновесным процессам
в телах.
Соотношение B.87) позволяет перейти к количественной
формулировке второго закона термодинамики применительно
к материальному континууму и получению
соответствующего дифференциального уравнения. С этой целью введем
такую величину, как удельная энтропия 5 — энтропия единицы
217

массы материального континуума. Тогда энтропия
индивидуальной частицы массой dm = р dV определится как Sp dV. В
соответствии с B.87) происходящее за малое время dt ф О
изменение энтропии индивидуальной частицы связано с ее
температурой Т, теплотой dQ, переданной этой частице со
стороны окружающих ее частиц, и теплотой dAT, выделившейся
в этой частице вследствие совершения над ней работы со
стороны окружающих ее частиц:
Td{SpdV) ^Td'SpdV = dQ + dAT. B.88)
Здесь передаваемая индивидуальной частице за время dt
теплота dQ = - <b q n dS* dt, где 5* — замкнутая поверхность,
ограничивающая бесконечно малую индивидуальную частицу
объема dV. Нетрудно видеть, что B.88) приводится к виду
где х = dAT/(dtpdV). Эта величина, имеющая размерность
удельной (отнесенной к единице массы) мощности, называется
некомпенсированной теплотой. Она всегда является
неотрицательной величиной (х > 0), характеризующей часть
удельной мощности деформирования
0<
которая определяет часть работы деформации (удельной \dt
в каждой частице или же полной / \dtpdV для всего тела),
V
необратимо переходящей в теплоту. Физическими причинами
перехода механической работы в тепловую энергию является
внутреннее трение в среде, связанное с вязкими,
пластическими и некоторыми другими свойствами конкретных сред.
Очевидно, что конкретное выражение для некомпенсированной
теплоты зависит от свойств той или иной среды. Например, в
218

идеально упругой среде работа, которую совершают
внутренние силы над каждой индивидуальной частицей, переходит в
потенциальную энергию деформации. Процесс нагружения и
последующей разгрузки индивидуальных частиц упругой
среды сопровождается возвратом к исходному состоянию, а
внутренние тепловые потери отсутствуют (х = 0). Напротив, в
несжимаемой жесткопластической среде вся работа
деформации переходит в теплоту и х = <*%*?ij/p-
Из дифференциального уравнения B.89), выражающего
второе начало термодинамики для материального
континуума, следует, что в общем случае удельная энтропия S
индивидуальных частиц может как увеличиваться, так и
уменьшаться. Если частица отдает теплоту и divq = V,*?* > 0,
как для индивидуальной частицы 2 на рис. 2.39, то
энтропия такой частицы может уменьшаться и dS/dt < 0.
Энтропия же индивидуальной частицы 1, получающей теплоту
(divq — Vtg* < 0),
изменяется в сторону увеличения, и
dS/dt > 0. В целом же эн-
тропия индивидуального
объема V материального
континуума при теплообмене лишь
между его индивидуальными
частицами изменяется в
сторону увеличения (по аналогии с
изменением энтропии системы
из двух тел при теплообмене
между ними).
Важным частным случаем деформирования
материального континуума является адиабатический процесс,
происходящий в отсутствие теплообмена как между различными
частицами сплошной среды, так и с окружающей данное
тело средой. Формальным выражением условия адиабатично-
сти процесса является равенство нулю дивергенции вектора
теплового потока divg = V,g* = 0. Для адиабатического
процесса выражение второго закона термодинамики сводится к
Рис. 2.39
219

следующему виду:
При адиабатическом деформировании сплошной среды
изменение энтропии ее индивидуальных частиц определяется
только внутренними тепловыми потерями, характеризуемыми
неотрицательной величиной %• Следовательно, в этом
случае энтропия частиц среды может изменяться только в
сторону увеличения или оставаться неизменной. Например, в
средах, лишенных внутреннего трения (идеальная жидкость,
газ, упругая среда), внутренние тепловые потери отсутствуют
(х = 0), т.е. при их адиабатическом деформировании
энтропия индивидуальных частиц остается неизменной. В таких
же средах, как вязкая, упругопластическая, жесткопластиче-
ская, существуют внутренние тепловые потери (х > 0), и при
адиабатическом деформировании этих сред энтропия
индивидуальных частиц изменяется только в сторону увеличения.
Вопросы и задачи
1. Определите понятия индивидуальной точки,
индивидуальной частицы, индивидуального объема сплошной среды.
2. В чем заключается отличие понятий индивидуальной
точки сплошной среды и точки пространства?
3. Определите понятия системы отсчета наблюдателя и
сопутствующей системы отсчета.
4. В чем состоит точка зрения Лагранжа на изучение
движения деформируемых сред? Что понимается под лагранже-
выми координатами?
5. В чем состоит точка зрения Эйлера на изучение движения
деформируемых сред? Что понимается под эйлеровыми
координатами?
6. Сформулируйте общую задачу определения движения
сплошных сред.
7. Изменяются ли во времени эйлеровы координаты
движущейся сплошной среды?
220

8. Изменяются ли во времени лагранжевы координаты
движущейся сплошной среды?
9. Чем принципиально различаются точки зрения Эйлера и
Лагранжа на изучение движения сплошных сред?
10. Как следует понимать утверждение об эквивалентности
описания движения среды с позиций Эйлера и с позиций
Лагранжа?
11. Перечислите основные физические величины,
описывающие движение сплошных сред.
12. В чем состоит физический смысл субстанциональной,
локальной и конвективной производных по времени?
13. В чем заключается принципиальное различие
субстанциональной и локальной производных по времени?
14. Определите понятие деформирования сплошной среды.
15. Каким образом вводится в рассмотрение характеристика
деформированного состояния в точке сплошной среды —
тензор деформаций?
16. Каков геометрический смысл компонент тензора
деформаций?
17. С помощью каких соотношений можно вычислить
компоненты тензора деформаций по известному полю
перемещений (укажите их в перечне основных формул к главе 2
(см. приложение 1))?
18. Охарактеризуйте тензор деформаций (ранг,
симметричность или антисимметричность, геометрический смысл
компонент).
19. Что понимается под физическими компонентами тензора
деформаций? С какой целью они вводятся в рассмотрение?
20. Какие составляющие механического движения сплошных
сред можно выделить? Какие из этих составляющих
присутствуют при движении абсолютно твердого тела, а какая
присуща лишь деформируемым средам?
21. Охарактеризуйте тензор поворота (ранг, симметричность
или антисимметричность, геометрический смысл
компонент).
221

22. В чем состоит геометрический смысл тензора поворота,
какую информацию о движении индивидуальной частицы
сплошной среды он позволяет получить?
23. Какую информацию о характере движения в окрестности
данной индивидуальной точки несет в себе тензор
деформаций?
24. Как следует понимать утверждение, что тензор
деформаций является характеристикой деформированного
состояния в точке материального континуума?
25. Определите понятия главных осей тензора деформаций и
главных деформаций.
26. Сформулируйте принцип определения главных
направлений и главных деформаций.
27. Какую форму записи имеет тензор деформаций в
декартовой прямоугольной системе координат, связанной с
главными осями тензора деформаций?
28. Каким образом вводится в рассмотрение геометрический
образ деформированного состояния в точке
материального континуума — поверхность деформации Коши? Какова
каноническая форма записи уравнений этой поверхности и
в какой системе координат она получена?
29. Каков геометрический смысл поверхности деформации
Коши и как по ее виду составить представление о
деформированном состоянии в точке материального континуума?
30. Какой вид будет иметь поверхность деформации для
деформированного состояния всестороннего растяжения?
31. Какой вид будет иметь поверхность деформации для
деформированного состояния всестороннего равноосного
растяжения?
32. Задано поле перемещений v} = f1 + а?2, v? = f2 + а?3,
и = f3 + а?1 в сопутствующей системе координат,
являющейся в начальный момент времени декартовой
прямоугольной системой координат. Считая деформации
малыми, определите поле тензора деформаций.
222

33. Задано поле перемещений и = (?l -?2JRl
—?}(?R? в сопутствующей системе координат,
являющейся в начальный момент времени декартовой прямоугольной
системой координат. При ограничениях, принятых в
теории малых деформаций, определите тензор деформаций и
тензор поворота в индивидуальной точке с лагранжевыми
координатами f1 = 0, f2 = 2, f3 = — 1.
34. Определите главные деформации тензора, заданного в
декартовой прямоугольной системе координат матрицей
35. Компоненты тензора деформаций (е) = е^тгг^ в
декартовой прямоугольной системе координат имеют значения
?12 = а> ?П = ?22 = ?33 = ?23 = ?13 = 0.
Найдите главные деформации ?ь ?2> ?з и главные направления
Я*, Я2, Д3, докажите инвариантность тензора
деформаций (е) = 6tirV = ?i R\R\ + ?2Л2 А2 + ез^Я3.
36. С какой целью при характеристике деформированного
состояния вводятся в рассмотрение инварианты тензора
деформаций?
37. Что такое инварианты тензора деформаций и как
определяются основные инварианты?
38. Как определяется производный инвариант тензора
деформаций — средняя деформация — и каков его физический
смысл?
39. Как определяется производный инвариант тензора
деформаций — интенсивность деформаций — и каков его
физический смысл?
40. Что можно сказать об изменении объема и формы
индивидуальной частицы сплошной среды, деформированное
состояние которой характеризуется тензором с матрицей
223

41. С какой целью тензор деформаций представляется в виде
суммы шарового тензора и девиатора деформаций, каким
образом осуществляется это разложение?
42. Каким образом доказывается, что шаровой тензор и деви-
атор деформаций (каждый в отдельности) характеризуют
только вполне определенную часть полных деформаций и
не касаются другой части?
(( \Л ff12 4 °11
43. Разложите тензор деформаций I |?t, I I = I I 4 9 —2II
11 )} [{О -2 3 J J
на шаровую и девиаторную части. Вычислите
интенсивности исходного тензора и девиатора деформаций.
44. Матрица деформаций [|?ij 1) = I I -1 4 О I
U П U-1 0 4 JJ

соответствует заданному в декартовой прямоугольной
системе координат тензору деформаций. Найдите компоненты
тензора деформаций в декартовой прямоугольной системе
координат, связанной с главными осями. Покажите
расчетом, что первый и второй основные инварианты тензора
деформаций в обеих системах координат совпадают.
45. Что понимается под уравнениями совместности
деформаций? Из каких соотношений следуют уравнения
совместности деформаций?
46. Почему компоненты тензора деформаций в сплошной среде
не могут быть совершенно произвольными функциями
координат, а должны быть взаимосвязаны между собой
уравнениями совместности деформаций?
47. В чем состоит физический смысл уравнений совместности
деформаций?
48. Каким образом вводится в рассмотрение тензор скоростей
деформаций?
49. С помощью каких соотношений можно вычислить
компоненты тензора скоростей деформаций по известному полю
скоростей (укажите их в перечне основных формул к
главе 2)?
224

50. Охарактеризуйте тензор скоростей деформаций (ранг,
симметричность или антисимметричность,
кинематический смысл компонент).
51. Какую информацию о характере движения в окрестности
данной индивидуальной точки сплошной среды несет в себе
тензор скоростей деформаций?
52. Охарактеризуйте тензор скоростей поворота (ранг,
симметричность или антисимметричность, кинематический
смысл компонент).
53. В чем состоит кинематический смысл тензора скоростей
поворота, какую информацию о движении индивидуальной
частицы сплошной среды он позволяет получить?
54. С какими физическими явлениями связано появление
внутренних сил в сплошной среде?
55. Какая физическая величина характеризует внутренние
силы, возникающие в сплошной среде, как эта величина
вводится в рассмотрение?
56. Каким образом вводится в рассмотрение тензор
напряжений, характеризующий напряженное состояние в точке
сплошной среды?
57. Охарактеризуйте тензор напряжений (ранг,
симметричность или антисимметричность, физический смысл
компонент).
58. Какую информацию о состоянии материального
континуума в данной индивидуальной частице содержит в себе
тензор напряжений, как выявляется эта информация?
59. Тензор напряжений (а) = а^гхг^ в точке сплошной среды
0 -S
задан матрицей [ I aty 11 = I I 0 5 0 II* Определи-
= ((_°2 J
те вектор полного напряжения <тп в данной точке на
площадке, ориентация которой задается единичным вектором
,221
нормали п = 71*гд. = - т\ - - т*2 + -гз-
о о о
8-9712 225

60. Тензор напряжений (а) = а^тхг3 в точке сплошной среды
a w ff1 2 °11
задан матрицей I I сг~ \ I = 2 3 5 I I . Определите
11 " Но 5 lJJ
нормальное напряжение в данной точке на площадке,
ориентация которой задается единичным вектором нормали
61. Тензор напряжений (а) = G{jr%r3 в точке сплошной среды
a w ff2 2 °11
задан матрицей I I "ty I I = I I 2 1 3 I I . Определите
U )} {{О 3 lJJ
касательное напряжение в данной точке на площадке,
ориентация которой задается единичным вектором нормали
п = пКгк = -Г! + — г3.
62. Тензор напряжений (а) — о^тхт3 в некоторой точке
сплошной среды задан в декартовой прямоугольной системе ко-
ординат матрицей
(( л\ ff5 ° 2Л
I I aij I I = 0 6 3 11. Определи-
VV п [{2 3 lJJ
те нормальное и касательное напряжения, а также модуль
вектора полного напряжения в данной точке на площадках,
ориентации которых задаются нормалями п = т\ и п = тч-
63. Напряженное состояние материального континуума в
декартовой прямоугольной системе координат задано тензо-
и \\ \\6ху Ь-
ром напряжении с матрицей
(Ы)= «j» о -]]
Определите вектор полного напряжения, действующего в
точке с координатами ж = 1,з/ = 2,2г = 3на площадке,
ориентация которой задается единичным вектором норма-
к 1 1
ли п = пКгк = -дгг ~ -j= г2.
64. Определите понятия главных площадок, главных осей
тензора напряжений, главных напряжений.
226

65. Сформулируйте принцип определения главных
напряжений и главных осей тензора напряжений.
66. Какую форму записи имеет тензор напряжений в
декартовой прямоугольной системе координат, связанной с
главными осями, и почему?
67. Тензор напряжений в точке задается в декартовой
прямоугольной системе координат матрицей I j <j{j 11 =
¦((is:))-
Определите главные напряжения.
68. Как определяется геометрический образ напряженного
состояния в точке сплошной среды — поверхность
напряжений? Как по виду поверхности напряжений можно судить
об особенностях напряженного состояния?
69. Каковы возможные формы поверхности напряжений для
различных напряженных состояний?
70. Каким напряженным состояниям соответствуют
сферическая и эллипсоидная формы поверхности напряжений?
71. Как будут выглядеть выражения основных инвариантов
тензора напряжений в произвольной системе координат, в
какой-либо ортогональной системе координат, в
декартовой прямоугольной системе координат главных осей?
72. В чем заключается физический смысл производного
инварианта тензора напряжений — среднего напряжения?
73. В чем заключается физический смысл производного
инварианта тензора напряжений — интенсивности
напряжений?
74. Тензор напряжений задан в декартовой прямоугольной си-
{< w [[ 6  °I
стеме координат матрицей I I crt, 11 = II -3 6 Oil.
lv )} (I 0 0 8))
Найдите главные напряжения и покажите, что
диагональная матрица приводит к тем же значениям первого и
второго основных инвариантов, что и исходная матрица.
8* 227

75. Определите главные значения девиатора напряжений для
тензора, заданного матрицей
76. Тензор напряжений задан в декартовой прямоугольной
системе координат матрицей
(Ы)=1Г10 ° 30|]
11 )} Но 30 -27JJ
Разложите его на шаровой тензор и девиатор напряжений.
Вычислите и сравните средние напряжения и
интенсивности напряжений для исходного тензора, шарового тензора
и девиатора напряжений.
77. Определите понятия внешних сил — объемных и
поверхностных. Какими физическими величинами количественно
характеризуются эти внешние силы?
78. Каков физический смысл граничных условий в
напряжениях, как записываются эти условия?
79. Каков принцип вывода дифференциального уравнения
равновесия в объеме тела, как записывается это уравнение
(укажите его в перечне основных формул к главе 2)?
80. Назовите фундаментальные законы, которым подчиняется
движение материального континуума.
81. Как называются и как записываются дифференциальные
уравнения, выражающие законы сохранения массы,
импульса и энергии применительно к сплошной среде?
82. Каков принцип вывода дифференциального уравнения
неразрывности, как записывается это уравнение (укажите
его в перечне основных формул к главе 2)?
83. Как получить уравнение неразрывности на основе
истолкования физического смысла дивергенции вектора скорости
потока жидкости?
84. Как устанавливается и как выглядит взаимосвязь
плотности и объемной деформации индивидуальной частицы
сплошной среды?
85. Что понимается под несжимаемым материальным
континуумом и однородным континуумом?
228

86. Как выглядит уравнение неразрывности для несжимаемой
среды, для однородной среды?
87. Получите запись уравнения неразрывности в декартовой
прямоугольной системе координат для трехмерного
пространственного течения среды (vx = vx(x, у, z, tf), vy =
= vy(x, у, z, t), vz = vz(x, у, z, t)), для двумерного
плоского движения (vx = vx(x, у, /), vy = vy(x, y, t), vz = 0) и
для одномерного плоского движения (vx = vz(x, i), vy = 0,
^ = 0).
88. Получите запись уравнения неразрывности в
цилиндрической системе координат (Г21 = Г^2 = 1/^5 Г^2 = ~7*) для
двумерного с осевой симметрией движения (vr = vr(r, z, /),
vz = v2(r, z, tf), V0 = 0) и для одномерного с осевой
симметрией движения (г>г = vr(r, t), vz = 0, v^ = 0).
89. Запишите закон сохранения импульса для
индивидуального объема материального континуума в виде
соответствующего интегродифференциального уравнения. Укажите
принцип перехода к дифференциальному уравнению,
выражающему этот закон сохранения применительно к каждой
индивидуальной частице сплошной среды. Как
записывается это уравнение (укажите его в перечне основных
формул к главе 2)?
90. Получите запись уравнений движения в декартовой
прямоугольной системе координат для течений: трехмерного
пространственного (vx = vx(x, у, z, t), vy = vy(x, j/, z, i),
vz = vz(x, y, z, *), aij = <Tij(x, y, z, *)), двумерного
плоского (vx = vx(x, y, <M V2/ = vy(x, y, /), vz = 0, ai;- =
= <7ij(x, y,t)) и одномерного плоского (vx = vx(x, t),
vy = 0, vz = 0, a^ = Gу(х, <)).
91. Получите запись уравнений движения в цилиндрической
системе координат (Г21 = Г^ = 1/^» Г22 = —г) для
двумерного течения с осевой симметрией (ут = vr(r, z, t),
vz = v^(r, z, <), v^ = 0, (T{j = &ij(r, z, t)) и одномерного
течения с осевой симметрией (vr = г;г(г, /), vz = 0, v^ = 0,
229

92. Справедливо ли утверждение об универсальности
уравнений неразрывности и движения, а если справедливо, то как
его понимать?
93. Сформулируйте принцип получения уравнения баланса
механической энергии (доказательство теоремы "живых
сил"). Укажите в перечне основных формул к главе 2
соответствующее интегродифференциальное уравнение и дайте
ему объяснение.
94. Как следует понимать название теоремы "живых сил"?
Что является аналогом этой теоремы в динамике
материальной точки? В чем состоит принципиальное отличие от
аналога?
95. Укажите путь доказательства утверждения, что объемный
интеграл / a%3kijdV определяет полную (для всего тела)
мощность деформирования.
96. Укажите в перечне основных формул к главе 2
интегродифференциальное уравнение, выражающее закон
сохранения энергии при отсутствии тепловых явлений, и дайте его
истолкование.
97. Определите понятие удельной внутренней энергии. Какие
составляющие содержит удельная внутренняя энергия для
чисто механических и для тепловых процессов?
98. Каким образом определяется и вводится в рассмотрение
физическая величина вектора теплового потока? Как при
известном векторе теплового потока в данной точке
сплошной среды определить количество теплоты, проходящей за
малое время dt через малую площадку dS, ориентация
которой задана единичным вектором нормали п?
99. Сформулируйте закон теплопроводности Фурье и дайте его
физическое обоснование.
100. Укажите в перечне основных формул к главе 2
интегродифференциальное уравнение, выражающее закон
сохранения энергии при наличии тепловых явлений, и дайте его
формулировку.
230

101. Каков принцип, с помощью которого получают
дифференциальное уравнение энергии, выражающее первый
закон термодинамики применительно к каждой
индивидуальной частице сплошной среды? Как записывается это
уравнение и каков физический смысл входящих в него
составляющих?
102. Какие процессы называются адиабатическими? Как
будет выглядеть уравнение энергии для адиабатических
процессов?
103. Перечислите физические величины, описывающие
состояние сплошной среды.
104. Сформулируйте второй закон термодинамики (в
качественной формулировке).
105. Определите понятия обратимых и необратимых
процессов. К какому типу относятся процессы: упругого
соударения двух тел; проникания срабатывающегося
металлического ударника в металлическую преграду;
передачи теплоты от более нагретого тела к менее нагретому;
взрывного превращения энергетических материалов?
106. Что следует понимать под необратимыми потерями
энергии в изолированной системе? Действительно ли
имеются в виду реальные потери энергии и отклонение от
закона сохранения энергии?
107. Почему внутренняя тепловая энергия не может являться
мерой накопления необратимых потерь энергии, а для
характеристики этих потерь необходимо вводить в
рассмотрение специальную физическую величину — энтропию?
108. На примере равновесного процесса прямого
теплообмена между телами, нагретыми до различной
температуры, обоснуйте необходимость введения понятия энтропии.
Как изменяется энтропия каждого участвующего в этом
процессе тела и системы в целом, чему физически
соответствуют эти изменения?
231

109. Сформулируйте принцип вывода дифференциального
уравнения, выражающего второй закон термодинамики
применительно к каждой индивидуальной частице
материального континуума, укажите его в перечне основных
формул к главе 2. Каков физический смысл входящих в
это уравнение составляющих?
ПО. Что понимается под величиной некомпенсированной
теплоты, используемой в записи дифференциального
уравнения второго закона термодинамики?
111. Как и за счет каких факторов может изменяться
энтропия индивидуальных частиц химически инертной среды в
общем случае и при адиабатических процессах?
112. В чем состоит сущность второго закона термодинамики?
В каком направлении в природе происходит
самопроизвольное развитие изолированных систем материальных
тел, каков конечный итог указанного процесса?

Глава 3
МОДЕЛИ СПЛОШНЫХ СРЕД,
ИХ ФИЗИЧЕСКИЕ СООТНОШЕНИЯ
3.1. Понятие модели сплошной среды
Во второй главе были получены дифференциальные
уравнения и соотношения, выражающие законы сохранения массы,
импульса, энергии и второй закон термодинамики
применительно к сплошным деформируемым средам, геометрические
и кинематические соотношения и т.п. Эти уравнения и
соотношения были выведены для общего случая независимо от
того, какими конкретными физико-механическими свойствами
обладает деформируемая среда, и в силу этого имеют
универсальный характер, т.е. справедливы для любых сред. Однако
при попытке математического описания движения какой-либо
конкретной деформируемой среды (газообразной, жидкой или
твердой) довольно легко установить, что имеющихся в
распоряжении универсальных дифференциальных уравнений и
соотношений не достаточно для составления замкнутой системы
уравнений, которая могла бы послужить основой для
последующего нахождения единственного решения и получения
количественной информации о характере движения и изменения
состояния деформируемой среды. При этом очевидна
закономерность: количество входящих в составляемую систему
уравнений неизвестных величин (характеристических функций)
на 6 единиц больше имеющихся в распоряжении уравнений,
где 6 — количество независимых компонент симметричных
233

тензоров напряжений и деформаций. Например, приведенная
ниже система уравнений адиабатического движения
деформируемой среды включает 20 уравнений (одно уравнение
неразрывности C.1), три уравнения движения C.2), одно
уравнение энергии C.3), три кинематических соотношения
взаимосвязи компонент скорости и перемещения C.4), шесть
геометрических соотношений C.5) и шесть кинематических
соотношений C.6)) и 26 неизвестных характеристических функций
(плотность, удельная внутренняя энергия, по три
компоненты векторов перемещения и скорости, по шесть независимых
компонент симметричных тензоров напряжений, деформаций
и скоростей деформаций):
4j 0i C.1)
X; C-2)
C.3)
Анализ приведенной системы уравнений показывает, что
в ней отсутствуют соотношения, учитывающие реакцию
деформируемой среды на процесс деформирования и
показывающие, какие внутренние напряжения возникают в ней в ответ
на деформации. Подобные соотношения в самом общем виде
можно записать как
°ij = °xj{?ij,?ij,T). C.7)
Соотношения вида E.7) называются физическими
соотношениями, они определяют специфику той или иной
деформируемой среды в отношении оказания сопротивления
деформированию и тесно связаны с понятием модели сплошной среды.
234

Модель сплошной среды — это некоторое
идеализированное представление реальной деформируемой среды,
учитывающее основные ее свойства сопротивления
деформированию и подчиняющееся определенному математическому
описанию в виде физических соотношений E.7). Выбор модели
сплошной среды для реальной деформируемой среды и
соответствующий выбор физических соотношений C.7) позволяет
составить замкнутую систему дифференциальных C.1)—C.6)
и конечных функциональных C.7) уравнений для
математического описания движения и внутреннего состояния
исследуемой среды.
3.2. Физическое и механическое поведение
деформируемых сред
При постановке вопроса об особенностях сопротивления
деформированию той или иной среды различают понятия
физического и механического поведения среды. Сущность и
содержание этих понятий определяются следующим образом.
При действии на материальный континуум внешних сил
(объемных F или поверхностных р) его индивидуальные
частицы получают определяемые уравнением движения C.2)
ускорения dv/dt, приводящие к движению и появлению
соответствующих полей скоростей v и перемещений и. В свою
очередь, появление поля перемещений приводит к изменению
расстояний между индивидуальными точками материального
континуума и к возникновению поля тензора деформаций (е)
в соответствии с геометрическими соотношениями C.5). И
наконец, изменение расстояний между индивидуальными
точками материального континуума влечет за собой появление в
деформируемой среде внутренних сил, количественной
характеристикой которых является тензор напряжений (<т), т.е.
деформированному состоянию соответствует вполне
определенное напряженное состояние, характеризуемое полем тензора
напряжений.
235

Как известно, тензор деформаций в целом может быть
представлен в виде суммы двух тензоров — шарового тензора
деформаций и девиатора деформаций:
(e) = (S?) + (De),
где шаровой тензор деформаций (Se) характеризует лишь ту
часть полных деформаций в данной индивидуальной частице
материального континуума, которая определяет изменение ее
объема и не связана с изменением формы, а девиатор
деформаций (D?), напротив, характеризует ту часть полных
деформаций, которая определяет формоизменение данной
индивидуальной частицы и не связана с изменением объема.
Необходимость подобного разделения тензора деформаций в целом
(е) на две составляющие обусловлена тем, что различные
деформируемые среды по-разному реагируют на изменение
объема и формы их индивидуальных частиц. В общем случае
каждый фактор (изменение объема индивидуальной частицы
— Eб) ф О или изменение ее формы — (^е) ф 0) вносит
свой вклад в возникающее в этой частице напряженное
состояние, что приводит к появлению шарового тензора
напряжений EV) / 0 и девиатора напряжений (Da) ф 0, в то время
как результирующее напряженное состояние в данной частице
определяется суммой двух этих тензоров
И = ($„) +(А,).
Именно с особенностями сопротивления сплошной среды двум
отмеченным факторам деформирования связаны понятия
физического и механического поведения деформируемых сред.
Физическое поведение деформируемых сред определяется
их способностью оказывать сопротивление изменению
объема индивидуальных частиц и характеризуется присущей
каждой среде взаимосвязью шаровых тензоров напряжений и
деформаций:
E,) = h(Se). C.8)
Механическое поведение деформируемых сред
определяется их способностью реагировать на формоизменение и
характеризуется присущей каждой среде взаимосвязью девиа-
торов напряжений и деформаций:
(Dff) = f2(De). C.9)
236

Тензорные уравнения C.8) и C.9) называются
определяющими уравнениями. Именно они характеризуют
индивидуальность каждой деформируемой среды в отношении
сопротивления деформированию, именно из них следует конкретный
вид физических соотношений C.7) для той или иной модели
сплошной среды.
3.2.1. Физическое поведение сплошных сред.
Уравнение состояния
Тензорному уравнению C.8) соответствует скалярное
уравнение, определяющее физическое поведение
деформируемой среды. В силу одинаковой структуры шаровых тензоров
напряжений и деформаций (E^) = (Tgijrxr^, (S?) = egijrWJ)
взаимосвязь этих тензоров характеризуется скалярным
соотношением а = а(е) между производными инвариантами
тензоров напряжений и деформаций — средним напряжением а
и средней деформацией е. В более общем случае скалярное
уравнение, определяющее физическое поведение
деформируемой среды, учитывает влияние температуры и имеет вид
а = сг(?, Т). Поскольку среднее напряжение с точностью до
знака равно давлению, возникающему в данной
индивидуальной частице материального континуума (а = —р), а средняя
деформация характеризует изменение объема индивидуальной
частицы и взаимосвязана с текущим и начальным значениями
плотности деформируемой среды как р = />о/A + Зе) (в
случае малых деформаций), скалярное уравнение, определяющее
физическое поведение среды, может быть представлено в виде
Р = р(р,Т) C.10)
и называется уравнением состояния деформируемой среды.
Уравнение состояния характеризует фундаментальное
свойство реальных деформируемых сред — их сжимаемость.
Сжимаемость — это способность деформируемых сред к
изменению объема {или плотности) их индивидуальных частиц
вследствие действующего в них давления (или, напротив,
237

это способность среды сопротивляться изменению плотности
посредством возникновения в частицах давления
противодействия).
За редким исключением, информация о сжимаемости
реальных деформируемых сред получается из опыта
посредством исследования поведения тел в специально организуемых
условиях всестороннего сжатия и последующего обобщения и
представления полученной информации в виде уравнений
состояния C.10). Так, например, уравнение состояния
достаточно разреженных газов получается как обобщение частных
газовых законов (Бойля — Мариотта, Шарля, Гей-Люссака) и
представляется в виде уравнения Клапейрона — Менделеева
р = pRT, где R = Ro/fji — газовая постоянная, определяемая
соотношением универсальной газовой постоянной Rq и
молярной массы ц данного газа. Это уравнение состояния лежит в
основе одной из моделей сплошных сред — модели идеального
совершенного газа.
В качестве еще одного примера рассмотрим методы
экспериментального исследования сжимаемости деформируемых
твердых тел (металлы, пластмассы и т.п.). Такие методы
разделяются на две группы, различающиеся как по уровню
достигаемых давлений, так и по используемым для
получения результатов технических средств.
Статическая сжимаемость твердых тел исследуется в
сосудах высокого давления посредством измерений
создаваемых давлений р в жидкости и объемной деформации в образца,
помещаемого в жидкость (рис. 3.1). Верхняя граница
получаемых таким образом давлений составляет около 10 ГПа.
Основные полученные результаты по сжимаемости твердых тел в
статических условиях связаны с именем Бриджмена, который
экспериментально получил, что вплоть до давлений р < 3 ГПа
сжимаемость твердых тел описывается уравнением
0 = -ар-Ър2, C.11)
где а и b — определяемые из опыта константы, соотносящиеся
для большинства твердых тел как b/a ~ 10 ГПа". С
учетом такого соотношения эмпирических констант аибиз(З.Н)
238

Рис. 3.1
Рис. 3.2
следует, что в диапазоне давлений р < 1 ГПа статическая
сжимаемость твердых тел с точностью до 10 % описывается
линейной зависимостью давления от объемной деформации в или
от средней деформации е:
где К — модуль объемного сжатия, определяемый по
опытным данным. Последнее уравнение может быть представлено
в виде уравнения Бриджмена
а = ЗКе C.12)
и является одним из определяющих уравнений для модели
идеально (или совершенно) упругой среды.
Динамическая сжимаемость твердых тел исследуется
путем проведения ударноволновых испытаний с помощью
экспериментальных методов физики быстропротекающих
процессов. Основным методом является создание в
испытуемом образце плоской ударной волны посредством взрывного и
ударного нагружения. Для примера на рис. 3.2 показана
схема нагружения образца 3 зарядом взрывчатого вещества 2 с
плосковолновым генератором i, формирующим в заряде
плоскую детонационную волну, которая генерирует
распространяющуюся в образце плоскую ударную волну. Ударная волна
239

представляет собой скачок параметров движения и состояния,
распространяющийся в среде со сверхзвуковой скоростью, при
этом значения параметров на фронте ударной волны
взаимосвязаны между собой и с параметрами покоящейся среды
определенной системой соотношений физики взрыва:
Р~Ро = PouD, p0D = p(D- и), C.13)
где и, р, р — соответственно массовая скорость движения
вещества, давление и плотность на фронте ударной волны; D —
скорость движения самого фронта; индексом 0 отмечены
параметры покоящейся среды. В подобных экспериментах
определяются скорость движения фронта ударной волны D (по
разности М\ времени прихода фронта ударной волны к
разнесенным на небольшое расстояние h\ электроконтактным
датчикам 5: D = hi/Ati) и скорость движения свободной
поверхности ип после отражения от нее фронта ударной волны (по
разности Л^2 времени замыкания разнесенных на расстояние
Л-2 электроконтактных датчиков 4: ип — ^2/^2)- Скорость
же свободной поверхности, как это показано в физике
взрыва, взаимосвязана с массовой скоростью движения среды на
фронте ударной волны: ип = 2и. Последующее
использование системы соотношений C.13) позволяет рассчитать
соответствующие данной интенсивности ударной волны давление
р и плотность р. Путем варьирования интенсивности
ударной волны удается получить уравнения динамической
сжимаемости твердых тел р = р(р), которые называются
ударными адиабатами (ударноволновое сжатие вещества на фронте
ударной волны происходит практически мгновенно и
вследствие этого в адиабатических условиях).
Экспериментально получаемые результаты по
динамической сжимаемости аппроксимируются, как правило,
степенными зависимостями вида
[] C-14)
(ударная адиабата в форме Тэта). Для примера,
коэффициенты ударной адиабаты железа в диапазоне давлений,
характерном для обычного взрыва, имеют значения А « 21,5ГПа,
п « 5,5, а меди — А « 30,2 ГПа, п«4,8.
240

При изучении сжимаемости твердых тел выделяют
несколько характерных диапазонов изменения давления.
1. Низкие давления (р < 1 ГПа). При давлениях в
пределах этого диапазона сжимаемость твердых тел
описывается линейным уравнением Бриджмена C.12), а при давлениях
вблизи верхней границы диапазона начинают проявляться
существенные отклонения от этой зависимости.
2. Средние давления A < р < 10 ГПа). При этих
давлениях в твердых телах происходят фазовые и полиморфные
превращения. Например, в железе при р = 13 ГПа
меняется структура кристаллической решетки и железо переходит из
а-фазы (кубическая объемноцентрированная решетка) в
?-фазу (гексагональная плотноупакованная решетка).
Наличием такого полиморфного превращения определяется
замечательная особенность железа, заключающаяся в возможности
распространения не только ударных волн сжатия, но и
ударных волн разрежения, приводящих к формированию гладких,
зеркальных, откольных поверхностей при разрушении
материала.
3. Высокие давления A0 < р < 100 ГПа). Верхней
границе этого диапазона соответствует начало разрушения
электронных оболочек атомов и превращения вещества в
электронно-ионный газ, описываемый статистическими
моделями.
4. Сверхвысокие давления (р > 100 ГПа).
Следует отметить, что в области техники, связанной с
использованием обычных взрывчатых веществ, реализуются
давления в пределах диапазонов 1—3. Сверхвысокие
давления достигаются в основном при ядерном взрыве. Например,
рекордное на сегодня давление около 104 ГПа достигнуто при
проведении сопутствующих подземному ядерному взрыву
экспериментов по соударению металлических пластин, при этом
скорость соударения составляла около 60 км/с.
Таким образом, путем экспериментального исследования
сжимаемости твердых тел в статических и динамических
условиях удается получить соответствующие уравнения
сжимаемости. Их обобщение позволяет установить уравнение
241

состояния C.10) твердых тел в широком диапазоне
изменения давления. Форма C.10) представления уравнения
состояния называется термической (давление зависит от
температуры) и не является единственно возможной. Достаточно
часто используются уравнения состояния в калорической форме
р ¦— р(р, Е)9 когда давление зависит от плотности и удельной
внутренней энергии, или в энтропийной форме р = р(р, S),
когда давление зависит от плотности и энтропии.
3.2.2. Механическое поведение деформируемых сред.
Диаграмма механического поведения.
Понятие о реономных и склерономных свойствах
Механическое поведение деформируемых сред связано со
способностью индивидуальных частиц реагировать на
изменение формы посредством возникновения в них
соответствующих напряжений и характеризуется тензорным
определяющим уравнением C.9) взаимосвязи девиаторов напряжений и
деформаций. Как известно из теории деформаций,
каждому девиатору деформаций соответствует скалярная величина,
интегрально характеризующая формоизменение
индивидуальных частиц материального континуума, — интенсивность
деформаций
где T2(D?) — второй основной инвариант девиатора
деформаций. Аналогично каждому девиатору напряжений
соответствует величина, обобщенно характеризующая касательные
напряжения в индивидуальной частице, — интенсивность
напряжений
аг =
где T2(Dcr) — второй основной инвариант девиатора
напряжений. На основании имеющегося однозначного соответствия
между девиаторами и интенсивностями механическое
поведение деформируемой среды может быть охарактеризовано
242

скалярным определяющим уравнением о± — сгДб,), в более
общем случае принимающим вид зависимости интенсивности
напряжений от интенсивности деформаций ?,*, интенсивности
скоростей деформаций к{ и температуры Т:
°i = 0i(euei,T). C.15)
Определяющие механическое поведение уравнения C.9)
или C.15) устанавливаются на основе опытных данных. Так,
для многих реальных газов и жидкостей, деформируемых при
относительно небольших скоростях деформаций, зависимость
C.15) имеет тривиальный вид О{ = 0. Такие среды не
реагируют на формоизменение [(Dp) = 0], сколь бы
существенным ни было изменение формы их индивидуальных частиц
((D?) ф 0J. Такое механическое поведение соответствует
модели идеальной среды. В большинстве же случаев
реальные деформируемые среды оказывают сопротивление
формоизменению и зависимость C.15) не является столь простой. В
частности, это характерно для реальных сред, проявляющих
основные механические свойства— свойства упругости,
пластичности и вязкости. Упругость — это способность
материала среды возвращаться к исходному состоянию после
снятия приложенных нагрузок; пластичность — это способность
материала после снятия нагрузок сохранять полученные в
результате нагружения деформации полностью или частично;
вязкость — это способность деформируемой среды оказывать
сопротивление наличию относительной скорости движения ее
частиц.
На примере мягкой стали (типа стали 10), по своим
свойствам близкой к модели упругопластической среды,
рассмотрим, каким образом из эксперимента получается информация
о механическом поведении деформируемых сред. При
медленном растяжении на разрывной машине стального
образца в изотермических условиях (ё, « 0, Г = const) может
быть найдена зависимость истинного растягивающего
осевого напряжения ст\ от осевой деформации Е\ с одновременным
243

б
Рис. 3.3
определением тангенциальной ?2 и радиальной ?з деформаций
(рис. 3.3, а). На рис. 3.3, б показана диаграмма растяжения в
виде зависимости а\ = сг1(е1), включающая линейный
(упругий) участок о\ = Ее\, где Е — модуль упругости первого
рода, или модуль Юнга, и нелинейный (пластический)
участок. Поскольку в данных условиях реализуется
напряженное состояние одноосного растяжения, для которого
интенсивность напряжений определяется единственной отличной от
нуля осевой компонентой тензора напряжений о± — о\, найдя
интенсивность деформаций по трем известным компонентам
тензора деформаций е\, ?2, ?з> диаграмму растяжения можно
перестроить и представить в виде зависимости сг,- = 0",-(?,-),
характеризующей механическое поведение материала в
изотермических квазистатических условиях (рис. 3.3, в). На
диаграмме механического поведения О{ = <?{(?{) выделяется ряд
характерных точек. Точка 0 соответствует исходному
состоянию материала. Линейный участок ОА диаграммы
механического поведения описывается прямо пропорциональной
зависимостью <7г = 3G?t, где G — модуль упругости второго
рода, или модуль сдвига (пояснения причин изменения
коэффициента пропорциональности при переходе от зависимости
о\ = сг1(?1) к зависимости О{ = 0|(е,*) см. в разделе 3.3.3).
Значение интенсивности напряжений Ор, соответствующее
завершению линейного участка, называется пределом
пропорциональности. Точка В на диаграмме соответствует пределу
текучести сгт — значению интенсивности напряжений, начиная с
которого дальнейшее деформирование на определенном
участке (площадке текучести ВС) происходит при неизменном или
244

незначительно изменяющемся значении напряжений. Участок
CD, соответствующий повышению интенсивности
напряжений, называется участком упрочнения, при этом точка D
соответствует достижению предела прочности ав — значения
интенсивности напряжений, при котором происходит
нарушение сплошности и разрушение стального образца.
Подобным же образом из экспериментов по
динамическому растяжению образцов на разрывных машинах
определяются диаграммы механического поведения материала с учетом
влияния скорости деформаций сг{ = а,-(е,-, ?,-), а из опытов по
растяжению нагретых образцов определяют влияние на
механическое поведение материала температуры: <т; = <7,-(?,-, Г).
Характер влияния скорости деформаций на механическое
поведение материала показан на рис. 3.4. Для большинства
металлов увеличение степени динамичности нагружения
оказывает "упрочняющее" влияние: с увеличением интенсивности
скорости деформаций (ег2 > ёц) увеличивается проявление
свойств упругости (ар2 > api) и прочности (сгт2 > aTi и
0"в2 > ^Bl) и уменьшается проявление пластических свойств
(разрушение происходит при меньшем значении
интенсивности деформаций ?1;J < Sipi). Температура же влияет на
механическое поведение противоположным образом (рис. 3.5): с ее
повышением (Т2 > 7\) происходит разупрочнение материала
(ор2 < cTpi, аТ2 < <тТ1, <7в2 < сгв1) и увеличение пластических
свойств (е;по >
6pZ'
bpf
О
?ipz Чр1
Рис. 3.4
Рис. 3.5
245

Таким образом, путем экспериментального исследования
раздельного влияния на механическое поведение материала
различных факторов с последующим обобщением полученной
информации получаются скалярные уравнения C.15),
определяющие механическое поведение деформируемой среды. Они
характерны для деформируемых сред, обладающих так
называемыми склерономными свойствами, когда способность
сопротивляться формоизменению в явном виде не зависит от
времени. С одной стороны, такие среды как бы "забывают"
предысторию своего деформирования, а с другой стороны,
значение интенсивности напряжений <7,-, возникающей в
индивидуальных частицах этих сред, зависит только от значений
интенсивности деформаций ?,-, скорости деформаций Е{ и
температуры Г. Склерономные свойства проявляют, например,
твердые тела при относительно невысоких температурах. На
рис. 3.6 на примере стали 10
показано, что независимо от
того, каким образом
получено значение интенсивности
деформаций,
соответствующее точке М на диаграмме
деформирования
(возможные "пути деформирования"
помечены цифрами 1—«?),
значение интенсивности
напряжений во всех случаях
одно и то же и
соответствует точке М на диаграмме
деформирования. Если
достигнутое к определенному
моменту времени значение
рис. з.б интенсивности деформаций
в дальнейшем будет
сохраняться неизменным, то столь же неизменным будет оставаться
и соответствующее значение интенсивности напряжений.
t
246

Однако при некоторых условиях (высокие температуры,
достаточно продолжительные временные интервалы) те же
твердые тела могут проявлять и реономные механические
свойства — свойства, в явном виде зависящие от времени,
когда характеристики напряженно-деформированного состояния
зависят от предыстории деформирования. К числу реономных
свойств относятся свойства релаксации и последействия.
Под релаксацией понимается процесс уменьшения с
течением времени интенсивности напряжений в индивидуальных
частицах деформируемой среды при неизменном значении
интенсивности деформаций (рис. 3.7). Подобные условия
неизменности интенсивности деформаций реализуются, например,
в металлическом стержне, растянутом в разрывной машине с
последующим прекращением относительного перемещения ее
захватов и их фиксацией относительно друг друга. Если
такой металлический стержень будет подвергнут воздействию
достаточно высокой температуры, то в нем при сохранении
неизменных деформаций с течением времени будут
уменьшаться (релаксировать) внутренние напряжения и интенсивность
напряжений в каждой из его индивидуальных частиц в
соответствии с зависимостью о± = &{ме~*1Т (закон релаксации
Максвелла), где г — характерное время или период
релаксации.
const
tl"const
1
Напротив, свойство последействия проявляется в виде
процесса увеличения с течением времени интенсивности
деформаций в индивидуальных частицах деформируемой среды
247

1
1
JP- const
h
61M=const
n
h
h
t
Рис. 3.8
при неизменном значении интенсивности напряжений.
Подобные условия неизменности напряжений реализуются,
например, в металлическом стержне с подвешенным к нему грузом
(рис. 3.8). Под воздействием температуры такой стержень
будет самопроизвольно удлиняться с соответствующим
увеличением деформаций и интенсивности деформаций в его
частицах.
Свойства релаксации и последействия — это проявления
на макроуровне физических процессов перестройки
структуры твердых тел, происходящей под влиянием высокой
температуры. При этом разные твердые тела проявляют подобные
свойства при различных температурах. Так, если для
металлов для этого необходима температура, соизмеримая с
температурой плавления, то резина способна к релаксации или
последействию даже при комнатной температуре (всем известен
пример релаксации — потеря упругости резинового
эспандера, оставленного на длительное время в растянутом
состоянии). Однако во всех случаях для проявления реономных
свойств необходимо достаточно большое время, а для
кратковременных, быстропротекающих процессов типа взрывных
или ударных проявлением релаксации или последействия
можно пренебречь.
248

3.3. Простые модели сплошных сред
Под простыми моделями сплошных сред понимаются
идеализированные представления реальных деформируемых
сред, учитывающие какое-либо одно из основных
механических свойств. К числу простых относятся следующие
четыре модели: модель идеальной среды (идеальная жидкость или
идеальный газ, не способные оказывать сопротивление
формоизменению); модель вязкой жидкости (учитывается лишь
свойство вязкости); модель упругой среды (принимается во
внимание лишь проявление свойства упругости); модель жест-
копластической среды (проявляется только свойство
пластичности). Рассмотрим перечисленные выше простые модели
сплошных сред, придерживаясь следующей
последовательности: определение модели, общие соображения относительно
сопротивления деформированию данной среды, определяющие
уравнения, физические соотношения, примеры использования
данной модели при физико-математическом моделировании и
ее термодинамические особенности.
3.3.1. Идеальная среда
(идеальная жидкость или идеальный газ)
Идеальная среда (идеальная жидкость или идеальный
газ) — это среда, не способная оказывать сопротивление
изменению формы своих частиц. Как уже отмечалось выше, в
такой среде отсутствуют касательные напряжения ((Da) = О],
сколь бы существенным ни было формоизменение ее
индивидуальных частиц f(J9?)^OJHc какой бы скоростью оно ни
происходило ((De) ф О J. Однако такая среда оказывает
сопротивление изменению объема или плотности своих частиц,
и при наличии изменения объема (E?)^0)в ней возникают
соответствующие внутренние напряжения (E<г) Ф 0J. Таким
образом, тензор напряжений в любой индивидуальной частице
идеальной среды является шаровым:
(а) = (S<r) = (rgijrW = -pgijrxri,
249

а напряженное состояние характеризуется, по существу, одной
скалярной величиной — давлением р.
Уравнения, определяющие физическое и механическое
поведение идеальной среды, выглядят соответственно как
р = р(р,Т), (Dff) = 0,
а физические соотношения для модели идеальной жидкости
приобретают вид
°ij = -P9ij = -Р{Р, Т) gij, C.16)
где текущее значение плотности р косвенным образом
учитывает компоненты тензора деформаций, так что физические
соотношения C.16) по структуре выражения соответствуют
общему виду физических соотношений C.7).
Из ряда реальных деформируемых сред к модели
идеальной среды наиболее близки большинство жидкостей и газов,
и этим определяется область применимости этой модели.
Например, при расчете параметров поля взрыва заряда
взрывчатого вещества в воде модель идеальной среды используется
как по отношению к жидкости, так и по отношению к
продуктам детонации заряда взрывчатого вещества. Воду в данном
случае в первом приближении можно рассматривать как
идеальную баротпропную среду, давление в которой зависит лишь
от плотности р = р(р), не принимая во внимание зависимость
давления от температуры. В качестве такого баротропного
уравнения состояния можно выбрать ударную адиабату воды
в форме Тэта C.14) при значениях опытных коэффициентов
Расчет взрыва заряда взрывчатого вещества в воздухе
можно проводить также с использованием в качестве модели
воздушной среды модели идеального газа с уравнением
состояния Клапейрона — Менделеева р = pRT. Такой газ
называется идеальным совершенным газом (термин "идеальный"
касается механических свойств газа, не способного оказывать
сопротивление формоизменению, а термин "совершенный"
относится к конкретному виду уравнения состояния).
Модель идеальной среды может использоваться и в том
случае, когда реальная деформируемая среда оказывает
250

значительное сопротивление формоизменению, однако
возникающие в ответ на изменение формы напряжения Da{j
существенно меньше напряжений а = -р, появляющихся
вследствие изменения объема индивидуальных частиц.
Классическим примером такого использования является
гидродинамическая теория кумуляции, разработанная академиком
М.А.Лаврентьевым в середине 1940-х годов и используемая
в настоящее время для описания процессов формирования
кумулятивных струй и их проникания в бронепреграды.
Несмотря на высокую сдвиговую прочность броневой стали (предел
текучести сгт ~ 1 ГПа), значение возникающего при
проникании кумулятивной струи давления р ~ 100 ГПа существенно
превышает значения компонент девиатора напряжений Daij ~
~ <72 ~ <тт, так что ими можно вполне обоснованно пренебречь
(Dpij/p ~ 0,01), и физические соотношения для броневой
стали в этих условиях принимают вид сг^- = -pgij + D^ij ~ ~P9ij >
характерный для модели идеальной жидкости.
Термодинамические особенности модели идеальной
среды определяются тем, что эта среда характеризуется
отсутствием касательных напряжений, а следовательно,
отсутствием какого-либо внутреннего трения и способности к
диссипации энергии при деформировании. Наиболее ясно это видно
на примере идеальной баротропной среды. Действительно, с
учетом физических соотношений C.16), кинематических
соотношений C.6), а также с помощью операций тензорной
алгебры (операций жонглирования индексами) уравнение энергии
C.3) в адиабатическом приближении преобразуется
следующим образом:
= -0,5р(р) (Viivjg* ) + V,W )) =
= -0, Ър{р) (УУ + V,V ) = -р(р) V.V,
а с учетом уравнения неразрывности C.1) приводится к виду
dE p(p) dp
dt p2 dV
251

свидетельствующему о зависимости удельной внутренней
энергии только от плотности: Е = Е(р). При нагружении
такой среды внешними силами и возникновении в ее
индивидуальных частицах давления р ф ро (здесь ро — давление в
недеформированной идеальной среде с начальной плотностью
ро) плотность частиц будет меняться от начального значения
ро до некоторого значения р ф ро при одновременном
изменении удельной внутренней энергии от начальной Е(ро) до
некоторой Е(р) ф Е{ро)- В случае снятия нагрузок
последуют разгрузка идеальной среды до начального давления р§
и возврат к моменту достижения этого давления к
начальным значениям плотности ро и удельной внутренней энергии
Е(ро). Подобное поведение идеальной среды при ее
адиабатическом нагружении и последующей разгрузке говорит о том,
что процесс дефбрмирования ее частиц является обратимым
и допускает самопроизвольное протекание в обратном
направлении с возвратом к исходному состоянию. Для такой
среды величина некомпенсированной теплоты х (часть удельной
мощности деформирования, определяющая часть работы
деформации, необратимо переходящую во внутреннюю
тепловую энергию) равна нулю. В соответствии со вторым законом
термодинамики B.89) удельная энтропия S (обозначаемая во
второй главе как 5 ) индивидуальных частиц идеальной среды
может меняться только за счет их теплообмена с
окружающими частицами:
Л "Х р ~ р '
Деформирование же идеальной среды в адиабатических
условиях (Vtg* = 0) происходит при неизменной энтропии ее
частиц (dS/dt = 0).
3.3.2. Вязкая жидкость
Вязкая (идеально, или совершенно, вязкая) жидкость —
это изотропная сжимаемая сплошная среда, сдвиговое и
объемное сопротивление которой линейно зависит от скоростей
252

деформаций. Подобная среда реагирует на изменение объема
ее частиц и на скорость его изменения, причем каждый из этих
факторов деформирования i(Se) ф О, Eg) ф 0J вносит свой
вклад в шаровой тензор напряжений EV). Вязкая жидкость
реагирует также на скорость изменения формы частиц, и
наличие фактора деформирования (D^) ф О вносит свой вклад
в девиатор напряжений (D^) ф 0. В то же время само
изменение формы частиц ({D?) ф 0J вязкой жидкости не
вызывает появления дополнительных касательных напряжений,
т.е. девиатор напряжений определяется только скоростным
фактором.
Согласно модели вязкой жидкости, уравнения,
определяющие физическое и механическое поведение среды, выглядят
соответственно как
C.17)
C.18)
где А и /I — динамические коэффициенты объемной и
сдвиговой вязкости; ё — средняя скорость деформаций. Из
определяющих уравнений C.17) и C.18) следуют физические
соотношения для модели вязкой жидкости, принимающие форму
закона Навье — Стпокса:
atj = -р(р, Т) gtj + (ЗА - 2/i) egij + 2^. C.19)
В частном случае при А = /х = 0 из закона Навье — Стокса
получаются физические соотношения C.16) для модели
идеальной жидкости, а сама модель идеальной жидкости может
рассматриваться как частный случай модели вязкой
сжимаемой среды.
Практически все реальные жидкости и газы в той или
иной степени обладают вязкими свойствами. Например, даже
при малых скоростях деформаций сильно проявляются
вязкие свойства у таких жидкостей, как масло, глицерин, нефть,
253

и для их описания необходимо использовать закон Навье —
Стокса C.19). Для таких же реальных деформируемых сред,
как вода, воздух, значения динамических коэффициентов
объемной и сдвиговой вязкости малы, что позволяет при малых
скоростях деформаций (ё, S{j) пренебречь вязкими
составляющими в законе Навье—Стокса и использовать, как уже
отмечалось в разделе 3.3.1, физические соотношения C.16)
для модели идеальной среды. Однако для описания физико-
механических свойств этих же сред при высоких скоростях
деформаций необходимо использовать уже полный закон
Навье— Стокса, так как вязкие составляющие C.19) могут
оказаться соизмеримыми с давлением р или даже превосходить
его, несмотря на малые значения коэффициентов вязкости А
и /i. Такая необходимость появляется, например, при физико-
математическом моделировании гиперзвукового обтекания
летательного аппарата воздушной средой.
С точки зрения термодинамических особенностей вязкая
среда существенно отличается от идеальной наличием
внутреннего трения, приводящего к диссипации энергии и к
необратимому переходу части работы деформации во
внутреннюю тепловую энергию. Покажем это на примере вязкой баро-
тропной среды, у которой возникающее в частицах давление
зависит лишь от плотности (р = р(р)) и не зависит от
температуры.
С учетом физических соотношений C.19) выражение для
удельной мощности деформирования приобретает вид
+ (ЗА -
Р
Р{р) dp (ЗА -
где Т\(ё) = g%^eij = 3ё — первый (линейный) основной
инвариант тензора скоростей деформаций, взаимосвязанный
со средней скоростью деформаций ё, а Т2(ё) = eX3kij —
второй (квадратичный) основной инвариант этого же тензора,
254

взаимосвязанный с интенсивностью скоростей деформаций
'а и с первым основным инвариантом как ё,- = (у/2/3) х
Хл/ЗТ2(?) - Т2(е) (полная аналогия с определением
производного инварианта тензора деформаций — интенсивности
деформаций, см. раздел 2.2.3). С помощью приведенных
взаимосвязей между основными и производными инвариантами
тензора скоростей деформаций выражение для удельной
мощности деформирования в вязкой баротропной среде может быть
преобразовано, а уравнение энергии в адиабатическом
приближении примет вид
dE ^ai4lj ^p(p)dp | 3ЗЛб2+/хб?
dt р p2 dt p
Нетрудно видеть, что находящаяся в правой части
уравнения энергии удельная мощность деформирования для
вязкой среды разделяется на две принципиально разные части
— обратимую и необратимую. Первая часть (р(р)/р2) (dp/dt)
описывает возможные случаи как увеличения, так и
уменьшения удельной внутренней энергии, меняя знак в зависимости
от того, нагружается ли индивидуальная частица вязкой
среды (увеличение плотности и удельной внутренней энергии)
или же в ней реализуются условия разгрузки (уменьшение
соответствующих значений). Вторая часть 3 C\e2+fie2)/p > О
"действует" только в сторону увеличения удельной
внутренней энергии независимо от того, нагружается или
разгружается данная индивидуальная частица. Эта существенно
положительная часть удельной мощности деформирования и
определяет величину некомпенсированной теплоты х Для вязкой
среды, а физически соответствует части работы деформации,
диссипируемой при деформировании вязкой среды и
переходящей во внутреннюю тепловую энергию. С учетом этого
дифференциальное уравнение второго закона термодинамики для
вязкой среды принимает вид
dS ЗАё2 + /хё? V.V
dt p p
откуда следует, что в адиабатических условиях (У,д* = 0)
энтропия идивидуальных частиц деформируемой вязкой среды
может изменяться только в сторону увеличения: dS/dt > 0.
255

3.3.3. Упругая среда
Упругая (идеально, или совершенно, упругая) среда —
это изотропная сплошная среда, сдвиговое и объемное
сопротивления которой линейно зависят от деформаций. В
качестве определяющих уравнений для модели упругой среды
выступают уравнения, устанавливаемые на основе опытных
данных по деформированию твердых тел (металлов и их
сплавов, пластмасс и т.п.) при малых деформациях. Этим же
обстоятельством определяется область практического
использования данной модели сплошной среды.
Так, из экспериментов по всестороннему сжатию
твердых тел при малых объемных деформациях
устанавливается прямо пропорциональная зависимость среднего напряжения
от средней деформации, выражаемая уравнением Бриджмена
C.12) и определяющая физическое поведение упругой среды.
В более общем случае, с учетом влияния температуры,
физическое поведение упругой среды описывается уравнением Дю-
амеля — Нейманна:
<T = 3K[e-ai(T-T0)], C.20)
где К — модуль объемного сжатия; а/ — коэффициент
линейного теплового расширения материала; Т и Го —
соответственно текущая и начальная температуры материала.
Уравнение Дюамеля — Нейманна может быть представлено в более
"прозрачном" для понимания виде: Зе = в = а/1Г+За/(Т-То),
показывающем, что вклад в объемную деформацию в при
деформировании индивидуальных частиц упругой среды вносят
всестороннее сжатие или растяжение и нагрев, при этом
влияние фактора нагрева проявляется в зависимости от
коэффициента объемного теплового расширения av — За/.
В то же время из экспериментов по кручению
тонкостенных металлических труб, в которых в индивидуальных
частицах среды реализуется напряженно-деформированное
состояние чистого сдвига, устанавливается прямо пропорциональная
256

зависимость касательных напряжений от сдвиговых
деформаций, приводящая к выводу о существовании следующей
взаимосвязи между девиаторами напряжений и деформаций:
(Da) = 2G(De), C.21)
где G — модуль упругости второго рода (модуль сдвига).
Уравнение C.21) принимается в качестве определяющего
механическое поведение упругой среды. Из уравнения C.21)
следует скалярное определяющее уравнение — прямо
пропорциональная зависимость интенсивности напряжений от
интенсивности деформаций:
ах =
= ^ 2G y/wi'Ddj = 3G ^
Из определяющих уравнений C.12) (или C.20)) и C.21)
следуют физические соотношения для модели упругой среды,
принимающие форму обобщенного закона Гука.
Компоненты девиатора напряжений (см. C.21)) могут быть
выражены через компоненты девиатора деформаций как <j{j - ад^ =
= 2G (eij — egij). Отсюда в случае выражения среднего
напряжения а через среднюю деформацию е из уравнения Бридж-
мена C.12) следуют прямые физические соотношения в
виде зависимостей компонент тензора напряжений от компонент
тензора деформаций:
= 2G [et; + (Ц - l) еду]. C.22)
Обратные физические соотношения (зависимости компонент
тензора деформаций от компонент тензора напряжений)
получаются аналогичным образом и имеют вид
4 (М8)
9-9712
257

Обобщенный закон Гука описывает все частные
проявления упругого поведения деформируемых сред,
реализующиеся в простых случаях напряженно-деформированного
состояния. Так, для деформированного состояния чистого
сдвига (?12 Ф О, ?И = ?22 = ?33 = ?13 = ?23 = 0) соглас-
но C.22) реализуется напряженное состояние <т\2 = 2G?i2,
0"ll = ^22 = ^33 = 03 = а23 = 0 с прямо пропорциональ-
ной зависимостью касательных напряжений от сдвиговых
деформаций. Деформированному состоянию всестороннего
равноосного растяжения или сжатия (бц = ?22 = ?33 =: ? Ф 0,
е- = 0 при г ф j) соответствует такое же напряженное
состояние: <7ц = Oil = 0*33 = & = 3i^?, G12 = СГ13 = G23 = 0.
Напряженному состоянию одноосного растяжения (аи ф 0,
02 = ^33 = 012 = ^13 = 03 = 0, G = 0"ц/3) отвечает
трехосное деформированное состояние: 6{j = 0 при г ф jf, и
C.24)
2G-ZK 3K-2G
?22 - ?33 -
где ? = 18KG/FK + 2G) — модуль упругости первого рода
(модуль Юнга), ai/ = CK - 2G)/FK + 2G) — коэффициент
Пуассона.
Модуль Юнга Е и коэффициент Пуассона и в дополнение
к модулю сдвига G и модулю объемного сжатия К являются
еще одной парой упругих характеристик, через которые
может быть представлен обобщенный закон Гука. Выражая
модуль объемного сжатия и модуль сдвига через модуль Юнга
и коэффициент Пуассона как
кё G=mvy C-25)
можно получить запись физических соотношений для модели
упругой среды в форме
Е
l + v
1 + v ( Zv
258

Следует отметить, что имеющаяся взаимосвязь между парами
упругих характеристик C.25) позволяет ограничиться
экспериментальным определением лишь двух из них с
последующим расчетом двух других. Наиболее просто определяются
из опытов значения модуля Юнга Е (одноосное растяжение
образцов) и модуля сдвига G (кручение образцов с
реализацией напряженно-деформированного состояния чистого сдвига).
Уравнения C.12), C.21) и C.24) позволяют истолковать
физический смысл упругих характеристик G,E,v, К. Как
следует из C.21), модуль сдвига G определяет касательные
напряжения, возникающие в упругой среде при чистом сдвиге.
В соответствии с C.24) модуль Юнга Е определяет
продольные деформации, возникающие при одноосном растяжении, а
коэффициент Пуассона и — соотношение поперечной и
продольной деформаций в этом же случае. Согласно уравнению
Бриджмена C.12), модуль объемного сжатия К определяет
среднее напряжение в зависимости от объемной деформации
в и, напротив, характеризует объемную деформацию,
возникающую в частицах упругой среды, когда в них существует
давление р = -а: в = 3? = а/К.
Важным частным случаем модели упругой среды
является так называемая несжимаемая упругая среда, объем
индивидуальных частиц которой не изменяется при любом уровне
давления (или среднего напряжения). Для такой среды 0 = 0,
модуль объемного сжатия К = оо, а коэффициент Пуассона
v = 0,5 в соответствии с C.25). Для реальных же
твердых тел, обладающих сжимаемостью и по своим свойствам
близких к модели упругой среды, коэффициент Пуассона v =
= 0,2. ..0,3.
Термодинамические особенности модели упругой среды
определяются тем обстоятельством, что процесс
адиабатического деформирования ее частиц является обратимым (по
определению свойства упругости, см. раздел 3.2.2) и в случае
снятия нагрузок сопровождается самопроизвольным
протеканием в обратном направлении с уменьшением до нуля
напряжений и деформаций и возвратом в исходное состояние. Для
о« 259

такой среды отсутствует переход механической работы
деформации во внутреннюю тепловую энергию (х = 0), энтропия
индивидуальных частиц может изменяться только за счет
теплообмена с окружающими частицами: Т dS/dt = Х~^Шг/Р =
= — V{ql/р. Деформирование же упругой среды в
адиабатических условиях (Vj^1 = 0) имеет изоэнтропический характер
dS/dt = 0.
3.3.4. Жесткопластическая среда
В рамках модели жесткопластической среды
учитывается проявление лишь одного из механических свойств —
свойства пластичности. Физические соотношения для модели
такой среды имеют вид
3 к{ ( ,
eij = 2^ ^*i " a9%jh
где ki — интенсивность скоростей деформаций; стт — предел
текучести материала.
Физические соотношения для модели жесткопластической
среды могут быть получены как частный (предельный)
случай одной из сложных моделей сплошных сред — модели упру-
гопластической среды.
3.4. Модель упругопластической среды
Под сложными моделями сплошных сред понимаются
модели, в которых учитываются два и более основных
механических свойства. К числу таких моделей относятся, например,
упругопластическая, вязкоупругая, вязкопластическая, упру-
говязкопластическая среды. В этом разделе
рассматривается одна из сложных моделей — модель упругопластической
среды, наиболее широко используемая при математическом
моделировании процессов деформирования твердых тел.
Модель упругопластической среды соответствует твердым
телам (главным образом, металлам и их сплавам), которые при
260

нагружении работают упруго, пока не выполняется
некоторое предельное условие, называемое условием пластичности,
а при дальнейшем нагружении такой среды в ней развиваются
не только упругие, но и пластические деформации.
Для реальных упругопластических сред характерны
диаграммы механического поведения (диаграммы
деформирования) сг{ = 0"j(e,-), подобные диаграмме, приведенной на
рис. 3.3, в для мягкой стали (типа стали 10). В ряде
случаев диаграммы деформирования реальных металлов могут
несколько отличаться от показанной на рис. 3.3, в в сторону
усложнения (например, включать участок нелинейной
упругости) или в сторону упрощения (например, для некоторых
металлов отсутствует площадка текучести и после
упругого участка сразу происходит переход к участку
упрочнения) и включать дополнительные характерные точки: в
первом случае такой точкой является предел упругости,
больший предела пропорциональности, а во втором —
условный предел текучести, соответствующий заданному уровню
остаточной пластической деформации. Однако при
построении модели упругопластической среды, как правило,
пренебрегают такими тонкими особенностями и
рассматривают идеализированные диаграммы механического поведения,
подобные показанным на рис. 3.9. Наиболее часто в
качестве таких идеализированных диаграмм механического
поведения рассматриваются диаграммы для идеальной упруго-
пластической среды, для которой пределы
пропорциональности, упругости, текучести и прочности ассоциируются с
одним и тем же значением ат (рис. 3.9, а), и для
упругопластической среды с линейным (рис. 3.9, б) или нелинейным
6U
4
Рис. 3.9
цв
261

(рис. 3.9, в) упрочнением. Возможными вариантами
упрощенных диаграмм механического поведения являются
диаграммы идеальной жесткопластической среды (рис. 3.9, г) или
жесткопластической среды с упрочнением (рис. 3.9, <?), причем
для двух последних случаев характерно отсутствие упругого
участка (упругими деформациями по сравнению с
пластическими пренебрегают).
Модель упругопластической среды является сложной не
только по формальному признаку (принимаются во
внимание свойства упругости и пластичности), но и с точки
зрения уровня сложности математического описания. Отметим,
что в случае малых деформаций (превышающих упругие, но
соизмеримых с ними) модель упругопластической среды
хорошо описывается деформационной теорией пластичности
(теория малых упругопластических деформаций). При больших
(конечных) деформациях для описания поведения
упругопластических сред более предпочтительна теория пластического
течения.
3.4.1. Деформационная теория пластичности
(теория малых упругопластических деформаций)
Деформационная теория пластичности справедлива для
малых деформаций и для случаев так называемого простого
нагружения. В рамках этой теории предпринимается и
реализуется попытка сформулировать определяющие уравнения и
физические соотношения для модели упругопластической
среды с учетом проявления пластических свойств материала, но
при минимально возможном отклонении от структуры
соответствующих уравнений для модели упругой среды.
Интуитивно ясно, что достичь компромисса в отношении двух этих
противоречивых требований (учесть пластичность без
существенного выхода за рамки структуры определяющих
уравнений для модели упругой среды) можно лишь при
незначительном выходе за рамки упругости. Именно этим
объясняются ограничения в применимости этой теории, которая
распространяется лишь на случаи малых деформаций.
262

Под простым погружением упругопластической среды
понимается такое ее нагружение, когда все внешние силы
изменяются пропорционально некоторому общему параметру
(чаще всего времени t), так, что соотношения между
компонентами нагрузок остаются постоянными и не зависящими от
этого параметра. Например, при нагружении
металлического бруса растягивающей силой Р и крутящим моментом М
(рис. 3.10, а) процесс нагружения будет простым, если
внешние силы изменяются как Р = k\t, М = k<it, т.е. в
плоскости (М, Р) закону совместного изменения внешних сил
соответствует прямая (рис. 3.10, б). Процесс нагружения не
будет простым, если, например, к нагружаемому брусу
вначале прикладывается только
крутящий момент, который
постепенно возрастает до
максимального значения, а - ^
затем при неизменном
моменте увеличивается
растягивающая сила. В этом
случае закон совместного
изменения внешних сил в
плоскости (М, Р) будет
изображаться ломаной линией с резким
изменением характера
приложения нагрузки (рис. 3.1, в).
Иначе говоря, простое
нагружение — это равномерный,
односторонний, монотонный
процесс приложения
нагрузок. При таком нагружении
столь же монотонно будут
изменяться характеристики
деформированного и напряженного состояний в любой
индивидуальной частице деформируемого тела, т.е. для любого
момента времени можно рассчитывать на пропорциональность
характеристик напряженно-деформированного состояния
подобно зависимостям для упругой среды (см. определяющие
уравнения C.12), C.21)).
М
Рис. ЗЛО
263

Уравнения, определяющие физическое и механическое
поведение упругопластической среды в рамках деформационной
теории пластичности, внешне очень похожи на
соответствующие уравнения C.12), C.21) для модели упругой среды и
выглядят как
о = ЪКг, (Dff) = B(De), C.26)
где, в отличие от модуля сдвига G в уравнении C.2.1),
коэффициент пропорциональности В между девиаторами
напряжений и деформаций не является постоянной величиной, но
представляет собой так называемый функционал
пластичности, который учитывает проявление пластических свойств.
Физическое поведение упругопластической среды
описывается чисто упругим уравнением Бриджмена C.12).
Подобная особенность математического описания
физико-механических свойств упругопластической среды учитывает
экспериментальные факты, согласно которым остаточные
пластические деформации связаны с изменением формы
индивидуальных частиц, но не с изменением их объема: после
полной разгрузки (полное исчезновение внутренних напряжений)
предварительно нагруженного выше предела упругости
металлического образца его объем остается неизменным и
равным исходному значению, что говорит об обратимом, упругом
характере изменения объемной деформации в = Зе в
зависимости от напряжений.
Выражение для функционала пластичности Б,
позволяющее вычислять конкретные его значения, может быть
получено с помощью специальной функции — функции пластичности
Ильюшина и = v(ei), вводимой в рассмотрение в
деформационной теории пластичности. Эта функция определяется
следующим образом. На рис. 3.11, а приведена
схематизированная диаграмма деформирования упругопластической среды с
упрочнением. На упругом участке О Л имеется прямо
пропорциональная зависимость между интенсивностями деформаций
и напряжений. За пределами упругости, на участке AD>
начинают проявляться пластические свойства, а зависимость
<7г- = сг{(в{) отклоняется от линейной. Это отклонение и
учитывается функцией пластичности Ильюшина
1 -и/), C.27)
264

где комплекс A — и) выполняет роль корректирующего
множителя по отношению к чисто упругому закону <7t = 3Get.
При заданной
диаграмме деформирования упруго-
пластической среды О{ —
= 0ifa) однозначно
определяется значение функции
пластичности
по соотношению
соответствующих отрезков M\M<i и
М0М2 на диаграмме
деформирования (см. рис. 3.11, а).
Характер изменения
функции пластичности и = u;fa)
показан на рис. 3.11,6: в
пределах упругости и = О
с последующим монотонным
возрастанием в области
пластичности.
Выражение для функционала пластичности В
конкретизируется следующим образом. Из уравнений C.26) следует
взаимосвязь между вторыми основными инвариантами девиа-
торов напряжений и деформаций:
Т2(Д.) =
= B2D?Deij = B2T2(D?).
С учетом известной из теорий напряжений и деформаций
взаимосвязи между вторыми основными инвариантами девиа-
торов тензоров напряжений и деформаций и интенсивностями
напряжений и деформаций
265

приходим к выражению В = 2G,-/C?,-) или с учетом C.27) — к
окончательному выражению для функционала пластичности
В = 2GA - и). В результате определяющие уравнения для
модели упругопластической среды, описываемой
деформационной теорией пластичности, приобретают вид
а = 3#?, (Da) = 2G A - и) (D?). C.28)
Очевидно, что определяющие уравнения C.28)
действительно отличаются от уравнений для модели упругой среды
некоторым корректирующим множителем A — а;),
учитывающим пластические свойства материала. Это же присуще и
физическим соотношениям, которые образуются из
определяющих уравнений C.28). Прямые физические соотношения для
модели упругопластической среды имеют вид
Ч = 2G [?у + (|| - l) ед;] - 2Gu> (etj - s9ij), C.29)
а обратные физические соотношения выглядят как
е« = h Ь+(i) Ч+2G(ib) (^-^)- C-30)
При этом также нетрудно видеть, что напряжения,
возникающие в упругопластической среде, меньше, чем они были бы
при чисто упругой работе материала при данных
деформациях Sijy и, напротив, деформации, возникающие при данных
напряжениях а|;, превышают деформации, реализующиеся в
упругой среде. Из обратных физических соотношений C.30)
следует условие аддитивности деформаций в
упругопластической среде, согласно которому полные деформации
складываются из упругих составляющих
2G -• <3-31>
266

подчиняющихся обобщенному закону Гука, и пластических
составляющих
(р) _
€;/ =
C.32)
2G(l-u)
зависящих от функции пластичности Ильюшина.
Прямые и обратные физические соотношения C.29) и
C.30) для модели упругопластической среды, описываемой
деформационной теорией пластичности, справедливы в
случае простого нагружения материала, находившегося в
исходном (недеформированном) состоянии. Простое нагруже-
ние является частным случаем более общего процесса —
процесса нагружения
упругопластической среды,
когда с течением времени
происходит увеличение
интенсивности деформаций в
индивидуальных частицах
среды (участок ОАВ на
рис. 3.12). Однако в упру-
гопластических средах
могут реализовываться и иные
процессы — процессы
разгрузки , сопровождающиеся
уменьшением интенсивности деформаций в частицах среды с
течением времени (участок ВМС на рис. 3.12).
Математическое описание процесса разгрузки в упруго-
пластических средах базируется на экспериментально
установленном факте: разгрузка упругопластической среды
происходит упруго по отношению к предварительно нагруженной
среде. Определяющие уравнения для процесса разгрузки
упругопластической среды соответствуют определяющим
уравнениям C.12) и C.21) для модели упругой среды, но с тем лишь
отличием, что записаны они по отношению к приращениям
компонент тензоров напряжений и деформаций:
До- = ШАе, Д(Ат) = 2GA(D?).
267

Соответственно и физические соотношения, описывающие
разгрузку упругопластической среды, являются обобщенным
законом Гука, записанным в приращениях:
= 2G
C.33)
где приращения напряжений и деформаций определяются по
их разности в текущем состоянии реализующейся разгрузки
(точка М на рис. 3.12) и в состоянии окончания процесса на-
гружения и начала разгрузки (точка В на рис. 3.12).
В частности, при полной разгрузке упругопластической
среды (точка С на рис. 3.12) соотношения C.30) и C.33)
позволяют показать, что остаточные деформации ef-' = E{j + A?tj
в упругопластической среде действительно определяются
соотношением C.32), тогда как часть деформаций e\j C.31),
возникших в результате нагружения, действительно
являются обратимыми и исчезают при исчезновении напряжений.
3.4.2. Критерий пластичности
и поверхность пластичности
Под критерием (или условием) пластичности
понимается некоторое предельное условие (взаимосвязь между
компонентами тензора напряжений или тензора деформаций), при
выполнении которого упругопластическая среда уже не
подчиняется только упругим соотношениям и в ней начинают
развиваться пластические деформации. В простейшем
случае напряженного состояния — при одноосном растяжении
— в качестве такого условия выступает условие достижения
единственной отличной от нуля компонентой тензора
напряжений некоторого предельного значения. На рис. 3.13 для
идеализированной диаграммы одноосного растяжения с
линейным упрочнением в качестве такого предельного
значения выступает значение предела текучести при одноосном
268

растяжении <7ц = <тт. В
более сложном случае, когда
напряженное состояние в
упругопластической среде
характеризуется тензором
напряжений (<т) с девятью
отличными от нуля
компонентами, предельное
условие не является столь
очевидным. Однако с учетом
того, что любое
напряженное состояние может
характеризоваться тензором
напряжений
(а) =
задаваемым в декартовой прямоугольной системе
координат главных осей (ту1, г/2, т/3) через свои главные значения
0*1 > a2i 0"з> поиск выражения для предельного условия может
быть существенно облегчен и сведен к установлению между
главными напряжениями а\, а2, <тз взаимосвязи
Рис. 3.13
, o2, сг3) = 0,
C.34)
соответствующей переходу от упругости к пластичности.
Иначе говоря, критерий пластичности удобно рассматривать
в пространстве главных напряжений.
Под пространством главных напряжений понимается
некоторое трехмерное пространство, каждой точке которого
соответствуют определенные значения каждого из трех главных
напряжений а\, о2 > ^3 • В пространстве главных напряжений
может быть введена декартова прямоугольная система
координат (рис. 3.14), в которой начало координат (точка 0)
соответствует ненагруженному состоянию, а по осям откладываются
возможные значения главных напряжений. В такой системе
269

6,
Упругое
состояние
V
Рис.
/
и
3.14
^^Ч. ? Ji dk
{ Пластическое
\ А состояние
} *
/ *
FFubz,63)=0
координат удобно изображать различные напряженные
состояния. Например, точки на координатных осях а\у o<i, &ъ
соответствуют напряженным состояниям одноосного растяжения
или сжатия, точки на пространственной диагонали системы
координат (прямая, равнонаклоненная к осям <ti, 0*2, сгз)
соответствуют всестороннему равноосному растяжению
(положительный октант) или сжатию (отрицательный октант).
Критерию же пластичности C.34) в пространстве главных
напряжений соответствует некоторая поверхность — поверхность
пластичности, при этом точки, расположенные внутри
поверхности пластичности, соответствуют упругому состоянию
материала, а точки на поверхности и за ее пределами —
пластическому состоянию.
Известно несколько критериев пластичности для
твердых тел с упругопластическими свойствами, однако среди них
выделяется критерий пластичности Мизеса, наиболее
распространенный и хорошо удовлетворяющий опытным данным
для металлов и их сплавов. По своей природе критерий
пластичности Мизеса является энергетическим критерием.
Согласно этому критерию, переход упругопластической среды
из упругого состояния в пластическое происходит тогда,
когда удельная энергия упругого изменения формы
достигает своего предельного значения. Этот экспериментально
подтверждающийся факт лежит в основе получения
математического выражения, конкретизирующего общий вид предельного
условия C.34).
270

Выражение для удельной энергии деформации упругопла-
стической среды, находящейся в упругом состоянии, может
быть получено с помощью интегрирования уравнения
энергии pdE/dt = cr%Hij с учетом естественного для упругого
состояния предположения о малых деформациях (tij dt = d?,j,
Р = />о/A + Зб) и ро), с использованием разложения тензоров
напряжений и деформаций на шаровую и девиаторную
составляющие и с учетом физических соотношений C.12), C.21)
для модели упругой среды. Учитывая указанные
предположения, а также равенство нулю первых основных
инвариантов девиаторов напряжений и деформаций, уравнение энергии
преобразуем к виду
dE = G%3de%>
Ро ро
_ За de + P{J dDetj _ За da/CK) + P{J dPaij/BG)
Ро Ро
из которого после интегрирования получим выражение для
удельной потенциальной энергии деформации
2Кр0 + 4Gp0 '
позволяющее выделить в ней две части, одна из которых
связана с изменением объема индивидуальных частиц Еу =
= <72/Bif/9o), а другая определяется их формоизменением
Как следует из результатов экспериментов, значение
удельной энергии формоизменения, предельно
"выдерживаемое" упругопластической средой при работе в упругом
режиме, не зависит от вида напряженного состояния и в силу этого
может быть определено по любому известному условию
перехода от состояния упругости к состоянию пластичности,
например по известным условиям предельного перехода при
одноосном растяжении:
^п = ^т; сг22 = ^зз = <7i2 = ^13 = <?23 = 0; а = сгт/3;
Aril = 2<тт/3; Аг22 = -*т/3; АтЗЗ = -*т/3;
Dcnj = 0, %ф j.
271

Предельно допустимое значение удельной энергии упругого
формоизменения определится как Е* = a^/FGpo)> и
математическое выражение для энергетического критерия
пластичности Мизеса Е3 = Е* применительно к произвольному
напряженному состоянию примет вид
D*JDaij = 2*2/3, C.35)
а с учетом взаимосвязи второго основного инварианта де-
виатора напряжений с интенсивностью напряжений (<7,- =
= (\/2/2)л/ЗТ2(Дх) = (л/2/2) y/w'jD^j ) его можно свести к
условию равенства интенсивности напряжений пределу
текучести при одноосном растяжении в{ — сгт. При представлении
интенсивности напряжений через главные напряжения B.47)
получается окончательное выражение для критерия
пластичности Мизеса в пространстве главных напряжений:
(*1 - °2? + (*2 ~ *3J + (*3 " "l)* = 2^т- C.36)
Геометрическим образом критерия пластичности Мизеса
C.36) в пространстве главных напряжений, или поверхностью
пластичности, является прямой круговой цилиндр, ось
которого совпадает с пространственной диагональю а\ = оъ — ^3
системы координат, а радиус R определяется значением
предела текучести ат. В этом легко убедиться, составив
каноническое уравнение такого цилиндра в декартовой прямоугольной
системе координат пространства главных напряжений.
Произвольному напряженному состоянию 0"ь 0*2, <7з в
пространстве главных напряжений соответствует точка А
(рис. 3.15), положение которой относительно точки 0,
принятой за начало координат, характеризуется радиус-вектором
а = crjг + СГ2j + а*з fc. Ориентация пространственной диагонали
системы координат (<ji, G2, 03) задается единичным вектором
п — i/y/З + j/л/З + fc/\/3, равнонаклоненным к
координатным осям. Проекция вектора о-, соответствующего данному
напряженному состоянию, на направление пространственной
272

R
Рис. 3.15
диагонали определится как otn\ = а • п = (crj + 02 + 0"з)/\/3.
Условие нахождения точки А в пространстве главных
напряжений на цилиндрической поверхности радиусом R
выражается как \<т\2 - о1, ч = Д2, где |а| = \1а\ + сг| + сг| — модуль
вектора а. Таким образом, в пространстве главных
напряжений уравнение цилиндрической поверхности радиусом R с
осью, совпадающей с пространственной диагональю системы
координат, определится как
°\ + *2 + ^з " (*1 + °2 + *зJ/3 = R2
или же как
Последнее выражение полностью соответствует записи
критерия пластичности Мизеса C.36), и это, с одной стороны,
подтверждает, что поверхность пластичности по этому
критерию является круговой цилиндрической с равнонаклоненной
к осям координат осью, а с другой стороны, позволяет
определить радиус этого цилиндра R = ат у/2/3.
Как уже отмечалось выше, важным частным случаем
модели упругопластической среды является модель
идеальной упругопластической среды с диаграммой механического
поведения, показанной на рис. 3.9, а. В рамках такой
модели предполагается, что пластическое деформирование
происходит при постоянном значении интенсивности напряжений
273

а\ = <jT, что соответствует непрерывному выполнению
критерия пластичности C.36) в процессе пластического
деформирования. Для такой модели в пространстве главных напряжений
упругим напряженным состояниям материала будут
соответствовать точки внутри цилиндра Мизеса (см. рис. 3.15), а
пластическим напряженным состояниям — точки на
поверхности цилиндра, при этом выход изображающих напряженные
состояния точек за пределы цилиндра Мизеса исключен.
3.4.3. Теория пластического течения
Представленная в разделе 3.4.1 деформационная теория
пластичности хорошо описывает поведение упругопластиче-
ских сред в случаях малых упругопластических деформаций
и простого нагружения, позволяя установить взаимно
однозначное соответствие между напряжениями и деформациями
согласно физическим соотношениям C.29) и C.30).
Однако достаточно часто, особенно в случаях динамического
нагружения элементов конструкций, процессы нагружения не
являются простыми: они сопровождаются многократными
разгрузками, повторными нагружениями и большими
деформациями. Характерным примером является процесс
высокоскоростного деформирования металлической облицовки
кумулятивного заряда под действием давления продуктов
детонации взрывчатого вещества, что приводит к
формированию металлической кумулятивной струи. При нагружении
кумулятивной облицовки продуктами детонации давление на
ее поверхности меняется как монотонно убывающая функция
времени, и уже одно это не позволяет отнести такой процесс
к случаю простого нагружения. Кроме того,
распространяющиеся в облицовке волны сжатия и разрежения
(чередующиеся нагружение и разгрузка) приводят к тому, что одному
и тому же значению интенсивности деформаций могут
соответствовать различные значения интенсивности напряжений
в зависимости от того, каким путем получена данная
деформация: в результате ли "первичного" нагружения (путь ОАВ
274

Рис. 3.16
на рис. 3.16) или же после упругой разгрузки (путь 0ABCD на
рис. 3.16). Последующее деформирование кумулятивной струи
в свободном полете
является экстремальным
примером реализации больших
деформаций, когда отдельные
элементы струи
испытывают к моменту ее разрыва
более чем двадцатикратные
удлинения, что
соответствует деформациям, примерно
в 104 раз превышающим
упругие. В таких
условиях применять для
описания поведения упругопла-
стических сред
деформационную теорию пластичности
не представляется возможным. Эта теория не описывает
поведение подобных сред в общем случае, но лишь характеризует
свойства частного и наиболее простого процесса — процесса
простого нагружения.
Следует отметить, что в настоящее время
отсутствует строго обоснованная теория поведения упругопластических
сред в случаях произвольных деформаций и сложного
нагружения. Более всего известным экспериментальным данным
соответствует теория пластического течения. В отличие от
деформационной теории пластичности теория
пластического течения является инкрементальной теорией (инкремент
— приращение). В ней рассматривается изменение
характеристик напряженно-деформированного состояния за каждый
бесконечно малый интервал времени dt и устанавливаются
взаимосвязи между соответствующими приращениями
компонент тензора деформаций deij и напряжений daij.
Определяющие уравнения для модели упругопластиче-
ской среды, раскрываемой в рамках теории пластического
течения, выражаются четырьмя предположениями, или
гипотезами.
275

1. Упругопластическая среда предполагается
изотропной.
2. Изменение объема упругопластической среды
предполагается малым, а физическое поведение — подчиняющимся
уравнению Бриджмена da = 3Kde> записаному в
приращениях.
3. Предполагается, что приращения компонент тензора
деформаций deij складываются из упругих de^ и пластиче-
j (р)
ских ае^- составляющих:
dexj = de\f + de\f. C.37)
При этом упругие составляющие приращений компонент
тензора деформаций связаны с приращениями компонент тензора
напряжений согласно обобщенному закону Гука, записанному
в дифференциальной форме:
(з-з8)
Эта гипотеза называется гипотезой аддитивности
деформаций и вполне соответствует особенностям физических
соотношений C.30)—C.32) для модели упругопластической среды
согласно деформационной теории пластичности.
4. Предполагается, что пластические составляющие
приращений компонент тензора деформаций определяются
компонентами девиатора напряжений согласно ассоциированному
закону пластического течения:
de\f = dX-Dffij, C.39)
где d\ — малый скалярный множитель.
Ассоциированный закон пластического течения обобщает
результаты опытов по сложному нагружению упругопласти-
ческих сред, из которых следует, что при сложном нагруже-
нии отсутствует пропорциональность девиаторов напряжений
276

и деформаций, подобная имевшей место при простом нагру-
жении и описываемой определяющими уравнениями C.26)
деформационной теории пластичности. В более сложном случае
имеет место приращение пластических деформаций,
пропорциональное девиатору напряжений. Ассоциированный закон
пластического течения C.39) учитывает уже отмеченный в
разделе 3.4.1 экспериментальный факт так называемой
пластической несжимаемости, согласно которому пластические
деформации связаны с изменением формы индивидуальных
частиц, но не с изменением их объема. Действительно, с
учетом условия аддитивности деформаций C.38) можно показать,
что вклад в изменение de средней деформации е вносят лишь
упругие составляющие приращений компонент тензора
деформаций:
de = de^/Ъ = (de\f + de\f) g* /3 =
тогда как пластические деформации не влияют на изменение
объема индивидуальных частиц: de^ = de^'g1* /3 = d\ x
Ассоциированному закону пластического течения может
быть дано простое физическое объяснение, основывающееся на
анализе поведения упругопластической среды в простейшем
случае напряженного состояния — случае одноосного
растяжения. На рис. 3.17 приведены три, казалось бы, возможных
варианта диаграммы g\ = cri(ei) для этого случая. Однако
опыт свидетельствует, что реально реализуются лишь
диаграммы, подобные показанной на рис. 3.17, а, и для
дополнительного пластического деформирования Ае\ > 0 требуются
дополнительные напряжения A&i > 0, т.е. удельная
работа дополнительных напряжений на дополнительных
пластических деформациях — существенно неотрицательная
величина:
> 0. C.40)
277

Обратная ситуация (рис. 3.17, б
и в) исключена, так как,
например, варианту диаграммы на
рис. 3.17, в соответствует
нарушение закона сохранения
энергии (нагружению
вертикального стержня дополнительным
грузом соответствуют
уменьшение деформаций, укорочение
стержня и подъем груза). Для
идеальной упругопластической
среды (см. рис. 3.9, а) условие
C.40) приобретает вид
= 0.
C.41)
В общем случае
напряженное состояние идеальной
упругопластической среды
характеризуется тензором напряжений,
который можно рассматривать
в некотором девятимерном
гиперпространстве как вектор с
компонентами а^ (рис. 3.18).
Поверхности пластичности в
этом гиперпространстве будет
соответствовать некоторая
гиперповерхность F(<Tij) = 0,
отвечающая критерию
пластичности Мизеса C.35). При
пластическом деформировании крайняя точка вектора с
компонентами G{j движется по поверхности пластичности, а в
случае бесконечно малого приращения напряжений dc{j
вектор можно считать направленным по касательной к
поверхности. Подобным же образом пластические составляющие
приращений компонент тензора деформаций de? ,
соответствующие данному приращению напряжений, могут рассма-
278

триваться как компоненты девятимерного вектора,
определенным образом ориентированного по отношению к вектору
приращения напряжений da {у По
аналогии с C.41) удельная
работа дополнительных напряжений
на дополнительных
пластических деформациях равна нулю
(da%:>de\j = О], что
свидетельствует об ортогональности
вектора defj вектору da {у а
следовательно, и поверхности
пластичности F((Tij) = 0. Учитывая, что
направление нормали к поверхности
пластичности в рассматриваемом
гиперпространстве определяется вектором градиента с
компонентами dF/daij = (dF/dDaij) (dD^j/daij) (суммирование
по г и j не подразумевается), и принимая во внимание уело-
(?)
Рис. 3.18
вие dDffij/do'ij = 1, условие ортогональности вектора defj
поверхности пластичности Мизеса C.35) можно привести к
виду
de\f = d\ (dF/doij) = d\ ¦ Daih
вполне соответствующему экспериментально
устанавливаемому соотношению C.39).
Из уравнений C.37)—C.39) следуют физические
соотношения для модели упругопластической среды согласно теории
пластического течения, которые могут быть записаны в
приращениях, т.е.
Sij = ^ \deij + (Ц "
или в скоростях, т.е.
C.43)
279

где e{j = deij/dt — компоненты тензора скоростей
деформаций; &{j = daij/dt — скорости изменения компонент тензора
напряжений; & = da/dt — скорость изменения среднего
напряжения; Л = dX/dt — скалярный множитель. Физический
смысл входящего в физические соотношения скалярного
множителя d\ (или Л) может быть установлен с помощью
ассоциированного закона пластического течения C.39).
Действительно, с помощью соотношений C.39) может быть получено
выражение для приращения удельной работы напряжений на
пластических деформациях
dAp = aij de\f = dX a{\a%i - agij) = dX (сг1>а^ - <r
= dX [T2(a) - Т?(*)/з] = dX [зГ2(сг) - T?(a)
которое с учетом известного из теории напряжений
выражения для производного инварианта тензора напряжений
(интенсивности напряжений) О{ — (л/2/2) л/ЗТ2(<т) - Т^(а)
позволяет установить, что значение скалярного множителя dX
определяется именно приращением удельной работы напряжений
на пластических деформациях и интенсивностью напряжений
как dX = 3dAp/Ba?). Соответственно скалярный множитель
Л будет определяться следующим образом:
где dAp/dt = сггуе\^ — удельная мощность пластического
деформирования.
Из выражений C.42)—C.44) следует, что при упругом
деформировании упругопластической среды (начальное
упругое нагружение — участок ОЛ на рис. 3.12, упругая
разгрузка и повторное упругое нагружение — участки В С и С В на
рис. 3.12), которому соответствует изменение лишь упругих
деформаций при отсутствии приращений или скоростей
пластических деформаций
dAp = 0, dAp/dt = 0, dX = 0, А = 0,
280

физические соотношения для модели упругопластической
среды согласно теории пластического течения сводятся к
закону Гука, записанному в дифференциальной форме, и, таким
образом, позволяют описывать и эти частные случаи
деформирования упругопластической среды, чем существенно
отличаются в лучшую сторону от физических соотношений C.29)
и C.30) деформационной теории пластичности, справедливых
лишь для частного случая простого нагружения из исходного
(недеформированного) состояния.
Важными и часто используемыми частными случаями
модели упругопластической среды являются идеальная упру-
гопластическая среда (см. рис. 3.9, а) и жесткопластическая
среда (см. рис. 3.9, г). Физико-механическое поведение
идеальной упругопластической среды описывается уравнениями
пластического течения Прандтля — Рейсса, также имеющими
вид C.42) и C.43), в то время как входящий в эти уравнения
скалярный множитель Л определяется соотношением
и, в частности, равен нулю при упругом нагружении или
разгрузке.
Физические соотношения для модели жесткопластической
среды (теория пластического течения Сен-Венана — Мизеса)
также следуют из общих уравнений теории пластического
течения в предположении реализации сильно развитого
пластического течения, когда упругими деформациями по
сравнению с пластическими можно пренебречь. "Скоростная" форма
C.43) записи уравнений теории пластического течения в
таких предположениях сводится к равенству
и может быть еще более конкретизирована с учетом
свойства пластической несжимаемости, приводящего к выводу об
отсутствии изменения объема индивидуальных частиц
жесткопластической среды: Ti(e) = tijg1* = tt gl* = ^Daijg%J = 0.
281

Действительно, выражение для удельной мощности
пластического деформирования в случае жесткопластической среды
(а,- = ат) может быть с учетом C.46) записано как
dAp/dt = aije\f = \{<xijatj - aa^gij) =
В то же время эта величина может быть
представлена и через производный инвариант тензора
скоростей деформаций — интенсивность скоростей деформаций
ё,- = (n/2/З) у/гТ2(ё)-Т1(ё) = (л/2/3) v/ЗВД - как
= ?%/А = Г2(ё)/А = Зё?/BА). C.47)
Из сравнения двух полученных различным путем выражений
для удельной мощности пластического деформирования
следует вывод: А = 3?|7B<7Т), а физические соотношения теории
пластического течения Сен-Венана — Мизеса для модели
несжимаемой жесткопластической среды приобретают
окончательный вид
?ij = v^-(°ij-°gij)- C.48)
Как уже отмечалось в разделе 3.3.4, модель
жесткопластической среды относится к числу простых моделей, при ее
описании учитывается лишь одно из основных механических
свойств — свойство пластичности. Отличительной
особенностью такой среды с точки зрения термодинамического
поведения является то, что при ее деформировании вся механическая
работа деформации необратимо переходит во внутреннюю
тепловую энергию. Это следует из анализа уравнения энергии в
адиабатическом приближении с учетом выражений C.47) для
удельной мощности деформирования и для значения
скалярного множителя А = 3?t/B<7T):
282

В случае жесткопластической среды удельная мощность
деформирования — существенно положительная величина
независимо от того, происходит увеличение или уменьшение
деформаций (перемещение по диаграмме деформирования,
представленной на рис. 3.9, г, вправо или влево). В силу этого
обстоятельства возврат жесткопластической среды к
исходному состоянию невозможен, процесс ее деформирования имеет
необратимый характер и происходит с увеличением энтропии:
> 0.
Вопросы и задачи
1. Что понимается под моделью сплошной среды? Какими
соотношениями описывается модель?
2. Что понимается под физическим поведением сплошной
среды, какого типа определяющими уравнениями оно
характеризуется?
3. Что понимается под уравнением состояния, какое
фундаментальное свойство деформируемых сред оно
характеризует и каким образом получается?
4. Определите понятие сжимаемости деформируемых сред.
5. В чем заключается основное отличие подходов к
экспериментальному исследованию сжимаемости деформируемых
сред в статических и динамических условиях? Каковы
уровни достигаемых давлений в обоих случаях?
6. Каким уравнением описывается сжимаемость твердых тел
при малых объемных деформациях (укажите их в перечне
основных формул к главе 3 (см. приложение 1))? В основе
какой модели сплошной среды лежит это уравнение?
7. Каков порядок максимального давления, достигаемого в
настоящее время в контролируемых условиях с
обеспечением соответствующих измерений?
283

8. Что понимается под механическим поведением сплошной
среды, какого типа определяющими уравнениями оно
характеризуется ?
9. В чем состоит особенность механического поведения
большинства реальных жидкостей и газов при малых скоростях
деформаций ?
10. Определите понятия упругости, пластичности, вязкости.
11. Как выглядит характеристика механического поведения
мягкой стали — ее диаграмма деформирования, какие
характерные точки можно указать на диаграмме?
12. Что понимается под пределами пропорциональности,
упругости, текучести и прочности?
13. В чем заключается и всегда ли существует различие
между пределами пропорциональности и упругости?
14. В чем состоит причина изменения коэффициента
пропорциональности на упругом участке диаграммы
деформирования металла при переходе от координат
"напряжение — деформация" при одноосном растяжении к
координатам "интенсивность напряжений — интенсивность
деформаций" ?
15. Каково влияние температуры на механическое поведение
металлов?
16. К чему сводится влияние скорости деформаций на
характеристики упругости, прочности и пластичности
металлов?
17. Что понимается под склерономными свойствами сплошных
сред? Как объясняется это название?
18. Что понимается под реономными свойствами сплошных
сред? Какие именно свойства относятся к числу реоном-
ных и как они проявляются?
19. Какие факторы являются определяющими при
проявлениях свойств релаксации и последействия?
20. Почему при взрывных и ударных процессах,
сопровождающихся высокими температурами, можно не учитывать
проявление свойств релаксации и последействия?
284

21. Определите понятия простой и сложной моделей сплошных
сред.
22. Какие модели сплошных сред относятся к числу простых?
23. Определите понятие идеальной среды (идеальной
жидкости или идеального газа).
24. Как выглядят определяющие уравнения и физические
соотношения для модели идеальной жидкости или идеального
газа?
25. Как следует понимать утверждение о том, что тензор
напряжений в идеальной жидкости или идеальном газе
характеризуется одной скалярной величиной? Какой именно?
26. Сколько главных осей тензора напряжений и главных
площадок можно указать в любой точке идеальной жидкости?
27. Что понимается под идеальной баротропной жидкостью?
28. Что понимается под идеальным совершенным газом?
Какой вид имеет уравнение его состояния?
29. Какие реальные деформируемые среды наиболее близки к
модели идеальной среды? В каких условиях эта модель
может использоваться для описания поведения
высокопрочной стали?
30. Могут ли в идеальной среде возникать внутренние
тепловые потери механического происхождения?
31. Как изменяется энтропия индивидуальных частиц
идеальной баротропной среды для непрерывных адиабатических
течений ?
32. В идеальной жидкости задано поле перемещений
и(х1, ж2, х3) = х1х2г1 + Зж3г2 - (ж1J/*3, которому
соответствует определенное поле деформаций ^(ж1, ж2, ж3).
Определите значение интенсивности напряжений в точке
с координатами ж1 = 2, ж2 = 3, ж3 = 4.
33. Определите понятие вязкой жидкости.
34. Как выглядят определяющие уравнения и физические
соотношения для модели вязкой жидкости (укажите их в
перечне основных формул к главе 3)?
285

35. Укажите в перечне основных формул к главе 3 закон На-
вье — Стокса. В каком частном случае он сводится к
физическим соотношениям для модели идеальной среды?
36. Верно ли утверждение об одностороннем характере
изменения энтропии индивидуальных частиц вязкой жидкости
для адиабатических течений? В чем причины этого?
37. Могут ли возникать внутренние напряжения в вязкой
жидкости при бесконечно медленном изменении формы
индивидуальных частиц? Если могут, то за счет каких факторов
деформирования ?
38. Определите понятие модели упругой среды.
39. Как выглядят определяющие уравнения, прямые и
обратные физические соотношения для модели упругой среды
(укажите их в перечне основных формул к главе 3)? Как
из определяющих уравнений получаются физические
соотношения?
40. Укажите в перечне основных формул к главе 3
обобщенный закон Гука. К каким частным случаям он
сводится для напряженно-деформированных состояний
одноосного растяжения, чистого сдвига, всестороннего равноосного
сжатия?
41. Охарактеризуйте физические величины, участвующие в
записи физических соотношений для модели упругой
среды.
42. Назовите упругие характеристики материала в рамках
модели упругой среды. Каков физический смысл каждой из
них и каков принцип установления взаимосвязи между
ними?
43. Чему равны модуль объемного сжатия и коэффициент
Пуассона для несжимаемой упругой среды?
44. Каков порядок коэффициента Пуассона для реальных
твердых тел?
45. Могут ли при деформировании упругой среды возникать
тепловые потери механического происхождения? Чему
равно значение некомпенсированной теплоты в упругой
среде?
286

46. Определите понятие упругопластической среды.
47- Какие идеализированные диаграммы деформирования
чаще всего используются при рассмотрении модели упруго-
пластической среды?
48. Что понимается под идеальной упругопластической
средой, упругопластической средой с линейным упрочнением
и жесткопластической средой?
49. Чем принципиально отличаются и для каких случаев
пригодны деформационная теория пластичности и теория
пластического течения?
50. Что понимается под простым нагружением
деформируемого твердого тела?
51. При каких допущениях справедлива деформационная
теория пластичности?
52. Как выглядят определяющие уравнения для модели
упругопластической среды согласно деформационной теории
пластичности (укажите их в перечне основных формул к
главе 3)? Что такое функционал пластичности, какое
поведение (физическое или механическое) он описывает?
53. На каком экспериментальном факте основано
математическое описание физического поведения упругопластической
среды в виде упругого уравнения Бриджмена? Почему
свойство пластичности учитывается лишь в
определяющем уравнении механического поведения?
54. Как вводится в рассмотрение функция пластичности
Ильюшина? Как она взаимосвязана с функционалом
пластичности?
55. Как выглядят прямые и обратные физические
соотношения для модели упругопластической среды согласно
деформационной теории пластичности для процесса нагружения
(укажите их в перечне основных формул к главе 3)?
56. Как следует понимать утверждение об аддитивности
деформаций в упругопластических средах?
287

57. Как ведут себя упругопластические среды при разгрузке?
Как выглядят соответствующие определяющие уравнения,
прямые и обратные физические соотношения (укажите их
в перечне основных формул к главе 3)?
58. Как следует понимать утверждение о том, что физические
соотношения деформационной теории пластичности
описывают не столько поведение упругопластической среды,
сколько свойства частного и наиболее простого процесса
нагружения этой среды?
59. Существуют ли ограничения на применимость теории
пластического течения, накладываемые значениями
деформаций или характером нагружения?
60. Как следует понимать утверждение о том, что теория
пластического течения является инкрементальной теорией?
61. Сформулируйте основные допущения теории
пластического течения.
62. Как следует понимать гипотезу пластической
несжимаемости в теории пластического течения? На каком
экспериментальном факте она основана?
63. Охарактеризуйте законы, в соответствии с которыми
упругие и пластические составляющие приращений
компонент тензора деформаций связаны с приращениями
компонент тензора напряжений, укажите соответствующие
соотношения в перечне основных формул к главе 3.
64. Какими соображениями можно обосновать
проявляющийся при проведении опытов ассоциированый закон
пластического течения ? Почему имеет место прямо
пропорциональная зависимость пластических составляющих приращений
компонент тензора деформаций от компонент девиатора
напряжений ?
65. За счет каких деформаций, упругих или пластических,
происходит изменение объема индивидуальных частиц
упругопластической среды?
288

66. Каков физический смысл скалярного множителя,
участвующего в записи ассоциированного закона пластического
течения и физических соотношений упругопластической
среды согласно теории пластического течения?
67. К чему сводятся уравнения теории пластического течения
при описании процессов разгрузки и повторного упругого
нагружения?
68. Что понимается под жесткопластической средой? Какой
вид имеет диаграмма деформирования для такой среды?
69. Что понимается под сильно развитым пластическим
течением? К какому виду сводятся уравнения пластического
течения в этом случае?
70. Как выглядят уравнения теории пластического течения
Сен-Венана — Мизеса (укажите их в перечне основных
формул к главе 3)? Откуда следует, что эти
уравнения описывают физико-механические свойства
несжимаемой жесткопластической среды?
71. В какой части верно, а в какой не верно утверждение о
том, что физические соотношения для модели
несжимаемой жесткопластической среды имеют много общего с
физическими соотношениями для модели вязкой жидкости?
72. Какую часть от удельной мощности деформирования в
жесткопластической среде составляет некомпенсированная
теплота (внутренние тепловые потери механического
происхождения)?
73. Каким образом изменяется энтропия индивидуальных
частиц жесткопластической среды при ее адиабатическом
деформировании ?
74. Определите понятия критерия пластичности,
пространства главных напряжений, поверхности пластичности.
75. Каков физический смысл критерия пластичности Мизеса?
76. Какую форму записи имеет критерий пластичности
Мизеса (укажите его в перечне основных формул к главе 3)?
'/2Ю-9712 289

77. Верно ли утверждение об энергетической природе
критерия пластичности Мизеса? Если верно, то как следует
понимать отсутствие в его записи энергетических
характеристик ?
78. Каким образом определяется предельно допустимое
значение удельной энергии упругого формоизменения
материала?
79. Как выглядит поверхность пластичности в пространстве
главных напряжений согласно критерию пластичности
Мизеса? Как ориентирована эта поверхность и каковы ее
характерные размеры?
80. Могут ли быть реализованы следующие напряженные
состояния для идеальной упругопластической среды с
пределом текучести ат: <?\ = g<i — 3<7Т, <7з = 2ат и о\ = -5<тт,
^2 = °Ъ = -3<тт?
81. В каком состояниии, упругом или пластическом,
находится идеальная упругопластическая среда с пределом
текучести сгт, если напряженное состояние характеризуется
главными напряжениями о\ = 1,5<тт, o<i — <7Т> 0"з = 0,5<тт?

Глава 4
ПОСТАНОВКА ЗАДАЧ
МЕХАНИКИ СПЛОШНЫХ СРЕД
Прикладное значение механики сплошных сред
заключается в том, что она создает фундамент для
физико-математического моделирования процессов взаимодействия
деформируемых тел и сред. С помощью формулируемых в механике
сплошных сред уравнений и соотношений удается составить
замкнутую систему уравнений, решение которых позволяет
исследовать поведение деформируемых сред и получать
информацию о параметрах их движения и состояния. В
настоящее время именно физико-математическое моделирование с
позиций механики сплошных сред является наиболее мощным
инструментом расчетно-теоретического исследования
функционирования различных технических объектов, как
существующих, так и проектируемых. В качестве примеров
прикладных задач, необходимость решения которых возникает при
изучении функционирования газодинамических импульсных
устройств, можно указать задачи обтекания тел вращения
воздушным потоком (рис. 4.1, а), проникания тел вращения в
плотные и прочные среды (рис. 4.1, б, в), метания
металлических облицовок продуктами детонации взрывчатого вещества
(рис. 4.1, г), схлопывания конических металлических
облицовок под действием приложенного давления с формированием
кумулятивной струи (рис. 4.1, д) и т.п.
Однако решению задачи обязательно предшествует
весьма важный этап формализации рассматриваемого
физического процесса: его описание в виде соответствующей системы
72 Ю* 291

Рис. 4.1
уравнений, соотношений и определенных условий, т.е.
решению задачи предшествует так называемая постановка задачи
или же формулировка физико-математической модели
изучаемого процесса взаимодействия деформируемых тел или сред.
Далее приведем общие принципы постановки задач
механики сплошных сред с различными физико-механическими
свойствами и последовательно проанализируем особенности
постановки задач механики идеальной и вязкой жидкостей,
упругой и упругопластической сред. При этом основное
внимание уделим этапам составления замкнутой системы
исходных уравнений, получению системы разрешающих уравнений
и различных частных ее видов, особенностям задания
граничных условий. Постановку задачи механики
упругопластической среды рассмотрим в полном объеме на примере процесса
проникания металлического тела в металлическую преграду.
4.1. Общие принципы постановки задач
Постановка задачи механики сплошных сред
заключается в составлении такой замкнутой системы уравнений и
соотношений, которая бы описывала движение и состояние
деформируемых сред с учетом их физико-механических свойств,
292

действия внешних сил, тепловых и других факторов и
позволяла определять зависимости характеризующих движение
и состояние физических величин от координат и времени:
и(х\ *), v(x\ i), еф\ *), Gij{x\ t), p(x\ t), Т(х\ t) и т.п.
Постановка любой задачи механики сплошных сред
включает следующие пять этапов:
— выбор системы отсчета и системы координат, по
отношению к которым будет описываться движение
материального континуума;
— выбор моделей сплошных сред для участвующих в
исследуемом процессе реальных деформируемых сред;
— составление системы исходных уравнений для
выбранных моделей и исследуемого процесса;
— выбор основных неизвестных характеристических
функций и переход к так называемой системе разрешающих
уравнений;
— формулировка начальных и граничных условий для
решаемой задачи.
Кратко рассмотрим содержание каждого этапа
постановки задачи.
4.1.1. Выбор системы отсчета
и системы координат
В большинстве случаев при постановке прикладных
задач выбираются инерциальные системы отсчета,
неподвижные относительно земной поверхности. Как известно, выбор
такой системы отсчета позволяет использовать при
математическом описании движения законы механики Ньютона, в
частности уравнение движения C.2), являющееся выражением
второго закона Ньютона применительно к сплошным
деформируемым средам. Например, для показанного на рис. 4.1, б
случая проникания тела вращения в плотную среду в
качестве точки отсчета удобно принять неподвижную
относительно Земли точку 0 начала взаимодействия проникающего тела
с плотной средой. В некоторых более редких случаях
допустимо и более удобно использование неинерциальных систем
10 - 9712 293

отсчета. Например, при решении задачи расчета
характеристик напряженно-деформированного состояния проникающего
тела — оболочки вращения — и оценке его прочности
удобнее связать систему отсчета с самим тормозящимся в
процессе проникания телом. Однако в этом случае в соответствии
с принципом Даламбера следует включить в число внешних
сил объемные силы инерции, для чего необходимо
предварительное определение ускорения проникающего тела.
Выбор конкретного вида системы координат ж1
(ж1,ж2,ж3) произволен и определяется прежде всего
соображениями удобства и простоты математического описания
движения. Так, при решении задачи пространственного обтекания
тела воздушной средой (см. рис. 4.1, а) все параметры
движения и состояния газа зависят от трех координат и времени
(трехмерная нестационарная задача). В этом случае
целесообразно выбрать наиболее простую систему координат — де-
картову прямоугольную систему координат (ж1 = ж, ж2 = у,
х3 = z). При проникании тела вращения в преграду по
нормали к ней (см. рис. 4.1, б) очевидна осевая симметрия
движения, в этом случае наиболее целесообразен выбор
цилиндрической системы координат (ж1 = г, ж2 = 0, ж3 = z), в которой
вектор скорости движения частиц имеет лишь две отличные
от нуля компоненты vr и vZi а также отсутствует зависимость
параметров движения и состояния деформируемой среды от
угловой координаты в (двумерная осесимметричная
нестационарная задача). В еще более геометрически простом случае
взрыва сферического заряда, инициируемого в центре,
движение обладает точечной симметрией, поэтому наиболее удобно
принять для описания движения сферическую систему
координат (ж1 = г, ж2 = 0, ж3 = <р), которая обеспечивает
зависимость параметров движения и состояния среды лишь от одной
радиальной координаты г и времени t (одномерная
нестационарная задача с центральной симметрией).
4.1.2. Выбор модели сплошной среды
Выбор модели сплошной среды для участвующей в
исследуемом процессе реальной деформируемой среды базируется
294

на анализе особенностей поведения этой среды в отношении
сопротивления деформированию, на выделении основных
факторов и игнорировании второстепенных. Этап выбора
модели заканчивается определением конкретного вида физических
соотношений C.7), ближе всего соответствующих
особенностям физико-механического поведения реальной
деформируемой среды.
Например, при решении прикладной задачи проникания
тела вращения в воду с относительно небольшой начальной
скоростью взаимодействия Vq « 100 м/с в качестве модели
реальной деформируемой среды (воды) вполне допустимо
принять модель идеальной жидкости. Действительно, реальные
жидкости обладают свойством сжимаемости и вязкости и в
то же время не оказывают сопротивления непосредственно
изменению формы своих частиц. При малых скоростях
деформации, соответствующих малым скоростям взаимодействия,
можно также пренебречь влиянием вязкости и вообще не
учитывать появление касательных напряжений, используя для
описания физико-механического поведения физические
соотношения aij = -p(/>, T)gij, присущие модели идеальной среды.
Следует отметить, что достаточно часто выбор модели
сплошной среды применительно к процессам, происходящим в
экстремальных условиях (например, к взрывным и ударным),
осуществляется итерационным путем, так как заранее
трудно предсказать, какие именно физико-механические свойства
реальных сред будут определяющими, а какими можно
пренебречь. В таких случаях последовательно используют все более
сложные модели, а критерием удовлетворительности выбора
является соответствие получаемых расчетным путем
результатов имеющимся экспериментальным данным.
4.1.3. Составление системы исходных уравнений
Система исходных уравнений — это замкнутая система
уравнений и соотношений, которая полностью описывает
движение и состояние деформируемых сред с учетом их физико-
механических свойств. В самом общем виде система исходных
уравнений имеет следующий вид:
'О* 295

J + />V,V = 0; D.1)
^ = Fi + VX; D.2)
^ = *% - V,g'; D.3)
? = *; D-4)
^ = ^(Vi^ + V^); D.5)
<Tij = <Tij{eij,eij,T). D.7)
Система исходных уравнений в обязательном порядке
включает основные общие для всех сплошных сред
дифференциальные уравнения механики, выражающие
фундаментальные законы сохранения массы D.1), импульса D.2), энергии
D.3), а также общие для всех сред кинематические
соотношения D.4) и D.5) и геометрические соотношения D.6).
Индивидуальные особенности рассматриваемой деформируемой
среды в отношении оказания сопротивления деформированию
учитываются физическими соотношениями D.7),
обязательно включаемыми в систему исходных уравнений согласно
выбранной модели сплошной среды.
В зависимости от конкретного вида физических
соотношений D.7) и от характера процесса деформирования среды
в систему исходных уравнений для обеспечения ее
замкнутости могут быть включены дополнительные уравнения и
соотношения. Например, при отсутствии влияния
температуры на физико-механическое поведение рассматриваемой
среды физические соотношения имеют вид оуу = Cij(sijy eij) и
для адиабатического процесса (V,g* = 0) система уравнений
D.1)—D.7) является замкнутой и содержит 26 уравнений и
296

соотношений и такое же количество искомых характеристи-
чесих функций (см. раздел 3.1). Напротив, в случаях
зависимости компонент тензора напряжений от температуры или
же при учете теплообмена между частицами сплошной среды
и необходимости определения температурного поля в
систему исходных уравнений необходимо включать
дополнительные соотношения, учитывающие закон теплопроводности
Фурье (ql = qjg%i = -\g%*VjTy где А — коэффициент
теплопроводности) и взаимосвязь между удельной внутренней энергией
и температурой (Е = Б(/>, Г)).
В ряде случаев система исходных уравнений может быть
и более узкой, нежели представленная выше система
D.1)—D.7). Например, при постановке задачи механики
идеальной жидкости, для которой компоненты тензора
напряжений не зависят напрямую от компонент тензора деформаций
(зависимость напряжений от деформаций имеет косвенный
характер через плотность, взаимосвязанную с объемной
деформацией (см. раздел 2.4.2)), не требуется включения в систему
исходных уравнений кинематических соотношений D.4) и
геометрических соотношений D.6). Однако в любом случае
следует обеспечивать замкнутость системы исходных уравнений
с равенством количества уравнений числу неизвестных
характеристических функций, описывающих движение и состояние
сплошной среды. Это является необходимым условием для
последующего нахождения единственного решения задачи.
4.1.4. Выбор основных неизвестных
и переход к системе разрешающих уравнений
Система разрешающих уравнений — это замкнутая
система уравнений и соотношений, содержащая минимальное
количество взаимно независимых искомых функций и
получающаяся исключением остальных неизвестных функций из
уравнений исходной системы.
При рассмотрении системы исходных уравнений
D.1)—D.7) нетрудно заметить, что она может быть
преобразована с исключением некоторых неизвестных функций. На-
297

пример, компоненты е1;- тензора скоростей деформаций,
участвующие в записи уравнения энергии D.3) и физических
соотношений D.7), могут быть выражены через компоненты V{
вектора скорости в соответствии с кинематическими
соотношениями D.5) и, таким образом, исключены из системы уравнений
при сохранении в качестве основных неизвестных компонент
вектора скорости. Аналогичным образом из уравнений
движения D.2) и энергии D.3) могут быть исключены и компоненты
&ij тензора напряжений в соответствии с физическими
соотношениями D.7) и т.п. Такой процесс преобразования
системы исходных уравнений сопровождается уменьшением
количества искомых функций и уравнений, а по существу,
соответствует получению из общих уравнений механики их частного
вида и построению замкнутой системы уравнений,
описывающей движение и состояние сплошной среды с
определенными физико-механическими свойствами (идеальной или вязкой
жидкости, упругой или упругопластической среды и т.д.).
В математическом отношении система разрешающих
уравнений представляет собой систему дифференциальных
уравнений в частных производных и конечных
функциональных уравнений. Например, входящие в уравнения движения
D.2) абсолютные производные компонент тензора напряжений
по координатам представляются в виде суммы частных
производных по координатам и дополнительных составляющих,
зависящих от символов Кристоффеля выбранной системы
координат и учитывающих искривленность ее координатных
линий (см. раздел 1.3.6). Входящие в эти же уравнения
субстанциональные производные компонент вектора скорости по
времени при использовании, например, подхода Эйлера
представляются в виде суммы локальной производной (частная
производная по времени, определяемая в фиксированных
точках пространства) и конвективной производной (зависящей от
частных дгроизводных по координатам) и т.п. К числу
конечных функциональных уравнений относятся в большинстве
случаев физические соотношения D.7).
Система разрешающих уравнений является
окончательной, результирующей системой, и именно эта система требует
298

своего решения путем нахождения всех входящих в нее
характеристических функций. С определением зависимостей
физических величин, входящих в систему разрешающих
уравнений, от координат и времени получает свое логическое
завершение феноменологический подход к изучению механического
движения деформируемых сред. В большинстве
представляющих практический интерес случаев системы разрешающих
уравнений, описывающие движение газов, жидкостей и
твердых тел, достаточно сложны, а их решение может быть
найдено при использовании методов вычислительной математики —
численных методов механики сплошных сред.
4.1.5. Начальные и граничные условия
Неотъемлемым и важнейшим элементом постановки
любой задачи механики сплошных сред является формулировка
начальных и граничных условий. Их значение определяется
тем, что та или иная система разрешающих уравнений
описывает целый класс движений соответствующей
деформируемой среды, и лишь задание отвечающих исследуемому
процессу начальных и граничных условий позволяет выделить из
этого класса представляющий интерес частный случай,
соответствующий решаемой практической задаче.
Начальные условия — это условия, которыми задаются
значения искомых характеристических функций в момент
начала рассмотрения исследуемого процесса. Количество
задаваемых начальных условий определяется количеством
основных неизвестных функций, входящих в систему разрешающих
уравнений, а также порядком входящей в эту систему высшей
производной по времени. Например, адиабатическое движение
идеальной жидкости или идеального газа описывается
системой шести уравнений с шестью основными неизвестными —
тремя компонентами вектора скорости v± = г;,(аг*, ?),
давлением р = р(ж\ ?), плотностью р = р(х%> t) и удельной внутренней
энергией Е = E(xl, tf), при этом порядок производных этих
физических величин по времени не превышает первый порядок
299

(см. раздел 4.2). Соответственно этому в качестве
начальных условий должны быть заданы начальные поля этих
шести физических величин: при t = О V{ = 17,B;*, 0), р = р(х*, 0),
р = р(хг, 0), Е = Е(х1у 0). В некоторых случаях (например,
в динамической теории упругости; см. раздел 4.4) в
качестве основных неизвестных в системе разрешающих
уравнений используются не компоненты V{ вектора скорости, а
компоненты щ вектора перемещения, а уравнение движения
содержит производные второго порядка компонент перемещения
сРщ/dt2, что требует задания двух начальных условий для
искомой функции щ = щ(хгу t): при t = 0 щ = щ(х%, 0) и
dui/dt = Vi(x\ 0).
Более сложным и разнообразным образом при постановке
задач механики сплошных сред задаются граничные условия.
Граничные условия— это условия, которыми задаются
значения искомых функций (или их производных по координатам и
времени) на поверхности S области, занимаемой
деформируемой средой. Различают граничные условия нескольких типов:
кинематические, динамические, смешанные и температурные.
Кинематические граничные условия соответствуют
случаю, когда на поверхности 5 тела (или ее части) задаются
перемещения и(ж^., 0 или скорости и(ж^, t), где х1^ = xlg(t)
— координаты точек поверхности 5, изменяющиеся в общем
случае в зависимости от времени.
Динамические граничные условия (или граничные
условия в напряжениях) задаются, когда на поверхности 5
действуют поверхностные силы р. Как следует из теории
напряжений, в этом случае на любой элементарной площадке
поверхности с единичным вектором нормали п вектор удельных
поверхностных сил рп принудительно задает вектор полного
напряжения ап = рп, действующий в сплошной среде в точке
на данном участке поверхности, что приводит к взаимосвязи
тензора напряжений (а) в этой точке с поверхностной силой и
ориентацией вектора п соответствующего участка
поверхности: (а) ¦ п = рп или O{jV? = рп{ (см. B.49)).
Смешанные граничные условия соответствуют случаю,
когда на поверхности 5 задаются значения и кинематических,
300

и динамических величин или устанавливаются взаимосвязи
между ними.
Температурные граничные условия подразделяются на
несколько групп (родов). Граничные условия первого рода
задают на поверхности 5 деформируемой среды определенные
значения температуры Г. Граничные условия второго рода
задают на границе вектор теплового потока д, что с учетом
закона теплопроводности Фурье q = — A grad Т, по существу,
накладывает ограничения на характер температурного
распределения в окрестности граничной точки д, = — AVjT.
Граничные условия третьего рода устанавливают зависимость между
вектором теплового потока д, направленным к данной среде
со стороны окружающей среды, и температурным перепадом
между этими средами и т.д.
Следует отметить, что постановка и решение
большинства задач физики быстропротекающих процессов, как
правило, осуществляются в адиабатическом приближении, поэтому
температурные граничные условия используются достаточно
редко, в основном в различных сочетаниях применяются
кинематические, динамические и смешанные граничные условия.
Рассмотрим возможные варианты задания граничных
условий на частном примере.
На рис. 4.2 схематично представлен процесс
взаимодействия при проникании деформируемого тела / в
деформируемую преграду П. Тело / ограничено поверхностями S\ и
5б, а тело II —
поверхностями 52, 5з, ?4, ^5- По-
верхность S$ является
границей раздела
взаимодействующих деформируемых тел.
Будем полагать, что
движение тела / до начала
взаимодействия, а также в его
процессе происходит в жидкости,
создающей определенное
гидростатическое давление ро и Рис. 4.2
301

задающей внешние по отношению к обоим телам
поверхностные силы рп = -роп = -рощг1, действующие на любой из
элементарных площадок поверхностей S\ тела / и 52
преграды Я, граничащих с жидкостью. Будем также считать, что
поверхность 5з преграды жестко закреплена, а поверхность
54 свободна от действия поверхностных сил (рп = 0).
Для приведенного примера на различных поверхностях,
ограничивающих деформируемые среды /иЯ, должны
задаваться граничные условия всех трех основных типов.
Очевидно, что на жестко закрепленной поверхности 5з следует задать
кинематические граничные условия v(S^) = v(xlg , t) = 0.
Граничные условия на поверхностях S\ и 52 однотипны и
относятся к динамическим условиям, накладывающим
ограничения на компоненты тензора напряжений в граничных точках
соответствующих тел: a^v? = —роЩ или («ту +Po9ij)n* = 0.
Компоненты тензора напряжений на поверхности 54
преграды также не могут быть произвольными, а взаимосвязаны с
ориентацией ее элементарных площадок как о^п* = 0.
Граничные условия на границе раздела (поверхность S$)
взаимодействующих деформируемых сред являются наиболее
сложными и относятся к условиям смешанного типа,
включающим, в свою очередь, кинематическую и динамическую
части (см. рис. 4.2). Кинематическая часть смешанных
граничных условий накладывает ограничения на скорости движения
индивидуальных точек обеих сред, находящихся в контакте
в каждой пространственной точке поверхности 5s-
Возможны два варианта задания этих ограничений,
проиллюстрированные на рис. 4.3, а и б. По наиболее простому
первому варианту предполагается, что скорости движения любых
двух находящихся в контакте индивидуальных точек
одинаковы (t?/ = vjf)y — это так называемое условие "прилипания",
или условие "сварки" (см. рис. 4.3, а). Более сложным и в
то же время более адекватным для рассматриваемого
процесса является задание условия "непроницаемости", или условия
"непротекания" (vj п = vn • п; см. рис. 4.3, б), которое
соответствует экспериментально подтверждающемуся факту:
взаимодействующие деформируемые среды не могут проникать
302

Рис. 4.3
друг в друга или отставать друг от друга, а могут
проскальзывать одна относительно другой со скоростью Vj-vn>
направленной по касательной к границе раздела ((vj - vn) • п = 0).
Динамическая часть смешанных граничных условий на
границе раздела двух сред формулируется на основе третьего закона
Ньютона с использованием соотношений теории напряжений
(рис. 4.3, б). Так, в каждой из двух находящихся в контакте
индивидуальных частиц деформируемых сред / и П
реализуется свое напряженное состояние, характеризуемое тензорами
напряжений (сгO и (v)w При этом в среде / на каждой
элементарной площадке границы раздела с единичным вектором
нормали п/, внешней по отношению к данной среде,
действует вектор полного напряжения сгп1 = (<т)/ • П/. В среде П
на той же площадке, но с единичным вектором нормали nff,
внешней по отношению к этой среде, действует вектор
полного напряжения сгпП = (сг)я-пл. С учетом взаимности действия
и противодействия сгп1 = -<тпп<> а также очевидного условия
71/ = —Пд = п устанавливается взаимосвязь между тензорами
напряжений в обеих взаимодействующих средах на границе их
раздела: (а)/ • п = (ст)ц • и или же {a^j - Gijn) nJ = 0.
Возможные варианты задания граничных условий не
исчерпываются рассмотренным частным примером.
Вариантов задания начальных и граничных условий столь же много,
сколь много существует в природе и технике процессов
взаимодействия деформируемых тел или сред. Они определяются
303

особенностями решаемой практической задачи и задаются в
соответствии с приведенными выше общими принципами.
4.2. Постановка задач
механики идеальной жидкости и газа
Основой системы исходных уравнений в данном случае
являются дифференциальные уравнения неразрывности,
движения и энергии D.1)—D.3), а также кинематические
соотношения D.5), справедливые для любой среды
независимо от ее физико-механических свойств. Особенности физико-
механического поведения рассматриваемой сплошной среды
будут учитываться физическими соотношениями вида C.16)
при использовании уравнения состояния в термической
(р = р(р, Г)) или калорической (р = р(/9, Е)) форме (в
зависимости от последующего выбора основных неизвестных). При
необходимости учета теплообмена между частицами
идеальной среды в систему исходных уравнений следует включить
и соотношения закона теплопроводности Фурье q% = qjgV =
= —Xg^VjT. В связи с тем, что дифференциальные
уравнения законов сохранения и физические соотношения для модели
идеальной среды не включают в явном виде компоненты
тензора деформаций, геометрические соотношения D.6) и
дифференциальные уравнения D.4) взаимосвязи перемещений и
скоростей в систему исходных уравнений могут не включаться,
если их определение не представляет интереса.
В итоге система исходных уравнений, составляемая при
постановке задач механики идеальной жидкости или газа,
имеет следующий вид:
304

p = p(p, E) или p = p(p, T);
Приведенная система исходных уравнений может быть
преобразована с помощью операций тензорной алгебры с
одновременным упрощением ряда уравнений и исключением из
системы некоторых "промежуточных" соотношений и
соответствующих характеристических функций. Например,
уравнение энергии с учетом кинематических, физических
соотношений, закона теплопроводности Фурье и уравнения
неразрывности преобразуется так:
dE
' ) + V, W
+ XgijS/iVjT = V- % + AV2T, D.8)
J p at
где V2T = AT = gl*ViVjT — оператор Лапласа, записанный
для случая произвольной системы координат. В этом
можно убедиться при использовании наиболее простой декартовой
прямоугольной системы координат, в которой метрические
коэффициенты образуют единичную матрицу (g%i = 1 при i = j
и д%э = 0 при г ф j), а абсолютные производные по
координатам совпадают с обычными частными производными (см.
раздел 1.3.6):
v2t = V! ViT + v2v2t + v3v3r =
В свою очередь, дифференциальные уравнения движения
с помощью физических соотношений для модели идеальной
305

среды также существенно упрощаются и приобретают
следующий вид:
= Fi + gjaVa(-Pgij) = Fi - gjagijVaP =
= Fi-gfVap = Fi-^ip. D.9)
Уравнения D.9) выражают собой частный случай закона
сохранения импульса для деформируемой идеальной среды и
называются уравнениями Эйлера. Этим уравнениям
соответствует одно векторное уравнение
И = g Р'
D.10)
позволяющее интерпретировать физический смысл уравнений
Эйлера (рис. 4.4). Действительно, вектор градиента
скалярной функции давления направлен по нормали к изобарной
поверхности, проходящей через точку М пространства, в
которой находится некоторая индивидуальная частица идеальной
жидкости или газа. При этом вектор градиента направлен
в сторону наиболее резкого возрастания давления. Согласно
\
dtt /,
Р-Рг>Р1
"p=p1~const
Рис. 4.4
306

векторному уравнению движения D.10), в случае отсутствия
объемных сил F каждая индивидуальная частица идеальной
среды получает ускорение в сторону наиболее резкого
убывания давления, и тем большее, чем интенсивнее изменяется
давление в окрестности данной частицы (см. физический смысл
градиента скалярной функции векторного аргумента в
разделе 1.2.2). Присутствие объемных сил F несколько изменяет
направление и модуль вектора ускорения, склоняя его в
соответствующую сторону.
В результате проведенных преобразований уравнений
исходной системы образуются системы разрешающих уравнений
для возможных частных случаев течений идеальной среды.
Так, адиабатическое течение идеальной жидкости или
идеального газа (Vtg* = 0 или коэффициент теплопроводности
А = 0), как правило реализующееся во взрывных и ударных
процессах, описывается системой уравнений
dp
dt
pd~dl
dE
dt
P =
= Fi
P
" P2
P(p^
V = 0;
- ViP;
dp
dt'
D.11)
содержащей пять дифференциальных уравнений,
выражающих основные законы сохранения (одно уравнение
неразрывности — закон сохранения массы, три уравнения Эйлера —
закон сохранения импульса, одно уравнение энергии —
первый закон термодинамики) и уравнение состояния в
калорической форме. Система уравнений D.11) является замкнутой
и содержит шесть неизвестных характеристических функций:
три компоненты v{ вектора скорости, давление р, плотность р
и удельную внутреннюю энергию Е.
Система разрешающих уравнений для адиабатического
течения идеальной среды может быть еще более сокращена в
случае более простых моделей идеальной среды. Например,
307

для идеальной баротропной среды, описываемой уравнением
состояния в виде р = р(р, Е) = р(р)> уравнение энергии
является изолированным от остальных уравнений системы D.11)
и может не включаться в систему разрешающих уравнений,
которая в этом случае будет содержать пять уравнений:
Р = Р(Р),
где пять неизвестных — и,-, р, р. Система разрешающих
уравнений для идеальной несжимаемой среды (р — рс = const)
приобретает еще более простой вид и сводится к четырем
дифференциальным уравнениям неразрывности и движения:
V.V = 0;
dvi _, _ D-13)
* "л = Fi - v'p;
где четыре неизвестных — г;,-, р.
Аналогичным образом может быть получена система
разрешающих уравнений, описывающая течение идеальной
среды, в которой теплообмен между ее частицами происходит
посредством теплопроводности. Например, для частного случая
модели идеальной среды (модели совершенного газа),
описываемой уравнением состояния Клапейрона — Менделеева р =
= pRT, уравнение энергии D.8) может быть преобразовано
с учетом существующей прямо пропорциональной
зависимости удельной внутренней энергии от температуры: Е = СуТ,
где су — постоянная величина, по своему физическому смыслу
соответствующая удельной теплоемкости при постоянном
объеме. После очевидного преобразования уравнения энергии,
приобретающего вид уравнения распространения теплоты,
система разрешающих уравнений будет состоять из следующих
308

шести уравнении:
? = *-*<* D.14)
dT Pdp
содержащих такое же количество неизвестных величин —
г>„ Р, />, Г.
Таким образом, все приведенные выше системы
уравнений D.11)—D.14), описывающие различные частные случаи
течения идеальных сред, имеют гораздо более простой вид,
нежели общие уравнения механики сплошных сред, и являют
собой, по существу, частные следствия этих общих уравнений
для случая, когда деформируемая среда не обладает
способностью сопротивляться формоизменению. Подобным же
образом для модели идеальной среды существенно упрощается и
запись граничных условий. Например, при расчете процесса
функционирования заряда самоликвидатора космического
аппарата, связанного с разлетом продуктов детонации
взрывчатого вещества в вакуум, на границе раздела газа с вакуумом
должны ставиться динамические граничные условия
отсутствия поверхностных сил: а^п? = рп, = 0. Учитывая это,
а также физические соотношения для модели идеальной
среды, приходим к выводу о необходимости ограничения
значения давления на границе раздела ((-pgij)ni = —рщ = 0) или
к простому и очевидному граничному условию р = 0.
В заключение отметим, что все получающиеся в итоге
системы разрешающих уравнений D.11)—D.14) записаны с
использованием тензорных величин (тензоры нулевого и первого
рангов) и тензорных дифференциальных операторов
(операторы Гамильтона и Лапласа), в силу этого они имеют
универсальный характер и справедливы для любой системы
координат (см. раздел 1.1). При постановке конкретной задачи
309

механики жидкости или газа и выборе конкретной системы
координат решению этих систем уравнений предшествует их
представление в координатной форме, получаемой уже чисто
формальным математическим путем с использованием
операций тензорного анализа, рассмотренных в разделе 1.3.
4.3. Постановка задач
механики вязкой жидкости
Основные моменты постановки задач механики вязкой
жидкости рассмотрим на частном примере вязкой баротроп-
ной среды в предположении, что определение полей
температуры и удельной внутренней энергии не представляет
особого интереса. Для такого случая система исходных уравнений
примет вид
dv'
ij = -P(p)9ij + (ЗЛ - 2/z) kgij + 2fieij;
(V + V)
и будет включать дифференциальные уравнения
неразрывности и движения, физические соотношения в виде закона На-
вье — Стокса, где давление зависит лишь от плотности
среды: р = р(р)> а также кинематические соотношения,
определяющие компоненты тензора скоростей деформаций через
компоненты вектора скорости и среднюю скорость деформаций,
записанную с помощью первого основного инварианта тензора
скоростей деформаций (основные инварианты тензора
скоростей деформаций определяются так же, как основные
инварианты тензора деформаций). Исключение из системы исходных
уравнений дифференциального уравнения энергии D.3),
конечно же, не означает невыполнения закона сохранения
энергии в процессе движения вязкой среды, а лишь соответствует
310

рассматриваемому частному случаю, для которого уравнение
энергии является изолированным от других уравнений
исходной системы, а специальное определение энергии не
представляет интереса.
Система разрешающих уравнений получается из
системы исходных уравнений путем преобразования физических
соотношений Навье — Стокса и выражения компонент тензора
скоростей деформаций через компоненты вектора скорости.
В дальнейшем проводятся преобразования уравнений
движения, в результате которых из них исключаются
компоненты тензора напряжений и получается частный вид уравнений
движения для вязкой жидкости — уравнения Навье — Стокса.
Так, физические соотношения Навье—Стокса после
исключения из них компонент тензора скоростей деформаций
приобретают вид
ЗА - 2j
°ij = ~P9ij + з
вследствие чего уравнения движения записываются как
\-pgij
Принимая во внимание постоянство компонент
фундаментального метрического тензора по отношению к абсолютному
дифференцированию, последующее преобразование уравнений
движения проводят, используя операции тензорной алгебры
(операции жонглирования индексами — опускания индекса и
замены одного индекса другим), учитывая независимость
результата двойного дифференцирования по координатам от
порядка дифференцирования и обозначая суммарное двойное
абсолютное дифференцирование компонент вектора скорости в
виде оператора Лапласа:
311

gja9ij Va (V.t,*) + /**» Ve V^,-
аЪщ = Ft- g?VaP + ZL-HgfVe(Vkv
В итоге система разрешающих уравнений, описывающая
течение баротропной вязкой жидкости, будет состоять из пяти
уравнений — уравнения неразрывности, уравнений движения
(уравнений Навье — Стокса), баротропной зависимости:
$ - f,-
D15)
и включать пять неизвестных характеристических функций
— V,-, р, />.
Нетрудно видеть, что в частном случае отсутствия
вязких свойств (А = /z = 0) уравнения Навье—Стокса
сводятся к уравнениям Эйлера D.9), а в целом система уравнений
D.15) сводится к системе уравнений D.12) течения идеальной
баротропной среды. Поэтому математическое описание
течения идеальной жидкости может рассматриваться как частное
следствие более общего описания движения вязких сред.
В связи с отсутствием в системе разрешающих уравнений
для вязкой жидкости компонент тензора напряжений и
использованием в качестве основных неизвестных скорости, давления
312

и плотности несколько видоизменяется запись динамических
граничных условий. Если в общем случае динамические
граничные условия GijTi3 = pni накладывают ограничения на
компоненты тензора напряжений на поверхности сплошной среды,
как бы приводя их в соответствие с поверхностными силами
pni и ориентацией границы п-?, то в данном случае, вследствие
выражения компонент тензора напряжений в соответствии с
законом Навье — Стокса через давление и абсолютные
производные компонент вектора скорости по координатам,
подобные ограничения накладываются на взаимосвязь
распределений скорости и давления в окрестности границы:
ЗА - 2/z / к\ ^ ъ \ i
-P9ij + jj [Vkv J gij + fiViVj + liVjViJ nJ = pni
Система разрешающих уравнений D.15) течения вязкой
жидкости, будучи записана с использованием тензорной
символики, имеет универсальный характер с точки зрения выбора
системы координат. При постановке конкретной задачи
механики вязкой жидкости и выборе некоторой системы координат
можно получить различные частные виды систем уравнений
в координатной форме представления. Например, при
изучении пространственного (трехмерного) нестационарного
течения вязкой жидкости наиболее удобно ввести декартову
прямоугольную систему координат, в которой система уравнений
приобретет следующий вид:
dp fdvx dvy
дх+ З дх\дх + ду
/4Л
11-9712 313

dvy dp ЗА + fJ> д /dvx dvy dvz
РИГ= y~~dy + 3 Ъу \дх + ~ду + ~dz
P~dT = Fz~~!h + ~~3 dz \!h~ + ~dy + 1h)
P = P(p)-
4.4. Постановка задач
теории упругости
В качестве примера рассмотрим математическое
описание динамического деформирования упругой среды,
пренебрегая влиянием температуры на ее физико-механическое
поведение и не ставя цель определить температурные поля
(адиабатическое приближение).
В данном случае в систему исходных уравнений
включаются дифференциальные уравнения неразрывности, движения
и физические соотношения в форме обобщенного закона Гука.
Так как напряжения в упругой среде зависят от деформаций,
а деформации — от перемещений, в систему исходных
уравнений дополнительно включаются геометрические соотношения
взаимосвязи компонент тензора деформаций и вектора
перемещений, кинематические соотношения взаимосвязи компонент
векторов перемещения и скорости, а также выражение
входящей в запись закона Гука средней деформации через
компоненты тензора деформаций. Тогда система исходных уравнений
приобретает следующий вид:
piit=Fi+Va^= Fi
314

Подобно тому как это было выполнено для вязкой
жидкости, в данном случае система разрешающих уравнений при
выборе в качестве основных неизвестных компонент
вектора перемещения получается из системы исходных уравнений.
Это достигается с помощью преобразования физических
соотношений (закона Гука) путем записи компонент тензора
деформаций через компоненты вектора перемещения и с
помощью последующего преобразования уравнений движения
путем исключения из них компонент тензора напряжений, в
результате чего получается частный вид уравнений движения
для упругой среды — уравнения Лямэ. Обобщенный закон
Гука после выражения компонент тензора деформаций через
компоненты вектора перемещения приобретет вид
+
i +
а уравнения движения на основе правил тензорной алгебры и
тензорного анализа преобразуются следующим образом:
= Ft + GVeVi( Vе) + GV2ut +3K~2Gg?Va(ykuk)
315

В итоге система разрешающих уравнений, описывающая
динамическое адиабатическое деформирование упругой среды,
имеет вид системы семи дифференциальных уравнений
dt - "
выражающих закон сохранения массы, закон сохранения
импульса (уравнения Лямэ) и кинематическую взаимосвязь
перемещений и скоростей, при точно таком же количестве
неизвестных характеристических функций — v^ щ, р.
В частных случаях система разрешающих уравнений для
упругой среды может принимать и более простой вид, как это
имеет место, например, при ее равновесии, когда уравнение
неразрывности и уравнения взаимосвязи перемещений и
скоростей становятся тривиальными тождествами, а вся система
сводится к трем уравнениям Лямэ
содержащим три компоненты щ вектора перемещения.
При выборе в качестве основных неизвестных компонент
вектора перемещения необходимо соответствующим образом
видоизменять и запись динамических граничных условий
(Tijn* = pn{. Учитывая физические соотношения для модели
упругой среды, получаем, что динамические граничные
условия в этом случае накладывают ограничения на
распределения перемещений в окрестности границы сплошной упругой
среды и
(V*j gij\ nj = Pni.
316

4.5. Постановка задачи
о динамическом взаимодействии
упругопластических сред
Особенности постановки задачи механики
упругопластических сред рассмотрим в полном объеме на примере процесса
проникания металлического ударника в металлическую
преграду (рис. 4.5). Будем полагать, что ударник
взаимодействует под углом а с броневой преградой с начальной скоростью
vq (рис. 4.5, а), соответствующей скоростям бронебойных под-
калиберных снарядов, и в процессе взаимодействия
срабатывается с образованием характерной грибообразной формы
(рис. 4.5, б). При взаимодействии под углом движение
индивидуальных частиц обоих тел имеет пространственный
характер, а все параметры движения и состояния зависят от
трех координат и времени. Это так называемая трехмерная
нестационарная задача. Для описания движения
взаимодействующих тел в таком случае рационально ввести наиболее
простую декартову прямоугольную систему координат, а
точку отсчета ассоциировать с неподвижной относительно
Земли точкой 0 преграды, в которой начинается взаимодействие
(см. рис. 4.5, а). При таком выборе системы отсчета
обеспечиваются ее инерциальность и возможность использования
Xs-Ч
Рис. 4.5
317

основных уравнений механики сплошных сред без учета
заранее неизвестных объемных сил инерции, при этом в связи с
прямолинейностью координатных линий уравнения механики
в координатной форме примут наиболее простой вид.
Материалы броневой преграды и бронебойного снаряда
являются высокопрочными металлами, оказывающими в
процессе деформирования существенное сопротивление
изменению как объема, так и формы своих частиц. При этом
очевидно, что при реализующихся в процессе
рассматриваемого взаимодействия больших деформациях металлы обоих тел
будут проявлять упругопластические свойства, а для
описания их физико-механического поведения необходимо
использовать модель упругопластической среды в соответствии с
теорией пластического течения. Будем полагать, что оба
деформируемых тела ведут себя как идеальные
упругопластические среды с присущим каждой из них пределом текучести
ат при одноосном растяжении и с характерной диаграммой,
показанной на рис. 3.9, а, а в качестве критерия пластичности
используется критерий Мизеса. Определяющие уравнения и
физические соотношения для модели упругопластической
среды согласно теории пластического течения в случае их
применимости для описания динамических процессов, связанных
с большими объемными деформациями, имеют определенную
специфику, несколько отличающую их от уравнений и
соотношений, приведенных в разделе 3.4. Действительно, в рас
сматриваемом случае взаимодействия тел с артиллерийскими
скоростями изменение объемов частиц ударника и преграды
может быть существенным, следовательно, физическое
поведение необходимо описывать не линейным уравнением Бридж-
мена, как это делается в классической теории пластического
течения, а имеющим более общий характер уравнением
состояния, например в калорической форме р — р(р, Е). В
качестве такого уравнения состояния может быть принято
экспериментальное уравнение состояния в форме Ми — Грюнай-
зена р = рх{р) + i(p)p[E - Ех(р)], где Ех(р) —
составляющая удельной внутренней энергии — удельная
потенциальная энергия объемной деформации; Е — Ех(р) = Ет —
составляющая удельной внутренней энергии — удельная тепловая
318

энергия; рх(р) — так называемая "холодная" составляющая
давления, связанная с взаимодействием молекул между собой;
у(р) р [Е — Ех(р)] = рт — "тепловая" составляющая давления,
связанная с хаотическим движением молекул; j(p) — так
называемый коэффициент Грюнайзена.
Допущения теории пластического течения, касающиеся
аддитивности деформаций, пластической несжимаемости и
ассоциированного закона пластического течения могут быть
записаны в "скоростной" форме, более удобной при решении
динамических задач. В соответствии с гипотезой
аддитивности деформаций компоненты тензора скоростей деформаций
могут быть представлены в виде суммы двух составляющих,
определяющих изменение во времени упругих (е) и
пластических (р) деформаций:
где упругие составляющие компонент тензора скоростей
деформаций связаны со скоростями изменения компонент девиа-
тора напряжений согласно прямо пропорциональной
зависимости, подобной зависимости (Dp) = 2GB?e), характерной для
модели упругой среды:
($М$ D.18)
Согласно гипотезе пластической несжимаемости,
пластические составляющие компонент тензора скоростей деформаций
ef» не вносят вклада в изменение объема индивидуальных
частиц, а средняя скорость деформаций определяется лишь своей
упругой составляющей
& = ёцд*/г = 4eV'/3 + t$gii/b = iWgii/3 = eW, D.19)
тогда как пластическая составляющая средней скорости
деформаций равна нулю: ё^ = ё^'дг*/3 = 0. И наконец, за-
319

кон пластического течения, записанный в "скоростной" форме,
приобретет вид
e\f = АЛ„у, D.20)
где А — скалярный множитель, определяемый удельной
мощностью пластического деформирования (см. раздел 3.4).
Из соотношений D.17)—D.20) с учетом ранее
использовавшейся взаимосвязи Ti(e) = Зг = ?{jg%* — Vjv1 =
— —(l/p)(dp/dt) средней скорости деформаций со скоростью
изменения плотности следуют дифференциальные уравнения
Прандтлл — Рейсса
;,- = 2G (ёу - t9ij) = 2G
dt
описывающие механическое поведение идеальной упругопла-
стической среды. Уравнения Прандтля — Рейсса в сочетании
с описывающим физическое поведение уравнением состояния
р — р(р^ Е) и известным разложением тензора напряжений
на шаровую и девиаторную составляющие сг,у = —pgij + Do-ij
представляют собой физические соотношения для описания
деформирования упругопластической среды,
сопровождающегося большими объемными деформациями.
Система исходных уравнений, описывающая
динамическое деформирование ударника и преграды, будет включать
дифференциальные уравнения основных законов сохранения,
кинематические и физические соотношения. При этом вполне
обоснованно рассмотрение задачи высокоскоростного
взаимодействия двух тел в адиабатическом приближении, когда
можно пренебречь достаточно медленным процессом теплообмена
между частицами (полагая в уравнении энергии V{ql = 0).
Как правило, при рассмотрении подобных процессов,
связанных с возникновением интенсивных полей внутренних
напряжений, пренебрегают и действием объемных сил типа сил
тяжести (в уравнениях движения F+ = 0). В целом система
исходных уравнений принимает следующий вид:
320

D.21)
dt
p = p(p, ?),
В отличие от рассмотренных выше постановок задач
механики более простых сред, система исходных уравнений
D.21) динамики упругопластических сред достаточно
сложна, и дальнейшее ее упрощение не представляется
возможным. Совершенно очевидна взаимосвязь входящих в эту
систему уравнений неизвестных характеристических функций.
Например, поле плотности р влияет на скорость изменения
самой плотности, на изменение скоростей г;,-, удельной
внутренней энергии ?*, компонент Daij девиатора напряжений и
напрямую через уравнение состояния определяет компоненты
шарового тензора и тензора напряжений в целом. Изменение
же с течением времени поля скоростей V{ контролируется
распределением напряжений сгг;- в упругопластической среде и, в
свою очередь, прямо или через кинематические соотношения
определяет эволюцию во времени полей плотности /9, удельной
внутренней энергии J?, давления р, компонент D^j девиатора
напряжений, компонент <7^ тензора полных напряжений и т.д.
Значительная сложность подобных систем уравнений
определяет практическую нецелесообразность минимизирования
количества искомых функций, т.е. система D.21), по существу,
является системой разрешающих уравнений.
321

В выбранной для описания движения взаимодействующих
сред декартовой прямоугольной системе координат система
уравнений D.21) принимает следующий вид:
dvx dvy dvz
dx dy dz
dvx doxx doXy d(jXz
di)y OOXy OCyy OGyz
P
dt - dx * ду ^ dz '
д
9 dt
dx dy dz
2стХубХу + 2crxzeXz
_ dvx
Sxx " 1^
D.22)
l(8vx
_l_(dv1,dvA.
~2\dz + ду)'
322
dDazz

~1Г +
^l + 2G\DffXZ = 2Gexz;
at
" + 2G\Dayz = 2Geyz; D.22)
p =
°\j — ~P9ij
Система уравнений D.22) описывает целый класс трехмерных
нестационарных течений упругопластических сред. Для
выделения из этого класса единственного течения, отвечающего
решаемой задаче проникания металлического ударника в
металлическую преграду, необходимо задать соответствующие
начальные и граничные условия.
Начальные условия для взаимодействующих тел
задаются исходя из того, что материалы обоих тел в момент начала
взаимодействия не деформированы, не возмущены, все
индивидуальные точки преграды находятся в покое, а
индивидуальные точки ударника движутся с одинаковой скоростью vo.
В соответствии с этим начальные поля параметров движения
и состояния в области пространства ж, у, z ? Z?y, занимаемой
ударником, задаются как
Щ = Vi(x\ 0) = vOi]
р = р(х\ 0) = /э0у;
р = р(х\0) = 0- D.23)
Dtnj = Daij{x\ 0) = 0;
Е = Е(х\ 0) = ?Оу,
а соответствующие начальные поля в области пространства
ж, у, z G An занимаемой преградой, отличаются значениями
323

скорости, плотности и удельной внутренней энергии:
у{ = vt{xl, 0) = 0;
р = р{х\ о) = роп;
p = p(zl,0) = 0; D.24)
Dffij = D^ix1, 0);
Е = Е{х\ 0) = ЕОп,
где роу, роп и ?оу> ^0п — начальные значения плотности
и удельной внутренней энергии материалов ударника и
преграды. Следует отметить, что начальные уровни удельной
внутренней энергии при нормальных условиях для удобства
обычно полагаются равными Е$у = -Еоп = 0 (это
соответствует отсчету значений удельной внутренней энергии от уровня
удельной внутренней тепловой энергии при нормальной
температуре), а уравнения состояния материалов строятся с
обеспечением выполнения условия р = р(ро? ^о) = р(ро> 0) = 0«
Граничные условия при постановке задачи проникания
ударника в полубесконечную преграду задаются на
поверхностях 5*1, 5^2, 5з, ограничивающих деформируемые тела (см.
рис. 4.5, б). Поверхность Si преграды и поверхность 52
ударника допустимо рассматривать как свободные от действия
поверхностных сил, пренебрегая силами атмосферного давления:
о{jitf — рп{ = 0. В координатной форме динамические
граничные условия на свободных поверхностях Si и 52 примут
следующий вид:
ОтхПх + ОхуПу + uxznz = 0;
сгхуПх + ОууПу + Gyz^z = 0; D.25)
crxznx + &yzny + 0
где a{j — компоненты тензора напряжений в точках на
поверхностях S\ и 52; пх, пу, nz — компоненты единичного вектора
нормали п к поверхности в данной ее точке.
Более сложным образом следует задавать граничные
условия на границе раздела (поверхность 5з)
взаимодействующих деформируемых тел. Граничные условия на поверхности
324

5з накладывают ограничения на скорости движения
индивидуальных точек обоих тел, находящихся в контакте, в
соответствии с условием непроницаемости vy • п = vn • п, а также
на напряженное состояние, реализующееся в этих точках в
соответствии с третьим законом Ньютона ((?ijy — &ijn)n'* — О
(см. раздел 4.1.5), где п = п%г{ — единичный вектор нормали
к границе раздела двух тел. В принятой для описания
движения декартовой прямоугольной системе координат указанные
граничные условия задаются следующими равенствами:
пу
[(vz)y ~ (v*)nj nz = 0;
Пу
+ \(Gxz)y - (<7хг)п\ Пг = 0;
1 г 1 D*26)
- {(ТХу)п\ Пх + [(<7уу)у - (^yyj
yz)y - (<v)nj n2 = 0;
[(<rxz)y - (°xz)n\ ПХ + [((Tyz)y - (<ryz)n\ Пу +
+ [(azz)y - (^zz)nj nz = 0.
Система уравнений D.22) с начальными условиями
D.23) и D.24) и граничными условиями D.25) и D.26)
определяет физико-математическую модель процесса динамического
взаимодействия металлических ударника и преграды,
формулируемую на этапе постановки задачи. Уравнения и
соотношения D.22)—D.26) необходимы и достаточны для
выполнения завершающего этапа реализации феноменологического
подхода к изучению движения взаимодействующих
деформируемых тел или сред — непосредственного решения задачи
и получения количественной информации о представляющих
практический интерес параметрах исследуемого процесса.
325

В силу сложности приведенных уравнений подобные
системы не могут быть решены аналитически, поэтому для
получения результатов используются специальные методы
вычислительной математики — численные методы механики
сплошных сред. Подобная ситуация в целом характерна и
часто встречается при решении задач динамического
деформирования сплошных сред, даже гораздо более простых,
нежели рассмотренные в этом разделе упругопластические среды.
В настоящее время наиболее эффективным и универсальным
средством решения задач механики сплошных сред являются
именно численные методы.
Основные численные методы решения задач механики
деформируемого тела на примере задач физики быстропротека-
ющих процессов рассмотрены в третьем томе комплекса
учебников серии "Прикладная механика сплошных сред".
Вопросы и задачи
1. Что понимается под постановкой задачи механики
сплошных сред? Каковы основные этапы постановки задачи?
2. На основании чего выбирается модель сплошной среды для
исследуемого процесса движения реальной деформируемой
среды? Какими соотношениями описываются
индивидуальные физико-механические свойства той или иной
сплошной среды?
3. Какие ограничения накладываются на выбор системы
отсчета при постановке задачи механики сплошных сред, чем
определяются эти ограничения?
4. Какими соображениями определяется выбор конкретного
вида системы координат при постановке задачи механики
сплошных сред?
5. Какие системы координат разумно выбирать при описании
движения в следующих случаях: пространственное
движение; двумерное плоское; одномерное плоское; двумерное с
осевой симметрией; одномерное с точечной симметрией?
326

6. Что понимается под системой исходных уравнений, какие
группы уравнений и соотношений она включает? Каково
основное требование к системе исходных уравнений?
7. Что понимается под системой разрешающих уравнений,
как она взаимосвязана с системой исходных уравнений?
8. Что понимается под начальными условиями, чем
определяется их количество?
9. Определите понятие граничных условий и назовите их
типы.
10. Какие кинематические граничные условия являются более
жесткими — условия "прилипания" или условия
"непроницаемости"? Какое граничное условие более адекватно на
границе раздела двух взаимодействующих сред в процессе
проникания одной в другую?
11. Каков физический смысл граничных условий
"непроницаемости" ?
12. Каков физический смысл динамических граничных
условий?
13. Каков физический смысл динамической части граничных
условий смешанного типа на границе раздела двух
взаимодействующих сред? Какой закон физики они выражают?
14. К каким соотношениям сводятся динамические граничные
условия на свободной поверхности в общем случае и для
модели идеальной среды?
15. Как следует задавать граничные условия на поверхности
абсолютно твердого тела при обтекании его
деформируемой воздушной средой?
16. Как следует задавать граничные условия на границе
жидкости и проникающего в нее с постоянной скоростью неде-
формируемого тела?
17. Как следует задавать граничные условия в задаче о
метании несжимаемой тонкой жидкой оболочки газом?
18. Как следует задавать граничные условия в задаче о
метании поршня газом, движущимся в закрытой с одного торца
трубе?
327

19. Как называются частные виды уравнений движения для
идеальной и вязкой жидкостей, для упругой среды?
20. Каким образом из общих уравнений механики можно
получить уравнения движения и уравнение энергии
идеальной среды? Сформулируйте принцип и укажите в перечне
основных формул к главе 4 (см. приложение 1)
используемые для этого уравнения и соотношения.
21. Дайте эвристическое обоснование уравнений Эйлера и
истолкуйте их физический смысл.
22. Поле давления для некоторого момента времени в
идеальной среде в декартовой прямоугольной системе координат
задано функцией р = —2ху + 3yz. Пренебрегая объемными
силами, определите направление вектора ускорения
индивидуальной частицы, находящейся в данный момент
времени в точке пространства с координатами х = 2, у = 3,
z = 4.
23. Как выглядит система разрешающих уравнений
адиабатического течения идеальной среды (укажите ее в перечне
основных формул к главе 4 и поясните физический смысл
каждого уравнения)? К чему сведется эта система
уравнений для идеальной баротропной и несжимаемой жидкости?
24. Справедливо ли утверждение, что уравнение
теплопроводности является частным случаем уравнения энергии? Как
получить уравнение теплопроводности из уравнения
энергии?
25. Как выглядит система разрешающих уравнений течения
совершенного газа с учетом теплопроводности (укажите ее
в перечне основных формул к главе 4 и поясните
физический смысл каждого уравнения)?
26. В чем состоит особенность динамических граничных
условий при постановке задачи механики идеальной среды?
27. Каким образом из общих уравнений механики можно
получить уравнения движения Навье — Стокса?
Сформулируйте принцип и укажите в перечне основных формул к
главе 4 используемые для этого уравнения и соотношения.
328

28. Как выглядит система разрешающих уравнений
адиабатического течения вязкой баротропной среды (укажите ее
в перечне основных формул к главе 4 и поясните
физический смысл каждого уравнения)?
29. Какова особенность динамических граничных условий при
постановке задачи механики вязкой жидкости с
использованием в качестве основных неизвестных давления,
плотности и компонент вектора скорости? На что в этом случае
накладываются ограничения?
30. Каким образом из общих уравнений механики можно
получить уравнения Лямэ? Сформулируйте принцип и
укажите в перечне основных формул к главе 4 используемые
для этого уравнения и соотношения.
31. Как выглядит система разрешающих уравнений
адиабатического течения упругой среды (укажите ее в перечне
основных формул к главе 4 и поясните физический смысл
каждого уравнения)? К чему сведется эта система
уравнений при постановке статической задачи теории упругости ?
32. Какова особенность записи динамических граничных
условий при постановке задачи механики упругой среды с
использованием в качестве основных неизвестных компонент
вектора перемещения? На что в этом случае
накладываются ограничения?
33. Какой системой уравнений описывается адиабатическое
деформирование упругопластической среды при больших
деформациях и сложном нагружении (укажите ее в перечне
основных формул к главе 4 и поясните физический смысл
каждого уравнения)?
34. Как следует задавать начальные условия для задачи
проникания металлического тела в металлическую преграду?
35. Как задаются граничные условия для задачи проникания
металлического тела в металлическую преграду?
36. В чем состоит особенность записи определяющих
уравнений и физических соотношений теории пластического
течения для динамических процессов, сопровождающихся
большими объемными деформациями?
329

37. В каком смысле можно говорить об универсальности
тензорной формы записи систем разрешающих уравнений
течения той или иной среды? Каким образом можно
получить различные частные формы представления этих
систем применительно к конкретной системе координат?

ПРИЛОЖЕНИЯ
1. Основные формулы
Глава 1
Преобразование координат и векторов основного базиса:
dr = ri dx{ = (rS dy\ dy{ = dxj
Инвариантность тензора первого ранга относительно
преобразования системы координат:
а = аУ = (а,)' (г')' = а'г, = (в*)' (г,-)'.
Представление тензора первого ранга через
контрвариантные компоненты и векторы основного базиса:
{ V дхк
( Л' it дУ{ ( V
через ковариантные компоненты и векторы взаимного базиса:
>V = r*
dxk'
Инвариантность тензора второго ранга относительно
преобразования системы координат:
(о) = аЧг;гу = («°)'('i)'(r,-)' = «urV =
331

Представление тензора второго ранга через
контрвариантные компоненты и диадные произведения векторов
основного базиса:
1 dyi /у дха / у f*
«У k
через ковариантные компоненты и диадные произведения
векторов взаимного базиса:
1 / ty а%* / у оду'
/ \' дж* дх1 / ty а%*
через смешанные компоненты и диадные произведения
векторов основного и взаимного базисов:
, дхк dyi ( л' а ду1 ^
Глава 2
ty = 0,5 (Vjtt,- + VjUi + ViUkVjUk).
u\ = u + dua + dun.
dua = (e) • dR = (eijlVR^ ¦ (df'Aj) = e{j d?RJ.
dun = dR ¦ (w) = (Л/df') • (uijR'Ri) = utj dCRj.
332

?«¦ =
2,( \2
+ («B2) - ?C3)J "
(зз)
uij = 0,5 (ViVj-VjVi).
dvn.
dva = (e) ¦ dr = (kijT%r*) ¦ (dxlr\ j = ё,-у ё,х1г}.
/ д / ,- л • i «'
\ / \ /
) • П = (<7ijrlrj) • (^njtr^J = <7ijnjr%.
а(п) = <7пП = СГцПгП3.
333

y/2
\2 / \2
~ °"B2)J + ^B2) - cr{33)j
+
+ ^23) +
y/2
i = -y V (<?1 -
= 0.
do
dv „ , . .
— = F+ div(a).
-+ f (Tij?ijdV= f FvdV + ipnvdS.
V V S
j(EK + U)= f F-vdV+ lpnvdS.
V S
: + U)= I FvdV+ ipnvdS- iqndS.
dE
dt p p
334

о<х<-^-
Глава 3
а = -р(р, Т) + ЗАё.
= -р(р, Т) 9ij + (ЗА - 2/х) egij +
о = ЗКе;
(D,) = 2G(D?);
<rtj = 2G
?tj ~ 2G
еа
ЪК
к =
Е
сг = ЗКе;
= B(De)=-±(De) = 2G(l
ое,-
= 2G
_ J_
~ 2G
ij + f go ~ 0
335

da = 3Kde;
de^deW + de®;
= deWgii/z = 0;
" 7 ^^'] + dX
3 ?,•
r —
Глава 4
^ + pvy = 0;
at
dtrr '
H dt '
pCvTt=-pTt
p = рДГ.
336

p = p(p)-
ij = ~P9ij

2. Примеры билетов
теоретических коллоквиумов
для контроля усвоения материала
(три коллоквиума, максимальная сумма баллов — 100)
Коллоквиум 1. Математический аппарат механики сплошных
сред — 30 баллов
Билет 1
№. п/п
Содержание задания
1
10
Покажите, что совокупность точек на сферической
поверхности не образует двумерного евклидова
пространства
Понятие координатных поверхностей
Векторное произведение векторов
Задано поле скалярной величины р = р(х, у, z) =
= 2xy + z. Для точки пространства с координатами
z = l,2/ = 2,2 = 3 определите значение производной
1.1.
по направлению единичного вектора 8 — —j=. % + —=. J
Какое значение имеет дивергенция вектора
скорости в любой точке потока несжимаемой жидкости в
случае отсутствия в потоке внутренних источников
массы ?
Различаются ли матрицы, составленные из
метрических коэффициентов смешанного типа в
декартовой прямоугольной, цилиндрической и
сферической системах координат ?
Преобразование векторов основного базиса. Кова-
риантный закон преобразования
Понятие ранга тензора
Определите результат (а) • F) = ( aijTlrJ J • lbkVk J,
где F) = lri -f 2Г2 + ЗГ3, a тензору второго ранга со-
( ( 1 0 2\\
ответствует матрица I I аи I I — I I 3 2 ill
I I 0 0 5 J J
Векторный символический дифференциальный
оператор Гамильтона в тензорном анализе (приведите
запись и поясните ее)
338

Билет 2
№ п/п
1
2
3
4
5
6
7
8
9
10
Содержание задания
Основные гипотезы механики сплошных сред
Понятие и примеры криволинейных систем
координат
Определите объем параллелепипеда, построенного
на отложенных от одной точки векторах а = li +
+ 2j + 3fc, b = -2* + 3j + lfc, с = 2i - 5j + 2fe
Постройте векторные линии поля скорости
движения частиц абсолютно твердого тела при
вращении его вокруг закрепленной оси
Использование векторного символического
дифференциального оператора Гамильтона при
проведении дифференциальных операций первого порядка
с векторами в декартовой прямоугольной системе
координат
Метрические коэффициенты основного базиса и
соответствующая метрическая матрица
Контрвариантные компоненты вектора.
Инвариантность вектора относительно преобразования
системы координат
Операция умножения тензора произвольного
ранга на скаляр
Чем объясняется тот факт, что компоненты дис-
криминантного тензора с любыми двумя
одинаковыми индексами равны нулю
Теорема Остроградского — Гаусса в тензорном
анализе (формулировка и запись в тензорном
виде)
Балл
3
1
2
3
3
3
5
2
4
4
Билет 3
№ п/п
1
2
Содержание задания
Почему при решении прикладных задач
взаимодействия деформируемых тел или сред время можно
считать абсолютным и не зависящим от выбора
системы отсчета ?
Задание координат точек пространства в
цилиндрической системе координат
Балл
to to
339

Окончание билета 3
№ п/п
3
4
5
6
7
8
9
10
Содержание задания
Разложение вектора на составляющие. Компоненты
вектора
Чему равно векторно-скалярное произведение
трех векторов, составляющих ортонормированный
базис в декартовой прямоугольной системе
координат ?
Задано скалярное поле р = р(х} j/, г) = х + 2zy.
Для точки пространства с координатами х = 1,
у = 2, 2 = 3 определите минимальное значение
производной по направлению
Скорость движения потока жидкости одинакова
для всех частиц. Чему равна дивергенция
вектора скорости в произвольной точке потока ?
Метрические коэффициенты основного базиса
в цилиндрической системе координат, их
геометрический смысл
Инвариантность вектора dr (дифференциала
радиус-вектора т) относительно преобразования системы
координат
Операция вычитания тензоров
Дифференцирование по координатам тензора
второго ранга, заданного своими
контрвариантными компонентами. Абсолютная производная
контрвариантных компонент тензора второго
ранга
Балл
1
1
4
3
3
5
3
6
Билет 4
№ п/п
1
2
3
4
Содержание задания
Что такое сплошная среда? Существуют ли такие
среды в реальности?
Почему математические объекты математического
аппарата механики сплошных сред должны быть
инвариантными относительно преобразования
системы координат ?
Понятие правой тройки векторов
Понятие годографа вектора
Балл
2
3
1
1
340

Окончание билета 4
№ п/п
5
6
7
8
9
10
Содержание задания
Ротор вектора (определение, физический смысл,
выражение через компоненты вектора)
Какие математические объекты определяются в
соответствии с выражениями Г; = ——г ?
дхг
Является ли фундаментальный метрический
тензор симметричным ? Если является, то почему ?
В чем состоит правило суммирования Эйнштейна ?
Определите результат перемножения тензоров
[(«) • № ¦ (Ь) = [(aOrv) • (б*г*)] • (б(г')
Чем отличается абсолютная (ковариантная)
производная от обычной частной производной ?
Каков геометрический смысл дополнительных
членов ?
Балл
5
3
4
2
5
4
Коллоквиум 2. Общие положения, уравнения и соотношения
механики сплошных сред — 30 баллов
Билет 1
№ п/п
1
2
3
4
Содержание задания
Понятие сопутствующей системы отсчета
Принцип определения главных направлений и
главных деформаций
Производный инвариант тензора деформаций —
средняя деформация — и его физический смысл
Тензор напряжений (сг) = <п^г1г3 в точке
( ( 1 2 ® Л Л
задан матрицей 1 1 а3А 1 = 1 1 2 3 5 1 1 .
1 1о 5 1 J J
Определите нормальное напряжение в данной точке
на площадке с единичным вектором нормали
k 1 1
\/2 у/2
Балл
2
4
3
3
341

Окончание билета 1
№ п/п
5
б
7
8
9
10
Содержание задания
Взаимосвязь тензора напряжений на поверхности
тела с вектором удельной поверхностной силы
и ориентацией поверхности — граничные условия
в напряжениях
Запись уравнения неразрывности в декартовой
прямоугольной системе координат
Как следует понимать утверждение об
универсальности уравнений движения ?
Закон теплопроводности Фурье
К каким процессам (обратимым или необратимым)
относится удар упругого тела о недеформируемую
преграду ?
Вывод дифференциального уравнения второго
закона термодинамики
Балл
3
3
2
3
2
5
Билет 2
№ п/п
1
2
3
4
5
б
Содержание задания
Понятие переменных Эйлера
Задано поле перемещений в сопутствующей
системе координат, являющейся в начальный момент
времени декартовой прямоугольной: и1 = (г + а?2,
и2 = ?2 + аC, и3 = ?3 + ас;1.- Считая деформации
малыми, определите поле тензора деформации
Геометрический смысл компонент тензора
деформаций с одинаковыми индексами (обоснуйте)
Геометрическое представление напряженного
состояния — поверхность напряжений
Производный инвариант тензора напряжений —
интенсивность напряжений — и его физический
смысл
Вид уравнения неразрывности для несжимаемой
среды
Балл
1
3
4
4
3
2
342

Окончание билета 2
N° п/п
7
8
9
10
Содержание задания
Охарактеризуйте физические величины,
участвующие в записи уравнения баланса механической
энергии (теоремы "живых сил"). Сформулируйте
эту теорему
Определение вектора теплового потока
Что понимается под необратимыми потерями
энергии при взрыве, при ударе ?
Вид уравнений движения в декартовой
прямоугольной системе координат
Балл
3
3
3
4
Билет 3
Ns. п/п
Содержание задания
Балл
Понятие переменных Лагранжа
Введение тензора деформаций
Что можно сказать об изменении объема и формы
индивидуальной частицы сплошной среды,
деформированное состояние которой характеризуется
тензором деформаций, заданным матрицей
а-)) -
Физический смысл тензора напряжений в целом
Производный инвариант тензора напряжений —
среднее напряжение — и его физический смысл
Получите уравнение неразрывности, исходя из
истолкования физического смысла дивергенции
вектора скорости течения сплошной среды
Какое уравнение в динамике материальной точки
является по физическому смыслу аналогом
уравнений движения сплошной среды ?
Какие физические величины описывают состояние
сплошной среды ?
343

Окончание билета 3
№ п/п
9
10
Содержание задания
Охарактеризуйте физические величины, входящие
в дифференциальное уравнение второго закона
термодинамики. Каков физический смысл
составляющих, входящих в это дифференциальное уравнение?
Как может меняться энтропия индивидуальных
частиц материального континуума в общем случае
и почему ?
Балл
со со
Билет 4
№ п/п
1
2
3
4
5
6
7
Содержание задания
Понятие местной или локальной производной по
времени
Характеристика тензора деформаций
Что можно сказать об изменении объема и формы
индивидуальной частицы сплошной среды, если
в ней реализуется деформированное состояние
всестороннего растяжения ?
Принцип определения главных напряжений и
главных осей тензора напряжений
Определите первый и второй основные инварианты
тензора напряжений, заданного в декартовой
прямоугольной системе координат матрицей
(( 6 -3 0 ЛЛ
1 1 O4j J] = || —3 6 0 II. Найдите главные
Но 0 8 ))
напряжения и покажите, что диагональная матрица
приводит к тем же значениям инвариантов
Назовите фундаментальные законы, которым
подчиняется движение материального континуума
Охарактеризуйте математические объекты,
участвующие в записи дифференциального уравнения
движения (название величины, ранг)
Балл
3
3
2
4
4
2
2
344

Окончание билета 4
№. п/п
8
9
10
Содержание задания
В точке материального континуума задан вектор
теплового потока q. Определите количество
теплоты dQy переносимой за малое время dt через
бесконечно малую площадку dS, ориентация
которой задана единичным вектором нормали п
Запишите интегродифференциальное уравнение,
выражающее закон сохранения полной энергии для
индивидуального объема материального
континуума. Каков физический смысл входящих в это
уравнение составляющих ?
К каким процессам (обратимым или необратимым)
относится процесс проникания срабатывающегося
металлического тела в металлическую преграду ?
Балл
4
4
2
Коллоквиум 3. Модели сплошных сред и постановка задач
механики сплошных сред — 40 баллов
Билет 1
№. п/п
1
2
3
4
5
6
7
Содержание задания
Понятие реономных свойств сплошной среды
Понятие идеальной баротропной жидкости
Модель упругой среды — прямые физические
соотношения
Основное отличие теории пластического течения
от деформационной теории пластичности
Выражение для критерия пластичности Мизеса
и его физический смысл (без вывода)
Какими соотношениями в системе исходных
уравнений учитываются физико-механические свойства
сплошной среды, а какие соотношения являются
общими для всех сред ?
Запишите систему разрешающих уравнений
адиабатического течения идеальной среды в
декартовой прямоугольной системе координат
Балл
3
2
4
4
3
4
5
12-9712
345

Окончание билета I
№ п/п
8
9
10
Содержание задания
Постановка задачи механики вязкой жидкости
(для вязкой баротропной среды)
Запишите конкретный вид уравнения
неразрывности, используемый для описания трехмерного
течения упругопластической среды
Как следует задавать граничные условия на
границе раздела двух взаимодействующих упругопласти-
ческих тел ?
Балл
7
3
5
Билет 2
№ п/п
1
2
3
4
5
6
7
8
Содержание задания
Понятие склерономных свойств сплошной среды
Оказывает ли сопротивление формоизменению
идеальная жидкость ?
Модель упругой среды (обратные физические
соотношения)
Обратные физические соотношения для модели
упругопластической среды согласно
деформационной теории пластичности
Представление различных видов напряженного
состояния в пространстве главных напряжений
Кинематические граничные условия
непроницаемости
Поле давления в идеальной среде в некоторый
момент времени задано функцией р = Ъху — 2yz.
Пренебрегая объемными силами, определите
направление вектора ускорения индивидуальной
частицы, находящейся в данный момент времени в
точке пространства с координатами х = 2, у = 1,
z = 5
Постановка задачи теории упругости (при
отсутствии влияния температуры на
физико-механическое поведение среды)
Балл
2
2
4
5
3
4
5
7
346

Окончание билета 2
№ п/п
9
10
Содержание задания
Запишите в декартовой прямоугольной системе
координат уравнения пластического течения,
используемые при постановке задачи о
динамическом взаимодействии упругопластических сред
В какой из моделей сплошных сред
используется коэффициент Пуассона ? Каков его физический
смысл ?
Балл
6
2
Билет 3
№ п/п
1
2
3
4
5
6
7
8
Содержание задания
Что понимается под определяющими уравнениями
сплошной среды ? Что они описывают ?
Напряженное состояние в идеальной жидкости
характеризуется тензором напряжений (<т) = <Т{3тхт*.
Определите главные оси тензора напряжений
Чему равны модуль объемного сжатия и
коэффициент Пуассона для несжимаемой упругой среды ?
Определение остаточных деформаций при нагру-
жении и последующей разгрузке упругопласти-
ческой среды (в рамках деформационной теории
пластичности)
Каким образом представляются напряженные
состояния всестороннего равноосного
растяжения-сжатия в пространстве главных напряжений ?
Какие граничные условия следует задавать на
границе раздела недеформируемого ударника и
деформируемой среды ?
Получите систему разрешающих уравнений
адиабатического течения идеальной несжимаемой
жидкости (в тензорной записи)
Запишите систему разрешающих уравнений
пространственного (трехмерного) адиабатического
течения вязкой баротропной среды в наиболее
подходящей для этого случая системе координат
Балл
2
2
4
7
2
5
5
5
12*
347

Окончание билета 3
№ п/п
9
10
Содержание задания
Получение уравнений Лямэ из общих уравнений
движения
В системе уравнений, описывающей адиабатическое
деформирование упругопластической среды,
укажите уравнения, выражающие законы сохранения
массы, импульса и энергии
Балл
6
2
Билет 4
№ п/п
1
2
3
4
5
6
7
8
Содержание задания
Физическое поведение сплошной среды и его
математическое описание. Понятие об уравнении
состояния
В идеальной жидкости задано поле перемещений
щ(х1)х2уХ3)} которому соответствует поле
деформаций eij^x1,^2,^3). Определите значение
интенсивности напряжений в точке с координатами
х1 = 2, х2 = 0, х3 = 5
Понятие идеально упругой среды
Физические соотношения для модели
упругопластической среды при разгрузке
В каком состоянии (упругом или пластическом)
находится идеальная упругопластическая среда
с пределом текучести <гт, если напряженное
состояние в ней характеризуется главными
напряжениями <г\ = 1,5о"т, <Т2 = 0т, 0"з = 0,5(Гт
Пример задания граничных условий в задаче об
одномерном метании поршня газом, находящимся в
трубе
Физическая интерпретация уравнений Эйлера
Преобразование уравнений движения для модели
вязкой жидкости — получение уравнений
Навье — Стокса
Балл
4
2
2
3
5
4
3
6
348

Окончание билета 4
№ п/п
9
10
Содержание задания
Постановка задачи механики у пру гоп ласти ческой
среды на примере процесса проникания
металлического тела в металлическую преграду
Влияние температуры на механическое поведение
сплошных сред
Балл
8
3

3. Примеры решения
типовых задач
1. Определите объем параллелепипеда, построенного на
отложенных от одной точки векторах а = 2i+5fc, Ь = 3i+j+k,
Решение. В соответствии с геометрическим
смыслом векторно-скалярного произведения трех векторов
искомый объем определяется модулем определителя,
составленного из компонент заданных векторов:
2 0 5
V = Ьт bl br = 3 1 1
2-5 0
+ 5
ах ау
az
bx by bz
Сх Су С%
. 3 1
> 2 -5
=
1
-5
5 (-15- 2-1) = |10-85| = 75.
2. Определите градиент скалярной функции координат
г = yjx1 + у2 + z2. Для произвольной точки пространства
определите производные по направлениям: от начала
координат к данной точке (si), от данной точки к началу координат
E2), по касательной к проходящей через данную точку
сферической поверхности с центром в начале координат (зз).
Решение. В соответствии с определением градиент
заданной скалярной функции в декартовой прямоугольной
системе координат для произвольной точки пространства
выражается как
дг . дг . дг , *>*
grad r=—t+—j+—k =
дх ду дг
+ У* +
•-J +
+ У2 + г2
хг + yj + zk
к =
yf*
Г
= - = пг,
350

где г — радиус-вектор данной точки, а пг — единичный
вектор, ко л линеарный радиус-вектору и сонаправ ленный с
ним. Согласно геометрическому смыслу градиента
скалярной функции координат, его проекция на произвольное
направление определяет значение производной заданной функции по
данному направлению: dr/dsi = 1, дг/дв2 = — 1, dr/ds^ = 0.
3. Поле скорости течения жидкости в некоторый момент
времени t задано в декартовой прямоугольной системе
координат как v = vxi + vyj + vzk = xi - Zyzj + 2zk. Что можно
сказать о движении бесконечно малой частицы жидкости,
находящейся в данный момент времени в точке пространства с
координатами х = 1, у = 2, z = 3?
Решение. Поле скоростей позволяет определить
поступательную, деформационную и вращательную
составляющие движения любой частицы жидкости. Скорость
движения данной частицы определяется тривиальным образом:
v = 1 • 2г - 3 • 2 • 3j + 2 • 3fc = 2г - 18j + 6fc.
Согласно физическому смыслу дивергенции вектора, для
векторного поля скорости течения жидкости при отсутствии
в потоке внутренних источников массы divu определяет
относительную скорость изменения объема V бесконечно малой
индивидуальной частицы:
г V ,. dvx dvy dvz
lim 77 = div v = -т^- + -г^ + -rr-1 =
V-+0 V дх ду dz
d(x) d(-3yz) 0B*) _
Для данной частицы div v = — 6 < 0, что говорит о
проявлении в данный момент времени тенденции к сжатию частицы,
уменьшению ее объема и увеличению плотности.
Согласно физическому смыслу ротора вектора, для
векторного поля скорости течения жидкости rot г? определяет
мгновенную угловую скорость и> вращательного движения
бесконечно малой индивидуальной частицы:
351

= rot v =
г
д
дх ду
к
д_
dz
Vz
dvz
ду
dVy
" dz
dBz)
ду
\ . (dvz
d(-Zyz)
dvx
dz
дх
dz
3 +
Для данной частицы ш = 6г — ось вращения, параллельная
оси х системы координат, и вращение происходит против хода
часовой стрелки по отношению к этой оси.
Зависимость величин г?, divv, rotv от координат
говорит о том, что частицы деформируемых сред в общем случае
движутся с разными скоростями, испытывают различные
деформации и вращательные движения.
4. На примере скалярного произведения тензора второго
ранга (а) = uj^r и тензора первого ранга F) = Ь%Г{ =
= 2r\ + 3i*2 + 5гз покажите, что операция скалярного
умножения тензоров в общем случае не обладает свойством
коммутативности. Тензору второго ранга соответствует матрица
Решение. Тензор второго ранга (а) = а^т^т*
представляет собой сумму девяти составляющих, а тензор F) = Ь%Г{
— сумму трех составляющих. При скалярном умножении
(а) • (Ъ) в соответствии с распределительным законом
получается сумма 27 составляющих (а) -F) = [ajk^rj ' y>%ri) =
= а^Ьгг3гк • г,, каждый член которой содержит
произведение компонент a,jh и Ьг исходных тензоров, а также скалярное
произведение базисных математических объектов — тензора
352

второго ранга (диадных произведений векторов взаимного
базиса г*тк) и тензора первого ранга (векторов г,-). По правилам
умножения диады на вектор результат скалярного умножения
Wr* • Г{ определяется скалярным произведением вектора тк
(ближайшего к базисному математическому объекту) и
вектора rj, является вектором, коллинеарным вектору т3
(дальнему от сомножителя гг), и представляется как г3тк • гг =
= rJ(rk • Г{ j = г3дк, где дк = 6к — метрические
коэффициенты смешанного типа, или символы Кронекера. С
использованием операции замены одного индекса другим получается
выражение для скалярного произведения (а)-F), которое
определяется вектором:
(а) • F) = ajkb^rk - rt = ajkbW3 (r* . r.) = ajk
= ajk (Ь{дк) г* = ajkbkr> = (anb1 + al2b2 + a
-f-^ib1 + a22b2 + a23b3) r2 + (аз^1 + a32b2 + a33b3) r3 =
= A-2 + 0-3 + 2. 5) r1+C-2 + l-3 + 2- 5) r2 +
+ A • 2 - 1 - 3 + 4 - 5) r3 = 12Г1 + 19r2 + 19r3.
Скалярное произведение (Ь) • (a) определяется
аналогичным образом, но с тем лишь отличием, что сумма (Ь)-(а) =
— (Ь*т*Л • (ayjtr>?r ) = ajkb*Ti r^rk содержит скалярные
произведения векторов гг и диад г^тк. Каждое из этих
произведений определяется как г, • г*гк = (г^ • W 1 rk = 5ir^ и является
вектором, коллинеарным вектору г*. Это изменение и
определяет отличие результата скалярного умножения тензора (Ь)
на тензор (а) от результата скалярного умножения (а) на F):
(б) • (a) = (blrt) - (азкг>гк) = а^Ь{тг - т>тк =
= азкЬг{тг ¦ т>) тк = ajkblg{rk = ajkVvk =
1 + a21b2 + а31Ь3) г1 + (а12Ьг + a22b2 + а32Ь3) г1 +
353

(a13b1 + a23b2 + a33b3) rz = A • 2 + 3 • 3 + 1 • 5) r1 +
+ @ • 2 + 1 • 3 - 1 • 5) r2 + B • 2 + 2 • 3 + 4 • 5) r3 =
5. В декартовой прямоугольной системе координат
определите векторное произведение двух тензоров первого ранга
(a) = aWi и F) = Vtj с использованием дискриминантного
тензора, убедитесь в идентичности найденного Вами
результата результату, получаемому с помощью известных правил
векторной алгебры.
Решение. Согласно правилам векторного
умножения тензоров, векторным произведением двух тензоров
первого ранга является тензор первого ранга
(с) = (а) х F) = () ()
= а^(тг х Tj) = alb>Aijkrk = ckr\
где компоненты дискриминантного тензора Л^д. = 0 при г = j,
или г = &, или j = к, а при одновременном выполнении
условия i ф j, i ф к, j ф к эти компоненты определяются
детерминантом метрической матрицы декартовой
прямоугольной системы координат д = 1 как Л,^ = ±\/^ = ^1> ПРИ этом
знак плюс используется в случае образования
соответствующими индексам г, j, к базисными векторами г,-, гу, гк правой
тройки, а знак минус — в случае образования базисными
векторами 7%, ry, rj., соответствующими индексам i,j,Л, левой
тройки.
Компоненты результирующего тензора ск = а1ЫА^к в
развернутом виде выражаются как
с* = аЧ1Аик + а1Ь2Л12* + ^
a363A33ib = а1
354

в частности
с2 =
+ аЧ1
a2b1A2n + а2Ь3Л231 +
+ аЧ1 Am + а362Л321 = а2Ь3Л231 + а3*>2Лз21
а263Л232 +
+ а362Л322 = a1bzAi32 + аЧ1 А312
= а1Ь3(-1) + о361(+1) = о3Ь1
= аЧ2(+1) + a2b\-l) = аЧ2 - аЧ1.
В декартовой прямоугольной системе координат
результатом векторного умножения двух векторов является вектор
с = axb =
г1 г2 г3
а1 а2 а3
б1 Ь2 б3
= т\аЧ3-аЧ2)-
компоненты с\, С2, сз которого идентичны компонентам,
полученным с использованием дискриминантного тензора. Это
является следствием того, что правила векторной алгебры —
частный случай более общих правил тензорной алгебры.
6. Определите производную тензора первого ранга (а) =
= агг{ по каждой из трех координат ж1, ж2, ж3, считая, что
тензор задан в цилиндрической системе координат (ж1 = г,
х2 = 0, х3 = z) как а1 = а1^1, ж2, ж3) = а1 (ж1, ж3) =
= a\ry z) = 2r2+3z, а2 = 0, а3 = а*(х\ ж2, ж3) = а3(жх, ж3) =
3 2
Решение. Производной тензора первого ранга по
координате является также тензор первого ранга
355

компоненты которого — абсолютные (ковариантные)
производные компонент исходного тензора:
i t да% к
6 =V>a = + аГ
где Г^. • — символы Кристоффеля второго рода, в
цилиндрической системе координат отличные от нуля лишь в случаях
*21 = М2 = 1/г> Г22 = —f.
С учетом этого обстоятельства, а также при заданном
а2 = О компоненты результирующего тензора в развернутом
виде запишутся как
2 5а 1Г2 ,.2Г2 , „3Г2 ЛГ2 .
3
В частности:
при j' = 1
1 2 + Зг)
Ъ2 = а1^ = 0;
з да*
b
Ъг 
и результирующий тензор первого ранга принимает вид
при j = 2
те— = 0;
356

и производной будет тензор первого ранга
при j = 3
б2 = а1Т\3 = 0;
з да3
и искомый результат представляется как
где гь Г2, гз — векторы основного базиса цилиндрической
системы координат в точке пространства с координатами г,
e,z.
7. Для некоторого момента времени закон движения
сплошной среды задается уравнениями ж1 = zj, х2 = Яд + аа^,
ж3 = Zq + ажд, где ж1, ж2, ж3 — эйлеровы координаты
индивидуальных точек, a xj, ж2, ж3 — их лагранжевы
координаты, понимаемые как начальные значения эйлеровых
координат. Определите поле перемещений сплошной среды, описав
его с позиций Лагранжа и Эйлера.
Решение.В соответствии с определением вектор
перемещения и = г — JR, где г — радиус-вектор текущего
положения индивидуальных точек, a R — радиус-вектор их
начального положения. Отсюда компоненты вектора
перемещения выражаются через эйлеровы и лагранжевы координаты
как иг = х% — Xq, что приводит к описанию поля
перемещений с позиций Лагранжа как и1 = 0, и2 — axjj, и3 = аж§. Это
описание определяет перемещение любой индивидуальной
точки, выделяемой тройкой значений своих начальных координат
Т1 Т2 Т3
х х х
357

Переход к описанию поля перемещений с позиций Эйлера
выполняется с помощью преобразования закона движения и
представления его в обратной форме:
19 9 1
ах ~~ х 3 _ ах ~~ х
Хо =
указывающей на то, какая именно точка среды,
индивидуализируемая лагранжевыми координатами xj, х2, ж3, находится
в данный момент времени в данной точке пространства с
эйлеровыми координатами я1, я2, ж3. С учетом этого
преобразования поле перемещений описывается с позиций Эйлера (для
каждой точки пространства) как
1 л 2 ах2 я3 ая3 я2
и = 0, и =
2 1
и =а—ту —, и =а
1 1
а1 - 1 а1 - 1
8, В сопутствующей системе координат (f1, f2, f3),
являющейся в начальный момент времени декартовой
прямоугольной, задано поле перемещений:
и = f 1^2Д1 + (f2 + ^3) Д2 - f2f3Д3.
Считая деформации малыми, сопоставьте три следующие
индивидуальные частицы с заданными лагранжевыми
координатами f1, f2, ^3 с точки зрения изменения их объема и формы:
Ml@, а, 2а), М2Bа, -а, 0), М3Bа, За, -За).
Решение. О степени изменения объема и формы
индивидуальных частиц следует судить по производным
инвариантам тензора деформаций — средней деформации и
интенсивности деформаций:
" "' 3
где первый и второй основные инварианты в декартовой
прямоугольной системе координат определяются как
^2^J — tijt — tj! -t- ?22 "• ?33 "+" Z?12 ' Z?13 "i Z?23*
2 +1\ + e\ + 2е\ + 2е2 + 2е\
358

Значения компонент тензора деформаций в
индивидуальных точках сплошной среды определяются согласно
геометрическим соотношениям, в данном случае приобретающим
следующий вид:
_ 1 (дщ , дщ\ _п
дщ
Для индивидуальной частицы Mi@, а, 2а)
((| ))
Г2(е) = 46а2, е = 2а, ?t- = -^р1 а;
для индивидуальной частицы МгBа, -а, 0)
(Г-а а 0))
((*<;)) = а а ~° ' Г1(е) = -2а,
для индивидуальной частицы МзBа, За, -За)
= \\ а ° 1.5а ,
Ц 0 1,5а -За JJ
49fl2 л >/147
359

Наибольшие объемную деформацию и формоизменение
испытывает индивидуальная частица Mi, наименьшее изменение
объема — частица Мз, а наименьшее формоизменение —
частица Мг.
9. Напряженное состояние сплошной среды в
декартовой прямоугольной системе координат задано полем
тензора напряжений (а) = сг^ггг^ с компонентами I I о^ 11 =
(Bху Ъу2 ОЛЛ
= Зу2 0 z • Определите вектор полного напряже-
Ц 0 z lJJ
ния, нормальное и касательное напряжения в точке
РB, 1, у/3) на площадке, касательной к цилиндрической
поверхности у2 + z2 = 4.
Решение. Вектор полного напряжения, нормальное
и касательное напряжения в любой точке сплошной среды на
произвольной площадке определяются тензором напряжений
в этой точке и ориентацией площадки как <гп = (а) • п =
( (nkrkj = (JijnJr1 = anir\ <7(n) = an n =
Тензор напряжений в данной точке среды РB, 1, \/3) при-
(( Л\ ff4 3 ° 11
нимает вид 11 a{j 1 ] = I I 3 0 л/3 , а единичный век-
11 )} [{О V3 1 JJ
тор нормали к заданной площадке определяется как нормаль к
цилиндрической поверхности Ф(я, у, z) = y2 + z2-4 = 0,
которая может рассматриваться как одна из поверхностей уровня
скалярной функции координат Ф(х, у, z) = у2 + z2 — 4.
В соответствии с физическим смыслом градиента
скалярной функции координат последний направлен по нормали к
заданной цилиндрической поверхности и позволяет определить
искомый единичный вектор нормали как n = grad Ф/lgrad Ф|.
В заданной точке
360

дФ
= ('2yr2 +
дФ
+ ду
2zrz)
n =
r2 +
p ~
1
2 r2
дФ
dzn
2t2 + \
^у/Ъ
+ 2 7
, |grad Ф| = 4,
В итоге вектор полного напряжения определится как
{а2\п1 + (Т22П2 + <T23«3) г2 + (1 И1 + 2Я2 +
а нормальное и касательное напряжения будут соответственно
равны:
(п) =crnn = aninx =
+ °п2П
з л з
10. Относительно неподвижной декартовой
прямоугольной системы координат (ж1, х2, я3) имеется плоский поток
несжимаемой жидкости
где г2 = (х1) + (х2) . Найдите во всем потоке компоненту
v2, если v2 = 0 при х1 = 0 для всех значений х2.
361

Решение. Уравнение неразрывности для плоского
потока несжимаемой жидкости V,v' = 0 в декартовой
прямоугольной системе координат сводится к виду
dv2
Эх2 ~ '
откуда
dv2 dv1 2ax2x1
дх2 Эх1 Г/ Л2 , / ,\2]2"
1Н + И J
Г/ Л2 , / ,\2]
1Н + И J
Интегрируя последнее выражение по ж2 при фиксированном
ж1 от некоторого ж2 до произвольного я2, получаем
[И + И1
, ахЧ\(х
J («о
(«о+ и ]
Заданному условию г;2 = 0 при х1 = 0 для Уж2 отвечает любая
функция С(ж1, ж2), удовлетворяющая требованию (^(ж1, ж2) =
z= С(ж1) = 0 при ж1 = 0, и, в частности, искомый результат
может быть представлен как
2 _ ах1 _ oar1
И+И"
11. Найдите зависимость скорости материального
континуума от времени и лагранжевой координаты его частиц, если
распределение напряжений в среде задано в декартовой
прямоугольной системе координат приведенным ниже тензором
362

напряжений, массовые силы отсутствуют и в
начальный момент времени материальный континуум неподвижен:
(( \\ iff 0к0Р о II
11 ач 11 = Ъ{х1Ур 0 2х6р I I , где р — плот-
II 0 2х*р О JJ
ность среды.
Решение. В соответствии с уравнениями
движения компоненты вектора ускорения индивидуальных точек
материального континуума определяются как
dv^__ \j_
р dt ~ ja ~
_ \j_^_ ^_ да13
dt ~ ja ~ + +
dv3 _ з,-
p dt ~Vj(T
С учетом начальных условий отсюда получаем, что в
направлении оси ж3 движение отсутствует: v3 = 0, в
направлении оси х2 оно является равноускоренным: v2 = 21, а в
направлении оси х1 — более сложным: dv1 /dt = 13x2, где
эйлерова координата х2 индивидуальных точек зависит от
времени и изменяется согласно дифференциальному уравнению
dx2/dt = v2 = 2t. Интегрирование последнего уравнения с
учетом определения лагранжевой координаты как начальной
позволяет получить закон изменения
эйэйлеровой х2 = х2
леровой координаты индивидуальных точек: х2 = Zq-И2. При
последующем интегрировании уравнения движения по
направлению х1 с учетом отсутствия движения в начальный момент
находим зависимость первой компоненты вектора скорости от
времени и лагранжевой координаты: v1 = 13(xq? + ?3/3).
12. В сплошной среде с теплопроводностью А в некоторый
момент времени существует температурное поле Т(х, у, z) =
= 5ху-Ъхг. Определите количество теплоты, передаваемой в
363

единицу времени через лежащую в плоскости хОу квадратную
площадку 0<ж<1, 0<у<1.
Решение. Искомая величина может быть определена
потоком вектора q через заданную поверхность:
=
Q = Ч'п
при этом единичным вектором нормали для всех
элементарных участков dS заданной площадки будет являться
направленный по оси z базисный вектор fc (в данном случае п = fc).
Согласно закону теплопроводности Фурье, вектор
теплового потока в любой точке сплошной среды определится как
= -А [E2/ - Зг) i + Ъх j - За: fc],
так что количество теплоты, передаваемой в единицу времени
через данную площадку, равно
Q = -A
5
= 3A
о о
13. В вязкой жидкости с динамическим коэффициентом
сдвиговой вязкости /х в направлении оси х равномерно
движется длинная тонкая пластина длиной L и шириной а. При
этом в окрестности пластины реализуется течение с
распределением скорости в направлении движения в виде vx = v$e~yl ,
где у — направление, перпендикулярное движению пластины,
а 6 — параметр, имеющий размерность длины. Какой
должна быть сила, прикладываемая к пластине для осуществления
такого движения ?
364

Решение. Искомую силу следует оценивать по
величине касательных напряжений ахуу действующих на
границе вязкой жидкости и пластины. В соответствии с законом
Навье— Стокса и кинематическими соотношениями
касательные напряжения в произвольной точке вязкой жидкости
определятся как
°ху = 2Aёху = 2/х - (v.-v,- + Vjt;;) = ix -щ- = -/х j е~*'6.
На границе раздела аху = -/xvq/й, и искомая сила равна F =
14, Для упругого состояния упругопластической среды
сопоставьте напряженно-деформированные состояния
одноосного растяжения (а\ ф 0, &2 — 0"з = 0, е ф 0, ?2 = ?з Ф 0)
и одноосного деформирования ((?i Ф 0, ^2==o'3^0,?i/0,
?2 = ?з=0)по значениям интенсивности напряжений. В
каком из этих случаев переход в пластическое состояние
произойдет при больших значениях а\ ?
Решение. Для одноосного напряженного состояния
О{ = — y/((Ti - СГ2J
Для одноосного деформированного состояния напряжения
сг2 = аз могут быть найдены из обобщенного закона Гука,
представленного через модуль Юнга Е и коэффициент
Пуассона и:
Е
Поскольку средняя деформация а = ?i/3, из соотношений
закона Гука, записанных при г = j = 1, г = j = 2 и при i = j = 3,
следует
_ G1 A + 1/) A-21/) V__
365

lor да (jj = <j\ — G2 = ai-j , что меньше, чем в случае
одноосного напряженного состояния. Используя критерий
пластичности Мизеса о± = ат, приходим к выводу: во втором
случае переход в пластическое состояние произойдет при больших
значениях &\, чем в первом.
15. Диаграмма деформирования упругопластической
среды включает линейно-упругий участок сг, = 3Gei при
в{ < ет и пластический участок с модулем пластического
упрочнения ddi/dsi = 3GeT/ei. Определите функцию
пластичности Ильюшина. Какие пластические деформации
возникают в такой среде при одноосном растяжении с <j\ = 6GeT ?
Решение. По определению, функция пластичности
Ильюшина
и для ее нахождения необходимо получить зависимость сг, =
= &{(?{) за пределами упругости. Это можно сделать,
проинтегрировав выражение для модуля пластического упрочнения
по деформациям от ?т до некоторого ?,-, а по напряжениям от
<тт = 3GeT до соответствующего а,:
О{ = 3G?i
В итоге функция пластичности Ильюшина представляется как
{О при а < 6Т>
ет ( л еш\
1 I 1 + In — I При ?{ > ?т.
При одноосном растяжении <Т{ = <ti> и для заданного случая
Si = 2,72l?T, и = 0,26. С учетом физических соотношений для
модели упругопластической среды согласно деформационной
теории пластичности пластические составляющие компонент
тензора деформаций можно определить как
Лр) _ и
366

Для данного случая одноосного растяжения а = а\/3 = 2GeT,
и искомые пластические деформации равны:
= 0, 7?Т;
е(р) = 6(Р) = " / ^ = w
$ = °> *V J-
16. Найдите распределения значений давления и
плотности в политропной атмосфере, для которой давление р и
плотность р взаимосвязаны соотношением р = ро(р/ро)к) гДе Ро и
ро — давление и плотность на поверхности Земли.
Определите высоту атмосферы.
Решение. На воздушную среду действуют
вертикальные объемные силы Fy = -ур, где д — ускорение
свободного падения. Тогда для неподвижной атмосферы уравнение
движения идеальной среды в направлении вертикальной оси у
принимает вид
0 = F -?l = -gp-?l.
Выражая из уравнения состояния плотность р через давление
р, приходим к дифференциальному уравнению
Интегрируя это уравнение по высоте в пределах от у = 0 до
у = /i, а по давлению от ро до р> получаем распределения
значений давления и плотности по высоте h:
-1ро
Высота атмосферы Н определяется из условия р = 0, откуда
"" fc-1 род'
367

17. Исследуйте течение вязкой несжимаемой жидкости в
поле тяжести между двумя неограниченными вертикальными
пластинами с зазором а. Найдите касательное напряжение,
действующее на эти пластины.
Решение. Уравнения движения вязкой жидкости в
общем случае имеют вид
Движение одномерное и направлено вертикально вниз.
Так как в бесконечной по высоте щели давление не должно
зависеть от высоты (V,-p = 0), движение должно быть
установившимся (dvi/dt = 0), а жидкость должна быть
несжимаемой (^kv = 0), то в декартовой прямоугольной системе
координат с осью у, направленной вертикально вниз, и осью
ж, перпендикулярной стенкам щели, уравнение движения
принимает вид
д\
p9 = ti^
Интегрируя это уравнение при граничных условиях vv —
х=0
= 0, получаем
х—а
Vy " 2^ ^ X)'
Согласно физическим соотношениям для модели вязкой
жидкости и кинематическим соотношениям, касательные
напряжения в жидкости определятся как
(JXy — ^Г^Ху _ ^
откуда при х = 0 и х = а аху = рда/2.
18. Сформулируйте физико-математическую модель
процесса метания осесимметричной тонкой металлической
368

оболочки продуктами детонации взрывчатого вещества,
приняв гипотезу мгновенной детонации.
Решение. Для описания движения газообразной
среды и тонкой осесимметричной металлической оболочки целе-
собразно ввести в рассмотрение цилиндрическую систему
координат (г, 0, г), ось z которой совпадает с осью симметрии
оболочки. В такой системе координат отсутствует движение в
тангенциальном направлении и вектор скорости частиц имеет
лишь радиальную и осевую составляющие — vr, vz.
В качестве деформируемой среды в данном случае
можно рассматривать лишь продукты детонации, приняв модель
идеального газа с уравнением состояния в калорической
форме р = р(/9, Е) или с политропным уравнением состояния
р = Apk. Тонкую же оболочку можно рассматривать
приближенно, учитывая из ее свойств лишь инерционные свойства,
характеризуемые плотностью материала /9об и толщиной 6oq.
Система уравнений, описывающая нестационарное
двумерное осесимметричное движение продуктов детонации,
включает:
уравнение неразрывности
h r dz
уравнения Эйлера, записанные в пренебрежении
массовыми силами,
dvr __ dp dv2 _ dp
уравнение энергии в адиабатическом приближении
dE _ p dp
~dt ~ ^2 И]
уравнение состояния
р = р(р, Е).
Данная система пяти уравнений замкнута и содержит пять
неизвестных функций координат и времени — vr, vz, p, p, E.
369

Граничные условия на границе раздела (поверхность 5)
газа и оболочки относятся к смешанному типу и задаются в
виде условия непроницаемости vT • п = vo^ • п и
дифференциального уравнения движения фрагмента оболочки под
действием давления газа р:
Pobbob—7— = рп,
at
где vT и г?Об — соответственно скорости взаимодействующих
частицы газа и фрагмента оболочки; п — единичный вектор
нормали к поверхности 5. Дополнительным уравнением
является уравнение dro^/dt — г>Об> позволяющее определять
изменение во времени координат точек поверхности 5.
Начальные условия при t = О задаются на основе
гипотезы мгновенной детонации как р = РоВВ> vr = vz = 0, Е = Q,
Р = Рм.д> где ровв — начальная плотность взрывчатого
вещества, рм.д — давление мгновенной детонации, Q — удельная
теплота взрыва.
19. На примере задачи проникания по нормали осесимме-
тричного абсолютно твердого тела в деформируемую
жидкость сформулируйте граничные условия на границе
раздела тела и жидкости.
Решение. Скорость проникающего тела vT и
скорость частиц жидкости v на границе раздела (поверхность 5)
должны быть взаимосвязаны граничным условием
непроницаемости vT • п = v • п, где п — единичный вектор нормали
к поверхности S. Кроме того, в соответствии со вторым
законом Ньютона ускорение проникающего тела определяется
силой противодействия со стороны деформируемой жидкости
и зависит от распределения давления по поверхности 5 тела,
от массы тела тт и от его формы:
5
где nz — осевая компонента единичного вектора нормали,
определяющая осевую компоненту поверхностных сил -рп.
В целом граничные условия на границе раздела тела и
жидкости являются условиями смешанного типа.
370

Список рекомендуемой литературы
Ионов В. Н., Огибалов /7. М. Прочность пространственных элементов
конструкций: В 2 ч. Ч. 1: Основы механики сплошных сред.
М.: Высш. шк., 1979. 384 с.
Мейз Дж. Теория и задачи механики сплошной среды: Пер. с англ.
М.: Мир, 1974. 318 с.
Седов Л. И. Механика сплошной среды: В 2 т. М.: Наука, 1973. Т. 1.
536 с.
Селиванов В. В., Зарубин В. С, Ионов В. Н. Аналитические методы
механики сплошной среды. М.: Изд-во МГТУ им. Н.Э. Баумана,
1995. 384 с.

ОГЛАВЛЕНИЕ
Предисловие 5
Введение 8
Глава 1. Математический аппарат механики сплошных сред 12
1.1. Характер математических объектов математического
аппарата механики сплошных сред 12
1.2. Основные элементы векторного исчисления 17
1.2.1. Элементы векторной алгебры 17
1.2.2. Элементы векторного анализа 21
1.3. Основные элементы тензорного исчисления 44
1.3.1. Характеристика системы координат 44
1.3.2. Преобразования координат и базисных векторов .... 56
1.3.3. Понятие тензора второго ранга 62
1.3.4. Ряд тензоров 67
1.3.5. Элементы тензорной алгебры 70
1.3.6. Элементы тензорного анализа 80
Вопросы и задачи 92
Глава 2. Основные понятия, уравнения и соотношения
механики сплошных сред 101
2.1. Представление движения материального континуума 101
2.1.1. Система отсчета наблюдателя и сопутствующая
система отсчета. Индивидуализация точек
материального континуума 101
2.1.2. Сущность точек зрения Лагранжа и Эйлера на
изучение движения сплошной среды 108
2.2. Основы кинематики материального континуума. Теория
деформаций 111
372

2.2.1. Тензор деформаций — характеристика
деформированного состояния материального континуума .... 111
2.2.2. Главные оси деформации и главные деформации.
Геометрическое представление тензора деформаций . 134
2.2.3. Инварианты тензора деформаций 141
2.2.4. Шаровой тензор деформаций и девиатор тензора
деформаций 147
2.2.5. Понятие об уравнениях совместности деформаций . . . 149
2.2.6. Тензор скоростей деформаций 152
2.3. Теория напряжений 157
2.3.1. Напряжение — мера интенсивности внутренних сил . 157
2.3.2. Тензор напряжений — характеристика
напряженного состояния материального континуума 158
2.3.3. Главные оси, главные площадки и главные
значения тензора напряжений. Геометрическое
представление тензора напряжений 164
2.3.4. Инварианты тензора напряжений 167
2.3.5. Шаровой тензор напряжений и девиатор тензора
напряжений 170
2.3.6. Условия равновесия материального континуума .... 172
2.4. Законы сохранения в механике сплошных сред. Элементы
термодинамики сплошных сред 177
2.4.1. Полная, локальная и конвективная производные .... 177
2.4.2. Закон сохранения массы — уравнение неразрывности 181
2.4.3. Закон сохранения импульса — уравнения
. движения 187
2.4.4. Баланс механической энергии — теорема
"живых сил" 191
2.4.5. Закон сохранения энергии при отсутствии
тепловых явлений 198
2.4.6. Закон сохранения энергии при наличии тепловых
явлений. Первый закон термодинамики, уравнение
энергии 199
373

2.4.7. Второй закон термодинамики, обратимые и
необратимые процессы, энтропия . 208
Вопросы и задачи 220
Глава 3. Модели сплошных сред, их физические соотношения .... 233
3.1. Понятие модели сплошной среды 233
3.2. Физическое и механическое поведение деформируемых сред 235
3.2.1. Физическое поведение деформируемых сред.
Уравнение состояния 237
3.2.2. Механическое поведение деформируемых сред.
Диаграмма механического поведения. Понятие о
реономных и склерономных свойствах 242
3.3. Простые модели сплошных сред 249
3.3.1. Идеальная среда (идеальная жидкость или
идеальный газ) 249
3.3.2. Вязкая жидкость 252
3.3.3. Упругая среда 256
3.3.4. Жесткопластическая среда 260
3.4. Модель упругопластической среды 260
3.4.1. Деформационная теория пластичности (теория малых
упругопластических деформаций) 262
3.4.2. Критерий пластичности и поверхность пластичности 268
3.4.3. Теория пластического течения 274
Вопросы и задачи 283
Глава 4- Постановка задач механики сплошных сред 291
4.1. Общие принципы постановки задач 292
4.1.1. Выбор системы отсчета и системы координат 293
4.1.2. Выбор модели сплошной среды 294
4.1.3. Составление системы исходных уравнений 295
4.1.4. Выбор основных неизвестных и переход к системе
разрешающих уравнений 297
374

4.1.5. Начальные и граничные условия 299
4.2. Постановка задач механики идеальной жидкости и газа . . . 304
4.3. Постановка задач механики вязкой жидкости 310
4.4. Постановка задач теории упругости 314
4.5. Постановка задачи о динамическом взаимодействии упруго-
пластических сред 317
Вопросы и задачи 326
Приложения 331
1. Основные формулы 331
2. Примеры билетов теоретических коллоквиумов для
контроля усвоения материала 338
3. Примеры решения типовых задач 350
Список рекомендуемой литературы 371

Учебное издание
ПРИКЛАДНАЯ МЕХАНИКА СПЛОШНЫХ СРЕД
Том 1
Бабкин Александр Викторович
Селиванов Виктор Валентинович
ОСНОВЫ МЕХАНИКИ СПЛОШНЫХ СРЕД
Редактор Е.В. Авилова
Художники С.С. Водииц, Н.Г. Столярова
Компьютерная верстка В.А. Товстонога
Оригинал-макет подготовлен в Издательстве
МГТУ им. Н.Э. Баумана
Подписано в печать 20.01.2004.
Формат 60x90/16. Печать офсетная. Бумага офсетная.
Усл. печ. л. 23,5. Уч.-изд. л. 23.
Тираж 500 экз. Заказ №. 9712
Издательство МГТУ им. Н.Э. Баумана. 105005, Москва, 2-я Бауманская, 5
Отпечатано с оригинал-макета в ГУП ППП «Типография «Наука».
121099, Москва, Шубинский пер., 6.
ISBN 5-7038-3344-2
9785703 833445