*•«**
" i"
1С
МИР
.Д>
'♦.^|i ^
* « вскии
l_l
Т РНДОИ
"■'*! 1МИЧ
I—-
У'^/JT)
»н»

hawk
СЛДужин, ЕДЯёботпаревский
от орнаментов
ДО ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИИ ПОПУЛЯРНОЕ
ВВЕДЕНИЕ
В ТЕОРИЮ ГРУПП
ПРЕОБРАЗОВАНИЙ
Минск "Вышэйшан школа" 1988

ББК 22Л51.5
Д81
УДК 514.74
Серия основана в 1982 году.
Рецензенты: кандидат физико-математических паук,
профессор МГПИ им. А. Л1 Горького А. А. Дадаян', кандидат
физико-математических наук, зав. отделом математики
журнала «Квант* А. Б. Сосинский,
1702040000-049
ДМ304{03)-88 ш~™
ISBN 5-339-00101-6 <g) Издательство «Вышэйшая школа», 1988

К ЧИТАТЕЛЮ
Эта книга предлагает отправиться в необычное
путешествие. Вступив на тропу у дворцового комплекса
Альгамбра, читатель совершит переход через несколько
столетий и приблизится к одному из современных разделов
математики.
Одна из при ел екательных особенностей матем атики
состоит в том, что в процессе решения различных задач
из областей, на первый взгляд не связанных между
собой, часто возникают совершенно аналогичные понятия,
идеи и методы. Это удивительное единство авторы
попытались продемонстрировать на примере элементарной
теории групп преобразований.
Группы преобразований, естественно, появляются
везде, где есть какая-либо симметрия (а она часто
присутствует в скрытом виде дазке там, где, казалось бы, ее нет
совсем). В предлагаемой книге понятие группы
иллюстрируется разнообразными примерами из области
элементарной теории чисел, геометрии и алгебры.
Перед началом путешествия заметим, что от читателя
не требуется специальной подготовки: достаточно
владеть основами школьного курса математики. По мере
продвижения произойдет знакомство с комплексными
числами, началами геометрической теории движений и
других преобразований плоскости, алгебраическими
понятиями и методами, связанными с этой теорией. Основ-
з

Ное понятие — группа преобразований — служит
инструментом для исследования самых разных вопросов: от
описания орнаментов до решения дифференциальных
уравнений.
Изложение ведется последовательно, с привлечением
большого числа примеров, при разборе которых и
происходит первое знакомство с новыми понятиями.
Разнообразные задачи показывают путнику, где ему следует
остановиться и оглядеться. При затруднениях можно
воспользоваться ответами и указаниями, помещенными
в конце книги.
Надеемся, что некоторые трудности и неудобства,
связанные с чтением этой книги, неизбежные при любом
путешествии, не испугают юного читателя, а
открывающиеся пейзажи и встречи со знакомыми и незнакомыми
^персонажами» взбодрят притомившегося путника и
оставят приятные воспоминания.
Авторы благодарны профессору А. А. Дадаяну и
доценту А. Б. Сосинскому, взявшим на себя труд по
рецензированию рукописи, за их советы и замечания, которые
способствовали ее улучшению, а также профессору
Т. Цудзисита (Япония), приславшему образцы японских
орнаментов.
Все отзывы и замечания просим направлять по
адресу: 220048, Минск, проспект Машерова, 11, издательство
«Вышэйшая школа».
Авторы

ВВЕДЕНИЕ
«В жизнь мою не забуду того впечатления, какое
испытал я, когда на другой день после моего приезда
сюда пошел я по Гранаде. Представьте себе, в
продолжение пяти месяцев привыкнув видеть около себя
природу суровую, почти всюду сожженную солнцем, небо
постоянно яркое и знойное, не находя места, где бы
прохладиться от жару,— вдруг неожиданно найти город,
утонувший в густой свежей зелени садов, где на каждом
шагу бегут ручьи и разносится прохлада... Нет! Это
можно оценить только здесь, под этим африканским
солнцем,..»,— так писал о своих впечатлениях при первом
посещении Альгамбры Василий Петрович Боткин,
путешествовавший по Испании в 1845 году. Альгамбра—это
старинный дворец (точнее, дворцовый комплекс)
мавританских королей на окраине испанского города Гранада,
построенный при калифе Мохамеде Абу-Абдалла-бен-
Хуснф-бен-Насере, который правил с 1231 по 1273 год.
Чтобы понять, какое отношение имеет этот дворец к
предмету нашей книги, обратимся дальше к
свидетельству В. П. Боткина: «Невозможно представить себе той
резкой противоположности, какая существует
обыкновенно между наружностью и внутреиностыо в мавританских
постройках. В этом отношении никакая архитектура не
может дать понятия о мавританской: снаружи все их
здания смотрят уныло, сурово и воинственно; они громоз-
5

дили их без всякого порядка, без симметрии, без
малейшего внимания к наружному виду, а всю роскошь
архитектуры и украшений сберегали только для внутренних
комнат: там расточали они весь свой вкус, стараясь
Рис. 1
соединить в них удобства роскоши с красотою природы,
мрамор, лепные украшения и дорогие ткани с
цветниками и апельсиновыми деревьями... Рисунок и узоры
деревянных мавританских потолков чрезвычайно похожи на
те, которые в прошлом веке делали под названием
рококо; но мавританская работа несравненно отчетливее и
изящнее. Стены залы покрыты раскрашенными
арабесками. Одна из главных особенностей мавританского
стиля — нигде не поражать глаза резкостью: только всмот-
6

ревшись хорошенько в эти украшения, вы увидите всю
отчетливую тонкость этой работы. С первого взгляда
кажется, будто потолок и стены обтянуты персидскими
коврами или вышитыми по канве обоями с мельчайшим
рисунком».
Именно в орнаментах Альгамбры, их разнообразии,
красоте и изощренности заключается главная ценность
этого дворца — ценность не только художественная, но
и, если можно так выразиться, математическая. Одного
взгляда на образцы орнаментов Альгамбры (рис. 1)
достаточно, чтобы понять нх тесную связь с геометрией:
изображенные фигуры очень симметричны. Более точный
смысл этого слова в данной ситуации таков: существует
много движений плоскости (в частности, поворотов,
переносов, осевых симметрии), переводящих каждый нз
рассматриваемых узоров в себя. Если найти для
приведенных орнаментов все центры симметрии (или, что то же
самое, центры поворотов на 180°) и центры поворотов
на 90°, то обнаружится много таких точек, чередующихся
в шахматном порядке. Иначе обстоит дело с осями
симметрии: у первого узора их пет, а у второго есть. В этом
состоит различие между этими орнаментами с точки
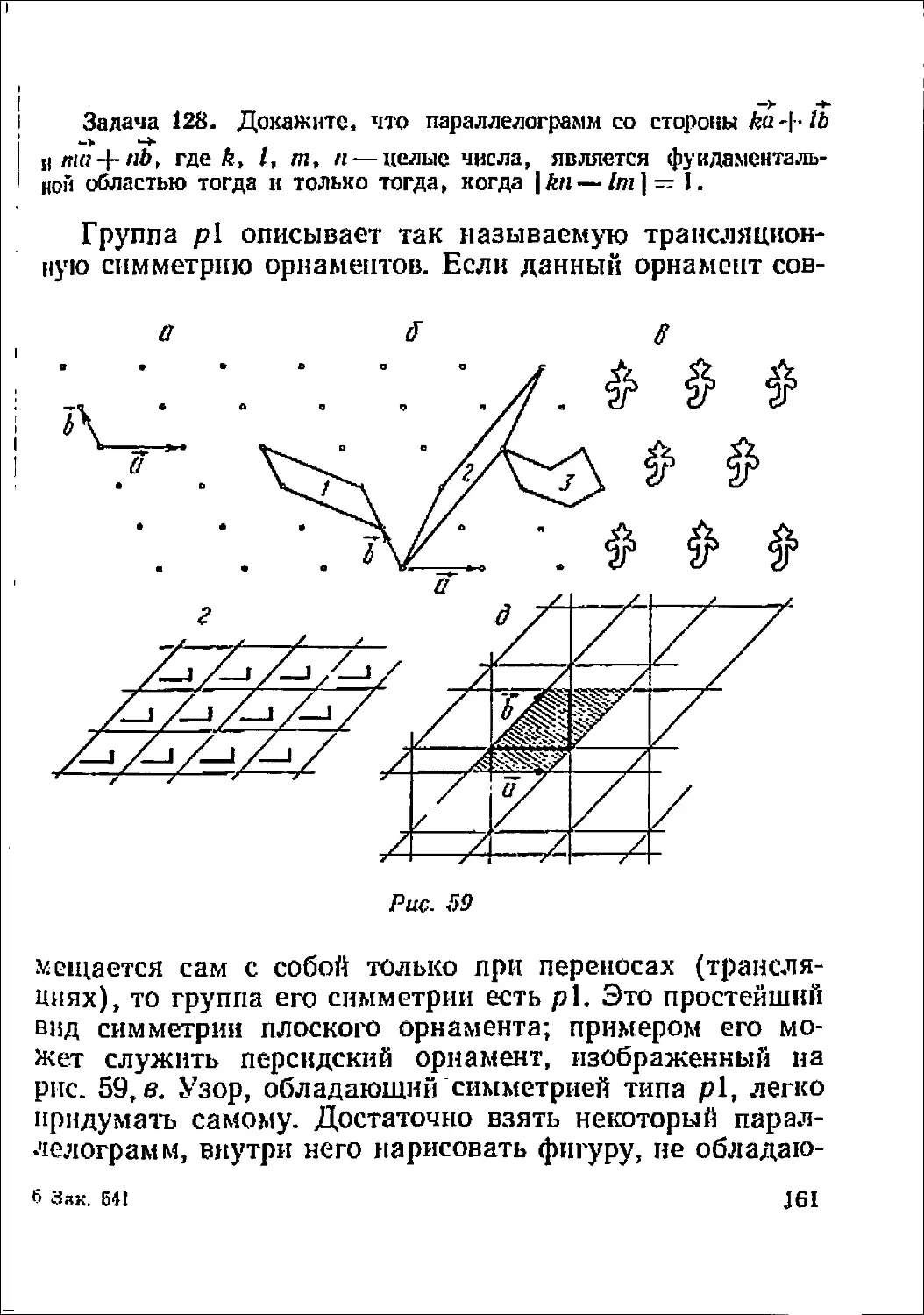
зрения геометрии.
Коль скоро замечено, что орнаменты бывают с точки
зрения симметрии одинаковые и разные, у математика,
естественно, возникает вопрос: сколько и какие
разновидности орнаментов принципиально возможны?
Конечно, чтобы этот вопрос был математически осмысленным,
нужно дать четкие определения геометрическому
понятию орнамента и тому, что означает выражение «два
орнамента одинаково симметричны». Оказалось, что эти
определения можно дать лишь в рамках теории групп,
зародившейся в 30-х годах XIX века в работах
замечательного французского математика Э. Галуа. А полный
ответ на поставленный вопрос был дан впервые в 1891 го-
7

ду русским ученым Е. С. Федоровым. Оказалось, что
всего существует 17 двумерных кристаллографических
групп и, следовательно, ровно 17 типов орнаментов на
плоскости.
По подсчетам известного современного геометра
Г, С. М Кокстера, всего в мозаиках Альгамбры
использовано 11 из 17 возможных групп. Высокоразвитым
искусством орнамента владели многие народы древности.
Вот что пишет по этому поводу одни из крупнейших
математиков XX века Герман Вейль: «Образцы всех
17 групп симметрии обнаружены среди декоративных
узоров древности, в особенности среди египетских
орнаментов. Вряд ли возможно переоценить глубину
геометрического воображения и изобретательность,
запечатленные в этих узорах. Их построение далеко не тривиально
в математическом отношении. Нет сомнения в том, что
вплоть до XIX века не существовало необходимых
понятий, с ломощыо которых можно было бы дать полную
абстрактную формулировку основной проблемы, а
именно, не было математического понятия группы преобразо*
ваштй. Только ыа основе этого понятия можно было
доказать, что 17 видов симметрии, в иеявном виде известных
еще египетским ремесленникам, исчерпывают все
возможные случаи».
Для того чтобы построить математический аппарат,
о котором говорит Г. Вейль, необходимо вначале изучить
геометрию и алгебру плоскости.

плоскость
Представьте себе огромный лист бумаги,
на котором Отрезки прямых, Треугольники,
Квадраты, Пятиугольники, Шестиугольники
и другие фигуры, вместо того чтобы
неподвижно оставаться на свопх местах,
свободно перемещаются по всем направлениям
вдоль поверхности, не будучи, однако, в
силах ни приподняться над ней, ни опуститься
под нее, подобно теням (только твердым
и со светящимися краями), к вы получите
весьма точное представление о моей стране
« моих соотечественниках.
Э. Э. Эббогт
Эти слова принадлежат юристу Квадрату, обитателю
Флатлаидни*. Представители низших слоев населения
имеют форму остроугольных равнобедренных
треугольников; остальные жители (мужчины)— правильные
многоугольники, число сторон которых тем больше, чем выше
их положение на общественной лестнице.
* Эта страна описана в книге Э. Э. Эбботта «Флатлакдия».
9

Продолжая фантазию автора, пред-
Клетчатая положим, что Флатландня представ-
Флатландия ляет собой лист бумаги в клетку,
как бы вырванный из огромной
тетради «по математике», а ее обитатели считают наиболее
удобным и приятным такое положение своего тела, при
котором все вершины попадают в узлы сетки. Можно
легко вообразить простого солдата и квадратного
джентльмена, расположнвщихся на отдых, как показано
на рис. 2. Спрашивается, могут ли подобным образом
расположиться на плоскости прочие граждане Флат-
ланднн.
Рис. 2 Рис. 8
Пример 1. Доказать, что не существует правильного
многоугольника, отличного от квадрата и имеющего
вершины в узлах клетчатой бумаги.
Пусть AiA2. ..An — правильный многоугольник,
удовлетворяющий условию задачи, О — его центр. С каждой
тройкой последовательных вершин Аи-и Ah, Ah+l свяжем
точку Вп так, чтобы фигура Ak-iAnAk+i^k была
параллелограммом. Фигура, изображенная на рис. 3, при
отражении от прямой ОАк и при повороте на угол 360э/я
ю

отображается на себя, поэтому каждая точка Bk лежит
на прямой OAh, а многоугольник BiBz... Вп —
правильный. При п > 6 этот многоугольник по размерам меньше
исходного. Действительно, в этом случае угол а= (я—2) X
X 1807^- больше угла р — 2 • 360°/л. и поэтому точка Bk
принадлежит отрезку OAk, Заметим (это очень важно!),
что точки Bi, Bz, ..., Bn тоже находятся в узлах сетки.
Проделаем описанную
процедуру с
многоугольником ВА ... Вп. Получим
правильный многоугольник
CiOi... Cm вершины
которого находятся: а) в узлах;
б) на отрезках OAk\ в)
ближе к точке О, чем Bh-
Поскольку на отрезках OAk
лежит конечное число узлов,
повторение этой процедуры
рано или поздно приведет
к противоречию.
В случае правильного пятиугольника рассуждение
остается в силе с той лишь разницей, что теперь точки Bk
будут располагаться не на отрезках ОАь, а на их
продолжениях»
Для п — 3 или б приведенное доказательство
неосуществимо (почему?). Заметим, что три вершины
правильного шестиугольника образуют правильный
треугольник, поэтому достаточно рассмотреть этот
треугольник. Допустим, нам удалось «удобно» его расположить
на клетчатой бумаге (рис. 4). По теореме Пифагора
квадрат длины стороны треугацьника AtAzAs— целое
число (размеры клетки считаем 1x1), значит, его
площадь S = аг у 3/4 — число иррациональное. С другой
стороны, треугольник AiA^As получается из некоторого
Рис. 4
И

прямоугольника с целочисленными сторонами
выбрасыванием прямоугольных треугольников с целыми
катетами, площадь которых — целое или полуцелос число. Но
тогда S = т или т -f- 0,5, где т —- целое число.
Задача 1. Может ли удобно расположиться на клетчатом
плоскости Нспрашгльпая фигура в виде прямоугольного треугольника,
длины сторон которого — целые числа? (Расположение, при котором
хотя бы одна сторона идет но линиям сетки, Неправильные фигуры
не считают удобным.)
При рассмотрении примера 1 мы ви-
Спожсние дели, что для любых трех узлов вся-
точек кая четвертая точка, дополняющая
этот треугольник до
параллелограмма, тоже попадает в узел. Говорят, что множество всех
узлов замкнуто относительно описанной операции.
Определим эту операцию.
Существует три способа дополнения данного
треугольника MNP до параллелограмма. Рассмотрим один
из них: соединяем точку Р с серединой К отрезка MN
и на полученной прямой откладываем отрезок KL « Р/С
Точка L — искомая. Эту точку назовем суммой точек М
и N (при выбранном полюсе Р). Запишем L = М ~f N
р
(читается; «М плюс N над Р») или, если полюс
подразумевается, L = М -\- N.
Дашюе.определение годится и в том случае, если
точки Mt N и Р лежат на одной прямой (тогда
параллелограмм MPNL как бы сплющивается в отрезок) или даже
если некоторые из них (или все три) совпадают.
Таким образом, сумма любых двух узлов сетки над
любым третьим узлом есть узел.
Задача 2. В плоскости даны два треугольника ABC и DEF
и точка Р. Пусть Ф — множество всех точек М -1-N, где М лежит
р
внутри треугольника ABC, а # —внутри треугольника DEF.
12

Докажите:
а) что фигура Ф — многоугольник; сколько сторон он может
иметь?
б) что его периметр равен сумме периметров исходных
треугольников,
Сложение точек тесно связано со сложением
векторов: L = М + N равносильно PL = РМ -f- PN и обладает
р
теми же свойствами. Перечислим их.
1°. Справедлив сочетательный (ассоциативный) закон
А -\-(В -f С) - {А +' В)+ С
р р р р
для произвольных точек Л, В и С.
2°. Точка Р служит нейтральным элементом, т. е. для
любой точки А
Р + А=А.
р
3°. По известной сумме и одному из слагаемых (при
заданном полюсе Р) можно восстановить другое
слагаемое, т. е. уравнение
А -|- X = В
р
разрешимо, каковы бы ни были точки А и В.
4°. Имеет место перемеетительный (коммутативный)
закон
А+В-В+А
р р
для всех А к В.
Все эти свойства, кроме первого, очевидны. Для
проверки свойства 1° построим сначала точки М = А -|- В
р
и N = В -}- С (рис. 5); Тогда отрезки AM, PB и СМ рав-
р
ны и параллельны, следовательно, середины отрезков
13

МС и AN совпадают, а значит, М 4 С = A -J- N, что и
р р
требовалось.
Как и для чисел, точка X, удовлетворяющая
уравнению А -\- X = В, называется разностью точек, В и А и
р
обозначается В — А. Свойство 3° означает, что вычита-
р
ние определено для любых точек А и В, причем X
определяется по Л и В однозначно (как и четвертая вершина
параллелограмма РАВХ),
Рис. 5 Рис. 6
При выкладках, в которых встречается сложение и
вычитание, можно пользоваться обычными
правилами раскрытия скобок, например /1 — (В — С 4-D) —
== А — В-\- С — D при одном и том же полюсе
(докажите это!).
Пример 2. Найти А + В 4 С, где М -- точка пересече-
м м
иия медиан треугольника ABC.
Точка D — А -|- 5 лежит на продолжении медианы
С/С, причем DK=*KM=MC/2. Следовательно, DM = МС
vD + C = M.
м ,,
Интересно, что точка пересечения медиан М — это
единственная точка, для которой А 4 В 4 С ~ Л4, Чтобы
14

в этом убедиться, нам нужно вначале научиться заменять
один полюс другим в суммах и разностях. Докажем
следующие равенства:
4+jB = i4+B-Q; А-В^А-В -|- Q.
Q P P Q Р Р
Первое соотношение, перепнсашгое в виде (Л ~\-В) -hQ—
Q я
= А -\- £?, легко доказывается построением (рис. 6).
р
Чтобы убедиться в справедливости второго равенства,
проверим, является ли точка А — В ~\- Q решением урав-
р р
нения В -\- X = Л. В самом деле, пользуясь первой из
Q
доказываемых формул, получаем
В +(А - В + Q) = В + (Л - В + Q) - Q = Л.
Q Р Р Р Р Р Я
Любопытно, что левые части рассматриваемых
равенств не зависят от точки Р. Следовательно, ее выбор
произволен.
Задача 3. Выясните, в каком случае точка
A t -f A z -f... + А а — В i ~ В* —.,. - В i,
где все операции выполняются над одним н тем же полюсом, не.
зависит от выбора последнего.
Продолжим обсуждение примера 2. Предположим,
что некоторая точка N обладает тем же свойством, что
и точка пересечения медиан, т. е. Л -|- В 4- С = N. Тогда
N N
A -J- В -\- С — N — JV"<= N (полюс нейтрален относитель-
N N N N
но сложения), но выражение в левой части этого
равенства, согласно результату задачи 3, не зависит от выбора
полюса. В частности, если в качестве полюса взять
точку М (пересечение медиан нашего треугольника),
получим M~N-N = N, т. e.N + N + N.=• М и N = А1.
AI М М М
15

Задача 4. Докажите, что A -f В -J- С =* И, где О — цедггр окруж-
0 О
ностл, оппслтюн вокруг треугольника /ШС, а Я — его ортоцситр
(точка пересечения высот).
Операцию умножения точек плоско-
Умиожвние точки сти на число а при выбранном
лона чиспо люее Р обозначим ар и определим
следующим образом. Точка арА=В
лежит на прямой РА па расстоянии |а||РЛ| от
полюса Р. Если а > 0, то точки А и ш>А лежат по одну
сторону от Р, а если а <С 0,— то по разные. Кроме того,
будем считать, что при умножении любой точки на нуль
получается полюс, так же как и при умножении полюса
на любое число.
Используя векторы, операцию умножения точки на
число можно определить равенством РВ = оРА, откуда
следует:
5°. 1рА = Л.
6°. ар{$рАу~-((ф)рА.
7°. (а + §)рА = арА + РрА
8°. ар{А +В)=арА -|- аРВ
р р
для любых чисел а и р и любых точек А, В и Р.
Умножение точек на числа связано со сложением
следующим образом: прА = Д + А-\- ...-\- А (п раз) для
р р р
натурального tu Отсюда и из свойства 6° следует, что
точку (1/2)рЛ можно определить как решение уравнения
Х-\-Х = А (проверьте это!).
р
Рассмотрим выражение
аРА -f frp£ + ... -f wpZ « S.
p p p
Вообще говоря, точка S зависит от выбора полюса,
однако, как видно из задачи 3, в некоторых случаях S
16

не зависит от выбора Р. Это может случиться и тогда,
когда коэффициенты а, р, ..., о в выражении точки 5
дробные. Например, точка М = 0,5Л -f 0,5#=0,5(Л -f- В)
независимо от положения полюса попадает в середину
отрезка АВ.
Задача 5 (обобщение задачи 3). Найдите необходимое и
достаточное условие, налагаемое на коэффициенты а, р, ..., а, при
котором точка арА -\- fti'B + ... 4- (OpZ не зависит от выбора полюса Р.
Р р Р
Кстати, через А и В легко ас в
выразить любую точку прямой
АВ. Пусть С делит отрезок АВ
в отношении k • I (это
означает, по определению, что 1-АС=
=/г-СВ). Возьмем на
плоскости произвольную точку Р, не рис. 7
лежащую на прямой ЛВ, и
будем считать ее полюсом. Проведем через С прямые,
параллельные РВ и РА, до пересечения с РА и РВ
соответственно в точках А' и В' (рис. 7). По теореме Фалеса:
\РА'\ _ \\ВС\ _ I \РВ'\ _ \АС\ /
\РА\ ~ \ВА\ ~~ ft-K ' \Р&\ ~~ \АВ\ ~ k + l '
I k
Обозначив k,l через а, а -щ^—Р, получим С — Л' +
-f- Br = оА 4- Р#» причем а -\- P = 1. Верно и обратное:
каковы бы ни были неотрицательные числа а и р,
причем а -Ь Р = 1, точка С — сИ -|- р/? принадлежит
отрезку АВ.
Если в выражении С = а Л -{- РВ, где а + р — 1, один
из коэффициентов а, р отрицателен, точка С по-прежнему
будет лежать на прямой АВг но теперь уже вне отрезка
АВ. Измешга должным образом рис. 7, проверьте, что и
17

в этом случае а — k ■ t , (5 — к;ь , если /г:/ —
отношение (теперь уже отрицательное), в котором С делит АВ.
Итак, прямая АВ — это множество всех точек вида
аА + (1 — а)В, где а — любое число, а отрезок АВ — это
множество точек такого же вида, где 0 ^ a =S 1.
Подчеркнем, что по построению (а также по результату
задачи 5) такое описание прямой и отрезка не зависит от
выбора полюса.
Задача 6. Определите подобным образом множество всех
внутренних точек выпуклого многоугольника с вершинами Ait Аг, ..., An,
в частности треугольника;
Теперь вы можете вернуться к задаче 2, так как
располагаете всеми возможностями для успешного ее
решения.
Задача 7. Докажите, что средние линии четырехугольника н
отрезок, соединяющий середины диагоналей, пересекаются в одной
точке и делятся этой точкой пополам.
Вернемся к примеру 2. Точка М
центр пересечения медиан треугольника
тяшестн ABC была описана неявно, как
(единственное!) решение уравнения
A -J- В -J- С = М. Сейчас можно явно выразить М через
м м
А, В и С. В самом деле, умножая обе части данного
уравнения на 1/3, получаем (1/3) м(А + В -J- С)= М. Соглае-
м м
но результату задачи 5, выражение в левой части этого
равенства не зависит от выбора полюса, поэтому ответ
можно записать так: М — (1/3) (А -\- В -J- С).
Точка М пересечения средних линий
четырехугольника ABCD (см. задачу 7) аналогично выражается через
его вершины: М = (1/4) (А + В -f С + />),
18

Среднее арифметическое нескольких точек называют
центром тяжести системы, состоящей из этих точек: М =
= (1/ft) (Ai + M -J-.., -f Л„) (независимо от полюса!).
Так, центр тяжести треугольника * — это точка
пересечения его медиан. Таким образом, задачи, связанные с
отысканием центра тяжести геометрических фигур,
удобно решать с помощью введенных нами операций над
точками.
Пример 3. Пусть точки А, В я С лежат на одной
прямой, а точки Е и F— произвольные. Доказать, что
центры тяжести треугольников AEF, BEFf CEF лежат на
одной прямой.
Выразим центры тяжести треугольников через их
вершины:
•Y(A + E + F)~K; -g-(В-|- Е -|- F) = L; -i-(C + £ +
+ F) = М.
Но, по условию, точка С лежит на прямой АВ. Поэтому
С = аА Н- (1 — а) В и, следовательно, а/С -Н (1 — а)Ь =
= ~-(А Н- Е + F) + -Цр- (В + Я + /0 =-g- (C +Д +
-J- F) =* М. А это означает, что точка М лежит на
прямой F(L.
Задача 8. Пусть Л, В, С, D, Е, F —середины последовательных
сторон некоторого шестиугольника. Докажите, что точки пересечения
медиан треугольников АСЕ н BFD совпадают.
Задача 9. В четырехугольнике ABCD точка Е — середина АВ,
К —середина CD. Докажите, что середины отрезков А К, СЕ, ВК
и ED являются вершинами параллелограмма.
Задача 10. Пусть ABCD — произвольный четырехугольник, К, L,
М, Af —центры тяжести треугольников BCD, ACD, AoDt ABC.
Докажите, что отрезки АК. BL, CM, DN пересекаются п одной точке и
каждый из них делится этой точкой в отношении 3:1.
* Точнее, системы его вершин. Следует различать центр тяжести
системы вершки треугольника, контура треугольника к сплошного
треугольника,
19

Пример 4. Доказать, что средняя линия
четырехугольника проходит через точку пересечения его диагоналей
тогда и только тогда, когда этот четырехутолышк
является трапецией.
Возьмем в качестве полюса точку О пересечения
диагоналей (рис. 8). Тогда С — аЛу D = $B для некоторых
а и р. Следовательно, К — -g- (Л -f В), £ — -§- (a^ +
А к В
Рис. 8
-f Р#). Если AB\\CD, то из подобия треугольников ОБА
и ODC а — р, поэтому L = а/С и точки К, L, О лежат на
одной прямой.
Если же, наоборот, точки /С и L лежат на одной
прямой с точкой О, то одна из них может быть получена из
другой умножением на некоторое число при полюсе О:
L = у К. Отсюда &А -\- рЛ = уА -f у В и (а — у) А =
— (у — ?>)В. Но точки (а —у)А и (у — р)5 лежат на
прямых ОА и 05 соответственно. Совпасть они могут
только в том случае, когда представляют собой точку
пересечения прямых, т. е. О, Следовательно, о — у — О
и у — р = 0, откуда а = р и, значит, прямые АВ и CD
параллельны.
20

Задача 11. Используя введенные операции над точками,
докажите, что центр тяжести треугольника делит каждую медиану в
отношении 1 :2.
Задача 12. Прямая отсекает от параллелограмма треугольник,
стороны которого составляют 1/3 и 1/4 соответствующих сторон
параллелограмма. Какую часть диагонали отсекает эта прямая?
Заметим, что для точек пространства сложение к
умножение на число можно определить точно так же, как
и для плоскости.
При разборе примера 4 мы исполь-
Координаты з овал и следующий важный факт:
если точки М и N не лежат на одной
прямой с полюсом, то равенство аМ -\- $N — уМ -j- &N
возможно лишь при а «= у и р = 6. Действительно, это
равенство можно переписать
в виде (a—y)M=(6—$)N,
а отсюда, как и в примере 4,
можно заключить, что а=^
и р*=6.
Выберем на плоскости
полюс Р и некоторые две
точки М и Л', не лежащие
с ним иа одной прямой.
Тогда любую точку Z можно
представить в виде Z—xM-\-
-fVN (рис. 9). Назовем
точки М и N базисными,
выражение данной точки Z через
М и N — ее разложением по
базисным, а числа х и у — координатами точки Z в
базисе Му N (при полюсе Р)*. Приведенное выше
рассуждение означает, что координаты хну определяются по
точке Z однозначно, поэтому мы получаем взаимно одно-
Рис 9
* Если угол MPN прямой и отрезки РМ и PN имеют единичную
длину, то получаются обычные декартовы координаты.
21

значное соответствие между точками плоскости и
парами действительных чисел.
Ясно, что при сложении точек их координаты
складываются, а при умножении на число — умножаются на это
число:
(аМ -f- bN) -f (cM -f- dN) = {а + с) M -f (Ь + d)N;
а(аМ + bN) = (аа)М +"(а&) W.
Использование координат позволяет отождествлять
точки плоскости с парами действительных чисел и
переводить геометрические понятия на язык алгебры. Тогда
под геометрической фигурой можно понимать множество
точек плоскости, координаты которых удовлетворяют
некоторому уравнению. Поскольку, например, любая
точка прямой MN имеет вид хМ -f- yN, где х -J- у = 1,
можно рассматривать последнее соотношение как уравнение
этой прямой.
Пример 5, Составить уравнение прямой, проходящей
через точку К с координатами af Ь параллельно
прямой ЛШ.
Пусть М? и N' — точки пересечения этой прямой с
прямыми РМ и PN соответственно. Так как M'N'\\MN,
то М' = Ш, N' = tN при некотором t (рис. 9). Любая
точка 7 прямой M'N' равна аЛГ -{- рЛР, где а + р — 1,
т. е. 7 — аШ + $Ш, причем а/ -f- (3/ — /. Таким образом,
координаты х = at, у = fit точки Z удовлетворяют
уравнению х -f- у = t, где /, однако, пока неизвестно. Чтобы
его найти, воспользуемся тем, что точка /С лежит на М'И'
и, значит, при подстановке в уравнение прямой ее
координат (а, о) получается верное равенство: a -f- b — t.
Итак, искомое уравнение х-\-у ~ а-\-Ь„
Задача 13. Найдите уравнение прямой, проходящей через
данную точку К(в, Ь) и параллельной РМ; параллельной PN;
проходящей через полюс Р,
22

Пример 6. Предположим, что внутри некоторого
треугольного участка Флатландии законы оптики таковы,
что луч света, параллельный одной стороне этого
треугольника, падая на вторую его сторону, после
отражения принимает направление третьей стороны. Доказать,
что флатландец, находящийся внутри этого треугольника
и пускающий луч света параллельно одной из его сторон,
освещает свою спину.
Рис. 10 Рис. 11
Введем во Флатландии систему координат, приняв
одну из вершин данного треугольника за полюс, а две
другие — за базисные точки (рис. 10). Пусть флатландец
находится в точке К(&, Ь) и направляет луч света
параллельно PN в сторону PAL Точка Л, в которой этот луч
отразится от прямой РМ, имеет координаты (а, 0),
поскольку, с одной стороны, KA\\PN и, значит, первая
координата точки А такая же, как и К (см. задачу 13), а
с другой стороны, А лежит на прямой РМ и, значит, ее
вторая координата — нуль.
Отрезок АВ отраженного луча параллелен MN.
Согласно примеру 5, уравнение прямой АВ х-\-у—а, ибо а
есть сумма координат точки А. Для точки В х = 0, по-
23

скольку она лежит на PN. Следовательно, вторая
координата точки В будет равна а.
Рассуждая подобным образом, получаем, что
координаты точек, в которых луч встречает стороны
треугольника MNP, таковы: С{1 — о, а), £>(! — а, 0), £(0,1 — а),
F(a, 1 — я). Прямая FK параллельна PN, поэтому луч
возвращается в точку К, причем с другой стороны.
Луч света, однако, может вернуться в точку /С
раньше, чем пройдет всю шестизвенную ломаную ABCDEF
и попадет флантландцу не в спину, а в бок.
Задача 14. Найдите множество всех точек внутри треугольника
MNP, для которых утверждение примера 6 ие выполняется.
Задача 15- Внутри треугольника ABC взята точка /С. Прямые
АК, ВК и СК пересекают стороны ВС, С А и АВ в точках D, Е,
„ „ KD KE KF
F. Докажите, что ^р--\~ ВЕ -\- -ggr = 1 (рис. 11).
Задача 16. Докажите, что прямые AD, BE, CF (рнс. 11) перс-
AF BD СЕ
секаются в одной точке тогда и только тогда, если -kjj- -утп—рт* ='■
= 1 (теорема Чевы). i и w, ьл
Задача 17. На сторопах АВ и СВ треугольника ABC
откладываются отрезки АП и CF одинаковой длины. Найдите множество
середин отрезков EF.
Мы научились умножать точки плос-
Умножение кости и а числа. Но действительные
точек числа можно изображать точками
некоторой прямой. Разместим эту
(числовую) прямую на плоскости так, чтобы ее нулевая
точка совпала с полюсом Р, относительно которого будем
рассматривать сложение точек и умножение их на
числа. Единичную точку числовой прямой обозначим Е
(рис. 12, я).
Если точки А и В изображают числа а и Ь, то а -f- b
изображается суммой точек А и В (рис. 12, б), т. е,
операции сложения чисел и сложения точек согласованы
между собой. Определим умножение точек лрямой РЕ
24

так, чтобы оно было тоже согласовано с умножением
чисел (рис. 12, в), т. е. АВ = аРВ = ЬРА.
Возникает естественный вопрос: можно ли
распространить операцию умножения на все точки плоскости
так, чтобы при этом оставались в силе обычные правила,
приведенные ниже.
а
X
0
А
а
в
р
о
р
о
р
А
——о-
П
/
Е
А+В
а+Ь
АВ
В
ъ
в
О
а 1 оЪ
Рис. 12
Рис. 13
9°. Ассоциативность умножения:
{АВ)С=*А(ВС).
10°. Коммутативность умножения:
АВ = ВА.
11°. Дистрибутивность умножения относительно
сложения:
А(В+С)^АВ-\-АС.
Кроме того, потребуем, чтобы новая операция была
следующим образом согласована с умножением точек на
числа: произведение точек плоскости на точки числовой
прямой (расположенной в плоскости!) должно совпадать
с произведением этих точек иа соответствующие
действительные числа, т. е. AZ = aPZt если точка А изображает
число а. В частности, должно выполняться равенство
EZ = IpZ = Z.
25

Пока неясно, сколькими способами можно ввести
умножение точек плоскости, удовлетворяющее всем
перечисленным требованиям, и возможно ли это вообще.
Оказывается, таких способов очень много, причем среди них
только три существенно различны. Вскоре мы в этом
убедимся.
Пример 7. Пусть EABCDK— правильный
шестиугольник с центром в полюсе Р (напомним, что Я — единичная
точка) и Л2 — В при некотором выборе операции
умножения. Найти все попарные произведения вершин
шестиугольника.
Разложим все вершины по базису Е, А при полюсе Р
(рис. 13): В = А — £, С=-Я, D = —A, K = E — A,
Попарные произведения базисных точек известны:
Ег = Е, ЕА = А, Аг = В. Пользуясь дистрибутишюстыо и
другими свойствами умножения, находим: ВК— (А—Е) X
X (Я—Л) - —AZ+2AE—В = —£+2Л—£ = (Л~-Я) +
+ (Л — Е) = Е -J- В — А. Подобным образом
определяются и все остальные произведения. Ответ можно
оформить в виде следующей таблицы умножения:
£
А
В
С
D
К
Е
Е
А
В
С
D
К
А
Л
Б
С
D
К
Е
В
В
с
D
К
Е
А
С
С
D
К
Е
А
В
D
D
К
В
А
В
С
К
к
Е
А
В
С
D
26

Отметим, что множество вершин шестиугольника при
выбранном нами способе умножения замкнуто, т. е.
произведение любых двух вершин снова является вершиной.
Задача 18. Является ли множество вершин шестиугольника
замкнутым относительно умножения, при котором: а) Л2 = А;
б) А1 — Р? Составьте соответствующие таблицы умножения.
Задача 10. Составьте таблицу умножения правильного
пятиугольника EABCD (его центром является полюс Р), если известно,
что Л2 «= В.
Возьмем на плоскости, кроме полюса Р и единичной
точки Е, еще одну (произвольную) точку F, не лежащую
на прямой РЕ, т. е. образующую вместе с точкой Е
базис. Как видно из примера 7, умножение точек плоскости
будет полностью определено, если мы будем знать
точку /•*, которую в свою очередь можно разложить по
базису: F2 — а£-г- р/7. Постараемся выбрать вторую
базисную точку (вместо F) так, чтобы разложение ее квадрата
по базису выглядело наиболее просто.
Пусть G = F 1-£. Так как FG || РЕ, точки Е и G
могут служить новым базисом и GZ = (F x-E)2=Fz—
-f>EF + -^E* = aE + $F-f>F f~ E = (a + JJ-) E.
При этом возможны три случая:
а) a-f--L- = 0 (сравните с задачей 1861). Тогда
произведение точек аЕ -\- bG и сЕ -f- dG равно асЕ -f-
■±(ad-^bc)G. Попробуем найти частное от деления Е
на G, т. е. такую точку Z = хЕ -j- yG, что GZ = Е. Но
GZ= G(xE -j- yG) — xG. Очевидно, что ни при каком
значении х (и у) эта точка не совпадает с Я. Значит,
разделить Е на 6 невозможно;
as 1
б) а + -~>0. Обозначая — G буквой Я,
27

имеем Я2 — Е (сравните с задачей 18а, в которой тоже
есть точка, отличная от Е и — £, а именно, Е — 2Л,
квадрат которой равен Е). Тогда произведение двух точек
записывается так:
(аЕ + ЬН) (сЕ + сШ) = (ас + bd)E + (ad -f bc)H.
При таком умножении деление тоже выполнимо не
всегда. Проверьте самостоятельно, что но существует точки Z,
удовлетворяющей равенству (Е -f- H)Z = H;
R2 I
в) а -f -^- < 0. Положим / = —====^- С Тогда
/2 _ _ £ Очевидно, что точки £ и / не лежат на одной
прямой с полюсом Рл поэтому по ним можно разложить
любую точку плоскости. Пусть hi—aE-yhl, N=cE-\-dE.
Тогда
MN = (аЕ + Ы) (сЕ -J- dl) = (ас — hd) E + (ad+ be)I.
Проверим, что в этом случае деление на любую точку,
кроме полюса, всегда выполнимо. Разделим точку М —
= аЕ ~\- Ы на точку Лг = сЕ -J- dl, отличную от Р (это
значит, что числа с и d не равны нулю одновременно).
Частное М : N — это такая точка Z = хЕ -j- yl, что
NZ = М, или
(сЕ н- rf/) (х£ + #/) = аЕ + bL
Это уравнение равносильно следующей системе:
сх — dtj = а, 1
dx + c# = &, J
acA-bd „ be — ad
решая которую, получаем: л*= •# + # > #^" си-цр '
Итак, на трех рассмотренных случаев только в одном
умножение точек обладает всеми свойствами умножения
чисел. Заметим, однако, что и в этом (третьем) случае
умножение определено далеко не однозначно: все зави-
28

сит от того, где находится точка /. Пусть, например,
РЕАВ (где Р — нулевая, а Я — единичная точка)—
квадрат. Чему равно Л2? Если / совпадает с точкой Л, то
Л2 = — Е. Если же / попадает в точку В, то
Л2 = (В + Я)2 = В2 + WE + £*=—Я + 2Я + £^ 25.
Мз всех возможных способов задания умножения
точек выберем один — будем считать, что расстояние PI
равно единице и угол EPI прямой,— и изучим его
подробнее.
Поскольку точки прямой РЕ отож-
Комппексные дествляются с действительными чис-
чкела ламп, естественно считать, что точки
всей плоскости, относительно
которых введены алгебраические операции, это тоже
некоторые числа, составляющие более широкое множество, чем
действительные. Назовем их комплексными* Будем
отождествлять точки действительной оси (прямой РЕ) с
соответствующими действительными числами (так, точку Р
обозначают 0, а Е— 1), а вместо / писать L В
соответствии с этими обозначениями определим операции над
комплексными числами:
(а+ W)+-(c + di) = (а + с) + {Ь + d)i;
(а + Ы) — (с + di) = (а — с) + (Ь — d)i\
(а + Ы) (с"+" di) = (ас — bd) + (ad -f be) i;
a-f & _ g£ + fc* , _bc—ad .
c+di "" V + d* ' "'" <? + <**
Заметим, что все действия выполняются так же, как
и над обычными числами (точнее, над многочленами от
«переменной» t), но при этом учитывается равенство
/а = — 1 *. Учитывая последнее равенство, число *', не
* Чтобы получить с помощью этого общего правила
приведенное выражение для частного, надо умножить числитель н
знаменатель дроби на с — di.
29

являющееся действительным, называют мтиюй
единицей.
Задача 20. Выполните действия:
а) -у+1—«(3+40-г-р б) УЗ-АЦ в) (-2--"V"
\I9B3
Пусть z = а -|- &/, Расстояние от точки г до 0
называется модулем комплексного числа z и обозначается |г|.
Поскольку о и Ь — декартовы координаты тошен г, имеем
| г I = 1Л*2-[-&2. Например, при любом/ модуль чисел
cos jf -(-1 sm f и 1_|_ .2 + -тпгтг"l равен 1.
Расстояние между двумя комплексными числами г
и w равно |z— ш|, так как точки Qt z, w, z — w
располагаются в вершинах параллелограмма.
Задача 21. Найдите множество точек г, для которых:
а) |г~|-3| = 5; б) |г-И| = [г-2г|;
в) сумма квадратов расстояний до двух данных точек равна
данному числу.
Принимая во внимание, что Уа2-\-Ь2 есть расстояние
между двумя точками плоскости, при решении
алгебраических задач можно использовать геометрические
методы и иллюстрации.
Пример 8. Доказать неравенство
}/а\ + Ь\ -ь/аПь Й + • - • + У А + Й >
> /(ei -I" а2 + . •. Ч- *«)» + (6i + Ьл +■,. - -!•■ Ьл)а-
Обозначим £i = aL + 6if, ..., zn = a„ + &,,* и
рассмотрим ломаную с вершинами в точках 0, г*, г4 + г&,...,
2i + гг -{-*•- 4~ ^п- Левая часть доказываемого
неравенства выражает длину этой ломаной, а правая —
расстояние между ее начальной и конечной точками.
30

Задача 22. Докажите неравенство
Угол, на который нужно повернуть луч 01 против
часовой стрелки так, чтобы он прошел через точку г,
называется аргументом комплексного числа z и
обозначается argz.
Рис. 14 Рис. 15
Задача 23, Найдите аргументы следующих комплексных чисел:
2, i\—3, — 2i, 1-f/, УН — U
Комплексное число полностью определено, если
известен его модуль г и аргумент ср. В самом деле, как видно
из рис. 14, z = х -j- yit где х — г cos q>, у = r sm cp и,
значит, z — rjcosip -f- / sin ф). Эта запись называется
тригонометрической формой комплексного числа.
Соответствие между комплексными числами и
парами (/*, ф) не вполне взаимно однозначно: аргумент
числа 0 не определен (его можно считать равным любому
углу), а для всех остальных чисел он определен лишь
31

с точностью до целого числа оборотов. Так, аргументом
числа 1 можно считать 0°, 360ь, —360°, 720° и т. д.
Пару (г, ф) можно все же считать координатами
точки г. Эти координаты называются полярными. Они
широко используются в радиолокации: чтобы определить
местонахождение самолета, сначала находят пеленг или
азимут (угол), а затем измеряют дальность
(расстояние).
Уравнения некоторых фигур удобно записывать в
полярных, а не в декартовых координатах.
Задача 24. Используйте полярные координаты для решения
следующих задач:
а) изобразить линию, заданную в полярных координатах
уравнением r=|cos3tp|;
б) найти уравнение цветка с шестью лепестками (рис. 15).
Попробуйте переписать это уравнение в декартовых координатах.
Понятия модуля и аргумента позволяют описать
умножение комплексных чисел весьма просто. Отмстим,
что справедливы следующие соотношения:
[2w| = |z||z®[; arg(zw)^ argz-|- arga>.
Первое из них следует нз тождества (ас—bd)2-\-
-f-(ad + be)* = (a* + fcz) (c*-f- №).
Докажем второе соотношение. Пусть z = г (cos ф 4
+ * sin ф), w = s(cos i}> + / sin яДО. Тогда zw = rs(cos ф -j-
-H sin ф) (cos ij)+£ sin t])) =«? ((cos ф cos -ф — sin ф sin tp) -j-
-j-i (sin ф cos op -j- cos ф sin "ф)) и на основании
тригонометрических формул
zw = rs (cos (ф + чМ +1sin (ф -+- Ф)) •
Это доказательство, несомненно, очень понравится
любителям тригонометрии. Чтобы не обидеть остальных
читателей, приведем другое доказательство, из которого,
кстати, можно получить формулы синуса и косинуса
суммы двух углов.
32

Рассмотрим два треугольника с вершинами в точках
О, I, z и 0, ш, zw (рис. 16). Так как \т\: 1 = |2ra>|:|z|^=
= \zw — ki|:|z— if, то стороны треугольников
пропорциональны, сами они подобны, а их соответственные углы
равны. Из равенства углов, отмеченных на рис. 16,
следует, что arg(zw) — arg z -f- arg w.
Рис. 16
Итак, при умножении комплексных чисел их
аргументы складываются, а модули перемножаются. Поэтому
(г (cos ф + / sin ф))п — rn (cos лф -|- i sin mp).
Задача 25. Зная, что г-f- ~ — 2eosa, докажите, что
г" -|- —уг = 2 cos «a.
Вернемся к задаче 20в. Использовав
тригонометрическую форму комплексного числа, можно решить ее без
I 1 •' 3~
всяких ухищрений. Обозначим -^ Ц?— '• буквой £.
Тогда |£|= 1, arg £ = —60° н, следовательно, |£1Ш| =
2 Зак. 54 J 33

= |£|1SS3 = 1, a arg £1983 = 1983(—60°) - —661 • 180°.
Значит, £19M=—1.
Заметим, что различные степени числа 'Q
располагаются только в шести точках — вершинах правильного
шестиугольника (рис. 17). Любопытно, что любое из этих
чисел может быть корнем шестой степени из 1, ибо
(£ft)6=(£6)'1 = 1Л = 1. Вообще, при любом натуральном п
существует ровно п корней /г-н степени из 1, которые
образуют правильный /г-угольник. В этом можно
убедиться, решив уравнение z71 — 1 в тригонометрической
форме.
Пример 9. Найти произведение всех диагоналей и
двух сторон, выходящих из одной вершины правильного
я-угольника, вписанного в окружность радиусом I.
Выберем полюс в центре данного многоугольника,
а данную вершину А\ примем за единичную точку. Все
вершины многоугольника удовлетворяют уравнению
2™ — 1 я= 0, и, следовательно, все вершины, кроме Л|,
являются корнями уравнения 2Tl-J-|-2n~2-h • .+z-f-l = 0,
полученного делением многочлена zn—1 на z— 1. У
многочленов zTlml -|-... + z + 1 и (г—А2) (г—As) * • ■ (г—Ап)
старшие коэффициенты равны 1, а корни одни и те же.
Следовательно, эти многочлены тождественно равны и их
значения при г = Ах совпадают: .
(А - А2) (А, - Л)... И, - Ап) = А'Г1 f ... + Л -|- 1
(напомним, что А±= 1). Поэтому |^li — A?r\ \Ai —■ Л3| - - ■
\Ai — An\ = n.
Задача 26. Правильный многоугольник ЛИг.-.^л вписан в
окружность единичного радиуса, А—точка на этой окружности.
Найдите сумму квадратов расстояний от Л до вершин много-
угольника.
Деление — действие, обратное умножению, поэтому
справедливы следующие тождества:
34

w
arg
w
= argz — arg dp.
Последнее соотношение позволяет выразить угол на
плоскости через его вершину и две точки, лежащие на
сторонах: <р — arg ** ~*9 (рис. 18). Приведем два при-
мера использования этой формулы: в первом
геометрическая задача решается с помощью алгебры
комплексных чисел, а во втором, наоборот, алгебраическая задача
решается геометрическими методами.
Пример 10. Доказать, что сумма углов DAH, FDH и
KFH (рис. 19) равна прямому углу.
Будем считать, что А — 0, D — 1 и В ~ L Тогда F —
-2, К=3, H*=3+L Следовательно, ££>ЛЯ=arg-£=-~ =
- arg (3 -|-i)f L FDH = arg-£=£- = arg (2 + i), откуда
L DAH -f A FDH = arg (3 -[- i) (2 -|- i) -- arg (5 + 57) =-45°,
что и требовалось.
Пример 11. Доказать, что если zu z2, z3, г4 —
различные комплексные числа, модули которых равны, то число
ч — ч
«3
~а
г4
действительное»
35

Данные четыре точки лежат на окружности с центром
О. Точки 2Х и 2а разбивают эту окружность на две дуги.
Если точки 2з и 24 находятся на одной дуге, то углы
zlz3z2 и 2i24z2 равны как вписанные углы, опирающиеся
на одну дугу. Значит, arg £i~^y— — arg Zl ~?fl и
argf 2l^gg : г*~г* )— 0t т.е. рассматриваемое отиоше-
ние — действительное положительное число. Если же
точки г3 и г4 принадлежат разным дугам, то углы 2, гя z^ и
Za^i отсчитываются в одном направлении и в сумме
составляют 180°, значит, argf ?|~"<а : -ilZLfi.] —
— argf Zy ~ч : gg~gO ^ 180°, т. е. в скобках стоит
действительное отрицательное число-
Утверждение примера 11 очевидным образом
обобщается: оно имеет место для любых четырех
комплексных чисел, лежащих на окружности либо на прямой.
Верно и обратное: если указанное выражение
представляет собой действительное число, то четыре точки лежат
на одной окружности либо на одной прямой.
Задача 27. Докажите, что из любых пяти точек плоскости,
никакие трк из которых не лежат на одной прямой, можно выбрать
три таким образом, что треугольник, ими образованный, будет иметь
хотя бы один угол, не больший 36°.
Задача 28. Пусть комплексные числа At, Azt .... Ап
расположены в вершинах выпуклого многоугольника. Докажите, что всякое
комплексное число г, удовлетворяющее соотношению
I , 1 . , I A
г —Л ~Г z-An -*-••• "Г г-Д, ~ и'
находится внутри этого многоугольника.

ДВИЖЕНИЯ
Так как природа есть начало движения и
изменения, а предмет нашего
исследования— природа, то нельзя оставлять
невыясненным, что такое движение; ведь незнание
движения необходимо влечет за собой
незнание природы.
Аристотель
Движения плоскости — это такие ее преобразования,
которые не меняют длины отрезков и как следствие
сохраняют многие характеристики геометрических фигур
(углы, площади), изменяя лишь их первоначальное по-
ложение. Сравнивая полученное положение фигуры с
первоначальным, часто можно легко прийти к выводам,
получить которые из других соображении затруднительно.
Даже Евклид, считавший, что «математические
предметы чужды движению»» несколько раз применял
наложение фигур в своих рассуждениях. Заметим, что если бы
великий геометр мог отказаться от своих философских
взглядов, ои значительно упростил бы некоторые
доказательства. Так, например, рассуждения о равенстве углов
37

при основании равнобедренного треугольника ABC*
становятся очевидными, если учесть возможность такого
наложения данного треугольника на себя, что вершины В
и С меняются местами.
Мы начнем эту главу с разбора примеров, решение
которых основано на применении движений плоскости,
хорошо известных читателю из школьного курса
геометрии. При этом почти во всех задачах обыгрывается одна
и та же идея: части чертежа, по условию расположенные
неудачно, нужно переместить друг относительно друга
так, чтобы прояснились скрытые до этого связи между
различными элементами.
* При доказательстве этого предложения Евклид использует
чертеж с дополнктелышмн построениями, напоминающими мост.
Это служит объяснением названия pons asinorum (мост для ослов),
данного этой теореме в средине века. Ослами считались студенты, не
усвоившие это доказательство.
38

Пример 12. Населенные пункты А
параллельный и В расположены по разные стороны
перенос прямолинейной реки с
параллельными берегами. Требуется построить
мост MNt перпендикулярный к берегам, чтобы расстояние
AMNB было кратчайшим.
Если бы реки не было, то кратчайший путь из Л в В
был бы прямолинейным. Попробуем «избавиться» от
реки. «Придвинем» берег, на котором находится В, к
берегу, на котором находится Л, перемещая его в
направлении, перпендикулярном к линии берегов (рис. 20).
Пусть В' — новое положение точки В. Тогда расстояние
AMNB равно расстоянию АМВ'В. Положение точки Вг
(а значит, и длина отрезка ВВ') не зависит от выбора
места для строительства моста. Остается выбрать
точку М на берегу так, чтобы ломаная АМВГ была как
можно короче. Для этого, очевидно, в качестве М нужно взять
точку пересечения прямой АВ' с линией берега.
Задача 20. Построите кратчайший путь, соединяющий пункты А
н В, которые разделены двумя реками (рис. 21).
Пример 13. Вписать данный вектор в данную
окружность (т. е. построить хорду данной окружности, равную
и параллельную данному отрезку).
Рис 20
Рис. 21
39

Требуется перенести данный отрезок АВ параллельно
самому себе так, чтобы о» вписался в данную окруж-
ность С с центром в точке О (рис. 22). Оказывается, что
проще, наоборот, перенести окружность к данному
отрезку так, чтобы он стал ее хордой. В нашем примере
вопреки известной пословице гора идет к Магомету.
Строим на отрезке А В как на основании равнобедренный
Рис. 22
треугольник с боковой стороной, равной радиусу г
окружности С. Вершина D этого треугольника служит центром
окружности, описанной около отрезка АВ. При перено-
се на вектор DO эта окружность перейдет в исходную
окружность, а образ отрезка АВ будет искомой хордой.
Предлагаем решить еще две задачи на параллельный
перенос. В первой можно воспользоваться способом,
который мы применили в примере 13.
Задача 30. Впишите данный вектор в данный треугольник (т. е.
постройте отрезок с концами на сторонах данного треугольника,
равный и параллельный" данному отрезку).
Задача 31. Постройте трапецию по ее основаниям и диагоналям.
Пример 14. На плоскости даны пря-
Отражения мая / и две точки А и В по одну
сторону от нее. Требуется на этой прям
мой указать точку Af, такую, чтобы длина ломаной АМВ ,
была минимальной. (Те из читателей, кто предпочитает
40

реальные задачи абстрактным, могут представить, что в
точке А находится человек с пустым ведром, в точке В —
горящий стог, а прямая I — это река.)
Если бы точки А и В располагались по разные
стороны от прямой /, решение было бы очевидным: нужно
просто соединить эти точки отрезком прямой. Попробуем
исправить ситуацию, имеющую место в данной задаче:
отразим точку В симметрично относительно прямой /
(рис. 23). Тогда при любом расположении точки М на
прямой / ломаные АМВ и АМВ' имеют одинаковую
длину. Точки же А и В', как нам того и хотелось,
расположены по разные стороны от прямой /, и выбрать из всех
ломаных вида АМВ' кратчайшую не составляет труда.
Именно, точку М следует взять на пересечении прямой /
41

с отрезком АВ\ Заметим, что отрезки AM н MB образуют
равные углы с прямой /; следовательно, по закону
отражения свет всегда распространяется по кратчайшему
пути.
Задача 32. Внутри угла даны две точки: А и В. Среди всех
ломаных вида AMNB, где М и Лг лежат на разных сторонах угла, пай*
днте кратчайшую *.
Рассмотрим еще один пример, связанный с
отысканием кратчайших линий.
° A U С
Рис. 23 Рис. 24
Пример 15. В данный остроугольный треугольник
вписать треугольник с наименьшим периметром.
Пусть WW— произвольный треугольник, вписанный
в данный треугольник ABC. Отразим точку U
симметрично относительно сторон АВ и ВС (рис. 24). Тогда длины
ломаных UVWU и KVWL совпадают. Поэтому из всех
вписанных треугольников с вершиной V наименьший
периметр имеет тот треугольник, для которого ломаная
KVWL является частью прямой, а именно &UMN. Если
теперь из всех «минимальных» треугольников UMN, соот-
* Можно предсташггь, что в точке А находится ворон, в
точке В — Иван-царевич, а стороны угла — это ручьи с мертвой и
живой водой.
42

ветствующих различным положениям точки U, выбрать
тот, периметр которого будет наименьшим, то этот
треугольник и будет, очевидно, искомым. Поэтому теперь
требуется найти такое положение вершины V, чтобы
отрезок KL имел наименьшую длину.
Замечаем, что ABRL— равнобедренный (BK=BU=*
= BL), А так как угол при вершине В не зависит от
положения точки U (ZKBL — 2ZABC), то основание
будет наименьшим в том треугольнике BKL, в котором
боковая сторона ВК (равная BVI) является наименьшей.
Отрезок же ВU является кратчайшим среди всех
отрезков, соединяющих точку В с точками прямой АС, в том
случае, когда BV А.ЛС.
Рис. 25
Так как результат «симметричен» по отношению ко
всем вершинам искомого треугольника, то точки U, V,
W — основания высот, проведенных из точек А, В, С.
Задача 33* Постройте треугольник, если известна одна его
вершина, а также прямые, на которых расположены три его
биссектрисы.
Задача 34. Внутрь угла с зеркальными сторонами, величина
которого 45е", пущен луч. Докажите, что после нескольких отражений
он примет направление, параллельное исходному. Для каких других
углов наблюдается то же явление?
Задача 35. Найдите закономерность и продолжтге ряд фигур,
изображенных на рис. 25.
Посмотрите на рис. 13. Очевидно,
Поворот что сумма всех вершин правильного
многоугольника с четным числом
сторон над его центром Р совпадает с Р (другими слова-
43

ми, сумма радиусов-векторов вершин равна нулю).
Попробуйте, однако, доказать аналогичное утверждение в
случае многоугольника с нечетным числом сторон,
например пятиугольника. Попытка решения этой задачи с
использованием координат сопряжена с громоздкими
тригонометрическими преобразованиями. Но трудной эта
задача кажется лишь до тех
пор, пока плоскость
неподвижна.
Пример 16. Доказать, что
сумма вершин правильного
многоугольника над его
центром Р совпадает с Р.
При повороте плоскости
вокруг точки Р на угол 360°/'*,
где п — число сторон, данный
многоугольник перейдет в себя.
Значит, сумма его вершин при
повороте не изменится. Но на
плоскости есть только одна
точка, которая переходит в себя
Рис. 26
при повороте: это центр поворота.
Задача 36. Из произвольной точки М, находящейся внутри
правильного многоугольника, проводятся перпендикуляры к его
сторонам и на каждом из них откладывается отрезок, равный
соответствующей стороне. НаЙд1гге сумму всех полученных точек нал М.
Пример 17. Построить равносторонний треугольник,
если известны расстояния с, Ь, с его вершин от данной
точки D.
Мы умеем строить треугольник по трем сторонам, но
на рис. 26 отрезки а, Ь, с треугольника не образуют.
Повернем плоскость вокруг точки С на 60°. При этом
точка В перейдет в Л, а точка D займет новое
положение D'. Так как при поворотах сохраняются расстояния,
44

то в треугольнике ADD' известны длины всех сторон. Его
мы и построим сначала. Затем найдем точку С (&CDD'—
равносторонний) и достроим отрезок Л С до
равностороннего треугольника ABC.
Задача 37. Постройте равносторонний треугольник, вершины
которого расположены по одной на трех данных параллельных нря!У5ых.
Пример 18. В остроугольном треугольнике ABC найти
такую точку К, сумма расстояний от которой до трех
вершин треугольника
является наименьшей.
Пусть К —
произвольная точка внутри
треугольника ABC.
Повернем ААСК вокруг точки А
на 60° (рис. 27). Так как
ААК'К равносторонний,
то АК = КК', и длина
ломаной С'К'КВ
представляет собой сумму расстоя- Рис. 27
ний от точки К до трех
вершин треугольника. Положение точки С от выбора
точки К не зависит. Поэтому сумма будет наименьшей,
когда К и К' находятся на отрезке ВС, причем угол
АКС' должен быть равен 60° и точка К. определяется
однозначно.
Заметим, что из точки К сторона АВ видна под
углом 120°. Вершины и стороны треугольника в нашей
задаче равноправны. Поэтому и углы ВКС и АКС также
равны 120°.
Задача 38. Внутри квадрата ABCD взята произвольная точка М.
Из вершины А проведен перпендикуляр к прямой ВМ, из
вершины В—-на СМ, нз С—на DM, а нз D~~на AM. Докажите, что все
четыре перпендикуляра (или их продолжения) пересекаются в одной
• очке.
45

Частный случай поворота — поворот на 180° — имеет
особое название: разворот, или центральная, симметрия.
Приведем две задачи на использование разворота.
Задача ЗУ. Через точку пересечения двух окружностей проведите
прямую, на которой эти окружности отсекают равные хорды.
Задача 40. Имеется круглый стол и неограниченное количество
одинаковых круглых монет. Двое играющих по очереди
выкладывают монеты на стол так, чтобы они не касались друг друга.
Выигрывает тот, кто положит последнюю люнету. Как должен поступить
игрок, делающий первый ход, чтобы выиграть?
Пример 16 можно решить и алгеб-
Функцин раически. Введем на нашей
плоскокомплексной сти комплексную структуру (т. е.
переменной описанное выше умножение точек
плоскости). Сделаем это так, чтобы
центр данного /г-угольника соответствовал числу 0, а одна
из вершин— 1. Пусть %—вершина, соседняя с 1, тогда
остальные вершины суть £?,..., £«-*. Поскольку 1п = \, то
Б (1 + £ +,... + Г'"1) = 5 + I2 + . • • + Г-' +' 1.
Из уравнения %х = х получаем л-= 1 + t + ■ ■. -+- £""*1=;0,
ибо*£ ф \. '
Это доказательство принципиально не отличается от
предыдущего, точнее, представляет дословный перевод
геометрических рассуждений на алгебраический язык.
Действительно, алгебраическое доказательство основано
на том, что единственное число, переходящее в себя при
умножении на £, т. е. удовлетворяющее уравнению pi'—x,
есть нуль. Но что происходит с комплексным числом
приумножении на £? Согласно общему правилу, его модуль
не изменяется, так как |£| — 1» а к аргументу
прибавляется Зб07«. Геометрически это означает поворот
данной точки на угол 3607« вокруг центра многоугольника.
Итак, если точки плоскости понимать как
комплексные числа, то геометрические преобразования и, в част*
46

кости, движения плоскости следует интерпретировать как
функции комплексной переменной w = f(z), где г —
произвольная точка плоскости, a w — ее образ. Например,
поворот с центром в нуле представляется функцией вида
w — аг, где |а[=*1 (при этом а = cosср-\- lsinф, где
(р — угол поворота). Очевидно также, что параллельный
перенос описывается формулой
w — z + а, (1)
где а — некоторое комплексное число.
Выведем теперь формулу поворота комплексной
плоскости вокруг произвольной точки /7. Из рис. 28 видно,
что поворот точки z вокруг р на угол ф можно
осуществить в три этапа:
1) точку z перенести в точку z — p;
2) точку z — р повернуть на угол <р вокруг О, в
результате чего она попадет в точку a (z — /?), где а —
-= cosq>-h'sin<i>;
3) точку а{г — р) перенести в точку a(z — р)-\- р.
Таким образом, поворот плоскости вокруг точки р на
угол ф задается функцией
w = az-b(l — a)p, (2)
где a ,!= cos ф + i sin ф.
Параллельные переносы и повороты называются
собственными движениями. Такое название объясняется тем,
что для физического осуществления этих преобразований
не надо выходить за пределы плоскости, тогда как
отражение требует ее переворота в окружающем трехмерном
пространстве. Из формул (1) и (2) видно, что
собственные движения плоскости описываются линейными
функциями
w = u,z -f- гп, (3)
где а и m — комплексные числа, причем |а| = 1.
47

Докажем и обратное: всякая линейная функция
вида (3) задает некоторое собственное движение. Если
а— 1, то формула (3) принимает вид (1), что
соответствует переносу. Если же а Ф 1, то из выражения
и>*=аг + т = a(z ^—) -[--г-^—
1 ^ I—a J ' I — a
Рис, 28 Рис. 29
видно, что данное преобразование есть поворот вокруг
точки mf{\ — а) на угол <р, такой, что cos <р-J- i sinq> — а.
Для описания несобственных движений (например,
отражения относительно прямой), помимо сложения,
умножения и перехода к пределу, требуется еще одно
действие: комплексное сопряжение. Сопряженным к
числу z = j:-f- Щ называется число z = х — iy.
Геометрически переход к сопряженному числу означает отражение
относительно действительной оси (рис. 29). Напомним,
что в главе «Плоскость» мы уже пользовались
сопряжением при выводе формулы для частного двух комплекс-
пых чисел.
48
i

Задача 41. Выведите следующие формулы, описывающие
отражение относительно прямой, заданной уравнением у = kx -j- b;
xv «= г +2W, если ft = 0, (4)
1—А8-|-2ft/ /_ b \ b
w = Г+¥ Г + T)~~T> еслн A^° <5>
I #a .l 2ft/
(заметим, что j i ^ — аг, где a = cos ф -{- / sfn ф, а ф —
угол наклона дайкой прямой к оси х).
А теперь рассмотрим
пример, иллюстрирующий
использование
алгебраической записи движений
как функций комплексной
переменной при решении
геометрических задач.
Пример 19. Искателю
сокровищ стало известно,
что местонахождение
клада можно определить по
положению трех
известных примет А, Вj С
следующим образом (рис. 30). В точке А нужно построить
прямой угол и отложить отрезок DA = ACf в точке В —
прямой угол и отложить отрезок BE = ВС и начинать
раскопки в точке К, являющейся серединой отрезка DE.
Искатель клада прибывает на место и видит, что приметы
А и В имеются, а примета С бесследно исчезла. Может
ли он тем ие менее определить точку К?
Пусть точке А соответствует нуль комплексной
плоскости, а точкам В и С — числа Ь и с. Согласно формуле
(2), точки D и Е суть числа — ic и Цс — Ь)-{-Ь, следова-
тельно, середина отрезка Е есть —^—Ь. Поскольку это
49

выралсение от с не зависит, местонахолсденне клада не
зависит от положения точки С. Из той же формулы
видно, что точку К можно найти как вершину
прямоугольного равнобедренного треугольника с гипотенузой ЛБ.
Это построение и должен выполнить искатель клада.
Задача 42. Дпс стороны треугольника повернуты вокруг их
общей вершины на 90° в противоположных направлениях. Докажите,
что прямая, соединяющая концы полученных отрезков,
перпендикулярна к медиане.
Поскольку движение плоскости есть,
Композиция по определению, преобразование,
движений сохраняющее расстояния между
точками, а при последовательном
выполнении двух движений (при нх композиции)
расстояния также не меняются, то композиция движений
является движением. Рассмотрим композиции изученных
движений: переносов, отражений и поворотов.
Пример 20. Найти композицию двух отражений.
Отражение относительно прямой I условимся
обозначать 5л Пусть даны две прямые / и т и требуется найти
50

композицию STn ° Si. Обозначим А' образ данной точки А
при St, а А" — образ точки А' при Sm.
Рассмотрим сначала случай, когда данные прямые
параллельны (рис. 31,а). Точки А, А', А" располагаются
на одной прямой, перпендикулярной к / и т, причем
независимо от положения точки А расстояние АА" равно
удвоенному расстоянию между прямыми / и т.
Следование 31
тельно, композиция отражений Si и Sm действует на
каждую точку плоскости так же, как и параллельный перенос
на вектор 2«, где вектор м, как показано на рис. 31, а,
перпендикулярен к данным прямым, равен по длине
расстоянию между ними и направлен от / к т, т. е.
Sm о 5/ = Tj£. (6)
Пусть теперь прямые / и т пересекаются в некоторой
точке С (рис. 31,6). Если ф — угол между данными
прямыми, то из чертежа видно, что ZACA" = 2ц>. Кроме
того, точка С равноудалена от точек А, А\ А". Значит,
51

точку А" можно получить из А поворотом на угол 2ср
вокруг точки С. Иными словами,
5«о5х«/8», (7)
где через Re9 обозначен поворот на угол 2ср вокруг
точки С против часовой стрелки, если <р >■ 0, и по часовой
стрелке, если ср «С 0.
Рекомендуем читателю наряду с рис. 31,5
рассмотреть другие случаи расположения точки А иа плоскости
и убедиться, что доказанное утверждение справедливо
для всех точек плоскости. Во избежание недоразумении
отметим, что угол 2ф, фигурирующий в формуле (7), от-
считывается в ту же сторону, что и угол <р.
Задача 43. Пусть /, т и п — прямые, пересекающиеся в одной
точке. Определите, что представляет собой движение (5« eSmoSi)2
(возведение в квадрат понимается как композит»! движения с. собой,
т. е. в данном случае как $п ©S,„ aSioSn <>Sm о St), Советуем вначале
решить задачу «экспериментально», т. е. применить указанную
композицию к точке плоскости, взятом наугад. Полученный результат
докажите с помощью формулы композиции отражений.
Формулы (6) и (7) можно прочитать и справа налево:
тогда они позволяют выразить перенос' и поворот через
отражения. При этом следует иметь в виду, что пара
прямых, отражения относительно которых дают искомое
движение, определяется неоднозначно, и этим
обстоятельством можно воспользоваться.
Пример 21. Найти композицию двух поворотов.
Если центры поворотов совпадают, ответ очевиден:
ЯЯ о /& = Я£*. (8)
Рассмотрим композицию поворотов R% и Rb с разными
центрами. Каждый из них можно представить в виде ком-
52
J

позиции двух отражений: /?л = 5^о5г (прямые / и т
пересекаются в точке А и образуют угол ф/2), а /& =
— Sp°Sn (прямые п и р пересекаются в точке В и
образуют угол я)>/2) (рис. 32, а). Тогда #V% #1=5,7, ^З/^п-
Это выражение упрощается, если прямые / и р
совпадают: в этом случае St <> SP = id является тождественным
Рис. 82
преобразованием * и из четырех «сомножителей»
остается только два. Чтобы так получилось, нужно в
качестве / и р взять прямую с, соединяющую точки Л и Б.
Обозначим через b прямую, полученную из с поворотом на
угол ф/2 вокруг точки А, а а—прямую, полученную, из с
поворотом на угол —ф/2 вокруг В. Если прямые а и b
пересекаются в точке С (рис. 32,6), то, согласно
сказанному выше,
или, обозначив a = ф/2, [5 = \р/2, у = 180° — a — р,
4 Тождественное преобразование переводит каждую точку п
себя. Его принято обозначать символом id, что в переводе с
латинского означает «это».
53

ЯЗГ-ЛУ-Кс*. (9)
где С — третья вершина треугольника, имеющего
вершины А, В и углы аир при этих вершинах; у— угол этого
треугольника при вершине С.
Если же прямые а и b параллельны (ф -f* Ф кратно
360°), то
/во/&-Га-, (10)
где вектор и определяется из рис. 32, в.
Равенство (9) можно переписать в более
симметричном виде, если домножить обе его части справа* на Rcy
(т. е. взять композицию обеих частей равенства с
поворотом Rcv в указанном порядке):
RfoRf*Rty~\&t (П)
Это равенство равносильно равенству (9), так как
получается из него домноженнем обеих частей на Rcv -
Справедливо и обратное утверждение: если точки А,
В, С и углы а, р, у, заключенные в пределах от 0° до 180°,
таковы, что имеет место равенство (11), то а, Р, у —
величины углов треугольника ABC.
В справедливости равенства (11) можно убедиться и
непосредственно. Так как а +р-f y = 180°, то
композиция 7$а ° ЙР ° #cv является параллельным переносом. Из
рис. 33 видно, что при последовательном выполнении
поворотов Rp, /?|e, #ла точка А переходит в себя.
* Порядок здесь пажен, поскольку композиция движении
зависит от последовательности их выполнения.
54

Можно вывести it алгебраическую формулу для
композиции двух поворотов. Согласно формуле (2), для
любых значений
R% (z) = q(z — b) 4 b; /Д И = P (» - a) -I-*.
где ^ = cosя]) + i sin ф; /7 = cos ф 4 /sin ф. Чтобы найти
композицию поворотов 1^[ и /?|, нужно во второе
равенство подставить значение w — ^1(2) из первого равенства:
Рис. 33 Рис. 34
— b) -j- b — а) 4- a ~ pqz — pqb -\- pb — pa + a =* де+(1 —
, a — pa -I- pl> — pgf»
Замечая, что pq = cos(cp4-^)+ i sin(q> + -ф)л и
сравнивая полученное выражение с формулой (2), видим, что
55

где точка С описывается комплексным числом
с= а-ра + рЬ-РЧЬ
1 — рд v '
Итак, геометрические и алгебраические рассуждения
привели нас к разным по виду формулам композиции
двух поворотов. Из сравнения этих формул получаем
следствие.
Точка С, являющаяся третьей вершиной треугольна- |
ка ABC, вершины А и В которого суть известные коми- •
лекспые числа а и b и углы которого при этих вершинах
ф/2 и -ф/2 даны, описывается комплексным числом с,
определяемым из соотношения (12).
Рассмотрим, как используются понятие композиции
движений и выведенные формулы при решении
геометрических задач.
Пример 22. На сторонах треугольника вне его
построены правильные треугольники (рис. 34). Доказать,
что их центры Mt N, Р также образуют правильный тре- '
угольник.
По условию, треугольники АМВ, BNC и СРА
равнобедренные с углами по 120° при вершинах. Рассмотрим
композицию трех поворотов /?р20° о #дг2°е и /Д20° — F
(напомним, что положительные углы отсчитываются против |
часовой стрелки). Из формул (9) и (10) видно, что двн- I
жение F должно быть поворотом или параллельным
переносом. Поскольку суммарный угол поворота
композиции F есть 120° +120° +120° = 360°, F представляет
собой перенос. Посмотрим далее на образ точки А при
этом переносе. Ясно, что Rm°°{A) =Bt R1n°°{B) — С,
R1p0°(C) — А, т. е. F(А) — А Отсюда следует, что F —
56

перенос на нулевой вектор, т. е. тождественное
преобразование
D120° Ы20° с»12**0 ;л
Сравнивая это равенство с формулой (11), делаем
заключение, что М — третья вершина треугольника с
вершинами в точках N и Р, имеющего углы по 60° при этих
вершинах, т. е. равностороннего треугольника.
Задача 44. Попробуйте доказать утверждение предыдущего
примера с помощью комплексных чисел. Предполагая числа,
соответствующие точкам Л, 13, С, данными, найдите по формуле (12) числа,
соответствующие точкам М, N и Р. Полученное решение будет более
громоздким, чем прнпеденное выше, но не менее интересным и
поучительным.
Задача 45. На сторонах четырехугольника вне его построены
кнадраты. Докажите, что их центры образуют четырехугольник,
диагонали которого взаимно перпендикулярны н равны.
Задача 46. Найдите композицию:
а) двух разворотов;
б) разворота н отражения.
Задача 47. Постройте пятиугольник по серединам его сторон.
Решая задачу 46, читатель уже имел
Скользящее возможность убедиться в том, что
отражение при композиции переносов и
отражений, а также поворотов и
отражений иногда получаются движения, не принадлежащие
ни к одному из перечисленных видов, а именно,
скользящие отражения (или скользящие симметрии). Скользя-
-у -Г
щей симметрией с осью I и вектором v (обозначим ее Vi)
называется движение, состоящее в отражении отиосн-
тельно прямой I и параллельном переносе на вектор у,
-*-
параллельный прямой / (рис 35). Иначе говоря, UVL =
— Т~£ о St = St о Г£. Движения Т^ и St перестановочны
57

относительно композиции, так как
АА\А'Ач—прямоугольник.
Скользящие отражения, так же как и другие виды
движений, могут с успехом использоваться при решении
геометрических задач.
Пример 23. Построить
прямую, параллельную стороне
АС данного треугольника ABC
и пересекающую его стороны
А В и ВС в таких точках D и Е
соответственно, что AD = BE.
Воспользуемся свойствами
скользящего отражения,
которые следуют из рис. 35:
I) при скользящем
отражении середина любого отрезка,
соединяющего точку с ее
образом, лежит на оси;
2) при скользящем отражении точки, лежащие на
оси, на ней же и остаются.
Рассмотрим скользящее отражение U, переводящее
луч АВ в луч ВС. Его осью служит прямая NK, где W —
середина стороны АВ, а К — такая точка ка стороне ВС,
что ВК = NB, По условию, AD = BE, так что U(D) = Е.
Середина отрезка DE должна лежать на прямой NK.
Но поскольку DE\\AC, середина DE лежит на
медиане ВМ. Поэтому отрезки DE, ВМ и NK должны
пересекаться в одной точке, и требуемое построение можно
выполнить в следующем порядке. Построим точки N и К
так, как было сказано выше, проведем медиану ВМ, а
через точку пересечения ВМ и NK — прямую,
параллельную АС. Это и есть искомая прямая.
Рис. 35
Задача 48. Даны три прямые и некоторая точка. Через эту точку
проведите прямую / так, чтобы ее образ при композиции трех отра-
58

HtCJiiift относительно данных прямых (в заданном порядке) был
параллелен прямой /.
Задача 49. Выведите алгебраическую формулу скользящего
отражения, заменяя точки плоскости соответствующими им
комплексными числами, а движения — действиями над этими числами.
Итак, мы познакомились с новым
Классификация видом движении плоскости. Возни-
движений кает естественный вопрос:
исчерпываются ли все движения четырьмя
описанными видами? Нельзя ли получить еще какое-либо
новое движение как композицию уже известных? Ответ
на этот вопрос дает теорема: все движения плоскости
исчерпываются поворотами, переносами, скользящими
(и обычными) отражениями *.
Докажем ее. Начнем наше рассуждение со
следующего замечания: движение плоскости полностью
определяется образами трех точек А, В, С, не лежащих на одной
прямой. Действительно, если А', В', С — образы точек
А, В, Су то для любой точки D существует ровно одна
точка £К, такая, что расстояния от нее до точек Л', В', С
соответственно равны расстояниям от D до А, В, С,
Второе свойство, которым мы будем пользоваться, состоит
в том, что для любой пары точек М, М' существует
отражение, переводящее М в М'\ осью этого отражения
служит серединный перпендикуляр к отрезку ММ*.
С учетом сделанных замечаний представим
произвольное движение плоскости как композицию нескольких
отражений — этим приемом мы уже пользовались при
выводе формулы композиции поворотов (см. пример 21).
Итак, пусть f — произвольное движение плоскости.
Выберем любые три точки А, В, С, не лежащие на одной
* Обычно в популярной литературе это утверждение называют
теоремой Шаля (М. Шаль — французский математик XIX века), хотя
оно было известно уже Эйлеру в XVIII веке. Шаль доказал яиало*
гнчкую теорему для движений пространства.
69

прямой, и обозначим их образы f(A)~ A', f(B)= В'7
f(C)^C. Пусть S/ — отражение, переводящее А в Аг.
Положим S[(B)~ Bi, Si(C)= C± (рис, 36). Если точка В±
не совпадает с В\ то существует отражение Sm, которое
их совмещает. При этом ось т проходит через точку А\
так что эта точка остается на месте, a Ci переходит в
новое положение С-г. Теперь ясно, что точки Сг и С или
совпадают, или симметричны относительно прямой
Рис. 36
А'В1 = п. Таким образом, данное движение f либо само
является отражением, либо равно композиции двух или
(самое большее!) трех отражений. Если f—композиция
двух отражений, то, согласно примеру 20, это поворот или
перенос. Разберем, наконец, случай композиции трех
отражений Si. Существует несколько способов
расположения трех различных * прямых на плоскости
(рис, 37). В случае «а» композиция Sm°Si представляет
собой поворот. Его можно представить также как Sm* ° S?,
где прямые тг и /' пересекаются в той же точке и иод
* Можно рассмотреть также случаи, когда две из трех прямых
совпадают. Читатель сможет сделать это самостоятельно.
60

тем же углом, что и прямые т и / (при этом учитывается
порядок, в котором берутся прямые). Пару т\ V можно
выбрать так, чтобы т' = п. Тогда
5ц ° Ощ 00/ = Oxi ° Ол о Sf = о/'.
0 rf ^
Р«с. 37
Аналогично проверяется, что и в случае «б»
композиция трех отражений также является отражением.
Рассмотрим теперь
случай «в». Заменим
композицию Sm о Si композицией
S»i' ° Si*, где прямая т'
выбирается перпендикулярной
к я (рис. 38); тогда Sn °Sm«
о St—Sn о Sm'« Si'.
Фигурирующую здесь композицию ^5?
Sn ° Sm' заменим Sn' ° Sm", '/
где прямая пг
перпендикулярна к V, Получим Рис. за
f = Sn о Sm о Si = Sn° Sm' ° Si' = Snf ° Sm>t о Sf.
Заметим, что прямые /' и т" параллельны, поэтому
композиция Sm" ° о> является переносом вдоль
перпендикулярной к ним прямой п', а все движение f, будучи
композицией этого переноса с отражением относительно я',
есть скользящее отражение.
61

Случай «г» сводится к случаю «в». Чтобы в этом
убедиться, достаточно одно из выражений Sm ° 5/ или Sn о Sm
заменить композицией отражений относительно чуть
повернутой пары прямых. Параллельность при этом
нарушится, и мы получим рис. 37, в.
Итак, существует четыре вида дви-
Орнентация жений плоскости: перенос, поворот,
отражение и скользящее отражение.
В ходе доказательства этой теоремы мы видели, что
движения первых двух видов, ранее названных
собственными, представляются композицией четного числа (двух)
отражений. Остальные два вида движений, которые
называются несобственными, так как для своего
физического осуществления требуют выхода в пространство,
соответствуют композиции нечетного числа отраженнй
(одного или трех). Чтобы лучше разобраться в причинах
этого явления, введем понятие ориентации.
Две упорядоченные тройки точек Л*, В\, Ct и Лг, В*,
Сг, не лежащих на одной прямой, называются одинаково
ориентированными, если обход контуров треугольников
AiBid и АъВзРъ, вершины которых берутся в указанном
порядке, в обоих случаях происходит в одну и ту же
сторону (оба раза по часовой или оба раза против часовой
стрелки). Если же этот обход производится в различных
(противоположных) направлениях, то говорят, что эти
тройки ориентированы по-разному (имеют разную
ориентацию).
Понятие ориентации хорошо иллюстрируется
следующей задачей.
Задача 50. На плоскости в вершинах треугольника лежат три
шайбы. Хоккеист выбирает одну из них н бьет по цен так, что она
проходит между двумя другими и останавливается в какоП-либо
точке. Могут лн все шайбы вернуться на свои прежние места после
25 ударов?
62

Замечательно, что всякое движение f либо сохраняет
ориентацию сразу всех троек точек (т. е. ориентация
любой тройки А, Ву С совпадает с ориентацией тройки f(A)f
f{B), f(C)), либо меняет ориентацию сразу всех троек.
Движения, которые можно представить как композиции
четного числа отражений (собственные движения)
сохраняют ориентацию, а движения, представимые как
композиции нечетного числа отражении (несобственные),
ориентацию меняют. Отсюда следует любопытный факт:
композиция нечетного числа отражений никогда не
может привести к тождественному преобразованию
плоскости.
Заметим, наконец, что понятие ориентации легко
интерпретируется на языке операций над комплексными
числами.
Задача 51. Докажите, что тройки точек (zi, 22, гз) и (0, 1, /) на
комплексной плоскости ориентированы одинаково тогда и только
тогда, когда аргумент ф числа (га — Zi)/(£2 — zi) заключен в
пределах от 0° до 180е.
63

Преобразование / некоторого мно-
Исчисление жества называется инволютвным
инволюций (или инволюцией), если само оно
нетождественно, но в квадрате дает
тождественное преобразование: / -ф id, f2 = f о / = id. Это
условие равносильно тому, что данное преобразование
совпадает со своим обратным (f~f~l), т. е. если f(A) ~Bf
то f(B) = А. Есть два вида ннволютивных движений
плоскости: I) отражения 5/; 2) развороты Ra
(условимся, что если угол поворота не указан, то он считается
равным 180°). Инволюции на плоскости взаимно
однозначно соответствуют элементам двух сортов: точкам и
прямым. Разным точкам и разным прямым отвечают при
этом разные движения плоскости, поэтому переход от
геометрических элементов к соответствующим
инволюциям не приводит к потере информации* любое
геометрическое утверждение, относящееся к точкам и прямым
плоскости, может быть сформулировано как некоторое
свойство отвечающих этим элементам инволюций.
Пример 24. Найти свойство отражений Si и 5ГО,
равносильное тому, что прямые / и т взаимно
перпендикулярны.
Рассмотрим композицию Sm ° St, представляющую
собой перенос, если т\\1, и поворот на угол 2q>, если / и т
пересекаются под углом ср. Квадрат этой композиции
(SmoSi)z в первом случае есть снова перенос (на
двойной вектор), а во втором — это поворот на угол 4ср.
Отсюда видно, что движение (Sm°S/)2 совпадает с
тождественным преобразованием тогда и только тогда, когда
Ф = 90°. Итак, искомое свойство
(Sm°S,)2 = id, (13)
т. е. движение Sm°Si инволютивно (заметим, кстати, что
это разворот с центром в точке пересечения данных
прямых).
64

Домножим равенство (13) на Si, а затем на Sm. Tor-
да, учитывая, что Si и Sm — инволюции, получаем другую
форму записи того же свойства:
Sm ° 5( = Si о Sm, (14)
т. е, отражения Sm и Si перестановочны (коммутируют).
Заметим, что композиция движении, как и любых
преобразований, всегда ассоциативна, как и умножение чисел
и точек, но в отличие от последнего она, вообще говоря,
не обладает свойством коммутативности. Например, как
мы только что увидели, отражения относительно двух
различных прямых коммутируют между собой тогда и
только тогда, когда эти прямые взаимно
перпендикулярны.
Здесь уместно сказать несколько слов по поводу
ассоциативности. Свойством ассоциативности обладают не
только движения и другие преобразования, но и
произвольные отображения (преобразованием называется
взаимно однозначное отображение множества в себя).
Точнее, пусть Vt W, X, У—некоторые множества и г, g,
h — их отображения согласно схеме
V + W *> X -> Y.
Тогда можно составить композиции (или, употребляя это
слово в переносном смысле, произведения) отображений:
gof: у-+Х, hog: W-+Y, h<>(g° f) : V-+Y, (Л*g) ° f: V-+Y.
Утверждается, что отображения ft о (go f) и (л eg) of
совпадают. Приведем сначала формальное
доказательство этого утверждения, а затем поясним его наглядно.
Для формального доказательства достаточно
несколько раз воспользоваться определением композиции
отображений, которое, например, для fug выражается
равенством (g°f) (»)— g(f(v)) для любого элемента v
множества V (т. е. к v применяется отображение /, а
3 Зак. 541
65

к f (v) отображение g). Проследите» как используется это
определение в следующей цепочке равенств:
(А* (g°f))(v) = h((g°f)(v))= h(g(f(v)))=*
= (h*g)(f(v)) = ((h°g)*f)(v). (15)
Поскольку значения отображений h ° {g ° /) и (Л ° g) of
иа любом элементе i/еУ совпадают, эти отображения
равны между собой.
Для понимания существа свойства ассоциативности
проведем следующую аналогию. Представьте себе, что !,
g и Л-—действия, состоящие в надевании носков,
валенок и галош соответственно. Чтобы составить
композицию h о {g°f)t нужно вдеть носки в валенки и надеть то,
что получится, на ноги, а сверху надеть галоши.
Композиция же (Л о g) о f осуществляется так: сначала
надевают носки, а затем валенки, на которые уже надеты
галоши. Результат в обоих случаях одинаков!
Этот же пример хорошо иллюстрирует пекоммутатнв-
ность рассматриваемых операций: надеть носки, а потом
валенки — это совсем не то же самое, что надеть сначала
валенки, а потом носки! Однако и здесь можно указать
66

коммутирующие действия, например надевание носка на
левую ногу и надевание носка на правую ногу.
С помощью этой аналогии легко найти формулу
действия, обратного композиции. Если, например, надеты
носки, валенки и галоши, то для того, чтобы все это
сиять, надо снять сначала галоши, затем валеики, а
потом носки- Таким образом,
(hcgof)-i = f-iog~io!rK
Вернемся теперь к исчислению инволютивных
движений плоскости»
Пример 25. Выразить посредством инволюций тот
факт, что четыре данные точки Л, В, С, D образуют
параллелограмм.
Согласно результату задачи 46, композиция Ra ° Re
есть параллельный перенос на вектор 2ВА7 а
композиция Rb о Rc — перенос на вектор 2 CD. Четырехугольник
ABCD (с этим порядком вершин!) является параллело-
—> — >•
граммом тогда и только тогда, когда ВА = CD, что
равносильно соотношению
Ra о Rb — Rd° Rc.
Это соотношение можно переписать в виде /?д ° RBo
с Rc ° Rd — id или
Ra°Rb°Rc = Rb. (16)
Последнее равенство можно рассматривать как формулу,
выражающую четвертую вершину параллелограмма
через три другие вершины.
Задача 52* Запишите следующие геометрические факты на языке
инволюций:
а) точка А лежит на прямой /; б) точка А — середина
отрезка ВС.

Задача 53. Укажите геометрический смысл следующих сосп-ио-
шении:
а) Rao St <= StoRu; б) (Sn *Sm »Sj)2 = id.
Исчисление инволюций часто обеспечивает краткую и
удобную форму записи геометрических фактов и
соотношений, полезную при
решении задач и
доказательстве теорем.
Пример 26. Пусть М,
N, P, Q — центры
квадратов, построенных на
сторонах четырехугольника
ABCD (рис. 39).
Определить, при каких условиях,
налагаемых на
четырехугольник ABCD,
четырехугольник MNPQ будет
квадратом.
Читателю уже извест-
Рис. 39 но, что диагонали
четырехугольника MNPQ
взаимно перпендикулярны и равны (см. задачу 45).
Следовательно, для того чтобы быть квадратом,
четырехугольнику MNPQ достаточно быть параллелограммом.
Пользуясь результатом примера 25, запишем это условие
в виде
Rm °Rn°Rp°Rq = id. (17)
Но, согласно формуле (9),
rm = Ra°Rb; Rn = Rb°R*c; Rp^R^-Rd; Rq = r1>°R%
где d — 90° (напоминаем, что если величина угла
поворота не указана, то имеется в виду разворот, т. е.
поворот на 180°). Подставляя эти выражения в формулу (17),
получаем
68
ч

RdAoRB*Rc*RDoRdA = i6. (IS)
Согласно формуле (16), произведение трех разворотов,
входящих в левую часть этого равенства, есть 7?е, где
В — четвертая вершина параллелограмма, тремя
вершинами которого являются Л, В и С. Если теперь умножить
обе части равенства (18) дважды на R^ (один раз
слева, другой раз справа), получим Re — Ra, а это
возможно лишь в том случае, когда точки А и Е совпадают.
Итак, если MNPQ— квадрат, то ABCD —
параллелограмм. Достаточность этого условия можно усмотреть,
проследив в обратном порядке проведенные выше
рассуждения, а еще проще проверить ее непосредственно,
заметив, что треугольники QAM, MBN} NcP и PDQ
в этом случае равны.

ГРУППЫ
Элементарная геометрия изучает свойства
фигур, которые не зависят от их частного
положения в пространстве. Прошло немало
столетии, прежде чем эта несколько
неопределенная формулировка была переведена на
точный язык: свойства, изучаемые
элементарной геометрией, являются теми, которые
остаются инвариантными относительно
некоторой совокупности преобразований,
образующей группу движений.
Э. Картон
В понятие группы входят общие свойства операций,
наиболее часто встречающихся в математике. Примеры
таких операций — умножение и сложение чисел и точек,
сложение векторов, композиция движений — были
рассмотрены в предыдущих главах. Идея группы является
математическим выражением общенаучного принципа
симметрии: чем больше преобразований не изменяет
рассматриваемый объект, тем более симметричным он
является. Так, например, круг более симметричен по
сравнению с квадратом.
70

I
Учет степени симметричности иозво-
перекашиание ляст решать довольно сложные за-
треугопькнка дачи.
Пример 27. На плоскости лежит
[равильный треугольник. Разрешается перекатывать его
ю плоскости, переворачивая на 180° вокруг любой сто-
юны. Доказать, что если в результате нескольких таких
Рис. 40
пераций треугольник вернется в исходное положение,
i: все его вершины займут первоначальные места.
Переформулируем условие задачи, используя понятие
'ижения плоскости. Очевидно, что при любых перека-
i знаниях стороны треугольника могут лежать только на
рямых, параллельных тем, на которых они
располагать вначале, и удаленных от них на расстояния,
кратче высоте треугольника. Все такие прямые образуют
i тку, изображенную на рис. 40, а. Преобразования, ко-
■■рые, по условию, разрешается выполнять с данным
[ еугольником, представляют собой композиции отраже-
ни относительно прямых этой сетки. Пусть G — мно~
ество всех движений плоскости, которые можно полу-
71

ijHTb композициями таких отражений. Это множество
содержит, например, повороты на 120° вокруг вершин
данного треугольника и скользящие отражения, оси
которых— средние линии треугольника (проверьте это!).
Задача будет решена, если мы докажем, что
единственное движение, принадлежащее G л оставляющее на
iJCCTe треугольник ABC, есть тождественное
преобразование. Легко понять, что существует пять
нетождественных преобразований, оставляющих треугольник ЛВС на
усеете: это три отражения относительно его высот и два
поворота вокруг его центра. Задача сводится, таким
образом, к доказательству того факта, что ни одно из
этих пяти движений не содержится в множестве G,
Нашим читателям, вероятно, приходилось встречаться
с задачами, для решения которых достаточно привести
itaKofi-либо пример или контрпример. Оказывается, что
-таким же образом можно решить и данную задачу.
Однако пример, который мы сейчас построим, будет не совсем
обычный. Это — узор, обладающий следующими двумя
свойствами. Во-первых, он симметричен относительно
.яюбой прямой, изображенной на рис. 40, а; во-вторых,
несимметричен относительно высот треугольника ABC, a
центр этого треугольника не является для него центром
(Юворотиой симметрии третьего порядка (т. е. при
повороте на 120° узор не совмещается с собой). Из первого
свойства следует, что такой узор переходит в себя при
^юбом движении из множества G. Тогда из второго
свойства получаем, что ни одно из пяти нетождественных
движений, сохраняющих ААВС, не может принадлежать G.
Примером такого узора служит древнекитайский
орнамент (решетка), нанесенный на сетку, повторяющую
рис;' 40, а (рис. 40,6);
Приведенный пример, разумеется, не единствен.
Опишем общий способ построения подобных примеров.
Внутри треугольника ABC нужно выбрать, как говорят в тео-
П

пни орнаментов, некоторый несимметричный мотив, т. е*
подмножество (рисунок), не обладающий осевой или
центральной симметрией, присущей всему треугольнику.
Б качестве такого мотива можно взять, например, одну
точку, не лежащую на высотах треугольника. Требуемый
узор получается из выбранного мотива путем
применения к нему многократных отражений от сторон
треугольника. Для наглядности можно представить, что мотив
нанесен краской с двух сторон на картонный треугольник
и при перекатывании оставляет след на бумаге.
Задача 54. Выберем на плоскости такую систему координат (см.
главу «Плоскость»), в котором точка А имеет координаты (0, 0),
точка В — координаты (6, 0), а точка С —координаты (0, 6)
(треугольник ABC ло-прежнему равносторонний!) В качестве мотпва
возьмем точку К (3, 1). Изобразите узор, получаемый из этого
мотива, и опишите координаты всех точек, принадлежащих этому
узору.
Задача 55. Остается ли верным утверждение примера 27, если
равносторонний треугольник заменить па треугольник с углами:
а) 45°, 45°, 90°? б) 30°, 60°, 90°? в) 120°, 30*. 30й?
Определенное при рассмотрении
Понятие примера 27 множество преобразова-
группы преобразований Ннй G плоскости обладает
следующими двумя свойствами: 1) если два
преобразования принадлежат G, то и их композиция
принадлежит G; 2) вместе с любым своим преобразованием
Множество G содержит и преобразование, ему обратное.
Заметим, что первое из этих свойств было весьма
существенным при решении примера 27. Этим свойством
множество G обладало по построению. Второе свойство
выполняется потому, что преобразование, возвращающее
все точки на свои места, есть последовательность тех же
отражений, выполняемых в обратном порядке.
Смысл этих свойств в том, что элементы множества G
связаны друг с другом и образуют нечто целое. Это целое
73

замкнуто (т. е. к нему ничего нового не добавляется) при
композиции и при переходе к обратному
преобразованию. С понятием замкнутости читатель уже встречался
в примере 8.
Множество преобразований, обладающее указанными
свойствами, называется группой преобразований^
Задача 56. Докажите, что всякая группа преобразовании
содержит тождественное преобразование
При разборе примера 27 мы имели дело еще с двумя
группами преобразований. Это группа £>з
самосовмещений правильного треугольника (движении, переводящих
правильный треугольник в себя) и группа Д всех
движений плоскости.
Группы /)з и G содержатся в Д; говорят, что они
являются подгруппами группы Д. Вообще, если на плоскости
задана фигура Ф, то можно рассмотреть множество
Sym (Ф) всех движений плоскости, при которых Ф
переходит в себя. Следовательно, Sym(O) есть подгруппа
группы Д, которая называется группой самосовмещений
или группой симметрии фигуры Ф. Так, описанная выше
группа Ds является группой симметрии правильного
треугольника: Sym(A)— Ds. Группа G, описанная в
примере 27, также является группой симметрии некоторой
фигуры, а именно узора, изображенного на рис. 40, б. Чтобы
убедиться в этом, достаточно доказать, что любое
движение, сохраняющее данный узор, является композицией
отражений относительно нескольких прямых сетки.
Задача 57. Проверьте это утверждепне, пользуясь рис. 40, б.
Понятие группы симметрии позволяет указать,
многочисленные интересные примеры rpyim преобразований.
Рассмотрим некоторые из них.
74

I
Пример 28. На рис. 41 изображены древнеяпонские
фамильные гербы. Найти группы симметрии этих фигур.
Какие фигуры имеют одинаковую, а какие — разную
симметрию?
Фигура Ф1 выдерживает отражение относительно
четырех осей, расположенных через 45°, а также повороты
на углы 90°, 180°, 270°. Добавляя к этим движениям
тождественное преобразование, которое является симметрией
Рис. 41
любой фигуры, получаем, что группа Sym <Dj (т. е.
группа симметрии фигуры uh) состоит из 8 элементов.
Группа 5ут(Ф2) также состоит из 8 элементов, из вращений
на углы, кратные 45°. Однако группа Sym(<D2) не
содержит отражений и тем отличается от группы (Sym<X>).
С другой стороны, на рис. 4.1 можно отыскать фигуру,
имеющую ту же группу симметрии, что и фигура Фи
Это — Фз. Таким образом, фигуры Ф1 и Фз имеют
одинаковую симметрию.
Наконец, Ф4 совмещается с собой только при
тождественном движении. В этом случае говорят, что ее группа
симметрии тривиальна, а фигура не имеет симметрии.
Задача 58. Найдите группы симметрии фигур, изображенных на
Рис, 42. Сравните эти группы между собой и с группами, отесанными
п примере 28.
75

Группы симметрии всех фигур, изоб-
Классификация раженных на рис. 41 и 42, состоят из
конечных групп нескольких вращений, либо из
недвижений скольких вращений и такого же чис-:
ла отражений. Это наблюдение мож- i
но сформулировать в виде общей теоремы. Для этого
введем некоторые понятия и обозначения.
Группа преобразований называется конечной, если
она состоит из конечного числа элементов. Так,
например, группы симметрии фигур, изображенных на рис. 41
Рис. 42
и 42, все конечны, а группы Д и G, описанные в
примере 27, бесконечны.
Группу, состоящую из п поворотов на углы, кратные
3607л, с общим центром, будем называть циклической
группой порядка п и обозначать Сп. Группу,
содержащую те же повороты, а также п отражений относительно
прямых, проходящих через центр поворотов и
расположенных через каждые 180°/я, назовем группой диэдра
порядка 2л и обозначим Dn.
Порядком группы называется число элементов в ней.
Таким образом, конечная группа — это группа, имеющая
конечный порядок.
Теорема, Всякая конечная группа движений плоскости
совпадает либо с Сп, либо с Dn.
76

Например, группы симметрии восьми фигур,
изображенных на рис. 41 и 42, суть соответственно £>4, Cs, 0«,
Ci, Сг, Е>и ®з> Сх.
Приступая к доказательству теоремы, отметим, что
конечная группа движений плоскости не может
содержать параллельного переноса. В самом деле, в
противном случае, обозначив этот перелое Т*, из первого
свойства группы (см. определение, приведенное в начале
главы) мы получили бы, что данная группа содержит
бесконечно много различных параллельных переносов
-*■
(на векторы, кратные а).
Поскольку квадрат скользящего отражения, т. е. его
повторное применение, есть параллельный перенос, то и
конечная группа движении не содержит и скользящих
отражений. Таким образом, она должна целиком состоять
из поворотов и отражений. Все вращения, содержащиеся
в конечной группе, имеют общий центр. Это вытекает из
следующей задачи.
Задача 59. Докажите, что если А и В — различные точки плос-
кости, то движение R^' ° R^ <? R'^ о R§ представляет собой
параллельный перекос.
Если данная конечная группа движений содерлшт
повороты Щ и R'b с разными центрами, то она содержит
и параллельный перенос /?вфо R^* °R%^ R§ (заметим, что
здесь используются уже оба свойства, входящие в
определение группы) и, следовательно, не может быть
конечной.
Итак, все повороты, входящие в данную группу,
имеют общий центр. Обозначим их R% Д^, ... , /?^, где
все углы ф,..., (й принадлежат промежутку от 0 до 360°.
Выберем из углов <р, ,,,, со наименьший; пусть это бу-
77

дет \\\ Докажем, что остальные углы являются
кратными ij>. Действительно, если, например, <р не делится
нацело на ipf то, выполняя деление с остатком, получим
(p — ipk-\-£, где О <С | < ijj, a k — некоторое целое число.
Поворот на угол £ также принадлежит рассматриваемой
группе, по, вопреки предположению, £ <; чр.
Заметим, что угол ф должен быть равен 3607", так
как в противном случае некоторая степень R'a (т. е.
результат последовательного выполнения нескольких таких
поворотов) была бы поворотом на угол, меньший ф. Итак,
все повороты, принадлежащие конечной группе, суть
/И?, где k■ = 0, 1, ..., п — I, ty = 360°/"- Если группа не
содержит отражений, то, следовательно, она
представляет собой циклическую группу Сп.
Предположим теперь, что конечная группа движений
плоскости G содержит некоторое отражение St.
Докажем, что в этом случае группа G состоит из некоторого
числа поворотов с общим центром А и такого же числа
отражений, оси которых проходят через точку Л.
Действительно, пусть в группе G имеется п
поворотов, включая тождественный; тогда композиции этих
поворотов с отражением Si дадут п отражений (в том
числе St). В самом деле, эти композиции являются
несобственными движениями, т. е. отражениями или
скользящими отражениями. Последний случай, согласно
сказанному выше, невозможен. Нетрудно видеть, что все
полученные отражения различны. Следовательно, число
отражений, содержащихся в группе G, не меньше числа
поворотов.
Подобным же образом можно убедиться и в том, что
чпсло поворотов не меньше числа отражений.
Действительно, композиции одного отражения St с различными
отражениями группы G представляют собой различные
собственные движения, принадлежащие G. Поскольку
78

переносов группа G не содержит, эти собственные
движения все являются поворотами.
Итак, группа О состоит из я поворотов с общим
центром Лип отражений. Если п — 1, то группа содержит
одно отражение и один поворот на нулевой угол.
Согласно принятым выше обозначениям, это есть группа Dim
Если же л > 1, то оси всех отражений группы должны
проходить через центр поворотов. В самом деле, если оси
некоторых двух отражений параллельны, то в группе
содержится некоторый перенос, являющийся их
композицией. Далее, композиция двух отражений с
непараллельными осями есть поворот с центром в точке пересечения
осей. Поскольку конечная группа не может содержать
поворотов с разными центрами, то оси всех отражений
данной группы должны проходить через центр поворотов.
Заметим, что поскольку композиция отражений, оси
которых образуют угол ср, есть поворот на угол 2ср, то оси
п отражений, принадлежащих G, располагаются через
углы 180в/л. Получаем, что группа G есть £)„.
Задача 60. Может ли фигура па плоскости иметь:
а) ровно две оси симметрии? б) ровно два центра симметрии?
Задача 61. Назовите самую симметричную (т. е. имеющую
наибольшую группу симметрии) ограниченную фигуру па плоскости.
Найденный нами перечень всех конечных групп
движений плоскости в неявном виде был известен еще
Леонардо да Винчи (XV век), который «систематически
занимался вопросом об определении возможных видов
симметрии для центрального здания, а также о том,
каким образом следует производить пристройку к ним
часовен и ниш, не разрушая симметрии ядра
архитектурного ансамбля» (Г. Вейль. Симметрия, с. 92).
79

Сопряженные
преобразования
Давайте задумаемся, в каком
смысле употреблен знак равенства в
соотношении Sym((Di) = Sym(<D3) (см.
пример 28). Это равенство имеет
буквальный смысл, т. е. соответствующие множества
движений совпадают в том случае, когда фигуры
расположены на плоскости так, что их центры и оси симметрии
совпадают. Если же фигуры расположены по-другому, то
множества G.— Sym(Oi) и /7=Sym(<Ds) различны.
Однако между ними имеется тесная связь, которую мы
сейчас выясним.
Рис. 43
Обозначим центр вращений и оси отражений,
принадлежащих группе G, через А и Ci, ..., с4 соответственно.
Те же объекты для группы И обозначим В и &i, ..., bt,
(рис. 43). Пусть f—некоторое движение плоскости,
переводящее В в А, а прямые &i, ..., Ьь. — в прямые
ai, ..., од. Тогда преобразования группы О можно
получить из преобразований группы И следующим образом.
Возьмем, например, отражение относительно прямой Ьз.
Перенесем фигуру Ф% посредством движения f-1, затем
отразим ее относительно прямой £»3 и, наконец, возвратим
ее на прежнее место с помощью /. После выполнения
80

этих действий обнаруживается, что фигура просто
отразилась от прямой а3.
Точно так же, взяв любое движение ft из группы Н,
мы увидим, что композиция f о haf-* принадлежит (?.
При этом» если ft — отражение от прямой Ьи то f с ft о f-1—
тоже отражение, но от прямой af (с тем же номером).
Если К — поворот воокруг Л, то [оЬ/-1 — поворот на
тот же угол, но вокруг В.
Говорят, что движение g — / « ft о f-i e G,
соответствующее движению ft <~ Я, получено из Л сопряжением
с помощью /. Движения g и ft называются
сопряженными.
Сопряженные преобразования нам уже встречались:
мы их использовали при выводе формулы для поворота
с произвольным центром и при решении задачи 41 (см.
главу «Движения»).
Две группы движений называются сопряженными,
если все элементы одной нз них получаются из элементов
Другой с помощью сопряжения одним и тем же
движением. Если бы мы в предыдущих рассуждениях взяли не
Две различные фигуры Ф4 и (1>з, а одну и ту же,
например (1^, и разместили ее на плоскости двумя различными
способами, то их группы симметрии были бы также
сопряженными подгруппами в группе движений плоскости.
Вообще, сопряжение можно понимать как рассмотрение
предмета (или преобразования) с новой точки зрения.
При этом преобразование f\ осуществляющее
сопряжение, как бы переводит старую точку зрения (систему
отсчета) в новую.
Отметим весьма важное свойство сопряженных
подгрупп. Сопряженные подгруппы имеют одинаковую
внутреннюю структуру: операции композиции
преобразований в обеих группах устроены одинаково. Точный
математический смысл этой фразы заключается в следующем.
Пусть подгруппа О сопряжена с подгруппой Н при по-
81

мощи преобразования f. Если g = f сА° f-\ то будем
считать g и h соответствующими друг другу и писать: g ■«-»■ А.
Легко понять, что это соответствие взаимно однозначно:
если А -«-»■ £,. то А определяется по # однозначно как
t~x с £ ° /• Тогда оказывается, что
композиции двух элементов
группы И соответствует композиция
соответствующих элементов
группы (?, а обратному элементу в
И — обратный элемент в G: если
^i ч""1, gi и Аа ^ gz, то
Рис. 44
Ац" Ах ** #й о £х и Ai <~>gi
Первое равенство проверяется так:
tf°/^1Mf°Ai°/-I) =
= fo(AfioA1)o/'-1-
Для проверю! второго достаточно заметить, что
(foA1o/-i)o(/:oA7lo^)-fo(AloAr1)^1=f^'-'1
есть тождественное преобразование.
Выведем формулы для сопряжения одних движений
плоскости с помощью других.
Пример. 29. Найти движение, сопряженное повороту
/?л посредством отражения St.
Пусть движение S]-1» совпадающее с St, переводит
точку уЦ, в точку M-l (рис. 44). Под действием поворота
Я5 Mi •переходит в Мй, а Мг под действием St — в М$.
Обозначим через А' точку, симметричную точке А
относительно прямой ./. Тогда ДМД'Мз — &MiAM2. Значит,
Л*з = Я**(М). Итак, S, ° *5 ° $ - Я?» где Л'=-5,(Л).
.82

Задача 62. Составьте полную таблицу сопряжении ь группе D,
1 т. е. найдите для каждого движения 7"-*, Д^, S^ Uf движение,
ему сонряжыпгое, с помощью Т-+л Щ$, Sm, Um*
При разборе примера 29 и решении задачи 62
полезно не забывать указанный выше смысл сопряжения как
перехода к новой системе отсчета. Вот еще одно
упражнение, которое поможет читателю понять эту важную
мысль. Вырежьте из картона правильный многоугольник
: и обозначьте его вершины с двух сторон числами 1, "2
и т. д. Группа симметрии правильного многоугольника
состоит из п. поворотов и л отражений. Последние можно
1 осуществлять как повороты в пространстве на 180°
вокруг осей симметрии. Эта группа ранее была названа
группой диэдра * и обозначена Dn. Манипулируя с
картонным многоугольником, легко проверить, что
движение, сопряженное в группе Dn некоторому повороту
посредством отражения, есть поворот на такой же угол, но
в противоположном направлении. Сопряжение же с
помощью другого поворота не меняет данного поворота.
Если дополнить картонный многоугольник таким же
многоугольником, нарисованным на бумаге, получится
удобный «прибор» для изучения группы Dn.
Нарисованный многоугольник должен быть чуть больше, чем выре-
занный; его вершины .также должны быть
пронумерованы. Композицию двух элементов fug группы можно
отыскать с помощью этого «прибора» следующим
образом. Положите диэдр на бумагу так, чтобы
соответствующие цифры совпали. Проделав с ним движение f,
положите многоугольник виовь па бумагу (в новом положе-
* Многоугольник, рассматриваемый как пространственная фпгу-
ГЧ представляет собой диэдр, т. е. двухгранник.
83

нии) и примените движение g. Сравнивая нумерацию i
вершин диэдра и нарисованного многоугольника, легко
понять, какое движение привело бы к такой же
перестановке вершин. Это и есть композиция gof,
Задача 63. Найдите все попарные композиции движсе-нй из грукп !
симметрии правильного треугольника и квадрата. Иначе говоря, с.и-1
ставьте таблицу композиций (или, как ее чаще называют, таблицу!
умножения) для групп D3 и D^
Глядя на таблицу сопряженных двнженнй"(ответ к агь
даче 62), можно заметить, что сопряжение посредством
переноса T-g не меняет переноса Т~>а:Т~%*Т-^оTZ1 =* Т-^
Это равенство можно переписать так: Т-$ с Т-* = Т-% о Т^
(мы домножилн обе части предыдущего равенства справа
на Г-j; напоминаем, что порядок, в котором выполняется
композиция, важен!). Последнее равенство означает, что
параллельные переносы Т* и Т-% перестановочны, или
коммутируют*.
Группа преобразований, в которой любые два
элемента перестановочны, называется коммутативной.
Пример 30. Найти все конечные коммутативные
группы движений плоскости.
Список всех конечных групп движений плоскости нам
известен: это группы Сп и Dn для всех п= 1, 2, 3, ...
'Коммутативность любой циклической группы
Сп_следует из коммутативности более широкой группы всех
вращений с общим центром*, композиция поворотов на
углы а и р в любом порядке есть поворот на угол а + р.
Группа А коммутативна, так как содержит всего два
различных элемента, один из которых — тождественное
преобразование — коммутирует с любым движением.
* Напомним, что перестановочность отражении обсуждалась при
разборе примера 24.
84

Докажем, что группа Dz также коммутативна, Она
состоит из двух отражений Si и S2 с взаимно
перпендикулярными осями, разворота R и тождественного
преобразования. Композиция S2°5i есть поворот на 180° в одну
сторону, а композиция Si с S2 — поворот на 180° в
другую сторону. Следовательно, S2 ° Sj = Si о S2> причем обе
эти композиции совпадают с R. Поэтому Si о R =
= Si о S2 о Si ~ R ° Si. Точно так же S2 о R = R о S2.
Рассмотрим теперь группу Dn при п >- 2. Она
содержит поворот на угол 360°/«, который мы обозначим R, и
некоторое отражение S. Тогда, согласно примеру 29,
SoRoS — R~* (в этом вы, конечно, убедились также с
, помощью описанного выше картонного «прибора»), а при
п > 2 поворот R-1 отличен от R. Значит, группа Dn
некоммутативна.
Итак, в полный список конечных коммутативных
групп движений плоскости входят группы Du D2 и все
группы Сп.
Для тех, кто решил задачу 63, заметим, что таблица
умножения позволяет легко определить, коммутативна ли
данная группа: у коммутативных групп таблица
умножения симметрична относительно диагонали, идущей из
левого верхнего угла в правый нижний. Если же таблица
в целом несимметрична, то в ней встречаются равные
элементы, стоящие на симметричных местах. Такие
элементы соответствуют парам перестановочных
преобразовании данной группы.
Задача 64. Укалигте все пары коммутирующих
(псрсстаковочных) преобразований в группах симметрии правильного треугольника
и квадрата.
Читатели, не решившие задачу 63, могут вернуться
к задаче 64 после того, как таблицы умножения для групп
будут рассмотрены ниже.
85

Коммутативность циклической груи-
Порождающне пы Сп можно объяснить и но-друго-
эпементы му. Обозначим R поворот на угол
ЗбО°/л. Тогда остальные движения
этой группы можно представить как степени R, т. е.
Я ° Я = Я2, Я с Я ° Я = Я3,..., Я" = id. Но очевидно, что
любые степени одного и того же элемента
перестановочны: Я* о & =•/?* о /?ft = RW.
Преобразование f, степенями которого являются все
преобразования группы G, называется порождающим или
образующим элементом группы G. Говорят также, что
преобразование f порождает группу G. Для лучшего
понимания смысла введенного термина представим, что
никакой группы пока нет, а есть одно преобразование f
некоторого множества М. Спрашивается, существует ли
группа преобразований множества М, содержащая
данное преобразование f? Ответ на этот вопрос положителен
всегда. Наименьшую группу преобразований,
содержащую /, можно построить следующим образом.
Если некоторая группа содержит преобразование f,
то, согласно своему первому свойству (замкнутость
относительно композиции), она должна содержать все
положительные степени р, /Зт ... этого преобразования. По
второму свойству 2 (замкнутость относительно перехода
к обратному), эта группа должна содержать также
обратное преобразование f-1 и, следовательно, его
степени (М)2, (Нз,...
Задача 65. Докажите, что (ffc)-1 = {f""*)*.
Преобразование (f-1)'', где к — натуральное число,
обозначают также f~h и называют отрицательной
степенью преобразования f. Нулевой степенью любого
преобразования считается тождественное преобразование.
Заметим, что множество всех целых степеней..., f~2, /-1,
86.

f°, fl, P,... данного преобразования / уже образует
группу. Это следует из равенств fkc fl = fk+l и (ffc)_1 = f~h,
которые справедливы не только для натуральных, но и
для всех целых значений к и L Это и есть группа, порож-
! денная преобразованием f.
Среди степенен /* могут оказаться равные. Так,
например, если преобразование/ инволютивное, то /*
совпадает с / при нечетных к и представляет собой тождест-
, венное преобразование при четных к. Следовательно,
! группа, порожденная /, состоит всего из двух элементов.
В общем случае есть две возможности.
1. Степени fh все различны. Тогда группа,
порожденная /, бесконечна и называется бесконечной циклической
группой.
2. Среди степеней преобразования f есть
совпадающие, скажем, /* = fl, где k>l. Тогда найдется степень f,
| совпадающая с тождественным преобразованием
(например, fh~l = id). Обозначим л наименьший положительный
показатель, такой, что fn = id. Число п называется
порядком преобразования f. В этом случае группа,
порожденная Д состоит из я различных преобразований f,
Р,...,р. (Эти преобразования действительно различны,
так как если бы оказалось, что /* = fLt где О <С I <. к^ я,
то мы имели бы fh~l — id вопреки выбору я.) Последова-
1 тельность степеней fk> где к изменяется от — оо до + со,
i содержит только эти л элементов, которые циклически
повторяются: р- совпадает с f\ где k — остаток от
деления / на я. По этой причине данная группа называется
I Циклической группой порядка я,
В случае, когда все степени данного преобразования f
различны, говорят, что его порядок бесконечен. Порядок
тождественного преобразования, но определению,
равен \г а группа, им порожденная, состоит из одного
преобразования и называется единичной или тривиальной
''Руппон.
87

Пример 31. Какие элементы группы С& порождают
эту группу? Какие подгруппы порождаются другими
элементами?
Группа Сп состоит из 12 поворотов на углы,
кратные 30°. Все эти повороты — степени поворота на 30°,
который является порождающим элементом группы Ск.
Легко понять, что поворот на
—30° также является
порождающим. Чтобы разобраться
с остальными элементами
группы, воспользуемся рис. 45, на
котором каждое движение
изображается вершиной
правильного 12-уголышка, причем
точка Ао соответствует
тождественному преобразованию,
вершина Ai—повороту на 30°
и т. д. Рассмотрим поочередно
все движения данной группы и
для каждого из них отметим на
рисунке вершины
12-уголышка, соответствующие всем его степеням. При этом
обнаружится, что еще два поворота — на углы 150° и 210° —
являются образующими элементами группы С&.
Повороты на 60° и 300° порождают группу Се, причем
вершины Л о, А% Ли, Л в, Л в, Л ю, соответствующие элементам этой
группы, на рис. 45 образуют шестиугольник, повороты
на 90° и 270° —группу С4 (квадрат ЛоЛзЛИэ),
повороты на 120° и 240° — группу С3 (треугольник АоАьАв),
наконец поворот на 180°, будучи инволюцией, порождает
группу Счу соответствующую отрезку ЛоЛв*
Полученные результаты исследования можно
оформить в виде таблицы, в которой под каждым числом k
(номер вершины 12-угольннка) указан порядок
элемента R\ где R — поворот на 30°:
Рис. 45
88

0
I
I
12
2
6
3
4
4
3
5
12
6
2
7
12
8
3
9
4
10
6
11
12
Задача 66. Используя понятие наибольшего общего делителя
(ИОД) двух чисел, выведите общую формулу для порядка
элемента fh в циклической группе СП) порожденной элемиггом /.
6 6 6 6
6
6 6 6
9 9 9
Рис. 46
Преобразование, принадлежащее конечной группе,
является порождающим для этой группы тогда и только
тогда, когда его порядок совпадает с порядком группы.
Количество порождающих элементов циклической
группы Сп обозначают ф(л), а фушщию ф называют функцией
Эйлера.
Задача 67. Отыскав значения функции ЭЛлера для чисел от 1
ДО 20, попытайтесь вывести какую-либо общую формулу для
функции ЭЛлера.
Посмотрим теперь, каковы порядки различных
движений плоскости. Ясно, что любой перенос и любое
89
6
9

скользящее отражение имеют бесконечный порядок: при
повторении этих движений всякая точка будет занимать
все новые положения (рис. 46, а, б).
Задача 68. Верно ли, что и любая фигура будет занимать при
этом осе новые и новые положения?
Всякое отражение имеет порядок 2 (рис. 46, в).
Повороты могут быть различных порядков. Если угол
поворота выражается рациональным числом градусов
360° m/я, где tnfn — несократимая дробь, то этот поворот
имеет порядок я; в противном случае порядок поворота
будет бесконечным.
Задача 69. Проверьте предыдущее утверждение для поворотов,
рассмотренных в примере 31. Докажите это утверждение в общем
случае.
Мы назвали циклической всякую
образующие и группу, порожденную одним преоб-
соотношення разованнем. С точки зрения этого
общего определения циклическими
являются не только группы вращений Сп, но и группа
переносов на векторы, кратные данному. Циклической же
будет и группа, порожденная одним отражением. Она
состоит из двух элементов и обозначается Dt. Заметим
(подробнее об этом будем говорить позже), что
внутреннее устройство групп Сг и Di одинаково: каждая из них
состоит из двух элементов, причем квадрат
нетождественного преобразования равен тождественному.
Докажем, что группы Dn при п ^ 2 не являются
циклическими. При п ^ 3 это очевидно, ибо тогда группа Dn
некоммутативна, а все циклические группы
коммутативны. Что же касается группы Dz, то каждый ее
нетождественный элемент имеет порядок 2 и, значит, ни одни
элемент не порождает всей группы.
80

В связи с этим возникает естественный вопрос: каким
наименьшим числом элементов порождается группа £>«?
Другими словами, через какое наименьшее число
элементов группы Dn с помощью двух действий — композиции
и перехода к обратному,— которые разрешается
выполнять неограниченное число раз, выражаются все
остальные элементы? Оказывается, для
этого достаточно двух элементов,
например поворота R на угол
360 °/л и некоторого отражения
S. В самом деле, всякий поворот
из группы Dn можно записать ,
в виде Rh, где O^.k^.n—1, а
произвольное отражение — в виде
ф о S.
Первое из этих утверждений
очевидно. Докажем второе. Для ""''
этого обозначим вершины пра- Рис 47
внльного многоугольника буквами
Ло, Ai,...., Лп-1, предполагая, что
ось отражения 5 проходит через вершину Л0 (рис. 47).
Тогда (flfteS) (Ло)— Rh(AQ)^= Ah- Кроме того, движение
Rh о S меняет ориентацию; следовательно, оно
представляет собой отражение, меняющее местами вершины Ао и
Ah. Его ось образует угол 180°/л с осью отражения S\
следовательно, при А—0, 1, ..,, п— 1 получим все
отражения из группы Dn.
Утверждение о том, что любое отражение из
группы Dn можно представить в виде Rh о S, можно доказать
следующим образом. Заметим, что все такие движения
при /е — 0, I, .♦.., ft — I различны. Действительно, если
бы имело место равенство Rh ° S — Rl<>S, то, домножая
его справа на S, мы получили бы, что Rh = RK Далее,
все эти движения несобственные (как композиции
собственного и несобственного движения), а так как в груп-
91

ne Dn всего п несобственных движений (отражений), то,
значит, все они попадают в список $, R « St..., Rnmi о S *.
Рекомендуем читателю сопровождать все
рассуждения, связанные с группой £)•„, действиями с описанным
ранее картонным «прибором». |
Итак, группа Dn состоит из 2п элементов вида Rh и .
Rh о S, где к принимает значения от 0 до п — 1:
Dn -{id, Я, Я2,..., Я"-*, S,RoS,&aS,..., /?«-* о 5}.
Постараемся найти все попарные композиции движений
из этого списка.
Композиция поворотов Rh и R1 есть 7?Л+г, причем если
k -J- I 5* л, то этот поворот совпадает с Яй+*-" и, таким
образом, является элементом нашего списка. Точно так
же имеем Rh° {Rl»5)= Rh+i« S, а если k + Iz&n, то
#ft с (/?' о S) = Rh-H-n о 5. Найдем теперь, какому элементу
из приведенного списка соответствует композиция
(Rk о 5) о /?'. Вспомним, что SoR* S = R-*. Возведем
обе части этого равенства в степень /:
(SoRoS)o(SoRoS)o... o(SoRvS)^R-1.
Учитывая ассоциативность композиции и равенство
S2 = id, приводим левую часть к виду S о R1 о S. Значит,
S ° Rlo $ =; /Н и, домножая обе части равенства на S,
получаем S *Rl « R-*o S. Следовательно,
{Rko$)oRl^Rko(SoRi) = RK(R-ioS)^Rli-*oS.
Если k ^ /, то элемент Rh~l ° S содержится в нашем
списке. Если же к < /, то Rh~l — ;?*-'+", а элемент /?'*-^+rt
таюке входит в наш список. Подобным образом можно
найти, что композиция (Rh° S) о (Ri о S) совпадает с
преобразованием R11-1.
* По поводу этого рассуждеггая уместно привести такую цитату:
«.И теперь мы можем решить задачу вообще без всякой
математики— с помощью одной лишь теории групп». (Ян Стюарт.
Концепции современной математики, гл. 7).
92

Итак, таблица умножения элементов группы
диэдра D7l1 выраженных через образующие R и S7 имеет вид
i?ft
Rk*S
Rl
Лл+/
Я*-'о 5
RloS
Rk+lcS
tf*~'
(При необходимости показатель степени /? можно
увеличивать или уменьшать на п, пользуясь тем, что Rn = id.)
Из этой краткой таблицы умножения можно получить
полную, выписывая все элементы группы в явном виде.
Например, для группы D& имеем
id
п120°
1ю
^240°
Sa
S&
Sc
id
id
nl20*
j?S40°
Sa
Sb
Sc
Rb20°
Rh20°
n24Q°
R0
id
Sc
Sa
■ sb
r,240°
*<0
p240°
id
Rh20°
St
Sc
Sa
Sa
Sa
St
Sc
id
R}?0°
R™°
Sb
Sd
Sc
Sa
#240°
id
K0
Sc
Sc
Sa
sb
'*!>**
#240°
id
93

•Обратим внимание читателя на тот факт, что при
выводе таблицы умножения для группы Dn мы опирались
только на следующие три соотношения между
образующими элементами R и S:
S2= id; (Sptf)2=id;/?» = i(L (19) |
(Второе соотношение, очевидно, равносильно
соотношению So R°S — R-*.) Элементы R и S связаны и другими,
соотношениями, например:
j
Оказывается, что любое такое соотношение между R и Si
является следствием формул (19). Для соотношения
54 = Id это очевидно: оно получается из равенства!
S2 = id возведением его в квадрат. Вывод второго соот-|
ношения несколько сложнее: id = 5 о R о S * R — S ° R.
oSol6oR=SoRoSo[(SoRoSoR)oR=SoRzoSoR^3jXecu>
мы также воспользовались соотношением S2 =* id. '
Соотношения (19) обладают замечательным свойсг-j
вом: исходя только из них можно доказать, что числа
элементов группы, порожденной преобразованиями R, S,
равно 2/1, и составить полную таблицу умножения для
этой группы. Построение такой таблицы и было
проделано выше. Заметим лишь, что число элементов группы
и закон их композиции нам были известны заранее,
поэтому в данном случае указанное свойство особого интс-:
реса не представляет. Приведем пример, в котором роль
образующих и соотношений (19) видна яснее.
Пример 32. Пусть А и В — некоторые
преобразования, удовлетворяющие соотношениям:
Л3 = id; В5 =* id, AB = В*А. (20)
Доказать, что группа, порожденная преобразованиями А
и В,— циклическая порядка 3. '
94

В условии (20) данного примера, а также в
последующих рассуждениях мы опускаем знак композиции
(кружок) и называем композицию произведением.
Любой элемент группы (?, порожденной
преобразованиями А и Ву можно записать в виде BklAuJ^ *Ah ■.. fl *М/д,
причем в сапу соотношений (20) можно считать, что
0 ^ hi =С 4, 0 ^ к ^ 2. Далее всякий раз, когда В
встречается рядом с А и справа от него, заменять
произведение АВ на SM. Рано или поздно мы сможем «перегнать»
все буквы В «сквозь» буквы А налево и, таким образом,
переписать данный элемент группы G как ВкА*. Здесь
опять-таки можно считать, что 0 ^ k ^ 4, 0 ^ I ^ 2,
Поскольку индекс k принимает пять значений, а
индекс / — три, не зависящих от к значения, то может
показаться, что группа G содержит 15 различных
элементов вида BhAl. Однако это не так, в чем легко
убедиться, получив некоторые следствия из
соотношений (20).
Б самом деле, из этих соотношений вытекает такая
цепочка равенств: В - А*В = А*В*А « АВ«А* = В™А* «■
— ВК Следовательно, В3 = id, откуда, используя
соотношение В" — id, заключаем, что В2 = id ий* id» Значит,
группа (?, порожденная преобразованиями А и В, имеет
одну образующую А, для которой А& — id, и представляет
собой циклическую группу порядка 3. Заметим, что
равенство А = id нельзя вывести из соотношений (20), так
как все они выполняются для А *= R(?°°, В — Id, а в
данном случае А ф id.
Соображения, подобные использованным в этом
примере, можно применить при решении следующей задачи,
и которой речь идет о предметах, на первый взгляд
весьма отдаленных от групп преобразований.
Задача 70. Пусть в одном из языков имеется четыре звука:
А, У, Ы и Е. Звук Е — особый. Употребленный сам по себе, он озиа-
95

чает некоторое слово, но если этот звук присоединить к любому
слову (в начале, середине или в конце), то значение этого слова не
изменится. Кроме того, если произнести cer.Sb раз подряд звуки А, У
или Ы, то получим синоним слова Е. Синонимами (словами
тождественными или близкими по смыслу) являются и пары: УУУЫ — Ь1У,
ААЫ--ЫА, УУУУА — АУ. В племени 400 туземцев. Могут лн у j
всех них быть разике имена? I
Задача 71. Найдите всевозможные пары образующих элементов .
в группе £>«. Для каждой из них nocrapaihrecb указать определяю- '
щне'соотношения.
Понятие определяющих соотношений относится,
конечно, не только к группам с двумя образующими.
Циклическая группа порядка п имеет один образующий
элемент и одно определяющее соотношение Rn — id.
Бесконечная циклическая группа имеет один образующий
элемент Т, который не связан никакими соотношениями.
Поясним смысл последней фразы. Здесь имеется в
виду, что образующий элемент циклической группы не
связан никаким нетривиальным соотношением, т. е.
соотношением, содержащим Т и id и не являющимся следствием
общих свойств групп преобразований. Приведем пример !
тривиального соотношения: Т~{Т^Т~& = id. I
Рассмотрим группу движений плоскости, которая в
примере 27 была обозначена G и которую сейчас мы
обозначим более сложным символом рЗш\, принятым в
кристаллографии (кристаллографические группы будут рас- |
смотрены ниже). Группа p3ml, no определению,
порождена бесконечным множеством отражений относительно
прямых, проведенных на рис. 40, а.
Оказывается, что наименьшее число образующих
группы рЪт\ равно трем: в качестве образующих можно
взять отражения Sfl, S<> и Sc относительно трех сторон
исходного равностороннего треугольника. Для того чтобы
это доказать, достаточно проверить, что через SQ> So, Sc.
можно выразить отражение относительно любой прямой,
изображенной на рис. 40, а. Действительно, в этом слу-
96

чае и произвольное движение группы рЪт\, если его
представить в виде композиции отражений относительно
этих прямых, можно будет выразить через Sa, 5ь, Sc,
Рассмотрим, например, отражение Si. Поскольку
прямая / симметрична а относительно с, то Si получается
из Sa сопряжением посредством 5С, т. е. Si ■— Sc ° Sa <* Sc
(напомним, что S71 — Sc). А это как раз то, что нужно.
Заметив, далее, что St(b) = т, представим Sm как
композицию Si о Si о Si, которая есть не что иное, как Sc о Sa °
о Sc ° Sb ° «Ьс ° «Ьа ° "с-
С помощью подобных рассуждений можно выразить
через Sa, Si, Sc отражения относительно всех прямых,
параллельных Ь, а также, разумеется, и относительно
всех остальных прямых.
Заметим теперь, что образующие S«, S*,, Sc подчинены
соотношениям
(Sa)Z = (Sb)Z = (5С)2 = (Sa с $Ь)3 =
= {Sa о Scy - ($ь о 5с)з = id. ;(21)
Задача 72. Пусть Fi, Fs, Fs— три движения плоскости, которые
порождают некоторую бесконечную группу, н справедливы
соотношения:
F\= Ff- F\= {Fi»Fty = (F,ef3)3 = (F2 o^= = id.
Покажите, что Fi, Fa. F3 — отражения от сторон правильного
треугольника.
Решив эту задачу, видим, что соотношения (21) с
некоторым небольшим уточнением полностью определяют
группу рЗт\ и в этом смысле могут быть названы ее
определяющими соотношениями. Последнему
высказыванию мы пока не придаем строгого математического
смысла: точное описание определяющих соотношений требует
знакомства с понятиями абстрактной группы, группы
слов и фактор-группы.
4 Зак. 541 97

Во многих приведенных выше рас-
общее понятие суждениях и вычислениях для нас
группы было совершенно не важно, что мы
имеем дело именно с движениями.
Существенными являлись лишь следующие свойства
группы движений:
1) композиция двух движений из данной группы есть
движение из этой же группы;
2) композиция движений обладает свойством
ассоциативности;
3) группа содержит тождественное преобразование,
характеризующееся тем, что его композиция с любым ;
другим преобразованием / дает снова f;
4) вместе с каждым движением группа содержит и
обратное ему движение.
Подобными свойствами обладают не только группы ;
движений (или других преобразований). Если вместо '
движений взять действительные числа, а вместо компо-
зиции движений — сложение чисел, то все эти свойства
также выполняются. Обращаем внимание читателя на i
то, что уже в главе «Плоскость» (примеры 1Т 7 и др.) мы
неоднократно использовали эти свойства для элементов i
различной природы (чисел, точек, векторов) и различных '
операций над ними (сложения, умножения).
Характерной в этом отношении является аналогия между
примером 32 и задачей 70. Все это говорит о целесообразности
формулирования общего понятия группы.
Группой называется множество G элементов
произвольной природы, в котором:
1) задано правило (групповая операция), согласно
которому любой паре (а, Ь) элементов G сопоставляется
некоторый элемент а * Ь того же множества;
2) групповая операция ассоциативна, т. е. для любых
элементов a, b и с из G {а * Ь} *с = а * (Ь * с);
98

3) в G имеется нейтральный элемент, т. е. такой
элемент е, что для любого a^G а*е = е*а = а;
4) у каждого элемента ав G есть симметричный, т. е.
такой элемент а\ что д * а' = о! * а = е.
Свойства 1—4 называют также аксиомами группы.
Полезно подумать, почему же всякая группа
преобразований является группой в смысле данного определения:
ведь понятие группы преобразований включает только
два свойства, являющихся аналогами аксиом 1 и 4. Дело
в том, что аксиома 2 для композиции преобразований
выполняется автоматически, а аксиома 3 следует в этом
случае из аксиом 1 и 4 (нейтральный элемент для ком-
; позиции — тождественное преобразование — существует
всегда, вопрос лишь в том, принадлежит ли он группе).
Вместо знаков * (звездочка) и ' (штрих), а также
терминов «нейтральный» и «симметричный», смысл
которых раскрыт в определении группы, в разных конкретных
ситуациях могут употребляться другие знаки и слова.
Так, в случае группы преобразований групповая
операция (композиция) обозначается кружком (°),
нейтральным элементом является тождественное
преобразование id, а элемент, симметричный данному
преобразованию /, называется обратным преобразованием и
обозначается f-1. Если рассматривать группу чисел
(целых, действительных или комплексных, т. е. точек
плоскости) с операцией сложения, то нейтральным элементом
I будет нуль (в случае точек плоскости — полюс Р), а
выражение «симметричный элемент» заменяется
словосочетанием «противоположное число». Для группы чисел
с операцией умножения знак операции не пишут,
нейтральным элементом служит единица, а симметричными
являются взаимно обратные числа а и 1/с = а~К
Система обозначений, применяемая в случае опера-
| Нин умножения, наиболее удобна, поэтому ее часто
используют н для произвольных групповых операций.
4* 99
I

В дальнейшем будем писать ab вместо а * Ь, называть
этот элемент произведением а и Ь, нейтральный элемент
называть единичным, а симметричный — обратным н
обозначать сгК Пользуясь этой системой обозначений,
необходимо помнить, что групповая операция в отличие
от обычного умножения не всегда коммутативна.
Пример 33. Являются ли следующие множества с
операциями группами:
1) все четные числа с операцией сложения?
2) все нечетные числа с операцией сложения?
3) все действительные числа с операцией вычитания?
4) все натуральные числа с операцией сложения?
5) все неотрицательные целые числа с операцией
сложения?
6) все действительные числа с операцией х*у^=
= х + у-1?
Первые пять случаев рассматриваются с помощью
простой проверю! выполнения групповых аксиом. Ясно,
что в первом случае все свойства групповой операции
выполняются. Во втором примере нарушается уже
первое свойство: сумма двух нечетных чисел есть четное
число. В третьем случае первое свойство выполнено, но
операция неассоциативна: 6 — (5 — 3) ф (6 — 5) — 3.
В четвертом примере имеем ассоциативную операцию,
которая, однако, не обладает нейтральным элементом:
единственное число, которое может служить
нейтральным элементом относительно сложения, есть, очевидно,
нуль, а он не входит в данное множество. Пятый случай
отличается от четвертого лишь тем, что к
рассматриваемому множеству добавлен нуль, поэтому операция
обладает нейтральным элементом. Однако ии для одного
числа, кроме нуля, противоположное ему число не
содержится в данном множестве, следовательно, свойство 4 не
выполнено.
Большего внимания требует последний пример, в ко-
100

тором предлагается рассмотреть необычную операцию
над числами. Ясно, что применив эту операцию к паре
действительных чисел (х, у), мы получим снова
действительное число х -+- у — 1, значит, первое свойство
выполнено. Для проверки ассоциативности достаточно
вычислить, согласно определению операции *, выражения
(х * у) *z\\ х * (у * z). Имеем:
(л- * у) * z « (л- -f У — 1) * z = х -f у — 1 + z — 1;
* * (У * z) = х * (у + z — I) = х -|- # -f £ — 1 — 1.
Далее, нейтральный элемент е должен удовлетворять
тождеству х-\-е — 1 = х при любом *♦ Отсюда в — 1.
Поскольку данная операция коммутативна, для
нахождения элемента, симметричного х, "мы имеем лишь одно
равенство вместо двух: х * х* — \, т. е. я -f- х' — 1 •— 1,
откуда х* = 2 — дг. Итак, операция обладает всеми
четырьмя свойствами групповой операции, и множество
действительных чисел с такой операцией образует
группу.
Задача 73. Проверьте, образуют ли группы следующие
множества с указанными операциями. Если ответ отрицателен, назовите то
из четырех свойств группы, которое в данном случае нарушается:
1) множество всех иррациональных чисел с операцией сложения;
2) множество всех действительных чисел из промежутка
] 1, + оо [ с операцией ху = ху — х — у + 2;
3) множество всех двоично-рациональных чисел (т. е. дробей,
зпаменатель которых — степень двойки, а числитель — любое целое
число) с операцией сложения;
4) множество непулевых двоично-ргциональпых чисел с
операцией умножения;
5) какое множество действительных чисел является группой
относительно операции л-*у = {х-\- г/)/(1 — ху)?
Приведем некоторые простые следствия четырех
групповых аксиом.
1. Нейтральный элемент в группе единствен, т. е. в
группе не может быть двух различных элементов, каж-
101

дый из которых обладает характеристическим свойством
нейтрального элемента (аксиома 3). Действительно,
пусть ех и ег — такие элементы, что для любого а g G
aeL = eia = ае% = е?а = о.
Полагая в этом равенстве сначала а = £i„ а затем а = е^
получаем е\ = е&ь = <?2, что и требовалось доказать.
2. В группе всегда однозначно разрешимо всякое
уравнение вида ах = Ь, т. е. для любых а, Ъ ^ G
существует единственный элемент х е G, такой, что ах = Ь.
Действительно, домножим слева данное уравнение на
элемент crL: а~1(ах) = a~lbt откуда, по аксиоме
ассоциативности и по определению обратного элемента, получим
х = arlb.
Задача 74. Докажите, что в группе всегда однозиачно разрешимо
ураппепке вида ха = Ь. Найдите его решение.
Из доказанных следствии и утверждения задачи 74
можно сделать два полезных вывода. Во-первых,
обратный элемент, определенный аксиомой 4, для каждого
о €= G единствен. Во-вторых, если рассматриваемая
группа конечна и мы составим ее таблицу умножения,
расположив первый сомножитель в левом столбце, а второй - -
в верхней строке, то в каждой строке таблицы должны
встретиться по одному разу все элементы группы. Это
следует из однозначной разрешимости уравнений вида
ах = Ь. А из однозначной разрешимости уравнения вида
ха = Ь следует, что и каждый столбец таблицы
умножения содержит по одному разу все элементы группы.
3. Из аксиом группы следует, что элемент (а-1)'1
является обратным ап. Поэтому, как и для
преобразований, можно ввести понятие любой целой степени данного
элемента группы, полагая а0 — е, ст™ — (й~!)п при п >■ 0.
Тогда для любых целых k и / будет выполнено соотно-
102

Из соотношения (22) видно, что множество всех целых
степеней данного элемента а образует группу. Элемент а
называется образующим элементом этой группы, а сама
группа — циклической. Определим порядок элемента а
как наименьшее натуральное число п, для которого
ап = е (если а = е7 то порядок, по определению, считают
равным единице; если ап при любом п отлично от е, то
говорят, что а — элемент бесконечного порядка).
Заметим, что порядок (т. е. число элементов) циклической
Рис 48
группы, порожденной элементом а, равен порядку этого
элемента.
До сих пор мы рассматривали группы, элементы
которых были или числами, или преобразованиями. Группы
преобразований и числовые группы играют важную роль
в математике. Приведем еще несколько примеров групп,
элементы которых имеют совсем другую природу.
Пример 34. Назовем переключателем электрическую
схему, имеющую три входа и три выхода, соединенные
между собой попарно в некотором порядке. Таких
переключателей всего шесть, они изображены на рис. 48.
Требуется определить на множестве переключателей
некоторую операцию, превращающую это множество в группу.
Естественная операция, которую можно производить
с переключателями—соединение. Например, при
соединении переключателей П2 и ГЦ * вход 1 будет соедн-
* Рассмотрение начинаем с ГЬ.
103

пяться с выходом 3, вход 2— с выходом 2, а вход 3—
с выходом /. Точно такое же соответствие между
входами и выходами осуществляет переключатель ГЬ.
Поэтому можно записать ГШй = Пе. Заметим при этом, что
результат соединения переключателей зависит от их
порядка: так, ГШг — Пе.
Убедитесь, что все соединения переключателей
представлены в таблице
Пх
П2
пэ
П4
По
пв
пх
П!
п2
п3
п4
п5
п0
п,
п3
Ц,
П!
Па
Па
ns
п3
п3
п,
п2
п5
Пе
Па
1\
Па
п5
п.
п,
п2
п3
пБ
п5
п0
п<
Пз
Пх
п*
пв
пв
П4
п,
п2
Ц,
ni
Оказывается, что множество из шести
переключателей с операцией соединения образует группу. Но как это
проверить? Если убеждаться в выполнении групповых
свойств непосредственно, то для доказательства
ассоциативности нашей операции потребуется проверить
справедливость 6s = 216 равенств вида Пг(ГГ?П/4) = (ШТ^Пл,
где /, /, k — номера от 1 до 6. К счастью, эту проверку
делать вовсе пе обязательно. Заметим, что если в данной
Ю4

таблице заменить Ui, П2, ГЪ, Пс, Па, Пе на id, /?o20*>
Rv°°> S«t 5б, $с соответственно, то она преобразуется
в таблицу умножения группы Da (см, с.93). Это означает,
что операции соединения переключателей и композиции
преобразований из группы Ds устанавливают одинаковые
связи между соответствующими элементами этих
множеств. Например, при соединении переключателей Пг
и ГЦ получается переключатель Пз, а при композиции
120°
соответствующих движении — поворота Яо и
отражения Sa — отражение S&, которое соответствует
переключателю Пц. Поэтому операция соединения ообладает
всеми свойствами, присущими операции композиции в
группе D3, а именно: она подчиняется ассоциативному закону,
переключатель П|, как и тождественное преобразование,
является нейтральным элементом, и для каждого
переключателя можно указать такой переключатель, что
после их соединения получается переключатель ГЪ. А это
и означает, что множество переключателей — группа.
Математическое содержание рассмотренного примера
заключается в описании всевозможных взаимно
однозначных соответствий на себя множества из трех
элементов, которые можно (как и входы и выходы
переключателей) занумеровать числами 1,2, 3.
Взаимно однозначное отображение множества чисел 1,
2, ... , п на себя называется в математике подстановкой
из п элементов. Подстановка, переводящая 1 в ilt 2 — в
/1 2 ... п \
h* --. , п — в/„, обозначается I . . . I. Подстановки
Vi W ■ - ■ in /
из п элементов образуют группу порядгса п! Композиция
подстановок — это композиция преобразований. Так,
например,
/1 2 3\ /1 2 3\ /I 2 3\
[\ 3 2J*U 2 1/~Ч2 3 l)'
105

Точно так же множество всех преобразований
(взаимно однозначных соответствий между элементами)
множества М относительно композиции преобразовании
образует группу, которую обозначают Тг(М).
Отметим важное следствие аксиомы ассоциативности:
произведение не только трех, но и любого числа
элементов группы не зависит от порядка, в котором пронзво-
дятся действия, т. е. от способа расстановки скобок в
выражении didf-an. Например, ((aia2)03)a& = (^1^2)X
X(4sa«)~ ^(^2(0^4))- ^ общем случае это утверждение
легко доказать индукцией по л. Из него следует, что
произведение нескольких элементов группы можно
записывать без скобок. Это соображение наряду с
рассуждениями, приведенными в примере 8, полезно иметь в виду
при решении следующей задачи.
Задача 75. На школьной доске нарисовано несколько
окружностей, квадратов и треугольников. Разрешается стереть любые две
фигуры, нарисован вместо них третью по такому правилу: вместо
пары окружностей — одну окружность, вместо пары квадратов —
треугольник, вместо пары треугольников — квадрат, вместо
окружности и квадрата — квадрат, вместо окружности и треугольника —
треугольник, вместо квадрата и треугольника — окружность.
Доказать, что форма фигуры, которая остаиется последней, не зависит от
того, в каком порядке стирают фигуры.
100

Задача 76. Рассмотрим множество всех рашюналытых алгебраи*
ческнх выражеикй с действительными коэффициентами, содержащих
одну букву х (эти выражения имеют вид отношения двух
многочленов от л-). Ьслн А п В — два таких выражения, то можно
образовать повое выражение А * В, подставив в А всюду вместо х
выражение В. Докажите, что совокупность всех выражений, которые
можно получить с помощью подстановок из двух выражений Ai «=. I — х
и Аз = \/х, образует группу, найдите ее порядок, составьте список
всех ее элементов и таблицу умножения для них.
Задача 77. Попытайтесь пайтн рациональное выражение В,
такое, что В*At = В*Аг = В, где Ai и А% определены в задаче 76.
При разборе примера 8 мы вывели
Изоморфизм все необходимые свойства операции
соединения переключателей из
аналогичных свойств композиции преобразовании, так как
обе операции в известном смысле устроены одинаково.
В математике существует точное понятие для того,'чтобы
характеризовать подобные ситуации.
Группы G и Я называются изоморфными, если между
их элементами можно установить такое взаимно
однозначное соответствие, что всякий раз, когда элементы g\
и hi, а также g2 и Лг соответствуют друг другу, элементы
gigz и /ii/te также будут соответствовать друг другу.
Говорят, что это соответствие не нарушается групповыми
операциями. Более точно это определение можно
сформулировать так: группы G и Я изоморфны, если существует
взаимно однозначное отображение ф: G-^Н, такое, что
ф(М*) = ф(в1)ф(#) (23)
для любых двух элементов gt и g2 из G. В этом случае
говорят, что ф есть изоморфизм группы G на группу Я.
На первый взгляд кажется, что второй вариант
определения отличается от первою несимметричным
подходом к группам G и Я. На самом деле это не так, ибо
если ф—изоморфизм G на Я, то обратное отображение
цг1 будет изоморфизмом Я на G. Действительно, обозна-
107

чая /ii=<p(g'*), Ы = ф(й'г) и применяя отображение tjr1
к обеим частям равенства (23), получим ф-^ОФ-1^) —
= <Г*(Л1Л2). *
Для конечных групп самым непосредственным
способом установления изоморфизма служит явное
перечисление пар соответствующих друг другу элементов и
проверка того свойства, что при замене в таблице умножения
одной группы каждого элемента на его «пару» из другой
группы получается таблица умножения другой группы.
Именно так мы поступили в примере 34 (когда не знали
даже, что переключатели образуют группу).
Задача 78. Проверьте, является лн изоморфизмом следующее
соответствие между элементами группы симметрии щ.аинльнсго
треугольника и группой переключателей: lu*+Tllt /?q20"<«-> llv>, Kq40' +*
4->Пя, Srt*+na, Sf,<-*n5, Sc*+nB.
Решим эту задачу, можно сделать два поучительных
вывода. Во-первых, при замене движений треугольника
на элементы группы переключателей, соответствующие
им по схеме, приведенной в условии задачи, из таблицы
умножения группы Ds получается следующая таблица:
п3
и.
пЕ
пя
Пл
п3
п2
nD
п4
П!
п2
п2
п,
Hi
п3
па
Ц,
пБ
п3
пв
п4
п2
пг
пэ
п<
Пь
п.
п.
108

Она не совпадает с таблицей, приведенной в примере 34,
но эквивалентна ей, так как отличается только
перестановкой строк и столбцов (проверьте это!). Во-вторых,
оказывается, что если группы изоморфны, то может
существовать несколько различных изоморфизмов первой
группы на вторую. В частности, могут существовать
изоморфизмы группы на себя, отличные от тождественного
отображения. К этому понятию мы еще вернемся, но уже
сейчас читатель может «поломать голову» над
следующей задачей.
Задача 79. Перечислите все изоморфизмы группы Дч на себя.
Понятие изоморфизма раскрывает смысл некоторых
аналогий, на которые вдумчивый читатель мог обратить
внимание при чтении предыдущих глав. Теперь можно
сформулировать соответствующие утверждения в виде
четких задач.
Задача 80. Докажите, что множество точек плоскости с
операцией сложения над некоторым полюсом (см. главу «Плоскость»)
образуют группу, изоморфную группе всех векторов плоскости.
Докажите также, что сопоставление каждой точке (или вектору) ее
координат в некотором базисе осуществляет изоморфизм каждой нз этих
групп с rpynnofi пар действительных чисел, в которой сложение
определено правилом
(Ли 6|)+(йа, Ь2) = (ei -f-«z, bt + Ьг).
Задача 81. Докажите, что множество вершин правильного шести-
угольника на комплексной ■ плоскости (сю таблица умножения
приведена в примере 7) образует труппу, изоморфную циклической
группе Сп, состоящей из поворотов с общим центром на углы,
кратные 60°,
Задача 82. Докажите, что множество, состоящее нз окружности,
треугольника и квадрата, с операцией, описанной в задаче 75,
образует группу, изоморфную циклической группе Сз. Сколькими
способами можно осуществить этот изоморфизм?
Задача 83. Докажите, что группа рациональных алгебраических
выражений с операцией подстановки, определенная в задаче 76,
изоморфна группе диэдра Х?з.
109

Результаты задач 81 и 82 можно обобщить. Заметим,
что в той и другой задаче речь идет об изоморфизме
между двумя циклическими группами одного порядка.
Любые такие группы изоморфны. В самом деле, пусть
g __ образующий элемент группы G7 a А— образующий
элемент второй группы Я. Зададим отображение <р:
G-кЯ формулой ф(£*) = А*. Тогда правило
перемножения степеней (22) справедливо в каждой из данных групп
и означает, что <р — изоморфизм:
vteW - ф (**+') = ьш = hm = ф(в*)ф(#).
С другой стороны, ясно, что две циклические группы
разных порядков неизоморфкы, так как между конечными
множествами, состоящими из разного числа элементов,
нельзя установить взаимно однозначного соответствия.
Ясно также, что если некоторая группа изоморфна
циклической, то и сама она циклическая: элемент,
порождающий одну группу, при изоморфизме переходит в
образующий элемент другой группы.
Предположим теперь, что даны две группы G и Я и
требуется определить, изоморфны они или нет. Найти
наугад или путем простого перебора взаимно
однозначное соответствие между элементами этих групп, которое
не нарушалось бы групповыми операциями, практически
невозможно (рассмотренные ранее примеры были,
конечно, специально подобраны так, чтобы это было легко
сделать). При исследовании этого вопроса полезно
учитывать следующее.
Доказать, что группы G и И изоморфны, как правило,
труднее, чем доказать их неизоморфность. Дело в том,
что в первом случае требуется обычно явно построить
изоморфизм между данными группами, тогда как во
втором достаточно указать некоторое свойство, которое
различает эти группы. Перечислим несколько свойств, совпа-
110

деиие которых является необходимым признаком
изоморфных групп.
1. Порядок. Конечные группы, имеющие разное число
элементов, не могут быть изоморфными.
Задача 84. Изоморфны ли группы всех целых чисел и четных
чисел (обе—с операцией сложения)?
2. Коммутативность. Коммутативная группа не может
быть изоморфна некоммутативной.
3. Цикличность. Циклическая группа не может быть
изоморфна нециклической.
Задача 85. Укажите все пары изоморфных между собой групп
среди конечных групп движений плоскости, т. е. среди групп из
следующего списка: Си Du Cz, Dzt Cj, Ds,...
4. Порядки элементов. Если в группе G имеется
несколько элементов порядка л, то в изоморфной ей
группе И должно быть столько же элементов порядка я, так
как соответствующие друг другу при изоморфизме
элементы двух групп имеют одинаковые порядки.
Докажем последнее утверждение, так как оно
несколько сложнее предыдущих. Заметим, во-первых, что
при изоморфизме единичные элементы групп
соответствуют друг другу. Действительно, если е — единичный
элемент группы G и <р: G-^H— изоморфизм, то из
равенства ее ~ е следует, что ф(е)<р(е) — ф(е). Домножая
обе части этого соотношения на элемент группы И,
обратный ф(е), получаем, что у(е) = е' — единичный
элемент группы //. Пусть теперь g — элемент группы G,
имеющий порядок п и Ф(#)=й. Тогда из равенства
ё11 — е следует, что /t" = е', т. е. порядок s элемента h
не превосходит я. Ест имеет место строгое неравенство
s <С я, то из равенства № = в' вытекает, что gs = е. А это
противоречит выбору п (порядок элемента — это наи-
П1

меньшая его степень, равная единичному элементу),
следовательно, S = TL
Например, в группе Da имеются один элемент
порядка / (тождественное преобразование), три элемента
порядка 2 (отражения) и два элемента порядка 3
(повороты). Б группе Се—один элемент порядка 1, один
элемент порядка 2 и по два элемента, имеющих порядки 3
и 6. Это лишний раз объясняет, почему эти группы неизо-
морфньт.
Список свойств, необходимых для изоморфизма двух
групп, можно продолжать неограниченно: и него входит
любое свойство группы, которое формулируется в
терминах групповой операции без обращения к конкретной
природе элементов группы. Мы, однако, перейдем к
обсуждению другой части вопроса об изоморфизме двух
групп. Предположим, что группы G и Н состоят из одного
и того же числа элементов, что они обе коммутативны
или некоммутативны, что входящие в них элементы
имеют одинаковые порядки и т. д. Тогда возникает
надежда, что данные группы могут оказаться
изоморфными. Но чтобы доказать, что они действительно изо- i
морфны, нужно построить изоморфизм. Дадим несколько ,
полезных советов, помогающих это сделать в простейших \
ситуациях. '
Начнем с того, что, как было доказано выше,
единичные элементы групп при изоморфизме соответствуют
друг другу, поэтому, если мы хотим построить
изоморфизм <р: б-*-#, следует положить <р(#)— е\ где е и е'—
единичные элементы в группах G и //. Далее, если
известен образ при отображении <р некоторого элемента g
из G, т. е. <р(£) = К то из соотношения (23)
последовательно ВЫВОДИТСЯ, ЧТО (p(g2) = Л2, ф(£3) = №, ... И ПО
индукции <p(£n) = hn при любом натура льном п.
Задача 86. Докажите, что равенство np(gn)=hn верно и для
отрицательных значений п.
112

Итак, если отображение <р определено на некотором
элементе g группы Gr то оно определено и на всей под-
группе, порожденной этим элементом. Подобным
образом, если известно, куда переводит <р несколько
элементов gu g?.,---, gh группы G, то можно однозначно указать
образы всех элементов, порожденных gi, g*, ..., gh (т. с.
имеющих вид g1} ■-- gfc). Если при этом элементы g±
#2» ♦ • -, gh являются образующими группы G, то
значения tp(gi) = hi, <p(ga) = Ла,..., ф(Ял) = Ла полностью
определяют отображение ср, В случае двух образующих
получаем формулу
Ф (rf£2 $Sli • • ■ £?*g*/) « Л.?1 /£hf h'i • • • /£/£. (24)
Итак, если группа G порождена двумя элементами gt
и #2, то для построения изоморфизма q>: G-^H
достаточно задать его значения на образующих: q>(gi)=ht,
Ф(£а)~ Ла, а затем, согласно формуле (24),
распространить отображение <р на все множество G. Как при этом
следует выбирать элементы hi и Лг? Ясно, что они
должны быть образующими группы Н, их порядки должны
совпадать с порядками элементов gi и gz соответственно
и что они должны удовлетворять любому соотношению,
которому удовлетворяют элементы gi и #2. Например,
если gf gl — е, то должно выполняться соотношение /i?fti =
^ е'. Заметим, что приведенные соображения позволяют
построить отображение (р, являющееся «кандидатом в
изоморфизмы». После того как отображение построено,
необходимо проверить, действительно ли оно
изоморфизм.
Пример 35. Пусть 1,ф 1 — комплексное число,
являющееся корнем третьей степени из единицы (£а = 1).
Рассмотрим две функции комплексной переменной: Fi(z) =
— t,zt Fz(z) = z. Доказать, что множество всех функций,
ИЗ

которые можно получить из Ft и F% с помощью операции
суперпозиции функций (образования сложной функции), |
является группой относительно этой операции, причем
эта группа изоморфна группе диэдра Ds.
Находим:
F3(z)^ Fl(F?.[z))= Ft{z) = t£;
Л И- F2(F2(z)) = Fz(z)^ z;
F*(z)= Л(/ч(2))~'• Ft(&)*"?{*)i
Рв M - ft (Pi (*)) « F, (fe) = £= £2J.
Все другие сложные функции совпадают с шестью, I
вычисленными выше. Таким образом, множество
функций Fu I = 1, ..., 6, замкнуто относительно
суперпозиции. Кроме того, для каждой из этих функций обратная
ей функция также принадлежит данному множеству.
Следовательно, мы получили группу. Роль нейтрального
элемента играет тождественная функция Fa, элементы
Fz, Fa, F0 имеют порядок 2, а элементы Fi и Fu —
порядок 3. Данная группа некоммутативна: например,
Fi{F2(z))= Fs[z), a F2(Fi(z))= F6(z). Все это наводит
на мысль, что рассматриваемая группа может быть
изоморфна группе Da- ,
Чтобы построить изоморфизм <р: G-+-Ds, заметим, что |
группа G, по определению, порождена двумя функциями '
Fi и F% порядки которых равны 3 и 2. В группе D3 также ,
есть система из двух образующих, имеющих те же
порядки: это некоторый поворот и некоторое отражение.
Положим, например, Fi <-+ RoZ0\ F21-> Sa. Тогда F9 <-> Sc,
Fu++id, FB<r+Ro4Q°, Fa^Sb. Заменяя каждый элемент
группы Da соответствующим ему элементом группы G, из
таблицы умножения для D3 (см. с. 76) получим таблицу,
которая представляет собой таблицу умножения для
группы G (проверьте это!).
114

Ft
Ft
Fb
F*
F„
Fa
F*
Fa
Fx
F5
Fz
F0
F*
Ft
Ft
F6
Л
F*
F*
F0
F*
F*
F<
Ft
F«
^
Fz
Fz
Fz
Fa
F3
F<
Ft
F*
Fa
Fa
F3
F*
F<
Ft
Fu
Fa
F*
Fa
Ft
F6
F,
Итак, изоморфизм найден. Оказывается, однако, что
его можно построить некоторым естественным способом,
не подбирая его значения на образующих.
Действительно, вспомним о том, что функции комплексной
переменной имеют простой геометрический смысл, т. е.
представляют собой аналитическую запись некоторых
преобразований плоскости (см. главу «Движения»), Рассмотрим на
комплексной плоскости треугольник с вершинами 1, £, £2,
где Е;— комплексное число, такое, что £3 = I. Тогда
функция T^z)» £2 соответствует повороту на 120° с центром
в нулевой точке, а функция Fz(z)= z— отражению
относительно оси а (рис. 49). Сопоставим всякой функции,
полученной из F\ и Fz с помощью суперпозиций,
соответствующее пробразование плоскости. Ясно, что
суперпозиция функций переходит при этом в композицию преобра-
115

зований*. Отсюда без всяких вычислений следует, что
функции Fi и F<i порождают группу, изоморфную группе,
симметрии правильного треугольника.
Изоморфизм, построенный вторым способом, можно
в отличие от первого назвать естественным. Естественный
изоморфизм вскрывает причину, в силу которой две
группы изоморфны.
Задача 87. Укажите естественный изоморфизм между группой
переключателей (см. пример 34) и группой D3.
Можно построить естественный изоморфизм с
группой D3 и для группы рациональных алгебраических
выражений, описанной в задаче 78.
Следует отметить, что
естественность, о которой идет речь, ни
в коей мере не является строгим
математическим понятием, а
носит чисто эвристический
характер. В некотором смысле
изоморфизм является естественным, по
для того чтобы понять
естественность некоторого обнаруженного
изоморфизма, требуется подчас
развить новую математическую
теорию. Стремление понять
причины, по которым в различных
областях математики появляются изоморфные
объекты, является мощным стимулом развития науки. Мы
не случайно употребили обобщающее слово «наука»-
Дело в том, что понятие изоморфизма существует и пло-
Рис. 49
* Более того, слова «композиция» и «суперпозиция» на самом
деле означают одно и то же, только первое принято d геометрии
когда говорят о преобразованиях, а второе — н анализе, когда ?сцЬ
идет о функциях.
116
i

дотворно используется не только в математике, но и
в других областях науки и даже в практической
деятельности, правда, там оно не имеет такого точного смысла.
Поясним это на примере.
Вступительная работа Всесоюзной заочной
математической школы при МГУ в 1970 г. была опубликована в
двух журналах: «Квант» и «Математика в школе».
В «Кванте» была приведена следующая задача:
«Один из трех гангстеров, известных в городе М под
кличками Арчи, Босс и Всели, украл портфель (с
деньгами). На допросе каждый из них сделал три заявления.
Арчи:
Я не брал портфель.
В день кражи я уезжал из города М.
Портфель украл В если.
Босс:
Портфель украл Весли.
Если бы я и взял его, я бы не сознался»
У меня и так много денег.
В е с л и:
Я не брал портфель.
Я давно ищу хороший портфель.
Арчи прав, говоря, что он уезжал из М.
В ходе следствия выяснилось, что из трех заявлений
каждого гангстера два верных, а одно — неверное. Кто
Украл портфель?»
В журнале «Математика в школе» была дана такая
задача:
«До царя Гороха дошла молва, что, наконец, кто-то
убил Змея Горыныча. Царь Горох знал, что это мог
сделать либо Илья Муромец, либо Добрыия Никитич, либо
Алеша Попович. А вот и они, запыленные, явились ко
Двору. Царь стал их спрашивать. Трижды каждый
богатырь речь держал. И сказали они так.
117

Илья Муромец:
Не я убил Змея Горыныча.
Я уезжал в заморские страны.
Змея Горыныча убил Алеша Попович.
Д о б р ы й я Никит и ч:
Змея Горыныча убил Алеша Попович.
Если бы я его и убил, то ие сказал бы.
Много еще нечистой силы осталось.
Алеша Попович:
Ие я убил Змея Горыныча.
Я давно ищу, какой бы подвиг совершить.
И взаправду Илья Муромец в заморские страны
уезжал.
Потом царь Горох узнал, что дважды каждый
богатырь правду говорил, а один раз лукавил. Кто убил Змея
Горыныча?»
Нетрудно заметить, что хотя в этих задачах речь идет
о совершенно различных вещах, логическая структура их
одна п та же. Точнее, можно составить следующий
словарик, в котором сопоставляются лица, предметы и
действия, фигурирующие в условии задач:
Арчи Илья Муромец
Босс Добрыня Никитич
Весли Алеша Попович
портфель Змей Горыныч
украсть убить
уехать из города М. уехать в заморские страны.
При замене в условии первой задачи всех слов из левого
столбца на соответствующие слова из правого столбца
мы получаем условие второй задачи. Исключение
составляют два высказывания (шестое и восьмое), которые в
каждой задаче не зависят от остальных высказываний
и которые, как выясняется в ходе решения, можно
считать истинными или ложными, смотря по обстоятельствам
1J8

I
(предполагается, что задача решается путем перебора
всех логически допустимых возможностей). В этом
смысле данные задачи изоморфны.
Подмеченный изоморфизм можно использовать еле-
дующим образом. Решив первую задачу, мы получаем
отпет: Босс. После этого вторую задачу можно уже не
решать: ответом па нее будет слово, соответствующее
слову «Босо, а именно Добрыня Никитич.
Подобным образом используется и изоморфизм
групп (и других математических объектов, о которых мы
не имеем возможности рассказать): если две группы G
и И изоморфны, то всякое утверждение, формулируемое
в терминах групповой операции, которое выполняется
Для G, будет выполняться и для Н.
Изоморфизм групп можно использовать и для другой
цели. Пусть установлен изоморфизм ср: .(?->•// между
группами G и Н. Операции в группах G и II обозначим
соответственно звездочкой (») и кружком (о).
Предположим, что выполнение операции ° проще, чем
операции *. Тогда, чтобы вычислить элемент gt * £2, можно
поступить так: возьмем элементы y>(gi), ф(ё"г) группы Я,
соответствующие элементам gi 11 gZl «перемножим» их в
группе //, т. е. найдем cp(gi) °ф(£2), а затем отыщем соот-
119

встствующий элемент в группе G — это и будет gi * gz.
В самом деле, согласно определению изоморфизма,
gi *Цг = «Г1 (<p(#i) оф(Ы). (25)
Изобретение логарифмов Дж. Иепером * в начале
XVII века явилось, по-видимому, первым в истории
применением изоморфизма в этом смысле. Логарифмы были
введены для того, чтобы заменить умножение чисел
более простой операцией — сложением. Если обозначить
десятичный логарифм числа х через \gx, то имеет места
тождество
XiX2 = ю^-не**, (26)
являющееся частным случаем соотношения (25).
Изоморфизм, который делает возможным все вычисления с
помощью логарифмов,— это изоморфизм \g:x~y\gx
группы положительных действительных чисел Rf по
умножению и группы всех действительных чисел R по
сложению. Два основных свойства логарифмической функции:
1) она определена на множестве R+, принимает значения
в R и взаимно однозначна; 2) она удовлетворяет
тождеству
\g{XiX-i)= Igxi + lgA*
и означает, что отображение lg:R|.-*-R представляет
собой изоморфизм указанных групп.
Задача 88. Укажите, как изменится формула (26), если вместо
десятичного логарифма у = lg х использовать функцию Непера у =*
= A\gx-{-В (иначе говоря, как сам Непер находил произведение
чисел с помощью таблиц значений функции ц = A\gx-{- В и
обратной ей), и придумайте такую групповую операцию * на множестве
* Точнее, его последователем Г. Бригеом, который впервые
составил таблицу десятичных логарифмов: логарифмы самого Дж.
Непера отличались от ныне употребляемых (вместо логарифма он
рассматривал функцию у = A Ig х -f- В, где А и В — некоторые
константы).
120

всех действительных чисел, чтобы функция Непера была изешорфнз-
иом группы R+ с умножением и группы R с операцией *.
В заключение укажем приложение изоморфизма к так
называемому переносу структуры.
Пусть G — некоторая группа с операцией D и Я —
некоторое множество, в котором операция не определена,
но такое, что его элементы можно поставить во взаимно
однозначное соответствие с элементами группы G, т. е.
существует взаимно однозначное отображение <р: II->-G.
Тогда групповую операцию можно перенести из О в II
следующим образом. Возьмем два произвольных
элемента из Я, перенесем их в G с помощью отображения <р,
эти образы перемножим, а результат перенесем назад
н IL Таким образом, в множестве И появляется
некоторая операция. Обозначая ее значком Л, описанные
действия можно записать в виде формулы h% Д Ite =
-ф-'(ф(Л1)П(/г2)).
Именно так были определены сложение точек
плоскости в главе «Движения» и необычная групповая
операция над действительными числами x*y = x-fy — I,
описанная в примере 33. Она получается нз обычного
сложения, если перенести его с помощью
отображения q>:R->-R, заданного формулой у(х) = х— 1. В
самом деле, л'*^-ф-1(ф(^)+ф6/)) = ((^-1)-Н(!/-П) +
+ 1 = х-\-у — 1.
Операция х * у — ? J , которая рассматривалась в
задаче 73, имеет такое же происхождение. Мы
попытались перенести обычное сложение с помощью
отображения y(x) = tgx (бросается в глаза, что формула,
задающая операцию *, похожа на формулу тангенса
суммы!), но это нам плохо удалось по той причине, что
тангенс не является взаимно однозначной функцией.
Выбирая на числовой прямой множество М7 образующее
группу по сложению, и такое, что на нем тангенс не принн-
121

мает одного к того же значения в разных точках, видим,
что значения тангенса образуют группу относительно
операции *.
Задача 89. Докажите, что:
- а) в качестве такого множества М можно взять совокупность
всех чисел, кратных данному ненулевому числу а,
несоизмеримому с я;
б) множество М с требуемыми свойствами не может содержать
никакого открытого интервала ]а, Р(.
Задача 90. Выясните:
а) какая операция получится на множестве действительных
чисел, если сложение перенести при помощи отображения у = хя?
б) как получена операция х*и^ху — лс ~ ff + 2,
рассмотренная в задаче 73?
В терминах переноса структуры изоморфизм можно
описать следующим образом: две группы G и Н
изоморфны, если в результате переноса групповой операции из G
в Н получается операция, которая уже была в И.
Сформулируем и докажем самую
Теорема первую теорему теории групп»
Лагранжа утверждение которой было
подмечено Лагранжем в конце XVIII века,
когда точного понятия группы еще не существовало.
Занимаясь исследованиями проблем теории чисел, Лаг*
ранж обнаружил закономерность, которая на языке тсо- <
рии групп может быть выражена так:
Теорема Лагранжа. Порядок конечной группы
делится на порядок любой ее подгруппы.
В частности, любой элемент группы порождает
циклическую подгруппу, порядок которой равен порядку
самого элемента. Поэтому частным случаем теоремы
Лагранжа является следующее утверждение: порядок
любого элемента конечной группы является делителем
порядка группы.
Внимательный читатель мог подметить эту
закономерность для группы Ci2 и для группы диэдра D3, pac-
122

1
смотренных выше. В первом случае, согласно примеру 5,
порядки элементов принимают значения 1, 2, 3, 4, 6, 12,
а во втором — I, 2 и 3,
Чтобы доказать теорему Лагранжа в наиболее общем
случае, нам понадобится важная в теории групп
конструкция разложения группы на смежные классы по
подгруппе.
Пусть G — группа порядка я; Н —{lht /i2, ..., fhn}—
ее подгруппа. Поскольку подгруппа должна содержать
единичный элемент группы, можно без ограничения
общности предположить, что Ы = е. Кроме того, будем
считать, что подгруппа Н — собственная, т. е. она не
совпадает со всей группой G и единичной подгруппой е, в
противном случае утверждение теоремы Лагранжа
тривиально.
Выберем некоторый элемент gt группы G, не
принадлежащий Я, и рассмотрим множество
glff = {gihh gih2f . .. , gjlm),
полученное умножением всех элементов подгруппы Я на
один и тот же элемент gi слева. Множество giH
называется левым смежным классом группы G по
подгруппе Н. Оно состоит из того же числа элементов, что и Я,
т. е. в списке grfiu gJhy. • -, g\hm все элементы различны.
Действительно, если предположить, что gjif = gihh для
некоторых i и /г, то после умножения этого равенства
слева на gjl получим Ы = 1цх. Кроме того, множества Я
и giH не имеют общих элементов. В самом деле, если
предположить, что Ы = gjis для каких-либо / и st то но:
лучим gi = hth~l. Элемент, стоящий в правой части этого
равенства, принадлежит //, ибо Л*еЯт /1*еЯ и Н—
подгруппа. Но, согласно выбору glt gf Ф Я.
Для группы Dti и ее подгруппы Н, состоящей из
поворотов па углы 0°, 120°, 240п, смежные классы (Я и SaH)
123

изображены на рис. 50. Воспользовавшись таблицей
умножения группы Ds, читатель легко убедится, что
классов ровно 2.
Если оказалось, что множества Я и g\H исчерпали
все G (именно так обстоит дело в только что рассмотрев
ном случае), то мы имеем G=^H\]gJi и утверждение
теоремы доказано: [0[ = 2[Я|. Если же существует хо-
Рис. 50
тя бы один элемент g2t который не попал ни в Я, ни
в gtH, рассмотрим смежный класс
gzH = {gjjfti, U2K • • • > йМ.
Как и раньше, проверяется, что множество gzH состоит
из т элементов и не пересекается с Я, Оно не
пересекается также и с g\H (докажите это самостоятельно:
рассуждение аналогично предыдущему).
Если окажется, что G = Я Ug\H U #Л то | G\ = 3\Щ
и теорема доказана. В противном случае продолжаем
процесс выбора элементов и построения смежных
классов Н. Так как группа G конечная, то на некотором таге
все элементы из G будут распределены по смежным
классам (подгруппу Я тоже можно считать смежным
классом, ибо еН = Н). КаждыГг такой класс содержит т
элементов, а разные классы ле имеют общих элементов
124

Следовательно, п (число элементов в группе) делится
на т (число элементов в подгруппе).
На рис. 51 изображено разложение группы D3 на
смежные классы по подгруппе порядка 2.
Рис. 51
Задача 91. Найдите все подгруппы в группе диэдра /)я.
Из теоремы Лагранжа легко получить следующее
важное утверждение.
Пример 36. Доказать, что всякая конечная группа,
порядок которой — простое число, является циклической.
Пусть g — произвольный элемент данной группы G
простого порядка р. Обозначим через Я подгруппу,
порожденную элементом g. Поскольку Я содержит
элементы е я g, ее порядок не меньше 2. А единственным
делителем простого числа /;, большим 1, является само
число /;. Поэтому, по теореме Лагранжа, порядок Я
совпадает с порядком G и, значит, О = Я. Таким образом,
группа G порождена одним элементом g и, по
определению, является циклической.
Следствием рассмотренного примера является
утверждение, что всякая группа простого порядка коммутативна.
Укажем теперь простейшие применения групповых
понятий, и в частности теоремы Лагранжа в
арифметике.
Простейшая группа, с которой мы сталкиваемся в
125

арифметике,— это группа всех целых чисел Z по
сложению. Поскольку групповая операция здесь сложение,
вместо степеней некоторого элемента (которые
получаются последовательным «умножением» этого элемента
на себя) говорят о кратных этого числа (которые
получаются последовательным сложением). Группа Z—
циклическая с образующим элементом 1, так как любое
целое число можно записать в виде п • 1.
Задача 92. Есть ли в группе Z другой образующий элемент?
Как и во всякой группе, любой элемент п группы Z
порождает некоторую подгруппу. Эта подгруппа состоит
из всех чисел, кратных п. Обозначим ее nZ.
Задача 93. Докажите, что любая собственная подгруппа в
группе 2 имеет вид пЪ для некоторого натурального числа п.
Результат этой задачи позволяет применить
теоретико-групповые соображения в арифметике. Докажем, что
если числа а и т взаимно просты, то найдутся такие
целые числа х и у, что ах -f ту « 1.
Рассмотрим в группе Z подгруппу И, порожденную
данными числами а и т. По определению, И состоит из
всех чисел вида ах -\- ту, где х, у е= Z (если бы
групповая операция записывалась как умножение и была
коммутативной, то вместо ах + Щ следовало бы написать
ахтУ). Согласно задаче 93, найдется такое
натуральное п, что Я ■— пХ. Поскольку подгруппа Я содержит
числа а и т, следовательно, они оба делятся на п. А так
как а и т взаимно просты, то п = I. Таким образом,
подгруппа Я содержит 1, т. е, единицу можно записать в
виде ах + ту, что и требовалось доказать.
Итак, общий вид подгруппы в Z есть nZ. К паре,
состоящей из группы Z и подгруппы «Z, теорема Лагран-
жа, разумеется, неприменима, так как группа бесконеч-
126

на. Однако конструкция разложения группы на смежные
классы, которую мы использовали, по-прежнему имеет
смысл. Более того, она приводит к важным понятиям
классов вычетов и к теории сравнений.
Пусть, например, п = 3, Прибавляя ко всем числам,
кратным 3 (т. е. ко всем элементам подгруппы 3Z),
единицу, получим все числа, дающие при делении на 3
остаток I. Складывая со всеми элементами той же подгруппы
число 2, имеем множество всех чисел, остаток которых
при делении на 3 равен 2. Поскольку других остатков при
делении на 3 быть не может, все целые числа можно
разбить на три класса. Это и есть разбиение группы Z на
смежные классы по подгруппе 32. Наглядное
представление об этом разбиении дает рис. 52. Поскольку
множества 3Z, 3Z -f- 1 и 3Z -f- 2 бесконечны, на рисунке
изображено лишь несколько представителей каждого
смежного класса.
Смежные классы по подгруппе mZ называются
классами вычетов по модулю /л. Класс, состоящий из всех
чисел, дающих при делении на т остаток kt принято
обозначать Ъ. Всего по модулю т имеется т. классов вычетов:
б^ Г, 7ii— 1. Например, по модулю 3 существует три
класса 0, 7, 2 (рис. 52).
Глядя на этот рисунок, можно заметить: если взять
Из некоторых двух классов по одному числу (или, как
говорят, по одному представителю), то их сумма будет
находиться в одном и том же классе независимо от вы-
127

бора этих представителей. Например, если в классе 1
взять представителей 1, —2, 7, а в классе 2 —
представителей —4, 5, 8, то все суммы 1 +(—4) = —3, (—2)-|-5 =
— 3, 7-f- 8 = 15 будут принадлежать одному и тому же
классу 0. В общем случае соответствующее
утверждение следует из равенства
(тх -J- A)'-|-(my -j- /)i= m(x -f- #)4* k-\-l.
Это наблюдение позволяет определить операцию
сложения непосредственно на множестве классов вычетов:
суммой двух классов Я и 1 по модулю т называется
класс, которому принадлежат все суммы вида к -f- /, где
число & выбрано из класса /г, а число / — из класса 7.
Например, для вычетов по модулю 3 имеет место следую-
щая таблица сложения:
6
т
2
0
0
I
2
Т
Г
2
6
2
2
0
I
Из этой таблицы видно, что множество классов вычетов
по модулю 3 образует циклическую группу порядка 3.
Задача 94. Докажите, используя определение группы *, что
классы вычетов по любому модулю т образуют циклическую группу
порядка т.
Можно ли подобным образом определить и
умножение классов вычетов? Можно. Рассмотрим классы к~ и 1
* В следующей главе рассказывается, как это можно доказать
без непосредственной проверки определении.
128

по модулю m. Произвольный представитель класса fi
имеет вид тх -{- к, класса Z — вид ту -\- I (все буквы
обозначают целые числа), а их произведение равно
m{nixy-\-xl + ky)-\-kl. Остаток при делении
полученного числа на т равен Ы и не зависит от выбора
представителей.
Составим таблицу умножения классов вычетов по
модулю 3:
0
б
0
I 1 0
2
б
Т
б
2
б
Т 2
2
I
Из таблицы очевидно, что умножение здесь не обладает
групповыми свойствами. Мешает нуль: в строке,
содержащей 0, все элементы одинаковы. А в таблице
умножения любой группы, как мы уже знаем, каждая строка
состоит из различных элементов. Однако, если
выбросить 0, то оставшаяся таблица
1
2
Г
т
2
2
2
I
Уже определяет группы (это циклическая группа
порядка 2).
Задача 95. Образуют ли группу все ненулевые классы вычетов
'"*<-> модулю 6 oTHoarreiiMio умножения?
За к. 541 129

Из предыдущих рассуждений и результата задачи 95 '
можно сделать вывод: если мы хотим получить группу j
классов вычетов по умножению, следует брать только
вычеты, взаимно простые с модулем. Например, для
вычетов по модулю 6 элемент 4, который имеет с числом 6
общий множитель 2, дает 0 приумножении на некоторый '
ненулевой вычет, а именно, на 3. Но включать 0 в нашу ,
группу нельзя, так как умножение на 0 несовместимо
с групповыми аксиомами.
Докажем теперь следующее важное утверждение:
множество всех классов вычетов Л по модулю т, таких,
что число к взаимно просто с т, образует группу но
умножению.
В самом деле, если два числа взаимно просты с м, то ;
и их произведение взаимно просто с т; это означает
замкнутость операции умножения на данном множестве,
Далее, ассоциативность умножения классов вычетов
следует из ассоциативности обычного умножения чисел. :
Класс 1 взаимно прост с числом т и служит единичным
элементом. Самое трудное — это доказать существование
для любого класса вычетов, ему обратного, т. е. доказать,
что для любого числа а, взаимно простого с т, найдется
число х, взаимно простое с т и такое, что ах при
делении на_/и дает в остатке 1 (т. е. принадлежит классу
вычетов I). Последнее утверждение можно записать в виде
ах-\- ту = 1, где у — некоторое целое число. Но мы уже '
доказывали это утверждение (в качестве следствии из
задачи 93). Там только не было сказано, что число X
взаимно просто с ш, но это очевидно.
Задача 96. Является _ли группой по умножению множество и3
двух классов вычетов 2 и 4 по модулю С? I
Построенную группу классов вычетов, взаимно
простых с модулем, но умножению обозначим Z*. Порпдо*
130

этой группы, т. е. число всех таких вычетов, ранее (когда
речь шла об образующих) обозначали ф(т) и называли
функцией Эйлера от числа т. Для того чтобы указать
одно интересное применение теоремы Лагранжа,
необходимо извлечь из нее некоторое следствие. Пусть g —
элемент порядка т в группе G порядка п. Тогда, по теореме
Лагранжа, п = mk, где k — целое число. Следовательно,
gn = gmii =(^n)ft,= eh = е. Таким образом, при
возведении любого элемента конечной группы в степень, равную
порядку группы, получается единичный элемент.
Б случае группы Z*M это означает следующее: если
о —число, взаимно простое с /и, то аРС") — 1. Иными
словами, число aW при делении на т дает остаток 1.
Это утверждение известно как теорема Эйлера. Обычно
ее записывают так:
atfm) == l(modm).
Это соотношение читается «art™) сравнимо с 1 по
модулю tn» и означает, что оба числа при делении на т дают
одинаковые остатки, т. е. принадлежат одному классу
вычетов по модулю т.
Поскольку всякое число, не делящееся на простое
число р, взаимно просто с ним, то в случае т = р
теорема Эйлера превращается в следующее утверждение:
ap-i = J (mod р)
и называется малой теоремой Ферма.
Конечно, ни Ферма, ни Эйлер не использовали в явном
виде попятил теории групп при доказательстве
утверждений, носящих их имена. Следует сказать, однако, что в их
рассуждениях некоторые соображения
теоретико-группового характера (например, разложение системы классов
вычетов по подгруппе) присутствовали в неявном виде.
Эти рассуждения были одним из источников, из которых
впоследствии выросла теория групп. Явное применение
Б»
131

понятий и конструкций теории групп позволяет внести
ясность в этот круг вопросов, лучше понять смысл дока-
здтельств и дать далеко идущие обобщения.
Приведем в заключение несколько задач, при
решении которых используют понятие класса вычетов и
теоремы Эйлера и Ферма.
Задача 97. Докажите, что уравнение ** = Зу2 -|- 8 не имеет
решений в целых числах.
Задача 98. Докажите, что а* = a(modp) при любом а, если р—
простое число.
Задача 99. Найдите две последние цифры числа 1987,в8Н.

ОРНАМЕНТЫ
Искусство орнамента содержит в неявном
виде наиболее древнюю часть известной нам
Высшей математики.
Г, Вейль
В этой главе появится определение орнамента.
Предварительно обсудим такие важные понятия, как действие
группы на множестве, орбита и инвариант.
Группы преобразований по самому своему
определению действуют на некоторых множествах. Так, группа
Движений плоскости действует на плоскости (на
множестве всех точек плоскости), а группа 53 подстановок
элементов 1, 2, 3—на множестве {1, 2, 3). Эта
способность преобразовывать некоторое множество настолько
присуща группе, что сохраняется в полной мере и для
произвольных групп. Для определения действия
абстрактной группы в множестве нам понадобится понятие
гомоморфизма.
133

Мы убедились, что группа 53 под-
Гомоморфизмы становок элементов 1, 2, 3
изоморфна группе Ds — Sym(A) симметрии
правильного треугольника. Занумеруем вершины
треугольника цифрами 1, 2, 3. Тогда всякой подстановке
/1 2 3\
V / h)
соответствует движение плоскости,
переводящее вершины 1, 2, 3 в вершины i, /, к соответственно.
Например, подстановке отвечает отражение
относительно высоты данного треугольника, проведенной из
вершимы 1.
Таким образом, каждой подстановке с ^ S3 мы
сопоставили некоторое движение плоскости, т. е. элемент
группы Тг(Я) всех преобразований плоскости. Иначе
говоря, оказывается, что подстановки трех элементов
могут действовать на плоскости. Точку TqA будем считать
образом точки А после применения преобразования о",
где Та — элемент группы Ds, соответствующий сг при
изоморфизме 5з на Da. Ясно, что поскольку мы «стартовали»
с изоморфизма Ss->-Da, описанное действие обладает
следующим свойством: результат последовательного
применения к точке А подстановок т и о (в этом порядке)
совпадает с точкой, в которую переходит А при действии
на нее элементом от. Символически это можно записать
так:
rw(i4)=rtf(r,(i4))
или
Тот ~ 1 а ° м.
Это равенство, собственно, и означает, что мы имеем дело
с изоморфизмом 5з-»-Оз. Если же в качестве области
значении рассматривать группу всех преобразований
плоскости /7, то в этом случае отображение, хотя и обла-
134

даст свойством Тот = То° /*, изоморфизмом, конечно, не
будет, ибо не является взаимно однозначным (S3 —
конечная группа, а Тг(#)—бесконечная). Встречаются и
такие отображения <р: G-+H, которые различным
элементам группы G сопоставляют не обязательно
различные в Я, однако при этом равенство (23) остается
справедливым. Их и называют гомоморфизмами.
Гомоморфизм групры G в группу II— это
отображение <|>: G ->- II, такое, что
ф(аЬ) = ф(а)ф(&) (27)
для любых а и Ъ из G (групповая операция обозначена
здесь как умножение, но может, разумеется, иметь
произвольную природу). Частным случаем гомоморфизма
является изоморфизм (взаимно однозначный
гомоморфизм). Доказательство того, что при изоморфизме
нейтральный элемент переходит в нейтральный (см. с. 111),
справедливо для произвольных гомоморфизмов, т, е.
если е—нейтральный элемент группы С, то
ф(е)—нейтральный элемент группы Я. Точно так же при любом
гомоморфизме
ФСГ^-ФСЯ)-1. (28)
Рассмотрим несколько примеров гомоморфизмов.
Пример 37. Пусть Z — группа целых чисел с
операцией сложения; Zm — группа классов вычетов по
модулю м (с операцией сложения классов). Отображениер,
которое сопоставляет каждому числу а его класс а,
является гомоморфизмом. Действительно, согласно
определению сложения классов, а -}- Б — a -f- b. Это
равенство означает, что р сохраняет операцию слооюения.
Отметим, что р сохраняет и операцию умножения: ab =
* Здесь удобнее обозпачать значение отображения Т0
вместо Г (с).
135

= a * 5. Эти два свойства и делают возможным прием
перехода к вычетам по данному модулю (см. задачу 97).
Отметим, что каковы бы ли были группы G и Н,
всегда существует так называемый тривиальный
гомоморфизм, определенный равенством q>(g)=e' для любого
элемента g e G. Иначе говоря, тривиальный
гомоморфизм — это такой гомоморфизм, образ (множество
значений) которого состоит из одного единичного элемента.
Образ произвольного гомоморфизма ф группы G в
группу II является в любом случае подгруппой в
группе Н (чтобы в этом убедиться, нужно прочитать справа
налево равенства (27) и (28)). Наиболее интересен
случай, когда этот образ совпадает со всей группой Я.
(Тогда говорят, что ф— гомоморфизм G на Н).
Рассмотренный выше гомоморфизм группы Z является
гомоморфизмом на Zm.
Задача 100. При каких т и п существует гомоморфизм 1М
па Zn?
Пример 38. Рассмотрим группу перестановок четырех
букв: а, Ьу с, d, которую будем обозначать 54. Пусть
а — с а — d
Х~ Ь — с : Ъ — а •
Любопытно, что при любой перестановке букв а, Ь, с, d
в этом выражении его новое значение может быть выра-
(а b с d\
жено через х. Например, при замене (. . 1(т. е. а >Ь%
b—>c> c-^-d, d-»-a) имеем
h — d . d — a _ х
c — d ' с —а ~ #— 1 *
Задача 101. Выразите через к все отношения, которые
возникают в примере 38 при выполнении различных перестановок букв
а, Ь, с, й.
136

Внимательный читатель, конечно же, вспомнил, что
множество получившихся функций образует группу
относительно замен переменной. Покажем, что отображение f,
ставящее каждой подстановке о в соответствие функцию
fe{x), является гомоморфизмом. Действительно,
поскольку
Г (у\ _ g(ft)-gfc) . о(<*) —с(d) „ ,.
Ic w а {Ь) - о {с) * и {{>) -о (d) —y
и
F /,Л _ т0" (°) ~ то (0 . то (<*) — ^ (rf)
IxaKi/) то (h) ~ to (с) ' xu(b) — w(d)'
то с учетом определения композиции подстановок fxa(x)
можно получить как U{U)~ U{h\u))- Значит, /то(лг) =
- /t{fa{х)), т. е. f-co = ftvfa. Следовательно, / —
гомоморфизм.
Тот факт, что f — гомоморфизм, облегчает решение
предыдущей задачи. В самом деле, любую подстановку
можно выполнить, переставляя достаточное число раз
только соседние элементы (буквы). Это означает, в
частности, что группа Si порождена тремя транспозициями:
fi •*-*6, Ь ++ с и C++ d. Этим транспозициям
соответствуют функции 1/х, 1 — х, 1/а'. А поскольку / —
гомоморфизм, то любой подстановке будет соответствовать
некоторая композиция указанных функций (см.
задачу 76). Заметим при этом, что поскольку функции 1/х и
1 — х являются образующими, то образ рассмотренного
гомоморфизма совпадает со всей группой замен.
Задача 102. Сопоставим движению, сохраняющему ориентацию,
число + 1, а движению, меняющему ориентацию,— число — 1.
Докажите, что полученное соответствие задает гомоморфизм группы
движений плоскости в группу чисел {-HI, —1} с операцией умножения.
Пример 39. Напомним, что всякое собственное
движение комплексной плоскости задается функцией v=f(z) =
=--=pz-\-at где |р|=1. Сопоставим этому движению
137

комплексное число р. Тем самым мы задаем отображение
множества собственных движений плоскости в
множество 5 комплексных чисел, по модулю равных 1. Это
отображение является гомоморфизмом. Действительно, для
всякого другого движения w = g(z)= qz-\- b будем
иметь g(!(г)) = q [pz -f a) -J- Ь = pqz + (aq + b).
Геометрический смысл рассмотренного гомоморфизма состоит
в том, что при композиции поворотов даже с различными
центрами углы поворота складываются (об этом уже
шла речь в главе «Движения»)» В частности,
композиция R% ° #дф дает параллельный перенос.
При решении задачи, приведенной ниже, полезно
иметь в виду, что угол между прямыми I к т равен
углу между прямыми Ra{1) и Rb{m)- В самом деле,
повороты сохраняют углы, поэтому угол между прямыми / и
и т равен углу между прямыми R% (l) и R% (m). Прямая
же Ri[tn) может быть получена из прямой R%(m) дви*
жеиием R%oRAPt которое представляет собой
параллельный перенос.
Задача 103. Пусть CF и BE—высоты треугольника ABC, О —
центр описанной окружности. Докажите, что AOJLFE.
Задача 104. Определителем матрицы (таблицы чисел) I ) ла*
зьшается число ad — 6с. Произведение матриц I I ы I J есть
(am + bp anA-bq\ „
матрица! , . I- Докажите, что псе матрицы с неиулс-
\cm-\-dp cn-\-dql
вым определителем образуют группу, а определшгель является
гомоморфизмом этой группы на группу ненулевых чисел по умножению-
Рассмотрим с более общей точки
Фактор-группа зрения группу классов вычетов Zm
И ГОМОМОрфИЗМ Z-^-Zm, КОТОрЫИ
числу а сопоставляет его класс а по модулю т. Грул*
138

па Ът состоит из смежных классов группы Z по
подгруппе mZ чисел, кратных т. Ее называют фактор-группой Ъ
по подгруппе mZ и записывают это так: Z,n ■= Z/mZ.
Пусть теперь G — произвольная группа, Н — ее
подгруппа. Попытаемся по образцу Ъщ построить
факторгруппу GJH. Элементами фактор-группы будем считать
смежные классы по подгруппе Я. Однако сразу же
возникает вопрос: рассматривать смежные классы левые еЯ,
gxHt... или правые Не, Hgu -..? Для группы Z этот
вопрос пс возникал, поскольку она коммутативна.
Напомним, что левый смежный класс gH образуют
всевозможные произведения пнда gh, где h e Я,
а правый смежный класс Hg— произведения вида gh,
где h e Я. Ясно, что если группа некоммутативна, то,
вообще говоря, gH Ф Hg. Например, для группы
переключателей (см. пример 34) и подгруппы Я ={Пи ПЛ с
помощью таблицы соединений находим, что Л2//«
*={Л&Пи Я2Я4}.= {Яа, Ла}, а ИШ={ПЛъ ЩП2}^
~{П2, Я0}. Если же взять подгруппу К ={ЯЬ Я», /7s},
то левый и правые смежные классы но этой подгруппе,
порожденные одним и тем же элементом, совпадают,
несмотря на то что операция соединения переключателей
некоммутативна.
Подгруппа Я в группе G, которая обладает
аналогичным свойством (для любого элемента g <= G
glf = Hg), называется нормальной. Именно для
нормальных подгрупп оказывается возможным повторить
конструкцию фактор-группы ZJmZ, ибо
(gdf) (gzH) - gi(Hg*)H = gi{g2H)H = gigzH
(H • H = H', поскольку Я — подгруппа). Ясно, что класс
вН является нейтральным элементом, а классы gH и
g~lH симметричны. Таким образом, если Я —
нормальная подгруппа в G, то множество смежных классов по Я
с операцией умножения классов, определенной правилом
139

(giH) (ёгН) = gigzH, образует группу, которую и
называют фактор-группой группы G по нормальной
подгруппе //. В случае группы переключателей и подгруппы К
таблица соединений (см. пример 34) разбивается на
четыре квадрата размером 3 X 3, в каждом из которых
содержатся элементы только одного смежного класса.
Схематически это можно изобразить так:
0
1
0
0
1
1
1
0
Нетрудно заметить, что эта таблица определяет
сложение в группе Z2- Следовательно, фактор-группа группы
переключателей по подгруппе К изоморфна группе Z2.
Пример 40. В группе G собственных движений
плоскости рассмотрим две подгруппы: N — поворотов вокруг
заданной точки А и К—переносов. Выяснить, являются
ли эти подгруппы нормальными и, если это возможно,
построить фактор-группы.
Условие нормальности gH = Hg можно переписать в
виде gHg-* = Я, откуда следует, что подгруппа //
нормальна в G, если она вместе с любым своим элементом
содержит и все элементы, сопряженные с ним. Поскольку
сопряжение — это взгляд на элементы с некоторой
другой точки зрения, то подгруппа нормальна, если она
выглядит одинаково независимо от точки зрения: ясно, что
жителю Флатландии переносы плоскости представляются
одинаково независимо от его местонахождения, в то
время как подгруппа поворотов Лг воспринимается им
по-разиому в зависимости от того, ближе или дальше от
точки Л он находится. Поэтому К— нормальная
подгруппа в группе движений плоскости Д, а N — нет. Эти
140

рассуждения можно провести более строго, если
воспользоваться результатами задачи 62. Подгруппа Л*
нормальна, ибо каждое движение, сопряженное с переносом, есть
перепое. Подгруппа N не является нормальной,
поскольку, сопрягая поворот движением f, мы получаем поворот
с'цептром f(A),
Построим фактор-группу Д/К и рассмотрим
гомоморфизм ф: Д-^S, описанный выше (см. пример 39).
Заметим, что два собственных движения fug находятся в
одном смежном классе по подгруппе К, тогда и только
тогда, когда им соответствует од по и то же комплексное
число, т. е. когда ф(П = ф(#)- Пусть <p(f) — <p(g) — p.
Если р — 1, то f и g — переносы и оба находятся в
классе К. Если же р = cos a -J-i sin а Ф I, то f и g—
повороты на угол а, скажем, f = R% и g — Rb- В этом случае
[=R% = R%» (Rlf'oR'fi s gH, поскольку R^o #« —
параллельный перенос. Если же h — параллельный
перенос nf^goh, то cp(f) = <p(g).
Таким образом, гомоморфизм ф определяет взаимно
однозначное соответствие ф между смежными классами
Д1К и элементами S, причем класс /(, называемый ядром
гомоморфизма, состоит из тех элементов группы Д,
которые при гомоморфизме переходят в 1. А поскольку ф
согласовано с групповыми операциями, то и ф согласовано.
Поэтому ф — изоморфизм группы Д1К на группу S.
Следовательно, смежные классы группы Д по подгруппе
переносов К можно представить как комплексные числа с
единичным модулем, а действия со смежными классами
интерпретировать как умножение комплексных чисел.
Отметим в заключение, что разбиение на смежные
классы по подгруппе К имеет простой геометрический смысл:
смежный класс состоит из всех поворотов на один и тот
же угол с различными центрами.
Обобщая эти рассуждения, можно получить следую-
141

щую теорему о гомоморфизме: если ф — гомоморфизм
группы G на группу Я и /С — ядро этого гомоморфизма
{т. е. множество всех элементов, которые переходят в
нейтральный), то фактор-группа GJK изоморфна Я.
Подгруппа К всегда является нормальной, поэтому
факторгруппа GJK. всегда определена. Действительно, если
к €= /С, то ф(£) = е и vigkg-t) = ф(|Г)ф(^)ф(^-1) = ф(#) X
X с • (p(g)"1 = е, т. е. gkg~^y^ К,
Из теоремы о гомоморфизмах следует, что если ф —
гомоморфизм конечных групп G на Я, то в G имеется
нормальная подгруппа, число смежных классов по
которой равно числу элементов в Я. Вследствие этого
порядок группы G делится на порядок группы Я.
Задача 105. Существует ли гомоморфизм группы Ds на
группу 22? на группу Zs?
Пример 41. Найти ядро гомоморфизма ф группы 5*
на группу Ф, описанного в примере 38.
Поскольку ф — гомоморфизм на (его образ совпадает со
всей группой Ф), то группы S4//( и Ф изоморфны (здесь
К — ядро гомоморфизма ф) и | /С I m 154| : ] Ф| — 24:6 —• 4.
Легко указать четыре подстановки, оставляющие
инвариантным (т. е. не изменяющие) выражение х:ь—I )
\аЬс d"
fa b с d\ (a b с d\ (a b с d\
р ~" \b a d с}* \с d a b) ~ \d с b at
ляя таблицу умножений элементов е, р, о, t, мы
убеждаемся, что она совпадает с таблицей умножения
группы Dz. Таким образом, ядро гомоморфизма изоморфно
группе диэдра ZV, получаем формулу S1JD2 <*> Dz (знак ^
используется для обозначения изоморфизма).
Задача 106. Найдите ядро и образ гомоморфизма f {x)-> f (х) ■¥
+ /(—*) группы функций в себя.
142

Задача 107. Пусть S— группа вращений плоскости с общим
центром, Сп — ее циклическая подгруппа порядка п. Докаяигге, что
SIC* a* & ^
Задача 108. Используя теорему о гомоморфизмах, представьте
группу S как фактор-группу группы (R, +).
С помощью понятия гомоморфизма
Действия можно дать точное определение дей-
групп и ствню группы на множестве.
орбиты Действие группы G на
множестве М — это некоторый гомоморфизм
Т группы G в группу преобразований Тг(М) множества
Af — Т: G-**Tr(Af). Под действием элемента g ^.G
точка m множества М переходит в точку Tg(m), которая
обозначается gm, если действие, о котором идет речь,
подразумевается.
Отметим сразу, что данная группа G может
действовать в данном множестве М разными способами, ибо
гомоморфизмов G-*Tr(M)
может быть много. Например,
действие группы S3 на
плоскости, о котором шла речь
выше, определяется
выбором правильного
треугольника, а точнее, его центра и
упорядоченной тройки
прямых, на которых лежат
высоты.
Обозначим. центр
правильного треугольника О,
высоты-—а, Ьу с. Действие
группы Z)3 на плоскости изо- Рис. 53
Сражено на рис. 53: точка О
под действием любого элемента группы D9 переходит
в себя; применяя элементы группы к точке,
расположенной на одной из прямых а, Ь, с, можно получить три раз-
а
из

личные точки; а из точки В, не лежащей ни на одной из
указанных прямых, шесть различных точек: Bit ..., i?6.
Множество точек, которые получаются из данной
точки М под действием всевозможных элементов группы Ог
называется орбитой этой точки (при рассматриваемом
действии):
0(M) = {M'-Tg{M)\ge-G}.
Так, в рассматриваемом случае встречаются орбиты
только трех типов: состоящие из одной, трех или шести
точек (орбиты длины 1, 3 и б).
Ясно, что орбита любой точки М всегда содержит эту
точку, ибо нейтральный элемент группы действует как
тождественное преобразование.
Точка, орбита которой состоит из нее самой,
называется неподвижной точкой действия. В нашем примере
имеется одна неподвижная точка — точка О.
На рис. 53 видно, что, применив к точке Ач элементы
группы Ds, получим точки Ai, Л?., Аз. Аналогично 0(Bi) —
— 0(B). Справедливо следующее утверждение (по
определению): орбита любой точки, взятой на орбите
точки М, совпадает с орбитой точки М. Из этого следует,
что любые две орбиты либо совпадают, либо не
пересекаются. В самом деле, если множества О(М) и 0(N)
имеют общий элемент Р, то 0{М)^0(Р) и 0(P)=0(N)
и, следовательно, в этом случае 0(М) = 0(N).
Множество, в котором действует группа, распадается, таким
образом, на непересекающиеся орбиты.
Еще нагляднее смысл введенных понятий и терминов
поясняется примером действия группы S комплексных
чисел с единичным модулем на комплексной плоскости
с помощью умножений. В этом случае имеется одна
неподвижная точка — нуль, другие орбиты —
концентрические окружности, заполняющие всю плоскость.
144

Задача 109. Постройте топки, соответствующие комплексным
числам: 0, ±2, ±1, i/J/T, ±4, ±2±2i}rW. Найдите действие
группы Dz на этом множестве- Укажите его разбиение на орбиты.
Пример 42. Рассмотрим группу замен ф, о которой
шла речь в задаче 76. Каждую замену переменной
можно понимать как функцию на числовой прямой, однако
некоторые из этих функций определены не иа всей
прямой. Чтобы определить действие этой группы на
прямой, можно либо исключить точки 0 и 1, либо добавить
новый элемент, обозначаемый оо (его полезно
представить себе как бесконечно удаленную точку на прямой).
Действие группы Ф, т. е. значения функций fi, иа
элементы 0, I, оо зададим таблицей
0
I
со
h
оо
1
0
h
1
0
со
fa
0
1
оо
h
1
со
0
/б | h
то 1 0
0 1 оо
1 1 I
Из таблицы, в частности, следует, что тройка точек О,
1, оо составляет одну орбиту. Кроме того, группа Ф
изоморфна группе подстановок нз трех элементов: О, I, оо.
Задача ПО. Найдите еще одну трехэлементную орбиту и дока-
Жите, что все остальные орбиты шестнэлементиые.
Задача Ш. Считая аргумент функций ft <=Ф комплексным, рас- "
смотрите действие группы Ф на пополненной (элементом оо)
комплексной плоскости. Найдите двухэлементную орбиту этого действия
и докажите, что все орбиты, кроме нее к двух указанных ранее
трехэлементных, состоят нз шести точек.
14S

Перечисление
орбит
Рассмотрим еще одни пример
действия группы.
Пример 43. Пусть О —
некоторый куб в пространстве, к G —
группа всех движений пространства, переводящих куб в себя
(группа симметрии куба). Помимо тождественного
преобразования, эта группа содержит 6 поворотов на 180°
вокруг прямых, соединяющих середины ребер (типа
АА' на рис. 54), 3 поворота на 180° вокруг прямых,
соединяющих центры граней
(типа ВВ'), 6 поворотов на 90й
вокруг тех же прямых и 8
поворотов на 120° вокруг прямых,
проходящих через пару
противоположных вершин куба
(типа СС). Порядок группы G,
таким образом, равен 24.
Группа G естественным
образом действует на
множестве Г всех граней куба Q* Это
множество насчитывает 6 эле- ,
меитов и состоит из одной up- |
биты, поскольку любую грань ;
можно перевести в любую
другую некоторым движением куба. Заметим, что для каж- ,
дой грани существует ровно 4 движения куба, которые
оставляют эту грань на месте: тождественное и три по- j
ворота вокруг прямой, проходящей через центр этой
грани. Любопытно, что 6-4=24, т. е. получаем порядок
группы G.
Задача 112. Рассмотрите действие группы G движений куба на
множестве Р его ребер и на множестве В его вершин.
Мы рассмотрели для группы G множества из 6, 8 Я
12 элементов, на которых она действует траизитиви0
14G
Рис. 54

I
(т. е, все множество представляет собой одну орбиту).
Все эти числа суть делители числа 24 — порядка группы.
Число 24 имеет и другие делители. На рис 55
изображены множества нз четырех, трех и двух элементов, на
которых группа G также действует транзитивно: это
множество Д диагоналей куба, множество С средних линий
и множество Т правильных тетраэдров, вписанных в куб.
В каждом нз этих случаев определен гомоморфизм груп-
Рис. 55
пы G в группу перестановок соответствующего
множества, т. е. действие группы G в соответствующем
множестве.
Задача ИЗ. Для каких из множеств Г, В, Р, Д, С, Т этот
гомоморфизм является:
а) гомоморфизмом «в? б) изоморфизмом?
Можно рассмотреть действие группы G и на более
сложных объектах, состоящих нз элементов
рассмотренных множеств.
Пример 44. Описать орбиты действия группы G на
множестве пар, состоящих из какой-либо грани и какого-
либо ребра куба Q.
Обозначим это множество Р X П («декартово произ-
147

ведение» множеств Р и Г) и опишем его элементы. Ребро
куба может либо лежать в данной грани (рис 56, с),
либо иметь с ней одну общую вершину (рис. 56, б), либо не
иметь общих точек (рис. 56, б). Ясно, что пару ребро —
грань одного нз этих трех видов нельзя перевести в пару
другого вида никаким движением, т. е. такие пары
принадлежат разным орбитам. Покажем, что пары одного
вида можно перевести друг в друга движением куба.
Пусть, например, даны две пары ребро—грань, причем
каждое ребро лежит в соответствующей грани. Сделаем
Рис. 56
сначала такое движение куба, которое переводит первую
грань во вторую. Тогда оба ребра окажутся в плоскости
одной и той же грани к можно будет найти
дополнительное движение (поворот вокруг средней линии, возможно,
тождественный), переводящее одно из инх в другое и не
изменяющее положения грани. Аналогично
рассматриваются остальные два случая.
Итак, множество Р X Г, состоящее из всех пар
ребро — грань распадается на три орбиты, типичные
представители которых изображены на рис. 56.
Задача 114. Найдите число орбит и укажите вид их элементов
для действия группы С на множествах:
а) В х Г (пары першнна— грань); б) Д X Г (пары диагональ —
грань); в) Р X Р (упорядоченные пары ребер).
148

Обобщим выводы, сделанные при рассмотрении
предыдущих примеров. Для этого нам потребуется понятие
стабилизатора (или стабильной подгруппы) точки.
Стабилизатор точки х — это совокупность всех элементов
группы, под действием которых элемент х никуда не
смещается: st(x) = {g e G\Tg(x) = х]. Стабилизатор
является подгруппой: если g и h находятся в st(x), то
Ых) = Tg(Th (х)) = Те(х) ~ х и 7_i (х) = Т~* (х) = х.
Стабилизатор неподвижной точки действия группы G
есть вся эта группа. Например, стабилизатор точки О
(см. рис. 53)—вся группа, а стабилизатор точки Л
состоит из двух преобразований: тождественного и
отражения относительно прямой а. Стабильная подгруппа
точки В тривиальна, т. е. состоит из одного тождественного
преобразования. Здесь можно заметить еще одну
закономерность, которую сформулируем в общем виде так:
произведение длины орбиты и порядка стабилизатора ее
точки всегда дает порядок действующей группы:
\0(х)\ |st(*)|HG|. (29)
Рассмотрим разложение группы G на левые смежные
классы по подгруппе Я — st(#):
G^giH{)gvH\J...\JgkH.
Элементы из одного смежного класса одинаково
действуют на элемент х: Т^(х)= Te(Th(x))= Tg(x) = xf, так
как АеЯ = st(x). Обратно, если некоторые элементы g
и k одинаково действуют на х, то они находятся в одном
смежном классе: так как k = gh, то Тп (х) = Т ~.\ (х) =
- v{Th (А)) ~ V{Th {х) )=х и hs* *~1** ^st (А'>*
аким образом, точек в орбите элемента а- столько же,
колько смежных классов в разложении группы по
стабилизатору этого элемента.
149

Из формулы (29) можно заключить, что стабильные
подгруппы у всех точек одной орбиты имеют одно и то
же число элементов. Оказывается, что эти подгруппы
между собой изоморфны и, более того, сопряжены.
Действительно, пусть х и у—точки одной орбиты,
Тогда у — Tg{x). Если теперь ft est (я), то Т s _i (у)^
= Tg(Tk(Tri(y))) = Tg (Th(x)) = Tjx) = y9 т. Tghg-^
€=st(r/) " gst(*)g~l csi(y). Рассуждая в обратном
порядке (от у к х), получим: g*1 st (у) g a st (а:) или st(r/)c
<zig&t(x) g~x. А это и означает, что подгруппы si (у) и
st(*) сопряжены с помощью элемента g.
Пример 45. Сколькими способами можно раскрасить
п красками круг, разделенный на р равных секторов
(р — число простое)? Раскраски, совпадающие при
поворотах круга, считаются одинаковыми.
Здесь идет речь о действии группы поворотов Ср на
множестве всевозможных раскрасок круга. Одинаковые
способы раскраски — это точки из одной орбиты.
Требуется найти число орбит. Какой длины могут быть эти
орбиты? Длина орбиты — делитель порядка группы.
В нашем примере это 1 и р. Орбита длины 1 — это такая |
раскраска, которая не изменяется при поворотах, т. &
одноцветная. Таких раскрасок ровно п. Число всех |
остальных раскрасок пр ~ п. Они разбиваются и а /7-элс-
ментные орбиты. Значит, число таких орбит (яр — п)1Р* !
а всего орбит, т. е. различных раскрасок (пр — п)/р 4~п'
Отметим, что по ходу решения этой задачи у нас
получилось, что число пР — п всегда делится на р. Это дрГ
гое доказательство малой теоремы Ферма (см. заДа'
чу 98).
Задача 115. Попробуйте решить эту же задачу, отказавшись оТ
предположения, что число р — простое.
150

Пользуясь «кустарными» соображениями, подобными
использованным при разборе примера 45, эту задачу
решить довольно трудно. Существует, однако, общая
формула, позволяющая находить число орбит — так
называемая формула Бернсайда.
Для данного элемента группы g обозначим N(g)
число неподвижных точек преобразования Tg, т. е. число
таких х е М, что Ts(x) = х.
Задача 116. При центральной симметрии цифры 0, 1, 8 лерехо*
Л«т в себя, цифры 6 и 9 меняются местами, а прочие теряют смысл.
Сколько существует пятизначных центрально-симметричных чисел?
Формула Бернсайда представляет число орбит г как
«среднее арифметическое числа неподвижных точек для
всех преобразований группы»:
(иначе говоря, сумма чисел N(g) по всем элементам
группы G в \G\ раз больше числа орбит).
Для доказательства этой формулы подумаем,
сколько раз учитывается в сумме J^N (g) некоторая
фиксировав
ванная точка х множества М. Она учитывается всякий
раз, когда g не сдвигает х, т. е. когда g^st(x). Таким
образом, точка х учитывается Ist(#)| раз. Другие точки
орбиты 0(х) входят в сумму J^/Nig) по столько же раз.
Общий вклад данной орбиты равен, следовательно,
|st(jc) | \0(х) | — \G\. Мы видим, что каждая орбита дает
один и тот же вклад, равный |0|, и вся сумма равна
г\ G\t что и требовалось доказать.
Применим формулу Бернсайда для решения приме-
151

pa 45. Здесь тождественный поворот имеет л?
неподвижных точек (он оставляет на месте все возможные
раскраски), а каждый нетождественный — п неподвижных
точек. Поэтому г = (др — {р — 1)п)1р. Легко видеть, что
этот результат не отличается от полученного выше.
Пример 46. Завод выпускает погремушки в виде
кольца с надетыми на него семью белыми и тремя черными
шариками. Сколько различных
погремушек может быть
выпущено?
Погремушки естественно
считать одинаковыми, если одну из
них можно получить из другой,
сдвигая шарики по кольцу и
переворачивая игрушку. Таким
образом, речь идет о действии
группы диэдра £>«) на множестве
погремушек; требуется найти число
орбит этого действия. Определим
для этого число неподвижных
точек различных преобразовании
группы. Для тождественного
преобразования все С?о=120 «точек» являются
неподвижными. Для отражения относительно диаметра а,
проходящего между двумя шариками (рис. 57), неподвижных
(т. е. имеющих а осью симметрии) погремушек нет, ибо
число белых шариков (7) нечетно. Для отражений от
диаметров вида b (проходящих через два шарика)
симметричные расстановки шариков возможны. Именно из
двух шариков А, В один должен быть черным, и, кроме
того, из четырех симметричных пар одна должна
быть черной. Для каждого из пяти подобных отражений
таких погремушек 8. По формуле Бернсайда, г =
-(120 + 5 -8)/20 = 8.
152

Задача 117. Решите пример 46 для четырех белых и шести
черных шариков.
Задача 118. Сколько существует различных игральных костеи?
(Две игральные кости считаются различными, если одну из них
нельзя поставить на место другой так, чтобы числа на
соответствующих гранях были равны.)
Задача 119. Сколькими различными способами можно
раскрасить в два цвета (с использованием ие более чем двух красок):
а) вершины;
б) ребра проволочной модели куба?
Задача 120. Сколько различных 6-угольпиков можно вписать
в правильный 15-у гол ызик?
Задача о погремушках — одна из
Инварианты популярных задач школьных
математических олимпиад. Школьник, не
знакомый с теорией групп, вероятно, стал бы решать ее
следующим образом.
' Три черных шарика разбивают все кольцо на три
i участка, в каждом из которых имеется некоторое
количество белых шариков, скажем, т, п, k. Числа m, n, k
\ заключены в пределах от 0 до 7, причем т + п -f- к — 7.
• Важен ли порядок, в котором берутся эти числа? Нет,
так как поворачивая и переворачивая игрушку, этот
порядок можно как угодно менять. Условимся считать, что
m^n^k. Задача, таким образом, свелась к перечне*
i лепию всех троек т, я, k неотрицательных целых чисел,
которые удовлетворяют условиям т -f- n -f- k ~ 7 и
tn ^ n ^ k. Вот они: 0, 0, 7; 0, 1, б; 0, 2, 5; 0, 3, 4; 1, I, 5;
1,2,4; 1,3,3; 2, 2,3.
Почему для решения задачи оказалось возможным
использовать тройку чисел т, п, k? Потому что, во-пер-
вьтх, у игрушек, которые считаются одинаковыми, эти
тройки совпадают, а, во-вторых, если тройки чисел у двух
игрушек одинаковы, то сами игрушки можно
расположить так, что они будут неразличимы. Первое свойство
можно переформулировать следующим образом: для
163

двух погремушек, принадлежащих одной орбите
группы D10, тройки чисел совпадают, т. е. значения т, я, k
постоянны на орбитах.
Рассмотрим общую ситуацию. Пусть группа G
действует на множестве М. Отображение множества М в
некоторое множество N называется инвариантом действия,
если его значения на элементах одной орбиты всегда
совпадают. Множество N при этом может состоять из
объектов любой природы. В рассмотренном выше примере это
множество состояло из троек чисел: mt n, k. Одно чис-
оо
Рис. 58
ло m (наименьшее) также будет инвариантом
рассматриваемого действия. Этот инвариант, однако, не
обладает вторым свойством: например для игрушек,
изображенных на рис. 58, m ~ 0. Таким образом, видим, что
с помощью одного числа нельзя различить, одинаковы ли
погремушки. В связи с этим инвариант действия группы,
который на различных орбитах принимает различные
значения, называют различающим.
Задача 121. Постройте различающий инвариант для
погремушек с четырьмя белыми и шестью черными шариками.
Рассмотрим группу движений плоскости. Эта группа
естественным образом действует на плоскости. Что
представляет собой орбита некоторой точки плоскости? Оче-
154

-. „доо, это вся плоскость: достаточно уже одних перено-
- сов, чтобы перевести данную точку в любую другую.
Нахождение инвариантов не представляет никакого инте-
- I леса: инвариантом может быть только постоянное ото-
* I бражение.
Действуя на точки плоскости, группа движений дейст-
I вуСТ к на множестве отрезков. В этом случае уже нельзя
совместить друг с другом два произвольных отрезка.
I Все зависит от их длин. Если длины отрезков равны, то
отрезки можно совместить движением, т4 е. отрезки ле-
1 иат в одной орбите. Если же длины отрезков различны,
то совместить отрезки движением нельзя. Таким
образом, длина отрезка представляет собой различающий
j инвариант действия группы движений на множестве всех
отрезков плоскости.
Задача 122. Рассмотрите действие группы движений плоскости
! ва множестве:
j а) всех треугольников; б) всех четырехугольников. Укажите
несколько различающих инвариантов этих действии.
i
i Если Н — подгруппа в группе движений, то она так-
I же действует на плоскости. Если она «достаточно мала»,
! то и ее орбиты будут «небольшими». В этом случае
могут появиться интересные инварианты. Так, при действии
на плоскости группы поворотов с центром А орбитами
являются окружности с центрами в точке Л. В этом слу-
1 чае появляется инвариант одной точки — расстояние от
I нее до центра поворота, причем инвариант различающий.
Если выбрать на плоскости полярные координаты,
совместив полюс с точкой А, то расстояние от точки до
полюса А превращается в полярную координату г этой точки,
а всякий инвариант является функцией различающего
инварианта, т. е. имеет вид f(r)f где г— произвольное
отображение.
Рассмотрим действие на плоскости группы £>3 симмет-
1Б5

рнй правильного треугольника (см. рис. 53). Центр трс*
угольника примем за полюс, луч ОМ — за полярную ось.
Ясно, что /- является инвариантом действия группы Д.
Однако этот инвариант не является различающим.
Функция cos Зф также является инвариантом. Чтобы в этом
убедиться, достаточно проверить, что выражение cos3ip
не изменяется при действии образующих элементов
группы. Группа Д-з порождена одним отражением от оси а
и одним поворотом на 120°. При отражении ф изменяется
на —ср, а при повороте — на q>+ 120°. Поэтому и в том
и в другом случаях выражение cos Зф не изменяется.
Пара чисел (г, cos3<p) может служить различающим
инвариантом. Действительно, система уравнений
cos3cp = fr,l
при с"> 0 л \Ь\^1 может иметь 3 или 6 решений,
соответствующих точкам одной орбиты.
Вероятно, каждый из наших читателей держал в
руках замечательную игрушку — кубик Рубика. Этот кубик
является хорошим наглядным пособием по изучению
групп и их действий. Как известно, игрушка состоит пз
шести неподвижных центральных кубиков и двадцати
подвижных (восьми угловых с тремя раскрашенными
гранями и двенадцати средних с двумя раскрашенными
гранями). Всего существует 12! • 212 • 8! • З8 способов
расстановки разноцветных кубиков по местам. Это число
получено следующим образом: 121 — за счет
произвольных перестановок средних кубиков, 212 — за счет их
разворотов на месте, 8! и 3s — за счет тех же
преобразований восьми угловых кубиков. На множестве всех
состояний кубика действует группа Г всевозможных
перестановок, которые можно осуществить согласно
правилам игры (путем последовательного выполнения любого
156

числа поворотов граней). Эта группа порождена шестью
элементами: поворотами на 90° вокруг центров каждой
из шести граней.
Уже из того наблюдения, что игра имеет групповую
природу, можно сделать интересные выводы.
Отправляясь от некоторого состояния и повторяя действия в
1 одной и той же последовательности, мы всегда рано или
поздно вернемся к исходному состоянию. Действительно,
I так как группа Г конечна, то, выписывая одну за другой
, степени элемента а е Г, мы в конце концов обнаружим
совпадающие, например а™ — ап. Поэтому а™-*1 =* е.
Второе наблюдение состоит в том, что при сборке ку-.
бика часто используются сопряжения, т. е. операции вида
; ttber1. Выще уже говорилось, что такая операция — это
та же операция Ь, но «в другой системе отсчета».
Состояние кубика, при котором все грани
одноцветные, считается начальным. Цель игры состоит в том,
чтобы перейти от заданного состояния к начальному.
Заметим, что не из всякого состояния можно перейти к
начальному (например, если после механической разборки
игрушки один из угловых кубиков повернзть на 120°).
Ясно, что все состояния куба, которые можно получить
из данного, образуют орбиту рассматриваемого действия.
Перейти от данного состояния к начальному можно лишь
п том случае, когда оба состояния находятся в одной
орбите.
Задача 123. Выберем па каждом ребре куба некоторое
направление (его можно представить стрелкой в пространстве), выберем
также на ребре каждого среднего кубика некоторое направление (его
можно представить стрелкой, нарисованной на этом ребре). Пусть
куб находите в некотором состоянии S. Сравним направления
стрелок на каждом среднем кубике с направлением на том ребре, на
котором он находится. Число пор стрелок, направленны* одинаково,
может быть четным или нечетным. Положим п (S)» I, если это
число четное, н n(S)= —I, если это число нечетное. Докажите, что
"(5)—инвариант.
157

Задача 124. Выдел км два цвета (которыми окрашены централь,
иые горнзоЕпалъные кубики), Одна грань каждого углового кубика
окрашена в один КЗ выделенных цветов. Мысленно поворачивая (про-
тив часовой стрелки) вокруг диагонали куба каждый угловой кубик
на 0°, 120° или 240°, можно добиться того, чтобы грань с
выделенной окраской заняла горизонтальное положение. Обозначим через
N($) суммарный угол (0, 120 или 240°) восьми поворотов, Докажите,
что Лг (5)— инвариант.
Имеется еще один инвариант («четность» расстановки
всех кубиков), который вместе с двумя описанными
составляет различающий инвариант действия группы Г.
Все состояния куба (в том числе и полученные при
механической его разборке и сборке) распадаются на
12 орбит.
Теперь мы владеем всеми необходи- ,
Крксгаппографнче- МЫМИ понятиями для ТОГО, чтобы •'
скне группы вернуться к вопросу о симметрии |
орнаментов, который был поставлен
во введении. Симметрия орнаментов описывается так
называемыми кристаллографическими группами.
Примером такой группы может служить группа перекатывания
правильного треугольника, подробно рассмотренная в
главе «Группы»,— она описывает симметрию узора,
изображенного на рис. 40,6.
Кристаллографическая группа—это дискретная
группа движений плоскости, имеющая ограниченную
фундаментальную область.
В этом определении имеются два термина, еще не
знакомые читателю: дискретная группа и фундаментальная
область. Поясним их.
Группа движений G называется дискретной, если для
любой точки плоскости А найдется круг с центром в А,
не содержащий других точек из орбиты точки А, Смысл
этого условия заключается в том, что точки любой
орбиты располагаются отдельно, не скапливаясь ни в каком
месте. Например, группа, порожденная одним парал-
1Й8

дельным переносом, дискретна. Группа же переносов,
содержащая два коллииеарньтх вектора с
несоизмеримыми длинами, не является дискретной. Действительно,
в этом случае орбита любой точки А всюду плотно
заполняет прямую, проходящую через А в направлении
векторов переноса, так что в любой сколь угодно малой
окрестности точки А найдутся другие точки ее орбиты.
Задача 125, Докажите, что группа, порождеина51 поворотом на
угол а градусов, дискретна тогда и только тогда, когда число а
рационально.
Задача 126. Докажите, что стабилизатор любой точки относп-
тельно дискретной группы движений конечен.
Второй термин, требующий
объяснения,—фундаментальная область. Говорят, что область * F на плоскости
является фундаментальной для группы движений G, если
она обладает приведенными ниже свойствами.
Г. Любая точка плоскости принадлежит орбите
некоторой точки (возможно, граничной) области F,
2°. Никакие две внутренние точки области F не могут
быть переведены друг в друга преобразованием
группы G.
Эти два свойства означают, что образы фигуры F под
Действием преобразований группы G различны и
заполняют всю плоскость без пропусков и наложений. Мы
получаем, таким образом, «замощение» плоскости
фигурами, равными F. Для группы G перекатывания
треугольника фундаментальной областью может служить
исходный треугольник. Действительно, его образы под
действием группы G, очевидно, покрывают всю
плоскость, а тот факт, что никакие две внутренние точки это-
* Точное определение понятия «область» требует некоторых
усилий. Читатель может без ущерба для понимания заменить всюду
слово «область» словом «многоугольник».
1БУ

го треугольника не лежат в одной орбите, был уже
доказан (см. пример 27). Мы убедились также, что если после
перекатывания треугольник занимает исходное место, то
он находится в первоначальном положении.
Задача 127. Найдите фундаментальные области для групп
Сп и Dn.
Название «кристаллографические группы» обязало
своим происхождением тому, что аналогичные (т. е.
дискретные и с ограниченной фундаментальной областью)
группы движений пространства описывают симметрию
кристаллов. Плоские кристаллографические группы
называют также орнаментальными группами, поскольку
именно они описывают симметрию орнаментов.
Существует специально разработанная международная система
обозначений кристаллографических групп. Например,
неоднократно упоминавшаяся группа, порожденная
тремя отражениями относительно сторон правильного
треугольника, обозначается символом pSm[. Приведем
другие примеры кристаллографических групп и
соответствующих им орнаментов.
Простейшая кристаллографическая группа,
обозначаемая р\, порождается двумя переносами на неколли-
неарные векторы я, Ь. Орбита точки под действием этой
группы, а также ее фундаментальная область
(параллелограмм) изображены на рис. 59, с. Фундаментальная
область группы pi, равно как и любой другой
кристаллографической группы, может выбираться .по-разному.
На рис. 59, б показаны еще три фундаментальные
области для той же группы р\. Две из них имеют форму
параллелограмма, а третья — шестиугольника. Стороны
параллелограмма / суть векторы о — а, о, а стороны
параллелограмма 2 — векторы a -j- 2b и 2a-\-3b.
160

-> ■*■
Задача 128. Докажите, что параллелограмм со стороны ka~\-lb
\\ttm-\-nb, где k, I, т, п — целые числа, является
фундаментальной областью тогда и только тогда, когда \kn—lm\—\.
Группа pi описывает так называемую
трансляционную симметрию орнаментов. Если данный орнамент сов-
а ff 6
Рис. 59
вещается сам с собой только при переносах
(трансляциях), то группа его симметрии есть pi. Это простейший
вид симметрии плоского орнамента; примером его
может служить персидский орнамент, изображенный на
рис. 59, е. Узор, обладающий симметрией типа pi, легко
придумать самому. Достаточно взять некоторый
параллелограмм, внутри него нарисовать фигуру, не обладаю-
б Ззк. 641
J6I

щую осями и центрами симметрии, и с помощью
параллельных переносов разнести эту фигуру по всей
плоскости (рис. 59, г). Правда, при этом может получиться
узор, обладающий дополнительной симметрией
(например, осевой), хотя первоначальная фигура внутри
параллелограмма такой симметрией не обладала. Такое
явление может наблюдаться лишь в том случае, если взятая
фигура лежит не строго внутри фундаментального
параллелограмма и выходит на его край (рис. 59,с?).
Группа р\ важна не только потому, что она является
простейшим примером кристаллографической группы, но
также и потому, что всякая плоская
кристаллографическая группа содержит подгруппу вида pi, т. е.
порожденную двумя неколлинеарнымн переносами. Докажем это.
Предположим, что некоторая дискретная группа G
движений плоскости содержит переносы, параллельные
только одному направлению, например прямой /. Тогда
оси всех скользящих отражений, входящих в G, также
параллельны прямой Z, ибо квадрат скользящего
отражения есть перенос. Группа G может содержать повороты
только на 180°, потому что если а^180°, то /?^° 7U о Rt*
есть перенос на вектор, не коллннеарный а (см. ответ
к задаче 62). Центры всех поворотов, принадлежащих
группе G, должны располагаться на одной прямой,
параллельной /; можно без ограничения общности считать,
что / проходит через центры разворотов.
Задача 129. Докажите, что группа G может содержать только
такие отражения, оси которых перпендикулярны к прямой / или
совпадают с не(1.
■■ Из всех этих наблюдений вытекает, что ннкаки'е две
точки луча, перпендикулярного к прямой / и
начинающегося на ней, не могут лежать в одной орбите. Значит,
фундаментальная область группы G должна содержать
162

I
весь этот луч и поэтому она не ограничена.
Следовательно, рассматриваемая группа G не является
кристаллографической.
Итак, мы доказали, что всякая орнаментальная
группа G содержит два иеколлинеарных переноса и тем
самым подгруппу типа pi, ими порожденную. На самом
деле справедливо более сильное утверждение:
совокупность всех параллельных переносов, принадлежащих (7,
есть группа типа р\ (т. е. с двумя образующими). Чтобы
доказать это утверждение, надо решить следующую
задачу.
Задача 130. Докажите, что всякая орнаментальная груша,
состоящая из переносов плоскости, порождается некоторыми двумя
нс-коллилеарнымн переносами.
Пусть G— некоторая орнаментальная группа.
Обозначим через Н подгруппу переносов, содержащихся в G.
Пусть Ф — фундаментальная область для группы G,
а Я — фундаментальная область для группы И (ее
можно выбрать в виде параллелограмма, поскольку Н имеет
тип р\). Область Ф называется мотивом орнамента,
имеющего группу симметрии G, а область Я—
элементарной ячейкой этого орнамента. Весь орнамент
получается из ячейки с помощью параллельных переносов.
Внутри ячейки мотив повторяется несколько раз (если
G ф Н). Отношение площади ячейки к площади мотива
выражается всегда целым числом и равно числу
смежных классов группы G по подгруппе Н. Допуская
некоторую вольность, можно сказать, что размер
фундаментальной области группы «обратно пропорционален
величине этой группы».
Пример 47. Найти мотив и элементарную ячейку
узора с группой симметрии G типа рЪш\. Описать смежные
классы группы С по подгруппе переносов Н.
&•
163

На рис. 60, а изображен узор, группа симметрии
которого имеет тип рЗт\, т. е. порождена отражениями
относительно трех сторон правильного треугааьника (вместо
рис. 60 можно было бы рассмотреть рис. 40,6). Узор
получен из мотива MNB путем этого треугольника по
плоскости. Из рисунка видно, что узор выдерживает парал-
Рис. 60
лельные переносы на векторы, соединяющие, например,
вершины А, В, D. В качестве элементарной ячейки
можно выбрать, например, параллелограмм ABCD, сто-
ромы которого АВ и AD служат образующими подгруппы
переносов Я. Легко видеть, что Здвсл^Зютл—б: 1.
Ячейку A BCD нельзя разбить на шесть треугольников,
каждый из которых является мотивом орнамента. Можно,
однако, выбрать фундаментальную область для
группы Я в виде шестиугольника, например BQCLDM,
состоящего из шести фундаментальных треугольников. Для
нахождения числа смежных классов группы G по Н
заметим, что элементы подгруппы Я не изменяют расло-
164

I
ложения мотива на плоскости (угол наклона и
направление «ноги»). Скажем, перенос ВС переводит треуголь-
I инк MNB в треугольник LCP, внутри которого мотив
i ориентирован точно так же. Далее, разные движения из
одного смежного класса G по II, например g о hi и g ° /?2,
где Ни Ы ^ ff, меняют характер расположения мотива
i одинаково, потому что в указанных композициях сначала
выполняется перенос h± или Ич, не меняющий ориентации
мотива. Следовательно, смежных классов ровно столько,
| сколько мы видим на рисунке различных расположений
мотива, а их ровно шесть. Эти расположения можно
занумеровать цифрами от 1 до 6 (рис. 60, б). Тогда все
движения из смежного класса gH, где g — отражение
относительно некоторой вертикальной оси, вызывают такую
перестановку этих цифр: 1 -*-»■ 6, 2 «-»■ 5, 3 ч_^ 4. Заметим
i еще, что подгруппа переносов Н нормальна в (7, поэтому
' множество смежных классов G/H составляет
факторгруппу. Таким образом, получаем, что фактор-группа
G/H действует на множестве мотивов, содержащихся в
элементарной ячейке, точно так же, как группа
симметрии правильного треугольника Ds (три поворота,
включая тождественный, и три отражения). Итог наших
рассуждений можно записать следующим образом: G/H ^
« D& Запись p&mlfpl c* D3 была бы ошибочной, так как
группа типа p3ml содержит много подгрупп типа pi,
содержащихся в //.
Задача 131. Каков порядок фактор-группы G/K, где G—рассмот-
-> —>-
репная группа, а К — группа переносов, порожденная АС и AR
(рис. 60)? Опишите структуру этой группы,
Для произвольной кристаллографической группы G
ее подгруппа переносов Н является нормальной-
Интересен вопрос о структуре фактор-группы G/II.
Оказывается, что, во-первых, она конечна и ее порядок равен от-
165

Обозначение
Pi
/>2
рт
Рё
166
Таблица плоских кристал
Рисунок
^в*
S3
Ыт--\~ L Г L Г
ill I г- I Г-
0LL+- L f L

лографических групп
Образующие
3
Два неколлинеарных
параллельных переноса Tl7 T2
Три разворота Rlt R2, R3
Две осевые симметрии Si, S8
и параллельный перенос Т
Два параллельных
скользящих отражения L/j, £/s
Соотиошелыя
4
TjT^T^
/?}Bal?J*/?§ = (i?1i?,Uil)« = £
Sr{ = S% = E't SjT^T^;
SzT*=TS2
u\^u\
167

cm
pmm
wm
-—"6-
^ff
I 1!
~Q 0-——ф-
pmg
4--
4-
i
ИШ
Ш
Peg
4—г -о—,—$-
j~ ll-^Pj-j
&Щ?4 \ i
«л-^—=-1-.-«ф~—! ft-
168

Продолжение табл.
Отражение S и скользящее
отражение U
Четыре отражения SLt S2,
&а> 54(от сторои квадрата)
Отражение S и два разворота
#1» #2
Два взаимно перпендикуляр*
ных скользящих отражения 1Л,
S2^E; SU*=:U*S
Si — S2 — Sq — SA = (S^^2 —
>2_ D2
= R±SRz
(UtU&={VTl UJ* = E
169

cmm
pi
pirn
P*g
y^<AJUC£jUtlJ^
x-
ЧР
X
i г
-x
X
X
-■ L -1 L
1Ш4 L i I '

Продолжение табя.
Два отражения Slt S2 п
разворот R
Разворот R и поворот Rt на
90°
S^Sl^Rz^&Stf
= (S1RS2R)* = E
Я4^д2==(ад).1==£
Три отражения Slt S2, Sa
(от стороп равнобедренного
прямоугольном треугольника)
Отражение S и поворот R на
90°-
,—1
Ss^^^^-^S^S)*-/:
171

+
/АЛ/
/Л/\~~/\
/л\У/л^У/
/Л\У/Л\У/Л
л л л
А.ЛЛЛ/,

Продолжение табл.
Три поворота на 120°
Отражение S и поио]>от R
на 120°
Три отражсшгя St, S2, Ss (от
сторон
инка)
правильного треуголь-
Разворот R п
120°
поворот Rt на
дЗ ^ ^з = ^ ^ RtR2R3 = £
,-1.
Rs = S*=(R-lSRSF = E
Si —' On = 5g ^= (Oj02/ :
#2 ^ #3 ^ (^i/?je ^ £
173

рвт
V
ношению площади элементарной ячейки к площади
фундаментальной области, и, во-вторых, эта фактор-группа
всегда изоморфна одной из групп Сп или Dn, где п --
~ 1, 2, 3, 4 или 6. Группа С„ или £)„., соответствующая
данной кристаллографической группе, называется ее
орнаментальным классом. Например, орнаментальный
класс группы p3ml есть Ds-
В заключение приведем (без доказательства) список
всех возможных типов кристаллографических групп на
плоскости, полученный впервые русским ученым Е. С.
Федоровым в 1890 году. Для каждой группы на рисунках
слева изображена ее фундаментальная ячейка с
заштрихованной фундаментальной областью и схематически
указаны содержащиеся в этой группе движения
(сплошная линия обозначает ось симметрии, пунктирная —
ось скользящего отражения, значки 0Т Л, D, О—"
центры поворотов 2-го, 3-го, 4-го и 6-го порядков), а
справа приведены примеры орнаментов с данной группой
симметрии (орнаменты получены путем применения
движений группы к исходному мотиву, имеющему форму
буквы Г). Пользуясь этой таблицей, читатель сможет
определить группу симметрии любого орнамента, начи-
174

Окончание табл.
3
Три отражений SlF S2, t9s
сторон половины правиль-
о треугольника)
4
s'j^sl ==: s§ = (ад,)* ^
пая с узора обоев, которыми оклеены стены его
комнаты.
Задача 132. Найдите группы симметрии узоров, изображенных
на рис. 1, и их орнаме1гтальные классы. Рассмотрите также орнамент
на обложке книги.

ПРЕОБРАЗОВАНИЯ
Преобразования умножают наши знания
к экономят усилия.
У, У. Сойер
Главный «персонаж» этой книги — группа
преобразований— до сих пор являлся перед читателями лишь в
весьма частном виде групп движений плоскости. В
настоящей главе мы рассмотрим преобразования плоскости
более общие, чем движения: гомотетии, подобия,
инверсии и дробно-линейные преобразования. При изучении
последних полезно ознакомиться с аналогичными
преобразованиями прямой. С них мы и начнем рассказ.
Отметим, что хотя преобразованием обычно называют
взаимно однозначное отображение некоторого множества
на себя, иногда этот термин понимают в более широком
смысле, как взаимно однозначное отображение одного
множества на другое (например, одной прямой на ДРУ'
тую).
176

Фотографирование (или рисование)
Рисование с математической точки зрения
является центральным
проектированием. Это такое отображение, которое точку А
переводит в точку А\ где луч света, идущий от А через
оптический центр объектива, пересекает плоскость фотопленки
(рис. 61). Рисуя, художник поступает аналогично с той
лишь разницей, что плоскость холста он мысленно
помещает между объектом и глазом. Ясно, что при иент-
Рис. 61
ральных проектированиях прямые изображаются
прямыми, поэтому имеет смысл изучить такие (проективные)
преобразования прямой в прямую. Постараемся найти
математическое описание этих преобразований.
Рассмотрим следующий пример. Вдоль дороги на одинаковых
расстояниях посажены деревья. Как определить,
правильно ли соблюдены промежутки между ними на
рисунке? Для начала уточним (и несколько обобщим)
вопрос. Пусть на прямой / имеется нсколько точек А, В,
С, ..., и прямая / проектируется из центра S иа
прямую V. Точке А при этом сопоставляется точка А1
пересечения прямой SA с /', точке В — точка В' пересечения
прямой SB с V и т. д. Требуется указать такую
количественную характеристику, связанную с расстояниями
между точками A, Bj С, ..., которая при проектировании не
177

изменится. Ясно, что эта характеристика относится более
чем к трем точкам, так как при проектировании
изменяется расстояние (функция пары точек) и отношение
трех точек (на рис. 62 точка В находилась между
точками'Л и С, а после проектирования точка- А' оказалась
между Вг и С). Решающее открытие состояло как раз
в том, что если на прямой даны четыре точкн Л, 5, С, Д
которые при проектировании переходят в точкн А', В\
Рис. 62
С, D' другой прямой, то некоторая величина,
называемая их сложным отношением, сохраняет свое значение.
Сложное отношение точек Л, В, С, D — это отношение
двух простых отношений:
МЯСО)-■&:-£
(здесь отрезки считаются направленными, их отношения
могут быть положительными и отрицательными).
Проверим, изменяется ли сложное отношение при
проектировании. Для этого вычислим площади
треугольников (рис. 63) двумя способами:
Smc = -\-h-AC = -t-SA-SCsin^ASC;
/ h\ \
178

Sasbc =-^li-BC = ^-SB- SCsin^BSC;
S^w^-^-h-AD = ~ SA-SDsm^ASD;
S^sbd = -j-h-BD -= -YSB-SDsm^BSD.
Теперь
AC . AD _ SCSAC . S£SAD _
ВС ' BD Sasbc ' S£$bd
_ SASC sin /, ASC-CB-SD sin Z ЯСР _ sin^,4SC . sin /, Л3£>
~ SJ3-SCsin/BSC-SA-SDsinZ^5D ~ sin^ #SC : sin /_BSD'
Получили, что сложное отношение зависит только от
углов, под которыми из точки 5 видны отрезки АС, ВС,
AD и BD. При проектировании же эти углы не
изменяются.
Пример 48. На изображении аллеи, о которой
говорилось выше, расстояние между первым и вторым деревом
3 см, между вторым и третьим — 1 см. Какое расстояние
между изображением третьего и четвертого деревьев?
Так как расстояния между деревьями А, В, С, D
одинаковые, то их сложное отношение
АС . АР _ 2-2 __4_
ВС * BD I -3 ~~ 3 *
Пусть х — искомое расстояние. Тогда сложное отиоше-
ние изображений ,; ; '- и должно равняться -*-, отку-
да дг = 0,5 см.
Предположим, что на прямых / и /' заданы системы
координат х и х?. Какими формулами выражается
зависимость координаты х' точки Мг от координаты х
точки М, если М* получается нз М при некотором
проектировании прямой / на /'? Для ответа на этот вопрос про-
179

ведем такое же рассуждение, как и в приведенном выше
примере. Пусть точки А(а)1 В(Ь), С(с) проектируются
в точки Л'(а'), Я'(Ь'), С'(с'). Тогда
(АВСМ) = (А'В'С'М')
н
с — а х~-а с' — а' х' — а'
С-~Ь ' х*-Ь с'—Ь' ' х' — Ь' '
Находя из полученного соотношения х\ получаем
функцию вида
Х' e J«£±2Lf (30)
которая называется дробно-линейной.
Задача 133. Проверьте задает лн некоторое преобразование
числовой прямой формула х' — тх * п , если та —tip Ф 0.
РХ + Ц
Например, точка 0 переводится в точку n/q. Однако
при х = — q/p (если р Ф 0) выражение тх 7"п теряет
смысл, т. е. эта формула, вообще говоря, не задает
преобразование прямой в буквальном смысле.
Задача 134. Укажите точку, которая не имеет прообраза при
преобразовании, задаваемом формулой х'
тх' -\- п
Для того чтобы устранить возникающие затруднения,
дополним числовую прямую еще одной точкой,
обозначаемой оо (бесконечно удаленной точкой), принимая по
определению следующие правила:
■
т-со4-п
* -—■
оо, если р — 0
p-co + q
н а : 0 ~ оо.
-^-, если рф0\
180

Прямую, к которой добавлена точка оо, будем называть
расширенной прямой. На этой прямой всякие дробно-ли-
нсйпые преобразования определены а являются ее
взаимно однозначными преобразованиями.
Задача 13J5. Проверьте, образуют ли группу всевозможные дроб-
Е«'линейные преобразования расширенной прямой.
Эта группа называется группой проективных
преобразований расширенной прямой.
Задача 136. Проверьте, является ли сложнее отношение
инвариантом действия группы проективных преобразовании на множестве
четверок точек.
Заметим, что по трем точкам нельзя определить
никакого выражения, которое было бы инвариантно при таких
преобразованиях. Действительно, повторив рассуждения,
проведенные при выводе формулы (30), мы можем
убедиться, что проективное преобразование расширенной
прямой задается двумя тройками соответствующих точек,
и, значит, любую тройку точек можно перевести в любую
Другую с помощью подходящего проективного
преобразования.
В задаче 76 вы рассматривали одну конечную
подгруппу этой группы, порожденную преобразованиями
х' = \fx и xf — 1 ~~х. Существуют и другие конечные
группы дробно-линейных преобразований»
Задача 137. Докажите, что преобразования х *= \{х и х =»
=•(*— 1 )/(*'-[- 1) порождают подгруппу из восьми элементов,
изоморфную группе Di.
Задача 138. Опишите все элементы группы проективных
преобразований прямой, имеющие конечный порядок.
А теперь перейдем к рассмотрению различных
преобразований плоскости. Подобием называется
преобразование плоскости, при котором все расстояния изменяются
181

в одно и то же число раз. Подобия изменяют форму
фигуры так, что расстояние между любыми точками
увеличивается или уменьшается в одно и то же число раз. '
Наиболее простое из преобразований подобия —
гомотетия.
Гомотетия Н\ с центром А и коэф-
Гомотетия фициеытом к Ф О — это такое
преобразование плоскости, которое
каждую точку М переводит в такую точку AV, что AAV -
= &«ЛМ. Проиллюстрируем применение гомотетии следу- !
ющими примерами.
Пример 49. В треугольник ABC вписать квадрат так,
чтобы две его вершины лежали на основании АС, а две
другие—на боковых сторонах.
Очевидно, нетрудно вписать квадрат, у которого две
вершины лежат на основании треугольника, а третья —
на боковой стороне (рис. 64). Только вот четвертая его
вершина Лг не попала на сторону ВС. Квадрат оказался
мал. Однако если «раздувать» его с помощью гомотетии
с центром в А так, чтобы вершины К, L7 M скользили по
сторонам треугольника, то в какой-то момент вершина N
займет необходимое положение в точке Е.
Задача 139. В данный треугольник ABC вписать треугольник,
стороны которого параллельны прямым U, 1% и U*
При гомотетии каждая прямая переходит в
параллельную ей прямую и, следовательно, углы сохраняются.
Кроме того, все расстояния увеличиваются или
уменьшаются в одно и то же число раз. Эти свойства гомотетии
часто используют при решении задач.
Пример 50. В сегмент вписано несколько
окружностей. Доказать, что прямые AiB\, AzB2, ... пересекаются
в одной точке (Аи Bi — точки касания 1-й окружности с
дугой и хордой соответственно).
182

Пусть О — окружность, a MAtN — ее дуга (рис. 65).
рассмотрим гомотетию И с центром в точке /U, которая
переводит окружность 0i в О (ее коэффициент k —
^ ОА\: OtAi). При этом хорда ЛШ перейдет в
касательную I к окружности О, точка Bt — в точку касания С,
через которую проходит прямая А\Вь Точно так же мы
убеждаемся, что через точку касания С проходит и
любая другая прямая AiBi.
Рис. 64 Рис. 65
Задача 140. Даны две концентрические окружности. Проведите
прямую I, пересекающую эти окружности последовательно в точках
А, В, С и Д таких, что АВ « 2ВС = CD.
Задача 141. Докажите, что три прямые, проведенные через
середины сторон треугольника параллельно биссектрисам
противолежащих углов, пересекаются в одной точке.
Задача 142. Докажите, что для произвольного треугольника
существует окружность, проходящая через середины сторон, осиоваЕ!НЯ
высот и середины отрезков КА, KB, КС, где К — точка пересечения
высот (окружность Эйлера или окружность девяти точек).
Очевидным частным случаем гюдо-
Спирапьные бия является спиральное подобие —
подобия композиция гомотетии с центром в
некоторой точке и поворота вокруг
этой точки. С такими преобразованиями читатель встре-
183

тился уже в главе «Плоскость»: там мы видели, что
умножение на комплексное число а сводится к растяжению
в |й| раз и повороту на угол argot вокруг нулевой точки.
Рассмотрим геометрические приложения спиральных
подобий.
Пример 51- На сторонах АВ и ВС треугольника ABC
как на гипотенузах построены вне его прямоугольные
треугольники АРВ и BQC с одинаковыми углами р при
их общей вершине В (рис. 66). Найти углы треугольника
PQK где К — середина стороны АС.
Рассмотрим два спиральных подобия: Fp — Ир с R%° и
HQ^HlQ/k a £>%>", где kr^PB:PA. Так как А АР В со
оо A CQB, то PB:PA = QB: QC и, следовательно, 1/К~
= QC:QB. Ясно» что FP(A) = B, a Fq[B)^C Значит,
(Fqo Fp) (А) — С. Но при последовательном выполнении
спиральных подобий их коэффициенты перемножаются,
а углы поворотов складываются (об этом будет сказано
чуть позже). Спиральное подобие F = Fq*Fp является
поворотом на 180°. А так как F(A)= С, то центр
поворота находится в точке К и F(K) —■ /С. Пусть FP(K) = Ки
184

тогда /7q(/<i)=/C. Тогда прямоугольные треугольники
(рис. 67) КРК\ и QKKt подобны, так как имеют
одинаковое отношение катетов К\Р : РК = KtQ : QK = k, а
значит, и равны. Из подобия следует, что ZPKiK —
= ZQKiK = ZQPK = ZPQK = p. Теперь ZPKQ =
= 180° - 20.
В ходе решения мы пользовались тем, что при
спиральных подобиях величины углов не изменяются и при
композиции спиральных подобий углы их складываются,
а коэффициенты перемножаются. Для доказательства
этих фактов воспользуемся комплексными числами.
Прежде всего заметим, что любое преобразование
подобия, сохраняющее ориентацию плоскости,
описывается формулой вида ну = pz -f а, где рис — некоторые
комплексные числа. В самом деле, пусть F —
собственное подобие, т. е. преобразование плоскости, при котором
все расстояния умножаются на одно и то же число /г,
а ориентация сохраняется. Пусть И—гомотетия с
коэффициентом k и центром в пуле. Преобразование Н~*°Р
сохраняет расстояния и ориентацию, т. е, является
собственным движением и, следовательно, описывается
формулой | — as*-f- b, где |а|= 1 (см. (3) в главе
«Движения»). Тогда преобразование F = Н о (#-i о F)
описывается формулой w = //(£) = k{az -f- b). Из равенства
pz + a - plz 1 ^ j _|. ^ в следует, что формула
w — pz -f- а задает на комплексной плоскости при р ф 1
спиральное подобие с центром в точке a/(l — р),
коэффициентом k \p\ и углом поворота <р= arg/з (см. с. 48).
Если выполнить еще одно спиральное подобие: u=qw-\-b,
то композиция будет определяться формулой
и = q{pZ-\-a)+b = р^ -f я<? + Ь,
из которой видно, что она снова задает спиральное
подобие с коэффициентом \р - q\ = \p\ \q\ и углом поворота
185

ar&(P<?)= arg/? -f- argq. Попутно мы доказали, что
всякое подобие, сохраняющее ориентацию и отличное от
параллельного переноса, имеет неподвижную точку — центр
спирального подобия.
Рассмотрим, как действует спиральное подобие j
(рис. 68). Равнобедренный прямоугольный треугольник
__г
0
н
_|_
-&$
п
I
-—
и
L
—
—
Рис. 68
ОН подобие / переводит в некоторый равнобедренный и
прямоугольный треугольник ABC, исходную
координатную сетку — в новую (тоже квадратную), в узлах
которой расположены точки Л, В, С. Действие подобия f
можно представить как выполнение растяжения
(гомотетии), которое координатную сетку и вместе с ней
любую фигуру увеличивает (или уменьшает) в
определенное число раз, н последующего поворота. Примечательно,
что если точка М' получена из точки М с помощью пр^'
образования f, то точка Mf имеет в системе координат
А, В, С те же координаты, что и точка М в исходной си-
186

стеме. Поэтому часто для задания преобразования
плоскости указывают новую систему координат и требуют,
чтобы исходная точка и полученная из нее
преобразованием имели одинаковые координаты в соответствующих
системах координат.
Задача 143. Две карты одной и той же страны, выполненные на
кальке в разных масштабах, наложены друг на друга так, что одна
из них целиком покрывает другую. Докажите, что существует п
точности один пункт страны, который на обеих картах изображается
одной н той же точкой.
О"
Рис 69
—*■ —*-
Задача 144. Даны точки А, В, С, D, такие что АВ ф CD.
Докажите, что существует такая точка Е, что &АВЕ ~ ACDE.
Задача 145. На сторонах А В, ВС и СА треугольника ABC вне
его построены квадраты с центрами в точках М, N и Р
соответственно. Докажите, что отрезки NP н СМ равны гг взаимно
перпендикулярны.
Пример 52. Пусть окружность S касается
одновременно двух окружностей St и <S2. Доказать, что прямая,
соединяющая точки касания, проходит через центр
подобия этих окружностей.
Пусть К—точка пересечения прямых АВ и 0±Оч
(рис. 69). Рассмотрим преобразование f, которое точке М
187

сопоставляет точку М', находящуюся на луче КМ и
такую, что КМ - КМ' — КА - KB = const. Очевидно, что
при этом точка А переходит в точку В, а В — в Л.
Вспомнив, что произведение KL * KLf отрезков секущей,
проходящей через точку /С, равно квадрату длины касательной,
проведенной через эту же точку, и не зависит от
положения секущей, убеждаемся, что окружность остается на
прежнем месте: f (S) — S.
А куда перейдет окружность S2? Точка М, взятая на
ней, перейдат в точку М' на луче КМ такую, что
КМ' - КМ = КА . KB, Значит,
W- кл'кв
км '
Пусть Mi — вторая точка пересечения прямой КМ с
окружностью S2. Тогда КМ - KMi = С = const.
Следовательно,
КМ' = КАСКВ КМг.
Точка М' — f (M) находится иа окружности 52,
гомотетичной S2l с центром К и коэффициентом (КЛ-КА)/С.
А поскольку окружность касается S в точке А и центр
окружности S!2 лежит на КОг, то он совпадает с Ои и»
значит, S!2 — Sx.
Присмотримся внимательнее к пре-
Инверсия образованию / из предыдущего
примера. Часто его определяют
несколько иначе. Пусть на плоскости дана окружность 5 с
центром О и радиусом R. Симметрией (или инверсией)
относительно окружности S называют преобразование,
которое точку М переводит в точку М' на луче ОМ,
такую, что Ом • ОМ' = R2-. В определении инверсии есть
один недостаток: преобразование для центра инверсии,
точки О, не определено. При движении точки М к центру
188 i

окружности инверсии ее образ М' уходит неограниченно
далеко. Поэтому часто говорят, что при инверсии
образом центра является бесконечно удаленная точка
(которая при инверсии переходит в центр). При таком
соглашении инверсия становится взаимно однозначным
соответствием на пополненной бесконечно удаленной точкой
плоскости.
Пополненную плоскость можно представить и так.
Поставим на «обычную» плоскость П сферу S. Пусть О—
точка касания («южный полюс» сферы). Каждой точке М
плоскости /7 соответствует отличная от «северного
полюса» N точка пересечения сферы с прямой Л1 Если
точка М неограниченно удаляется от точки О, то
соответствующая ей точка на сфере неограниченно
приближается к точке Л\ Поэтому «северный полюс» N
189

естественно считать соответствующим бесконечно
удаленной точке и представлять пополненную плоскость как
сферу 5. Прямые из плоскости Я будут изображаться
окружностями, проходящими через точку N. Как и
обычное отражение, инверсия — ннволютивное
преобразование. Рассматривая пример 52т мы убедились, что при
инверсии окружность преобразуется в окружность
(правда, если исходная окружность не проходила через центр
инверсии).
Свойства инверсии позволили одному из персонажей
рассказа Г. Петарда «К математической теории охоты»
предложить такой способ поимки льва: наблюдатель в
пустыне находится в круглой клетке. Лев находится вне
клетки. Производится инверсия. Тогда лев попадет в
клетку, а наблюдатель окажется вне ее.
Задача 146. В какую фигуру при инверсии / преобразуется
окружность, проходящая через центр инверсии?
Задача 147. В какую фигуру прн инверсии преобразуется
прямая?
Таким образом, из примера 52 п задач 146 и 147
следует, что при инверсии окружности и прямые переходят
в окружности или прямые. Это свойство преобразования
называют круговым: если прямые линии считать
«окружностями с бесконечным радиусом» (бесконечно
удаленная точка как бы склеивает «концы» прямой, превращая
ее в окружность), то инверсия преобразует окружности
в окружности.
Пример 53. Доказать, что если каждая из четырех
окружностей касается двух соседних, то четыре точки
касания лежат на одной окружности (рис. 70, а).
При инверсии / с центром А окружности S3 и 54
преобразуются в окружности 5з и S',„ a 5t и S2 — в
прямые Si и Sa. Линии S3 и S'4, Si и S'4, S'2 и Sa будут
иметь по одной общей точке и касаться в точках "С =
190

=/(C), D'=f(D) и £'= /(B) соответственно (рис. 70,6).
Прямые S,' и S'2 параллельны, так как окружности St
н 52 общих точек, кроме точки Л, не имеют. (Точка А ни
в какую точку плоскости не переходит!) Таким образом,
осталось доказать, что точки Вг, О и D* лежат на одной
прямой. Пусть MN — отрезок общей касательной к
Рис. 70
окружностям S$ и Si, заключенный между
параллельными прямыми S[ и S£. Треугольники MD'O и NOB' —
равнобедренные (MD' — МО, NB' —■ NO как
касательные, проведенные из одной точки), и, кроме того,
ZD'MO = ZONB'. Поэтому ZD'OM =-^-(180° —
— ZD'MO) - -i-(l80° - ^C'NBf) - ZB'ON. А так как
точки В' н Dr лежат по разные стороны от MN, то углы
D'OM и B'ON— вертикальные. Точки В', О, D' лежат
на одной прямой. При инверсии \~х — \ прямая В'О пре-
191

образуется в окружность, проходящую через центр иииср-
сми А н точки В, С и D.
В рассмотренном примере использовался тот факт, что
касающиеся окружности (и прямые) при инверсии
преобразуются снова в касающиеся.
Задача 148. Нязонем углом мезкду двумя окружностями угол,
образованный их касательными, проведенными через общую точку.
Докажите, что при нниерсин сохраняется угол между двумя
окружностями.
Пример 54. На плоскости даны
Дробно-линейные окружность С и точка Л, лежащая
преобразования на середине некоторого ее
радиуса ОБ. Разрешается делать два
преобразования: инверсию относительно окружности С и
симметрию (разворот) относительно точки А. Сколько точек
может получиться из данной точки М плоскости с
помощью этих двух преобразований, если разрешается
выполнять их в любом порядке неограниченное число раз?
(Точка М, конечно, должна быть отличной от О и В.)
Опишем каждое из преобразований с помощью
комплексных чисел, взяв центр О окружности за нуль, а
точку В — за единицу. Тогда точке А отвечает число 1/2.
Разворот вокруг точки А описывается формулой fi (z) —
= 1 — z. Из определения инверсии следует, что если г
и it'—соответствующие точки при инверсии, то \z\ |ic?| =1
и argt<y = argz. Число ty, удовлетворяющее уравнению
z - w = 1, обладает этими свойствами. А так как
инверсия относительно окружности единичного радиуса с
центром в нуле этими двумя свойствами определяется
однозначно, то она задается формулой
И разворот, и инверсия — преобразования инволю-
тнвные. Поэтому при рассмотрении всевозможных ком-
192

I
позиций /i и f2 их нужно чередовать. Получаем
последовательно zt lfz,_ 1 — 1/2, z/(z — 1), 1/(1—2), 1 — 2, z,
1/z, 1 — I/2t 2/(2— 1), 1/(1—2), 1—2. Далее
преобразования будут повторяться. Следовательно, инверсия и
разворот порождают конечную группу G из 12 элементов.
Поэтому из одной точки плоскости ие может получиться
более 11 новых точек. Конечно, орбита одной точки под
действием группы G может содержать и меньшее
количество точек.
Задача 149. ИсслсдуПте, какое количество точек может
содержаться в одной орбите Как располагаются эти точки?
А теперь решим более интересную задачу. Найдем
фундаментальную область этой группы, т. е. наименьшую
часть плоскости, из которой при всевозможных
композициях преобразований
инверсии относительно
окружности С и разворота
вокруг точки А можно
получить всю плоскость. При
развороте Ra окружность
С перейдет в окружность
С, которая при инверсии
преобразуется в прямую,
проходящую через точки
М и М' пересечения
окружностей СнС (в
перпендикуляр к ОВ,
проходящий через точку Л).
Кроме того, отражение от
прямой ОВ (оно описывается функцией w=z) меняет
местами верхнюю и нижнюю полуплоскости (рис. 71).
Таким образом, вся плоскость разбивается на 12 областей.
Проследите, какими преобразованиями можно, например,
из области 1 получить все остальные. Особенно интерес-
Рис. 71
7 Зпк. И1
193

но наблюдать за точками, расположенными на границе
области. Так, из отрезка ОА получаются еще 5 отрезков,
которые заполняют прямую ОВ* Поэтому орбита каждой
внутренней точки отрезка ОА состоит из шести точек.
Орбитой же точки А будет набор: 1/2, 2, —1. (Орбита
точки О также состоит из трех элементов: 0, 1, оо.)
Отрезок AM (как и дуга ОМ) «порождает» еще пять
линий. Они отмечены пунктиром. Здесь, как и раньше,
орбита каждой внутренней точки отрезка состоит из
6 элементов. Орбита же точки М содержит только 2
элемента: М и М' (1/2 ± i У 3/2).
Выясним геометрический смысл дробно-линейных
преобразований плоскости, задаваемых формулами вида w —
= ■■? "*~ и w— g , . (A = ad—ЬсфО). Мы знаем,
cz + d « + <* v '
что функция ш = -=- задает инверсию относительно
единичной окружности с центром в точке О. При с = 0и
йФЪ получаются функции вида w = az-\- Ъ и w —
— az-\- bt которые задают спиральное и зеркальное
подобия. Для получения формулы инверсии с
произвольным центром можно воспользоваться сопряжением
сдвигом, как и при выводе формулы для поворота с центром
в точке а (см. с. 48): w = ——— -|- а.
z — а
Постараемся представить произвольное
дробно-линейное преобразование в виде композиции уже известных
нам преобразований. Так как
„ __ аг-\-Ь с с ос — ad . ji_
^~ cH-d ~~ & + d " #(- ±\ ~"~~
Д / 1 d\ . _а A d
^~ с* [ z + dfc с ) с * с
- »
194

то соответствующее преобразование является
композицией инверсии относительно единичной окружности с
центром в точке — die и спирального подобия. А так как
az-\-b с с be —ad 1 ,
cz+d cz-\-d c2 z-\-djc '
. с _ А /' I ~й \ . _а A d
"1_ с ~~ * \ 1 + 3/5 с /"'" с ' с* с '
то в этом случае преобразование является композицией
инверсии относительно единичной окружности с центром
в точке —die и зеркального подобия.
Таким образом, каждое дробно-линейное
преобразование является круговым, т. е. окружности и прямые
переводит в окружности и прямые. Верно и обратное:
каждое круговое преобразование комплексной плоскости
является дробно-линейным. Поэтому всевозможные
дробно-линейные преобразования образуют группу (группу
круговых преобразований). Так как каждое круговое
преобразование является композицией инверсии и
подобия, то при круговых преобразованиях не изменяются
углы между линиями (т. е. углы между касательными
к линиям в их общих точках).
Задача ISO. Проверьте, образуют ли группу все дробно-линейные
преобразования вида w = (az-\-b)f(cz-\~d), т. е, «собственные»
дробно-линейные преобразования.
Задача 151. Докажите, что всевозможные преобразования, за-
дашше функциями
f (2) = аг + Ь при ad —ЬОО (31)
сг + d
И
ф (z) = _££±i при ad — bc< 0, (32)
cz-\-d
где a, b, c, d — действительные числа, образуют группу.
7* 195

Плоскость
Лобачевского.
и -|- iv
Убедимся, что вес
преобразования вида (31) и (32) переводят
точки верхней полуплоскости в точки
этой же полуплоскости. Пусть z =
= х -f- it/, w = и + iv. Тогда
— а & "Ь *У) ~^ ^ — (о^' -1- ^ Н- f'ff«) (ex -f~ ^ — /gj/) _,
e(*+«0) + d '" (gAr-f-d)2 +1/8 ~"
— (в* + 6) (с* + Ф +mif _._ . //а (ел; + d) — су (ax-f b)
Получим, что формула (31) равносильна системе
и — (gx-l-^^ + ^ + Qgy3 .
и " "' ' (ac + dy + i?
(ad —be) у
откуда видно, что у и v имеют одинаковые знаки.
Аналогичный результат получается и для преобразований
вида (32). Рассмотрим группу
L всех преобразований,
действующую на точки верхней
4д1 полуплоскости W, вида (31)
и (32). Преобразования из
группы L окружности
(прямые линии) переводят в
окружности (или прямые),
причем углы между ними
сохраняются. На полупло-
q л скости W рассмотрим
полупрямые и полуокружности,
Рис. 72 перпендикулярные к оси Ох*
Через две различные точки,
принадлежащие этой полуплоскости, проходит
единственная такая линия (рис 72), аналогично тому, как на
обычной плоскости через две различные точки проходит
У'
в
А
o/V
196

единственная прямая. По этой причине полупрямые и
полуокружности в W, перпендикулярные к оси Ох, назыв.а-
,;ir L-прямьши.
Аналогию с обычной плоскостью можно
продолжить, если движениями W (/.-движениями) считать пре-
сбразования вида (30) и (31). Отличие появится только
тогда, когда мы перейдем к рассмотрению параллельных
(не пересекающихся) прямых (рис. 73). На W через точ-
Рис. 78
ку Л, не лежащую на L-прямой а, можно провести
бесконечное множество L-прямых, не пересекающих а. К их
числу относится, например, прямая k. На рис 73
/--прямые т и п касаются L-прямой а в точках,
лежащих на оси Ох (точки оси Ох не входят в WI). L-прямые,
проходящие через точку А в одной паре вертикальных
углов, не пересекают L-прямой а, а те прямые, которые
проходят через точку Л в другой паре вертикальных
углов, пересекают а (например, /).
Крайние непересекающие прямые называются
параллельными L-прямой а.
Вычислим сумму углов какого-либо треугольника на
плоскости Лобачевского. Пусть Л (0,7), В (4,3), К(0,5)
(рис. 74). Угол К в этом треугольнике прямой: радиус
перпендикулярен к окружности, т. е. к соответствующей
касательной. Легко догадаться, что если М — «центр»
197

L-пряыой АВ, то угол В в треугольнике 71В К равен углу
ОВМ, а угол Л—углу ОМА (ZOMA -= ZBOBi-
- ZBMBi).
Задача 152. Найдите координаты точки М.
Вычислим tg ZOMA и tg ZOBM: igZOMA = 1$t
tg ZOBM = tg (ZBOBi — ZBMBi) = 9/37.
Теперь *(^ + ^В) = тВД^- "»
1—7/3-9/37
Поэтому ^Л -j- ZB < 90° и сумма углов в ДЛЯ/С
меньше 2d. Интересно, что сумма углов равнобедренного
треугольника ABC, у которого ось Оу — высота и медиана,
будет еще меньше. Эти результаты не случайны: в
плоскости Лобачевского сумма углов треуголышка
непостоянна, она всегда меньше 2d на величину,
пропорциональную площади треугольника. Поэтому чем больше
площадь треугольника, тем меньше сумма его углов.
Б группе L всех движений плоскости Лобачевского
можно выделить подгруппу Н, состоящую из
преобразований
198

I
t целыми я, b, с, d. Сюда входят, в частности,
преобразования
5:гi->— 1/2 и Т:г.->Н-г>
которыми эта подгруппа порождается.
Задача 153. Проверьте соотношения SZ=>(ST)3 = Е.
Из рис 75 видно, как преобразуется область
(b={z = a + bi\ |z|> I, ]й.|^1/2}
под действием преобразований Е, Т, 5, 7м, 75, ST, T-*S,
57'-*, ... Можно доказать, что фигурами, полученными
из области Ф под действием преобразований группы Я,
можно «замостить» всю плоскость Лобачевского без
пропусков и перекрытий. Группа И является дискретной
группой движений плоскости Лобачевского с конечной
(в смысле этой геометрии) фундаментальной областью.
Таким образом, эта группа представляет собой аналог
кристаллографических групп в случае геометрии
Лобачевского. Выбрав в области Ф некоторый мотив, можно
нарисовать на плоскости Лобачевского соответствующий
орнамент. Попробуйте!

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
...Надеюсь, что моя теория групп окажется
плодотворной во многих областях
математики и в большей или меньшей степени
изменят ее лицо. Я нмею в виду геометрию,
теорию дифференциальных уравнении,
механику.
С. Ли
В этой гласе мы рассмотрим применение
разработанного ранее аппарата групп преобразований к решению
дифференциальных уравнений. Мы предполагаем, что
читатель знаком с понятием производной и интеграла, знает
производные и интегралы элементарных функций и
встречался с простейшими дифференциальными уравнениями.
Обыкновенное дифференциальное
Обыкновенные уравнение первого порядка — это
дифференциальные уравнение вида
"—" ,у = и*, у), (33)
правая часть которого — некоторая данная функция двух
200

переменных, т. е. некоторое выражение, содержащее х
]{у*. Решением этого уравнения называется такая функ-
иИЯ у = у(х), которая при.подстановке в уравнение обрат
щает его в тождество, т. е. такая, что при любом х - ,.;
ф'(*) = /Ч*,ф(*)).
Поскольку мы интересуемся зависимостью у от х, то
переменная у называется зависимой, а х — независимой.
Уравнение (33) записывают также в виде dy/dx=f(x, у),
где dy и dx — «бесконечно малые» приращения
переменных у и л*, отношение которых по определению равно
производной у'.
Везде, где в этой главе встречаются дифференциалы
(бесконечно малые величины), мы рекомендуем
понимать их интуитивно, как малые переменные величины,
стремящиеся к нулю. Всякое равенство, содержащее
дифференциалы, является приблизительным, если вместо dx
и dy подставлять некоторые конечные значения. При этом
точность такого равенства возрастает по мере стремления
бесконечно малых к нулю и в пределе равенство
становится точным. Однако заменять дифференциалы нулями
нельзя, так как в этом случае получается либо
бессодержательное равенство вида 0 — 0 (см., например, формулу
(54)), либо выражение вида 0/0 (как в определении
производной dy/dx). В этом противоречии и состоит
основная трудность понимания анализа бесконечно
малых. В XVII — XVIII веках новорожденный
математический анализ часто подвергался нападкам со стороны
многих ученых и философов, которые видели сплошные
логические противоречия в манипулировании бесконечно
малыми величинами. Так, Дж. Беркли писал: «Я
признаю, что можно заставить знаки обозначать что-либо
* Есть и более общее понятие обыкновенного дифференциального
Уравнения первого порядка, однако мы ограничимся приведенным
определением.
201

или ничто, и, следовательно, в первоначальной записи
х -f- dx dx может означать либо приращение, либо нуль.
Но затем, какое бы из этих двух значений вы ему ни
придали, вы должны рассуждать последовательно в
соответствии с этим значением, а не исходить из двойного I J
значения; делать так было бы явным софизмом». Впо- '
следствии, в трудах математиков XIX столетия (главным i
образом, О. Коши (1789—1857) и К. Вейрштрасса |
(1815—1897)) математический анализ получил строгое '
обоснование в рамках теории пределов, опирающейся на i
теорию действительных чисел. А в XX веке Э. Картаиом I
была создана теория дифференциальных форм, являю- ,
щаяся современным математическим языком анализа I
бесконечно малых.
В этой книге мы не можем, однако, касаться вопросов
обоснования дифференциального исчисления и призываем I
читателя вместе с нами стать на точку зрения классиков |
XVII века, которые понимали дифференциал буквально
как бесконечно малую величину, одновременно равную и
неравную нулю, и при этом достигли огромных успехов
в решении задач естествознания, несмотря на то что
недостаточное обоснование и определение понятий матема- ,
тического анализа приводило их к парадоксам и
ошибкам.
Примером дифференциального уравнения может
служить уравнение
У' = У-К (34)
решением которого являются, например, функции у =*
= х+ 1 н^ае*+дг+1,в чем легко убедиться
подстановкой.
Отметим сразу, что всякое дифференциальное уравне- |
нне имеет, как правило, бесконечное множество решений, |
которое обычно можно описать одной формулой у — j
= ty(#, с), содержащей, кроме переменной хг еще неко- I
202 '

торую постоянную с, причем с может выбираться
произвольно. Такая функция fy(x, с) называется общим
решением данного дифференциального уравнеииия.
Например, уравнение (34) имеет общее решение у=се*-^х-\-\,
из которого при с = 0 и с = 1 получаем указанные выше
частные решения.
Задача 154. Выясните, существуют ли дифференциальные
уравнения, частными решениями которых были бы функции:
а) У = 0 и у = 1 (постоянные);
б) у = х и "у= I.
Функция/(х, у) в правой части уравнения (33) может
не зависеть от неременной х или от переменной у (или
ни от одной из них). Например, можно рассмотреть
дифференциальные уравнения
У' - 2; (35)
у' = cos х\ (36)
tf - 'А (37)
Задача 15S. Попробуйте найти общее решение уравнений (35)
и (36) и угадать какое-либо частное решение уравнения (37).
Мы предполагаем, что читателю известен способ
нахождения общего решения уравнения вида
М* = /М (38)
(примерами уравнений этого вида являются уравнения
(35) и (36)). Как известно, для решения таких
уравнений используется операция интегрирования*
(нахождения первообразной функции)
y = ff(x)dx, (39)
* Терминологии этого простейшего случая используется и для
произвольных дифференциальных уравнений: вместо «решить»
дифференциальное уравнение говорят «проинтегрировать» его, а в
качестве синонима общего решения используют выражение «общий
интеграл».
Ш

причем в соотношении (39) правая часть определена
«с точностью до аддитивной константы». Точный смысл
этого выражения состоит в следующем: если
F(x)—некоторая первообразная функция f(x), т. е. F'(x)*=* f(x),
то общее решение уравнения (38) задается формулой
y = F{x)-fC. (40)
уу
У
У
у
s
У
У
— \
— \
— \
_. • -*%,-
— \
— \
• ^
А
.—.
При различных значениях С мы получим все возможные
решения уравнения (38). Графики всех функций вида
(40) друг с другом не пересекаются и заполняют всю
плоскость с координатами х, у. Например, для
уравнения (36) мы получим картину, изображенную на
рис. 76, а.
'. Представить графически полезно не только семейство
решений дифференциального уравнения, но и само
уравнение. Как это сделать? Равенство у* = f(x, у) означает,
что наклон (тангенс угла наклона) касательной к
графику искомого решения в точке (х, у) равен известному
числу f(x, у). Таким образом, в каждой точке плоскости
известно направление, в котором должен проходить
график решения (интегральная кривая). Поэтому геометри-
204
Рис. 76

ческий объект, связанный с дифференциальным
уравнением вида (33), есть поле направлений на плоскости.
На рис. 76, б изображено поле направлений для
уравнения (36), Геометрически задача интегрирования
дифференциального уравнения формулируется следующим
образом: дано ноле направлений, требуется провести
семейство линий (интегральных кривых) так, чтобы они
всюду касались этого ноля, т. е. в каждой своей точке
а
У
/ /
/ /~
/~\
Рис. 77
имели то же направление, что и заданное поле.
Нетрудно видеть, что семейство кривых, изображенных на
рис. 76, а, соответствует в этом смысле полю
направлений, указанному на рис. 76,6. На рис. 77 представлены
подобные иллюстрации для уравнения (34).
Задача 166. Нарисуйте иоле направлений и семейства
интегральных кривых для уравнений (35) и (37).
Задача 157. Какие шггсгральныс кривые у поля направлений,
изображенного на рис, 78? Соответствует ли это поле направлений
какому-либо дифференциальному уравпешею?
С помощью обычного интегрирования можно найти
и общее решение произвольного уравнения вида
У' = 1Ш{У). (41)
205

Для этого применяется следующий классический прием.
Вместо производной у' пишут отношение
дифференциалов dyfdx, а затем переписывают уравнение (41) в виде
dy/g(y)^f{x)dx.
(42)
У*.
Как видим, здесь переменные разделились: в левой части
сюит выражение, содержащее только у, а в правой —
только х. По этой причине
уравнение (41) называют
уравнением с разделяю-
^"-ч щнлшся переменными.
-•ъ. \ Если проинтегрировать
\ \ обе части соотношения
\ \ \ (42), получим
Ч
ко
ч.^^_
т
$7W = UMdx (43)
У
Рис, 78
/ (подразумевается, что в
У одну из частей этого
равенства входит
произвольная аддитивная
постоянная С), Это и есть
общее решение уравнения
(41), записанное в
неявном виде. Если выразить у через х, получим решение
в явном виде.
Пример 55. Проиллюстрируем эту процедуру на
уравнении
0'«(*+-l)W). (44)
Имеем ЪуЫу = (х + 1 )dx. Интегрируя, получаем #3 =
= х2/2 + х -\- С, откуда у = /х*/2 + х -]~ С. Придавая
постоянной С всевозможные значения, можно получить
все решения уравнения (44).
206

Частным случаем уравнений с разделяющимися
переменными являются уравнения, правая часть которых
зависит только от одной из переменных.
Задача 168. Найдите общее решение уравнения (37).
Перейдем теперь к выяснению связи
Замена между дифференциальными уравне-
переменных ниями и основной темой нашей
книги — преобразованиями плоскости.
Оказывается, что для решения дифференциальных
уравнений большое значение имеют замены переменных, т. е.
переход к новым переменным и, v no формулам вида
""?!*• *!:1 (46)
v = У(х, у),\ v
где ф и -ф — некоторые функции. При замене (45)
уравнение у' = f(x, у) преобразуется в некоторое другое
уравнение
V = £(«, V) (46)
(здесь штрих обозначает производную по аргументу и\).
Если при этом окажется, что в уравнении (46)
переменные разделяются, то ыы его решим, а затем,
возвратившись по формулам (45) к переменным х, у, получим
решение исходного уравнения (33). В этом и состоит
простейший, но очень действенный прием интегрирования
дифференциальных уравнений: сделать такую замену
переменных, после которой переменные разделяются.
Пример 56. Проиллюстрируем сказанное на примере
уравнения (34). Мы видим, что в этом уравнении
переменные не разделяются. Сделаем такую замену:
и = х; 1 х — и;
} или
v = y — x—l) y-=u-\-v-\-
207

Поскольку здесь и — х, производная no х и производная
по и — это одно и то же и, значит, yr — t/ 4- 1.
Подставляя выражения для х,.у, у* .в уравнение (34), получаем
vr -\- 1 = v -|- и + 1 — и, т. е. v' = v. Здесь . переменные
разделяются; общее решение этого уравнения'—-v = Сеи,
где С—произвольная постоянная. Выражая и, v через
х, у, получаем формулу общего решения исходного
уравнения (34): у = Се* + х'^_ 1, которую мы уже приводили
читателю без выхода.
Задача 159. Найдите замену, разделяющую переменные и
уравнении tf =уг-\- 2ху -{- & — U
Геометрически на формулы замены переменных (45)
можно смотреть двояко.
Во-первых, считая х, у декартовыми координатами на
плоскости, можно рассматривать и, v как другую
криволинейную систему координат на этой плоскости.
Например, формулы
o=arctg-|-
или равносильные им формулы
яГ *= hcos и,*|
у = «sin li J
вводят на плоскости полярную систему координат, т. е.
замена равносильна преобразованию координат.
. Во-вторых, можно считать, что мы имеем дело с
преобразованием самой плоскости (точечным
преобразованием), при котором точка с координатами {и, v)
переходит в точку с координатами (х, у), где х = у(и, с),
# = т1)(м, и). Чтобы представить такие преобразования
наглядно, полезно нарисовать на плоскости образы пря-
208

I
мых координатной сетки и = const, v = const под
действием этого преобразования (см., например, рис. 68).
Исторически первым примером ис-
Уравнснне пользования преобразования при
Бернулли интегрировании дифференциальных
уравнений было решение Иоганном
Бернулли (1667—1748) следующего уравнения:
tf =, Ay + By», (47)
где А и В — данные функции переменной х. С помощью
замены переменных ему удалось свести это уравнение к
линейному уравнению
У' = РУ + Q, (48)
где Р и Q — определенные функции от х.
Рассмотрим вначале, как решается линейное
уравнение (48). Представим неизвестную функцию у в виде
у — uvf где к и о — неизвестные функции от х.
Подставив ttv вместо у в уравнение (48), получаем и'-о -f- их/ =
— Puv + Q. Для того чтобы это равенство было
справедливо, достаточно выполнения двух соотношений:
и' — Ри, vr = Qftt. Первое соотношение представляет
собой уравнение с разделяющимися переменными, из
которого мы найдем функцию и{х). Подставив найденное
выражение для и во второе соотношение, мы простым
интегрированием найдем функцию v{x). Следовательно,
можно найти и решение исходного линейного уравнения*
Задача 160. Найдите общее решепие уравнения
tf = 2ylx — х* + х.
Пример 57. Покажем теперь, каким образом
уравнение (47) можно преобразовать к уравнению (48). Не
меняя независимую переменную х, произведем такую
замену зависимой переменной: у = yiAi-n). в этом случае
209

у' = l j- ри/а-и)!/1'f и после подстановки в формулу (47)
получим
1 — п
или
Задача 161. Найдите общее решение уравнения
у Wj
Читателя не должно смущать, что в ответе этой
задачи встречается интеграл, который ие выражается через
элементарные функции. Одна из первообразных для
функции е~х2& отличается постоянным множителем от
функции, называемой интегралом вероятности. Для нее
составлены подробные таблицы, эта функция изучена так
же хорошо, как и широко известные функции типа синуса
или логарифма. В настоящее время, однако, таблицами
для вычислений почти не пользуются. С помощью ЭВМ
можно найти значение первообразной для любой
функции с любой степенью точности. В связи с этим считают,
что дифференциальное уравнение решено, если для
получения его общего решения достаточно найти конечное
число значений элементарных функций и интегралов.
В этом случае говорят, что уравнение решено в
квадратурах.
Однако далеко не каждое дифференциальное
уравнение решается в квадратурах. Например, уже такое
уравнение, как
не интегрируется в квадратурах. Это уравнение является
частным случаем так называемого специального
уравнения Риккати:
^ = а (**+■*«). (49)
210

A3tf
2
x*v
ах
"' -i- '
X2V2 QX2
Задача 162. Найдите общее решение уравнения (49) при п = 0.
В 1724 году Д. Бериулли и Я. Риккатн открыли серию
значений п, при которых уравнение (49) интегрируется
в квадратурах. Они нашли такую замену переменной у,
которая сводит это уравнение с данным п к уравнению
того же вида с другим показателем» При замене
имеем
и после подстановки в уравнение (49) получаем
2 • _ _^= /J__ , _J 2_ л
дг2у д;2^2 ' ах2 I л'о2 ' а3л2 сх3!' у
или
я' e а f—_^ дл+2 А (50)
Произведем теперь замену независимой переменной,
полагая и = хп+3 (или х = wl/(n+3>). Для того чтобы
отличать производные по х от производных по и, последние
будем записывать в виде отношения дифференциалов.
По правилу дифференцирования сложной функции
dv dv da = dv (п + 8) хП+2 ^ {п + 3) wJg_ dv
dx du dx du K ' \ ■ / ju
В результате замены из уравнения (50) получим
* — ттт^+'ГЩ.
du n -f-
(51)
Уравнение (51) является уравнением Риккатн вида
(49), однако вместо показателя п возник показатель
-(п + 4)/(п+,3).
211

Если в уравнении (49) п = — 4, то после
преобразования получим уравнение Риккатн с показателем 0,
которое, как мы знаем, интегрируется (см. задачу 161).
Задача 163. Проинтегрируйте уравнение уг = у2 + А'-4.
Задача 164. Найдите еще одно значение для п, при котором
уравнение (49) интегрируется в квадратурах.
Если известно, что уравнение (49) интегрируется при
показателе nt то, используя описанные преобразования,
его можно иронитегрировать н при показателе т, таком, что
т 4- 4 3/1-4-4
г-%- — п, т. е, при т — т-г--
Рассмотрим дробно-линейную функцию
«<") = —TFT- <52>
Тогда, согласно нашим рассуждениям, из
интегрируемости уравнения Риккатн (49) для некоторого
показателя п следует его интегрируемость и для показателя
q{n). Повторяя приведенные выше преобразования,
найдем, что уравнение Риккатн (49) интегрируется и для
показателей q(q(n)) и q(q(q(n))), и вообще для
показателей <7Л(Л)» гае qh обозначает /г-ю степень
преобразования q (его /е-кратное применение).
Задача 166. Выведите явную формулу для qk («.).
Заметим, что преобразование q~l обладает тем же
свойством, что и q: переводит всякий интегрируемый
случай уравнения Риккати (49) снова в интегрируемый.
Формула для qh(ri) остается справедливой и при
отрицательных значениях /г. Возникает бесконечная
циклическая группа, порожденная дробно-линейным
преобразованием q. Эта группа действует во множестве
действительных чисел (показателей уравнения (49)) н
212

замечательна тем, что под действием ее показатель, для
которого уравнение (49) интегрируемо, преобразуется в
показатель, обладающий этим же свойством. Таким
образом, для действия этой группы в множестве показателей
свойство уравнения (49) быть интегрируемым в
квадратурах является инвариантным. А раз так, то орбита
любого числа состоит либо из чисел, для каждого из
которых уравнение (49) не интегрируемо в квадратурах, либо
из чисел, для каждого из которых уравнение (49)
интегрируется.
В частности, орбита числа 0 доставляет нам
бесконечную серию уравнений Риккати (49), интегрируемых в
квадратурах. Их показатели имеют вид
f*(0)«4ft/(l-2ft).
Заметим, что если к стремится к бесконечности, то qk{0)
стремится к —2.
Задача 166. Докажите, что уравнение (49) интегрируемо и при
п = — 2.
Если читатель попытается, отправляясь от
показателя п = — 2, найти новые случаи интегрируемости, то его
ждет разочарование. Дело в том, что число —2 остается
неподвижным под действием преобразования q, и его
орбита состоит из одной точки.
Таким образом, мы нашли две орбиты показателен,
для которых уравнение (49) интегрируемо. Французский
математик Ж- Лиувилль (1809—1882) в 1841 году
показал, что при всех остальных показателях п уравнение
(49) не может быть решено в квадратурах.
До сих пор нам встречались только такие замены, при
которых новая функция выражается только через новую
независимую переменную. Однако чрезвычайно
распространены и общие замены координат;
213

* = q>(«, vU и = К(х, у),)
y = ty{u, v),i v?=\.i(x, у)4
Чтобы найти выражение для dyjdx через функции от и,
v и производную dv/du, нам потребуется понятие
частных производных. Пусть 2 — А (х, у)— функция двух
переменных. При неизменном значении у = Уо величина z
зависит только от х, и мы получаем функцию от одной
переменной л" z = h(xr y0). Производная этой функции
при х = Xq и называется частной производной функции
h(x,y) no x в точке (лг0,*Л>). Она обозначается -щг (•*<>, #о).
Пишут также -^- или zx, подразумевая, что z есть
функция х и у. Таким образом,
Пример 58. Найдем частную производную функции
z = V9—xz — у* в точке (2, 1).
При у — 1 получается функция одной переменной:
z = \f8—х%. Ее производная по х будет —х/У 8 — хг и
при х = 2
0,2 (2, 1) = -^=^ = — 1.
Выражение -%— (а-0, #0) определено при любых Л'0 и Уо
и представляет собой новую функцшо двух переменных
хи> Уо* Эта функция обычно обозначается dz/дх, а ее
аргументами считают х и 1/ (фиксированную точку (дг0, у0)
заменяем произвольной точкой (л:, у)). Так, для функции
z sis ]/9 —jc2 — у2 имеем
дг __ х
214

Таким образом, для нахождения частной производной
-—if' tJ' нужно, считая у обозначением некоторого
постоянного числа, продифференцировать Л(х, у) как
функцию одной переменной.
Частная производная по у определяется аналогично
н находится по правилам дифференцирования функции
одной переменной, при этом х— некоторое постоянное
число.
Для функции г — Y§ — *2 — У2 получаем дг/ду —
= --y/V9-xz-yi.
По аналогии с графиком функции одной переменной,
можно рассмотреть и график функции h — (xt у) двух
переменных а* и у. Он
располагается в трехмерном
пространстве и состоит из точек (х, уг
Л (*» У)) • Иа рис. 79 изображен
график функции z= У 9—х2—уг.
Он представляет собой
верхнюю половину сферы.
Геометрический смысл
частной производной функции
h {х> у) по х в точке (х0, у0)
заключается в следующем.
Рассмотрим плоскость у=уо. Она
пересекает график функции по
некоторой кривой. Тангенс угла
между положительным направлением оси ох и
касательной к этой кривой в точке (х0, у0) и есть -^ {Хъ,у0).
Аналогичный смысл имеет и частная производная по у
от h(x, у) в точке (х0, //о). На рис. 79 изображены эти
два сечения для функции z — ")/9 — хг— г/2 в точке (2,1).
Если через две касательные к построенным сечениям про-
215

вести плоскость, то эта плоскость будет касаться графика
функции. Ее уравнение имеет вид
г — 2о = р(х — Хо)+ q(y — y0)t (53)
где г0-Л(^, у0); P--§jr(^ УоУ* Я = ~о^(хо* Уо)-
В самом деле, если х = Хо, то получим уравнение
касательной к графику функции h(x0, у), а если у — уо, то
получим уравнение касательной к графику функции
h(x,y0).
Точка графика и точка касательной плоскости к этому
графику, лежащие над точкой (л*, у), почти не
отличаются друг от друга, если точка (я, у) очень близка к
точке (jco, уо). Поэтому разность z— Zq, вычисленную из
уравнения (53)t можно понимать как приращение
функции fi(x, у) при сдвиге от точки (х0, уо) к точке (х, у),
если этот сдвиг «бесконечно мал». Обозначая бесконечно
малые приращения переменных через dx, dy и dzt
получаем следующее выражение:
dz = Zxdx -f Zydy (54)
(формула дифференциала функции двух переменных).
С помощью формулы (54) можно получить закон
преобразования производной при замене переменных общего
вида.
Пусть (х, у)—исходная система координат на
плоскости, («, v)—другая система координат, связанная с
исходной равенствами:
х = Ф(и, v);\ u^K(х, у)'Л
у=,ц> fa v),\ v = p(x, y)4 *° '
Будем считать, что в «старых» координатах х является
независимой переменной, а у — зависимой, а в «но-
216

вых» и—независимой, a v — зависимой.
Соответствующие производные будем обозначать tf — dy/dx, v' =
= dv/au (обратите внимание, что штрихи при у \\v имеют
разный смысл!).
Тогда, по формуле (54),
• dv
У и ~г Чт>
dy __ У иd" + Уv dv * du _ yu-\ryvvr
** dx x^du-^Xadv ч. i .. dv
(56)
du
Рис. 80
Таким образом, производная уг в «новых»
координатах записывается как дробно-линейная функция от у',
коэффициенты которой суть функции от и, v.
Если формулы (55) описывают не замену координат,
а преобразование плоскости, при котором точка (и, v)
переходит в точку (я, у), то формула (56) показывает,
как при этом преобразовании изменяется наклон кривых
(»' — это тангенс угла наклона касательной к
некоторой кривой, у* — тангенс угла наклона касательной к ее
образу (см. рис. 80)).
217

Назовем касательным элементом точку плоскости
вместе с некоторым направлением, «прикрепленным»
к ней. Такой элемент описывается тремя числами
(х1 уу р), где (х, у)—координаты данной точки, ар —
тангенс угла наклона. Множество всех касательных
элементов образует, таким образом, трехмерное
пространство (пространство касательных
элементов). Несколько его
элементов («точек») изображены на
рис. 81. Формулы (55), (56) задают
некоторое преобразование
пространства касательных элементов.
_w /^ Пример 59. Найти преобразова-
/\ ние пространства касательных
элементов при инверсии в плоскости
х, у относительно окружности xz-\-
Координаты точек плоскости при инверсии
относительно дайной окружности изменяются по формулам:
У U
^
*
Рис. 81
U =
v —
хЧ-у2 '
У
Воспользуемся формулой (56). Имеем:
и = У2—** . „ _ — 2x,J • г, - -^ •
[х* + tff ' и» - (х2 -|- tfy ' и* - (** + г/2)2'
v„ —
сг — if
у (*• + **)*
и, следовательно,
, = Vy + УуУ' = № — tf)!f—2xg
"д: + "у У' — 2*//.'/ +!?- *г '
218

Преобразования вида (55)—(56) могут с успехом
использоваться при интегрировании дифференциальных
уравнений.
Пример 60. Решить уравнение
,/ = *2 w - **>+^ № - (*2+т ч- (yg+*а) (** ■+ уф
у у* (*2 - у2) -|- atjr (* + (*2 + ^)2) + W + х-2) (х-2+^ •
Сделаем замену:
г _ и , р . ../ _ (ка-о«)о'--2цр
Л «г + о21 и ~ tfl + tfi1 * ~ —2uwr + tP — uf
Подставляя эти выражения в исходное уравнение,
после упрощений получаем
«4-1
у2— 1
Здесь переменные.разделяются— {v2— \)dv=^ («2-f-1)dtt,
и общий интеграл (записанный неявно) имеет вид
и3 «3 , . ^
_ v= -g- + tt + Clt
где G — произвольная постоянная. Выполняя обратную
замену, получаем общее решение исходного уравнения:
# - х? - 3(* + у) (* + Я2 + с(*2 + 0е)3.
где С — произвольная постоянная.
Задача 167, Найдите выражение для drfdy через dy/dxt если, г,
Ф — полярные координаты.
Предположим, что задано некоторое
Однопараметриче- действие группы действительных чи-
енне группы сел R с операцией сложения на
плоскости. Это значит, что для любого
действительного числа / определено преобразование
плоскости gi, причем для любых двух чисел t и s имеет
место равенство gi° gs = gt+s. Другими словами, мы
219

имеем дело с гомоморфизмом группы чисел в группу
преобразований плоскости, который числу t ставит в
соответствие преобразование gL. В этом случае говорят, что
задана однопараметрическая группа преобразований
плоскости. Простейшим примером однопараметрической
группы преобразований плоскости может служить
группа переносов вдоль оси х: для всякого t преобразование
-»- -»-
gt есть параллельный перенос на вектор teif где ei —
единичный вектор оси х.
Задача 168. Докажите, что любые два преобразования gt u gt
однопараметрической группы коммутируют.
Чтобы перейти к более сложным примерам, полезно
ввести координатную запись одиопараметрнчееких групп
преобразовании плоскости. Такая запись дается парой
функций трех переменных:
*i - ф (x,ry,rJ);)
Здесь (х, у)— координаты произвольной точки
плоскости, a (*i, #i)— координаты ее образа при
преобразовании gt. При любом фиксированном значении
группового параметра t получается пара функций двух
переменных, т. е, формулы вида (55), задающие одно
определенное преобразование. На языке функций (57)
групповой закон, т. е. равенство glogs = gi+Ss записывается
в виде соотношений
Ф(ф(*, y,Zs), ty(x, yt s), £) = q>(x, у, Н s)l] .
которым должны удовлетворять функции q> и tp при
произвольных значениях аргументов для того, чтобы они
определяли некоторую одно параметрическую группу
преобразований.
220

Например, группа переносов по оси х задается парой
функций
для которых тождества (58) проверяются тривиально.
Задача IC9. Образуют ли однопараметрическуто группу
преобразований псе гомотетии с положительным коэффициентом и общим
uesnpoM?
Внимательный читатель обнаружит, что приведенных
условий недостаточно для решения этой задачи. Дело
в том, что задание однопараметрической группы
преобразований включает в себя не только указание
некоторого множества преобразований, но и приписывание
каждому преобразованию некоторого действительного
числа /. Если, например, сопоставить числу t гомотетию
с коэффициентом t, то мы не получим одиопараметри-
ческую группу в смысле данного выше определения, ибо
композиции гомотетий с коэффициентами ins будет
отвечать гомотетия с коэффициентом ts, а не t-\-s.
Однако мы знаем способ, как превратить умножение в
сложение: нужно воспользоваться показательной
функцией. Если числу t сопоставить гомотетию с
коэффициентом с1, то мы получим настоящую однопараметрическую
группу преобразований. Если общий центр
рассматриваемых гомотетий поместить в начало координат, то эта
группа может быть описана формулами
для которых равенства (58) легко проверяются.
Наглядное представление об однопараметрической
группе преобразований плоскости дает семейство орбит
221

этой группы. На рис. 82, а, б изображены орбиты двух
рассмотренных групп: переносов и растяжении. Следуег,
однако, отмстить, что две различные однопараметри-
ческие группы могут иметь одно и то же семейство орбит,
поэтому различить их по рисункам орбит невозможно.
а У-
О
.
X
Рис. 82
Простейшим примером такой ситуации может служить
группа переносов вдоль оси х с удвоенной скоростью:
хг = х + 2t] |
Уг = У- )
Ее орбиты такие же, как на рис. 82, а.
Задача 170. Определите однопараметрическую группу попоротое
с фиксированным центром, опишите ее координатными формулами и
изобразите ее орбиты.
Задача 171. Проверьте, задают ли равенства
хх = eat (х cos bt — .jysiii bt) \ \
уг == efl/ (x sin bt -j- i/coa bt) J
однопараметрическую группу. Выясните се геометрический смысл и
нарисуйте ее орбиты.
Задача 172. Пусть лч и j/i— корпи квадратного уравнения
(относительно неизвестной w) (w — х) (w — */)+ / = 0. Тогда ач и yi явля-
222

ртся функциями трех переменных: х, у, t. Докажите, что эти
функции определяют одноггараметрическую группу преобразований плос-
» костл. Изобразите се орбиты.
Дифференциальное уравнение на
Симметрии плоскости, понимаемое как поле на-
дифференциальных правлений, может обладать опреде-
уравнений ленной симметрией. При первом
взгляде на ряс. 76, б видно, что он
не меняется при сдвигах на любое расстояние вдоль
оси у, а также при сдвигах на числа, кратные 2л, вдоль
оси л'. Преобразования первого типа образуют однопара-
метрическуго группу (ее можно описать формулами
Л| = х, yi — y-{-t)t преобразования второго типа одно-
параметрической группы не порождают (а образуют
дискретную группу, см, с. 158). Оказывается, зная одно-
параметрическую группу симметрии дифференциального
: уравнения, можно найти его общий интеграл» тогда как
1 наличие дискретной группы симметрии никак не
облегчает эту задачу.
Уточним сказанное. Пусть даны дифференциальное
уравнение вида (33) и преобразование плоскости (55).
Это преобразование называется симметрией уравнения
(33), если при подстановке выражений (55) вместе с
соответствующим выражением для производной (56)
в равенство (33) вместо х, yt if мы получим такое же
уравнение для переменных и, v и vr: v' = \{и% v). Геомет-
• рически это означает, что преобразование пространства
касательных элементов (55)—(56) нри действии на эле-
, менты поля направлений, соответствующего данному
дифференциальному уравнению, переводит их в элементы
того же поля направлений (но «прикрепленные», вообще
I говоря, в других точках плоскости). Если изображать
i касательные элементы в настоящем трехмерном
пространстве (откладывая координату р = у' по вертикали),
то дифференциальное уравнение можно представить
223

в виде поверхности в этом пространстве, а его
симметрию— как преобразование этого пространства,
заданное формулами вида (55)—(56), которое эту поверхность
оставляет на месте (точнее, сдвигает ее по себе).
На рис. 83 в виде поверхности изображено упомянутое
выше уравнение tf = cos xt причем видно, что
преобразования
Л'1 — х\ ] хх = х -|- 2nk\
0i-0 + fi • и У\=&
Pi^P J Рх = Р J
переводят эту поверхность в себя.
Ставится два вопроса о связи дифференциальных |
уравнений и однопараметрическнх групп их симметрии:
1) дано дифференциальное уравнение. Найти все (или
хотя бы одну) группы его симметрии; 2) дана однопара- ,
метрическая группа преобразовании плоскости. Найти
все дифференциальные уравнения, для которых эта
группа является группой симметрии (или, говоря иначе,
уравнения, допускающие эту группу).
Практически более важным является первый вопрос,
но он и более труден. Поэтому вначале обсудим второй
вопрос. Приведем два примера однопара метрических
групп, для которых построение соответствующих им
уравнений очевидно.
Общий вид уравнения, допускающего группу
переносов вдоль оси а.*:
tf-fiy). (59) ,
Его частным случаем является уравнение (37).
Уравнения, допускающие группу переносов вдоль
оси */, имеют вид tf = /(я)» частным случаем которого
является уравнение (36).
Обратимся теперь к более содержательным задачам.
224 '

Пример 61. Найти общий вид дифференциального
уравнения, допускающего группу вращений с центром
в начале координат.
При повороте на угол а всякий касательный элемент
преобразуется так, что его новое направление
оказывается повернутым по отношению к исходному также на
угол а (рис. 84), т. е. его угол с радиусом-вектором
Рис. 83 Рис. 84
остается неизменным. Следовательно, поле направлений
(дифференциальное уравнение) допускает группу
вращений, если угол между направлением поля в любой точке
и ее радиусом-вектором является функцией только
расстояния от этой точки до начала координат. Значит,
тангенс этого угла есть некоторая функция расстояния (или
его квадрата х2-)-//2). Тангенс угла наклона поля
направлений равен у\ тангенс угла наклона
радиуса-вектора— у/х; искомый угол есть разность двух этих углов.
Пользуясь формулой тангенса разности, получаем
уравнения, допускающие группу вращений:
8 Зак. 641
225

где / — некоторая произвольная функция, или, разрешив
относительно производной:
Задача 173. Найдите все дифференциальные уравнения, дону-
екающие одно пара метрическую группу гомотетий.
Задача 174. Найдите вес дифференциальные уравнения,
допускающие одиопараметрнческую группу спиральных подобии,
описанную в задаче 171.
Оказывается, что если для некото-
Интегрирование Рош Дифференциального уравнения
дифференциальных известна однопараметрическая груп-
уравненнй па симметрии, то можно сделать
с известной группой такую замену координат, после ко-
симметрии торой переменные разделяются. При
нахождении новых координат
используется понятие инварианта группы преобразований
(см. главу «Орнаменты»). Рассмотрим его для случая
одиопараметрических групп преобразований плоскости.
Напомним, что инвариантом группы преобразований
называется всякая функция, постоянная на орбитах этой
группы, т. с. такая функция, значения которой в точках А
и В совпадают, если точка А может быть получена из
точки В некоторым преобразованием рассматриваемой
группы. Ясно, например, что функция у, сопоставляющая
каждой точке плоскости ее ординату, является
инвариантом группы переносов вдоль оси х. Действительно, у
точек, полученных друг из друга переносом вдоль оси х,
ординаты совпадают. Инвариантом этой группы является
также произвольная функция /(*/), так как всякая
функция инварианта снова является инвариантом. Нетрудно
заметить, что функция у в этом примере представляет
собой универсальный инвариант: ее значения на всех
орбитах различны и, следователыю, любой инвариант
226

группы переносов по х для некоторой функции / имеет
бил f(y). Аналогично функция х является универсальным
инвариантом группы переносов вдоль оси у.
Универсальным инвариантом для группы гомотетий,
рассматриваемой на плоскости с выброшенным началом
координат, хотелось бы назвать полярный угол q>.
Действительно, на каждом луче, выходящем из начала
координат, угол ф принимает одно и то же значение (см.
рис. 82,6), причем разным лучам соответствуют разные
значения <р. Следует, однако, отметить, что угол ф не
является однозначно определенной функцией на
плоскости: точке (—1, 0) можно с равным успехом сопоставить
углы 180° и —180°. Можно, конечно, условиться брать
значения полярного угла ф так, что 0° ^ ф < 360°, но
тогда полученная функция ф будет разрывной, что не
очень приятно. На самом деле непрерывного
универсального инварианта группа гомотетий не имеет. Функция
у/х, определенная при х ф О, является инвариантом
группы гомотетий на своей области определения.
Задача 175. Найдите какой-либо инвариант группы вращений с
центром в начале координат. Обладает ли эта группа универсальным
инвариантом?
К проблеме нахождения инвариантов данной однопа-
раметрической группы преобразований существует два
подхода. Первый (формульный) состоит в следующем.
Предположим, что группа преобразований задана в
координатах парой соотношений вида (57). Тогда задача
заключается в том, чтобы из выражений ц>(х, у, t) и
ty(x, yt t) составить такую комбинацию, в которой
переменная t уничтожается, т. е. подобрать функцию Л(ф, \\)),
не зависящую от t.
Второй подход — геометрический. На плоскости
проводят некоторую кривую, пересекающую каждую орбиту
8*
227

ровно в одной точке (рис. 85). На этой кривой
определяют произвольную функцию, принимающую различные
значения в разных точках кривой, а затем доопределяют
эту функцию на всей плоскости, полагая ее значение
в точке А равным, по определению, значению этой
функции в точке В, в которой орбита пересекает выбранную
кривую.
Рис 85 Рис. 86
Пример 62. Найти инвариант однопараметрической
группы преобразований, заданной формулами
Ух = е*У- I
Искомый инвариант нетрудно найти «формульным»
способом. Действительно, выражение егу • е-(*+') не
зависит от t, поэтому функция уе~х является инвариантом.
Построим этот инвариант также из геометрических
соображений. Орбиты данной группы показаны на рис. 86.
В качестве кривой, пересекающей каждую орбиту в
одной точке, можно взять прямую — ось у. Функция
v = у принимает различные значения в точках этой кри-
22В

вой. Для того чтобы определить значение этой функции
в произвольной точке A(xt у) плоскости, проведем
через А орбиту данной группы до пересечения с осью у
в точке В (О, v). Из уравнений группы получаем: х± — t,
tji = elv при некотором t Отсюда находим v = yte-ъ.
Значение искомой функции в точке А равно ее
значению в точке В, т. е. v = ye~x. Таким образом, искомый
инвариант есть функция #е-*.
Задача 176. Найдите инвариант группы спиральных подобий,
описанной d задаче 171 двумя способам».
Рассмотрим, наконец, вопрос об использовании одно-
параметрических групп симметрии дифференциальных
уравнении при их интегрировании. Оказывается, что если
известна одиопараметрическая группа симметрии
дифференциального уравнения, то следует перейти к новым
переменным, одна из которых является инвариантом
данной группы. После такой замены часто (но не
всегда!) переменные разделяются и, значит, уравнение
можно решить. Так обстоит дело с уравнениями вида if =
= f(x) и tf — fiy), при решении которых переходить
к новым переменным не нужно, ибо х и у обладают
указанным свойством (в первом случае х, а во втором у есть
инвариант соответствующей группы переносов).
Рассмотрим задачу, которая часто встречается в приложениях.
Пример 63. Найти общее решение дифференциального
уравнения вида
if - Ш1*). (61)
Уравнение (61) называют однородным. Как известно
из результата задачи 173, однородные уравнения
инвариантны относительно однопараметрической группы
растяжений с центром в начале координат. Поскольку
выражение у/х является инвариантом этой группы, примем
его за одну из новых переменных (зависимую); незави-
229

симой переменной по-прежнему будем считать х. Таким
образом, полагаем, что v = у/х или у = xv. Отсюда
if = v -\-xv\ и, подставляя в уравнение (61) значения ij
и у, получаем v + хх/ = f(v) или vr = JJELzlL.
Переменные действительно можно разделить!
Задана 177. Доведите до явного ответа рассуждения
предыдущего примера в случае уравнения у' = 1 -}- 2у/х.
Задача 178. Раздели ются ли переменные н уравнении (61) при
нереходе к полярным координатам?
Задача 179. Модифицируйте рассуждения, использованные в
примере 63 применительно к уравнению вида
„г _ f / ах+Ьу + с \
У ~4Q^ + &^ + cW*
Следует отметить, что указанный выше способ
интегрирования дифференциальных уравнений е известной
группой симметрии не всегда приводит к успеху (т. е.
к разделению переменных). Например, если в
уравнении (60), допускающем группу вращений, перейти к
полярным координатам, получится уравнение с
разделяющимися переменными: udvfda = f{v). Если же сделать
замену по формулам и = х, v — х2 + Уг (вторая
функция— инвариант!), то разделить переменные не удастся
(проверьте это). Таким образом, недостаточно, вообще
говоря, правильно выбрать одну из новых координат;
разделение переменных зависит также от выбора второй
координаты.
Чтобы получить универсальное правило
интегрирования дифференциального уравнения с известной однопа-
раметрической группой симметрии, постараемся найти
новую криволинейную систему координат (и, v) так,
чтобы в ней преобразования данной группы выглядели
как можно проще, а именно, являлись переносами вдоль
одной из осей координат, например и. Общий вид урав-
230

нений, выдерживающих группу переносов по
независимой переменной, нам известен: это уравнения dvfdu =
— ф(и). Переменные здесь, очевидно, разделяются.
Остается понять, как же построить требуемую систему
координат.
Пусть функция v — инвариант данной однопарамет-
рической группы G ={gi}, так что орбиты последней
описываются уравнениями v — v0 с различными значениями
величины ио- Выберем кривую К, пересекающую каждую
орбиту группы в одной точке и не касающуюся их (при
этом, возможно, нам придется рассматривать не все
орбиты, но лишь орбиты, заполняющие некоторую область
плоскости). Примем кривую К за ось v новой системы
координат, т. е. будем считать, что на ней и — 0. Тогда,
чтобы получить точку Л с координатами («о, щ),
необходимо взять на кривой К точку В с координатами (0, v0)
и подействовать на нее преобразованием gV9. Таким
образом, одно семейство линии новой координатной сетки
(жирные линии на рис. 85)— суть орбиты группы G,
а другое (тонкие)— сдвиг кривой /( под действием
преобразований группы.
Если вместо определенной выше функции и взять
другую координатную функцию wf линии постоянства
которой w = w0 такие же (т. е. сдвиги кривой К), то мы
также получим разделение переменных, ибо в этом случае
w = w(u) и уравнение dvfdu = ф(и) примет вид dv/dw =
= Ф(у)"Ф(ш).
Сформулируем полученный результат.
Теорема о разделении переменных. Пусть известна
однопараметрическая группа симметрии G = {gt}
некоторого дифференциального уравнения. Тогда данное
уравнение допускает разделение переменных в любой системе
координат (и, v) такой, что координатные линии v =
= const — суть орбиты группы G, а линии и = const
переходят друг в друга под действием преобразований gt.
231

Пример 64. Проинтегрировать дифференциальное
уравнение у'—-§-(#*-f-a~2).
Заметно, что если у умножить на некоторую
постоянную kr а х — на А-1, то вид уравнения не изменится.
Поэтому данное уравнение допускает следующую одно-
параметрическую группу преобразований:
У1 = е{У- I
Рас. 87
Ее называют группой гиперболических поворотов.
Орбитой любой точки будет ветвь гиперболы ху = а
(рис. 87). Произведение ху является инвариантом этой
группы. Поэтому в качестве одной из новых
координатных функций возьмем v = ху. Заметим теперь, что
вертикальные прямые х = const переводятся друг в друга
преобразованиями группы G. Действительно, образ прямой
232

x — Хо есть прямая х = е~1Хо. Поэтому в качестве
координаты и можно взять просто х. Итак, искомая замена
и — х; \
v — xy.j
Применим ее к данному уравнению. Имеем
, v _2t>8-f5H-2
' и ~ 5и
Разделим переменные: ^.^.л — -g^-. Осталось взять
интегралы от левой и правой частей (левую часть при
этом полезно представить в виде -j- ( р4-1/2 Т~2)):
2 -С«3/5.
о + 2
Подставляя сюда и, v. получаем ответ: #~ гге
2(*—С*8'5)
2
. Это общее решение данного уравнения в области
#>0.
Задача 180. Найдите общий интеграл уравнения у'= (x+y2)j(xy).
Наконец, рассмотрим еще одно уравнение, в котором
разделить переменные заменой только х или только у
невозможно.
Пример 65. Решить дифференциальное уравнение
У ™ (рВ_дЛ)а + 5& — *) + 4'
233

используя однопараметрическую группу симметрии
_ е1 + е~* с'-е-'
xi — g Х ' 2 ^'
i/i = —2—* "*—\—J-
Эти преобразования представляют собой не что иное,
как уже рассмотренные гиперболические повороты, но
в системе координат, повернутой на 45°. Инвариантом
группы является функция v = у2— хг (проверьте!).
Заметим, что семейства вертикальных и горизонтальных
прямых не выдерживают преобразований группы, так что
выбор и = х или и = у не приводит к успеху.
Оказывается, однако, что линии у — х = const переходят друг в
друга. Положим и = у — х. Тогда, согласно формуле,
dv _ 2 (tjdy — xdx) _ 2{yi/ — x) ~ , у — х
du """ dy — dx "~ if —I y^ y' — 1
__ 5p —t>a~-4
"~ и
Переменные разделяются! Интегрируя обе части равенст-
ва [ ■ —- ■ _. )dv — , получим решение
исходного уравнения (в неявном виде):
/уг_Л*-4 -С^ А> *
Задача 181. Проинтегрируйте уравнение у' = уЧ~* — у + е* с
помощью группы симметрии Xi <=* *" +*, #iв* £'#-
Итак, если известна однопараметрическая группа
преобразований обыкновенного дифференциального
уравнения первого порядка, то его можно решить. «Это, однако,
никоим образом не означает, что можно
проинтегрировать любое дифференциальное уравнение Xdy— Ydx — 0.
234

Трудность состоит в том, что для интегрирования такого
дифференциального уравнения нужно найти одноиара-
метркческую группу, которая оставляет его
инвариантным». Эти слова, которыми мы заканчиваем главу,
принадлежат выдающемуся норвежскому математику Со-
фусу Ли (1842—1899), создателю теории симметрии
дифференциальных уравнений. Следует отметить, что со
времен С. Ли положение несколько изменилось:
усилиями математиков последнего поколения созданы новые
мощные методы исследования дифференциальных
уравнений на основе понятия симметрии, и в частности
методы нахождения симметрии заданных уравнений.
Однако рассказ об этом выходит за рамки этой книжки.

ЕЩЕ НЕСКОЛЬКО ЗАДАЧ
Предлагаем читателю самостоятельно найти решения следующих
задач, связанных с обсуждаемыми в книге вопросами.
1. Существует ли прямоугольный треугольник с целыми
странами, ни одиа из сторон которого не идет по линиям квадрзТЕЮй
сетки, а вершины лежат в ее узлах?
2. На сторонах АВ и ВС треугольника ABC выбираются
точки М н N. Найдите множество середин отрезков MN.
3. Пусть ABCD— произвольный четырехугольник, /(, Lt M, N —
центры тяжести треугольников BCD, ACD, ABD, ВСА. Докажите, что
четыре прямые, соединяющие середины противоположных стороп п
четырехугольнике A BCD н в четырехугольнике KLMN, пересекаются
п одной точке,
4. На сторонах выпуклого четырехуголышка как на основаниях
построены во внешнюю сторону квадраты, центры которых
обозначены М, rV, Р, Q. Докажите, что середины диагоналей
четырехугольников MNPQ и ABCD образуют квадрат.
6. Докажите, что если zv ■+• zt -f- . . . + zn = 0, то среди
комплексных чисел zt, %г, ^ - -, 2,i найдется два таких, у которых
аргументы отличаются не менее, чем на 120°.
6. Нанднте сумму k-x степеней корней уравнения хп —1=0.
7. Комплексное число % является корнем многочлена f(x)=>
= xv -f- aix"-1 + .. . + Cit с действительными коэффициентами,
причем 1 > ai > oz > .. - > fln > О, |Я| > L Докажите, что Я —
корень степени п из единицы,
8. Функция d(x, у) определена равенством d(x. у) --
— -./1 . ^гг; а • Докажите, что d(x, y)+d{y, z)> d(x, г).
У 1 + *3 У I Ч- у3
9. Дан произвольный центрально-симметричный шестиугольник.
На его сторонах как на основаниях построены по внешнюю сторону
правильные треугольники. Докажите, что середины отрезков,
соединяющих вершины соседних треугольников, являются вершинами
правильного шестиугольника.
10. Сколько ocefi симметрии может' иметь шестиугольник?
семиугольник?
11. Дан угол и точка М внутри его. Постройте отрезок с
концами на сторонах данного угла, середина которого находилась бы
в точке М.
236

12. На биссектрисе внешнего угла С треугольника ABC взята
точка Л!, отличная от С. Докажите, что MA -|- MB >■ СА -|- СВ.
13. Даны прямая MN и две точки А и В. Постройте ка прямой
такую точку К, что АЛКМ = 2/LBKN.
14. У борта прямоугольного бильярда стоит шар. В каком
направлении надо его толкнуть, чтобы он, отразившись от трех бортов,
лопал в начальную точку? А если шар не стоит у борта?
15. Докажите, что площадь четырехугольника не превосходит
полусумму произведений противоположных сторон.
16. Докажите, что выпуклый центрально-симметричный
многоугольник можно разрезать на параллелограммы.
17. В трапеции ABCD ADftBC, М —точка пересечения
биссектрис углоо А и В, N — точка пересечения биссектрис углов С и D.
Докажите, что 2MN = \АВ -[- CD — BC — AD\.
18. Точка М лежит на диаметре АВ окружности. Хорда CD
проходит через М и пересекает АВ под углом 45°. Докажите, что сумма
СМг + DM2 не зависит от выбора точки М.
19. Можно ли 31 прямоугольником I X 2 закрыть шахматную
доску 8 X 8, от которой отрезали моля а\ и Л8?
20. Т-образная фигура составлена из четырех квадратов 1X1.
Можно ли девятью Т-образными фигурами закрыть квадрат 6X6?
21. Можно ли девятью полосками 1 Х4 закрыть квадрат 6 X 6?

ВМЕСТО ЗАКЛЮЧЕНИЯ
Закончен наш рассказ о преобразованиях плоскости
и их приложениях. На хорошо знакомом материале мы
постарались раскрыть и проиллюстрировать ряд важных
понятый современной математики, сконцентрированных
вокруг идеи группы преобразований. Надеемся, что
знакомство с этой книгой побудит читателя к дальнейшей
работе. Самым юным мы рекомендуем вышедшую в
серии «Библиотечка «Квант» увлекательно написанную
книгу О. Оре из приведенного ниже списка. В книгах
Г. Вейля и Л. В. Тарасова обсуждаются сущность и
проявления идеи симметрии, ее роль в науке и искусстве.
«Классическое» сочинение Г. Радемахера и О. Теплица —
своеобразная «математическая хрестоматия»-— содержит
несколько этюдов на тему симметрии. Идеи симметрии,
группы преобразований связывают воедино популярное
изложение Г. С. М. Кокстером основ почти всех разделов
геометрии. Богатую подборку задач на геометрические
преобразования содержит книга И. М. Яглома.
О великом русском математике Н. И. Лобачевском и
о созданной им геометрии рассказывается в вышедшей
к 150-летию ученого книге Б. Л. Лаптева. Связи
геометрии с группами преобразований можно изучать по книге
В. В. Никулина и И. Р. Шафаревича. Основные понятия
теории групп излагаются П. С. Александровым, И.
Гроссманом и В. Магнусом, В. Б. Алексеевым. Книга
В. Б. Алексеева знакомит также с комплексными
числами, функциями комплексной переменной и связанными
с ними группами Галуа. Элементарные функции
комплексной переменной рассматриваются в книге А. И. Мар-
кушевича. М. М. Постниковым изложена теория Галуа.
Этой же темы, а также анализа различных комбинатор-
238

ных игр, в том числе и кубика Рубика, касаются в своей
книге Л. А. Калужнин и В. И. Сунданский. Различного
рода комбинаторные задачи приведены в книге Н. Я. Вн-
ленкина* Для знакомства с геометрическим подходом
к теории дифференциальных уравнений советуем
использовать первые главы книги В. И. Арнольда. Наконец,
невозможно не порекомендовать уникальный по
богатству идей сборник задач московских математических
олимпиад.
Мы указали лишь несколько тропинок, ведущих в
богатый и разнообразный сад математики. Авторы желают
каждому лз вошедших в этот сад подобрать букет по
своему вкусу.

ОТВЕТЫ И УКАЗАНИЯ К ЗАДАЧАМ
1. Может. Рассмотрите треугольник, вершины которого имеют
координаты: (0, 0), (12, 9), (24, —7).
2. Для начала попробуйте решить задачу с помощью прямого
построения. Если не получится, воспользуйтесь результатом
задачи 6 и выразите произвольную
точку фигуры Ф через
вершины данных треугольник».
Многоугольник Ф имеет 3, 4, 5
или 6 сторон.
3. Тогда и только тогда,
когда k'-'l— 1. Представьте
данное выражение в виде Av\-
+Л2—Bi-\-Az—Вг+ ... н
воспользуйтесь замечанием па с. 13.
4. Из примера 2 следует,
что эта задача равносильна
следующей теореме (Эйлера):
при гомотетии с центром в
точке пересечения медиан М и
коэффициентом —2 центр О
описанной окружности пере*
ходит в ортоцентр Н. Для
доказательства этой теоремы
нужно заметить, что середин*
совпадают с высотами ААВС
Рис. 88
AAiBiCi
4- й — 1 • Рассмотрите векторное равенство
кыс перпендикуляры
.(рис 88).
5. а-г-р-г-
аРА + $РВ +
-f ...+ю)Р$.
6. Это множество всех точек вида cHi + агАг -f-... + апАп, где
«i + й% + •.. -f- яп = I.
7. 0. Выразите через точки А, В, С, D середины указанных в
условии отрезков.
8. Выразите эти точки через точки Л, В, С, D, £, F.
10. Для каждого из перечисленных отрезков выразите точку,
делящую его в отношении 3 :1, через А, В, С, D.
11. Возьмите за полюс точку пересечения двух медиан и
воспользуйтесь примером 2.
240

12. 1/7. Возьмите одну нз вершин параллелограмма за полюс,
дое другие — за базисные н выразите точку пересечения этой прямой
с диагональю двумя способами.
13. у = Ь; х = а-, ау = Ьх.
14. Объединение трех медиап.
15. 16. Возьмите точку К за полюс, а точки А и В— за базисные.
Через координаты {а, Ь) точки С выразите координаты точек D, Е, i\
17. Примите середину стороны АС за полюс, а точки А и В —за
базисные. Покажите, что точки описанного в задаче множества
удовлетворяют уравнению вида ау ■= Ьх, и используйте результат
задачи 13в.
18. Ни в том ни в другом случае множество вершин не является
замшгутым.
19. Разложите точку К (0, 1) по базису Е, А н докажите, что
/<* в= — Я. Следовательно, это умножение совпадает с умножением
комплексных чисел (чтобы сделать этот вывод, вам нужно
прочитать еще несколько страниц). Представляя вершины пятиугольника
в тригонометрической форме, получаем такую таблицу умножения:
Е
А
В
С
D
Е
Е
А
В
С
D
А
А
В
С
D
Е
В
В
с
D
Е
А
С
С
D
Е
А
В
D
D
Е
А
В
С
20. а) 0; б) ±(1 — 2(); в) —-1 (заметьте, что куб этого числа
равен —I).
21. а) окружность радиусом 5 с центром в точке —3;
б) серединный перпендикуляр к отрезку [—4; 2«'J;
в) окружность (воспользуйтесь тождеством | т |2 +1 п \г = -— X
X(|'H-f-n|2-f-jm — «|2), где m н п — комплексные числа).
22. Сумма, стоящая в левой части неравенства, есть длина
некоторой ломаной, соединяющей точки 0 и 5 -f- 5f на плоскости. Восполь-
241

зуйтесь тем, что сумма чисел *i +(1 ~Хг)1, (1 ~ *») + X&, .,., хъ +
+ (1 —x\a)i, (1 — л"») + Х1п/ равна 5 -Ь 5f.
23. 0°, 90", 180°, 270°, 45е, 330°.
24. а) см. рис. 89; б) (г— 2) (г— 2 — |sin3<p|) = 0, (^з.}./у2_
(х2 -f- ifft2
■н-
Рас. 89
25. Покажите вначале, что z = cos ф ± I sin ф.
2G. 2п; следуйте примеру 9.
27. Рассмотрите аргумент числа ... а — ~ g £ZZ£. °~~g. x
С—a d — а е — а 6 —е
а — Ь
28. Еслн точка 2 лежит вис многоугольника, то аргументы вскх
разностей 2 —ЛЛ, а следовательно, и всех чисел 1/(г — ЛЛ) попадают
в один промежуток величиной 180°.
29. Используйте дбэ переноса.
SO. Сначала параллельным переносом сдвиньте треугольник так,
чтобы концы данного отрезка оказались на его сторонах.
ЗК Сделайте перенос на вектор ВС (ВС — основание трапеции)
и рассмотрите треугольник ACD', где DD* = ВС.
242

32. Используйте два отражения от сторон утла и пример 3.
S3. Воспользуйтесь тем, что точки, симметричные вершине
относительно двух других биссектрис, лежат на противоположной стороне
(или ее продолжении).
34. ]80°/Л1 п ^ 2. «Перекатите» угол по плоскости четыре раза
и сравните действительный ход луча с прямой, на которой
расположен входящий луч,
35. Разрежьте каждую фигуру вдоль вертикальной оси
симметрии.
36. Покажите, что получившиеся точки лежат в вершинах
правильного многоугольника.
37. Используйте поворот на 60° с центром на средней прямой,
38. Пусть К—такая точка, которая переходит в М при
повороте квадрата на 90° вокруг центра (при котором А переходит в В).
Покажите, что А К ± ВМ, ВК -L СМ, СК ± DM, DK ±АМ.
39. Используйте разворот вокруг точки пересечения окружностей,
40. Первый игрок выкладывает монету в центр и затем
использует симметричность.
41. По аналогии с выводом формулы (2) используйте поворот
вокруг точки пересечения прямой с осью х.
42. Введите на плоскости подходящую комплексную структуру.
43. Тождественное преобразование. Используйте формулу (7).
45. Легко проверит!., что R^ ° RJ/° RP ° Rq = id (см. рис. 39).
Запишите это условие с помощью комплексных чисел и убедитесь,
что это возможно лишь тогда, когда отрезки MP и NQ взаимно
перпендикулярны и раины.
46. Используйте пример 21. Отоет: a) RB°RA"^йЗя*
б) St ° RA —скользящее отражение с осью ЛК. и вектором 2АК,
где К—основание перпендикуляра, проведенного из точки А к
прямой /.
47. Используйте композицию пяти разворотов относительно
последовательных середин сторон. Убедитесь, что получается разворот
и его центр — одна из вершин пятиугольника.
48. Найдите ось скользящего отражения, получающегося при
композиции трех отражений, н через данную точку провед1Гте
прямую, параллельную осн.
49. Используйте результат задачи 41.
50. Нет. При каждом ударе меняется ориентация тройки шайб.
51. 23. Используйте определение аргумента.
52. a) RA*S, = SI»RA; б) RacRc = Rc°Rb'
53. а) см. задачу 52а; б) прямые /, т, п пересекаются в одной
точке,
243

54. Точки, принадлежащие этому узору, можно получить из
точек Лх(5, 3), Л2(7, 2), Д»(3, 1), Д,(4, -I), А-,(2, 9), Д,(3, 10)
-*--»■-♦• ^
переносами на всевозможные векторы fca-^lbt где я =(—б, 12), b =>
= (12, —6), ft, /e=Z. Так, например, из точки Л» получаются точки
с координатами (5 — 6М- 12/, З-f- 12Л — 6/), где k, I — яепые числа.
55. а) да; б) да, ибо Syru(A)= id; в) нет.
56. Пусть g е= G. Тогда, согласно свойству 2), g~l e G, а
согласно свойству 1), g~l »g = id e G.
57. Движение полностью определяется образами трех точек, не
лежащих на одной прямой.
58. Бее stu группы различны.
59. Воспользуйтесь результатом примера 21.
60. а) да. Наприг.5ер, ромб; б) нет. Убедитесь, что если при
разворотах RA и Ru фигура переходит в себя, то она переводится в
себя и при развороте Re, где C = Rb(A) (сравните композиции
RboRa и RcoRb).
61. Окружность — «королева геометрии», в частности точка С
(«окружность нулевого радиуса»), или объединение концентрических
окружностей.
62. Ответ представлен в таблице
'Л*
а
«5
Si
ь
а
sr-40
UTfil)
RPla)
S а
sm
т ->
о—а
ssmw
'-'in
T +
Ubm<A)
m '
63. Таблица умножения для группы D3 приведена на с 93.
64, В каждой группе тождественное преобразование
коммутирует с любым, все пары одинаковых преобразовании, разумеется,
244

перестановочны, кроме того, в группах /)„ коммутируют все
попороты. Б группе Ds других коммутирующих преобразованкГ» нет, а
в группе Dt. к ним добавляются отражения от взаимно
перпендикулярных осей.
65. Проверьте равенство {/"*')* *fh *= id.
66. Порядос элемента fh равен частному от деления п на НОД
Oh *).
67.0) ф(т)•='«(! — 1/jpi)...(I — lllh), где ри .... /)* — все
различные простые делители т.
08. Нет. Например, подходящим обраяом расположенная прямая.
69. Композиция из п поворотов /?5 даст тождественное
преобразование, если результирующий угол поворота кратен 360°, т. е.
па = 360°/и, откуда а = Л- 360°.
и.
70. Всякое слово можно заменить равнозначным ему словом вида
ЕУУ ... УАА ... АЫЫ ... Ы, где k, I» т могут изменяться от 0
к I m
до 6.
71. Например, отражения 5А и Sz, удовлетворяющие
соотношениям sf = S| — (Sj« S2)" — id.
72. Убедитесь, что ни одно из движений не может быть
разворотом.
78. 1) нет: —У5 -J- )Лз^- чнсло не иррациональное; 2) да;
3) да; 4) нет: (3/4)-1 = 4/3.
74. Решением является элемент х = Ьа~1.
75. Убедитесь, что эта операция ассоциативна.
76. Воспользуйтесь аналогией с примером 34.
77. Например, сумма квадратов всех функции, полученных в
задаче 76.
78. Да.
79. Элементы Sa, S&, Sc можно переставюь в любом порядке.
Таким образом, получается шесть изоморфизмов.
80. Убедитесь, что при выбранном базисе соответствие,
сопоставляющее каждому вектору его координаты, является взаимно
однозначным, и при этом координаты суммы векторов равны суммам
соответствующих координат слагаемых.
82. Двумя способами.
84. Да. Изоморфизмом является соответствие /е-^-*-2Л.
85. Изоморфны только группы Dt н Cj.
86. Так как е* = q>(t?) = q>(g - g~')= Ф(£)ф(#-1) = л ■ Ф(£"'), то
ф(£~') = Л"1. Поэтому q>(g-") = Ф(§-1)" = (л-1) *» - Л-п.
245

87. Занумеруйте вершины правильного треугольника.
88. Если уи уг—логарифмы Непера чисел Xi, x*t то логарифм
Непера числа Х|*2 есть yi + 'jz — В; yi*yz = УхЛ-Цг — В.
89. б) если М — группа по сложению, содержащая открытый
интервал ]«, р[, то М содержит все действительные числа.
90. a) x*y — y/&-\'tf-t б) умножение перенесено с. помощью
отображения у = х — I.
91. В группе £>3 три подгруппы порядка 2 и по одной —
порядков 1, 3 и 6.
92. Есть. Это число —1.
93. Убедитесь, что подгруппа в Z порождается своим
наименьшим положительным элементом.
95. Нет: 2*3=6^0.
9G. Да. Составьте таблицу умножения.
97. Каждое целочисленное решение уравнения хг= 3#24-8
является решением уравнения л2 ся 3#24-8(mod3) или jc2=2(tnod3).
Однако последнее сравнение решений не имеет.
98. Воспользуйтесь теоремой Ферма.
99. 21. Требуется найти такое число х, что 0 г^ х < 100 и х н=?
=з 1987,HSB(mod 100). Воспользуйтесь свойством почленного
умножения сравнений и теоремой Эйлера.
100. Тогда и только тогда, когда т делится на п. Один из
возможных гомоморфизмов задается соответствием U-+U, где слева
стоит класс по модулю т, а справа — класс по модулю п.
101. I/*, 1-х, х, 1/(1 —х), 1 — Цх, xf(x ~ 1). Ср. с
результатом задачи 76.
108. Докажите, что jLOAC «= jLBEF, и рассмотрите поворот
отрезка BE вокруг точки Е, а отрезка АС вокруг А на этот угол.
104. Оба утверждения задачи следуют из того, что определитель
произведения двух матриц равен произведению нх определителей.
105. Да. Нет.
106. Ядро составляют все нечетные функции, а образ--четные,
107. Рассмотрите гомоморфизм ф(2}= г»,
108. Рассмотрите отображение <p(*)= cos 360°*+ t sin360°Jc.
109. Всего 5 орбит.
110. —1, 2, 1/2._
111. 1/2 + г'КЗ/г.
113. а) Д. С, Т; б) Д.
114. 15. а) 2; б) 1; в) 7. Пели совместить первое ребро первой
пары с первый ребром второй пары, то для совмещения вторых
ребер в нашем распоряжении останется только одно движение:
поворот па 180° вокруг реи, проходящей через середину первого ребра,
246

Этот поворот не изменяет положения первого ребра и ему
противоположного, а остальные 10 ребер позволяет совмещать попарно.
На множестве неупорядоченных пар ребер орбит было бы 5.
т
115. ]► „(A. »0f Где ^ mj — наибольший общин делитель
чисел k и т.
116. 60.
117. 16.
118. 30.
119. а) 23; б) 218.
«._£&+iii^±L£L-«.
30
121. Тройка чисел (/«, л, /г), таких, что т—наибольшее число
идущих подряд белых шариков, п и к — число белых шариков слева
н справа (до очередного синего). При этом m + n-f-ft^ 6=^ 2т -\-
+ п -\-k, m ^ n ^ ft, набор (2, 2, 0) не рассматривается.
122. а) признаки равенства треугольников дают примеры
различающих инвариантов; б) инвариантом является набор из длин
сторон и угла (для выпуклых четырехугольников это различающий
инвариант).
123. 124. Проверьте инвариантность ti(S) и JV(S) при действии
шести образующих элементов группы,
125. См. с. 77—78.
126. Воспользуйтесь тем, что бесконечное множество точек на
окружности не является дискретным.
127. Угол величиной 360°/« или 1807ft с вершиной в центре
диэдра.
128. Гео метрический смысл этого условия состоит в том, что
такой параллелограмм, отложенный от тощей А, не содержит внутри
себя и на сторонах точек, принадлежащих орбите А, кроме перший.
129. Используйте таблицу сопряжений.
130. Используя свойство дискретности, выберите среди всех век-
»>
торов переноса, параллельных некоторому направлению, вектор а
наименьшей длины. Отложите все векторы данной группы от одной
-*■
точки А и возьмите второй вектор b так, чтобы его конец был как
можно ближе к прямо!!, проходящей через А в направлении вектора
«* -+■ -*■
а. Докажите, что пара о, Ъ— искомая.
181. Группа порядка 18 с образующими о, Ь, с и соотношениями
а* = Ъ* «= с2 = {oby = (6с)3 = (со)а - (abc)2= е.
132. рА, p4g, pmg; C*. Dit Z)2.
247

134. т/р (при рф 0).
135. Напишите явные формулы для композиции и обратного
преобразования.
136. Проверьте равенство
ft г г
*3~~Х1 . *4~"**1 _ XS — A"i . Хц — Xi
Л"3 — Х2 Х4 — *2 *а — Лй *■* — **
mxt -f- и
если jc,- =s ■ „ , „ .
137. Воспользуйтесь соотношениями (19) на с. 94.
138. Преобразование (30) имеет конечный порядок тогда и толь-
ко тогда, когда ;" 'г<7 -г пр ._cosa Где а — угол, измеряемый
2 (/и<? — пр)
рациональным числом градусов.
139. Легче построит!» треугольник, описанный около данного, со
сторонами, параллельными данным прямым.
140. Используйте гомотетию с центром на внешней окружности
и коэффициентом 3/4.
141. Используйте гомотетию с центром в точке пересечения
медиан и коэффициентом —2.
143. Искомая точка — центр подобия. Убедитесь, что она
находится внутри меньшей карты.
144. Точка £ — центр подобия, переводящего точку А в точку В,
а С—d D.
145. Найдите образы отрезков МС и PN под действием спираль
иых подобий РА(У2, 45s) и FC(V2, 45?) соответсгвенно.
146. 147. Прямая, не проходящая через центр инверсии,
преобразуется в окружность, проходящую через центр инверсии, и обратно.
148. Сведите задачу к случаю, когда одна из линий — прямая,
проходящая через центр инверсии.
149. См. рис. 71.
150. 151. Напишите явные формулы для композиции и
обратного преобразования.
152. (-3, 0).
154, а) у' « 0; б) нет.
1Б6. у — 2х + С, у = sinх + С, у = — 1/х.
150. Для уравнения (35) получаем семейство прямых, для
уравнения (37)—семейство гипербол.
157. Окружности с центром в начале координат. Это поле
соответствует дифференциальному уравнению у' «= — х/у, которое
определено всюду, кроме оси х. На всей плоскости такого
дифференциального уравнения ис существует.
248

158. r/ = l/(C-x).
169. ~v = x-\-y, u = x.
160. у = -хЧЪ-\-хг + Сх.
161. д=[*Ч*\е-*1*ах)Ш
162. i/ = tg(ax+C).
m'U^ x4g(l)x + C) "4
164. Выберите n пз условия — (л + 3)/(л + 4)= — 4.
165. Заметьте, что — = — 1. Отсюда
■* •
q (n) + 2 п+2 4*(«)+2
fz-J-2
166. Замена //о \}(хи) переводит это уравнение п олнородное
(см. пример 63). Другой способ решения указан в формулировке
задачи 181.
167. Согласно формуле (G6), J£_ = У** + *£Jx + 1Ш'), т
168. gt »gt = £,+в = gt+t = fa«gt.
170. a'i •=> x cos / — у sin t, tjt — x sin f + tf cos f.
171. Это группа спиральных подобий. Ее
орбиты—логарифмические спирали с центром в начале координат.
172. Воспользуйтесь теоремой Биета.
17S. //=/(///*).
174. и' = *f№fj , где | в arctg X — A In У'х*4-у*.
x—yfil) х а
175. Функция х*-\- у* — универсальный инвариант.
176. Функция % (см. ответ к задаче 174). ■
177. ц = Сх*~х.
17& Да.
170, Воспользуйтесь группой гомотетий с центром в точке
пересечения прямых ах + Ьу + с = 0 и ахх -f- bty -\- ct => 0,
180. Используйте группу xl=e2ix, yl—e'y. Ответ: // =
— YCx*—2x.
x+C—l v
181. U—
jc 4- с

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Александров П. С. Введение в теорию групп.— М.: Наука,
I9S0.—144 с.
Алексеев В. Б. Теорема Абеля в задачах и решениях.— М.:
Наука, 1976.—207 с
Арнольд В. И. Обыкновенные дифференциальные уравнеЕзи»,—
М,: Наука, 1971.—239 с.
Вейлъ Г. Симметрия.— М.: Наука, 1968.—191 с.
Виленкин Н. Я. Популярная комбинаторика.—М.: Наука, 1975.—
208 с
Гальперин Г. А., Толпыго А. К,- Московские математические
олимпиады.— М.: Просвещение, 1986.—303 с.
Гроссман И., Магнус В. Группы и их графы.— М.: Мир, 1971.—
247 с.
Калужшш Л. А., Сущанский В. И. Преобразоиання н
подстановки.— М.: Наука, 1985.—160 е.
Кокстер Г. С. М. Введение в геометрию.— М.: Наука, 196G,—
648 с.
Лаптев Б. Л. Н. II. ЛобачсискиК и его геометрия.— М.: Проспе-
щеиие, 197й—112 с.
Маркушевич А. И. Комплексные числа и конформные
отображения.—М.: Наука, 1979.—56 с.
Никулин В. В., Шафа^вич И. Р. Геометрии и группы,—М.:
Наука, 1983—239 с.
Оре О. Приглашение в теорию чисел.— М.: Наука, 1980.—128 с.
Постников М. М. Теория Галуа.—М.: Фнз.чатгиз, 1963.—218 с.
Радемахср Г., Теплиц О. Числа и фигуры.—М.: Фнзматгнз,
1962.—263 с.
250

Ст/оарт Яи. Коггцепции современной математики.— Мн.: Выш.
шк., 1980.— 382 с.
Тарасов Л. В. Этот удивительно симметричный мир.—М.:
Просвещение, 1982.—174 с.
Эбботг Э. Э. Флатлаядия, Сферландия.—М.: Мир, 1976.—360 с,
Яглом Л. М. Геометрнчсскис преобразошшия: В 2 т.—М.: Гос-
техиздат, 1955—1956 — Т. 1.—283 с; Т. 2.—611 с.

СОДЕРЖАНИЕ
К читателю , , 3
ВВЕДЕНИЕ 6
ПЛОСКОСТЬ 9
Клетчатая Флатландня 10
Сложение точек 12
Умножение точки па число 16
Центр тяжести . . . * 18
Координаты 21
Умножение точек .. 24
Комплексные числа 29
ДВИЖЕНИЯ 37
Параллельный перенос . 39
Отражения 40
Поворот . . . 43
Функции комплексной переменкой 4(>
Композиция движений 50
Скользящее отражение 57
Классификация движений 59
Ориентация 62
Исчисление инволюций 64
ГРУППЫ 70
Перекатыиание треугольника 71
Понятие группы нреобразований 73
Классификация конечных групп движении ...... 76
Сопряженные преобразования ......... 80
Порождающие элементы .......... 86
Образующие и сооткошешся . 90
Общее понятие группы 98
Изоморфизм 107
Теорема Лагранжа 122
ОРНАМЕНТЫ .133
Гомоморфизмы . 134
Фактор-группа 138
252

Действия групп и орбиты 143
Перечисление орбит 146
Инварианты 153
Кристаллографические группы 158
ПРЕОБРАЗОВАНИЯ 176
Рисование 177
Гомотетия , 182
Спиральные подобии 183
Инверсия 188
Дробио-лпнейные преобразования 102
Плоскость Лобачевского 196
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 200
Обыкновенные дифференциальные уравнения . 200
Замена переменных . . , 207
Уравнение Беркулли 209
Однопараметрнческне группы 219
Симметрии дифференциальных уравнений 223
Интегрирование дифференциальных уравнений с известной
группой симметрии 226
. ЕЩЕ НЕСКОЛЬКО ЗАДАЧ 236
ВМЕСТО ЗАКЛЮЧЕНИЯ 238
Ответы и указания к задачам 240
Рекомендуемая литература 250

Научно-популярное издание
Дужин Сергеи Васильевич
Чеботаревский Борис Дмитриевич
ОТ ОРНАМЕНТОВ
ДО ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Зав. редакцией
Л. Д. Дцхоалов
Редактор
Л. II. Баэулько
Мл. редактор
Я. В. Моховикова
Художник
С. В. Вайченка
Худож. редактор
10. С, Ссргачев
Техн. редактор
ЛГ. //. Кислякава
Корректор
И. И. Ганелес

И Б К» 2530
Сдано в набор 30.ОЯ.87. Подписано в печать 13.С4.8Б. Формат
70X106'/,». Бумага тнпогр. Л& I- Гаржггура литературная. Высокая
печать. Усл. псч. л. 11,2. Усл. кр.-отт. 11,46. Уч.-изд. л. 10,58.
Тираж 18300 лкз. Зак. 541. Цена 50 к.
Издательство «ВыиЫ1шая школ»» Государственного комитета
БССР по делам иэлателыяп, нолпгряфш! н ккпкнсП торговли.
230048. .Минск, проспект Машеровя. 11.
Орлгпа Трудового Крпсиого Знамени типография издательства Щ<
КП Белоруссии. 220MI, AinncK, Ленинский проспект, 71).

Дужнн С. В., Чсботаревскии Б. Д.
Д81 От орнаментов до дифференциальных
уравнений: Попул. введ. в теорию групп
преобразований.— Мн.: Выш. шк., 1988.—253 с: ил.— (Мир за-
кимат. науки).
ISBN 5-339-00101-6.
Книга знакомит с такпглз важными понятиями соврсмсшюП
математики, как группа, инвариант, симметрия дифференциального
уравнения, которые об'ькенхкясм на доступных примерах л связи с оГлдеА
темой геометрических преобразовании плоскости. Поксзздю еди!1Стло
трех основных математических дисциплин: алгебры, геометрии и
анализа. Изложение сопровождается большим количеством упражнений,
среди которых испило задач ог.импиадного характера.
Для студсИтои, учащихся старших классов, всех, иго любит Мате-
МЕТНКУ.
„ 1702040000—049
Д М304(03)-86 10П~88 ББК 22151'5
i