С. Г. КРЕЙН, В. Н. УШАКОВА
МАТЕМАТИЧЕСКИЙ
АНАЛИЗ
ЭЛЕМЕНТАРНЫХ
ФУНКЦИЙ
Ш
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕР
МОСКВА 1963

517.2
К 79
Селим Григорьевич Крейн, Валентина Николаевна Ушакова,
Математический анализ элементарных функций.
М., Физматгиз, 1963 г., 168 стр. с илл.
Редактор А. Н. Копылова.
Техн. редактор Я. Ш. Аксельрод.
Корректор
Сдано в набор 8/IX 1962 г. Подписано к печати 11/1 1963
Физ. печ. л. 5,25. Условн. печ. л. 8,61. Уч.-изд. л. 7,
Т-01508. Цена книги 33 коп. Заказ №
Государственное издательство физико-математическУ,
Москва, В-71, Ленинский проспект, 15;
Типография № 2 им. Евг. Соколовой УЦБ и ПП Ле
Ленинград, Измайловский пр., 29.

ОГЛАВЛЕНИЕ
Предисловие 8
Глава I
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
§ 1. Понятие функции 11
1. Определение функции по Лобачевскому A1). 2. Система
координат A2). 3. График функции и уравнение кривой A3).
4. Однозначные и многозначные функции A6). 5. Область
определения функции A6).
§ 2. Линейная функция у = kx + b 18
1. График линейной функции у = kx A8). 2. График общей
линейной функции B0). 3. Приращение линейной функ-
функции B2). 4. Возрастание и убывание линейной функции B3).
5. Задачи на построение линейной функции B4).
§ 3. Геометрические задачи для двух линейных функций . 26
1. Параллельность графиков линейных функций B6).
2. Точка пересечения графиков линейных функций B6).
3. Угол между графиками линейных функций B7). 4. Пер-
Перпендикулярность графиков линейных функций B8).
§ 4. Линейная интерполяция 29
§ 5. Квадратичная функция 30
1. Симметрия графика функции у = х2 C1). 2. Иссле-
Исследование функции на возрастание и убывание C1).
3. Экстремум функции у = х2 C2). 4. Исследование
графика функции у = х2 на выпуклость и вогну-
вогнутость C4). 5. Функция у = ах2 C5). 6. Уравнение пара-
параболы с вершиной в заданной точке C6). 7. Исследование
общей квадратичной функции у = ах2 + Ьх + с C7).
8. Примеры зависимостей, выражающихся квадратичной
функцией C8).

4 ОГЛАВЛЕНИЕ
§ 6. Кубическая функция 40
1. Исследование функции у *= хг D0). 2. Исследова-
Исследование функции у =* хг + kx D2). 3. Исследование
функции у = хъ + Ьх + Ь D6). 4. Исследование общей
кубической функции у = аох* + а{х2 -\-а2х-\-аг D8).
5. Пример зависимости» выражающейся кубической фун-
функцией D8).
§ 7. Многочлены 49
1. Сравнение графиков степенных функций у = х11 при чет-
четных и нечетных показателях D9). 2. Многочлен. Корни
многочлена. Разложение на множители E0). 3. Поведение
многочлена у = Рп(х) на бесконечности E2). 4. Примеры
графиков многочленов E2).
§ 8. Обратно-пропорциональная зависимость и дробно-ли-
дробно-линейная функция 53
1. Исследование функции у = — E3). 2. Гипербола
с центром в заданной точке E6). 3. Дробно-линейная функ-
функция E7).
§ 9. Дробно-рациональная функция 58
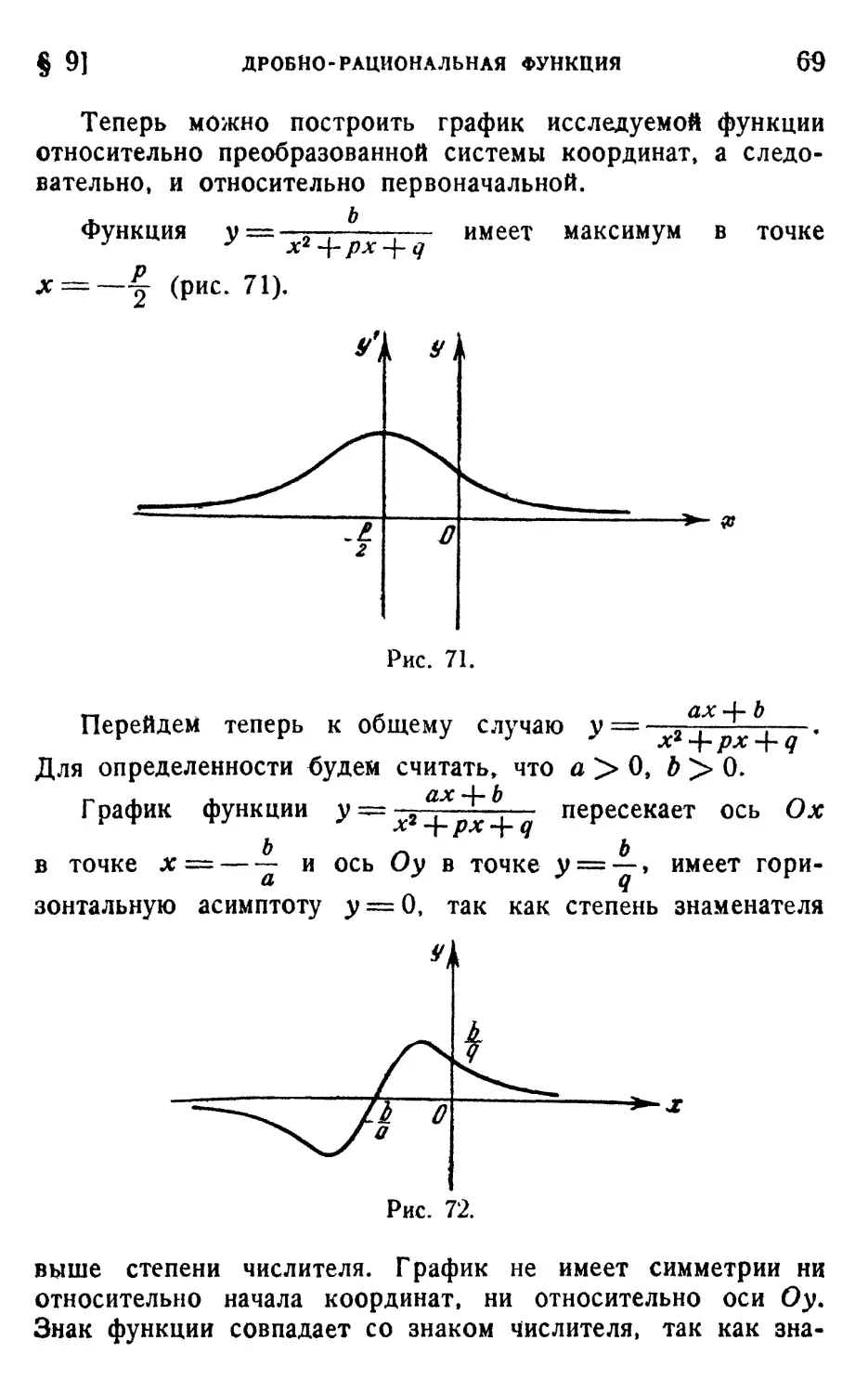
1. Отрицательные степени х E8). 2. Дробно-рациональная
функция F1). 3. Асимптоты графика дробно-рациональ-
дробно-рациональной функции F2). 4. Разложение на простейшие дроби F4).
5. Графики простейших дробей F6). 6. Пример зави-
зависимости, выражающейся дробно-рациональной функ-
функцией G0).
§ 10. Показательная функция 71
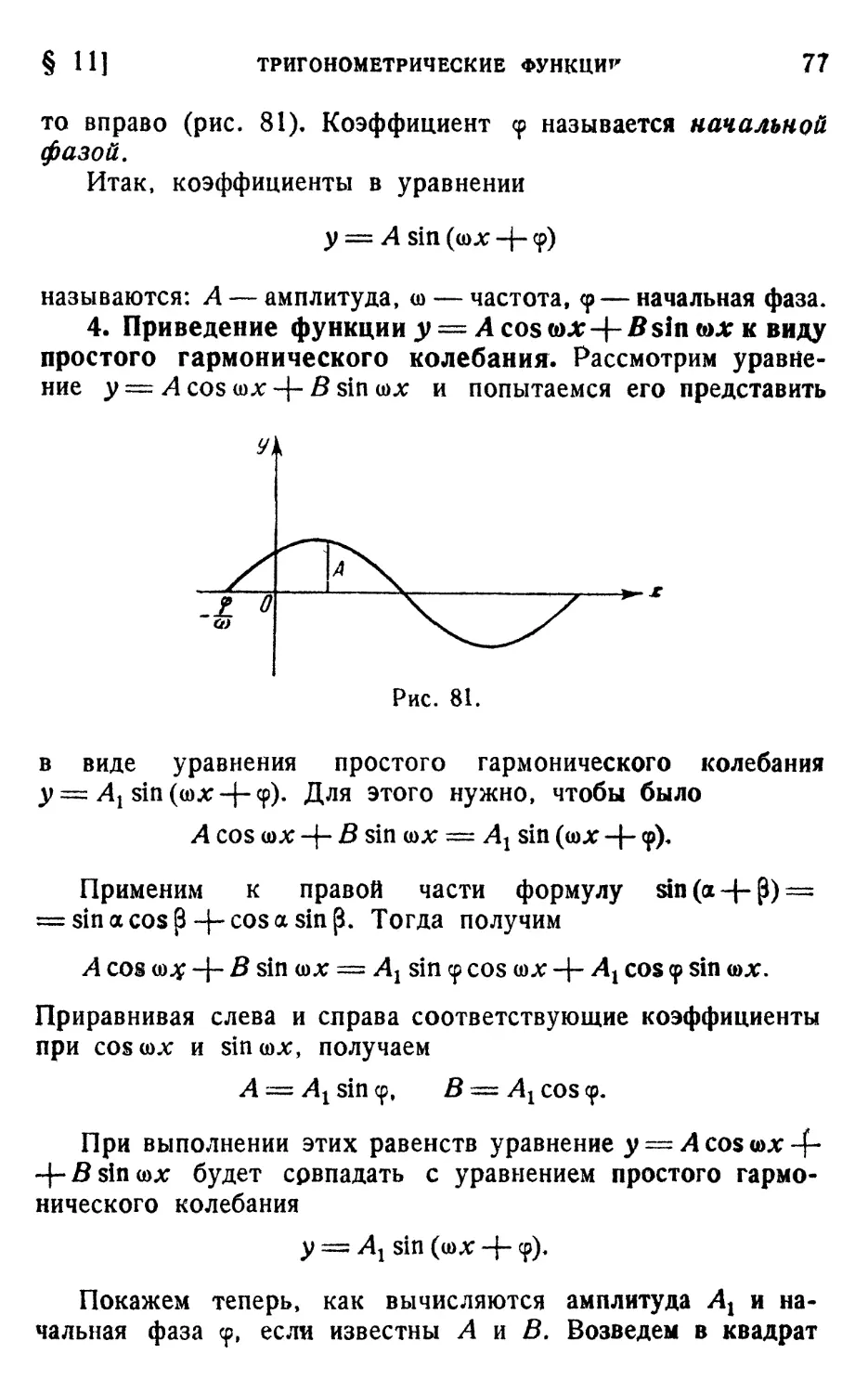
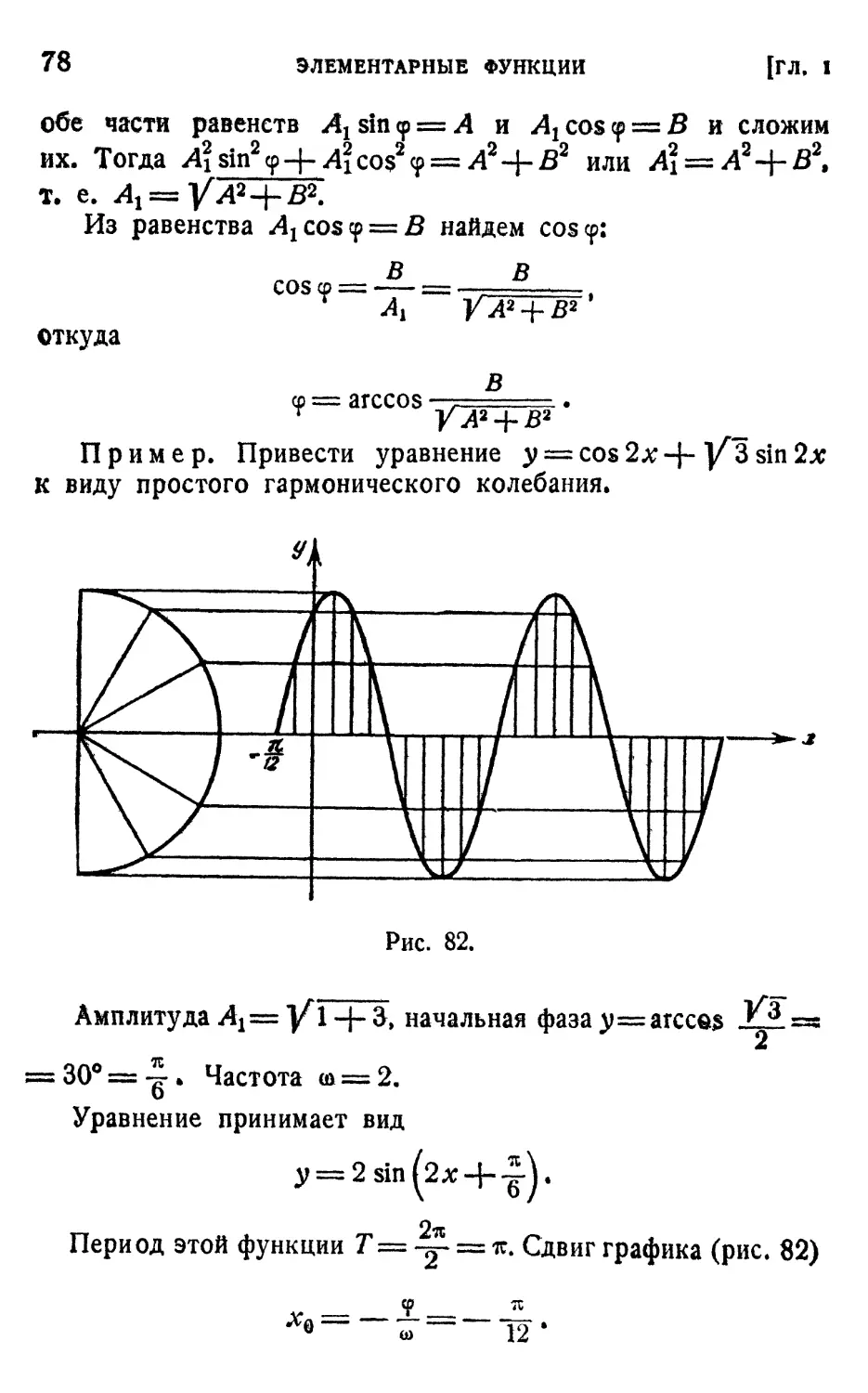
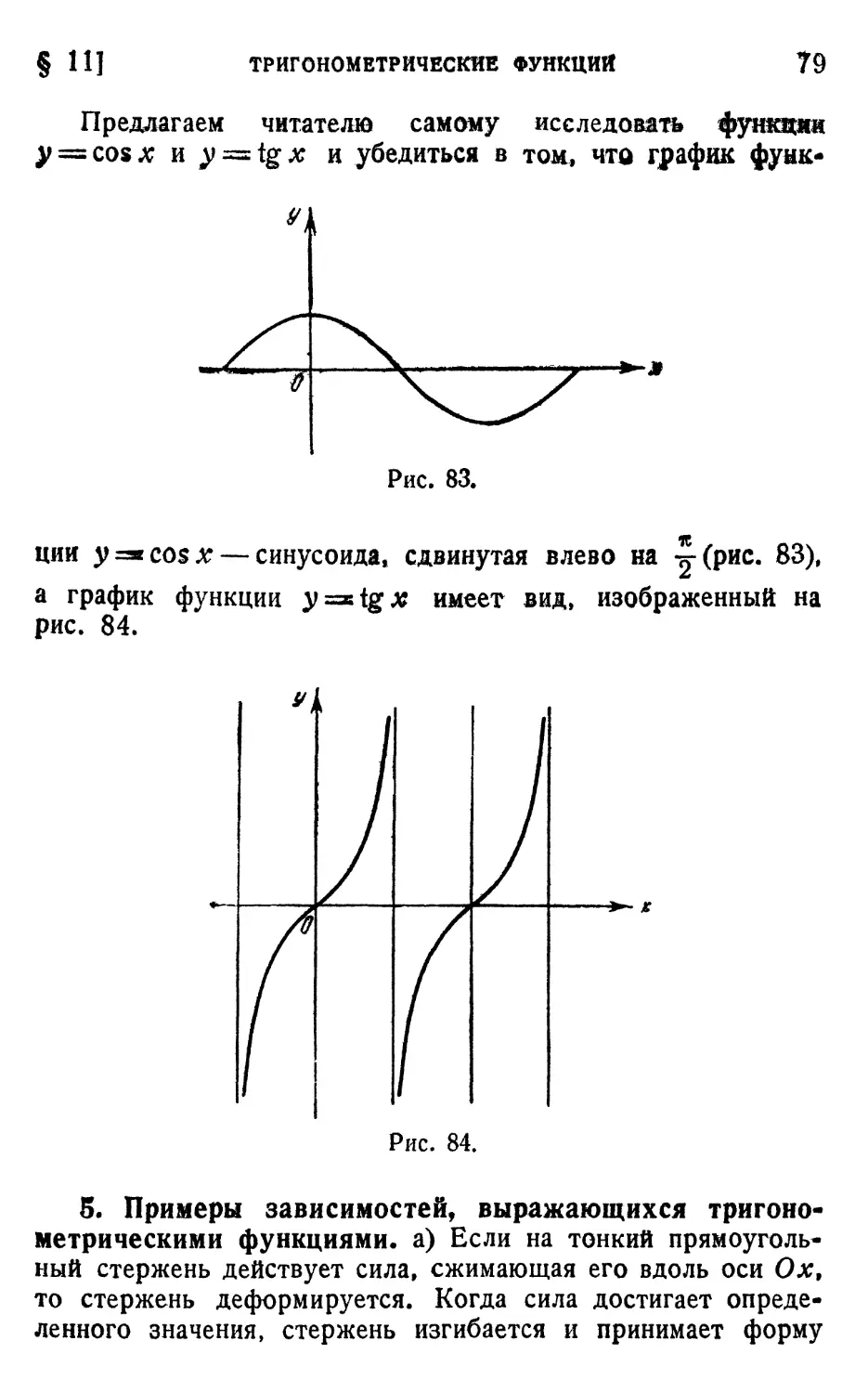
§ 11. Тригонометрические функции 72
1. Исследование функции у = sin x G3). 2. Исследование
функции у = sin &х G5). 3. Уравнение простого гармо-
гармонического колебания G6). 4. Приведение функции
у = A cos odx + В sin ФХ к виду простого гармонического
колебания G7). 5. Примеры зависимостей, выражающихся
тригонометрическими функциями G9).
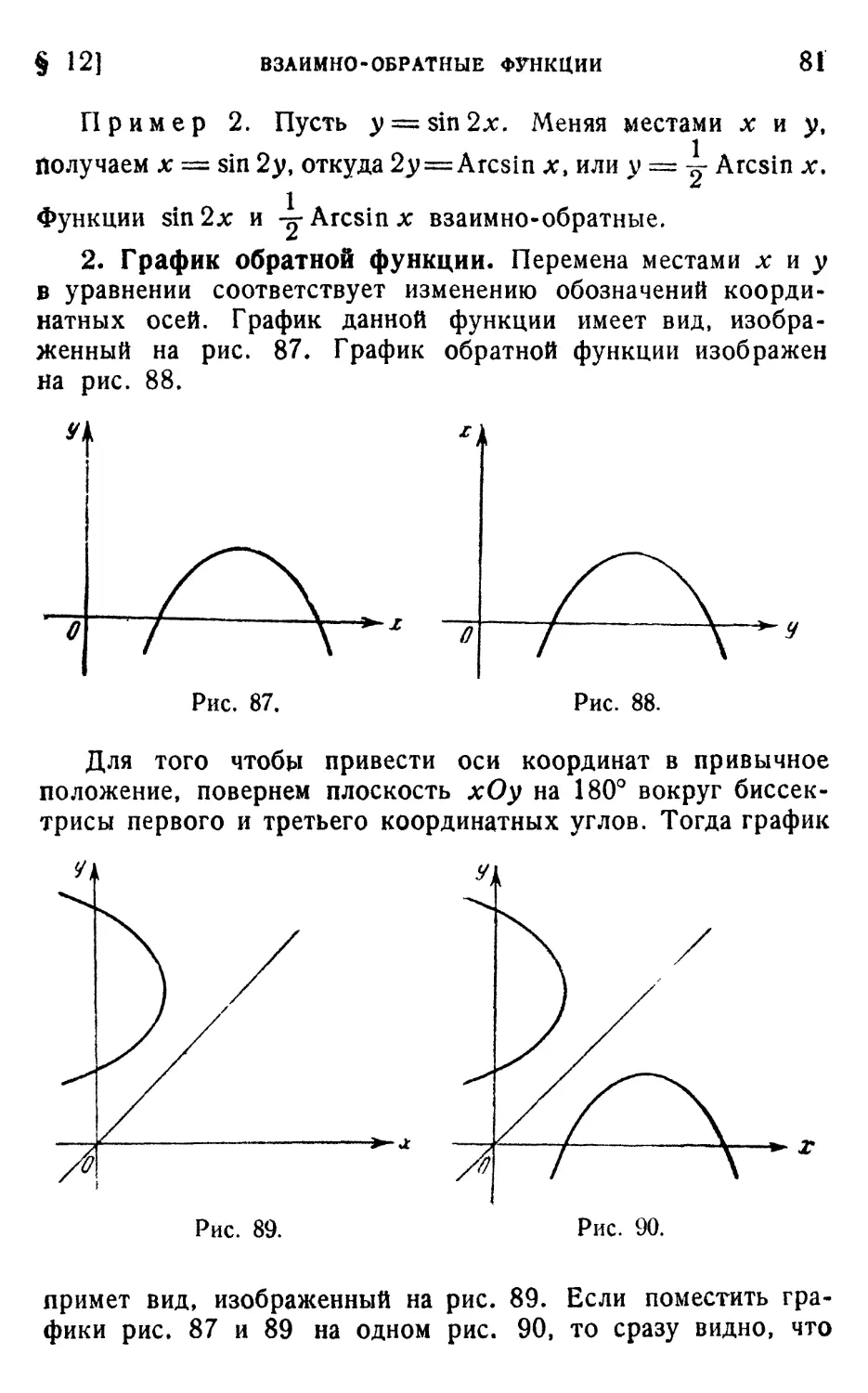
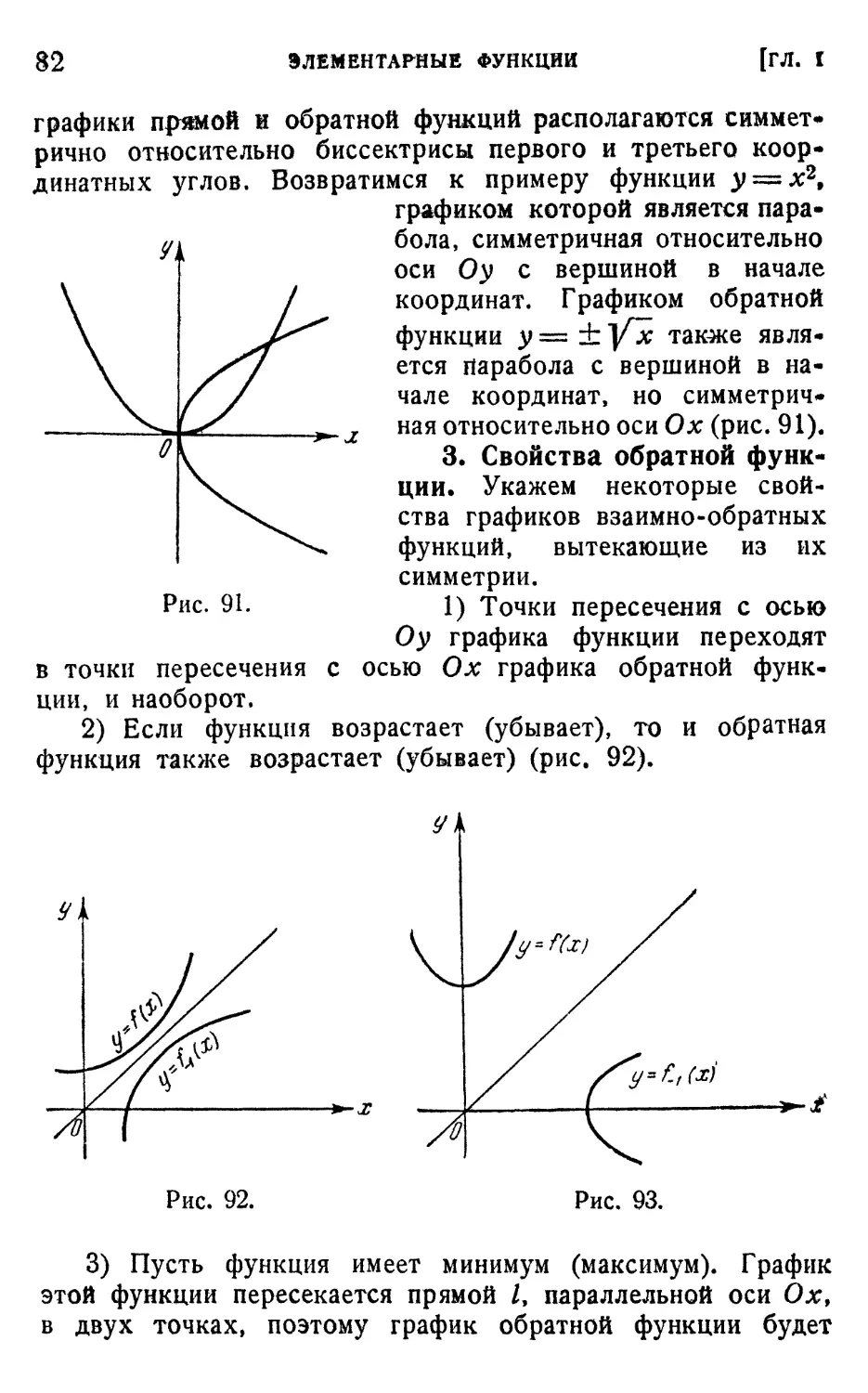
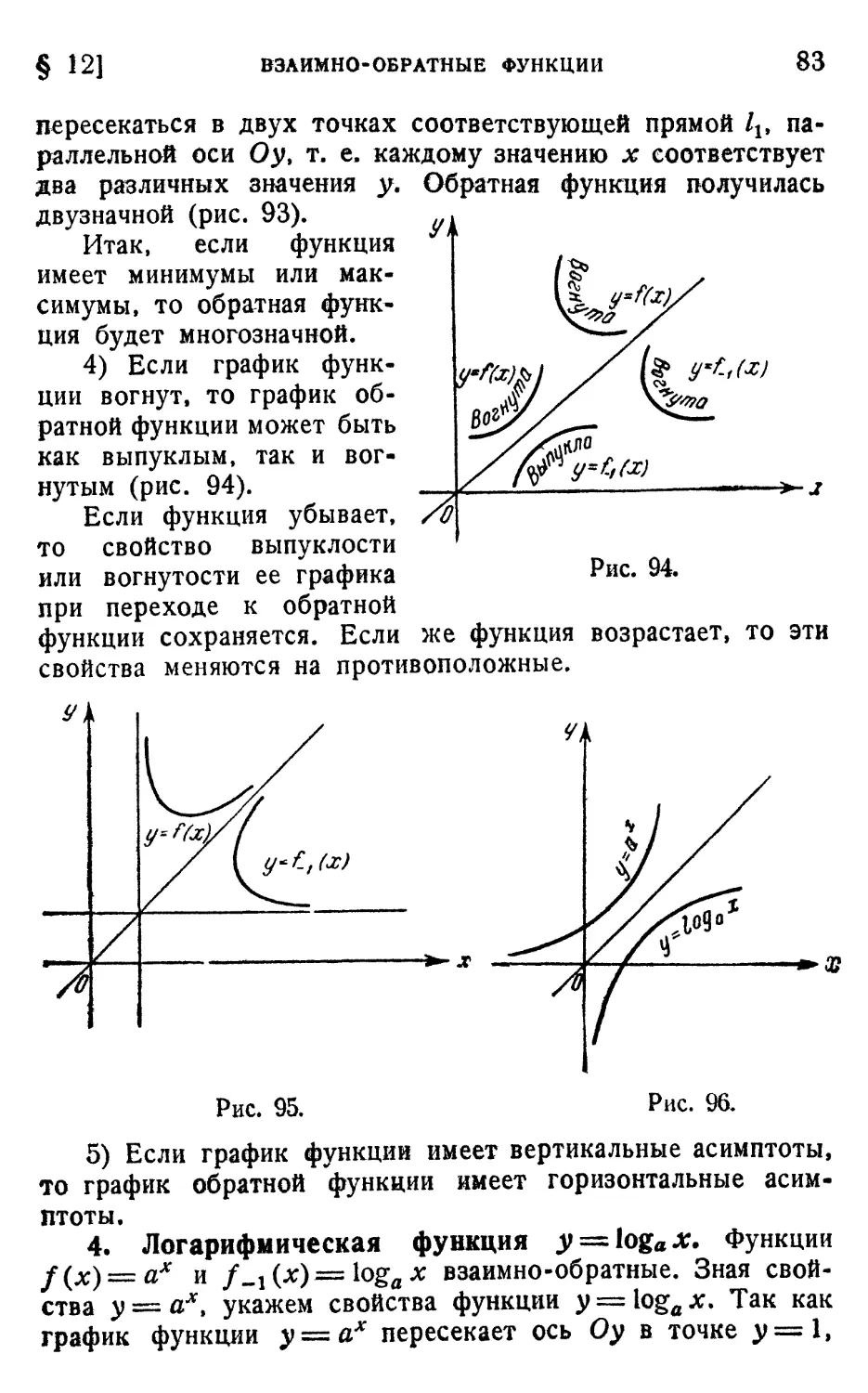
§ 12. Взаимно-обратные функции 80
1. Понятие обратной функции (80). 2. График обратной
функции (81). 3. Свойства обратной функции (82).
4. Логарифмическая функция у = logQ x (83). 5. Обратные
тригонометрические функции и их главные значения (84).
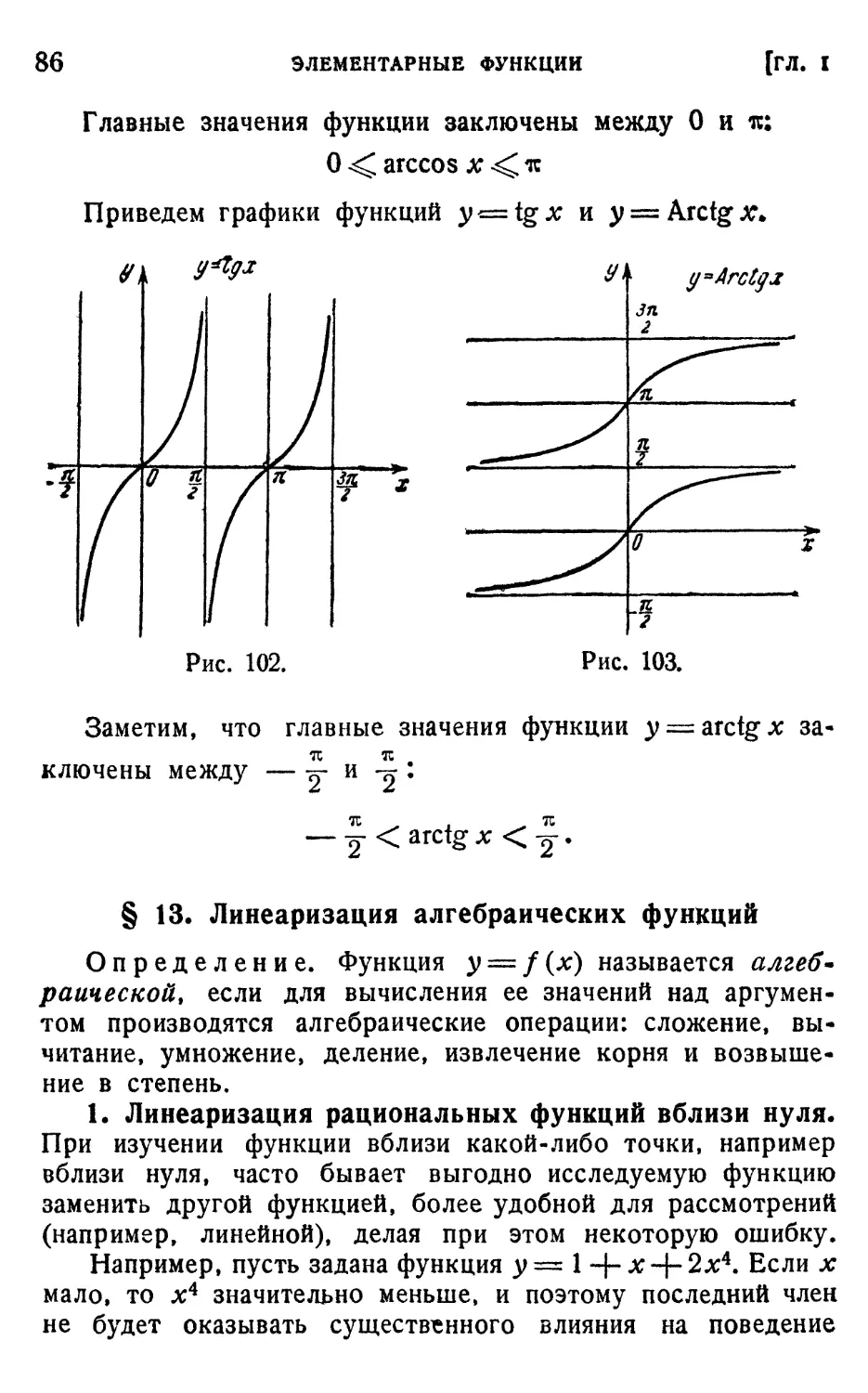
§ 13. Линеаризация алгебраических функций 86
1. Линеаризация рациональных функций вблизи нуля (86).
2. Линеаризация иррациональных функций (88). 3. Лине-
Линеаризация вблизи данного значения аргумента (щ.

ОГЛАВЛЕНИЕ О
Глава II
ТЕОРИЯ ПРЕДЕЛОВ
§ 1. Предел функции в точке 91
1. Понятие бесконечно малой (91). 2. Свойства бесконечно
малых (92). 3. Понятие предела функции (93). 4. Свой-
Свойства пределов (93). 5. Понятие непрерывной функции (97).
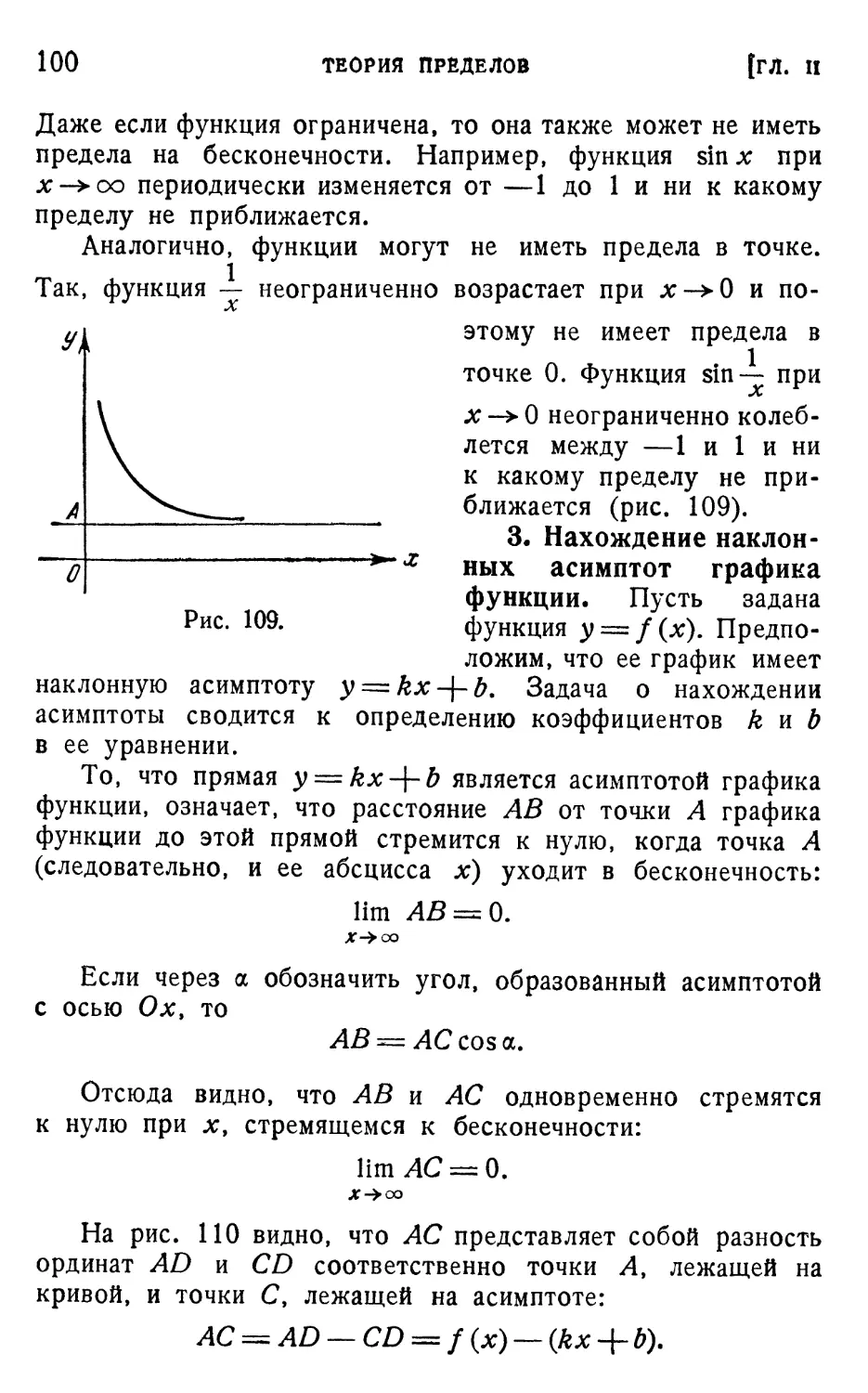
§ 2. Предел функции на бесконечности 99
1. Понятие функции, бесконечно малой на бесконеч-
бесконечности (99). 2. Предел функции на бесконечности (99).
3. Нахождение наклонных асимптот графика функции A00).
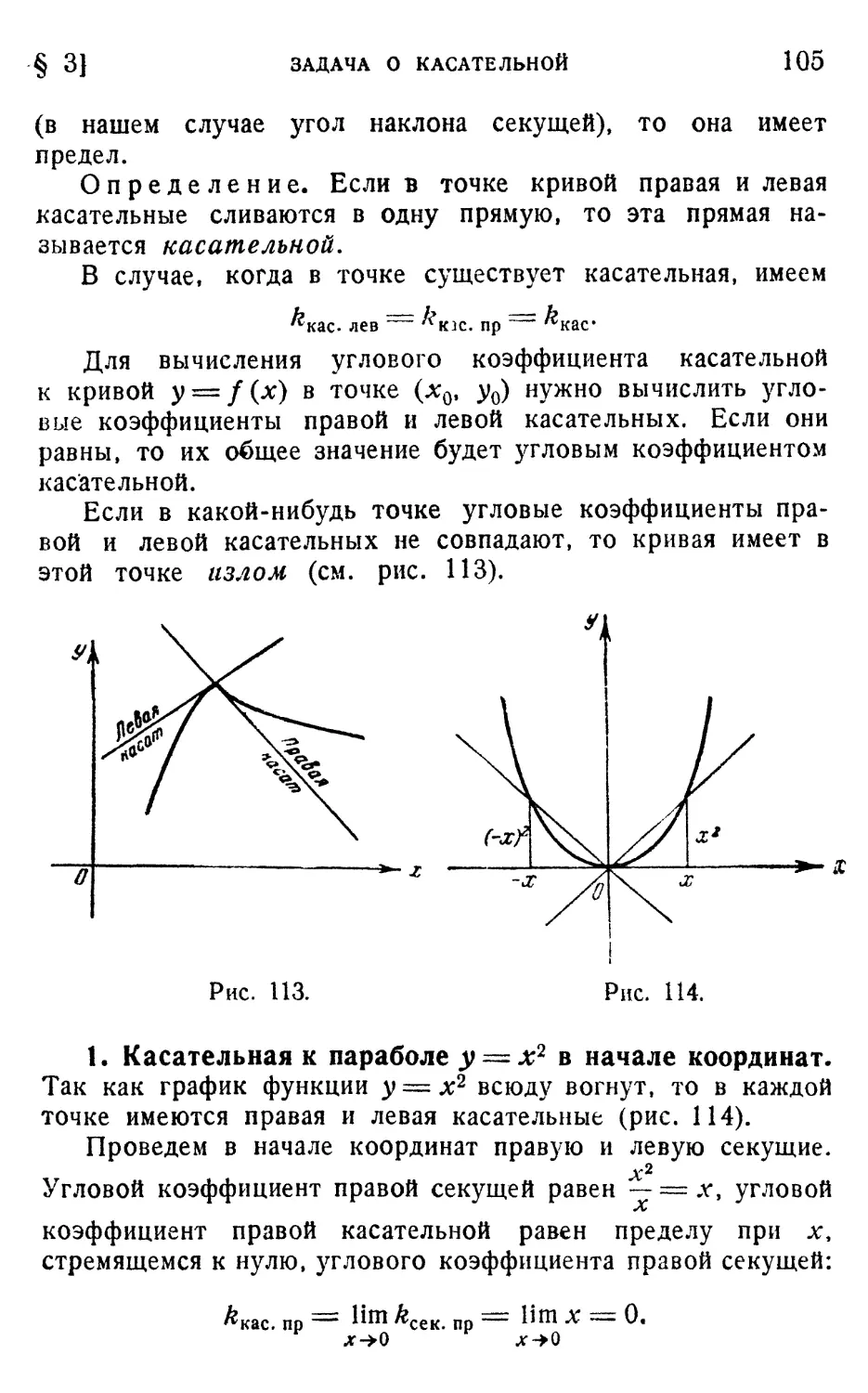
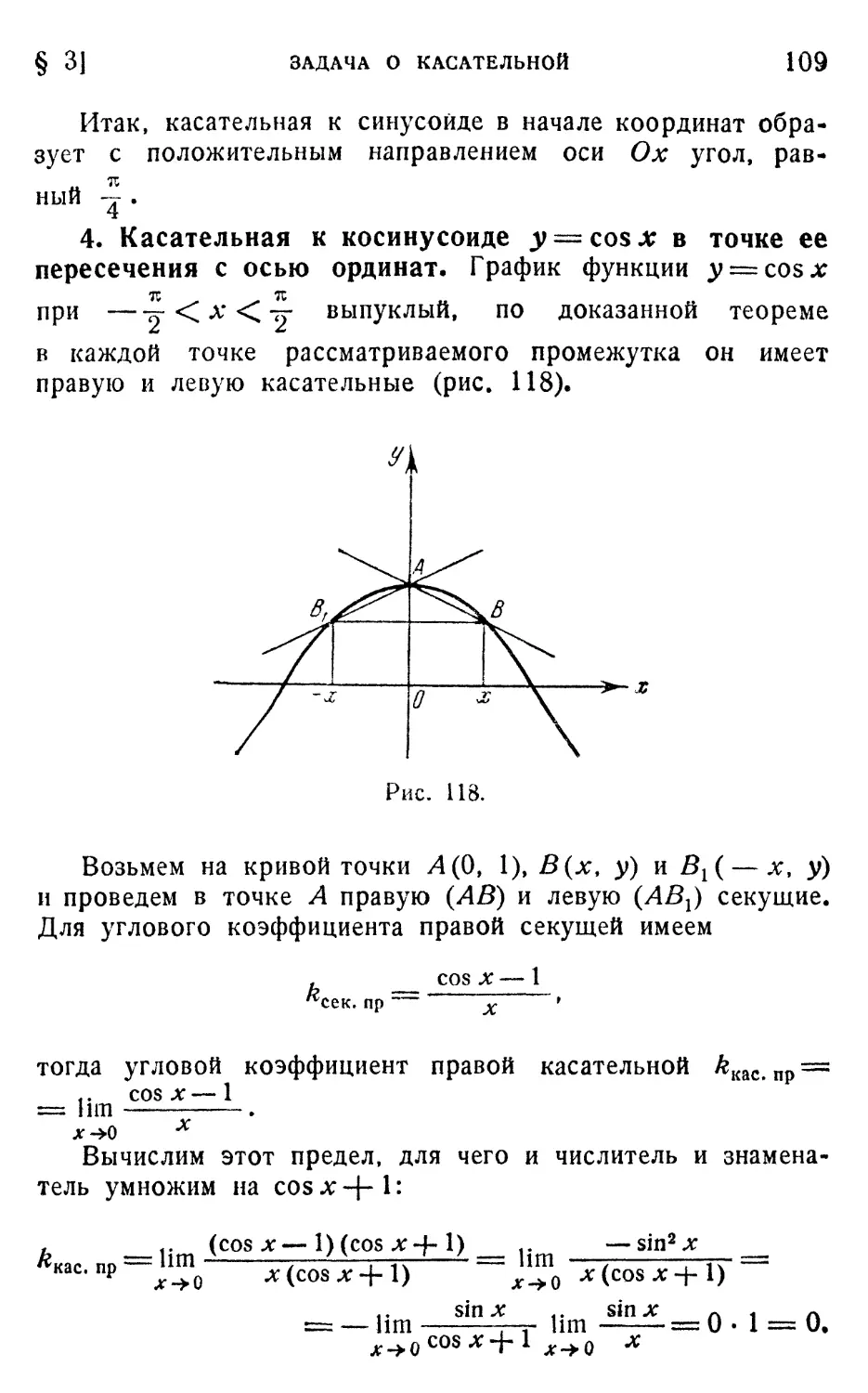
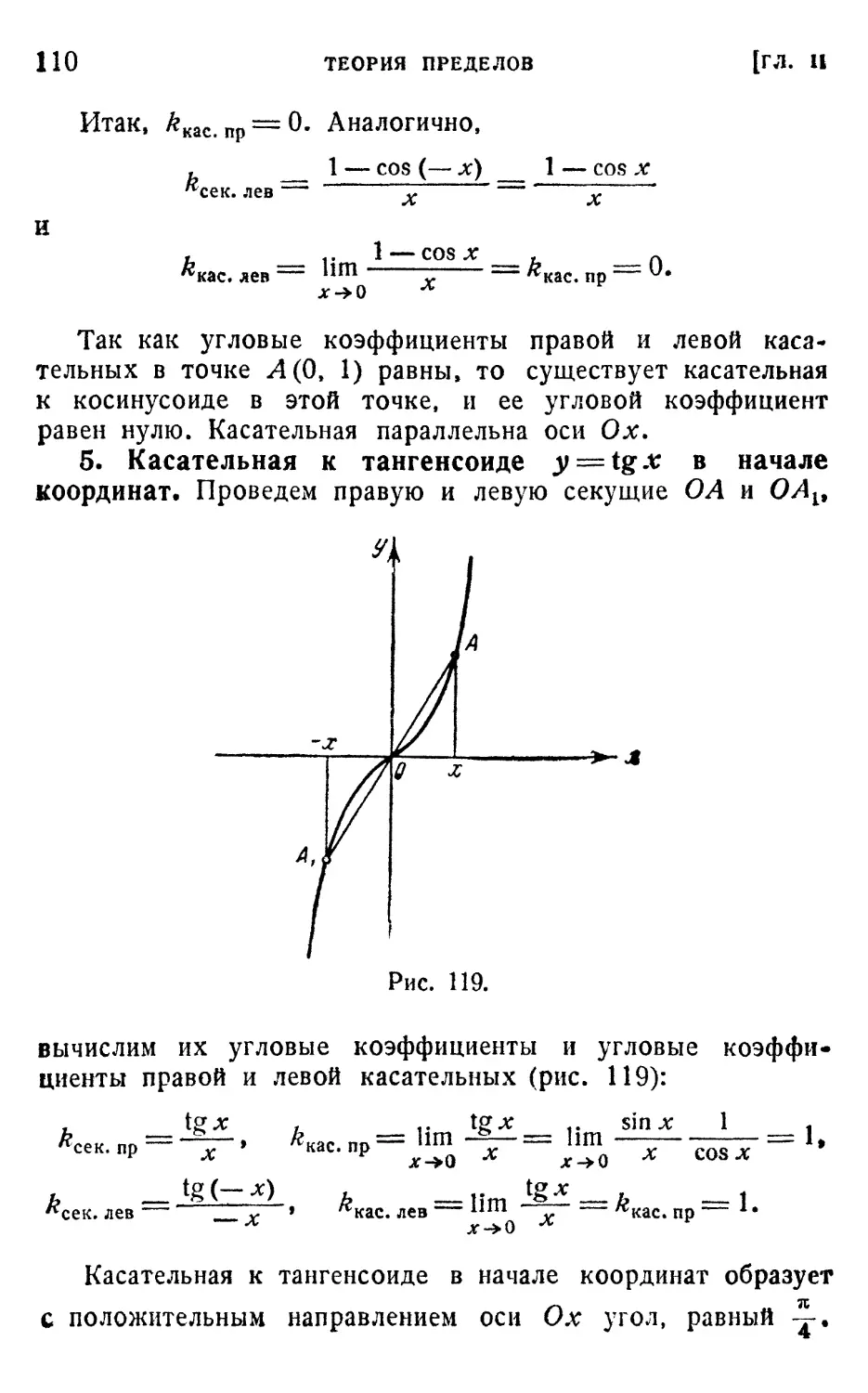
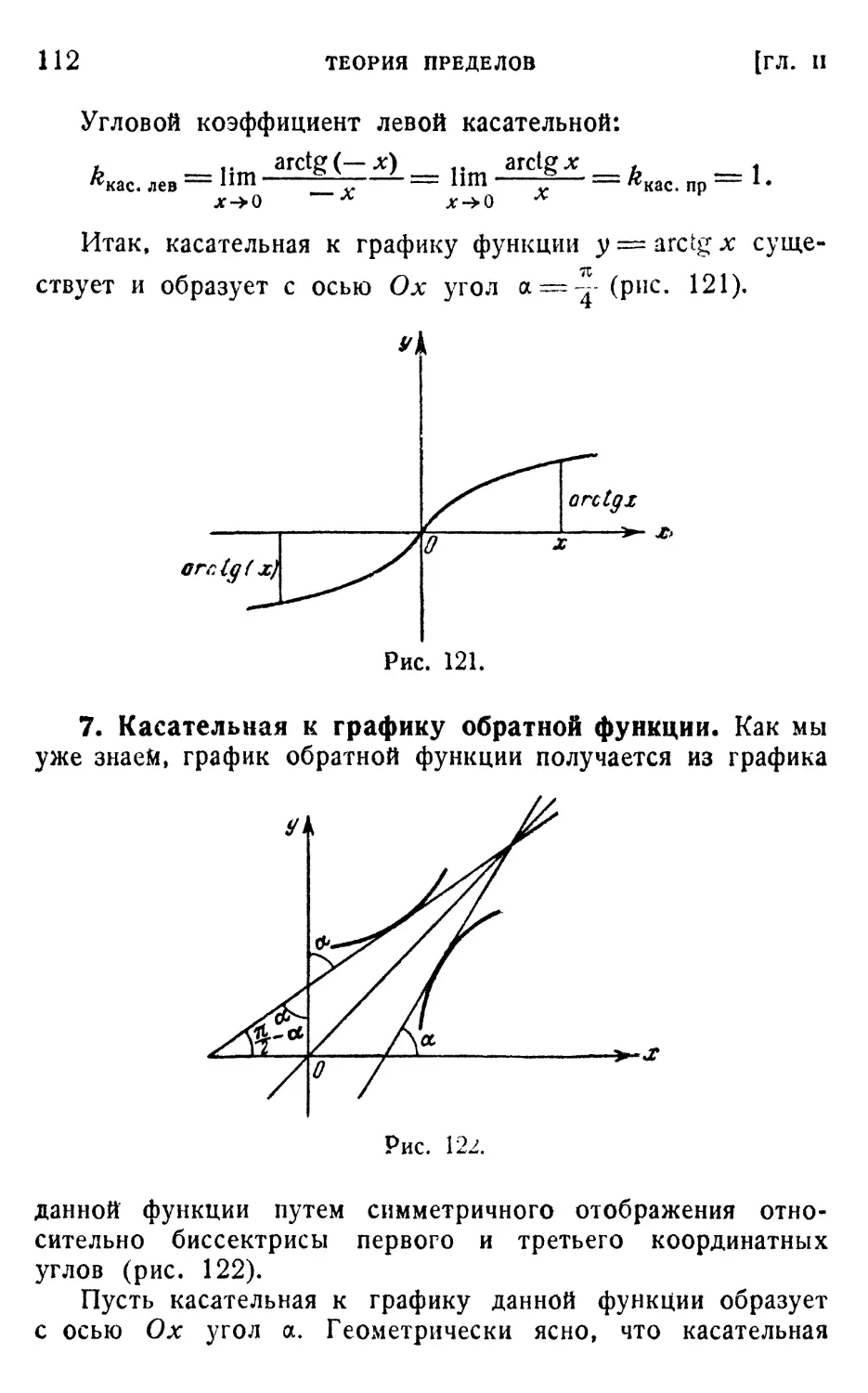
§ 3. Задача о касательной 103
1. Касательная к параболе у =* х2 в начале координат A05).
2. Касательная к параболе у = У х A06). 3. Касательная
к синусоиде у = sin x в начале координат. Первый заме-
замечательный предел A06). 4. Касательная к косинусоиде
у =* cos х в точке ее пересечения с осью ординат A09).
5. Касательная к тангенсоиде у = tg x в начале коорди-
координат (НО). 6. Касательные к графикам обратных тригоно-
тригонометрических функций A11). 7. Касательная к графику
обратной функции A12). 8. Касательная к графику пока-
показательной функции в точке его пересечения с осью орди-
ординат A13). 9. Касательная к графику логарифмической
функции в точке пересечения с осью их A16). 10. Число е
как предел A17).
§ 4. Гиперболические функции 117
Глава III
ЛИНЕАРИЗАЦИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
§ 1. Сравнение бесконечно малых функций 120
1. Свойства бесконечно малых более высокого порядка
малости, чем данная A21). 2. Основная теорема об экви-
эквивалентных бесконечно малых A21).
§ 2. Линеаризация вблизи нуля 122
1. Линеаризация функции у = (\-\~х)п A23). 2. Линеари-
Линеаризация функции у = -г~т— A23). 3. Линеаризация функ-
1 -у" X
ции у =*У~\ -{-х A24). 4. Линеаризация функции
у = sin х A24). 5. Линеаризация функции у = cos л: A24).
6. Линеаризация функций у = ех и у ±= а* A25). 7. Линеа-
Линеаризация функции у = loga A + х) A25). 8, Формулы линеа-
линеаризации вблизи нуля A25), 9. Примеры применения
линеаризации A26).

6 ОГЛАВЛЕНИЕ
§ 3. Линеаризация функции вблизи данной точки .... 126
1. Производная и дифференциал линейной функции в дан-
данной точке A28).
§ 4. Формулы линеаризации основных элементарных
функций. Производные 129
1. Линеаризация степенной функции f(x) = хп при це-
целом положительном п A29). 2. Линеаризация функции
f(x) = — A30). 3. Линеаризация функции f(x) = Yx A30).
4. Линеаризация функции f(x) = sinx A31). 5. Линеари-
Линеаризация функции f(x)~co$x A31). 6. Линеаризация пока-
показательной функции f(x) = ax A31). 7. Линеаризация лога-
логарифмической функции/(х) = \ogax A31).
§ 5. Общие свойства производных 132
1. Производная суммы A32). 2. Производная произведе-
произведения A33). 3. Производная дроби A33). 4. Производная и
дифференциал сложной функции A35). 5. Производная сте-
степенной функции при любом показателе степени A37).
6. Производные обратных функций A37). 7. Производные
обратных тригонометрических функций A38).
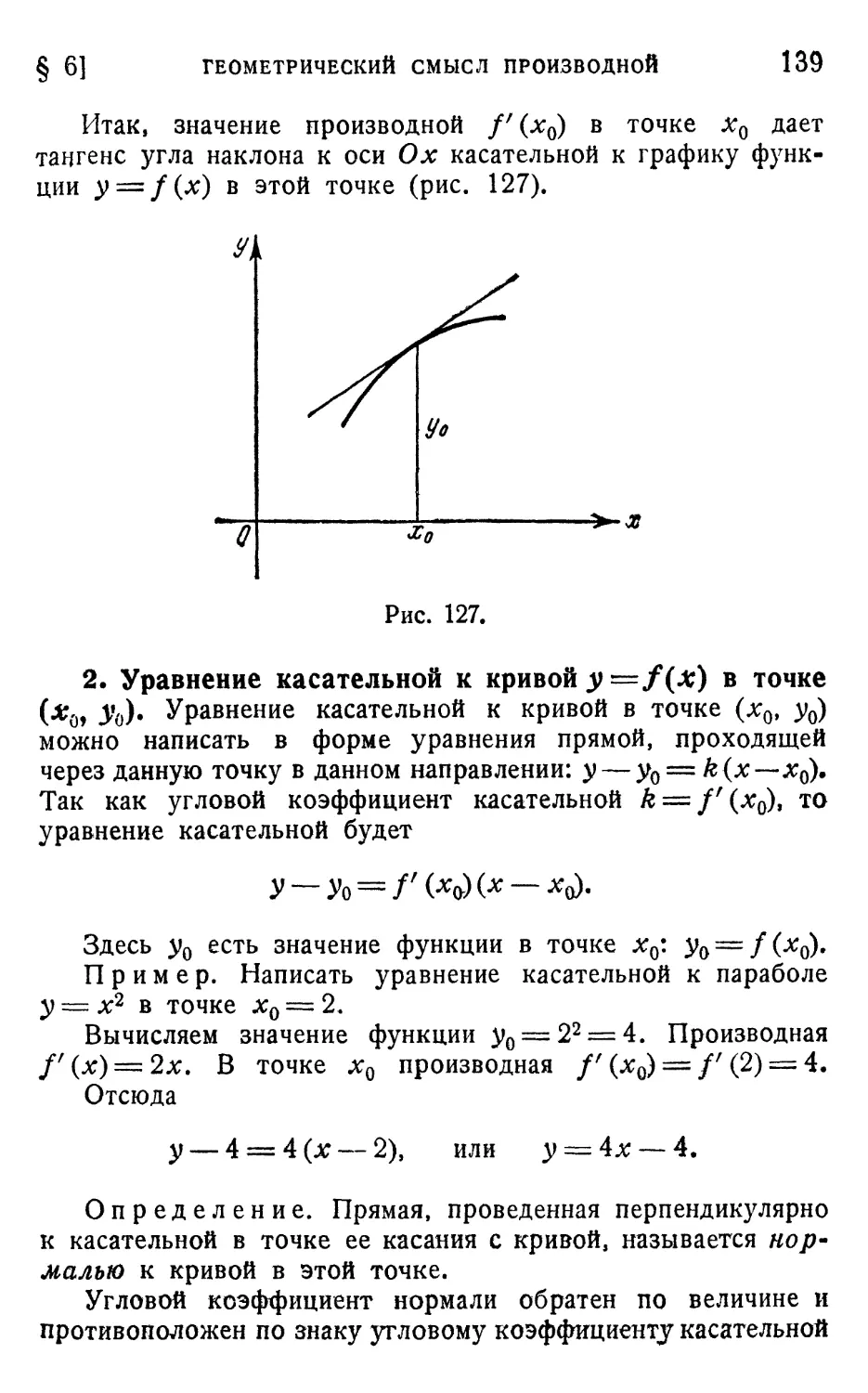
§ 6. Геометрический смысл производной и дифференциала 138
1. Геометрический смысл производной A38). 2. Уравнение
касательной к кривой у=/(х) в точке (х0, у0) A39).
3. Геометрический смысл дифференциала A40).
§ 7. Понятие о производных и дифференциалах высшего
порядка 140
§ 8. Механический смысл производной 141
Глава IV
ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ
К ИССЛЕДОВАНИЮ ФУНКЦИЙ
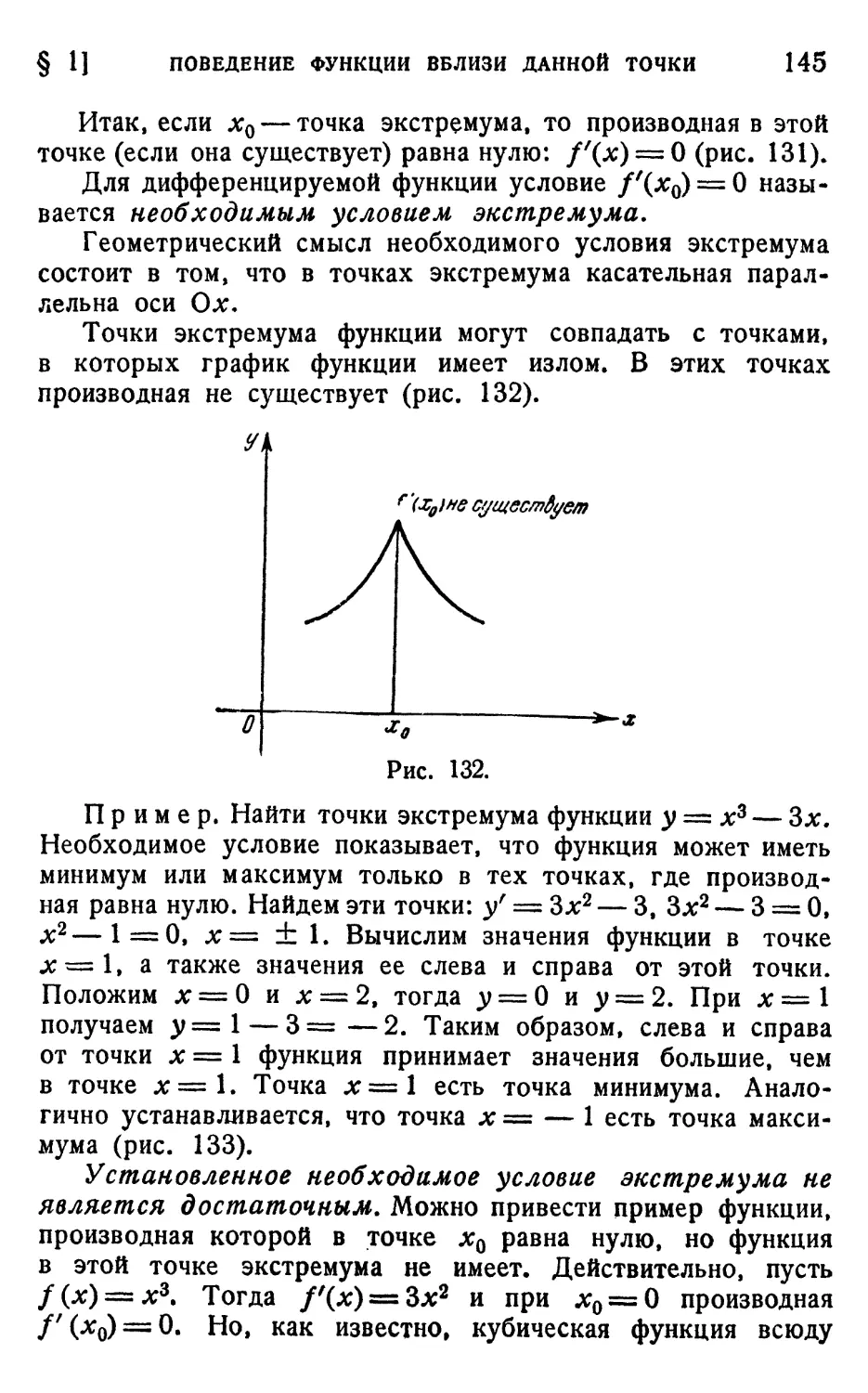
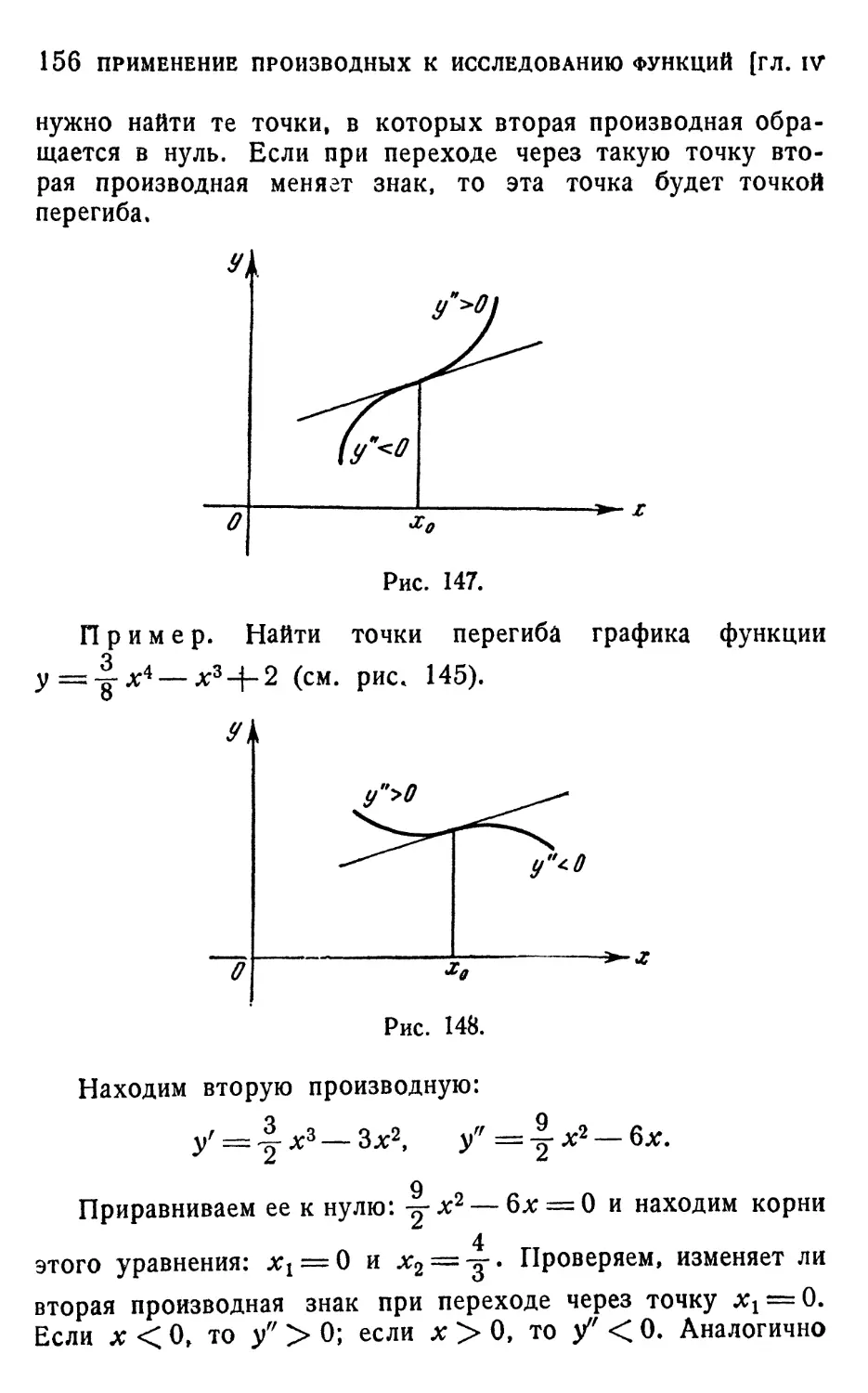
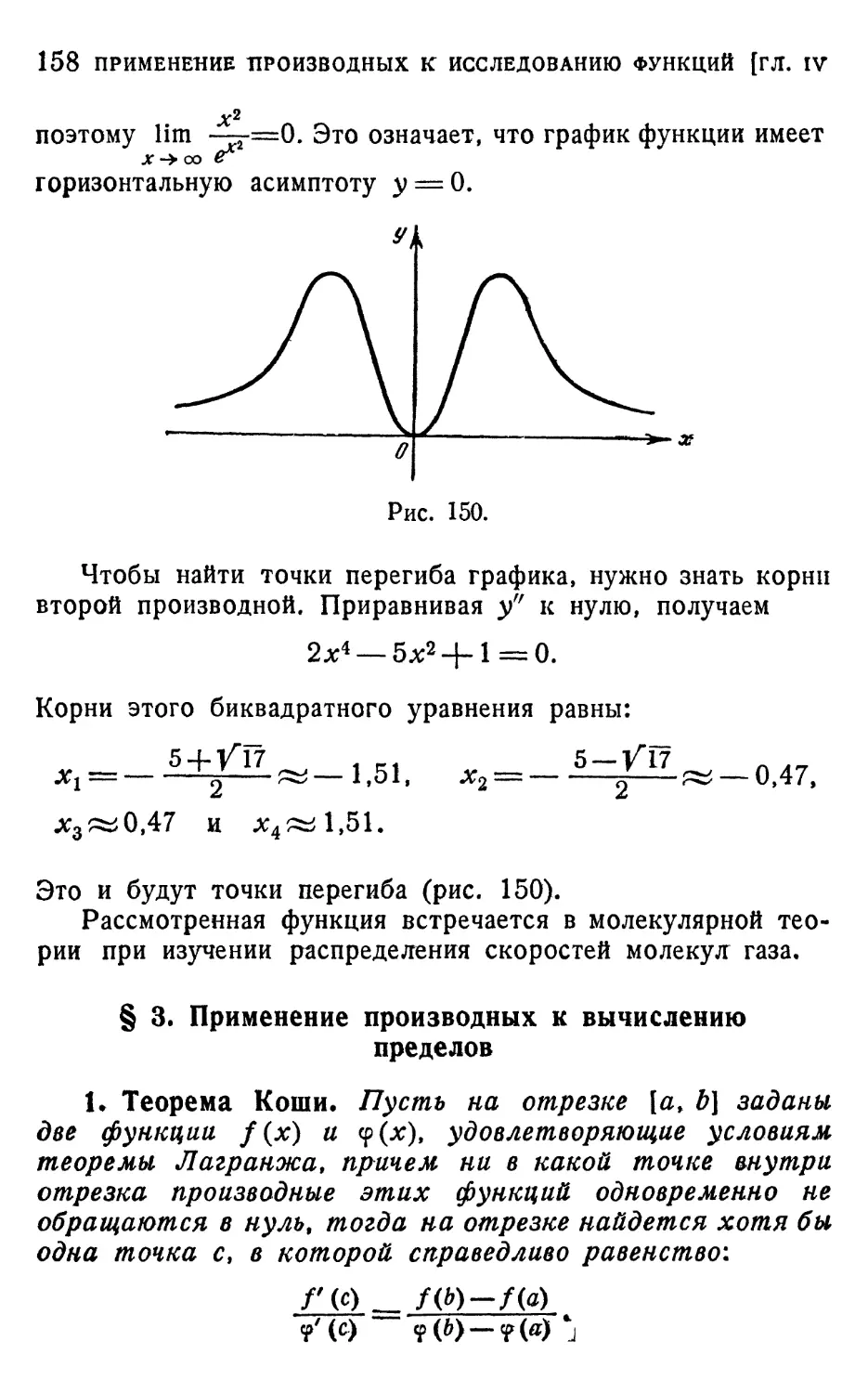
§ 1. Поведение функции вблизи данной точки 143
1. Условие возрастания и убывания функции в точке A43).
2. Точки экстремума A44). 3. Отыскание наибольшего и
наименьшего значений функции на отрезке A46).
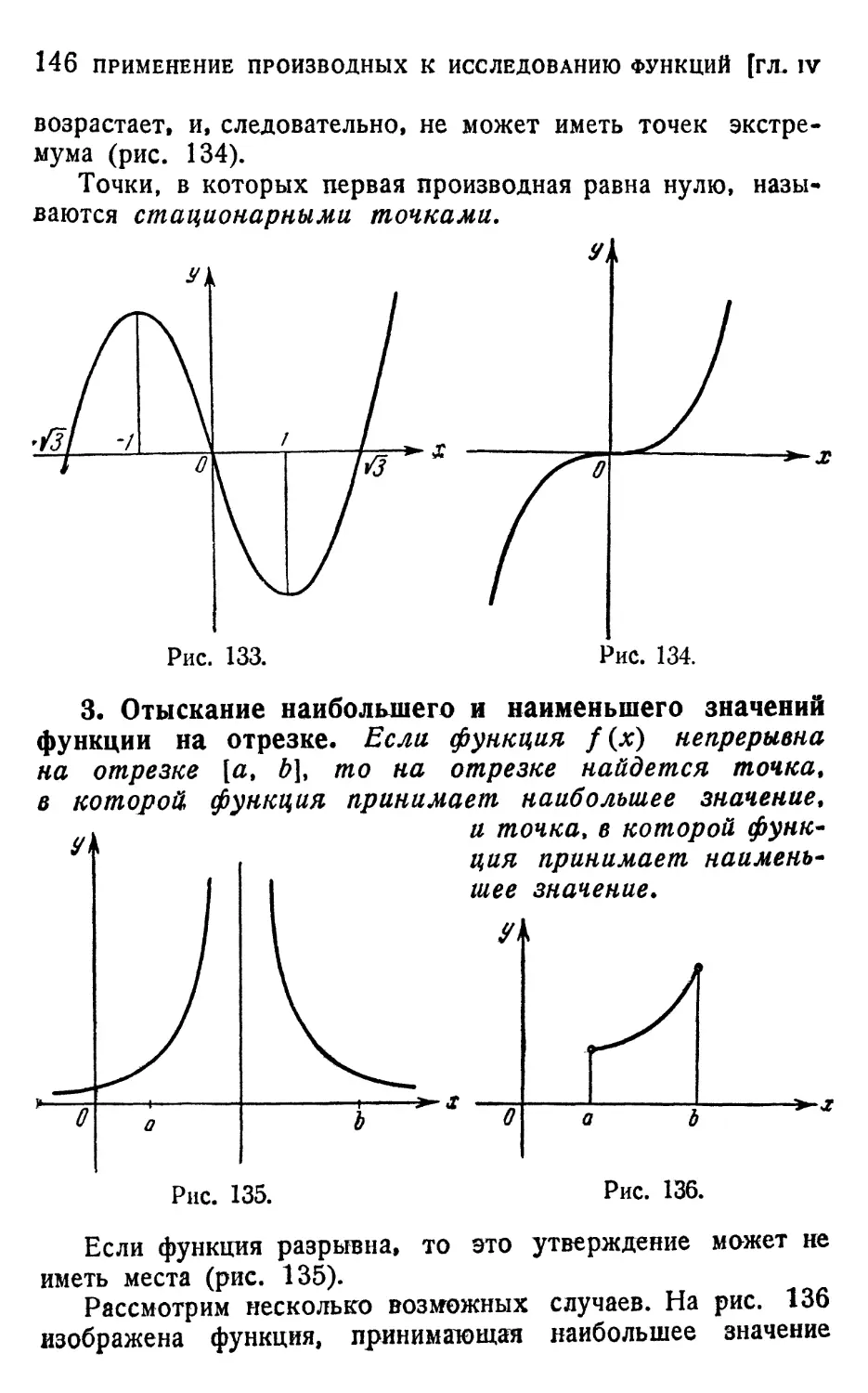
§ 2. Теорема Лагранжа и ее применения 148
1. Теорема Лагранжа A48). 2. Возрастание и убывание
функции на отрезке A50). 3. Классификация изолированных
стационарных точек A51). 4. Достаточное условие экстре-
экстремума по второй производной A53). 5. Выпуклость и вог-
вогнутость дуги кривой A54). 6. Пример. Исследование
функции у = *2

ОГЛАВЛЕНИЕ 7
§ 3. Применение производных к вычислению пределов . 158
1. Теорема Коши A58). 2. Правило Лопиталя A59).
3. Сравнение поведения на бесконечности степенной, пока-
показательной и логарифмической функций: хп, еху \ъх A60).
§ 4. Представление функции по формуле Тейлора ....
1. Формула Тейлора A61). 2. Геометрический смысл фор-
формулы Тейлора при п = 2 A64).
§ 5. Представление элементарных функций по формуле
Тейлора вблизи нуля 164
1. Представление многочлена A64). 2. Представление фун-
функции A -\- х)т. Бином Ньютона A65). 3. Представление
функции -у-р— A66). 4. Представление функции
у 1 + х A66). 5. Представление функций sin x и cos x A67).
6. Представление функций е* и ах A67). 7. Представление
функций 1пA+л:) и loga(l+*) A67). 8. Таблица про-
простейших представлений основных элементарных функций
по формуле Тейлора A68).

ПРЕДИСЛОВИЕ
Настоящая книга написана на основе лекций по курсу
высшей математики, которые читались одним из авторов
в течение ряда лет в Криворожском горнорудном и в Воро-
Воронежском лесотехническом институтах.
Общеизвестно, что при изучении курса высшей матема-
математики учащийся встречает ряд трудностей. Особенно трудно
усваивается первая часть математического анализа, содер-
содержащая теорию пределов и дифференциальное исчисление
Эти трудности, с одной стороны, объясняются обилием
новых понятий и методов, с другой, по нашему мнению, —
недостатками в построении курса. Главным из них мы счи-
считаем отсутствие ясности в том, что является основным
объектом исследования. Создается впечатление, что наиболее
важным является изучение логической взаимосвязи между
различными новыми понятиями.
Нам кажется, что основное содержание любого курса
определяется не общностью понятий и теорем, которые
в нем вводятся, а запасом примеров и приложений, которые
рассматриваются в самом курсе, на практических занятиях
и в смежных курсах. Можно применять все более и более
общий подход к изложению понятий числа, функции, пре-
предела и т. п., однако, если при этом не изменится круг
задач, решаемых на лекциях, практических занятиях и
в смежных курсах, то это только приведет к отрыву
метода изложения от объекта исследования.
Авторы считают, что основным объектом исследования
в курсе математического анализа во ВТУЗе являются функ-
функциональные зависимости между величинами, выражающиеся
точно или приближенно с помощью элементарных функций.
Те небольшие выходы за рамки класса элементарных функ-
функций, которые имеются в теории интегралов, рядов и диф-

ПРЕДИСЛОВИЕ 9
ференциальных уравнений, еще больше подчеркивают основ-
основное содержание курса. Если подготовка инженера требует
большего, то вводят такие дополнительные разделы или
курсы, как «Специальные функции», «Аналитические фун-
функции» и т. п.
Точка зрения авторов отразилась в названии и содер-
содержании книги. В ней излагается не математический анализ
вообще, а математический анализ элементарных функций.
Изучение математического анализа в ВУЗе осложняется
тем, что выпускники средней школы имеют чрезвычайно
скудный запас сведений об элементарных функциях. С целью
пополнить этот запас в книгу введена большая глава «Эле-
«Элементарные функции», в которой приводится детальное иссле-
исследование основных элементарных функций методами «школь-
«школьной математики» (даже без использования бинома Ньютона).
При этом рассматриваются уже все основные характе-
характеристики функций и их графиков, изучаемые в курсе анализа
(область определения, участки возрастания и убывания,
точки экстремума, участки выпуклости и вогнутости гра-
графиков, точки перегиба, асимптоты и т. д.). Все свойства и
соответствующие им понятия вводятся не «про запас», а по
мере их обнаружения при изучении той или иной функции.
В конце первой главы затрагивается вопрос о линеаризации
простейших алгебраических функций. Линеаризации функции
путем отбрасывания степеней малой величины выше первой
авторы придают важное значение, так как именно таким
образом она производится большей частью в прикладных
задачах.
Во второй главе изложены основы теории пределов.
Вычисление наиболее важных пределов привязано к задаче
о нахождении касательной к графикам основных элементар-
элементарных функций. Так, число е вводится как основание показа-
показательной функции, угловой коэффициент касательной к гра-
графику которой в точке пересечения с осью ординат равен
единице.
В третьей главе («Линеаризация элементарных функций»)
на базе вычисленных пределов получаются формулы для
линеаризации основных элементарных функций вблизи нуля,
а затем и для линеаризации вблизи любой точки. Произ-
Производные получаются как коэффициенты при Ах в формулах
линеаризации. Вызод всех формул для производных одно-

10 ПРЕДИСЛОВИЕ
типен и основан на применении «теоремы сложения» и фор-
формулы линеаризации вблизи нуля для соответствующей функ-
функции. Широко используются понятия эквивалентных беско-
бесконечно малых и порядка одной бесконечно малой относи-
относительно другой.
Четвертая глава — «Применение производных к исследо-
исследованию функций» — написана сжато. Основные задачи на
исследование функций уже поставлены в первой главе и
быстро решаются с помощью теоремы Лагранжа. Формула
Тейлора выводится как дальнейшее естественное развитие
формулы линеаризации и применяется к разложению основ-
основных элементарных функций.
Изложение иллюстрируется небольшим числом примеров
физического характера.
Уровень строгости изложения разный в разных главах.
Если в первой главе используется только интуитивное
понятие предела функции, то во второй главе оно вводится
строго. Свойства непрерывных функций и непрерывность
основных элементарных функций используются без их
доказательства.
Авторы еще раз подчеркивают, что они пытались по-
построить изложение так, чтобы максимально сузить разрыв
между построением аппарата математического анализа и
основным объектом, к которому он применяется, — элемен-
элементарными функциями. Насколько им удалось это, будет
судить читатель.
С. Г. Крейа
В. Н. Ушакова

ГЛАВА I
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
§ 1. Понятие функции
При изучении различных явлений природы приходится
иметь дело с самыми разнообразными величинами: темпера-
температурой, объемом, массой, весом, длиной и др. При этом
в каждом рассматриваемом случае одни из этих величин
остаются неизменными, другие изменяются.
Величина называется переменной, если она принимает
различные численные значения.
Известно, что отношение длины окружности к ее диа-
диаметру остается неизменным, равным тг, какую бы окруж-
окружность мы ни рассматривали, в то время как площадь круга
и длина окружности могут принимать разные значения.
Заметим, что одна и та же величина при одних условиях
может рассматриваться как постоянная, при других — как
переменная. Так, при грубом измерении длину металличе-
металлического стержня можно считать неизменной. Но при точном
измерении оказывается, что она изменяется при тепловом
воздействии.
Среди переменных величин различают независимые и
зависимые. В вышеприведенном примере независимой перемен-
переменной можно считать температуру, зависимой — длину стержня.
1. Определение функции по Лобачевскому. Величина у
называется функцией величины х, если каждому значению х
соответствует одно или несколько определенных значений у.
Величину х при этом называют аргументом.
Если величина у есть функция величины х, то усло-
условимся это записывать так: y = f(x) и читать: игрек есть эф
от икс. Для каждой конкретной функции знак / определен-
определенным образом расшифровывается.

12
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
[ГЛ. I
Чаще всего функция задается уравнением, из которого
при каждом значении х находится соответствующее значе-
значение у. В таком случае говорят, что функция задана анали-
аналитически. Если при этом уравнение, задающее функцию,
разрешено относительно у, то говорят, что функция за-
задана явно.
Например,
—-—
X -f-
или у = sin3 л;-f-cos3 л;.
При явном задании функции y — f(x) значок / указы-
указывает совокупность тех математических операций, которые
должны быть произведены над х, чтобы получить у.
В конкретных задачах зависимая и независимая пере-
переменные могут обозначаться другими буквами. Например,
в уравнении s = vt, определяющем зависимость длины
пути s от времени t при равномерном движении, независи-
независимая переменная обозначена через t, а зависимая — через s.
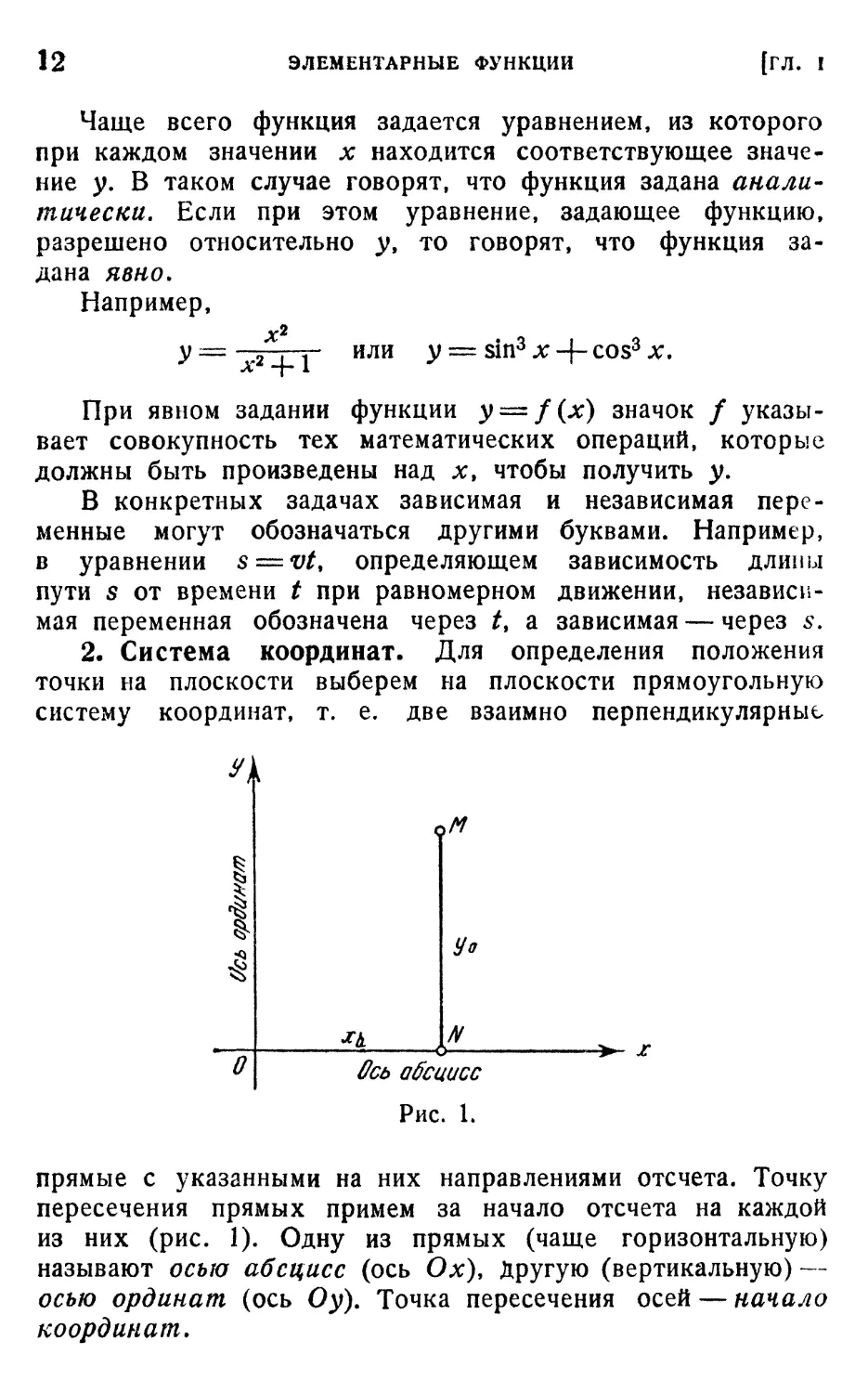
2. Система координат. Для определения положения
точки на плоскости выберем на плоскости прямоугольную
систему координат, т. е. две взаимно перпендикулярные
I
Уо
N
Ось абсцисс
Рис. 1.
прямые с указанными на них направлениями отсчета. Точку
пересечения прямых примем за начало отсчета на каждой
из них (рис. 1). Одну из прямых (чаще горизонтальную)
называют осью абсцисс (ось Ох), Другую (вертикальную) —
осью ординат (ось Оу). Точка пересечения осей — начало
координат.

§ п
ПОНЯТИЕ ФУНКЦИИ
13
Пусть на плоскости имеется некоторая точка М. Опустим
из этой точки на ось абсцисс перпендикуляр MN. Абсцис-
Абсциссой л:0 точки М называется длина отрезка ON, если точка N
лежит правее точки О (т. е. расположена от точки О
в сторону заданного направления отсчета). Если же точка N
лежит левее точки О, то абсциссой точки М называется
длина отрезка ON, взятая со знаком минус.
Ординатой yQ точки М называется длина отрезка MN,
если точка М лежит выше оси абсцисс. В противном случае
ордината точки М — длина отрезка MN, взятая со знаком минус.
Отметим, что точки, лежащие на оси абсцисс, имеют
ординаты, равные нулю, а точки, лежащие на оси ординат —
равные нулю абсциссы.
Два числа, абсцисса х0 и ордината у0, называются коорди-
координатами точки М и это принято записывать так: М (х0, у0).
x > О
(/ > О
->- х
X :
У
Рис. 2.
На рис. 2 указано, какие знаки имеют координаты
точек в каждом из четырех координатных углов, называе-
называемых четвертями.
3. График функции и уравнение кривой. Если задана
функция y — f(x), то каждому значению х соответствует
значение у — значение функции в точке х. По двум
числам хну можно построить точку М(х, у). Совокуп-
Совокупность всех таких точек образует график функции. Этот
график обычно представляет собой одну или несколько
кривых.

14 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ [ГЛ. I
Если задается кривая, а по ней восстанавливается функция,
то полученное уравнение y — f(x) называют уравнением
кривой.
Итак, всякая функция имеет свой график и, наоборот,
всякая линия имеет свое уравнение. Вместо линий можно
рассматривать уравнения, исследовать их и полученные ре-
результаты переводить на язык геометрии. Наука, решающая
задачи геометрии алгебраическими методами, называется
аналитической геометрией.
Приведем примеры геометрических задач, решаемых
алгебраически.
Задача 1. Пусть даны уравнение кривой y = f(x) и
точка М(х0, у0). Требуется узнать, лежит ли точка М
яа данной кривой.
Вычислим значение y = f(x), при х = х0 сравним полу-
полученное значение y = f (х$) с у0. Если / (х0) будет больше у0,
то точка М лежит ниже кривой, если / (х0) меньше у0,
то точка М лежит выше кривой. Равенство уо = /(л;о) яв-
является условием того, что точка лежит на данной кривой.
Итак, для того чтобы узнать, лежит ли точка Л4(лг0, у0)
на кривой у = / (л:), нужно в уравнение кривой подставить
координаты точки М. Если координаты удовлетворяют урав-
уравнению кривой, то точка лежит на кривой, если не удовле-
удовлетворяют, то не лежит.
Пример. Дано уравнение кривой у = х3 + 5л:2 — 1.
Требуется проверить, лежат ли на этой кривой точки
МгB, 3) и Ж2A, 5). Абсцисса точки Мг равна 2. При хо = 2
будет у—8 + 20—1=27. Точка Мг лежит ниже кривой.
При *0=1 будет у =1 + 5—1=5. Точка М2 лежит на
кривой.
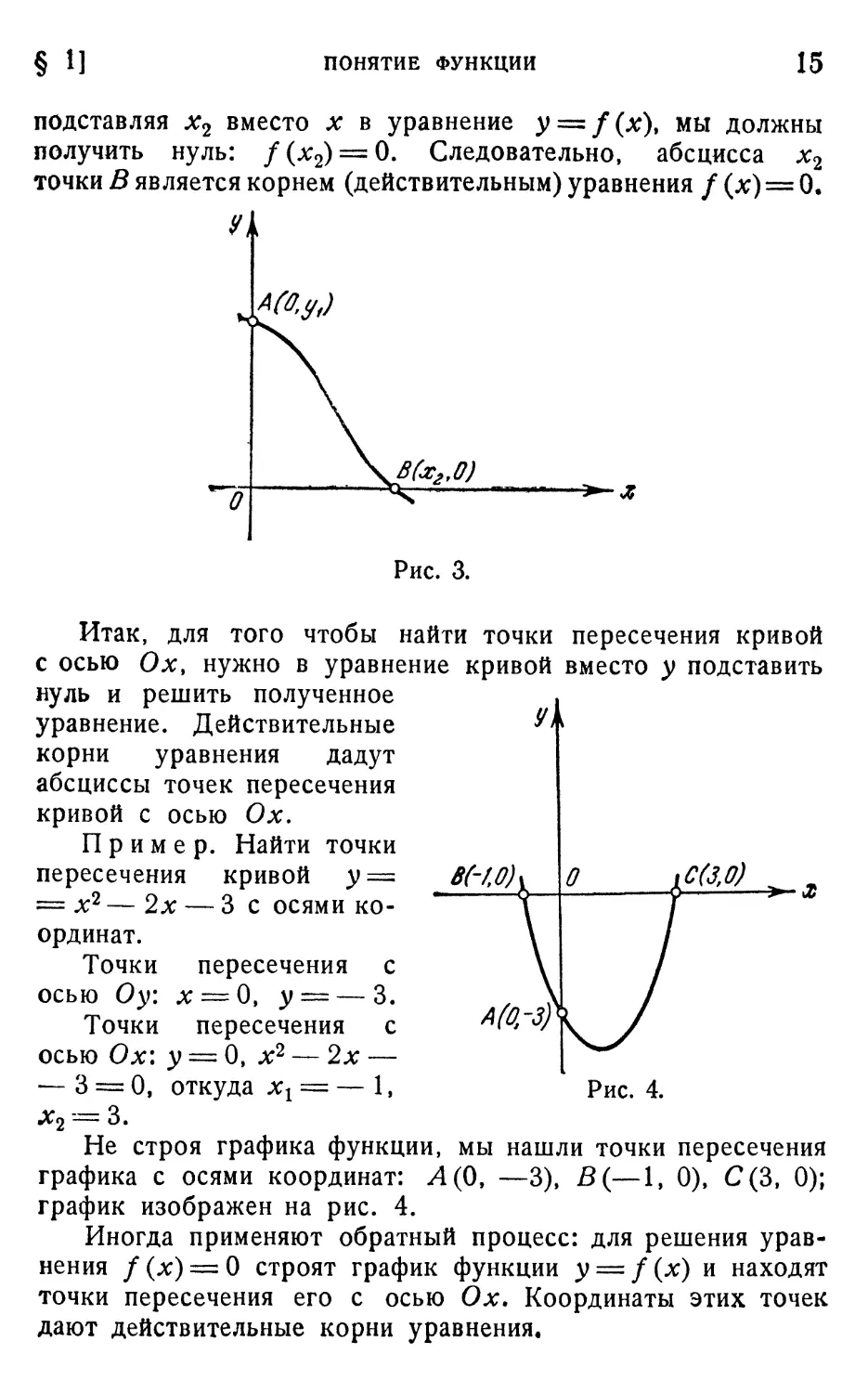
Задача 2. Найти точки пересечения кривой y = f(x)
с осями координат.
Пусть кривая y = f(x) пересекает ось Оу в точке
A{xv ух), ось Ох — в точке В(х2> у2) (рис. 3). Так как
точка А лежит на оси Оу, то абсцисса ее равна нулю:
Ar1 = O, но точка А лежит и на кривой, поэтому ординату ее
мы можем найти из уравнения кривой. Для этого подставим
в него вместо х нуль и вычислим соответствующее значе-
значение у: y1 = /(x1) = /@).
Точка В лежит на оси Олг, поэтому ордината ее равна
нулю: у2 = 0. Так как точка В лежит и на кривой, то,

§ 1]
ПОНЯТИЕ ФУНКЦИИ
15
подставляя х2 вместо х в уравнение у = /(#), мы должны
получить нуль: f(x2) = 0. Следовательно, абсцисса х2
точки В является корнем (действительным) уравнения / (х) = 0.
Рис. 3.
Итак, для того чтобы найти точки пересечения кривой
с осью Ох, нужно в уравнение кривой вместо у подставить
нуль и решить полученное
уравнение. Действительные
корни уравнения дадут
абсциссы точек пересечения
кривой с осью Ох.
Пример. Найти точки
BHOh
А@,-3)
О
\СC,0)
Рис. 4.
пересечения кривой у =
= х2 — 2х — 3 с осями ко-
координат.
Точки пересечения с
осью Оу: лг = О, у = — 3.
Точки пересечения с
осью Ох: у — 0, х2 — 2х —
— 3 = 0, откуда хг = — 1,
х2 = 3.
Не строя графика функции, мы нашли точки пересечения
графика с осями координат: Л@, —3), В(—1, 0), СC, 0);
график изображен на рис. 4.
Иногда применяют обратный процесс: для решения урав-
уравнения /(л;) = 0 строят график функции y = f(x) и находят
точки пересечения его с осью Ох. Координаты этих точек
дают действительные корни уравнения.

16
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
(ГЛ. 1
4. Однозначные и многозначные функции. Опреде-
Определение. Функция называется однозначной, если каждому
значению аргумента соответствует одно значение функции.
Функция называется многозначной, если некоторым значе-
значениям аргумента соответствует несколько значений функции.
В примере, изображенном на рис. 5, значению аргу-
аргумента х0 соответствуют три значения функции. Геометри-
Геометрически это означает, что пря-
прямая, параллельная оси Оу,
пересекает график функции
в трех точках.
График однозначной
функции (рис. 6) пересе-
пересекается каждой прямой, па-
параллельной оси Оу, только
в одной точке.
б. Область определе-
определения функции. Опреде-
Рис. 6. ление. Совокупность всех
значений аргумента, кото-
которым соответствуют определенные действительные значения
функции, называется областью определения функции.
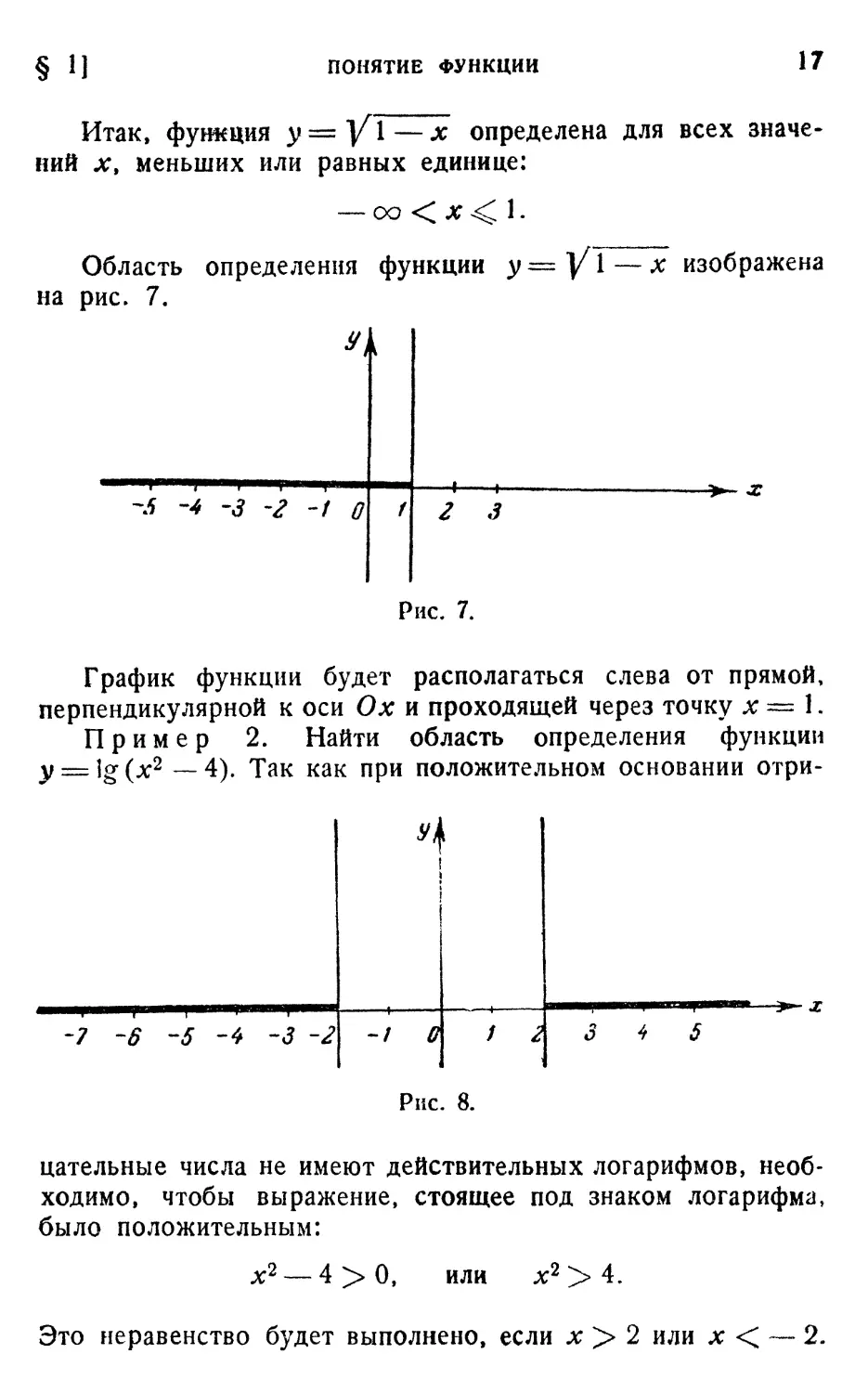
Пример 1. Найти область определения функции
y — yi—х, т. е. те значения х, которым соответствуют
действительные значения у. Очевидно, подкоренное выраже-
выражение для этих х не должно быть отрицательным:
1—*>0
или

§ 1]
ПОНЯТИЕ ФУНКЦИИ
17
Итак, фугаеция у=у\—х определена для всех значе-
значений лг, меньших или равных единице:
— оо<лг< 1.
Область определения функции
на рис. 7.
— х изображена
-.* -4 -з -г -/ о
г з
Рис. 7.
График функции будет располагаться слева от прямой,
перпендикулярной к оси Ох и проходящей через точку х = 1.
Пример 2. Найти область определения функции
у = \g (х2 — 4). Так как при положительном основании отри-
-7 -8 -5 ~4 -J -2
D
Рис. 8.
цательные числа не имеют действительных логарифмов, необ-
необходимо, чтобы выражение, стоящее под знаком логарифма,
было положительным:
4>0,
или
х2>4.
Это неравенство будет выполнено, если х > 2 или х < — 2.

18 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ [ГЛ. I
Область определения исследуемой функции состоит из
двух частей: — оо < л; < — 2 и 2 < х < оо (рис. 8), а гра-
график имеет две ветви, которые располагаются слева от прямой
х== — 2 и справа от прямой х = 2.
§ 2. Линейная функция y = kx-{-t>
Уравнение y — kx-\-b задает линейную функцию, здесь
k и b — действительные числа. Так как при этих условиях
функция y — kx-\-b дейст-
действительна для всех действи-
действительных х% то, следова-
следовательно, область ее определе-
определения — вся числовая прямая:
— оо < х < оо.
1. График линейной
? ^х функции y = kx. Покажем,
Л1 хг что графиком функции
y = kx является прямая,
Рис. 9. проходящая через начало
координат (рис. 9).
Дадим х произвольное значение хх и вычислим соответ-
соответствующее значение у:
Через начало координат и точку Ах(хг, уг) проведем пря-
прямую. Обозначим через at угол, образованный этой прямой
с положительным направлением оси Ох и отсчитываемый от
оси Ох против часовой стрелки. Из прямоугольного тре-
треугольника ОАХВ находим
Х\ -^i
При этом мы воспользовались тем, что yl=kxl.
Дадим теперь х новое значение х2, вычислим соответ-
соответствующее значение у: У2 = кх2 и покажем, что точка
Л2 (х2, у2). лежит на той же прямой. Для доказательства
проведем через начало координат и точку А2(х2, у2) пря-
прямую. Тангенс угла, образованного этой прямой с осью Ох,
найдем из треугольника ОА2С:
у2 kX2 ,

§ 21
ЛИНЕЙНАЯ ФУНКЦИЯ у = kx + Ь
19
Следовательно, tga2==tga1, т. е. 04 = 012 илиа1 = а2±1г.
Это значит, что точка А2 лежит на прямой, проходящей
через точки О@, 0) и Ax(xv yt), что и требовалось доказать.
Таким образом, графиком функции y = kx является
прямая, проходящая через начало координат и образующая
с положительным направлением оси Ох угол а, тангенс кото-
которого равен k (рис. 10).
Проведем теперь через начало координат прямую, не
совпадающую с осью Оу> и покажем, что уравнение ее имеет
вид y = kx.
Возьмем на прямой произвольную точку М(х, у). Опу-
Опустим из нее перпендикуляр на ось Ох, Из прямоугольного
треугольника 0MN найдем у = х tg a. Если обозначить
= &, то у = кх.
\
у,
'0
м
<
У
N
ОС -
Рис. 10.
Рис. 11.
Для прямой, совпадающей с осью Ox, a = 0, tga = O,
^ = 0 и уравнение ее y = Q.
Итак, уравнение всякой прямой, проходящей через начало
координат и не совпадающей с осью Оу, имеет вид y = kx,
где коэффициент k — тангенс угла, образуемого прямой
с положительным направлением оси Ох.
По знаку к можно установить, какой угол образует пря-
прямая с осью Ох: если k < 0, т. е. tga<0, то угол тупой;
если &>0, — острый (рис. 11, 10). Число k называется
угловым коэффициентом.
Если прямая совпадает с осью Оу, то ее уравнение не
может быть написано в виде y — kx. Для всех точек этой
оси лг = О, и это уравнение можно рассматривать как

20
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
[ГЛ. I
уравнение оси Оу. Уравнение прямой, параллельной оси Оу,
имеет вид х = а, где а — расстояние прямой от оси Оу.
2. График общей линейной функции. Рассмотрим функ-
функции y = kx и y = kx-{-b. При одном и том же значении х
значения этих функций отличаются на Ь, причем значения вто-
второй функции больше соответствующих значений первой, если
b > 0, и меньше, если b < 0. В частности, если х = 0, то для
первой функции у = 0, а для второй >> = &. Следовательно,
чтобы построить график функции y = kx-\-b, нужно пря-
прямую y^kx поднять вверх параллельно самой себе на Ь%
если b > 0, и опустить вниз,
если b <0 (рис. 12).
Итак, графиком всякой
линейной функции является
/о
/
Рис. 12.
Рис. 13.
прямая линия. Коэффициент k представляет собой тангенс угла
наклона этой прямой к оси Ох. Абсолютная величина коэф-
коэффициента b дает длину отрезка, отсекаемого прямой на
оси Оу, а знак Ь указывает на расположение этого отрезка:
при ?>0 отрезок расположен выше оси Ох; при #<0 —
ниже.
Справедливо и обратное утверждение: всякая прямая, не
параллельная оси Оу, имеет уравнение у = kx -f- b. Доказа-
Доказательство предоставляем читателю.
Укажем частный случай, когда /г = 0. Тогда функция
имеет вид у = 6. Ее графиком является прямая, параллель-
параллельная оси Ох (рис. 13).
Приведем примеры линейных зависимостей.
а) При равномерно-ускоренном движении с нулевой на-
чальной скоростью скорость движения прямо пропорцио-

§ 2}
ЛИНЕЙНАЯ ФУНКЦИЯ у = kX + Ь
21
нальна времени. Зависимость скорости от времени выра-
выражается в этом случае линейной функцией
где v — скорость, а — ускорение, t — время.
Графически эта зависимость изображается прямой, про-
проходящей через начало координат, причем рассматривать
нужно ту часть прямой, которая располагается над поло-
положительной частью оси абсцисс:
0</< оо (рис. 14).
О
Рис. 14.
Рис. 15.
б) В физике изучается зависимость объема газа v от тем-
температуры t. Эта зависимость выражается линейной функцией
где vQ— объем газа при ? =
Г
— коэффициент объемного
теплового расширения. Графически (рис. 15) эта зависимость
изображается прямой, отсекающей от положительной части
оси ординат отрезок, равный v0.
в) Аналогичная зависимость существует между длиной
стержня L и температурой t:
где Lo — длина стержня при ^ = 0°, а—коэффициент ли-
линейного теплового расширения.
Понятие приращения функции и его геомет-
геометрический смысл.
Определение. Приращением функции называется
величина, на которую изменяется значение функции при пере-
переходе от одного значения аргумента к другому.

22
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
[ГЛ. I
Пусть л:0 и хг— два значения аргумента, Уо = /(•%) и
у{ — f (xx) — соответствующие значения функции, тогда при-
ращением аргумента назовем разность
xi хо>
а приращением функции — разность
Для различных хг и х0 значение ylf вообще говоря,
отличается от у0, поэтому удобно ввести обозначения
- —"
0
Уо
У,
x0 x, "
Теперь приращение функции
примет вид
где Дл: = хх — х0 — прираще-
ние аргумента.
На рис. 16 изображен график
Рис. 16. некоторой функции у = /(лг)
и на нем точки М0(х0, у0) и
Мх (аг1, ух). Приращение функции Ау = у1 — у0 представляет
собой разность ординат этих двух точек кривой.
Заметим, что приращение функции может быть положи-
положительным, отрицательным или равным нулю.
3. Приращение линейной функции. Вычислим прира-
приращение линейной функции
Имеем
) -\-b = kxQ + * Ад:
Вычитая из второго равенства первое, получаем
Ду = kx0 -f- k Ад: -f- Ь — kxQ — Ь = k Ад:.
Это равенство показывает, что приращение линейной
функции пропорционально приращению аргумента, причем

§ 2]
ЛИНЕЙНАЯ ФУНКЦИЯ у = kx + Ъ
23
коэффициент пропорциональности равен угловому коэффи-
коэффициенту к.
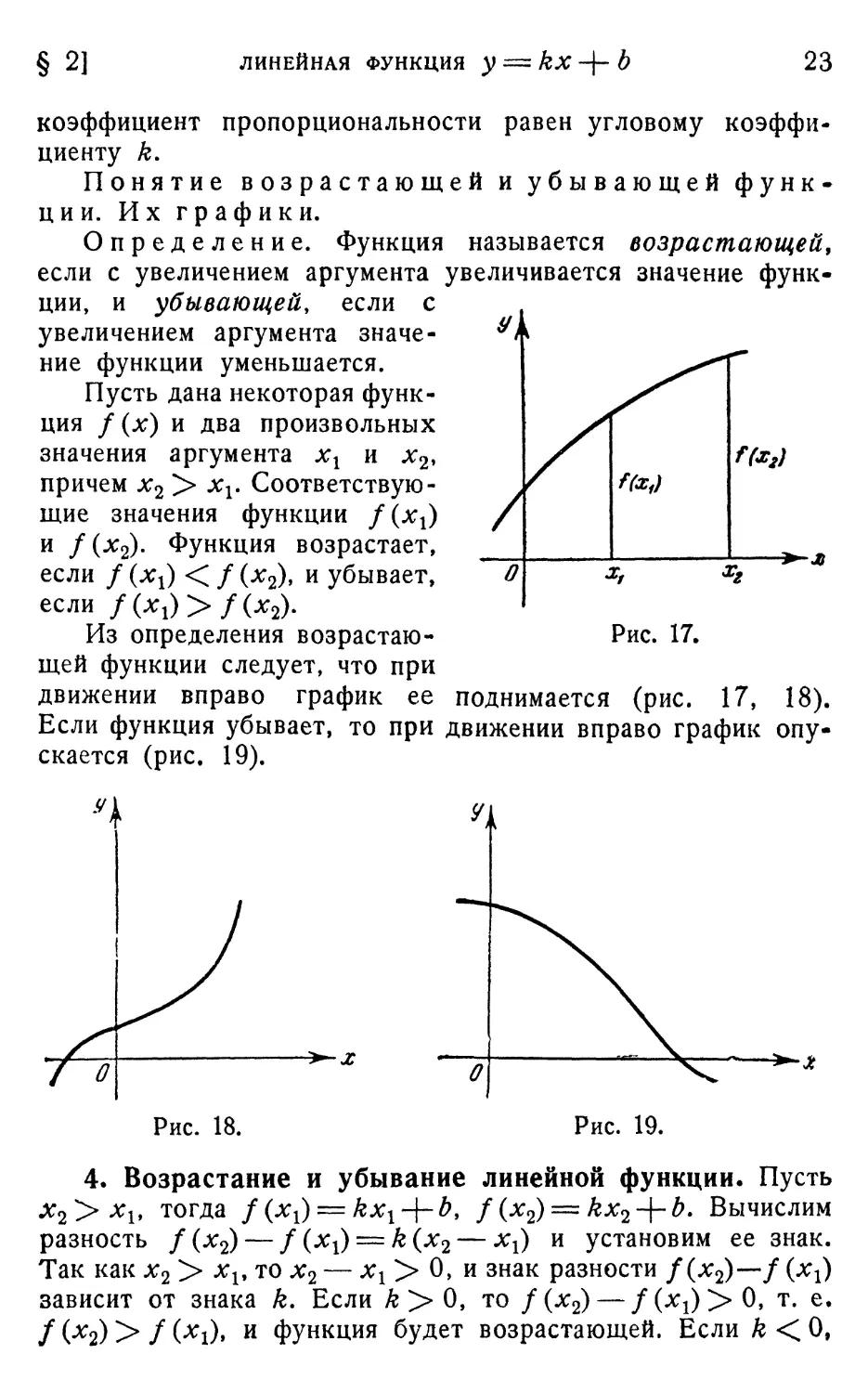
Понятие возрастающей и убывающей функ*
ции. Их графики.
Определение. Функция называется возрастающей,
если с увеличением аргумента увеличивается значение функ-
функции, и убывающей, если с
увеличением аргумента значе-
значение функции уменьшается.
Пусть дана некоторая функ-
функция f (х) и два произвольных
значения аргумента хг и х2,
причем х2 > хг. Соответствую-
Соответствующие значения функции f(xx)
и f(x2). Функция возрастает,
если / (хх) < / (лг2), и убывает,
если f(xx)>f(x2).
Из определения возрастаю- Рис. 17.
щей функции следует, что при
движении вправо график ее поднимается (рис. 17, 18).
Если функция убывает, то при движении вправо график опу-
опускается (рис. 19).
/
0
ffrf)
f(x2)
Т о
Рис. 18.
Рис. 19.
4. Возрастание и убывание линейной функции. Пусть
Х2> хх, тогда f(xl) = kxl-{-b, f {x2) = kx2-+-b. Вычислим
разность f(x2) — f(xx) = k(x2 — хх) и установим ее знак.
Так как х2 > х1% то х2 — хх > 0, и знак разности f(x2)—f (xx)
зависит от знака k. Если k > 0, то f (х2) — /(^i)>0, т. е.
/ (Х2) > / (-^i). и функция будет возрастающей. Если k < О,

24 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ [ГЛ. I
то / (х2) — / (*!>< 0f т. е. /C*2)</(*i). и функция убы-
убывающая.
Итак, если угловой коэффициент k больше нуля, то ли-
линейная функция возрастает. Если угловой коэффициент k
меньше нуля, то линейная функция убывает. При & = 0 ли-
линейная функция постоянна, и графиком ее является прямая,
параллельная оси Ох.
б. Задачи на построение линейной функции. Под тер-
термином «построение линейной функции» мы будем понимать
отыскание уравнения y — kx-\-bt задающего эту функцию.
Для составления этого уравнения необходимо знать два коэф-
коэффициента k и Ъ. Эти коэффициенты могут быть определены
из двух заданных условий, которым должна удовлетворять
функция.
Рассмотрим три наиболее распространенные задачи.
Задача 1. Построить линейную функцию по угловому
коэффициенту и значению ее в некоторой точке.
Пусть даны угловой коэффициент k искомой функции и
значение у0 функции в точке х0 : yo = f(xQ). Чтобы найти
линейную функцию у = kx-\-b, необходимо найти Ь (k нам
известно). Для этого воспользуемся вторым условием, т. е.
тем, что yQ — kx0-\-b. Отсюда Ь = у0 — kx0.
Подставляя это в уравнение, задающее функцию, получим
y=z kx-\-y0 — kXQ, ИЛИ
У — Уо = * (х — *<>)•
Геометрический смысл этой задачи таков: требуется найти
прямую, проходящую через заданную точку и образующую
с осью Ох заданный угол. Действительно, нам известны
координаты (х0, у0) и известен тангенс k угла прямой
с осью Ох.
Пример 1. Найти линейную функцию, угловой коэф-
коэффициент которой равен 2 и которая при х0= 1 принимает
значение Уо=3. Подставляя данные в уравнение, получаем
у — 3 = 2 • (лг— 1) или у = 2*+1.
Пример 2. Найти уравнение прямой, проходящей через
точку ЛA, 2) и образующей с осью Ох угол 45°. По
условию fc = tg45°=lf jc0 == I, уо = 2. Поэтому
у — 2= 1 (jc — I), y = x-fl.

§ 2]
ЛИНЕЙНАЯ ФУНКЦИЯ у ™ kX + Ь
25
Задача 2. Построить линейную функцию по двум ее
значениям, принимаемым в двух заданных точках.
Пусть даны значения функции у0 и ух в двух точках х0
/() /( kjb
у
и хг: Уо = /(*о)» У1 =
П
0
и пусть y — kx-j-b— искомая
1 1
Подставляя вместо х значения х0 и x
о
линейная функция.
получаем
Вычитая первое равенство из второго, имеем
i9
Отсюда находим угловой коэффициент к:
к_ У\ — Уо ш
Х\ ""¦*" Xq
Зная значение функции в точке х0 и угловой коэффи-
коэффициент, можем подставить их в уравнение у — у0 = к (х — лго)#
Тогда получим
У ~ Уо — l[Z.ll (х — хо)-
Разделив обе части уравнения
на уг — у0, запишем уравнение
в симметричной форме
У УО ___ -У Xq
Геометрический смысл за-
задачи состоит в том, что мы
находим прямую, проходящую Рис, 20.
через две данные точки.
V t —— Va
Формула к = ——— для вычисления углового коэффи-
Х\ """" Xq
циента имеет простой геометрический смысл. На рис. 20
У1—У0
Х\ ""-" Xq
в прямоугольном треугольнике ЛВС и, следовательно, равно
тангенсу угла а, т. е. угловому коэффициенту.
Пример. Найти уравнение прямой, проходящей через
точки B, 3) и A, 0).
видно, что отношение
является отношением катетов
— 3
0-
X — 2
Т^2
= 3(лг —2), у^Злг — 3.

26
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
[ГЛ. I
§ 3. Геометрические задачи для двух линейных функций
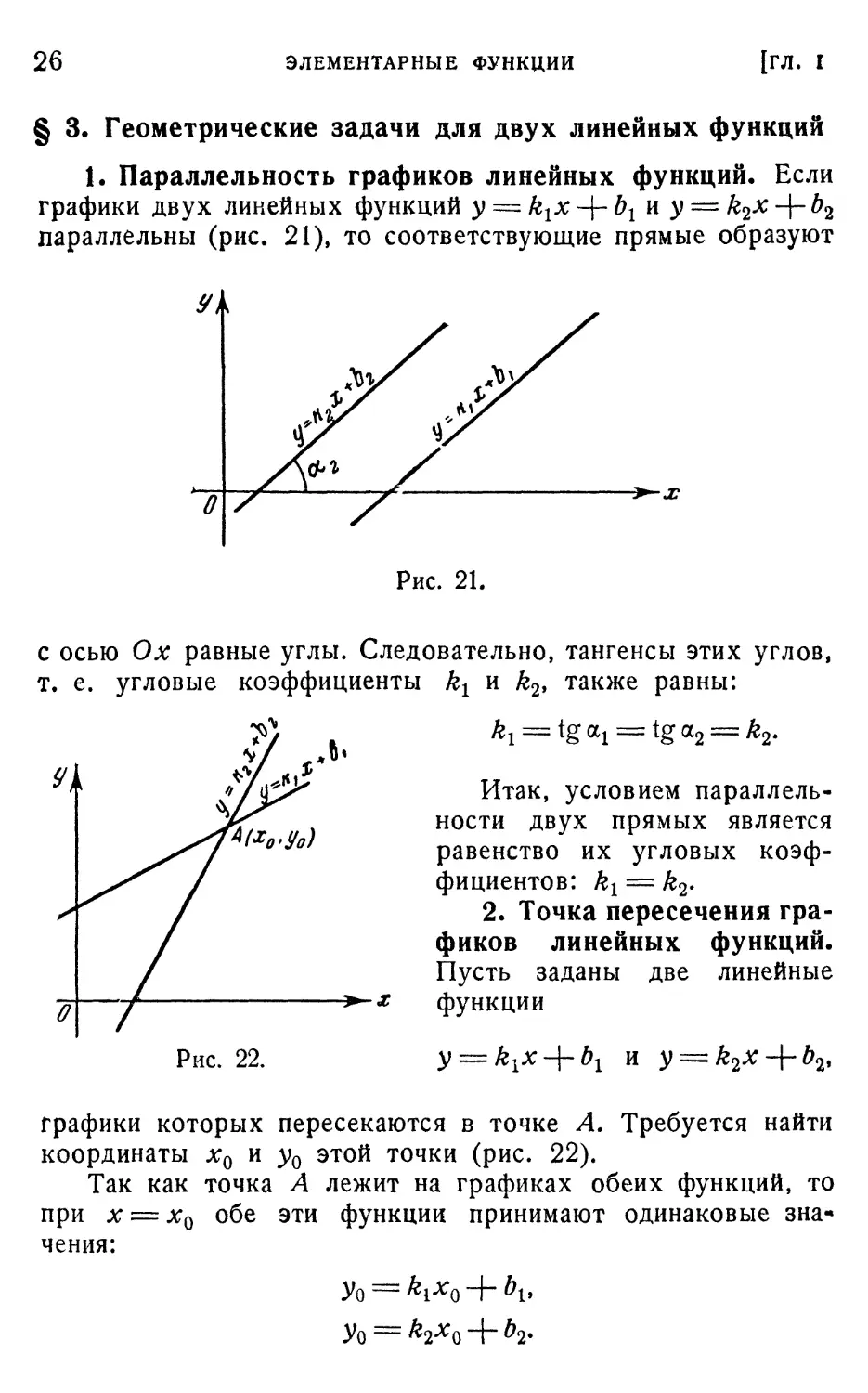
1. Параллельность графиков линейных функций. Если
графики двух линейных функций y — k^x-^-b^ и y = k2x-\-b2
параллельны (рис. 21), то соответствующие прямые образуют
-*-x
Рис. 21.
с осью Ох равные углы. Следовательно, тангенсы этих углов,
т. е. угловые коэффициенты кг и k2i также равны:
Рис. 22.
Итак, условием параллель-
параллельности двух прямых является
равенство их угловых коэф-
коэффициентов: kx — k2.
2. Точка пересечения гра-
графиков линейных функций.
Пусть заданы две линейные
функции
и у =
графики которых пересекаются в точке А. Требуется найти
координаты х0 и у0 этой точки (рис. 22).
Так как точка А лежит на графиках обеих функций, то
при x = xQ обе эти функции принимают одинаковые зна-
значения:

§ 3] ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ ДЛЯ ДВУХ ЛИНЕЙНЫХ ФУНКЦИЙ 27
Приравнивая правые части, получаем
откуда
Зная л:0, находим
Ь2 — Ь1
У
l {
Итак, для отыскания точки пересечения графиков линей-
линейных функций следует решить совместно уравнения, задающие
эти функции.
Если kx = k2% то графики параллельны, точки пересече-
пересечения не существует, что подтверждается найденными форму-
формулами.
3. Угол между графиками линейных функций. Пусть
даны линейные функции y = klx-\-bv у — k2x-\-b2. Тре-
Требуется найти угол ср между
прямыми, являющимися графи-
графиками этих функций. Обозна-
Обозначим через 04 и а2 углы, обра-
образованные соответственно пер-
первой и второй прямой с осью
Ох (рис. 23).
При определении угла ср
воспользуемся свойством внеш-
внешнего к треугольнику угла а2,
равного сумме внутренних, не
смежных с ним: а2 == ср —(— а1э
откуда ср = а2 — ах.
Так как из уравнений у == Рис. 23.
известны не сами углы аг и а2, а их тангенсы tga1 = ft1 и
tg a2 = k2% то находят не угол ср, а тангенс этого угла. Тогда
«l)= l+tgajga, =
По этой формуле вычисляется тангенс угла, отсчитываемого
против хода часовой стрелки от графика функции у = ^jc -J- ^
до графика функции y — k2x-\-b2.

28
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
[ГЛ. I
Пример. Найти угол между графиками функций
y = 2jc-f-3 и у — х-\-\.
Предварительно построим графики, для чего найдем их точки
пересечения с осями координат (рис. 24). Прямая 4у==2л: + 3
пересекает ось Оу в точке 3, а ось Ох — в точке — -^.
Прямая у — х ~\-1 пересекает ось Оу в точке 1, а ось
Ох — в точке —1.
Рис. 24.
Построив найденные точки, проведем прямые. Будем
искать острый угол между прямыми. Он отсчитывается про-
против хода часовой стрелки от прямой у=х~\-\ к прямой
. Поэтому, так как ^=1, k2 = 2t получаем
4. Перпендикулярность графиков линейных функций.
Если графики функций y = klx-\-bl и y — k2x-\-b2 перпен-
перпендикулярны /ср = -^}, то котангенс угла между ними равен
нулю: ctgcp = O. Из формулы для tgcp находим
Отсюда следует, что при перпендикулярности графиков
1 -f- k2kx = 0 или k2= т- •
Итак, если прямые перпендикулярны, то их угловые коэф-
коэффициенты обратны по величине и противоположны по знаку.

§4]
ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ
29
я
§ 4. Линейная интерполяция
Пусть y = f(x) — некоторая функция, вид которой нам
неизвестен, но известны два значения этой функции в точ-
точках х0 и хх\
Уо = /(*о) и У\ = / по-
потребуется найти значение функции в точке х, находя-
находящейся между л:0 и хг. Это значение может быть найдено
приближенно, если неизвест-
неизвестную нам функцию мы заме-
заменим линейной, принимающей
в точках xQ и хх те же значе-
значения у0 и уг.
Пусть х = хо-\~кх, а ис-
искомое значение функции у =
= уо4-Ду (рис. 25). Для того
чтобы найти значение функции
в точке х, достаточно найти
Ду. Если приближенно заме- Рис. 25.
нить функцию линейной, то
приращение последней мы можем легко вычислить. Оно про-
пропорционально приращению аргумента:
Ранее было доказано, что для линейной функции k= ——:
XI —-— Л
Тогда
Ду = ~~Г Лх*
Вычисляя приближенное значение функции, получаем
У1 — Уо а*.
или
<1—Х0
У ~ Уо + — т- (У1 - Уо)-
Л\ — Ло
Замена функции на отрезке линейной функцией, прини-
принимающей те же значения на концах отрезка, называется ли-
линейной интерполяцией. Она применяется для приближенного
вычисления промежуточных значений функции.
Пример. Вычислить значение функции y = \gx при
х = 4,537, если известны \g 4,53 = 0,6561 nig 4,54 = 0,6571.

30
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
[ГЛ.
В этом примере д:0 = 4,53, уо = 0,6561, дг1 = 4,54, ух =
= 0,6571, Ах = х — хо = 4,537 — 4,53 = 0,007. Подставляя
Ал:
в формулу у^уо+у ___у (Ух — Уо) значения х0, Arlf y0,
и Ад:, получаем
0,007
= 0,6561
lg 4,537 ^lg 4,53 + 4 54 — 453 (°>6571 —°»6561) =
0,007
0,01
0,001=0,6568.
§ 5. Квадратичная функция
Функция вида у = ах2-{-Ьх-\-с называется квадратич-
квадратичной. Она определена для всех х(—со < х < со), так как
любые действительные числа можно возводить в квадрат,
перемножать и складывать, и при этом получаются опреде-
определенные действительные числа.
Изучение квадратичной функции начнем с наиболее про-
простого случая: а—1, 6 = 0, с = 0, т. е. с функции у = х2.
График этой функции проходит через начало координат,
так как при х = 0 из уравнения следует, что у = 0.
Понятие четной и нечетной функции.
Определение. Функция называется четной, если при
изменении знака аргумента значение функции не изменяется
(рис. 26), и нечеткой, если при изменении знака аргумента
значение функции изменяет только знак (рис. 27).
Это определение можно записать так: функция f (х)
четна, если / (— x) = f (x)t и нечетна, если / (—х) =* —/ (х).

§5]
КВАДРАТИЧНАЯ ФУНКЦИЯ
31
На графике функции y = f(x) построим точки А и В
с координатами (х, f(x)) и (—х, /(—л:)). Если /(х) =
= /(—х)> то точки А и В будут расположены симметрично
относительно оси Оу. Если /(—х) = — /(¦*:), т0 точка В
будет симметрична точке А относительно начала координат.
В
Рис. 27.
Итак, график четной функции симметричен относительно
оси ординат, график нечетной функции симметричен отно-
относительно начала координат.
1. Симметрия графика функции у = х2. Изучаемая функ-
функция f(x) — x2 четная, так как /(—х) = (—хJ — х2 = / (л:).
Следовательно, график этой функции симметричен относи-
относительно оси Оу.
2. Исследование функции на возрастание и убыва-
убывание. Возьмем два значения аргумента хх и х2 (х2 > хх), вы-
вычислим соответствующие значения функции f (хг) = Х\,
f(x2)=xl и най^ем разность f(x2) — f {х\)~ х\ — х\ш
Как известно, если f (x2) > f (Х\)> то функция возрастает,
если f(x2Xf(x1)> то функция убывает. Для определения
разности f(x2) — f(x\)—xl — х\ заметим, что
= (х2-^~ хМх2 — хХ Так как х2 > хг> то второй со-
сомножитель положителен, х2 — х{^> 0, и, следовательно, знак
произведения зависит от знака сомножителя х2~{-хх.
Знак суммы х2-\-хх при всевозможных значениях х не-
непостоянен. Поэтому рассмотрим функцию отдельно при
отрицательных и положительных значениях х.
знака
х\ —

32
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
[ГЛ. I
1) Если хх > О и х2 > О, то лг2 + хх > О и / (лг2) —
— /C*i)>0» T- е- функция возрастает при положительных
значениях аргумента.
2) Если х{ < О и л:2<0, то х2-\-х1<0 и /(х2) —
— /(Л)<0» т- е- функция убывает при отрицательных
значениях аргумента.
Итак, функция f(x)=x2 возрастает при х > 0 и убы-
убывает при х < 0.
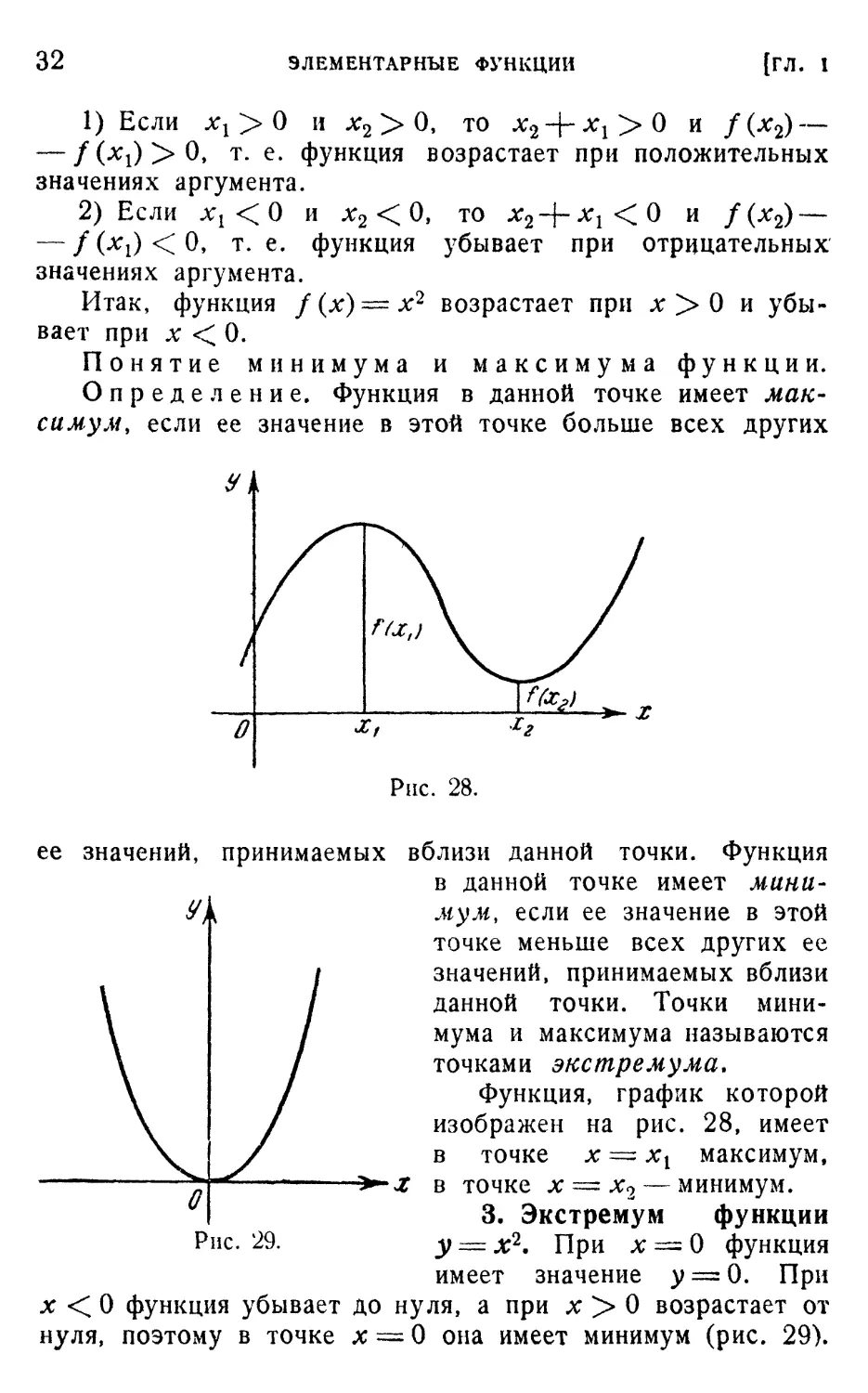
Понятие минимума и максимума функции.
Определение. Функция в данной точке имеет мак-
максимум, если ее значение в этой точке больше всех других
Рис. 28.
ее значений, принимаемых вблизи данной точки. Функция
в данной точке имеет мини-
минимум, если ее значение в этой
точке меньше всех других ее
значений, принимаемых вблизи
данной точки. Точки мини-
минимума и максимума называются
точками экстремума.
Функция, график которой
изображен на рис. 28, имеет
в точке х = хх максимум,
-**-? в точке х — х2 — минимум.
3. Экстремум функции
у — х2. При х = 0 функция
имеет значение у==0. При
х < 0 функция убывает до нуля, а при х > 0 возрастает от
нуля, поэтому в точке # = 0 она имеет минимум (рис. 29).
О
Рис. 29.

§ 51
КВАДРАТИЧНАЯ ФУНКЦИЯ 33
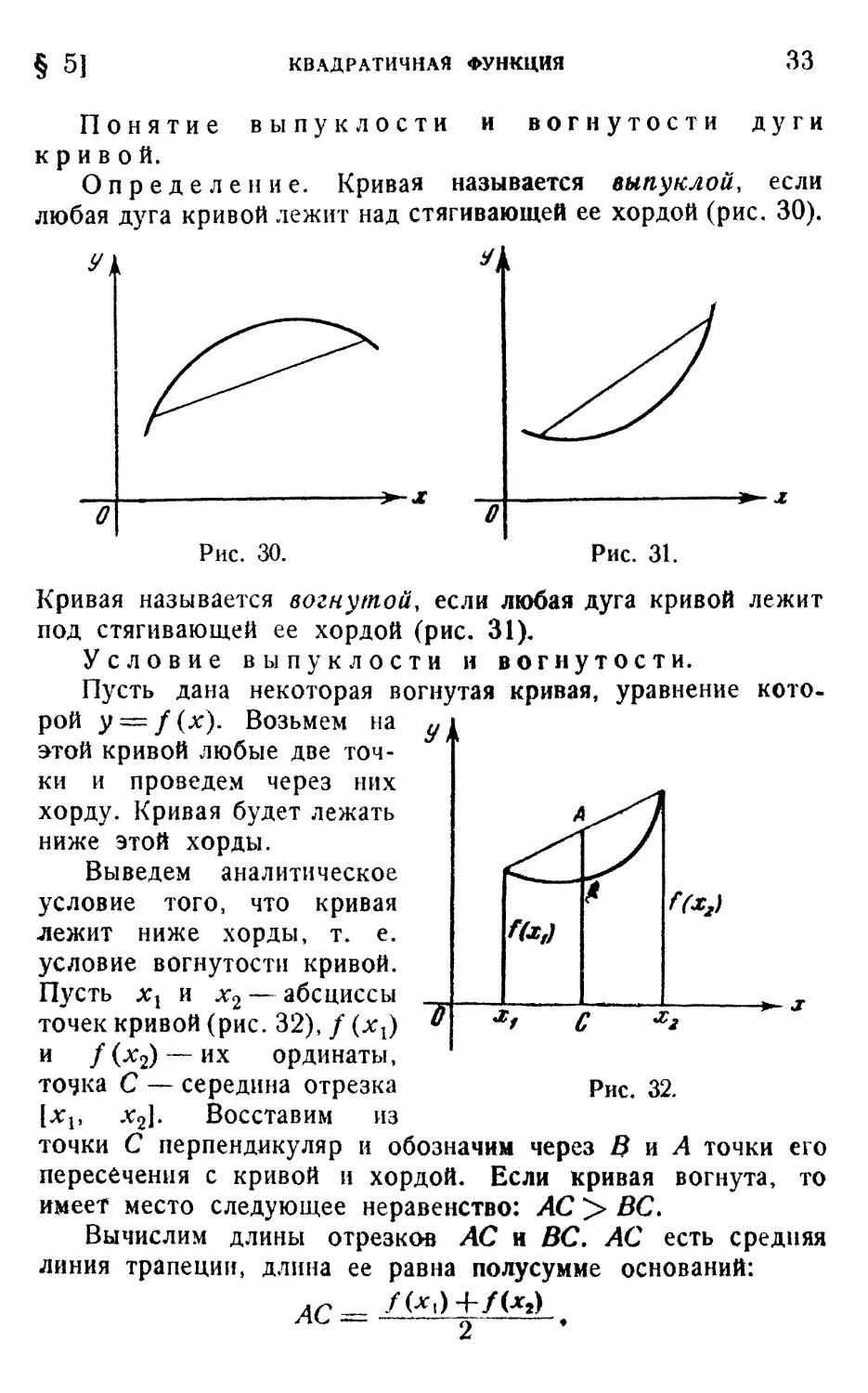
и вогнутости дуги
Понятие выпуклости
кривой.
Определение. Кривая называется выпуклой, если
любая дуга кривой лежит над стягивающей ее хордой (рис. 30).
п
Рис. 30.
Рис. 31.
Кривая называется вогнутой, если любая дуга кривой лежит
под стягивающей ее хордой (рис. 31).
Условие выпуклости и вогнутости.
Пусть дана некоторая вогнутая кривая, уравнение кото-
которой y — f(x). Возьмем на
этой кривой любые две точ-
точки и проведем через них
хорду. Кривая будет лежать
ниже этой хорды.
Выведем аналитическое
условие того, что кривая
лежит ниже хорды, т. е.
условие вогнутости кривой.
Пусть хг и х2 — абсциссы .
точек кривой (рис. 32), / (хг)
и / (хт) — их ординаты,
точка С — середина отрезка Рис. 32.
[лгр х2]. Восставим из
точки С перпендикуляр и обозначим через В и А точки его
пересечения с кривой и хордой. Если кривая вогнута, то
имеет место следующее неравенство: АС > ВС.
Вычислим длины отрезков АС н ВС. АС есть средняя
линия трапеции, длина ее равна полусумме оснований:
ас — /(*!)+/<*»)
/к>— 2

34 ЭЛЕМЕНТАРНЫЕ ФУНКЦИЙ [ГЛ. X
Точка С делит отрезок [xv х2] пополам. Длина этого
отрезка равна х2 — xv Поэтому абсцисса ОС = хг-\-
Ч~~ *2 "о"Х{ = Xl о *2~ • Абсцисса точки В также равна—[ ^ 2-.
Ее ордината ВС может быть найдена из уравнения кривой:
Тогда неравенство АС > ВС можно записать в виде:
2 >'\ 2
Итак, если дуга кривой вогнута, то
2
если дуга кривой выпукла, то
2 ^
Справедливо и обратное утверждение: если при всех Xj и х2
2
или ^-
то дуга кривой вогнута (соответственно выпукла).
4. Исследование графика функции у = х2 на выпук-
выпуклость и вогнутость. Вычислим значения функции у = 2
в произвольных точках хг, х2 и в точке Х{
2
_ 2 f/v4_r2 r / Xi + X2 \ / xx + X2 \
— x\t f (X2) — x2, f I—2—) == 1 2 / *
Определим знак разности /(Xl) +/(^z) — / ( X{ +x* \;
4
2 4
x\ — x\ — 2хгх2 — ^ (хг — x2
0.

§ 5]
КВАДРАТИЧНАЯ ФУНКЦИЯ
Следовательно, /<*'>+/<*»>
35
и график
вогнут.
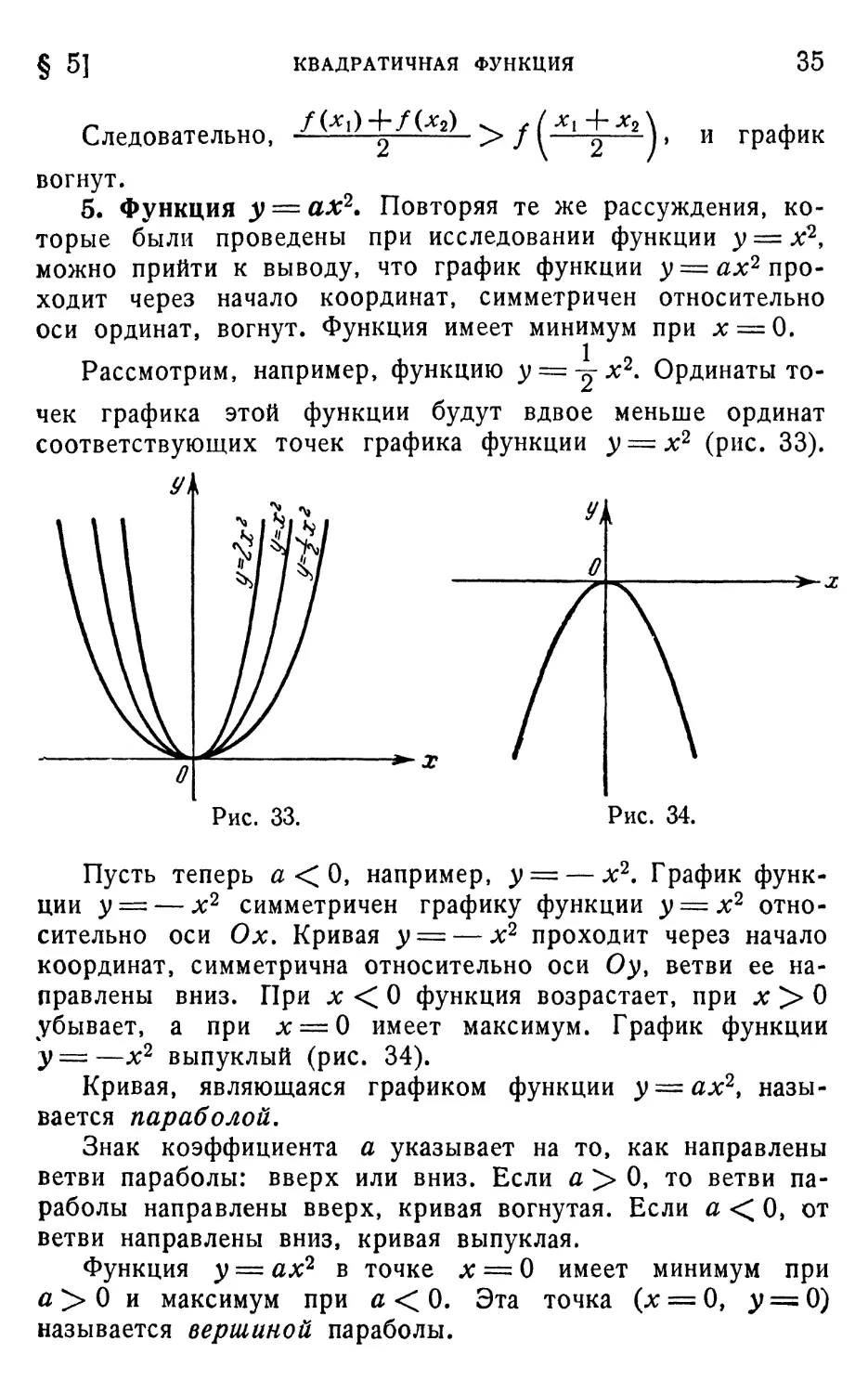
5. Функция у = ах2* Повторяя те же рассуждения, ко-
которые были проведены при исследовании функции у = х2,
можно прийти к выводу, что график функции у = ах2 про-
проходит через начало координат, симметричен относительно
оси ординат, вогнут. Функция имеет минимум при л; = 0.
Рассмотрим, например, функцию у — ^х2. Ординаты то-
точек графика этой функции будут вдвое меньше ординат
соответствующих точек графика функции у = х2 (рис. 33).
У\
Рис. 33.
Рис. 34.
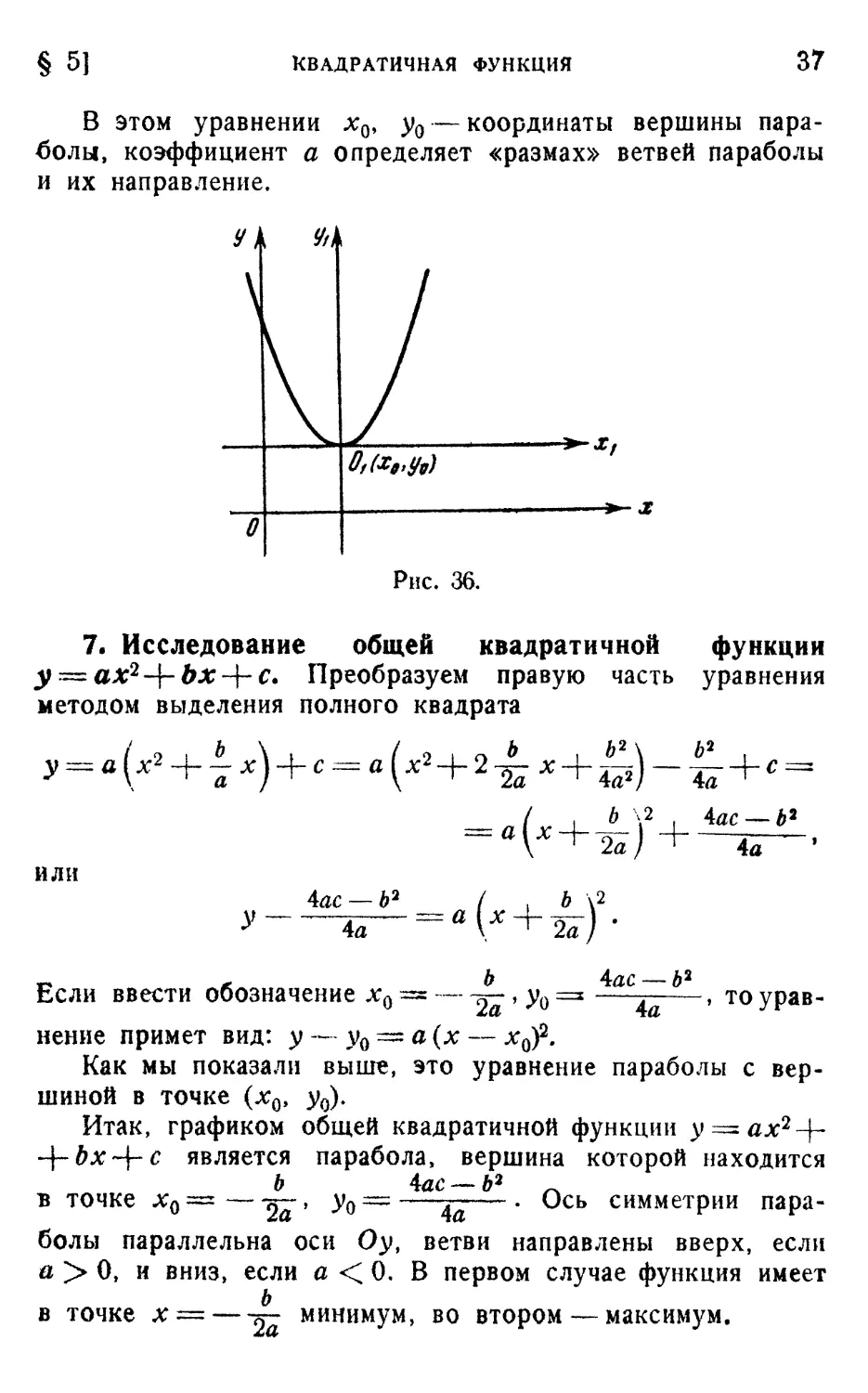
Пусть теперь а < О, например, у =— х2. График функ-
функции у = — х2 симметричен графику функции у — х2 отно-
относительно оси Ох. Кривая у — — х2 проходит через начало
координат, симметрична относительно оси Оу, ветви ее на-
направлены вниз. При х < 0 функция возрастает, при х > О
убывает, а при л; = 0 имеет максимум. График функции
у = —х2 выпуклый (рис. 34).
Кривая, являющаяся графиком функции у = ах2, назы-
называется параболой.
Знак коэффициента а указывает на то, как направлены
ветви параболы: вверх или вниз. Если а > 0, то ветви па-
параболы направлены вверх, кривая вогнутая. Если а < 0, от
ветви направлены вниз, кривая выпуклая.
Функция у —ах2 в точке л; = 0 имеет минимум при
я>0 и максимум при а < 0. Эта точка (х = 0, у = 0)
называется вершиной параболы.

36
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
(ГЛ. Г
Параллельный перенос системы координат.
Выберем на плоскости систему координат х'Оху\ на-
начало которой находится в точке Ox(xQi у0), а оси Oxxf и
Оху' параллельны осям Ох и Оу,
Рис. 35.
Найдем координаты любой точки А в системе х'Оху\
На рис. 35 видно, что
X = X — Xq,
где х, у — координаты точки А в системе хОу, а
х\ у1 — координаты точки А в системе х'Оху'.
Эти формулы называются формулами преобразования
координат при параллельном переносе системы координат.
6. Уравнение параболы с вершиной в заданной точке*
Пусть вершина параболы находится в некоторой точке Оь
координаты которой jc0, y0 (рис. 36). Требуется найти вид
уравнения, этой параболы.
Выберем вспомогательную систему координат с началом
в вершине Ох параболы. Тогда в этой системе координат
парабола будет иметь уравнение
Уравнение в исходной системе получаем, подставляя вместо
хг и у' их выражения через х и у, т. е.

§ 5]
квадратичная функция
37
В этом уравнении л;0, у0 — координаты вершины пара-
параболы, коэффициент а определяет «размах» ветвей параболы
и их направление.
Рис. 36.
7. Исследование общей квадратичной функции
у~ах2-\-Ьх-\-с. Преобразуем правую часть уравнения
методом выделения полного квадрата
или
У —
4ас — Ь2
4а
Если ввести обозначение
4ас
Аа
тоурав-
нение примет вид: у — у0 — а (х xof.
Как мы показали выше, это уравнение параболы с вер-
вершиной в точке (jc0, y0).
Итак, графиком общей квадратичной функции у=^ах2-\-
-\-bx~\-c является парабола, вершина которой находится
Ось симметрии пара-
л:0——^, уо=
болы параллельна оси Оу, ветви направлены вверх, если
п > 0, и вниз, если а < 0. В первом случае функция имеет
в точке х~ — -^ минимум, во втором — максимум.

38
ЭЛЕМЕНТАРНЫЕ ФУНКЦИЙ
[ГЛ. I
Пример. у== — Зл;2+6л; + 2 (рис. 37).
1. Графиком этой квадратичной функции является пара-
парабола.
2. Ось симметрии параллельна оси Оу.
3. Ветви параболы направлены вниз, так как а = — 3 < 0.
4. Вершина параболы смещена, координаты ее находятся
методом выделения полного квадрата.
у = —
= — 3(х2 — 2л;+1 —
= _3(JC— 1J+6.
у — 5 = — 3(лг— IJ.
Координаты вершины: л;0=1, уо — 5.
Задача. Представить число 10
в виде суммы двух чисел так, чтобы
сумма квадратов этих чисел была наи-
наименьшей.
Разобьем число 10 на два слагае-
слагаемых: х и 10 — х, тогда сумма их
квадратов у = л;2 + A0— хJ, или
у = 2л:2—20х+100. Выделяем полный квадрат у =
= 2 (л: — 5J + 50, откуда следует, что при х — 5 функция
имеет минимум (а = 2 > 0), равный 50.
Если 10 представить, например, в виде суммы 4 и б, то
сумма квадратов этих чисел, равная 52, уже больше пяти-
пятидесяти.
8. Примеры зависимостей, выражающихся квадратич-
квадратичной функцией, а) Количество тепла, выделяемого при про-
прохождении тока в проводнике с сопротивлением R и силой
тока /, выражается квадратичной функцией
Рис. 37.
Графически эта зависимость изображается правой ветвью
параболы (/^>0), симметричной относительно оси ординат
с вершиной в начале координат (рис. 38).
б) Бомба, сброшенная с самолета на высоте h с началь»
ной скоростью v0, при своем падении описывает правую
ветвь параболы

§5]
КВАДРАТИЧНАЯ ФУНКЦИЯ
39
Вершина этой параболы находится на оси Оу в точке у = ht
ветви параболы направлены вниз (рис. 39).
в) Во время работы сепарирующей центрифуги поверх-
поверхность вращающейся жидкости принимает форму так назы-
Q
Рис. 38.
ваемого параболоида вращения. Если взять сечение, прохо-
проходящее через ось цилиндра, то в сечении получается пара-
парабола. Уравнение этой параболы
где со — угловая скорость, g — ускорение свободного па-
падения.
Рис. 39.
Рис. 40,
Парабола симметрична относительно оси Оу, ветви направ-
направлены вверх, а вершина лежит на оси Оу в точке yQ (рис. 40),

40
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
[ГЛ. t
г) Пусть тело брошено под углом а к горизонту с на-
начальной скоростью v$. Полет тела будет происходить по кривой
cos2 a
Как было установлено ранее, эта кривая — парабола.
Рис. 41.
Ветви ее направлены вниз (рис. 41). Выделяя полный квад-
квадрат, находим, что вершина параболы имеет координаты:
V7{ sin a cos a
Уо
sin a
Ордината у0 соответствует наибольшей высоте полета тела.
Для того чтобы определить дальность полета, нужно найти
вторую точку пересечения параболы с осью Ох:
хл —¦
sin a cos a
i
§ 6. Кубическая функция
Кубической функцией называется функция вида
Рассмотрим простейший случай, когда a=lf b = 0t c — 0t
d Q:
у — л:3.
1. Исследование функции у — хъ. Для вычисления у
нужно величину х возвести в куб, и так как возводить

§ 6j КУБИЧЕСКАЯ ФУНКЦИЯ 41
б куб можно любые числа, то функция y = x3 опреде-
определена при всех х. При лг = О также у = 0, поэтому график
функции проходит через начало координат. Функция f(x) = л;3
нечетная, так как (—хK = — л:3, следовательно, ее график
симметричен относительно начала координат.
Исследуем функцию у = х3 на возрастание и убывание.
Возьмем два значения аргумента хх и х2(х2 > х^, вычислим
соответствующие значения функции f(xl) = X\, f(x2) — X2,
найдем их разность и установим ее знак.
о о
Для этого разложим разность x<i— Х\ на множители:
/ (x2) — f (хх) = xl — x\ = (х2 — хх)
Первый сомножитель х2 — хх положителен, так как х2
Второй сомножитель xl-{-x2xL + х? также положителен,
так как произведение ххх2 по абсолютной величине не прево-
превосходит квадрата большей из абсолютных величин чисел хх и х2.
Итак, х\ — х\ > 0, т. е. х\ > х\ и, следовательно, функ-
функция всюду возрастает.
Если функция всюду возрастает, то она не имеет ни макси-
максимума, ни минимума.
Исследуем выпуклость и вогнутость графика функ-
функции у = л:3. Для этого проверим, выполняется ли для функ-
функции у = jc3 неравенство
2 >7\ 2 /'
являющееся условием вогнутости ее графика. Для функ-
функции /(л:) = л:3 имеем /(хг) = хЬ f(x2) = xi fyXl ~^X 2j =
r^ 1 Х{ 2 *2) ' Установим знак разности:
—А—3^ix2—^1^1—*
2 8 == 8
= [
= 8 — =8" [
= |-(лг2 — ^^(л:! — л:?) = ~{х2 — xxf{x2 + xx).
Знак полученного произведения зависит от знака сомножи-
сомножителя x2-\-xv Рассмотрим функцию отдельно при отрицатель-
отрицательных и положительных значениях х. Если хх > 0 и х2 > О,

42
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
[ГЛ. 1
то х2+хх>0 и разность
вогнутый. Если хх < 0 и х2 < 0, то разность
— ( 2 2) < ^; гРаФик выпуклый.
> 0; график
1 = л:3 выпуклый при х < 0,
2
Итак, график функции
вогнутый при х > 0.
Понятие точки перегиба.
Определение. Точка, которая отделяет участок вы-
выпуклости графика однозначной функции от участка вогну-
вогнутости, называется точкой пе~
региба *).
При исследовании было
установлено, что функция
у = х3 всюду возрастает, в на-
начале координат график ее имеет
точку перегиба, так как при
х > 0 график вогнутый, при
х < 0 — выпуклый (рис. 42).
Располагается график этой
функции в первой и третьей
четвертях.
График функции у = х3 на-
называется кубической парабо-
параболой.
функции у =x3-\-kx. Рассмотрим
при k > 0.
Рис. 42.
2. Исследование
сначала функцию у = x3-\-kx
Функция у = x3-\-kx определена при всех х. График ее
проходит через начало координат, так как при л: —0 у = 0.
При у—0 имеем x3-\-kx = 0y откуда л:1 = 0, x2f 3= ± V"—k .
Так как k > 0, то других (кроме начала координат) точек
пересечения с осью Ох график не имеет. Функция y—x3-{-kx
нечетная. Действительно, / (— х) = (— xf + k (— х) =
=— я3 — kx = —/ (jc). График симметричен относительно
начала координат.
Исследуемая функция ^==^3 + ^л: состоит из двух сла-
слагаемых л;3 и kx, каждое из которых возрастает. Поэтому
функция у = x3-{-kx также возрастает.
*) В дальнейшем это понятие будет уточнено.

§ 6] КУБИЧЕСКАЯ ФУНКЦИЯ 43
Для исследования графика функции у = х^-\-кх на выпук-
выпуклость и вогнутость составляем выражение
(хг + x2f + 4k (хг + х2) 4x1 + *4 - (Х1 + Х2?
8
->- X
Все члены, содержащие к, уничтожаются, и поэтому выра-
f(Xl) + f(X2) r I X\ + Х2 \
жение ¦ v '—-^- /\~^~Ь— ) получается такое же, как
и для функции у = jc3. Сле-
Следовательно, при х < 0 график
выпуклый, при х > 0 вогнутый.
В начале координат график
имеет точку перегиба (рис. 43).
Заметим, что добавление
к любой функции линейной щ
kx-\-b не изменяет ни выпук-
выпуклости, ни вогнутости графика.
Пусть теперь к < 0. Функ-
Функция у = хг-\-кх определена
при всех х, график ее про-
проходит через начало координат
и пересекает ось Ох в трех ' Л
л л г ~^г- Рис- 45-
точках: jc1 = O, x2—y—к,
хг = — у — к. График симметричен относительно начала
координат, выпуклый при х < 0 и вогнутый при х > 0.
Исследование возрастания и убывания функции у=хг^-кх
при к < 0 будет более сложным. Первое слагаемое л:3
возрастает, второе кх (линейная функция) — убывает. При-
больших значениях |jt| величина |л:|3 будет значительно
больше величины \кх\, поэтому можно предполагать, что
при больших \х\ функция у — х3-{~кх возрастает. При зна-
значениях *, близких к нулю, наоборот, | jc|3 будет значи-
значительно меньше \кх\, поэтому следует ожидать, что функция
у = х3-\-кх убывает.
Полученные данные позволяют нарисовать график функ-
функции у = хъ-\-кх (рис. 44).
Для уточнения вида кривой следует найти точки макси-
максимума и минимума. Возьмем на графике какую-нибудь точку

44
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
[ГЛ. t
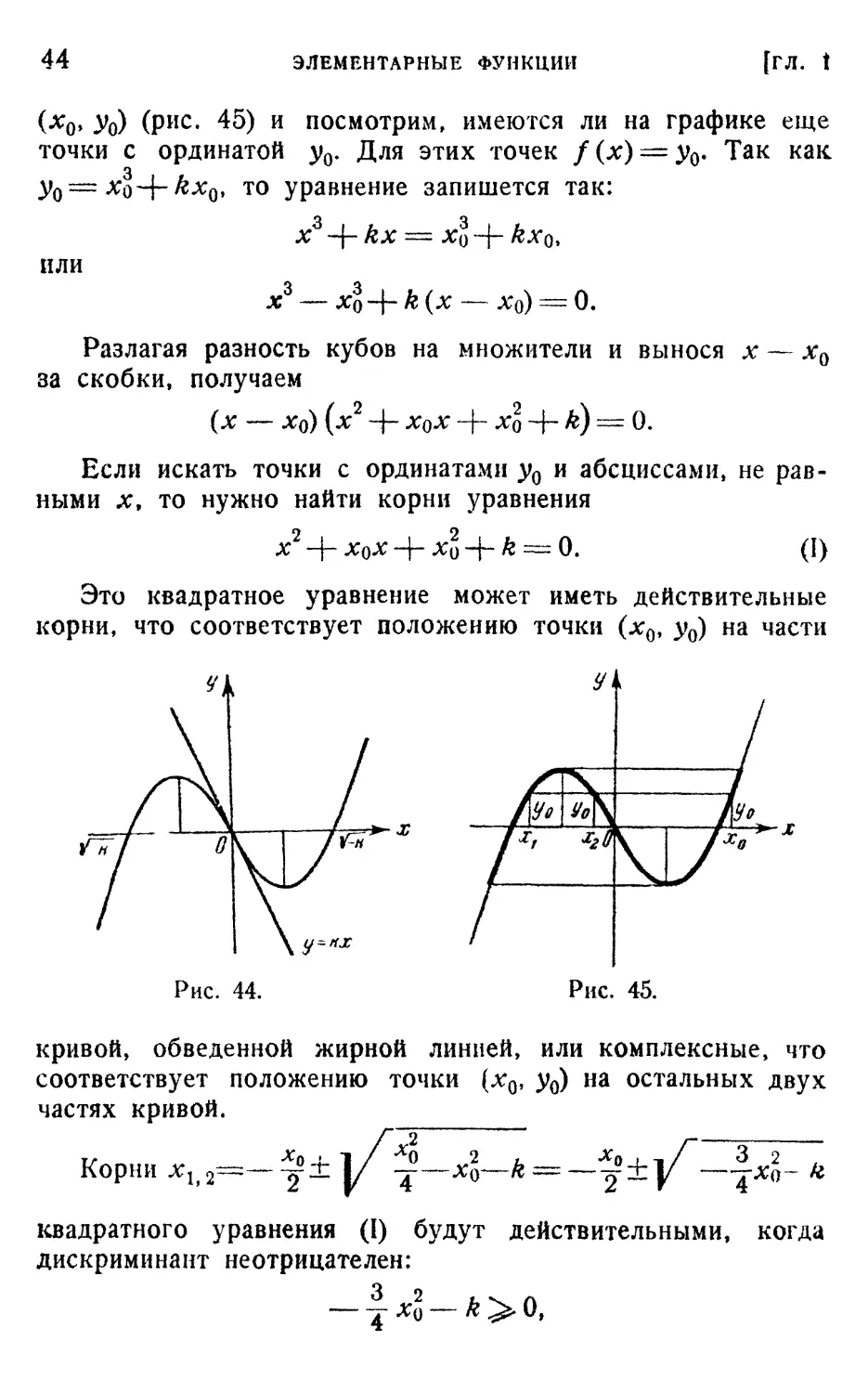
(д:0, у0) (рис. 45) и посмотрим, имеются ли на графике еще
точки с ординатой у0. Для этих точек f(x) = y0. Так как.
уо~ xl~\-kxQi то уравнение запишется так:
xs -f- kx =
или
XZ — #0+ k (X — Xq) = 0.
Разлагая разность кубов на множители и вынося х — х0
за скобки, получаем
(* — Х0) (
= 0.
Если искать точки с ординатами у0 и абсциссами, не рав-
равными х, то нужно найти корни уравнения
Это квадратное уравнение может иметь действительные
корни, что соответствует положению точки (х0, у0) на части
Рис. 44.
Рис. 45.
кривой, обведенной жирной линией, или комплексные, что
соответствует положению точки (xQ, y0) на остальных двух
частях кривой.
Корни
1|2=-^± у J—4—* = —§±
квадратного уравнения (I) будут действительными, когда
дискриминант неотрицателен:
т" Xq
ft ^> U,

§ 61
КУБИЧЕСКАЯ ФУНКЦИЯ
45
или
A
"з
Таким образом, вся проведенная жирной линией часть
кривой располагается по оси
Ох от * = — /~
Если хо=2у —j,
дискриминант уравнения (I)
равен нулю и, следовательно,
на кривой есть еще только
одна точка с ординатой у0. Для
нее лг1>2= — ~к = —у ~ it-
В этой точке функция у = л:3+&лг, очевидно, будет иметь
максимум
Рис. 46.
Г ~~ "^(з"
будет минимум, равный
Аналогично, при х = у — -тг
2 / /Г
Or О
— со < х < —у —^-, убывает при — l/ —
и возрастает при у —-^-<л:<сх>. При х = — у — -^
максимум, при х=у —-^ — минимум. График функции
изображен на рис. 46.
Итак, при &>0 функция y=:x3-\~kx возрастает
и не имеет точек экстремума, при k < 0 имеет точку ми-
минимума и точку максимума. В обоих случаях в начале коор-
координат точка перегиба.
имеет

46
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
[ГЛ. !
3. Исследование функции у = xs~-\-kx~\-b. Рассмотрим
теперь график функции у = хъ-]-кх-\-Ь. Он отличается от
графика ранее рассмотренной функции у = x3-{-kx тем,
что ординаты всех его точек
увеличены на Ь% т. е. график
сдвинут по оси Оу на Ъ (рис.
47—49).
Абсциссы точек максимума,
минимума и точки перегиба
при этом не изменяются. Абсцис-
Абсциссы точек пересечения с осью Ох
изменяются. Более того, на
рис. 48 видно, что при боль-
больших Ь график пересекает ось
Ох только в одной точке,
причем ее абсцисса отрица-
отрицательна. Аналогично, при боль-
большом по абсолютной величине,
но отрицательном Ъ график y = xz-\-kx-\-b имеет также
только одну точку пересечения с осью Ох, но в ее поло-
положительной части. Очевидно, что график будет пересекать
*- х
Рис. 47.
Рис. 48.
Рис. 49.
ось Ох в одной точке при тех значениях Ь, которые по
абсолютной величине больше значений функции y = ^{
в точках максимума и минимума, т. е.

§ 6J КУБИЧЕСКАЯ ФУНКЦИЯ 47
Возводя в квадрат обе части этого неравенства, получаем
- -o=- k3, или
Ь2
Итак, мы приходим к выводу:
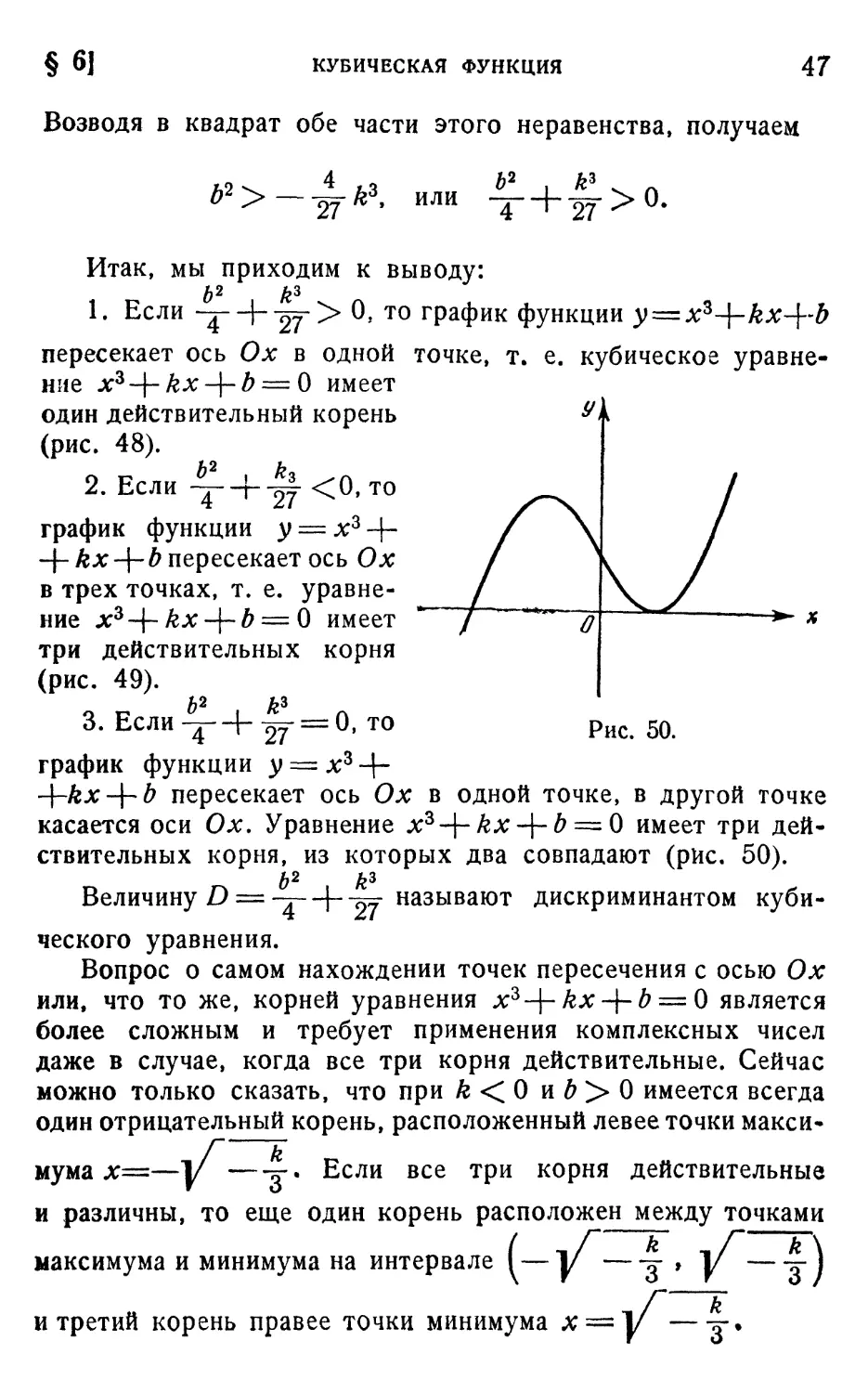
Ь2 №
1. Если -^-\-~2f> О* то график функции у = л:
пересекает ось Ол: в одной точке, т. е. кубическое уравне-
уравнение xz-\-kx-\-b — О имеет
один действительный корень
(рис. 48).
2. Если -^--f-^f
график функции у = х3 -\-
-f-&;t + ^ пересекает ось Ол:
в трех точках, т. е. уравне-
уравнение xz-\-kx-\-b — 0 имеет
три действительных корня
(рис. 49).
3. Если -j- 4- 27" = 0, то Рис 50.
график функции у = хг-\-
-\-kx-\-b пересекает ось Ох в одной точке, в другой точке
касается оси Ох, Уравнение х3+/гл: + ^ = 0 имеет три дей-
действительных корня, из которых два совпадают (рис. 50).
b2 k3
Величину D = -j- + -97" называют дискриминантом куби-
кубического уравнения.
Вопрос о самом нахождении точек пересечения с осью Ох
или, что то же, корней уравнения xz-\-kx-\-b = 0 является
более сложным и требует применения комплексных чисел
даже в случае, когда все три корня действительные. Сейчас
можно только сказать, что при к < 0 и b > 0 имеется всегда
один отрицательный корень, расположенный левее точки макси-
к
^-. Если все три корня действительные
и различны, то еще один корень расположен между точками
максимума и минимума на интервале (— у — 'з f V — Т
и третий корень правее точки минимума х=у —-q-*

48
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
[ГЛ. I
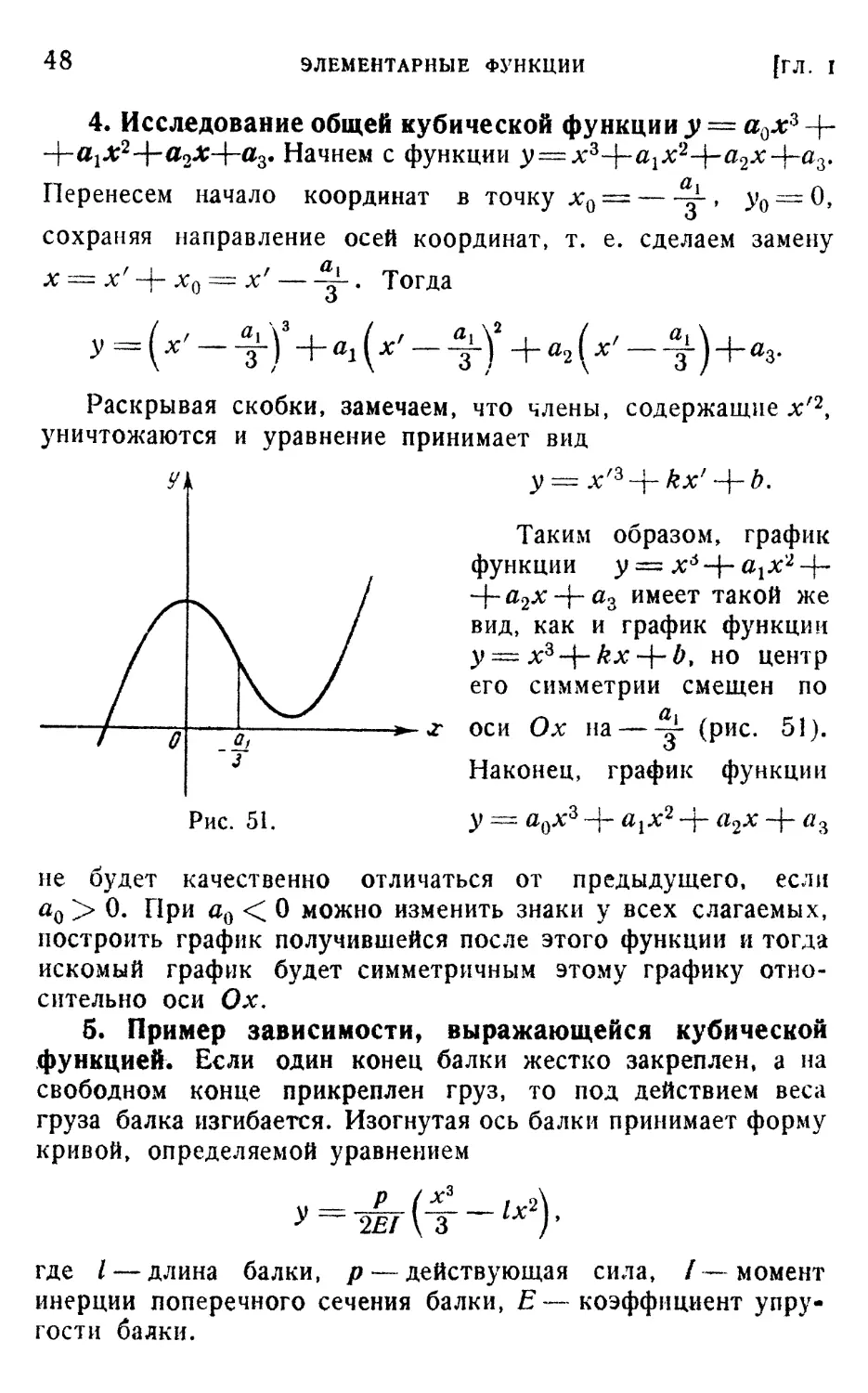
4. Исследование общей кубической функции у — адх3 -j-
2-f-^2Jt+a3- Начнем с функции y = x*-\~alx2-\-a2xJra^
Перенесем начало координат в точку xQ = — ~t у0 = О,
сохраняя направление осей координат, т. е. сделаем замену
х
х0 = х' — -—-. Тогда
Раскрывая скобки, замечаем, что члены, содержащие х'2,
уничтожаются и уравнение принимает вид
Рис. 51.
Таким образом, график
функции у = х6 + агх2 -f-
+ а2х + аг имеет такой же
вид, как и график функции
)) = xs~$~kx>-{-b, но центр
его симметрии смещен по
х оси Ох на ^- (рис. 51).
Наконец, график функции
у = а0л:3 -f- ajjc2 -)- а2х -{- аг
не будет качественно отличаться от предыдущего, если
а0 > 0. При а0 < 0 можно изменить знаки у всех слагаемых,
построить график получившейся после этого функции и тогда
искомый график будет симметричным этому графику отно-
относительно оси Ох.
5. Пример зависимости, выражающейся кубической
функцией. Если один конец балки жестко закреплен, а на
свободном конце прикреплен груз, то под действием веса
груза балка изгибается. Изогнутая ось балки принимает форму
кривой, определяемой уравнением
где / — длина балки, р— действующая сила, /—момент
инерции поперечного сечения балки, Е—коэффициент упру-
упругости балки.

* 7)
МНОГОЧЛЕНЫ
49
График кубической функции y=z -Jet(^s Iх} прохо-
проходит через начало координат, так как у = 0 при л* = 0,
и пересекает ось Ох в точке jt —3/ (рис. 52).
У
31/
^-x
Рис. 52.
В точке х = 0 функция имеет максимум, равный нулю,
в точке х — 21 — минимум, равный ШГ'
При х — / (на свободном конце балки) кривая имеет
точку перегиба.
§ 7. Многочлены
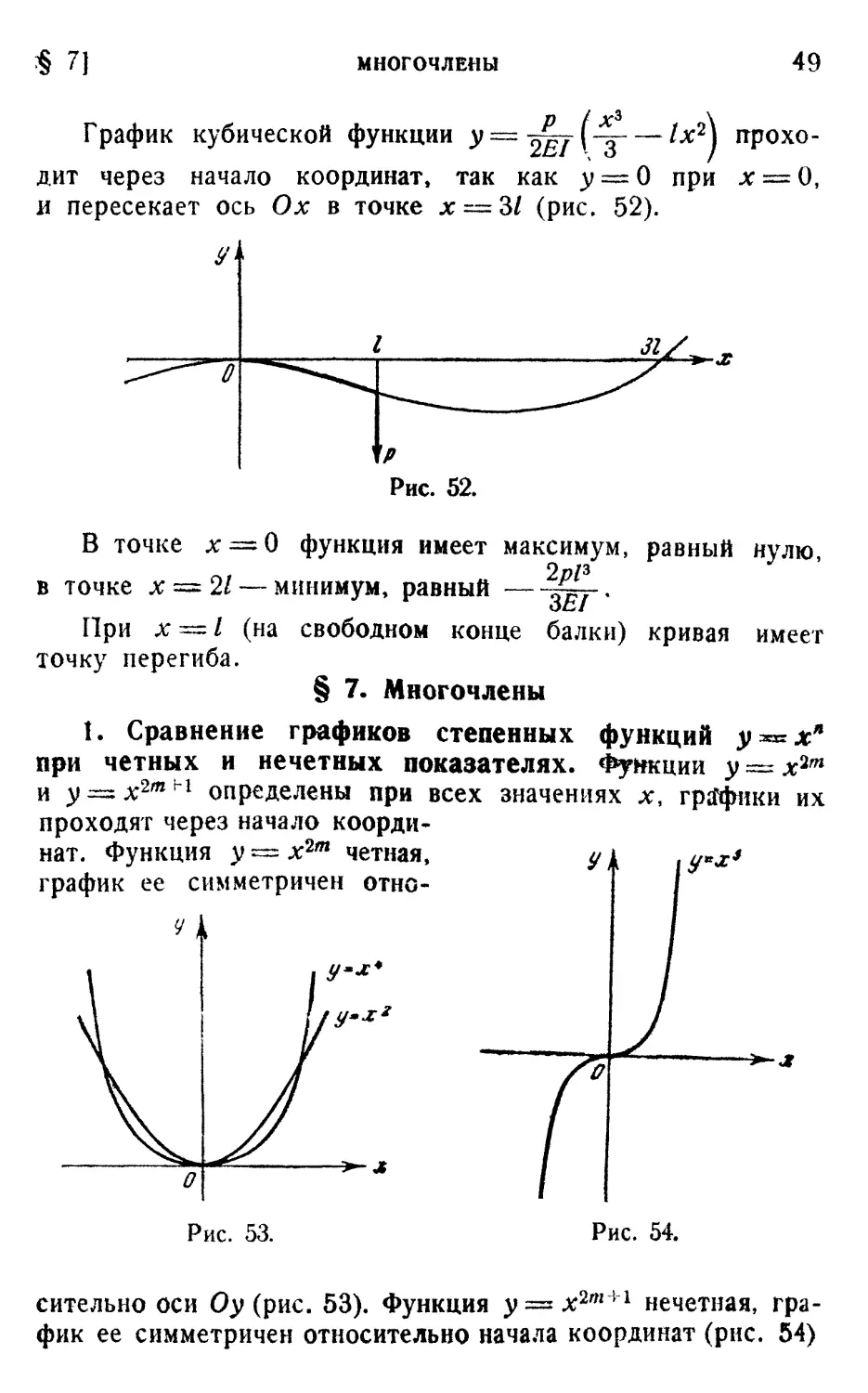
I. Сравнение графиков степенных функций у^хп
при четных и нечетных показателях. Фикции у = хы
2ml
и y
=zx2mrl
определены при всех значениях х, гр^Гфики их
проходят через начало коорди-
координат. Функция у^х2т четная,
график ее симметричен отно-
Рис. 54.
сительно оси Оу (рис. 53). Функция у=» х2|Я+1 нечетная, гра-
график ее симметричен относительно начала координат (рис. 54)

50 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ [ГЛ. I
Функция у = х2т при х = 0 имеет минимум, функция y=x2m+i
не имеет ни максимума, ни минимума. График функции
y=x2m+i имеет точку перегиба х = 0.
График функции у = хп называется параболой п-го по-
порядка.
2. Многочлен. Корни многочлена. Разложение на мно-
множители. Определение. Функция у = аохп-\~аххп~1-\-...
.. . + ап_гх -f- ап (а0 ф 0), где п — целое положительное
число, называется многочленом степени п.
Многочлен степени п сокращенно будем обозначать через
Рп(х). В дальнейшем рассматриваются многочлены только
с действительными коэффициентами.
Так как возводить в степень, перемножать и складывать
можно любые действительные числа, то многочлен опреде-
определен для всех значений х.
Если многочлен содержит только четные степени jc, то
он является четной функцией и график его симметричен отно-
относительно оси Оу. Если многочлен содержит только нечетные
степени х, то он является нечетной функцией и график его сим-
симметричен относительно начала координат. В общем случае
многочлен не является ни четной, ни нечетной функцией, и
график не имеет симметрии.
График функции у = Рп(х) пересекает ось Оу в точке
лг = О, у = ап. Для определения точек пересечения графика
функции у = Рп(х) с осью Ох нужно найти действительные
корни уравнения
Определение. Действительное или комплексное число
а называется корнем многочлена Рп(х), если при подста-
подстановке а вместо х многочлен Рп(х) обращается в нуль:
Л, (*) = 0.
Теорема. Всякий многочлен имеет хотя бы один
корень.
Доказательство этой основной теоремы алгебры здесь
не приводится.
Если известны корни многочлена, то его можно разложить
на множители. Пусть ах — корень многочлена Рп(х):Рп(<х1)=0.
Тогда по теореме Безу этот многочлен разделится без остатка
на х — oij, причем частное в свою очередь будет многочле-

§ 7] многочлены 51
ном степени п— 1:
т. е.
Так как Рп_г(х)— многочлен, то он имеет хотя бы один
корень, который обозначим через а2.
Тогда
откуда
Подставив найденное выражение для Рп-г(х) в исходный
многочлен, получим
Рп (х) = (х — аг) (х — ос2) Рп_2 (х).
Относительно Рл_2(.к) можно повторить приведенные выше
рассуждения.
После п-то шага получим
Рп (*) = (х — аг) (х — а2)...(х — ап) а0.
Числа а2, а3, ..., ал являются корнями многочлена Рп(х),
так как при подстановке <xk (/г = 2, 3, ...) вместо х много-
многочлен Рп(х) обращается в нуль. Они могут быть как ком-
комплексными, так и действительными.
Итак, если употреблять комплексные числа, то много-
многочлен степени п можно разложить на п линейных множи-
множителей вида х — ал, где ak— корни многочлена. Некоторые
из этих множителей могут повторяться. Если некоторый
множитель встречается один раз, то соответствующий корень
называется простым. Если какой-нибудь множитель повто-
повторяется k раз, то соответствующий корень называется крат-
кратным, а число k — его кратностью. Заметим без доказатель-
доказательства, что если многочлен Рп(х) с действительными коэф-
коэффициентами имеет комплексный корень вида а-\-Ы> то он
имеет и комплексно-сопряженный корень а — Ы.
Пусть «j = а -|-Ы и аз = а — Ы — корни многочлена. Рас-
Рассмотрим произведение соответствующих линейных множи-

52 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ {ГЛ. 1
телей (х — aj) • (х—а2) и преобразуем их так:
(дг—a!)(jc—a2) == (* — а — Ы)(х—а + Ы) = (х — аJ
здесь
р = — 2а, ^ =
Пусть многочлен степени п имеет & пар комплексных
корней, которые обозначим через (alt ctgjog, а4; . . ., a2ft-1, а2Л),
и (я— 2&) действительных (обозначим их через а2Л+1,
+2, .. ., ал).
Тогда, объединяя в разложении многочлена попарно все
комплексно-сопряженные множители, получаем
. .(* —ая).
Если при разложении многочлена употреблять только
действительные числа, то многочлен можно разложить на
линейные и квадратные множители.
Отметим, что практически разложение многочлена на
множители является столь же трудной задачей, как и
нахождение его корней.
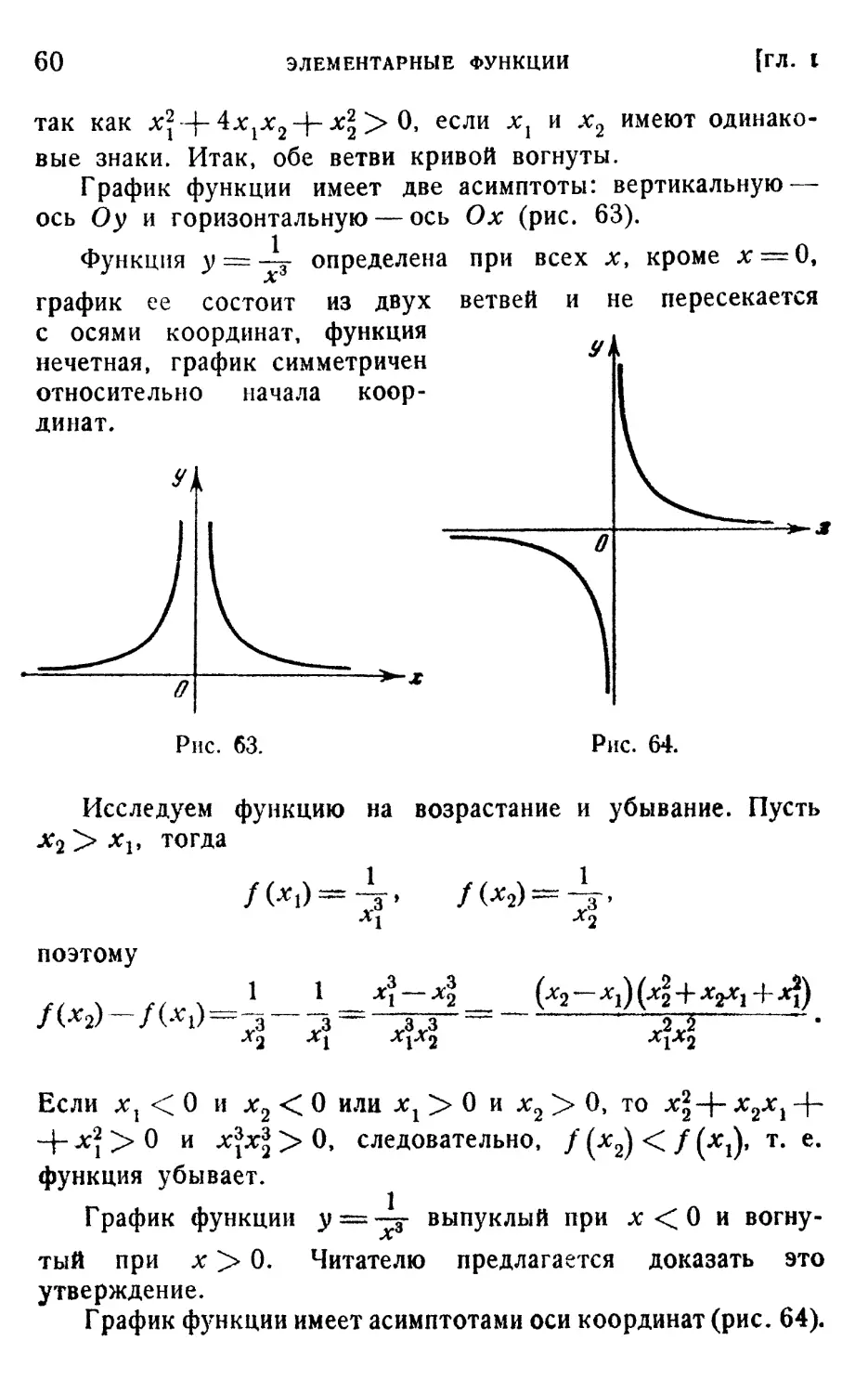
3. Поведение многочлена у = Рп (х) на бесконечности.
Представим многочлен в виде
При больших значениях |д:| величина, стоящая в скобках,
близка к единице, поэтому многочлен у = Рп {х) будет
вести себя подобно степенной функции у = аохп.
4. Примеры графиков многочленов. Рассмотрим много-
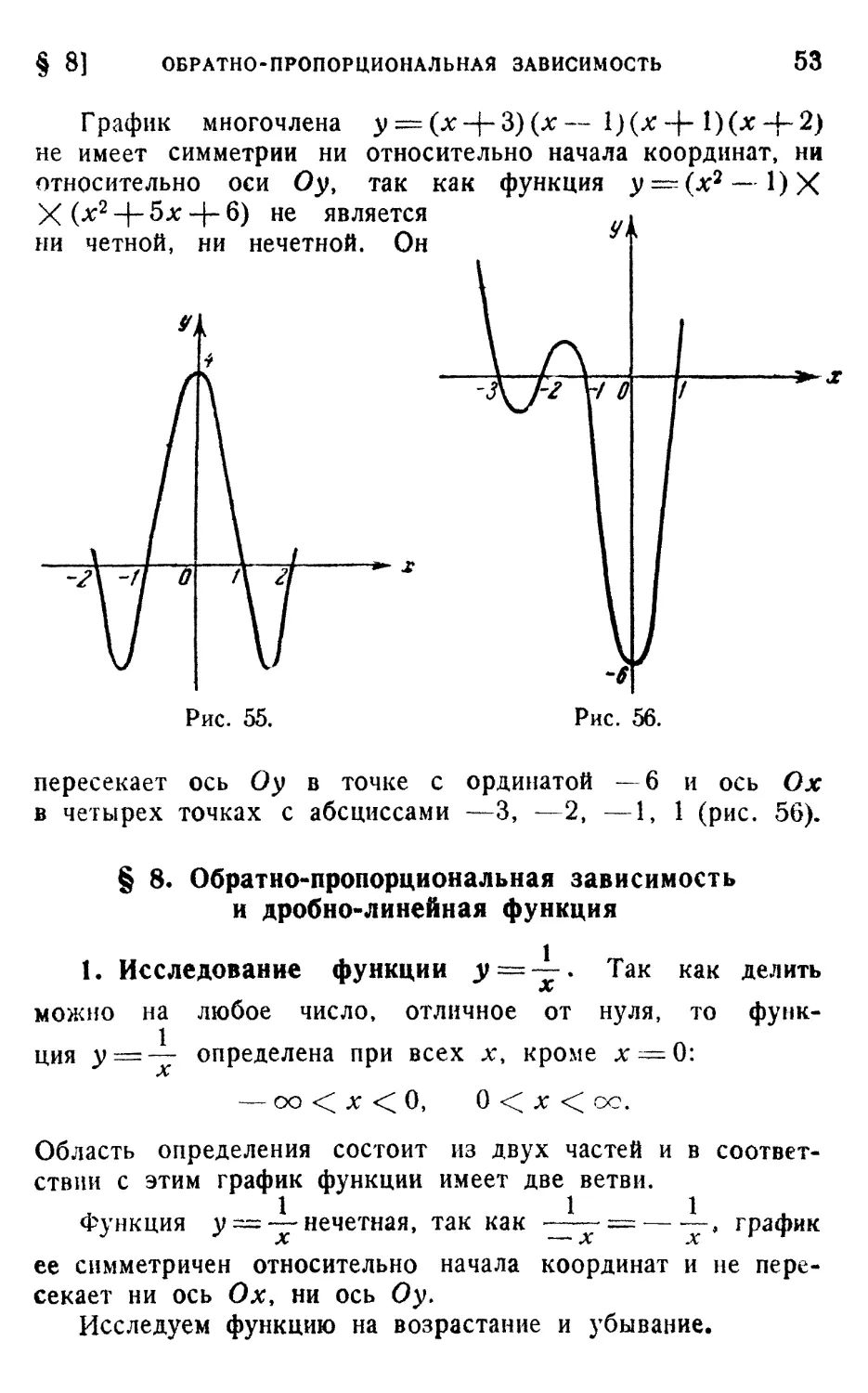
многочлен у — (х—1) (л: —|— 1) (jc — 2)(jc + 2). Этот многочлен
является четной функцией, так как у = {х2—1)(х2 — 4).
График этого многочлена симметричен относительно оси Оу,
пересекает ось Оу в точке с ординатой 4 и ось Ох в четы-
четырех точках с абсциссами —2, —1, I, 2 (рис. 55),

§ 8)
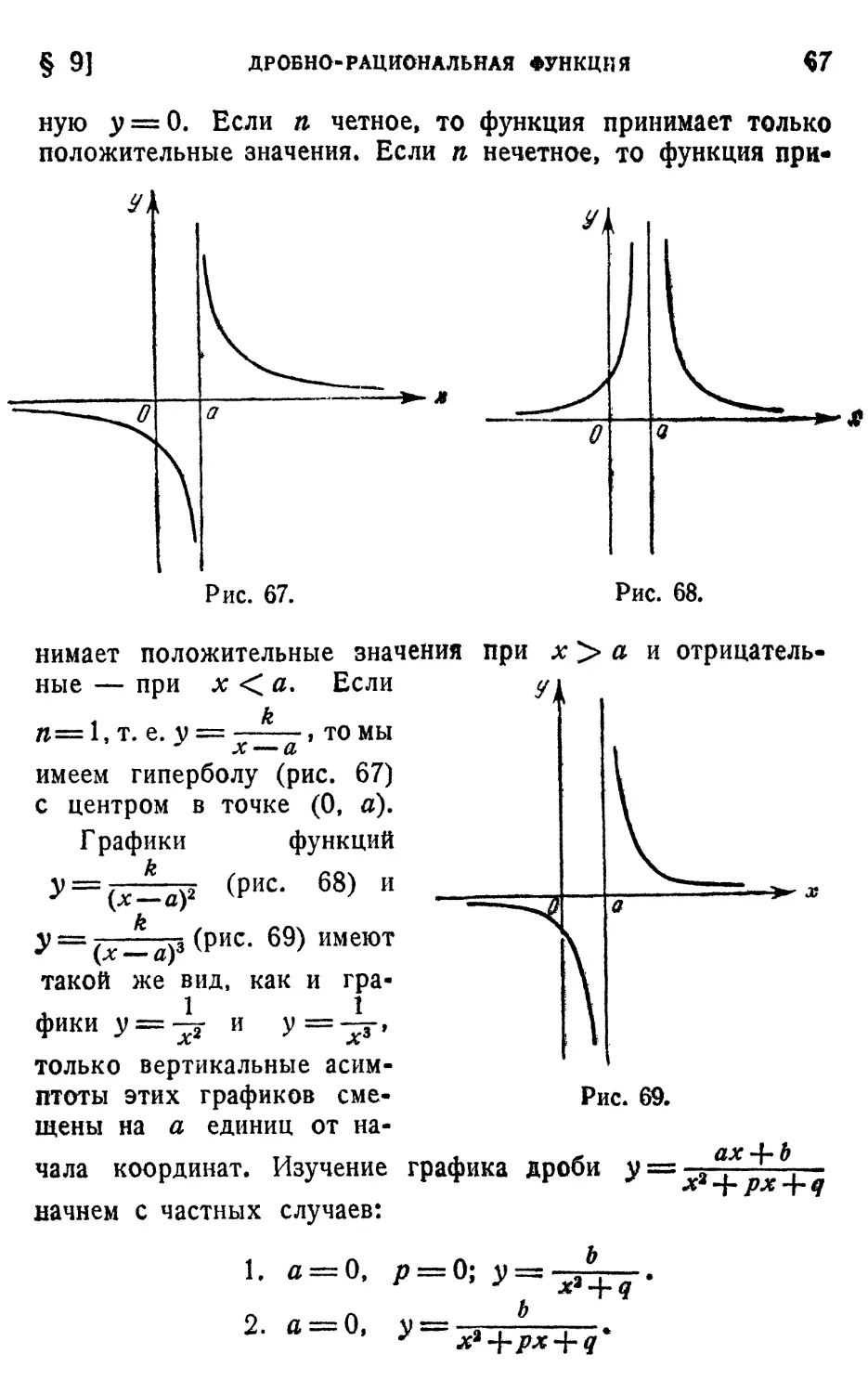
ОБРАТНО-ПРОПОРЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ
53
График многочлена у = (х + 3) (х — \){х ~\-\){х-\~2)
не имеет симметрии ни относительно начала координат, ни
относительно оси Оу, так как функция у=г.(х2 — 1)Х
X (х2 -+- 5x -|~ 6) не является
ни четной, ни нечетной. Он
Рис. 55.
Рис. 56.
пересекает ось Оу в точке с ординатой —6 и ось Ох
в четырех точках с абсциссами —3, —2, —1, 1 (рис. 56).
§ 8. Обратно-пропорциональная зависимость
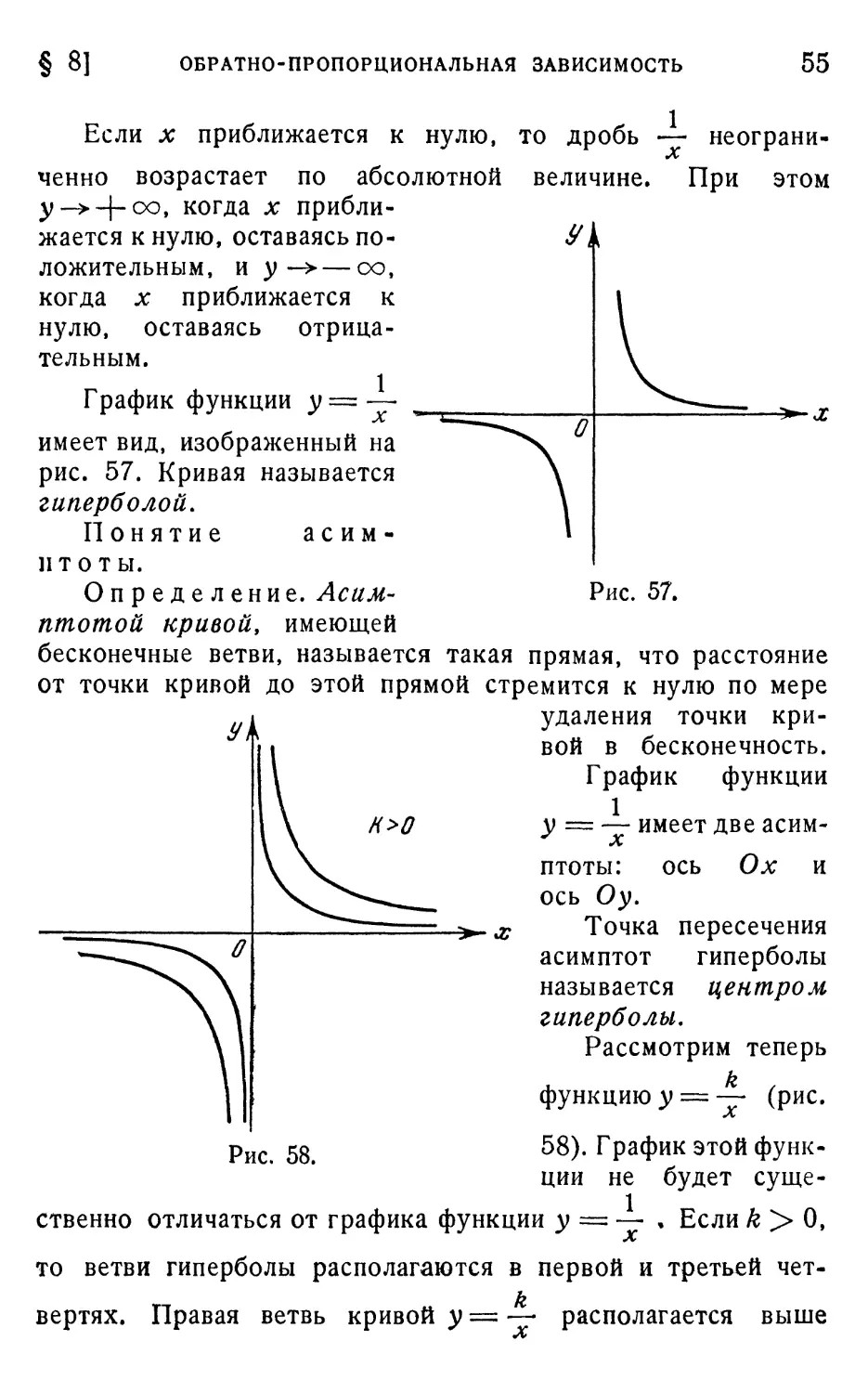
и дробно-линейная функция
!• Исследование функции у —
1
Так как делить
можно на любое число, отличное от нуля, то функ-
функция у — — определена при всех л*, кроме х —0:
— оо<л;
0<л:<сс.
Область определения состоит из двух частей и в соответ-
соответствии с этим график функции имеет две ветви.
Функция у^= — нечетная, так как = • , график
X "—**• X X
ее симметричен относительно начала координат и не пере-
пересекает ни ось Ох, ни ось Оу.
Исследуем функцию на возрастание и убывание.

54 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ [ГЛ. I
Пусть х2 > xv Имеем
— — f(x)~ —
Xi Х2
Рассмотрим разность
/(*) — /(*) = — — = Xl~~ *2
и установим ее знак в каждой части области определения.
Числитель этой дроби х2 — хг положителен, так как х2 > xv
Поэтому знак дроби зависит от знака знаменателя: если
х{ > 0 и х2 > 0, то ххх2 > 0, и, следовательно, — < 0.
1 I*2 Хх
Если хх < 0 и д;2<0, то ххх2>0 и < 0. Итак,
Х2 ¦*!
мы пришли к выводу, что функция у = — убывает в
X
обеих частях своей области определения.
Исследуем график функции на выпуклость и вогнутость.
Вычислим значения функции в точках хг, х2, *х "t" ^2 •
и установим знак разности:
f(*l)+f(*2) f(*l + **\_ l I J
J ) ^~ x2
f( J
2 J \ 2 )~ 2x{^~ 2x2
_ (Xf— X2J
2xxx2 xx + x2 2xxx2 (xx + x2) 2xxx2 (xx + x2) *~
Так как (*! — дг2J всегда больше нуля, то знак этой дроби
определяется знаком знаменателя. Имеем
>°. если ^i>0 и лг2>°.
(х\ + *г) i < 0, если хг < 0 и х2 < 0.
Итак, график функции вогнутый при д: > 0 и выпуклый
при х < 0.
При неограниченном возрастании лг(л:->оо) значение
дроби —• приближается к нулю. Это означает, что график
функции у = — неограниченно приближается к оси Ох при
удалении х в бесконечность.

§ 8]
ОБРАТНО-ПРОПОРЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ
55
о
Если х приближается к нулю, то дробь — неограни-
неограниченно возрастает по абсолютной величине. При этом
у-> + оо, когда х прибли-
приближается к нулю, оставаясь по- У l
ложительным, и у —>— со,
когда х приближается к
нулю, оставаясь отрица-
отрицательным.
График функции у = —•
имеет вид, изображенный на
рис. 57. Кривая называется
гиперболой.
Понятие асим-
асимптоты.
Определение. Асам- Рис. 57.
птотой кривой, имеющей
бесконечные ветви, называется такая прямая, что расстояние
от точки кривой до этой прямой стремится к нулю по мере
удаления точки кри-
кривой в бесконечность.
График функции
Н>0
1
у = — имеет две асим-
асимптоты: ось Ох и
ось Оу.
-# Точка пересечения
асимптот гиперболы
называется центром
гиперболы.
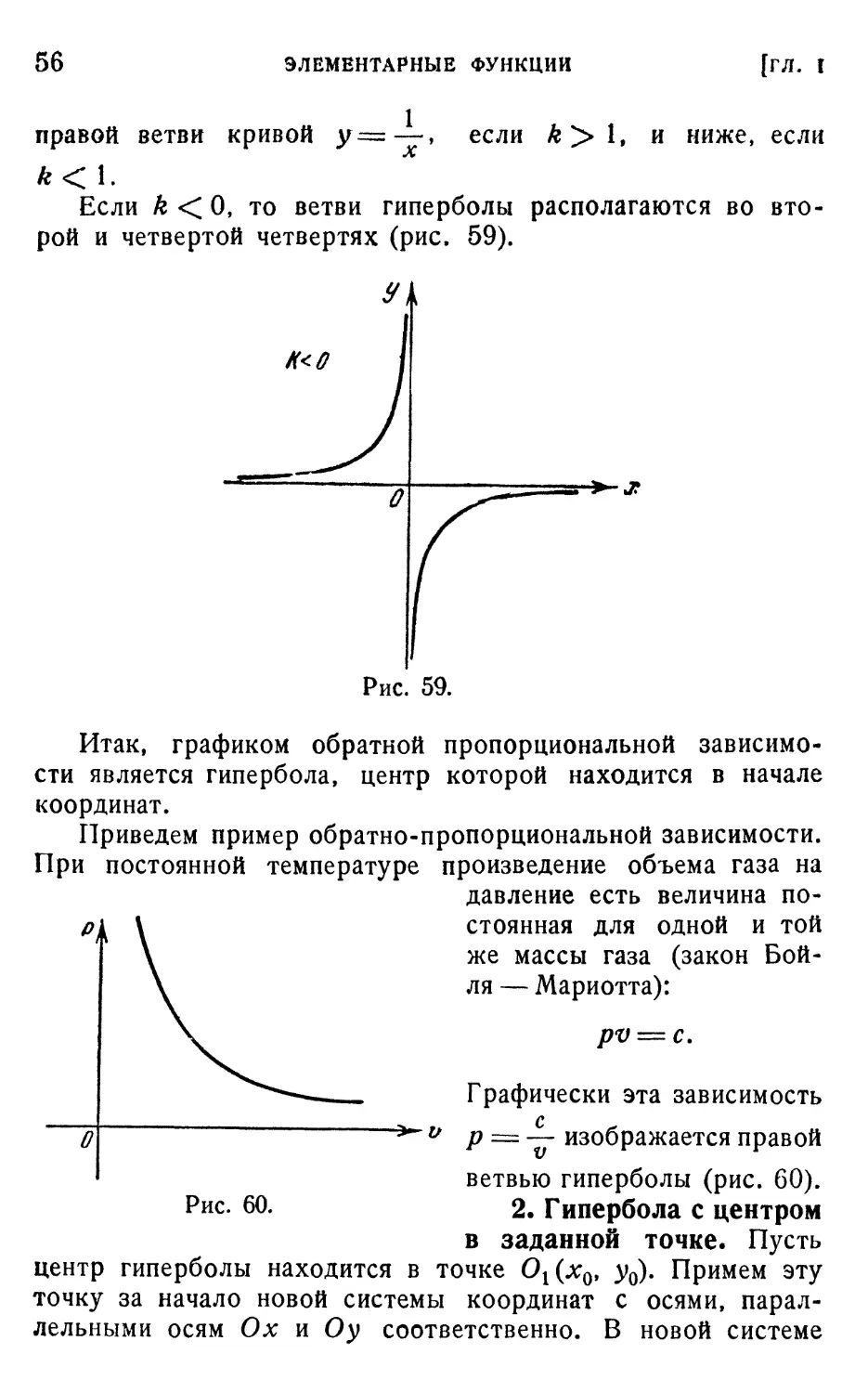
Рассмотрим теперь
функцию у — — (рис.
рис 58 58). График этой функ-
функции не будет суще-
существенно отличаться от графика функции у = — , Если k > О,
то ветви гиперболы располагаются в первой и третьей чет-
k
вертях. Правая ветвь кривой у =—• располагается выше

56
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
[ГЛ. I
правой ветви кривой У=—» если *>*• и ниже» если
Если k < О, то ветви гиперболы располагаются во вто-
второй и четвертой четвертях (рис. 59).
Н<0
Рис. 59.
Итак, графиком обратной пропорциональной зависимо-
зависимости является гипербола, центр которой находится в начале
координат.
Приведем пример обратно-пропорциональной зависимости.
При постоянной температуре произведение объема газа на
давление есть величина по-
постоянная для одной и той
же массы газа (закон Бой-
ля — Мариотта):
pv = с.
Графически эта зависимость
»- v p = JL изображается правой
ветвью гиперболы (рис. 60).
Рис. 60. 2. Гипербола с центром
в заданной точке. Пусть
центр гиперболы находится в точке Ох(х0, у0). Примем эту
точку за начало новой системы координат с осями, парал-
параллельными осям Ох и Оу соответственно. В новой системе

§ 81
ОБРАТНО-ПРОПОРЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ
57
координат кривая имеет уравнение у' — —т * Чтобы получить
уравнение кривой в первоначальной системе, нужно вместо xf
->-<г
Рис. 61.
и у' подставить в уравнение их значения:
Уравнение гиперболы (рис. 61) с центром в точке Ог (лг0, у0)
(в системе хОу) будет
X — Xq
3. Дробно-линейная функция. Дробно-линейной функ-
функцией называется дробь, числитель и знаменатель которой
линейные функции:
у cx + d *
Преобразуем уравнение, задающее функцию, методом
выделения целой части (в числителе выделим слагаемое,
кратное знаменателю):
у —
(-+4)
be —ad

58 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Введем обозначения
[гл. I
a d
~Y= Уо» T ~
be— ad
тогда У =
k k
, или у — Уо = ~z—
><</<))
Рис. 62,
Итак, графиком дробно-линейной функции является
d a
гипербола с центром в точке хо = —. Уо^"^» асимп-
асимптоты которой параллельны осям координат.
Пример.
У —
Зх + 8
+4)
16
Здесь (рис. 62)
16
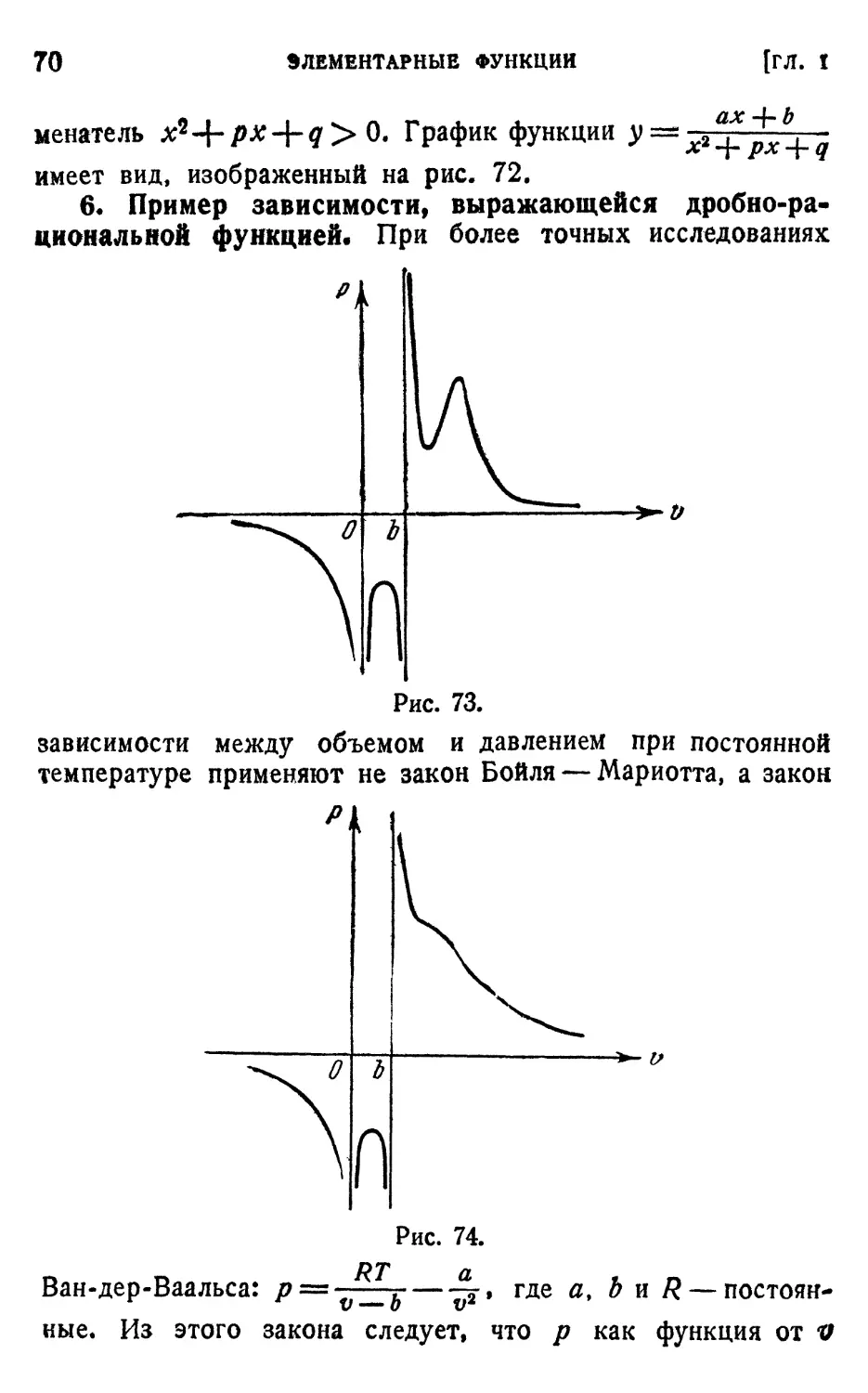
§ 9. Дробно-рациональная функция
1. Отрицательные степени х. Исследуем функции У = ^
и у = ~. Функция у = -г- определена при всех х, за
х х

§ 9] ДРОБНО-РАЦИОНАЛЬНАЯ ФУНКЦИЯ 59
исключением х = 0. С осями координат график функции не
пересекается, функция четная, график ее симметричен отно-
относительно оси Оу.
Исследуем функцию на возрастание и убывание. Пусть
х2 > хх, тогда
/(*> /(*)Л
пээтому
f(\ ff^ L 1 А-А
L
о Л — XJ~" — ~2~2
п Aj Л]Лп
Знак этой дроби зависит от знака числителя, точнее, от
знака сомножителя х2-\-хх. Числитель будет положительным,
если хх > 0 и лг2>0, тогда f (х2) — /(л:1)<0, т. е. функ-
функция убывает. Если же хх < 0 и х2 < 0, то / (лг2) — / (хх) > 0,
т. е. функция возрастает.
Итак, функция у = —^ возрастает при х < 0 и убывает
при х > 0.
Исследуем функцию на выпуклость и вогнутость. Так как
то
о „2 „2 » •/ I
2 2*?ж«
Установим знак разности
/ -
2 ' \ 2 / 2x*x* (x I y \2
^ — 2х\
дс2J
% + ЛГ
2х21х22(х1+х2J
{х\ - 4f + 2хЛ (.»! - ж2J ^ (^ - ж2J(^ + 4хЛ + 4)

60
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
[ГЛ. I
так как x\~\-±xlx2Jt~x\ > 0, если хг и х2 имеют одинако-
одинаковые знаки. Итак, обе ветви кривой вогнуты.
График функции имеет две асимптоты: вертикальную —
ось Оу и горизонтальную — ось Ох (рис. 63).
Функция у = —т определена при всех х, кроме х = 0,
график ее состоит из двух ветвей и не пересекается
с осями координат, функция
нечетная, график симметричен
относительно начала коор-
координат.
О
Рис. 63.
Рис. 64.
Исследуем функцию на возрастание и убывание. Пусть
> хг, тогда
~JL /( )_JL
*-3 J \ if з
х\ хъ
поэтому
„з,.з
ЛчЛ2
Если xt < 0 и х2 < 0 или х1 > 0 и х2 > 0, то ^ + X2xi "Ь
-f- ^1 > 0 и jc^x| > 0, следовательно, / (л:2) < / (х^, т. е.
функция убывает.
График функции у = —g- выпуклый при д: < 0 и вогну-
тый при х > 0. Читателю предлагается доказать это
утверждение.
График функции имеет асимптотами оси координат (рис. 64).

9] ДРОБНО-РАЦИОНАЛЬНАЯ ФУНКЦИЯ 61
2. Дробно-рациональная функция. Функция
у которой числитель и знаменатель многочлены, называется
дробно-рациональной.
Дробь пп) [ называется правильной, если степень чис-
лителя ниже степени знаменателя (п < т). Если же т^п,
то дробь называется неправильной.
Мы будем рассматривать только несократимые дроби.
Дробно-рациональная функция у = -пу\ определена
при всех х, за исключением тех х, при которых знамена-
знаменатель обращается в нуль: Qm(x) = Q.
График дробно-рациональной функции пересекает ось Оу
в точке у = ~ и ось Ох в точках, абсциссы которых
являются корнями уравнения Рп(х) = 0. Правильная дробь
при неограниченном возрастании \х\ стремится к нулю.
Действительно, если числитель и знаменатель дроби раз-
разделить на хт, то будем иметь
откуда видно, что при неограниченном возрастании \х\ чис-
числитель приближается к 0, а знаменатель к Ьо, т. е. дробь
стремится к нулю. Следовательно, ось Ох является асимп-
асимптотой графика такой функции.
Если дробно-рациональная функция представляет собой
неправильную дробь, то ее можно представить в виде
Q (x)
где S(x) есть частное от деления Рп(х) на Qm{x), a
R{x) — остаток. S(x) называется целой частью дробно-
рациональной функции.

62 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ [ГЛ. Г
Пример. Выделить целую часть функции у = '¦
Разделим числитель на знаменатель
_л;3+2л;2 + 4
Xs-\- Х2-\-Х
X2— X
— 2x-f-3
Итак, здесь S(х) = х +1, R(x) = — 2х + 3, т. е.
3-2*
3. Асимптоты графика дробно-рациональной функции.
Р (х)
Определение вертикальных асимптот графика функции у=пп, (
связано с определением действительных корней многочлена
Qm(x). При приближении х к этим корням знаменатель
приближается к нулю и дробь неограниченно возрастает.
Если, например, знаменатель представляется в виде
Qm « = ( Ъ
= m)> где квадратный трехчлен не
Р (х)
имеет действительных корней, то функция у=*-пп \ ' имеет 5
вертикальных асимптот: д: = а27.+1, д;==а2г+2 х — ап
(см. рис. 62 и 63).
Р (х)
При изучении поведения функции у=пп\ '
на бесконечности удобно воспользоваться тем, что эта функ-
Р (х\ 7? (х\
ция может быть представлена в виде ¦ пп\ \- — S(x)-\-п \ \.
jR (x}
Так как при л;->оо правильная дробь п \\ стремится
к нулю, то о поведении функции на бесконечности мы
можем судить по поведению ее целой части S(x).
Если степени числителя и знаменателя равны, т. е.
Р (х)
т — п, то график функции у = пп\ \ имеет горизонталь-
Vffl \х)
ную асимптоту. Действительно, если т = п, то целая часть

§ 91
ДРОБНО-РАЦИОНАЛЬНАЯ ФУНКЦИЯ
63
а°
--—- при
>оо, т. е.
прямая y = -~- является асимптотой графика функции.
Если степень числителя на единицу больше степени зна-
знаменателя, то график дробно-рациональной функции имеет
наклонную асимптоту. Действительно, если л = /ю+1, то
S(x) = kx-\-b и исследуемая функция будет вести себя
при х->со как линейная функция. Прямая y = kx-\-b есть
Pnix)
наклонная асимптота графика функции у =
2,6
-^ X
Рис. 65.
Если степень числителя больше степени знаменателя на
два и больше, то график дробно-линейной функции не имеет
асимптот при х—>оо. В этом случае S(x) будет многочле-
многочленом и дробь -пп\с\- При лг-^оо будет вести себя как мно-
гочлен.
Пример 1. Рассмотрим дробно-рациональную функцию
График ее (рис. 65) имеет две вертикальные

64
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
[ГЛ. I
асимптоты х =
3-/5
и х =
3 + /5
i 2,6, так как
при этих значениях знаменатель обращается в нуль. Выделяя
6л:— 2 „
целую часть, получаем у=1-| 5—^—хт- Следовательно,
график рассматриваемой функции имеет горизонтальную
асимптоту у = 1.
хг
Пример 2. График (рис. 66) функции у —-$—т имеет
две вертикальные асимптоты, так как знаменатель дроби
ГИТ
1 и # = 1. Выделяя
' Наклонной асимпто-
асимптоРис. 66.
имеет два действительных корня лг
целую часть, получаем у=:х]
той является прямая у^=х.
4, Разложение на простейшие дроби. Простейшими
дробями называют дроби, имеющие вид
* * г
*
х — а (х — а)*
г . При этом предполагается, что
+ p + q (+p + q)r F F
квадратный трехчлен х2~\- рх ~\-q не разлагается на дейст-
действительные линейные множители.

$ 9) ДРОБНО-РАЦИОНАЛЬНАЯ ФУНКЦИЯ 65
Всякую правильную дробь можно представить в виде
суммы простейших дробей.
х%-\-2х 2
Пример. Разложить на простейшие дроби ,
х\х l
б
Попытаемся представить эту дробь в виде суммы трех дро-
дробей со знаменателями х% х — 1, лг + 2. Числители этих
дробей обозначим соответственно через Л, В и С и опре»
делим их так, чтобы выполнялось равенство
-2 _ А , В . С
X (X— '
Приведем правую часть этого равенства к общему знамена-
знаменателю. Две дроби с равными знаменателями равны тогда и
только тогда, когда равны их числители, поэтому, прирав-
приравнивая числители, получаем
В левой и правой частях стоят многочлены 2-й степени»
Они будут равны, если будут равны коэффициенты при
одинаковых степенях х. Приравнивая коэффициенты при
одинаковых степенях, получаем:
при л:2
2Л — А + 2В — С = 2,
2Л = 2.
3
при х
при х°
Решая эту систему, находим, что Л=1,
С — 5 > и» следовательно,
о
—2 1
х~Т~ 3(х — 1) 3(д:
Как видно на примере, для разложения дроби на сумму
простейших дробей прежде всего нужно разложить знаме-
знаменатель на множители. Оказывается, что каждому простому
действительному корню знаменателя соответствует одна дробь
—^7~i каждому кратному корню кратности k соответствует
Сумма k дробей
Аналогично, каждой паре простых комплексных корней

66 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ [ГЯ. I
соответствует дробь ¦ 2 * , ¦» а паре кратности k соот-
соответствует сумма k дробей:
, M2x + N2 ¦ . Mkx + Nk
Итак, если Q(#) = (a;—^(jc —a2) ... (.?— an)t то
¦PC*) __. ^i | Лг | | -Д/г
Q (x) x — otj > x — a2 ' '" ' ' л: — а„ *
Если
Q(x) = (x — 04) (x — a2) ... (л; — ал)(д: — afe+1)r....
то
P(x) = A, , A
' X — a2 x — ak
Если Q(jc) = (a: — a)<x — p/(x2+ />* + ?), то
Наконец, если
q (^) = (x — a) (* — p/ (л;2 + рл: + ?) (x2 + Лх + q{f.
TO
Q(x) ~ x — <%''r(*-.p)''"r (^ —
Br Mx + N
Возможность разложения дробно-рациональной функции
на сумму простейших дробей требует доказательства, кото-
которое мы не приводим.
k
б- Графики простейших дробей. Функция у = -( г^-
\Х — &)
(k > 0, п^>1) определена при всех х за исключением х = а.
k
График функции пересекает ось Оу в точке у— , .п9
имеет две асимптоты — вертикальную х = а и горизонталь-

§ 9]
ДРОБНО-РАЦИОНАЛЬНАЯ ФУНКЦИЯ
ную у = 0. Если п четное, то функция принимает только
положительные значения. Если п нечетное, то функция при-
Рис. 67.
Рис. 68.
нимает положительные значения при х > а и отрицатель-
отрицательные — при х < а. Если
k
л=1,т. е. у = - , томы
имеем гиперболу (рис. 67)
с центром в точке @, а).
Графики функций
У = / * 42 (Рис 68) и
k —""
у = rj—тчз (рис. 69) имеют
такой же вид, как и гра-
графики у = —2- и у=~т,
только вертикальные асим-
асимптоты этих графиков сме- рис# §9.
щены на а единиц от на-
начала координат. Изучение графика дроби у= %ах'
начнем с частных случаев:

68
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
{ГЛ. I
Функция у =*
2~г— определена при всех х (считаем
х -\- q
q > 0), четная, график симметричен относительно оси Оу,
пересекает ось Оу в точке у== — и имеет горизонтальную
асимптоту у —0.
Исследуем функцию на возрастание и убывание. Пусть хг
и х2(х2> Х\)— два значения аргумента, f(xx) и f{x2) —
соответствующие значения функции. Установим знак разности
b Ь
Он зависит от знака второго сомножителя в числителе. Если
^<0 и х2<0, то f(x2) — /(^i)>0, т. е, функция воз-
о
Рис. 70.
растает. Если хх > 0 и х2>0, то f(x2) — /(*i)<0, т. е.
функция убывает. Итак, при х < 0 функция возрастает, а
при х > 0 убывает, следовательно, точка л: = 0 является
точкой максимума функции (рис. 70).
Для изучения функции у = -щ- -— в знаменателе
дроби выделим полный квадрат; у =
Если перенести начало координат в точку (—--, 0Ь т. е.
сделать замену хг = х-\--29 У* ~ У» то в новой системе урав*
нение запишется так: у' =
-, где #' =
х<*+д<* I"w/ —«/ —^>0.так
как знаменатель x2-{~px-i~q не имеет действительных корней*

§ 9]
ДРОБНО-РАЦИОНАЛЬНАЯ ФУНКЦИЯ
Теперь можно построить график исследуемой функции
относительно преобразованной системы координат, а следо-
следовательно, и относительно первоначальной.
Функция у = 2Л п — - имеет максимум в точке
X = —4 (рис. 71).
Рис. 71.
ах-\-Ъ
Перейдем теперь к общему случаю у ¦
Для определенности будем считать, что а > О, b > 0.
График функции У==7ОГ^Т^ГТ пересекает ось
г Z г ^
в точке х = и ось Оу в точке у = —, имеет гори-
горизонтальную асимптоту у = 0, так как степень знаменателя
Рис. 72.
выше степени числителя. График не имеет симметрии ни
относительно начала координат, ни относительно оси Оу.
Знак функции совпадает со знаком числителя, так как зна-

70
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
[ГЛ. I
менатель x*-\-px-\-q> 0. График функции У —
имеет вид, изображенный на рис. 72.
6. Пример зависимости, выражающейся дробно-ра-
дробно-рациональной функцией. При более точных исследованиях
Рис. 73.
зависимости между объемом и давлением при постоянной
температуре применяют не закон Бойля — Мариотта, а закон
п
Рис. 74.
Ван-дер-Ваальса: р = v__b—-—-, где я, Ъ и R — постоян-
постоянные. Из этого закона следует, что р как функция от V

§ 10] ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ 71
является дробно-рациональной функцией, представленной
JRT а.
в виде двух простейших дробей: у и -j-. График этой
функции имеет три асимптоты: горизонтальную — ось абсцисс
и две вертикальные — ось ординат v = 0 и v = Ъ (рис. 73,74).
§ 10. Показательная функция
Функция у — ах, где а— действительное положительное
число, называется показательной.
Так как положительное число а можно возводить в лю-
любую степень, то функция у = ах определена при всех х:
— оо < х < со. График этой функции располагается над
всей осью Ох.
Найдем точки пересечения графика функции с осями
координат. Если # = 0, то у = а°=1, т. е. график пере-
пересекает ось Оу в точке у==1. С осью Ох кривая у — ах
не пересекается, так как ни при каком значении х вели-
величина у не обращается в нуль.
Выясним, имеет ли график функции симметрию:
т. е. функция ах при изменении знака аргумента сохраняет
знак, но изменяет величину, поэтому функция у = ах не
является ни четной, ни нечетной. График функции не имеет
симметрии ни относительно оси Оу, ни относительно начала
координат.
Исследуем функцию на возрастание и убывание. Вычислим
ее значение в точках хх и х2 (х2 "> хх): f (хг) = ах>,
f (х2) = ах*, найдем разность ах* — ах* = aXl (ах*~х* — 1) и
определим ее знак. Так как ах* всегда больше нуля, то
знак произведения будет зависеть от знака второго сомно-
сомножителя. Имеем х2 — хг > 0 и, следовательно, a^-^i>l,
если а> 1, и ах*-х* < 1, если а< 1. Отсюда следует, что
{> 0, если а > 1,
< 0, если а < 1.
Если а > 1, то функция у = ах возрастает, и если
а < 1, то функция у = а убывает,

72
ЭЛЕМЕНТАРНЫЙ ФУНКЦИИ
Для того чтобы выяснить, является ли график выпуклым
или вогнутым, установим знак разности
Значения функции1 в точках х{, лг2, ! "]Г 2-
= а*».
— 2а
Поэтому
таковы:
Следовательно, график функции у = а^ вогнут (рис. 75, 76),
Найдем асимптоты графика. Если а>1 их-* — оо,
то ах уменьшается, приближаясь к нулю. Это означает* что
Рис. 75.
Рис. 76.
ось Ох является асимптотой графика. Если а< 1, то при
возрастании д: число, меньшее единицы, возводится все
в большую степень и значение функции уменьшается: лс->оо,
у->0. Ось Ох и в этом случае является асимптотой.
§11. Тригонометрические функции
Понятие периодической функции.
Определение. Функция называется периодической
с периодом Tt если при значениях аргумента, отличающихся
друг от друга на Г, она принимает равные значения.

§ 11] ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 73
Итак, если при определенном Т выполнено тождество
/(х)ss/(х¦+-Г)*), то функция у = /(лг) является периоди-
периодической с периодом Т.
Изучив периодическую функцию на отрезке, длина кото-
которого равна периоду, мы тем самым будем знать ее свойства
во всей области определения.
1. Исследование функции .у —sin*. Функция y = sinx
периодическая, так как для этой функции имеет место
тождество sin(x + 2TC)^sinx. Период этой функции Т=2ъ.
Функция y = sinx определена при всех х: —оо < х < оо.
Для определения точек пересечения графика функции
у = sin х с осью Ох решим уравнение sin х = 0, находим
л; = 0, ±тг, ±2я, ..., ±лте, ... График функции у = sin x
проходит через начало координат.
Функция у = sin х нечетная, так как sin (— х) = — sin x$
поэтому ее график симметричен относительно начала коор-
координат.
Как известно из тригонометрии, функция sin x возрастает,
если угол х находится в первой или четвертой четвертях,
т. е. при 0 < х < -ц при -о- тс < х < 2тс, и убывает во вто-
рой и третьей четвертях, т. е. при ~ < лг < у те, поэтому
« 3
точка x = y является точкой максимума, а точка ути —
точкой минимума. Так как функция y=slnjc периодиче-
периодическая, то точками максимума будут также точки х = -^-\- 2&тс
(k=±l, ±2,...). а точками минимума — также точки
jc = ^«+2ftic (ft=±l, ±2, ...).
Исследуем график функции на выпуклость и вогнутость.
Для этого установим знак разности *(х\)+ *{**) —/р1 ^ х*\:
sin Xj + sinA:2 . xx+x2
S1"
т
х9
*) Знак ^означает, что равенство справедливо при всех зна-
значениях аргумента х, т. е. является тождеством.

74
ЭЛЕМЕНТАРНЫЕ ФУН1ЩИИ
{ГЛ. I
Заметим, что сомножитель cos*! 2*3' — 1 либо отрицателен,
либо равен нулю, так как |cosx|<;i. Кроме того, если
углы хг и х2 находятся в одной четверти, то их полусумма
х -4- х
- '"Г 2 будет также находиться в этой четверти. Таким
образом,
х,+х2
2
< 0 в 1-й и 2-й четвертях,
> 0 в 3-й и 4-й четвертях,
т. е. в первой и второй четвертях, при 0 < х < тс график
выпуклый, а в третьей и четвертой, т. е. при тс < х < 2тс
Рис. 77.
график вогнут. Точка х = тс является точкой перегиба гра-
графика функции.
Пользуясь периодичностью функции sin x, можно пока*
зать, что точки 0, —тс, ±2тс, ..., ±&тс, ... будут также
точками перегиба графика функции.
Используя полученные результаты, можно построить
график функции у = sin x. Этот график называется сину-
синусоидой (рис. 77).
Понятие ограниченной функции.
Функция y=zf(x) называется ограниченной, если все
ее значения по абсолютной величине не превосходят неко*
торого положительного числа:
Функция у = sin х ограниченная, так как

§11] ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 75
2. Исследование функции у — $\пых. Найдем точки
пересечения графика этой функции с осью Ох. Полагая
j> = 0, получаем sina)Ar==O, (ux = rnzt или д: = —(#=:0,
± 1, ±2, ...). Пусть, например, y=sin2Ar. Тогда х = ~,
т. е. расстояния между соседними точками пересечения
с осью Ох графика функции у = sin 2x вдвое меньше соот-
соответствующих расстояний для графика функции у = sin x
Рис. 78.
(рис. 78). Изменится и период функции. Если для sin x
он равен 2т:, то для sin 2x он будет в два раза меньше:
Покажем, что период Т функции sinwA: равен —, т. е,
что в точках х и х -| функция sin ых принимает рав-
равные значения. Действительно,
in со (х + Т) = sin a) f х -f- -^ j = sin (шд: + 2тг) = sin аздг,
sin о (х + Г) ^ sin (ax.
sin со
т. е.
Максимумы функция у = sin сод; имеет в точках х = -^- +
-) , а минимумы — в точкдх ^==-9—I * Из про-
проведенных рассуждений следует, что график функции
у = sin wx может быть получен из графика функции у = sin x

76 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ {ГЛ. I
сжатием (о> 1) или растяжением («) < 1) вдоль оси Ох.
Коэффициент ш называется частотой. Как было показано,
период связан с частотой соотношением
Рассмотрим теперь функцию y = Asin(ox, например, у —
= 2 sin (ох. Точки пересечения графика этой функции оста-
останутся такими же, как и
у графика sin (ox, но зна-
значения функции в точках
максимума и минимума
увеличатся по абсолютной
величине вдвое (рис. 79).
— ? Наличие коэффици-
коэффициента А приводит к растя-
растяжению или сжатию кривой
вдоль оси Оу. Этот
коэффициент определяет
* '"• максимальное отклонение
кривой от оси Ох и
называется амплитудой.
На рис. 80 изображен
график функции
->- * y = __sinjc D = — 1).
3. Уравнение про-
Рис 80 стого гармонического
колебания. Уравнением
простого гармонического колебания называется уравнение
вида у == Л sin (о>х -f- cp).
Преобразуем его так: у —Л 5т(о>х-|-<р)=Л sinon x-f- —-J.
Обозначим i = — х0. Тогда y=^Asmai(x — х0). Отсюда
видно, что кривая у = Л sin (wx -f- cp) получается из кривой
у = A sin шх смещением по оси Ох на хо= — ~. Заметим,
что если ~ > 0, то сдвиг происходит влево, если -~- < 0,

§ 11] ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 77
то вправо (рис. 81). Коэффициент ср называется начальной
фазой.
Итак, коэффициенты в уравнении
у = A sin (сол: -f- <р)
называются: А — амплитуда, ш — частота, ср— начальная фаза.
4. Приведение функции у = A cos оух-^В sin wx к виду
простого гармонического колебания. Рассмотрим уравне-
уравнение у = A cos шх -f- В sin сох и попытаемся его представить
"со
Рис. 81.
в виде уравнения простого гармонического колебания
у= Ах sin (шл: —(- ср). Для этого нужно, чтобы было
A cos шаг -f- 5 sin coat = Л! sin (ш
Применим к правой части формулу sin (a-j-(J) ==
= sin а cos p -|- cos а sin p. Тогда получим
A cos ш# -j- В sin (ojc = ^2 sin ср cos шх -+- >4i cos cp sin шд:.
Приравнивая слева и слрава соответствующие коэффициенты
при cos аи; и sin (djc, получаем
А = Ах sin ср, В — Ах cos ср.
При выполнении этих равенств уравнение у — A cos сод: -f-
-f-Z* sin шлт будет совпадать с уравнением простого гармо-
гармонического колебания
у = Ах sin (шл: -f- ср).
Покажем теперь, как вычисляются амплитуда Ах и на-
начальная фаза ср, если известны А и В. Возведем в квадрат

78
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
[ГЛ. I
обе части равенств
их. Тогда ЬЧ
т. е. Л, = 1
Из равенства Агсо$у = В найдем coscp:
= Л и А1со$<$ = В и сложим
22 или А{ = 22
в в
cos 9 = = ¦. -
т Л! УА* + В2
откуда
) = arccos •
J3
Пример. Привести уравнение у==:СО52л;4-1^3 sin 2д:
к виду простого гармонического колебания.
Рис. 82.
Амплитуда Л1==
, начальная фазау=агссаз
У =
30° ===-?• • Частота ш = 2.
о
Уравнение принимает вид
Период этой функции Г== -^~ = тс. Сдвиг графика (рис. 82)

§ 111
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИЙ
79
Предлагаем читателю самому исследовать функвди
у = cos л; и y = tgx и убедиться в тол, что график функ-
Рис. 83.
ции y=»cosx — синусоида» сдвинутая влево на -^(рис. 83),
а график функции y=xtgx имеет вид, изображенный на
рис. 84.
Рис. 84.
S. Примеры зависимостей, выражающихся тригоно-
тригонометрическими функциями, а) Если на тонкий прямоуголь-
прямоугольный стержень действует сила, сжимающая его вдоль оси Ох,
то стержень деформируется. Когда сила достигает опреде-
определенного значения, стержень изгибается и принимает форму

ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
{ГЛ. It
волны синусоиды
половины
б) В цепи переменного тока зависимость между силой тока /
у = A sin — х (рис. 85).
Рис. 85.
и временем t выражается формулой
Рис. 86.
Графически эта зависимость изображается синусоидой,
сдвинутой от начала координат на величину (рис. 86).
§ 12. Взаимно-обратные функции
1. Понятие обратной функции. Пусть функциональная
зависимость между величинами а: и у задана уравнением
У = /(х), Если в этом уравнении поменять местами х и у,
то получим функциональную зависимость х = /(у), которая
называется обратной к исходной. Чтобы привести эту зави-
зависимость к привычной форме, решим уравнение # = /(у)
относительно у. Тогда получим y~f_i(x). Функция f^i(x)
называется обратной к функции f(x). Для того чтобы
найти функцию, обратную к данной, нужно в уравнении,
задающем данную функцию, поменять местами х и у и по-
полученное уравнение решить относительно у.
Пример 1. Пусть
у — х2.
Меняя местами х и у, получаем х = у2. Решим это уравне-
уравнение относительно у :
Таким образом, ±]/х является обратной функцией к х2.

§ 12]
ВЗАИМНО-ОБРАТНЫЕ ФУНКЦИИ
81
Пример 2. Пусть y = sin2jc. Меняя местами л: и у,
Получаем х = sin 2у, откуда 2з>=Arcsin #, или у = ~~ Arcsin лг.
Функции sin2x и -2* Arcsin х взаимно-обратные.
2. График обратной функции. Перемена местами хну
в уравнении соответствует изменению обозначений коорди-
координатных осей. График данной функции имеет вид, изобра-
изображенный на рис. 87. График обратной функции изображен
на рис. 88.
Рис. 87.
Рис. 88.
Для того чтобы привести оси координат в привычное
положение, повернем плоскость хОу на 180° вокруг биссек-
биссектрисы первого и третьего координатных углов. Тогда график
Рис. 89.
Рис. 90.
примет вид, изображенный на рис. 89. Если поместить гра-
графики рис. 87 и 89 на одном рис. 90, то сразу видно, что

82
ЭЛЕМЕНТАРНЫЕ ФУНКЦИЙ
[ГЛ. I
графики прямой и обратной функций располагаются симмет*
рично относительно биссектрисы первого и третьего коор-
координатных углов. Возвратимся к примеру функции у = х29
графиком которой является пара*
бола, симметричная относительно
оси Оу с вершиной в начале
координат. Графиком обратной
функции у — ± У~х также явля-
является парабола с вершиной в на-
начале координат, но симметрич-
симметричная относительно оси Ох (рис. 91).
3. Свойства обратной функ-*
дни. Укажем некоторые свой-
свойства графиков взаимно-обратных
функций, вытекающие из их
симметрии.
1) Точки пересечения с осью
Оу графика функции переходят
с осью Ох графика обратной функ-
0
Рис. 91.
в точки пересечения
ции, и наоборот.
2) Если функция возрастает (убывает), то и обратная
функция также возрастает (убывает) (рис. 92).
У >
Рис. 92.
Рис. 93.
3) Пусть функция имеет минимум (максимум). График
этой функции пересекается прямой /, параллельной оси Ох,
в двух точках, поэтому график обратной функции будет

§ щ
ВЗАИМНО-ОБРАТНЫЕ ФУНКЦИИ
83
пересекаться в двух точках соответствующей прямой 1г, па-
параллельной оси Оу, т. е, каждому значению х соответствует
два различных значения у. Обратная функция получилась
двузначной (рис. 93). „.
Итак, если функция *
имеет минимумы или мак-
максимумы, то обратная функ-
функция будет многозначной.
4) Если график функ-
функции вогнут, то график об-
обратной функции может быть
как выпуклым, так и вог-
вогнутым (рис. 94).
Если функция убывает, /и
то свойство выпуклости
или вогнутости ее графика Рис 94.
при переходе к обратной
функции сохраняется. Если же функция возрастает, то эти
свойства меняются на противоположные.
~>~jr
Рис. 95.
Рис. 96.
5) Если график функции имеет вертикальные асимптоты,
то график обратной функции имеет горизонтальные асим-
асимптоты.
4. Логарифмическая функция y = loga^. Функции
f(x) — ax и f~i(x)—logax взаимно-обратные. Зная свой-
свойства у — а*, укажем свойства функции y—logax. Так как
график функции у — ах пересекает ось Оу в точке у=1,

ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
[ГЛ. I
то график y — \ogax пересекает ось Ох в точке лг= 1. Да-
Далее, при а > 1 функция у — ах возрастает, график ее вогнут
и имеет горизонтальную асимптоту у = 0. Обратная функция
возрастает, график ее выпуклый и
имеет вертикальную асимптоту х — 0.
5. Обратные тригонометрические
функции и их главные значения* N
Пусть / (х) = sin х, тогда обратная
функция /_, (х) = Arcsin x.
V У
Рис. 97.
\
\
Рис. 98.
При изучении функции у = sin x было установлено, что
график ее пересекает ось Ох в точках 0, ± ir, ± 2тс, ... ,
±лтс, .... имеет максимумы в точках J
и мини-
мумы в точках -s-it~f-2i:#, кроме
того, он заключен между двумя
прямыми у= 1 и у — — 1 (рис. 97).
График обратной функции
у = Arcsin х пересекает ось Оу в
точках 0, dus, ±2тс, ..., ±птс, ...
- * Обратная функция многозначная:
каждому значению х соответствует
бесконечно много значений функции
(точки пересечения с прямой, парал-
параллельной осиОу). График у = Arcsin к
заключен между прямыми jc=1 и
х = — 1 (рис. 98).
Из графика многозначной функции у = Arcsin x можно
выделить часть, которой соответствует уже однозначная
рис# 99

§ 12]
ВЗАИМНО-ОБРАТНЫЕ ФУНКЦИИ
85
функдия. Удобнее всего взять часть графика, расположен-
расположенную ближе к началу координат (рис. 99). Полученную та-
таким образом функцию называют главным значением арк-
арксинуса и обозначают
у = arcsin х.
Эта функция определена при \х\?С 1» значения ее заклю-
заключены между —
и ~:
— ^< arcsin
Пусть /(лг) = сО8л; (рис. 100), тогда f_x(x) — Arccos x
(рис. 101).
График функции y = cosjc пересекает ось Оу в точке
у=1, а ось Ох — в точках ±тр i-o"^' *#t> имеет мак"
симумы в точках 0, ±2тг, ±3тс, ...
и минимумы в точках ±тг, ±3тс, ...
График обратной функции
у = Arccos х мы получим, если ото-
отобразим график у = cos х симмет-
симметрично относительно биссектрисы
Рис. 100.
-*-x
Рис. 101.
первого и третьего координатных углов. График обратной
функции пересекает ось Ох в точке х = 1, а ось Оу — в
точках i-H-t ± -к я, ... Функция у = Arccos x многознач-
многозначная. Однозначная часть графика arccos x выделена на ри-
рисунке жирной линией.

86 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ [ГЛ. I
Главные значения функции заключены между 0 и тс;
О <^ arccos х ^ ъ
Приведем графики функций y = tgx и у =
зп
2
Рис. 102.
Рис. 103.
Заметим, что главные значения функции y = arctgx за-
заключены между — -н- и -н •
— ~2< arctg a: < 2" •
§ 13. Линеаризация алгебраических функций
Определение. Функция y = f(x) называется алгеб»
раической, если для вычисления ее значений над аргумен-
аргументом производятся алгебраические операции: сложение, вы-
вычитание, умножение, деление, извлечение корня и возвыше-
возвышение в степень.
1. Линеаризация рациональных функций вблизи нуля.
При изучении функции вблизи какой-либо точки, например
вблизи нуля, часто бывает выгодно исследуемую функцию
заменить другой функцией, более удобной для рассмотрений
(например, линейной), делая при этом некоторую ошибку.
Например, пусть задана функция у= 1 -\-х-\-2хА. Если х
мало, то х4 значительно меньше, и поэтому последний член
не будет оказывать существенного влияния на поведение

^ 13] ЛИНЕАРИЗАЦИЯ АЛГЕБРАИЧЕСКИХ ФУНКЦИЙ 87
нашей функции при малых х. Отбросим член 2л;4, тогда
функция заменится линейной: yttl-^-x.
Этот процесс замены функции линейной функцией на-
называется линеаризацией.
Определение. Линеаризацией функции вблизи нуля
называется замена функции линейной функцией путем отбра-
отбрасывания всех степеней х выше первой.
Пример, у = ао+ахх + а2х2 + • •• ~{-апхп. Отбра-
Отбрасываем все члены, содержащие степень х выше первой,
и получаем
Эта линейная функция получена в результате линеари-
линеаризации многочлена вблизи нуля.
В качестве важного примера рассмотрим линеаризацию
вблизи нуля степени линейной функции. Пусть y — (kx-\-b)n.
Если п = 2, то
у = (kx + bJ = b2 + 2bkx + k2x2 я^ b2 + 2bkx.
При n — 3 имеем
у == {kx + *K =
Покажем, что при любом п
Эта формула справедлива при й = 2 и 3, Предположим,
что она справедлива при п = т. Покажем, что она спра-
справедлива также при л = /ю+1. Действительно,
у = (kx + b)m+l = (kx + ftI" (Aa: -f- ft)«
mbm~lkx) (kx + *) =
mbm~lk2x2
Особо важен тот частный случай, когда &=1 и й=
Тогда
Рассмотрим пример. При нагревании твердого тела объем
его увеличивается. Если тело имеет форму куба, то закон
изменения объема v от температуры t выражается формулой

88
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
[ГЛ. I
где vQ — первоначальный объем тела, а — коэффициент ли-
линейного расширения.
Величина at весьма мала, поэтому, применяя формулу
линеаризации при & = ос и 6=1, получаем закон в следую-
следующем виде:
Коэффициент р = За называется
коэффициентом объемного рас-
расширения.
Линеаризуем теперь в нуле дроб-
дробно-рациональную функцию
... +апхп
Рис. 104.
Отбросим в числителе и знаме-
знаменателе все степени х выше первой,
тогда исследуемая функция заменится
дробно-линейной функцией
Остается получившуюся дробно-линейную функцию заме-
заменить линейной. Для этого умножим числитель и знаменатель
на разность Ьо — Ьхх\
-- Ьхх)
До t
ь\
X.
Пример (рис. 104). у = t
Геометрический смысл линеаризации функции вблизи нуля,
как это будет выяснено в дальнейшем, состоит в том, что
кривая, изображающая функцию вблизи ее точки пересечения
с осью Оу, заменяется касательной прямой.
2. Линеаризация иррациональных функций. Заменим
функцию у = j/l -f- ax линейной y —
УТ+ax^kx + b.

§ 13] ЛИНЕАРИЗАЦИЯ АЛГЕБРАИЧЕСКИХ ФУНКЦИЙ 89
Вычислим теперь k и ft. Для этого возведем обе части
равенства в квадрат:
1 + ах да (kx + bf = ft2 + 2ftAx + k2x2
и приравняем слева и справа коэффициенты при х и сво-
свободные члены:
Получаем ft = 1 > а = 2& или ^ = ~.
Теперь мы можем записать формулу линеаризации
Пример.
Повторяя рассуждения, приведенные выше, можно полу-
получить формулы линеаризации для корней третьей степени,
четвертой и т. д.
В общем случае yi-f-ejt»l + ~*« Пусть у 1-|--Д*да
да^х + ft. Тогда \-\-ax^{kx-*rb)n<^bn-\-nkbn-lx.
Приравнивая коэффициенты при равных степенях jc, по-
получаем Ьп==\, nkbn~l = a, откуда следует, что ft=l,
t = i,T. e.
3. Линеаризация вблизи данного значения аргумента.
Пусть нам задана функция y — f(x). Требуется изучить эту
функцию вблизи некоторой точки х0. Для точки дг, близкой
к jc0, рассмотрим малую величину Длс = х — х0. Тогда
х = аг0—j-~ Да;. Подставим вместо х в уравнение, задающее
функцию, хо-\-кх и линеаризуем функцию, отбрасывая уже
не степени х, а степени Дл; выше первой:
Определение. Линеаризацией функции вблизи дан-
данной точки называется замена функции линейной функцией
путем отбрасывания членов, содержащих степени Дл; выше
первой.

90 ЭЛЕМЕНТАРНЫЕ ФУНКЦИЙ [ГЛ. I
Геометрический смысл линеаризации состоит в том, что
вблизи данной точки кривая заменяется касательной.
Пример. Линеаризовать функцию у = 2 + *— Зх2
вблизи точки хо==2.
Пусть х = 2 + Дх. Тогда, подставляя это выражение
в функцию вместо х, получаем
у = 2 + 2 + Дх — 3B + ДхJ=2 +2 + Д-*: — 12— 12 Дх —
— 3 Дх2« — 8 — 11 Дх = — 8 — 11 (х — 2) = 14 — 1 1х.
Вблизи точки х = 2 функция у = 2 + х — Зх2 заменяется
линейной у =14 — Их.
В этом параграфе мы показали, как можно производить
линеаризацию алгебраических функций. Линеаризацию не-
неалгебраических функций, например таких, как sinx, 2х и др.,
нельзя уже производить, пользуясь только средствами алгебры.
Соответствующие формулы мы получим ниже с помощью
теории пределов.

ГЛАВА II
ТЕОРИЯ ПРЕДЕЛОВ
§ 1. Предел функции в точке
1. Понятие бесконечно малой. Определение. Функ-
Функция а(х) называется бесконечно малой вблизи точки х0,
если ее значения по абсолютной величине становятся и про-
продолжают оставаться меньше любого наперед заданного поло-
положительного числа, как только значения аргумента становятся
достаточно близкими к х0.
Если функция бесконечно мала вблизи точки х0, то это
означает, что при значениях аргумента, близких к л:0, зна-
значения функции близки к
нулю, т. е. к точке х0 можно
подойти так близко, что
абсолютная величина значе-
значений функции окажется (и
будет оставаться по мере
приближения к д:0) меньше
наперед заданного положи-
тельного числа. Такое по-
положительное число принято
обозначать через е (эпсилон).
То, что значения функции
по абсолютной величине меньше е, геометрически озна-
означает, что отрезок кривой вблизи точки д:0 будет заключен
в полосе [—е, е) (рис. 105).
Из определения бесконечно малой функции ясно, что
если функция вблизи точки х0 постоянна, то она может быть
бесконечно малой только в том случае, когда эта постоянная
равна нулю. Функция а(лг)==гО есть бесконечно малая.
Различие между бесконечно малой величиной и постоян-
постоянной можно пояснить следующим примером. На льдине лежит
Рис. 105.

92 ТЕОРИЯ ПРЕДЕЛОВ [ГЛ. tl
копейка, льдина попадает в теплое течение и начинает таять.
Размеры монеты малы, но постоянны; льдина при таянии
уменьшается и, наконец, вся растаивает в момент времени Го.
Размер тающей льдины, как функция времени 7\ и будет
бесконечно малой величиной вблизи момента Го.
2. Свойства бесконечно малых* 1°. Сумма двух функ-
функций, бесконечно малых вблизи данной точки, есть
функция бесконечно малая вблизи этой же точки.
Пусть а (л:) и §{х) — две функции, бесконечно малые
вблизи точки х0. Докажем, что а(д;) + р(л;) будет также
бесконечно малой функцией вблизи той же точки, т. е. что
значения функции по абсолютной величине станут и будут
оставаться меньше любого наперед заданного е.
Так как функции <х(л:) и р(лг) бесконечно малы, то их
значения становятся и продолжают оставаться по абсолютной
величине меньше любого наперед заданного положительного
числа, в частности меньше -&;
С того момента, когда абсолютные величины <х (д:) и р (я)
становятся меньше у, абсолютная величина их суммы будет
меньше е:
Отсюда следует, что а (д:) + Р (х) бесконечно малая
функция.
й\ Произведение постоянной на функцию бесконечно
малую вблизи данной точки есть функция бесконечно
малая вблизи этой точки.
Пусть а(х) бесконечно малая вблизи точки xQt с — неко-
некоторая постоянная. Докажем, что са(х) также бесконечно
малая функция вблизи л:0.
Так как функция а (л:) бесконечно мала, то ее значения
становятся и продолжают оставаться по абсолютной величине
меньше любого наперед заданного положительного числа,
в частности меньше -г-т : |а(д:)| < -А-г» С этого момента

§ 1] ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ 93
|са(л;)| = |с||а(л:)| < |с|-~ = е, т, е. са(х) по абсолютной
величине становится и продолжает оставаться меньше е.
Следовательно, са(х) является бесконечно малой функцией.
3°. Произведение ограниченной функции на бесконечно
малую вблизи данной точки есть бесконечно малая
функция вблизи этой точки.
Пусть ср(лг) — ограниченная функция: |cp(jc)|<;Af,
а а(х) — бесконечно малая вблизи лг0. Докажем, что произ-
произведение ф (л:) а (л;) бесконечно мало вблизи той же точки л;0.
Так как а (л:) бесконечно малая, то вблизи х0 |а (лг)| ста-
становится и продолжает оставаться меньше любого положи-
положительного числа, в частности меньше -уг • |а(*)| <"аГ#
Тогда
т. е. <?(х)а(х)— бесконечно малая функция вблизи х0.
Следствие. Произведение двух функций, бесконечно
малых вблизи данной точки, есть функция бесконечно
малая вблизи этой точки,
3. Понятие предела функции. Определение. Число А
называется пределом функции f(x) в точке х0, если функ-
функция / (х) отличается от этого числа на функцию, бесконечно
малую вблизи точки х0.
Это определение может быть записано следующим образом:
число А есть предел f(x) в точке д:0, если /(дг) = А-\-а(х),
где а (л:) — бесконечно малая вблизи х0.
Для предела функции принято обозначение
А= lim
Иначе еще говорят, что функция f(x) стремится к А
при xt стремящемся к х0, что короче записывается так:
/(лг)->Л при jc->jc0.
4. Свойства пределов. 1°. Если функция в данной точке
имеет предел, то она вблизи этой точки ограничена.
Пусть Л= lim /(*), т. е. / (х) — А ~\- а (х).

94 ТЕОРИЯ ПРЕДЕЛОВ [ГЛ. II
Так как- а (л:) — бесконечно малая функция, то ее значе-
значения вблизи х0 на абсолютной величине становятся и продол-
продолжают оставаться меньше любого положительного числа,
в частности, меньше единицы. Поэтому
|/(*)| = |Л + а(х)|<|Л| + |а(*)| < \А\ + 1.
Отсюда следует, что все значения функции вблизи точки х0
меньше |Л|-{-1, т. е. функция ограничена.
2°. Предел постоянной функции равен самой по*
стоянной.
Пусть f(x)=zzc, тогда можно написать, что f(x)=c-\-a, (x)t
где a(#) = 0, т. е. lim f(x) = c.
3°. Предел бесконечно малой функции равен нулю.
Пусть f(x) — a(x) — бесконечно малая функция. Она
может быть представлена как сумма числа 0 и бесконечно
малой функции а(лг) :/(лО = О-|-<х(л:), т. е. lim /(л:) = 0.
4°. Предел суммы двух функций в данной точке равен
сумме ах пределов.
Пусть
lim Д (х) = А и lim /2 (х) = В.
Покажем, что
Так как lim ft(x) = А, то fx(л:) = А + a(jc). Анало-
гично /2(*) = # + РС*:)- Отсюда
Функция Д (х) •+• /2 (х) представлена в виде суммы числа
+ B и бесконечно малой а(лг) + Р(лг) (сумма двух беско-
бесконечно малых), т. е. она отличается от числа А-\-В на функ-
цию бесконечно малую. Из определения предела следует, что
или
lim {/!(*) +Л(*)]= Нт fx{x) + Ит /2(х).
5°. Предел произведения двух функций равен произ*
ведению их пределов.

§ 1] ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ 95
Пусть lim/1(jc) = -4 и lim /2 (х) = В. Покажем, что
9
Так как Ит/1(л:) = Л, то /г (х) = Л + а (л:). Анало-
гично /2(#) =-6 + f*C*O- Отсюда
Функции Лр (х) и Bcl (x) бесконечно малые как произве-
произведения постоянных величин на бесконечно малые, а(х)ф(х)
также бесконечно малая функция как произведение двух бес-
бесконечно малых. Сумма их будет также бесконечно малой
функцией.
Итак, функция fi(x)/2(x) отличается от числа АВ на
бесконечно малую, т. е. lim fl(x)f2(x) — AB1 или
lim fx(x)f2(x)= lim fx(x)- lim
Х >X
Следствие. Постоянный множитель можно вино»
ситъ за знак предела.
Действительно, по доказанному предел произведения равен
произведению пределов, поэтому
lim cfx {x) = lim с • lim fx (x) = с lim /х (х).
Х->Х9
6°. Предел частного равен частному их пределов,
если предел знаменателя не равен нулю.
Пусть lim /х (х) = Л и lim /2 (л:) = В, причем В Ф 0.
Покажем, что
Мы имеем /г(х) — А-+-а(х),
Разделим почленно первое равенство на второе и в пра-
правой части прибавим и вычтем -g-:
/,(*) __ Л А + а(х) Л _
— В ^ Б В —
А . Ва (х) — А? (х) А

96 ТЕОРИЯ ПРЕДЕЛОВ {ГЛ. II
Множитель Во. (х)— А$(х) бесконечно мал как разность
бесконечно малых. Множитель D0 . PQ. ч ограничен, так
в* -+- я? \х)
как его знаменатель отличается от J52 на бесконечно малую
функцию, причем В Ф 0. Произведение бесконечно малой на
ограниченную бесконечно мало.
Итак, функция } ]\ отличается от числа -~- на функцию
/2 Vх) &
бесконечно малую, т. е.
ит
Пример. Вычислить Нт
>0
Воспользоваться непосредственно теоремой о пределе
частного нельзя, так как предел знаменателя равен нулю.
Предварительно преобразуем функцию
fT+зз—i ,.m
hm ¦—2 = ^ltn
jr->0 x •*-><)
К полученной функции уже можно применить теорему
о пределе частного: предел знаменателя равен 3. Искомый
предел равен -g-.
7°. Теорема о пределе промежуточной функ-
функции. Пусть даны три функции fl(x)t /2(*)» /3D причем
значения одной из них, например f^(x)t заключены между
значениями двух других:
Если функции fi(x) и /3С*0 имеют в некоторой точке
одинаковые пределы, то и промежуточная функция /гС-к)
имеет в этой точке такой же предел.
Итак, lim /г(х) = А, lim /3(лг) = Л. Надо показать,
X -» Хо X -> Xq
что Нт /2 (х) = А.

§ 1]
ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ
Вычтем из всех частей неравенства fx{x)</2(x)</3(л:)
величину fi(x). Тогда получим
О < /2 (х) - /г (х) < /3 (*) - Л (л:).
Так как lim [fz(x) — fx(x)] = A — Л = 0, то функция
/г(х) — fi(x) является бесконечно малой. Из последнего
неравенства тогда следует, что f2(x) — f\(x) также беско-
бесконечно малая функция, т. е. lim [f2(x)~fx(x)] = 0. Отсюда
lim f2(x)— lim fx(x)~Q, или lim f2(x) — Л = 0.
Таким образом, lim f2(x) = A.
б. Понятие непрерывной функции. Определение.
Функция y = f(x) называется непрерывной в точке х0,
йу
о хо+Дх
Рис. 106с
хв zo
Рис. 107.
если бесконечно малому приращению аргумента соответствует
бесконечно малое приращение функции: lim Ay = 0, или
Д0
lim [
Длт->0
На рис. 106 изображена функция, непрерывная в точке лг0,
а на рис. 107 — разрывная.
Пусть функция y = f(x) непрерывна в точке xQi т. е.
HmAy= tt
Д0 Д
Так как /(л:0) не зависит от Ал:, то
lim /(

98 ТЕОРИЯ ПРЕДЕЛОВ [ГЛ. II
Отсюда следует, что
lim /С*0 + д*) = /(*<>)• или lim
Д.дг->0 х->х0
Итак, если функция непрерывна в точке х0, то предел
функции при х~>х0 равен ее значению при х — х0.
Последнее равенство можно записать в виде
lim
im / (л:) = / f lim x\
>х0 \х-*>х0 )
X-*>Xq
откуда следует, что для непрерывной функции знак функции
и знак предела можно менять местами.
Пользуясь свойствами пределов, можно доказать, что
сумма и произведение непрерывных функций являются не-
непрерывными функциями. Частное двух непрерывных функций
непрерывно за исключением того случая, когда знаменатель
обращается в нуль.
В качестве примера докажем непрерывность функции
у = х2. Вычислим ее приращение в некоторой точке х0:
Отсюда
HmAy= limBxQJlrkx)kx= lim Bл:0 + Ал:) lim Ал: = 0.
Д0 Д0 Д>0 Д0
Это равенство справедливо при любом х0. Бесконечно
малому приращению аргумента соответствует бесконечно
малое приращение функции. Функция у = х2 непрерывна при
любом значении х.
Так же просто можно доказать непрерывность функции
у = хп. Непрерывность других элементарных функций до-
доказывается сложнее.
Оказывается, что функции sinx, cosjc, ax непрерывны
при всех значениях х, а все другие элементарные функции
(tgA;, ctgx, arcsinA:, arccosx, logaAr)
непрерывны при всех х, принадлежащих их областям опре-
определения. Например, функция у —loga.v непрерывна при всех
положительных значениях х.

§ 2] ПРЕДЕЛ ФУНКЦИИ НА БЕСКОНЕЧНОСТИ 99
§ 2. Предел функции на бесконечности
1. Понятие функции, бесконечно малой на бесконеч-
бесконечности. Определение. Функция называется бесконечно
малой на бесконечности, если ее значения по абсолютной
величине становятся и продолжают оставаться меньше любого
наперед заданного положительного числа, как только значе-
значения аргумента становятся достаточно большими.
Если задать сколь угодно малое положительное число е,
то график функции, бесконечно малой на бесконечности, при
достаточно больших х будет заключен между прямыми
Рис. 108.
у = — е и у— в. Следовательно, если функция бесконечно
мала на бесконечности, то ее график имеет асимптоту у = 0
(ось Ох) (рис. 108).
2. Предел функции на бесконечности. Определение.
Число А называется пределом функции y = f(x) на беско-
бесконечности, если функция f (х) отличается от этого числа на
функцию, бесконечно малую на бесконечности.
Итак, если / (х) = А -)- а (х), причем а(л:) бесконечно
мала на бесконечности, то A— lim f (x).
Геометрический смысл того, что функция имеет предел
на бесконечности, состоит в том, что график такой функции
имеет горизонтальную асимптоту у = А. Следовательно, чтобы
найти горизонтальную асимптоту графика функции, нужно
вычислить ее предел на бесконечности.
Из геометрического смысла предела на бесконечности
ясно, что не всякая функция имеет предел на бесконечности.
Если функция неограниченно возрастает на бесконечности,
то она, естественно, не имеет предела на бесконечности.

100 ТЕОРИЯ ПРЕДЕЛОВ {ГЛ. II
Даже если функция ограничена, то она также может не иметь
предела на бесконечности. Например, функция sin x при
лг->со периодически изменяется от —1 до 1 и ни к какому
пределу не приближается.
Аналогично, функции могут не иметь предела в точке.
Так, функция — неограниченно возрастает при л;->0 и по-
поэтому не имеет предела в
точке 0. Функция sin— при
х—>0 неограниченно колеб-
колеблется между —1 и 1 и ни
к какому пределу не при-
приближается (рис. 109).
3. Нахождение наклон -
~ *~х ных асимптот графика
функции. Пусть задана
Рис- 109- функция у = f (x). Предпо-
Предположим, что ее график имеет
наклонную асимптоту y — kx + b. Задача о нахождении
асимптоты сводится к определению коэффициентов к и b
в ее уравнении.
То, что прямая y = kx-\-b является асимптотой графика
функции, означает, что расстояние АВ от точки А графика
функции до этой прямой стремится к нулю, когда точка А
(следовательно, и ее абсцисса л:) уходит в бесконечность:
lim AB=zO.
Л"->оо
Если через а обозначить угол, образованный асимптотой
с осью Ох, то
1 = AC cos а.
Отсюда видно, что АВ и АС одновременно стремятся
к нулю при х, стремящемся к бесконечности:
lim ЛС = 0.
На рис. ПО видно, что АС представляет собой разность
ординат AD и CD соответственно точки Л, лежащей на
кривой, и точки С, лежащей на асимптоте:
= AD — CD = f(x) —

l\ ПРЕДЕЛ ФУНКЦИИ НА БЕСКОНЕЧНОСТИ 101
Следовательно, lim [/ (х) — kx — b] = 0.
jtr-»oo
Так как предел разности равен разности пределов, то
т. е.
lim [/ (х) — kx\ — b = Qt
JT-»OO
b= l\m[f(x)—kx].
ДГ->00
Для нахождения k запишем равенство lim [f(x) —kx—b] =0
JtT-»OG
в несколько ином виде:
lim л
ХЧЮО
W_A_!i о.
X XJ
Предел произведения равен нулю, и так как первый
множитель неограниченно растет, то предел второго множи-
множителя должен равняться нулю, т. е. lim Г/(*) ^ А]_0
0
\
С
D
Рис. ПО.
Воспользовавшись свойством предела разности, получим
Так как lim — = 0, то из последнего равенства следует,
что

102 ТЕОРИЯ ПРЕДЕЛОВ [ГЛ. II
Итак, мы доказали, что для прямой y = kx-\- bt являю-
являющейся асимптотой кривой y = f(x)t коэффициенты k н b
находятся по формулам:
k — Hm Л^1, ъ = lim [/(*) — kx].
X-+QQ Х Х-+ОО
Справедливо и обратное утверждение: прямая у— kx-{-b
является асимптотой графика функции y — f(x), если числа
k и b связаны соотношением 6 = lim[/(x)— kx].
Действительно, если ft = lim [f(x) — kx], то lim [/ (х)—
Х->оо Jf-»oo
— kx — b] = 0, т. e, lim AC = 0. Отсюда следует, что и
Jf-»oo
lim ЛВ = 0, т. е. прямая y = kx-\-b есть асимптота графика
функции y = f(x).
Заметим, что задача о нахождении асимптоты равносильна
задаче о линеаризации функции для больших значений аргу-
аргумента.
Пример. Найти наклонные асимптоты графика функции
-з •
X-+OQ Л
= lim
Прямая y=zx-±--j есть асимптота.

§ 3]
ЗАДАЧА О КАСАТЕЛЬНОЙ
§ 3. Задача о касательной
103
Пусть дана функция y = f (x), график которой изображен
на рис. 111, и точка А{х0> у0) на этом графике. Возьмем
на кривой справа от точки А(х0, у0) точку В и проведем
через эти точки прямую, которую назовем правой секущей.
Рис. 111.
Угловой коэффициент этой секущей найдем из треуголь-
треугольника ЛВС:
_ Ду
^сек — Щ асек — д^- •
Если точка В перемещается по кривой, приближаясь
к точке Л, то секущая поворачивается вокруг точки А.
Предположим, что она приближается к некоторому пре-
предельному положению.
Определение. Предельное положение правой секущей,
когда ее переменная точка пересечения с кривой приближается
к точке (х0, у0), называется правой касательной в точке
(*о> Уо).
Из определения правой касательной следует, что ее угло-
угловой коэффициент &кас,пр равен
ес
Возьмем теперь на графике функции y = f(x) точку
Вх (xv уг) слева от точки A (xQi уд) (рис. 112) и проведем через

104
ТЕОРИЯ ПРЕДЕЛОВ
[ГЛ. И
точки А и В{ секущую, которую назовем левой секущей.
Угловой коэффициент левой секущей есть
А ...
и —
•VfPlT ПРИ —
лев
0 — Х\ Х\ "— Xq &Х
причем Дл; < 0.
Определение. Предельное положение левой секущей,
когда ее переменная точка пересечения с кривой прибли-
приближается к точке (х0, у0), называется левой касательной
в точке (х0, у0).
У t
У
0
/
У»
X,
А
С
\yo-yt
Уо
Рис. 112.
По определению левой касательной ее угловой коэффи-
коэффициент
^ (Д* < 0).
л
Теорема. Всякая выпуклая (вогнутая) кривая имеет
в каждой точке правую и левую касательные.
Доказательство проведем для правой касательной.
Пусть график функции y = f(x) выпуклый. Проведем
в точке А(х0, у0) правую секущую АВ. При приближении
точки В к А секущая вращается против часовой стрелки,
при этом угол, образуемый ею с положительным направле-
направлением оси Ох, увеличивается и приближается к некоторому
предельному значению. Этот угол и будет углом наклона
касательной к оси Ох.
В наших рассуждениях мы использовали без доказатель»
ства тот факт, что если величина возрастает и ограничена

§ 3}
ЗАДАЧА О КАСАТЕЛЬНОЙ
105
(в нашем случае угол наклона секущей), то она имеет
лредел.
Определение. Если в точке кривой правая и левая
касательные сливаются в одну прямую, то эта прямая на-
называется касательной.
В случае, когда в точке существует касательная, имеем
и ь ъ
/ькас. лев лкзс. пр "'кас*
Для вычисления углового коэффициента касательной
к кривой у = /(лг) в точке (л;0, у0) нужно вычислить угло-
угловые коэффициенты правой и левой касательных. Если они
равны, то их общее значение будет угловым коэффициентом
касательной.
Если в какой-нибудь точке угловые коэффициенты пра-
правой и левой касательных не совпадают, то кривая имеет в
этой точке излом (см. рис. 113).
ы>
Рис. 113.
j
Рис. 114.
1. Касательная к параболе у = х2 в начале координат.
Так как график функции у = х2 всюду вогнут, то в каждой
точке имеются правая и левая касательные (рис. 114).
Проведем в начале координат правую и левую секущие.
х2
Угловой коэффициент правой секущей равен — = .г, угловой
коэффициент правой касательной равен пределу при х,
стремящемся к нулю, углового коэффициента правой секущей:
. пр
сек. п
= lim х = 0.

106
ТЕОРИЯ ПРЕДЕЛОВ
[ГЛ. XI
Для того чтобы вычислить угловой коэффициент левой
касательной, проведем через начало координат левую секу-
секущую. Она пересечет график функции в точке, абсцисса
которой отрицательна (обозначим ее через — х). Тогда утло-
вой коэффициент левой секущей равен
littl (— X) =х 0.
0
х и
Так как угловые коэффициенты правой и левой касатель-
ных равны, то парабола у=*х2 имеет в начале координат
касательную, совпадающую с осью Ох.
2* Касательная к параболе у = Ух. Функция у = Ух
определена при х^О, поэтому можно говорить только
о правой касательной в точке х = О. Угловой коэффициент
Vx
правой секущей в начале координат равен ~—=
—^=,
тогда
при а*->0 угловой коэффициент правой секущей неогра-
неограниченно возрастает; kctK по = —^= -> оо. Это означает, что
р У х
угол наклона секущей стремится к -н", т. е. касательная
совпадает с осью Оу (рис. 115).
Рис. 115.
Рис. 116.
3. Касательная к синусоиде у = sin x в начале коор-
координат. Первый замечательный предел. При исследовании
функции у = sin х было установлено, что справа от начала
координат график ее выпуклый, а слева — вогнутый. При-
Применяя теорему, приходим к выводу, что в начале координат
существуют правая и левая касательные к ее графику. Пока-
Покажем, что эти касательные совпадают. Проведем через начало
координат правую и левую секущие: ОА и OAV Для угло-

§ 3] ЗАДАЧА. О КАСАТЕЛЬНОЙ 107
вого коэффициента правой секущей имеем ^Сек.пр
тогда для углового коэффициента правой касательной
^кас.пр= lim"^~ (РИС. 116).
лг-»О х
Угловой коэффициент левой секущей равен -п *"~"х*,
угловой коэффициент левой касательной равен:
*каслев = limftceK
.. и ,. sin (—х) ,. sinx
= limftceK> лев = 111П * ' = lim"-T~"*
лг-»О Л jtr->0 •*
u - , f. sin x
Итак, лкас, пр = ^кас# лев = hm ——, следовательно,
лг-»О х
. t. sin x
Вычислим этот предел.
Первый замечательный предел: \im ^а х¦. При вычис-
о х
лении этого предела нельзя воспользоваться теоремой о пре-
пределе частного, так как предел зна-
знаменателя равен нулю. Восполь-
Воспользуемся геометрическими соображе-
соображениями.
Возьмем круг единичного ра-
радиуса, построим острый угол х
(в радианах), проведем линии тан-
тангенса ВС и синуса AD и соеди-
соединим точки А и С прямой. Рас-
Рассмотрим следующие фигуры: тре-
треугольник О АС, сектор О АС и Рис. 117.
треугольник ОВС. Так как эти фи-
фигуры вложены одна в другую, то для их площадей спра-
справедливы неравенства (рис. 117)
5<з оас < 5д овс» (О
Вычисляя площади этих фигур, получаем
= -2 sin*,
5д овс = -?г ОС • ВС = -g- tg л;.

108 ТЕОРИЯ ПРЕДЕЛОВ [ГЛ. II
Напомним, что площадь кругового сектора с радиусом г и
углом а вычисляется по формуле
(угол измеряется в радианах!).
Для сектора ОЛС получаем
So оас = -ту ОЛ2х =->х.
Подставив найденные выражения для площадей в нера-
неравенства A), получим
1 . ^ 1 ^ 1 ,
у sin х <  •* < ^ te *•
или
sin х < д: < tgx.
Разделив все части неравенств на sin x% получим
sin л: cos x
В этих неравенствах перейдем к обратным величинам. При
этом знаки неравенств изменятся на противоположные:
1 ^ sin х ^
1 > > cos х.
X
Так как пределы левой и правой частей неравенства
при х->0 равны единице, то на основании ранее доказан-
доказанной теоремы о пределе промежуточной функции предел
sin х
также равен единице:
f. sin x *
lim = 1.
Заметим, что в предыдущем рассуждении мы использо-
использовали то, что функция cos х непрерывна, и поэтому lim cos x =
O
= cosO=l.
Возвращаясь к задаче о касательной к синусоиде, полу^
чаем, что
, ,. sin х л % п
ftKac= Urn——=1, т.е. tgaKac=lt акас = т.

§ 3|
ЗАДАЧА О КАСАТЕЛЬНОЙ
109
Итак, касательная к синусоиде в начале координат обра-
образует с положительным направлением оси Ох угол, рав-
равный
 *
4. Касательная к косинусоиде у = со$х в точке ее
пересечения с осью ординат. График функции y = cosx
при —~ < л* < у выпуклый, по доказанной теореме
в каждой точке рассматриваемого промежутка он имеет
правую и левую касательные (рис. 118).
. /
' ' V
Рис. 118.
Возьмем на кривой точки Л@, 1), В(х, у) и Вх{ — х, у)
и проведем в точке Л правую (ЛВ) и левую (АВХ) секущие.
Для углового коэффициента правой секущей имеем
COS X-
\
. пр
тогда угловой коэффициент правой касательной &кас# пр =
.. COS X — 1
= Hm .
д:->0 х
Вычислим этот предел, для чего и числитель и знамена-
знаменатель умножим на cosx-f-1:
— sin2x
_ t._ (cos х — 1) (cos x + 1) _ ь
•ПР „тЛ л: (cos л:+ 1) *™0 ^(cosAr+l)
= — Hm
sm x
lim =0 • 1 =

ПО ТЕОРИЯ ПРЕДЕЛОВ
Итак, kmz. Пр = 0. Аналогично,
[ГЛ. 11
И
?кас.лев= Ни
1 — cos (— х)
X
1 — COS X
1 — COS X
. np'
Так как угловые коэффициенты правой и левой каса-
касательных в точке Л @, 1) равны» то существует касательная
к косинусоиде в этой точке, и ее угловой коэффициент
равен нулю. Касательная параллельна оси Ох.
б. Касательная к тангенсоиде y — tgx в начале
координат. Проведем правую и левую секущие ОЛ и OAi9
О
Рис. 119.
вычислим их угловые коэффициенты и угловые коэффи-
коэффициенты правой и левой касательных (рис. 119):
. пр"
« Ир
X COSX
.h 1
¦ ^кас. пр — *•
Касательная к тангенсоиде в начале координат образует
с положительным направлением оси Ох угол, равный ~.

§ 3]
ЗАДАЧА О КАСАТЕЛЬНОЙ
111
6. Касательные к графикам обратных тригонометри-
тригонометрических функций. Рассмотрим функцию y = arcsin.x; и вы-
вычислим угловой коэффициент правой касательной к ее гра-
графику в начале координат:
ь — цт arcsin x
^. пр 11ГП
Обозначим arcsin х через а, тогда х = sin а и
.. arcsin x ,. a *
\im — hm-r—= I,
x „_^sina
*кас.пр—*•
л:->0 •* a->0
Вычислим угловой коэффициент левой касательной:
, f. arcsin (—х) t.
^кас лев = "m " = "m
jr->0
arcsin at
Итак, касательная к графику функции у = arcsin л: в на-
начале координат существует и образует с осью Ох угол,
равный ~ (рис. 120).
arcstn(-x)
4,
arc sinх
О х
Рис. 120.
Рассмотрим функцию у = arctg x и вычислим угловой
коэффициент правой касательной к ее графику в начале
координат:
. t. , t. arctg x
^кас. пр — lim Лсек. пр — lim Z " •
Обозначим arctg л: через а, тогда x = tga и
=

112
ТЕОРИЯ ПРЕДЕЛОВ
[ГЛ. II
Угловой коэффициент левой касательной:
Ь — п~ arctg(-*> _ i:~ аг<^* _
. пр
— 1
Итак, касательная к графику функции у = arctg x суще-
существует и образует с осью Ох угол а —-^ (рис. 121),
orctgx
Рис. 121.
7. Касательная к графику обратной функции. Как мы
уже знае&, график обратной функции получается из графика
Рис. 12л
данной функции путем симметричного отображения отно-
относительно биссектрисы первого и третьего координатных
углов (рис. 122).
Пусть касательная к графику данной функции образует
с осью Ох угол а. Геометрически ясно, что касательная

§ 3]
ЗАДАЧА О КАСАТЕЛЬНОЙ
113
к графику обратной функций в соответствующей точке
будет образовывать с осью Ох угол ~ — а. Поэтому
с. обр :
Итак, угловой коэффициент касательной к графику
обратной функции в некоторой точке есть обратная вели-
величина к угловому коэффициенту касательной к графику дан-
данной функции в соответствующей точке.
Применим это соображение к рассмотренным нами функ-
функциям. Функции х2 и
2
Ух
взаимно обратны. Касательная
O
у У р
к графику у = х2 в начале координат совпадает с осью Oxt
касательная же к графику у = Ух совпадает с осью Оу.
Угловые коэффициенты касательных к графикам функ-
функций sin х и tg х в начале координат равны единице, следо-
следовательно, угловые коэффициенты касательных к графикам
обратных функций arcsin x и arctg x также равны единице,
и касательные образуют с осью Ох угол -у.
8. Касательная к графику показательной функции
в точке его пересечения с осью ординат. Как известно,
график показательной функции вогнутый. Из доказанной
Рис. 123.
в начале параграфа теоремы следует, что в любой точке
этого графика существуют правая и левая касательные.
Покажем, что в точке пересечения графика с осью ординат
они совпадают. Для определенности будеи считать а > 1
(рис. 123).

114 ТЕОРИЯ ПРЕДЕЛОВ [ГЛ. II
ах ]
Угловой коэффициент правой секущей равен и,
следовательно, угловой коэффициент правой касательной
равен
дХ 1
^кас. по 11Ш
а-х |
Угловой коэффициент левой секущей равен —— =
и, следовательно, &кас# лев = lim .
х ' x-*Q х
Преобразуем выражение, стоящее под знаком предела:
При д:->0 первый множитель а~х имеет пределом еди-
единицу, а предел второго множителя равен &каСш пр. Таким
образом, &кас# лев = кШСш пр, и график имеет касательную
в точке пересечения с осью Оу, угловой коэффициент ко-
которой обозначим через ka.
Рассмотрим, как изменяется угловой коэффициент каса-
касательной в зависимости от основания показательной функции.
Возьмем функцию у = Ьх. Для углового коэффициента кь
имеем
IjX ]
kh = lim .
О у
Введем переменную а такую, что Ьх = аа. Беря от обеих
частей логарифм при основании Ь, получаем
Подставляя выражения для Ьх и х под знак предела
для kb и замечая, что а—>0 при х—>0, получаем
kh = lim —j = -j hm
\ogba
Таким образом, при переходе от основания а к основа-
основанию Ъ угловой коэффициент уменьшается в logb а раз.
Так как \ogb а при Ь > 1 принимает все возможные положи-
положительные значения, то и коэффициент kb при различных
основаниях Ь принимает все возможные положительные
значения*

§ 3]
ЗАДАЧА О КАСАТЕЛЬНОЙ
115
Оказалось, что во многих случаях особенно удобной
является та показательная функция, для которой угловой
коэффициент касательной в точке пересечения с осью Оу
равен единице. Основание такой функции условились обозна-
обозначать буквой et а саму функцию ех.
По определению числа е угловой коэффициент &e = 1, или
lira —
х-Ю л
С другой стороны, для любого а feg = |og а' к& Откуда
следует, что ka = logea.
Логарифм при основании е условились называть нату*
ральным и обозначать так: In. Поэтому последнюю формулу
можно сокращенно записать в таком виде: &д = 1
У/0
/
Рис. 124.
Вспоминая предел, который нас привел к величине ka%
получаем
ах I
ka= lim =ln#.
Х
Можно доказать, что число е является иррациональным
числом и, следовательно, имеет вид бесконечной непериоди-
непериодической десятичной ароби. Позднее мы получим возможность
вычислять число е с любой степенью точности. Сейчас же
оценим лишь приближенно величину е. Для этого восполь-
воспользуемся тем, что угловой коэффициент касательной к гра-
графику функции ех в точке пересечения с осью Оу равен
единице (см. рис. 124). Из вогнутости кривой у = ех

116 ТЕОРИЯ ПРЕДЕЛОВ [ГЛ. II
следует, что угловой коэффициент любой правой секущей
больше, а коэффициент любой левой секущей меньше, чем
угловой коэффициент касательной в точке А. Отсюда полу-
получаем, что
рХ 1 р-Х I
X ^ —X ^
Напомним, что согласно нашим обозначениям в обоих
неравенствах х > 0.
Из первого неравенства следует е* > 1 + х. Во втором
неравенстве при умножении на — х знак неравенства изме-
изменяется на противоположный, следовательно, е~х > 1 — х.
Положим в первом неравенстве х= 1, тогда получим е > 2.
1 — 1
Из второго неравенства при х = -^ получим е 2 >-н-. Отсюда
< 2 и, следовательно, е < 4. Итак мы показали, что
Придавая в неравенствах г* > 1 + л: и е~^> 1 — jc
переменной л: значения, более близкие к нулю, можно сузить
границы, между которыми заключено число е.
В действительности е — 2,718 ...
9. Касательная к графику логарифмической функции
в точке пересечения с осью Ох. Функция у — \щах яв-
является обратной к показательной функции у = ах. Точке
пересечения графика у = ах с осью Оу соответствует точка
пересечения графика y — \ogax с осью Ох. Угловой коэф-
коэффициент касательной к графику показательной функции
в точке пересечения с осью Оу равен In а. Поэтому угловой
коэффициент к графику логарифмической функции в точке.
пересечения с осью Ох равен -|—. Если вычислить его
как предел углового коэффициента секущей, то получим
Следовательно,
hx — In a

§ 4] ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ 117
Если рассматривать функцию у = In xt то
10. Число ^ как предел. Формулу для углового коэф-
коэффициента касательной к графику функции у = \пх можно
переписать в виде
kxt<xc:===' Hm -
Преобразуем выражение, стоящее под знаком предела:
Отсюда
lim
±fI_ iimln(l+aO = ln lim(l+a)H = 1.
a a-»0 La->0 J
При перемене местами знаков предела и логарифма была
использована непрерывность логарифмической функции.
Итак,
In lim (I + aO =1 =lne.
Lo->0 J
Отсюда следует, что
l
lim A-faO z=e.
Иногда этот предел записывают в другой форме, за-
заменяя а на —, т. е.
§ 4. Гиперболические функции
В приложениях часто встречаются следующие комбинации
функций ех и е~х:

118
ТЕОРИЯ ПРЕДЕЛОВ
[гл. и
В связи с этим функциям
_—., дали
специальные названия. Первая из них называется гиперболи-
гиперболическим косинусом, вторая — гиперболическим синусом.
Обозначаются они так:
2
¦ sh х.
Функции ch х и sh л: определены для всех значений х.
Исследуем функцию y = chx. График функции пересе-
пересело _l. е°
кает ось Оу: при х = 0 имеем у = ch 0 = —~— = 1. Функ-
Функция ch х четная, так как
ch(-*) = -
График функции ch x симметричен относительно оси Оу.
При неограниченном возрастании х значения е~х будут
Рис. 125.
становиться сколь угодно малыми, и значения ch x приблизи-
приблизительно будут равны значениям функции у^*.
Построим вспомогательный график функции у = ^ех.
График у = ch х расположен выше графика у = -g- ex\ так как
ех + е~* ^ ех
При больших положительных значениях х эти графикц
сближаются (рис. 125).

§ 4] ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ 119
Аналогично исследуем функцию у = sh x. Так как
¦—~— = 0, то shO = O, т. е. график проходит через
Рис. 126.
начало координат (рис. 126). Функция нечетная, так как при
изменении знака х функция меняет знак:
sh (-*)=
е-л — <
-в"
2 — 2
Если х велико, то е~х мало и
y=shx пройдет ниже графика у — ^е*, так
. = — sh л:.
-n ех. График
как
Легко проверить, что гиперболические синус и косинус
связаны соотношением
ch2 х — sh2 x = 1.

ГЛАВА III
ЛИНЕАРИЗАЦИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
§ 1. Сравнение бесконечно малых функций
Пусть а (л:) и Р(лг) — две функции, бесконечно малые
вблизи одной и той же точки х0.
Определение. Две бесконечно малые называются
бесконечно малыми одного порядка малости, если
В частности, две бесконечно малые называются эквива-
эквивалентными, если предел их отношения при х->х0 равен
единице:
Нт 444
Если а(х) и р (jc) — эквивалентные бесконечно малые
функции, то это записывают так: а(х) — $(х) (читается а(х)
эквивалентна [3 (х)).
Определение, а (л:) называется бесконечно малой
более высокого порядка малости, чем р(х), если
lim
К -> Xt
Итак, если
О, то а (л:) более высокого порядка малости,
чем
Л, то а(х) и P(jc) одного порядка малости;
1, то а (л:) и $(х) эквивалентные бесконечно
малые*

§ 1], СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ ФУНКЦИЙ 121
1. Свойства бесконечно малых более высокого порядка
малости, чем данная. 1°. Сумма двух бесконечно малых
более высокого порядка малости, чем данная, есть бес-
бесконечно малая более высокого порядка малости, чем
данная.
Пусть ах(х) и а2(х) — бесконечно малые более высокого
порядка малости, чем Р(х), т. е.
.. Oti (х) ~ 1- а2 (х) г\
hm ' ; ч; = 0 и hm 2V ' =zQ.
Р(*) PW
Тогда
al(x) + a2(x) ,. a, (x) , t. a2 (x) л
PW ^->^0 PW *->*0 PW
Свойство доказано.
2°. Произведение бесконечно малой более высокого
порядка малости, чем данная, на ограниченную функ-
функцию есть снова бесконечно малая более высокого порядка
малости, чем данная.
Читателю предлагается самому доказать это свойство.
Сравним некоторые бесконечно малые.
1. Пусть а (л:) = sin х, ф(х) = х, х0 = 0.
Так как Hm smx = 1, то sin jc и х эквивалентные бес-
х
конечно малые: sin jc — х.
Эквивалентными бесконечно малыми будут tgx и х,
arcsin х и х.
2. Пусть а(дг)= 1 — cosa;, $(x) — x2t xQ = 0.
Тогда
t 2 sin2— 2~ Л
.. 1— cos л1 ,. 2 t. 4 1
hm -5 = hm -2—= hm —_ = T.
Итак, бесконечно малые 1—cosx и х2 одного порядка
малости.
2. Основная теорема об эквивалентных бесконечно
малых. Т е о р е м а* Если две бесконечно малые эквива*
лентны, то разность между ними есть бесконечно малая
более высокого порядка малости, чем каждая из них.
И, наоборот, если разность двух бесконечно малых

122 ЛИНЕАРИЗАЦИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ [ГЛ. Ш
есть бесконечно малая более высокого порядка малости,
чем одна из них, то эти бесконечно малые эквивалентны.
Пусть <х(лг)—$(*)> т. е. lim -?-рг=1. Докажем, что
х-*х0 rW
а (л:) — $(х) есть бесконечно малая более высокого порядка
малости, чем, например, §
Действительно,
Это и означает, что <х(л:) — $(х) — бесконечно малая более
высокого порядка малости, чем ф(х).
Доказательство обратного утверждения. Пусть
Докажем, что а (л:) и $(х) эквивалентны:
Так как первый предел по условию равен нулю, то
lim в; \' — 1» т« е- а(л:) и PW эквивалентные бесконечно
малые.
Обозначим разность а(х)—$(х) через ч(х): а(х)—$(х) =
— Т (^)- Тогда
Доказанная теорема утверждает, что из эквивалентности
а (л:) и Р(л:) (а (л:) ^-^ ^ (л:)) следует, что т(х) является бес-
бесконечно малой более высокого порядка малости, чем ф(х)
(или а(;е)).
§ 2. Линеаризация вблизи нуля
Линеаризацию функций вблизи нуля мы будем теперь
проводить, основываясь на теореме об эквивалентных бес-
бесконечно малых. Если функция f(x) бесконечно мала вблизи
нуля и эквивалентна функции kx, то по теореме об экви*

§ 2J ЛИНЕАРИЗАЦИЯ ВБЛИЗИ НУЛЯ 123
валентных бесконечно малых f(x) отличается от kx на бес-
бесконечно малую более высокого порядка малости:
Пользуясь равенством / (х) = kx -f- T (х), можно дать
такое определение: линеаризацией функции вблизи нуля
называется замена ее линейной функцией с точностью
до величины более высокого порядка малости, чем х.
Линеаризация элементарных функций вблизи
нуля.
1. Линеаризация функции y==(t-$-x)n. Как было по-
показано,
A -{- х)п» 1 -Ь пх
с точностью до членов со степенями х выше первой. Эти
отброшенные члены представляют собою бесконечно малые
более высокого порядка малости, чем х. Если, например,
ах2
отброшен член вида ах2, то Игл —==аНтлг=0, т. е.
*->0 х лг->0
ах2 более высокого порядка малости, чем х. Таким образом,
где 7 — бесконечно малая более высокого порядка малости,
чем х.
2. Линеаризация функции У = тт—• Функция , , -
1 -f- X 1 штт X
вблизи нуля не является бесконечно малой, поэтому рассмо-
рассмотрим вспомогательную функцию -j-j- 1, которая вблизи
нуля будет уже бесконечно малой.
Сравним две бесконечно малые -Г-Е 1 и х:
1 -f- х
_j !
t. 1 +Х .. 1 — I —X t
Из полученного равенства следует, что эти бесконечно
малые не эквивалентны. Однако, если сравнить функцию
._— — 1 с —х, то предел их отношения при х->0
1 -J- X

124 ЛИНЕАРИЗАЦИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ [ГЛ. III
окажется равным единице, т. е. у-г- 1 и — х эквивалентны.
Тогда по доказанной теореме -г-у- 1 = — х-\- f , где
1 -f- х
7 — бесконечно малая более высокого порядка малости, чем х.
Итак,
3. Линеаризация функции у = ]/l -\-х. Функция ]/ l-f-jc
вблизи нуля не является бесконечно малой, поэтому рассмо-
рассмотрим функцию "JA+a;—1, бесконечно малую вблизи нуля,
и сравним ее с бесконечно малой х:
,. l/T+T—l ,. 1+* —1 ,. 1 1
Um ! = lim ' -= hm =
x ifl + I)
lim hm -
x->0 Xifl+X + I) x^qY\+x+1 2
Бесконечно малые не эквивалентны. Если же сравнить
У\-\-х—1 с -у, то предел их отношения окажется рав-
равным единице, т. е. "j/l + х — 1 — -к> или
4. Линеаризация функции y — sinx. Сравним sin*
и х вблизи нуля. Получим первый замечательный предел
lim = 1, т. е. sin х >—х, или sin л; = л; + т.
х ' •
5. Линеаризация функции .у = cos л;. Функция cos л:
вблизи нуля не является бесконечно малой, поэтому рассмо-
рассмотрим функцию cos х — 1, которая вблизи нуля бесконечно
мала.
Сравнивая cos л; — 1 и л:, получаем
,. cos х—1 ,. —sin2 л: л
hm = hm 0
х
x(cosx + l)
Таким образом, cos л:—1—бесконечно малая более
высокого порядка малости, чем х. Обозначим cos л:—I
через т» тогда cos х — 1 == т» откуда
cosa:=

§ 2] ЛИНЕАРИЗАЦИЯ ВБЛИЗИ НУЛЯ 125
где y — бесконечно малая более высокого порядка малости,
чем х.
6. Линеаризация функций у = ех и у = ах. Вместо
функций ех и ах рассмотрим бесконечно малые вблизи нуля
функции ех—1 и ах—1.
ех i
По определению числа е имеем lim = 1. т. е.
о х
ех— 1 —х, или
ах i
Как было показано ранее, lim = lna. Отсюда сле-
0 х
ах i
дует, что lim —-. =1, т. е. ах—1^—х 1п а, или
J ^^0 х\па
ах = 1 -f-jcln а + у.
7. Линеаризация функции у = loga A + х). Функция
l°&aO~bx) бесконечно мала вблизи нуля. Как было пока-
показано ранее, lim ogg ^ "*"х' = -,—. Отсюда следует, что
о х {па
= 1, т. е. 10^A+*)-^, или lo
lna
ina ^ »•
Если рассматривать функцию у = 1пA+д:), то
Заметим, что функции \ogax и In x нельзя линеаризовать
вблизи нуля, так как вблизи х = 0 они не ограничены,
8. Формулы линеаризации вблизи нуля.
1. (l + *)rt=l+ttA: + -f; 5.
2.
3. /
9. In A +.*) =

126 ЛИНЕАРИЗАЦИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ [ГЛ. III
9. Примеры применения линеаризации. 1°. Пусть тре-
требуется приближенно вычислить |/82. Представим число 82
в виде суммы 81 + 1. Тогда
2°. Вычислить sin 10°. Угол в 10° содержит ^ радиан,
т. е. является малой величиной, поэтому
МП 1 \J МП "То" *~--^ "То" /"""*-' ^» * ' "^ •
В четырехзначных таблицах sin 10° = 0,1736.
3°. В атомной физике изучается формула, дающая зави-
зависимость распределения энергии излучения от частоты;
1
eW —\
Формула эта сложна, поэтому при малых частотах v, т. е.
при малых -Л?* величина екТ линеаризуется и заменяется
на 1+ту* Тогда получается более простая формула
ьт
л л
называемая формулой Релея — Джинса.
§ 3. Линеаризация функции вблизи данной точки
Рассмотрим функцию у = /(х) вблизи точки х0, т. е.
при л: = д:0 + Д^. Вблизи точки х0 величина Дл: будет бес-
бесконечно малой.
Определение. Говорят, что функция у = f(x) допу-
допускает линеаризацию вблизи точки х0, если эту функцию
можно заменить линейной функцией с точностью до бес-
бесконечно малой более высокого порядка малости, чем
Ах = х — xQ.

§ 3] ЛИНЕАРИЗАЦИЯ ФУНКЦИИ ВБЛИЗИ ДАННОЙ ТОЧКИ 127
Если функция допускает линеаризацию, то ее можно
представить следующим образом:
где т — величина более высокого порядка малости, чем Дат.
Выведем формулы для вычисления k и Ь. Предполагая,
что предыдущая формула справедлива при Да: = 0 *), найдем,
что # = /(л;0). Теперь можно записать:
или
В левой части последнего равенства написано приращение
функции, поэтому, используя сокращенные обозначения,
пишем:
Из этой формулы видно, что приращение функции состоит
из двух частей: линейной части ккх и бесконечно малой у
более высокого порядка малости, чем Да;.
Определение. Линейная часть приращения k Да; называ-
называется дифференциалом функции и обозначается dy: dy = k Дат.
Приращение функции, допускающей линеаризацию, отли-
отличается от ее дифференциала на бесконечно малую более
высокого порядка малости, чем Да;. Этот факт записывается
следующим образом:
Из равенства Ду = &Дл;-{-Т можно найти:
~ Ах
Переходя в этом равенстве к пределу при
получаем
*) Это предположение эквивалентно предположению о непре-
непрерывности функции f(x) в точке аг0.

128 ЛИНЕАРИЗАЦИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ [ГЛ. Ш
Так как *у — величина более высокого порядка малости,
чем Ajc, to
lim х __ л
и, следовательно,
*= lim
Этот предел называют производной.
Определение. Производной функции в данной точке
называется предел отношения приращения функции к при-
приращению аргумента, когда приращение аргумента стремится
к нулю.
Этот предел обозначается через f'(x0) или у'. Таким
образом,
Hm ? = lim
X
Теперь основную формулу для линеаризации функции
можно записать так:
/ (*0 + Дх) = f (xQ) + /' (^о) ^ + Ъ
Соответственно формулы для приращения функции и ее
дифференциала примут вид
Ду = /'(хо)д* + Т и dy =
Дифференциал функции в данной точке равен произ-
произведению производной (в этой точке) на приращение
аргумента.
Функции, допускающие линеаризацию, называются диф-
дифференцируемыми.
1. Производная и дифференциал линейной функции
в данной точке. Пусть дана линейная функция / (л*) = b~\- kx.
Полагая x — xQ-\-bx, получаем
х) =
Как известно, коэффициент при Ах есть производная, т. е.
производная линейной функции равна ее угловому коэф-
коэффициенту:
ф + kx)' = k.

§ 4} ФОРМУЛЫ ЛИНЕАРИЗАЦИИ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ 129
Дифференциал линейной функции равен ее приращению:
dy =
Рассмотрим частные виды линейных функций. Пусть к = О,
т. е. f(x) = b, тогда производная равна нулю в любой
точке х.
Итак, производная и дифференциал постоянной равны
нулю.
Пусть теперь / (х) = х, т. е. /5=1, тогда производная
равна единице, а дифференциал равен Ах:
dx = Ax.
Итак, дифференциал функции х равен ее прираще-
приращению Ах.
Это обстоятельство позволяет ввести другое обозначение
для дифференциала любой функции и ее производной.
Заменяя Ах на dx, получаем dy = f (x)dxt откуда
§ 4. Формулы линеаризации основных
элементарных функций. Производные
Для получения формул линеаризации конкретных элемен-
элементарных функций выражение /(xo-f-Ax) будем преобразовы-
преобразовывать так, чтобы к нему можно было применить одну из
формул линеаризации вблизи нуля. При этом следует иметь
в виду, что основной малой величиной является Ах.
1. Линеаризация степенной функции f(x) = xn при
целом положительном п. Имеем /(xo-f-Ax) = ( /I
Так как — величина бесконечно малая, то, полагая
Х° Дх
в первой формуле линеаризации вблизи нуля х = —,
получаем
«-» А*+

130 ЛИНЕАРИЗАЦИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ [ГЛ. III
Коэффициент при Ад; дает производную f (хЛ = $
Вывод справедлив при д;0, отличном от нуля. Если л;0 = 0,
то / (д;0 -]~ Ад;) = Ад;'* и коэффициент при Ад; равен нулю,
т. е. f @) = 0. Это же значение для производной получается
по предыдущей формуле.
Таким образом,
n) = tixn~ldx.
2. Линеаризация функции f(x) = — • Имеем
х
\ *о/
Так как — величина бесконечно малая, то, полагая
Х° Ах
во второй формуле линеаризации вблизи нуля х = —, по-
XQ
лучаем
" 2 • 2
Д*0 ^q Xq Д*0 Л"^
Коэффициент при Ал; дает производную f'(xo) = ^.
Вывод справедлив при любом х0, за исключением дг0 = О,
т. е. при всех х из области определения функции — имеем
х
/ IV 1_ . / 1 \ _ dx
\ х} х \ х / х
3. Линеаризация функции f(x) = Ух. Воспользуемся
третьей формулой линеаризации вблизи нуля, полагая в ней
Ах „
х = —. Получаем
f (х0 + Ддс) =
Коэффициент при Ад; дает производную //(д;0) =

4] ФОРМУЛЫ ЛИНЕАРИЗАЦИИ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ 131
При выводе формулы мы делили подкоренное выраже-
выражение на xQ, т. е. предполагали, что х0 Ф 0. Поэтому при
любом х Ф 0
(YJY _ !_ и *'*/~r\ dx
4. Линеаризация функции f(x) — sinx. Пользуясь
четвертой и пятой формулами линеаризации, получаем, что
/ (хо Н~" &х) = s*n (*о Ч~ &х) — s*n *о cos ^х + cos хо s*n А* ==
5= sin л:0 A + id) + cos xQ(Дл: -f- Ъ)== s^n xo + cos лг0 ^x + 7*
Коэффициент при Дат дает производную. Таким образом,
(sin х)' = cos х и d(s\nx) = cosx dx.
б. Линеаризация функции f(x) = cos д:# Аналогично
предыдущему получаем
/ (*о "Ь Д-^) = cos (хо ~Ь &х) = cos -^о cos ^x —
«= cos x0 A -f- Ti) — sin xo (^x + T2) = cos ^0 —
Коэффициент при Ikx дает производную. Таким образом,
(cos x)f = — sin x и rf (cos x) = — sin x dx,
6. Линеаризация показательной функции f(x) = ax%
По шестой формуле линеаризации вблизи нуля получаем:
f (д;о _|_ Дд;) = аЛ-0 +ДЖ _ axoabx = Л-Гв A + ДАТ In а + 7) =
= а^ + а*« In а Дд: + ^i-
Коэффициент при Дл: есть производная. Таким образом,
(axy = ax\na и d(ax) = ax\nadx.
В частном случае, для функции ех получаем
(ех)г = ех и d(ex) = exdx.
(Напомним, что 1п^=1.)
7. Линеаризация логарифмической функции f(x)=*
— 1°8а*9 ^° восьмой формуле линеаризации вблизи нуля,
полагая в ней х = —, получаем
Л^о
/ (х0 + Д х) = loga (*0 + Дл:) = loga xQ

132 ЛИНЕАРИЗАЦИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ [ГЛ. III
Поэтому
В частном* случае для натурального логарифма In x
имеем
)
Aпх)' = 1 и d(\nx) =
Из рассмотрения основных элементарных функций видно,
что производная от каждой из этих функций существует для
всех точек из области определения, за исключением, быть
может, отдельных точек (хо = О для функции Yx)' Поэтому
производную можно рассматривать как функцию f'(x). Про-
Производные элементарных функций снова являются элементар-
элементарными функциями.
§ 5. Общие свойства производных
Пусть даны две функции g(x) и h(x\ причем для
каждой из них известна формула линеаризации вблизи
ТОЧКИ Xq.
1. Производная суммы. Напишем формулы линеари-
линеаризации:
= g (х0) + gf (x0) Д* + 7i.
h {xQ -+-bx) = h (x0) -+- h!
Складывая эти равенства, получаем
= g (*o) + A (x0) + \g'
Коэффициент при Lx является производной суммы
g(x)-\-h{x) в точке х0.
Итак, производная суммы двух функций равна сумме
их производных:
(x)Y = g' (x) + V (х).
Пример. (х3+ sin x)f = Зх2-\- cos x.

§ 5] ОБЩИЕ СВОЙСТВА ПРОИЗВОДНЫХ 133
2. Производная произведения. Пусть снова
g (х0 + Ax) = g (х0) + gr (лг0) Ал: + Tl
h (х0 -\-Ax) = h (х0) + К (л:0) Ал: + Ъ.
Перемножая эти равенства, получаем
= g (*о) h {x,) + [g' (л:0) h (xQ) + g (x0) hr (x0)] Ax + T.
Коэффициент при Ах является производной произведе-
произведения g(x)h(x) в точке л:0. Таким образом,
[g (х) h (x)\f = g' (x) h(x) + g (x) hr (x).
Производная произведения равна сумме произведений
производной первого множителя на второй без измене-
изменения и производной второго на первый без изменения.
Пример. у = х2cosх + Inx,
yr = 2x cos х — х2 sin x -| .
Рассмотрим частный случай, когда одна из функций
тождественно равна постоянной: g(x) = c. Так как с' = 0, то
[ch (x)Y = c'h (х) + cW (x) = chf (x).
Итак, постоянный множитель можно выносить за
знак производной.
3. Производная дроби. Рассмотрим частный случай,
когда числитель дроби равен единице, а знаменатель g(x)
является функцией, допускающей линеаризацию:
g (х0 + А х) = g (*0) + gf (xQ) Ал: + Т-
Предположим, что g(xo)=?O. Тогда

134 ЛИНЕАРИЗАЦИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ [ГЛ. Ill
Дробь \ х-гЧ является бесконечно малой того же
g \хо)
порядка малости, что и Ал:. Поэтому к дроби ,, л
1 4- & \хо) ^х ~г 7
g
можно применить вторую формулу линеаризации вблизи нуля,
« gf \хо) &х + 7
полагая в ней х = s v , ч ^ ' .
Тогда получаем
1 1 и' (х0) Ал- + т . _ 1 ^^ (^0) .
Подставляя это выражение в начальное равенство, по-
получаем
i
g (х0 + Ьх) - g (х0) [ g (х0)
_J g'(x0)
Коэффициент при Ал: является производной:
1Т *'{х)
Рассмотрим общий случай: f(x) = —j-~. Эту дробь
можно рассматривать как произведение h(x)—т^-, тогда
lg(x)l— Г w ^)J" " w g (x) g> (x) " ^ -
_ h'(x)g{x)-g'(x)h(x)
g2 (x)
Производная дроби есть дробь, числитель которой
равен разности произведений производной числителя на
знаменатель и производной знаменателя на числитель,
а знаменатель равен квадрату знаменателя функции.
Применим это правило к выводу производных функций
igx и ctgx:
а у ,__ / s*n х V cos х cos x — (— sin x) sin x
v s ) \ cos л / =ж cos2 л*
cos2 x + sin2 x 1
ж eos2x COS2 X *

§ 5] ОБЩИЕ СВОЙСТВА ПРОИЗВОДНЫХ 135
Таким образом,
8ес2*
d(tg x)= sec2 xdx.
Аналогично получаем
(ctg ху = — ^r^j = — cosec2 x
d (ctg x) = — cosec2 x dx.
4. Производная и дифференциал сложной функции.
Рассмотрим функцию
Функция такого вида называется сложной. Знак ср определяет
внутреннюю функцию, знак F— внешнюю.
Для того чтобы вычислить значение функции f(x) при
х = х0, нужно сначала вычислить значение <р(х0), которое
обозначим через ио(ио = у(хо)), а затем — значение F(uQ).
Тогда f(xo) = F(uo).
Дадим теперь х значение хо-\-кх, тогда
Применяя формулу линеаризации к внешней функции,
получаем
В этой формуле ио = ср(л;о) и Ай = ср(л:0 + Ал:) — <f(xQ).
Применяя формулу линеаризации к внутренней функции <f(x),
получаем
Д« = <Р (^о) + <?' (хо) ДлгЧ-Т1 — Т С-^о) = ? (хо) Ьх + ft.
Подставив в формулу для f{xQ~\-kx) выражение для
и0 и Aw, получим
= F [ср (х0)] + F' [ср (л:0)] [ср^ (х0) Д^ + ft] + Т -
+ Та-
Коэффициент при Ах дает производную:

136 ЛИНЕАРИЗАЦИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ [ГЛ. III
Итак, производная сложной функции равна произве-
произведению производной внешней функции на производную
внутренней.
Для дифференциала сложной функции получим
dy = F' [ср (х)] ср' (х) dx.
Введем вспомогательную переменную и = у(х). Тогда
du = ср' (х) dx и формулу для дифференциала можно -записать
в виде
dy = F' (и) du.
Таким образом, дифференциал сложной функции запи-
записывается через вспомогательную переменную в обычной
форме (произведение производной на дифференциал пере-
переменной).
Примеры.
1) f(x)— ysinje. Функция сложная, корень квадрат-
квадратный— внешняя функция, синуе — внутренняя
/'(*)= i_^ cos*.
2) f(x) = \ncosx. Здесь внешняя функция логарифм,
внутренняя — косинус
3) f(x) = cos2x. Здесь внешняя функция косинус,
а внутренняя — линейная функция 2х
/' (х) = — 2 sin 2x.
4) f(x) = e~x. Здесь внешняя функция — показательная,
внутренняя — линейная, равная — х
5) Производные гиперболических функций
ОХ \_ о — X рХ а — X
Y и /(x) = shA; = i—~~
(chx/=**"'"* ^shA:; (sh x)' = il^fll = ch x.

§ 5} ОБЩИЕ СВОЙСТВА ПРОИЗВОДНЫХ 137
5. Производная степенной функции при любом пока-
показателе степени. Пусть f(x) = xa. Из тождества х = е1пх
следует ха = (е1п х)а = е*1пх.
Тогда
/' (а:) = е*1пх ~ = х* j = ах*
I- производная внутренней функции а1пдм.
№ак,
(xa)f = ал;01", d (л;а) = ал:01" dx.
Эта формула совпадает с выведенной ранее формулой
для производной степенной функции с целым положительным
показателем степени.
6. Производные обратных функций. Пусть функция
У = /_1(х) является обратной к функции у = /(лг). Поло-
Положим лг = лг0 и вычислим уо== /__t (лг0), тогда xo = f(yo).
Полагая лг=лг(Г+Дл;> получаем уо-}-Ду = /_1(.?о + Д*)
или л:0 + Дл: = /(у0 + Ду).
Воспользовавшись формулой линеаризации для прямой
функции, получим
отсюда
Д* =
Предполагая, что /' (у0) Ф 0, находим
Величина fi является бесконечно малой более высокого
порядка малости, чем Ду. Однако для функций, допускаю-
допускающих линеаризацию в точках, где производная отлична от
нуля, величины Дл: и Ду имеют одинаковый порядок малости.
Поэтому Yi является бесконечно малой более высокого по-
порядка малости, чем Дл:. И, следовательно, в предыдущей
формуле коэффициент при Дл: дает производную
_ 1

138 ЛИНЕАРИЗАЦИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ [ГЛ. III
7. Производные обратных тригонометрических функ-
функций. Пусть у = /_1(л;) = arcsin х> тогда л; = / (у) = sin у.
По выведенной формуле
. ч, 1 1 1 1
(arcsin х) = = = — = ¦ - , ,-.
sin' у cos у у \ — sin2 у У \ — х2
Таким образом,
(arcsin x)r = г и d (arcsin x) = -
Аналогично можно показать, что
"—',/•? г и d (arccos x) = — -rjM^
Пусть теперь у = /в1 (л:) == arctg л:, тогда д; = / (у) = tg у.
По формуле производной обратной функции
(arctgху = -j^y = -^j =
1+tg2y =
Таким образом,
1
(arctg л:)' = 1 + ;g2 и d (arctg л:) =
Аналогично
(arcctg л:O = — у^г и rf (arcct? *) = — у
§ 6. Геометрический смысл производной
и дифференциала
1. Геометрический смысл производной. Пусть функ-
функция у = /(х) такова, что график ее в данной точке имеет
касательную. Угловой коэффициент касательной, как было
установлено ранее, равен
= lim *с«к. пр = lim *с
Д* — Нп,
~Кх 11Ш
По определению, предел отношения приращения функ-
функции к приращению аргумента при Дл;->0 есть производная.

§ 6]
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
139
Итак, значение производной f'(xQ) в точке х0 дает
тангенс угла наклона к оси Ох касательной к графику функ-
функции y = f(x) в этой точке (рис. 127).
Уо
Рис. 127.
2. Уравнение касательной к кривой y=f(x) в точке
(д;оэ д?0). Уравнение касательной к кривой в точке (л:0, у0)
можно написать в форме уравнения прямой, проходящей
через данную точку в данном направлении: у— уо = k(x—x0).
Так как угловой коэффициент касательной k = f'(xQ), то
уравнение касательной будет
у — Уо =
Здесь у0 есть значение функции в точке х0: Vo^
Пример. Написать уравнение касательной к параболе
у = х2 в точке х0 = 2.
Вычисляем значение функции уо = 22 = 4. Производная
f'(x) — 2x. В точке х0 производная /' (xQ) = /' B) = 4.
Отсюда
у —4 =
—2),
или
3? = 4л: — 4.
Определение. Прямая, проведенная перпендикулярно
к касательной в точке ее касания с кривой, называется нор-
нормалью к кривой в этой точке.
Угловой коэффициент нормали обратен по величине и
противоположен по знаку угловому коэффициенту касательной

140
ЛИНЕАРИЗАЦИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
[ГЛ. III
и, следовательно,
имеет вид
у-Уо = —т^
Уравнение нормали
— АГ0).
0
А
Лх
D
Хд X,
3. Геометрический смысл дифференциала. Рассмотрим
функцию у = /(*), график которой изображен на рис. 128.
Проведем в точке А (л:0, у0)
касательную. Обозначим
угол наклона этой касатель-
касательной к оси Ох через а, тогда
Из прямоугольного тре-
треугольника ACD найдем
CD = AD tg a = Д*/' (х0).
Произведение производной
на приращение аргумента
есть дифференциал функции:
f'(xQ)tix = dy.
Рис. 128. Итак, геометрический
смысл дифференциала со-
состоит в том, что он представляет собой изменение орди-
ординаты точки при ее перемещении по касательной.
Напомним, что приращение функции Ду есть изменение
ординаты точки при ее перемещении по кривой.
Приращение функции отличается от дифференциала на
величину бесконечно малую, более высокого порядка малости,
чем Дд:: Ду = dy-\- у. На рисунке величина f изображается
отрезком ВС.
Замена приращения функции дифференциалом этой функ-
функции в некоторой точке геометрически эквивалентна замене
кривой касательной к ней в этой точке.
§ 7. Понятие о производных и дифференциалах
высшего порядка
Так как производная функции в свою очередь является
функцией, то можно вычислить от нее производную. Произ-
Производная от производной называется второй производной, или
производной второго порядка и обозначается у" : (у')' = у"

§ 8] МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ 141
Аналогично, производная от второй производной назы-
называется третьей производной и обозначается у"г: (у")' — ут.
Пример. 1. у = х*-+-5х2-\-\, у1 = За:2 + 10*. у" =
= 6*4-10, /"=6, ylv = 0.
2. у ==: sin jc, y' = cosje, у" =— sin лс, yw = — cos л:,
yv = sin x.
Вообще производная от производной порядка п — 1 на-
называется производной п-го порядка и обозначается
(у{п-1)у — у(п)ш
Дифференциалом п-го порядка называется произведе-
произведение производной п-то порядка на п-ю степень приращения
аргумента:
dny = yW Д" W n
Отсюда получается другая запись для я-й производной:
- dxn '
§ 8. Механический смысл производной
Пусть точка совершает какое-то движение. Длина пути,
пройденного точкой, изменяется в зависимости от времени
и, следовательно, является функцией времени: $ = s(t).
Пусть за время t точка прошла путь s, а за время
?-f-A?— путь s-f"As» т. е. за время Ы: точка прошла
путь As. Отношение -дт- характеризует скорость движения
точки на данном отрезке пути в том смысле, что если бы
движение было равномерным, то скорость движения равня-
равнялась бы отношению пройденного пути As ко времени А/.
As
Отношение -гг называется средней скоростью на от-
отрезке As.
Однако, если движение неравномерное, то средняя ско-
скорость на каком-то отрезке As не будет характеризовать
движение точки в любой момент времени.
Истинная скорость движения будет тем меньще отли-
отличаться от средней, чем меньше промежуток времени Д?.
Чтобы получить скорость v в данный момент времени,
рассмотрим предел — при Л?->0: lim ~ = <у.

142 ЛИНЕАРИЗАЦИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ [ГЛ. III
С другой стороны, этот предел представляет собой пре-
предел отношения приращения функции 5 (t) к приращению аргу-
аргумента t и, следовательно, является производной от функ-
функции s(t).
Таким образом, скорость есть производная длины
пути по времени
ds
Пример. Пусть s — ^y-. Тогда скорость v = sf = at.
Скорость движения связана с изменением величины прой-
пройденного пути со временем. Понятие скорости вводится и
для других процессов, протекающих во времени. Если не-
некоторая величина в этом процессе изменяется, то ее про-
производную по времени называют скоростью изменения. Про-
Производную по времени от скорости естественно назвать
ускорением:
dv d2s
Ускорение есть вторая производная длины пути по
времени,
В предыдущем примере w = s" = а, т. е. движение равно-
равнопеременное.

ГЛАВА IV
ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ
ФУНКЦИЙ
§ 1. Поведение функции вблизи данной точки
1. Условие возрастания и убывания функции в точке.
Функция возрастает в данной точке дг0, если ее значения
вблизи этой точки справа больше, чем значение в самой
точке, а слева — меньше (рис. 129). Функция убывает в
точке х0, если ее значения вблизи этой точки справа меньше,
чем значение в этой точке, а слева — больше (рис. 130).
v
Рис. 129.
Рис. 130.
Теорема. Если в данной точке производная поло*
жителъна (отрицательна), то функция в этой точке
возрастает (убывает).
Пусть проиаводная функции f(x) в точке х0 положительна:
оО Докажем, что функция в этой точке возрастает.
Для сравнения значений функции f(x) справа и слева от
точки х0 воспользуемся формулой линеаризации этой функция:
f(xQ + А х) = /(*о) + А*о) Д х + т-

144 ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ ФУНКЦИЙ [ГЛ. IV
Пусть Ад: >0. По условию/'(д:0)> 0, поэтому f'(xQ) А х>0.
Так как f — величина более высокого порядка малости, чем
Ал;, то при малых Ад: сумма f'(xQ) А х +1 также положи-
положительна.
Следовательно, значение /(л:0-4-Дл:) равно сумме f(x0)
и положительной величины f'(x0) A x -f- *у Отсюда сле-
следует, что /(*о + АлО>/(*о)» т- е- Функция f(x) принимает
справа от д:0 значения большие, чем в точке х0.
Пусть А х < 0, тогда f'(x0) А х < 0 и сумма f'(xQ) A a: -f- T
отрицательна. Отсюда вытекает, что f(x0 -f- А х) < f(x0).
Таким образом, функция f(x) принимает справа отточки
х0 значения большие, а слева меньшие, чем ее значение
в точке х0. Функция возрастает.
Пример. Пусть у — х*-{-Ъх—1, тогда в любой точке
у' = Зл;2-{-3>0. Производная положительна, функция всюду
возрастает.
2. Точки экстремума. Напомним, что функция в данной
точке имеет максимум (минимум), если ее значение в этой
точке больше (меньше) всех
ее других значений, прини-
принимаемых вблизи этой точки.
Точки, в которых функция
имеет максимум или мини-
минимум, называются точками
экстремума.
Теорема. Если в не-
которой точке функция
имеет экстремум, то в
этой точке производная
или равна нулю, или вооб-
вообще не существует.
рис. 131. Пусть функция y = f(x)
в некоторой точке х0 имеет
экстремум. Если в этой точке существует производная, то
она или положительна, или отрицательна, или равна нулю.
Если бы производная в точке х0 была положительной, то
функция в этой точке возрастала бы и, следовательно, не
имела экстремума. Если бы производная была отрицательна,
то функция в этой точке убывала бы и, следовательно,
также не имела экстремума. Остается единственная возмож-
возможность— производная равна нулю.

§ 1]
ПОВЕДЕНИЕ ФУНКЦИИ ВБЛИЗИ ДАННОЙ ТОЧКИ
145
Итак, если х0— точка экстремума, то производная в этой
точке (если она существует) равна нулю: //(jc) = O (рис. 131).
Для дифференцируемой функции условие /'(л:0) = 0 назы-
называется необходимым условием экстремума.
Геометрический смысл необходимого условия экстремума
состоит в том, что в точках экстремума касательная парал-
параллельна оси Од;,
Точки экстремума функции могут совпадать с точками,
в которых график функции имеет излом. В этих точках
производная не существует (рис. 132).
п
'(zg)He сущес/пдует
Рис. 132.
Пример. Найти точки экстремума функции у = х3 — За:.
Необходимое условие показывает, что функция может иметь
минимум или максимум только в тех точках, где производ-
производная равна нулю. Найдем эти точки: у' = За:2 — 3, За:2 — 3 = 0,
Х2—1=0, х= ±1. Вычислим значения функции в точке
jc = l, а также значения ее слева и справа от этой точки.
Положим х = 0 и х = 2, тогда у = 0 и у = 2. При х = 1
получаем у=1 — 3=—2. Таким образом, слева и справа
от точки х = 1 функция принимает значения большие, чем
в точке х=1. Точка дг=1 есть точка минимума. Анало-
Аналогично устанавливается, что точка х = — 1 есть точка макси-
максимума (рис. 133).
Установленное необходимое условие экстремума не
является достаточным. Можно привести пример функции,
производная которой в точке х0 равна нулю, но функция
в этой точке экстремума не имеет. Действительно, пусть
f(x) — x3. Тогда /'(*) = За:2 и при л;0 = 0 производная
/'(а:0) = 0. Но, как известно, кубическая функция всюду

146 ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ ФУНКЦИЙ [ГЛ, IV
возрастает, и, следовательно, не может иметь точек экстре-
экстремума (рис. 134).
Точки, в которых первая производная равна нулю, назы-
называются стационарными точками.
Рис. 133.
Рис. 134.
3. Отыскание наибольшего и наименьшего значений
функции на отрезке. Если функция f(x) непрерывна
на отрезке [а, Ь\, то на отрезке найдется точка,
в которой функция принимает наибольшее значение,
и точка, в которой функ-
функция принимает наименъ-
I шее значение.
Рис. 135.
Рис. 136.
Если функция разрывна, то это утверждение может не
иметь места (рис. 135).
Рассмотрим несколько возможных случаев. На рис. 136
изображена функция, принимающая наибольшее значение

§ и
ПОВЕДЕНИЕ ФУНКЦИИ ВБЛИЗИ ДАННОЙ ТОЧКИ
147
на правом конце отрезка и наименьшее значение на левом
конце.
Функция, изображенная на рис. 137, принимает наиболь-
наибольшее значение в точке д:0, лежащей внутри отрезка.
ВC,18)
Рис, 138.
На рис. 138 изображена функция, принимающая и наиболь-
наибольшее и наименьшее значения внутри отрезка.
Если функция принимает наибольшее (наименьшее) зна-
значение внутри отрезка, то эта точка будет точкой максимума
(минимума). Следовательно, наи-
наибольшее (наименьшее) значение
функция может принимать или
в точках максимума (минимума),
или на концах отрезка. Отсюда
вытекает правило для определе-
определения наибольшего и наименьшего
значений функции.
Чтобы найти наибольшее и
наименьшее значения функции
на отрезке, следует вычислить
значения функции в точках
максимума, минимума и на кон-
концах отрезка. Большее из полу-
пившихся чисел будет наиболь-
наибольшим значением функции на от-
отрезке, а меньшее—наименьшим.
Пример. Найти наибольшее и наименьшее значения функ-
функции y = xz — Зл: на отрезке [0,3] (рис. 139). Как было пока-
показано ранее, эта функция имеет максимум при х — — 1 и
Рис. 139.

148 ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ ФУНКЦИЙ [ГЛ. IV
минимум при х=1. На отрезке [0,3] лежит только одна
точка минимума х=\. В ней функция принимает значение
ут1п = — 2. Вычислим теперь значения функции на концах
отрезка: при д: = 0 у = 0; при х = 3 у =18. Сравнивая
получившиеся значения функции —2, 0, 18, устанавливаем,
что наибольшее значение функции 18, наименьшее —2.
§ 2. Теорема Лагранжа и ее применения
1. Теорема Лагранжа. Если на отрезке [а, Ь] задана
функция /(х), непрерывная во всех точках отрезка
и имеющая во всех внутренних точках производную,
то на отрезке [а, Ь] найдется хотя бы одна точка с,
в которой справедливо равенство
(а<с< Ь).
Выясним геометрический смысл теоремы Лагранжа. Пусть
дуга кривой, изображенной на рис. 140, есть график функ-
функции у = /(х) на отрезке [а, Ь]. Функция на концах отрезка
принимает значения f(a) и f(b). Проведем хорду MN, стя-
стягивающую данную дугу, и вычислим тангенс угла наклона
хорды к оси Ох:
a
ахорды

§ 2] ТЕОРЕМА ЛАГРАНЖА И ЕЕ ПРИМЕНЕНИЯ 149
Итак, правая часть равенства f\c) = ^?~ предста-
вляет собою тангенс угла наклона хорды. В левой части
этого равенства стоит производная f'(c)t которая равна тан-
тангенсу угла наклона к оси Ох касательной к графику функ-
функции в точке х = с:
Из равенства /'(с) = ^ a Z следует, что
Итак, геометрический смысл теоремы Лагранжа состоит
в том, что на дуге кривой найдется хотя бы одна точка,
в которой касательная параллельна хорде, стягивающей дугу.
Докажем теорему Лагранжа.
Прежде всего напишем уравнение хорды MN как урав-
уравнение прямой, проходящей через две данные точки (а, /(а))
и Ф, *
Решая это уравнение относительно у, получаем
Введем в рассмотрение новую функцию ср (х), равную раз-
разности ординат точек, лежащих на кривой y = /(jc) и на
хорде:
9 W = Укр -
(Функция ср (х) равна величине вертикального отрезка, заклю-
заключенного между хордой и кривой).
Установим свойства вспомогательной функции у== ср(дг).
1) На концах отрезка функция ср(дг) обращается в нуль:
ср(а) = О, ср(#) = О. Действительно,

150 ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ ФУНКЦИЙ [ГЛ. IV
2) Функция ср(х) непрерывна, так как она является раз-
разностью двух непрерывных функций: f(x) и линейной функции.
3) Функция ср(дг) принимает свое наибольшее или наимень-
наименьшее значение внутри отрезка [а, Ь]. Действительно, на кон-
концах отрезка функция равна нулю, и если она не тождествен-
тождественный нуль, то наибольшее или наименьшее значения она
достигает не на концах отрезка, а внутри его.
В случае, когда ср(лг)=О, кривая совпадает с хордой, функ-
функция f (х) линейная, и для нее теорема Лагранжа очевидна.
Обозначим через с точку внутри отрезка (а < с < Ь),
в которой функция ср(д:) принимает наибольшее или наимень-
наименьшее значение. В точке с функция cp(x) имеет максимум или
минимум, т. е. точка с является точкой экстремума функции
cp(x). В точках экстремума производная равна нулю, следо-
следовательно, при х = с производная ср'(с) = 0.
Вычислим производную ср' (х)\
~/ /v\ _ /// у\ f(b)—f(a)
Подставляя с вместо х, получаем
ИЛИ
Теорема Лагранжа доказана.
Последнее равенство можно записать в другом виде, умно-
умножив обе его части на Ъ — а. Тогда получим
/(*) — /(«) = /'(*) (* — *)•
Эту формулу называют формулой конечных приращений.
Согласно формуле конечных приращений, приращение
функции равно приращению аргумента, умноженному на
значение производной в некоторой промежуточной точке.
2. Возрастание и убывание функции на отрезке.
Теорема. Если во всех точках внутри отрезка
производная функции положительна (отрицательна), то
функция на отрезке возрастает (убывает).
Пусть дано, что f\x) положительна во всех точках отрезка.
Возьмем на этом отрезке два значения аргумента хг и х2, х2>х1$
вычислим соответствующие значения функции f(x{) и f(x2)

ТЕОРЕМА ЛАГРАНЖА И ЕЕ ПРИМЕНЕНИЕ
151
и рассмотрим разность f(x2) — f(X\). Если воспользоваться
формулой конечных приращений при Ь — х2 и a = xlt то
получим:
/ (х2) — / (*х) = Г (с) (х2 — хг).
Знак этой разности зависит от знака fr(c), так как
Х2 — хг > 0* По условию в любой точке отрезка производ-
производная положительна и, следовательно, f'{c) > 0.
Итак, f(x2)— /(#i)>0, т. е. функция возрастает.
Аналогично доказывается, что при f\x) <0 функция
убывает.
3. Классификация изолированных стационарных точек.
Напомним, что стационарной точкой называется точка,
в которой первая производная обращается в нуль. Геометри-
Геометрически это означает, что касательная к графику функции
в стационарной точке параллельна оси Ох.
Стационарная точка называется изолированной, если
вблизи нее нет других стационарных точек. Слева и справа
от такой стационарной точки производная отлична от нуля.
Рассмотрим знаки производной слева и справа от изо-
изолированной стационарной точки.
-*~J?
Рис. 141.
Рис. 142,
Пусть слева и справа от стационарной точки производ-
производная положительна. Это означает, что функция и слева и справа
возрастает. Такая точка называется точкой слабого возра-
возрастания (рис. 141).
Если слева и справа от стационарной точки производ-
производная отрицательна, то функция убывает, а точка называется
точкой слабого убывания (рис. 142).

152 ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ ФУНКЦИЙ [ГЛ. IV
Если слева от стационарной точки производная поло-
положительна, а справа отрицательна, то точка является точкой
максимума. Действительно, слева от стационарной точки
функция возрастает, и, следовательно, ее значение в этой
точке больше ее значений, принимаемых в точках слева*
Н
Рис. 143.
Справа функция убывает, и поэтому ее значение в стацио-
стационарной точке больше ее значений, принимаемых в точках
справа. Таким образом, значение функции в стационарной
точке больше всех ее значений вблизи этой точки. Функция
имеет максимум (рис. 143).
Ри?. 144.
Если слева от стационарной точки производная отрица-
отрицательна, а справа положительна, то слева функция убывает,
а справа возрастает. Аналогично предыдущему заключаем,
что в этой точке функция имеет минимум (рис. 144).

§ 2]
ТЕОРЕМА ЛАГРАНЖА И ЕЕ ПРИМЕНЕНИЕ
153
Проведенное рассмотрение изолированных стационарных
точек позволяет сформулировать следующее достаточное
условие экстремума: если при переходе через данную
точку первая производная меняет знак, то в этой
точке функция имеет экстремум. Если при этом знак
меняется с плюса на минус, то функция имеет мак-
максимум, если с минуса на плюс, то — минимум.
Пример. Найти стационарные точки функции у —
= -g-jc4 — jc3+2 и определить их характер.
Находим первую производную
и приравниваем ее к нулю: -кх* — Зл:2 = 0 или х2 (х — 2) = О.
Отсюда х1 = 0, х2=2.
Проверяем, изменяет ли первая производная знак при
переходе через точку хг = 0. Если х < 0, то уг < 0; если
х > 0, то У < 0. Точка хх — точка слабого убывания. В этой
точке функция принимает значение, равное 2.
Рис. 145.
Аналогично исследуем точку х2 = 2. При х < 2 у' < 0;
при х > 2 уг > 0. Точка х2 — точка минимума. В этой точке
;у 3
График функции у = -g-л:4 — Я3+ 2 изображен на рис. 145.
4. Достаточное условие экстремума по второй про-
производной. Если в некоторой точке xQ первая производ-
производная равна нулю, а вторая производная отлична от
нуля, то в этой точке будет экстремум. В точке х0

154 ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ ФУНКЦИЙ [ГЛ. IV
будет минимум, если вторая производная положительна,
и максимум, если вторая производная отрицательна.
Действительно, пусть первая производная в точке л:0
равна нулю: //(д:0) = 0, а вторая производная больше нуля:
f"(xo)i>Q' Вторая производная есть производная от первой
производной. Поэтому, если вторая производная положи-
положительна, то первая производная возрастает. Но в точке xQ
производная /'(л;0) = 0, поэтому слева от этой точки произ-
производная fr{x) отрицательна, а справа положительна, т. е.
точка х0 является точкой максимума. Аналогично доказы-
доказывается, что в точке х0 будет минимум, если /"(л;0)<0.
Пример. Исследовать стационарные точки функции
у — ех-\-е-х.
Находим первую и вторую производные: у' = ех— е"х
и у" = ех-\-е~*. Первая производная обращается в нуль при
х = 0. Вторая производная в этой точке равна двум и, сле-
следовательно, положительна. В точке х = 0 функция у=ех-\-е~х
имеет минимум.
Если при исследовании стационарной точки окажется, что
вторая производная в ней равна нулю, то по второй произ-
производной судить о характере этой стационарной точки нельзя.
5. Выпуклость и вогнутость дуги кривой. Теорема.
Если в каждой точке отрезка вторая производная поло-
положительна {отрицательна), то график функции на этом
отрезке вогнутый {выпуклый).
с, с,
Пусть f {х) > 0 во всех точках рассматриваемого от-
отрезка. Покажем, что на этом отрезке график будет вогнутым.
Пусть х2 > хг. Рассмотрим разность, по знаку которой
определяется выпуклость или вогнутость графика:

§ 2] ТЕОРЕМА ЛАГРАНЖА И ЕЕ ПРИМЕНЕНИЕ 155
Применим формулу конечных приращений к каждой раз-
разности, стоящей в квадратных скобках:
4" /' (С2) (*2 — *l) — -4
Точка с2 лежит между точками —1 ^ 2- и #2, точка Cj —-
между точками ^ и ^
Применяя еще раз формулу конечных приращений, полу-
получаем
= i (х2 - хх) (с2 - сх) Г (с3).
Так как #2> xv 7(^ С2 > ci« Отсюда дг2 —xt>0 и
^2—ci > ^* ^° условию f"{c^)> 0 и, следовательно, произ-
произведение -j(x2 — хг)(с2—сг)/"(с^ положительно. Итак,
x + х2
2
График функции вогнут.
Напомним, что точка, отделяющая участок выпуклости
графика функции от участка вогнутости, называется точкой
перегиба. Из последней теоремы вытекает следующее до-
статочное условие того, что точка является точкой
перегиба: если при переходе через данную точку вторая
производная меняет знак, то эта точка является точ-
точкой перегиба.
Если вторая производная меняет знак с минуса на плюс,
то слева кривая выпукла, справа вогнута (рис. 147). Если
вторая производная меняет знак с плюса на минус, то слева
кривая вогнута, а справа выпукла (рис. 148).
Если в точке перегиба вторая производная существует,
то otfa равна нулю. Поэтому для отыскания точек перегиба

156 ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ ФУНКЦИЙ [ГЛ. IV
нужно найти те точки, в которых вторая производная обра-
обращается в нуль. Если при переходе через такую точку вто-
вторая производная меняет знак, то эта точка будет точкой
перегиба.
Рис. 147.
Пример. Найти точки перегиба графика функции
у=-|Л;4_А;3_4-2 (СМ. рис, 145).
у">0
у"<0
Рис. 148.
Находим вторую производную:
/=4г*2 —6*.
9
Приравниваем ее к нулю: -^-^ —6х = 0 и находим корни
4
этого уравнения: #! = 0 и х2 = -g- • Проверяем, изменяет ли
вторая производная знак при переходе через точку д:1==0.
Если х < 0, то f > 0; если х > 0, то у" < 0. Аналогично

§ 2]
ТЕОРЕМА ЛАГРАНЖА И ЕЕ ПРИМЕНЕНИЕ
157
4 4
исследуем точку #2 = — . Если х<-~, то у" < 0; если
о о
4 4
лг>-тг, то у">0. Следовательно, точки *! = () и х2 = -ъ
являются точками перегиба. Слева от точки хг = 0 график
^огнутый, между точками хх и л:2 — выпуклый и справа от
точки х2 = ~о- — вогнутый (рис. 149).
Рис. 149.
6* Пример. Исследование функции у — 6х2е~х\ Функ-
Функция у = 6х2е~х2 определена при всех х> график ее симмет-
симметричен относительно оси Оу и проходит через начало коор-
координат. Найдем стационарные точки. Вычисляем производные
у' и у":
у' = 6 Bх — 2х3) е-* = 12 (х — л:3) е~х\
/=12A— З*2 —2*2+ 2л:4)^^2= 12A—
Первая производная обращается в нуль при хг = —1,
х2 = 0, дГз = 1.
Если лг = —1 или jt=l,.TO /' = — 24^-1 < 0 и, сле-
следовательно, функция имеет в этих точках максимум. Значе-
Значение функции в этих точках б^. Если х = 0, то у" = 12 > 0
и, следовательно, функция имеет минимум. Значение функции
в этой точке равно нулю.
Исследуем поведение функции при больших значениях
аргумента. При л:—>оо множитель х2 неограниченно растет,
1
а ?-*2=— стремится к нулю. Как будет показано ниже,
показательная функция растет быстрее любой степенной,

158 ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ ФУНКЦИЙ [ГЛ. IV
X2
поэтому lim —г=0. Это означает, что график функции имеет
X -> 00 е
горизонтальную асимптоту у = 0.
Рис. 150.
Чтобы найти точки перегиба графика, нужно знать корни
второй производной. Приравнивая у" к нулю, получаем
' — 0,47,
-1=0.
Корни этого биквадратного уравнения равны:
! 51 х— 5~Vn
г* 1.61.
2
и хА
Это и будут точки перегиба (рис. 150).
Рассмотренная функция встречается в молекулярной тео-
теории при изучении распределения скоростей молекул газа.
§ 3. Применение производных к вычислению
пределов
1» Теорема Коши. Пусть на отрезке {а, Ь] заданы
две функции f(x) и <р(лг), удовлетворяющие условиям
теоремы Лагранжа, причем ни в какой точке внутри
отрезка производные этих функций одновременно не
обращаются в нуль, тогда на отрезке найдется хотя бы
одна точка с, в которой справедливо равенство'.
Г (с) _ f(b)-f(a)

§ 3] ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ВЫЧИСЛЕНИЮ ПРЕДЕЛОВ 159
Теорема Лагранжа является частным случаем теоремы
Коши: если <р (*) = *. ?'(*)= 1. то /' (с) = l^J
Доказательство теоремы Коши аналогично доказательству
теоремы Лагранжа и здесь не приводится.
2. Правило Лопиталя. Пусть заданы две функции
f(x) и ср (х), удовлетворяющие условиям теоремы Коши,
и пусть в точке a f(a) = 0 и ср(а) = О, тогда предел
отношения этих функций в точке а равен пределу отно-
отношения их производных, если последний существует:
fix) f. fix)
Итак, дано /(a) = 0, <p(a) = O и Jim Стт = А тРе-
f(x}
буется доказать, что lim ~\ = ^ Рассмотрим отношение
функций -^r- Так как /(а) = 0 и у(а) = 0, то
f(x) = f(x)-f(a)
По теореме Коши между точками а и х найдется такая
точка с, что
Перейдем к пределу при х—>а. Если х->а, то и с—>а,
поэтому
По условию
Ш
Ч
следовательно,
Игл 44 = Л.
Правило Лопиталя позволяет заменить вычисление пре-
предела отношения двух функций, обращающихся в пределе
в нуль, вычислением предела отношения производных этих
функций.

160 ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ ФУНКЦИЙ \ГЛ. IV
Пример. Вычислить lim ~—.
х-+о х
При # = 0 числитель и знаменатель обращаются в нуль.
Поэтому по правилу Лопиталя искомый предел будет равен
lim cos * ~~ . в этом пределе снова и числитель и знаме-
*->о 6Х
яатель при х = 0 обращаются в нуль. Поэтому, применяя
еще раз правило Лопиталя, приходим к пределу
— sin л: 1
Нт —g— = — ¦§¦ •
Итак,
lim sinx-x — _ I
1X111 q ¦ л
С соответствующими изменениями правило Лопиталя при-
применимо и в том случае, когда и числитель и знаменатель
в некоторой точке обращаются в бесконечность, а также,
когда предел вычисляется при л:->оо.
3. Сравнение поведения на бесконечности степенной,
показательной и логарифмической функций: хп, ех, \пх.
Все эти функции возрастают при х->оо. Установим, какая
из них растет быстрее.
Рассмотрим предел отношения показательной и степенной
функций. Предел будем вычислять по правилу Лопиталя:
lim -^-= Hm —prj-
X -> оо •* * -» оо "л
tfC gX
= lim —t п—zr-«-= ... = lim —r=oo.
Итак, показательная функция ех растет быстрее/
степенной хп.
Сравним теперь логарифмическую функцию In x со сте-
степенной хп\
J_
,. 1пд: .. х |. 1 л
1ш —jr= hm = l»m 0
X -> оо л X -> оо
Итак, логарифмическая функция растет медленнее
любой положительной степени аргумента.

§ 4] ПРЕДСТАВЛЕНИЕ ФУНКЦИИ ПО ФОРМУЛЕ ТЕЙЛОРА 161
§ 4. Представление функции по формуле Тейлора
1. Формула Тейлора. Формулу Тейлора можно рассмат-
рассматривать как дальнейшее развитие формулы линеаризации
/ (х0 + А*) =* / (
Во многих случаях замена функции линейной не является
достаточно точной. В связи с этим возникает вопрос об уточ-
уточнении формулы линеаризации и более детальном изучении
величины fi- При этом из величины fi выделяют часть, про-
пропорциональную Ал:2 так, чтобы оставшаяся часть была более
высокого порядка малости, чем Ал:2. Тогда величина fi пред-
представляется в виде 71 == & А*2 + 72» гДе А — некоторяа по-
постоянная, а величина *[2 обладает тем свойством, что
lim -r2^ = 0. Тогда из формулы линеаризации получаем
f (х0 + Д *) = / (*0) + /' (*ь) Ал: + А Ал:2 + ъ.
Коэффициент А пока неизвестен, и задача состоит в том,
чтобы найти его.
Из последнего равенства находим
Аде) —/(хв) —Г (*0) Ал:^
^_
л ~ Ал:2 Ал:2 #
Это выражение для А нельзя считать окончательным,
так как в него входит неизвестная функция у2- Чтобы изба-
избавиться от этой неизвестной функции, перейдем к пределу
при Дл:->0:
А= lim
Предел последней дроби равен нулю, поэтому
При непосредственной подстановке вместо Ал: его пре-
предельного значения числитель и знаменатель дроби обра-
обращаются в нуль. Воспользуемся правилом Лопиталя. При этом
следует иметь в виду, что величина х0 является постоян-
постоянной, а Д# — переменной. Производная числителя по пере-
переменной Ал: равна /'(*о + Д*) — f'(xo)* знаменателя

162 ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ ФУНКЦИЙ [ГЛ. IV
Поэтому
Л— lim
/i ИГЛ
В числителе стоит приращение функции f'(x). Предел
отношения приращения функции к приращению аргумента
есть производная от /'00» т. е. вторая производная. Итак,
л _ f" (*о>
Л~" 1-2 '
Подставив вместо А найденное значение, получим
/ (*0 + А*) = / (дг0) + Г
Эта формула есть дальнейшее уточнение формулы линеари-
линеаризации функции и называется формулой Тейлора при п = 2.
Если последняя формула недостаточно точна, то из вели-
величины 72 выделяют член, пропорциональный Ад;3 так, чтобы
оставшаяся часть ^з была величиной более высокого порядка
малости, чем Ад;3. Тогда ^2 = В Ад;3 -f- Тз» гДе & — постоян-
постоянная, а 7з обладает тем свойством, что
Формула для представления функции примет вид
Как и выше, из этого равенства найдем
Ах*
= lim
Предел последней дроби равен нулю, для вычисления
предела первой дроби применяем правило Лопиталя, тогда
В= lim
ЗАх2

§ 4] ПРЕДСТАВЛЕНИЕ ФУНКЦИИ ПО ФОРМУЛЕ ТЕЙЛОРА 163
Подставляя найденное значение В, получаем
/ (лг0 + Длг) = / (*«,) + /' (*0) Дд: +
Эта формула называется формулой Тейлора при п = Ъ.
Процесс последовательного выделения членов со степе-
степенями Ах можно продолжить. Для любого п формула Тей-
Тейлора имеет вид
/ (х0
где Т/г — бесконечно малая более высокого порядка малости,
чем кхп:
При выводе формулы Тейлора мы предполагали, что все
производные, которые в ней участвуют, существуют.
Запишем формулу Тейлора в другой форме, заменяя
хо-{-&х через х: хо-{-кх = х. Тогда Ах = х — дг0 и фор-
формула принимает вид
Это равенство показывает, что формула Тейлора позво-
позволяет заменить функцию многочленом степени п так, что
ошибка тЛ будет бесконечно малой величиной выше я-го
порядка малости относительно величины х—х0.
Если в формуле Тейлора положить л;0 = 0, то она при-
примет вид
Эта формула для представления функции вблизи нуля
называется формулой Маклорена. Если в ней ограничиться
первыми двумя слагаемыми, то мы получим формулу линеа-
линеаризации функции вблизи нуля.

164 ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ ФУНКЦИЙ [ГЛ. IV
2. Геометрический смысл формулы Тейлора при п = 2*
Напишем формулу Тейлора для п = 2:
Ч f (x)=f (xo)+f (х0) (х~хо)+
Отбросим f2 и рассмотрим
квадратичную функцию
У = / (*о)+/' (*о) (* — *о)+
Рис. 151. Графиком этой функции яв-
является парабола. Следователь-
Следовательно, геометрический смысл формулы Тейлора при п=2 состоит
в том, что она позволяет заменить график вблизи данной
точки параболой с точностью до бесконечно малой выше
второго порядка малости. Парабола, которая при этом по-
получается, называется соприкасающейся, В точке х0 кривая
y = f(x) и парабола имеют общую касательную.
§ 5. Представление элементарных функций
по формуле Тейлора вблизи нуля
При применении формулы Тейлора для представления
конкретной функции вблизи нуля нужно вычислить значения
при х = 0 самой функции f (х) и ее производных f'(x),
/"(*), • •.. /{п) (х), а найденные числа /@), /'@), /"@), ...
... , fw @) подставить в коэффициенты формулы Тейлора.
Проделаем это для основных элементарных функций.
1. Представление многочлена. Пусть дан многочлен
Его представление по формуле Тейлора для п = 2 будет:
/ (х) =./ @) + /' @) х + ?$- х* + Ь.
Находим, что при х = 0 / @) = а0 Вычисляем производные
Подставляя х = 0, получаем //@) = а1, ///@) = 2а2. Отсюда
/ (х) = ао-{- ахх + а2х2

§ б] ПРЕДСТАВЛЕНИЕ ПО ФОРМУЛЕ ТЕЙЛОРА ВБЛИЗИ НУЛЯ 165
Таким образом, представление многочлена по формуле
Тейлора дли я = 2 получается, если в f2 объединить члены
со степенями х выше второй.
Аналогично получается представление многочлена по
формуле Тейлора для любого п. В частности, при
Таким образом, при п^пг формула Тейлора дает точ-
точное представление многочлена: ?л = 0.
2. Представление функции A+д:)т. Бином Ньютона.
Функция /(л;) = A -j-x)m является многочленом степени т%
поэтому для нее формула Тейлора при п = т дает точное
представление. Находим /@)=1. Вычислим производные
функции A + л:)т и их значения при л; = 0:
f(x) =m(l + x)m~\ /'@) =т,
Г(х) =т(т-\)A + х)т-2, /"@) =m(m-l),
/(«) (^) = m (m — 1) (m —- 2) ... 2.1, /W @) = m!
Подставляя выражения для /'@), /"@), . ••> /(m)@)
в формулу Тейлора для п = т, получаем
m(m-l)(m-2)...3-2-1 „
...-i ^l ^ .
В этой формуле коэффициент при xk обозначается через Скт:
Ст = y\ •
Из формулы видно, что Сда=1, а С^"*1^^. Вообще
Полученное представление для (\г\-х)т является частным
случаем бинома Ньютона, которое из него легко получается.
(Ь \т
^ Н ) • Применяя пред-
представление для A + л:)т при х = —, получаем

166 ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ ФУНКЦИЙ [ГЛ. IV
Это и есть формула бинома Ньютона.
3. Представление функции -г——. Находим: /@)=1.
1 ~у~ X
Вычислим производные и их значения при лг = О:
/'(*) »-A+*)-*, /'@) =-1,
/(х) =Ь2A+^Г3, /"@) =1.2 = 2!,
/'" (х) = —1.2-3A -f- х)~\ /'" @) = — 1 • 2 • 3 = — 3!,
• ••••••• •••
/(я) (х) = (—1)" 1.2 • 3 ... п A + х)~п~\ /(«) @) = (--1)" л1
По формуле Тейлора получаем
Получившийся многочлен можно рассматривать как гео-
геометрическую прогрессию со знаменателем — д;.
4. Представление функции ]Л -\-х. Находим: /@)= 1.
Вычислим производные и их значения при х = 0:
- 1
2, /'@) =i.,
444
/С) @)=(—1)я+1 Ь35-Bя—
По формуле Тейлора получаем
1 , . 1-3 , ЬЗ-5
22-2! ~^23-3! 24-4!
Ь3'5..,Bд>-3) „ ,
^^ х ¦+¦*'

§ 5] ПРЕДСТАВЛЕНИЕ ПО ФОРМУЛЕ ТЕЙЛОРА ВБЛИЗИ НУЛЯ 167
б. Представление функций sin л: и cos*. Находим;
/ @) = sin 0 = 0,
f'(x) =cosx, /7@) =cosO=l,
f{x) = —sinx, /'"(О) = — sin 0 = 0,
f" (x) = — cos x9 /'" @) = — cos 0 = — 1,
/iv (X) = sin x, /iv @) = sin 0 = 0,
В дальнейшем значения производных 1, 0, —1, 0 будут
периодически повторяться. Отсюда получаем
Аналогично для функции cos л: получаем
Полученные формулы для sin x и cos x могут служить
для вычисления значений этих функций с большой степенью
точности.
6. Представление функций е* и а*. Находим: /@) =
f'(x) =e*. /40) =*°=lf
f(x) =e\ f'@) =eo=lt
(x) = ex,
По формуле Тейлора получаем
e*==l_j_* + _. + ___i_ ... +-JJJ-+T.
Для функции а^ имеем ах = e*In a и, следовательно,
7. Представление функций 1пA-(-дг) и loga(l -\-x).
Находим: / @) = In 1 = 0;
, /"@) = —1.
, /"'@) = Ь2,
/(») (х) = (-I)""J(я-1)! A-НгЧ /<«) W^C-l)"-1 (и-1)!

168 ПРИМЕНЕНИЕ ПРОИЗВОДНЫХ К ИССЛЕДОВАНИЮ ФУНКЦИЙ [ГЛ. IV
По формуле Тейлора получаем
Для функции loga(l+x) имеем loga(l + *) = 1
и, следовательно,
X2
8. Таблица простейших представлений основных эле-
элементарных функций по формуле Тейлора.
3.
4. si
5. cos л;
6. ех
7. а*
8.
9.
1 —
1+
х3
з
х2
В каждой из этих формул выписан член, следующий за
главной линейной частью функции. Величина f является
бесконечно малой более высокого порядка малости, чем
предшествующий ей член. ~~