Оглавление
Предисловие 13
1 Введение ' 16
1.1 Логические знаки 16
1.1.1 Вступление 16
1.1.2 Примеры использования логических знаков ... 16
1.2 Элементы теории множеств • 17
1.2.1 О понятии множества 17
1.2.2 Примеры 18
1.2.3 .Упражнения 19
1.2.4 Действия над множествами 19
1.3 Общее понятие отображения или функции 22
1.3.1 Историческая справка 25
1.4 Мощность множества. Счётные множества 25
1.4.1 Историческая справка 30
1.5 Действительные числа 31
1.5.1 Введение 31
1.5.2 Определение действительных чисел 33
1.5.3 Числовая прямая 34
1.5.4 Элементарные свойства действительных чисел . 35
1.5.5 Точные грани множества действительных чисел . 36
1.5.6 Действительное число как точная грань чисел
рациональных 39
1.5.7 Теорема о существовании точных граней .... 40
1.5.8 Действия над числами 41
1.5.9 Неравенства для модуля суммы и Я. Бернулли . 42
1.5.10 Определение корня натуральной степени из по-
положительного действительного числа 43
1.5.11 Лемма о вложенных отрезках 45
1.5.12 Неравенства Коши 46
1.5.13 Историческая справка 50

Оглавление
Предел последовательности действительных чисел 51
2.1 Определения и примеры 51
2.1.1 Определения 51
2.1.2 Примеры 54
2.2 Свойства сходящихся последовательностей 57
2.2.1 Доказательства теорем 57
2.2.2 Примеры применения 59
2.2.3 Линейное регулярное преобразование последо-
последовательности 61
2.2.4 Теорема Штольца 63
2.3 Монотонные последовательности 64
2.3.1 Существование предела монотонной последова-
последовательности 64
2.3.2 Операции над действительными числами и предел 67
2.3.3 Число е 68
2.4 Подпоследовательности и их свойства 70
2.4.1 Подпоследовательности и частичные пределы . 70
2.4.2 Существование монотонной подпоследователь-
подпоследовательности 72
2.4.3 Верхний и нижний пределы последовательности 74
2.5 Фундаментальные последовательности и критерий Коши 77
2.5.1 Фундаментальные последовательности и их сво-
свойства '. 77
2.5.2 Критерий Коши 78
2.5.3 Определение предела последовательности век-
векторов 79
2.5.4 Историческая справка 80
Предел функции в точке. Непрерывные функции 81
3.1 Предел функции в точке 81
3.1.1 Предельная точка множества 81
3.1.2 Определение Коши предела функции в точке и
примеры 83
3.1.3 Определение Гейне предела функции в точке.
Эквивалентность определений Коши и Гейне . . 87
3.1.4 Свойства пределов функции 88
3.1.5 Односторонние пределы 91
3.1.6 Существование предела функции в точке . ... 92
3.2 Исследование локального поведения функций 93
3.2.1 Предположения 93
3.2.2 Отношение подчинённости 94
3.2.3 Свойства отношения "О" 95
3.2.4 Отношение пренебрежимости 95

•давление
3.2.5 Свойства отношения "о" 96
3.2.6 Эквивалентные функции 97
3.2.7 Свойства отношения эквивалентности 97
3.2.8 Порядок одной функции относительно другой . 98
3.2.9 Шкала сравнения 99
3.2.10 Главная часть. Асимптотическое разложение . . 99
3.3 Непрерывные функции 101
3.3.1 Определения и примеры 101
3.3.2 Элементарные свойства непрерывных функций . 105
3.3.3 Обратные функции к некоторым элементарным 108
3.3.4 Свойства логарифмической функции и замеча-
замечательные пределы 110
3.3.5 Свойства функций, непрерывных на отрезке . . 112
3.3.6 Равномерно непрерывные функции 117
3.3.7 Разрывы функций 120
3.4 Теорема Вейерштрасса 121
3.4.1 Вспомогательные тождества 121
3.4.2 Теорема Вейерштрасса о приближении *122
3.4.3 Историческая справка 123
Производная и её приложения 125
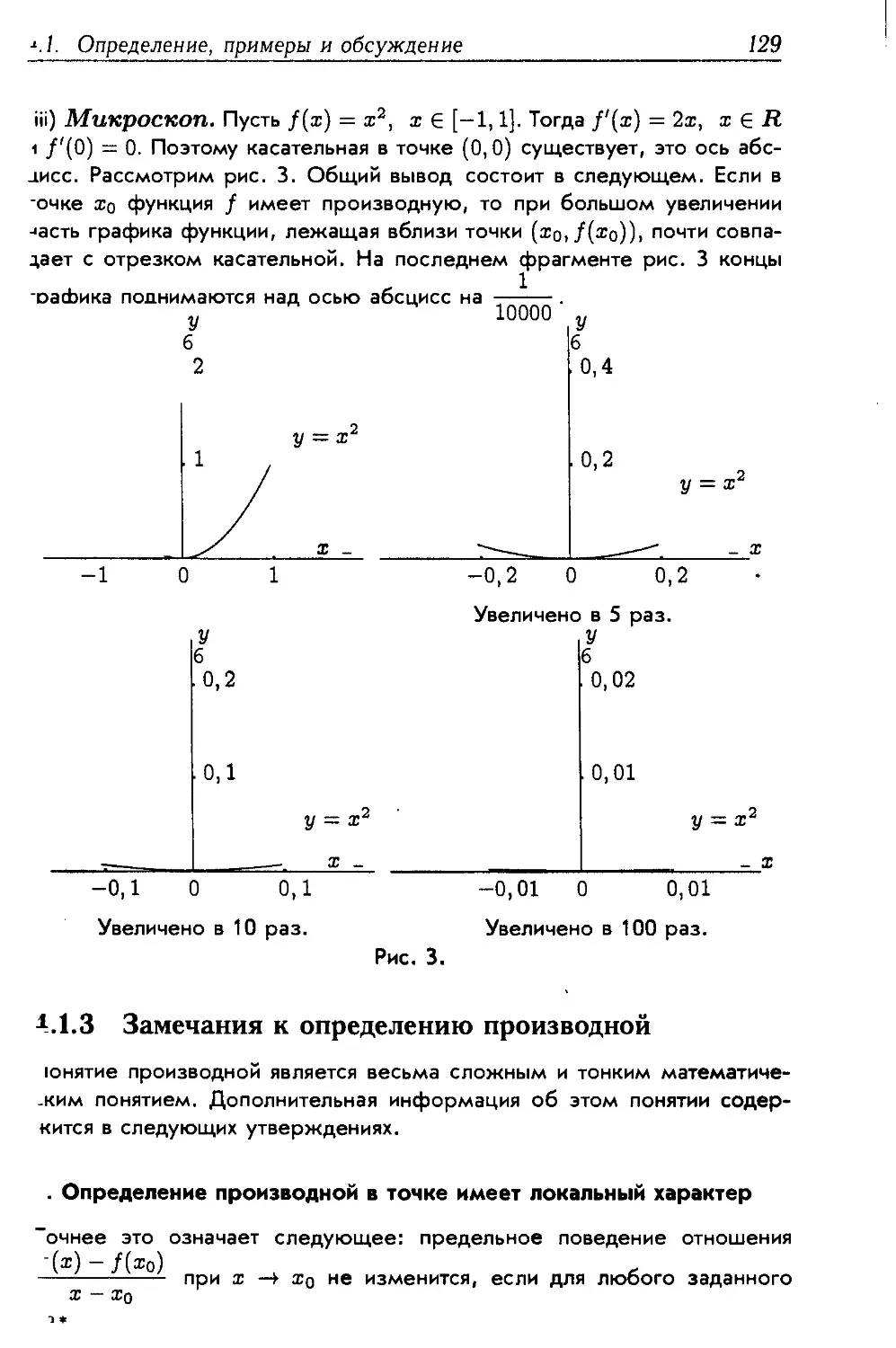
4.1 Определение, примеры и обсуждение 125
4.1.1 Определение и примеры 125
4.1.2 Интерпретации производной 126
4.1.3 Замечания к определению производной .... 129
4.2 Правила вычисления производных и примеры 132
4.2.1 Правила вычисления производных 132
4.2.2 Примеры вычисления производных 135
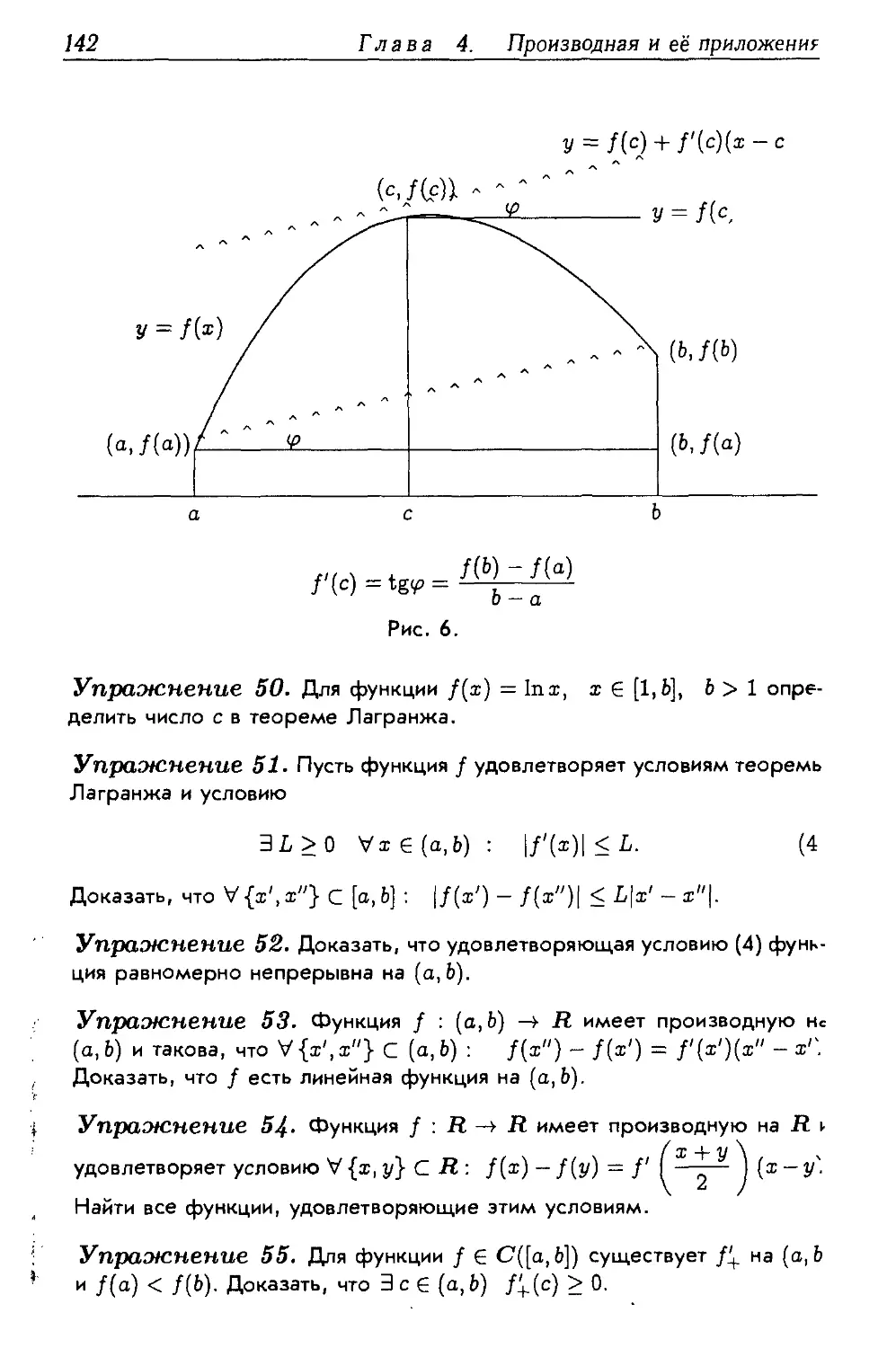
4.3 Теоремы о функциях, имеющих производную 139
4.3.1 Доказательства теорем 139
4.3.2 Первые применения теоремы Лагранжа .... 144
4.3.3 Дифференциал функции 148
4.4 Производные старших порядков . . . .' 150
4.4.1 Определение и примеры 150
4.4.2 Свойства производных старших порядков .... 151
4.4.3 Дифференциалы старших порядков 153
4.4.4 Историческая справка 154
4.5 Приложения производной 155
4.5.1 Формула Тейлора 155
4.5.2 Правило Лопиталя 159
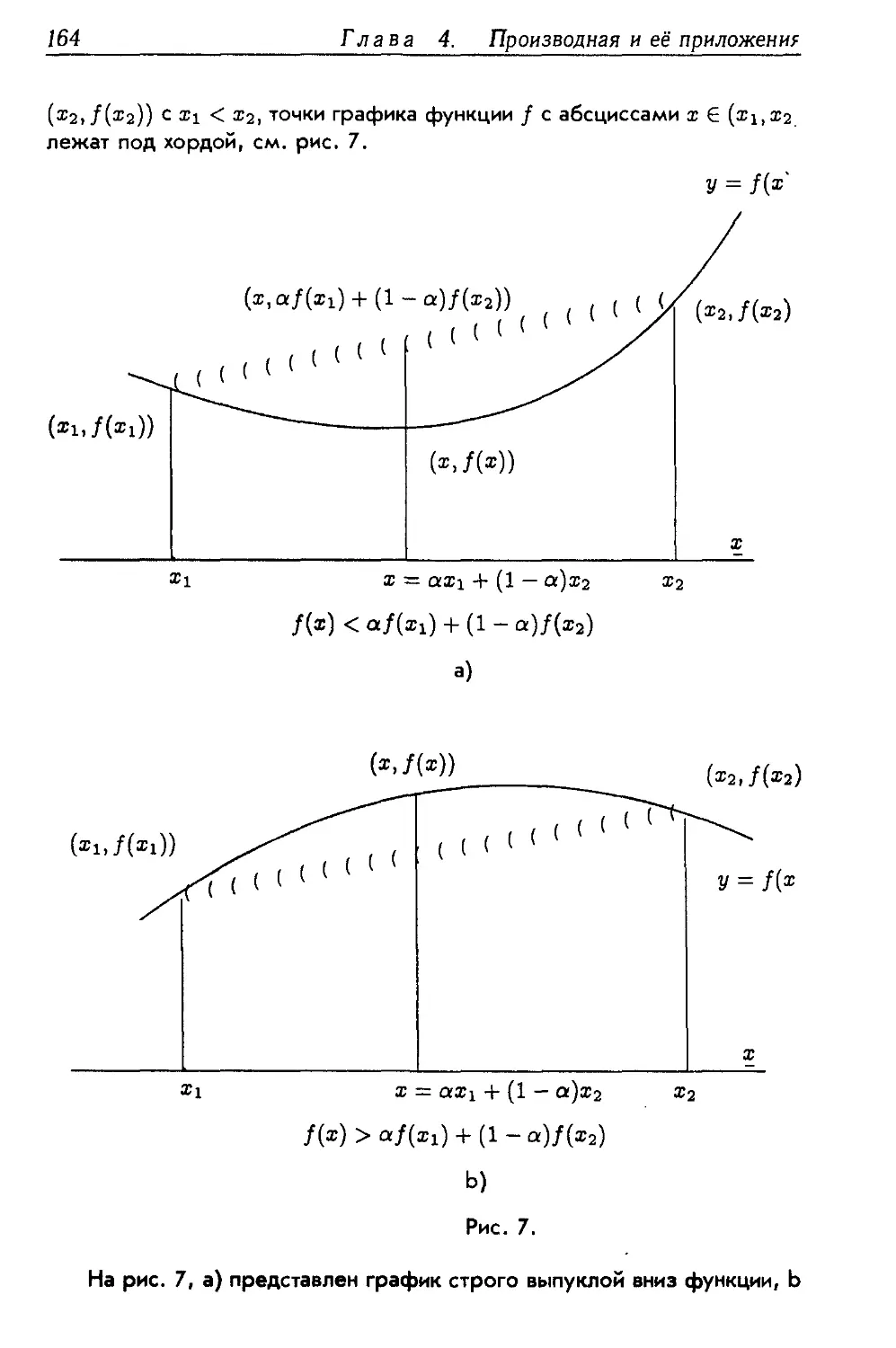
4.5.3 Выпуклые функции 163
4.5.4 Условия локального экстремума 169
4.5.5 Точки перегиба 174

Оглавление
4.5.6 Асимптоты 175
4.5.7 Построение графика функции 176
4.5.8 Историческая справка 176
4.6 Дополнительные задачи к главам 1—4 177
5 Примитивная и неопределённый интеграл 183
5.1 Определения и элементарные свойства 183
5.1.1 Определение и свойства примитивной 183
5.1.2 Свойства неопределённого интеграла 186
5.1.3 Таблица основных интегралов 186
5.1.4 Интегрирование с помощью подстановки .... 188
5.1.5 Интегрирование по частям 190
5.2 Интегрирование функций из некоторых классов функций 191
5.2.1 Рациональные функции 191
5.2.2 Разложение на элементарные дроби. Метод не-
неопределенных коэффициентов 193
5.2.3 Интегрирование элементарных дробей 194
5.2.4 Интегрирование рациональной функции
от sin и cos 196
5.2.5 Интегрирование функций, включающих ирраци-
иррациональности 197
5.2.6 Историческая справка 197
6 Интеграл Римана 198
6.1 Введение 198
6.1.1 Задача о вычислении площади криволинейной
трапеции 198
6.1.2 Задача о вычислении величины пройденного пути 199
6.2 Определение интеграла Римана 200
6.2.1 Вспомогательные определения 200
6.2.2 Определение интеграла и интегрируемой функ-
функции 202
6.2.3 Свойства сумм Дарбу 203
6.3 Критерий интегрируемости 205
6.3.1 Необходимое и достаточное условие интегриру-
интегрируемости функции 205
6.3.2 Другая формулировка критерия интегрируемости 206
6.4 Классы интегрируемых функций 207
6.4.1 Интегрируемость монотонной функции 207
6.4.2 Интегрируемость непрерывной функции .... 208
6.4.3 Интегрируемость некоторых разрывных функций 208
6.5 Интеграл как предел интегральных сумм 209
6.5.1 Предел интегральных сумм 209

Оглавление
6.5.2 Теорема Дарбу 211
6.6 Свойства интеграла Римана 214
6.6.1 Линейность и аддитивность интеграла 214
6.6.2 Неравенства и теорема о среднем значении . . 216
6.6.3 Интеграл как функция верхнего предела .... 218
6.7 Формула Ньютона-Лейбница и следствия из неё .... 219
6.7.1 Основная формула интегрального исчисления . 219
6.7.2 Формулы замены переменной и интегрирования
по частям 221
6.7.3 Формула Тейлора с остаточным членом в инте-
интегральной форме 224
6.8 Предельный переход под знаком интеграла 225
• 6.8.1 Поточечная и равномерная сходимость последо-
последовательности функций 225
6.8.2 Теорема о предельном переходе 226
6.9 Примеры применения определённого интеграла .... 228
6.9.1 Площадь криволинейной трапеции 228
6.9.2 Приближенное вычисление интегралов 230
6.9.3 Длина дуги кривой 231
6.9.4 Объём тела вращения 233
6.9.5 Площадь поверхности тела вращения 234
6.9.6 Координаты центра масс и теоремы Гюльдена . 235
6.10 Историческая справка 238
Т Ряды 242
7.1 Элементарные свойства сходящихся рядов 242
7.1.1 Основные определения 242
7.1.2 Свойства сходящихся рядов 245
7.2 Ряды с неотрицательными членами 246
7.2.1 Критерий сходимости и следствие 246
7.2.2 Признаки сравнения 247
7.2.3 Признаки сходимости рядов 250
7.3 Сходимость рядов с произвольными членами 255
7.3.1 Ряд Лейбница 255
7.3.2 Абсолютно и условно сходящиеся ряды 256
7.3.3 Признаки сходимости рядов 258
7.4 Другие свойства сходящихся рядов. Произведение рядов 261
7.4.1 Группировка членов ряда 261
7.4.2 Перестановка членов ряда 262
7.4.3 Умножение рядов 263
7.5 Бесконечные произведения 265
7.5.1 Определения. Сведение к ряду 265
7.5.2 Достаточные условия сходимости 266

Оглавление
Функциональные ряды 268
8.1 Равномерная сходимость последовательности функций . 268
8.1.1 Определения 268
8.1.2 Свойства равномерно сходящихся последовате-
последовательностей 269
8.2 Равномерная сходимость функционального ряда .... 270
8.2.1 Определения 270
8.2.2 Признаки равномерной сходимости 272
8.3 Свойства равномерно сходящихся рядов 275
8.3.1 Основные теоремы 275
8.4 Степенные ряды 277
8.4.1 Множество сходимости 277
8.4.2 Равномерная сходимость степенного ряда . . . 280
8.4.3 Свойства суммы степенного ряда 280
8.4.4 Ряд Тейлора 282
8.5 Степенные ряды с комплексными членами 287
8.5.1 Определения 287
8.5.2 Показательная функция в комплексной плоскости 288
8.5.3 Историческая справка 290
Функции ограниченной вариации. Интеграл Стилтьеса 292
9.1 Монотонные функции 292
9.1.1 Элементарные свойства 292
9.1.2 Теорема о разложении 293
9.2 Функции ограниченной вариации 294
9.2.1 Определение и примеры 294
9.2.2 Свойства функций ограниченной вариации и ва-
вариации 296
9.2.3 Спрямляемые кривые 298
9.3 Интеграл Стилтьеса 299
9.3.1 Определения 299
9.3.2 Свойства нижних и верхних сумм 301
9.3.3 Классы интегрируемых функций 301
9.3.4 Свойства интеграла Стилтьеса 302
9.3.5 Интеграл Стилтьеса относительно функции огра-
ограниченной вариации 304
9.3.6 Вычисление интеграла Стилтьеса 305
9.3.7 Теорема Хелли о предельном переходе .... 306
9.3.8 Историческая справка 308
9.4 Дополнительные задачи к главам 5 — 9 308

1 Оглавление_Ш
10 Элементы анализа в метрическом пространстве 317
10.1 Метрическое пространство 317
10.1.1 Определения метрики и метрического простра-
пространства 317
10.1.2 Примеры метрических пространств 318
10.1.3 Свойства расстояния 320
10.1.4 Декартово произведение пространств 321
10.1.5 Предел последовательности элементов метри-
метрического пространства 321
10.1.6 Сходимость в некоторых конкретных простран-
пространствах 322
10.1.7 Шары, ограниченное множество, предельная
точка 322
10.1.8 Открытые множества 325
10.1.9 Структура открытых множеств на прямой (R,p)
и в (Rm, р) 326
10.1.10 Замкнутые множества 327
10.1.11 Сепарабельные метрические пространства . . . 328
10.1.12 Полные метрические пространства 329
10.1.13 Пополнение метрических пространств 331
10.2 Функции на метрическом пространстве 332
10.2.1 Предел функции в точке 332
10.2.2 Свойства пределов действительных функций . . 333
10.2.3 Понятие о повторных пределах 333
10.2.4 Непрерывные функции 334
10.2.5 Элементарные свойства непрерывных функций . 335
10.2.6 Примеры действительных непрерывных на Rm
функций 336
10.2.7 Теорема о характеризации непрерывности . . . 337
10.2.8 Равномерно непрерывная на множестве функция 338
10.3 Компактные множества и их свойства 338
10.3.1 Определения 338
10.3.2 Свойства компактных множеств 339
10.3.3 Критерий компактности 341
10.3.4 Компактные множества в (Rm,p) 343
10.3.5 Компактные множества в C([a, b]),р) 343
10.4 Свойства непрерывных функций на компактах 345
10.4.1 Основные теоремы 345
10.5 Принцип сжимающих отображений 347
10.5.1 Определения 347
10.5.2 Теорема Банаха 348
10.5.3 Применение принципа сжимающих отображений 349

Оглавление
10.5.4 Теорема Стоуна-Вейерштрасса 353
10.5.5 Историческая справка 355
11 Функции нескольких переменных 357
11.1 Производная по направлению. Частные производные . . 357
11.1.1 Определения 357
11.1.2 Свойства производных по направлению. Част-
Частные производные 359
11.1.3 Основные теоремы о производных по направле-
направлению 360
11.2 Дифференцируемые функции 361
11.2.1 Понятие дифференцируемости 361
11.2.2 Достаточное условие дифференцируемости . . 363
11.2.3 Свойства дифференцируемых функций 364
11.3 Производные и дифференциалы старших порядков . . . 365
11.3.1 Производные второго порядка 365
11.3.2 Производные порядка п 366
11.3.3 Формула Тейлора 367
11.3.4 Экстремум 369
11.3.5 Достаточное условие строгого локального экс-
экстремума 370
11.3.6 Условия выпуклости функции 372
11.3.7 Историческая справка 374
12 Векторные функции от нескольких переменных 375
12.1 Непрерывные отображения 375
12.1.1 Линейные отображения 375
12.1.2 Непрерывные отображения 376
12.2 Дифференцируемые отображения 377
12.2.1 Определения 377
12.2.2 Свойства дифференцируемых функций 379
12.2.3 Теоремы о неявной и обратной функциях .... 380
12.3 Локальный относительный экстремум 384
12.3.1 Определения 384
12.3.2 Необходимое условие локального относитель-
относительного экстремума (правило множителей Лагран-
жа) 385
12.3.3 Достаточное условие 386
12.3.4 Собственные числа симметрической матрицы . 386
12.3.5 Историческая справка 387
12.4 Дополнительные задачи к главам 10—12 387

Оглавление
13 Несобственные интегралы, зависящие от параметра 394
13.1 Несобственные интегралы 394
: 13.1.1 Определение интегралов по неограниченным
интервалам 394
13.1.2 Элементарные свойства 395
13.1.3 Сходимость интегралов от неотрицательных
функций 396
13.1.4 Абсолютно и условно сходящиеся интегралы . . 398
13.1.5 Несобственные интегралы от неограниченных
функций 400
13.2 Функции, определяемые с помощью интегралов .... 402
13.2.1 Введение 402
13.2.2 Теоремы о непрерывности, интегрировании и
дифференцировании функции J 402
13.2.3 Равномерная сходимость и теорема о предель-
предельном переходе 404
13.3 Равномерная сходимость несобственных интегралов . . 405
13.3.1 Определение равномерной сходимости несоб-
• ственных интегралов 405
13.3.2 Признаки равномерной сходимости несобствен-
несобственных интегралов 407
13.4 Свойства функций, определяемых интегралами 410
13.4.1 Основные теоремы 410
13.4.2 Вычисление интеграла Эйлера-Пуассона .... 414
13.4.3 Несобственные интегралы от неограниченных
функций, зависящие от параметра 415
13.5 Гамма-функция. Бета-функция 416
13.5.1 Определение гамма-функции. Элементарные
свойства 416
13.5.2 Основная теорема теории гамма-функции . . . 418
13.5.3 Основные формулы для гамма-функции .... 419
13.5.4 Разложение синуса в бесконечное произведение 421
13.5.5 Формула Стирлинга 421
13.5.6 Бета-функция 423
13.5.7 Историческая справка 424
14 Кратные интегралы 425
14.1 Кратные интегралы по брусу 425
14.1.1 Определения и обозначения 425
14.1.2 Суммы Дарбу и их свойства 426
14.1.3 Верхний и нижний интегралы. Определение кра-
кратного интеграла по брусу 428
14.1.4 Интегрируемость непрерывной функции .... 429

10 ' Оглавление
14.1.5 Свойства интеграла от непрерывной функции . 430
14.1.6 Формула приведения m-кратного интеграла к
последовательным однократным 432
14.2 Множества, измеримые в смысле Жордана. Мера Жор-
дана 435
14.2.1 Разбиение пространства Rm 436
14.2.2 Измеримые множества. Мера 437
14.2.3 Свойства измеримых множеств 439
14.2.4 Свойства меры Жордана 441
14.2.5 Цилиндрические множества и их измеримость . 442
14.3 Кратные интегралы по измеримым множествам .... 444
14.3.1 Определение интеграла 444
14.3.2 Свойства интеграла 446
14.3.3 Вычисление интеграла по цилиндрическим мно-
множествам 447
14.4 Отображения множеств. Формула замены переменных 449
14.4.1 Отображения специального вида 449
14.4.2 Измеримость образа при отображении специ-
специального вида 450
14.4.3 Формула замены переменных для отображения
специального вида 452
14.4.4 Локальное сведение общего отображения к су-
суперпозиции отображений специального вида . . 454
14.4.5 Формула замены переменных 455
14.4.6 Следствие и примеры 457
14.5 Несобственные кратные интегралы. Определения и при-
примеры 459
14.5.1 Интегралы от неограниченных функций 459
14.5.2 Интегралы по неограниченным множествам . . 463
15 Интегралы по многообразиям и теорема Стокса 465
15.1 Основные определения 465
15.1.1 Допустимые координатные пространства. Ори-
Ориентация 465
15.1.2 Дифференциальные формы степени т в про-
пространстве Rm. Новая форма формулы замены
переменных 468
15.1.3 Многообразия 469
15.2 Интеграл по многообразию от дифференциальной фор-
формы 472
15.2.1 Дифференциальные формы степени р в про-
пространстве Rm 472
15.2.2 Интеграл от формы по многообразию 474

Оглавление
15.3 Внешний дифференциал формы. Ориентация границы . 479
15.3.1 Внешний дифференциал дифференциальной
формы 479
15.3.2 Ориентация границы множества, состоящего из
конечного числа брусов 481
15.4 Формула Стокса в специальном случае 482
15.4.1 формула Стокса для множества, состоящего из
конечного числа брусов 482
15.4.2 Частные случаи 485
15.5 Общая формула Стокса 487
15.5.1 Вывод формулы Стокса 487
15.5.2 Следствия из общей формулы Стокса 490
15.6 Криволинейный интеграл от формы 1-вой степени . . . 491
15.6.1 Криволинейный интеграл второго рода от диф-
дифференциала 491
15.6.2 Замкнутые дифференциальные формы. Одно-
связные множества 492
15.7 Мера на многообразии , 497
15.7.1 Частный случай многообразия — гиперплоскость
вГ...: 497
15.7.2 Определение меры на многообразии 499
15.7.3 Длина дуги 500
15.7.4 Длина дуги как предел 501
15.7.5 Площадь поверхности 501
15.7.6 Площадь поверхности как предел 503
15.8 Интегралы первого рода по многообразию 504
15.8.1 Общее определение 504
15.8.2 Связь с интегралом второго рода 504
15.8.3 Криволинейный интеграл первого рода, связь с
криволинейным интегралом второго рода . . . 505
15.8.4 Криволинейный интеграл первого рода как пре-
предел 506
15.8.5 Поверхностный интеграл первого рода 506
15.8.6 Связь между поверхностными интегралами пер-
первого и второго рода 507
15.8.7 Историческая справка 509
16 Элементы теории рядов Фурье и интеграла Фурье 510
16.1 Ряд Фурье по ортонормированной последовательности . 510
16.1.1 Основные определения 510
16.1.2 Задача о наилучшем приближении в смысле
среднеквадратического расстояния 513

12 Оглавление
16.1.3 Коэффициенты Фурье. Ряд Фурье. Элементар-
Элементарные свойства 515
16.2 Ряд Фурье по тригонометрической последовательности 519.
16.2.1 Обозначения. Следствия из общей теории . . . 519
16.2.2 Вспомогательные утверждения 521
16.2.3 Сходимость ряда Фурье в точке 525
16.2.4 Теорема Фейера 528
16.3 Дифференцирование и интегрирование ряда Фурье . . 529
16.3.1 Понятие тригонометрического ряда. Свойства
коэффициентов Фурье 529
16.3.2 Равномерная сходимость и почленное диффе-
дифференцирование ряда Фурье 530
16.3.3 Интегрирование ряда Фурье 531
16.3.4 Случай функции с произвольным периодом . . 533
16.4 Интеграл Фурье 534
16.4.1 Формальный вывод интегральной формулы Фу-
Фурье 534
16.4.2 Сходимость интеграла Фурье в точке 535
16.4.3 Преобразование Фурье 537
16.4.4 Элементарные свойства преобразования Фурье 538
16.4.5 Пример применения преобразования Фурье . . 539
16.4.6 Историческая справка 540
16.5 Дополнительные задачи к главам 13 — 16 541
Список основных обозначений 548
Указатели 551

Предисловие
Настоящая книга представляет собой переиздание с некоторыми изме-
изменениями и дополнениями книги автора, изданной в 1985 г. Киевским из-
издательством «Выща школа» под заглавием Математический ана-
анализ. Справочное пособие. Изменения состоят в следующем. Усо-
Усовершенствовано изложение ряда разделов курса, добавлены новые при-
примеры и задачи, исправлены некоторые неточности в тексте и опечатки.
Автор благодарит преподавателей и студентов, обративших его внима-
внимание на погрешности. Педагогические намерения автора, методические
установки и особенности изложения материала представлены в ниже-
нижеследующем предисловии к первому изданию. Содержание книги полно
представлено в детальном оглавлении.
Л Заметим также, что изданная в 1987 году книга автора Матема-
Математический анализ. Сборник задач (Киев. Выща школа) содер-
содержит задачи для практических занятий по курсу анализа, по содержанию
и расположению материала соответствующая настоящей книге.
Мз предисловия к первому изданию
[ Книга содержит краткое и вместе с тем достаточно полное по охва-
охвату материала изложение современного курса математического анализа.
Она рассчитана на студентов университетов и технических вузов и пред-
предназначена для первоначального изучения курса. Поэтому главное вни-
внимание сосредоточено на разъяснении основных понятий, идей и фактов,
а также примеров их использования.
При отборе материала учтены современные тенденции развития ма-
математики и её приложений, модернизировано изложение ряда разде-
разделов, в том числе тем, посвященным функциям многих переменных,
кратным интегралам, интегралам по многообразиям и др.
Автор использовал многолетний опыт чтения лекций по курсу мате-
математического анализа на механико-математическом факультете Киевско-
Киевского университета. В книге меньше, чем обычно, уделено внимания мате-
материалу технического или второстепенного для понимания основных идей

14 . Предисловие
характера, а также вопросам чисто логического обоснования. По педа-
педагогическим соображениям автор не стремился доказывать теоремы при
наиболее общих условиях, выбирая в каждом случае предположения,
которые хорошо выявляют идею теоремы и в определённом смысле
типичны.
Одной из целей автора было достижение единого уровня изложения,
в том числе единого разумного уровня строгости изложения, уровня де-
детализации доказательств, формализации и т. п. Работа над математиче-
математическим текстом должна побуждать к самостоятельному продумыванию ма-
материала, вызывать посильное участие читателя в получении результатов
Поэтому определённая часть работы по усвоению материала постояннс
оставляется читателю, хотя все принципиальные моменты, в частнооп
доказательства, детально изложены. Этим же частично объясняется ла
коничность изложения, в частности, отсутствие многочисленных огово
рок, которые часто не соответствуют индивидуальным представлениял
новичков и только уводят в сторону, создавая дополнительные помех!
усвоению.
Изучение курса математического анализа, как и любого математи
ческого предмета, невозможно без систематического самостоятельно
го решения задач. Именно процесс активного продумывания материал
при попытках решения задач помогает выработать правильные интy^
тивные представления о глубоких и абстрактных понятиях анализа, дг
понимания которых недостаточно обычных внематематических предста!
лений. Поэтому настоящая книга представляет собой и задачник. Beer
книга содержит около 1500 примеров и упражнений. Часть из них д«
тально разобраны в тексте, другие предназначены для контроля усв<
ения материала или содержат предупреждающие от неверного npej
ставления примеры. Ряд других включают разъясняющие или дополн!
тельные факты. Расположение задач таково, что подавляющая их час
вполне посильна для самостоятельного решения при условии усвоен!
предшествующего материала. Кроме того, имеется ряд задач олимп
адного характера, они отмечены звёздочкой. Материал книги разбит i
четыре цикла, которые соответствуют четырём семестрам при полис
двухгодичном чтении лекций. Каждый такой цикл заканчивается наборе
дополнительных задач, для решения которых, как правило, использует
весь предшествующий материал. Это задачи семестрового экзамена
задачи олимпиад, которые могут быть использованы в работе мател/
тических кружков и для курсовых работ. Большинство этих задач бол
трудны для решения нежели задачи из текста глав.
В отношении методики изложения ряда разделов автор следовав
первую очередь известным курсам:
Кудрявцев Л. Д. Математический анализ. В 2-х т. М<

Предисловие 15
ква. Высш. шк., 1970.
Рудин У. Основы математического анализа. Москва.
Мир. 1966.
Tutschke W. Grunlagen der reelen Analysis. Berlin. VEB
Deutscher der Wissenschaften. 1972. Vol. 1 — 2.
Blatter C. Analysis. Berlin. N.-Y. Heidelberg. Springer Verlag.
1974. Vol. 1 - 3.
Настоящее пособие является весьма кратким. Однако, опыт работы
показывает, что студенты, активно усвоившие курс в предлагаемом объ-
объёме, успешно владеют основными идеями и методами математического
анализа и могут без особого труда читать современные абстрактные
курсы. Этого вполне достаточно для продолжения математического об-
образования и дальнейшей самостоятельной работы.
Автор.

Глава 1
Введение
1.1 Логические знаки
1.1.1 Вступление
Современный математический текст состоит из математических формул
и собственно текста, написанного, например, на русском языке. При
этом ряд слов и словосочетаний, которые выражают наиболее важные
и часто используемые в математических рассуждениях отношения меж-
между объектами, получили специальные обозначения и называются логи-
логическими знаками. Далее используются следующие общеупотреби-
общеупотребительные логические знаки:
=>■ — «влечёт за собой», «следует»;
-Ф=*> — «тогда и только тогда», «равносильно»,
«если и только если»;
V — «для всех», «для каждого»;
3 — «существует»;
3 ! — «существует только один»;
:= — «равно по определению».
Замечание. Знак V представляет собой перевёрнутую первую
букву английского слова АН - все. Знак 3 представляет собой перевёр-
перевёрнутую первую букву английского слова Exist - существует. Знаки
V и 3 называются также кванторами общности и существо-
существования соответственно.
1.1.2 Примеры использования логических знаков
Приведём примеры утверждений о свойствах натуральных чисел и
их записей с помощью логических знаков. Проверить справедливость
16

1.2. Элементы теории множеств 17
следующих утверждений и равносильность записей.
1а. Из неравенства m < п следует неравенство т2 < п2.
1b. т < п =>■ т2 < п2.
2а. Неравенство m < п равносильно неравенству т2 < п2.
2Ь. т < п -Ф=Ф- т2<п2.
т т2
За. Число — целое тогда и только тогда, когда число —г- целое,
п п2
m m2
3b. — целое -Ф=> —— целое,
п п2
4а. Для каждого п число п2 — 1 неотрицательно.
4Ь. Vn: п2-1>0.
5а. Существует число п такое, что |п — 3| = 1.
5Ь. Эп: |п-3| = 1.
6а. Существует точно одно число п такое, что Зп = 2п + 1.
6Ь. 3 \п : Зп-2п + 1.
7а. Для любого п число п(п + 1) четно, то есть представимо в виде
п{п + 1) = 2т с натуральным числом т.
7b. Vn 3m: n(n + 1) = 2m.
Замечание. Двоеточие после знака Vn следует читать как «вы-
«выполнено» или «справедливо». Двоеточие после знака 3 п следует читать
как «такое, что».
Упражнение 1. Проверить следующие утверждения.
I.Vn: 1 + 2 + 3+.. . + („-1) = П£±!).
2. Vn>9: n2-9n-l>0. 3. Vn 3m: n(n + l)(n + 2) = 6m.
4. Vn Vfc 3m: n(n + l)(n + 2) •... ■ (n + к - 1) = m ■ k\,
здесь k\ := 1 • 2 • 3 •... • k.
1.2 Элементы теории множеств
1.2.1 О понятии множества
Понятие множества является одним из важнейших исходных и неоп-
неопределяемых понятий современной математики. Можно говорить о мно-
множестве N всех натуральных чисел, о множестве Q всех рациональ-
рациональных чисел, о множестве всех изданных к настоящему времени книг и т.
п. Создатель теории множеств Г. Кантор использовал следующее
«определение»:
2*

18 Глава I. Введение
мномсество или совокупность — это собрание опреде-
определённых и различных объектов нашей интуиции или ин-
интеллекта, мыслимое в качестве целого.
Как синонимы слова «множество» часто используются слова семей-
семейство, совокупность, класс. Составляющие множество объекты
называются элементами или точками этого множества. Множе-
Множество будем считать определённым, если о каждом рассматриваемом
объекте можно сказать, что он либо принадлежит, либо не принадле-
принадлежит множеству.
Пусть А - множество. Тот факт, что элемент х входит в множество
А, или что элемент х принадлежит множеству А, обозначается одним
из символов х G А, А Э х. Тот факт, что элемент х не входит в
множество А, обозначается одним из символов х (£ А, х£А.
Далее используются следующие способы задания множества.
(i) Задание множества с помощью перечисления или
указания его элементов. Например, множество А состоит из
элементов а, Ь, с,..., к. При этом используется следующее обозначе-
обозначение А — {а, Ь,с,..., к}. Для множества всех натуральных чисел исполь-
используется обозначение N = {1, 2, 3,..., п,...}, а для множества всех целых
чисел — обозначение Z = {..., -п,..., -1,0,1, 2,..., п,...}.
(ii) Задание множества указанием свойства его эле-
элементов. В каждой математической задаче обычно рассматривают-
рассматриваются элементы некоторого вполне определённого множества X, которое
называется основным. Нужные множества при этом выделяют с по-
помощью любого свойства Р, удовлетворяющего специальному
условию: для каждого элемента х из X либо свойство Р выполнено
(в этом случае будем говорить, что элемент х обладает свойством Р,
и писать Р{х)), либо свойство Р для элемента х не выполнено (эле-
(элемент х не обладает свойством Р). С помощью каждого такого свойства
выделяется множество всех тех элементов из X, которые свойством Р
обладают. Это множество обозначается {х £ X \ Р{х)} = {х \ Р{х)}.
Множество, не содержащее элементов, называется пустым и
обозначается символом 0.
1.2.2 Примеры
Справедливы утверждения.
1. 1 G N, -1 £ N, -1 G Z, I <£ N. 2. Vn е N : 2{lL±i) e jy.
\ 3. N — {х G Z | х > 0}. Здесь свойство Р означает «быть положи-
* тельным», это свойство специальному условию удовлетворяет: каждое
целое число либо положительно, либо неположительно.

1.2. Элементы теории множеств /9
4. Пусть Р означает «быть чётным». Тогда {2,4, 6,..., 2к,...} = {а; £
N | Р{х)}.
Q ' ~ln n ' m г
1.2.3 Упражнения
'Следующие простые упражнения рекомендуются для обязательного ре-
Йдения.
^Упражнение 2. Перечислить элементы множества:
Ь a){n£N | (п-3J<72}; Ь) {п € Z \ (п + ЗJ < 72};
с) {n G ЛГ | п3 > 4n}; d) {п 6 Z | п3 > Юп2};
. г лт п2 + Зп-12 ЛТ1 /ч г _7 п + 9 -7i
e)^n£iV (ЕЛ/Ч; f)^n£iV —— £iV^;
g){x£ Z \3y £ Z : \x\ + \y\ = 2}.
Упражнение З. Верны ли утверждения:
s|.2.4 Действия над множествами
,4.
({рпре деление 1. Множество А называется подмно-
УЫсеством множества В, если V х е А : х £ В.
Обозначение: ЛСВ или В D Л.
|/ По определению для любого множества А справедливо следующее
.•включение 0 С А.
Тримеры. Проверить утверждения.
1. N С Z С Q.
2. Для множества {а,Ь,с} всеми его подмножествами являются
0, W. {Ь}, {с}, {а,Ь}, {а, с}, {Ь,сУ, {а,Ъ,с}.
Определение 2. Множества А и В равны, если
,s.- ЛСВ и В С А.
^рбозначение: А = В.
|: Таким образом, А = В <=> А С В и В С Л.
^Пример. 3. {а, Ь, с} = {а, с, Ь} = {Ь,с, а}.
щО пре деление 3. Объединением множеств А и В на-
Шывается множество С, состоящее из всех тех элемен-
imoe, которые принадлежат по крайней мере одном/у из
1множ:еств А, В.

20 . Глава I. Введение
Обозначение: С = A U В.
Таким образом, Ли В = {х | х G А или х G В}.
Определение 4- Пересечением двух множеств А и В
называется множ.ество С, состоящее из всех тех эле-
элементов, которые принадлемсат камсдому из мномсеств
А и В.
Обозначение: С = А П В.
Таким образом, АГ\В = {х\х&А и х G В}.
Определение 5. Разностью множеств А и В назы-
называется мноок.ество С, состоящее из всех тех элементов
мноок.е.ства А, которые не принадлеэ+сат множеству В.
Обозначение: С = А\В.
Таким образом, А\ В = {х Е А и х £ В}.
Пусть X — основное множество и А С X.
Определение 6. Дополнением к множеству А назы-
называется мномсество А -.— X \ А.
Таким образом, А = {х G X \ х £ А}.
Определения объединения и пересечения двух множеств обобщают-
обобщаются на случай любого семейства множеств. Пусть Т — некоторое мно-
множество индексов и для каждого t G Т задано множество At.
Определение 7. Объединение и пересечение семей-
семейства мномсеств At, t eT определяются соответственно
соотношениями
\jAt~{x | 3*о GT: At03x}, f) At := {х \ Vi G Т : At Э х}.
teT ter
Примеры.
5. Пусть для каждого п £ N множество Ап = {1,2,...,п}. Тогда
Ап С Ап+х для п Е N и U Ап = N, f] Ап = {1}; и для фиксиро-
ngJV n£N
ванного m G N имеем (J An = N, f] An = Am, (J An = Am.
n>m n>m n<m
6. Пусть для каждого n G N множество Ап — {n, n+1,...}. Тогда для
каждого фиксированного m G N справедливы следующие равенства
U An = Am, П Ап = 0, U An = N.
п~>т п>тп п<.т
Упражнение 4- Аи 0 = А, Аи А = А, Аи В — В и А,
A U (В U С) = {А и В) U С =: А и В U С.
Упражнение 5. АП0 - 0, АГ\А = А, АпВ = ВпА, Ап(ВпС) =
(ЛПВ)ПС=: ЛПВПС.

1.2. Элементы теории множеств 21
Упражнение 6. А п (В и С) - (А П В) и (А П С), А и (В П С) =
= (Аи В) П {Аи С).
Упражнение 7. А с В <=> АпВ - А <£=> АиВ = В <=> В с
А.
Из определений действий над множествами следует ряд свойств этих
действий. В упражнениях ниже перечислены наиболее существенные из
свойств.
Правила двойственности. Для любых множеств А, В спра-
справедливы следующие равенства: Аи В = An В, An В = Аи В.
[Доказательство первого равенства: х £ A U В •<=> х £ (АиВ)
х $ а и i <£ в <=$■ х е ~А и х е в ч=> хе(Лпв). J
Упражнение 8. Доказать утверждения: А С В С С =>• С =
= A U (В \ А) и (С \ В), Л и В = (Л \ В) U (В \ А) и {А П В).
пражнение 9. Доказать, что (J At — f] At, f] At = [j At. •
ter ter ter ter
Определение 8. Упорядоченной парой (a,b) элемен-
элементов а и b называется множество {{а}, {а,Ь}}. Декарто-
Декартовым произведением множеств АиВ называется мно-
мсество А х В := {{а,Ь) \ а £ A, be В}. Аналогично, упо-
упорядоченный набор (а,Ь,с) из трех элементов а,Ь,с есть
мноок.ество {{а}, {a,b}, {a,b,c}}, а декартово произведе-
произведение мномсеств А, В, С есть множество А х В х С :=
{(а,Ъ,с) | а£ А, ЬеВ, с £ С}.
Декартово произведение п £ N множеств определяется аналогично.
Далее используются также следующие обозначения
" А2 :- А х А, А3 := А х А х А, Ап := А х А х ... х А, п £ N.
п раз
Упражнение 10. Если а ф Ь, то (а,Ь) ^ (Ь,а). В общем случае
Ах В ФВ х А.
Упражнение 11. (А\ х Bi) П (Лг х Вг) = (j4i П А2) х (Bi П
Определение 9. Множество, состоящее из конечно-
конечного числа элементов, называется конечным.
Обозначения. Для конечного множества А число его элементов обо-
обозначается символом \А\. Для множества А семейство всех его
подмножеств, включая 0 и А, обозначается символом 2А.
Упражнение 12. Для конечных множеств Л и В доказать следую-
следующие равенства:

22 Глава I. .Введение
а) \А\В\ = \А\ -\АПВ\, Ъ)\АхВ\ = \А\ ■ \В\,
с) \AuB\ = \A\ + \B\-\AnB\, d) \2A\ = 2W.
it
1.3 Общее понятие отображения
или функции
Определение 1. Пусть X и Y — два множества.
Отображением f множества X в мноэ+сество Y на-
называется правило или предписание, которое каждому
элементу х £ X ставит в соответствие точно один
элемент у G У. Множество X называется множеством
определения отобрамсения f и обозначается D(f). Мно-
жество R(f) := {у G Y | Зх G £>(/) : f{x) = у} называется
множеством значений отобрамсения /. Элемент у, ко-
который отобраснсение f ставит в соответствие элемен-
элементу х, называется образом элемента х при отобрамсении
f или значением отображения f в точке х и обознача-
обозначается символом. f(x), при этом будем, писать х ь-> f(x).
Обозначения. Каждая из следующих записей 1) / : X —¥ Y; 2) X —> Y;
3) у = f{x), х £ X означает, что / есть отображение множества X в
множество Y.
Далее слова отображение, функция, преобразование,
соответствие, оператор употребляются как синонимы.
Замечания. 1.Часто рассматривается случай, когда множество
определения D(f) есть часть более широкого множества.
2. Задание функции / согласно определению 1 предполагает зада-
задание следующих трех объектов: D(f), Y и правила, ставящего в соот-
соответствие каждому элементу из £>(/) точно один элемент из Y.
Упражнение 13. Определить R(f) для функций:
a)X = Y=Z, /(x) = x + l, i6 Z;
b)X = Y = Z, f(x) = |x| + l, zeZ;
с) X = Y = Z, f(x) = х2 - 6х + 5, i 6 Z.
Определение 2. Функции /i : Xi -> Yi, /2 : Х2 -> Y2
называются равными, если выполняются следующие ус-
условия 1) Хг = Х2 и 2) Vx G Xi : Д(х) = /2(х).
Обозначение: /1 = /2.
Определение 3. Пусть f : X -» Y и Хо С X. Функция
/о : Хо -> Y, определяемая соотношением Vi G Хо : fo{x) —
= /A), называется сужением функции f на м,номсество

j$.3. Общее понятие отображения или функции
Хо, а функция f называется продолжением функции /0
на мномсество X.
Определение 4- Пусть f : X -» У. График функции f
есть множество G{f) := {(х,у) G (X х У) \ х G X, у = f{x)}.
Отметим, что график функции / есть подмножество декартового
Произведения X х У.
Определение 5. Пусть f : X -> У и g : У -> Z. Функция
fi : X —> Z, определяемая равенством, h(x) := <7(/(я)), х G X,
называется сложной функцией или суперпозицией} фун-
функций fug.
Обозначения: h = g{f) или h = g о f.
Определение 6. Пусть /: X ^ Y и А С X, В С Y.
Образом множества А при отобрамсении / называется
множество f(A) := {у G Y | 3 х G А : }{х) = у} = {/(i) | x G Л}.
Прообразом множ.ества В при отображении / называ-
называется мномсество f~l(B) := {х Е X \ Зу £ В : у = f{x]} =
= {х G X | /(s) G В}.
Замечание. Обратим внимание на то, что f(A) С Y, /~1(В) С X.
Упражнение 14- Для каждой из функций упражнения 13 найти
f(N) и f
Упражнение 15. Пусть / : X -> Y и Ai С X, А2 С X. Проверить
соотношения:
а) /(Лх U А2) = /(Аг) U /(Л2); Ь) f(Ax П Л2) С (/(^) П f(A2));
с) (/(ЛО \ /(Л2)) С /(Л! \ Л2); d) Л! С Л2 ^ f(A,) С /(Л2);
е) Ах С /^(/(ЛО); f) (f(X) \ /(А,)) С /A7).
Упражнение 16. Пусть / : X -» У и Bi С У, В2 С У. Прове-
Проверить следующие соотношения: a) f~l{B\ U В2) = f~l(Bx) U/~1(В^);
Ь) Г1(в1пв2) = ГЧВОПГЧ-В.); с) гЧ-ВДг) = r1(Bi)\f-1(B2);
d)B1C_B2
Определение 7, Отображение f : X -> У наз-ывает-
сл ото5раэ/сениел» л*ноэ«:ес7тгва X на .мно:ж:ество У или
сюрвекг^ией, если /(X) = У.
О пре деление 8. Отображение f : X -> У называется
взаимно однозначным отобрамсением, мноок.ества X в
мномсество У или инвекг^ией, если Vii £ X Vi2 G I :
f{x2).
'От лат. suppono — подставлять.

24 Глава I. Введение
Определение 9. Отобрамсение /, которое является
сюръекцией и инъекцией, называется биекцией. В этом
случае таксисе говорят, что функция / осуществляет
взаимно однозначное соответствие мемсду мномсест-
вами X и У.
Упражнение 17. Какие из функций упражнения 13 являются сюръ-
екцией? Инъекцией? Биекцией?
Упражнение 18. Доказать, что суперпозиция биекций есть биекция.
Упражнение 19. Проверить следующие утверждения:
а)/: X -» У есть сюръекция Ч=» У у G У : /^({у}) ф 0;
b) / : X -¥ Y есть инъекция •£=>• V у € У : множество /-1({у}) = 0
либо состоит из одного элемента;
c) / : X -> Y есть биекция <£=> Vy G У : множество f~l({y})
состоит из одного элемента.
Упражнение 20. Пусть X и Y конечные множества, причем \Х\ =
т G N, \Y\ = п £ N. Проверить утверждения:
a) существует сюръекция / : X —¥ Y -Ф=> т > п;
b) существует инъекция / : X —¥ Y <==$■ т < п;
c) существует биекция / : X —¥ Y <=> т — п\
в) в случае с) существует п! биекций;
e) в случае а) существует т{т — 1)... (т — п + \)пт~"п сюръекций;
f) в случае Ь) существует п(п - 1)... (п - т + 1) инъекций;
д) всего существует пт отображений / : X —¥ Y.
Упражнение 21. Доказать, что
/ - инъекция <=> V С X : /-1(/(Л)) = А <=>
<=> \/АсХ \/ВсХ: f{AHB) = f(A)nf{B) <=>
<=>VACX VBCX, ADB: f(A\B) = f(A)\f(B).
Упражнение 22. Пусть отображения / : X ^> Y и g : Y -» X
таковы, что Vi G X : g{f{x)) = x. Доказать, что / — инъекция, aj-
сюръекция.
Определение 10. Пусть f : X -» У ес7тгъ (тегс-цил.
Тогда VjE/ 3!iGl: /(г) = у, поло:ж:ш^ /-1(у) := а;-
Z" : У -> X казъ1вае7тгсл обратной к функции /.
Упражнение 23. Если / : X -> 7 - биекция, то f~l — также
биекция с обратной функцией /. Доказать это утверждение.
Упражнение 2£. Доказать, что в условиях определения 10 справед-
справедливы утверждения: VigX: /-1((/(а;)) = х; Vy G У : f(f~1{y)) = У-

1.4. Мощность множества. Счётные множества 25
Упражнение 25. Пусть функции /: X -> У и g : Y -> X таковы,
что \/х £ X : g(f(x)) = x, Vy £Y : f(g{y)) = У- Доказать, что / и д
биекции и д = f~x.
Определение 11. Отображение вида / : N -> X на-
называется последовательностью элементов из X.
Обозначения: {сц, а2,..., ап,...}, {ап : п > 1} или {ап | п > 1}, где
ап := /(п) есть n-ый член последовательности.
11.3.1 Историческая справка
!i
Слово «функция» происходит от лат. functio — выполнять. Этот термин,
а также обозначение 3) функции ввёл в математику Г. Лейбниц.
Ртметим также, что определение 1 не является определением в обыч-
обычном для современной математики смысле. Оно лишь подменяет слово
(«функция» словами «правило», «предписание», которые более близ-
близки нашей интуиции. Это определение было предложено ещё в 1817 г.
Б. Вольцано A781 — 1848), однако оно стало использоваться после
' его введения П. Г. Дирихле A805 — 1859). Тем не менее, это
определение является исключительно важным этапом развития понятия
«функция» и этого определения вполне достаточно для нашего изложе-
изложения. О развитии понятия функции можно прочесть в интересной статье
i Г. Е. Шилова «Что такое функция?» (Математика в школе. 1964.
, N.1. С. 7-15). Формальное определение приведено, например, в книге
.Ж\ Дъедонне «Основы современного анализа» (М.: Мир. 1964.).
1.4 Мощность множества. Счётные
множества
Конечные множества сравниваются по запасу их элементов просто —
нужно сравнить числа элементов в этих множествах. Представляет ин-
интерес другой способ сравнения, относящийся к случаям, когда числа
элементов велики и фактический подсчёт числа требует много време-
времени. Контролёр в кинотеатре перед началом сеанса по наличию пустых
кресел делает вывод о том, что не все билеты проданы, то есть, что
число зрителей меньше числа мест в зале. При этом фактически ис-
используется тот факт, что между множеством зрителей и занятыми ими
креслами устанавливается взаимно однозначное соответствие. В связи с
этим вторым способом сравнения чисел элементов множеств полезно
рассмотрение упражнения 20.
Как сравнивать по запасу элементов бесконечные множества? Оди-
Одинаковы ли по запасу элементов множества N, Z, Q? Следует обратить

26 Глава I. Введение
внимание на то, что N С Z С Q- Поставленный вопрос и ответ на него
не являются простыми. Г. Кантор построил естественную и изящ-
изящную математическую теорию, которая содержит ответ на поставленный
и другие подобные вопросы. Исходным пунктом этой теории является
следующее определение.
Определение 1. Множества А и В равномощны или
имеют одинаковую мощность, если существует биек-
цил f : А —> В. То, что мноысества А и В равно мощны,
обозначается следующим образом, А ~ В.
Замечания. 1. Таким образом, А ~ В, если между множествами
Л и В можно установить взаимно однозначное соответствие.
2. С помощью определения 1 точные определения конечного и бес-
бесконечного множеств формулируются следующим образом. Множество
А конечно <=> Зп Е N : А ~ {1,2, ...,п}. Множество 0 так-
также конечно и |0| := 0. В остальных случаях множество А называется
бесконечным.
3. Пусть А и В конечные множества. Тогда А ~ В <=> \А\ = \В\.
Примеры.
1. N = {1,2,3,4,...,п,...} и В = {0,1,2,3,..., п - 1,...} = {0} U N
— равномощные множества, так как отображение TV Э п \-¥ (п — 1) £ В
есть биекция. Отметим, что N С В и что N ф В.
2. Множества N = {1,2,3,..., п,...}, В = {2,4,6,... ,2п,...} рав-
равномощны, так как отображение N Э п \-¥ 2п £ В есть биекция. Отме-
Отметим, что В С N.
Упражнение 26. Доказать следующие утверждения. Множество
А конечно тогда и только тогда, когда не существует множества В С
Л, В ф А такого, что В ~ А. Множество А бесконечно тогда и только
тогда, когда существует множество В С А, В ф А такое, что В ~ А.
Упражнение 27*. Доказать, что множества А и 2А не равномощны.
Указание: пусть / : А —> 2 - биекция. Рассмотреть множество {х £
Л | i $ /l1)} Для получения противоречия.
Определение 2. Мномсество А называется счётным
множеством, если А ~ N.
Замечание. 1. Если А ~ iV, то говорят, что элементы множества
А можно занумеровать. Пусть / : N -» Л — некоторая биекция,
с этой биекцией связана следующая нумерация: элементу /(и) £ Л ста-
ставится в соответствие номер п G iV. При этом все элементы множества
Л получат номера, различным элементам будут отвечать разные но-
номера и все номера из N будут использованы. Другая биекция между
множествами N и Л приведёт к другой нумерации множества Л.

\А. Мощность множества. Счётные множества
U бОрема 1. Бесконечное подмножество счётного
•^мномсества также счётно.
■'; \ Пусть А счётное множество, занумеруем его каким-нибудь обра-
образом А = {ai, a.2, аз, ..., а„,...}. Пусть В бесконечное подмно-
подмножество А. Занумеруем элементы В следующим образом. Пусть a.k(i)
<- первый элемент в последовательности А, который входит в В. Со-
Сопоставим элементу ац^ номер 1. Пусть ац2) ~ первый из элементов
bfc(i)+i, afc(i)+2, ••• i который входит в В. Сопоставим элементу a.kB)
номер 2. Продолжая аналогично, мы занумеруем все элементы В, при
Ьтом все номера из N будут использованы, так как В бесконечно. J
Теорема 2. Бесконечное мноэ+сество codepotcum счё-
шьное подмножество.
Ц \ Пусть А - бесконечное множество и ai - произвольный элемент из
■А. Тогда множество А \ {ах} также бесконечно, так как А = {ai} U
(А \ {ai})- Пусть а2 - произвольный элемент из множества А \ {ai}.
Множество ((А \ {ai}) \ {а2}) = А \ {ai,a2} также бесконечно. Пусть
из - произвольный элемент из А \ {01,02} и т. д. Получим счётное
множество В := {ах, 02, аз,...} С Л. J
Определение 3. Мномсество конечное или счётное
называется не более чем счётным.
ТеОремаЗ. Если для множества А существует инъ-
инъекция f : А -¥ N, то мномсество А не более чем счётно.
|" По теореме 1 множество f{A) не более чем счётно. Поскольку / :
А —> f(A) есть биекция, то множество А также не более чем счётно. J
Упражнение 28. Пусть А - бесконечное множество и х $ А. До-
Доказать, что (A U {х}) ~ А.
Упражнение 29. Пусть А - бесконечное множество и В - счётное
множество. Доказать, что (A U В) ~ А.
Теорема 4. Объединение счётного семейства счёт-
счётных мноок.еств счётно.
\ Пусть А\,Аъ,-. ■ ,Ап,... - счётные множества. Тогда для каждого п >
1
оо
Ап = {ani,an2,an3,...,ann,...}, а объединение \J Ап = {атп \ т £
п=1
N, n G N} есть множество, состоящее из всех элементов таблицы
рис. 1, которые можно занумеровать, например, в порядке, указанном
стрелками на рис. 1.

28 Глава I. Введение
12 6
аи -> а12 а13
4 9
a31 a32 a33 a34 ■ • • a3n
10
a41 a42 а4з a44
ап3 ап4
Рис. 1.
Предыдущая теорема имеет следующее обобщение.
Теорема 5. Объединение не более чем счётного се-
семейства не более чем. счётных м/номсеств не более чем.
счётно.
Упражнение 30. Другое доказательство теоремы 4. Проверить,
оо
что функция / : (J Ап —> N, определённая следующими равенствами
п=1
f(amn) := 2m3n, m G N, п £ N, есть инъекция.
Упражнение 31. Объединение двух счётных множеств счётно.
Теорема 6. Декартово произведение двух счётных
мномсеств счётно.
[ Пусть А = {а1,а2>...,ап,...}, В = {Ьь Ь2,... ,Ь„,...}, тогда множе-
множество Ах В состоит из пар (ат,Ьп), т £ N, n G N, которые распола-
располагаются в таблицу, аналогичную изображённой на рис. 1, и могут быть
аналогично занумерованы. J
Приведём теперь следующий важный принцип, часто используемый
в математических рассуждениях.

1.4. Мощность множества. Счётные множества 29
Принцип математической индукции. Пусть М — та-
такое множество, что:
1) 16М;
2) Vn 6 N из того, что п £ М => (п + 1) б М. Тогда
М D N. В частности, если М С N, то М = N.
Этот принцип (иногда говорят метод математической ин-
индукции) является аксиомой натуральных чисел.
Упражнение 32. Доказать, что принцип математической индукции
равносилен утверждению: любое непустое подмножество множества
N имеет наименьший элемент.
Упражнение 33. Доказать неравенства:
аJп>п, п>1; ЬI + ^+^+... + \<2--, п > 1;
2 6 п
Упражнение 34- Доказать, что для любого п € N число бп +72?+3
делится на 43.
Упражнение 35. Вывести из принципа математической индукции
такое утверждение. Пусть к £ N — фиксированное число и М — мно-
множество такое, что:
\)кЕМ;
2) V п £ N, п > к из того, что п € М => (п + 1) € М.
Тогда М Э {к, к + 1, к + 2, к + 3,...}.
Пусть А = {ах, а-2,..., ап,...} — счётное множество и для фиксиро-
фиксированного те N Ат = {{ак{1),ак{2),---,ацт)) \ k(j) e N, 1 < j < m}
— множество всех упорядоченных m-членных цепочек элементов из А.
Теорема 7. Для каждого m £ N мноэ+сество Ат счё-
оо
тно. Множество В := (J Ат такмсе счётно.
т=1
\ Пусть число т £ N фиксировано. Тогда следующая функция
си \\ fc(l) fcB) Цт) ,
f{{ak(i),akB),---,dk(m))) :=Pi 'р2 ■■■Рш ', где рир2,... ,рт - фик-
фиксированные попарно взаимно простые натуральные числа, есть инъек-
инъекция множества Ат в множество N. Второе утверждение есть следствие
теоремы 4. Другое доказательство следует и теоремы 6 и принципа ма-
математической индукции. J
Упражнение 36. Доказать, что множества Z и Q счётны.
Упражнение 37. Доказать, что множество всех многочленов с ра-
рациональными коэффициентами счётно.

30 Глава 1. Введение
Упражнение 38. Алгебраическим числом, называется корень
многочлена с целыми коэффициентами. Рациональные числа являют-
являются алгебраическими. Доказать, множество всех алгебраических чисел
счётно.
Указание: многочлен степени п не может иметь более, чем п
корней.
Теорема 8. Существуют несчётные множества.
\ Пусть А - множество всех возможных бесконечных последовательно-
последовательностей, составленных из двух символов, например, из 0 и 1, следующего
вида х = @,1,1,0,1,0,... ,0,...). Множество А несчётно. Действитель-
Действительно, допустим, что элементы множества А занумерованы:
xi = (ап, аг2, ..., а1п, ...),
Z2 = (а2Ь а22, • • •> а2п, ■ ■ ■),
хп = (а„1, ап2, ..., апп, ...),
где каждое из чисел атп равно 0 или 1. Однако следующий элемент
У = (bi, Ь2,.-., Ь„ ,...)• в котором Ъх ф а1Ь Ь2 ф а22, ••• ,Ьп ф а„„, ••• и
каждое Ьп равно 0 или 1, принадлежит согласно определению множе-
множеству А, однако не совпадает ни с одним из занумерованных. Полученное
противоречие показывает, что элементы множества А нельзя зануме-
занумеровать. J
Замечания. 1. Метод рассуждения, использованный при доказа-
доказательстве теоремы 7, называется диагональным методом Кан-
Кантора.
2. Следует сравнить доказательство теоремы 8 и упражнение 27.
Упражнение 39. Доказать, что множество 2^ несчётно.
Упражнение 40* • Доказать, что множество А из доказательства
теоремы 8 и множество 2^ равномощны.
1.4.1 Историческая справка
Кантор Георг A845 — 1918) — выдающийся немецкий мате-
математик (родился в Петербурге), создатель теории множеств — основа-
основания всей современной математики. Его революционные математические
идеи были встречены непониманием и необоснованной критикой со сто-
стороны многих ведущих математиков того времени. Работы Кантора были
по достоинству оценены и признаны лишь спустя несколько десятиле-
десятилетий после их опубликования. Они оказали исключительно плодотворное
влияние на развитие современной математики. Позже теория бесконеч-
бесконечных множеств, предложенная Кантором, была названа наивной теорией

1.5, Действительные числа 31
множеств. Она приводит к ряду логических противоречий, которые бы-
были известны и самому Кантору. Защищал теорию Кантора величайший
математик всех времён Д. Гильберт A862 — 1943), в частности
заявивший, что «Никто не изгонит нас из рая, созданного Кантором».
Дальнейшее развитие математики подтвердило правоту Д. Гильберта.
1.5 Действительные числа
1.5.1 Введение
Натуральные и положительные рациональные числа, а также их свой-
свойства, известны около 4 000 лет. Однако, ещё в древности математикам
пришлось столкнуться с необходимостью введения чисел иной природы.
Обнаруженная в школе Пифагора E70 - 496 г. до н.э.) несоизмери-
несоизмеримость диагонали и стороны квадрата означает, что длина диагонали не
может быть выражена рациональным числом, если в качестве единицы
длины взять длину стороны квадрата. Необходимость введения чисел,
отличных от рациональных, возникает и при решении простейших урав-
уравнений типа х2 — 6 = 0.
Пример. 1. Не существует числа х £ Q такого, что х2 = 2.
[ Назовём число — ст£ЛГип€ЛГ "настоящей" дробью, если
п
п > 1 и числа тип взаимно просты. Если — "настоящая" дробь,
п
2
то —г- также "настоящая" дробь. Следовательно, v2 не может быть
п2
"настоящей" дробью. Кроме того, число \/2 $ N, так как I2 < 2, 22 =
4>2ит. д. J
Упражнение ^1. Доказать, что: а)\/б ^ Q; Ь)(у/2 + \/3) £ Q.
Упражнение £2*. Пусть а = гтг, г £ Q, 0 < а < — . Доказать,
что: а) если г ф — , то sin a (£ Q; Ь) если г ф — , то tg a ^ Q.
Упражнение £3. Для каждого п £ N число -Jn б N или -Jn £ Q.
Упражнение 44- Для любых {т,п} С N число mlln £ N или
т}'п $ Q.
Далее предполагаются известными свойства нату-
натуральных, целых и рациональных чисел, а также прави-
правила перевода простой рациональной дроби в десятичную
и десятичной периодической дроби в простую.
3 — 4-1168

32 Глава I. Введение
К понятию действительного числа приводит задача об измерении от-
отрезка. Пусть задана единица длины, например метр, и мы хотим изме-
измерить длину заданного отрезка J. Предположим, что 1 м укладывается
целиком на J 13 раз и при этом остаётся отрезок J\, длина которого
меньше 1 м. Тогда длина отрезка J приближённо равна 13 м: длина
J и 13 w. Если такая точность неудовлетворительна, то можно рас-
рассмотреть — единицы измерения, то есть 1 дм, и определить, сколько
раз 1 дм укладывается целиком в остатке J\. Пусть 1 дм укладывается
целиком в остатке J\ 7 раз и при этом получается остаток J2, длина
которого меньше 1 дм. Так получаем более точное приближённое зна-
значение длины J : длина J к 13, 7 м. Продолжая процедуру получения всё
более точных приближений для длины J, приходим к реализации одной
из следующих двух возможностей:
(i) либо на каком-то шаге, например на (п 4- 1)-ом, —- единицы длины
отложится на остатке предыдущего шага Jn точно ап раз. В этом случае
процесс измерения приведёт к точному значению длины J :
длина J = 13, 7«2 • • • &п м. A)
(ii) Либо процесс измерения будет продолжаться неограниченно2 (на-
4
пример, если длина J равна - м) и тогда точным значением длины J
следует считать бесконечную десятичную дробь
длина J = 13, 7«2 .. .ап ... м.
Упражнение 4-5. Проверить, что в результате процесса измерения
отрезка бесконечная десятичная дробь с цифрой 9 в периоде получена
быть не может.
Заметим теперь, что конечную десятичную дробь A) можно рас-
рассматривать как бесконечную, считая равными 0 все знаки после п-го:
13, 7а2 ... ап = 13, 7а2 . ■. а„000 ... О ....
Таким образом, процесс измерения отрезка приводит
рассмотрению бесконечных десятичных дробей вида
ао,а1а2...ап ■■■, B)
где
a06(iVu{0}); VneN: an £ {0,1,2,3,4,5,6,7,8,9}, C)
причём дробь B) цифры 9 в периоде не содержит.
Упражнение 4^6. Что означает для дроби B) утверждение:
Предположение о неограниченности процесса измерения ивлиетси типичным примером
математичеекой абстракции. Для реальной процедуры измерения па определенном этапе
начнёт сказываться дискретность вещества.

/.5. Действительные числа 33
a)VneJV3m>n: am ^ 9? Ь)Эп€ЛГУт>п: ат = 9?
Рассмотрим прямую с фиксированной точкой О — началом коорди-
координат и фиксированной единицей длины. Тогда каждой точке Р, лежащей
на этой прямой справа от точки О, можно поставить в соответствие
бесконечную десятичную дробь вида B), не содержащую цифры 9 в
периоде, как результат измерения отрезка ОР. Точке О поставим в
соответствие дробь 0,00 ... О ... .
Это соответствие между точками полупрямой и дробями вида B),
удовлетворяющими условию C) и не содержащими цифры 9 в периоде,
взаимно однозначно. В частности, среди этих дробей есть и та, которая
отвечает отрезку, равному диагонали квадрата со стороной 1.
Все дроби вида B), удовлетворяющие условию C) и не содержащие
цифры 9 в периоде, можно разбить на два класса:
(i) периодические, в том числе дроби вида A), они переводятся в
неотрицательные рациональные числа и их можно отождествить с этими
рациональными числами;
(ii) дроби непериодические. Они представляют новые, нужные для
решения математических задач, числа, зто иррациональные числа.
В частности, длина диагонали квадрата с единичной стороной есть ир-
иррациональное число.
1.5.2 Определение действительных чисел
Определение 1. Неотрицательное действительное
или вещественное число есть бесконечная последовате-
последовательность цифр с одной запятой меснсду ним/а, то есть
бесконечная десятичная дробь вида а = ао>а1а2 • • -ап ■ ■ ■ ,
где числа аое(ЛГи{0}); У п £ N : an € {0,1,2,3,4,5,6,7,8,9}.
Неотрицательное действительное число а называет-
называется положительным, если Зп € (ЛГи{0})': ап > 0.
Отрицательное действительное число есть по опре-
определению полоэ+сительное действительное число со зна-
знаком "-".
Множество всех действительных чисел обозначается символом R.
Замечания. 1. С учётом обсуждения в п.1.5.1 имеем следующие
включения N С Q С R.
2. Правила действий со знаком "—" в Н те же, что и в множестве
Q. Поэтому далее в настоящем п.1.5.2 рассматриваются только неот-
неотрицательные действительные числа.

34 Глава 1. Введение
Определение 2. Числа из множества R\Q называ-
называются иррациональными3.
Определение 3. Неотрицательные действительные
числа а — ao,aict2 .. .ап... и b = /3o,/3i/32 • ■ -Рп ■ ■ ■ называются
равными (обозначение: а = Ь) в одном из следующих двух
случаев:
(г) Vn£(JVu{0}): ап = 0„;
(и) 3 п е (ЛГ U {0}) : ак = /3fc, 0 < к < п, ап - /3„ + 1;
\/т>п: ат = 0, рт = 9
(при п = 0 равенство с индексом, к следует опустить).
Далее, рассматривая действительные числа, ограничимся деся-
десятичными дробями, не содержащими цифры 9 в периоде.
Определение 4- Пусть числа а = ao,otiot2 ■ ■ .&п ■ ■■ и
b = Po,Pip2 ■ ■ -Рп ■ ■ ■ — неотрицательны. Число а меньше
числа b (обозначение: а < Ъ) или число b больше числа а
(обозначение: Ъ > а), если
3 п £ (AT U {0}) : ак = j8fcl 0 < к < п, ап < рп
( при п = 0 равенство с индексом, к следует опустить).
Упражнение £7. Проверить, что:
а) для чисел вида A) п. 1.5.1 неравенство из определения 4 совпа-
совпадает с обычным неравенством в Q;
б) для периодических бесконечных дробей неравенство определе-
определения 4 совпадает с обычным неравенством между соответствующими
рациональными числами.
Упражнение ^8. Доказать, что для любых {а, Ь} С R справедливо
одно и только одно из соотношений: а = Ь, а < Ъ, а > Ь, то есть
любые два действительных числа сравнимы.
Упражнение 49. Доказать, что для любых {а,Ь, с} С R а > b и
Ь > с =Ф- а > с.
1.5.3 Числовая прямая
Рассмотрим прямую с фиксированной точкой О — началом координат.
Пусть также задана единица длины. Множество R можно поставить во
взаимно однозначное соответствие с точками прямой следующим об-
образом. Точке Р, лежащей на прямой справа от точки О, поставим в
соответствие число х £ R, равное длине отрезка ОР\ точке Q, лежа-
лежащей на прямой левее точки О, — число —у, где у — длина отрезка QO;
От лат. irracionalis — неразумный.

1.5. Действительные числа 35
точке О — число 0=0,00. . . 0. . . . Число я, которое отвечает точке Р,
называется координатой точки Р, а прямая с описанным соответ-
соответствием называется числовой прямой.
Многие свойства действительных чисел имеют простую геометриче-
геометрическую интерпретацию на числовой прямой. Например, неравенство а < b
равносильно тому, что точка с координатой а лежит слева от точки с ко-
координатой Ь. Эта же геометрическая интерпретация может быть исполь-
использована для геометрического определения суммы действительных чисел,
как это делали древние греки и их последователи.
Пусть а £ R, b £ R и а < i. Далее постоянно используются следую-
следующие понятия:
[а, Ь] :— {я £ R | а < я < 6} — отрезок;
(а, Ь) := {я £ R \ а < х < Ь} — интервал;
[а, Ь) := {я £ R | а < х < 6} — полуинтервал;
(а, Ь] := {я £ R | а < я < Ь} — полуинтервал;
1IИсла а и b называются концами.
■" Кроме того, для а £ R положим [а, +оо) := {я £ R \ х > а},
f— со, а) := {я 6 R \ я < а}, (-оо, +оо) := R.
1.5.4 Элементарные
свойства действительных чисел
Следующие два простых утверждения весьма важны для дальнейшего
изложения.
1°. Аксиома Архимеда. V а £ R Зтп £ JV : т > а.
[ Пусть а = аО1 а1 ■ ■ ■ ап ■ ■ ■ > 0. Положим т := ао + 1, тогда т £ JV и
согласно определению 4 получим а < т. J
2°. Уа£Я УЬ£Я,а<Ь: (а,Ь)^0.
[ Докажем, что существует число г £ Q, для которого г £ (а, Ь). Пусть
а = ао,«1«2 .. .а„ ... > 0, Ь = Po,PiP2 ■ ■ -(Зп ■ • ■, причём для некоторо-
некоторого числа т £ (JVu{0}) ао = ро, ах-рх, ..., ат^х = 0т_ь ат < рт-
Пусть к - минимальный номер из тех, которые больше т и для которых
Qfc < 9. Положим г := ао, ах ... атат+х ... («& + 1). Тогда число г £ Q
и а < г < b. J
Упражнение 50. Доказать, что множество (а, Ь) П Q счётно.
Упражнение 51. Доказать, что любое семейство попарно непере-
непересекающихся интервалов на прямой не более чем счётно.
Упражнение 52. Доказать, что любое семейство интервалов с кон-
концами из Q на прямой не более чем счётно.

36 Глава 1. Введение
Упражнение 53. Доказать, что любая система попарно непересе-
непересекающихся кругов в плоскости не более чем счётна.
Упражнение 54- Доказать, что множество [0,1] несчётно.
Определение 5. Мноэ+сестео, равномощное мноэ+се-
ству чисел [0,1], называется множеством, мощности
континуум.
Упражнение 55*. Доказать, что @,1) ~ [0,1] ~ R ~ Я2 ~ Я3.
Относительно третьего утверждения Г. Кантор в 1877 г. писал Р.
Дедекинду «Я вижу зто, но не могу в зто поверить». Тем не менее Г.
Кантор поверил в правильность полученного им результата. Об этом и
других интересных деталях см. книгу М. Клайна Математика. Утрата
определённости. Москва. Мир. 1984.
1.5.5 Точные грани множества действительных чисел
Определение 6. Пусть Ac R. Если БаеАЧЪеА: Ъ <
а, то число а называется наибольшим или максималь-
максимальным элементом мноэ+сества А и обозначается одним, из
символов а = max А = тах{х | х £ А} = max х.
Если 3c€AVb€A: b > с, то число с называет-
называется наименьшим или минимальным элементом множе-
множества А и обозначается одним из следующих символов
с = min.A = min{x | х € А} = min x.
Примеры.
1. Для А — {1,2,3,4,5} имеем min A = I, max A = 5.
2. Для множества А = N имеем min A = 1 и максимального эле-
элемента не существует, так как Vn€JV 3(n + l)£JV: n + 1 > п, то
есть любой элемент множества А не является максимальным.
3. Пусть А - конечное множество чисел из R. Проверить, что min A
и max .А существуют.
4. Пусть А = Z. Проверить, что для множества Z наибольшего и
наименьшего элементов не существует.
5. Пусть А = f I i , i .... - ,...}= {- п 6 JV}. Тогда max A = 1,
12 6 п Jin i
так как Vn £ N : — < 1 -Ф=Ф- п > 1. Наименьшего элемента множе-
множество А не имеет, так как Vn £ N 3 (п + 1) £ JV : < — ■£=>• п <
п + 1 п
п + 1, то есть любой элемент — £ А не является наименьшим.
п

1.5. Действительные числа
Упражнение 56. Найти min А и max A :
Определение 7. Пусть А С R. Если Зс£ЯУя£.А: с <
х, то множество А называется ограниченным снизу, а
число с называется нижней гранью множества А.
Если 3d6 й Vi e A: х < d, то мномсество А называ-
называется ограниченным, сверху, а число d — верхней гранью
множества А. Множество, ограниченное снизу и свер-
сверху, называется ограниченным..
Примеры.
1. Для множества А = N любое число с < 1 является нижней гра-
гранью, следовательно множество N ограничено снизу. Множество JV
не имеет ни одной верхней грани, так как согласно аксиоме Архимеда
Vd£.R3n£iV: n > d. Следовательно, множество N не ограничено
сверху и не является ограниченным.
2. Множество А = Z не ограничено и снизу и сверху.
3. Множество А= \— п 6 N> ограничено снизу, так как любое
In >
число с < 0 является нижней гранью множества А. Оно ограничено
сверху, так как любое число d > 1 является верхней гранью множества
А. Следовательно, множество А ограничено.
Упражнение 57. Доказать, что конечное множество А С R огра-
ограничено.
Упражнение 58. Доказать, что множество А ограничено тогда и
только тогда, когда 3 с € R Vie А: -с < х < с -Ф=Ф- |х| < с.
Упражнение 59. Доказать, что следующие множества ограничены:
a) {sinn | п £ N}, Ъ) {—^~r n £ Лг|,
Определение 8. Пусть Ас Д. Число с* £ Я называет-
называется точной нижней гранью множ.ества А, если:
1) с» — нижняя грань мномсества А;
2) Vc — нижней грани множ.ества А: с < с».
Число с* £ Я называется точной верхней гранью мно-
ж.ества А, если:
1) с* — верхняя грань множ.ества А;
2) Vd — верхней грани мномсества А: с* <d.

38 Глава 1. Введение
Обозначения: с» = inf A — inf{x | х G А} = inf х, с* — sup A =
xdA
sup{x | х £ А} = supx.
Замечания. 1. Согласно определению 8, точная нижняя грань
множества есть наибольшая из нижних граней этого множества. Ана-
Аналогично, точная верхняя грань множества есть наименьшая из верхних
граней этого множества.
2. Точные грани могут не существовать. Например, N не имеет
точной верхней грани, так как оно не имеет ни одной верхней грани.
Упражнение 60. Проверить утверждения: а) если с* = inf А, то
любое число с < с* является нижней гранью множества А; Ь) если
с* = sup А, то любое число d > с* является верхней гранью множества
А. Таким образом, если с* = inf А, с* = sup .А, то А С [с*, с*].
Упражнение 61. Если существует min.A, то inf A = minA Если
существует max А, то sup A = max А Проверить эти утверждения.
Упражнение 62. Если множество А не ограничено сверху, то зто
множество не имеет точной верхней грани. Если множество А не огра-
ограничено снизу, то это множество не имеет точной нижней грани. Прове-
Проверить эти утверждения.
Теорема 9. Число с* = inf А тогда и только тогда,
когда:
1) с* — нижняя грань множества А;
2) Va>c, 3i6 А: х < а.
Число с* =supA тогда и только тогда, когда:
1) с* — верхняя грань множества А\
2)Va<c* Зх Е А: х > а.
\ Доказательство рассмотрим для нижней грани. Пусть с» = inf А Тогда
условие 1) теоремы выполнено согласно определению нижней грани.
Условие 2) также выполнено. Действительно, если для некоторого числа
а > с, не существует х £ А такого, что х < а, то, следовательно, для
любого х £ А имеем х > а и потому а есть нижняя грань, большая, чем
с». Последнее противоречит определению точной нижней грани.
Предположим теперь, что условия 1) и 2) выполнены. Тогда выпол-
выполнены оба требования из определения точной нижней грани, поскольку
из 2) следует, что любое число а > с* нижней гранью не является.
Следовательно, с* - наибольшая нижняя грань. J
Пример. 1. Пусть А—{—
Докажем, что inf A = 0.
п £ ЛГ}. Тогда sup A = max A = 1.

1. 5. Действительные числа 39
Г Воспользуемся теоремой 9. Условие 1) выполнено, поскольку 0 < —
п
для любого п £ N. Рассмотрим теперь любое число а > 0. Тогда су-
существует г G Q, для которого 0 < г < а и существует п Е N такое, что
1 г, - ! !
— < г < а. Действительно, — < г -Ф=> п > - и можно воспользо-
п п г
ваться аксиомой Архимеда. Поэтому условие 2) также выполнено. J
Обратим внимание на то, что гшпЛ не существует, а также на то,
что inf А = 0 $ А.
Условимся дальше писать sup A = +оо или inf A = —оо, если мно-
множество А не ограничено сверху или если множество А не ограничено
снизу соответственно.
1.5.6 Действительное число как точная грань
чисел рациональных
Рассмотрим представление любого действительного числа как точной
грани множества чисел рациональных. Пусть а = ао,а\а2 ■ ■ -ап ... —
произвольное неотрицательное число. Для каждого п Е (Nu{0}) обо-
обозначим а'п := ао, aia2 ... ап; а'п := ао, aja2 ... (ап + 1). Здесь запись
для числа а'п условна, если ап = 9, в этом случае n-ый знак после запя-
запятой равен 0, а предыдущий увеличен на 1. Числа а'п и а'п суть конечные
десятичные дроби. Согласно определению неравенства между действи-
действительными числами для любого п £ [N U {0}) имеем такие неравенства
Теорема 10. Для любого неотрицательного действи-
действительного числа а выполняются следующие равенства:
а = supa^,, a = inf a'n.
n>0 n>°
f Рассмотрим доказательство только первого равенства. Множество
{an I n ^ 0} ограничено, поскольку для любого п > 0 имеем 0 < а'п < а.
Если a = 0, то а'п = 0 для всех п > 0 и утверждение верно. Предполо-
Предположим теперь, что a > 0. Воспользуемся теоремой 9. Число а удовлетво-
удовлетворяет условию 1) этой теоремы. Проверим выполнение условия 2). Пусть
b = Ро,Р1Р2 ■■ -Рп ■■■ — любое число такое, что 0 < Ъ < а Согласно
предположению Ъ < a 3m£ (ЛГи{0}) : Рк = а*, 0 < к < т; рт < ат.
Но тогда а'т > Ъ. Таким образом, условие 2) теоремы 9 для числа а так-
также выполнено. J
Упражнение 63. Доказать второе утверждение теоремы 10.
Упражнение 64- Пусть А С В и В ограничено сверху. Доказать,
что sup A < sup В.

40 Глава I. Введение
Упражнение 65. Множества А и В ограничены сверху. Доказать,
что sup( A U В) = max(sup A, sup В).
Упражнение 66. Пусть А = {а — а0, aia2 ... ап ... | ао = 0, ац =
1,а2 = 5}. Найти inf А и sup А.
1.5.7 Теорема о существовании точных граней
Теорема 11. Непустое ограниченное сверху множе-
множество действительных чисел имеет точную верхнюю
грань. Непустое ограниченное снизу множество дейст-
действительных чисел имеет точную нижнюю грань.
[ Докажем первое утверждение, доказательство второго аналогично.
Достаточно рассмотреть случай, когда А С [0, +оо) и А ф 0. По усло-
условию теоремы множество А ограничено сверху, следовательно имеем
ЗсЕ-RVaE-A: а < с. С учётом аксиомы Архимеда можно считать,
Пусть Во := {а0 £ [N U {0}) | 3 a G А : а = а0, c*i.'■.}. Множество
Во ф 0 и ограничено сверху числом с. Следовательно, Во — огра-
ограниченное подмножество множества N U {0}, то есть Во — конечное
множество неотрицательных целых чисел. Поэтому существует верхняя
грань тахВ0 =: ш0, ш0 € (ЛГи{0}).
Положим теперь Ао := {a G А | а = ш0, ai...}, Ао С А, Ао ф 0.
Пусть далее Вх := {сц G {0,1,2,3,4,5,6,7,8,9} | 3a G Ло : а =
= wo,Q:ia2 • • •}• Тогда множество Bi ф 0 и конечно. Поэтому существу-
существует тахВх =: wi, wi G {0,1,2,3,4,5,6,7,8,9}.
Положим далее i4i := {a G Ло | а = ш0, ш\а2 .. ■}, Ai С Ао, Ai ф 0.
Аналогично, пусть В2 := {а2 € {0,1,2,3,4,5,6,7,8,9} | За G i4i :
а = ша,ш\а2аг ■ ■ •}, множество В2/0и конечно, следовательно, су-
существует тахВ2 =: ш2, ш2 G {0,1,2,3,4,5,6,7,8,9}.
Определим множество А2 := {a G Ai | a = wo,wiw2Q3 • • •}, -^2 С
Ai, ^2 ф 0-
Продолжая аналогично построение чисел шз,ш^,Ш5 и т. д., получим
действительное число z := шо, ш\ш2 ... wn ... .
Докажем, что z = sup Л. Для этого проверим выполнение условий
теоремы 9. Для проверки условия 1) заметим, что согласно определе-
определению числа Wo для любого а = а^,а\... из А справедливо неравенство
"о < ^о. Если при этом ао < и>о, то а < z. Если же ао = и>о, то число
а = и>о,ас\... входит в Ло и по определению шх имеем ai < ш\. Если
"l < wi, то а < z. Если же а-\. = uiy, то число а = и>о,Шуа2... входит
в А\ и по определению числа ш2 имеем а2 < ш2 и т. д. В результате
возможны следующие два исхода:

3|.5. Действительные числа 41
(i) 3 п е N : ао=шо, а1=ш1, ... , an_j = wn-i, an < шп;
тогда а < z;
(ii)VnG(iVu{0}): an=wn,
тогда а = z. Таким образом, в обоих случаях a < z и z — верхняя грань
<1 множества А.
Для проверки условия 2) теоремы 9 рассмотрим любое число d —
&>.<М2 • • -Ьп ■.. < z. Согласно определению неравенства между числа-
числами
' 3mG(iVu{0}): 60 = ш0, 61 = Wi, ..., 6m-i = шт-1, Sm < шт,
тогда для любого х G Ат С А имеем х > d. J
", Замечания. 1. Построенное при доказательстве теоремы с помо-
'щью определённого процесса число z может иметь цифру 9 в периоде.
' 2. Число z может принадлежать, так и не принадлежать, множеству А.
] Упражнение 67. Найти число z для множества А = [0,1).
ч,, *
Упражнение 68. Проверить, что теорема 11 не верна в Q. Точнее.
Непустое ограниченное множество А С Q согласно теореме 11 имеет
sup .А, однако число sup А не обязательно рационально.
Упражнение 69. Пусть А — {О.сцаг .. .ап ... | Vn G N : а„ 6
{1,2,3,4,5,6,7,8}} Найти sup А и inf A.
1.5.8 Действия над числами
Арифметические действия над числами из Q и над конечными десятич-
десятичными дробями предполагаются известными.
Пусть а и Ъ — произвольные положительные числа.
Определение 9. Положим по определению а + Ъ :=
sup(a^ + Ь'п), а-Ь:= sup« • Ъ'п), г := sup -£ ; для а > Ь а - Ь :=
п>0 n>0 ° п>0 °п
sup(a'n - Ь£); а0 := 1; V п е N : ап := а-а-. ..а.
п>0 " ч/ '
— п
Зал«ечамгхя. 1. Все числа, фигурирующие в определении 9 под
знаком sup, рациональны и для них арифметические операции опреде-
определены.
2. Выше было показано, что sup А не всегда существует. Однако,
в определении 9 все точные верхние грани существуют. Рассмотрим,
например, случай суммы двух чисел. Для каждого п Е (ЛГи{0}) имеем
а'п < а < а'п, Ъ'п < Ь < Ь'п, следовательно, а'п < aj,', b'n < Щ; откуда
следует, что а'п + Ъ'п < а'о' + Ь'о'. Таким образом, число Oq + bg — верхняя

42 Глава I. Введение
грань множества {а'п + Ь'п \ п £ (N и {0}), поэтому это множество
ограничено и по теореме 11 имеет точную верхнюю грань.
Упражнение 70. Доказать существование всех точных граней в
определении 9.
Относительно свойств, введенных в определении 9 операций над дей-
действительными числами, заметим следующее. Все известные свойства
арифметических операций над рациональными числами справедливы и
для операций из определения 9 над любыми действительными числами.
Однако.теперь эти свойства нуждаются в доказательстве. Например,
для любых положительных чисел а и Ь справедливо такое равенство
а + b = b + а, то есть равенство sup(a^ + b'n) ~ supF^ + а'п). Послед-
п>0 п>0
нее равенство очевидно, поскольку для рациональных чисел а'п + Ь'п =
Ь'п + а'п, п > 0. Более сложным является доказательство того, что
а + а = 2а, которое равносильно следующему равенству sup(a^ + a^) =
sup(B)'n-а'„), которое, однако, сводится к просто проверяемому равен-
п>0
ству supBa^) = 2sup(a^) с учётом того, что B)^ = 2, п > 0.
п>0 п>0
Упражнение 71. Доказать равенства:
а) a ■ Ъ = Ъ ■ а, Ъ) а + {Ь + с) - {а + Ъ) + с =: а + b + с,
с) a • (b ■ с) = (a • b) ■ с =: a • b ■ с.
d)a + b= inf« + b;0, a>0, 6 > 0.
n>0
В настоящей книге доказательства всех свойств операций над дей-
действительными числами из определения 9 не приводятся.
1.5.9 Неравенства для модуля суммы и Я. Бернулли
Для числа a E R положим а\ := < ' ~ . Отметим, что
[ —a, a < 0.
— \а\ < а < \а\, а также то, что \а\ < с <=> —с<а<с. Эти утвержде-
утверждения систематически используются в дальнейшем. Кроме того, \а\ = \ — о.\-
Теорема 12. Для любых a G R, b G R справедливы нера-
неравенства: 1) |о + Ь| < |a| + |b|, 2) \а-Ь\ > ||а|-|Ь||. Для любых чи-
чисел 01,02,... ,ап из R справедливо следующее неравенство
|о! + а2 + ... + о„| < |ai| + |а2| + ... + \ап\.
f Поскольку — \а\ < а < \а\, —\Ь\ < Ъ < \Ь\, то после сложения этих
неравенств имеем — [\а\ + \Ь\) < а + b < \а\ + \Ь\, то есть справедливо
неравенство 1). Заметим теперь, что в силу 1) \а\ = \а — b + b\ <

IJ.5. Действительные числа 43
<\a-b\ + \b\, откуда \a\ - |Ь| < \a - b\. А поскольку \a— b\ = \b- a\ > \b\ -
\\a\, то получаем 2). Последнее неравенство теоремы получается, как и
(неравенство 1), сложением неравенств — |afc| < а*; < |ctjt|, 1 < к < п. J
Теорема 13. Для любых чисел a > -1 и п G N справед-
справедливо неравенство A + а)п > 1 + па, (неравенство Я. Бер-
Бернулли), в котором знак равенства имеет место тогда
и только тогда, когда п = 1 или а = 0.
[ При п = 1 и а = 0 неравенство выполнено со знаком равенства. Пусть
а ф 0, тогда при п = 2 имеем A + аJ = 1 + 2а + а2 > 1 + 2а. Используем
теперь принцип математической индукции. Утверждение теоремы 13
верно для п = 2. Предположим, что неравенство верно для индекса
п > 2. Тогда получим A + a)n+1 = A + a)(l + a)n > A + a)(l + па) =
.= 1 + (n + l)a + na2 > l + (n + l)a. J
Унраменепис У^-Пусть a > О, Ь > -a и n G N. Доказать, что
(a + b)n > an + пап~1ъГ\ (неравенство Я. Бернулли), причём
:гггТ<~равенства возможен тогда и только тогда, когда п = 1 или Ь = 0.
Укозомгхе. Положить в теореме 13 число a = — и умножить по-
a
лученный результат на положительное число ап.
Упражнение 73. Доказать, что:
аJп>п + 1, п>1; bKn>2n + l, n > 1; с) 2п > {^2-1Jп2, п > 1;
с!)дляА;е]У: Зп > (^3 - l)fcnfc, n > 1.
Указание к с), d). Использовать неравенство Бернулли и пред-
представление 2п = {{-ЛуJ = (A + [у/2 - 1))пJ.
Упраэктение 74- Пусть а\, аг,..., ап — положительные числа. До-
Доказать, что A + ai)(l + a2) •... • A + an) > 1 + а\ + а2 + ... + аи-
Упражнение 75. Пусть: a > 0, п € N, 0 < Ь < —. Доказать, что
1
1.5.10 Определение корня натуральной степени из
положительного действительного числа
Теорема 14. Пусть а > 0 и п е N. Тогда
3 \х > 0 : in = a.
\ Достаточно рассмотреть случай, когда а ф \ и п > 1. Введём множе-
множество Л := {у > 0 | уп < а}. Множество А ф 0. Действительно, если
а < 1, то ап < а и потому а £ Л. Если же а > 1, то 1П = 1 < а и

44 Глава I. Введение
1 € А. Множество А ограничено сверху числом с := тах{1,а}. Дей-
Действительно, если у £ А и у < 1, то у < с. Если же у £ А и у > 1,
то у < у™ < а и снова у < сдПоэтому к множеству А применима
теорема оч"сущёс^ованШ~*г&ч?гбйг верхней грани. Пусть х := sup А, при-
причём х > 0. Поскольку {я", а} С R, то возможен один из трёх случаев:
(г) хп > a, (ii) ж" < а, (ш) жп = а.
Предположим сначала, что верно неравенство (i) xn > а. Тогда чис-
ло Д := хп — а > 0. Пусть т £ N таково, что х > — -Ф=> m > — . Co-
Corn х
гласно неравенству Бернулли, имеем I х ] > хп . Подчи-
\ m J m
пхп'1
ним теперь число т дополнительному условию < Д *\ у т >
птп"~1 г 1 гтгп~^ 1
lltdr . ~ [1 Ibdr \
—-— , то есть возьмем m таким, чтобы т > тах< —, —-— >, Тогда
Д L х Д )
х ) > хп — Д = а, и, следовательно, (х )^ А. Потому
m J V m '
Vz > х — 1/m : z ^ Л, откуда ж = sup A < х — 1/m, что противоречит
определению числа ж.
Рассмотрим теперь случай (ii) хп < а. Тогда число 6 := а — хп > 0.
1 ж 2п
Для числа т такого, что — < — •■£=> m > —, согласно неравен-
т 2п х
п
( 1 У 2м
ству упражнения 72, имеем i H < х -\ . Если теперь
\ т J m
Bп 2м"-1 -. / 1 \п
число т взять таким, чтобы т > < — , z >, то \х -\ <
I i о J у т J
< хп + 6 — а. Следовательно, число (х-\ )€. А и х -\ > х, что
\ т) т
противоречит определению числа х.
Таким образом случаи (i) и (ii) приводят к противоречиям и, сле-
следовательно, справедливо равенство хп — а. Число, удовлетворяющее
последнему равенству, является единственным. J
Теорема о существовании корня натуральной степени является осно-
основой следующего определения.
Определение 10. Пусть а > 0 и п € N. Корнем п-ой
степени из положительного числа а называется един-
единственное положительное число х, удовлетворяющее ра-
равенству хп = а.
Обозначения для числа х: ^/а = а1//п. Условимся также считать, что
{/0 = 0, neN.
Определение 11. Пусть а > 0 u r e Q, г>0. По опре-
определению аг := (а771I/", где г = — , m G N, n G N.
п

1.5. Действительные числа 45
Определение 12. Пусть a > 1 и Ъ > 0. Положим по
определению ab := sup аЬп.
п>0
Введенная выше операция возведения в степень обладает всеми из-
известными из школьного курса математики свойствами.
Упражнение 76. Доказать существование точной верхней грани в
определении 12. Доказать также, что аь = sup(a'n)bn.
. ■ п>0
. "Упражнение 77. Привести определение аь для случая 0 < а < 1.
Упражнение 78. Пусть А С R, В С R - ограниченные сверху
множества. Доказать, что sup(i4 + В) = sup A + sup В, где А + В :=
s={x + y\xeA, у € В}.
Упражнение 79. Доказать, что sup{N/n} = 1. Здесь {а} := а - [а],
:■•'! п>о
*t [а] - наибольшее целое число, не превосходящее а.
Упражнение 80*. Доказать, что inf sinn = -1, sup sin n = 1.
-.i n>° n>0
' Указание. Использовать без доказательства то, что тг ^ Q.
-Упражнение 81*. Числа, которые не являются алгебраическими,
называются трансцендентными4. Доказать, что множество транс-
трансцендентных чисел имеет мощность континуум.
Упражнение 82. Для числа у/2 = а0, ахагаз • ■ • найти значения а0,
ai,a2 и аз-
Указание. Поскольку 1 < V^2 < 2 <=J* I < 2 < 4, то а0 =
1. Затем проверить, что число у/2 — 1 = —■= лежит в интервале
v 2 + 1
/4 5 \
( —,— ). Таким образом, а\ = 4. После этого легко проверить, что
1 2 3-2ч/2 / 1 2 \
TfTT " 5 = гТ^Д е (loo' loo )• откуда следует а2 =: и т" д"
1.5.11 Лемма о вложенных отрезках
Теорема 15. Пусть {[ап,Ьп] '■ п > 1} — последователь-
последовательность отрезков, удовлетворяющая условиям,: 1) Vn > 1 :
[an+ubn+i] С [ап,Ьп]\ 2;Ve>0 3 п G N : Ъп - ап < е;
оо
Тогда 3!i6fiVn>l: ж € [а„, Ъп], то есть f] [а„, Ь„] = {х}.
4От лат. transcendo — ныходящий за пределы, пренышающий.

46 Глава 1. Введение
\ Поскольку [а, Ь] С [с, d] •*=>■ с < a < b < d, то в силу условия 1)
Vn > 1 : ai < а2 < ... < а„ < Ьп < bn_i < ... < bi. Рассмотрим
множество Л := {ai, a2,..., an, ■..} и докажем, что при любом т е N ■
число Ът есть верхняя грань для множества А. Действительно, если п <
т, то по условию 1) [ат, Ьт] С [ап, Ьп] <=$■ ап < ат <Ьт < Ьп, откуда
ап <Ьт. Если же п > т, то по условию 1) [ап, Ьп] С [ат, Ът\ <=> ат <
ап <Ьп < Ьт, и снова ап < Ьт.
По теореме о существовании точных граней Зх е R : х = sup Л,
причём, согласно определению точной верхней грани, Vn £ N : an <
i и Vm£ N: i<bm. Поэтому Vn G ЛГ : if [an,bn].
Пусть у (E. R такое число, что Vn 6 N : у G [an,bn]. Допустим,
что у > i. Из условия 2) следует, что Ve>03n£iV-. 0<y-i<
Ьп ~ an < е, то есть Ve>0: 0 < j/ — х < е, откуда у = х (если у > х,
то достаточно взять е = (у — х)/2 для получения противоречия). J
Упражнение 83. Доказать, что теорема 15 не верна, если вместо
отрезков рассматривать интервалы или полуинтервалы. Рассмотреть по-
последовательность @,1/п], п > 1.
Упражнение 84- Как изменится утверждение теоремы 15, если
опустить условие 2)?
Упражнение 85*. Приняв утверждение теоремы 15 в качестве ак-
аксиомы, доказать теорему о существовании точных граней.
Упражнение 86. (Теорема Хелли). Любая система отрезков,
каждые два из которых имеют общую точку, имеют непустое пересе-
пересечение.
1.5.12 Неравенства Коши
Для суммы и произведения действительных чисел 01,02,03,... ,ап вве-
п п
дём обозначения £] Ofc := аг + а2 + ... + ап\ П а* := <ц • а2 •... ■ an.
fc=i fc=i
Упражнение 87. Проверить, что
п п п п п п
а) Е ак = Е aj, Ь) Е a»c = ai + Е °fc. с) Е (са»с) =с Е ак,
fc=l jr=\ fc=l fc=2 fc=l fc=l
1m mm n n n
d)E"*=E a2j + E a2j_i, e) E (a* + 4=E«k+E h-
fc=i j=i j=i k=i k=i fc=i
Теорема 16. (Неравенство Коши). Пусть для п е N
{аь а2, ..., ап; Ьь Ь2> •■•. Ьп}5 С Д.
5Здесь и далее обозначение {а, Ь} С R , и аналогичные ему, не предполагает, что эле-
элементы а и Ь различны,

1.5. Действительные числа47
, п ч 2 п п
Тогда справедливо неравенство (Е akbk) < Е а1'Е Ч,>
4=i ' fc=i fc=i
в котором, знак равенства возмомсен тогда и только
тогда, когда 3 А е R Э /х G Д, |Л| + |/х| т^ 0 : Aafc = ^bfc, I < к < п.
п
\ Если А := Е afc = ° ч*=>' Vfc G {1,2, ...,n} : afc = О или
fc=i
аналогично В := J2 Ь\ = 0 <=^ V к G {1,2,... ,п} : Ък = 0, то
fc=i
неравенство выполняется со знаком равенства. При этом, если А = О,
то можно положить А = 1, \i = 0, а если В = 0, то А = 0, /х = 1.
f Пусть теперь А > 0 и В > 0. Тогда можно считать, что А = В = 1.
Если это не так, перейти к числам ак := —jzz, р* := —= ; 1 < к < п.
у/А \/В
': Заметим теперь, что для любых действительных чисел а и Ь имеем
0лЬ\ < - (a2 + Ь2) <=> 0 < (|а| — |Ь|J, пичём знак равенства возможен
I
,'тогда и только тогда, когда \а\ = \Ь\. С помощью этого неравенства
/имеем
afcbfc
fc=i
< £ |afc6fc|< £ \(а1 + Ь2к) = ^(Л + В) = 1, причём
fc=l fc=l
!'§нак равенства возможен тогда и только тогда, когда \ак\ = \Ьк\ для всех
к = 1,2,... , п. Таким образом, ( Е akbk) < 1. J
Упражнение 88. Пусть {ai,a2, ■. ■ ,ап} с R. Доказать неравенства
fc=i 4=i ' fc=i
Упраэ/смемгхе 59. Пусть {ai,a2,... ,а„} С @,+oo). Доказать нера-
п п 1
венство Е ак • Е — — п2 ■
fc=i fc=i afc
Упражнение 90. Рассмотрим наборы {01,02,... ,an} такие, что
п
Е а*; = 1. Для таких наборов определить наименьшее значение суммы:
fc=i
п п
а) Е afc> Ь) Е Pfcafc. гДе Pi,P2i--->Pn — фиксированные положи-
fc=i fc=i
тельные числа.
Упражнение 91. Определить минимальное значение следующей
п / п \ 2 п
суммы Е afc + ( Е °ь ) ПРИ условии Е Pfc°fc = 1 с заданными чис-
k=i Vfc=i у fc=i
ламирьр2,...,р„.
Упражнение 92. Для любых чисел {а,Ь,с} С Я доказать неравен-
неравенство \у/а? + Ь2 - \/а? + с2! < \Ъ - с\.
4 — 4-1168

48 Глава 1. Введение
Указание. Домножить на сумму; неравенство имеет простую гео-
геометрическую трактовку.
Упражнение 93. Доказать, что для п > 1 справедливо неравенство
3 \п
~7п) >п'
Указание. Согласно неравенству Бернулли имеем неравенство
>
. Далее ,/1 + -= - 1 > -=
>A + -P
фг)
Упражнение 94- Пусть {ак, Ьк, ск \ 1 < к < п} С R. Доказать
/n \* n n /п\2
справедливость неравенства I J2 akbkCk ) < S at S ^t ( S
Vfc=i / fc=i it=i \fc=i
Упражнение 95. Пусть {ai,a2,... ,an} С R. Доказать следующее
/ n \2 / n \
неравенство ^ afc ^ (n ~ !) Z! afc + 2aia2 .
\fc=i У \fc=i /
Определение 13. Предположим, что {ai, a2,..., an} с Д.
Средним арифметическим чисел ai,a2,...,an называется
ai + a2 + ... + а„
число
n
Упражнение 96. Доказать, что: а) min a^ < An < max а^; b)
l<fc<n l<fc<n
min ak < An < max afc, если не все числа ai,a2,... ,an одинаковы.
l<fc< l<fc<n
Определение i^. Пусть {ai,a2)... ,an} С [0,+oo). Сред-
Средним геометрическим чисел ai,a2,...,an называется сле-
следующее число Gn := ^/aia2 ... an.
Упражнение 97. Доказать, что min ajt < Gn < max afc. В каком
l<fc<n ~ ~ l<fc<n
случае оба неравенства строгие?
Определение 15. Пусть {ai,a2,...,an} С @, +оо). Сред-
Средним гармоническим чисел ai,a2,...,an называется такое
число Нп := -г j j— .
— Н + ...Н
ах а2 ап
Упражнение 98. Доказать, что min ak < Нп < max afc.
Kfc<n Kfc<n

1.5. Действительные числа 49
Теорема 17. (Неравенство Коши). Для любого набо-
набора чисел {аь а2,... ,ап} С [0, +оо) справедливо неравенство
. . а„ <.
+ а2 + ■ ■ ■ +
п
причем, знак равенства возмоо+сен тогда и только то-
тогда, когда а\ = а2 = ... = а„.
\ Заметим, что неравенство выполняется со знаком равенства, если
ai = a2 = ... = ап, поскольку тогда Ап = Gn = a\, и что имеет место
строгое неравенство, если хотя бы одно из чисел ai,a2,... ,а„ равно О
и они не все одинаковы. При п = 1 утверждение очевидно.
Пусть теперь числа а\, а2,..., а„ положительны и п > 1, тогда имеем
А А
> О -Ф=>- - 1 > — 1. С помощью неравенства Бернулли
A
—I
An—1
получим следующее неравенство
. , , , А„ Л А„-! +пАп -пАп-х
? 1 ■+■ п \ — — 1 1 _
И, следовательно, А% > anA^Z\. Отсюда А% > anAnZ\ > anan_iA"I2 >
... > anan_i... а2А{ = Gn, поэтому Ап > Gn.
Поскольку n > 1, то знак равенства в неравенстве Бернулли возмо-
жен тогда и только тогда, когда — 1 = 0, то есть когда Ап = An-i,
•An—1
откуда следует, что ап = А„-\ = Ап. Поэтому знак равенства в нера-
неравенстве An > Gn возможен тогда и только тогда, когда
ап-Ап- An-i, an_i = An-i = Ап-2, ■ ■ ■, <h = A2 = M = ai- J
Упражнение 99. Вывести неравенство Бернулли из неравенства Ко-
Коши теоремы 17.
Указание. Рассмотреть величину /A + пх) • 1 ■... • 1. Таким об-
образом, неравенства Бернулли и Коши равносильны.
Упражнение 100. Доказать, что Я„ < Gn, причём знак равен-
равенства возможен тогда и только тогда, когда аг = а2 = ... = а„. Таким
образом, Н„ < Gn < А„.
11 12
Упражнение 101. Доказать, что Vn > 1 : - н +.. +— > - .
п п +1 2п 3
Упражнение 102. Многочлен i13 - 13i12 + ... - 1 имеет 13 поло-
положительных корней. Найти зти корни.
4*

50 Глава I. Введение
Упражнение 103. Доказать, чт</ —- < \fn\ < .X V\}1
V fу
Упражнение 104- Для любого набора чисел^аь о2,..., о„} с @,1)
71 П
справедливо неравенство f] A — а&) > 1 — ]Г) о^.
it=i fc=i
1.5.13 Историческая справка
Бернулли Якоб A654 — 1705) — представитель замечатель-
замечательной семьи швейцарских математиков Бернулли. Один из основателей
методов математического анализа и вариационного исчисления. Решил
ряд задач комбинаторики (ввёл числа Бернулли), автор первого закона
больших чисел (теорема Бернулли) в теории вероятностей. Среди его
учеников был П. Эйлер — отец Л. Эйлера. О семье Бернулли см. кни-
книгу В. А. Никифоровского Великие математики Бернулли. Москва.
Наука. 1984.
Когии Огюстен Луи A789 — 1857) — выдающийся французский
математик. Много внимания уделял логическому построению математи-
математического анализа. Автор ряда основополагающих понятий и результатов
математического анализа, теории аналитических функций, геометрии,
математической физики. Написал свыше 800 научных работ.
Являющееся основным для математического анализа глубокое и аб-
абстрактное понятие действительного числа оказалось исключительно тру-
трудным для понимания. К этому понятию математики пришли после вве-
введения производной, интеграла, теории рядов и т. п., и это обстоятель-
обстоятельство до середины XIX в. лишало логического обоснования новейшие и
эффективные достижения математики того времени. Различные теории
иррациональных чисел были построены только в семидесятые годы XIX
в. ЯГ. Мерэ A835 - 1911), К. Вейерштрассом A815 - 1897),
Р. Дедекиндом A831 - 1916), а затем Э. Гейне A821 - 1881)
и Г. Кантором.

Глава 2
Предел
последовательности
действительных чисел
2.1 Определения и примеры
2.1.1 Определения
В этой главе изучаются свойства последовательностей действительных
чисел. Эти свойства характеризуются тем, что они не зависят от любого
произвольного конечного числа членов последовательности.
Определение 1. Последовательность {ап | п > 1} =
= {ai,a2,...,an,...} с R называется ограниченной последо-
последовательностью, если 3C>0 Vn> 1: \а„\ < С.
Замечание. Иными словами, последовательность {а„ | п > 1}
ограничена тогда и только тогда, когда существует отрезок [—С,С],
на котором лежат все члены последовательности {а„ | п > 1}. Если
последовательность {а„ | п > 1} ограничена, то полученная из нее
произвольной заменой произвольного конечного числа членов после-
последовательность также ограничена.
Примеры. 1. Последовательность {(—l)n | n > 1} ограничена и её
члены лежат в отрезке [—1,1].
2. Последовательность {sinn | n > 1} ограничена и её члены лежат
в отрезке [—1,1].
3. Последовательность {n | n > 1} не является ограниченной, так как
для любого С > 0 в силу аксиомы Архимеда существует п € N : п > С.
51

52 Глава 2. Предел последовательности действительных чисел
4. Последовательность {n2~n | n > 1} является ограниченной и ле-
лежит в отрезке [0,1] в силу результата упражнения 73 гл. 1.
Упражнение 1. Доказать ограниченность последовательности:
а)
n>l}; Ь) [ап = у 2 + у 2 + ... + ^2 + -Л | n > l};
пкорней
с) {а„ = 1+-+22 +... + ^- n > l}; d) {\/n2 + nsinn+ 1-n | n >
!}•
Указания, с) Заметить, что - on = ап - -а„. d) Использовать
неравенство </2 < 2.
р 2. Определить значения х € R, для которых последо-
последовательность { (— ) +х~п п>1> ограничена.
Упражнение 3*. Доказать, что последовательность {an | n > 1}
ограничена тогда и только тогда, когда ограничена последовательность
{а3п-ап\п> 1}.
Определение 2. Пусть х £ R ие > 0 - заданы.. Окрест-
Окрестностью гми е-окрестностью точки х называется ин-
интервал В{х, е) := (х - е, х + е) = {у € R | \у - х\ < е}.
Упражнение 4- Проверить, что: а) (а,Ь) = в( , ■ ■ J; Ь)
пересечение конечного числа окрестностей точки х есть окрестность
точки х; с) пересечение двух окрестностей есть либо 0, либо окрест-
окрестность.
Определение 3. Число а б R называется пределом
последовательности {ап \ п > 1}, если
Ve>0 3N€ R Vn> N : \ап - a\ < e.
Обозначения: a = lim an или ап -4 a, n-»oo.
n—too
Замечания. 1. Если число а удовлетворяет определению 3, то
говорят, что последовательность {а„ | п > 1} сходится к числу а
или стремится к числу о, а сама последовательность {an | n > 1}
называется сходящейся. Если для последовательности {an | n > 1}
числа а, удовлетворяющего определению 3, не существует, то после-
последовательность {an | п > 1} называется расходящейся.
2. Обратимся к числовой прямой. Определение 3 означает следую-
следующее: число а есть предел последовательности {an | п > 1}, если любая

2.1. Определения и примеры 53
е-окрестность точки а содержит все члены этой последовательности,
начиная с некоторого. Действительно, \ап — а\ < е •$=> а — е < а„ <
а + е <==> а„ 6 В(а,е).
3. Заметим, что 3N €NVn>N... <f==> 3N£RVn>N... .
4. Если некоторого е0 > 0 3 No € JV Vп > No : \ап - а\ < е0)
то для любого е > Со имеем 3 N = Л/о V n > JVo : |а„ — а| < Со < £■
Таким образом, для любого числа е0 > 0 определение 3 равносильно
следующему: а = lim а„ -*=^ Ve € @,е0) 3N£NVn>N:
п—+оо
|оп - а| < е.
5. Обратим также внимание на то, что имеют место равенства сле-
следующего вида lim an = Нш аи = Hm an_i = lim an+i.
n—>oo fc—юо n—>oo n—>oo
6. В определении 3 для каждого е > 0 любое из чисел некоторого
множества Ае С R можно взять в качестве N. Например, если число
N удовлетворяет условию определения 3, то любое число N + С, где
С > 0, также удовлетворяет этому условию. Число N в определении
3 есть одно (любое) из чисел Ае. Обычно множество А£ изменяется
с изменением е, а именно, "сдвигается" вправо с уменьшением е. В
некоторых случаях удаётся найти inf Ae, тогда можно положить N =
Упражнение 5. Для каких последовательностей {an | n > 1} число
N в определении 3 можно взять одним и тем же для любого е > О?
■ • Ответ: BmgJV V п >т : а„ = а.
Упражнение 6. Доказать, что предел последовательности не зави-
;Сит от порядка следования её членов. Точнее, для сходящейся к числу
"Л последовательности {а„ | п > 1} и любой биекции а : N —» N
последовательность {а^п) | те > 1} также сходится к числу а.
Указание. Это несколько неожиданное на первый взгляд утвер-
утверждение становится простым, если обратиться к числовой прямой: для
любого £ > 0 вне е-окрестности точки а лежит только конечное чис-
число членов последовательности {an | п > 1}, следовательно, и членов
последовательности {о<г(п) | те > 1} также.
Упражнение 7. Доказать утверждения:
a) an -» a, n -» оо <=$■ \ап - а\ -» 0, п -» оо;
b) ап -4 0, п -> оо <=> \ап\ -» 0, п -4 оо;
c)an->a, П-4О0 <=$■ V е > 0 3 N € N : {aN,aN+i,...} С В(а,е);
d) а„ -> 0, п -> оо <=> sup |afc| -4 0, n -> оо;
k>n
e) а„ -) а, п -4 оо => |а„| -4 |а|, п —> оо.
Указание к е). Воспользоваться неравенством ||а„| — |а|| < |а„ —а|.

54
Глава 2. Предел последовательности действительных чисел
Упражнение 8. Какое свойство последовательности содержится в
утверждении Зоб Д Зе > О 3N£N Vn>iV: |а„ - а| < е?
Упражнение 9. Привести пример последовательности {ап | п > 1},
для которой 3aeR Ve > О 3N£N V n > N : |а„ - а| > e.
Теорема 1. Последовательность действительных
чисел мож.ет иметь только один предел.
\ Пусть ап —» а, п —> оо и а„ —> Ь, п —^ оо. Тогда согласно определению
3 имеем Ve > 0 3Nr Vn > Nx : \ап - а\ < е и Ve > О 3N2 Vn > N2 :
\o-n-Ц < е. Поэтому Ve > 0 Vn > max(Ni,N2) : \а-Ъ\ = \а-ап+ап-
Ц < |а — in! + |in — Ь\ < 2е. Таким образом, Ve > 0 : |а—Ь| < 2е. Если
1 2 1
о ф Ь, положим е = - |о-Ь| > 0. Тогда \а—Ь) < - \а—Ь\ ===> - |а-Ь| < 0,
о о о
что невозможно. Следовательно, а = Ъ. J
2.1.2 Примеры
3. Последовательность {а, а,..., а,...}, где а€ Д сходится к числу а. В
определении 3 для любого е > 0 можно положить N = 1.
Теорема 2. Справедливо равенство lim — = 0.
га—юо И
-0
f Заметим сначала, что для любого е > 0 :
-. Поэтому Ve> 0 3N:=(-+l\eR Vn>N:
= - < е
0
п
Следствие 1. Для любого к е N lim —г = 0.
п-юо п
[ Действительно,
Ve>0 3N:=(-+l)eR Vn > N : -^ - 0
n
Следствие 2. Для любого к £ N
[Действительно,
lim
п-юо
= 0.
n >
J
-0
/п
Следствие 3. Для любого а > 0 lim — =0.
n-юо па
Указание. Для любого а > 0 существуют натуральные числа к и
m такие, что - < а < т.
к ~ ~

2.1. Определения и примеры 55_
Теорема 3. Пусть а € R, \а\ > 1, а е R. Тогда lim — = 0.
п—+оо а
[ Пусть к € N таково, что к > I + а. Согласно неравенству Бернулли
для любого п 6 N получаем |o|n = (|a|n/fc)fc = (A + (|a|Vfc - l))")fc >
> nfc(|o|Vfc - l)fc. Поэтому 2- - 0 = £r- < ?-— < .. ..}.—-г <
Vl ' ' a" |a|n ~ |a|" n(|a|Vfc - 1)*=
< e <=> n > , — . Следовательно, можно утверждать, что
J
Следствие 4- Справедливы, утверждения:
1) УобЯ.Н > 1: Нш— =0; 2) У а 6 R, \а\ < 1 : lim an = 0;
п—»оо а" п—+оо
:3; Va€ Д|а| < 1 Уа£Й: Urn (naan) = 0.
n-+oo
Указание к 2) и 3). При а = 0 утверждения очевидны. Если же
о ф 0, то положить Ь := - , тогда |Ь| > 1.
a
Теорема 4. Справедливо утверждение lim =0.
(" Пусть произвольное е > 0 задано. Заметим, что для любого п £ N
имеем 0 < -=— < е ■$=> п < 10пЕ <$=> — < 1. Согласно тео-
~ п A0Е)п
п
реме 3 имеем -* 0, п —> оо, откуда на основании определения
,
J
J
3 для числа е = 1 : 3^ Vn > N\ : < 1. Таким образом,
1
п
Теорема 5. Справедливо утверждение lim ^/n = 1.
п—+оо
1 Н—7= ) > ni п > 1, откуда
3
следует, что 1 < %/п < 1 Н—т= > п > 1- Тогда можно утверждать, что
Ve>03N :=^т +l\/n>N : \\/п-1\ = ^п - 1 < 4= < = < £- J
Упражнение 10. Доказать, что:
1)Va>0 V/3>0 : -^— -+0, п -> со; 2) lim ^/nT2 = 1;
3)Va>0 : 70 -4 1, п -» оо; 4) lim ?/п 4-1 sinn| = 1;
п—+00

56 Глава 2. Предел последовательности действительных чисел
5) ton v/n2 + 1 = 1; 6) lim ~= = 0.
n>оо n>oo !
Пример. 4. Последовательность {а„ = n | n > 1} предела не имеет. '
\ Согласно определению 3 нужно убедиться, что любое число а б
R не удовлетворяет этому определению. Действительно, для любого
а 6 R и любого е > 0 окрестность В(а,е) содержит не более 1 +
[2е] целых чисел. Поэтому, начиная с некоторого номера, все члены
последовательности лежат вне B(a,e). J
Замечания. 1. Определение 1 - это определение ограничен-
ограниченной последовательности. Последовательность {an | n > 1}, не удо-
удовлетворяющая этому определению, обладает следующим свойством
VC>0 Эп> 1 : |о„| >С.
2. Тот факт, что число а не является пределом последовательности
{ап | п > 1}, можно записать следующим образом 3 е* > 0 V N 6
N Зп > N : \ап — а| > е*. Последнее означает, что вне окрестности
В(а,е*) лежит бесконечное множество членов последовательности.
Определение 4- ton а„ =+оо <*=> VCeR3NVn>N:
а„>С. lim а„ = -оо <^£ \/C€R3NVn>N: an < С.
n—юо
Упражнение 11. Доказать, что следующая последовательность
1 , 11, 11, 1
111
Упражнение 12. Пусть {а„ | п > 1} С R \ {0}. Доказать, что
lim |а„| = +оо <=> lim — =0.
га—>оо п—too an
Упражнение 13*. Доказать, что lim —1= =0.
n->oo 2v"
Упражнение 14- Проверить, что предел последовательности не за-
зависит от произвольного изменения произвольного фиксированного ко-
конечного числа членов последовательности.
Упражнение 15. Доказать утверждение. Последовательность чисел
{а„ | п > 1} не сходится к числу а тогда и только тогда, когда 3 е* > 0 :
множество {п 6 N | |а„ — а\ > е*} бесконечно.
Упраэ«;кекие 16. Последовательность {а„ | п > 1} такова, что
— -» 0, п -> оо. Доказать, что ^-^—'■ !—- -» 0, п -> оо.
п п
Упражнение 17. Предположим, что an-)a, Ъп -> Ь, п -> оо.
Доказать, что тах{а„,Ьп} -> тах{а, Ь}, -> оо.

2.2. Свойства сходящихся последовательностей 57
Упражнение 18. Доказать, что последовательность {{</п} | п > 1}
предела не имеет.
Упражнение 19. Доказать, что последовательность {sinn | n > 1}
предела не имеет.
а"
Упражнение 20. Доказать, что Va€ R : lim —- = 0.
n—>oo n\
Указание. V a б R Зк е N : fc + l>|a|n для пук имеем
\а\ \а\ \а\ \а\к ( \а\ \п~к .. \а\
n! fc! fc + 1 fc + 2 ■•■ n ^ fc! \k + lj ' r fc + 1
\а\ \а\ ( \а\ \ .. \а\
21*. Пусть a > 0. Для произвольного xq > 0 рассмот-
рассмотрим последовательность {an j n > 1}, члены которой определяются
1 ( а \
равенствами а„ = — an_i Н 1 , п > 1; ао = io. Доказать, что
2 V an-i /
а„ -» -^а, п -» оо.
Указание. С помощью математической индукции проверить, ра-
венство ^т= = ^т= , п > 1, откуда -;= -» 0, п ->
an + л/a V ao + Va / a" + Va
оо. Из этого соотношения получить нужное утверждение.
Упражнение 22*. Привести пример ограниченной последователь-
последовательности {а„ | п > 1}, которая не имеет предела и для которой an+i — ап —»
0, п -> оо.
2.2 Свойства сходящихся
последовательностей
2.2.1 Доказательства теорем
Теорема 6. Сходлщалсл последовательность ограни-
ограничена.
I" Пусть а„ -) а Е й, п -4 оо. Согласно определению предела по-
последовательности для числа е = 1>0: 3 N £ N Vn>iV:
\а„ - а\ < 1. Положим С := тах(|а!|, |а2|,..., |ajv_i|, |a| + 1). Тогда
для п € {1,2,3,... ,N — 1} по определению числа С имеем |а„| < С.
Для значений п > N справедливы неравенства |а„| = |о„ — а + а| <
\а„ - а| + |а| < 1 + \а\ < С. Таким образом, \/п € N : \а„\ <С. J
Упражнение 23. Привести пример ограниченной последовательно-
последовательности, не имеющей предела.

58 Глава 2. Предел последовательности действительных чисел
Теорема 7. Пусть an -> а € R, п -> оо и число Ь > а.
Тогда 3NeN Vn>N: an <Ь. Аналогично, Vc<a ЭКе
N Vn>/C: с<а„.
[ Докажем первое утверждение. По определению предела последова-
последовательности для числа е = Ь — a > 0 3NENVn>N: \an — а\ <
£ <$=>• a-e<an<a + e =>• а„ < Ъ. J
Упражнение 24- Пусть а„ -> а > 0, п -» оо. Доказать, что 3 .W 6
iV Vn>N: an>0.
Упраэ/снекие 25. Пусть а„ -> а ^ 0, п -> оо. Доказать, что 3 N 6
iV Vn>N: апф0.
Теорема 8. Предположим, что длл последователь-
последовательностей {ап \ п > 1} и {Ъп | п > 1} вЪ1полненъ! условг4л: i.)
а„ -» а, Ь„ -> Ь, п -^ оо; 2) V п 6 N : ап < Ь„. Тогда а < Ъ.
\ Пусть произвольное е > 0 задано. Согласно неравенству a - е < a
по теореме 7 имеем 3 N\ 6 JV V п > N\ : а — е < ап. Аналогично
3 N2 6 JV Vn > N2 : Ьп < Ь + е. Таким образом, Ve > О 3N :=
= max(J\fi,J\r2) Vn>iV: а-е<а„<Ь„<Ь + е. Следовательно,
Ve>0: a-e<b + e -i=> а - Ъ < 2е, откуда следует, что а - Ь < 0,
то есть а < Ь. J
Упражнение 26. Пусть ап = 0, bn = 1/n, n > 1; а = 0, Ъ = 0. При
этом ап < Ьп, п > 1. Этот пример показывает, что замена условия 2)
теоремы 8 строгим неравенством не приводит к строгому неравенству
для пределов.
Упражнение 27. Доказать, что утверждение теоремы 8 сохраня-
сохраняется, если условие 2) заменить более слабым Зт Е N V п > т :
ап < Ь„.
Теорема 9. (О трех последовательностях). Пусть
последовательности {ап \ п > 1}, {Ъп | п > 1}, {с„ | п > 1}
удовлетворяют условиям: i j ип -> а £ Я, с„ -> а, п -^ оо;
2.) Vn > 1 : а„ < Ь„ < с„. Тогда Ьп -» а, п -^ оо.
[ Для каждого е > 0 согласно теореме 7 имеем 3 Ni £ N V n > Ny :
a-£<anM3W2 6JVVn>A/2: с„<а + е. Поэтому с учётом условия
2) получим такое утверждение Ve > 0 3N := max(Ni,N2) Vn > TV :
a - e < а„ < Ь„ < с„ < a + e, откуда имеем \/e>03N£NVn>N:
a-e<bn<a + e Ф=> jbn - a| < e. J
Теорема 10. Пусть ап -> a 6 -R, bn -+ 6 € Я, п -4 оо.

2.2. Свойства сходящихся последовательностей 59
Тогда а) V с € R: lim (can) = с lim а„; Ъ) lim (ап + Ъп) =
п—»оо п—юо n—too
lim ап + lim bn; с.) lim (а„ • bn) = lim ап ■ lim bn;
n—юо n—*oo n-+oo n-+oo n—юо
а lim an
d) если дополнительно b Ф 0, тпо lim — = "~*°° .
n-+oo bn lim on
n—юо
- \ Доказательство с). Сначала заметим, что для любого п > 1
\апЪп - аЪ\ = \апЪп - аЪп + аЪп - аЪ\ < \ап - а\ ■ \Ъп\ + \а\ ■ \Ъп - Ъ\. A)
; Пусть произвольное е > 0 задано. По теореме 63С>0 Vn > 1 :
|Ь„| < С, а согласно определению предела последовательности 3 N\ £
N Vn > ^ : \ап - а\ < ^- , и 3 N2 £ JV Vn > N2 : \bn -b\ < £ .
20 2(|a| + 1)
Таким образом, с помощью A) имеем Ve > 0 3 JV := max[Ni, N2) Vn >
Доказательство d). Для определённости пусть b > 0. По теореме 7
с учётом неравенства - < b имеем 3 N% 6 N \f n > N\ : - < bn, a
согласно определению предела последовательности для е > 0 получаем
3 N2 € N Vn > N2 : |а„ - а\ < — и 3 N3 € iV Vn > N3 : |Ь„ - b| <
< ТТЛ—Гч • Таким образом, Ve > 0 3 N := max(.Ni, JV2l N3) Vn > N :
4(|a| + ' >
Ьп
апЪ- аЬп
ъъп
еЪ 2 2\а\ еЪ
+
2
_ \anb - ab + ab — abn\ \an - a\ \a\ ■ \bn - b|
4 b b2 4(|a| + lj J
Упражнение 28. Доказать утверждения а) и b) теоремы 10.
Упражнение 29. Последовательность {ап \ п > 1} ограничена, а
последовательность Ъп —> 0, п —► со. Доказать, что anbn —► 0, п —^ со.
Упрагисненке 30. Последовательность {an | n > 1} ограничена, а
последовательность Ъп —> +со, п —^ со. Доказать, что ап + Ъп —> +со
при п —^ со.
2.2.2 Примеры применения
Рассмотрим примеры применения теорем предыдущего пункта.
1. Докажем, что lim \ 1 -\ \- - + ... Н— =1.
п-+оо У 2 3 П

60 Глава 2. Предел последовательности действительных чисел
[ Пусть в теореме 9 для п е N an = 1, bn = Г/1 + - + - +...+ -,
V 2. о п
сп = \/п\ при этом а„ < Ь„ < с„, п > 1 и а„ -+ 1, с„ -+ 1, п -> со. J
2. Докажем, что lim \Jv?2n + 5n = 5.
n—too
f Заметим сначала, что для любого п > 1 : 5 = \/S" < {/п22п + 5" <
< v2n^5". Положим в теореме 9 для п > 1 а„ = 5, Ьп = {/п22п + 5",
сп = \/2п25п. Тогда an < bn < cn, n > 1 и, кроме того, имеем
an -4 5, с„ = 5^2( ^/пJ -> 5, п -юо в силу теоремы 10 и того, что
{/2->1, ^п->1, п-^оо. J
n2 + nlgn + 3 1
3. Докажем, что lim =
z:= .
2пг + smn + 1 2
\ Теорема 10 непосредственно не применима. Однако, стоящую под
п2 + n lg n + 3
знаком предела дробь можно представить в виде —-х : =
2n2+sinn+l
. К правой части последнего равенства можно приме-
4
— —
sin п 1
J 2
n п
нить теорему 10. Действительно, сначала с помощью теоремы 4, след-
следствия 1 и теоремы 10 имеем lim A н 1—г )= 1 + lim Ь
п—юо \ П П I n-too n
i 1
+3 lim —- = 1. Далее с учётом неравенств -г < —г— < —х, п > 1
п—юо П2 nJ nJ nJ
и теоремы 9 получим lim —г— = 0. По теореме 10 имеем также
п-юо п
t sinn 1 \ ,. sinn ,. 1 . „ _
lim 2 Н г- н =2+ lim —ъ 1- lim —г =2^0. Применив
п—+оо V п П / n—>oo n п—юо П
теорему 10 ещё раз, получим требуемое. J
Упражнение 31. Найти пределы:
sin2n n + sinn /
a) hm —7=-, b) hm ?, с) hm ?/n+(-l)n,
I.1 n—юо Л/п п—юо П + COS П n—юо
d) hm
/
, a > 0, b > 0, e) Urn ."/ E
" П—ЮО U j^
\) ЦШ. ^_^ . — , э/ *.**.». д , ^_^ - w I '*/ *"— _„
П—>OO u_, s/fl6 А- к П-ЮО \/ ь_-1 П-*ОО ^
) , m) lim "+^, n) Urn -"/ £ fcn, где a = 1, a = 2.
П—ЮО П П—>OO П—+OO U fc — i
Упражнение 32. Пусть и„ > 0, n > 1 и а,, -m, n -^ со. Доказать,
что VfceiV : Л/а^-^-Уа, п-^ со. \

2.2. Свойства сходящихся последовательностейб/
Упражнение 33*. Пусть а0 = ах = 1; ап = an__i + an_2, n > 2.
Найти lim
2.2.3 Линейное регулярное преобразование
последовательности
Пусть
{спк I 1 < к < п, п > 1} С R A)
— набор фиксированных чисел. Для последовательности {ап | п > 1}
рассмотрим последовательность {Ь„ | п > 1}, общий член которой име-
п
ет вид Ъп — £2 cnfcifc, n > 1. Представляет интерес вопрос: при каких
fc=i
условиях на числа A) справедливо утверждение: для любой сходящейся
последовательности {ап \ п > 1} последовательность {bn \ n > 1} также
сходится к тому же пределу?
Теорема 11. (Теорема Теплица о регулярном преоб-
преобразовании последовательности). Пусть числа {с„к \ 1 <
к < п, п > 1} с R удовлетворяют условиям:
l)\/k€N : Спк^О, п-^ со;
П
2) Е спк -> 1, п -¥ со;
fc=i
З; ЭС>0 Vn> 1 : £ |cnfc| <С.
fc=l
Тогда длл любой сходящейся последовательности чи-
сел {а„ | п > 1} последоватпелъностпъ < Ьп = Е cnfcifc n > 1 >
fc=i J
такэ+се сходится и lim bn = lim an.
n—юо n—юо
f Для последовательности {an = a | n > 1}, a 6 H, имеем bn =
n
a E cnfc —^ ai n —► ooi в силу условия 2). Поэтому достаточно рассмот-
fc=i
реть случай, когда ап -> 0, п -^ со.
Следующее неравенство
\Ъп - 0| = |Ь„| =
m-l
Ы B)
fc=l k=m
справедливо для каждого т, 1 < т < п.
Пусть теперь е > 0 задано. Согласно определению предела после-
последовательности,
N!-. К|<^, C)

62 Глава 2. Предел последовательности действительных чисел
кроме того, по теореме 6
3£»>0Vn>l: |а„|<£». D)
Пусть далее в неравенстве B) n > Ni и m = N\. По условию 1)
теоремы У к,1 < к < Ni - I : с„к -> 0, п -^ со, -£=>■ |cnfc| -4 0, п ->
со, =Ф- £} |с„к| -» О, п -^ со. Следовательно,
fc=i
^- . E)
Тогда для номеров п > N := max{Ni, N2} из неравенства B) с учётом
Wi-i
неравенств C) — E) и условия 3) получим |Ь„ - 0| < D j^ |cnfc| +
fc=i
+2^ Д |c-fcl < Dh+ h £|с^! < I+ ^с=е- J
Упражнение 34- Доказать, что условия 1) и 2) теоремы Теплица
необходимы.
Указание. Рассмотреть, например, такие последовательности:
{а„ = 1 | п > 1}, {а„ = 6пк | п > 1}, 6пк = 1, если n = fc, 5nfc = 0,
если п ф к, для фиксированного к.
Замечание. Условия 1) — 3) теоремы Теплица необходимы и до-
достаточны. Однако, доказательство необходимости условия 3) несколько
сложнее и здесь не приводится.
У применение 35. Доказать, что если в теореме Теплица спк >
О, 1 < к < п, п > 1, то условие 3) можно опустить. Кроме того,
тогда ап —* +оо, п —> оо =Ф- Ъп —> +оо, п —> оо.
Упражнение 36. Доказать, что сходимость ап —* а, п —> оо влечёт
а.1 + а2 + ■. ■ + ап
сходимость -4 а, п -> оо.
п
Упражнение 37. Пусть ап -^ а, п -^ оо. Доказать сходимость
пах + (п — 1)а2 + ... + 1 • а„ а
Упражнение 38. Пусть а„ > 0, п > 1, и а„ -> а, п -^ оо. Доказать,
что ^aia2 ... ап —t а, п —■> оо.
Упражнение 39. Пусть an > 0, п > 1, и -^^ -ю, п -^ оо.
Доказать, что г/а~^ —> а, п —■> оо.

2.2. Свойства сходящихся последовательностей 63
Упражнение 40* • Пусть ап -¥ а, Ь„ -> b п -> оо. Доказать, что
— — — -— —> ab, п —> оо.
п
2.2.4 Теорема Штольца
Теорема 12. Предположим,, что последовательно-
последовательности {х„ | п > 1} и {у„ | п > 1} удовлетворяют условиям,:
1) Vn > 1 : уп < уп+1;
2) уп -¥ +оо, п -^ оо;
3) существует lim — г^- = а е (Ни {-оо, +оо}).
п-+°° Уп — Уп-i
Тогда lim — = а.
П-+00 Уп
[ Можно предположить, что у\ > 0. Положим Хо = 0, уо = 0 и
7/ь — 1/», ч 3J*i — 3<*i 1
cnfc = , 1 < к < n, n > 1; an = , n > 1.
Уп Уп - Уп-1
Числа {спк} удовлетворяют условиям теорема Теплица. Действительно,
У к — У к—1
спк > 0, 1 < к < п, п > 1; Vfc > 1 : спк = —>■ 0, п -^ оо,
Уп
,. Л Л Ук - Ук-i Л v. i n
в силу условия 2) и 2_, cnfc = 2_, = 1> ^ > 1- Поэтому,
fc=l fc=l Уп
согласно теореме Теплица,
v-> v-> Ук ~ Ук—1 ""fc ~ 2>fc—I 2>n I
Е cnfcafc = Е = ►а. п -> °°- J
fc=i fc=i Уп Ук - Ук-i Уп
п2
Упрагисненые 4-^- Доказать, что lim — =0.
П-+ОО 2"
Указание. Применить дважды теорему Штольца.
Упражнение 4%" Вычислить пределы:
а) Jim f^fl + ^+4r+--. + ^
,. .. 1 + 1а + 2а + ... + па
d) hm -— . а > 1;
n—too 7Ш +
5 — 4-1168

64 Глава 2. Предел последовательности действительных чисел
Упражнение 43. Пусть ап —t a, n —> оо. Вычислить пределы:
1-2 2-3 3-4 n(n+1O '
Упражнение 44- Последовательность {an | n > 1} удовлетворяет
условию an+i — an —¥ a £ H, n —► со. Доказать, что lim —— = a.
n-»oo n
Упрагисненые ^5. Предположим, что последовательности {хп \ п >
1} и {уп | п > 1} удовлетворяют условиям:
1) Vn> 1 : у„<у„+1;
2) in -> 0, у„ -> 0, п ->• оо;
3) существует lim — ^^ = a € (Яи {-оо,+оо}).
"■^°° Уп - Уп-1
_ .. 1„
Тогда lim — —а.
П-+ОО уп
Упражнение 46*- Для последовательности {an | n > 1} последо-
последовательность и„ := 2an + an_ll n > 2, сходится: ип ~* и, п -^ оо.
Доказать, что последовательность {an | n > 1} также сходится, и найти
её предел.
2.3 Монотонные последовательности
2.3.1 Существование предела монотонной
последовательности
Определение 1. Последовательность {ап | п > 1} на-
называется монотонно возрастающей в строгом смысле,
если Vn>l: an < an+i.
Последоватпелъкостпъ {an | n > 1} называется монотон-
монотонно неубывающей, если Vn > 1 : an < an+i.
Лоследоватпелъкостпъ {an | n > 1} назъ1ваетпсл монотон-
монотонно убывающей в строгом смысле, если Vn > 1 : а„ > an+i.
Последоватпелъкостпъ {а„ | п > 1} назъ1ваетпсл лсонотон-
но невозрастающей, если Vn > 1 : ап > ап+1.

2.3. Монотонные последовательности
\
Последовательность, удовлетворяющая хотя бы од-
одному из приведенных условий, называется монотонной.
Пример. 1. Последовательность {1,2,3,4 п,...} возрастает в
строгом смысле, последовательность {1,1,2,2,3,3,..., п, п,...} неубы-
неубывающая, а последовательность {1, -1,1, -1,..., (—l)n+1,...} не является
монотонной.
Упражнение ^7. Доказать, что монотонно неубывающая последо-
последовательность чисел ограничена тогда и только тогда, когда она ограниче-
ограничена сверху.
Упражнение £8. Доказать, что последовательность {n2~n | n > 2}
убывает в строгом смысле.
Упражнение 49. Доказать существование числа т £ N такого, что
последовательность {n2-v/" | n > т} строго убывает.
Упражнение 50. Последовательность {ап | п > 1} удовлетворяет
условию Vn > 1 : an+i > an — . Доказать, что последовательность
монотонна. Доказать также, что последовательность {ап | п > 1} огра-
ограничена <=$■ {Ьп | п > 1} ограничена.
Упражнение 51*. Пусть для числа с > 2 аг= с?, an+1 = (an -
fJ! n > 1. Доказать, что последовательность {а„ \ п > 1} строго
возрастает.
Теорема 13. Монотонная и ограниченная последова-
последовательность действительных чисел имеет предел.
\ Доказательство проведём для случая неубывающей последовательно-
последовательности, то есть предположим, что Vn £ N : ап < an+i- По условию
теоремы ЭС £ й Vn>l : ап < С. Поэтому множество значений
последовательности А := {01,02,03,... ,an,...} непусто и ограниче-
ограничено. По теореме о существовании точной верхней грани 3 a 6 R :
sup А = supan = а. Докажем, что ап —ь а, п —> оо. Пусть произволь-
п>1
ное е > 0 задано. Согласно определению точной грани и теореме о
её характеризации для числа а — е < а имеем а) V п 6 N : ап < а;
Ь) 3 ат : ат > а — е. С учётом условия теоремы отсюда получаем
Ve>03JV :=mVn> N :а-£ <ат <ап <а =» \ап - а\ < е. J

66 Глава 2. Предел последовательности действительных чисел
Упражнение 52. Если в теореме 13 последовательность {а„ | п >
1} строго возрастает, то Vn£iV: ап < а = lim an. Проверить это
п—«о
утверждение.
Упражнение 53. Доказать теорему 13 для монотонно невозраста-
ющей последовательности.
Упражнение 5^. Проверить, что теорема 13 остаётся верной, если
вместо условия монотонности {ап \ п > 1} потребовать только монотон-
монотонность последовательности {ап | п > т}, где т — произвольное число
из ЛГ.
Замечание. 1. Таким образом, для монотонно неубывающей ог-
ограниченной последовательности {ап \ п > 1} имеем равенства а =
= supan = lim ап, аналогично для монотонно невозрастающей огра-
п>1 п-*°°
ничейной последовательности {ап I п > 1} a = inf an = lim an.
П>1 П-+ОО
П2
Примеры. 1. Докажем равенство lim —- = 0.
п—»оо 2
Г Сначала заметим, что ^П < — <=> 2 < (n-1J <=^ n > 3.
2
Поэтому последовательность < — п > 3 > строго убывает и ограниче-
п2
на. По теореме 13 получим За £ R : а = lim — . С учётом этого
in (n + lF°° п2 (п + IJ
утверждения, теоремы 10 и равенства -— = — -1 ^— , п > 1
.. (п + 1J п2 (п+1J " 1
имеем lim п ,,— = lim — ■ lim ■* —— , то есть а = а- , откуда
п->оо 2"+1 "-+ОО 2" "-+ОО 2п2 2
следует, что a = 0. J
10"
2. Докажем, что lim. —— = 0.
п—>оо п!
10n+1 10"
Г Сначала заметим, что — < —— -$=Ф- 10 < п + 1 <=£► п > 9.
(п + 1)! п!
г 10"
п > 10| строго убывает и
Следовательно, последовательность <
I п!
10"
ограничена. По теореме 11 За £ Н : lim —— = а. Отсюда и из
п—»оо
1Ог 1О 10
равенства — = , п > 1, аналогично примеру 1, имеем
10n+1 ,. 10" ,.Ю ,
lim т rrr = lim —- • lim , то есть a = a • 0 или a = 0. J
n—»oo \n + 1)! n—>oo n! n-too П + 1
7l! 72
Упрагиснекые 55. Доказать, что: а) lim —^ = 0; b) lim —■= = 0.
П-+ОО 2" П-+ОО 2"

2.3. Монотонные последовательности 67^
Упражнение 56. Найти предел следующей последовательности
2
(In —
Упражнение 57. Пусть ai = 1; ап = /''К2"~Г *' д"-ь п - 2-
Bп)
Доказать, что последовательность {а„ \ п > 1} сходится.
Упражнение 58. Пусть ai = - ; a^ = 3an_i -2, n > 2. Доказать,
что последовательность {an | n > 1} сходится, и найти её предел.
Упражнение 59. Последовательность {ап \ п > 1} такова, что
Vn > 1 : 0<an<l,(l- an+1)an > - . Доказать сходимость этой
последовательности и найти её предел.
Упражнение 60. Последовательность {а„ | п > 1} ограничена и
такова, что \/п € N : an+i > an — . Доказать сходимость этой
последовательности.
Упражнение 61*. Последовательность {an | n > 1} ограничена и
1 2
такова, что V п £ N : an+2 < — an+i H— an. Доказать сходимость этой
последовательности.
Упражнение 62*. Пусть {ajfc | j > 1, fc > 1} С Я, причём при каж-
каждом фиксированном к > 1 последовательность {a^fc | j > 1} монотонно
не убывает и при каждом фиксированном j > 1 последовательность
{ajfc | & > 1} монотонно не убывает. Доказать следующее равенство
lim ( Um a,jk I = lim I lim a,-fc ) .
fc—»oo \j—wo j j—>oo yfc—юо у
2.3.2 Операции над действительными числами и предел
Пусть a = ao,ai(X2 ... ап ... неотрицательное Действительное число,
при этом а0 £ (ЛГи{0», Vn £ ЛГ: ап € {0,1,2,3,4,5,6,7,8,9}. Для
п > 0 пусть а'п := а0, аха2 ... ап; а1^ := а0, а\а2 ... (а„ + 1). Тогда
для любого п > 0 имеем: а'п £ Q, а'^ £ Q, а'п < а < а'^, а'п =
= «о, aia2 ... ап < а0, оца2 ■.. апап+г = a'n+1, а'^ = а0, аха2 ...{ап +
1) > ao,aiQ;2 • •-«71(^+1 + 1) = a^+1. Таким образом, для каждого
п > 0 получим а{, < а'х < а'2 < ... < а'п < а < < < а'^ < ... < а'{ < <.
Отметим также, что для чисел а <Ь имеем а'п < b'n, n > 0.
Теорема 14. Пусть а - неотрицательное действи-
действительное число. Тогда а — lim a' = lim
n—+00

68 Глава 2. Предел последовательности действительных чисел
\ Теорема 10 гл. 1 утверждает, что а = supa^, a = inf а'^. Так
„>о ">о
как последовательности {a'n | n > 1} и {a^ | n > 1} монотонны
и ограничены, то по теореме 13 получаем a = sup a' = lim a' и
n>0 "-+00
a = inf a'^ = lim <. I
n>0 n-»oo " J
Замечание. Теорема 14 даёт представление всякого неотрица-
неотрицательного действительного числа с помощью предела последовательно-
последовательности рациональных чисел, а с учётом знака "—" и любого числа. Соглас-
Согласно теореме 14, например, имеем для любых a > 0, b > 0 a + b —
= lim (a + b)'n, ab = lim (ab)'n. Кроме того, как и в теореме 14
доказывается, что a + b = lim (a'n 4- b'n), ab = lim (aj,b'n). Отсюда
nlim (a + b)'n = fcn. (a; + ^C^lim (ab)'n = ^m (K)-
Последние равенства и свойства пределов позволяют просто дока-
доказывать свойства действительных чисел. Докажем, например, что для
любых а>0, Ь>0, с>0 справедливо равенство a(b+c) = ab+ac. Дей-
Действительно, с помощью теоремы 10 имеем a(b + c) — lim (a'n[b + c)') =
n—юо
= lim aj,- lim {b+c)'n = a lim (b^ + c7,,) = a lim b'n+a lim dn = ab+ac.
2.3.3 Число е
Рассмотрим следующие две последовательности положительных чисел
A \п
1+п)
Докажем следующие свойства этих чисел.
/ 1 \ п
1°. Vn £ N : а„ <Ьп; 2°. { ( 1 н— ) п > 1} строго возрастает;
\ п )
п > 1 > строго убывает.
l\n+1
f Поскольку bn=an(lH )= а„ -\—— > а„, п > 1, то свойство
1° доказано. Для доказательства 2° применим для п > 2 неравен-
_ ап /n+nVn-lT1 n (л
ство Бернулли = = 1 —
an_! Vn/Vn/ "-I I
> г A о ) = 1- Отсюда, ап > а„_ь п > 2.
п — 1 \ п2 /
Для доказательства 3° с помощью аналогичнь1Х рассуждений полу-
Ьп-1
чаем также
ь„ Vn-iy W + i/ n

2.3. Монотонные последовательности 69
n-1 / I \n+1 п-1 / п + 1 \ л
= 1 + —2—г > 1 + -= г = 1, п > 2, а потому
п \ п2 - 1 / п \ п2 — 1 у
Ьп_! > Ьп, п > 2. J
Из свойств 1° — 3° для любого п > 1 следуют такие неравенства
ai < a2 < ... < а„ < а„+1 < 6n+i < bn < . ■ ■ < b2 < h.
Таким образом, последовательности {an | n > 1}, {bn | n > 1} моно-
монотонны и ограничены, следовательно, по теореме 13 сходятся. Обозна-
Обозначим буквой е1 предел последовательности {an | n > 1}. Таким образом,
e := lim 1 4— . Известно, что число е трансцендентное, его зна-
п-+оо у П J
чение с точностью до 10~15 равно е « 2,718281828459045. Число е -
одна из важнейших фундаментальных постоянных в математике.
Поскольку Ъп = ап [ 1 ч— ) , п > 1, то Ь„ -» е, п -> со. Отметим
V п У
/ 1\п / 1 "■'
также, чтоУп>1: 1 + - < е < 1 Ч- -
~ \ п J \ п
Логарифмы при основании е называются натуральными и обо-
обозначаются символом In := loge .
Прологарифмировав последнее неравенство, получим
Vn>l : -^-<Ь 1 + ± <-. A)
( 1 \П 3
Упрасмснение 63. Доказать, что Vn > 1 : 0 < е— ( 1 Ч— ) < — •
\ п; п
Упражнение 64- Доказать, что первая из следующих последова-
тельностей < [ 1-\—- ] п>1>, |AН— | п > l\ строго
I \ п2 j ~ i У\ п) )
убывает и сходится к 1, а вторая - строго возрастает и не ограничена.
Упражнение 65. Доказать, что lim [ nln [ 1 Ч— ] ] = 1.
7WOO ^ V П ) )
Упражнение 66. Доказать,что монотонно неубывающая и неогра-
неограниченная последовательность сходится к +оо.
Упражнение 67. Для г 6 Q, г > 0, найти предел lim 1 Ч—
n»oo \ n
Г™
'Это обозначение, как и обозначение числа тг и оо, принадлежит Л. Эйлеру.

70 Глава 2. Предел последовательности действительных чисел
Упражнение 68. Доказать, что для каждого х > 0 последователь-
последовательность |(lH— ) | гс > l| строго возрастает и ограничена.
Упражнение 69. Вычислить пределы:
a) lim 2 3 ——a_; b) lim ? §-
n—юо ШТ1 n-too
el/n + e2/n + . _ + en/n
c) lim — ; d) lim (n{\/e-l)).
n—>oo П n—>oo
70. Пусть an —> a, n —> со. Доказать справедливость
/1 afc \
равенства lim ; Y^ —- = a.
n>oo \lnn ^ fc j
Упражнение 71. Доказать, что ппе~пе < n! < nn+1e~ne, n > 1.
/ n! \1/n
Упраснснение 72. Вычислить пределы: a) lim ;
/fnM\ / fnH \
b) Jim. ( Щ- ) ; c) Jim. -g- ) ; d) Jim.
n3n
2.4 Подпоследовательности и их свойства
2.4.1 Подпоследовательности и частичные пределы
Пусть {ап | п > 1}. Рассмотрим произвольную последовательность
{ro(fc) | к > 1} С N такую, что 1 < тA) < тB) < ... < m(fc) <
m(fc + l) < ... . Отметим, что V к > 1 : m(fc) > к; т(к) —> +оо, fc —> со.
Примерами таких последовательностей натуральных чисел являются сле-
следующие последовательности:
1.m(fe) = fe, fe>l; {m(fe) | fc > 1} = {1,2,3,... ,fe,...},
2.m{k) = 2k, к > 1; {m(*) | fc > 1} = {2,4,6,... ,2fe,...},
3.m(fc) = fc2, fe>l; {m(fe) | fc>l} = {1,4,9,16,...},
4. m(fc) = 2fc, fc>l; {m(fe) | к > 1} = {1,4,8,16,32,...}.
Определение 1. Последовательность {ат(к) I к > 1}
назыеаетсл подпоследовательностью последовательно-
последовательности {ап | п > 1}.
Пример. 1. Подпоследовательностями последовательности {an | n >
1}, например, являются: а) {а2, а4,а6,... ,а2к, ■ ■ ■} = {^2к \ к > 1}, Ь)
{oi,O4,o9,...,ofca,...} = {ак2 | к > 1} и с) {а3,а6,а9,...,азк,...} =
к > 1}.

2.4. Подпоследовательности и их свойства 71
Из определения подпоследовательности следуют такие свойства под-
подпоследовательностей.
1°. Если последовательность ограничена, то любая её подпоследова-
подпоследовательность также ограничена.
2°. Если последовательность сходится к а (возможно а = +оо или а =
—оо), то любая её подпоследовательность также сходится к а.
3°. Пусть а„ -у а, п -у со; {v(k) \ к > 1} С N, i/(k) -> +оо, к -у со.
Тогда а„(&) —> а, к —» со.
f Доказательство 3° для a £ R. Пусть произвольное е > 0 задано.
По определению предела последовательности 3N£NVn>N:
|о„ - а| < е; 3 К £ ЛГ V к > К : v{k) > N. Таким образом, Ve > О
BKeN \/к>К: lo^) - о| < е. J
Упражнение 73. Доказать утверждения 1° и 2°. Чем отличаются
утверждения 2° и 3°?
Упражнение 74- Последовательность, которая является монотон-
монотонной и содержит ограниченную подпоследовательность, является ограни-
ограниченной (поэтому и все её подпоследовательности ограничены). Доказать
это утверждение.
Упражнение 75. Доказать, что последовательность {а„ | п > 1}
сходится тогда и только тогда, когда сходятся следующие три ее подпо-
подпоследовательности {a2fc | к > 1}, {a2fc-i | к > 1}, {а3к | к > 1}.
Упражнение 76. Доказать, что последовательность а„ -у а, п -ь
со тогда и только тогда, когда каждая её подпоследовательность содер-
; жит в себе подпоследовательность, которая сходится к а.
! Упражнение 77. Привести пример не имеющей предела последо-
последовательности {а„ | п > 1}, для которой для каждого m > 2 подпоследо-
': вательность {ат.к \ к > 1} сходится.
Определение 2. Число a б R называется частичным
пределом последовательности {ап \ п > 1}, если суще-
: ствует подпоследовательность {aTO(fc) | к > 1} такал, что
I Om(fc) —► a, fc —> со. Значение +со (—со) назыеаег7гсл частич-
; ныл* пределом последовательности {an | n > 1}, если су-
s гцесг7геуег7г подпоследоеаг7гелъносг7гъ {am(fc) | fc > 1} гтгакал,
что om(fc) -» +со, fc -»• со (am(fc) ->• -со, fc ->• оо).
Пусть А — множество всех частичных пределов после-
последовательности {а„ | тг > 1}.
Примеры. 1. Для последовательности {1,2,3,... ,тг,...} множество
всех частичных пределов А = {+со}.

72 Глава 2. Предел последовательности действительных чисел
2. В силу свойства 2° подпоследовательностей для последовательно-
последовательности an -> а € R, п -> со множество А = {а}.
Упражнение 78. Доказать, что для следующей последовательности
{1, -1,1, -1,..., (-1)", • • •} множество А = {-1,1}.
Упражнение 79. Доказать, что для ограниченной последовательно-
последовательности множество А также ограничено.
Упражнение 80. Привести пример последовательности, для кото-
которой множество А состоит из: а) трёх чисел, b) n чисел, n G N.
Упражнение 81. Доказать следующие утверждения: а) -со £ А
<=> {ап \ п > 1} не ограничена снизу; b) +co 6 А <=>■ {an | n > 1}
не ограничена сверху.
Упражнение 82*. Привести пример последовательности, для кото-
которой множество А = Ни {—со, +оо}.
Упражнение 83*. Определить множество А для последовательно-
последовательности: a) {sinTrna | n > 1}, а 6 Q; b) {sinTrna | n > 1}, а £ Q;
с) {па - [па] | п > 1}, a G Q; d) {па - [па] | п > 1}, а ^ Q;
е) < ——• — —г— п > 1 >; f) {ап | п > 1}, состоящей из занумеро-
занумерованных в каком-либо порядке элементов множества {\/п — \/тп \ п G
N, m€ N}.
2.4.2 Существование монотонной
подпоследовательности
Теорема 15. (Харакгперизация частичного предела).
Число а е R есть частичный предел последовательно-
последовательности {ап | п > 1} тогда и только тогда, когда
Ve> О VN£ N Зпе ЛГ: n>N, |ои--о|<е. A)
f Необходимость. Пусть a € А. Тогда существует подпоследователь-
подпоследовательность am(fc) -> a, fc -4 со.
Предположим, что числа е > 0 и N £ N заданы. По определению
предела последовательности 3 К\ 6 ЛГ Vfc > К\ : |am(fc) — a| < £,
аналогично ЗК2 G ЛГ Vfc > Кг : m(fc) > iV. Положим теперь
fc := meLx(iCi, X2), n := m(fc). Тогда n > N, |a^- — a| < e.
Достаточность. Предположим, что условие A) теоремы для чис-
числа а выполнено. Тогда для е = 1, N = 1 по условию A) ЗтA) > 1 :
|am(i) — a| < 1. Аналогично, для е = -, N = гпA) + 1 по условию A)

2.4. Подпоследовательности и их свойства 73
3 тB) > тA) + 1 : |атB) - а| < - . Далее, для е = - , N ~ тB) + 1
^ о
по условию A) ЗтC) > тB) + 1 : |ат(з) — а| < - . и т. д. В ре-
о
зультате получим подпоследовательность {aTO(j.) | к > 1}, для которой
|om(fc) ~ а| < г > fc > 1- Следовательно, am(fc) -> a, fc -> со. J
Упражнение 84- Определить множество А для последовательно-
последовательности, занумерованных каким-либо образом множества всех рациональ-
рациональных чисел.
Упражнение 85. Доказать, что +оо £ А (-со 6 А) -Ф=» VC 6
R VNeN ЗпбЛГ: п > N и а* > С (ад < С).
Теорема 16. Любал последовательность действите-
действительных чисел содержит монотонную подпоследователь-
подпоследовательность.
\ Рассмотрим множество М := {n G N | Vm > n : am > an}.
Если М бесконечно и М = {пA),пB),... ,n(fc),...}, при этом пA) <
< пB) < пC) < ..., то согласно определению множества М имеем
<*n(i) < а„B) < < On(fc) < • • • , и {an(fc) | к > 1} — строго возрастаю-
возрастающая подпоследовательность.
Если М конечно, то пусть пA) - наименьшее натуральное число та-
такое, что Vm > пA) : т (£ М. Так как пA) ^ М, то ЗпB) > пA) :
an(i) > anB)l аналогично, так как пB) ^ М, то ЭпC)/> пB) : апB) >
°п(з) и т- Д- Таким образом получим невозрастающую подпоследова-
подпоследовательность {an(jt) | fc > 1}. б?гш? £/<?^5' ^^^ / J
Упрасмснение 86. Указать строго монотонную подпоследователь-
подпоследовательность последовательности {^/п — [\/п] | п > 1}.
Следствие 5. Для любой последовательности {ап | п >
1} множество всех её частичных пределов А ф 0.
f По теореме 16 существует монотонная подпоследовательность {an(fc) |
к > 1}. Если эта подпоследовательность ограничена, то по теореме о
существовании предела монотонной ограниченной последовательности
она сходится к некоторому действительному числу а. Тогда а £ А. Если
же подпоследовательность не ограничена, например, сверху, то она
сходится к +со и +со G A. J
Теорема 17. (Болъцано-Вейерштрасса). Любая огра-
i ниченная последовательность действительных чисел
\ содержит сходящуюся к действительном/у числу под-
; последовательность.

74 Глава 2. Предел последовательности действительных чисел
[ Следствие теоремы 16 и теоремы 13. J
Упражнение 87. Доказать, что любое бесконечное ограниченное,
множество действительных чисел содержит сходящуюся к действитель-
действительному числу последовательность.
2.4.3 Верхний и нижний пределы последовательности
Определение 3. Пусть {ап | п > 1} С R — последова-
последовательность и А — множество её частичных пределов.
Нижним пределом последовательности называется ве-
величина
-со, если {ап \ п > 1} не ограничена снизу;
inf А, если {ап \ п > 1} ограничена снизу и
А
+оо, если А = {+оо}.
Верхним пределом последовательности называется
величина
lim an = <
п—>оо
+оо, если {ап \ п > 1} не ограничена сверху;
sup .А, если {ап \ п > 1} ограничена сверху и
Аф{-оо};
—оо, если А = {-оо}.
Замечание. Если {an | n >_1} — ограниченная последователь-
последовательность, то Шп а„ = inf A 6 R; lim а„ = sup A 6 R.
п-юо п->оо
Пример. 1. Если последовательность {а„ | п > 1} сходится к а, то
lim а„ = lim а„ = а.
п—>оо п—юо
Упражнение 88. Доказать, что ап -¥ а, п -> оо -Ф=Ф- lim а„ =
11 lim ап = а.
' Примеры. 2. Для последовательности {an = n | n > 1} множество
А = {+оо}, поэтому Цт а„ = lim а„ = +оо.
п-юо п-*°°
3. Для ограниченной последовательности {( — l)n | n > 1} множество
А = {—1,1}. Действительно, любая её подпоследовательность либо со-
содержит конечное число членов, равных —1, либо содержит конечное

2.4. Подпоследовательности и их свойства 75
число членов, равных 1, либо содержит бесконечно много членов, рав-
равных — 1, и бесконечно много, равных 1. В первом случае подпоследова-
подпоследовательность сходится к 1, во втором — к —1, в третьем предела не имеет.
Таким образом, lim (-1)" = -1, lim (-1)" = 1.
П-»ОО П-+ОО
• Упражнение 89. Определить нижний и верхний пределы последо-
последовательностей: а) |(-1)п + - n > lj; Ь) In - 5[|] n > lj; с)
|^ d) {{^г7} | п > 1}; e){sinn|n>l}.
Теорема 18. Пусть длл последовательности чисел
{ап I п > 1} а = lim ап, /3 = lim ап. Тогда а £ А, @ 6 А.
п-юо п-^°°
(" Достаточно рассмотреть случай а 6 R, /3 G R. Доказательство про-
проведём для числа а. Докажем, что а = inf A 6 А, то есть, что а есть
частичный предел последовательности {an | n > 1}. Воспользуемся тео-
теоремой о характеризации частичного предела. Пусть е > 0 и N €; N
заданы Тогда, согласно определению inf.A = a, 3 a G А : а < а + е.
Поскольку а — частичный предел, то для чисел а+е — а > 0 и N получим
Зп: п > N и \а„ - а| < а + е — а. Тогда |a^ — a| < \а„ - а\ + \а — а\ <
<a + e — a + a — a = e. J
Замечание. Из теоремы следует, что для ограниченной после-
последовательности множество А содержит минимальный и максимальный
элементы и lim an = min A, lim an = max A.
n-too п->°°
Теорема 19. ^О жарактеризаг^ии нижнего и верхнего
пределов). Пусть {а„ | п > 1} — ограниченная последова-
последовательность. Тогда
а = Цт а„ •<=>•
п—»оо
1) мноэ+сество {п € ЛГ | а„ < а - е}
конечно и
<==> Ve > 0 : <
2) мноэ*сество {п € N | а„ < а + е}
бесконечно.
= lim а„ <=>
п—>оо
1) множ.ество {тг € N \ ап> Р + е}
конечно и
Ve > 0 : <
2) множество {тг 6 ЛГ | ап > Р — е}
^бесконечно,
\ Доказательство рассмотрим для верхнего предела.

76 Глава 2. Предел последовательности действительных чисел
Необходимость. Пусть /3 = lira an = sup А и е > 0 задано. Со-
П—ЮО
гласно теореме 18/3 6 А, поэтому существует подпоследовательность
о-т(к) —► Р, fe —> оо. По определению предела последовательности для
числа е имеем 3 К £ N V к > К : \ат(к) — Р\ < £ ==>■ am(fc) > /3 — е
и, таким образом, условие 2) выполнено.
Предположим, что условие 1) не выполняется. Тогда существуют
е* > 0 и подпоследовательность {aTO(fc) | fe > 1} такие, что
Vfe>l: am(fc) >/3 + е\ A)
По теореме о существовании монотонной подпоследовательности су-
существует монотонная подпоследовательность {<im(fc(j)) I j > !}■ Пусть
7 := lim Om(fc(j))i заметим, что 7 ё й и 7 £ А Кроме того, согласно
j—юо
неравенству A), 7 > /3 + £*, поэтому /3 = sup А > 7 > /3 + £*, что невоз-
невозможно. Противоречие показывает, что условие 1) также выполнено.
Достаточность. Пусть число /3 удовлетворяет условию теоремы.
Докажем сначала, что /3 G А. Используем теорему о характеризации
частичного предела. Согласно условиям 1) и 2), для любого заданного
е > 0 множество {п £ N \ /3 — е < an < 0 + е} бесконечно, поэтому
/3 е А. Докажем теперь, что /3 = sup Л. Предположим, что существует
7 6 А, 7 > /3- Тогда для числа е = G - /3)/2 > 0 множество номеров
{п £ N | 7-£ < an <7 + £} бесконечно, так как 7 € А. Однако, 7 —e =
= G + /3)/2 > /3, и, таким образом, получаем противоречие с условием
1). Следовательно, предположение о том, что З7 Е А : 7 > Р, приводит
к противоречию, Поэтому /3 = sup A. J
Упраоюнение 90. Проверить равенства: а) lim an = lim (inf at) =
n->oo n-+oo fc>n
= sup(inf at); b) lim an = lim (supafc) = inf (sup at).
n>! k>n n-+oo П-+ОО fc>n n>l fc>n
Упражнение 91*. Для последовательности {an | n > 1} пусть Ап :=
+ + n
, n > 1. Доказать справедливость следующих нера-
O
n
венств lim an < lim An < lim An < lim an.
n->oo n->oo n->0° n-*°°
Упражнение 92*. Доказать, что lim lan + bn) < lim an + lim bn.
n—юо n—too n—юо
S5*. Пусть о„ > 0, n > 1. Доказать неравенство
lim n+1 > lim ?/a^.
n—юо an n-too
Упражнение 94* • Доказать, что справедливо следующее равенство
lim тах(ап,Ь„) = тах( lim an, lim Ь„).
n—юо n—»oo

2.5. Фундаментальные последовательности и критерий Коши 77
2.5 Фундаментальные последовательности и
критерий Коши
2.5.1 Фундаментальные последовательности
и их свойства
Определение 1. Последовательность {ап \ п > 1} С
R называется фундаментальной или последователь-
последовательностью Коши, если справедливо такое утверок.дение
Ve>0 3N £ N Vm>N V n > N : \ат - ап\ < е.
Примеры. 1. Последовательность {а, а,..., а,...}, где а 6 R, фунда-
фундаментальна, так как в определении 1 для любого е > 0 можно положить
N = 1.
2. Последовательность < — n > l| фундаментальна. Действитель-
Действительно, поскольку — —> 0, п —> со, то для заданного е > 0 3 N £ N V'n >
N : — < е. Тогда Vm>NVn>N:
2
m
2n
- 2k
е>
k := min(m,n) > N.
3. Последовательность {ап = n | n > 1} не является фундаменталь-
фундаментальной, поскольку для е* = - VN£NVm>N3n = m+l>N:
\ат - ап\ = 1 > - .
4. Последовательность {а„ = (-1)" | п > 1} не является фундамен-
фундаментальной, поскольку для е* = 1 имеем VN£N'Vm>N3n = m+l>
N: \ат - ап\ = 2 > 1.
5. Пусть {i(k) | к > 1} - фиксированная последовательность, причём
Vfc £ N : i(k) e {0,1,2,3,4,5,6,7,8,9}. Докажем, что последователь-
ность < а„ := -*— -\—— + ... + —— п > 1 > фундаментальна.
\ Сначала заметим, что для любых натуральных чисел т, n, m <
1 \ат — Qn\ = нл^ . 1 Н нЛ™ , о + • • . + ——
1Q 1Q 10
9 9 10 1 1
< lo^iy = ^'Поскольку — -.0, т-^оо.то
Ve > 0 3Wi G N Vn > Wi : -|- < е, и потому Ve > 0 BN =
JVi Vm> W Vn > N : |om - on| < e. J
Замечание. Пусть а = О.ахаг-.- - действительное число такое,
а^ = i{k), к > 1. Тогда по теореме 14 ап = а'п —> а, п —> со.

78 Глава 2. Предел последовательности действительных чисел
Упражнение 95. Доказать, что монотонная последовательность, со-
содержащая фундаментальную подпоследовательность, фундаментальна.
Упражнение 96. Доказать, что следующая последовательность чи-
f sin I sin 2 sinn . i ,
сел ian = — h — \-... + —— | n > 1 j фундаментальна.
Упражнение 97. Доказать, что неограниченная последовательность
не фундаментальна.
Упражнение 98. Последовательность {а„ | п > 1} фундаментальна
тогда и только тогда, когда sup \am — ап\ —» О, N —» оо.
m>N,n>N
Следующие свойства фундаментальных последовательностей часто
используются.
1°. Сходящаяся к действительному числу последовательность фундамен-
фундаментальна.
[ Пусть ап —» а £ R, п —> оо. Пусть произвольное е > 0 задано. По
определению предела для числа - Э iVi G ЛГ Vn > Nx : |on - о| < - .
Поэтому имеем Ve>03iV = iViVm>iVVn>iV: \am - ап\ =
= \am - а + а - ап\ < \ат - а\ + \ап - а\ < - + - = е. J
2°. Фундаментальная последовательность ограничена.
[ Пусть {ап | п > 1} — фундаментальна. Тогда согласно определе-
определению 1 для e = l3NVm>NVn>N: \ат — ап\ < 1. Положим
С := max(|ai|,|a2|,...>|aw_1|,|aw| + 1), тогда Vn > 1 : |а„| < С. Дей-
Действительно, последнее неравенство выполнено для n < N по определе-
определению числа С. Если же n > N, то \ап\ = \ап— un + un\ < |an-a^| + |a^| <
<1 + Ы<С. J
1
2.5.2 Критерий Коши
Теорема 20. Для того чтобы последовательность
"действительных чисел сходилась к действительном/у
Числу, необходимо и достаточно, чтобы она была фун-
фундаментальной.
Г Необходимость. Содержится в свойстве 1° п. 2.5.1.
Достаточность. Пусть {an | n > 1} — фундаментальная последо-
1ательность, тогда в силу свойства 2° п. 2.5.1 она ограничена. По тео-
теореме о существовании монотонной подпоследовательности существует
монотонная подпоследовательность {aTO(fc) | k > 1}, которая также огра-
ограничена. По теореме о существовании предела монотонной последова-
последовательности 3 a £ Н : aTO(j.) —> а, к —¥ оо.

2.5. Фундаментальные последовательности и критерий Коши 79
Докажем, что ап -4 a, n —» оо. Пусть произвольное е > 0 задано.
Поскольку последовательность {an | n > 1} фундаментальна, то для
числа Е- > 0 3 Nx £ N \/m > Ni Vn > Ni : \am ~ an\ < Е- По
определению предела последовательности имеем 3K&NVk>K:
\am(k) — а\ < - ■ Таким образом, Ve>OziN = NxVn>N: \an — а\ —
ее
- \Оп ~ a.m(k) + am(k) - а] < \an - am(k)\ + \am(k) — a| < — + — = е, где
m(k) - какое-нибудь из чисел таких, что к > К, m(k) > Ni. J
Упражнение 99. Последовательность {ап | п > 1} такова, что
ЗЛ 6 [0,1) Vn > 1 : \ап+1 - ап+2\ < Х\ап - ап+1\. Доказать, что
эта последовательность сходится.
Упражнение 100. Пусть для п > 1 и х 6 [0,3] величина Рп(х) =
апх2 + Ьпх + с„, где {а„,Ьп,с„ | п > 1} С Я. Предположим, что
Vi £ [0,3] : -Рп(^) -> -Р(х) 6 й, п -4 оо. Доказать, что каждая из
последовательностей {а„ | п > 1}, {Ьп | п > 1}, {с„ | п > 1} сходится
и что Р — многочлен на [0,3].
Упражнение 101. Последовательности {ап | п > 1}, {Ь„ | п > 1}
таковы, что Vn 6 /V : \ап — Ьп\ < —^-. Доказать, что сходимость одной
п
последовательности влечёт сходимость второй и что их пределы равны.
Упражнение 102. Пусть a > 0. Для произвольного Xq > 0 рассмот-
рассмотрим последовательность {а„ \ п > 1}, члены которой определяются
1 / а \
равенствами ап = - [ап-х -\ , п > 1, а0 = х0. Доказать, что
2 \ an_! /
а-п -» \/a, n -4 оо.
Указание. Рассмотреть отношение — -=., п > 1.
an + у/а' ~
2.5.3 Определение предела последовательности
векторов
Пусть йт := {х = (хь х2,..., хт) | х0 е R, 1 < j < m}.
Определение 2. Последовательность векторов
{£(") = (х^.х^,...,!^) | п > 1} сходитсл к вектору х =
= (xi,x2,...,xm), если V.7,1 <j < т: х^п) -» Xj, n-4 оо.
Используются обозначения: х*(п) -4 х, п -4 оо; lim x^n) = 3.
П-+0О
6 — 4-1168

SO Глава 2. Предел последовательности действительных чисел
Упражнение 103. Доказать справедливость следующего утвержде-
п .
ния atfn) -» х, п -» оо -<=>• £2 IXL — а;*;| —*■ 0, n -» с».
fc=i
2.5.4 Историческая справка
Теплиц Отто A881 — 1940) — немецкий математик.
Больцано Бернард A781 — 1848) — чешский математик. Его
основные математические работы, опубликованные спустя столетие по-
после его смерти, содержали точные формулировки ряда основных по-
понятий математического анализа, а также доказательства многих суще-
существенных теорем. Эти результаты не были замечены современниками.
Вейерштрасс Карл Теодор Вильгельм A815 — 1897) —
выдающийся немецкий математик. Внёс большой вклад в логическое
обоснование математического анализа. Именно К. Вейерштрассу при-
принадлежат определения предела с помощью е и 6, он же ввёл общепри-
общепринятое теперь обозначение предела
lim а„.
П—+ОО
Разработал основы теории функций комплексного переменного, автор
многих плодотворных идей в алгебре, дифференциальной геометрии, в
вариационном исчислении. Постоянно занимался педагогической рабо-
работой, лекции К. Вейерштрасса пользовались исключительной популярно-
популярностью. Большая часть его математических работ была впервые опубли-
опубликована только в 1898 г.

Глава 3
Предел функции в точке.
Непрерывные функции
3.1 Предел функции в точке
3.1.1 Предельная точка множества
Определение 1. Пусть А с R. Число х0 € R называет-
называется предельной точкой множества А, если
Ve>0 Зу е А,у фхо : \у-хо\<е.
Примеры. 1. Для множества А = [0,1] множество всех предельных
его точек есть множество А.
2. Для множества А = @,1] U {2} множество всех предельных его
точек есть множество [0,1].
3. Для множества А = < — п > 1 > множество всех предельных его
In J
точек есть множество {0}.
4. Множество А — \l,-,-,...,— \, ngJV, .предельных точек не
12 3 п J
имеет.
Таким образом, предельная точка множества А может принадле-
принадлежать множеству А, а может не принадлежать А.
Определение 2. Значение +оо есть предельная точка
множества А, если VC€H 3y€A: у > С.
Значение —оо есть предельная точка мноок.ества А,
если V С ей ЗуеЛ: у < С.
Примеры. 1. Для множества N значение +оо есть предельная точка.
2. Для множества Z значения +оо, —оо — предельные точки.
6* 81

82 Глава 3. Предел функции в точке. Непрерывные функции
Определение 3. Точках £ А, которая не является пре-
предельной точкой MHOotcecmea А, называется изолирован-
изолированной точкой множества А.
Замечание. Точка х 6 А есть изолированная точка множества А,
если 35 > 0 : В(х,6) П А = {х}.
Упражнение 1. Доказать, что множество всех предельных точек
множества Q есть Ни{—оо, +оо}.
Упразднение 2. Пусть xq £ R — предельная точка множества А.
Доказать, что в любой окрестности точки хо лежит бесконечно много
точек из множества А.
Теорема 1. Значение х0 — предельная точка множе-
множества А с R тогда и только тогда, когда существует
последовательность {хп \ п > 1}, удовлетворяющая усло-
условиям: 1) Vn > 1 : хп 6 А, хп ф х0; 2) хп -» х0, п -» оо.
[ Рассмотрим случай, когда х0 6 R.
Необходимость. Пусть хо — предельная точка для А. По опре-
определению предельной точки для числа е = 1 имеем следующее утвер-
утверждение 3xi 6 A,Xi ф Хо : |xi — Хо| < 1. Аналогично, для чис-
числа е = ~ получим 3x2 6 А,Х2 ф хо : |хг - хо| < ^, для числа
е = — 3Хз 6 А,хз Ф хо : |хз — хо| < - , и т. д. Получим последова-
3 3
тельность {х„ | п > 1}, удовлетворяющую условию 1) по построению.
Кроме того, из неравенств Vn > 1 : \хп — Xq\ < — следует, что
Х„ -4 10| П-ЮО. П
Достаточность. Это часть утверждения теоремы следует из опре-
определений предела и предельной точки. J
Упражнение 3. Проверить, что среди членов последовательности
удовлетворяющей условиям теоремы 1 бесконечно много различных.
Упражнение 4* • Определить множество предельных точек множе-
множества: а) А = {{\/п} | п > 1}; b) {sinn | п > 1}; с) {\/т - tfn \ m €
N, п 6 N}.
Замечание. Наиболее частым расположением предельной точки
хо € Н множества А относительно множества А являются следующие:
(i) 3 6 > 0 : (В{хо,5) \ {хо» С А; (Н) 3 6 > 0 : (х0 - 6,х0) С А; (ш)
3 5 >0: (х0,х0 + 5) с А
Удобно положить В(хо,6) := B(xo,<J) \ {^о}. Говорят, что B(xq,6)
— "проколотая" 5-окрестность точки xq.

3.1. Предел функции в точке 83
3.1.2 Определение Коши предела функции в точке
и примеры
Пусть Ас Д, А ф 0, далее рассматриваются функции вида / : А —» R.
Определение 4- Пусть хо 6 R — предельная точка
м.нож.ества А и / : А -» R. Число р 6 R называется пре-
пределом (или предельным значением) функции / в точке
х0, если Ve>0 3<5>0 Vx 6 (An B{xQ,S)) : |/(x)-p|<e.
Обозначения: p= lim /(x); /(x)-*p, x —» Xo.
I—»Xq
Залеечакил. 1. Заметим, что имеет место следующее равенство
А П В(х0,6) = {х 6 А | |х - хо| < 8, хф х0}.
2. Определение 1 можно представить в таком виде р = lim /(x)
<=> Ve>0 35>0: /(An В(хО)<5)) С В(р,е).
3. Из определения 1 следует единственность числа р, доказательство
будет приведено ниже.
4. Следующие 4 утверждения равносильны:
(i)Ve>0 3<5>0 Vie {АпЁ{хо,5)) ....
(ii)Ve>0 3 5 € @,1) Vie [Ar\B{xo,6)) ...,
(iii) V e 6 @,1) 3<5>0 Vx 6 (An 5(xo>5)) ...,
(iv)Ve6@,l) 356@,1) Vx 6 (An B{xo,6)) ...,
Равносильность утверждений (i)-(iv) весьма полезна в рассуждениях,
связанных с понятием предела.
Примеры. 1. Пусть А = R, се fin Vi £ Я: /(х) = с (/ —
постоянная функция). Тогда Vxo 6 й : lim /(x) = с или lim с = с.
f Для каждого е > 0 в определении 1 можно положить 6 = 1 > 0. J
2. Пусть А = R, /(х) = х, х 6 й. Тогда Vx0 6 й : lim х = хо.
X—Яо
[ Действительно, для значения р = хо имеем Ve>035 = eVx6
£(х0,6) : |/(х) - хо| = |х - хо| < 5 = е. J
3. Пусть А = R и /(х) = х2, х 6 Д. Тогда VioeH: lim x2 = х2,.
X—+Хо
[ Можно ограничиться только теми х, для которых |х - хо| < 1. Тогда
|x2-xg| = |х+хо|-|х-хо| = |х-хо+2хо|-|х-х0| < (|х-хо|+2|хо|)|х-хо| <
< A + 2|хо|)|х - хо|. Поэтому Ve 6 @,1) 3 6 := -—%—- > 0 Vx €
1 + 2|хо|
В(х0,6) : |х2 - х2| < A + 2|хо|)|х - хо| < A + 2\хо\N = е. J
Упражнение 5. Доказать, что VfcGiV VxogH: lim xk = x§.

84
Глава 3. Предел функции в точке. Непрерывные функции
Примеры. 4. Пусть А - R \ {1}, х0 = 1, /(х) =
х2 - 1
х2 - 1
—,
х € А.
Тогда lim
1
1-1
= 2.
[ Действительно, Ve>O3<5 = e>OVx€
5. Пусть А = R\ {0}, х0 = 0, /(х) =
X2 -1
2
J
x £ А. Тогда
справедливо равенство lim
I+0
sinx
= 1.
I-+0 X
f Сравнивая площади треугольников и сектора в круге радиуса 1, с
помощью определения функций sin, tg приходим к следующим нера-
1 . 1 1 х / тг\
венствам — sinx < — х < — tgx, x € 10,— к из которых следует, что
sinx тг „ _
cosx < < 1, 0 < |x| < — с учетом четности функции. Поэто-
sinx Л . 2 х пх2 х2
му 0 < 1 < 1 — cosx = 2sin — < 2— = -т- для значении
х 2 4 2
х, 0 < \х\ < ^. Таким образом, Ve € @,1) 3<5 := е > 0 Vx e В@,6) :
sinx x2 82 ,
—<т<т<£- J
smx
Следствие 1. Справедливо следующее неравенство
Vx 6 Я: |sinx| < |х|, причём знак " =" •*==>• х = 0.
Упражнение 6. Доказать, что Vn6JVVx€H: | sinnx| < п\ sinx|.
Упражнение 7. Доказать, что Vx 6 R : cos(sinx) > sin(cosx).
Упражнение 8. Для х € Л такого, что sinx Ф 0, доказать неравен-
w хт л "^ sinBm +l)a; ,
ство Vn€JV : 1+ У) —^ — <п2.
m=i smx
Пример. 6. Докажем, что для любого х0 € й lim sinx = sinxo,
I—Но
lim cosx = cosxo-
1-+X0
[ Положим A = R, p = sinxo для доказательства первого утвержде-
утверждения. Имеем Ve>O3<5:=e>OVx€ B(xo,<5) : j sinx — sinxo| =
= 2
cos •
Xo
sm -
x —
J
Упражнение 9. Доказать второе утверждение примера 6.
Пример. 7. Пусть а > 0. Тогда Vx0 € R : lim a1 = а10, в частности
Х-+Х0
lim ax = 1.
х-+0

ЗЛШредел функции в точке 85
\ Рассмотрим случай а > 1. В этом случае функция f(x) = ах, х €
R строго возрастает на R, то есть xi < х2 => а11 < аХ2. Пусть
произвольное е > 0 задано. Так как а1/™ = ■у/а —> 1, а~11п = —р -4 1,
{/а
п -4 оо, то в силу теоремы 7 гл. 2 имеем 3N\ € ЛГ Vn > N\ :
а-V" > 1 _ еа-«о; 3N2 E N Vn > N2 : а1/" < 1 + еа-*о. Тогда
.. . > 0 Vx 6 В(хо,5) : |а | ^
i, YV2J
—1| < а10еа~10 = е, поскольку для значений х € В(хо,<5) имеем также
-еа~х° <a~s - К а10 - 1< а5 - 1 < еа0. J
Упражнение 10. Провести доказательство в примере 7 для числа
а 6 @,1).
Определение 5. Пусть xq б R — предельпал точка
множества А и f : А -» Д. Значение +оо есть предел
функции f в точке х0, если V С еДЗ<5>0Ух€ (Ап5(хо,5)) :
/(х) > С. Значение -оо естъ предел функции / в точке i0,
если VCe Д 35>0 Vx€ (АпВ(хо,5)) : /(х) < С.
Пример. 8. Пусть А = Й \ {0}, х0 = 0, /(я) = —, х ^ 0. Тогда
lim -r = +сх).
Упражнение 11. Доказать, что -гт-г -4 0, х -4 х0, если /(х) -»
/(а:)
+ 00, X -4 10.
Определение б. Пусть +оо — преЗелънал точка мно-
ж.ества А. Число р € R называется пределом функции f
при х -4 +оо, если Ve>0 ЭСбН Vx>C : |/(я) — pj < e.
Упражнение 12. Привести определения пределов:
a) lim /(х) = р € R, b) lim fix) = +оо; с) lim fix) = +оо.
I-»-0O I—>+0О Х-»-0О
Пример. 9. Пусть А = @, +оо), /(х) = - , х > 0. Тогда lim - = 0.
X I-++0O X
Г Действительно, Ve>03C:=->0Vx>C: 0 = - < е. I
е хх
Упражнение 13. Пусть а > 0. Доказать, что lim — =0.
х-ч+оо ха
Пример. 10. Пусть а > 1, А - R, meN, f(x) = хтагх, х € А.
хт
Докажем, что lim — = 0.
++0 ах

86
Глава 3. Предел функции в точке. Непрерывные функции
I Пусть е > 0 задано. Поскольку согласно теореме 3 гл. 2
(n + !)m
~— =
(п
а -» 0, п -у оо, то в силу определения предела последо-
вательности для числа е имеем 3N£NVn>N:
™ хт
Поэтому Ve>03C:=iVVx>C:
так как [х] > С = iV.
х~-о
ах
(п + 1)
а!*
< е.
Упралскекгхе 1Л. Пусть а > 1, а £ R. Доказать, что lim — =0.
i—>+oo ах
Упражнение 15. Пусть а 6 @,1), а е й. Доказать следующее
утверждение lim (x^a1) = 0.
1» + О
In з?
Пример. 11 .Докажем, что lim = 0.
х->+оо х
\ Пусть е > 0 задано. По теореме 4 гл. 2
1п(п + 1) 1п(п + 1) п + 1
п п +1 п
—> 0, п —> оо, следовательно, по определению предела последователь-
последовательности для числа е имеем 3 N 6 N V п > N : — < е. Поэтому
Ve>03C:=iVVx>C:
[х] > С = N.
lnx
п
-О
lnx ln([x] + 1)
< е, поскольку
J
lnx
Упражнение 16. Пусть а > 0. Доказать, что lim — = 0.
х-> + оо ха
/ 1 Y
Пример. 12. Докажем, что lim I x H— = е.
х—> + оо V X /
[ Пусть £ > 0 задано. По определению числа е имеем
п
1 +
= 1 +
п + 1
n+lj n+2
при п -4 оо, поэтому по определению предела последовательности для
£ получим 3NeNVn>N: е - е < ( Ц ] , A + - ) <
V п+1J \ п)
< е + £. Таким образом, доказано такое утверждение Ve > 0 ЗС :=
NVx>C: е-е < 1 +
< е + е
х
< ' Ы
1 + - 1 -е
х
< е.
<
J

3.1. Предел функции в точке 87
Упражнение 17. Доказать, что:
a) lim A+-) =е; b) lim A + хI/х = е.
х->0
Упраэюнение 18. Доказать, что: a) lim [ xsin- ) = 1; Ь) предел
х—у+оо у х }
у ■ г
lim sin — не существует.
х->0 X
Указание. Проверить, что существуют последовательности
{х„ ] п > 1} с @, +оо) и {уп | п > 1} С @, +оо) такие, что: х„ -¥ О,
sin — -» 1; уп -» 0, sin — ~» 0, п -¥ оо.
Упражнение 19. Доказать, что: a) lim /(х) = а -4=»- lim /(х3) =
I—»0 I—>0
= а; b) lim /(х) = а =Ф- lim /(х2) = а. Привести также пример к Ь),
показывающий, что обратное утверждение не верно.
Упражнение 20*. Предположим, что для функции / : R *-> R
выполнено условие Va Е й : /(-)-* 0, п -4 оо. Существует ли
предел lim /fx)?
х—>0
Упражнение 21. Для функции / : R-* @,+оо) справедливо соот-
соотношение /(х) + ——г -> 2, х -» 0. Доказать, что /(х) -» 1, х -» 0.
3.1.3 Определение Гейне предела функции в точке.
Эквивалентность определений Коши и Гейне
Определение 7. Пусть х0 — предельная точка ыно-
снсества А, / : А —» R. Значение р (возможно, что р = —оо
или р = +00.) называется пределом функции / в точке х0,
если для любой последовательности {хп | n -> ij, удовлё^-
творяющей таким, условиям,: 1) Vn > 1 : хп б А, хп ^ х0;
2^ х„ -» х0, п -> оо, справедливо следующее соотношение
. Определение Гейне охватывает ситуацию всех трёх
определений п. 3.1.2.
Теорема2. Определения Коши и Гейне предела функ-
функции в точке эквивалентны.
\ Доказательство проведём для случая {хо,р} С R.
(О Предел в точке по Коши есть предел по Гейне. Пусть
р = lim /(х) в соответствии с определением 4 и пусть {хп | п > 1} -

88 Глава 3. Предел функции в точке. Непрерывные функции
произвольная последовательность, удовлетворяющая условиям 1) и 2)
определения 7. Докажем, что /(хп) -4 р, п —> оо. Пусть число е > О
задано. По определению Коши 3 6 > 0 Vx 6 А, \х - хо| < 6,х ф хо :
|/(х) — р\ < е. Теперь по определению предела последовательности для
числа 6 имеем 3N £ N Vn > N : |хп - хо| < <5. Таким образом,
получим такое утверждение \/e>03N€N\/n>N: \f{xn)-p\ < e.
(ii) Предел по Гейне есть предел по Коши. Пусть р есть пре-
предел функции / в точке Xq по определению 7. Допустим, что р не есть
предел функции / в точке хо по определению 4. Это означает, что
Зе* > О У 5 > 0 Зх(<5) 6 А, |х(<5)-хо| < 5,х{6) ф х0 : |/(х(<5))-р| > е\
Пусть х„ := х(— ), п > 1. Последовательность {х„ | п > 1} удовле-
творяет условию 1) определения 7, кроме того, выполнено и условие
2), поскольку |хп - хо| < — , п > 1. Поэтому f{xn) -* р, п -4 оо, что
противоречит следующему неравенству |/(хп) - р\ > е*, п > 1. J
Упраэ*скекгхе 22. Доказать теорему 1 для следующих случаев: а)
Хо & R, р = +оо; Ь) хо = —оо, р = +оо.
Упражнение 23. Доказать, что предел функции sin — в точке х0 = О
не существует. х
Упражнение 2А. Вычислить предел: a) lim (xsin- ) ;
х—>0 \ х J
Ь) lim (х \-\) ■ с) lim fsin— +sin— + +sin —
I-+0 \ [x J J ' п-юо ^ n2 П2 П2
d) lim sinGrv/n2~+T); e) lim зт2(тг\/п2 +n).
3.1.4 Свойства пределов функции
Пусть Хо - предельная точка множества А.
Т е О р е М а 3. Если lim /(x)=pi, lim f(x) = рг, mo pi =рг-
I—»X(J X—+X0
f Пусть {xn I n > 1} — произвольная последовательность, удовлетворя-
удовлетворяющая условиям 1) и 2) определения Гейне. Тогда в силу эквивалентности
определений Коши и Гейне имеем /(xn) -» pi и /(х„) -» р2, п -» оо.
Однако, по теореме 1 гл. 2 предел последовательности определяется
единственным образом, поэтому pi = Р2- J
Теорема 4. Пусть х0 6 Я, lim /(х) = р € Н и число
X—+Хо
д>р. Тогда 3<5 > 0 Vi € (АпВ{хо,6)) : f(x)<q.

3.1. Предел функции в точке 89
[ Согласно определению Коши предела функции в точке для числа е :=
= д-р > 0 имеем 3<5 > 0 Vx € (АГ)Ё(хо,8)) : |/(х)-р| < е =$> f{x) <
<p + e = q. J
Упражнение 25. Пусть для некоторого 7 > 0 имеем Ё(хо,'у) С А и
предел lim fix) > 0. Доказать, что 3<5 > 0 Vi 6 Ё(хо,8) : fix) > 0.
I-H0
Упражнение 26. Пусть +оо - предельная точка множества А и
lim f(x) > 0. Доказать, что 3 С е Л V х > С, х е А : /(х) > 0.
X—У + ОО
Упражнение 27. Пусть а > 1, а € Л. Доказать, что 3 С > 0 Vx >
С : ха < ах.
Указание. Воспользоваться следующими известными утверждени-
утверждениями: а) хаа~х -» 0, х -+ +оо; Ь) 0 < 1.
Упрадаснение 25. Доказать, что 3C>0Vx>C: lnx< y^-
Упразднение 2Р. Доказать следующее утверждение 3 С > 0 V.x >
С: х3+7х2-Зх + 1<2х3.
Теорема 5. Предположим, что функции f : А-* R,
g : А-* R удовлетворяют условиям.: 1) Vх б Л : /(х) < д(х);
2,) lim /(х) = р, lim g(x) = q.
X—Но I—Mo
Тогда р < q, то есть lim /(x) < lim o(x).
I-H0 ~ X—>X0
f Пусть {xn | n > 1} - произвольная последовательность значений аргу-
аргумента х, удовлетворяющая условиям 1) и 2) определения Гейне. Тогда
для последовательностей {/(х„) | п > 1}, {g{xn) \ n > 1} имеем а)
Vn > 1 : /(xn) < 5(in); Ь) f(xn) -+ p, 5(in) -+ g, n -+ со. Согласно
теореме 8 гл. 2 имеем р < q. J
Следствие 2. Если для функций f : А-> Д j: A -+
Л 3<5 > 0 Vx е (ЛпВ(хо,E)) : |/(х)-р| < з(х), 5(х) -+ 0, х -+ х0,
lim /(x) = р.
Теорема 6. Предположим, что для функций f,g : A -+
Л суг^ест7гвутот7г пределъ4 lim /(х) =р£ Д, lim р(х) = q б Л.
XНо 1-Ио
lim (C/(x)) = С lim /(x);
2; lim (/(х) + з(х))= lim f(x) + lim 3(
I—»Хо I-Ио I—»X0
3^ lim (/(x)-g(x))= lim /(x) • lim g(x);
XHo X—VXo X—Ho
X—VXo
А) если дополнительно q Ф 0, too lim
^ x»x
/(x)
—7—- =
lim g[x)
X-+XO

90 Глава 3. Предел функции в точке. Непрерывные функции
\ Пусть {хп | п > 1} — произвольная последовательность, удовлетво-
удовлетворяющая условиям 1) и 2) определения Гейне. По условию теоремы 6
f{xn) ->• р, g{xn) -* q, n -> оо, а потому на основании теоремы 10 гл. 2
имеем Cf{xn) -» Ср, /(х„) + g(xn) -+р + q, f{xn)g(xn) -+ pq, n -» oo
и при условии g ^ 0 ~Г\ -> - , п -» оо. J
Упразднение 30. Пусть хо 4. vZ. Доказать, что lim ctgi =
В—Но
Указание. Использовать пример 6 п. 3.1.2.
Упражнение 31. Доказать, что lim tgi = tgx0, х0 4. \ — + vZ\.
Упражнение 32. Доказать, что lim (я3 + 7x2 + 2x + 1) = x3, + 7i§ +
I—►XO
2i0 + 1.
Упражнение 33. Доказать, что для m 6 iV и i0 ^ 0 справедливо
г 1 1
равенство lim — = —.
Упражнение 34- Доказать, что для х0 > 0 lim sfx —
IНО
I—НО
\x — Xn\ 1
Указание. Для x > 0 имеем \%/х- Jx^\ =-^= -р= < —у= |х-хо|.
Vх + vхо vxo
Упражнение 35. Вычислить предел:
X _L_ Vn д> 1 1
a) Urn . ; Ь) lim {x{s/x2 + 2x + 2 - х - 1));
sin x — 1
/2 1 \
) lim —5 ^ ! d) lim
z-+0 \sin X 1 —COSX/ i-nr/2 COSS
■\/l + x sin x — cos 2x x2 + x
■ 0 bm
tg2§
e) l
9) Нш v-~~ \/cosx Um
j- э/ х-+о sin x x-»+c»v
;| {m,n} С N; a > 0.
f Упразднение 36. Пусть для функций /: А -4 й и j : Л-)й
| выполнены условия: 1) lim f(x) — Vq, lim g(y) — zq\ 2) Vx ф хо :
P ' x-no V->Vo
i f{x) ф Уо (x0 e R, Уо е Л). Доказать, что lim g{f{x)) = zQ.
Упражнение ЗТ. Функция / : @,+oo) -+ @,+oo) такова, что
Vi > 0 Vy > 0 : f(x + у) < f(x) + f(y). Доказать существование

^л функции в точке 9f
предела lim ——.
Х->+ОО I
3.1.5 Односторонние пределы
Пусть множество А С R и точка х0 б R таковы, что 3j > 0 :
(хо-1,хо) С А
Определение 8. Число р б Я называется пределом
слева функции f в точке х0, если Ve>03<5>0Vx6
(io-iS.io) : \f{x)-p\ <e.
Обозначения: р = f{x0-), p= lim /A), р= lim /(z)-
Пусть множество А С йи точка хо € R таковы, что 3j > 0 :
(хо,яо+7) С А
Определение 9. Число р 6 R называется пределом
справа функции f в точке х0, если Ve>0 3<5>0Vx€
(х0)х0+<5) : \f(x)-p\ <£.
Обозначения: р = /(хо+), р= lim /(х), р = lim /(x).
X—>Х0+ X—»ХО,Х>Хо
Пример. 1. Для функции /(х) = 1, х > 0, /(х) = -1, х < 0, /@) = 0,
имеем /@-) = -1, /@+) = 1.
Упражнение 38. Доказать, что существование предела lim /(x)
X—+Хо
равносильно существованию обоих односторонних пределов /(х0-),
/(хо+) и их равенству.
Упражнение 39. Дать определение пределов f(xo-) = +00 и
7(хо+) = +оо.
Упражнение 40. Найти пределы:
х-+т/2,х<т/2 У1 — sillX
) lim (|7r-x|tg|); d) lim (|тг-i|tg^);
x—nr,x<ir\ 2 / x-»r,x>ir V 2 /
e-l/x
e) lim e~Vx; f) lim .
; x-»0,x>0 x—>0,x>0 X
1 Указание к e), f)- Положить z = — и заметить, что z -» +00 равно-
равносильно тому, что х -+ 0, х > 0. Тогда lim [ - e~llx)= lim (ze~z) =
х->0,х>0\х / z-> + oov
= lim —. см. пример 10 п. 3.1.2.
? z-ч+оо ez г- г-

92 Глава 3. Предел функции в точке. Непрерывные функции
Упражнение А1. Пусть а > 0. Найти lim a1/1, lim а1/1.
i-tO,i>O z->0,z<0
3.1.6 Существование предела функции в точке
Пусть А С Л, f : A-+R.
Определение 10. Функция f называется монотонно
неубывающей на А (монотонно невозрастающей на А),
если V{xi,x2} С А: хх < х2 =>■ /(ii) < /A2) (/(^1) > /(^2))-
Функция f называется строго возрастающей на А
(строго убывающей на А), если V{xi,x2} С A: ii < х2 =>
/Ы < /(*а) (f(xi) > f(x2)).
Пример. 1. Функция f(x) — х2, 1 6 Л строго убывает на (-оо,0] и
строго возрастает на @,+оо).
Определение 11. Функция f : А ->• Л называется огра-
ограниченной на множестве А, если множество f(A) огра-
ограничено, то есть, если ЗС>0 УхбЛ: |/(х)| < С.
Теорема 7. Пусть для множ.ества А существует,
число 7 > 0 : (зо — 7>хо) С А, и функция / : А -» Л удовле-
Т7гворлет7г условилл*; J^ / монотонно не убывает на А; 2)
f ограничена на А. Тогда существует предел lim f{x).
I—>Х0,1<10
f Пусть В := {f(x) | i € (An{x < xq})}. Множество В непусто и ограни-
ограничено. По теореме о существовании точных граней Зр 6 Л : sup В = р.
Докажем, что /(io~) = Р- Для е > 0 по теореме о характеризации точ-
точных граней Эх < х0 : f(x) > р - е. С учётом условия 1) имеем
Ve>O3<5:=xo-x>OVxe {{xo-S,xo)n(xo-'y,xo)) : p~e<f(x) <
<f(x)<p=>\f(x)-p\<e. J
Упражнение ^2. Доказать аналог теоремы 6 для монотонно невоз-
невозрастающей функции.
Упражнение 43. Пусть числа {а, Ь, с} С Л. Для следующей функции
f(x) =i + l, х < 1, f(x) = ax2 + bx + с, х > 1, определить значения
а, Ь, с, при которых функция / монотонна на Л.
, Упражнение 44- Пусть / — монотонно неубывающая на отрезке
[а, Ь] функция, а £ R, Ь 6 Л. Для любого с € (а, Ъ) доказать существо-
существование пределов f(a+), /(с—), /(с+), f(b—). Проверить неравенства
/(о) < /(о+) < /(с-) < /(с) < /(с+) < /(Ь-) < /(Ь). Доказать также,
что Дт+ f(x-) = f(c+), ]im_f(x+) = f(c-).

3.2. Исследование локального поведения функций 93
Теорема 8. (Критерий Коши). Пусть х0 е R — пре-
предельная точка множества А и f : А -> R. Конечный пре-
предел функции f в точке х0 существует тогда и толь-
только тогда, когда Ve > О 3<5>0 V{i,y}c (An B(xo,S)) :
\f(x)-f(y)\<e.
f Необходимость. Пусть е > 0 задано. По определению предела
функции в точке для числа е/2 имеем 3<5i > 0 Vi 6 (АП B(xo,6i)) :
|/(х) -р| < е/2, где р := Km f{x). Тогда Ve > 0 3<5 := Si V{i,y} С
(АпЁ(хо,6)) : |/(х)-/(у)|1=Т/A)-р+р-/(у)| < |/A)_р| + |/(у)_р| <
<е/2 + е/2 = е.
Достаточность. Предположим, что условие теоремы 8 выполне-
выполнено. Для доказательства существования предела функции / в точке х0
воспользуемся определением Гейне. Пусть {хп \ п > 1} и {yn | n > 1}
— две произвольные последовательности, удовлетворяющие условиям
1) и 2) определения Гейне. Тогда этим условиям удовлетворяет также
последовательность {zn \ п > 1} := {х1,у\,х2,У2,---,хп,уп,...}. До-
Докажем, что последовательность {f{zn) | n > 1} сходится. Для этого
согласно критерию Коши сходимости последовательности нужно прове-
проверить её фундаментальность. Пусть для е > 0 число <5 > 0 удовлетворяет
условию теоремы 8. Поскольку zn —» хо, п —> оо, то по определению
предела последовательности для числа 6 имеем 3 Ni 6 N V n > N\ :
•zn -zo| < 6. Таким образом, We > О 3N := Ыг Wm>NWn>N:
\f{zm) - f{zn)\ < £• Следовательно, f(zn) -tpefi, n -+ оо. Тогда
/(х„) -л р, f(yn) -+ р; п -+ оо. По определению Гейне р — lim /(x). J
I—НО
Упражнение 45. Доказать утверждение lim /(х) =рбй
X—У + ОО
Ve>0 ЗС>0 Vx>C Vy >С: |/(х) -/(у)| < e.
Упражнение 46. Вычислить предел lim (tg(sin(tgx)) ctg(tg(sinx))).
3.2 Исследование локального поведения
функций
3.2.1 Предположения
Пусть А С R и хо — предельная точка множества А. В настоящем
разделе все рассуждения проводятся в одной из следующих ситуаций:
1)х0бЛ; З7 > 0 : (В(хо,7) \ {^о}) С А;
2)хоеЛ; 37 > 0 : (х0 - J,х0) С А;
3) х0 е R, 3 7 > 0 : (х0, х0 + 7) С А;

94 Глава 3. Предел функции в точке. Непрерывные функции
4) х0 = +оо; 3 с € R : (с, +оо) С А; 5) х0 = +оо; А = N.
Ниже рассматриваются функции / : А —¥ R, поведение которых при
х —> хо таково, что: (i) /(х) —> О, s —> io либо (ii) f(x) —» +oo, i —» s0-
3.2.2 Отношение подчинённости
Пусть io — предельная точка множества Ли/: А-* R, g : А -* R.
Определение 1. Пусть xQ e Л. Функция f подчинена
функции g при х -> х0, если выполняется следующее усло-
условие 3L>0 36 > 0 Vx<E{AnB{xo,6)): |/(i)|<L|j(i)|.
Пусть х0 — +оо. Функция f подчинена функции g при
х0 ->• +оо, если 3L>0 3ceilVi>c: \f{x)\ < L\g(x)\.
Обозначения: /(i) = 0CA)), x —» io; / = 0(g), 1 —>• io-
Упражнение ^7. Верно ли , что f(x) = 0(/(i)), 1 ->• i0?
Упразднение 4<^- Проверить, что для любого с ^ 0 / = 0(g), x -+
f - O(cg), x -¥ хо-
Упражнение ^9. Пусть х0 6 Д. Доказать, что / = 0A), х -> i0,
тогда и только тогда, когда / ограничена на В(хо,6) П А \ {хо} при
некотором 6 > 0.
Упражнение 50. Пусть хобЯиУх€(.А\ {аг0}) : 5(а:) 7^ °- Дока-
Доказать, что / = О(р), х —> ioi тогда и только тогда, когда — ограничена
9
на S(soi E) П Л \ {хо} при некотором <5 > 0.
Упражнение 51. Проверить, что для функции д, отличной от 0 на
A, f = О(д), х —» +оо, тогда и только тогда, когда — ограничена на
9
(с,+оо) при некотором с £ R.
Упражнение 52. Верно ли утверждение: для любых двух функций
/ и д имеем / = О(д), х ->• х0, либо д — О(/), х -+ х0?
Указание. Рассмотреть пример: хо = +оо, /(х) = 2х, д(х) =
= 3Isinx, х е R.
Пример. Пусть т € N, {ai, аг,..., ат} С R- Докажем утверждение
1 2 + ...+ат= О(хт), х -+ +оо.
с :
Поскольку, 1+— +-| +... + —-> 1, i -» +оо, то 3ceilVx>
X Х'2 хт
1н Н—Г-+...Н
X
< 2. Отсюда приходим к утверждению

3.2. Исследование
Vx>c: |sm +
Xm
< 2|xm|
Упражнение
a) sinx = 0(x)
c) x2 = 0{x),
e) lnx = 0(x),
g)VmeJV:
локального поведения
aixm~l +a2xm-2 + ...
53. Доказать, что:
, i-+0;
x -» 0;
x -> +oo;
xm = OBX), x -> +oo;
функций
+ an
b)
d)
f)
b)
x ■
1 — l-rml
i| — \x |
sinx = 0A)
x = O(x2),
+
X
nlnn = 0Bn),
x sin x + ■Ух
-»■ +00.
=
95
X X
x -> +oo;
-» +oo;
n —> oo;
O(x),
3.2.3 Свойства отношения "О"
ttx\
1°. Если существует предел lim —p-f = р 6 Л, то имеет место соот-
х-+во <7(Х)
ношение /(i) = 0CA)), х ->• х0.
f Доказательство следует из того, что |р| 6 Я и свойства предела функ-
функции в точке, см. теорему 4. J
Упражнение 54- Утверждение, обратное к 1°, не выполняется.
Привести пример.
Упражнение 55. В каком случае при условиях 1° имеет место со-
соотношение д[х) — O(f(x)), х -+ хо?
2°. Если / = О(д), х —» хо, и д = O(/i), х —>• хо, то / = O(/i), х —> хо.
Таким образом, O(O(/i)) = O(h), x —)• хо.
3°. Если / = О(р), х -^ х0, и /i = О(р), х -> х0> то f+h = 0{д), х ->• х0.
Таким образом, Oi(p) + Ог(р) = О(р), х -+ х0.
4°. Если fk = O(gk), x -+ х0, для fc = 1,2, то Д/2 = 0{gig2), х -)• хо.
Таким образом, O(ffi)O(p2) = 0C132), х -> х0.
f Пусть х0 £ R. Согласно условию, для fc = l,23Lfc>03Efc>0Vx€
{АГ)В(хо,6)\{хо}) : \fk{x)\ < Lk\gk{x)\. Поэтому для L := ЬуЬ2, 6 :=
= min(<5i,<52) > 0 получим утверждение Vx € (АГ) В(хо,6) \ {хо}) :
|/i(x)/2(x)|<L|3i(xK2(x)|. J
Упражнение 56. Доказать утверждения 2° и 3°.
3.2.4 Отношение пренебрежимости
Пусть хо — предельная точка множества А и / : А -* R, д : А-+ R.
7 — 4-1168

96 Глава 3. Предел функции в точке. Непрерывные функции
Определение 2. Функция f называется пренебре-
жимой по сравнению с функцией g при х -> х0 е R, ес-
если Ve>0 35 > 0 Vx€{An6(xo,8)) : |/(х)| < e\g{x)\.
Функция f называется пренебрежимой по сравнению
с функцией д при х -» +оо, если Ve > О Зс е Я Vi > с :
|/(х)|<ф(х)|.
Обозначения: f(x) = о(д(х)), х ->• х0] f = о(д), х -> х0.
Упражнение 57. Доказать, что:
а)/(х)=оA), х-»х0 <=>■ Дх)-»0, х-»х0;
Ь) /(х) = о(х), х -> +оо -Ф=Ф- ^^ -> О, х -4 +оо;
X
с)/ = о(р), х->х0 <^=^ f = o{cg), i -Но, с 6 й, с ^ 0.
Упраэ«;нение 55. Пусть Vx е (Л \ {х0}) : д(х) ф 0. Тогда f(x) =
= 0EA)), х-+х0 <=3> lim ^44 = °-
Упражнение 59. Верно ли утверждение: для любых двух функций /
и д справедливо утверждение / = о(д), х —» хо, либо д = о(/), х —> хо?
Для каких функций / = о(/), х -> х0?
Указание. Рассмотреть следующий пример: х0 = +оо, /(х) = 1,
д{х) = 1, х е Я.
Упрагиснение 60. Доказать, что: a) s2 = o(x), i ч 0; b) x =
= о(х2), х -» +оо; с) х3 = оBх), х -)• +оо; d) lnx = о(-у/х), х -> +оо;
е) п2 + п + 1 = оBп), п -» оо; f) s - sinx = o(z), x -» 0.
3.2.5 Свойства отношения " о"
1°. Если / = о(д), х -> х0, то / = О{д), и%
2°. Если / = о(д), х -» х0, и 5 = О(^), х -> х0, то / = o(h), х ->• х0.
Таким образом, o(O(/i)) = o(h), x -)• х0, O(o(/i)) = o(/i), x -4 х0.
3°. Если fk = 0E), х -> хо, для к - 1,2, то Д + /2 = 0E), х -> х0.
4°. Если Д = 0E1), х -)• хо, и /2 = О(зг), х -» х0, то Д/2 =
= o{gig2), х ->• х0.
Таким образом, 0E1HE2) = 0E152), х-> i0.
I" Пусть х0 € R. Согласно определениям отношений " о" и " О" имеем
Vt? >0 3<5х>0 Vx€HnB(xO)<5i)) : |Д(х)| < fi\gi(x)\, A)
3L>0 3<52>0 Vxe(AnS(xo,<52)) : |/2(x)| < L|52(x)|. B)

3.2. Исследование локального поведения функций 97
Для заданного е > 0 положим r\ = e/L и <5 = min(<5i,<52). Тогда из
A) и B) имеем Vx е {АПЁ{хо,6)) : \h{x)f2{x)\ < Lrj\gi{x)g2{x)\ =
= e\gi(x)g2(x)\. j
Упражнение 61. Доказать свойства 2° и 3°.
5°. Имеет место соотношение / — g = o(f), i ч io •*=> / — 9 =
= 0C), i -> i0.
f Достаточно доказать, что из утверждения / - g = o(f), x -» х0,
следует / — g = 0C), 1 -t 10. Для этого с учётом свойства 2°
достаточно показать, что / = О(д), х —>• хо. По определению от-
отношения "о" для числа е = 1/2 > 0 имеем 3<5 > 0 Vi € (АП
В(хо,<5)) : \f{x)-g{x)\ < |/(х)|/2, отсюда следует, что |/(х)| - \д(х)\ <
< |/(х)|/2, поэтому имеем неравенство |/(х)| < 2|g(x)|. J
Упражнение 62. Пусть те N, {ao,ai,a2,... ,ат} С R. Доказать,
что аохт + ац™ + а2хт + ... + ат - o(xm+1), x -> +оо.
Упражнение 63. Пусть а > 1, д(х) -* +оо, х -» х0, и / =
= о(д), х ->• х0. Доказать, что а^1) = о(а9'1)), х ->• х0.
3.2.6 Эквивалентные функции
Определение 3. Функции fug называются эквива-
эквивалентными при х ->• х0, если f - g — o(f), i-+i0.
Обозначения: /(x) ~ ff(s), s —> Xq', f ~ 3, x —)• xo.
Упразднение <Ц. Доказать, что: a) x2 + x ~ x, x -» 0; b) x2 + x ~
x2, x —> +oo; c) 1/x2 + x + 1 ~ x, x —>• +oo; d) sinx ~ i, i -t 0; e)
xm+aixm~1 + ...+am ~xm, x -+ +oo; me N, {00,01,02,... ,am} С Л;
1
•0 ч/х + 1 - ,/x ^
3.2.7 Свойства отношения эквивалентности
fi°. Пусть Vx е {А \ {х0}) : д{х) ф 0. Тогда f ~ д, х -> х0
? f Если / ~ 3, i-Яо, то, согласно определению f — д = о(д), х ->•
xn =^ Z _ 1 - £(*) х _ 1П=^ Ит № _Л _ о
fix) f(x) fix)
Um Ц-i = 1. Если же lim ±4-f = 1, то ^Ц-f - 1 = o(l)
то з(х) i—no д(х) з!1)
T 7*

98 Глава 3. Предел функции в точке. Непрерывные функции
х0 =$- f(x) - g{x) = 3(i)o(l) = O(g(x))o(l) = o(g(x), x -t i0. Поэтому
/ ~ g при i —> so. J
2°. Для любой функции / : / ~ /, x —> io.
3°. Если / ~ g, 1 -> io, и g ~ h, x ->• io, то / ~ /i, 1 -> i0.
[ Из соотношения / ~ g, x ->• s0, следует, что / = О(з), 3 = O(/), z ->•
i0. Согласно предположению f-g = o(g), x -> i0; 5 —h = o(g), x -> т0,
откуда на основании свойства 3° п. 3.2.5 / — h = o(g), x —> io, и,
согласно свойству 2° п. 3.2.5 / — h = о(/), х —> i0. Следовательно,
/~h, i-иц. J
4°. Если /fc ~ pfc, 1 ->• io, Для к = 1,2, то /i/2 ~ Д1Д2, z -»i0.
Г Имеем /1/2-Р1Р2 = /1/2-/1З2 + /1З2-З1З2 = /i(/2-3a) + (/i-/2)fl2 =
= 0l(fllHl(fl2) + O2Cl)O2(g2) = OCl32), I -> S0. J
Теорема 9. пусть vi e (a\{io>) •. /(i) ^ o, 5(i) ^ o,
/~3, i —Ho u /i: Л —> R — произвольная функция.
Тогда ялз существования одного из следующих преде-
пределов lim (f(x)h(x)); lim (g(x)h(x)) следует существование
второго и их равенство.
Аналогично, из существования одного из следующих
пределов lim —7-х; lim -7-f слеоуеттг существование
1-чхо /(i) i-+so з(а;)
второго и их равенство.
[ Пусть существует lim (/(i)/i(i)). Тогда получим lim Ы1Ш1)) =
XУХо X>Х
тт «■_■-■• v 1-COSI . 1-COSI
Пример. 1. Найдем предел lim :—-—. Имеем lim : =
х-»о i sin 3i z-»o ism3s
2sin2f . 2т 1
= lim —о 2 ~ m о 2 ~ д ' ПРИ этом использованы такие эквива-
i i2
лентности sin3i ~ 3i, sin2 - ~ — , i -)• 0.
Упраэ«;ненг1е 65. Из того, что f ~ д, х —> io не следует, что
2-^ ~ 2s, s -4 i0. Привести пример.
Упражнение 66. Из того, что Д ~ 3fc, я ->• i0, fc = 1,2 не следует,
что Д ± Д ~ 3i i 32, i -> io- Привести пример.
3.2.8 Порядок одной функции относительно другой
Пусть функция д : А -> R такова, что Vi 6 (А \ {х0}) : д(х) > 0.

3.2. Исследование локального поведения функций 99
Определение 4- Функция f имеет порядок р £ R от-
относительно функции g при х —> хо, если существует
lim j^~ = a£R, a ф 0.
x-4xo {g{x))P
Примеры. 1. Пусть х0 = 0. Функция f(x) — sina:2, x £ R имеет
порядок 2 относительно функции д(х) = х, х £ R при х —> 0, а функция
h(x) = —т, х ф 0 имеет порядок —2 относительно <?•
а;
2. Пусть а:0 = +оо. Функция f(x) = o;m + a1a;m~1 + .. . + om, x € R, где
т £ N, {oi, a2,..., om} с Я, имеет порядок m относительно функции
5(г) = х, х £ R при а: -> +оо, а функция h(x) = \/х + 1 — -Jx, x > О
1
имеет порядок — — относительно д при а: —> +оо.
3.2.9 Шкала сравнения
Пусть А С R, х0 — предельная точка множества А. Рассматриваются
функции вида / : А -* R.
Определение 5. Семейство функций G называется
шкалой сравнения при х ~» х0, если: 1) ^{f,g} С G ли-
либо f = o(g), x -» zo, либо g = о(/), а; -> хо, либо f = g; 2)
V/eG V<5>0 Эге(ЛпВAо,г)\Ы): /(*)^0.
В случае Xq = +oo определение аналогично с очевидным изменени-
изменением в условии 2).
Примеры. 1. Пусть х0 = О, А = R \ {0}. Семейства функций
Gi - {А Э х ^ хп \ п £ Z}; G2 = {А э х i-> хп \ п £ (N U {0}}
являются шкалами сравнения при х —> 0.
2. Пусть хо = О, А = @,о), 0 < о < +оо. Семейство функций
G = {A3xt->xa\a£ R} есть шкала сравнения при х -» 0 + .
3. Пусть а;о = +оо, А = (о,+оо), a > 0. Семейства функций
d = {Л Э 1 и i" | п £ Z}; G2 = {А 3 х н-> хп \ п £ {N и {0}}
являются шкалами сравнения при х —> +оо.
3.2.10 Главная часть. Асимптотическое разложение
Пусть G — шкала сравнения при х —> xq, / — некоторая функция.
Определение 6. Если 3L Ф 0 Зд £ G : f{x) ~ Ь^а:), х -»
а;0, то функция Lg называется главной частью функции
f относительно шкалы G при х -» х0,
Замечание. Главная часть / относительно заданной шкалы может
не существовать. Привести пример.

100 Глава 3. Предел функции в точке. Непрерывные функции
Теорема 10. (О единственности главной части).
Если f(x) ~ Lkgk{x), х -» х0, к = 1,2, где Ьх Ф 0, L2 Ф 0 и
5*: € G, fc = 1,2, mo Li — L2 и g\= g2.
\ Поскольку Li^i ~ Ьг52> я —> Ясь согласно 3°, то Lxgi — L252 =
= o(Ligi), x -4 i0. и Ligi - L252 = 0C1), x -» i0, Если 5! ф g2,
то получаем равенство L2g2 = £i5i + o(gi), x -4 хо- Из него следу-
следует, что предположение g2 — 0E1), х —> хо приводит к соотношению
дх = 0E1), х —> Хо. что невозможно для функции из шкалы. Анало-
Аналогично отвергается случай д^ — о(д2), х —> хо- Поэтому <?i = 521 откуда
(Li — L2)g\ = 0E1), х —> Хо, и, таким образом, L\ = L2. J
Последовательное выделение главной части относительно соответ-
соответствующим образом подобранной шкалы позволяет детально изучить по-
поведение функции при х -» х0. Опишем кратко эту процедуру и рассмот-
рассмотрим её на примере.
Пусть / — некоторая функция и G — шкала сравнения при х —> xq.
Определим сначала главную часть L\g\ функции / относительно
шкалы G при х -» х0- Тогда Li ф 0, #i £ G; f ~ Ь\д\, х -> х0;
/ - bigi = 0E1), х -» а;0- Тогда /(i) = Li5i(a;) + 0E1A)), х -> г0-
Пусть далее L2g2 — главная часть функции / — L\g\ относительно
шкалы G при х —> яо- Тогда L2 ф 0, ^2 € G; / — Li^i ~ L2g2, х —> го-
Поэтому 52 = °Ci)i ^ ~^ хо- Кроме того, / — Li^i — L2g2 — о(д2), х —>
хо, и f{x) = Ligi(x) + L2g2{x) + 0E2A)), я -» а;0-
Поступая аналогично, после п шагов получим следующее представ-
представление для функции /
f(x) = Ligi(x) + L2g2{x) + ... + Lngn{x) + o{gn{x)), x -» x0, A)
где Ькф0, gk€ G, 1 < fc < n; 5^+1 = o(gk), x -> x0, для 1 < fc < n - 1.
Правая часть формулы A) называется асимптотическим раз-
разложением при х —* хо функции / относительно шкалы G с точно-
точностью до 5п-
Упражнение 67. Доказать, что асимптотическое разложение функ-
функции / с точностью до дп определяется единственным образом.
Пример. Найдём предел
lim
f Для числа а £ R, а ф 0 и функции f(x) = ^/х + о, а: > —о, найдём
асимптотическое разложение при х —> +оо относительно следующей
шкалы G = {@, +оо) Эг их" \ а £ Д}. Сначала определим главную
часть / относительно G при х —> +оо, то есть определим числа L\ ф
0, ал £ R так, чтобы lim — = 1. Для этого нужно положить
z-Ч-оо LiXai
Li = 1, Qfi = — . При этом получим ^/х + а ~ ^/х, х —> +оо.

3.3. Непрерывные функции
101
Найдём теперь главную часть функции tyx + о— ^/х, х > тах@, —о)
при х —> +оо относительно шкалы G, то есть определим числа Ьг Ф
О, а.2 € -R так, чтобы
v'a: + о - tfx
2
при а; —> +оо. Для этого нужно положить Ьг = — , с*2 = — т- Таким
образом, имеем 1/х + а = 1/х -\ j= + о I —р= \ , х -* +оо. Этого
«3 v **• \ v *** /
разложения достаточно для вычисления предела
Следовательно, искомый предел равен — .
о
Упражнение 68. Доказать, что:
а) Иш
х^+о
b) lira (xl'z (Ух2 + 5а: + 1 + Ух2 + х + 1 - 2а:2/3)) = 2;
с) lim
g
d) lim
I-4 + 0O
4
3.3 Непрерывные функции
3.3.1 Определения и примеры
Пусть А С R, Хо € А — предельная точка множества А, причём хо € А,
и / : А -» Д.
Определение 1. Функция f называется непрерывной
в точке хо, если lim /(я) = /(х0) ■$=>• lim /(г) = /(lim я).
Ж~ЧХо X—VXo X—VXo
С помощью определений Коши и Гейне получаем следующие две
равносильные определению 1 формулировки определения непрерывно-
непрерывности в точке.

102 Глава 3. Предел функции в точке. Непрерывные функции
Определение 2. Функция f непрерывна в точке х0,
если Ve>0 3 <5 > О Vz € (АпВ(хо,5)) : \f(x) - f(xo)\ < e.
Определение 3. Функция / непрерывна в точке х0,
если для любой последовательности {хп \ п > 1}, удовле-
удовлетворяющей условиям,: 1) Vn G N : хп £ А и 2) хп -» яо,
п -» оо еътолнлетсл соотношение /(хп) -* /(^о), п -> оо.
3aAte4OKue. Наибольший интерес представляет случай, когда для
точки х0 существует 5 > 0 такое, что {ю - 5,х0 + 5) С А. Тогда опре-
определению непрерывности в точке можно придать следующую форму
Ve > 0 35 > 0 : f(B(xo,5)) С B(/(io),e). то есть, для любой
окрестности V точки f(xo) существует окрестность U точки хо такая,
что /([/) С V.
Пусть А и Хо таковы, что 3 S > 0 : (хо — S, Хо] С А.
Определение 4- Функция f называется непрерыв-
непрерывной слева в точке х0, если f{x0-) = f{xo), то есть, если
Ve>0 35 > 0 Vze (!Го-*,!Го]: |/(*) -/(*о)| < е-
Пусть А и Хо таковы, что 3 5 > 0 : [хо, хо + 6) С А.
Определение 5. Функция f называется непрерывной
справа в точке х0, если f{xo+) = f{x0), то есть, если
Ve>0 3<5>0Va:e [а:о, хй + 6) : \f{x) - f(xo)\ < e.
Упражнение 69. Пусть для некоторого 5 > 0 окрестность В(х0,6) С
А. Функция / непрерывна в точке Хо тогда и только тогда, когда /
непрерывна слева и справа в точке хо- Доказать это утверждение.
Определение 6. Каж.дая функция непрерывна в изо-
изолированной точке. Функция f называется непрерывной
на мномсестве А, если она непрерывна в ка&сдой точке
м.нож.ества А.
Обозначение: / £ С{А) *v==> / непрерывна на А.
Теорема 11. Пусть функции /: А -» R, g : А -» R
непрерывны в точке х0 € А. Тогда:
1) Vc G R : (с/) непрерывна в точке Хо\
2) f + g непрерывна в точке хо\
3) fg непрерывна в точке хо\
4) если дополнительно значение д{х0) Ф 0, то f/g непре-
непрерывна в точке Хо-
\ Доказательство этих утверждений непосредственно следует из опре-
определения 1 и теоремы 5 о свойствах предела функции в точке. J

3.3. Непрерывные функции ДОЗ
Примеры. 1. Пусть для некоторого с £ R /(я) = с, х £ R. Тогда
/ е c(R).
[ Действительно, для любого фиксированного Хо 6 -R имеем Ve >
>035 = e>0Va:G В(я0, *) : |/(*) - /(*о)| = |с - с\ = 0 < 5 = е. J
2. Пусть f(x) =х, х £ R. Тогда / 6 С(Д).
[ Пусть Хо G Я фиксировано. Имеем
Ve>0 3<5=е>0 V а: е В(аго, E) : |/(х) - /(аго)| = |х - хо| < 5 = e.J
3. Пусть Р(х) :— аохт + аххт~1 + ... + ат-\Х + ат, х £ R, где
т £ N и {oo.oi,... ,om} С -R. Функция Р есть многочлен от я.
Тогда Р G С(Д).
f Следствие примера 2 и теоремы 11. J
4. Роциоколькоя функция есть отношение многочленов Р и Q :
P(i)
ЯС*) = ^7~Т i а; е {z G Я I Q(z) ^ 0}- Из примера 3 и теоремы 11
следует, что рациональная функция непрерывна во всех тех точках, в
которых она определена.
5. {sin, cos} с C(R), а функции tg, ctg непрерывны на множестве
определения.
[ Пусть произвольное Xq £ R фиксировано. Заметим, что Ve > 0 3 5 =
X ~\~ Xq II X — Xq
= е > 0 Vz £ В(хо,6) : |sina; - sinzol = 2 cos —-— • sin —-— <
< |a; — xq\ < 5 = e. Для функции cos рассуждения аналогичны, для
функций tg и ctg применить теорему 11. J
6. Пусть a > 0 и f(x) = ах, х £ R. Тогда / G C(R).
[ Следствие примера 7 п. 3.1.2. J
Упражнение 70. Найти пределы:
х2 + 2cosх + 1х + 1 , , ,. х sinх + 1
a) lim : ; b) lim 5—-— .
' i->2 i + smi + З1 »-»з a;3 +1
Упражнение 71. Пусть для {а, Ь}сй f{x) =z + l, г<0и /(г) =
ах + b, х > 0. а) Для каких значений о, Ь функция / монотонна на R?
b) Для каких значений a, b функция / £ C(R)?
Упрамснение 72. Пусть f(x) — [zjsinTra:, x £ R. Доказать, что
/ £ C(R) и построить график функции /.
Указание. Если х £ [к, к +1), к £ Z, то [х] = fc и /(я) = fcsin7пг.
В точках а: = fc £ Z найти /(fc-) и /(fc+).
Упрамснение 73. Пусть /(я) = [я] + (я - [я])^, я > 1/2. Доказать,.
что функция / £ С([1/2,+оо)) и строго возрастает на [1,+оо).

104 Глава 3. Предел функции в точке. Непрерывные функции
Упражнение 74- Функция / : R —> R непрерывна на Ли
\/r£Q : /(г) = г3 + г + 1. Найти /.
Указание. Пусть о £ (R \ Q), о > 0. Тогда по теореме 12 гл. 2
о = lira а'; о' 6 Q, п > 1. Следовательно, в силу непрерывности
функции / в точке а и свойств предела последовательности /(а) =
= lim /(о'„) = lim (Ю3 + а'п + 1) = а3 + а + 1.
п—»оо п—»оо
Ответ: /(z) = i3 + i + 1, 16Й.
Упражнение 75. Если / £ С(Д), то |/| € С(Д). Доказать это утвер-
утверждение и рассмотреть пример, показывающий, что обратное утвержде-
утверждение неверно. Пример: f(x) = —1, х < 0 и /(г) = 1, о; > 0.
Упрамснение 76. Для функций {/,5} С С(А) положим ft(i) :=
= mm(f(x),g(x))t k(x) := max(f(x),g(x)), x £ А. Доказать включение
{h,k}cC(A).
Указание. Воспользоваться следующими равенствами
min(a, b) = - (a + b - \а — b\), max(o, b) = - (a + b + ]o - b|).
Упроэкгкекие 77. Для функции / : R -* R положим g(x) :=
= f(x3), h(x) := f(x2); x £ R. Какие из следующих утверждений верны:
а)/€С(Я) =* {g,h}cC{R), b) g € C(R) =► / G С(Д),
с) h G С(Я) =► / G С(Я)?
Упражнение 78. Пусть / £ С(Д) иЭс>0Уг£(?: |/(г)| < с.
Доказать, что функция / ограничена на R.
Упрамснение 79. Пусть {/, д} с С([0,1]). Могут ли функции fug
быть различными: а) только в конечном числе точек отрезка [0,1], Ь)
только в счётном множестве точек отрезка [0,1]?
2хх2п + х2 + 1
Упражнение 80. Пусть f{x) = lim ^— , i£R По-
Построить график функции / и исследовать её на непрерывность.
Упражнение 81*. Функция / : R -» R непрерывна в точке 0 и
такова, что \/ х £ R: f(x) + f(— ]= х. Доказать, что f(x) = - х, х € R.
Упрамснение 82*. Функция / : @,+оо) -4 @,+оо) такова, что
V{a:,j/} С @,+оо) : f(x + у) = f(x) + f(y). Доказать утверждение
Зс>0 Vz>0: f(x) = cx.
Упражнение 83*. Функция / £ C(R) удовлетворяет соотношению
A)

3.3. Непрерывные функции 105
Доказать, что f(x) = /A)я, х 6 R. Уравнение A) относительно функ-
функции / называется функциональным уравнением Коши.
Определение 7. Если функция f не является непре-
непрерывной в точке хо, то говорят, что функция / разрывна
в точке х0 и что точка х0 есть точка разрыва /.
Пример. Пусть f(x) = -1, х < 0, f(x) = 1, х > О, /@) = 0. Тогда
/ € С(Я\ {0})), /@-) = -1, /@+) = 1 и / разрывна в точке 0.
Упраэкгкекие 84- Доказать, что функция f(x) = sin - , х ф 0, /@) =
X
0 разрывна в точке 0.
Упражнение 85. Пусть f(x) = 1, i6Q, /(i) = 0,i G {R\Q) —
функция Дирихле. Доказать, что / разрывна в каждой точке.
Упражнение 86. Пусть f(x) = sina:, i 6 Q, f(x) = 0, ie(R\
<5). Доказать, что функция / непрерывна в точках nZ и разрывна в
остальных точках.
Упражнение 87. Пусть функция / : R -> R такова, что Уже
R \/ п € N : fix )</(а:Н ) ■ 1) Является ли функция / моно-
тонной? 2) Доказать, что / монотонна на R, если / £ (
3.3.2 Элементарные свойства непрерывных функций
Теорема 12. Пусть функция / непрерывна в точке
хо и q — произвольное число такое, что q > f(x0). Тогда
36 > 0 Ухе{АпВ{хо,6)) : f{x)<q.
Г Следствие теоремы 4 для р = f(xo). J
Теорема 13. (Ч? пределе сложной функции). Пусть
х0 — предельная точка м.нож.ества А (возм.ож.но х0 = —оо
или х0 = +00.), длл функции / : А -> Я сг/гцестег/em предел
lim f(x) = р е R; для м.нож.ества В э ({/(я) | a; G А} и {р})
X—Но
пусть g : В -* R — функция, непрерывная в точке р.
Тогда lim g(f(x)) = g(p) <=> lim g(f(x)) - g( lim /(*)).
X—VXo X—VXo X—>Xo
f Для любой последовательности {xn | n > 1}, удовлетворяющей усло-
условиям 1) и 2) определения Гейне, согласно предположению теоремы
f{xn) -» Р, ти оо, а с учётом непрерывности функции g в точке р,
имеем g{f{xn)) -» p(p)i n -> оо. J

106 Глава 3. Предел функции в точке. Непрерывные функции
Теорема 14. (О непрерывности суперпозиции). Пре-
дполоэ*сим, что функция f : А —> R непрерывна в точке
xq £ А, мноэ+сество В э {/(я) | х € А} и функция g : В —> R
непрерывна в точке f[x0).
Тогда функция h(x) := g(f(x)),x £ А непрерывна в точке х0.
\ Следствие теоремы 13 с р = f{x0). J
Пусть (а,Ь) С R, возможно, что -оо < о и (или) b < +oo. Пусть
/ : (о, Ь) —> R — монотонно неубывающая на (а,Ь) функция. Согласно
теореме 6 существует предел lira f(x) —: с € R, если / ограничена
х—>а+
снизу на (о, Ь), и /(я) -> -оо —: с, х -» о+, если / не ограничена снизу
на (а,Ь). Поведение функции / при i -> d- аналогично, существует
предел lim fix) =: d, d < +oo.
х->Ь-
Теорема15. (О существовании и непрерывности об-
обратной функции). Пусть функция / : {a,b) -> R удовле-
удовлетворяет условиям,: 1) f строго возрастает на {а,Ь) и
2) f е С((а,Ь)).
Поломсим. с := lira f(x), d:= lira f(x); — оо < с < d < +oo.
Тогда существует единственная функция g : (c,d) —>
(о,Ь), г/довлетворл'югцаА условилм:
a^ 5 строго возрастает на {c,d); b) g € C((c,d));
cJ>Va:e(a,b): <;(/(*)) = *; Vye(c,d): /E(y)) = y.
f I. Докажем сначала, что Vj/0 € (с, d) 3 ]x0 £ {a,b) : f{x0) = Уо- Пусть
произвольное j/o £ (с, d) фиксировано, при этом с < уо < d. Рассмотрим
множество М :— {х € (о, Ь) | f(x) < j/o}> множество М обладает следу-
следующими свойствами, (i) М ф 0. Действительно, поскольку lira fix) =
I—*O +
= с < j/oi то для фиксированной последовательности {х'п | тг > 1}, удо-
удовлетворяющей требованиям определения Гейне: х'п Е (о, Ь), п > 1 и
ij, ч о, п -ч оо, имеем f{x'n) —> с < уо> тг —> оо, откуда соглас-
согласно теореме 7 гп. 2 3NX £ N \/п > Ыг : f(x'n) < у0 => х'п £ М.
(ii) Множество М ограничено сверху. Пусть {х1^ | п > 1} — произволь-
произвольная фиксированная последовательность такая, что: х„ £ (a,b), n > 1
и х"п —> b, n —> оо. Тогда f{x'^) —> (i > j/Oi n —> оо. Поэтому
; ЗЯ2 € ЛГ Vn > N2 : /«) > у0 =» «^ ^ М. Тогда х'{,2 есть верх-
|йяя грань для М, поскольку по условию 1) имеем х > x"N =>■ /(г) >
■|>/(!Г^)>УО=>!Г^М.
»>. Применим теперь к множеству М теорему о существовании точной
«рерхней грани. Получим 3 хо £ R : supM = Хо- Отметим также, что
.^'Wl <xa<x'i,a, хо£{а,Ь).

3.3. Непрерывные функции 107
Докажем теперь, что /(яо) — Уо- Пусть Uq £ N такое, что V п>п0 :
а < Хо < Хо < Хо Н— < Ь. Поскольку хо = sup M, то по условию 1)
п п
для п > По имеем [хо )£ М =>■ f(xo )< Уо- Воспользуемся
теперь теоремой 8 гл. 2 и непрерывностью функции / в точке хо, см.
условие 2), f(x0) = lira f(x0 )< у0. Отсюда f(x0) < Уо- Кроме
того, для п > по имеем (х0 Н— )$ М =>■ /(го Н— )> 2/о- Откуда,
V п / V п /
как и выше, получим f(xu) = lim /(zo H— )> Уо- Следовательно,
п—юо \ П /
/(а:о) > г/о- Таким образом, /(i0) = Уо-
Если z € (о, Ь) такое число, что f(z) — у0, то из предположения
z < Хо имеем по условию 1) уо = /(z) < f{xo) = Уо, что невозможно.
Аналогично приводит к противоречию и предположение z > хо- Следо-
Следовательно, z = Хо-
II. Определим теперь функцию д : {c,d) -» (о,Ь), положив для у €
(c,d) значение ^(у) равным тому единственному числу х £ (о,Ь), для
которого /(я) = у. При этом Vz G (о, Ь) : ^С/С^)) = х', Vj/ € (c,d) :
/(^(у)) = У. а функция g является обратной для функции /.
III. Пусть с < 2/i < у2 < d. Докажем, что д{у\) < 5(Уг)- Предполо-
Предположим, что последнее неравенство неверно, то есть, пусть 5B/1) > 5(Уг)-
Положим г*; = д(Ук), к = 1,2, при этом a < Z2 < £i < Ь- Тогда по усло-
условию 1) теоремы f(x2) < f(xi) <=> /($(у2)) < f{g{yi)) ==> У2 < У1,
что невозможно. Таким образом, функция д строго возрастает на (с, d).
IV. Докажем теперь, что д G C((c,d)). Пусть произвольное зна-
значение уо € (с, d) фиксировано. Воспользуемся определением Гейне.
Для произвольной последовательности {уп \ и > 1}, удовлетворяю-
удовлетворяющей условиям: уп £ (с, d), п > 1 и 2/„ -» 2/0) п -> оо, нужно дока-
доказать соотношение д(Уп) -> 5(Уо)> п -> оо. Можно предположить, что
Уп € [/(z'ati)> /(^Arjli n > 1. Положим хп := 5(Уп), п > 1; х0 := д{Уо),
при этом хп € [г'^, z'^-J с (о, Ь), п > 0. Предположим, что последова-
.тельность {хп | п > 1} не сходится к х0- Это означает, что существует
число е* > 0 такое, что неравенство \хп — хо\ > е* выполняется для бес-
бесконечного набора номеров п = n(fc), fc > 1. Выберем из ограниченной
■ последовательности {xn(fc) | к > 1} монотонную подпоследовательность
: {xn(k(j)) I 3 > 1}, тогда in(fc(j)) -» z, j -> 00, причём z £ [a;'Wi, 1'^]
и \z — Xo\ > £*- Согласно условию 2) теоремы f{xn(k(j))) —* /(z) 7^
/(^o), J -> 00. Следовательно, j/n(fc(j)) -» /(z) # Уо> j -> oo, что невоз-
невозможно. J
Замечания. 1. Утверждение, аналогичное теореме 15 , справед-
справедливо для строго убывающей и непрерывной функции.

108 Глава 3. Предел функции в точке. Непрерывные функции
2. Если о £ R, то теорема 15 верна для множества [a,b), при этом
непрерывность в точке о есть непрерывность справа в точке о.
3.3.3 Обратные функции к некоторым элементарным
Здесь приводятся определение и свойства логарифмической и обратных
тригонометрических функций в качестве применения теоремы 15.
Примеры. 1. Определение и свойства степенной функ-
функции с показателем — , т Е N. Пусть число т & N фиксирова-
т
но, [а,Ь) = [0,+оо), /(х) = хт, х £ [0,+оо). Функция / удовлетворя-
удовлетворяет условиям теоремы 15, именно, строго возрастает и непрерывна на
[О,+оо). При этом с— lim хт - О, d - lim xm - +оо.
i->0+ х-»+оо
Согласно теореме 15 существует единственная строго возрастающая
и непрерывная на [0, +оо) функция д, обратная к /. Функция д обычно
обозначается следующим образом д(у) — rq/y = у1/™, у > 0, причём
V х > 0 : \/х™ = х; V у > 0 : ( ^/у)т = у.
Замечания. 1. Таким образом, функции вида /i(a;) = \fts /2B:) =
s/x, x>Q непрерывны на [0,+оо).
2. Если т — 2fc — 1 с числом fc £ N, то утверждение примера 1
справедливо для интервала (о, b) = R. Тогда (с, d) = R. Следователь-
Следовательно функции /i(a;) = \/x, /2B) = v^i x £ R строго возрастают и
непрерывны на R.
ъг оо п г </я + ^Х2 + X + 1
Упражнение во. Вычислить предел lim
X» 1
2 + v4in x
Упражнение 89. Применить теорему 15 к функции f(x) — х2, х <
О и найти обратную функцию.
2. Определение и свойства логарифмической функ-
функции. Пусть d > 0, d ф 1, и f(x) — dx, x £ R. Докажем, что
функция / имеет обратную, которая называется логарифмической
функцией. Рассмотрим случай, когда d > 1. Для d > 1 функция / строго
возрастает на Ли согласно результату примера 7 п. 3.1.2 непрерывна
на R. При этом с = lim сР = О, d = lim d1 = +оо. По теореме 15
I—У —ОО I—У + ОО
V у £ @, +оо) 3 \х £ Д : dx = у, число а: называется логарифмом
числа у при основании d и обозначается символом а: = logd у. Функция
; д(у) — logdy, у > 0, обратная к /, строго возрастает и непрерывна на
| "(О, +оо). Кроме того, V х £ R : logd d1 = х\ V у £ @, +оо) : dl°&*у =у,
в частности, d° = 1, logd 1 = 0.
;" Таким образом, для d > 1 логарифлшческая функция logd
определена, строго возрастает и непрерывна на @,+оо).

3.3. Непрерывные функции НЮ
Аналогично, для d G @,1) логарифмическая функция logd опре-
определена, строго убывает и непрерывна на @,+оо).
Упражнение 90. Построить график логарифмической функции для
d > 1 и d < 1.
3. Определение и свойства обратных тригонометри-
тригонометрических функций.
a) Пусть [а,Ь] = [—тг/2, тг/2]; /(х) = sinx, х G [—тг/2,тг/2]. Со-
Согласно определению синуса, функция sin строго возрастает, а в си-
силу результата примера 5 п. 3.1.2 она непрерывна на [-тг/2, тг/2]. При
этом с = lim sinz = sin(-7r/2) = —1, d = lim sinx = 1. По
1-+-7Г/2 x-nr/2
теореме 15 Vy G [—1,1] 3 !x G [-тг/2, тг/2] : sinx = у, число х
называется арксинусом числа у и обычно обозначается символом
х = arcsiny. Обратная к / = sin функция g(y) = arcsinj/, у G [-1,1]
строго возрастает и непрерывна на [—1,1]. Кроме того, имеем равенства
Vx G [-7г/2,тг/2] : arcsin(sinx) — х; Vy £ [-1,1] : sin(arcsiny) = у.
b) Пусть [a,b] = [0, тг], /(х) = cosx, x G [0, тг]. Функция cos стро-
строго убывает на [0, тг], согласно примеру 5 п. 3.1.2 она непрерывна на
этом отрезке и с = -1, d — 1. По теореме 15 Vy G [-1,1] 3 !х G
[О,тг] : cosx = у, число х называется арккосинусом числа у и обо-
обозначается символом х = axccosj/. Обратная к / = cos функция д(у) =
= arccosy, у G [—1,1] строго убывает и непрерывна на [—1,1]. При этом
Va;G[0,7r] : arccos(cosx) = х; Vy G [—1,1] : cos(arccosу) = у.
c) Пусть (а,Ь) = (-■7г/2,тг/2); /(х) = tgx, x G (-7г/2,тг/2). Функция
/ = tg строго возрастает и непрерывна на (— тг/2,тг/2). Кроме того,
с = -оо, d = +оо. По теореме 15 V у G (-оо, +оо) 3 !х G (-т/2, тг/2) :
tgx = у; число х называется арктангенсом числа у и обозначается
символом х = arctgy. Обратная к / = tg функция д(у) = arctgj/, у £ R
строго возрастает и непрерывна на R. При этом справедливы равенства
Vx G (-7г/2,7г/2) : arctg(tgx) = x; Vy G Я : tg(arctgy) = у. В
частности, tgO = 0, tg — = 1, arctgO = 0, arctg I = — .
d) Пусть (a,b) = (О,тг), f(x) = ctgx, x G @, тг). Функция / = ctg
строго убывает и непрерывна на (О,тг), а значения с = — оо, d = +оо.
По теореме 15 Vy G (-оо,+оо) Э !х G @,тг) : ctgx = у, число
х называется арккотангенсом числа у и обозначается следующим
символом х = arcctgy. Обратная к / = ctg функция с?(у) = arcctgj/, j/ G
Я строго убывает и непрерывна на R. Кроме того, имеем равенства
Vx G @, тг) : arcctg(ctgx) = х; У у G R : ctg(arcctgy) = у, в частности,
ctg - = 0, ctg ! = 1, arcctgO = - , arcctg 1 = - .

110 Глава 3. Предел функции в точке. Непрерывные функции
Упражнение 91. Построить графики следующих функций: arcsin,
arccos, arctg, arcctg.
Упражнение 92. Найти пределы:
. ,. 1пA + х) + arcsinх2 arctgx . arcsinx
a) hm — ; b) hm 2-—=■; с) hm ;
x-+o arccos x + cos x z-+i 1 + arcctg xi ^->o x
arccosx-| arctgx „,. arctgx-|
d) hm — ; e) hm — ; f) hm 3
x+0 X x*0 X x»l
hm — ; e) hm — ; f) hm ;
x-+0 X x-*0 X x-»l X — 1
| -arctgx sin(arctgx)
g) hm ; h) hm —^ —- .
X-++00 x x-+0 tgX
tr \ t arcsinx у
Указамил. с) hm = hm -— = 1, с учетом того, что
х-»о х v-+o smy
х -> О -Ф=>- у = arcsinx -+ 0.
arccosx-- y
d) lim й- = lim , v _ . = - lim -Л- = -1.
х-чо x »-*oCOB/y + l\ v-vo sin у
arctgx ,. У у ( У \ 1
e) lim = hm = hm -— • cost/ = 1.
x-+o x y-+o tgy y-+o Vsiny /
arctgx-- y--
f) lim —4- = lim i
H X 1 /
im lim
-H X — 1 y-V7T/4tgy-l
7Г 7Г
= lim = - hm -.— - т- = -
у-*т/4 sin у - cosy 2 v-"t/4 sin (y — — J
-.— - т-
sin (y — — J
Упражнение 93. Пусть /(х) = x при x < 1 и /(x) = x2 при x > 1.
Применить к / теорему 15 и найти обратную функцию.
3.3.4 Свойства логарифмической функции и
замечательные пределы
Теорема 16. Пусть а > 0, а ф 1. Тогда lim °g°^ + X'
1 Z-40 X
= log.e, в частности, при а = е hm *"v~ = 1.
х-+0 X
f Применим теорему 12 о пределе сложной функции для А — ( — 1, +оо),
/(х) = A + хI/1, х > -1, х0 = 0, р = lim A + хI/1 = е > 0; В =

3.3. Непрерывные функции III
(О, +оо), д(у) — logaj/, у > 0. В примере 2 установлено, что функ-
функция д непрерывна на @,+оо), а, следовательно, и в точке р = е. Со-
n r bga(l + х)
гласно теореме 12 получаем следующее равенство lim —- =
= hm log A + x)l/x — loga e. J
x-+0
Теорема 17. Пусть a > 0. Тогда lim = lno, в
1 x-iO X
ex — 1
частности, при а = e ujneeju lim = 1.
x-+0 X
[ При a = 1 утверждение верно, пусть a ф 1. В силу непрерывности и
монотонности показательной функции z :— ах — I —> 0 •<=>■ х —» 0,
при этом х = loga(l + z). Поэтому в силу теоремы 15 lim =
х—+0 X
= lim г——г = = In a. J
z-+o loga(l + z) loga e
Теорема 18. Пусть a e R. Тогда lim — = q.
r x-+0 x
[Для a = 0 утверждение верно. Пусть a ф 0. Тогда, используя непре-
непрерывность логарифмической функции, имеем 1пA + х) —> 0, х —» 0. С
A + х)" - 1
помощью теорем 15 и 16 получаем такое равенство lim ^ =
х->0 X
lim г—7- г = a lim ——7 г- lim = a.
х->о xaln(l + x) x->o aln(l + i) х~+° х
Теорема 19. Пусть а е Я и /(х) = ха, х > 0. Тогда
/€С(@,+оо)).
[Поскольку для любого х > 0 справедливо равенство /(х) = е1'111, то
непрерывность / следует из теорем о непрерывности суперпозиции и
непрерывности показательной и логарифмической функций. J
Упражнение 94- Найти пределы:
а) lim (cosxI; b) lim (x(ln(l + x) - lnx));
x—+0 i—++oo
. ,. Л + зтгхч1/* 1-cosx
c) hm I — ; d) hm —-;
x-+o v cos 2x / x->a 1 — cos 2x
ln(l + x) + ex - cosx ,, з
e) hm ——~- : ; f) lim (cosxI'1 ;
a,_>o ex - 1 + smx x-+o
. ,. arcsinfx - 1) l-cos2xcos2x
g) hm —:—- , me N; h) hm 5 ;
Vl + sin2x-l
. ,. Vl + sinxl .. ,.
i) hm z ; k) hm
' x40 X2 ' xvO
x-40 X2 ' х-Ю ^1 + x2 - 1 '
8 — 4-1168

112 Глава 3. Предел функции в точке. Непрерывные функции
l-(cosmx)m __. . ,. 1 - (cosmxI/m
I) lim ^—5 — > meN; m) lim * ;—'- , m € N;
x-+0 X2 x-+0 X2
n) lim arete x; o) lim axcsinf— cosx);
p) lim —--■, если an > 0, bn > 0, n > 1; bn -> +oo, n -> 00; -^ -+
n-юо mon on
cG @,+oo), n -+ 00.
Упражнение 95. Пусть / — монотонно неубывающая и непрерывная
на R функция и {хп | я > 1} С Я. Доказать следующие равенства
Ит f[xn) = /( lim хп); Ш f{xn) = /( Шп хп).
Упраэ*смемие 96. Пусть / — монотонно невозрастающая и непре-
непрерывная на R функция и {х„ | п > 1} С R. Доказать следующие равен-
равенства lim f(xn) = /( Пт xn); Gm /(xn) = /( lim xn).
3.3.5 Свойства функций, непрерывных на отрезке
Далее —оо < а < Ь < +оо, непрерывность функции / на отрезке [а, Ь]
означает для точек а и b непрерывность справа и слева соответственно.
Теорема 20. (Первая теорема Вейерштрасса). Пред-
поло&сим, что f G С([а,Ь\). Тогда функция f ограничена на
отрезке [а,Ь].
\ Предположим, что утверждение теоремы неверно, то есть, что функ-
функция / не является ограниченной на [о.,Ь]. Это означает, что Vn £
N 3xn G [а,Ь] : |/(хта)| > п. Ограниченная последовательность
{хп | п > 1} в силу теоремы Больцано-Вейерштрасса содержит схо-
сходящуюся подпоследовательность xn^) —t xo, k —> оо. С учётом нера-
неравенств а < xn(fc) < Ь, к > 1 и теоремы 9 гл. 2 имеем а < хо <
Ь. По условию теоремы функция / непрерывна в точке хо и пото-
МУ /(^n(fc)) -+ /(^о), к -> оо, что, однако, невозможно, так как
|/(zn(fc))| > n(fc)-»+оо, fc^oo. J
Примеры. 1. Функция / G С((а,Ь]) не обязательно ограничена на
множестве (a, b].
\ Пусть (а,Ъ] = @,1], Дх) = -, х G @,1]. Тогда / G С(@,1]), /(х) =
= - -» +оо, х -^ 0 + . J
2. Пусть / € С([0,+оо)) и существует lim /(х) =: р G R. Тогда
функция / ограничена на [0,+оо).
[Согласно определению Коши предела функции в точке |/(х)| -> \р\,
х -» +оо; Эс> 0 Vi > с : |/(х)| < |р| + 1. К отрезку [0, с] и

3.3. Непрерывные функции ИЗ
функции / применима первая теорема Вейерштрасса, следовательно,
3d > О Vz G [0,с] : |/(х)| < d. Таким образом, имеем ЗС :=
= max(d, \р\ + 1) VxG[0,+oo): |/(х)| < С. J
3. Пусть функция / G C(R) и периодична с периодом т > 0, то есть
Vx G R: f(x + т) = /(х). Тогда / ограничена на R.
\ На отрезке [0, г] к функции / применима первая теорема Вейерштрас-
Вейерштрасса и потому 3 С > О V х G [0, г] : |/(а:)| < С. Тогда для любого х G R
в силу периодичности |/(х)| = |/(х - [х/т]т)| < С, (х - [х/т]т) G [0, г],
где [а] — целая часть числа а, то есть, [а] есть наибольшее целое число,
не превосходящее a. J
( 1 А1
Упражнение 97. Доказать, что функция fix) = 1 + - I , х > О
V х)
ограничена на @, +оо).
Указание. Теорема 20 к интервалу @, +оо) не применима. Найти
пределы / при х —» 0+ и при х —> +оо. Затем см. пример 2.
Упражнение 98. Доказать, что функция — многочлен чётной степе-
степени Р(х) = x2m+aix2m~1 + .. .+а2т, х е R, гр,ете N, {аьа2,... ,а2т}
С R, ограничена снизу на R, то есть, ЗС G R VxG-R: P{x) > С.
Упражнение 99. Доказать, что функция /(х) = е"'11р(х), х G Я,
где Р — произвольный многочлен, ограничена на R.
Определение 8. Функция f : А -> R принимает в точ-
точке х* G А наибольшее или максимальное на множестве
А значение, если Vx G А : /(х) < /(х*). Функция f : А —> R
принимает в точке х„ G А наименьшее или минималь-
минимальное на множестве А значение, если Vx G А : /(а;*) < f{x).
Отметим, что /(х«) = min/ = min/(x); /(x*) = max/ = max/(x).
.A I6A >1 igA
Примеры. 4. Функция /(х) = {х} = х - [х], х G [0,2] принимает
наименьшее значение 0 в каждой из точек 0,1,2 и не принимает наи-
наибольшего значения. При этом /@) = min {x}, sup {х} = 1, Vx G
»е[0,2] 1б[0,2]
[0,2]: {х}<1.
Упражнение 100. Функция /(х) = -, х G @,1) не принимает
наименьшего значения, так как mf — = 1; Vx G @,1) : — > 1.
16@,1) X X
Теорема 21. (Вторая теорема Вейерштрасса). Пре-
Предположим, что f G С([а,Ь]). Тогда функция f принима-
принимает наибольшее и наименьшее значения на [а,Ь], то есть,
3{x,,x'}c[a,b] VxGM]: /(*,)</(*)</(*')•
8*

114 Глава 3. Предел функции в точке. Непрерывные функции
\ Докажем существование точки х*. Множество /([а, Ъ]) значений функ-
функции / на отрезке [а, Ь\ ограничено по первой теореме Вейерштрас-
Вейерштрасса, следовательно, по теореме о существовании точных граней Эр G
R : sup /(х) = р. В силу теоремы о характеризации точной грани
х6[о,Ь]
Vn G N Зхп € [а, Ь] : р— — < f{xn) < р. К последовательности
{^п | те > 1} С [а, Ь] применим теорему Больцано- Вейерштрасса, со-
согласно которой существует сходящаяся подпоследовательность хп^ —>
х*, fc —> оо, причём число х* G [а>Ь]. По условию / £ С([а,Ь]), сле-
следовательно, непрерывна в точке х*, потому /(xn(fc)) —> /(e*)i & —> оо.
Кроме того, по построению Vfc > 1 : р — < /(хпш) < p и в
n(k)
силу теоремы 9 гл. 2 /(xn(fc)) —^р, А: —» оо. Поэтому р = f(x*). Таким
образом, /(х*) = sup /(x) = max /(x). J
101. Доказать существование точки х» в теореме 21.
Примеры. 6. Функция / £ C(R) и периодическая с периодом г > О
принимает наибольшее и наименьшее значения.
[ К функции / на отрезке [0, г] применима вторая теорема Вейерштрас-
Вейерштрасса, согласно которой 3{х*,х*} С [0,т] Vx е [0,т] : /(х*) < /(х) <
< /(х*), а поскольку для любого х £ R в силу периодичности /(х) =
/(х - [х/т}т), (х- [х/т]т) G [0, г], то V х G Я : /(*,) < /(х) < /(х*). J
7. Пусть Р(х) = x2m + a1x2m-1 + ... + a2m, x G R, где m G JV,{ai,a2,
• • •,&2m} С Н. Докажем, что Эх, £ RViG Д: Р(х„) < Р(х).
[ Заметим, что Р G С"(Я) и что Р(х) -> +оо, х -> -оо; Р(х) ->
+оо, х -> +оо. Поэтому Эс > 0 Vx, |х| > с : Р(х) > Р@) + 1.
Применим к отрезку [—с, с] и функции Р вторую теорему Вейерштрасса.
Получим Эх» G [—с, с] Vx G [-с, с] : Р(х») < Р(х), причём Р(х„) <
< Р@). Следовательно, Vx G R : Р(х*) < Р(х) или Р(х«) = minP. J
R
Упражнение 102. Пусть Р — произвольный многочлен. Доказать,
что Эх, G Я VxG-Я: \Р{х,)\<\Р{х)\.
Упражнение 103. Пусть / G С([0,+оо)) и /(х) -> +оо, х -+ +оо.
Доказать, что Э х, G [0,+оо) : /(а;,) = inf / = rain /.
[О.+оо) [0,+оо)
Упражнение 104*. Для функции / G С{[а, Ь]) введём функции
3(х):=тах/, h(x); = min/, x G [а,Ь]. Доказать, что {g,h} С С([а,Ь]).
[а,х] [а,х]
Указание. Проверить для a < xj < x2 < Ь справедливость нера-
неравенств g(xi) < g{xi) < g(xi) + max |/(x) — f{xi)\. Заметить, что
X<X<X

3.3. Непрерывные функции П5
= шах(з(х1), max /J= maxf3(x1),/(xi)+ max
• max |/(x) ■
Упражнение 105. Для функции / : Я -> Я, точки х0 G Я и 6 > О
пусть ui(xq,6) := sup \f{x) — /(хо)| < +оо. Доказать, что функция
х: |x-io|<i5
/ непрерывна в точке хо тогда и только тогда, когда uj(xq, 5) —> 0, 5 —» 0. .
Упражнение 106. Пусть G C(R) и /(х) -» -оо, х -» -оо; /(х) ->
+оо, х -> +оо. Положим д(х) := sup{£ G Я | /(£) < х}, х е Я.
Является ли функция д непрерывной?
Теорема 22. Предположим, что функция f удовле-
удовлетворяет условиям: 1) f G C([a,b\) и 2) f(a) < 0 < f(b) либо
f{a) > 0 > f{b). Тогда 3 х0 G [а, Ъ] : /(х0) = 0.
Г Рассмотрим случай, когда f(a) < 0 < f(b). Определим множество
М — {х G [а, Ь] | /(х) < 0}. Множество М ф 0, поскольку a G М, и
ограничено, так как М С [а, Ь]. По теореме о существовании точных
граней существует supM =: х0. Проверим, что а < х0 < Ь. С учётом
условий 1) и 2) и теоремы 3 имеем 3 6"i > 0 Vx G [а,а + 5\) : /(х) <
0; 3 6 > О V х G {Ь — 6, Ь] : f(x) > 0; откуда следует, что [а, а + 6"i) С
М, supМ < Ь - 52. Таким образом, а < х0 < Ь.^~^ ($- fz £~)(\^^ 0
Докажем теперь, что /(х0) = 0. По теореме о характеризации точ-
точных граней Vn £ N Зхп £ М : х0 <xn<x0 = supM, откуда
п
in -> хо, п -¥ оо; Vn G N : /(х„) < 0. На основании условия 1)
и теоремы 4 имеем f(xn) —> /(хо), п —> оо; lim /(xn) < 0, откуда
следует, что /(хо) < 0. Кроме того, из неравенства хо < х следует, что
х ^ М, /(х) > 0. Поэтому lim /(х) > 0; /(х0) = lim fix) >
X—>Х0)Х>Х0 1-+Хо,Х>Хо
0. Следовательно, /(х0) = 0. J
Примеры. 8. Пусть Р(х) = х2 +а!Х2т-2 + .. .+а2т_ь х б Я, где
m£N, {ai,a2,...,a2m_i} С Я Доказать, что Эхо G Я: Р(х0) = 0.
Таким образом, многочлен нечётной степени имеет по крайней мере
один действительный корень.
[ Поскольку Р(х) -> -оо, х -> -оо и Р(х) -> +оо, х -+ +оо, то
3c>0Vx<-c: Р(х) < -1, и Vx > с : Р(х) > 1. Для отрезка
[—с, с] и функции / выполнены условия 1) и 2) теоремы 22, поскольку
Р{—с) < —1, Р(с) > 1. Следовательно, согласно этой теореме 3 хо G
{-с, с]: Р(хо) = 0. J
9. Пусть {/,<?} С С{[а,Ь}) и /(а) < g{a), f{b) > д{Ь). Тогда Эх0 G
(a,b) : f{xo)=g{xo).

116 Глава 3. Предел функции в точке. Непрерывные функции
\ Для функции h := f — g выполнено условие 1) теоремы 22, кроме
того, h(a) < 0, h{b) > 0 и условие 2 ) также выполнено. J
10. Теорема о хорде. Пусть / G С([0,2]) и /@) = /B). Доказать,
что 3 {ц.^г} С [0,2] : 12-11 = 1 и f(xi) = f{x2).
\ Если /@) = /A), то можно положить xi =0, х2 = 1. Далее /A) ф
/@). Функция g(x) := f(x + 1) — f(x), x G [0,1] удовлетворяет условию
1) теоремы 22, а поскольку д{0) = /A) - /@), д{1) = /B) - /A) =
/@) — /A), то и условию 2). По теореме 22 имеем Зх\ G [0,1] :
g(xi) = 0 •$=>• f(xi + 1) = f{x\) и, положив х2 '•= ^i + 1, получим
утверждение примера 10. J
Теорема 23. (Теорема Коши о промеснсуточном зна-
значении). Пусть функция f G С([а,Ъ]). Тогда для каждого
числа L из отрезка с концами f(a) и f(b) справедливо
утверждение 3 х0 6 [a, b] : f{x0) = L.
\ Если /(а) = /(Ь), то L = /(а) и х0 — а. Далее пусть f(a) < f(b) и
•^ 6 (/(а)> /(Ь))- Тогда функция g(x) := f(x)-L, x G [а, Ь] удовлетворяет
условию 1) теоремы 22 и, поскольку д(а) < 0, д{Ь) > 0, то и условию
2). По теореме 22 Зх0е{а,Ь): д(х0) - 0 4=» /(х0) = ^- J
Примеры. 11. Для функции / G С([а, Ь\) множество её значений
f([a,b]) есть отрезок.
[ Согласно второй теореме Вейерштрасса 3{х»,х*} С [a,b] Vx G
[a,b] : /(x») < f(x) < f{x*), а в силу теоремы Коши о промежу-
промежуточном значении для любого L € [f{x*),f{x*)] существует точка х на
отрезке с концами х* их*, для которой /(х) = L. Таким образом,
ДМ]) = [/(*,),/(**)]■ J
12. Пусть /(х) = х3 — х, i Е Л. Доказать, что / : R —> R есть
сюръекция, но не инъекция.
[ Отметим сначала, что /(х) —> —оо, х —¥ —оо; /(х) —> +оо, х —» +оо.
Пусть произвольное L £ R задано. Тогда З^^хг} С R ■ /(xi) <
L < /(хг). Для определённости пусть xi < х2- Тогда к отрезку [х^Хг]
и функции / применима теорема 23, согласно которой Зхо G [xi,X2] :
L = /(х0). Следовательно, / есть сюръекция. Функция / : й-»Яне
есть инъекция, так как 0 ф 1, а /@) = /A) = 0. J
Замечание. Обратим внимание на то, что определение непре-
непрерывности в точке является локальным. Непрерывность в заданной точке
определяется, грубо говоря, только значениями функции, лежащими в
как угодно малой окрестности этой точки. Теоремы 20 — 23 показыва-
показывают, что непрерывным функциям и их' графикам действительно присущи
те интуитивно угадываемые свойства, которые обычно описываются сло-
словом непрерывный.

3.3. Непрерывные функции . Н7
Упражнение 107. Функция / : [a,b] -* R строго возрастает на [а, Ь]
и такова, что V L G [/(a), f(b)] 3 х0 G [а, Ъ) : /(^о) = Ь. Доказать, что
/€С([а,Ь]).
Упражнение 108. Пусть Р(х) = х2т + щх2™ + ... + а2т, х € Я,
где т G ЛГ, {aj, аг,..., а2т} С Я. Доказать, что функция Р : Я -» Я
не есть сюръекция и не есть инъекция.
109. Функции /, д : [0,1] -> [0,1] непрерывны на
отрезке [0,1] и / является сюръекцией. Доказать, что 3 Хо 6 [0,1] '•
/(х0) =
Упражнение 110. Пусть / : [-1,1] -+ [-1,1], / G С([-1,1]).
Доказать, что Э{хьх2} С [-1,1] : /(xi) = Xi и /(х2) = -х2.
Упражнение 111. Функции /,д : [0,1] -> [0,1] непрерывны на [0,1]
и 5@) = О, 5A) = 1- Доказать, что Эх0 G [0,1] : /(х0) = д{х0).
Упражнение 112. Пусть Р - произвольный многочлен и /(х) =
ех +Р(х), х G Я. Доказать, что функция / : Я —> Я не есть сюръекция
и не есть инъекция.
Упражнение 113. Пусть для п G N ап — такое число, что выпол-
п+ап
няется равенство 1 Н— I = е. Найти lim an.
\ П J п-+оо
3.3.6 Равномерно непрерывные функции
Пусть ЛсЯи/: А -» Я.
Определение 9. Функция f называется равномерно
непрерывной на множестве А, если Ve>0 35>0 V{x',x"}
СЛ|х'-х"|<5: |/(х')-/(х")|<£.
Замечание. Если функция / равномерно непрерывна на множе-
множестве Л, то / G С{А). Обратное неверно, см. ниже пример 3.
Примеры. 1. Функция /(х) = х, х G Я равномерно непрерывна
на Я, поскольку Ve>035 = e>0 V{x',x"} С Я, |х' - х"| < 6 :
\f{x')-f{x")\=:\x'-x"\ <6 = е.
2. Функции sin и cos равномерно непрерывны на Я.
[ Рассмотрим функцию sin, она равномерно непрерывна на Я, так как
Ve>0 Э5:=е>0 V{x',x"} С Я, |х' - х"| < 6 :
I sin x' - sin x" I = 2
sin
х' - х"
cos •
х' + х"
<\х'-х"\<6 = е. J

118 Глава 3. Предел функции в точке. Непрерывные функции
3. Функция f(x) = — , х 6 @,1] не является равномерно непрерыв-
ной на @,1].
[ Действительно, для числа е* = - > 0 имеем V 5 > 0 3 1 х' := — , х" :=
2 » L тт.
где п 6 ЛГ, п > 1/5. J
4. Функция f(x) = х2, i£ Дне является равномерно непрерывной
на Я, поскольку Зе* = - > О V5 > 0 3{х' := ^/п, х" := \/п + 1} С
R,\x'-x"\ <6: |(x'J-(x"J| = ]n-(n + l)] = l> I , где n > 1/D<52).J
Упражнение 11^. Доказать равномерную непрерывность на соот-
соответствующих множествах следующих функций:
a)f[x)=lnx, x£[l,+oo); b) f(x) = sin(cosx), x G R,
c)f{x) = Jx, xG[0,+oo); d) f{x) = x sin - , x G @, +oo).
x
Упражнение 115. Доказать, что следующие функции не являются
равномерно непрерывными на заданных множествах:
a)/(i)=lni, iG@,l]; Ь) f{x) = Xy/x, xG[0,+oo);
с) f(x) = sinx2, хб[0,+оо); d) f(x) = xsinx, xg[0,+oo);
e) /(x) = sin(xsmx), x > 0.
Упражнение 116. Доказать, что:
a) сумма равномерно непрерывных на некотором множестве функций
равномерно непрерывна на этом множестве;
b) произведение равномерно непрерывных на некотором множестве
функций не обязательно равномерно непрерывно на этом множестве.
Теорема 24. (Теорема Кантора). Пусть { е С([а,Ь\).
Тогда функция f равномерно непрерывна на [а,Ъ].
\ Предположим, что / не является равномерно непрерывной на [а, Ь].
Это означает по определению 9, что Эе* > 0 V5 > 0 3{х'F),х"F)} С
[а,Ъ],\х'{6) - х"{6)\ < 6 : \f{x'{5)) - /(х"(*))| > е'. Зафиксируем та-
кое число е* и рассмотрим для него следующую последовательность
\— | п > 1 \ значений 6, а также соответствующих пар х'(8),х"E). По-
ложим х' :— х'(— ), х" := х"(— ); п G N. Последовательность
{х'п | " > 1} по теореме Больцано-Вейерштрасса содержит сходящу-
сходящуюся подпоследовательность х',к-. —> Xq G [а,Ь], к —> оо. Поскольку

3.3. Непрерывные функции 119
\xL[k\ — x'',i,\\ < —ттт i fc > 1, то имеем также x'L,ks —> Xn, k —> со. В
" п\к) п{к)> щ/с) П\К1
силу непрерывности функции / в точке Xq f{x'n,k\) —> f(xo), }{x'Lk\) —>
/(x0); fc -»• со, следовательно, /(x'n(fc)) - /(x£(fc)) -> 0, fc -»• со. Од-
Однако, по построению |/(x'n,fcs) - f{x'Lk^)\ > e*, fc > 1. Противоречие
показывает, что исходное предположение о функции / неверно, а, сле-
следовательно, функция / является равномерно непрерывной на [a,b]. J
Примеры. 5. Предположим, что для функции / £ C(R) существуют
пределы lim /(х) =: с £ R, lim /(x) =: d £ R. Докажем, что
X—-> — ОО X—>+0О
функция / равномерно непрерывна на R.
Г Для произвольного е > 0 по определению предела 3 С > 1 V х < -С :
|/(х)-с|<| иУх>С: |/(i) - d|<|. Так как/еС([-С-1,С + 1]),
то по теореме Кантора для числа е 3 5 £ @,1) V {х1, х"} С [—С — 1, С +
1],|х'-х"| <5: |/(х')-/(х")| <£. Пусть теперь {х',х"> с Я, |х'-х"| <
S. Если при этом {х',х"> П [-С,С] ф 0, то {х',х"> С [С - 1,С + 1] и
потому |/(х') - /(х")| < е. Если же {х',х"}п [-С,С] = 0, то либо
а) {х',х"} с (-00,-6), либо Ь) {х',х"} с [С,+оо). В случае а) имеем
|/(x')-/(s")l = \f(x')-c+c-f(x")\ < |/(x')-c| + |/(x")-c| <|+£=е,
а в случае Ь) аналогично |/(х') - /(х")| = |/(х') - d + d - f{x")\ <
|/(x-)-d| + |/(x")-d|<|+| =e. J
6. Пусть функция / £ C(R) и периодична с периодом т > 0. Тогда
функция / равномерно непрерывна на R.
[ По предположению / £ C([0,2t]) и, следовательно, по теореме Кан-
Кантора функция / равномерно непрерывна на [0,2т] и Ve > 0 3<5i £
@,т) V{z',z"} с [0,2т],|г' - z"\ < <5i : \f{z') - f{z")\ < e. Заметим
теперь, что для любых х', х", х' < х" имеем z' := (х' — [х1 /т]т) €
[О, т], z" := (х" - [х'/т]т). z' - z" =x' - х", причём z" £ [0,2т], если
|х'-х"| <5i. При этом |/(х')-/(х")| = l/(z')-/B")l в силу периодич-
периодичности /. Таким образом, V е > 0 3 5 := их > О V {х1, х"} С R, |х' - х"| <
5: \f(x')-f(x")\ = \f(z')-f(z")\<e. j
Упражнение 117. Пусть / £ С([0,+оо)) и (/(х)-х) -> 0, х -> +оо.
Доказать, что / равномерно непрерывна на [0,+оо).
Упражнение 118. Доказать, что функция /(х) = , х >
In а;
2 равномерно непрерывна на [2,+сх>).
Упражнение 119. Предположим, что функция / : [а,Ь] ->■ R удо-
удовлетворяет условию Ve > 0 Зд £ С([а,Ъ]) Vx £ [a,b] : \f(x)-g(x)\ < е.
Доказать, что / £ С([а,Ь]).

120 Глава 3. Предел функции в точке. Непрерывные функции
У применение 120*. Предположим, что функции /, g : R ->■ R пе-
периодичны и Нт (/(я) — д[х)) = 0. Доказать, что эти функции имеют
х—»4-оо
одинаковый период и совпадают на R.
Упражнение 121*. Для функции / : R-* R выполняется условие
3 A g [0,1) V {*', х"} с R : |/(х') - /(х")| < А|х' - х"\.
Проверить, что / равномерно непрерывна на R. Для произвольного
х0 Е R положим xn+i = /(х„), п > 0. Доказать, что уравнение /(х) =
х имеет единственное решение х* и что in ч г*, п —>■ oo.
Упрамснение 122. Функция / : @, +оо) -* R непрерывна в точке
1 и удовлетворяет условию Vx > 0 : /(х) = /(х2). Доказать, что
х>0.
Упрамснение 123. Функция / 6 C(R), отлична от 0 на R и такова,
что V{x,y} с R: f{x+y) = /(х)/(у). Доказать, что /(х) = /A)х, х g
R, где /A) > 0.
3.3.7 Разрывы функций
Пусть / : (а,Ь) -> Д, -оо < а < b < +оо, и х0 £ (а, Ь). Функция /
непрерывна в точке Хо тогда и только тогда, когда существуют пределы
слева и справа
/(хо-), /(хо+) A)
в точке xq и справедливы равенства
/(*„-) = /(х0) = /(х„+). B)
Если функция / в точке Хо не является непрерывной, то точка Хо есть
точка разрыва функции /.
Определение 10. Если оба предела в A) существуют
(конечны), но хотя бы. одно из равенств B) нарушает-
нарушается, то точка х0 называется точкой разрыва первого ро-
рода. При этом говорят, что функция имеет в точке х0
скачек. Если хотя бы один из пределов A) не существу-
существует (в частности, бесконечен), то точка х0 называется
точкой разрыва второго рода.
Замечание. Иногда выделяют случай, когда оба предела A) суще-
существуют и равны, но /(хо—) = /(хо+) ф /(хо)- Тогда точку xq называют
точкой устранимого разрыва.

3.4. Теорема Вейерштрасса 121
Примеры. 1. Для функции /(я) = sign я, х £ R, имеем для xq = О :
ff(O) = О, /(О-) = —1, /@+) = 1. Точка 0 есть точка разрыва первого
; 2. Для функции /@) = {я}, х £ R, каждая из точек множества Z
;есть точка разрыва первого рода.
3. Пусть f(x) = sin - , если i/Ои /@) = 0. В точке 0 функция /
х
\не имеет пределов слева и справа, поэтому точка 0 есть точка разрыва
второго рода.
Замечание. В случаях, аналогичных примеру 3, значение в точке
Хо иногда не рассматривают. Например, о функции f(x) = —, х Ф 0,
говорят, что она в точке 0 имеет разрыв второго рода.
Теорема 25. Пусть {а,Ь} с R и f : [а,Ь] ->■ R — мо-
монотонная на [а, Ь] функция. Функция / момсет иметь в
качестве точек разрыва только скачки.
| Пусть / монотонно не убывает на [а,Ь]. Согласно теореме 7 существу-
существуют f(a+), f(b-); Vc £ (а,Ь) : /(с—), /(с + 0), причём справедливы
неравенства /(а) < /(о+) < /(с-) < /(с) < /(с+) < f{b-) < f{b). J
Упражнение 124- Доказать, что утверждение теоремы 25 остаётся
верным и для монотонной функции на (а, Ь), —оо < а < b < +оо.
Упражнение 125. Доказать, что монотонная функция может иметь
не более чем счётное множество точек разрыва первого рода.
3.4 Теорема Вейерштрасса
3.4.1 Вспомогательные тождества
Пусть п £ N и х £ [0,1].
(i) £ Cknxk{\ - x)n-k = 1.
fc=0
Г Это равенство следует из тождества 1П = (х + A — х))п и формулы
бинома Ньютона. J
00 Е сц(--х)хкA-хГ-к = о.
к=0 \п I
\ Поскольку кСк = nCkZ\ при к > 1, то £ Ск-хк{\ - х)п~к =
к=0 п
= Е CkZ\xk{l-x)n-k =xnJ2 C]n_1xj{l-x)n-i-j = х. Отсюда следует
к=0 j=0

122 Глава 3. Предел функции в точке. Непрерывные функции
нужное тождество
(iii) E l ( )(r
f Сначала, как и при доказательстве (ii) имеем
£ C*k{k-\)xk{l-x)n-k = nx^ Ci.^i^l-i)"-1-^ = n(n-l)x2.
fc=0 j=0
" /fc \2
Далее с помощью (i) и (ii) получим Y\ Ck I ~ ~~ x I xfc(l ~ x)"~fc =
fc=o Vn /
= Л f E C*k(k - l)xfc(l - х)»"* + £ Cknkxk{l - x)"-k) -
n \fc=0 fc=0 /
Л V"^ ^fc fc fc,« ,„ I s> П(П — 1) 2 ПХ „ 9 9 X(l — X)
2x > C^-xfc l-x)n~fc+x2 = v o ; x2 + -^- -2x2+x2 = -i '-.
fc=0
Упражнение 126. Пусть Р — многочлен. Доказать, что функция
Q{t) = P(at + b), t G R, где числа а и Ь фиксированы, также есть
многочлен по t.
3.4.2 Теорема Вейерштрасса о приближении
Теорема 26. Пусть f e C([a,b]). Тогда для каждого
е > 0 существует многочлен Р£ такой, что справедливо
утверждение Vxe[a,b]: |/(х)-Р£(х)| < е <=> тах|/-Р£| < е.
[оЬ]
[ Достаточно доказать теорему для отрезка [0,1]. Действительно, если
теорема справедлива для отрезка [0,1], то для функции / £ С([а, Ь])
и заданного е > 0 существует многочлен Р£ такой, что Vf E [0,1] :
\f{a+t[b-a))-Pe(t)\ <£, и потому Vx£ [а,Ь] : |/(х)-Р£ ( т—-^ ) I < е-
Пусть функция / £ С*([0,1])- Введём многочлены
Bn(f\ х) := £ Ckf (- ) xk(l - x)n~k, х е [0,1], nEN.
Здесь 0° := 1, Bn(f; •) — многочлен Бернштейна степени п для
функции /. Положим pn/t(x) := C£xfc(l - x)"~fc > 0, x £ [0,1], n e N.
Пусть e > 0 задано. По теореме Кантора для числа е/2 > 0 имеем
35 > 0 V{x',x"}c [0,1],|х'-х"| <5: |/(х') - /(х")| < ^/2. Используя
тождества (i) — (iii), получим
Ё Pnk(x)-Bn(f;x)\= £ (f(x)-f(-))Pnk(x)
=0 fc=0V V^/'/

3.4. Теорема Вейерштрасса 123
fc:|*-*|<«
, у^ f(T\ — f(—-*\\ ( \ <? — V*
+2L ^ Pn/t(a;) < - 2^ Pnfc(.a;J + 77 L
fc:|x-i|>,5 2 fc=O d fc=O
£ 2iifl-i) e L
Пусть теперь N таково, что Vn > N : —— < -. Тогда Vn >
А71О А
Упрамснение 127. Для функции / G С([0,1]) доказать утверждение
Vie [0,1]: f^ C*{-l)kf (-)хк{1-х)п-к->0, п-юо.
fc=o \п/
Упрамснение 128*. Функция / удовлетворяет условию
3L>0 V{i',i"}c[0,1] : \f{x') - f{x")\ < L\x' - x"\.
С помощью неравенства Коши и тождеств (i) — (iii) доказать, что
Vn>l Vie [0,1] : |/(x)-Bn(/;x)|< L
3.4.3 Историческая справка
Гейне Генрих Эдуард A821 — 1881) — немецкий математик.
Теорема Кантора была доказана Гейне.
Центральным понятием этой главы является понятие предела функ-
функции в точке, включающее в себя и понятие предела последователь-
последовательности. Идея предельного перехода возникла фактически у математи-
математиков древней Греции, наиболее существенными были работы Евдокса
(~ 408— ~ 355 г. до н.э.) с "методом исчерпывания" и Архимеда
(~ 287 — 212 г. до н.э.). Однако формальное определение преде-
предела было введено в математику позже, например, таких по существу
определяемых с помощью понятия предела понятий, как производная
и интеграл. При этом творцы дифференциального и интегрального ис-
исчисления Ньютон и Лейбниц постоянно возвращались к обоснованию
предельных переходов, но их основное внимание было поглощено раз-
развитием методов исчисления и его эффективными приложениями в фи-
физике. Слово "предел" — limes ввёл в математику Ньютон. Отсутствие
точных и определённых понятий дифференциального и интегрального

124 Глава 3. Предел функции в точке. Непрерывные функции
исчисления вызвало критику не только математиков, английский фило-
философ Док.. Беркли A685 — 1783) издал памфлет с резкой критикой
работ Ньютона и Лейбница. Современное понятие предела функции в
точке принадлежит Больцано и Коши. Близок к современному понятию
предела последовательности был также К. Ф. Гаусс (U77 — 1855).
Коши был первым, кто попытался построить математический анализ с
помощью понятия предела.
Непрерывными функциями сначала называли функции, определяе-
определяемые одним аналитическим выражением. Так понимали непрерывность
Л. Эйлер A707 — 1783) и некоторые его предшественники. Совре-
Современное определение принадлежит Больцано и Коши. Интуитивное пред-
представление о непрерывной функции, как о функции, график которой
можно начертить одним росчерком пера, не отрывая его от бумаги,
является следствием этого определения.
Понятие равномерной непрерывности было введено Д. Г. Сток-
сом A819 - 1903) и Ф. Л. Зейделем A821 - 1896), а затем Коши.
Различие между непрерывностью и равномерной непрерывностью яв-
является весьма тонким, этого различия вначале не замечал Коши.
Дирихле П. Г. Л. A805 — 1859) - немецкий математик. Ему при-
принадлежит ряд основополагающих результатов в математическом анали-
анализе, теории чисел, вариационном исчислении и математической физике.
Бернштейн Сергей Натанович A880 — 1968) — выдающий-
выдающийся советский математик, получивший ряд фундаментальных результатов
в теории приближения функций, теории вероятностей и в других разде-
разделах математики. Предложенное им в 1912 г. доказательство теоремы
Вейерштрасса основано на изящной теоретико-вероятностной идее, оно
весьма элементарно и обладает тем преимуществом, что приближаю-
приближающие функцию многочлены строятся явно.

Глава 4
Производная и её
приложения
4.1 Определение, примеры и обсуждение *
4.1.1 Определение и примеры
Пусть А с R, хо £ А, причём 3 5 > 0 : (хо — 5,х0 + 5) С А. Пусть
/ : А —>■ R. Введём для х Е А, х ф xq разности Дх := х — Хо,
Д/(аО := f(x) - /(хо), при этом Д/(х) = f{x0 + Дх) - /(х0).
Определение 1. Если существует конечный предел
/()/() ( )()
lim :LLJ—tmi = lim ^"u ""'—i+^LL mo этот предел
x-+Xo X — Хо ЛЖ-+0 Дх
называется производной функции f в точке хо-
Обозначения: /'(хо), —^—- ,
Таким образом, /'(xq) = lim
Определение 2. Если существует конечный предел
/(х) - /(х0)
слева lim —— *—- , то этот предел называется
х-+хо,х<хо X — Хо
производной слева функции / в точке хо и обозначает-
обозначается символом. /1(х0). Если существует конечный предел
справа lim ^—'— , то этот предел называется
х-+хо,х>жо X — Хо
производной справа функции f в точке хо и обозначает-
обозначается символом f'+(x0).
125

126 Глава 4. Производная и её приложения
Замечание. Таким образом, производная /'(х0) существует тогда
и только тогда, когда существуют /1(х0), /+(х0) и f'-Ы) = Г+{х0)-
Рассмотрим теперь примеры типичного поведения отношения (роз-
()()
постного отношения) —— —- при х —> хо.
х - х0
Примеры. 1. Для функции /(х) = х, х £ R и любой точки хо £ Я
имеем lim ^—^—~—- = lim = lim 1 = 1. Следовательно,
х—>жо X — Xq х—»Xq X — Xq х-+а;о
х1 = 1, х £ R.
2. Для функции /(х) = |х|, х £ /? и точки хо = 0 имеем равенства
х—>0,ж<0 X — 0 х-+0,х<0 X ж->0,х<0 ' х-+0,х>0 X — 0
lim - = lim 1 = 1. Таким образом, /1@) = -1, /1@) = 1, а
х->0,ж>0 X ж-+0,х>0
производная /'@) не существует.
3. Для функции /(х) = х2, х £ R и любой точки хо 6 /2 имеем
х2 - х2
lim = lim (x + xo) = 2хо. Таким образом, (х2)' = 2х, х 6 R-
х—Но X — Хо х—Яо
4. Для функции /(х) = ^г, х £ R и точки Хо = 0 справедливо ра-
,. $х-Уд .. 1
венство lim — = lim = +оо. Следовательно, производная
£-+0 X — 0 I—>0 A^j2
функции / в точке 0 не существует.
5. Для функции /(х) = xsin — для х ф 0 и /@) = 0 и точки Хо = 0
х
отношение —^—^ — = —■ = sin — при х —> 0 предела не
х - 0 х - 0 х
имеет. Поэтому производная функции / в точке 0 не существует.
Упражнение 1. Проверить, что (х|х|)' = 2|х|, х £ R.
Упражнение 2. Для функции /(х) = |х2 — х|, х £ Д найти /'(х) для
х £ (Д\ {0,1}). В точках 0 и 1 найти производные слева и справа.
Упражнение 3. Для функции /(х) = |х2 - 2|х||, х £ R найти /'(х)
для х £ (R\ {-2,0,2}). В точках -2, 0 и 2 найти производные слева и
справа.
4.1.2 Интерпретации производной
Понятие производной было введено в математику для решения задач
математики и других наук, в первую очередь для описания законов дви-
движения и решения задачи о построении касательных.

4.1. Определение, примеры и обсуждение
127
(i) Физическая интерпретация. Точка Р движется по числовой
прямой, s(t) — координата точки Р в момент времени t. Пусть t\, t2
— два момента времени, причём t\ < t2. Средняя скорость движения
точки за период времени [ti,ta] равна , где s(t2) — s{t\) —
путь, пройденный за время от момента t\ до момента t2. Если движение
не является равномерным, то мгновенная скорость в точке £i
определяется как предел lim —— -—- . Таким образом, мгно-
t2 - J
венная скорость v(t) точки Р в момент t есть производная в точке t от
пути s, именно v(t) = s'(t). Если мгновенная скорость точки в момент t
известна, то приближённое значение пути, проходимого за промежуток
времени [t,t + At], равно s'(t)At.
(ii) Геометрическая интерпретация. Пусть / : (а, 6) -> R, х0
G (а,6). Прямая, проходящая через точки Ро = (хо,/(хо)), Р(х) =
(х, /(х)) графика функции /, называется секущей. Положение секу-
секущей определяется точкой Ро и углом наклона секущей а(Р(х)), который
отсчитывается от положительного направления оси абсцисс. Тангенс это-
этого угла равен
tga(P(x))=nx)~f{Xo) , A)
при этом достаточно ограничиться следующими значениями угла
а(Р(х)) G (—7г/2,тг/2], см. рис. 2. Если абсциссу х приближать к хо,
то точка Р(х) будет приближаться, перемещаясь по графику функции
/, к точке Ро. При этом может оказаться, что секущая приближается к
некоторому определённому положению. Точнее это означает, что угол
о(Р(х)) -¥ а0, х ->■ х0. касательная
- X
Рис. 2.
9 — 4-1168

128 Глава 4. Производная и её приложения
Определение 3. Если существует предельное поло-
положение секущей при х ->■ х0, то есть существует предел
lira a(P(x)) =: oto, то прямая, проходящая через точку Ро
X—+£(]
и образующая угол ао с положительным направлением,
оси абсцисс, называется касательной к графику функ-
функции / в точке Ро-
Замечание. Возможно, что существует lim a(P(x)) = а0 -
X—iX0,X<X0
( lim а{Р{х)) = ао+). Тогда прямая, проходящая через точку Ро с
углом наклона ао — (ао+) к положительному направлению оси абсцисс
называется левой (правой) полукасательной в точке Ро. Ес-
Если ао— = ао+, то существует lim а(Р(х)) — а0— = ац и существует
касательная в точке Ро.
Теорема 1. Касательная к графику функции / в точ-
точке Ро = (хо,/(хо)) с углом, наклона ао £ (—тг/2, тг/2) к поломси-
тельному направлению оси абсцисс существует тогда и
только тогда, когда существует производная /'(х0), при
этом tga0 = /'(хо)-
\ Пусть существует производная /'(хо). Тогда согласно равенству A) и
определению производной существует предел lim tg a(P(x)) — /'(хо),
Х~+ XQ
а так как arctg £ C(R), то а(Р(х)) = arctg(tgа(Р(х))) ->■ arctg/'(х0),
х -¥ х0, причём arctg/'(х0) £ (-тг/2,тг/2). Следовательно, касательная
в точке Ро существует и ао = arctg /'(хо).
Пусть существует касательная в точке Ро, то есть а(Р(х)) —¥ а§ £
(-тг/2,7г/2), х -> х0. Отсюда с учётом того, что tg £ С((-тг/2,тг/2)),
получим с помощью равенства A) ———- = tgа(Р(х)) —> tgao £
R, х —¥ xq. Поэтому существует /'(хо) = tgao- J
Упражнение 4- Рассмотреть поведение секущей при х —>■ хо = 0 в
примерах 2 и 5 п. 4.1.1.
Упражнение 5. Доказать, что функция / имеет вертикальную каса-
касательную с ао = 7г/2 к графику в точке (хо,/(хо)) тогда и только тогда,
когда —¥ +00 (—со), х —> Хо. Поэтому в этом случае иногда
говорят о бесконечной производной и пишут /'(х) = +со (-со).
Упражнение 6. Доказать, что функция /(х) = x2sin-, i/Ои
/@) = 0 имеет /'@) = 0.

хЛ. Определение, примеры и обсуждение
129
iii) Микроскоп. Пусть f(x) = х2, х е [-1,1]. Тогда f'(x) = 2x, x G R
1 /'@) = 0. Поэтому касательная в точке @,0) существует, это ось абс-
-1исс. Рассмотрим рис. 3. Общий вывод состоит в следующем. Если в
"очке xq функция / имеет производную, то при большом увеличении
-■асть графика функции, лежащая вблизи точки (xq, f(xo)), почти совпа-
совпадает с отрезком касательной. На последнем фрагменте рис. 3 концы
-оасЬика поднимаются над осью абсцисс на .
У
6
2
х -
0,4
0,2
у = х2
- X
-1
0,2
0,1
у = х2
-0.2
0
0,2
Увеличено в 5 раз.
У
6
0,02
0,01
-0,1 0 0,1
Увеличено в 10 раз.
-0,01 0 0,01
Увеличено в 100 раз.
Рис. 3.
4.1.3 Замечания к определению производной
юнятие производной является весьма сложным и тонким математиче-
-ким понятием. Дополнительная информация об этом понятии содер-
кится в следующих утверждениях.
. Определение производной в точке имеет локальный характер
"очнее это означает следующее: предельное поведение отношения
()Ы ,
при х —¥ xq не изменится, если для любого заданного
X —

/30 Глава 4. Производная и её приложения
6 > О произвольно изменить значения функции / вне <5-окрестности
ТОЧКИ Xq.
2. Близость к касательной
Если в точке Xq существует производная, то график функции / в окрест-
окрестности точки (xo,f(xo)) близок к прямой. Точнее, если существует про-
производная f'{x0), ТО f(x) = f(xQ) + f'(xO)(x - Xq) + o(x - X0), X -> X0-
[ Действительно, поскольку f'(xo) = lim — , то разность
x->x0 X — Xq
a(x) := —— —— - f'(x0) -4 0, x -> x0. Поэтому имеем f(x) —
X — Xq
f{x0) + f'{xo){x - x0) + a{x){x - x0) = f(x0) + f'{xo){x - x0) + o{x - x0)
При X —¥ Xq. J
Упражнение 7. Если 3 L £ R : f(x) = f(xQ) + L[x - x0) + o(x -
Xo), x —> xq, to существует производная f'{xo) — L. Доказать это утвер-
утверждение.
3. Определение касательной
Формальное определение касательной к графику функции состоит в
следующем.
Определение 4- Прямая вида д(х) — f{xo) + L(x-x0), x £
R, где L £ R — фиксированное число, называется каса-
касательной к графику функции f в точке (xo,f(xo)), если
f(x)-g(x) = o(x-x0), x-+x0.
Упражнение 8. Проверить, что определения 3 и 4 равносильны.
4. Непрерывность
Существование у функции производной в точке влечёт непрерывность
функции в этой точке.
Теорема 2. Если в точке хо существует производная
f'(x0) £ R, mo функция f непрерывна в точке х0.
\ Согласно замечанию 2 f(x) = f(xo) + f'(xo)(x — xq) + o(x — xq), x —> xq,
поэтому f{x) -> /(io), x -t xo. J
Упражнение 9. Привести пример непрерывной в точке функции, не
имеющей производной в этой точке.

4.1. Определение, примеры и обсуждение 131
5. Дифференцирование
Определение 5. Если для каждого х£А существует
производная /'(х), то функция /', определяемая соотно-
соотношением. Аэхи /'(я) называется производной функции /
на множестве А. Операция определения функции /' на-
называется дифференцированием функции /.
Упражнение 10. Функция / имеет производную /'(хо) в точке Хо-
Выразить через значения /(то), /'(^о) значения следующих пределов:
lim /(sq + 2Ax)-/(x0) ^ /(sp + Ax) - /(sp - Ax)
Д1-+0 As
g) lim —, если x0 ^0; xn ф x0, n > 1, xn -¥
n-»oo Xn — Xq
X0, П -> OO;
Упражнение 11*. Обязательно ли при условии предыдущего упра-
r f(Xn)f(zn)
жнения существует предел lim —-— 5—- для последовательно-
п-»оо хп - Zn
стей хп -> s0, zn -> хо> п -> °°\ хп ф zn, n > 1?
Указание. Рассмотреть для точки для точки so = 0 функции /(s) =
х3, х £ R; g(x) = s2 sin - для i/Ои g@) = 0.
Упражнение 12. Доказать, что из существования обоих односто-
односторонних производных fL{xQ), /+(s0) следует непрерывность функции /
в точке So.
Упражнение 13. Функция / : R -> R имеет производную /' на R. В
каких точках функция |/| имеет производную? Найти эту производную. В
тех точках, в которых производная не существует, найти односторонние
производные.
Упражнение Ц. Для функций /,g : й->й существуют производ-
производные f',g' на R. В каких точках функция h(x) := max(/(s),з(а:)), s G R
имеет производную? Найти эту производную. В остальных точках опре-
определить односторонние производные.

132 Глава 4. Производная и её приложения
4.2 Правила вычисления производных
и примеры
4.2.1 Правила вычисления производных
Следующие теоремы содержат основные средства для вычисления про-
производных.
1°. Производная суммы, произведения и частного.
Теорема 3. Пусть функции f,g : А -> R имеют про-
производные f'{xo), g'{xo) в точке xq £ А. Тогда:
1) для любого числа с £ R функция cf имеет производную
в точке х0, причём, (cf)'(x0) = cf'(xo);
2) функция f + g имеет производную в точке х0, причём.
3) функция fg имеет производную в точке х0, причём.
(МЫ = f'(xo)g(xo) + f(xo)g'(xo);
4) если дополнительно значение д{хо) ф 0, то имеет ме-
(f\. , /'(so)g(xo) - f(xo)g'(xQ)
сто равенство - (х0) = ————f
\д)
гп i\ n
I Доказательство утверждения 3). Поскольку
X — Xq
- _ f(x) ~ fixo) , ч ,
X — Xq X — Xq
g(x)-g(x0)
+j(xq) , то с учетом определения производной, теоремы
X — Xq
2, согласно которой д(х) —> д(хо), х —» xq, и теоремы 6 гл. 3 получаем
утверждение 3).
Доказательство утверждения 4). Поскольку д(хо) ф 0, то по теоре-
теореме 4 гл. 3 д(х) / 0 в некоторой окрестности точки xq. Для значе-
1 /70=) /Ы\
;—- =
нии х из этой окрестности имеем равенство , .
x-xq \д(х) д[хо)
_ f(x)9Jxo) ~ f{xo)g{xo) + f{xo)g{xo) — fixo)g{x) _
д{х)д(хо)(х - х0)
1 /70=)-
- 9(x)9(x0) { x-xQ 9{X0) /(Д0) x-Xq ) '
вая часть аналогично имеет нужный предел при х —> xq. J
Упражнение 15. Доказать утверждения 1) и 2) теоремы 3.
Упражнение 16. Пусть для каждого j G {l,...,n} функция /; :
А —¥ R имеет производную /j(a:o) в точке xq £ А. Доказать, что:

4.2. Правила вычисления производных и примеры 133
«) ( Е fi 1 Ы = Е />Ы; Ь) I П /; 1 Ы = ЛЫ/2(*о) ■ ■ ■ /п(*о)
■ • • /n(io) + • • • + Ы*оI2Ы ■ ■ • №о).
Упражнение 17. Пусть дополнительно к условиям предыдущего
упражнения /j(xo) 7^ 0, j € {1,2,... ,п}. доказать следующее равен-
равенУпражнение 18. Пусть Р — многочлен степени п с различными
действительными корнями Х\,Х2, ■ ■ ■, хп. Доказать, что для любого х ^
Р'(х) п 1
{хг, х2,..., хп} справедливо равенство -~~ = Е ;■
2°. Правило дифференцирования сложной функции или
цепное правило.
Теорема 4. Пусть функция f : Л -> J? имеет произ-
производную f'{x0) в точке xQ G Л, множество В D {/(я) | х £ А}
и функция g : В -> R имеет производную з'(Уо) в точке
Уо := /(а:о)- Тогда функция g{f), определяемая соотношени-
соотношением Лэхи ^(/(я1))! имеет производную в точке xq, причём.
f Согласно утверждению п. 4.1.3, 2 имеем д(у) - д(уо) = з'(Уо)(у -
Уо) + ос(у)(у — уо), причём а(у) —> 0, у —> уо- Положим в этом равенстве
у = /(а:), уо — /(^о) и разделим его на а: — х0 при а: ^ х§. Получим
следующее равенство
gV{o)){f{)) ()
X — Xq X — Xq X — Xq
По теореме 2 f(x) -> /(io) = Уо, а: -> х0, а потому а(/(а:)) ->0, х ->
a:0. Переходя к пределу при а: -> а:0 в равенстве A), имеем существо-
существование производной функции g(f) в точке aio и нужное равенство. J
Упражнение 19. Сформулировать и доказать правило дифферен-
дифференцирования суперпозиции трёх функций.
Упражнение 20. Для функции / : й-»й существует производная
/' на R. Доказать утверждения:
a) производная /' чётной функции / есть нечётная функция;
b) производная /' нечётной функции / есть чётная функция;

134 Глава 4. Производная и её приложения
с) производная /' периодической с периодом Т > О функции / есть
периодическая с периодом Т функция.
Упражнение 21. Функции /, g : А -> R имеют производные f'{x0),
g'(x0) в точке х0 £ А, причём }{х) > 0, iGA. Доказать равенство
(П'(х0) = f(xoyM (^± f{xo) + g'{
Указание. Воспользоваться равенством f9 =
3°. Правило дифференцирования обратной функции.
Теорема 5. Пусть -со < а < b < +00 и функция / :
(a,b) -> R удовлетворяет условиям,: 1) f £ С((а,Ь)) и 2) f
строго возрастает на (а,Ь). Пусть (c,d) := {/A) | х £ (а, 6)},
при этом, -со < с < d < +00. Пусть такмсе g : (с, d) -> (а, 6)
— функция, обратная к {.
Если в точке хо е (а,Ь) сугцествует производная f'(xo) ф
О, то функция g имеет производную д'(уо) в точке уо :—
/(хо), причём д'Ы = ~ = j^y
\ Обратная функция д существует в силу теоремы 15 гл. 3, при этом
д строго возрастает. Пусть у ф уо, тогда д(у) ф д{Уо)- Согласно опре-
определению обратной функции и утверждению п. 4.1.3, 2 имеем у — Уо =
1Ш) - /(з(уо)) = Г(дЫ)Ш - дЫ) + <*{д(у))Ш - з(уо)), где
а{9{у)) -> 0 при д(у) -> д(уо). Поскольку д £ C((c,d)), то у ->
() ()
Уо =>■ з(у) -> з(Уо) =>■ a(fl(y)) -> 0. Поэтому получим
У ~ Уо
д{у)-д{уо) 1
/'C(УО))C(У) - ЗЫ) + a(S(y))(s(y) - s(yo))
1 .
правая часть последнего равенства сходится к —-——— при у —> Уо- J
/ЧЗ(Уо))
Отметим, что геометрически утверждение теоремы 5 очевидно, см.
рис. 4 на следующей странице.
Замечание. Допустим, что в теореме 5 для каждой точки х £
(а,Ь) существует производная f'(x) ф 0. Тогда для каждого у £ (с, d)
существует д'(у) и связь между производными /ид можно получить,
дифференцируя по х или по у соответственно тождества g(f(x)) —
х, х £ (a,b); f{g{y)) = У, у £ (с, d) на основании теоремы 4. Получим
5'(/(х))/'(х) = 1, х £ (а, 6); /'(<?(у))<7'(у) = 1, У £ (с, d).
Упражнение 22. Доказать существование обратной функции д к
функции / и найти производную g'(f(x)) :
a)/(z) = 7T^> I>1; b)/(x) = x3 + 3x, xeR;
c) f(x) = x + sina:, a: £ J?; d) }{x) = a: + In a:, 1 > 0.

4.2. Правила вычисления производных и примеры
135
Касательная
d
с
0
У
6
9
f
->
i
a
i
A
t
x0
i
i
i
j
i
f
x = 5(y)
.
_ X
b
= f'{x0), tg/3o = g'{yo),
Рис. 4.
4.2.2 Примеры вычисления производных
В следующих примерах содержится необходимый для дальнейших рас-
рассуждений набор производных,
i. Пусть а £ Я. Тогда Vi>0 : (xa)'= ax"-1.
Для a = n e N имеем Vi £ R : (xn)' = m".
Для a = m £ Z имеем Vi G (Я\ {0}) : (xm)' = mi1"'1.
f С помощью теоремы 18 гл. 3 для х > 0 получаем
— т
— X
а —1
Дх
а:
■Xе-а, Да:->0. J
Упражнение 23. Доказать, что (а0 + aix + а^х2 +.. . + апхп)' = ai +
2а2х + .. .+папхп~1 для любого х £ R, где п £ N, {ao,ai,... ,а„} С R.
2. Пусть а > 0. Тогда Vi £ J? : (а1)' = а11па, в частности, для
а = е ViG R : (е1)' = ев.
f С помощью теоремы 17 гл. 3 имеем
-)• axlna, Да: -> 0.
а
х+Ах
Да:
= а
Да:

136 Глава 4. Производная и её приложения
3. ViG-R: (since)' = cos a:, (cos a:)' = -sin a:;
Vie(J?\7rZ): (ctgi)' = -—
[ Для любого х £ R имеем утверждение
sm x
sin(a: + Ax) — sin a:
Ax
Ax
2 . Ax i Ax\ sm о i Ax
sm-
Да:
. l\x / ui\ — p / l\x \ .
m —- cos I x + —— I = —. * cos I x H I -> cos x, Ax -> 0.
2
Отсюда с учётом теоремы 4 для любого х £ R получаем (cos а:)' =
(sinf— — х J j = cos Г — — re J (— 1) = —sinx. Применим теперь теорему
... /since \ cos x ■ cos x — sin x • (— sin a;) 1
3. Получим tga:)' = = ^ '- = —5—
\ COS X ) COS^ X COS^ X
дляяе (Я\(| +ttZ)). J
4.. Пусть a > 0, a ^ 1. Тогда Vi > 0 : (loga a:)' = —; . В частности,
a; ma
Va:>0: (lniI = -.
x
\ Рассмотрим случай a > 1 и воспользуемся теоремой 5, положив
(a,b) = R, f(x) = ax, x £ R, (c,d) = @,+oo). Согласно теореме
19 гл. 3 функция / £ C(R), а с учётом примера 2 Vi € й : f'(x) —
ax In a ф 0. Применим теорему 5 к логарифмической функции — функ-
функции, обратной к /, получим g'{y) = (loge уI = -щ = ^j^
где у = /(а:) > 0. J
Упражнение 24- Доказать утверждение примера 4 для а £ @,1).
5.VxeR: (arctgz)' = —^.
[ Воспользуемся теоремой 5, положив в ней (а,Ь) = (—тг/2, тг/2),
/(а:) = tga:, а: £ (а,Ь), (c,d) = Я. При этом имеем tg £ С((тг/2,7г/2)),
(tga:)' = —г~ # 0, а: £ (тг/2,7г/2), и з(у) = arctgy, у € Д. Поэто-
cos а:
му для любого у £ R имеем <?'(у) = (arctgy)' = = cos2i =
J (a:)
= cos2(arctgy) = 2 г = ——j-, где а: = 5(у), tga: = у. J
l + tg2(arctgy) 1 + Г
6.\/x£R: (arcctga:)' = -^
X "т"
Vi£ (-1,1) : (arcsinx)' =

4.2. Правила вычисления производных и примеры 137
1
Vie (-1,1) : (arccosi)' = --
l\ -х2
Упражнение 25. Доказать утверждения примера 6 с помощью тео-
теоремы 5.
Упражнение 26. Доказать формулу бинома Ньютона
п
(а + b)n = J2 Ckakbn~k, где числа п £ N, {а, 6} С R и использованы
обозначений := 1, Ск := -(п - 1)(п - 2).. .(п - к + 1) _ х < fc < „_
Указание. Достаточно доказать следующее тождество (z + а)п =
п
Е Ckzkan~k, z £ R. Заметить, что многочлен (a + z)n имеет вид
fc=0
{a + z)n = bQ + blZ + b2z2+ ... + bnzn, z£R A)
и нужно определить лишь числа bo,bi,... ,bn. Положив в A) z = О,
находим Ьо = ап. Найдём теперь производную по z от A)
n(a + z)n-1=61 + 2b2z + ... + nbnzn-1, z £ R, B)
положив в B) z = 0, находим 6i = nan~l и т. д.
п п
Упражнение 27. Вычислить сумму: а) J2 kekx, х £ R; Ь) J2 kCk;
fc=i fc=i
fc=0
z — zn+1
Указания, а) Для производной от z + z2 + .. . + zn — — , z ф
1 — (n + l)zn + nzn'lrl
1 имеем 1 + 2z + 3z2 + ... + nzn~l = ^—-1— , z ф 1,
A-zJ
откуда после умножения на z получим z + 2z2 + 3z3 + ... + nzn =
z-{n + l)zn+l + nzn+2 '
= ^ — , z Ф 1. Затем положить z = e , x ф 0.
{1-zJ
Случай i = 0 рассмотреть отдельно.
n
b) Найти производную суммы ]Г) Ckzk = (l + z)n, а затем положить
fc=0
z = 1. Ответ: п2п..
c) Ответ: 2"-1(п + 2).
Упражнение 28. Пусть Р — многочлен степени п с действитель-
действительными корнями xi,X2, ■ ■ ■ ,хп и старшим коэффициентом 1. Вычислить
Р'(хк), к = 1,2,...,п.

138
Глава 4. Производная и её приложения
Упрамснение 29. Вычислить производные на R следующих функций:
a) f(x) = ! sini| sim, x £ R; b) f(x) = [i]sm27ri, x £ R.
Упражнение 30. Привести пример отличных от постоянных функций
f,g, для которых справедливо следующее "правило"вычисления произ-
производной произведения двух функций (fgI = f'g'.
Упражнение 31. Пусть f(x) = х2 при х < 1 и f(x) = ах + Ъ при
х > 1. При каких значениях {а,6} С й : а) функция / £ C(R)\ b)
функция / имеет производную на J?? Найти /'.
Упражнение 32. Пусть f(x) = |sini|a, x £ R, а > 0. При каких
значениях а функция / имеет производную на R? Найти /'.
Упражнение 33. Пусть f(x) = - при 0 < х < 1 и /(ее) = ах2 -
4
— х + b при i > 1. Определить значения а и Ь, при которых функция /
а
имеет на @, +оо) производную и найти её.
Упражнение 34- Пусть }{х) = — е~1/х2 при а: ^ 0 и /@) = 0.
X
Доказать, что /'@) = 0.
Упражнение 35. Определить числа Ь, с так, чтобы графики функций
f(x) = 4-х2, д(х) = х2 + Ьх + с имели в точке A,3) общую касательную.
Упражнение 36. Пусть f(x) = ^/х для х £ [0,1] и f(x) = ах2 +
Ьх + За3 + b для х > 1. Определить а,Ь, для которых функция / имеет
производную на @,+оо).
Упражнение 37. Доказать, что
d
dx
an(x)
a2i(s:)
,(r\ ni (T\ n i.
il\x) ■■■ anj\x) ■■■ ann{-
если элементы исходного определителя имеют производную в точке х.

4.3. Теоремы о функциях, имеющих производную
139
4.3 Теоремы о функциях, имеющих
производную
4.3.1 Доказательства теорем
Теорема 6. (Ферма). Пусть / : (а,Ь) -»■ R, х0 6 (а,Ь)
и /(io) = max /(i) или /(io) = min f(x). Если в точке io
существует производная /'(io), то /'(in) = 0.
[ Предположим, что f(x) = max /(i). Тогда Vi € (а, Ь) : /(ж) <
х6(а,Ь)
/(in). Поэтому
X—>Х0,Х<Х0
X — In
аналогично
/'(Ю) = Д(ю) =
I - In
< 0.
A)
• B)
Из неравенств A) и B) следует, что /'(in) = 0. J
Замечания. 1. Геометрически утверждение теоремы Ферма оче-
очевидно. Оно означает, что если в точке минимума или максимума суще-
существует касательная, то она параллельна оси абсцисс. См. рис. 5.
2. В теореме Ферма существенно, что а < х0 < Ь. Утверждение
теоремы неверно, например, для функции f(x) = i, i £ [0,1], для
которой max i = 1 = /A).
*€[0.1] (So,/(SO))
У = f(x)
a in b
tga0 = /'(so) = 0, a0 = 0
Рис. 5.
Упражнение 38. Предположим, что для функции / :
существуют f'+{a) и /L(b). Доказать утверждения:
а) Д(а) > 0, если /(a) = min{/(i) | х £ [а,Ь]};
[о,Ь]

140 Глава 4. Производная и её приложения
b) f'+{a) < 0, если /(а) = max{/(z) | х £ [а,Ь]};
c) /1(Ь) > О, если f(b) = max{/(z) \ х € [а,Ь]};
d) /-(ь) < О, если /(Ь) = min{/(x) | х £ [а,Ъ]}.
Упражнение 39. Обобщение теоремы Ферма. Пусть / :
(а,Ь) -> R, х0 £ {а,Ь) и f(x0) = max /(i). Если точке х0 существуют
Г_Ы и f'+(x0), то /1(х0) > 0, /;%„) < 0.
Теорема7. (Ролля). Пусть функция / : [а,Ь]->й удо-
елетеорлет условиям: 1) f £ C([a,b]); 2) Vi G (а,Ь) сугце-
cmeyem f'{x); 3) /(а) = /(Ь). Тогда 3 с е (а, Ь) : /'(с) = 0.
Г Если Vie[a,6]: f{x) = f{a) => Vc£{a,b): /'(с) = 0.
Пусть теперь
3i'G[a,b] : /(x')^/(a). C)
С учётом условия 1) и второй теоремы Вейерштрасса В{х*,х*} С [а,Ь] :
/(i*) = min f{x), f{x*) = max f{x). Согласно условию З) и предпо-
хе[а,Ь] хе[а,Ъ]
ложению C) либо /(i*) ф f{o), либо f{x*) ф /(а). Рассмотрим случай,
когда f{x*) ф /(а), второй случай рассматривается аналогично. Тогда
х* ф а и х* ф Ь, и, следовательно, i* £ (a,b). Для функции / на интер-
интервале (а,Ь) и точки xq = х* выполнены все условия теоремы Ферма, по
которой f'{x*) = 0. Положим с = х*. J
Упражнение J^O. Пусть для / £ С[[а,Ь]) существует /' на (а,Ь),
причём Vi € [а, Ь) : /'(i) ф 0. Доказать, что /(а) ф f(b).
Упражнение ^1. Доказать, что уравнение х13 + 7х3 — 5 = 0 имеет
точно один положительный корень.
, Упражнение ^2. Функция / € С([а,Ъ}) имеет производную на [а,Ь)
и /(а) = /(Ь). Доказать, что для каждого а £ R следующее уравнение
ctf(x) + f'(x) = 0 имеет по крайней мере один корень на (а, Ь).
Указание. Применить теорему Ролля к функции g(x) = f(x)eax на
отрезке [а,Ь].
Упраж.нение 43. Пусть Р — многочлен степени п, все корни ко-
которого различны и действительны. Доказать, что все корни Р' также
действительны.
Упражнение 44-' Числа ao,ai,... ,ап удовлетворяют следующему
а0 а1 а2 - п
условию н н + ... + ап = 0. Доказать, что многочлен
п+1 п п-\
Р(х) = аохп + аух71 + а2хп~2 + ... + ап имеет по крайней мере один
корень на @,1).

4.3. Теоремы о функциях, имеющих производную 141
Упражнение ^5*. Пусть ai,a2, ■ ■., ап - отличные от 0 действитель-
действительные числа, ai, а2,. ■ ■, осп ~ попарно различные действительные числа.
Доказать, что функция f(x) = сце* + а2еа2Х + ... + апеа"х, х £ R
может иметь не более чем п — 1 корень на R.
Указание. Применить теорему Ролля и метод математической ин-
индукции.
Упражнение ^6. Пусть {ai_,a2,..., а„; а^ а2,..., а„} С R и f(x) —
aix + агх + ... + апхап, х > 0, — функция, отличная от 0 в некото-
некоторой точке. Доказать, что функция / может иметь не более (п — 1)-го
положительного нуля.
Упражнение ^7. Функции / и g удовлетворяют условиям теоремы
Ролля. Доказать, что 3 с G (а, Ь) : /'(с) + f(c)g'(c) = 0.
Теорема 8. (Лагранмса). Предположим, что функ-
функция / : [а,Ъ] -> R удовлетворяет условиям.: 1) / G С([а,Ь]);
2) Vi € (a,b) существует f'{x).
Тогда Зс£{а,Ь): f{b)-f(a) = f'(c)(b-a).
fill) _ f(a)
\ Функция g(x) := f(x) - f(a) - ^-^ ^—^ (i - a), x G [a, Ь] удовлетво-
удовлетворяет условиям теоремы Ролля, причём g'(x) = f'[x) - ^-{—=^—^ , х £
о — а
{а,Ь). По теореме Ролля существует число с G (а,Ь) : <7'(с) = 0 <=^
№)_ЛЬЬЖ _„ ^ Лс)=/М1 «. /w_/w =
= №)(»-«)• J
Замечания. 1. Теорема Лагранжа называется также теоремой
о среднем значении или теоремой о конечном прираще-
приращении.
f(b) - На)
2. Отношение — есть тангенс угла наклона к оси абсцисс
о — a
секущей, которая проходит через точки [a,f(a)) и (Ь, f[b)). Теорема
Лагранжа утверждает существование точки с такой, что касательная
к графику в точке (с, /(с)) параллельна секущей. См. рис. 6 на сле-
следующей странице. Существование точки с становится наглядным, если
проследить за поведением касательной в точке графика (х, f(x)) при
передвижении точки х от точки а до точки Ь.
Упражнение ^-8. Доказать, что теорема Ролля следует из теоремы
Лагранжа. Таким образом, теоремы Ролля и Лагранжа равносильны.
Упражнение 49. Пусть f(x) = х2 + 2рх + q, x € [a,b]; {p, q} С R.
Определить число с в теореме Лагранжа.

142
Глава 4. Производная и её приложение
У = f(c) + f'(c)(x - с
»-/
л л л
/-/(с
(ъ,№
(Ь /(а)
/'(с) =
Ь-а
Рис. 6.
Упражнение 50. Для функции /(i) = Ini, x G [1,Ь], 6 > 1 опре-
определить число с в теореме Лагранжа.
Упраж.нение 51. Пусть функция / удовлетворяет условиям теоремь
Лагранжа и условию
3L>0 Vi G (а,Ь) : |/'(i)| < L.
Доказать, что V{i/1a:"} С [а,Ь] : \f(x') - f{x")\ < L\x' - х"\.
D
Упражнение 52. Доказать, что удовлетворяющая условию D) функ-
функция равномерно непрерывна на (а, Ь).
Упражнение 53. Функция / : (а, Ь) -> R имеет производную не
(а, Ъ) и такова, что V {а:', х"} С (а, Ъ) : f{x") - f{x') = f'{x'){x" - х'\
Доказать, что / есть линейная функция на (а,Ь).
Упрамснение 54- Функция / : R —> R имеет производную на R >■
удовлетворяет условию V {х, у} С R : f(x) - f(y) = /'
Найти все функции, удовлетворяющие этим условиям.
х+у
[х-у.
Упражнение 55. Для функции / £ С([а,Ь]) существует Д на (а,Ь
и /(а) < /(Ь). Доказать, что 3 с G (а,Ь) Д(с) > 0.

4.3. Теоремы о функциях, имеющих производную 143
Указание. Существуют числа а,0, а < а < /3 < b такие, что
/(а) < /(/3). Если f'+(x) < 0 для х 6 [а,/3], то существует х0 £ (а,/3) :
f{x0) < /(а). Поэтому min/ = /(i»), I* € (а,/3). Тогда Д(х») > 0.
Упражнение 56. Для функции / £ С([а,Ь]) существует Д на {а,Ь)
и /(а) = /(Ь). Доказать, что 3cie(a,b): ДЫ > 0, 3c2e(a,b):
ЛЫ < 0.
Упражнение 57. Для функции / G C([a,b]) существует Д на (а,Ь).
Доказать, что 3 {Cl) с2} С (а, Ь) : Д(С1) < /(&^ f ^ <
Упражнение 58*. Для функции / : (a,b) -> R существует Д. 6
С((а,Ь)). Доказать, что существует производная /' и /' = Д на [а,Ь).
Теорема 9. (Когии). Пусть функции /,g : [а,Ь] -> R
удовлетворяют условиям.: 1) {f,g} С С([а,Ь])\ 2) Vi 6 (a.b)
сугцествутот /'(i),5'(a;); 3^ Vi 6 (a,b) : 5'(i) / 0.
g{b)~g[a) g'{c)
\ Сначала заметим, что g(a) ф g(b), так как если бы д[а) — д(Ь), то по
теореме Ролля существовала бы точка с 6 (а,Ь), для которой д'(с) = 0.
Последнее же противоречит условию 3).
Функция h(x) := /(*) - /(a) - ^j I g(!) E(l) ~ д{а))' Х £ [a'b]
^j (
удовлетворяет на отрезке [a,b] условиям теоремы Ролля. Согласно этой
теореме 3 с 6 (а, Ь) : h'(c) = 0 ^=^ /'(с) - ^jl^j 5'(с) = 0. J
Замечания. 1. Теорема Лагранжа есть частный случай теоремы
Коши для функции д(х) = х, х £ [а,Ь]. Поэтому теоремы Ролля, Ла-
Лагранжа и Коши равносильны.
2. Следует обратить внимание на то, что теорема Ферма, а следо-
следовательно, и важнейшая теорема Лагранжа, фактически является след-
следствием определения производной.
Упражнение 59*. Пусть функции fj : [а,Ь] -»■ R, j = 1,2,3 удо-
удовлетворяют условиям: 1) {/ь/г./з} С С([а,Ь\); 2) Vi £ (a,b) существу-
существуют производные f[(x), f^x), f^x). Доказать утверждение Зс 6 (а,Ь) :
/() fi(b) f[(c)
/2@) Mb) fi(c)
/з(а) /з(Ь) /3(c)
в качестве частных случаев.
= 0. Получить теоремы Ролля, Лагранжа и Коши
10 — 4-1168

144 Глава 4. Производная и её приложения
Упражнение 60. Функция / : [а,Ь] -» R удовлетворяет усло-
условиям теоремы Лагранжа. Доказать, что 3 с £ {a, b) : f(b) — /(а) =
е-с/'(с)(еь-еа).
4.3.2 Первые применения теоремы Лагранжа
1. Определение функции по производной
Следствие 1. Функция / : (a,b) -> R имеет производ-
производную /' на (а, Ь) и такова, что выполняется следующее
условие V х 6 (а, Ь) : f'(x) - 0. Тогда 3 L £ R V i £ (а,Ь) : f(x) = L.
I Пусть Xq £ [a,b) — произвольная фиксированная точка и х ф xq.
Применим к отрезку с концами i к io теорему Лагранжа. Получим
f(x) - f(x0) = f'{c)(x - i0) = 0. Положим L = f[x0). J
Следствие 2. Функции f,g : (a,b) —t R имеют производ-
производные /' и g' на (a,b) и, кроме того, Vi £ {a,b) : f'(x) = g'(x).
Тогда 3 L £ R Vi G (a, b) : /(i) = 5A) + L.
[ Применить предыдущее следствие к функции / — g. J
Следствие 3. Функция f : (a,b) -> R имеет производ-
производную на (а,Ь) и 3 L £ R V х £ {a,b) : f'(x) — L. Тогда справед-
справедливо утверждение 3 М £ R V х € (a,b) : f(x) = Lx + М.
\ Применить предыдущее следствие к функциям / и g{x) = Lx. J
Упражнение 61. Пусть числа а,Ь фиксированы. Определить все
функции / : R—*R, для которых f'(x) = ax + b, x £ R.
Упражнение 62. Определить все функции / : R —> R, для которых
f'(x) = f(x), xeR.
Указание. Заметить, что (f(x)e~x)' = {f'(x) - f(x))e'x, x £ R.
Упражнение 63. Функции f,g : (a,b) -> @, +00) имеют производ-
производные на (а,Ь), причём Vi£(a,6) : = -7—- . Доказать, что в этом
/(я) 9(х)
случае 3 L > 0 Vi £ (а,Ь) : /(i) = Lg(x).
Указание. Рассмотреть функции In/ и 1п<7-
2. Существование односторонней производной
Следствие ^. Функция f : (a,b] -> R удовлетворяет
условиям: 1) f £ C((a,b]); 2) Vi £ (a,b) существует f'(x);
3) существует lira. f'{x) =: L. Тогда существует произ-
1->Ь,з:<Ь
водная слева /1(Ь) и /1(Ь) = L.

4.3. Теоремы о функциях, имеющих производную 145
[ Пусть а < х < Ь. Применим теорему Лагранжа к функции / на отрезке
[х,Ь]. Получим Зс = с(х) £ (х,Ъ) : ^ ~ (^ = f'(c(x)). Отсюда с
1 — 0
учётом условия 3) и того, что с(х) —> Ь— при х —> о—, получим утвер-
утверждение следствия. J
3. Доказательство неравенств
Приводимые ниже неравенства постоянно используются в математиче-
математических рассуждениях.
Пример. 1. Докажем, что: V{x',x"} С R :
| arctgi' - arctgi"| < \х' - х"\;
V {х1, х"} С [1, +оо) : \у/х> - \№\ < \ \х' - х"\
\ Доказательства этих неравенств аналогичны. Докажем первое и по-
последнее из них. Пусть для определённости х' < х". Применяя теорему
Лагранжа к функции sin на отрезке [i',i"], получим Зс G (х',х") :
|sini" — sinx'| = | cosc|(a;" — x'), а поскольку |cosu| < 1 для любого
и £ R, то |sini' -sini"| < \x' - x"\.
Для доказательства последнего неравенства применим теорему Ла-
Лагранжа к функции }{х) = -Jx, х > 1 на отрезке [i',i"], получим
Зс £ (х',х") : \\/х"-\/х1\ = —■7={х"-х1), отсюда, поскольку с > х' > 1,
2 /с
/
имеем \у/х17-у/х1\<-\х"-х'\. J
Упражнение 64- Доказать второе и третье неравенства примера 1.
Пример. 2. Докажем, что: a) Vi £ R : ех > 1+х, " = " <=$■ х = 0;
2
Ь) Vi >0: ех > 1-Ы+
х2
[ а) Для случая х > 0 применим теорему Лагранжа к функции /(и) =
еи, и £ [0, х], получим 3 с £ @, х) : ех - е° = ес(х - 0) > х, поскольку
ес > 1 для с > 0. Если х < 0, применим теорему Лагранжа к функции
/(и) = еи, и G [i, 0]. Получим 3 с 6 (i, 0) : е° - ех = ес@ - х) < -х,
так как -i > 0, а ес < 1 для с < 0. Таким образом, ех > 1 + х, х ф 0.
Ь) Применим теорему Коши к функциям /(и) = еи, д(и) — 1 + и +
и2 е1 - е° ес
-| , и £ [0,:г]. Получим Зс 6 @,а;) : 2 = • ^
2 X 1 + С
1+Х+—-1
X2
учётом неравенства а) отсюда имеем ех > 1 + х + — . J

146 Глава 4. Производная и её приложения
Упражнение 65. Доказать такое неравенство VnGJVVi>0:
е*>1 + х+» +3! +--- + ^!'
Указание. Использовать математическую индукцию и пример 2.
Упражнение 66. Доказать, что Vi > -1 : < ln(l + х) < х,
1 + 1
" " х = 0.
Упражнение 67. Обобщение неравенства Бернулли. Для
а > 1, доказать, что Vi > -1 : A + х)а >1 + ах, " = " <=$■ х = 0.
Упражнение 68. Доказать, что:
X3 X2
a) Vi > 0 : х - -— < sin a; < x; b) Vi > 0 : 1 - — < cosx < 1.
Упражнение 69. Предположим, что функции /, g : [а, Ь] —> Д
удовлетворяют условиям теоремы Лагранжа и условию V х G (а, Ь) :
/'(i) < 5'(i). Доказать, что f(b) - /(а) < g(b) - g(a).
Упражнение 70. Доказать неравенство Ve>0 3i0 >0 Vi>io:
In a; < хс.
4. Исследование монотонности функции
Теорема 10. Пусть -оо < а < Ь < +оо и функция f :
{а,Ь) -¥ R имеет производную f'(x) для каждого х е (а,Ь).
Для того чтобы функция / была монотонно неубываю-
неубывающей на (а,Ь), необходимо и достаточно, чтобы
Vx£(a,b) : /'(!)> 0. A)
[ Достаточность. Пусть условие A) выполнено и а < х' < х" < 6.
Применяя к функции / на отрезке [а;', а;"] теорему Лагранжа, получим
Зс£ {х',х") : f{x") - f(x') = f'{c)[x" - х') > 0. Следовательно, имеем
неравенство f(x") > f(x').
Необходимость. Пусть / монотонно не убывает на (а,Ь). Тогда для
числа х £ (а, Ь) имеем f'(x) = f'(x) = lim Л^±^1и!М > 0,
поскольку Да; > 0, f(x + Да;) > f(x). J
Теорема 11. Пусть -оо < а < b < +00 и функция / :
(а, Ь) -> R имеет производную f'(x) для каждого х £ (а,Ь).
Для того чтобы функция / строго возрастала на (а,Ь),
необходимо и достаточно, чтобы выполнялись условия:
1) Vx£(a,b) : f'(x)>0;
2) не существует интервала (а,/3) С (а,Ь) такого, что

4.3. Теоремы о функциях, имеющих производную 147
\/х€(а,0) : /'(*) = 0. B)
Г Необходимость. Пусть функция / строго возрастает на (а,Ь). Тогда
/ монотонно не убывает на (а,Ь) и согласно теореме 10 условие 1)
выполнено. Условие 2) также выполнено, поскольку из существования
интервала (а,/3) С (а, Ь), для которого выполнено равенство B), следует
согласно следствию 1, что функция / постоянна на (а,@). Последнее
противоречит предположению о строгом возрастании /.
Достаточность. Предположим, что условия 1) и 2) выполнены.
Тогда по теореме 10 функция / монотонно не убывает. Пусть теперь
а < х1 < х" < b, f(x') = f[x")- Тогда получим следующее утверждение
Vi6 [x',x"] : f{x) = f(x') ^=» Vi£ {x',x") : f'{x) = 0, что
противоречит условию 2). Поэтому f(x') < f{x"). J
Упражнение 71. Доказать аналоги теорем 10 и 11 для убывающей
функции.
Указание. Применить теоремы 10 и 11 к функции -/.
Примеры. 1. Функция f(x) ~ ex, x (E R строго возрастает на. R
согласно теореме 11, поскольку f'(x) = ех > 0, х £ R.
2. Функция f(x) = х2 + Ъх + с, х 6 R строго убывает на (-со, -Ь/2]
и строго возрастает на [—Ь/2,+оо) согласно теореме 11, поскольку
Ь Ь
f'(x) = 2х + Ь<0, х < -- ; f'(x) = 2x + b>0, x> --.
3. Функция f(x) = sini, x G R строго возрастает на [-тг/2, тг/2]
согласно теореме 11, поскольку f(x) = cos а; > 0, х € (-7г/2,тг/2).
4- Функция f(x) — lni, x > 0 строго возрастает на @,+со) согласно
теореме 11, поскольку f'(x) — 1/х > 0, х > 0.
5. Функция f(x) = tgi, x G ( —7г/2, тг/2) строго возрастает на
(—7г/2, тг/2) согласно теореме 11, поскольку f'(x) = l/cos2a; > 0 на
интервале х £ (-я/2,п/2).
6. Функция f(x) = aurctgi, x G R строго возрастает на R согласно
теореме 11, поскольку f'(x) = 1/A + х2) > 0, х-е R.
7. Функция f(x) = х + sina;, x £ R строго возрастает на R согласно
теореме 11.
In х
8. Функция f(x) = , х > 0 строго возрастает на @,е] и строго
х
1 — In х
убывает на [е,+оо) согласно теореме 11, поскольку f'[x) = ^—,
х > 0 положительна на @, е) и отрицательна при х > е.
9. Функция f(x) = хх, х > 0 строго убывает на @,1/е] и строго
возрастает на [1/е, +оо) согласно теореме 11, поскольку f'(x) — iI(l +
lni), x > 0 положительна на A/е,+оо) и отрицательна на @,1/е).

148 Глава 4. Производная и её приложения
Упражнение 72. Определить интервалы монотонности функции:
d) f(x) = x+
Упражнение 73. Определить значения а £ R, для которых функция
f(x) = х + a sin i, i £ Л монотонна на Д.
Упражнение 7£. Какое из чисел тге, е* больше?
Упражнение 75. Доказать неравенство: а) 1пA + х) < -; -^
2{х + 1)
х > 0; Ь) х2 cos i < sin2 x, x £ @, тг/2).
Упражнение 76. Пусть a > 0, Ь > 0. Доказать, что следующие
функции строго возрастают на @, +оо) :
'а<Ь;
Упражнение 77. Пусть / : [61,62] -> @,+оо), существует /' на
(#1,02) и /(^i) = /(^г)- Доказать существование значения 0о 6 (^ь^г)
такого, что касательная к графику г = f(9), 9 £ [^1,^2] в точке (#о, /(^о))
перпендикулярна к радиусу-вектору этой точки.
Упражнение 78. Исследовать на монотонность следующие функ-
ции Ш = 1 -
определённые при х > 0, и доказать следующее полезное неравенство
2п + 2 V п ) 2п + 1
4.3.3 Дифференциал функции
Пусть / : Л-»Ли точка х0 такова, что 3 6 > 0 : (хо — E, хо + 5) С Л.
Определение JL Функция f называется дифференци-
дифференцируемой в точке хо, если
3 L £ R : /(х) = /(xq) + L(x — хо) + о(х — хо), х —> хо. A)
Для дифференцируемой в точке xq функции f линей-
линейная функция у = L(x - х0), х 6 R называется дифференци-
дифференциалом в точке х0.
Обозначения: х - х0 = dx, L(x — х0) = Ldx = df(x0).

4.3. Теоремы о функциях, имеющих производную 149
Более логичным является не очень распространённое обозначение
) = Lh, heR.
Замечания. 1. Дифференциал функции / в точке х0 есть главная
часть (линейная по х — хо) приращения f(x) — f(xo) функции / относи-
относительно шкалы сравнения {R э м- (х — Xo)n \ n G ЛГ} при х —¥ xq.
2. Число L в A) определяется единственным образом.
Теорема 12. Функция f дифференцируема в точке х0
тогда и только тогда, когда в точке х0 существует про-
производная
\ Необходимость. Если / дифференцируема в точке хо, то из A)
f(x) - f{x0) o(x - хо)
при х ф х0 имеем —— —L = L -\—J , х -4 х0. Поэтому
х - х0 х - х0
.. f{x)-f{x0) .
существует предел lim. —— = L, следовательно, существует
х—*хо X — Хо
производная f'(xo) = L.
Достаточность содержится в замечании 4.1.3, 2. J
Замечания. 3. Таким образом, df(xo) = f'(xo)dx. Поэтому обо-
()
значение производной ———- можно понимать, как отношение диффе-
ах
ренциалов. Из правил вычисления производных легко получить правила
вычисления дифференциалов. Например, d(fg) — gdf + fdg и т. п.
4. Представляет интерес правило вычисления дифференциала слож-
сложной функции. Предположим, что выполнены условия теоремы 4. Тогда
dg(Vo) = g'(yo)dy> dh(xo) = dg(f(xo)) = g'(f(xo))f'(xo)dx, где h = g(f).
В правой части первого равенства имеем дифференциал функции g в
точке г/о, в правой части второго — дифференциал сложной функции в
точке х0. Причём правые части имеют одну и ту же форму, посколь-
поскольку f(xo) = г/о и dy = df(xo) = f'(xo)dx. Это свойство часто называют
инвариантностью формы дифференциала.
5. Введенные выше производная и дифференциал называются также
производной и дифференциалом первого порядка.
Упражнение 79. Если функция у = f(x), x 6 А задана параметри-
параметрически х = x(t), у = y(t), t G Т, то —— =
ах
и x'(t) ф 0. Доказать это утверждение.
чески х = x(t), у = y(t), t G Т, то —— = —\-^-, если х' и у' существуют
dx х(t)

150 Глава 4. Производная и её приложения
4.4 Производные старших порядков
4.4.1 Определение и примеры
Предположим, что для функции / : (а, 6) -4 R в каждой точке х € (а, 6)
существует производная f'{x). Функцию g = /' : (а,£>) -4 i? определим
равенством g(x) = f'{x), х Е (а, 6).
Определение 1. Если в точке х0 Е (a,b) существует
производная д'(х0) функции д в точке х0, то эта произ-
производная называется производной второго порядка функ-
ции f в точке х0 и обозначается символами /"(х0), —-г-^— .
Если производная порядка п Е N на (а, 6) определена, ее
обозначения /(п)(х), , х € (а,Ь), то производная по-
ахп
А , Л #<">(*)
ряока и|1 в точке х определяется как , если по-
ах
следняя существует.
Примеры. 1. Пусть а > 0. Для каждого х Е R получаем равенства
(a'J^a'lna, (a1)" = {axlnx)' = ax(ba)a,..., (ax)W = ax(ba)n, nE
N. В частности, для a = е имеем (е1)^ = ех, х Е R, п Е N.
2. Проверим, что для п Е N и х Е R
(n) = sinfz тп-1, (cosz)(n) = c
f Действительно, (sinx)' = cosx = sinlxH— J, (sinx)" = (cosx)' =
= - sinx — sinfx + 2— J, (sini)'" = (—sini)' = - cosx = sinfx + 3— J
и так далее. J
3. Пусть a E R- Проверим, что для n E N и х > 0
(ia)(") = a(a - l)(a - 2)... (a - n + l)x<*-n.
Г Имеем для х > 0 : (xa)' = ai", (xa)" = (ai"-1)' = a(a - I)!01-2,
(xa)'" = (a(e - l)xa-2)' = a(a - l)(a - 2)x°-3, и т. д. J
Заметим, что для а Е N и п > a (xa)(n) =0, х Е R.
4' Пусть а Е R. Для п £ iVw i> -1 имеем
(A + x)a)W = а{а - 1)(а - 2)... {а - п + 1)A + х)а~п.
5. Для п Е N и х > 0
1 /1 у
f Действительно, для х > 0 имеем (lnx)' = —, (lnx)" = ( — J =

4.4. Производные старших порядков 151
Упражнение 80. Найти производную п-го порядка:
a) /(х) = 2х'1, х G Я; Ь) /(х) = 2ХЪ~Х, х е Я; с) /(х) = ~, х > 0;
\]Х
d) f{x) = y/l + х, х > -1; е) /(х) = ln(l + х), х> -1;
f) f(x) - sin - cos - , x G Я; g) /(i) = arctg x, x £ R.
4.4.2 Свойства производных старших порядков
Теорема 13. Пусть функции f,g имеют на (а,6) про-
производные порядка п Е N.
Тогда справедливы равенства:
1) V*€{lf2,...,n} : (/(»-*))(*) = (/(*))(»-*) = /(»), /W := /;
2) VcG Я : (c/)W =c/(n);
3) (/Tg)H=/HTSH;
4) (/(aa!+j9))W = an/(n)(aa: + j9I {а,/3} С R.
Упражнение 81. Привести подробное доказательство теоремы 13.
Примеры. 1. Для чисел п е N и х е Я имеем (sin2 z)(n) =
Г(
2. Для пбЛГих^-1 имеем
/ 1_г\(п)
итЕ (-М) : (in ) = (ln(l-i)-ln(lTi))(n) =
4. Для n £ N и x £ ( — 1,1) имеем
Упражнение 82. Найти производную порядка п :
а) /(х) = sin х cos2 х, х 6 Я; Ь) /(х) = — , х € Я;
Х'' + ОХ + 6
«=)/(«) = Й- N^2= ""<*>=(,-ik,-2)' ^{1'

152 Глава 4. Производная и её приложения
Упражнение 83. Пусть f{x) = expf—j- J, i/Ои /@) = 0. Найти
\ X У
производную /(п'@) для п > 1.
Определение 2. Пусть А с R и п е N.
f£C{n){A) <=> Ухе А существует f^{x) и /<п> Е С{А).
Замечание. Если А — [а,Ь], то под производными функции / в
точках а,Ь будем понимать /+(а) и /iF) соответственно. Аналогично —
со старшими производными.
Теорема 14. длл любого п g n
С{п\А) С С{п~г\А) С. С Сг{А) С С(А).
\ Следствие определения производных и того, что имеющая производ-
производную в точке функция непрерывна в этой точке. J
Упражнение 8^. Пусть {f,g} С С'П^(Д). Доказать следующее
утверждение g(f) G C{n)(R).
Упражнение 85. Функция / £ С^п\(а,Ь)) имеет обратную д, при-
причем f'(x) ф 0, х G (а,Ь). Доказать, что д G C(n)((c,d)), где (c,d) :=
{f(x) \ х е (а,Ъ)}.
Определение 3. С{оо)(А) := f] С
п=1
Упражнение 86. Проверить, что функции sin, cos ,arctg, ех, x £ R
принадлежат классу C^°°'{R).
Упражнение 87. Пусть f{x) = expf—j, x > 0 и f{x) = 0 при
х < 0. Доказать, что f^{0) = 0, п > 1 и что / £
Упражнение 88. Для функции g е С(оо)(Я) функция / G ^((а.Ь))
удовлетворяет соотношению f'(x) = 5(/(^)). х £ (а.Ь). Доказать, что
Теорема 15. (Формула Лейбница). Длл числа п е N
пусть {f,g} С С^{{а,Ь)). Тогда (fg) G C^n\{a,b)) и на (а,Ъ)
справедливо равенство
(fg){n) = E c*/(fcVn-fc)- A)
fc=0
[ Воспользуемся методом математической индукции. При п = 1 име-
имеем {fgI = С?/(°MA) + ClfWgV-V = fg' + fg, что верно согласно
теореме 3.

4.4. Производные старших порядков 153
Предположим, что формула A) верна для индекса п. Тогда
fc=o
fc=0
fc=i
)
fc=i
+
fc=0
поскольку согласно определению С° = C°+1 = 1 и
n(n- l)...(n-fc + 2) / n-fe + 1
^ 1 I
2) _ fc
_ _
Упражнение 89. Найти: a) (z^1)^), x G Д; b) {x3smx)(-n\ x e R;
c) (ine*)(n), хеД; d) {xn lnx)(n), x > 0.
Упражнение 90. Доказать, что (e1 sinx)(n) = 2n/2ex sin (x + n— J ,
x G R, n > 1.
4.4.3 Дифференциалы старших порядков
Предположим, что для функции / : (a, b) -» R существует /' на (а, 6).
Рассмотрим первый дифференциал df(x, /ц) = f'(x)hi, x G (a, b), hi €
R функции /, как функцию от х, считая hi фиксированным. Первый
дифференциал, если он существует, этой функции, то есть
d(df(x)) = d(df(x,hi)) = df'(x,hi)hi - f"(x)hih2, hj G R, j - 1,2,
называется вторым дифференциалом функции / в точке х и обо-
обозначается символом d?f(x, /ii,/i2). Дифференциал порядка п есть
дифференциал первого порядка от dn~1 f(x, hi,..., 7in_i). Имеет место
формула
dnf{x, hu..., hn) = /(п)(х)/ц ... hn, hj G R, 1 < j < n, n > 1.
Иногда дифференциалом порядка п называется также функция

154 Глава 4. Производная и её приложения
Упражнение 91. Вычислить дифференциал d?F, где F — f{g) для
функций {/,<?} С С2(Я).
Упражнение 92. Для функции у = f(x), х G А, заданной парамет-
параметрически х = x(t),
и x'(t) ф 0, t G Т.
рически х = x(t), у = y(t), t G Т, вычислить —— , если {х,у} С С (Т)
4.4.4 Историческая справка
Основы дифференциального исчисления были разработаны в основном
в течение семнадцатого столетия. Это было время создания удобных
алгоритмических процедур и общих методов эффективного решения
задач механики, физики и собственно математических, таких как задачи
о построении касательных, нахождения максимумов и минимумов и т. п.
Ферма Пьер A601 — 1665) — известный французский математик.
Юрист по профессии, он изучил математику и занимался ею в свобод-
свободное время. Ферма — один из творцов аналитической геометрии, автор
выдающихся работ по теории чисел. В частности им была сформулиро-
сформулирована знаменитая последняя теорема Ферма, попытки доказательства ко-
которой способствовали развитию многих разделов математики. П. Фер-
Ферма предложил метод определения наибольших и наименьших значений
функций, а также метод нахождения касательных до введения понятия
производной, к которому подошёл весьма близко. Получил существен-
существенные результаты в алгебре, теории вероятностей, оптике и др.
Ролль Мишель A652 — 1719) — французский математик, теоре-
теорему Ролля он доказал для многочленов, как и свои результаты Ферма,
чисто алгебраическими методами,
Лагранж Жозеф Луи A736 — 1813) — выдающийся фран-
французский математик, автор основополагающих работ по математическо-
математическому анализу, теории дифференциальных уравнений, вариационному ис-
исчислению, теоретической механике, алгебре и теории чисел. Лагранж
участвовал в работе комиссии по разработке метрической системы мер,
которой ныне пользуется весь мир. Он был прекрасным преподавате-
преподавателем, членом нескольких академий наук.
В разработке методов дифференциального и интегрального исчис-
исчисления принимали участие почти все выдающиеся математики — пред-
предшественники И. Ньютона и Г. В. Лейбница, которые по праву считаются
теперь творцами дифференциального и интегрального исчисления.
; Лейбниц Готпфрид Вильгельм A646 — 1716) — великий не-
I, Мецкий математик и философ. К основным понятиям дифференциаль-
дифференциального исчисления Лейбниц пришёл в связи с задачей отыскания касатель-
касательной к кривой. Опубликованная в 1684 г. его краткая работа содержала

4.5. Приложения производной 155
интуитивную формулировку понятия производной с помощью бесконеч-
бесконечно малых, правила дифференцирования функций, применение произ-
производных к отысканию наибольших и наименьших значений функций и к
исследованию выпуклости функций. Формулу Лейбница он доказал в
1685 г. Понятие интеграла было им введено в 1686 г. Лейбниц получил
много других основополагающих результатов в математическом анали-
анализе, его логические идеи стали исходным пунктом развития математиче-
математической логики. Лейбниц сконструировал одну из первых счётных машин.
Ему принадлежит также значительная часть современной математиче-
математической символики, оказавшейся очень удобной (в том числе обозначения
производной и интеграла, термины "функция", "координата"и др.). Су-
Существенный вклад в распространение и развитие революционных мате-
математических идей Лейбница внесли братья Бернулли и Лопиталь.
■ Ньютон Исаак A643 — 1727) — великий английский физик и
математик. Ньютон в связи с исследованием фундаментальных задач
механики и физики разработал основы дифференциального и интеграль-
интегрального исчисления, привёл важные примеры решения дифференциальных
уравнений. Для Ньютона производная — это фактически скорость. Диф-
Дифференциальному исчислению он посвятил только три работы, опублико-
опубликованные в 1704, 1707 и 1736 гг., позже публикаций Лейбница.
Современная формулировка понятия производной появилась у Б.
Больцано и О. Л. Коши, хотя связь между понятиями производной и
непрерывностью ещё не была установлена в работах Коши.
4.5 Приложения производной
4.5.1 Формула Тейлора
1. Формула Тейлора для многочлена.
Пусть п £ N и числа {ao,ai,a2,... ,а„} С R. Для произвольной точки
х0 Е R многочлен Р(х) — а0 + а\х + а2х2 + ... + апхп, х £ R можно
представить в виде
Р(х) = Ь0 + Ьг(х - х0) + Ъ2{х - х0J + ... + Ъп{х - хо)п, х £ R A)
с некоторыми числами {£>о, bi, • • •, &п} С R. Эти числа можно определить
следующим образом. Положим в равенстве A) х = хо, получим £>о =
Р(хо). Затем найдём производную от обеих частей A)
Р'(х) = Ъг + 2Ъ2{х -хо) + ... + пЪп{х - ео)"-1, х G R. B)
Положив теперь х = хо в B), получим равенство £>i = Р'(хо). Найдём
теперь производную от обеих частей B)
Р"{х) = 2Ь2 + ... + п{п - 1)Ьп{х - хо)п~2, x£R. C)

156
Глава 4. Производная и её приложения
Р"(Хп)
Положив в C) х = хо, приходим к равенству Ьг = —г;—- • Продолжая
г;
аналогично, получим Ьт =
т\
, т > 0.
Таким образом, для каждого х £ R справедливо представление
Р(х) = D)
Формула D) выявляет следующий интересный факт: многочлен Р
определяется на оси полностью заданием его значения и значений его
производных в одной точке xq. При этом точка Хо может быть взята
любой. Для функций, отличных от многочлена, формула D) не верна.
Однако, если ограничиться значениями х, близкими к Xq, to для доста-
достаточно широкого класса функций правая часть D) оказывается близкой к
значениям функции.
2. Формула Тейлора с остаточным членом в форме Пеано.
Теорема 16. Пусть функция / : (а,6) -> R и точка
х0 £ (а,Ь) для числа n G N удовлетворяют условиям: 1)
Vie (а,Ъ) существует /("""^(х); 2) существует /(п'(х0).
Тогда
= Е
fc=0
о((х -
E)
Слагаемое о((х-х0)п) называется остаточным членом
в форме Пеано.
f Напомним, что 0! := 1. Рассмотрим следующую функцию г„(х) :=
Г f№ ~ Е —и\—(х ~ хо)к> х £ (а>^)- Согласно условиям 1) и 2)
к=0
Существуют Гп {х), х £ (а,Ь) и Гп(х0). Кроме того, легко видеть,
jm> гп(х0) = г^(х0) = г'£(х0) = ... = ri.n)(x0) = 0. Пусть х > х0,
(Применяя последовательно теорему Лагранжа, а затем определение
Производной, при х —¥ хо получим
(х - хо)п
~ гп(х0)
(х - хо)п
<(ci)(x-x0)
(а; - xo)n
(x - xoO1-1
C(c3)(c2-xo)
(x-xo)n-2
(n) = 0,
<(C2)(C1-XO)
(x-xo)n-2
X - X0

4.5. Приложения производной 157
где х0 < cn_! < сп_2 < ■ • • < с2 < С! < х. При этом, с„_1 -4 х0, х -+ х0.
Таким образом, гп(а;) = о((х — Хо)п)> х —> Xq. J
Замечание. Формула E) является обобщением утверждения п.
4.1.3, 2, которое означает, что функцию, имеющую производную в
точке xq, можно приблизить такой линейной функцией gi(x) := f{xo) +
{'{xq){x — Xq), x G R в окрестности точки xq с точностью до о(х — хо).
По теореме 16 функцию, имеющую производную порядка п в точке хо,
можно приблизить многочленом gn(x) := У) — (х — хо)к, х £ R
в окрестности точки х0 с точностью до о((х — Хо)™)-
3. Формула Тейлора с остаточным членом в форме Лагранжа.
Теорема 17. Пусть пе (ЛГи{0}) и f : {а,Ь)-> Я Предпо-
Предположим, что длл каждого х б (а, 6) существует /(п1)
Тогда
V{*,х0} С(а,Ъ)Зве @,1) : f(x) = £ ^-^ (x - xo)fc + rn(x), F)
fc=O *•
гп(х) .-
Слагаемое гп(х) в F) мазъбваетпсл оетаточмыл* члеиоле
в форме Лагранжа.
[ Если х = х0, то формула F) справедлива. Пусть х ф х0- Введём
функцию g(z) := f(x) - ^ Щ^- (х - z)k - j^-^ (x - z)n+' для
значений z из отрезка с концами х и х0. Здесь L — пока произвольное
число. Согласно условиям теоремы 17 функция g непрерывна и имеет
производную g'(z) = (д — г)п Н—r(x —z)n в точках отрезка
с концами х и хо. При этом д(х) = 0. Возьмём теперь число L таким,
чтобы выполнялось равенство ^(^о) = 0. К функции д на отрезке с
концами х и хо применима теорема Ролля, по которой 39 6 @,1) :
д'(х0 + в(х - хо)) = 0, или _/()(*о + *(**о)) _ ^^ _ ,)П +
+ — {х - хо)п{1 - в)п = 0. Таким образом, L = f{n+1){x0 + в{х - х0)).
Формула F) теперь совпадает с равенством ^(^о) = 0. J
Замечания. 1. Формула F) является обобщением теоремы Ла-
Лагранжа, которая получается при п — 0.
2. Обе формулы Тейлора E) и F) в случае х0 = 0 называются также
формулами Маклорена.

158 Глава 4. Производная и её приложения
4. Примеры.
В следующих примерах xq = 0.
1. Vn€ JVVxG R36e @,1) :
„n
2! n! (n + 1)!
f Это формула Тейлора с остаточным членом в форме Лагранжа для
функции f(x) = ех, х G R, для которой f^(x) = ех,х 6 R; в частности
/<п>@) = 1, п € ЛГ. J
Замечание, формула примера 1 позволяет получать приближён-
X2 ХП
ные значения е , вычисляя значения многочлена 1 + х -\ +...Н .
2! п!
евх
Ошибка при этом равна — xn+1. Например, для х G [0,3] и п = 12
(п + 1)!
имеем следующую оценку
е
9х
г.п+1
(п + 1)!
e3313 1
е3
< -ггг- <
13! 1000
2. Vfc £ (ЛГи{0>) VxGii Звб@,1):
sin а: =
х
2fc+l
-X__+Z \ ( \\k i ч 2 /
3! 5! '" v ; BJfc + l)! Bifc + 3)!
, s2 x4 fc a:2fc cos{ex + {к + 1)тг) 2fc+2
2fc+3
3. Vn£ ЛГ Vi>-1 Эв G @,1) :
Справедливо утверждение: V п G N V х > -1 3 в G @,1) :
A + х)а = 1 + С\х + С\х2 + ... + С%хп + С£+1A + вх)а-пхп+1.
Упражнение 93. Если при условиях теоремы 16 для {ao.ai,... ,an}
С R справедливо соотношение
/(*) = Е afc(x - хо)к + о((х - хо)п), х -4 х0, G)
fc=O
то пк = —п— ' ^ — ^ — П- Д°казать это утверждение.
Указание. Рассмотреть разность между E) и G).

4.5. Приложения производной 159
Упражнение 94- Применить теорему 17 или воспользоваться пре-
предыдущим упражнением, чтобы получить формулу Тейлора следующих
функций в точке xq = 0 : a) sin2; b) f(x) — iln(l + x), x > — 1;
c)f(x) = xsinx, d)f(x) = ex\xeR; e) /(*) = ^ ,x ф 0, /@) = 1;
ch«:=
Упражнение 95. Пусть (а, 6) = R, x0 = 0, / — чётная функция,
удовлетворяющая условиям теоремы 16. Доказать, что основная часть
формулы Тейлора (то есть правая часть F) без остаточного члена) со-
содержит только чётные степени х. Какова особенность формулы Тейлора
для нечётной функции?
Упражнение 96. Пусть f(x) - ехрГ—^\х ф 0, /@) = 0. Дока-
Доказать, что / 6 С^°°^(Д) и записать формулу Тейлора для функции / в
точке х0 = 0.
4.5.2 Правило Л опита ля
Правила вычисления пределов функции в точке, приведенные в гл. 3,
применимы при определённых ограничениях. Однако, в ряде важных
случаев эти ограничения не выполняются. Типичными являются следую-
следующие ситуации определения предела lim h(x), где:
х->х0
f(x\
1) hlx) = -~-х , когда fix) -¥ 0, д(х) -» 0 при х -» х0;
д(х)
2) h(x) = —7—f , когда f(x) -¥ +00, д(х) -¥ +оо при х -» х0;
9{х)
3) Цх) = }{х) - д(х), когда }{х) -* +оо, д(х) -> +оо при х -^ х0;
4) h(x) = /(iK(x), когда f(x) -^ 0+, g(i) -> 0+ при i -^ х0;
5) h(i) = /(iK^x\ когда f(x) -> 1, g(i) -» +00 при i -> х0;
6) /i(i) = /AMB:). когда f(x) -¥ 0, ^l1) -* +°° ПРИ ^ ~> Не-
Неэффективным средством вычисления этих и подобных им пределов
является производная, впервые использование производной для вычис-
вычисления пределов было предложено Иоганном Бернулли и Лопиталем.
Теорема 18. Пусть Ь £ R и функции f,g : (а,Ъ) -> R
удовлетворяют условиям: 1) lim fix) = 0, lim glx) = 0;
x-vb,x<b х-»Ь,х<Ь
2; Vi 6 (a,b) существуют f'{x), g'{x); 3jVit (a,b) : ^(i) ф 0;
f'(i)
^^ сушествует lim ,. . = L £ R.
1->ь,х<ь g'(x)
11 — 4-1168

160
Глава 4. Производная и её приложения
Тогда существует lim
д(х)
= L.
\ Продолжим функции / и д на полуинтервал (а,Ь), положив }{Ь) =
д(Ь) = 0. С учётом условия 1) функции f и д будут непрерывными в
точке Ь. Для любого х 6 (а>Ь) значение 5B:) ^ 0, так как равенство
д(х) = 0 с помощью теоремы Ролля приводит к существованию точки
с € (я,Ь), для которой д'(с) = 0, что невозможно по условию 3).
Пусть теперь произвольное е > 0 задано. Согласно условию 4) име-
ем 38 > 0 Vi б (Ь- 6,Ь) :
9'(х)
- L
< е. Применим теперь к
функциям / и д на отрезке [х, Ь], х £ (Ь — 8,Ь) теорему Коши, получим
/(Ь) -
-L
f'(c)
g'(c)
-L
, ce(x,b)c(b-6,b).\
Замечание. Утверждение, аналогичное теореме 18, справедливо
и для предела справа в точке а £ R.
Упраснснение 97. Доказать: a) lim = 1; Ь) lim —Ц = 1;
х->0 X х->0 Sini
i-e e
-arctgij -I
d) lim -^ i- = — , a € -R;
»-+i In а; 7Г
1 - cosQ i a
e) lim —r-5 = — , a 6 it;
x->o sin21 2
g) lim
x*o
/ sin i
1ТП
x-*o у x
1/x
f) lim
x->0+
Указание. Использовать тождество f9 = effln^ и непрерывность
показательной функции.
Упраснснение 98. Вычислить пределы:
. ,. х — sini
a) lim
х—>0 Xй
, . ,. sini' - sin х
b) lim —rz , n 6 N.
x—>0 X ^
Упраснснение 99. Пусть Ь £ il и функции /, ^ : (а,Ь)-»й удовле-
удовлетворяют условиям: 1) Vх 6 (<J,b) существуют f^n\x) и <7^(:r), n £ iV;
2)Vxe(a,b):5(")(x)^0; 3) Vj € {0,1,2,... ,n-l} : Urn /w(x) = 0,
lim
x—>b—
= 0; 4) существует lim
х->Ь-
= L £ R. Доказать, что

4.5. Приложения производной 161
х->Ь- д(х) х->Ь- д'(х) х->Ь- gin-1)(x)
Упражнение 100. Вычислить пределы: a) lim — ;
ех-е*'тх arctg(x2 - 1) arcsin(x + 2)
b) lim : ; с) lim —— - ; d) lim r-^——- .
x->0 I -Sin I x_tl X-l s-v-2 X2+2x
Теорема 19. Утверждение теоремы 18 остается
верным, и для Ь = +оо.
[ Пусть Ь = +оо и функции fug удовлетворяют условиям 1) — 4)
теоремы 18. Можно считать, что а > 0. Положим z — l/x, x > а.
Заметим, что z £ @, I/a); z —» 0+ •<==>■ х -> +оо. Определим функции
F и G следующим образом F(z) := f(l/z), G(z) := g{l/z); z G @, I/a).
При этом F'(z) = f'(l/z)(-l/z2), G'(z) = 5'(l/z)(-l/z2); z <E @, I/a) и,
кроме того, в силу условий 1) и 4) имеем F(z) -> 0, G(z) -> 0, ^ =
= —> £f, z -¥ 0 + . Поэтому к функциям F и G на интервале
.F(z)
@, I/a) применима теорема 18, согласно которой -> L, z -> 0+,
G(z)
что равносильно соотношению . . —> L, х -> +оо. J
fll1)
Упражнение 101. Найти пределы: а) lim (ам— -arctgi));
,. .. / з/т . 1 \Л " ч ,. Ь(д +1) - 1п(х -1)
b) lim [ х3[ arctg х ; с) lim , / .
' Х-++00 \ \2 6 X I) ' «-И-оо у/х* + \ - у/х2 - 1
Указание. Для а) воспользоваться равенством хук 12 — arctg x) =
7г/2 - arctg х
'—гГ*—>х>
Упражнение 102. Доказать, что утверждения теорем 18 и 19 верны
и для L = +оо.
Теорема 20. Пусть функции f,g : (a,b) -» R удовле-
удовлетворяют условиям,: 1) д(х) -» +оо, х -> Ь—\ 2) Vx € (<х, Ь)
}'{х) и д'(х); 3) Vx € (а,Ь) : g'l1) ^ 0; 4-^ сугце-
предел lim —r-f =LgH.
*->*- fl'(a;)
/(i)
Тогда cyiuecmevem предел lim —7-r = L.
х>ь 5A)
[" Пусть произвольное е > 0 задано. По условию 4) и определению
предела функции в точке для числа е/2 имеем 3ci € (а,Ь) Vx 6 (с\,Ь) :

162 Глава 4. Производная н её приложения
9'(х)
-L
е е fix) e , .
<> L <±У Ь + A)
2 2 g'(x) " ' 2'
Аналогично из условия 1) следует 3 с2 € (а, Ь) V х G (с2| Ь) : 5A) > О,
д(х) — д{с\) > 0. Пусть х > max(ci,C2). Применим к функциям / и
д на отрезке [ci,i] теорему Коши. Получим следующее утверждение
3 0 G (ci.i) : -7-с Нт = -^Т> откуда с учётом неравенства A)
g(x)-g(Ci) д'(В)
имеем
Т £ г- Л») /(Cl) , £ ,^
2 fl(l)-fl(ci) 2
После умножения B) на д(х) - g{ci) > 0 и деления на д(х) > 0
f(x)
приходим к неравенству и(х) < < v(x), в котором и{х) :=
По условию 1) и(х) —» (L j, v(x) —> f Z, 4— ); 1—> b—,
поэтому согласно теореме 4 гл. 3 3 с3 € {a,b) Vi € (сз,Ь) : и(х) >
> L — е, г»(х) < L + е. Положим теперь с :— тах(с1,С2,сз). Тогда
Vi € (с,Ь) : L - е < u(i) < —-г < v(x) < L + е, откуда следует, что
д(х)
Vie (с,Ь) :
-L
J
. 2. Утверждение теоремы 20 остаётся верным для L =
+оо и для правостороннего предела в точке а.
Упражнение 103. С помощью теоремы 20 доказать, что для е > 0:
1 X X2
a) lim — = 0; Ь) lim — = 0; с) lim — = 0;
х
lim = 0; Ь) lim 0; с) lim
х-»+оо 2х 1->+оо 2х в-Ц-оо 2
х In х
d) lim —у= =0; е) lim =0; f) lim (i£lni) = 0;
у ; ) ; )
g) lim xx = 1; h) lim (cosiI/1' = e/2; i) lim (ln(l + x))x = 1.
Упраэ*сненг*е 104- Вычислить пределы: a) lim (xsin —
в-»+оо у X
( 1 1 \X ( 1 1 \X
b) lim [ x sin - -\— ; c) lim [ x sin —I—-I ;
x-H-00 ^ XX) n+00 \ XX2)
/
^ ) \
.. .. A + sI/x-e / . и
d) lim ; e) lim sin ——- + cos
X 1-++00 ^ 6l + l 3x
y
f) lim sin у= + cos1

4.5. Приложения производной 163
9) lim ^ ; ^K " ^ " , {a,/?, 7} С Я
z->0 \ 3 J
Упражнение 105. Доказать, что для каждого п 6 N существу-
существует число а„ £ @,1) такое, что ( 1 -\— ) = е, и найти предел
V п)
lim (п(ап- -)).
Упражнение 106. Для функций /,5 : @,1) -» Я существуют /',5'
на @,1), д' ф 0 на @,1) и /(i) -> 0, 5A) —> 0, х -> 0. Доказать, что
<n5.
{х) "->о° 5Ч1)
4.5.3 Выпуклые функции
1. Определения и примеры
Пусть -со < а <Ь < +оо и / : (а, Ь) -¥ R.
Определение 1. Функция f называетсл выпуклой
вниз на (а,Ь), если V{11,12} С (а,Ь) Va б [0,1] :
/(стая + A - o)i2) < af(xi) + A - о)/(х3).
Фуптсцил / называется выпуклой вверх на (а,Ь), если
функция —/ выпукла вниз на (а,Ь).
Определение 2. Функция } называется строго вы-
выпуклой вниз на (а,Ь), если V{ii,i2} С (a,b),xi ф х2 Va б @,1) :
/ называется строго выпуклой вверх на
(а, Ь), если функция —f строго выпукла вниз на (а,Ъ).
Замечание. Геометрическая интерпретация. Пусть / —
строго выпуклая вниз функция на (а,Ь). Рассмотрим произвольные числа
a < xi < Х2 < Ь, a € @,1). Тогда число х :~ аху + A - а)х2 удовлетво-
удовлетворяет неравенствам ах-^ +{\-а)х\ < aii + (l-a)i2 < ai2 + (l-a)a;2, то
есть х\ < i < i2. Заметим теперь, что у = a/(ii) + A — a)/(i2), 1 =
aix + A — a)i2; a 6 Д суть параметрические уравнения прямой, ко-
которая проходит через точки плоскости (ii,/(ii)) и (a^)/!2^)), a зна"
чениям a G [0,1] соответствует хорда, соединяющая эти точки. Для
точки а 6 @,1) точка (x,f(x)) лежит на графике функции /, а точка
(x,af(x1) + A — a)f(x2)) лежит на хорде. Согласно предположению
о строгой выпуклости f(x) < af(xi) + A - a)f(x2)- Таким образом,
для любой хорды, соединяющей точки графика функции (xi,f(x{)) и

164
Глава 4. Производная и её приложени?
с Х1 < Х2, точки графика функции / с абсциссами х £ (ii,i2
лежат под хордой, см. рис. 7.
У = fix
x = axi + A — a)x2
f{x) < a/(xi) + A - a)/(x2)
a)
(*./(*))
(X2,/(X2)
Xl
+ A - a)x2 x2
b)
Рис. 7.
На рис. 7, а) представлен график строго выпуклой вниз функции, b

4.5. Приложения производной 165
представлен график строго выпуклой вверх функции.
Примеры. 1. Пусть {L, М} С R. Функция f(x) = Lx + М, х £ R
выпукла вниз на Д и выпукла вверх на R, так как справедливы равенства
V{x1,x2}cRVa £ [0,1] : f(ax1 + (l-a)x2) = L{ax1 + (l-a)x2) + M =
= a(Lxi + М) + A - a){Lx2 + М) = a/(xi) + A - a)f{x2).
2. Функция f(x) = \x\, x £ R выпукла вниз на R, так как имеем
V{ibi2}cflVa6 [0,1] : / (aii + A - а)х2) = |aii + A - а)х2\ <
< a\Xl\ + A - a)|z2| = af(xy) + A - a)f{x2).
Замечание. Следует проверить, что функция примера 2 не явля-
является строго выпуклой на R. Кроме того, f(x) = тах(—х,х), х£Й, это
наблюдение приводит к интересным обобщениям. Например, функция
f(x) = maxf-i-2, -x,x — 2j, x 6 il выпукла вниз на R. Если функции
f,g выпуклы вниз на (а,Ь), то функция h(x) := max(f(x),g(x)), x 6 R
выпукла вниз на {а,Ь). Если функции /,g выпуклы вверх на (а,Ь), то
функция к(х) := roin(f(x),g(x)), х £ R выпукла вверх на (а,Ь). Напри-
Например, функция к(х) := minf-i - 2, -х,х - 2J выпукла вверх на R.
3. Функция f(x) = х2, х £ R строго выпукла вниз на R, так как
согласно элементарному неравенству 2iii2 < х\ + х2, %\ Ф Х2> имеем
следующее: V{ii,i2} С R,хх ф х2 Va 6 @,1) : }{ахг + A - а)х2) =
+ A - а)х2J = а2х\ + 2аA - a)iii2 + A - olJx\ < а2х\ +
а){х\ + х2) + A- аJх2 = ах2 + A - а)х\ = а/(ц) + A - a)f(x2).
4. Функция /(i) = - , х > 0 строго выпукла вниз на @, +оо,) так
как V{ii,i2} С @,+oo),ii ф x2 Va £ @,1) : f{axx + A - a)i2) =
= (ац + A - a)x2)-y < ax + A - a)^1 = a/(n) + A - a)f{x2)
в силу того, что х\х2 < ai2(aii + A — a)i2) + A — a)ii(aii + A —
a)i2), то есть x\x2 < a2iii2 + a(l - a)x\ + a(l - a)x\ + A - aJiii2.
Последнее неравенство равносильно неравенству Коши 2a(l — a)
2. Условия выпуклости
Теорема 21. Футсцил / : (a,b) -* R выпукла (строго
выпукла) вниз на (а,Ь) тогда и только тогда, когда для
любой точки х0 £ (а,Ь) функция наклона относительно
точки х0 д(х) := —— ^-^- *' х £ ((а,Ь) \ {х0}) монотонно не
х - х0
убывает (строго возрастает) на (а,Ь)\{х0}.
[" Рассмотрим случай строго выпуклой вниз функции. Пусть произ-
произвольная точка Xq фиксирована и точки х^,х2 таковы, что a < Xq <

166 Глава 4. Производная и её приложения
, _ Э?2 — Х\ Х\ — Хп
< ху < х2 < о. Положим a := , 1 — a = , при этом
\ Х2 — Xq X2 — Xn
a 6 @,1) и 2i = aio + A \ а)х2. Следующие неравенства равно-
равносильны: f{ax0 + A - а)х2) < a/(i0) + A - a)f(x2) <=> /(ii) <
<^-Z^Lf{x0) + ^—^-f{x2) <=> {x2-x0)f{x1) < {x2 -xq + xo-
X2 — Xq X2 — Xq
-zi)/(io) + {xi - xo)f{x2) <=^ {x2 - xo){f{x1) - f{x0)) < {xx -
—xo){f(x2) - f(xo)) <==> g(xi) < g(x2). Для других случаев располо-
расположения точек х\ и х2 рассуждения аналогичны. J
Упражнение 107. Дать геометрическую интерпретацию утвержде-
утверждения теоремы 21.
Упражнение 108. Сформулировать и доказать аналог теоремы 21
для выпуклой вверх функции.
Упражнение 109. Доказать, что функция f(x) = х3, х > 0 строго
выпукла вниз на [0, +оо).
Теорема 22. Пусть для функции f : {a,b) -» R для
каж.дого х £ (а,Ь) существует производная f'{x). Функция
f выпукла (строго выпукла) вниз на (а, Ь) тогда и только
тогда, когда функция f монотонно не убывает (строго
возрастает) на (а,Ь).
[" Рассмотрим только случай выпуклой вниз функции.
Необходимость. Пусть / выпукла вниз на (а,Ь) и a < х\ < х2 < Ь.
По теореме 21 для точек a<u<ii<i2<^<b имеем
=f(x1)-f(x2) <f{vt
U - Xi ~ Х2 - Xi Х\—Х2 ~ V — Х2
Отсюда при и —» Xi~ и v —> х2+ имеем f'_{x{) < —-— <
< ДA3), поэтому f(Xl) = f'_{Xl) < }'+{х2) = f'(x2).
Достаточность. Пусть /' монотонно не убывает на {ч,Ь). Для
произвольной точки хо € (а, Ь) рассмотрим функцию наклона д{х) =
—^— —- , х 6 ((а, Ъ) \ {х0}), для которой с помощью теоремы Ла-
х — xq
гранжа получим д'(х) - v ; у1 Ц^ ——— = L-i-L — ,
v (x-xQJ x-Xq
где с лежит между числами х и xq. Поэтому д'(х) > 0 для х 6 ((<J,b) \
{in})- Следовательно, функция 5 не убывает на каждом из интерва-
интервалов (а,х0) и (хо,Ь). Кроме того, д{х0-) = }'_{х0) = f'(x0) = f'+(x0) =
— д(хо+)- Таким образом, функция д не убывает на множестве (a,b) \
{х0} и по теореме 21 функция / выпукла вниз на (a,b). J

4.5. Приложения производной 167^
Упражнение 110. Доказать теорему 22 для строго выпуклой функ-
функции.
Указание. При доказательстве необходимости дополнительно рас-
рассмотреть точку w £ {xltx2).
Теорема 23. Пусть для функции f : (a,b) —> R для
каждого х £ (а,Ь) существует производная f"{x). Функция
f выпукла вниз на (а,Ь) тогда и только тогда, когда Vx £
(a,b) : f"(x) > 0. Функция f строго выпукла вниз на (а, Ь)
тогда и только тогда, когда 1) \/х £ (а,Ь) : f"{x) > 0;
и 2) не существует интервала (а,/3) С (а,Ь) такого, что
Vx'e(o,j9): f"{x)=0.
\ Следствие теоремы 22 и критерия монотонности функции. J
Упражнение 111. Сформулировать и доказать аналог теоремы 23
для выпуклой вверх функции.
Упражнение 112. Определить интервалы выпуклости функций:
а) ех, х £ R; Ъ) \пх, х > 0; с) sin; d) cos; e) tg; f) ctg;
g) arctg; h) arcsin; i) }{x) = xa, x > 0, a £ Я;
j) f(x) = x2 + ax + P, x £ R, {a,/3} С R.
Упражнение 113. Функция / : й-»й- выпукла и ограничена на
R. Доказать, что / постоянна на jR.
Упражнение 114- Функция / выпукла вниз на R. Доказать, что
имеет место одна из следующих возможностей: 1) / возрастает на оси; у
2) / убывает на оси; 3) существует точка а £ R такая, что / убывает на
( —оо,а] и возрастает на [а,+оо).
Упражнение 115. Пусть г > 1 и {а, 6} С R. Доказать неравенство
ч |о + ЬГ<2'-1(|оГ + |Ь|Г).
( JVff.
3. HepafeeHcrio Иенсена '
Теорема 24. Пусть f — выпуклая вниз на (а,Ь) функ-
функция. Тогда Vn > 2 V{ii,i2, • ■ • .г„} С {а,Ъ) \/{ау,а2, ■ ■. ,ап} С
[0,1], £ ofc = 1 : / ( Е akxk) < £ akf(xk). A)
fc=i \fc=i / fc=i
Для строго выпуклой вниз функции неравенство A)
является строгим., если числа xi,x2,. ■■ ,хп не все одина-
одинаковы, а числа ai,a2,...,an положительны.

168 Глава 4. Производная и её приложения
\ Для п = 2 неравенство A) совпадает с неравенством из определения
выпуклой функции.
Предположим, что неравенство A) справедливо для любого набора
из п точек. Рассмотрим для п > 3 произвольные наборы
п+1
{x1,x2,...lxn,xn+l} С {a,b); {ai,a2,... ,an,an+i} С [0,1], Е ak =
fc=i
1. Среди чисел ai, аг,..., an+i хотя бы одно отлично от 1. Пусть
1. Согласно предположению
) = / an+1xn+i + A - а„+1) X)
*=1 У V fc=l
< an+1f(xn+1) + A - а„+1)/ ( £ "fc
< an+i/(in+i) + A - а„+1) Е -, f(xk) = E OLk}{xk).
k—\ 1 ~ Q!n+1 fc=l
Таким образом, согласно принципу математической индукции теоре-
теорема 24 доказана. J
Замечание. Неравенство Иенсена имеет следующий физиче-
физический смысл. Разместим в точках (ij, /(i1)),(i2, f{x2)), ■ ■ ■ > (in, f(xn))
графика функции / соответственно массы а\}а2,- ■ ■ ,ап. Координаты
п п
центра масс этой системы точек равны Е ctfc^fc, E akf{xk)- Для
fc=l к—1
выпуклой вниз функции центр масс лежит над кривой и потому его ор-
п / п \
дината Е akf{xk) больше ординаты / I Е акхк I точки на графике
fc=i \fc=i У
п
с абсциссой Е акхк- Таким образом, имеем неравенство A).
fc=i
Примеры. 1. Пусть f(x) = |i|, i 6 Я выпукла вниз на Д, поэтому
п
: Е I1*!- Это неравенство следует из
" fc=i
A) при значениях ах = а2 = ... = ап = — .
п
2. Функция /(i) = lni, i > 0 строго выпукла вверх на @,+оо),
поскольку /"(а;) = j < 0, i > 0. Поэтому из неравенства A) для
функции —/ и чисел
(О.+оо) :
неравенство есть неравенство Коши между средними значениями.
3. Докажем, что Vn > 2 V {xi,x2>... ,хп}-С @,+оо)
= a2 = ...=Q!T, = — имеем V{ii,i2)- • • ,a;n} С
п

4.5. Приложения производной /69
V{a1)a3l...,aTl}c[0,l], E a* = 1 = Ё afcifc > ft ХТ ■
f В решении примера 2 использовать произвольные ai,.. • , an. J
Упражнение 116. Пусть р>1, j > 1 и —Ь- = 1. Доказать, что
Р 9
хр у9
V {х, у} С @, +оо) : ху < 1 .
р q
Указание. Использовать результат примера 3 для следующих чи-
чисел п = 2. ari = - , а2 = - и Xi = хр хо = V9.
Р 9
Упражнение 117. Функции /ид выпуклы вниз на {а,Ъ). Доказать,
что: а) для любых положительных чисел Cj, сг функция Ci/ + C2<? выпукла
вниз на {а,Ь); Ь) функция h := тах(/,д) выпукла вниз на {а,Ь).
Упражнение 118. Доказать , что для любых {j>x > Vi > ■ ■ ■, Рп} С
/ п \2 п п
[О, +оо) и {хь х2,..., х„} С Я : J2 pkXk ) < Е Р* Е Р*Х1-
\k=l J k=l fc=l
Упражнение 119*. Пусть n € N и р > 1 фиксированы. Для х =
/ п \х/р
(хь...,хп) £ Я" положим ||х||р := Yl \xk\p I ■ Доказать нера-
неравенство Минковского V {х, у} с Я" : ||х + у\\р < \\х\\р + \
Упражнение 120*. Пусть п 6 JV и р > 1, 9>1, - Н— =1
Р 9
фиксированы. Доказать, что V{x, у*\ с Я" :
^керавекстпво Гёльдера).
fc=i
<
4.5.4 Условия локального экстремума
Пусть А с Я.
Определение 3. Точка х0 € А называется точкой ло-
локального максимума функции / : А —> Я, если
V<S>0 : 1) B(zOi*)Cj4 tt 2) Vx G В(хо,<5) /(х) < /(xo).
Точка x0 £ А называется точкой строгого локального
максимума функции f : А —> Я, если
V<S>0: 1)В(хо,<5)сЛ и 2) Vx € (В(хо,<5)\{хо}) : /(х) </(х0).
определлютсл точки локального минимума
и строгого локального минимума.

170 Глава 4. Производная и её приложения
Точки локального минимума и локального максимума
называются точками локального экстремума.
Примеры. 1. Для функции /(х) = х2, х € R точка х0 = 0 есть точка
строгого локального минимума и точка, в которой функция / принимает
наименьшее на R значение.
2. Для функции /(х) = х, х € [0,1] точки х, = 0 и х* = 1 суть
точки, в которых функция / принимает соответственно наименьшее и
наибольшее на [0,1] значения. Однако, точки 0 и 1 не являются точками
локального экстремума.
Упражнение 121. Пусть для функции / : [а,Ъ] -> R 3{х,,х*} С
[a,b] : /(z*) = inf/, fix*) — SUP/- Когда точки х» и х* — точки
Ml [а,ъ]
локального экстремума?
Упражнение 122. Пусть Е - множество всех точек локального
максимума функции / : [а,Ь] —> R. Доказать утверждение. Если 3 х* €
[а, Ь] : /(х*) = max/, то х* £ {Еи{а, Ъ}) и f(x*) = max{/(x) | x € {Ей
{а, Ь})у. Аналогичное утверждение справедливо и для точки, в которой
принимается наименьшее значение.
Упражнение 123*. Доказать, что множество всех точек, в которых
функция / : R—>R имеет строгий локальный экстремум, не более чем
счётно.
Теорема 25. Если длл функции f A -> R точка х0 € А
есть точка локального экстремума и в точке х0 суще-
существует производная /'(х0), то /'(хо) = 0.
if Пусть хо — точка локального максимума. Тогда согласно определению
13 5 > 0 : В(хо,6) С Ли VxG В{хо,8) : /(х) </(х0), при этом /(х0) =
ц— max /(х) и к функции / на интервале (хо - 6,х0 + 6) применима
s ieB(io,s)
I Теорема Ферма. Согласно теореме Ферма /'(х0) = 0. J
: Замечания. 1. Теорема 25 даёт необходимое условие для точ-
точки локального экстремума. Если в некоторой точке хо производная
,/'(хо) = 0, то точка хо не обязательно — точка локального экстре-
экстремума. Например, для функции /(х) = х3, х £ R точка х0 = 0 не есть
точка локального экстремума, хотя /'@) = 0.
{,. 2. Точки, в которых производная не существует, также могут быть
j точками локального экстремума. Так для функции /(х) = |х|, х 6 R
*fto4Ka хо = 0 есть точка строгого локального минимума, производная в
этой точке не существует.

4.5. Приложения производной 171
Определение 4- Точки, в которых производнал фун-
тции f равна О, называются критическими или стаци-
Фнарными точками функции /.
Замечание. 3. Таким образом, точки локального экстремума фун-
функции / лежат в объединении множества критических точек и множества
Точек, в которых производная не существует.
Определение 5. Функция g сохраняет знак левее
Ъючки хо, если либо 3 5 > 0 Vx £ (х0 - 5, х0) : д(х) > О
"либо 3 5 > 0 Ух £(хо-5,хо) : д(х)<0.
Определение того, что функция g сохраняет знак
правее точки хо, аналогично. \
Тборема 26. Предположим, что функция f : А —> R
удовлетворяет одному из условий:
1) @ 35 > 0 Vx G В(хо,5) существует /'(х);
(п) точка х0 — критическая, то есть /'(хо) = 0;
(Hi) /' сохраняет знак левее и правее точки х0;
2) (i) / 6 С {A) u3<5>0VzG B(xOli5) существует f'[x);
(ii) /' сохраняет знак левее и правее точки х0.
Если при переходе через точку хо производная /' меняет
знак, то хо есть точка строгого локального экстрему-
экстремума. Если ж.е при переходе через точку xq производная /'
знака не меняет, то х0 не есть точка локального экс-
экстремума.
\ Заметим, что выполнение условия 1) влечёт выполнение условия 2).
Поэтому достаточно доказать теорему при условии 2).
I. Предположим, что для некоторого 5 > 0 Vx € (хо — 5,хо) :
f'{x) > 0; Vx £ (хо,хо + 5) : f'(x) < 0, то есть предположим,
что производная /' меняет знак "+" на "—". Тогда функция / стро-
го возрастает на (хо — 5, хо] и строго убывает [хо,хо + 5). Поэтому
Vx £ (В(хо,5) \ {х0}) : /(х) < /(х0) и, следовательно, х0 есть точ-
точка строгого локального максимума.
В том случае, когда производная меняет знак "—" на "+", точка хо
есть точка строгого локального минимума.
II. Предположим, что производная /' знака при переходе через точ-
точку хо не меняет. Пусть, например, 3 5 > 0 Vx G (В(хо,5) \ {хо}) :
/'(х) > 0. Тогда функция / строго возрастает на каждом из интервалов
(хо - 5,х0) и (хо,хо + 5), и с учётом непрерывности функции / в точке
хо, строго возрастает на В(хо,<5). Поэтому хо не есть точка локального
экстремума. J
Примеры. 1. Для функции /(х) = х3 - Зх, х € R точки -1 и +1 кри-
критические, то есть нули производной /'(х) = 3(х2 - 1), х £ R. Поскольку

172 Глава 4. Производная и её приложения
/' при переходе через точку -1 меняет знак с "+" на "-", то точка
— 1 есть точка локального максимума. А поскольку при переходе через
точку 1 производная меняет знак с "—" на "+", то точка 1 локального
минимума. Других точек локального экстремума у / нет, так как суще-
существующая на R производная /' не имеет иных корней, кроме —1 и 1.
2. Для функции /(х) = х2е~х, х € R производная /'(х) = хB — х)е~х
обращается в 0 для значений 0 и 2. Поскольку /' меняет знак с "—" на
"+" при переходе через точку 0, то точка 0 есть точка строгого локаль-
локального минимума. Производная /' меняет знак "+" на "—" при переходе
через точку 2, следовательно, точка 2 есть точка строгого локального
максимума.
Упражнение 124- Найти точки локального экстремума функции: а)
/(х) = х3е~х, х G R; Ь) /(х) = х + - , х > 0; с) /(х) = хх, х > 0;
d) /(x) = |х|е-*2, х 6 R.
Упражнение 125*. Пусть /(х) = х4B + sin - V х ф 0; /@) = 0.
Ч х /
Доказать, что: а) 0 есть точка строгого локального минимума, Ь) про-
производная /' не сохраняет знака ни левее, ни правее точки 0.
т -,-, ,2/Оюст. ус-е.
I е О р е М а 2/. Пусть функция / и точка хо £ А удовле-
удовлетворяют условиям: 1) 3 5 > 0 Vх £ В{хо,5) существует
/'(х); 2) /'(х0) = 0; 3) существует /"(х0) и /"(х0) ф 0.
Тогда точка xq есть точка строгого локального мак-
максимума, если /"(х0) < 0, и точка строгого локального ми-
минимума, если /"(хо) > 0.
\ Рассмотрим для функции / и точки хо формулу Тейлора с остаточным
членом в форме Пеано для п = 2
откуда с учётом условий теоремы для х ф хо имеем /(х) — /(х0) =
о((х-х0J\ _ о((х-х0J)
;; ) Поскольку ^ /
x - x0J \, ' + -^ =£- . Поскольку -у —■ -4 0 при
\ 2! (х - xQy J [х - xQy
х -». xOl то 35 > 0 Vx 6 (В(хо,5) \ {х0}) : 0^^-~^°)--)
" 2-2!
Поскольку для любого х 6 (В{хо,5) \ {хо}) знак разности /(х) —
совпадает со знаком /"(хо), то имеем утверждение теоремы 27. J
Пример. 3. Для функции /(х) = (х- 1)е~х , х £ R нулями производ-
ной /'(х) = (l-2x2+2x)e~l2, х € R являются числа

4.5. Приложения производной 173
в которых производная /"(я) = -2хA - 2х2 + 2х)е~х2 + (-Ах + 2)е~х ,
х € R принимает значения /" ( ) > 0, /" ( —-— ] < 0. Поэто-
Поэтому точка есть точка строгого локального минимума, а точка
-Уз-
а
v/3+l
—-— — точка строгого локального максимума.
Теорема 28. Пусть / : А -> R, х0 € А, то G ЛГ, то > 2.
Предположим, что выполнены следующие условия: 1)
В5 > 0 Vx £ В(хо,<5) С Л существует f^m~^{x); 2) существу-
существует ^т)Ы); 3) /'(х0) = /"(х0) = ... = ^т~1Цх0) = 0, /(тНх0) ф 0.
Тогда длл то = 2к, к £ N точка х0 есть точка локаль-
локального экстремума, а именно точка строгого локального
максимума при /(т'(х0) < 0 и точка строгого локального
минимума при /(т^(х0) > 0. Для значений т = 2k + 1, к £ N
точка xq не является точкой локального экстремума.
\ Формула Тейлора с остаточным членом в форме Пеано для функ-
функции / и точки х0 имеет такой вид /(х) = Y1 П— (х ~ хоУ +
j=o 3-
+о((х - хо)т), х —> х0, или, согласно условию 3), вид /(х) = /(х0) +
/Нх0)
Н \—- (х - хо)т + о((х - хо)т), х -> х0, откуда при х ф х0
то!
/(,) - /Ы = (. - «)- (££& + ff^> ) , . ^ ^ с„-
гласно определению "о" для числа -—r|/^m^(x0)| >035>0 Vi £
2то!
(В(хо,5)\{хо}):
о((х ~
(х-хо)
< -—- |/^т'(х0)|. Заметим теперь, что
2то!
имеют ненулевые значения одного знака. Учитывая формулу A), мож-
можно утверждать, что знак разности /(х) - /(х0) для х € (В(хо,<5) \ {хо})
совпадает со знаком произведения
^<—.г. и
Поскольку при т = 2к разность /(х) — /(х0) > 0, если /'т'(х0) > 0,
и, следовательно, хо является точкой строгого локального минимума
Разность /(х) -/(х0) < 0, если /'т'(х0) < 0, и тогда х0 является точкой
строгого локального максимума. Если же то = 2к + 1, то произведение
B) меняет знак при переходе через точку хо в B(xq,8') для любого
0 < 51 < 5. Поэтому Xq не является точкой локального экстремума. J

174 Глава 4. Производная и её приложения
Упражнение 126. Найти точки локального экстремума на R функ-
ции: а) /(х) = х4A - хK; Ь) /(х) = у - \ + 4BJ+1) I с) /(*) =
У\ = 0.
4.5.5 Точки перегиба
Пусть А С R и хо £ А.
Определение 6. Точка х0 называется точкой переги-
перегиба функции f (точнее, точка {xo,f(xo)) называется точ-
точкой перегиба графика функции f), если: 1) f непрерывна
в точке хо; 2) 3 8 > 0 : В(хо,5) С А и на каэ+сдом из интер-
интервалов (х0 - 5, х0) и (хо,хо + 8) функция f выпукла, причём,
направления выпуклости различны.
Примеры. 1. Для функции /(х) — х3, х € R точка хо = 0 есть
точка перегиба, поскольку /"(х) = 6х < 0 на (—оо,0) и, следовательно,
функция / выпукла вверх на этом интервале, и /"(х) > 0 на @,+оо) и
функция / выпукла вниз на @,+оо).
2. Для функции /(х) = sinx, х £ R каждая точка множества nZ
есть точка перегиба. Действительно, для точки вида 2/гтг, k £ Z имеем
/"(х) = -sinx > 0, х € Bтг/г - тг,2тгА:); /"(х) = -sinx < 0, х £
Bжк,2жк + ж). Следовательно, при переходе через точку 2кж выпук-
выпуклость вниз сменяется на выпуклость вверх. Аналогично проверяется,
что при переходе через точку вида Bк + 1)тг, к £ Z выпуклость вверх
сменяется на выпуклость вниз.
3. Для функции f(x) = arctgx, x £ R точка 0 является точкой пере-
перегиба, поскольку /"(х) = -J-—^-^ > 0, х < 0; /"(х) < 0, х > 0 и,
следовательно, функция / выпукла вниз на ( —оо,0) и выпукла вверх на
(О.+оо).
Упражнение 127. Пусть для функции / : А -> R и точки х0 £ А
3 5 > 0 \f х £ В(хо,5) : существуют /'(х), /"(х), причём /" сохраняет
знак левее и правее точки х0 Доказать что хо — точка перегиба /, тогда
и только тогда, когда точка хо — точка локального экстремума /'.
Теорема 29. Пусть функция f : А —> R и точка х0 £ А
таковы, что: 1) 3<5>0 Vx€ В(хо,5) С А существует f'(x);
2) х0 — точка перегиба /. Если существует f"{x0), то
Г'Ы = о.
[ Предположим, что при переходе через точку хо выпуклость вниз
сменяется на выпуклость вверх, второй случай рассматривается ана-
аналогично. Согласно теореме 22 функция /' монотонно не убывает на

4.5. Приложения производной 175
(xq — 8, xq) и монотонно не возрастает на (xq,xo +8). Следовательно,
f'(x0) = max /'(х) и в силу теоремы Ферма f"{x0) = 0. J
Х£В(ХО,5)
Замечания. 1. Теорема 29 даёт лишь необходимое условие для
того, чтобы точка Xq была точкой перегиба. Для функции /(х) = х4, х 6
R точка хо = 0 не является точкой перегиба, хотя /"@) = 0.
2. Согласно теореме 29 точки перегиба функции / лежат в объеди-
объединении множества точек, в которых /" равна 0, и множества точек, в
которых /" не существует.
Теорема 30. Предположим, что функция f : А -» R
и точка хо € А удовлетворяют условиям: 1) 3 5 > 0 Vi £
В(хо,5) существует /"(х); 2) /"(х0) = 0; 3) f" сохраняет
знак левее и правее точки х0.
Точка хо есть точка перегиба функции /, если произ-
производная /" меняет знак при переходе через точку х0. Точ-
Точка х0 не является точкой перегиба, если производная /"
не меняет знак при переходе через точку хо.
f Следствие теоремы 25. J
Упражнение 128. Найти точки перегиба функций: cos, tg, ctg,
arcsin, arccos, x + sinx, x £ R.
4.5.6 Асимптоты
Пусть А С R, a £ (Ди{-oo, +oo}) — предельная точка множества А.
Определение 7. Прямая у — kx + l, x € R называется
асимптотой графика функции f при х -> +оо (при х -¥
-ооЛ если lim (/(х) - кх - I) = 0 ( lim (/(х) - fcx - I) = о).
Прямая х = а € R называется асимптотой графика
функции /, если выполняется хотя бы одно из соот-
'■ ношений: lim fix) = +оо; lim f(x) = —oo; lim f(x) =
1-Ю,1<О V ' 1-Ю,Х<О V ' I-+O,I>O V '
+oo; lim fix) — -oo.
Примеры. 1. Для функции /(х) = — , х ^ 0 прямые х = 0 и у = О
являются асимптотами. х
2. Для функции f(x) = ,i^0 прямая у = 0 является асимпто-
X
той при х —> —оо и при х —► +оо.
X2 + 1
3. Для функции /(х) = , i/О прямая у = х является асимп-
X
тотой при х —> —оо и при х —> +оо.
12 — 4-1168

176 Глава 4. Производная и её приложения
Замечание. Согласно определению параметры к и I наклонной
асимптоты у = кх +1 при х —> +оо определяются следующим образом
к= lim , 1= lim f/(x) - fcx).
X-» + OO X 1-» + ОО
Упражнение 129. Найти асимптоты следующих функций: а) /(х) =
е) f{x)=x+y/\\-x*\,
4.5.7 Построение графика функции
Производная может быть использована при построении графика функ-
функции. При этом удобно выделить следующие этапы:
1) определение поведения функции при приближении к предельным точ-
точкам, определение асимптот;
2) определение интервалов монотонности, критических точек и точек
локального экстремума;
3) определение интервалов выпуклости и точек перегиба.
Упражнение 130. Построить графики функций:
a) f(x) = х3 + Ъх2 - 9х + 1, х G R, Ь) /(х) = х3е~х, х £ R;
с) /(*) = \ + ~^ - * i {0. О: d) Дх) = 2VU-z),!/!;
f) /(х) = х2^, х ^ 0;
111 3!
g)/(x) = xln|x|, x^O; h)/(x)=—, x>0.
Упражнение 131. Для каждого а £ R определить число действи-
действительных корней уравнения: а) ах = lnx; Ь) х3 + Зх2 - ах + 5 =
0; с) х3Ьх - х + а = 0; d) 1 + х + —- = аех.
4.5.8 Историческая справка
Тейлор Брук A685 — 1731) — английский математик. В 1715 г.
опубликовал общую формулу разложения функции в степенной ряд,
которая носит его имя. Этот ряд был известен ранее Дж. Грегори
A638 - 1675) и И. Ньютону.
Пеано Джузеппе A858 — 1932) - итальянский математик. По-
Построил непрерывную кривую, заполняющую квадрат. Ему принадлежит
общая теорема о существовании решения дифференциального уравне-
уравнения, результаты по обоснованию геометрии. Дж. Пеано в 1889 г. пред-
предложил аксиоматическое построение множества натуральных чисел, чем

4.6. Дополнительные задачи к главам 1 — 4 177
было завершено построение теории действительных чисел, основанной
на теории целых и рациональных чисел.
Маклорен Колин A698 — 1746) — шотландский математик, уче-
ученик и последователь И. Ньютона. Получил частный случай ряда Тейлора,
носящий его имя. Этот случай был известен И. Ньютону и Б. Тейлору
ранее. Ему принадлежат новые известные результаты в математическом
анализе и геометрии. В 1740 г. К. Маклорен, Д. Бернулли и Л. Эйлер
получили премию Парижской АН за работы о приливах и отливах.
Маркиз Гийом Франсуа де-Лопиталь A661 — 1704) — фран-
французский математик. Овладел дифференциальным исчислением с помо-
помощью Иоганна Бернулли. Лопиталь задумал написать книгу, которая бы
позволила легче усвоить воззрения Лейбница по дифференциальному
исчислению. В результате в 1696 г. появился первый и на долгое вре-
время единственный учебник по дифференциальному исчислению "Анализ
бесконечно малых для изучения кривых", неоднократно переиздавав-
переиздававшийся. В нём содержалось "правило Лопиталя", которое было сообще-
сообщено ему Иоганном Бернулли.
Иенсен Иоганн Людвиг A859 — 1925) — датский математик.
Автор известных результатов в теории аналитических функций, геомет-
геометрии и др.
Минковский Герман A864 — 1909) — немецкий математик, ав-
автор работ по теории чисел, геометрии, топологии, теории относитель-
относительности и др.
Гёльдер Отто Людвиг A859 — 1937) — немецкий матема-
математик, автор работ по алгебре, математическому анализу, теории рядов,
теории потенциала, теории чисел и др.
4.6 Дополнительные задачи к главам 1 — 4
1. Пусть / : X -> X и для п € N fl(x) := /(я), fn+l(x) := /(/"(я)).
Если Вт £ N \/х £ X : /т(я) = я, то / биекция Доказать зто
утверждение.
2. Является ли функция / : N2 —> N, определяемая соотношением
N2 Э {т,п) н-> min(m,n) 6 N, сюръекцией? Инъекцией? Определить
f{A) для А - {Bfc,n) | k G N, n £ N} и f~l{{k}) для к £ N.
3 Доказать, что функция / : Z —» Z, определяемая соотношением
/(п) = п-'- ( —l)n, n G Z есть биекция.
4- Определить мощность следующих множеств:
а){я€ N\ Бу £ R: 10siny = a;}; Ь) {х £ R\3y £ N : у = log2 я};
d){x£R\3n£N 3{ai,...,an}C Zn : xn+alxn~1+ . .. + an = 0}.

178 Глава 4. Производная и её приложения
5*. Доказать, что следующие множества имеют мощность континуум:
а) множество иррациональных чисел; Ь) объединение счётного семей-
семейства множеств мощности континуум; с) декартово произведение счёт-
счётного семейства множеств мощности континуум; d) множество всех
бесконечных последовательностей натуральных чисел; е) множество
всех бесконечных последовательностей действительных чисел; f) мно-
множество 2^; д) множество всех функций из N в N; \) множество всех
сходящихся последовательностей действительных чисел; j) C([a,b]).
6. Пусть А, А ф 0 — ограниченное подмножество R и J — пересечение
всех отрезков, содержащих множество Л, то есть 3 — f] I.
Доказать, что J = [inf Л, sup A].
7. Пусть / : X х У —> R, где X и У — некоторые непустые множества.
Доказать, что inf sup f(x,y) > sup inf f(x,y).
8*. Пусть А, А Ф 0 — произвол^ноелодмножество Ни/: А —> R
— функция, удовлетворяющая^условию Липшицар постоянной L > 0 :
V{i,y}Ci4: i/(z) - f{y)\ S Цх - у1ГДоказать существование продол-
продолжения /, удовлетворяющего условию Липшица на Л с постоянной L.
Указание. Рассмотреть функцию g(x) := inf (f(y) + L\x — y|), x £ R.
9. Из двух последовательностей
I П
n>1
П
п>2
I J I
первая строго убывает, а вторая строго возрастает. Доказать это утвер-
утверждение.
10. Последовательность {ап | п > 1} сходится, а последовательность
{pn I n > 1} ограничена и удовлетворяет условию Vn > 1 : bn+i >
Ьп + Qn+i — o.n. Доказать, что последовательность {bn | n > 1} сходится.
11*. Последовательность {an \ n > 1} сходится, а последовательность
{Ьп | п > 1} ограничена и удовлетворяет условию
3 1 3 1
V п > 1 : Ьп+2 - - Ьп+1 + -zK> an+2 - г an+i + « a"-
Доказать, что последовательность {bn | n > 1} сходится.
/ 1 n a, \
12. Вычислить предел lim -—; V .. . ) , если ап —> а, п —) оо.
n-»oo \ lnlnn j^2 J In j I
Ответ: а.
n 1
13. Определить функцию f(x) = lim ^ : , x £ @,1], и по-
П—»0O j_j 1 + J X
строить её график.

4.6. Дополнительные задачи к главам 1 — 4 179
14- Предположим, что для каждого п £ N выполняются условия
an > 0, sn := ai + a2 + ... + an\ an+i < — — , n > 2.
Sn+l
Найти предел lim а„.
n—юо
Ответ: 0.
15. Для числа x > 0 вычислить сумму X) I 2 < Цг^ > + 1 I 2~n~1.
"=1 V I 2 J /
Ответ: ~{{х} + 1).
16. Пусть Vn £ N : an £ @,1); an->0, n-> со. Вычислить предел
i^o (a"+ a«-i+ а"-з + • • • + a?)-
Ответ: О.
17. Определить действительные числа a, b, с так, чтобы существовал
конечный предел lim [n(an + у 2 + bn + en2)) .
n->oo \ /
18. Положим для х > 0 : ai := у/х, a2 := у/х + a2, ..., an+1 :=
л/х + ani ■ • • • Доказать существование предела lim an =: fix) и
n-юо
определить функцию /.
Ответ: f(x) = - + ^ - + х, х > 0.
19. Функция / : R —)• К имеет производную в точке а. Вычислить
/ п / ^. \ \
предел lim Е / а + ~Т ~ п/(а) •
Ответ: i/'(а).
. Доказать, что не существует непрерывной биекции R на отрезок
1-1. !]■
21*. Доказать, что не существует непрерывной биекции R на окруж-
окружность в плоскости.
, 22*. Доказать, что не существует функции / £ C(R), которая прини-
принимает каждое своё значение дважды.
23. Привести пример функции из C(R), которая принимает каждое
своё значение трижды.
24' Доказать, что многочлен чётной степени со старшим коэффициен-
коэффициентом 1, как функция из R в R, не есть инъекция и не есть сюръекция.
о_ . ТТХ о
x2n sin h х
25. Построить график функции f(x) := lim ^-* , х £ -R.
Верно ли, что / £ C(R)? Является ли / дифференцируемой?

180 Глава 4. Производная и её приложения
/„1,21, , пх \ 1/х
26. Доказать, что для п £ N lim + + ■ • • + е = е„(п+1)/2
х->0 \ П )
27*. Пусть xi > 0 и хп+1 = 1пA + х„), п > 1. Доказать, что пх„ -»•
2, п —> оо.
Указание. Сначала проверить, что х„ > О, п > 1, и что х„ -»•
О, п -> оо. Далее
Ша (-±--±)= lim Д":1П!1 + Д?) = lim
n-*oo 1.,, Х„ У n->oo Xnlnl + Xn) a-»0 zln(l + Z^ 2
.. /If,/1 X \\ l l l
Поэтому km - £) = n • откУДа ->
"-♦" \" k=l \lt+l Xk J J 2 ПХ„ ПХ!
- , n -»• оо. Следовательно, пх„ -»• 2, n -»• оо.
Другой подход см. в книге Г. Полиа, Г. Сеге Задачи и теоремы
из анализа. В 2-х т. Москва. Наука. 1978. Т. 1. 392 с.
28*. Пусть Xi > 0 и xn+i = arctg:rni n > 1. Доказать что xns/n —>•
/г
-, п->оо.
Указание. Аналогично решению задачи 27 вычислить следующий
предел km
+
29. Пусть п 6 ЛГ и {ai,... ,an; xi,... ,хп} С @, +со). Вычислить предел
1/Р
Ответ: тах(хх,..., хп).
30*. Пусть х = 0,xiX2.. .х„... — запись числа х € [0,1] в систе-
системе счисления с осноаанием 3, а / — функция [0,1] Э х ь-> f(x) —
0,2/12/2 ■ • -2/п • • • , где /(х) записано в системе счисления с основанием
2, причём ух - 1 <£=> xi = 1; уп+1 = у„ «<=> xn+i = xn, n > 1.
Доказать, что / £ С([0,1]), и что / не является дифференцируемой в
каждой точке отрезка х £ [0,1].
31. Функции / и д равномерно непрерывны на множестве А. Являются
ли равномерно непрерывными на А функции: а) с/, с £ R; Ь) / + д; с)
/^ в случае Л = [а, Ь]? А = [а, +со)?
Ответ: а) и Ь) "да" для [а,Ь] и для [а,+оо).
32. Пусть Р — многочлен степени п > 2 с различными действительными
п 1
корнями xi,х2,...,хп. Найти сумму £) ——-.
it=i г (xk)
Ответ: 0.
33. Пусть /(х) = х2 - 2х, х < 0 и /(х) = ах2 - 2х, х > 0. Определить
все значения а £ К, при которых функция / имеет обратную функцию
д. Найти д.

4\6. Дополнительные задачи к главам 1—4 Ш
Ответ: а < 0.
34' Доказать, что функция /(х) = — г^, х > -1, имеет обратную
д. Найти д'.
35. Определить главную часть функции:
а) /(х) = l-cos(l-cosx), х £ R; b)/(x) = xsin(sinx)-sin2x, x £ R,
при х —> 0 относительно шкалы {хп}.
х4 х6
Ответ: а) у ; Ь) - .
36. Найти предел lim xx .
х->0+
Ответ: 1.
37. Функция / : А -> R называется алгебраической на множе-
множестве А, если для некоторых n £ N и многочленов Р0)Plf..., Рп, Р„ ^
0, справедливо равенство Pn(x)(/(x))n+Pn_i(x)(/(x))"-1+.. -+Р0{х) =
0, х & А. Доказать, что функции f(x) = sinx, g(x) = ех, х £ R, .не
являются алгебраическими на множестве вида [а, +со), а £ R.
38. Пусть / : [0,1] -+ [0,1], / £ С([0,1]). Доказать, что 3 х £ [0,1] :
/(х)=х.
39. Для функции / : [а, Ь] —> К существует /' на [а, 6], причём /(а) =
/F) = 0, /'(а) = Д(а) > 0, /'F) = /1F) > 0. Доказать, что Зс £
40. Для функции / : (а, 6) —> R существует /" на (а, 6) и для трёх
различных точек Х1,Х2,Хз из (а, 6) /(х*,) = 0, fc = 1,2,3. Доказать, что
41. Пусть функции / : (а, 6) -» (-1, +со), д : (a,b) -» R удовлетворяют
условиям: 1) Vx £ (а, 6) : /(х) ^ 0; 2) существует lim (f(x)g(x)) =
L £ R, L ф 0; 3) существует lim A + f{x))9^ = eL. Доказать, что
х-+Ь-
/(i)-»0,s-»6-.
42. Пусть / £ C([a, 6]) и /(a) = /F). Доказать существование отрезка
[а,Р] С [а, 6] такого, что /3 - а = - F - а), /(а) = /(/3).
43. Пусть {/,5} С С2([0,1]), причём Vx £ @,1); д'(х) ф 0 и /'@)у"@)
Ф /"(О)^'(О). Пусть ^(х) для х £ @,1] какое-либо из чисел в теореме
/(х) - /0) f'(9{x)) u _ ,. б(х)
Коши —^—^ ^—^ = ^ ' " . Найти предел lim —i—^ .
Ответ: \ .
44- Функция / : R -> R строго выпукла и 3i, 6 Д: /(z*) = min/.
Доказать, что /(х) -»• +оо при |х| -> +оо.

i.82 Глава 4. Производная и её приложения
Указание. Показать, что / выпукла вниз, затем сравнить величины
1 х-х*
45. Доказать, что для любых п £ N, {xi,..., хп} С @, тг/2) справедли-
„/-! ! : ^ . ^1 + Х2 + . . . + Х„
во неравенство {/sinxi sinx2 .. .sinxn < sin .
n
Указание. Рассмотреть функцию f(x) = In sin x, x £ @,тг/2).
46. Для каждого а £ R определить число корней уравнения х3 + Зх2 —
ах + 5 = 0.
47. Доказать, что функция / : R -»• Я, /(х) = Зх5 + 7х3 + 2х + 1 есть
биекция.
48. Является ли функция / : R —> R, /(х) = х3 — Зх2 + 2 инъекцией?
Сюръекцией?
49. Функция / £ С([—1,1]) и четна (нечётна). Доказать, что для каж-
каждого е > 0 существует многочлен Р, включающий только чётные (нечёт-
(нечётные) степени х и такой, что max |/(x) - Р(х)| < е.
50. Функция / : @,+со) -» R такова, что существует /' на @,+со) и
/(г) + /'(х) -> 0, х -> +00. Доказать, что /(х) -> 0, х -» +оо.
51. Функция / е С2([0,+оо)) и для некоторого к £ N xkf(x) -»•
О, xkf"(x) -¥ 0, х -» +00. Доказать, что xkf'(x) -> О, х -> +оо.
52. Функция / : [а,Ь] —» [а, Ь] удовлетворяет условию V{x',x"} С
[а,Ь] : |/(х') - /(х")| < |х' - х"|. Для хх £ [а,Ъ] положим хп+1 =
х ~\- fix )
= Л—_—И- ^ п > 1. Доказать, что хп —> z E [а,Ь],п —^ оо, и что
справедливо равенство f(z) = z.
Указание. Показать, что для z = f(z) справедливы утверждения:
1) Nn+i - z\ < |х„ - z|, n > 1; 2) х„ < z => xn+i < z, n > 1.
Обратить внимание на то, что множество {z | /(z) — z} есть отрезок
или точка.
53*. Функция / : (a, b) -> R имеет /' на (а, Ь) и удовлетворяет условиям
f[x) -> -co, х -> а+; /(х) -> +оо, х -> Ь-; Vie (а,Ь) : /'(х) -
/2(х) < 1. Доказать, что Ь - а > п.
54* • Функция / : [a,b] -> R удовлетворяет условию V х £ [а, Ь] 3 6 >
О 3L £ R V{x',x"} С [а,Ь] П В{х,6) : |/(х') - /(х")| < L|x' - х"\.
Доказать, что / удовлетворяет условию Липшица на [а,Ь].
55*. Функция / : R -> R имеет /" на Ли ограничена на R. Доказать,
что 39 £R: f"{9) = 0.
56. Функция f : R-> R выпукла вниз на R, дифференцируема в точке
xt и f'(xt) = 0. Доказать, что функция / принимает наименьшее на R
значение в точке х+.

Глава 5
Примитивная и
неопределённый интеграл
5.1 Определения и элементарные свойства *
5.1.1 Определение и свойства примитивной
Пусть / : А -» R — функция, имеющая для каждого х € А производную
f'(x). При этом операция дифференцирования ставит в соответствие
функции / новую функцию /' : А —> R. Физическая интерпретация этой
операции — определение скорости движения по функции, задающей
пройденное расстояние, как функция времени. С точки зрения прило-
приложений не менее естественной является обратная операция — опреде-
определение пройденного пути по известной скорости движения, как функции
времени. Формально последняя операция есть операция определения
функции по ее производной.
Далее в настоящей главе буква J обозначает одно из следующих
подмножеств R : [а,Ъ], [а,Ъ), [а,Ь], [а,Ь), (-со,а], (-со,а),
[6,+со), (Ь,+оо), (-оо,+оо) = R, где а <Ь.
Кроме того, для функции <р : [a,b] -> R положим <р'{а) := <р'+(а),
*>'(*>):= V>'-(b).
Определение 1. Для функции f : J -> R функция F :
J -> R называется примитивной или первообразной фун-
функции f на J, если Vx € J существует F'(x) и F'(x) = f{x).
Замечание 1. Поскольку функция, имеющая производную в некото-
некоторой точке, непрерывна в этой точке, то примитивная функции
f на J непрерывна на J.
183

184 Глава 5. Примитивная и неопределённый интеграл
Примеры. 1. Для функции f(x) — х, х £ R примитивной на R явля-
1 /1 \'
ется функция F{x) = - х2, х £ R, поскольку V х £ R : I - х2 ) = х.
2 \2 )
Функция G{x) = - х2 + 1, х £ R также является примитивной функции
/1 А'
/ на R, так как V х £ R : ( - х2 + 1 ) = х.
2
/
2. Для функции /(х) = ех, х £ R функция F{x) = ех, х £ R есть
примитивная функции / на R, так как Vx £ R : (ех)' — ех.
3. Для функции /(х) = 0, х < 0, /(я) = ж, х > 0 примитивной на
R является функция ^(а;) =.0, х > 0, F[x) ~ -х2, х > 0, поскольку
^'(х) = 0, х < 0; F'(x) -1-х2\ = х, 1>0и кроме того,
FL{0) = 0, F|@) = 0, а потому и ^'@) = 0.
Всякая ли функция имеет примитивную? Следующий
пример показывает, что ответ на этот вопрос отрицателен.
Пример. 4- на J = (-1,1) функция f(x) = -1, а; < 0, /@) = 0,
f{x) = 1, х > 0 не имеет примитивной.
f Предположим, что это утверждение не верно. Тогда существует функ-
функция F : (-1,1) -> Я такая, что ^'(х) = -1, х < 0, jF"(O) = 0, ^'(х) = 1,
х > 0. К функции F на отрезке [0, х] с х > 0 применим теорему Ла-
гранжа, получим Эв £ @,х) : F(x) ~ F@) = F'@)x = f(9)x - x.
Отсюда следует, что FL @) = lim —— — = 1. Однако, по
т 0!-»0, 1>0 X
предположению ^+@) = F'(Q) = 0. J
Замечание 2. Справедливо более общее утверждение — теорема
ГДарбу, если для каждого х £ [а,Ъ] существует /'(х), то функция /'
I принимает в качестве значения каждое промежуточное число, лежащее
\ между /'(а) и f'(b). Это утверждение здесь доказываться не будет.
^""Пример 4 показывает, что простые функции могут не иметь прими-
примитивной. Поэтому нужно иметь условия, гарантирующие существование
примитивной, эти условия будут приведены в главе 6.
Для того, чтобы рассматривать и такие функции, как в примере 4,
иногда используется следующее определение, более общее, чем опре-
определение 1.
Определение 2. Пусть f : J -» R. Функция F : J ~> R
называется примитивной функции f на J, если: 1) F £
,C{J)\ 2) Vx 6 (J\A) существует F'(x) и F'(x) = /(x); 3)
множество А не более чем счетно, причем Vn € N :
\А П [-п, п]\ < +00.

5.1. Определения и элементарные свойства 185
Далее, если не оговорено специально, используется опреде-
определение 1.
Если примитивная для функции / существует, то она
определяется не единственным образом. Действительно, ес-
если F — примитивная функции / на J, то для любого числа С € R
функция F + С также есть примитивная для функции / на J, поскольку
Vx 6 J : {F(x) + С)' = F'(x) + 0 = /(х). Кроме того, если функции
F и G — примитивные функции / на J, то Vx £ J : (F(x) - G(x))' =
= F'(x) — G'(x) — f(x) — f(x) — 0. Отсюда по следствию из теоремы
Лагранжа ЭСе-RVxeJ: F(x) - G[x) - С ^=^ F(x) = G(x) + С
Таким образом, для функции, имеющей примитивную,
набор всех возможных её примитивных получается из
какой-либо одной из них с помощью всевозможных её
сдвигов вдоль оси ординат. Одну из примитивных F можно вы-
выделить, задав её значение F(x0) в какой-нибудь точке х0 £ J.
Определение 3. Неопределённым интегралом от
функции f на J называется вырамсение F(x) + С, х € J,
в котором F — примитивная функции f на J, а С —
символ, обозначающий произвольную постоянную.
Неопределенный интеграл от функции f no J обозначается следую-
следующим символом
f{x) dx, х £ J.
/■
Таким образом, неопределенный интеграл от функции f no J пред-
представляет собой общий вид функции с производной f на J.
Процедура определения примитивной или неопределенного интегра-
интеграла для функции / называется интегрированием функции /.
Упражнение 1. Найти примитивные на R для функций: a) f(x) =
|х|; Ь) /(z) -max(l,z2); с) f(x) = \smx\\ d) F(x) = sinx + |sinx|.
Упражнение 2. Функция / имеет примитивную на R. Доказать, что:
a) для чётной на R функции / существует нечётная примитивная;
b) для нечётной на R функции / существует чётная примитивная;
c) для периодической с периодом Т функции / существует периодиче-
периодическая с периодом Т примитивная.
Упражнение 3. Функция / : R -> R имеет примитивную F на R и
Vx 6 R: F(x) = f(x). Найти функцию /.
Указание. Поскольку Vx £ R : F(x) — F'(x), то после умножения
на ех имеем Vx € R : F(x)e~x - F'(x)e~x = 0, то есть Vigil:
(F(x)e~1)' = 0, откуда согласно следствию из теоремы Лагранжа 3 С £

186 Глава 5. Примитивная и неопределённый интеграл
R ViEfl: F{x)e~x = С. Таким образом, F(x) = Сех, х б R и
/(х) = Сех, х 6 К.
Упраснснение 4- Функция / : R —> R имеет примитивную F на К.
Найти /, если: a) F(x) = \ /(*); Ь) F(x) = /(х) + 1; с) 2xF(x) = /(»);
d)F(x) = /(x) + cosx.
Упраснснение 5. Найти ошибку в следующем рассуждении. Посколь-
Поскольку Vx £ 12 : (sin2 x)' = 2sinxcosx, (cos2 x)' = 2cosx(— sinx), то на
R имеем f 2 sin x cos x dx — sin x + C; J 2 sin x cos x dx = — cos2 x + C.
Следовательно, sin2 x — - cos2 x, i£fi, откуда 1 = 0!
5.1.2 Свойства неопределённого интеграла
Следующие утверждения являются непосредственными следствиями оп-
определений 1 и.З при условии существования примитивных.
2. ff'(x)dx = f(x)+C, xeJ;
3.Va£R,a^0 : f{af(x))dx = af f[x)dx, x e J;
4- {
5. Если ff[x)dx = F{x) + C, x £ J, и {a,6} С R,a ф 0, тогда
/ f{at + Ь) dt = - F{at + b) + C, teJ, где J := {t \ {at + b)e J}.
Упраснснение 6. Найти ошибку в следующем рассуждении /
х ~ 1.
dx ,. dx
= ln|x-l|+C = ln|l-x| + C = J = — f , следовательно,
i. X X ~~ 1
x-
Упраснснение 7. Для функции / : J -> @. + со) существует произ-
производная /' на J. Найти / f^ 11 ^ dx, x 6 J.
5.1.3 Таблица основных интегралов
На первый взгляд с фактическим вычислением интеграла дело обстоит
просто. Именно, из определений 1 и 3 имеем утверждение
F'(x) = f(x), xeJ <=Ф J7(x)dx = F(x) + C, xeJ. A)
С помощью этого утверждения и набора основных производных из гл.
4 получаем следующие важные формулы.

$.1. Определения и элементарные свойства 187
/xa+1
xa dx = -—- + С, х £ @, +со).
f xn+1
Уп£(ЛГи{0}): / xndx=-—- + С, х £ К.
Г xn+1
Vn £ (Z \ {—1}) : / xn dx = + С на каждом из интервалов
(-оо,0), @,+оо).
2. I — = 1п|х| + С на каждом из интервалов (-со,0), @,+со).
3. V а > 0, а ^ 1 : / axdx — -— + С, х £ R. В частности при a =■ е
J lna
получаем / exdx = ex + С, х £ R.
4- / cosxdx = sinx + C, x £ Я. 5. / sinxdx = -cosx + C, x £ К.
б. / —г— = tgx + С, на каждом из следующих интервалов
J cos2x .
(—тг/2 + птг,тг/2 + птг), ngZ.
/dx
—5— = — ctgx + C, на каждом из интервалов (птг,п7г + 7г),п £ Z.
sin х
/" dx
8. / j = arctg x + С, х £ R.
f dx
t7• / ■ :=: ^ 3XCS1U X -f~O. X t (—1,1).
J s/l-x2
Утверждение A) позволяет продолжать эту таблицу неограниченно.
Однако, положение существенно меняется, если для заданной функ-
функции / требуется найти примитивную на J. Можно вычислить производ-
производные большого числа функций и не встретить функции F, для которой
F'(x) = f(x), x £ J. Более того, такой поиск может оказаться напрас-
напрасным. Приведем без доказательства следующий известный факт, напом-
напомнив сначала определение элементарных функций. Элементарными
функциями являются: многочлены, рациональные функции, степен-
степенная, показательная и логарифмическая функции, тригонометрические
и обратные тригонометрические функции, их суммы, произведения и
частные, а также всевозможные суперпозиции этих функций в конечном
числе. Согласно цепному правилу производные элементарных функций
также являются элементарными функциями. Упомянутый выше факт со-
состоит в том, что примитивные элементарных функций могут не быть эле-
элементарными функциями. Например, не являются элементарными функ-
функциями примитивные следующих простых функций /i(x) = ех , /2A) =
= sinx2, /3(х) = cosx2, х £ Я; /4(х) = — , /5(х) = — , х > 0.

188 Глава 5. Примитивная и неопределённый интеграл
Доказательство существования примитивных этих функций будет полу-
получено в следующей главе.
В следующих разделах настоящей главы приводятся некоторые наи-
наиболее общеупотребительные приёмы, которые позволяют эффективно
находить в явном виде примитивные функций из некоторых определён-
определённых классов элементарных функций.
Упражнение 8. Найти /P(x)dx, x 6 R для многочлена Р(х) —
= аохп + aix"--1 + ...+ an_iz + ап, x G R, n G N, {a0,oi,...,an}cB.
Упражнение 9. Найти интегралы:
a)/sin2xdx, x G-R; b)/cos2xdx, x £ R;
c) / sin az sin fcxdx, x G H; d)/sinax cosfczdz, x G R, где{а,Ь}СЙ;
e)/sin3 ids, xGK; f) / , 3 dX , 16@,1/2).
sin z cos^ z
izn z > 0
1 - .
U, X \ U
(ax + bI+1
Доказать, что J (ax + fc)"dx = ^— -^r hC, x G R, где a > 0, 6 G R.
a(n 4~ lj
5.1.4 Интегрирование с помощью подстановки
Теорема 1. Пусть функции f : J\ -> R, f G C{Ji), g :
J -> Ji, 5 G C^J) u F — примитивная функции f, то есть
ff{t)dt = F{t)+Ct teJv Тогда f f{g{x))g'{x)dx = F{g{x))+C, x e
J; CeR.
\ Действительно, согласно цепному правилу
(F(g(x))Y = F'(g(x))g'(x) = /(g(x)M'(z), z G J. J
Зал«ечамие. При практическом вычислении интеграла удобно ис-
использовать следующую формализованную запись f f(g(x))g'(x)dx =
(х) dz = dt
ворят, что переход от переменной х к переменной t осуществляется с
помощью подстановки или замены переменной g(x) — t.
Примеры. 1. Вычислить f2xex dx, x £ R.
[ Согласно теореме 1 имеем
Х~ = f etdt = et + C = ex'i+С, х G R. J
2xdx = dt J
dt = F^) + С = F(^2)) + С- ПРИ этом

5.1. Определения и элементарные свойства
189
f(x)f'(x)
2. Вычислить интеграл f - ——- dx, где / — функция, имеющая
производную /' и такая, что 1 + / > 0 на J.
[ Согласно теореме 1 имеем
f'{x)dx = dt
l+t
+t
= [dt-[^-=t-
J J i + t
I6J.J
Теорема 2. Пусть функции / : J -* R, f £ C(J); y> :
Jo —> J, (/5 £ C1(Jo), причёл* длл (^ ст/гцестпет/ега обратная
функция <р~1. Предполоэ+сим такэ+се, что G — примитив-
примитивная для функции g(t) := f{f{t))ip'(t), t £ Jo. Тогда
f /(x) dx = f f{tp(t))ip'(t) dt = G{t) + С = G(v?"(x)) + C, x £ J; С £ R.
\ Действительно, пусть F — примитивная для функции / на J. Тогда
согласно цепному правилу (F(tp(t)))' = F'(tp(t))ip'(t) = j:(tp(t))ip''(t), сле-
следовательно, с некоторым числом С имеем G(t) = F(ip(t)) + С, t £ Jo
или G((p~l{x)) = F{x) + C, x £ J и / f(x) = G{(p~x{x)) + С J
Примеры. 3. Вычислить интеграл f v^l — x2dx, x £ [—1,1].
x — sini
ГПо теореме 2 имеем Г vl — х2 dx — = Г cos tdt —
dx = cos t dt J
, 1 1 . „ 1 • 1/ , Л ,
dt = -1 + - sin 2t + С = - arcsm a; + - x V1 - x2 + C. J
4- Вычислить интеграл f \/l + x2 dx, x £ -R.
ex _ e-x
f Введем функции shx := z > chz :=
x e R,
2 ' 2
для которых для х £ R справедливы равенства (shx)' = chx, (chx)' =
= shx, 1 + sh2 x = ch2 x, sh2x = 2 shx chx. По теореме 2 имеем
x = shi
dx = ch t du
1
= fch2tdt= j
для х £ Я поскольку sh2u = 2shuchu = 2shuv 1 + sh2u = 2xi/l + x2,
u = ln(x + i/l + а;2)! последнее следует из уравнения для величины
Упражнение 11. Найти интегралы:

190
Глава 5. Примитивная и неопределённый интеграл
a) f u cos u2 du, u G R;
g) / v/1 - 3x dx, x<-;
О
m)
x3, xeR,
b) / -A-, х€@,7г);
J smi
, xG@,7r/2);
j) f sin5 x cos3 x dx, x G -R;
xdx
I)
(x + lO>
dx
x2 +x + 1
, x e R.
5.1.5 Интегрирование по частям
Теорема 3. Пусть функции и,v : J -> R таковы, что
для каждого х G J ст/гцествук>7п u'(a;) it u'(x). Предполо-
э+сим, что функция uv' хилеет примитивную на J. Тогда
функция u'v также имеет примитивную на J и справед-
справедливо равенство J u'(x)v(x) dx = u{x)v{x) — f u(x)v'{x) dx, x G J.
\ При предположениях теоремы 3 функция uv является примитивной
функции u'v + uv' на J, следовательно f(u'(x)v(x) + u(x)t/(x)) dx =
= u(x)v(x) + С, x G J. Добавляя на основании свойств 3 и 4 п. 5.1.2
к обеим частям последнего равенства интеграл f(—u(x)v'(x))dx =
— j u(x)v'(x)dx, получим нужную формулу. J
Примеры. 1. Вычислить интеграл Jxexdx, x E R.
v(x) = х, v'(x) = 1
[ По теореме 3 имеем f xex dx =
- j exdx = хех - е1 + С, х € R.
2. Вычислить интеграл flnxdx, x > 0.
[ По теореме 3 для х > 0 имеем f In x dx =
= xlnx — f x ■ — dx = xlnx — х + С.
u'{x) = ex, u(x) = ex
= xex -
J
v(x) — lnx, v'(x) — —
X
u'(x) = 1, u(x) = x
Упражнение 12. Вычислить интегралы:

5.2. Интегрирование функций из некоторых классов функций 191
/г
xsmxdx, х G R, Ь) x2sinxdx, x G R,
с) (lnxJdx, х > 0; d) ln(x2 + х + l)dx, ' х £ R.
•Упражнение 13. Найти ошибку в следующем рассуждении. На
основе теоремы 3 f — =
х
и'(х) = 1, и(х) = х
/"/In f dx
I x[ —г I dx = 1 + / — . Следовательно, 0=1.
J \ x2 I J x
1
= I • - —
X
/
— I x
J
5.2 Интегрирование функций из некоторых
классов функций
5.2.1 Рациональные функции
Национальной функцией называется отношение двух многочленов.
Эта функция определена на всей оси, исключая нули знаменателя. Раци-
р
ональную функцию — , где Р и Q — многочлены, всегда можно предста-
Р Р
»ить с помощью деления в виде — — S+ — , где S и Рх — многочлены,
причём степень Р± меньше степени Q. Поэтому далее рассматриваются
только рациональные функции, у которых степень числителя Р меньше
степени знаменателя Q, такую рациональную функцию называют также
правильной дробью.
Непосредственным следствием основной теоремы алгебры является
^следующая лемма.
Лемма 1. Пусть Q{x) = aoin + a1in~1 + . .. + an_1x + an, x G R,
— мпогочлеп с действительными коэффициентами по,
ах,...,ап, причём. а0 Ф 0. Существует единственный с
точностью до перестановки набор комплексных чисел
zi,z2)... ,*„ такой, что
VzG-R : Q(x) = ao(x-z1)(x-z2,)...(x-zn). A)
Преобразуем разложение A), учтя кратность корней и то, что каж-
каждый комплексный корень z = а + г/3,- {«,/?} С й, /3^0 входит в
произведение A) вместе с ему сопряжённым z = a-г/З. Пара комплекс-
комплексно сопряженных корней гиг приводит к множителю (х — z)(x — Т) =
= (х - аJ + /З2 = х2 + рх + q, где р = -2а G R, q = а2 + /З2 6
R, р2 — Aq = —Ар2 < 0. Поэтому из представления A) имеем
13 — 4-1168

192 Глава 5. Примитивная и неопределённый интеграл
Q(x) = a0 П (* - ^)в" П (*2 + Рм* + 9мГ". * € Л, B)
где {ao;x1,a;2,...,a;r;p1,g1,...1ps,gs} С Я; р\ - 4дм < 0, ^ G
{1,2,... ,s}; {ui,...,ur; Ui,...,us} С N. При этом, если г = 0 или
s = 0, то в B) отсутствует второй или третий соответственно множи-
множитель.
Обратим внимание на то, что в отличие от представления A), в
представлении B) все числа действительны.
Общее утверждение — лемма 1 опирается на основную теорему ал-
алгебры, однако, в конкретных случаях нужное для проведения интегри-
интегрирования рациональной функции представление B) обычно получается
без труда.
В следующих двух леммах Р и Q — многочлены с действительными
коэффициентами.
Лемма 2. Пусть степень многочлена Р меньше степе-
степени многочлена Q, многочлен Q имеет вид Q(x) =
(х - a)mQi(x), х € R с некоторыми числами а е R и т е N,
причём, Q\(a) ^ 0. Тогда правильная дробь P/Q единствен-
единственным образом, представляется в виде
где А е R и Р\ — многочлен с действительными коэффи-
коэффициентами такой, что вторая дробь в правой части C)
правильная.
(" Для произвольного А £ R рассмотрим разность
P(s) _ A = P{x)-AQ1(x)
Q{x) (x-a)m (x-a)mQx{x)' {>
Выберем теперь число А так, чтобы многочлен Р(х) — AQi(x) делится
Р(а)
на х — а, то есть так, чтобы Р(а) - AQx(a) — 0 <;=?■ А = ———.
QiW
Положим теперь Рх{х) := —— ^ . J
х — а.
Лемма 3. Пусть степень многочлена Р меньше сте-
степени многочлена Q, многочлен Q имеет следующий вид
Q(x) = (х2 + рх + q)mQ\{x), х £ R с некоторыми числами
р, q С R, m e N, р2 - iq < 0, причём, многочлен Q\ не
делится на х2 +px + q. Тогда правильная дробь P/Q един-
единственным, образом, представима в виде
Р(х) = Ах + В Рг(х) (
. Q{x) (x2+px + q)m + (x2+px + q)m-lQx{x)' {>

5.2. Интегрирование функций из некоторых классов функций 193
где х е {u e R \ Q(u) ф 0}, {А, В} С R и Рх — многочлен с
действительнъьми коэффициентами такой, что вторая
дробь в правой части равенства E) правильная.
\ Рассмотрим разность
' ЕМ Ах + В P(s)-(^g
Q(x) (x2+px + g)m Q(x)
Подберем теперь числа А и В так, чтобы многочлен Р(х) - (Ах +
B)Qi(x) делился на x2 + px + g = (x-z)(x-I), где z = а + г'/З, {a,P} С
R, Р ф 0; р = -2а, q = а2 + /З2. Тогда должны выполняться равенства
P(z) -Р(-г)
, = Ла + В + г/3 .А, = Ла + В -г/3 Л, из которых имеем А =
Q\{z) Qi(z)
х2 + рх + q
5.2.2 Разложение на элементарные дроби.
Метод неопределенных коэффициентов
Использование представления B) п. 5.2.1, а также последовательное
применение утверждений лемм 2 и 3 позволяет представить любую
правильную дробь единственным образом в виде суммы слагаемых вида
л
, гпеае R, AeR, me N, A)
(ж _
и вида
Х~ q)m ' гДе{А-В,Р,д}СЯ, m€iVHp2-4g<0. B)
(х2
Дроби вида A) и B) называются элементарными.
"■ При этом для правильной дроби P/Q со знаменателем Q из форму-
формулы B) п. 5.2.1 с a.Q = 1 получим следующее представление
Р{*) М А2 AUl
( О^1 +
Q(x) [x - n)«i (х- хО^-1 x-Xl +'"
Ех Е2 EUr
' ■ (х - xr)u- (x - х,.)"--1 х-хг
| Crx + Dx CVix + DVl
(x2+p1x + g1)"i ■" х2+р1Х + дг
Мхх + Nx Mv,x + NVs
(x2 + ps + qs)v> ■" x2+psx + gs'
13

194 Глава 5. Примитивная и неопределённый интеграл
Для фактического получения разложения правильной дроби на элемен-
элементарные обычно используется не последовательное применение лемм 2 и
3, а так называемый метод неопределенных коэффициентов.
Этот метод состоит в следующем. Сначала записывают знаменатель Q
р
в виде B), п. 5.2.1, а затем представляют правильную дробь — в виде
суммы дробей A) и B) с неизвестными коэффициентами. После приве-
приведения полученного равенства к общему знаменателю и его отбрасыва-
отбрасывания, получается равенство двух многочленов. Приравнивая коэффици-
коэффициенты при одинаковых степенях х, получают систему линейных уравнений
для неизвестных коэффициентов.
Пример. 1. Представим в виде суммы элементарных дробей дробь
х -4- т. -4- 1
/(х) = 1—-— , х G {R\ {—1,1})- Согласно леммам 2 и 3 имеем с
х* — 1
некоторыми, пока неизвестными, числами А, В, С, D
х3+ж + 1_ х3 + х+1 _ А В Cx + D
после приведения к общему знаменателю и его отбрасывания получим
тождество z3+x + l = >l(x + l)(a;2 + l) + B(a;-l)(x2 + l) + (Ca; + jD)(x2-l),
откуда, приравнивая коэффициенты при одинаковых степенях х в левой
и правой частях, приходим к следующей системе уравнений
-3 1 = А + В + С
0=A-B+D
х*
X2
X1
1=А+В-С
1 = A-B-D.
Решая полученную систему, получаем следующие значения для коэф-
3 1 1
фициентов А - - , В =-, С = 0, D =--. J
ft ft £i
Замечание. Таким образом, интегрирование произволь-
произвольной рациональной функции сводится к интегрированию
многочлена и элементарных дробей вида A) и B).
Упражнение Ц. Разложить на элементарные дроби следующую
х2 + 3
рациональную функцию , х ф -1.
5.2.3 Интегрирование элементарных дробей
Элементарные дроби вида A) п. 5.2.2 легко интегрируются. При m = 1
А
имеем Г dx = Л1п|х — а| + С на каждом из интервалов (-оо,а),
х — а

5.2. Интегрирование функций из некоторых классов функций
195
(a, +00). Если m £ JV и m > 1. то Г -. г— dx = --, -г-. ; г
J (x-a)m (m-l)(x-a)
+ С на каждом из интервалов (—оо, а), (а,+оо).
Переходя к интегрированию дробей вида B) п. 5.2.2, сначала заме-
заметим, что
. , Р _.
1
Ах + В
(х2 + рх -
-А [
-2}
dx =
2tdt
{t2
1.2 \т
dt
A)
где a := q - — > 0. Для первого интеграла правой части A) для числа
m = 1 имеем f — = ln(i2 + a2) + С, t G R и для числа m > 1
г 2tdt п 1 _
Интегрирование второго слагаемого в правой части A) сложнее,
приведём простую рекуррентную формулу для его вычисления. Пусть
^т := / Ш гшГ ' * е -**> m e -^' C помощью формулы интегриро-
интегрирования по частям для^т > 1 получаем
?)m
a?)
-m2t
v =
2)m
2m
{t2+a
Отсюда находим
{t2 + a2)m+1
\-2тКт — 2та Кт+х.
2m-J.
2ma2(t2 + a2)m 2ma2
Кт, m > 1.
B)
Кроме того, ifi = — arctg - + C, t £ R. Таким образом, зная К\ из
а а
B) при m = 1 находим К2, по ^Гг из той же формулы при m = 2 найдем
#з и т- Д-
Зал«ечание. Таким образом, интегралы от рациональных функций
вычисляются эффективно и результатом является сумма рациональной
функции, логарифмической функции и арктангенса.
Упражнение 15. Вычислить интегралы:
x3dx f xdx f xdx
b) )y
X2 + X + 1
(l + lI3
di.

196 Глава 5. Примитивная и неопределённый интеграл
Упразднение 16. Указать метод вычисления интеграла fR(ex)dx,
где R — рациональная функция.
Упразднение 17. Найти интеграл / ——- .
6 т -1
5.2.4 Интегрирование рациональной функции
от sin и cos
Определение 1. Многочленом от двух переменных х
и у называется функция Р : R2 -> R следующего вида
Р(х, у) = аОо + ахох + аоху + а2ох2 + апху + аО22/2 + ...
... + апОхп + ап-1Лхп-ху + ... + аопУ"; (*, у) G Я2,
где {а00, aw,..., ао„} С R.
Определение 2. Рациональной функцией от двух пе-
переменных называется отношение двух многочленов от
двух переменных; это отношение определено в тех точ-
точках точках R2, в которых знаменатель отличен от 0.
Упражнение 18. Пусть R — рациональная функция от двух пере-
переменных, a Rx и i?2 — рациональные функции от одной переменной. До-
Доказать, что функция R(R\,R2){x) := R(Rx(x), Лг(х)) есть рациональная
функция от х на -R.
Пусть Я — рациональная функция от двух переменных. Интеграл вида
f R(cos х, sin x) dx эффективно вычисляется путем сведения к интегралу
от рациональной функции с помощью следующей замены переменной
г
/ R(cosx,sinx)dx =
L x . „ . . , 2dt
tg -x = *, * = 2 arctg f, dx = -—-
л 1 T t
2
Замечание. Следует иметь в виду, что общая замена переменной
п. 5.2.4, как и следующего, при фактическом вычислении часто приво-
приводит к громоздким вычислениям, и что структура функции R во многих
случаях позволяет использовать более простые замены переменной.
dx
Упражнение 19. Вычислить интеграл Г- : .
r J 3 cos х + sin х + 1
1 —1~ ЯШ Ж
Упражнение 20. Вычислить интеграл Г dx.
J 1 - COS X
Упражнение 21. Пусть Л — рациональная функциягот двух пере-
переменных. Указать метод интегрирования интеграла f R(sb.x,ch.x)dx.

5.2. Интегрирование функций из некоторых классов функций
197
5.2.5 Интегрирование функций, включающих
иррациональности
Пусть R — рациональная функция от двух переменных.
1. Интегрирование иррациональностей
Пусть {a,b,c,d} С R и n G N. Интеграл вида fR\x, ..
1 " ex + а
сводится следующим образом к интегралу от рациональной функции
b-tnd
dt
И
= R
ctn -a ' j \ctn -a
2. Интегрирование иррациональностей. Продолжение
Пусть {a, b, с, d} £ R, аф 0. Интеграл f R(x, s/ax2 + bx + с) dx с помо-
b
щью замены х -\ = zd сводится к одному из следующих интегралов
2а
(^)fR(t,^ir^l)dt, B)fR(t,ViTTT)dt, C) / H(i, yi^F) di, с раци-
рациональной функцией от двух переменных R. Интеграл A) — это интеграл
п. 5.2.5, 1 с учётом того, что \/t2 — 1 = (t — 1)
. Для вычисления
интеграла B) можно использовать подстановку t = shu, см. пример 4
п. 5.1.4. Для интеграла C) можно использовать либо подстановку п.
5.2.5, 1, либо подстановку t = sinu.
5.2.6 Историческая справка
Первые таблицы примитивных были составлены И. Ньютоном. За-
Затем были разработаны разнообразные методы вычисления примитив-
примитивных. Более существенным оказалось введение и изучение новых, так на-
называемых трансцендентных функций, как примитивных. В этой ра-
работе принимали участие многие выдающиеся математики, например, Л.
Эйлер A707-1783), К. Ф. Гаусс A777-1855), А. М. Лемсандр
A752-1833). Процедура интегрирования рациональных функций была
известна уже Ж. Лиувиллю A809-1882) и Ш. Эрмиту A822-
1901).

Глава 6
Интеграл Римана
6.1 Введение
Рассмотрим сначала две задачи, приводящие к понятию интеграла.
6.1.1 Задача о вычислении площади криволинейной
трапеции
Определение 1. Пусть /-непрерывная и неотрица-
неотрицательная на отрезке [а,Ь] функция. Множество F точек
плоскости, ограниченное осью абсцисс, проходящими че-
через точки а и Ъ вертикальными прямыми, и графиком,
функции f, называется криволинейной трапецией.
Таким образом, F := {{х,у) £ R2 \ а < х < Ь, 0 < у < f{x)}.
Предполагая известной площадь прямоугольника, к вычислению площа-
площади криволинейной трапеции можно подойти следующим образом. Раз-
объём отрезок \atb] точками а = хо < xj_ < хг < ... < zn-i < хп = Ъ
на п частей и проведем через эти точки вертикальные отрезки. При
этом криволинейная трапеция будет разбита на п меньших криволи-
криволинейных трапеций. В каждую из этих меньших криволинейных трапеций
впишем прямоугольник и около каждой из них опишем прямоугольник.
Высоты вписанного и описанного прямоугольников соответственно равны
rrifc := min f(x), Mk := max f(x) для криволинейной трапе-
Xk<X<Xl, + 1 Ifc<I<Ifc + l
ции с основанием [zft,Zfc+i]; 0 < fc < n — 1, см. рис. 8 на следующей
странице, на котором для п = 6 заполнены точками вписанные пря-
прямоугольники. Тогда суммы площадей вписанных и площадей описанных
прямоугольников соответственно равны
198

^ведение
199
у = /(*)
а = х0
х2
х3
Х4
Х5
хб=Ь
Рис. 8.
п-1
п-1
— Xfc+1 - 2k. A)
fc=O fc=O
Эти суммы можно рассматривать как приближенные с недостатком и с
избытком соответственно значения для площади криволинейной трапе-
трапеции F.
Поскольку функция / на отрезке [а,Ь] непрерывна, то для меньше-
меньшего отрезка [zjt,Xfc+i] ее ординаты будут меняться мало, то есть малой
будет разность Мк — тпк. Поэтому суммы A) будут тем точнее давать
значение площади, чем меньше длина каждого из отрезков [xjt, Xfc+i].
Таким образом, можно ожидать, что точное значение площади получа-
получается как предел
п-1
lim ___
fc=0
при условии, что max Дх*, -> 0.
0<fc<n-l
= Hm
п-1
Y1
fc=0
B)
6.1.2 Задача о вычислении величины пройденного пути
Предположим, что точка Р движется по прямой с известной в каж-
каждый момент времени t мгновенной скоростью v(t). Определим величи-
величину пути, пройденного точкой Р за время [tj,^], предполагая функцию
v непрерывной. Разобьем отрезок [<i,£2] точками i\ = т0 < Ti < т2 <
... < rn_i < тп = t2 на п частей. В каждом из отрезков [rfc,rfc+1]
выберем произвольно точку £к- Приближенно скорость точки Р на ма-
малом отрезке [7"jfe,Tfc+i] постоянна и равна v(£k), а пройденный за время

200 Глава 6. Интеграл Римана
путь приближенно равен у(£к)&тк, Дтк := тк+1 - тк. При
этом приближённое значение пути, пройденного точкой Р за время
[ti,t2], равно
(з)
fc=0
Точность приближения C) будет тем большей, чем ближе значение v(£k)
к значениям v(t) для t € jYfc,Tfc+i]- Для непрерывной функции v эта
близость достигается малостью отрезка [тк,тк+1].
Таким образом, можно ожидать, что точное значение проходимого
за время [ti,ta] пути получается, как
D)
fc=0
при условии, что
max Атк -> 0. E)
0<fc<n-l V '
Пределы типа B) и D) при условии E) действительно существуют, эти
пределы изучаются в настоящей главе.
6.2 Определение интеграла Римана
6.2.1 Вспомогательные определения
Определение 1. Пусть [a,b] — отрезок и п е N. Набор
точек xo,xi,X2,... ,хп таких, что а = х0 < х\ < хг < ... <
хп_1 < хп = b называется разбиением отрезка [а,Ь] и обо-
обозначается одним, из символов {xo,xi,X2,... ,in}, Л([а,b]), Л.
Диаметром или мелкостью разбиения Л называется
число |Л| := max{Axfc | 0 < к < п — 1}, где Дх*, := xfc+1 - Хк для к €
Отметим, что для каждого к £ {0,1,2,... ,п — 1} Дхь > 0 и что
п-1
]Р Дхк = Ъ — а. Пусть / : [а,Ь] —> R — ограниченная на отрезке [а,Ь]
fc=0
функция. Тогда V х € [а, Ь] : т < f(x) < М, где т := inf /, М := sup /,
[°.Ч [а,Ь]
при этом mei?, М € R-
Пусть Л = {хо.хьхг,... ,х„} — некоторое разбиение отрезка [а, Ь].
Для каждого к £ {0,1,2,..., п — 1} определим следующие числа т*, :=
= mfc(/) := inf{/(x) | х € [xfc,xfc+i]} = inf /, Мк := Affc(/V:=
[Sfc,Sfc+l] '
= sup{/(x) | x € [xfc,xfc+i]} = sup /.
Отметим, что все введенные точные грани определены в силу тео-
теоремы о существовании точных граней. Кроме того,

6.2. Определение интеграла Римана 201
Vfce{0,l,2,...,n- 1} : m<mk<Mk<M. A)
Определение 2. Нижней суммой Дарбу для ограни-
ограниченной на отрезке [а,Ь] функции f и разбиения X называ-
п-1
ется число L(f\X) := £! mkAxk.
fc=O
Верхней суммой Дарбу для ограниченной на отрез-
отрезке [а,Ь] функции f и разбиения X называется следующее
п-1
число U(f;X) := ]Г MkAxk.
fc=O
Определение 3. Пусть X = {х0,х1,х2,--.,хп}-некоторое
разбиение. Произвольный набор точек {£o,£i,. ..,£n-i} та-
таких, что У к е {0,1,2,... ,п - 1} : £к £ [xfc,Xfc+i], называет-
называется набором, отвечающим разбиению X, и обозначается
символом. {&|А} = {&}.
Для любого набора {&|А} с учетом неравенств A) имеем
т<тк< /(&.) <Мк<М, 0 < к < п - 1. ' B)
Определение 4- Интегральной суммой для функции
f : [а, Ь] -у R, разбиения X = Л([а,Ь]) и набора точек {£»|А}
п-1
: называется число S(f; X,{£i\X}) :— S(f\X) :— ^ f(Zk)Axk.
fc=0
i Упражнение 1. Пусть а = -1, Ъ = 1; /(х) = |х|, х G [-1,1];
Вычислить L(/;Л), С/(/;Л), 5(/; Л, {
Введенные суммы Дарбу и интегральные суммы обладают следую-
следующим свойством
т(Ъ -а)< L(f; X) < S(f; X, {^|А}) < U(f; Л) < M(b - а). C)
j Для доказательства неравенств C) нужно помножить на положительное
I число Axk fc-oe неравенство из B), а затем сложить все полученные
неравенства.
Упразднение 2. Дать геометрическую интерпретацию для нера-
неравенств из C).
Упражнение 3. Пусть [а,Ь] = [0,1]; /(х) = х2, х G [0,1]. Для про-
произвольного разбиения Л записать суммы L(/;A), U(f;X), а также сумму
S{f; X, {£|Л}) для набора £fc = —= \Jx\+1 + xfc+ixfc + х\, 0 < fc < n -1.

202 Глава 6. Интеграл Римана
6.2.2 Определение интеграла и интегрируемой
функции
Пусть / : [а, Ь] —> R — ограниченная на отрезке [а, Ь] функция.
Согласно неравенствам C) множества действительных
чисел {L(/;A) | Л}, {U(f;X) | А}, то есть множества всех нижних
и всех верхних сумм Дарбу, отвечающих всевозможным разбиениям Л
отрезка [а,Ь], ограничены.
Определение 5. Нижним интегралом от функции f
по отрезку [а,Ь] называется число Jf(x)dx :— supL(/;A).
А
Верхним интегралом от функции f по отрезку [а,Ь]
называется число J f(x)dx := inf U(f;\).
При этом, точные верхние и ниснсние грани берутся
по всем возможным разбиениям А отрезка [а,Ь].
Упражнение 4- Найти нижний и верхний интегралы для постоянной
на [а,Ь] функции.
Упражнение 5. Найти нижний интеграл от f(x) = х, х € [0,1].
Указание. Использовать неравенство Хк < - {хк + Xk+i).
Пример. 1. Пусть f(x) = 1, х е Q и /(х) = 0, х е (R \ Q)
— функция Дирихле. Для функции /, рассматриваемой на отрезке
[0,1], и любого разбиения Л = {х0, хь ..., х„} этого отрезка для любо-
любого к е {0,1,2,... ,п - 1} имеем Шк = 0, Мк = 1, поскольку любой
отрезок [ifc,Xfc+i] содержит как рациональные так и иррациональные
числа. Таким образом, L(f; Л) = 0, U(f; Л) = 1 для любого разбиения
Л. Следовательно, f f(x) dx = О, J f(x) dx = 1.
Определение 6. Если для функции f -. [а,Ь] -> R выпол-
выполняется равенство J f(x)dx = Jf(x)dx, то функция f на-
л*"
врывается интегрируемой по Риману по отрезку [а,Ь], а
/общее значение верхнего и нижнего интегралов называ-
называется интегралом Римана от функции f no отрезку [а,Ь]
ш обозначается символом f f(x)dx.
а
1 Замечания. 1. Далее рассматриваются только интегрируемые по
!риману функции и интеграл Римана, поэтому будем говорить об инте-
й*рируемых функциях и интеграле.

6.2. Определение интеграла Римана 203
ь
2. Согласно определению 2 интеграл J f(x)dx есть число, опреде-
а
ляемое функцией / и отрезком [a,b]. В частности, это число не зависит
ь ь
от х и можно писать J f(x)dx = J f(u)du и т. п. Более логичным яв-
а
Ь
ляется обозначение J /. Однако, общеупотребительное обозначение
а
связано с логикой преобразований интеграла и потому полезно.
3. Числа а и Ъ в обозначении интеграла называются нижним и
верхним пределами интеграла соответственно.
Обозначение: / G Д([а,Ь]) <=> функция / интегрируема по [а,Ь].
Примеры. 2. Пусть /(х) = С, х G [а,Ь], где С G R. Тогда для
любого Л = Л([а, Ь]) имеем L(f; X) = U[f\ X) = С{Ъ-а). Следовательно,
ь
/ G Щ[а,Ь]) и jCdx = C{b-a).
а
3. Для функции Дирихле / на отрезке [0,1] 0 = / / dx ф J f dx = 1,
следовательно, функция Дирихле не является интегрируемой.
: Упражнение 6. Для функции / е ^([0,1]) ЭСе Д VА = Л([0,1]) :
L(f; Л) = С. Доказать, что /(х) = С, х е [0,1].
Упражнение 7. Пусть /(х) = 1, х G [0,1] и /(х) = 2, х G A,2].
2
Доказать, что / G Д([0,2]) и найти J f(x)dx.
о
6.2.3 Свойства сумм Дарбу
Согласно неравенству C) п. 6.2.1. имеем
1°. Для любого разбиения Л = Л([а,Ь]) справедливы следующие нера-
неравенства: m(b - а) < L{f; X) < U{f; Л) < М{Ь - а).
Определение 7. Пусть X и Л' — разбиения отрезка
[а,Ь]. Разбиение X' называется подразбиением разбиения
X, если Л С Л', то есть если разбиение X' мож.но получить
из разбиения X добавлением новых точек.
2°. Для произвольного разбиения Л и произвольного его подразбиения
Л' справедливы неравенства: L{f; X) < L(f; Л'), U{f\ X) > U{f; X').
\ Достаточно рассмотреть случай, когда разбиение Л' отличается от
разбиения Л = {xo,Xi,..., х„} добавлением одной точки х'. Пусть точка
х' принадлежит отрезку [xk,xk+1], точнее Xfc < х' < Xk+i- Тогда

204 Глава 6. Интеграл Римаяа
; Л) = т0Дх0 + ■ • • + mfc_i Axfc_i + mkAxk + mk+1Axk+1 +
L(f; A') = ШоДхо + ■ • ■ + mk-i6.xk-i + m'k{x' - xk) + m'l{xk+i - x')
+mk+1Axk+i + ... + mn_iAin_b
где m'k := inf / > mk, m'l := inf f > mk. Отсюда имеем нера-
[«*.«'] [x'.Xk + l]
венства Ь(/;Л') - Ь(/;Л) = т'к(х' - хк) + m'l(xk+i - х') - ткАхк >
> mfc(x' — Xfc) +mfc(xfc+i — at') — тпкАхк = 0. Доказательство для верхних
сумм Дарбу аналогично. J
5°. Для произвольных разбиений Лх и Л2 отрезка [a,b] справедливо
неравенство L(f; Ai) < U(f\ Л2).
[ Положим Л' := Л1 U Лг. Тогда Л' есть подразбиение каждого из раз-
разбиений Aj и А2. Поэтому на основании 1° и 2° имеем
Hf; АО < L(f; A') < U(f; A') < U(f; A2). J
Следствие 1. Для любой ограниченной на отрезке [а,Ь]
функции f J f(x) dx < f f(x) dx.
\ Согласно определению верхнего интеграла из 3° для любого фик-
фиксированного Aj имеем L(/;Aj) < inf У(/; Лг) = / f(x)dx, отсюда
dx = eupL(/;A1)<;/(x)dx. J
Упразднение 8. Пусть а > 0 и /3 G R. Доказать следующие равен-
равенства L{af+p; A) = aL(/; А)+0(Ь-о); U{af+p; A) = aU(f; \)+0{Ь-а).
Упраэюнение 9. Пусть /(х) < д{х), х £ [а,Ь]. Доказать, что для
любого разбиения А = А([а,Ь]) выполняются следующие неравенства
L{f;X)<L{g;X); U(f;A) < U(g;A).
Упражнение 10. Доказать, что для любого разбиения А :
+ д; А) > L(f; А) + Цд; А); С7(/ + 5; А) < U(f; A) + U(g; A).
Упражнение 11. Пусть / е С([а,Ь]). Доказать, что для каждого
разбиения нижняя и верхняя суммы Дарбу для / являются интегральными
суммами. Доказать также, что аналогичным свойством обладают суммы
Дарбу для монотонной функции.
Упражнение 12. Пусть / G С([а,Ъ}). Для х G (а,Ь] пу^ть .F(x) и С?(х)
есть соответственно нижний и верхний интегралы от функции по отрезку
[а, х], положим также F(a) := 0, G(a) := 0. Доказать, что существуют

6.3. Критерий интегрируемости 205
производные F' и G1 на [а,Ь], причём F'(x) = G'{x) = f{x), x G [a,b].
Рассматривая функцию G - F доказать, что / € R([a,b]).
Указание. По свойству 2° имеем для Дх > 0 : ^(х + Дх) < ^(х) +
+ max f(u)Ax, F(x + Дх) > ^(х) + min /(и)Дх. Аналогичные
неравенства верны и для G.
6.3 Критерий интегрируемости
6.3.1 Необходимое и достаточное условие
интегрируемости функции
Теорема 1. / G Д([а,Ь]) <=> Ve>0 ЗЛ = Л([а,Ь]):
\ Необходимость. Пусть / G R([a,b], то есть J f(x)dx = j f(x)dx =
ь
= f f(x)dx. Предположим, что произвольное е > 0 задано. Согласно
а
определению нижнего интеграла 3 Ai = Aj([a, b]) : J f(x)dx — e/2 <
< L(/;Ai). Аналогично по определению верхнего интеграла получим
3A2 = A2([a,b]) : U(f;X2) < j f(x)dx + e/2.
Пусть A := Ai U A2, А есть подразбиение каждого из разбиений Ai
1м А2. С учетом свойств 1° и 2° сумм Дарбу для разбиения А имеем
и- —
f/ /(x) dx - ~ < L{f; Ax) < L(f; A) < U(f; A) < U(f; А2) < j f(x) dx + £-.
Таким образом, Ve > 0 3A:=AiL)A2: U{f; A) - L(/; A) < е.
Достаточность. По определению нижнего и верхнего интегралов
и следствию 1 VA : L(/;A) < Jf(x)dx < Jf{x)dx < U{f;\), сле-
следовательно VA : 0 < //(x)dx - Jf{x)dx < U{f;\) - Ь(/;А). По
условию теоремы 1 Ve > О ЗА : U(f;\) — L(/;A) < е. Таким
образом, Ve > 0 : 0 < J f(x)dx — J f(x)dx < e. Следовательно,
//(x)dx = //(x)dx и функция / G Щ[а,Ь]). J
Замечание 1. Следует обратить внимание на то, что существен-
существенная для дальнейшего теорема 1 есть следствие определения интеграла

206 Глава 6. Интеграл Римана
и свойств сумм Дарбу.
6.3.2 Другая формулировка критерия интегрируемости
Определение 1. Колебанием функции / на отрезке
[а,/3] называется число u/(f, [а,/31) := sup / — inf / > 0.
[а,/3] [°.0]
Упражнение 13. Доказать следующее равенство w(/, [a,/3]) =
= sup{/(x') - /(»») | х' G [а,/3],х" G [а,/3]}.
Для функции / : [а, Ь] —> Д и разбиения Л = {хо, xi,..., х„} положим
""*(/) := w(/, [xfc, xfc+1]), A = 0,1,..., n - 1.
Теорема 2. Справедливо утверж.дение f G R([a,b])
Ve>0 ЭА = А([а,Ь]): Jf uk{f)bxk < e.
fc=0
[ Поскольку для любого разбиения А имеем следующее равенство
U{f\X) - L(f;X) = "ff (Mk(f) - mk(f))Axk = "ff wfc(/)Axfcl то тео-
fc=0 Jfc=0
рема 2 есть переформулировка теоремы 1. J
п-1
Замечание 2. Сумма ]Р о/к(/)Дхк в теореме 2 имеет простой
fc=0
геометрический смысл. Это есть суммарная площадь прямоугольников с
основаниями над [хь, xjt+i], k = 0,1,2,..., п — 1 и высотами u>k{f), к =
0,1, ...,п— 1, которые накрывают график функции /, см. рис. 9 на
следующей странице, на котором накрывающие график прямоугольники
заполнены точками. Для интегрируемой функции график можно накрыть
прямоугольниками упомянутого вида со сколь угодно малой суммарной
площадью.
Упражнение 14- Пусть / G R([a,b]). Доказать, что: а) |/| G R([a,b});
Ь) sin/ G Л([о,Ь]); с) /2 € Я([о,Ь]); d) /+ := max@,/) G Л([о,Ь]);
е) привести пример функции / такой, что |/| G R{[a,b]) и / ^ Д([а, Ь]).
0/(х2)еЯ([0,11)для/еЛ([0,1]).
Упражнение 15. Пусть функции /,р С R([a,b]). Доказать, что функ-
функция (fg) e Л([а,Ь]).
Упражнение 16*. Функция / : [a,b] -> R удовлетворяет условию
Ve>0 3geR{[a,b}) Vx G [a,b] : \f{x) - g{x)\ < e.
Доказать., что / G Л([a, b}). ,

6.4. Классы интегрируемых функций
207
a =
= Ь
Рис. 9.
Упражнение IT. Функция / е R([a,b]) и равна 0 во всех точках
ь
непрерывности на [а,Ь]. Доказать, что f f(x)dx = 0.
6.4 Классы интегрируемых функций
6.4.1 Интегрируемость монотонной функции
Теорема 3. Пусть f : [a,b] -> R — монотонная на
отрезке [а,Ь] функция. Тогда f € R([a,b]).
f Предположим, что / монотонно не убывает на [а,Ь] и что /(а) < f(b).
Используем критерий интегрируемости. Для произвольного заданного
числа е > 0 рассмотрим произвольное разбиение Л отрезка [а, 6] с
размером |Л| < е/(/(Ь) — /(а)). Для такого разбиения имеем
*
[/(/; Л) - L(f; Л) = £ {Мк - тк)Ахк = £ (f{xk+1) - f(xk))&xk <
fc=0 fc=0
fc=0
- f(a)) < e. J
Упражнение 18. Дать геометрическую интерпретацию доказатель-
доказательства теоремы 3 на основе теоремы 2.
14 — 4-1168

208 Глава 6. Интеграл Римана
Упразднение 19. Для произвольной ограниченной на отрезке [а,Ь]
функции / положим д(х) := sup /(u), h(x) := inf /(и); х G [а,Ь].
а<и<х а<и<х
Доказать, что {д, К} С R{[a,b]).
6.4.2 Интегрируемость непрерывной функции
Теорема 4. с{[а,ь\) с Щ[а,щ).
\ Используем критерий интегрируемости. Пусть произвольное число
е > 0 задано. Функция / G С([а, Ь]) по теореме Кантора равномер-
равномерно непрерывна на [а,Ь]. Поэтому для числа {s/(b — а)) > 0 имеем
3 5 > О V {х1, х"} С [а, Ь], |х' - х"| < 6 : |/(х') - Дх")| < ^ .
Для произвольного разбиения Л = Л([а, Ь}) с \Х\ < 5 имеем для каждого
he {0,l,...,n-l} Mk-mk= sup /- inf / = /(х*) - /(х*) < е
в силу второй теоремы Вейерштрасса. При этом {x*,x*} С [xfc,Xfc+i]>
I1* -1*1 < |^| < 5. Таким образом, Ve > 0 3<5 > О VЛ, |Л| < 5 :
U(f; Л) - L(f; Л) = "е (Mfc - тк)Ахк < -±— "ff Axfc = e. J
fc=0 О - а fc=0
Упражнение 20. Пусть / е С([а,Ь]). Доказать, что:
a)/2GH([a,b]); Ь) arctg/6 Д([а,Ь]).
6.4.3 Интегрируемость некоторых разрывных функций
Справедлива следующая теорема.
Теорема 5. Пусть фупкцчмл / : [а,Ь] -> R и точки
{zi,z2)... ,zm} из [a,b] удовлетворяют условиям,: 1) f огра-
ограничена на [а,Ь]; 2) f G C([a,b]\{z1,z2,. ■. ,zm}). Тогда функция
/€Д([а,Ь]).
f Условие 1) означает, что ЭС > 0 Vx G [а,Ъ] : |/(х)| < С. Вос-
Воспользуемся критерием интегрируемости. Пусть произвольное е > 0 за-
задано. Положим 5 := е/A6тС) > 0. Множество [a,b] \ G, где С? :=
m
(J (zfc — S, Zfc +5), либо пусто, либо состоит из конечного числа от-
Срезков. Ниже рассматривается второй случай. По условию 2) функция
', f G C([a, b] \ G). По теореме Кантора для числа е/B(Ь - а)) > 0 суще-
. ствует число 7 > 0 такое, что дх<я любых точек х' и х", принадлежа-
1 гдих одному из составляющих множество [a, b] \ G отрезков и таких, что
|х' - х"| < 7> выполняется неравенство |/(х') — /(х")| < е/B(Ь - а)).

6.5. Интеграл как предел интегральных сумм 209
Пусть теперь А — произвольное разбиение отрезка [a,b], размер
которого |А| < min(E,7)- Для этого разбиения имеем
п-1
k:[xk,xk+1]nG=0 fc:[xfc
E ^+™ E
k:\xktxk+1]r\Gj:<!l
2(^) £- J
Упражнение 21. Доказать, что / e Я([0,1]) для следующих функ-
функций: а) Дх) = [5i], х € [0,1]; b) f(x) = {5i}, x € [0,1]; с) f(x) =
= sin-, ie@,1], /@) = 0; d)/(z) = sign(emi), zG@,l], /@) = 0.
X \ X I
Упражнение 22. Пусть функция / £ Я([а,Ь]), а функция g получает-
получается из / произвольным изменением значений функции / в произвольном
конечном числе произвольных точек на отрезке [а,Ь]. Доказать, что
6.5 Интеграл как предел интегральных сумм
6.5.1 Предел интегральных сумм
п-1
Интегральная сумма S(/;A,{&|A}) = X) /(бОД1*: Аля Функции / :
fc=0
[а,Ь] -> R, разбиения Л = {хо.Хх,... ,х„} и соответствующего этому
разбиению набора {&|Л} была определена в п. 6.2.1, см. также п.
6.1.2. Для определения интегральной суммы ограниченность на [а,Ь]
функции / не нужна.
Определение 1. Число J e R называется пределом
интегральных сумм при |А| -> 0, если Ve>0 35>0 VA,
|А| < 6 V{fc|A} : |S(/; A,«i|A}) - J\ = Ге №ь)Ьхк - J\ < e.
Обозначение: J — lim S(/; A,{
|A|+0
Замечание. Предел интегральных сумм определяется единствен-
единственным образом. Прямое доказательство получается из определения по-
подобно доказательству единственности предела последовательности. Ни-
Ниже доказательство единственности следует из теоремы Дарбу.
Далее используются такие свойства предела интегральных сумм.
14*

210 Глава 6. Интеграл Римана
1°. Если существует lim S(/; А,{&|А}), то для любого с £ R суще-
существует lim S(cf; А, {&|А}) = с lim S(f; X, {^|
2°. Если существуют lim S(f; А,ША}), lim S{g; А,{&|А}), то су-
|А|-+0 | А|—>-0
ществует предел
lim S(/+5;A,{£|A})= lim S(f; A,{fc|A}) + lim S(g; A,{fc
|A|->0 | A]—j-0 | A|—vO
Упражнение 23. Проверить, что S(cf; A, {&|A}) = cS(/; A, {&|
S{f + 3;A,{&|A}) = S(/;A,{fc|A}) + 5(з; A,{£|A}) и доказать свойства
1°и2.°
3°. Для функции / : [а,Ь] —* R существует предел интегральных сумм
lim S(/; А,{&|А}) — J £ R. Тогда функция / ограничена на [a,b].
|А|-»0
f Согласно определению предела интегральных сумм для числа е = 1
В 6 > О VA,|A| < 5 V{£|A} : |S(/; A,{fc|A}) - J\ < 1. Зафиксируем
произвольное разбиение А = {xo,xi,... ,х„} с размером |А| < 8. Для
двух отвечающих разбиению А наборов {&|А} и {^|А}, равных соответ-
соответственно {£o,£i,-.,6:,->£n-i}, {^o.6i---.^fc.---^n-i} с фиксиро-
фиксированным к £ {0,1,2,..., п — 1} и различающихся только точками {^, £J|.} С
[zfc, xk+1], имеем |S(/; A, {^|A}) - S{f; A, {^|A})| < |S(/; A, {^t|A}) - J| +
+|5(/;А,{^|А}) - J| < 2, откуда |(/(ffc) - /(^))Aifc| < 2, и следова-
следовательно |/(&)| = |/F) - /(ft) - /FI < 1/FI +2/Дх*. Фиксируя
значение £*, получаем sup |/(ft)| < |/F)| + 2/Дхь. Таким об-
разом, для каждого к £ {0,1,2,... ,п — 1} функция / ограничена на
отрезке [хь,хь+1], следовательно, функция / ограничена и на [a,b]. J
4°. Если существует предел интегральных сумм lim S(/; A, {&|A}) = J,
|А|-»0
то значение интеграла J можно получить, как предел числовой после-
последовательности.
[ Для каждого п £ N фиксируем некоторое разбиение отрезка [а, Ь]
А™ = {xq.x™, ... ,3wn)}, зти разбиения фиксируются произвольно, ис-
исключая условие |АП| -> 0, п -> оо. Для разбиения А™ фиксируем произ-
произвольно соответствующий ему набор {£™|An}; n £ N. Получим числовую
последовательность
",Ч m(n)—1
"* 5(/;A",{CiA"})= E /(ftn)A^, n £ ЛГ, A)
•j fc=O
сходящуюся к J при п —> оо. J
Упражнение 24- Доказать, что последовательность A) сходится к
числу J.

6.5. Интеграл как предел интегральных сумм 211
6.5.2 Теорема Дарбу
Теорема 6. Справедливо следующее утверэ+сдение:
f £ Щ\а,Ь]) <==> существует lim S(/; А,{&|А}). При этом.
|Л|+0
\ Необходимость. Пусть / G Д([а,Ь]) и произвольное е > 0 зада-
задано. Согласно критерию интегрируемости для числа е/2 имеем 3 Ло =
Л0([а, Ь]) : U(f;\o) - L(/; До) < е/2. Зафиксируем разбиение Ао, пусть
т - число точек разбиения Ао, а число С > О таково, что Vx £ [a,b] :
|/(х)| < С.
Рассмотрим теперь произвольное разбиение А с размером |А| <
5 := е/{8Ст), пусть также А' := A U Ао- С учетом свойств сумм Дарбу
имеем [/(/; А) = [/(/; А') + ([/(/; А) - [/(/; А')) < U{f; Ао) + (U(f; A) -
~U{f\ А')) < U{f; Ао) + 2Ст\\\ < U(f; Ао) + е/4. Следовательно
ТГо) + |. A)
Аналогично доказывается, что
L(/;A)>L(/;A0)-|. B)
Из A) и B) имеем VA,|A| < 8 V{^|A} : L(/;A0)-e/4< L(f; A) <
< 5(/;А,{^|А}) < [/(/;A) < [/(/; Ao) + е/4. Кроме того, согласно
ь
определению интеграла для любого A L(/;A) < J f(x)dx < [/(/;A).
а
Таким образом, VA,|A| < 5 V{&|A} : \S{f; A,{^|A}) - J f{x) dx\ <
<[/(/; Ao)-L(/;Ao)+e/2<e.
Достаточность. Предположим теперь, что существует предел
lim S(/; А,{&|А}) = J- Согласно свойству 3° п. 6.5.1 функция / огра-
ничена на отрезке [а,Ь}. Для доказательства того, что / G Д([а,Ь]) ис-
используем критерий интегрируемости. Пусть произвольное е > 0 зада-
задано. По определению предела интегральных сумм для числа е/4 име-
ем 3 5 > О VA,|A| < 5 V{£,|A} : \S{f; A,{£|A}) - J| < е/4. Пусть
A = {xo, xi,..., х„}. По теореме о характеризации точных граней 3 x'k G
[хк,хк+1]: f(x'k) > Мк - е/D(Ь - а)); 3 х'^ £ [xfc,xfc+1] : Цх1') <
<тк + е/D(Ь - а)). Тогда
U{f, А) = "Е МкАхк < "ff f(x'k)Axk + - < J + |;
fc=0 fc=O 4 ^
' Hf, A) = "e mkAxk > "e /(x'DAxfc - £ > J - £
; fc=o fc=o * ^

212 Глава 6. Интеграл Римана
откуда имеем [/(/; Л) - L(f\ Л) < е. J
Замечание 1. Согласно теореме Дарбу для функции / £ Д([а,Ь])
ь
интеграл Jf(x)dx является пределом интегральных сумм. Поэтому
а
свойство 4° п. 6.5.1 указывает путь вычисления интеграла, как пока-
показывают простейшие примеры, этот путь является технически сложным и
редко осуществим эффективно. Эффективным средством вычисления
интеграла является формула Ньютона-Лейбница, приводимая ниже.
Рассмотрим примеры вычисления интегралов на основе свойства 4°
п. 6.5.1.
1
Примеры. 1. Вычислим интеграл fxdx.
о
[ Функция /(х) = х, х £ [0,1] непрерывна на [0,1] и, следовательно,
/ £ Я([0,1]). По теореме Дарбу искомый интеграл есть предел инте-
интегральных сумм и можно воспользоваться свойством 4° п. 6.5.1.
Для п £ N пусть Л" = (о, -,-,...,-) и £? = - для к £
inn п i п
{0,1,2, ...,п - 1}. Тогда |А"| -> 0, пчоои
fc=O fc=O
при n —¥ oo. Следовательно, f x dx — — . J
о 2
l
2. Вычислим /x2dx.
0
f Функция /(x) = x2, x £ [0,1] непрерывна на отрезке [0,1], следова-
следовательно / £ -R([0,1]), и по теореме Дарбу искомый интеграл есть предел
интегральных сумм. Воспользуемся свойством 4° п. 6.5.1.
Для п £ N пусть А" = /о, -,-,...,- } и для к £ {0,1,2,... ,п
Inn п j
1} пусть с? = д —II — I Ч— • -+- . Заметим, что
Тогда |АП| -> 0, пчоои
п-1
К—О
fc + 1 _^
п

6.5. Интеграл как предел интегральных сумм 213
fc\3
Этот интеграл, точнее соответствующую площадь криволинейной
трапеции, впервые вычислил Архимед. J
3. Представим предел следующей последовательности чисел
г 1 1 1 ,1
^ — н + ... Ч : п > 1 ^ в виде интеграла.
lnn + 1 2n - 1 ~ J
f Функция /(х) = 1/A + х), х £ [0,1] непрерывна на [0,1], а потому
1 fa
f £ -R([0,1]). По теореме Дарбу интеграл J := J- есть предел
о 1 + х
интегральных сумм. Воспользуемся свойством 4° п. 6.5.1. Для п £ N
пусть Л" = (о, - , - ,..., - ) и $? = - для к £ {0,1,2,... ,п - 1}. Тогда
inn п ) п
|Л»| -> 0, п -> с» и S(/ А»{€Г|А»}) "^ ^ ^ ^
fc=0 [ , 1 " fc=0
,./11 1 \ } di
при п -> оо. Потому hm — Ч Ч-... Ч- I = I •
Г ' п-+оо \п П + 1 2п-1/ о 1 + 1
Замечание 2. Аналогично определению предела интегральных
п-1
сумм определяются пределы lim V /(ffc)sinДхь, lim L(/;A)
1Л1-+о jt=o 1Л1-*°
м т. п. Например,
lim L(/;A) = J <^> Ve > 0 3,5 > О V А, |А| < E : \L(f;\)-J\ < e.
|Aj>0
Упражнение 25. Доказать неравенство B) в теореме Дарбу.
. Упражнение 26. Функция / : [а,Ь] —» R ограничена на [а,Ь] и число
п-1
о > 0. Доказать, что lim V f(^k)Axl+a = 0.
|Л|—>0 fc=0
Упражнение 27. Для функции / £ _R([a,b]) найти пределы:
а) lim "e f(tk)smAxk; b) lim "е ЬA + f(b)bxk).
1>1-+о ь=о 1А1->0 ь=о
Упражнение 28. Пусть / £ С([о,Ь]) и /(х) > 0, х £ [а,Ь]. Найти
предел lim "ff /(^)Alfc-
l*l-+o fc=0
Упрасмснение 2Р. Для функций {/,д} С Я([а,Ь]) вычислить предел
п-1
lim E f{ik)g{Vk)Axk, где {&} и {ту*;} — наборы точек, отвечающие
1Л1->° ь=о
разбиению А.

214 Г л а в а 6. Интеграл Римана
Упражнение 30. Пусть fug — функции из упражнения 22. Дока-
ь ь
зать, что f f(x)dx = Jg(x)dx. Таким образом, интеграл не зависит от
а а
значений функции в любом конечном наборе точек.
Упражнение 31. Доказать для ограниченной на [а, Ь] функции /
равенства: a) lim L(/; A) = //(x) dx; b) lim U{f; A) = J f(x)dx.
Упражнение 32. Неравенство Эрмита - Адамара. Пусть
/ — выпуклая вниз на (а,/3) функция и [а,Ь] С (<*,/3)- Тогда
6.6 Свойства интеграла Римана
6.6.1 Линейность и аддитивность интеграла
С помощью теоремы Дарбу простые свойства интегральных сумм пе-
переносятся на интеграл.
1°. Если / е Щ[а,Ь\) и с £ Я, то (с/) е Щ[а,Ъ}) и
ь ь
fcf{x)dx = cff(x)dx.
а а
\ Заметить, что всегда S(cf; A,{&|A}) = cS(f; Л, {&|А}) и дважды вос-
воспользоваться теоремой Дарбу. J
2°. Если {/,з} С Щ[а,Ь]), то (f + g) € Ща,Ъ}) и
+ 5(х)) dx = J f{x) dx + }д(х) dx.
Г Заметить, что S(f + д; А,{(^|А}) = S(/; A,{(^|A}) + S(g; A,{^|A}), и
трижды использовать теорему Дарбу. J
1
Упражнение 33. Вычислить интеграл /(х2 + Зх + 2) dx.
о
3°. Если / е Я([а,Ь]) и с £ (о,Ь), то / £ Я([а,с]) и / £ Я([с,Ь]), причём
\ I. Докажем сначала более общее утверждение, представляющее са-
самостоятельный интерес:

6S. Свойства интеграла Римана 215
для любой ограниченной на отрезке [а, Ь] функции / справедливы сле-
следующие равенства для нижних и верхних интегралов
dx, A)
jfix)dx = ffix)dx + jfix)dx, B)
а а с
Доказательства зтих равенств аналогичны, поэтому докажем только ра-
равенство B). Пусть произвольное е > 0 задано. По определению верх-
верхнего интеграла имеем 3 Ai = Ai([a,c]) : Uif;\\) < //(x)dx + - и
о 2
3 Аг = А2([с, Ь]) : [/(/; А2) < / /(х) dx + - . Поэтому для разбиения А =
с ^
А([а, Ь]) := Ах U А2 получаем / /(*) dx < U(f; A) = U(f; Xi) + U(f; A2) <
a
с Ь Ь
< //(x)dx + //(x)dx + e. Таким образом, Ve > 0 : .//(x)dx <
ас а
с Ь
<< j fix) dx + f f[x) dx + e, откуда
a c
//(x)dx<//(x)dx + //(x)dx. C)
а а с
Аналогично, для произвольного е > О ЗА = А([а,Ь]) : [7(/;А) <
ь
j fix) dx + е. Пусть теперь А' := A U {с}, Ai = А' П [а, с], А2 = А' П [с, Ь].
а
J
Тогда / /(х) dx + J f(x) dx < U(f; \r) + [/(/; A2) = U{f; A') < U(f; A) <
a c
b
< f f(x) dx + e. Отсюда
a ч
ff(x)dx + Jf(x)dx<jf(x)dx. D)
аса
Теперь из неравенств C) и D) имеем равенство B).
II. Пусть равенства A) и B) имеют место. Согласно условию / €
-R([a,b]) левые части равенств A) и B) равны, кроме того, всегда име-
ем / f{x) dx<f f{x) dx, f fix) dx<] fix) dx. Поэтому / /(x) dx =
о а с с а
£ Ь Ь
= J fix) dx, f fix) dx — f fix) dx и все утверждения 3° доказаны. J
а с с

216 Глава 6. Интеграл Римана
Упражнение 34- Доказать равенство A).
Упражнение 35. Доказать, что / G Щ[а,Ь}), если / £ Я([а, с]) и
/ея[с,ь]).
Упражнение 36. Доказать, что функция /(х) = [х], х £ [0,5/2]
5/2
интегрируема по отрезку [0,5/2] и вычислить интеграл f [x] dx.
о
6.6.2 Неравенства и теорема о среднем значении
Следующие факты постоянно используются в математических рассуж-
рассуждениях, связанных с интегралами.
1°. Пусть {f,g} С Л([о,Ь]) и /(х) < д(х), х £ [а,Ь]. Тогда справедливо
ь ь
неравенство J f(x) dx < J g(x) dx.
а а
Ь
\ Для произвольного разбиения Л имеем L(/; А) < L(g; А) < J g(x) dx =
ь ъ ъ ъ
= fg(x)dx, откуда ff(x)dx — J/(x)dx < fg(x)dx по определению
а а о а
нижнего и верхнего интегралов, интегрируемости функций /ид. J
2°. Пусть / € Я([а,Ь]) и m := inf /, M := sup/. Тогда справедливы
[».Ь] [а,Ь]
Ь
неравенства m(b - а) < J }{x) dx < М{Ъ - а).
а
f Воспользоваться неравенствами m < /(х) < М, х £ [а,Ь], свойством
1° и примером 2 п. 6.2.2. J
Упражнение 37. Если / £ Д([а,Ь]) и Vx £ [о,Ь] : /(х) > 0, то
ь
J f(x) dx > 0. Доказать это утверждение.
а
Упражнение 38. Пусть / £ Д([0,1]) и Vx € [0,1] : }{х) - х > 0.
1 1
Доказать, что / /(х) dx > - .
о 2
3°. Теорема о среднем значении. Для функции / € С([а,Ь\)
,BB€[a,b]: f f{x)dx = f(9)(b-a).
а
1 Ь
[ Согласно свойству 2° m < L := т Г /(х) dx < М. Из условия / £
! о-а о
'С([а,Ь]) следует согласно второй теореме Вейерштрасса 3{х,,х*} С

6.6. Свойства интеграла Римана 2\7_
[a,b] : m = f{xt), М = f{x*). Следовательно, /(х*) < L < f(x*)
и по теореме Коши о промежуточном значении существует число в,
лежащее на отрезке с концами х« и х*, для которого f(9) = L. J
Упражнение 39. Пусть функция / удовлетворяет таким условиям:
1) / £ С([а,Ъ\); 2) Vx £ [а,Ъ] : Дх) > 0; 3) Зх0 е [а,Ь] : /(х0) > 0.
ь
Доказать, что J f(x)dx > 0.
а
Упражнение 40- Пусть {f,g} С R([a,b}) и m := inf/, M :=
[о,Ь]
sup/; д(х) > 0, х £ [а,Ь]. Доказать, что {fg) G R([a,b}) и имеют место
Jb]
ь ь ь
ь ь ь
неравенства m J g(x) dx < f f(x)g(x)dx < M J g(x)dx.
a a a
Упражнение 1^1. Пусть / £ C([a, Ь]), д £ -R([a,b]) и д{х) > 0,
,x £ [о,Ь]. Доказать, что 3 в £ [a,b] : }f(x)g(x)dx = f{6)fg{x)dx. .
Упражнение 4%- Для функций {f,g} С R([a,b\) вычислить предел
lim E /F0 / 9{x)dx.
1*И° fc=O xfc
^°. Неравенство для модуля интеграла. Для функции / €
Я([а, Ь]) имеем |/| £ Я([а, Ь]) и I / /(х) dx < / |/(х)| dx.
I а а
[ Интегрируемость |/| есть следствие интегрируемости /, критерия ин-
интегрируемости и оценки Шк{\}\) — sup{|/(x')| - |/(х")| | {х',х"} С
[хк>хк+1]} < eup{|/(z')-/(*")| | {х',х"} С [xk,xk+l)}=wk(f). Неравен-
Неравенство для модуля интеграла является следствием неравенств Vx £ [a,b] :
-\f{x)\ < f{x) < |/(x)|. и свойства 1°. J
Упражнение 43. Для функции / £ Я([0,1]) доказать равенство
lim / /(x)dx = //(x)dx.
n~~>°° l/n 0
Упражнение 44- Доказать, что lim Г sin" x da: = 0.
п—voo _
7Г
П—УОО
Упражнение 45. Для функции / £ С([0,1]) вычислить предел:
a) lim //(xn)dx; b) Urn //(xn(l - x)n) dx.
Упражнение 46- Вычислить предел:

218 Глава 6. Интеграл Римана
( /+1 xdx \ / 32р xdx
a) lim n4 Г ; b) hm п3 Г -
Упражнение £7. Неравенство Коши. Для {f,g} С R([a,b])
,ъ \2 ь ь
справедливо неравенство (ff(x)g{x) dx) < J /2(x)dx J g2{x)dx.
a 'a a
Упражнение J^8. Функция / £ C([a,b}) и Vg £ C([a,b}) :
ь
f f(x)g(x)dx = 0. Доказать, что /(х) = 0, x £ [a,b].
a
b
Упражнение J^9. Функция / £ C([a,b}) и ff(x)dx = 0. Доказать
\I ь
неравенство Jf2(x)dx < -mM(b — a), m=min/, M = max/.
Упражнение 50. Для {/,g} С R([a,b}) положим для каждого х £
[а,Ь] h(x) := min(/(x),g(x)); Я(х) := max(/(x),g(x)). Доказать, что
{h,H}CR([a,b}).
Упражнение 51*. Для / £ С([а,Ь]) доказать равенство
( Л \
hm Г fzn{x)dx\ =max|/|.
6.6.3 Интеграл как функция верхнего предела
а
Определение 1. Положим V/ : Jf(x)dx := 0. Длл
а
функции f е Я([а,Ь]), где а < Ь, положим.
Sf{x)dx:=-}f(x)dx.
Ъ а
Пусть / £ Я([а, Ь]). Согласно свойству 3° п. 6.6.1 / £ Я([а,х]) для
х
любого х £ (о,Ь]. Определим функцию <р, положив <р(х) := J f(u)du,
а
х £ [a,b]. Заметим, что ip(a) = 0.
Теорема 7. Если f £ R([a, b]), то <р £ С([а, Ь]).
f Для любых {х',х"} С [а, Ь] имеем такое неравенство |у(х') - у(х")| =
Jf(u)du-ff(u)du
ff(u)du
< sup |/| -|x'-x"|. Следователь-
, но, функция / равномерно непрерывна на [а, Ь]. J

6.7. Формула Ньютона-Лейбница и следствия из неё 219
i х
, Упражнение 52. Построить график функции <р(х) = f sign и du,
-i
х € [—1,1] и проверить, что ip'_@) = —1, </з+@) = 1. Таким образом,
производная </з'@) не существует.
Теорема 8. Если / € С([а,Ь]), то <р € Сх{[а,Ь]), причём
Vx€[o,b]: р'(х) = /(х).
\ Пусть произвольное х € [а,Ь] фиксировано и Да; таково, что (х + Дх) €
X' I
[a, bj, Дх ф 0. Поскольку — ~—r^—- = — / /(u)du, то со-
согласно теореме о среднем значении
Дх
где значение в(х, Дх) лежит между х и х + Дх. Поскольку / непре-
непрерывна в точке х, то существует предел /@(х,Дх)) —> /(х) при Дх —> 0
и, следовательно, существует предел lim — = f(x)-
* - ■" Ах
Таким образом, <р'(х) = /(х), х € [a,b]. J
' Упражнение 53. Найти предел:
/X \ / X \
A /'uarctgu \ / 1 Г и2 \
' a) lim - / — du ; b) hm -г / (eu - 1) du \ .
x^+oo Ix) 1 + U ) x^O 1 X3 J j
\ 0 / \ 0 /
Указание. Использовать правило Лопиталя.
Теорема 9. (О существовании примитивной). Фун-
Функция f 6 С([а,Ь]) имеет примитивную на [а,Ь].
! Г Согласно теореме 2 примитивной для / на [а, Ь] является функция <р.\
Упражнение 54- Доказать, что функция / € С([0,+оо) имеет при-
примитивную на [0,+оо).
6.7 Формула Ньютона-Лейбница и следствия
из неё
6.7.1 Основная формула интегрального исчисления
Теорема 10. (Формула Ньютона-Лейбница). Пред-
Предположим, что функция f удовлетворяет условиям,: 1)
f € Н([а,Ь]); 2) f имеет примитивную на [а,Ь]. Пусть G —
произвольная примитивная функции / на отрезке [а, Ь].
Тогда / /(х) dx = G{b) - G{a).

220 Глава 6. Интеграл Римана
[ Первое доказательство для / £ С([а, Ь]). Функция
tp{x) = ff{u)du,xe[a,b] A)
-^ о
согласно теореме 9 п. 6.6.3 есть примитивная функции / на [а,Ь]. При
этом с учётом результатов п. 5.1.1 гл. 5
3CeRVxe[a,b]: G(x) = <p{x) + C. B)
Поскольку <р(а) = 0, то G(a) = С. Положив в B) х = Ъ получим
G{b) = </?(Ь) + G(a), откуда tp(b) — G(b) — G(a), и с учётом A) получаем
}f(u)du = G(b)-G(a).
а
Второе доказательство в общем случае. Пусть Л = {хо, xi,...,
хп} — произвольное разбиение отрезка [а,Ь]. Сначала заметим, что
G(b) - G(a) = C)
= (G(xi) - G(x0)) + (G(x2) - G(xi)) + ... + (G(xn) - G(in_i)),
затем к каждой разности в правой части C) применим теорему Лагран-
жа. Тогда G{b) - G{a) = G'{to)&xo + G'(fi)An + ■ • • + G'(^n_!)Axn_i =
= /(^o)Aa:o + /F)Дал + ■ • ■ + /F.-i)Axn_i, где $k € [xk,xk+1], к €
{0,1,..., n — 1}. Таким образом,
G(b)-G(a) = S(/; A, {fc|A}), D)
и согласно теореме Дарбу из D) при |А| —> 0 получим следующее ра-
ь
венство G(b) - G(a) = //(х) dx. J
a
х=Ь
Замечание. Часто обозначают G(x) := G(b) — G(a).
I
I=O
Упражнение 55. Пусть / € C^Ql.+oo)). Доказать следующее ра-
X
венство f[u]f'(u)du — [х]/(х) - J2 /(*)> х ^ 1| гДе W "~ Целая
1 fc:l<fc<x
часть числа а.
Упражнение 56. Пусть / : R —> R — периодическая с периодом
Т функция, которая имеет примитивную на R. Тогда для любой прими-
примитивной G функции /най ЗС€Й Vx€il: G(x + T) = G(x) + С. В
частности, V х € Н : G{x + T)- G(x) = G(T) - G@).
Указание. Заметить, что функции G(-) и G(- +T) являются прими-
примитивными функции / на R.
Упражнение 57. Функция / € C(R) и периодична с периодом Т.
о+Г Т
Доказать, что Уа€Я: / f(x)dx = f f{x)dx.
а О

6.7. Формула Ньютона-Лейбница и следствия из неё 221
Пример. Формула Лейбница. Пусть функция / : R -> R имеет
примитивную на Я и интегрируема по Риману на каждом конечном
отрезке, а функции a,b : R —> R дифференцируемы на R. Тогда
Ь(х)
£ I f(u) du = f(b(x))b'(x) - f(a(x))a'(x), x € R.
a(x)
[ Пусть G — некоторая примитивная функции / на R. По формуле
Ньютона-Лейбница
;'; / f(u) du = G(b(x)) - G(a(x)), x € R, E)
причём правая часть E) имеет производную, которая равна по цеп-
цепному правилу £ (G{b{x)) - G{a{x))) = G'(b(x))b'(x) - G'(a(x))a'(x) =
= ДЬ(х))Ь'(х) -/(a(x))a'(x), x € R. J
6.7.2 Формулы замены переменной и интегрирования
по частям
Теорема 11. Предположим, что : 1) f € С {{А, В)); 2)
и€С1[[а,0\); 3) и([а,/3}) С (А,Б).
/3 и(/3)
Тогда справедлива формула f f(u(t))u'(t)dt = f f{x)dx.
f Функция / непрерывна на отрезке с концами u(a) и и(/3), поэтому /
имеет примитивную на этом отрезке. Пусть G — некоторая примитивная
для /, тогда по формуле Ньютона-Лейбница
«(/3)
/ f(x)dx = G(u(C))-G(u(a)). A)
u(a)
Кроме того, функция G(u) есть примитивная функции /(u)u' на отрез-
отрезке [а,/?], причем (/(u)u') € С{[а,C]). Поэтому по формуле Ньютона-
Лейбница имеем
/ f(u(t))u'(t) dt = G(u(p)) - G(u(a)). B)
Из равенств A) и B) следует утверждение теоремы 11. J
Упражнение 58. Пусть a > 0, g : [0, a] -» [0,+оо) и g € C([0,a]),
о /t \P-1 /о \Р
р > 1. Доказать равенства: а) р f g(t) I f g(s)ds I dt = I f g(s)ds I ;
о \o У \o У

222 Глава 6. Интеграл Римана
Ь) f f^ dt = \n(l +fg(s)ds); с) /cos(ff(s)ds)f(t)dt =
1 + fg{s)ds
0
= sm(/f(s)ds); d)/exp(//(s)ds)/(i)d* = exp(//(s)ds)~l.
i
55. Пусть а > 0. Доказать, что /
/ .
_i ax + 1 5
Пример. 1. Решение функционального уравнения Когии
в классе локально интегрируемых по Риману функций.
Определим функцию / : R -» R, которая интегрируема по каждому
конечному отрезку и такую, что
У{х,у}сЯ: f(x + у) = f(x) + /(у). C)
f Зафиксируем в равенстве C) произвольное значение х и полученное
равенство проинтегрируем по у по отрезку [0,1], получим равенство
1 1
/ /(х + y)dy — f{x) + С, С := / f{y) dy, которое после замены пере-
о о
менной в интеграле примет вид
i+i
f №& = f{x) + C, D)
X
здесь х G R. По теореме 7 п. 6.6.3 интеграл в D) есть непрерывная
функция от х € -R, поэтому в силу равенства D) функция / € C{R).
Тогда по теореме 8 п. 6.6.3 интеграл в D) есть функция, имеющая про-
производную для х G R, следовательно функция / имеет производную /' на
R. По формуле Лейбница из D) имеем /(х + 1) — /(х) = f'(x), х € -R,
откуда с учетом C) следует, что /A) = f'{x), x € R. Следовательно,
/(х) = /(l)x+L, х € R с некоторым числом L £ R. Число L — 0, так как
при х = 1 имеем /A) = /A) + L. Окончательно, /(х) = /A)х, х € -R. J
Теорема 12. Пусть {u,v}£ C^Qa.b]).
ъ ъ
Тогда / u(x)r/(x) dx = и(Ь)«(Ь) - u(o)«(a) - / u'(x)v{x) dx.
a a
|" Поскольку функция uv есть примитивная для суммы uv' + u'v на [a, b],
ь
то по формуле Ньютона-Лейбница имеем /(u(x)v'(x) + u'{x)v{x))dx =
a
= u(b)vF) - u(a)v(a), откуда с учетом свойства 2° п. 6.6.1 получим
нужную формулу. J
ж/2 п/2
Пример. 2. Вычислим интеграл In = f sin" x dx = f cos" x dx для
ne(JVu{o}). ° .

6.7. Формула Ньютона-Лейбница и следствия из неё 223
[ При п > 2 применим теорему 12 к интегралу 1п
sin"! = и(х); sinx = r/(x)
(п — 1) sin"" х cos x = u'(x); - cos x = v(
x=*/2
In = f sin" x dx =
= - sin" x x cos x
1=0
+ (n-l) / sin" 2 x cos2 xdz =
5Г/2
= (n - 1) / sin" x(l - sin2 x) dx = (n- l)Gn_2 - Л»).
0
Поэтому In = In-2> ti > 2. Поскольку интегралы Jo = — и
n 2
/
= — COS X
= 1,то
1=0
_ Bfc)!! .
Bfe)!! ' 2 '
Здесь для к > 1 использованы обозначения Bfc)!! := 2 ■ 4 ■ 6 • ... • Bfc);
B* + l)!!:=l-3-5-...-BJfe+l). • J
Замечание. Формула Валлиса. Поскольку имеют место не-
неравенства 7гп+1 < hn < hn-i, n > 1, то из формул E) имеем
Bп)!! Bп-1)!! тг Bп - 2)!!
< <
Bn+l)!! Bn)!! 2 Bn — 1)!!
откуда получаем такие неравенства для числа 7г/2
Bп)!! \2 1 т _
2п + 1 2
причём разность между правой и левой частями неравенств F) равна
2га - 1)!! ) 2п{2п +1) 2 2га '
.Поэтому существует предел
Bп)!! \2 1 тг
Равенство G) известно как формула Валлиса.
Упражнение 60. Пусть / £ Я([а,Ь]). Доказать, что:
а) / Дх) dx = ff(a + b-x) dx; b) / f(x) dx = /'/(с + x) dx, с € R.
а а а а—с
15 — 4-1168

224 Глава 6. Интеграл Римана
Упражнение 61. функция F € С([а, Ь]) и для некоторого разбиения
А = {х0, xi,..., хп} отрезка [а, Ь] для каждого к G {0,1,..., п - 1} удо-
удовлетворяет условиям: 1) F £ C1((xfc,Xfc+i)); 2) существуют конечные
пределы lim F'(x), lim F'lx). Доказать обобщённую
Х-УХк,Х>Хк X—>Xfc+1,X<Xj,+ l
b
формулу Ньютона-Лейбница / ^'(х) dx = F{b) - F(a).
а
Указание. См. упр. 22 и 30.
Упражнение 62. Для функций и и г», удовлетворяющих условиям
предыдущего упражнения на функцию F, доказать правило интегриро-
интегрирования по частям.
1
Упражнение 63. Вычислить предел : a) lim. f exxndx;
n->oo 0
/ 1 x fexxn+1dx
/ l \ J l Re>
b) lim [nfexxndx); c) lim ~ ; d) lim Г dx;
) lim //(x")dx, f) lim fn/x"/(x)dxV /€C([0,l]).
п-юо 0 n-юо у 0 у
6.7.3 Формула Тейлора с остаточным членом
в интегральной форме
Теорема 13. Для п е (JVU{0}) пусть / G С(п+1)((а,/?)).
Тогда для любых а £ (а,/3) и х € (а,/?) справедливо равен-
равенство
n!
[ Для фиксированного х € (а,/3) рассмотрим функцию

6.8. Предельный переход под знаком интеграла 225
для s G (а,/3). Для функции g имеем д(х) — /(х) и
•*<-«■
Из формулы Ньютона-Лейбница имеем равенство д(х) — у(а) =
X
Jg'{s)ds, которое совпадает с равенством теоремы. J
а
Упражнение 64- С помощью теоремы 13 доказать формулу Тей-
Тейлора с остаточным членом в форме Лагранжа.
Упражнение 65. Доказать, что при условиях теоремы 13 для любых
{а,Ъ,х} С (а,/3) справедливо равенство
i ±
п- a k=Q "■■
Упражнение 66. Функции и и v имеют примитивные U и V на [а, Ь]
соответственно, причём (uV + Uv) € Д([о,Ь]). Доказать, что {uV) €
Л[а, Ь]) тогда и только тогда, когда (Uv) £ R[a, b]), при этом справедли-
ь ь
во равенство / U(x)v(x) dx = u(b)v(b) - u(a)v(a) - J u(x)V(x) dx.
6.8 Предельный переход под знаком
интеграла
6.8.1 Поточечная и равномерная сходимость
последовательности функций
Пусть ЛСД/: Л->Яи/п: А-> R, п£ N.
Определение 1. Последовательность функций {/„}
хсходитсл поточечно на м.нож.естве А к функции /, если
Vx G А : /п(а;) —► /(х), п —у оо.
|Яримеры. 1. Пусть Л = [0,1]; /„(х) = хп, х € [0,1], п > 1; /(х) = О,
х G [0,1), /A) = 1. Последовательность {/„ | rt > 1} сходится к /
поточечно на [0,1].
J 2. Пусть А = R, /(х) =0, х € Я; /„(х) = 0, х < п, /(х) = 1, х >
п; п > 1. Тогда {/п | п > 1} сходится к / поточечно на Я.
15*

226 Глава 6. Интеграл Римана
3. Пусть А = [0,1]; /(х) = О, х € [0,1]. Рассмотрим последователь-
последовательность /п(х) = 0, xG([0,l]\[l/n,2/n]), /(x) = n2, xG[l/n,2/n]; n > 1.
Последовательность {/„ | п > 1} сходится к / поточечно на [0,1].
Определение 2. Последовательность функций {/„}
сходится равномерно на множестве А к функции /, ес-
/iuVe>0 3NeN Vn>N Vx € A : |/n(x) -/(z)| < e.
Замечания. 1. Условие определения 2 может быть записано в
следующей равносильной форме dn := sup |/n(x) — /(х)| —> 0, n —> со,
А
удобной для практического исследования равномерной сходимости.
2. Из равномерной на множестве сходимости следует поточечная на
множестве сходимость. Обратное утверждение неверно. Так, в приме-
примерах 1 — 3 равномерной сходимости нет. Действительно, в примерах 1 и
2 dn = 1, п > 1, а в примере 3 dn = п2, п > 1.
6.8.2 Теорема о предельном переходе
Сначала докажем лемму о том, что равномерный на отрезке предел
интегрируемых функций есть интегрируемая функция.
Лемма 1. Предположим, что выполнены условия: 1)
Vn G N : fn£ R([a,b]); 2) последовательность {/„ | п > 1}
сходится равномерно на [а, Ь] к некоторой функции / :
[а,Ь] -> R. Тогда f € Щ[а,Ъ]).
[ Используем критерий интегрируемости. Пусть е > 0 задано. Согласно
условию 2) леммы
3N£N Vx€[a,b] : \fN(x)-f{x)\<-^±-^ «=>
-i^)</(x)</W(x)+i^y. A)
Теперь зафиксируем N в соотношении A). Так как /дг € Н([а,Ь]), то
3 А : U(fN] A) - L(ftr; A) = "^ (Mk(fN) ~ mk(fN))Axk < |.
fc=0 г
Из равенства A) для каждого к, 0 < к < п — 1, имеем неравенства
mk(f) > mk(fN) - цЬ£а) , Mk{f) < Mk(fN) + ^~^) • ПоэтомУ
[/(/; А) - L(/; А) = "^ (мк(/ы) - mk(fN) + —±_-W < е. J
fc=o v 2(Ь - a) /
Теорема 14. Предполоснсим, что выполнены условия:
1) Vn £ ЛГ: /„£ Я([а,Ь]); 2.) последовательность {/„ | п > 1}
сходится равномерно на [а, Ь] к функции /.

6.8. Предельный переход под знаком интеграла 227
Тогда f € Я([а,Ь]) u справедливо равенство
ь ъ
lim Г /n(z) dx = Г f(x) dx.
п->о° о о
Г Интегрируемость функции / содержится в лемме 1. Для доказатель-
доказательства равенства заметим, что
\ffn(x)dx-ff(x)dx<f\fn(x)-f(x)\dx
'о о о
< sup |/п(х)-/(х)|(Ь-а)-> О, n->oo. J
хе[о,ь]
Замечание. Теорема 14 даёт простое достаточное условие для
предельного перехода под знаком интеграла Римана, Более полезным
является такое утверждение, которое приводим без доказательства.
Предположим, что: 1) Vn е N : /„ e R([a,b])\ 2) f &
R{[a,b]) и /„->/, n -> оо, поточечно на [а.Ь]; 3) ЗС > 0 Vn>
lVi€[o,b]: |/„(х)| < С. Тогда lim Jfn{x)dx = Г Дх) dx.
п-*°° о о
Упражнение 67. Доказать, что при условиях теоремы 14 для лю-
любой функции g G R{[a, Ь]) справедливо также следующее равенство
ь ь
lim / fn{x)g(x)dx = J f{x)g{x)dx.
n^°° a a
Упражнение 68. С помощью теоремы Вейерштрасса доказать, что
для каждой функции / £ С([а,Ь]) существует последовательность мно-
многочленов, равномерно на [а,Ь] сходящаяся к функции /.
ь
Упражнение 69*. Пусть / € С{[а,Ъ]) и f xnf{x)dx = 0 для каждого
п € (JVu{0}). Доказать, что /(х) = 0, х € [а,Ъ].
1
Упражнение 70. Пусть / е С([-1,1]) и / x2n/(x) dx = 0 для каж-
-1
дого п G (Nu{0}). Доказать, что / — нечётная функция на [—1,1].
Указание. Принять во внимание, что условие задачи выполнено
также для функции /(—х), х £ [—1,1], следовательно, и для чётной
функции /(х) + /(-х).х € [-1,1]. Поэтому / xm{f{x) + f{-x))dx = 0
-1
для всех т € (JVu{0}).
1
Упражнение 71. Пусть / € С([-1,1]) и f x2n+1f{x)dx = 0 для
каждого п € (ЛГи{0}). Доказать, что / — чётная функция на [—1,1].

228 Глава 6. Интеграл Римана
ь
Упражнение 72. Пусть / € С([а,Ь\) и /enxf(x) dx — 0 для каждого
а
п € (NU {0}). Доказать, что /(х) = 0, х € [а,Ъ].
Упражнение 73. Пусть / € С([а,Ь]) и для фиксированного m £ N
ь
выполняется условие Vn£ N,n > m : fxnf(x)dx = 0. Доказать, что
/(х) = 0, хе[а,Ъ].
ь
Упражнение 7^. Пусть / € С([0,1]) и /х3"/(х) dx = 0 для каждого
а
п € (ЛГи {0}). Доказать, что /(х) = 0, х € [а, Ъ].
6.9 Примеры применения определённого
интеграла
6.9.1 Площадь криволинейной трапеции
1. Определение криволинейной трапеции
Пусть / : [а, Ъ] -» R — неотрицательная и ограниченная на отрезке [а, Ь]
функция.
Определение 1. Множество точек плоскости
F := {(i,y) eR2 \ a<x<b, 0<y< f{x)}
называется криволинейной трапецией.
Упражнение 75. Изобразить на плоскости криволинейные трапеции
над отрезком [0,1], соответствующие функциям:
a) f{x) = х; Ь) fix) = у/2; с) Дх) = х2.
2. Определение плоедади криволинейной трапеции
Пусть Л = {xo,xi,x2l... ,хп_1,х„} — произвольное разбиение отрезка
[а,Ъ]. Проведенные через точки с абсциссами, равными xo,xi,... ,х„,
вертикальные прямые разбивают криволинейную трапецию F на п кри-
криволинейных трапеций Fq,F\, ..., Fn-i, основаниями которых являются
соответственно отрезки [xo,xi], [xi,X2],..., [xn_i,xn]. Для каждого к £
{0,1,...,п— 1} в криволинейную трапецию Fk впишем прямоугольник
Р'к и около Fk опишем прямоугольник Р'к'.
Далее предполагаем известной площадь прямоугольника.

6.9. Примеры применения определённого интеграла 229
При этом для прямоугольников Р'к и Рк, имеющих общее основание
[xk,xk+i], их высоты соответственно равны mk = mk(f) := inf /,
[хк,хк+1]
Mk = Mk{f) := sup /, здесь к £ {0,1,..., п - 1}. Поэтому площади
прямоугольников Рк и Р'к' соответственно равны тпкАхк и МкАхк, а
суммарные площади всех вписанных и всех описанных прямоугольников
п-1 п-1
соответственно равны J2 "ifcAzit = L(/;A), ^ МкАхк = U{f\X).
fc=0 fc=0
Определение 2. Внутренней площадью криволиней-
криволинейной трапеции F называется число s,(F) :=supL(/;A), вне-
х
гиней площадью криволинейной трапеции F называет-
называется число s*(F) := miU(f;X), где точные верхняя и нижняя
грани берутся по всем, разбиениям, А отрезка [а,Ь]. Если
s,(F) = s*(F), то криволинейная трапеция F называет-
называется квадрируемой, а число s(F) := s*(F) = s*(F) называется
площадью криволинейной трапеции F.
Упражнение 76. Привести пример криволинейной трапеции, не
имеющей площади.
3. Формула для вычисления плоздади криволинейной трапеции.
Теорема 15. Если f е С([а,Ъ]), f > 0 на [а,Ъ], то криво-
криволинейная трапеция F квадрируема и ее площадь равна
s(F) = ff(x)dx.
■ ■ О
ь ь
[ Согласно определению s,(F) = f f(x)dx, s*(F) = f f(x)dx, a no
о а
условию / G C([a,b]), а потому / £ il([a,b]) и, следовательно,
ь
с I p\ — c*( p\ — f f(T\ dr I
a
Примеры. 1. Площадь криволинейной трапеции F иэ упр. 75 с) равна
1 Т3 i=l
3
1 ,., „ „ „
= -. Площадь этой криволинейной трапеции впервые
1=0 3
вычислил Архимед.
х2 у2
2. Пусть G — фигура, ограниченная эллипсом —^ + -j = I, a >
О, Ъ > 0. Из геометрических соображений ясно, что для вычисления
площади G достаточно вычислить площадь следующей криволинейной

230 Глава 6. Интеграл Ркыана
{/ Х ]
(х,у) 0 < х < а, О < у < Ь\ 1 ^ г- По теореме 15'
имеем для площади s[G) фигуры G
ax = a cos £ ей
о
х = asini. . , i. 3jji
\ 4ab / cos tdt =
. /l + cos2t
= 4ao J at — nab.
о
Упражнение 77. Пусть {/,g} С C([a, b]), f{x) < g(x), x G [a,b] и
G := {(x,y) G il2 | a < x < b, f(x) < у < д{х)}. Доказать, что фигура
ь
G квадрируема и ее площадь равна s(G) = f{g{x) — f{x)) dx.
a
Упражнение 78. Предположив известной площадь кругового сек-
сектора, доказать, что криволинейный сектор F, определяемый в полярных
координатах формулой F = {{9,г) | вх < 8 < 02, 0 < г < р{9)}, р G
1 е2
^]), является квадрируемым с площадью s(F) = - f p2(9)d9.
2
6.9.2 Приближенное вычисление интегралов
Для использования формулы Ньютона-Лейбница при вычислении инте-
интеграла нужно знать примитивную. Если эта примитивная через элемен-
элементарные функции не выражается, то для вычисления интеграла исполь-
используются приближенные формулы, основанные на идеях, аналогичных ис-
использованным в п. 6.9.1.
1. Формула прямоугольниковч
ь
Для вычисления интеграла f f(x)dx, представляющего при условиях п.
a
6.9.1 площадь криволинейной трапеции, используют суммарную пло-
Ь-а n~l fxk + xk+1 \
щадь прямоугольников Jn := 2_ 7 7, • полученных
" ;ь=о V 2 /
следующим образом. Пусть разбиение А имеет вид А = {х0, хх,..., хп},
Хк = а-\ к, к = 0,1,...,п, при этом |А| —> 0, п —> оо. Над основа-
п
г , - г { Хк +
нием [хй,х^+1] рассмотрим прямоугольник с высотой /
2
к = 0,1, 2,... ,п — 1, при этом суммарная площадь полученных прямо-
прямоугольников равна Jn. Число Jn есть интегральная сумма для функции
/ G il([a,b]) и потому Jn -t J, n -> оо в силу теоремы Дарбу.

6.9. Примеры применения определённого интеграла 231
2. Формула трапеций
Используем обозначения п. 6.9.1, 1. Рассмотрим в качестве прибли-
приближения для площади криволинейной трапеции с основанием [х*;,х*:+1]
площадь трапеции с вершинами в следующих точках плоскости (х^О),
{xkJ(xk)),{xk+i,f(xk+1)),(xk+1,O), площадь этой трапеции равна
s«- (/(xjt) + f[xk+i)) . Так получаем формулу трапеций
2 и
f{xk+1) Ь - a
fc=0 2
(f(x0) + 2/A0 + 2/(х2) + ... + 2/(хп_!) + /(!„)).
Поскольку К„ = - E(/; A, {xk\X}) + S(f; A, {xfc+i|A})), то по теореме
ь
Дарбу для функции / G Л([а, Ь]) К„ -> / /(х) dx, n -> оо.
а
Упражнение 79. Для / G С^2)([а,Ь]) доказать неравенство
1 Указание. Для каждого к = 0,1,...,п — 1 оценить с помощью
_■_ т - Xkr'1 ti \ j b - а (хк + xk+i \
формулы Тейлора разность J /(х) ах / I ' —
6.9.3 Длина дуги кривой
1. Определение непрерывной кривой.
Определение 3. Пусть {y.V1} С С([а,Ь]). Mnootcecmeo
точек плоскости Г := {(х, у) е il2 | х = <^(£), у = ^(*)>а < * < ^}
наз'Ываетсл непрерывной кривой в плоскости.
Упражнение 80. Изобразить на плоскости следующие кривые:
а) Г = {{х,у) | x = at + P, у = >yi + 5; t G Щ,
b)V = {{x,y)\x=t, y = 2t, te[0,l]},
c)r = {(x,y)\x=t, y = t2, *еЯ},
d) Г = {(х,у) | x = cosi, у = sint, t G [0,2тг]},
e) Г = {{x,y) | x = cost, у — s'mt, t G [0,тг]},
f) Г = {(х,у) | i = acosi, y= bsmt, t G [0,2тг]}, а > 0, b > 0.

232 Глава 6. Интеграл Римана
2. Определение спрямляемой кривой и длины кривой
Пусть А = {to,ti,... ,tn} — некоторое разбиение отрезка [а, Ь], а ГЛ
— ломаная, которая получается соединением каждой пары соседних
точек ((<p(tfc), V(tfc)) и (<^(£fc+i),T/>(£fc+i)) на кривой Г отрезком прямой,
к — 0,1,..., п — 1. Длина /(Га) ломаной Га равна
п-1
'(Га) =
fc=0
Определение 4- Если существует конечный предел
lim /(Га) =: КГ), то есть, если
|А|-Ю
31(Г)£Й Ve>0 3E > 0 VX, |А| < 5 : |1(ГЛ) - 1(Г)| < е,
то кривая Г называется спрямляемой, а предел 1(Г) на-
называется длиной кривой Г.
Упражнение 81*. Построить пример непрерывной кривой Г, для
которой предел в определении 2 равен +оо.
Упражнение 82. Доказать, что /(Г) = sup/(Га).
А
3. Формула для вычисления длины кривой
Теорема 16. Пусть {tp,ip} С С1{[а,Ь]). Тогда кривая Г
спрямляема и её длина 1(Г) равна
[ С помощью теоремы Лагранжа для /(Га) имеем
п-1
«(Га) = Е
fc=0
где {^jbTjfc} С [£it,£k+i], Ыу. — ifc+i ~^к, 0 < fc < п — 1; и
п-1
к=0
Поскольку \/[<р'J + (т/>'J £ ^([а>Ь]), то по теореме Дарбу
Кроме того, согласно неравенству
|ч/и2 + v2 - Vu2 + w2\ <\v-w\ A)
для любых {и, г», ш} С -R имеем для га
"Б
fc=0 fc=0

&9. Примеры применения определённого интеграла 233
• В силу критерия интегрируемости для ip' имеем lim r\ — 0. J
Упражнение 83. Доказать неравенство A).
Упражнение 84- Пусть / е Сх([а, Ь]) и Г = G{f) = {{х,у) \ х G
[а,Ь], у — f{x)}. Доказать, что Г есть спрямляемая кривая и что спра-
справедливо равенство 1{Г) — f \J\ + f'{xJ dx.
Упражнение 85. Для p G C1{[01,82]) пусть Г := {{в,г) | в G
[^ii^2]i г — р{8)} — кривая, заданная в полярных координатах. До-
Доказать, что Г есть спрямляемая кривая и 1{Г) = f \/р2{8) + р'{8J d8.
6.9.4 Объём тела вращения
1. Тело вращения
Пусть ^—криволинейная трапеция из п. 6.9.1. Ниже рассматривается
тело G, которое получается при вращении трапеции F относительно
оси абсцисс.
Упражнение 86. Какое тело G получается при вращении следую-
следующей криволинейной трапеции F :
s)F = {{x,y) G R? | а < х < Ь, 0 < у < г};
b) F = {{х, у)е R2 \ а<х<Ъ, 0 < у < х - а};
c) F = {{х, у)£ R2 \ а<х<Ь, 0 < у < х + с}, О 0;
d) F = {{х,у) & R2 \ -а<х<а, 0<у< у/а2 - х2}, а > 0;
e) F = {{х, у) G R2 | 0 < х < а, 0<у < <Ja2 - х2}, а > 0?
2. Определение объёма тела вращения
Воспользуемся обозначениями из п. 6.9.1. При вращении относитель-
относительно оси абсцисс прямоугольников Ро,Р{,..., P^_i возникает тело С?'(А),
состоящее из прямых круговых цилиндров, которое содержится в G.
Аналогично, при вращении прямоугольников Pq', Р",..., P^'_i возникает
тело С?"(А), состоящее из прямых круговых цилиндров, которое содер-
содержит тело G.
Предположим известным объём прямого кругового цилин-
цилиндра. Тогда для объемов V{G'(\)) и V{G"{\)) тел G'{\) и G"{\) имеем
значения V{G'{b)) = "z nm2{f)Axk, V{G"{\)) - "e nM2{f)Axk co-
fc=0 fc=0
ответственно.

234 Глава 6. Интеграл Римана
Определение 5. Числа V,(G) := supV(G'(A)) и V*{G) :=
А
= inf V(G"(X)), где точные грани берутсл по всем возмож-
возможным, разбиенилм X, называются соответственно внут-
внутренним и внешним объёмами тела G.
Если для тела G выполняется равенство V»(G) = V*(G),
то тело G называется кубируемым, а число V(G) :=
= V*(G) = V*{G) называется объёмом тела G.
3. Формула для вычисления объёма
Теорема 17. Пусть f е С{[а,Ъ]), / > 0 на [а,Ъ]. Тогда
тело G является кубируемым и объём G вычисляется
по формуле V(G) = п fa f2{x) dx.
(" Заметим, что при условии теоремы тп£(/) = "ifc(/2)i Mk(f) —
Mk{f2)\ 0 < * < n - 1. Поэтому V(G'(A)) = *L{f2;X), V(G"(A)) =
ь ь
= nU(f2;X), кроме того Vt(G) = ж f f2{x)dx, V*{G) = nf f2(x)dx.
a a
Согласно предположению теоремы f2 G С([а,Щ), а следовательно /2 G
ь
Д([а,Ь]). Таким образом, V,(G) = V*(G) = wff2{x)dx. J
a
Упражнение 87. С помощью последней теоремы вычислить: объ-
объём конуса, объём усечённого конуса, объём шара, объём шаровых
сегмента и слоя, объём эллипсоида вращения.
Упражнение 88. Тором называется тело, получающееся при вра-
вращении относительно оси абсцисс круга {{х,у) \ х2 + (у - RJ < г2}, где
О < г < R. Вычислить объём тора.
6.9.5 Площадь поверхности тела вращения
1. Определение плоцади поверхности тела вращения
Пусть Р есть поверхность, полученная при вращении относительно оси
абсцисс кривой Г = {{х, у) \ х G [а, Ь] у = f{x)}, где функция
/ G С([а,Ц), / > 0 на [а,Ь]. Г = G(/) есть непрерывная кривая. Пусть
А = {хо,х\,Х2,-.. ,хп} — некоторое разбиение отрезка [a, b]. Для каж-
каждого k G {0,1,... ,п-1} соединим точки Г (xk,f(xk)), (xk+1, f(xk+1))
отрезком прямой. При вращении этих отрезков вместе с Г получает-
получается поверхность Р(Х), составленная из боковых поверхностей усечённых
конусов.

§fc9. Примеры применения определённого интеграла 235
Предположим известной площадь боковой поверхности
усечённого кругового конуса.
Площадь s(P(A)) поверхности Р(А) равна
s(P{\)) = Е2,г
l| fc=0 *
Определение 6. Если существует конечный предел
flim s(P(A)), то этот предел называется площадью по-
поверхности Р и обозначается s(P).
l
%. Условие существования плоэдади и формула для её вычисления
Теорема 18. Пусть f G С1 [[а, Ъ]). Тогда поверхность Р
имеет площадь, которая равна s(P) = 2тг / /(i)>/l + f'[xJdx.
' а
f Функция / G C([a,b}) и для каждого k G {0,1,... ,п - 1} значение
\f{xk) + f{xk+1))/2 лежит между f(xk) и f{xk+1). По теореме Коши
to промежуточном значении 3£к G [хк,хк+х] ■ (f{xk) + /(zfc+1))/2 =
г f(tk)- По теореме Лагранжа Эг]к G [xfc,ifc+i] : /(ifc+i) - /(xfc) =
«t= /'(?;fc)Axfc. Таким образом, для любого разбиения А
5(Р(А)) = 2^
fc=0
n-l
.где га := 2тг Е (/F0 ~ /(i?it))\/l + f'{VkJ&xk. В силу оценки
fc=0
n-l
ч (
[о,6] fc=0
критерия интегрируемости для / и теоремы Дарбу имеем
lim 5(Р(А)) = 2*
|А|HJ
HJ
6.9.6 Координаты центра масс и теоремы Гюльдена
1. Физические предположения
Если в точках плоскости (xlt ух),(х2,У2), ■ ■ ■ 1 {хп,Уп) размещены мас-
массы Pi,p2, ••■ ,Рп соответственно, то координаты хс,ус центра масс этой
системы точек определяются равенствами

236 Глава 6. Интеграл Римана
«.= Eft E ft**. Ус = E ft E
\fc=i / *=i \fc=i / k=i
Если J? — фигура в плоскости, которая имеет однородное распре-
распределением масс и имеет ось симметрии, то центр масс фигуры F лежит
на оси симметрии. Если F имеет центр симметрии, то центр масс сов-
совпадает с центром симметрии. Если фигура F имеет однородное рас-
распределением масс и состоит из двух частей Fi и F% ( которые имеют
соответственно массы Pi и р2 и центры масс (x^s/i), (x2, у2), то центр
. г, ziPi + х2рг 2/1Р1 + У2Р2
масс фигуры F имеет координаты , .
Pi +P2 Pi +P2
2. Координаты центра масс однородной криволинейной трапеции
Пусть F — криволинейная трапеция F = {(х,у) \ х G [а, Ь], 0 < г/ <
/(х)}; / G С([а,Ь]), по которой однородно распределена масса, по
величине равная площади F.
Для определения координат центра масс фигуры F можно рассуж-
рассуждать следующим образом. Воспользуемся обозначениями из п. 6.9.1.
Пусть Л — некоторое разбиение отрезка [а, 6]. Для каждой из криволи-
криволинейных трапеций Fk, 0 < fc < п — 1, как и для фигуры F, координаты
центра масс неизвестны. Однако, для фигуры, составленной из вписан-
вписанных прямоугольников PoiPi,-■ • i Pn-i ЧентР масс определяется легко.
Именно, прямоугольник Р'к имеет массу mfc(/)Aifc и центр масс прямо-
прямоугольника Р,£ совпадает с центром симметрии прямоугольника, который
имеет координаты (х^ + xfc+i)/2, mfc(/)/2; 0 < fc < n — 1. Поэтому
центр масс системы прямоугольников Pq, Р[,..., Рп-\ имеет координаты
хс(А)= (
\fc=0 / fc=0
Л»-1 \
Уе(А) = Е mk(f)Axk)
\к-0 I
fc=0 г-
'■ Естественно предполагать, что при А —\ 0, фигура, составленная из
вписанных прямоугольников, будет приближаться к фигуре F, а коорди-
координаты хс(Х),ус(Х), будут приближаться к координатам центра масс фигу-
фигуры F.
Таким образом, координаты хс,ус центра масс однородной фигуры
F определяются формулами
}Н)ь //а()^ (p) }я)<ь- A)
s(F)

6.9. Примеры применения определённого интеграла 237
3. Вторая теорема Гюльдена
Теорема 19. Объём тела, описываемого плоской фи-
фигурой при вращении её около оси, лемсащей в плоско-
плоскости этой фигуры и не пересекающей её, равен произве-
произведению площади фигуры, на длину окруэ+сности, описыва-
описываемой при вращении центром, масс этой фигуры.
\ Доказательство рассмотрим для случая, когда фигура F есть криволи-
криволинейная трапеция. Тогда утверждение теоремы получается из равенства
для ус в A) после его умножения на 2ns(F). При этом получим равен-
равенство s(F)-Bnyc) = nff2(x)dx. J
а
Упражнение 89. Определить координаты центра масс полукруга, а
затем с помощью теоремы Гюльдена найти объём шара. Аналогичным
образом вычислить объём конуса, усечённого конуса, шаровых сегмен-
сегмента и слоя, эллипсоида вращения.
Упражнение 90. Найти объём тора.
4. Координаты центра масс однородной кривой
Пусть Г = {(х,у) | х G [а,Ъ], у = f[x)}, /€ С{[а,Ц) - непрерыв-
непрерывная кривая. Используем обозначения п. 6.9.3. Если / £ Cl([a, b}), то
согласно п. 6.9.3 кривая Г спрямляема и её длина 1(Г) равна /(Г) =
ь
я= f i/l + f'{xJ dx. Предположим, что вдоль Г однородным образом
распределена масса, равная по величине длине дуги Г. Пусть Га — ло-
ломаная, вписанная в Г для разбиения А отрезка [а, Ь]. При этом центр
Масс отрезка с концами {xk,f(xk)), (xk+1,f(xk+1)) имеет координа-
координаты (xk + xk+1)/2, (f{xk) + f(xk+1))/2, а масса этого отрезка равна
его длине л/Дх| + (/(xfc+1) - f{xk)J, здесь 0 < fc < п - 1. Поэтому
координаты хс(Х), ус{\) центра масс Га равны
1 ^/Ы-
Таким образом, если / £ С1([а,Ь])) то координаты хс, ус центра
масс кривой Г определяются формулами
хс = Jim хс(А) =
—
1A )

238 Глава 6. Интеграл Римана
b
1
Ус = |ЙтпУс^ = 77п ff(x)V1 + f'(xJdx- (!)
|A|->0 1{Г) а
5. Первая теорема Гюльдена
Теорема 20. Поверхность тела, описываемая, плос-
плоской кривой при вращении её около оси, лемсащей в плос-
плоскости этой кривой и не пересекающей ее, равна произ-
произведению длины кривой на длину окруэ*сности, описывае-
описываемой при этом вращении центром, масс кривой.
[ Доказательство проведем для кривой Г из п. 6.9.3 и поверхности Р,
полученной при вращении Г около оси абсцисс. В п. 6.9.3 было доказа-
доказано, что поверхность Р имеет площадь s(P) = 2тг f f[x)y/l + f'(xJ dx.
a
Умножив равенство A) на 2тг/(Г), получим /(Г) • Bтп/с) = s[P). J
Упраэюнение 91. Определить координаты центра масс полуокруж-
полуокружности.
Упражнение 92. Найти площади поверхности шара и тора.
6.10 Историческая справка
Первыми примерами использования методов, которые сейчас относят к
интегральному исчислению, были методы решения геометрических за-
задач, предложенные Евдоксом и Архимедом.
Евдокс Книдский (~ 408 — ~ 355 до н.э.) — древнегреческий
математик и астроном, автор "метода исчерпывания", вычислил объёмы
конуса и пирамиды. Его не дошедшие до нас сочинения Евклид исполь-
использовал при создании ряда своих книг "Начал".
Архимед (~ 287 — 212 до н.э.) — древнегреческий математик,
механик, физик, астроном, изобретатель. Многие его работы посвя-
посвящены вычислению площадей, объёмов, центров тяжести. Архимед, на-
например, вычислил площадь параболического сегмента, поверхности и
объёмы шара, шарового сегмента и цилиндра. Хорошо известны: акси-
аксиома Архимеда, спираль Архимеда, архимедов винт, закон Архимеда в
гидростатике, полиспаст.
Дифференциальное и интегральное исчисление было создано Нью-
Ньютоном и Лейбницем. Они также первыми эффективно применили новые
методы в механике, физике, геометрии.

$.10. Историческая справка 239
Ньютон Исаак A643 — 1727) — английский физик, матема-
математик, астроном. Открыл законы механики и закон всемирного тяготения,
изобрел первый зеркальный телескоп.
Современное интегральное исчисление базируется на взаимодей-
взаимодействии двух концепций: определении интеграла как предела интегральных
сумм и определении функции по ее производной. Ньютон использовал в
основном неопределенный интеграл, для него интегрирование есть опе-
операция, обратная к дифференцированию. Лейбниц развивал и первую
концепцию, интересную с теоретической точки зрения и эффективную
в приложениях.
Первое определение интеграла, которое можно считать точным, дал
в 1823 г. Коши. Для функции /, непрерывной на отрезке [а,Ь], и разби-
разбиения Л = {хо, xi, i2, • • • i £п} этого отрезка Коши вводит сумму
S = f{xo)(x1 - х0) + f{x1)(x2 - хх) + ... + /(xn_j)(xn - xn_i),
т. е. интегральную сумму специального вида, и доказывает существо-
существование предела S при |Л| -* 0. Этот предел и называется определённым
интегралом и обозначается по словам Коши "придуманным г-ом Фурье"
ь
символом f f(x)dx. Отметим также, что символ интеграла f исполь-
а
зовал еще в 1690 Як. Бернулли, который впервые ввёл термин "инте-
"интеграл". Доказательство Коши существования интеграла, т. е. предела
интегральных сумм S при |А| -* 0, содержало пробел, оно становится
корректным после применения теоремы о равномерной непрерывности
непрерывной на отрезке функции, которая была доказана позже. Коши
распространил свое определение на некоторые разрывные функции,
однако, изучением разрывных интегрируемых функций он не занимал-
занимался. Отметим, что суммы S использовал также Эйлер, как приближенные
значения соответствующих интегралов, однако, вопрос о пределе инте-
интегральных сумм S при |А| —¥ 0 Эйлер не рассматривал.
Определение интеграла у Римана то же, что и у Коши, с той разни-
разницей, что вместо сумм S рассматриваются интегральные суммы общего
вида
где £ь £ [xfc,a;fc+1], k — 0,1,... ,n - 1. Однако, Риман исследует все
функции, для которых существует предел интегральных сумм, и полу-
получает критерий интегрируемости.
Риман Георг Фридрих Вернхард A826 — 1866) — немецкий
математик, автор широкого круга выдающихся результатов в различ-
различных областях математики. Ьго именем названы: римановы поверхности
и многообразия, гипотеза Римана о нулях дзета-функции, матрица Ри-
Римана, функция Римана, геометрия Римана.
16 — 4-1168

240 Глава 6. Интеграл Римана
В 1875 г. появилась новая форма условия интегрируемости функции.
Почти одновременно математики Дарбу, Томе, Г. Смит, Ас-
коли и Дюбуа-Реймон ввели суммы Дарбу L(f; А) и £/(/; Л) для
ограниченной функции, нижний и верхний интегралы, определение ин-
интегрируемости и получили критерий интегрируемости, доказана была и
теорема Дарбу.
Дарбу Жан Гастон A842 —1917) — французский математик,
автор известных результатов в дифференциальной геометрии и тео-
теории дифференциальных уравнений. Отметим, что первым суммы Дарбу
£(/; ^) и U(f\ А) для ряда простых функций использовал Архимед.
И Ньютон и Лейбниц вводили определенный интеграл как разность
значений примитивной, т. е. функция / : [а,Ь] —> R имеет интеграл
ь
f f(x) dx, если она имеет примитивную F на [а,Ь], и тогда по определе-
а
Ь
нию f f(x)dx := F(b)-F(a). Остается, однако, неясным, какие функции
а
имеют примитивную. Если же принять определение интеграла, как пре-
предела интегральных сумм, то доказательство существования примитивной
проводится просто. При таком подходе формула Ньютона-Лейбница бы-
была впервые доказана Коши. С другой стороны, существование прими-
примитивной у непрерывной функции, которое не использовало бы понятия
интеграла, впервые было получено А. Лебегом только в 1905 г.
Естественным развитием идей и методов дифференциального и ин-
интегрального исчисления можно считать почти всю современную мате-
математику: дифференциальная геометрия, дифференциальные уравнения,
вариационное исчисление, теория кратных интегралов, тригонометриче-
тригонометрические ряды, уравнения с частными производными и другие разделы.
Дальнейшее развитие понятия интеграла связано с именами Стилтье-
са и Лебега.
Стпилтъес Томас Иоганнес A856 — 1894) — нидерландский
математик.
Лебег Анри Луи A875 — 1941) — французский математик.
Методы и идеи интегрального исчисления оказались исключительно
плодотворными как в самой математике, так и в ее приложениях. Для
решения ряда типичных задач было создано много различных вариаций
понятия интеграла, причём этот процесс введения в математику новых
интегралов продолжается и в настоящее время.
К вопросу о геометрических применениях понятия определенного
интеграла нужно отметить следующее. Задачи о вычислении площади,
объёмов тел, длин дуг и площадей поверхности, а также координат цен-
центров тяжести, на протяжении более 2000 лет до создания интегрального
исчисления Ньютоном и Лейбницем, были трудными математическими

6.10. Историческая справка 241
проблемами и привлекали внимание всех математиков. Например, Ар-
Архимед считал одним из наиболее важных своих результатов доказатель-
доказательство того, что объём шара относится к объёму описанного цилиндра как
2:3, и попросил своих друзей изобразить соответствующий рисунок на
могильной плите. По этому рисунку спустя 100 лет Цицерон нашел мо-
могилу Архимеда. К началу XVII в. математиками было решено огромное
количество задач, которые можно отнести к интегральному исчислению.
Однако, ни Архимед, ни его последователи, вплоть до работ Ньютона
и Лейбница, не видели в решениях отдельных задач, которые обыч-
обычно остроумно использовали специальные свойства объектов, зародыша
единого метода. Одним из важнейших достижений дифференциального
и интегрального исчисления было то, что с его помощью исключитель-
исключительно просто вычисляются длины дуг, площади, объёмы и т. п. Сейчас
эти вычисления посильны школьнику. Для самой математики оказалось
важным следующее. До последней четверти XIX в. математиков инте-
интересовал только вопрос о вычислении площади, длины, объёма и т. д.,
предполагалось,что, например, фигура имеет площадь и т. п. Однако,
с развитием понятий функции и интеграла оказалось, что формально
определённые объекты включают в себя нечто такое, что интуицией
не предвиделось и сознательно в определение не закладывалось. На-
Например, развитие понятия функция привело Жордана к следующему
определению непрерывной кривой:
линией называется совокупность точек плоскости,
координаты, которых суть непрерывные функции х =
tp(t), у = ip(t) параметра t, заданные на отрезке 0 < t < 1.
Те линии, длину которых определяли математики, оказались линиями
и по определению Жордана. Однако, в 1890 г. итальянский математик
Пеано показал, что среди непрерывных кривых Жордана есть кривые,
заполняющие квадрат, в частности они имеют бесконечную длину. Те
линии Жордана, для которых можно определить длину, были названы
спрямляемыми. Аналогичная история произошла с понятиями : площадь
фигуры, площадь поверхности и т. п.
Жордан Камил A838 — 1922) — французский математик, автор
меры Жордана — понятия, которое на плоскости обобщает понятие
площади на весьма широкий класс плоских фигур.
Гюлъден Пауль A577 — 1643) — швейцарский математик. Тео-
Теоремы, носящие имя Гюльдена, были известны без доказательств еще
древнегреческому математику Паппу.

Глава 7
Ряды
7.1 Элементарные свойства сходящихся рядов
7.1.1 Основные определения
Пусть {ап | п > 1} — последовательность действительных чисел. Рядом
называют выражение
аг + а2 + ...+ ап + ...= £ ап. A)
Это выражение пока точного смысла не имеет, поскольку бесконечное
число сложений осуществить нельзя.
Для каждого п € N положим sn := а\ + а2 + ... + ап.
Число ап называется п-м членом, а число sn — п-ой частичной
суммой ряда A). Заметим, что sn+i = sn + an+i, n > 1.
Определение 1. Две последовательности {ап \ п > 1} и
{sn | п > 1} называютсл числовым рядом и обозначают-
сл символом A). Если последовательность частичных
сумм {sn | п > 1} сходитсл к действительном/у числу s,
то рлд A) называется сходящимся, а число s называет-
оо
ел суммой ряда A) и обозначается символом, s = £) ап.
п=1
Если последовательность {sn I n > 1} конечного предела
не имеет, то рлд A) называется расходящимся.
_ оо
Теорема 1. Если ряд £) а„ сходится, то ап -> 0, п -> оо.
п=1
Г Действительно, поскольку ап = sn-sn-i, n > 2, и sn -У s € R, п -у оо,
то ап —> s — s = 0, п —> оо. J
242

ftjt, Элементарные свойства сходящихся рядов 243
Теорема 1 даёт простое необходимое условие сходимости ряда,
Аналогично можно получить другие условия такого типа, Привдём ещё
один полезный факт.
оо
Теорема 2. Если рлд Yl an сходится, то
п=1
ап + ап+1 + ... + а2п -+ 0, п -> оо.
Упражнение 1. Провести доказательство теоремы 2.
Пример. 1. Ряды
1 + 1 + 1 + ... + 1 + ... B)
1-1 + 1-1 + ... + (-1)п+1 + ... C)
расходятся, поскольку последовательности частичных сумм sn — п, п >
1, для ряда B), и sj = 1, s2 = 0, s3 = 1, s4 = 0, ... для ряда C) предела
не имеют. Можно также воспользоваться теоремой 1.
оо
Упраж.нение 2*. Доказать, что ряд £) sinn расходится.
п=1
Примеры. 2. Геометрический ряд. Так для if fi называется
следующий ряд
1_i_T_|_T2iT3i | тп . /л\
частичная сумма которого равна sn(l) = n, sn(i) = A — хп)/A — х),х ф
1; п > 1. Ряд D) сходится к сумме 1/A — х) для \х\ < 1, и расходится
для \х\ > 1.
[ Если \х) < 1, то хп —¥ 0, п —> со. Следовательно, при \х\ < 1 ряд D)
сходится к сумме 1/A —ж) : 1 + х + х2 + х3 + .. . + хп + ... = , \х\ < 1.
При |х| > 1 последовательность {sn(x) | тг > 1} конечного предела
не имеет, следовательно, при \х\ > 1 ряд D) расходится. Заметим, что
сумму геометрического ряда впервые нашёл Архимед. J
3. Докажем, что -—- + —— + —— + ... + -г—, -г + ... = 1.
[ Действительно, для п > 1 имеем
1 1 1 1
Sn~ 1-2 +2-3 +3-4 + • • • + п • (п + 1)
^ ' 1 2 I • \2 3 I • V3 4
Следовательно, sn —> 1, п —> со. J
4. Гармонический ряд. Так называется следующий ряд
. 111 1

244 Глава 7. Ряды
\ Докажем, что этот ряд расходится. Используем теорему 2. Заметим,
что для п > 1 справедливо неравенство
- 1 1 _L > JL _ I _ i I I I
Следовательно, S2n — sn ■/* 0, n —¥ оо. Поскольку последовательность
{sn | n > 1} возрастает и не имеет предела, то sn -> +оо, п -> оо.
Однако, возрастание частичных сумм sn с ростом п происходит очень
медленно. Л. Эйлер подсчитал, что Sjoooooo ~ 14- Обратим внимание
на то, что члены гармонического ряда, убывая, сходятся к 0. J
Упражнение 3. Доказать, что частичные суммы гармонического ря-
ряда удовлетворяют неравенствам 0 < sn - ln(n + 1) < 1, n > 2.
Указание. Использовать неравенства для членов последователь-
последовательности, определяющей число е.
Пример. 5. Обобщённый гармонический ряд. Так называется
следующий ряд
где а € R. Докажем, что ряд E) сходится при а > 1.
\ Пусть sn{a) := 1 + — + — +•■■+—, п > 1. При а = 1 ряд
E) является гармоническим и sn(l) —¥ +оо, п —¥ оо. При а < 1 имеем
sn(a) > sn(l), n > 1, следовательно, ряд E) расходится и при а < 1.
При а > 1 ряд E) сходится. Действительно, сначала имеем
откуда следует неравенство s2n(a) < rj^ 7 i n > 1- Поэтому
s2n(a) -» С(«) € R, п -^ оо; s2n+i(a) = s2n(a) + ,^ + ^a -+ С(«),
при п -> оо. J
Замечание. Пусть ^(а) — сумма ряда E) для а > 1. Функция £ —
знаменитая дзета-функция Римана, которая часто встречается в
различных разделах математики. Ряд предположений о поведении этой
функции не доказаны и не опровергнуты до настоящего времени.
Упраэюнение 4- Найти суммы рядов (к € N фиксировано):
оо J оо I оо ^
Э) Si (v^+v/^TT)N/n(n+l) ; Ь) Si 4n2l ; C)

7.1. Элементарные свойства сходящихся рядов 245
7.1.2 Свойства сходящихся рядов
оо
1°. Пусть ряд Yl an сходится и имеет сумму s. Тогда для любого с € R
оо оо оо
ряд Y1 (сап) также сходится и имеет сумму cs, т. е. £) [сап) = с £) ап.
п=1 п=1 п=1
[ Доказательство следует из определений. J
оо оо
ОР. Пусть ряды Y1 а'п и Y2 ап сходятся к суммам s' и s" соответ-
п=1 п=1
оо
ственно. Тогда ряд £) (а'п + ап) также сходится к сумме s' + s", таким
n=l
образом, g « + <)= g a'n+ g <.
n=l n=l n=l
Определение 2. Для ряда
al + а2 + аЗ + • • • "Ь ап + ■ • • A)
14 числа m E N ряд
am+l + O.m+2 + Ягп+3 + • • ■ + ап + • • • B)
называется остатком исходного ряда.
Если ряд B) сходится, то пусть гт — его сумма.
3°. Если ряд A) сходится к сумме s, то сходится любой его остаток,
причём VmEiV: s = sm + rm. Если для некоторого т € N сходится
остаток B), то ряд A) сходится.
Упрамснение 5. Доказать, что для сходящегося ряда его остаток
гт -+ 0, m -> оо.
4°. Критерий Коши сходимости числового ряда. Для того,
чтобы ряд A) сходился, необходимо и достаточно, чтобы
Ve>0 3NeN Vn>N Vp € N : \ап+1+ап+2+.. -+an+p\ < e.
Г Этот критерий представляет собой перефразировку критерия Коши
сходимости последовательности частичных сумм ряда. J
Упражнение 6. Доказать, что ряды
а1 "Ь а2 "Ь аз ~Ь • • • ~Ь ап "Ь • • • i
сходятся или расходятся одновременно.
Упражнение 7. Доказать сходимость ряда
sinl2 sin22 sin32 sinn2

246 Глава 7. Ряды
1
7.2 Ряды с неотрицательными членами
7.2.1 Критерий сходимости и следствие
Теорема 3. Пусть члены ряда
ai +a2 + ... + а„ +... A)
удовлетворяют условию: ап > 0, п > 1.
Рлд A) cxod-итсл тогда и только тогда, когда последо-
последовательность его частичных сумм {sn \ n > 1} ограничена
\ Заметим, что для ряда с неотрицательными членами последователь-
последовательность его частичных сумм не убывает sn+x = sn + an+i > sn, n > 1.
Необходимость. Если ряд A) сходится, то последовательность его
частичных сумм ограничена, как сходящаяся последовательность. При
этом условие неотрицательности членов не обязательно.
Достаточность. Последовательность {sn | n > 1} монотонно не
убывает и ограничена, следовательно, сходится. J
Замечание. Обратим внимание на следующие факты, относящи-
относящиеся к теореме 3. Если sn —> s, n —¥ оо, то Vn > 1 : sn < s; если,
кроме того, V п > 1 : ап > 0, то V п > 1 : sn < s.
Вместо теоремы 3 часто используется следующее утверждение, со-
содержащее простое достаточное условие сходимости ряда с неотрица-
неотрицательными членами.
Лемма 1. Пусть ряд A) с неотрицательными членами
сходитсл, а последовательность чисел {dn | n > 1} удо-
удовлетворяет условию 3 L > О V п > 1 : 0<dn<L. Тогда
ряд
оо
Z) dnan B)
n=l
сходится.
Г Доказательство основано на применении теоремы 3. Введём частич-
п п
ные суммы sn = Yl ak, $п — Yl dkcik, n > 1. Согласно теореме
fc=i fc=i
3, Vn > 1 : sn < s = lim sn. Учитывая условие леммы, получим
V n > 1 : 3„ = J2 dko-k < Lsn < Ls. J
Замечание. Заметим, что при условиях леммы выполняется нера-
оо оо
венство Yl dnan < L Y2 ап-
п=1 п=1
Упражнение 8. Пусть ряд A) с неотрицательными членами схо-
сходится, а последовательность чисел {dn | n > 1} ограничена. Доказать

7\2. Ряды с неотрицательными членами 247
сходимость ряда B).
Указание. Использовать критерий Коши сходимости ряда.
1 °° 1
Упражнение 9. Доказать сходимость ряда J2 ~~7= ■
2vn
п=\
Указание. Использовать неравенства
1 1 1 1 2fc+l
+ + + Н <
Упражнение 10. Доказать сходимость следующих рядов:
»=1 V n / n- n% П* ■
Упражнение 11. Доказать, что для любой последовательности по-
положительных чисел {<in | п > 1} такой, что dn -у +оо, п -4 оо суще-
существует сходящийся ряд с неотрицательными членами A), для которого
ряд B) расходится. Это означает, что условие леммы 1 в определённом
смысле необходимо.
7.2.2 Признаки сравнения
/^^\ оо оо
1°. Предположим, что члены рядов A) 52 ап и B) 52 ^« удовлетворя-
^/ п=\ п=1
ют условию: 0 < ап < Ьп, п > 1. Тогда из сходимости ряда B) следует
сходимость ряда A) (из расходимости ряда A) следует расходимость
ряда B)).
[ Пусть ряд B) сходится. Положим dn :— -^ , если Ьп ф 0 и dn — 0, если
On
Ьп = 0; п > 1. Тогда 0 < dn < 1, dnbn — ап, п > 1. По лемме 1 ряд A)
сходится. J
, оо 1
Примеры. 1. Ряд 5Z nsin— сходится, так как в силу неравенства
п=1 п
0 < sinх < х, х G @,тг/2) имеем nsin— < —, п > 1, причём ряд
оо 1
52 ~Ч сходится.
п=1 П
оо 1
2. Ряд J2 sin— расходится, так как в силу неравенства sini >
n=l П
2 12 1 °° 1
> — х, х € @,7г/2) имеем sin — > , п > 1, и ряд 52 ~~ расходится.
7Г П 7Г П n=i П
3. Утверждение 1° остаётся верным при следующем более слабом
условии 3N € N V п > N : 0<ап<Ь„.

Глава 7. Ряды
» ln3n _ „
Докажем, например, что ряд 2_, —5~ сходится. Действительно,
71=2 П
1 3 1 3
поскольку —-=- -4 0, п -4 оо, то 3NeNVn>N: _ < 1
ln3n 1 ^1
=Ф- —— < —^ , причем ряд Е ~Т/2 СХ°ДИТСЯ-
°° 1 ( 1 \
Упражнение 12. Доказать сходимость ряда: а) Е — In I И— i
71=1 П V П /
Ь) Е ( 1 ~ cos ~ ) i с) X) ( 7 ) ! d) E ~ arctg —j= .
71=1 V П J «=1 У71 + 1 / « = 1 П V71
Упражнение 13*. Определить все значения а > 0, для которых
оо я^(п)
сходится ряд Е —5~ > где "(п) ~ число нулей в десятичной записи
71=1 П
числа п.
Ответ: 0 < а < 91.
Упражнение 14- Пусть ап > 0, п > 1 и существует а > 0 такое,
оо
что an+i < аап, п > 1. Предположим, что Е а« = +00- Доказать,
71=1
ОО
что для любого р € N имеем Е апр — +оо.
~ 71=1
Пусть члены рядов A) и B) удовлетворяют условию: ап > 0, Ьп >
^п > 1 и существует конечный или бесконечный предел
lim р = С, 0 < С < +оо.
71-4ОО Ьп
Тогда гайи С/< +00^ из^ход^мост^ ряда/B) следует сходимость ряда
A). При/С7 >/о из/расзюди«Хости ряда B) следует расходимость ряда
A). Таким образом, при 0 < С < +оо оба ряда одновременно сходятся
или расходятся.
[ Пусть С < +ОО и ряд B) сходится. Положим dn = т~, п > 1. После-
Последовательность {dn | п > 1} ограничена, как сходящаяся, и по лемме 1
оо оо Ьп 1
ряд Е ^"Ьп = Е ап сходится. Если С > 0, то lim — = — < +оо и
П=1 71=1 П^ОО пп С/
по доказанному из сходимости ряда A) следует сходимость ряда B). J
оо
Примеры. 4. Пусть а > 0. Ряд Е (Vn2 + 1 — п)а расходится при
, 71=1
■ а < 1, и сходится при а > 1.
[ Действительно,

7.2. Ряды с неотрицательными членами 249
2а пс
па
причём обобщённый гармонический ряд расходится при а < 1, и схо-
сходится при а > 1. J
Пример. 5. Докажем, что -уп := 14 \-— +...-{ Inn —> 7, п —> 00.
2 3 п
Число 7 ~ 0,577215... — постоянная Эйлера. Интересно отме-
отметить, что до сих пор неизвестно, является ли число -у рациональным.
I" Для доказательства заметим, что
00 /1 п \
есть частичная сумма ряда 1 + У' ( — — In 1 , для которого име-
п=2 \П П-\ )
1 . П 1
ем In ■ —— , п -> оо. J
п п - 1 2п2
Упрасмсмение 15. Пусть {а,/3} С Я. При каких а и /3 сходится сле-
оо
дующий ряд J] n" circtg n'3.
n=l
Упражнение 16. Доказать сходимость последовательности
(——- + —— + . . . + —; In 1ПП I П > 2).
I21n2 31n3 nlnn ' - I
y Пусть члены рядов A) и B) удовлетворяют следующим условиям:
ап > 0, Ьп > 0; —-— < -^—, п > 1. Тогда из сходимости ряда B)
следует сходимость ряда A).
(" Пусть ряд B) сходится. Положим dn = 7~ >0, п>1 и заметим, что
Ьп
dn+i = -~^— < -р = dn < dn_i < ... < di, n > 1. Таким образом,
Ьп+1 Ъп
последовательность {dn \ п > 1} ограничена и, согласно лемме 1, ряд
fln СХОДИТСЯ. J
оо
п=1 п=1
п
Пример. 5. Ряд Е г сходится. Действительно,
n=i е"п!
ап+i
en+1(n + l)!nn~2

250 Глава 7. Ряды
п V (п + 1J Ь„+1 1
У применение 17. Доказать сходимость следующих рядов:
2 2
оо „2
ОО jj™
Упражнение 18. Доказать, что ряд Y1 ~^~1 Расх°Дится.
в П
п=1
1
П.
Упражнение 19. Пусть ряд A) с неотрицательными членами сходит-
сходится. Доказать сходимость рядов: а) ^/а-^а^Л- ^/а^а^Л- ... + y/anan+i +... ;
- +- =1.
Р 9
7.2.3 Признаки сходимости рядов
1°. Признак д'Аламбера. (Первая формулировка.) Если члены
оо
ряда A) J2 ап удовлетворяют условиям: 1) Vn > 1 : а„ > 0; 2)
п=1
=3р, 0<р<13п0бЛГУп>п0: n+1 < р, то ряд A) сходится. Если
при условии 1) 3 По 6 N V п > По : —-— > 1, то ряд A) расходится.
SP. Признак д'Аламбера. (Вторая формулировка.) Пусть чле-
члены ряда A) удовлетворяют условиям: 1) Vn > 1 : ап > 0; 2) существует
lim " = г. 0 < г < +оо. Тогда при г < 1 ряд A) сходится, а при
п->оо ап
г > 1 ряд A) расходится.
[ Утверждение 2° есть следствие 1° и определения предела после-
последовательности. Например, при г<1 Vp, г < р < 1 3n0 Vn >
По : "+ < р. Доказательство 1° следует из неравенств Vn > по :
:: о-п
"+ < р = ; an+i > а„, п > По, признака сравнения 3 и сходи-
О-п РП
мости геометрического ряда, а также теоремы 1. J
х2 х3 хп
Пример. 1. Ряд 1 + 1+ — +Т7 + • •.Н г +••• сходится для любого
2! 3! п!
' ап+1 хп+1п\ х
х > 0, так как —— = -, г;— = -> 0. п -л сх>.
ап (п + 1)!хп п + 1

7.2. Ряды с неотрицательными членами 251
Упражнение 20. Доказать сходимость рядов:
~ 3"(п!J , ~ 7"(п!J
Упражнение 21. Если для ряда A) с положительными членами
lim —-— < 1, то ряд A) сходится. Если lim —— > 1, то ряд A)
п-юо ап п-*оо ап
расходится. Доказать зти утверждения.
Упражнение 22. Доказать следующее утверждение. Если для по-
последовательности {а„ | п > 1} положительных чисел существует предел
lim "+1 = г, то существует предел lim ?faZ = г. Привести пример,
П-+ОО пп П-*ОО
показывающий, что обратное утверждение не имеет места.
3°. Признак Коши. (Первая формулировка.) Если члены ряда
A) удовлетворяют следующим условиям: 1) Vn > 1 : ап > 0; 2)
=3p,0<p<13n0GiVVn>no: {/а^Г < р, то ряд A) сходится. Если
при условии 1) неравенство tfa^ > 1 справедливо для бесконечного
числа номеров п, то ряд A) расходится.
4°- Признак Коши. (Вторая формулировка.) Пусть члены ряда
A) удовлетворяют условиям: 1) Vn > 1 : ап > 0; 2) существует
lim ?/а^ = г, 0 < г < +оо. Тогда при г < 1 ряд A) сходится, а при
П—+ОО
г > 1 ряд A) расходится.
Г Утверждение 4° есть следствие 3° и определения предела после-
последовательности. Доказательство утверждения 3° следует из неравенств
Vn > По : ап < рп\ ап > 1 для бесконечного числа номеров п, при-
признака 1°, сходимости геометрического ряда и теоремы 1. J
ОО fji 2П
Пример. 2. Ряд J2 7 Г~=" сходится, так как справедливо
п=1 (П + 1)п
_ / п \п 2 ,
такое утверждение уап = 2 —> - < 1, п —> оо.
\п + 1 / е
Упражнение 23. Доказать сходимость рядов:
оо дЗ оо 2П
Упражнение 24- Пусть для ряда A) с неотрицательными членами
г := lim s/aZ. Доказать, что при г < 1 ряд A) сходится, а при г > 1
П—+ОО
ряд A) расходится.
5°. Логарифмический признак. Пусть члены ряда A) удовле-
удовлетворяют следующим условиям: 1) Vn > 1 : ап > 0; 2) существует

252 Глава 7. Ряды
lim ( nln —— 1 = г, — оо < г < +оо. Тогда при г > 1 ряд A) сходит-
п^оо ^ а„+1 )
ся, а при г < 1 ряд A) расходится.
[ Используем неравенства V п > 1 : [ 1 Ч— < е < [ Ц— ,из
V п I V п I
которых следует, что Vn > 1 : < In I 1 Л— 1 < — . Пусть г > 1
~ п + 1 \ п ) п
и 1 < р < г фиксировано. По определению предела последовательности
имеем 3 по V п > по : п 1л —— > р, откуда V п > no : n In >
> рп In 1 + - , или > <=$■ <
V п ) а„+1 \ п ) an
п
Теперь утверждение о сходимости получается из признака сравнения 3°
и сходимости обобщённого гармонического ряда с а = р > 1.
Пусть г < 1. Тогда 3n0 Vn>n0 : nIn —^— < 1 < пIn A -\
а \
(
а„+1 \ п -
1
ап+1
откуда < -£=>■ > —y— • Для доказательства
o-n+i n — 1 an i
n-1
расходимости можно использовать признак 3° и расходимость гармони-
гармонического ряда. J
Пример. 3. Ряд J2 п сходится, поскольку nln—— =
п=1 е п- ап+1
епп\(п+1)п \ V п J / 2
цри п -> оо.
Упраэ/сиеиие 25. Доказать сходимость ряда ^ —-
: —-—^__ n=1 ^
Упражнение 2Щ. Признак Раабе.У|усть члены ряда A) удовле-
удовлетворяют следующим услбвиямП) Vn >i : an > 0; 2) существует
lim ( n I —^— — 1 1 ] = г, —оо < г < +оо. Доказать, что при г > 1
ряд A) сходится, а при г < 1 ряд A) расходится.
Указание. Использовать логарифмический признак.
б°. Интегральный признак Маклорена-Коши. Предполо-
Предположим, что функция / : [1, +оо) —> R удовлетворяет таким условиям:
«.) Vx > 1 : f(x) > 0; 2) V{x',x"> С [1,+оо),х' < х" : /(х') > Дх").

7.2. Ряды с неотрицательными членами 253
оо оо
Пусть an := f(n),n > 1. Ряд S a« = S /(п) сходится или расходится
71=1 П=1
X
в зависимости от того, конечен или бесконечен предел lim ff(u)du.
х
\ Положим .F(x) := //(u) du, х > 1. Функция F не убывает на [1,+оо),
1
х" х"
поскольку по условию 1) .F(x") = / f(u)du = F(x') + f f(u)du >
1 x'
> F(x'), 1 < x' < x". Поэтому существование предела lim .F(x) <==>
существование lim F(n) <=> supF(n) <+oo. B)
"-*00 n>l
oo n+1
: Ряд ^ Ь", где Ь„ := F{n + 1) - F{n) = f f{u)du, n > 1, имеет
l
частичные суммы sn := ^ bk = ^(n + 1) - ^A) = ^(n +1), n > 1, и
fc=i
Поэтому сходится тогда и только тогда, когда предел B) конечен. Кроме
Того, поскольку
г п+1
f{n + l)<F{n + l)-F{n)= f f{u)du<f{n), n>l, C)
9 п
п
то для sn ■= Y^ ак, п > 1, имеем неравенства sn+i - /A) < sn <
fc=i
^ *п, n > 1. Отсюда получаем следующие утверждения
supsn<+oo <=$>■ supsn<+oo -<=> зир^(п) <+оо. J
оо
Замечание. Пусть rm ~ J2 /(n)> яг > 1. Из C) следует также
J n=m+l
" х
I такая оценка rm < lim F(x) - F(m) = lim Г f(u) du.
x-*+oo x-* + oo ^
;> °° 1 x du
Примеры. 4. Ряд У] — a > 1 сходится, поскольку lim Г — =
l Па х-+ + оо ^ Ua
= lim
и
]
n=l Па
-a+l U=I
x-++oo —a + 1
u=i a — 1
. Кроме того, для остатка имеем оценку
ОО J
5. Ряд У) сходится при a > 1 и расходится при а < 1.
2 n(lnn)Q
„=2
? du ^dz (lnx) (In2)
Действительно, — -— = Г — = - при
? du
a/ln f —— = lnlnx - Inln2.
^ ulnu

254 Глава 7. Ряды
Упражнение 27. Для ряда из примера 4 найти lim (ma 1гт).
ть оо
Упражнение 28. Пусть ап > 0, sn = ах + а2 + . ■. + ап, п > 1, и
оо
ряд Е ап расходится. Доказать, что первый из двух следующих рядов
п=1
Е ——— ; Е \— расходится, а второй сходится.
n=l Sn In Sn n=\ Sn In Sn
Упражнение 29. Найти а, при которых сходится ряд:
оо оо
п=1 п=1
оо / / 1 \ "+1 \ а оо
с) Е 1 + 1 ~е ; d> E
п=1 у \ п ) ) п=1
Упражнение 30. Признак Коши. Предположим, что Vn > 2 :
an-i > а„ > 0. Доказать, что ряды
а1 + а2 + аЗ + а4 + • • ■ + ап + • • ■ j
2а2 + 4а4 + 8а8 + ... + 2па2« + ...
сходятся или расходятся одновременно. Использовать этот результат для
исследования сходимости гармонического ряда.
оо
Упражнение 31*. Пусть ап > 0, п > 1, и ряд Е °п сходится.
п=1
оо
Доказать сходимость ряда Е ^/а1а2 . • ■ о,п .
п=1
Упражнение 32. Доказать, что при условиях упражнения 28 ряд
Е ~ сходится для а > 1 и расходится для а < 1.
n=l sn
оо
Упражнение 33. Пусть а„ > 0, п > 1, и ряд Е а" сходится. Пусть
п=1
оо оо йп
г„ = Е afc. " > 1- Доказать, что ряд Е — сходится при а < 1 и
fc=n+l п=1 гп
расходится при а > 1.
оо
Упражнение 34.. Пусть а„ > 0, п > 1, и ряд Е а" расходится.
п=1
Исследовать сходимость ряда:
ОО л ОО <-, ОО л ОО п
а\ р а" ■ Ь) У -2=—: с) Г " ; d) Г — ■
Упражнение 35. Пусть ап > 0, п > 1, и для т & N фиксированного

7.3. Сходимость рядов с произвольными членами 255
существует предел lim = а. Доказать, что ряд Е ап сходится
n-ioo an п-1
при а < 1 и расходится при а > 1.
Упражнение 36. Пусть ап > 0, п > 1, и ит„_юо '"Л'а^ < - . Дока-
е
оо
зать сходимость ряда Е а«-
п=1
Упражнение 37. Пусть а„ > 0, п > 1, и Пт 11>1°^/па„ < -. Дока-
оо
зать сходимость ряда ^ ап.
п=1
7.3 Сходимость рядов с произвольными
членами
7.3.1 Ряд Лейбница
Рассмотрим следующий ряд
1111
+
)"
называемый рядом Лейбница. Докажем, что ряд A) сходится и найдём
111 1
его сумму. Положим sn = l + -+-H h ... Н— , 7n = sn - Inn;
2 3 4 n
i 1111 ("I)" ^ , о
sn = 1 — — + — — - H— —... + -1 г ; n > 1. Заметим теперь, что
2 3 4 5 n
Л 111 11
1+ +
= hk
72fc -lnfc-7fc, fc>,l,
Следовательно, поскольку 7„ -* 7, n —> oo, то sn -> In2, n —> oo.
Таким образом, ряд A) сходится и
Е ^ =1п2. B)
Оказывается, что сходимость ряда Лейбница, и, в частности, его
сумма, зависят от порядка следования его членов. Рассмотрим ряд
, 11111 1 11 /ОЧ
1+3-2+5+7-4+--- + 4TT3+4fc3T-2ifc+--- ' C)
17 — 4-1168

256 Глава 7. Ряды
который отличается от ряда A) только порядком следования членов.
Для частичной суммы ряда C) с номером Зк имеем
- —1 - -- I 1 -- 1 1 1
111 I _^_
1 1 ]
_ 1 _ 1 _
- S4fc - 2 S2k - 2 Sk -
= 74fc + lnDfc) - \Ък - I bBfc) - 17fc - - lnfc, fc>l.
3 1
Поэтому получим S3fc —> - In2, к —> oo; s%k+\ = s$k + ——- —>
- In2, fc -> oo; s3k+2 = s3k + ——- + ——- -> - In2, к -> oo;
3
а, значит, и sn —> - In2, n —> oo. Таким образом,
1 1 1 1 _ (-1)"-1 _3
~ 2 + 3 ~ 4 + 5 ~ '"+ n +'"~2П'
Ряд Лейбница обладает новым свойством, присущим рядам: в от-
отличие от конечной суммы сумма ряда зависит от порядка
следования слагаемых.
Упражнение 38. Доказать, что
1 I I _ I _ I I I J^ _ 3. _ 1
Упражнение 39. Доказать, что
. 1111111 1
Упражнение 40*. Доказать, что
11111111 11 1
3+5+7-3+9+TT-5+T3+^-7+---=2
Замечание. Если "привести подобные члены", как в конечной сум-
сумме, то в левой части получим 0.
7.3.2 Абсолютно и условно сходящиеся ряды
Определение 1. Ряд
ах + а2 + ... + а„ + ... A)

7.3. Сходимость рядов с произвольными членами 257
называется абсолютно сходящимся, если ряд
Ы + \а2\ + ... + \ап\ + ... B)
сходится.
Определение 2. Сходящийся ряд A) называется ус-
условно сходящимся, если ряд B) расходится.
Примером условно сходящегося ряда является ряд Лейбница.
Теорема 4. Если ряд A) абсолютно сходится, то он
сходится, причём. J] а„ < £) |а„|.
оо
п=1
оо
п=1
[ Члены ряда
ЕК + Ы) (з)
п=1
удовлетворяют неравенствам 0 < ап + \ап\ < 2\ап\, п > 1. Следова-
Следовательно, ряд C) сходится. Прибавим к сходящемуся ряду C) сходящийся
оо оо оо
ряд £ Нап|), получим сходящийся ряд £ (ап + |ап| - |ап|) = Е а"-
п=1 п=1 п=1
Неравенство для сумм рядов получается с помощью предельного пере-
перехода в неравенствах
ak
lafcl> n > 1 с учётом сходимости
рядов A) и B). J
Положим ип := а„, а„ > 0, ип := 0, ап < 0; vn := -а„,
о-п < 0, vn := 0, а„ > 0. Отметим, что для каждого п > 1 :
\)ип>0, vn>0, 2)an = un-vn, 3) \ап\ = ип + vn.
Теорема 5. Ряд A) сходится абсолютно тогда и то-
только тогда, когда ряды
оо оо
Е «», Е Vn D)
п=1 п=1
сходятся, при этом, справедливы следующие равенства
оо оо оо оо оо оо
Е *»=Е«»-Е «», Е К1=Е«»+Е «». E)
п=1 п=1 п=1 п=1 п=1 п=1
f Если ряд A) сходится абсолютно, то сходимость рядов D) следует из
неравенств ип < \ап\, vn < \ап\, п > 1, и признака сравнения 1°. Из
D) равенства E) получаются из свойств сходящихся рядов.
оо оо
Если же ряды D) сходятся, то сходится ряд Е (un + vn) = Е la«l- J
Теорема 6. Пусть ряд E a™ сссодитсл условно. То-
n=l
оба ряда из D) расходятся.
17

258 Глава 7. Ряды
оо
[ Допустим, что ряд J2 ип сходится. Тогда по свойствам сходящихся
п=1
оо оо оо оо
рядов ряд £ ип ~ Т, an = Z) («п - а„) = £ г/„ также сходится.
п=1 п=1 п=1 п=1
Однако, сходимость обоих рядов D) по теореме 5 влечёт абсолютную
сходимость исходного ряда. Аналогично, к противоречию приводит и
оо
предположение о сходимости ряда Yl vn. J
n=l
7.3.3 Признаки сходимости рядов
1°. Признак Лейбница. Пусть числа а„, п > 1, удовлетворяют
условиям: 1) Vn > 1 : ап > an+i > 0; 2) ап —> 0, гг —> оо. Тогда ряд
оо
ai - а2 + а3 - а4+ ...= £ (-l)"^ (б)
п=1
сходится к сумме s, причём 0 < s < oi.
f Для частичных сумм с чётным индексом из 1) имеем
s2k = а.1 — а2 + а3 - а.4 + ... + a2k-i ~ a2k =
= (<*i - а2) + (а3 - а4) + ... + (a2fc_i - a2fc) > s2fc_2, к > 2.
Аналогично,
s2* = oi - (a2 - a3) - (a4 - a5) - ... - (a2fc_2 - a2fc_!) - а2к, к>1
Таким образом, последовательность {s2k | к > 1} монотонно не убывает
и ограничена: 0 < s2^. < aj, к > 1. Пусть s := lim S2fc, s 6 R. Тогда
к—»оо
на основании 2) s2fc+i = s2^ + a2fc+1 -> s, fc -> cx>. J
Замечание. Пусть rm = (-l)mam+i+(-l)m+1am+2+... — остаток
ряда F). Тогда \rm\ < am+i, m > 1.
oo oo
Упрамснение 41 • Привести пример рядов J^ ап и Z) ^n> первый
п=1 п=1
из которых "сходится" к +оо, второй сходится условно, и таких, что
lim — = 1.
n-юо 0п
Упражнение 4.2. Исследовать сходимость рядов:
оо / / 1 \ ™\ оо П+1 • °° f-l^n/3]
а) E(-l)n(e-(i + i) ); Ь) £(-l)nln^i; с) Е ^-^—-,
п=1 \ \ п / / п=1 п п=1 "
[а] — целя часть числа а.
Упрамснение 43. Доказать, что ряд
11111
1 I I I
•Д -Д -А -Л -Л '"

7.3. Сходимость рядов с произвольными членами
259
сходится, а ряд, полученный перестановкой слагаемых,
1 +
1
Т" /—
1
1 1
+
■Л -Л у/Ъ у/7 уД у/§ у/П ч/б
расходится.
Упражнение 44*• Пусть числа ап, п > 1, удовлетворяют условиям
признака Лейбница. Доказать сходимость ряда
ui + 0,2 О\ + 0,2 + Оз Oi + О2 + О3 + О4
Ol 2 + 3 4^ + • • • •
Упражнение 45. Привести пример сходящегося ряда, для которого:
оо оо
а) ряд Е °п расходится; Ь) ряд Е °п расходится.
п=1 п=1
Пусть {n,p}C JV и {on+llon+2,...,on+p; 6n+1,bn+2,-• ■ >ЬП+Р} С Н,
положим a(n + l,fc):= E bji fc > п + 1; <т(п + 1,п) := 0.
Лемма 2. (Тождество Аб*ё%я). Справедливо равенство
п+р п+р-1
» Р>2-
fc=n+l fc=n+l
f Для доказательства используем такое равенство Ьк = сг{п + 1, к) —
ar(n + l,k — 1), к > п + 1, и перегруппировку слагаемых. J
2°. Признак Дирихле. Пусть последовательности чисел {on | n > 1}
и {6П | п > 1} удовлетворяют условиям: 1) {on | n > 1} монотонна; 2)
о„ -ч 0, п -ч оо; 3) Э С > 0 Vn > 1 :
£ ап6п
fc=i
< С- Тогда ряд
G)
п=1
сходится.
\ Для доказательства сходимости ряда G) применим критерий Коши. Из
условия 3) имеем оценку |сг(п + l,fc)| < 2С, к > п + 1, с помощью
которой из тождества Абеля получим
п+р
Е
fc=n+l
<2С _
fc=n+l
6 силу условия 1) справедливо равенство
п+р-1
|, P>2.
п+р-1
Поэтому
Е
к=п+1
п+р
\ак - ак+1\ =
п+р-1
к=п+1
(Ofc - Ok+l)
afcbfc
< 2C(|on+i| +2|оп+р|). Отсюда с помощью усло-
вия 2) получаем условие критерия Коши сходимости ряда.
J

260
Глава 7. Ряды
Пример. Докажем, что ряд
]Г) сходится для любого х 6 R.
п=1 П
\ Если х = ктг, к G Z, то утверждение верно. Пусть х 7^ 'c7ri гДе к (z Z.
Положим в признаке Дирихле ап = —; 6n = sinnx; n > 1. Тогда
п
условия 1) и 2) выполнены. Кроме того,
sin fcx
fc=i
sin -
fc=1
2 sin — • sin kx
2
sin —
1 / 1 \
cos — — cos in + — jx
<
. X
sm-
n > 1,
поэтому условие З) также выполнено. J
Замечание. Признак Лейбница следует из признака Дирихле.
Упражнение 46. Доказать сходимость на R следующих рядов:
а)
sinn2i • sinni
n=l
cosn x • sinnx
n
cos n ■ sin nx
n
~ sin nx
п=1 П
1 - cos 2a
Упражнение 41- Доказать что для х ф ктг, к £ Z, ряд
сходится условно.
Указание. Использовать неравенство | sin a\ > sin2 a =
признак Дирихле и расходимость гармонического ряда.
Упражнение 48* • Определить, при каких х е R сходится следую-
щии ряд
sinn2x-cosnx
п=1 П
3°. Признак Абеля. Пусть последовательности чисел {an | n > 1}
и {Ьп | п > 1} удовлетворяют условиям: 1) {ап | п > 1} монотонна;
оо
2) {а„ | п > 1} ограничена; 3) ряд J2 ^п сходится. Тогда ряд G)
п=1
сходится.
[ Признак Абеля следует из признака Дирихле, который нужно приме-
применить к последовательностям {ап — а \ п > 1}, {bn | n > 1}, где о — пре-
оо
дел последовательности {ап \ п >!}. Из сходимости ряда J2 (°п-о)Ьп
п=1
оо оо оо
и условия 3) следует равенство Y1 (°п — аNп + о J2 Ьп = £ °nbn- J
п=1 п=1 п=1
Упражнение 49. Доказать сходимость ряда ]Г) (-1)™—Т117
п=1 V"

7.4. Другие свойства сходящихся рядов. Произведение рядов 261
7.4 Другие свойства сходящихся рядов.
Произведение рядов
7.4.1 Группировка членов ряда
Значение конечной суммы чисел не изменяется при выполнении сле-
следующих операций: группировки слагаемых, перестановки слагаемых,
раскрытия скобок. Для бесконечных рядов положение несколько иное.
Некоторые операции в общем случае недопустимы, например, в бес-
бесконечном ряду нельзя раскрывать скобки. Точнее, если члены ряда яв-
являются конечными суммами, то ряд, членами которого есть слагаемые
этих сумм, ведёт себя иначе чем, исходный. Например, следующий ряд
A-1)+ A-1) + .. . + A-1) + ... сходится, однако, ряд 1-1 + 1-1 + ...
расходится. Для ряда Лейбница было доказано, что его сумма зависит
от порядка слагаемых.
Определение 1. Пусть {т(к) | к > 1} — строго возрас-
возрастающая последовательность натуральных чисел и ■
oi + а2 + а3 + ... + о„ + ... A)
— некоторый ряд. Поломсим bi = 01 + 02 + ... + am{i), fo =
1m(l)+l + <*m(l)+2 + ■ • • + HmB), h = 0-mB) + l + OmB)+2 + . ■ • + OmC),
bj = Om(j-i)+i + ат(у_1)+2 + ... + am(j), j > 1 Говорят, что ряд
Ь1 + Ъ2 + Ъ3 + ... + Ъп + ... B)
получается из исходного ряда A) группировкой членов
(без изменения их порядка) или расстановкой скобок, а
ряд A) получается из ряда B) раскрытием скобок.
Теорема 7. В сходящемся ряду допустима произ-
произвольная расстановка скобок (т. е. группировка членов
без изменения их порядка). Полученный ряд сходится и
имеет ту ж.е сумму, что и исходный.
\ Пусть sn = Oi + 02 + ... + on, n > 1, — частичные суммы сходящегося
ряда A). Для ряда B), полученного с помощью группировки членов ряда
A), n-я частичная сумма есть &i + 62 + ... + bn = sm(n). Следовательно,
частичные суммы ряда B) представляют собой подпоследовательность
последовательности {sn \ n > 1} и потому сходятся к тому же пределу,
что и последовательность {sn | n > 1}. J
Упражнение 50. Доказать, что скобки раскрывать можно, если
полученный в результате ряд сходится.
Упражнение 51. Доказать, что для произвольного ряда допустима
группировка членов с одинаковыми знаками. Например, ряды

262 Глава 7. Ряды
1 _ 1 1 1 _ 1.
сходятся к одной сумме.
7.4.2 Перестановка членов ряда
Определение 2. Пусть т : N -> N — некоторая биек-
ция (говорят так&се, что m(l),mB),...,m(fc),... есть пе-
перестановка чисел 1,2,..., п,...) и
i i i i /Ъ\
"l + Oj "г ■ • ■ + Оп + • • • W)
— некоторый ряд. Говорят, что ряд
°m(l) + ОтB) + . . • + Om(fc) + . . . D)
получен из ряда C) с помощью перестановки членов.
Теорема8. (Дирихле). В ряду с неотрицательными
членами допустима произвольная перестановка членов
ряда. Точнее, ряд, полученный после перестановки сла-
слагаемых, сходится к той ж.е сумме (расходится), если
исходный ряд сходится (расходится).
\ Пусть тпA), тпB),..., т{к),... — некоторая перестановка чисел N, т.
е. Vifc е N : т(к) G N; Vn G N 3\к £ N : т(к) = п. Пусть
оп > 0, п > 1. Ряды C) и D) имеют частичные суммы
Sn = Ol + 0,2 + • • • + ап, П > 1; Sfc = am(!) + OmB) + . . . + Om(fc)i k > 1
соответственно. Если ряд C) сходится, то Vn > 1 : sn < s := lim Sj,
J-+OO
а потому Vfc>l: h < sn < s для N := max(m(l),mB),... ,m(k)).
Следовательно, ряд D) также сходится к некоторому числу 5 и s < s.
Однако, можно считать, что ряд C) получен из ряда D) с помощью
перестановки его членов (с помощью биекции т). Тогда, согласно
доказанному, s < s.
Таким образом, ряды C) и D) сходятся одновременно и s — s. j
Теорема 9. В абсолютно сходящемся ряду допусти-
допустима произвольная перестановка членов ряда.
оо
[ Пусть ряд J2 оп абсолютно сходится. Используем обозначения п.
п=1
оо оо оо
7.3.2 и теорему 5. Тогда Е °п = Е ип - Е vn, ип > 0, vn >
n=l n=l n=l
0, n > 1. Согласно теореме Дирихле, для любой перестановки m имеем
оо оо оо оо
Е ип = Е um(fc), Е vn = Е um(fc). Следовательно,
n=l fc=l n=l fc=l

ТА. Другие свойства сходящихся рядов. Произведение рядов 263
оо оо оо оо оо оо
Е Дп = Е Un - Е Vn = Е Um(fc) - Е Vm(k) = E °m(fc)- J
n=l n=l n=l fc=i fc=l fc=l
Таким образом, обычные свойства конечных сумм переносятся толь-
только на абсолютно сходящиеся ряды
оо
Упражнение 52*. Теорема Римана. Пусть ряд J2 ап сходится
п=1
условно и s G (Ru {-оо,+оо}). Доказать существование перестановки
оо
m множества N такой, что ряд ]>2 am(fc) сходится к s. Доказать так-
fc=i
же существование перестановки m множества N такой, что частичные
суммы переставленного ряда ограничены, но не имеют предела.
оо
Упражнение 53. Пусть J2 °п — расходящийся ряд с положитель-
п=1
ными членами, причём ап —> 0, п —> оо. Доказать, что для любого числа
s 6 R существует последовательность {еп \ п > 1} чисел таких, что каж-
каждое еп = -1 или еп = 1, и таких, что ряд £iOi+e2a2 + - • -+епап + -.. = s
сходится к сумме s.
оо
Упражнение 54- Ряд Е °п обладает свойством: для любой пе-
п=1
оо
рестановки m множества N ряд ]>2 am(fc) сходится. Доказать, что
fc=i
исходный ряд сходится абсолютно.
7.4.3 Умножение рядов
Произведение двух сумм а0 + ах + а2 + ... + ап, Ьо + 6Х + 62 + ... + Ъп
есть сумма всех произведений вида о; -Ьк, 1 < J,fc < п, которые можно
расположить в виде таблицы
(\\
Порядок сложения этих произведений при этом не существенен. При
переходе к рядам аналог таблицы A) содержит бесконечно много строк
и столбцов. Естественно и для рядов определить произведение двух
рядов, как ряд составленный из всех произведений вида о; ■ Ьд.> j,k > 1,
при этом, однако, порядок суммирования оквзывается существенным.
Определение 3. Произведением в смысле Коши -рядов

Щ Глава 7. Ряды
оо оо
Е *п, Е Ъп B)
fc=O fc=O
называется ряд
оо / п \
Е Е «А-,- • (з)
n=0 \j=0 у
Упражнение 55. Если ряды B) сходятся, то ряд C) не обязательно
сходится. Привести пример рядов с таким поведением.
Упражнение 56. Доказать, что если для сходящихся рядов B) ряд
C) сходится, то сумма ряда C) равна произведению сумм рядов B).
оо оо
ТеоремаЮ. (Коши). Пусть ряды Е °п = о, Е Ъп = 6
fc=O fc=O
сходятся абсолютно. Тогда ряд, составленный из всех
произведений а: -bk, j,k > 1, занумерованных в произволь-
произвольном порядке, в частности, ряд-произведение по Кохии,
сходится абсолютно и его сумма равна аЬ.
N N
[" По условию теоремы ЗС £ R V W > 1 : Е М < С, Е \ьп\ < С.
п=0 п=0
Рассмотрим ряд
оо
Е Oj(n)bfc(n), D)
п=0
составленный из занумерованных в каком-либо порядке всех произведе-
произведений Oj bfc, j, k > 1. Докажем, что ряд D) сходится абсолютно. Действи-
m N N N
тельно, Vm>l: Е к(п)Цп)| < Е 1^1'1^1= Е Kl E |bfc|<C2,
n=0 J,fc=O j=0 fc=O
где /7 := max(j(n), k(n) | 0 < n < m).
Таким образом ряд D) сходится абсолютно, и его сумма s не зависит
от порядка слагаемых. В частности, по теореме 9
s =
Частичная сумма sn с номером п последнего ряда имеет вид sn =
п—1 п—1 п—1
= Е аА = Е °j E &fc. n > 1. Поэтому sn ->■ 06, п -+ оо. J
j,fc=0 j=0 fc=O
00 2;i
Упражнение 57. Для любого i £ R ряд Е "Т =: оA) сходится
п=0 п!
абсолютно. Доказать, что V{i,t/}Cfl: 0A +у) = о(х)о(у).
Упражнение 58. Доказать, что при условиях теоремы Коши
lim (о06„ + О!бп_1 + о26„_2 + ... + оп60) = 0.

7.5. Бесконечные произведения 265
7.5 Бесконечные произведения
7.5.1 Определения. Сведение к ряду
Пусть {о„ | п > 1} — последовательность действительных чисел. Произ-
Произведение р„ := а^ ■ ■ ■ ап называется n-м частичным произведе-
произведением, п > 1. Заметим, что pn+1 = pnan+i, n > 1.
Определение 1. Две последовательности {а„ | п > 1}
^ {Рп I " > 1} называются бесконечным произведением и
обозначаются символом
П «п. A)
п=1
Если последовательность {pn | n > 1} сходится к числу
об Д, а^О, то произведение A) называется сходящим-
сходящимся, а число а — его значением и обозначается символом
оо
а — YI °п- В остальных случаях произведение A) назы-
п=1
вается расходящимся.
Замечания. 1. Если произведение A) сходится, го 3 N Vn >
N : Рп ф 0, следовательно, Vfc > 1 : afc ф 0.
2. Если произведение A) сходится, то а„ -4 1, п -» оо. Действитель-
рп а
но, если рп -» а ^ 0, то а„ = -> - = 1, п -ч оо.
Pn-i a
Далее произведение A) рассматривается только при
условии, что а„ > 0, п > 1.
Теорема 11. Длл того, чтобы произведение A) сссо-
дилось к значению а, необходимо и достаточно, чтобы
оо
сходился ряд Y1 1и°п = s, при этом а = es.
п=1
[ Положим sn = boi + 1по2 + ... + 1поп =-1прп, п > 1. Тогда
рп = es", п > 1. Если рп -> о, п -» оо, то Ьр„ = sn -> In a, n -ч оо,
в силу непрерывности логарифмической функции на @,+оо). Если же
sn -> s Е R, п -ч оо, то eSn = рп -> е5, п -> оо, в силу непрерывности
показательной функции. J
Упражнение 59. Доказать, что для х, \х\ < 1, следующее произве-
произведение A + х)A + 12)A + я4)A + I8) • • ■ сходится и найти его значение.
Упражнение 60. Доказать, что произведение \\ { 1 Ч— I рас-
п=1 \ П )
ходится.

266 Глава 7. Ряды
00 (
Упражнение 61. Найти значение произведения J~[ I 1 н
п=2 \
—
7.5.2 Достаточные условия сходимости
Теорема 12. Пусть ип > 0, п > 1. Произведение
ПA + «п) A)
п=1
сходится тогда и только тогда, когда сходится ряд
Е «». B)
Е
[ По теореме 11 произведение A) сходится тогда и только тогда, когда
сходится ряд
Е b(i + «n). (з)
п=1
Пусть ряд C) сходится, тогда 1пA + и„) -4 0, п-4оо, откуда имеем
un = elnA+u") - 1 -+ 0, п -ч со. Следовательно,
ln(l+ un)~un, n -+ оо, D)
и ряд B) сходится в силу признака сравнения 2°.
Если же сходится ряд B), то и„ —> 0, п ->оо, и снова справедливо
соотношение D), из которого следует сходимость ряда C). J
Замечание. Теорема остаётся верной и тогда, когда выполняются
такие неравенства — 1 < un < 0, п>1.
00 ( 1
Упражнение 62. Доказать сходимость J~[ I Ц—-
п=1 \ п
Упражнение 63. Определить значения х > 0, для которых сходится
оо
произведение f] (l + xn).
п=1
Теорема 13. Пусть числа ип > —1, п > 1, удовлетво-
оо оо
рлтот условиям: 1) ряд Y^ un сходится; 2) ряд J^ u\
п=1 п=1
i. Тогда произведение f] (l + un)
n=l
\ Докажем сходимость ряда C). Ряд
■«n)) E)
оо
п=1
сходится, поскольку согласно условию I) и„ -4 0, п —> оо, и потому
ип— ln(l + un) ~ -uj, n -4 оо. Учитывая условие 2), для доказательства

7.5. Бесконечные произведения 267
сходимости ряда E) применим признак сравнения 2°. Сходимость ряда
C) теперь следует из условия 1) и сходимости ряда E). J
Упражнение 64- Определить значения х £ R, при которых сходится
произведение из упражнения 63.
Упражнение 65. Исследовать сходимость произведения:
ОО 1 ОО / 1 \ ОО /ж 1
а) П cosi; Ь) П l™^ Ь О П tg (\ + ±
n=l n n=l \ П J n=l V4 n
Произведение J~[ on называется абсолютно сходящимся,
n=l
oo
если абсолютно сходится ряд J2 lnon- Для абсолютно сходящегося
п=1
произведения допустима произвольная перестановка сомножителей без
изменения его значения.

Глава 8
Функциональные ряды
8.1 Равномерная сходимость
последовательности функций
8.1.1 Определения
Пусть AcRh fn: A->R, п>1; f : А -+ R.
Определение 1. Последовательность функций {fn{x),
х е А | п > 1} сходится поточечно на множестве А к
функции /, если Vx £ А : fn{x) —► /(я), п —> оо.
Пусть множество В С А
Определение 2. Лоследователъностпъ функций {fn(x),
х е А | п > 1} сазодится равномерно на множестве В к /,
если Vg>0 3JVeiVVn>JVVxeB: |/„(х) -/(i)| < e.
Определение 2 равносильно следующему.
Определение 3. Последовательность функций {fn(x),
i S Л | п > 1} сходится равномерно на множестве В к
функции /, если dn := sup \fn{x) - f[x)\ ->0, n -+ oo.
хев
Замечание. Отметим, что dn < +oo, n > 1. Из равномерной на
множестве В сходимости последовательности следует её поточечная
сходимость на В.
Примеры. 1. Пусть А = [0,1]; /„(х) = хп, х £ [0,1], п > 1;
/(х) = 0, х G [0,1), /A) = 1. Последовательность {хп, х е [0,1] | п > 1}
сходится поточечно на [0,1] к /. Эта сходимость на [0,1] не является
равномерной, так как dn = sup |/n(x) —/(х)| = sup |хп - 0| = 1/> 0,
хе[од) хе[од)
при п —> оо.
268

8.1. Равномерная сходимость последовательности функций 269
На множестве Ва = [0,а], 0 < а < 1, последовательность функций
{zn, х 6 [О,1] | га > 1} сходится равномерно на [0, а] к /, так как
dn = sup \xn - 0| = а" -> 0, га -> оо.
Замечание. Обратим внимание на то, что в примере 1 поточечный \ /
предел последовательности непрерывных на [0,1] функций на является
непрерывной на [0,1] функцией.
2. Последовательность \ — , х Е R I n > 1 > сходится поточечно
I га2 + х2 )
на А к f(x) = О, х 6 R. Эта сходимость равномерна на -R, так как
dn = sup
-0
= SUP
п*
3. Последовательность < —, х £ [0,1] | га > 1 \ сходится по-
L 1 -)- 71 X «*
точечно на [0,1] к f(x) = 0, х € [0,1]. Эта сходимость не является рав-
ГЛ ,i , 2гаг . 2пх
номерной на [0,1J, так как а„ = sup ^—- — 0
= max
хб[0,1] 1 + П2Хг
1^0, га —> оо. Сходимость равномерна на множестве Ва = [а, 1], О <
а < 1, поскольку в этом случае dn = max ^—j = —-,
n > — , и поэтому dn —> 0, га —> оо.
Упражнение 1. Доказать, что последовательность функций /n(z) =
О, х < га, /(г) = 1, г > га, га > 1, сходится равномерно на любом
ограниченном множестве В и не сходится равномерно на R.
Упражнение 2. Пусть fn(x) = raln(l + - ) , х > 0, га > 1. Найти
\ га /
поточечный на [0, +оо) предел этой последовательности и доказать, что
сходимость равномерна на любом множестве В = [0,с], где О 0, и не
является равномерной на [0,+оо).
8.1.2 Свойства равномерно сходящихся
последовательностей
Теорема 1. (Критерий Когии равномерной сходимо-
сходимости последовательности функций). Для того, чтобы
последовательность функций {fn(x), x e A | га > 1} сходи-
сходилась равномерно на множ.естве А, необходимо и доста-
достаточно, чтобы
V£>03W6JVVm>WVn>WVi£^ : \fm{x)-fn{x)\ < е.A)
Г Необходимость. Пусть е > 0 задано. По определению 2 3 N £

270 Глава 8. Функциональные ряды
NVn>NVx£A: \}п{х) - }{х)\ < -. Тогда Vm > N Vn > N
Ухе В: \fm(x) - fn(x)\ < \fm(x) - f(x)\ + \f(x) - fn(x)\ < e.
Достаточность. Пусть х £ А фиксировано. Выполнение условия
теоремы для каждого значения х означает фундаментальность последо-
последовательности чисел {fn{x) | п > 1}. Согласно критерию Коши сходимости
числовой последовательности 3f(x) £ R : fn(x) —> f(z), n —> оо.
Пусть теперь е > 0 задано. Перейдя к пределу при т -> оо в неравен-
неравенстве A), получим Vn>N Vie А: \}п{х) - }{х)\ < е. J
Упражнение 3. Доказать, что равномерный на оси предел после-
последовательности многочленов есть многочлен.
Лемма 1. Пусть {fn(x), х е А \ п > 1}, / : А -> R, х0 е А.
Предполоок.им, что выполнены следующие условия:
1) {fn{x), х £ А | п > 1} сходится равномерно на А к /;
2) Vn > 1 : функция /„ непрерывна в точке х0.
Тогда f непрерывна в точке х0.
\ Пусть е > 0 задано. Согласно условию 1) имеем 3N £ N
Vn>NVx£A: \fn{x) ~ f(x)\ < е/3. По условию 2) 36 > 0 Vz £
А,\х-хо\ < 6 : \fN{x) -Ыго)| < е/3. Тогда Vz € А, \х - хо\ < 6 :
Лемма 2. Пусть {fn{x), х е [а,Ь] \ п > 1}, / : [а,Ь] -> -R.
Предполомсим, что выполнены следующие условия:
1) {/n(z), х e[a,b) | n > 1} сазодитсл равномерно на [а,Ъ\ к /;
2)Vn>l: /nG R{[a,b}). Тогда f £ R([a,b]).
\ Лемма 2 была доказана в п. 6.8.1 гл. 6. J
8.2 Равномерная сходимость
функционального ряда
8.2.1 Определения
Пусть А С R; а„ : А -> R, п > 1. Для г е А рассмотрим ряд
£ ап(х), хЕА. A)
п=1
Пусть sn{x) := ai(z) + a2(z) + ... + ап(х), х £ А, п > 1.
Определение 1. Множ.ество всех тех точек х е А,
для которых ряд A) сходится, называется множест-
множеством сходимости ряда A).

8.2. Равномерная сходимость функционального ряда 271
Замечание. Множество сходимости ряда A) есть множество, на
котором последовательность частичных сумм сходится поточечно.
Упражнение 4- Определить множества сходимости и абсолютной
сходимости ряда: a) g 2" sin ± ; Ь) jg ^—J^-—— ;
ОО (~, _ 0\П ОО ~П ОО
) е ^ ) е db^ > s ()
ОО
Определение 2. Фз/нк-цгюналънът рлд J2 а,„(г), i б А,
п=1
пазъ1ваетсл равномерно сходящимся на мномсестве В С
Л, если последовательность {sn(x), х € А \ п > 1} сазодитсл
равномерно на мноэ*сестве В.
Замечание. Равномерно сходящийся на некотором множестве ряд
сходится на этом множестве. Поэтому при исследовании равномерной
сходимости можно ограничиться рассмотрением рядов, сходящихся на
этом множестве.
ОО ОО
Положим а(х) := £ ап(х), гт(х) := £ ап(х), х € А.
п=1 п=т+1
Следующее определение равносильно определению 2, однако, бо-
более удобно при использовании.
ОО
Определение 3. Функциональный ряд £) ап{х) — а(х),
п=Х
х £ А, называется равномерно сходящимся на множе-
множестве В С А, если dn = sup \a(x) -sn{x)\ = sup (г„(ж)| -4 0, п -* оо.
I6B х&В
Пример. Ряд £) ^"i г € (—1,1), сходится равномерно на мно-
п=0
ОО
жестве Ва — \-а,а\, где 0 < а < 1, поскольку dn = sup £) x
х6[-а,а] fc=n+l
= sup —■ < ~r -> 0, n -> oo. Ha множестве (-1,1) равно-
«€!-«,«] 1 - я: - 1 - о v . ^
мерной сходимости нет, так как при этом dn = +оо, п > 1.
Непосредственным следствием теоремы 1 является следующее утве-
утверждение.
Теорема 2. (Критерий Коши равномерной сходимо-
сходимости функционального ряда). Для того, чтобы ряд A)
сходился равномерно но. множ.естве В С А, необходимо и
достаточно, чтобы Ve>0 3Nei
f |an+i(z) + an+2{x) + ... + an+p(z)| < e.
18 — 4-1168

272 Глава 8. Функциональные ряды
Упражнение 5. Доказать утверждение: если ряд A) сходится рав-
равномерно на множестве А, то последовательность функций {ап(х), х £
А | п > 1} сходится равномерно на А к 0.
Упражнение 6. Доказать утверждения: 1. если ряд A) сходится
равномерно на множестве А, а функция Ь : А —> R ограничена на А,
то ряд
£ (Ъ(х)ап(х)), х£А, B)
п=1
сходился равномерно на множестве А; 2. если ряд B) сходится рав-
равномерно на множестве А, а функция 1/Ь ограничена на А, то ряд A)
сходился равномерно на множестве А
Упражнение 7. Доказать что из равномерной на множестве А схо-
оо оо
димости рядов J3 ап(я), J3 Ъп[х), х £ А следует равномерная на
п=1 п=1
оо
множестве А сходимость ряда £ (an(z) + bn{z)), x £ А.
п=1
Упражнение 8. Доказать утверждение: если ряд A) сходится рав-
равномерно на каждом из множеств А и В, то он сходится равномерно на
множестве A U В.
8.2.2 Признаки равномерной сходимости
1°. Признак Вейерштрасса. Пусть функции а„ : А -> R, п > 1,
и числа сп £ R, п > 1, удовлетворяют условиям: 1) Vn > 1 Vi € А :
оо
1ап(я)| < сп; 2) ряд £ сп сходится. Тогда функциональный ряд
п=1
f an(x), х£А, A)
п=1
сходится равномерно на множестве А.
\ Из условий 1), 2) и первого признака сравнения для числовых рядов
следует сходимость ряда A) для всех х £ А. Кроме того,
dn = sup
оо
fc=n+l
оо оо
< sup ^2 \ak{x)\< Yl cfc->0,n->oo. J
fc=n+l fc=n+l
oo
Пример. 1. Если числовой ряд £ an сходится абсолютно, то ряд
п=1
оо
£ ancosnz, х £ R, сходится равномерно на оси.
п=1

8.2. Равномерная сходимость функционального ряда
273
Упражнение 9. Доказать равномерную на оси сходимость ряда:
b)
П=1
а) Е *2е-
ОО
d) E е-*1'
п=1
Указание к d). При каждом х £ Д предложенный ряд есть ряд
Лейбница и допускает потому простую оценку остатка. Обратить внима-
внимание на то, что ряд сходится условно при каждом х £ Д, и, следователь-
следовательно, к нему признак Вейерштрасса не применим, поскольку признак Вей-
ерштрасса обеспечивает равномерную и абсолютную сходимость ряда.
ОО 1 2
Упражнение 10. Доказать что ряд Е ~ е~п{х~п) , х £ R, схо-
п=1 П
дится равномерно на оси.
2°. Признак Дирихле. Пусть функции ап : А -> -R, Ь„ : .А -> Д,
п > 1, удовлетворяют таким условиям: 1) Vz £ А последовательность
{an(z) | п > 1} монотонна; 2) последовательность {an(z), г £ А | п >
1} сходится равномерно на А к 0, т. е. dn = sup|an(i)| —> 0, n —> тэо;
3) ЗС£ Д Vn> 1 Ухе А:
Тогда функциональный ряд Е ап(г)Ьп(г), х £ А, сходится равно-
равного 1
мерно на множестве А.
\ Из тождества Абеля следует неравенство
п+р
Vn>lVp£iWz£A: E о*(я)Ч:
fc=n+l
Согласно условию 2) и критерию Коши равномерной сходимости функ-
функционального ряда, получаем утверждение признака Дирихле. J
Замечание. Направление монотонности в условии 1) признака Ди-
Дирихле при разных х может быть разным.
„ _ _ ^ sinnz _ „
Пример. 2. Ряд 2_, , х £ Д, сходится равномерно на любом
п=1 п
множестве вида В = [2nk + 5,2п(к + 1) - 5], где fc £ Z, 0 < S < тт.
[ Все условия признака Дирихле для функций а„(х) — 1/п, Ьп(х) =
sinnz, г £ Д, п > 1, и множества В выполнены, в частности имеем
г £ В, п > 1.
Е sin fez
fc=i
em-
-l
Упражнение 11. Доказать, что ряд V
сходится равномерно на оси.
sinn2z • sinnz
п + xJ
_
х £ Д,
18*

274 Глава 8. Функциональные ряды
_. .Л _ ££, cosnx _
Упражнение 12. Доказать, что ряд 2_, —т=~ i * € Я, сходится
п=1 V"
равномерно на [<5,2тг — 6], 0 < 6 < 7Г.
_. . _ _ S sinnz • arctgпх _
Упраэ*скекие 13. Доказать, что ряд J2 =—, х е R,
п=1 П
сходится равномерно на [5,2тг — 6], 0 < 6 < 7Г.
5°. Лризкок Абеля. Пусть функции an : А -> Д, Ь„ : j4 -^ -R, п > 1,
удовлетворяют условиям: 1) Vx € А последовательность {ап{х) \ п >
1} монотонна; 2) ЭС £ Д Vn > 1 Vi £ Л : |an(i)| < С; 3)
с»
ряд Y1 Ьп(*) сходится равномерно на А. Тогда функциональный ряд
п=1
оо
ап(х)Ь„(г), х £ А, сходится равномерно на множестве А.
п=1
[ Доказательство основано на тождестве Абеля и аналогично доказа-
доказательству признака Дирихле. J
Упражнение 14. Провести доказательство признака Абеля.
Примеры. 3. Ряд £) -— хп, х G (-1,1], сходится равномерно
п=1 П
на [0,1].
[ Для доказательства в признаке Абеля положим А = [0,1]; ап(х) =
(_1)п+1
г", Ъп(х) = -— , х € [0,1], п > 1. Тогда все условия признака
п
Абеля выполнены. J
то (_1)п+1
4. Ряд Y1 > х > 0. сходится равномерно на [а, +оо), а > 0.
71=1 П
f Для доказательства в признаке Абеля положим А = [а, +оо); ап(х) =
(+1
1 (l)
= х_а/2 i Ьп(а:) = ^уз— > г — a> n — ^- ^огДа все условия признака
Абеля выполнены. J
Упражнение 15. Доказать, что ряд £) -—-—— arctgnz, x e Я,
сходится равномерно на оси.
Упражнение 16. Пусть функции а„ : A—*R,n>l, удовлетворяют
условиям: 1)Vn>lVze.A: ап(х) > ап+1(г) > 0; 2) supai(z) < +оо;
3) ряд 5Z апB;) сходится равномерно на А. Доказать, что для любого
п=1
оо
a > 0 ряд £) а^+а(гI * € Д сходится равномерно на множестве А.
п=1

8.3. Свойства равномерно сходящихся рядов 275
8.3 Свойства равномерно сходящихся рядов
8.3.1 Основные теоремы
ТеоремаЗ. (О непрерывности суммы функциональ-
функционального ряда). Пусть функции а„ : А -» R, п > 1, удовлетво-
оо
ряют условиям.: 1) Vn > 1 : а„ € С(А); 2) ряд £) ап{х) = а{х)
п=1
сходится "равномерно на А. Тогда а € С(А).
[ Достаточно доказать непрерывность функции в каждой точке. Эта
непрерывность есть следствие леммы 1 п. 8.1.2. J
Замечание. При условиях теоремы 3 для каждой точки Хо € А
имеем а(х) —> a(z0), х —¥ xq, или
оо
lim £ an{x) = X) lim an(x) = £ an{x0).
x~+xo n=l n=l *-*Bo n=l
oo f_t
Упражнение 17. Доказать равенства: a) lim У)
x-t-1 n=1 П
oo (_i\n+l oo f_1in+l oo (_11n+l
= £ LiL-; b) lim E Lir- = E U~ ■
n=l n X-+-1 „_! П1' n=i П
Упрасиснекие 18*. Пусть функции an : [a,b] —> R, n > 1, удовлетво-
удовлетворяют условиям: 1) Vn > 1 Vz e [a,b] : an(x) > 0; 2) Vn > 1 : an e
oo
C([a, Ь]). Доказать, что равномерная на [a, b] сходимость ряда Е ап(з)
п=1
есть необходимое и достаточное условие непрерывности на [а, 6] его
суммы.
Упражнение 19. Пусть ai(:r) = х, ап(х) = a.i/Bn-i)_a.i/(an-3)) д. е
оо
[—1,1], п > 2. Доказать, что ряд £) а„(г) не сходится равномерно на
п=1
отрезке [—1,1].
Указание. Показать, что сумма ряда равна signz, x € [—1,1].
Теорема 4. (О почленном интегрировании функци-
функционального ряда). Пусть функции ап : [а,/3] -> R, п > 1,
t/довлетворлкзт условиям.: 1) Vn > 1: an G Д([а,;0]); 2^ рлд
оо
Е а„(г) = а(х), х € [а,/3], сходитсл paenoAtepMo на отрезке
п=1
/3 оо /3
[а,Р]. Тогда ае R([a,p)) и fa(x)dx= Е Jan(x)dx, т. е.
а п=1 а

276 Глава 8. Функциональные ряды
/3 / оо \ оо /3
/ Е ап{х) ) dx = Е jan(x)dx.
а \п=1 / n=la
f Для доказательства заметим, что sn '■= (oti + - • ■+<*„) G -R([a,/3]), n > 1.
Теперь используем лемму 2 п. 8.1.2 и теорему о предельном переходе
под знаком интеграла. J
оо (_2}п+1
Пример. 1. Докажем, что 1пA + х) = Е хП> х £ (—1,1].
п=1 п
Этот ряд был открыт в 1668 г. Меркатором.
f Если |и| < 1, то
1 оо
~- = Z (-l)n«n, A)
I + U п-0
причём ряд A) сходится равномерно на [—а, а] для любого а, 0 < а < 1.
Пусть х G (—1,1) фиксировано, для определённости положим х > 0.
К ряду A) на отрезке [0,х] применима теорема 4, согласно которой
1 du °° х
f - = Е /(~l)nundu. Таким образом, справедливо равенство
о 1 + и п=о о
оо (_-]\п+1
W1 4-И- Г ' г" г Р ( — 1 1^ (!Л
п=1 "
Кроме того, в силу непрерывности логарифмической функции
lim ln(l + z) =ln2, C)
оо ^_2^п+1
а в силу равномерной на [0,1] сходимости ряда Е х™ и тео~
п=1 1
ремы 3 имеем также
оо (_]^п+1 оо (_^)п+1
I-+1- n=l П „=i П
Из равенств C), D) и B) следует, что формула B) верна и при х = 1.J
оо
Упражнение 20. Найти сумму следующих рядов: а) Е (n + l)*ni
|х| < 1; Ь) Е "*". 1*1 < 1-
Ответ: а) A-х); Ь) х{1 - х)~2.
Теорема5. (О почленном дифференцировании функ-
функционального ряда). Пусть функции ап : [а,C] -> R, п > 1,
удовлетворяют условиям,: 1) Эг0 G [а,0\, для которого
оо
ряд Е ап{хо) сходится; 2) Vn > 1 : а„ G С ([а,/3]); 3^ ряд
п=1
оо
Е а'пB;), х € [а,/б], сходитсл равмол^ерно па [а,/3]. Тогда рлд
п=1

8.4. Степенные ряды 277
an(z) = а(х) сходится па [а,/3], причём его сумма а 6
n=l
oo
C1([a,/3]) и справедливо равенство а'(х) = £] a'n(x), x £ [a,/3],
n=l
m. e. — I 2_\ cLn[x) 1= YJ — £2nf2?), x £ [o;,pl.
<*x ^n=i ^ n=i :
f Пусть
Ь(*):= £ <(*). *е[о,|9]. E)
n=l
Из условий 2) и 3) и теоремы 3 следует, что Ь £ С([а,/3]).
Пусть z £ [а,/3] фиксировано, для определённости предположим,что
z > хо. К ряду E) на отрезке [го,-г] применима теорема 4, из кото-
г оо г
рой следует равенство J" Ь(г) dx = Yl f a'n(x) dx. Применяя формулу
г оо
Ньютона-Лейбница и условие 1), получим J b(x) dx — J^ an(z)+c, с :=
n=l
oo
= — J3 anBo)- Из этой формулы следуют оба утверждения теоремы.]
тг=1
Упражнение 21. Доказать, что при условиях теоремы 5 исходный
оо
ряд J3 ап{х), х С [ai/3] также сходится равномерно на [а,/3].
п=1
оо
Упражнение 22. Пусть произведение П A + **п) сходится. Найти
п=1
lim f[(l + unxn).
I-*1~ n=l
oo I
Упражнение 23. Пусть a(z) = J2 — j, x e R. Доказать, что
n=l П + X
а' можно получить с помощью почленного дифференцирования.
8.4 Степенные ряды
8.4.1 Множество сходимости
Пусть {а„ | п > 0} с R и хо G R- Степенным рядом называется
оо
функциональный ряд вида J3 ап{х — хо)п, а; £ Д. Далее вместо этого
п=0
ряда рассматривается ряд вида
£ апхп, xeR, A)
п=0

278 Глава 8. Функциональные ряды
который получается из предыдущего линейной заменой переменной.
Частичные суммы ряда A) являются многочленами. Ряд A) всегда схо-
сходится для х = 0.
Упражнение 24- Лемма Абеля. Пусть {an | n > 0}, х0 Ф 0
таковы, что последовательность {апх^ \ п > 0} ограничена. Тогда ряд
A) сходится абсолютно для х 6 (—|zo|, l^ol)- Доказать это утверждение.
Положим:
р := lim л/jo^J, 0 < р < +оо; B)
П-+ОО
г := 0, р = +оо; г := - , 0 < р < +оо; г =+оо, /? = 0. C)
/>
Теоремаб. (Коши-Адамара). Пусть {ап \ п > 0} — по-
последовательность действительных чисел, риг — вели-
величины, определё'ннъ4е по этой последовательности фор-
формулами B) и C). Тогда:
a) при г = 0 ряд A) расходится для любого х ф- 0;
b) при г = +оо ряд A) сходится абсолютно для любого
х е R,
' с) при 0 < г < +оо ряд A) сходится абсолютно для х, \х\ < г
и расходится для х, \х\ > г.
[ а) г = 0 •<=> р = lim^oo л/|ап| = +оо. Следовательно, существует
подпоследовательность, для которой nih^/\(in(k)\ —> +oo, fc —> оо. Пусть
произвольное х ф 0 фиксировано. Тогда
3 fc0 V fc > fc0 : "(VF^)I > Л ^^
I
поэтому а„хп -ft 0, п -> оо.
b) г = +оо -<=Ф- р = lim v/|an| = 0. Пусть произвольное х ф 0
П-+ОО
фиксировано. Тогда
Эп0 Vn>n0 : vlan|<^| ^=> \о-пх\<—.
Из первого признака сравнения следует абсолютная сходимость ряда
D) для числа х.
c) 0 < г < +оо <=>■ 0 < р = linin^oo ^/|an| < +oo. Пусть произ-
произвольное х, \х\ > г фиксировано. Тогда р > т~т и существует такая
подпоследовательность, что
Vfc>l: ■'" т Х
" " х\

8.4. Степенные ряды 279
Таким образом, anxn ■/* О, п —> оо, и ряд A) в точке х расходится.
Пусть теперь произвольное х ф 0 таково, что |а;| < г, т. е. \х\р < 1.
Рассмотрим какое-либо а такое, что \х\р < а < 1. Поскольку р < —,
N
то Зп0 Vn > п0 : \/|ап| < —- -$==>• |anxn| < а™. Отсюда, как и
|х|
выше, получаем абсолютную сходимость ряда A) для числа х. J
Определение 1. Величина г, определённая формулами
B) и C), называется радиусом сходимости ряда A).
Упражнение 25. Доказать, что каждый из следующих рядов: а)
ж оо оо 2
2^ п\хп; Ь) J2 ппхп\ с) J2 2П хп имеет равный 0 радиус сходимости.
га=0 п=0
Упражнение 26. Доказать, что каждый из следующих рядов:
У] —г; У(—1)п+17 г: имеет равный +оо радиус сходимости.
п=о п' ~х Bп - 1)!
Таким образом, эти ряды сходятся абсолютно для каждого i£ Д. .
Упражнение 27. Доказать, что каждый из следующих рядов:
ОО Ю j« " j»
J2 xn; Y1 — ; 2_\ ~ имеет равный 1 радиус сходимости, а мно-
п—0 n=l n n=1 n
жества сходимости соответственно равны ( —1,1), [—1,1), [—1,1].
Упражнение 28. Определить радиус сходимости ряда:
n=0 n=o("+l)n n=0
Упражнение 29. Последовательность {ап \ п > 0} такова, что ап
О, п > 0, и существует предел lim
ап+1
оо
. Тогда г = lim.
Упразднение 50. Ряд £2 ал:сП имеет радиус сходимости г > 0. По-
п=0
оо
казать, что радиус сходимости каждого из следующих рядов: J2 папхп;
ОО ОО д
£2 {п2 + l)an!En; Y1 —^ хП также равен г. Определить радиус схо-
п=0 п=0 п + 3
~, ~, °°
ОО ОО д л
димости каждого из рядов: J2 2nanxn; £ Т^Г1"; /^"Т21"-
п=0 п=0 ^ „=0 п-
Упраэ<скекие 51. Определить множество сходимости ряда:
а) £ 2^хп; Ь) £ *п J с) £ 2"(х
п=0 п=0

280 Глава 8. Функциональные ряды
Упражнение 32. Пусть ri и г2 — радиусы сходимости двух рядов
оо оо
£2 апхп и £2 Ьпхп . Каким может быть радиус сходимости ряда:
п=0 п=0
а) £ (ап±Ьп)хп; Ь) £ ап6пх"?
п=0 п=0
Упражнение 33. Пусть 0 < рх < р2 < • • • < Рп < ■ ■ ■, Рп -* 9, «
сю. Найти радиус сходимости степенного ряда
оо Хп~^
n=l PlP2 Рп
8.4.2 Равномерная сходимость степенного ряда
Далее рассматриваются степенные ряды с положительным ра-
радиусом сходимости.
Теорема 7. Степенной ряд сходится равномерно на
любом, отрезке вида [а,/?], а & R, 0 G R, содерж.ащем,ся в
множестве сходимости.
\ Пусть г — радиус сходимости ряда
£ апх\ A)
п=0
Если а £ @, г), то ряд A) сходится равномерно на отрезке [—а, а] в
силу признака Вейерштрасса равномерной сходимости, поскольку Vn >
1 V х £ [—а, а] : |ап!Еп| < |апап| и для х = а ряд A) сходится абсолютно.
оо
Если ряд A) сходится при х = г, то £2 anxn = Y1 апгп
х
Рав-
n=0 n=0 r
номерную на [0, г] сходимость ряда A) получаем с помощью признака
Абеля равномерной сходимости.
Из доказанного легко следует утверждение теоремы. J
Упражнение 34- Найти все степенные ряды, сходящиеся равномер-
равномерно на оси.
8.4.3 Свойства суммы степенного ряда
Теорема 8. Сумма степенного ряда непрерывна на
множестве сходимости.
[ Теорема 8 есть следствие непрерывности членов ряда, теоремы 7 и
теоремы о непрерывности суммы функционального ряда. J
_ оо
Теорема 9. Пусть Y1 апХп — а(х), х £ А — степенной
ряд с радиусом, сходимости г и мноэ+сеством сходимо-
сходимости А. Тогда

$.4. Сгепенные ряды 281
Ухе A: Ja(u)du= £ ^ГТ^+1. A)
причём, радиус сходимости рлда в A) равен г.
\ Доказательство следует из теоремы 7 и теоремы о почленном инте-
интегрировании функционального ряда. Утверждение о радиусе сходимости
следует из теоремы Коши-Адамара lim \ = lim v/|an|. I
n-юо V П + 1 n->oo
1 1цП — x) °° 1
Упражнение 35. Доказать, что - Г — dx = У\ —.
О Х п=1 П2
Следствие 1. На множестве сходимости степенной
рлд моэ+сно интегрировать почленно произвольное число
раз, полученные при этом, степенные рлды, будут иметь
тот мсе радиус сходимости, что и исходный рлд.
оо
ТеоремаЮ. Пусть Y1 апХп = а(х), х е А — степенной
п=0
рлд с радиусом, сходимости г. Тогда а е С1((—г, г)) и
ViG(-r.r): a'(s)= £ no»*". B)
n=l
причёл* степенной рлд в формуле B) имеет радиус схо-
сходимости г.
\ Степенной ряд в формуле B) имеет радиус сходимости г в силу тео-
теоремы Коши-Адамара lim л*/|пап| = lim v/la»»l- Теперь утверждение
п—>оо п—>оо
теоремы следует из теоремы 7 и теоремы о почленном дифферен-
дифференцировании функционального ряда, применённым к отрезку [—a, a], где
О < а < г. J
Следствие 2. Сумма а степенного рлда с радиусом,
сходимости г принадлежит классу С°°{(-г,г)). Производ-
Производные функции а мо&сно получать с помощью почленного
дифференцирования исходного рлда.
Напомним, что для многочлена Р степени п для любого хо € R
справедливо равенство
Теорема 11. Пусть
£ апхп = а(х), хеА C)
п=0
— степенной рлд с радиусом сходимости г. Тогда

282 Глава 8. Функциональные ряды
Vn>0 ; пп = ^р. D)
Г При х = 0 в формуле C) имеем а0 = а@). После почленного диффе-
дифференцирования C) получим формулу B), из которой при х = 0 найдём
а.} = а'@) и т. д. J
Замечание. Таким образом, сумма степенного ряда есть функ-
функция класса С°°, обладающая тем свойством, что её значения на {-г, г)
восстанавливаются с помощью формул D) по значениям функции и её
производных в одной точке.
Теорема 12. Предполомсим,, что для степенных ря-
оо оо
дов £2 апхп = а(х), £2 Ъпхп = Ь(х) существует последова-
п=0 п=0
телъностъ чисел {tk \ к > 1}, принадлежащих множ.е-
ствам сходимости обоих рядов и таких, что Vfe > 1 :
tk ф 0; tk ->• 0, к ->• оо; a(tfc) = b{tk), к > 1. Тогда Vn > 0 : а„ = bn.
[ Равенство а^ = Ьо получим, перейдя к пределу при к —> сю в условии
a(ffc) = b(tk), к > 1, на основании теоремы 7. Учитывая полученное
равенство, имеем j^ ап^-1 = £2 ^n^fc) fe > 1- Далее как и выше
находим ai = 2>i, и т. д. J
Упраоюнение 36. Пусть а0 = аг = 1, an = an_! + an_2, n > 2.
с»
Доказать, что степенной ряд £2 апа;П =: s(x) имеет положительный
п=0
радиус сходимости и найти s.
Упраэ»скекие 57. Пусть а0 = а^ = 1, an = an_i + (n — l)an_2, n > 2.
00 in
Доказать, что степенной ряд J2 —7 х" =- s(x) имеет положительный
п=0 п-
радиус сходимости и найти s.
Упраэ»скекие 58. В множестве последовательностей {а„ | п > 0}
действительных чисел, удовлетворяющих условию по — 1, lim. v/|an| <
n-»oo
п
+сю, найти последовательности, для которых: а) £2 акап^к — 2п, п>
к=0
0; Ь) J2 afcan_fc = (n + l)an+1, n > 0.
fc=0
8.4.4 Ряд Тейлора
Согласно следствию 2 и теореме 11, сумма степенного ряда есть функ-
функция класса С°°, а частичная сумма ряда является основной частью фор-
формулы Тейлора для суммы ряда. Вследствие того, что степенные ряды

8.4. Степенные ряды 283
являются простейшими функциональными рядами, а свойства их сумм
особенно просты и потому легко могут быть использованы, возникает
вопрос: какие функции являются суммами степенных рядов? Или иначе:
какие функции можно представить степенным рядом? Принадлежность
классу С°° не является достаточной, как показывает следующий при-
пример.
Пример. 1. Пусть f(x) — ехр(-1/х2), х ■£ 0, /@) = 0. Доказать, что
/ G Cca{R) и что /<пН0) =0, п > 0.
Определение 2. Пусть х0 G R, 0 < г < +оо, и f G С°°((х0-
г, хо + г)). Степенной ряд
(xxoL (ххо)+...+p (х1оГ+...
= fl^~(x-xo)n, xe(xo-r,xo+r)
n=0 n-
называется рядом Тейлора (при х0 = 0 — рядом Макло-
рена) функции f в окрестности точки х0.
Замечание. Ряд Тейлора многочлена в окрестности точки хо сов-
совпадает с разложением этого многочлена по степеням х — хо- Ряд Тей-
Тейлора функции примера 1 в окрестности точки 0 равен 0. Степенной ряд
является рядом Тейлора для своей суммы, согласно теореме 11.
Теорема 13. Пусть х0 € R, 0 < г < +оо. Предположим.,
что функция f удовлетворяет следующим условиям,: 1)
f £ С°°((хо -г,х0 +г)); 2) ЗС G R Vn > 1 Vx G (x0 - г,х0 + г) :
|/(п)(х)| <Сп. Тогда
VxG(xo-r,xo+r): f(x) = Z , ' {* - »o)w, A)
n=0 n-
причём для г < +oo сходимость ряда равномерна на (х0 —
г,хо + г), а для г = +оо сходимость равномерна на любом,
отрезке вида [х0 - г, х0 + г], 0 < г < +оо.
Г По формуле Тейлора для любого п G N имеем представление
V х G (х0 - Л х0 + г) : /(х) = sn(x) + pn{x), B)
в kotodm s (х) - f fi){Xo) (x xn)k- о (х) - /
в которм sn(X) .— 2^ ,, ^х —xoj i pn^x; .— fn + l)!
• (x-xor+1, ве\о°,1).
Для х G (хо — г,Хо + г), учитывая условие 2), имеем неравенство
Cn+1
|р„(х)| < т гтг |х-х0Г+1 -ч 0, п -ч оо. Поэтому формула A) следует
(п + 1)!
из B) при п —> сю. Утверждения относительно равномерной сходимости
получаются аналогично. J

284 Глава 8. Функциональные ряды
Примеры. 2. Пусть /(х) = cosx, х € Я; х0 = 0, г = +оо. Поскольку
Vi 6 Д VnGiV: |/(n)(x)| = cosf x + n— J < 1, то условия теоремы
О Л Эк
X X ь, X
13 выполнены и cosx = l-— +— - ... + (-1) 7^7 + ••• .^А
3. Аналогично sinx = х-~ +^- -.. . + (-1)* * + +... , х € Я.
4. Пусть /(х) = ех, х G Я; хо = 0. Докажем, что
е = 1 •+■ х + ~гг + ■.. Н г + .. • . I с л.
2! п!
[ Для произвольного х G Я заданного пусть г таково, что |х| < г. Тогда
Vn > 1 Vx G [—r,r] : |/^(х)| = ех < ег и применима теорема 13. J
Упражнение 39. Пусть функция / представима рядом Тейлора на
{—г,г). Каким свойством обладает ряд Тейлора, если: а) / — чётная
функция на (—г,г)? Ь) / — нечётная функция на (—г,г)?
Упражнение ^0*. Доказать, что число е иррационально.
Теорема 13 даёт метод разложения функций в ряд Тейлора. Од-
Однако, условия этой теоремы не всегда выполняются или не могут быть
просто проверены.Тогда эффективным методом получения разложения
является использование свойств степенных рядов и их сумм. Этот метод
иллюстрируется на примерах 5 — 7.
; Примеры. 5. Справедливо представление
х2
Упомянутым выше методом зто представление получено в п. 8.3.1, при-
пример 1.
6. Докажем, что
X3 X5 x2k+l
+ + (l)fc
,«€[-1,1].
' Г Поскольку arctg' х = , х £ R, то
1 + х2
arctg'х = = 1-х2 + х4-х6 + .. . + (-l)*x2fc + ... , х G (-1,1).
1 + х*
На основании теоремы о почленном интегрировании функционального
X XX X
ряда имеем J arctg' u du = J du + Ju2 du +... + (-l)fc f u2k du+... для
о oo о
x G (-1,1), или
x3 x5 k x2k+1

8.4. Степенные ряды 285
Степенной ряд в C) сходится на [—1,1]. Следовательно, по теореме
8 его сумма непрерывна на [—1,1] Из этого, учитывая непрерывность
функции arctg и равенство C), получим верность равенства C) и для
значений х = —1, 1 = 1. J
Замечание. Из равенства C) при х = 1 получаем
ж 1 1 1 1 , ..,, 1
4=1-3+5-7+- + (-1J*П+- •
Упражнение 41- Доказать, что
Упражнение 4%> Разложить в ряд Тейлора в окрестности точки
х0 = О функции: a) shx, х G R; b) chx, x G R, с) sinx3, x e R;
d) sin3 х, х G Я; е) \ In ^ , х G (-1,1); f) ln(l - х2), х £ (-1,1);
2 1 + х
g)ln(l+x + x2), xG (-1,1); h) (I + x)sinx2, x G R;
0 1 + » + »' ' Х G (~1( 1); Ю A ~ 5X I
Упражнение 43. С помощью разложений в ряд Тейлора функций
sin и cos на оси доказать, что sup |sinx| < +оо, sup )cosa:| < +оо.
Указание. Подсчитать сумму sin2 x + cos2 x.
оо -j.3
Упражнение 44* • Найти сумму ряда Y1 1—\Т ■ a: G
п=0 (ЗП)
с»
Упражнение 4&- Найти сумму рекуррентного ряда J2 о,пхп, где
п=0
а0 = ai = 1; ап - an_x - ап_2 =0, п > 2.
оо
Упражнение 46. Найти сумму рекуррентного ряда J2 anxn, где
п=0
а0 = 1, ai = 2; an - - ап^ - - an_2 =0, n > 2.
Пример. 7. Биномиальный ряд. Пусть a G Д. Докажем, что
(l + i)e= Е Q=n. i6(-M), D)
где Со;:=1; cg;a;a(a-l)..ja-n+l)i ^L
Зал«ечакие. Частичные суммы ряда D) фигурируют в формуле
Тейлора для функции A + x)Q, х > —1. Если a G N, то Vn > a :

286 Глава 8. Функциональные ряды
С£ = 0 и тогда равенство D) превращается в формулу бинома Ньютона.
Ньютон первым получил формулу D) для целых отрицательных а.
\ Пусть а ^ (N U |{0}). Радиус сходимости ряда D) равен 1, так как
lira
CS+1
= 1. Пусть /(х) := Е С>п, * € (-1,1).
п=0
Покажем, что функция / удовлетворяет уравнению
т x)j \х) — ajyx), х t ^ — 1, i.). \o)
Согласно теореме о почленном дифференцировании степенного ряда
A + х)/'(х) = A + х) g nC2xn~l = Е пС2хп~1 + Е
п=1 п=1 п=1
оо оо
п=1 п=1
для x 6 (-1,1) в силу того, что пС^ + {п + 1)C^+1 = aC£, n > 1.
После умножения равенства E) на A + х)"", получим
A + х)-»/'(х) = a(l + x)-a-V(x), х € (-1,1).
Отсюда находим (A + х)~а/(х))' = 0, х £ (—1,1). Следовательно,
Зс € R Vx € (-1,1) : A + x)~af{x) = с. Число с = 1, так как
/@) = 1. Таким образом, /(x) = (l + x)a, x€(-l, I). J
Упражнение ^7. С помощью рассуждений, аналогичных использо-
использованным в примере 7, получить разложение в степенной ряд для функции
/(х) = е*, х € R.
Упражнение ^8. Разложить в ряд Тейлора в окрестности точки 0
функции: а) /(х) = ^, |х| < 1; Ь) /(х) = у/1-х2 \х\ < 1;
v -1 х;
.... 3-4х + 2х2 1
Упражнение А9. Доказать, что arcsinx = Е ,п " ^/i'\.. x2n+1,
n=i Bn + l)Bn)!!
|х| < 1. Получить аналогичную формулу для arccos.
Указание. Рассмотреть производные и использовать биномиаль-
биномиальный ряд.
оо
Упражнение 50*. Функция f(x) = Е e~n cos(n2x), х € R, при-
надлежит классу С°° и обладает тем свойством что её ряд Тейлора в
точке 0 сходится только в одной точке. Доказать это утверждение.

8.5. Степенные ряды с комплексными членами 287
8.5 Степенные ряды с комплексными членами
8.5.1 Определения
Пусть С — множество комплексных чисел. Число z € С имеет вид
z = a+bi, {a,b} С R; i = Vе!; a = Rez, b = Imz; \z\ := \/a2 +b2.
Справедливы неравенства
шах(|о|,|Ь|)<|г|<|о|+|Ь|; \zx + z»\ < Ы + \z2\. A)
Определение 1. Пусть {zn | n > 1} с С, z 6 С. Число
z называетсл пределом последовательности {zn | n > 1}
комплексных чисел (при этом такок.е говорят, что по-
последовательность {zn | п > 1} сходится к числу z), если
\zn — z\ —> 0, п —> оо.
Обозначения: z = lim zn, zn -4 z, n -» oo.
n—+c»
Пусть zn = an + £>ni, n > 1; z + a + bi. Из неравенств A) следует
утверждение:
>1°. zn -> z, n -» оо ^=Ф а„ -> а, Ь„ -> b, n -> оо.
Определение 2. Рлд с коллплекскьини членами
'■ 2 ^ (з)
п=1
" " п
'Назьбваетпсл сссодягцгхмся, если sn := ^2 Zk -> z £ С, п -» оо.
fc=i
Число z — сулглга рлда C). В остальных случаях ряд C)
называется расходящимся.
ЯР. Ряд C) сходится тогда и только тогда, когда сходятся следующие
оо оо
два ряда £} <*„, J2 Ь„; zn = а„ + Ь„г, п > 1, причём имеет место
п=1 п=1
оо оо оо
равенство J2 zn= E a« + * £ b«-
п=1 п=1 п=1
Определение 3. Ряд C) сходится абсолютно, если
оо
сходится ряд J2 \z*\-
п=1
3°. Ряд C) с zn = а„ + bni, n > 1, сходится абсолютно тогда и только
оо оо
тогда, когда сходятся ряды £} l°n|i Z) 1^1-
n=l n=l
4°. В абсолютно сходящемся ряду допустима произвольная перестанов-
перестановка членов ряда.
Пусть G С С; ап\ G -^ С, п> 1.
Определение 4' Функциональный ряд
19 — 4-1168

288 Глава 8. Функциональные ряды
an(z), z € G, D)
п=1
сходится равномерно на G, если sup f^ аЛг)
О, п -у оо.
z€G fc=n+l
5°. Признак Вейерштрасса. Если Vn > I VzgG: |an(z)| <
оо
с« 6 -R, причём ряд £2 сп сходится, то ряд D) сходится равномерно
п=1
на множестве G.
Упражнение 51. Если ряд C) сходится, то zn -ч 0, п -у оо,
оо
Определение 5. Рлд вида £) anzn, где ап е С, п > 0, z G
п=0
С, называется степенным.
Из определения 3 и теоремы 6 следует такое утверждение.
б°. Георема ЛГоши-Адал«ара. Пусть г \л р определены формулами
B) и C) п. 8.4.1. Тогда:
a) при г = 0 ряд E) расходится для любого z £ С, z ф 0 + Ог;
b) при г = +оо ряд E) сходится абсолютно для любого z £ С;
c) при 0 < г < +оо ряд E) сходится абсолютно для z, \z\ < г и расхо-
расходится для z, \z\ > г.
Величина г, определённая формулами B) и C) п. 8.4.1, называется
радиусом сходимости ряда E).
Упражнение 52. Лемма Абеля. Пусть {ап \ п > 0} с С, zo £
С, \zo\ ф 0 таковы, что последовательность {|anZo | | n > 0} ограничена.
Тогда ряд E) сходится абсолютно для z £ С, \z\ < \zo\. Доказать зто
утверждение.
Упражнение 53. Определить множество сходимости ряда
£(! + »)"(*-0я. г ее.
п=0
8.5.2 Показательная функция в комплексной плоскости
Показательная функция f(x) — ех, х £ R, обладает следующими свой-
свойствами:
2) показательная функция непрерывна на Д;
х2 х3
3)VGK 1 1 + +++

8.5. Степенные ряды с комплексными членами 289
Легко проверить, что свойства 1) и 2) определяют показательную
функцию с точностью до основания.
Определение 6. Показательной функцией на С назы-
называется сумма следующего ряда
e>:=l + z + ^+Zl+. .. + £+... , *6С. A)
Ряд в формуле A) сходится абсолютно для любого z б С.
Отметим следующие свойства показательной функции.
1°. Для z = x + 0i = x£R определённая формулой A) показательная
функция совпадает с показательной функцией ех, х € R-
° 2}cC : eZl • ez= =
[ По теореме об умножении абсолютно сходящихся рядов имеем
°° -п °° -п
£-"_ п\ {-"_ п!
,2 \
JP. Формулы Эйлера. Для любого х £ R справедливы равенства:
егх = cos а: + isinx, e~lx = cosx-iaiax;
gix , g-ix gi* _ g~*x
COS X = , ■ sin X = : .
2 2г
• Пусть sn{z) — частичная сумма ряда A) с номером п. Имеем
elx = lira Sin(ix) =
п—»оо
^3 ^4п-1
= lira 1 -—+... + 77—^ +«1ш U ~ -гг + ■ • • -
х3 а;4"-1
2! '■■■■' Dп)!у ' "п^о у 3! ' ■" Dп-1)!
= cos а: + isini. J
1 В качестве следствия отметим, что ez = ex(cosy + isiny), z =
:t + iy, {x,y}cR.
Г oo !
^Упражнение 5^. Доказать, что ряд ((z) := ]Г] — сходится аб-
|-< п=1 п
.солютно для значений z E С, Rez > \.
19*

290 Глава 8. Функциональные ряды
8.5.3 Историческая справка
Первым рядом, с которым имели дело ещё древнегреческие математи-
математики, была сумма членов бесконечной убывающей геометрической про-
прогрессии. Этот ряд встречается уже у Архимеда. Сколько-нибудь точ-
точное понимание вопросов сходимости отсутствовало у математиков ещё
в течение всего XVIII века. Например, для ряда
1-1 + 1-1 + 1-...
на основании расстановок скобок следующими двумя способами
A-1) +A-1) +A-1) + ... , 1-A-1)-A-1)-... ,
суммой считали и 0 и 1. Гранди делал из "доказанного" таким образом
равенства 0 = 1 вывод, что мир мог быть создан из ничего. Позже
Гранди, полагая в известном равенстве
1х+хх+х... ,
1 + 1
1 = 1 получил ещё одну сумму — . С этим выводом Гранди согласился
Лейбниц, приведя при этом свои соображения. Затем к ним при-
присоединились Якоб, Иоганн и Даниил Бернулли, а также Ла-
гранмс.
Важным для математики событием стало разложение Меркато-
ром в 1668 г. функции 1пA +х) в степенной ряд. После этого, к изуче-
изучению и использованию степенных рядов приступили Ньютон и Лейб-
Лейбниц. В частности, именно они впервые использовали степенные ряды
для решения дифференциальных уравнений. Формальная теория рядов
интенсивно разрабатывалась также в работах Я. и И. Бернулли,
Б. Тейлора, К. Маклорена, Л. Эйлера, Ж. Даламбера,
Ж. Лагранжа и др.
Современная теория рядов, основанная на понятии предела, была
разработана, в первую очередь, К. Гауссом, Б. Больцано, О.
Когии, П. Дирихле, Н. Абелем, К. Вейерштрассом и Б.
Риманом. Создание важной для приложений теории тригонометри-
тригонометрических рядов связано с именем Ж. Фурье.
Гвидо Гранди A671 — 1742) — итальянский математик, автор
работ по геометрии.
Николаус Меркатор A620 — 1687) — немецкий математик,
астроном и инженер.
Леонард Эйлер A707 — 1783) — один из наиболее выдающихся
математиков всех времён. Был также физиком, механиком и астроно-
астрономом. Значительную часть жизни провёл в России, был членом Петер-
Петербургской АН.

$.5. Степенные ряды с комплексными членами 291
Жан Лерон Д'Аламбер A717 — 1783) — один из самых раз-
разносторонних и влиятельных учёных XVIII в. Математик, физик, механик
(принцип Д'Аламбера), автор физико-математической части "Энцикло-
"Энциклопедии" Д. Дидро, а также ряда трудов по музыке и эстетике.
Жозеф Людвиг Раабе A801 — 1859) — швейцарский математик
и физик, основоположник сферической тригонометрии.
Колин Маклорен A698 — 1746) — шотландский математик, уче-
ученик И. Ньютона. Вместе с Д. Бернулли и Л. Эйлером по-
получил премию Парижской АН за теорию приливов и отливов. Первым
опубликовал работу о разложении функции в ряд.
Нильс Генрик Абель A802 — 1829) — норвежский математик.
Доказал невозможность решения общего алгебраического уравнения
выше четвёртой степени с помощью явных формул, аналогичных фор-
формулам решения квадратного уравнения.
Жак Адамар A865 — 1963) — французский математик и педа-
педагог. Ему принадлежит ряд выдающихся результатов во многих разделах
современной математики.

Глава 9
Функции ограниченной
вариации. Интеграл
Стилтьеса
9.1 Монотонные функции
9.1.1 Элементарные свойства
Определение 1. Функция f : [о,Ь] ->• R называется
монотонно неубывающей на [а,Ь], если V{x',x"} с [а, 6] :
х'<х" =>■ /(*')</(*")■
Положим по определению /(а—) := /(а), /(&+) = /(&)•
Если для точки х0 6 [о,Ь] : /(io+) — /(^о—) > 0. то величина
/(^0+) — /(so—) называется скачкол* (^ункг^кк в точке х0.
В настоящем разделе рассматриваются монотонно неубываю-
неубывающие функции, заданные на отрезке.
Лемма 1. Пусть х\, х2,..., хп — различные точки отрезка
[а, Ь], neN. Тогда £ (/(**+) - f(xk-)) < (Ь - о).
fc=i
f Предположим, что Х\ < х^ < ... < хп. Требуемое неравенство
— следствие следующих неравенств: /(а) < /(ii—), f{xn+) <
)" Г
1еистви-
тельно, Е (/(**+) - /(**-)) <
fc=i
292

&i. Монотонные функции 293^
+/(*„+) - / (a:"2+gn) = /(*„+) - /(*i-) < № ~ f(a). J
Лемма 2. Множество точек разрыва монотонной фун-
функции не более чем счётно.
[ Монотонная функция в качестве точек разрыва может иметь только
точки скачка. Пусть для заданного е > 0 имеется п точек xltх2, ■ ■ ■,хп,
скачек в каждой из которых не менее е. Учитывая лемму 1, имеем
п
f(b) - f(a) > £ (f{xk+) - f[xk-)) > пе. Отсюда следует, что число
точек со скачком, не меньшим е, конечно. Для fc £ N пусть Ак —
множество точек разрыва со скачком, не меньшем, чем \/к. Тогда
А = У Ак — множество всех точек разрыва функции / на [а, Ь], причём
множество А не более чем счётно. J
Следствие 1. Пусть {хп \ п > 1} — мномсество всех
точек скачка функции f на [а,Ь]. Тогда
Е (/(**+)-/(**-)) </(ь)-/(«)■ (!)
Замечание. Функция / может быть непрерывной на [а, Ь]. Тогда
множество точек скачка пусто и в этом случае считаем, что левая часть
неравенства A) равна 0. Левая часть неравенства A), вообще говоря,
есть ряд с положительными членами.
Определение 2. Пусть {хп \ п > 1} — мноок.ество всех
точек скачка функции f на [а,Ь]. Если Е {f{xk+) — f[xk—)) =
= f(b) — f(a), то функцил f называетсл функцией скачков.
Упражнение 1. Пусть с £ (а, Ъ). Найти lim f{x+), lim f{x—).
X—► С— i X—^C-f-
Упражнение 2. Пусть {г„ | n > 1} — последовательность всех раци-
рациональных чисел отрезка [0,1]. Положим /@) := 0; f{x) := ]П 2~п,
п: гп<х
0 < х < 1. Доказать, что: 1) функция / строго возрастает на [0,1]; 2) /
разрывна в рациональных точках, именно /(rn+) — f{i"n~) — 2~п, п > 1;
3) / есть функция скачков на [0,1].
9.1.2 Теорема о разложении
Теорема 1. Пусть f — монотонно неубывающал на
[а,Ь] функцил. Справедливо следующее представление

294 Глава 9. Функции ограниченной вариации. Интеграл Стилтьеса
f(x) = g(x) + h(x), x 6 [a, b], в котором д — функцил скачков,
имеющая скачки в тех о+се точках и той о+се величи-
величины, что и функцил /, a h — монотонно неубывающая
непрерывная на [а,Ь] функцил.
f Пусть {х„ | п > 1} — множество всех точек скачка функции / на [а,Ь].
Положим: д[а) := 0, д{х) := £ (/(**•+) - /(*„-)) + /(*) - f{x~),
п : х„<х
а <х<Ь; h{x) := f(x) - д{х), х G [а, Ь]. Если а < х' < х" < Ь, то
g(x")-g(x') = f(x'+)-f(x')+
+ Е (/(*»+)-/(*»-)) + /(«")-/(«"-)■ B)
п:х'<х„<х"
Отсюда в силу леммы 1, имеем
О <fl(*")-P(*') </(«")-/(*') C)
и /(а;') — д(х') < /(а;") — д[х"). Поэтому д и h монотонно не убывают на
[а, Ь]. Следствием равенства B) является также неравенство
g(xl')-g(x')>f(xl+)-f(x'). D)
Из неравенств C) и D) при х" -> х'+ получим:
д(х'+) - д(х') < /(*'+) - /(*'). 9{х'+) - д(х') > /(х'+) - /(*')•
Следовательно, g(a:'+) - g(a:') = f{x'+) - /(а:') и h(x') = h(x'+). Ана-
Аналогично доказывается, что h(x') = h(x'—). Непрерывность в точке b
доказывается аналогично. Поэтому h 6 С([а,6]). J
9.2 Функции ограниченной вариации
9.2.1 Определение и примеры
Определение 1. Функция f : [a,b] -> R называется
функцией ограниченной вариации (или ограниченного
изменения) на отрезке [а,Ь], если
3L€R VA([o1b]) = {*0,*i,...,xn} : "fl \f(xk+1)-f(xk)\ < L.
fc=O
Обозначение: / 6 BV([a,b]) <=Ф- / имеет ограниченную
вариацию на [a,b].
Для / 6 JBV([a,b]) вариация функции / на [а,Ь] есть величина
п-1
V(f,[a,b]) := sup ^ \f[xk+i) - f[xk)\, где верхняя грань берётся по
A fc=O
всем возможным разбиениям Л = {а;о, xit..., хп} отрезка [a, b].
V(f, [a, b]) := +оо, если / не имеет ограниченной вариации на [a, b].
Примеры. 1. Пусть / монотонная на [а,Ь] функция. Тогда функция
feBV([a,b}) и V(f,[a,b]) = \f{b)-f(a)\.

$Д Функции ограниченной вариации
295
J Пусть / монотонно не убывает на [a,b]. Тогда для любого разбиения
X = {х0, xlt..., х„} отрезка [а, Ь] имеем
"е l/(*fc+i) - Я**I = "е (/(*fc+i) - /(**)) = Я*») - Я*о) =
fc=O fc=O
= f{b)-f{a). J
1 2. Функция / определена на [0,1] следующим образом: /@) =
0, /(l/Bfc - 1)) = 0, /(l/Bfc)) = l/Bfc), fc G N, и линейна на каждом
из отрезков [l/Bfc+l),l/Bfc)], [l/Bfc), l/Bfc-1)], fc G N. Докажем,
что V{f,[a,b]) = +oo.
f Действительно, для любого п & N рассмотрим разбиение
2п + \'2пУ2п\'-'Ъ'2' }'
для которого имеем равенство
1
2п
-Яо)
1^-
2n-l
->^Yn
1
= - +
2n + l
1
2
n n — 1
Г +r +1-
3 2
Заметим, что / G C([a,6]).
Упражнение 3. Доказать, что V(f,[a,b]) = О
/(*) = /(a).
J
V* G [o,b] :
Упражнение 4- Найти вариацию функции: а) f(x) = sini, x G
[о,я-]; b)/(*) = *2, *e[-i,i]; с)/(*) = *3-*, *e[-i,i].
Упраэ«;ненг1е 5. Доказать, что V(/, [о,Ь]) = f{b) - /(a) •<=> /
монотонно не убывает на [а,Ь].
Упражнение 6. Пусть /(г) = isin-, х ф 0, /@) = 0. Доказать,
что 7(/, [0,1]) = +оо.
Упражнение 7. Пусть / € BV([o,6]). Для {а,/3} С R определить
вариацию функции д(х) — af{x) + /3 через V(/,[a,b]).
Упраэ«;ненг1е 8. Доказать, что / G BV([a,b})
\f\eBV{[a,b})-
Упражнение 9*. Доказать, что для / G С([а,Ь]) имеем |/| G
ВУ([а,Ь]) => / G BV{[a,b]). Привести пример, показывающий, что
условие непрерывности нельзя опустить.

296 Глава 9. Функции ограниченной вариации. Интеграл Стилтьеса
9.2.2 Свойства функций ограниченной вариации и
вариации
&.\f(b)-f(a)\<V(f,[a,b})-
\ Следует из определения для разбиения Л = {а, Ь}. J
3°. функция / £ BV([a, b]) ограничена на [a,b].
Г Пусть х 6 [а,Ь]. Тогда имеем |/(i)| < |/(а)| + \f{x) - f{a)\ < |/(а)| +
+ |/(«) - /(о)| + \f(b) - f(x)\ < |/(о)| + V(f, [а, б]). Таким образом, V х G
КЧ: |/(*)< |/(а)| + У(/,[а,Ч). J
4°. Если {/,Э} с BV([o,4), то: a) Vc 6 Я : (с/) G ВУ([а,Ь]);
b) (/ ± д) 6 BV([o,b]), (fg) 6 BV([o,b]); с) если дополнительно
3 a > О V х 6 [а, Ь] : |р(*) > а, то (//<?) 6 В V([o, Ч).
f Доказательства утверждений а) — с) элементарны и одинаковы. На-
Например, доказательство утверждения с) основано на оценке
< ± (\f(x")g(x') - f(x')g(x')\ + \f(x')g(x') -
< -^ (sup\д\ ■ |/(х") - /(х')| + sup|/| ■ \д(х") -д(х')\)
и использовании свойства 3°. J
Упражнение 10. Доказать, что / 6 Lip^a^b]) =>■ / 6 ВУ([а,Ь]).
Упрасмснемие ii. Пусть функция / имеет производную /' на [а,Ъ],
причём /' 6 Д([а,Ч)- Доказать, что / 6 J3V([a,4) и следующую фор-
a
Указание. Использовать для значений х' < i" следующее нера-
х" х"
венство |/(а;") - f(x')\ — f /'(и) du < J |/'(u)| du и теорему Лагранжа
X
Упраэ«;ненг4е i2. Пусть ^-6 Д([о, Ч) и f(x) = fip(u)du, x G [а,Ч-
а
Ь
Доказать, что V(/, [a, Ь]) = / \(р{и)\ du.
а
5°. Аддггтивностъ вариации Пусть / G BV([a, 6]) и с G (а,Ь). То-
гда/бВУ([а,с]), /gBV([c,4); V(f,[a,b]) =

9.2. Функции ограниченной вариации 297
\ Пусть Ai = Ai([a,c]) = {ио,иг,... ,un(i)}, A2 = А2([с,Ь]) = {vo,v1}...,
vn{2)} и А := Ai U A2 — разбиение отрезка [a, b]. Из неравенства
Е l/(«fc+i) ~/(«01 + Е \f[vk+i)~ f[vk)\<V(f,[a,b]) (I)
fc=O fc=O
следует, что
fc=0 fc=O
и тем самым первые два утверждения доказаны. Кроме того, согласно
неравенству A), имеем также
V(f,[a,c]) + V(f,[c,b])<V(f,[a,b]). B)
Пусть теперь А = А([а, Ь]) = {xq, Х\,..., хп} — произвольное разбие-
разбиение отрезка [a,b], причём с€ [х„,х„+\\. Тогда
П-1 I/-1
Е \fixk+i) - fixk)\ = Е |/(a;fc+i) ~ f(xk)\+
fc=0 fc=0
fc=I/+l
V — I
~ fc=0
n—1
fc=v+l
Отсюда
Из неравенств B) и C) следует третье утверждение свойства 5°. J
Замечание. Вторая часть доказательства свойства 5° показывает,
что / 6 BV([a,c]) и / б BV([c,b]) =» /еЩа,6]).
id. Вычислить вариацию функции:
а) f(x) = sin2i, ж€[0,27г]; Ь) f{x) = \sia.x\, x G [0,
Упраэкнение 1^. Пусть /(ж) = iasin—g-, a; 9^ 0, /@) = 0;{а,/3} С
R, j3 > 0. Доказать, что V(/, [0,1]) < +оо, если а > /3, и V(/, [0,1]) = 00,
если а <C.
Упражнение 15. Пусть / : [о,+оо) -> йи V6 > а : /6
BV([o,6]). Определим V(f,[a,+oo)) := lim V(^[o,b]) < +00. До-
b—*-\-oo
казать, что из неравенства V(f,[a,+oo)) < +00 следует существование
конечного предела lim /(я)- Привести пример, показывающий, что
X—►+ОО
обратное утверждение неверно.

298 Глава 9. Функции ограниченной вариации. Интеграл Стилтьеса
б°. Теорема Жордана. Функция / 6 BV([a,b]) тогда и только то-
тогда, когда / можно представить в виде разности монотонно неубываю-
неубывающих на [а,Ь] функций.
(" Достаточность. Следует из свойства 4° и результата примера 1 п.
9.2.1.
Необходимость. Пусть / 6 JBV([a,b]). Определим функции
д{а) := О, д(х) := V(f, [а,*]), х 6 [а,Ь}; h(x) = д(х) - /(*), х 6 [а, Ь].
функция д монотонно не убывает на [а,Ь], поскольку для a < х' < х" <
Ь имеем, согласно свойству 5°, д(х") = V{f,[a,x"]) = V(f,[a,x']) +
+V(f,[x',x"}) > V(f,[a,x']) = g[x'). Функция h монотонно не убывает
на [а, Ь], так как для в силу свойств 5° и 2° h{x") - h{x') = g{x") - f(x") -
-9(х') + f(x') = V(f, [*', х"}) - (/(*») - f{x")) > 0. J
Упражнение 16*. Доказать, что множества точек разрыва функций
/ и д в теореме Жордана совпадают. Доказать также, что функция
/ 6 BV([a, b]) может иметь не более чем счётное множество точек
разрыва первого рода.
Упражнение 17. Пусть / £ С1([а,6]). Доказать справедливость ра-
£а,х]) = |/'(х)|, х€[а,Ъ].
Упражнение 18. Представить в виде разности монотонно неубыва-
неубывающих функций следующую функцию: а) f[x) = sini, x 6 [0,27г]; Ь)
/(*) = sin2!, х G [0,2тг]; с) f{x) = х - [х], х 6 [0,3];
d) f(x) = s'mx — xcosx, а;б[0,47г].
Упражнение 19. Пусть / 6 BV([a,b}) и положим д(а) := /(а),
1 х
/ f{u)du, x 6 (а,Ь]. Доказать, что д б BV([a,b])
X О,
Упражнение 20. Пусть / 6 (BV([a,b\) Г)С([а,Ь})). Доказать, что /
можно представить в виде разности непрерывных монотонно неубыва-
неубывающих на [а,Ь] функций.
9.2.3 Спрямляемые кривые
Определение 2. Мномсество точек в пространстве
R3 Г = {{x,y,z) | х = <pi(t), у = ч>№), z = <p3(t); t g [a,/3]}, г<Эе
{^1>^2,<Рз} С C([a,/3]), козмеаетсл непрерывной кривой.
Пусть Л = \([а,C]) = {to,ti,... ,£„} — разбиение отрезка [а,0\ и
(Vi(*j).^2(*i)i V»3(*j)), 0 < j < п — точки на Г. Для каждого j, 0 < j <
п-1, соединим точки (vi(ij((

|>.3. Интеграл Стилтьеса 299
отрезком прямой. Пусть Г(Л) — полученная ломаная, её длина 2(Г(Л)),
в силу теоремы Пифагора, равна
«г(А)) = пЕ t/
fc=O у i=l
Определение 3. Непрерывная кривая Г называется
спрямляемой, если 1(Г) := вщ>1{Г(\)) < +оо, где верхняя
х
грань берётся по всем, возможным, разбиениям. А отрез-
отрезка [а,р]. Число 1(Г) называется длиной кривой Г.
^Упражнение 21. Доказать, что supZ(P(A)) = lim *(Г(А)).
А |А1—+0
Теорема 2. (Жордана). Кривая Г спрямляема тогда
и только тогда, когда {<Р1,ч>2,<Рз} С BV([a,p]).
\ Доказательство следует из определения функции ограниченной вари-
ации и неравенств
.max Е* |w(*fc+i) ~ Ы**)| < '(Г(>)) < £ if lw(*fc+i) ~ Vi(*fc)j- J
,. »-1,2,3 fc=0 i=1 k=0
9.3 Интеграл Стилтьеса
9.3.1 Определения
;. Пусть [а, Ь] — отрезок на Я, / : [а, Ь] -»• R — ограниченная на отрезке
[а,Ь] функция и а : [а,Ь] —>• Н — монотонно неубывающая на [а,Ь]
функция.
Для разбиения Л = Л([а,Ь]) = {xo,Xi,X2.- • • ,хп} и функции / для
О < к < п - 1 положим Дхк := я*,+1 — хц,; mj, := mfc(/) := inf
Mfc := Mfc(/) := sup /. Пусть |A| := max{Axfc | 0 < к < n - 1}.
Определение 1. Нижней суммой Дарбу-Стилтьеса
для ограниченной на отрезке [а, Ь] функции f и разбиения
п-1
Л называется число L(f,a;\) := Е mfc(a(xfc+i) ~ a(xfc))-
fc=0
Верхней суммой Дарбу-Стилтьеса для ограниченной
на отрезке [а,Ь] функции / и разбиения Л называется чис-
число U{f,a;\) := "e Mfc(a(xfc+1) - a(xfc)).
fc=0
Для набора точек ffc € [xfc,Xfc+i], 0 < к < п — 1, сумма
:= S(/,o;A) := "е f(b)(a(xk+1) - а(хк))
fc=0

300Глава 9. Функции ограниченной вариации. Интеграл Стилтьеса
называется интегральной суммой.
Замечание. Для ск(х) = х, х € [а, Ь], определение 1 содержит,
как частный случай, суммы Дарбу и интегральные суммы, введенные
при определении интеграла Римана.
Если неравенства inf / < тгц, < /(&) < Mk < sup/ умножить на
1».ь] [о.Ь]
a(xk+i) — a(xfc) > 0 и просуммировать по fc, 0 < к < п — 1, то получим
следующее свойство введенных сумм.
1°. VA = А(М1) V{£|A} : inf / ■ (а(Ь) - о(о)) <
< 5(/, а; А) < [/(/, а; А) < sup / ■ (о(Ь) - о(о)).
[о.Ч
Из свойства 1° следует, что AtHOcwcecmea чисел {L(/, a;A) | А},
{[/(/, а; А) | А} ограничены.
Определение 2. Нижним интегралом Римана-Сти-
Римана-Стилтьеса от функции f no отрезку [а, Ь] называется число
//(x)da(x) := supL(/, а; А), Верхним интегралом Римана-
х
Стилтьеса от функции f no отрезку [а, Ь] называется
число ff(x)da(x) := inf U(f, а; А). При этом, точные верхние
и нижние грани берутся по всем возможным разбиени-
разбиениям А отрезка [a,b].
Если для функции f f f(x)da(x) = J f(x)da(x), то функ-
функция f называется интегрируемой относительно функ-
функции а по отрезку [а,Ь], а общее значение верхнего и ниж-
нижнего интегралов называется интегралом Римана- Сти-
Стилтьеса от функции f по отрезку [а, Ь] и обозначается
ь
символом, f f(x)da(x).
Обозначение: / 6 RS(a, [а, Ь]) <=> f интегрируема относительно
а по [а,Ь].
Упражнение 22. Для функции Дирихле на [0,1] и функции а, для ко-
которой аA) — а@) > 0, для любого разбиения определить суммы Дарбу-
Стилтьеса, а также нижний и верхний интегралы.
Упражнение 23. Функции / и а определены на [—1,1] следующим
образом f(x) = -1, х < 0, /(х) = 1, х > 0, а(х) =0, х < 0, а(х) =
1, х > 0. Доказать, что f f(x)da(x) = -1, / f(x)da(x) = 1.

9.3. Интеграл Стилтьеса 301
9.3.2 Свойства нижних и верхних сумм
1°. Для произвольного разбиения Л и произвольного его подразбиения
Л' справедливы неравенства
L(f, а; Л) < L(f, а; Л'); U(f, а; А') < U(f, a; А).
[ Доказательство этого утверждения использует монотонность функции
айв точности совпадает с доказательством аналогичного утверждения
для сумм Дарбу. J
SP. Для произвольных разбиений Ai и Аз отрезка [а, Ь] справедливо нера-
неравенство L(/, a; Ai) < [/(/, а; А2).
3°. Для любой ограниченной на отрезке [а, Ь] функции /
ff(x)da(x)<jf(x)da(x).
4°. Критерий интегрируемости. Функция / 6 RS(a, [а, b}) то-
тогда и только тогда, когда V е > О ЗА: U(f, a; A) — L(/, а; А) < е.
[ Доказательство то же, что и для интеграла Римана. J
ь
Упражнение 24- Доказать для любого с € R равенство f cda(x) =
c(a(b) - а(о)).
Упражнение 25. Доказать утверждение: если а(а) — а(Ь), то V/ :
ff(x)da(x) = 0.
а
Упражнение 26. Пусть {f,g} С RS([a, Ъ]). Доказать, что:
а)Ус€Д: (с/) € RS([o,b]); Ь) |/| € RS([a,b]);
с) (/ ±д) € RS([a,b}); d) (fg) € RS([a,b}).
9.3.3 Классы интегрируемых функций
1°. С([а,Ъ)) с JRS(a,[a,b]). Кроме того, имеем также Ve>0 3 6 > 0
VA, |A|<<5 V{^|A} :|5(/,o;A1{fi|A})-
a
\ Пусть / € С([а, Ь]) и а(Ь) - а(а) > 0. Пусть задано е > 0. Функция / €
С([а,Ь]) по теореме Кантора равномерно непрерывна на [а,Ь]. Поэтому
для числа (е/(а(Ь) - а(а))) > 0 имеем
3<5>0V{x',x"}c[a,b], \x'-x"\<6: \f(x')-f{x")\<e/(a(b)-a(a)).

302 Глава 9. Функции ограниченной вариации. Интеграл Стйлтьеса
Для произвольного разбиения Л = Л([а,Ь]) с |Л| < 6 имеем:
[/(/, а; Л) - L(/, а; Л) = *£ (Mk - mk)(a(xk+l) - a(xk))
fc=0
Согласно критерию интегрируемости, / € Д£(а,[а,Ь]). Поскольку
ь
всегда имеют место неравенства L(/, a;A) < f f(x)da(x) < U(f, а; Л);
а
Ь(/, а; Л) < 5(/, а; Л) < [/(/, а; Л), то I / f(x) da(x) - S(f, a; Л) < e. J
1 a
Упражнение 27. С помощью утверждения 1° вычислить интеграл
1
/ х2 da{x), a@) = 1, a(x) = 2, 0 < х < 1, a(l) = 3.
2°.;Пусть функция / монотонна на [а,Ь], а функция а монотонно не
убывает на [а,Ь] и a € C([a,b}). Тогда функция / € RS(a, [a,b]) и
f Предположим, что / монотонно не убывает и /(Ь) — /(а) > 0. Пусть
е > 0 задано. По теореме Кантора 3 6 > 0 V{x',x"} С [а,Ь],|х' — х"\ <
6 : |а(х') - а(х")| < е/(/(Ь) - /(а))- Для любого Л, |Л| < 6, имеем
[/(/, а; Л) - L(/, а; Л) = "ff (/(xfc+1 - /(xfc))(a(xfc+1) - а(хк)) <
fc=0
г n-l
J
/(b) - /(a) fcf0
25. Пусть / и а удовлетворяют условиям утвержде-
утверждения 2° и а(а) > 0. Доказать, что для р > 1 справедливо равенство
9.3.4 Свойства интеграла Стйлтьеса
Доказательства следующих утверждений аналогичны доказательствам
соответствующих утверждений для интеграла Римана и потому не при-
приводятся.
1°. Если / € RS{a, [а, Ь\) и с € R, то (с/) € Л5(а, [а, Ь]) и
ь ь
/c/(x)da(x) = c//(x)da(x).

9.3. Интеграл Стилтьеса 303
2°. Если f,g и а удовлетворяют условиям 1° п. 9.3.3 или 2° п. 9.3.3, то
/(/(*) + 9{х)) da(x) = } f{x) da(x) + } д(х) da(x).
a a a
S°. Если / € RS(a, [a,b]) и с € (а,Ь), то справедливы следующие вклю-
включения / € RS(a, [а, с]) и / € RS(a, [с, Ъ]), причём
/ f{x) da(x) = f f{x) daix) + / /(x) daix).
■ а а с
,4°. Пусть {f,g} С Д5(а, [a,b]) и /(х) < g(x), x € [a,b]. Тогда
5°. Пусть / € RS{a, [a,b]). Тогда
inf / • (о(Ь) - aia)) < f fix) da(x) < sup / • (c«(b) - o(o)),
laM a [o,b]
, b b
и |/| € HS(a, [a, b]), кроме того, / /(x) daix) < f |/(x)| da(i).
'a a
б°. Пусть ctj — монотонно неубывающая на [a,b] функция и
/ей%„[а,Ь]), i = 1,2. Тогда
/ fix) d(ai(x) + a2(x)) = / /(x) dai(«) + / /(x) da2(x).
Упразднение 29. Если / € ^([a.b]) и Vx e [a,b] : fix) > 0, a
ь
a(b) - a(a) > 0, то / /(x) da(x) > 0.
a
b
Упрадаснение 30. Если / e C([a, b]), то 3в £ [a,b] : / /(x) da(x) =
1Г
Упрадаснение 31. Пусть / sin xda(x) = а(тг) - a@). Доказать, что
о
функция а постоянна, исключая точку тг/2, в которой справедливо ра-
равенство а(тг/2+) - а(тг/2-)) = а(тг) - а@).
Упражнение 32. Пусть V/ € С([0,1]) : //(х) da(x) = /A/2).
о
Доказать, что функция а постоянна, исключая точку 1/2, в которой
Упражнение 33. Для функции / б С([а,Ь]) и любой монотонно
б
неубывающей на [а, Ь] функции а справедливо равенство J fix) daix) =
a
20 — 4-1168

304 Глава 9. Функции ограниченной вариации. Интеграл Стилтьеса
= a(b) — a(a). Доказать, что Vx € [а,Ь] : /(х) = 1.
Упражнение 34- Пусть / € С([а,Ь]), функция а монотонно не убы-
вает и непрерывна на [а,Ъ], a F(x) := f f(u) da(u), x £ [a, b]. Доказать,
a
что F 6 (C([a,b]) П JBV([a, b])). Остаётся ли верным это утверждение
для a <£С{[а, b])?
Упражнение 35. Если в точке с € (а, Ь) хотя бы одна из функций /, a
с Ь
непрерывна, то из существования интегралов //(х) da(x),//(x) da(x)
а с
Ь
следует существование интеграла //(x)da(x).
\i
36. Если последовательность {/„ | п > 1} С C([a, b])
^ходится равномерно на [a, b] к функции /, то имеет место равенство
llim
и—юо
Упражнение 37. Предположим, что выполняются следующие ра-
1 1
венства /хA - x)da(x) = 0, fxda(x) = (a(l) - a@))/3. Определить
о о
функцию а.
9.3.5 Интеграл Стилтьеса относительно функции
ограниченной вариации
Если a £ BV([a,b}), то, согласно теореме Жордана, a = /3 - 7> гДе
Р и 7 монотонно неубывающие на [a,b] функции. Поэтому интеграл
6
/ /(х) da(x) естественно определить как разность
a
) da(x) := / /(х) d/3(x) - / /(х) d7(x). A)
a a a
Однако, определение A) нуждается в разъяснении. Во-первых, разло-
разложение Жордана a = /3 - 7 не является единственным; во-вторых, следу-
следует требовать интегрируемость / относительно всевозможных компонент
разложения Жордана. С помощью утверждений 1° и 2° п. 9.3.3 суще-
существование интеграла можно гарантировать в следующих двух случаях:
1)/GC([a,b]), a e BV([a,b});
2) / £ BV([a, Ь]), a € (BV([a, b]) П С([а, Ь]),
когда имеет место интегрируемость / относительно компонент разло-
разложения. В этих случаях разность A) не зависит от различных представ-

9.3. Интеграл Стилтьеса 305
лений а. Действительно, пусть также а = /3 — 7- Тогда /3 + 7 = /3 + 7 и,
ь ь
следовательно, / /(я) d(/3(x) + 7A)) = //(x)d(/3(x) + 7B:)). Теперь,
а а
Ь Ь
учитывая свойство 6 п. 9.3.4, получим //(x)d/3(x) - / f(x)drf(x) =
a a
Ъ _ Ъ
— f f(x)dC(x) — f f(x)d;y(x). Заметим также, что в обоих рассмат-
а а
риваемых случаях интеграл A) есть предел интегральных сумм.
ъ ъ
Упражнение 38*. Доказать, что / f(x)da(x) < f \f(x)\dv(x) <
а
а
< sup |/| V{a, [а, Ь]), где v{x) := V{a, [a, x}), x £ [a, b].
[a,b]
Упражнение 39. Правило интегрирования по частям.
Пусть / £ (BV([a,b))nC([a,b\), a € BV([a,b]). Доказать, что
/ f(x) da(x) = f(b)a(b) - /@H@) - / а(х) df(x).
%
Указание: lim X) /(^^(«(^fc+i) ~ «(^fc)) = /Wa(b) - f{a)a{a) -
\M-*o fc=0 \ г
-lim ПЕ«(^)(/F)-/F-1)), a = &, b = ^n-
1ЛН° fc=i
9.3.6 Вычисление интеграла Стилтьеса
Теорема 3. Пусть f € R[[a,Ь]), а € С([а,Ь\) и, исключая
конечное число точек отрезка \а,Ь], существует a' u a' €
R([a, b]). Тогда существует предел интегральных сумм,
lim S(f,«; А) = / /(*) ао(«) = / /(х)о'(х) а*.
[А|—>0 а а
f Для разбиения Л = Л([а,Ь]) = {xo,xi,x2, • • • ,1»}, включающего точки,
в которых а' не существует, имеем с помощью теоремы Лагранжа
S(f, «I A, tfi|A}) = if /(ffc)(a(*fc+i) - o(xfc)) = "ff /Ы"'^)^*,
fc=O fc=O
где ?7fc € [xfc,ifc+i], 0 < fc < n — 1. Отсюда получаем утверждение
теоремы, принимая во внимание, что (fa1) € R([a,b}). J
Л е м м а 3. Пусть функция / : [a, b] -» R непрерывна в точ-
точке с е [а,Ь], и а(х) = а(с-), х < с, а(х) = а(с+), х > с, а(с-) <
ъ
< а{с) < о(с+). Тогда / /(х) da(x) = f{c){a{c+) - о(с-)).
а
20* __

306 Глава 9. Функции ограниченной вариации. Интеграл Стилтьеса
\ Действительно, сумма 5(/,а; А,{&|А}) равна либо одному слагае-
м°му /(ffc)(a(zfc+i) - а(хк)), если с € {xk,xk+1), либо сумме двух
/(ffc-i)(a(c) - a(ifc_i)) + f{tk){a{xk+1) - a(c)), если с = xk. J
Лемма 4. Пусть f e C([a,b]), a = zx < z2 < ... < zm = b u
функция a : [a, b] -»• R постоянна на каж.дом из интерва-
интервалов (zfclzfc+i), l<fc<m-l. C/wrxW ivWwM3
Тогда jf(x)da(x) = £ /(zfc)(a(zfc+) - a(zfc-)).
a fc=l
f Лемма есть следствие леммы 3 и свойства 3° п. 9.3.4. \дулМ-
Теорема 4. Пусть f € C([a,b]), a непрерывна на [а,Ъ],
кроме конечного числа точек zi,z2t... ,zm — точек разры-
разрыва первого рода, за исключением, конечного числа точек
существует а', причём а1 € R([a,b]).
Тогда f f{x) da(x) = f /(x)a'(x) dx + £ f(zk)(a(zk+) - a(zk-)).
a a fc=l
Указание. Представить a в виде суммы функций из теоремы 1 и
воспользоваться леммой 4. Заметим также, что в леммах 3, 4 и теореме
4 монотонность функции а не требуется.
2
Упражнение 40' Вычислить интеграл /21 d(xsign costtx).
о
9.3.7 Теорема Хелли о предельном переходе
Теорема 5. (Хелли). Пусть f € С([а,Ь]), а а и ап, п >
1, — монотонно неубывающие на [а,Ь] функции. Пред-
Предположим, что an(x) -» a(x), n -» оо, для всех тех то-
точек х € [a, b], в которых функция а непрерывна, и что
ап{а) -»• а(а), an(b) -* ot(b), n -» оо. Тогда
ь ь
п-+о° о "о
[ Заметим, что все интегралы в A) определены. Для разбиения Л =
A([a,b]) = {xOlxi,i2.---.a:m}, в котором xi,x2,...,xm_i — точки непре-
непрерывности функции а, рассмотрим следующее вспомогательное нера-
неравенство:
//(x)dan(x)-//(x)da(x)
ш-1 /zfc+l +
£ / f(x)dan(x)- f f(x)da(x)
fc=O \ it xk t

9.3. Интеграл Стилтьеса
m-l
fc=O
(f(x)-f(xk))dan(x)+ f f(xk)dan(x)-
/(xfc)do(*)- f (f(x)-f(xk))da(x)
m-l
< E
fc=O
+ Ё
fc=O
m-l
+ E /
fc=O xb
Пусть e > 0 задано. Поскольку / € C([a, b]), то по теореме Кантора
36 > 0 V{x',x"} с [a,b], \x' - x"\ < S : |/(x') - /(x")| < e/C(l +
a(b) - a(a))). Предположим теперь дополнительно, что разбиение Л в
неравенстве B) имеет размер |Л| < 6 и фиксировано. Тогда
m-l
[o,b] fc=O
{\an{xk+1) - a{xk+1)\ + \an{xk) - a(xk)\)+
Выберем теперь число N таким, чтобы: 1) Vn > N : an(b) — an(a) <
m-l
<a{b)-a(a) + l; 2)Vn>W: sup/ £ (|an(xfc+i)-a(xfc+1)| + |an(xfc)-
[a,b] fc=O
-a(xfc)|) <e/3. Тогда Vn > N : Д„ < e. J
Пример. Пусть a — монотонно неубывающая на [a, b] функция скач-
скачков, xn, n > 1 — все точки скачка функции а, причём a(a) = 0, а(Ь—) =
а(Ь). Тогда а(х) = £ (a(xfc+)-a(xfc-))+a(x)-a(x-), х€[а,Ь].Для
ne N введём функцию ап(х) = Y. (a(xfc+) - a(xfc-)), x € [a, b].
k<n:xk<x
Заметим теперь, что для любого х € [а, Ь) — точки непрерывности
функции а имеем ап(х) —>• а(х), п —>• оо, поскольку
|а(х) - а„(х)| = J2 (a(xfc+) - a(xfc-)) <
к>п:хк<х
< Е (a(a;fc+) ~ а(хь-)) -»• О, п -»• оо
к>п
Здесь использовано то, что ряд из положительных скачков сходится.
Согласно лемме 4 и теореме Хелли, имеем для / € ^([а, Ь]) следую-

308 Глава 9. Функции ограниченной вариации. Интеграл Стилтьеса
Ъ оо
щую формулу //(x)da(x) = £ f(xk)(a(xk+) - a(xfc-)), причём ряд
a fc=l
в правой части абсолютно сходится.
Замечание. Пример показывает, что сумма любого абсолютно
сходящегося ряда может быть представлена в виде интеграла Стилтьеса.
9.3.8 Историческая справка
Камиль Мари Эдмон Жордан A838 — 1922) — французский
математик. Ему принадлежит ряд основных понятий и идей современ-
современной математики (жорданова форма матрицы, кривая Жордана, теорема
Жордана о простой замкнутой кривой в плоскости, признак Жордана
сходимости ряда Фурье, функция ограниченной вариации, разложение
Жордана, мера Жордана и др.). Автор точных и сжатых курсов по тео-
теории групп, теории Галуа, "Трактата о подстановках", трёхтомного "Кур-
"Курса анализа", широко известных в своё время и оказавших существенное
влияние на развитие математики.
Томас Иоанес Сгпилгпьес A856 — 1894) — нидерландский ма-
математик. К обобщению понятия интеграла Римана Т. Стилтьеса приве-
привела задача, связанная с неоднородным распределением масс на отрез-
отрезке прямой, в некоторых точках которого сосредоточены положитель-
положительные массы. Полученные им результаты относятся к теории непрерыв-
непрерывных дробей, проблеме моментов, теории ортогональных многочленов
и другим разделам анализа.
Эдуард Хелли A884 — 1943) — австрийский математик, автор
работ по топологии и функциональному анализу.
9.4 Дополнительные задачи к главам 5 — 9
1. Пусть /(х) = sin -, х ф 0, /@) = 0; g{x) = sin2 - , х ф 0, д@) =
! х х
1/2; h(x) = sin2 - , х ф 0, h@) = 0. Доказать, что функции /ид имеют
х
примитивные на R, а примитивная на R для функции h не существует.
2. Пусть {f,g} С Щ[а,Ъ]) и Цх) := inf /(*), Я(х) := sup /(*).
e<t<s: a<t<x
Доказать, что {h, Н} С R[[a, Ъ])
3. Функция / € -R([0,1]) удовлетворяет условию
причём /A/2) = 1. Определить /.
Ответ: f(x) = 1, х € [0,1].

9.4. Дополнительные задачи к главам 5 — 9 309
4- Вычислить предел:
a) lim (- £ sinf- +-)); Ь) lim £ i(+
Ответ: а) 1-cos 1; Ь) 1/2.
l
5. Пусть / £ XipiQO.lJ.L), f f(x)dx = 0. Доказать следующее нера-
о
n-1 /к \ I
венство V п > 1: У^ / ( ~ ) ^ Ь/2.
fc=O Ч П ' '
6. Пусть / £ С(Д). Доказать, что / нечётна на R тогда и только тогда,
X
когда ЗсЕЙ Ух £ R: J f(u)du = c.
— X
7. Определить функцию / £ С([0,1]), удовлетворяющую равенству
О Л О
Ответ: /(ж) = у/х, х е [0,1].
8. Пусть функция / £ С([а,Ь]) выпукла вверх и неотрицательна на [а,Ь].
1 * 1
Доказать неравенство Г f(x)dx > - max/.
о - a a 2 [о,ь]
5. Доказать, что для возрастающей на (a,b) функции / функция F(x) :=
X
/ f(u) du, x £ (a, b), с £ (a, b), выпукла вниз на (а, Ь).
с
10. Для функции / G BV([a, b]) определим функцию g следующим
1 x
образом: g(a) := /(a); g(x) := ^ f f(u)du, x £ (a,b]. Доказать,
x-a a
что g £ BV({a,b]).
Указание. Использовать теорему Жордана.
11. Функция £ C^QO.l]) строго возрастает на отрезке [0,1] и /@) = 0,
пусть g — функция, обратная к /. Доказать, что
X /(»)
jf{u)du+ J g{u)du = xf{x), же [0,1].
о о
ь
12. Для функции / £ С([а, Щ) имеем равенство J f(x) dx = 0. Доказать,
a
b
что Г/2(х)dx < mM(b — a), m:=-min/, M:=max/.
а М М
13. Пусть / £ С([0,2]). Доказать, что последовательность функций
*е[о,1] -. п>Л
fc=o
сходится равномерно на отрезке [0,1], и найти предельную функцию.

310 Глава 9. Функции ограниченной вариации. Интеграл Стилтьеса
1
Ответ: / f[x + u) du, х £ [О,1].
о
14- Пусть функция / £ С1([о,Ь]) монотонна на отрезке [a,b], a g £
C([a,b}). Доказать, что
39£{a,b) : Jf{x)g{x) dx = f{a) Jg(x) dx + f{b) Jg{x)dx.
a a в
Указание. Сначала в левой части проинтегрировать по частям,
затем к полученному интегралу применить теорему о среднем значении.
15*. Доказать, что Va> 0 Va;>0 :
х+а
f sin u3 du
4
1 1
/1 п к \ f f
16*. Доказать, что lim - Г In- = Inxdx := lim / lnidi. С
n-»oo Vn £±1 П / J e->0+ J
О с
помощью этого равенства установить, что lim f — vn!j= -.
IT. Пусть D = {f £ C2([0,l]) | /@) =7Tl) = 0. /'@) = «}. W
l
число a £ R фиксировано. Найти значение min /(/"(я)J dx и функцию,
доставляющую минимум.
Ответ: За2, f(x) = | (ж3 - Зж2 + 2х), х G [0,1].
. Для функции /, которая дифференцируема в некоторой окрестно-
окрестности точки х, и для которой /' непрерывна в точке х, доказать равенство
1
19*. Пусть / G С^ЦО, 1]), причём /'@) ^ 0. Для каждого х £ @,1] пусть
X
0(а;) — какое-либо число из теоремы о среднем значении J f(u)du =
о
= f(9(x))x. Доказать, что lim -^—- = - .
х-»о+ х 2
20. Пусть {/, д} С С([0,1]). Доказать неравенство
(//(u)duJ+(/«7(u)duJ< (/y/2(u
()() (
Указание. Рассмотреть в плоскости кривую х = F(t), у = G{t),
t £ [0,1], где F и G — примитивные функций fug соответственно. Нера-
Неравенство означает, что длина хорды, соединяющей точки (F@),G@)) и
(F(l),G(l)), не больше длины кривой.
/1 х A 4-иI/13 - 1 \
21. Вычислить предел lim I — Г du 1.
х-»0 \ X о U /
Ответ: 1.

9.4. Дополнительные задачи к главам 5 — 9 311
22. Функция / £ Д([О,Ь]) и имеет предел lim f(x) = р. Для 0 < a < Ь
Ь/n flx\
вычислить предел lim / ——- dx.
Ь
Ответ: pin-.
a
a/n
/Iх \ „ .1
23. Вычислить предел lim ( — Г f(u) du) для функций: a) f(x) = sin — ,
х-»0 \l J / X
х^О, /@) = 0; Ь) /(*) - sin2 i , z ^ 0, /@) = 0.
Ответ: а) 0; Ь) 1/2.
2^. Пусть функции {f,g} С С([0,1]); p(i) > 0, х £ [0,1] и, кроме того,
lim /g(u) du = +00; lim -j-т = а. Тогда lim — = a.
0
25. Найти предел lim I J eu du I
X—» + 0O \q /
Ответ: е.
26. Пусть / G C([0,+oo)) и /(a;) -4 a, a; -> +00. Доказать, что
/ 1 A \
lim (— [ f{x)dx)— а. Привести пример функции /, для которой су-
А—»+оо \А q /
ществует последний предел, и которая не имеет предела при х —> +оо.
1
27. Найти предел lim /(I - a;2)" dx.
/A - x2)n d
п->оо
Ответ: 0.
28. Пусть функция / : R —> R такова, что: Vi 6 Д : f(x + 1) =
1
/(ж); / £ й([0,1]); J f(x)dx = 0. Доказать, что для любых а, Ь, а <
о
| ь '2 1
Ь, Л > 0 справедливо неравенство J /(Лж) dx < — f \f{x)\ dx.
Ь
29. Для функции / G C^da^}) доказать, что lim Г f(x) cos nxdx = 0.
n-»oo o
Указание. Проинтегрировать по частям.
ь
ь if
30. Пусть/ б ^([а.Ь]). Доказать: lim Г/(я) sin2 па; da; = - f(x)dx.
п-»оо 2 J
а 2 J
а
1
51*. Для / £ С([0,1]) доказать, что lim //(a;)(sin7rna;)+da; =
п-»оо 0
у

312 Глава 9. Функции ограниченной вариации. Интеграл Стилтьеса
= -} /(*) dx, (f(x))+ := f(x), f(x) > 0, (f(x))+ := 0, f(x) < О.
ж о
1
32. Пусть / £ С([0,1]). Вычислить предел: a) lim fxnf(x)dx;
П—ЮО q
Ь) lim (nfxnf{x)dx); c) lim (n f e-"x/(a:)da:V
И—ЮО \ л / И—ЮО \ л /
1 1
Jxnf(x)dx f f (x) sin2n 2irx dx
d) lim -, ; e) lim -, .
Jxnex2dx f e*2 sin2n 2irx dx
о о
Ответы: a) 0; b)/A); c)/@); d) /(l)/e; e)
33. Пусть / 6 C([0,1]). Вычислить предел lim f /(sin2n a;) di.
П—fOO л
Ответ: 2тг/@).
3^. Для функции / £ С([—1,1]) доказать равенства:
a) lim (— f f(sinx) dx)=— f f(smx) dx;
n—»oo \Tl о ' 2?T q
A n \ 1 T
— //(|sina;|)da;)= - f f(smx) dx;
c) lim I— fa;/(sina;) da; )=— f /(sin a;) da;.
n-»oo \nJ q / 4?r q
35*. Для функции / G C([-l,l]) вычислить пределы:
l l
a) lim /a;/(sin27rna;)da;; b) lim Jcosx ■ f(sm2imx)dx.
n-»oo 0 n-»oo 0
Ответы: а) - J/(sin27ra;)da;; b) sinl • J/(sin27ra;)di.
2 о о
1 Tl —1 1 jU _l_ 4»
Указание, а) Интеграл равен — £) / /(sin2?ru) du.
ifcOO n
l
36. Пусть / G Щ[0,1]) и ufc = fxkf(x) dx, k > 1. Вычислить следующий
о
предел lim V -—.
n-^oo fc=1 fc
1 1-е
Ответ: - / f(x) ln(l - x) dx := - lim / f(x) ln(l - a;) da;.
О e-»0+ 0
oo
37. Ряд ^2 an сходится условно. Доказать, что существует сходящаяся
п=1

9.4. Дополнительные задачи к главам 5 — 9 313
к 0 последовательность {bn | n > 1}, для которой ряд £ anbn pacxo-
п=1
дится. Существует ли такая последовательность положительных чисел?
38*. Числа ап, п > 1, отличны от и таковы, что —ц ;г —> 1, п —» со.
а
Доказать, что ряд £ ~~" сходится.
п=1 "
39. Исследовать сходимость ряда:
С)
п=1
2
n=l
40. Пусть для ai = 1, a G @,1) : an+i = -—2—, п > 1. Доказать
1 + а»
оо
Сходимость ряда J2 ап •
п=1
' Указание. Проверить, что Вс £ R Vn>l:an< —щ
41. Исследовать на абсолютную сходимость ряд:
оо п2 j_ 00 n+1
1^ /
) е (D /
n=l n—1
£ (-l)n+1/*narctg^ dx; d) £ (-
оо
е) El
n=l
rin, [0, тгп)) '
42. Пусть ряд £ — сходится. Доказать существование предела
fc=i *
/1 n \
lim (- Е <*Л
п-»оо \П fc^ /
Указание. Выразить члены последовательности через частичные
суммы ряда.
43. Предположим, что: 1) Vn > 1 : а^п -> «n, iV -> со; 2) Vn >
> 1 : |а^п| < bn; 3) ряд £ К сходится. Доказать, что тогда
п=1
оо оо
справедливо равенство lim £ aWn = Z) an-
^-^°° n=l n=l
44- Исследовать на равномерную сходимость ряд:

314 Глава 9. Функции ограниченной вариации. Интеграл СтиЛплся
а) Е 7"ln(l + u2)du, *€ [0,3]; Ь) £ { *ши2 du, «€[-3,3];
n=l 0 n=l -x
оо (n+l)x j оо (n+l)x2
E / —-а; С [0,3]; d) E I t
n=l nx 1 4" U ' n=l nI2
X\/n+l
оо
. Доказать, что сумма ряда Е \fn\vin{x + 1) принадлежит классу
оо епх
46. Пусть а(х) = Е 1 2 ' х - °- Д°казать' что а ^ С([0,+оо)) и
п=0 1 + П
аеС°°(@,+оо)).
47. Доказать, что £] -|^L = 1 (е« + 2е"г/2 cos ^ а), г G R.
п=0 *• '■
45. Доказать, что последовательность чисел {ап \ п > 0} является по-
последовательностью коэффициентов степенного ряда с радиусом схо-
сходимости г = +оо для некоторой функции тогда и только тогда, когда
lim v/jaJ = 0.
п—»оо
49. Функция / — сумма степенного ряда с радиусом сходимости г > О
dn/n, ,/1\\ 1 ./1 \ 1
удовлетворяет уравнению у— [х f I - = ——7 /1 - ),х > - , для
некоторого n G N и условиям /^fc^@) = 1, 0<fc<n — 1. Найти /.
Ответ: f(x) = ех, х£ (-г,г).
50*. Пусть числа ао>0, ап>0, п>1, таковы, что
Ап := а0 + ai + ... + ап ->• +оо, >• 0, п -^ оо.
■An
00
Доказать, что степенной ряд £) ani" имеет радиус сходимости 1.
п=0
У^казамие. Обратить внимание на следующее:
а д
—— -> 0, п ->• оо => —— >• 0, п ->• оо, => уАп -> 1, п -> со.
/in -*in—1
00
51*. Пусть ап £ С, Хп £ R, п > 1. Пусть ряд £) а„е2Лп, 2 G
п=1
С, сходится абсолютно в некоторых точках Zi,Z2,...,zn плоскости С.
Доказать, что этот ряд сходится абсолютно и равномерно на замкнутом
выпуклом многоугольнике, натянутом на точки Zi,Z2,... ,zn.
l/n
52*. Вычислить предел lim cos" z + cos"(z + i) + cos"(z + 3i) ,
n—*oo
z =а + Ы, a G R, Ь > 0.

9.4. Дополнительные задачи к главам 5 — 9 315
Ответ: y/(ch.2(b + 3) + cos2a)/2.
53. Пусть А С С, f : А -> С. Функция / называется амалитине-
ской в точке z0 £ А, если 3 6 > О : ВB0,<5) := {z е С \ \z - zo\ <
6} С А и / на BBo><S) есть сумма степенного ряда по степеням z — го-
Функция / аналитична на множестве А, если она аналитич-
аналитична в каждой точке множества А. Пусть / — сумма степенного ряда
оо
f{z) — X) anZn, an £ С, п > 0, с положительным радиусом схо-
п=0
димости г. Доказать, что / есть аналитическая функция на множестве
В@,г). В частности, функции ez, sinz, cosz, z £С, аналитичны на С.
54' Проверить, что аналитическая в точке z0 функция / непрерывна в
этой точке. Доказать, что функция f(z) = e~1//z ,2^0, f(z) = 0, опре-
определённая на С, не аналитична в точке 0. Доказать также, что сужение /
функции /наЯ есть функция класса C°°(R), причём /^"^@) =0, п > 1.
Замечание. Таким образом, / не есть сумма ряда Тейлора (если
/ есть сумма степенного ряда в некоторой окрестности (-6,6), то этот
же степенной ряд сходится для z £ В@,6).
Указание. Функция / разрывна в точке 0. Рассмотреть значения
на мнимой оси.
55. Определить множество точек сходимости произведения:
оо
/•j-2 I п2■ Ы П A+ т1птМ
п=1
оо
56. Пусть ап > 0, п > 1, и произведение J~[ A + ап) = р сходится.
71=1
ОО
Найти предел lim П (^ + ап.хп).
х->1- п=1
Ответ: р.
оо
Указание. Доказать, что существует lim £) ln(* + ап2;п)-
^"^ п=1
57. Определить множество А точек сходимости- произведения
оо
П A + епх) = р(х) и доказать, что р £ С(А).
71=0
58. Определить множество А точек сходимости произведения
°° ( п2 \
П y"^—2п }= Р(х}' х ^ ^' и Д°казать существование р'(х) для х £ А.
п=1 ^ X п I
59. Для последовательности {an | n > 1} положительных чисел выпол-
выполняется соотношение —>■ 1, п —> со. Доказать расходимость
оо
произведения J~[ (l + an).
п=1

316 Глава 9. Функции ограниченной вариации. Интеграл Стилтьеса
60. Доказать существование функции / G (С([0,1]) П jBV([0, 1])), кото-
которая не удовлетворяет условию Липшица на [0,1] ни при каком показателе
а<Е[0,1].
61. Пусть {f,g} С BV{[a,b}) и h{x) :=max{f{x),g{x)), х <Е [а,Ь]. Дока-
Доказать, что h G BV([a,b}).
62. Представить в виде разности монотонно неубывающих на отрезке
[-1,2] функций следующие функции: a) f(x) = х3—х; Ь) д(х) — sin27ra;.
63 Вычислить интеграл Стилтьеса:
1 1
а) / х d(sign sin47ra;); b) J x d(a;2sigii sin47ra;).
о о
64. Пусть / £ C([0,+co)) и f(x) > 0, x > 0. Доказать, что для любого
х £u
а > 0 функция д(х) := f(x) f , х > 0, не ограничена на [0, +оо).
о / (и)
Указание. Рассмотреть предположение , что функция да ограни-
ограничена на [0, +оо).
65. Пусть / £ С"([а,Ь]). Доказать, что для каждого е > 0 существует
многочлен Р такой, что max max \f^kHx) - Р^кЦх)\ < е.
0<к<пхе[а,Ь] V '
Указание. Пусть Q — многочлен, приближающий равномерно на
[а,Ь] функцию /("). Рассмотреть многочлен

Глава 10
Элементы анализа в
метрическом пространстве
10.1 Метрическое пространство
10.1.1 Определения метрики и метрического
пространства
Логический анализ понятий предела последовательности действитель-
действительных чисел, предела функции в точке, непрерывности и ряда важнейших
связанных с этими понятиями теорем показывает, что все эти понятия
и факты основаны на использовании расстояния на прямой. Перечень
необходимых свойств расстояния при этом оказывается очень коротким
и содержит следующие свойства:
l°.V{x,y}cR ■ \х - у\ > 0, причём \х-у\=0 •$=>• х = у;
2°.У{г,у}сЯ : \х - у\ = |у - х\;
P.\/{x,y,z}cR : |г-у|<|а!-2| + |2-у|.
Здесь |а; — у\ — расстояние между точками на прямой с координа-
координатами а; и у. Свойствами 1° — 3° обладает также обычное расстояние
в трёхмерном пространстве. Оказывается, что формальное введение
расстояния со свойствами 1 ° — 3° на множестве элементов произволь-
произвольной природы приводит к возможности построения ряда понятий и фактов
анализа на этом множестве. При этом в качестве конкретных случаев
охватывается широкий круг различных известных математических ситуа-
ситуаций.
Пусть X — некоторое множество, далее всегда предполагается, что
X ^ф. 0. Элементы множества X называются также точками, а само
317

318 Глава 10. Элементы анализа в метрическом пространстве
множество X — пространством.
Определение 1. Расстоянием или метрикой р на
пространстве X называется функция р : X х X -у R,
удовлетворяющая следующим условиям:
1)У{х,у}сХ : р{х,у) > 0, причём р(х,у) = 0 <*=>■ х = у;
2)V{x,y}cX : р(х,у) = р(у,х);
3)V{x,y,z}cX : p(x,y)<p(x,z) + p{z,y).
Множество X с метрикой р называется метриче-
метрическим пространством и обозначается символом (Х,р).
Замечания. 1. Условия 1) — 3) называются также аксиомами
расстояния. Условие 2) называется аксиомой симметрии, а условие
3) — неравенством треугольника.
2. Пусть р\ и р2 метрики на X. Метрические пространства (Х,р\) и
(Х,р2), вообще говоря, различны.
3. Пусть (X,р) — метрическое пространство и Y С X. (Y,p) есть
также метрическое пространство, вообще говоря, отличное от (Х,р).
4. Условие 2) в определении расстояния есть следствие условия
4) V {х,y,z}cX : р(х, у) < р{х, z) + р{у, z).
Таким образом, условия 1) — 3) равносильны двум условиям 1) и 4).
10.1.2 Примеры метрических пространств
1. Пространство {R,p). Пусть X = R; р{х,у) := \х - у\, {х,у} С
R. Тогда (R, р) — метрическое пространство — числовая прямая с обыч-
обычным расстоянием.
2. Пространство (Rm,p). Пусть для т £ N фиксированного
X = Rm:={x = {xux2,...tXm) \xkER, I < k < m};
Л"
p{x,y) := Л £ {xk-VkJy{x = (xltx2,...,xm),y= (У1,У2, • ■-,Ут)},
V*=i
где {х, у} С Rm.
\ Покажем, что р есть метрика на Rm. Условия 1) и 2), очевидно,
выполнены. Согласно неравенству Коши для {ж = (х\,Х2,- ■ ■ ,хт),у =
{У1,У2,---,Ут),2 = {zi,z2,...,zm)} С Rm имеем
т т
Р2{х,у) = £ (Xfc-yfcJ = £ Ы - zk + zk - yfcJ =
fc=l fc=l
m
= p2(a;,2) + 2£ {xk - zk){zk - yk) + p2{z,y) <
fc=i
< p2{x,z) +2p(x,z)p(z,y) + p2(z,y) = {p{x,z) + p{z,y)J.

ЮЛ. Метрическое пространство 319
Отсюда, учитывая условие 1), получаем неравенство 3). Таким об-
образом, р — метрика на Rm, a (Rm,p) — метрическое пространство.
Далее, чтобы не выписывать явно выражение для р будем называть рас-
расстояние р евклидовым или обычным. J
3. Пространство (h,p)- Пусть X = 12 := (я = {xn} = (xi,x2t...,
in,...) xn£R, п>1; f)x2<+ooj; р{х,у) := J § (х„ - у„J,
n=l J у n=l
{х = {х„},у = {у„}} С 12.
\ Для проверки условий 1) — 3) сначала заметить, что
{х = {хп},у = {у„}} С h => x-y = {xn-yn}ch- J
4. Пространство (C([a,b]),p). Пусть X = С([а,6]); р(х,у) :=
= max |x(t) - y[t)\, {х,у} С C([a,b]). Расстояние р между функци-
a<t<b
ями х и у имеет простой геометрический смысл. Условия 1) — 3) для р
легко проверяются.
Упражнение 1. Пусть X = R; d(x,y) := min(l,|x-y|), {x,y} С R.
Доказать, что d — метрика на R, а (R, d) — метрическое пространство.
Упражнение 2. Пусть X = R; d(x,y) := \х3 - у3\, {х,у} С R.
Является функция d метрикой на ft?
Упражнение 3. Пусть X = [0,+оо); d(x,y) := \х2-у2\, {х,у} С R-
Является функция d метрикой на R?
Упражнение 4- Пусть X = {х = (cos6,sin6) | 0 < в < 2п}\
d(xltx2):=\61-62\, xfc = (cosefc,sinefc) cX, k =1,2.
Является функция d метрикой на XI
Упражнение 5. Доказать, что каждая из функций
т
\хк-Ук\, <к{х,у) = jn.axm\xk - ук\,
где {х = {xi,x2,...,xm),y = (У1,У2,---,Ут)} С Rm, — метрика на Rm.
Упражнение 6. Доказать, что каждая из функций
d1(*,y) = /Hu)-y(u)|du, d2(x,y)=
а чо
где {х,у} С С([а,Ь]), есть метрика на С([а,Ь]).
Упражнение 7. Пусть X = {х = {хп} = (хх,х2,... ,х„,...) \ хп е
R, п > 1; sup|xn| < +oo}, d(x,y) := sup|xn-yn|, {x,y} С X.
п>1 п>\
Доказать, что (X,d) — метрическое пространство.
21—4-1168

320 Глава 10. Элементы анализа в метрическом пространстве
Упражнение 8. Пусть X - произвольное множество, d(x,y) — 1,
х ф у, d(x,y) = О, х = у, {х,у} С X. Доказать, что (X,d) — метриче-
метрическое пространство. Метрика d называется дискретной.
ОО |g — ty I
Упражнение 9. Пусть d(x,y) = £ — -, {х = {хп},у =
п=1
{уп}} С h- Доказать, что (i2,с2) — метрическое пространство.
10.1.3 Свойства расстояния
Пусть (X, d) — метрическое пространство. Из аксиом расстояния легко
получается ряд свойств расстояния, привычных для расстояния в трёх-
трёхмерном пространстве. Рассмотрим те из них, которые часто использу-
используются.
Свойство 1°. (Неравенство треугольника).
У{х,у,г}сХ : \d(x,z) - d(z,y)\ < d(x,y).
\ Действительно, на основании аксиом 3) и 2) имеем
d[x, z) < d{x, у) + d{y, z) = d(x,у) + d{z, у) ==►
=► d(x,z)-d(z,y)<d(x,y). A)
Аналогично
d(z, у) < d(z, x) + d{x, y) = d{x, z) + d{x, у) =Ф-
=► d(z,y)-d(x,z)<d(x,y). B)
Согласно определению модуля числа, неравенства A) и B) вместе
равносильны требуемому \d{x,z) - d(z,y)\ < d(x,y). J
Свойство 2°. (Длина отрезка прямой, соединяющего две
точки, не больше длины любой ломаной, соединяющей
эти снсе точки). Для любого конечного набора xltx2t. .■ ,хп точек
из X справедливо неравенство
d{xi,xn) < d{xi,x2) +d(x2,x3) + d(x3,x4) + ... + d(xn_uxn).
\ Последовательно применить аксиомы расстояния 3). J
Свойство 3°. (Неравенство четырёхугольника). Для лю-
любых элементов x,y,u,v из X справедливо следующее полезное нера-
неравенство \d(x,u) - d(y, v)\ < d(x,y) + d(u,v).
\ Действительно, на основании аксиом 3) и 2) имеем
d(x, и) < d(x, у) + d(y, и) < d(x, у) + d(y, v) + d(v, и) = C)
= d(x, у) + d(y, v) + d(u, v) =>• d(x,u) - d(y, v) < d(x,y) + d{u, v).
Аналогично получаем
d(y,v)-d(x,y)<d(x,y) + d{u,v). D)

ЮЛ. Метрическое пространство 321
Неравенства C) и D) вместе равносильны требуемому. J
Замечание. Свойство 1° есть частный случай свойства 3° (поло-
(положить и = v = г).
10.1.4 Декартово произведение пространств
Пусть (Xk,dk), к = 1,2 — метрические пространства и X = Х\ х Х2 —
декартово произведение множеств Х\ w Х2. Положим для элементов
{х = {хих2),у = {у
d(x,y) = d{{x1,x2),{ylly2)) ■= V^ifai.yi) + dl(x2ly2).
Функция d есть расстояние на X, а (X, d) — метрическое пространство,
называемое декартовым произведением пространств (Xk,dk),
к — 1,2. (проверьте аксиомы расстояния!).
Метрика на X может быть определена и иным способом. Метрикой
является, например, функция d(x,y) = di(zi,yi) +^2(хг,У2)-
Аналогично определяется декартово произведение любого конечно-
конечного числа метрических пространств.
Упражнение 10. Получить пространство примера 2, как декартово
произведение пространств примера 1, см. п. 10.1.2.
10.1.5 Предел последовательности элементов
метрического пространства
Пусть (X, d) — метрическое пространство и {хп \ п > 1} — последова-
последовательность элементов из X.
Определение 2. Последовательность элементов
{хп | п > 1} пространства (X,d) сходится в (X,d), если су-
существует элемент х е X, такой, что d(xn,x) -4 0, п -4 оо.
При этом, элемент х называют пределом последова-
последовательности {хп | п > 1} в (X, d) и используются обозна-
обозначения: х = lim х„, или х„ -> х, п -4 оо.
п—>оо
Упражнение 11. Если хп -4 х, п -4 оо в (X,d), то для любой
подпоследовательности zn(fc) -я, к -4 оо в (X,d). Доказать.
Упражнение 12. Последовательность элементов {хп \ п > 1} про-
пространства (X, d) удовлетворяет условию: любая её подпоследователь-
подпоследовательность содержит в себе подпоследовательность, сходящуюся в (X, d)
к некоторому фиксированному элементу i El Доказать, что хп -4
-. п -4 оо.

322 Глава 10. Элементы анализа в метрическом пространстве
Теорема 1. (О единственности предела последова-
последовательности). Если 1„->г, п —► оо и хп -» у, п -4 0О в (X,d),
то х = у.
\ Согласно аксиомам расстояния, имеем 0 < d(x,y) < d(x,xn)+d(xn,y),
n > 1. Поскольку d(x, xn) --» 0, d(xn,y) -4 0, n -» оо, то d(x,y) = 0. По
аксиоме 1) х = у. J
Теорема 2. Пусть хп ->• х, уп —► у, п —► оо, в (X,d). Тогда
d(zn, у„) -^ d(x, у), п -^ оо.
[ Использовать неравенство четырёхугольника для оценки разности
\d(xn,yn) - d(x,y)\. J
Следствие 1. Пусть хп -4 х, п —> оо, в (X,d). Длл лто5ого
у 6 X имеем d(xn,y) -> d(x,y), n -4 оо.
Упражнение 13. Какие последовательности метрического простра-
пространства из упр. 8 являются сходящимися?
10.1.6 Сходимость в некоторых конкретных
пространствах
1. Сходимость в пространстве (Rm,p) равносильна по-
покоординатной сходимости.
ГПуСТЬх(") = (хAП),х(П)>...,Х^)-4(х1,Х2,...,Хт) П-4 00, B(Rm,P),
Y, (Ч> - xfcJ) -► 0, п -4 оо. Поскольку р(х("), х)
^ 1Х1 ~ ж*|| 1 < А; < т, п > 1, то Xf?' -Я1, п -» оо для каждо-
каждого 1 < к < т. Обратное утверждение следует из свойств сходящихся
последовательностей. J
2. Сходимость в пространстве (С([а,Ь]),р) равносильна
равномерной на [а,Ц сходимости.
Упражнение 14- Пусть (X, d) — декартово произведение метри-
метрических пространств из п. 10.1.4. Доказать, что х(") = [х™ ,ху') -4
(xi,x2) = z, п-4 оо, в(Х,d) •<=>■ x^'-^xi, n-4 оо, B(Xi,di) и
lj -t lj, П -4 00, В (X2,d2).
10.1.7 Шары, ограниченное множество,
предельная точка
Пусть (X, d) — метрическое пространство, х0 — фиксированный элемент
из X и г > 0.

ЮЛ. Метрическое пространство 323
Определение 3. Замкнутым шаром В(хо,г) с цен-
центром в точке xq и радиусом, г называется множество
Б(хо,г) = {х е X | d(x,x0) < г}.
Определение 4- Открытым шаром В(х0,г) с центром
в точке xq и радиусом, г называется множество
В{хо,г) = {х £ X | d{x,x0) <r}.
Определение 5. Множество А С X, Аф0 называет-
называется ограниченным, если d(A) := sup d(x,y) < +оо. Число
хвА.увА
d(A) называется диаметром мпожества А. Множество
0 такж.е ограничено и d@) := 0.
Замечания. 1. Легко проверить, что множество ограничено тогда
и только тогда, когда оно содержится в некотором шаре.
2. То, что хп —» х, п —> оо, в (X, d) можно сформулировать в следу-
следующей равносильной форме Vr>03JV6iV: {xn,xn4-i,...} С В(х,г).
Упражнение 15. В пространстве (R,p) изобразить следующие ша-
шары: БA, 2), ВB,|).
Упражнение 16. В пространстве (R2,p) изобразить следующие ша-
шары: Б(A,1),2), В(A,0),3). В каждом из пространств (R2,dk), k = 1,2
где d1((x1,x2),(yi,y2)) = \xi - yi| + \х2 - Ут], d2{{xl,x2),{y\,y2)) =
= max(|xi-yi|,|x2 -Уг!), изобразить шары В(A,1),2), В(A,0),3).
Упражнение 17. Доказать, что d(B(xo,r)) < 2г. Возможен ли слу-
случай, когда d(B{xo,r)) < 2г?
Упражнение 18. Для пространства (С([а,Ъ]),р) и функции xo(t) =
0, t £ [а,Ь] описать шары В(хо,1), В(хо,1).
Упражнение 19. Пусть А С X, А ф 0, лх 6 X и d(x,A) :=
= inf d(x,y). Доказать, что d(xn,A) -4 d(x,A), n -4 оо для любой
уел
последовательности хп —¥ х, п -4 оо, в (X, d).
Определение 6. Пусть А с X, х0 6 X. Точка х0 назы-
называется предельной точкой множества А, если выполня-
выполняется условие Vr>0 Зх£А, хфхо,'- х G B(xQ,r).
Примеры. 1. Для множества А = [0,1) U {2} в (R, р) множество всех
его предельных точек есть множество [0,1].
2. Пусть А = {(хьХг) I xk £ Q, к — 1,2} множество в (R2,p).
Множество всех предельных точек множества А есть ft2.

324 Глава 10. Элементы анализа в метрическом пространстве
3. Пусть А — множество всех многочленов, рассматриваемых на
[a,b] в пространстве (С([а,6]),р). В силу теоремы Вейерштрасса мно-
множество всех предельных точек множества А есть C([a,b]).
Упражнение 20. Какие точки пространства упр. 8 являются пре-
предельными точками множества А = XI
Упражнение 21. Пусть хп -> х, п -4 со, в (X,d). При каком условии
точка х является предельной точкой множества {xi,X2,...} — множе-
множества значений последовательности {х„ | п > 1}?
Упражнение 22. Привести пример множества в (R, р) имеющего
ровно три предельные точки.
Теорема 3. Точка х0 лвллетсл предельной точкой
м,ноок.ества А тогда и только тогда, когда существу-
существует последовательность {хп \ п > 1}, удовлетворлющал
условиям: 1) Vn > 1 : хп G А, х„ ф х0; 2) хп —> х, п —► оо, в
пространстве (X,d).
[ Необходимость. Пусть хо — предельная точка множества А. Со-
Согласно определению предельной точки для шара B(xq, 1), имеем 3 х\ G
A, Xi ф хо '■ х\ G В(хо, 1) •<==> d(xo,Xi) < 1. Положим г =
— d(xo,xi)/2 и для шара В(хо,г) снова используем определение пре-
предельной точки Зх2 £ А, х2 ф х0 : х2 £ B(xo,r) =^~ d(xo,x2) < 1/2 и
т. д. Продолжая аналогично, получим последовательность {хп \ п > 1},
удовлетворяющую условиям 1) и 2).
Достаточность. Пусть {хп \ п > 1} последовательность, удовле-
удовлетворяющая условиям 1) и 2). Поскольку, d(xn,xo) —» 0, п —> оо, то
Vr>0 3n Vn>n: d(xn,xo)<r <=> хп G B(xo, г). Согласно
условию 1), хп G А, хп ф х0, п > 1. J
Упражнение 23. Пусть {Ап \ п > 1} — некоторая последователь-
последовательность подмножеств метрического пространства (X, d). Определим
lim Ап := {х £ X I x = lim х„ для некоторой последовательности
п-юо п~>°°
хп G Ап, п > 1} и lim Ап := {х G X \ существует некоторая подпосле-
п—юо
довательность п(к), к > 1 последовательности iV и элементы xn(fc) G
■^n(fc). к > 1, lim a;n(fc) = х}. В пространстве (Л2,р) найти lim An и
fc-юо п-юо
lim Ап для последовательности: а) Л„ = В[0,— ), п > 1; Ь) Ап =
n-too \ п /
B@,n), n>l; c)i£

ЮЛ. Метрическое пространство 325
10.1.8 Открытые множества
Пусть (X, d) — метрическое пространство и А С X.
Определение 7. Точка х0 е А называется внутренней
точкой множества А, если 3 г > 0 : В(хо,г) с А.
Примеры. 1. Для множества А = [0,1) в пространстве (R, р) множе-
множество внутренних точек есть @,1).
2. Множество А = {(xi,x2) \ х\ = х2} в пространстве (R2,p) внут-
внутренних точек не имеет.
Определение 8. Множество А с X называется от-
открытым в (X,d), если каждая точка мноок.ества А есть
внутренняя точка множества А.
Согласно этому определению, множество X открыто (оно содер-
содержит все шары), множество 0 также будем считать открытым (как не
содержащее невнутренних точек).
Пример. 3. Множество А = @,1) открыто в (R,p).
Упражнение 24- Доказать, что множество [0,1) открыто в про-
пространстве ([0,+оо),р), р — обычное расстояние.
Упражнение 25. Описать все открытые множества в пространстве
упр. 8 п. 10.1.2.
Упражнение 26. Доказать, что для открытого множества А и любо-
любого конечного набора точек {xi, Хг,..., х„} из X следующее множество
А \ {xi, X2,..., хп} также открыто.
Упражнение 27. Доказать, что множество {х | х@) > 1} в про-
пространстве (С([0,1]),р) открыто.
Упражнение 28. Доказать, что классы открытых множеств про-
пространства (R2,p) и пространств (R2,dk), k = 1,2, введенных в упр. 16
п. 10.1.7, совпадают.
Теорема 4. Открытый шар есть открытое множе-
множество.
\ Пусть В(хо,г) — некоторый открытый шар и точка z ф хо, z 6 В(хо,г).
Тогда d(z,Xo) < г. Положим г\ = г — d(z,Xo) и докажем, что
B(z,ri) CB(xo,r) ^=^ Vy : d{y,z)<r1 =>■ d(y,xo)<r.
Действительно, на основании аксиомы 3) расстояния имеем
d{y,х0) < d{y, z) + d{z, хо) < гч + ф, х0) = г. J

326 Глава 10. Элементы анализа в метрическом пространстве
Теорема 5. Объединение произвольного семейства
открытых множеств есть открытое множ.ество.
\ Пусть Т — произвольное множество индексов и для каждого а £ Т
множество Аа открыто. Предположим, что х0 £ IJ Аа. Далее имеем
сет
х0 £ U Аа ■$=>■ 3 а0 € Т : -Аао Э х0, а так как Аао открыто, то
получим Зг>0: В{хо,г) С Аао С [j Aa. J
Теорема 6. Пересечение конечного числа открытых
множеств есть открытое множество.
п
\ Пусть Ai,A2,.. ■ ,А„ — открытые множества и точка xq G f| Ak.
Имеем x0 6 П -^fc ■£=*■ Vfc, l<fc<n: xo£ ^л, a no-
скольку Ak — открытое множество, то 3rk '■ В(хо,Гк) С Ак- Пусть
г — min(ri,r2l... ,rn), r > 0. Тогда Vfc, 1 < fc < n : B(zOlr) =
n n
= П B(xo,rk) С B(a;o>''fc) С Ак. Следовательно, B{xo,r) С fl A*>- J
fc=i fc=i
Упрагхснение 29. Пусть Л„ = (-l/n,l+ 1/n) — открытое в (R,p)
oo
множество, n > 1. Доказать, что f] Ak не есть открытое множество в
fc=i
пространстве (R,p).
10.1.9 Структура открытых множеств на прямой (R,p)
Теорема 7. Любое непустое открытое мноэюество в
(R,p) есть объединение не более чем. счётного семейства
открытых непересекающихся интервалов.
\ Пусть А — открытое в (R,p) множество и xq £ А. Поскольку А откры-
открыто, существует интервал, который содержит точку xq и содержится в А.
Пусть J(xq) — объединение всех таких интервалов. По теореме 5 J(xq)
есть открытое множество, кроме того, J(x0) С А и J(x0) — интервал,
как объединение интервалов с общей точкой х0. Таким образом, J(xo)
— открытый интервал.
Пусть теперь J{x\) и J(x2) — открытые интервалы, соответствую-
соответствующие точкам х\ и х2 из А. Докажем, что либо J(xi) П J(x2) = 0, либо
J{x\) = J(x2). Действительно, если J(xi) П J(x2) ф 0, то J{x{) U J(x2)
— открытый интервал, содержащий обе точки Xi и х2- Поэтому, по

10.1. Метрическое пространство 327
построению, J(xi) = J(xi) U J(x2) — J(a;2). Таким образом, А состо-
состоит из объединения попарно непересекающихся интервалов, семейство
которых на прямой не более чем счётно. J
Теоремз8. Любое непустое открытое множество в
(Rm,p) есть объединение счётного семейства открытых
шаров.
\ Пусть Р := {B(z,r) | z = (zuz2,... ,zm), zk G Q, 1 < k < m; r G
Q}, P — счётное семейство открытых шаров. Для любой точки х из
открытого множества А существует шар B(zx,rx) G P, такой, что спра-
справедливо включение х £ B(zx,rx) С A. J
10.1.10 Замкнутые множества
Пусть (X, d) — метрическое пространство и А С X.
Определение 9. Множество называется замкнутым
в (X,d), если оно содержит все свои предельные точки.
Множество X замкнуто, 0 замкнуто (не имеет предельных точек).
Множество, состоящее из конечного числа точек, замкнуто (не имеет
предельных точек).
Упражнение 30. Описать все замкнутые множества в пространстве
упр. 8 п. 10.1.2.
Упражнение 31. Доказать, что замкнутый шар есть замкнутое мно-
множество.
Теорема 9. Множ.ество А замкнуто в (X,d) тогда
и только тогда, когда его дополнение X \ А открыто в
пространстве (X,d).
\ Необходимость. Пусть А замкнуто. Тогда х G (X \ А) <=> х ^
А. Следовательно, х не есть предельная точка множества А и потому
3 г > 0 : В(х, г)Г\А- 0 =^ В(х, г) С {X \ А). Таким образом, любая
точка дополнения является внутренней точкой этого множества.
Достаточность. Пусть Х\А открыто. Тогда любая точка х е (-■f \-<4)
является внутренней точкой этого множества, т. е. Зг > 0 : В(х,г) С
(X \ А) =4- В(х,г) П А = 0. Поэтому х не есть предельная точка
множества A. J
Теорема 10. Пересечение любого семейства замкну-
замкнутых множеств есть замкнутое множ.ество. Объеди-
Объединение конечного числа замкнутых мноок.еств есть за-
замкнутое множ.ество.
\ Доказательство следует из правил двойственности и теорем 5 и 6. J

328 Глава Ю. Элементы анализа в метрическом пространстве
Определение 10. Множество А, состоящее из всех
точек множества А и всех предельных множества А,
называется замыканием множества А.
Упражнение 32. Пусть А замкнуто, А ф 0 и х £ А. Доказать, что
d{x,A) = inf d(x,y) > 0.
Упражнение 33. Доказать, что для любого множества его замыка-
замыкание есть замкнутое множество.
Упражнение 34- Доказать, что А = А.
Упражнение 35. В пространстве [R,p) при любом п > 1 множе-
оо
ство [1/п, 1 + 1/п] замкнуто. Является ли множество (J [1/п, 1 + 1/п]
71=1
замкнутым?
Упражнение 36. Доказать, что А= {х 6 X \ d(x, A) = 0}.
Упражнение 37. Доказать, что А = f] F.
, F-замкнуто
10.1.И Сепарабельные метрические пространства
Пусть (X, d) — метрическое пространство и А С X.
Определение 11. Множество А называется всюду
плотным в (X,d), если VxeXVe>0 3y£i4: d(x,y)<e.
Теорема 11. Следующие утверждения равносильны:
1) А — всюду плотно в (X, d); 2) А имеет непустое пере-
пересечение с любым, открытым, шаром; 3) V х 6 X 3 {хп \ п >
1} С А : х„ -> х, п —> оо; ^) А = X.
Определение 12. Метрическое пространство (X,d)
называется сепарабельным, если оно содержит счёт-
счётное и всюду плотное подмноэ*сество.
Примеры. 1. Пространство (R, р) сепарабельно, множество Q счётно
и всюду плотно в (R,p).
2. Пространство (Rm,p) сепарабельно, множество Qm счётно и
всюду плотно в (Rm,p).
3. Пространство (С([а,Ь\), р) сепарабельно. Счётным и всюду плот-
плотным множеством является множество всех многочленов с рациональ-
рациональными коэффициентами.

10.1. Метрическое пространство 329
Упраж.нение 38. В каком случае пространство упр. 8 п. 10.1.2
сепарабельно?
Упражнение 39. Доказать, что декартово произведение сепара-
бельных пространств сепарабельно.
Упражнение 4-0- Доказать, что непустое открытое множество в
сепарабельном метрическом пространстве есть объединение счётного
семейства открытых шаров.
Упражнение 4-1*. Доказать, что пространство (Ь,р) сепарабельно.
Упражнение 4%- Доказать, что пространство упр. 7 п. 10.1.2 не
является сепарабельным.
10.1.12 Полные метрические пространства
При изучении предела последовательности действительных чисел фунда-
фундаментальную роль играет критерий Когии: последовательность дей-
действительных чисел сходится тогда и только тогда, когда она фундамен-
фундаментальна. Понятие фундаментальной последовательности можно ввести в
любом метрическом пространстве. Однако, критерий Коши не имеет
места в любом метрическом пространстве. Например, он не имеет
места в пространстве (Q, р) (рассмотреть последовательность прибли-
приближений к числу \/2 $. Q. В пространствах, в которых критерий Коши не
имеет места, теряют силу многие утверждения анализа. Поэтому есте-
естественно выделить класс метрических пространств, в которых критерий
Коши справедлив.
Определение 13. Последовательность {хп | п > 1} эле-
элементов метрического пространства {X,d) называется
фундаментальной или последовательностью Коши, ес-
если V е > 0 3N£N Vm>N V n > N : d{xm,xn)<e.
Упражнение ^.3. Доказать, что фундаментальная последователь-
последовательность ограничена.
Упражнение 44- Доказать, что сходящаяся последовательность
фундаментальна.
Упраж.нение ^5. Пусть {хп \ п > 1} — фундаментальная последо-
последовательность в (X, d). Доказать, что для любого х 6 X числовая после-
последовательность {d(xn,x) | п > 1} сходится в (R, р).
Определение 14- Метрическое пространство (X,d)
называется полным, если каж.дая фундаментальная по-

330 Глава 10. Элементы анализа в метрическом пространстве
следовательностъ элементов пространства сходится к
некоторому элементу этого пространства.
Примеры. 1. Пространство {R,p) полно в силу критерия Коши
сходимости числовой последовательности.
2. Пространство {Rm, р) полно, так как фундаментальная в
(Rm,p) последовательность векторов покоординатно фундаментальна
и наоборот,
3. Пространство {С([а, Ь]), р) полно в силу критерия Коши рав-
равномерной сходимости последовательности функций.
4. Пространство (@,1),р), где р(х,у) = \х — у\, не является полным.
5. Пространство {Q,p), где р(х,у) = \х — у\, не является полным.
Упражнение ^6. Декартово произведение конечного числа метри-
метрических пространств полно тогда и только тогда, когда все сомножители
полные метрические пространства.
Упраоюнение ^7. Доказать, что пространство {h,p) полно.
Упраоюнение 48. Пусть X = R, d(x,y) = |arctgz-arctg2/|, {x,y} С
R. Проверить, что (R, d) — метрическое пространство. Является ли это
пространство полным?
Упражнение 4-9- Пусть (X, d) — полное метрическое пространство
и А замкнутое множество в нём. Доказать, что (A,d) — полное метри-
метрическое пространство.
Теорема 12. (Обобщение принципа стягивающихся
отрезков). Пусть {B(xn,rn) | п > 1} - последовательность
замкнутых шаров в полном, метрическом пространстве
{X,d), удовлетворяющая условиям.: 1) Vn > 1 : В(х„+1,г„+1)
CB(zn,rn); 2) г„ -» 0, п -» оо.
ОО
Тогда 3!x€X:Vn>l х е В{хп, г„) или П В{хп, г„) = {х}.
71=1
[ Докажем, что последовательность \хп \ п > 1} центров шаров фунда-
фундаментальна. Пусть е > 0 задано. Согласно условию 2), 3^ V п > N :
гп < е. Далее, учитывая условие 1), имеем
Vm>NVn>m: B(in, г„) С B(im, rm) =$■ d{xn, хт) < гт < е. A)
Таким образом, последовательность {хп \ п > 1} фундаментальна,
а поскольку (X, d) полно, то существует элемент х 6 X такой, что хп —*
х, п —> оо, в (X,d). Перейдём при п —> оо к пределу в неравенстве A),
принимая во внимание следствие 1. Получим неравенство d(x,xm) <
гт < £, т > N, из которого следует^ что х € B(xm,rm), m > N.
Отсюда, в силу условия 1), имеем х 6 В(хп,гп), п > 1.

10.1. Метрическое пространство
Осталось установить единственность точки х. Пусть у £ X такой эле-
элемент, что у € B{xn,rn), n > 1. Тогда d{x,y) < d{xn,x) + d(xn,y) <
2rn -> 0, n -» oo. Следовательно, d(x,y) = 0 и i = у. J
Замечание. Справедливо также и утверждение, обратное к тео-
теореме 12: если любая последовательность замкнутых шаров, удовлетво-
удовлетворяющих условиям 1) и 2), имеет непустое пересечение, то пространство
(X, d) полно. Прямое и обратное утверждения составляют теорему
Кантора.
Упражнение 50. Пусть (X,d) — полное метрическое пространство.
Пусть также Vn > 1 : Ап Ф 0, Ап замкнуто, An+i С Ап, d(An) ->
оо
О, п —► оо. Доказать, что 3 \х £ X : р| Лп = {i}.
71=1
10.1.13 Пополнение метрических пространств
Определение 15. Два метрических пространства
(Xi,di) и (X2,d2) называются изометричными, если.су-
если.существует биекцил f : Хг -» Х2 такал, что V{i,y} С Х\ :
— di{x,y). Функция f называется изометрией.
Упраоюнение 51. Пусть (Xi,dx) и {X2,d2) — изометричные про-
пространства, причём пространство (Xi,di) полно. Доказать, что простран-
пространство (X2,d2) полно.
Теорема 13. (О пополнении). Пусть {X,d) — произ-
произвольное метрическое пространство. Существует пол-
полное метрическое пространство {Y,d) с подмножеством
X С У такое что: 1) [X,d) изометрично {X,d)\ 2) X всюду
плотно в (У,d). Пространство (У, а) называется пополне-
пополнением пространства {X,d).
Доказательство этой теоремы, выходящее за рамки программы,
здесь не приводится.
Упражнение 52. Построить пополнение пространства примера 4 п.
10.1.12.
Упражнение 53. Построить пополнение пространства упр. 48
Упражнение 5^.. Пусть X — множество всех многочленов р на
отрезке [0,1], d(pi,p2) := max(|pi(x) - р2{х)\ \ 0 < х < 1). Проверить,
что пространство {X,d) неполно и найти его пополнение.
Упражнение 55*. Доказать, что любое непустое открытое множе-
множество в (Rm,p) можно представить в виде счётного объединения "за-

332 Глава 10. Элементы анализа в метрическом пространстве
мкнутых интервалов" вида [ai,bi] х [а2,Ь2] х ... х [ап,Ь„], {a.k,bk} С
R, a/c < bk, 1 < к < го без общих внутренних точек.
Упражнение 56. Пусть А — всюду плотное в (R, р) множество,
а 6 (Н\{0}) И|в£Й- фиксированные числа. Доказать, что множество
В := {ах + /3 | х € А} всюду плотно в (R, р).
10.2 Функции на метрическом пространстве
10.2.1 Предел функции в точке
Пусть (X, di) и (У, d.2) — метрические пространства, А С X, хо —
предельная точка множества А. Далее рассматриваются функции вида
/ : А —> У. Наиболее важные частные случаи:
1) Х = У = Д; / : Л-»Я — действительная функция, определённая
на множестве А действительных чисел;
2) X = Rm, У = Л; / : Л->Д — действительная функция от m
переменных;
3) X = Дт, У = Дп; / : А —> Дп — векторная функция от тп пере-
переменных:
4) (X, d) — метрическое пространство, Y = R, f : А -» Д — дей-
действительная функция, определённая на множестве Л метрического про-
пространства.
Определение 1. Пусть х0 — предельная точка мно-
множества А. Элемент р € У называется пределом функции
в точке хо, если Ve > 0 35 > 0 Vx е А х ф х0, di(x,x0) < 5 :
da(/(*),p)<e.
Обозначения: /(х) —> р, х —> хо, или р = lim /(x).
X—>Хо
Теорема 14. Элемент р является пределом, функ-
функции f в точке х0 тогда и только тогда, когда для лю-
любой последовательности {хп | п > 1} такой, что Vn >
1 : х„ g А, х„ ^ х0 и х„ -» х0, п -» оо в (X, cii), iU/tee.A/t
/(х„) ->р, п->оо в (y,d2).
I" Доказательство теоремы в точности повторяет доказательство анало-
аналогичной теоремы для действительной функции. J
Упражнение 57. Провести доказательство теоремы 14.
Теорема 15. (О единственности предела). Пусть
/(х) -» р, х -> хо, и /(х) -» д, х -> х0. Тогда р = д.
[ Доказательство следует из теоремы 14 и теоремы 1. J

10.2. Функции на метрическом пространстве 333
Упраоюнение 58. Пусть У = йи lim /(x) > 0. Доказать существо-
существование шара В(х0,г), для которого Vx € (В(хо,7")ПЛ\{хо}) : /(х) > 0.
10.2.2 Свойства пределов действительных функций
Пусть (X, d) — метрическое пространство, А С X, Хо — предельная
точка множества А, и У = R, d2(x, у) = р(х, у) = \х - у\ для {х, у} С R.
Пусть f : X -* R, д : X -» R — две функции. Утверждения следую-
следующей теоремы доказываются просто с помощью теоремы 14 и свойств
сходящихся последовательностей действительных чисел.
Теорема 16. Пусть lim f(x) = p € Я, lim $(х) = g e Д.
Тогда: i; Vc € Я : lim (°c/(z)) = с lim /(x);
2; lim {f{x)+g{x))= lim /(x) + lim 5A);
X—*XQ X—>Xo X—*Io
З; lim (/(xM(x)) = lim /(x) • lim ff(x);
X—>Xq X—>Xo X—>Xq
fix) x^S f№ "
А) если дополнительно q Ф 0. mo lim —7-7 = ^^—7^- .
x-*x0 g(x) lim 5A)
I—HO
Упражнение 59. Пусть У = Rm, d.2 = p — обычное расстояние в
Ят. Доказать, что f(x) = (/i(x),/2(x),... ,/m(x)) -> (pi,P2,-- • ,Pm) =
p, i-hob {Rm,p) <=$■ Vk,l<k<m: fk{x) ->pfc, x -> x0.
10.2.3 Понятие о повторных пределах
Пусть (Xic,dic), k = 1,2 — метрические пространства и X = Xi x X2
— декартово произведение множеств Х\ и Хг- Определим для то-
точек {х = (х1,хг),2/ = B/1,2/2)} С X расстояние, положив d(x,y) =
Заметим, что х^ = (х{ , х2п ) -* (xi,x2) = х, п -> оо, в (X,d)
хр -» хь п -> оо, s(Xi,di) и Xjn) -> х2", п -> оо, в(Х2,^2)-
Пусть (х°,х°) € X — некоторый элемент, f : {X \ {{х°,х°)}) -» -R.
Определение 2. Предел lim /(xi,x2)=p e (X,d)
(ii,x2)-»(x°,x§)
называется двойныл* пределом. Используется так&се
обозначение р= lim /(xi,x2).
xi~*xi
х%->х%
Зафиксируем теперь значение х\ ф х\ и рассмотрим исходную
функцию /(xi,-) : Х2 —> R, как функцию от х2 € Х2. Предположим,
что существует предел lim /(xi,x2) =: g{x\) в (X2,d2).

334 Глава 10. Элементы анализа в метрическом пространстве
Определение 3. Если существует предел lim g(x\)
= q в (Xi,dx), mo q называется повторным пределом в
точке (х5,х°) и обозначается q= lim lim /(х1,хг).
1 1^2
Аналогично определяется повторный предел lim lim /(xi,x2).
Двойной предел и повторные пределы в точке {х°,х2), вообще го-
говоря, различны.
Упражнение 60. Пусть Х\ = Х2 = R, d\ = d2 = р — обычное
2
расстояние, (х°,х°) = @,0) и }{х\,х2) — 2 : 2 , (х1(х2) Ф @,0).
Х1 + Х2
Существует ли двойной предел в точке @,0)? Чему равны повторные
пределы в точке @,0)?
10.2.4 Непрерывные функции
Пусть (X,dx) и (Y,d2) — метрические пространства, А С X, х0 € А и
/ : А -» У.
Определение 4- Точка х0 € А называется изолирован-
изолированной точкой мноснсества А, если выполняется условие
Зг > 0: В(хо,г)ПА = {х0}.
Определение 5. Пусть х0 € А — пределънал точка
мноок.ества А. Функция f : А -» У называется непре-
непрерывной в точке х0, если /(х) -» /(х0), х -» х0| т. е. если
Ve>0 3 5 > 0 VxeAdi(x,xo)<5 : d2(/(x),/(x0)) < e.
Определение б. Пусть xq £ А — изолированная точка
мноснсества А. Условимся считать, что каок.дая фун-
функция f : А -> У wenpejmewa в точке х0.
Определение 7. Фт/мк'цил / : А -» У — nenpepbtewa на
ji4.wowcecmee Л, если / wenpeybiena в камсдой точке мно-
множества А.
Обозначения: / € C(A,Y). C(A,R) =: С(А) для R с евклидовым
расстоянием.
Примеры. 1. Пусть J/0 € У — фиксированный элемент и V х € А :
f(x) = 2/0- Функция / непрерывна на X (d2(f(x\),f(x2)) = 0 для любых
элементов {a;i,i2} С X).
2. Пусть а £ X — фиксированный элемент, У = R и /(х) =
= di(x,a), х £ X. Функция / непрерывна на X в силу неравенства
треугольника |<ii(x,a) — dy(y,a)\ <di(x,y). В определении непрерывно-
непрерывности можно положить 8 = е.

10.2. Функции на метрическом пространстве 335
Замечание. Пусть х0 — внутренняя точка множества А. Определе-
Определение непрерывности функции / : А —> У в точке Хо допускает такую экви-
эквивалентную формулировку Ve>0 35>0: f(B(xo,S)) с В(/(хо),е).
Упражнение 61. Доказать, что функция / из определения 15 п.
10.1.13 непрерывна на Х\.
Упражнение 62. Пусть А С X, А ф 0, — фиксированное множе-
множество и для х е X f(x) := di(x,A) := inf di(x,z), lEl Доказать, что
z&A
функция / непрерывна на X.
10.2.5 Элементарные свойства непрерывных функций
Пусть Y = R, d2{x,y) = р{х,у) = \х-у\, {х,у} С R.
Теорема 17. Пусть f : 1->Д, д : 1->Д - непрерыв-
непрерывные в точке х0 6 ^ функции. Тогда:
a) Vc € R функцил cf непрерывна в точке х0;
b) функцил f + g непрерывна в точке х0;
c) функцил fg непрерывна в точке хо\
d) если дополнительно ff(xo) ф 0, то функцил f/g непре-
непрерывна в точке х0.
[" Использовать определение непрерывности и теорему 16. J
Пусть У = Ят, di — р — евклидово расстояние в Rm.
Теорема 18. Пусть функция f = (Л,/2,. ■. ,/т) : X ->
Rm. Функцил f непрерывна в точке х0 б X тогда и только
тогда, когда длл каждого к, 1 < к < т функцил Д непре-
рывна в точке хо-
[ Для доказательства использовать равносильность сходимости в Rm
покоординатной сходимости. J
Теорема 19. (О непрерывности слооюной функции).
Пусть (X,di), {Y,d2) и {Z,d3) — метрические простран-
пространства и f : X -» У, g : Y -¥ Z. Пусть h(x) := g{f{x)), x € X,
функцил h называется слооюной функцией или суперпо-
суперпозицией функций fug. Предположим, что длл некото-
некоторого х0 € X функцил f непрерывна в точке хо, а функцил
g непрерывна в точке уо := f{xo). Тогда функцил h непре-
непрерывна в точке х0.
\ Доказательство следует из теоремы 16. J
22 — 4-1168

336 Глава 10. Элементы анализа в метрическом пространстве
10.2.6 Примеры действительных непрерывных
на Rm функций
Пусть X = Rm и У = R с евклидовыми расстояниями.
1. Постоянная функция. Пусть уо € R — фиксированное чис-
число и f(x) = уо, х € Rm- Функция / непрерывна на Rm.
2. Непрерывность координат. Пусть к, 1 < к < т, фикси-
фиксировано и функция жк : Rm —> R определена следующим образом
жк(х) = 7rfc(ii, х2,..., хт) = хк, х = (ii, х2,..., хт) € Дт.
В силу неравенства |7rfc(i) - пк{у)\ = \хк - ук\ < р{х,у), {х,у} С Rm,
функция жк непрерывна на Rm (в определении непрерывности можно
положить 5 — е). Таким образом, координата точки есть непрерывная
функция точки.
3. Непрерывность многочленов. Многочленом от т
переменных называется функция Р : Rm —> R, определяемая с
помощью набора неотрицательных целых чисел ni, пг,... ,пт и набора
действительных чисел {a(ki,k2,... ,кт) \ 0 < kj < rij, I < j < m}
следующим образом
Р{х) = Р{х1,х2,...,хт)= J2 а,{к1,к2,...,кт)х\1х^ ...х*»,
где х = {xi,x2 хт) € Rm-
Частным случаем многочлена от т переменных является линейная
функция от т переменных Р{х) — а\Х\ + а2х2 + ... + атхт, х =
(ii, х2,..., хт) 6 Rm, где ai, а2,..., ат — действительные числа.
Любой многочлен от т переменных — непрерывная на Rm функ-
функция. Действительно, поскольку жк — непрерывная на Rm функция, то
утверждение примера следует из теоремы 17.
4- Рациональные функции от переменных. Пусть Р и Q
— два многочлена от т переменных и А — {х € Rm \ Q{x) ф 0}. Функ-
Функция S : А —> R, определяемая равенством S(x) = P(x)/Q(x), x £ А,
называется рациональной функцией от т переменных. Из теоре-
теоремы 17 следует, что рациональная функция от т переменных непрерывна
на множестве определения.
5. функция f{x\,x2) = e-\Ai+I2 sin(ii + xix%), {xi,x2) € R2 непре-
непрерывна на R2. Доказательство следует из непрерывности многочленов и
теоремы 19.
Упражнение 63. Доказать, что функция / : С([0,1])-» Д: а) f(x) —
1
ft3x2[t)dt; b) f(x) - i@) + max x(t); непрерывна в (C([0, l]),p).
0 1/2<*<1

10.2. Функции на метрическом пространстве 337
10.2.7 Теорема о характеризации непрерывности
Пусть (X, di), (V, (£2) — метрические пространства и / : X —> Y. Для
множества А С X его образ при отображении / есть множество f(A) =
{у € У | Э х € А : f(x) = у}. Для множества В С У его прообраз при
отображении / есть множество f~1(B) — {х € X | Зу 6 В : f(x) = у}.
Теорема 20. Функция f : X -» У непрерывна на X
тогда и только тогда, когда для, любого открытого в
{Y,d2) множества G множество f~1(G) открыто в (X,di).
\ Необходимость. Пусть / — непрерывна на X. Предположим, что
G — открытое множество, G С У и G Ф 0. Пусть хо G f~l{G) —
произвольная фиксированная точка. Положим уо — /(^о) G G. По-
Поскольку G открыто, то Зе > 0 : В(уо,е) С G. Из непрерывности
функции / в точке Хо следует также, что 3 5 > 0 Vx 6 В(хо,8) :
Дя) € В{уо,е) => В{хо,5) С /-1(ВB/0,е))- Таким образом, В{хо,6) С
/-^В^о.е)) С /"ЧС). Если G = 0, то /-1(С) = 0 - открыто.
Достаточность. Пусть хо € X — фиксированная точка и е > О
задано. Множество G — В(уо,е), где у0 = f{xo), открыто в (Y,d2).
Следовательно, по условию теоремы f~1(G) = f~l(B(y0,e)) открыто в
(X, dx). Поэтому для х0 € f~1{B(y0,e)) имеем
i 35 > 0 : В(хо,5)сГ1(В{уо,£)) =► /(В(хо,5)) С В(/(хо),е). J
^Згпросхснение 04- Доказать, что / € С;(а,У) тогда и только тогда,
когда для любого замкнутого в (У, ^) множества F множество f~1{F)
замкнуто в (X, dx).
Упраоюнение 65. Привести пример пространств X, У, функции / €
C(X,Y) и открытого в (X,di) множества А, для которых множество
/(Л) не является открытым в (У, d2).
Упраоюнение 66. Пусть У = {yi,y2,---,yn}, d2 — метрика на У.
Описать функции класса C(X,Y). Рассмотреть случай X = R.
Упражнение 67. Пусть (У, d2) — пространство с дискретной метри-
метрикой. Описать класс функций C{R,Y).
Упражнение 68. Доказать замкнутость в (С([0,1]),р) множества:
а) {х е С([0,1])| Vt е [0,1] : x(t) > 0}; Ь) {х € С([0,1])| /ix2(i)<if > 3}.
Упраоюнение 69. Доказать, что множество: а) {х 6 ^([0,1]) |
x{O) + f{l-t)x{t)dt > 0}; Ь) {х € С([0,1]) | х@) > 1, fx{t)dt < 0}
о о
открыто в (С([0,1]),р).
22

338 Глава 10. Элементы анализа в метрическом пространстве
Определение 8. Отображение f : X -> У называется.
гомеоморфизмом, если: 1) f — биекцил между X и У; 2,)
/€С(Х,У); З^
Упражнение 70. Биекция / : X -* У есть гомеоморфизм тогда и
только тогда, когда множество А открыто в (X, dx) тогда и только тогда,
когда f(A) открыто в (У, d2).
10.2.8 Равномерно непрерывная на множестве функция
Пусть (X, di), (У, d2) — метрические пространства иЛсХ
Определение 9. Функцил f : А -ь У называетсл рав-
равномерно непрерывной на множестве А, если:
Ve>0 35 > О 4{x',x"}cA,d1{x',x")<5: d2(f{x'),f{x"))<e.
Упражнение 71. Доказать, что функции упр. 61, 62 и примера 2 п.
10.2.6 равномерно непрерывны на множестве определения.
10.3 Компактные множества и их свойства
10.3.1 Определения
Пусть (X, d) — метрическое пространство, Т — произвольное непустое
множество индексов и Ас X.
Определение 1. Семейство мноэ*сеств О = {Оа \ Vа 6
Т : Оа С X} называетсл покрытием множества А, если
УхеАЗаеТ: Оа Э х ( <=> А С \J Оа) ■ Длл подмно-
v ает '
мсества 7" С Т семейство О' = {Оа \ а б Т'} называетсл
подпокрытием, покрытил О, если О' — покрытие длл А.
Если мпомсество Т конечно, то покрытие О называ-
называетсл конечным. Покрытие О = {Оа | а € Т} называетсл
открытым, если длл любого а £ Т множество Оа от-
открыто в (X,d).
Упражнение 72. Пусть (R, р) — прямая с обычным расстоянием.
Является ли семейство множеств {(l/n,2— 1/n) | n > 1} покрытием
(открытым покрытием) множества: а) @,1); Ь) [0,1)?
Определение 2. Пусть F с X. Множество F называ-
называетсл компактным в {X,d), если любое открытое покры-
покрытие множества F содержит конечное подпокрытие.
Примеры. 1. Произвольное конечное множество компактно.

IQ.3. Компактные множества и их свойства ' 339
. 2. Множество Z в (R, р) не является компактным.
Указание. Рассмотреть покрытие {(п - 1/2, п + 1/2) | n € Z}.
3. Множество @,1] не является компактным в (R,р).
Указание. Рассмотреть покрытие {A/п, 1 + 1/n) j n > 1}.
4. Множество {1/п | п > 1}и{0} компактно в [R,p).
5. Открытый шар БA,г) в пространстве (Rm,p) не является ком-
компактным множеством.
Указание. Рассмотреть покрытие {B(i,rfc) j 0 < rk < г, & >
1; rfc -> г, fc -> оо}.
Определение 3. Если X компактно в {X,d), то мет-
метрическое, пространство (X, d) называется компактным.
10.3.2 Свойства компактных множеств
ТеоремЗ 21. Компактное множество ограничено.
\ Пусть F — компактное в (X, d) множество. Для любого х £ F рассмот-
рассмотрим открытое множество В(х, 1). Семейство {В{х, 1) | х 6 jF1} является
открытым покрытием F. Согласно определению компактного множе-
множества, существует конечное подпокрытие B(xi,l),B(x2,l),. ..,B(xn,l),
т. е. F С U B(ifc,l). Пусть С := 1 + max(d(illifc) | 1 < к < п}.
fc=i
Покажем, что F С В{х\,С). Действительно, для х € F
Зк : В{хк,1)Эх => d{x,xi) <d(x,xk) + d{xk,xi) <C. J
Теорема 22. Компактное множество замкнуто.
\ Пусть F — компактное в (X, d) множество. Докажем, что множе-
множество X \ F открыто в (X,d). Пусть xq € (X \ F) — фиксированная
точка. Каждой точке х € F сопоставим два открытых шара В(хо,г(х))
и В(х,г(х)), где r(x) := -d(xo,x). Семейство {В(х,г(х)) | х £ F} есть
открытое покрытие компактного множества F. Следовательно, суще-
существует конечное подпокрытие {B(xi,r1),B(x2,r2), ■ ■., B(xn,rn)}\ F С
п
U B(ik,rt)i rK-r(xk), 1< fc <n. Пусть r:=min(rllr2l...,rn) > 0.
fc=i
Заметим, что B{xOtr) = f] B{xo,rk); B(xo,r)n[ [j B{xo,rk) = 0, так
fc=i vfc=i ;
как B(xQ, г) П B(xk, rk) = 0 для 1 < k < п. Поэтому B(xQ, г) П F — 0, т.
e.B(xo,r)c{X\F). J
Теорема 23. Замкнутое подмножество компактно-
компактного множества компактно.

340 Глава 10. Элементы анализа в метрическом пространстве
\ Пусть F — компактное в (X, d) множество и G С F, G — замкну-
замкнуто в (X, d). Пусть О = {Оа | а € Т} — открытое покрытие множе-
множества G. Тогда семейство О U (X \ F) есть открытое покрытие компакт-
компактного множества F. Следовательно, существует конечное подпокрытие
i, Оаз,..., 0Оп, X \ F. Поэтому {Оа1, 0а2,..., Оап} — конечное под-
подпокрытие для G. J
Теорема 24. (Обобщение теоремы Болъцано-Вейер-
штрасса). Пусть F — компактное в {X,d) множество.
Камсдая бесконечная последовательность элементов из
F содержит сходящуюся в (X, d) к некоторому элементу
из F подпоследовательность.
Замечание. В условиях теоремы для последовательности {хп \ п >
1} не предполагается, что хт ф хп при т ф п.
\ Пусть {хп | п > 1} С F — произвольная последовательность. Если
для точки х существует подпоследовательность {zn(fc) | k > 1} такая,
что in(fc) 4i, к —> оо, то для любого е > 0 неравенство d(xn,x) < e
выполняется для бесконечного числа индексов п. Поэтому, тот факт, что
для точки х требуемой подпоследовательности не существует, означает
существование е(х) > 0 такого, для которого неравенство d(xn,x) <
е(х) выполняется только для конечного числа номеров п.
Предположим, что утверждение теоремы неверно, т. е., что для
любой точки х € F не существует сходящейся к ней подпоследователь-
подпоследовательности. Тогда Vх е F 3e(a;)>0 3N = N(x) Vn > N : d{xn,x) >
е{х). Семейство шаров {В(х,е(х)) | х € F} есть открытое г^Ькрытие
компактного множества F. Пусть набор {B(xi, e(a;i)), В(х2, ерг)), • ■ •,
В(хт,е(хт))У составляет конечное подпокрытие F. Тогда, coi/ласно оп-
ределению, FC U В(хк,£{хк)). Кроме того, хп $ \J B(xk,E(xk)) для
fc=i fc=i
n > max{N(x1),N(x2),... ,N(xm)), т. е. хп $. F. Получили противоре-
противоречие с условием теоремы. J
Пример. 1. Докажем, что замкнутый шар в (С([а,Ь]),р) не есть ком-
компактное множество.
[ Достаточно рассмотреть случай [а, Ь) — [0,1], Xo(t) = 0, t € [0,1] и шар
В(х0,1). Последовательность функций
{*"|п>1} A)
принадлежит шару B(xq, 1). Допустим, что шар B(xq, 1) компактен. То-
Тогда по теореме 24 последовательность A) содержит равномерно на
[0,1] сходящуюся к некоторой функции / € В(х0,1) подпоследователь-
подпоследовательность {*"(") | * > 1}. Поэтому p{f,tnW) = max |/(t) - tn^\ -> 0, к ->
оо; 1/A) - 1| < max \f(t) - tnW\ -> 0, к -> оо, и для каждого
0<t<l

10.3. Компактные множества и их свойства 341
t 6 [0,1) |/(*)-*n(fc)| < p(/,*n(fc)) -> О, к -> оо. Таким образом, /A) = 1
и f(t) = 0, t € [0,1), что невозможно, так как / 6 В(х0,1) С С([0,1]). J
Упражнение 73. Пусть (Xk,dk), к = 1,2 — метрические простран-
пространства и (X, d) — их декартово произведение. Предположим, что Fk —
компактное множество в (Xk,dk), к = 1,2. Доказать, что множество
F\ х i* компактно в (X, d).
Упражнение 74- Доказать, что замкнутый шар в (i2,p) не есть
компактное множество. ..,-^
Замечание. Из утверждений примера 1, упр. 74 следует, что ком- I
пактные множества в этих пространствах не могут содержать открытых i
или замкнутых шаров. __>
Упражнение 75. Доказать, что компактное метрическое простран-
пространство полно и сепарабельно.
10.3.3 Критерий компактности
Пусть (X, d) — метрическое пространство и А С X. Пусть е > 0 задано.
Определение 4- Множество С с X называется е-се-
тъю для множества Л, если Vi € А Зу £ С : d(x,y) < e
(» \J B(y,e)Z>A).
Теорема 25. (Критерий Хаусдорфа). Для того, что-
чтобы замкнутое множество F метрического пространст-
пространства (X, d) было компактным необходимо, а для полного
пространства {X,d) и достаточно, чтобы для любого
числа е > 0 существовала конечная е-сеть для F.
\ Необходимость. Пусть F компактно. Тогда по теореме 22 F замкну-
замкнуто. Пусть е > 0 задано.Открытое покрытие {В(х,е) | х £ F} множества
F должно содержать конечное подпокрытие: {B(xi,e),B(x2,e), ...,
В(хп,е)}. Тогда множество {ii.ia» • • ■ ,хп} есть конечная е-сеть для F.
Достаточность. Пусть полно (X,d), a F замкнуто. Предположим,
что F не является компактным. Согласно определению, это означает,
что существует открытое покрытие О = {0а \ а £ Т}, не содержа-
содержащее конечного подпокрытия для F. Пусть для е = 1 Сх — конечная
1-сеть для F (она существует в силу условия теоремы). Хотя бы одно из
множеств {В(х, 1) П F | а: € С{} не может быть покрыто конечным на-
набором множеств из О. Допустим, что это множество Ft = B(xi, 1) П F.
Пусть для е — 1/2, С% — конечная A/2)-сеть для F, а, следователь-
следовательно, и для Fx. Хотя бы одно из множеств {В(х, 1/2) П jF\ | х £

342 Глава 10. Элементы анализа в метрическом пространстве
не может быть покрыто конечным набором множеств из О. Пусть это
множество F2 = В(х2,1/2) П Fi. Продолжая аналогично, получим по-
последовательность множеств {Fn \ п > 1} таких, что: 1) Fn С F, n > 1;
2) Fn С B(zn,2~n+1), n > 1; 3) Fn не может быть покрыто конечным
набором множеств из О (в частности Fn бесконечно), п > 1.
Рассмотрим теперь последовательность {yn | n > 1} таких элемен-
элементов, что:
y1e(B(x1,l)nF)) = F1;
yn G (B(xn, 2 n+1) П Fn-i)) = Fn, Уп^Ук, 1 < к < п - 1;
;- A " iT
Последовательность {у„ | n > 1} фундаментальна, что следует из
неравенства d(ym,yn) < 2~~т+\ т < п. Поскольку (X, d) полно, то
существует элемент у € X"такой, что уп —> у, п -> оо в (-X\d). За-
Замкнутость F влечёт включение у € F. Открытое покрытие О множества
F содержит множество Оа> Э у. Поскольку Оа> открыто, то 3 6 > 0 :
В{у,8)С Оа>. Пусть теперь п таково, что 2~n+1 < S/3, d{yn,y) < 8/3.
."с B(xn,2~n+1)iC B(y,S), так как для любого х Е Fn имеем
d(x, хп) + d(xn,% < 2~п+1 + d(xn, уп) + d(yn, у) < 2 ■ 2~n+1 +
+d(yn,y) < S. Таким образом, множество Fn покрывается одним мно-
множеством Oai из О. Полученное противоречие доказывает теорему. J
TorfLaj
d(x,y)
Теорема 26. Пусть {X, d) — метрическое простран-
пространство u F С X. Если ка&сдал последовательность элемен-
элементов из F содержит подпоследовательность, сходлщую-
сл к некоторому элементу из F, то множество F ком-
компактно.
\ F замкнуто, поскольку содержит все свои предельные точки. Дока-
Докажем, что для каждого е > 0 существует конечная е-сеть. Предполо-
Предположим, что для некоторого е* > 0 не существует конечной е-сети для
F. Пусть xi — любой элемент из F, множество {В(х1)е*)} не есть
покрытие для F. Поэтому существует х2 € F, x2 (fc B(xi,e*). Набор
{В(х1)е*)) В(х2,е*)У также не образует покрытия для F и т. д. Полу-
Получим последовательность {хп | п > 1} С F такую, что d(xm,xn) > e* для
т ф п. Последовательность {хп \ п > 1} не может содержать сходя-
сходящейся подпоследовательности (противоречие с фундаментальностью).
Полученное противоречие с условием теоремы показывает, что пред-
предположение о несуществовании конечной е*-сети неверно. Далее см.
доказательство теоремы 25. J

IQ.3. Компактные множества и их свойства 343
Замечание. Теоремы 24 и 26 вместе дают ещё один критерий
компактности в метрическом пространстве — теорему Кантора ■
Упражнение 76. Пусть для каждого а € Т множество Fa компакт-
компактно И ДЛЯ Любого КОНечНОГО набора ^е*A), ^е*B), ■■■ ,Fa(n)
• • • П Fa(n) ф 0. Доказать, что П
10.3.4 Компактные множества в (Rm,p)
Теорема 27. Подмномсество метрического простра-
пространства (Rm,p) компактно тогда и только тогда, когда
оно замкнуто и ограничено.
\ Необходимость. В силу теорем 21 и 22 компактное множество в
любом метрическом пространстве замкнуто и ограничено.
Достаточность. Пусть F замкнуто и ограничено. Воспользуемся
критерием Хаусдорфа. Предположим, что е > 0 задано. Множество с
есть е-сеть для Jf?m. Поскольку F ограничено, то оно содержится в{
гиперкубе вида J = {(хг,х2, ■ ■ ■ ,хт) | \xj\ < р, 1 < j < т; р > 0}.^
Множество С — С C\J конечно и является е-сетью для F. J
Упражнение 77. Пусть А — произвольное замкнутое множество в
(Rm,p). Доказать существование последовательности {а(п) \ п > 1} С
Rm такой, что для неё множество всех частичных пределов равно А.
Доказать также, что эта последовательность может быть взята такой,
что {аA),аBI...,а(п),...} = Л.
Упражнение 78*. Описать компактные множества в (f2l р)- \/
10.3.5 Компактные множества в С([а,Ь]),р)
Пусть АсС{[а,Ь]).
Определение 5. Семейство функций называется ра-
равномерно ограниченным если 3L е R Vx e A Vi G [а,Ь] :
\x(t)\ < L, т. е. если множество А ограничено в метриче-
метрическом пространстве (С([а,Ь]),р).
Определение 6. Семейство функций называется ра-
равностепенно непрерывным, если
Ve>0 36 > 0 Vie Л Vt',t" C[a,b],\t'-t"\<6: \x{t') - x(t")\ < е.

344 Глава 10. Элементы анализа в метрическом пространстве
Теорема 28. (Теорема Асколи-Арцела). Для. того,
чтобы замкнутое множество F С С([а,Ь]) было компакт-
компактным в (С([а,Ь]),р), необходимо и достаточно, чтобы:
1) множество F было равномерно ограниченным.;
2) множество F было равностепенно непрерывным.
[ Необходимость. Пусть F — компактное множество в метриче-
метрическом пространстве (С([а,Ь]),р). Тогда F — ограниченное множество
и, следовательно, условие 1) теоремы выполнено. Пусть е > 0 за-
задано. Согласно критерию Хаусдорфа, существует конечная A/3)-сеть
{xi, х2,.. ■, хп} для F, п = п(е). В силу теоремы Кантора
36 > О V*. l<k<n, Vt',t"C[a,b],\t'-t"\<6: \xk(t')-xk(t")\ < £- .
О
Пусть теперь х € F задано. Тогда для некоторого к, 1 < к < п,
имеем р(х,хк) < е/3, т. е. Vi € [a,b] : \x(t) - Xk(t)\ < е/3. Поэтому
Vt'.t" С [а,Ъ], \t'-t"\ < 6 : \x(t')-x(t")\ = |a(t')-afc(t')+afc(t')-*fc(*") +
xk{t") - x(t")\ < \x(t') - xk(t')\ + \xk(t') - xk(t")\ + \xk(t") - x(t")\ < e.
Таким образом, условие 2) также выполнено.
Достаточность. Пусть F — замкнутое множество, удовлетворя-
удовлетворяющее условиям 1) и 2). Используем теорему 26. Предположим, что
{a:n | n > 1} С F, {гп | п > 1} — множество всех рациональных чисел
отрезка [а,Ь], занумерованных в каком-нибудь порядке. Последователь-
Последовательность чисел {in(^i) | п > 1} ограничена по условию 1), следовательно,
она содержит сходящуюся к некоторому числу х(гх) подпоследователь-
подпоследовательность a:n(fc) -> z(fi). к -> оо. Обозначим хп(к) ='■ a=ifc, к > 1. Последо-
Последовательность {х\к | к > 1} С F и такова, что X\k{ri) —> х(г\), к —> оо.
Рассмотрим теперь последовательность чисел {яц^гг) | к > 1}, ко-
которая также ограничена. Поэтому существует подпоследовательность
{Iifc(i)(I%2) I j > 1}. сходящаяся к некоторому числу x(r2) : xlk{j)(r2) ->
I(r2), j -> оо- Обозначим хщ}) =: хц, j > 1. Для последовательности
{х2п | п > 1} имеем: х2п(п) -> х^^), х2п(г2) -> х(г2), п -> оо.
Продолжая аналогично, построим для каждого т Е N последова-
последовательность {хтп | п > 1}, которая является подпоследовательностью ис-
исходной, и для которой V j, 1 < j < m : a;mn(^j) —> x{rj) € H, n->oo.
Последовательность {inn |n > 1} является подпоследовательностью
исходной, причём хпп £ {хпк \ к > 1}, п > 1. Поэтому Vj > 1 :
Inn(rj) ~> z(r,) € Н, n —> оо. Действительно, для j заданного Xjn(rj)
—> a;(r_j), n —> оо, и, следовательно, для каждого е > 0 только для ко-
■ нечного числа номеров \xjn(rj) — x(rj)\ > e. Все последовательности
' {.хтп | п > 1}, m > j; {xnn |n > j'} по построению есть части после-
последовательности {xjn | n > 1}. Поэтому неравенство |а;пп(г;) — i(ry)| > е
может выполняться только для конечного числа номеров п.

10.4. Свойства непрерывных функций на компактах 345
Пусть теперь е > 0 задано, а 8 > 0 — соответствующее число из
определения равномерной непрерывности F. Пусть для числа 6 набор
rfc(i)>rfcB)i ■ • • .rfc(s) есть 6-сеть для [a,b] из рациональных чисел. Для t €
[a,b] обозначим через r(t) элемент этой сети такой, что \t — r(t)\ < 6. То-
Тогда Vt 6 [a,b]V{m,n} С N : |xmm(t)-a!nn(OI < \xmm(t)-xmm{r{t))\ +
\xmm{r{t)) - Xnn(r(t))\ + \xnn(r{t)) - Xnn(t)\ < 2e + £ \xmm{rk(i)) -
3 = 1
xnn{^kU)))\- Таким образом, последовательность {xnn \n > 1} удовле-
удовлетворяет условию критерия Коши равномерной сходимости и, следова-
следовательно, сходится к непрерывной на [a,b] функции, лежащей в F силу
его замкнутости. J
Упражнение 79. Доказать, что условие 1) теоремы можно заме-
заменить следующим, более простым 3L€l? Vi £ F: |z(a)| < L.
10.4 Свойства непрерывных функций
на компактах
10.4.1 Основные теоремы
Теорема 29. Пусть (Х,йх) — компактное метриче-
метрическое пространство, (Y, йъ) — метрическое пространство.
Пусть f eC{X,Y).
Тогда множество f(X) компактно в (Y, й2).
\ Пусть О = {Оа} — открытое покрытие f{X) в (Y, d2). Согласно теоре-
теореме 20 множество f~1(Oa) открыто при каждом а. Семейство множеств
\1 (Оа)} есть открытое покрытие компактного множества X и суще-
существует конечное подпокрытие {/~1(°a(i))./~1(c'<»B))i--^/"Ч^оСп))}-
Поэтому имеем X С U Г1(Оа{к)) =► f(X) С f(\J ГНО^к)))^
fc=i 4fc=i '
= U НГЧоа{к))) с и оа(к). ' J
fc=i k=i
Замечание. Пусть (X, di) и (У, d2) метрические пространства, F —
компактное множество в (X, dx) и / € C(F,Y). Тогда f{F) компактно.
Рассмотрим теперь в качестве пространства (У, d2) числовую прямую
R с обычным расстоянием.
Теорема 30. Пусть (X,di) — метрическое простран-
пространство, F — компактное множество в X и f € C(F).
Tozda:aKLeR Vi e F : \f{x)\ < L; Ъ) 3{xt,x*} С F :
f(x.) = ixdfix), /(a')=eup/(x).
x£F F

346 Глава Ю. Элементы анализа в метрическом пространстве
f Доказательство следует из компактности множества /(F) и того, что
компактное множество ограничено и замкнуто. J
Теорема31. Пусть (X,di), (У,d2) — метрические про-
пространства и выполнены следующие условил: 1) X — ком-
компактное мномсество в (X, di); 2) f биекцил между X и
У; 3) f £ C(X,Y). Тогда обратная функция f'1 £ C(Y,X).
f Обратная функция f : У —> X существует в силу условия 2). Пусть А
— открытое множество в (X, d\). Прообразом множества А при отоб-
отображении /-1 является множество (f~1)~1(A) = {у | 3 х £ А : f~1{y) =
х} = {у | у = f(x), хеА} = /(Л).
Замкнутое подмножество X \ А компактного по условию 1) множе-
множества X является компактным. Поскольку / £ C(X,Y) по условию 3), то
f{X \ А) компактно в (У, d2). Следовательно, f(X \ А) =Т/(Х) \ f(A) =
— Y\f(A) замкнуто, a f(A) открыто в (У,d2)- ", ^в^«у»у\. ■ttwf J
Теорема 32. (Теорема Кантора). Пусть (X, di), (У, d2)
— метрические пространства и выполнены следующие
условил: 1) X — компактное мноэ*сество в (X, di); 2) f €
C(X,Y). Тогда функция f равномерно непрерывна на X.
\ Пусть е > 0 задано. Согласно определению непрерывности в точке,
имеем Vz€X Э6 = 6{х) > О Vz £ В{х,6{х)) : d1(f{z),f{x)) < е/2.
Семейство шаров {B{x,5{x)/2) \ х £ X"} является открытым покры-
покрытием компактного по условию 1) множества X. Поэтому существует
конечное подпокрытие В(х1,6{х1)/2), В(х2,6{х2)/2),..., В{хп, 6{хп)/2)
п
такое, что X С U B(xkiS(xk)/2). Положим 6 := vam(S(xk)/2, 1 <
fc=i
ifc < п). Пусть теперь {х',а;"} С X, dx(x',х") < 6. Для точки х' Зк :
B(afc, E(ifc)/2) Э *'-«=*• di(i', ifc) < E(*fc)/2. Тогда а" 6 B(ifcl <5(afc))-
Следовательно, d2(/(x'), f(x")) < d2{f{xl),f{xk)) + d2{f(x"),f{xk)<e.\
Определение 1. Пусть {X,d) — метрическое простра-
пространство и S с X. Мноэ*сество S называется связным мно-
множеством в {X,d), если не существует открытых мно-
э+сеств А и В, удовлетворяющих условиям.:
1)АПВ = 0, 2)AnS^0, 3)BnS/0, 4) S С (Ли В).
Пример. В пространстве (R,p) множества (а,Ь), (а, +оо) и Я связны,
а множество [0,1] U [2,3] несвязно.
[ Докажем, что интервал (а, Ь), {а, 6} С R, есть связное множество.
Предположим, что множество {а,Ь) несвязно. Достаточно рассмотреть
случай, когда а € Л, Ъ € В, где А и В множества из определения
, 1. Тогда непустое множество А П (а, Ь) ограничено сверху числом b и
потому имеет точную верхнюю грань с := sup(A П (а,Ь)). Поскольку

jf0,5. Принцип сжимающих отображений 347
An(a,b) открыто, то с ^ (АП (a,b)), в частности, с > а. Аналогично,
поскольку В П (а,Ь) открыто, то с (£. (В П (а,Ь)), и с < Ь. Поэтому точка
с 6 (а,Ь), но с$({АП (а,Ь)) U (В П (а,Ь))) = (а,Ь). J
Упражнение 80. Описать связные множества пространства (R, р).
Упражнение 81. Пусть S\ и S2 — связные множества, причём
Si П ^2 ф 0. Доказать, что S\ U S^ также связно. /( ^
Теорема 33. Пусть (X,di), (Y,d.2) — метрические про-
пространства и выполнены следующие условия: 1) X — свл-
аное мноысество; 2) f € C(X,Y).
Тогда множество f{X) связно в (У.йг)-
f Предположим, что f(X) несвязно. Тогда существуют открытые в
(X,di) множества Ли В такие, что АпВ = 0, f(X)f)A^0, f(X)n
В Ф 0. f(X) С (Л U В). Переходя к прообразам, получим f~1{A) П
\ 1 11
Кроме того, множества / 1(А) и / 1{В) открыты, следовательно., X
несвязно, что противоречит условию теоремы. J
Упраоюнение 82. Пусть Y = R, р — обычное расстояние. Доказать,
что тогда теорема 33 утверждает, что f(X) — интервал (возможно
бесконечный).
Упраоюнение 83. Пусть / е C{Rm) и 3 а 6 Я : {х G Rm | f(x) <
а} ф 0 и ограничено. Тогда 3 х* € Rm : niin/ = f(xt).
Упражнение 84*. Пусть (X, d) — полное сепарабельное метриче-
метрическое пространство и / € С(Х). Функция / называется компактной,
если для каждого а € R множество {х € X \ f{x) < а} компактно.
Построить примеры компактных функций.
10.5 Принцип сжимающих отображений
10.5.1 Определения
Пусть (X, d) — метрическое пространство и / : X -4 X — отображение
этого пространства в себя.
Определение 1. Точка х £ X называется неподвиж-
неподвижной точкой отображения /, если f(x) = х.
Определение 2. Отобрамсение называется сжимаю-
сжимающим (отображением сжатия), если
ЗА, 0 < А < 1 VieX VyeX d{f{x),f{y))<\d{x,y).

348 Глава 10. Элементы анализа в метрическом пространстве
Упражнение 85. Доказать, что в пространстве (R2,p) преобразо-
преобразование f{xi,x2) = (ал + 1,3:2 + 3), B:1,12) € R2 не имеет неподвижных
точек и не является сжимающим.
Упражнение 86. Доказать, что в пространстве {R2,p) преобразо-
преобразование f(x\,X2) = {xiCOSlf - X2Sin(p,XiSill(p + X2COStf), (li,l2Nfl2,
где ip £ R — фиксировано, имеет неподвижную точку, но не является
сжимающим.
Упражнение 87. Имеет ли в пространстве (С([а,Ь]),р) преобразо-
преобразование: a) f(x) — —х; Ь) f(x) = \x\; с) f{x)(t) = maxx(u) неподвижные
[а.*]
точки. Является ли это преобразование преобразованием сжатия?
Упражнение 88. Рассмотрим в пространстве (С([а,Ь]),р) преоб-
t
разование f{x)(t) — fx(u)du, a < t < b; x g C{[a, b)). Определить
а
неподвижные точки /. Является ли это преобразование преобразовани-
преобразованием сжатия?
Упражнение 89. Доказать, что сжимающее отображение простра-
пространства X в себя равномерно непрерывно на X.
10.5.2 Теорема Банаха
Теорема 34. (Теорема Банаха). Пусть (X, d) — полное
метрическое пространство и f : X —> X — отобрамсе-
ние смсатил. Тогда отображение f имеет единствен-
единственную неподвижную точку.
\ Пусть х0 — произвольный элемент из X. Рассмотрим последователь-
последовательность хх = f{x0), х2 = f(xi), ..., хп = /(in-i) Элемент хп
есть результат n-кратного применения преобразования / к элементу
Xq : хп = fn(xo). Докажем, что последовательность {хп \ п > 1}
фундаментальна. Для этого сначала отметим неравенство d(a:n+1,a:n) =
= d{f{xn),f{xn-i)) < Xd{xn,xn-i) < ... < And(x!,x0),n > 1. Учиты-
Учитывая это неравенство, для любых т, п, т < п, получим d(xm, xn) <
< d(xm,xm+1) + d{xm+1,xm+2) + ... + d{xn-2,xn-i) + d(xn_!,xn) <
Am
d(xux0).Ta-
)xo) + ... + Ad(x1,xo) <
; ким образом,
ДТП
V{m,n}c N,m< n : d{xm,xn) < -d(xltx0). A)
1 — A
Из неравенства A) следует фундаментальность последовательности
{хп | п > 1}. Поскольку (X, d) полно, то существует элемент х* £ X

10.5. Принцип сжимающих отображений 349
такой, что х„ —> х*, п-юов (X,d). Устремив в неравенстве A) п —> оо,
получим следующее неравенство
что
d(x;xm)<^—^d(xux0). B)
, . Элемент х* есть неподвижная точка /, так как в силу непрерывности
/ из равенства гп+1 = f(xn), n > 1, при п —> оо получим г* = f(x*).
Элемент г* есть единственная неподвижная точка /. Действительно,
если для некоторого z £ X : f(z) = z, то d(x*,z) = d(f(x*),f(z)) <
< \d(x*,z). Таким образом, х* = z. J
Замечание. Следует обратить внимание на конструктивный ха-
характер доказательства теоремы Банаха. Элементы последовательности
\хп | п > 1} являются приближениями к неподвижной точке х*, причём
точность приближения оценивается неравенством B).
Следствие 2. Пусть (X,d) — полное метрическое про-
пространство и f : X -> X. Предположим, что для некото-
некоторого т £ N отобрамсение fm есть отобраэ+сение сэ+сатил.
Тогда отображение f имеет единственную неподви-
о*сную точку.
\ Отображение / может иметь только одну неподвижную точку, по-
поскольку неподвижная точка для / есть неподвижная точка и для fm.
Пусть х* — неподвижная точка fm : fm{x*) = х*. Тогда d(x*, f(x*)) =
= d{fm{x*), fm+1{x*)) < \d{x*,f{x*)). Отсюда х* = f(x*). J
Упражнение 90. Пусть X = [а,Ь], р(х,у) = |i-y|; (X, p) — полное
метрическое пространство. Пусть / : [a,b] -> [a,b] — дифференциру-
дифференцируемая на [а,Ь] функция. Доказать, что / есть преобразование сжатия
тогда и только тогда, когда 3 Л < 1 : sup |/'(x)| < Л.
х€[а,Ь]
Упражнение 91. Доказать, что требование теоремы Банаха Л < 1
существенно. В пространстве (Я, р) рассмотреть преобразование f(x)
= 7г/2-arctg 1|1,1бй, для которого \f{x)-f(y)\ < \х-у\ при х фу.
Упражнение 92. Проверить, что f2 для преобразования / упр. 88
есть преобразование сжатия при Ь — а < 1.
10.5.3 Применение принципа сжимающих отображе-
отображений
I. Решение уравнений вида f(x) — х.
Определение 3. Функция f : [о,Ь]-»й удовлетворяет
на [а, Ь] условию Липшица порядка а > 0 с постоянной L,
если V {х,у} С [a,b] : \f(x) — f{y)\ < L\x — у\а. Класс функций,

350 Глава 10. Элементы анализа в метрическом пространстве
удовлетворяющих на [a,b] условию Липшица порядка а,
обозначается символом. Lipa([a,b]).
Упражнение 93. Описать класс Lipa([a,b]), a > 1.
Упражнение 94- Показать, что С1^^}) С Lipa([a,b]), и что об-
обратное включение неверно.
Упражнение 95. Доказать, что из включения / £ Lipa([a,b]) сле-
следует равномерная непрерывность / на [а,Ь].
Теорема 35. Пусть f [а,Ь] -» [а,Ь] и f e Lipa([a,b\) с по-
постоянной L < 1. Тогда 3 \х* € [а,Ь] : f(x*) = х*.
\ Применить теорему Банаха к пространству X = [а, Ь] с обычным рас-
расстоянием и отображению /. Заметим, что утверждение этой теоремы
может быть получено элементарно, однако, теорема Банаха фактиче-
фактически даёт больше: начиная с любой точки хо £ {а>Щ> мы получаем по-
последовательность {хп | п > 1}, сходящуюся к I*, причём справедливо
Ln
неравенство \х - х*\ < |/(х0) - хо\, п > 1. J
1 — L
II. Решение уравнений вида F(x) = 0.
Теорема 36. Пусть F : [а, Ъ) -> R, причём
F(a) < 0 < F(b); Зт 3 М, 0 < т < М Vi € [а,Ъ] : m<F'{x)<M.
Тогда 3\х*£[а,Ъ] : F{x*) = 0.
|" Применить теорему Банаха к пространству ([а, Ь], р) и преобразованию
f(x) = х - XF(x), х в [а,Ъ], с числом А, 0 < А < М. См. также
замечание к п. I. J
III. Решение системы линейных уравнений.
Пусть А = (ajk)Jlk=1 — матица размера т х т с действительными
m
элементами такими, что А2 := Yl (ajk + 5jkJ < 1, 5jk ■= 0, j ф
>,fc=i
fc, 5jk ■= 1, j = к. Удобно использовать векторные обозначения. Пусть
х — вектор-столбец с компонентами х\, х2, ■. ■, хт; х £ Rm.
Теорема 37. Для любого а е Rm существует един-
единственное решение х* € Rm системы Ах = а.
|" В полном метрическом пространстве (Rm,p) отображение, опреде-
определяемое формулой f(x) — Ах + х — а, х £ Rm, есть преобразова-
преобразование сжатия, так как для любых х и у с компонентами Жг.хг,... ,хт и
!/ii !/2i • • • i Ут соответственно имеем неравенство
= Е (Л(г) -

Ю.!$$Принцип сжимающих отображений 351
m , m m ^2
= Е Е ajkXk + Xj - Oj ~ Е aikVk - Vj + 9j ) =
j=l 4=1 V__ _ у k=l - -• / '
= E
i
< E E (a* + 8jkJ E (** - VfcJ = А2Р2(^,У)-
i=i fc=i *=i
Согласно теореме Банаха, существует единственная неподвижная
точка х* преобразования / : f(x*) = х*, т. е. Ах* = а. Причём
для произвольной точки г(°) е Rm имеем f(n+1) = ,4i(n) + f(n) -a, n>
0; lim i^n^ = f* в (Rm,p). Кроме того, для любого j, 1 < j < m,
справедливо неравенство
Ю-х^Крр^К^р&Ч,*0)), п>1. J
IV. Теорема о существовании и единственности реше-
решения дифференциального уравнения.
Теорема 38. Пусть функция F : [а, Ь) х R -ь R удовле-
удовлетворяет условиям.: 1) F е С([а, Ъ] х R); 2KLeR\/xE
[а,Ъ] V{у1,у"} : \F{x,y') - F{x,y")\ < L\y' - у"\. Тогда для любого
начального значения у0 £ R задача Кохии
[y(a) = Уо-
имеет единственное решение. , о i л
| Заметим, что решение задачи A) равносильно решению интегра-
X
лъного уравненияу(х) = уо'+ /F(u,y(u))du, a < х <Ъ, относитель-
a
но функции у £ С([а,Ь]). Для применения теорем Банаха в пространстве
С([а,Ъ]) введём метрику d(f,g) = тале («"*«—»>|/(я:) - g(x)\), {f,g} С
а<х<о
С([а,Ь]), где к > 0 — фиксированное число, которое будет выбрано
позже. Обратим внимание на неравенства pp{f,g) < d(f,g) < p{f,g),
fj. := е~к^ь~а\ из которых следует полнота (C([a,b\),d) при любом к > 0.
В пространстве (C([a,b]),d) рассмотрим следующее преобразова-
преобразование А : C([a,b]) —> C([a,b]), задаваемое формулой (Af)(x) = уо +
X
+ / ^(u,/(u)) du, a < x < b; f £ C([a, Ь]), есть преобразование сжатия
a
для соответствующим образом выбранного значения к. Действительно,
поскольку для любого х € [а,Ь] справедливо неравенство \(Af)[x) —
~(Ад)(х)\ = \JF(u,f(u))du-JF(u,g(u))du\< Lf\f(u)-g(u)\du,
{f,g}cC([a,b]),Jo
23 — 4-1168

352 Глава 10. Элементы анализа в метрическом пространстве
x) - {Ад)(х)\ < bje-k^-u^e-^u-a)\f(u) - g{u)\ du<
Отсюда следует, что d(Af,Ag) < Xd(f,g), {f,g} С С([а,Ъ]), где
Л = L/fc. Если k таково, что Л < 1, то Л есть преобразование сжатия.
Применяя теорему Банаха получаем заключение теоремы.
Заметим также, что теорема Банаха позволяет в сложной ситуации
(когда отсутствуют алгоритмические способы определения точного ре-
решения задачи A)) просто строить приближения к неизвестному решению
с произвольной точностью. J
V. Существование решения уравнения Фредголъма вто-
второго рода.
Теорема 39. Пусть функция К : [а, Ъ] х [а, Ъ] -» R, К €
C([a,b]x[a,b]) и число X £ R таково, что \Х\ < (М(Ь-а)) длл
М :— тах(\К(х,у)\ \ {х,у) е [а,Ь]2)- Тогда длл любой g е С([а,Ь])
существует единственна а функция f G С([а, Ь]) такая,
что справедливо равенство
f(x) = XjK(x,y)f{y)dy + g(x), х£[а,Ъ). B)
а
Замечание. Для заданных функций К и g уравнение B) относи-
относительно функции / называется интегральным уравнением Фред-
Фредголъма второго рода.
\ К полному метрическому пространству (С([а,Ь]),р) и преобразова-
ь
нию сжатия Л, задаваемому формулой A(f)(x) = X JK(x,y)f(y)dy +
а
+g(x), x £ [а,Ь]; / £ С([а,Ь]), применить теорему Банаха. J
Упражнение 96. Пусть (X, d) — компактное метрическое простран-
пространство, а преобразование / : X —> X удовлетворяет условию
V{х, у} С X, х ф у : d(f(x), /(у)) < d(x, у). C)
Доказать, что / имеет единственную неподвижную точку .
Упражнение 97. Пусть (X, d) — метрическое пространство, а пре-
преобразование / : X —> X удовлетворяет условию C) и таково, что /(X)
компактно в (X, d). Доказать, что / имеет единственную неподвижную
точку.
Упражнение 98*. Пусть (X, d) — полное метрическое простран-
пространство, функция / £ С(Х,Х), а функция р : X —> [0 + оо) удовлетворяет

10.5. Принцип сжимающих отображений 353
условию d{x,f(x)) < р(х) -p(f(x)), х € X. Доказать, что для лю-
любой точки х0 Е X последовательность итераций.in+i = f(xn), n > О
сходится к неподвижной точке /.
Упражнение 99*. Пусть (X, d) — компактное метрическое про-
пространство, а преобразование / : X —» X удовлетворяет условию
V{x,y} С X : d{f{x)J(y)) > d(x,y). Доказать, что /(X) = X и
что / — изометрия.
VI. Теорема о существовании неявной функции
Теорема 40. Пусть функция F : [а,Ь] х R -> R удо-
удовлетворяет следующим, условиям,: 1) F £ С([а,Ь] х Я);
2) Зт ЭМ, 0 < т < М Vi £ [а,Ъ] V{yi,y2} С R, ух ф у2 ■
2/1 ~У2
Тогда Э!/еС([о,Ь]) : F{x,f{x))=0, хе[а,Ъ].
\ В полном метрическом пространстве (С([а,Ь]),р) следующее преоб-
2
разование {Ад)(х) = д(х) —— F(x,g(x)), х 6 [а,Ъ], д 6 С{[а,Ъ]),
т -\- М
есть преобразование сжатия. v J
10.5.4 Теорема Стоуна-Вейерштрасса
Пусть (X, d) — компактное метрическое пространство. Введём в про-
пространстве С{Х) непрерывных действительных функций расстояние
p{f,g) := max\f(x)-g(x)\, {f,g} С С(Х).
Xt-Л
Пространство (С(Х),р) — полное метрическое пространство. Доказа-
Доказательство этого утверждения полностью аналогично доказательству пол-
полноты пространства (С([о,Ь]),р).
Определение 4- Пусть А С С(Х). Мно&сество А на-
называется алгеброй, если V{/,g} с A Va £ R : (af) £ A,
(/ + 9) 6 A, {fg) e А.
Определение 5. Пусть АсС(Х), А — алгебра. Алгеб-
Алгебра А отделяет точки мноэ*сества X, если выполняется
условие \/{х,у}сХ,хфу 3f £А: }{х)ф}(у).
Теорема41. (Стоуна-Вейерштрасса). Пусть (X,d) -
компактное метрическое пространство, {С(Х),р) — про-
пространство непрерывных действительных функций на X
с равномерной метрикой, А с С{Х). Предположим, что:
1) А — алгебра: 2) А отделяет точки мноо*сества X;
23*

354 Глава 10. Элементы анализа в метрическом пространстве
3) функция /, определяемая равенством f(x) = 1, х € X,
принадлежит А.
Тогда мноок.ество А всюду плотно в (С(Х),р).
\ Докажем, что замыкание А равно С(Х). В силу теоремы Вейер-
штрасса для функции g(t) = \Д, t £ [0,1] имеем Ve > 0 ЭР -
многочлен от t V< £ [0,1] : \\Д - P{t)\ < £• Поэтому для функции
/ £ А со значением ||/|| := тгис|/(а;)| > 0 получим
п/н mi/ii2 я- v ii/ii2 mi/ii2
и, следовательно, |/| 6 j4.
Поскольку для {а, 6} С Я справедливы очевидные равенства min(a, Ь)
= (о + Ъ — \а - Ь\)/2, тах(а, Ь) = (а + Ъ + \а - Ь|)/2, то для любых
{/, дУ С А на основании доказанного заключаем, что функции h(x) =
= min(/(a;),g(i)); H(x) = max{f(x),g(x)), x £ X, принадлежат Л.
Если{а:1у}сХ и х ф у, а {а,/3} С Я, то 3 / £ .4 : f[x) = а, /(у) =
/3. Действительно, по условию Эд 6 А : д(х) ф д{у). Можно положить
Пусть теперь / £ С(Х) и е > 0 заданы. Зафиксируем х £ X и для
г £ X положим а = f(x), /3 = /(г). Согласно доказанному, 3 hz £ А :
hx(x) = а = f(x), hz(z) = p = f(z), а поскольку {hz - f) £ С(Х), то
3r(z) >0Vy £ B(z,r(z)) : hz(y) < /(у) +е. Семейство {B{z,r(z)) \ z £
X} есть открытое покрытие компакта X и потому содержит конечное
п
подпокрытие Хс |J B(zk,r(zk)). Определим функцию дх следующим
fc=i _
образом дх(у) := min {hZlt(y)), у £ X. Заметим, что дх £ А, дх{х) =
= f{x) и что Vy £ X : дх(у) < /(у) + е.
Поскольку (дх-/) £ С(Х), то 3 s(a;) > 0 V у £ В(х, s(x)) : дх(у) >
f(y)-e. Семейство {B(x,s(x)) \ х £ X} есть открытое покрытие компак-
N
та X и потому содержит конечное подпокрытие (J B(xk,s(xk)) D X.
fc=i _
Пусть h(y) := max {дХк{у)), у Е X. Для функции h имеем h £ А и
V у £ X : /(у) - е < /i(y) < /(у) + е. Таким образом, 34 = С{Х). J
Рассмотрим теперь наиболее важные приложения теоремы Стоуна-
Вейерштрасса.
Примеры. 1. Пусть X — компактное множество в (Ят,р), А — мно-
множество всех многочленов от т переменных, рассматриваемых на X.
Множество А удовлетворяет всем условиям теоремы Стоуна-Вейершт-

10.5. Принцип сжимающих отображений 355
расса. Следовательно, непрерывная функция от m переменных на ком-
компакте является равномерным на этом компакте пределом последова-
последовательности многочленов от m переменных.
2. Пусть X = [0,27г], причём точки 0 и 2ir считаются равными. Для
{х,у} С [0,2тг] положим d(x,y) := min(|a; - у\, 2тг — |х — у\), {X,d)
— компактное метрическое пространство. Тогда справедливо равен-
равенство С(Х) = С([0,2гг]) П {/ | /@) = /Bir)}. Это множество можно
рассматривать как сужение на [0,2тг] множества непрерывных на R 2тг-
периодических функций. Множество
п
А = {р\р(х) = ao+Y. {akcosкх+Ъкsinkx), n е (ЛГи{0>,{ajtbk} С R},
fc=i
так называемых тригонометрических многочленов, удовле-
удовлетворяет всем условиям теоремы Стоуна-Вейерштрасса. Таким обра-
образом, непрерывная на R 2тг-периодическая функция есть равномерный
на R предел последовательности тригонометрических многочленов. Это
утверждение впервые было доказано Веиергитрассом и обычно на-
называется теоремой Вейерштрасса.
Упражнение 100. Проверить выполнение условий теоремы Стоуна-
Вейерштрасса в примерах 1 и 2.
Упражнение 101. Пусть {/„ | п > 1} С С([а,Ь]) — последова-
последовательность функций, разделяющая точки [а,Ь]. Доказать, что для любой
функции / £ С{[а,Ъ\) \/e>03m£N 3F£ C{Rm) Vi € [о,Ь] :
\f(x)-F(f1(x)J2(x),...,fm(x))\<e.
Упражнение 102. Пусть [а,Ь] С [0, +со) и А — семейство всех ко-
конечных линейных комбинаций функций fn{x) = х2п, х £ [а,Ъ], п > 0.
Применить теорему Стоуна-Вейерштрасса к множеству А в простран-
пространстве (С([о,Ь]),р).
Упражнение 103. Две функции f(x) = 1, д{х) = х, х € [а,Ъ],
разделяют точки [а, Ь]. Построить алгебру функций, включающую /ид.
10.5.5 Историческая справка
Метрические пространства возникли в результате развития и обобще-
обобщения на более общие ситуации идей Коши, Вейерштрасса, Гейне и Кан-
Кантора, предложенных для строгого определения действительных чисел,
сначала в частных случаях, а затем и в виде общей теории. Само по-
понятие метрического пространства и ряд других понятий современного
анализа (компактность, полнота, сепарабельность, производная Фре-
ше) ввёл в 1906 г. известный французский математик Морис Рене

356 Г л а в а /0. Элементы анализа в метрическом пространстве
Фреше A878 — 1973), который в общей ситуации отметил важность
критерия Коши. Значительный вклад в разработку теории метрических
пространств внёс Феликс Хаусдорф A868 — 1942), который анало-
аналогично Кантору построил пополнение произвольного метрического про-
пространства. Ф. Хаусдорф создал теорию топологических пространств,
получил основополагающие результаты в теории множеств, топологии,
функциональном анализе, теории чисел, теории непрерывных групп.
Дмсулио Асколи A843 — 1896) — итальянский математик. Ввёл
понятие равностепенной непрерывности и доказал теорему о компакт-
компактности множества непрерывных функций. Автор работ по теории функ-
функций и тригонометрическим рядам.
Чезаро Арцела A847 — 1912) — итальянский математик. Автор
работ по теории функций, в частности получил критерий непрерывности
предела сходящейся на отрезке последовательности непрерывных функ-
функций. Одновременно с Асколи получил условия компактности множества
непрерывных функций.
Стефан Ванах A892 — 1945) — выдающийся польский матема-
математик, один из создателей современного функционального анализа (бана-
(банахово пространство, банаховы алгебры, банахова решётка). Ряд резуль-
результатов Банаха стали классическими и входят в учебники.
Рудольф Липшиц A832 — 1903) — немецкий математик. Его
работы посвящены различным разделам анализа. В частности, получил
достаточные условия сходимости ряда Фурье, предложил достаточное
условие единственности решения дифференциального уравнения.
Эрик И вар Фредголъм A866 — 1927) — шведский математик,
основоположник теории интегральных уравнений. Он рассматривал ин-
интегральные уравнения как пределы систем линейных уравнений.
Теорема Стоуна-Вейерштрасса представляет собой элегантное и глу-
глубокое обобщение теоремы Вейерштрасса о равномерном на отрезке
приближении непрерывной функции многочленами. Эта теорема была
получена американским математиком Маршаллом Гарвеем Сто-
Стоуном A903 г. р.), автором работ по топологии и функциональному
анализу.

Глава 11
Функции нескольких
переменных
11.1 Производная по направлению.
Частные производные
11.1.1 Определения
В этой главе рассматриваются свойства действительных функций, опре-
определённых на подмножествах пространства Rm, m £ N. Поскольку в
дальнейшем будут систематически координаты точек из Rm, то мы бу-
будем придерживаться следующих обозначений. Элемент-вектор из Rm
будем обозначать символом х = {xi,X2,. ■ ■ ,хт), хк £ R, 1 < к <
т; 0 = @,0,..., 0). Таким образом, Rm — {х = (хг, х2,..., хт), хк £
^i 1 <• fc ^ гп-} Пространство Rm будем рассматривать как линей-
линейное с обычными (покоординатными) операциями сложения, а также
умножения на действительные числа На Rm будем рассматривать ев-
клидово расстояние р{х,у) = [Y, (zfc - Ук) ) , {$,$)} С Rm,
4 '
при этом (Rm,p) — полное метрическое пространство. Для вектора
/ оо \ 1/2
х = (xi,x2,. ■ ■ ,хт) £ Rm число ||£|| := ( ^ х\\ называется дли-
71=1
ной или нормой вектора х. Отметим следующие, получаемые из
определения, утверждения:
:)р(х,у) = \\х-у\\, {x,y}cRm;
2)Va£fl V£eHm: ||af|| = |a| • ||f||;
,-y).

358 Глава 11. Функции нескольких переменных
Эти утверждения постоянно используются в дальнейшем.
Пусть А С Ята и / : А —> Я. Функция / обычно называется дей-
действительной функцией от т переменных. Значение функ-
функции / в точке х — [xi,X2i ■ ■■ ,im) £ А обозначается следующим обра-
образом }{х) = f(xi, х2,..-, хт).
Фиксированный вектор a £ Rm, а ф 0, будем называть также на-
направлением, а множество {х \ х = х° + ta, t £ Я} — прямой
линией, проходящей через точку i° £ Rm в направлении а. Заметим,
что р(х° + ta, 5°) = \t\ ■ |\а\|. )H/
Упражнение 1. В пространстве R изобразить прямую, проходя-
проходящую через точку i° = B,1) в направлении а = A,3).
Определение 1. Пусть f : А -> R, х° — внутренняя
точка мноок-ества А и а — направление. Производной
функции в точке х° по направлению а называется предел
Ж») :-& "*' + '?-"*>,
если он существует. Удобно положить /i := 0.
Определение 2. Пусть А — открытое мноэ*сество в
Rm. Если для любого х £ А существует f's(x), то гово-
говорят что производная f's no направлению а определена на
мномсестве А, }'-: А -л R.
Далее предполагаем, что А — открытое множество.
Упражнение 2. Для функции f(xi,x2) = х\ + х\, B:1,2:2) € Я2,
точки (ii,2:^) = B,1) и направления а — A,1) вычислить }'й{х\,х%).
Упражнение 3. Пусть /B:1,2:2) = \/\х\ - х\\, {xi,x2) £ Я2 и
(х°,х^) = @,0). Определить те направления а, для которых существует
/i@,0) и вычислить её значение.
Замечание. Предположим, что выполнены условия определения
2. Поскольку i° — внутренняя точка множества А, то существует число
5 > 0 такое, что Vt, \т\ < 5 : (х° + та) £ А. Определим функцию
(р : (—5,5) -> Я следующим образом
Ф) = Д*° + та) = /(г:? + таи х° + та2,..., х°т + тат), т £ (-S, 6),
где х° = (i?, *:§,..., z£i), a = {alta2,... ,am). Для т £ (-6,6) имеем
= +
t-»o t
Таким образом,
A)

11.1. Производная по направлению. Частные производные 359
в частности1 <р'@) — /-(z0).)Формула A) часто используется.
11.1.2 Свойства производных по направлению.
Частные производные.
Теорема 1. Пусть f : А -> R, g : А -> R, х 6 A, a —
направление. Предположим, что существуют производ-
производные fg[x) и g's[x). Тогда существуют следующие производ-
производные по направлению а и справедливы равенства:
1) Vс 6 R : (cf)L(x) = cfL(x); 2) (f + g)'s(x) = fL(x) + &(£);
3) (fg)'d(x) = }'E{x)g{x) + f(x)g'5(x); J^) если дополнительно
[ Перейти к функции <р, введенной в замечании, и использовать свойства
производный действительных функций. J
Теорема 2. (О среднем значении). Предположим,
что для некоторых t > 0, точки х и направления а :
V т, 0 < т < t : (х + та) G А и существует f~(x + та).
Тогда 36 6@,1): }{х + та) - f(x) = fl{x + 6тЗ)г.
\ Рассмотрим функцию (р{т) — }{х + та), т G [0,<], для которой,
согласно предположению, существует (р'(т) = f'~{x + та), т € [0,t].
Применим теорему Лагранжа к функции ip на отрезке [0,t]. Получим
36 6@,1) : ip{t)-(p{0) = ip46t)t. J
Определение 3. Частной производной по k-й пере-
переменной называется производная f~k no направлению ёк,
где ёк := @,0,..., 1, 0, ...,0), 1 < к < т. Частная производ-
к
пая функции f в точке х по k-й переменной обозначается
одним, из следующих символов: , /fc(z), Dkf{x).
охк
Таким образом, для х — [х\,Х2,... ,хт) имеем
? (х) = lim ttXl>X2> ■■■>xk+t,---,xm)- f{x!,x2, ...,xk,...,xm)
Из теоремы 1 получаем следующие правила вычисления частных
в точке х.

360 Глава II. Функции нескольких переменных
11.1.3 Основные теоремы о производных
по направлению
ТеоремаЗ. Пусть точка х и направление а фиксиро-
фиксированы. Если существует f's{x), то для любого с £ R суще-
существует f'ca{x) и
fcM = cfs№- B)
f Доказательство следует из определения. J
Теорема 4. Пусть х е А, а иЪ — два направления.
Предположим, что: 1) 3 6 > О Vz £ B(x,S) существует
/~(z); 2) f's непрерывна в точке х; 3) существует fg[x).
Тогда существует производная по направлению a-bb в
точке х и f's+i(x) = f's(x) + fi(x).
[ Используя условие 1) и теорему 2, имеем f(x + t(a+ b)) — f(x) =
= f{(x + tb) + to)) - f[£+t$) + f[x+tS) - f{x) = f's((x + tS) + 9ta)t +
+f(x + tb) — f(x), в £ @,1). Разделив полученное равенство на t, с
учётом условий 2) и 3) перейти к пределу при t —> 0. J
Следствие 1. Пусть А — открытое множество, х° £
А, /: A—t R и V к, 1 < k < m, Vz £ А существует производ-
производная Dkf{x) и функция Dkf непрерывна в точке х°.
Тогда для любого направления а существует f's(x°) и
/s(*°)=E £7TLiafc, S=(a1,a2,...,am). C)
fc=l ОХк
Определение 4' Производной функции f в точке х на-
называется вектор — градиент функции в точке х, равный
fdf(x) df(x) df(x)\ , „ Л
-— , — -т-^— , обозначаемый одним, из символов
\ дх1 дх2 дхт )
f(x), grad/E), V/(f).
Для двух векторов а и b из Rm их скалярное произведение (а, о), в
силу неравенства Кош и, удовлетворяет неравенству \(а, о)\ < ||а|| • ||о||.
Если ||а|| • ||6|| ф 0, то величина !—=г- называется косинусом
угла между векторами а и b и обозначается символом cos(a6). Фор-
Формулу C) можно записать в виде }'d{x) = ||grad/(:r)|| • ||a||cos(agrad/(:r)).
Замечание. Пусть точка х фиксирована. Рассмотрим различные
направления а единичной длины, т. е. такие, что ||а|| = 1. Тогда f's(x) =
||grad/B)|| cos(agrad/(£)). Поэтому направление градиента функции /

11,2. Дифференцируемые функции 361
в точке х есть направление, для которого производная по направлению
в точке х максимальна.
т.
Упражнение 4- Для функций a) f{x) — J2 ak^k\ b) g(x) =
т
,■; х = (хх,х2,...,хт), {ak, akj} С Я, найти /', д1.
Упражнение 5. Доказать формулы: 1) V(c/) = cV/, с G R;
5) = V/ + V5; 3) V(/5) = gS7f + fS7g;
предполагая существование производных в правых частях равенств.
Упражнение 6. Пусть f(xx,x2) := х\/х2, х2 ф 0, f(xi,0) := 0;
B1,12) 6 Я2- Найти /'@,0). Проверить, что функция / не является
непрерывной в точке @,0).
Упражнение 7. Доказать, что: 1) а -» 0 <=> \\a\\ -> 0; и
° ° \\х-Х°\\->0.
11.2 Дифференцируемые функции
11.2.1 Понятие дифференцируемости
Определение 1. Функция L : Rm —> R называется ли-
линейной, если: 1) Va e R Vх е Rm : L{ax) = aL(x); 2)
V{x,y}cRm: L{x + y) = L{x) + L{y).
Легко проверить, что для линейной функции L существуют числа
m
Li,L2l. ..,Lm из R такие, что Vx = (xltx2,.. .,^m) : L(x) = J2 Lkxk.
k=X
Упраж.нение 8. Определить все линейные функции L такие, что
L(x) = о(\\х\\), х-+б.
Определение 2. Пусть А С Rm, x — 'внутренняя точ-
точка множ.ества А и f : А -» R. Функция f называется
дифференцируемой в точке, если существует линейная
т
функция L(a) = Y^ Lkak, a = (ai,a2,... ,ат) £ Rm\ {Lk} C R,
fc=i
такая, что
f(x + a)-f(x)-L{a) = o(\\a\\), ||3||-> 0, A)

362 Глава II. Функции нескольких переменных
или, что равносильно A), такал, что выполняется ра-
,. f(x + a)-f(x)-L(a)
венство lim — ,',, — = 0.
\\а
Функция L называется дифференциалом (полным
дифференциалом) функции f в точке х и обозначает-
т
сл символом, df(x) = df(x;a) = L(a), или df(x) = J2 Lkdxk с
заменой ak на dxk, 1 < fc < m.
Дифференциал определяется единственным образом, см. упр. 8.
Замечание. Функция L (или определяющие её числа Lj, Ьз,...,
Ьт) зависит, вообще говоря, от точки х.
Теорема 5. Пусть f — дифференцируемая в точке х
функция. Тогда для любого направления а = (ai,a2,... ,am)
существует f'Jx), в частности существуют , 1 <
дхк
df(x)
к < т. При этом, Vfc, 1 < fc < тп : Ьк = , а производная
дхк
т dflx)
по направлению f's{x) — L{a) = J2 afc.
дх
\ Пусть направление a ф 0 задано. Заметим, что L(ra) = rL(a) для
т € R, и что та -л 0, если т —¥ 0. Поскольку / дифференцируема в
,. f[x + Ta)-f{x)-TL{a) n f
точке х, то hm р———г ^— = 0. Отсюда следует суще-
т^О |т|-||а|| /
ствование f~(x) и равенство f~{x) = L(a). Положив a = ек, получим
Теорема 6. Пусть f — дифференцируемая в точке х°
функция. Тогда f непрерывна в точке х°.
[Действительно, f{x) - /E°) = L(x - х°) + о(\\х - 2°||), х - х° -> 0.
Кроме того, согласно неравенству Коши,
/ т ч 1/2
\L(x- S°)| < ||L|| • \\L(x - а°)||, где ||L|| := ( Ц L\) .
■**Ш*?\ к=х
, Поэтому \f(x)-f(f)\ <\\L\\-\\L(x-x*)\\+o(\\x-x°\\),x-xO ->0.
Следовательно, f(x) —► f{x°), х -л х°. J
к
Упражнение 9. Пусть /(iiva;2) = ^/jxia32|, (г1,г2) € Я2. Показать,
; что / £ C(R2). Найти /^@,0) и /jl0!0)- Доказать, что / не является
дифференцируемой в точке @,0).

it.2. Дифференцируемые функции 363
/ m \a/2
Упражнение 10. Пусть /(х) = I £ x\) , х = (х1,х2,...,хт) £
vfc=i '
Rm, a > 0. При каких а функция / дифференцируема в точке 0?
11.2.2 Достаточное условие дифференцируемое™
Пусть / : А —¥ R, и х — фиксированная точка из А.
Теорема 7. Предположим, что: 1) Зе > 0 Vz G В(х,е)
Vfc, 1 < к < т, существует —^■; 2) Vfc, 1 < к < тп,: ^:^
• непрерывна в точке х.
Тогда функция f дифференцируема в точке х.
f Для любого а£ Rm, для которого ||а|| < е, имеем ,, ^^^ ^.^,
- . ; ^Г' . B)
X2 +а2.---.:ст + ат) -/(xi,x2 + а2)..., zm + ат))+
2,... ,хт + ат) - f{xi,x2,x3 + а3 ..., хт + ат)) + ...
,- •., xTO_i, хто + ат) - f{xi,x2,..., хт)),
х = (х^хг,... ,хт), а = (ai,a2,... ,ат).
Применяя к каждой разности в правой части B) теорему 2 получим
f(x + a) - f(x) - L{a) = £ 5kak, L(a) = £ -^ ofcl
fc=i fc=i
+afc+1(...)xm4-am),^G@,l), 1 < fc < m. .. ^'
Заметим теперь, что ||u^|| < ||a||/Следовательно, <5j^—> 0, a —>
^i 1 < fc < тп. Таким образом, I qI\,0 -^ ^?»j \
/ m v 1/2
EП ->0,S->0. J
Следстеие 2. Пусть А — открытое множ.ество, f :
A-> R. Предположим, что Vfc, 1 < fc < m,: -— £ C(A).
axfc
Тогда: a) f дифференцируема в каж.дой точке множ.е-
ства А, Ъ) f € С [А).
Упражнение 11. Пусть функция / : В{й, г) -л R удовлетворяет
условиям: 1) Vz* € В(й,г) f дифференцируема в точке z; 2) Зс €
R Vz G В(й,г) : ||V/(f)|| < с. Тогда имеем V{zi,z2} С В(й,г) ;
|/(^i) — /(^г)| <-c||zi — z2||. Доказать это утверждение.

364 Глава П. Функции нескольких переменных
Упражнение 12. Пусть функция / : В(й,г) —> R удовлетворяет
условиям: 1) Vz* £ В(й,г) f дифференцируема в точке z; 2) Vz* €
В{й,г) Vfc, I < k < т : 4~ = 0. Доказать, что 3 с € Я V/ €
ox k
В{ч,г) : }{z)=c.
Определение класса функций СХ(А). Пусть А — открытое
множество. Рассматриваются функции вида / : А —► R.
feC'iA) <=> Vfc, l<fc<m,: |^ € С {А).
Ох к
Заметим, что С1 (А) С С(А).
11.2.3 Свойства дифференцируемых функций
Теорема 8. Пусть f : А -» R, g : А -» Я — функ-
функции, дифференцируемые в точке х £ А. Тогда функции
cf, eg R; f + g; fg и f/g, если дополнительно g(x) ^0, диф-
дифференцируемы в точке х.
f Воспользоваться соотношением A) для функций / и g. J
Теорема 9. Пусть функция f : А -» R дифференци-
дифференцируема в точке х° — {х\,х\,... ,х%^) £ А. Предположим, что
функция g = (si,fl2,... ,gm) : (t0 - e,t0 + е) -> А такова, что
Vfc, 1 < fc < т, : gk{to) = x°k, существует g'k(t0), t0 £ R, e > 0
фиксировано.
Тогда сло&сная функция h(t) := f(gi(t),... ,gm(t)), t G (to -
£,<о+£) дифференцируема в точке to, причём.
fc=l OXk
(" Поскольку / дифференцируема в точке х°, то
fc=l
Отсюда, положив г = g(t0 + At), x° — g(to), At ф 0, и разделив на Д<,
h(to + At) - ) (( W)
имеем такое равенство
Д* At
„ vj ^ j tf)c^o -r At)) - gkjtp)) o{}\x - x°\\)
= 2-, —д л ^ л ' Заметим,
f fc=1- -or 4k V^ <>£6&/ «'(-/.^
': ' Производные и дифференциалы, введенные ранее, называются со-
соответственно производными и диффереыциапдми_тгврвого порядке
V I'*-veil"

П.З. Производные и дифференциалы старших порядков 365
Упражнение 13. Пусть А С Rm — открытое множество, причём
8f d m df
-^- eC(A), l<k<m. Тогда — f[x,x,...,x) = £ t^-(i,i i).
CcCfc ax ic—i OXk
11.3 Производные и дифференциалы старших
порядков
11.3.1 Производные второго порядка
Пусть А — открытое множество в (Rm,p), а а и О — фиксированные
направления. Предположим, что для любого х € А существует f'^{x).
Тогда f'~: А-> R.
Определение 1. Производная функции f's no направле-
направлению b в точке х £ А, если она существует, называется
производной второго порядка функции в точке х по на-
направлениям, а, Ь.
Обозначение: (/^(z) = f'^(x).
Определение 2. Частными производными второго
порядка функции f в точке х называются производные
2f!x)
Обозначения: я я ' , f"k(x)-
OXjОХк
Пример. Пусть А = R2J{xux2) = ^1^ ^ , (xi,x2) Ф @,0),
п* ^ г, dfio,o) a2/(o,o)
/@,0) = 0. Производные второго порядка ——^—, -z—т— суще-
дх\ дх2 дх2 дхх
ствуют, но различны.
Теорема 10. Предположим, что /1'- G С (A), /i'_ € С (А).
Тогда ДО = /&(*), г е Л.
[ Пусть х € А — фиксированная точка. При всех достаточно малых по
модулю значений s и t имеем (х + so) € A, (x + tb) £ A, (x + sa +
tb) € А. Положим g(x) := f(x + sa) - f(x), h(x) := f{x + tb) - f(x).
Применяя дважды теорему 2, получим g(x + tb) — д(х) = tgU S
£ £ S 0
Аналогично, h(i + so) — h(x) = stf"-(x + ri2tb + riisa), 0 < т?ь т?2 < 1.
Заметим, что д(х + tb) — д(х) = h(x + sa) — h(x). Таким образом,
fy(x + e2sa + 6itb) — f"-[x + rfctS+r)isa). Отсюда, учитывая условия
теоремы, получим f'lAx) = f~~(x). J

366 Глава П. Функции нескольких переменных
Определение 3. Пусть А — открытое мноэ+сество.
f € С2(А) <=> Vj, k, I <j,k < т существует производ-
д2} д2}
нал на А и G С (А).
OXjOXk OXjOXk
Заметим, что С2(А) С Сг[А) С С(А).
Упражнение 14- Теорема Шварца. Проверить, что для функ-
d2f д2 f
ции / € С2 (А) справедливо равенство ——-— = ——-— на А,
OXj OXk OXk OXj
l<j,k<m.
Определение 4- Производная второго порядка функ-
I д2 fix) \m
ции f в точке х есть матрица fix) := (-—~- )
\OXj OXk ' j,k=l
Пусть / 6 С2(А) и а = (ау,...,ат), Ь = (bi,...,bm) — два направ-
2
(
Я2 f(zt\
ления. Тогда /l'-(f) = f'J (x) = Е ТТ» aibk> a матрица ?'&
j,k=l OXj OX^
m d2fix)
симметрична. В частности, f~s(x) = ^ ——^—ctjO-k-
j,k=l OXj OXk
Определение 5. Для функции f € С2(А) дифференци-
дифференциал второго порядка в точке х называется такая форма
т d2f(x)
d2f(x) := У) -—-— a,ja,k, a € Rm, или после замены а, на
i,fc=i oxjdxk
f(
- форма*f(£):= E f1^-dxjdxk.
j,k=i oxjdxk
Следует также иметь в виду, что d2f(x) = d(f's(x)) = /i'-(
m m
Упражнение 15. Для функции f(x) =
fc=l j,k=l
x = (xu...,xm) £Rm, {co,ck,Cjk}cR, найти/'(£), /"(*)■
11.3.2 Производные порядка п
Пусть А — открытое множество в (Rm,p), а аA),аB),... ,а(тг) — фик-
фиксированные направления. Предположим, что для любого х € А опреде-
определена производная порядка п — 1 по направлениям аA),аB),... ,а(п-1) :
JB.(l)aB),..S(n-l)\X>-
Производной порядка п функции / по направлениям аA), аB),
... , а{п) в точке х € А называется производная
/ _ч Лп) /-»ч
X) -'■ Ja(l)aB)...5(n){X)-

П.З. Производные и дифференциалы старших порядков 367
Частными производными порядка п функции / в точке х
называются производные
* f(n) ал -
2) . . . Эхк{п) ~"
1 <fc(l),fcB),...,fc(n) <m.
1 Производной порядка п функции / в точке х Е А называется
/ дп}(х) \т
Пгмерная матрица f^n\x) := (- )
\dxk^)dxk^2) ■ ■ ■ ОХЦП) /fc(l)fcB),...,fc(n)=l
Класс функций Сп(А) определяется следующим образом
Vl<fc(l),fcB),...)fc(n)<m: /g)fcB),..fc(n) G C(A).
Из теоремы 10 следует, что для функции / G Cn(i4) значение про-
. dnf(x)
изводнои не зависит от порядка хци,.. .,xkin\.
» ОХЦ1)С)ХЦ2) ОХЦ)
Отметим включения Сп(А) С С"-1 (А) С ... С СХ{А) С С {А).
Замечания. 1. Пусть / G Сп(А) и а = (oi,...,am) — некоторое
направление. Тогда для г G А имеем
/й'5(г) = ЬA,,ц£,Ь(»,в1 дхН1)8хН2)...8хНп)
2. Для производной -—-— часто употребляется обозначение —j .
ОХ\ ОХ\ ОХ л
Аналогично, в упрощённом виде используются обозначения старших
производных.
3. Введём следующее обозначение
/<»>(£)*» := £ д //(£) д afcA)afcC)... afc(n).A)
fc(i),fcB) fc(n)=i 9ifc(i)aa;jB)9a;fc()
11.3.3 Формула Тейлора
Теорема 11. Предположим, что функция f G Сп(А).
Пусть точка х £ А и направление а £ Rm таковы,, что
Vt € [0,1] : (x + ta) eA.
Тогда существует число в G @,1) такое, что
+ i /(»>(£+ 9а)ап, B)
Замечание. Внешне формула B) напоминает формулу Тейлора
для функции одной переменной. Следует, однако, иметь в виду, что
каждое слагаемое суммы B) является суммой, см. обозначение A).
24 — 4-1168

368 Глава П. Функции нескольких переменных
\ Для функции tp(t) = f(x + ta), t € [0,1], имеем
V{k){t) = fik}.s(*+tZ), *G [0,1], l<fc<m. C)
Запишем фармулу Тейлора для функции <р относительно точки t — 0 с
остаточным мленом в форме Лагранжа
4,A) = т + <р'(о) + \^"(о) +... + ^4ijT^(n}(o) + ±<р(п)№, D)
где 9 Е @,1). Формула B) получается теперь подстановкой в равенство
D) значений производных из C). J
Замечания. 1. Из неравенства Коши следует такая полезная оцен-
оценка — f(s'(x)as < L(s)||a||s с некоторым числом L(s), зависящим от
производной f(shx). В частности, — f(shx)as = 0(||a||s), a -» 0.
s!
2. При условиях теоремы с учётом неравенства Коши из B) получаем
/(£+ о) = }{х) + f(x)a + \ f(x)a2 + • • • + ^ /(n)(x)a" + E)
+гвC), rn(a) = O(||a||"),a-4 0.
Упрадаснекие 15. Доказать, что для функции / G Cs(i4)
VI < fc(l), fcB),... ,k(s) < m :
дхц1)дхц2) ■ ■ ■
Упражнение 17. Предположим дополнительно к условиям теоре-
теоремы 11, что выполняется условие 3С G R VI < fc(l), fcB),... ,fc(s) <
т Vz€i4: |/jm5B) 5(s)(г)| < С. Доказать следующее неравенство
Для открытого множества А определим семейство функций С°°(А),
оо
положив С°°(А) := ("") С (А). Таким образом, справедливо утвержде-
fc=i
ние /€С°°(Л) <!=> VfcGiV: / G Ск[А).
Пусть / G С°°(А), х и а удовлетворяют условию теоремы 11 и
Тогда справедливо следующее разложение в ряд Тейлора
f(x + a)= g 1/(»)(*)*», /(°Ь=/.
п=0 п!
Для доказательства перейти к пределу в E), учтя оценки упр. 17.

//.3. Производные и дифференциалы старших порядков 369
Упражнение 18. Пусть / G Cl{R2). Доказать формулу
/(хьх2) = /@,0) + /(/i(ixi,fx2)xi + /2(ia;i1fx2)x2)cff.
о
11.3.4 Экстремум
Пусть А С Rm, } : А-> R.
Определение 6. Если существует точка х° € А та-
такая, что Vx € А : f(x) < /(x°), то функция f имеет в точ-
точке х° абсолютный максимум. Значение /(х°) = тах/(х)
называется наибольшим значением функции f на мно-
ж.естве А.
Определения абсолютного минимума и наименьшего
значения аналогичны.
Определение 7. Функция f имеет в точке х° € А ло-
локальный максимум, если существует число г > 0 такое,
что: 1) В{х°,г)сА; 2) Vx € B{x°,r) : f{x*)<f{x°).
Локальный максимум называется строгим, если су-
существует число г > 0 такое, что: 1) В(х°,г) С А; 2)
Vx€(B(x*V)\{x0}): Дх)</(х°).
Определения локального минимума и строгого локаль-
локального минимума аналогичны. Точки локального максимума и локаль-
локального минимума называются точками локального экстремума.
Теорема 12. (Необходимое условие локального экс-
экстремума). Предположим, что: 1) х° есть точка ло-
локального экстремума функции /; 2) существует f'{x°)
(а потому существуют все частные производные пер-
первого порядка функции f в точке х°). Тогда /'(х°) = 0.
[ Предположим для определённости, что х° — точка локального мак-
максимума. Тогда Зг > 0 : В(х°,г) С А и Vx € В(х°,г) : /(х) < /(х°).
Пусть fc, 1 < к < т, — фиксировано. Функция
обладает следующими свойствами: gk{t) < 5fc@), t € (—'",'"); суще-
существует 5^@) = f'k(x°). Таким образом, функция д^ имеет локальный
максимум в точке t = 0 и существует 5JU0). Тогда д^{0) = 0. Следова-
Следовательно, /£(х°) = 0. J
Определение 8. Пусть х° — внутренняя точка мно-
множества А. Если /'(х°) = 0, то точка х° называется кри-
критической.
24»

Ч
370 Глава 11. Функции нескольких переменных
Замечания. 1. Критическая точка не обязательно — точка экстре-
экстремума. Например, при т — 2 функция f[xi,x2) = xix2, (zbz2) € Я2, в
точке х° = @,0) не имеет экстремума, но Л@,0) = /^@,0) = 0.
2. Точки, в которых /' не существует, могут быть точками экстре-
экстремума. Например, при т — 2 точка @,0) есть точка абсолютного мини-
минимума каждой из следующих функций f{xi,x2) = \ху\ + \х2\, g{xi,x2) =
2
11.3.5 Достаточное условие строгого локального
экстремума
Определение 9. Пусть D = {djk)^k-i, djk = dkj 1 < j,к < го,
— симметрическая матрица размера т х т с действи-
действительными элементами. Матрица D называется поло-
положительно определённой, если Va € Rm, а ф 0 : a1 Da > О
(произведение в определении — произведение матриц, а
— вектор-столбец, а* — вектор-строка). Матрица D
называется отрицательно определённой, если -D есть
полож.ительно определённая матрица. Матрица D на-
называется неопределённой, если За £ Rm : a1 Da < 0 и
ЗЬе Rm :Ь*£>Ь>0.
Обратим внимание на то, что в обозначениях п. 11.3.2 a*Da = Da2.
Предполагается известным критерий Сильвестра. Положим
п t\ ^ = detR A)
Критерий Сильвестра. Матрица D положительно
определена тогда и только тогда, когда dk > 0, 1 < к < т.
Лемма 1. Пусть А — открытое множество и функции
{djk | 1 < j,k < т} С С(А); D(x) = (djk(x))™k=1, x € А; х° € А.
Предположим., что матрица D(x°) положительно опре-
определена. Тогда Зг > 0 : В(х°,г) с А и Vх € В(х°,г) : матрица
D(x) положительно определена.
I Функции dk > 0, 1 < к < т, определённые в формуле A), принадле-
принадлежат классу С[А). Согласно критерию Сильвестра, D(x°) положительно
определена тогда и только тогда, когда dk(x °) > 0, 1 < к < т. Поэтому
Vfc, l<fc<m 3rk >0
т
Положим г := min(ri,r2,...,rm) > 0; B[x°,r) = f\ B{x°,rk). То-
гда Vfc, I < It < m Vi 6 B(x°,r) : dk(x) > 0. Следовательно, для

11.3. Производные и дифференциалы старших порядков 37/
Vx £ B(x°,r) матрица D(x) положительно определена в силу критерия
Сильвестра. J
Теорема 13. Пусть А — открытое множество иг°6
А. Предположим,, что f € С2(А), и что х° — критическая
точка f, т. е., что /'(х °) = A Тогда:
fd2 fix0) \m
a) если матрица f"(x°) := (————- 1 положительно
\ axj oxk I j,k-i
определена, то точка х° — точка строгого локального
минимума;
b) если матрица /"(а?0) отрицательно определена, то
точка х° — точка строгого локального максимума;
c) если матрица /"(х°) является неоределённой, то точ-
точка х° не является точкой локального экстремума.
\ а) Пусть В(х°,д) — такой шар, что VaT £ В(х°,8) матрица }"{х)
положительно определена. Такой шар существует согласно лемме 1.
Для каждого х € В(х°,8) рассмотрим формулу Тейлора, положив
п = 2, а = х - х° : /(£) = f(x°) + \ f"(x° + в(х - £°))(af- S°)\ в =
в(аТ) € @,1). Поскольку точка (а:0 + 9{х - х°)) 6 В{х°,5), то матри-
матрица f"(x°) + 9(х — х0)) положительно определена и, следовательно,
V $ & В{х\6), х ф х° : f(x)>f(x°).
b) Применить доказанное утверждение а) к функции —/,
c) Заметим, что в этом случае для любого шара 13@,5)
За€В{б,6) : f"{x°)a2 > 0 и 3b€B@,5): /"(f°)Ь2 < 0. J
Приведём формулировку теоремы 13 для частного случая т = 2.
Следствие 3. Ят/стпъ Л — открытое множ.ество в R2
и х° & А. Предположим, что f € £?2(j4)i и что частные
производные f'x{x°) = 0, /г(г°) = 0. Тогда:
a) если f^(x°) > 0 и Г^°)Ш^°) - (/i'2(*°))a> 0, то точка
х° — точка строгого локалъкого минимума;
b) если /^(x0) < 0 и /^(г0)/^!0) - (Л'2(х0)J> 0, то точка
х° — точка строгого локального максимума;
c) если Гп{х°)М2(х°) - (Я'2(:е0)) < 0, то точка х° не явля-
является точкой локального экстремума.
Упражнение 19. Найти точки локального экстремума следующей
функции /(хьх2) = 2х\ - х2(х2 - IJ, (ii.ij) € Я2.

372 Глава 11. Функции нескольких переменных
Упражнение 20. Найти наименьшее и наибольшее на Я значения
функции f(xu х2) = fa + х2)е-х1-х2, (хьх2) € R2.
Упражнение 21. Пусть {аA),...,а(п)} С Rm. Найти наименьшее
на Rm значение функции /(х) = £ ||£-3(fc)||2, x 6 Ят.
fc=i
Упражнение 22. Пусть А и В — точки на графиках функций у = х2
и у — х — 6, х € Я, соответственно Для каких Л и В расстояние между
А \л В будет наименьшим?
Упражнение 23. Доказать что сумма, произведение и суперпози-
суперпозиция функций из класса Сп(А) принадлежит классу Сп(А).
11.3.6 Условия выпуклости функции
Определение 10. Множество Ac Rm называется вы-
выпуклым, если V{x,y} С А : {ах + A - а)у \ а € [0,1]} С А.
Множество 0 выпукло.
Замечание. Множество {ах + A - а)у \ а € [0,1]} есть отрезок
прямой, соединяющий точки х, у. Поэтому множество А выпукло, если
для произвольных точек х, у из Rm соединяющий их отрезок также
лежит в А.
Упражнение 24' Пусть {ai,a2l... ,am;b} С Я. Доказать, что мно-
множество {х € Ят | aixi + a2x2 + ... + атхт < b} выпукло.
Упражнение 25. Доказать, что шары В(х,г), В(х,г), х € Ят, г >
0, — выпуклые множества.
Упраоюнение 26. Доказать, что пересечение произвольного семей-
семейства выпуклых множеств есть выпуклое множество.
Упражнение 27. Пусть А — выпуклое множество, х £ Ят, и по-
положим х + А := {х + у | у € .А}. Доказать, что х + А — выпуклое
множество.
Упражнение 28. Пусть А = {х \ \\x\\ < 1}. Доказать, что для каж-
каждого ус |Jy|| = 1 полупространство Ну := {х | хьу < 1} содержит
множество Л и A— f] Hy.
v.llvINi
Упражнение 29. Пусть А — выпуклое множество, {xi,...,£n} С
A, {ai,...,an}C [0,1], ai + ...+an = 1 Доказать, что £
4=1

П.З. Производные и дифференциалы старших порядков 373
Замечание. Таким образом, множество А выпукло тогда и только
тогда,когда Vn € N V{xlt. ■ ■ ,Sn} С A V{ab... ,an} С [0,1], "l +
а„ = 1 : (J2 akxk)e A.
Упражнение 30. Для выпуклого множества А пусть А0 — множе-
множество всех его внутренних точек и А — замыкание множества А. Дока-
Доказать, что множества А° и А выпуклы.
Упражнение 31. Пусть А — замкнутое подмножество Я, для ко-
которого множества А и Rm \ А выпуклы. Доказать, что А есть полупро-
полупространство.
Определение 11. Пусть А — выпуклое и открытое
множество в Rm. Функция f : А -> Я называется выпук-
выпуклой вниз на множестве А, если выполняется условие
У{£,у}сЛ Va€[0,l]: f{ax + A - а)у) < af{x) + A - a)f{y).
Функция f : А -> Я называется строго выпуклой вниз
на м,нож.естве А, если выполняется следующее условие
У{х,у}сД£#у Va 6@,1): f(ax + (l- a)y) < af(x) + A -a)f(y).
Определение выпуклой вверх и строго выпуклой вверх
функций аналогично (с заменой знаков <, < на >, > соответствен-
соответственно). Функция, удовлетворяющая одному из приведенных определений,
называется выпуклой.
Лемма 2. Функция f выпукла (строго выпукла) вниз
на множестве А тогда и только тогда, когда для произ-
произвольных {а,х} С А, аф х функция (p(t) := f(a+t(x — a))}t £ [0,1],
выпукла (строго выпукла) вниз на отрезке [0,1].
[ Необходимость. Пусть / выпукла вниз на А. Для значений {ii,^} С
[0,1] и a € [0,1] имеем следующее неравенство ip(at\ + A - a)t2) =
= f(a+(ah+(l-a)t2){x-a)) = /(a(a+i1(x-a)) + (l-a)(a+i2(x-a))) <
< af{a + ty{x - a)) + A - a)f{a + t2{x - a)) = cupfa) + A - a)<p{t3).
Достаточность. Рассмотрим произвольные {х,у} С А и a £ [0,1].
Предположим, что функция ip(t) := f(x+t(y — х)), t € [0,1] выпукла
вниз на [0,1]. Тогда (р{1-а) = <р{а-0 + {1-а) ■ 1) < а<^@) + A-а)<^A).
Отсюда имеем f[ax + A - а)у) < af{x) + A - a)f{y). J
Теорема 14. Пусть А — открытое выпуклое м.ноже-
ство, функция / G С2(А) и производная второго порядка
/" положительно определена на множ.естве А.
Тогда функция f строго выпукла вниз на А.
\ По лемме достаточно проверить, что для любых {а, х} С А, а ф х
функция ip(t) := f(S+t(x-a)), t € [0,1], строго выпукла вниз на [0,1].
Однако, tp"{t) = f"(a + t{x-a))(x-aJ и потому <p"(t) > 0, t € [0,1].J

374 Глава 11. Функции нескольких переменных
Замечание. Пример функции f(xi,x2) = х\ + х\, {xi,x2) € R2,
показывает, что обратное к теореме 14 утверждение неверно (имеет
место только утверждение, что /" неотрицательна на А).
Упражнение 32. Пусть А ф 0 — выпуклое множество и положим
f(x) := inf ||х-у||, х £ Rm. Доказать, что функция / выпукла вниз на
уел
множестве Rm.
Упражнение 33- Доказать, что строго выпуклая вниз на выпуклом
открытом множестве функция не может иметь более одного локального
экстремума.
Упражнение 34- Пусть / — выпуклая вниз на А функция. Доказать,
что для каждого с € Я множество {х € А | /(£) < с} — выпукло и
открыто.
Упражнение 35*. Функция / выпукла на открытом множестве А.
Доказать, что / £ С(А).
Упражнение 36. Пусть функции fug выпуклы вниз на А и с > 0.
Доказать, что функции с/; / + 3! max(/(^)i3(^))> x & А выпуклы
вниз на А.
Упражнение 37. Пусть А — открытое и выпуклое множество и
/ € С2{А). Доказать, что функция / выпукла вниз на множестве А
тогда и только тогда, когда /" неотрицательно определена на А.
11.3.7 Историческая справка
Джеймс Джозеф Сильвестр A814 — 1897) — английский ма-
математик. Наиболее важные его работы посвящены алгебре и теории
чисел. Он ввёл ряд общепринятых терминов алгебры: "инвариант", "дис-
криминант" и др.

Глава 12
Векторные функции от
нескольких переменных
12.1 Непрерывные отображения
12.1.1 Линейные отображения
В настоящей главе рассматривается ряд основных понятий дифферен-
дифференциального исчисления функций (отображений, преобразований) одного
конечномерного пространства в другое. Пусть тип — фиксированные
натуральные числа. Пространства Ят и Я™ будем рассматривать как
линейные метрические пространства с евклидовым расстоянием, а эле-
элементы этих пространств — как векторы-столбцы. Евклидово расстояние
в пространствах Rm и Я™ обозначаются рт и рп соответственно. Умно-
Умножение матриц на число и их сложение понимаются обычным образом.
Пусть А С Я и отображение / : А -> Rn. Задание / означа-
означает, что для любого х = (xi, X2, ■ ■ ■, ХтУ € А поставлен в соответствие
вектор /(£) = (/i(x),/2(x),... ,/„(£))* € Я". Таким образом, задание
/ на А равносильно заданию упорядоченного набора п действительных
функций fx, f2,..., /„ на А, где Д — fc-я компонента отображения /.
Примеры. 1. Постоянное отображение. Пусть А — Rm и у0 €
Я" — фиксированный элемент. Положим /(£) = у*0, х € Ят, / —
постоянное ч>тображение.
2. Линейное отображение. Отображение /: Ят -» Яп на-
называется линейным, если: 1)Vc£ R Vi 6 Ят : /(сх) = с/(х);
2) V {и, V) С Ят : /(и + v) = /(и) + />).
Легко проверить (доказательство проводится в курсе линейной ал-
375

376 Глава 12. Векторные функции от нескольких переменных
гебры), что отображение / линейно тогда и только тогда, когда су-
существует матрица D = (dj fc)j=i£Li размера m x n с действительными
элементами такая, что Дх) = Dx, х € Нт, т. е. когда для любого
х = (xi,X2i • • • ,im)' € Rm, j-я компонента fj отображения / задаётся
го
равенством Д(х) = £ djkxk.
Пусть /: Rm -4 R" и 5 : Rn -* Rk — линейные отображения с
матрицами D(f) и D(g) соответственно. Тогда их суперпозиция h(x) :—
g(f(x)), x € Rm, есть линейное отображение со следующей матрицей
D(h) = D(g)D(f).
В том случае, когда / : Rm —> Rm — линейное отображение с мат-
матрицей D с det D ф 0, то отображение / взаимно однозначно и обратное
отображение f~l линейно с матрицей D~l.
, п го \1/2
Для матрицы D = (d,-fc),-=iE=i положим ||D|| := Е Е4 ■
Согласно неравенству Коши, для линейного отображения / с матрицей
D имеем ||/(х)|| < ||£>|| • ||х||, х € Rm, при этом \\f\\ — норма /в
Rn, а ||х|| — норма х в Rm. Далее в аналогичных случаях оговорка о
пространстве, в котором рассматривается норма, делаться не будет.
12.1.2 Непрерывные отображения
Пусть А С Rm — открытое множество.
Определение 1. Пусть f: A->Rn, x° € А. Отображе-
Отображение f называется непрерывным в точке х°, если
Ve > 0 3 8 > 0 Vx, Рго(х,х°) < 8 : р„(/(х*), Дх°)) < е.
Отображение f непрерывно на множестве А, если
оно непрерывно в каждой точке множества А.
Приведенное определение есть перефразировка общего определе-
определения п. 10.2.4 в частном случае, когда X = Rm, Y = Rn с обычным
расстоянием.
Примеры. 1. Постоянное отображение непрерывно на Rm.
2. Линейное отображение /(х) = Dx, x £ Rm, непрерывно на Rm,
так как справедлива такая оценка Pn{f{x),f{xQ)) = \\f{x) — /(х°)|| =
= \\D(x - х°)|| < ||D|| • р- х°|| = ||D||pm(x,x0).
Теорема 1. Пусть f = (Д, /2,..., /„)* : А -> Я". Отобра-
Отображение f непрерывно на А тогда и только тогда, когда
V fc, 1 < fc < n : fk € C{A).

12.2. Дифференцируемые отображения 377
\ Поскольку сходимость в (Rn,pm) равносильна покоординатной схо-
сходимости, то / непрерывно в точке х° <=*• f{x) -» f{x°), х -» х°
<=* Vfc, I < fc < n :/fc(x) ^/fc(x°), i^f°. J
Следствие 1. Пусть f : А -> Я" непрерывно на A, D
— матрица размера к хп с действительными непрерыв-
ным.и на А элементам.и. Тогда отображение Df: A -> Rk
непрерывно на А.
Упражнение 1. Пусть D — матрица размера п х т с действи-
действительными элементами и у — фиксированный вектор. Отображение
/(х) = у° + Dx, х € Rm называется аффинным. Доказать, что аф-
аффинное преобразование непрерывно на Я.
Упражнение 2. Пусть f: Rm -> Rm преобразование таково, что
^{£,У} С Rm : ||/(х) - /(у) || = ||£-у||. Преобразование /называ-
/называется изометрическим. Доказать, что f непрерывно на А. Можно
также доказать, что / есть аффинное преобразование с ортогональной
матрицей D.
12.2 Дифференцируемые отображения
12.2.1 Определения
Пусть А С Rm — открытое множество.
О пред еление 1. Пусть f: А -> Я", х € А. Отображе-
Отображение f называется дифференцируемым в точке х, если су-
существует линейное отображение Rm в Я" с матрицей
D = (d,-0i=i7=i такое, что \\f{x + a)-f{x)-Da\\ = о{\\а\\), а -> 0.
Матрица D называется производной отображения f в
точке х и обозначается символом D — ?{х).
Упражнение 3. Рассмотреть частные случаи определения 1, когда:
a) m = n = 1; b) n = 1.
Упражнение 4.. Определить производную аффинного преобразо-
преобразования.
Упражнение 5. Проверить, что производная дифференцируемой в
точке функции определяется однозначно.
Теорема 2. Отображение /= (Д, /2,..., /„)* дифферен-
дифференцируемо в точке х тогда и только тогда, когда каждая
компонента fk — дифференцируем.ая функция в точке

378 Глава 12. Векторные функции от нескольких переменных
я> 1 < fc < п. При этом производная отображения f равна
fix) = ( ) . Дифференцируемое в точке отобра-
V oxk />=ifc=i
жение непрерывно в этой точке.
(" Действительно, Vj, 1 < j< п : fj — дифференцируема в точке х
т df(x)
<=> Vj, 1 < j < п : fj(x + a) - fj{x) - £ у afc = г;||а||, где
г,- -> 0, а = (ai, a2,..., ато)* -> 0. Поэтому имеем следующее неравен-
ство
\х + а) - fj{x) - £ -^— afc < ||/(х + а) -
= f £ г>) 11^11- Отсюда следуют первые два утверждения теоремы.
Учитывая теперь теорему 1 и непрерывность компонент в точке х имеем
непрерывность отображения / в точке х. J
Упражнение 6. Пусть / и g — дифференцируемые в точке х отоб-
отображения. Доказать, что: 1) Vc € Я : (с/)'(х) = с/'(х); 2) [f+g)'{x) =
= /'(ж) +5'(^)! 3) если h : Я" —» Я — дифференцируемая в точке
х функция, то справедливо равенство (hf)'(x) = h(x)f'{x) + f(x)h'(x),
где /i'(x) — вектор-строка.
Упражнение 7. Пусть /: А -» Я" — дифференцируемое в точке
х отображение, D — матрица размера fc x n с действительными по-
постоянными элементами. Тогда Df : А -* Rk. Доказать, следующее
равенство {Df)'(x) = Df'(x).
.1 Определение 2. Пусть f: А -» Я" — дифференциру-
емая в точке х функция. Матрица f (х) = ( —^—- )
V OXfc /j=lfc=l
казъ1ваетсл матрицей Якоби. Если т = п, то опреде-
j лителъ i> 2. ■ • ■ ■ mj :=det/1(x) называется якобианом.
Точка х, в которой det/'(x) = 0, каэъ4ваетсл точкой вы-
вырождения отображения /*.
Определение 3. Пусть А с Ят — открытое м.ноже-
• ство, f: A^Rn uke(N\j{0}). /= (Д./з,... ,/„)* € Ск(Д Яп)
Vj, l<J<n: fj€Ck(A).
Упраэ«;нение S. Пусть m = п = 2, А = {(г, ip) \ г > 0, 0 <
2тг}, f[r,f) = (r cosyj, r sinyj)*. Доказать, что det/^ = г.
Упражнение 9. Пусть m = п = 3, у! = {(г, у>, z) | г > 0, 0 < <р <
2тг, z £ Я}, f[r,(p,z) = (гcosip,rsinyj,z)*. Доказать, что det/^ = г.

12.2. Дифференцируемые отображения 379
Упражнение 10. Пусть m = п = 3, А = {(т\0,<р) | г > О, О < в <
"■. О < ip < 2тг}, f{r,6,tp) = (rsin0cos<p,rsin0sin<p,rcos0)*. Доказать,
что det у — г2 sin б.
12.2.2 Свойства дифференцируемых функций
Теорема 3. (Правило дифференцирования сложной
функции). Предположим, что: А — открытое мноэ*се-
ство в Rm, В — открытое мпоэ*сество в Rn, f: A -» В
— функция, дифференцируемая в точке х°, g ; В -> Rk —
функция, дифференцируемая в точке $° := f[x°).
Тогда функция h := g(f) : A -» Rk дифференцируема в
точке х° и h'{S°) = g'{f{x°))f'{x°).
Г Поскольку /дифференцируема в точке х°, то
||/(а?° + 3) - />°) - />(^°)S1| = o(||5||), S -» 0. . A)
Аналогично, поскольку <f дифференцируема в точке у, то
Положим Ъ = /(ж0 + а) — f{x°) и заметим, что по теореме 1 Ь —> 0
при а —> 0. Из равенств A) и B) следует
\\h(xo + a)-h(xo)-g>(yo)f'(x°)a\\= ^ И1> C)
= Ю° + ь) - 5(у°) - 5'(у°)ъ + g'iy0)?- д'(у°)Г(г°)з\\ <
<о(\\Ъ\\) + \\д"(у°)\\-о(\\а\\), а^б. uj|-f'#*l'
Кроме того,
l|b||<o(||S||) + ||/'(x0)||-P|, 3^6. D)
Из формул C) и D) имеем
Если m = n = А;, то из теоремы 3 и правила вычисления опре-
определителя произведения матриц получаем следующее утверждение для
якобианов.
.Следствие 2. При условиях теоремы. 3 и т = n = k
..d{hl,h2,...,hm) _ d(gl,g2,..-,gm) d{fl,f2,...,fm)
имеем — - — -tt-j j т—г '7J7 Г • ^оесъ
d{xi,x2,...,xm) d{fuf2,...,fm) д{х1,х2,...,хт)
h = (hlt..., hmy = (gx(f),... ,дти~)У, f= (Л, /a,.... /m)*.
Упражнение 11. Используем обозначения теоремы 3. Пусть функ-
функции {/д} С С для некоторого г £ N. Доказать, что Я € С.

380 Глава 12. Векторные функции от нескольких переменных
Упражнение 12. Пусть f{r,tp) = (г cos tp, r sirup)*, {r,tp) € ([0, +оо)
х[0,2тг]; g£C2(R2), h{r,<p) = g{f{r,<p)), (r,<p) € ([O.+oo) x [0,2тг].
Доказать равенство д'^ + g'in = h'(i Л—~ h'L h'1} r > 0.
т т
Теорема 4. Пусть A — открытое мноок.ество e Rm,
f : A -» Rn, f € Cl{A,Rn) и точки х и а таковы, -что
{x + та | 0 < г < 1} С А. Тогда имеет место следующее
неравенство \\f(x + а) - f(x)\\ < sup \\f(x + та)\\ ■ \\a\\.
0<т<1
[ Для любого фиксированного z € Rm рассмотрим действительную
функцию уэ(т) = £*/(£+ та)), т € [0,1], для которой производная
(р'(т) = гг?(х + та))а, т £ [0,1], ц>' € С([0,1]). По теореме Лагранжа
|¥>A)-¥>(О)| = И0)|< sup W[t)\, flG[0,l]. E)
0<т<1
Поэтому |£*(/(£+а)-/(£))| < ||£Ц sup ||/'(£+га)||-||а||. Если величина
0<т<1
\\f(x + a) - f(x)\\ = 0, то требуемое неравенство выполнено. Если же
\\f{x + а) - f{x)\\ ф 0, то положив £= f(x + а) — f{x), из формулы E)
после сокращения на \\z\\ также получаем требуемое неравенство. J
Упражнение 13. При условиях теоремы 4 доказать неравенство
||/(i + о) - /(£) - f'(S)a\\ < sup \\f(x + та) - f'(x)\\ ■ \\a\\.
0<т<1
Упражнение 14. Пусть f(x) = (sinx.cosa;)*, x € [0,2тг]. Доказать,
что не существует в € [0,2тг] такого, что /Bтг) - /@) = /*'@)Bтг - 0).
12.2.3 Теоремы о неявной и обратной функциях
В этом разделе приведены две наиболее важные и наиболее часто упо-
употребляемые теоремы о дифференцируемых отображениях.
Лемма 1. Пусть А — открытое множество в Rm, f:
А -> Rm, fe Cl{A,Rm), x° eA и detf'[x°) ф 0.
Тогда f — гомеоморфизм меж.ду некоторым, откры-
открытым, множеством в Rm, которое содержит точку х°, и
некоторым, открытым. мноок.еством в Rm, которое со-
содержит точку у0 := f{x°).
Г I. Из условий леммы имеем 3 е > 0 Vaf € В(х°,е) •£=>• \\х — х°\\ < е :
\, E = (8jk)™k=l A)

12.2. Дифференцируемые отображения 381
2
II. Положим
C)
а также определим функцию Vy, Ну*— у*°|| — ||!Г—/(*0)|| < V '■ 9y{%) '■=
= х + (?(го))~1Ш- /(*)), х € В(а?°,е)-
Докажем, чтр_для каждого у € В(у°,т]) отображение д$ переводит
замкнутый шар В(х°,е) в себя. Действительно, из B) и C) имеем
Ш*) - х°\\ = \\х-х°
1 (р(х°)(х-х°) + Д*°) - /(£
|| \\(Г()у\\г, < е.
Заметим теперь, что (&(£))'..= £- (/'(х0))'1/^^), *€ 5(х°,е).
Для каждого у*€ B{y°,rf) отображение д$ сжимающее, так как с учё-
учётом теоремы 4 и A) имеем для любых векторов {х',х"} С В(х°,е) :
1 |
III. Таким образом, по теореме Банаха для каждого у € В(у°,т])
получим 3 \х € В(£0,е) ду(ж) = ж -4=>- /(ж) = у. Следовательно на
открытом множестве f~l(B(y°,ri)) П В(х°,е) отображение / взаимно
однозначно и имеет обратное /-1.
IV. Проверим, что обратное отображение /-1 непрерывно на шаре
B(y°,i]). Действительно, пусть для произвольных {у1,у"} С В(у°,т])
векторы {х",х"} С f~l(B{y°,r])) П В{х°,е) таковы, что /(£') = у",
f(x") = у*". Тогда с учётом B) сначала имеем неравенство \\х' — х"\\ =
= ||ду-(х') - ^«(£")|| < \\Ы2') - 9у(х")\\ + \\ду-(х"') - дуМ*")\\ <
< ^ \\х' - х"\\ + \\(?{х°)\ 1\\ ■ \\у' - у"||, а затем неравенство
\\х' - f "|| < 2\\{?(х°))~1\\ ■ ||у' - у"||. D) J
Теорема 5. (О существовании обратной функции).
Пусть А — открытое м.-и.оок.ество в Rm, f : A-* Rm, x° €
А и у0 := f(x°). Предполоэ+сим, что выполнены, условия:
1) /*€ С1^,^); 2) detf'{x°) ф 0. Тогда существуют от-
открытое в Rm множество О(х°) С А, которое содержит
точку х°, и шар В(у°,г) такие, что: а) отображение
f : 0{х°) -> В[у°,г) — гомеоморфизм; Ъ) обратная к f

382 Глава 12. Векторные функции от нескольких переменных
функция д = f~l : В(у°,г) -» 0(х°) удовлетворяет условию
g£C\B{y\r),Rm); с) Vy € В(у°,г) : д'(у) = (/'Ш)))^-
|" I. Утверждение а) теоремы содержится в лемме 1.
II. Заметим, что при доказательстве леммы 1 число е > 0 можно
взять таким, чтобы матрица f (x) была невырожденной для каждого
х € В(х°,е). Далее предполагаем, что такое е фиксировано, и положим
г:=т,, О(х°) := f-i(B(y°,r,))nB(xo,e). Пусть g : B(y°,rj) -» О(х°)
— обратное к / отображение и произвольное значение у1 € В(у°,т])
фиксировано. Докажем, что отображение д дифференцируемо в точке
у, и что справедливо равенство с). Положим
тогда
По условию теоремы отображение / дифференцируемо в точке х1
и потому
Отметим, что по лемме х —> х 1 -4=>- у —> у*1. Из равенств E) — G)
имеем
Для оценки левой части (8) используем неравенство D)
\Ш-9(У1)-
1\№- у Ml • ||ёТ5(УОI1, 1Г-> У1-
Поскольку е{д(у)) —> 5, у —у у1, то отображение д дифференцируе-
дифференцируемо в точке у1 и имеет производную (f (х1)) = \f'(g{yl)) . J
Перед формулировкой следующей теоремы введём некоторые обо-
обозначения. Далее рассматриваются пространства Я, Rn и Ят х Я" =
jjm+n c евклИдОВЬ,ми расстояниями. Их элементы будем обозначать со-
соответственно символами х, у, (х,у) (возможно с индексами), таким
образом, (х, у) есть вектор-столбец ( -I ■ Матрица F~(x,y) определя-
определяется как производная отображения F при фиксированном у. Аналогично
определяется Р^(х,у)
Теорема 6. (О существовании и свойствах неяв-
неявной функции). Пусть G — открытое множество в про-
пространстве Rm+n, (x°,y°) £ G. Предположим, -что функ-
функция F : G -» Rn удовлетворяет условиям: 1) Р[х°,у°) = 0;

12.2. Дифференцируемые отображения 383
2)PeCl(G,Rn); 3)
A,У2.---.Уп)
F = [FltF2,.... Fn)\ y = (yb ya,.... у„)*.
Тогда существует шар В(х°,г) С Rm и единственная
функция h: B(x°,r) -» Я", Я € С1(В(£>0,г), Я"), удовлетворя-
удовлетворяющая условиям,: a) h(x°) = у°; Ъ) Vz € B(x°,r) : F(x,h(x)) = 0;
1
(" Введём отображение f{x,y) := \ в(- -л ) > (£>У) € G. для которого
\Р (x,y)J
Отображение / удовлетворяет всем условиям теоремы 5. Поэтому в
некотором шаре B(f(x°,y°),5) С Rm+n определено обратное отоб-
отображение g = (Ki,K2), причём g(x°,0) = (х°,у°) и
/(Й1(**).Яа(*.*)) = №«). №«) € B(f(x°,y°),6); <9)
кроме того, **$($)</)
ge Cl(B{f(S°,y0),S)); д'Ы.Ъ = (/'(^(гГ^.ЯгК^))'1. A0)
Рассмотрим теперь какие-либо открытые шары В(х°,г) С i?m и
В(Р(х°,у°),г) = В{б,г) С Я" такие, что&ь
Я := (В(*о,г) х В(РB°, j?0),r))c B(f(x°,y%6).
Согласно равенству (9), имеем
hx(u,if) = U, F{uMu,v)) = v, {utv)cH. A1)
Аналогично, в силу равенства A0), /^Р )' /
в о\ ( в о V1
Для £ € В(х°,г) положим h(x) := ^2A,0). Заметим, что отобра-
отображение h : B(x°,r) —> it". Теперь из равенств A1), A2) следуют та-
такие утверждения для отображения h: h(x°) = y°\ Va? € B(x°,r) :
(Y1
(())Y(())
Упражнение 15. Пусть л — открытое подмножество Я, /j, €
С1(А), 1 < fc < т. Предположим, что существует функция ц> € C1(Rm)
такая, что \\tp'\\ ф 0 и Уж€а: ^(/1(ж),/2(г),... ,fm(x)) = 0, функции
/ь/г.. ..,/т в этом случае называются функционально зависи-
У)
. Доказать, что V £ € Л : У'/а.-.-./т) (f) - 0.
d(xi,x2,...,xm)
25 — 4-1168

384 Глава 12. Векторные функции от нескольких переменных
Упражнение 16. Пусть А — открытое подмножество Rm, f €
Cl(A,Rm), detf'(x) ф 0,x € А. Тогда для любого открытого мно-
множества В С А образ f(B) есть открытое множество в Rm.
Упражнение IT. Пусть /€ C{Rm,Rm) и V{z,y} С Rm : \\f{x)-
/(у)Н ^ Н^~У||- Доказать, что: 1) / взаимно однозначно; 2) Vaf € R
йеЬр(х)фО; 3)
m
Упражнение 18. Пусть В{б,г) С Я, ВE,р) С Rn — открытые ша-
ры^отображение F € С(Б@, г)хБ@, р), Я") и V £ € Б@,г) V{yi,у2} С
В(С1,р) : 11^A,^) - ^(£,у2)|| < A||yi - у2\\ с некоторым числом Л €
[0,1). Предположим, что Ух £ В(б,г) : \\F(x,S)\\ < рA - Л). Тогда
3!/еС(Б@,г),Б@,р)): F(x,f(x)) = f(x), хеВ(б,г).
Замечание. Применить теорему Банаха. Из этого утверждения
легко получается основная часть теоремы 6.
12.3 Локальный относительный экстремум
12.3.1 Определения
Пусть А — открытое подмножество Rm и / : А -» R. Для натурального
s < m пусть tpj; : А —> R, 1 < j < s — заданные функции. Введём
множество М = {х £ А \ 4>j(x) = 0, 1 < j' < s}, иногда говорят,
что множество М определяется с помощью s уравнений связи;
Vi = 0, ц>2 = 0,...,ips =0.
Определение 1. Пусть х° е М. Функция f имеет в
точке х° локальный относительный максимум при ус-
условиях или ограничениях <pi = 0, (р2 = 0,..., tps = 0, если
3r >0 Vie {В(х°,г)ПМ) : f{x) < f{x°).
Локальный относительный максимум называется
строгим, если последнее неравенство выполняется со
знаком. " < " для х ф х°.
Аналогично определяются понятия локального относитель-
относительного минимума и строгого локального относительного
минимума. Все введенные выше понятия описываются также сле-
следующими общими терминами: локальный относительный или
условный экстремум.
Упражнение 19. Определить наименьшее на R? значение функции
f{xx,x2) = х\ + х\, {хх,х2) € R2. Определить наименьшее значение
функции / при условии Xi + х2 = 1.

12.3. Локальный относительный экстремум 385
12.3.2 Необходимое условие локального относительно-
относительного экстремума (правило множителей Лагранжа)
Теорема 7. Предположим, что: s < т, f € С1 (A), <pj €
Iди> (х®) \ * m
С (А), 1 < j < s, и матрица ( —^—- ) хилеет ранг s
\ OXk I j=l fc=l
в точке х° — точке локального относительного экстре-
экстремума функии f при ограничениях щ = 0, ц>г = 0,..., tps = 0.
Тогда существуют действительные числа Ai, Л2,. •., As,
для которых точка х° лвллетсл критической точкой
функции F = f + \i<pi + \2ч>2 + ■ ■ ■ + Aj¥>s.
Замечание. Функция F и числа Ai, А2,..., As называются соответ-
соответственно функцией Лагранснса и множителями Лагранжа.
\ Допустим, что
+i,Xm-.s+2,. . . ,Хт)
I. Определим теперь действительные числа Aj., Aj,.. .,А, так, чтобы
В силу предположения A), эти числа определяются единственным об-
образом.
II. Ограничения 4>j{xi,..., xm_s, xm-s+x,..., хт) = 0, (ii,..., xm) €
А, 1 < j < s, согласно теореме о существовании и свойствах неявной
функции, можно разрешить относительно переменных гт_8+1,... ,хт
как функций от Хх,... ,xm-s в некотором шаре В с центром в точке
(х°,... ,x^n_s). В этом шаре на основании правила дифференцирования
сложной функции для каждого j, 1 < j < s получим
М+ £ d^f=0, l<k<m-s. C)
OXk Vzzm-i+l OXV OXk
III. Для (xi,..., xm-.s) e В функция f(xlt..., xm) =
x, ■ . . ,Xm-s),. . . ,Xm(xx,. . . , 2m_s))
имеет локальный экстремум в точке (х^,..., x^n_s). Поэтому
| D,
Учитывая равенства B) и C), из равенстваD) находим
'-'■Efc 1/=тп—14-1 ч 1 = 1 УХ,,
X-imi^, l<fc<m-s.
OXk

386 Глава 12. Векторные функции от нескольких переменных
12.3.3 Достаточное условие
ТеоремЭ 8. Предположим, что: 1) f € С2(А), ipj €
С2{А), 1 < j; < s; 2) х° £ М — критическая точка функ-
5
г^гш F = / + J2 ^jV> <Элл петеоторого набора действителъ-
3 = 1
/dtpjix0) \ s m
ных чисел Ai, А2,..., Л,; 3) матрица ( —£ име-
\ дхк >з—^ fc=i
em ранг s, далее предполагаем, выполнение условия A)
п. 10.3.2. Для любого элемента [а.\,... ,ат_5) 6 Rm~s no-
т d2F(x°)
лож.им Q(ai,...,am..s) := £ "Б—5—а>аь> где am-s+i,- ■ ■ ,а
т
d(pj(x)
определяются из уравнений }2 —а— afc = 0, 1 < j < s.
fc=l O^fc
Если g(all...,am_s) > 0, (аь ... ,am_s) ^ @,...,0), то х° —
точка строгого относительного локального миниму-
минимума для функции f. Если Q{ai,... ,am_s) < 0, (аь.. .,am_s) ^
(О, ...,0), то i° — точка строгого относительного ло-
локального максимума для функции /.
[ Пусть а € Rm таково, что (i° +a) 6 А. С помощью формулы Тейлора
имеем для некоторого в € @,1)
^ i,fc=i o
О = ^(*°+3)-W(i0) = £ g^(y+g>5) afcl 9k G @,1), 1 < k < 5,
Далее нужно дважды использовать лемму 1 гл. 11. Первый раз —
для того, чтобы определить am_J+i,..., ат через ах,..., am_Sl а второй
раз — чтобы получить утверждение теоремы. J
12.3.4 Собственные числа симметрической матрицы
Пусть D = (djfc)j%i; {djk} С R\ djk = dkj, 1 < j,k < т. Чис-
Число A € R называется собственным числом матрицы D, если
det(£> - ХЕ) = 0. Вектор х € Rm, i/?, называется собственным
вектором , соответствующим собственному числу А матрицы D, ес-
т
ли Dx = \х. Пусть f(x) := xbDx = Е djkXjXk, x = (ii im)' €
j,k=i
Rm; f € C{Rm).
Рассмотрим множество Mi := {x € i?m | ||ж|| = 1}. Оно компакт-
компактно, так как ограничено и замкнуто. Следовательно, существует вектор

12.4. Дополнительные задачи к главам 10 — 12 387
гГA) € Мх такой, что /(гГA)) = max/. По теореме 7 существует чис-
число Ai € R такое, что вектор tf(l) является критической точкой сле-
следующей функции Fi(x) - f(x) + А:A - р||2), x € Ят. Поэтому
Dv{l) - Xxv{l) = 0, откуда А: = гГA)*Г>гТA) = /(t7(l)).
- Множество Мг := {х € Rm | ||ж|| = 1, х*гТA) = 0} также компактно
и существует vB) € М2 такой, что /(гТB)) = max/. Заметим, что
М2 С Mi и /(гТB)) < /(гТA)). Существуют числа {Х2,(л2} С -R такие,
что вектор v{2) является критической точкой функции F2(x) — f(x) +
+Х2{1-\\х\\2)+ц2х*ьA), хе Rm. Поэтому 2(DvB)-X2v{2)) + fi2v{l) =
= 5, и, следовательно, \i2 = 0; Dv{2) = А2гТB); /(^B)) = А2 < Ai.
Таким образом, наибольшее собственное число матрицы D равно
наибольшему значению функции / на Mi и достигается на собственном
векторе, соответствующем этому собственному числу. Следующее по
величине собственное число равно наибольшему значению / на М2 и
достигается на соответствующем собственном векторе и т. д.
12.3.5 Историческая справка
Якоби Карл Густав Якоб A804 — 1851) — немецкий матема-
математик. Создатель теории эллиптических функций. Внёс большой вклад в
разработку математических методов механики.
12.4 Дополнительные задачи к главам 10 — 12
1. Пусть Pn({a,b]) — множество всех многочленов с действительны-
действительными коэффициентами не превосходящей п степени, рассматриваемых
на отрезке [а,Ь]. Для двух многочленов {р,q} С Pn{[a,b]), р(х) =
п п п
Е Pixl, Ч{*) = Е ffj^. х ^ [а. Ь], положим d{p,q) = J2 \Pi ~ 4j\-
j=0 J=0 j=0
Доказать, что (Pn([a,b]),d) — полное сепарабельиое метрическое про-
пространство. Является ли множество всех многочленов с коэффициентами
из [0,1] замкнутым? Компактным?
2. Пусть J3V([a,b]) — множество всех действительных функций ограни-
ограниченной вариации на [а,Ь]. Положим
d(f, 9) = |/(a) - g(a)\ + V(f - g, [a, b}), {/, g} С BV([a, b}).
Доказать, что (BV([a,b]),d) — полное метрическое пространство. Яв-
Является ли это пространство сепарабельным?
3. Для функции / : [a,b] -^ R положим ВЦ[а,Ь]) := {/ | ||/||si < +00}

388 Глава 12. Векторные функиии от нескольких переменных
|Bi:=«ip|/|+ sup l/(f~/(v)l. Пусть также d(/,g):=
II/ -5||si, {/,5} С J3L([a,b]). Доказать, что:
a) (BL([a,b]),d) — полное сепарабельное метрическое пространство;
b) множество BL([a,b]) всюду плотно в (C([a,b]),p).
4- Пусть V — множество всех многочленов, рассматриваемых на отрез-
отрезке [iifb]. Определить множества внутренних и предельных точек множе-
стваР в (С([а,Ь]),р).
5. Пусть В(х,г) — замкнутый шар с центром в точке х и радиусом г в
метрическом пространстве [X, d), C(x,r) — замыкание открытого шара
В(х,г). Доказать, что С(х,г) С В(х,г). Привести пример метрического
пространства (X, d) такого, что С(х,г) ф В(х,г) для некоторых жиг.
6. В пространстве (С([1,2]),р) определить замыкание множества всех
функций вида f(x) = a0 + axx^2 + a2x3/2 + ... + anx^2n~1^2, x G
[1,2]; n£N, {ao,a1,...,an}cR.
Ответ: С([1,2]).
7. Пусть А + В:={{х1 + у1,х2+у2)\{х1,у1)еА,{х2,У2)еВ}, ЛС
R2, В СИ2. Доказать, что: а) А + В открыто, если А или В открыто;
Ь) А + В замкнуто, если А и В замкнуты.
8. Какие из следующих подмножеств пространства (С([0,1]),р) :
а) {х | i@) = 0}; Ь) {х \ max x{t) > 1}; с) ix Jx2{t)dt < l);
0<х<1 О
d) {х | Vz € [0,1] : x{t) > t} замкнуты? Открыты?
9. Доказать, что метрическое пространство (X, d) сепарабельно тогда и
только тогда, когда каждое открытое покрытие множества X содержит
счётное подпокрытие.
10. Доказать, что в метрическом пространстве любое открытое мно-
множество есть счётное объединение замкнутых, а любое замкнутое —
счётное пересечение открытых множеств.
11. Пусть F и G — непересекающиеся замкнутые множества метри-
метрического пространства. Доказать существование открытых непересекаю-
непересекающихся множеств А и В таких, что F С A, G С В.
12. Пусть Aj — компактное множество в метрическом пространстве
(Xj,dj), j = 1,2. Доказать, что множество А\ х А2 компактно в декар-
декартовом произведении (Xi x X2, d = d\ + d2).

12.4. Дополнительные задачи к главам 10 — 12 389
13. Пусть К — компактное множество в метрическом пространстве
(X,d) и / € С {К). Доказать, что график {{х,у) \ х € К, у = f{x)}
— компактное множество в метрическом пространстве (X х R,di), где
2) + \yi - у2\.
14- Какие из следующих подмножеств пространства (C([a,b]),p) всюду
плотны в нём: а) множество всех многочленов; Ь) С ([а, Ь]); с)
}x(t)dt = o\; e) BV([a,b}) П С([а,Щ)?
{х \ х(а) + х(Ъ) = 1}; d) {x
15. Пусть (X,d) — полное метрическое пространство и {xjk \ 1 < к <
nj> 3 > 1}) nj £ N, j > 1, — произвольный набор элементов из X.
ОО "j
Доказать, что множество f] (J B(xjk,l/j) компактно.
>=ifc=i
16. Предположим, что множества А и В компактны в (Rm,p) и С :=
{ах | х € А}, а € Я; D := {аж + у | х е Л, у £ В}. Доказать, что
множества С и D компактны в (Rm,p).
17. Пусть {Кп | п > 1} — последовательность связных компактных мно-
множеств в метрическом пространстве, причём Кп+\ С Kn, n > 1. Дока-
оо
зать, что множество f] Kn связно. Привести пример, показывающий,
п=1
что условие компактности множеств нельзя заменить их замкнутостью.
18. Пусть А — компактное подмножество (Rm,p). Доказать, что сле-
Г п
дующее множество <х \ Зп € N Э{а1,...,а„} С [0,1], ^2 ак = 1,
1 fc=i
3{J<1)|fB),.,.,I»}cA:i = £ afci(fc)} компактно.
fc=i >
19. Пусть и А = {A1,3:2) | 0 < Xi < 1, х2 — 0}, О — открытое покрытие
множества А в (R2, р). Доказать существование е > 0 такого, что О есть
покрытие множества Ае := {(х\,х2) \ — е < ii < 1 + е, |аг2| < е}-
20. Пусть (X,d) — метрическое пространство и / € С(Х). Предполо-
Предположим, что для некоторого с € -R множество {х \ f(x) < с} непусто и
компактно, Доказать, что За:* € X Vi € X : f(x*) < f{x).
21. Пусть А — некоторое преобразование полного метрического про-
пространства (X, d) в себя, Т — гомеоморфизм этого пространства в себя.
Предположим, что Т~ХАТ — преобразование сжатия. Доказать, что А
имеет единственную неподвижную точку.
22. Пусть (X, d) — компактное метрическое пространство, а преобра-

390 Глава 12. Векторные функции от нескольких переменных
зование А : X —> X удовлетворяет условию d(Ax,Ay) < d(x,y), для
{х, у} С X, х ф у. Доказать, что преобразование А имеет единствен-
единственную неподвижную точку.
23. Пусть /A1,12) = (х[/3 + х\'Л , (xltx2) € Я2. Доказать, что:
а) / G C(R2); Ь) существуют /{@,0), /з@,0); с) / не является
дифференцируемой в точке @,0).
24- Пусть А — симметрическая матрица размера m х m, o£ Rm,
/(£) = xlAx - З'х, x e Дт. Доказать, что /'(£) = 2Лх -5, х е Ят.
25. Пусть /(х) = ||х||, х G Ят. Проверить, что для любого a G Ят
не существует /^@). Доказать, что функция / недифференцируема в
точке 0 и что /'(х) = i/||^|| для х ф О.
26. Вычислить /"(х) : а) /(х) = ||х||, х ^ 0; Ь) /(х) = (а'хJ, а е Rm-
Ответ: а) ЦгЦ-1^ - ||f||-3^i*; Ь) 233*.
27. Пусть В = {х е Ят | ||х|| < 1}. Предположим, что функция / €
С(В) дифференцируема во внутренних точках В и /(х) = 0 для точек
х, ||i|| = 1. Доказать, что 3 х°, ||х°|| < 1 : /'(х°) = б.
28. Пусть D — замкнутое подмножество Rm, / G C(D). Предполо-
Предположим, что для любой последовательности {xn | n > 1} С D такой, что
||х„|| —> +оо, п -* оо, справедливо соотношение /(хп) —> +оо, п —> оо.
Доказать, что 3i,eDV£eD: /(£*) <
2Р. Пусть / € С(Ят) и для некоторого о£Я множество {х | /(х) < а}
непусто и ограничено. Доказать, что функция / принимает наименьшее
на Rm значение.
30. Для функции F: ([а, Ъ] х R) -» Я существует f>FJe С([а, Ь]хД).
Предположим, что для функций {51,02} С C([a,b]) : F(x,gk(x)) = 0, х G
[a,b], k = 1,2, и 3!х0 G [а,Ь] : £i(x0) = 52A0) =: Уо- Доказать, что
31. Найти наименьшее и наибольшее значения функции /(xi,x2) = xix2
на кольце {(xi,x2) G R2 \ 1 < х\ + х\ < 4}.
32. Найти кратчайшее расстояние от точки A,4) до параболы у2 =
2х, убй.
33. Найти наибольшее значение произведения х\х\ ... х2т при условии
^ 2

12.4. Дополнительные задачи к главам 10 — 12 391
34- Пусть (ojfc)™fc=i ~ симметрическая положительно определённая
матрица с действительными элементами. Доказать, что существует а >
m m
О такое, для которого £) ajkXjXk > a £) х2, (xi, х2,..., xm) G Дт.
j,fc=i j=i
35. Пусть (ujk)Jtk=.1 — симметрическая положительно определённая
матрица с действительными элементами, {а, Ь\, Ь2,..., Ьт} С йи
m
f(xi,x2,.. .,xm) = а+ J2 bjXj +
>=X >,fc=l
Доказать, что / принимает наименьшее на Rm значение.
36. Пусть Р — многочлен от х\ и Х2. Верно ли, что существует точ-
точка, в которой \Р\ принимает наименьшее значение на R2? Аналогичное
утверждение верно для многочлена от одной переменной на R. Рас-
Рассмотреть пример: Р(аг1)х2) = (zix2 - IJ + x\, {xi,x2) G Я2.
37. Для фиксированного a G -Rm определить max а1х.
38. Определить расстояние от точки х ° до гиперплоскости {х | 5*х =
Ь}, вектор а и число Ь е -R фиксированы.
39. Определить наименьшее и наибольшее значения функции
= (xi - х2J + xix2 - xi, (x!,x2) G -R2, на следующем множестве
2)|0<х1<1, 0<х2<1}.
,2ir 2ir . t
40. Для отображения .F(x) = If x(t) cost dt, f x(t) sin tdt J , где х €
о о
С([0,2тг]), определить ^(С([0,2тг])).
41. Для отображения j?(x) = (ftx(t)dt,ft2x(t) dt,ft3x(t) dt)*,x G
C([0,1]), определить #(С([0,1])).
Ответ: Я3.
/1 . 1 \
/ — sinxi cos x2 + 2
^2. Доказать, что отображение/(xx,x2) = ":
\ — cosxi H— sinx2 — 1
\6 2 '
является сжимающим в (R2,p).
43. Доказать, что отображение /(х!,х2) =
единственную неподвижную точку.

392 Глава 12. Векторные функции от нескольких переменных
44- Пусть / : Rm -> Rn — дифференцируемое на Rm отображение.
Положим д(х) = \\f(x)\\, х G Rm. Доказать, что функция д диффе-
дифференцируема в точках множества Rm \ {х | /(х) = 0}.
45. Пусть / : Rm —> Rn — дифференцируемое на Rm отображение,
для которого матрица Якоби /' постоянна. Доказать, что /— аффинное
отображение.
46. Для отображения / : Rm —> Rm существует у на Rm, причём
у(х) положительно определена для каждого х £ Rm. Доказать, что
V {х, у} с Rm : (/E) - Щ*B - у) > 0.
47. Пусть А — сжимающее в (Rm,p) преобразование и ^(х) = х-
А(х), х € Rm- Доказать, что Р — гомеоморфизм (Rm,p) на себя.
48. Для отображения / : Rm -> Rm существует р на Rm, и для неко-
некоторого а > 0 имеет место ||/(х) - /(у)|| > а||х - у||, {х,у} С Rm.
Доказать, что для любого i£ Rm матрица f(x) обратима.
49. Отображение / : Rm —t Rm непрерывно дифференцируемо на
Rm и удовлетворяет условию Липшица 3 L G R V{x, у} С Rm '■ ||/(^) —
f(y)\\ < L\\x - у\\. Доказать, что sup П/фиИ < Ь, ZeRm.
И«И<1
50. Пусть /:Й-4Й, / G C*(R) и 3 А € [0,1) Vx е Я : \f'{x)\ < A.
Доказать, что отображение F(x\,x2) = (xi + /(x2),x2 + /(xi))* есть
биекция R2 на себя. •
51. Пусть Л С Rm, f:A^Rn, a € Дт, отрезок / = {х + та | 0 < т <
1} С А, и /е С1 [A, Rn). Доказать, что /(х+а)-/(х) = /?{х+та)а<1т.
о
52. Предположим, что выполнены условия предыдущей задачи и, кро-
метого.ЗЬеЯ V{U,tT}cJ: \\f'{u)-f'{v)\\ < L\\u-v\\. Доказать,
что ||/(х + а) - /(х) - ?(х)а\\ < Ц\а\\2.
53. Отображение А : Rm -+ Ят имеет единственную неподвижную
точку х * и удовлетворяет условию: для любого компакта К существует
число a G [0,1) такое, что \\А{х) - А{у)\\ < а\\х - у]\, {х,у} С К.
Доказать, что для любого х° € Rm последовательность х°, х1 =
А{х°), х2=А(х2), ..., хп = Л(хп-1), ... сходится к х*.
54- Пусть /: Rm -+ Ят, /е С^Я, Дт), Б(а,г) - замкнутый шар.
Предположим,что существует А € @,1), удовлетворяющее условиям:

12.4. Дополнительные задачи к главам 10 — 12 393
а) ||/(а) - а|| < A - Л)г; b) sup \\f[x)\\ < А. Доказать, что 3 \х* €
1бВ(о,г)
В(а,г) :/(£*) = х*.
55*. Пусть /: Ят -> Ят, /б C(Rm,Rm) и К - компактное множе-
множество. Предположим, что для некоторого Л G @,1) справедливо нера-
венство ||Да) - f(y)\\ < А||х - уЦ, {£,у} С (Дт \ if). Доказать, что
отображение / имеет неподвижную точку.
х-1 <'"
56- (Теорема Дини). Пусть (X, d) — компактное метрическое про-
пространство и функции /n G C"(X), n > 1, удовлетворяют условиям:
1) V* е X Vn > 1 : fn(x) < fn+1(x); 2)VxeX: fn(x) -> /(x), n -> oo;
3) / € C(JT). Доказать, что последовательность {/n(a:), i £ X | n > 1}
сходится равномерно на X к функции /.

Глава 13
Несобственные интегралы,
зависящие от параметра
13.1 Несобственные интегралы
13.1.1 Определение интегралов по неограниченным
интервалам
Пусть функция / : [а,+оо) —> R и число а € R таковы, что
а : f G Д([а,Л]). Далее это условие предполагается выполненным и не
А
оговаривается. Пусть <р(А) := J f(x) dx, A>a.
а
Определение 1. Несобственным интегралом
+Ff{*)dx A)
а
от функции f no множеству [а, +оо) называется конеч-
конечный предел
lim <p{A)= lim ff{x)dx, B)
Л->+оо Л->+оо „
если этот предел существует. При этом говорят, что
несобственный интеграл A) сходится. Если ж.е предел
в B) не существует или бесконечен, то несобственный
интеграл A) называется расходящимся.
Замечание. Если интеграл A) сходится, то для любого b > a
сходится несобственный интеграл
+ОО
f f(x)dx, C)
ь
394

13.1. Несобственные интегралы 395
причём
+оо Ь +оо
/ f(x)dx = ff(x)dx+ f f(x)dx. D)
a a Ъ
Если для некоторого b > а сходится интеграл C), то сходится инте-
интеграл A) и справедливо равенство D). Оба эти утверждения следуют из
А Ь А
равенства / f(x) dx = / f{x) dx + f f(x) dx, a < b < А, и определения
a a Ь
несобственного интеграла. Далее утверждения замечания используются
без оговорок.
+0О
Примеры. 1. Интеграл f е~х dx сходится и имеет значение 1, так
о
А
как lim ш(А) = lim [e~x dx = lim (l-e~"A)=l.
А-++оо А-++оо 5 А-Ц-оо
+ ОО fa jj.
2. Справедливо равенство f ^ = —, так как lim (p{A) =
А dx ж
= lim Г 7г dx = lim (arctg A - 0) = — .
А-++оо о 1 + Х2 А-Ц-ооV 6 У 2
+°° dx
3. Пусть а > 0. Несобственный интеграл f — сходится и имеет
п
значение при а > 1 и расходится при а < 1, поскольку (р{А) =
= /-—=< A~a+l
'x+oo,
+oo
4. Интеграл J sinicte расходится, поскольку для функции (р(А) =
о
А
= / sin х dx = 1 — cos А, Л > 0, не существует предела при А -> +оо.
о
13.1.2 Элементарные свойства
Приводимые ниже утверждения следуют из свойств интеграла Римана и
определения несобственного интеграла.
+ ОО
1°. Предположим, что несобственные интегралы f fk(x)dx, к =
a
+ОО +0О
1,2 сходятся. Тогда имеем f [cfi(x))dx — с f fi(x)dx, с 6 Я и
a a
+ ОО +ОО +0О
/ {h(x) + f2(x))dx = / fi(x)dx+ f f2(x)dx, т. е. сходятся несоб-
несобственные интегралы в левых частях равенств и справедливы равенства.

396 Глава 13. Несобственные интегралы, зависящие от параметра
Предположим, что функция / имеет примитивную F на [а,+оо).
ели существует конечный предел
lim F{x) =: F{+oo), A)
X—У+ОО
+ОО
то / f(x)dx = F(+oo) — F(a). Если предел в A) не существует или
а
+оо
бесконечен, то несобственный интеграл / f(x) dx расходится.
а
Упражнение 1. Пусть / : [0, +оо) -> [0, +оо), / е С([0, +оо)),р > 1.
,+оо .р +оо ,+оо .р_1
Доказать равенство ( / f(x) dx) — р f f(x) I / /(u) du) dx при
раедположении существования интеграла в левой части равенства.
(^З^Предположим, что {f,g} С С1([а,+оо)). Если один из несобствен-
несобственных интегралов
+ОО +ОО
/ f(x)g'(x)dx, f f'(x)g(x)dx B)
а а
сходится и существует конечный предел lim (f(x)g(x)), то сходится
х+foo
второй из интегралов B) и справедливо равенство
+ОО +ОО
/ f(x)g'(x) dx = Jim^ (f(x)g(x)) - f(a)g(a) - J f'[x)g(x) dx.
+OO
Пример. Для а = 0, f(x) = i, g'(x) = e~x, x > 0, имеем / xe di =
о
+oo
; = lim (-же-1) - 0 + f e-1 dx = 1.
^°. Критерий Кохии. Для того, чтобы несобственный интеграл
. +ОО
f f(x) dx сходился, необходимо и достаточно, чтобы
a
А"
Ve>0 ЗЛ0 >а
ff{x)dx
13.1.3 Сходимость интегралов от неотрицательных
функций
В настоящем разделе изучается сходимость несобственных интегралов
от неотрицательных функций.
+оо
Теорема 1. Несобственный интеграл f f{x) dx от не-
а
отрицательной функции f сходится тогда и только
тогда, когда ЭСейУА>а: <р{ А) < С.

13.1. Несобственные интегралы // ,-/ ° 397
г/
f Функция <р монотонно не убывает и ограничена на [а, +оо), следова-
следовательно, существует предел lim 4>{A). J
А-++оо
Замечание. Для неотрицательной функции справедливо неравен-
А +оо
ство (р(А) = / /(х) dx< f f(x) dx, A>a.
a a
Упражнение 2. Для каких функций последнее неравенство является
строгим?
Теорема 2. Пусть f : [а, +оо) -> R, д : [а, +оо) -> R, при-
причём 0 < f(x) < д(х), х > а. Тогда сходимость интеграла
+ 0О +0О
f g(x) dx влечёт сходимость интеграла f f(x) dx.
а а
\ Доказательство состоит в использовании теоремы 1 и следующего
А А +оо
неравенства f f(x)dx < f g(x) dx < f g(x) dx, A>a. J
+00 cog2 x
Примеры. 1. Интеграл f ^ dx сходится, поскольку применима
О 1 + 2!
теорема 2 для а = 0; f{x) = ——г-, д(х) = ——- , х > 0.
1 + Ж 1 + 2IJ
+00 2
2. Интеграл / е~х dx сходится, поскольку применима теорема 2
1
для а = 1; /(з;) = е"*2, д(х) = e-I, 2; > 1.
+00
3. Интеграл f e~xlnxdxcxopync*, поскольку применима теорема
1
2 для а = 1, f(x) = е~х1п2;, д(х) = хе~х, х > 1, и справедливо
неравенство lnx < з;, я > 1.
Следствие 1. Предположим, что для некоторых чи-
сел 0 < С < +оо, а > 0 /(х) ~ — , х -> оо ^fc=> lim (ха/B;)) = С.
+оо
/Три а > 1 интеграл f f(x)dx сходится, при а < 1 этот
а
интеграл расходится.
\ Пусть а > 1. По определению предела функции в точке 3 Aq >.a Vi >
2С
Ао : f(x) < —. Теперь применим теорему 2 для а = Aq и функций
х"
2С
Q
Пусть а < 1. Аналогично, 3 Ао > о Vx > Aq : f(x) > -—. При этом
2ха
+?° С -fl
интеграл J —— расходится. Следовательно, по теореме 2, расходится

398 Глава 13. Несобственные интегралы, зависящие от параметра
+OO
интеграл f f(x) dx J
Ao
13.1.4 Абсолютно и условно сходящиеся интегралы
Определение 2. Интеграл
+ОО
/ f(x)dx A)
а
называется абсолютно сходящимся, если сходится ин-
интеграл
Г \fl-r\\dT О\
J \J\x)\ax- \*)
а
Если интеграл A) сходится, а интеграл B) расходится,
то интеграл A) называется условно сходящимся.
Теорема 3. Абсолютно сходящийся интеграл сходи-
сходится.
f Пусть интеграл B) сходится. Для неотрицательных на [а,+оо) функций
/_(*) = (-/(re) + |/0c)|)/2, f+(x) = (f(x) + I/0OD/2, х > а, спра-
справедливы соотношения: 0 < f~(x) < \f(x)\, 0 < f+(x) < |/(x)|, f(x) =
= f+ix) ~ f-ix)> x>a-
+ 0O +OO
По теореме 2 сходятся оба интеграла f f-{x)dx, f f+(x)dx, a
a a
+OO +OO
вместе с ними сходится и интеграл / (f+(x) — f~(x))dz — f f(x)dx.\
a a
Пример. Интеграл
/ -— Ac C)
о x
сходится условно (подынтегральная функция равна 1 при х = 0).
\ I. Интеграл C) сходится. Достаточно доказать сходимость интеграла
+sini
/ dx. Согласно формуле интегрирования по частям, имеем
1 х
+оо +оо
/sin х ( cosin cosl f cos ж , /J4
dx= hm +— / —— dx. D)
X I-++OO \ X ) 1 J X2 '
l l
В правой части D) предел существует и равен 0, а интеграл сходится
абсолютно. Следовательно, сходится интеграл в левой части D).
. +?|siiiz| .
I. Интеграл J dx расходится, так как
о х
fc=0 к*

ЩЛ. Несобственные интегралы 399
I 2 п 1
> £ 7ГТ-тг- I |smx|dz = - £ Г ^+оо, n ^ oo. J
Теорема 4. (Признак Дирихле). Предположим., что
функции fug удовлетворяют таким условиям: 1) ВС £
I A
R V.A > а : \ff(x)dx < С; 2) функция g монотонна на
' а
[а, +оо); 3) д(х) -> 0, х -> +оо. Тогда следующий интеграл
+ 0О
/ f(x)g{x)dx E)
а
f Доказательство проведём при следующих дополнительных предполо-
предположениях: существует д', V А> а : д' € Щ[а, A]); f € С([а, +оо)).
X
Положим F{x) = / f{u)du, x > a; F{a) = 0, F'(x) = /(х), х > а.
а
Применим к интегралу E) формулу интегрирование по частям
+ ОО +ОО
/ /(xM(x)dx= / i?'(xM(x)<fx= F)
а а
+оо
= lim (F(x)g(x))-0-J F{x)g'(x)dx.
Согласно условиям 1) и 3) теоремы 4, предел в правой части F)
существует и равен 0. Интеграл в правой части F) сходится абсолютно,
+ОО +ОО [,-v +ОО
так как / \F(x)\ ■ \д'{х)\ dx < С / \g'{x)\dx±C / g'{x)dx = С\д{а)\,
в силу условий 2) и 3). Поэтому сходится интеграл из левой части F). J
^~°° sin х
Примеры. 1. Интеграл / dx сходится. Достаточно доказать
о х
+?°sinx
сходимость интеграла J dx которая следует из теоремы 4 для
i х
а = 1, функций /(х) = sinx, д(х) = 1/х; х > 1, условия 1) — 3) теоре-
теоремы 4 выполняются с числом С = 2.
+оо
2. Интеграл f sinx3 dx сходится. Достаточно доказать сходимость
о
+оо
интеграла J sinx3 dx. Для доказательства в теореме 4 положим
1
а = 1, /(х) = х2since3, д[х) = 1/х2; х > 1. Условия 1) — 3) выпол-
выполняются с числом С = 2/3.
Теорема 5. (Признак Абеля). Предположим, что
функции/ ид удовлетворяют условиям: 1) f f(x)dx exo-
а
26 — 4-1168

400 Глава 13. Несобственные интегралы, зависящие от параметра
дится; 2) функция g монотонна на [а, +оо); 2) функция
g ограничена на [а, +оо).
Тогда интеграл Г f(x)g(x)dx сходится. „sfy'X*" ^. * Л
\ Доказательство следует из признака Дирихле. , * г(а-^Я^ а J ^
О п * " ч +r°°COSX
3. Доказать сходимость интегралов: a) J —■=- ах;
1 Vх
+°° +°° +°° sin 2х ■ sin ж +о°
b) J sinx2 dx; с) / cosx2dx;d) f dx; e) / xsinx3dx.
о о ix о
Упражнение 4- Пусть / £ C(R) — периодическая с периодом 2Т >
Т 2Т
О функция и J f(x)dx > 0, / f(x)dx = 0. Доказать, что интеграл
о о
+оо t/x\
J -^—— dx сходится условно.
о 1 + х
а
Замечание. Определение и свойства интеграла f f(x)dx анало-
—оо
+ ОО
гичны приведенным выше. Интеграл / /(х) dx = f f(x) dx определяет-
-ce R
a +oo
ся как сумма интегралов f f(x) dx + f f(x) dx для любого а € R.
—oo a
13.1.5 Несобственные интегралы от неограниченных
функций
Рассмотрим обобщение интеграла на случай, когда функция определена
на отрезке, исключая конечное число точек, и является неограниченной
в окрестностях этих точек. Поскольку обобщение интеграла должно
сохранять свойство аддитивности при разбиении отрезка на части, то
можно предполагать, что на заданном отрезке имеется только одна
точка — конец отрезка, в окрестности которой функция неограничена.
Пусть {о, 6} С R и a < Ь. Будем рассматривать функции / : [а, Ъ) ->
R такие, что Vc € (а,Ь) : / € й([а,с]), и такие, что в интервале (с,Ь)
они неограничены. Примерами таких функций являются:
1) /(*) = ^~ , х € [0,1); 2) /(«) = TL= , х € [ir/2, it).
1-х Vsin x
Случай, когда функция неограничена в окрестности точки а рассмат-
с
ривается аналогично. Пусть (р(с) := f f(x)dx, с € {a,b).
а
Определение 3. Несобственным интегралом

13.1. Несобственные интегралы 4Ш
ff(x)dx A)
а
от функции f по множеству [о, Ь) называется конечный
предел
]im_ff(x)dx, B)
если этот предел существует. При этом говорят, что
несобственный интеграл A) сходится. Если э*се предел
в B) не существует или бесконечен, то несобственный
интеграл A) называется расходящимся.
ь dx
Примеры. 1. Несобственный интеграл Г — —, а > 0, сходится
о {Ь-Х)а
при а < 1 и расходится при а > 1. Действительно, <р(с) = Г — г— =
о (о-х)а
1п(Ь-а)-1п(Ь-с), ' а = 1; Г+оо, а > 1,
и |
_а + 1 _а + 1 • ^'
при с —> Ь — .
1
2. Несобственный интеграл flnxdx сходится. Действительно,
о
1
/lnxdi =-1 - clnc +с->-1, с -> 0 + .
с
Приведём некоторые свойства интегралов от неограниченных функ-
функций, Доказательства этих свойств аналогичны доказательствам свойств
интегралов по неограниченному интервалу.
ъ
1°. Пусть f[x) > 0 для х € [а, Ь). Несобственный интеграл f f(x)dx
а
с
сходится тогда и только тогда, когда ЗСб-R Vc<b: / /(ж) dx < С
а
Ь
2°. Пусть 0 < /(х) < д[х) для х б [а, Ь). Сходимость интеграла J g[x) dx
а
Ь
влечёт за собой сходимость интеграла f f(x) dx.
а
Q
3°. Если для некоторых а>0и0<С< +оо /(х) ~ — г~ ,х ->
[о — х)а
ь
Ь — •£=>■ (/(х)(Ь- х)а) -> С, х -> Ь—, то при а < 1 интеграл J/(x)dx
а
сходится и при а > 1 расходится.
4°. Если функция / имеет примитивную F на [а,Ь) и существует конеч-
26*

402 Глава 13. Несобственные интегралы, зависящие от параметра
ь
ный предел lim F(x) =: F(b-), то / f(x) dx = F{b-) - F{a).
5°. Интеграл f — sin— dx сходится условно,
о i x
dx
Упражнение 5. Доказать сходимость интеграла f
о
Упражнение 6. В чём заключается ошибочность следующего рас-
i dx I
суждения J — = —
-1
-1
= -2?
13.2 Функции, определяемые с помощью
интегралов
13.2.1 Введение
Пусть {a,b,c,d} С R, причём о < Ь, с < d, f : ([а,Ь] х [с,d]) -> R.
Если для любого у € [c,d] функция f{-,])) : [a,b] -> R, f{-,y) G
ь
R([a,b]), то интеграл f f{x,y)dx =: J(y), у € [с, d], определяет функ-
a
цию J на [с, cfj. Величина у в интеграле для J(y) называется парамет-
параметром. Определяемые таким образом функции часто используются в ма-
математических рассуждениях и приложениях математики. Далее приво-
приводятся типичные условия, обеспечивающие для функции J такие свойства,
как непрерывность, дифференцируемость и т. п., а также приводятся
формулы для вычисления J' и т. п.
13.2.2 Теоремы о непрерывности, интегрировании
и дифференцировании функции J
Теорема 6. Предположим, что f € С([а,b]x[с,d]). Тогда
JeC([ctd\).
[ Для любого у € [c,d] функция f(-,y) € R([a,b]). Следовательно,
значение J(y) определено для любого у € [c,d]. Пусть произвольное
Уо £ [c,d] фиксировано. Докажем непрерывность J в точке у0. Пусть
е > 0 задано. Множество [a,b] x [с,d] ограничено и замкнуто в (R2,p),
следовательно, компактно. По теореме Кантора функция J равномерно
непрерывна на [a,b] x [c,d]. Поэтому
36 > 0 V{(si,y1),(s3,ya)} С {[а,Ъ] х [c,d]

13.2. Функции, определяемые с помощью интегралов 403
i) - /(зз,У2)| < е/(Ъ - а). Положим ц = х2 = х, ух = у, у2 =
Уо- Тогда из следующего неравенства р{{х,у),(х,у0)) = \у - уо\ < 8
получаем Vx € [а,Ь] : |/(х,у) -/(х,уо)| < е/(Ь-а). Отсюда
\J{y) - J(yo)\ = \}(f(x,y) - /(«.уо))dr </!/(*,») - f(x,yo)\dx < е. J
'а а
Теорема 7. Предположим, что функция f : ([а,Ь] х
[с, d]) -> R удовлетворяет таким, условиям: 1) У у £ [c,d\ :
f{-,y) € С([а,Ь]); 2) V(s.y) € ([а,Ь] х [c,d]) сг/гцестег/em /i(s,y);
5^ /г £ С([а,Ь] х [с, d\). Тогда существует производная J'(y),
ъ
у е [c,d\, и J'(y) = / f'2{x,y)dx, у e[c,d\ (формула Лейбница).
а
Г Пусть уо £ [c,d\- Согласно формуле Ньютона-Лейбница получим та-
кое равенство J{y° + ^ " J(Vo) = ± /(/(*, »о +A»)-/(*,»o))dx =
= /("т~ / /2(xi2/)^2/) dx,Ax ф 0. Используя зто равенство, имеем
Уо
Уо+Ду
J \f2\x^y) ~ /г(;
Уо
в силу равномерной непрерывности f2 на [a,b] x [c,d], как и при дока-
доказательстве теоремы 6. J
Теорема 8. Пусть f € С([а,Ъ] х [с,d]).
Тогда fJ(y)dy = }(ff(x,y)dy)dx.
с о чс '
Г Согласно теореме 6, J — непрерывная на [c,d\ функция, а интеграл
в скобках — непрерывная на [а,Ь] функция. Поэтому все интегралы в
утверждении теоремы определены. Для каждых z £ [с, d] и (x,z) €
[[a,b] x [c,d]) положим
g(z):=}j(y)dy, h(z):=}(jf(x,y)dy)dx, F(x,z) := /f(x,y)dy.
с а чс ' с
Поскольку J £ C([c,d\), то существует g'[z) = J[z), z € [c,d]. Функ-
Функция F{x, z) при каждом z € [с, d] непрерывна по х на [a, b] по теореме
6. Для любой точки (x,z) существует F2{x,z) = f{x,z) и i^ € C([a,b] x
[c, d]), поэтому, в силу теоремы 7, для каждого z € [c,d] существует
h'{z) и h'[z) = J(z). Таким образом, g'(z) = h'(z) = JB), z € [c,<f],

404 Глава 13. Несобственные интегралы, зависящие от параметра
причём д(с) = h{c) — 0. Следовательно, g(z) = h(z), z £ [c,d]. Доказы-
Доказываемое равенство получается при z = d. J
1 хь - х°
Пример. Вычислим интеграл f — dx, 0 < а < b.
хь-х°
Г Согласно правилу Лопиталя, имеем fix) := —: —> 0, х —> 0+;
шх
/(х) —> b—a, х —> 1—. Поэтому можно считать, что /@) = 0, /A) = b—a.
ь
Поскольку /(х) = f xy dy, x £ [0,1], то, применяя теорему 8, получим
а
1 <*Ь _ „а 1 / Ь \ Ь , 1
0 Vo ' о ч0
Упражнение 7. Пусть / е ^([ayb] х [с, d]), а : [с, d] -> [а, Ь], ^ :
[c,d] —> [а,Ь], причём а' и /3' существуют на [с, d]. Доказать следующую
формулу Лейбница
d Р(у) 0(у)
У а(у) а(у)
где у е [c,d].
13.2.3 Равномерная сходимость и теорема о предельном
переходе
Пусть / : {[a,b] x [c,d]) -»• R и Vy € [c,d) : /(-,y) € С([а,Ь]). Пред-
Предположим также, что Vx 6 [а,Ь] : /(х,у) -> д(х) € Н, t/ -+ d-.
Естественно ожидать, что J(y) = J f(x,y)dx —> f g(x)dx, у —> d — .
a a
Однако, это утверждение не всегда верно. Рассмотрим следующий
пример функции /(х,у) = - (l - s1/»)»1^, (х>у) € ([1/2,1] х @,1]);
/ € С([1/2,1] х @,1]), для которой Vx е [1/2,1] : /(х,у) -»• 0, ес-
1 1 / \
ли у -4 0+, и / - ix1ly - х2/") dx -> 1/2, у -> 0 + . Следовательно,
1/2 У V У
Определение 1. Пусть Y с R, уо — пределънал точ-
точка множества Y в {R,p) и f : {[a,b] x У) -> R. Семейство
функций {/(х,у), х € [а, Ь] | у € У} сходитсл равномерно на

13.3. Равномерная сходимость несобственных интегралов 405
[a,b] при у -> уо к функции g : [a,b] -> R, если Ve > О 3<5 >
О Vy е У, |у-уо| < S, у ^ уо Vi € [a,b] : \f{x,y) - g{x)\ < e, m. e.
если sup |/(x,y) - g{x)\ -> О, у -> y0.
i6[o,b]
Замечание. В качестве уо можно рассматривать +оо или — оо с
соответствующим изменением формулировки.
Упражнение 8. Доказать, что семейство функций {/(х,у), х € [а,Ь]
| у £ Y} сходится равномерно на [а,Ь] при у -> у0 к функции g то-
тогда и только тогда, когда для любой последовательности {yn | n >
1} С У, у„ -> Уо, п -> оо, последовательность функций {f(x,yn), x e
[а, Ь] | п > 1} сходится равномерно на [а, Ь] к функции д.
Упражнение 9. Пусть X := {у : [а,Ь] -> Я | 3L = L(y>) G Д :
|v(i)| < L}, d(<p,ip) := sup |v(i) - V(a=)|t {^.V1} С Х. Доказать, что
х6[а,Ь]
(X, d) — полное метрическое пространство. Показать, что семейство
{f{x,y),x £ [о,Ь] | у £ У} ограниченных на [а,Ь] функций сходится
равномерно на [а,Ь] при у —> уо к функции д тогда и только тогда, когда
/(-, У) -> 9 в (.X, d) при у -> у0.
Теорема 9. Пусть Y С R, уо — пределънал 7почка У и
/ : ([а,Ь] х Y) -> Я. Яредполоотсил*, что: 1) Vy Z.Y : /(-,у) £
Я([а,Ь]); 2.) сел*ейс7пво {/(х,у), х G [а,Ь] | у е У} функций
сходится равномерно на [а,Ь] при у -> уо к функции д.
ь ь
Тогда д £ R{[a,b\) и lim / f(x,y)dx = Jg{x)dx.
[ Доказательство того, что д € й([а,Ь]) следует из леммы 1 гл. 6. Из
,ь ь ь
неравенства И f(x,y)dx - Jg{x)dx < /|/(х,у) - g{x)\dx, у £ У, и
а а а
определения равномерной сходимости получаем нужное равенство. J
Упражнение 10. Пусть / е С^ЦО, 1]) и .F(x) := //(t)sign sin(xt),
*■ о
х > 0. Вычислить F'.
13.3 Равномерная сходимость несобственных
интегралов
13.3.1 Определение равномерной сходимости
несобственных интегралов
Пусть a € -R, М — некоторое множество и / : ([а,+оо) х М) —¥ R.

406 Глава 13. Несобственные интегралы, зависящие от параметра
Предположим, что для каждых А > а, а 6 М : /(-,а) € Я([а, 6])
и несобственный интеграл J{ot) —\ f f(x,a)dx сходится. В п. 13.3.1 и
а
13.3.2 эти предположения считаются выполненными.
Определение 1. Несобственный интеграл J{a),a е М,
сходится равномерно на мноок.естве М, если имеет ме-
место sup
J{a)-ff(x,a)dx
= sup
J f(x,a)dx
-> 0. А -¥ +оо.
Примеры. 1. Несобственный интеграл
J(a)=+/°— A)
1
сходится для а > 1. В случае множества Mi = [2, +оо) имеем для А > 1 :
sup
ае[2,+оо)
: sup
ae[2,+oo) (.a -
+ 0О.
Следовательно, интеграл A) сходится равномерно на М\. Для множе-
множества М2 = A, +оо) равномерной сходимости нет, поскольку для А > О
+°°dx 1 ^
sup J — = sup ,, .. , = +оо.
ae(l,+oo) A X «e(l,+oo) (a "
2. Несобственный интеграл
+r° sin ax ,
I dx
B)
сходится для каждого а € R в силу признака Дирихле. Интеграл B)
сходится равномерно на множестве МG) = {а | \а\ > 7}> 7 > 0>
поскольку для А > 0 имеем
sup
'sinai
dx
= sup
+ 0O
/
A
sin a x
a] dx
— sup
+°°sinx ,
f — dx
\a\A X
= sup
B>yA
sinx
dx
0,
+oo.
Интеграл B) не сходится равномерно на М = R, так как для А > О
+ ОО
sup
+5° sin ax
sup
+ O
/
sinx
/• sinx
> 0.
Замечание. Согласно определению, равномерная на М сходи-
+°°
мость несобственного интеграла J f[x,a)dx, a £ М, равносильна
+оо
равномерной на М сходимости несобственного интеграла / /(х, a) dx,
ь
а € М, для любого Ь > а.

13.3. Равномерная сходимость несобственных интегралов 407
С помощью критерия Коши равномерной сходимости последователь-
последовательности функций получаем следующий критерий равномерной сходимости
несобственного интеграла.
Теорема 10. Для того, чтобы несобственный инте-
грал / f(x,a)dx, а £ М, сходился равномерно на мноо*се-
а
стве М, необходимо и достаточно, чтобы Ve > 0 3 Ло >
А"
ff(x,a)dx
A'
<e.
13.3.2 Признаки равномерной сходимости
несобственных интегралов
Теорема 11. (Признак Вейерштрасса). Предполо-
снсим, что функции f : [[а, +оо) х М) -> R, g : [а,+00) —> R
удовлетворяют условиям: l)Vx>aVa£M: \f(x,a)\ < g{x);
+00
2) J g(x)dx сходится. Тогда несобственный интеграл
а
+оо
f f(x,a)dx, a € M, сходится равномерно на М.
а
\ Интеграл сходится абсолютно при любом а € М. Утверждение о рав-
равномерной сходимости следует из оценки
+ ОО +ОО /£
sup
J f{x,a)dx< / g(x)dx-+0, А-У+00.
А
+оо sjn ax
Примеры. 1. Несобственный интеграл J j dx, a £ R, сходит-
о 1 + х
ся равномерно на А в силу признака Вейерштрасса для а = О, М =
R, /(x,a) = ^^, x>0, aeR, g(x) =-J—, х>0.
, x>0, aeR, g(x) =-J—, х>
1 Т* о-
2. Несобственный интеграл J dx, a E [2,10J, сходится
! а + ха
равномерно на [2,10] в силу признака Вейерштрасса для о = 1, М =
Q. COS Q. X 10
[2,10]; f(x,a)= , х > 1, а £ [2,10]; д(х) = —^ , х > 1.
OL -Г X Z -г А
Теорема 12. (ЛризиакДириазле^. Предположим, что
функции f : ([а,+00) х М) —yR,g: ([а,+00) х М) -> Л удовле-
А
творяют условиям: 1) ЗС £ R sup sup f f(x,a)dx < С; 2)
аеМ А>а а

408 Глава 13. Несобственные интегралы, зависящие от параметра
Va € M функция д(-,а) монотонна на [а,+оо); 3) h(x) :=
sup |з(х,а)| -> 0, х -> +оо. Тогда несобственный интеграл
+оо
A)
f{x,a)g{x,a)dx, a£M,
а
сходится равномерно на М.
Г Доказательство проведём при следующих дополнительных ус-
условиях: V (х, а) е ([а, +оо) х М) существует g[(x,a), V a € М V А>
a: 5i (•-«)€ Я([а, Л]); Va€M: /(-,«)€ С([о, +оо)).
Интеграл A) сходится для каждого a € М, в силу признака Дирих-
х
ле сходимости несобственного интеграла. Пусть .F^a) := J f(u,a)du,
а
F[(x,a) = /(x,a), x > а, а £ М. Применяя формулу интегрирования
по частям, получим:
+ ОО
sup
/ f{x,a)g(x,a)dx
= sup
+ ОО
/ F{{x,a)g{x,a)dx
= sup
F(x,a)g(x,a)
+ оо
- / F(x,a)g'1(x,a)dx
А
+oo
J g'1{x,a)dx <2Ch{A)-+0, A -> +oo. J
Примеры. 3. С помощью теоремы 12 легко устанавливается рав-
равномерная сходимость интеграла B) п. 13.3.1. Нужно положить a =
1, /(x,a) = sinax, g(x,a) = l/x, x > 1, a £ M(~f). Условия теоре-
теоремы 12 проверяются легко.
4. Несобственный интеграл f sin ж" dx, a € M(j) := {a G R | а >
о
7}, 7 > li сходится равномерно на МG)- Для доказательства в тео-
теореме 12 можно положить о = 1, /(x,a) = axa~1sinxa, <?(x,a) =
-, х > 1, а £ ММ. Тогда sup sup) f axa~1smxa dx < 2.
ax01-1 ~
Условие 2) выполнено и /i(x) = sup
ах*
— -¥ 0, x -> +oo.
Упражнение 11. Доказать равномерную сходимость на М = {а €
+оо
R | |а/| > 1} несобственного интеграла J sin(ax3) dx, a € R.
Упраэгсиеиие 12. Пусть / : [0,+оо) -> Я, УЛ > 0 : /€ Я([0,А|) и
I
sup / е~а°х/(х) dx < +оо; а0 € Я. Доказать, что для любого е > О
0<Л<+оо1 О

13.3. Равномерная сходимость несобственных интегралов
409
+оо
+
интеграл J e~axf(x)dx, a > ао, сходится равномерно на множестве
о
[ао+е,+оо).
Теорема 13. (Признак Абеля). Предположим, что
функции f : ([а,+оо) х М) -* R, g : ([а,+оо) х М) -* R удовле-
удовлетворяют следующим условиям: 1) несобственный ин-
теграл f f(x,a)dx, а € М, сходится равномерно на М; 2)
а
Va 6 М функция д(-,а) монотонна на [а,+оо); 3) ВС 6 R :
+ОО
sup sup ^(я.а)! < С. Тогда интеграл J f(x,a)g(x,a)dx, а € М,
1>ао6М о
сходится равномерно на М.
\ Доказательство проведём при том же дополнительном предпо-
предположении, при котором доказывалась теорема 12. Введём функцию
F(x,a;A) := j f(u,a)du, x > А > а, а € М. Применив формулу
А
интегрирования по частям, получим
sup
f f{x,a)g(x,a)dx
= sup
«ем
+оо
lim {F{x,a;A)g{x,a))- f F{x,a;A)g[{x,a)dx
< С sup
+oo
f f(u,a)du + swp sup\F(x,a; A)\ ■ f g[(x,a)dx
a£M x>a
+oo
+oo
< С sup f f(u,a)du + sup sup\F(x,a; A)\2C-> 0, A->+00. J
A
+00 _:
Примеры. 1. Несобственный интеграл J
sin г
е ах dx, a > 0, схо-
дится равномерно на [а, +оо) в силу теоремы 13 для а = О, С =
1; /(s,ot) = —, g{x,a) = e-ax, х > 0, ае[0,+оо).
х
-> и il - +?°sinx dx
2. Несобственный интеграл / , а > 0, сходится рав-
5 а; 1 + ах2 ~
номерно на [0,+схэ) в силу теоремы 13.
Упражнение 13. Функции /п : [а, +оо) -¥ R, п > 1 удовлетворяют
Ь оо оо b
условиям: 1) V6 > а : J Yl fn(x)dx= ^2 ffn{x)dx; 2) сходятся инте-
а n=l n=l a
+оо оо оо +оо оо +оо
грал / 2 fn(x)dx и ряд 2 / fn(x)dx; 3) lim £ / /»(*)<** =
a n=l n=l a b-++oo n=1 ь

410 Глава 13. Несобственные интегралы, зависящие от параметра
+ ОО С» С» +ОО
^0. Тогда / £ /»(*)& = £ / fn(x)dx.
a n=l n=l a
13.4 Свойства функций, определяемых
интегралами
13.4.1 Основные теоремы
Предположим, что М = [с, d] С R. В этом разделе рассматриваются
свойства несобственного интеграла J(a) = f f(x,a)dx, a G [с, d], как
a
функции от a.
Теорема 14. (О непрерывности несобственного ин-
интеграла по параметру). Предполоэюим, что выполня-
выполняются условия: 1) f G С([а, +оо) х [c,d]); 2) несобственный
+ ОО
интеграл J(a) = f f(x,a)dx, a £ [с, d], сходится равномерно
на [c,d]. Тогда J E C([c,d]).
п
[ Для п £ N, п > а положим Jn(a) = /f(x,a)dx, a £ [c,d]. По
a
теореме 6 функция Jn G C([c, d]) для каждого п > а. Кроме того,
+ ОО
по условию 2) теоремы sup |J(a) — Jn{ot)\ — sup J f(x,a)dx —>
ae[c,d] <*e[c,d] n
0, n —» схэ. Следовательно, функция J есть равномерный на [с, d] предел
последовательности {Jn \ n > а} непрерывных на [с, d] функций и по
лемме 1 п. 8.1 — непрерывна на [c,d]. J
Теорема 15. (О предельном переходе под знаком не-
несобственного интеграла). Пусть М с R, а0 — предельная
точка М. Предположим,, что функции f : ([а, +оо) х М) -» R
и g : [a,+oo) -» R удовлетворяют условиям; 1) VA > а :
sup \f(x,a)-g(x)\ -» 0, а-»а0; 2) несобственный интеграл
хе[а,А]
+ оо
J(a) = J f(x,a)dx, a G М, сходится равномерно на М. Тогда
а
lim. f f(x,a)dx= f g(x)dx.
а^а° а а
+оо
f Несобственный интеграл f g(x) dx сходится в силу критерия Коши.
a
Действительно, для заданного е > 0, согласно условию 2), имеем

t3.4. Свойства функций, определяемых интегралами
411
■ 3A0>aVA'> Ao \/A"> Ao Va£M: ff(x,a)dx<s.
A'
Применяя к последнему интегралу теорему 9 получаем неравенство
А"
f g(x) dx < е. Заметим теперь, что при любом А > а справедливы
А'
+оо +оо
также следующие неравенства
f{x,a)dx- f g(x)dx
f f[x,a)dx-Jg(x)dx + J f[x,a)dx + f g(x)dx
+00
+00
J
+00
| Л Л | Т°° "ТОО
<\ff{x,a)dx-fg{x)dx\+sup f f{x,a)dx + J g{x)dx.
I а «Ш a ' argM A A
Теперь, используя теорему 9, условие 2) и сходимость интеграла
J
J g(x) dx, получаем утверждение теоремы.
а
Замечание. Случай, когда ао = +оо, также возможен.
Теорема 16. (Об интегрировании по параметру).
Предположим, что длл функции f : ([а, +оо) х [с, d]) -> R
выполнены, условия: 1) f £ С([а, +оо) х [с, d]); 2) интеграл
J(a) = J f(x,a)dx, a £ [с,d], сходится равномерно на [c,d].
а
Тогда J £ C[c,d]) и
d d ,+cx> . +оо , d .
fj(a)da = f(ff{x,a)dx)da= f (ff{x,a)da) dx. A)
f To, что J £ C[c,d])t следует из теоремы 14. Далее для любого А > a
d d.A .
имеем равенство fj(a)da = JlJf(x,a)dx)da + r(A), где г (А) :=
= / / f{x,a)dx)da и \г{А)\ < sup / f(x,a) dx {d - с) -> О, А ->
с Ч А ' ae[c,d] A
+оо, согласно условию 2). На основании теоремы 8 заключаем, что
d A^d^ Г -"
J J(a)da = П f f(x,a)dx] da + r(A). Отсюда при А -> +oo получаем
с a ^c '
сходимость несобственного интеграла из правой части равенства A) и
требуемое равенство. J
Теорема 17. (О дифференцировании по параметру).
Предположим, что для функции f : ([a, +oo)x[c,d]) -> R вы-
выполнены условия: 1) существует f'a и f'a £ С([а, +00) x [c,d]);
+00
2) существует число а0 £ [c,d], для которого J f(x,ao)dx

412 Глава 13. Несобственные интегралы, зависящие от параметра
+оо
сходится; 3) f f'a{x,a)dx, a e [с, d], сходите а равномерно
+оо
на [c,d]. Тогда интеграл J(a) = f f(x,a)dx сходится для
а
каждого a e [c,d], существует производная J' на [c,d] и
справедливо равенство J'(a) = f f^(x,a)dx, a G [c,d].
a
\ Можно положить ао = с. Согласно условиям 1) и 3) теоремы и утвер-
утверждению теоремы о непрерывности несобственного интеграла по пара-
параметру, функция
Дв):= / f'a{x,a)dx, a£[c,d], B)
a
непрерывна на отрезке [c,d]. Применим к несобственному интегралу B)
теорему об интегрировании по параметру, а затем формулу Ньютона-
а +оо ,а , +оо &• V^ IX-)
Лейбница fl{u)du = / [f f'a(x,u) du) dx = / (f(x,a) - f(x,c))dx.
с a Vc ' а «Г
Учитывая условие 2), получаем сходимость интеграла J(a), a 6 [c,d], и
a
следующее равенство J(a) = JI(u)du + C, a G [c,d], где I € C([c, d])
+ ОО
и число С = f f(x,c)dx. Из свойств интеграла как функции верхнего
а
предела получаем утверждение теоремы. J
тт . « +?°sina; , тт
Примеры. 1. Докажем, что J dx = — .
о х 2
+оо
sinaa;
f Для a £ R рассмотрим сходящийся интеграл F(a) := f da;.
о x
Легко проверить, что Va £ R : F(-a) = -F(a); F@) = 0, ^(a) =
^A), a > 0. Пусть /3 > 0. Введём интеграл J(a) := / e~px dx,
о x
a £ R, к которому после естественного доопределения подынтеграль-
подынтегральной функции / в точке 0 применима теорема о дифференцировании по
параметру для любого отрезка [с, d], поскольку для f'a{x,a) = cos ax •
е~Рх, х > 0, a £ R, условия этой теоремы выполнены. Получим Va 6
+ ОО
R : J'(ot) = J cosaz • e~Px dx. Теперь, дважды интегрируя по ча-
стям, получим J'(a) = —^——j, а £ R. Таким образом, J(a) =
= arctg — + С, a G R. Поскольку J@) = 0, то С = 0. Пусть далее
о = 1. Интеграл 7A) сходится равномерно относительно /3 > 0 в силу
признака Абеля равномерной сходимости. Согласно теореме 14 инте-

13.4. Свойства функций, определяемых интегралами 413
грал J(l) — непрерывная функция от /3 на [0,+оо). Поэтому
х;- ,. .„, ,. +?°smx _g +?°siiix
hm J(l) = lim f e px dx = j dx.
/Э-Ю+ /Э-+0+ о X о I
Кроме того, lim J(l) = lim arctg — =-. J
2. Интеграл Фруллани. Пусть / e С1 ([0, +оо)), причём / мо-
монотонна на [0, +оо) и существует lim /(x) =: /(+оо).
X—V+OO
Тогда +f°l№lz.M^l dx = (/(+oo)-/@))ln-, a > 0, Ь > 0.
0 х а
+оо
\ Пусть а < Ь. К интегралу J f'(ax)dx, а 6 [а, Ь], равномерно схо-
о
дящемуся согласно признаку Вейерштрасса равномерной сходимости,
применим теорему об интегрировании по параметру
g = f G f(«*)**) ^ = Tf{bX) ~ HaX) **. J
a a^O ' 0 X
жг . , +?° cos ax — cos ba; ,
Упражнение 14- Вычислить интеграл J 5 ax, где
о x
{a,b}cR.
Упражнение 15. Для a > 0, 6 > 0 вычислить интеграл:
+ оо р—ax _ «—Ьх +с» р—ах2 _ _—6х2
а) / £ ! dx; Ь) Г * dx.
Jo х Jo х
Теорема 18. (Об интегрировании по бесконечному
промежутку). Предположим, что функция/: ([а, +оо) х
[с,+оо)) -» R удовлетеорлет следующим условилм: 1) f £
+00
С([а,+00) х [с, +оо)); 2) V d > с : / f(x,a)dx сходится рав-
а
+ оо
номерно на [c,d]\ 3) Vb > a : / f(x,a)da сходится рав-
с
номерно на [а,Щ; J^) для х > а, а> с сходятся интегралы
/ |/(z,a)|dx, / |/(a;,a)|da и сходится хотя бы один из ин-
интегралов
/ ( / !/(*, а)\ da) dx, I ( / !/(*, а)\ dx) da. C)
Тогда справедливо равенство
+oo,+oo N +сю,+оо ч.
/. ( / /(*, a) dx) da = I (J f(x, a) da) dx,
в котором все интегралы сходятся.

414 Глава 13. Несобственные интегралы, зависящие от параметра
\ Предположим, что сходится первый из интегралов в C). Сначала ис-
используем условия 1), 2) и теорему об интегрировании несобственного
интеграла по параметру для d > с :
d ,+oo v +оо d
/(/ /(x,a)dz)da = f F(x,d)dx, F(x,d):=ff(xla)da, x > a.
с ^ a 'a c
+oo
Заметим, что Vi > a Vd > с : \F{x,d)\ < g{x) := / |/(x,a)|da, и,
с
+ OO
согласно условию 4), интеграл f g(x)dx сходится. Поэтому, в силу
a
+оо
признака Вейерштрасса, интеграл f F(x,d)dx, d> с, сходится равно-
a
+оо
мерно на [с, +оо). Кроме того, V А > a : sup F(x,d)- J f(x,a)da =
[A]
= sup J f(x,a)da\—> 0, d —» +00. Согласно теоремте" о предельном
переходе под знаком несобственного интеграла, существует предел
^m^ +fF(x,d)dx = TCjj», F(x>d))dx = 7GЛ1»a)da)dl- J
13.4.2 Вычисление интеграла Эйлера-Пуассона
Докажем равенство f e~x dx = —- .
о 2
[ В сходящемся интеграле J := f e~x dx сделаем замену переменной
х = at, где число a > 0; J = f e~a * a dt. Далее имеем с учётом
о
2
a
2
свойств интеграла как функции нижнего предела J2 = J Je~a da =
о
+°° 2 +О0,+О0 .
= Иш f Je'a da = Ит / ( f e~a * ~a adt) da.
e-+0+ Je e-fO+ J V ^ /
Теперь для произвольного фиксированного е > 0 к следующему
+ 00 ,+00 2 2 2 \
интегралу f I J e~a * ~a adt) da применим теорему 18. Условие 1)
e ^ 0 '
теоремы 18 выполнено, кроме того, Vd > 0 : sup f ae~a f* +1^ d< <
e<a<d yl
-f-OO -r-OO
< d / е-«а(*а+1) Л -> 0, A -> +oo; V6 > 0 : sup / ae-a^^ da <
A 0<t<b A

'43.4. Свойства функций, определяемых интегралами
< J ae~a da —> О, А —> +оо. В силу теоремы 14 имеем такое утвер-
А
+00.+00 N +ooe-e2(t2+l) _
ждение / ( / ae~^^ da) dt = f L3 , .,<* -* \ , e -> 0 + .
0 v e 7 0 zl' + ^-N
Таким образом, J2 - 7r/4. ^. (euocu**i  T'^- J
Упражнение 16. Доказать, что: а) / е ах dx = - J — , а > 0.;
о 2 у а
i . +?°cosax , +?°xsinax ж _„ „ , _
Ь) Г г dx = j — dx = — е , а>0 (интегралы Ла-
'Jii~2 ^ 1-1- -г2 О
"*' +°° +о° 1 piT
пласа); с) J sinx2dx= / cosx2dx = -w— (интегралы Фре-
•/• о о 2 у 2
.иеля).
+оо
Упражнение 17. Пусть J |/,(x)|fcdx < +oo, j,к = 1,2; положим
—оо
+ ОО +ОО
Л(х) := J /i(x — и)/г(и)du. Вычислить / /i(x)dx.
—оо —оо
Упражнение 18*. Обосновать следующее вычисление интеграла
+оо 2 +оо / д.2 . п
Эйлера-Пуассона: Г е~х dx = f lim 1 ) dx =
о о п->°° ^ п ^
= lim И 1 - — ) dx = lim (x/n / sin2n+11dt ]= ^- .
n^oo J V rt / n-oo VV J У 2
Указание. Использовать формулу Валлиса.
13.4.3 Несобственные интегралы от неограниченных
функций, зависящие от параметра
Пусть М С R; f : ([а,Ь) х М) -»Я- функция такая, что при неко-
некоторых а £ М функция /(-,а) : [а,Ь) -»Яне является ограниченной в
окрестности точки 6. Предположим, что для каждого а £ М интеграл
ъ
J f(x,a)dx сходится.
a
Определение 1. Интеграл
ь
//(x,a)dx, a eM, A)
a
Ь
сходится равномерно на М, если sup / f(x,a)dx -» 0 при
agM Ъ—е
£-»0 + .
27 — 4-1168

416 Глава 13. Несобственные интегралы, зависящие от параметра
Исследование свойств интегралов вида A) вполне аналогично иссле-
исследованию свойств интегралов по неограниченно промежутку. На инте-
интегралы вида A) переносятся утверждения пп. 13.3 и 13.4, в частности,
справедлив признак Вейерштрасса.
13.5 Гамма-функция. Бета-функция
13.5.1 Определение гамма-функции. Элементарные
свойства
Гамма-функция Г определяется для значений а > 0 следующим обра-
зом Г(а) := f e~xxa~1 dx. Интеграл, определяющий значение функ-
о t
ции Г(а), есть сумма -*/d»C)
1 +оо е •>
Г{а) = fe-xx°-1dx+ I е-'х^Чх^Х т*' A)
о 1 *■ У1- )
в которой первый интеграл сходится при а > 0, так как е~хха~1 ~
ха~х, х -¥ 0+, а второй — сходится для любого а£Й.
Используя равномерно сходящийся на [0,1] ряд Тейлора для функции
f(x) = е~х, х 6 R, из равенства A) получаем следующее представле-
представление для Г(а)
Заметим, что формула B) позволяет дополнительно определить функ-
функцию Г для всех значений а, исключая числа 0, — 1, — 2, — 3,..., — п,...,
поскольку при всех таких а правая часть равенства B) определена.
Перечислим простейшие свойства функции Г.
1°. Из определения следует, что Г(а) > 0 для а > 0.
2°. Функция Г имеет на @,+оо) производные всех порядков, которые
можно получать с помощью дифференцирования под знаком интеграла.
Например,
+ ОО +ОО
Г(а):= / e-*xa-1]jixdx, Г"(а) := / e-1Bse-1(liis)ads, a > 0.
о о
[ Для доказательства дифференцируемости в фиксированной точке од
нужно применить к интегралам в равенстве A) и а 6 [/0,7], гДв 0 < /3 <
а0 < 7, теорему 17. J
5°. Функциональное уравнение для гамма-функции.
Va>0 : Г(а+1) = аГ(а).
[ Для доказательства используем формулу интегрирования по частям

13.5. Гамма-функция. Бета-функция 417
+ ОО
Г(а + 1) = Km (-see-")-O + a / e!0 dx = аГ(а), a > 0. J
Замечание. Из свойства 3 следует, что функция Г на @, +оо)
определяется своими значениями на @,1]. Более того, функциональ-
функциональное уравнение позволяет доопределить гамма-функцию на всю ось, ис-
исключая точки 0, —1,—2,...,—п, Именно, для значений а £ (—1,0)
положим Г(а) := -, где (а + 1) 6 @,1), затем для значений
а £ (-2, -1) положим Г(а) := — , где (а + 1) £ (-1,0), и т. д.
Далее предполагаем, что функция Г определена на множестве R \
{0, —1, -2, -3,..., —п,...} с помощью интеграла для а > 0 и с помощью
функционального уравнения для остальных значений.
4°. ГA) = 1, ГB) = 1, Г(п) = (п - 1)!, n e N,
\ Последнее равенство получается с помощью следующей замены пе-
переменной х — t2 и использования интеграла Эйлера-Пуассона. J
Упражнение 19. Построить график гамма-функции.
Упражнение 20. Для п е N вычислить Г(п + 1/2).
Упражнение 21. Доказать, что Г(а) ~ —, а -► 0+, Г(а) -*
+со, а —> со.
Упражнение 22. Проверить, что гамма-функция строго выпукла
вниз на @,+со).
Определение 1. Пусть А — интервал Функция f :
А -» @,+со) называется логарифмически выпуклой на А,
если функция In/ выпукла вниз на А.
5°. Гамма-функция логарифмически выпукла на @,+со).
Г Чтобы убедиться в выпуклости вниз функции In Г рассмотрим произ-
производную AпГ)" = Г~2(Г"Г - (Г'J), принимая во внимание свойства 1°
и 2°. Используем теперь неравенство Коши следующим образом
(Г»J =
/ (e-/aa.(«-i)/a^e-*/aa.(«-i)/a]na.^dl^ < Г(а)Г"(а).
Следовательно, (InГ(а))" > 0, а > 0. f'fl*~(f') 7° J
27-

418 Глава 13. Несобственные интегралы, зависящие от параметра
Упражнение 23*. Доказать, что сумма и произведение логариф-
логарифмически выпуклых на А функций логарифмически выпуклы на А. Рас-
Рассмотреть случай функций класса С2(А).
Упражнение 2^*. Доказать, что положительный поточечный на А
предел последовательности логарифмически выпуклых на А функций
есть логарифмически выпуклая на А функция.
13.5.2 Основная теорема теории гамма-функции
Теорема 19. Предположим, что функция f : @, +оо) ->
@,+со) удовлетворяет условиям,: 1) /A) = 1; 2) Va > 0 :
/(а + 1) = а/(а); 3) f логарифмически выпукла на @,+оо).
Тогда
Va>0: /(в) = Г(в). A)
[ Из условий 1) и 2) следует, что /(п) = (п — 1)!, п £ N. Равен-
Равенство A) достахочно_дЙказать только для a 6 @,1]. Отметим, что Va 6
@,1] V п > 2 : n-l<n + a<n + l. Поскольку функция In / выпукла
вниз на @, +оо), то для наклона этой функции относительно точки х = п
. имеем
№] Ь/(п-1)-1п/(п) 1п/(п + а)-1п/(п) ln/(n
f
Ло (n-l)-n {n + a)-n ~ (n
Ч* => 1П(П - 1) < ^M»-r«J-mUT.-x;!; < bn
+ а) <па(п-1)!
(п- 1)а(п^1)! <'F>7^"t*ije * "Л(" - 1)!
а(а + 1)... (а + п - 1) - J v ' - а(а + 1)... (а + п - 1)
B)
так как, согласно условию 2), ([- п) ТТГ^"^ "^ *-41* с<-'"'
/(n + a) = (n+a-l)/(n + a-l) = ... = (n-l + a)(n-2+a).. .a
то из B) имеем :—/(a) < —. ——'-. r < /(a). Таким обра-
' a + n v ' ~ a(a + l)...{a + n) ~ K ' K
зом, для любого a 6 @,1] существует предел
lim —. ^-. = /(a). C)
Следовательно, функция / определяется на @,1] единственным об-
образом, Поскольку гамма-функция удовлетворяет условиям 1) — 3) тео-
теоремы, то / = Г. . J

13.5. Гамма-функция. Бета-функция 419
13.5.3 Основные формулы для гамма-функции
1°. Формула Эйлера.
а(а + 1^!(а + п). A)
( ^( + )
[ Формула A) для а € @,1] была доказана в п. 13.5.2, соотношение C).
Положим Г„(а) '•= а/а + д? П',а + пч ■ об(Д\{0,-1,...,-п,...}).
Для/3 6 A,2] имеем Г„@) = "(f ~ ^ Гп(^-1), причём @-1) 6 @,1].
р + п
Следовательно, существует предел lim Г„(^) = (>5— 1)Г(/3 — 1) = Г(/3).
n-юо ati
Далее аналогично рассматривается интервал B,3] и т. д. KL_i£L
Если же р £ (-1,0), то Гп@) = Р я Г„()9 + 1), гДе (j9 +' 1)
@,1). Поэтому существует предел lim Г„(/3) = - Г(р + 1) = Г@). J
2°. Представление Вейерштрасса.
n=i
где С := lim A + -+... Ч In n\ С и 0,577215..., С — посто-
п-юо \ 2 П J
янная Эйлера. £ ^ j&w-
f Представим Г„ в следующем виде
^ л.^-^
а1Т
fc=i k
где 7п := 1 + г + ... Н Inn, п > 1. Как было доказано в п. 7.2.2,
2 п
последовательность {7n | n > 1} сходится. Следовательно, сходится
произведение в равенстве B) и это равенство справедливо. J
3°. Формула Лемсандра удвоения аргумента.
Va>0: 2-1
[ Положим /(а) := —= 2а~1Г(— )Г( ), а > 0, и докажем, что
у/"п \ 2 / \ 2 /
функция /удовлетворяет условиям теоремы 19. Действительно,

420 Глава 13. Несобственные интегралы, зависящие от параметра
1
Кроме того, функция
(|) (^^) a > О,
есть сумма с положительными коэффициентами функций, выпуклых
вниз. Следовательно, функция In/ выпукла вниз. По теореме 19 полу-
получаем равенство / = Г. J
4° • Функциональное уравнение Эйлера. Верно равенство
^ C)
[ Для а 6 (Н\ Z) положим ip(a) := Г(а)ГA - a)sin7ra. Функция ip
периодична с периодом 1, так как для а £ {R\ Z) верно равенство
<р{а + 1) := r(a + l)r(-a)sin7r(a+l) = аГ(а)Г^_~ ^ (-sin™) = ip(a).
Кроме того, поскольку имеем tp(a) := — ГA + а)ГA - a)sin7ra =
_. . / тг3а2 тг5а4 \
= ГA + а)ГA - а) I тг — 1—— ... I, то существует следующий
предел lira ip(a) = тт.
Доопределим теперь функцию tp, положив её равной тг в точках
из Z. Доопределённая функция <р имеет в точке a = 0 производные
всех порядков, поскольку такие производные имеют следующие функ-
функции ГA + а), ГA — а) и сумма сходящегося на оси степенного ряда.
Поэтому ip 6 С°°(Я). Функция ip положительна на R. Применив дважды
формулу Лежандра, получим равенство
^ D)
сначала для a E @,1), а затем, учитывая периодичность и определение
на Z, и на R.
Рассмотрим теперь функцию ф := (lnp) 6 C°°(R), периодическую
с периодом 1. Из формулы D) для функции яр' имеем уравнение
Отсюда для любого п 6 N получаем равенство
H'W, «е [0,1],
fc=0
из которого на основании теоремы Дарбу следует соотношение
1
fip'(u)du — ф'(а),а 6 [0,1]. По формуле Ньютона-Лейбница имеем
о
0 = V(l) - V'(O) = Ф'{а), a € [0,1]. Таким образом, ф(а) = ф@), а 6
[0,1], а для значения ф@) = lnip(Q) = In тт. Следовательно, ip(a) =
eV(a) = е1лтг _ 7Г> а 6 |о,1], и потому <р(а) = тг, а е R. Если a ^ Z, то
последнее равенство приводит к формуле Г(а)ГA — а) = — . J
smxa

13.5. Гамма-функция. Бета-функция 42J
Упражнение 25. Доказать, что г(- +а)г(- - а\ =
cos тга
13.5.4 Разложение синуса в бесконечное произведение
Согласно уравнению Эйлера, имеем следующее равенство Va 6 (Н \
Z) : Г(а)ГA - a)sin7ra = тг, или -аГ(а)Г(-а) sinTra = тг^Отсюда с
I too—е±и/п
помощью представления Вейерштрасса Г(±а) = етСа—— \\ ■ а ■
1 оо ! Л. ffffinM)M
а 6 (.Г1\ Z), получим равенство — {j 5" sinira = тг, из которого
следует представление sinTra = тга ]"[ 11 —^ 1 сначала для a 6 (H\Z).
n=i^ п '
В точках из Z равенство также имеет место. Таким образом, получено
следующее представление \/а € R: sinTra = тга J~[ A — ®т J.
п=1 ^ '
Упражнение 26. Доказать, что для любого а £ R справедливо
представление cos тга = ]~[ f 1 — Bn-iJ ) •
оо п(п — — )
Упражнение 27. Найти значение произведения ]~[
n=l I™ - 4 Г
Упражнение 28. Доказать, что для о > 0 справедливо равенство
о
13.5.5 Формула Стирлинга
Теорема 20. (Формула Стирлинга). Справедливо
следующее равенство Va > 0 : Г(а) = %/2тгаа-* e-«ee(«)/(i2<«))
где 0 < 0(а) < 1.
Г I. С помощью ряда Тейлора для функции f(x) = ln(l + х), \х\ < 1,
1 1 + х ^^ х2п
имеем Vx 6 R, х ф 0, |х| < 1 : r~ In z = Yj 7, 7 ■
2х 1-х n=Q 2n +1
II. Введём функцию F(a) := (a+r )Wn— ) —1, a > 0. Учитывая
I, получим
i 1 +
2a+ 1 2a+ 1
Поэтому

422 Глава 13. Несобственные интегралы, зависящие от параметра
. 1 ^ 1 11
< 3
i
III. Используя теперь последнюю оценку для следующей функции
оо
/*(а) := Л Fin + а)> Ма + !) ~ А4!") = --^Х0). а > 0, получаем
п=0
такие неравенства 0 < /л(а) < ——, а > 0, из которых имеем
/х(а) = j~ , а > 0; 0(а) := 12а/х(а), 0 < в {а) < 1, а > 0.
Заметим также, что по теореме о почленном дифференцировании фун-
оо
кционального ряда /х"(а) := ^ F"(n + а) > 0, а > 0.
п=0
IV. Рассмотрим положительную функцию /(а) := ao"se"o+'1'e',
а > 0, и докажем, что функция ///A) удовлетворяет условиям основ-
основной теоремы теории гамма-функции. Действительно, для а > 0 имеем
f(a + 1) := (а + i)«+i-i/2e-«-i+M(««+i) =
= (а + 1
1 = af{a).
Кроме того, (In/(а))" = Ь —- + //'(а) > 0, а > 0, и потому
функция / логарифмически выпукла на @, +оо).
Таким образом, на основании основной теоремы теории гамма-фун-
гамма-функции имеем /(а)//A) = Г(а), а > 0.
Для определения постоянной 1//A) используем для функции Г фор-
формулу Лежандра
2-1J Г^Г/2/2-/2+^/2) J
^ ае _ Q > 0_
откуда J_ = ^V2f_^_r/2el/2eM(a)-M(a/2)-M((a+l)/2)] Q > „_ По.
/A) \а + 1 J
скольку 1х{а) -)■ 0, а -» +оо, то 1//A) = %/2тг. J
Следствием доказанной теоремы является известная формулу Стир-
линга для п! с п 6 JV, а именно
ra! = v/27rnnne-nee(n)/A2n), 0 < 0(п) < 1.
Для доказательства нужно использовать равенство п! = пГ(п), п £
N, и доказанную выше формулу для Г(а) с а = п.

13.5. Гамма-функция. Бета-функция 423^
13.5.6 Бета-функция
Бета-функция В : (@, +оо) х (О, +оо)) -л R определяется равенством
B{a,p):=}xa~l{\-xf-1dx, a > 0, р > 0. A)
о
Приведём некоторые свойства бета-функции.
1°. Интеграл A) сходится при а > 0, @ > 0, и для любых фиксиро-
фиксированных ао > 0, Ро > 0 сходится равномерно на следующем множестве
([а0,+оо) х[/30)+оо)).
2°.В€С(@,+оо) х@,+оо)).
3°.Va>0V/3>0 : В(а,/3) = В(/3,а).
Доказательство получается заменой 1 - х = t в интеграле A).
5°. В(а,)9 + 1) = -~-B(a,P), ao>Q,po>0.
\ Доказательство этого равенства следует из формулы интегрирования
по частям
Л!D1)
x=l
0;B(£.,« = ™.
[ Пусть f3 > 0 фиксировано. Докажем, что функция
Па):=щВ(а,р)Г(а+р), а > 0,
удовлетворяет условиям основной теоремы теории гамма-функции.
Действительно,
В(а + llj9)r(a
Функция В(а,Р), а > 0 логарифмически выпукла на @,+оо), что
доказывается аналогично случаю гамма-функции. Поэтому / логариф-
логарифмически выпукла как произведение логарифмически выпуклых функций.
Следовательно, / = Г. J

424 Глава 13. Несобственные интегралы, зависящие от параметра
Упражнение 29. Выразить через значения гамма-функции интегра-
+оо т/2
лы: а) / е~х dx; Ь) / sin01 ucos^'1 udu, a > 0, /? > О;
о о
1 dx "I2
с) / -jP== ; d) / (tguJ" du, 0 < a < 1.
Упражнение 30. Предположим, что о < Ъ. Вычислить следующий
ь
предел lira ( —== Ге ^ dx).
13.5.7 Историческая справка
Джеймс Стпирлинг A692 — 1770) — шотландский математик.
Первым получил асимптотическое разложение для логарифма гамма-
функции, установил ряд свойств бета-функции и гипергеометрической
функции.
Адриен Мари Лежандр A752 — 1833) — французский мате-
математик. Автор работ по теории специальных функций (многочлены Ле-
жандра), вариационному исчислению, теории чисел, также известных
учебников, в частности "Теории чисел".
Симеон Дени Пуассон A781 — 1840) — французский физик и
математик. Автор основополагающих работ по небесной механике, по
многим разделам математической физики, теории упругости, матема-
математическому анализу, теории вероятностей и др.
Гамма-функция принадлежит к числу наиболее удивительных объек-
объектов математики. Эта функция и связанная с ней бета-функция, которые
часто встречаются в различных математических задачах и приложениях
математики, привлекала к себе внимание самых выдающихся математи-
математиков. Многие существенные результаты об этих функциях получены Эйле-
Эйлером, в частности Эйлер получил формулу связи гамма и бета-функции,
частные случаи формулы Лежандра. Существенные результаты принад-
принадлежат Гауссу в связи с его работами о гипергеометрической функции,
ему принадлежит общая теорема умножения для гамма-функции. Осо-
Особый раздел теории этих функций составляют работы, посвященные про-
продолжению гамма-функции в комплексную плоскость. То, что свойство
логарифмической выпуклости характеризует гамма-функцию, обнару-
обнаружено недавно. Э. Артин в 1931 г. показал, как можно получить все
основные теоремы о гамма-функции, исходя из этого факта.

Глава 14
Кратные интегралы
14.1 Кратные интегралы по брусу
14.1.1 Определения и обозначения
В настоящей главе рассматриваются подмножества пространства Rm и
действительные функции, определённые на этих подмножествах. Про-
Пространство Rm рассматривается как линейное полное метрическое про-
пространство с евклидовым расстоянием. Необходимые определения, в
частности, определения расстояния, нормы и т. п. см. в п. 11.1.1. Пред-
Предлагаемая ниже конструкция определения интеграла является ещё одним
обобщением схемы определения интеграла Римана на случай функций
от нескольких переменных.
Определение 1. Прямоугольным параллелепипедом в
Rm (или т-мерным интервалом или брусом) называет-
т
сл множество Q = [ai.bi] х [a2,b2] х ... х [om,bm] = П [ofc,bfc] =
fc=i
= {£ = (n,...,im) e Rm | ak < xk < bk, 1 < к < m},{ofc, bk} С
R, ofc < bk, 1 < к < т. Диаметром бруса Q называется
число
d{Q) := sup(p(z, у) | х 6 Q, у 6 Q) = Ц (bk - akf
Vfc=i
Объёмом (точнее т-мерным объёмом) или мерой (т-
мерной мерой) бруса Q называется положительное чис-
т
ло m(Q) := П (h - о»,).
fc=i
Упражнение 1. Пусть Qi и Q2 — брусы в Ят. В каких случаях
множества Qi П Q2, Qi U Q2, Qi\ Q2 являются брусами в Ят?
425

426 Глава 14. Кратные интегралы
Упражнение 2. Пусть Q — брус в Rm, Q° — множество всех внут-
внутренних в [Rm,p) точек Q и dQ =: Q\Q° — граница бруса Q. Предста-
Представить 8Q в виде объединения 2тп брусов из Д, каждая пара которых
не имеет общих внутренних точек в (Я"^). Отдельно рассмотреть
случаи m = 1, m = 3.
m
Пусть Q = П [afc,bfc] — брус. Для каждого к, 1 < к < т, рассмот-
fc=i
рим для отрезка [afc,bfc] некоторое его разбиение, т. е. набор точек
Хк = {xfc(O), Xfc(l),..., Xfc(nfc)}, ak = ccfc(O) < ifc(l) < . < Xfc("fc) = bfc,
и положим Дц(^) := Xk[v + 1) - Xfc(i'), v = 0,1,2,..., Пк - 1; при этом
i/=0
Для любого набора целых чисел v\, V2,. ■ ■ ,vm таких, что Vfc, 1 <
к < m : 0 < ик < пи — 1, рассмотрим брус
= П [xfc(i'fc),Xfc(i'fc + l)] с объёмом m(Q{v1,v2,...,vm)) - П Axfc(^fc)-
fc=l fc=l
Определение 2. Набор брусов Л = {Q{vuv2,■ ■ • ,vm)} -
= {Q{yi,v2,---,vm) | 0<i/fc <nfc- 1, 1 <fc<m}
называется разбгхемиел* бруса Q. Диаметром или разме-
размером разбиения Л называется число
|Л| = max{d(Q(i/i, 1/2,..., I'm)) | 0 < vk < nk - 1, 1 < fe < m}.
Заметим, что ^ rn(Q{ullu2,..., vm)) = m(Q).
Пусть ш(Х) := {(i^i, u2,..., i/m) | 0 < i/fc < nit - 1, 1 < fc < m}.
14.1.2 Суммы Дарбу и их свойства
Пусть Q — брус, функция / : Q -л R, } ограничена на Q. Предпо-
Предположим, что Л = {Q(^i,i/2i • • ■ ,Vm)} — некоторое разбиение бруса Q.
Определение 3. Нижней суммой Дарбу для функции
f и разбиения X называется сумма
L(f;X):= E inf / -m{Q{vltVi,...,um)).
(t/i,t/2 vm)£u(\)QV/l'v*'"'v™)
Верхней суммой Дарбу для функции f и разбиения X
называется сумма
U(f;X):= £ sup / ■m(Q(vliv2,...,vm)).
(x,v2,-..,vm)

'44.1- Кратные интегралы по брусу 427
"Пусть V (i/!, v2,._.., vm) 6 ш(Х) : f(i/i, i/2)..., vm) £ Q{vlt v2,..., vm).
Набор точек {({vu v2,..., vm)} = {£*0i, Щ, ••■,vm) I ("l, v2, ■ ■ ■, vm)
£ w(X)} называется набором, соответствующим разбие-
разбиению X. Интегральной суммой для функцииJ, разбиения
X и соответствующего разбиению набора {£{yi,v2,---,vm)}
называется сумма
Е f(((vi,V2,.--,vm)) ■m{Q{vuv2,...,vm)).
Поскольку для любого набора индексов {v\, v2,..., vm) € и{Х) спра-
ведливы неравенства
inf/< inf /</U>i,^,...^m))< sup /<sup/, A)
Q Q^u,-,Vm) Q(vX,V2,.,.,Vm) Q
то, умножив неравенства A) на m(Q(yi, v2, ■ ■ ■, Vm)) > 0 и просум-
просуммировав по всем наборам (i/1( v2,..., vm) из ш(Х), получим следу-
следующее свойство введенных сумм: для любого Л и любого набора
{^(^li V2, ■ ■ ■, vm)}, соответствующего разбиению Л, верны неравенства
inf/ ■m(Q)<L(f]X)<S(f;X,{fcuV2,...,Vm)})<
<C/(/;A)<sup/ m(Q). B)
Q
Из неравенств B) следует, что множества всех верхних и
нимсних сумм Дарбу, соответствующих всем возмож-
возможным разбиениям бруса Q, являются ограниченными.
Заметим теперь, что разбиение Л бруса Q из определения 2 по-
получается с помощью разбиений Ai,A2,...,Am соответственно отрезков
[oi,bi], [ог.Ьг], ..., [<Jm,bm]- Рассмотрим теперь для каждого из раз-
разбиений Ai, А2,. -., Am соответствующие им подразбиения А'1( А'2,..., А'т,
(которые получаются из Ai, А2,..., Ат добавлением новых точек).Пусть
А' разбиение бруса, полученное с помощью разбиений А^, А'2)..., А^,.
При этом каждый брус Q{vi,V2, ■ ■ ■ ,Vm) разбиения А окажется раз-
разбитым на части-брусы {Q(^i,^2. • • • > ^m/Mi.M2, • ■ ■ .Mm)}, которые со-
составляют разбиение X'(vi, v2,..., i/m) бруса Q{vi, v2,..., v-т)- Таким об-
образом, имеем А' = {Q(i/i, v2,..., vm/ini, ц2, ■ ■ ■, цт) \ (мь Мг, • • •, Mm) 6
, v2,..., vm) 6 w(A)} и следующее равенство
V2, ....
= m{Q{vltv2,...,vm)).
Определение 4- Разбиение Х' бруса Q, полученное опи-
описанным, выше способом., называется подразбиением раз-
разбиения X.

428 Г л а в а 14. Кратные интегралы
Суммы Дарбу, соответствующие разбиению Л и любому его подраз-
подразбиению Л', связаны следующими неравенствами:
Hf;X) < L(f-X') <U(f;X') <U(f;X). C)
Для доказательства неравенств C) используем неравенство B) для
бруса Q(vj., v2,..., vm), функции / и разбиения X'(vi, v2,..., vm) :
inf / ■m(Q(v1,v2,...,vm)) <
,V2 t/m)
inf J ■m(Q{u1,u2,...,um/fj.i,H2,...,IJ.m)
.Q(VI,V2 t/m//li,/J2,...,/lm)
l,M2 Mm)
SUp f ■m{Q(vllV2l...>Vm/l*uH2 Mm)
sup / ■m{Q{v1,v2,...,vm)),
i,t/2,...,t/m)
где суммы по (/ii,/i2, ■ ■ ■, Mm) берутся по всем возможным брусам раз-
разбиения \'{vi,V2, ■ ■ ■, vm)- Просуммировав полученные неравенства по
всем наборам (i'i, v2, ■ ■ ■, vm) из ы{\), получим формулу C).
Пусть А' и А" — два разбиения бруса Q, полученные с помощью раз-
разбиений A'lt А'2)..., Х'т и А", А-;,..., А^, соответственно отрезков [ai,bi],
[02,62], • • •, [о-т,Ьт]. Положим А^ = A'fc U AJJ, 1 < к < т, и пусть А —
разбиение бруса Q, полученное с помощью Ai, A2,.. ■, Am. Разбиение А
является подразбиением каждого из разбиений А', А". Учитывая нера-
неравенства A) и C), получим L(/;A') < L(/;A) < U(f;X) < U(f;X").
Таким образом, для любых двух разбиений А', А" бруса Q справед-
справедливо неравенство
Ь(/; А') <Щ/; А"). D)
Упражнение 3. Пусть при m = 2, А — разбиение прямоугольника
Q, полученное с помощью разбиений Ai и Ад отрезков [ai,bi] и [02,62]
соответственно. Пусть Д : [ofc,bfc] -> Я, к = 1,2 — ограниченные функ-
функции. Доказать равенства: а) L(g; A) = L(/i; Ai)(b2 - ^2) + Ь(/2;Аг)(Ь1 -
oi), U(g;X) = C/(/i;Ai)(b2 - o2) + U{f2;X2)(b1 - 01) для g(xltx2) =
h(xi) + f2(x2), (xx,x2)eQ; b)L(/i;A) = L(/1;A1)L(/a;A3), U(h;X) =
W(/iiAi)C/(/2iA2) для h(xi,x2) = /i(xi)/2(x2), (xi,cc2) € Q при усло-
условии, что /i > 0, /2 > 0.
Чр
14.1.3 Верхний и нижний интегралы. Определение
;; кратного интеграла по брусу
5Пусть Q — брус и / : Q —>• R — ограниченная на Q функция.
Определение 5. Нижним интегралом от функции f
по брусу Q называется число J, = supL(/;A).

14.1. Кратные интегралы по брусу 429
Верхним интегралом от функции f no брусу Q называ-
называется число J* = inf U(f; A).
Точные грани берутся по всевозможным разбиениям.
А бруса Q.
Из неравенств D) п. 14.1.2 следует, что справедливо неравенство
Л < J*. A)
Определение 6. Функция f называется интегриру-
интегрируемой по брусу Q (обозначение f 6 R(Q)), если J* = J*.
Для интегрируемой функции f число J := J» = J* называ-
называется интегралом (точнее т-кратным интегралом) Ри-
мана от функции f no брусу Q и обозначается одним.
из следующих символов: J f(x) dx, J f{x\,..., xm) dx\... dxm,
Q Q
bl b2 bm
J J ... J J\X\j x2i • • -, xm) dx\dx2 ... uxm.
При m = 2 и m = 3 интеграл часто называют также
двойным и тройным соответственно.
Упражнение 4- Пусть дополнительно к условиям упр. 3 функции
/fc 6 R[[ak,bk]), k = 1,2. Доказать, что {g, h} С R{Q) и определить
двойные интегралы от g и h no Q.
Упражнение 5. Для т = 2 привести пример функции, для которой
имеет место неравенство Jt < J*.
Упражнение 6. Доказать, что / 6 R{Q) тогда и только тогда, когда
Ve>0 ЗА : U[f; A) - £,(/; А) < е.
Упражнение 7. Интеграл от постоянной функции. Пусть
с 6 R и /(х) = с, х 6 Q. Доказать, что J cdx — cm{Q).
Q
14.1.4 Интегрируемость непрерывной функции
Лемма 1. Пусть функция f : Q -> R удовлетворяет длл
некоторого числа е > 0 условию
36>0V{x,y}cQ,p(S,y)<6: \f(x)-f(y)\<e. A)
Тогда VA,|A|<5: U{f; A) - L(/; A) < em(Q).
f Пусть разбиение А имеет размер |А| < 6. Тогда для любого бруса
Q[vi,u2,...,um) разбиения А : d(Q(ui,u2,... ,ит)) < 6, и потому
SUP / ~ „, inf J = SUP (/(*) ~ /(У)) <e-
J.-.l-m)

1Л430 Глава 14. Кратные интегралы
С помощью этого неравенства получаем оценку U(f] А) — L(f; А) =
£ (sup /- inf f)m{Q{ultV2,...,um))<
("i,^ ^)eu(A)vQ("i.,-,"m) W-^ ^m) / /.^W
< em(Q). захчгмГа*, 1>(t. $-mu<1 ^^^j. 0,)P*' J
Теорема 1. Функция f 6 C(<?) интегрируема no Q.
\ Брус С? — ограниченное замкнутое подмножество в (ilm,p), сле-
следовательно, компактное в этом пространстве. По условию теоремы
/ 6 С(<5), поэтому по теореме Кантора функция / равномерно непре-
непрерывна на Q. Следовательно, условие леммы 1 для функции / и любого
е > 0 выполнено. Из определения интегралов Jt, J*, неравенства A)
п. 14.1.3 и утверждения леммы 1 для любого разбиения А, |Л| < 6
имеем 0 < J* - Л < U(f;\) — L(f;\) < em(Q). Отсюда получаем
О < J* - J* < em(Q) для любого е > 0. Таким образом, J* - Л = 0. J
Теорема 2. Пусть f б C[Q). Тогда
Ve>0 36>0 VA, |Л] < <5 (
//(x)dx- £ f(((vllV2,...,vm))m(Q{vi,v3,...,vm))<
Q (V1,V3 l-m)ew(A)
< em{Q).
f Теорема утверждает, что для непрерывной функции кратный инте-
интеграл совпадает с пределом интегральных сумм. Для функции / выпол-
выполнено условие A) леммы 1. Кроме того, согласно определению J, и J*
имеем неравенства VA : L(/;A) < Л = //(x)dx = J* < U{f;X), и
Q
V А V {fallV3, ...,vm)}: L(f; A) < S(/; A, {£>!, v2>..., *m)}) < ВД ^)-
Отсюда следует неравенство \f f{x)dx - S[f;X,{({v1,u2,... ,vm)})\<
< U[}\ A) — L(/; А). Согласно лемме 1 теперь получим
Ve>0 3E>0 VA,|A|<<5: [/(/; A) - L(/; A) < em{Q). J
Следствие 1. Пусть f e C(Q), {\W \ n > 1} — последо-
вательность разбиений бруса Q, удовлетворяющая усло-
условию |А(")| -> 0, п -> со. Пусть для каждого натурального
п {$n1(vi,V2, ■ ■ ■ ,vm)\ — некоторый набор, соответствую-
соответствующий разбиению а'").
Тогда lim S(f; A^, {|t»)(Vlf V2, •. •, vm)}) = / /B) dx.
n—voo л
14.1.5 Свойства интеграла от непрерывной функции
Теорема 3. Для любого с£ R /cdx = cm{Q).
Q

14.1. Кратные интегралы по брусу 431
Теорема 4. Пусть Q — брус в Rm u Q = Qi U Q2, где
Qi) Q2 — брусы в Rm, не имеющие общих внутренних
точек. Пусть f £ C[Q).
Тогда //(£) dx = / f(x)dx + / /(£) dx.
Q Qi O2
f В силу теоремы 1 все интегралы в утверждении теоремы определены,
Построим последовательность {Л'п' | п > 1} разбиений бруса Q следу-
следующим образом. Пусть А'1' состоит из брусов Qlt Q2] разбиение А'2' —
разбиение Q, которое является подразбиением А'1); вообще, разбиение
\(п) — разбиение Q, которое является подразбиением А'п-1'. Последо-
Последовательность разбиений можно взять такой, что |А'П)| —^ 0, п —> оо. Для
каждого п > 1 брусы разбиения А^"\ лежащие в брусе Qk, составляют
разбиение Aj. бруса Qk, k — 1,2. При этом |А^| -4 0, п -> со, к = 1,2.
Заметим также, что
S(f; \(n\{£n4"W2, • ■ ■, I'm)}) = Е S(f; \{kn), {£»(*!, u2,..., un)}).
it=i
Остаётся к последнему равенству применить следствие 1. . J
Теорема 5. Пусть fk е C{Q), ckeR, к = 1,2.
Тогда ДС1Д(£) + c2f2(x)) dx = Cl / Д(£) dx + c2f }2{x) dx.
Q Q Q
f Доказательство следует из равенства
S(c1/1 + c2/2;A) = c1S(/1;A) + c2S(/2;A). J
Теорема 6. (Теорема о среднем значении). Пусть
функция / е C(Q). Тогда Зв £ Q : / f{x)dx = f{$)m{Q).
Q
\ Поскольку / € C(Q) и Q — компакт в (Rm,p), то 3{xt,x*} С
Q : inf/ = f(xt), sup/ = }[х*). Теперь из определения интеграла и
Q q
неравенств A) п. 14.1.2 имеем f{xt)m(Q) < Jf(x)dx < f{x*)m{Q),
Q
или /(i.) < ——- J f{x)dx < f{x*). Отрезок {x*+t{x* - x») | t £
[0,1]} С Q. Рассмотрим функцию ip(t) := f{xt + t{x* - £,)), t £ [0,1].
По теореме о непрерывности суперпозиции непрерывных функций ip £
С([0,1]). Кроме того,
По теореме Кош и о промежуточном значении имеем равенство Зв £
[0,1] : (р(в) = ——-г f }{x)dx. Положив в :=■ х„ + в(х* — х»), получим
Tn[Q) q
утверждение теоремы. . J
28 —4-1168

432 Глава 14. Кратные интегралы
Теорема 7. Пусть / е c{Q) u Дх) > о, х е Q.
Тогда ff{x)dx>0.
Q
[Для доказательства воспользоваться теоремой 6. J
Теорема 8. Пусть Д 6 C{Q), к = 1,2 и Д(х) < Д(х), х 6 Q.
Тогда / Д(х) dz < / /2(£) dx.
Q Q
f К функции Д — Д применить теоремы 7 и 5. J
Теорема 9. Пусть / 6 C(Q). Тогда I/ Дх) dx < / |/(х)| dx.
f Использовать неравенства —1/| < / < |/| и теорему 8. J
Упражнение 8. Пусть / 6 C(Q) и /(х) > 0, х £ Q. Доказать, что
//(x)dx>0.
Q
Упражнение 9*. Пусть Q = [О, I]2, функция / е -R(Q) и равна 0 во
всех точках непрерывности. Доказать, что J/(xi,X2)dxidx2 = 0.
14.1.6 Формула приведения m-кратного интеграла к
последовательным однократным
Для вычисления m-кратного интеграла J Дх) dx по брусу Q имеется
Q
простая формула, сводящая вычисление этого интеграла к последова-
последовательному вычислению однократных интегралов Римана.
Пусть т > 1. Для бруса Q = {(хь ..., хт) \ ак < хк < Ьк, 1 < к <
т} в Rm и каждого к, 1 < к < т, рассмотрим также следующий брус
Qk ■= {(xi,...Jxfc_i,xfc+i1...)xm) | а, < Xj < bj, 1 < j < m, j фк} в
Д, Qk — проекция бруса Q на гиперплоскость хк = 0.
Упражнение 10. При m = 2 и т = 3 для бруса Q определить все
брусы {Qk}-
Пусть / 6 C{Q). Тогда Vfc,l<fc<mVc6 [ак,Ък] : / 6 C(Q П
{х | Xfc = с}). Поэтому для любого х 6 [afc.bfc] определён (т — 1)-
кратный интеграл по брусу Qk
дк{х) := / /(xi,..., Xfc_i, х, хк+1,..., xm) dxj... dxfc_idxfc+i... dxm.
Л е м м а 2. Пусть f e C(Q).
Тогда для каждого к, 1 < к < т : дк £ С([ак,Ьк]).
\ На основании теорем 5 и 9 для любых {х',х"} С [ait,bfc] имеем

14.1. Кратные интегралы по брусу 4с№
■•,*«)- A)
О*
.. ,a;fc_i,x",Xfc+i,... ,xm)j dxi.. . dxn!_1dxfc+i... dxm.
Пусть произвольное число е > 0 задано. Поскольку / 6 C{Q) и Q-
компакт, то по теореме Кантора для числа е
j-- 36 > 0 V{x,tf}CQ,p(x',y)<6: |/(х) - f(y)\ < —^— . B)
""* Пусть теперь {х',х"} С [ajt, bfc], |x' - х"| < 6. Тогда для векторов
X ' = (ХЬ . . . , Xfc_i, X', Xfc+i, . . . , Xm), X " = (Xi, . . . , Xfc_1( X", Xfc+1, . . . , Xm),
где (x1,...,Xfc_i1xfc+i1...,xm) 6 Qk, имеем p(x',x") = |x' - x"| < 5, и
поэтому согласно неравенству B) |/(х') - /(х")| < e/m(Qk). Из этого
неравенства, формулы A) и теорем 8 и 3 находим
jgfc(x') - git(x")| < / dxi... dxfc_idxfc+1... dxm = e.
; Таким образом, дк равномерно непрерывна на [ajt, bfc]. J
Теорема 10. Пусть f e C(Q). Тогда для любого к, 1 <
ьк
к<т справедливо такое равенство / }{x)dx= f gk(x)dx =
Q *k
-bf(rt( \j \
— J I / J№l 3Tfc—1) Xfci Xk+i, • . . , Xm) aX\ . . . d.Xk—idXk+1 • ■ ■ dXm I
«* V Q* I
f Пусть произвольное число е > 0 задано. Поскольку / 6 R{Q), то
существует разбиение Л бруса Q такое, что U(f;X) - L(/;A) < e.
Разбиение Л естественным образом разбивает брус Qk- Сначала имеем
Ьк Ik — I Ik(l'fc + 1)
fgk{x)dx= E / ffk(x)dx<
а» "к—(
nfc-l
< E SUP
< e «up М*)Д**Ы<^(/;*).
Vk=0 x£[ik(
где /iit(x) :=
E sup /(xi xk_ux,xk+1,...,xm)YlAxj(vj)
"" ()
и второе неравенство получено путём замены (т — 1)-кратного инте-
Ьк
грала дк{х) верхней суммой Дарбу. Аналогично, J gk(x)dx > L(f;X).
28

434 Глава 14. Кратные интегралы
Поскольку L(f; А) < / /(x)dx <U(f;X), то |//(x)dx - /gk(x)dx <
П 1О rt,_
Следствие 2. Пусть feC(Q). Тогда
Ьт . Ьт-l . , Ь\ ч v ч
//(x)dx=/( / (...(//(xll...)xm)dx1)dz2...)dxm_1)dxm.
Q ат Ча„_! Ч 4<ц til
\ Доказательство получается с помощью последовательного примене-
применения теоремы 10. Заметим, что порядок интегрирования может быть
произвольным. J
Следствие 3. Пусть f £ C(Q). Тогда длл любого к, 1 <
к < т, справедливо равенство
J /(х) dx = J ( / /(х) dxit) dxi... dxk-idxk+i... dxm.
\ Для доказательства достаточно дважды применить следствие 2. J
Следствие 4- Пусть f e C(Q), существует f'k на Q и
f'keC{Q). Тогда
dx = J }{x\,.. ..Xfc-i.bfc.Xfc+i,... ,xm) Y[jj:kdxj-
Qk
- f /fail- ■ •,2;jt-i.ajfc,xjfc+i,... ,a;m) f] dxj. C)
Qk ЗФЬ
\ Для доказательства использовать следствие 3 и формулу Ньютона-
Лейбница. J
Простая формула C) представляет собой некоторый аналог форму-
формулы Ньютона-Лейбница для m-кратного интеграла. Она также является
частным случаем общей формулы Гаусса-Остроградского, которая до-
доказывается далее на основании формулы C).
Упражнение 11. Для функции / 6 Cm(Q) вычислить интеграл
Q
Упражнение 12. Пусть / е C[Q) и Q{x1}..., xm) := {(щ,..., um) |
ак < ик < хк, 1 < к < т}, {хх хт) 6 Q. Положим g(xlt..., хт) :=
= f f(u)du, (xi,...,xm) 6 Q°. Вычислить следующие произ-
Q(xi xm)
dg dmg
водные -х— , 1 < к < т; -— — .
дхк дх1дх2..дхт
Упражнение 13. Пусть Q = [ai.bi] x [аг.Ьг], {1,9} С C2(Q) и

14.2. Множества, измеримые в смысле Жордана. Мера Жордана 435
f{xlta2) = f{xllb2) = 0, xi 6 [ai.bi]; g{ai,x2) = g{bux2) = 0, x2 6
[а2,Ьг]- Доказать равенство
d2g(xi,x2) rd2f{x1,x2)
«») dxdx=l
I №*'«») dxidx2 dxidx*=l dxxdx2
^применение 14- Пусть Q = [0,2тг]2, / e C([-l,l]2). Вычислить
^зедел lim //(sinna;1,cosnX2)da;idx2.
15. Пусть / e C1^), Q = [ОД]2. Вычислить предел
lim (n(//(
x1)x2)dx1dx2--i El /f.
Упражнение 16*. Пусть / 6 C(Q), Q = [0,l]2. Вычислить предел
Упражнение 17. Пусть / 6 С([0,1]), Qn = [0,1]". Вычислить предел
lim / }{хгх2 ...хп) dxjdx2 ... dxn.
woo
rwoo Q
Указание. В задачах 16 и 17 использовать теорему Вейерштрасса
для / соответственно на [0,1]2 и [0,1].
Упражнение 18. Пусть функция / : (a,/3) -> R выпукла вниз на
(а,/3) и [а,Ь] С (а,/3). Для п > 2 доказать неравенство
14.2 Множества, измеримые в смысле
Жордана. Мера Жордана
Для однократного интеграла отрезок является основным естественным
множеством, на котором определяется интеграл. При переходе к крат-
кратным интегралам положение существенно меняется. Например, в случае
двойного интеграла желательно уметь определять интегралы не только
по прямоугольникам, но и по таким множествам, как треугольник, круг
и т. п. Для определения кратного интеграла по множествам, более
сложным, чем брусы, нужно сначала распространить понятие объёма
на эти множества. Первое распространение понятия меры (т. е. дли-
длины в случае множеств на R, площади для подмножеств R2 и объёма
для подмножеств R3) на довольно широкий класс подмножеств при-
принадлежит французскому математику К. Жордану. Множества из этого
класса называются измеримыми по Жордану, а их объём-мера

436 Глава 14. Кратные интегралы
называется мерой Жордана. Мера Жордана обладает обычными
свойствами, которые присущи длине, площади и объём/.
14.2.1 Разбиение пространства Rm
Определение 1. Разбиение нулевого порядка прост-
пространства Rm есть следующее его представление в виде
объединения брусов Rm = (J <?'°'(ni>-- • >nm). где
nfceZ,l<fc<m
Qi0)(nb..., nm) := {? = (xlf..., xm) | nfc < xfc < rifc + l, 1 < fc < m}.
Пусть п е N. Разбиение п-го порядка пространства
Rm есть следующее его представление в виде объедине-
объединения брусов Rm = U Q(n)("i. •■•>пт), где QW{nu...,nm)
— <xfc < 2n , 1 <fc<m|.
Разбиение нулевого порядка можно получить следующим образом.
На каждой из координатных осей отметим точки, координаты которых
есть целые числа, и через эти точки перпендикулярно к осям проведём
гиперплоскости. При т = 2 получим разбиение плоскости на конгруэнт-
конгруэнтные квадраты со стороной 1 (бумага в клетку). Для получения разбиения
первого порядка нужно дополнительно отметить на осях точки, коорди-
координаты которых кратны 1/2.
В дальнейшем используются следующие свойства разбиений про-
пространства Rm.
1°. Пусть F С Rm — ограниченное множество в (Rm,p). Для каждого
п 6 (ЛГ и {0}) набор брусов разбиения порядка п пространства Rm,
имеющих хотя бы одну общую точку с F, конечен.
J80. Для каждого п 6 (ЛГ U {0}) брусы разбиения порядка п + 1 полу-
получаются иэ брусов разбиения порядка п разбиением последних на 2т
конгруэнтных бруса.
5°. Диаметр и объём бруса разбиения порядка п соответственно равны
4°. Два различных бруса разбиения порядка п не имеют общих внут-
внутренних в (Rm,p) точек.
5°. Разбиение порядка п пространства Rm определяет естественным
образом разбиение порядка п таких подпространств, как подпростран-
подпространство RT-1 = {(X! Хт_!)}, Я2={(Х1,Х2)>ИТ. П.
Разбиение порядка п пространства Rm будем обозначать следую-
следующим образом тг(п) := 7г£° := {Q(n>(ni,... ,nm) | пк 6 Z, 1 < к < т},
при этом U Q = Rm.

14.2. Множества, измеримые в смысле Жордана. Мера Жордана 437
Для бруса Q 6 тг'") через Q0 будем обозначать множество всех его
внутренних в (Rm,p) точек.
Упражнение 19. В R2 изобразить множество точек, координаты
которых xi,X2 удовлетворяют условию sinBn7rxi) • sinBn7rx2) > 0, п£
(ЛГи{0>).
14.2.2 Измеримые множества. Мера
Определение 2. Объёмом (точнее т-мерным объё-
объёмом) или мерой (точнее т-мерной мерой) бруса Q =
т т
Y[ [afc.bit] называется число m(Q) := ]"[ (Ьк - ait)-
fc=i fc=i
s
Если G С Rm и G - U Qk, Qk 6 т(п\ 1 < к < m, при неко-
fc=i
тором, п, и все {Qk} различны,, то мера (точнее т-мерная
мера) множества G есть число
т
m(G) := E m(Qk). A)
Будем, также считать, что т@) := 0.
Упражнение 20. Проверить корректность последнего определения
(дело в том, что представление для G не единственно!).
Далее используется определение A) и связанные с ним элементар-
элементарные свойства.
Пусть F С Rm, F ограничено в (Rm,p). Для каждого п 6 (ЛГи{0})
определим множества F(n) := U Q\ F^ '■= U Q\
AF(n) := U Q. В том случае, когда бруса Q £ n^n\ для
которого Q С F, не существует, будем считать, что F(n) := 0.
При этом F(n) С F С FW, (F \ F(n)) С (F(») \ F(n)) С Щп)-
Упражнение 21. Для т = 2 рассмотреть геометрическую иллю-
иллюстрацию приведенных выше включений.
Мера множеств F(n), F^ и AF(n) определяется с помощью равен-
равенства A), справедливы следующие соотношения
m(F(n)) < m(F^), m(AF{n}) = m(F(")) - m(F(n)); n > 0.
Заметим, что определение чисел m(F(n)) и m(F(n^) для множества
F в плоскости является естественной конструктивной процедурой полу-
получения реальных приближений для площади множества F.

438 Глава 14. Кратные интегралы
Рассмотрим теперь разбиения порядков п и п + 1 пространства Rm
и соответствующие F множества F(n), F^n\ i^n+i), F^n+1\
Из свойства 2 следуют включения
F{n)CF{n+l}, F'n+1'CFW. B)
следовательно для мер этих множеств справедливы следующие нера-
неравенства
О < m(F{n)) < m(F{n+1)) < m(F<n+l>) < m(F<n>). C)
Согласно свойству 1° меры m(F^) и m(F^) конечны, и мы прихо-
приходим к следующему заключению: последовательность чисел
{m(F(n)) | n > 0} монотонно не убывает и ограничена, а
последовательность чисел {m(F'n') | гг > 0} монотонно не
возрастает и ограничена.
Определение 3. Внутренней мерой ограниченного
мноо+сества F С Rm называется неотрицательное число
mt(F) := Jim^ m(F{n)) = supm(F(n)).
Внешней мерой ограниченного мноок.ества F с Rm на-
называется число m*(F) := lim m(F^) = inf m(F^).
v n-*oo n>0
Из неравенств C) следует, что 0 < mr(F) < m*(F) для каждого
ограниченного множества F.
Определение 4- Ограниченное множество F С Rm на-
называется измеримым в смысле Жордана, если справед-
справедливо равенство mt(F) = m*(F). Для измеримого мноо*се-
ства F число m(F) := mt(F) = m*(F) называется мерой
Жордана (точнее, т-мерной мерой Жордана) мноэюе-
ства F.
Класс всех подмножеств Rm, измеримых по Жордану, обозначим
% — %т. Класс % не пуст, в него входят множества, составленные
из конечного числа брусов разбиений пространства Rm, поскольку для
такого множества F имеем F = F(n), m(F^) = m(F(n)) + Sn для всех
п, начиная с некоторого, причём <5П -» 0, п -» оо. Множество 0 также
будем включать в ЭС, полагая при этом тп{И:1 := 0. Заметим, что для
любого F € % : m(F) > 0.
Пример. Пусть тп > 1, с, L — фиксированные числа из R и
F = {£=[xll...,xm)\x1 = c, \xk\ < L, 2<k<m},
F — ограниченное множество, лежащее в гиперплоскости Zi = с. До-
Докажем, что m*(F) = m*(F) и m(F) = 0.
\ Множество F не имеет внутренних в {Rm,p) точек, поэтому F(n) = 0
для любого п > 0. Кроме того, для меры F^ имеем следующую

14.2. Множества, измеримые в смысле Жордана. Мера Жордана 439
оценку m(F^) < 2BL2n + 2)m~12-mn, n > 0. Поэтому m(F^) ->•
0, п -» оо, и, следовательно, mt(F) = m*(F) = 0. J
Упражнение 22. Множество F G DC и F° = 0. Доказать, что
ш(^) = 0.
Теорема11. Пусть F — ограниченное подмножество
Rm. Тогда F еХ <=> m(AF(n)) = m{F^n)) - m{F{n)) -> О, n ->• оо.
f Теорема представляет собой перефразировку определения измери-
измеримого множества. J
Упражнение 23. Доказать, что для любого i £ Я одноточечное
множество F = {х} G Х\ и m(.F) = 0.
Указание. Для каждого п > 0 имеем .F(n) = 0. Поскольку мно-
множество F^ состоит из одного или двух отрезков разбиения тг^ имеем
также m(F(n)) < 2 ■ 2~п -^ 0, п -> оо.
Упражнение 2^.. Доказать, что любой отрезок [а,Ь] G Х\ с мерой
пг([а, Ь]) = Ъ - а.
Указание. Учесть неравенства Bп(Ь — а) - 2J~n < m([a, £](„)) <
< 2"(Ь-аJ~п, и то, что Д([а,Ь](„)) состоит из одного или двух отрезков
разбиения тт^ , п > 0.
Упражнение 25. При m = 2 пусть F = {(zbZ2) | it £ (Qfl
[0,1]), А; = 1,2}. Найти mt(F) и m*(F). Множество F не является из-
измеримым по Жордану.
Упражнение 26. Доказать, что любой брус есть измеримое мно-
множество и его мера совпадает с определённой в п. 14.1.1.
Упражнение 27. Пусть F = {(xr, x2) \ xi>0, х2> 0, хх + х2 < 1}.
Найти m(F(n)), m(F(n)) для п > 1. Доказать, что F G ЭС2 и найти m(F).
Упражнение 28. Пусть F — замкнутое счётное подмножество от-
отрезка [а,Ъ]. Доказать, что F G Х\ и что m(F) = 0.
Упражнение 29. Пусть множество F G ЗС и число е > 0 заданы. До-
Доказать существование замкнутого измеримого множества G и открыто-
открытого измеримого множества Н таких, что G С F С Я, m{H)-m(G) < e.
14.2.3 Свойства измеримых множеств
Теорема 12. Пусть {А,В} С ЭС. Тогда имеют место
включения: а) (А и В) 6 ЭС; bj (Л \ В) G ЭС; с) (А П В) G ЗС.

/
440 Глава 14. Кратные интегралы
[ Докажем сначала, что для каждого п > 0 справедливы включения
Д(ЛиВ)(п) С(ДЛ(п)иДВ(п)), A)
Д(Л \ В)(п) С (ДЛ(П) U ДВ(П)), B)
Действительно, если брус Q £ ir^n\ Q С Д(Л U В)(п), то
Эх : xe{Qn{A0B)) и Эу : у £ (Q П {Rm \ {A UB))).
Если при этом i £ Л, то i G (QHi4) и у € (QP\(Rm\A)). Следовательно,
Q С ДЛ(„). Аналогично, если х £ В, то Q С ДВ(П)- Таким образом,
включение A) доказано. Если Q £ ir'n\ Q С Д(Л \ В)(п), то Эх : х €
(Q П {А \ В)) и Э у : у £ (Q П (Нт \ (Л \ В))). Если при этом у $ А,
то х £ (Q П А) и у £ (Q П (Hm \ Л)). Следовательно, Q С ДЛ(п). Если
же у £ Л, то у £ В, и поэтому у £ (Q П В), х € (Q П_ГЯт \ В)). Таким
образом, Q С ДВ(П). Тем самым включение B) доказано.11 <3г>1} и^/(-
Из A) и B) следуют неравенства: '
О < тп(Д(Л U В)(п)) < тп(ДЛ(п)) + тпД(В(п))Чо
О < тп(Д(Л \ В)(п)) < тп(ДЛ(п)) + тД(В(п)).
Применив дважды теорему 11, получаем утверждения а), Ь). Из
утверждений а) и Ь), а также из представления А П В = Л\(Л\В)
следует утверждение с). J
Замечание. Из теоремы 12 следует, что объединение и пере-
пересечение конечного числа измеримых множеств являются измеримыми
множествами. Класс множеств %} удовлетворяющий условиям а), Ь), с)
теоремы 12 назь\вается(колъцому Таким образом, класс множеств из-
измеримых по Жордану является кольцом, включающий б русы и конечные
объединения брусов.
Упражнение 30. Объединение счётного набора множеств из DC
может не принадлежать DC. Рассмотреть следующие примеры.
a) Пусть тп=1. Доказать, что любое одноточечное множество {х} €
%i и имеет меру 0. Множество, состоящее из конечного числа точек,
измеримо и имеет меру 0. Доказать, что множество {1/n | n £ JV} £ DCj
и имеет меру 0. Доказать также, что (Q Q [0,1]) ^ %i.
b) Пусть m = 1 и {rn | п > 1} — занумерованные каким-либо об-
образом все рациональные числа интервала @,1). Для числа г\ суще-
существует е > 0 : B(ri,e) С @,1)._^Цля произвольного фиксированно-
фиксированного 5, 0 < 5 < е, положим F± := B(ri,8/2). Пусть rmB) — первая из
оставшихся точек гг.^з,..., не попавших в F%. Пусть теперь F2 — за-
мкнутый шар с центром в точке гтB) и радиусом, меньшим 52~2 и
такой, что F2 С @,1), F\ П F% = 0. Аналогично строятся множества
-Pn, n > 3. Доказать следующие утверждения: 1) Vn > 1 : Fn £ DCj;
(ОО \ ОО
U Fn № OCi; 3) замыкание в (R,р) множества- (J Fn совпадает с
п=1 ' п-\

14.2. Множества, измеримые в смысле Жордана. Мера Жордана 441
отрезком [0,1]. Поскольку множества Fn, n > 1 попарно не пересека-
пересекаются, то их объединению естественно приписать "длину", равную сумме
оо
ряда Yl m{Fn), который сходится и имеет сумму, меньшую 25, так как
п=1
m(Fn) < 2-2~п5, п > 1.
14.2.4 Свойства меры Жордана
Заметим, что согласно определению, гп(А) > 0, A £ X.
1°. Полуаддитивность. Для любых {А, В} С X справедливо нера-
неравенство
тп(ЛиВ) <т{А) + т{В). A)
[ Согласно теореме 12, (A U В) £ X. Заметим, что
{A U В)(п) С {А(П) U AA{n) U B(n) U ДВ(п)),
так как входящий в левую часть брус содержит только точки A U В,
а в правой части представлено объединение всех тех брусов, которые
имеют по крайней мере одну общую точку хотя бы с одним из множеств
А, В. Поэтому
т{{А U В)(п)) < т{А{п)) + т(ДЛ(п)) + тп(В(п)) + т(ДВ(п)),
откуда, с помощью определения меры и теоремы 11, имеем
m(AuB)= lim m{{AU B)in)) <
П—+ОО
< lim тп(А(п)) + 0+ lim m{Bin\) + 0 = m(A) + m(B). I
~ п-юо v ' n-юо v '
Для множества А С Hm пусть А0 — множество всех его внутренних в
(Rm,p) точек. Заметим, что при любом п > 0 два различных бруса раз-
разбиения 7г(п) могут иметь общие точки, но не имеют общих внутренних
в (Rm,p) точек.
SP. Аддитивность меры Жордана. Пусть {А, В} С X и
А°ПВ° = 0. Тогда
т(ЛиВ) = т{А) + т{В). B)
[ Достаточно доказать неравенство т(АиВ) > тп(Л)+тп(В), поскольку
из этого неравенства и полуаддитивности A) следует равенство B).
Для любого п > 0 имеем (Л(п) U В(п)) С (Л U В)(п), причём мно-
множества А(п) и В(„) общих брусов из тИ") не имеют (в противном случае
А9) П В°п) ^ 0, следовательно, и А0 П В0 ^ 0). Поэтому
т(Л(п) U В(п)) = т{А(п)) + гп(В{п)) < т{{А U В)(п)).
Поскольку {Л, В, A U В} С ЗС, то т(Л) + n*{B) = lim т(Л(п)) +
+ lim т(В(„)) < lim m{{A U BW)^m(i4 U В). J
3°. Монотонность' Aiep*t. Пусть {Л, В} С ЭС, Л С В. Тогда

442 Глава 14. Кратные интегралы
m{A)<m{B), m{B\A) = m{B)-m(A).
\ Заметим, что В = A U (В \ А), причём А £ DC, (В \ А) £ DC, А П (В \
Л) = 0. Из аддитивности имеем равенство гп(В) = тп(Л) + тп(В \ А).
Используем теперь неравенство тп(В \ А) > 0. J
Упражнение 31. Доказать, что {[0,1), @,1)} С ЭСХ и, кроме того,
m([0,l)) = m(@,l)) = l.
Упражнение 32. Пусть {А, В} С DC. Доказать справедливость ра-
равенства тп{А и В) = т(А) + т(В) - т(А ПВ).
Упражнение 33. Для Л е DC доказать, что т(А) = 0 <$=>■ Л° = 0.
Упражнение 3^. Доказать справедливость следующего соотноше-
соотношения т(А U В) = т{А) -ф=ф- (В \ Л)° = 0.
Упраэ/смемие 35. Пусть Л*, £ DC и тп(Лк) =0, 1 < к < п. Доказать,
что m(Ai U A2 U ... U Л„) = 0.
14.2.5 Цилиндрические множества и их измеримость
Пусть Rm = {{х\,..., хт) | Xfc G И, 1 < А; < т}. В пространстве Я771 =
= {(xi,..., xm_i) | Xfc G Я, 1 < A; < m — 1} рассмотрим множество Л и
две функции Uj : А -> Я, j = 1,2 такие, для которых справедливо нера-
неравенство V(x1,...,xm_1) 6 Л : u1(x1,...,xm_1) < u2(ii,...,im_i).
Определение 5. Цилиндрическим в направлении оси
0хт мноясеством, с основанием А называется следующее
подмножество Ят С :- {(xi,... ,хт_ьхт) | (xi,...,xm-i) G
Л, «!(!!,...,!,„_!) < Хт <U2{xi,...,Xm-l)}-
Для цилиндрического множества С его основание будем обозначать
следующим образом ЬаС := Л.
Пример. При m = 2 цилиндрическими множествами являются круг,
треугольник, а при т = 3 — шар, часть цилиндра с осью, параллельной
оси Охз, полученная с помощью двух крышек.
т
Замечание. Брус Q = Y[ [afc,bfc] является цилиндрическим множе-
к=1
т-1
ством с основанием baQ = ]~[ [afc,bfc] — брусом в Я171 и функциями
fc=i
•^Ui(xll...,xm_1) = am, u2{xi,...,xm-i) = bm; (xlt...,xm-i) GbaQ.
; Очень широким является класс множеств, которые можно получить
■|.;как объединение конечного числа цилиндрических множеств. В практи-
практических приложениях можно обычно ограничиться только такими множе-
множествами.

14.2. Множества, измеримые в смысле Жордана. Мера Жордана 443
Теорема 13. Пусть С - цилиндрическое множество с
основанием, ЬаС и функциями и\, u2. Предполоо+сим, что:
1) ЬаС компактно в (Rm~l,pm_i) и ЬаС £ 0Ст-ъ 2) Uj £
C7(baC), J = 1,2.
Тогда множ.ества С компактно в (Rm,pm) и С Е Хт.
[ В конечномерном пространстве с обычным расстоянием множество
компактно тогда и только тогда, когда оно ограничено и замкнуто.
Ограниченность С следует из ограниченности ЬаС и ограниченности
непрерывных функций щ, и2 на компакте ЬаС. Замкнутость С следу-
следует из замкнутости ЬаС, непрерывности функций щ, и2 и определения
цилиндрического множества. Действительно, если последовательность
{(а^,...,!^) £ С | п > 1} сходится^: (х^!..,хт), то (хь... ,хт-\) £
ЬаС, поскольку (х<п\... .х^) £ ЬаС, п > 1; (х^,... .х^) ->
(ij,... ,xm_i), n -¥ оо. Кроме того, имеем ь&сцаСЬ / 4 ?
Отсюда следуют неравенства Ui(x\,..., xm_i) < xm <
Доказательство измеримости более сложно. Пусть Жт разбиение /-^
порядка п пространства /£"". Зто разбиение определяет также разби-
разбиение тг^!_1 порядка п пространства Rm~l = {(xi,... ,xm_i)}. Оцени,
величину т(ДС(п)). Заметим, что
ДС(П, = U Q
Пусть произвольное е > 0 задано. Согласно условиям 1) и 2), име-
имеем 3L > 0 V(xi,...,xm_!) £ ЬаС : -L < ui(ib... ,xm_i) <
< L, и к функциям ub U2 на ЬаС применима теорема Кантора. Сле-
Следовательно, 35 > 0 V{x = (xi,...,xm-i), У - (yi,---,ym-i)} CbaC,
р{х,у) <6:\uk{x)-uk{y)\<e, k = 1,2.
Далее рассматриваются ^только п, для которых у/т2~п < min(e,<5).
Пусть baQ G ^m-i и baQ С A(baC)(n). Брус baQ является осно-
основанием некоторого количества брусов Жт из ДС(П). Высота наиболь-
наибольшего "столбика" — бруса с основанием baQ, содержащего точки С,
не больше 2(L + 2~тЦ1амера — объём этого "столбика" не больше
2{L + 2-n)m(baQ). ^Q^ ^/
Пусть теперь baQ G Щ^-i и baQ С (ЬаС)(п). При этом baQ является
основанием не более чем двух "столбиков", высота каждого из которых
не большеШе + 2~п) и состоящих из брусов Жт , лежащих в ДС(П).
Таким образом, £( _ vi^xzut. % гр. ccndoutd ^ и«*г*Г с С -каш,

444 Глава 14. Кратные интегралы
т(ДС(п))=
baQCA(baC)(n) 1 baQC(baC)(n)
Q 2-n)m(A(baC)(n))"+Xe + 2-n)m((baC)(n)) <
2(L + 1)т(Д(ЬаС)(п)) + 8em(baC).
Поскольку baC S 3Cm-i по условию 1), to тп(Д(ЬаС)(п)) < е для
всех n, начиная с некоторого. Поэтому Эп0 Vn > no : т(ДС(п)) <
< B(L + 1) + 8тп(Ьас))е. Следовательно, С Е DCm. J
Упражнение 36. Доказать, что множество
0 < Xi < 1, 0 < *2 <
Упражнение 37. Пусть Г = {(хьх2) | з;г £ [а, 6], х2 = /(xi)} для
/ £ С7([а,6]). Доказать, что Г Е ЗС2> и что плоская мера тгг(Г) = 0.
Упражнение 38. Пусть yfc £ С1{а,0\), к - 1,2; (vi@
0, f G [а,/3]. Регулярная кривая есть множество
Г = {(ii,n) | xfc = <pk{t), t £ [a.jS], fc = 1,2}.
Доказать, что Г G 3C2, и что плоская мера тп(Г) = 0.
J
Упражнение 39. Пусть / £ СЦа^^] х [a2)b2]). Доказать, что по-
поверхность в R3
S = {(xltx2,x3) | (xi,x2) £ ([ai.bi] x [a2lb2]), x3 = }{xltx2)}
есть измеримое множество и имеет объём 0.
Упражнение 40*. Привести пример компактного неизмеримого по
Жордану множества в В?.
14.3 Кратные интегралы по измеримым
множествам
14.3.1 Определение интеграла
Пусть DC = %т — множество всех измеримых подмножеств Rm, множе-
множество A G DC и / : А —> R — ограниченная и непрерывная на А функция.
Для каждого п > 0 для разбиения Жт пространства Rm определим
множество А(п).
Определение интеграла по измеримым множествам включает ряд
этапов.
I. Определение интеграла от непрерывной функции по
брусу. Это определение было приведено и детально изучено в п. 14.1.

14.3. Кратные интегралы по измеримым множествам 445
II. Определение интеграла от непрерывной функции по
множеству А(п). Интеграл от непрерывной на А функции по мно-
множеству Л(п) определяется равенством
/ f(x)dx:= £ jf{S)dx, A)
где в правой части каждое из конечного числа слагаемых есть инте-
интеграл от непрерывной функции по брусу. Если множество А(п) = 0, то
положим f f(x) dx := 0.
Лемма 3. Пусть А Е X, функция f € С{А) ограничена на
А. Тогда последовательность чисел I f f{x) dx п > 0 >
фундаментальна.
Пусть к < п, тогда А(к) С Л(„) и , согласно определению A), имеем
f f(x)dx- f f(x)dx\=\ f f(x)dx
По условию леммы 3 L > 0 ViGj4: |/(i)| < L, а по теореме 9 для
бруса Q С А справедлива оценка
f(x)dx<Lm(Q). C)
Из формул B) и C) получаем следующее неравенство ^
/ f(x)dx- f f(x)dx\<m{A{n)\A°ik}) = L(m(A{n))-m(A{k))),
из которого следует утверждение леммы, так как последовательность
чисел {тп(Л(п)) | п > 0} сходится и, следовательно, фундаментальна. J
III. Определение интеграла от непрерывной и ограни-
ограниченной на А функции по измеримому множеству А.
т-кратным интегралом от функции / по множеству А называ-
называется число
//(£)<*?:=nlim / f(x)dx. D)
А А(п)
Если А £ DC и т(А) = 0, то Л(п) = 0 для п > 0 и / /(i) di := 0.
Приведенное определение допускает некоторое обобщение.
IV. Пусть А еХ, функция / ограничена на Л, В С А, В ЕХ с т{В) =
0 и /£ С(А\В). Интеграл от функции / по множеству А определяется
формулой D), если в качестве Л(п) взять объединение всех тех брусов
Жт i которые целиком лежат в множестве Л и не содержат точек из В.

446 Глава 14. Кратные интеграл^
14.3.2 Свойства интеграла
А £ X, с £ R и /(х) = с, х £ Л. Тогда
fcdx^cm(A). E)
[ Равенство E) справедливо для бруса, см. теорему 3, и, следователь-
следовательно, согласно определению A), для Л(п) имеем / cdx = стп(Л(п)).
Переходя к пределу при п —> оо в последнем равенстве, с учётом опре-
определений величин J cdx и m(A), получаем равенство E). J
А
А £ X, fk £ С(Л) и ограничена на Л, к — 1,2. Для любых
С R справедливо равенство
ciji[x) + C2j2[x)j ax = ci J /i(xj ax + C2 J /2C;) ax. [bj
A A A
f Справедливость равенства F) для Л(п) следует из определения инте-
интеграла A) и теоремы 5. Перейдя в этом равенстве к пределу при п -» оо,
&^чнётом определения III получаем равенство F). J
3°. Ьусть {А, В} С X и т(Л П В) = 0; функция / 6 С(А U В) и ограни-
""чена на Л U В. Тогда
АиВ А В
\ При любом п > 0 множества Л(п) и В(п) общих брусов разбиения тгт
не содержат. Поэтому, согласно определению A), имеем
/ /(x)dx+ / f(x)dx=A f f(x)dx. (8)
Кроме того, С„ := (Л U В)(п) \ (Л(п) U В(п))° С (АЛ(п) U AB(n)), откуда
f f{x)dx<
n) < 1,(т(ДЛ(п)) + т(ДВ(п)), L := sup |/|. (9)
лив
Нужное равенство получается из равенства (8) с помощью предель-
предельного перехода при п —> оо с учётом определения III, неравенства (9) и
эримости множеств А и В. J
4 . jiycTb Л G DC, / S С7(Л) и ограничена на А. Тогда
А
А
(" Сначала получаем равенство A0) для множества Л(п), используя опре-
определение A) и теорему 9. Затем, осуществляя предельный переход при
п —> оо, получим A0). J
\При условиях свойства 4° пусть f(x) > 0, х G Л. Тогда / /(£) dx > 0.
А

14.3. Кратные интегралы по измеримым множествам
[ См. теорему 7. J
Упражнение J^l. Теорема о среднем значении. Пусть мно-
множество А £ ОС компактно и обладает следующим свойством связности
\/{х,у} С А Зд £ С {[0,1],А), д{0) = х, д{1) = у. Тогда для функции
/ £ С(А) справедливо утверждение 39 £ А : //(х) dx = f($)m{A).
А
Упражнение ^2. Пусть {А, В} С ОС, В С А и гп(В) = 0. Функция
/ : А -» Я ограничена на Л и / £ С7(Л \ В). Пусть {Ах,.. .,Ап} С
п
DC, причём [j Ак = А и m(Aj П Л*;) = 0 для j 7^ k- Пусть также
lit € i4fc, I < К п, и А„ := max(d(i4fc) | 1 < к < п). Доказать, что
п _^
справедливо равенство lim Yl f{ik)m(Ak) = Г f(x)dx.
Упражнение J^3. Пусть выполнены предположение свойства 5° и
//(£) dx = 0. Доказать, что V х £ Л° : /(£) = 0.
14.3.3 Вычисление интеграла по цилиндрическим
множествам
Пусть А — цилиндрическое множество в Rm с компактным основанием
ЬаЛ С Rm-1 и непрерывными на ЬаЛ функциями их и иг, и / G С7(Л).
(Х1 Жт-l)
ПОЛОЖИМ ^(^Ь-- -.Xm-l) := / f[xi,.. ■ ,Xm-i,Xm)dxm ДЛЯ
Лемма 4. де С(ЪаА).
\ В том случае, когда функция / является многочленом, утверждение
леммы есть следствие теоремы о непрерывности сложной функции.
В общем случае применим теорему Вейерштрасса. Пусть произ-
произвольное е > 0 задано. Тогда существует многочлен Р€ от m пере-
переменных такой, что тах|/(х) - Ре{х)\ < е. Пусть he{xi,... ,zm_i) :=
xgA
U2(xi,--,Xm-l)
= / Pc{xi,... ,xm-i,xm)dxm, {xi,...,xm-i) £ baA Тогда
ui(xb...,xm_i)
функция he S С(ЬаЛ). Кроме того, имеем
V(xll...,xm_1) £ ЬаЛ : \д{хх,... ,xm-i)-he{xi,... ,xm-i)\ <£(L2-LX),
где Li :- minui, L2 := maxu2. iwlUi^i)
ba А ЪлА Hafr
Пусть теперь точка (хь ... ,xm^i) S ЬаЛ фиксирована и 6 > 0 взято
таким, что V(x'1)...,x^_1) € baA, p{{xlt... .Xm-i)^^,.. .,^1)) <
29 — 4-1168

448 Глава 14. Кратные интегралы 1
< 8 : \hc{x1,...,xm-i)-hc{x'1,...,x'm_1)\ < е. Тогда I^C^i, - ■ ■ ,<i-i)-
-g{x1,...,xm-1)\<2e{L2-L1) + e. J
Теорема 14. Пусть А — цилиндрическое мно&сество
в Rm с компактным измеримым основаниемЪаА и непре-
непрерывными на ЬаЛ функциями щ и и2- Тогда
u2(xi,...,zm-i) m_!
ff(x)dx= f ( / f(xi,...,xm~i,xm)dxm) П dxk-
А ЫА VUl(X! xm-i) ' fc=l
[ Для разбиения -Km определим множества Л(п) и (ЬаЛ)(п). По тео-
теореме 13 множество А измеримо и, согласно определению интеграла,
получим f f(x) dx = lim f f(x) dx.
A п-юо A(n)
Рассмотрим случай, в котором проекция множества Л(п) на подпро-
подпространство хт = 0 совпадает с (Ьа А)(пу
Множество Л(п) составлено из цилиндрических множеств — "стол-
"столбиков", основаниями которых являются брусы Q £ я"}£-1> Q С (ЬаА)(п).
Определим на (ЬаЛ)(п) две функции пх и пг следующим образом
п2(хь ..., im_i) := max{im | (хь ..., im_b im) £ Л(п)},
где {xi,...,xm-i) £ (ЬаЛ)(„). Функции пу и п2 постоянны на каждом
Q°, ge»^, Qc(ba^)(n).
Из следствия 3 и свойства интеграла G), получаем равенство
U2(ll,...,Xm_l) m_l
/ }{x)dx= f ( / f(xu...,xm-i,xm)dxm) П da;fc-
A(») (baA)(n) Чгн(х1 xm_i) У fc=l
Пусть теперь е > 0 задано. Определим 5 > 0 так, чтобы
V{z' = (zi.-.-.z^), f" = «'...-X-i)} С ЬаЛ, p(r,f") < 6 :
Такой выбор 6 возможен в силу равномерной непрерывности функций
их и и2 на компакте ЬаЛ. Если 2~пу/т < 6, то c^z. 2pJ^««
О < «,(«, xm_l} - МЗТЧ55^ « + 2'1-«; 8
О < и2(ц,..., im_i) - п2(хь ..., xm_i) < e + 2 • 2-n.
для (xb...,xm_1) £ (ЬаЛ)(п). Поэтому
m-l
f{x)dx- f g(xu...,xm-i) П dc
fc=l
Xm-l) m_l
(ЬаА)(„) 4ui(xi xm_i) *=1

14.4. Отображения множеств. Формула замены переменных 449^
< 2L(e + 2-"+1)тп((Ьа A){n)) < 2Lm(ba
Переходя к пределу при п->оо в последнем неравенстве, получим
| ТП —1
Uf(x)dx- / 5(xi,...,xm_i) П difc < 2Ьтп(ЬаЛ)е,
U ЬаЛ fc=l
откуда при е -> 0+ следует утверждение теоремы. J
Следствие 5. Пусть А — ■цилиндрическое множест-
множество, удовлетворяющее условиям, теоремы 14- Тогда
т-1
/
А ЬаА к=\
Упражнение 44- ^ помощью формулы A1) вычислить площадь кру-
круга и объём шара.
Упражнение 45- Пусть В — компактное измеримое множество в
Rm~1 = {(xi,... ,xm-i)} и / G G(B). Доказать, что множество
{(xi,... ,ira-i,im) | (ii, • • • ,xm-i) G B, xm = f(xi,... ,xm-i)}
имеет тп-мерную меру 0.
14.4 Отображения множеств.
Формула замены переменных
14.4.1 Отображения специального вида
Пусть А — открытое подмножество Rm, число к, 1 < к <т, фиксиро-
фиксировано и функция и G С1 (А). Отображение g : А -> Rm, определяемое
формулой — ~/ ~ 1
(k{x) := (ii,..., xk~i(u(x)Jxk+i, ■ • ■, з-m), x = (xi,...,xm)EA, A)
задаёт отображение подмножеств множества А в некоторый набор под-
подмножеств Rm : g{B) = {g(x} \ x G В}, В С А.
Множества В С А удобно рассматривать в одном пространстве
Rm = {(xi,... ,xm)}, а их образы — д(В) — в другом пространстве
Rm = {{Уи ■ ■ • ,Ут)}, полагая у = (уи ... ,ут) = д{х).
Упражнение 46. Пусть т — 2, А = R2 и a) ^(ii.xj) = {xi,xlx2),
(xi,x2) G Л2, fc = 2; b) h{xux2) = (-xiXa.xa), (x_i,xa) ЕЙ2, fc = 1.
Для Q = [ai.bi] x [02,62] определить образы g{Q), h(Q).
29.

450 Глава 14. Кратные интегралы
Определение 1. Отображение вида A) называется
отображ.ением специального вида.
Далеегщадпооагаем, что для отображения A) выполняются следу-
следующие два условия:
T=supK(z)|<+oo, B)
j либо
—Нам
еЛ: и'к(х)>0, либо УхбЛ: и'к(х) < 0. C)
ам понадобится следующая лемма.
Лемма 5. Пусть отображение h = (hi,...,hm) : А -> Rm
удовлетворяет условиям,: 1) h — взаимно однозначное
отображение (инъекция) множества А в Rm\ 2) h e
C(A,Rm). Тогда для любых G С A, F С A, G0 П F° = 0 спра-
справедливо равенство h(G)° П h(F)° — 0.
\ Предположим, что утверждение леммы неверно. Пусть вектор у G
(h(G)° Dh{F)°). Тогда Зе > 0 : В(у,е) С {h{G)° Г) K(F)°). Пусть
х G А тот вектор, для которого h(x) = у. Поскольку h G C(A,Rm), то
3 5 > 0 : h{B{x,5)) С В{у,е), а так как В{у,е) С h{G), B(y,e) С h{F),
то h(B(x, 6)) С £(G), Я(В(х, 5)) С /^(J7). Отсюда, согласно условию
1), В(х,5) С G, В(х,5) С i^, что противоречит условию G°nF° = 0. J
14.4.2 Измеримость образа при отображении
специального вида
Теорема 15. Пусть g — отображение специального
вида A), удовлетворяющее условиям B), C), и являюще-
являющееся взаимно однозначным.. Предположим, что множ.е-
ство В С А, В£ Хт и компактно. Тогда образ д(В) есть
компактное измеримое мноэ*сество.
Г Доказательство теоремы разделим на три части. .
I. Рассмотрим сначала случай, когда В брус в Rm. Именно, пусть
В = <? = [ai.bi] х [а2М] х ... х [ат,Ьт],
Ьа<? = {xi,...,Xfc-i,xfc+1,...,xr7l) | aj < Xj• < Ь 1 < j < т, j ф k}.
При условии u'k > 0 на А образ g(Q) есть такое цилиндрическое
множество g(Q) = {{yi,...,ym) \ {Vi,-■ ■ ,Ук-1,Ук+1,-■ ■ ,Ут) G baQ,
и{У1,...,Ук-1,ак,Ук+1,---,Ут) < Ук < "(Vl Ук-1,Ьк,Ук+1,---,Ут)}
в Rm с компактным и измеримым основанием baQ и непрерывными
функциями г*1 и иг. Согласно теореме 13 g(Q) есть компактное изме-
измеримое множество в Rm. С учётом следствия 5 для меры g(Q) имеем
m(g(Q)) =

14A. Отображения множеств. Формула замены переменных 451
.., х=Ьк
Ш J ЩХх, . . . ,Xfc_i,X,Xfc+i, . . . ,Хт) _ Yl d.Xj.
baQ х=аъ ]фк
{ Отсюда с помощью следствия 4 и теоремы 6 о среднем значении,
получаем равенство
т(№)) = I K(*)l dx = \u'k(x(Q))\m(Q) D)
Q
для некоторой точки x(Q) G Q.
II. Для разбиения тг&г определим множества В(„), В'"', ДВ(„)
и рассмотрим их образы cf(B(n)), g(B^), д(ДВ(„)). Поскольку мно-
множество А открыто, то B^n) С А для всех п, больших некоторого No-
Далее п > No.
Заметим, что отображение д при условиях теоремы есть непрерыв-
непрерывная инъекция из А в Rm, и что справедливо следующее утвержде-
утверждение В(п) С В С ВН =>. g(B(n)) С д(В) С g(B(n)). Кроме того,
д(В(п-)) = (J ff(Q)- Поэтому согласно части /доказательства
и свойствам измеримых множеств, множество g(B(n)) измеримо. -На
основании леммы 5 и аддитивности меры
m(g(B(n)))= £ m(g(<?)). E)
Аналогично, множества д(В^) G 0Cm, д(ДВ(„)) G ЭСт и их меры
вычисляются так же как в E). Покажем ещё, что тп(д(АВ(п))) —> 0,п —>
оо. Действительно, для любого бруса Q С j4 имеем Tn(g(Q)) < Lm(C3)
из формулы D) и условия B). Отсюда
т(д(ДВ(п)))< £ т(д((?)) < Ьт(ДВ(п)).
Правая часть зтого неравенства стремится к 0 в силу измеримости мно-
множества В.
///. Докажем теперь измеримость д(В). Пусть числа п и е > О
фиксированы. Поскольку множества g(B(nj) и д(В^) измеримы, то
BNi = Ni{n,e) VN>Ni :
C g(B(n)) С д(В) С д(ВЫ) С
)) <
Поэтому т(Дд(В)(„}) < m{{g{B^))^)) - m((g(B(n)))(w)) =
m(g(B{n)))+
Если n таково, что тп(д(ДВ(п))) < е, то тп(Др(В)(^)) < 2е для N > Nx.
Это означает, что тп(Дд(В)(^)) -» 0, iV -> оо, т. е. д(В) G ЭСт.

452 Глава 14. Кратные интегралы
Поскольку m(g(B(n))) < m(g(B)) < m(g(B^)), то имеем неравенство
тп(д(В)) - m(g(B(n))) < т(д(ДВ(„))), откуда следует, что
тп(д(В)) = lim m(s(B(n))). F)
п—*оо
Кроме того, д(В) компактно как непрерывный образ компакта. J
Упражнение 47. Пусть при m — 2, А = R2, В - {(xi,x2) I х\+х\ <
1}, g(xi,X2) = (a^i,а;|), (х1,хг) G Я2. Доказать измеримость д(В) (хотя
не все условия теоремы 15 выполнены).
Упражнение 48- Пусть д — отображение вида A), удовлетворяю-
удовлетворяющее условиям B) и C). Пусть Q С А — брус и / G C(g(Q)). Доказать,
что 30! G д(<Э) Зв2 G <? : / /(х) dx*= r^
14.4.3 Формула замены переменных для отображения
специального вида
Теорема 16. Пусть д — ото6рао*сение специально-
специального вида A), удовлетворяющее условиям B), C) п. 14.4.1 и
являющееся взаимно однозначным. Предположим, что
множество В С A, Be Xm и компактно, а функция f e
С{д(В)). Тогда
I f(y)dy = ff(g(x))\u'k(x)\dx. A)
г(в) в
Формула A) называется формулой замены переменных
или формулой перехода от интегрирования по перемен-
переменным, xi,...,xm к интегрированию по новым, переменным
J/ii ■ • • ,Ут, о, переход осуществляется функцией у = д(х).
\ В силу теоремы 15 множество д(В) компактно и измеримо По тео-
теореме о непрерывности суперпозиции непрерывных функций функция
(/(ff)lu'fcl) £ С{Щ- Поэтому оба интеграла в формуле A) определены и
нужно только доказать их равенство. Для разбиения Жт пространства
Rm рассмотрим множество В(п) и для каждого бруса Q G тгпг-, Q С
В(п) выберем пока произвольную точку x(Q) G Q. Затем запишем оче-
очевидное неравенство
/ f{y)dy-f f(g(x))\uk{x)\dx<Ji + JZ + jz + J*, B)
д(В) В
где
- f
g(B) g(B(n))
f f(y)dy- £ f(№Q)))KWQ))\™(Q)

14.4. Отображения множеств. Формула замены переменных
453
ь(х)| dx ,
QCB(n)
В(„) В
Докажем, что правая часть B) стремится к 0 при п —> оо. Пусть L :=
= max{max|/|, max \f(g)u'k\}. Из неравенства A0) п. 14.3.2 и формулы
г(в) в
оо.
F) п. 14.4.2 имеем_ 7* < L(m(g(B)) - m(g(B{n)))) -> 0, n
Аналогично, J* < L(m(B) - m(B(n))) -> 0, n -> оо.
Для оценки 7^ сначала выберем для каждого Q точку x(Q) таким
образом, чтобы выполнялось равенство D) п. 14.4.2. Тогда
\ QCB
/ (
g(Q)
(f(y)-f(g(x(Q))))dy
С помощью равномерной непрерывности функций / на д{В) и и'к на В
легко показать, что J^ -*• 0, п -> оо.
При оценке величины /^ нужно сначала применить теорему 6 о сред-
среднем значении. Получим J% <
[f(g(x(Q)))\u'k(x(Q))\ - f(g(e(Q)))\u'k(e(Q))\)m(Q)
для 9(Q) G Q, а затем воспользоваться равномерной непрерывностью
функции f{g)\u'k\ на В. J
Замечание. Для отображения д = (<7i,..., <7т) вида A) п. 14.4.1
имеем -гу—'-''' т = и'к. Поэтому формулу A) можно записать в
виде
i я/ п. г, ^
х. C)
Упражнение 49. Пусть В = {(zi,z2) | 1 < z\ + z\ < 4, z2 > zx, z2 >
-zi} и / € CE). Пусть Q = {{r,<p) \ 1 < r < 2, тг/4 < ^ < Зтг/4}
— брус в пространстве {(г, (р)}. Для следующего отображения g =
(У1.У2) : (л^) •-* {rcos<p,r) с якобианом ^/' ^ = rsin<p построить
о(г, (р)
g{Q). Далее для отображения h = (zi,z2) : B/1,2/2) •-»• (y
= (у1,У2у1-(У1/У2) J= (У1,л/у| -V?) построить образ
Я 1г 2 = :. Применив
показать, что h(g) = (r cos(p,r simp),
дважды теорему 16, доказать равенства
/ f{zi,z2)dzidz2 =

454 Глава 14. Кратные интегралы
т
— J /(г cos(p, г sin (p) . \т sin </?| drdip =
Q \JT2 — Г2 COS2 ip
= f rf(r cos </?, r sin <p) drdip.
Q
o d{zi,z2)
Заметим, что -^ ^- =
d{r,ip) 8{y1,y2) d(r,<p)
= r.
14.4.4 Локальное сведение общего отображения к
суперпозиции отображений специального вида
Пусть А — открытое множество в Rm, д = {gi,--.,gm) : А -> Rm,
причём д е С(А, Rm) и
f(g- 'gm)(x)^0. A)
■ • i Em)
Лемма 6. Vx0 G A 3r > 0 Vi £ B(x°) := B(i°,r) : g\x) =
= ff(m)E(m-i)(--.E(i)(f)) ■■■)). 2(^e отображение g*w — отобра-
ок.ение специального вида A), удовлетворяющие услови-
условиям B) и C) п. 14.4.1, к = 1,..., т.
[ Согласно условию A), определитель detg'(£o) 7^ 0. Следовательно,
существует минор (т — 1)-го порядка, отличный от 0. Не ограничивая
общности, можно предположить, что —.——'■—' т . (асо) Ф 0- Ана-
9(xx)
()
логичное рассуждение показывает, что можно считать выполненными
следующие неравенства
Для х £ А положим
[1] yi1) = x2, .... y^ = xmi C)
При этом
{)
В силу предположения B), существует открытый шар Bi(vo ) с цен-
центром в точке % и единственным образом определяемая действитель-
действительная функция hi G C1(Bi(yo ')) такая, что для каждого у*1) G Bi(yQ1 )
набор
I x1 = h1tfV),xa=yi1\...,xm = ylm) D)
' Является решением системы C) относительно xi,..., xm, т. е.

ЩА. Отображения множеств. Формула замены переменных 455
A) II. I A) A)\ A) A) A) A) ГГ\
У\ =9l{hl{y\ ',...,Ут), УУ =УЪ ',..., Ут =Ут. E)
Пусть Й! := (hi.yi4,...,^) : B^yf >) -> Я™, и
н- открытое множество, содержащее точку а?о-
Для х £ А положим
F)
Для некоторого открытого шара Вг(Уо ) с центром в точке Уо си~
ему F) мо
согласно F),
) цр
стему F) можно разрешить относительно у[ ,...,Ут ■ Действительно,
кроме того, из E) следует, что
_ dg
9* ' [ '
dx2 ■
5у
Поэтому —j-r ф 0, так как иначе однородная система G), (8) с отлич-
0Уз
ным от 0 по предположению B) определителем имела бы отличное от
нулевого решение —-ггг, 1. Как и выше, получаем открытое множе-
ду{21]
ство 1>2{хо), содержащее точку хо, и такое, что для каждого х G D :=
Di(£o)nD2(fo) имеем у<2)(х)
причём отображения дA) : D
удовлетворяют всем нужным условиям. Дальнейшие рассуждения ана-
аналогичны проведенным выше. J
14.4.5 Формула замены переменных
Теорема 17. Пусть А с Rm — открытое множество,
В С А — компактное измеримое множ.ество. Пусть
отобрамсение д = (<?i,..., <7m) : j4 -> Я771 удовлетворяет сле-
следующим, условиям: 1) отображение g мноо*сества В на
д(В) взаимно однозначно; 2) g G C(A,Rm)\ 3) либо Vx G
В : J(f) := f{gl Jmj (x) > 0, либо V x £ В : 7(x) < 0.
C(xi,.. .,xm)
Пусть такэ+се функция f G C(g(B)).

456
Глав а14. Кратные интегралы
Тогда множ.ество g(B) компактно, измеримо и спра-
справедлива следующая формула
/
g(B)
[ Согласно лемме 6,
VxGB3«5>OVuGB(x,E):
причём 6 = 8(х), а отображение д
... ,Хт)
dx.
A)
B)
есть отображение специально-
специального вида A), удовлетворяющее условиям B) и C) п. 14.4.1, 1 < к <
т. Семейство шаров {В(х, 5(х)/2) \ х G В} есть открытое покрытие
компактного множества В. Поэтому существует конечное подпокрытие
{В(х(»,<5(х(»)/2) | 1 < j < в}. Пусть 7 := (l/2)min{*(z«>) | 1 < j <
s} > 0. Рассмотрим теперь такие разбиения ттт пространства Rm, для
которых диаметр брусов меньше 7- Пусть Q(l), ■ ■., Q(N) — все те бру-
сы разбиения тгт , которые имеют непустое пересечение с множеством
В. Положим B{j) := В П Q(j), 1 < j < N. При этом
В = U B(j); B{j)° П B(fc)° = 0, зф к. C)
3=1
Поскольку Vi', I < v < N 3 jp = jo(v) ■ B{v)nB(x(-:io\5(xi':>^)/2) ф 0
и B{v) С Q{v), то B{v) С B(x^Jo\E(i^Jo)).
Таким образом, рассматривая отображение g на B(f) можно пред-
предполагать, что оно имеет вид B) и что образ g(B(v)) получен таким обра-
образом: g(B(i/)) = g(m)(B^m~1^(i')),..., B^(u) := gr2)(B^(i/)), B^(u) :=
= g(i)(B(v)). Множества В^(и), 1 < j < т - 1; g(B(v)) компактны и
измеримы на основании теоремы 16. Применяя теперь последовательно
теорему 17 и следствие 2 п. 12.2.2, имеем
/ }{y)dy= D)
ЯВИ)
= /
du = ...
= в{)
/ /(Г*
dx —
dx.

ЩЛ. Отображения множеств. Формула замены переменных 457
Поскольку д{В) = [) g(B(j)), то д(В) компактно и измеримо. С
Помощью представления C), леммы 5 и равенств D) находим оконча-
окончательно / /(у) dy =
= Е / f(y)dy=JT / /(g(£))|7(x)|dx = //(g(x))|7(x)|dx. J
"=1 g{B{u)) "=1 B(v) В
Замечание. Формула замены переменных A) часто записывается
также в следующей форме. Пусть D := д{В), тогда В := g~1(D) и
формула A) примет вид J f{y)dy = f f(g(x))\J(x)\dx, при этом
D д-ЦО)
вместо условий на множество В нужно потребовать компактность и
измеримость множества D.
14.4.6 Следствие и примеры
Следствие 6. При условиях теоремы 17 на мно&се-
ство В и отображение g справедливо равенство
Площадь фигур в плоскости обладает следующим свойством: кон-
конгруэнтные фигуры имеют одинаковую площадь. Аналогичным свойством
обладают длина и объём. Для введенной ранее меры Жордана такое
свойство не является непосредственным следствием определения, по-
поскольку это определение зависит от системы координат пространства.
Следующее утверждение содержит это свойство меры Жордана.
Следствие 7. Пусть D — матрица размера тх т с
действительными элементами, для которой |detZ?| = 1;
g — аффинное преобразование, определяемое формулой
g(x) = Dx + a, x£Rm; a G Rm.
Тогда для любого компактного измеримого множ.е-
ства В С Rm справедливо равенство т(В) = т(д(В)).
Условия теоремы 17 могут быть ослаблены. Следующий пример по-
показывает, что формула замены переменных остаётся верной, если усло-
условия 1), 3) этой теоремы нарушаются на множестве меры 0. Приведенные
при рассмотрении этого примера рассуждения могут быть использованы
для обобщения теоремы 17 и в общем случае.
Пример. Переход к полярным координатам,. Пусть В =
{(</?,г) | ip G [0,2тг], г G [0,ri]} — брус-прямоугольник в R2, х± =
</?, х2 = г; а отображение g = C1,32) = B/1,2/2) задаётся равенствами

458 Глава 14. Кратные интегралы
Ух ■= gi(<p,r) = rcoscp, t/2 = ^(Vi7") = г sin ср. Для этого отображения
d(gi, 32)
J = —. г- = — г и J = 0 на нижней стороне прямоугольника В. Кро-
о((р,г)
ме того, отображение д : В —> (?(В) не является взаимно однозначным,
так как упомянутая сторона переходит в точку @,0) — центр круга д(В).
Однако, для любой функции / £ С(д(В)) справедлива формула
/ 1(У1,У2) dyidy2 = //(г cos (p, г sin (p)rd(pdr, B)
д(В) В
или
ri 2тг
// f{yuV2)dyidy2 = / / /(гcos<p,rsincp)rd(pdr.
§° °
f Докажем формулу B). Сначала заметим, что оба интеграла в B)
определены, поскольку множество В и круг д(В) — компактные изме-
измеримые множества, а подынтегральные выражения непрерывны. Пусть
число 0 < £ < пипGГ,Г!) задано. Положим Ве = {(ip,r) | (р Е [е,2тг —
e]i r € [е, ri]}. Имеем Ве С В; т(В \ Ве) = 2тге + 2(гг - е)е -> 0, е -»■
О + . Тогда
/ /(г cos <^, r sin cp)r dipdr < ri max |/| тп(В \ Ве) —> 0, е —> 0 + .
в\вс ^в)
Для множества Ве и отображения д : Ве —> д(Ве) все условия тео-
теоремы 17 выполнены, и, следовательно,
/ f(yi,y2)dyidy2 = J /(гcos<p,r sinф)г dipdr.
§{в.) вс
Кроме того, из равенства д(В) \ g(Bs) = д(В \ Ве) имеем также
/ /(Уь 2/2) Ж/1 Л/2- / f{yi,y2)dyidy2 <
< max |/| т(д(В \ Ве)) < max |/| (тге2 + г2 tge) -> 0, е -¥ 0 + .
Таким образом,
/ f{yi,V2)dyidy2 = /
S(B) ?(Ве) j(B\Be)
= / /(г cos<p,r siny)r dipdr + / f{yi,y2)dy1dy2 =
Be д(в\вс)
~ f f {r cos ip, r sin ip)r dipdr + J /A/1,1/2)^1/1^1/2-
- f f(r cos ip,r sin ip)r dipdr.
B\BC
Устремив е —> 0+ в этом равенстве, получим формулу B).

14.5. Несобственные кратные интегралы. Определения и примеры 459
Упражнение 50. Пусть Bt = {{х\,х2) \ х\ + х\ < t2}, t € [0,1], и
для функции / € C(Bi) пусть F(t) = ff f{xi,x2) dxxdx2. Вычислить F'.
Bt
Упражнение 51. Пусть Bt = {{хх,х2) \ t2 < x\ + x\ < <4, txx < x2 <
2tii}, t > 1. Доказать, что для каждого t > 1 множество Bt измеримо
и для функции F(t) = m(Bt), t > 1, вычислить F'.
52. Пусть В£ = {{хг,х2) \ \xi\ + \х2\ < 1, \хх - х2\ >
е}, е > 0, Вычислить предел lim ffln\xi — x2\dxidx2.
е~>0+ в.
Упражнение 53. Пусть Ва = {(ii,i2) | x\{\+x\) < 1, х\ < а2}, а >
^ г. ., .. dx\dx2
1. Вычислить предел lim 11 ^-.
•-*+«> я. 1 + ^2
14.5 Несобственные кратные интегралы.
Определения и примеры
14.5.1 Интегралы от неограниченных функций
Пусть А С -Rm — компактное измеримое множество, х° € А — фикси-
фиксированный вектор, положим В = j4.\{i0}. Пусть функция / € С{В). Нас
интересует случай, когда функция / не является ограниченной на В.
Пример. Для то = 2, А = ~В{{х°,х°2), пусть i° = (x?,i^), r =
:a) = ^, a > 0.
Пусть {J5n | п > 1} — последовательность измеримых открытых под-
подмножеств Rm, удовлетворяющая условиям: 1) Vn > 1 : Еп Э х°;
2)d{En)= sup pm(i,y)->0, n -> со.
Такие последовательности существуют. Например, условиям 1) и
2) удовлетворяет следующая последовательности открытых измеримых
шаров
Еп = В{х°,5п), <5„>0, п>1; <5„ -»• 0, п -»• оо. A)
Каждое из множеств А \ Еп, п > 1, компактно и измеримо. Кроме
того, [3(Л\Д0= \J{B\En) = B; Vn>l: /
l
Определение J. Несобственным т-кратным инте-
интегралом от функции f no множеству А называется пре-
предел
lim / f(x)dx, B)
П^°° А\Еп

460 Глава 14. Кратные интегралы
который обозначается символом
ff(x)dx. C)
А
Если предел B) существует, конечен и не зависит от
выбора последовательности {Еп | п > 1}, то несобствен-
несобственный интеграл C) называется сходящимся, в остальных
случаях — расходящимся.
Для некоторых расходящихся интегралов предел B) существует для
некоторых специальных последовательностей {Еп \ п > 1}. Важным
является случай последовательности A).
Определение 2. Предел lim f f(x)dx, если он су-
П^°° А\В(х°,6„)
ществует и конечен, называется главным значением
расходящегося интеграла C) и обозначается символом,
v.p. f f(x) dx.
A
Примеры. 1. Пусть для то = 2, А = {(хг,х2) I х\ + х\ < 1}> х° =
@,0); f{x1,x2)= (zi,z2) т-ЧО.О); а > 0. Для п > 1 опреде-
[Х1 +Х2]____
лим числа 5'п := min{-\/if + х\ \ {xi,x2) ^ Еп}, 5'^ :— тах{л/х! + х\ \
(ati,xa) € Еп}, где Еп — замыкание Еп. Предположим, что множества
Еп ограничены. Согласно условиям 1) и 2), 5'п —> 0, 5п —> Q, п —> со.
Имеем
Я , 2 L < Я , 7 ах, < Я
л\в((о,о),ед lxi + хг) л\в„ txi + хг) л\в((о,о),«;) Iх! + Х2)а
.. dx\dx2
Переходя к полярным координатам, получим JJ —^ ^
А\В(@,0),6'п) 1Х1+Х2У
12* г }
= f f-^drdip = 2ir r
2-2а ' ^
2 - 2а = 0.
Из этого равенства и формулы D) следует, что при 2 — 2а > 0, т. е.
, - ,. г г dxxdx2 7Г
при а < 1, существует конечный предел lim JJ —^ j-t— = .
Для а > 1 предел не существует.
2. Пусть то = 1, А = [-1,1], х° = 0, f{x) = -, i^O. Интеграл
\ dx . dx
J — расходится, однако, существует предел lim J — =
— 1 Х ""tM l_1 11W_* К \ Х
(?n dx i di \
Г V I — = 0, 5n > 0, {„ -> 0, n —> oo. Таким образом,
-l * бп х '

ф4.5. Несобственные кратные интегралы. Определения и примеры 461
Г — -О
Для функции / со значениями одного знака на всём В проблема
сходимости интеграла
ff(S)dx E)
А
решается следующей теоремой.
Теорема 18. Для того чтобы несобственный инте-
интеграл E) от непрерывной и неотрицательной на множ.е-
стве В функции f сходился, необходимо и достаточ-
достаточно, чтобы для некоторой последовательности {£>„ | п >
1}, открытых измеримых мноясеств, удовлетворяющих
условиям. 1) и 2) и таких, что Dn+i С Dn, n > 1, последо-
последовательность
г / f(x)dx, п>1, F)
A\Dn
была ограниченной.
f Необходимость. Согласно определению сходящегося интеграла,"по-
интеграла,"последовательность F) сходится для любой последовательности {Еп \ п >
1}, удовлетворяющей условиям 1) и 2). Следовательно, она ограничена.
Неотрицательность функции при этом не обязательна.
Достаточность. Для каждого п > 1 множества А\ Dn иА\ Dn+i
компактны и измеримы, причём (А \ Dn) С (A\Dn+i)- Неотрицатель-
Неотрицательность / влечёт следующее неравенство
/ f{x)dx= J f{x)dx+ J f{x)dx> f f{x)dx.
A\Dn+l A\Dn Dn\Dn+1 A\Dn
Таким образом, последовательность F) не убывает и ограничена. По-
Поэтому существует конечный предел lim / f(x) dx =: J.
n-*°° A\Dn
Пусть теперь {En \ n > 1} — произвольная последовательность от-
открытых множеств, удовлетворяющая условиям 1) и 2), и число е > О
задано. Сначала заметим, что
Зп0 Vn>n0 : 0<J- / f{x)dx<e. G)
A\Dn
Множество Dno открыто и Dno Э х°, поэтому 3р > 0 : В(х°,р) С
Dno- Дэлее в силу условия 2), 3 N Vn > N : d(En) < р. Следова-
Следовательно, Vn>JV: En C Dno.
Аналогично, множество Еп открыто и содержит точку х°. Как и
выше, заключаем 3rn(n) Vm > т{п) : Dm С Еп. Положим теперь
то{п) := max{rn(n),n0}. Тогда Vn > N : Dmo(n) С Еп С Dno, и,
в силу неотрицательности /, получаем f f(x) dx < f f(x) dx <
A\Dno A\En

462Глава 14. Кратные интегралы
^ / /(£) dx. Отсюда, учитывая неравенства G), имеем Vn>N:
J-e< f f(x)dx<J. J
A\En
Пример. Пусть то = 2, A — компактное измеримое подмножество
Я2, f° = (z?,z§) - внутренняя точка Аи/: Л -> [О.+оо), / € С [А).
Докажем, что несобственный интеграл
сходится для а € @,2), а интеграл JJ — с а > 2 расходится.
А *"
\ Предположив, что В(х°,1) С А, рассмотрим последовательность
Я Щ& dxldx2 = (9)
А\В{х°,1/п) Г
= Я %£2l dxidx2 + ц ^
А\В(х°,1) Г J3(i°,l)\J3(c°,l/n) Г
Оба интеграла в правой части (9) определены как интегралы от непре-
непрерывных функций по измеримым множествам, причём первый из них не
зависит от п. Для второго интеграла правой части (9) имеем
Я ' ^I'a2' dxidx2 < max/ Я ^ dxidx2 =
J3(x°,l)\J3(z°,l/n) т л J3(x°,l)\J3(i°,l/n) '
„ „2-OC 1 Om-
max /, n —> сю
= max/ / / — drdcp = 2»max/ -—-
r2~a i 2tt
i/n 2 - a a
l/n 0
для 0 < a < 2. Поэтому последовательность (9) ограничена и по теоре-
теореме 18 интеграл (8) сходится.
Для второго интеграла аналогично доказывается неограниченность
последовательности (9) для f(xi,x2) = 1. J
Определение 3. Несобственный интеграл E) назы-
называется абсолютно сходящимся, если сходится несоб-
несобственный интеграл f\f(x)\dx.
А
Легко проверить, что абсолютно сходящийся интеграл сходится.
Несобственные кратные интегралы обладают рядом свойств, анало-
аналогичных свойствам одномерных несобственных интегралов, Однако, из-
за существенного различия определений, при то > 2 несобственный
j интеграл сходится тогда и только тогда, когда он сходится абсолютно.
: ■ Доказательство этого утверждения и подробная теория несобственных
' кратных интегралов здесь не приводятся.

14.5. Несобственные кратные интегралы. Определения и примеры 463
Упражнение 54- Вычислить интеграл //A — ^\)а^2 dx\dx2 по мно-
А
жеству А = {{хих2) | 0 < х2 < х1 < 1}, а > -1, /3 > -1.
Упражнение 55. Вычислить интеграл //х?г§ dx\dx2 по множеству
А
А - {{xi,x2) | 0 < х2 < 1 - xi, xi > 0}, а > -1, /3 > -1.
Упражнение 56. Вычислить //(xf + х\)а{\ ~ ^i ~ ^l)*3 dxxdx2, где
2) | xj+xl < 1, X! >0, х2 >0}, а > -1, /3> -1.
14.5.2 Интегралы по неограниченным множествам
Пусть В С Rm — неограниченное множество, для которого существует
последовательность {Dn | тг > 1} компактных измеримых множеств,
удовлетворяющая следующим условиям: 1) Vn > 1 : Dn С Вп+г С В;
2)Vc>0 3NVn>N : (В П В{б,с)) С £>„.
Такую последовательность {£>„ | п > 1} будем называть исчерпыва-
исчерпывающей для множества В. Пусть / € С7(В).
Определение 4- Несобственным интегралом от
функции f no мноысеству В называется предел
x, A)
обозначаемый символом
//(x)dx. B)
А
Несобственный интеграл B) называется сходящимся,
если предел A) конечен и не зависит от выбора исчер-
исчерпывающей последовательности {Dn | п > 1}, в остальных
случаях интеграл B) называется расходящимся.
Для интеграла B) справедлив аналог теоремы 18.
При вычислении несобственных интегралов из пп. 14.5.1 и 14.5.2
можно пользоваться формулой их сведения к повторным при условии
сходимости повторных интегралов от абсолютной величины функции, а
также формулой замены переменных. Эти утверждения, как и теория
интеграла B), здесь рассматриваться не будут.
Пример. Пусть при т = 2, В = [0,+ооJ, /(xi,x2) = е~х^~х^, (xi,x2)
€ В. Несобственный интеграл
+оо+оо 2 2
J = ff f(xi,x2) dx\dx2 = / / e~xi~x* dxxdx2
в оо
30 — 4-1168

464 Глава 14. Кратные интегралы
сходится. Доказательство независимости предела от исчерпывающей
последовательности проводится аналогично соответствующей части тео-
теоремы 18. После перехода в интеграле J к повторным интегралам, по-
получим формулу
+оо ,+оо ч ,+oo . 2
J = I е~х* ( / е~». dx1) (tea = ( / е- dx) . C)
о ч о ' v о '
Доказательство равенства C) получается просто, если рассмотреть
в качестве исчерпывающей последовательности Dn = [0,п]2, п > 1, и
применить правило перехода к повторным интеграла для бруса Dn :
е
П—+ОО
J= lim Г е xi Х2 dxidx2 = lim Ге
П-+ОО ^ п+оо
= lim (fe-*2dx) =(/ e-l2dx) .
П-+ОО \q / \ q /
С помощью формулы перехода к полярным координатам для исчер-
исчерпывающей последовательности
„2 . -2 <- „2
2) | х\+х\ <п2, хг >0, х2 >0}, п> 1,
аналогично доказательству равенства C) получаем формулу
7Г
г-И-оо
J= f f e-rrdrd(p=--e-r =-. D)
оо 4 г=о 4
Из равенств C) и D) находим значение интеграла Эйлера-Пуассона
о ^
57. Доказать, что абсолютно сходящийся интеграл схо-
сходится.
Упражнение 58. Пусть функция / : В —> R непрерывна на В и
удовлетворяет условию Эс > 0 За > 2 V(ix>a;2) € В : |/(xi,хз)| <
< — , г2 = х\ + х\. Доказать абсолютную сходимость интеграла
ff f(x1,x2)dxidx2.
в
Упражнение 59. Для а > — 1 вычислить интеграл:
+ОО+ОО +ОО+ОО
а) / / e-t'i+'a) (fax(tea, « > 0; b) / / (a? + i|)ae-Ii-^ dxxdx2.
0 0 0 0
Упраэ/скекие 60*. Доказать сходимость интеграла
+оо+оо +ооdx1dx2...dx
+ +
1 11 Xix2...xm(max{xi,x2,...,xm})a '

Глава 15
Интегралы по
многообразиям и теорема
Стокса
15.1 Основные определения
15.1.1 Допустимые координатные пространства.
Ориентация
Пусть П? = {х = (ij,..., хр)} — р-мерное пространство. Это простран-
пространство будем называть также х-пространством, чтобы отличать от других.
Пусть А — некоторое множество в х-пространстве. Любая точка Р £ А
в я-пространстве задаётся набором координат Х\,..., хр. Однако, точки
из А могут задаваться и другими способами.
Пусть G — открытое в пространстве (Rp,p) множество, причём G Э
А. Пусть д = (gi,... ,др) : G —>■ Rp — отображение, удовлетворяющее
следующим условиям: 1)^6 Cl{G, Rp); 2) десть взаимно однозначное
соответствие между множествами G и g{G); 3) либо VaT £ G : J(x) :—
0.
(i,,p)
Определение 1. Отобрао+сение g = E1,•• -,gp) : G-> Яр,
удоелетеорлтогцее условиям. 1) — 3^ называется регу-
регулярным или диффеоморфизмом.
Регулярное отображение имеет обратное, которое также регулярно.
Упражнение 1. Доказать последнее утверждение, Доказать, что
зо • 465

466 Глава 15. Интегралы по многообразиям и теорема Стокса
суперпозиция регулярных отображений есть регулярное отображение.
Любая точка Р £ А, имеющая координаты х\,..., хр в х-пространстве,
может быть также задана с помощью образа (j/i, ■.. > Ур) = д{£) —
{дг(х),... ,др(х)) при регулярном преобразовании д. Этот образ будем
считать расположенным в у-пространстве — другой копии Rp, отличной
от х-пространства. Значения yi,...,yp будем называть координатами
точки Р в у-пространстве, а переход от координат х\,...,хр к координа-
координатам ух,..., ур — заменой или преобразованием координат. Преоб-
Преобразование координат, осуществляемое с помощью регулярного преоб-
преобразования, называется допустимым. Далее рассматриваются толь-
только допустимые преобразования координат. Иногда у-пространство, в
котором расположен образ д(А), называют допустимым коорди-
координатным пространством для множества А. Тогда х-пространство
допустимо для д{А), если у-пространство допустимо для А.
Таким образом, множеству G соответствует класс координатных
пространств, получаемых из i-пространства (а также и друг из друга) с
помощью допустимых преобразований координат.
Определение 2. Допустимые для множества А
х-пространство и z-пространство называются одина-
одинаково ориентированными, если
>0
..,zp) д(уи...,ур)
и противоположно ориентированными, если
(и--,УР)
Мноок.ество А называется ориентированным, если
какое-нибудь допустимое координатное пространство
для А фиксировано и названо положительным или про-
пространством, знака +1. При этом все одинаково ориен-
ориентированные с фиксированным, пространством допусти-
допустимые пространства такмсе полоо+сителъны (имеют знак
+1). Пространства, противоположно ориентированные
с фиксированным, пространством,, называются отрица-
отрицательными или пространствами знака —1.
Согласно этому определению, любое подмножество х-пространства
ориентировано, если х-пространство названо, например, положитель-
положительным. При этом допустимое у-пространство имеет
знак+1, если д^"-^\ > 0, и знак -1, если f,(Vl'"""'^ < 0.
д{хи...,хр) д(хи...,хр)
Заметим также, что у-пространство и z-пространство, для которых

15.1. Основные определения 467
9{У1,--,УР) > 0 d{zlt...,zp) > 0
d{xlf...,xp) '
одинаково ориентированы, поскольку
d{yi ур)
..,zp) d{zu. ..,zp)'
Примеры. 1. Пусть при р = 1 множества G = R, А = [а, Ь] — отрезок
на прямой R в х-пространстве, которое будем считать положительным.
Пусть g € С1 (Л), причём д'{х) > О, х £ R. Образ д{А) = [д{а),д{Ь)]
dy dg
лежит в положительном у-пространстве, поскольку — = — > 0. Если
ах ах
h € ^(R) и h'(x) < 0, х € R, то регулярное преобразование h при-
приводит к отрицательному z-пространству, в котором h(A) = [h(b), h(a)].
Поэтому положительную ориентацию отрезка на прямой можно интер-
интерпретировать, как задание начальной а и конечной b точек отрезка (или
задание направления движения от а к Ь). При этом в положительном
у-пространстве этот порядок сохраняется: д(а) < д{Ь). В отрицательном
z-пространстве порядок изменяется на противоположный: h(b) < h(a).
2. Пусть для р = 2 множества G = R?, А = [0,2] х [0,1] лежат
в положительном х-пространстве. Отображение у = g(xi,X2) = {х\ +
1,2x2 +2), (a;i,X2) € R , является регулярным, причём
d(yi,y2)
д{хих2)
J 2 =2>0; (х1,х2)€Я2.
Поэтому образ д(А) = [1,3] х [2,4] лежит в положительном у-простран-
у-пространстве. Отображение z = h(xx,x2) = {x2lxi), {xi,x2) G R2, также регу-
регулярно и
а образ h(A) = [0,1] x [0,2] лежит в отрицательном z-пространстве.
Множество А ориентировано.
Ориентацию множества А можно интерпретировать как задание на-
направления обхода его границы (одного из двух возможных: по часо-
часовой стрелке, если смотреть на плоскость сверху, или против часовой
стрелки). При переходе к положительному у-пространству направление
обхода сохраняется, при переходе к отрицательному z-пространству —
меняется на противоположное.
Упражнение 2. Пусть Rp — положительное х-пространство и у =
= §{*) = (^A), ^B), ■ • •, Za(P)), 2 € RP, где а = (<тA), сг{2),..., а{р)), -
некоторая перестановка чисел 1,2,...,р. Определить, для каких пере-
перестановок а регулярное преобразование д приводит к положительному
у-пространству.

468 Глава 15. Интегралы по многообразиям и теорема Стокса
15.1.2 Дифференциальные формы степени га
в пространстве Rm. Новая форма формулы
замены переменных
Пусть А С Rm — компактное измеримое ориентированное множество
в х-пространстве. Пусть G D А и у = д : G —> Rm — регулярное
преобразование, переводящее множество А в д{А). Множество д{А) по
теореме 17 п. 14.4.5 компактно и измеримо, и лежит в у-пространстве.
Пусть / G С(д(А)).
Определение 3. Дифференциальная форма степени
т ш = f(yi, у2,.. ■, ут) dyi Л dy2 Л ... Л dym на д{А) в т-мерном
у-пространстве есть символ, определяемый равенством
и = fdy1Ady2A-..Adym= A)
{f dytdy2 . ■ ■ dym, если у-пространств о знака +1,
-/ dy\dy2 ■. -dymt если у-пространств о знака -1.
Выражение в правой части A) есть подынтегральное выражение т-
кратного интеграла по множеству д{А) от функции / или —/.
С помощью определения C) формулу замены переменных в т-
кратном интеграле из теоремы 17 п. 14.4.5 можно записать в более
удобной для дальнейшего форме
dyiAdy2A.. .Adym = ff ^У1'У2' ■■■' Ут\ dx1Adx2A...Adxm.B)
д(А) А д{Х1,Х2,...,Хт)
Упражнение 3. Доказать равенство B).
Далее используются следующие свойства дифференциальных форм
степени то в пространстве Rm. Эти свойства фактически описывают пра-
правила преобразования подынтегральных выражений при регулярных пре-
преобразованиях (заменах) координат.
1°. Если у-пространство — допустимое координатное пространство для
множества А, лежащего в х-пространстве, то будем считать, что
/(у) dyi A dy2 А ... A dym =
= /(УФ) У1' У2> "" Ут\ dxxAdx2A...A dxm. C)
d[xi,x2,...,xm)
Равенство C) есть формула связи для выражений дифференциаль-
дифференциальной формы в разных координатных пространствах. Оно представляет
собой удобную формализованную запись равенства B) и реально ис-
используется только в равенствах типа B).
2°. Если у-пространство и z-пространство — допустимые координатные
пространства для множества А, то

15.1. Основные определения ^ 469
/(у) dyi Л dy2 Л ... Л dym =
= f{№) ^Vl'V2'-""Vi dz1 Л dz2 Л ... л dzm. D)
O(Zi,Z2,... ,Zm)
Равенство D) получается формально двукратным применением C)
Л dy2 Л ... Л dym = / ^УьУа,---,Ут) dxi Л dx2 Л ... л
= / „, ' ''''' ( -^r-2—'-^^ г dzi A dz2 A ... A dzm =
= J —. uZi A UZ2 A ... A aZm.
d{z1,z2,...,zm)
3°. Пусть a = (cr(l),crB),... ,cr(m)) — некоторая перестановка чисел
1,2,..., т. Положим S(cr) := 1, если а — чётная перестановка, и S(cr) :=
— 1, если и — нечётная перестановка. Тогда у-пространство для отоб-
отображения у — (xa(i),xaB),... ,ха(т)) является допустимым для любого
множества А, причём
" ' =S(«r).
д(х1,х2,...,хт)
Согласно равенству D), имеем
/ xa(i) Л хаB) Л ... Л ха(тп) = S(a)/ dxi Л dx2 Л ... Л dxm. E)
Например, для т — 2 получим следующее равенство дифференци-
дифференциальных форм /(xi,X2)dxi A dx2 = — /(xi,X2) dx2 Л dxi.
Упражнение 4- Проверить равенство E).
Упражнение 5. Множество F - {(уьУг) | 1 < у\ + у\ < 4, yi >
0| Уг > 0} лежит в положительном у-пространстве. Определить вид
дифференциальной формы w = {у\у2 +у|)%2 A dylt (у1,уг) € F, в
полярных координатах.
15.1.3 Многообразия
Многообразиями размерности р называют такие подмножества
пространства Rm, которые "в малом" подобны пространству Яр. Одно-
Одномерное многообразие "в малом" устроено примерно так, как прямая
— пространство R, двумерное — как плоскость и т. п. Понятие много-
многообразия включает в себя такие понятия, как гладкая кривая на плоскости
или в пространстве (одномерное многообразие), гладкая поверхность в
пространстве (двумерное многообразие).
Здесь и в дальнейшем в случае множества Т С Яр, не являющегося
открытым в (Rp,p), обозначение / G Cr(T,Rp) понимается следующим

470 Глава 15. Интегралы по многообразиям и теорема Стокса
образом: существуют открытое в (Rp,р) множество G Э Т и функция
д € Cr(G,Rp) такие, что g{i) = /*(i), f G Г.
Определение 4- Пусть 1 <р < т. Мномсесгпво М С Rm
называется многообразием размерности р или р-мер-
ным многообразием, если существуют мпоснсество Т С
Rp и функция и £ (^(Т, .Rm) такие, что й(Т) ~ М. При
этом, говорят, что функция й задаёт параметрическое
представление многообразия на множестве парамет-
параметров Т. Числа ti,...,tp называются координатами точ-
точки u(ti,... ,tp) многообразия М. Допустимое координатное
пространство для параметрического мноснсества Т на-
называется допустимым координатным пространством
многообразия М.
Пусть М — многообразие из определения 4. Если s-пространство
— допустимое координатное пространство для Т, получаемое с помо-
помощью регулярного преобразования s = g(i), t G T, то М = v(S), где
S := з(Т), v := {[(д*1). Поэтому функция v также задаёт параметри-
параметрическое представление многообразия М на множестве параметров S.
Представления многообразия с помощью функций й и v называются
эквивалентными, при этом говорят, что функция д осуществляет
преобразование параметров многообразия.
Многообразие М называется ориентированным, если какое-
нибудь допустимое координатное пространство фиксировано и названо,
например, положительным.
Далее на функцию й будут налагаться дополнительные условия глад-
гладкости, а в качестве Т будут рассматриваться компактные измеримые
множества. Приведём наиболее типичные примеры многообразий.
1°. Ориентированная кривая. Пусть р = 1 и множество Т =
[а, Ь] лежит в положительном i-пространстве. Ориентацию множества
Т будем трактовать, как задание направления движения вдоль Т от а к
Ь. Пусть гГеС^аДЯ).
Одномерное ориентированное многообразие Г = й(Т) называется
ориентированной кривой в пространстве Rm. Ориентацию
кривой Г можно трактовать, как задание направления движения по Г
от гГ(а) к й(Ь). При этом переход к положительному допустимому ко-
координатному s-пространству приводит к параметрическому множеству,
для которого движение в сторону возрастания нового параметра также
соответствует ранее заданному движению по Г, поскольку — > 0 й,
at
следовательно, £х < г2 <=$■ sx < s2. Если перейти к отрицательно-
отрицательному допустимому координатному пространству, то движение в сторону

15.1. Основные определения 471
уменьшения нового параметра соответствует ранее заданному движе-
движению по Г.
Примеры. 1. Пусть т — 2, Т = [О,яг], u(t) — (cost,smt), t e [0,яг],
f-пространство положительно и 0 — начало отрезка [0, я-]. Тогда Г =
й([0, я-]) — ориентированная полуокружность с центром в @,0) и ра-
радиусом 1, расположенная в верхней полуплоскости Я2. Ориентацию Г
можно трактовать как задание движения по Г от A,0) к ( — 1,0). Если
ds
преобразовать параметр t с помощью равенства s = —t, то — = —1 < 0
at
и s-пространство отрицательно для [О,тг], а эквивалентное параметриче-
параметрическое представление для Г задаётся функцией v(s) — (coss, -sins), s G
[—я",0]. Поскольку s-пространство отрицательно, то движение от 0 к —я"
вдоль [—я", 0] соответствует заданному движению по Г.
Приведём ещё одно параметрическое представление для Г, кото-
которое получается с помощью следующего преобразования параметра
z = cost, t е [0, яг]. При этом Г = {(z, у/1- z2) | z € [-1,1]}, a z-
пространство отрицательно, поскольку ■— = — sini, t G [0,я-].
at
2. Пусть m — 3, T — R, ^-пространство положительно, ориентация
Т есть движение вправо вдоль Т. Винтовой линией называется
кривая Г = {(cos£,sin£,£) | t G Я} в Я3. Ориентация Г есть движение
вверх по Г.
2Р. Ориентированная поверхность. Пусть р = 2, Т = [ai.bi] x
[аг.Ьг], и 6 Cl{T,Rm). Двумерное многообразие S = й(Т) называется
поверхностью в Rm. Если Т — ориентированное множество, то
поверхность 5 называется ориентированной.
Пример. Пусть т = 3, Т = {{г,(р) \ г е [0,2], ip £ [О,яг]},
й(г, ip) = (r cos ip, r sin ip, 4 - г2), (г, ip) £ Т.
Здесь S = й(Т) — часть параболоида вращения. Предположим, что Т
ориентировано, ориентация множества Т есть задание обхода его гра-
границы против часовой стрелки. При зтом поверхность 5 ориентирована.
Ориентацию S можно трактовать как выбор верхней стороны S, ес-
если смотреть из точки @,0,5). Тогда обход контура S, соответствующий
обходу границы Т, будет также происходить против часовой стрелки.
3°. Определение. Многообразие М, определяемое с помощью фун-
функции it € Сг(Т, Rm) на множестве параметров Т, называется соб-
собственно р-мерным в точке u{t°) G M, t° G Т, если матрица

472 Глава 15. Интегралы по многообразиям и теорема Стокса
ои 1 {t ) dxi i {t )
Cti dtp
dum(t°) dum(t°)
\ dt\ dtp I
имеет ранг р.
Это определение описывает свойство многообразия М в точке u(t°),
которое не зависит от выбора параметрических координат. Действи-
Действительно, пусть s-пространство — допустимое координатное пространство
для Т, причём s*= g{t), te T\ s° = g{t°); M = v{S), S = g{T), v =
(t>i,...,vm) ■= u[g~^) = ■u(£(s)I u(t°) = t?(s*°).
Если, например, ^''''' "p) (Г0) ^ 0, то
■ • ■ ■, vp) (-.оч
15.2 Интеграл по многообразию от
дифференциальной формы
15.2.1 Дифференциальные формы степени р в
пространстве Rm
Пусть 1 < р < m, T — ориентированное компактное измеримое мно-
множество в ^-пространстве Яр, й= {их um) G С*{Т, Rm). Тогда М =
и(Т) — ориентированное р-мерное многообразие в х-пространстве
Rm. Рассмотрим функции fj G С(М), 1 < j < q, q e N.
Определение 1. Дифференциальной формой степени
р на р-м,ерном, ориентированном, многообразии М в Rm
называется выраснсение
w = /i(xi,..., хт) dxv(i) Л ... Л dxv(p) + ...
... + fq(x1,...,xm)dxliA) A...Adx^p), A)
в котором, каждый из индексов {^(j), ^(A;)} принимает од-
одно из значений 1,2,... ,т. Для каждого параметрического
представления многообразия М, задаваемого функцией и
на множ.естве параметров Т, значение ш равно
^ = /i(xi,..., xm) dxvA) Л ... Л dxv(p) +...
■ ■■ + fq{xl,- ■ ■ . xm) dx^i) Л ...
d(h,...,tp)

15.2. Интеграл по многообразию от дифференциальной формы 473
^^)dt1A...Adtp. B)
O(ti,...,tp) j
Функции fi,...,fq называются коэффициентами диф-
дифференциальной формы ш.
Заметим, что в правой части B) фигурирует определённая в п. 15.1.2
дифференциальная форма степени р на множестве Т С Rp.
Хотя в дальнейшем дифференциальные формы почти всегда встре-
встречаются под знаком интеграла, целесообразно установить некоторые
правила формального проведения операций над ними.
1°. Каждая дифференциальная форма A) может быть записана в фор-
форме, называемой канонической, в которой: а) отсутствуют слагаемые
вида / dxx(i) Л ... Л dxx(p) с совпадающими индексами; Ь) каждое сла-
слагаемое в A) имеет вид f dxx(i) Л- • • AdiA(P) для 1 < АA) < АB) < ... <
< Чр) < т-
\ Действительно, если, например, АA) = АB), то
^;X^)] dt1A...Adtp = 0
O(ti,t2, . ■ ■ ,tp)
для любого параметрического представления многообразия, поскольку
якобиан в этом выражении содержит две одинаковые строки. Если же
индексы АA), АB),..., А(р) различны, то
(i) A- ■ ■ Ad«V(p),
где / = fS(a), a — перестановка чисел A(l), AB),... ,A(p) такая, что
переставленные индексы А'A), А'B),..., А'(р) упорядочены: А'A) <
А'B) < ... < А'(р). Напомним, что S(cr) = 1, если перестановка а
— четна и S(ct) = —1, если перестановка а — нечётна. J
2Р. Дифференциальная форма равна 0, если в её канонической форме
все коэффициенты равны 0. Две дифференциальных формы w\ и и>2
равны (w\ = UI2), если в канонической форме равны их соответствующие
коэффициенты. Сумма ш\ +и/2 форм w\ и ш^ определяется как форма,
равная сумме соответствующих выражений из A). Функция / : М —I R
называется дифференциальной формой степени 0.
Упражнение 6. Привести к канонической форме следующую диф-
3
ференциальную форму ш = ]Г] fjkdxj Adxk степени 2 в R . Прове-
i,fc=i
рить, что любая дифференциальная форма второй степени в R? имеет
такой вид

474 Глава 15. Интегралы по многообразиям и теорема Стокса
ш = Рdx2 Л dx3 + Q dx3 Л dxi + Rdxi A dx2.
Упражнение 7. Доказать, что ^ fjk dxj A dxk = 0 тогда и только
j,k=i
тогда, когда fjk = fkj, j, k - 1,2 m.
Упражнение 8. Пусть ш = Pdx2 Л dx3 + Qdx$ Л dxi + Rdxi A dx2
— дифференциальная форма второй степени на многообразии М =
{(xi,x2,x3) | xi = 1} — плоскости в Я3. Доказать, что ш = Pdx2 Adx3
на многообразии М.
Упражнение 9. Пусть ш = /i dxi + f2 dx2 — дифференциальная
форма первой степени на многообразии М = {(xi,X2) | Х\ + х2 = 1}.
Доказать, что ш = (Д - f2)dxi на многообразии М.
15.2.2 Интеграл от формы по многообразию
Пусть М — ориентированное многообразие размерности р в Rm, a
ш = Д <&„(!) Л ... Л dxv(p) + ...+/, dxM(i) Л ... Л dxM(p)
— дифференциальная форма степени р на многообразии М.
Определение 2. Интегралом от дифференциальной
формы ш степени р по ориентированному многообразию
М размерности р в Rm называется число
A)
[p) )
где и — функция, которая осуществляет параметриче-
параметрическое представление многообразия М на множестве па-
параметров Т.
Замечание. Интеграл в правой части A) есть интеграл от диф-
дифференциальной формы степени р по множеству Т в RF. Однако, для
заданного многообразия М параметрическое множество и функция,
■| осуществляющая параметрическое представление, могут быть выбраны
; разными способами. Существенным обстоятельством, оправдывающим
' определение 2 является то, что значение интеграла f w не зависит от
м
выбора параметрического множества и соответствующих эквивалентных
представлений многообразия М.
Действительно, пусть s-пространство — допустимое пространство
для Т, полученное с помощью регулярного преобразования д, и

't5.2. Интеграл по многообразию от дифференциальной формы 475
s=g(t),teT; S = g(T); ь = й(д-гУ, М = u(T) = v(S).
Тогда с помощью формулы замены переменных получим J ш :=
м
f J л—от: 7~ч— + • ■ • + /9—^r. n— 1 «i л... л dtp -
1 T\ o\tx,...,tv) O{t\,...,tp) J
. Л ■ ■ ■ л 4» -
S V O{slt...,Sp) O(Si,...,Sp)
Рассмотрим следующие два частных случая определения 2.
I. Если р = m vi w — f dx\ Л ... Л dxm) то
М Т <J{li, . . . ,Zm)
что представляет собой формулу замены переменных.
II. Если многообразие М может быть задано с помощью специаль-
специального параметрического представления
хх = щ =ti,...,xp- up = tp\ xp+i - up+1(t),...,xm - um(t), te
Т, то якобиан *'" '' р = 1 и справедливо следующее равенство
o(ti,...,tp)
f f(xlt...,xm)dx1A...Adxp= B)
м
i, • ■ •, tP, up+1{t) um{t)) Ai Л ... Л dtp =
ii Л... AdXp, x = (ij,...,xp).
T
J°. криволинейный интеграл второгоро^о. Предположим,
что Г — u([a,b}) — ориентированная кривая в Rm, причём функция
u e ^([a.bj.R). Кривая Г, для которой u G ^([о.Ь], Дт), называ-
называется гладкой кривой. Пусть fj G С'(Г), 1 < J < т. Рассмотрим
следующую дифференциальную форму первой степени на Г
ш = /i(x) dxi + ... + Лп(х) dxm.
Определение 3. Криволинейным интегралом второ-
второго рода от формы ш по ориентированной кривой Г назы-
называется число

476 I Глава 15. Интегралы по многообразиям и теорема Стокса
^^dt, C)
где j = +1, если t-пространство имеет знак +1, и j = —1,
если t-пространство имеет знак —1.
Заметим, что интеграл в правой части C) есть интеграл Римана от
непрерывной функции по отрезку [а,Ь].
Примеры. 1. Пусть т = 2, множество Т = [О,тг] лежит в положи-
положительном ^-пространстве и Г = {(cos£,sin£) | t € [0,яг]}. При этом х\ =
ut = cost, х2 — и2 = sini, t G [0,яг]. Для функций Д = -x2l h = xi
7Г
имеем /(—i2 dii + Xi di2) = (+1) /(— sin^ ■ (— sint) + cosi • cosi) dt = ж.
г о
Заметим, что движение в сторону возрастания t по [0, яг] соответствует
движению против часовой стрелке по Г.
2. Вычислить криволинейный интеграл /(Bа — 12)^X1+ Zi йх2), а > О,
г
где Г — арка циклоиды над отрезком [0,2яга], пробегаемая в направле-
направлении от точки @,0) к точке Bяга, 0). Рассмотрим следующее параметри-
параметрическое представление для Г
Г = {(хьх2) | xi = o(<-sin<), x2 = a(l -cost), t G [0,2яг]}.
Поскольку возрастание параметра t на [0,2яг] соответствует движе-
движение в заданном направлении по Г, то ^-пространство следует считать по-
2т
ложительным. Поэтому имеем /(Bа — х2) dxi + Xi dx^) = (+1) /(Bа —
г о
—аA — cosi))a(l — cosi) + a(t — sint)asini) dt = —2тга2.
Замечание. Криволинейный интеграл fat обладает многими обыч-
ными свойствами интеграла Римана. Например, f(uj\+uj2) = f wi+f Ш2-
г г г
Далее, если с G (а,Ь), и Г\ := «([а,с]), Г2 := и{[с,Ъ}), то Г = Гх U Г2 и
/ ш = / ш + / ш.
ггиг2 гг г2
2°. Криволинейный интеграл второго рода как предел
интегральных сумм. Пусть Г = гГ([а,Ь]) — ориентированная кри-
кривая в R3. Предположим, что i-пространство для [а, Ь] положительно.
Ориентацию Г будем интерпретировать, как задание движения по Г, со-
соответствующего возрастанию параметра t. Пусть F — векторная функ-
функция, заданная на Г, т. е. F = (/ь/2,/з) : Г —> R3. Пусть А = {а =
to,ti,... ,tn = by — разбиение [а,Ь], \Х\ — его размер. В каждом из от-
отрезков [iw,iv+i] рассмотрим точку £„; 0 < v < п — 1. Для участка кривой
Г, соответствующего параметрическому множеству [ij/,ij/+i], рассмот-
рассмотрим скалярное произведение вектора F{u(£v)) на вектор u(tv+i)—u(tv),

15.2. Интеграл по многообразию от дифференциальной формы 477
который направлен в сторону движения по этому участку. Это скаляр-
скалярное произведение равно такой сумме (F(u(£v)),(u(tv+i) - u(tv))) =
з
= Е fj{ui(iv)>u2(^v),'^3{iv)){'Uj(tv+i) —Uj(tv)). Следующая величина
п-1
Е
i/=0
(F(U(£v)),(U(tv+1)-U(tv))) D)
n-l
есть сумма трёх сумм вида Si := £] h{u(£v)){ui(tv+i) -щA„)). Если
Г — гладкая кривая, a F G С(Г, Я3), то, по теореме Лагранжа, Si =
при |Л| —> 0. Таким образом, криволинейный интеграл второго рода
допускает следующее представление
Д/i dxi + /2 dx2 + /з dx3) = lim "e №(&)). (^(^+i) ~ «(<^))) E)
Г |Aj—уО у-о
Представление E) позволяет получить ряд важных физических •ин-
•интерпретаций криволинейного интеграла второго рода.
Пример. Предположим, что на материальную точку Р, помещённую
в точке х е Я3, действует сила Р = {fi{x),f2(x),f3(x)). Пусть Г —
гладкая кривая в Я3, задаваемая с помощью функции й на [a,b]. Пред-
Предположим, что точка Р движется от одного конца Г к другому, причём
направление движения соответствует возрастанию параметра t. Какая
работа затрачивается на перемещение точки Р по кривой? Приближён-
Приближённое значение даёт сумма D), а точное значение равно криволинейному
интегралу второго рода из формулы E).
Замечания. 1. Криволинейный интеграл второго рода был опре-
определён в 1° по гладкой кривой. Непрерывная кривая называется кусоч-
кусочно-гладкой, если она составлена из конечного числа гладких кусков.
Криволинейный интеграл второго рода по кусочно-гладкой кривой опре-
определяется как сумма интегралов по гладким кускам.
2. Заметим также, что переход к противоположной ориентации из-
изменяет знак интеграла fw. Точнее, если Г — ориентированная кривая,
г
а Г' — та же кривая с противоположной ориентацией, то fw = — f w.
Г Г'
Упражнение 10. Пусть m = 2 и кривая Г = {(х, и(х)) \ х е [а, Ъ], и е
С1([а,6])} пробегается в направлении возрастания параметра х. Дока-
Доказать, что для {Р, <3} С С"(Г) справедлива формула
J(Pdx1+Qdx2) = }(Р(х,и(х)) +Q(x, «(*))«'

478 Глава 15. Интегралы по многообразиям и теорема Стокса
Упражнение 11. Вычислить интеграл f ш, если w = x\dx\ ~
г
и Г = {(xi,x2) | |zi| + |х2| = 1} — кривая, пробегаемая по часовой
стрелке.
3°j Поверхностный интеграл второго рода. Пусть т = 3,
р = 2, Т — компактное измеримое Пбдмножество К , положим й(Т) =
= {(хих2,х3) = {ui(ti,t2),u2{ti,t2),U3{t1,t2)) | {tut2) € Т} для функ-
функции й £ C1(T,-R3). Допустим, что множество Т ориентировано, тогда
S — й(Т) — ориентированная поверхность в R3. Пусть fj G C(S), j =
1,2,3.
Определение 4- Интеграл f ш от дифференциальной
s
формы, второй степени
w = fi(x) dx2 Л dx3 + /2(х) dx3 Л dxi + /3(х) dxi Л dx2
по ориентированному многообразию — поверхности S
называется поверхностным интегралом второго рода.
Заметим, что согласно общему определению 2 интеграла от формы
по многообразию, поверхностный интеграл второго рода вычисляется
по следующей формуле
/(/i(x) dx2 Л dx3 + /2(х) dx3 Л dXl + /3(х) dxi Л dx2) = F)
s
Пример. Пусть T = {{hM) | t? +i| < 1}, xx =ui(ii,t2) = <i, ^2 =
«2(<1,<2) = <2, 2з = из(<1,<2) = l-t\-t\\ \tut2) € Г, Причём t-
пространство имеет знак +1. Тогда S = й(Т) есть ориентированная
поверхность — верхняя сторона параболоида вращения, расположен-
расположенная в полупространстве Хз > 0. Для функции /(х1,Х2,Хз) = Хз вычис-
вычислим интеграл J f(xi,x2,x3)dxi Adx2. На основании формулы F) имеем
S
/ х3 dxj Л dx2 = f(l -t\- t\) dt1dt2 = -кJ2.
s т
Упрамснение 12. Вычислить интеграл f(dxi Adx3 +2xi dx\ Adx2) no
s
внешней стороне поверхности цилиндра х\ + х\ < 1, |хз| < 1.
Упражнение 13. Пусть F(t) = f (x1x2dxi +x2dx2), t > 0, где
r(t)
F(t) = {(xi,x2) | x\+x\ = t2, Xi > 0} с началом в точке @,t). Вычислить
производную F'.

/5.3. Внешний дифференциал формы. Ориентация границы 479
Упражнение 14- Пусть F[t) — f (xix2x3 dx2 Л dx3 + х2 dx3 A dxx),
S(t)
где S[t) ={{xi,x2tx3) | xl+xl + xl = t2, x3 > 0}, t > 0. Вычислить F'.
15.3 Внешний дифференциал формы.
Ориентация границы
15.3.1 Внешний дифференциал дифференциальной
формы
Пусть ш = fi(x)dxv(i)A.. .Adxv(p) + .. . + /,(х) dx^A.. .Adx^ — диф-
дифференциальная форма степени р < m на ориентированном множестве
М С ЯГ, причём fk Е СХ{М), l<k<q.
Определение 1. Внешним дифференциалом формы
ш степени р называется, следующая, дифференциальная
форм.а степени р + 1
dw := Е ^^ da;fc Л dxv(D л • • • л
• • • + Е "^-^ dxk A dx^i) Л ... Л dxM(p).
fc=l OXk
Внешним дифференциалом функции f (т. е. форм.ы
т д}(х)
степени СО называется её дифференциал df = V dxfc.
fc=i dxk
■ Заметим, что форма записи формы dui в определении 1 не является
канонической и что, согласно, определению d(uix +102) = duj^ +duj2.
ПримерыП) Пусть т = 2,р = 1и ш = P(xi,x2)dxi + Q(xi,x2)dx2—
дифференциальная форма первой степени на R . Согласно определе-
определению A), её внешний дифференциал равен
ЭР , , ЭР , , dQ , , dQ ,
du = -— dxx A dxx + -— dx2 A dxx + -— dxx A dx2 + -r— dx2 A dx2,
axi ax2 axx ax2
откуда после приведения к канонической форме получим
Q дР
2.уПусть т = 3, р — 1. Внешний дифференциал формы первой
степени на R3 ш = Р(х) dxx + Q{x) dx2 + R{x) dx3 после упрощения
имеет вид
. fdR dQ\ ^(дР dR\ , Л . ^
dui = —— — —— dx2 A dx3 + I —— — —— dxi A dxx +
\ox2 dx3 J ' \dx3 dxx J
dQ &P\
я я~~ ) dx1Adx2.
OXi OX2
31 —4-1168

480 Глава 15. Интегралы по многообразиям и теорема Стокса
3. Пусть m = 3, р = 2 и
ш = Р(х) dx2 Л dx3 + Q{x) dx3 Л dai]. + R{%) dx\ A dx2
— дифференциальная форма второй степени на R . Её внешний диф-
дифференциал после приведения к канонической форме равен
(дР dQ dR \ ,
duj = Ь н -— dx\ Л dx2 Л
V^x 9x2 дх3 J
Следует обратить внимание на "циклическую" запись форм и их
внешних дифференциалов в примерах 1 — 3. Заметим также, что со-
гяасно определению внешний дифференциал любой формы степени m
в Rm равен 0.
Теорема 1. Пусть ш — дифференциальная форма
степени р на М с коэффициентами, принадлежащими
классу С2(М). Тогда d(dw) = 0.
[ Достаточно рассмотреть случай дифференциальной формы вида ш —
f(x) dxv(i) Л ... Л dxv(py На основании определения 1 сначала имеем
5Л dxv(X) Л ... Л dxv(p),
fc=l OXk
а затем
m fdf(x) \
d{dw) = 2 d[ — dxk Л dxv(i) Л ... Л da;v(p) ) =
fc=i V c'a:fc /
m m d2f(x)
= E E ^~^- da:i Л dlfc л ^«-(l) Л ... Л dxv{p) =
fc=lj=l OXjOXk
поскольку для / 6 С2(М) справедливо равенство
dxkdxj dxjdxk - >j -
Доказанную теорему иногда называют теоремой Пуанкаре.
"Упражнение 15. Определить внешний дифференциал формы:
a) х\ dx2 Л dx3 + х2 dx3 Л dxx + х3 dxx Л dx2;
b) /i(zi)dz! + f2{x2)dx2 + ... + fm{xm)dxm;
c) /1B:2,2:3)^x2 Adx3 + f2{x
m
fk dxk+i Л ... Л dxm Л dxi Л ... Л
в) Е (-1)" f/il^- -/al^) dx1A...Ada;fc_1Ad:rfc+1A...Adxm.
oxk axk J

15.3. Внешний дифференциал формы. Ориентация границы 481_
Упражнение 16. Привести примеры дифференциальных форм ш,
для которых dui = dxx Л dx2 Л ... Л dxm.
15.3.2 Ориентация границы множества, состоящего из
конечного числа брусов
Пусть для множества А в пространстве (Rm,p) A0 — множество всех
его внутренних в (Rm,p) точек.
Определение 2. Пусть F — замкнутое в (Rm,p) мно-
множество. Границей dF множ.ества F называется мно-
множество dF:=F\F°.
Пример. Брус Q = {(хх,..., хт) | а* < хк <Ък, 1 < к < т} в Rm есть
замкнутое множество. Его граница dQ есть объединение 2т (т. — 1)-
мерных брусов следующего вида
[obbi] х ... х [ak~i,bk-i] x {cfc} x [ofc+i,bfc+i] x ... x [ат,Ът],
где cfc = оь или Ск = Ък, 1 < к < т.
Пусть М — множество, которое является объединением конечного
числа брусов некоторого разбиения пространства Rm.
Граница дМ множества М состоит из конечного числа (т — 1)-
мерных брусов. Пусть для каждого к, 1 < к < т., дкМ есть та часть гра-
границы дМ, которая располагается в гиперплоскостях вида Хк = constant.
Все брусы размерности т — 1, составляющие дкМ, разделим на две ча-
части 9fc~M и д£М следующим образом. Предположим, что Q — (т— 1)-
мерный брус, лежащий в гиперплоскости Хь = с и Q С дкМ. Брус Q вхо-
входит в д£М {дк~М), если Vf = (хх,... ,xk-i,xk = с,хк+1,... ,хт) 6 Q°
при всех достаточно малых положительных 8 имеем
xs := (i1,...,a;fc_1,c-|-E,a;fc+i1...,a;m) $ М (xs £ М).
Здесь Q0 — множество всех внутренних точек Q в гиперплоскости
Хк = с, которая является (т — 1)-мерным пространством с обычным
расстоянием.
Предположим теперь, что A1,12, ■ • ■, хт)-пространство имеет знак
j. При этом множество М ориентировано. Заметим теперь, что при
этом (а:*.,... ,xm,Xi,..., а:к_1)-пространство есть пространство, получа-
получаемое с помощью регулярного преобразования — перестановки коорди-
координат из (xi,x2,.. ■ ,а:т)-пространства, и имеет знак j(-l)(m-1)(fc"). К
Определение 3. Длл любого к, 1 < к < т., множество
дкМ лежит в {xk+i,... ,xm,xi,.. .,хк-1)-пространстве, ко-
которое есть, согласно определению, пространство знака
j(_l)(m-i)(fc-i) для множества д^М и знака -j{-\)(m-W-V
для множества д^М. При этом граница дМ множ.ества

482 Глава 15. Интегралы по многообразиям и теорема Стокса
М называется ориентированной. Эта ориентация гра-
границы, дМ называется ориентацией, соответствующей
ориентации множества М.
Упражнение 17. Доказать следующие утверждения:
a) Если брус Q принадлежит (хк+1,... ,хт,х1,..., ^-^-пространству
знака +1 и одновременно принадлежит (i)i+1,...,im,i1,...,i|C_i)-
пространству знака —1, то Q не входит в дМ.
b) Пусть Q — брус, Q — ориентированный брус Q и Q — брус Q с
ориентацией, противоположной Q. Условимся считать, что Q UQ = 0.
Для множества М = \J Qj, N 6 N доказать равенство дМ — \] dQy
c) Доказать, что д(дМ) = 0.
Упражнение 18. Пусть при т = 2 множество М лежит в поло-
положительном (а:ь ^-пространстве. Положительную ориентацию отрезка
в одномерном пространстве будем трактовать как задание направления
движения в сторону возрастания координаты. Доказать, что ориентацию
дМ, соответствующую ориентации М, можно интерпретировать как за-
задание обхода дМ в таком направлении, при котором ближайшая часть
множества М оказывается слева. Обратить также внимание на то, что
дМ состоит из конечного числа замкнутых ломаных. Если лежит М в
отрицательном (х1,а:2)-пространстве, то обход дМ следует заменить на
обратный.
Упражнение 19. Пусть при т = 3 множество М лежит в положи-
положительном (а^яг.хзЭ-пространстве. Доказать, что ориентацию дМ можно
трактовать как выбор внешней по отношению к М стороны поверхности
дМ, поскольку, если смотреть на грани — части дМ извне М, то их
ориентация будет такой, как описано в упр. 18.
15.4 Формула Стокса в специальном случае
15.4.1 Формула Стокса для множества, состоящего из
конечного числа брусов
Пусть т > 1, Q = [oi, bi] х... х [om, bm] — брус в Rm, и число к, 1 < к <
т, фиксировано. Для множества Q рассмотрим части границы d£Q =
}... ,хк-1,Ьк,хк+и ... ,хт) | а; < Xj < bj,l <j< m,j ф к}, d^Q =
..,xm) | Oj < Xj <bj,l <j <m,j ф к}.

15.4. Формула Стокса в специальном случае
483
н На основании формулы C) п. 14.1.6 для функции </, —— >С C(Q),
I ах к J
имс
имеем
,. ■ ■ ,xm)dxi.. .
A)
Здесь брус Qk := [оь bi] x ... x [ak-i, bk-i] x [ofc+1)bfc+i] x ... x [om, bm].
Предположим теперь, что (xi,..., хт)-пространство имеет знак j, то-
тогда (ifc,... ,xm,Xi,... ,a:fc_i)-npocTpaHCTBO имеет знак j(—l)(m~1)(*~1).
Рассмотрим ориентацию 5Q, определённую в п. 15.3.2. При этом
(zfc+L---.a:m,:ri,---,:Efc_:l)-npocTpaHCTBO имеет знак j(-l)(m-1)(fc-1)
для множества d£Q и знак —j( — 1)("а—1)(fc—x) для множества d^Q. Учи-
Учитывая теперь определения дифференциальной формы и интеграла по
многообразию, запишем формулу A) в следующем виде
а/
J -— dxk Л
л ... Л xm A xi Л ... Л Xk-i =
B)
fdxk+iA...AxmAx1A...SCxk-i+
fdxk+iA...AxmAxiA...Axk-i.
Заметим также, что согласно определени1сгйнтеграла по многооб-
многообразию, для j ^ k имеем '
/ fdxk+iA...AxmAx1A...Axk-i =
C)
_Л 0|
поскольку якобиан в правой части содержит следующую строку из ну-
dxj
лей -~ =0, I ■= j + 1,..., т, 1,..., j — 1. Аналогично, для j ф к
OX
D)
Равенства (З) и D) позволяют представить формулу B) в виде
Г -— dxk A dxk+i Л .. . Л Хт A Xi А .. . A Xk-i =
q дхк
= / fdxk+1A...AxmAx1A...AXk-i. n n
E)

484 Глава 15. Интегралы по многообразиям и теорема Стокса
Рассмотрим теперь два бруса Qi и Q2 с общей (т - 1)-мерной
гранью, лежащей в гиперплоскости хк = constant :
Qi = {(zi,..., xm) | o,k <xk < bk; Oj < xj < bj, 1 < j < m, j Ф k},
Qi = {{xi,...,xm) \bk<xk <ck; Oj <Xj <bj, 1 < j <m, j ^ fc},
Объединение Q = Qi U Q2 есть также брус, причём d^Qi — d^Q,
9+Q2 = d£Q. Общая грань брусов Qi и Q2 есть множество 9^"Qi =
9kQ2, которое не имеет внутренних точек в (Rm,p). Как часть границы
бруса Qi это множество лежит в пространстве знака j[ — l)(m~1)(fc~1I a
как часть Q2 — в пространстве знака -j(-l)(m-1)(fc-1). Пусть </, -— г
L дхк >
С C{Q). Если теперь записать формулу B) для каждого их брусов
Qii <?2> то правые части полученных равенств будут содержать два ин-
интеграла от функции / по d^Qi и ддГфг, т- е. по одному множеству,
имеющему противоположную ориентацию в интегралах. Тогда сумма
этих двух интегралов будет равна 0. Следовательно, учитывая формулу
E), получим
/ -— dxk Л dxk+i Л ... Л хт Л х1 Л ... Л Zfc_i =
O1UO2 dXk
= f fdxk+iA...AxmAx1A...Axk-i. F)
Из равенства F) следует такое утверждение.
Лемма 1. Пусть М — множество, которое лвллетсл
объединением, конечного числа брусов в Rm. Предполо-
Предположим, что М ориентировано и пусть дМ — граница мно-
otcecmea M, ориентиров аннал соответствующим ориен-
ориентации М способом, Пусть \f,-=— \сС(М). Тогда
I- дхк ) \
а/ ^<х)
f -— dxk A dxk+1 Л ... Л im Л i! Л ... Л xk-i = р
М дхк
= / / dxk+1 Л ... Л im Л it Л ... Л ifc_i. G)
дМ
Полученную формулу G) можно записать в иной форме. Предполо-
Предположим, что {Д,..., /m} С С1(М). Положим в G) / = fk и затем сложим
все полученные равенства, получим
т Qfk
f Y, -— dxk A dxk+1 Л ... Л im Л i! Л ... Л o:fc_i =
M fc=l dxk
m
= / E fkdxk+1A...AxmAx1A...Axk-1. (8)
дМ fc=l
Пусть

5.4. Формула Стокса в специальном случае 485
ш ■'= Е) fk dxk+1 Л ... Л Im Л Ix Л ... Л Xk-i
fc=l
|8- дифференциальная форма степени m - 1 на дМ — (т. — 1)-мерном
Многообразии.Тогда внешний дифференциал ш равен
Y, J2 — &XJ Л dxk+i Л ... Л im Л ii Л ... Л xk-i =
fc=l j=l C*2;
Qfk
- Y. a— dxk Л da:fc+1 Л ... Л хт Л Xi Л ... Л хк-1-
fc=l <JXk
Поэтому формулу (8) можно записать в виде
fdcj=faj. (9)
м ам
Полученное равенство представляет собой специальный случай об-
|Дей формулы Стокса.
15.4.2 Частные случаи
Формула (9) п. 15.4.1 представляет собой интересный результат, охва-
охватывающий ряд классических утверждений анализа.
I. Формула Ньютона-Лейбница. Определим 0-кратный инте-
интеграл от функции / по 0-мерному множеству, состоящему из одной точ-
точки {о}, как /(о). Пусть отрезок [о, Ь] = М лежит в положительном
х-пространстве R, функция / 6 С1([о,Ь]) и ш = f — дифференци-
дифференциальная форма степени 0 на [о, Ь]. В этом случае дМ = {а,Ь}, причём
д~М = {а}, д+М = {Ъ}.
Кроме того, dui = f'dx и формула (9) принимает вид
М а. дМ
Это равенство представляет собой формулу Ньютона-Лейбница.
II. Формула Грина. Пусть М — множество, которое является объ-
объединением конечного числа прямоугольников — брусов в положитель-
положительном (х1,а:2)-пространстве. При этом дМ есть объединение конечного
числа отрезков, а ориентацию дМ, соответствующую ориентации М,
можно интерпретировать как задание обхода дМ в таком направлении,
что ближайшая часть множества М остаётся слева, если смотреть на
плоскость сверху.
Пусть {Р, Q} С СХ(М) и ш = Рdxx + Qdx2 — дифференциальная
форма первой степени с внешним дифференциалом
/ дО дР \
dcj = — dxxAdx2.
\0Xi 0X2 J
В этом случае формулу (9) п. 15.4.1 можно записать в виде

486 Глава 15. Интегралы по многообразиям и теорема Стокса
*{ш~М;)dXldX2 = !
Это равенство называется формулой Грина. Интеграл в левой
части A) есть двойной интеграл по М от непрерывной функции, а инте-
интеграл в правой части A) есть криволинейный интеграл второго рода по
границе дМ, ориентированной указанным выше способом.
Замечание. Для отрицательного (ij, а^-пространства интеграл в
левой части формулы A) следует взять со знаком "—", а интеграл пра-
правой части рассматривать по дМ с противоположной ориентацией.
III. Формула Гаусса-Остроградского. Предположим, что
множество М является объединением конечного числа брусов в по-
положительном (хх, а^а^-пространстве. При этом дМ есть объедине-
объединение конечного числа прямоугольников, а ориентацию дМ можно ин-
интерпретировать как выбор внешней стороны поверхности дМ. Пусть
{P,Q, R} С Сг{М). Для дифференциальной формы второй степени
ш = Р(х) dx2 Л dx3 + Q{x) dx3 Л dxx + R(x) dxx A dx2
с внешним дифференциалом
(дР dQ dR \ ,
duj = — + ^- + — dxx Л dx2 Л dx3
\oxi ax2 ox3 J
формулу 9 п. 15.4.1 можно записать в виде
г (дР ^dQ &R\
J a— + -^~ + -^~ dxidx2dx3 =
li \dxi дх2 дх3 J
B)
дМ ~i
Равенство B) называется формулой Гаусса-Остроградского.
Интеграл в левой части B) есть тройной интеграл по М от непрерыв-
непрерывной функции, а интеграл правой части B) есть поверхностный интеграл
второго рода от формы ш по внешней стороне поверхности дМ.
Замечание. В случае отрицательного B1,22, яз)-пространства ин-
интеграл в левой части B) следует взять со знаком "—", а интеграл в
правой части рассматривать по внутренней стороне дМ.
Пример. Пусть {(p,ip} С С1(М). В формуле Грина положим Р =
О, Q = (pip, получим Г I (р—— +^— ) dx\dx2 — Г ipipdx2, откуда
м \ dxi dxi J эм
C)
D)
м
Аналогично
и
0— UXiCLX2
дхх
dip
дх2
м
м
vdxx
д(р
рдГя
dx\
dx\
dx2
dx2
+
+
/
дМ
I
ЭМ
(pipdx2.
(piPdx,.

/5.5. Общая формула Стокса 487
Формулы C) и D) являются для кратных интегралов аналогами од-
одномерной формулы интегрирования по частям. Эти формулы допускают
различные обобщения. Например, если {VjV'} С CS(M), p + q = s, р>
О, q > 0, то
^ d"d"+
С помощью формулы Гаусса-Остроградского легко получить аналоги
формул C) — E) для тройных интегралов.
Упражнение 20. Пусть {ip,ip} С С2(М) и Aip := —-у + —у . До-
Доказать следующую формулу Грина: f(tpAip - ipAip) dxi Л dx2 —
м
дМ
Упражнение 21. Пусть (zj,... ,а:т)-пространство положительно и
m
U> = ^ ( — l)(m~X)(k~l)XkdXk+l Л ... Л Хт Л Xi Л ... Л 2fc_i.
Доказать для меры тп(М) множества М следующую полезную форму-
формулу т(М) = — J" ш. Записать полученную формулу для т — 2, m = 3.
15.5 Общая формула Стокса
15.5.1 Вывод формулы Стокса
Формула (9) п. 15.4.1 была доказана для множества М, которое являет-
является объединением конечного числа брусов в Rm, и дифференциальной
формы степени т — 1. Эта формула допускает обобщение на случай
произвольной формы на многообразии более общего вида.
Пусть Т — объединение конечного числа брусов в (ij,... ,<p+i)~
пространстве Rp+1. Пусть Т — ориентированное множество и дТ —
граница Т, ориентированная соответствующим ориентации множества
Т образом.
Пусть р<ши {ui,..., um} С С2(Т). Множество

I
488 Глава 15. Интегралы по многообразиям и теорема Стокса
м = й(Т) = {(u^i),...,um@) I f eт}
есть (р + 1)-мерное ориентированное многообразие в (ij,... ,xm)-
пространстве Rm. Множество й(дТ) называется ориентированной
границей многообразия М, й(дТ) — ориентированное многообразие
размерности р в Rm.
Теорема 2. (Общая формула Стокса.) Пусть функ-
функции {/i /,}CC'(W) и
ш = fi(x) div(i) Л ... Л dx^p) + ... + fq{x) diM(i) Л ... Л dx^(p)
— дифференциальная, форм.а степени р. Тогда
f duj= f ы. A)
й(Т) й(дТ)
[ Согласно определению интеграла по многообразию, доказательство
достаточно провести для формы вида ш = }{х) dz^i) Л.. ./\dxv(p), внеш-
ний дифференциал которой равен du> = £2 ^— dxkf\dxv^f\.. .Adxv(py
fcl 9Xk
На основании определения интеграла по многообразию, для инте-
интеграла из левой части A) имеем
m Qf
f dcj = f Е^-^Л 4в„A) Л ... Л dxv(p) = B)
п(Т) п(Т) *=1 OXk
J L х:^777 f Г" *1 Л сй2 Л ... Л dip+i.
т k=i dxk d{t1,t2,- •• ,tP+i)
С помощью разложения якобиана в B) по элементам первой строки
_ Р+1 /_1у+1 Ё5*. g(a:^(i)-a:^B)----ia:^(p))
а также формулы для вычисления производной сложной функции
™ df дхк df
У. т; ^— = ■^— i равенство B) запишем в следующем виде / аи =
к=1 дхк dtj dtj _(JT)
_ rP£-, Ui+ldf dixu(l),XvB),---,Xv(p))
- J L, [~1У^ дт- ^т -. : :—г dtx л dt2 л... л dtp+1. C)
T j-1 Otj atl>-■■<tj-l,tj+l>-■ ■ >1р+1)
Для интеграла в правой части A) на основании определения интегра-
р+1
ла по многообразию получим такое равенство f ш — J2 f ш =
й(дТ) k=l й(дкТ)
2^ J
fc=l 3fcT
Г
J
^ Г f
k=idT "I'll- ■ • >rfc-i.rfc+ii • • • >гр+1;
p+1 =

15.5. Общая формула Стокса 489
= / а, D)
ет
где
.ы:= £ f-яп +—Ч Т—Т dtiA...Adtk-1Adtk+1A...Adtp+1
fc=i °4'i> • ■ ■ iEfc—iiEfc+i> • • • irp+ij
— дифференциальная форма степени p с внешним дифференциалом
p+ip+i 5 / d(xvll),xv{3),...,xv(p)) \
fc=l j=l Otj \ C(tb. . . , tfc—i, tfc+i, - - t) J
xdtj A dtx A ... A dtk-i A difc+i... Л dtp+1 =
поскольку форма
j=l OIj Oti, ■ • • ,bj-l>rJ+l> ■ • • irP+lJ
Действительно,
p+i
Е
fc=l
i f
' Применим теперь к множеству Т и дифференциальной форме й>
формулу (9) п. 15.4.1 f ш = f diu =
дТ Т
= /Е аГ от:—"—.' " ,' '—?-£—- di л ... л dip+i- F)
Т j=l j '-'I'll • • • )'j —1)'j + li • • • i'p+l/
Из формул C), D) и F) следует равенство f dw = f ш. J
п(Т) п{дТ)
Заметим, что частные случаи A) и B) п. 15.4.2 также справедливы
для й(Т) и дМ = ЩдТ).

490 Глава 15. Интегралы по многообразиям и теорема Cioft&6
15.5.2 Следствия из общей формулы Стокса
I. При m = 2 и р = 1 й(Т) = М — множество точек плоскости, а
й(дТ) =: Г — кривая или набор кривых, ограничивающих множество М.
Предположим также, что на множестве Т \ Ф отображение и взаимно
однозначно и , 1> 2' -ф- О, тп(Ф) = 0; ш = Pdxi + Qd$2- Пусть
0A1,12)
{P,Q} С Сг(М). Предположим, что х-пространство положительно. То-
Тогда формула Стокса имеет вид
)то равенство называется формулой Грина. Интеграл в левой ча-
:ти формулы есть двойной интеграл по М, а интеграл в правой части
- криволинейный интеграл второго рода по Г, пробегаемой в таком
«вправлении, что ближайшая часть М остаётся слева.
Положив Р = —Х2, Q — Xi в формуле Грина, получаем следующее
выражение для площади — меры Жордана тгг(М) = - J(xidx2-X2<ix\).
1 г .
| II. Пусть m = 3, р = 2. Допустим, что на множестве Т \ Ф отобра-
|кение и взаимно однозначно и
т(Ф)=0; ш =
Предположим, что функции {P,Q,R} С C1(Af) для М = й(Т), и что
х-пространство положительно, a S := й(дТ). Тогда формула Стокса
принимает вид
Р 6Q dR
s
'. Полученная формула называется формулой Гаусса-Острог-
Гаусса-Остроградского. Интеграл в левой части этой формулы — тройной интеграл
по М, а интеграл правой части — поверхностный интеграл второго рода
по внешней стороне поверхности S.
Положив в формуле Гаусса-Остроградского Р = Xi, Q = х^, R = хз,
получим формулу
т(М) = - f(xidx2 A dxs + X2dx3 A dxi + x$dxi Л dxj),
3 s
дозволяющую вычислять объём с помощью поверхностных интегралов
второго рода.

j|5.6. криволинейный интеграл От формы 1-вой степени 491
III. Пусть m = 3, р = 1. При этом S := й(Т) = {(tii(<i,t2),U2(*i,<2),
Шз(*11<2)) I (*ii*a) G Т} — поверхность в Д3, а Г := и(9Т) — край
поверхности 5. Обычно Г — кривая или набор кривых. Для дифферен-
дифференциальной формы первой степени ш = Pdx\ + Qdx2 + Rdx3 внешний
дифференциал определён в п. 15.3.1. В этом случае общая формула
Стокса принимает вид
f(Pdxx + Qdx2 + Rdx3) = s((^--^-\ dx2Adx3 +
дР 8R \ , д . (8Q ЭР
JdAd+[
Это равенство есть классическая формула Стоках.
/применение 22. Вычислить площадь круга с помощью криволиней-
юго интеграла.
{Упражнение 23. Вычислить объём шара с помощью поверхностно-
•fo интеграла.
Упражнение -2\. Вычислить интеграл / Г —|- dx2 \ dxA , где Г —
пробегаемая против часовой стрелки окружность радиуса 1 с центром
р точке @,0) и г2 = х\ + х\. ^-
1 Предостережение. Формулу Гринв к кругу, ограниченному Г,
^применить нельзя. ^
^Упражнение 25*. Пусть А = {(ii,i2) I *? + ** ^ х} и / е
1 'Вычислить предел
15.6 Криволинейный интеграл от формы
первой степени
15.6.1 Криволинейный интеграл второго рода от
дифференциала
Пусть G С Rm — открытое множество.
Определение 1. Определённом на G дифференциаль-
дифференциальная форма ш называется точной на G, если она являет-
является внешним дифференциалом некоторой формы, в G.
; Пример. Важным примером точной формы первой степени является
дифференциал функции g 6 C1(G)

492 Глава 15. Интегралы по многообразиям и теорема Стокса
, дд(х) , дд(х) ,
ax\ oxm
Криволинейный интеграл от дифференциала обладает следующим
простым, но важным свойством.
Теорема 3. Пусть функция д £ Cl(G) и Г = {u{t) \ t e
[a,b]} С G — кусочно-гладкая кривал в G, причём, отрезок
[а,Ь] лежит в положительном t-пространстве. Тогда
(" Согласно определению криволинейного интеграла второго рода, име-
имеем следующее равенство
dUl{t) dg(u(t)) dum(t) \
~dT+--- + ^xZ dT)dt-
J
Замечание. При условии теоремы 3 ориентацию Г можно интер-
интерпретировать как задание движения по Г, соответствующего возрастанию
параметра t. При этом й(а) и й(Ь) — соответственно начало и конец
кривой Г. В случае, когда ш = dg в G, теорема 3 утверждает, что кри-
криволинейный интеграл f dg по кривой Г в G зависит только от начала
г
й(а) и конца й(Ь) кривой Г. При этом говорят, что интеграл f dg не
г
зависит от пути интегрирования.
Определение 2. Кусочно-гладкал кривал Г = {u(t) \ te
[a,b]} называется замкнутой, если й(а) = й(Ь) (т. е. если
начало и конец кривой совпадают).
Следствие 1. Если g e C^G) и Г — кусочно-гладкая
замкнутая кривая в G, то f dg — 0.
г
(" Доказательство следует из формулы A). J
15.6.2 Замкнутые дифференциальные формы.
Односвязные множества
Определение 3. Дифференциальная форма ш, опреде-
определённая на открытом мноснсестве G С Rm, с коэффициен-
коэффициентами из класса CX(G) называется замкнутой в G, если
dcj = 0 в G.
Примеры. 1. Пусть g 6 C2(G) и ш = dg. Форма ш = dg — замкнута в
G, поскольку, согласно теореме Пуанкаре, dw = d(dui) — 0.

1&.6. Криволинейный интеграл от формы 1-вой степени 493
прит = 2, {P,Q}C C^G) и
-£—=-£—, C=1,2:2) € G. A)
Для формы первой степени ш = Pdx1JrQdx2 внешний дифференциал
rip и условии A) равен
dcj = I -r-^- - -г— ) dxi Л di2 = 0.
\oii ai2 /
Следовательно, ш — замкнутая форма. Заметим, что условие A) необ-
необходимо для замкнутости формы и.
(ъ) Пусть m = 3, {Р,Q, R} С Cl(G), причём на множестве G выпол-
выполняются равенства
dQ_ - ЭР_ ^_^. дР_ _ dR_
дх1 дх2 ' дх2 дх3 ' дх3 Эац
.Форма первой степени ш = Pdx\ + Qdx2 + Rdx3 при условиях B)
замкнута, поскольку
(BR dQ \ , , (ЭР dR \ _,
dw= я ^- ) dx2Adx3+[- д— dx3Adxi+ *
\ох2 дх3 ) \ох3 охх J
dQ ЭР \
-г-2- - ^— dn Л dx2 = 0.
Условия B) необходимы для замкнутости формы ш в G.
Ы] Точная дифференциальная форма первой степени с коэффициен-
коэффициентами из класса C'1(G) является замкнутой, согласно теореме Пуанкаре.
Пусть Г = {u(t) \te[a, b]} - кривая в Rm.
Определение 4- Кривал Г называетсл кусочно два-
дважды непрерывно дифференцируемой, если Г непрерывна
и отрезок [а,Ь] можно представить в виде объединения
в конечном числе отрезков [а,/3] таких, что й£ С2([а,/3])
■ (в точках а и /3 рассматриваютсл соответствующие
односторонние производные).
В этом разделе далее под замкнутой кривой будем
подразумевать замкнутую кусочно дважды непрерывно
дифференцируемую кривую.
Определение 5. Пусть М с Rm, Г = {u(t) \ t e [а,Ь]} —
замкнутал кривал в М. Замкнутал кривал Г гомотопна
точке в М, если длл множества D := [a,b] x [0,1] суще-
существуют точка х0 е М и функицл ф € C(D,Rm), удовлетво-
удовлетворяющие следующим, условиям: 1) \f(t,a) £ D : 0{t,a) € М;
2) Vt € [a,b] : 0(t,O) = u(t), <p(t,l) = x0; 3) Va € [0,1] : <p(a,cx) =
<р(Ъ,а); 4) За = t0 < tr < ... < ts = b \fk,0<k<s-l : <p £
C2(Dk,Rm), Dk:=[tk,tk+1]x[0,l].

494 Глава 15. Интегралы по многообразиям и теорема Стокса
Определение 6. Множество М называетсл линейно
связным, если длл любых его двух точек существует
пепрерывнал кривал, лежащал в М и соединлющал эти
точки. Множ.ество называетсл односвязным, если оно
линейно свлзно и любал замкнутал кривал, леок.ащал в
М, гомотопна точке в М.
Примеры. 1. Множество М С Rm называется звёздным относи-
относительно точки xq, если для любой точки х € М следующий отрезок
{xq + т(х — xq) | т £ [0,1]} С М. Звёздное множество односвязно,
причём ip(t, а) — ах0 + A - a)u(t), (t, a) 6 D.
2. Множество М = {B:1,2:2) | 0 < х\ + х\ < 1} С R2 не является
ОДНОСВЯЗНЫМ.
Теорема 4. Пусть М — односвлзное множество в
Rm, ш — замкнутал дифференциальнал форма первой
степени с коэффициентами из класса ^(М). Тогда длл
любой замкнутой кривой Г, лежащей в М, f ш = 0.
г
[ Кривая Г = {u(t) | t € [а, Ь]} гомотопна точке в М. Пусть (р : D —> Rm
— соответствующее отображение из определения 5. Множество <p(D) —
) двумерное многообразие, т. е. поверхность в Rm, лежащая в М; ф{О)
естественно интерпретировать как поверхность, натянутую на контур
Предположим, что (t, а)-пространство положительно для D и для
каждого {Dfc} из определения 5. Для каждого к, 0 < к < s — 1, рас-
рассмотрим соответствующую ориентацию границы dDk- Любой отрезок
{{t,a) | t = tk, a 6 [0,1]}, 1 < к < s - 1, ориентирован положительно
в качестве части dDk-i и ориентирован отрицательно в качестве части
dDk.. При каждом fc,0<fc<s — 1,к ориентированному многообра-
многообразию <p(Dk) и дифференциальной форме ш применима теорема Стокса
f dw = f ш. В полученном равенстве левая часть равна нулю.
Складывая правые част(+ и используя аддитивность криволинейного ин-
интеграла по множеству интегрирования, получим
к=0 0(dDk) Ф(дО) Г
Следствие 2. При условилх теоремы 4 криволиней-
криволинейный интеграл второго рода от формы ш не зависит от
кривой — пути интегрирования, лежащей в М. Точнее,
длл любых двух кусочно двасисды непрерывно дифферен-
дифференцируемых кривых Г\ иГ2, лежащих в М и таких, что
они имеют общее начало и общий конец, справедливо ра-
равенство f ш — f ш.

15.6. Криволинейный интеграл от формы 1-вой степени 495
\ Доказательство следует из теоремы 4, которую с учётом ориентации
нужно применить к кривой Г — ГЛ U Гг. J
Следствие 3. Теорема 4 справедлива длл точной фор-
формы ш = dg, g Е С2(М).
Замечание. Очевидно также следующее утверждение. Если для
множества М и формы ш криволинейный интеграл fu — 0 для любой
г
замкнутой кривой Г С М, то криволинейный интеграл от ш не зависит
от пути интегрирования.
Теорема 5. Пусть М — открытое односвлзное мно-
множество в Rm и ш = /i(z) dx\ + ... + /m(z) dxm — дифференци-
альнал форма первой степени, коэффициенты которой
{/ii---i/m} С ^(М). Длл того, чтобы форма ш была точ-
точной на М, необходимо и достаточно, чтобы
= *Ш. C)
oxj axk
I" Необходимость. Если ш — точная форма, то существует функция
g такая, что на М имеем ш = dg = Д dxx + ... + fmdxm. Тогда Д. =
дд
■^—1 1 < Л < т, на М. Поскольку, согласно условию, {Д,...,/т} С
охк
то -—-— € С(М), 1 < k,j < т. Тогда на М справедливо
OXkOXj
d2g d2g dfk(x) dfj{S) Л ^ , . ^
равенство -—|— = -—^— , откуда J = -J~L , Kk,j < т.
OXkOXj axdx oxj ax ~ ~
Заметим, что при доказательстве необходимости односвязность
множества М не использовалась.
Достаточность. Из условий C) теоремы 5 следует, что du) = О
на М. Поэтому для формы ш справедливо утверждение теоремы 4, из
которого следует, что криволинейный интеграл от ш не зависит от пути
интегрирования в М. Пусть xq — произвольная фиксированная точка
М и для точки х 6 М пусть Г(х) — некоторая дважды непрерывно
дифференцируемая кривая с началом xq и концом х, лежащая в М.
Рассмотрим функцию д : М —> R, определённую таким равенством
д(х) := f ш, х € М, заметим, что для каждого х € М значение д(х)
Г(х)
не зависит от вида кривой Г(х).
дд(х)
Докажем, что ш = dg, т. е. что = Д(х), х € М, 1 < к < т.
Рассмотрим точки вида z = (х^ + т,Х2, ■ ■ ■ ,хт), лежащие в М при всех
г, \т\ < 6, где 6 — некоторое положительное число, х = (i1(...,im).
Пусть Fi = {(xi +tT,x2,... ,xm) | t € [0,1]} — кривая — отрезок прямой
32 — 4-1168

496 Глава 15. Интегралы по многообразиям и теорема Стокса
с началом в точке х* и концом в точке z. Для T(z) := Г(х) U
имеем
g{z) - g{x) _ ff(xi + т, x2, ■ ■ ■, xCT) - g(xi, x2,...,
r r
•i Г(х) ' T J
Г(х)
.. ,xm)Tdt = f/i(xi +ir,a;2.---,a;m)dt.
Отсюда с помощью теоремы о среднем значении и предельного пе-
дд(х)
рехода приходим к равенству ——- = Д(х). Дальнейшие рассуждения
С'СС 1
аналогичны. ^(С ГГ«]^ '^,Ы&&-г,) J -~*£§-К) С>\<0( J
Часто оказывается полезной следующая теорема, содержащаяся в
приведенных выше утверждениях.
Теорема 6. Длл того чтобы криволинейный инте-
интеграл от формы и = Л dxi + • •. + fmdxm, {A,..../m} С Cr{M),
не зависел от пути интегрирования в односвлзном. от-
открытом, множестве М, необходимо и достаточно вы-
выполнение условий C).
Упразднение 26. Форма ш = sinx^dii + 2х:х2 cosx^ dx2 точна в
R2. Доказать это утверждение и найти функцию д, для которой ш = dg.
Упражнение 27. Доказать, что следующая форма
ш = fan) dx! + /2(i2) ^з + Д(х3) dx3, {Л, /а, /з} С С(Д),
точна в Д3. Найти ^, для которой ш = d^.
Упражнение 28. При каком условии на функцию / форма ш =
f(xi,..., хт) dx\ замкнута?
Упражнение 29. На множестве Д2\{@,0)} для следующей формы
xi dx2 - х2 dx\
ш = s ^ вычислить aw. Вычислить также интеграл от ш :
х\ + х\
х\ + х\
\
1) по замкнутой кривой, не охватывающей точку @,0);
2) по замкнутой кривой, охватывающей точку @,0).
Упражнение 30. Доказать, что множество {(xi,x2) | 0 < х\ + х% <
1} не односвязно.
Упражнение 31. Является ли вектор (—Х2,Х1,хз) градиентом неко-
некоторой функции в Д3?

15.7. Мера на многообразии 497
15.7 Мера на многообразии
15.7.1 Частный случай многообразия —
гиперплоскость в Rm
Напомним, что многообразиями размерности р в Rm называют подмно-
подмножества Rm такие, которые в малом подобны или близки пространству
RP. При р = 1 это гладкая кривая, которая в малом подобна прямой,
при р = 2 это гладкая поверхность, которая в малом подобна плоскости
и т. п.
Цель настоящего раздела состоит в том, чтобы ввести понятие меры
многообразия размерности р в Rm, которое бы при р = 1 было обоб-
обобщением длины кривой, при р = 2 — площади поверхности. Это новое
понятие удобно рассмотреть сначала для случая, когда многообразие
размерности р есть гиперплоскость в Rm.
Пусть Т= Rp, u = (tti,..., um) : Т -4 Rm, причём
р _
Uk{t) -xk{t) = £ akjtj+ak0> k = l,2,...,m; t = (ib ... ,tp) € Rp,
3 = 1
и akj, l<fc<m, 0 < j < p — фиксированные числа из R. р-мерное
многообразие М := u(R ) есть гиперплоскость в Rm. Предположим,
что М собственно р-мерно, т. е. что матрица (akj)^ij=i имеет ранг
р. Далее предполагается, что р < т.
Каждое измеримое множество А С М имеет m-мерную меру Жор-
дана 0. Однако, М есть гиперплоскость размерности р, и для её под-
подмножеств можно рассматривать р-мерную меру Жордана. Построим
в М систему координат следующим образом. Пусть t° = (t°,...,t°)
— фиксированная точка из Т и х° = u(t°) = {х°,... ,х^п) € М — её
образ на М. Каждой точке х € М поставим в соответствие вектор
г := х — х°. Из-за предположения собственной р-мерности М множе-
множество Н := {г* = х — х° | х € М} содержит р линейно независимых
векторов и является р-мерным линейным пространством. Если рассмот-
рассмотреть некоторый ортонормированный базис в Н, то для определённого
класса подмножеств Н можно определить р-мерную меру Жордана.
Согласно следствию 7 п. 14.4.6 значения этой меры не будут зависеть
от выбора точки х° и базиса в Н. Нас интересует связь между значе-
значением меры Жордана измеримого множества А С Т = RP и значением
меры множества й(А) на многообразии М.
Построим в Я специальный базис, используя то, что, согласно пред-
предположению, р векторов а, = (aiy,a2j,... ,атз), 1 < j < p, линейно
независимы. Сначала заметим, что
Уг€Я : f=f-£°=£a,-(t,--*5). A)
.7=1
32*

498 Глава 15. Интегралы по многообразиям и теорема Стокса
С помощью процесса ортогонализации Шмидта векторы ai,u2,... ,Зр
можно ортонормировать. Положим
е2 :=
02 ~
01
|o*i|
-1
О2,
Д1
Здесь (а, Ь) — скалярное произведение векторов а и Ь. Получим орто-
нормированный базис ei, ё*2)..., ер, при этом
Действительные числа djk, 1 < k < j < p определяются известным
образом по набору alf S2,..., Зр, причём djj > 0, 1 < j' < р. Для dn и
d.22 имеем
dn == ||oi||)
@*2,0*1) .
а2 -
lalll
1/2
Ц01
B)
Используя представление A) для векторов из Я, получаем следую-
следующее равенство
г= Е ЧЬ ~ Ъ) = Е *fc^. г"€ Я, C)
fc
в котором
fc=l
51= dii(*i - <?)+
s2 =
4pi(*p-*S),
dp2(*p-*P). ш
Заметим, что якобиан преобразования от переменных ti,...,tp к
переменным si,..., sp равен
= dud22... dpp > 0.
E)
* d(tlt...,tP)
В качестве координат точки f=x — x° = u(i) — u(t°) в Я ("внутренних"
координат многообразия М) рассмотрим координаты si,...,sp, связан-
связанные с координатами точки t в Т равенствами D). Если F — измеримое
подмножество Т = ЯР с р-мерной мерой m(F), то образ u(F), ле-
лежащий на многообразии М, согласно формуле замены переменных,
измерим и его р-мерная мера m(u(F)) равна

15.7. Мера на многообразии 499
m(u{F)) = / ldsy...dsp= f ldsi...dsp =
u(F) ?(F)
%\ F)
Таким образом, для измеримого множества F С Т с мерой m(F)
образ u(F) на многообразии М имеет меру, равную pm(F). Поэтому
величина р из формулы E) называется коэффициентом искаэюе-
ния меры. Заметим, что допустимых координат Ту,..., тр
Е
Щ<я множества Т значение коэффициента искажения р связано со зна-
ч#нием р следующим образом
- = Э(Д1,---,»р) = d{Sll...,sp) d{tu...,tp) = d(tr,...,tp)
9 din^) a(tt) d{TT) рд{тт)'у '
ib.7.2 Определение меры на многообразии
ПустьТсНр; u£Cl{T,Rm)\ М :~ й{Т). Множество М - р-мерное
многообразие. Предположим, что М собственно р-мерно на Т.
При этих предположениях в окрестности любой точки Г° € Т зна-
значения й{ъ) близки к значениям v(t) следующего отображения, рассмот-
рассмотренного в п. 15.7.1,
vk(?) := uk(t°) + Е ^г1 & - fy, l<k<m. (8)
"Близость" состоит в том, что ||гГ(£) - г)(г)|| = o{\\t- t°\\), Г-+ Г°. Если
множество F лежит в окрестности точки t°, то образ u(F), лежащий на
многообразии М, близок к образу v[F). Меру же образа v(F) можно
определить так, как это было сделано в п. 15.7.1, и считать приближён-
приближённым значением "меры" u(F). Точность такого "приближения" тем выше,
чем меньшая окрестность точки Г° рассматривается. Замети ещё, что в
преобразовании (8) роль чисел {ctfc;} играют числа
Замечание. Если р = 1, то М — кривая, а равенства (8) есть
параметрические уравнения касательной к М в точке u(t°). Если р = 2,
то М — поверхность, а равенства (8) есть параметрические уравнения
касательной плоскости к М в точке ^(Г0).
После приведенных выше рассуждений становится понятным следу-
следующее формальное определение.

500 Глава 15. Интегралы по многообразиям и теорема Стокса
Для каждой точки t£ Т пусть aj.,-(i) = ——— , 1 < к < т, 1 < j < р;
atj
j
числа dkj(i), 1 < j < к < р, и p(t) определены так, как в п. 15.7.1. В
частности, числа du(i), d.22{t) определяются формулами B). Значение
p(i) называется коэффициентом искаоюения меры в точке
t. Заметим, что р € С(Т).
Определение 1. Пусть Т — компактное измеримое
множество в t-пространстве RF и и € C^T.R). Предпо-
Предположим, что р-мерное многообразие М — й(Т) собственно
р-мерно на Т. р-мерной мерой р-мерного многообразия М
называется, число
m(M):=JP(t)dt1...dtp. (9)
т
Замечания. 1. Определённая формулой (9) мера многообразия
М не зависит от допустимых координат для параметрического множе-
множества Т. Действительно, для допустимых координат Ту,... ,тр и S = т[Т)
с помощью формул замены переменных и G) получим
df = fp(f(*))^■•••'Гр.) dt= f
S T O[ti,...,tp) J
T
2. Многообразие М может не быть в некоторых точках собствен-
собственно р-мерным. Формула (9) относится к многообразию М такому, что
для любой точки t либо М собственно р-мерно в точке u(i), либо в
точке Г существует предел lim р(т). Более того, условие собственной
р-мерности, а также условия гладкости, могут не выполняться на под-
подмножестве Т с нулевой мерой, если й непрерывна и < —— \ непрерыв-
ны и ограничены на остальной части Т.
Упраоюнение 32. Пусть Т — компактное измеримое множество,
Т = Ti U Т2, причём Ти Т2 измеримы и Т? П Т2° = 0. Пусть М =
й{Т), Мк = й(Тк), к = 1,2. Доказать, что т{М) = т{М{) + т(М2).
15.7.3 Длина дуги
Пусть р = 1, Т = [а,Ь], и € C([a,b],Rm). Одномерное многообразие
Г := Qa,b]) есть непрерывная кривая в Rm. Предположим также, что
[а,Ъ] можно представить в виде объединения конечного числа отрез-
отрезков [а,р] таких, что и £ С1([а,/3]) (в точках а и /3 рассматриваются
соответствующие односторонние производные).
В этом случае

15.7. Мера на многообразии 501
Ofci(*) = ofc@ = -^ , 1 < к < ш; НохСОП = Т -^ ) '■
и p(t) = ||ai(t)|| для всех t на [а, Ь], исключая, возможно, конечное число
точек, в которых существует предел р. Заметим, что криаая Г одномер-
одномерна в тех точках t, в которых ||Si(t)|| Ф 0, т. е. в тех точках, в которых не
обращаются в нуль одновременно все производные u'k[t), 1 < к < т.
Обратим также внимание на то, что для точки to следующая функция
v(t) = u(to) + u'(to){t — to), t € R, определяет касательную к кривой Г
в точке u(to).
Мера 1{Г) := тп(Г) одномерного многообразия Г называется дли-
длиной кривой Г. Согласно формуле (9), имеем
J
Пример. Пусть Г = {{xi,x2,x3) \ xi = cost, i2 = sint, 13 = 2t; t £
[0,2тг]}, Г — часть винтовой линии. Для длины кривой Г имеем
2*
15.7.4 Длина дуги как предел
Длина дуги может быть также определена как предел вписанных ло-
ломаных. Рассмотрим это определение при условиях п. 15.7.3. Пусть
a = to < t\ < ... < tn = b — разбиение А отрезка [a,b], включаю-
включающее точки, в которых й' не существует. В пространстве Rm рассмотрим
точки u(to), u{t\), ... , u(tn), лежащие на кривой Г. Соединим каж-
каждую пару точек u(tk), u(tk+i) отрезком прямой, 0 < к < п — 1. Получим
п—1 Гт
ломаную Г„, длина которой 1(Гп) =]£»/]£ ("j(*fc+i) - "j(*fc)J- Есте-
fc=o у j=i
ственно следующее определение: если при |А| —> 0 существует предел
lim 1(Г„), (И)
|А|—+0
то кривая Г называется спрямляемой, а предел A1) называется
длиной кривой Г.
При предположениях о функции й с помощью теоремы Лагранжа легко
доказать, что предел A1) существует и совпадает с интегралом A0).
15.7.5 Площадь поверхности
Пусть р = 2, Т — компактное измеримое подмножество R2, й £
С1(Т, Rm). Двумерное многообразие S := й(Т) есть поверхность в Rm.

502 Глава 15. Интегралы по многообразиям и теорема Стокса
Предположим, что поверхность S собственно двумерна в точках Т, т.
,-, _ (dv.-j.fy du2(i) dum(i) \
■ ' ~ ~~я* > ~~я* ''''' ai и
у Cti OTi ati J
—— 1 линейно независимы для любого
е. что следующие векторы
вектора t = (ti,^) € Т. Согласно формуле E), в этом случае
p(t) =
где
it=i
fc=l Cti Cl2
есть коэффициенты первой квадратичной формы поверхности 5.
Заметим, что функция
задаёт касательную плоскость к S в точке u{t°).
Мера тE) =: <гE) поверхности S называется плогцадъю по-
eepxHOCmii S. Согласно формуле (9),
ct{S) = JVEG-F2dt1dt2. A2)
т
Кроме формулы A2) при m = 3 часто используется также следующая
формула
a{S) = fVA2 + B2+C2dt1dt2, A3)
т
1) ~ d{ui,u2)
С:=
Ж^Г Ж^ ЖлГ
A3) следует из равенства EG-F2 = А2 + В2 + С2, которое проверяется
прямым подсчётом.
Полезным для применения является частный случай формулы A3),
относящийся к поверхности S, задаваемой следующим образом S =
{(ii,i2,x3) | ii = ui = ti, x2 - u2 - t2, i3 = щ = /(ii,t2); (*i,<2) €
T}. В этом случае А = -/{(хьх2), В == -/2(xi,a:2), С = 1 и
потому
(ЛJ + (/2J ^1^2- A4)
т
Заметим, что в A4) Т — проекция поверхности S на плоскость (xi,x2).
Пример. Определим площадь сферической "шапочки"

15.7. Мера на многообразии
S = {{x1,x2,x3) \х\+х\Л-х\ = r2, i3 >г0},
где г0 € [0,г]. Пусть Т = {(<£>, 0) | О < у> < 2тг, 0 < в < arccos — },
)
() { y u^(ip,8) = rcosB, )
Т. Тогда S = u[T) и A = -r2cos<psin20, В = -г2 sintpsin2 б, С =
-г2 sine cose, a2 + в2 + c2 = r4 sin2 e.
С помощью формулы A3) находим
2ir.arccos(r0/r)
tr(S) = /г2 sinec^d0= /( / r2sinede)(i^ = 27rr2(l- —).
При го = 0 получим площадь полусферы, откуда следует, что пло-
площадь поверхности сферы радиуса г равна 4тгг2.
15.7.6 Площадь поверхности как предел
Площадь даже совсем простых поверхностей нельзя определить как
предел площадей вписанных многогранных поверхностей при условии,
что диаметры всех граней стремятся к нулю. Первый пример, в котором
для цилиндра предел площадей вписанных многогранных поверхностей
может быть произвольным числом или +оо, был построен Шварцем.
Возможен следующий подход к определению площади поверхности,
приводящий к интегральным суммам для интеграла (9).
Пусть S — поверхность, удовлетворяющая условиям п. 15.7.5, при-
причём m = 3 и Т = [cti,fci] х [02,62]- Представим прямоугольник Т в виде
Т = \JQk,Qk = [<*(*),£(*)] х [7(*),*(*)], 1 < к < n; Ql ng° = 0, к ф j.
fc=i
Пусть А := max d(Qk). Тогда S = if (Г) = Q 5fc; Sk :- u{Qk), 1 < к < п.
l<fc<n k—i
Зафиксируем некоторые точки f<fc) = (t^ ,t{2k)) € Q°k, 1 < к < п. В
каждой точке u(t^) £ Sk рассмотрим касательную плоскость
(tl^) + ^(i2^r(tlli2)€tf.
Кусок поверхности Sk = u(Qk) близок к образу v{Qk), лежащему в ка-
касательной плоскости, так как ||i?(t)-t/(t)|| = o(||f-f(fc>||), Г-* №. Пло-
Площадь образа v(Qk), согласно п. 15.7.1, равна cr(v(Qk)) = p(t^)m(Qk).
Рассмотрим сумму сг„E) := Yl p(t^)m{Qk). Площадью поверхности
fc=i
S естественно назвать предел
lim an{S) = tr(S), A5)
если он существует.
Используя непрерывность функции р на Q, легко проверить, что пре-
предел A5) существует и равен интегралу A2). Действительно, величина

504 Глава 15. Интегралы по многообразиям и теорема Стокса
Дп := \tr{S) - an{S)\ =
в силу аддитивности интеграла может быть записана в следующем виде
An = Е 1Ш -p(tW))dt\, откуда Дп < Е / \Р(?) ~ p(tW)\df.
fc=l Qfc ' fc=l Qfc
Далее с помощью обычных рассуждений получим Д„ -4 0, А —> 0.
Упражнение 33. Вычислить поверхность тора S =
= (R + г cos <p) cos в,
= { (xi,i2lx3)
х2 = {R + г cos tp) sin в, {(р,в) £ [0,2тг]2,0 < г < R
i3 = г sin ip,
15.8 Интегралы первого рода по
многообразию
15.8.1 Общее определение
Пусть Т — компактное измеримое подмножество EF, й € C1(T,Rm).
Предположим, что р-мерное многообразие М = й[Т) собственно р-
мерно на Т, и пусть p(i) — коэффициент искажения меры в точке f G Т.
Пусть также / € С{М).
Определение 1. Интегралом первого рода от функ-
функции f по многообразию М называется интеграл
ffdm:=ff(u(?))p(i)dt. A)
м т
Замечания. 1. Введенный интеграл A) не зависит от допустимых
координат для Т. Пусть тх,... ,тр — допустимые координаты для Т, при-
причём т(Т) = S. С помощью формулы замены переменных получаем
?(!ii---'?>) dt= f
O(ti, . . . ,tp) J
T
2. Если f(u) = 1, и G М, то интеграл A) равен мере многообразия
М, т. е. f dm — m{M).
м
15.8.2 Связь с интегралом второго рода
Предположим, что ^-пространство положительно для Т. Интеграл от
формы /(х) с2х„(х) Л ... Л с2х„(р) по ориентированному многообразию
ранее был определён формулой
/ /(х) с2х„A) Л ... Л dxV(p) = f f(u(i)) -ztt^ '-rx dt.
м т

15.8. Интегралы первого рода по многообразию 505
Этот интеграл называется интегралом второго рода, он связан с
интегралом первого рода следующей формулой
М Т O(ti,...,tp)
Упраэюнение 34- Интеграл второго рода из левой части последнего
равенства зависит от ориентации множества М, интеграл же правой ча-
части есть интеграл по множеству М. Как реагирует на смену ориентации
подынтегральное выражение правой части?
'15.8.3 Криволинейный интеграл первого рода, связь с
криволинейным интегралом второго рода
Пусть р = 1, Т = [а, Ь], и[Т) = Г — одномерное многообразие — кривая
в Rm. Интеграл A) в этом случае называется криволинейным ин-
интегралом первого рода от функции / по кривой Г и обозначается
символом
г
Значение этого интеграла вычисляется по формуле
Г о \
Предположим, что Т лежит в пространстве знака +1. Пусть
ш = A(i) dx1 + ... + /m(i) dxm; /fc € С(Г), 1 < к < m,
.*- дифференциальная форма первой степени. Криволинейный интеграл
второго рода от формы ш по ориентированной кривой Г (движение по
Г соответствует возрастанию t) был определён равенством
ДД(х)dx1 + ... + /m(x)dxm) = fZ /fc(tT(t))*^*i dt,
Г a fc=l at
рткуда
Г a fc=l Ot /J(f) r fc=1 dt p(t)
f(t) — единичный вектор касательной к кривой Г в точке u(t), направ-
направленный в сторону заданного движения по Г. Тогда формула C) может

506 Глава 15. Интегралы по многообразиям и теорема Стокса
быть записана в виде Jw = f(f,r)dl. Если t-пространство для [a,b]
_. 1 /dui(t) dum{t)\
отрицательно, то вектор r(t) := —г- I ^ ,..., —-£— ) .
15.8.4 Криволинейный интеграл первого рода
как предел
Используем обозначения из п. 15.7.4. Пусть Г\ = u([tk,tk+i]), (к €
п-1
[*fc,*fc+i]i 0 < к < п - 1. Рассмотрим сумму JA = £ /(uF0)Krfc)> в
fc=0
которой fc-e слагаемое есть произведение значения функции / в точке
u(£fc) € Гк на значение длины куска Гк- При предположениях о функциях
/ и и предел сумм Ja при |А| -+ 0 существует и равен интегралу из
правой части B). Определение интеграла с помощью предела сумм JA
позволяет получать такие физические интерпретации интеграла первого
рода, как значение массы кривой, определяемое по заданной плотности
распределения масс и т. п.
15.8.5 Поверхностный интеграл первого рода
Пусть р = 2, Т — компактное измеримое подмножество R2, й €
С1(Т, R3). Предположим, что поверхность S = й(Т) собственно дву-
двумерна на Т. Пусть / € C(S).
Интеграл A) в этом случае называется поверхностным инте-
интегралом первого рода от / функции по поверхности S и обозначается
символом
S
Значение этого интеграла вычисляется по формуле
/ f{x) dcr = f f(u(t)WEG-F* dt, D)
S T
где функции E, G и F определены в п. 15.7.5.
Интеграл D) также может быть олпределён как предел сумм типа
интегральных. Используем обозначения п. 15.7.6. Для точки u(t^) pac-
смотрим значение /(u(fW)) и составим сумму J* = ^ f(u[t^))cr{Sk),
fc=i
в которой cr{Sk) — площадь куска Sk = #(<?*:)•
Если существует конечный предел
то он называется поверхностным интегралом первого рода
от функции / по поверхности S.

Л5.8. Интегралы первого рода по многообразию
507
ч * При предположениях о функциях /, и предел E) существует и равен
(интегралу D). Действительно,
ff(x)dcr-Jx
J7(tT(t))p(t)df-JA
<£ f\f(u(i))-f(u(№))\P(i)dt,
::}эткуда с помощью теоремы Кантора имеем lira J\ = Г f(x) da.
|А|->0 JS
Отметим ещё частный случай формулы D) для поверхности S, за-
: данной следующим образом
S = {{хих2,х3) | (хьх2) € Т, х3 = и{хих2)}, и 6 С1^).
. 1ри этом / f[x) da = f /(хь х2, u(xb x2))\/l + КJ + КО2 dxxdx2.
S т
•I
15.8.6 Связь между поверхностными интегралами пер-
первого и второго рода
Пусть параметрическое множество Т и поверхность S удовлетворяют
.условиям п. 15.8.4, Т лежит в положительном пространстве, тогда S —
ориентированная поверхность. Пусть {/ъ/2,/з} С C(S).
Поверхностный интеграл второго рода от формы
ш = /i(x) iix2 Л dx3 + /2(х) dx3 Л dxi + /з(х) dxi Л iix2
по ориентированной поверхности 5 ранее был определён равенством
(х) ихз Л dx\ ~\~ j3[x) uXi Л дх2) ==
J(fi(x) dx2 Л dx3
s
F)
Введём вектор п = (пьп2,Пз), где
._ 1 э(ц2,Цз)
L d[u3,ui)
п2 :=
= сов(Я,11);
= cos(n,x2);
p(ti,t2) d(tltt3)
П3 := „и j. ч а/?' Л = cos (Й> хз)-

508 Глава 15. Интегралы по многообразиям и теорема Стокса
.. 1 - - .. -
Заметим, что n = -aixa2l где ai x а2 — векторное произведение
Р
векторов Si и а2. Вектор п перпендикулярен к плоскости, которая опре-
определяется векторами 2i и а2 и касается поверхности S в точке u(ti,t2).
При этом ||п|| = 1. Вектор п называется вектором нормали к
поверхности в точке u(ti,t2). Положим также / = (Л./г./з)-
Формулу F) теперь можно записать в виде
ДЛ(х) dx2 Л dx3 + /2(х) dx3 Л dxr + /3(£) dxx Л dx2) = /(/, п) Аг. G)
S S
В формуле G) левая часть содержит интеграл второго рода по ори-
ориентированное поверхности S, а правая — поверхностный интеграл пер-
первого рода. Если бы множество Т лежало в отрицательном простран-
пространстве, то вектор п имел бы координаты —ni, -п2) -п3. Таким образом,
ориентация поверхности 5 учитывается в правой части равенства G) век-
вектором нормали п.
Рассмотрим расположение вектора п более подробно в следующих
двух случаях.
I. Пусть S = {(хьхг.хз) | {хих2) € Т, х3 = u(xi,x2)}, и G С\Т).
Тогда
p(xltx2) = 4/l + (u'1J + (u2J; ni = —u'n n2 = —u'2, n3 = -.
P P P
Напомним, что Т лежит в положительном пространстве. Поскольку
пз = cos (n, хз) > 0, то вектор п образует острый угол с положительным
направлении оси Ох3. Ориентированная поверхность 5 есть верхняя сто-
сторона поверхности S, поскольку при обходе Т против часовой стрелки
соответствующий обход поверхности S происходит так, что ближайшая
к наблюдателю часть поверхности S расположена слева, если смотреть
сверху. Таким образом, при движении наблюдателя в положительном
направлении при обходе S вектор п направлен от ног к голове.
II. Пусть А С R3 — множество, состоящее из конечного числа брусов
некоторого разбиения пространства R3. Предположим, что простран-
пространство R3 положительно для А. Тогда ориентированная соответствующим
ориентации множества А граница дА есть внешняя сторона дА. Предпо-
Предположим, что функция г? € С1 (A, R3), а замкнутая поверхность S = й(дА)
собственно двумерна. Ориентированная поверхность 5 — зто внешняя
сторона S, если ^-пространство для А и х-пространство для S одинаково
d(ui,u2,u3)
ориентированы, т. е. если —г-—-——г- > 0.
d(ti,t2,t3)
Покажем, что в этом случае вектор нормали п направлен во внеш-
внешнюю сторону S. Пусть Q — брус-прямоугольник, лежащий в д+А в плос-
плоскости £з = С) (^1>*2|*з) ~ внутренняя точка Q. При всех достаточно

15.8. Интегралы первого рода по многообразию 509
малых 6 > 0 точки (*i,<2.*з + 6) $ А. Рассмотрим в точке u(*i,*2,*з)
на S касательную плоскость к S. Эта плоскость определяется линейно
независимыми векторами ai и о.?,. Векторы Si, a2, n образуют базис в
R3. Рассмотрим в этом базисе координаты точек u(ti,t2tt3 + S) £ u(A).
Пусть u(ti,t2,t3 + 5) = u(ti,t2,t3) + zxa\ + z2a2 + z3n. Тогда
z3 = №x,t2>t3 + 5)- U(tut2,t3),n) « -dilUU.2'^6.
, Отсюда следует, что если \ 1;———^- > 0, т. е. если t-пространство
o{ti,t2tt3)
и т-пространство одинаково ориентированы, то z3 > 0. Следовательно,
вектор п направлен во внешнюю сторону. Таким образом, при движе-
движении наблюдателя по контуру S в положительном направлении вектор п
направлен от ног к голове. Это правило справедливо во всех случаях и
позволяет связывать выбранную сторону поверхности с направлением
нормали п в формуле G).
15.8.7 Историческая справка
Грин Джордж A793 — 1841) — английский математик и физик,
автор классичеких работ по математической физике. Формула Грина
была известна ещё Л. Эйлеру.
Остороградский Михаил Васильевич A801 — 1862) — рус-
русский математик, один из основателей петербургской математической
Школы. Его работы посвящены различным вопросам математики и ме-
механики.
Стоке Джордж Габриэль A819 — 1903) — английский ма-
математик и физик. Формула Стокса A854) устанавливает связь между
потоком векторного поля через ориентированную поверхность и цир-
циркуляцией этого поля по ориентированному краю поверхности. Позже
рбобщение этой формулы получило название общей формулы Стокса.
, Пуанкаре Анри Жюль A854 — 1912) — выдающийся француз-
. ский математик, физик, астроном и и философ. Его работы касались
почти всех разделов математики и содержали новые идеи и методы ис-
исследований.
Шварц Карл Герман Амандус A843 — 1921) — немецкий
математик.

Глава 16
Элементы теории рядов
Фурье и интеграла Фурье
16.1 Ряд Фурье по ортонормированной
последовательности
16.1.1 Основные определения
В этом разделе на пространство функций, интегрируемых по Риману
на заданном отрезке, переносятся с определёнными видоизменениями
те понятия и факты геометрии конечномерного пространства, которые
определяются с помощью скалярного произведения: ортогональность,
норма, ортонормированный базис, теорема Пифагора и др.
Пусть [а, Ъ] — фиксированный отрезок на R. Относительно класса
функций R([a, Ъ]) напомним, что С([а,Ь]) С Д([а, Ь]), и что сумма и
произведение функций из R([a,b]) также функции из R([a,b}). Кроме
того, в дальнейшем полезно иметь в виду следующие утверждения.
ь
I. Если / е Щ[а,Ъ]); f{x) > 0, х£ [а, Ъ\; f f{x) dx = 0, то функция /
а
равна нулю во всех точках непрерывности.
II. Если функция / € R([a,b}) и равна нулю во всех точках непрерывно-
ь
сти, то f f(x) dx = 0.
а
Следующее определение покажется естественным обобщением ска-
скалярного произведения в конечномерном пространстве, если функции
приблизить векторами значений, взятых в конечном числе точек, и для
векторов-приближений рассмотреть скалярное произведение, которое
510

16.1. Ряд Фурье по ортонормированной последовательности 511
после умножения на некоторые числа будет сходится к интегралу.
Определение 1. Пусть {f,g} С R([a,b]). Скалярным
произведением функций fug называется число
(f,9)-=Sf{t)9(t)dt.
а
Из определения 1 следуют такие свойства скалярного произведения.
1°.У/€Я([а,Ь]) : (/,/)>0.
b}) : (f,g) = (g,f).
fi: (af,g) = a(f,g).
4°-4{h,f2,g}cR{[a,b]) -. (h + f2,g) = (h,g) + (h,g).
5°. Неравенство Коши. V {/,<?} с Щ[а,Ь}) : (f,gJ < (f,f)(g,g).
^Определение 2. Нормой функции f € Щ[а,b]) называ-
называэтого определения и свойства 5° следует, что:
H: ||а/|| = \а\ ■ ||/||;
||/ + д\\ < \\f\\ + \\g\\.
Заметим, что равенство ||/|| = 0 равносильно тому, что функция f
равна нулю во всех точках непрерывности. Далее будем
считать функции fug совпадающими, если \\f - д\\ =
О, т. е. если функция f - д равна нулю во всех точках
непрерывности.
Определение 3. Пусть {f,g} С Я([а,Ь]). Функции f и
g называются ортогональными на [а,Ь], если скалярное
ъ
произведение {f,g) = / f{t)g(t)dt = 0. Функция f называется
формированной, если \\f\\ = 1.
■ - Среднеквадратическим расстоянием между функци-
функциями fug называется число \\f — g\\.
1 Среднеквадратическое расстояние обладает всеми свойствами рас-
• Стояния (с учётом договорённости о совпадающих функциях), а множе-
множество с расстоянием (K([a, b]), \\f — g\\) — метрическое пространство. Су-
'щественным обстоятельством является тот факт, что метрическое про-
пространство (Я([а,Ь]), ||/ - д\\) неполно.
) Упражнение 1. Доказать, что функция / € Я([а, Ь]) ортогональна к
^ любому многочлену степени не больше по на [а,Ь] тогда и только тогда,
когда / ортогональна каждой из функций <?&(<) = tk, k = 0,1,2,..., по-
33 — 4-1168

512 Глава 16. Элементы теории рядов Фурье и интеграла Фурье
Упражнение 2. Доказать, что пространство (Я([а,Ь])) неполно.
Определение 4- Набор функций ipi,4>2, ■ ■ ■, ч>п называет-
называется ортонормированным набором, если эти функции по-
попарно ортогональны и нормированы, т. е. если выпол-
выполняются равенства (<pj,ipk) = l,j = к, (ipj,ipk) = 0,j Ф к.
Последовательность функций называется ортонор-
мированной последовательностью, если выполняются
равенства {ipj,4>k) = l,j = к, {tpj,tpk) = 0,j Ф к; j > 1, к > 1.
Упражнение 3. Доказать, что функции последовательности
1, cost, sint, cos2£, sin2£, ..., cosnt, sinnt, ... ,£ € [0,2тг],
попарно ортогональны на отрезке [0,2тг], а последовательность
1 cost sinf cos2f sin2f cosnf sinnt
,/тг ' y/if ' ' y/n ' у/ж '"' у/тР у/п ' "'
ортонормирована на этом отрезке.
Определение 5. Функции Д, /2,..., /п из Щ[а, Ь]) при п >
2 называются линейно зависимыми на отрезке [а,Ь], если
существует набор {ci,c2,... ,сп} с Я, |ci| + |c2| + .. .+|сп| ф 0, для
которого ||ci/i + с2/2 + ... + с„/„|| = 0. Функции /i,/2> •••»/n, не
являющиеся линейно зависимыми на [а,Ь], называются
линейно независимыми на [а,Ь].
Заметим, что для линейно независимых функций /i,/2,...,/n спра-
справедливы неравенства ||Д|| ^ 0, 1 < к < п.
Последовательность функций {/n | n > 1} С Н([а,Ь]) называется по-
последовательностью линейно независимых функций, если
любой конечный набор /j(i), /jB)i ■ • ■, fj(n) есть набор линейно незави-
независимых функций (j(l),jB),..., j(n) — различные натуральные числа).
Лемма 1. Пусть [а,Ь] — любой отрезок. Последователь-
Последовательность функций fn(t) = tn,t € [a,b]; n = 0,1,2,... — последова-
последовательность линейно независимых функций на [а,Ь].
[ Докажем, что для любого п > 2 функции /o,/i,/2, • ■ • ,/п линей-
линейно независимы на [а,Ь]. Действительно, пусть действительные числа
co,Ci,C2,...,cn таковы, что ИГ] CjtA\ = 0 <=> Vi G [а,Ь] : £ CjV = 0.
n
Следовательно, для многочлена P(t) = J2 с$ степени не выше п
j=o
каждое значение t £ [а,Ь] является корнем. Так как отличный от нуля
многочлен не может иметь более п корней, то Cq — с\ = ... = сп = 0. J
Упражнение 4-- Доказать, что любой набор ортонормированных
функций есть набор линейно независимых функций.

16.1. Ряд Фурье по ортонормированной последовательности 513
Упражнение 5. Пусть а1,а2,...)ап — различные действительные
числа. Доказать, что наборы функций а) fk{t) = tak,t £ [a,b],a > 0; к —
1,2,..., n; b) fk{t) = eatt, t E [a, b]; fc = 1,2,..., n, есть наборы линейно
независимых функций на [а,Ь].
Упражнение 6. Пусть функции Д, /г,..., /п линейно независимы на
[а,Ъ]. Доказать, что det((/fc,/j))]JJ=1 ф 0.
Упражнение 7. Пусть функции Л, /г. • ■ • ■ /п линейно независимы
на [а,Ь]. Доказать, что для любых действительных чисел Ci,c2,...,cn
существует функция / € R([a, b}) такая, что (/, fk) = ск, к = 1,2,..., п.
ь
Упражнение 8*. Пусть / € Д([а, Ь]) и / tnf{t) dt = 0, п = 0,1,2,... .
а
Доказать, что ||/|| =0.
Замечание. Любую последовательность {/n | n > 1} линейно
независимых на [а,Ь] функций из Щ[а,Ь}) можно преобразовать в ор-
тонормированную последовательность следующим образом. Положим
Ч>\ '•— ИДИ/!- Тогда ]|<pi|| = 1 {||/i|| ф 0 из-за линейной независи-
независимости). Пусть далее <р2 := ||/2 - {f2,<Pi)<Pi\\~1{f2 ~ (/2,Vi)<Pi)- ТогДа
\\<р2\\ = 1 и ((p2>Vi) = 0 (||/2 - {f2,<Pi)<Pi\\ Ф 0 из-за линейной незави-
независимости Д и /2) и т. д. Полученная последовательность {ipn \ n > 1}
будет ортонормированной, причём справедливы представления вида
4>п = cnifi+cn2f2 + - ■ . + cnnfn, fn = dnlip1 + dn2ip2 + . ■ . + dnntpn, n > 1,
где {cjk, d]k} С К. Процесс построения последовательности {tpn \ n >
1} называется процессом ортогонализации Шмидта.
16.1.2 Задача о наилучшем приближении в смысле
среднеквадратического расстояния
Пусть {<pi,<P2i • ■ • I <Рп} С Д([а,Ь]) — ортонормированный на [а,Ь] набор
Г п 1
функций, Нп := < J2 акфк ifc G Н, 1 < к < п, >. Семейство функ-
U=i J
ций Нп — п-мерное подпространство Щ[а,Ь\). Функции из Я„
называются многочленами относительно функций ^i, <Р2, ■ • •! <Рп-
Пусть / 6 Д([а,Ь]) — фиксированная функция.
Рассмотрим задачу определения такого многочлена Р* € #„, для
которого
Многочлен Р* называется проекцией f на подпространство Нп.
зз*

514 Глава 16. Элементы теории рядов Фурье и интеграла Фурье
/ п \
Лемма 2. Для любого Р = I Е <*кЧ>к 1 € Нп справедливо
Vfc=i /
равенство
II/ - РЦ2 = II/II2 " Е (/, V*J + £ (а* - (/,ЫJ- A)
fc=i fc=i
\ Действительно, используя свойства скалярного произведения, имеем
\\f-P\\2=(f- E akVk,f- £ afcVfc) =
V *=i fc=i /
= II/H2-2E ak(f,Vk)+ Ё
fc=l
fc=i
Следствие 1. Для любого многочлена Р= Е afcVfc € Н„
fc=i
справедливо неравенство
||/-Р||2>|1/||2-Е(/.Ы2. B)
fc=l
в котором, знак равенства имеет место тогда и только
тогда, когда
ак — (/i фк), 1 < fc < П. C)
Таким образом, проекция Р* функции / на подпространство Нп
определяется единственным образом
Р* = Е (/> Ч>к)Ч>к D)
fc=l
и имеет такой же вид, как и проекция вектора в конечномерном про-
пространстве. Кроме того,
-Ё(/.Ы2. E)
fc=i
Внешне все приведенные определения и утверждения представляют-
представляются вполне аналогичными фактам и понятиям конечномерного простран-
пространства со скалярным произведением. Однако, эта аналогия не является
полной. Особенно следует обратить внимание на то, что в простран-
пространстве Я([а,Ь]) существуют бесконечные последовательности ортонорми-
рованных функций, см. упр. 3.
Упражнение 9. Для функции f(t) = (тг —1)/2, t € [0,27г] и заданного
п 6 N определить тригонометрический многочлен вида Тп =

'{6.1. Ряд Фурье по ортонормированной последовательности 515
п
«о+ Е (afccosfct+/3fcsinifct), t £ [0,2тг]; {otk,Pk} С R, минимизирующий
fc=i
расстояние ||/ -Т„||.
16.1.3 Коэффициенты Фурье. Ряд Фурье.
Элементарные свойства
Пусть {tpn | п > 1} — фиксированная ортонормированная последова-
последовательность функций из Н([а,Ь]).
Определение 6. Для функции f £ R([a,b}) числа
а
/называются коэффициентами Фурье функции f относи-
относительно ортонормированной последовательности функ-
функций {<рп | п >1}. Ряд Е с„(/)<рп или Е cn(/)<Pn(t), t£[a,b]
n=l n=l
называется рядом Фурье функции f относительно ор-
ортонормированной последовательности {ipn | п > 1}.
Отметим следующие свойства коэффициентов Фурье.
1°. Для любой функции / G Д([а,Ь]) справедливо неравенство
Е 4(Я = 2 (/,VnJ < Ц/112 (неравенство Бесселя). A)
п=1 п=1
[ Действительно, при каждом п > 1 из равенства E) п. 16.1.2 имеем
п
неравенство ||/||2 - Е (/,VfcJ > 0, откуда и следует A). J
fc=i
SP. Пусть / € Ща,Ъ]). Тогда
е„(/) -» 0, n -v оо. B)
Определение 7. Последовательность {/„ | п > 1} С
*И([а, Ь]) называется замкнутой в {R{[a, Ь}), ||/ - д\\), если
*VfeR([a,b}) Ve>0 ЗР= Ё afc/fcl n € iV{afc} С Д : ||/ - Р|| < е,
fc=i
^m. e. если ceAteucmeo ececc копечпъиз липейпъюз
сций членов последовательности {/„ | п > 1} всюду плотно
Ге простпранстпве (R([a,b]), ||/ - д\\).
) Замечание. Пусть {/n | n > 1} — замкнутая последовательность
' в Н([а, Ь]) и {(рп | п > 1} — ортонормированная последовательность,
■ полученная из {/п | п > 1} с помощью процесса ортогонализации.
;|'Тогда {ipn | п > 1} замкнута в Я([а,Ь]).
^Примеры. 1. Для любого отрезка [a, b] последовательность функций
' fn(t)=tn, t£[a,b]\ n = 0,1,2,... замкнута в Я([а,Ь]).

516 Глава 16. Элементы теории рядов Фурье и интеграла Фурье
\ Утверждение этого примера не является тривиальным. Доказательство
состоит из следующих двух частей.
I. Сначала докажем, что
У/€Я([а,Ь]) Ve>0 3 he € C([a,b}) : ||/ - Л,|| < е.
Поскольку / € Д([а,Ь]), то sup|/| = L < +оо; V<5*> О ЗА = А([а,Ь]) :
[».ь]
ь
О < f f(t)dt - L(/;A) < 5. Пусть функция g\ определена равенством
а
g\{t):=mk, t£[tk,tk+1), 0 < к < п ~ 1; 9\{Ь)=тп-1,
при этом sup|gA| < L, g\{t) < f(t), t € [а,Ь]. Пусть число 6г :=
[а.»]
1шп{E/п, Atk/Bn), 0<fc<n-l}n определим функцию g5 € C([a, b])
следующим образом: gs(t) := mfc, f € [tfc + 5i, ifc+i - <Si], 0 < fc < n - 1,
и доопределим g{ на каждом из отрезков [tk — 5\,tk + Si], 0 < к <
n - 1; [io,fo + Si], [tn - 5i,tn] линейно так, чтобы д5 £ C{[a,b]). Тогда
li/ - 9s\\2 =
< 2L ( / \f(t) - gx(t)\ dt + f \gx(t) - gs(t)\ dt) <
<2b(s+ П£ Ь2*Л < Д L := 2LA + 2L).
Поэтому для заданного е > 0 функцию he можно положить равной
gs c<5 = L-1e2.
II. Пусть е > 0 задано. Рассмотрим функцию Ле/2 € С([о, Ь]), для
которой ||/ - Ле/2|| < е/2. Согласно теореме Вейерштрасса, для функ-
N
ции he/2 существует многочлен Pe(t) = J2 aktk, t € [а>&]| {а*} С К,
fc=0
такой, для которого Vt € [a,b] : |^e/2(i) - Pe{t)\ < е/B%/Ь - a). Тогда
11 he/2 ~ ■Pell < e/2, и из неравенств C) и D) получим
|1/-Ре||<11/-Ье/2|| + ||Ле/2-Ре||<е- J
Замечание. Следуя доказательству части I примера 1, легко до-
доказать, что V/ е Щ{а,Ъ]) Ve > 0 ЭЙе € C([a,b]), fc,(a) = ^(ь) :
\\f-K\\<e.
2. Замкнутой в Н([—7Г,тг]) является последовательность функций
1, cost, sint, ,cos2t, sin2t, ..., cosnt, sinnt, ... .E)
f Пусть £ > 0 задано. Согласно доказанному в части I примера 1, для
любой функции / € Я([-7Г,7г]) справедливо такое утверждение

16.1. Ряд Фурье по ортонормированной последовательности 5Y7_
3 К/2 е С([-тг, тг]), ht,2(-ir) = ht/2(ir) : ||/ - h«/a|| < \ ■
В силу теоремы Вейерштрасса существует многочлен вида
п
Pe{t) = a0+ Yl iak cos kt+pk sinkt), {ak,pk} С Я,
fc=i
для которого V* € [-тг, тг] : |/ie/2(i) - Pe(f)l < е/B\/2тг)- Тогда ||Ле/2 -
Р,|| < е/2, и, следовательно, ||/ - Р,|| < ||/ - he/2\\ + \\he/2 - Ре\\ < е. J
Замечание. Система E) замкнута в R([a,a + 2тг]) для любого
числа а £ R.
Упражнение 10. Доказать, что для любого а > 0 последователь-
последовательность fn(t) = t2n, te[a,b], n = 0,1,2,... замкнута в Ща,Ь]).
Упражнение 11. Доказать, что последовательность fn(t) = t2n+1,
t e [a,b], n = 0,1,2,... замкнута в Я([а,Ь]) при а > 0.
Упражнение 12. Доказать, что каждая из последовательностей
I,cosf,cos2f,... ,cosnt,...; sinf(sin2t,... ,sinnt,...; i € [0, тг],
замкнута в Я([0, тг]).
Упражнение 13. Доказать, что последовательность функций из
упр. 10 не является замкнутой в Я([—1,1]).
1 ( п \2
Указание. Рассмотреть интеграл J I t — J2 ckt2k dt, {ck} С Я.
-i V fc=o J
Упражнение 14- Последовательность {ipn \ n > 1} замкнута в
Я([а,Ь]). Замкнута ли последовательность {<pn | n > 2} в Я([а,Ь])?
Указание. Рассмотреть последовательность упр. 12.
Следующее свойство ряда Фурье сформулируем в виде теоремы.
Теорема 1. Пусть {tpn | n > 1} — замкнутая орто-
нормироваинал последовательность функций в Щ[а,Ь]).
Тогда длл любой функции f € R([a,b}) её рлд Фурье
n=l
cn(f)ipn(t), te[a,b],
сходитсл в среднем, квадратическом, к функции /, т. е.
II/ - Е ck(f)<pk\\ = Jf (f(t) - £ ck(f)<pk(t)) dt -v 0, n -v oo.
jt=i v ° V fc=i /
При этом, имеет место равенство
оо
II/II2 = Е 4(/) (равенство Парсеваля). F)
п=1

518 Глава 16. Элементы теории рядов Фурье и интеграла Фурье
\ Пусть / е Щ[а,Ъ}), положим sn{t) := £ ck{f)<pk{t), t € [а,Ь], n > 1.
fc=i
Функция sn (см. п. 16.1.2) является проекцией функции / на подпро-
подпространство, порождённое функциями tpi,tp2, ■ ■ ■ ,4>п- Поэтому sn = Р* и
fc=i
Пусть е > 0 задано. Поскольку последовательность {<рп | п > 1}
m
замкнута, то 3 Ре = £ afc<pfcl {afc} С Я : ||/ - Ре\\ < е. Отсюда для
fc=l • ___ .
п>гп получим ||/ - sn\\2 < ||/ - P/j|2 < е2. ~—-^ ^to
Следовательно, Vn > m : 0 < ||/ - sn||2^ ||/||2 - £ "с|(/) < е2-
fc=i
Поэтому ||/ - sn||2 -> 0, п -у оо =» Ц/112 = g с2(/). J
п=1
Замечание. Следует иметь в виду, что утверждение о средне-
квадратической сходимости ряда Фурье не влечёт за собой его равно-
равномерную или хотя бы поточечную сходимость на [а,Ь].
Упражнение 15. Доказать, что при условиях теоремы 1 для {/,<?} С
оо
Я([а,Ь]) справедливо равенство (/,g) = Yl cn(/)cn(ff) (обобщённое
fc=i —
равенство Парсеваля).
Упражнение 16*. Привести пример функций /, /„, п > 1 из мно-
множества Я([0,1]), для которых: а) ||/ - /п|| -+ 0, п —> оо; Ь) последо-
последовательность функций {/п | п > 1} не сходится к функции / ни в одной
точке отрезка [0,1].
Определение 8. Последовательность {/„ | п > 1} с
Я([а,Ь]) называется полной в R([a,b]), если длл любой фун-
функции f £ Щ[а,Ъ}) имеем Vn > 1 : (/,/„) = 0 =4> ||/|| = 0.
Замечание. Замкнутая в Я([а,Ь]) последовательность {/„ [ п > 1}
полна в Щ[а, Ь]). Действительно, пусть для функции / £ R([a,b]) выпол-
выполняются равенства (/, /„) = 0, п > 1. В силу замкнутости последователь-
последовательности {/„ | п > 1} справедливо следующее утверждение
п
Ve>0 3Pe= E akfk,{ak}cR : ||/- Р,|| < е.
fc=i
Тогда 11/Ц2 = (/,/) = (/,/- Ре) < Н/П • ||/ - Р£|| < е||/||. Отсюда
следует, что ||/|| =0.
1
Упражнение 17. Пусть / € С([-1,1]) и Vn > 0 : / f{t)t2ndt = 0.
-i
Доказать, что / — нечётная на [—1,1] функция.

16.2. Ряд Фурье по тригонометрической последовательности 519
Упражнение 18. Пусть / е С([-1,1]) и Vn > 0 : / f(t)t2n+1 dt =
-i
О. Доказать, что / — чётная на [—1,1] функция.
Упражнение 19*. Пусть / е й([0,Зтг]) и
Vn>0 : f f(t) cos ntdt = f f{t) sin.ntdt = 0.
00
Доказать, что функция / в точках непрерывности совпадает с функцией
д, для которой g(t) = 0, t G (тг,2тг); g(t) + д{2ж + t) = 0, *€[О,тг].
Упражнение 20. Пусть функция / € С([а,Ь]), а > 0, и удовлетворя-
ь
ет условию Vn > 0 : / f(t)ent dt = 0. Доказать, что f(t) = 0, t G [а,Ь].
а
Упражнение 21. Пусть / € С([0,2тг]) и /@) = /Bтг). Предполо-
Предположим, что для некоторого тп € N справедливы равенства
Vn>m : f f(t) cos ntdt = f f(t) sin. ntdt = 0.
о о
Какой может быть функция /?
Упражнение 22*. Пусть функции {/ь/2, ■ • ■ ,/п} С JR([a, Ь]) линейно
независимы на [а,Ь]. Доказать существование е > 0 такого, что
функции ipi, ip2, ■ ■ ■, <pn линейно независимы на [а, Ь].
16.2 Ряд Фурье по тригонометрической
последовательности
16.2.1 Обозначения. Следствия из общей теории
Функции последовательности
-, cost, sint, ,cos2t, sin2t, ..., cosnt, sinnt, ... A)
имеют на отрезке [—7Г, 7г] нормы Л — , */ъ, */ъ, ..., ^/п, */ъ, ...
ветственно и попарно ортогональны на [—тг,тг]. Последовательность A)
замкнута в JR([—тг.тг]). Первыми в математике и её приложениях появи-
появились ряды Фурье относительно тригонометрической последовательно-
последовательности A). Эти ряды уже встречались в работах Д. Бернулли, Даламбера,
Лагранжа и Эйлера, относящихся к первой половине XVIII века. Ж. Фу-
Фурье в опубликованной в 1822 г. книге "Аналитическая теория тепла"
систематически использовал ряды относительно последовательности A)
соот-

соот520 Глава 16. Элементы теории рядов Фурье и интеграла Фурье
и продемонстрировал пользу и важность таких рядов. Разработка тео-
теории рядов Фурье несколькими поколениями математиков привела к на-
настоящему времени к созданию глубокой и обширной теории, имеющей
исключительно важное значение как для самой математики, так и для
её приложений. Весьма существенным оказалось также влияние зтой
теории и возникавших в ней проблем для развития других разделов ма-
математики, например, теории интеграла.
По сложившейся традиции для функции / £ JR([—тг,тг]) её коэффи-
коэффициенты Фурье относительно тригонометрической последовательно-
последовательности A) определяются равенствами
ап := оп(/) := - / /(*) cos nt dt, п>0;
Ж ~Z B)
bn ■= bn(f) := - j f(t)smntdt, n > 1.
я" --n
Функции / при этом сопоставляется следующий функциональный ряд
Ц- + £ (о„ cos nt + bn sin nt), t€[-*,n], C)
^ n=l
называемый рядом Фурье.
Замечание. Все члены ряда C) — периодические с периодом 2тг
функции. Если ряд C) сходится на [—тг, тг], то такой же будет его сумма.
Поэтому часто удобно считать функцию / заданной на Ди периодиче-
периодической с периодом 2тг, сохранив предположение / € JR([—тг,тг]).
Пусть Rq — множество всех функций / : JR -> JR, периодических с
периодом 27Г и таких, что / € JR([—тг,тг]). При фактических вычислениях
часто удобно использовать тот факт, что интеграл от периодической
функции по любому отрезку, длина которого равна периоду, принимает
одно и то же значение.
Последовательность функций A) не является нормированной, нор-
нормировка приводит к следующей ортонормированной последовательно-
последовательности функций
1 cosi sint cos2f sin2f cos nt sinnt . .
на отрезке [—тг, тг],относительно которой коэффициенты Фурье из п.
16.1.3 определяются равенствами
тг тг
dt' с>п := 7т? /f{t) cos nt dt]
—тг —тг
тг
< = -т= [ f(t) sinnt dt; п>1. E)

JJ6.2. Ряд Фурье по тригонометрической последовательности
Из результатов п. 16.1.3 для функции / € JR([—тг,тг]) имеем:
(") (<4(/)J + E (K(/)J + (<(/)J) = /
n=l -ir
Заметим теперь, согласно B), C) и E) справедливы такие равенства
" do{}) = \f^
^ + (
Поэтому из утверждений (i) — (iii) следует, что для любой функции
/ € Я([-7Г,тг]) для её ряда Фурье по тригонометрической последова-
последовательности справедливы следующие утверждения:
(i') an -> О, Ь„ -> 0, гг -> оо; F)
00 5 ао(/) + £ (aKf) + Ш) = - [ f4t) dt (равенство Парсе-
2 fc=i * ]
— V
валя); G)
4p £
II 2 fc=1
, т. е. ряд Фурье сходится в среднем квадратичном.
Упражнение 23. Пусть {f,g} С Я([-тг,тг]). Доказать обобщённое
равенство Парсеваля:
1 ОО 1 1Г
« «о(/М$) + Е (efc(/)«fcE) + bk(f)bk(g)) = - f f(t)g(t)dt.
2 fc=l . 7Г _w
Указание. Записать равенство Парсеваля G) для двух функций
7 + 5, f-g-
'Упражнение 24- Доказать, что ряд Фурье для многочлена Tn(t) =
п
= ао + Е (afccoskt + Pk sinkt), t € R, совпадает с многочленом Тп.
16.2.2 Вспомогательные утверждения
; Основной задачей дальнейшего изложения является изучение ряда Фу-
Фурье C) как функционального ряда. При этом нас интересуют вопросы,

522 Глава 16. Элементы теории рядов Фурье и интеграла Фурье
подобные следующим: при каких условиях ряд C) сходится в задан-
заданной точке? Чему равна его сумма? При каких условиях ряд C) можно
интегрировать или дифференцировать почленно? Сначала рассмотрим
некоторые утверждения, играющие в дальнейшем основную роль в до-
доказательствах.
Утверждение (i') п. 16.2.1 о стремлении к нулю коэффициентов Фу-
Фурье интегрируемой функции имеет ряд обобщений и первоначально по-
появилось в следующей форме.
1°. Лемма Римана. Пусть [а,Ь] — некоторый отрезок, а / — функ-
функция такая, что функция |/| интегрируема по [а,Ь] хотя бы в несобствен-
ь ь
ном смысле. Тогда / f(t) cos At dt -* 0, / f(t) sin. At dt -y 0, X -> +oo.
a a
f Оба утверждения доказываются одинаково. Поэтому рассмотрим до-
доказательство первого из них.
I. Утверждение очевидно для постоянной функции f(t) = с € JR, t £
г л г, - г ч, f, sinAb-sinAa
[а,о]. Действительно, тогда J ccos At at = с у 0,А -4 +оо.
а А
II. Утверждение леммы справедливо для кусочно-постоянной на [а,Ь]
функции /, т. е. такой, что существует разбиение a = to < t\ < • • • <
tn = b, для которого на каждом из интервалов (tk,tk+i) функция /
постоянна и принимает значение Ск € R, 0 < к < п — 1. Действительно,
в этом случае
/ f(t) cos At dt = Л У f(t) cos At dt = *£ ck sinA*fc+1~sinA*fc -> 0
a fc=0 tk fc=O A
при A —у +oo.
III. Пусть теперь / € Я([а,Ь]) и е > 0 задано. Тогда
3М = {а = t0 <t!<...<tn = b} : }f(t)dt-L(f-^)<£-.
a *
Определим функцию fe следующим образом
fe(t) := mk = inf /, te[tfc,tfc+i), O^fc^n-l, /,(b):=mn_i.
Заметим, что /e(t) < /(t), t € [a, Ь]. Согласно доказанному в части II
имеем 3 Л V A > Л : / /e(t) cos At dt < — . Теперь для А > Л имеем
'a 2
< /1/@ - /«@1 • I cos At| Л + I//,@ сое At dt
a 'a
3 nuiZ. Ift? .

Щ.2. Ряд Фурье по тригонометрической последовательности 523
<ff(t)dt-L(f;n) + - <e.
a z
IV. Пусть теперь |/| интегрируема в несобственном смысле. Пред-
Предположим, что Ъ — единственная особая точка. Пусть е > 0 задано.Тогда
35 > 0 : / \f{t)\dt < - , а в силу доказанного в III ЗЛ VA > Л :
ъ-6 2 ^
Ъ-6
J f{t) cos Xtdt
< - . Тогда для А > Л получим следующее неравенство
I/ f(t) cos Xtdt< f f{t) cos Xt dt + f |/(f)| dt < e. J
In a. h—X
Ъ-6
f(t) cos Xtdt 4
6-4
Упражнение 25. Пусть для функции / : R -¥ R несобственный
•интеграл f \f(t)\ dt сходится. Доказать, что имеет место сходимость
— оо
+0О +ОО
/ f(t) cos Xt dt^O, f f(t) sin Xt dt -> О, Л -> +oo.
—oo —oo .
Указание. Для любого е > 0 существуют а и Ь такие,что
■fSP. Интегральное представление для частичной суммы
ряда Фурье. Пусть / £ Rq- Положим для х € R
sQ(f,x):=s0(x)~ -ao(/);
1 п
sn{f,x):=sn(x) := -ао(/)+ £ (ak(f) coskx + bk(f)sinkx), n > 1.
2 fc=i
; Л е м м a 3. Длл любых функции f e Rq и числа п>0 спра-
справедливо представление
sn(x)=2-jf{x-vI;fiX + V)Vn(v)dv, x€R, (8)
■к г
■in(n + )t, tltrtit.
г котором T)n(v) = — ■$-!— , v e (О,тг), — ядро Дирихле.
2 sin-
С помощью определения B) сначала имеем
11
1 l
— f f(u) cos ku du cos fcx H— f f(u) sin feu du sin kx =
71" * /
11»
= ~- f f(u)du+
-v
-7Г

524 Глава 16. Элементы теории рядов Фурье и интеграла Фурье
1 v (l n \
= - I Ди) о + У, cosfc(* ~ ■") du.
1 n sm\n+-)v
Используем теперь тождество - + Yl cos kv = v • v ^
2 fc=i 2 sin-
2жп, n € Z. Это тождество справедливо на всей прямой, если его пра-
правую часть доопределить в точках v = 2жп, п € Z так, чтобы получилась
непрерывная на оси функция. Нужные пределы существуют.
Учитывая периодичность функций / и Dn, а также чётность Dn, по-
получим
sn(x)=- J f(x-v)Vn(v)dv =
Я —к
= - / /(* - v)Vn(v) dv+-jf(x- v)Vn(v) dv =
К -я К О
ж о
и формула (8) доказана. J
Замечание. Следующие свойства ядра Дирихле часто использу-
используются Ъп{у) = Vn{-v), v€@,7r); -JVn(v)dv=- j Vn(v)dl = l
______
Второе равенство следует из представления (8) для функции f[x) =
1, х € JR, для которой ао = 2, а„ = Ъп = 0, гг > 1.
5°. Интегральное представление для средних по Чезаро
частичных сумм ряда Фурье. Пусть / € Яо> для гг > 1 положим
гг
Заметим, что для каждого п > 1 функция ап — тригонометрический
многочлен.
Лемма 4. Длл любых функции f £ Rq и числа п > 1 спра-
справедливо представление
'п(я) = /2(/(х - 2t/) + /(х + 2v))Fn(v) dv, (9)
° ,^)t... ^(
_ . ч 1 sin2 nv . . > " „ y.^ i
в котором ■/Vi(v) := n—i v ^ (О,тг), — яоро Феиера.
ггтг sin г»
f Согласно формуле (8) имеем
1 w/2
Sn(x) = - / (/(х - 2t/) + /(х + 2v))DnBvJ dv.
Отсюда

16.2. Ряд Фурье по тригонометрической последовательности 525
*»(*) = ^ 7 (/(* - 2«) + /(* + 2v))^- "e sinBfc + l)v dv.
/17Г q 5111V fc=Q
Теперь формула (9) получаем с помощью тождества
"^, t/€@,*). J
k=0
Замечание. Отметим следующие свойства ядра Фейера:
Tn{v) > 0, Tn{v) = Tn{-v\ v 6 (О.тг); 2 /V»(«)*' =
о
16.2.3 Сходимость ряда Фурье в точке
Пусть / € До и х € [—тг, тг] — фиксированная точка. Для числа сбйс
помощью (8) получим равенство
*„(«) - с = - /9с(и)Ъп(и) du, A0)
Я" О
в котором
дс(и):=дс(х,Ц)^/C;-Ц);/C; + Ц)-с. A1)
Теорема 2. Длл того чтобы ряд Фурье C) функции
f сходилсл в точке х к числу с € R, т. е. чтобы
sn(x)-¥c, n->oo, <=> ~^-^ + Е (an(/) cosnx+bn(f) sinnx) = с,
* n=l
необходимо и достаточно, чтобы
3 5 > 0 : jgdu)—^-—^— du -> 0, гг ->• оо.
f С помощью формулы A0) для любого 5 € @, тг), имеем
2 * , . sin Ли , 2 ' . . sin Ли
sin Аи
Покажем, что ко второму и третьему интегралам правой части A2)
при любом 5 € (О,тг) применима лемма Римана. Действительно, функ-
функция 5с € Щ[5, тг]), функция h(u) = 2 sin j непрерывна и положительна
на [5,тг]. Следовательно, функция -^ € JR([5,тг]). В силу леммы Римана,

526 Глава 16. Элементы теории рядов Фурье и интеграла Фурье
о } sm(n + 5 )u
V5>0 : - 9c(u)—; . „ ' du -» 0, n -4 oo. A3)
7Г у <£ Sill «
2
о
Далее заметим, что
11 1 / и3 \ n
„ . ц =-—г-г- (u-u+ — -... )-» 0, и-»0 + .
2sin| u 2usmf v 24 /
Поэтому, согласно лемме Римана,
S^) A4)
V5>0: f9c{u)(^
"■ о V 2 sin 2 u
Из соотношений A3), A4) и A2) получаем утверждение теоремы.]
Замечание. Из теоремы 2 вытекает следующее, неожиданное на
первый взгляд, заключение. Пусть 5' € @,7г) задано. Рассмотрим функ-
функцию / такую, что f(t) = f(t), t € (х — 5',х + 5'), а в остальных точках
определённую произвольно, но так, чтобы / £ До. Положим в условии
теоремы 2 5 = 5'. Тогда функция дс на отрезке [0,5] одна и та же для
функций / и /. Следовательно, в силу теоремы 2 сходимость и предел у
последовательностей {sn(f, x)} и {sn(/, x)} одинаковы. Таким образом,
предельное поведение последовательности {sn(/,x)} зависит только от
поведения функции вблизи точки х. Это утверждение часто называют
принципом локализации Римана.
Упражнение 26. Пусть {/,д} С Rq и для фиксированного х 35 >
Sr\f(x + u)-g(x+u) ,
0 : J — ' * аи < +оо. Доказать, что тогда справедливо
-«I «
утверждение (sn(f,x) - sn(g,x)) -> 0, гг -> оо.
Теорема 3. (Признак Дини). Пусть для числа с
J^4U A5)
(,) /
о и
Тогда sn{x) -»с, п -* оо.
Г Для доказательства согласно теореме 2 достаточно проверить, что
* sinn+| )tx
J 5c(u) — du -* 0, гг -> oo.
о u
Однако, при условии теоремы 3 последнее утверждение следует из
леммы Римана. J
Замечание. Пусть условие A5) выполнено. Если предположить
дополнительно существование предела lim gc(u), то из A5) следует,
и—»0+
что этот предел равен нулю.

$2. Ряд Фурье по тригонометрической последовательности 527
•■*' Поэтому, если выполнено условие A5) и точка х - точка
разрыва первого рода функции /, то с = — .
Если выполнено условие A5) и х - точка непрерывно-
непрерывности функции /, то с = f(x). «-
Заметим также без доказательства, что ряд Фурье для непрерывной
в точке функции не обязательно сходится в этой точке.
Теорема 4. (Признак Липшица). Пусть функция / в точке
х удовлетворяет для некоторого числа а € @,1] условию Липшица
3LeR 36>0 Vue(-6,6) : \f(x + и) - f(x)\ < L\u\a. A6)
Тогда sn(x)->/(x), n ->• oo.
f Из условия теоремы следует, что для числа с = /(я) справедливо
неравенство |5с(и)| = A/2)|/(х - u) + f(x + и) - 2f{x)\ < L\u\a, и €
(—5, 5). Поэтому условие A5) признака Дини выполняется для с = f(x).\
Следствие 2. Если в точке х функция f имеет про-
производную, то sn(x) -> f(x), n -¥ оо.
Следствие 3. Пусть х — точка разрыва первого ро-
рода функции /. Предположим, что существуют конечные
f(x + u)-f{x-) ,. f{x + u)-f{x+)
пределы lim ^ '-—^—'-, lim ^ ———-.
u->0- U u-»0+ U
Тогда Sn{x) _> /(«-) + /(« + ) ,„_«,.
Пример. Рассмотрим следующую функцию из i?o f(x) = (тг - х)/2,
х е @,2тг); /@) = /Bтг) = 0. Для неё имеем /'(х) = -1/2, х <Е @,2тг);
/(^/() = 1 (-§+!)= О = /@). Кроме того, ап = 0, „ >
1 ^^ sin тъсс
0; Ь„ = — , п > 1. Следовательно, /(х) = J] , х € Н.
" n=i "
' ' °° 1 7Г2
Упражнение 27. Доказать формулу Эйлера J2 ~z = ~z~ ■
n=l " б
( [ж2 " 1 \\
Упражнение 28. Доказать, что lim \п\ У] — = 1.
n-voo ^ ^ б fc=i fc2 J J
"Следствие 4. Для любой функции g € -Ro ряд £
*' n=l П
сходится.
\ Действительно, запишем для функции g и функции / из рассмотрен-
рассмотренного выше примера обобщённое равенство Парсеваля
34 — 4-1168

528 Глава 16. Элементы теории рядов Фурье и интеграла Фурье
Следствие 5. В классе Rq не существует функции,
ОО Q1T) f) ГЕ
для которой сходлщиисл на R рлд Y) — , х б JR, был
п=2 1пгг
бы рлд ом Фурье.
Упражнение 29. Пусть в е @,2тт). Доказать, что
в ~ /sinn0 l-cosn6 \
— + > cos пх н sin ггх =
2тг ^! \ тггг тггг /
'1/2, i = 0,
sinn@-x) ~ sinnx
"Ь z_<
тггг п=1 тгп
1/2, ж =
0,
16.2.4 Теорема Фейера
Теорема 5. Пусть функция f 6 C(R) и периодична с
периодом, 2тг. Тогда max|/(z) — <7n(z)| —¥ 0, n —¥ оо.
f Из леммы 4 сначала имеем для х 6 JR
<тп(х) - /(х) = / (f{x - 2v) + f{x + 2w) - 2/
0
Пусть теперь е > 0 задано. Поскольку функция / Е C(R) и периодична,
то она равномерно непрерывна на JR. Следовательно,
3 5>0 V{x',x"}cK) \х'-х"\<5 : \f(x') - /(х")| < |.
Поэтому имеем следующую оценку для величины <тп(х) — /(я)! ^
г/2 я/г
< / |/(x-2v) + /(x + 2t;)-2/(x)|^n(U)<iU+ / 4шах
о г/2 я
о R J тгп sin v
г/2
- - Ifl X n г
Z /Г it S1H 77 " "I
Следствие 6. (Теорема Вейерштрасса). Пусть функ-
функция f € C*(JR) u периодична с периодол* 2тг. ТогдаУ е 3Те(х) =
),{ак)&}сД,У*€Я: |/(х)-Т£(х)| < е.
Следствие 7. (Теорема Вейерштрасса). Пусть функ-
ция f G СЦа,Ь]). Тогда

16.3. Дифференцирование и интегрирование ряда Фурье 529
Ve >0 ЗРе{х) = £ akxk,{ak}cRVxe[a,b}): \f(x)-Pe(x)\<e.
fc=O
[ Достаточно рассмотреть случай, когда [a,b] = [0,тг]. Пусть функция
g e C([0,2ir]),g@) = gBn), g(t) = f(t), t € [О,тг]. Согласно следствию
6 для каждого е > 0 существует тригонометрический многочлен Те
такой, что Va; G [0,2тг] : \д(х) - Те{х)\ < е/2. Многочлен Т£ есть конеч-
конечная линейная комбинация функций вида cosfca;, sin kx, каждая их кото-
которых есть сумма ряда Тейлора на R, равномерно сходящегося на каж-
71
дом отрезке. Поэтому 3 Ре(х) = Y1 секхк, {c*fc} С -R Va; G [0, 27г]) :
fc=0
\Те(х) - Ре{х)\ < е/2. Следовательно, \д(х) - Р£(х)\ < е, х G [0,2тг]. J
16.3 Дифференцирование и интегрирование
ряда Фурье
16.3.1 Понятие тригонометрического ряда. Свойства
коэффициентов Фурье
Ряд вида
оо
«о + £ {akcoskx+pksmkx), t G R, {ak,/3j} С R, A)
fc=i
называется тригонометрическим. Как показывает следствие 5
существуют сходящиеся тригонометрические ряды, которые не явля-
являются рядами Фурье функций из Rq. Однако, справедливо следующее
утверждение.
Теорема 6. Равномерно сходящийся, на оси тригоно-
тригонометрический ряд есть ряд Фурье своей суммы.
\ Заметим сначала, что сумма равномерно сходящегося на R тригоно-
тригонометрического ряда непрерывна на R. Пусть ряд A) сходится равномер-
кр на R к сумме / G C(R) :
• оо
\ ао+ J2 {ak cos kx+Pk sin kx) = f{t), t G R. B)
§■, fc=i
Умножим равенство B) на ~ cos mi, где m > 0. Полученный в левой
части ряд также сходится равномерно на R, поэтому допустимо его
почленное интегрирование по отрезку [—7г,7г]. В результате получим
1 *
ао~ f cosmtdt+
оо / 1 it i тг \
+ 12 \ ап~ J cosnt ■ cosmt dt + +@n — f sinnt ■ cosmtdt) =
n=l V T -* v T -ir 4V. У
34* ° °

530 Глава 16. Элементы теории рядов Фурье и интеграла Фурье
= - / f{t)cosmtdt = am(f).
— IT
В силу ортогональности функций тригонометрической последователь-
последовательности, это равенство принимает вид §^то = am(f). Аналогично /?то =
Лемма 5. Пусть функция f € C(R), периодична с пери-
периодом, 2ж и, исключал, возмож.но, конечное число точек
отрезка [—тг, тг], существует /', причём /' €
^Тогда ап{{) = — \,
[ Обе формулы доказываются с помощью интегрирования по частям. J
Лемма 6. Пусть / € Cr~1(R) длл г > 1, периодична с пе-
периодом, 2л- и, исключая, возможно, конечное число точек
отрезка [—7г, тг], существует f^r\ причём, f^ € Rq.
f Для доказательства последовательно применить лемму 5. J
Упражнение 30. Пусть {/,$} С До, {а,Р,Ч>} С R, gv(t) = f(t +
tp), t € R. Доказать, что a) an(af + pg) = aan(f) + pan(g), n >
0; bn{af +pg) = abn(f)+pbn{g), n > 1; b) aQ(gv) = o0(ff), an(ff¥>) =
an(f) cosn(p + bn{f)smntp, Ьп(з¥>) = bn{f)cosn<p- an(f)smntp, n > 1.
16.3.2 Равномерная сходимость и почленное
дифференцирование ряда Фурье
Теорвма7. Пусть функция f € С'(Д), периодична с пе-
риодом, 2тг и, исключал, возмоэ+сно, конечное число точек
отрезка [—7г,7г], сугцествует /', причёл* /' € До- Тогда
оо
f{x) =-j- +2_/(an cos nx+ bns'mnx), x & R, C)
n=l
причёл* рлд C) сходится равномерно на R.
\ Докажем равномерную на R сходимость ряда C). Согласно призна-
признаку Вейерштрасса равномерной сходимости, достаточно доказать сходи-
сходимость ряда
Е(М/I + М/I)- D)
п=1
Из леммы 5 и неравенства Коши имеем

16.3. Дифференцирование и интегрирование ряда Фурье
" '
Из этого неравенства следует сходимость ряда D). В точках, в ко-
которых существует /', равенство C) справедливо. Поскольку функция /
и сумма равномерно сходящегося ряда из непрерывных функций есть
непрерывные функции, то равенство C) выполняется на R. 9j<*a>*{%?q1 и*е
Замечание. Из теоремы 7 следует также такое неравенство
£ £
< £ (мяыы/I)= £ мл|;*;|ь*(л| <
k=n+l k-n+\ K
4;
где
f °o \1/2
£п := ( £ (М/')| + |bfc(/')lJ -> 0, п -^ оо.
\fc=n+l /
Неравенство E) даёт представление о скорости сходимости частичных
сумм {sn} к функции /. При условиях леммы 6 аналогично получается
неравенство
max |/(i) - sn(x)\ < пГ_/2) . п>1; еп -> 0, п -юо.
Теорема 8. Пусть функция f € C^JR), периодична с
периодом 2тг и, исключал, возмомсно, конечное число то-
точек отрезка [—тг, 7г], ст/гцествует /", причём. /" G Ло- Тогда
рлд Фурье C) длл ^утсции л*оэ«:но почленно дифферен-
оо
•цироват7гъ и f'(x)= Yl {nbn cos пх - nansmnx), x 6 R, причём,
n=l
полученный рлд сходится равномерно на R.
[ Утверждение теоремы есть непосредственное следствие теоремы о
почленном дифференцировании функционального ряда и теоремы 7. J
16.3.3 Интегрирование ряда Фурье
Пусть f £ Rq. Тогда ряд Фурье
Щр- + £ (an(f)cosnx + bn(f)sinnx), a: € Я, F)
* n=l
не обязательно сходится поточечно. Однако, в силу следствия 4 ряд
п=1
всегда сходится.

532 Глава 16. Элементы теории рядов Фурье и интеграла Фурье
Заметим теперь, что интеграл f f(t)dt, x £ Д, от периодической
о
функции / £ До не является периодической функцией. Например, для
функции /(<) = 1 + cost, t £ Д, этот интеграл равен х + sin ж, а; £ Д.
Однако, функция
F(x):=jf(t)dt-^P-x, x£R, (8)
периодична с периодом 2тг и F £ C(R). Действительно,
x+2-ir
F{x + 2n)= J f(t) dt - {aQ{f)/2)(x + 2тг) =
о
х x+2ir
= J f(tj dt — (flo(/)/2)a; 4- J /(i) dt — ^ao{f) = F[x)t x £ Д.
о x
Пусть x £ @,2тг). Рассмотрим^лериодическую с периодом 2тг функ-
функцию д £ До, равную на периоде g(t)J= тг/2, i = О, i = x; g{t) = я", t £
(О, a;); g(t) = 0, i G (a;,27r]. Коэффициенты Фурье функции g равны
ао(д) = х] ап(д) = — Гтг cos nidi = , bn (g) =— Г тг sin ni di =
7Г 0 .
1 - cos па; Я
■ n > 1. уд ■
n
Применим теперь к функциям '/, д из До обобщённое равенство
Парсеваля
1 г sr^ jx a°(/) v2' / , ,4sinni l-cosna;\
- / 7r/(i) dt = —^ x + JC k(/) —^— + bn{f) J , (9)
где x € [0, 2тг]. Теперь, учитывадлиюДимость ряда G) и определение (8)
функции F, получим равенство
F(x) = £ ГПШ + V -ОЛШ cosnx + ^ПШ sinna; (ю)
n=l П „=i V n n J
для a; £ [0,2тг].
Заметим, что равенство (9) получается с помощью формального
почленного интегрирования ряда Фурье F), который для функции / £
До не обязательно сходится поточечно. Однако, ряды в (9) и A0) схо-
сходятся равномерно на отрезке [0, 2тг] в силу признака Вейер
\ak{f)\ + \bk{f)\£\JZU
номерной сходимости, поскольку > ' ——— < +оо.
аметим также,-что вследствие периодичности функции F равенство
A0), а вместе с ним и равенство (9), справедливы на Д. Из теоремы 6
теперь заключаем, что ряд A0) есть ряд Фурье функции F и что
£ , ^) , ю

16.3. Дифференцирование и интегрирование ряда Фурье 533
Ъ- Полученный интересный результат сформулируем в виде следующей
•теоремы.
Теорема 9. Пусть f G Но- Ряд, полученный из ряда
Фурье функции } формальным почленным интегрирова-
X
нием., сходится равномерно на R к функции J f(t) dt, t E R.
о
Таким образом, формальное почленное интегрирование, возможно,
расходящегося в некоторых точках, ряда Фурье для функции /, приводит
к ряду, равномерно сходящемуся на оси к интегралу от функции /.
16.3.4 Случай функции с произвольным периодом
Рассмотрим функцию / : R —» R, которая периодична с периодом
21, I > 0, т. е. такую, что f(x + 2l) = f{x), x G R. Пусть / G R([-l,l]).
Для таких функций можно рассматривать ряд Фурье по несколько ви-
видоизменённой тригонометрической последовательности и и получить
все факты, доказанные выше для 2тг-периодических функций. Прведём
основные формулы.
1 Функция g(t) ;= fl — t), t £ R, имеет период 2ir, поскольку
\7Г /
g(t + 2тг) = /(-(* + 2тг))= f(-t + 2l)=f(-t)= g(t), t G R.
Коэффициенты Фурье для функции g и её ряд Фурье имеют вид:
1 * 1 т
ап(д) := — f g(t)cosntdt,n > 0; bn(g) := — / g(t)sinntdt,n > 1;
7Г _„• 7Г _n
9(t) ~ ^TT- + £ (fln(g) cosnt + bn{g) sinnt), t G R. A1)
^ n=l
Положив в формуле A1) t = — x, получим
+ E (MS) cos ^ +Mfl)rin^), «6 A A2)
n=l v ' ' '
7Г
Кроме того, замена t — — x в интегралах A1) приводит к следующим
выражениям для коэффициентов Фурье {an(f), Ь„(/)} функции /
an{f) = ап(д) - - / /(i) cos -у- di, n > 0;
1 ;' A3)
Ь„(/) = Ъп(д) = j J f(x) sin —- dx, n > 1.

534 Глава 16. Элементы теории рядов Фурье и интеграла Фурье
Формулы A3) определяют коэффициенты Фурье, а формула A2) —
ряд Фурье, для 2/-периодической функции / относительно последова-
последовательности функций
1 ТГХ . 1ГХ ТТПХ . ТТПХ
-, cos—, smT' "■"'
-, cos—, smT' "■"' C°S~' Sm~' •" '
попарно ортогональных на [-1,1]- Эта последовательность функций за-
замкнута в R([-l,l]).
16.4 Интеграл Фурье
16.4.1 Формальный вывод интегральной формулы
Фурье
Пусть функция / : R—> R такова, что / G R([-l,l]) для каждого / > 0.
При определённых условиях, приведенных выше, функцию / на отрезке
[—1,1] можно представить в виде суммы ряда Фурье
., . а0 ~ / кпх , . ппх \ г , л
I п=1 V' ' /
Используя формулы A3) п. 16.3.4 для коэффициентов Фурье, запишем
зто представление в виде
1 ' Ло с» I
f(x) = ±-ff(u)du+ E у /
•<" -I п=1 ' -I
= i//(«)**+i 2 «(т)т- *€Н,ч. A)
Л _1 7Г n=l \ I / I fy,
где /^-^
i
Fi(A) := / /(u) cos А(я! - и) du. B)
j
+ ОО
Предположим теперь, что f \f(u)\ du < +оо. Тогда для каждого А € R
— оо
имеем
+ ОО 1 I
Fi{\)^ J f{u)cos\{x-u)du, -ff{u)du^0, l^+oo.
-oo 2i -I
Поскольку сумма в правой части A) аналогична интегральной сумме
для функции F+oo) интервала [0,+оо), разбиения < 0, ж/1,2п/1,... > и
соответствующего набора точек < п/1, 2ж/1,... >, то можно ожидать, что
правая часть равенства A) при / —к+оо сходится к такому интегралу
1 +ОО / +0О \
- / / /(u)cosA(a;-u)du dA.

16.4. Интеграл Фурье 535
Эти рассуждения приводят к следующей формуле
f(x) = - 7° ( T/(u)cos Л(* - «) du ] dX, xeR, C)
* о \-оо у
которую также часто записывают в виде
}{х) = - /°(а(А) cos Хх + Ь(Х) sin Хх) dX, x € R, D)
"" о
где
+ОО +ОО
а(А) := / /(u)cosAudu, Ь(А) := / /(u)sinAudu, A G Я. E)
— оо —оо
Каждая из формул C) и D) называется интегральной форму-
формулой Фурье, а правая часть из C) или D) — интегралом. Фурье.
16.4.2 Сходимость интеграла Фурье в точке
Пусть функция / : R —> R абсолютно интегрируема по R, т. е.
+оо
/ |/(u)|du < +оо.
— оо
При этом условии функции а и Ь, определяемые равенствами E), непре-
непрерывны по А на R, поскольку определяющие их интегралы сходятся рав-
равномерно по А на R, в силу признака Вейерштрасса. Согласно лемме
Римана, а(А) -> О, Ь(Х) -> О, |А| -»■ +оо.
Заметим также, что а — чётная, а Ь — нечётная функции на R.
Упражнение 31. Доказать, что функции а и Ь равномерно непре-
непрерывны на R. Таким образом, для каждого х £ R функция
+оо
д(Х) := а(А) cos Ая + Ь(А) sin Хх = f f (и) cos Х(х— и) du, X > О,
непрерывна по А на [0,+оо). [tJutfpfy'^
Для числа А > 0 положим J(A) :- С^З •vte? 'w<9 =9
= - jf(o(A) cos Аа; + Ь(А) sin Хх) dX = - / ( / f{u) cos X{x -u)du) dX.
Из теоремы об интегрировании по параметру равномерно сходяще-
сходящегося несобственного интеграла следует такое представление для J
Учитывая равенство J dv = — , А > 0, получаем следующее
о 'У 2
представление для J(A) — с, с Е R :

536 Глава 16. Элементы теории рядов Фурье и интеграла Фурье
J(A) - с = - / ffc(u) du, F)
7Г о U
. . , . f{x-u) + f(x + u)
в котором gc(u) := gc(u, х) := — —- - - с.
Теорема 10. (Признак Дини). Пусть f |/(u)| du < +оо,
— оо
число х б R — фиксировано и для некоторого числа с £ R
справедливо утверждение 3 8 > 0 : J" c du < +оо.
о и
Тогда J(A) -> с, Л -> +оо, т. е. справедливо равенство
- / ( / /(u)cosA(a;-u)du)dA=:c.
"" ° °° • ^
Г Согласно представлению F) имеем г ^ ^jf. s5 Л,^' "
,,,. 2l. sin Ли ,
J(A) - с = - / дс(и) du+
7Г 0 U
2 +~/(а: - и) +/(а: + и) . . , 2с +?> sin Ли
+ - Г — —— sin Аи du-— Г du. G)
п j 1u п j и
Первый и второй интегралы правой части G) сходятся к нулю при А —>■
+оо по лемме Римана. Кроме того,
+г° sin Аи , +?°smt; , „ . .
I du = I dv —> 0, Л —> +оо.
Замечание. Если выполнены, условия, теоремы 10 и х —
« . f{x-) + f(x+)
точка разрыва первого рода /, то с = .
Если выполнены условия теоремы 10 и х есть точка
непрерывности /, то с= f(x).
Теорема 11. (Признак Липшица). Предположим,
что f |/(u)|du < +оо и функция f в точке х удовлетворя-
—оо
ет для некоторого а е @,1] условию Липшица
3LeR 36>0 VuG(-<5,E) : \f{x + и) - f{x)\ < L\u\a.
Тогда J(A) —>■ f(x), A —> +oo, т. е. справедливо равенство
1 +0O/ +OO .
f(x) = - /( / /(u)cosA(a;-u)du)dA =
— ~ I iaW cos ^ж
^ 0
\ Доказательство следует из теоремы 10.

16.4. Интеграл Фурье 537
+ ОО
С лед с те ие 8. Если f \f(u)\du < +00 и функция f имеет
— оо
в точке х производную f'{x), то J{A) —> f{x), A-+ +00.
Замечание. Справедлив аналог следствия 3.
Упраснснение 32. Пусть }{х) = —■e~°lx\ x G R, о > 0. Вычислить
2а
. , 7г _ , | +?° cosAz
функции а и о и доказать такое равенство — е =1 —5 г? "^
2сг о ^ + А
для х & R.
16.4.3 Преобразование Фурье
+оо
Пусть функция / : R —> R такова, что J |/(u)| du < +00.
—00
Определение 1. Преобразованием. Фурье функции f
называется комплексная функция
+ ОО +ОО +ОО ,
/(А) := / eiXxf{x)dx= J /(x)cosXxdx + г f f(x)smXxdx,X G R.
—00 —00 —00
Теорема 12. (Формула обращения). Пусть функция
f непрерывна в точке х, удовлетворяет условию призна-
+ ОО
ка Дини в точке х и J \}{u)\du < +00.
—00
1 А
Тогда }{х) = — lim f e-lAx/(A)dA.
2ТГ А->+оо _JA
[ Для доказательства заметим, что е~гАх/(А) = (cosAa;-ismAa;)-(a(AL-
+ib(X)) — a(A)cosAa; + b(A)sinAa; - ia(A)sinAa; + ib(A)cosAa;. Поэтому
J e~tAx/(A) dX = J (a(X) cos Aa; + b(X) sin Aa;) dA = 2irJ(A). Затем нуж-
-A -A 3[iti^C*$
но использовать признак Дини сходимости интеграла Фурье и учесть
непрерывность функции / в точке х. J
Упражнение 33. Вычислить преобразование Фурье следующих
функций: а) }(х) = 1/{2а),х G {-а,а), }{х) = Q,\x\ > а, а > 0; Ь)
f(x) - ае-ах,х > 0, }(х) = 0,а; < 0, а > 0; с) fix) = ; 5 , х £ R;
1 4- х
d) }{х) = —^= ехр (- ~э 1 - * е Д, a G Я, а > 0.
С\/2п \
Ответы, a) ^^ , A G Я; b) —i— , A G Я; с) тге-1А1, А 6 R\
Xa a —iX

$38 Глава 16. Элементы теории рядов Фурье и интеграла Фурье
6) exp (ia\ - ?—— ] , А € Я.
Замечание. В том случае, когда преобразование Фурье / так-
также абсолютно интегрируемо по Я, формулы, выражающие / и / друг
через друга, принимают следующий вид
/(А) = +/W(*) dx, A € R, /(*) = I- +/ViA'/(*) dX, x € А
-оо z7r -то
16.4.4 Элементарные свойства преобразования Фурье
^~^\ +0°
kl0.) Пусть J" |/(u)|du < 4-оо. Тогда преобразование Фурье / равно-
V-У -оо _ ^П.
мерно непрерывно на оси, причём /(А) —> О, |А| —> +оо. J ^й«в1'' Д
[ Утверждение о непрерывности следует из теоремы о непрерывно-
непрерывности по параметру равномерно сходящегося интеграла, то, что /(А)
О, |А| —>■ +оо следует из леммы Римана. ivummMI ^
Г 2° J Если для некоторого числа п € N справедливо неравенство^
+ОО
то преобразование Фурье / имеет производные до порядка п включи-
включительно (каждая из них удовлетворяет 1°), причём j^i
**(гх)к/(х) dx, \eR;l<k<n. I (
-оо -•* СУ. р':
+ОО '
В частности, /(fc)@) = t* / xkf{x) dx, 1 < к < п. м 7
—оо
\ Это свойство есть результат последовательного применения теоремы
одифференцировании несобственного интеграла по параметру. J
уПусть / € С1 (Я), существует /<п) на Я, причём
, 0< fc<n-l; /°|/(fc)(a;)|(ia;< +oo, 0 < fe < п.
Тогда /Н(А)=ГМ /(А), А € Я.
f Рассмотрим только случай п = 1. Используя формулу интегрирования
Л +оо
по частям, получим следующее равенство /'(А) = / elXxf'(x)dx =
-оо и v/
+ОО Л
-tA / elXxf{x)dx=*f{\), A G Я. J
-оо ^ ^ »
Замечание. Заметим, что при условии 3° АП/(А) -> О, |А| -> +оо.

16.4. Интеграл Фурье '" 539
[4 ] Пусть функции Д и Д. таковы, что
\У +оо +оо
/ |/fc(u)|du<+oo, / /fc2(u)|du<+oo; fc = l,2.
—оо —оо
Тогда свёртка функций Д и /2
I +О0
—оо
имеет следующее преобразование Фурье Д. * /а = Д • /г-
[ При предположениях 4 выполнены условия теоремы об интегриро-
интегрировании по параметру по неограниченному промежутку несобственного
интеграла. Поэтому Д * Д>(Л) = i ^
+О0 •**( +О0 / +О0 \
• -u)dx\ /2(u) du =
ЛеД. J
16.4.5 Пример применения преобразования Фурье
Найдём решение и: (Ях [0, +оо) —> R уравнения теплопровод-
'ности
с начальным условием
+оо
• u(i,0) = /(i), г£Й; J \f{x)\dx <+оо. (9)
—оо
Задачу решения уравнения (8) при условии (9) рассмотрим при следу-
следующих дополнительных предположениях: 1) для каждого t > 0 функция
u(-,t) абсолютно интегрируема по R, при каждом t > 0 : u(x,t) —>
+ ОО
О, u[(x,t) -> 0, |i| -* +оо. Пусть u(X,t) :-. J elXxu(x,t)dx для
—оо
Л £ R, t > 0. Заметим, что
й(л,о) = /(л), лед. (ю)
Рассмотрим теперь преобразование Фурье равенства (8), учитывая
формулу —д-j— = — А2й(А,£). Получим следующее равенство
ОХ
^1=-X4(\,t), о о, лед,
которое, в силу формулы A0), можно при каждом Л е R рассматри-
рассматривать как дифференциальное уравнение относительно функции й(Л, ■) на

540 Глава 16. Элементы теории рядов Фурье и интеграла Фурье
[0,+со). Решение этого уравнения имеет вид u(X,t) — /(А)е~л ', t >
0; A 6 R. Заметим теперь, что для t > 0, х £ R имеем
1 +°° 1 +°° 1
— f e-iXxe^2td\=— f e-AtcosAxdAU
2тг _JTO 2тг _JTO
Последнее равенство можно получить следующим образом. Пусть
J(x) := / е~Л *cosA2dA, гей, t > 0. Тогда
о
+ °о 2 / \ 2 А—»+°о х
О \ 2t ) А=0 2t
откуда J(x) = ce~x ^At\ х £ R, с £ R. Заметим, что при х = 0
:, t > 0.
о
В силу свойства_4£_находим
du, *>0. х б Д. ^
Упраэ«;кекие 3^. Пусть дополнительно к условиям (9) / е С (Я).
Доказать, что lim u(x,t) = /(г), х Е R.
16.4.6 Историческая справка
Фурье Жан Батист Жозеф A768 — 1830) — французский
математик. Его математические работы с новыми оригинальными мето-
методами посвящены математическому анализу, дифференциальным урав-
уравнениям, теории теплоты и численным методам. Эти работы послужили
основой создания теории тригонометрических рядов и разработки ряда
других современных проблем математики. И хотя Фурье предполагал,
что всякая функция может быть представлена тригонометрическим ря-
рядом, его результаты и новые методы оказались исключительно плодо-
плодотворными для многих разделов математики и её приложений. Точные
условия сходимости тригонометрических рядов были получены затем
Дирихле. Связанные с исследованием рядов Фурье работы Дирихле, а
затем и Римана. оказали большое влияние на анализ многих понятий
математики (непрерывность, дифференцируемость, понятие функции и
др.) и разработку теории интеграла. Фурье участвовал в военном похо-
походе Наполеона в Египет, был губернатором Нижнего Египта и секретарём
института, организованного Наполеоном в Каире. В 1827 г. занял место
П. Лапласа в должности ректора Политехнической школы.
Парсевалъ М. А. A755 — 1836) — французский математик, ав-
автор работ по теории дифференциальных уравнений и теории функций.

16.5. Дополнительные задачи к главам 13 — 16 541
Равенство Парсеваля было установлено им чисто формально для три-
тригонометрической последовательности ещё в 1799 г. Из этого равенства
следует неравенство Бесселя. Идеи Парсеваля позже привели Гильберта
к введению пространств, названных позже именем Гильберта.
Бесселъ Фридрих Вильгельм A784 — 1846) — немецкий ма-
математик и астроном. Неравенство Бесселя было сформулировано им
для тригонометрических рядов. Его именем назван класс цилиндриче-
цилиндрических функций и ряд других результатов.
Дини Улисс A845 — 1918) — итальянский математик, автор ра-
работ по теории функций, специальным функциям, теории поверхностей,
теории дифференциальных уравнений и алгебре.
Чезаро Эрнесто A859 — 1906) — итальянский математик, автор
работ по теории расходящихся рядов и геометрии. Предложил метод
суммирования, названный его именем.
Фейер Липот A880 — 1959) — венгерский математик, автор ра-
работ по теории функций, теории тригонометрических рядов, теории ин-
интерполяции и специальным функциям.
16.5 Дополнительные задачи к главам 13 — 16
1. Пусть F{a) = fe~a2x2 dx, a G R. Доказать, что F € C(R).
о
2. Пусть F(a) — f ln(a2 — sin x)dx, a > 1. Доказать, что функция
о
F£ C^l.+oo)), и найти F'.
с2
3. Пусть F(a) = / sin(z2 + 2a)dx, оЕЙ. Доказать, что F G С1 (Я) и
а •
найти F'.
4- Определить те значения а € R, для которых сходится интеграл
_ з/\ха _
_ 1 3
Ответ, а < — - , а > - .
1
5. Доказать сходимость интеграла Г
о *
+оо(_1)И
6. При каких значениях а£Л сходится интеграл j — dx?
l xa
Ответ. Сходится абсолютно при а > 1 и условно при 0 < а < 1.
7. Доказать сходимость интегралов:

542 Глава 16. Элементы теории рядов Фурье и интеграла Фурьё
+ОО +ОО
a) f exp(-z4sin2 x)dx; Ь) / х2ехр(-ха sin2 x)dx.
о. Доказать сходимость интеграла J
о х + sin г
+оо г _|_ J
5. При каких значениях a £ R сходится интеграл / sinzdx?
1 г
Ответ. Сходится абсолютно при a > 2 и условно при 1 < а < 2.
10. Доказать сходимость интеграла Г — dx.
Jo ж2 -х2
\ dx
11. Исследовать сходимость интеграла J —-^т- тг , а > 0, /3 > 0.
Ответ. Сходится при а < 1 и /3 < 1.
+оо 5
12. Доказать сходимость интеграла f ijsinxjx dx.
о
13. Доказать сходимость интегралов:
a) J cos(x + х3) dx; Ь) f cosB2 + sin2x) dx; c) / sin(i2+sini)dx.
0 0 0
1J).. Доказать условную сходимость интегралов:
+оо +оо +оо sin2i
а) / cosx3dx; b) / exsine2xdx; с) / esiax dx.
x
. _ „ . .. ( +?°sinu , \
15. Вычислить следующие пределы: a) lrni x j —r— du ;
i-»+oo \_ Jx U2 J
,. / +г°°8т2и \ /2 "Binu \^
b) lim [x I —r— du] ; c) lim - Г du
x-»+oo \_ Jx U2 J x-4+oo \1X I U J
Ответ, a) 0, b) - , c) 1.
16. Для функции / G С (R) интеграл J \f'(x)\dx сходится. Доказап
—oo
существование пределов lim fix), lim f[x).
X—i — OO X—»+O0
+ O0 +O0
17. Для функции / G С1 (Я) интегралы / /(х) dx, / I/'C1)! dx сходят
—oo —oo
ся. Доказать, что /(х) —> 0, |x| -* +oo.
15. Для функции / G C([0,+oo)) /@) = 0 и sup|/(i)| < +oo, а дл
x>0
+OO
функции g сходится интеграл f IffC1)! dx. Доказать, что
о

16.5. Дополнительные задачи к главам 13 — 16 543
lim ff(-)g(x)dx = O.
+ OO
/
О
19. Для функции / 6 С([0, +оо)) сходится интеграл f |/(х)| dx, а функ-
о
ция д 6 С([0, +оо)) и ограничена на [0, +оо). Доказать, что
lim J f{x + X)g(x) dx — 0.
20. Функция / абсолютно интегрируема по [0, +оо) и при каждом Л > 0
Ь(А)
отрезок [а(Л),Ь(Л)] С [0,+со). Доказать: lim / /(x)cosAxdx = 0.
А^+°° а(А)
+оо г
21. Доказать, что интеграл / е~ах (a3 +x)dx, а > 0, сходится равно-
о
мерно на отрезке [1,10].
+°° а2 _ Х2
22. Доказать, что интеграл / -т—^ ^ dx, a £ R, сходится равно-
равномерно на R.
+ sinai
23. Доказать, что интеграл J dx, a € R, сходится равномерно
о &
на множестве [1,+оо).
+ ОО
24. Доказать, что интеграл / cos(aa:3) dx, а^О, сходится равномерно
1
на множестве {а | \а\ > 1}.
25. Исследовать на равномерную сходимость интегралы:
+оо а +оо
a) J sinx-sin— dx, a £ [0,1]; b) f sin(aex)dx, |a| > 1.
ox о
Ответ, а), Ь) сходится равномерно.
26. Доказать, что функция F(ct) := J dx, a < 2, непрерывна на
о х<*
множестве [0,2).
+оо е-х
27. Пусть F(a) := Г — — dx, а < 1. Доказать, что F € С(@,1)).
0 | sinx|a
1 e~xdx
28. Пусть F{a) := / -7== , a € [0,1]. Доказать, что F £ С([0,1]).
о у/\х - а\
29. Доказать равенства:
+oo_-ijt +00
а) lim / —— = 0; Ь) Um f e~* dx = 1.
35 — 4-1168

544 Глава 16. Элементы теории рядов Фурье и интеграла Фурье
~*~?° 1 / ее \
'. Вычислить интеграл J ехр( — —j J dx, a > 0, n > О.
30
Ответ. 2("-
31. Вычислить пределы:
Ответ, а) yfi, Ь) Г(сг).
32. Пусть Л = {A1,12) I (xi - IJ + x2, < 1}- Рассмотрим множества
■Bn = {C1,3:2) fxi J +х| < —j, n > 1. Доказать, что множество
oo
A \ |J Бп измеримо и определить его площадь.
п=1
33. Пусть / G С([0,1]2). Доказать, что равномерно по {xltx2) £ [0,1]2
справедливо утверждение
Е C^(^,x2)xJ(l-x1)"-fc^/(x1)x2), п^оо.
34. Пусть М — компактное измеримое множество в Rm такое, что
для любых х и у из М существуют точки x*i, х2,..., хп из М такие, что
отрезки, соединяющие точки х& и x*fc+ii к — 0,1,... ,п, х*о = х, xn+i =
у*, лежат в М. Пусть / G С(М). Доказать, что справедливо следующее
утверждение: 3 в£ М : J f(x) dx = f(&) тп(М).
м
35. Вычислить интегралы:
а) / min(xi,X2)dxidx2; Ь) / тах(х1,хг) dxi dx2.
[0,l]2 [0,1]»
_ . 1 , . 2
Ответ, а) - , Ь) - .
36. Доказать, что для / G Щ[0,1])
/ (J (Jf{x1)f(x2)f(x3)dx3^j dx2SJ dx, = I Qf(x)dx\ .
37. Вычислить интеграл f Xixldxidi2, где А = {(i!,i2) | x2 + x\ <
4, xi > 0}.
26
Ответ. - .
38. Найти интеграл
J J ...J cos2 (— (xi + x2 + ... + xm)) dxi dx2 ... dxm.
00 0 \^m j
Указание. Сделать замену х*, = 1 — у^, k = 1,2,..., m.

16.5. Дополнительные задачи к главам 13 — 16 545
Ответ. 1/2.
39. Для функции / € С([0,1]) вычислить предел
1
Ответ, тг J f(x)dx.
о
ег
^0. Вычислить интеграл f -—= dx\ dx2, z = х\ + ix2, А = {z \ \z\ < 1}.
А 2- z
Ответ. *(el/a - 1).
41. Пусть / G С(Д), /(х) > 0 для х € Я и / /(х) dx = 1. Для фиксиро-
я
п
ванного а > 0 вычислить предел lim /•••/ П /(я1*:)^1*!-
Ответ. 0.
42. Для функции / G С([0,1]2) положим F(£) := f f(xi,x2)dxi dx2
At
с множеством At = {(ii,i2) I 0 < Xy < t, 0 < x2 < *}• * ^ [0,1].
Определить i<".
Ответ. F(t) = / f(t,x2)dx2 + } }{xut)dxu t G [0,1].
о о
43. Для функции / G C([0,+ooJ) положим F(t) := J /(x1,x2)dx1dx2
л.
с множеством At = {(xi,x2) | xi > 0, x2 > 0, xx + x2 < t}, t > 0.
Определить i5".
t
Ответ. F'(f) =//(xi,f-xi)dxb t > 0.
о
44' Для функции / G С(Д3) положим F(t) := J /(xi, х2| Х3) dxi dx2 йхз
At
с множеством At = {(хь x2)x3) | t2 < x\ + x\ + x\ < 4t2}, t > 0.
Определить F'.
Ответ.
2ir x/2
F'(t) = &t2f J fBtcos</>cost/1,2tsinv»cosip,2tsin 1/»)cosipd<pdip~
0 -x/2
-t2 J J f (t cos (pcos %p,t sin tpcos ip,t sin%p) cos ipd<pdil).
0 -ir/2
45. Вычислить для a > —1,/3 > —1 интегралы:
35*

546 Глава 16. Элементы теории рядов Фурье и интеграла Фурье
a) /x?xf dx1dx2,A = {(xi,x2) | 0<х2 < 1-хь ii > 0};
А
b)/e-»»x?da:idx3l Л = {(xi,x3) | 0 < х2 < xi};
с) /A - xi)exf dxi dx2, А = {(xi, х2) | 0 < х2 < xi < 1}.
Ответ, a) 5fe±M+i) ; Ь) Г(« + 1); с)
' a + 0 + 2 ' v ;' '
4.6. Вычислить интеграл /((xi — x2)dxi + dx2), где Г — граница мно-
г
жества {(xi,x2) | х\ + х\ < 2xi, x2 > 0}, пробегаемая против часовой
стрелки.
47. С помощью криволинейного интеграла вычислить:
а) площадь, ограниченную эллипсом; Ь) площадь множества, ограни-
ограниченного кривыми Х!Х2 = 1, xix2 =2, х2 = х2, х2 = 2х2.
48. Вычислить интеграл §(х\ + х\ + х\) dl, где Г — граница треугольника
г
с вершинами A,0,1), @,0,2), @,1,1).
49. Пусть S - граница симплекса с вершинами @,0,0), A,0,0), @,1,0),
@,0,1). Вычислить интегралы:
a) J(xi dxi Л dx2 + xix2 dx2 Л dx3 + x2x3 dx3 Л dxi) по внешней стороне
s
поверхности S;
b) /(xi + x2 + x2) da.
s
50. Найти ряд Фурье для функции f(x) — —тг/4, — тг < х < 0, f(x) =
■4, 0 < х < тг и исследовать его сходимость. Доказать, что
тг _ 1 1 _ 1
51. Найти ряд Фурье для функции /(х) = |х|, х G (—тг, тг], и исследовать
его сходимость. Доказать, что
^-1 + 1+1+1 +
8 + З2 52 + 72 '
52. Доказать равенство
sin3x sin5x тг .„ .
sinx+———+—-—+... =-, хе@,тг).
о о 4
53. Найти суммы рядов:
°° cosBn + 2)х °° cos nx
п=о 2п +1 ' ' n=1 n
о
54- Доказать, что: a) J —i dx = — — ; b) I - ш dx = —
nX 6 n X 1 — X 4

16.5. Дополнительные задачи к главам 13 — 16 547
55. Пусть / 6 С7([0,1]). Вычислить интеграл
j „ jx1 + x2 + ... + xk д 1<*<п, п>1.
г Х1 + Х2 + + Х / ^ " "
г О
Ответ. - f ff{x)dx\ .
$6. Пусть / € С([0,1]). Доказать равенство
1 1 п
/.?. /min(xi,...,xn) П f{xj)dxj=.
О 0 j=l 0 \х
57. Доказать равенство
/ .». /(xix2... х„)Вя-"- ft dxj = 1 /11 In" - dx, n > 1.
о о j=i \п ~ Ч- о х
55. Доказать равенство
+оо П. Ат С оо 1-»п+1
J v __ _21 \^ / 1 ЛП 6У *!> О
(асимптотическое разложение интеграла при а —> 0).
59. Доказать равенство
+оо i
nun j б~хA + п\Х + ... 4~ Qfi&nj dx = i Tt ^ 1.
{oi ап}СЙ 0 П + 1
60. Пусть / € С([0,+оо)) и V(/, [0,+оо)) < +со. Доказать, что ряд
ОО +О0
£2 f(n) и интеграл J f(x) dx сходятся или расходятся одновременно.
п=1 О
61. Пусть / G Д([0,1]) и f(x) -+Q, х -* 0 + . Доказать, что
lim ( а Г ^тр- dx ) =0.
62. Доказать равенство
г—v sinnxsinny . , . „ .
ху + 2> г =7rmin(x,y), 0<аг,у<7Г.
п=1

Список основных
обозначений
V - для всех, для каждого
3 - существует
3 ! - существует точно один
:= - равно по определению
N - множество всех натуральных чисел
Z - множество всех целых чисел
Q - множество всех рациональных чисел
R - множество всех действительных чисел
С - множество всех комплексных чисел
Rm - m-мерное векторное пространство
c°-i ck- <*(<*-1)-->-fc + 1) k£N
А1 для матрицы (в частности, вектора) А обозначает транспониро-
транспонированную матрицу
/ : А —¥ В - функция (отображение, преобразование), определёная
на множестве А и принимающая значения во множестве В
f(A) := {/(*) | х € А}
:= {х | f(x) € В}
max/ (min/) - наибольшее (наименьшее) значение функции / на
А А
множестве А
аир A (inf A) - точная верхняя (нижняя) грань множества А действи-
действительных чисел
[1, о>0,
sign а := < 0, а = О,
[-1, а<0
548

Список основных обозначений 549
[а] - целая часть числа а
А
*■ f(a-) = lim /(i) - предел функции / слева в точке а
X—*в —
/(а+) = lim /(х) - предел функции / справа в точке а
х—>а+
О - отношение подчинённости
* ' о - отношение пренебрежимости
/ ~ з, х —¥ хо - отношение эквивалентности функций / и д при
х —¥ xq
С(А) - множество всех функций / : А —> R, непрерывных на мно-
множестве А
Сь(А) - множество всех функций / : А —> R, непрерывных и огра-
ограниченных на множестве А
С(А,В) - множество всех функций / : А -4 В, непрерывных на
множестве А
/1(а) (/+(а)) - производная слева (справа) действительной функции
/ в точке а
СП{А) {СП{А, Я)) - множество всех функций / : А -» R (/ : Л -4
Ат), имеющих непрерывные на А производные порядка п (компоненты
которых имеют непрерывные на А производные порядка п)
С°°(А) := П СП(А)
п=1
*■ Ltpa([a,b]) - класс всех функций / : [а,Ь] —> Д, удовлетворяющих
На отрезке [a, b] условию Липшица с показателем a
R([a, b]) - множество всех действительных функций, интегрируемых
по Риману по отрезку [а, Ь]
RS(a,[a,b]) - множество всех действительных функций, интегриру-
интегрируемых по отрезку [а, Ь] относительно функции а
BV([a, b]) - множество всех функций ограниченной вариации на [а, Ь]
V(/, [а, Ь]) - вариация функции / на отрезке [а, Ь]
'" {ап(х), х 6 А | п > 1} - последовательность действительных функ-
функций, заданных на множестве А
(X, р) - метрическое пространство с метрикой (расстоянием) р
В{хо,г) := {х £ X | р(х,хо)<г}
~В(хо,г) := {х G X | р{х,х0) < г}

550 Список основных обозначений
S{x0, г) := {х € X | р[х, хо) = г}
хп -4 х, п —¥ оо в (Х,р) - последовательность элементов {xn \ n >
1} С X сходится к элементу х £ X при n-юов метрике р
/i(z) - производная по направлению а действительной функции нес-
нескольких переменных в точке х
fk*[x) - dxkdxj
V/(i) := grad/(x) = ( -—^ ,..., -^^ ) - фадиент действител»г-
\ oxi дхт j
ной функции от m переменных в точке х

Указатели
е-сеть, 341
Артин Э., 424
Архимед, 35, 123, 229, 238
Арцела Ч., 356
Асколи Дж., 356
Банах С, 356
Беркли Дж., 124
Бернулли Д., 177
Бернулли И., 159, 177
Бернулли Я., 50
Бернулли братья, 155
Бернштейн С.Н., 124
Больцано Б., 25, 80, 124, 155
Валлис Д., 223
Вейерштрасс К. Т. В., 50, 80
Гёльдер О. Л., 177
Гаусс К. Ф., 124, 197
Гейне Г. Э., 50, 123
Гильберт Д., 31
Гранди Г., 290
Грегори Дж., 176
Грин Дж., 509
Гюльден П., 237, 241
Дарбу Ж. Г., 201, 240
Дедекинд Р., 50
Дини У., 393
Дирихле П. Г. Л., 25, 124
Дюбуа-Реймон П., 240
Евдокс, 123, 238
Жордан К. М. Э.( 241, 308
Зейдель Ф. Л., 124
Иенсен И. Л., 167, 177
Кантор Г., 17, 26, 30, 50
Коши О. Л., 46, 50, 124, 143,
155, 239
Лагранж Ж. Л., 141, 154, 157
Лебег А. Л., 240
Лежандр А. М., 197, 424
Лейбниц Г. В., 25, 154
Липшиц Р., 356
Лиувилль Ж., 197
Лопиталь Г. Ф., 155, 159, 177
Маклорен К., 157, 177
Мерз Ш., 50
Минковский Г., 177
Ньютон И., 123, 137, 154, 155,
176, 197, 239
Остроградский М. В., 509
Папп, 241
Пеано Д., 156, 176, 241
Пифагор, 31
Пуанкаре А. Ж., 509
Пуассон С. Д., 424
Риман Г. Ф. Б., 202, 239
Ролль М., 140, 154
551

552
Указатели
Сильвестр Дж. Дж., 374
Смит Г. Д. С, 240
Стилтьес Т. И., 240, 299, 308
Стирлинг Д., 424
Стоке Дж. Г., 124, 509
Стоун М. Г., 356
Теплиц О., 80
Тейлор Б., 155, 176
Томе, 240
Ферма П., 139, 154
фредгольм Э. И., 356
Фреше М. Р., 356
Фруллани Д., 413
Хаусдорф Ф., 356
Хелли Э., 308
Шварц К. Г. А., 509
Шилов Г. Е., 25
Эйлер Л., 69, 124, 177, 197
Эрмит Ш., 197
аксиома Архимеда, 35
алгебра, 353
асимптота, 175
биекция, 24
бином Ньютона, 137
вариация функции, 294
гомеоморфизм, 338
градиент, 360
граница, 481
ориентированная, 488
грань множества
верхняя, 37
верхняя точная, 37
нижняя, 37
нижняя точная, 37
график функции, 23
группировка членов ряда, 261
дзета-функция Римана, 244
диагональный метод
Кантора, 30
диаметр
множества, 323
разбиения, 200
диффеоморфизм, 465
дифференциал внешний, 479
длина кривой, 232
дополнение к множеству, 20
дробь
десятичная, 31
десятичная бесконечная, 32
десятичная конечная, 32
периодическая, 31
правильная, 191
рациональная, 31
элементарная, 193
интегрирование, 194
знаки логические, 16
значение функции
наибольшее, 113
наименьшее, 113
изометрия, 331
интеграл
т-кратный, 429
Римана, 202
Римана-Стилтьеса, 300
Фурье, 534
верхний, 202, 300
двойной, 429
как функция верхнего пре-
предела, 218
неопределённый, 185
несобственный
расходящийся, 394, 401
сходящийся, 394, 401
нижний, 202, 300
тройной, 429

Указатели
553
интегрирование, 185
по частям, 190
с помощью
подстановки, 188, 189
интервал, 35
инъекция, 23
касательная, 128
вертикальная, 128
определение, 130
класс Rq, 520
колебание функции, 206
кривая
гладкая, 475
гомотопная точке, 493
замкнутая, 492
непрерывная, 231, 298
ориентированная, 470
спрямляемая, 232, 298
критерий , ■
Коши, 78, 93
интегрируемости, 205
лемма Абеля, 278, 288
линия винтовая, 471
логарифм натуральный, 69
матрица Якоби, 378
мелкость разбиения, 200
метрика, 318
микроскоп, 129
многообразие, 469
ориентированное, 470
многочлен от двух переменных,
196
множества равномощные, 26
множество, 17
бесконечное, 26
всюду плотное, 328
выпуклое, 372
замкнутое, 327
звёздное, 494
значений, 22
конечное, 21, 26
линейно связное, 494
мощности континуум, 36
ограниченное, 37, 323
ограниченное сверху, 37
ограниченное снизу, 37
односвязное, 494
определения, 22
ориетированное, 466
основное, 18
открытое, 325
пустое, 18
связное, 346
сходимости, 270
множители Лагранжа, 385
набор упорядоченный, 21
набор, отвечающий разбиению,
201
неравенство
Бернулли Я., 43
обобщение, 146
Гёльдера, 169
Иенсена, 167
физический смысл, 168
Коши, 46, 218
Минковского, 169
Эрмита-Адамара, 214
для модуля интеграла, 217
для модуля суммы, 42
треугольника, 320
норма вектора, 357
нумерация элементов
множества, 26
образ множества, 23
образ элемента, 22
обратные тригонометрические
функции, 109
объединение множеств, 19, 20
окрестность, 52
оператор, 22
ориентация, 466

554
Указатели
остаток ряда, 245
отношение
подчинённости или О, 94
пренебрежимости или о, 96
эквивалентности, 97
отображение, 22
взаимно однозначное, 23
регулярное, 465
сжимающее, 347
отображение в, 23
отображение на, 23
отрезок, 35
пара упорядоченная, 21
первообразная, 183
пересечение множеств, 20
перестановка членов ряда, 262
площадь
криволинейной
трапеции, 199
поверхности, 235
поверхность
ориентированная, 471
подмножество, 19
подпоследовательность, 70
подразбиение разбиения, 203
полуинтервал, 35
полукасательная
левая, 128
правая, 128
пополнение метрического про-
пространства, 331
последовательность, 25
Коши, 77
монотонно
возрастающая, 64
невозрастающая, 64
неубывающая, 64
ограниченная, 51
расходящаяся, 52
сходящаяся, 52
поточечно, 268
равномерно, 268
фундаментальная, 77, 329
постоянная Эйлера, 249
правило
Лопиталя, 159
двойственности, 21
предел
двойной, 333
интеграла
верхний, 203
нижний, 203
интегральных сумм, 209, 211,
301, 302
повторный, 334
последовательности, 52
последовательности
частичный, 71
слева функции в точке, 91
справа функции в точке, 91
функции в точке, 83, 332
преобразоавание, 22
преобразование Фурье, 537
признак
Абеля, 260, 274
Вейерштрасса, 272, 288
Дини, 526, 536
Дирихле, 259, 273
Коши, 251, 254
Лейбница, 258
Липшица, 527, 536
Раабе, 252
д'Аламбера, 250
интегральный, 253
логарифмический, 251
примитивная, 183
принцип локализации, 526
продолжение функции, 23
произведение
бесконечное, 265
декартово, 21, 321
расходящееся, 265
рядов, 263
рядов по Коши, 263

Указатели
555
сходящееся, 265
производная
бесконечная, 128
второго порядка, 150
геометрическая
интерпретация, 127
доказательство неравенств,
145
исследование
монотонности, 146
обратной функции, 134
слева функции в точке, 125
сложной функции, 133
справа функции в
точке, 125
суммы, произведения и
частного, 132
физическая интерпретация,
127
функции в точке, 125
функции на множестве, 131
производные старших порядков,
150
прообраз множества, 23
пространства
изометричные, 331
пространство
компактное, 339
метрическое, 318
полное, 330
сепарабельное, 328
радиус сходимости, 279
разбиение, 200
разность множеств, 20
расстояние, 318
ряд, 242
Лейбница, 255
Тейлора, 283
абсолютно
сходящийся, 256, 287
гармонический, 243
геометрический, 243
равномерно
сходящийся, 271
расходящийся, 242
степенной, 277
сходящийся, 242, 287
тригонометрический, 529
условно сходящийся, 257
сектор криволинейный, 230
площадь, 230
секущая, 128
скачек функции, 292
скорость мгновенная, 127
соответствие, 22
соответствие взаимно однознач-
однозначное, 24
сравнение чисел, 34
сужение функции, 23
сумма
Дарбу
верхняя, 201
нижняя, 201
Дарбу-Стилтьеса
верхняя, 299
нижняя, 299
интегральная, 201, 299
сумма ряда, 242
суперпозиция функций, 23
сюръекция, 23
тело вращения, 233
объём, 234
теорема
Банаха, 348
Больцано-Вейерштрасса, 73
Вейерштрасса вторая, 113
Вейерштрасса первая, 112
Гюльдена
вторая, 237
первая, 238
Дарбу, 211
Дирихле, 262
Жордана, 298, 299

556
Указатели
Кантора, 118, 331
Коши, 143, 264
Коши о промежуточном
значении, 116, 217
Коши-Адамара, 278, 288
Лагранжа о конечном при-
приращении, 141
Лагранжа о среднем значе-
значении, 141
Пуанкаре, 480
Римана, 263
Ролля, 140
Ферма, 139
обобщение, 140
Хелли, 306
Шварца, 366
о среднем значении, 216
о существовании и свойст-
свойствах обратной функции,
106
о существовании корня, 43
о существовании монотон-
монотонной подпоследователь-
подпоследовательности, 73
о существовании примитив-
примитивной, 219
о существовании точных
граней , 40
о трёх последовательно-
последовательностях, 58
о характеризации частично-
частичного предела, 72
о хорде, 116
тождество Абеля, 259
тор, 234
точка
внутренняя, 325
вырождения, 378
изолированная, 334
критическая, 171, 369
локального
максимума, 169
максимума строгого, 169
минимума, 170
минимума строгого, 170
экстремума, 170
неподвижная, 347
перегиба, 174
предельная, 323
разрыва функции, 105
стационарная, 171
трапеция
криволинейная, 198, 228
площадь, 228
уравнение Коши
функциональное, 105, 222
условие Липшица, 350
форма
дифференциаль-
дифференциальная, 468, 472
замкнутая, 492
точная, 491
формула
Валлиса, 223
Гаусса-Остроградского, 486,
490
Грина, 485, 487, 490
Лейбница, 152, 221
Маклорена, 157
Ньютона-Лейбница, 219, 485
обобщённая, 224
Стокса, 491
Стокса общая, 488
Тейлора, 155, 367
для вычисления
длины кривой, 232
меры Жордана, 457
объёма, 234, 490
площади, 229, 490
замены переменной, 188,
189, 221
интегрирования по частям,
190, 222

Указатели
557
основная интегрального ис-
исчисления, 219
прямоугольников, 230
трапеций, 231
формулы
Эйлера, 289
для вычисления
координат центра масс,
236
функции равные, 22
функция, 22, 25
Дирихле, 105, 202, 203
Лагранжа, 385
аналитическая, 315
выпуклая вверх, 163
* выпуклая вниз, 163, 373
дифференцитруемая, 361
интегрируемая
по Риману, 202
по Риману-Стилтьесу, 300
компактная, 347
линейная, 336
логарифмическая, 108
монотонно
невозрастающая, 92
неубывающая, 92, 292
непрерывная, 334
в точке, 101
на множестве, 102
слева точке, 102
справа в точке, 102
обратная, 24
ограниченной
вариации, 294
показательная, 289
равномерно
непрерывная, 117, 338
рациональная, 103,191, 336
от двух переменных, 196
скачков, 293
сложная, 23
степенная, 108
строго возрастающая, 92
строго выпуклая вверх, 163
строго выпуклая вниз, 163
строго убывающая, 92
трансцендентная, 197
элементарная, 187
центр масс, 236
цепное правило, 133
циклоида, 476
числа
действительные
алгебраические, 30
иррациональные, 33, 34
натуральные, 16, 31
неотрицательные, 33
операции, 67
отрицательные, 33
положительные, 33
равные, 34
рациональные, 31, 33
трансцендентные, 45
комплексные, 287
число е, 68
числовая прямая, 34
элемент
максимальный, 36
минималный, 36
наибольший, 36
наименьший, 36
элементы множества, 18
ядро Дирихле, 523
якобиан, 378

Дороговцев А. Я.
д g<) Математический анализ. Краткий курс в современном изложи
нии. — Издание второе. — К.: Факт, 2004. — 560 с.
ISBN 966-8408-44-6
Книга содержит краткое и вместе с тем достаточно полное по охвату
териала изложение современного курса математического анализа. (
рассчитана в первую очередь на студентов университетов и техни1
ких вузов и предназначена для первоначального изучения курса. П
ведено модернизированное изложение ряда разделов: функции мно
переменных, кратные интегралы, интегралы по многообразиям, o6i
формула Стокса и др. Теоретический материал иллюстрируется бс
шим числом упражнений и примеров. Всего книга содержит около 1
примеров и упражнений.
Для студентов вузов, преподавателей математики, инженерно-тех
ческих работников.
УДК 517(
ББК 22.16
ДОРОГОВЦЕВ Анатолий Яковлевич
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Краткий курс в современном изложении
Киев, «Факт», 2004, 560 с.
Редактор Анатолий Чуприн
Корректор Евгения Колодко
Технический редактор Оксана Кравченко
Компьютерное макетирование Александр Скопко
ООО «Издательство „Факт"»
Регистрационное свидетельство
ДК №1284 от 19.03.2003
04080, Украина, Киев-80, а/я 76
Тел./факс: @44) 417 1366, 416 8754
E-mail: office@fact.kiev.ua
Отдел .сбыта: @44) 468 6887
E-mail: sbyt@fact.kiev.ua
www.fact.kiev.ua
Зак.№4-пб8 Тираж 2 000
Сдано в набор 02.05.2004. Подписано в печать 16.05.2004. Формат 60x90/"
Бумага офсетная. Печать офсетная. Усл.печ.л. 26,8
ЗАО"ВИПОЛ",ДК№15
03151, г. Киев, ул. Волынская, 60

Анатолий Яковлевич Дороговцев
Математический анализ
Краткий курс
в современном изложении
«...Книга является эффективным введе-
введением в математический анализ»
Zentmlblatt MATH
Дорогой читатель!
Автора книги, которую ты держишь в своих руках, сегодня уже нет в жи-
живых. Мой отец, Дороговцев Анатолий Яковлевич, немного не дожил до семи-
семидесятилетия и до выхода в свет второго издания своего учебника по математи-
математическому анализу 40 лет отец проработал в Киевском университете
им. Т. Г. Шеченко, где с 1973 по 1998 г. г. заведовал кафедрой математического
анализа. Анатолий Яковлевич является автором 24 учебных пособий для сту-
студентов вузов, учителей и учащихся средних школ, двух монографий, более 200
научных работ. Главными своими учебниками он всегда считал курс матема-
математического анализа и задачник к этому курсу Отец самостоятельно разработал
программу курса, который читался им на протяжении многих лет. Будучи чле-
членом бюро секции математики Научно-методического совета при Минвузе
СССР, он использовал и обобщил традиционные подходы к изложению мате-
материала, а также учел современные тенденции. Некоторые разделы были вклю-
включены им в нормативный курс впервые. Стремление к современному изложе-
изложению, соответствию сегодняшнему развитию математики привело отца к пере-
переработке и подготовке настоящего переиздания, работа над которым была за-
завершена в 2003 году Книга во многом сохраняет дух лекций Анатолия Яков-
Яковлевича. Он всегда стремился не только ясно и четко изложить необходимый
материал, но и передать собственное отношение к предмету, который он страс-
страстно любил всю жизнь. До конца своих дней отец работал как профессиональ-
профессиональный математик, и его последняя статья датирована 2004 г.
Я думаю, что настоящая книга будет полезна любому студенту, изучающе-
изучающему математический анализ, преподавателю, ведущему такой курс, каждому,
кто хочет серьезно познакомиться с математикой.
Доктор физ.-мат. наук, профессор
Андрей Анатольевич Дороговцев