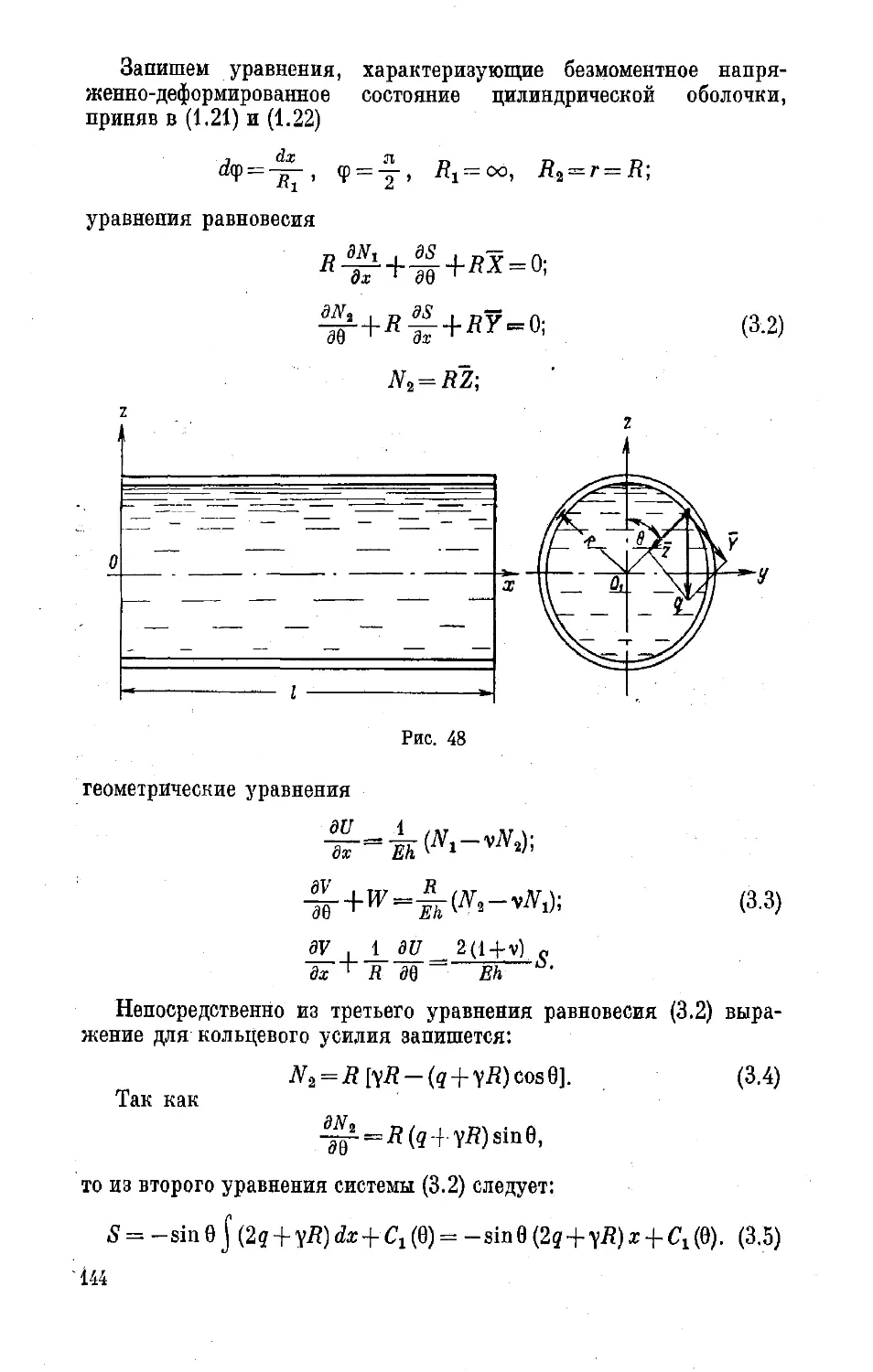
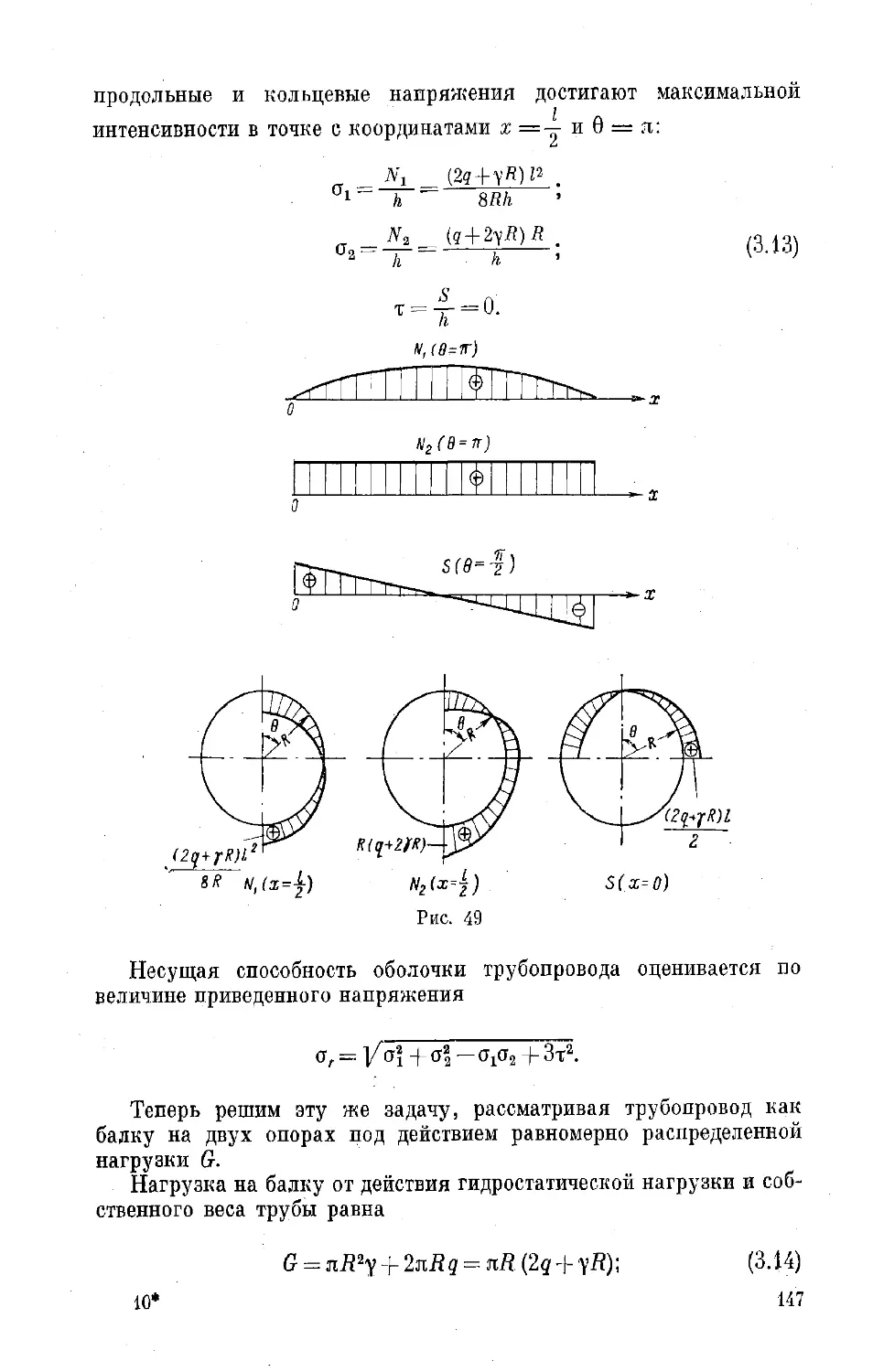
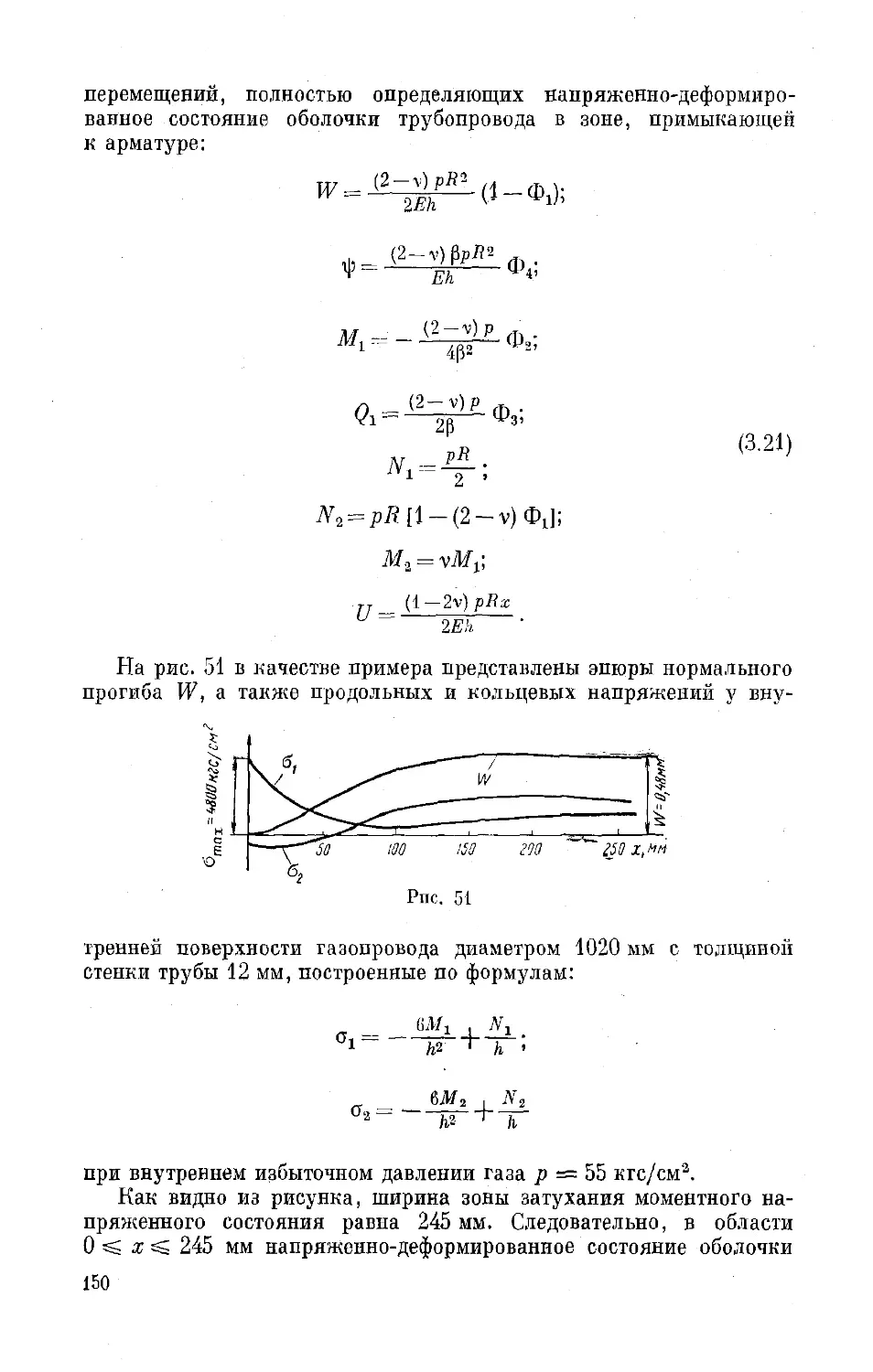
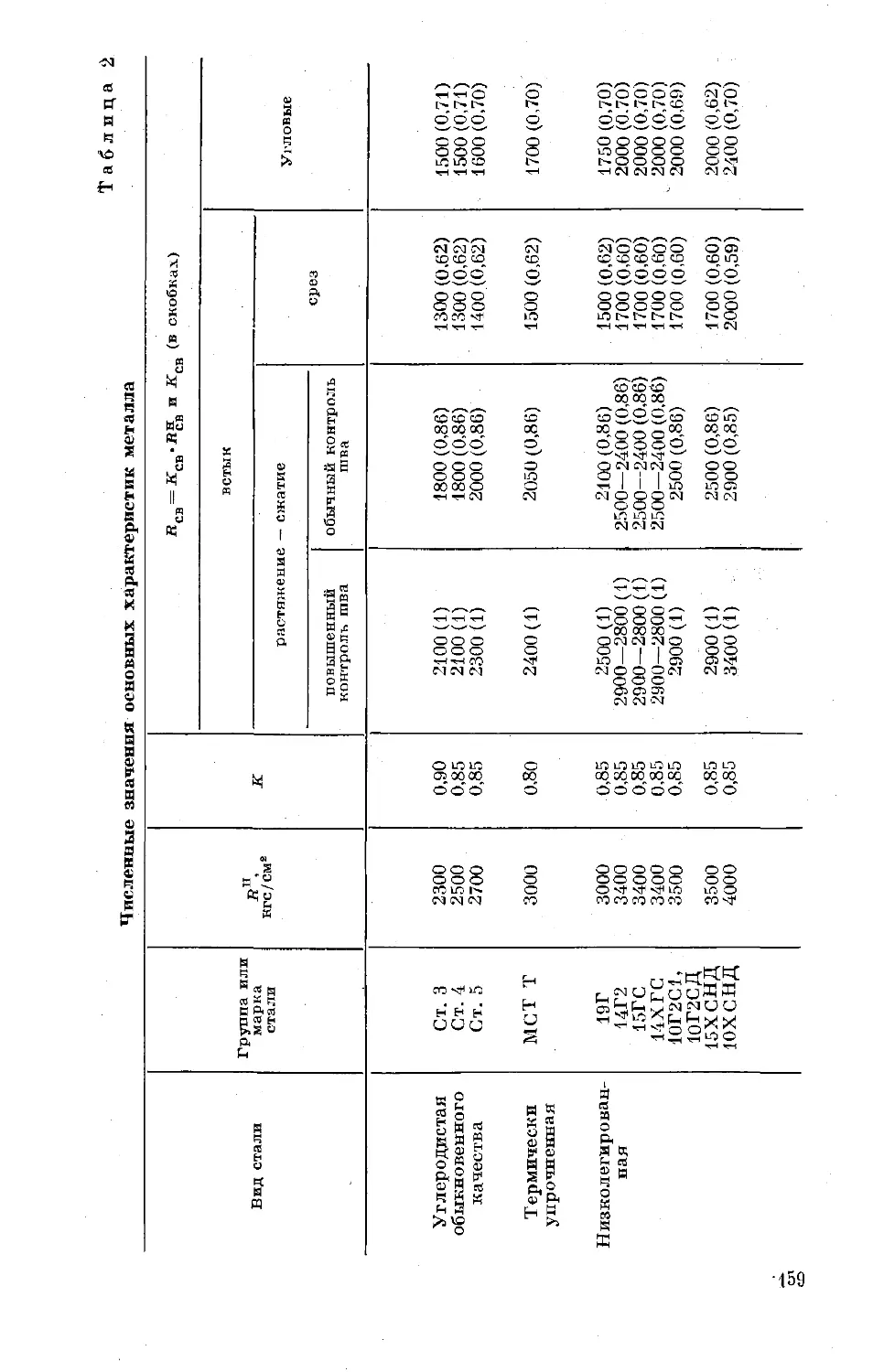
Текст
В. Л. БЕРЕЗИН, В. Е. ШУТОВ
ПРОЧНОСТЬ
И УСТОЙЧИВОСТЬ
РЕЗЕРВУАРОВ
И ТРУБОПРОВОДОВ
ИЗДАТЕЛЬСТВО «НЕДРА»
МОСКВА, 1973
УДК 622.692.23/43 : 539.4
Березин В. Л., Шутов В. Е. Прочность и устойчивость ре-
зервуаров и трубопроводов. М., «Недра», 1973, 200 с.
В связи с бурным развитием нефтяной и газовой промышлен-
ности в нашей стране интенсивно увеличивается емкость резерву-
арных парков для хранения нефти и газа и протяженность маги-
стральных трубопроводов. Однако до настоящего времени несущая
способность конструкций резервуаров и трубопроводов исследо-
вана недостаточно полно.
В книге изложены современные методы расчета на прочность
и устойчивость оболочек газонефтехранилищ и трубопроводов.
Главное внимание уделено исследованиям несущей способности
основных типов вертикальных цилиндрических резервуаров при
различных условиях эксплуатации.
Приведены результаты исследований ветрового воздействия
на резервуары большой вместимости (до 100 тыс. м3). Рассмотрены
некоторые вопросы прочности и устойчивости оболочек магистраль-
ных трубопроводов.
Книга предназначена для инженерно-технических и научных
работников нефтехимической и газовой промышленности, занима-
ющихся вопросами транспорта и хранения нефти и газа.
Таблиц — 4, иллюстраций — 64, список литературы — 22 на-
звания.
Б 043(01) -73 278 73
Всеволод Леонидович Березин,
Вадим Евгеньевич Шутов
ПРОЧНОСТЬ И УСТОЙЧИВОСТЬ
РЕЗЕРВУАРОВ И ТРУБОПРОВОДОВ
Редактор издательства А. Б. Латай Технический редактор В. Л. Прозоровская
Корректор П. А. Денисова
Сдано в набор 2/Х 1972 г. Подписано в печать 11/11973 г. Т-01128.
Формат 60 х 90>/,«. Бумага № 2. Печ. л. 12,5. Уч.-изд. л. 11,75. Тираж 3300 экз.
Заказ № 2036/4558—8. Цена 1 р. 29 к.
Издательство «Недра», 103633, Москва, К-12, Третьяковский проезд, 1/19.
Ленинградская типография М 6 «Союзполиграфпрома» при Государственном Комитете
Совета Министров СССР по делам издательств, полиграфии и книжной торговли.
196006, г. Ленинград, Московский пр., 91.
ПРЕДИСЛОВИЕ
Открытие новых богатейших месторождений и интенсивный рост
добычи нефти и газа в нашей стране требуют развития трубопро-
водного транспорта и увеличения объема резервуарных парков.
В ближайшем будущем проблема интенсификации трубопровод-
ного транспорта и емкости резервуарных парков будет решаться
путем применения в практике строительства трубопроводов больших
диаметров (до 2,5 м) и резервуаров большой вместимости (до
100 тыс. м3).
С увеличением диаметра трубопроводов и емкости газонефте-
хранилищ возрастает отношение толщины стенки к радиусу кривиз-
ны, т. е. оболочка этих сооружений становится более тонкостенной.
В этих условиях традиционная теория расчета, например трубо-
провода как стержня, наиболее распространенная в настоящее
время как в отечественной, так и в зарубежной литературе, может
привести к серьезным ошибкам.
Существенно изменяется подход к оценке несущей способности
газонефтехранилищ, так как с увеличением их объема наряду с про-
блемой прочности весьма актуальной становится проблема устой-
чивости формы оболочек.
В настоящей работе авторы стремились восполнить те пробелы,
которые еще имеются в теории расчета- оболочек трубопроводов
и газонефтехранилищ. Особое внимание обращено на анализ совре-
менных методов расчета, формулировку граничных условий на верх-
ней кромке корпуса вертикальных цилиндрических резервуаров,
1* 3
сопряженной с упругим кольцом жесткости и разнообразными кон-
струкциями покрытий, на исследование прочности и устойчивости
оболочек трубопроводов, резервуаров и газгольдеров при разнооб-
разных видах загружения (гидростатическое давление столба жид-
кости, снеговая и ветровая нагрузки, вакуум и т. д.).
Все решения выполнены в замкнутом виде. В ряде случаев при-
ведены примеры численных расчетов трубопроводов и газонефте-
хранилищ.
Книга является первой цопыткой систематизированного изложе-
ния вопросов прочности и устойчивости оболочек трубопроводов
и газонефтехранилищ при различных условиях эксплуатации.
Глава 1
ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ
ТОНКИХ УПРУГИХ ОБОЛОЧЕК ПРИМЕНИТЕЛЬНО
К РАСЧЕТУ РЕЗЕРВУАРОВ И ТРУБОПРОВОДОВ
Геометрические характеристики
оболочек резервуаров и трубопроводов
Оболочкой называется тело, ограниченное двумя криволинейными
поверхностями, расстояние между которыми мало по сравнению
с прочими размерами тела.
Геометрическое место точек, равно удаленных от обеих поверх-
ностей, является срединной поверхностью оболочки. Эта поверхность
в теории оболочек играет такую же роль, как и геометрическая ось
балки в сопротивлении материалов.
Длина перпендикуляра, восстановленного в произвольной точке
срединной поверхности, между двумя ограничивающими поверх-
ностями определяет толщину оболочки, которую обозначим через h.
Форма срединной поверхности, толщина стенки и граничный
контур полностью определяют оболочку с геометрической стороны.
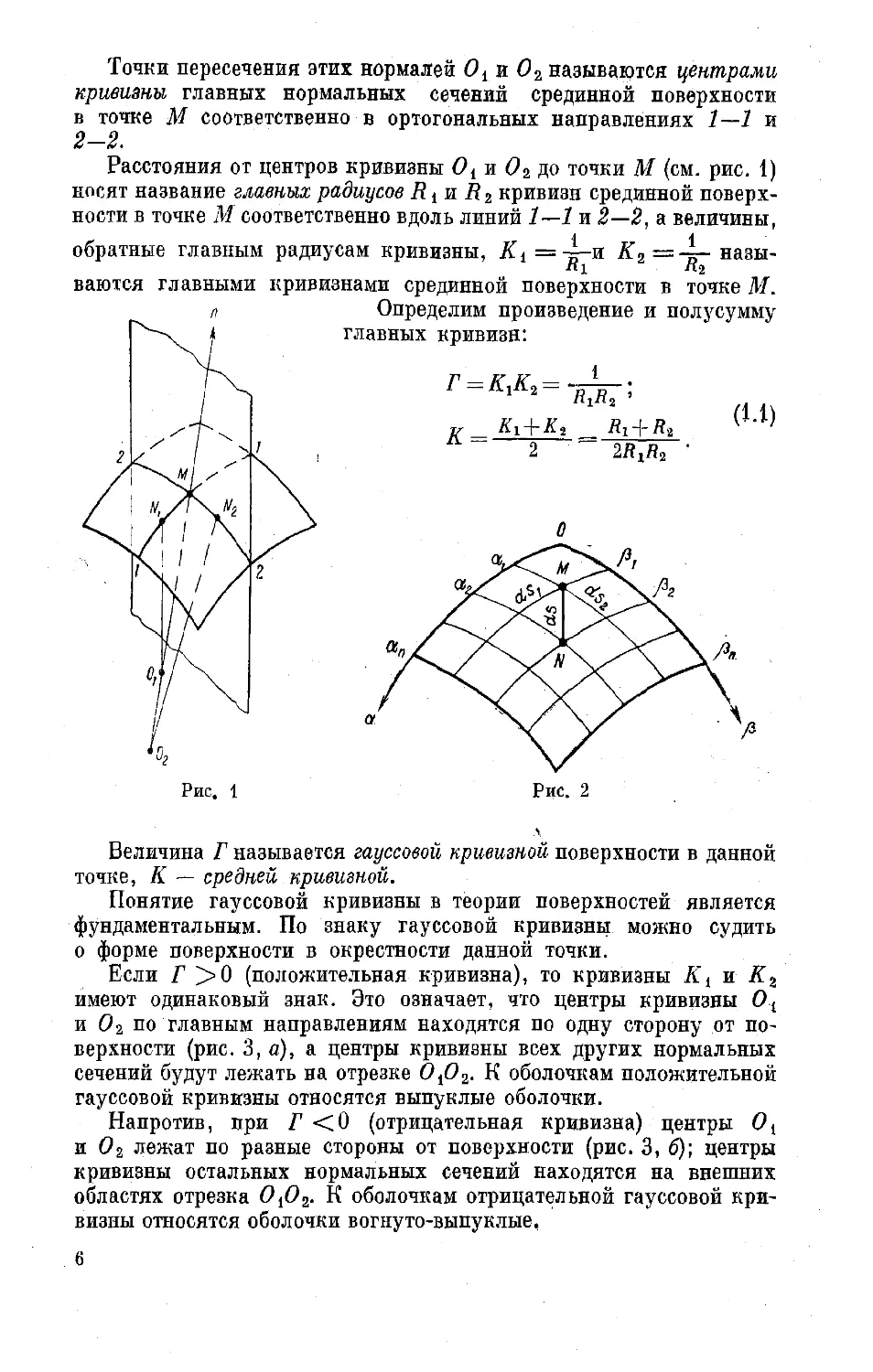
Проведем в некоторой точке М срединной поверхности произ-
вольной формы нормаль и плоскость, содержащую эту нормаль
(рис. 1). Точки пересечения плоскости, содержащей нормаль, и сре-
динной поверхности образуют некоторую кривую линию, которая
называется нормальным сечением в точке М.
Проведем на срединной поверхности произвольной формы се-
мейство линий alt a2, • • ., a„ и р15 р2, . . ., |3Л (рис. 2). Если ли-
нии систем аир пересекаются под прямым углом, т. е. угол между
касательными к этим линиям равен 90°, то сетка этих линий назы-
вается ортогональной.
Семейство ортогональных линий аир называется линиями кри-
визны. Через каждую точку пересечения проходит одна кривая каж-
дого семейства.
Предположим, что на ортогональных линиях 1—1 и 2—2 семей-
ства аир лежат две точки N t и N2, бесконечно мало удаленные от
точки пересечения этих линий М (см. рис. 1).
5
Точки пересечения этих нормалей О1 и О2 называются центрами
кривизны главных нормальных сечений срединной поверхности
в точке М соответственно в ортогональных направлениях 1—1 и
2—2.
Расстояния от центров кривизны и О2 до точки М (см. рис. 1)
носят название главных радиусов R{ и R2 кривизн срединной поверх-
ности в точке М соответственно вдоль линий 1—1 и 2—2, а величины,
обратные главным радиусам кривизны, К4=4-и К2=-^— назы-
/?1 к2
Величина Г называется гауссовой кривизной поверхности в данной
точке, К — средней кривизной.
Понятие гауссовой кривизны в теории поверхностей является
фундаментальным. По знаку гауссовой кривизны можно судить
о форме поверхности в окрестности данной точки.
Если Г > 0 (положительная кривизна), то кривизны Kt и К2
имеют одинаковый знак. Это означает, что центры кривизны Ot
и О 2 по главным направлениям находятся по одну сторону от по-
верхности (рис. 3, а), а центры кривизны всех других нормальных
сечений будут лежать на отрезке ОХО2. К оболочкам положительной
гауссовой кривизны относятся выпуклые оболочки.
Напротив, при Г <0 (отрицательная кривизна) центры
и О2 лежат по разные стороны от поверхности (рис. 3,6); центры
кривизны остальных нормальных сечений находятся на внешних
областях отрезка C>iO2- К оболочкам отрицательной гауссовой кри-
визны относятся оболочки вогнуто-выпуклые,
6
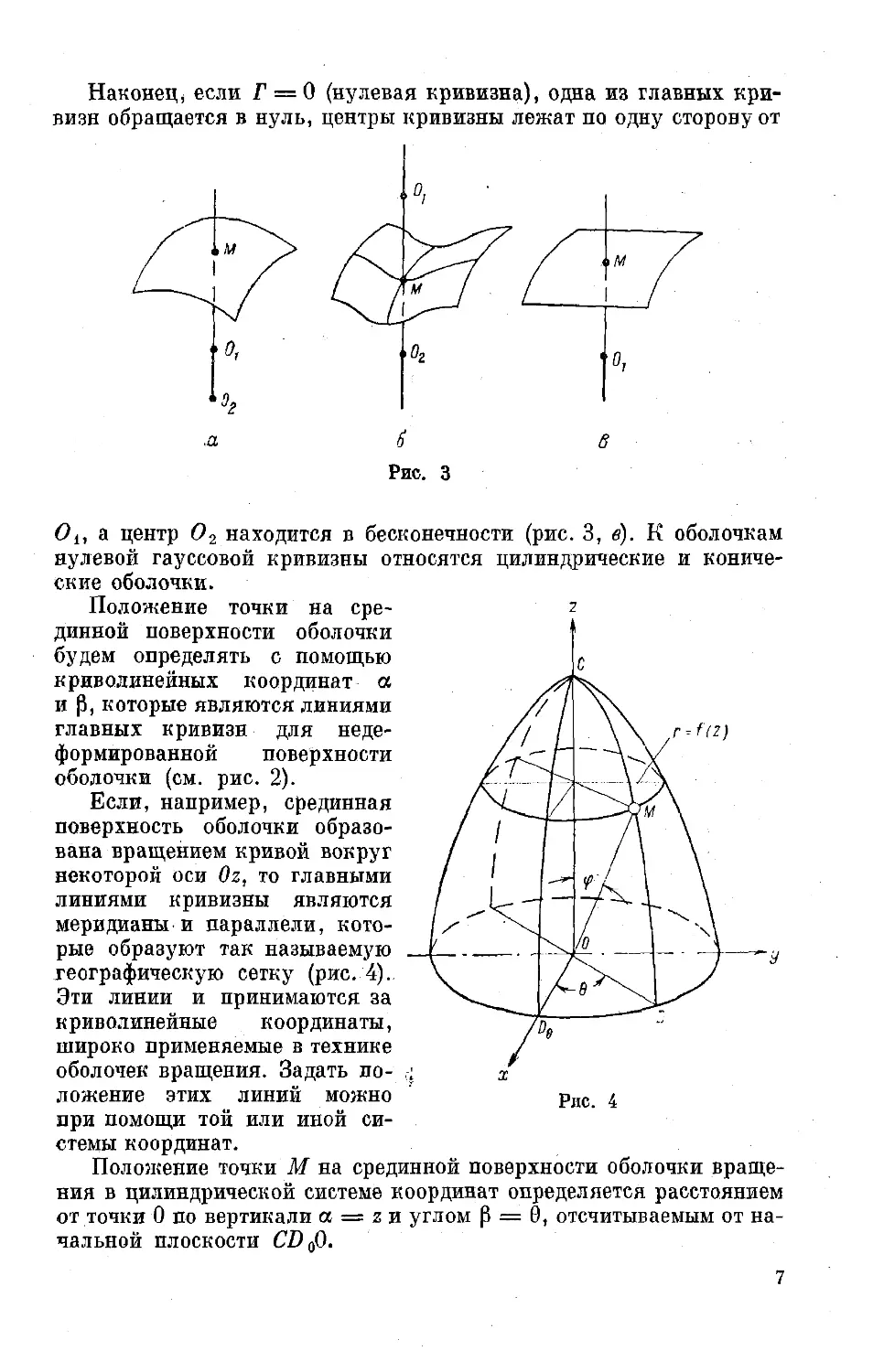
Наконец, если Г = 0 (нулевая кривизна), одна из главных кри-
визн обращается в нуль, центры кривизны лежат по одну сторону от
Рис. 3
Oi, а центр О2 находится в бесконечности (рис. 3, в). К оболочкам
нулевой гауссовой кривизны относятся цилиндрические и кониче-
ские оболочки.
Положение точки на сре-
динной поверхности оболочки
будем определять с помощью
криволинейных координат а
и р, которые являются линиями
главных кривизн для неде-
формированной поверхности
оболочки (см. рис. 2).
Если, например, срединная
поверхность оболочки образо-
вана вращением кривой вокруг
некоторой оси Oz, то главными
линиями кривизны являются
меридианы и параллели, кото-
рые образуют так называемую _
географическую сетку (рис. 4).
Эти линии и принимаются за
криволинейные координаты,
широко применяемые в технике
оболочек вращения. Задать по-
ложение этих линий можно
при помощи той или иной си-
стемы координат.
Положение точки М на срединной поверхности оболочки враще-
ния в цилиндрической системе координат определяется расстоянием
от точки 0 по вертикали а = z и углом р = 0, отсчитываемым от на-
чальной плоскости CD0O.
7
Каждому значению z = const соответствует некоторая параллель,
а углу 0 = const — меридиан.
Положение точки М на срединной поверхности оболочки вращения
в сферической системе координат определяется углом <р, характери-
зующим положение меридиана.
В окрестности точки М срединной поверхности произвольной
формы выделим четырьмя координатными линиями бесконечно ма-
лый элемент (см. рис. 2). Так как при линеаризации в малом беско-
нечно малые отрезки кривых можно заменить прямыми линиями,
выражение для квадрата линейного бесконечно малого элемента
в ортогональной системе координат запишем:
ds2~ ds{ +ds2, (1.2)
где dst, ds2 — линейные элементы, соответствующие приращениям
криволинейных координат в направлениях аир. Так как приращения
в направлении а и Р бесконечно малы, то линейные элементы ds,
и ds2 будут пропорциональны дифференциалам независимых пере-
менных
ds^Ada, ds2~Bd$. (1.3)
где Л, В — коэффициенты искажения, преобразующие приращения
криволинейных координат в линейные отрезки.
После подстановки (1.3) в (1.2) выражение для квадрата линей-
ного элемента примет вид:
ds2 = H4afi + 52dp2. (1.4)
Выражение (1.4) носит название первой квадратичной формы
поверхности, а величины А и В — коэффициенты первой квадратич-
ной формы. Эти коэффициенты зависят от криволинейных координат
точки М поверхности, но не зависят от их дифференциалов, следова-
тельно, для данной точки поверхности А и В определяются одно-
значно. Например, значения коэффициентов первой квадратичной
формы для рассмотренной нами произвольной оболочки вращения
запишутся:
а) в цилиндрической системе координат
л=/‘+(£У:
б) в сферической системе координат
А=—^— 1 В = г; (1.6)
cos <р ♦ ' '
где г — функция от <р (см. рис. 4).
Теория расчета оболочек в зависимости от отношения толщины
стенки h к радиусу срединной поверхности R делится на теорию
оболочек произвольной толщины и на теорию тонких упругих обо-
лочек. Обычно считают тонкими такие оболочки, укоторых max
8
sg-^г, а толстостенными, —у которых это неравенство не соблю-
20
дается.
При выводе основных формул для тонких оболочек можно от-
, h
брасывать члены, содержащие относительную толщину стенки
для толстостенных оболочек эти члены сохраняются.
Оболочки газонефтехранилищ и магистральных трубопроводов
удовлетворяют рассматриваемому условию, поэтому расчет этих
сооружений основывается на теории упругих тонких оболочек.
Основные уравнения линейной теории тонких упругих оболочек
В основу теории оболочек положены упрощения, имеющие опре-
деленный физический смысл и вполне очевидную преемственность
от хорошо проверенной теории балок.
Эти допущения и гипотезы формулируются следующим образом:
прямолинейные волокна оболочки, перпендикулярные к средин-
ной поверхности до деформации, остаются после деформации также
прямолинейными и перпендикулярными к изогнутой срединной по-
верхности, сохраняя при этом свою длину;
нормальные напряжения на площадках, параллельных средин-
ной поверхности, пренебрежимо малы по сравнению с прочими на-
пряжениями.
Эти гипотезы впервые обосновал в теории пластин Густав Роберт
Кирхгоф (1824—1887 гг.).
Смысл гипотез весьма близок к гипотезе плоских сечений, при-
нятой в элементарной теории изгиба бруса.
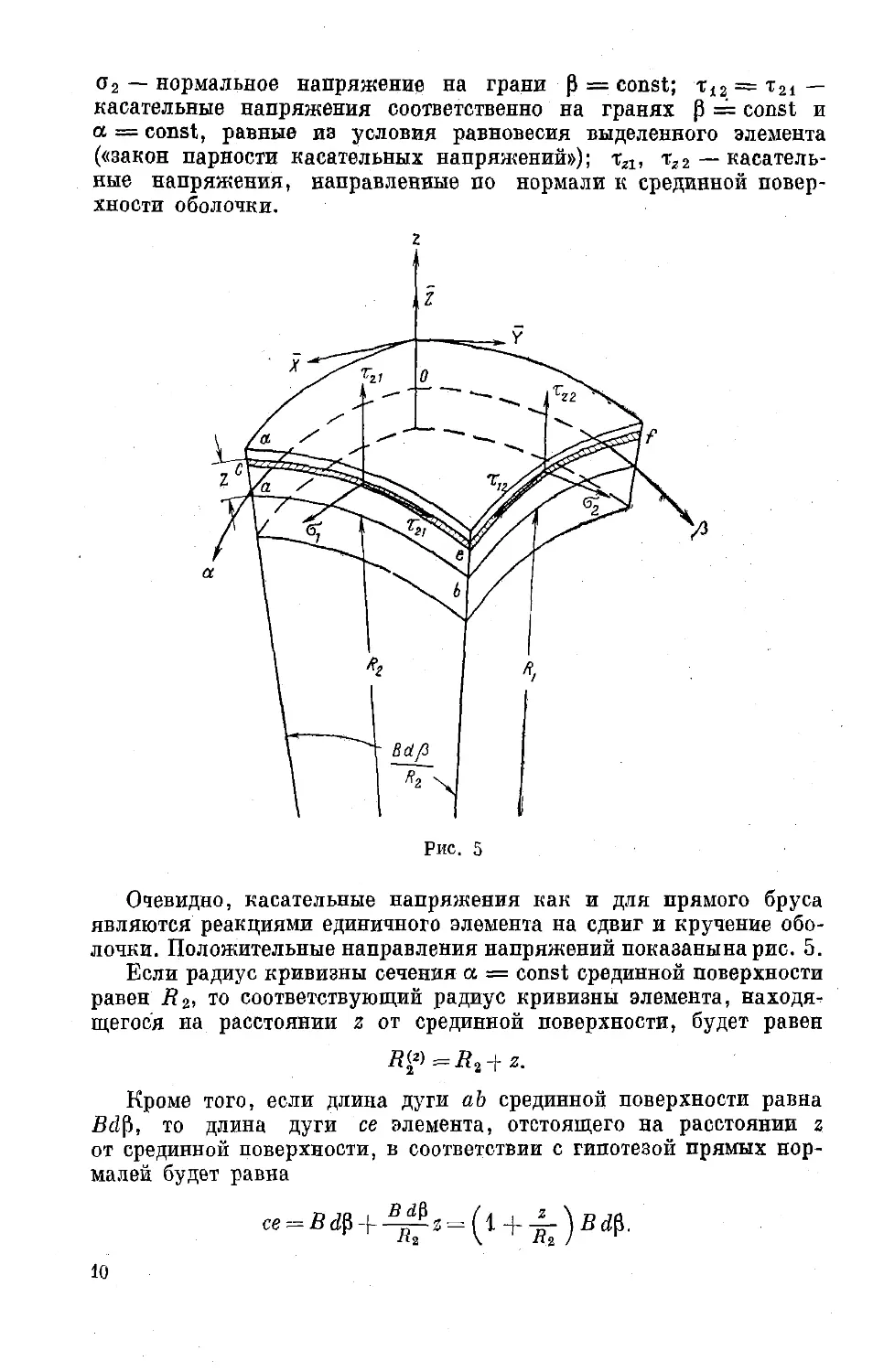
В оболочке произвольной формы, заданной в системе координат
а, р, z, выделим нормальными плоскостями а = const, а + da =
= const, р = const, р -J- dp = const бесконечно малый элемент
и рассмотрим условия его равновесия под действием всех внешних
и внутренних сил (рис. 5).
Внешние силы, непрерывно распределенные по поверхностям,
ограничивающим оболочку, действуют нормально к ее срединной
поверхности (давление жидкости или газа). Обозначим внешнюю
силу, приходящуюся на единицу площади срединной поверхности,
через q, а ее компоненты, совпадающие с направлениями касатель-
ных к координатным линиям а, р и z в точке 0 соответственно через
X, Y и Z. Эти составляющие нагрузки — произвольные непрерывные
функции независимых переменных аир. Например, для стенки
цилиндрического резервуара в качестве нагрузки Z принимается
давление жидкости и ветровое давление, а нагрузки X — собствен-
ный вес резервуара и кровли на единицу периметра. Внутренним
силам соответствуют напряжения, действующие на соответствующие
боковые грани элемента.
Обозначим:
Oj — нормальное напряжение на грани a == const;
9
о2 — нормальное напряжение на грани 0 = const; т12 = т21 —
касательные напряжения соответственно на гранях 0 = const и
а — const, равные из условия равновесия выделенного элемента
(«закон парности касательных напряжений»); т21, tz2 — касатель-
ные напряжения, направленные по нормали к срединной повер-
хности оболочки.
Очевидно, касательные напряжения как и для прямого бруса
являются реакциями единичного элемента на сдвиг и кручение обо-
лочки. Положительные направления напряжений показанына рис. 5.
Если радиус кривизны сечения а = const срединной поверхности
равен 7?2, то соответствующий радиус кривизны элемента, находя-
щегося на расстоянии z от срединной поверхности, будет равен
Кроме того, если длина дуги аЪ срединной поверхности равна
.Bd0, то длина дуги се элемента, отстоящего на расстоянии z
от срединной поверхности, в соответствии с гипотезой прямых нор-
малей будет равна
10
Аналогично определяются радиус кривизны и длина дуги эле-
мента, отстоящего на расстоянии z от срединной поверхности, в се-
чении Р = const:
R[!> = z;
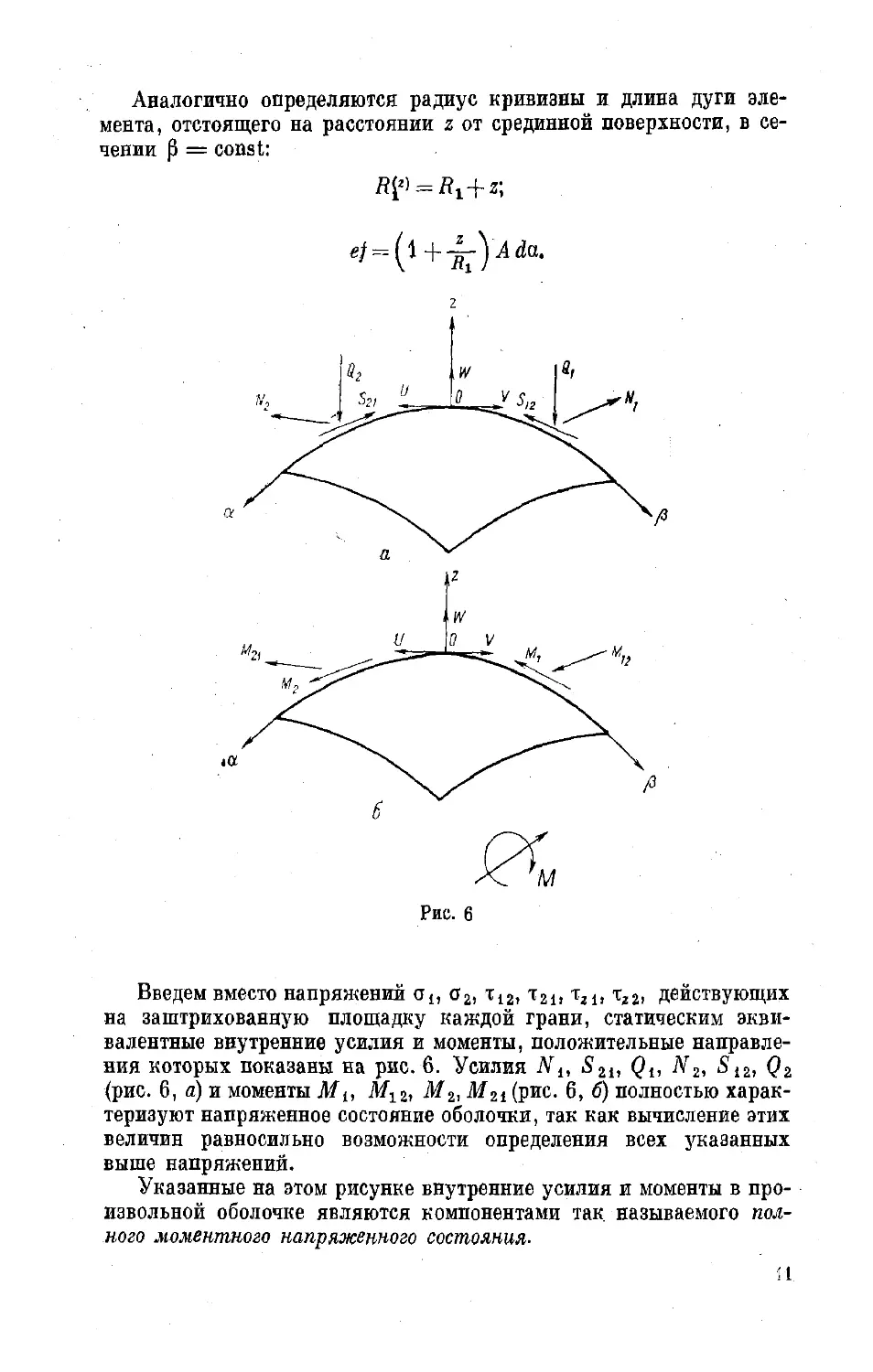
Введем вместо напряжений ot, о2, т12, т211 тг1, тг2, действующих
на заштрихованную площадку каждой грани, статическим экви-
валентные внутренние усилия и моменты, положительные направле-
ния которых показаны на рис. 6. Усилия Nв S21, Qt, Nz, S12, Qz
(рис. 6, а) и моменты Mt, M12, M2, М21 (рис. 6, б) полностью харак-
теризуют напряженное состояние оболочки, так как вычисление этих
величин равносильно возможности определения всех указанных
выше напряжений.
Указанные на этом рисунке внутренние усилия и моменты в про-
извольной оболочке являются компонентами так называемого пол-
ного моментного напряженного состояния-
И
Нормальное усилие Ni на грани а = const, отнесенное к единице
длины сечения оболочки, определяется путем суммирования нор-
мального напряжения Oj по площади грани а = const
Л/2
-h / 2 2
ИЛИ
ft/2
-ft/2
Нормальное усилие N2 на грани £ = const, отнесенное к единице
длины сечения оболочки, определяется путем суммирования нор-
мального напряжения <т2 по площади грани |3 = const
или
ft/2
h/2
N«Ada = § о2 A da dz
-h/2 1
A^ = J -h / 2
Аналогично находим сдвигающие усилия, действующие ственно на гранях а = const и |3 = const: h/2 $21— J X21(^ + -h/2 h/2 S-12,— ^12 ) dz. -h/2 1 соответ- (1.7)
Линейное распределение нормальных : напряжений по высоте
сечения оболочки, вытекающее из гипотезы о прямых нормалях
(первой гипотезы Кирхгофа), дает возможность записать изгибающие
моменты в форме:
h/2 )' °‘( 1 + я2) zdz;
-h/2 h/2
м2 = = S0 ,2 -h/2 h/2 С1' ^zdz;
м12= Т12 -h/2 h/2 V1- ) zdz;
Т21 -ft/2 А ! ^zdz.
(1.8)
12
Поперечные силы получаются путем суммирования по высоте
сечения соответствующих касательных напряжений
(1.9)
Так как внутренние усилия и моменты отнесены к единице длины
сечения оболочки, то размерность усилий будет кгс/см или тс/м,
а размерность моментов кгс-см/см или тс -м/м.
В общем случае при =£ R2 из закона парности касательных
напряжений, когда т12 = t2i согласно формулам (1.7) и (1.8), не сле-
дует равенство сдвигающих сил *512, S2i и крутящих моментов М12,
М21 в сечениях а = const и р = const. В частном случае, при R t =
= R2, т. е. для сферической поверхности, сдвигающие и крутящие
моменты на двух взаимно перпендикулярных сечениях равны между
собой (<$12 = S21 и Ш12 - М21).
Если учесть, однако, что для тонких оболочек z<^RiHz^R2,
то величиной членов и по сравнению с единицей можно с доста-
точной точностью пренебречь. Тогда из формул (1.7) и (1.8) в общем
случае следует:
512 — S2i — S;
М12 = ТИ21 = К
(1.10)
Для определения десяти неизвестных внутренних усилий и мо-
ментов в общем случае должна быть составлена система из десяти
уравнений.
Из рассмотрения условий равновесия элемента, вырезанного из
оболочки нормальными сечениями а = const, а + da = const, р =
= const и р + dp = const, можно получить только шесть уравнений.
Следовательно, задача о равновесии элемента оболочки является
статически неопределимой.
Остальные четыре дополнительных уравнения, так же как и в эле-
ментарной теории статически неопределимой балки, можно соста-
вить из рассмотрения геометрических уравнений и соотношений
упругости.
Геометрические уравнения связывают компоненты упругих пере-
мещений и деформаций срединной поверхности оболочки, а соотно-
шения упругости устанавливают зависимость внутренних усилий
и моментов с деформациями срединной поверхности.
В данной работе нет смысла останавливаться на составлении
уравнений равновесия элемента оболочки, геометрических и физи-
ческих уравнений. Подробный вывод их очень широко представлен
13
как в отечественной, так и в зарубежной литературе (например, в ра-
ботах [4, 12]), поэтому воспользуемся уже готовыми уравнениями.
Уравнения равновесия:
(5JV.) - Д', -g + А- (Л5„) + +QtK,AB + А ВХ = 0;
(AN,)—N, ^-+ A. (BS„) + S„ ^+Q,K,AB + АВУ=0;
-(xJV'+^2V’)+^-[^(a?‘>+^m]+z=o; (i.H)
(BM„) + M„ £ + Л- (ЛM.) - M, % - Q,AB=0;
(ЛИ„)+M„ +Л (BM,) - M, % - QiA В = 0.
Для задач динамики компоненты нагрузки X, Y, Z включают
инерционные силы.
Уравнения (1.11) могут быть использованы также для решения
задач устойчивости оболочек резервуаров и трубопроводов. Однако
в этом случае необходимо учесть изменения коэффициентов первой
квадратичной формы при деформации поверхности.
Шестое уравнение равновесия вследствие закона парности каса-
тельных напряжений обращается в тождество. Из 2}тотг = 0
следует
521-512 + ^M21~^3M12-0. (1.11, а)
После подстановки значений усилий (1.7) и моментов (1.8)
в соотношение (1.11, а) получим
J Тц (1 -F K2z) dz — f т12 (1 + Krf dzJrK1^ t21z (1 + K^z) dz —
— K2 J t12z (1 + Кгг) dz — \ (t2i — r12) (1 + K2z) (1 + KjZ) dz = 0.
На основании закона парности касательных напряжений т12 =
= т21, поэтому последнее соотношение тождественно удовлетво-
ряется.
Геометрические уравнения:
„j_ ___v ад , ж
81 А да АВ ар “Г 7?t >’
1 dV . U дБ , W
е'2~ А ер + АВ да + R2 ’
S д (V\(A д /U\'
А да к В / "* В ЗР \ А / ’
=_±2 / ___L(_ d 121
1 А да к РчУ А да J АВ \ В2 Г В ар ) ар ’
14
1 д / V . 1 dW \ if и I 1 dW \ дВ .
в ар v я2 в ар ) лв \ в1*' а да ) аа »
1 г а а 1 / v 1 ж \ г a a i / и i aim
Х “ 2 L В да В v Л2 В ар ) + В ар А к R1 А да ) J ’
где еь е2 — относительные удлинения срединной поверхности со-
ответственно в направлениях а и 0; у — сдвиг срединной поверх-
ности (косинус угла между линиями а и Р после деформации); xlf
и2 — параметры, характеризующие изменение кривизны срединной
поверхности соответственно в направлениях а и Р; % — параметр,
характеризующий «кручение» срединной поверхности; под «круче-
нием» понимают предел отношения угла взаимного закручивания
двух противоположных сторон элемента срединной поверхности
к расстоянию между ними при стремлении размеров элементов к ну-
лю; U, V — перемещения срединной поверхности оболочки, совпа-
дающие с направлениями касательных соответственно к линиям а
и Р; W — перемещение срединной поверхности, совпадающее с на-
правлением нормали к срединной поверхности.
Относительно уравнений (1.12) следует заметить, что они отве-
чают условиям малых перемещений U h, V h, W h. В тех
случаях, когда эти условия не выдержаны, необходимо учитывать
нелинейные составляющие деформаций, рассматриваемые в рамках
нелинейной теории оболочек [И].
Физические уравнения:
Ni=r=^(8i+ve2);
(e2+vei);
5 = 512 = 521 G/гу;
Af1 = Z)(x1-ll-vx2), ' f
M2 = Z)(x2 + vXi);
M = M12 = M21 = Z)(l-v)X,
где
n Е1‘я
l) = ,j2 (i _vs) — цилиндрическая жесткость;
G = 2(i~pvj — модуль сдвига; (1.14)
E — модуль упругости; v — коэффициент Пуассона.
Таким образом, имеются пять уравнений равновесия (1.11),
шесть зависимостей, связывающих деформации с перемещениями
(1.12), и восемь соотношений закона Гука (1.13). Неизвестны три
перемещения (U, V, W), четыре усилия в срединной поверхности
2, 512, S2l), четыре момента (Мь М2, М12, М21), две попереч-
ные силы (Q^ Q2), три деформации в срединной поверхности (е1(
15
s2>?) и три параметра кривизны (Xj, и2, у). Перечисленным девятнад-
цати неизвестным соответствуют девятнадцать уравнений.
Решение системы уравнений (1.12)—(1.13) при заданных гранич-
ных условиях; — задача значительной математической трудности,
которая для ряда оболочек в общей постановке не решена до сих пор.
Но для конкретных геометрических параметров оболочек и заданной
нагрузки путем оправданных упрощений, отображающих действи-
тельную работу оболочки под нагрузкой, почти всегда удается по-
строить более простые теории. В частности, анализ методов расчета
упругих тонких оболочек на произвольную нагрузку применительно
к конструкциям резервуаров и трубопроводов показывает, что, как
и для большинства других тонкостенных конструкций, общее напря-
женное состояние можно разделить на безмоментное и краевой аф-
фект. Это означает, что для большей части поверхности оболочки,
достаточно удаленной от краев (например, от верхнего и нижнего
узла сопряжения цилиндрического резервуара), изгибающими, кру-
тящими моментами и перерезывающими силами можно пренебречь,
т. е. единственными компонентами напряженного состояния будут
тангенциальные усилия (N, S), а компонентами перемещений —
тангенциальные перемещения U, V. Моментное напряженное состоя-
ние возникает только вблизи краев. Расчет резервуаров и трубопро-
водов может быть построен следующим образом:
проводится расчет оболочки по безмоментной теории на заданную
поверхностную нагрузку с удовлетворением тангенциальных гра-
ничных условий на ее краях;
строятся для каждого края оболочки независимо друг от друга
простые краевые эффекты;
усилия, моменты и перемещения полного напряженного состоя-
ния получаются путем суммирования результатов расчета по без-
моментной и моментной теории;
произвольные постоянные общего решения определяются из
удовлетворения нетангенциальных граничных условий на краях
оболочки.
Безмоментное напряженное состояние оболочек
При проектировании пространственных конструкций, в част-
ности газонефтехранилищ и трубопроводов, всегда следует стре-
миться к тому, чтобы в оболочке этих сооружений отсутствовали
изгибающие и крутящие моменты, приводящие к изгибным напряже-
ниям, а напряженное состояние оболочек складывалось только от
действия нормальных и сдвигающих усилий. От действия только
нормальных и сдвигающих усилий напряжения в оболочке полу-
чаются значительно ниже, чем от действия крутящих и особенно из-
гибающих моментов, поэтому чисто изгибающий тип напряженного
состояния опасен и технически невыгоден для тонкостенных про-
странственных сооружений. Это объясняется тем, что внутренняя
энергия деформации оболочки при изгибе значительно больше, чем
16
при растяжении или сжатии. Это можно показать на простейшем
примере из элементарной теории бруса. Если на свободном конце
консольной балки приложить сосредоточенную силу сначала в на-
правлении, перпендикулярном оси балки (изгиб,) а затем вдоль
оси (сжатие или растяжение), то внутренняя энергия деформации
балки при изгибе будет значительно больше, чем при сжатии или
растяжении.
Предположим, что в сечениях а = const и |3 = const оболочки
действуют только сдвигающие S и нормальные и N2 усилия,
а поперечные силы, крутящие и изгибающие моменты отсутствуют,
т. е.
M1 = M2 = Q1 = Q2 = M1S = M21 = O. (1.15)
Тогда напряженное состояние оболочки зависит только от дей-
ствия нормальных и сдвигающих усилий и называется безмоментным.
К сожалению, прийти к безмоментному напряженному состоянию
оболочки удается не всегда, а только в тех случаях, когда соблю-
даются следующие условия его существования:
оболочка должна иметь плавно изменяющуюся непрерывную
поверхность. Действительно, в зонах резкого изменения формы (пе-
релом поверхности, скачкообразное изменение толщины оболочки)
величина деформаций элементов оболочки различна, а это, в свою
очередь, приводит к изгибу;
нагрузка на оболочку должна быть плавной и непрерывной;
условия закрепления краев оболочки должны иметь возможность
свободно перемещаться в направлении нормали к срединной поверх-
ности. Например, если не учитывать местные изгибные напряжения
в стыках поясов стального вертикального цилиндрического резер-
вуара с плавающей крышей вследствие скачкообразного изменения
толщины стенки, то средняя часть его корпуса при действии эксплу-
атационной нагрузки будет находиться в безмоментном напряженном
состоянии. Нижняя кромка оболочки резервуара жестко сопряжена
с окрайками днища, верхняя — с упругим кольцом жесткости,
поэтому края оболочки не могут свободно смещаться в направлении
нормали к срединной поверхности, что приводит к появлению в зонах,
примыкающих к краям, изгибающих моментов и резкому увеличению
величины напряжений;
силы, приложенные к краям оболочки, должны лежать в пло-
скости, касательной к ее поверхности.
Основные уравнения безмоментной теории
оболочек вращения
спроизвольной формой меридиана
Рассмотрим оболочку, срединная поверхность которой является
поверхностью вращения. У такой оболочки линиями главной кри-
визны будут ее меридианы и параллели. Положение произвольной
точки М на срединной поверхности оболочки вращения можно
2 Заказ 2036 17
задать как в цилиндрической, так и в сферической системе координат.
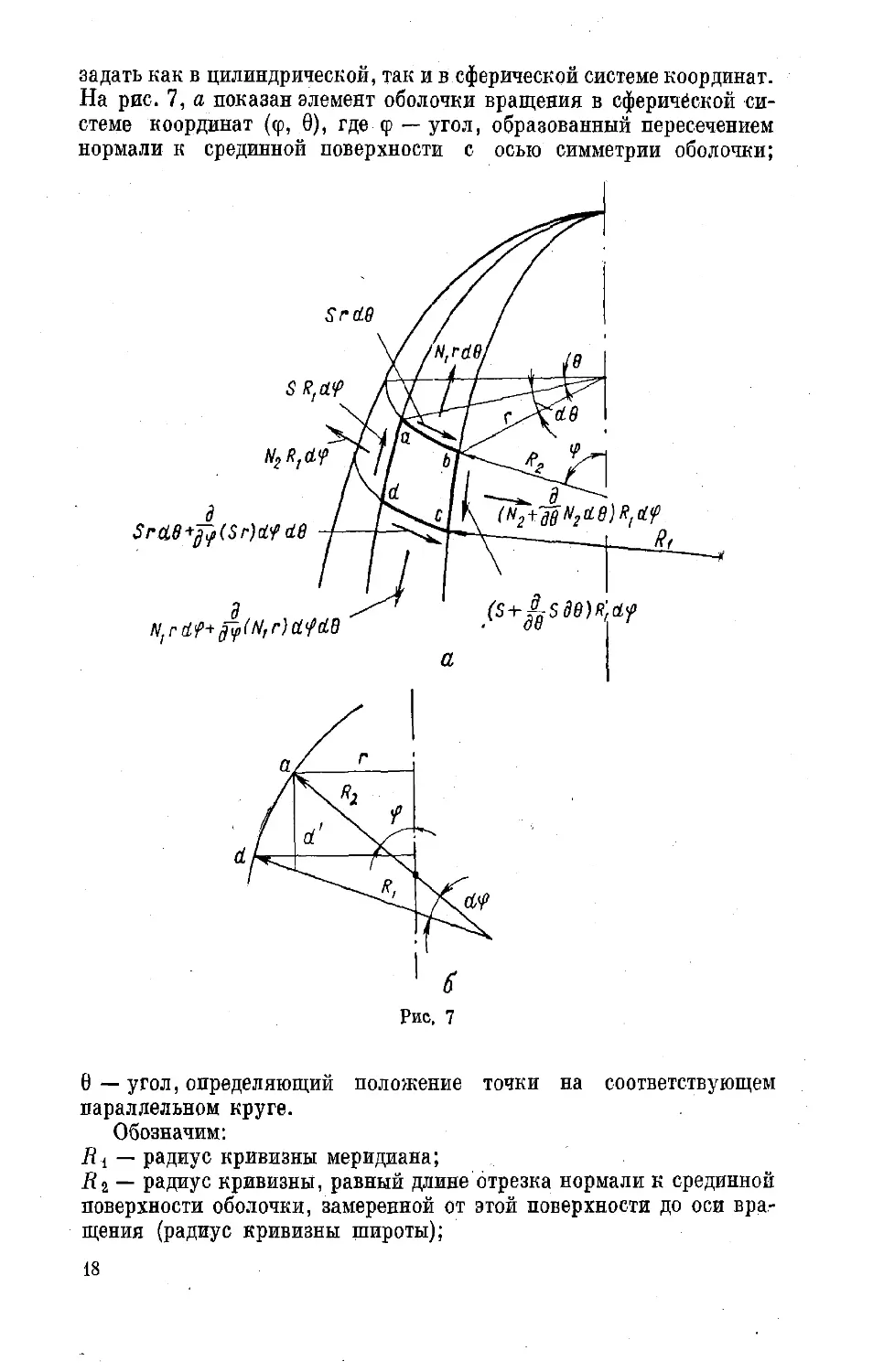
На рис. 7, а показан элемент оболочки вращения в сферической си-
стеме координат (<р, 0), где <р — угол, образованный пересечением
нормали к срединной поверхности с осью симметрии оболочки;
0 — угол, определяющий положение точки на соответствующем
параллельном круге.
Обозначим:
У?4 — радиус кривизны меридиана;
У?2 — радиус кривизны, равный длине отрезка нормали к срединной
поверхности оболочки, замеренной от этой поверхности до оси вра-
щения (радиус кривизны широты);
18
г — радиус параллельного круга, для произвольной формы мери-
диана г = / (ф).
Ввиду симметрии оболочки вращения коэффициенты квадратичной
формы А и В являются функциями лишь координаты <р и не зависят от
от 0.
Из рис. 7, б для элемента дуги меридианов можно записать
ad = ds1~ Ridff,
откуда согласно формуле (1.3) с учетом, что da = d<p, следует
Л-Лр (1.16)
Соответственно элемент дуги параллельного круга будет равен
ab = ds2 = rdQ,
но из рис. 7, б можно установить, что
r = -ff2sni<p, (1.17)
поэтому
ab — ds2 — В2 sin ф с/0,
и, следовательно, с учетом формулы (1.3) и = d0
В — /?2sin<p = r. (1.18)
Если подставить условия (1.15) в уравнения (1.11) с учетом, что
А = В = г, и заменить а на <р, |3 на 0, то уравнения равно-
весия в этом случае примут вид:
^№ + ^<-^^+^ = 0;
следует, что
d'd = dtp^ad cos <pi = R± dtp cos <p,
(1.19)
Но из рис. 7, б
поэтому
-т— ; /tiCOStp.
d(p it
(1.20)
После подстановки (1.20) в (1.19) окончательно запишем уравнения
равновесия элемента оболочки вращения в следующей форме:
4g-- ВД cos ф + rR.X = 0;
+ RrS c°s Ф + z-flj = 0; (1.21)
2*
19
Таким образом, имеем три уравнения относительно трех неиз-
вестных усилий (S, Ni и 2V2)> которые являются функциями обеих
независимых переменных <р и 0.
Подставив аналогично условия (1.15) и4=Й1, В = г с заменой
а на ф и р на 0 в уравнения (1.12) и (1.13), получим геометрические
уравнения:
'= = -R № - ^.) = 7 Йг + ° ) + Ъ W: (tM)
Y Gh d<f \r r dQ ‘
Применение тригонометрических рядов
к расчету оболочек вращения
Дифференциальные уравнения равновесия (1.21) и геометриче-
ские уравнения (1.22) безмоментной теории оболочек вращения со-
держат две независимые переменные ф и 6 и записаны в частных
производных, что значительно усложняет их интегрирование. Но
так как оболочка вращения замкнута в окружном направлении, то
компоненты поверхностной нагрузки X, У и Z и все факторы напря-
женно-деформированного состояния оболочки можно представить
в виде периодических функций угла 0 (с периодом 2л). После под-
становки этих функций дифференциальные уравнения в частных
производных сводятся к обыкновенным дифференциальным урав-
нениям относительно одной независимой переменной <р, решение
которых значительно проще. В этом и заключается сущность метода
разделения переменных, основанного на разложении величин как
искомых, так и заданных в тригонометрические ряды по перемен-
ной 0.
Любую непрерывную нагрузку, действующую на оболочку вра-
щения, функция которой вдоль меридиана непрерывна и монотонна,
можно разложить в тригонометрические ряды (ряды Фурье) по пере-
менной 0:
_ 00
Х(ф, 0) = 2 хп (ф)cos и0;
п«0
У (ф, 0) = 2 Уп (ф) sin (1.23)
П«о
Z (ф, 0) = У zn (ф) cos пв,
п=о
где п — 0, 1, 2, . . ., ©о — целое число; х„(ф), г/„(ф), zn(cp) — функ-
ции распределения нагрузки по ф, не зависящие от 0, кгс/см2.
Представление функций X (ф, 0), У (ф, 0) и Z (ф, 0) тригоно-
метрическим рядом называется гармоническим анализом.
20
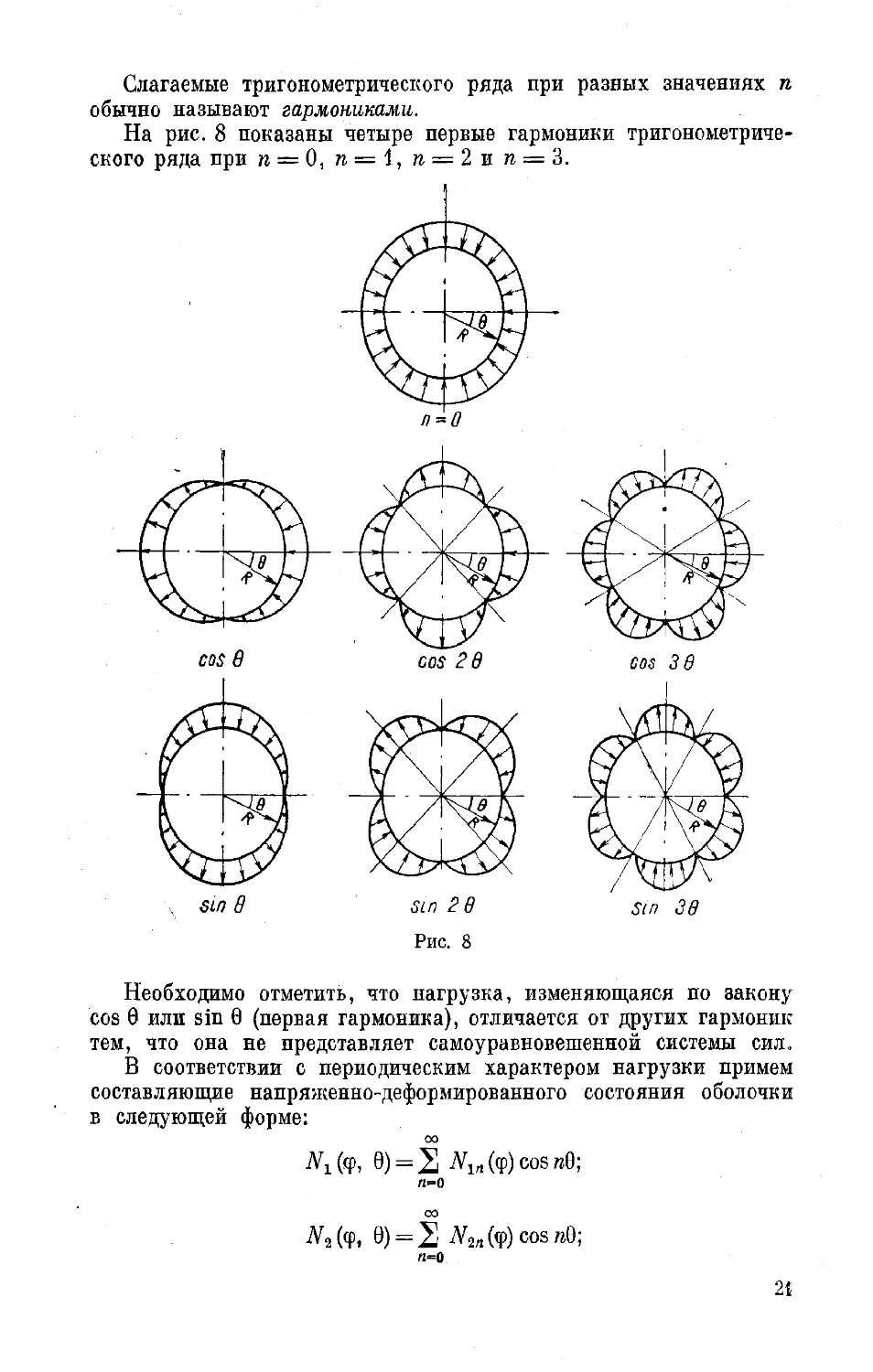
Слагаемые тригонометрического ряда при разных значениях п
обычно называют гармониками.
На рис. 8 показаны четыре первые гармоники тригонометриче-
ского ряда при n = 0, п = 1, п = 2 и п = 3.
Необходимо отметить, что нагрузка, изменяющаяся по закону
cos 9 или sin 9 (первая гармоника), отличается от других гармоник
тем, что она не представляет самоуравновешенной системы сил..
В соответствии с периодическим характером нагрузки примем
составляющие напряженно-деформированного состояния оболочки
в следующей форме:
00
Л\(<р, 9) = 2 ЛГщ (ф) cos «0;
JV2((p, 9) = 2 jV2zi(<p) cos тгб;
n-0
21
S (<p, 0) = 2 5„(<p)sinn0;
n-0
U (<p, 0) = 2 (<p) cos 7/0;
rt-0
(1-24)
00
v (<p, 0)=2 vn (<p) sin «0;
«=0
W (ф, 0) = 2 Wn (<p) cos nQ,
n-0
где N 1л(ф),^2Я(ф)> ^„(ф), [7„(Ф)> ^л(ф), Wn(ф) — функции одной
независимой переменной ф. В дальнейшем во избежании громозд-
кости обозначение переменной ф, стоящей в скобках, будет опущено.
После подстановки выражений (1.23) и (1.24) в (1.21) и (1.22)
и дифференцирования по 0 получим:
уравнения равновесия
— (rNln) cos и0 -f- nR^n cos nd~Rt N2n cos ф cos nd — rR^ cos n0 = 0;
-- (rSn) sin n0 — nRrN2fl sin «0 4- RL Sn cos ф sin «0 4 sin n0 = 0;
cos n 0 cos n0 — 2„ cos n0 = 0;
-**2
геометрические уравнения
— (Nin cos «9 — vN2„ cos n0) = 4- ^2- cos n0 4 Wn cos «0;
Eh ' z d(p лх
1 л 1
-jT- (N2n cos «9 — vNln cos ?i9) = — Vn cos n0 -j— Un cos ф cos nQ 4
thrl г T
-f-4- 1Упсози9;
Л2
— Sn sin n0 = sin nd — — Un sin «0.
Gh n Ri dtp \ r J r n
Все уравнения равновесия и геометрические уравнения могут
быть сокращены на sin «0 и cos «9. Это означает, что при задании
усилий и перемещений в форме выражений (1.24) уравнения равнове-
сия и геометрические уравнения будут удовлетворены при любом
значении 0 и будут содержать только одну независимую перемен-
ную ф:
22
уравнения равновесия
(r^in) + Лг N2ncosф-+ rRtxn = 0;
~ (rSJ-nRJ^ + R1 Sn costp + rRxyn --- 0; (1.25)
^1П I 7 Л-
—+ -ДГ 2"-u-
геометрические уравнения
4г (Ntn — vNln) = nV„ 4- Vn cos ф + 4~ Wn; (1.26)
ЫЬ it 2
1 0 rdf Vn X n
Gh n~ Rt dq \ r ) r n'
где
r = flasinq>, 7?1 = /(ф).
Обыкновенные дифференциальные уравнения (1.25) и (1.26)
описывают напряженно-деформированное состояние произвольной
оболочки вращения для n-го члена разложения в тригонометрические
ряды. Каждому слагаемому ряда (гармонике) соответствует некоторое
напряженно-деформированное состояние оболочки вращения. В даль-
нейшем ограничимся расчетом оболочки на нагрузку, представлен-
ную одним членом ряда. Если же нагрузка задана несколькими чле-
нами ряда, то, применяя принцип наложения (суперпозиции), можно,
сложить решения нескольких задач, соответствующих нагрузке при
разных значениях п, и получить общее решение.
Уравнение безмоментной теории
цилиндрических, сферических
и конических оболочек
Уравнения (1.25) и (1.26) соответствуют безмоментному напря-
женно-деформированному состоянию оболочки вращения с произ-
вольной формой меридиана. Но конструкции газонефтехранилищ
п трубопроводов состоят в основном из замкнутых оболочек более
простой геометрической формы: цилиндрической, сферической и ко-
нической. Цилиндрические оболочки преобладают в качестве кон-
струкций стенок резервуаров. Сферическую форму имеют стенки
резервуаров высокого давления, покрытия цилиндрических резервуа-
ров. Для ряда покрытий используются оболочки, в которых можно
выделить элементы конической формыПутем соответствующих гео-
метрических преобразований составим для n-го члена разложения
основные уравнения для замкнутых цилиндрической, сферической
и конической оболочек.
23
Цилиндрическая оболочка
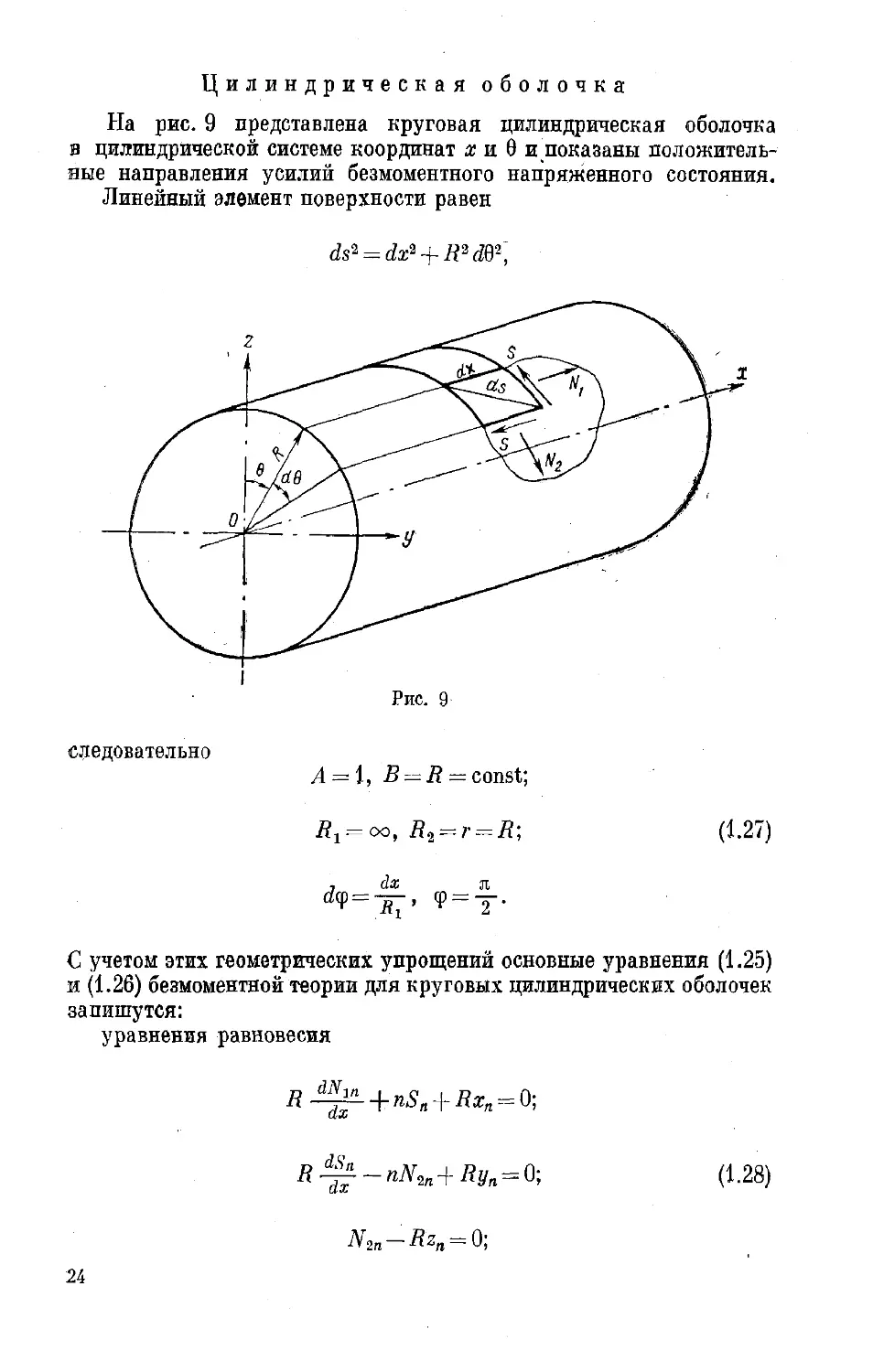
На рис. 9 представлена круговая цилиндрическая оболочка
в цилиндрической системе координат х и 9 и показаны положитель-
ные направления усилий безмоментного напряженного состояния.
Линейный элемент поверхности равен
ds2 = dx2 + R2d92,
следовательно
4 = 1, B — R = const;
й1 = оо, Ri = r = R‘,
(1.27)
c/cp
dx
С учетом этих геометрических упрощений основные уравнения (1.25)
и (1.26) безмоментной теории для круговых цилиндрических оболочек
запишутся:
уравнения равновесия
R^.-nN^Ryn^Q-
(1.28)
TV2ra —/?z„ = 0;
24
геометрические уравнения
Eh ' 1п dx ’
1 (Лг2п _ v7Vin) = 1 (nVn + Wn)
Xi ft
1 c _ dVrl n TT
Gh йп~ dx R Un'
(1.29)
Сферическая оболочка
Для сферической облочки геометрические параметры оболочки
вращения с произвольной формой меридиана приобретают следу-
ющий вид:
Rr — R2-~ R, r — Rsin<p. (1.30)
Тогда уравнения равновесия (1.25) преобразуются
+"557 s" + ctg ’’— ЛГ’” °18 V ' R х’ ” °’
^+2S,etg<p-^rJV„ + fl!,„ = 0; (1.31)
—^zn — 0;
геометрические уравнения (1.26) —
jrW.-vlV1J = 4(1i?r„ + clg41^ + ir,); (1.32)
-4т-5Л =-4-Esin <р(ДМ-----Un~\.
Gh п R L <*ф \ sin ф ) sm ф " J
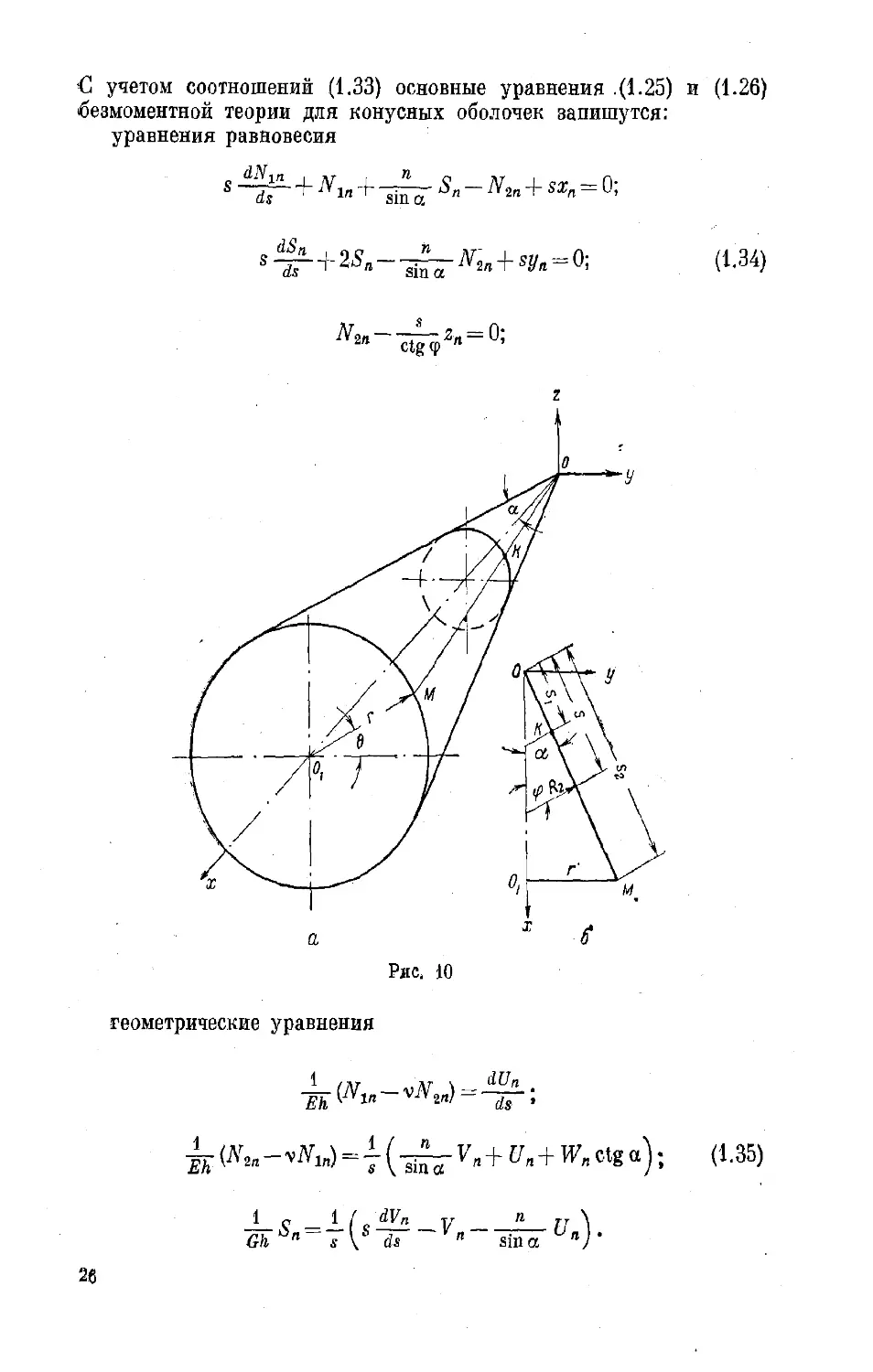
Коническая оболочка
Расположим начало координат в вершине конуса (рис. 10, а),
тогда положение произвольной точки К на срединной поверхности
оболочки конуса будет определяться двумя координатами: отрезком
образующей 5 и углом 0, а коэффициенты первой квадратичной фор-
мы равны
A = i, В = Г" ssina.
Из рис. 10, б следует, что
x = scosa, R1 = oo;
г. s . ds и
л = dm = __ m = —--а
2 ctg а ’ т 7?! ’ т 2
(1.33)
25
•С учетом соотношений (1.33) основные уравнения .(1.25) и (1.26)
юезмоментной теории для конусных оболочек запишутся:
уравнения равновесия
s + + _Д- sn - N2n + sxп = 0;
ds lrI sma
s + 2Sn - N2n + syn = 0; (1.34)
~z„ = 0;
ctg <p
Nin
геометрические уравнения
И'-СН;
— X — — (s — ~V — ”. - A
Gh As ds n sina °ПГ
(1.35)
26
Моментное напряженное состояние оболочек
при осесимметричном загружении
Основные уравнения теории
краевого эффекта оболочек вращения
Конструкции резервуаров и трубопроводов невозможно пол-
ностью рассчитать по безмоментной теории. Это объясняется тем, что
в узких зонах, примыкающих к краям оболочки, ребрам жесткости,
местам резкого изменения формы поверхности и т. д., условия без-
моментного напряженного состояния нарушаются и возникает быстро
затухающее моментное напряженное состояние — краевой эффект.
При этом величина изгибных напряжений краевого эффекта значи-
тельно больше велииины безмоментных напряжений и чем меньше
толщина стенки оболочки, тем больше интенсивность изгибных на-
пряжений и короче ширина зоны затухания краевого эффекта.
Составим основные уравнения, описывающие моментное напря-
женное состояние оболочки вращения с произвольной формой мери-
диана при действии осесимметричной нагрузки (внутреннее давление,
вакуум, гидростатическое давление столба жидкости и т. д.).
При действии осесимметричной нагрузки деформации оболочки
будут также осесимметричны, поэтому все факторы напряженно-де-
формированного состояния не зависят от угла 9 и производные по 9
равны нулю, а также отсутствуют сдвиг у и «кручение» % срединной
поверхности оболочки
512 = 521 = 7И21 = 0. (1.36)
Кроме того, отсутствуют тангенциальные перемещения в кольце-
вом направлении
7 = 0, (1.37)
а так как М2 не зависит от 0, a Q2 есть производная по 0 от М2г
то и
<?2 = 0. (1.38)
Учитывая это и принимая во внимание, что в сферической сис-
теме координат
а = ф, А = Иг, l? = r = /?2sin(p, -^- = /?1созф,
запишем в следующем виде уравнения равновесия (1.11):
(N\R2 sin <р) — N2R1 cos ф -J- R2 sin ф -j- T?2^i % sin Ф = 0?
— Л\/?2sii^ — 81пф ;--^7 (<2X-R2sinф)-J-7?x/?2 Zsincp =0; (1.39)
(A/j/h sin ф) — M2Rt cos ф — RtR2 sin ф = 0;
27
геометрические уравнения (1.12):
61 = X (£L + иЛ = 1 (ДГ _ VAT2);
1 /?! \ dtp 1 J Eh ' 1 2/’
П W 1
8* = Щ ct^ + 1Г2 =~Ёк ~ vN^
1 а ( и-. 1 aw \
Х1 ~ /?! dtp йх “г йг dtp ) I
(1.40)
и2 =
_ _£te£. / _ тт I .
R2Rt u dtp / ’
^ = (e1-s2)ctg(p-^4^’
где ф — угол наклона касательной к меридиану оболочки.
Определив деформации оболочки вращения при осесимметричном
загружении, можно с помощью соотношений (1.13) записать физи-
ческие уравнения:
лг Eh Г 1 / dU тт,\ . / и . , W \-]
L я; (+ W) + ’ (х «8 Ф + лу) J;
лт Eh Г CZctgcp . W , v / dU . W\T /4 zi\
= й? + *rUir+WjJ’ (1Л1)
,r Eh? [ 1 йф , ф . \
M1~ 12(l-v2) ( Й! 1ф +V Й? ct8(P);
ТИ2 =
Eh? / лр ctg <р
12(1—V2) \ й2
V йф \
Й! dtp /
Таким образом, имеем систему из двенадцати уравнений (1.39) —
(1.41) для определения двенадцати неизвестных: усилий и моментов
{Nj, N2, Qi, М2)', деформаций (elt е2, х2), перемещений {U,
W) и угла поворота ф.
Краевой эффект в замкнутых
цилиндрических оболочках
Рассмотрим круговую цилиндрическую оболочку (рис. 11) в си-
стеме координат х, 6 при осесимметричном загружении.
В цилиндрической системе координат
d<p = ~, Ф = Rr — oa, R2=r = R,
/11 «й
и поэтому уравнения равновесия (1.39), геометрические (1.40) и
физические (1.41) уравнения оболочки вращения принимают вид:
28
уравнения равновесия
геометрические уравнения
d^W
И1“ dx2 ’
х2 = 0;
т d.x dx ’
физические уравнения
N _ Eh !\dU vW \
j_v2 dx R /’
- Eh / W , dU\
m __ Eh3 W „ Efl3 'd2W.
Д2 (1-л2) dx — 12(l-v2) dx^ ’
(1.43)
(1.44)
Мг = vMv
29
Приведем систему уравнений (1.42)—(1.44) к виду, удобному для
решения практических задач.
Дифференцируя по х третье уравнение равновесия (1.42) и нод-
dQr d*Mi
ставляя во второе — —г-Л, получим
цД? й,Х“
d-45)
Первое уравнение равновесия (1.42) интегрируется непосред-
ственно
N^-fxdx + C, (1.46)
о
причем постоянная интегрирования С имеет простой механический
смысл — это осевое усилие, действующее в сечении х = 0. Если
обозначить результирующую всех внешних сил, действующих вдоль
оси Ох, через Ро, то
С=2Й-- ('•«>
При решении практических задач по расчету круговых цилиндри-
ческих оболочек обычно компонента поверхностной нагрузки X =
= 0, поэтому уравнение (1.46) с учетом (1.47) примет вид
= (1.48)
Если направление результирующей внешней нагрузки совпадает
с положительным направлением оси Ох (см. рис. 11), то продольная
сила — растягивающая, в противном случае — сжимающая и
Ро следует брать со знаком минус.
С помощью физических уравнений (1.44) исключим из уравнения
(1.45) Mi и Nг- Тогда
-----— diW.---------—ZApp-L v _LZ = o (149)
12(l-v2) dxi (l-v2)7? иг-T v dx и.
Определим из первого физического уравнения (1.44)
^-N --W
dx Eh 2V1 R™'
и после подстановки его значения в уравнение (1.49) с учетом (1.48)
получим
Ehs diw Eh vPp (150)
12(1—№) dxi R- 2лЯ2 ’ ' '
Это дифференциальное уравнение четвертого порядка линейное
неоднородное с постоянными коэффициентами. Оно является урав-
нением нормального прогиба замкнутой цилиндрической оболочки
и получено из общих уравнений (1.11)—(1.13) оболочек вращения
30
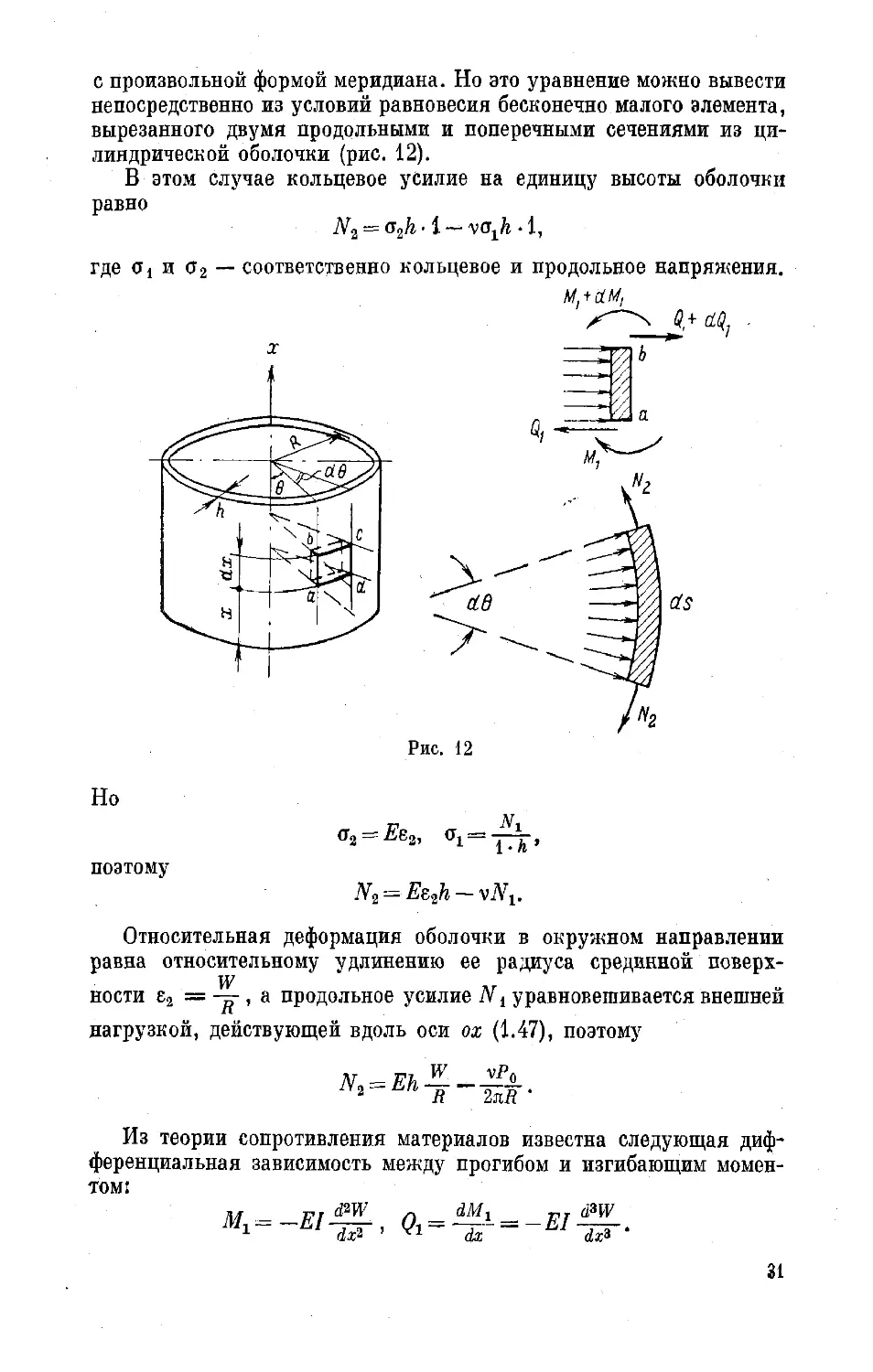
с произвольной формой меридиана. Но это уравнение можно вывести
непосредственно из условий равновесия бесконечно малого элемента,
вырезанного двумя продольными и поперечными сечениями из ци-
линдрической оболочки (рис. 12).
В этом случае кольцевое усилие на единицу высоты оболочки
равно
N2 --= 62h • 1 — • 1,
где Oj и б2 — соответственно кольцевое и продольное напряжения.
Но
<т2 = #82,
поэтому
N2 — Ee2h — vNr.
Относительная деформация оболочки в окружном направлении
равна относительному удлинению ее радиуса срединной поверх-
ности е2 = —, а продольное усилие уравновешивается внешней
нагрузкой, действующей вдоль оси ох (1.47), поэтому
м = Eh — — —А
R 2jiR .
Из теории сопротивления материалов известна следующая диф-
ференциальная зависимость между прогибом и изгибающим момен-
том:
1 dz2 dx dx3
31
Если бы элементарные полоски, вырезанные вдоль образующей
оболочки, изгибались независимо друг от друга, то жесткость в ука-
занных зависимостях была бы справедлива и для цилиндрических
оболочек. Но в действительности при симметричной деформации
оболочки любому изменению формы поперечного сечения полоски
препятствуют смежные полоски. Поэтому, чтобы учесть взаимное
влияние элементарных полосок друг на друга вместо жесткости
El = Е 1 необходимо ввести цилиндрическую жесткость обо-
n 77 1 • fc8|
лочки D = £ J2(i_v2) . тогда:
M^-D
WW
dx%
Q1=-D
d?W
dx*
Спроектируем на направление радиуса все силы, действующие
на бесконечно малый элемент abed оболочки (см. рис. 12)
(<2i + <*<2i) ds — Qxds — 2N2dx ~ Zdx ds = 0.
Если учесть, что dQ =-^-, то после сокращения каждого члена
Л
равенства на ds получим
>-4лг,+г = о.
Исключая из последнего равенства перерезывающее Q [ и кольце-
вое У2УСИЛИЯ! получим дифференциальное уравнение прогиба замк-
нутой цилиндрической оболочки, аналогичное (1.50):
ndiW ; Eh иг у vP0
U dxi + 7?2 W Z 2n7?2 •
Таким образом, цилиндрическая оболочка при осесимметричном
загружении может рассматриваться как совокупность изгибающихся
элементарных полосок, связанных между собой упругими силами.
Отсюда видно, что элементарная полоска оболочки при изгибе
находится в тех же условиях, что и балка на сплошном упругом
основании с коэффициентом постели К = ~^- Покажем это. Уравне-
ние прогиба стержня, нагруженного поперечной нагрузкой, согласно
теории сопротивления материалов равно
Так как балка лежит на упругом основании, то со стороны его
на балку действуют реактивные силы, пропорциональные величине
оседания грунта
q(x) ~ Р (x) — KW (х),
32
где Р (ж) — внешняя нагрузка на балку, отнесенная на единицу
длины; К — коэффициент постели основания (сопротивление грунта
оседанию, когда оседание равно 1).
Таким образом, дифференциальное уравнение прогиба балки,
лежащей на упругом основании, принимает вид
EI
(4
Если обозначить
EI = D, К = -Е^, p{x) = Z—^-, (1.50,а)
то получится дифференциальное уравнение прогиба цилиндрической
оболочки при осесимметричном загружении, аналогичное (1.50).
Следовательно, при расчете замкнутых цилиндрических оболочек
на осесимметричную нагрузку можно использовать хорошо иссле-
дованный аппарат теории расчета балок на сплошном упругом осно-
вании [17].
Общее решение дифференциального уравнения (1.50) состоит
из двух частей: из решения 1¥<1<р) однородного уравнения, когда
нагрузка на оболочку равна нулю, и частного решения РРб>
Ж=Ж<кр, + Иг<6’. (1.51)
В качестве частного решения может быть принят прогиб оболочки,
полученный при решении задачи по безмоментной теории. рркр’
определим из решения однородного уравнения, приняв в (1.50)
й!41у(кр) dxi 1 (1.52)
Если обозначить Eh _ 4РД2 3(1 —V2) : 04 Д2Д2 Р ’ (1.53)
то уравнение (1.52) запишется в виде
,74Щ(кр) dx& 4-4₽4ГР‘к₽» = 0. (1.54)
Решение уравнения (1.54) ищем в форме:
РЕ<кр) = е‘х. (1.55)
Подставляя (1.55) в (1.54), получим следующее характеристиче-
ское уравнение для определения t
+ = (1.56)
Корни характеристического уравнения (1.56) равны:
2 = (1 — О Р>
^з, 4 = — (1 ± О р.
3 Заказ 2036
33
Так как корни характеристического уравнения комплексные,
то решение (1.55) запишется как
= + + + (1.58)
Но
ez-v = cos х 4- i si n x, e~Cx = cos x — i sin x,
поэтому
A&x 4- Ве~№ = A-+B (e‘₽* 4- e^x) 4- (e'₽x — e-№) =
== A^~~ 2 cos fix 4-
4- AT-B- 2i sin 0x.
Обозначим
A + B = Dlt i(A~B) = D2.
Преобразовав таким же обра-
зом вторую скобку выражения
(1.58) и обозначив
C + D = DS, i(C-D) = Dl,
получим
Ж(кр’ = еЗ“ (Z\ cos 0x4-
4- £>а sin 0х) 4- е’₽х (Н8 cos 0х 4-
4-P4sin0x). (1.59)
Таким образом получен интег-
рал однородного уравнения
(1.54), характеризующий прогиб
быстро затухающего моментного
напряженного состояния цилин-
дрической оболочки (краевого
эффекта).
Нормальный прогиб оболочки при краевом эффекте представляет
собой по форме две пары быстро затухающих функций.
Первая пара, содержащая множитель e|3JC, быстро затухает по
мере удаления от края х = Н. Вторая пара, содержащая множитель
e_₽*, быстро затухает по мере удаления от края х = 0 (рис. 13).
Из рисунка можно определить ширину зоны затухания краевого
эффекта Z или длину полуволны затухающих функций
поэтому
sin 0Z = sin л,
Z = 2,44 VRh.
(1.60)
34
Обычно, в конструкциях резервуаров и трубопроводов ширина
зоны затухания крарвото эффекта оболочки значительно меньше
длины оболочки Н.
При L <zH обе 4a<W выражения для прогиба, содержащие мно-
жители еэ* и е_;м', не зависят друг от друга. Первая часть, содержа-
щая множитель е₽*, описывает напряженно-деформированное состоя-
ние оболочки у края х «s Н, вторая, содержащая множитель е"^, —
у края х — 0. Используя это, будем рассматривать напряженное
состояние оболочки у одного какого-либо края независимо от дру-
гого.
Для нижнего края оболочки
выражение прогиба (1.59) запи-
шется как
17‘кр) =
_ е-0х (£)д cos p-j. gjn
(1.61)
для верхнего —
jyupi = е₽(х- я) [ Di cos р (я _ #) +
+ Z>2sinp(z — Я)]. (1.62)
Таким образом, получено решение однородного уравнения (1.52)
для каждого края цилиндрической оболочки независимо друг от
друга. Соответственно этому общее решение (1.51) также следует
записывать отдельно для каждого края оболочки:
И/н = epx(£)3cosPa: + Z)4sinpл;) + J7<б,; (1.63)
Wa = е₽<*-я) [2?!cos р (а:-Я) + sin 0 (я-Я)] + W16'. (1.64)
Следовательно, на каждом краю длинной цилиндрической обо-
лочки следует определить лишь две произвольные постоянные неза-
висимо друг от друга. При практических расчетах цилиндрических
оболочек определение произвольных постоянных существенно упро-
щается, если применять метод начальных параметров.
Предположим, что внешняя нагрузка Z = Ро = 0 и, следователь-
но, W<6y = 0, W = И/кр, а на одном из краев оболочки, например
при х = 0, действуют равномерно распределенные момент Мй
и перерезывающее усилие Qo (рис. 14), тогда при х = 0 соблюдаются
условия: (^О)=Мо; ()<кнр> (а; = 0) = (?0, (1.65)
но Л/$кр> D d2W • ЛТ1Н - и dx2 ,
3*
35
(1.66)
поэтому нужно трижды продифференцировать выражение прогиба
(1.63) для нижнего края оболочки:
— = ₽е-Рх [(- D3 + Р4) cos рж - (Р3 + Р4) sin рх];
d2WfIKP) По, йи/л . д л о \
—— = 2p-e_Pr (D3 sin p.r — Р4 cos pF);
—=2рзе-₽х [(Лз+Di} cos px-+ (_Da+Di) sin px].
Тогда
1WihP) = — 2P2Pe~px (D3 sin Рж — Z)4 cos Px);
-2P3Z)e-P* [(P8 + Da) cos par + (-P8 + PJ sin Par]. (1.67)
Раскрывая условия (1.65) с помощью уравнений (1.67) при х =
= 0, получим:
(1.68)
D3 — 2₽3Л (<2o+P-^o)>
n _ M°
4 2P-D '
Подставив полученные значения коэффициентов в выражения
(1.63) и (1.66), найдем:
, е“‘3х
И^кр) = >зо (sin — C0S “ *?о C0S
dWdx = ТрЖ [2₽Af0cos Par + <?0(cos P^-j- sin pa;)]; (1.69)
, e-3*
MihP) = —p— [Cosin ₽£ + Wo (sin |3z + cos Pa:)];
<2ih₽) = e“3* [<?0 (cos — sin fta) — 20МО sin 0x].
При х = 0, т. е. на загруженном конце, из (1.69) следует, что
ж‘крч* = 0) = -^Ф<о+<2о);
(•г=°)=Wd (Wo+<2o); (1-70)
М^(х = О) = Мо-,
Q{^>(x = O) = Qo.
Знак минус (—) в выражении для прогиба указывает на то, что под
действием момента М0 и усилия Qo кромка цилиндрической оболочки
прогнется внутрь, т. е. в сторону отрицательного направления нор-
мального перемещения WH.
36
Обозначив
Ф4 = е“?х (cos рх + sin рх);
Ф2 = e-1'* (cos 0x — sin |3x);
Ф3 = e"^ cos |3x;
Ф4^= e"'*sin |3x,
(1.71)
и приняв во внимание, что между функциями Ф! — Ф4 (табл. 1)
существуют дифференциальны^ зависимости:
ф;=-2₽Фа, Ф^ = -20ф3, Ф^-рФ^
Ф1 = рФ2, (1.71, а)
запишем выражения (1.69) в следующем окончательном виде:
= - w = - 4 «Фа+<Ж);
4F"=W (2РМ»фз + <2оф1) = ?- (2РМофз + СоФт); (1-72)
(?1кнР’ = -2₽М0Ф4 + (?0Ф2.
Следовательно,
= = _2рЯ (Р>0Ф2 I <?0Ф3);
ЛГ<кнр> = vM‘khp>.
Таким образом, соотношения (1.72), определяющие краевой
эффект у края х 0 круговой цилиндрической оболочки, выражены
через начальные параметры Мо и Qo.
Аналогично записываются выражения для усилий, моментов
и перемещений моментного напряженного состояния цилиндрической
оболочки у края х -С Н:
w<K₽)=4(-P^ + ^);
^Тк=-4-^оф2-2^оФз);
ВД1-М0ф:+-^Ф*4;
да = ^Ф1-2₽М0ф*4;
Л?вр,-2РадФз-|Ж0ФГ); (1.72, а)
М^р) = vM$P),
37
Таблица 1
Численные значения функций Фг— Ф4
Ф, Ф2 Фз Ф<
0 1,000000 1,000000 .1,000000 0
0,1 0,990650 0,809984 0,900317 0,090333
0,2 0,965067 0,639754 0,802411 0,162657
0,3 0,926657 0,488804 0,707731 0,218927
0,4 0,878440 0,356371 0,617406 0,261035
0,5 0,823007 0,241494 0.532281 0,290786
0,6 0,762836 0,143071 0,452954 0,309882
0,7 0,699718 0,059900 0,379809 0,319909
0,8 0,635379 -0,009278 0,313051 0,322329
0,9 0,571205 -0,065749 0,252728 0,318477
1,0 0,508326 —0,110794 0,198766 0,309560
1,1 0,447646 -0,145668 0,150989 0,296657
1,2 0,389865 -0,171585 0,109140 0,280725
1,3 0,335502 -0,189698 0,072902 0,262600
1,4 - 0,284922 -0,201096 0,041913 0,243009
1,5 0,238355 -0,206788 0,157784 0,222571
1,6 0,195915 . -0,207706 -0,005895 0,201810
1,7 0,1*57623. —0,204699 -0,023538 0,181161
1,8 0,123420 -0,198532 -0,037556 0,160976
1,9 0,093183 -0,189891 -0,048354 0,141537
2,0 0,066740 -0,179379 -0,056319 0,123060
2.1 0,043884 -0,167527 -0,061821 0,105706
2,2 0,024376 -0,154792 -0,065208 0,089584
2,3 0,007963 -0,141564 -0,066800 0,074764
2,4 —0,005618 -0,128171 -0,066895 0,061277
2,5 —0,016636 —0,114887 -0,065762 0,049126
2,6 -0,025356 -0,101932 -0,063644 0,038288
2,7 -0.032036 -0,089481 -0,060759 0,028722
2,8 -0,036926 -0 077667 -0,057297 0,020371
2,9 -0,040261 -0,066590 -0,053425 0,013164
3,0 -0,042263 -0,056315 -0,049289 0,007026
3,1 -0,043137 -0,046883 -0,045010 0,001873
3,2 -0,043072 -0,038313 —0,040693 —0,002379
3,3 -0,042239 —0,030603 -0,036421 —0,005818
3,4 -0,040793 -0,023737 -0,032265 —0,008528
3,5 -0,038871 -0,017686 -0,028279 -0,010593
3,6 -0,036594 -0,012411 -0,024503 -0,012091
3,7 -0,034067 -0,007868 -0,020968 -0,013099
3,8 -0,031382 -0,004007 -0,017695 -0013688
3,9 —0,028616 -0,000773 -0,014694 -0,013922
4,0 —0,025833 0,001889 —0,011972 • -0,013861
4,1 -0,023087 0,004035 -0,009526 -0.013561
4,2 —0,020422 0,005718 -0,007352 —0,013070
4,3 -0,017869 0,006993 -0,005438 -0,012431
4,4 -0,015456 0,007910 -0,003773 -0,011683
4,5 -0,013201 0,008518 -0,002342 -0,010859
4,6 -0,011116 0,008861 -0,001127 —0,009988
4,7 —0,009207 0,008982 -0,000113 -0,009095
4,8 —0,007478 0,008918 0,000720 -0,008198
4,9 -0,005927 0,008705 0,001389 -0,007316
5,0 -0004550 0,008372 0,001'911 —0,006461
5,1 —0,003340 0,007949 0,002304 -0,005644
38
Продолжение табл. 1
fix Ф1 ф2 Фз ф.
5,2 -0,002289 0,007458 0,002585 -0,004874
5,3 -0,001387 0,006922 0,002767 —0,004154
5,4 -0,000624 0,006357 0,002867 -0,003490
5,5 0,000013 0,005780 0,002896 -0,002883
5,6 0,000534 0,005202 0,002870 -0,002334
5,7 0,000950 0,004635 0,002793 -0,001843
5,8 0,001274 0,004088 0,002681 -0,001407
5,9 0,001517 0,003565 0,002541 -0,001024
6,0 0,001687 0,003073 0,002380 -0,000692
6,1 0,001797 0,002614 0,002205 -0,000409
6,2 0,001854 0,002191 0,002022 -0,000169
6,3 0,001867 0,00180а 0,001836 0,000031
6,4 0,001844 0,001457 0,001650 0,000194
6,5 0,001792 0,001145 0,001468 0,000323
6,6 0,001716 0,000869 0,001293 0,000424
6,7 0,001624 0,000627 0,001126 0,000498
6,8 0,001519 0,000418 0,000968 0,000550
6,9 0,001405 0.000239 0,000822 0,000583
7,0 0,001287 0,000088 0,000687 0,000599
где между функц ф; = е₽<*-н) [с ф* = еР(*-Н) |с ф* = ( Ф*4-< ИЯМИ Ф1 — Ф’ os |3 (х—/7)4- OS Р (х — Н) — ;₽( v-H)cos р в₽(*-н) sin Р (х имеются еле; sin Р (х — Н)]; sin р (аг — Я)]; -Я); -Я). дующие дифф (1.72, б) вренциальные
зависимости: ф?=2Рф;, ф*8'=-; !РФ4, Фз'-| }ф8, Ф^^РФр (1.72, в)
Краевой эффект в сферических оболочках
Рассмотрим сферическую оболочку в системе координат ср, 0
при осесимметричном загружении (рис. 15, а).
Ввиду симметрии действия нагрузки все факторы напряженно-
деформированного состояния оболочки не зависят от 0, поэтому
М12 = М21 — 812 = S2) = Q2 = О, U ~ 0; нулю равны также все
производные по) 0. Если учесть, что в сферической оболочке 7?! =
= 7?s = R, и принять компоненты нагрузки X = Y = Z = 0, то
исходные уравнения равновесия оболочки вращения произвольной
формы (1,39) примут вид;
sin <р) — N2 cos ф + sin ф = 0;
- sin ф - TV2 sin ф+—((?! sin ф) = 0; (1.73)
(Л^зшф)—М2созф—7? (>!sin^=0.
39
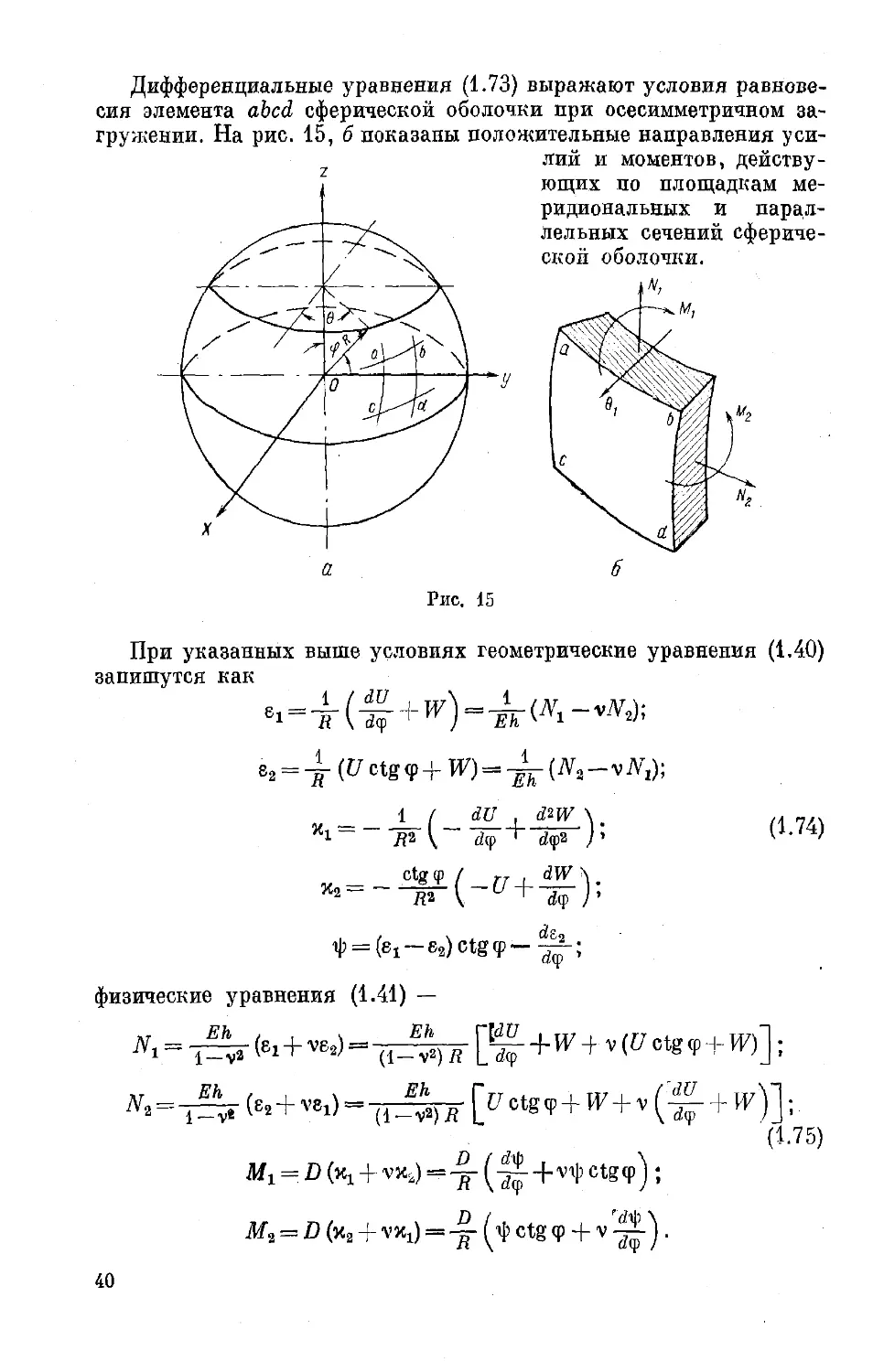
Дифференциальные уравнения (1.73) выражают условия равнове
сия элемента abed сферической оболочки при осесимметричном за
гружении. На рис. 15, б показаны положительные направления уси
лий и моментов, действу-
ющих по площадкам ме-
ридиональных и парал-
лельных сечений сфериче-
ской оболочки.
При указанных выше условиях геометрические уравнения (1.40)
запишутся как
t, = 4 (V otg <р + W) - -±- [N.-vff,);
_ i ( dU , dW \.
X1 “ J?2 \ d<p ' d<p2 ) *»
x!=^(^+«);
ф = (е1-в2) ctg<p-^-;
физические уравнения (1.41) —
nr Eh t t \ Eh
(61+V62)=
--Д- fe + V.,)-[cetg ф + Ж + v
(1.74)
(1.75)
Mx = D (xx + vx2) =
Ma = D (x2 + v%j) = -£- (ф etg <p + v -
40
Таким образом, для определения двенадцати неизвестных: пяти
силовых факторов (N t, N2, Мlf М2, (?i)> четырех деформаций (е1г
g2, х2), двух перемещений (U, И7) и угла поворота ф, имеем си-
стему из двенадцати уравнений (1.73)—(1.75).
Примем за основное неизвестное системы перерезывающее усилие
Qi и приведем ее к более простому виду. Исключим из первого и вто-
рого уравнений (1.73) кольцевое усилие N2
(Л\ sin ф) + Nt cos ср - (Qt sin ф) ctg <p + <2i sin ф = 0.
Вводя cos ф и Qi sin q> под знак дифференциала, получим
------(N, sin2 ф) Д— -%- (Q, sin ф cos ф) = 0.
sm<p dtp ' 1 sin ф dtp
Проинтегрируем последнее равенство по ф
^1-<?1с1иф + ^? = 0.
*
Физический смысл произвольной постоянной С можно легко вы-
яснить, если при безмоментном решении (>j=0. В этом случае
Также как и в цилиндрической оболочке, произвольная постоян-
ная С представляет собой результирующую внешних сил, распре-
деленных по поверхности оболочки. Но так как в данном случае
Х = У = Z = 0, то С = 0.
Тогда
Л\ = (?1^ф. (1,76)
Подставим (1.76) во второе уравнение равновесия
- Qi cos ф - N2 sin ф + ~ (Qi sin ф) = 0.
Принимая во внимание, что
(<?i sin ф) = sin ф + Qi cos ф,
запишем последнее равенство в виде
^=-V- (»•”)
Таким образом, меридиональное и кольцевое усилия выражены
относительно основного неизвестного Q^
Перед тем как выразить остальные факторы напряженно-дефор-
мированного состояния сферической оболочки относительно (?i,
сделаем некоторые упрощения, основанные на том, что при диффе-
ренцировании функций, изображающих затухающее колебание,
41
с большим коэффициентом затухания значение производной всегда
больше значения самой функции на величину коэффициента затуха-
ния. Следовательно, производными низшего порядка по сравнению
с высшими для данной функции можно пренебречь. На этом допу-
щении основана приближенная теория краевого эффекта в сфери-
ческой оболочке, которая по своему физическому смыслу аналогична
теории расчета краевого эффекта в цилиндрической оболочке: у края
возникает напряженное состояние, которое быстро затухает вдоль
меридиана, имея форму кривой затухающего колебания.
Пренебрегая ei и е2 в (1.74) по сравнению с
выражение для угла наклона касательной к меридиану в
ной форме
запишем
упрощен-
, ^2
Ф -----
т dcp
После подстановки (1.76) и (1.77) в (1.74) получим следующее
приближенное значение деформации оболочки в кольцевом напра-
влении:
Eh
Исключая с помощью (1.79) из (1.78) е2, получим
Eh <7ф2 '
Из третьего уравнения равновесия (1.73) следует
R Q1 sin <р = sin <р Мг cos <р — М2 cos <р.
Так как > ЛГ t и М2, последнее выражение для
ющего усилия запишется:
п _ 1 dMt
Согласно третьему физическому уравнению (1.75)
или, пренебрегая ф по сравнению с
= R dtp
Подставляя (1.82) в (1.81), а полученное выражение в (1.80),
находим
(1.78)
(1.80)
перерезыва-
(1.81)
(1.82)
D
— ~ Eh№ ТфГ •
42
Обозначим
EhR4 _3(1-\>2)Я2_
iD /i2 _ ’
(1.83)
тогда последнее уравнение перепишется:
=°-
(1.84)
Уравнение (1.84) описывает краевой эффект в сферической оболочке.
Если вместо ф ввести новую переменную — дугу меридиана s, свя-
занную с ф выражением ds' — Rdq>, уравнение (1.84) примет вид:
dsi Г !1< * ‘
Это уравнение совпадает с одно-
родным уравнением (1.52),
описывающим краевой эффект
в замкнутой цилиндрической
оболочке при условии
R4 н
Следовательно, поворот ка-
сательной к меридиану сфери-
ческой оболочки можно опреде-
лить приближенно как поворот касательной, «заменяющей» цилиндр,
радиус которого равен радиусу сферы (рис. 16).
Такая аналогия позволяет получить все факторы напряженно-
деформированного состояния сферической оболочки непосредственно
из формул (1.42)—(1.44).
Так как основной неизвестной (разрешающей функцией) в данном
случае является перерезывающее усилие Qit то в уравнении (1.84)
с помощью (1.80) выразим ф через Qi
(1.85)
Решение уравнения (1.85) известно из рассмотренной выше тео-
рии краевого эффекта цилиндрической оболочки
(Ci cos tap + С2 sin Хф) ф- (С3 cos Хер ф- С4 sin Хф). (1.86)
Если обозначить ф4 ==а — ф, ф2 = ф — р, то интеграл (1.86)
запишется
Qi — (Л cos Хф1 + 2?з1п Хф1)ф-е^ч>2 (С cos Х'ф2ф- D sin tap2). (1.87)
Таким образом, решение уравнения (1.85) состоит из двух пар
быстро затухающих знакопеременных функций: первая пара (функ-
ция от ф() затухает от левого края, а вторая (функция от ф2) — от
правого края (рис. 17).
43
Обычно верхняя часть оболочек сферических резервуаров и газ-
гольдеров свободна от закреплений и находится в безмоментном
напряженном состоянии. Нижняя часть сопряжена с опорным по-
стаментом, который препятствует свободному смещению оболочки
в радиальном направлении, что приводит к краевому эффекту. По-
этому для определения краевого эффекта в зоне, примыкающей
к опорному постаменту, следует пользоваться первой частью реше-
ния (1.87), содержащей функ-
цию ОТ фр
Qx = е(A cos Хфх +
+ .Bsin Хф^. (1.88)
Тогда из уравнения (1.80)
можно определить ф
и Eh Йф2
= - •^re'x<P1 (“ tfcostapx -F
Eh
+ A sin Хф^). (1.89)
Выражение для изгиба-
ющего момента найдем из
(1.82)
£/гЗ йф _
12(l-v2)7? dtp ~
= -«7i—-5Г-Д- [(Л + Б) cos Хф! + (-Л + #) sin tapj. (1.90)
г» ( 1 —V6\ Н 1 4 1 /
Из равенства (1.76) определим выражение для меридионального
усилия:
JVX = Qx ctg <р = ctg ф е'А<Р’ (Л cos Хф! + В sin Хфх), (1.91)
а из соотношения (1.77) найдем выражение для кольцевого усилия:
е в _[(_А + В)cos-(А А-В) sin .
Ф Ф1 (1.92)
Выражение для изгибающего момента в кольцевом направлении
определим из уравнений (1.75):
" 12(Х)Д Ч> etg <р+vJH. = 6(1“Ъг е‘1” К® с‘8 *+ЛА +
+ укВ) cos Хфх — (Л ctg ф — vXB-| уХЛ) sin . (1.93)
При практических расчетах оболочек сферических резервуаров
и газгольдеров необходимо знать смещение оболочки в плоскостях
параллельных кругов 6.
4
Из второго геометрического уравнения (1.74) выражение для пере-
мещения в плоскости параллельного круга равно
6 = Т?е2 sin ф — U cos ср 4- И7 sin (р — Д |(,п (N^-vN^. (1.94)
Hl fl
После подстановки в (1.94) значений из (1.91) и из (1.92)
выражение для горизонтального смещения оболочки запишется как
б =Д е-^* [(- КА + КВ 4- vA ctg <р) cos +
Л n
+ (—L4 — X^ + v^ctgqjJsinJwpj]. (1.95)
Таким образом, получены все факторы краевого эффекта в зоне,
примыкающей к нижнему краю сферической оболочки.
Аналогично можно получить усилия, моменты и перемещения
в зоне, примыкающей к верхнему краю оболочки:
Qi — е^°2 (С cos Л.<р2 + D sin Z<p2);
ф =—^~е'%!р!( — 7? cos Z<p2 + С sin Х<р2);
И п>
M1 = - е'**‘ Kc+D>!cos Z-<p2 + (-С + 7)) sin Хф2];
^2 = -j^z^fj^“e'’l’’!(-7Jc°sZ<p2-|-6,smZ(p2) + vMi; (1.95, а)
Ni = ctg ф (С cos Хф2 + D sin Ц>2);
N2 — — Хе'^2 [(С—D) cos 1ф2 + (С + D) sin 1ф2];
6 = —Д е“хь [(ХС — KD + v ctg фС) cos Хф2 -J-
Lil
+ (КС + KD + v ctg ф7)) sin Хф2].
Краевой эффект в конических оболочках
Определим моментное напряженное состояние конической обо-
лочки (см. рис. 10) при действии осесимметричной краевой нагрузки.
В этом случае
/?1 = оо; T?2 = stga; d^ = ^\ Ф = у-a;
X=F = Z = 0.
Основные уравнения оболочки вращения (1.39)—(1.41) при осе-
симметричной деформации для конической оболочки принимают вид:
45
уравнения равновесия
s-^- + Ci-tf2ctga = 0; (1.96)
s^+M.-Mt-sQ^O-,
геометрические уравнения
'.=т4м;
e2 = 4-(^ + Wctga) = ^(JV2-vA\);
dW
Ki ~ ;
1-------dW
я2 =----3—:
i s ds ’
. dW
ф =---j— >
T ds
физические уравнения
(v+—clsa)J;
» /i+2L„tga+v "LY
2 1— № \ s * s ° ds J ’
(1.97)
(1.98)
ds
м,
я|> -J- v
Второе уравнение равновесия системы (1.96) можно представить
как
(1.99)
Вычтем из третьего физического уравнения (1.98) четвертое
(1.100)
и, учитывая, что
ds ds% 1 \ as s J
запишем третье уравнение равновесия (1.96) в следующем виде:
Ds о. (1.101)
ds- \ (aS S J
46
Обозначим
(1.102)
тогда уравнение (1.101) примет окончательный вид:
dty . i|>____L = o
ds s D
(1.103)
Уравнение (1.103) является одним из разрешающих уравнений для
конической оболочки.
Другое разрешающее уравнение можно получить, если рассмот-
реть условие равновесия отсеченной части конической оболочки,
которая из-за отсутствия внешней нагрузки будет уравновешиваться
лишь усилиями N{ и Qi, действующими на ее кромке (рис. 18, а)
cos а — Qt sin а = 0. (1.104)
Тогда
= СМё а = 7" tg а- (1.105)
Из соотношений (1.99) и
(1.105) следует, что
JV,—=
(1.106)
Но, с другой стороны, из первых
двух геометрических уравнений
(1.97) можно составить следу-
ющее соотношение:
fJW
= —Eh—j— ctg a = Ehty ctg a.
CIS
(1.107)
Следовательно, второе разрешающее уравнение можно получить,
если приравнять правые части выражений (1.106) и (1.107)
+77 - т)tg a = “£/z^ctga- (I-108)
Если ввести дифференциальный оператор
_d2_ _d_______1_
d«2 > ds s’
(1.109)
47
то разрешающие уравнения (1.103) и (1.108) примут вид:
A(t|>) = -f; (1.1Ю)
A(y)tga = — £7ii]>ctga. (1.111)
Проделав операцию А над уравнением (1.111) с учетом (1.110),
окончательно получим разрешающее уравнение для конической обо-
лочки, загруженной осесимметрической краевой нагрузкой,
(1.112)
Обозначим
(1.113)
(1.114)
Eh — у
D tg2 a
тогда уравнение (1.112) перепишется
AA(y) + Vy = 0.
Уравнение (1.114) эквивалентно системе двух уравнений второго
порядка:
Л(у) + г^2У = 0;
А (г/) — г Х2г/ = 0,
(1.115)
следовательно,
,4&+4'_А±й«!(=0.
ds% 1 ds s а
Если обозначить
(1.116)
(1.117)
8 - 4X2 ’
то уравнение (1.116) преобразуется в известное уравнение Бесселя:
dty ; 1 dy
d& "Г I dl
(1.118)
(1.119)
-Щ)
решение которого имеет вид:
У=(В) + см)+caf3 (В)+с4/4 (В),
г
где h (В) — функции Кельвина [19].
Как показал С. П. Тимошенко [15], для функций Л (В)
и их производных в окрестности нуля, т. е. при В С 1, справед-
ливы следующие асимптотические зависимости:
/, (В) - Л=- cos -4=-- 4);
еЕ/ /2 /е я \
48
(1.120)
Поведение функций ft (i = 1, 2, 3, 4) и их производных напоми-
нает поведение гиперболотригонометрических функций из теории
цилиндрических оболочек при осесимметричном загружении.
При достаточно большой длине образующей конической оболочки
общее решение (1.119) по аналогии с цилиндрической оболочкой
можно разделить на две пары быстрозатухающих периодических
функций: первая пара с коэффициентом eV описывает картину
напряженного и деформированного состояния оболочки корпуса
у края s= s2, вторая — с коэффициентом e'V^a у края s= st (см.
рис. 10). Определив решение однородного уравнения (1.118), не-
трудно построить выражение для всех внутренних усилий и переме-
щений.
С учетом (1.117) выражение для перерезывающего усилия опре-
деляется непосредственно из равенства (1.102)
<2i=fIGA (В) + CJ, (?)+c3fs (?) + (В)], (1-121)
а продольного — из соотношения (1.105):
М = IG/i(В) + G/з(В) + ШВ) -bG/i(В)1. (1-122)
4 Заказ 2036
49
Из второго уравнения равновесия (1.96), записанного в форме
(1.99), с учетом 'зависимости (1.117), получим выражение для коль-
цевого усилия
дт tn п 2Х- tg ос dy ______ 2Z- tg a r/-, : >. /%\ ।
Л2 = 77 tg а =---11-----------------[<-1/1 (s) + с272 (S) +
+ С3Ш-г-С^)]. (1.123)
Имея выражения для продольного и кольцевого усилий, опре-
делим согласно (1.35) величину горизонтального перемещения кони-
ческой оболочки:
6=- vN^ = sin^^-1С1Л8’ ®® +
+ (1-124)
где
i=l, 2, 3, 4. (1.125)
Для определения выражения угла поворота ф =-----------— восполь-
зуемся выражением (1.111)
V Eh Eh \ ds4 ds s )'
?2
Так как s = , то оператор
принимает вид: _
А = ХаА, (1.126)
где
*=>+т4--г <U27>
После подстановки в первое уравнение системы (1.115) (1.128)
у = 1Д1^ = ШЯ1Ш
с учетом (1.126) получим
^Ш + ih^ + ilfdlHih (5)1 = 0, (1.129)
откуда Д [/1(B)] =/а(5); А[/3(В)] = -/1(B)- (1.130)
По аналогии А[/з(В)]=/4(В), Д[/4(&)1 = -/8(?). (1.131)
50
Следовательно,
Ф = - А (у) = - 2^. [С1/2 (?)_ с2а (Ю 4-
+ С3Ш~С4Ш], (1-132)
тогда изгибающие моменты в соответствии с формулами (1.98) при-
мут вид:
мD (+—ф ) = 2ZA2 4- (4г + 4- ф') =
1 \ ds ' s ) g \ dl 1 I т /
= — С^3М^ (1.133)
м, = D (4+v -g-) = - -f- [с^ (g) - c2tfhi (£) +
+СзАМг)(?)-сЛМ!)(5)], (1-134)
где
(g) = Л (I) + у- Л Ю; i = l,2, 3, 4; (1.135)
/^^(1) = v/2 (В)+-|-Л(Ю; * = 1, 2, з, 4. (1.136)
Таким образом, получены все факторы напряженно-деформиро-
ванного состояния короткой конической оболочки, содержащие
четыре произвольные постоянные Clt . . ., С4.
Если длина конической оболочки вдоль образующей такова, что
s2 и Sj (см. рис. 10) подчиняются условию
(/Г2-/^> 1,2(1.137)
то с ошибкой менее 5% оболочку можно считать длинной. В этом слу-
чае решение (1.119) можно разделить на два независимых решения:
у края s st
У = С3/3® + С414®; (1.138)
у края з з2
У = СМ1) + С3Ш, (1.139)
содержащих только по две произвольных постоянных.
Предположим, что на краю s = s2 длинной конической оболочки
приложены равномерно распределенные усилия Qo (рис. 18, б).
Тогда во всех выражениях для внутренних усилий и перемещений,
определяющих напряженно-деформированное состояние конической
оболочки у края s з2, члены, содержащие С3 и С4, обращаются
в нуль.
Граничные условия при z = ° или з — з2 — запишутся:
Qn-a -- Qo cos а; Л/1>а^0. (1.140)
4’
51
Раскрывая эти условия с помощью зависимостей (1.121) и (1.133),
получим С1/1 (а) + С2/2 (а) = <2о cos а; (1.141)
G/^1’ (а)-СгАМ,) (й) = 0.
Откуда <2«cosa- G = 4Х2 <2о cos а F(a) ' (1.142)
где F (а) = Л(а)АМ1,(а) + /2(а)/(аМ1)(а). (1.143)
После подстановки значений произвольных постоянных в формулы
для внутренних усилий и перемещений получим:
=- <?о sin а [ЛМ1) (а) Л (?) + 4М1) (а) Л (Ю] !
= Q2FWl (й) К ® + (Я) ® 1;
4* \U/9
М1 - [/"'> (“>(Е) - /“'1 (“> Л"'1 ©1:
"»=- [/“‘) (о) © А" ©1; <U44>
a=[/“’ © а ©+1"" м a ©I •
6=4е4М°7 [Ам,> © Л” (5)+Ам,> («)/“’©];
* - - °’ © А © - Л" © А ©I •
При больших значениях аргумента а, входящего в формулы
(1.144), можно воспользоваться асимптотическими формулами для
функций Д (^) и их производных. Покажем это.
Введем безразмерную координату ц, связанную с расстоянием х
вдоль образующей зависимостью
» = (1.145)
и предположим, что х + s = s2> тогда
52
Для длинных конических оболочек в зоне, примыкающей к краю,
справедливо соотношение: — 1, поэтому «2
У 1 а2 2а • (1.147)
Как и в цилиндрических оболочках, обозначим
тогда с учетом (1.112) R4 = _£L R4 № tg2 а Р 4р2 ’ (1.148)
(1.149)
где Р = $а tg а, (1.150)
поэтому
2а - = -^- = ]/2Pz. V s2 (1.151)
Принимая во внимание равенство (1.151), представим безразмер-
ную координату £ (1.147) в следующем виде:
£ = а-/2рж. (1.152)
Тогда при достаточно больших значениях аргумента а справед-
ливы следующие приближенные равенства для соотношений (1.135)
и (1.136):
F!)(a)^v/J(«).
Формула (1.143) запишется:
F (а) = А («) Л(«) + /2 («)Д(«). (1.154)
После подстановки зависимостей (1.122) в формулу (1.154) при
£ = а получим:
Аналогично
ЛМ,)|(«) А а) = Г1 (а) fl (« - /2 0z) =
53
2ла
2a
е
. / а
8Ш —7=
-^-?Х
у 2 / О' I Л \ / О I Л
e COS -7=г + -^- COS -7=--f—3-
г = (/2 8/ \/2 8
ря);
2па
2ла
ЛМ1)(«)/2(?)^/2 («)/;(«-/2 м=
е __________sin
Л /2|3а
d । «ГС
75 ’“8
Подставив зависимости (1.155) и (1.156) в выражение для про-
дольного усилия (1.144), получим:
е~.«
Л\ = sin а—
cos
== cos
2 Ра L
а
cos X
а JT
7Т “
и п
72~~8
<20sina е pj. (cog _ g.n „ )
. V2Ba
или, принимая во внимание (1.71).
Qo sin a
V2 В'с
(1.157)
Так как — 1, то
а
Г]2
2а2
1,
и выражение для продольного усилия (1.157) примет окончательный
вид:
Л\ = Qo Фгвш «
(1.158)
54
Аналогичным образом определяются все остальные факторы на-
пряженно-деформированного состояния у нижнего края длинной
конической оболочки, загруженной силами Q0:
т/'о _ _____
Л’2 — aQ0 O3sin а — |/2 1 ]/s2 <20 ®3sin а = 2рр<?0 Ф3соз а;
Mr = - ae-»x sin = - C-° °-Sa Ф4;
W2 (1.159)
М2= - V^0Stt ф4;
= _g0COSao.
2{PD 3’
. _ Qq cos а ф
'р- 2pD Ф1'
Теперь предположим, что на краю s = s2 длинной конической
оболочки приложены равномерно распределенные вдоль окружности
изгибающие моменты Мд (рис. 18, в). Тогда граничные условия при
| = а запишутся:
M^a=M0-
Qll=a — 0.
Раскрывая эти условия с помощью зависимостей (1.121) и (1.113),
получим:
(1.160)
откуда следует:
Cifi (a) + Qa (a) = °;
4
аМ0
(1.161)
Сг
(1.162)
аМ0 f (а) .
2 Р (а) ’
аМ0 /1 (а)
2 F (а) ’
где F (а) определяется по формуле (1.143).
Исключая из выражений для внутренних усилий и перемещений
произвольные постоянные Сг и С2 с помощью соотношений (1.162),
получим:
W /* («) h ©];
111 (а) (5)- /*(а) ®];
Mi=W t/i /^'’ +/2 /(2М,) ’
55
И, = 1/1 ®+h (а) ftM’’<Е,|; <1Лв3)
8="•"IW-r 1А /“’ ® ~ л (а} >“ ®,:
* = Тш* (А <“) А ©+/«(“) А ©1-
Прибегнув к асимптотическим упрощениям формул (1.163) при
больших значениях а (как и в случае загружения усилиями Qo)
и складывая полученный результат на основании принципа супер-
позиции с выражениями (1.158) и (1.159), получим окончательно
следующие выражения для внутренних усилий и перемещений кони-
ческой оболочки, на краю которой приложены перерезывающие
силы Qo и изгибающие моменты Мо:
Nr = - 20 tg а (М0Ф4 + ф2);
N, = N, - 202р (М0Ф2 - ф3);
М1 = М1)Ф1 — -^^-ф4;
M^vM^ (1.164)
^-^ = -2Р^оф4 + ^^ф2);
W = ~ Рмоф2 + <?о cos аФ3);
Ф = -1^0 (20ЛГОФ3 - (?о cos аФ4).
Из сравнения формул (1.164) с формулами для цилиндрических
оболочек (1.72) можно сделать вывод, что при большом значении
параметра а расчет конической оболочки, находящейся под дей-
ствием краевых нагрузок, совпадает с расчетом цилиндрической
оболочки радиусом р = s2 tg а (см. рис. 18).
Граничные условия при расчете оболочек резервуаров и трубопроводов
С помощью статических (1.11), геометрических (1.12) и физиче-
ских (1.13) уравнений невозможно полностью рассчитать напряжен-
но-деформированное состояние оболочки до тех пор, пока они не
подчинены граничным условиям на краях а, = const и 0 = const.
Если оболочка замкнута и не имеет границ, то граничные усло-
вия заменяются условиями периодичности. В этом случае на реше-
56
ние статических и физических уравнений накладываются следующие
условия: перемещения при обходе замкнутого контура оболочки
вдоль координатных линий в заданной точке ее срединной поверх-
ности должны быть периодичными функциями а и |3 и однозначны.
Срединная поверхность вертикальных цилиндрических резер-
вуаров и трубопроводов замкнута в направлении координаты р
и не замкнута в направлении координаты а. Поэтому для коорди-
наты Р будет иметь место условие периодичности, а для координаты
а — граничные условия.
В теории упругих тонких оболочек доказано [12], что если края
оболочки совпадают с линиями главных кривизн (это почти всегда
имеет место на практике), то на каждом краю оболочки а = const
и р = const в общем случае должно быть четыре граничных условия,
являющихся линейными комбинациями следующих четырех величин:
на краю р = const
^2, ^=<22 + 4^’ = +
на краю а = const
Л\, Й-й+l-^s-. S„ = S1S+^,
где (?!, (?2> *512> *^2i — соответственно обобщенные перерезывающие
и сдвигающие усилия.
Разумеется, необязательно, чтобы граничные условия были вы-
ражены именно через представленные четыре величины на каждом
краю оболочки. Усилия и моменты могут быть заданы косвенно,
через перемещения или углы поворота.
Рассмотрим наиболее распространенные варианты граничных
условий при расчете трубопроводов и резервуаров, на краю а =
= const.
Свободный край:
>1==0, 2VX = О, ^ = ^ + 4-^ = 0, ^ = ^ + 4^=0;
0 О р • Д 2
шарнирно опертый неподвижный край:
М1 = 0; 7 = J7=?7 = 0;
свободное опирание:
М1==0, Х = 0, £7 = 7 = 0;
шарнирный, свободный в нормальном направлении край:
М1 = о, ^1 = (?1 + 4^ = 0, 77 = 7 = 0;
57
Шарнирно опертый край, имеющий возможность свободно сме-
щаться в касательной плоскости:
Мх = 0, Л\ = 0, 512 = S13 + ^ = 0, W =
Абсолютно заделанный край:
H'-C'-V = 0,
где т|> — угол поворота края оболочки.
В чистом виде ни одно из этих условий на практике не встре-
чается. Однако в большинстве случаев реальные граничные условия
могут с определенной точностью быть аппроксимированы ими. На-
пример, стенку цилиндрического резервуара большой емкости можно
считать абсолютно заделанной по нижнему краю, аналогичное за-
крепление может быть принято для верхней кромки стенки резер-
вуара со щитовой кровлей.
Оболочки в инженерных сооружениях очень часто сопрягаются
с упругими элементами (кольцами жесткости, диафрагмами, оболоч-
ками другой формы и различной толщиной стенки и т. д.), жесткости
которых соизмеримы с жесткостью края оболочки.
В этом случае составление граничных условий в значительной
степени усложняется, так как необходимо, чтобы в каждой точке
края оболочки обобщенные перемещения были равны соответству-
ющим обобщенным перемещениям упругого элемента и чтобы при-
веденные краевые усилия и моменты оболочки были равны соответ-
ствующим нагрузкам, действующим на упругий элемент. Число не-
зависимых граничных условий в этом случае также должно быть
равно четырем.
Глава 2
РАСЧЕТ РЕЗЕРВУАРНЫХ КОНСТРУКЦИЙ НА ПРОЧНОСТЬ
Вертикальные цилиндрические резервуары состоят из следующих
основных элементов: днища, корпуса и покрытия. Покрытие опи-
рается либо на центральную стойку и корпус, либо только на
корпус. В зависимости от конструкции покрытия цилиндрические ре-
зервуары подразделяются на резервуары с жестким покрытием, пла-
вающей крышей и безмоментной кровлей. Таким образом, конструк-
ция кровли предопределяет тип резервуара и вместе с тем расчетную
схему узла сопряжения корпуса с кровлей.
Следуя схеме расчета, намеченной в гл. 1, рассмотрим предвари-
тельно безмоментное напряженное состояние и краевые эффекты
вертикального цилиндрического резервуара от действия основных
эксплуатационных нагрузок: внутреннего давления и веса покрытия
с учетом вакуума, снеговой и ветровой нагрузок. Полные напряже-
ния определим суммированием соответствующих напряженных со-
стояний.
Безмоментное напряженное состояние вертикального цилиндрического
резервуара
Основными нагрузками, определяющими безмоментное состоя-
ние корпуса, являются внутреннее давление продукта, вес кровли
и корпуса. Для резервуаров с плавающей крышей единственной на-
грузкой, действующей в направлении оси резервуара, является вес
корпуса.
Дифференциальная система (1.21), определяющая в безмомент-
ной теории усилия, имеет второй порядок.
Соответственно второй порядок имеет и система (1.22), определя-
ющая перемещения. Однако входящие в левые части уравнений
(1.22) усилия сами являются решениями системы второго порядка,
поэтому перемещения в безмоментной теории подчиняются дифферен-
циальной системе четвертого порядка, которую можно получить,
если подставить в уравнения (1-21) усилия NN2, S, выраженные
с’помощью уравнений (1.22) через перемещения.
59
Важно отметить, что для перемещений в безмоментной теории
получаются дифференциальные уравнения вдвое более низкого по-
рядка, чем в общей (моментной) теории оболочек, следовательно,
и число граничных условий в безмоментной теории на каждом краю
оболочки будет вдвое меньше, чем в моментной.
Таким образом, на каждом краю оболочки при безмоментной тео-
рии может быть задано лишь два условия, составленных из танген-
циальных усилий Ni и S и перемещений U и V.
При упругом сопряжении края оболочки с кольцом жесткости
или с оболочкой, имеющей другие геометрические или упругие пара-
метры, два граничных условия при безмоментной решении должны
состоять также только из тангенциальных усилий и перемещений.
Отмеченное относится к резервуарам любой конструкции (сфери-
ческим, каплевидным и др.).
Предположим, что в процессе эксплуатации резервуара со ста-
ционарным покрытием на цилиндрическую оболочку корпуса оказы-
вают осесимметричное воздействие следующие нагрузки: в радиаль-
ном направлении (вдоль оси Oz) гидростатическое давление столба
хранимой жидкости Р и избыточное давление газа в газовом про-
странстве р, а в продольном направлении (вдоль осиОж) — собствен-
ный вес корпуса у(?к и покрытия Qn, снеговая нагрузка qcil и из-
быточное давление газа р.
Нагрузки, действующие в продольном направлении оболочки
корпуса, уравновешиваются постоянным по высоте резервуара про-
дольным усилием, которое определяется по формуле (1.48)
__ <2п + 0.5(>к 0сн —р) Р ^2 1)
где F = nR2 — площадь поперечного сечения корпуса резервуара
в свету.
Так как компоненты поверхностной нагрузки
х„ = уп-=0, z = p + P*=p + y(H—x), (2.2)
(где у — удельный вес хранимой жидкости; Н — высота цилиндри-
ческого корпуса резервуара), то нагрузка, действующая в радиаль-
ном направлении, согласно формуле (1.28) будет уравновешена коль-
цевым усилием
N«' = Rz = R[p + y(H-x)]. (2.3)
Тогда из первого геометрического уравнения (1.29) получим
U(6) - J (Л^6’ - dx + С(6> =
= [ <2п-ЮЖ+^сн-рИ. + vRy ±) + vpR] + С<6>
60
Произвольную постоянную С<б> определим из граничного условия
в опорном сечении резервуара при х = 0:
U(6) (0) =0 и С(б)^0,
поэтому
U(6)=Sh + ?сн + (2v-1)P + ту(2Я-*)]. (2.4)
Максимальное перемещение верхней кромки оболочки при х =
= Н равно
= Р40,-5(?К + ?сн + (2v-1)Р + vyH]. (2.5)
Знак минус (—) в формуле (2.5) указывает на то, что верхний край
оболочки корпуса резервуара при действии нагрузки смещается вниз.
Из второго геометрического уравнения (1.29) определим выраже-
ние для нормального прогиба оболочки
W^ = ~{N2-vN1) = ^[2y(H~x) + (2-v)p +
। л. „ । ч((?п + 0,5Ск) 1 /(у
+ ^сн +-------------J- (2.6)
Так как нормальный прогиб оболочки резервуара при безмомент-
ном решении меняется по линейному закону, стенка резервуара при
деформации останется прямолинейной и повернется на угол:
dW^ _ yR2 ,
dx Ek ’ >
В действительности нижняя кромка корпуса резервуара жестко
приварена к окрайкам днища, а верхняя жестко сопряжена со ста-
ционарным покрытием, так что края оболочки не могут свободно
смещаться в радиальном направлении и одно из условий существо-
вания безмоментного напряженного состояния нарушается (см. гл. 1).
Поэтому в узких зонах, примыкающих к краям оболочки, неизбежно
возникнут дополнительные осесимметричные краевые моменты М
и перерезывающие усилия Q, которые существенно повлияют на пере-
распределение усилий безмоментного состояния.
Максимальное радиальное перемещение оболочки корпуса при
безмоментном решении имеет место при х — 0:
«X = [2уН + (2 - v) р + yqm v((?n+°2’5g-K)-] . (2.8)
J-srtf I JUl“ __I
Обозначив в формуле (2.6)
61
запишем окончательное выражение для радиального перемещения
оболочки корпуса в следующем виде:
Wf6) ^ + (2.10)
Таким образом, нормальный прогиб оболочки от гидростатиче-
ской нагрузки складывается с прогибом 6 от нагрузки, действующей
вдоль оси Ох
При расчете нижних поясов резервуара следует учитывать полный
вес корпуса (коэффициент 0,5 перед QK исключается). При расчете
верхних поясов необходимо иметь в виду, что QK = 0.
Для определения безмоментного напряженно-деформированного
состояния резервуара с плавающей крышей во всех предыдущих фор-
мулах следует принять, что (?п == 0, qm = 0.
Для построения полного напряженного состояния рассмотрим
отдельно основные конструктивные элементы вертикальных цилин-
дрических резервуаров. Здесь следует учитывать особенности работы
верхних и нижних узлов в зависимости от конструктивного исполне-
ния основания и кровли.
Расчет узла сопряжения стенки с днищем резервуаров большой
вместимости
Особенностью резервуаров большой вместимости (F > 10 тыс. м3)
является усиленное основание. Днище 2 выполняется из двух частей:
центральной и окрайков, сваренных друг с другом в единое кольцо.
Рис. 19
Внутренняя кромка кольца внахлестку приварена к центральной
части днища. Окрайки днища свободно лежат на гидрофобном грун-
те 5 толщиной 50 мм, под которым заложено железобетонное кольцо
из плит 4 с цементной выравнивающей подливкой 3 толщиной 50 мм
(рис. 19).
Стыки плит связаны цементным раствором марки М150. Под
железобетонным кольцом находится бетонная подготовка 6 из бе-
тона марки М50.
62
Железобетонное кольцо и бетонная подготовка покоятся на пес-
чаной подушке 7, ниже которой идет слой грунтовой подушки 8
и, наконец, земляной грунт 9, уплотненный щебнем.
Такая конструкция позволяет предотвратить опасные осадки
корпуса резервуара 1.
Нижняя кромка корпуса резервуара с внутренней и наружной
сторон жестко приварена к окраинам днища. Как показали практи-
ческие наблюдения, сила
веса корпуса и кровли
резервуара выдавливает
наружу некоторую часть
гидрофобного слоя между
окрайками и железобетон-
ными плитами, а остав-
шуюся часть плотно опрес-
совывает. На рис. 20, а
показан нижний узел ре-
зервуара до деформации
основания, на рис. 20, б—
после деформации.
Таким образом, наблю-
дается плотное прилегание
окраек днища к железобе-
тонным плитам, перемеще-
ния окраек
но
относитель-
железобетонных плит
J
Рис. 20
Рис. 21
практически равны нулю, поэтому в первом приближении можно
считать, что нижняя кромка корпуса резервуара большой вмести-
мости защемлена полностью. Расчетная схема нижнего опорного
узла резервуаров большой вместимости представлена на рис. 21,
где — толщина стенки цилиндра.
Приняв, что перемещения нижней кромки корпуса резервуара
равны нулю, получим следующие граничные условия:
= V = =
- 1 dW л
ф- я =°-
(2.11)
63
При осесимметричных деформациях оболочки резервуара гра-
ничные условия (2.11) перепишутся в виде:
РИ = О;
v 1 dW
7Г d£
(2.12)
Построим общее решение для области, примыкающей к нижней
кромке корпуса резервуара (ж >=()), складывая соответствующие
факторы безмоментного напряженного состояния (2.1)—(2.10) с мо-
ментным (1.61), (1.66) и (1.67):
WH = № + W(6) = (D3 cos 0ж + Di sin 0ж) + уДЗ(Д--)- + б;
dWH dW&P> . с7ГГ<6’ о г, , г, ч о
—J-2- == —/-------------— = Be (— D3 + D.) cos б.г —
dx dx ' dx r l\ j । а/ r
— (Ds -i £>4) sin 0x] —
М1а — Л/]нр) = — 2Z)02e“|3x (£>3 sin 0ж — Z)4 cos 0ж);
Я2н = <1H;
C1B = Cir - - 2Л03е-'« [(D3 + Z?4) cos 0ж +
+ ( — Z)3 +Z)4) sin 0ж]; (2.13)
N = N(6} — On+ 0»5<?к-К^сн — p) .
1 1 ~ 2nR ’
#2H = MKHP) + e-^ (D3 cos 0Ж + Di sin ₽ж) +
+ 7? [р + ?(Я-ж)1;
[7H = U(^ ^Ul6> = - f Nffl'dx H- C^Kp> + H(6> =
a ft j
= —2^д е'р* [ - (D3 + Z)4) cos 0ж + (D3 - sin ₽ж] -
jn Г ецт. + +(2v „ t) p+VY (2/f _ я)! + Ci»>'.
| . Г _J
Произвольные постоянные D3 и Z)4 определим из граничных усло-
вий на нижней кромке оболочки. Согласно принятой расчетной
схеме нижняя кромка корпуса резервуара большой вместимости
имеет жесткое защемление, поэтому граничные условия формули-
руются в форме (2.12).
При х = 0
им°) = °,
64
Раскрывая эти условия с помощью уравнений (2.13), получим:
4 Eh § ) °'
Произвольную постоянную С(нкр> также определим из граничных
условий на нижней кромке оболочки.
При х = О, Ян (0) = 0 из (2.13) с учетом (2.14) следует
- W (2 т +26 - w) -I- снкр) = °’
\ Ln pLn /
откуда
(2Л5)
После подстановки значений произвольных постоянных D3, D4
и С(£р) в формулы (2.13) получим следующие выражения для внутрен-
них усилий, моментов и перемещений, характеризующих напря-
женно-деформированное состояние оболочки в зоне у нижней кромки
корпуса:
Af2H = v7l/1H;
й.--«^[(}-2Я-^)^+^]:
N, - - . (2д6)
Я2Н = - уЯе^ [ (Я + ) cos + (я -1 ) sin fk +
+ Я[р+У(Я-а:)];
и* = -да е’зх [(2Я+W ~ l)cos Рж “ Isin ₽а0 “•
5 Зака» 2036 65
rgn+0,5£K + ?сн + (2 v _ 1} р + (2Я _ х} И
Рис. 22
Пример. На рис. 22 представлены результаты расчета напряженно-дефор-
мированного состояния нижнего пояса резервуара вместимостью 50 тыс. м3
но формулам (2.16) при следующих исходных данных:
Высота корпуса Я, м....................................... 18
Радиус срединной поверхности корпуса R, м............... 30,35
Толщина стенки по поясам (считая снизу вверх), см . . . = 2,6; Я2 = 2,4;
Ztg = 2,2; Я4 == 1,9;
Лг = 1,7; Л,=1,6;
^7 — Л12 — 1,2
Коэффициент Пуассона v . . .................................. 0,3
Модуль упругости Е, кгс/см2.......................... 2,1-10е
Удельный вес хранимой жидкости (нефти) у, тс/мз .... 0,9
Избытонное давление газа р, мм вод. ст.................... 200
Снеговая нагрузка дсН, кгс/м2............................ 1,4 • 102
Вес покрытия (?п, т....................................... 170
Собственный вес корпуса <?к, т............................ 320
Как видно из рисунка, изгибине напряжения Oj имеют наибольшую интен-
сивность в нижнем опорном узле и затухают на расстоянии 600—700 мм от
нижней кромки. В стыках сопряжения поясов с различной толщиной стенки
функция кольцевых напряжений о2 претерпевает разрыв непрерывности, так
как в этих сечениях не учитывалось влияние изгибающих моментов вследствие
их малой интенсивности.
66
Напряженное состояние нижнего узла резервуара на грунтовом
основании
Резервуары вместимостью менее 10 тыс. м3 ввиду сравнительно
небольшого давления на основание по окружности корпуса устана-
вливаются на гидрофобном песчаном основании без железобетонных
плит.
Это означает, что при действии нагрузки перемещением стенки
и днища пренебречь нельзя и следует рассматривать совместную
работу корпуса с днищем. Расчетная схема сопряжения показана
на рис. 23.
Составим граничные условия
для такого сопряжения корпуса
с Днищем при действии осесиммет-
ричной эксплуатационной на-
грузки.
Сделаем сечение между корпу-
сом и днищем резервуара и для
обеспечения неразрывности дефор-
мации приложим в сечении лиш-
ние неизвестные: перерезывающее
усилие хх и изгибающий момент х2
(рис. 24).
Рис. 23
Неизвестные xt и х2 данной дважды статически неопределимой
пространственной задачи определим, воспользовавшись методом сил
строительной механики.
Канонические уравнения метода сил имеют следующий вид:
бцЯй + 612ж2 + А1р -- 0; I?)
621^1 + 622^2 “Ь А2р = 0.
При этом каждое единичное перемещение 81к и перемещение от
внешней нагрузки Az р состоит из суммы перемещений корпуса (ци-
линдра) и днища.
, 612 = 612 + 6?2;
622 — 622 4- 621; (2.18)
Alp = Alp + AiP;
А2р — А2Р + А 2р.
Таким образом, граничные условия в случае упругого сопряже-
ния корпуса с днищем формируются в виде системы канонических
уравнений (2.1/).
Определим усилия, моменты и перемещения в опорном узле ре-
зервуара со стационарным покрытием вместимостью менее 10 тыс. м3,
5* 67
у которого нижняя кромка корпуса упруго сопряжена с окрайками
днища (см. рис. 24).
Для решения данной дважды статически неопределимой про-
странственной задачи необходимо сначала найти единичные переме-
щения б/ к и грузовые члены Az к корпуса и днища, которые являются
коэффициентами при неизвестных xt и х2 в канонических уравне-
ниях (2.17). Затем из решения этих уравнений можно определить
лишние неизвестные: момент х2 = Мо и перерезывающее усилие
Ряс, 24
Xi = Qo, а по ним с помощью формул (1.72) все остальные факторы
напряженно-деформированного состояния оболочки резервуара.
Так как сопротивление окраек днища растяжению значительно
выше, чем изгибу, то фактически линейные деформации днища вдоль
оси Ох равны нулю (см. рис. 24). Поэтому
б^б^б^А^О, (2.19)
а суммарные единичные перемещения и грузовые члены согласно
(2.18) примут вид:
бц-6^;
612 631 = 6121
А1Р-А?Р; (2.20)
622 — баз 622'1
А2р = А§р ~г Мр-
68
После подстановки (2.20) в (2.17) получим:
Sii^i ~Ь 612^ + Л1р = 0; (2 21)
Фи3! + (^22 4" ^22) Х2 + Мр 4* Мр = О-
Но как видно из основной системы (см. рис. 41), угловая дефор-
мация днища А2Р складывается из угловой деформации днища A^N1
от действия усилия Nь передаваемого стенкой на днище, и из угло-
вой деформации днища Д§? от действия гидростатического давления
столба хранимой жидкости высотой Я, т. е.
Д?р = А^1+А§«. (2.22
Система канонических уравнений (2.21) примет следующий окон-
чательный вид:
бхА + 612^2 4~ А1Р = 0; ?2 23)
+ (622 ~Ь 622) х2 4~ Аар 4~ ЛгМ, 4_ Mg — 0.
При определении 6/к и Д/к условимся все перемещения считать
положительными, если их направление совпадает с направлением
соответствующего усилия х^ или момента х2.
Перемещение края цилиндра в направлении силы Xf
ствием силы Xt = 1 согласно (1.72) равно
ян ______________________________L_
11 2₽»ДЦ •
Введем фиктивный коэффициент постели (1.50, а)
тг _
ЛЦ~ Д2 ’
тогда характеристика гибкости (1.53) запишется:
а4_ 3(1-v2)
Рц 4ЛЦ ЯЩ, ’
а формула (2.24) примет вид
6?! = 2-^.
Лц
Перемещение края цилиндра в направлении силы Xi под дей-
ствием момента х2 ~ 1 согласно (1.72) равно
хц _ 1
12 2₽«оц
или с учетом (2.25)
6?2 = 2-^ = 651. (2.27)
а
Перемещение края цилиндра в направлении силы под дей-
ствием нагрузки определяется по формуле (2.10):
АЬ=-т^-8=-т^-в- <2-28>
под дей-
(2-24)
(2.25)
(2.26)
69
Угол поворота края цилиндрической оболочки в направлении дей-
ствия момента х2 под действием момента х2 = 1 определяется по
формуле (1.72):
6!!-ж-4Д- <2-29>
Угловая деформация края цилиндрической оболочки в направле-
нии действия момента х2 под действием внешней нагрузки согласно
формулы (2.7) равна
A»=-w=~i- <2-30’
Для определения Д^2, 6$n, и достаточно рассмотреть дефор-
мации элементарной полоски днища, лежащей на сплошном упругом
основании. Ширина полоски равна единице.
Используя аналогию в напряженно-деформированном состоянии
цилиндрической оболочки при осесимметричном загружении и балки
на сплошном упругом основании, при определении угловых дефор-
маций днища воспользуемся формулами (1.72) для цилиндрических
оболочек, заменяя в них цилиндрическую жесткость D на балочную
Е1, фиктивный коэффициент постели на коэффициент постели
песчаного основания К и принимая положительное направление
прогиба днища согласно рис. 24.
Тогда выражение для нормального прогиба, угла поворота и из-
гибающего момента полубесконечно.й балки, лежащей на сплошном
упругом основании и загруженной на расстоянии I от края сосредо-
точенным моментом Мо = 1, вертикальной силой и равномерно
распределенной нагрузкой q, определится следующими зависи-
мостями.
Прогиб:
УМа = [Ф4 (Рд*) - Ф1 (РдО Фз (IV + Рд^) -
- Фз(РдО Ф2(Рдх+Рд/)];
=(М + 2фз (IM) фз (Рд*+м +
+ Ф2(рд/)Ф2(рд*4 ₽«/)]; (2,31)
= [2 —Фз (Рд^) + Ф2 (Рд^) Фз (Рдж +Рд^)
-ф4(Рд№(Рд* + рдг)1.
Угол поворота:
dyw М(ф;?
4г —F[Фг +ф* < ф1 +№+
+ 2Ф8(рд?) Ф3(рдх + рд/)];
-7Т = “ | ф4 (М + ф3 (№ Фг (Рд3- + РдО +
|-фа(₽д0 Фз(Рд*+Рд*)];
70
[Ф1М - ф2 (РдОФх (IV+м +
+ 2Ф4(|У)Ф3(Рдя+|Зд0]. (2.32)
Изгибающий момент:
ММа = 41 [ф3 (М + Ф! (РдО Ф4 (IV + V) +
+ фз (РдО Ф1 (V + РдО 1!
MNl = [Ф2 (Рдх) - 2Ф3 (₽до ф4 (IV+м -
-®2(VWIV+M1; (2.зз)
MQ- [Ф4 (₽дя) - ф2 (рдО ф4 (IV + Рд0 +
+ ф4(рд/)ф1 (Рд/) ф! (Рд^+Рд/)],
f к
где Рд=У^7-------характеристика гибкости днища; Ф4—Ф4—
гипербодотригонометрические функции, определяемые по формулам
(1.71). Численное значение этих функций дано в табл. 1.
При х — 0, т. е. в точках сопряжения днища резервуара с кор-
пусом, выражения для прогиба, угла поворота и изгибающего мо-
мента запишутся следующим образом.
Прогиб:
г/мо(0)=-^Ф!(Рдг);
(°)=-^г+ 2Ф« +ф’ (2-34)
мон^+фирж
Угол поворота:
[1 + ф| (м + 2Ф| (Ml; Ф2з (рд0;
т21 # и - ф1 (М Ф2 (Эд 0:+2фз (РдО ф4 (рдО ]. (2.35)
Ц/Л>
Изгибающий момент:
^„(0)=^- [1+ф1(Рд01;
MNl (0) = [1- 2Ф3 (М Ф4 (Рдо - фх (Рд0 ф2 (рд01; (2.36)
мИ°) = 1|гф’(Рд0.
Таким образом, угловые деформации днища от действия Мй = 1,
Л\ и q определяются формулами (2.35).
71
Принимая, что угол поворота положительный, если направление
его вращения совпадает с направлением момента Мо, из формул
(2.35) получим:
бд2 = [1 + ф2 (1У) + 2ф2 (|у)];
Д^ = - (М; (2.37)
Д^ = - [1 - Ф1 (М ф2 О+2Ф3 (М ф4 (Ml.
Если обозначить
Л=Ц-ФНРд0 + 2Ф?(Рд/);
Л=Ф8’(М; (2.38)
. Л = 1 - Ф1 (РдО Ф2 (М + 2Ф3 (М Ф4 (М,
то соотношения (2.37) с учетом, что М0 = 1, q = у Н, перепишутся
6Д
22 К ’ “
A»Wl = -®L; (2.39)
дд _ уЯРд^з '
Л2’“ 2К~'
После подстановки значений единичных перемещений б/к и гру-
зовых членов Д( к корпуса и днища в систему канонических уравне-
ний (2.23) получим:
2 -|з-+ 2 х2- 6 = 0;
Лц Дц Лц
Из решения этой системы следует:
-г ~м________________Г AR । уЯРц ( 1 I 1 ।
2Xp9 + xupjF1L 0Рц + ~х7-(, + Ж "г
। Дцвд^з \ _ ~|.
f 2ЛГ₽ц J К J’
*1= *?°= Ж + Х
х/Глй I У#0Ц (1 1 \ I Рд-^Л "]
хГРц± I/ Ярц 2ЯРц /+—к—_]• (2.40)
72
Таким образом, определены выражения для момента Ма и пере-
резывающей силы Qo (лишние неизвестные), действующие по линии
упругого сопряжения оболочки корпуса резервуара с днищем.
Если в формулах (2.40) принять = F?=FZ = 0, то упругая
заделка корпуса в днище станет абсолютно жесткой и выражения
для момента и перерезывающей силы в нижнем опорном сечении
примут вид:
(2.41)
Полученные значения полностью совпадают со значениями мо-
мента и перерезывающей силы (2.16) в опорном сечении при х — 0
резервуара большой вместимости со стационарным покрытием, у ко-
торого нижняя кромка корпуса имеет жесткое защемление. Интен-
сивность максимальных продольных изгибных напряжений Gj в опор-
ном сечении, например, резервуара вместимостью 50 тыс. м3 при
жестком защемлении корпуса согласно рис. 22 равна —3600 кгс/см2,
а при упругой заделке, когда Мй определяется по формуле (2.40),
составляет —1880 кгс/см2.
Определив значения Мо и Qo в нижнем опорном узле, можно
с помощью формулы (1.72) вычислить усилия, моменты и перемеще-
ния в любой точке оболочки корпуса и днища резервуара вмести-
мостью менее 10 тыс. м3.
Расчет резервуара с плавающей крышей
В настоящее время в практике резервуаростроения как за рубе-
жом, так и в СССР широкое распространение получили понтоны как
средства снижения потерь от испарения.
Несмотря на то, что стоимость сооружения таких резервуаров
по сравнению с обычными оказывается несколько выше, экономиче-
ские расчеты показывают, что разница в стоимости окупается в тече-
ние 1,5—2 лет за счет уменьшения потерь нефтепродукта. Понтоны
целесообразно применять для оперативных резервуаров большой
вместимости, работающих с большим коэффициентом оборачивае-
мости при хранении сырой нефти и легкоиспаряющихся жидкостей.
Весьма часто понтон используется в качестве специального обо-
рудования резервуара без изменения его конструктивной схемы.
Однако он может служить также в качестве покрытия резервуара
(резервуары с плавающей крышей). Очевидно, использовать такую
конструкцию целесообразно в районах с низкой нормой снеговых
осадков. Плавающая крыша резервуара состоит из коробов-понто-
нов, сваренных друг с другом в единое кольцо, и днища. Кромки
днища по всей окружности приварены к коробам-понтонам.В опорож-
ненном резервуаре плавающая крыша находится в нижнем положе-
нии и лежит на опорных стойках, при залитом — плавает на зеркале
73
нефтепродукта и перемещается вместе с ним вверх и вниз. Для гер-
метизации в зазоре между краем плавающей крыши и корпусом
резервуара установлен уплотняющий затвор, препятствующий про-
хождению паров нефтепродукта в атмосферу.
Для придания верхней кромке корпуса резервуара с плавающей
крышей пространственной жесткости и обеспечения цилиндрической
формы предусмотрено кольцо жесткости, которое приварено к верх-
ней кромке корпуса снаружи. Таким образом, условия работы верх-
них поясов таких резервуаров существенно отличаются от условий
работы верхних поясов резервуаров со стационарным покрытием.
Необходимые расчетные формулы для нижних поясов резервуа-
ров получим непосредственно из (2.16) с учетом, что 6=0. Ввиду
незначительного влияния на напряженное состояние резервуара
веса корпуса его можно не учитывать* Тогда напряженно-деформиро-
ванное состояние опорной части корпуса резервуара с плавающей
крышей большой вместимости, у которого нижняя кромка жестко
защемлена в основании, будет определяться зависимостями:
w«= "ёг е“₽ж [~ н cos + (т ~ si.n Ю+7~Уг~- J
Фн = е-₽к Г - cos рж + (1 -20Я) sin 0ж) + ;
ХУ ГЪ | xLIh
е'рж - 1) cos Pz 4- sin 0г];
Л/2н = vM1H;
A\ = 0; (2.42)
<2ih = - бй—8Й)е Рж ~cos +sin
Я3н = — уЯЯе^ £ cos {Зж(Ч------------------sin 0а:J -f-y/? (Я — х);
и- = -ж е'рж [(1 - W cos + sin ₽ж] +
В резервуарах с плавающей крышей вместимостью менее 10 тыс. м3,
у которых нижняя кромка корпуса упруго сопряжена с окрайками
днища, выражения для изгибающего момента и перерезывающего
усилия в опорном сечении согласно формулам (2.40) запишутся:
' ps в;
(2.43)
74
где
„ — f -1 1 । \ (2 ЛЛ)
11 ' 2£рзц+ядак ярц ' 2Крц г (2л)
Подставив зависимости (2.43) в формулы (1.72) и сложив получен-
ное моментное напряженное состояние с безмоментным, определяе-
мым соотношениями (2.3), (2.7) и (2.10) с учетом S = 0, найдем выра-
жения для внутренних усилий, моментов и перемещений в нижней
зоне корпуса резервуара
ТУН - Wр) + w<6) = [Н (2рФ4 - Ф3) + Я - X];
Фи = Ф^р) + Ф(б) = [- Ярц (2р,Ф2 + Фх) +1 ];
М1н=М(«Р) = ^-(2рФ3-РФ4);
M2„ = vM]H; (2.45)
е1а = ^р>-^(ф2-2рф3);
Я2н = </ + Я<б> = УН [Н (2рФ4 — Ф3) + Н-х].
Из формул (2.45) нетрудно увидеть, что при х = 0
W (0)^0;
Ф(°) = ^Ц-Я|}ц(Ц-2р)], (2.46)
т. е. в соответствии с принятыми в расчете допущениями нижняя
кромка корпуса, упруго сопряженная с окрайками днища резервуара,
в горизонтальной плоскости не перемещается в радиальном напра-
влении, а лишь поворачивается в пространстве на угол ф (0).
Напряженно-деформированное состояние верхнего пояса ре-
зервуара с плавающей крышей зависит от совместной работы обо-
лочки и упругого кольца жесткости. На рис. 25 представлена схема
75
Рис. 26
сопряжения цилиндрической оболочки корпуса с упругим кольцом
жесткости. Для составления граничных условий в верхнем узле
сопряжения корпуса с упругим кольцом жесткости необходимо
иметь уравнения равновесия, геометрические и физические ура-
внения криволинейного стержня.
В вертикальных цилиндрических резервуарах с плавающей кры-
шей отношение радиуса кривизны к высоте сечения упругого кольца
жесткости в зависимости от объема колеблется в диапазоне 80—230,
так что при выборе уравнений деформации можно использовать ос-
новные гипотезы призматического бруса малой кривизны [6]. Пред-
положим, что ось стержня
имеет начальные кривизны
в двух плоскостях ход и xoz,
т. е. в ненапряженном состоя-
нии ось стержня представляет
собой пространственную кри-
вую.
Пусть, кроме того, стержень
скручен (главные оси сечения
вращагртся вокруг оси стержня
с изменением положения сече-
ния вдоль координаты ж) и его
начальный относительный угол
закручивания определяется
функцией 0О.
Рассечем стержень. пло-
скостью, нормальной к оси,
и рассмотрим внутренние силы
на площадке, нормаль к ко-
торой направлена в сторону
рассмотрим действие правой части
положительной оси Ох, т. е.
стержня на левую. Внутренние силы в сечении могут быть предста-
влены в виде главного вектора Р и главного момента М.
Проектируя их на координатные оси, получим три внутренних
усилия: нормальную (продольную) силу N и поперечные (перерезы-
вающие) силы ()г и Qy, а также три момента: крутящий момент Мх
и изгибающие моменты Му и Мг (рис. 26).
Связывая усилия и моменты с напряжениями, определим их
по величине и знакам:
N= \<JxdF;
F
(2-47)
F
(2.48)
(2.49)
F
76
Мх = J (W - W) dF-, (2.50)
F
My= \(j>:zdF; (2.51)
F
M^^a^dF,
F
(2.52)
где F — площадь поперечного сечения стержня.
Чтобы с помощью этих формул определить положительные на-
правления моментов, нужно в сечении взять точку с положитель-
ными координатами у и z, показать в ней компоненты напряжения
ах,\у и тх2 и проследить, в каком на]
сительно осей местной координатной
системы Oxyz.
Главный вектор и главный момент
в проекциях на оси координат могут
быть представлены следующим об-
разом:
P^Ni^QynQzk-, (2.53)
М = Мх1^М^-Мгк, (2.54)
где i, 7, /с—орты координатных осей
Ох, Оу и 0z соответственно. Знак
минус перед Мг означает, что этот
момент, если он положителен вращает
вокруг оси в отрицательном напра-
влении, т. е. против хода часовой
стрелки, если смотреть в положи-
тельном направлении этой оси.
Вырежем из стержня элемент
длиной ds (рис. 27). На левый торец
этого элемента действуют силы, ко-
торые выражаются через главный
вектор — Р и главный момент
—М. Знак минус необходим здесь
потому, что соответствующие положительные векторы Р и М пред-
ставляют собой действие той части стержня, которая расположена
справа от сечения, на остальную часть стержня.
Пусть на стержень действует распределенная нагрузка, интен-
сивность которой выражается вектором q, и внешний момент интен-
сивностью т.
77
Приравнивая нулю векторную сумму всех сил, приложенных
к элементу, и сумму моментов всех сил относительно точки 0, полу-
чим два векторных уравнения равновесия:
— Р 4- (Р 4- dP) -J-qds = Q;
— dsi X (— Р) — М-\- (М 4- dM)----х qds -!-mds =^0.
Здесь —dsi представляет собой радиус-вектор точки приложе-
ния силы — Р, проведенный из моментной точки 0. На бесконечно
малом отрезке интенсивность нагрузки q и т принимается постоян-
ной, и поэтому точка приложения силы qds и момента mds находится
посередине отрезка ds. Слагаемое — -jdsi х qds во втором урав-
нении можно отбросить как величину второго порядка малости при
наличии величин первого порядка малости.
Приводя подобные члены и разделив оба равенства на ds, будем
иметь:
(2.55)
j—-1 хР-т = 0,
as 1 1
Равенства (2.55) выразим в проекциях на координатные оси.
Принимая во внимание, что одноименные оси, проведенные в началь-
ном (левом) сечении элемента и его конечном (правом) сечении, будут
непараллельны, т. е. в равенствах (2.53) и (2.54), выражающих глав-
ные векторы внутренних сил и их моментов через проекции, орты
осей г, / и к не будут постоянными векторами, так как их направле-
ния меняются от сечения к сечению. Поэтому, подставляя выраже-
ния (2.53) и (2.54) в уравнения (2.55), нужно производные
4г (ж 4w)
и т. п. находить по правилу дифференцирования произведения двух
функций.
Подставив еще выражение для вектора интенсивности нагрузки
д = ?/4-ад'4-
и для вектора интенсивности внешних распределенных моментов
т — mxi ту] 4- тгк,
78
получим два следующих векторных уравнения:
7 I 7 । d®2 к \ N di \ О — + О ~
ds 'ds ‘ 1 ds й rfs ' ' * ds
+ + QyJ т (hk — 0;
(2.56)
iMx 7 I ^My 7— dMz L\M & I
ds ' ds 1 ds ' x ds '
M +
У ds z ds 1
H-1 x (Ni + Qyj + Qzk) +
+ m = 0.
Теперь найдем произ-
водные от ортов. Произ-
di
водную — можно предста-
вить как отношение при-
ращения (его главной
части) di вектора i к дли-
не ds элемента оси стер-
жня. Приращение вектора
постоянной длины может
произойти только за счет
вращения этого вектора
вокруг осей Оу и 0z, при-
чем вектор di можно счи-
тать перпендикулярным
к орту i.
На рис. 28, а изобра-
жены приращения векто- рис 28
ров i и к при вращении се-
чений, а вместе с ними и координатной системы вокруг оси Оу
в положительном направлении на угол xOyds, определяемый началь-
ной кривизной стержня хоу. Имея в виду, что длина вектора г равна
единице, найдем угол поворота
ds
а отсюда модуль производной
I di
I ds
— хоу.
79
Вектор di, а вместе с ним и вектор параллельны оси Oz, но
направлены в отрицательную сторону этой оси. Следовательно,
Однако это не полная величина производной ~, так как следует
учитывать и вращение сечения вокруг других координатных осей
системы.
На рис. 28, б изображены приращения векторов i и j при враще-
нии сечения вокруг оси Oz в положительном направлении на угол
n01ds, определяемый начальной кривизной стержня ког. При этом
вращении
а вектор di имеет направление ; и поэтому ,
dl
Естественно, при вращении сечения вокруг оси Ох орт i прираще-
ния не получает (рис. 28, в).
Суммируя полученные результаты, найдем полную величину
производной
= (2.57,а)
Таким же способом найдем значение двух других производных:
A = 80fc-xJ; (2.57,6)
~ = (2.57,в)
Подставим эти значения производных в уравнения (2.56), сгруп-
пируем слагаемые по ортам и приравняем нулю множители при каж-
дом орте в отдельности.
Тогда получим шесть уравнений равновесия:
—Q^z + Qz^y-i ^=°;
-^+^хо2-(?Д + д1/ = 0;
80
^-^+<2Д + ?г=-0;
— Му%ог — Мгхоу -}- тх = 0;
+ Млх 4 Мг0о — Qz — ти — 0;
Jn ( л 1 и X <ь у '
(2.58)
+ Мхкоу - MyQ0 - Qy - mz = 0.
Эти уравнения в несколько другом виде в 1859 г. были опублико-
ваны Кирхгофом, а спустя 3 года в данном виде Клебшем, поэтому
их обычно называют уравнениями Кирхгофа — Клебша.
Если начальные искривления и начальное кручение стержня
считать равным нулю
^01/= иог = 00 = 0»
интенсивность внешнего момента также приравнять нулю
тх = ту — тг = О,
а элемент дуги ds заменить на dx, то будут получены следующие
уравнения равновесия для прямого стержня:
dN п.
dx °’
Тг+«’ = °;
dMx Q.
dx ’
dMy
dx
^--Qy = Q.
dx y
<?г = 0;
Теперь установим зависимости между деформациями и перемеще-
ниями кривого стержня.
В результате упругой деформации поперечные сечения стержня
изменяют свою ориентировку в пространстве, повернувшись на
угол а вокруг оси Ох, на угол 0 вокруг оси 0у и на угол у вокруг
оси 0z местной системы координат. Эти углы можно считать проек-
циями вектора угла упругого поворота А в пространстве, т. е.
Л — аг 4 0/ 4 ук.
6 Заказ 2036
81
Каждое сечение поворачивается на свой угол и приращение угла
поворота на длине элемента ds стержня можно оценить дифферен-
циалом dA. Разделив эту величину на ds, мы получим взаимный
dA
угол упругого поворота двух сечении, отстоящих одно от дру-
гого на расстояние, равное единице. Этот взаимный угол поворота
до деформации можно изобразить вектором
/it = 0ог 'Яду] 4- xozZc,
после деформации — вектором
K“ = e'oi +Ху/ + ХгЛ:.
Разность этих векторов равна приращению вектора на длину
единицы
Введя для упругих деформаций обозначения:
ок=о*-е0;
= Ку хог/;
= иг ИОг,
последнее векторное равенство напишем в виде
6кг + = “J? (ai + М +'УЙ-
Выполняя дифференцирование в правой части равенства, следует
помнить, что орты г, у, к — переменные векторы.
В результате получим:
е 7+ 4 г+ 4т Г+ 4т
+• а (иОг/ - >о/Л) + Р (0<Л - «огО + Y 0W - 0оЬ
Приравнивая множители при одинаковых ортах, получим ра-
венства, связывающие упругий относительный угол закручивания
и упругие кривизны с упругими углами поворота сечения:
0к = -^Г-иог₽ + ио</У;
к,/ = -^- + хО2а-0оу; (2.59)
82
Теперь линейную деформацию е и углы поворота (3, у нужно
связать с упругими перемещениями сечения. На рис. 29 изображена
ось стержня в недеформированном и деформированном состояниях.
Элемент ab, длина которого равна ds, в результате деформации пере-
местился в положение а'Ь', так что длина его стала ds'.
Вектор перемещения сечения а равен
U = Ui + Vj + Wk.
Элемент ds можно с точностью до бесконечно малых второго
порядка считать прямым отрезком и приписать ему направление
орта i, аналогично элемент ds' считать направленным отрезком, сов-
падающим с ортом г'. Так как из точки а в точку Ъ можно попасть
двумя путями: через а' или
через Ъ, то
аа" + а’Ь' = ab’ — ab-\- bb';
U + ds'T = (U + dU),
откуда следует, что
dU = ds'i'‘ — dsi
или
dU ds' + "t
—- = i —i.
ds ds
Рис. 29
Дробь ds’/ds представляет собой отношение длины деформирован-
ного элемента к его длине до деформации, поэтому
ds' .
=1 + 8,
as 1 ’
(е — относительное удлинение оси стержня),
-^ = (1 + е) Г —i = i' —i +ei".
Так как деформации малы и I' отличается от i на малый вектор,
то 8i' отличается от ei на вектор второго порядка малости, поэтому
ei'ei и последнее равенство запишется:
= (2.60)
Запишем равенство (2.60) в проекциях
dU _ dU
ds ds
+ ^-k + U^- + V^-±W^- .
ds ds 1 ds ds ds
6*
83
Использовав равенства (2.57) и сгруппировав слагаемые по ортам,
получим
#-(^-Гх» + И'МГ+(т->
UH02-we0)7+
+(^r+F0o-^)*-
(2.61)
Теперь рассмотрим проекции вектора i'—i. Ввиду того, что мо-
дуль вектора г не изменится, малое приращение этого орта i’—i
следует считать перпендикуляр-
ным самому орту г. Следовательно,
вектор i'—i параллелен плоскости
Oyz и может быть разложен по
ортам j и к. Поскольку модуль i
равен единице, модуль вектора
i'—i измеряет угол поворота се-
чения относительно начала коор-
динат, т. е. центра тяжести сече-
ния (рис. 30). Отсюда следует,
что проекции вектора на оси Оу
и Oz должны быть равны углам
упругого поворота сечения вокруг
этих осей. Из рисунка видно, что
ось Оу дает угол поворота вокруг
проекция этого вектора на
оси Oz, т. е.
(Г - г% = у,
а проекция на ось Oz дает угол поворота вокруг оси Оу в отрицатель-
ном направлении:
(?-Т)г=-р.
Таким образом, правая часть равенства (2.60) принимает вид
ei+yj — pfc. (2.62)
Приравнивая множители при одинаковых ортах в равенствах
(2.61) и (2.62), получим:
е = -^—V^oz+Wnoy;
y=-^-+u^-w^
(2.63)
84
Равенства (2.59) и (2.63) дают возможность относительный угол
закручивания и упругие кривизны выразить через перемещения и на-
чальные искривления стержня.
Если в равенствах (2.63) принять начальные искривления стержня
равными нулю, т. е.
^02 = — % — 0,
и заменить ds на dx, то получим зависимости между деформациями
и перемещениями прямого стержня:
Полученные условия равновесия (2.58) и геометрические зависи-
мости (2.63) должны быть связаны между собой с помощью физиче-
ских зависимостей, которые в теории упругости являются зависи-
мостями закона Гука:
N = eEF: (2.64)
Mz= — v.zEJz, (2.65)
My = v^EJy, (2.66)
ЛЛ = 9к£7кр. (2.67)
Совокупность уравнений равновесия (2.58), двух групп геометри-
ческих уравнений (2.59) и (2.69), а также физических уравнений
(2.64)—(2.67) позволяет вывести уравнения упругого сопряжения
кольца жесткости со стенкой резервуара.
85
Если сделать сечение между кольцом жесткости и верхней кром-
кой цилиндрического корпуса резервуара согласно расчетной схеме
(см. рис. 25), то на бесконечно малый элемент кольца жесткости со
стороны оболочки резервуара будут действовать реактивные силовые
факторы 7VK, SK, QK, Мк (рис. 31). В результате действия этих внеш-
них силовых факторов в кольце жесткости возникнут неизвестные
внутренние усилия N, Qy, Q2 и моменты Мх, Му, Мг, положитель-
ные направления которых даны на рис. 31.
Положительные направления усилий и моментов, действующих
яа площадках поперечных и продольных сечений оболочки корпуса,
показаны на рис. 32.
В точках сопряжения уп-
ругого кольца жесткости
с верхней кромкой цилиндри-
ческого корпуса резервуара
соблюдаются следующие
условия:
77 — _ V •
с/ к ' ц,
wK=~w^,
ЛГК = Л\Ц; (2.68)
о _ о [ 'Инц .
— °12ц — °12ц Т д ,
мк-м1ц,
где Рк, Ук, WK — перемещения кольца жесткости в направлении
юсей Ох, Оу, Oz (см. рис. 31); Йц, Тц, — перемещения верхней
кромки корпуса резервуара в направлении осей Ох,Оу, Oz (см. рис. 32);
«к — угол поворота вокруг оси Ох сечений кольца жесткости (ак >>
> 0, когда поворот сечения происходит по часовой стрелке, если
смотреть в сторону отрицательного направления оси Ox); R — радиус
кривизны срединной поверхности оболочки корпуса резервуара;
е =— безразмерная координата; N 1ц, 512ц, <?1Ц, М 1ц — соответ-
ственно продольное усилие, обобщенное сдвигающее усилие, обоб-
щенное перерезывающее усилие и изгибающий момент, действующие
на верхней кромке оболочки корпуса.
Составим для данной пространственной задачи уравнения равно-
весия бесконечно малого элемента ds кольца жесткости. Для этого
воспользуемся уравнениями равновесия кривого стержня (2.58), вы-
«6
веденными для общего случая. В нашем частном случае следует при-
нять: 6о — И0г — 1_е И0й— д » Qx = *^к> ^ = 7VK; (2.69)’ Qz = Qw тх = Мк', т,. = тг = 0. У А
После п следующие юдстановки условий (2.69) в уравнения (2.58) получим уравнения равновесия упругого кольца жесткости: т+^=0; L]yjn =о- (2.70> &=0;
ds Т р тх Чу и-
Исключим из уравнений (2.70) перерезывающие усилия Qy и Qzt
-?-+4’-^+1?к=0;
ds 1 R 8s к
д2Мг , 1 8МХ । ЛГ- _fj.
+ = (2.71).
l-Mz + MK = Q.
87
С помощью уравнений (2.59) и (2.65)—(2.67) с учетом условий
первого и второго уравнений (2.69) выразим моменты через упругие
углы поворота сечения кольца жесткости:
Му = Е1уу.у = Е1у~\ (2.72)
Учитывая условия первого и второго уравнений (2.69), запишем
геометрические уравнения (2.63) в следующем виде:
. - ds + R
avK
6 = — (9Wk_____—й )
P \ ds R U&]'
Тогда выражения для продольной силы и моментов согласно
уравнениям (2.64) и (2.72) примут вид:
х кр \ R ds 1 ds / ’
/ - ' (2-73)
Му=—Е1у ;
у у \ ds% R ds ] ’
М РГ I 1 \
Мг~ EIZ дз., д «Не-
обычно при расчете кривых стержней в случае пространственной
деформации ось стержня принимается несжимаемой. При этом до-
пущении первое равенство (2.63), в котором следует положить е = О,
преобразуется в условие нерастяжимости стержня:
ds R
Физическое уравнение (2.64) при этом теряет смысл.
В нашем случае радиус кривизны оси упругого кольца жесткости
резервуаров с плавающей крышей в зависимости от емкости равен
10—30 м при достаточно малой площади поперечного сечения (50—
200 см2), поэтому в результате действия продольной силы N ось
кольца жесткости может получить некоторые продольные деформа-
ции. В данном случае допущение о несжимаемости оси стержня
38
может привести к значительной погрешности в расчетах, поэтому
е 0.
Подставляя соотношения (2.73) в (2.71), получим:
\ Ely ( №WK_____
( ds* г R ds j R \ aS3 f{ 0S2 U’
vi / 1 02aK \ , <?7Kp ( 1 d2TK । д2<Хк \ । м _
~EI* \-0^--r-^}^-r-\-r-0^- + ^)^N^'
vj ( 1 d»ZzK \ EF / 0UK . 1
Jy\ 0si R 0s3 ) R \ ds ‘ R
Cl 7 1 , a2gK \ / а2Ук______1
KP \ R 5s2 T 5s2 )T Д ( &2 R
Принимая во внимание условия совместности деформаций (2.68),
перепишем эти уравнения в следующем виде:
Ely ( 03W4 1 Й2Уц \ „ 7 02йц 1 dWn, \
R \ 3s» R 0s2 ) \ dst R 0s J 1
pj ( diuu____1 \ czKp (ажц
/г\ Osl RV 3g3s2 ) R2 \ 0S2 "Г 3gds2
«к) + ^к = о.
^12Ц __ Q.
(2.74)
^^12Ц А.
0s ’
dsi R ds^ R \ ds R
Е1г / Wu 1 Жц \ 67кр ( dWu, , Жд
R \ dsi R2. 0% )~T R \ a«2 + 01012
Таким образом, для данной пространственной задачи получены
четыре условия совместности деформаций верхней кромки цилин-
дрической оболочки корпуса и кольца жесткости — граничные усло-
вия. Так как оболочка корпуса цилиндрических резервуаров замк-
нута в окружном направлении, то компоненты поверхностной и крае-
вой нагрузок, внутренние силы, моменты и перемещения должны
быть периодическими функциями угла 0 с периодом 2л.
Отсюда выражения для внутренних усилий, моментов и пере-
мещений в точках сопряжения корпуса с упругим кольцом жесткости
можно представить в виде тригонометрических рядов:
С7Ц= 2 U cosn0;
п-0
Уц = 2 V sin 7i0;
n=0
Жц = 2 W cosnG;
(2.75)
л\ц = 2 ^ricos ”9;
89
co
<У12ц = 2^12 sin п0;
n«0
00
<?1ц = 2 Qi cos n0;
я=0
М1Ц = 2 Дхcos п0;
П=0
^12Ц = 2^12 sin П0,
п-0
® которых коэффициенты являются функциями только независимой
переменной £.
Принимая во внимание, что s = 7?0, подставим выражения (2.75)
в уравнения (2.74), продифференцируем последовательно по 0 и после
сокращения на тригонометрические множители sin «0 и cos «0 полу-
чим для га-го члена разложения следующие граничные условия:
(nW + V) + (W + nV) + S12 +4М12 = 0; (2.76)
^(?г2^+4г)+тЕ(ЛГ+^г)+ЛГ1=0; (2'77)
^{nW+V) + ^{W^nV) + Qi + ^^Q. (2.78)
#(n2t/+4r)+^£’(t7+^)“Jli=0- (2-79)
Для исследования граничных условий (2.76)—(2.79) ограничимся
первыми тремя гармониками, т. е. отрезком тригонометрического
ряда из трех первых членов. Точность такой аппроксимации функций
наиболее характерных нагрузок, действующих на резервуар, вполне
достаточна для инженерных расчетов.
п = 0. При п = 0 нагрузка, внутренние усилия, моменты и пере-
мещения должны быть симметричны относительно вертикальной
оси резервуара. Следовательно, внутренние усилия, моменты и пере-
мещения, содержащие множитель sin nQ в выражении (2.75), при
несимметричной деформации превращаются в нули
V-512 = M12 = 0.
Тогда уравнения (2.76) и (2.78) при п = 0 тождественно удовлет-
воряются, а (2.77) и (2.79) принимают вид:
+ = (2.80)
90
С физической стороны уравнение (2.80) выражает растяжение-
кольца поперечной нагрузкой, передаваемой с верхней кромки обо-
лочки корпуса резервуара; уравнение (2.81) — кручение кольца
жесткости с равномерно распределенными вдоль оси Ох моментами.
Уравнение, аналогичное (2.81), получено С. П. Тимошенко [16]
в случае кручения кругового кольца крутящими моментами, равно-
мерно распределенными вдоль его оси.
Здесь уместно отметить, что существует критическое значение
момента Mt, при котором происходит потеря устойчивости кольца
при кручении, так называемое «опрокидывание». Рассмотрим это
явление подробнее. Предположим, что поперечное сечение кольца
имеет форму круга. Тогда
лМ
~Т'
где г — радиус окружности поперечного сечения кольца.
Учитывая, что угол поворота сечения кольца из-за малости
деформации равен
1 dW
“к ~ R dl
—sin а,
запишем уравнение (2.81) в виде
«г _ 2?Hr4sina
При 0 ' а с' А момент М {
максимального значения
возрастает, достигая при а = —-
А
^1 max
Enri
HP •
Для дальнейшего увеличения угла а требуется меньший момент.
При а = л (кольцо «вывернуто наизнанку») М1 = 0. Кольцо при
этом находится в состоянии неустойчивого равновесия и при малей-
шем отклонении возвращается в начальное положение.
При а л момент Mt <0. Это означает, что для удержания
кольца в заданном положении в этом случае необходимо приложить
момент обратного знака.
Полученное выше значение 7iflmax можно рассматривать как кри-
тическое значение момента, при котором кольцо теряет устойчивость
и «опрокидывается».
Для кольца, имеющего в сечении произвольную форму, крити-
ческое значение момента равно:
(2-82>
91
п — 1. При и = 1 уравнения JX76)—(2.79) принимают вид:
(2.83, а)
4-(ЕЛ + й/кр)(р +™L)=-^; (2.83,6)
•^-(4т(-(')(«'+И-(2.83, в)
^(E!,+gi„i(v+4г)=м‘- (2.83,г)
Уравнения (2.83, а) и (2.83, в) содержат совершенно одинаковые
левые части. Если умножить почленно уравнение (2.83, б) на R,
то левая часть его также будет совпадать с левой частью уравнения
(2.83, г). Вычтем из уравнения (2.83, а) уравнение (2.83, в), а из
уравнения (2.83, б) уравнение (2.83,'г).
После вычитания получим:
<?i-S12 = 0; (2.84)
RNt 4-М! = 0. (2.85)
Уравнение (2.84) с физической стороны означает, что проекции
всех сил на ось 0z, действующих на кольцо жесткости со стороны
оболочки, равны нулю. Уравнение (2.85) показывает, что сумма
моментов всех сил относительно оси Оу, действующих на кольцо
жесткости со стороны оболочки, равна нулю.
Уравнения (2.84) и (2.85) можно получить непосредственно из
условий равновесия всех сил, действующих на верхней кромке обо-
лочки корпуса резервуара с плавающей крышей (см. рис. 32).
Из = 0 следует:
л л
2 j SKR sin0cZ9 — 2 j QrR cos9d9 = 0,
о о
а из 2momj/ = 0 имеем:
2 J MKR cos 9cTO + 2 J 7VK7?2 cos 0d9 = 0.
о о
Используя пятое — восьмое соотношения (2.68), получим:
Л л
2 j (512ц + 4 М12ц) R sin 0Й9 - 2 J (<?1Ц + R cos 9(/9 = 0;
о о
2 [ M1UR cos 0cZ0 2 [ 2 cos QdQ = 0.
о о
92
Принимая во внимание тригонометрические ряды — четвертое—
восьмое уравнения (2.75) — при п = 1, запишем уравнение в сле-
дующем виде:
(& + 4 М12) j cos2 0d6 - ( 512 + 4 M12) У sin2 0dQ = °;
0 0
(Mj+RNJ j cos2 OdO = 0.
о
Так как
j sin2 ode = у cos2 ede=у,
о о
то
Qi ~ ^12 — 0;
RN. +Af1 = O,
т. e. мы пришли к уравнениям (2.84) и (2.85).
Таким образом, для данной пространственной задачи при п = 1
составлены два граничных условия. Но для определения произволь-
ных постоянных, входящих в общие интегралы исходных дифферен-
циальных уравнений цилиндрической оболочки, число граничных
условий на верхней кромке оболочки должно быть равно четырем.
Следовательно, не хватает еще двух граничных условий. Это несоот-
ветствие объясняется тем, что поверхностная нагрузка, представлен-
ная первым членом разложения в тригонометрический ряд (при п —
= 1), является неуравновешенной системой сил, под действием
которой кольцо жесткости вместе с оболочкой перемещается в про-
странстве с двумя степенями свободы, т. е. данная пространственная
задача дважды кинематически неопределима.
Для устранения кинематической неопределимости необходимо
с помощью метода перемещений строительной механики определить
перемещения кольца жесткости й тем самым получить два недоста-
ющих граничных условия.
Раскрытие кинематической неопределимости при действии по-
верхностной нагрузки, представленной первой несамоуравновешен-
ной гармоникой, будет дано ниже в общем виде для резервуара со
стационарным покрытием и, в частности, при соответствующих пре-
образованиях может быть использовано для резервуара с плава-
ющей крышей.
п = 2. При п — 2 уравнения (2.76)—(2.79) принимают вид:
(2W+ V) + (W+2V) +Sl2+4- M12 = 0;
^Elz ( / T7 I A I ^KP [ T7 1 \ I ЛГ П.
TrT- t4u + ~dT J+-R4-1u + J+0’
93
(2IV + Г) + (W + 2 V) + Q,+4 М„ = 0; (2.86)
-^•(4£/+4г)+^(^+О-лг‘=°-
Уравнения (2.86) можно записать в более компактной форме:
-^-(IV + 2V) + 25x2-<2x^0;
(2PF + V) + 2<?t -s12 + 4 = °;
ЗЕ12 (,тт , dW \ . ,, R п (2'87)
(и+чг) ~NiR ~
Этим же способом можно получить граничные условия в точках
сопряжения корпуса с упругим кольцом жесткости резервуара с пла-
вающей крышей для любого номера члена тригонометрического
ряда. Так как при любом значении п (кроме п = 1) поверхностная
нагрузка самоуравновешена, то всегда будем иметь четыре граничных
условия, что соответствует числу произвольных постоянных, входя-
щих в общие интегралы исходных дифференциальных уравнений
цилиндрической оболочки корпуса.
Используя выведенные условия сопряжения кольца жесткости
со стенкой резервуара, определим напряженно-деформированное
состояние оболочки резервуара в области, примыкающей к верхней
кромке корпуса. Для этого сложим безмоментное решение (2.1) —
(2.7) при 6 = 0 с моментным (1.62). Тогда выражения для полных
усилий, моментов и перемещений верхней части оболочки корпуса
резервуара с плавающей крышей запишутся:
= еР(х-Я) [Dxcos р (х — Н) + D> sin р (х— Н)\ 4- (Н—х);
^в. = ре₽ (Х-Н) [(£>1 cog р _ Я) + ( _ D1 + Sin р (Ж _ Я)] -
у/?2 .
Eh •
М1Ъ -- — 27)р2е₽ (А’И) [Z)2cos р (х — Н) — sin р (х — Н)];
М2в = v7IT1B;
Л\=0-,
(?1В = -2£>рзе₽ (х-н) [(£)2 — -Ox) cos Р (^ — Я) — (D1 + Z)2) sin р (ж — Я)];
(2.88)
94
Я2в = ~ ев (х’н) [Лх cos р (х— Н) 4- D2 sin р (х - Я)] + yR (Н-х)-,
= W ®Р (х~Н) [(Dx - D2) cos р (х - Н) + (Рх + Я2) sin р (х - Я)] -
^р/1
vyRx(2H— х)
2Eh
Произвольные постоянные Ях и Я2, входящие в формулы (2.88),
определим из граничных условий в точках сопряжения верхней
кромки корпуса с упругим кольцом жесткости.
При осесимметричной деформации оболочки при х — Н эти
условия согласно (2.80) и (2.81) имеют вид:
^>в(Я) + <21в(Я) = 0;
Е1г dWB(H) м п
-Jp-Tx-------М11;(Я) = 0,
(2.89)
где
где F, 12 — соответственно площадь и момент инерции относительно
оси 0z поперечного сечения кольца жесткости.
Раскрывая эти условия с помощью уравнений (2.88), получим
п Удг
1 (1^С01Ш3)₽^ ’
п - М1Уда
2 (l + oiiCOa)^ ’
“2=1 + '2₽я7‘
Подставляя значения произвольных постоянных D х и D 2 в урав-
нения (2.88), получим выражение для усилий, моментов и переме-
щений, определяющих напряженно-деформированное состояние кор-
пуса резервуара в зоне сопряжения с упругим кольцом жесткости:
=Ti+£)Whе₽ (ж’я) icos р -я)+«1sin р (^ - я)]+
(2.90)
+т(я-ж>;
^в = - (1 + X"pgfe е₽ (Х’Н) [ (1 + “1) C0S Р(^-Я) +
+ (®1-1)^пР(^-Я)1 + ^-;
М1В = ~ W + ^) е₽ {Х~Н) cos Р (z ~ Я) — sin р (ж — Я)];
95
^2в —
У1 = 0;
(2.91)
ft-- - *В<'~Н>1-1)°М(*-Я)+
+ (coi + 1) sin р (ж — Н)];
= (i+SoJfi е₽ ("Н) Iе03 ₽(*-#)+«! sin ₽ (х-Н)] + yR (Н-хУ,
Ub = 2(1 + й1(о2) &Eh е₽ <Ж Н> 1(1 — ®1) cos Р (ж - #) +
+ (Oh + 1) sin ₽ (a - Н)] - Л5-х (2Н - х).
Пример. Определим величину полных продольных и кольцевых напряжений,
действующих по линии сопряжения корпуса с упругим кольцом жесткости,
а также численное значение радиального перемещения верхней кромки обо-
лочки и кольца жесткости резервуара с плавающей крышей (вместимость 50 тыс.
м3) при следующих исходных данных:
Удельный вес нефтепродукта у, кгс/см3................... 0,95-IO*3
Радиус срединной поверхности оболочки корпуса R, см......... 3035
Толщина стенки верхнего пояса Л, см ........................ 1,2
Модуль упругости стали Е, кгс/см2........................... 2,1 • 10®
Коэффициент Пуассона у...................................... 0,3
Площадь поперечного сечения кольца жесткости F, см2......... 100
Момент инерции поперечного сечения кольца жесткости Iz отно-
сительно оси z, см4.......................................... 4-24 • 105
1. По формуле (1.53) определим характеристику гибкости оболочки верх-
него пояса резервуара
ft _ 1[. $ _____2 14 • Ю’2 1 /см
Р Г 30352Х1,22 ’ 1 ’ '
2. Коэффициенты, характеризующие упругие и геометрические свойства
кольца жесткости, согласно формулам (2.90) равны:
„ , 2 X 2,14 • IO’2 X 100 .
®i = 1-1--------гй--------= 4,56;
1,2
“2 1+2 (2,14-10-2)3x4,24-106 ll26'
3, С помощью зависимостей (2.91) вычислим значения усилий моментов
и перемещений в сечении х = Н:
Л\=0;
.. 0,95-10-3Х3035 „п .
^"" 2,14-10-2(1+4,56x 1,26) 20 кгс/см.
0,95 • IO-3 X 4,56
2 (2,14-10-2)3 х (1 + 4,56 XI,26) ~ 34 см • кгс ’ см/см;
Л/2 = —0,3 X 34 = —10,2 кге • см/см;
0,95-10-3x30352 ______ _
ТД/ — .----_• • z 4 * ч (1 СМ
2,14-10-2x2,16-103x 1,2(1+4,56x 1,26) ’
96
4. Величину полных продольных и кольцевых напряжений в точках сопря-
жения верхней кромки оболочки с кольцом жесткости определим по формулам:
Nt 6X34 , ,
----j-rr- = -143 кгс/см2;
6 X 10,2 .20 кгс
1,22 ' 1,2 ~ см2 •
6Л/1
, 6JH2 , JV2
+—=
Рис. 33
Напряженное состояние верхнего пояса резервуара
со стационарным покрытием
Стационарное покрытие цилиндрических резервуаров выпол-
няется в настоящее время в основном трех видов: щитовое, сфери-
ческое и складчатое. Конструкция жесткого покрытия состоит из
системы мощных радиальных
и кольцевых двутавровых
балок, жестко сваренных
друг с другом и сверху по-
крытых настилом из листо-
вого железа. Уторный коль-
цевой уголок кровли сплош-
ным швом приварен к верх-
ней кромке корпуса резер-
вуара. Данная конструкция
покрытия обладает значи-
тельной жесткостью как на сжатие, так и на изгиб, поэтому можно
с достаточной точностью считать, что покрытие резервуара является
абсолютно жестким.
Расчётная схема верхнего узла резервуара с жестким, например
сферическим покрытием, показана на рис. 33.
Согласно расчетной схеме верхняя кромка корпуса данного типа
резервуара сопряжена с абсолютно жестким стационарным покры-
тием. В этом случае граничные условия по линии сопряжения корпу-
са с покрытием можно получить непосредственно из условий сов-
местной работы корпуса и упругого кольца жесткости резервуара
с плавающей крышей, выполнив предельный переход от конечной
жесткости упругого кольца жесткости к бесконечной.
Принимая во внимание, что G = , граничные условия
(2.76)—(2.79) при £ оо запишем в следующем виде:
(nW + V) + F (W + nV) = 0;
(nW + 7) + F (W 4 «V) = 0;
I ( n2U 4- \ I ( U J-
M 2d + v) c 1 dl )
(2.92, а)
(2.92, б)
(2.92, в)
(2.92, г)
7 Заказ 2036
97
После последовательного вычитания из уравнения (2.92, а) урав-
нения (2.92, в), а из (2.92, б)—(2.92, г) получим:
nW + V^O; (2.93, а)
^ + ^ = 0. (2.93.6)
Остальные два условия получатся, если уравнение (2.93, а)
подставить в уравнение (2.92, а) или (2.92, в), а (2.93, б) в (2.92, 6)
или (2.72, г).
Итак, на верхнем краю оболочки, сопряженном с абсолютно
жестким стационарным покрытием, соблюдаются следующие кине-
матические граничные условия для n-го члена разложения в тригоно-
метрический ряд:
п17 + 7 = 0;
Т7 + и7 = 0;
^ + ^ = 0; (2.94)
dW . „тт п
-^-+п и-0.
Нетрудно убедиться в том, что система уравнений (2.94) опреде-
лима при всех значениях п, кроме и = 1. Например, при п = 0,
т. е. при действии осесимметричной нагрузки, условия (2.94) при-
мут вид:
U=^V = W^~^0, (2.95)
При п = 1, т. е. при действии несамоуравновешенной нагрузки,
из условий (2.94) получаются только два кинематических условия:
17+7 = 0;
[7 + ^ = 0. (2.96)
Остальные два условия тождественно удовлетворяются, следо-
вательно, при п = 1 задача становится дважды кинематически не-
определимой.
Два недостающих условия можно получить, рассмотрев движение
покрытия как жесткого целого в пространстве под действием несамо-
уравновешенной нагрузки на корпусе резервуара и на самом покры-
тии.
Предположим, что поверхность стационарного покрытия имеет
сферическую форму (практически раскрытие кинематической не-
определимости можно будет провести по аналогии для любой гео-
метрической формы покрытия).
98
Произвольную поверхностную нагрузку на сферическом покры-
тии резервуара можно представить в виде тригонометрического ряда
СО
Qn (ф, 0) = 2 Чп (ф) соя га0, (2.97)
/г-0
где ср, 0 — угловые координаты соответственно в меридиональном
и кольцевом направлениях; qn (<р) — известная функция, выража-
ющая интенсивность поверхностной нагрузки в меридиональном
сечении сферического покрытия. Интенсивность считается положи-
тельной, если нагрузка действует по нормали внутрь покрытия.
При п = 1 формула (2.97) перепишется:
*21 (ф, 0) = д1(ф)с°8 0. (2.98)
Систему сходящихся сил в каждой точке сферического покрытия
целесообразно заменить эквивалентными: горизонтальной силой
Рэ, направленной вдоль оси Oz, и моментом М3 относительно оси об-
ратной симметрии Оу, вращающим против хода часовой стрелки
(рис. 34). Вертикальная составляющая системы сходящихся сил, дей-
ствующая вдоль оси Ох, равна нулю, так как проекции сходящихся
сил на ось Ох взаимно уравновешиваются.
Под действием горизонтальной силы Р3 и момента М3 сфери-
ческое покрытие сместится как жесткое целое на расстояние I па-
раллельно плоскости yoz (см. рис. 36) и повернется на угол со вокруг
оси обратной симметрии Оу (см. рис. 37).
Горизонтальная составляющая системы сходящихся сил опре-
деляется по формуле:
Рэ= — J J <?1 (ф, 0) ds cos (га, z), (2.99)
где ds = p2dcpsin фйб — элемент поверхности сферического покры-
тия; cos (га, z) = sin cpcos 0 — направляющий косинус внешней нор-
мали к поверхности сферического покрытия; р — радиус кривизны
сферического покрытия.
После подстановки в формулу (2.99) значений <21(ф,0),ds и cos (га, z)
получим
2Я ап ап
Р3 — — р2 J соз20 dQ J q-i (ф) sin^tp tfrp = — яр2 qx (ф) sin2<pc?<p. (2.100)
0 0 o'
Момент от действия сходящихся сил произвольной поверхно-
стной нагрузки на сферическом покрытии равен
а с учетом (2.100)
М3
Мэ — Рэр cos а,
ап
— — лр3 cos а J (ф) sin2 ф йф.
в
(2.101)
7*
99
Зная Р3 и Мэ, эквивалентные действию на сферическом покры-
тии произвольной нагрузки, представленной первым членом разло-
жения в тригонометрический ряд, можно перейти к определению
движения верхнего края корпуса вместе со сферическим покрытием.
А-А
у
Рис. 34
Для определения перемещений сферического покрытия в про-
странстве применим метод перемещений строительной механики.
Чтобы препятствовать перемещению покрытия как жесткого
целого на расстояние I и повороту на угол ю под действием силы
100
Рэ и момента Мэ, закрепим сферическое покрытие, добавив соот-
ветственно две дополнительные связи 1 и 2 (рис. 35, а). Связь 1
препятствует перемещению покрытия в горизонтальном направлении
параллельно плоскости yoz,
а связь 2 — повороту покры-
тия вокруг оси обратной
симметрии оу.
Составим канонические
уравнения метода перемеще-
ний, смысл которых заклю-
чается в том, что реакции
первой и второй связей равны
нулю:
| QJ + Qa® + Qpi — Рэ “
I Mil -f-Л/щО) MPl -|-Мэ = О,
(2.102)
где (?,, QPl, Mt, Мш,
МР1 — реактивные силы и
моменты связей 1 и 2 соответ-
ственно от смещения I = 1,
угла поворота ю = 1 и дей-
ствия внешней нагрузки на
цилиндрическом корпусе ре-
зервуара (/’1), представлен-
ной первым членом разложе-
ния в тригонометрический
ряд.
На основании свойства
взаимности реакций должно
соблюдаться условие Qa =
= Mt.
Для определения реак-
ций связей Qi, Q<o, Qp,, Mt,
Ma и MPl, а следовательно,
и неизвестных перемещений I
и и необходимо рассмотреть
условия равновесия сфери-
ческого покрытия. Но чтобы
рассмотреть эти условия равновесия, следует определить внутренние
усилия и моменты, передаваемые с цилиндрической оболочки корпуса
на сферическое покрытие в трех случаях: при горизонтальном пере-
мещении его на расстояние I — 1, при повороте его на угол ® = 1
и при действии на цилиндрическом корпусе резервуара нагрузки Р{,
когда верхний край оболочки корпуса жестко защемлен. Следова-
тельно, нужно трижды рассчитать цилиндрическую оболочку и найти
внутренние усилия, действующие на ее верхнем крае, а для этого
101
требуется предварительно составить граничные условия на верхней
кромке оболочки при / = 1,со = 1ир1 = 0, а также при защемлении
верхнего края, когда 0.
При смещении покрытия как жесткого целого на расстояние I =
= 1 параллельно плоскости yoz (рис. 35, б) граничные условия
при % = на верхней кромке оболочки запишутся:
U = t/cos0 = 0;
а =
1 dW
R dl
cos 0 = 0,
где Н — высота цилиндрического корпуса резервуара.
Рис. 36
Третье и четвертое условия
определятся геометрически из
разложения перемещения Z=1
на две составляющие в нор-
мальном и тангенциальном на-
правлениях (рис. 36):
W= — Zcos0;
V = Z sin 0.
Если принять во внимание,
что W = W cos 0, V = V sin 0,
а I = 1, то третье и четвертое
условия запишутся:
Ж=-1; Е = 1.
Таким образом, граничные условия при смещении сферического
покрытия как жесткого целого на расстояние I = 1 имеют вид:
^=4^-=°; (2.1°з)
Ж=-1, V=l.
При повороте сферического покрытия как жесткого целого на
угол й = 1 вокруг оси обратной симметрии оу (рис. 35, в) граничные
условия формулируются с учетом того, что перемещения оболочки
малы по сравнению с толщиной стенки (обычное допущение теории
оболочек), поэтому при 1=-^-.
Ж = Ё = 0.
На этом же основании при составлении двух других граничных
условий будем с достаточной точностью считать, что компонента
перемещения U во всех точках верхней кромки оболочки направлена
вдоль оси ОХ.
102
Тогда согласно рис. 37 будем иметь
U = AM tgco. (2.104)
Так как угол со достаточно мал, то
Кроме того, tgft) «SCO = 1. (2.105)
t/=67cos0; (2.106)
AM = R cos 0.
Подставляя (2.105) и (2.106) в (2.104), получим
U = R.
Но с другой стороны, согласно рис. 37
U — AM * sin со = R cos 0 tg co R® cos 9;
sina = — ?«cocos0.
it
Если учесть, что при повороте сферического покрытия
образующая цилиндра направлена внутрь оболочки, то
<0 = 1
на
Рис. 37
1 dW
smci- R
следовательно,
1 dW „
«ifticosO.
R dl
Подставляя в последнее
равенство W = VPcos 0 и со-
кращая на cos 0, получим
1 dW ,
R dt, ~ “ 11
Итак, при повороте сферического покрытия на угол со = 1 во-
круг оси оу имеем следующие граничные условия на верхней кромке
оболочки корпуса:
U-=R-,
1 dW _ ,
R dl
17 = 7 = 0.
Граничные условия при защемлении верхнего края оболочки
в точках сопряжения со сферическим покрытием (рис. 35, г) запи-
шутся:
U = V = W = — = О
и v и R dl
(2.107)
(2.108)
103
При данных граничных условиях (2.103), (2.107) и (2.108) путем
интегрирования разрешающей системы уравнений замкнутой цилин-
дрической оболочки можно определить все усилия и моменты на вер-
хней кромке корпуса резервуара.
Определив значения внутренних сил и моментов на верхней кром-
ке оболочки при I = 1, со = 1 и от действия нагрузки Pi на цилинд-
тывать не следует, так как реакции от
в канонических уравнениях (2.102),
рическом корпусе, можно
найти все шесть неиз-
вестных реакций связей 1
и 2.
Для этого отсечем
сферическое покрытие от
корпуса, заменим связи
реакциями Q и М и соста-
вим условия равновесия
сферической кровли (рис.
38). При этом силу Р3
и момент Мэ, эквивалент-
ные действию на покры-
тии поверхностной на-
грузки, при составлении
условий равновесия учи-
них уже учтены отдельно
2 2 = 0;
Л л
2 J 512ц/? sin 0 <20 — 2 J Q1VR cos 920 = 0;
о 0
2 monij = 0;
M + 2 J MlaR cos 0 <20 + 2 J 7У1ЦЯ2 cos 0 <20 = 0
о о
Но принимая во внимание, что
<^12Ц = sin 0;
+ Wia^cosG;
М1Ц = Мг cos 0;
Л\ц — JVic°s0,
104
получим
Q = nR(Q-Sli'); (2.109)
М= -nR^ + N^. (2.110'
По формулам (2.109) и (2.110) можно определить значения реак-
ций связей 1 и 2, Qt, Qa, QPl, Mt, и MPt при смещении I = 1,
повороте и = 1 и действии нагрузки Pi на корпусе резервуара.
Определив все шесть неизвестных реакций связей, можно под-
ставить их значения в канонические уравнения (2.102), найти дей-
ствительное перемещение I и угол поворота <о сферического покрытия
как жесткого целого и вычислить все действительные силы, моменты
и перемещения в любой точке оболочки резервуара.
Например, действительное нормальное напряжение в попереч-
ном сечении оболочки резервуара определится по формуле
01 =<Уц1 H-fTiaOJ-J-Crip,, (2.111)
где аи, о1ш, <J1P1 — нормальные напряжения в поперечном сечении
оболочки резервуара соответственно при единичном смещении (Z =
= 1), единичном угле поворота (со = 1) сферического покрытия и при
действии на корпус резервуара (основную систему) нагрузки Рр
Таким образом, после определения методом перемещений строи-
тельной механики движения сферического покрытия в пространстве
при действии несамоуравновешенной произвольной нагрузки (при
п = 1) получены два недостающих условия на верхней кромке обо-
лочки. Следовательно, число граничных условий на верхней кромке
корпуса резервуара со стационарным покрытием при п = 1 соот-
ветствует числу произвольных постоянных, входящих в общие ин-
тегралы исходных дифференциальных уравнений цилиндрической
оболочки.
Расчет порожнего вертикального цилиндрического резервуара
со сферическим покрытием вместимостью 50 тыс. м3 по данным гра-
ничным условиям на действие несимметричной ветровой нагрузки
был выполнен численным методом на БЭСМ-2М [14].
Ветровая нагрузка аппроксимировалась тремя первыми членами
тригонометрического ряда. При интенсивности скоростного напора
ветра 100 кгс/см2 сферическое покрытие переместилось в горизон-
тальной плоскости на расстояние I = 1,03-10"5 м и повернулось
вокруг оси обратной симметрии Оу на угол о = 3,34-10“ 7 рад.
Данный алгоритм построения граничных условий на верхней
кромке корпуса резервуара со стационарным покрытием при дей-
ствии несамоуравновешенной нагрузки, представленной первым
членом разложения тригонометрического ряда, можно применить
и для резервуара с плавающей крышей, заменив абсолютно жесткое
покрытие упругим кольцом жесткости и приравняв нулю Рэ и Мэ
в канонических уравнениях (2.102).
Аналогично предыдущему, складывая безмоментное решение
(2.3)—(2.7) с моментным (1.62), определим все факторы напряженно-
105
деформированного состояния оболочки в зоне, примыкающей к верх-
ней кромке (х sZ Н), жестко сопряженной со стационарным покры-
тием:
WB = Ж'кр’ И7'6’ = е9 (ж'н) [Dj cos ₽ (x-ff) + D2 sin р (х- Н)] +
+^.(Я-а:) + й;
dWs dW№> . dW«* 0 B(x-H)r/n , о/ m ,
-^Г=-^-+^Г-=Ре 4(D1 + D2)c0S$(x-H) +
-Н-/А + Я2) sin P (г-Я)]
Lilli
Mv = M = - 2Dp2e3 (X'H) [Z?2 cos p (x - Я) - Dx sin p {x- H) ];
M2a = vM1B;
Q1B = QiT = -2£p3e₽ (X’H) [(P2^PX) cos p (x—H) -
-(J^ + DJsin^x-H)]; (2.112)
дт ___ (?п4-0,5^к-К^сн~Р) F .
1 2лЯ
я2а = <BP> + N«> = (X-H) [Dt cos P (ж-Я) + D, sin P (x-H)] +
4- R [р + у(Я-«)];
UB = = -- e₽ (X~H} [(Z), - Z>2) cos p (x-H) +
+ (D14-P2)sinP(a:-^]-^[-^^-4-?CH + (2v-l)p +
4-yv(2ff-a;)]+O‘.
Произвольные постоянные D x и D 2 найдем из граничных условий
по линии сопряжения верхней кромки корпуса с абсолютно жестким
стационарным покрытием:
При х = Н wB(H)=^^ = Q.
Раскрывая эти условия с помощью уравнений (2.112), получим:
^=-6;
С1=1Й'+«- <2.ИЗ>
Произвольную постоянную С<кр) определим из условия, что
продольное перемещение верхней кромки оболочки вместе со стацио-
нарным покрытием равно (№> (2.5):
При х = Я uB(H)^U^x.
106
Тогда из выражения для продольного перемещения оболочки
(2.112) при этом условии следует
«р’=-₽(ж+28)- (2-Ш)
После подстановки значений произвольных постоянных в формулы
(2.112) получим следующие зависимости, характеризующие напря-
женно-деформированное состояние оболочки корпуса резервуара
в зоне сопряжения со стационарным покрытием:
W, - ее* [ - eos 0 (I - Я) + (1 + -Jg.) sin 0 (г - Я)] +
+ (1 + ^)31„₽(.-Я)] + ^;
Л^Зв ”
С,. = - е» «-*> [(1 + ^) cos 0 (ж—Я)— sin 0 (ж—Я)^
м ___ Qn ~ЬО>5(?к -|-(<?сн +р) ,
2л7?
^2в ер <х-н) Г -cos ₽ (х-Н) + (1 +-S-) sin р (х — Н)~\ +
--/?[/> +у (Я-я)];
U. = е& ("Н) [ ~ (1 + C0S Р“ Я) + Sin Р (Х ~ Я)] “
_^^^^+?сн+(2¥_1)д+^(2Я_^ + ^(-^ + 26).
(2.115)
С помощью формул (2.16) и (2.115) можно определить усилия,
моменты и перемещения в любой точке корпуса резервуара со ста-
ционарным покрытием.
На рис. 22 в качестве примера представлены эпюры радиальных
перемещений (W), продольных (Oj) и кольцевых (о2) напряжений,
подсчитанных по формулам (2.16), (2.115) по всей высоте корпуса
резервуара.
107
Вертикальный цилиндрический резервуар
с «безмоментной» кровлей
В практике отечественного резервуаростроения резервуары с «без-
моментной» кровлей получили широкое применение для хранения
мазута и темных нефтепродуктов.
Несмотря на некоторые затруднения, возникающие при монтаже,
«безмоментная» кровля
является весьма перспективной конструк-
цией. К основным ее достоинствам
можно отнести: снижение расхода
металла при изготовлении кровли
на 40% по сравнению со щитовым
покрытием; снижение потерь нефте-
продукта от малых дыханий за счет
вертикальных перемещений кровли
при телескопической конструкции
центральной стойки; большую кор-
розионную стойкость кровли из-за
отсутствия металлического каркаса
и улучшения условий нанесения
антикоррозионного покрытия на
внутреннюю поверхность покрытия.
Расчетная схема нижнего узла
такого резервуара не имеет никаких
особенностей по сравнению с рас-
смотренными ранее конструкциями.
Следовательно, расчет нижнего узла
резервуара с «безмоментной» кровлей
вместимостью 10 тыс. ма и более
можно выполнять по формулам
(2.16), менее 10 тыс. м3 — по фор-
мулам (2.40), (1.72).
Таким образом, остается опре-
делить все факторы напряженно-де-
формированного состояния верхней части корпуса резервуара и обо-
лочки кровли.
Но конструкция узла сопряжения корпуса с кровлей резервуара
данного типа зависит от вместимости: меньше 1000 м3 — верхняя
кромка корпуса упруго сопрягается с оболочкой; 1000 м3 и более —
кровля с корпусом сопрягается через упругое кольцо жесткости
(периферийный каркас), т. е. расчетная схема для верхнего узла
сопряжения корпуса с кровлей имеет два варианта. Первый вариант
соответствует резервуарам вместимостью менее 1000 м3 (рис. 39, а),
второй — пригоден для резервуаров вместимостью 1000 л3 и более
(рис. 39, б).
При выводе граничных условий ограничимся действием осесим-
метричной нагрузки, являющейся основной при проектировании
вертикальных цилиндрических резервуаров.
108
Сформулируем граничные условия для первого варианта расчет-
ной схемы, когда верхняя кромка цилиндрического корпуса резер-
вуара упруго сопряжена с «безмоментной» кровлей.
Предположим, что на оболочке корпуса и покрытия действует
осесимметричная нагрузка интенсивностью соответственно р и q.
В результате действия этой нагрузки в узле пересечения оболочек
корпуса и покрытия возникает напряженное состояние, которое можно
определить методом сил строительной механики.
Рис. 40
Отсечем покрытие резервуара от корпуса по линии сопряжения
(рис. 40), и для обеспечения неразрывности деформаций приложим
в сечении неизвестные усилия Х(иХ2' Для того чтобы отсеченное
покрытие находилось в состоянии равновесия, по краю его следует
приложить равномерно распределенное усилие Хо, величина кото-
рого будет получена по безмоментной теории оболочек.
Неизвестные усилия Xt и Х2 могут быть определены путем ре-
шения системы канонических уравнений метода сил:
Зц-X’i + 612Х2 4- А1р = 0;
621Х1 + 622Х24-Д2р = 0. '
В уравнениях (2.116) 6 н означает суммарное перемещение кромок
корпуса и покрытия в направлении силы X i под действием X 2 = 1,
612 — суммарное перемещение кромок корпуса и покрытия в напра-
влении силы X1 под действием момента X 2 = 1 и т. д. Соответственно
Д1р и Д2р означают суммарное перемещение кромок корпуса и по-
крытия в направлениях сил X 2 и X2 под действием внешних нагрузок,
которыми являются р, q и N0.
109
Все перемещения считаются положительными, если их направле-
ния совпадают с направлением соответствующих усилия Xt и мо-
мента Х2-
На основании теоремы о взаимности перемещений следует, что
612 = 521. Кроме того, •
б12 = бу2 + б^б21;
б22 = б?2 + б?2; (2.117)
\Р = А?р + Л1"р;
где индекс «ц» относится к цилиндрическому корпусу резервуара,
а индекс «и» — к покрытию.
Рис, 41
Коэффициенты 6“к и б"к и грузовые члены Д-р и Д"р определяются
из расчета оболочек корпуса и покрытия по безмоментной теории
плюс краевой эффект по линии сопряжения корпуса с покрытием
(методом асимптотического интегрирования). Методика определения
коэффициентов и грузовых членов будет дана в гл. 2 при расчете кон-
струкции резервуара с безмоментной кровлей на действие осесим-
метричной нагрузки.
Определив коэффициенты канонических уравнений (2.116), из
решения системы можно найти действительные значения момента X 2
НО
и поперечной силы Х1г действующих в точках сопряжения корпуса
с кровлей, а по ним все остальные факторы напряженно-деформи-
рованного состояния оболочек корпуса и покрытия.
Таким образом, граничными условиями в данном случае являются
канонические уравнения (2.116), которые с физической стороны вы-
ражают условия совместности деформаций корпуса резервуара и по-
крытия.
Аналогично составляются граничные условия для резервуаров
с «безмоментной» кровлей вместимостью 1000 м3 и более, у которых
корпус с покрытием сопрягается через упругое кольцо жесткости.
В этом случае необходимо сделать два сечения: по линии сопряжения
корпуса с кольцом жесткости и по линии сопряжения кольца же-
сткости с покрытием (рис. 41). Так же как ив первом случае для обес-
печения неразрывности деформаций приложим в сечениях неизве-
стные усилия X j и Х3 и моменты Х2 и Х4, а для обеспечения равновесия
покрытия— равномерно распределенные по его краю усилия N0.
Канонические уравнения метода сил, выражающие условия сов-
местности деформаций корпуса, упругого кольца жесткости и покры-
тия (граничные условия) в этом случае запишутся:
6цХ4 + 642Х3 + 613X3 + 614Х4 4 Aip = 0;
62iX4 4- 822X2 + 633Х3 + 634Х4+ Д2р = 0;
4' 832X2 + 633Х3 + 634Х4 + А3р = 0;
6«Xi 642 Х2 4- 643Х3 4 644Х4 4- А4р = 0.
Смысл коэффициентов 6; к и грузовых членов А(- к в канонических
уравнениях (2.118) и правило знаков те же, что и в первом случае,
но при их вычислении следует иметь в виду, что
611 = 6^4- б-
612 = 621 = 6ц+^2;
613= 631 = 633;
6ц = 641 = 634;
б22 = 6gg + 62к2;
623 — 632 — 623;
X — X _____Хк •
24 42 24’ (2.119)
6зз = 63"з+6“;
634 = 643 = 631 4 634;
644 = 6^4 6?4;
AiP = A4p+A?p;
A2p = A«p + A*p;
lit
Азр ’ AJp Д'зр’
д4р-л?р + л$р.
Здесь индекс «ц» относится к цилиндрическому корпусу, индекс «к» —
к кольцу жесткости, а индекс «п» — к покрытию.
Следовательно, для того.чтобы найти лишние неизвестные X t,
X 2, Xз, Х4, необходимо определить 16 коэффициентов и 8 грузовых
членов, т. е. перемещения и углы поворота кольца жесткости, обо-
лочек корпуса и покрытия от действия единичных сил и нагрузки.
Громоздкость этой задачи существенно снижается, если учесть,
что большая часть этих коэффициентов и грузовых членов будет
известна из решения предыдущей задачи для резервуара с «безмо-
ментным» покрытием вместимостью менее 1000 м3.
Статический расчет верхнего узла
резервуара с «безмоментной» кровлей
(V < 1000 м3)
Конструкция кровли представляет собой самонесущую оболочку
вращения отрицательной гауссовой кривизны, выполняемую из
листов толщиной 2,5—3 мм, меридиан которой можно описать урав-
нением гибкой нити с небольшой величиной провисания.
Приближенный расчет безмомент-
г ной кровли приведен в работе [13].
По методике этого расчета безмо-
П ментная кровля считается работа-
r=f(z) I Ющей на одноосное растяжение, т. е.
учитываются только меридиональные
_________I усилия, возникающие в оболочке
г л______д кровли под действием внешней на-
r ff — грузки. Однако в этой же работе
рнс 42 при анализе экспериментальных
исследований указывается, что в про-
цессе нагружения в безмоментной
кровле возникают также кольцевые усилия, которые в неко-
торых случаях приводят к образованию волн в кольцевом на-
правлении. В особенности это заметно в местах радиальных нахле-
сточных швов, где вследствие отступления от плавности геометриче-
ской формы поверхности оболочки происходит нарушение безмомент-
ного состояния и возникает местное моментное напряженное состояние.
Приведем расчет «безмоментной» кровли с учетом ее работы как в ме-
ридиональном, так и кольцевом направлениях, что дает более пол-
ную картину напряженно-деформированного состояния кровли.
Возьмем за исходное уравнение меридиана поверхности кровли
уравнение гибкой нити с различными уровнями точек подвеса
(рис. 42). Будем считать, что внешняя нагрузка интенсивностью q
равномерно распределена по длине проекции нити на горизонталь-
ную ось. Это вполне допустимо, так как разница в длине меридиана
112
оболочки и его проекции составляет величину, не превышающую 3%.
Тогда уравнение меридиана поверхности кровли в цилиндрической
системе координат будет:
1 I
(2.120)
Для последующего изложения удобно записать исходную систему
обыкновенных дифференциальных уравнений (1.25), описывающих
напряженное состояние оболочки вращения с произвольной формой
меридиана при осесимметричном загружении (п = 0 и 5 = 0),
в цилиндрической системе координат (г, z).
Приняв в этих уравнениях согласно рис. 7
, dz 1
а<р = —g-, sin<р = —- ,
smcpT?! Y Г / dr \2
F, + U)
получим:
' (Гдг(б))' _ /ту(б) _г /ГГдТ
' № , Af’ у <2-121)
Л1 + Л2 Z’
где ________
7?! = ; R2 - -Г ]/Т+РЛ (2.122)
Из решения системы уравнений (2.121) с учетом (2.122) следует:
Х<б> = - £l±(r? j г (X - r'Z) dz + Су
. о
(2.123)
Принимая во внимание, что компоненты поверхностной нагрузки
в цилиндрической системе координат равны
/1 + (г'? ’
Z = 9,1'
И+0Д2
перепишем соотношения (2.123) в форме
(2.124)
N* =
/1 + (г')2
Г
/1Д (r'j2 dz + Cy ;
Мб) = тгй'У1б) + 9"'Л'
(2.125)
8 Заказ 2036
113
Произвольная постоянная С, определяется из условий на контуре,
которому соответствует координата z = 0. Из первого соотношения
(2.125) видно, пто при z = 0 -р==== = 0, поэтому =0.
Тогда после подстановки (2.120) в (2.125) и интегрирования по z
получим:
у(б) дКДа + 41г
1 1 ' 41 Кг (К/ -Кг)
Viz (fi2-\-ilz)
, Д2 , С Vl K^2 + 4iz + 2!/г \ . К(Д2+41г)з Дз
+ 2 Д yi ) + (Я 1
7у(б) __ R2 (УТ — (У &) __ дД2 . qRz
2 ~ УТ (Д2 + 4/г) 1 ~ 2 KIz '
(2.126)
Функции NV и N% определены только в диапазоне 0 < z <1,
а на краях оболочки при z — 0 или г = I претерпевают бесконечный
разрыв или принимают неопределенные значения. Например, при
2 = 0Л^=Л.
Эго объясняется тем, что при задании уравнения меридиана
в форме (2.120) на краях оболочки кровли претерпевают разрыв
непрерывности кривизны Кг и Кг. :
«Неопределенность» функций Л^б)и УУ на краях оболочки можно
легко раскрыть, например, по правилу Лопиталя. В частности,
limM6) = -=-тг lim 8Z]/Zz-(
УТ Kfl2 + 4/z + 2iKF \ .
Д кг р
____21R^ Уz__
(КГ-2/Г) КД2 + 41г
2 КГ Д2
кг-КГ+
X In
. Уz (ЩДЧ-з2г22)________________________
' 3/ (КГ -2 /Г) 3 (КГ-2 КГ) Кд2+4!г _
Следовательно,
2Дз Кг
qRZ
IT'
д/(б) (0) - "У2
21 •
(2.127)
Но устранить разрывы непрерывности этих функций при задании
уравнения меридиана оболочки в форме (2.120) практически невоз-
можно. Поэтому, точное уравнение (2.120) целесообразно аппрокси-
мировать, например с помощью метода наименьших квадратов
[5], следующим степенным полиномом:
г = az2 — bz с.
(2.128)
114
В частности, для резервуара вместимостью 5000 м3 численные
значения коэффициентов равны: а — 1,9957 1/м; b = 8,7716; с —
= 9,9656 м.
Геометрическая форма меридиана, заданная уравнениями (2.120)
и (2.128), представлена на рис. 43 (сплошная линия соответствует
уравнению (2.120), пунктирная — (2.128).
Как видно из рисунка, сходимость функций, заданных уравне-
ниями (2.120) и (2.128), на всем протяжении меридиана (за исключе-
нием краев, где Ni (z) mN2(z) имеют неопределенные значения) вполне
удовлетворительна.
Подставляя (2.128) в соотношения (2.125) и интегрируя по z,
получим:
М‘> = |(Ь-2“)/1 + №124
+ 16ас — 8&2 + 1] + (8&2 +1 - 16ас) In
2az-b + /l + (2az-&)2
/1 + ^2 -fc
+ h ]/1+~^ (6fr2 - 16дс - 1) + J: (2.129)
= № -bz + c) + + <1 (2я2 “ •
Эпюры меридионального и кольцевого усилий при безмоментной
решении представлены на рис. 44. Сплошные линии на рисунке по-
строены по уравнениям (2.129), пунктирные — по (2.120).
Имея выражение для меридионального и кольцевого усилий,
определим перемещение срединной поверхности оболочки кровли
в направлениях касательной к меридиану (С7) и нормали к поверх-
ности (И7).
Согласно (1.26) геометрические уравнения при осесимметричной
деформации (и = 0 и 7 = 0) примут вид:
».=S (М« - V2V<°>)=(тг+и™);
, . (2.130)
е2 = А- (ЛГ(б) _ v^(6)) = -L (и (б) ctg ф + И7(б)).
8*
115
Исключая из соотношений (2.130) W(6), получим [15]
- pm otg<p = Л да» (Я,+uR,) - Л'»> (Я,+чл,)|
(2.131)
Из решения уравнения (2.130) следует:
г *
' 1
Eh sin ср
(2.132)
£7<6)=:sni(p
JV(6)7?2){Z(p + C2 .
.о
В цилиндрической системе координат уравнение (2.132)
(2.122) можно записать в следующем виде:
(2
^J[(i+(/)2)M6)+^6)]^+ca .
После подстановки NSp* в уравнение (2.133) получим
учетом
(2.133)
г?(б)
с
1
2
о
р N<& + grW]dz + С2 .
(2.134)
Исключая из (2.134) меридиональное усилие 1У[б), функцию г (z)
и ее производные и интегрируя полученное выражение по частям
без учета членов наивысшего порядка малости, запишем выражение
для тангенциального перемещения в следующем виде:
С/(б) _---- ? _ 2asbz6 + 2а2 (2 Ь2 - Зас) г4 -
EhVl + {2az-b^[ 3 '
- (18ас - 62) z3 +1 (Ь* 4- 8аЬ2с + 4й2с2) г2 - (62 + 2ас) z +
116
4-TST1 [6 + ьг <86! - )в“-Ч + ти^г] х
х In 1 (2.135)
/1 + 62 -& J
Произвольная постоянная С2 = О, так как из граничных условий
на контуре при z = 0 U(6> =0.
Выражение для нормального прогиба оболочки кровли опреде-
лим из второго уравнения (2.130)
W’ = да - v7V<6)) - U™ ctg <р =
- Г r£h{r')2[(v - ) Мб) ~ (2.136)
где г’ = 2az — b.
Теперь определим зависимость для угла наклона касательной к ме-
ридиану после деформации оболочки.
По формуле (1.40) имеем:
Ф(б) = (8Х - е2) ctg ср - = (ех - е2) r‘ + v .
U-ip ил
Исключая из этого выражения и е2 с помощью соотношений
(2.130), получим
ф(6)=да - да>) /•"+ih 4 (Мб) - *да>). (2.137)
Подстановка выражения Л'2б,в уравнение (2.137) и дифференциро-
вание по z приводит к
1Ь(б)__L f _ 2 (2+V) аг' уг' . 2а 8а2г'г )
Eh\ 1 + (г')2 “Г г “Г 1-[1 + (г')2р
хда--^-[2аг+(3 + ^(/)2 + 1]. (2.138)
LJtV
Таким образом, получены зависимости для усилий и перемещений,
определяющие безмоментное напряженное состояние оболочки
кровли.
Выражения для усилий и перемещений оболочки цилиндриче-
ского корпуса резервуара при безмоментной решении можно полу-
чить из соотношений (2.1), (2.3), (2.4), (2.6), (2.7), приняв р = 0:
ДГ(б) Qп + 0,5(?к + <?сн
1Ц " 2лЯ
да=у7? (Н-х);
W + VY (2Я - х) + g"+°,5QK -1 (2 139)
117
Полное напряженно-деформированное состояние оболочки кор-
пуса и кровли складывается из безмоментного и краевого эффекта.
Безмоментное напряженное состояние оболочек кровли и корпуса
•определяется соответственно по формулам (2.129), (2.135), (2.136),
(2.138) и (2.139), а моментное — по формулам (1.164), (1.72, а).
Но в зависимости (1.164) и (1.72, а) входят неизвестные перерезы-
вающие усилие Qо и изгибающий момент Ма (начальные параметры),
действующие по линии упругого сопряжения корпуса с покрытием.
Эти неизвестные определяются из решения системы канонических
уравнений метода сил (2.116), выражающих условия совместности
деформаций корпуса и кровли (граничные условия).
Основная трудность при этом заключается в определении коэф-
фициентов 6/ к и грузовых членов Лг- к, которые являются суммарными
перемещениями корпуса и кровли.
Перемещения верхнего края корпуса резервуара под действием
единичных сил Х1 = <20 = 1 и Х2 = MQ = 1 и внешней нагрузки
определяются по формулам (1.72, а) и (2.139):
SH _ 2Рц
611 - ка ’
сц _ 2Рц t
012
in _ 4рц #
°22' Кц ’
^P = 5u->^oSinai;
Л2₽= ~ i;+^vosiliai
где
тг _________________________ E}la .
ЛЦ- Д2 >
4 —
ц 4ПЦ •
(2.140)
(2.141)
Продольное усилие No, действующее по линии сопряжения кор-
пуса и кровли, определяется по формуле (2.127)
jVo = A\(O) =
1Г
118
поэтому соотношения (2.140) запишутся:
кц ______________________________ 2^ц ,
611 ~ Хц ’
612 ~ “ Ац ’
хи _ Ш .
622' Т/’
*ц Л 9fl2pusinai
А1Р“°Ц К~1 ’
ЛЦ _ V I дЯ2ЙSinai
а2₽ /сц + Яц/
(2.142)
Для определения единичных перемещений кровли во избежание
сложных и громоздких вычислений малые отрезки меридиана, при-
мыкающие к краям оболочки кровли и равные по величине ширине
зоны затухания краевого эффекта, заменим прямыми линиями.
Тогда узкие зоны у краев кровли будут иметь форму конуса с углом
конусности у нижнего края at, у верхнего — а2 (см. рис. 40). Пра-
вомерность такого допущения станет вполне очевидной, если учесть,
что оболочка кровли имеет весьма малую толщину стенки (2,5—3 мм)
и, следовательно, малую ширину зоны затухания краевого эффекта,
при котором криволинейный отрезок меридиана близок к прямой
линии.
Если обозначить толщину оболочки кровли через h„, то, вводя
параметр
п = (2-143)
можно цилиндрическую жесткость, коэффициент постели и характе-
ристику гибкости для «конической» оболочки кровли выразить через
соответствующие величины цилиндрической оболочки корпуса ре-
зервуара:
Dn = naD^
Кп = пКа cos2 а; (2.144)
О о 1 /cos a
Рп = Рц|/—•
Тогда, согласно формулам (1.164), (2.136) и (2.138) для нижнего-
края оболочки кровли при z = 0 и a = a15 получим:
6?1 = 2-^со82а1 = 6?1]/'^-;
6;2 = 6^ = 2Acosai=--±6“2;
622 = 4^- = ------ ^2;
• Лп у «5 cosai
1191
лп Г. . / 2ас \ Ri "I
Alp~' nEhu L? + V l + ia) 2Zc& J ’
п __ qc^2 v& 2(2 + v)a6 2a
Л2р~ 2nlEh^ [V Г+&2 (1 + 62)’A +
. 8a2&c . 2Z+4flcZ + 2(3 + v) &2/П
+ (l+&2)2 + Д2 J-
(2.145)
На основании (2.117) суммарные перемещения точек сопряжения
корпуса и кровли равны:
би = б?1 + 6?! ]/(«2 + /и cos ах);
х — а _ хц 1 ха _ 2(га2 —1)PJ _
О12-О21-О12 -^-012- ,
42 = б§2 4- = —-,Д= — (14-И2 (2.146)
V пъ cos ах «2 V п cos ах дц
л — л 4_ ' ?6с2 Г1 — (_ 2gg А Д2 _ ”IWM sin й11.
1р иЦ^ „£цД2 [/ \V 1 + &2 J 2lcb lc*b _]>
д _ у . qc Г 2гаР^Я2 sin «1 . vb 2(24-v)ab
Лг₽ А4" + 2ШК^ L Гр2
2а . 8а26с 2/ 4-4acZ + 2 (34-v) ЬЧ "1
(1 + &2)’/2 + (1 + 62)2 + Я2 J-
Определив значения коэффициентов 81к и грузовых членов А/к,
можно из решения системы канонических уравнений (2.116) найти
.лишние неизвестные Х( и Х2:
у __ Agp^ia —A1P^22 .
1 W22—612 ’ (2.147)
у __ Д1рв12~ А2р6ц
Л2 6цд2а-д?а •
Теперь, складывая соответственно результаты расчета по без-
моментной теории и краевого эффекта с учетом направления коорди-
натных осей при каждом решении, можно получить выражение для
полных усилий, моментов и перемещений в различных зонах.
В зоне, примыкающей к верхнему краю корпуса:
^3=-^ (-₽л2ф;11+Х1Ф*8Ц)+
Лц
i vn » У(0п + 0Ж)П.
+ 2Яц L2Y'# 3:)+ v?ch+ лд2 J,
гр = (Х1Ф*ац - 2РД2Ф‘зц)+-Ь ;
Лц Лц
120
М1В = Х2Ф^+^Х1Ф:Ц;
Рц (2.148):
<21» = «ц - 2₽цХ2ф;ц;
лг2в = 2М (Ххф;ц- рцХ2Ф?ц) + yR (Н-х)-,
кт (?п +0,5^к4~?сн^ .
Л1 2лЯ
и‘ ’V (2Я - *) + -2=^] ;
Л^2В = V>1B.
Функции Ф*1Ц — Ф4Ц определяются по формулам (1.72, б) при р =
В зоне, примыкающей к нижнему краю кровли:
Wa=-^T (₽пХ>Ф2п + cosа^Фзн) + .<?^z+-c.y<1+(2az-b)2 X
Л-П ЛЛп
< {(? ~ 21+(17^\У'] n[6) ~q ~bz+с) (2й2 ~ 6)} - и'бу (2й2 _ 6);
“ Т7 (2Р"Х2фзп + cos «1Ф1п)+(аг2-^+с) X
[ 2 (2-|-у) a (2az —6) . v (2az — b) ._2а_________,
( l + (2az— 6)2 "г az2— bz^c [1-|_(2аг — Ь)2]‘/а
. 8a2 (2az—6) (az2—6z + c)) y(6)
[l+(2az-6)2]2 j7V1
g^-bz + c) [2a ^22_ bzc) + (3_|_ (2az-b)2 +1 ];
M1H = ^Фщ+Т- Х1Ф4П; (2.149}
4рл
<21H == -20п (х2Ф4п - ХАп) ;
= sin Ф8П + Ф2П) - 2₽п tg аЛ Ф2П + Ф4п W
\ vvS 0*1 / \uva(Ai /
+ (®2-bz kс)[1+(^-б)2 + Я(2«-*)];
Nin= -2Pntga1(x2®4n--^l- XAn) + Мб>;
^2H = vM1H.
Функции Ф1п — Ф4п определяются по формулам (1.71) при
р = рп; х = —, а N{6) по формуле (2.129).
121
Верхняя кромка оболочки «безмоментной» кровли приварена
к наружной поверхности короткой конической оболочки зонта.
Внутренняя поверхность зонта также с помощью электросварки
жестко, через косынки, сопрягается с центральной стойкой [13].
Так как жесткость такой конструкции зонта значительно выше
жесткости тонкостенной оболочки кровли, то можно считать, что
верхняя кромка кровли имеет жесткое защемление. Тогда граничные
условия по линии сопряжения оболочки кровли и зонта (при z = I)
запишутся:
Te(7)-4F^'(?)xJV<«)(0.0;
Фв(/)<кр) (z) + ^6,(z) = o. (
Раскрывая эти условия с помощью зависимостей (1.164), получим:
' 2Р7П ?2 (- Mz/o + Qo cos а2) + Ж‘б’ (Z) = 0;
J (2-151)
-g-(-2PnM0 ! Q0c°sa.2) ; <6>(Z) = 0.
Из решения системы уравнений (2.151) определим неизвестные
изгибающий момент и перерезывающее усилие, действующие по
линии сопряжения оболочки кровли и зонта:
Численные значения функций (Z) и фв (Z) определяются по
формулам (2.136) и (2.138) при z = I.
Выражения для полных усилий, моментов и перемещений, опре-
деляющих напряженно-деформированное состояние верхней части
оболочки кровли, найдем путем подстановки значений Мо и Qo
в формулы (1.164) и суммирования полученного решения с безмомент-
ным (2.129), (2.136) и (2.138):
Г(Z) (Ф5п - Ф*п cos а2) +
Рп CDS C*2 L
+ cos ~ 2фзп) 1 + х
S1H ОС2 "Лп
х([v- ]N^-q(az2 bz+c)&az-6))~
— (2az — b) U(6>;
<>. = (/) if?’ (o
J _ 2 (2+v) a (2az—b) . v(2az—b) ,_____2a______.
X( l + (2«z-b)2 "r az2-bz + c "f" [1 + (2oz_b)2]’/« *"
122
. 8a2 (2az —b) (az2—bz-}-c) 1 g(az2—ЬгЦ-с)
[l + (2az - &)2]2 jyvi ЁКп X
x [2a (az2 — bz + c) + (3 -j- v) (2az — &)2 +1];
m1b=-§- [Ч® <!> *" -tst ф‘>"й'“’ <'));
^Pn L- bill «2 J
M2B = vM1B; (2.153}
<21B = [ - <’ (О Ф*1П + w<6> (D Ф*зп];
x1B - F^F2 Г - <> (/)Ф1п+и-Т (/) ФэЛ +<’;
*РП L w2 J
x2B = ^б) (I) ФЗп-ф*1п) +
"|-‘n \VU&W2 /
+w-“ <l> (ф- - ф;")++c> x
*[<+ (£->) H(2«=-6),
где функции Ф£п — Ф4П определяются по формулам (1.72, б) при
В = В Н = —-—, х =—-—, а выражения IV)6’ и U(6) соответствен-
1 В * 1 11 cos a2 cos a2 r 1
но по формулам (2.127) и (2.135).
Таким образом, зависимости (2.148), (2.149) и (2.153) полностью
определяют напряженно-деформированное состояние верхней
части корпуса и оболочки покрытия резервуара с безмоментной
кровлей вместимостью менее 1 тыс. ма при действии эксплуатацион-
ной нагрузки.
Статический расчет верхнего
узла резервуара с «безмоментной» кровлей
(V 5? 1000 м3)
В резервуарах с «безмоментной» кровлей вместимостью 1000 ма
и более оболочки корпуса и кровли сопрягаются друг с другом через
упругое кольцо жесткости (периферийный каркас).
Напряженное состояние в этом узле можно получить обычным
путем, отсекая корпус и кровлю от кольца жесткости, прикладывая
в месте разреза неизвестные усилия Xf, Х3 и моменты Х2, Х4и обес-
печивая неразрывность деформации. На рис. 41 представлена расчет-
ная схема верхнего узла резервуара.
Неизвестные усилия и моменты Xt — Х4 определяются путем
решения системы канонических уравнений метода сил (2.118).
Для коэффициентов 6/к и грузовых членов Д;к, входящих в эти
уравнения, справедливы соотношения (2.119). Если пренебречь
эксцентриситетом Лк/2 приложения сил Х(, Ха и No, считая, что
123
эти силы действуют на уровне срединной плоскости кольца же-
сткости, и принять во внимание, что поверхностная нагрузка на
кольце отсутствует, получим:
а?2 = si4 = 641 - 623 - 632 = 6“4 = Д2Р = Д?р = 0. (2.154)
Тогда соотношения (2.119) существенно упростятся:
= + 834=643 = 6^;
812 — 821 — 812! 844 = 624+644;
81з = 631 = 623; Д1р = Д?р + Д;р; (2.155
632 = 622 = 632! Д2р = Азр>
824= 842 — 824; Д3р = Д2Р + Дзр;
833 = 633 + б33; Д4р = Д2Р,
где по-прежнему индекс «ц» относится к цилиндрическому корпусу,
индекс «п» — к покрытию (кровле), индекс «к» — к кольцу же-
сткости.
Значения единичных перемещений 8iK и грузовых членов Д(К
с учетом правила знаков определяются:
для цилиндрической оболочки корпуса по формулам (2.140)
при Na = 0:
622=~; (2.155, а)
Aip= 8Ц;
д______Y_.
Л2Р- Кц ’
для кольца жесткости по формулам (2.80) и (2.81):
би — -6£3 = 651;
6?3=-8£i; 6?4 = 6?2;
Я2 дк Л^оД2Sinai . (2’ 56)
°22 Е1г ’ EF
хк _ SK . ЛК _ ЛК .
О24— О22, /Л3р— 1Л1р,
124
для оболочки кровли по формулам (2.145):
яп __ 2рц т/ cosax .
°33-_я7 V
21+
Лп - - ц •
°34‘ П2ЛЦ’
ЯП ЭД
О44 — — /. 1 t
Кц V cos ах
(2.157)
дп = № г / 2ас \ Д2 у
Лзр nEh^ L1+V 1 + b2 / 2lcb J’
,n qc№ Г vi 2(2 + v) ab . 2a .
Д1р 2nlEh^ L“ 1 + &2 Г (1 + 62j«7T+
8a2&c 21 bad 2(3+v)b2Z
+ d + b2) *" Д2 + Д2 T" 7?2
После подстановки значений коэффициентов б/к и грузовых чле-
нов Л/к в систему канонических уравнений (2.118) получим:
где
2В2
+ ^ГЦХ4 + АзР = 0;
Д2 2Й2 / Д2 46» \
-^^+^/з+(^+хтаг)х
ХХ4+Д4Р = 0,
Л - Л I 3Д4 sin «1 .
^1Р °цт 21EF
Д =J--
Дц’
. оМ Г Д2 / 2ас . \ , g/?4sinoti
A>p“+sLTa+_TW+'’)+1J—
Л qcR2 I” vb 2(2-|-v)ab 2a ,
Л4Р = 2nlEh^ Г+*2 (1 + &2)*Л +
, 8a2bc , 21 . bad . 2(3 + v)b2Z“l
+ (1-рЬ2)2 "г да+да+ Д2 J*
(2.158)
(2.159)
125
Из решения системы уравнений (2.158) следует:
— 0ц(8у2у3у4
huv3 4у2 ) Л
ад п4 ;л1р
Лц ( Ц I F ! \ Л
«2₽^z ,V2VJ:-!:
у*Ц
1 -
д2р +22L
। Лц ( 2у2
М к пз
₽ц (^~4v3v4 +
1- v3 V4 — Др2' ) Д^Р + 0Ц ( 3^8^ [ф-) Дэр 4
I ( _ ^цУЛ'з . hq . Ьц
"Ч 0^г «w “Гад/’а
v _ Го ( Ь-г___।__hq
3- 1РЧ «ад +4₽^/|
। ( 2)?цу4 _М1 \ д , о / ^цУх
М М Ц3₽34;а2р + Рц^
.1 ( 4у4у2 2
Г \ «2 «2
у __ Г К ( ~^цД)2
4- RpIJMnw
2п2|3^/г
Л 2
к*
РКр L
2v.
4ВД
Уз? VI.
/ J’
—_____ |Д .2
2«ад/2) '
-^«-)д1р+ (2.160)
+ Д3р4-
2₽*7*
А2н
' 2^Р1г
hbv3 \ л _l.
' 1р'
I / ^Uvlv3
+к ₽^z
hi_______hu. \ Л 4
4₽6ЦР4 «W J U2p "r
n2 2 “ 20«F/z rtf') A3P + (2v3 — 4v1v2v3+ ^)A4p]»
где
p = Vt 16v2v3v4 — -ф| ) 4 n3^FIz + — 8V3V4 +
I Лц / । F z \
+ \ 4Z“₽fi *" " W; 4V3V^;
V4 -14-
K .
2M ’
(2.161)
VП COS 0-1 , Лц
Vs - * ;
__ 1 i
4 K«5 cos ctj 4₽JZ2
126
Таким образом, определены зависимости для перерезывающих
сил и изгибающих моментов (лишние неизвестные) в сечениях между
упругим кольцом жесткости, корпусом и кровлей резервуара вме-
стимостью 1000 м3 и более.
Выражения для полных усилий, моментов и перемещений в верх-
ней части корпуса и нижней части кровли резервуара можно полу-
чить, если подставить значения Х{ и Х2 в (1.72, а), а значения Х3
и Xt в (1.164) и полученные краевые решения сложить с безмомент-
ным соответственно по формулам (2.129), (2.136) и (2.138).
Усилия, моменты и перемещения верхней части оболочки кровли,
сопряженной с зонтом, определяются так же, как и для резервуара
вместимостью менее 1000 м3, т. е. по формулам (2.153).
Пример. Рассмотрим важный в практическом отношении вопрос о влиянии
периферийного каркаса на напряженное состояние верхнего узла резервуара
с «безмоментной» кровлей. Для этой цели определим сначала изгибные напря-
жения в верхнем узле резервуара с «безмоментной» кровлей, например вмести-
мостью 5000 м3 в двух случаях: когда оболочки корпуса и кровли сопрягаются
непосредственно друг с другом и через периферийный каркас.
Геометрические и упругие параметры резервуара с безмоментной кровлей
вместимостью 5000 м3 равны: R = 1142 см; hn= 0,3 см; Лц= 0,4 см; I = 200 см;
= 1,53; F = 60 см2; 1 z = 1,67 Ю4 5 * * см*; v ~ 0,3; Е = 2,1 • 10е кгс/см2.
Удельный вес хранимой жидкости у = 10"3 кгс/см3. Коэффициенты поли-
нома (2.128): a s 2 10- 2 1/см, b = 8,77, с 1000 см.
Интенсивность поверхностной нагрузки на кровле:
<1 = 2 • 10’2 кгс/см2.
По формулам (2.143), (2,141) и (2.146) получим:
6,05-10-2 1/см;
v 2,1-10е X 0,4 ,
=-----Й422----= 01645 кгс/см3;
6ц = л+г’^й/ч (°’75г + ,Z°’75 X °-035) = 01232 см2/кгс;
IN (О* A UiV'lJ
А 2(0,75 —1) X 0,06052 .
= < 0.752 X 0,645---= -8’9-IO"3 см/кгс;
4 X 0.0605^(1+0552/0^0035) = 1В7..1П-2
0,752 /о,75 X 0,035 X 0,645
. ппг , 2 10-2 х 8,77 X 10002 Г. ./+„ 2x2-10-2X1000
Д1Р = 0’°° + 0,75 X 0,645 Х~ 1422- + к°’3----Г+8572-----
11422 о,75 X 6,05 • 10-2 х ц/,24 Х 0,99 "1
Х 2 X 200 X 1000 X 8,77 200 X 10002 X 8,77 J- 1
_ 10-3 । 2- 10-2X 1000 Г 2ХО75ХО,О6О52Х 11422 ХО,99
Азр 0,645 ' 2 0,75 X 200 X 0,645 |_ 1000
,7 см;
127
, 0,3 x 8,77 2 (2 + 0,3) X 2 • IO-2 X 8,77 2x2-10-2
"Г 1000 l + 8,772 (I + SJ?2)*/*
8 (2 • IO'2)2 X 8,77 X 1000 ,
(1+8,772)2
। 2X200+4X2 • IO-2 x 1000x200+2 (3 + 0,3) X 8,772 X 200 П
+ 11422 J—0,725.
Тогда величина изгибающего момента в точках пересечения корпуса с кро-
влей согласно (2.147) будет равна:
„ ,, 11,7 X 8,9 • Ю-3 —0,725 X 0,232 лег . ..
М° 0,232 X 1,67- 10-2-(—8,9-10'3)2 16,3 <кг'см)/см-
Этой величине изгибающего момента соответствуют напряжения у внут-
ренней поверхности корпуса:
(п) 6X16,5 „
°i ~ —оТр— = 619 кгс/см2
и кровли
(П) 6X16,5 .„
а1 —-----------= 1100 КГС/СМ2.
UiOz
Аналогично при сопряжении кровли резервуара с корпусом через перифе-
рийный каркас из зависимостей (2.161), (2.160) и (2.159) получим:
0,4
V1 = 1 + 2 X 6,05 • 10-2 х во = 1,055;
0,4
V2== 1 + 4 X 0,06053 X 1,67 • 105 = 1,002;
_ V 0,75 X 0,035 ._________0,4_______= , „, .
0,752 "Г 2 X 6,05 • IO'2 X 60 и’641’
__________1____________|____________™____________
0,752 /0,75 x0,035 4 X 0.06053 X 1,67 • 103
=4.055 (1вх 1ДЙХ0М X «MS—одтХХ1°^‘.1О1. ~ +
+ 0.752 х 0,0605* X 60 X 1,67 X 10s "I" 0.75* ~ 8 Х 0,341 Х 11,15 +
. 0,42 / о,42 . 60
0,06052 х 602 \ 4 X 1,672 • 105 X 0.0605е 0,752 х 0.06052 х 1,67 • Ю5
-4X 1,002 X 11,15) ) = 19,2;
Ajp —0,05
2-10-2Х11424Х0,99
2 X 200 X 2,1 • 106 х 60
IO"3
= ^645 “ Ш • 10'3;
2-10-2 x8,77X 10002 Г 11422
Лзр ~ 0,75 X 2,1 • 106 х 0,4 2 х 200 X 8,77 X 1000
2x2- IO'2 X 1000
1 + 8,772
2-IQ-2 X 11424 х 0,99
2x 200 X2,1 -1О6Х6О
128
л 2.10-2X 1000X11422 Г 0,3 X8,77 _ 2(2+0,3)X 2« Ю^Х 8,77
)р- 2 X 0,75 X 200 X 2,1-ДОХОД L 1000 1 + 8,772
2X2-10-2 , 8 X (2 10-2) X 8,77 х 1000 , 2 x 200 .
(1-+8 772)*/г "Г (1 + 8,772)2 ' 11422 +
, 4x2-10-2x1000x200 , 2(3+0,3) X 8,772X 200 1 д дп
11422 ' + 11422 J 1ЛЬ’10 ’
*2 = 0,06053х 19,2 [6’05'10“2 ("0J54 4X0.341 X11,15 +
_|--------:----2^!---------------- у о 71 _l
“ 2X0,752 X 0,06054 X 60 X 1,67 • 105 /л ’ т
+ (4 X 1,055 X 0,341 X 11,15 * 1.55-10-»-
-“S' ‘"-(o^xow’xtfc^- одиоУхи )°Д +
, / 0,4X1,055X0,341 ।________ОД________,
"Г \ 0.06053 х 1,67 • 105 Т 9,752 х 0,0605 X 60 +
+ 4 X 0,0305-X I,07 • 10* X SO-) КГС ’
0,645 Голг ||К / 2 X 0,4X1,0021
4 0,0605» X 19,2 L \ 0,752 х 6,05-10-2 х 60
0,4 X 0,341 Ч , / 0,4 X 1,055 X 0,341
0,0605s X 1,67 • 105 / ’71 + \ 0,0605» X 1,67 • Ю6
_____________0,4»_________________04________Ч
4 X 0,0605» X 6Q2 X 1,67 • 10s 0,752 х 6,05 • 10"® X 60 J Х
X 1,55 10-3-6,05 • 10-2 X ( 4Х1’О55 Х°'341. _
\ U,7oz
-2X03605. Х60Х1.67.10,-0^')М1+(2ХМ41-4Х1'1)55Х1да2Х
Х "М1+оОДО5>‘^) Х 1-“ Н
Тогда величина изгибных напряжений у внутренней поверхности оболочек
корпуса и кровли резервуара будет равна соответственно:
°1Ц) = ^042^ = 1670 кгс/см2;
°1П) = 6^J’9 = ~ 525 кгс/см2.
1 0,32
Из сравнения интенсивности изгибных напряжений в кровле в двух рассмот-
ренных случаях видно, что наличие периферийного каркаса приводит к пере-
распределению внутренних усилий и моментов в верхнем узле резервуара
и существенно повышает несущую способность «безмоментной» кровли.
9 Заказ 2036
129
Шаровой резервуар
В настоящее время как в СССР, так и за рубежом для хранения
сжиженных нефтяных газов широко применяются шаровые резер-
вуары.
В практике отечественного резервуаростроения наибольшее
распространение получили шаровые емкости объемом 600—4000 м3,
работающие под давлением 2,5—18 кгс/см2. Шаровые резервуары
опираются либо на систему трубчатых опорных стоек (по экватору
или несколько ниже), либо на цилиндрический постамент (ста-
кан) [9]. Число опорных стоек в зависимости от емкости колеблется
от 8 до 16, а диаметр постамента равен радиусу резервуара.
Придерживаясь установленного
в гл. 1 порядка расчета упругих тонких
оболочек, определим сначала напря-
женно-деформированное состояние обо-
лочки шарового резервуара, опертого
на упругий цилиндрический постамент
при действии
грузки.
эксплуатационной на-
безмоментной
е о р и и
эксплуатации на обо-
Расчет по
т
В процессе
лочку шарового резервуара симмет-
рично относительно вертикальной оси
оказывает воздействие гидростатическое давление жидкости с удель-
ным весом у и избыточное давление р, поэтому:
^=г/п = 0;
Z„ = p + y7?(l-cos<p);
(2.162)
n = 0; 5„=Уп = 0.
Условие равновесия части оболочки, расположенной выше сече-
йия, определяемого углом <р (рис. 45), соответствует уравнению
2nnVfB) sin <р Qa — 0.
На рис. 45 видно, что
r = Z?sin<p,
поэтому последнее условие запишется
2л R sin2 + Q3 = 0.
(2.163)
130
Равнодействующая QB давления этой части оболочки выразится
интегралом:
<р v
= —2nR2 j znsin<p cos ф (ftp = — 2л7?2 j [p + yR (1 — совф)] x
о 0
Хз1пфСО8ф(/ф = — п7?2р81п2ф — 2nRay ----COS2 ф ^1--у СО8ф)^ .
(2.164)
После подстановки (2.164) в (2.163) выражение для продольного
усилия примет вид
дг(б) Qb ____ pR । yR2 / л 2cos2<p \
7V1B “ ~ 2itffsin2(p-6~ k l+cos<p ?
Выражение для кольцевого усилия определяется из третьего
уравнения равновесия (1.31):
= Rzn - (5 - 6 cos ф + ). (2.166)
Тогда горизонтальное перемещение верхней части оболочки
резервуара будет равно
«» = ялр +
+-1g. F5_v-6 с08ф+ 2(1,+ v)eosa<p'lSiny. (2.107)
1 QEh L l + costp J T v '
Угол поворота касательной к меридиану резервуара определяется
соотношением:
*“,=-4[w+(1+v)I“]=-Slsi”'f' (2168)
Аналогично определяются внутренние усилия и перемещения
нижней части оболочки резервуара, когда ф >а. Только в этом
случае следует учитывать не только внутреннее давление, но и сумму
вертикальных реакций со стороны постамента. Эта сумма равна
полному весу жидкости, хранимой в резервуаре, т. е.
G = ±n7?Y (2.169)
О .’
Тогда суммарная равнодействующая вертикальных реакций со
стороны постамента и внутреннего давления, действующих на обо-
лочку при ф ^>а, будет равна
<2н= -G + QB = - ул7?3у —2л7?3у — у соз2ф(1-у созф)] —
—- nR2p sin2 ф. (2.170)
9* 131
Производя действия, аналогичные верхней части оболочки
резервуара, получим:
V(6)_ PR । уЛ2 / к , 2cos2(p \
1Н 2 6 \ “г 1—cos ср )’
Я® =4-+^ (1 - 6cos3 ф _ 2£S*i_);
2 1 6 \ т 1 — cos ф / ’
с(б) (1— V) р/?2 sin <р , уДз Г- 2(l + v)cos2 (р"1 .
«" = J—2И—51+тег L1 -Sv -6 cos ’+-T-cU JSl” t:
(2.171)
.(6) Y^2 •
W” = - sin ф.
Таким образом, безмоментное напряженно-деформированное
состояние оболочки сферического резервуара определяется для
области ф <а формулами (2.165)—(2.168), а для области ф >а —
зависимостями (2.171).
' Теперь определим безмоментное напряженно-деформированное
состояние цилиндрической оболочки опорного постамента;
На торец оболочки цилиндрического постамента в направлении
оси Ох (рис. 46) оказывает равномерно распределенное по окруж-
ности воздействие вес резервуара с жидкостью:
Р = ^ у + 4л/?2Лур, (2.172)
и
132
где h — толщина стенки резервуара; у, ур — соответственно удель-
ный вес жидкости и материала резервуара.
Так как поверхностная нагрузка на оболочке постамента отсут-
ствует, то компоненты хп = уп = zn — 0 и, следовательно,
^б) = Мц = <2цб) = О, а = (2.173)
где г — радиус кривизны оболочки постамента.
Тогда из первого геометрического уравнения (1.29) выражение
для продольного перемещения запишется:
= A f*+с = - Asr1 +с-
Произвольную постоянную С определим из граничных условий
в нижнем сечении постамента: при х = Н U^y (Я) = 0, откуда
с PH
2ягЕцкц
и, следовательно,
= (2-174)
Из второго геометрического уравнения (1.29), принимая во вни-
мание, что при осесимметричной деформации Уцб) = 0, следует:
^б'=А' (2Л75)
т. е. радиальное перемещение цилиндрической оболочки при без-
моментном решении постоянно по всей высоте постамента и поэтому
угол поворота касательной к образующей ф^б) = 0.
Построение краевого эффекта
При (р = а, т. е. в опорном сечении сферической оболочки как
продольные, так и кольцевые усилия изменяются скачком на вели-
чину 38-П2~ф 1 а это приводит к разрыву непрерывности горизонталь-
ных перемещений и нарушению условий безмоментного напряжен-
ного состояния шарового резервуара. Поэтому в узких зонах, при-
мыкающих к постаменту, должно возникнуть моментное напряженное
состояние — краевой эффект.
Моментное напряженное состояние верхней части сферической
оболочки определяется формулами (1.88)—(1.95), а нижней —
(1.95, а).
Исключая с помощью начальных параметров Q* и М 0 произволь-
ные постоянные А, В в формулах (1.88)—(1.95) и С, D в формулах
(1.95, а), запишем выражения для внутренних усилий, моментов
и перемещений сферической оболочки в следующем виде:
133
для-области ф а
б,кр)= [/ЩЧУ+ v^T4B)M0B +
+ (vctg<pT3B-2XT3B)(?0*B];
’ ^КР’ = ~ + AW0ЛЗП);
М{Т =~(-2QMB + КММ; (2.176)
«’ = yr I ~ (ctg фЧ\3 4 2vlT4B) <?0*а +
+ ^(ctg?¥3E4-vX'F1B)M№];
<?-КР’ = ^*Л + КМ^’
ctg ф ($BW2в + АЛ70п¥41.) ;
Мквр’ = X (-ЛГМввТ2в + 2(?^ЗВ);
для области ф а
б(Кр) = £|пф [К _ v ctgфY4h) Mqн +
4-(2X¥3„ + vctg<p¥2H)(2*0H];
Пр’=-^Мн+О0Т8й);
м®> = 4 (2ЩЛ + 2<2*Ончт4Н);
ад’ - 4г i(ctg л+2vX4f«)Q «н+к <ctg Л+v ХТ1н) Л/»"];
(2.177)
*?-’ =iib
TVir - ctg ф ($нТ2н - ЯМЛ);
Л-= - X (Ж,нт2н + 2(?;Л);
•.с
_____________________6 (1—у2)Д_
К~ W R' (2.178)
„ _ 3(1-у2)Я~
л V №
<2ов = (<?ов — <2ов) Sin Ф = ((?ов — N1^ cos ф) sin ф; (2.179)
<2Sh = «?он - <2он) 81Пф = (&Н- Мн COS ф) ЭЫф.
134
г1г]в = е~^: (cos Mi4-sin Mi);
чм = (cos Mi—sin Mi);
Т3в = е~Хч>* cos Mi!
^4в = е'кч>1 sin Mi.
Tjh = e'A<P2 (cos М2 + sin М2);
T2h = e-^2 (cos М2— sin М2);
4f3H = e^4’2cos Мг!
Чг4и = e'x<f)2 sin Мг5
(2.180)
<Pi = a-<p;
ф2 = <р — a.
Функции ф1в — ф4н затухают по мере удаления от сечения ф = а
в направлении по часовой стрелке вдоль меридиана верхней части
сферической оболочки (0 ig <pt а).
А функции ф1н — ф4н затухают по мере удаления от сечения ф =
= а в направлении против часовой стрелки вдоль меридиана нижней
части оболочки (а ф2 л) (см. рис. 17).
Между функциями фч — ф4 существуют следующие дифферен-
циальные зависимости:
Т1 - 2Х¥4, Т2 - - 2 VF3. 4% - - Т; = /Лг2. (2.181)
Моментное напряженно-деформированное состояние цилиндриче-
ской оболочки опорного постамента в области, примыкающей к краю,
х^г 0 определяется по формулам (1.72).
Построение общего решения
Для любой емкости сферического резервуара параметр тонко-
стенной оболочки Л 2> 1. Поэтому, пренебрегая в зависимостях
(2.176) и (2.177) величиной v ctg ф по сравнению с л и складывая
моментное решение с безмоментным, получим:
для области ф а
6в = - WA - 2$В^в) +
(l-v) pfl2 Sintp Г 2 (1 + v) cosZcp -1
+ 2Eh г 6Eh |_э v b cos <p -j- {+cos ф J sin ф,
~ (- <?*ЛВ + WOaT3B) - sill ф;
М1В = а (_ 2(?*0вф-4в _ АМОВ¥1В); (2.182)
135
M2B = -^[- (ctg<pT1B + 2vX'F4B)^B-1-
+ /C(ctg<p¥3B + v^1B)Jf0B];
□111 Ц/
tfM=ctgT(«»T»+«M.Yu)+^+-!^(i--
^. = X(2Q;p4'„-».,V„)+4-+J^(5-ecos<P+^^);
для области <p a
fi«= ~ (KM^ + 2<?0иУ3н) + U ~ V)2^2 81П Ф +
, vfls Г, c c , 2(l + v)cos2<p-| .
+ fe? L1 - 5v - 6-C0S + 1-СО8Ф "J Sin
(<2S Л1Н 4- ЖЛ„) - Sin <p;
11 г h Eilt.
M2H = [(ctg <p¥1H + 2vXV4h) $h + £(ctg фТ3н 4- v X^) M 0H];
(2.183)
□ 111
7V1H = ctg q> (<2*OhY2h - «НЧ%) + ( 5 + );
U \ 1 VU3 /
^„= -Х(2№ЧГзн + ^онТ2н) + 4 4-1(2 (1-6со82ф_.
для области x 0 цилиндрической оболочки опорного поста-
мента
и'-->(('.ф.+₽Лф!)+2^1;;
Ф^-^(<20Ф1+2рцМ0Фз);
лц
Рц
Qi = —2рцМ0Ф4+ <?0Ф2;
M2 = v^ (2.184)
J 36
(2.185)
(2.186)
JV2 = - 2рцг (рцМ0Ф2 + <20Ф3);
и Р{И-х)
Рассечем узел сопряжения сферической оболочки резервуара
и цилиндрической оболочки опорного постамента, как показано
на рис. 46. Тогда условия совместности деформации и уравнения
равновесия рассматриваемого узла при <р = а и х = 0 запишутся:
6B(a) = 6H(a) = W(OWo;
Фв(а) = фн(а) = ф(О) = фо;
Л^ов -^он —
Qo» Qo = °-
При ф = а и х == 0 выражения для горизонтальных перемещений
и углов поворота оболочек сферического резервуара и цилиндри-
ческого постамента принимают вид:
6В (a) = Rs^ a ( — ЬКМОВ + 2Х sin а(?ов — 2XJV^) sin a cos а +
£t п I
+ + r5_v_6cosa+ 2(1+V)
1 2 1 6 L 1 +COS a J)’
6Я (a) — л^1,пое / _ XKM0B — 2X sin a()0H 4- 2?^V{h) sin a cos a 4-
.Ctrl I
+ (l-v)p«+IBtr1_5v_6cosa+ (2.187)
и'<°)=-^^+₽Л)+Д^:
Фв (a) = ( — sin a^0B 4- КМйв 4- sin a cos a —
“ wsina);
Фи (a) = ( — sin a(?0H — КМйв 4- sin a cos a — 1^-sin a);
ф(О)=-Ж(ео + 20цМо).
Лц
Исключая из формул (2.187) МОв и QOb с помощью условий равно-
весия (2.186) и раскрывая условия совместности деформации (2.185),
получим:
4Z sin а()Он 4- 2Х sin а()0 — К\Мй 4-^ = 0;
Pi(?o — 2ЛГХМ0н4- ЛГр,дЛ/04- ?2 = о>
- sin а(?0 4- 2£М0н 4- КМй 4- q3 = 0;
2 sin и^он -j- Р-2^?0 + 4“ ?4 ~
(2.188)
137
где
и __ iEh^
к K^R sin а
4- 2ksin а;
2Eh№
^2“ Ац>.2 SinCl’
_ _W__i
/СА'цЛяша
_ 4ЯЭД
114 ~ кк^ •
(2.189)
ср = - - X sin a cos apR 4- 2yR2 [ — 2A, sin a cos a x
v /1 2cos3a A i (!+у) /л cos3a 4~| t
X \ + 3 sin2 a 3 V sin2a/J’
,. = (i-v)pR- +Tyx
Olli (л
X j- 4X ctg «+1_v_2cosa+2 (1 + v) ctg2 a J . (219Q)
_ 2y/?2 ctg a
93 - F~ 5
'flS7“S°+Y^Si.a[-X + ^(l -44^)].
Из решения системы уравнений (2.188) получим:
<2он = 4<osina ["Г (^з ~ РтШ + fyh + Чч sin а) +
+ (?2 + ^?з) (Нг + 2р4 sin а) — д4 (К sin а 4- р4 2ц3 sin a) j ;
Со = 1Н(4^ + М + Нз) + (92 + Мз) (1 - 2^)]; (2.191)
М°« = 7^ [("V + 2?4) (Hi + Из sin а) - д2 (2ц2 + sin а -4
+ 2|i4 sin а) 4- 2<73 (р.2Из — Н1Н4 + 0,5 sin а 4 р3 sin а)^|;
М°= [( + qi) (^ sin а — Hi) + (?2 + ^?з) (sin а + ш)],
где
со = ~ (2|л4 — 1) — Z,|i2 — р3 (р2 + sin а) — Хр4 sin а —. (2.192)
Остальные два неизвестных определяются по формулам:
М()В = -Мон 4“ Мд',
Q0B = Q0H + Q0. (2Л93)
138
Таким образом, получены выражения для шести неизвестных
усилий и моментов, действующих в опорном сечении сферического
резервуара. Если подставить соответствующие значения этих усилий
и моментов в формулы (2.182)—(2.184) с учетом равенств (2.179),
можно получить выражения для внутренних усилий, моментов
и перемещений, полностью определяющих напряженно-деформиро-
ванное состояние оболочки сферического резервуара при действии
эксплуатационной нагрузки.
Пример. Определим величину изгибных напряжений в опорном сечении
сферического резервуара вместимостью 600 м3, опертого на упругий металличе-
ский постамент для хранения сжиженного бутана, при следующих исходных
данных: Я = 525 см; г = 262,5 см; h = 1,6 см; h„ = 1 см; v = = 0,3;
а — 150°; £ = 2?ц = 2,1 10е кгс/см2; р = 6 кгс/см2; у = 10“3 кгс/см3;
1Z3
ур = 7,85 • 10“ 3 кгс/см3; sin а = 0,5; cos а =-— .
Определим прежде всего основные расчетные параметры:
4ВтПТ~7’и>:,’'! 1/с“;
3(1-0,32) X 5252
1,62
К = 2 Х 28,28 = 8,87 X 10-2 1/см;
525
р= 4ХЗ,14Х 5233 Х10-3|4 х зд4 х 5252 х 1)6 х 7185 х 10-з =
= 6,33 X 105 кгс.
Так как Е = £ц и Л'ц = , то формулы (2.189) можно записать так:
0,5=2,06;
. 4 X 1,6 X 7,93 • IO"2 X 262,52
haR sin« IX 525 X 0,5
4-2 x 23,28 X 0,5= 156,56;
2ОДг2 . 2 X 1,6 X (7,93 • IO'3)2 X 262,52
И2 = а =---------------------------------
„ - 1 - 4 X 1,6 X (7,93 - 10-2)2 х 262,52
И ОцЯвта 8,87-10-2 X 1 X 525 X 0,5 3,8 93,J3,
4/iPV2 i, 4 X 1,6 X (7,93 • 10-2)3 х 262,52
Щ ЛТгцХз"’'1 8,87-10’2 X 1 X 23,282 4-1-5,58.
Грузовые параметры согласно (2.190) равны:
9l = - 23,28X0,5
X 6Х5254-2. Ю-з х5252Х
X — 2 х 23,28 X 0,5 X
3X0,5*
з
139
з
(1 + 0,3)
3
= 2145*104 кгс/см;
1 _ 1-------
0,52
(1-0’3) X 6 X +10-3 X 5252 X
'4X23,28 (-Уз)
4-1—0,3 —2
3
= — 1,16 • 104 кгс/см;
2 X Ю-з X 5252 X (-/З) ,
?з =-------------5----1----- = 318,26 кгс/см;
3
I vT
6 X 525 X 0,5 X-------f-
-----=-^ + Ю-з х 5252 х 0,5 X
, 2х\ i
2
1
23,282
— —479,44 кгс/см.
Коэффициент
<о= - (2 X 5,58-1)- 23,28 X 2,06-95,93 X
X (2,06 + 0,5) -23,28 X 5,58 X 0,5 —23,28>SM. — 430.
и
Значения усилий и моментов в опорном сечении равны:
= 4X0,5X430 <2-06 х 95,93-156,50 X 5,58 +
+ 23,28 X 2,06 + 23,28 X 0,5 X 5,58) + (-1,16 • 104 + 23,28 X 318,26) X
X (2,06 + 2 X 0,5 X 5,58) + 479,44 X (23,28 X 0,5 +156,56 +
X 2 X 0,5 X 95,93) ] — —577 кгс/см;
Q. = т+й [+ftr- 2 * /‘79’/‘4) <23'28 + + <-1,1в. ю< +
+ 23,28 X 318,26) (1—2 X 5,58)] = 62,15 кгс/см;
М —__________1________Г( 2,45 ‘— 2 х 479 44 X
4 X 8,87 IO-2 X 430 L \ 23,28 ^X/HU./AJX
X (156,56 + 95,93 X 0,5) +1,16 • 104 (2 X 2,06 + 0,5 + 2 X 5,58 X 0,5) +
+ 2 X 318,26 (2,06 X 95,93 -156,56 X 5,58 + 0,5 X 0,5 +
+0,5x95,93)] ==-1716 кгс- см/см;
140
«>- 3.87.W-X430[(ъгэ!-««•«) <23,28 х 0,5 -156,56) +
+ (—1,16-101+ 23,28 X 318,26) (0,5+ 2,06)] =—456 кгс-см/см;
Л/Ов —1716 —456=—2272 кгс-см/см;
(?ов=-557 + 62,15=-514,85 кгс/см.
Следовательно, интенсивность изгибных напряжений, например, у наруж-
ной поверхности в верхней и нижней областях сферического резервуара и на
верхней кромке цилиндрического постамента будет равна соответственно:
<,,,=-5^» _1<=®а_-5315 вгс/см2;
= 4020 кге/ом2;
6(~р6) -"2740 „гс/ом-.
Значительная интенсивность изгибных напряжений в опорном
сечении шаровых резервуаров вызывает необходимость приме-
нения высокопрочной стали с расчетным сопротивлением не
менее 4500 кгс/сма. Интенсивность изгибных напряжений в опорном
сечении шарового резервуара можно несколько снизить, если опорное
сечение выбрать у экватора, т. е. при <р =~^-> а постамент заменить
системой из п опорных стоек.
В этом случае оболочка шарового резервуара будет находиться
в более благоприятных условиях, так как нормальная компонента
реактивной силы на опорах будет равна нулю.
Безмоментное напряженно-деформированное состояние верхней
части оболочки шарового резервуара, как и в первом случае, опре-
деляется по формулам (2.165)—(2.168). На опорах продольные уси-
лия возрастают на величину, равную весу резервуара вместе с жидко-
стью, деленному на число опор и ширину опоры:
= (2.194)
где 0О — центральный угол, соответствующий ширине опоры.
При заданном числе опорных стоек, а также геометрических
размерах шаровых резервуаров между опорными стойками у эква-
тора усилие (а) равно нулю. Следовательно, несмотря на то,
что эксплуатационная нагрузка оказывает осесимметричное воздей-
ствие на оболочку резервуара, напряжённо-деформированное состо-
яние ее будет функцией как <р, так и 0.
141
Так как функция продольного усилия у экватора изменяется
в окружном направлении периодически (рис. 47), то ее можно пред-
ставить в виде тригонометрического ряда по углу 0.
Л\(а, 0)
__ Xi (а)
2я
ш=1
~2~cos (m, 0)
-—sin
т
(2.195)
Скачкообразное изменение усилия Ni (а, 0), а следовательно
N2 (а, 0) и S (а, 0), у экватора приводит к разрыву непрерывности
радиального перемещения и из-
гибу оболочки в зоне опорных
стоек. Оценка величины изгиб-
ных напряжений в зонах, примы-
кающих к опорным стойкам, свя-
зана с серьезными затруднениями.
Как показано в работе [12], схо-
димость ряда (2.195) существенно
п9п
зависит от величины —у-, т. е. от
2л ’
отношения ширины опоры к расстоянию между опорами: чем
меньше это отношение, тем хуже сходимость ряда. Например,
при = 0,25 для получения достаточно точного результата
необходимо удержать в ряде (2.195) около 15 членов.
Громоздкость данной задачи станет очевидной, если учесть, что
для каждого члена тригонометрического ряда необходимо:
рассчитать верхнюю и нижнюю части оболочки резервуара по
безмоментной теории;
наложить на безмоментное решение краевые эффекты;
определить из условий совместности деформации и равновесия
у экватора ^при <р = произвольные постоянные (начальные
параметры);
получить общее решение, т. е. фактически нужно 15 раз проводить
расчет оболочки сферического резервуара. Поэтому данный алгоритм
расчета целесообразно реализовать на ЭВМ.
Глава 3
ПРОЧНОСТЬ ОБОЛОЧЕК ТРУБОПРОВОДОВ
Напряженно-деформированное состояние висячего перехода
нефтепродуктопровода
В практике проектирования и эксплуатации трубопроводов (осо-
бенно больших диаметров) весьма часто возникают задачи, решение
которых методами сопротивления материалов может привести к серь-
езным ошибкам.
Дело в том, что элементарная теория стержня дает достаточно
точные результаты расчета только для таких тел, у которых наи-
больший размер поперечного сечения по крайней мере в пять —
шесть раз меньше продольного. Если при расчете трубопровода это
условие не соблюдается, то следует применять теорию оболочек.
Чтобы иметь качественное и количестйенное представление
о погрешности расчета трубопровода как стержня, определим
напряженно-деформированное состояние, например, висячего пере-
хода нефтепродуктопровода пролетом I С 127? методами теории упру-
гих тонких оболочек и для сравнения методами сопротивления
материалов.
Предположим, что трубопровод, заполненный нефтепродуктом
удельного веса у, покоится на опорах абсолютно жестких в своей
плоскости и подвижных в направлении Ох (рис. 48).
В этом случае на краях трубопровода равны нулю: продольная
сила N i и перемещения W и V.
Компоненты нагрузки от собственного веса q для горизонтальной
трубы и гидростатического давления жидкости равны:
Т=0;
Y = sin 0;
(ЗЛ)
Z — yR — (q + yR) cos 0.
143
Запишем уравнения, характеризующие безмоментное напря-
женно-деформированное состояние цилиндрической оболочки,
приняв в (1.21) и (1.22)
= = Rt^r = R;
уравнения равновесия
геометрические уравнения
»+1г4№-,Ч1 (3.3)
dV , i dU 2(l+v) c
dx "r R dQ Eh °'
Непосредственно из третьего уравнения равновесия (3.2) выра-
жение для кольцевого усилия запишется:
N2 = R [yR — (g + y7?)cos0J. (3.4)
Так как
^==7?(g4Y7?)sine,
то из второго уравнения системы (3.2) следует:
5 = — sin 9 J (2? + у7?)Й2: + С1(6)= -sinO (2g' + y7?)x-|-Ci(0). (3.5)
144
Учитывая, что
л /п I I (®)
-= - cos 0 (2 q + у В) х Н-Jg—,
из первого уравнения системы (3.2) получим
ЛГ, = 4- J[c«s 6 Ш + ?Я) х-тг] * + <! <0) =
- 4- [cos0 (2g + уЯ) /]+С, (в).
Задав функции С { (0) и С2 (0) в форме
(^(OH^sinO;
C2(0) = C2cos0, L ’
определим произвольные постоянные С i и С 2 из следующих гранич-
ных условий на опорах трубопровода: при х — О N = 0; х=1
NX = Q.
Из этих условий следует, что
С2 = 0; С1= (2д+^Д) г_ (37)
Тогда выражения для сдвигающего и продольного усилий при-
мут вид:
S = (2?+уВ} — я) sin 0;
(2g+7Д) х cojg g
Теперь определим перемещения трубопровода. Из первого гео-
метрического уравнения системы (3.3) следует:
и=4h ~vNi) dx+G (0)=[ (2?12лд )'2, (2х + cos 0+
4-уЯ (g-i-Y-ff) cos0 — уу/?2ж^4-С3(0);
Так как
dU sin0 Г(2д + уД)я2 /г» , on । о / । о Я г df3(6)
7Г = - -ЁГ L 12Я <2Z + 3Z> + VRX J + T-1 ’
то из третьего геометрического уравнения с учетом (3.8) получим:
= (/-x)|3in 0+-SA (|+()*•+
+ V» -у (9 + уЯ) —г + С. (0).
10 Заказ 2036
145
Принимая во внимание, что функции
Сз (0)= Сзcos 0; „ п
г c4(0)-c4sine,, (3,9>
определим произвольные постоянные Cs и (\ из граничных условий
на опорах трубопровода при х = О, V = 0; х = Z, V — 0.
Раскрывая эти условия, получим:
С3 = - -JL. Г(2д + Тд).г2. + VjR + уд)-]
3 2Eh L 47? 1 ’ (3.10)
С4 = 0.
Тогда выражения для перемещений оболочки трубопровода вдоль
осей жиг/ запишутся:
U - [ (2g1j^--)- (4z3 - 3Z3 + 6Л) +
+ vR (q + yfl) (2x - Z)] cos 9 - ;
V = 124Л2 (1 + v) (I-x) 4- (3’И>
+ ж2 (x + 21)- 3Z3] sin 0 + v(9+vW-Z)^ sin 9
Выражение для нормального прогиба оболочки трубопровода
(перемещение вдоль оси z) определим из второго геометрического
уравнения (3.3):
112(2+ v)Д’(;-») +
4-х2 (х + 21) — 3Z3] cos9 — [2Д2 —va:(Z — ж)] cosQ-f--^ •• (3.12)
Непосредственно на опорах трубопровода при х = 0 и х = I
И7 = [у/? — (д 4- уЯ) cos 9],
т. е. граничные условия относительно нормального прогиба оболочки
не выполняются: труба стремится сместиться с опор в радиальном
направлении.
Но так как конструкция опор препятствует радиальным пере-
мещениям оболочки трубопровода, то непосредственно у опоры
должно возникнуть моментное напряженное состояние.
С помощью формул (3.4), (3.8), (3.11) и (3.12) можно определить
усилия и перемещения в любой точке трубопровода, заполненного
жидкостью, с учетом его собственного веса. На рис. 49 представлены
эпюры внутренних усилий в продольном (9 = л) и кольцевом ( х = )
направлениях оболочки трубопровода. Из этих эпюр видно, что
146
продольные и кольцевые напряжения достигают максимальной
интенсивности в точке с координатами х и 0 = л:
1' h 8Rh
+ (3.13)
2 h h ’ 4 '
N2(B=n)
Несущая способность оболочки трубопровода оценивается по
величине приведенного напряжения
о, = V°i + — ^1^2 + Зт2.
Теперь решим эту же задачу, рассматривая трубопровод как
балку на двух опорах под действием равномерно распределенной
нагрузки G.
Нагрузка на балку от действия гидростатической нагрузки и соб-
ственного веса трубы равна
G = aR2y + 2nRq = aR(2q + yR); (3.14)
10*
147
Изгибающий момент в сечении а: == -у балки —
Л
пл- (№ nR (уД H~2g) I2 .
8 8
напряжения в сечении х = у трубопровода —
М _ (2?+уДН2
°х ~ - лД2Л - 8ДЛ
(3.15)
(3.16)
Из сопоставления формул (3.13) и (3.16) видно, что напряженное
состояние «трубопровода — балки» отличается от напряженного
состояния «трубопровода — оболочки» на величину кольцевых на-
пряжений, не зависящих от длины пролета трубопровода. Чем
больше отношение (чем «тоньше» оболочка), тем значительнее
это отличие. Но так как при больших пролетах трубопровода (при
I > 122?) интенсивность продольных напряжений <т( значительно
выше кольцевых о2, т0 последними можно с достаточной точностью
пренебречь, в этом случае расчет трубопровода сводится к расчету
балки.
Расчет сопряжения магистрального трубопровода и арматуры
Определим (рис. 50) напряженно-деформированное состояние
длинной цилиндрической оболочки трубопровода, жестко сопряжен-
ного с арматурой (задвижкой, клапаном, краном и т. п.) при дей-
ствии внутреннего избы-
точного давления (газа или
нефтепродукта).
Так как избыточное
давление р оказывает осе-
симметричное воздействие
на оболочку трубопровода,
то п = 0, а компоненты
поверхностной нагрузки
л?о = Уо = °* го = Р- (317)
Тогда усилия и перемещения безмоментного напряженного состо-
яния оболочки трубопровода согласно (1.28) и (1.29) запишутся:
N^ = RZ(i^pR-,
дг(б> рлД2 _ рД т
1 2лД 2 ’
5(б) = 0;
И””=4
148
V<6, = 0;
U<6) = 4г f - ^26)) dx + C = -~^Х + C.
I-t ft J £ri!L
Из условия на границе сопряжения трубопровода (при х = 0)
и арматуры следует, что С7(б,= 0 и С = 0.
Складывая безмоментное решение (3.18) с моментным (1,72),
получим:
w = - f (рмвф2 + <20Фз);
ip = -f-(2₽^s + ^);
л/^л/оФх+’уФ*;
(?1=-2рм0Ф4 4 (?0Ф2;
2V1 = -^- = const; (3.19)
Лт2= -207? (₽М0Ф2 + е0Ф3) + рЯ;
Я2 — vMx]
,т_ (1 —2у) pRx
U ~ 2Eh
Неизвестные начальные параметры: момент 7И0 и перерезыва-
ющее усилие (?о определим из граничных условий в точках сопря-
жения трубопровода с арматурой. Так как жесткость арматуры
значительно превышает жесткость оболочки трубопровода, то можно
считать, что край трубопровода жестко защемлен, т. е. при х = 0
соблюдаются следующие условия:
И7 (0) = ф (0) = 0.
При этих условиях из уравнений (3.19) получим значения изги-
бающего момента и перерезывающего усилия по линии сопряжения
трубопровода и арматуры:
и _ _ (2-у) pR*K _ _ (2 -у) р .
0 iEhp 4Р« ’
Подставляя значения начальных параметров в формулы (3.19),
будем иметь выражения для внутренних усилий, моментов и
149
перемещений, полностью определяющих напряженно-деформиро-
ванное состояние оболочки трубопровода в зоне, примыкающей
к арматуре:
w _ (2 —т) рД2
2Eh
(1-Фт);
(2-у)рРД2
* Eh
Ж1~ ф2>
О - (2— У)Р ф .
Vi - 2р Фз’
= [1 —(2 —v) (Dj;
М2 = vMt;
р _ (1 — 2v) pRx
U 2ЁЬ '
(3.21)
На рис. 51 в качестве примера представлены эпюры нормального
прогиба W, а также продольных и кольцевых напряжений у вну-
тренней поверхности газопровода диаметром 1020 мм с толщиной
стенки трубы 12 мм, построенные по формулам:
СЛ/х , N,
„ 6М2 . n2
ff‘2“ Eir + тг
при внутреннем избыточном давлении газа р = 55 кгс/см2.
Как видно из рисунка, ширина зоны затухания моментного на-
пряженного состояния равна 245 мм. Следовательно, в области
0 х 245 мм напряженно-деформированное состояние оболочки
150
газопровода соответствует краевому эффекту, а в области х >
245 мм — безмоментное. В сечении х = 0 величина продольного
напряжения у внутренней поверхности оболочки превышает предел
текучести материала трубопровода и в этих точках появляются
пластические деформации. Если принять нижний предел текучести
стали <тг = 3500 кгс/см2, то длина зоны распространения пластиче-
ских деформаций в данном случае составит 2,2 мм. Несущая способ-
ность трубопровода в сечении х = 0 будет исчерпана, когда давление
в трубопроводе превысит предельное значение, при котором все
поперечное сечение оболочки будет охвачено пластической дефор-
мацией.
Расчет сопряжения труб с различной толщиной стенки
Магистральные нефте- и продуктопроводы, транспортирующие
нефть и нефтепродукты всегда"в одном направлении, проектируются
из труб с различной толщиной стенки (в соответствии с падением
давления по длине трубопровода) ступенчатыми.
В этом случае из-за скачкообразного изменения толщины стенки
оболочки трубопровода в зонах, примыкающих к узлу сопряжения,
возникают изгибные напряжения, интенсивность которых в зависи-
мости от разности толщин может достичь большой величины.
Приняв начало координат по линии сопряжения труб с различной
толщиной стенки, определим напряженно-деформированное состо-
яние их оболочек в зонах, примыкающих к стыку, при действии
внутреннего избыточного давления интенсивностью р (рис. 52).
При действии осесимметричной нагрузки р усилия и перемещения
безмоментного напряженного состояния оболочек трубопровода с раз-
личной толщиной стенки вычисляются по формулам (3.18), а краевого
эффекта — для оболочек I и II — соответственно с помощью зависи-
мостей (1.72) и (1.72, а).
В точках сопряжения оболочек трубопровода с различной тол-
щиной стенки соблюдаются следующие условия: при х = 0
Фо^'Фо1-
(3.22)
151
Складывая безмоментные перемещения (3.18) с моментными
(1.72, а) и (1.72) и раскрывая условия (3.22), получим:
(2-у)р^ 2ga (2—у) pH2
2Eh2 + К2( P^o+Vo)- 2Eh1
«+<?„); (3.23)
^(^-2W = -f-(2₽1Mo+-^,
где Мв, Qo — соответственно изгибающий момент и перерезыва-
ющее усилие, действующие по линии сопряжения оболочек трубопро-
вода с различной толщиной стенки:
гл Eh*, 2
Л1. 2~
(3-24)
. _t/3(1-v2>
•1.2- И "ЖТ
Уравнения (3.23) можно записать:
2 (ед - ед) м0 - 2 (ед+ед) <?«+(^ ед) -о;
2 (3.25)
2 <ед+ед> м0- (ед ед И) <?«=о.
Из решения системы уравнений
(3.25) следует:
п _(2~v)PVRhAt
Vo — о •
(3.26)
пл __ (2 — у) pRhxh2
— 4 >
где
g а (i-б) [1+бЧ1+а)]
1 V3(1~V2) [2бЗ(1 + б2) + (1+61)2] •
S U-62)(l-S4)_______ .
2 V3 (1 - v2) [263 (1 62) + (1 + 64)2] ’
(3.27)
(3.28)
Определив неизвестные начальные параметры Мо и Qo, с помощью
соотношений (3.18), (1.72) и (1.72, а) можно получить зависимости,
характеризующие напряженно-деформированное состояние оболо-
чек трубопровода с различной толщиной стенки.
152
Например, для оболочки I эти зависимости запишутся:
^-^[1+й^ф--ьЖФа)Ь
,= е=Ж(9>ф,£Ф1);
(2 + ф X
4 \ Pi У Rfh )
^=|2~Тм(Аф«+рГЖф‘); f3-29»
Мг = vMp
Зависимость изгибных напряжений Oj в оболочке I от отношения
меньшей толщины стенки трубопровода к большей представлена
на рис. 53.
Напряженное состояние трубопровода при наварке хомутов и корыт
Для ликвидации течей и негерметичностей, ремонта сильно кор-
родированных участков на магистральных трубопроводах произ-
водится наварка хомутов, латок, корыт. При этом в точках сопря-
жения указанных элементов с оболочкой нарушаются условия без-
моментного напряженного состояния трубопровода (плавность
геометрической поверхности и скачкообразное изменение толщины
стенки) и появляются под действием нагрузки дополнительные
изгибные напряжения.
Для определения величины этих напряжений рассмотрим участок
трубопровода, примыкающий к хомуту, как полубесконечную обо-
лочку с краевыми нагрузками Мо и Qo, равномерно распределенными
по контуру сечения трубы (рис. 54).
Примем положительное направление нормального прогиба обо-
лочки трубопровода внутрь, тогда согласно формуле (1.65) общий
интеграл дифференциального уравнения изгиба цилиндрической
оболочки при осесимметричном загружении запишется
W — е~?х (Д3 cos pre 4- Z)4sin pz) — , (3.30)
где p — внутреннее избыточное давление в трубопроводе.
153
Принимая во внимание зависимости (1.72), выразим прогиб
и угол поворота трубопровода на границе сопрягаемых участков через
начальные параметры Qo и Мй (лишние неизвестные):
wo=^j(2₽<2—2₽гЛГ0—/>); (3.31)
Ч = ТГ(-«.+ 2«.
(3.32)
Решение уравнения для участка трубы, на которой расположен
хомут, запишем в виде
Рис. 54
Поместив начало координат посередине длины хомута, получим
G = C3 = 0.
Прогиб и угол поворота оболочки трубы по краям хомута будут
ттт го X 2О0₽,Я2 2М0В?Л2
----b(2a)-fg—; (3.34)
W v (9а) 2<?°Р1Л2 4-v (2d) ^оР?#2.
Пр - Х2 (2а) —НХ8(2а) Eh ,
\ ch 2а + cos 2а /Q \ sh 2 а sin 2а
b<2°)= ai.2«+8i.2« ; bW- sh2a+sCT-; (3-35)
. ch 2а —cos 2а
Хз(2а)- Sh2a + sin2a ’
где 2a = PiZ, I — длина хомута.
154
Приравнивая соответственно правые части равенств (3.31) и (3.33),
(3.32) и (3.35) с учетом правила знаков для угла поворота и решая
полученную систему относительно Мй и Qo, получим:
' Р 2[*1 + tх.<2«>]ph + tz,И-]-;
„ ____________________________________
(3.36)
(3.37)
Рассматривая крайние случаи, получаем непосредственно:
при = оо (жесткая заделка полубесконечной трубы)
М ~ р
О — 2р2 ’
при h = оо (короткий цилиндр, жестко защемленный по концам)
= Хг(2а);
при hi = h (гладкая оболочка)
7Ио = 0.
В случае, когда длина хомута I 4-, значение функций Xi (2а)
Х2(2а)^Хз(2а)~1;
°^2(>1+4)(^Н‘‘-Л;
(hL_h)(hl+h$L\
Qo — -я 7 Pi \ / ВГ\ 7 вГ\~ (3.39)
В качестве примера определим величину добавочных изгибных
напряжений в трубе диаметром 1020 мм с толщиной стенки 12 мм,
сопряженной с хомутом толщиной 12 мм.
Для одинаковых толщин хомута и трубопровода
Ь_=1
₽ ’
и выражение для изгибающего момента с учетом того, что v = 0,3,
согласно формуле (3.38) запишется
М = р
° 34Р2 ’
155
Тогда величина добавочных изгибных напряжений при внутрен
нем избыточном давлении р = 55 кгс/см2 будет равна
„ 0,107рЯ 0,107-55-61 ,
о =-----4-— = ——------------= 300 кгс/см2.
п 1,2
Теперь рассмотрим напряженное состояние трубопровода при
наварке корыта. В случае достаточно длинного корыта напряжения
в средней части его можно приближенно рассчитать по схеме кольца
с разной толщиной стенки, находящегося под действием внутреннего
давления.
В качестве основной примем систему, изображенную на рис. 55.
Уравнением связи является равенство нулю осевого смещения угла
поворота ключевого сечения.
Момент и продольная сила в произвольном сечении равны:
Мт=М+Nr (1 — cos <р) 4-ргл (1 — cos <р); (3.40)
= TV cos <р-|-(1 — costp). (3.41)
Система канонических уравнений для ключевого сечения имеет
вид:
МЬхц N$xn Дх0 — 0;
жем-' -л^+де^о. ч (3-42)
Согласно теореме Максвелла — Мора имеем
ч>
с С ММ-! J
= J ~ЁГ ds'
о
где М — единичный момент; М, — момент от единичной продольной
силы:
с г Г (1—COS ср) , 7-2 , .
8хм = j Ei г (*Ро - sm Фо);
о
То ч”» .
. (* Ml , . Г N1 ,
= j ~Eids+ J ~Eids'
о о
156
где Ni — единичная продольная сила:
<Ро <р»
е Г Г2(1“С03ф)2 , , С COS2 <р
' El rd<P+ J ~^}Trd(f =
о . о
=it (4 ’р» -2 sin <ро+4sin 2<р°)+ih (4г+4sin 2(Ро)
?О
д1р= J +
о
То
I С pr (1 — COS ф) COS ср J рг* / 3 о . I 1 п \ I
+ J ---------Eh ----~rd^ = -ET\i: <Ро—2 sin<p0 + — sin 2<р0 J +
о
+54 (sin Фо - - 4sin М •>
То
66м = f
J Л-А 1 1J1
о
?» То
fin (* ММ, , г r(l— coscp) , г2 .
60N= J ~^±ds=j EI (<p0-sin<p0);
0 0
То
Д0 = С ^ргЧ1^созф)rd = _g_ _sin
r t) £1 £u
О
Таким образом, имеем систему
-^-(«Po-sinToJM + (jq>0-2sinq)0 + ^sin2<р0) N +
+5г ( 4г + Т sin 2(Ро) N + 5т (4 (Ро- 2 sin ^0+4 sin 2<Ро) +
+ ( sin Фо - - 4 sin 2<Ро) = °’
Л fl \ кА /
5г <РоМ + 5г ((Ро “ Sin Ч’о) N + IT ('Ро - sin <Ро) = °-
Получаем для ключевого сечения
М = ------------1-----j-------; (3.43)
_Л2____ф0 ФО + Т^ФО
24г2 sin фо фо—sin ф0
JV=-pr+-g----------------------<Р,^?0-7-----(3.44)
(Фо-sin фо) sin Фо + 2^-фо (^Фо+у Sin 2ф0
157
Момент в сечении заделки будет
М^о — М—Nr (1 — cos<p0) — pr1 (1 — cos tp0);
до = M2 sin ф0 (sin фр-tpo cos <p0)
12 7,2 m Фо + у8т2фо
! , Фо______f_______
’r 24r2 sin фо ф0— sin ф0
Как следует из формул, напряжения от изгиба в продольных
сечениях, вызываемые наваркой длинного корыта, незначительны
и могут не учитываться в расчетах.
Этими напряжениями тем более можно пренебречь для коротких
латок. Для них напряжения от изгиба можно рассчитывать только
в кольцевых сечениях по формулам как для хомута.
Проверка прочности оболочек газонефтехранилищ
и трубопроводов
Основной задачей теории расчета тонкостенных пространственных
сооружений и, в частности, оболочек газонефтехранилищ и трубопро-
водов, подверженных тому или иному силовому, температурному
или другому воздействию, является обеспечение надежной работы
конструкции в процессе эксплуатации, что достигается путем раци-
онального подбора материалов оболочки и толщины стенки при
заданных условиях работы конструкции. Толщина стенки оболочки
газонефтехранилищ и трубопроводов может быть определена из
расчета на прочность (основной вид расчета), устойчивость или
жесткость.
При расчете конструкций газонефтехранилищ и трубопроводов
на прочность определяются выражения усилий и моментов в наиболее
напряженной точке поверхности. Но степень загружения материалов
оболочки и, следовательно, опасность наступления разрушения
характеризуются не величинами усилий и моментов в сечении,
а величинами наибольших нормальных и касательных напряжений.
Для изотропного материала оболочек величины продольных, коль-
цевых и касательных напряжений определяются соотношениями:
ГТ - 6М1
O1 h - № ’
п Nz . Шг .
S 6М12
т = т±т->
В формулах (3.46) знак «плюс» соответствует наружной поверх-
ности оболочки, знак «минус» — внутренней.
Равномерно распределенные по толщине оболочки напряжения
N-Jh, N2/Ди S/h обычно называют тангенциальными (мембранными,
158
Численные значения основных характеристик металла
Таблица 2
Вид стали Группа или марка стали -НП, кгс/см2 К = и ксп <в скобках)
встык Угловые
растяжение — сжатие срез
повышенный контроль шва обычный контроль шва
Углеродистая Ст. 3 2300 0,90 2100 (1) 1800 (0,86) 1300 (0,62) 1500 (0,71)
обыкновенного Ст. 4 2500 0,85 2100 (1) 1800 (0,86) 1300 (0,62) 1500 (0,71)
качества Ст. 5 2700 0,85 2300 (1) 2000 (0,86) 1400(0,62) 1600(0,70)
Термически упрочненная МСТ Т 3000 0,80 2400 (1) 2050 (0,86) 1500 (0,62) 1700 (0,70)
Низколегирован- 19Г 3000 0,85 2500 (1) 2100 (0,86) 1500 (0,62) 1750 (0,70)
пая 14Г2 3400 0,85 2900—2800 (1) 2500—2400 (0,86) 1700 (0,60) 2000 (0,70)
15ГС 3400 0,85 2900—2800 (1) 2500—2400 (0,86) 1700 (0,60) 2000 (0,70)
14ХГС 3400 0,85 2900—2800 (1) 2500—2400 (0,86) 1700 (0.60) 2000 (0,70)
10Г2С1, 10Г2СД 15ХСНД 3500 0,85 2900(1) 2500 (0,86) 1700 (0,60) 2000 (0,69)
3500 0,85 2900(1) 2500 (0,86) 1700 (0,60) 2000 (0,62)
10ХСНД 4000 0,85 3400 (1) 2900 (0,85) 2000 (0,59) 2400 (0,70)
цепными), а линейно меняющиеся по толщине оболочки напря-
жения 6М{/№, QMz/h? и QM2/h2 — изгибными.
С физической точки зрения очевидно, что материал оболочек
резервуаров и трубопроводов не в состоянии выдерживать сколь
угодно большие напряжения, поэтому напряженное состояние этих
конструкций в наиболее опасной точке поверхности оболочки (исходя
из условий надежности работы) должно быть ограничено некоторым
предельным напряженным состоянием. Оценку прочности оболочек
газонефтехранилищ и трубопроводов по известному напряженному
состоянию в наиболее опасной точке поверхности целесообразно
проводить по энергетической теории прочности, которая для сталь-
ных конструкций дает результаты, наиболее близкие к эксперимен-
тальным данным. Согласно этой теории при двухосном напряженном
состоянии прочность оболочки будет обеспечена, если соблюдается
условие
<уг = /ol + ol-пл + Зт2 =5 R”, (3.47)
где аг — приведенное напряжение, кгс/см2; К — коэффициент одно-
родности материала; т — коэффициент условий работы; R* — нор-
мативное сопротивление материала, кгс/см2; п — коэффициент
перегрузки.
Для стальных листовых конструкций коэффициент однородности
материала определяется отдельно для основного металла (К) и на-
плавленного металла (А7СВ)Т а нормативное сопротивление мате-
риала представляет собой минимальные статистически вероятностные
значения предела текучести с учетом минусовых допусков проката,
уменьшающих расчетную площадь сечения [9]. Для газохранилищ
и нефтехранилищ коэффициент условий работы т принимается по
СНиП II. В-3—62, а коэффициент перегрузки п определяется по
следующим данным:
Вид нагрузки п
Гидростатическое давление жидкости....................1,1
Избыточное давление газа или вакуум.................., 1,2
Собственный вес конструкции...........................1,1
Собственный вес оборудования........................... 1,2
Снеговая нагрузка.....................................1,4
Ветровая нагрузка.....................................1,2
Численные значения основных характеристик различных
групп и марок сталей, применяемых в конструкциях газонефтехра-
нилищ и трубопроводов, представлены в табл. 2.
Глава 4
УСТОЙЧИВОСТЬ РЕЗЕРВУАРОВ И ТРУБОПРОВОДОВ
В предыдущих главах рассматривались вопросы прочности обо-
лочек резервуаров и трубопроводов при действии тех или иных
видов статической нагрузки. Однако соблюдение условий проч-
ности полностью не обеспечивает несущую способность конструкции.
При действии нагрузки оболочка резервуара и трубопроводов может
не сохранить свою первоначальную геометрическую форму и перейти
в некоторое новое положение равновесия. Процесс перехода в новое
равновесное состояние — потеря устойчивости — в подавляющем
большинстве случаев сопровождается большими перемещениями
оболочки, возникновением пластических деформаций или полным
разрушением, хотя напряжения к моменту потери устойчивости
не достигают предела текучести.
Наиболее ярко явление потери устойчивости проявляется в лег-
ких тонкостенных конструкциях и, в частности, может иметь место
в оболочках вертикальных резервуаров большой емкости, у которых
отношение радиуса кривизны срединной поверхности R к толщине
стенки h достигает 3000. Поэтому при проектировании этих кон-
струкций одновременно с расчетом на прочность ведется расчет на
устойчивость как отдельных узлов, так и системы в целом.
В данной главе рассмотрим некоторые часто встречающиеся
в практике проектирования и эксплуатации задачи устойчивости
оболочек, резервуаров и трубопроводов. Причем при определении
критических нагрузок будем считать исходную форму оболочек
идеальной. Влияние начальных неправильностей формы учитывается
коэффициентами, которые определяются по эмпирическим формулам
в зависимости от R/h, полученным в результате аппроксимации
экспериментальных данных, представленных в работе [3].
Устойчивость цилиндрической оболочки при действии
внешнего равномерного давления
В практике проектирования и эксплуатации резервуаров и трубо-
проводов нередко возникают случаи, когда цилиндрическая оболочка
этих конструкций подвергается сжатию при действии равномерно
11 Заказ 2036 161
распределенной поперечной нагрузки. Такой вид нагрузки харак-
терен, например, для оболочек трубопровода, уложенного в грунт,
и вертикального резервуара, находящегося под вакуумом.
При выборе расчетной схемы для определения величины крити-
ческого внешнего давления следует учитывать длину цилиндриче-
ской оболочки, j
Рассмотрим случай весьма длинной цилиндрической оболочки,
когда Н » R (где Н — длина цилиндрической оболочки).
В этом случае влиянием крае-
вых условий можно пренебречь,
а задача сводится к расчету на
устойчивость кольца единичной
ширины.
а б
Рис. 56
Предположим, что на замкнутое кольцо, у которого момент
т №
инерции поперечного сечения 1 действует сжимающая
равномерно распределенная радиальная нагрузка q (рис. 56, а).
Тогда для вывода уравнений равновесия и физических уравнений
кольца можно воспользоваться теорией кривого стержня, рассмо-
тренной в гл. 2.
В данном случае начальные искривления стержня будут равны
(см. рис. 27):
%=xO2 = 0; = <4,1>
Компоненты внешней нагрузки:
4,= }, = 0;
тх = ту = т2 = 0. 4 '
Тогда, согласно уравнениям (2.58), (2.59) и (2.63), получим:
уравнения равновесия в плоскости кольца —
^--^+4.-0; (4.3)
^Z_()z=o-,
as Y 4
162
физические уравнения —
М,= Ых,= -И(^+-^-).
Первое физическое уравнение (4.4) выражает условие несжима-
емости оси кольца единичной ширины (е = 0).
В докритическом состоянии осевая сила равна
N0=-qR. (4.5)
При выпучивании кольца возникает радиальная составляющая
усилий
Qz— N0Ky— qR у +д2). (4.6)
Исключая последовательно из трех уравнений равновесия (4.3)
перерезывающее Qz и продольное N усилия, получим
d3My ! 1 dMу dqz „ ,,
ds3 т- д2 ds 'r ds ‘
После подстановки значений Mb и q2, определяемых зависи-
мостями (4.4), (4.6) и (4.7), получим дифференциальное уравнение
для радиального перемещения кольца
dWV 2 <W 1 dW . qR / dWV .1 dW \ Q ,,
ds* т~ Д2 dsa "Г ri ds El \ dsa + Д2 ds
Решение дифференциального уравнения (4.8) будем искать
в форме
Ж^/sin^-, (4.9)
где п — число полных волн, образующихся при выпучивании по
окружности кольца.
При п = 1 задача теряет смысл, так как эта гармоника несамо-
уравновешена, и мы получим перемещение кольца как жесткого
целого.
После подстановки (4.9) в (4.8) и дифференцирования по «получим
(4.Ю)
Из соотношения (4.10) следует, что минимальное значение, соот-
ветствующее критической нагрузке, будет при п — 2. Тогда из (4.10)
9кр = ^-. (4.И)
11* 163
Следовательно, выпучивание кольца произойдет по двум вол-
нам (рис. 56, б).
Результаты, полученные для кольца, без труда распространяются
на длинные цилиндрические оболочки, нагруженные внешним давле-
нием р. В данном случае q = pH, а жесткость оболочки на изгиб
будет равна п „ _ Eh^H 12(1 — №) ‘
Таким образом, Ркр (4-12)
Формула (4.12) справедлива лишь для длинных оболочек. Если
длина оболочки Н соизмерима с диаметром, как это имеет место,
например, в оболочке корпуса вертикальных резервуаров, то кра-
евыми условиями пренебрегать нельзя.
В этом случае интенсивность критической поперечной нагрузки
согласно исследованиям, проведенным в работе [3] для цилиндри-
ческих оболочек средней длины, у которых
(4.13)
определяется по формуле
Ркр "
или при v = 0,3
Ркр = 0,92 4^]/-^. (4.15)
Соответственно этому критическое кольцевое напряжение равно
а2=--^ = -0,92^-(4)’/5- (Ш
Данный результат получен в рамках линейной теории. Однако
при потере устойчивости следует считаться с большими деформа-
циями.
Как показали экспериментальные исследования и расчеты на
устойчивость по линейной теории оболочек, в формулу (4.16) следует
ввести поправочный коэффициент, пропорциональный отноше-
нию R/h. Тогда
_ KER / h \’/«
°гкр - я k R J ’
(4.17)
где
К = 0,92Яг.
В зависимости от отношения R/h цилиндрической оболочки
коэффициент Kt имеет следующие значения:
Rfh ................... 250 500 1000 1500
К,.................... 0,7 0,6 0,5 0,4
164
Для оболочек вертикальных резервуаров, у которых
500 А 3000,
h
коэффициент К определяется по эмпирической формуле
(4.18)
Устойчивость цилиндрической оболочки при 'действии равномерно
распределенной продольной нагрузки
Предположим, что замкнутая цилиндрическая оболочка (шар-
нирно опертая) по краям нагружена
деленной по контуру продольной на-
грузкой интенсивностью q. При дости-
жении критического значения дкр на-
пряженное состояние оболочки претер-
певает качественный скачок: из безмо-
ментного оно становится изгибным —
моментным, а в период потери устой-
чивости оболочки появляется новая
форма равновесия, отличная от перво-
начальной — прямолинейной (рис. 57).
Будем считать, что изогнутая по-
верхность оболочки после выпучивания
является осесимметричной, т. е. по-
равномерно распре-
перечные сечения остаются круговыми.
Тогда дифференциальное уравнение,
описывающее напряженно-деформиро-
ванное состояние цилиндрической обо-
лочки в момент потери устойчивости,
соответствует однородному разреша-
ющему уравнению (1.52). Однако при
выпучивании постоянные силы сжатия
дают нормальную составляющую —
dW с„.
q которая в уравнении (1.52)
играет роль поперечной нагрузки.
Следовательно, разрешающее уравнение задачи об устойчивости
цилиндрической оболочки при осевом сжатии имеет вид:
d*W d*W
dxi dx%
— W=0
Д2
(4-19)
Решение уравнения (4.19) будем искать в форме, соответствующей
характеру выпучивания:
W = /sin-^, (4.20)
где п — число полуволн изогнутой поверхности вдоль образующей.
165
Выражение (4.20) удовлетворяет граничным условиям на краях
оболочки. Очевидно, при таком характере выпучивания каждая
продольная полоска оболочки находится в тех же условиях, что
и сжатый стержень на упругом основании. Таким «основанием»
здесь служат кольцевые волокна.
Подставляя уравнение (4.20) в (4.19) и приравнивая к нулю
множитель при sin , получим выражение для критического
усилия
/ п п2л2 EhH2 \ .. ...
?кр— \В Д2 + (4-21)
Исследуя функцию <?кр на минимум, получим
dq^p 2n2nZ> । 2EhH2
dn Н2 ' n2n3R2 ’
откуда минимальному значению критической силы соответствует
следующий номер гармоники:
После подстановки (4.22) в (4.21) действительное значение кри-
тического усилия будет равно
Е h2 / / о Q \
9кр ~ ” R /3(1-т2Г'
Приняв для стали v = 0,3, запишем формулу (4.23) в следующем
виде:
<7кР ~ -0,605-^. (4.24)
Тогда критическое напряжение при осевом сжатии будет равно
Eh
или при v = 0,3
а1кр = -0,605(4.25, а)
Длина полуволны оболочки при выпучивании равна
И n^Rh (4.26)
п |/12(1- V2)
или при v = 0,3 / = 1,7/Ж (4.27)
Если цилиндрическая оболочка весьма короткая и )•« 1,
то п — 1 и из (4.21) следует - ( n2D ЕН2 °1КР hH2 1 n2R2 1 ’ (4.28)
166
Так как 7?2 2> Я2, то в (4.28) вторым членом можно пренебречь
по сравнению с первым, отсюда:
ffiKp = — • (4.29)
Мы получили формулу Эйлера для полоски, вырезанной из обо-
лочки в направлении образующей.
Следует отметить, что результат (4.25, а) имеет только каче-
ственное значение. Экспериментальные величины критического на-
пряжения отличаются (в 3—4 раза) от рассчитанных по (4.25, а).
Это объясняется значительным влиянием начальных прогибов обо-
лочки и большой ролью нелинейных составляющих деформаций при
потере устойчивости.
Согласно результатам нелинейной теории оболочек, подтвер-
жденной экспериментальными данными, расчет на устойчивость
от осевой нагрузки следует выполнять по формуле
П1КР=-С~. (4.30)
Значения коэффициента С, полученные из сопоставления данных
статистической теории устойчивости оболочек с результатами много-
численных опытов [3], зависят от отношения R/h:
R/h...................................... 250 500 750 1000 1500
С . .................................... 0,18 0,14 0,12 0,10 0,09
Но в оболочках вертикальных резервуаров отношение R/h дости-
гает 3000, поэтому результаты экспериментальных данных следует
аппроксимировать в диапазоне 3000 ^R/h^ 250 следующим степен-
ным полиномом:
С = 0,23094 - 2,37996 • 10'4 А +1,33693 10;’ -
-2,51572- 10-н^-. (4.31)
Если начальные прогибы оболочки достигают величины по-
рядка h, расчетные значения следует снижать примерно вдвое.
Необходимо отметить, что формула (2.25) в точности совпадает
с формулой критического напряжения для сферической оболочки
при действии внешнего давления q\
°к₽_ /3 (1-v2) 7? ’
где R — радиус кривизны срединной поверхности сферической
оболочки.
Тогда выражение для внешнего критического давления (вакуума)
равно
__ 2/Юкр 2Е№_____
®кр R R2 f3(l-v2) '
167
или при v = 0,3
(4.33)
Чкр R2 •
Вводя поправку на начальные неправильности формы оболочки,
запишем последнюю формулу в следующем виде:
„ _ Р ЕЮ
Чкр— Ч д2 »
где коэффициент С1 согласно [3] зависит от R/h:
R/h......................... 250 500 750 ЮОО
G ........................ 0,30 0,24 0,20 0,16
1500
0,15
Устойчивость корпуса вертикальных цилиндрических резервуаров
Цилиндрический корпус стальных вертикальных резервуаров,
у которого в зависимости от вместимости отношение радиуса к тол-
щине стенки (R/h) колеблется в диапазоне 1000—3000, относится
к разряду очень тонких оболочек. Поэтому при проектировании
этих тонкостенных конструкций помимо расчета на прочность (при
действии эксплуатационной нагрузки) следует проверять устойчи-
вость оболочки незаполненного резервуара.
В общем случае при эксплуатации вертикальных цилиндрических
резервуаров потере устойчивости корпуса могут способствовать
одновременно следующие нагрузки:
собственный вес корпуса (<?к) и покрытия (Qn)',
вакуум при охлаждении и сливе нефтепродукта из герметически
закрытого резервуара (?В9К);
снеговая нагрузка (<?сн);
ветровая нагрузка (дв).
Следовательно, цилиндрическая оболочка корпуса вертикальных
резервуаров подвергается одновременному воздействию продольных
и поперечных нагрузок. В этом случае согласно исследованиям
А. С. Вольмира [3] устойчивость формы цилиндрической оболочки
проверяется по формуле
gl | g2
ClKp 02KP
где olt ст2 — соответственно расчетные продольные и кольцевые
напряжения; <т1кр, сг2кР — соответственно критические продольные
и кольцевые напряжения.
Из всех перечисленных выше нагрузок на вертикальные цилин-
дрические резервуары неизвестной является ветровая qQ.
Вес корпуса и покрытия известен из расчета резервуара на проч-
ность при действии эксплуатационной нагрузки, а интенсивность
ветровой и снеговой нагрузок определяется в соответствующих
Строительных нормах и Правилах. Причем данные ветровой на-
грузки, представленные в СНиП II-A.11—62, пригодны лишь для
цилиндров, у которых отношение высоты к диаметру равно или
(4.34)
168
больше единицы, без учета влияния конструкции покрытия на рас-
пределение аэродинамического давления ветрового потока как по
поверхности корпуса, так и по поверхности самой кровли.
Отношение высоты цилиндрического корпуса к диаметру, напри-
мер, у резервуаров большой вместимости может достигать 0,25. Для
таких отношений высоты к диаметру, как показали эксперименталь-
ные исследования, закон распределения аэродинамического давле-
ния по высоте корпуса существенно отличается от данных, пред-
ставленных в Строительных нормах и Правилах, и зависит от гео-
метрической формы покрытия.
Ветровая нагрузка на вертикальные
цилиндрические резервуары
Ветровая нагрузка представляет собой случайное поле аэродина-
мических давлений, неоднородное по поверхности сооружения.
Практически удобная гипотеза представления турбулентного потока
ветра состоит в том, что на некоторую, в среднем установившуюся
скорость потока воздуха накладываются скорости порывов, т. е.
на установившееся в среднем давление, которое практически по-
стоянно, накладывается пульсация давления, носящая случайный
характер. Случайный характер порывистости ветра обусловлен
многими факторами: неоднородность атмосферы, изменчивость рель-
ефа местности и т. д. Пульсации скоростного напора, вызванные
порывами ветра, оказывают на сооружение динамическое воздей-
ствие, которое учитывается путем умножения скоростного напора
на коэффициент |3:
= (4.35)
где р — коэффициент увеличения скоростного напора, зависящий
от пульсации ветрового потока и динамических характеристик соору-
жения; К — аэродинамический коэффициент; (Эв — расчетный ско-
ростной напор ветрового потока, кгс/м2.
Коэффициент увеличения расчетного скоростного напора опре-
деляется по формуле
Р = 11-ет,
где е — коэффициент динамичности, зависящий от периода соб-
ственных колебаний сооружения Т и логарифмического декремента
затухания колебаний сооружения; m—коэффициент пульсации
скоростного напора ветра.
Период собственных колебаний корпуса вертикальных цилиндри-
ческих резервуаров составляет весьма малую величину (например,
у резервуара вместимостью 50 тыс. м3 Т = 5,8-10“3 с), поэтому
е = 1, а при высоте корпуса Н = 18 м m — 0,35. Следовательно,
р = 1,35.
При определении ветровой нагрузки на сооружение различают
среднюю скорость ветра в данном географическом районе при
169
наиболее сильных ураганах и максимальную скорость в поры-
вах. Средняя из максимальных скоростей ветра принимается как
нормативная; по ней устанавливается нормативный скоростной
напор
<?н = -ф-’ (4.36)
где р — плотность воздуха, (кг-с2)/м4; VH — нормативная скорость
ветрового потока, м/с.
Коэффициент перегрузки, учитывающий изменчивость скоро-
стных напоров ветрового потока, равен 1,2, поэтому
<2в = 1,2<?н. (4.37)
Теперь перейдем к определению значений аэродинамического
коэффициента на поверхности вертикальных цилиндрических резер-
вуаров.
Малая относительная высота цилиндрического корпуса <1),
наличие покрытий разнообразной геометрической формы вызывают
необходимость экспериментального определения аэродинамиче-
ского коэффициента по всей поверхности резервуаров, величина
которого есть отношение избыточного давления (аэродинамического
давления) р на поверхности сооружения к нормативному скоро-
стному напору <?н:
К = Ъ <4-38)
Тогда выражение для ветровой нагрузки на сооружение с учетом
зависимостей (4.37) и (4.38) можно записать так:
?в = 1,2рр (4.39)
или для вертикальных цилиндрических резервуаров:
& = 1,62р. (4.40)
Таким образом, задача исследования ветровой нагрузки на вер-
тикальных цилиндрических резервуарах сводится к определению
аэродинамического давления р по всей поверхности корпуса и по-
крытия.
Известно, что опыты по определению аэродинамического давления
делятся на натурные и модельные. Натурные опыты позволяют
выдерживать полное аэродинамическое подобие, но требуют гро-
моздкой и дорогостоящей аппаратуры, связаны с большой затратой
времени на выжидание сильного ветра и не позволяют исследо-
вать различные емкости резервуаров с разнообразными формами
покрытий.
Главным методом исследования, определившим успех аэромеха-
ники как науки и широкое внедрение ее во многие области промыш-
170
ленности, является метод испытания на моделях в аэродинамических
трубах. И тот факт, что во всех существующих нормах ветровых
нагрузок учтены результаты модельных исследований, не случаен.
С целью исследования распределения аэродинамического давле-
ния на поверхности резервуаров с различными геометрическими
формами покрытий в аэродинамической трубе ЦАГИ им.
проф. Н. Е. Жуковского были проведены испытания геометрически
подобных моделей резервуаров. Согласно геометрическим пара-
метрам резервуаров для испытания в аэродинамической трубе были
изготовлены в масштабе 1 : 100 четыре сдвоенные модели корпуса
с относительными высотами Н/D, равными 0,15, 0,25, 0,35, 0,45,
и по две модели покрытий следующих типов конструкций: сфери-
ческая, коническая, складчатая, безмоментная и плоская. Каждая
из четырех сдвоенных моделей цилиндрического корпуса последова-
тельно исследовалась совместно с пятью указанными типами по-
крытий.
Таким образом, было исследовано 20 вариантов моделей, которые
охватывают всю серию резервуаров большой вместимости (от 10
до 50 тыс. м?) со всеми наиболее распространенными в практике
резервуаростроения типами покрытий (кроме резервуара с плава-
ющей крышей); этот тип резервуара одновременно исследовался
в лаборатории НИИМеханики МГУ).
Модели резервуаров (наружный диаметр 500 мм) изготовлялись
из древесины. Цилиндрический корпус выполнялся в виде деревян-
ного каркаса, обшитого трехмиллиметровой фанерой. Модели по-
крытий вытачивались на станке из предварительно склеенных фанер-
ных болванок. Соединение цилиндрических корпусов с покрытиями
осуществлялось внутри модели с помощью специальных винтов.
Внешняя поверхность тщательно зачищалась шкуркой и покрыва-
лась лаком.
Метод испытания сдвоенной модели, т. е. модели, воспроизводя-
щей резервуар и его зеркальное отражение относительно плоскости
земли, позволяет учитывать влияние последней на обтекание резер-
вуара в условиях аэродинамической трубы без воспроизведения
пограничного слоя земной поверхности.
Аэродинамическое давление по внешней поверхности моделей
резервуаров воспринималось дренажными медными трубками с внеш-
ним диаметром 2 мм и внутренним 1 мм.
Один из торцов трубки заделывался заподлицо к внешней поверх-
ности модели в заданной точке, а другой выводился через внутрен-
нюю полость наружу и посредством резиновых трубок соединялся
с батарейным спиртовым микроманометром. Дренажные точки, т. е.
точки, в которых измерялось давление, располагались вдоль одной
образующей верхней половины цилиндрического корпуса и покры-
тия. Положение продольного сечения модели с дренированной обра-
зующей корпуса и покрытия относительно направления ветрового
потока определяется углом 0. При 0=0 направление ветрового
потока совпадает с дренированной образующей.
171
Испытания проводились в аэродинамической трубе Т-1 ЦАГИ
с закрытой рабочей частью, поперечное сечение которой — правиль-
ный восьмиугольник с диаметром вписанного круга, равным 3 м.
Модель резервуара устанавливалась в аэродинамической трубе
на центровом приборе (рис. 58), при этом державка прибора и жгут
дренажных трубок проходили через кровлю той части сдвоенной
Рис. 58
модели, которая воспроизводит зеркальное отображение резервуара
относительно плоскости земли. Таким способом практически пол-
ностью устраняется влияние поддерживающего устройства на обте-
кание и, следовательно, на распределение давления по поверхности
верхней части сдвоенной модели. При испытании задавались поло-
жительные углы 0, равные 0, 10, 20, . . ., 180°, поворотом модели
по часовой стрелке вокруг центральной оси.
Результаты экспериментальных исследований представлены
в виде безразмерного аэродинамического коэффициента К. На рис. 59
и 60 показаны эпюры аэродинамического коэффициента в четырех
172
поперечных сечениях: -^ = 0;
и в продольном сечении, совпадающем с н
потока (в = 0°), резервуаров со сферическим пок®
ющей крышей при = 0,35 (рис. 59, а и 59, б —сое
1,56
0.19
0,62
1.0 0,9 0,8 0,7 0,6 о,
— =0,3
D
s 0,0
x
О и
0,3
О,
^-0.9
— -0.2
вуз- ; 1,о 7. 0
У . J
R
продольное и поперечное сечение резервуара со стационарным покры-
тием; рис. 60, а и 60, б — соответственно продольное и поперечное
сечение резервуара с плавающей крышей). Из рассмотрения этих
эпюр видно, что большая часть поверхности корпуса резервуара со
сферическим покрытием находится под разряжением, а резервуара
с., плавающей крышей — под давлением. Причем интенсивность
давления в продольном сечении 0 = 0° резервуара с плавающей
крышей на 35% выше, чем резервуара со сферическим покрытием.
Этот факт объясняется тем, что в резервуаре с плавающей крышей
173
аэродинамическое давление складывается из давления на наружной
поверхности корпуса и разряжения на внутренней.
Что касается сферического покрытия, то вся площадь поверх-
ности его находится под разряжением, максимальным на наветренной
области и минимальным на заветренной. Так как цилиндрический
корпус вертикальных резервуаров имеет конечную длину H/D,
равную 0,15—0,45, то на верхней кромке корпуса происходит срыв
ветрового потока и соответственно этому резкое падение аэродина-
мического давления. Наличие кровель приводит к еще более интен-
сивному падению давления, которое в области сопряжения корпуса
и кровли переходит в разряжение.
В дальнейшем для практических расчетов вертикальных цилин-
дрических резервуаров на устойчивость необходимо будет иметь
численные значения аэродинамического коэффициента вдоль обра-
зующей корпуса, совпадающей с направлением ветрового потока,
т. е. при 0 = 0° (табл. 3).
Экспериментальные исследования ветровой нагрузки на моделях
при различных отношениях высоты Н к диаметру D показали, что
174
величина аэродинамического коэф-
фициента на цилиндрическом кор-
пусе резервуара почти не зависит
от отношения Н/D, а в узкой зоне
корпуса, примыкающей к покры-
тию (2—2,5 м), и на самом по-
крытии, где преобладает разря-
жение, существенно зависит от
этого отношения. Степень зави-
симости величины аэродинами-
ческого коэффициента от отноше-
ния Н/D в верхней части корпуса
и на покрытии характеризуется
коэффициентом ц (рис. 61). Чем
меньше относительная длина ци-
линдрического корпуса, тем ниже
величина аэродинамического коэф-
фициента К и коэффициента гр
Следовательно, численные зна-
чения аэродинамического коэффи-
циента при ~ = 0,3, представлен-
ные на рис. 59 и 60 и в табл. 3,
можно использовать и для других
отношений HjD. Причем коэффи-
циенты аэродинамического раз-
ряжения в верхней части корпуса
и на покрытии умножаются на
поправочный коэффициент в зави-
симости от отношения Н/D (см.
рис. 61), а коэффициенты аэроди-
намического давления на цилин-
дрическом корпусе резервуара
переносятся без изменения.
Для того чтобы использовать
результаты модельных исследова-
ний при определении ветровой
нагрузки на вертикальные цилин-
дрические резервуары, необхо-
димо определить: не меняется ли
картина распределения аэроди-
намического коэффициента при
переходе от модели к натуре,
не имеется ли практически ощу-
тимого «масштабного эффекта»,
искажающего эту картину.
При обтекании турбулентным
ветровым потоком внешней по-
од со
S
ж-
ST о
и 3
4 о
о ю
а
Ь 2
ь
ч
я
а
S
О)
й
о
н
S
и
153
и —
ч
м
Я
я
ь
я
я
ВТ
я
>&
е
п
о
я
с
fa
о
я
с
ff
S
я
со
я
я
и
о
Рч
ft
я
я
S
я
£>
в*
л
X
со
Координаты точек вдоль образующей, м □о ЫД ГД яг-l 04 t- О ОД 00 СО 1 ч4т4 1 Оф ’ll1!'
£ ФФ идиДФ о 04 ид *<н тЧ QQ ф ® ^0 I Ф ф" ф О О 1 1 1
£ иД О О ид о О СО чн т-ч t— ф 04 ОД О тн СО 1- О 6 О С С 6
16,2 . СДОО1Д О •О 04 04 Г— Ф 04 иД ид ИД иО иД ОО о о о о о 6
кЛ иД иД СД иД ф Ф •«О sj ST ф о 04 ф ф ф CD Р-ф О С О О О 6
14,4 ф о ид ид ид о тн о тн тн Р- [> t- Гф Гф О Ф Ф Ф Ф Ф^
13.5 иД ID О ид НД О Ф СО Ф Ю 04 со г-. 1-~г Ф ф Ф ф о
12,6 ' ООиДиД ФО тн о тн ФСО^И 00 00 СО со 00 04 Ф Ф Ф о о
10,8 ид ид иД ф ф ф ид Р- Ф Ф О оо. оо оо оо оо О О О О 6
а Ф ид Q ид Ф ф тн О тн ф 04 04 Ф 00 ф 00 ф ид 6о666^
7,2 00ф ид ид фф СО 04 СО о4 Ю sf Ф Ф сд сд Ф ид ООООО^
3,6 О ид ид ф о ф СО СО CD Р- СО иД Ф Ф Ф ф сд ид ОО ффф*4
о чН тН тч тн тЧ ТЧ
£
S
2
ft
Я
о
й
с
л!
Я
ft
№
А*
и
ч
ч
175
верхности резервуаров условия физического подобия (критерий
подобия) представляются соотношениями:
ф = const;
Не =— = const,
ц
где ф — угол атаки; Re — число Рейнольдса.
При моделировании этого явления результаты опытов с моделью
можно переносить на натуру только для одинаковых фи Re. В дан-
ном случае предполагается, что движение ветрового потока как
в натурных, так и в искусственных условиях поступательное плоско-
параллельное, поэтому первый
критерий подобия с достаточ-
ной точностью удовлетворяется.
Результаты, приведенные
в табл. 3, получены при ско-
рости воздушного потока v =
= 50 м/с, что соответствует
Re = 1,67-10е. В натурных
условиях число Рейнольдса бу-
дет значительно выше. Так,
например, для резервуара вме-
стимостью 50 тыс. м3 при ско-
ростном напоре ветра QB ~
= 100 кгс/м2 Re = 1,68 • 108, что
значительно выше максималь-
ного значения Re = 8,4-10е,
достигнутого в настоящее время
при обдувке цилиндра беско-
нечной длины.
Это обстоятельство указывает на то, что второй критерий подобия
практически удовлетворить очень трудно, поэтому встает вопрос
о величине погрешности (масштабного эффекта), которая возникает
при переходе от модели к натуре. Ввиду указанных выше трудностей
проведения натуральных опытов затруднена и непосредственная
проверка величины масштабного эффекта.
Экспериментальные исследования по обдувке цилиндров, описан-
ные в работе [21], показывают, что величина аэродинамического
коэффициента в лобовой области цилиндра ^0 = 0± почти не
зависит от числа Re, поэтому для этой области результаты модельных
исследований можно без изменения переносить на натурные резер-
вуары. Но именно в этой области корпуса моделей аэродинамический
коэффициент имеет положительные максимальные величины, которые
следует учитывать при проверке цилиндрической оболочки корпуса
резервуаров на устойчивость. Следовательно, численные значения
аэродинамического коэффициента, представленные в табл. 3, при
0=0 можно переносить на натурные резервуары без изменения
в качестве расчетных. Этот вывод остается в силе и для аэродинами-
176
ческого разряжения на покрытиях резервуаров, где не наблюдается
отрыва ветрового потока от поверхности и Re = const.
Зато на боковых и заветренных областях корпуса моделей проис-
ходит отрыв ветрового потока от поверхности, поэтому величина
аэродинамического коэффициента зависит от числа Re.
Дополнительные продувки моделей резервуаров при различных
скоростях ветрового потока показали, что изменение числа Re в диа-
пазоне 1,33-10е—2-10е не вызывало заметного изменения величины
аэродинамического коэффициента на боковых и заветренной областях
поверхности корпуса моделей.
На цилиндре бесконечной длины в этой области чисел Re наблю-
дается резкое повышение величины аэродинамического коэффи-
циента [21]. Такое различие в поведении функции К =f (Re) при
указанных числах Re можно объяснить малой относительной высотой
цилиндрического корпуса резервуаров, поэтому в первом прибли-
жении можно считать, что при дальнейшем увеличении числа Re
не произойдет существенного изменения величины коэффициента К,
т. е. результаты модельных испытаний на заветренной и боковых
областях цилиндрической поверхности корпуса резервуара можно
переносить на натурные объекты без изменения.
Таким образом, распределение аэродинамического коэффи-
циента в области цилиндрического корпуса (9 = 0 45°) и на
покрытиях может с достаточной точностью применяться в качестве
ветровой нагрузки на натурные резервуары, а для остальной части
корпуса лишь в первом приближении.
Проверка устойчивости корпуса
резервуара со стационарным покрытием
Предположим, что на оболочку корпуса незаполненного вер-
тикального резервуара со стационарным покрытием (например,
сферическим) оказывают осесимметричное воздействие собственный
вес покрытия Qn и корпуса QK, вакуум внутри резервуара <jBaK,
снеговая qCH и ветровая qa нагрузки.
Тогда согласно безмоментной теории в i-ом поясе корпуса резер-
вуара возникнут продольные и кольцевые напряжения:
ej .
1 2лШц ’
(4.41)
02
RZj
hi
где Qi — суммарная вертикальная составляющая всех внешних сил
на уровне i-го пояса резервуара; Zt — компонента поверхностной
нагрузки на уровне i-ro пояса резервуара; ht — толщина стенки
i-ro пояса резервуара; R — радиус срединной поверхности кор-
пуса.
12 Заказ 2036 177
Суммарная вертикальная составляющая всех внешних сил на
уровне г-го пояса резервуара равна
2" а
Qi = -<2п - <2к (n-i) — лЯЧзк- f J [?сн - ?В (ф)I Р3 sin <р cos ф da,
о о
(4-42)
где п — число поясов в резервуаре; р — радиус кривизны сфери-
ческого покрытия; а — У2 центрального угла сферического покры-
тия; ф, 9 — угловые координаты соответственно в меридиональном
и кольцевом направлениях; фв(ф) — известная функция, выража-
ющая интенсивность ветровой нагрузки в меридиональном сече-
нии сферического покрытия.
'Принимая во внимание равенство (4.35), запишем соотношение
(4.42) в следующем виде:
2« а
Qi- ~Qn— Qk (n-i)— — J J [?CH— Р#(ф)(?в|р2Йф8П1фСОЗ(рСда,
0 0
где К (ф) — функция, характеризующая изменение аэродинамиче-
ского коэффициента в меридиональном сечении сферического покры-
тия (см. рис. 59, а).
После интегрирования получим
Qi Qu Qk (n-i) лЯ2^вак яр2
и
qcii sin2 а — |3()Б j* К (ф) sin 2ф dtp .
(4.43)
Так как функция аэродинамического давления в меридиональном
сечении сферического покрытия К (ф) задана не аналитически, а чис-
ленно, при практическом определении Qt целесообразно применить
приближенные формулы численного интегрирования прямоуголь-
ников или трапеций [5].
Тогда, разбив меридиональный участок покрытия в диапазоне
от 0° до а, например на двадцать равных отрезков, получим
“ /=2О
Кп= I Л’(ф) sin2ф^ф— 2 ^,-sin2ф; Афу, (4.44)
О /=1 .
где Kj — значение аэродинамического коэффициента на j-ом мери-
диональном участке покрытия; Дф, — приращение централь-
ного угла.
Для резервуара вместимостью 50 тыс. м3, у которого относитель-
ная высота цилиндрического корпуса равна 0,3, Кп = 0,75.
Таким образом, с учетом (4.44) формула (4.43) окончательно
перепишется:
Qt=- [<?п + <?К(п-о + л:7?2фвак + лр2(?сн81п2а-Р^п(2в)|. (4.45)
178
Так как компонента поверхностной нагрузки
— (?вак 4 Р-^-н(?в),
(4.46)
где Ки — значение аэродинамического коэффициента в i-ом поясе
корпуса резервуара со стационарным покрытием (см. табл. 3), то
с учетом (4.45) выражения для продольных и кольцевых напряжений
в i-ом поясе корпуса резервуара примут окончательный вид:
_ *?п + Qk <л-г)"Ь лЛ2<?вак Ц- яр2 (gCH sin2 а—р/?п9в) , // /лк
- 2^Rht '
п R (?вак + Р^1£*?в)
°2'=------------hi-------*
Знак «минус» в выражениях (4.47) говорит о том, что в оболочке
корпуса резервуара действуют сжимающие напряжения.
Критические напряжения при осевом сжатии и внешнем давлении
согласно (4.30), (4.17) и (4.18) равны:
„г CiEhi _
°1кр - д— ,
Л _ R \ER/hi\al2 (4’48>
2кр 0,644 (1 35№ ) я ( д ) •
После подстановки (4.47) и (4.48) в соотношение (4.34) получим!
Оп + Ок (n-i) (<7си sin2 сс—Р-А?пС?в) ।
_ Г
, я (?вак +Р^и'Ов) 1/~ДЗ .< 1 ('449'
Т / д \ у * v1-1'';
0,644 (l~-^—)Ehi '
\ 3500л£ /
Необходимо отметить, что формула (4.49) получена при условии,
что сжимающие напряжения действуют по всей оболочке корпуса
за исключением узких областей, примыкающих к краям, где напря-
женное состояние моментное. В действительности при действии
несимметричной ветровой нагрузки напряженное состояние оболочек
резервуаров является резко переменным [14]. Например, кольцевое
напряжение о2 на лобовой, наветренной области корпуса резервуара
со сферическим покрытием сжимающее, а на боковых и заветренных
областях — растягивающее. Это обстоятельство несколько повы-
шает величину критической нагрузки. Количественная оценка
расхождения в величинах неравномерной и равномерной критических
радиальных нагрузок затруднена тем, что в настоящее время как
в отечественной, так и в зарубежной литературе отсутствуют простые
формулы для подсчета критического параметра неравномерного
радиального давления.
12*
179
Точное решение данной задачи связано с математическими труд-
ностями (пока непреодолимыми), так как приходится решать задачу
нахождения минимального собственного значения дифференциаль-
ного уравнения в частных производных восьмого порядка с пере-
менными коэффициентами. Поэтому неизбежно применение различ-
ных приближенных методов, с помощью которых исходная задача
сводится к определению минимального собственного значения бес-
конечной матрицы. Но и здесь возникают трудности, связанные
с необходимостью раскрывать определители высоких порядков,
лежащие за пределами возможности стандартных программ совре-
менных ЭВМ.
Наиболее оптимальный алгоритм определения величины не-
равномерного критического радиального давления построен в ра-
боте [18]. При этом алгоритме заданная ветровая нагрузка раз-
лагается в тригонометрический ряд по косинусам. Численные зна-
чения коэффициентов разложения ветровой нагрузки в тригономе-
трический ряд для различных типов вертикальных цилиндрических
резервуаров имеются в работе [14]. Общее решение разрешающего
дифференциального уравнения также ищется в форме тригонометри-
ческого ряда, содержащего косинусы, что приводит к задаче нахо-
ждения наибольшего собственного значения бесконечной характери-
стической матрицы. Далее для нахождения наибольшего собственного
значения бесконечной матрицы последняя редуцируется последова-
тельностью конечных матриц. Если число полных волн вдоль окруж-
ности, которые возникают в момент потери устойчивости, невелико,
то при таком подходе хорошее приближение к наибольшему соб-
ственному значению исходной матрицы получается из характеристи-
ческой матрицы невысокого порядка. Если число полных волн вдоль
окружности велико, то приходится обращаться к характеристической
матрице более высокого порядка. Но и в том и другом случаях суще-
ственно снижается громоздкость задачи, что облегчает машинный
счет.
Численная реализация этого алгоритма на ЭВМ «МИР-1» поз-
волила определить коэффициенты перехода X от равномерной крити-
ческой радиальной нагрузки к неравномерной для различных типов
вертикальных цилиндрических резервуаров. Например, при H/D =
= 0,3 среднее для всех поясов значение коэффициента перехода
для резервуара со сферическим покрытием Х2 = 1,791, а для резер-
вуара с плавающей крышей Xi = 1,542.
Внося значение Xj в формулу (4.49), окончательно получим сле-
дующую расчетную формулу для проверки устойчивости корпуса
со стационарным покрытием: * I
(п-1)-Ьяй2?вакН~Лр2 (gciiSill2 И — Р/кпСв) ।
2nCtEh*
I___H (9вак 1 /~ Д3 - л
Т / R \ V h3
•-“('-ж)"' ‘
(4.50)
180
Проверка устойчивости корпуса
резервуара с плавающей крышей
В резервуаре с плавающей крышей отсутствует стационарное
покрытие, поэтому
Qn ~ 9сн ~ ?ВОК = 0- (4.51)
Заменяя Л\;на на Ц, получим
Qk. (n~i)
2nCiEh?
$K2iHQB
0,644Х2(1-^-Ш-
\ 3500ty /
1.
(4.52)
Но даже при i = 1, т. е. с учетом собственного веса всего корпуса
резервуара, первое слагаемое в левой части соотношения (4.52)
на два порядка ниже второго, поэтому можно принять QK(n-C) 0.
Тогда соотношение (4.52) перепишется:
---—------------------— ==s 1. (4.53)
Следовательно, для резервуара с плавающей крышей расчетной
нагрузкой при проверке на устойчивость является только ветровая,
величина которой есть сумма разряжения и давления соответственно
на внутренней и наружной поверхностях оболочки корпуса.
При практических расчетах на устойчивость необходимо знать
толщину стенки каждого пояса резервуара, поэтому формулу (4.53)
следует записать в следующей форме:
<4'54)
Решение уравнения (4.54), а также (4.50) целесообразно выпол-
нять на ЭВМ.
Пример. Определим, исходя из расчета на устойчивость, необходимую тол-
щину стенки каждого пояса резервуара со сферическим покрытием вместимостью
50 тыс. м8 и с плавающей крышей вместимостью 100 тыс. м3 при следующих
исходных данных:
Резервуар со сферическим покрытием
Число поясов п ................
Вес покрытия Qn, кг...................
Вес корпуса на уровне i-го пояса резервуара
Qk (л-1) • Ю5, кг.....................
Интенсивность вакуума 9вак, кгс/см2...
Радиус кривизны сферического покрытия р, см
Угол а, град..........................
Интенсивность снеговой нагрузки дсн, кгс/см2
Скоростной напор ветрового потока QB, кгс/см2
Коэффициент увеличения скоростного напора р
Среднее значение аэродинамического коэффи-
циента на сферическом покрытии Кп ....
12
1,7 • 105
3,811; 3,273; 2,781; 2,355; 1,973;
1,615; 1,346; 1,076; 0,8076;
0,538; 0,269; 0
3 • IO'2
9820
18
1,4 IO'2
1 • IO'2
1,35
0,75
181
Коэффициент Ci IO-2....................
Модуль упругости материала резервуара Е,
кгс/см2 ...................................
Высота корпуса резервуара Я, см ...........
Радиус кривизны корпуса Я, см .............
Значение аэродинамического коэффициента
в г-м поясе резервуара ....................
Коэффициент перехода от равномерной крити-
ческой нагрузки к неравномерной Xj . . . .
9,53; 9,29; 9,1; 8,94; 8,9; 8,88;
7,72; 7,72; 7,72; 7,72; 7,72;
7,72
2,1 106
1800
3035
1; 0,98; 0,96; 0,944; 0,938;
0,91; 0,875; 0 81; 0,765; 0,645;
0,54; -1,56
1,791
Резервуар с плавающей крышей
Число поясов п.........................
Высота корпуса резервуара Я, см............
Радиус кривизны корпуса й, см .............
Коэффициент увеличения скоростного напора |3
Скоростной напор ветрового потока Q-,, кгс/см2
Значение аэродинамического коэффициента в
i-м поясе резервуара ......................
Модуль упругости материала корпуса Я, кгс/см2
Коэффициент перехода от равномерной крити-
ческой нагрузки к неравномерной %2 ....
10
2000
4000
1,35
1 • 10-2
1; 1,55; 1,55; 1,54; 1,48; 1,4;
1,24; 1,04; 0.84; 0,61
2,1 • 106 '
1,542
В результате подстановки этих данных в уравнения (4.50) и (4.54) и решения
уравнений на ЭВМ «МИР-1» были получены численные значения толщины стенки
каждого пояса резервуаров со сферическим покрытием и с плавающей крышей,
представленные в табл. 4.
Таблица 4
Значения толщины стенки поясов (в мм)
Таким образом, при проектировании вертикальных цилиндри-
ческих резервуаров большой вместимости расчет толщины стенки
корпуса следует проводить в два этапа. На первом этапе, исходя
из условий прочности при действии эксплуатационной нагрузки,
определяется необходимая толщина стенки каждого пояса резер-
вуара.
182
На втором этапе полученные значения толщины стенки поясов
корректируются с учетом устойчивости каждого пояса порожнего
резервуара.
Например, при расчете на прочность резервуара со сферическим
покрытием вместимостью 50 тыс. м3 пояса корпуса имеют следующие
значения толщины стенки (данные института Проектстальконструк-
ция) — 26, 24, 22, 19, 17, 16, 12, 12, 12, 12, 12, 12 мм, а при расчете
на устойчивость — значения толщины стенки поясов представлены
в табл. 4. В итоге при совместном учете прочности и устойчивости
несущая способность оболочки корпуса резервуара будет обеспечена,
если толщина стенки каждого пояса будет равна 26, 24, 22, 19, 17,
17, 16, 16, 16, 15, 15, 12 мм.
Устойчивость верхних поясов вертикальных цилиндрических
резервуаров со стационарным покрытием при действии
эксплуатационной нагрузки
Исследование напряженно-деформированного состояния обо-
лочки резервуара со стационарным покрытием при действии эксплу-
атационной нагрузки, проведенное в гл. 2, показало, что на верхнюю
кромку корпуса оказывают осесимметричное воздействие изгиба-
ющие моменты и перерезывающие усилия со стороны покрытия.
Эти изгибающие моменты приводят к появлению в верхнем поясе
корпуса резервуара локальных кольцевых напряжений — сжима-
ющих, если изгибающий момент направлен изнутри оболочки на-
ружу, и растягивающих при противоположном направлении (см.
рис. 14). Например, согласно рис. 22 (узел Б) в резервуаре со сфери-
ческим покрытием вместимостью 50 тыс. м3 сжимающие кольцевые
напряжения действуют в узкой зоне шириной 25 мм от верхней
кромки корпуса и имеют максимальную величину, равную 80 кгс/см2,
по линии сопряжения корпуса с покрытием.
Естественно, эти напряжения при определенных значениях кри-
тических изгибающих моментов 7И1кр вызывают местную (локаль-
ную) потерю устойчивости оболочки с образованием впадин и выпу-
чиваний в основном только у верхнего края корпуса. На рис. 62
показан резервуар типа РВС-5000 после того, как произошло выпу-
чивание верхнего пояса. Выпучивание оболочки сопровождается
интенсивными перемещениями в кольцевом направлении по большому
числу волн в области, непосредственно примыкающей к покрытию.
Эти данные подтверждаются экспериментальными исследованиями
на моделях из медной фольги [1 ].
Определим величину критических изгибающих моментов, дей-
ствующих равномерно по линии сопряжения корпуса со стационар-
ным покрытием. Анализ конструкций вертикальных цилиндрических
резервуаров с жестким стационарным покрытием, проведенный
в гл. 2, показал, что граничные условия в этом сечении соответ-
ствуют жесткому закреплению.
183
Если принять начало координат по линии сопряжения корпуса
с покрытием, то в этом сечении при х = О
1У(0) = ^М. = 0.
Сделаем поперечное сечение по линии сопряжения корпуса с по-
крытием. Тогда на верхнюю кромку данной оболочки корпуса со
стороны покрытия окажут осесимметричное воздействие изгибающие
моменты Мо и перерезывающие усилия Qo. Положительное направле-
ние этих усилий показано на рис. 14.
Рис. 62
Согласно (Г.72) выражение для нормального прогиба длинной
цилиндрической оболочки, равномерно загруженной на краю мо-
ментом М0 и усилием Qo, имеет вид:
№=-^(PMA + <W
где ______
о 4/3(1-Т2) .
Р У R2h2 ’
Т7 _ Eh .
Ф2 = е"3* (cos рж — sin рж);
Ф3 — е“3х cos Рх.
184
Так как при х = О РГ(О) =0, то из последнего уравнения сле-
дует:
<?о=-Р^о- (4.55)
и прогиб оболочки определится уравнением
Иг= 2₽W!Le-3xsinpa; (4 56)
Л
Вводя безразмерную координату
% = (4.57)
и обозначив
ц = ₽Я, (4.58)
запишем уравнение (4.56) в форме
Ty = -^-Moe“^sinpg. (4.59)
Тогда кольцевое усилие будет равно
jV2 = ЛГое_|1’ sin pg. (4.60)
Из соотношения (4.60) следует, что если изгибающий момент М0
действует в положительном направлении, как показано на рис. 14,
то оболочка резервуара испытывает растягивающие кольцевые на-
пряжения. Сжимающие кольцевые напряжения могут иметь место
только при обратном направлении изгибающего момента, тогда Мо
в формуле (4.60) следует брать со знаком «минус»:
N2 = - sin pg. , (4.60, a)
Рассмотрим несимметричную деформацию цилиндрической обо-
лочки корпуса резервуара при действии кольцевых осесимметричных
сжимающих усилий (4.60, а).
Итоги работы [20], показавшие возможность пренебрежения
докритическим моментным состоянием в пределах «средних» (по клас-
сификации [И]) прогибов, позволяют использовать для решения
линейное дифференциальное уравнение устойчивости пологой обо-
лочки, полученное В. 3. Власовым [2].
Основное разрешающее уравнение для замкнутой цилиндрической
оболочки имеет вид
(W + 2va +1) vV-F - 2а! (1 - V!) (-jp—аДг) V2 F +
+ (l-*2)>-= (4.61)
где
2 да , да ,,
v — 4 да-; (4.62)
185
F — функция перемещения, определяющаяся уравнением
w = v4^; (4.63)
W — прогиб оболочки в направлении нормали к ее поверхности при
потере устойчивости; а2 — безразмерный параметр
(4.64)
Для оболочек вертикальных цилиндрических резервуаров вели-
чина а2 составляет (в зависимости от вместимости) 10"5 -4-10-8.
Поэтому, если в уравнении (4.61) отбросить члены, содержащие
множитель а2, которые не оказывают существенного влияния на
внутренние усилия и моменты, а из моментных членов сохранить
только главный, имеющий наивысшие (восьмого порядка) произ-
водные, то основное разрешающее уравнение примет вид
+ (4.65)
Если положить, что
Z = - ^ = - vV F (4 66)
Д2 902 д2 50 V V Vi.uu,
то уравнение (4.65) запишется в форме
V’FW 4? + ^ ©ТГ = 0. <4.67)
где D = 12 — цилиндрическая жесткость оболочки.
Выполняя над уравнением- (4.67) линейную операцию V4 и при-
нимая во внимание (4.63), получим
veTy + 4(r^ + ^v4[^a)-^] = 0. (4.68)
Если воспользоваться обратным дифференциальным оператором
V'4 = ^Г’ введенным Батдорфом [22], то
уравнение (4.68) можно
записать в форме
+ (4.69)
Решение уравнения (4.69) будем искать в виде
H7 = PE(g)cosnO, (4.70)
где п — число окружных волн при выпучивании оболочки.
Действительно, в окружном направлении функция (4.70) удо-
влетворяет условию замкнутости деформаций и разрешающему
уравнению (4.69). Что касается функции W (£), то она, очевидно,
удовлетворяет граничным условиям в начале координат, требующим
186
W (I) = 0. Если функцию представить в виде синус-преобразования
Фурье
W (?) = J / (2) sin & dz, (4.71)
о
то в силу теории Римана — Лебега [7] функция W (?) удовлетворяет
также и условию затухания прогиба с удалением от начала координат
[при £(?)->0 и И7'(?)->0]. После подстановки (4.71)
и (4.70) в (4.69) получим
00 00
f Г (z2 + м2)2 + / (2) sin & dz = N2 (?) n2 f / (z) sin ?z dz.
о 0
(4.72)
2
Умножив обе части равенства на — sin ?а d ( ?) и проинтегрировав
от нуля до бесконечности, получим в левой части синус-формулу
Фурье для функции
ф (а) = / (а) [(а2 + п2)2 + (• (4-73)
Так что для (4.72) имеем
00 00
Ф(а) = ^7Г J AM£)sin?aJ / (z) sin ?zdzd?. (4.74)
о о
Выражение под знаком второго интеграла умножим и разделим на
и, полагая У2 (В) — 470^'20 ( ?) (У2о ( Ю — функция кольцевых
•сжимающих усилий при действии единичного момента, а М 0 — пара-
метр, подлежащий определению), получим
00
, , . 2/г27?Ш0 f (z2_Lra2)2
• W = —j (Z2+n3)4 + 4^4 Ф(г. «)Ф(2Ж (4.75)
о
где
00
Ф(г,а)= J 7V2o(?)sin?zsin?ad?. (4.76)
о
Таким образом, уравнение равновесия (4.67) приведено к ин-
тегральному уравнению Фредгольма второго рода [10] для полу-
бесконечного промежутка.
Умножив обе части равенства (4.75) на
а2 | пг
/(а2 + я2)* + 4р«а »
187
и рассмотрев
/2|-п2
ф (£) — _____________
/(г2 + п2)4+4р4а4
в качестве новой функции, получим
оо
Q (а) = Л J <р (z, a) Q (z) dz,
о
(4-77)
где
д2-|-га2
22_|_и2
ф (Z, а) = ^'г'“ = = ф (Z, а); (4.78)
' /(а2 + м2)4-|-4(Л4а4 /(Z2 +„2)4+ 4^24
. 2и2Д2М,)
Л ~ nD
(4.79)
Уравнение (4.77) имеет отличное от нуля решение, когда Л при-
нимает собственные значения, наименьшее из которых соответствует
критической нагрузке.
Для функции сжимающих кольцевых усилий, определяемых
по формуле (4.60), будем иметь
’ а> R L4c4+(a-z)4
2c2-(a4-z)2 -|
4c4 + (a + 2)4 J *
(4.80)
Собственные значения уравнения (4.77) определим по способу
нахождения наименьшего собственного значения через
ядра [10].
Используя след второго итерированного ядра, получим с
статном
следы
недо-
(4.81)
где след
00 со
А2 = J j <p2(z, a)dzda.
о о
Таким образом, приближенное собственное значение равно
(4.82)
С С («2 + п2Р . (22 + ^2)2 ф2 (z а} dz da
Д2 J («2 + „2)4 + 4jx4a4 (Z2_|_„2)4 + 4B424 (Z,U)aZatt.
0 0
Для вычисления квадратур используем косинус-преобразование
Фурье и метод вычетов. С этой целью представим выражение
(г2 + „2)2
(«2+ „2)4 +4|х4Л4
(4.83)
по формуле Фурье:
(^ + „2)2 2 f’ „ . , ,
"г .л г=— 1 F (и) cos zu du,
(ж2 + „2)4 4|.t4_4 nJ'7 ’
О
(4.84)
1
/л? ’
188
где
F (и) = С -т „ cos У11 ^У- (4.85)
' J (</2 + na)4 + 4p4?/4 а » v >
О
Знаменатель последнего интеграла имеет следующие корни в по-
ложительной полуплоскости комплексной области:
Zl, 2 = ?1± Р1^>
Z3,4~ ?2 ± Pii,
где ______________
?х = у (с ± iZ/F-bc4—2^;
q2 = j(-c + ^y^-2');
Pi = 4H//U?+2); '(4.86)
Pi = ~2 (~с + V"/41 с41 2^;
C = i.
И
Согласно теореме о вычетах, получаем
оо
F (и) — К § f (u) cos хи du, (4.87)
о
где
___________________________л___,
8«2р. jil<.4
f (и) = еР1“ (Лх cos qxu + Br sin qru) 1 е"Р!“ (А2 cos q$u 1 В % sin q2u)\
Aj, = с]/ V'WT2-i/'4Tc5;
Л2 = с'|Л/4+74+2+ /41с4,
Вг=-с//4+^+2 + /4+?;
В3 - с /^ic4!^ - /4+74.
Подставляя (4.87) в (4.84), а полученное в (4.83) и вычисляя
с помощью вычетов квадратуры
00
j Ф2(з, a) cos zudz,
о
189-
л2
найдем
со со
1 =4~ f •; 9 л л &Ни) [5 (и, а)+ 7? (и, a)] du da,
2п J (а2 + п2)4-j-4fi4ai J 11 v ' v "
0 0
(4.88)
где
S (и, а) — [(1 — 2|ш) cos ри — 3 sin ри] cos аи;
R(u, а) nin(«+H)^+sin(«-R)q_
' ’ ' 2 L а+ц 1 а—fi J
п „ (а+fi) sin (а + ft) и , (а — ,u) sin (а —ft) u "I
“Те L (a + (1)2 + iLl2 -Г (а_и)2 + (12
’^"^a"e'!lU (а + И) w-i-sin (а — рО И1 —
“ 2(а"+р)е'^ [COS <а + U + C0S(« — И)«] +
+ 4С"Ш „Л „2 [sin(a + H)w + sin(a-fi)u],
Li \м** '"l"" Ц<
Принимая во внимание (4.85), окончательно для момента полу-
чаем
<4-89)
где
СО
J у /2 (it) е~с“ [(1 — 2cu) cos си + 3 sin си] du +
О
1 9с2
ш2" ~ 4(4 + с2)
ОО V)
Ци>) J Ци)е-си
О о
(cos cw — cos си) du dw 4-
СО 00
+ J/(M?)j / (м) е~с11 (cos си — cos cw) du dw
o w
(4.90)
Минимизацией по взятии квадратур на ЭВМ окончательно
получено
^окР=О,763тг5^
(4.91)
При тех же исходных данных этот результат получен энергети-
ческим методом в работе [8]. Если верхний край цилиндрической
оболочки свободен от всяких закреплений, но загружен продольными
осесимметричными изгибающими моментами, то величина крити-
ческого изгибающего момента существенно снижается:
м _ 0,312E/i3
Жокр (J_V2) Н •
190
Устойчивость оболочки магистрального трубопровода при
бесподъемном способе укладки
Открытие новых богатейших месторождений нефти и газа
в СССР, быстрый рост добычи и переработки нефти требуют интенсив-
ного развития трубопроводного транспорта. Проблема интенсифи-
кации трубопроводного транспорта решается в настоящее время
путем увеличения производительности каждого вновь строящегося
газонефтепровода. Уже сейчас успешно эксплуатируются трубо-
проводы диаметром более 1 м, а в ближайшем будущем диаметр
трубопровода возрастет до 2,5 м.
С увеличением диаметра существенно повышаются жесткость
и собственный вес трубопровода, а следовательно, изменяется вся
технология строительства. Из всех существующих способов укладки
трубопровода большого диаметра в траншею наиболее предпочтитель-
ным с экономической точки зрения оказался так называемый «бес-
подъемный» способ, при котором отпадает необходимость в подъеме
трубопровода, так как рабочий орган машины роет траншею на за-
данную глубину непосредственно под лежащим на поверхности
земли трубопроводом, который под действием собственного веса
опускается на дно траншеи.
В начальный период укладки, когда консольная часть трубо-
провода еще не коснулась дна траншеи, может произойти выпучива-
ние трубопровода в опорной зоне, где интенсивность изгибающего
момента максимальна. Определим критическую длину консольной
части трубопровода при «бесподъемном» способе укладки.
Предположим, что в начальной стадии укладки трубопровода
в траншею высотой Н при вылете консольной части I свободный край
трубопровода еще не коснулся дна траншеи.
Тогда, если расположить начало координат на краю трубопро-
вода (точка 0), то на участке I х 0 трубопровод будет работать
на изгиб под действием собственного веса, как обыкновенная кон-
сольная балка, а на участке х I — как балка на сплошном упругом
основании (рис. 63).
При равномерно нагруженной консоли изгибающий момент
и перерезывающее усилие в поперечном сечении, отстоящем
191
на расстоянии х от левого свободного конца, соответственно
равны
(4.92)
(4.93)
<2л(^) =
Тогда, если отсечь левую консольную часть трубопровода от
правой, то в сечении х = I
4i
Q^-Q0=~qI-
С учетом (4.94) дифференциальное уравнение изогнутой оси
консольной балки запишется:
«тЗ^-тг- <4-м>
Дважды последовательно интегрируя уравнение (4.94), получим:
EI
ах 6
EIwa = ^-+ Ax-f- В,
"4
(4.95)
где А, В — произвольные постоянные интегрирования.
В гл. 1 было показано, что дифференциальное уравнение изогну-
той оси балки на сплошном упругом основании полностью совпадает
(в смысле гипотезы коэффициента постели) с дифференциальным
уравнением прогиба замкнутой цилиндрической оболочки при осе-
симметричном загружении. Поэтому выражения для внутренних
усилий и перемещений в произвольном сечении правой части трубо-
провода, лежащего на сплошном упругом основании и загруженного
равномерно распределенной нагрузкой q, а на краю изгибающим
моментом Мо——и перерезывающим усилием Q0 = —ql, можно
-определить по формулам (1.72):
^ = ^(Фз+-^Ф2)+1;
4?-=- т <ф1+0/фз); <4-96)
Мп=-^-(ф4 + >Ф1);
<?„=-дЦФ2-р/Ф4);
где К — коэффициент постели основания; Ф4 — Ф4 — гиперболо-
тригонометрические функции, определяемые по формулам (1.71):
192
В сечении х = I, расположенном на границе левого и правого
участков трубопровода, соблюдаются следующие условия непрерыв-
ности:
__ dn’n
dx dx ’
= “’и-
Раскрывая эти условия с помощью отношений (4.95) и (4.96),
получим:
Л = ^лш+М. (4.98>
в=т('‘+4т+6-г+4>+тН- <4-м>
Тогда выражения для угла поворота и прогиба консольной части
трубопровода запишутся:
? г х3~13 Ш+РП т
dx El L 6 2р3 J’
____?_ Г __ 4^(1 + РО , 4
л 8£7 L 3 р "т" “г
+4Т+вТ-+4-р+|Н (4Л00>
Касание краем трубопровода дна траншеи возможно только в том
случае, если его перемещение равно Н — R. Следовательно, при
х = 0 должно соблюдаться условие
8EHH~R) 4 ,,*3*2 | 1 । 2
q +4 ₽ +4 рз + р4 •
Обозначим
,,п ,4 , , I3 I д *2 | , I , 2 8ЕЦН — П) ..
y = 7(Z) =/4 + 4 __|_6 _ _|_4 —-------------(4.101)
Уравнение (4.101) заведомо будет иметь единственный корень Zlf
так как производная /' (Z) существует и сохраняет постоянный знак
внутри интервала (0, со), т. е. при > Z >0 /' (Z) >0.
Например, для трубопровода диаметром 1020 мм с толщиной
стенки 12 мм при коэффициенте постели К = 200 кгс/мма из решения
уравнения (4.101) на ЭВМ «МИР-1» методом пропорциональных
частей [5] получено значение корня Ц = 43,95 м. График зависи-
мости у =j (Z) для этого частного случая представлен на рис. 64.
Таким образом в сечении х = Ц максимальный изгибающий
момент равен
(4.102)
13 Заказ 2036
193
От действия изгибающего момента в поперечном сечении трубо-
провода возникают нормальные напряжения, изменяющиеся по
закону плоскости:
_ MmaxR cos 0 qljR cos 0
j 2/
(4.103)
Определим критическую длину консольной части Ц трубопро-
вода, при которой может произойти выпучивание оболочки. Для
этого зададимся функцией радиального перемещения оболочки
в следующей форме:
W (.г, 0) = / (х) Т Ап cos п 0,
п
(4.104)
где / (х) — функциональная
неизвестная переменная по
длине оболочки; Ап — постоян-
ный коэффициент, зависящий
от номера гармоники тригоно-
метрического ряда.
Так как при изгибе сдвиг у
и компонента относительного
удлинения в окружном напра-
влении оболочки 82 равны
нулю, при подстановке в гео-
метрические уравнения (1.22)
зависимости (1.27) получим:
аи
81 дх ’
»>=-Н45-+и,)=°; (4-‘°5)
av . 1 аи л
дх R дЪ °'
Тогда из уравнений (4.105) с учетом (4.104) следует:
f = — / (г) 2 —sin п в;
п п
<4-,06>
п
D rRF (z) V An А
8, =- - R 'Л 7, -Г- cos K0-
1 dx% n2
n
194
Изменение кривизны срединной поверхности оболочки в про-
дольном и кольцевом направлениях вследствие деформации опре-
деляется соотношениями:
= eosnQ.
п
(4.107)
х2 —
у ( TF- + w ) = Т 2 А‘("2 -“s '
п
Этим кривизнам соответствуют изгибающие моменты:
М, = D,x1 — — D -d { У Ап cos «9;
1 dx2 £ (4.108)
М2 == Ох2 = D У Ап («2 — 1) cos «0,
11
а деформациям et — продольные напряжения:
<т = ЕЧ = -ER c°s (4-W9)
п
Записав выражение потенциальной энергии системы на единицу
длины в форме
п=4$ а ie ih -а крй (4г У -
-акрА(44У]Лйе <4Л10>
и подставив соответствующие величины, получим
п = 4 фИМ 12 4(п- -1) e»s »е]!+X
( п
* 2 cos и0Т ~Окр/г cos 0 [(2Ап cos ”02+
n n
+(2 4rsinra0y]Wo.
n J
Если обозначить длину участка оболочки трубопровода, нахо-
дящуюся в условиях изгиба через L и учесть, что L R, то функ-
циональную неизвестную, характеризующую изменение радиальных
перемещений W по длине L, можно представить в форме
/\х) — sin t (4.Ш)
где т. — число полуволн вдоль оси аг (т = 1, 2, 3, . . .).
13* 195,
Выражение полной потенциальной энергии системы
L
9 = \Hdx. (4,112)
о
Так как в выражение для П входит потенциал внешних сил,
взятый с обратным знаком, то условие
ь
Э = J Шх = О
о
означает равенство работы внешних и внутренних сил оболочки,
находящейся в безразличном равновесии при наличии малых ради-
альных перемещений W.
Раскрывая это условие с учетом (4.111), получим
£ 2 (»! --»)!+£л!* (тг)‘ 2 -4 -
п п
-’к-4 (-Н
. п п
откуда
_ D 1__________п_______________I
кр R*h ’ / тл у у у 4п Лп+1
< L ) £ А п(« + 1)
п п
2 а
nJ
ERi / тл у. -----„ ---- j 13
\ / V* . . . у AnAn+i • ' '
п п
Из условий минимума окр следует:
9<Ткр __ Q
/ тл \2 ’
Ч—)
откуда
^Y2-1)2
----п--------- (4114)
\ L J ERVi у
2j
п
После подстановки выражения из уравнения (4.114)
в (4.113) получим
__/г 1У
196
где
J2- * П_______«__________
п п
Коэффициент Кп имеет минимальную величину при Ап = Ап+1 =
== const, поэтому при определенном числе членов сумм Кп 1.
Тогда при v = 0,3 выражение (4.115) запишется:
<ткр^ 0,605^. (4.116)
Данное значение критического напряжения полностью совпадает
с верхним критическим напряжением для центрально сжатой обо-
лочки, Такой результат легко объяснить, если принять во внимание,
что характер потери устойчивости в обоих случаях один и тот же.
Поэтому при практических расчетах следует пользоваться прибли-
зительно теми же данными, что и при продольном сжатии.
Для стальных трубопроводов отношение составляет 50—100,
и, как следует из формулы (4.30), критические напряжения оказы-
ваются значительно выше предела текучести. Расчет на устойчивость
при изгибе в этом случае следует выполнять по теории упруго-пла-
стических деформаций тонкостенных оболочек. К сожалению, в на-
стоящее время отсутствуют достаточно проверенные теоретические
результаты в области устойчивости оболочек при изгибе за пределами
упругости. Поэтому для расчета следует рекомендовать эксперимен-
тальные данные, представленные в работе [3].
В общем случае внецентренного сжатия при изгибе оболочки
критическое напряжение будет равно:
= (4.117)
где С — расчетный коэффициент, определяемый по данным, при-
веденным на с. 167 в зависимости от отношения R/h\ сг+ — максималь-
ное напряжение сжатия; а“ — напряжение у противоположного
конца диаметра (с учетом знака).
В случае чистого изгибало* = —ОТ, поэтому
акр = 1,25С^7 (4.118)
Если принять во внимание, что максимальное напряжение в сече-
нии х = Zj равно
о =Л
мтах 27 ’
197
и сравнить его значение с критическим (4.118), то выражение для
критической длины консольной части трубопровода при бесподъем-
ном способе укладки запишется:
/1КР = /1,25С^, (4.119)
где у — удельный вес материала трубопровода.
Пример. Определим критическую длину консольной части трубопровода
диаметром 1020 мм с толщиной стенки 12 мм при бесподъемном способе укладки.
Удельный вес трубопровода у = 7,85 тс/м3, а модуль упругости Е = 2,1 х
X 107 тс/м2.
R
Отношение — = 42,5 < 250, поэтому, согласно данным, приведенным
на с. 167, С = 0,18.
Тогда по формуле (4.119) получим
, •. Г 1,25 X 0,18 X 2,1 X 10’ X 12 X 10'» „
Z1KP = ]/----------------------------- = 85 и.
Расчетная максимальная длина консольной части трубопровода Zlmax =
= 43,95 м, поэтому коэффициент запаса устойчивости равен 1,93.
СПИСОК ЛИТЕРАТУРЫ
1. Березин В. Л. Устойчивость верхних поясов вертикальных ци-
линдрических резервуаров. НТС УНИ, вып. 3, Уфа, изд. УНИ, 1968, 316—
326 с.
2. Власов В. 3. Избранные труды, т. 1. М., изд-во АН СССР, 1962,
528 с.
3. В о л ь м и р А. С. Устойчивость деформируемых систем. М., «Наука»,
1967, 984 с.
4. Гольденвейзер А. Л. Теория упругих тонких оболочек. М.,
Гостехиздат, 1953, 544 с.
5. Демидович Б. П., Марон И. А. Численные методы анализа.
М., «Наука», 1967, 368 с.
6. Д и н н и к А. Н. Устойчивость арок. М. —Л., Гостехиздат, 1946,
128 с.
7. Д и т к и и В. А., П р у д н и к о в А. П. Интегральные преобразо-
вания и операционное исчисление. М., Физматгиз, 1961, 524 с.
8. К ан С. Н., Б ы р с а н К. Е. Устойчивость цилиндрических обо-
лочек при локальных нагрузках. «Расчет пространственных конструкций»,
вып. XI, М., изд-во литературы по строительству, 1967, 127—144 с.
9. Лессиг Е. Н., Л и леев А. Ф. Листовые конструкции. М.,
изд-во литературы по строительству, 1970, 487 с.
10. Михлин С. Г. Интегральные уравнения. М., Гостехиздат, 1947,
304 с.
И. М у ш т а р и X. М., Галимов К. 3. Нелинейная теория упру-
гих оболочек. Казань, Таткнигоиздат, 1957, 431 с.
12. Новожилов В. В. Теория тонких оболочек. М., Судпромгиз,
1962, 344 с. .
13. С а ф а р я и М. К., Иванцов О. М. Проектирование и соору-
жение стальных резервуаров. М., Гостоптехиздат, 1961, 328 с.
14. С а ф а р я н М. К., Ш у т о в В. Е. Расчет стальных вертикальных
цилиндрических резервуаров большой емкости на действие ветровой нагрузки.
Экспресс-информация «Строительство магистральных трубопроводов и газо-
нефтепромысловых сооружений», № 1, 1968, 15—23 с.
15. Тимошенко С. П. Пластинки п оболочки. М., «Наука», 1966,
635 с.
16. Тимошенко С. П. Сопротивление материалов, т. 2. М., «Наука»,
1965, 480 с.
17. Уманский А. А. Специальный курс строительной механики,
ч. I. М., изд. ОНТИ, 1935, 238 с.
18. Ширинский В. И. Устойчивость цилиндрической оболочки под
действием неравномерной радиальной нагрузки. «Строительная механика п
расчет сооружений», № 1, 1971, 44—48 с.
19. Янке Е., Э м д е Ф. Специальные функции. М., «Наука», 1968,
344 с.
20. Я с и н Э. М. Устойчивость моментного состояния равновесия обо-
лочек. Тр. Уфимского авиационного института. Уфа, изд. Уфимского авиацион-
ного института, 1967, 23—27 с.
21. Roshko A. Experiments on the Flow past a Circular Cylinder at
very high Reynolds Neember. J. of Fluid Mechanics, v. 3, part 3, 1961, 63—69 p.
22. S e i d P. Weingarten v. I. Buckling of a Cylindrical Shell under
pure Bending. Trans. ASME, 1961, E 28, No 1, 86—92 p.